;.^г

К. А. Рыбников
ВВЕДЕНИЕ
В КОМБИНАТОРНЫЙ
АНАЛИЗ
ИЗДАНИЕ ВТОРОЕ
Ж
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО УНИВЕРСИТЕТА
1985

УДК 519.1
Рыбников К. А. Введение в комбинаторный анализ / 2-е изд. — М.: Изд-во
Моск. ун-та, 1985 — 308 с.
В книге (1-е издание вышло в 1972 г.) излагаются построенные на
единой теоретической основе методы исследования дискретных систем л решения
соответствующих комбинаторных задач. Рассмотрены: начала теории дискретных
множеств, основные комбинаторные понятия и операции, логические методы,
таблично-матричный аппарат, дискретные геометрические системы, методы
решения экстремальных задач и методы вероятностного характера. Содержание
взаимосвязано со сборником «Комбинаторный анализ: задачи и упражнения»
(«Наука», 1982).
Для студентов математических специальностей университетов.
Рецензенты:
чл.-кор. АН КазССР В. М. Амербаев,
д-р физ.-мат. наук В. А. Малышев
Печатается по постановлению
Редакционно-издательского совета
Московского университета
1702070000—082
р — 97—85
077(02)-85
© Издательство Московского университета. 1985 г.

ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Теоретические основы комбинаторного анализа 6
§ 1.1. Что изучают в комбинаторном анализе н какие типы задач
решают 6
§ 1.2. Необходимые сведения из теории множеств и алгебры 7
§ 1.3. Выборки и упорядочения 15
§ 1.4. Распределения и заполнения 21
§ 1.5. Системы множеств 29
Глава 2. Производящие функции 33
§ 2.!. Основы метода производящих функций 33
§ 2.2. Виды производящих функций и нумераторов 36
§ 2.3. Операторный аппарат метода производящих функций 48
§ 2.4. О приложениях метода производящих функций 58
§ 2.5. Теория Редфилда—Пона 62
Глава 3. Комбинаторно-логический аппарат 69
§ З.1.. МР.ТПЛ ИК.ЛЮИГНИЙ И ■к-Ушпчпчий 69
§ 3.2. Системы представителей множеств 73
§ 3.3. Начала теории Рамсея 77
Глава 4. Табличио-матричный аппарат комбинаторного анализа 82
§ 4.1. Системы инцидентности и специальные матрицы 82
§ 4.2. Латинские прямоугольники и квадраты 88
§ 4.3; Блок-сдамы— -ЗЬ...
§ 4.4* Перманенты 106
Глава 5. Геометрические системы 123
§ 5.1. Геометрические интерпретации 123
§ 5.2. О проективных пространствах 125
§ 5.3. Конечные проективные плоскости 128
§ 5.4. Графы 135
Глава 6. Методы решения экстремальных задач 150
§ 6.1. Экстремальные комбинаторные задачи и подходы к их
решению 150
§ 6.2. Метод ветвлений и ограничений 156
§ о.З. Эвристические методы 164
§ 6.4. Оптимизация иа графах 170
§ 6.5. Потоки в сетях 174
Глава 7. Вероятностные методы в комбинаторном анализе 183
§ 7.1. Примеры применения вероятностных методов 183
§ 7.2. Задачи планирования эксперимента 186
§ 7.3. Энтропийный метод 191
§ 7.4. Метод случайного баланса 195
§ 7.5. Разделяющие системы подмножеств 201
3

Глава 8. Комбинаторный анализ на частично упорядоченных
множествах 208
§ 8.1. Частично упорядоченные множества 208
§ 8.2. Решетки 228
§ 8.3. Функции инцидентности и обращение Мебиуса 248
§ 8.4. Матроиды 270
Заключение 303
Литература
304

ПРЕДИСЛОВИЕ
В учебных планах математических и других
специальностей высших учебных заведений, во всей практике их
учебно-научной деятельности возрастает роль тех
математических дисциплин, в которых изучают дискретные
системы. Тем самым вьГсшая школа учитывает важнейшую
сторону будущей работы своих выпускников. Эта работа чаще
всего происходит в условиях широкого использования ЭВМ.
Последние же в большинстве, как известно, работают на
основе принципов дискретного счета.
Студентам приходится изучать самые разные виды
дискретных систем: графы, блок-схемы, матрицы, электрические
сети, транспортные потоки, потоки информации, системы
организации производства, логические системы и многие
другие. Несмотря на кажущуюся непреодолимой разнородность
и специфичность, они в своих основах имеют много общего.
Их математические модели показывают это со всей
очевидностью.
В настоящей книге широкие классы дискретных систем
рассматриваются как части единой теории дискретных
множеств. В рамках этой теории (сохраняющей исторически
сложившееся наименование: комбинаторный анализ) они
занимают свое место в соответствии с тем, как
интерпретированы их объекты, какие классы задач выделены для
исследования или какие виды методов выбраны для их
решения.
В главе 1 водятся основные понятия и операции
комбинаторики, демонстрируются типичные комбинаторные задачи
и приемы решения наиболее простых из них. В главах 2—7
последовательно описываются различные группы
комбинаторных методов. С содержанием этих глав
скоординированы соответствующие разделы задачника [7]. Последняя, 8-я
глава содержит материал о распространении задач и методов
комбинаторного анализа на множества возможно более
общей природы. Она имеет целью ориентировать читателя
в некоторых направлениях развития современной
комбинаторной теории, что необходимо и для приложений.
Первое издание настоящей книги появилось в 1972 г.
в Издательстве МГУ. В последующем бурном развитии
комбинаторного анализа в СССР она свою роль сыграла. Сейчас
ее содержание остро нуждается в обогащении и даже в
обновлении, хотя, по нашему мнению, структура общей
комбинаторной теории изменилась мало. В подготовке
настоящего, второго, издания автору оказывали помощь его
ученики и коллеги: А. М. Ревякин (гл. 5 и 8), М. В.
Меньшиков (гл. 6 и первые три параграфа гл. 7), В. Н. Лузгин
(■§ 4.5, 7.4 и 7.5), В. И. Большаков (§ 6.3 и новая редакция
гл. 2). Всем им автор выражает свою благодарность и
считает их соавторами указанных частей книги. Он также
благодарит рецензентов чл.-кор. АН КазССР В. М. Амербаева,
д-ра физ.-мат. наук В. А. Малышева и редактора А. Ф.
Сидоренко.
Автор примет с благодарностью замечания читателей.

Глава 1
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ
КОМБИНАТОРНОГО АНАЛИЗА
В этой главе даются разъяснения, имеющие целью
сформировать у читателя начальные представления о комбинаторном
анализе. Речь идет об объектах, изучаемых в комбинаторном анализе
(т. е. об его предмете), и задачах, которые при этом ставятся и
решаются. Здесь же вводятся основные понятия, операции,
символика. Наконец разъясняются приемы решения несложных
комбинаторных задач как в теоретической, так и в практической
постановках.
1.1. ЧТО ИЗУЧАЮТ В КОМБИНАТОРНОМ АНАЛИЗЕ И
КАКИЕ ТИПЫ ЗАДАЧ РЕШАЮТ
Сформулируем для начала несколько задач. Мы сделаем это
для того, чтобы читатель интуитивно воспринял их
комбинаторный характер и был лучше подготовлен к восприятию общих
формулировок.
а) Поступающий в университет должен сдать четыре экзамена
при пятибалльной системе оценок. Для поступления достаточно
набрать 17 баллов. Сколькими способами он может сдать
экзамены (разумеется, не получив ни одной двойки)?
б) Как отыскать кратчайший маршрут для письмоносца или
киномеханика, обязанного обслуживать заданное число
населенных пунктов? Расстояние между каждой парой пунктов известно.
в) Сколько ферзей или других шахматных фигур достаточно,
чтобы они держали под боем все клетки шахматной доски?
Сколькими способами они могут быть расставлены?
г) На сколько частей делят пространство п плоскостей, из
которых никакие четыре не проходят через одну и ту же точку,
никакие три не проходят через одну и ту же прямую и никакие две
не параллельны, а любые три плоскости имеют общую точку?
Подобные задачи роднит в первую очередь то, что в них
изучают дискретные (составленные из отдельных, обособленных,
элементов) множества. В большинстве случаев эти множества
конечны. Из комбинаторного анализа не исключаются также
множества бесконечные, составленные из неограниченно большого
числа элементов, но при наличии достаточной информации
о структурных особенностях этих множеств. Структура дискрет-
6

ных множеств может быть очень сложной в зависимости от того,
какие связи и отношения существуют между ними. Изучение
таких дискретных структур, выражение их свойств принятыми
в математике способами (аналитическими, графическими,
табличными, геометрическими) — такова первая, главная, задача
комбинаторного анализа.
Над дискретными множествами производят операции. Одни
из них вызывают изменение структуры множеств, другие —
изменяют их состав. Простейшими операциями первого типа являются
обычные перестановки элементов, второго — выделение
подмножеств элементов, или, как принято говорить, их выборки.
Операции применяют в задачах чаще всего неоднократно и в самых
разнообразных комбинациях, при наложении различных условий.
Это создает практически неисчерпаемые возможности дискретных
построений, которые нередко называют конфигурациями (иногда
комбинаторными конфигурациями).
В зависимости от характера предмета исследования и
вводимых операций определяется специфическая совокупность задач,
решаемых средствами комбинаторного анализа. Самыми ранними
являются задачи о числе дискретных построений,
удовлетворяющих поставленным условиям. Методы их решения получили
название перечислительных. Кроме задач перечислительного типа
в комбинаторном анализе рассматриваются вопросы
существования или несуществования конфигурации, удовлетворяющей
заданным условиям, отыскиваются алгоритмы построения
конфигураций, а также выделения из заданной совокупности конфигураций
или алгоритмов таких, которые обладали бы избранным
свойством в наибольшей или в наименьшей степени (задачи и методы
оптимизации).
Комбинаторный анализ связан со многими разделами
математики или даже имеет с ними взаимопроникающие, общие части.
Дело в том, что элементы комбинаторных суждений появились
давно, еще в глубокой древности, на заре формирования
математической науки. Однако в ходе истории они развивались
совместно с другими разделами математики, входя в различных случаях
в их состав. Нетрудно увидеть, что в ряде областей современной
математики: теории чисел, алгебре, геометрии, математической
логике и др. — многие основные понятия и методы имеют
дискретную природу и обладают устойчивыми связями. Это позволяет
рассматривать задачи комбинаторного анализа в различных
интерпретациях, исследовать проблемы различной, казалось бы,
природы с единой, наиболее подходящей существу задачи точки
зрения.
В наше время возможности дискретных методов исследования
резко возросли. Выросло и их значение. Наряду с исторически
сложившейся общей комбинаторной теорией (комбинаторный
анализ) в современной математике существуют: теория графов и
гиперграфов, геометрия чисел, дискретный и конечный анализы,
исследование операций и др. В книгах и статьях рассматривают
7

отдельные классы задач, что свидетельствует о широкой
разветвленное™ и богатстве комбинаторных исследований.
Задачу настоящей книги мы видим в изложении
комбинаторного анализа как математической теории исследования
дискретных множеств в их различных интерпретациях, исходящей из
единых принципов, достаточно богатой в части используемых
методов и могущей служить также общей теоретической основой
дискретных методов исследования в математике.
1.2. НЕОБХОДИМЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
МНОЖЕСТВ И АЛГЕБРЫ
Сведения, которые мы включаем в настоящий раздел книги,
предназначаются для описания свойств объектов, изучаемых
в комбинаторном анализе, операций, производимых над ними, и
для установления единообразной символики. Как правило,
определения, термины и символы выбираются из числа
общепринятых в математике. Вводиться они будут постепенно.
Основное понятие: множество. Ему определения мы не даем
виду неизбежной тавтологичности. Все множества,
рассматриваемые в книге (если нет специального уточнения), — дискретные
и конечные. Множества будем обозначать прописными
латинскими буквами: А, В, ..., а их элементы — малыми: а, Ь, ... . Будем
писать аеЛ, если элемент а принадлежит множеству А, и а^А,
если а не принадлежит множеству А. Подмножеством А
множества 5 (Л^5) называется любое множество, все элементы которого
принадлежат 5. Другими словами, А<=5, если из а^А следует,
что ое5. Множества А и В совпадают или равны (А = В), если
они состоят из одних и тех же элементов. Иначе говоря, А = В
тогда и только тогда, когда А<=В и В=Л. Если А<=В, но АФВ,
то говорят, что А — собственное подмножество множества В, и
записывают: Лс=В.
Множества и подмножества можно вводить и обозначать раз- •
ными способами. Например, подмножество А множества 5 часто
определяется как множество всех тех элементов ое5, которые
обладают некоторым определенным свойством. Если это
свойство обозначить через Р(а), то определение А можно записать
символически: А = {а^З\Р(а)}, или (просто) А = {а\Р(а)}. Эти
записи читаются так: «А есть множество всех элементов а множества
5, для которых справедливо условие Р(а)». Например, запись(
'А={а\а^№ и а = 2Ь для некоторого Ье1М}, где N — множество
натуральных чисел, описывает множество всех положительных
четных чисел.
Введем символ 0 для обозначения пустого множества, т. е.
множества без элементов. Очевидно, любое множество содержит
в качестве подмножества пустое множество. Через Р(5) будем
обозначать множество всех подмножеств множества 5, которое
содержит в качестве элементов все собственные подмножества
А, удовлетворяющие условию 0с=Лс=5, а также пустое множест-
8

во 0 и само множество 5. Например, если 5 = {а, Ь, с}, то Р(5)
содержит, кроме 0 и 5, шесть собственных подмножеств {а}, {Ь},
{с}, {а, Ъ}, {а, с), {Ь, с}. Вообще, если 5 состоит из п различных
элементов, то Р(5) содержит 2" различных подмножеств.
Поэтому в литературе Р(5) обозначают также через 25.
Скажем, что задано отображение ц> из множества А в
множество В, если каждому элементу из множества А поставлен в
соответствие некоторый элемент из множества В. Для обозначения
отображения ф из А в В будем пользоваться символом ф : Л->-В.
Если аеЛ, то поставленный ему в соответствие элемент из В
обозначается через ф(а) и называется образом элемента а при
отображении ф. Если Ь^В, то всякий элемент а из А, для
которого справедливо равенство Ь = ц>(а), называется прообразом
элемента Ь. Множество А называется началом отображения ф, а
множество В — его концом. Разумеется, каждый элемент из
начала отображения ф имеет в точности один образ. Однако не у
каждого элемента из конца этого отображения должен быть
прообраз. С другой стороны, конец отображения может содержать
элементы, имеющие несколько прообразов. Подмножество конца
отображения ф, состоящее из всех его элементов, имеющих
прообраз, или тоже самое, представимых в виде ц>(а) для некоторого
а&"Л, называется образом отображения ф и обозначается 1т ф.
Для конечного множества А = {а\, аг, •.., ап) часто используется
двустрочная форма записи отображения ф : Л->-5, а именно
ф = / °1 а2 ■ ■ ■ ап \
\ф(а1) ф(а2) ... ф(а„)У
Два отображения ф1 :/^-)-5^ ф2 : А^-^-В^ считаются равными,
если Л 1=.(42, В\=В2 и ц>\(а) =ц>2(а) для всех аеЛь Отображение
ф' : А/-*-В является сужением на А' отображения ф : А-+В, если
А'<=А и ф'(а)=ф(а) Для каждого а<=А'.
Отображение ф : А—>-В называется вложением, если каждый
элемент из В имеет не более одного прообраза, т. е. ф(а)=ф(Ь)
влечет за собой а = Ь, Если каждый элемент из В имеет хотя бы
один прообраз, или, другими словами, 1тф = В, то отображение
Ф называется наложением. Наложение ф : А—>-В называют также
отображением А на В. Отображение, являющееся одновременно
вложением и наложением, называется взаимно-однозначным.
Если А = В, то взаимно-однозначное отображение ф : А^-А
называется подстановкой.
Множества могут быть конечными (т. е. состоящими из
конечного числа элементов) и бесконечными. Число элементов в
множестве А называется мощностью множества А и обозначается
\А\. Говорят, что множество А равномощно множеству В, если
существует взаимно-однозначное отображение ф : А-+В.
Очевидно, два конечных множества равномощны тогда и только тогда,
когда они содержат одинаковое число элементов. Конечные
множества А такие, что \А\=п, будем называть также п-множества-
ми. Бесконечные множества могут быть равномощны какому-
9

нибудь своему подмножеству; например, множество натуральных
чисел равномощно множеству положительных четных чисел и
множеству с&оих квадратов. Среди бесконечных множеств
выделяют счетные и несчетные множества. Счетным называется всякое
бесконечное множество, равномощное множеству натуральных
чисел. В дальнейшем, когда речь будет идти о бесконечных
множествах, они будут считаться счетными.
На множестве Р(5) определим операции.
Объединением (или суммой) А\]В множеств А и В называется
множество всех элементов, принадлежащих либо А, либо В (либо
и Л, и В одновременно):
А\]В = {а<=3\а<=А или а<=В}.
Пересечением (или произведением) А(]В множеств А и В
называется множество всех элементов, принадлежащих как А, так
и В:
А(}В = {а<=3\а<=А и а<=В}.
Аналогично определяются объединения и пересечения
произвольной (в том числе бесконечной) системы множеств.
Дополнением множества А называется множество
А = {а<=5\а^А}.
Разностью множеств А и В называется множество Л\В =
= {а<=5\а<=А и а^В}. Очевидно, Л\В = Л(~)В.
Симметрической разностью множеств Л и В называется
множество
ЛЛВ= (А[}В) \(А(]В) = (Л\В)ЩВ\>1).
Множество Р(5) с определенными на нем операциями
объединения, пересечения и дополнения называется булеаном. При
этом справедливы следующие алгебраические законы:
1. Л(~)Л = Л; Л^|Л = Л (идемпотентность);
2. А[\В = В[\А\ А'[]В = В[]А (коммутативность);
3. А[\(В[\С) = (А[\В)[\С; АЦ(ВЦС) = (АЦВ)ЦС (ассоциативность);
4. А(\(А[}В)=А[}{А{\В)=А (поглощение);
5. Если А<=С, то А[](В[\С) = (АцВ)[}С (модулярность);
6. А[\(В\]С) = (А[\В)\ЛА[\С);
Ли (В()С) = (А[}В) П (А[}С) (дистрибутивность);
7. Л(~)0 = 0; А[]0 = А; (универсальные
Л(~]5 = Л; Лу5_=5 границы);
8. А[\А = 0; А\]А = 3 (дополняемость);
9. А = А (инволютивность);
10. А(]В = А[}В; А[]В = А(]В (законы де Моргана).
Если А[)В = 0, то Л и В называются непересекающимися
множествами. Представление множества 5 в виде объединения
попарно-непересекающихся подмножеств называется разбиением
10

множества 5. Другими словами, Аи А2 Ак является разбиени-
к
ем множества 5, если 5 = у Д- и А1(]А,--^0 для всех 1ф]. Со-
вокупность всех упорядоченных пар (а, Ъ) таких, что а^А, Ь<=В,
называется прямым (декартовым) произведением множеств А и
В и обозначается Лхй, т. е.
АхВ = {(а, Ъ)\а^А, ЬсаВ}.
Если А = В, то прямое произведение АхА обозначается А2.
Аналогично определяется прямое произведение к множеств:
Л1хЛ2Х...хЛА = {(аг, а2 ак)\а1<=Аи а2^А2, ..., о6еЛ},
а при совпадении множеств: Ак = АхАх.-.ХА.
Сформулируем очевидные правила, лежащие в основе многих
комбинаторных вычислений и оценок.
Правило суммы. Если 5 — конечное множество и 5 = у А{,
гдеЛе^(5),( = 1,2 А, то
к к
|5|==1ил-кУ|д-|>
причем равенство достигается, когда А\, А2, ..., Ак образуют
разбиение множества 5.
Правило произведения. Для конечных множеств А\, А2, ..., Аь\
к
14 а л2х ... хЛ1 = П1Л-1-
1=1
Бинарным соответствием между множествами А и В
называется любое подмножество а^АхВ. Если (а, &)еа, то говорят,
что а находится в отношении а к Ъ, и пишут ааЬ. Понятие
бинарного соответствия между А и В служит обобщением понятия
отображения ф : А-+В. Действительно, каждое отображение ф : А-^-В
определяет бинарное соответствие аФ между А и В: аа^Ь означает,
что & = ф(а). Обратно, пусть дано бинарное соответствие а между
множествами А и В. Рассмотрим для каждого аеЛ множество
всех ЬеаВ со свойством ааЬ. Это соответствие определяет
отображение ф : А—>В тогда и только тогда, когда для каждого аеЛ
существует ровно один элемент &еВ со свойствами ааЬ. Таким
образом, понятие бинарного соответствия включает понятие
отображения как частный случай (очень важный).
При А—В бинарное соответствие р^АхА называется
бинарным отношением на множестве А. Примерами бинарных
отношений являются отношение равенства Д = {(а, а) |аеЛ}, называемое
оиагональю множества А, и отношение, совпадающее со всем
множеством АхА, называемое единичным.
Бинарному отношению р на конечном множестве А можно
поставить в соответствие геометрический объект, называемый
11

ориентированным графом или диаграммой. Каждому элементу
аеЛ ставится в соответствие точка на плоскости, называемая
вершиной. Если арЬ, то точки, отмеченные как а и Ъ, соединяются
стрелкой, идущей из а в Ъ, называемой дугой. Совокупность
вершин и дуг, построенных таким образом, представляет собой
диаграмму Г (Л, р) отношения р. На рис. 1.1 приведены
соответственно диаграммы Г(Л, Д) и Г(Л, /),
О а О а где А = {а, Ь, с}, 1 = АхА.
/Тук Пусть А' — непустое подмноже-
/I \\ ство множества А, на котором за-
I/ ^Л дано бинарное отношение р: об от-
0 с *) (№*~ -^Ъ ношении р' на А', задаваемом ус-
Ь ^ь с ловием
р . . ар'Ь = арЬ для всех а, Ь^А',
ис" " говорят, что оно индуцировано
отношением р.
Сформулируем свойства, которыми могут обладать бинарные
отношения. Отношение р называется рефлексивным, если ара для
всякого оеЛ. Другими словами, отношение рефлексивно, если
А^р. Если арЬ влечет Ьра, то отношение р называется
симметричным. Если же ар& и Ьра влечет а = Ь, то р называется
антисимметричным отношением. Отношение р называется транзитивным,
если арЬ и Ьрс влечет аре. Нетрудно убедиться, что диагональ
обладает всеми четырьмя перечисленными свойствами, а
единичное отношение—всеми, кроме антисимметричности. Впрочем, если
А состоит только из одного элемента, то единичное отношение
совпадает с диагональю.
Смежным классом бинарного отношения р, определяемым
элементом оеЛ, называется множество всех таких элементов Ь^А,
что Ьра.
Бинарное отношение р на множестве А называется
отношением эквивалентности, если оно одновременно рефлексивно,
симметрично и транзитивно. Отношения эквивалентности играют важную
роль в комбинаторном анализе, так как они тесно связаны с
разбиениями множеств. В самом деле, легко можно доказать, что
совокупность смежных классов отношения эквивалентности на
множестве 5 является его разбиением и что каждому разбиению
множества 5 соответствует отношение эквивалентности р, классы
которого совпадают с блоками указанного разбиения (арЬ тогда
.и только тогда, когда а и Ь принадлежат одному и тому же
подмножеству разбиения множества 5).
Бинарное отношение р на множестве А называется
отношением частичного порядка, если оно рефлексивно, антисимметрично
и транзитивно. Отношение частичного порядка будем обозначать
символом ^. Запись а^Ь означает, что &^а. Иногда мы будем
говорить, что А (или (А, ^)) является частично упорядоченным
множеством, подразумевая, что отношение частичного порядка
уже известно (это звучит не совсем корректно, поскольку на
одном множестве можно зафиксировать различные порядки).
12

Частично упорядоченное множество называется тривиальным,
если а=0 тогда и только тогда, когда а = Ь. Частично
упорядоченное множество (А, ^), которое обладает свойством, что для
любых а, Ь<=А выполняется либо а^Ь, либо Ь^а, называется
цепью (его называют также линейно упорядоченным
множеством).
Напомним еще некоторые алгебраические понятия, которые
понадобятся нам в дальнейшем. Бинарной операцией на
множестве А называется отображение / : АхА->-А. Если /(а, Ь)=с, где
а, Ъ, с^А, то этот факт записывается следующим образом: а*Ь =
= с. Бинарная операция называется ассоциативной, если для
любых а, Ь, с^А:
(а*Ь)*с = а*(Ь*с).
Если бинарная операция удовлетворяет условию
а*Ь = Ь*а
для любых а, Ь^А, то она называется коммутативной. Элемент
ееЛ называется единичным (или нейтральным) относительно
операции *, если для любого а^А:
а#е = е*а = а.
Если такой элемент существует, то он единствен. Пусть
множество Л с заданной операцией обладает единичным элементом е.
Тогда элемент аг1 называется обратным (или симметричным)
к элементу оеЛ относительно этой операции, если а*а~[ =
= аг{*а=е. Множество А с бинарной операцией *, в котором
уравнения а*х = Ъ и у*а = Ъ однозначно разрешимы относительно
х и у для любых, а, Ъ^.А, называется квазигруппой. Непустое
множество Л, на котором задана ассоциативная бинарная
операция, называется полугруппой. В случае коммутативности
операции полугруппа называется абелевой. Полугруппа, в которой
существует единичный элемент и для каждого элемента существует
обратный, называется группой. Число элементов группы
называется порядком группы. Группа, все элементы которой являются
степенью одного элемента а (т. е. могут быть получены
последовательным применением операции с использованием одного
и того же элемента а, отличного от нейтрального), называется
циклической. Циклические группы всегда абелевы.
Пусть Л и В — конечные группы с произвольными порядками
с бинарными операциями * и ° соответственно и ср : А—>-В —
отображение, при котором для любых а, а'щА имеет место равенство
ф(а*а/) = ф(а)°ф(а/).
Такое отображение ф называется гомоморфизмом группы А
в группу В. Если ф — взаимно-однозначное отображение, то
гомоморфизм называется изоморфизмом.
Пример. Множество подстановок ф : Х-*-Х образует группу,
если операцию * определить как результат последовательного
действия двух подстановок, т. е. ф*а^=л, где Ух^Х : л(х) =
13

= а|з(ф(х)). Эта группа носит название симметрической группы
степени п=\Х\. Легко показать, что все симметрические группы
одного порядка изоморфны. Заметим, что при л^З
симметрические группы не являются а'белевыми.
Если в подмножестве В^А результат операции двух любых
элементов из В также принадлежит В, то говорят, что В замкнуто
относительно данной операции. Подгруппой называется непустое
подмножество группы, замкнутое относительно бинарной
операции и содержащее для каждого элемента обратный ему.
Множество А с двумя бинарными операциями + и о
называется кольцом, если оно образует абелеву группу относительно
операции + , полугруппу — относительно операции о и если °
дистрибутивно относительно +, т. е. если для любых а, Ъ, с^.А:
(а+Ь)°с = аос+Ь°с,
со (а+Ь) = с°а+ с°Ь.
В кольце нейтральные элементы относительно операций + и °
называются соответственно нулем и единицей. Элемент кольца
называется обратимым, если для него существует обратный
относительно операции о.
Если совокупность отличных от нуля элементов кольца
относительно операции ° образует абелеву группу, то в этом случае
кольцо называется полем. Поле, содержащее конечное число
элементов, называется конечным. Конечное поле из п элементов
существует тогда и только тогда, когда п = ра, где р — простое
число, а — натуральное. Такое поле единственно с точностью до
изоморфизма, сохраняющего обе бинарные операции. Оно
называется полем Галуа и обычно обозначается ОР(ра). Если а=1, то
ОГ(р) изоморфно полю вычетов по простому модулю р.
Примерами бесконечного кольца и бесконечного поля служат
кольцо целых чисел 2 и поле действительных чисел К.
Бинарными операциями здесь являются обычные сложение и умножение.
Линейным пространством Ь над полем Р называется
множество, снабженное бинарной операцией ц>: ЬхЬ—>-Ь, обычно
обозначаемой как сложение ф(а, Ъ)=а+Ъ для а, Ъ^Ь и внешней
бинарной операцией /: ЯX/,-»-/,, обычно обозначаемой как
умножение /(р, а)=ра, которые удовлетворяют следующим аксиомам:
а) относительно сложения Ь является абелевой группой. Ее
нейтральный элемент обозначается 0; элемент, обратный к а, обыч-
>но обозначается —а;
б) умножение векторов на элементы поля Р, или скаляры,
унитарно, т. е. \а=а для всех а, и ассоциативно, т. е. р(да) =
= (/?<?) а для всех р, ч^Р; а^Ь;
в) сложение и умножение связаны законами
дистрибутивности, т. е.
р(а-\-Ь) =ра+рЬ,
(р+д)а=ра+да
для всех р, д<=Р; а, Ь<=Ь.
14

Выражение вида р\а\ +... +рпап называется линейной
комбинацией векторов а,\, а2, ..., ап\ скаляры р{ — коэффициентами этой
линейной комбинации.
Алгеброй над полем Р называется ассоциативное кольцо с.
единицей А, содержащее поле Р, и такое, что Р лежит в центре А,
т. е. коммутирует со всеми элементами А. В частности, А
является линейным пространством над полем Р.
Новые понятия мы будем вводить ниже по мере
необходимости. Перейдем теперь к разъяснению смысла простейших
комбинаторных операций. Для начала ограничимся рассмотрением
линейно упорядоченных множеств. Однако постепенно мы будем
рассматривать множества более сложной структуры.
1.3. ВЫБОРКИ И УПОРЯДОЧЕНИЯ
С понятием выборки связывают как саму операцию выделения
подмножества заданного множества, так и ее результат:
выбранное подмножество. Если в тексте не будет специальной оговорки,
то далее будет иметься в виду именно вторая трактовка.
Пусть из «-множества Ап получена г-выборка:
(аь а2, ..., аГ), где а,-еЛп; 1 = 1, 2, ..., г; г<гс.
Число г называют объемом выборки.
В г-выборках в зависимости от условий задачи либо
учитывают порядок следования в них элементов (и тогда они называются
/-перестановками), либо не учитывают (и в этом случае их
называют г-сочетаниями). Например, две 5-выборки из множества
Л„(я>5);
(аь а2, аз, а4, а5) и (а5, а4, а3, а2, а{)
представляют собой равные 5-сочетания и в то же время
различные 5-перестановки. Вообще, две г-перестановки а= (аь а2, ..., аг)
и &=(&ь ^2 Ьг) равны: а=Ъ лишь если щ = Ьг, £=1, 2, ..., г.
В г-выборках возможно повторное появление элементов, и в таком
случае они называются соответственно г-сочетаниями с
повторениями и г-перестановки с повторениями, г-перестановку (с
повторениями) элементов множества А называют также словом длины
г над алфавитом А.
Очевидно, что понятия г-перестановки и г-сочетания и их
комбинации охватывают все возможные типы выборок. Поэтому нет
необходимости в понятии размещения, хотя оно все еще
появляется в литературе, преимущественно в учебной.
Неоднозначность решения комбинаторных задач, замеченная
на очень ранних этапах развития математики, породила
естественный вопрос: сколькими путями может быть осуществлено
требуемое комбинаторное расположение? В частности, подсчет числа
/-выборок из «-множества исторически был одной из первых
задач комбинаторики.
15

Найдем число всех возможных г-перестановок (без
повторений) из «-множества. Обозначим искомое число через Р (п, г).
Задача сводится к последовательному применению правила
произведения. В самом деле, в «-множестве имеется « возможностей
для выбора первого элемента г-перестановки. Как только такой
выбор сделан, остается «—1 возможностей для выбора второго
элемента, затем «—2 возможностей для выбора третьего
элемента и т. д.; для выбора г-го элемента будет «—г+\ возможностей.
По правилу произведения
Р(п, г) = «(«— 1)...(«—/" + 1),
откуда следует
Р(п, п)=п\
Для полноты результата примем
Р(п, 0)=01 = 1.
Подсчитаем теперь число возможных /"-перестановок с
повторениями. В этом случае после выбора любого элемента
/"-перестановки остаются все те же « возможностей для выбора
следующего элемента. Следовательно, по правилу произведения число
/•-перестановок с повторениями из «-множества равно «г.
Приведенные здесь рассуждения легко проиллюстрировать
на примере урновой схемы, различные типы которой
используются в теории вероятностей: имеется урна, в которую помещены п
одинаковых шаров и из которой поочередно вынимают г шаров.
При этом возможны два случая: вынутый шар либо возвращают
(выбор с возвращением), либо нет (выбор без возвращения).
Другой пример: сколько существует подмножеств у
«-множества 5, т. е. чему равно |Р(5)|? Ответ: |Р(5)|=2". В самом
деле, любая л-выборка Я — (5.,, 5,-., ... ,5.),где г=1, 2, ..., «, входит
в Р(5). Этой /"-выборке можно поставить в соответствие
«-выборку, состоящую из элементов двух видов: нулей, если элемент
не входит в К, и единиц, если элемент
входит в /?. Таким образом, единицы должны
У,г стоять на местах 1\, г2, ..., 1Г, а нули — на
остальных местах. Но число таких
«-выборок (т. е. «-перестановок с повторениями)
из 2-множества {0, 1} равно 2", что и явля-
— ется искомым результатом. Эта же задача
может быть интерпретирована как задача
о числе вершин гиперкуба в пространстве
« измерений (случай « = 3, 5 = {л:, у, г)
показан на рис. 1.2, где все подмножества
Р(5) суть вершины куба).
Упражнение. Сколько существует матриц размера кх1, составленных
нз нулей н единиц?
Подсчитаем теперь число г-сочетаний, обозначая его (")
л, г
V
■,У,г
Х,У
Рис. 1.2
16

или С/. Начнем со случая, когда все элементы в /--сочетаниях^
различны. Легко видеть, что число /"-сочетаний из «-множества
в г! раз меньше, чем число /"-перестановок из элементов того же.
множества. Следовательно,
('п \ = р(п>г) = п(п—\) ... (я —г+1) = п\
Г '; г! г! г! (л — г)! '
отсюда следует, что (п\ ~ (п гу, в частности,
(") = (2)!- '•
Заметим, что /"-сочетания из «-множества являются его
/"-подмножествами. В связи с этим рассмотрим задачу о числе {г\, г2, ...
. ., гк)-разбиений «-множества 5, т. е. упорядоченных разбиению
вида 3 = Т]\]Т2\}...\УГк, в которых Т{(]Т,=0 при 1Ф\\ £, /=1, 2, ...,&,,
причем Т,- есть /уподмножество множества 5, £=1, 2, ..., к. Оче-
видно, У* г( = п. Будем рассуждать аналогично тому, как мы;
1 = 1
это делали при нахождении числа Р(п, г), для выбора
/^-подмножества Т\ из 5 имеется \ \ возможностей; после этого Гг-под-
множество Т2 можно выбирать только из остальных «—Г\
элементов (так как Т\[\Т2 = 0), и значит имеется 1п Г1) способов
для выбора Т2 и т. д.; /"^-подмножество Тк можно выбирать
только после того, как выбраны л-множества 7,-, £=1,2,..., к—1,следо-
вательно, из « — V /•; оставшихся элементов можно выбрать его
1=1
/ к~1 \
I ?^1 ') способами. Применяя теперь правило произведения,.
\ гк /
получим, что искомое число (ги г2, ..., /а)-разбиений «-множества.
3 равно (с учетом выражения для
Ц=(п\(п-г1\11п-^гЛ== «I
«=1 / гх\ га! • . • гк\
гк
/-сочетание из «-множества может быть интерпретировано как
(/", «—г)-разбиение, а (1, 1, ..., 1)-разбиение является просто
перестановкой. Подсчитаем, наконец, число /--сочетаний с
повторениями из «-множества 5. Мы дадим три разных способа получения
этого числа, чтобы полнее показать специфику комбинаторных
рассуждений.
17

1-й способ. Пусть элементы множества 5 занумерованы
числами 1, 2, ..., п (т. е. 5 находится во взаимно-однозначном
соответствии с множеством первых п натуральных чисел), тогда
вместо г-выборок из множества 5 мы можем рассматривать
соответствующие им (взаимно-однозначно) г-выборки из множества
5' = {1, 2, ..., п}. Всякая г-выборка из 5' может быть записана
в виде А=(а1, а2, ..., аг), где а^аг^...^^ (равенство номеров
отвечает случаю одинаковых элементов в соответствующей г-вы-
борке из 5). г-выборке А (элементы в ней не обязательно
различны) поставим в соответствие /-множество А'= {щ+0, а2+1, ...
..., аг + г—1}, в котором все элементы, очевидно, различны.
Это соответствие, как легко видеть, взаимно-однозначное, при
этом г-множества А' являются г-сочетаниями без повторений из
(п + г—1)-множества {1, 2. ..., п, л+1, ..., п + г—1}, число которых,
как было показано, равно (п~^г .. Это и есть искомый
\ г )
ответ.
2-й способ состоит в получении рекуррентной формулы *.
Обозначим число г-сочетаний с повторениями из «-множества
5 через /(л, г). Очевидно, что
[(п, 1)=л и Д1, г) = 1
(для любого целого л>0 из п элементов можно выбрать п
различных 1-сочетаний, т. е. п различных элементов; и для любого
целого г>0 из одного элемента можно получить только одно
г-сочетание: г-выборку, составленную из г одинаковых элементов).
Зафиксируем в 5 некоторый элемент, тогда каждое г-сочетание
либо содержит этот элемент, либо нет. Если имеет место первый
случай, то остальные г—1 элементов этого /"-сочетания (а значит,
г-сочетаний, содержащих фиксированный элемент) можно
выбрать {(п, г—1) способами. Если имеет место второй случай, то
/•-сочетание выбирается из п—1 элементов, и тогда число таких
г-сочетаний равно /(л—1, г). Используя правило суммы, получим
}(п, г)=!(п, г-1)+/(л-1, г). (1)
В частности, зная /(л, 1) и /(1, г), имеем
Дл, 0)=Дл, 1)—/(/1-1, 1) = 1,
что согласуется с ранее полученным результатом. Теперь
последовательно получаем
/(л, 2) = /(л, 1) + /(л-1,2) =
= /(л, 1) + /(л—1, 1) + /(« — 2, 2)= ...
* Рекуррентными (гесштепсе . — возвращение) называются соотношения
(формулы), позволяющие, вычислять значения искомой величины шаг за
шагом, исходя из известных «начальных» значений и значений, подсчитанных
ранее.
18

. . . -= л + (л — 1) + (л — 2) + . .. + 1 =
- я(я+1) _ /л+ П.
2 ~[ 2 }'
/(л, 3) = /(/г, 2) + /(л -1,2)+ ... ^/(1,3) =
/л + Г\ , /л\ , , 1 _ /л + 2\
-=( 2 )^(2) + --- + 1^ 3 ;
и т. д. Легко убедиться, что
Г.(п.г) = (п + Гг-1)
удовлетворяет соотношению (1) и начальным условиям:
/(л, 1) = л; /(1, /-) = 1.
3-й способ. К г-сочетанию с повторениями из л-множества 5
(например, к ЬсЪ из 5 = {а, Ъ, с, й, е}) припишем все п элементов
множества 5 и полученные п + г элементов запишем по порядку,
помещая одинаковые элементы рядом: (аЪЪЬссйе). Затем
подмножества одинаковых элементов разделим гь—1 черточками:
(а\ЪЪЪ\ее\(1\е). Наконец, заменим все элементы между
черточками на точки: (--1---1--1-1-)- Таким образом, мы сопоставляем
/•-сочетанию расстановку л—1 черточек в п + г—1 промежутках
между п + г точками. Обратно, по каждой такой расстановке
однозначно восстанавливается соответствующее ей г-сочетание.
Например:
(• • | • | • ■ | • | • -)->(аа\ Ь\сс\с1\ее)->(ааЬсс^ее)->{а, с, е}.
Всего существует 1п ^~ т ~ 1 = 1^1 т М способов
расстановки п—1 черточек на п + г—1 местах. Значит, и г-сочетаний
с повторениями из «-множества существует ровно столько же.
В заключение этого параграфа рассмотрим понятие, связанное
с операцией упорядочения, — перестановку. Последняя может
рассматриваться с двух позиций: а) как упорядоченная еовокуп-
ность элементов данного множества или б) как нарушение
стандартного порядка, называемого обычно естественным (например,
алфавитным, числовым). Случай а) приводит к уже описанным
выше /--перестановкам, ге^л. Случай б) приводит к л-перестанов-
кам (в смысле определения /--перестановки), называемым просто
перестановками (или подстановками) и изучаемым в теории
групп.
Пусть, например, имеется перестановка
Р=(4, 3, 7, 5, 6, 9, 2, 8, 1, 12, 11, 10),
являющаяся нарушением естественного порядка первых 12 чисел
натурального ряда. Ее можно записать в виде подстановки
19

(в первой строке — естественный порядок, во второй —
нарушенный) :
р_ (I 2 3 4 5 6 7 8 9 10 11 12\
^43756928112 11 Ю,1'
Эта запись показывает, что при перестановке Р элемент 1
перешел в 4, 2 — в 3, 3 — в 7 и т. д. Перестановка Р может быть
записана иначе:
Р=(1, 4, 5, 6, 9)(2, 3, 7) (10, 12) (8) (11), (2)
где каждая скобка есть перестановка, действующая только на
элементы, заключенные в данной скобке, и не затрагивающая
элементы, не заключенные в ней (например, подстановка (2, 3, 7)
переводит 2 в 3, 3 — в 7, а 7 — снова в 2). Представление
перестановки в виде (2) называется разложением на циклы. Любая
перестановка может быть разложена на циклы. Это разложение
единственно с точностью до циклических перестановок элементов
внутри циклов. Например, (2, 3, 7), (3, 7, 2), (7, 2, 3) есть
различные записи одного и того же цикла.
Пусть некоторая перестановка содержит к\ циклов, состоящих
из одного элемента, т. е. 1-циклов, затем к% 2-циклов, кг 3-циклов
и т. д. Тогда она называется (к\, кг, ■■-, кп) перестановкой, или
перестановкой вида
\к'2к'...пп, (3)
где, очевидно,
п
2 Щ = п.
1 = 1
Теорема. Число перестановок вида (3) равно
Р (к,, к2, ... , кп) = -г ~ г . (4)
V * "; 1^2¾^ ... пкпкп\ х '
Доказательство. Рассмотрим запись разложения на
циклы для перестановки вида (3), а именно: вначале к\ скобок для
записи циклов длины 1, затем &2 скобок для записи циклов длины
2 и т. д. На имеющихся внутри всех скобок п позициях можно
расставить п элементов п\ способами, и всякий раз мы получим
запись перестановки вида (3). Однако среди этих п\ записей
встречаются различные записи одной и той же перестановки.
Выясним, сколько различных записей имеет одна перестановка. Во-
первых, как мы заметили выше, каждый цикл длины, I можно
записать в пределах данной скобки I способами. Во-вторых, Ы
способами можно переставлять скобки, где записаны циклы длины й
По правилу произведения получаем, что семейство циклов длины
I может быть представлено I 1-к{\ способами. Заставляя I
пробегать значения от 1 до л и снова применяя правило произведения,
получаем, что существует
20

# = 1^12^1 ...п*"Ля!
способов записи каждой перестановки вида (3). Следовательно,
всего имеется п\/М таких перестановок, ч. т. д.
Представление перестановок в виде произведения циклов
служит источником многих комбинаторных задач, например: найти
число перестановок «-множества, имеющих заданное число
циклов (без учета длины циклов); оставляющих заданные элементы
неподвижными; имеющих данное число циклов заданной длины
и т. д.
1.4. РАСПРЕДЕЛЕНИЯ И ЗАПОЛНЕНИЯ
Во многих задачах некоторая совокупность элементов
(например, зерен, болтов, гаек и пр.) распределяется по некоторому
множеству ячеек (коробок, ящиков и т. п.), которые вследствие
этого заполняются. Оба основных понятия — распределение
(синоним: разбиение) и заполнение — используются как для
обозначения операций, так и их результата — полученной ситуации.
Задачи этого класса существуют с давних пор и имеют
разработанную методику решения. Интерес к ним не затухает ввиду их
практического значения. Они появляются в самых различных
постановках: разбиениях множеств, рассечениях графов, сетей,
группировках станков, автоматов-роботов и т. д.
В теоретическом плане они могут быть интерпретированы как
отображения одного множества (элементов) на другое множество
(ячеек). Их можно также трактовать как взятие выборок.
Сложившиеся способы решения этого класса задач зависят от
условий, накладываемых на виды распределяемых элементов,
способы распределения, виды и вместимость ячеек. Очевидно, что
богатство возможных условий определяет разнообразие методов
решения задач. Приведем ниже некоторые сведения, вводящие
читателя в этот круг вопросов.
Для подсчета числа распределений необходимо уточнить,
являются ли элементы данного множества и ячейки различимыми
(например, занумерованными) или нет. В соответствии с этим
задачи делятся на следующие четыре класса.
(А) элементы множества различимы, ячейки также
различимы;
(В) элементы множества неразличимы, ячейки различимы;
(С) элементы множества различимы, ячейки неразличимы;
{О) как элементы множества, так и ячейки неразличимы
между собой.
Внутри каждого из этих классов задачи в свою очередь
различаются видом отображений, задаваемых конкретными
условиями. Пусть всюду в дальнейшем N означает «-множество
элементов, а ^ есть г-множество ячеек. Поскольку в настоящем разделе
речь идет лишь о теоретических основах операции распределения
и заполнения, мы рассмотрим эти классы задач в общих чертах,
21

не стремясь к полному и детальному изложению всех возможных
подходов к решению соответствующих задач.
(А) Как сказано выше, все элементы множества N и все
ячейки множества ^ различимы. Для нас здесь несущественно,
отличаются ли они формой, цветом, объемом или даже номером.
Важен только факт различия. Укажем несколько эквивалентных
форм этой задачи: а) образование слов длины г из алфавита,
состоящего из п букв; б) последовательный выбор г шаров из урны,
содержащей п шаров, с немедленным их возвращением; в)
образование г-перестановок с повторениями из п символов.
Характер отображения, на которое мы еще не наложили
никаких ограничений, позволяет сразу же указать число возможных
распределений:
Р = п\
поскольку для каждой из г ячеек имеется возможность
помещения в нее любого из п элементов. Частный вид отображений —
взаимнооднозначные — соответствует дополнительному
ограничению: каждая ячейка вмещает один и только один элемент. В этом
случае
Р = п(п-1)... («-/■+ 1) = "' .
(п ~ г)\
К классу (А) относятся, в частности, следующие случаи
различимости элементов и ячеек.
(Д) Множество N имеет (к\, к2, ..., кт)-спецификацию, если
оно имеет к\ элементов первого вида (например, цвета), к2
элементов второго вида, ..., кт элементов т-го вида (при этом &1 +
+ к2 + ... + кт = п).
(А2) г-множество # имеет (пи п2, ■-, пг) .-спецификацию, если
в 1-й ячейке помещаются щ элементов, £=1, 2, ..., г.
(Л3) Элементы в ячейках упорядочены, т. е. две ячейки
считаются заполненными по-разному, если различно упорядочение
помещенных в них (даже одних и тех же) элементов; ограничение
на объем ячеек не накладывается.
Не претендуя на полное описание всех возможных ситуаций,
приведем лишь один пример. Пусть, например, множество .V
имеет (р, 9) -спецификацию, т. е. содержит р элементов первого
вида и ц элементов второго вида; р + <7 = гс. Требуется узнать,
сколько существует распределений элементов множества N по г
различным ячейкам без ограничений на число элементов в
каждой из ячеек. Элементы первого вида могут быть размещены по г
ячейкам
способами, а элементы второго вида —
(<^7'Н'%~')
22

способами. Общее число распределений в силу правила
произведения равно
(р+ г — \ | (я + г — 1\
\ Р )\ Я У
Если имеет место (к\, к2, ..., кт) -спецификация множества Ы, то
число распределений п элементов его по г различным ячейкам
равно
П
( Г + Л,-
I
1
У
п элементов
СП
Рис. 1.3
Перейдем к задачам класса (В).
Как было сказано, в задачах этого
типа элементы множества Л^
неразличимы, а множества ^ —
различимы. Рассмотрим различные
случаи:
1. Элементы множества N
размещаются по ячейкам множества ^
так, что ни одна ячейка не пуста (на
рис. 1.3 показано распределение п =
= 10 элементов по г=4 ячейкам).
Как видно, задача сводится к определению числа способов
провести г—1 линий в п—1 промежутках между элементами;
это число равно (п I. К этому же типу задач относятся
следующие: найти число способов окрашивания г цветами п
одинаковых объектов (например, шаров); найти число г-сочетаний
с повторениями, в которых каждый элемент использован.
2. Элементы из Л^ размещаются по ячейкам из Л так, что могут
быть пустые ячейки. Метод решения задач этого типа в основном
тот же. К множеству элементов АЛ присоединяют г символических
«пустых элементов». При этом задача сводится к определению
числа способов провести г—1 линий в п + г—1 промежутках
между элементами. Это число равно
(п+ г — Г, _ !п+ г—\\
[ г-\ )-[ п )■
К задачам данного типа относится, например, следующая:
найти число решений уравнения
Х1+Х2 + .: + Хг = П
в неотрицательных целых я,- : 1 = 1, 2, ..., г.
3. Наконец, к этому классу относятся задачи, связанные с
подсчетом числа г-выборок из я-множества.
Оставшиеся два типа задач, (С) и (Б), в которых
неразличимыми оказываются ячейки для заполнения, представляют, при
попытках их решения, значительно большие трудности. Их обычно
называют объединенным именем неупорядоченных разбиений.
Задачи типа (С), где неразличимы только ячейки, а распределяе-
23

мые элементы различимы, поддаются, впрочем, решению.
Приведем некоторые формулы.
1. В случаях, когда не допускаются при заполнении пустые-
ячейки и когда учитывается порядок попадания элементов в
ячейки, искомое число распределений равно
2. Если предыдущее разбиение видоизменяют так, что
допускают 1, 2, ..., г пустых ячеек, то искомое число распределений
равно
(А')'п = Агп + ЛГ' -т- • • • + А\. (2)
3. Если пустых ячеек нет, а порядок расположения элементов.
в ячейках не учитывается то число распределений равно
К = \ V , ,"' , =3(п,г). (3)
г! А^ 5!! 52! ... 5Г!
5,+ ... + 5,=/1
5 .-> 1
Число 5 (п, г) называют числом Стирлинга 2-го рода (см. ниже
§2.3).
4. Когда в случае 3 допускаются 1, 2, ..., г пустых ячеек, то
число распределений равно
(В')« = В^ + ВТ'+ ... +В1 (4)
Дадим набросок доказательства этих утверждений. В самом
деле, пусть в случае 1 распределяются элементы множества Л' =
= {(11, (12, ..., (1п}- Распределения Ь имеют вид:
Ь = {а1; а2, . . . , а,-, | а,;!+! ,а,1+2, ■ ■ ■ , «г I • • • |««,_!+ь агг.,, +2. • ■ • .«„)-
Число \Ь\ этих распределений можно подсчитать двумя
способами:
а) \Ь\ = п\ ( I, т. е. число перестановок в множестве N
умножается на число распределений г—1 линий в п—1
промежутках;
б) \Ь\=Апг-г\, т. е. искомое число умножается на число
возможных перенумераций ячеек.
Приравнивание а) и б) дает формулу (1).
В случае 3, как и в случае 1, применим два способа подсчета
числа распределений по различным ячейкам:
\ Вп-Г\ = V (П)(П-5Л. .. (П—Ъ—З,— ... — 5,_1^
51+-..+5г==П
^ VI п\ (п — %)! ^. ] (п — В?—!Ъ— ...~Вг.д'.
^1 вг\(п — в{)\ «г! (л — «! — «г)! { % вг\ (л — %"— %'—\ .. — $,у,
~~ 2^ %! 52! ... вг\ "
откуда следует (3).
/
24

Формулы (2) и (4) очевидным образом следуют из (1) и (3)
соответственно.
Рассмотрим, наконец, случай (И), т. е. тот класс задач о
распределениях, когда множества N п К оба состоят из
неразличимых элементов. Эти задачи оказались наиболее трудными и
теория их решения еще далеко не разработана. Наиболее известной
интерпретацией данного случая является теоретико-числовая
задача о разбиении натуральных чисел на натуральные слагаемые.
Прежде всего заметим, что задачам из класса (О) нельзя
сопоставить задачи из предыдущих классов, как это было сделано
выше: связи оказываются значительно более сложными, и найти
подходящее аналитическое выражение для получения искомого
числа не удается.
Для подсчета числа разбиений, относящихся к задачам типа
(О), основным средством пока является следующий рекуррентный
метод.
Пусть «-множество 5 разбивается на к непустых частей
а\. а.2. ..., ак, причем |аг|>1, 1=1, 2, ..., к. Обозначим через Рк{п)
число таких разбиений. Очевидно, что Л(«) = 1; Рк(к)=\,
Рк{п) = 0 при п<к,
ь
]Г а-1 = п. (5)
Предположим, что |а!|>|а2|> ... >|а/г| (перенумеруем, если
иужно, части разбиения). Ясно, что
£(0,-1) =л-6. (6)
Получили разбиение (п—к) -множества на части, число которых
«:& (равенство в том случае, если любое а,: содержит не менее
2 элементов). Число таких разбиений равно по правилу суммы
V Р1 (п — к), а в силу равенства (6) это число равно числу раз-
« = !
биений «-множества на к частей, т. е.
^Р({п-к) = Рк{п). (7)
1 = 1
Эта рекуррентная формула позволяет с учетом значений (5)
получить последовательно значения для Рк(п), сводя их, если надо,
в таблицу 1.4.
При малых значениях к можно получить формулы для Рк(п),
например:
Р1(п) = \; Л.(2) = 1; Р2(1) = 0;
Р2(п) =Р2(я-2) +/>,(я-2) =Р2(п—2) + 1;
25

Таблица 1.4
Числа Рк (п)
123456789 10
1
2
3
4
5
6
7
8
9
10
1 1
1
1
1
1
1
2
1
1
1
2
2
1
1
1
3
3
2
1
1
1
3
4
3
2
1
1
1
4
5
5
3
2
1
1
1
4
7
6
5
3
2
1
1
1
5
8
9
7
5
3
2
1
1
Я(и) = Е^а(") И 2 3 5 7 11 15 22 30 42
откуда
Р2(п) = —, если п — четное;
Рг(п) = , если п— нечетное.
Но уже для к — Ъ формулы получаются довольно громоздкие.
Нега
следование поведения величин Ри{п) и Я (я) = ^ Я6 (я) (число
всевозможных разбиений числа п) для больших значений к
сопряжено с большими трудностями. Найдено приближенное
значение
Рк{п)~-}-.(п-\\
которое на практике часто оказывается достаточным. Для Р(п)
найдено рекуррентное соотношение
Р(п) = Р(п — \) +Р{п — 2) — Р(п — Ь) — Р(п — 7)+ ■..
Ж- ± к \ ,
...+(— I)*"1 /5 "
-;
и подсчитаны первые последовательные значения этой величины.
Все эти и подобные им вопросы исследуются в теории
разбиений (см. [16]).
П'римерно с половины прошлого века усилиями Дарфи, Ферре,
Сильвестра, а позднее Макмагона и др. в теорию разбиений во-
26

шла интерпретация их с помощью точечных графов. Например,
разбиение 29 = 7 + 7 + 5 + 3 + 3 + 2 + 2 изображено на рис. 1.5.
Части разбиений располага-
ооооооо г '
ют, как правило, сверху вниз в
порядке убывания. Непосредст-
0000000 венно из рассмотрения
соответствующих «-точечных графов (на-
° ° ° о о зываемых также графами Фер-
ООО С^ОО'ООООО,
\
„ „ о ^Э о о о о
\
о о \ о о
о о ^
\
Рис. 1,5 Рис. 1,6
ре) можно получить следующие результаты.
1. Число разбиений «-множества, в которых наибольшая часть
имеет к элементов, равно числу разбиений «-множества на к
частей, т. е. Рк(п). Эта теорема доказывается транспонированием
графа Ферре относительно главной диагонали; такие графы
называются сопряженными. Так, на рис. 1.6 множество из 10 элементов
разбито на 5 частей: 10 = 3 + 3 + 2+1+1; после транспонирования
получаем: 10 = 5 + 3 + 2, т. е. разбиение 10-множества, в котором
наибольшая часть 5 элементов (аналогичная картина на рис. 1.7:
10 = 3 + 2 + 2+1 + 1 до транспонирования и 10 = 6 + 3+1 после
транспонирования).
2. Число самосопряженных
разбиений «-множества (разбие- о , о о оооооо
ние называется самосопряжен- 0 0 о о о
ным, если соответствующий ему
граф Ферре симметричен относи- ° ° °
тельно главной диагонали)
равно числу разбиений того же
множества на неравные подмножест- о
ва, состоящие из нечетного числа Рис. 1.7
элементов. Верна и обратная
теорема.
Так, например, самосопряженному разбиению 20-множества
20 = 6 + 4 + 4 + 4+1+2 (рис. 1.8) взаимно-однозначно соответствует
разбиение 20=11 + 5 + 3+1, если точки из 1-го столбца, лежащие
ниже диагонали, перенести на 1-ю строку, из 2-го столбца — во
2-ю строку и т. д.
3. Число разбиений «-множества на неравные между собой
части равно числу разбиений того же множества на части,
состоящие из нечетного числа элементов.
Пусть дано разбиение «-множества (например, « = 34) на не-
27

о^--о- —о о о-—-о о
! N
ф ^--О О
I I I \
ф сЬ А Ъ
I
6
о о о
о о о
о о о
о о о
Рис. 1.8
Рис. 1.9
четные составляющие (34 = 5 + 5+5+5+3 + 3+3+1 + 1 +1 + 1-г 1).
Все равные нечетные компоненты собираем в группы (4 пятерки,
3 тройки и 5 единиц) и числа их повторений (4, 3 и 5)
записываем в двоичной системе (4 = 22; 5 = 22 + 2°; 3 = 2' + 2°). Запишем
новое разбиение с учетом полученного двоичного представления
(34 = 5-4 + 3-3 +1 -5 = 5-22 + 3-21 + 3-2°+ 1 -22+-1 -2° = 20 + 6+3 +
+ 4+1). Эта процедура всегда осуществима, так как любое число
единственным образом записывается в двоичной системе.
Обратный ход рассуждений также всегда возможен.
4. Если С}п и 0,п — числа разбиений «-множества на четное
и соответственно нечетное число неравных между собой частей,
то
<г,.
Оп, если п Ф—(3& + 1);
<2„ -г (— 1)*, если п = — (ЗА ± 1);
где к=\,2, ...
Пусть граф Ферре разбиения я-множества на неравные части
имеет вид, показанный на рис. 1.9. 5 есть наименьшая часть
разбиения, а .Е-множество точек (линия), расположенных,
начиная с наибольшей части, под углом 45°. Если |5|е^|.Е|, то
перенесем 5 к Е; если же |5|>|Е|, то, наоборот, Е перенесем к 5.
Результатом таких переносов будет изменение четности числа
неравных частей разбиения. Каждому четному разбиению
сопоставляется нечетное, и притом взаимно-однозначно: (2п=(2п-
Читателю рекомендуется проделать эту операцию на следующем
примере: 7 + 6+5 + 3 + 2^8 + 7 + 5+3.
Однако операция не будет возможна, если линии 5 и Е
пересекутся друг с другом и
|5| = |Я| или |.5| = |Я| + 1.
Пусть \Е\=к. Тогда в первом из исключительных случаев имеем
п = к + (к+ 1) + . . . + (2к — 1)
(ЗА—1);
28

а во втором
п = (к+ 1) + (£ + 2)+ ... +2^ = -(3^+1),
что и доказывает наше утверждение.
1.5. СИСТЕМЫ МНОЖЕСТВ
Выше был определен предмет комбинаторного анализа, даны
некоторые сведения из теории конечных дискретных множеств,
введены операции, основные для комбинаторных исследований,
разъяснены методы подсчета числа основных комбинаторных
объектов: выборок и упорядочений, распределений и заполнений.
Все это было проделано только для множеств линейно
упорядоченных, и не для всех возможных случаев. Такие ограничения
были продиктованы вводным характером главы.
Однако было бы неверным заключить, что и вопросы,
затронутые в настоящей главе, тоже имеют лишь ограниченное
значение и что их роль чисто педагогическая. Общая теория конечных
дискретных множеств — развивающаяся математическая
дисциплина со своей собственной проблематикой. При этом часто
случается так, что к теоретическим исследованиям конечных
множеств сводятся задачи в высшей степени практические.
Возьмем, например, одну из задач о разбиениях конечного
«-множества 5 на непересекающиеся подмножества. Рассмотрим
разбиения л\ и л2. Для элемента 5е5 обозначим через /,-(8)
число элементов в том блоке разбиения щ, который содержит 5 (г =
= 1, 2). Разбиения т и я2 назовем сопряженными, если
упорядоченные пары чисел (/1(5), /2(з)) при всех 5е5 различны.
Пример. Пусть 5 = {1, 2, 3, 4, 5, 6}. Зададим два разбиения:
я,:5 = {1, 2, ЗМ4, 5,}1Д6};
я2:5 = {1, 4, 6}У{2, 5}1ДЗ}.
Для них получим
1
Л (О- Л (0 {3,3} {3,2} {3,1} {2,3} {2,2} {1,3}
Так как все упорядоченные пары {МО. Ы0) различны, то Я1 и
л2 — сопряженные разбиения множества 5. Относительно этих
сопряженных разбиений было доказано [35], что пара этих
разбиений существует тогда и только тогда, когда пф2, 5, 9.
Результат этот был получен при решении следующей задачи о «прозва-
нивании» многожильных телефонных кабелей.
Пусть задан кабель из п неразличимых жил. Требуется
определить на его концах А и В соответствующие каждой жиле
клеммы; Л,-, В,; 1=1, 2, ..., п. Метод решения состоит в соединении
29-

У
трупп концов жил на одной стороне кабеля и испытаний на
прохождение тока, производимых с другой его стороны. Разъясним
•его подробнее на примере 6-жильного кабеля.
Возьмем конец А с клеммами
А\, А2, ..., Л6 и соединим .его
клеммы в соответствии
разбиением щ (положение I на рис.
1.10). Пусть в результате
проверки со стороны конца В (с
клеммами Ви В2, ..., В6) получили
ситуацию, показанную на рис.
1.10 положением П. Неразличи-
I Л Ж Ж мне клеммы Вь В2, В3 обозна-
рис. 1 10 чим через х, В4 ий5 — через у, а
В6 — через г и соединим
клеммы на конце В в соответствии с разбиением яг (положение
III). Затем, произведя разъединение клемм на конце А,
проверяем, сколько и каких жил со стороны А оказались соединенными
на конце В. Пусть, например, жила А\В\ оказалась соединенной
с одной только клеммой на конце В. Поскольку мы знаем, что
клемма А\ принадлежит множеству {Аи А2, Л3}, а клемма на
конце В находится в множестве из двух соединенных клемм (а
именно В2 и В5), и поскольку пара {МО. Ы0} = {3, 2} соответствует
лишь 1 = 2, мы заключаем, что А\ соединена с В2. Аналогично,
если клемма Аь соединена с двумя другими клеммами на стороне
В (т. е. жила Л5В5 принадлежит к множеству трех жил, что были
соединены), то Л5 должна быть соединена с В4 (поскольку паре
(2, 3) соответствует 1 = 4) и т. д.
Этот алгоритм был распространен и на общий случай. Пусть /
есть «-множество целых чисел: / = {1, 2, ..., п). Предположим, что
для / существуют два сопряженных разбиения:
я, :1 = Р1\]Р2[]...ЦРк;
я2:/ = Р1'1|Р2'11...11Р*'.
На конце А соединим сначала жилы в соответствии с разбиением
Я], т. е. жилы, номера клемм которых принадлежат некоторому
РгбЕяь /=1, 2, ..., к. На конце В проверкой подбираем
подмножества 5ь 52, ..., 5« клемм тех жил, которые были соединены на
конце А, и перенумеруем клеммы на конце В так, чтобы для
любого 5Г множество индексов у клемм В*, встречающихся в 5Г,
было в точности подмножеством из Л\. Теперь соединим жилы на
конце В в группы Ти Т2, ..., Тк, где 7,- состоит из всех тех жил
с клеммами В,-, для которых геР/. Разъединяя все соединения
на конце А, подбираем, какие жилы со стороны А соединены на
конце В.
После проделанной процедуры можно найти «левую» и
«правую» клеммы для одной и той же жилы. В самом деле, пусть мы
взяли какую-нибудь жилу, скажем Аи, и пусть на конце В она
30

входит в Г/, которое имеет, скажем, р элементов (откуда и
находим это р). Поскольку мы знаем число элементов в
подмножестве 5/, содержащем Аи (пусть оно, например, равно <?), то из
способа построения 5,- и Т,- и из того, что все пары (р, (?) = {[!("),
Ы")} различны, мы можем найти единственное Дц такое, что
Аи и Вс суть концы одной и той же жилы.
Во многих областях математики и в прикладных областях
ставят и решают задачи, не только сводящиеся к исследованию
дискретных множеств и их систем, но и непосредственно
формулируемые в их терминах. Так, например, обстоит дело в теории
конечных автоматов, дискретной вычислительной технике,
прикладных проблемах алгебры и др. Опишем несколько типичных
задач, встречающихся весьма часто.
Шпернеровы семейства. Говорят, что подмножества 5), 52, ...
..., 5т конечного множества 5 образуют шпернерово семейство,
если из них ни одно не содержится в другом. Пусть |5|=л;
каково максимально возможное число пг членов в шпернеровом
семействе? Ответ на этот вопрос носит название теоремы Шпер-
нера (см. гл. 8): тп = \т^2л) ■
Разделяющие системы. Это понятие было введено А. Реньи
[36] в связи с задачами теории информации. Система
подмножеств {51, 52 5т} конечного множества 5 называется
разделяющей, если в ней для любых двух различных элементов
множества 5 существует подмножество 5,-, содержащее только один
из этих элементов. А. Реньи поставил задачу нахождения
минимальной разделяющей системы при условии, что каждое
подмножество этой системы состоит в точности из заданного числа
элементов. Эта задача была исследована в [37].
Задачи о пересекающихся подмножествах. Существует много
задач, в которых вводятся ограничения на мощность самих
подмножеств 5Ь 52, ..., 5т^5 и их пересечений. Требуется
определить максимальное число ш подмножеств, удовлетворяющих этим
условиям, при фиксированном га=|5|. В этом отношении
рекомендуем обзор [38]. Приведем классический результат Эрдеша,
Чао Ко, Радо [39]. Пусть
1) каждое из подмножеств 5ь 52, ..., 5т содержит не более к
элементов, где к^.п/2;
2) ни одно из подмножеств не содержится в другом;
3) любые два подмножества пересекаются.
Тогда максимально возможное число подмножеств есть I " ,М
' к— 1 /
Именно такое число членов имеет система всех ^-подмножеств
л-множества 5, содержащих некоторый фиксированный элемент
Через [л:] обозначается наибольшее целое число, не превосходящее х\
через \х\ — наименьшее целое число, большее или равное х.
31

Покрытия и упаковки. Задачи построения наилучших кодов
-приводят к следующей комбинаторной проблеме: определить
наибольшее число т, при котором существует система г-элементных
подмножеств {5Ь 3?,, ..., 5т} я-множества 5, где |5,Г|5/|<^ для
любых 1^1</^т. Другими словами, требуется, чтобы каждое
г'-подмножество множества 5 содержалось не более чем в одном
из подмножеств системы, Эта задача называется задачей об
упаковках. Часто рассматривается и противоположная задача,
Потребуем, чтобы каждое г'-подмножество содержалось не менее чем
:з одном из подмножеств системы; спрашивается, какое
минимальное количество г-подмножеств п-множества 5 необходимо для
образования такой системы, Эта задача называется задачей о
покрытиях. Как и задача об упаковках, она решена пока лишь
в частных случаях (например, при г = 3, 1 = 2; г = 4, 1 = 2), Если
вместо подмножеств 5ь 52, ..,, 5т рассмотреть их дополнения
•5/, 52', ,.., 5т', где 5,-' = 5\5,', и положить к = п—I, 1 = п—г, то
получим другую форму задачи о покрытиях: какое минимальное
число /-подмножеств «-множества 5 необходимо, чтобы в любом
£-подмножестве множества 5 содержалось по меньшей мере одно
из выбранных /-подмножеств. Это число называется числом
Турами Т(п, к, I). В 1941 г, Туран [40] доказал, что
/ (п, к, 2) = тп - (к — 1) при т < ■< т -)- 1,
Несмотря на простоту формулировки, в общем случае задача
нахождения чисел Турана оказывается исключительно трудной. При
/>3 результатов получено мало, Известно (см. [41]), что
Т(п, к,1)г=п — (к—\) при 1 < —-—<——.
Т(п, к,1) =
Г _1_
I 2
Свойство 98. Говорят, что система подмножеств 5Ь 52, ..., 5т^
^5 обладает свойством 98, если существует такое разбиение
множества 5=5Ц5" (5'П5" = 0), что 5,^5', 5,^=5" (1 = 1, 2, ..., тп).
Накладываются ограничения |5|=гг и |511 = |52| =,,.= |5т| —к
и ищется минимальное число тп = т(п, к) подмножеств в системе,
не обладающей свойством 98. Эта задача рассмотрена в гл. 7,
Еще один важный класс задач о системах множеств связан с
теоремой Рамсея, которой посвящен отдельный параграф гл, 3.
Изучение систем множеств — главная задача в
комбинаторном анализе, От успехов этой работы зависит как обогащение его
теории, так и расширение области приложений,
31
2
— 1
I— 1
«. I
2 I

Глава 2
ПРОИЗВОДЯЩИЕ ФУНКЦИИ
Долгое время основным содержанием комбинаторного анализа
был подсчет количества конфигураций определенных типов. Часть
комбинаторной теории, изучающая эти вопросы, и поныне играет
важную роль в приложениях,
В § 1.3 и 1.4 мы рассматривали прямые («элементарные»Л
методы подсчета. Настоящая глава посвящена косвенным
методам, с помощью которых подсчитывают количество
комбинаторных конфигураций.
2.1. ОСНОВЫ МЕТОДА ПРОИЗВОДЯЩИХ ФУНКЦИЙ
Метод производящих функций является одним из наиболее
развитых комбинаторных методов. Главные его идеи были
впервые высказаны в конце XVIII в. в работах Лапласа по теории
вероятностей. Поясним их на следующем простом примере.
Рассмотрим произведение конечного числа линейных биномов
г=0
где
йг (Хр . . . , Хп) — \ ХцХ^ . . . XI^
1<1,<|а<...<1 <|л
суть элементарные симметрические функции от переменных
хи ..., хп. Заметим, что слагаемым коэффициента ат можно
сопоставить г-сочетания из п элементов х\, ..., хп. Выражение (1)
назовем нумератором г-сочетаний из п элементов. Если положим в (1|
Хг = 1 для 1= 1,..., п, то получим
£(^ = (1^)-. (2)
так как аг(1,..., 1) есть число г-сочетаний из п элементов.
Разложим функцию (1 + 0п по степеням I по формуле Тейлора:
2 К. А. Рыбникоз
лз

(1 + Оп = У ^—-Г. (3)
У ' £1 г\(п — г)\
г=0
(Этот результат можно также доказать индукцией по п.)
Из (2) и (3) вытекает
г=0 г=0
Приравнивая коэффициенты при одинаковых степенях I в (4)',
снова получаем (теперь уже аналитически) результат гл. 1: число
г-сочетании из п элементов равно . Ьсли же применить
Н г! (л - г)! Р
этот результат гл. 1 к формуле (2), то мы получим еще одно
доказательство тождества (3). Подобный метод нахождения
коэффициентов разложений функций в первой половине XIX в. был
общепринят и назывался комбинаторным анализом в отличие от
математического анализа, к которому относили аналитические
методы нахождения разложений.
В выражении (2) функция \(1) = (\-\-1)п взаимно-однозначно
связана с последовательностью чисел
{(^)|, г = 0, 1,2, ... ,п.
Такая связь оказывается весьма полезной: придавая в формуле (2)'
различные частные значения переменной I, можно получить
многие важные тождества. Так, при 1=\ и 1=—1 имеем
соответственно:
*■-$(;)-■+»+(;) + $ + ... + (:;).
• -2(-|)-(;)->-«+(5)-(;) + - + (-|)-(;):
=0
их почленное сложение и вычитание дает
[т] т
г=0 г=0
а простая разбивка сомножителей
(1+*)п=(1+0т(1 + 0.п~т
приводит к тождеству
34

г
п\ _ V1 [п — т\ ( т
г)~1л\ к )\г-к
известному как свертка Вандермонда. И наконец, заменой в (2)
1=а\Ъ и домножением левой и правой частей на Ъп сразу же
получаем биномиальную теорему (биномиальную формулу):
в связи с этим числа (п) называют биномиальными
коэффициентами.
Упражнение. Индукцией по т доказать полиномиальную теореиу:
1 = 1
где сумма берется по всем решениям уравнения Л| + л2 + .,. +лт=л в целых
неотрицательных числах; коэффициенты в правой части называются
полиномиальными коэффициентами, они уже появлялись в гл. 1 как числа (Л|,
Л2,.... пт) -разбиений л-множества,
Функцию 1(1) = (1-\-1)п называют производящей функцией
последовательности чисел | : ' или, короче, производящей
функцией числа г-сочетаний из п элементов, г = 0, 1, 2 п.
Пусть теперь рассматривается числовая последовательность
а= (а0, аь а2,...), или, иначе, функция ап целочисленного
аргумента п. Ей взаимно-однозначно соответствует ряд
00
/в(0 = 1>,Л (5)
оперировать с которым гораздо удобнее и проще, особенно когда
он сходится к функции, обладающей удобной аналитической
формой. Ряд /а(0 называют производящей функцией последователь-,
ности а. Таким образом, производящие функции позволяют
перейти от рассмотрения отдельных величин (например, г-сочетаний для
частного значения г) к рассмотрению их последовательностей и
даже классов последовательностей.
Для большинства комбинаторных задач ряд (5) является
конечным. Если же такой ряд бесконечен и радиус его круга
сходимости равен нулю, то оперировать над ним можно лишь в рамках
алгебры формальных степенных рядов, которую мы рассмотрим
в следующем параграфе.
2*
35

2.2. ВИДЫ ПРОИЗВОДЯЩИХ ФУНКЦИЙ
И НУМЕРАТОРОВ
Пусть # есть некоторое кольцо с единицей. Кольцо 5(#)
последовательностей над # и изоморфное ему кольцо #[[^]]
формальных степенных рядов над # определяются следующим
образом. Элементами кольца 5(^) являются последовательности
{а} = {(а0, аи а2, ...)}, (1)
а соответствующими элементами кольца &['[^]] — ряды
{?а№, РаЦЬ-^а*. (2)
Суммой последовательностей а= (а0, щ,...) и Ь=(Ьо, &!,...)]
назовем последовательность
с = а+Ь= (а0+Ь0, 01+Ьь ...) = (с0, си ...),
а суммой рядов Ра(1) и Ръ(1), принадлежащих классу (2), ряд
РсУ)=РаУ)+Рь(Ц:
Рс (О = ^ ^',
где ст = ат-\-Ът.
Произведением (или сверткой) последовательностей а и Ъ из
класса (1) назовем последовательность аХЬ = с1=(с1о, ^1,...),
у которой
йг = а0Ьг+-а1бг_1+- ... +агЬ0, г = 0, 1 (3)'
а произведением (сверткой) рядов РаЩ и Рь(1) из класса (2)—
ряд
^(0=^(0x^(0 = 2^',
/■=0
где йг определяется по формуле (3).
Определим далее: нуль в классе (1) как (нулевую)'
последовательность
О=(0, 0,...),
тогда нуль в классе (2) есть соответствующий О ряд
^0(0=0;
единицу в классе (1) как (единичную) последовательность
е=(1, 0, 0,...),
тогда единица в классе (2) есть соответствующий е ряд
/40 = 1-
36

Наконец, обратный элемент дли ое5(^) относительно сложения
в классе (1? есть —а=(—Оо, —аь ...),_ а соответствующий ему
обратный элемент для Ра{Ц в классе (2)' ееть
Со
- Ра (0 =Р-а (0 = ^(-^.
Легко видеть, что все аксиомы кольца для 5(1?) и #[[*]]
имеют место.
Пусть а0 является обратимым элементом кольца Я, тогда ищем
аг1 = а' из условия аХа' = е, т. е.
а0а'о=1,
аАа'о + аА^а^ + ай-га'гЧ- ... +а0а'А = 0,
откуда находим а'ь(& = 0, 1,...) из первых к-\-\ уравнений
последовательным вычислением по методу Гаусса (либо по правилу
Крамера). Таким образом, лишь для последовательностей а,
таких что а0 обратим, существуют от* и Ра~1^) в кольцах 5 ДОТ и
На кольцах 5(#) и #[[^]] можно ввести дифференцирование
Б: для а=(а0, аи ...), Ба= (а1; 2аг,..., пап, ...),
ОРа{*)=ЪПа"1 '
и интегрирование \:
р= (0,а0,^-,
ап
л+1
+1
^.<(>-1]ттг'"
л=0
Упражнение 1. Доказать следующие свойства отображений й и
/ в 5(Я):
1) Д(а + 6)=Да+Д6; 2) /(а + 6) =/а+/й;
3) 0/а=а; 4) /Оа = а;
5) Д(аХб) = (Да)хо+аХД6;
и соответствующие свойства в кольце Я [[<]].
Если кольцо # является алгеброй над полем Р, то, вводя в
5(Я) и #[|7]] операции умножения на аеР:
ал= (аСо, ааь ...),
0^(0 = 2^^^
превращаем 5 (Я) и КЩ]] в изоморфные алгебры.
37

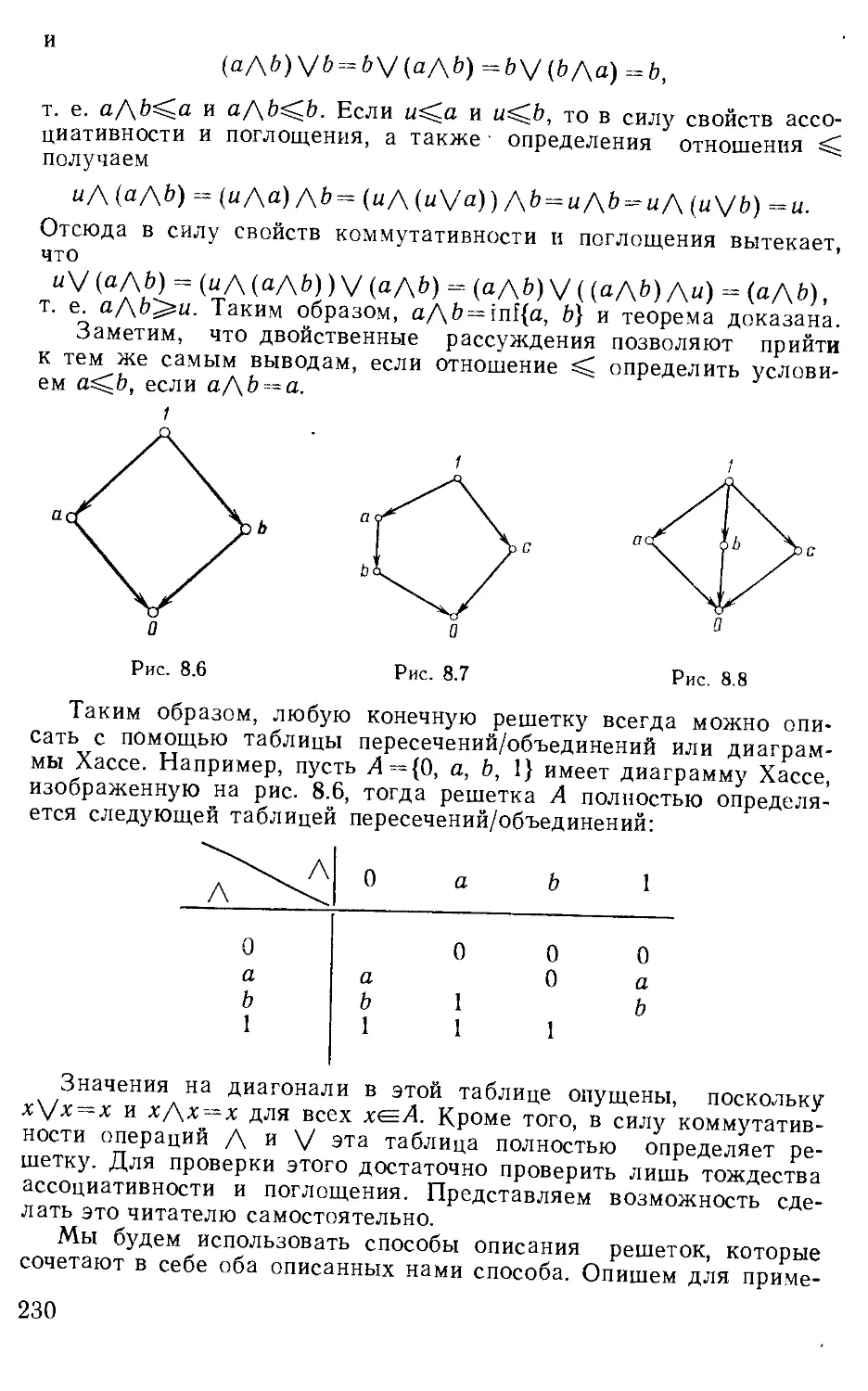
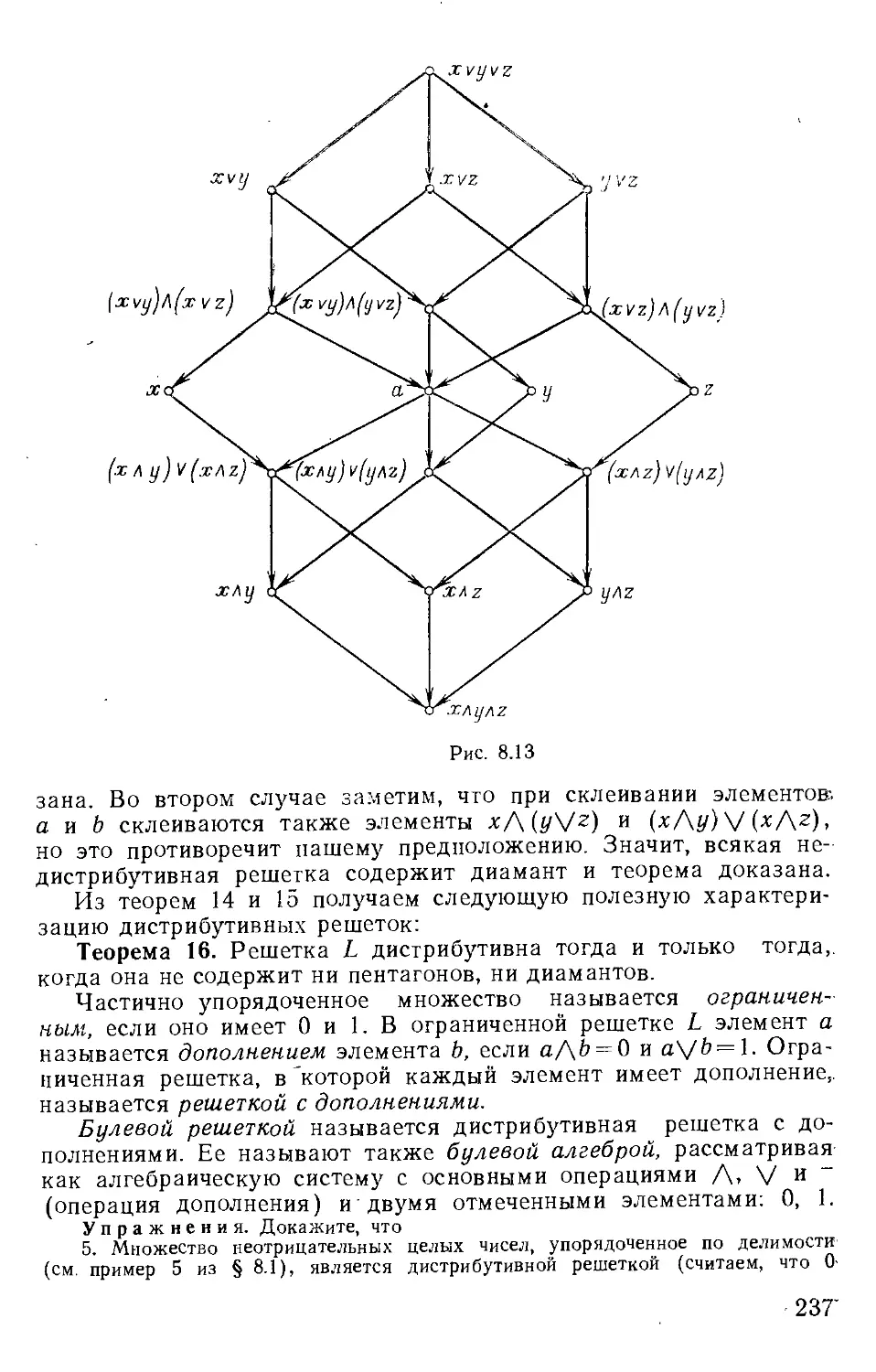
Вернемся теперь к последовательностям, появляющимся в
комбинаторных задачах, т. е. к алгебре 5 (К) последовательностей
над полем К действительных чисел. Для последовательности
ае5(К) ряд /^(О^'ЩО] называется обычной производящей
функцией, а сама алгебра К|[[0] называется алгеброй Коши.
Обычные производящие функции используются при исследовании
семейств последовательностей, элементами которых являются
функции неупорядоченных г-выборок (г-сочетаиий).
Для построения самих комбинаторных объектов (г-сочетаний)
мы будем пользоваться алгеброй К(х; {)—Щхи Хг,...] [[^]]
формальных степенных рядов над алгеброй Н[*ь х%,...] многочленов
от переменных х={х1, х%,...} над полем действительных чисел.
Алгебру К(х; I) будем называть нумераторной, а ряды,
коэффициентами которых будут многочлены, перечисляющие построенные
нами комбинаторные объекты, — нумераторами этих объектов.
Напомним, что отображение М : А\-+Аг из алгебры Л4 иад
полем Р в алгебру А2 над Р называется линейным оператором,
если М(а-\-Ь) =Ма + МЬ и М(аа)=аМа для всех а, Ь^А^ иеР.
Отображение М называется мультипликативным оператором, если
М(аЬ) = (Ма) (МЬ) для всех а, Ь^А\. Мы будем часто
пользоваться отображением Т : К(х; 0~*"ЭДШ> обращающим все х, в 1.
Упражнение 2. Доказать, что отображение Т является
мультипликативным линейным оператором.
Упражнение 3. Доказать, что отображения й и / на алгебре К(х; г)
являются линейными операторами.
Пример 1. Найти нумератор и производящую функцию для
г-сочетаиий из п элементов.
Эта задача уже решена нами в § 2.1: нумератор г-сочетаний из
п элементов задан рядом (1) в нумераторной алгебре К(х; I),
а производящая функция — рядом (4) в ее подалгебре К[[^]].
Пример 2. Найти нумератор и производящую функцию для
г-сочетаний с повторениями типа (Л1 Ап) из п элементов, где
Л* есть подмножество множества N0 неотрицательных целых
чисел; элемент а, может присутствовать в г-сочетаиии К раз, если
только Я.еЛг-
Сопоставим элементу а, из «-множества 5 переменную x^ в
К(х; I), тогда появлению элемента а% либо %1 раз либо Хг раз
в г-сочетании будет соответствовать ряд х('Л'+ х\Н 2+ ....
Поэтому искомый нумератор будет иметь вид:
Е^ = ПЕ^- (4)
Производящая функция в этом случае имеет вид:
^) = П I **■ (5)
£=1 А.6-\.
38

(к левой и правой частям (4) применили линейный оператор Т,
обращающий все х{ в 1). Раскладывая (5) по степеням I,
получаем, что число г-сочетаний типа (Л1,..., Лп) из п элементов равно
числу решений уравнения г/1+... +Уп = г с неизвестными «/г^Л<,
1=1,..., я.
Пример 3. Найти нумератор и производящую функцию для
г-сочетаний с неограниченными повторениями из п элементов.
Мы сведем нашу задачу к предыдущей, если положим
Л,-=М0, 1=1, ...,«. Нумератор (4) принимает вид:
Отсюда (или из (5)) находим производящую функцию:
/(0 = (1 +^+12 + ...)" = (1-0-" =
= У (~п)(—п — 1)...(—п~г+1) ,_ ^ур =
г=0
%(» + '-»)? = %(-»)(-,у.
=0 г=0
где положили по определению
— п\ = /_ п, (п + г — 1
г) \ г
Отсюда имеем последовательность Ь=(Ь0, Ь±,...), где
Ьг = |п + т ) — число г-сочетаний с повторениями из п
элементов. Этот результат согласуется с полученным ранее (см.
§ 1.3).
Пример 4. Найти нумератор и производящую функцию
г-сочетаний с повторениями, в которых присутствует хотя бы один
элемент каждого вида.
В условиях примера 2 положим Л,-=^{1, 2,...}, 1=1,..., п.
Тогда из (4) получаем искомый нумератор:
а> п п
Ус*' = п ш + х*р+...) = г Пт^Ч-
Отсюда имеем производящую функцию:
00
/(*) = (* + /■+ ...)" = ^(1-0^ ='"]Г(л+ ^
/•=0
Сделав замену п+г = к, получаем
О
39

'и-Е^-Б^!)*-
Следовательно, число искомых г-сочетаний равно 0 при г<п и
(п-{) приг>"-
Пример 5. Найти нумератор и производящую функцию для
г-сочетаний из п элементов, где допускается лишь четное число
появлений для каждого из элементов.
Полагая в условиях примера 2 Лг={0, 2, 4,...}, £=1 п,
имеем из (4) искомый нумератор:
со П Л
2°^ = П о + хт + **<4+ ---) = 11 ттлт-
/■=0 1=1 ' = ! "'
Отсюда получаем производящую функцию:
/(*) =(1+р + Ц+ ...)« = (!_ 12.уп = У(п + г — \\ рг
/■=0
Теперь можно получить интересное тождество: поскольку
(1—1г)~п=(\—1)-п(\+1)-п, сравнение коэффициентов при
степенях I в правой и левой частях дает:
г
У<—1)к(п + г — к—1 \ (п + к— 1 \ _
ЛЛ ' \ г —к ) \ к ~
6=0 ' ~
' 0, для нечетного г,
(" + 5-1'), для Г = 25.
Упражнение 4. Найти нумератор н производящую функцию для
г-сочетаний из п элементов, где допускается не более / повторений каждого
элемента.
Перейдем теперь к построению аналитической теории для
перечисления упорядоченных г-выборок или г-перестаиовок.
В алгебре К[хь *2,...] [[^]] формальных степенных рядов с
. коэффициентами из алгебры многочленов К[хи х% ...] над полем К
с переменными х\, Хг не коммутирующими между собой,
рассмотрим выражение
л л
~^Г Б П (1 + **«>') = Ба"{%ъ х*' ■■■)]7' (6)
П65П 1=1 /-=0
где сумма в левой части берется по всем подстановкам из
симметрической группы 5П подстановок «-множества. Нетрудно видеть,
40

что в коэффициенте при Р в разложении по степеням I выражения
£11(1 +*««>о
я€5„ 1=1
одночлен Х[1...Х1 появляется столько раз, сколько существует
подстановок яе5п таких, что яг* (п) <лг* (к) < — <я~* (ь).-
Строить такие подстановки можно следующим образом: г мест
для прообразов элементов к, ..., 1Г выбираем ("] способами, а
остальные п—г элементов могут переставляться (п—г)! способами.
Поэтому рассматриваемый одночлен появляется всего ("] (я—-/•)! =
= п\/г\ раз. Следовательно, многочлен аг* (хи х%,...) в (6)
состоит из одночленов, соответствующих всем г-перестановкам из
элементов х\,..., хп. Назовем ряд (6) экспоненциальным
нумератором г-перестановок из п элементов.
Далее, полагая в (6) Хг=1, 1=1 п (применяем к левой и
правой частям линейный мультипликативный оператор Т,
обращающий все х\ в 1), получим
п
(1-М)" = $]Я(га,/0-^-, (7)
г—О
где Р(п, г) есть число г-перестановок из п элементов. Функцию
1(1) = (1-\-()п назовем экспоненциальной производящей функцией
для числа г-перестановок из п элементов. Заметим, что
формулу (7) можно было вывести сразу из формулы (2) § 2.1, так как
Р(п, г)=аг(\,...)г\. Раскладывая (\+1)п по степеням I, получаем
—I Г\ ^ (/1--/-)1 Л
и отсюда снова находим число г-перестановок из п элементов:
Р(п, г)=п\/(п—г)\.
Пусть Я есть некоторое кольцо с единицей. Кольцо 5*(#)
экспоненциальных последовательностей над Я и изоморфное ему
кольцо ^?*[[^]] экспоненциальных формальных степенных рядов
над Я строятся таким образом. Как аддитивная группа, 5*(#),
совпадает с аддитивной группой кольца 5(#). Операцией
произведения в 5*(/?) является биномиальная свертка
последовательностей: аЪ = й=(й0, ^,...), гдеа=(а0, аи...), Ь=(Ь0, Ъи...),
Г
1=0
Единица и нуль в 5* (Я) такие же, как и в кольце 5 (Я). Обрат-
41

ный элемент относительно умножения для последовательности
а= (а0, аи ...) существует лишь в случае обратимости элемента а0
и вычисляется из системы уравнений, аналогичной уже
рассмотренной системе уравнений в кольце 5(#)'.
Упражнение 5. Доказать, что в 5*(./?) выполнены все аксиомы кольца
и отображение а= (ао, 01 а„, ...)—»а'= (ао, Д1 ап/п\,„.) есть изоморфизм
колец 5(Я) и 5*(Я).
Элементами кольца ^*[[^]] являются экспоненциальные
степенные ряды
/•=0
соответствующие последовательностям а=(а0, а\, ...). Операции
сложения и умножения определяются таким образом:
со
Ь= (Ь0, Ьи ...). сг = аг+Ьг',
00
где йг определяется формулой (8). Нуль и единица в #*['[^]]
такие же, как и в кольце #[|[?]]; обратный элемент относительно
сложения определяется аналогично; обратный элемент
относительно умножения вычисляется так же, как и в кольце 5*(#). Если #
есть алгебра над полем Р, то (так же, как и в случае 5 (^))
кольцо 5* (#) превращается в алгебру над Р. Аналогичное построение
проводится и для кольца #*[[^]] над алгеброй #.
Упражнение 6. Провести для кольца Л*[М] опущенные в тексте
построения и доказательства.
Из определения кольца #*['[^]] видно, что в случае
сходящихся рядов формальное произведение совпадает с обычным
произведением. Ряд Еа(1) называется экспоненциальной производящей
функцией для последовательности ае5*(К)', а сама алгебра
К*[[^]] называется алгеброй экспоненциальных производящих
функций.
Упражнение 7. Показать, что алгебры К*[[<]] и К*[[']] изоморфны.
Опять же с целью алгебраического конструирования^
упорядоченных г-выборок рассмотрим алгебру К*(х; 1) =
= (К[хь хг, ...])*[|[01 экспоненциальных степенных рядов над
алгеброй К[хь хг,...] многочленов с некоммутирующими
переменными, которую назовем экспоненциальной нумераторной алгеброй,
42

и алгебру К*(х; I) = (К|>, х2, ...])*[ДО] экспоненциальных
степенных рядов над алгеброй К[*ь х2,...] обычных многочленов,
которую назовем приведенной экспоненциальной нумераторнои
алгеброй. Терез Т* обозначим отображение из К*(х; I) в К* [ДО],
заменяющее все Хх на 1.
Упражнение 8. Доказать, что Т* является мультипликативным
линейным оператором.
Через V обозначим отображение, переводящее ряд из К* (х; I)
в тот же ряд из К* (х; I) т. е. позволяющее переменным х%
коммутировать между собой.
Упражнение 9. Доказать, что V является линейным
мультипликативным оператором.
Через Т* обозначим отображение из К*(х; I) в К* [[<]],
заменяющее все хг на 1.
Упражнение 10. Доказать, что Т* является мультипликативным
линейным оператором.
Рассмотрим отображение V : К* (х; ^)->К*(х; I), которое
каждый одночлен дс(,дс(, ... х^ со спецификацией (Ль ..., %п) (это
значит, что х, встречается }ч раз, хг—Х2 раз и т. д.) в коэффициенте
при 1к1'к\ переводит в многочлен
где сумма берется по всем перестановкам (/ь ...,/V) элементов
М,..., и.
Упражнение 11. Доказать, что V есть линейный оператор, но свойство
мультипликативности для него не имеет места.
Упражнение 12. Доказать, что 1)У есть тождественный оператор на
алгебре К::(х; ().
Каждой г-перестановке н^ ... 1Т из элементов 1,..., п с
повторениями сопоставим в экспоненциальной нумераторнои алгебре
одночлен Х{1 . .. х/1г/г1. Соответствующий ряд р(х\, х2, ... ; I) для
данного класса перестановок назовем экспоненциальным
нумератором этого класса. Образ 11р{х\, х2,...\1) при действии
оператора V назовем приведенным экспоненциальным нумератором
данного класса перестановок и ряд Т*р(х\, х2, ... ; I) —
экспоненциальной производящей функцией
Пример 6. Найти экспоненциальный нумератор,
приведенный экспоненциальный нумератор и экспоненциальную
производящую функцию для г-перестановок из п элементов.
Экспоненциальный нумератор уже найден нами в виде (6),
приведенный экспоненциальный нумератор есть многочлен
ПО + *Л
!=1
43

и экспоненциальная производящая функция для числа г-пере-
становок из п элементов найдена наии в виде (7).
Пример 7. Найти экспоненциальный нумератор,
приведенный экспоненциальный нумератор и экспоненциальную
производящую функцию для г-перестановок с повторениями типа (Ль ..., Ап)
из п элементов.
Под (Ль ..., Лп)-перманентом (см. [42]¾ (гХп)-матрицы
\ап ... агп)
с элементами из кольца # будем понимать элемент
Рег(Л1)...,лп) А = 2 аи%а211 . .. а,^,
где сумма берется по всем г-перестановкам (н,..., 1Т) из
элементов \,...,п с повторениями типа (Ль ••., Лп), или, другими
словами, в произведении могут участвовать К элементов из столбца I
лишь в случае К^Аг, если сумма имеет пустое множество
слагаемых, то положим ее равной нулю. Теперь мы можем записать
искомый экспоненциальный нумератор в виде:
СО
р(х±, х2, ... ; I) = ^Рег(Л1 а„)Хг,„ — ,
/•=0
где Хг,п есть (гХп)-матрица с г одинаковыми строками (Х\, ...,хп).
Приведенный экспоненциальный нумератор 11р(хи лг2, ... ; 0 можно
теперь представить следующим образом:
£//,(^,...-.0 = 2 X -^4...^, (9)
Г1&&1 ГП^АП
откуда
^(^,^,...-,:0 = 11(5)^-^-)- (1°)
1=1 Х€Л1
Наконец, искомая экспоненциальная производящая функция
имеет вид:
(=1 %€Л,-
Т*р{х1, хл, . .. ; 0 = ТЮр{х1, х2, ...'; 0 = П ( X
поэтому
р(1,1,...;0 = 5) 2
I]
/■=0 /-,+ ...+/•„=/•
Г'6Л> гп$Ап
гх! ... Ы г!
44

Отсюда находим, что число г-перестановок из п элементов с
повторениями типа (Ль .... Лп) равно
Л П\ ... г„\ '
'■6Л- гп6Л„
Можно также найти экспоненциальный нумератор из
приведенного экспоненциального нумератора (10), представив его в
каноническом виде (9) и применив линейный оператор V.
Пример 8. Найти экспоненциальный нумератор,
приведенный экспоненциальный нумератор и экспоненциальную
производящую функцию для г-перестановок с неограниченными
повторениями из п элементов.
В этом случае в условиях предыдущего примера Лг = М0 для
1=1, .... п, и
Рег(Мо цо) ХГшП = (хх+ ... + хг)г.
Поэтому экспоненциальный нумератор имеет вид экспоненты:
р(х1, хг, .. . ; 0 = Л (¾ + . . . + х,У -^- = ехр ((хг + . . . + хп) I).
/•=0
Такой же вид в этом случае имеет и приведенный
экспоненциальный нумератор, а экспоненциальная производящая функция
получается в следующем виде:
оо
р (1, 1, .. . ; 1) = ехр (гй) = V пг .
Таким образом, число г-перестановок с неограниченными
повторениями из п элементов равно пг, что согласуется с результатом из
§ 1.3. Видом производящей функции этого примера и обусловлен
термин «экспоненциальная», употребляющийся нами в
рассматриваемой аналитической теории перечисления г-перестановок.
Пример 9. Найти экспоненциальный нумератор,
приведенный экспоненциальный нумератор и экспоненциальную
производящую функцию для г-герестановок из п элементов с
повторениями, где каждый элемент должен появиться хотя бы один раз.
В этом случае в условиях примера 7 имеем Л{ = М, 1=1,..., п,
следовательно, приведенный экспоненциальный нумератор имеет
вид:
р"(Х1, х2, . . . ; {) = П (|]-^) = П <ехР(^) - О-
1=1 ^=1 1=1
Теперь можно выписать экспоненциальную производящую
функцию:
45

/(1, I, .. . ;0= (е* —П" = 5] (—!)*(") в/<л-*) =
*=о
2-й-2<-1)*(а«.-«г.
6=0
соответствующие числа, таким образом, равны
Р(п, г) = %(-!? Цип-к)'. (П)
*=о
Наконец, экспоненциальный нумератор можно найти с помощью
линейного оператора V:
р (х1У а-2, . . . ; 0 = уу (хх, х2, . . . ; () = У П («*'* - 1)-
1 = 1
Упражнение 13. Найти экспоненциальный нумератор, приведенный
экспоненциальный нумератор и экспоненциальную производящую функцию для
/■-перестановок с повторениями из п элементов, где каждый элемент может
встречаться лишь четное число раз.
Производящая функция Дирихле для последовательности чисел
а= (аи а2,...) — это формальный ряд
л.<0=Е-Ь
г'
/■=1
Определим, как и выше, операции сложения и умножения для
этих рядов. Суммой ОаЦ) и Бь{1) назовем ряд
00
оаС) -г оь(0 = Ос(0 = 2тг- ъ = &• 6*> ■ ■ ■)■
/■=1
где сг=аг + Ьг, а произведением их — ряд
СО
0в(Ох0ь(О=А*(О = 5)-^-.
где
^ = Е аА = 2 аЛл
1/=/-
(суммирование производится по целым делителям г). Отсюда легз
ко видеть, что 0= (0, 0, ...) определяет нуль относительно
сложения; е=(1, 0, 0,...) определяет единицу относительно умножения:
46

Д,(^) = 1; обратный элемент относительно умножения Ба 40
ищется из равенства
или, что то же, из системы уравнений:
^20^ + 01^2 = 0,
а3а'1+0.10.'3 = О,
а4а'1+а2а'2+а1а'4 = О,
откуда, в частности, имеем: а[ = , а2 = , а'г = *-, а\ =
а1 а\ а\
2
= — —и т. д., т. е. необходима и достаточна обратимость
элемента а^ Нетрудно проверить, что совокупность производящих
функций Дирихле также является кольцом. А если определить
естественное умножение ряда ДДО на действительное число, то
это кольцо становится алгеброй К{^} над полем К. Изоморфная
ей алгебра Дирихле Р(Щ последовательностей определяется
аналогично.
Понятие производящей функции Дирихле возникло в теории
чисел, где широко используется дзета-функция Римана:
Три вида производящих функций, введенных выше, являются
основными для комбинаторного анализа, но далеко не
единственными. Разнообразие видов производящих функций происходит
вследствие разнообразия постановок задач. Рассмотрим для
примера одну задачу о построении производящих функций для
размещений и заполнений, а именно задачу типа (/Ь) (см. § 1.4),
Имеется «-множество различных элементов и /и-множество
различных ячеек спецификации (пи п2,...,Пт), требуется построить
производящую функцию для числа размещений п элементов по т
ячейкам. Пусть символ
х11Х2г • • ■ х>
означает, что в 1-ую ячейку помещают я, элементов, 1=\,...,т.
Если п=\, т. е. имеется только один элемент, то
соответствующий символ размещения есть я,, если элемент помещен в 1-ю
ячейку. 1 = 1,..., т. По правилу суммы возможность разместить одни
элемент в любую из т ячеек описывается полиномом
47

*1+*2+ - +Х
Если имеется п элементов, из которых каждый может быть
помещен в любую из т ячеек, то соответствующий полином есть
(Х1 + Х2+ ■.. +Хт)п,
а соответствующей производящей функцией является
экспоненциальная функция
т
Е({) = У (хг -- хг+ ...+ *„,)" -- = ехр (I V х1
/1=0 ' 1=1
/71 /П
= ехр ( Р 1х^ г= ["] ехр (/*,).
Если речь идет лишь о числе возможных размещений, то полагаем
Хг = \, 1 = 1, 2, ..., т, и тогда производящая функция принимает
вид:
Е ({) =ехр(т<).
В соответствии с полиномиальной теоремой:
(У^1" = У =1 л«
\^ 1 I • &Л 71,! «2! ... пг/1!
откуда получаем, что число размещении п различных элементов
по т различным ячейкам с (щ, пг Пщ) -спецификацией равно:
Пу1 ;.а! . . . пт\
2.3. ОПЕРАТОРНЫЙ АППАРАТ МЕТОДА
ПРОИЗВОДЯЩИХ ФУНКЦИЙ
Использование производящих функций позволило с большой
общностью подходить к комбинаторным задачам
перечислительного типа. Однако производящие функции, построенные для
разных видов выборок, оказались в большом числе довольно
громоздкими. Поэтому для более удобной записи производящих функций
применяют специальные операторы, символические исчисления,
'специальные числа и специальные функции.
Пусть имеется последовательность а=(а0, аь ...), которую мы
будем записывать иначе: а = а(п), т. е. как функцию
целочисленного аргумента п (п = 0, 1, 2, ...). Для множества
последовательностей {а{п)} чаще других используются следующие специальные
операторы:
а) оператор сдвига Е:
Еа(п)=а(п+1), п = 0, 1, 2,...,
48

Е~1а{п)=а(п—\), л=1, 2,..., £-^(0)=0:
б) оператор разности А:
Аа(п)=а(п+1)—а(п);
в) оператор усреднения б:
Ьа{п) = «С-!) + "(" +О,, „ = 1, 2 ба(0) = -^-.
Эти операторы связаны некоторыми соотношениями, например:
Да(«)= (Е—1)а(п),
Да (л) =— (г + г-')а(«),
где / — тождественный оператор.
Повторные применения операторов к элементам
последовательности могут привести к полезным и удобным формулам.
Например, обозначим через пг последовательность с общим членом
а(п)=пг. Запись Ьпг, где Ь есть некоторый линейный оператор
на множестве последовательностей, будем понимать как {Ьа)(п\,
где а(п)=пг. Тогда
Еп(0)=п; Еп(0г)=пг; А0Г= 1Г—0Г= 1Г;
Д20г = 2'-_2; дз0г=зг_3-24-3
и т. д. Числа А"0Г называются числами Моргана.
В качестве примера использования операторов в
комбинаторных формулах приведем задачу о числе г-перестановок с
повторениями из «-множества при условии, что каждый элемент
появляется не менее одного раза.
Преобразуем число р(п, г), полученное нами в § 2.2 в виде
(И) следующим образом:
п п
Р("'Г) = Е < " ) (-1)'("-«У = X {■) (-1)'^П-'0Г =
1=0 ' 1=0
= {Е — 1)п0г = А"(У.
Докажем, что
ДпО^1 = п А"0' + иА"-10г.
В самом деле
п п
Д«0'+> = ^ (>!) (_!)<(„ _ог+! ="Ц (") (--1)'(п- 0' -
£=0 1=0
1 = 0
49

Первое слагаемое есть пАпОг, что очевидно из предыдущего. Что
же касается второго слагаемого, то, произведя подстановку
.1 = /+1, получим
п п—Л
^(^(-1).^-0^ = -2(.^)(-1/^-/-1)^(/+1) =
1=0 1=о
= -У п(п-1)!(/ + 1) (_1)/( -_1Г =
7' (/+!)/!(„- 1-/)! V '
/=о
л—1
= -пЕ(п7') (-^-1 -/т= -пд1-^.
Упражнение 1. Доказать, что число /--перестановок нз п элементов с
неограниченными четными (включая 0) повторениями равно б"0г.
Частые повторения одних и тех же выражений привели к
появлению специальных чисел и специальных функций. Специальные
числа, например, открывают и переоткрывают в разных частях
математики: исчислении конечных разностей, теории чисел, теории
вероятностей, математической статистике. Приведем некоторые
сведения об этих числах.
Рассмотрим нижний факториал (^)п = ^—1) ••• (^—га+1) как
производящую функцию:
(0„ = 28(М)'*. л>0.
й=0
Коэффициенты 8(п, к) в этом разложении называются числами
Стирлинга 1-го рода. Так как {1)и есть полином степени к, то
можно разложить 1п по системе многочленов (1)0, {1)ь у)„:
п
*» = 2 5 (л. *)(*)*. п>0. (1)
Коэффициенты 5 (п, к) называются числами Стирлинга 1-го рода.
Для обоих видов чисел произведем доопределение:
(Оо = *°=8(0, 0)=5(0, 0) = 1.
Числа Стирлинга появляются во многих задачах. Вернемся,
например, к выше рассмотренной задаче о числе «-перестановок с
повторениями из к элементов при условии, что каждый элемент
появляется в указанных выборках хотя бы один раз (см. пример 9
из § 2.2). Мы получили, что производящая функция в этом случае
имеет вид:
(=0 л=0 (=0
50

= Уд*оп —.
п=0
Напомним, что эта задача допускает интерпретацию, как задача
о числе размещений п различных элементов в к различимых ячеек,
таких, чтобы не оставалось пустых ячеек. При всех натуральных
1>-п имеем
*» = Е'О» = (1 + Д)'0» = ^ (*Л Д*0" - ^ Ц)к'-
к\
к=0 6=0
п
к\
к=о
= Ц^
так как Д"0П = 0 при к>п (Дл0" — число «-перестановок из к
элементов с повторениями, где каждый элемент присутствует не
менее 1 раза). Поскольку многочлен степени п имеет п корней,
то равенство
2>
6=0
будет справедливо при всех действительных значениях I.
Учитывая разложение (1), получаем
Ак0п = к\ 5(л, к).
Это означает, что число размещений п различных элементов по к
различимым ячейкам, при которых не остается пустой ячейки
(задача типа (А)), равно к\ 5(п, к), а соответствующее число для
неразличимых ячеек (задача типа (С)), (или, что то же самое,
число разбиений «-множества на к непустых частей) равно
5(л, к).
Числа Стирлинга часто встречаются в комбинаторных
рассуждениях, поэтому сделаем о них еще несколько замечаний.
Можно получить полезные рекуррентности для этих чисел, на^
пример:
а) из {1)п+1=(1—п)(1)п вытекает
я(л+1, к) =з(п, к—1)—пз{п, к);
п+1
I
к=0 к=0
б) *»+! = 2 5 (л + 1, Л) (1)к = * Е 5 (л, к) (Цк
= У 5Кл, Л) ((*)*+1+ *(/)*),
«ней
А=0
откуда получаем
51

5(л+1, *) =5(л, к—1)+кЗ(п, к).
Одно из двух выражений
лодставим в другое:
Г = 2 5 (п, к) ^ 5 (Л, ш) ^ = ^ ^ 5 (п, к) 5 (к, т) Г-
^ 8{п,к)з{к,т) = Ъп,т =
6=т I
ъ ъ
6=0 т=0 6=0 т=0
Приравнивание коэффициентов при одинаковых степенях I дает:
1, если п = т,
б=т { О, если пфт.
Число 8п,т называется дельтой Кронекера.
Дадим некоторые сведения о других специальных числах.
Числами Фибоначчи называются числа /(я), где
/(0)=/(1)=1, !{п)=1{п-\)+!{п-2), л>2.
Их производящая функция имеет вид:
Р (1) = \ + 1 + 2Р+?,15 + Ъ^ + Ыъ+\?,^ + ....
Учет рекуррентного соотношения приводит к аналитическому
выражению для производящей функции:
/40 = 1+4-(/(1)+/(0))^+.,. +(?(п-1) +
+ /(П-2) )*»+... =1 + у + Р)Ру),
откуда
Р {1) = {\—1—Р)-К
Эту функцию можно также представить в виде
^(0 = ((1-00(1-60)-1. (2?
где а и Ь определяются из соотношений:
а + Ь=\, аЪ= —1,
откуда
— Л.+ЗСК ь — 1~" ' ^~
2 ~~ 2 "
Раскладывая (2) на простейшие дроби, получаем
-о; \ — Ы 2 /5 ' 2 /5
(аир находятся методом неопределенных коэффициентов).
Отсюда получаем формулу Бине:
/ 1+У"5-\"+' (1-/Г\п+1
!(п) = оса" + рЬ"= -^ —
52

Числа Фибоначчи образуют специфическую
последовательность, нередко встречающуюся в комбинаторных задачах.
Например, число Фибоначчи /(я), я>1, есть число (п—1)-перестановок
из нулей и единиц, не содержащих двух нулей подряд.
Дальнейшим усовершенствованием аппарата производящих
функций является использование символического исчисления
Блиссара. Мы приведем его строгую версию, основанную на идеях
Маллина и Рота [43] об использовании для целей обоснования
исчисления Блиссара аппарата линейных операторов.
Напомним, что линейный оператор из векторного
пространства в поле, над которым оно построено, называется линейным
функционалом.
Основная идея исчисления Блиссара состоит в операции
«поднятия индексов»: экспоненциальная производящая функция
Е^=1^
последовательности а= (а0, а4, ...) заменяется рядом
ехр (а1) = V ап -^-
и после проведения нужных преобразований с участием этого
ряда степени вновь заменяются индексами (вместо ап пишем а„).
Для обоснования этих переходов введем алгебру К*(а; I) =
= (К[а])*[[^]] экспоненциальных формальных рядов с
коэффициентами в алгебре многочленов Ща] от переменной а и
линейный функционал Ьа : Ща]—*-Ц такой, что Ьаап = ап> естественно
продолженный до линейного оператора Ьа : К*(а; 0~»-К*[[*]], так
что Ьаехр(а() =Еа(1).
Пример 1. Рассмотрим последовательность чисел Бернулли
В={В0, #1,...), определенную их экспоненциальной функцией
Уд
п=0
Тогда для линейного функционала Ьв : К[В]-»-К такого, что
ЬвВп = Вп, имеем
1вехр(В0 = —!—. (3)
Р \
Отсюда получаем
( = Ьв (ехр ((В + 1) I) - ехр (Ш)) = ^(^ ((В + 1)" - В") -^Л =
53

л-1
-42 (Е(,")» )^) = В (20* )2-
п=0 г—0 л=0 г=0
и таким образом имеем рекуррентную формулу:
п—1
ЕС
Г 1 при я = 1
\ 0 при п = 0, 2, 3, 4,
г=0
Заменяя в (3) I на —I получаем
1вехр(-В*) = ^~- = ^ 1 = ^вехр((Б + 1) I).
Приравнивая коэффициенты при степенях I, имеем
Ьв(В + \)п= Ьв{—В)п,
т. е.
» ) В, = (-1)"Вп. (4)
г=0
Из (3) и (4) теперь получаем В„=(— \)пВп для пф\ и В4 =
= —В4—1. Следовательно, В1= —1/2, В3 = б5=В7= ... =0.
Упражнение 2. Доказать, что в алгебре К*(я; 0 имеют место
свойства перестановочности между линейными операторами Б, / и Ьа-
1. йЬа^Ьай;
2. /ьа = ьа;.
Рассмотрим теперь случай, когда в рассматриваемых
выражениях участвуют две последовательности а=(а0, аь ...) и Ь =
= (60, Ьи--.)- Тогда для каждой из них строим свой линейный
функционал: Ьа ; ап^-ап и Ьь : Ьп^-Ьп (работаем уже в алгебре
К*(а, Ь; I) = (К[а, &])*[[*]] с многочленами от двух переменных
в качестве коэффициентов). Рассмотрим, например,
последовательность с=(с0, Сь ■■•). являющуюся их биномиальной сверткой.
Предполагая, что Ьа(р(Ь)ап) =р(Ь)Ьаап для любого полинома
р(Ъ) (и аналогично для Ьь), имеем
п п
с:! = V (" ) акЬ^к = 41, | • (« | а*6»-* = ЬаЬь (а + Ь)«.
Вводя линейный функционал Ьс: сп^-сп, получаем отсюда
Ьссп = ЬаЬь(а+Ь)п.
Для произведения соответствующих экспоненциальных
производящих функций имеем
1сехр(сО=Яс(0=Яа(0'Яь(*) =
54

= ЬаЬьехр (а^)ехр (Ы) = ЬаЬьехр ((а + Ь)1).
Основная трудность классического исчисления Блиссара состояла
в необходимости при рассмотрении свертки
после поднятия индексов:
2!
П \ акап-к
6=0
запрета перемножения акап~к = ап, так как это приводит к
абсурдному результату:
п
6=0
Здесь, следуя идеям А. П. Гуинанда [44], мы эту возможность
ликвидируем, потребовав при поднятии индексов у сверток
одинаковых последовательностей вводить для них разные переменные.
В данном случае берем Ьа : ап—>-ап и Ьа' ; (а )п-*-ап. Тогда
2 (пЛ ака^к = Ьаи> (а + а')".
А=0
Пример 2. Докажем тождество Эйлера для суммы
произведений чисел Бернулли Вп:
2(2^В2гВ2п_2г=,-(2« + 1)В2п.
Это тождество может быть переписано в виде:
т
^(-1у^ВеВт_в = (1-т)Вт (5)
5=0
(при нечетных т левая и правая части равны нулю). Вводим
линейные функционалы Ьв:Вп—>-Вп пЬа' : В'п-*-Вп, тогда (5)
можно записать в виде:
ЬвЬв> (В — В')т = (\—т) ЬвВт. (6)
Рассмотрим экспоненциальную производящую функцию для левой
части (6):
ЬвЬв' У (В — В')т — = ЬвЬв' ехр ((В — В') *) =
т=0
55

= ЬвЬв' ехр (ВО ехр (—В'1) * * **е
е*—\ е'1 — 1 (е<—I)2
" ЧЁ ^--^--2 В"+' ^Г] = 42 <' -1^^)-
т=0 т—0 т=0
Отсюда получаем тождество (6), что и требовалось.
Упражнение 3. Доказать следующее тождество для чисел Борнулли:
2П ' 2п
^ (_1)* | I 2*В*В„„.Й = (1 -2п) В*,.
*=0
Развитие теории и аппарата производящих функций привело
к введению не только степенных рядов, но и аналогов теоремы
Тейлора; иными словами, к выражению производящих функций
через их производные. Пусть дана сложная функция Л(?)*=
= /(2(0). 2(0="- Для ее производных введем обозначения:
-^--0,. 0?'А® = А.:,
тогда имеем в этих обозначениях:
^2 = ^2 + /2212.
^3 = А2з + 3/22122 + /з213,
"4«"=Е ЬАп.ь^ё* ■■■ , 2,Ь
где Лп,й зависят только от §4 (1 = 1, 2, ..., л) и не зависят от /¾.
Для функции / выберем вид, близкий к экспоненциальным
производящим функциям; при этом найдем удобное выражение для
Ап,к. Пусть
?(§) = ехР(а2)> а = сопз1.
Тогда
/л=а*ехр(а#), 2 = 2(0.
Е л».* (21. 22 2«) а* = ег°Ч$е*я = Л„ (а; £,^, ...,2-),
л
где правая часть есть сокращенная запись левой части равенства.
Выражение для А„ запишется так:
56

4=М»(/;й,й ^. У* = /*, £ = 0,1,...
В соответствии с определением Л(^) добавим:
А0=Т0=АЦ).
Полиномы А„ (а; §ь ^2, ...,Яп) (или иногда их частный вид при
а=1) называются полиномами Белла; в обозначениях Белла:
Ап = (1; г/ь г/2, ..., у„) = У (#ь г/2, ..., г/п) =
= е-УОхпеУ, у=у(х).
Эти полиномы оказались важным оперативным средством в
математической статистике, а затем в комбинаторной теории.
Найдем рекуррентное соотношение для полиномов Белла.
Введем сокращенное обозначение:
Лп(а)=Л„(а; §1 §п).
Тогда
Ап+1 (а) = е^Вп {Веа$) = е~а^аВп {ё\^е) ■
Отсюда по формуле Лейбница о дифференцировании произведения
имеем
п «
Ац., (а) = а У] (^ (е-^-%^) ^ = а^ ^) Л,_,(а)^+! =
= Ь(0) 1дИИ +^]п. (7)
Ь(«) И (а)]* = Л (а), ^ §* = &, * = 0, 1,2
Рассмотрим теперь ряд
п-=1
и экспоненциальную производящую функцию для полиномов
Белла:
Из (7) получаем
ОР(х)=аС(х)Р(х),
отсюда, интегрируя это уравнение, получаем
Р(х) = ехр(аС(х)).
Теперь по полиномиальной теореме имеем
57

где & = &!+ ... +кп и сумма берется по всем решениям в целых
числах уравнения к\ + 2к2+ ... +пк„=^п. И наконец, получаем
выражение:
известное как формула Фаа ди Бруно.
2.4. О ПРИЛОЖЕНИЯХ МЕТОДА ПРОИЗВОДЯЩИХ
ФУНКЦИИ
Как было отмечено выше, метод производящих функций
применяется для решения задач перечислительного характера, т. е.
когда определяется число объектов в некотором классе.
Непосредственные комбинаторные рассуждения типа тех, которые мы
использовали в гл. 1, играли и продолжают играть большую роль
в качестве основных методов, но производящие функции внесли
большую общность суждений и расширили область возможных
приложений комбинаторного анализа.
Исторически сложилось так, что прежде всего комбинаторные
методы нашли применение в теории вероятностей и
математической статистике. Это легко объяснимо. В современной
аксиоматической теории вероятностей сами вероятности мыслятся лишь в
связи с пространствами элементарных событий. Последние
являются понятиями первоначальными, неопределяемыми и
интерпретируются как точечные множества. Если пространство
элементарных событий состоит из конечного или счетного множества
точек, то это пространство называют дискретным.
По существу весь аппарат исследований дискретных
пространств элементарных событий комбинаторный. Более того, мы
можем говорить о теоретико-вероятностных интерпретациях
определенной части комбинаторного анализа.
В самом деле, /--выборки могут быть интерпретированы
различными урновыми схемами. Случаи, когда допускаются повторения
элементов в выборках, соответствуют урновым схемам с
возвращением. Производящие функции вида
Е 'А
1=1
где У* р( = 1, р1 ^ О, (I = 1, ... ,5), появляются в теории вероят-
1 = 1
ностей, когда случайная величина X (функция на множестве
элементарных событий) может принимать значения д;,-, £=1, 2,...,5,
с вероятностями р,-, £== 1, 2, ..., 5 соответственно. Одна из
простейших производящих функций в теории вероятностей связана с
бросанием монеты и другими событиями с двумя исходами:
58

Р(1)=ч + р1, р + ?=1, Р, ?>0
{случайная величина принимает значение 0 с вероятностью ц и
значение 1 с вероятностью р). Производящая функция бросания
одной шестигранной кости с равновероятными выпадениями очков
имеет вид:
6 ^ 6(1—0
Пусть Х1 есть случайная величина, принимающая значения
0, 1,2,..., 5 с вероятностями р0, рь рг, ..., рв соответственно, и пусть
Х2 — другая случайная величина, принимающая значения
О, 1, 2,..., г с вероятностями р'0, р'и р'г,—,р'т соответственно. Их
производящие функции:
Е р<р и Е ^-
1=0 6=0
Если два события независимы, то вероятность одновременного
их наступления равна произведению их вероятностей.
Соответствующая производящая функция двумерной случайной величины
(Хи Х2) имеет вид:
РаРо + (РхРо) * + (РоР'О *' + (Р1Р1) «'+■■■ + (р5Рг) ^'' =
ЧЕ^ИУрПО*).
Если рассматривается распределение суммы Х^ + Хг, то 1—1' и
произведение имеет вид:
Ер^) (Ер*'*)= роРа + ^°р'+ р*р°)1 + ^Р1р'+ р°р2 ~Ргр^ ?+■■■ ■
Эта конструкция легко распространяется на распределения п
независимых случайных величин. В частности, для п независимых
испытаний (с 2 исходами) производящей функцией числа исходов
определенного вида будет
>Р(0= (<7 + р0". р+ч=1 р, ?>о.
В теории вероятностей могут применяться и производящие
функции несколько иного вида. Например, пусть четыре частицы
влетают в камеру, где находятся центры притяжения с силами,
пропорциональными 8:9:11:12. Будем говорить, что производящая
функция вероятностей распределения одной частицы по центрам
есть
40 х г 40 2 40 40 *
Тогда при обеспечении независимости частиц, производящая
функция вероятностей попадения четырех частиц имеет вид:
59

1 4 \ 40 ' 40 2 40 3 40 4 /
1—1
А если мы интересуемся лишь тем, сколько частиц попадет в
заданные центры, то соответствующая производящая функция суть
^ 40 40 2 40 40 / У
Например, вероятность того, что частицы попадут на разные
центры, будет равна коэффициенту при 1\1гЫк в (1).
Комбинаторные задачи о размещениях в их
теоретико-вероятностной трактовке приводят к введению понятий моментов. Пусть
дано распределение вероятностей, т. е. последовательность
с*
р0, рх, р2, . . . ; 0 < рг < I; I =- 0, 1, 2, . . .; ]Г р1 = 1.
Для него могут быть введены моменты различных видов:
а) обычные моменты
(=0
& = 0, 1, 2, ..., в частности
/ПО=РО+РН"Р2+ - .
т1 = р1 + 2р2-гЗрз+ ...,
тк = р1 + 2кр2 + Зкр3+ ....
Обычные моменты отождествляют с математическими
ожиданиями: если дана случайная величина X с распределением {((Х()} и
если математическое ожидание величины ХТ (г>0) существует, то
оно называется моментом /--го порядка для X;
б) факториальные моменты:
(тк) = ^ Ц)кР!,
/=о
где (/)& = /(/— 1) ... (/—к+\), к = 0, 1, 2,...; обозначение (т)к
обусловлено тем, что (т)и = Ьтт(т—1) ... (т—к-\-\), где
Ьт{т1)=тг, при этом гП{ — обычный момент 1-го порядка;
в) биномиальные моменты:
*=Ы)р» й=ол
,'=0
Между моментами (гп)к и Вк имеется очевидная связь:
60

Очевидно, что выражение факториальных моментов через обычные
порождает числа Стирлинга 1-го рода, а обратное выражение —
числа Стирлинга 2-го рода;
г) центральные моменты:
Мк = 1т(т—т{)к, 1т(т')=т1, 1 = 0, 1, 2,...,
или, иначе,
к
Мк = ^\ (к) тк-,(—щ)К к = 0, 1, 2
/=о
Наиболее простым является второй центральный момент,
называемый иначе дисперсией: Мг = т.г—т42. Основная идея,
приведшая к рассмотрению центральных моментов, состоит в том, что
вместо самой случайной величины рассматриваются ее
отклонения от среднего значения.
Приведем некоторые виды производящих функций из числа1
наиболее употребляемых в теории вероятностей:
а) для распределения вероятностей:
к
б) для обычных моментов:
т (I) = Ьт ехр {т1) = ^ тк —; Ьт (тк) = тк, к = 0, 1, ... ;.
к
в) для факториальных моментов:
(т) (0 = ^ (т) к —;
г) для биномиальных моментов:
В(*)=2]ВА**;
к
д) для центральных моментов:
М(
к
(О = 1« ехр (АН) = ^ Л14 ~, ЬМ (М*) = /И„ А = 0, 1.
Операции формального характера над различными
производящими функциями приводят к открытию многих полезных соотно-:
шений, например: ■
1) т(1) = Р(ег). В самом деле,
»м-2>.-2-Е-5-3>;
к
61,

-ЕлЕ^-Е""-"*'»
/ * 1
12) (т)(1)~Р(\+1), что видно из следующих равенств:
И(0-ЕМ.-^-22(Лл-5-
/ к 1
2.5. ТЕОРИЯ РЕДФИЛДА-ПОЙА
Вид производящих функций зависит от конкретных условий
задач, и построение их во многом является искусством. В течение
долгого времени не существовало регулярного подхода к
построению производящих функций. Существенные шаги в этом
направлении были сделаны Редфилдом и Пойа, разработавшими метод
построения производящих функций для неэквивалентных
комбинаторных объектов весьма общего вида. Перечисляемым объектам
придавались веса, а понятие эквивалентности вводилось через
группы подстановок. Поясним этот вопрос подробнее.
Рассмотрим некоторую группу С подстановок элементов
«-множества, т. е. подгруппу симметрической группы 5„. Каждая
подстановка порождает разбиение «-множества на циклы, т. е.
подмножества, элементы которых циклически переставляемы;
количество элементов в подмножестве называется длиной цикла.
Пусть, например, подстановка § имеет к1 циклов длины 1, к2
циклов длины 2 и т. д., тогда говорят, что она обладает циклической
структурой (&ь кг, ...) и ставят ей в соответствие моном р (§) =
= 1к4к^ ■ ■ ■ . Цикловым индексом группы О называется среднее по
таким мономам от всех §^С:
Ра&.Ъ, ...)=101-1 V %&....
260
Пример. На основании формулы (4) из § 1.3 для числа
подстановок обладающих заданной циклической структурой, находим
цикловой индекс симметрической группы 5П всех подстановок
«-множества:
1л К\ ...кп\ \ 1 ) " ' [ п ) '
где суммирование производят по всем решениям в
неотрицательных целых числах уравнения 1-к1 + 2-к2 + ... + пкп — п, иначе говоря,
по всем разбиениям числа п.
62

Каждой группе подстановок можно сопоставить ее цикловой
индекс единственным образом. Обратное утверждение, однако,
будет неверным. В 1937 г. Пойа построил две неизоморфные
группы подстановок порядка р3 (р>2, простое) с одинаковыми
цикловыми индексами.
Пусть заданы конечное множество О и конечная группа С с
ее гомоморфным отображением л в симметрическую группу
подстановок множества Д т. е. каждому §^0 соответствует
подстановка л3 множества И и лее' = лЁЩ' (для всех §, §'еС).
Не требуется, чтобы отображение я было вложением.
Эквивалентность элементов множества О введем через
группу С:
если существует элемент §^С такой, что лгй\-=й2. Все
требования эквивалентности при этом определении соблюдаются. В самом
деле:
а) й~й для всех йеД так как ле, где е — единичный элемент
О, является тождественной подстановкой;
б) из с?1~с?2 следует с?2~^ь поскольку из условия гомоморфно-
сти следует, что если §'=д~\ то щ> = (я^)-1;
в) из с?1~с?2, с?2~с?з следует с?1~с?з, поскольку если ле&\-=<1%
Ле'С12 = <^з> то лё'2 ^1 =1 л2' (лг^1/ =1 Я,&'й2 = С?з-
В силу определения эквивалентности множество О оказывается
разбитым с помощью группы С на классы эквивалентности
(транзитивные множества). Элементы эквивалентны тогда и только
тогда, когда они входят в один и тот же класс эквивалентности.
Лемма Бернсайда. Число классов эквивалентности,
определяемых конечной группой С, действующей на конечном множестве Д
равно
-щ-3>(г)'
260
где \С\ —число элементов О; $(§) —число элементов Д
инвариантных относительно л8, т. е. таких, что л8(1 = д, а суммирование
производится по всем элементам §^С.
Это утверждение впервые появилось в работах Коши, Фробе-
чиуса и Бернсайда.
Доказательство. Рассмотрим все пары (§, (1), для которых
лйд,~й {ё^О, (1еО), тогда:
а) мы можем фиксировать § и сосчитать, сколько существует
А, для которых л&й-=й;
б) для каждого фиксированного б, сосчитаем все §, при
которых лай-=б,; обозначим эти числа через г\{й). Ясно, что
2 Л (<*) = У] г|>(2).
<*ео гее
63.

'Элементы #еО, фиксирующие й, образуют подгруппу 6а группы С:
|Ой|=г,(^).
Если взять другой элемент из того же класса эквивалентности
й\~(1, то число элементов §, для которых пей=йх, тоже равно
\Оа\. В самом деле, имеется Н^О, для которого л,нй\ = й, и значит
из того, что лей — йх, следует Н§^6а- Таким образом, группа С
может быть разделена на непересекающиеся подмножества по
\Оа\ элементов в каждом (левые смежные классы группы 6 по
подгруппе Ой); каждое подмножество соответствует в точности
одному элементу класса эквивалентности, в который входит элемент д..
Отсюда, чтобы найти г\{й), надо разделить |0| на число
элементов класса эквивалентности, к которому принадлежит й.
Суммируем: а) Ет)(^)= |0|, если сумма берется по всем й, входящим в
один и тот же класс эквивалентности; б) сумма V Л (^) равна
лей
произведению |С[ на число классов эквивалентности, откуда
следует доказываемый результат.
Итак, мы ввели понятие эквивалентности для элементов через
группу подстановок и вывели формулу для числа классов
эквивалентности.
Введем отношение эквивалентности для отображений. Пусть
даны конечные множества О и К. Множество всех отображений из
О в К обозначим К°. Число этих отображений равно |^|1г>1, так
как для каждого й^И существует |#| независимых возможностей
для образа. Пусть у нас имеется группа 6 подстановок
множества О. Отображения /1 и /2 эквивалентны (/1~/г), если существует
подстановка §^С такая, что /1(^)=/2(^) Для всех <2еД или
/1^ = /2. Условия эквивалентности: а) /~/; б) если /1~/г, то /г~/ь
в) если /1~/г, /г~/з, то /1~/з — все выполняются. Первое условие
следует из существования в 6 тождественной подстановки;
второе— из того, что вместе с § в С входит н §~и, третье — из того,
что если §,еО, §2^С то §1§2^С.
Эквивалентность отображений, введенная таким образом,
разбивает множество Я° на классы эквивалентности (или модели).
Введем теперь веса; они дадут нам возможность перечислять
специальные классы комбинаторных объектов. Сначала каждому
элементу г^К приписывается вес а(г), где а (г) есть элемент
коммутативного кольца над полем рациональных чисел. Вес
отображения №(/), где 1^К°, определяется как произведение:
^(/)=П »(/И).
где /(<2) —образ элемента йеВ при отображении /, а ©(/(с?)) —
его вес. Эквивалентные отображения имеют одинаковые веса.
В самом деле, если /1^=/2(5^6), то
П «(/.И) = П "(/г» = П «(/.И)-
<*€о ибо <*ео
64

Равенство очевидно, так как первое и последнее произведения
отличаются лишь порядком сомножителей. Поскольку все
отображения / класса эквивалентности Р обладают одинаковым весом,
припишем этот вес всему классу Р, обозначив его через Щ/7).
Сумму весов
ген
элементов множества # назовем (следуя де Брейну) инвентарем
(туеп!огу) множества # и будем обозначать ту О.
Теперь мы можем вычислить инвентарь множества Я°
отображений:
т\К° = £^(/) - (2 о>(г))1В| = (ту #)1В|.
/ ген
Покажем, что это так. В правой части имеем \К\1в1 членов. Можно
установить соответствие между \П\ сомножителями и элементами
множества В. Выбор члена из каждого сомножителя и
образование одного члена разложения интерпретируются как отображение
\:Б-*-Я. Но для каждого / имеем №(/) = П ш (/(^)). Все
произвел
ведение равно сумме всех №(/), что и требовалось доказать.
Если же рассмотреть множество 5 отображений, постоянных на
подмножествах Пи ..., Пь, образующих разбиение множества Д то
Шу5=П2 И'))'0'1 , (1)
г=1 ген
что показывается рассуждением, аналогичным предыдущему.
Теперь, когда все необходимые понятия уже введены, мы
можем сформулировать основную теорему. В ней речь идет о
переходе от весов функций к весам моделей (классов эквивалентности).
Теорема Пойа. Пусть О и К — данные конечные множества, а
О — группа подстановок элементов О; пусть, кроме того, элементам
г^К приписаны веса а(г), а отображениям ^К° и моделям
(классам) Р соответственно веса №(}) и №(Р). Тогда
£^(/=) =Яо Д "(О, Е («С"))2, ^ («И)3,...),
р ген ген г$к
где Ра — цикловой индекс группы С. В частном случае, когда все
веса равны 1, число классов эквивалентности равно
Ро(\К\, |Я|,...).
Доказательство. Из К°, т. е. из множества всех
отображений /:/)->■/?, выберем множество 5 тех отображений, веса
которых одинаковы, скажем, равны ш. Для /е5 имеем: $7(/) =о), а
число классов эквивалентности для множества 5 равно
3 К. А. Рыбников
65

тггЕ *•<*>•
. М
2 60
где $•*(§) обозначает число отображений /, для которых
№(/)=«, !=Ы (или [§-1 = [).
В самом деле, было доказано, что если §^С и /1 = /2^, то /1 и /2
имеют одинаковый вес. Значит, если /^5, то и /^-'сеЗ. Таким
образом, каждому §^С соответствует отображение ле множества
5 на себя, определяемое соотношением:
Если два элемента /1 и /г множества 5 эквивалентны, то это
утверждение равносильно такому: существование элемента §^С, для
которого пеи = 1ъ эквивалентно существованию элемента £6^0, для
которого и = !\ё- Теперь осталось только сослаться на лемму
Бернсайда, чтобы убедиться, что число классов эквивалентности
выражено верно.
Все классы эквивалентности, входящие в 5, имеют вес ш.
Следовательно, если умножить
на о) и просуммировать по всем ш, то получим
р (й 2€0
Но очевидно, что
где суммирование производится по всем ^Н°, удовлетворяющим
равенству /=/§; значит
И^)=7ч21>(/)- <2>
Р 260 {
(2)
Вычислим теперь 2^^(/)- Подстановка § разбивает В на цик-
{
лы. Условие ? = }§ означает, что
т. е. / = сопз! для каждого цикла. Верно и обратное утверждение:
всякое отображение /, постоянное на каждом цикле,
удовлетворяет равенству /§ = /, так как §(с!) и с! всегда принадлежат одному
циклу. Так что если Би В2, ..., !>*— циклы §, то по (1) имеем
66

(£) *
/ 1=1 ген
Пусть подстановка § имеет циклическую структуру (Ьи Ь2,---),
тогда
(в) *■ . *2
/ ген ген
Подставив это выражение в (2), получаем
2™-7ггЕ(Е-">Г(3: <""»')■•••■
ч. т. д.
Теорему эту Д. Пойа опубликовал в 1937 г. Позднее было
замечено, что такую же теорему, но в несколько иной форме
опубликовал в 1927 г. Дж. Редфилд (см. в [12]). Однако в силу
сложившейся уже привычки за теоремой сохранилось имя Пойа.
Позднее эта теорема была доказана при общих
предположениях. Как было отмечено выше, при отображениях /:!)-»-/?
эквивалентность вводилась через группу С подстановок элементов ЛеаО.
Если добавить вторую группу Я подстановок элементов ге^, то
введение эквивалентности с помощью обеих групп О и Я
производится следующим образом: две функции (два отображения)
!1^КВ и /2^#д эквивалентны: /1-/2, если существуют элементы
^еО и йеЯ такие, что /1^ = /1/2, т. е.
/1(^)=^/2(^) для всех йеВ,
Из других обобщений теоремы Пойа упомянем то, которое
связано со сплетением групп. Пусть имеем группы подстановок О и Я
для множеств 5 и Г соответственно. На прямом произведении
множеств 5x7' образуем подстановки специального вида. Именно
выбираем §е^0; для каждого зе5 выберем элемент /г8еЯ. Эти
элементы определяют подстановку:
(5, 0-(25, Н4), 5е5, ^Т.
Всего таких подстановок \С\- |Я|1Я1; они и образуют группу,
названную Пойа сплетением групп (Огиррепкгапг). Термин «группы
Кранца», появившийся в литературе на русском языке, возник в
результате ошибки в переводе.
Удачное разъяснение теорем Пойа, снабженное примерами,
Дано в [10]. Последующее развитие мало обогатило теорию Ред-
фильда — Пойа и не изменило ее принципиально.
В заключение приведем несложный пример, разъясняющий
применение теории Пойа. Речь пойдет о перечислении изомеров
органических молекул заданной структуры. Рассматриваются
молекулы вида:
3*
67

X
I
X —С —X
I
X
где С — атом углерода, а на местах, обозначенных крестиками,
могут находиться: СН3 (метил), С2Н5 (этил), Н (водород) и С1
(хлор). Например,
СН3
С1-С-С2Н5
!
С1 (дихлорбутан).
Математической моделью этих молекул будет являться
тетраэдр, в центре которого расположен атом углерода. Задача о
перечислении молекул будет трактоваться как задача о числе классов
эквивалентности О (для 4 вершин):
/:Я+# = {СН3, С2Н5, Н, С1}.
Группа О будет группой вращений тетраэдра, состоящей из:
одной идентичной перестановки вершин;
восьми вращений на 120° вокруг вершин;
трех вращений на 180° вокруг осей, проходящих через середины
непересекающихся ребер. Тогда
Ра (хх, х2, х3) =~(х\ + 8хгх3 + 3x1).
Положим все веса равными единице и получим общее число
молекул:
Ра (4, 4, 4)=36.
Подставим частные виды молекул данной структуры: пусть,
предположим, надо подсчитать число таких молекул, в которое не
войдет атом водорода. В этом случае для СН3, С2Н5 и С1 веса будут
равные единице, а для Н — нулю:
Ра (3,3,3) = — (3* + 8-3-3 + З-З2) = 15 искомых молекул.
Чтобы классифицировать остальные 21 молекулу, придадим,
как и ранее, единичные веса для СН3, С2Н5 и С1 и вес Н для атома
водорода:
Ра (И + 3, Н2 + 3, № + з) = -у((Н + 3)* + 8(Н + 3) (№ + 3) +
+ 3(Н2 +3)2) = Н* + ЗН3 +6Н2 + ПН + 15.
Следовательно, существуют: 1 молекула СН4 (метан); 3 молекулы
с 3 атомами Н; 6 молекул с 2 атомами Н; 11 молекул с 1
атомом Н; 15 молекул, не имеющих атома Н.
Теория производящих функций является частью
комбинаторного анализа, наиболее продвинутой в теоретическом и в
практическом плане для решения перечислительных задач. Состав и
возможности этой теории уже определились.

Глава 3
КОМБИНАТОРНО-ЛОГИЧЕСКИЙ
АППАРАТ
В этой главе мы опишем характерные логические приемы,
составляющие основу многих комбинаторных доказательств.
3.1. МЕТОД ВКЛЮЧЕНИЙ И ИСКЛЮЧЕНИИ*
Пусть дано «-множество ^ некоторых элементов и
^-множество свойств рь р2,..., ри, которыми элементы множества могут как
обладать, так и не обладать. Требуется найти число элементов, не
обладающих ни одним из вышеперечисленных свойств.
Выделим какую-либо г-выборку свойств (рс„рс, ...,р;г).
Число элементов множества 5, каждый из которых обладает всеми
выбранными свойствами, обозначим через п (Р;,, р(2, ..., р;).
Отсутствие у элементов свойства р; будем обозначать через рг. Таким
образом, число элементов, обладающих, скажем, свойствами рь р3,
рь и не обладающих свойствами р2, р4, ре, запишется как п(ри р2,
рг, р4, рь, рб) ■
Рассмотрим сначала два простых случая:
а) имеется только одно свойство р; тогда, очевидно,
п(р)=п—п(р);
б) имеется конечное число свойств рь р2 ря, несовместимых
друг с другом; снова очевидно, что
_ _ _ N
п (р1? р2, . . . , ры) = п— ^ п (рс).
1 = 1
Перейдем к более общей постановке вопроса, когда элементы
множества могут обладать комбинациями совместимых свойств.
В этом случае имеет место
Теорема 1. Если даны «-множество элементов и ^-множество
свойств рг, 1= 1, 2, ..., А/', то
_ _ _ N
п (рг, р2, . . . , ры) = п— ][] п (р() + 2 п (Л, Р/) —
— 2 "(Л. Р1'Рк) + ■■■ +(— ^п(Рг,р2, ... ,рц). (1)
* Встречается также под названиями: метод решета, логический метод,
принцип перекрестной классификации, символический метод.
69

Доказательство. Чтобы получить элементы, не
обладающие ни одним из указанных свойств, необходимо из «-множества
исключить элементы, обладающие свойством рь затем — свойством
рг и т. д., т. е. У\п(р() элементов. Однако при этом элементы,
имеющие два свойства, скажем р\ и р2, оказались исключенными
дважды (сначала как обладающие свойством р\, затем как
обладающие свойством р2). Значит, надо возвратить все множества,
элементы которых обладают двумя свойствами, т. е. прибавить
У "(р<, р;) элементов. Но при этом элементы, обладающие
тремя свойствами, скажем рь р2 и р3, оказались включенными,
следовательно, надо вычесть 2с п(р1,р1>рк)- Рассуждая далее
аналогичным образом, получим алгоритм для вычисления
п{р\, р2, •••, рм), состоящий в попеременном отбрасывании и
возвращении подмножеств. Это определило одно из названий метода:
метод включений и исключений. Его мы и будем придерживаться.
Помимо простых рассуждений, приведенных выше,
доказательство можно провести индукцией по N. Теорема справедлива для
N=1:
п(Р)=п—п(р).
В соответствии с формулировкой теоремы мы можем написать
также:
П(ри р2, ... , рн)=П(р\, р2, ... , рЫ-\)—П(ри р2, .- , рЛГ-1, рх) ■
Пусть теорема верна для Л^—1 свойств, т. е.
" (рр рь ... , рдг-0 =я-Л»(й)+^п (а. Р/) — • • •
... +(—1)"-1п(рх,р2 рц_1).
Перейдем к случаю, когда имеется Л^ свойств. Применим
полученное соотношение для числа п(р\, р2, ..., ры-и ри):
" (р1> р2 рлг-1. рн) = " (рм) — ^] " (Рр Рм) + • • •
I
... +(—1)^-1п(р1,р2 ры).
Вычитая это равенство из предыдущего, получим утверждение
теоремы.
Характер доказательства таков, что его можно применить для
любой комбинации свойств. В левой части доказанного равенства
может стоять не только п{р\, р2, ..., рх), но и, например,
"(рь р2, рз, р4). Теорема формулируется при этом относительно
совокупности свойств рг и р4 с обязательным выполнением свойств
Р\ и рз следующим образом:
"(рь рз, р2, Ра) = ",(рь рз)—«(рь рз, рг) —
—"(рь рз, Р4) +п(ри рз, р% р4)-
70

Дальнейшие усложнения метода связаны с введением весов
элементов. Как и в гл. 2, мы никаких ограничений или уточнений
для понятия веса вводить не будем. Для нас веса — это числовые
характеристики элементов множеств, определяемые условием
задачи.
Итак, пусть задано «-множество 5 и каждому элементу 5,-е5;
1=1, 2, ..., п, приписан вес У(л).Из ^-множества свойств рир2у...
рн возьмем г-выборку р,, р,г и обозначим сумму весов
элементов, обладающих всеми г выбранными свойствами, через
У(рс1, р1г Рг )• А сумму весов, распространенную на все
возможные /--выборки свойств, обозначим через
2У(р(1,р1ш Р1) = У(г).
Для случая г = 0 соответствующий символ У(0) будет обозначать
сумму весов всех элементов множества 5.
Предыдущая теорема при этом переформулируется так.
Теорема 2. Если даны ^множество 5, каждый элемент
которого имеет вес, и Л^-множество свойств, то сумма У^(0) весов
элементов, не обладающих ни одним из заданных свойств,
определяется по формуле
Уп(0) = У(0)>-У(1) +1/(2)-...+ (—1)"К(А0.
Заметим, что теорема 2 обобщает теорему 1. Если все элементы
5*е5 имеют единичный вес, то сумма весов равна числу слагаемых
в сумме. В этом случае У(0)=Ы, а У^(0) равно числу элементов
множества 5, не обладающих ни одним из N свойств; формула,
получающаяся при этом, есть формула (1).
Теорема 2 в свою очередь может быть обобщена.
Теорема 3. Сумма весов элементов, обладающих в точности г
свойствами из свойств рь р2, ..., р№ находится по формуле
Ум (г) = V(г) - (г + 1) V(г + 1) + ^ + 2) V (г + 2) - .. .
или, что то же самое,
Ун (г) = У(г)-(г+Х)У{г + \)+^г + 2\У(г+2)-...
••• +(-1)^(^1/(^.
Теоремы 2 и 3 доказываются аналогично теореме 1. Читателю
предлагается найти эти доказательства самостоятельно или
обратиться к § 8.3, где приводятся дальнейшие обобщения метода
включений и исключений.
Рассмотрим в качестве примера задачу о беспорядках, иначе
называемой задачей о встречах. Пусть имеется конечное
упорядоченное множество чисел 1, 2, 3, ..., п. Для них могут быть обра-
71

зованы перестановки: а,\, а2, ..., а„. Число всех перестановок з = п\
Среди этих перестановок имеются такие, где ни один элемент не
сохранил своего первоначального места: щФц £=1, 2, ..., п. Такие
перестановки называются беспорядками. Сколько существует
беспорядков?
Множество п элементов рассматривается по отношению к
множеству свойств элементов оставаться на своем месте: р;~{а; = 1'|
£=1, 2, ..., п). Очевидно, что если 5 элементов закрепляются на
своих местах, то число Л^(5) соответствующих перестановок равно
(п—5)!. Число беспорядков тогда находится с помощью метода
включений и исключений:
N(0) =п\- (7) (и - 1)! + (з) (я - 2)! - . . .
••• + (-1)8 (")("-^)!+ ••• =
\ 2! 3! п\ )
что является целым числом, ближайшим к п\е~1.
Если речь идет не о беспорядках, а о числе перестановок, в
которых остаются на своих местах 5 элементов, то
ЛГ(5) = — (1—1 +- - + ... +(—I)"-8 Ц-У
V ; 5! \ 21 3! ^ У ' (я —5)! I
Легко заметить ход рассуждений при решении: из п элементов
выбирают 5 неподвижных элементов (™) способами, а затем
умножают (по правилу произведения) на число беспорядков среди
оставшихся (п—5) элементов.
Приведем теоретико-вероятностную интерпретацию метода
включений и исключений. Множество элементов при этом
трактуется как дискретное пространство элементарных совместных или
несовместных событий а.\, а2, ..., ап, а веса элементов — как
вероятности. Вероятность одновременного появления событий а,-,,
а/.> ••• > а!к обозначим через Р(аи, ..., а1к). Для случая
непоявления событий используется так называемое символическое
уравнение Пуанкаре:
Р(аи Й2, ...а„)=[1—Р(а!)][1—Р(а2)]...П—Я(ап)];
раскрытие скобок в котором может быть произведено по правилу:
Р(щ)Р(а;) = Р(а«, а/). Это уравнение является обобщением
формулы для вероятностей независимых событий на случай событий
зависимых и совместных. Общая формула метода включений и
исключений
"(Р1-Р2- ... ,~Рп) = п — 2«(А) + ^«(Л.Р/) —...
... + (—1)пп(р1гр2, ... ,рп)
72

при этом видоизменяется: обе части делятся на п, чтобы получить
не абсолютные, а относительные величины —вероятности
л-« п (^, ра, •'• • -Й = 1 — я"1 2 я (р() +
+ "-'2"(Р;-Р/)— ••' +(—1)"л~1п(Р1.Р«. ••• ,Рп)-
I. I
Ниже мы приведем приложения метода включений и
исключений к вычислению перманентов (§ 4.4) и к подсчету значений
специальных функций теории чисел (§ 8.3).
3.2. СИСТЕМЫ ПРЕДСТАВИТЕЛЕЙ МНОЖЕСТВ
Здесь мы рассмотрим один из комбинаторных подходов к
характеристике структуры конечных множеств. Уже по названию
можно понять, что основной идеей является замена системы
множеств собранием их представителей.
Постановка задач этого типа и методы их решения зависят от
того, каким требованиям должны эти представители
удовлетворять.
Системы различных представителей. Пусть имеются
«-множество 5 и множество Р(5) всех его подмножеств. Пусть М =
= (51, 52, ..., 5т) есть некоторая т-выборка из Р(5), а а =
= (а\, а2, ..., ат) есть некоторая т-выборка из 5. Если выборке
М можно сопоставить (не обязательно однозначно) выборку а
такую, что элементы щ, 1 = 1, 2, ..., т, попарно различны и при этом
а*е5,, 1 = 1, 2, ... , т, то говорят, что элемент щ представляет
множество 5„ а вся выборка (аи а2, ..., ат) называется системой
различных представителей (сокращенно с.р.п.) для М. Заметим сразу
же, что если 1ф\, то щфа/, даже если 5* = 5/. Если множество
появляется несколько раз, то всякий раз оно должно иметь
представителя, отличного от всех других.
Сразу же оказывается, что с.р.п. может существовать не для
всяких совокупностей множеств. Если в конечной системе
множества не пусты и не пересекаются, то с.р.п., очевидно, существует.
Возьмем более сложный случай. Например, если 5= (а, Ъ, с, й, е),
а М есть совокупность четырех множеств 51= (а, Ъ, с, й)\ 52 =
= (а, Ъ, е)\ 53 = 54=(&, е), то существует две с.р.п.: (с, а, Ъ, е) и
(Ь, а, е, й). Но стоит изменить лишь одно из подмножеств,
например, вместо 52 взять 52'=(Ь, е), и мы уже не сможем получить ни
одной с.р.п. На вопрос о том, существует ли с.р.п. для заданного
семейства множеств, отвечает теорема Ф. Холла, найденная
последним не позже 1935 г. и дающая необходимые и достаточные
условия существования с. р.п.
У Теорема Ф. Холла. Подмножества 51, 52, ..., от имеют с. р. п.
тогда и только тогда, когда объединение любых к из этих
множеств содержит не менее к элементов. Иными словами, с.р.п. для
5ь 52, ..., 5т существует тогда и только тогда, когда 5,-,05^...(^1
73

состоит не менее чем из к элементов, при этом к = \, 2, ..., т, а
(н, 12, •••, (т) — любая ^-выборка из 1,2, ..., т.
Доказательство. Необходимость почти очевидна, так как
существование с.р.п. обеспечивает наличие необходимого числа
элементов в качестве различных представителей. Что касается
достаточности, то приведем усовершенствованную формулировку,
которая дает нам также нижнюю грань для числа самих с.р.п.
Теорема. Пусть семейство М=(5и 52, ..., 5т) удовлетворяет
'необходимому условию существования ср.п., и пусть каждое из
множеств 5Ь 52, ..., 5т состоит не менее чем из I элементов. Тогда:
а) если 1<ст, то М имеет не меньше чем И ср.п.; б) если 1>т, то
М имеет не менее чем Д/(<—т)\ ср.п.
й Доказательство проведем по индукции относительно т.
Для т=\ (и даже для т = 2) теорема очевидна. Докажем, что она
верна для любого конечного т, исходя из ее справедливости для
т'<т.
Рассмотрим объединение некоторой ^-выборки множеств:
тогда следует рассмотреть два случая: когда число элементов в
объединении равно к и когда число элементов больше, чем к.
Начнем со второго случая, когда в рассматриваемом объединении
имеется не менее к+1 элементов, каковы бы ни были к: к =
= 1, 2, ..., т, и набор м, 12, ..., г'д из чисел 1, 2, ..., т. Выберем
какой-либо элемент а^^ и удалим его из 52, 5з, ..., Зт, если он
там встречается. Придем таким образом к М* = (52*, 5з*, ..., 5т*).
Эта (т—1)-выборка удовлетворяет необходимому условию
существования ср.п., так как 5^ 1)5^11 ... I) 5 содержит не менее
к элементов и, кроме того, М* имеет либо не менее (Ь—1)! ср.п.,
если ^<т (и значит, I—1<:т—1), либо (Ь—1)!/(<—т)! ср.п., если
1~>т (и значит, I—1>т—1). Искомый результат достигается, если
учесть, что в 51 имеется по меньшей мере I возможностей
фиксировать элемент а,\ и что этот элемент вместе с с.р.п. для М*
составляет ср.п. для М.
Вернемся к первому случаю, когда вышеприведенное
доказательство применить нельзя из-за того, что существует некоторая
^-выборка 5. , 5, , .... 5; такая, что 5, У 5,. ^) ... И 5г. содержит
точно к элементов (1<:&<:т—1). Перенумеруем множества 5Ь
$2, •••. Зт так, чтобы 5(. стало 5Ь 5, стало 52, ..., 5(Л стало
5А, и запишем эти множества в новом порядке:
5], Ог, ... ; О*, 5й+1, ... , 8т.
Поскольку 5^520..^5¾ содержит точно к элементов, то ^<:&.
Следовательно, по предположению индукции (5Ь 52, ..., 5А) имеет
не меньше чем Л ср.п. Возьмем одну из этих ср.п.: (аи аг, ... , а*)>
где аге5;; 1 = 1, 2, ..., к. Удалим элементы аи а2, ..., ак из
5А+1, ..., 5т, если они там встретятся. Получившаяся (т—к)
-выборка М*=(3*к+и ..., 5*т) удовлетворяет необходимому условию
74

существования ср.п. В самом деле, если это не так и если
объединение какой-нибудь &*-выборки 5^,^)... [}5*к+к, имеет меньше
к* элементов, то объединение
имело бы менее чем к + к* элементов, что противоречит условию
теоремы. Итак, М* имеет хотя бы одну ср.п., и, следовательно, М
имеет не меньше чем И с.р.п.
Алгоритм выбора с р. п. Практически очень трудно проверить,
выполняются ли в данном конкретном случае условия теоремы
Ф. Холла. Приведенное только что доказательство, основанное на
полной математической индукции, не дает никаких указаний,
которые помогли бы найти ср.п. Это неудивительно. Теоремы
существования чаще всего появляются там, где бывает трудно или
невозможно найти алгоритм, приводящий к нахождению решения.
Алгоритм, который позволяет подобрать ср.п. для конечного
числа множеств или показать, что такой системы для данного набора
множеств не существует, дал М. Холл в качестве доказательства
теоремы Ф. Холла о различных представителях.
Пусть задано п множеств: 5Ь 52, ..., 5„. Требуется найти для
них ср.п. или показать, что этой системы не существует.
Произвольным образом выберем элемент первого множества 0^51 в
качестве его представителя. Поочередно будем выбирать
представителей других множеств: о2е52; а3^5з;..., заботясь только о
том, чтобы все они были различными. Если мы доведем этот
процесс до о„е5„ включительно, то получим искомую с.р.п.
Может случиться, что на г-и шаге мы дойдем до некоторого
^-множества 5Г, все элементы которого Ьи Ь2, ... , Ьг уже были
выбраны представителями других множеств. Это, однако, еще не
означает, что ср.п. не существует. Будем брать поочередно все те
множества, представителями которых являются элементы Ь{
(1=1, 2, ...), и удалять из них все элементы последовательности
Ьи Ь2, ..., Ь(, а оставшиеся приписывать в конец этой
последовательности. Так будем поступать до тех пор, пока не случится одно
из двух: либо 1) мы достигнем элемента Ь{, который не может
служить представителем; либо 2) последовательность
исчерпывается элементами Ьи Ь2, ..., Ь3 как представителями множеств.
В случае 2) мы можем быть убеждены, что с.р.п. не существует.
В самом деле, элементы Ъ\, Ь2, ..., Ь3 являются представителями 5
множеств, и по построению каждый элемент этих 5 множеств
содержится в данной последовательности. Но тогда эти 5 множеств,
а также множество 5Г образуют 5+1 множеств, которые содержат
только 5 различных элементов, что противоречит условию теоремы.
Если же имеет место 1), то на некотором этапе мы находим
элемент Ь1 = 6,-, е 5/, (м><), не являющийся до сих пор
представителем. Это означает, что представителем 5/, уже был выбран
Другой элемент Ыг (12< ^). Если 12>1, то значит Ь,\, е5/„
представителем которого является &;„ (13 < 12). и т. д. Таким образом,
возникает последовательность Ь^, Ь-н, . .. , Ь{/ , индексы которой
75

убывают (1т<0> причем в этой последовательности каждый ее
член входит в множество, представителем которого является
следующий член. Заменяем представителей, выбирая элементы: Ь^ для
5/а- *(, для 5/,' • • • • Чп-1 Для 5/т-1 • Элемент Ь-1т в результате
этой замены освобождается для выбора в качестве представителя
5Г. Итак, 5ь ..., 5Г имеют различных представителей, и мы можем
следовать тем же путем, имея в виду либо возможность дойти до
5К и получить полную с.р.п., либо встретить случай 2) и установить
несуществование с.р.п.
Заключение о числе ср.п. получается из приведенного
алгоритма как следствие. В самом деле, если ср.п. существует, то это
значит, что существует также некоторое множество, каждый элемент
которого может быть выбран в качестве его представителя в с.р.п.
Значит, если множества данного семейства п элементов имеют I
или больше элементов, то существует по меньшей мере 1\ с.р.п.,
если 1<п, или 1(1—1).-.(^—п + 1), если 1^>п (поскольку выбор
первого представителя может быть осуществлен по меньшей мере
I способами; вычеркнув этот выбранный нами представитель из
всех других множеств, придем к системе множеств 5г*, ..., 5К*,
наименьшее из которых имеет не менее I—1 элементов. Продолжая
шаг за шагом, мы и получим указанный результат).
Условие конечности является здесь важным. Если его снять, то,
например, для бесконечной системы множеств
50 = {1, 2,3, ...,*, ...};
5, = {1};
нет с.р.п., хотя она есть для любой его части.
Другие системы представителей множеств. Задачи о разбиении
множеств привели к понятию систем общих представителей
множеств. Пусть даны два различных разбиения одного и того же
множества 5 на к непустых составляющих:
5=А1ЦА2Ц...ЦАк; 5 = В,1|В211... 1|В*.
Если существует подмножество О множества 5, состоящее из к
элементов и такое, что его пересечение с любым из составляющих
не пусто:
О(\Аф0; О[\ВФ0\ 1=1, 2, ..., к,
то оно называется системой общих представителей (с.о.п.) данных
разбиений. При этом каждое из пересечений оказывается
состоящим только из одного элемента. Попарно взятые множества
первого и второго разбиений, подобранные, если надо, соответствующим
образом, имеют один и только один общий элемент, который и
является их общим представителем.
Разумеется, совсем не обязательно, чтобы соблюдалось
требование существования только одного общего элемента. Можно ставить
и учитывать разные условия: существование заданного числа
общих элементов, заданного множества их и т. п. Например, если
76

потребовать, чтобы каждый элемент 5(е5 входил в с.о.п. не менее
ки и не более к2с раз {к21>ки>>\), то такую систему называют
системой ограниченного числа представителей [28]. Ясно, что задача
о с.р.п. является частным случаем такой задачи при кц = 0, к21=1.
Другой частный случай, когда
а _ ( * Для 1 = 1.2,...,/;
11 I 0 для I = / + 1. / + 2, ... , т;
к2( = 1 для 1=1, 2, .... т,
носит название задачи о существовании с.р'.п., содержащей
данное множество маргинальных элементов 5Ь 52, .... 5;.
Критерий существования или несуществования с.о.п. близок
к критерию, применяемому к с.р.п.
Теорема. Два разбиения множества
З^АМц ... 11^ = 5^11... \]Вк
тогда и только тогда имеют с.о.п., когда объединение любых т из
множеств Л,- пересекаются не менее чем с т из множеств В;, где
т=\, .... к.
Доказательство. Необходимость, как и в случае ср.п.,
очевидна. Достаточность доказывается простым сведением к
теоремам о ср.п.
Действительно, для каждого В и 1 = 1, 2, ..., к, выберем
множество 5,- всех индексов /е/С={1, ..., к}, таких, что А;(]В[Ф0.
Получим т-выборку М=(8и 52, ..., 5¾) подмножеств множества К.
Для М существует ср.п. (сформулированный критерий
существования ср.п. является критерием существования ср.п. для М).
Выбор различных представителей дает для каждого В{ свое Л/,
причем пересечение их не пусто. В этом пересечении можно выбрать
хотя бы один элемент, общий для Л/ и Вь т. е. их общий
представитель.
Понятие о представителях множеств и о системах
представителей находит в математике многочисленные и разнообразные
приложения; например, это представители классов эквивалентности.
Метод систем представителей встречается также в теории сетей
при исследовании допустимости потоков и в теории расширения
латинских квадратов.
3.3. НАЧАЛА ТЕОРИИ РАМСЕЯ
Операция разбиения множеств лежит в основе бесчисленного
количества практических задач. В этом параграфе описывается
подход, позволяющий получить данные о характере самих
разбиений и о возможности осуществлять разбиение заданного
заранее типа.
Пусть имеется «-множество 5, элементы которого должны быть
размещены по двум ящикам. Каким должно быть число п, чтобы
обеспечить попадание либо в первый ящик ^^ элементов, либо во
второй ящик ц2 элементов? Ответ почти очевиден: п>-цх + ц2—1-
77

Чг
г- I
оооооооооооо
I .—I
Таким образом, минимальное число элементов, обеспечивающих
решение задачи, равно
Л/(<7Ь ц2; 1)=91 + 92-1-
Если ставится задача о распределении не в два, а более (скажем,
I) ящиков, причем соответственные числа, характеризующие
требуемое заполнение ящиков, суть 9ь Цг, ■■■. Ци то
1=1
В 1930 г. Рамсей [45] доказал теорему, в которой эти частные
результаты были обобщены. Вместо распределения единичных
элементов «-множества в этой теореме имеют дело с распределением
его /--подмножеств. Обозначим через 5„ множество из п
элементов, а через Рг(8„) —совокупность его /--подмножеств.
Теорема Рамсея. Пусть /->1, ц^г (1=1, ... , I). Существует
такое наименьшее натуральное М=М(д\, ..., щ; г), что для любого
п^>Ы и любого упорядоченного ^-разбиения Рг(8п) = А\[] ... \)А*
найдется (при некотором 1-е{1, ..., 1}\ (9;, Л,-)-подмножество, т. е„
такое ^/'Подмножество множества 5„, все /--подмножества которого
содержатся в Л,-.
Сделаем предварительно три замечания с целью облегчить
понимание постановки теоремы и ее доказательства.
1. Приведенные выше примеры, относящиеся к разбиениям
множеств, являются частными случаями теоремы Рамсея при /"=1,
Рг(3)=3, а (9;, Л/)-множество есть просто ^^подмножество
множества Л,-.
2. Для частного случая, когда 1=\, имеем #(91, г)=9ь что
тривиально.
3. Если теорема Рамсея будет доказана для 1=2, то она
окажется справедливой и для 1=3. В самом деле, пусть
Яг(5) =А,\]А2\]АЪ = А,\]{А2\]АЪ).
Обозначим Л211Лз = Л2*. Положим 9г* = Лг(92, Цъ, г). Если гсз^Л^ь
9г*; г), то либо 5 содержит (91, А\)-подмножество, либо 5
содержит (92*; Л21|Л3) -подмножество. Первый случай соответствует
утверждению теоремы. Если же имеет место второй случай, то 92*-
подмножество множества 5 в силу предположения будет
содержать либо (92, Л2)-подмножество, либо (93, Л3)-подмножество.
Следовательно, наше утверждение справедливо. Отсюда следует,
что теорему Рамсея достаточно доказать для 1=2, а затем
заключить по индукции, что она верна для всякого целого 1>2.
Доказательство теоремы для случая 1=2 начнем с
того, что выпишем в качестве исходных следующие равенства:
78

#(9ь 92; 1)=91 + 92-1;
М(диг,г)=ди (Ч
М{г, 9г; г) =92-
Первое из равенств уже известно. Во втором равенстве любое
разбиение Л^Лг приводит либо к (г, А2) -подмножеству, если Л2
непусто, либо к (ди Рг(5)) -подмножеству. При этом 91 не меньше,
чем г. Любой из случаев точно соответствует Формулировке
теоремы. Несложные рассуждения покажут справедливость и третьего
равенства. Кроме того,
г>\\ 91>'; 42>г. (2)
Таким образом, мы уже можем утверждать, что существуют
числа N(2, 2, 2), N(3, 2, 2), N(4, 2, 2) и т. д., а также N(2, 3, 2),
#(2, 4, 2) и т. д. Равенства (1) и неравенства (2) служат
исходными данными для доказательства теоремы Рамсея по индукции.
Первый шаг, таким образом, уже сделан. Второй шаг,
завершающий доказательство, будет состоять в доказательстве
существования N(91, 92; г) при условии существования
р!='ЛГ(91—1, 92; г);
Р2 = Л^(91, 92—1; /-);
К(ри р2, г—1).
Смысл доказательства состоит в том, чтобы, поскольку точно
подсчитать N(91, 92; г) пока не удается, оценить это число сверху,
доказав неравенство:
ЛЧ9ь 9г; г)^Ы(ри р2; /--1)+1.
В самом деле, возьмем множество 5„, где п>-Ы(ри р2\ г—1) +1,
и зафиксируем в нем элемент а0; тогда 5^4(0()) = 5^-1. При этом от
разбиения Рг(Зп) =АХ[}А2 перейдем к разбиению Рг_1 (5„_1) =
= В1[}В2 следующим образом: в множестве 5п-1 берем поочередно
(г—1)-подмножества; если объединение такого подмножества,
скажем В', и фиксированного элемента а0 входит в А\, то отнесем
это (/-—1)-подмножество В' в класс В,, а если объединение входит
в А2, то отнесем В' в класс В2.
Множество 5„-1 имеет не менее N (ри р2; г—1) элементов, и для
этого множества теорема верна по предположению индукции.
Следовательно, в нем содержится либо а) (р,, В,)-подмножество, либо
б) (р2, В2)-подмножество. Пусть имеет место случай а). Это
значит, что в 5„_1 входит р,-множество Т, все (г—1)-подмножества
которого находятся в В,. Но ^, = ^(9,-1, 9г; г); Т^8„, и в этом
множестве Т существует либо (91—1)-подмножество, все
/--подмножества которого входят в Л,, либо 92-подмножество, все
/--подмножества которого входят в А2. Если имеет место последний
случай, то мы получили 92-множество, удовлетворяющее условиям
теоремы. Если же имеет место первый случай, т. е. существует
(91—1)-подмножество, все /--подмножества которого входят в А\,
79

то объединим его с фиксированным элементом ао. Получим
^-множество, входящее в 5. Рассмотрим его /"-подмножества. Если
какое-либо из них не содержит а0, то оно есть /--множество,
входящее в Ль Если же оно содержит ао, то оно состоит из этого
элемента и (г—1)-подмножества, входящего в В\. Значит, оно входит
в Л,. Получили ^-подмножество множества 5П, все
/--подмножества которого входят в Ль
Мы рассмотрели случай, когда (рь В,)-множество содержится
в 5п-1. Случай б) доказывается аналогично. Теорема Рамсея
доказана.
Казалось бы, что для любого ^-разбиения и при любых
подходящих (<7ь <72, - , 9<"> г) можно определить ттга=# (91,92. —.9^0.
существование которого в силу теоремы Рамсея обеспечено. Но это
оказалось исключительно трудным делом, так как еще нет
никакого метода подсчета этих чисел. При 1 = г=2 все известные числа
#(91, 92'. 2) содержатся в таблице 3.1 (там, где точное значение
неизвестно, приводятся границы, в которых оно заключено):
Таблица 3.1
3
4
5
6
7
8
9
3
6
9
14
18
23
28—29
36
4
9
18
25—28
37—44
5
14
25—28
42—55
57—94
6
18
34—44
57—94
102—169
7
23
8
28—29
9
36
Случаи, когда ^>2, еще совсем мало изучены. Известно,
например:
N(3, 3, 3; 2) =17; N(5, 5, 5; 2)>257;
N(4, 4, 4; 2) > 128; N(6, 6, 6; 2) >906.
Еще меньше известно о значениях чисел Рамсея для г>2.
Заслуживает внимания следующий результат:
13<#(4, 4; 3)<15.
Несмотря на исключительные трудности и медленность
продвижения, усилия в части отыскания чисел Рамсея или их оценок
(верхних и нижних) не прекращаются. Это объясняется
особенностью проблемы, допускающей многочисленные интерпретации и
разнообразные приложения. В теории графов, например, она
интерпретируется как задача об окрашивании ребер графов. Сама
проблема отыскания чисел Рамсея часто рассматривается для
отдельных классов графов.
Другим направлением, в котором развивают теорию Рамсея,
80

является изучение условий существования, т. е. таких ограничений,,
при которых обобщенные постановки проблемы оказывались
обоснованными, а доказательства — осуществимыми.
Задачи теории Рамсея рассматриваются сейчас с высокой
степенью общности. Пусть символ п~^ (1х 1Г) означает: если к-
подмножества «-множества 5„ разбиты на г классов, то для
некоторого I существует /,-подмножество Ь^5п такое, что все к-под-
множества из Ь[ входят в 1-й класс Тогда теорема Рамсея
записывается так:
Теорема. Для любых натуральных к, г, 1и ... , 1Г существует
Ы~Ы(к, г, 1[, ..., 1Т) такое, что если «>ЛГ, то п-*" (1г, ... , 1Г).
Вообще, теоремы рамсеевского типа имеют вид утверждений
^~*~ (Сг, ... ,СГ), где символы А, В, Си ..., Сг обозначают объ-
екты (множества) с определенной структурой. Последние могут
быть множествами с отношениями порядка на них, графами и
гиперграфами, конечными векторными пространствами, множествами
решений систем линейных уравнений, булевыми алгебрами,
разбиениями конечных множеств. Обобщения на случай бесконечных
множеств приводят к рассмотрению высказываний с
кардинальными числами. Результаты здесь еще невелики.

Глава 4
ТАБЛИЧНО-МАТРИЧНЫЙ АППАРАТ
КОМБИНАТОРНОГО АНАЛИЗА
В настоящей главе рассматриваются комбинаторные понятия
:и методы, связанные с представлением систем конечных множеств
щ виде таблиц. В основе таких табличных представлений лежит
общее понятие систем инцидентности.
4.1. СИСТЕМЫ ИНЦИДЕНТНОСТИ И СПЕЦИАЛЬНЫЕ
МАТРИЦЫ
Системой инцидентности называется упорядоченная тройка
(М, 5, ф), где ф — бинарное соответствие между множествами М
и 5 (см. ^ 1-1)- Например, плоскость можно представить как
систему инцидентности, если взять в качестве 5 множество точек
плоскости, М — множество прямых, а в качестве ф — множество пар
(а, Ь)еМх5, удовлетворяющих условию «точка Ъ лежит на
прямой а». Бинарное соответствие ф в системе инцидентностюшзыва-
ют также отношением инцидентности. В большинстве случаев
элемента множества М трактуются как некоторые подмножества
множества 5, при этом отношение ф есть попросту отношение
принадлежности элементов множества 5 подмножествам из семейства М.
Если М = {51, ..., 5т}, 5 = {51, ..., 5„}, то отношению ф будет
взаимно-однозначно соответствовать матрица Л = ||о;/|| порядка тХп,
где щ,- — элемент 1-й строки и /-го столбца — равен единице, если
(5;, 5,) еф, и нулю в противном случае. В частности, когда М =
= {3[ ..., 5т} интерпретируется как система подмножеств
множества 5, то
_ | 1, если 3; (= 5;;
I 0, если 8,-^5(.
Эта матрица называется матрицей инцидентности для семейства
подмножеств М = {51, ..., 5т} по отношению к множеству 5.
Единицы, расположенные в 1-й строке, обозначают элементы
подмножества 5;, а единицы, находящиеся в /-м столбце, указывают на
подмножества, содержащие 5,-. Матрица А дает полное описание
системы инцидентности (М, 3, ф). Она является бинарной, т. е.
состоит из символов двух видов. Для удобства при вычислениях мы
выбрали здесь в качестве элементов матрицы 0 и 1 (такие матрицы
мы дальше называем (0, 1) -матрицами), хотя иногда выбирают и
другие пары величин, например, +1 и —1.
82

Область применения матриц инцидентности весьма широка. Так,.
Кирхгоф ввел их для исследования электрических цепей; А.
Пуанкаре привнес это понятие в топологию и т. д.
Теоремы комбинаторного анализа очень часто
интерпретируются и даже доказываются с помощью матриц инцидентности.
Приведем пример. В § 3.2 сформулирована теорема Ф. Холла о
системе различных представителей. Ее матричным аналогом является
Теорема Кё'нига [46]. В прямоугольной матрице минимальное
число т линий (строк и столбцов), содержащих все ненулевые
элементы, равно максимальному числу М этих элементов, выбираемых
так, чтобы никакие два из них не были расположены на одной
линии.
Доказательство. Достаточно рассмотреть случай, когда
задана прямоугольная (0,1)-матрица Л = ||аг/||, £=1, 2, ..., /г; / =
= 1, 2, ..., /. Доказательство того, что т = Л1, состоит из двух
частей; вначале доказывается, что т>М, затем — Л1>т. Первое
неравенство очевидно, так как ни одна линия не содержит более
одного из М выбираемых элементов. Докажем второе неравенство..
Пусть т линий составлены из г строк и 5 столбцов: т = г + з.
Переставим эти строки и столбцы так, чтобы они попали на первые
места. Каждой 1-й строке (£=1, ■■■ , г) сопоставим множество
номеров столбцов /, для которых ац=\, />5. Полученные множества
удовлетворяют условиям теоремы Ф. Холла. В самом деле, если
бы это было не так, т. е. если к из этих множеств содержат ь<к
элементов, то эти к строк могут быть заменены V столбцами и все
единицы войдут в меньшее число линий, а это противоречит
условию минимальности числа т. Поскольку условие теоремы Ф.
Холла выполняется, можно выбрать г различных представителей из
т строк, т. е. г единиц, так, чтобы не было двух единиц в одной
строке и ни одной в первых 5 столбцах. Рассуждая аналогично,,
можно получить 5 представителей из 5 первых столбцов так, чтобы
не было их в первых г строках. Это множество из /- + 5 = т единиц
выбрано так, что нет двух, расположенных на одной линии.
Значит, т<М, что и требовалось доказать.
Доказательство, приведенное здесь, опирается на теорему
Ф. Холла. Последняя также может быть доказана, если опираться
на теорему Кёнига. Пусть имеем множество 5 и систему из п его
подмножеств. Строим (0,1)-матрицу инцидентности. Пусть все ее
единицы размещены в г строках и 5 столбцах. Если г+з=п, то, по
теореме Кёнига, существует п единиц, никакие две из которых не
лежат на одной линии, и они образуют с.р.п. для п множеств. Если
же г + з<п, то справедливость теоремы Ф. Холла нарушается, так
как для к = п—г строк единицы найдутся только в 5<п—г = к
столбцах.
Бинарные матрицы используются в комбинаторном анализе при
исследовании структуры дискретных множеств. Теория бинарных
матриц за последние годы получила существенное развитие
именно вследствие возросшей роли (практической и теоретической)
комбинаторного анализа.
83,

В зависимости от типа комбинаторных задач при их решении
'появляются различные типы матриц. Оперирование с ними
производится, разумеется, по общим правилам теории матриц. Так,
кроме обычных сумм и произведений для них определены прямые
(или кронекеровы) суммы и произведения. Напомним, что прямой
суммой матрицы Л = ||аг/|| порядка п и матрицы В порядка т
является матрица порядка п + т вида
п-
а прямым произведением этих матриц является матрица порядка
-ят вида
ГоцВ ... а1пВ
ап1В . . . апПВ
Ниже мы рассмотрим некоторые специальные виды матриц,
наиболее часто применяющихся в комбинаторном анализе.
Матрицы перестановок (перестановочные матрицы). Это —
матрицы инцидентности для того случая, когда 3 = М = {\, ..., п), а
отношение инцидентности 1ф/ означает, что элемент I находится на
у'-м месте в некоторой фиксированной перестановке чисел 1, ..., п.
Пусть, например, дана перестановка (5, 3, 4, 1, 2). Тогда
соответствующая матрица суть
0 0 0 10^
0 0 0 0 1
0 10 0 0
0 0 10 0
-1 0 0 0 0'
Ее строки соответствуют номерам элементов перестановки, а
столбцы— порядковым номерам мест.
Таким образом, матрица перестановки есть квадратная (0,1)-
матрица, у которой в каждой линии (строке и столбце) имеется
ровно по одной единице. Матрица перестановки Р обладает тем
свойством, что
РРТ = 1,
где РТ — транспонированная матрица, а / — единичная матрица.
Это свойство нередко используют в качестве определения матрицы
перестановки.
Матрицы перестановки, как наиболее простые, интересны в
первую очередь тем, что через них могут быть выражены другие,
более сложные матрицы (см. ниже теорему Биркгофа).
Матрицы попарных сравнений. Это — матрицы инцидентности
для случая, когда М = 8, а отношение инцидентности ф
антисимметрично и удовлетворяет условиям:
а) для любого 5е5: (5, 5) ^ф (иррефлексивность);
б) для любых различных 5,-, 5/е5 (£=^/): либо (5,-, 5,)еф, либо
(5/, 5;) Еф.
84

Такое отношение можно интерпретировать как результат
кругового турнира с участием |5| игроков. Матрица инцидентности есть
таблица этого турнира. По диагонали в ней стоят нули (а,-« = 0).
Выигрыш 1-го игрока у /-го отмечается как а,-/=1, ац = 0-
Таким образом, матрицы попарных сравнений являются
бинарными, квадратными, с нулями на главной диагонали. Они
удовлетворяют матричному уравнению
Л+Лт = 7—/,
где Л — матрица попарных сравнений, Лт — транспонированная
матрица А, I — единичная матрица, а / — матрица, составленная
из единиц.
Матрицы Адамара. Так называются бинарные квадратные
матрицы Я (сокращенно от Нас1атагс1), составленные из
положительных и отрицательных единиц, удовлетворяющие матричному
уравнению:
НН*=п1,
где п — порядок матрицы Я, / — единичная матрица п-то порядка,
Я1 — транспонированная матрица Я. Из определения вытекает,
что каждые две строки матрицы Я ортогональны, а также, что
,\йе{Н\ =л"'2 и Н-'-^п-'Н7, откуда
Если в матрице Адамара какую-либо линию (строку или столбец)
умножить на —1, то свойство матрицы быть адамаровой
сохранится. Полученные таким образом матрицы считаются
эквивалентными. Если Нх и Я2 эквивалентны, то
где Р и С} — матрицы перестановки, в которых, однако,
единственный ненулевой элемент в линии равен +1 или —1. Умножением
строк или столбцов на —1 матрицы Адамара можно
нормализовать, т. е. привести их к виду, когда первая строка и первый
столбец состоят только из положительных единиц. Нормализованные
матрицы Адамара порядков 1 и 2 суть
<■>■(:_:)•
Что касается таких матриц порядка гс>3, то оказывается, что если
они существуют, то гг = 0(тос14). В самом деле, переставим в
матрице Адамара столбцы так, чтобы во второй строке первая
половина членов состояла из положительных единиц, а вторая — из
отрицательных. Рассмотрим третью строку. Пусть на первых п/2
местах мы найдем I положительных единиц, а на вторых — г".
Тогда из определения
21 + 21'= п\
21—2Г=0; ■
85

откуда п = М. Однако- доказательство существования матриц в
смысле их эффективного построения продвигается медленно
несмотря на многочисленность изобретаемых методов.
Отметим, что прямые произведения матриц Адамара также
являются матрицами Адамара. Известно, что матрицы Адамара
порядка п существуют, в частности, в следующих случаях (см. [47]):
1. п = 2г-
2. п = рг+ 1 = 0(тос14), где р— простое число;
3. п= (к—1)3+1, где к— произведение чисел вида 1 и 2;
4. п = к(к + 3), где к и к + 4 — произведения чисел вида 1 и 2;
5. п = к(к—1), где к — произведение чисел вида 1 и 2;
6. п = 92, 116, 156, 172;
7. п = ^(^ + 2) + \, где ц и ¢ + 2 — степени простых чисел;
8. п равно произведению каких-либо чисел, упомянутых выше.
Стохастические матрицы. Этот тип матриц появился и
используется в комбинаторном аппарате теории вероятностей. Матрица
называется стохастической по строкам (столбцам), если ее
элементы неотрицательны и их сумма в каждой строке (столбце)
равна 1. Матрица называется дважды стохастической, если она
является стохастической и по строкам, и по столбцам. Нетрудно
показать, что дважды стохастическая матрица — квадратная.
Произведение дважды стохастических матриц одинакового порядка
является дважды стохастической матрицей. В самом деле, если
С=||с//||1», Л = ЫЛ В=НМЛ С=АВ, то
сг, = Е аиЪа > 0, ^ си =2^2 Ъи = 1
1=1 /=! 1=1 /=1
п
и аналогично ^ сп = '•
£=1
В квадратной матрице порядка п будем называть трансвер-
салью набор из п элементов, где никакие два не расположены в
одной линии (строке или столбце).
Лемма. Дважды стохастическая 'матрица имеет трансверсаль,
состоящую из ненулевых элементов.
Доказательство. Пусть Л=||а,7|| — дважды стохастическая
матрица. Заключим все ненулевые элементы матрицы в р столбцов
и ц строк так, чтобы сумма р + ц принимала наименьшее
возможное значение. По теореме Кёнига максимальное число ненулевых
элементов А, никакие два из которых не находятся в одной линии,
равно р + 7- Так как все ненулевые элементы А можно заключить
п
в п строк, то р + <7<^я. С другой стороны, п= V а,-/-<р + 9.
Следовательно, р + ц = п, и в матрице найдется трансверсаль,
состоящая из ненулевых элементов.
Теорема Биркгофа. Для любой дважды стохастической МатрИ-
цы А порядка п справедливо разложение: А = V ХСР1У где Р; —
1 = 1
ас

к
перестановочные матрицы, Я,>0, V Я,- = 1, & < гс2 — я + 1.
£=1
Доказательство. Согласно лемме в матрице А существует
трансверсаль, состоящая из ненулевых элементов. Пусть
наименьший из них равен ?ч>0 (^^=1, иначе матрица А будет
перестановочной и утверждение теоремы сделается тривиальным); Р\ —
перестановочная матрица, соответствующая трансверсали. Так
как матрица (1—%\)~1(А—%\Р)—дважды стохастическая, то в
матрице А—К[Р существует трансверсаль, состоящая из ненулевых
элементов. Наименьший из них обозначим Я2 и т- Д- Так как мат-
рица А — V] Я;Р,- содержит не менее у нулевых элементов, то
1=1
указанный процесс конечен и закончится не позднее (п2—гг + 1) -го
шага. Это потому, что после (п2—я+1)-го шага матрица
П-—П + 1
А— V Я;Р;, имеющая одинаковые суммы элементов в стро-
1 = 1
ках и столбцах, содержала бы не более (п—1) ненулевых
элементов, а, следовательно, все элементы этой матрицы были бы нулями.
Отметим, что оценку числа к в теореме Биркгофа можно
уточнить: к<п2—2гс + 2, причем существуют дважды стохастические
матрицы порядка п, которые не представимы в виде линейной
комбинации менее чем п2—2п + 2 перестановочных матриц.
При решении задач комбинаторного характера появляется
необходимость использования и других видов специальных матриц.
Мы не будем стремиться к их перечислению и описанию.
Рассмотрим ниже лишь некоторые общие подходы к исследованию таких
матриц.
В математике давно уже принято изучение свойств классов
объектов начинать с поисков инвариантов и их анализа. Одним из
самых важных инвариантов матрицы является ее перманент. Мы
посвящаем ему специальный раздел этой главы.
Рассмотрим далее другие заметные направления. В последние
годы в теоретических исследованиях бинарных матриц все чаще
переходят от анализа частных видов матриц к изучению их
классов. При этом используют понятия граничного ранга (или терм-
ранга), а-ширины и др. Следом матрицы называют сумму
элементов, составляющих ее главную диагональ; максимальное значение
для следа, полученное при всевозможных перестановках строк и
столбцов матрицы, называется граничным рангом, а-шириной
матрицы называется минимальное число столбцов, которые можно
выбрать из нее так, чтобы сумма их значений в каждой строке была
не меньше а.
Укажем один из способов выделения классов матриц. Пусть А
есть (0,1)-матрица размера тХп. Суммы ее элементов по строкам
обозначим через гг. 1=1, 2, ... , т, а по столбцам — через 5;:
./'= 1, 2, ..., п. Очевидно, что
87

т п
(=1 1=1
Из совокупности сумм строк и сумм столбцов матрицы А
образуем соответствующие векторы:
#= (Л, г2, ..., гт); 5= (8Ь 82, ■■-, зп).
Обратно, фиксируя векторы # и 5, чьими компонентами являются
целые неотрицательные числа, мы найдем, что они определяют
класс (тхя)-матриц А, который мы обозначим через з&(Я, 8).
Для классов зФ(В., 8) найдены необходимые и достаточные
условия непустоты. Однако в этой части комбинаторного анализа
исследования только начаты. Еще нет даже регулярного способа для
подсчета числа всех матриц заданного класса или хотя бы
нормализованных матриц, т. е. таких, где линии, состоящие из одних
нулей, вычеркнуты, а оставшиеся линии переставлены так, что
Г\^>Г2^> ... >Гт>0; 81>82> ... >8„>0.
Для классов матриц изучают максимальные и минимальные
значения перманента, граничного ранга, а-ширины и т. п.
4.2. ЛАТИНСКИЕ ПРЯМОУГОЛЬНИКИ И КВАДРАТЫ
Так называют расположения элементов по строкам и столбцам,
где элементы в линиях (как в строках, так и в столбцах) не
повторяются. Название «латинские» восходит, по-видимому, к
Эйлеру, который при изучении расположения данного вида использовал
в качестве его элементов буквы латинского алфавита.
Пусть задано «-множество 5. Задача построения на нем (из его
элементов) латинского (гХ 8)-прямоугольника означает, что
нужно построить (гХ8) -прямоугольную таблицу, в которой линиями
являются соответственно г- и 8-перестановки без повторений
элементов множества 5 (очевидно, что г, 5<я). Например,
расположение
2 15 7 3
13 2 4 5
7 4 18 2
5 2 3 16
является латинским (4X5)-прямоугольником для 5={1, 2, ..., 8}.
В латинских (гХп)-прямоугольниках строками являются
перестановки, выбранные так, чтобы элементы в столбцах не повторялись.
Например,
12 3 4 5 6
3 12 6 4 5
2 4 6 5 3 1
5 3 4 1 6 2
есть латинский (4x6)-прямоугольник для 5 = {1, 2, ..., 6}. Если
первая строка латинского прямоугольника такова, что ее элементы
расположены в заранее фиксированном порядке (чаще всего 1,
2, ..., п), то прямоугольник называется нормализованным. Только
88

что приведенный пример можно рассматривать как пример
нормализованного латинского прямоугольника. Иногда рассматриваются
латинские прямоугольники, нормализованные не только по первой
строке, но и по первому столбцу.
Латинские прямоугольники, которые могут быть получены один
из другого при помощи перестановок линий и перенумерации
элементов, называются эквивалентными. Легко видеть, что для
каждого латинского прямоугольника существует эквивалентный ему
прямоугольник, нормализованный по первой строке и по первому
столбцу.
Естественно поставить вопрос о том, сколько может
существовать латинских прямоугольников заданного вида. Пусть Ь(г, п)—
число всех латинских (гХп)-прямоугольников, а Ы(г, п)—число
нормализованных латинских (гХп)-прямоугольников. Очевидно,
что
Ь(г, п)=пШ(г, п);
причем
Ц1,п)=п\; #(1, л) = 1.
Поскольку двухстрочные нормализованные латинские
прямоугольники суть беспорядки, то их число равно числу беспорядков:
*№„ = я1(Х-Л. + А_...+_ИЕ.)=д„
и соответственно
Ь(2, п)=п\ N(2, п)=пЮп.
Однако уже для подсчета числа 3-строчных латинских
прямоугольников потребовалось преодолеть гораздо большие трудности.
Рассмотрим сначала частный вид таких прямоугольников:
1 2 3 4...П—1 п
2 3 4 ... п I
1Л[ 0,2 ИЗ • • • йп
и попробуем найти их число. Поставленная таким образом задача
эквивалентна, в частности, задаче о числе коммутаторов, 2п гнезд
которых расположены по кругу, соединены попарно, причем
никакие два соседних гнезда не соединены между собой. Эта задача
получила известность в другой трактовке как задача о числе
размещений п супружеских пар за круглым столом с условием, чтобы
ни одна из пар не сидела вместе. Вначале, естественно, заботятся
о дамах, рассаживая их (2п)! способами и оставляя пустые
стулья справа и слева от каждой дамы. Пустые стулья нумеруют:
1, 2, ..., п. Теперь ясно, что первый супруг не может сесть на 1-й
и 2-й стулья, второй — на 2-й и 3-й и т. д., вплоть до п-то супруга,
которому «запрещены» стулья 1-й и п-п. Задача решается по
формуле метода включений и исключений со свойствами р,: а,= 1 или
£+1 (£=1, 2, ..., п—1), ап = п или 1. Искомое число:
г/„ = п1-2п(п-1)| + ... +(-1)г 2п2^г (2гг-г)(гс-г)1+...
... +(—!)».2.
89

В общем случае число всех 3-строчных латинских
прямоугольников, составленных из п элементов, определяется по формуле
(см. [48]):
И
Числа латинских (ЗХп) -прямоугольников оказались очень
большими. Вероятно, именно ввиду сложности доказательств и
громадности чисел соответствующих латинских прямоугольников
последние изучены еще довольно слабо. Что же касается
латинских прямоугольников с большим числом строк, то здесь вообще
мало что известно (см. [49]). В этой связи не уменьшается
значение асимптотических формул. Исходя из известных результатов:
Ь(2, п)=пШп~(п\)2ег1;
1(3, л)~(л!)3е~3;
было сделано предположение:
Ь (к, п) ~ (п\)к е~ (2>.
Эту гипотезу при к<п1;3 доказал Ямамото [50].
Несмотря на то что попытки оценить сверху число возможных
латинских (кХп)-прямоугольников еще не привели к точным
результатам, уже можно видеть, что это число весьма велико и
быстро растет с ростом к. Это подтверждается тем, что можно
получить оценку снизу посредством использования идеи расширения
латинских прямоугольников.
Расширить латинский прямоугольник — значит дописать строки
и столбцы к нему так, чтобы прямоугольник оставался латинским.
Это возможно только если число строк и столбцов не превысит
числа элементов п. Доказательство возможности расширения
осуществляется простым повторением рассуждений, приводящих к
дописыванию одной строки снизу или одного столбца справа.
Пределом расширения является латинский квадрат порядка п.
Пусть дан латинский прямоугольник 2 (г, п) из п элементов,
которые мы обозначим через 1, 2, ..., п. Поставим задачу
расширить 2{г, п) до 3?(г+\, п). Рассмотрим столбцы /=1, 2, ..., п и
каждому /-му столбцу сопоставим множество 5,, состоящее из
п—г элементов, не вошедших в состав данного столбца. Получим
совокупность М= (5[, 52, ..., 5„), где каждое множество 5, состоит
из п—г элементов.
Задача расширения 3?(г, п) до 5^(/-+1, п) сводится теперь к
построению с.р.п. для совокупности М. Покажем, что такая с.р.п.
существует. В самом деле, возьмем 3? (г, п). Каждый элемент I из
п элементов встречается в нем г раз. Во множествах 5[, 5г, ... , 5„
он встречается (п—г) раз. Выбираем любые к множеств из 5Ь
5д, ... , 5„. В них будет к(п—г) элементов, считая и повторяющиеся.
Но каждый элемент встречается не более п—г раз. Значит, к
выбранных множеств имеют не менее к различных элементов. Усло-
90

вие существования с.р.п. выполнено, что и доказывает возможность
требуемого расширения.
Решение проблемы расширения латинских прямоугольников
позволяет дать оценку снизу для их числа. Именно существует га!
латинских прямоугольников 3?(1, га), каждый из которых может
быть расширен по меньшей мере до (га—1)! латинских
прямоугольников 9? (2, га). Следовательно, прямоугольников 5^(2, га)
существует по меньшей мере га! (га—1)!. Рассуждая далее таким же
образом, придем к выводу, что существует по меньшей мере
я! (я—1)1... (га—/-+1)!
латинских прямоугольников 3? (г, га).
Латинские квадраты, на которых мы теперь сосредоточим наше
внимание, являются частным случаем латинских прямоугольников
2?(г, з) при г=з = п. Другими словами, латинские квадраты —
это квадратные (пХп)-расположения из га элементов, где строки и
столбцы являются перестановками этих элементов. Так, все 4
возможных дважды нормализованных латинских квадрата 4-го
порядка суть:
12 3 4
2 3 4 1
3 4 12
4 12 3
12 3 4
2 14 3
3 4 12
4 3 2 1
12 3 4
2 14 3
3 4 2 1
4 3 12
12 3 4
2 4 13
3 14 2
4 3 2 1
Существование латинских квадратов любого порядка
обеспечивается не только общими комбинаторными рассуждениями, но и тем,
что каждый латинский квадрат может быть интерпретирован как
таблица Кэли, т. е. таблица умножения в некоторой конечной
квазигруппе. Для подсчета числа латинских квадратов и оценки
этого числа сверху приходится преодолевать практически те же
трудности, что и для случая латинских прямоугольников, в
частности, оценки снизу имеет вид (/-=га):
га! (га— 1)!... 2! 1!.
Подсчеты числа латинских квадратов показали, что эта оценка
очень грубая. Обозначим через /-(га) число дважды
нормализованных, а через Г(га) — число неэквивалентных латинских квадратов
порядка га. Тогда число всех латинских квадратов порядка га равно
га!(л—\)\Ь(п). Все известные числа Ь(п) и Г (га) содержатся в
следующей таблице (см. [20]):
га
1
2
3
4
5
6
7
8
9
Таб
Цп)
1
1
1
4
56
9 408
16 942 080
535 281 401 856
377 597 570 964 258 816
лица 4.1
1(п)
1
1
1
2
2
22
563
1 676 257
91

Наибольший интерес в теории латинских квадратов вызывают
проблемы, связанные с понятием ортогональности. Два латинских
квадрата называются (щшгоиальныШл ,если при наложении
одного из них на другой получаются все неповторяющиеся
упорядоченные пары элементов. Другими словами, два латинских квадрата
порядка п:
А=[а<>>]; Л = И?»]; £,/ = 1,2 «,
называются ортогональными, если все п2 пар (аН>,а}?>) различны.
Изучение ортогональности латинских квадратов ведет свое
начало от широкоизвестной задачи Эйлера о 36 офицерах,
прибывших из 6 полков. Каждый полк выделял по 6 офицеров, имеющих
6 различных воинских рангов. Этих офицеров требовалось
построить в каре так, чтобы ни в одной линии не было повторения
ни рангов, ни названий полков. Иначе говоря, ставилась задача
построения двух ортогональных латинских квадратов 6-го
порядка.
Задача о построении пары ортогональных латинских квадратов
6-го порядка не поддавалась решению, и Эйлер пришел к выводу,
что такой пары не существует. В опубликованном в 1782 г.
сочинении на эту тему Эйлер высказал гипотезу, что та же
невозможность распространяется на случаи гс=10, п=14 и вообще на
п = 2(тос14), т. е. п = 2, 6, 10, 14, 18, ... .
Первый ответ на гипотезу Эйлера был найден только через
118 лет. В начале XX в. Терри [51] подтвердил ее для гс = 6 путем
построения и перебора всех латинских квадратов 6-го порядка.
Дальнейшая проверка гипотезы снова затянулась. Лишь к 1960 г.
было доказано, что пары ортогональных латинских квадратов
существуют для любого порядка, кроме п = 2 и я = 6, которые
оказались единственными исключениями (см. [53]).
Естественным обобщением понятия пары ортогональных
латинских квадратов является множество, состоящее более чем из двух
латинских квадратов, попарно ортогональных. Такое множество
также получило название ортогонального. Перенумеруем
элементы квадратов так, чтобы нормализовать у каждого первую строку
(при перенумерации элементов свойство ортогональности
сохранится). Тогда первые элементы вторых строк должны быть
различны и не равны 1. Следовательно, число попарно ортогональных
татинских квадратов порядка п не может превышать п—1. Ортого-
лальное множество называется полным, если оно содержит в
точности п—1 квадрат.
В теории ортогональных латинских квадратов выделяются две
'большие проблемы: проблема существования пар и семейств
ортогональных латинских квадратов и проблема их построения. Эти
проблемы тесно связаны, так как доказательство существования
*ередко оказывается и построением. Проблема существования
множеств ортогональных латинских квадратов оказалась довольно
грудной, а доказательства соответствующих теорем — сложными и
громоздкими. Мы приведем здесь лишь некоторые результаты.
92

1. Не для всякого латинского квадрата существует другой
латинский квадрат, ортогональный ему.
Этот факт, равно как и условия существования, был
установлен в [52].
2. Если п=ра, где р— простое, а а — натуральное число, то для
гс>3 существует полное множество из п—1 ортогональных
латинских квадратов.
Доказательство. Для всякого п = ра существует поле Галуа.
Пусть а0 = 0, а1 = 1, а2, аз, ..., ап-\— элементы поля Галуа.
Построим п—1 матриц порядка п следующим образом:
А = \\ацЩ; I, / = 1, 2, .... п—1; /=1, 2, .... и—1,
где
а,7(/) = а/а, + а/.
Это семейство матриц Л/ и будет полным множеством
ортогональных латинских квадратов. В самом деле:
а) каждая из построенных матриц есть латинский квадрат, ибо
если какая-нибудь из этих матриц, скажем Л/, имеет два равных
элемента в одной строке, то существуют / и /' такие, что
щщ + а,- = а а( + а,',
откуда
а,- = аг.
Если же допустить, что два равных элемента существуют в одном-
столбце, то должны существовать различные I и I', такие, что
щщ -{- а,- = ащ' + ау-;
и так как щФО, то 0.1 = 0.1- и значит 1 = 1';
б) каждая пара этих матриц ортогональна. Пусть 1 </</<«—1,
и пусть Л/ не ортогональна Ац тогда существуют такие £, I', /, /',
что
(аФ,а!|>) ==(^),, «</>,),
т. е.
а^аг + а/ = а1а[- -г а,» ;
а^ + а1 = а}0{1 + а,' .
Отсюда
01{а1—а{)=01 (о1—а{),
а так как щфщ, то а; = ас, откуда 1 = 1' и, следовательно, / = /'.
Искомое множество, таким образом, построено.
3. Теперь выскажем более общее утверждение. Дано
произвольное натуральное число п и его разложение по натуральным
степеням различных простых чисел: п = р^*ра* . .. ра^ . Пусть
I = тт(/Я< — 1); £ = 1,2, .... АЛ
93'.

Если ^>2, то существует семейство I ортогональных латинских
квадратов порядка п.
В самом деле, выше мы показали, что для каждого "г = Р^1'
1 = 1, 2, ... Ы, существует семейство щ—1 (а значит, и I) искомых
квадратов. Чтобы перейти к произведению величин, надо доказать
промежуточную теорему (справедливость общего утверждения
доказывается последовательным применением этой теоремы).
%, Теорема. Если даны два семейства, состоящие каждое из I
ортогональных латинских квадратов порядков п и п'
соответственно, то существует семейство из I ортогональных латинских
квадратов порядка пп'.
Ь Доказательство. Каждому семейству из I ортогональных
латинских квадратов порядка п (^>2, гс>3) можно сопоставить
[п2Х (^ + 2)]-таблицу, построенную из тех же п элементов
(обозначенных: 1, 2, ..., п) таким образом, что любая пара столбцов
содержит все п2 2-выборок элементов (такую таблицу мы будем
называть таблицей силы 2). Переставим в этой таблице строки так,
чтобы в первых двух столбцах (читая сверху) содержались пары
в таком порядке: (1, 1), (1, 2), ..., (1, п), ..., (п, 1), (п, 2),..., (п, п).
Тогда следующие I столбцов, переписанные поочередно сверху, по
п штук в строчку, образуют I латинских квадратов порядка п.
В самом деле, первый столбец таблицы построен так, что ни в
одном из I латинских квадратов не окажется в строке двух
одинаковых элементов. Второй столбец таблицы построен так, что нет
двух одинаковых элементов и в столбцах квадратов. Например,
(9x4)-таблица
1111
12 2 2 соответствует двум ортогональным ла-
13 3 3 тинским квадратам:
2 12 3
2 2 3 1
2 3 12
3 13 2
3 2 13
3 3 2 1
Построим две таблицы, соответствующие двум ^-семействам
ортогональных латинских квадратов порядков п и п'. Размерности
этих таблиц будут соответственно п2Х (^ + 2) и (п')2Х (^ + 2).
Возьмем из этих таблиц соответственно 1-ю и /-ю строки:
сил <к.2 ■ ■ ■ СЦЛ+2,
II I
а/,1 а/.2' • • • а/,Н-2
и построим из них строку, состоящую из пар элементов:
аМа/.Р а1,2а],2> ••• >а1,1+2а',;1+2-
Таким образом, получим всего (пп')2 строк, образующих
1 2 3
2 3 1 и
3 1 2
1 2 3
3 1 2
2 3 1
94

[{пп')2Х (< + 2)]-таблицу, в которой каждые два столбца образуют
все пары из следующих пп' элементов:
(1, 1), (1,2),..., (1,/0.-. (п, 1), (и, 2),..., (п, п').
Тогда этой таблице соответствуют I ортогональных латинских
квадратов порядка пп'.
Монография [20] содержит богатую информацию по
рассматриваемым в настоящем разделе вопросам.
4.3. БЛОК-СХЕМЫ
Тот вид комбинаторных конструкций, о котором пойдет речь в
настоящем параграфе, появился в математической литературе
примерно в середине прошлого века. И. Штейнер опубликовал в
1853 г. маленькую заметку [54], в которой речь шла о такой задаче:
какое число символов можно разбить на тройки так, чтобы любая
пара оказалась в одной и только одной тройке?
Без особого труда было найдено, что только числа гс = 6&+1 к
п = 6к + 3, т. е. я=1, З(тоаб), являются решением этой задачи.
Действительно, поскольку каждый элемент входит в тройку с
двумя другими, п—1 должно быть четным числом, и значит п —
нечетным, т. е. гг=1(тос12). Во-вторых, в каждой тройке есть три
я(я—1)
пары. Каждая пара появляется один раз. Всего пар: ~ •
Это число должно быть кратно 3. Отсюда я=1, З(тоаб), т. е.
я = 3, 7, 9, 13, 15, 19, ... . Эти условия являются необходимыми-
Штейнер ставил вопрос: являются ли они также достаточными?
В 1859 г. Раисе [55] ответил на этот вопрос утвердительно.
Ни Штейнер, ни Раисе не знали, что аналогичная
комбинаторная задача была поставлена и решена несколько раньше, в 1847 г.,
Киркманом [56]. Через 3 года появилась другая комбинаторная
задача Киркмана [57]: учительница ежедневно выводит класс из
15 девочек на прогулку, при этом, она строит их в 5 рядов по 3
человека; надо организовать тройки так, чтобы в течение 7 дней
каждая ученица встречалась с каждой лишь однажды.
Описанная в этой задаче система троек получила название
троек Киркмана. По сравнению с системой троек Штейнера
здесь присутствует дополнительное условие (так называемое
условие разрешимости): множество троек должно быть разбито на
и—1
2 компонент (в задаче Киркмана 7 компонент, каждая
соответствует одному дню недели) так, что каждый из п
элементов появляется ровно по одному разу в тройках каждой
компоненты.
Возникает вопрос: сколько существует систем данного типа?
Для троек Штейнера известно следующее. Если я = 3, 7, 9, то
существует только один тип такой системы, а именно:
а) при я = 3 — система из одной тройки
1 2 3
б) при я = 7 — система из семи троек
95

12 3
145 246 347
167 257 356
в) при п = 9 — система из 12 троек
1 2 3
145249348
168 256 357 467
179 278 369 589
Для гс = 13 оказалось, что существуют две системы иеизо-
тиорфных решений, т. е. такие, которые не могут быть получены
друг из друга подстановкой элементов или перестановкой троек.
Эти системы состоят из 22 одинаковых троек
1 2 3
1 4 5
1 6 7
1 8 9
1 10 11
1 12 13
2 4
2 5
2 8
2 9
2 11
6
7
10
12
13
и четырех неэквивалентных
3
3
а для второй —
3
3
6 10
9 13
6 13
9 10
5
5
5
5
4 3 8
4 7 9
4 10 13
4 11 12
: для пер!
6 13
9 10,
6 10
9 13.
7
7
7
ЗОЙ
3
8
10
—
11
13
12
8
8
6
3
5
6
9
5
11
12
11
12
К 1925 г. были закончены подсчеты систем троек Штейнера для
п=15: таких различных систем оказалось 80. Насколько
известно, пересчет троек Штейнера для я>15 не производился. Что же
касается числа неизоморфных систем троек Штейнера, то оно
леограничено возрастает с ростом п (см. [58]).
Решение задачи Киркмана, известное с 1921 г., таково:
*
12 5 13 9 1 4 15 1 6 11
3 14 15 2 8 15 2 9 11 2 7 12
4 6 12 4 11 13 3 10 12 3 8 13
7 8 11 5 12 14 5 7 13 4 9 14
9 10 13 6 7 10 6 8 14 5 10 15
1 8 10 1 7 14 1 12 13
2 13 14 2 4 10 2 3 6
3 473511 458
5 6 9 6 13 15 7 9 15
11 12 15 8 9 12 10 11 14
\
Методы построения систем троек в основном рекурсивные,
т. е. строятся «начальные» системы троек для малых значений
параметров, а затем используются методы, опирающиеся на этот
уже имеющийся в наличии запас. Приведем некоторые из этих
методов.
96

.Если существуют две системы троек Штейнера А и В
порядков VI и V2 соответственно, то можно построить еще одну
систему Штейнера С порядка V = V^■^2, содержащую подсистемы,
изоморфные данным.
Пусть (щ, а}, ак) — тройка из системы А, (Ьг, Ь$, Ьи) —
тройка из системы В. Строим систему троек С из элементов Сц(1 = \,
2, ....оь /=1, 2,...,^2), которые образуют тройки (с<г, с]8, ски),
если выполнено какое-либо из следующих условий: 1) /- = 5 = и,
{аь щ, ак)е=А; 2) 1 = ] = к, (Ьг, Ь8, Ьи)<=В; 3) (а*, щ, ак)<=А, (Ьг,
Ь8, Ьи)^В. Системой, изоморфной системе Л, является первая из
них с условием: /-=5 = и=1, а системой, изоморфной В, будет
служить вторая с условием: 1 = \ = к = \.
В 1893 г. Мур [59] предложил метод построения троек
Штейнера, основанный на изложенных выше принципах.
Пусть даны системы Штейнера: 5г порядка о2, в которую
входит 5з порядка ^3, и 51 порядка 1>1>1; тогда можно
построить систему Штейнера 5 порядка V=^3-\-V^(V2—о3),
имеющую подсистемы, изоморфные 5ь 5г, 53.
Возьмем множество из V = Vз+^^(^2 — о3) элементов и
представим его в следующем виде:
М0: аг а2 . .. а0з;
Мг: Ьп Ь12... &1,0г_0,;
М2: Ь21 Ь22 . . . Ь2,02-0з;
Мщ : Ъщ\ ЬЩ2 . . . Ь-а^-сг—V,-
Образуем тройки по следующим правилам.
1. Поставим элементы М0 во взаимно-однозначное
соответствие элементам 5з и выберем все тройки (а,-, щ, ак), если они
соответствуют тройкам системы 5з.
2. Поставим элементы пары множеств М0 и М,-, 1=1, 2,..., Оь
во взаимно-однозначное соответствие системе 5г так, чтобы _М0
соответствовало его подсистеме 5з- Тройки из элементов М0 уже
найдены по предыдущему правилу. Остальные тройки должны
содержать не более одного элемента из М0 и, значит, имеют вид:
(От, Ьц, Ь{к) или (Ъц, Ь{к, Ь{Г). Они, разумеется, должны
соответствовать оставшимся тройкам системы 5г.
3. Определим систему 51 на числах 1, 2,..., оь Если (/, к, г) —
тройка этой системы, то образуем все тройки вида (Ь}Х, Ъку, Ъгг),
где х+у+г=0 (тойо2— Уз).
Эти правила дают все тройки системы 5 порядка о=оз+
Что же касается троек Киркмана, то найдены методы, с
помощью которых можно их строить для порядков (см. [60]):
о=15, 15-3", 3", 22»—1.
Можно рассматривать и тройки других типов, отличных от
троек Штейнера и Киркмана. Так, латинский квадрат порождает
4 К. А. Рыбников
97

множество п2 упорядоченных троек, где каждая тройка (I, /, к)
соответствует тому, что в 1-й строке, /-м столбце находится
элемент к; I, /, к=\, 2,..., п. Условие, что совокупность троек (ь, /,
к) {и /, к=\, 2,...,п) образует латинский квадрат, состоит в том,
что любая пара компонентов тройки должна встречаться один и
только один раз.
После введения систем троек Штейнера и Киркмана задачи в
области комбинаторных выборок, казалось бы, должны были
сосредоточиться на следующих направлениях:
а) на разработке методов эффективного построения
различных систем, в первую очередь троек Штейнера и Киркмана;
б) на обобщениях задач о тройках на системы 4-, 5-, 6-
и т. д. подмножеств. И хотя эти проблемы остаются
актуальными и в наши дни (см. [61]), такой путь постепенного развития
был нарушен. Произошел логический скачок, не столь уж
редкий в математике. Преодоления трудностей стали искать на
путях построения более общей теории.
В настоящее время из систем инцидентности наибольший
интерес вызывают блок-схемы. Их изучение ведется весьма
активно, что объясняется как потребностями практики, так и чисто
научными интересами.
В упрощенном виде происхождение блок-схем может быть
описано следующим образом. Результаты эксперимента,
производимого в одно и то же время при определенных условиях,
записываются столбиком (блоком). Повторные результаты при
измененных условиях дают новые блоки. Совокупность блоков дает
двумерную таблицу, называемую блок-схемой (сокращенно ВО
от Ыоск-аез^п).
Из статистической обработки результатов вырастает подход к
проблеме планирования эксперимента, т. е. составления его
схемы (плана) с целью получения оптимальных результатов при
наименьшем числе опытов.
Для комбинаторного анализа из большого круга проблем,
относящихся к блок-схемам, наибольший интерес представляют
задачи существования, классификации, изучение свойств
различных видов блок-схем, способы их построения, взаимосвязи,
разработка смежных вопросов дискретной математики, конечных
геометрий, конечных групп и т. д. Эти теоретические проблемы
исследуются интенсивно с конца 30-х—начала 40-х гг.
Пусть имеется о-множество элементов т.\, т^,..., тК.
Элементы этого множества распределены по Ь блокам-подмножествам
А{ь М2,...,Мь, пересечение которых не обязательно пусто. Число
элементов в блоке М$ называется объемом блока и обозначается
через к$. Элементы могут появляться в нескольких блоках; пусть
/-,•— Число появлений элемента т,- (т. е. число блоков,
содержащих т,), 1 = 1, 2,..., V, наконец, введем число повторений
(неупорядоченных пар) элементов: Кр (р=1, 2,..., (у/2)). Тогда
говорят, что множество блоков Ми...,Мь образует блок-схему с
параметрами V, Ь, /-,-, к], Кр (если вместо пар рассматривают трой-
98

ки или /-выборки элементов, то соответствующее расположение
называют тактической конфигурацией). Итак, блок-схема
характеризуется параметрами V, Ь, ги к{, 1Р.
Различных типов блок-схем может быть очень много.
Поэтому введем начала классификации блок-схем в том виде, как она
сложилась к настоящему времени. Прежде всего, блок-схема
называется полной, если в каждом блоке содержатся все элементы
множества, т. е. к^ = ь, /=1, 2,...,6, и неполной, если к]<а, /=1,
2,...,6. Латинские квадраты могут служить примером
полных б.-с.
Неполные блок-схемы делятся в свою очередь на два
больших класса: класс уравновешенных неполных блок-схем
(сокращенно ВШ-схем, от Ьа1апсес1 шсотр1е!е Ыоск аезщп) и класс
частично уравновешенных неполных б.-с. (сокращенно РВ1В-
схем, от рагИаПу Ьа1апсес1 шсотр]еге Ыоск аез1дп).
Блок-схема называется В1В-схемой, если кх = к2 = ... = кь = к<
<с; г\= ...=/-„ = /- и ХР = К для всех р; иными словами,в В1В-схе-
ме все элементы имеют одно и то же число повторений, все
блоки имеют одинаковый объем и каждая пара элементов
появляется в одном и том же числе Я = сопз1 блоков. РВ1В-схемы
отличаются тем, что в них А=^сопз1. Это обстоятельство порождает
большое число различных типов РВ1В-схем и создает
значительные трудности для их исследования.
Частично уравновешенной неполной блок-схемой с тп
классами, или короче РВ1В(т)-схемой, называется блок-схема, у
которой множество всех (2) пар ее элементов можно разбить на
тп непересекающихся классов (пару элементов, относящуюся к
1-му классу, мы назовем ^-связанной) так, что
а) любая пара ^'-связанных элементов содержится ровно в Я*
блоках (£=1, 2,..., тп);
б) для любого элемента существует в точности щ элементов,
^'-связанных с ним (£=1, 2,..., тп);
в) для любой пары ^'-связанных элементов а и Р число
элементов, /-связанных с а и одновременно /-связанных с р,
равно р^х, при этом р{л=р{ц (£, /, 1=1, 2 тп\.
Таким образом, параметрами РВ1В(т)-схемы являются
числа:
V, Ь, к, г, %и щ, р*п (£, /, 1=1, 2,...,гп).
Чтобы облегчить восприятие большого числа новых и порой
сложных комбинаторных конструкций, мы предлагаем читателю
схему первоначальной классификации блок-схем с указаниями
на возможные продолжения (рис. 4.2).
Современная теория блок-схем огромна по числу и объему
фактических исследований, зачастую еще разбросанных и слабо
организованных. Ниже будут изложены основы этой теории, без
стремления к полноте освещения фактов.
В начале настоящей главы мы уже рассматривали в общем
4»
99

Блок-схемы
Полные
6.-г..
Симметрические
В1В-схемы
Несимметрические
В1В -схрмы
РВ1В-схеиь,
А=/
(Классификация
па числу и виду
I -сЛязпнипсти)
Конечные
нроркшвныр.
плоское г и
Рис. 4.2
виде метод матричного представления структуры множества.
Применим его к блок-схемам. Пусть имеется некоторая блок-
схема с параметрами V, Ъ, к, г *. Положим
1, если 1-й элемент находится в /-м блоке,
О, в противном случае,
1=1, 2,..., V, /=1, 2, ...,&;
(оХЬ)-матрица N=11^,11 называется матрицей инцидентности
данной блок-схемы; при этом каждая строка матрицы Л^
содержит г единиц, каждый столбец содержит к единиц (Хр равно
скалярному произведению двух строк). Например, ВШ-схема с
параметрами: а = 6, 6=10, к = 3, г = 5, Я=2 — имеет следующее
матричное представление (матрицу инцидентности):
Блок-схема
Г- 1 1 1 1 2
2 3 4 5 2 3
3 4 5 6 6 5
3 2
4 4
6 5
-
3 2
5 4
6 6
Матрица
1 1 1
1 0 0
1 1 0
0 1 1
0 0 1
0 0 0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
1
0
1
0
0
0
1
1
0
1
0
1
0
1
1
0
0
0
1
0
1
1
0
1
0
1
0
1
* Мы не будем писать параметр X, если не указывается о какой именно
б.-с, уравновешенной или частично уравновешенной, идет речь.
100

Приведем еще один пример: пусть для 9-множества
рассматривается следующая система подмножеств:
В, =(1, 2, 3)
Въ = (2, 5, 8)
В9 =(3, 4, 8)
В2=(4, 5, 6); В3=(7, 8, 9); В4=(1, 4, 7);
В6=(3, 6, 9); В7=(1, 5, 9); В8=(2, 6, 7);
В!0=(1, 6, 8); Вц = (2, 4, 9); В!2= (3, 5, 7).
Нетрудно видеть, что эта система является В1В-схемой с
параметрами у = 9, 6=12, к = 3, г = 4, Я=1. Запишем блок-схему,
как и выше, в виде прямоугольной (кхЬ)-таблицы:
14712312 3123
258456564645
369789978897
Матрица инцидентности этой блок-схемы:
100100100100
100010010010
100001001001
0
0
0
10 10 0 0 0 10 10
0 0 0 0 1
10 10 0
10 0 10 1
10 0 0 10
001 100010001
001010001 100
001001100010
Несмотря на кажущуюся громоздкость, бинарные матрицы
инцидентности весьма просты для оперирования. Из
рассмотрения их структуры Можно непосредственно получить ряд свойств,
в том числе соотношения между параметрами. Например, для
блок-схем вообще:
»=1 ,=1
что очевидно. В частности, для В1В-схем имеем
Ък = ы\ (1)
г(*—1)=А,(о—1). (2)
Первое из соотношений выражает простой подсчет числа
элементов в блок-схеме (т. е. число всех единиц в матрице
инцидентности). Во втором соотношении ход рассуждений таков:
каждый элемент встречается г раз и всегда соседствует с к—1
элементами. Этот же элемент встречается % раз в паре с
каждым из у — 1 элементов.
Рассмотрим соотношения между параметрами
РВ1В(т)-схемы. Очевидно, что по-прежнему имеет место равенство (1).
Установим некоторые другие равенства:
1=1
о-1; ^ К(пс = г(к-\);
101

^ I .,. если 1ФГ, (3)
ТЗ ( п; — 1, если I = /'; ь, / = 1, 2, . . . , ш;
П1р1ц = п,-р1и = П1р11;; и /, /=1, 2, ..., т.
Первое из соотношений очевидно. Второе является
видоизменением (2) и доказывается аналогичными рассуждениями. В
слега
дующем равенстве }[] р;5 обозначает число элементов, /-связан-
ных с любым из двух ^-связанных элементов. Оно,
следовательно, равно П] (если (ф\) или П)—1 (если ! = /'). Что же касается
.последнего соотношения, то оно доказывается следующим
образом: возьмем некоторый фиксированный элемент а. Согласно
определению, существует п\ элементов р\, |52, . . . , р\гЛ 1-связан-
ных с а, а также п> элементов у^ у2, ... , у„., /-связанных с а.
Построим бинарную матрицу:
гь1\ ....бЧ
V..» у1<ь
ье' „.... ьЧ
УпГ" уп.,Ь
в которой
/А _ | 1, если р\ и у.^ /-связаны;
у^'1 I 0, в противном случае.
Подсчитаем число единиц в каждом столбце матрицы:
и в каждой строке:
Г=1
Из двух способов подсчета числа всех единиц в матрице
получаем
П1р*з,1 = П)р>11{.
Соотношения (1), (2) и (1), (3) являются необходимыми
условиями для существования В1В- и РВ1В(т)-схем соответственно.
Пусть N=11^11 есть (уХЬ)-матрица инцидентности
уравновешенной неполной блок-схемы с параметрами V, Ь, г, к, К. Тогда
N удовлетворяет матричному уравнению
Л^Л/т=(г— Я)/+Л/,
где Л/т — транспонированная матрица Ы; 1 — единичная матрица
порядка V; / — матрица, целиком состоящая из единиц, также
порядка V.
102

Действительно, подсчитаем произведение
#.ЛР = В = ||&„||; 1,/=1,2, ..., V.
Элемент Ьц равен скалярному произведению 1-й строки из N на
/-й столбец из Ыт, следовательно
Отсюда
Ьц
г=1 I А,
если I = /;
если 1ф\\
I, /=1, 2, ..., V.
В =
= г/ + к (У—/) = (г ^- я) / + и.
Для матрицы В можно найти значение ее детерминанта:
йе* В= (г—1)*>-1 (VI—К + г).
Чтобы получить этот результат, достаточно вычесть первый
столбец из всех других столбцов, а затем прибавить сумму всех строк,
начиная со второй, к первой строке. Тогда выше главной
диагонали будут одни Нули; а'п=г+(ь—1 )Я; а'22= ... =а\к = г—К, что и
дает искомый результат. Так как из к<и следует К = г
к—\
у—1
<г,
то с1ехВ=^0. Используя (2), имеем
(1е1 В = (г—I )*~1гкфО.
Ранг матрицы В, таким образом, равен V. С другой стороны,
ранг N (и ранг Л^т) не превосходит Ь. Как известно из теории
матриц, ранг произведения не превосходит рангов сомножителей.
Отсюда следует важное неравенство:
называемое неравенством Фишера, которое также является
необходимым условием существования ВШ-схемы.
Из рассмотрения матриц инцидентности N и матрицы В — Ы-Ыг
может быть выведено много теорем, относящихся к частным видам
блок-схем (см. [62]).
Матрицы инцидентности — не единственный способ описания
блок-схем; другим аналогичным методом является применение
квадратичных форм. Этот метод особенно интересен потому, что
теория квадратичных форм достаточно разработана. В самом деле,
соотношение Ы-Ыт=(г—Я)/ + Я/ сразу переформулируется в
квадратичных формах. Введем неопределенные переменные: Х\, Хг, ...,
.... х-е, соответствующие элементам блок-схем, и каждому блоку Ь,
сопоставим линейную форму:
и
Е пцхс
1=1
/=1,2,
■ V,
103

где пц — кратность элемента [ в блоке Ь}. Тогда матричному
уравнению Ы-Мт=(г—К)1 + К1 будет сопоставлена квадратичная форма:
1=1 1=1 1=1
В теории комбинаторного анализа и в его приложениях блок-
схемы играют весьма большую роль. Многие из известных нам
комбинаторных расположений являются частными видами блок-
схем или эквивалентны им. Поясним это на примерах.
Латинские квадраты, как было уже сказано, оказываются
полными блок-схемами. Тройки Штейнера суть В1В-схемы, для
которых к = 3, Я=1. Для них соотношения (1) и (2) между
параметрами принимают вид:
ЗЬ = уг; 1г = ь—1;
откуда
и, следовательно,
г=0,1(тос!3); о=1,3(тос16).
Матрицы Адамара Я эквивалентны частным видам блок-схем.
В самом деле, возьмем матрицу Я порядка п>3. Известно (см.
§ 4.1), что п = 0(той 4). Нормализуем Я, т. е. умножая
соответствующие строки и столбцы на —1, приведем ее к виду, когда
первая строка и первый столбец будут состоять из положительных
единиц. Такая матрица Я порядка гс = 4^>8 оказывается
эквивалентной симметричной В1В-схеме с параметрами:
у = Ь = А1—\; к = г = 21—\; "к = 1—\.
В самом деле, каждой нормализованной матрице Я можно
сопоставить (0,1 )-матрицу А порядка ь = А1—1, в каждой линии
которой имеется к = 2Л—1 единиц. Способ сопоставления состоит в
том, что в нормализованной матрице Я вычеркивают первую
строку и первый столбец, а в оставшейся матрице заменяют все
единицы на нули. Матрица А удовлетворяет соотношению
и является, таким образом, матрицей инцидентности
уравновешенной неполной блок-схемы с г—"к = 1 и К=1—1. Рассуждение легко
можно обратить, что и докажет наше утверждение.
В § 4.2 при доказательстве теоремы о существовании семейств
ортогональных латинских квадратов было показано, что
построение такого семейства эквивалентно построению ортогональной
таблицы силы 2. Оказывается, однако, что существование последней
влечет за собой существование блок-схемы определенного вида.
Разъясним это подробнее, но прежде дадим общее определение
ортогональной таблицы.
Пусть дана (тХЛ^)'-матрица А с элементами из множества 5 =
104

= {0, 1, 2, ..., 5—1}. Всего существует 5' различных столбцов
длины I с элементами из этого множества. Если во всякой ^-строчной
подматрице матрицы А столбец (хи х2, ..., х{)т появляется
Х(хь х2, ..., Хг) раз, где число А положительно и не меняется при
перестановках х\, х2, ..., х<, то матрица А называется частично
уравновешенной таблицей силы I с N столбцами, тп строками, 5
символами и параметрами К(хи х2, ..., х{), или, короче, таблицей
(Ы, т, 8, I) с параметрами Х(х\, х2, ..., хг). Если Л=сопз1 для всех
столбцов (х\, х2, ..., х<), то таблица (./V, т, з, {) называется
ортогональной таблицей индекса К.
Приведем в качестве примера ортогональную таблицу (18, 7,
3, 2) индекса Я = 2 с символами 0, 1, 2:
Таблица 4.3
Номера
строк
1
2
3
4
5
6
7
1 2 3
0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
0 1 2
0 0 0
Номер
4 5 6 7 8 9
0 12 0 12
0 12 12 0
12 0 0 12
2 0 12 0 1
12 0 2 0 1
2 0 1 12 0
0 0 0 111
а столбцоЕ
10
0
2
2
0
1
1
1
11
1
0
0
1
2
2
1
12
2
1
1
2
0
0
1
13
0
1
2
1
0
2
2
14
1
2
0
2
1
0
2
15
2
0
1
0
2
1
2
16 17 18
0 1 2
2 0 1
1 2 0
1 2 0
2 0 1
0 1 2
2 2 2
Отделение от этой таблицы трех первых столбцов и последней
строки приводит к частично уравновешенной таблице (15, 6, 3, 2)
с параметрами:
» , ч I, если х1 Ф х2;
л (Хг, х2) — <
I 1, если хг = х2.
Существование к взаимно ортогональных латинских квадратов
порядка 5 эквивалентно существованию ортогональной таблицы
(52, к + 2, 8, 2) индекса л=1.
В самом деле, пусть имеем ортогональную таблицу (52, к + 2,
5, 2), и пусть элементы в этой таблице обозначены числами
1, 2 5. Переставим столбцы в таблице так, чтобы элементы
столбцов в первых двух строках оказались в порядке:
(1, 1), (1, 2) (1, 5) (5, 1), (5, 2) ,..., (5, 5).
Для каждого 1 = 3, 4, ..., к + 2 построим таблицу Лг=(52, 5, 5, 2)'
следующим образом: первый столбец Аг состоит из первых 5
элементов строки / исходной таблицы, второй столбец — из
следующих 5 элементов и т. д. до последнего столбца, составленного
из последних 5 элементов той же строки. Составленные подобным
образом таблицы Л3. -^4. ■••. Ак+2 образуют множество, состоящее
105

из к взаимно ортогональных латинских квадратов порядка 5. То,
что таблица Ах не имеет двух одинаковых элементов в столбце,
видно из рассмотрения первой строки исходной таблицы.
Аналогичное свойство строк видно из рассмотрения второй строки. Если
1ф\, то Л; и А; ортогональны, что следует из способа построения
соответствующих строк. Доказательство, как нетрудно показать,
обратимо.
Научные исследования в области блок-схем группируются в
настоящее время вокруг проблемы существования (или
несуществования) отдельных видов блок-схем, изучения их свойств,
нахождения методов их построения. Комбинаторная теория здесь
находится в начале развития. Заинтересованному читателю можно
рекомендовать для дальнейшего изучения гл. 10—16 книги [4].
Современные исследования в области комбинаторных
расположений и блок-схем, в частности, требуют привлечения теории
чисел, теории групп, теории матриц, теории выпуклых тел и т. д.
4.4. ПЕРМАНЕНТЫ
Это понятие приобрело в современном комбинаторном анализе
настолько большое значение, как теоретическое, так и
практическое, что представляется необходимым выделить для его
рассмотрения отдельный раздел.
Пусть задано множество 5={5ь ..., $„} и некоторое семейство
его подмножеств М={5и 52, ..., 5т}. Теорема Ф. Холла дает
необходимые и достаточные условия существования у семейства М
системы различных представителей и нижнюю границу для числа
таких систем. Однако во многих задачах комбинаторного анализа
возникает необходимость получения более точных оценок этого
числа. Эта цель достигается введением нового понятия —
перманента матрицы — и изучением его свойств.
Пусть задана матрица А = ||а,^||, 1=1, 2, ..., т\ /=1, 2, ..., п,
элементами которой являются действительные числа. Ее перманентом
называется выражение (число)
т
регЛ = ]|]Па'-<т»).
а 1=1
в котором суммирование производится по всем вложениям а из
{1, 2, ..., т) в {1, 2, ..., п). Естественно, при этом предполагается,
что пк п.
Пусть А — матрица инцидентности для М по отношению к 5,
тогда регЛ будет являться числом систем различных
представителей, которыми обладает семейство подмножеств М.
Перманенты были введены в 1812 г. почти одновременно в
мемуарах Бине [63] и Коши [64] в связи с развитием теории
определителей как специального вида знакопеременных симметрических
функций. Термин «перманент» впервые появился в работе Мюира
[65], где выведены также некоторые его свойства.
106

Очевидно, что перманент инвариантен относительно
перестановок строк и столбцов в матрице Л; умножение элементов какой-
либо строки матрицы Л на скаляр а заменяет регЛ на арегЛ;
разложение Лапласа на миноры по строкам справедливо и для
перманентов.
Набор (01,,(1), а2а{2) Ото(т)) элементов матрицы А, никакие два
из которых не находятся в одной линии (строке или столбце),
будем называть трансверсалью. Перманент матрицы А, таким
образом, представляет собой сумму по всем я!/(п—т)\ трансверсалям
произведений элементов матрицы А, лежащих на одной трансвер-
сали.
Определение перманента и его свойства указывают на близость
этого понятия к понятию определителя. Однако, если техника
вычисления определителей к настоящему времени хорошо
разработана, то вычисление перманентов является технически трудной
задачей, в решении которой предстоит продвинуться. Пека известен
метод, состоящий в применении формулы включений и исключений.
Обозначим через Лг матрицу, получающуюся из матрицы Л
заменой г ее столбцов на столбцы, составленные из нулей. Пусть
5(ЛГ) — произведение сумм строк Лг, а 25(Лг) — суммы 5(ЛГ)[
по всем выборам для АТ. Тогда справедлива следующая формула
Г. Дж. Райзера:
т—1
регЛ=Л(-1)'("-7 + Г)5]5(Л„_т+1-).
1=0
В самом деле, обозначим через М множество всех т-перестановок
(/! /т) с повторениями из натуральных чисел 1, 2 п. Пусть
т
вес такой перестановки равен I I а*;> а свойство р* означает, что
1 = 1
эта перестановка не содержит целого числа г (1 = 1, 2, ..., п).
Предположим теперь, что Аг получено из Л заменой столбцов с
номерами II, 12 1Г на столбцы, составленные из нулей. Тогда сумма
весов перестановок из М, которые обладают каждым из свойств
Рн,Р1*, •-. >Р,Г, равна
У(р{1,р1„...,р1г)=5(Аг).
Следовательно,
у(г)= е у(р.-,./*, Р1Г) =^5(4).
!<11<г'2<... <»,.<«
Функция регЛ равна сумме весов элементов из М,
удовлетворяющих п—т свойствам рх (£=1 п). Воспользовавшись формулой
метода включений и исключений, приходим к приведенной выше
формуле Райзера. Для квадратной матрицы Л порядка п эта
формула принимает вид:
РегЛ = ]Е (_1)« £5(,4,).
1=0
107

Если / есть матрица порядка п, составленная целиком из единиц,
то рег / = «1, и мы в качестве следствия получаем тождество:
и—1
Если рассмотреть матрицу /—/, где / —> единичная матрица, то
рег
(У-/) = п! 2(-1)'-^=^.
(=0
где Бп — число беспорядков. Воспользовавшись формулой Райзе-
ра, можно получить другую формулу для числа беспорядков:
л—1
^=^(-^(1)^-17(1-(-1)1^.
(=0
Укажем на интересную связь между перманентом квадратной
матрицы Л = ||ау|| (I, /=1, 2 п) порядка п и перманентами и
определителями ее главных подматриц. Обозначим через 0.к<п
множество всех возрастающих последовательностей /=(/1, ..., /ь)
длины к из натуральных чисел 1, 2 п: 1<:/1</2< ... </ь<я.
Пусть }^0.к<п\ через Л[/] обозначим подматрицу \\а,- ;- || (г, 5 =
= 1, 2 к) матрицы Л, а через Л(/) — подматрицу матрицы Л
порядка (п—к), дополнительную к АЩ.
Справедливо следующее соотношение (см. [66]):
п
регЛ= Л (—1)*-> ^ регЛ(/)(1еЫ[/']. (1)
*=! 7е<г*,„
Действительно, нетрудно заметить, что выражение, стоящее в
правой части этой формулы, представляет собой сумму произведений
элементов матрицы Л, лежащих на одной трансверсали, с
некоторыми целыми коэффициентами. Следовательно,
I (-!)*-' ^ реМ(Г)(1еМ[Л = Е ^Па(„(0,
где суммирование производится по всем подстановкам а из
симметрической группы @„ степени п. Покажем, что йа=\ для
любой подстановки яе6„. Тем самым формула (1) будет доказана.
Разложим а в произведение циклов: а=(с!) ... (ст) — и заметим,
что выражение ащг) ... ап^п) входит в те и только в те
произведения рег Л(/) с1е{Л[|] правой части формулы (1), для которых
существуют натуральные числа 1и ..., /4 (1«:/1< ...</;<т, 1<1<:т)
т
такие, что!^, ... , }к}= У сг , где с* — множество натуральных
чисел, образующих запись /Р-го цикла. Следовательно,
108

«°=2 2 (-О" ^.(-1)"
'=1 Тед.
гп т
= 2 2 (-^ = 2(7)(-^ = ^
где |Л, ..., /4| — суммарная длина циклов сг,, .. . ,^.
Утверждение доказано.
Отметим, что тождество (1) может быть записано в
следующем виде:
II
6е\А = ^(—1)к~1 Л йе!Л(/)регЛ[/]. (2)
*=! Гб<г6,„
Приведем два тождества Мак-Магона [72], которые могут быть
получены как простые следствия формулы (1):
РегА = £(-1 )"-*.*! 2 П4е1Л[ЛМ, (3)
п к
6е\А= ^ (—1 )"-**! ^ ПРе^[^]. (4)
6=1 Л/Л, ^й'=1
Здесь сумма берется по всем разбиениям множества N={1, 2,...,«}
на А частей АА. ..., Ык. Действительно, заменяя регЛ(/) в правой
части формулы (1) соответствующим выражением по той же
самой формуле и так проделав конечное число раз, после простых
преобразований получаем (3). Тождество (4) доказывается
аналогично с использованием формулы (2). Трудности с
вычислениями перманентов привели к появлению неравенств, которые
сыграли фундаментальную роль при исследовании ряда проблем
комбинаторного анализа: проблемы Ван дер Вардена о минимуме
перманента дважды стохастической матрицы, задачи оценки числа
неизоморфных троек Штейнера, латинских прямоугольников,
задачи о числе покрытий двумерного решетчатого графа димера-
ми и др.
Хронологически первое нетривиальное неравенство для
перманентов было получено в 1961 г. Маркусом и Ньюменом [18]. Пусть
А есть (тХя)-матрица, а В — (яХт)-матрица. Тогда
|рег (Л-В)|2<рег {А-АТ)-рет (В-В*),
причем равенство достигается в том и только в том случае, когда
У А найдется нулевая строка или у В — нулевой столбец либо
А = ОРВт для некоторой диагональной матрицы Б и
перестановочной матрицы Р. Знак Т обозначает операцию
транспонирования матрицы. Для квадратной матрицы порядка п отсюда следует
(если положить В = 1):
109

|регА12«рег (А-Ат).
Равенство здесь имеет место в том и только в том случае, когда Л
имеет нулевую строку или А = ПР.
В 1980 г. Г. П. Егорычев [67], пользуясь представлением
перманента в виде смешанного дискриминанта, перенес из геометрии
в теорию перманентов классические неравенства Александрова и
Брунна — Минковского. Это позволило ему доказать
справедливость известной гипотезы Ван дер Вардена *.
Мы приводим эти неравенства для перманентов, оставляя в
стороне их первоисточник: геометрическую теорию смешанных
дискриминантов А. Д. Александрова, развитую им в 30-е годы и
использованную для изучения объемов выпуклых тел в евклидовом
пространстве.
Нам потребуются некоторые факты из линейной алгебры.
Пусть Ь есть конечномерное линейное пространство над К, ф —
симметрическая билинейная форма на Ь. Тогда говорят, что
(Ь, ф) — пространство с метрикой. Сигнатурой ф называется
тройка (&1, к2, &з), где к\ — число положительных, к2 — число
отрицательных и кг — число нулевых собственных значений
матрицы формы ф в некотором базисе. Теорема Сильвестра (закон
инерции) утверждает, что эта тройка не зависит от базиса. Говорят,
что пространство с метрикой (Ь, ф) есть пространство
Минковского, если сигнатура ф равна (1, п—1, 0).
Лемма 1. Пространство с метрикой (Ь, ф) является
пространством Минковского тогда и только тогда, когда выполнено
условие Ф: существует вектор а^Ь такой, что ф(а, а)>0, и для
любого Ъ^Ь из ф(а, Ь) = 0, ЬФО, следует ф(Ь, Ь)<0.
Доказательство. Напомним, что вектор ае/, называют
невырожденным, если существует Ь^Ь такой что ф(а, Ь )ф§.
Подпространство М^Ь называют невырожденным, если любой
ненулевой его вектор невырожден. Пусть теперь (Ь, ф) —
пространство с метрикой, для которого выполнено условие Ф. Так как
вектор а — невырожденный, то можем разложить Ь= {а)@Ьа,
где {а} — линейная оболочка а, Ьа — ортогональное дополнение
к а (см. [69]). Построим в Ьа ортогональный базис Ь2, ...., Ьп. Тогда
а, Ь2, ..., Ьп есть ортогональный базис в Ь, где ф(а, а)>0 и
<р(Ь/, Ьс)<0 для всех !'е{2, ..., п), т. е. (Ь, ф) — пространство
Минковского. Обратное также, очевидно, имеет место (из
существования ортогонального базиса в пространстве с метрикой). Лемма
доказана.
Пусть (Ь, ф) — пространство с метрикой. Вектор ае/,
называют положительным (отрицательным), если ф(а, а)>0 (ф(а, а)<
<0), и изотропным, если ф(а, а)=0.
Теорема. (Неравенство Коши — Буняковского для
пространства Минковского.) Пусть (Ь, ф) — пространство Минковского, а —
* Д. И. Фаликманом [68] было независимо получено решение проблемы
Ван дер Вардена (без доказательства единственности минимизирующей
матрицы).
110

положительный вектор, Ь — произвольный. Тогда
Ф2(а, 6)>ф(а, а)-ф(Ь, Ъ) (5)
и равенство имеет место тогда и только тогда, когда Ъ = %а для
некоторого ЛеК.
Доказательство. Если Ь=Ка для некоторого Л<=К, то в
(5) имеет место равенство. Если ф(Ь, Ь)<0, то (5) очевидно
выполнено. Пусть Ь<=ё.{а}, ф(Ь, Ь\>0; в этом случае рассмотрим
плоскость Р={а, Ь). Покажем, что в Р имеется отрицательный
вектор. Если для некоторого уеР, уфО, имеем ф(г/, г/) = 0, то по
лемме 1 имеем ф(а, у)ФО. Отсюда получаем, что выражение
у(а + ку, а + А,г/) = ф(а, а) + 2Лф(а, у) будет меньше нуля при
соответствующем Я, т. е. мы нашли отрицательный вектор в Р.
Предположим теперь, что для всех хеР, хфО, имеет место
ф(л', х)>0. В этом случае Р — невырожденное подпространство.
Поэтому строим разложение в прямую сумму: Ь = Р@Р{, где Р{ —
ортогональное дополнение к Р. Возьмем ортогональные базисы:
{еь ег} в Р и {ез, ..., еп) — в Л. Их объединение есть
ортогональный базис для Ь. В этом базисе ф(ег, е: )>0, ф(е2, е2)>0,
следовательно, сигнатура Ь есть (&,, к2, &з) с &1>2, а это противоречит
тому, что (Ь, ф) — пространство Минковского. Таким образом,
исходное предположение неверно и в Р всегда имеется
отрицательный вектор. Рассмотрим теперь выражение ф(а+АЬ, а + КЬ) =
= ф(а, а) + 2Лф(а, Ь) + %2у{Ь, Ь); при некотором % оно
отрицательно, поэтому квадратный трехчлен от К имеет действительные
корни. Следовательно, его дискриминант неотрицателен:
Ф2(а, Ъ)—ф(а, а)-ф(Ь, Ь)>0,
что доказывает (5). Случай равенства исследуется подобными же
рассуждениями и читателю предлагается сделать это в качестве
упражнения. Теорема доказана.
Теорема (неравенство Александрова — Егорычевч для
перманентов). Пусть ач>0 при г, ] = !, ..., п. Тогда справедливо
неравенство:
#1,1 ••• &1,П—2 #1,,1-1 0-1,п
рег
О-пЛ ■ ■ • 0-п,п—2С1п,п—1 0-п,п_
> рег
#!,1
0-1,п—2®1,п~ 1 &1,п—I
\_&П,1
О-п, п—2 Чп, п—I О-п, п—1
■рег
4,1
. #1,п—2 ®1,П &1,П
М,1
0-п,п—2@-п,пС1п,п
(6)
Матрицы, стоящие в правой части, отличаются только двумя
последними столбцами: в одной последний столбец является
повторением предпоследнего, в другой — наоборот. Если а^>0 при
1=1, ..., п; / = 1, ..., п—2, то равенство достигается тогда и только
тогда, когда при всех 1=1, 2, ..., п имеет место а{п^[=Ха{п, где
А,еЦ. Для доказательства теоремы потребуются две леммы
Д. И. Фаликмана [68].
Ш

Лемма 2. Пусть ф(х, у) — симметричная билинейная
функция на векторном пространстве V такая, что существует
ненулевой вектор оеУ, обладающий свойством ф(а, а)=0, а для всех
х<=У, хФЫ^^К), из того, что у{х, а) = 0, следует, что ф (х, х)<
<0. Тогда, если Ь, се1/, Ъ, с=И=0, и ф(Ь, с) = 0, <р(Ь, Ь)>0, то
ф(с, с)<0.
Доказательство. Если для некоторого хе1/ выполняется
условие ф(х, с) = 0, то ф(х, х)<0. Из ф(Ь, Ь)>0 следует ф(Ь, а)=?^
^=0. Положим т) = —ф~'(^ а)-ф(с, а). Тогда у{с+г\Ъ, а)=0 и,
следовательно,
0>ф(с + т)6, с + т]Ь)=ф(с, с) + т)2ф(Ь, Ь).
Если т)^=0, то ф(с, с)<—т)2-ф(Ь, Ь)<0. Если же т) = 0, то ф(с, а) =
= 0. Векторы с и а не коллинеариы, так как иначе из условия
<р(Ь, с)=0 следовало бы ф(Ь, а) = 0, что неверно. Поэтому ф(с, с)<
<0 и в этом случае.
"й1,1 . . . 0:,,-,-2 Л.\ : !
Лемма 3. Пусть ф (*, #) = рег где
Оп,\ • ■ ■ 0-п,п—2 хп Уп
с,-,->0 при I, / таких, что 1<1<я, 1 </'«:«—2, я>2.
Тогда, если Ь, сеК", Ъ, сФО, ф(Ь, с) = 0, ф(Ь, Ь)>0, то
ф(с, с)<0.
Доказательство леммы будем вести индукцией по я>2.
При п = 2 Ф (*.«/) = Р61"!^1^1 =*1#2 + *2#1- Имеем: 0 = го(Ь, с) =
/ ' Х2 У* \
= Ь\С2 + Ь2С\, ф(Ь, 6) = 2&1&2>0. Следовательно, Ь^О, Ьг^О и
С1=т^=0, С2=т^=0. Умножив обе части равенства —6^2 = 62^1 на Ъ\С2,
получим —Ь[2С22 = Ь[Ь2С[С2. Следовательно, С1С2<0 и ф(с1, Сг) =
= 2с,с2<0.
Пусть теперь я>2 и для всех натуральных к: 2<&<я—I,
утверждение леммы справедливо. Положим а= (0, ..., 0, 1). Тогда
~а[}[ . . . а[?п_2 0 0"
Ф (а, а) = рег
= 0.
ап_1.1 . • . ап_1.>1_2 0 0
#П,1 . . . &п,п— 2 ' 1„
Выберем произвольный вектор #=(^,, ..., х„)еК" такой, что
ф(х, а) = 0, а векторы х и а не коллинеарны, т. е. х'= {х{,..., х„^ )=^=
=^=0. Тогда ф(х, х)<0. В самом деле
"«1,1 • • • «1.П-2 хг 0
Ф (х, а) = рег
&пА ■ ■ ■ 0-п,п—2 Хп 1
Следовательно,
рег
#1,1 • • • #1,П—2 Х1
_#га—1,1 ■ ■ • 0-П—1.П—2 Хп—\
0.
Ф (х, х) = рег
#1,1 • • • #1,п—2 *! -^1
#п.1 • . . йп,п—2 Хп Хч_
— Ха^ф.ф'.У),
112

где
^1,1 . . . а[.;—[ #1,,-+1 • • • #1
ф, (х',х ) = рег
_0п-1,1 • • • аП-.1,1-\ ап—мч-1 ■ ■ ■ ап.
П—2 Х1 Х1 I
-1,Л—2-*-П—I Хп— I ^
Ясно, что ф,-(х', а,-')=ф(х, а) =0, а также фг(аг', аг')>0 (так
как а,/>0 при 1=1, ..., гг, /=1, ..., я—2), где а/=(а1,(, ..., ап-1,,-).
Следовательно, по предположению индукции ф,(х', х')<0, откуда-
ф(х, х)<0. Применение предыдущей леммы завершает
доказательство леммы 3.
Докажем теперь (6). Предположим сначала, что все элементы
матрицы Л = ||0,-/11 — положительны. Для функции ф, построенной
в лемме 3, существует положительный вектор а=(1, ..., 1).
Согласно лемме 3 из того, что ф(а, Ь)=0, ЬФО, следует ф(Ь, Ь)<0.
Поэтому по лемме 1 пара (К", ф) — пространство Минковского,
а неравенство (6) является неравенством Коши-Буняковского (5)
для этого пространства. ,
Случай, когда среди элементов ац могут встретиться нулевые,,
следует из рассмотренного посредством предельного перехода.
Однако знак равенства при этом не обязательно имеет место
только тогда, когда векторы Ь и с коллинеарны. Общий случай,
когда в неравенстве (6) достигается равенство, исследован:
А. А. Пановым [70].
В 1926 г. Ван дер Варден [71] поставил вопрос: каково
минимальное значение функции перманента на множестве &п всех
дважды стохастических матриц порядка п? Положительный ответ
на этот вопрос был известен как гипотеза Ван дер Вардена.
Предполагалось, что если Л — дважды стохастическая матрица
порядка п, то рег А~^п~п-п\, причем равенство достигается тогда
и только тогда, когда Л есть матрица /п, все элементы которой
равны п~1. Доказательство справедливости гипотезы было
найдено в 1980 г. Его изложение начнем с ряда вспомогательных лемм
(см. [18]). Введем предварительно некоторые понятия.
Неотрицательную матрицу порядка п назовем частично
разложимой, если она содержит нулевую подматрицу размера АХ(л—
—к). Другими словами, матрица Л частично разложима, если
существуют матрицы перестановок Р и С? такие, что
РАНо О
где В и Б — квадратные матрицы. Если матрица не содержит
кулевой подматрицы размера кх\п—к) ни при каком к = \, ...
■••, п—1, то она называется вполне неразложимой.
Отметим, что если Л — частично разложимая дважды
стохастическая матрица, то найдутся матрицы перестановок Р и С)
такие, что РАС) разлагается в прямую сумму дважды
стохастических матриц.
Действительно, предположим, что
113,

рщ =
в
о
Я-
где В и О — квадратные матрицы и порядок О равен к.
Обозначим через з(Х) сумму элементов в матрице X. Так как РАС) —
дважды стохастическая матрица, то сумма элементов,
находящихся в ее первых п—к столбцах, равна п—к, т. е. 8(В) =п—к.
Аналогично 8(П)=к. Следовательно, з(С) =з(РА(2)—х(В)—з(О) —
= п—(п—&)—& = 0. Поскольку С неотрицательна, то С = 0.
Очевидно, что матрицы В и Б дважды стохастические.
Лемма 4. Пусть А — матрица порядка п. Для того чтобы
каждая ее трансверсаль содержала нуль, необходимо и достаточно,
чтобы в А существовала нулевая подматрица размера ^X^, где
г + 1 = п+ 1.
Справедливость утверждения леммы вытекает из теоремы Ке-
нига (см. § 4.1).
Будем обозначать через Ац подматрицу матрицы А,
полученную вычеркиванием /-й строки и /-го столбца.
Лемма 5. Неотрицательная матрица А порядка п^2 вполне
неразложима тогда и только тогда, когда для всех I, /=1, ..., п
выполняется неравенство: регЛ,/>0.
Доказательство. Согласно лемме 4 рег Л,/= О тогда и
только тогда, когда подматрица Ац, а следовательно, и матрица
Л содержат нулевую подматрицу размера гХ^, где г + 1=(п—1) +
+ 1. Другими словами, регЛ,/ = 0 гогда и только тогда, когда Л
частично разложима.
Назовем дважды стохастическую матрицу Л порядка п
минимизирующей, если регЛ = ттрегВ.
В60„
Лемма 6. Минимизирующая матрица вполне неразложима.
Доказательство. Пусть
Лейл — минимизирующая
матрица, и предположим, что Л
частично разложима. Тогда найдутся
У ■ гЧ матрицы перестановок Р и С1
такие, что РАС1 есть прямая сумма
1РЯ \ матриц ВеЙл-4 и .ОеЙ*.
Обозначим А' = РА01. Понятно, что Л'ейп
и Л' — минимизирующая матрица.
Выберем на трансверсали матрицы Л',
состоящей из ненулевых элементов, эле-
и а'Рц, принадлежащие соответственно матрицам В и £):
Имеем: а'^фО, а'рдфО, а'1ч = а'р1^Ъ, регЛ';,>0, рег А'Рд>Ъ. Из
леммы 4 следует, что регЛ',д = рег Л'р/ = 0. Рассмотрим матрицу
А'(г) :а'ц(%)=а'ц—Е, а'Рд(е) =а'рд—е, а',-„(е) =а'р/(е) =е, а'г<(е) =
= а'Г(, если гф[, р или 1Ф\, д. Ясно, что Л'(е)ейл при достаточно
малых значениях е>0. Непосредственно убеждаемся, что
-^- рег Л' (е) |Е=0 = — рег Л!у + рег А\ц — рег А'рц + рег А'р/ = — ргг А'(1. —
I В
аРГ
О
I
менты а
114

— регЛ^<0. Следовательно, рег А'(г) <рег А' при достаточно-
малых значениях е>0. Это противоречит тому, что матрица А'—
минимизирующая.
Лемма 7. Если матрица АеО« — минимизирующая и ар17>0,.
то рег Арч = рег А.
Доказательство. Рассмотрим следующее множество,
матриц размера пХп : С (А) ={Х= \\хц\\ |х,7>0 для всех и /=1, •••
.... п; х,/ = 0 при (I, /)е2}, где 2 = {(/, /) |а,/ = 0}. Будем
рассматривать С (Л) как множество точек в евклидовом пространстве
размерности п2—\2\; тогда А — внутренняя точка этого множества.
На С(А) имеем гладкую задачу (см. [111]):
рег Х^ипГ
с ограничениями
Г х(/ = 1> 1= I, ... ,п;
(7>
%хс,-= 1, /= 1, . . . ,п — 1
1=1
П
(заметим, что условие V х{п = 1 является следствием условий
1 = 1
(7)). Матрица А является решением этой задачи, поэтому
существуют множители Лагранжа Яо, Яь ..., Яп, Ць •••. Ця-ь не равные-
нулю одновременно, такие, что функция Лагранжа
Р (X, Я0, Яь . .. , Я„, щ, . .. , Цп-0 = \> Рег -^ —
(=1 6=1 /=1 6=1
в точке Х = Л удовлетворяет условиям стационарности по х (см-
[111, с. 47—481):
Р (X, Я0, Я2, . .. , Я„, И1> • • ■ /Ия-О 1х=/5 = 0 для всех ('> /)^2,
т. е. имеем:
Г Я0 рег А,- = к; + ц; при I = 1, ... , п; / = 1, ... , п — 1; {и /) *$2,
\ Я0 рег А1п = Я,- при I = I, ... ,п; (I, п)Ер 2.
Предположим, что Яо = 0. Тогда (8) сводится к
I Я, + ц,/ = 0; I = 1, .. . , л; / = 1, . .. , п — 1; (*', /) ^ I,
\ Я, = 0; 1=1,..., я; (I, п)^ 2.
Из наличия (;, я) таких, что а,„^=0, вытекает, что имеются /, при
которых Я, = 0. Пусть Я! = ... = Яб = 0. Если к = п, то согласно (9) из
115

•существования (*, ])^2, для каждого /=1 п—\, получаем:
^! = ... = ^1„_1 = 0, а это противоречит тому, что не все множители
-Лагранжа нулевые. Пусть к<п и Кк+\Ф0 Яя^О (этого можно
добиться перестановкой строк в А). Если существует ненулевой
элемент щ„ где !'е{1 к), ]<п, то из (9) получаем: ц, = 0.
Переставим столбцы А так, чтобы выполнялись условия: ^1 = ...=
= ц„_1_г = 0 и ц/=т^0 при всех п—1—1<]<п. Если /=0, то ^1 = ...=
= ц„_1 = 0 и, следовательно, %к+1 = 0, так как существует (к +
+ 1, ])^2, где ]<п (снова применяем (9)). А это противоречит
предположению о том, что Яь+^О. Пусть />0, тогда подматрица
матрицы А, образованная ее первыми строками и столбцами с
номерами п—/, ..., п—1 — нулевая и имеет размеры кХ1. Так как
А вполне неразложима, то согласно лемме 5 регЛп,„>0 и отсюда
по лемме 4 получаем
к + 1<п. (10)
Докажем теперь, что подматрица А', образованная строками
■к+ 1, ..., п и столбцами 1, ..., п—/—1, — нулевая. Действительно,
если в этой подматрице существует ненулевой элемент Щ], то в
силу ц; = 0 и равенства Я/+ц,- = 0 (из (9)) получаем Я, = 0, но это
невозможно по построению. Эта подматрица имеет размеры
(п—к) X (п—/—1). Отсюда и из неравенства (10): п—к + п—/—
— 1=ят(я—к—/—1)^«, так как п—к—/—1^0. А это
противоречит полной неразложимости матрицы А. Стало быть, равенство
.Яо = 0 невозможно. Разделив соотношения (8) на Яо, получим
рег Л,-,= Я, + ц/ для всех (/, ])&2, /, /е{1, ..., п)
(здесь мы взяли цп = 0).
Переставляя, если это необходимо, строки и столбцы матрицы
А, добьемся выполнения неравенств: Я^Яг^.-.^Я,,, ^1=¾^5¾.-5¾
^^„. Разлагая рег Л по первой строке и последнему столбцу, а
также используя то, что сумма элементов в любой строке
(столбце) матрицы Л равна единице, получим
п п
К + Ц« > У] «1/ Рег Л1у- = V ах1 рег Аи = рег Л =
;=1 ;=1
(1./)ег-2
п п
= ][] а1п рег А{„ = ^ а,, рег Аы > \ + \ьп.
1=1 1=1
Следовательно, Я1 + (1п = рег Л = рег Л!у = рег Л,„ при всех /, /' таких,
что (1,/)^2, (I, п)*$2.
Предположим, что для всех I, / таких, что ]^-)\, 1^Л\, (х, ']) &2,
мы уже доказали, что рег Л,у = рег Л. Рассмотрим (м + 1) -ю строку
матрицы Л. Если найдется Т^\\ такое, что (11+1, ])^2, то при
всех ]^~] таких, что (11+1, ])^2, имеем: рег Л,1+1 у = рег Л (по
116

предположению) и при всех /</ таких, что (11+1, ]')^%> имеем:
регЛ/,+1,/ = %1+1 + (I/ < %1+1 + р]- = рег А-,+1,7 = рег А. Следова-
п
тельно, регЛ = ^| щ+и1- рег А-1+!,/ <регЛ и при всех / таких, что
/=1
(»1 + 1, /) ^"2, выполняется равенство:
регЛ,1+и = рег Л.
Аналогичные рассуждения справедливы и для (/1—1)-го
столбца матрицы А. Если же для всех ]^\\ и для всех 1=¾^
выполняется:
(11+1, ])е=2 и (/, /1—1) е2, т. е. а(,+,,/= О и а(,/,_, =0, то
_, ~ ''-'
^.+1 + ^/,-1^= 5] а<,+М рег /4(,+1,,- = регЛ =
/=1
Т Я;,/,-! регД,/,-! > Лц+1 +|А/,-
. .. -1
1 = 1,+1
и, следовательно, для всех /, / таких, что (/, /1—1)^2, (^ +
+ 1, /') ^7., имеем: рег Л; /,_1 = рег Д-,+1,/ = рег Л.
Таким образом, если (/, /') ^2, то рег Л,у = рег Л, ч.т. д.
Лемма 8 (неравенство Лондона). Если Л — минимизирующая
матрица в Й„, то для любых г, /=1, ..., п выполняется
неравенство рег Л,/^рег Л.
Доказательство. Для любой матрицы перестановок Р =
= ||р,/|| и числа 6е[0; 1] положим /Р(6) =рег((1—6)Л+6Р). Так
как Л — минимизирующая матрица, то /р (0)^0 для любой
матрицы перестановки Р. Пусть а — перестановка, соответствующая
Р. Имеем
/р(°)= Е (—ап + Рп) рег Ап = ^ рп рег Аи — я рег Л =
л,<=1 г,<=1
= V рег Лга(г) — га рег Л > 0.
Следовательно,
2] рег Ага(г) > и рег Л (11)
для любой перестановки а. По лемме 6 матрица Л вполне
неразложима, и поэтому по лемме 5 любой элемент Л лежит на
некоторой трансверсали, все остальные элементы которой
положительны. Иными словами, для любой пары (»", /) найдется такая
перестановка а, что / = а(0 и аго(Г)>0 при г=\, ..., I—1, /+1, ..., п.
Но в силу леммы 7 это означает, что рег ЛГо(0 = рег Л при г= 1, ...
117

.... 1—1, 1+1, ..., п. Так как / = а(0, то из (11) получаем: рег Л,-/>
>рег Л, ч. т. д.
Теперь, следуя Г. П. Егорычеву, покажем, как,
воспользовавшись неравенством (6), можно доказать справедливость
предположения Ван дер Вардена.
Пусть Л — минимизирующая матрица. Покажем, что рег /4,-,- =
= регЛ для всех I, /=1, ..., п. Предположим противное: пусть
существует хотя бы одна пара г,$е{1, ..., п} такая, что регЛГ8>
>регЛ. Так как матрица А — дважды стохастическая, то
существует ?е{1, ..., п} такое, что аг*>0. Тогда в силу неравенства (6)
и леммы 8 имеем
п п
рег2 Л > (2 а*5 рег Ан) (^ ан рег А„3) >
4 6=1 '6=1
5 п
> (2 акз ргг Л) (2 ан рег л) = рег2|Л
6=1 6=1
(то что неравенство здесь строгое, вытекает из аГ1~>0, регЛг5>
>регЛ>0).
Докажем теперь, что если Л — минимизирующая матрица, то
а11 = п~1 (I, /=1, ..., п). Пусть столбец матрицы Л с номером п
отличен от (гг1, ..., гг~')т. Поскольку Л не разлагается в прямую
сумму ненулевых матриц, то каждый элемент п-то столбца А
меньше единицы. Следовательно, среди первых п—1 элементов
каждой строки матрицы Л есть хотя бы один ненулевой.
Переходя от Л к матрице, получающейся из Л заменой 1-го и /-го
столбцов их полусуммой (1ф], I, /=1, ..., п—1), мы за конечное число
шагов получим матрицу Л', у которой все элементы первых п—1
столбцов положительны, а п-и столбец совпадает с п-м столбцом
матрицы Л, причем регЛ' = регЛ, гак как при каждом шаге
перманент не изменится (что вытекает из формулы разложения
перманента матрицы по столбцам и равенства всех перманентов
подматриц (п—1)-го порядка).
Обозначим через Л (Ъ) матрицу, полученную из А' заменой
/
/-го столбца на столбец Ь. Мы выяснили, что в неравенстве
рег2 Л' > рег А' (а!) рег Л' (а„)
п I
реализуется равенство. Положительность компонент а'\, ..., а'п-\
дает основание утверждать, что ап^К^аи (1=1, ..., п—1).
Поскольку суммы компонент векторов равны все 1, то ап=а'1 (1=1, ...
..., п—1). Так как матрица А' дважды стохастическая, то а\ = ...
... = а'п-1 = ап= (п~1, ..., п~1)т, что означает противоречие.
Следовательно, все столбцы матрицы Л равны (гг1, ..., гг1)'1, что и
доказывает наше утверждение.
Рассмотрим состояние проблемы о верхних оценках для
перманентов. В 1960 г. Райзер предположил, что в классе (0, 1)-
118

матриц порядка тк, содержащих к единиц в каждой линии,
максимум перманента достигается на прямой сумме матриц порядка
к, составленных из единиц. Минк в 1963 г. высказал более общее
предположение, что если Л есть (0, 1)-матрица порядка п, имею-
п 1
щая суммы гь ..., г„ по строкам, то регЛ< П(г<0'7 • Из этого
1=1
неравенства сразу же следует гипотеза Райзера.
Неравенство Минка доказал впервые в 1973 г. Брэгман [73].
Ниже мы приводим более простое доказательство этого
неравенства, принадлежащее Шриверу [74].
Лемма 9. Для неотрицательных действительных чисел хь ...
.,.., хг справедливо неравенство:
г
1=1 1=1
(в этой формуле подразумевается, что 0° = 1).
Доказательство. Воспользовавшись выпуклостью
функции у = х\о§2х, получим:
г-' ^ х, 1о§2 (г-' ^ х{) < г-» ^ х, 1о§2х„
1=1 1=1 1=1
откуда результат леммы тотчас следует.
Пусть Л = ||а,/|| есть квадратная (0, 1)-матрица порядка п,
8 — множество всех перестановок я чисел 1, ..., п таких, что
п
I I а»жо = 1 ■ Тогда
п
П (регЛг,.)регЛ<7= П ПрегЛад,
1,1 ■ Я65 ;=1
1=1 яе$ 1=1
В справедливости этих тождеств легко убедиться
непосредственной проверкой. Воспользуемся ими для доказательства
неравенства Минка. Применим метод полной математической
индукции по п. Из леммы 9 имеем
п
п п 2 аЧрСтА'1
(рег А)" р<а = П (Рег А)**А = П (£) аи Рег Л/)'-1 <
; = 1 1=1 /=1
<П(ТЛ П (регЛ(/)р'=П[(П^)(ПрегЛя(о)].
1=1 V. П€5 1=1 1=1
в,Г!
119

Применим теперь предположение индукции к каждой из матриц
п п 1 1
ПрегЛ,Я(о<П( П (г/!р)( П (Г/—1)1?р)) =
»=1 1=1 ' /*( /*1
а/я(0=0 а/Я(0=1
= П( П (г,-1у,-) П (^-1)^-^) = 111^ 'I (г/-1)1]-
/=1 <*/ (*/ /=1
а/я(<)—° а]гЦ1)—1
Последнее равенство получено подсчетом сомножителей (г!)'/г;
и (г/— 1)11^--^. При фиксированных я и / число индексов IV
для которых гФ\, равно га—г/, если а/я{1) = 0, и равно г;— 1, если
о/я(()=1. Таким образом,
(регЛ)«ре^<П[(Пг1)(П01 ''' (0-1)')] =
я€5 1=1 /=1
|_!_\ п рег Л
-П(П'.'")-(ПМ7-)"'
я€5 1=1 1=1
что и требовалось доказать.
Обратимся к приложениям неравенств для перманентов.
Обозначим через Ь{г, га) число латинских
(гХга)-прямоугольников, составленных из элементов множества 5 = {1, 2, ..., га}.
Рассмотрим какой-нибудь латинский прямоугольник размера 1Х.пу
1^<г. Сколькими способами он может быть расширен до
латинского (1+ 1) X га-прямоугольника? Ясно, что число таких
способов равно рег А, где А — матрица инцидентности системы
подмножеств (51, ..., 5«), где 5; — подмножество тех элементов 5,
которые не встречаются в 1-м столбце расширяемого
прямоугольника (1= 1, ..., га).
В каждой строке матрицы А содержится га—I единиц; матрица
(я—1)~1А будет дважды стохастической. Применяя неравенства
Минка и Ван дер Вардена, получим
п
— (га — I)" < рег А < (п — О !"""'■
пп
п
При ^= 1 регЛ = га! \ (—1);—= Д„— число беспорядков на га
1=0
элементах. Следовательно,
пп(г-2)
■°пТ\(п — *)п<1'{г> л)<л1Ц,[~[ (я —*)1"
1=2
120

Если положить г — п, то получим Ь(п, п) ^(п\)2пп-п' У(е~2п)п'.
Здесь мы воспользовались известным неравенством: п\>е~ппп.
Уилсон [58] использовал приведенное неравенство Ь(п, п) > (е"2п)пг
для определения нижней границы числа N(V) неизоморфных
троек Штейнера порядка у и получил следующую оценку:
В заключение рассмотрим приложение перманентов к задачам
о димерах, возникших в физике и химии. Назовем п-кирпичом
А-мерный параллелепипед (&^2) объема п, длины ребер которого
целочисленны: а,\, ..., а&. Пусть п четно. Ставится вопрос:
сколькими способами гг-кирпич можно сложить из 2-кирпичей (диме-
ров)? Обозначим это число через N. Разобьем гг-кирпич на
единичные кубики и занумеруем их: 1, 2, ..., п. Пусть Л = ||а,-,-|| есть
матрица инцидентности, характеризующая взаимное
расположение кубиков: а,ц = \ или 0 в зависимости от того, имеют ли кубики
с номерами г и / общие грани или нет {аи = а22= ■■■ = аПп = ^) ■
Утверждается, что Л^2 = регЛ. В самом деле, каждой
упорядоченной паре разбиений гг-кирпича на димеры соответствует
взаимно-однозначно трансверсаль матрицы А, состоящая из единиц.
Пусть, например, п = 6, к = 2, а\ = 2, а2 = 3. Матрица инцидентности
будет иметь следующий вид:
/
2
3
4
5
Б
1 г
0 1
И о
0 /
1 0
0 [7]
0 0
3
0
1
0
0
0
ш
4
Ш
0
0
0
;
0
5 6
0 0
1 0
о [7]
ш °
0 1
1 0
Рнс. 4.4
Упорядоченной паре разбиений кирпича на рис. 4.5
взаимнооднозначно соответствует подстановка
_ _/1 2 3 4 5 6\
V4 16 5 2 3^
и трансверсаль матрицы А, состоящая из единиц, обведенных на
рис. 4.4.
121
/
4
2
5
3
6

Заметим, что все суммы по
строкам и столбцам матрицы
инцидентности Л равны 2к, за исключением тех,
что соответствуют кубикам на
поверхности. Рассмотрим вместо я-кирпича
соответствующий тороидальный кирпич, который получается
склеиванием противоположных граней исходного кирпича. Матрица
инцидентности А' тороидального кирпича имеет 1к единиц в каждой
строке и каждом столбце. Воспользовавшись неравенством Мин-
ка, получим: рег Л^рег А'^(2к) \п/2к и, следовательно, А^
<(2к)\п/*к.
Хаммерсли [75] показал, что если а,->-оо для всех »=1, ..., ку
то величина п~11п N стремится к некоторому пределу Я*. Таким
образом,
Хк<±\п[(2к)\]^<±\пк.
Применение неравенства Ван дер Вардена к матрице Л' при-
1 2к
водит к оценке снизу Кк ^—1п (см. [75]). Следовательно,
1 9*>
%к = — 1п -==-(1 +о(1)) при к^оо.
1
4
2
5
3
6
1 г
Ч 5
3
6

Глава 5
ГЕОМЕТРИЧЕСКИЕ СИСТЕМЫ
5.1. ГЕОМЕТРИЧЕСКИЕ ИНТЕРПРЕТАЦИИ
Комбинаторные задачи и теоремы нередко формулируются в
терминах геометрии. Наглядность геометрических интерпретаций
помогает лучше понять сущность комбинаторных высказываний,
а соединение геометрических и комбинаторных средств
оказывается плодотворным для обеих частей математики.
Дискретная структура и конечность множеств, являющихся
объектом комбинаторного анализа, определяют то, что
соответствующие геометрические объекты также состоят из конечного
числа элементов. Некоторые из таких специфических
геометрических систем описаны ниже (см. § 5.2—5.3).
Теоремам комбинаторного анализа придают геометрическую
интерпретацию не только для того, чтобы облегчить их
понимание или придать им наглядность. Такая интерпретация создает
дополнительные возможности для приложений. Примером может
служить теорема Рамсея (см. § 3.3).
Напомним, что теорема Рамсея обобщает представление о
разбиении множеств. Пусть Рг(5) = Л1 Ц/4 211 ••• ЦЛ4— некоторое
разбиение множества всех г-подмножеств множества 5. Пусть,
далее, заданы целые числа д^ такие, что 1=^>^<7,; £=1, 2 I.
Если существует ^-подмножество 5, все г-подмножества
которого содержатся в Аи то его называют (д,, Л^ -подмножеством
множества 5. Теорема Рамсея утверждает, что существует
минимальное натуральное число N (д\, <72,..., <7*; г), начиная с
которого (т. е. при п^-Ы) множество 5 содержит {ди
Л,)-подмножество для некоторого £^( 1, 2,..., Ц.
Рассмотрим частный случай теоремы Рамсея, когда г = 2.
Геометрическая интерпретация здесь такова: п элементов
соответствуют п точкам на плоскости; таре точек отвечает отрезок, их
соединяющий; включение отрезка в подмножество А± отмечается
окраской его в 1-й цвет (£=1, 2, ...,^), Теорема Рамсея
гарантирует при гС^-Я{р, д; 2) существование р точек, соединенных
между собой отрезками только первого цвета, или д точек,
соединенных отрезками только второго цвета.
Та же идея лежит в основе приложения теоремы Рамсея к
выпуклым многоугольникам. Рассматриваются «-множества то-
123

чек на плоскости такие, что никакие три точки не лежат на
одной прямой. Оказывается, что на точках этого множества, как
на вершинах, можно построить любой выпуклый т-угольник,
если только п достаточно велико.
а б в
Рис. 5.1 Рис. 5.2
Теорема. Для данного целого числа т существует
минимальное целое число Ыт такое, что любые Ыт точек в плоскости, из
которых никакие три не лежат на одной прямой, содержат т
точек, образующих выпуклый т-угольник.
Доказательство. Заметим сначала, что среди любых
5 точек можно выбрать 4, являющиеся вершинами выпуклого
4-угольника. Доказательство легко усмотреть на рис. 5.1. Как
видно, даже «вырожденный» случай (рис. 5.1, в) дает выпуклый
четырехугольник (внутри треугольника).
Далее, справедливо утверждение, что если среди
рассматриваемых т точек любые 4 являются вершинами выпуклого
4-угольника, то эти т точек образуют выпуклый т-угольник.
В самом деле, предположим, что существует, самое большее,
выпуклый <7-угольник (<7<т). Диагоналями, проведенными из
одной и той же вершины, разобьем его на треугольники, при
этом (т — <7) точек попадут внутрь треугольников, что
противоречит условию выпуклости всех 4-угольников. Значит, ц = т и
т-угольник будет выпуклым.
Теперь рассмотрим общее утверждение. Пусть т^4; гС^-
~^Ы{т, 5; 4). Разобьем 4-множества (их Цмна выпуклые и
невыпуклые. Тогда по теореме Рамсея либо: а) существует
5-угольник со всеми невыпуклыми 4-угольниками, что
противоречит доказанному выше; либо б) существует один т-угольник,
все 4-угольники которого выпуклы, и, следовательно, по
доказанному выше этот т-угольник выпуклый.
Геометрические интерпретации существуют почти для всех
комбинаторных объектов. Например, для латинских квадратов
геометрическую интерпретацию строят следующим образом.
Каждый из п2 элементов латинского квадрата рассматривается
как точка на 2-координатном многообразии. Через множество
точек, составляющих латинский квадрат, проведем три «-семейства
124

линий, проходящих: 1) по строкам, 2) по столбцам, 3) по
одинаковым элементам. Эти семейства образуют 3-сеть с п2 узлами.
Обратно, каждая такая 3-сеть может быть интерпретирована как
латинский квадрат.
Условие эквивалентности латинских квадратов в настоящей;
интерпретации выглядит как сохранение 3-сетей при
перенумерации линий каждого семейства. Иногда допускают взаимную
замену семейств и этим расширяют понятие эквивалентности.
Заметим, наконец, что геометрическая интерпретация, видимо,
послужила причиной появления понятия ортогональности в
применении к латинским квадратам.
Последовательное применение геометрических интерпретаций,
привело к тому, что оказались выделенными классы дискретных
систем, изучение которых производится без отрыва от их
геометрических свойств, а также символики и терминологии. Это —
конечные геометрии и графы. Ввести читателя в эти обширные-
области математики в интересах основной цели книги — такова
задача настоящей главы.
5.2. О ПРОЕКТИВНЫХ ПРОСТРАНСТВАХ
Проективные пространства можно строить из линейных
пространств по крайней мере двумя способами. Во-первых,
реализацией проективного пространства как множества прямых в
линейном пространстве. Пусть Ь — линейное пространство над
полем К\ через сПт Ь будем обозначать размерность Ь. Множество
Р{Ь) прямых (т. е. одномерных линейных подпространств) в Ь
называется проективным пространством, ассоциированным с Ь,
а сами прямые в Ь называются точками Р(Ь). Число АхтЬ—1
является размерностью Р(Ь) и обозначается а\т Р(Ь).
Одномерные и двумерные проективные пространства называются
соответственно проективной прямой и проективной плоскостью.
Множества вида Р(А), где А^Ь, называются проективными
подпространствами в Р(Ь). Очевидно, Р{А\[\А2) = Р {А\)[\Р {А2),
т. е. семейство проективных пространств замкнуто относительно
пересечений. Поэтому во множестве проективных подпространств.
Р(А), содержащих данное множество 5^Р(Ц, имеется
наименьшее—пересечение всех таких подпространств. Оно
называется проективной оболочкой 5, обозначается 5 и совпадает с
Р(А), где А — линейная оболочка всех прямых, отвечающих
точкам «е5, в Ь. Можно показать, что если Р\ и Р2—два
конечномерных проективных подпространства в проективном
пространстве Р, то
сНт (Р,Г)Р2) + сНт (Р7ЦР2) = сНт Р, + сНт Р2.
В дальнейшем нам понадобятся два конкретных проективных,
пространства, так называемые конфигурации Дезарга и Паппа.
Конфигурация Дезарга. Пусть А — семейство точек в
проективном пространстве. Символ А будет обозначать его
проективную оболочку. Рассмотрим в трехмерном проективном простран-
125.

<:тве упорядоченную шестерку точек (а\, а2, а3, Ь\, Ь2, Ъъ).
Предполагается, что точки попарно различны и что а\а2аг и Ъ\Ь2Ъг
■суть плоскости. Далее, пусть прямые а\Ъ\, а2Ь2 и аъЬъ
пересекаются в одной точке р, отличной от аи а2, а3, Ъи Ь2, Ъг (рис. 5.2).
В этом случае будем говорить, что треугольники (а\а2аг) и
(Ь\Ь2Ьг) перспективны относительно точки р и каждый из них
есть проекция другого из центра р, если они лежат в разных
плоскостях. Тогда для любой пары индексов {и /}е{1, 2, 3}
прямые а-1Щ и Ьф$ не совпадают, иначе имели бы а,-=Ь{, ибо аг- и
Ь{ — точки пересечения этих прямых с прямой раф{. Кроме того,
прямые а.{<1] и Ь{Ь] лежат в общей плоскости ра^а-у Поэтому они
пересекаются в точке, которую обозначим с,-,-. Точки с\2, с\ъ, с2з
•суть точки пересечения продолжений пар соответствующих
сторон треугольников {а\а2аг) и {Ь\Ь2ЬЪ).
Скажем, что треугольники (а.\а2аг) и {Ь\Ъ2Ъ$) перспективны
относительно прямой /, если точки С\2, с!3, с2г лежат на прямой /.
Теорема Дезарга. Если два треугольника перспективны
относительно некоторой точки, то они перспективны относительно
прямой.
Конфигурация Паппа. Рассмотрим в проективной плоскости
две различные прямые 1\, 12 и две тройки лежащих на них
попарно различных точек аи а2, а3 и Ьи Ь2, Ь$ (рис. 5.3). Для
любой пары индексов {г, /}е{1, 2, 3} таких, что К], обозначим
через сц точку пересечения прямых а,Ь3- и а3Ь,-.
Теорема Паппа. Точки с\2, с^, с2$ лежат на одной прямой.
Доказательство теорем Дезарга и Паппа, а также другие
подробности читатель может найти в книге [69].
Во-вторых, проективные пространства можно строить путем
добавления к аффинному пространству «бесконечно удаленных
точек». Этим способом достигается единообразие в
формулировках и доказательствах ряда теорем аналитической геометрии и
некоторых других геометрических результатов. Этот способ
привел к созданию классической проективной геометрии. С
развитием аксиоматического метода были созданы различные
аксиоматические описания проективных пространств. Дальнейшие ис-
126

следования показали, что геометрические системы,
подчиняющиеся этим аксиомам, имеют самостоятельное значение и их
теория оказывается весьма глубокой (см. [4, 21, 76, 77]). С тех
пор под классическим проективным пространством обычно
понимают именно такую геометрическую систему. Например,
трехмерное пространство определяется как множество, элементы
которого называются точками, снабженное двумя системами
подмножеств, элементы которых называются соответственно
прямыми и плоскостями. При этом должны выполняться следующие
аксиомы инцидентности:
1. Две разные точки принадлежат единственной прямой.
2. Три разные точки, не лежащие на одной прямой,
принадлежат единственной плоскости.
3. Прямая и плоскость имеют общую точку.
4 Пересечение двух плоскостей содержит прямую.
5. Существуют четыре точки, не лежащие в одной плоскости,,
и такие, что любые три из них не лежат на одной прямой.
6. Каждая прямая состоит не менее чем из трех точек.
В дальнейшем мы рассматриваем лишь классические
проективные геометрии, называя их для простоты проективными
геометриями.
Классическая проективная плоскость определяется как
множество, элементы которого называются тшсамщ снабженное
системой подмножеств, элементы которой называются прямыми.
При этом должны выполняться следующие аксиомы;
1. Две разные точки принадлежат единственной прямой.
2.' Пересечение двух прямых непусто.
3. Существуют три точки, не лежащие на одной прямой.
4. Каждая прямая состоит не менее чем из трех точек.
Множество Р(Ь), где Ь— линейное пространство над
полем К размерности 4 или 3, вместе с системами проективных
плоскостей и прямых в них, как они были определены выше,
удовлетворяют аксиомам классического трехмерного
проективного пространства и классической проективной плоскости
соответственно. Однако не всякое классическое проективное
пространство или плоскость изоморфно одному из наших
пространств Р(Ь). Более того, оказывается, что существуют
классические проективные плоскости, не изоморфные даже никакой
плоскости вида Р{Ь), где Ь—трехмерное проективное
пространство над каким-нибудь телом. Причина этого состоит в том, что
в проективных плоскостях вида Р(Ь) теорема Дезарга
по-прежнему верна, тогда как существуют недезарговы плоскости, где
она не выполняется. Сформулируем без доказательства
следующий результат:
Теорема 1. Три свойства классической проективной плоскости
равносильны:
а) в ней выполняется плоская теорема Дезарга;
б) ее можно вложить в классическое проективное
пространство;
127

в) существует линейное трехмерное пространство Ь над
некоторым телом Л', определенным однозначно с точностью до
изоморфизма, такое, что наша плоскость изоморфна Р(Ь).
Даже в дезарговых плоскостях теорема Паппа может не
выполняться. Назвав соответствующее утверждение аксиомой
Паппа, мы можем сформулировать следующую теорему, которую
также приведем без доказательства:
Теорема 2. Если в классической проективной плоскости
выполнена аксиома Паппа, то она является дезарговои. Дезаргова
классическая плоскость удовлетворяет аксиоме Паппа тогда и
только тогда, когда связанное с ней тело коммутативно, т. е. эта
плоскость изоморфна Р(Ь), где Ь — трехмерное линейное
пространство над полем.
Во всяком классическом проективном пространстве
размерности выше двух справедлива теорема Дезарга. Теорема Дезарга
позволяет координатизировать классическое проективное
пространство с помощью некоторого ассоциативного тела К. Таким
образом, изучение классических проективных пространств,
размерность которых превышает два, сводится к алгебраическому
вопросу — к теории ассоциативных тел. В проективных же
плоскостях теорема Дезарга может не иметь места, и вышеуказанное
сведение к алгебре в общем случае не удается. В связи с этим
изучение классических проективных плоскостей представляет
самостоятельный интерес, и их теория успешно развивается с
начала нынешнего столетия. В следующем параграфе мы
остановимся подробнее на результатах этой теории и ее связях с
другими разделами комбинаторного анализа.
5.3. КОНЕЧНЫЕ ПРОЕКТИВНЫЕ ПЛОСКОСТИ
Легко проверить, что определение классической проективной
плоскости, данное в § 5.2, эквивалентно следующему:
Проективной плоскостью называется множество точек и
прямых, между которыми установлено соотношение инцидентности,
подчиняющееся следующим требованиям:
1. Две различные точки инцидентны с одной и только с одной
прямой.
2. Две различные прямые инцидентны по крайней мере с
одной точкой.
3. Существуют четыре точки в общем положении, т. е. такие,
что никакие три из них не инцидентны с одной прямой.
В самом деле, для этого достаточно доказать следующее
утверждение.
Теорема 3. Каждая прямая содержит не менее трех точек.
Доказательство. Из аксиомы 3 следует, что существуют
четыре точки щ, а2, аз, а4, никакие три из которых не лежат на
одной прямой. Этим точкам соответствуют шесть различных
прямых, соединяющих их попарно 1\\ ахафх; 1ч\ а\афч\ 1ъ'. а\а^Ъг\
Ц: ага3Ьз; к- сцсцЬ^; /е.- агаф\. Здесь Ьи Ь2, Ьг — точки пересече-
128

ния этих прямых. Из того, что все шесть прямых различны,
легко получается, что все точки Ьи Ь2, Ъъ различны и все они
отличны от точек щ; 1=1, 2, 3, 4. Каждая из прямых /,- (1=1, 2,...,6)
содержит по крайней мере три точки. Если произвольная
прямая / не содержит щ, то она пересекается с прямыми 1\, 12, к в
трех различных точках. Если / не содержит а2, то она пересекает
прямые /], и, 15 в трех различных точках. Если же прямая /
содержит и аи и аъ то / = /ь но прямая /1 содержит, во всяком
случае, три различные точки аи а2, Ъ\. Теорема доказана.
Заметим, что из аксиомы 1
следует, что две различные прямые
инцидентны не более чем с одной точкой.
На рис. 5.4 изображена конечная
проективная плоскость, содержащая
семь точек и столько же прямых,
причем помимо сторон и медиан
равностороннего треугольника «прямой»
приходится считать вписанную
окружность. Эта конкретная
проективная плоскость часто называется
конфигурацией Фано. Другой пример
проективной плоскости мы уже
рассмотрели в § 5.2, а именно Р(Ц,
когда Ь — линейное пространство над полем размерности 3.
Аксиома 3 в определении проективной плоскости служит
главным образом, для отбрасывания «вырожденных» плоскостей
таких, как пустая плоскость; прямолинейный ряд точек (в
частности, прямая); пучок прямых (в частности, точка);
прямолинейный ряд точек, через одну из которых проведено несколько
прямых; пучок прямых, пересеченный прямой.
Введем еще несколько определений. Подмножество л' точек и
прямых проективной плоскости л называется подплоскостью,
если вместе с каждыми двумя точками (прямыми) л' содержит
прямую (точку), инцидентную с ними. Две плоскости называются
изоморфными, если между их точками и их прямыми можно
установить взаимно-однозначное соответствие, сохраняющее
.инцидентность. Специфическим для проективных плоскостей
является понятие двойственности. Две плоскости называются
двойственными, если между точками (прямыми) одной плоскости и
прямыми (точками) другой можно установить
взаимно-однозначное соответствие, сохраняющее инцидентность. Плоскость,
двойственную данной, можно получить, объявив «точками» прямые
данной плоскости, а «прямыми» — ее точки, сохранив
существующие инцидентности. Нетрудно убедиться, что плоскость,
изоморфная плоскости, двойственной плоскости л, сама будет
двойственной по отношению к л. Плоскость, двойственная двойственной,
изоморфна исходной. Изоморфное отображение плоскости на
себя называется коллинеацией. Однозначное (не обязательно
взаимно-однозначное) отображение точек и прямых плоскости я
5 К. А. Рыбников
129

на точки и прямые плоскости я' с сохранением инцидентности
называется гомоморфизмом.
Теорема 4. Пусть п^1 — произвольное целое число. Тогда
следующие свойства проективной плоскости я эквивалентны:
а) некоторая прямая содержит ровно п-\-\ точек;
б) некоторая точка принадлежит ровно п-\-\ прямым;
в) каждая прямая содержит ровно гг—(— 1 точек;
г) каждая точка лежит ровно на п-\-\ прямых;
д) в плоскости я ровно гг2+гг+1 точек;
е) в плоскости я ровно н2+гг+1 прямых.
Доказательство. Пусть а\, а2, а%, а4—четыре точки, из
которых никакие три не лежат на одной прямой. Этим точкам
соответствуют шесть различных прямых, соединяющих их
попарно (см. доказательство теоремы 3). Предположим теперь, что
выполняется свойство а), т. е. в я существует прямая /,
содержащая ровно гг+1 точек, скажем, для определенности с\, с2,...
...,сп+1. Если Ь — точка, не лежащая на /, то прямые Ьси £=1,
2,...,гг+1, различны, так как если Ьс< = Ьс] для некоторых 1ф},
то Ь лежит на /, что противоречит предположению. Далее,
каждая прямая, проходящая через Ь, .пересекает / и, значит, должна
быть одной из гг+1 прямых Ьс,-, £=1, 2,..., гг+1. По крайней мере
две из точек аь а2, аз, а* не лежат на прямой /, и поэтому такая
точка Ь существует. Пусть теперь Ь — точка, лежащая ровно на
гг+1 прямых: ть т2, ...,тп+\. Если /* — некоторая прямая, не
проходящая через 6, то /* пересекает Ш],..., т„+1 в точках й\,...
...,йп+\, которые все различны, поскольку Ь — единственная
точка, лежащая более чем на одной из прямых ть..., тп+1. Если бы
на /* существовала еще одна точка йп+2, то существовала бы
прямая Ьйп+2, не совпадающая ни с какой т;, /=1, 2,..., гг+1, так
как в противном случае прямая Ьйп+2 содержала бы некоторое
й5: ]фп-\-2 и тогда Ьйп+2 = Ьйп+2(1) = (1п+2(1, = 1*, что противоречит
предположению, что Ь не лежит на прямой /*.
Наша исходная прямая / содержала ровно гг+1 точек;
следовательно, каждая точка, не лежащая на /, лежит ровно на гг+1
прямых; к таким точкам относятся по крайней мере две из
точек щ, ач, аз, а4, например, а\ и а2. Поэтому каждая прямая, не
проходящая через а\ или через а%, содержит ровно п+1 точек,
т. е. каждая прямая, исключая, быть может, прямую 1\\ а[а2Ь1!
содержит ровно гг+1 точек. Тогда /2: агазЬ2 содержит ровно
га+1 точек, и точка Ъъ, не лежащая на /2, лежит ровно на гг+1
прямых; следовательно, 1\, которая не содержит Ь3, также
должна содержать гг+1 точек. Таким образом, свойство а) влечет
за собой свойство в).
Но для любой точки Ь можно найти прямую, не проходящую
через нее, и поэтому так же, как и выше, существует ровно гг+1
прямых, проходящих через Ь, чем доказаны свойства б) и г).
Докажем теперь свойство д), исходя из а). Пусть Ь0 —
некоторая точка плоскости я, и пусть 1\, /2,..., 1п+\ — гг+1 прямые.
130

проходящие через Ь0. Эти прямые содержат все точки плоскости
л, причем каждая из них содержит Ь0 и п других точек. Ь0 —
единственная точка, принадлежащая любым двум из прямых 1\,
12,...,1п+и Следовательно, плоскость я содержит 1-\-(п-\-\)п =
= я2+я+1 точек. Установим теперь свойство е). Пусть /о—
некоторая прямая плоскости я, и пусть Ьи...,Ьп+1 суть я+1 точек
этой прямой. Каждая из этих точек лежит на /о и на п других
прямых. Таким способом мы получаем все прямые плоскости я;
их, следовательно, 1 + ("+1)" = "2+"+1- Итак, из свойства а)
вытекают все остальные свойства, указанные в теореме.
В силу двойственности из б) также следуют все остальные
свойства. Очевидно, что из в) следует а), а из г)—б). Если
справедливо свойство д) и некоторая прямая состоит из т+1
точек, где т — натуральное число, то плоскость я состоит из
т2+#г+1=я2+я+1 точек, откуда т = п, т. е. из д) следует а).
Аналогично из е) следует свойство б). Теорема доказана.
Условимся называть порядком конечной проективной
плоскости число п, если каждая прямая этой плоскости содержит га+1
точек. Заметим, что плоскость имеет порядок п, если она
обладает любым из шести свойств, отмеченных в теореме 4.
Наименьший порядок конечных проективных плоскостей равен 2. «Самая
маленькая» конечная плоскость — это конфигурация Фано,
каждая прямая которой содержит ровно 3 точки, изображена на
рис. 5.4. Всего в этой плоскости 7( = 22+2+1) точек и столько
же прямых. Прямыми в этой плоскости являются: 1\\ 1, 2, 6; /2:
1, 3, 5; /3: 2, 3, 7; /4: 1, 4, 7; /5: 3, 4, 6; /6: 2, 4, 5; /7: 5, 6, 7.
Уже на этом простейшем примере проявляются возможности
интерпретации конечных проективных плоскостей. А именно
конечная проективная плоскость порядка 2 оказывается системой
троек Штейнера порядка 7. Заметим, что эта система является
блок-схемой с параметрами о = Ь = 7, к = г=3, Х=\. В общем
случае плоскости порядка п являются блок-схемами, параметры
которых имеют вид: а = Ь = п2 + п+\, к~г=п + \, Я=1, т. е.
симметрическими уравновешенными неполными блок-схемами. Обратно,
блок-схемы с такими параметрами являются конечными
проективными плоскостями, так как, очевидно, выполняются все аксиомы.
Установим еще одну полезную связь между конечными
проективными плоскостями и полными семействами ортогональных
латинских квадратов.
Теорема 5. Пусть п^З — произвольное целое число.
Проективная плоскость порядка п существует тогда и только тогда,
когда можно построить полное семейство п—1 ортогональных
латинских квадратов порядка п.
Доказательство. Пусть дана конечная проективная
плоскость я порядка п. Рассмотрим на ней прямую /. На этой
прямой, как известно, имеется п-\-\ точек: щ, а,2,...,ап+и Пусть
Ь1г Ь2, . .. , ЬП' — остальные п2 точек плоскости я, не лежащие
на /. Каждая точка а, (/=1, 2, ...,л+1) лежит на п прямых, не
5*
131

считая прямую /. Пронумеруем произвольным образом
натуральными числами от 1 до гг все п прямых, проходящих через точку
а,-. И так поступим для каждого /=1, 2,..., гг+1. Пусть прямая
Ьхщ пронумерована натуральным числом а^-. Тогда Л = ||а^||, где
1=1, 2,..., гг2; /=1, 2,...,л+1, есть п2Х (га+1) -таблица из
элементов 1, 2,..., п.
Строки любой (гг2Х2)-подтаблицы, выбранной из А,
представляют п2 пар из элементов 1, 2,..., гг. Если предположить, что
аи = ап и а1к = агь, где 1ф)\ ]фк, то ^ = ^" и&д = Ьгай.
Но в этом случае прямая Ьф-/ содержит как точку а/,
так и ак, т. е. прямая '^Ь1, совпадает с прямой /, что
противоречит нашему предположению. Значит, матрица Л=||а^-|| является
ортогональной п2Х (я+1) -таблицей силы 2, которая, как было
доказано в гл. 4, эквивалентна полному множеству п—1
ортогональных латинских квадратов порядка п.
Докажем обратное утверждение. Пусть дано полное
множество п—1 ортогональных латинских квадратов порядка п. От
него переходим, как было сделано в гл. 4, к таблице
А = \\ац\\; 1=1, 2,.... п2; /= 1, 2,...,л+1.
Каждый из гг2 строк таблицы Л сопоставим точки Ъи Ь2,. .. ,Ьпг,
а столбцам — точки щ, а2, ..., ап+\. Определим прямую /1
как состоящую из точек щ, а2,...,ап+1. Через каждую точку а;-
проведем п прямых /1з-, содержащих те точки Ь{, где в /-м
столбце стоит число I. Получается конечная проективная плоскость
порядка п, в которой п2-\-п-\-\ прямых и такое же число точек,
причем каждая прямая содержит ровно гг—(— 1 точек и каждая
точка лежит на гг + 1 прямых. В самом деле, пусть /,-;- и /(-/ —
две прямые, причем 1Ф1'. Эти прямые инцидентны с одной и
только с одной точкой а,. Прямые /,;- и / также инцидентны с
одной и только с одной точкой. Это доказывает требование 3 в
определении проективной плоскости. Четыре точки: (1, 1), (1, 2),
(2, 1), (2, 2)—удовлетворяют требованию 3 определения
проективной плоскости. Значит, построенная плоскость л
действительно является проективной плоскостью порядка п. Теорема
полностью доказана.
Введение координат. Выберем в проективной плоскости я
четыре точки А, В, О, Е в общем положении (см. рис. 5.5). Будем
называть пучком А множество прямых, проходящих через
точку а. Поставим в соответствие каждой прямой пучка А ту
прямую пучка В, с которой она встречается на прямой ОЕ.
Каждую из прямых пучка А (кроме АВ) снабдим особым
символом а и тот же самый символ припишем соответствующей
прямой из пучка В. Прямой АО припишем символ 0, прямой АЕ —
символ 1. Прямые ВО и ВЕ получат те же символы. Таким
образом определяется некоторое множество символов М = {0,
1, {а}}.
Пусть точка Р не принадлежит прямой АВ (рис. 5.5). Через
132

0(0,0)
Рис. 5.5
нее проходит по одной прямой из каждого пучка А и В, а
именно прямые АР и ВР. Пусть прямой АР приписан символ а, а
ВР—символ Ь. Тогда точке Р поставим в соответствие
упорядоченную пару символов (а, Ь) из М, которые назовем
координатами этой точки. Легко видеть, что соответствие между точками,
не лежащими на АВ, и парами (а, Ь) будет
взаимно-однозначным. При этом у точек, расположенных на ОЕ, обе координаты
окажутся равными. Снабдим теперь координатами точки
прямой АВ, отличные от А. С этой целью соединим точку С (см.
рис. 5.5) с О и посмотрим, где прямая 00 пересечется с АЕ.
Вторую координату точки пересечения и будем считать
координатой точки О-
Заметим, что тем же самым построением можно получить
декартовы координаты в обычной действительной плоскости.
Точкой А следует считать несобственную точку оси у, точкой В —
несобственную точку оси х, О — начало координат, Е — точку
(1. О-
Определим над получившимся в результате координатизации
множеством М тернарную операцию, т. е. каждой упорядоченной
тройке элементов х, т, Ь из М поставим в соответствие
некоторый элемент
у — х-т°Ь,
лежащий в М. Этот элемент у по данным элементам х, т, Ь
определяется как вторая координата точки пересечения
прямой х из пучка А с прямой (т), (О, Ъ) (рис. 5.6). Очевидно, что
таким способом у определяется однозначно.
Теорема 6. Всякое задание четырех точек А, В, О, Е в общем
положении определяет тернарную операцию со следующими
свойствами:
1. 0-т°с~а-0°с = 0.
2. 1 -т°0 = т- 1°0 = т.
3. а-т°г=С однозначно разрешимо относительно г.
4. Х'т\°Ъ\=х-тч°Ъч однозначно разрешимо относительно х.
5. Система
а\-т°Ъ = с\; а2-т°Ь^с2; аг=а2,
однозначно определяет пару (т, Ъ).
133

Доказательство. Выбрав четыре точки А, В, О, Е,
никакие три из которых не лежат на одной прямой плоскости я,
мы образуем тернарное кольцо с операцией х-т°Ь так, как это
делалось выше. Свойства 1 и 2 немедленно следуют из
определения. Свойство 3 означает, что прямая, соединяющая точки
(т) и (а, с), пересекает ОВ во вполне определенной точке (О,
г). Смысл требования 4 заключается в том, что две прямые: у =
= х-гп\°Ь\ и у=х- т2°Ь2 с различными направлениями т\ и т2 —
пересекаются в единственной конечной точке. Требование 5
говорит о том, что если (щ, сг) и (а2, Сг)—две конечные точки
при а.\фа.ъ то существует единственная прямая у=х-т°Ь,
проходящая через эти две точки.
Множество М с тернарной операцией, обладающей
свойствами 1—5 из теоремы 6, называют тернаром. Если данный тернар
построен над плоскостью я по вышеуказанному правилу, то он
называется тернаром плоскости я.
Приведем без доказательства следующий результат.
Теорема 7. Если дан тернар М, то с его- помощью можно
определить проективную плоскость с точками: (а, с), (т), А и
прямыми у = х-гп°Ь, х=а, 1Х, где а, Ъ, с, гп — всевозможные
элементы из М, А и /оо — некоторые вспомогательные символы, а
инцидентность определяется следующим образом: (а, с)
инцидентна с у=х-гп°Ь тогда и только тогда, когда с=а-т°Ь; (а, с)
инцидентна с х = а при всех с; (т) инцидентна с у = х-т°Ь при
всех Ь; (т) при всех т инцидентна с 1Х\ А инцидентна с х=а
при всех о и с /оо.
Введем для данной плоскости я натуральные операции —
сложение и умножение, определяемые, исходя от одного из
тернаров этой плоскости, по следующим правилам:
а-\-Ъ = а- \°Ь;
аЬ = а-Ь°0.
Множество М с так определенным сложением и умножением
называют натуральным телом плоскости л.
Заметим, что натуральное тело, вообще говоря, не определяет
породивший его тернар и теорема, аналогичная теореме 7, в
этом случае места не имеет.
Итак, конечные проективные плоскости допускают различные
интерпретации: через тернары, блок-схемы и полные семейства
ортогональных латинских квадратов. Однако теория конечных
плоскостей еще далеко не разработана. Не получен даже
полный ответ на вопрос об объеме этого класса комбинаторных
объектов, о том, при каких условиях конечные плоскости
существуют, а при каких — нет.
Известно, что конечная проективная плоскость существует,
если ее порядок п имеет вид ра, где р — простое число, а а —
натуральное число. В самом деле, было доказано (см. гл.. 4), что
если п=ра, п^З, то существует полное семейство из п—1
ортогональных латинских квадратов. А существование такого множе-
134

ства эквивалентно существованию искомой конечной
проективной плоскости.
Из остальных результатов отметим: а) конечная плоскость
не существует, если п=1, 2 (той 4) и если свободная от
квадрата часть п имеет хотя бы один простой множитель р =
= 3(тос14); б) необходимым условием существования конечной
проективной плоскости, порядок которой имеет вид га=1,
2 (той 4), является существование целых чисел х и у таких, что
п = х2-\-у2 (теорема Брука—Райзера). Мы не приводим
доказательств; они довольно сложны. Из этих результатов, в частности,
следует отсутствие плоскостей для я = 6, 12 и 14. Вопрос
относительно я=10, 18 и 20 остается открытым. Чтобы дать
почувствовать трудность проблемы, укажем, например, что задача
построения плоскости 10-го порядка требует построения семейства
из 9 попарно-ортогональных латинских квадратов того же
порядка.
Важным направлением теории конечных проективных
плоскостей являются подсчет числа плоскостей данного порядка и
изучение их различных видов. К 1956 г. было доказано, что при
я<9 (п=2, 3, 4, 5, 7, 8) существует единственная проективная
плоскость порядка п, а именно дезаргова. Три плоскости,
построенные Вебленом и Веддербарном в 1907 г., вместе с дезар-
говой плоскостью, построенной годом раньше Вебленом и Бас-
си, являются единственными, известными для порядка 9 и в
настоящее время. Новых плоскостей не получено, как не доказано,
что их нет вообще. В этом направлении предпринимаются
многочисленные исследования. Похоже, что близко к завершению
решение вопроса о существовании проективных плоскостей
порядка 10.
5.4. ГРАФЫ
На языке теории графов хорошо описываются многие типы
комбинаторных задач. При этом графические представления
являются не просто иллюстрациями, но и позволяют получать
новые результаты. В этом параграфе мы дадим необходимые
сведения из теории графов, которые используются в настоящей
книге.
Ориентированным графом (или просто орграфом) называется
тройка С=(Х, А, ф) состоящая из непустого множества X,
элементы которого называются вершинами, множества А дуг и
функции ф: А^-ХхХ, которая ставит в соответствие каждой дуге
оеЛ упорядоченную пару (р, д) вершин, называемых концами
этой дуги. Дуга с концами (р, р) в одной и той же вершине
называется петлей. Граф, у которого нет таких дуг, называется
графом без петель.
На рис. 5.7 изображены четыре орграфа; каждый с четырьмя
вершинами. Все эти графы не имеют петель. Кроме того, они
просты: последнее по определению означает, что любая пара вер-
135

шин р, д соединена не более чем одной дугой. В простых
орграфах будем обозначать единственную дугу с концами р, д (если
она существует) через рд.
Рис. 5.7 Рис. 5.8
Опишем два важных семейства простых орграфов, каждый из
которых зависит от параметра п. Простой путь длины п состоит
из гг+1 вершин: Х\,...,хп+\ и п дуг, соединяющих соседние
вершины: хкхк+1. Простой контур длины п состоит из п различных
вершин: Х\,...,хп и п дуг вида хкхк+1 для к<п и, кроме того,
хпХ\ (в частности, простой контур длины 1 является петлей с
■вершиной Х\). Все простые пути длины п изоморфны, и все
простые контуры длины п изоморфны (см. определение ниже). На
рис. 5.7, а изображен простой путь длины 3, а на рис. 5.7,6 —
простой цикл длины 4.
Изоморфизмом орграфов С=(Х, А, ф) и С*=(Х*, А*, ф*)
называется такая пара биекций р: Х-^-Х* и /: А—>-А*, что в О
дуга а идет от вершины р к вершине д в том и только в том
случае, когда в С* дуга /(а) идет от вершины р(р) к вершине
р(д). Иными словами, ф(а) = (р, д) в О равносильно условию
Ф*(/(а)) = (р(р), р(д)) в О*. Два орграфа называются
изоморфными, если между ними существует изоморфизм. Изоморфные
орграфы естественно отождествлять.
Всякий орграф 0=(Х, А, ф) определяет на множестве своих
вершин бинарное отношение следования а. По определению рад
означает, что ф(а) = (р, д) для некоторого а^А. Обратно, всякое
бинарное отношение р на множестве X определяет простой
орграф С(р) = (Х, А(р), 1|з), у которого Л(р)={(р, д)\р<=Х, де=Х,
рад} и у$>(рд) = (р, д). Отсюда непосредственно следует, что класс
множеств с одним бинарным отношением (X, р) находится в
естественном биективном соответствии с классом простых
орграфов.
Неориентированным графом (или просто графом) называется
тройка С=(Х, Е, 0), состоящая из непустого множества X,
элементы которого называются вершинами, множества Е ребер, и
136

функции в, ставящей в соответствие каждому ребру ое^
неупорядоченную пару вершин (р, ¢) = (^, р), которые называются
концами этого ребра. Ребро (р, р) называется петлей.
Понятия, введенные для орграфов, можно распространить на
неориентированные графы, если считать, что неориентированное
ребро (р, д) отвечает паре дуг рц и цр.
Простая цепь длины п состоит из п+1 различных вершин
хи..., хп+1 и п ребер, соединяющих соседние вершины. Простой
цикл длины п состоит из п различных вершин: хх,...,хп и п
ребер вида (хь, хк+\) для к<п и, кроме того, ребра (хп, Хг).
Орграф О можно рассматривать также как пару 0=(Х, Г),
образованную множеством X и многозначным отображением
множества X в себя (т. е. отображением X в множество Р(Х) всех
подмножеств множества X). Для графа, изображенного на
рис. 5.8, имеем: Г(хг)={х2, Хь}\ Г(х2)~0. Через Г_! (хк) будем
обозначать множество вершин хк графа, для которых в С
существует дуга (хк, Х{). Пусть Хд = {хи ...,хд}. Тогда под Г(Х())
понимают объединение Т(х1)[}... [}Т(Хд). Отображение Г(Г(л:1))
записывается как Г2 (я,-). Аналогично «тройное» отображение
Г (Г (Г (я,-))) записывается как Г3(л:г) и т. д. Например, для
нашего орграфа имеем:
Г2(х1)=Г(Г(л:1))=Г({хь х2, хе})={хи х2, х5, х6};
Г3(.Г,)=Г({хь Х2, ХЪ, *б} ) = {*!, Х2, Хь х5, х6}.
Граф (X', А') называется подграфом графа (X, А), если X'
и А' содержатся соответственно в X и А. Остовным подграфом
(частичным графом) Ор графа С=(Х, А) называется граф (X,
Ар), для которого АР<=А. Таким образом, остовной подграф
имеет то же множество вершин, что и граф О, но множество дуг
подграфа Ср является подмножеством множества дуг исходного
графа. Пусть дан граф С=(Х, Г). Порожденным подграфом С8
называется граф (Х8, Г,5), для которого Х$^Х и Г5(х,) =Г(х,)П
Л^.5 для каждой вершины х^Х8. Таким образом, порожденный
подграф состоит из подмножества вершин Хв, множества вершин
исходного графа и всех таких дуг графа О, у которых конечные
и начальные вершины принадлежат подмножеству Х8. На
рис. 5.9, а, б приведены соответственно порожденный подграф,
остовный подграф и подграф, не являющийся ни порожденным,
ни остовным графа О, изображенного на рис. 5.8.
«4- Лс -А*
Рис. 5.9
137

Пусть 0= (X, А)—орграф с множеством вершин X,
множеством дуг А. В случае, когда мы хотим пренебречь
направленностью дуг из множества А, то неориентированный граф,
соответствующий О, будем обозначать как С=(Х, А) и называть его
неориентированным двойником графа О. Неориентированный
граф С называется связным, если каждая пара его вершин
может быть соединена цепью. Конечный граф, который не является
связным, может быть разбит на конечное число связных
подграфов, называемых его компонентами. Неориентированный граф С
называется полным, если для каждой пары его вершин
существует ребро, их соединяющее. Полный граф на п вершинах
принято обозначать через Кп- Неориентированный граф называется
двудольным, если множество его вершин можно разбить на
такие два подмножества Х\ и Х2, что каждое ребро имеет один
конец в Хи а другой в Х2; здесь Хх[\Х2 = 0. Двудольный граф С =
= (^11^2, А) называется полным, если для любых двух вершин
Х{^Хг и х^Х2 существует ребро (х^ х^^А. Если |Лп|=и и
\Х2\=гп, то полный неориентированный граф 0=(^1^1^, А)
обозначается через Кп,т- Орграф С называется связным
(соответственно двудольным), если таковым является его
неориентированный двойник С.
Степенью вершины в неориентированном графе называется
число тех ребер, концом которых она является.
Рассмотрим неориентированный граф С=(Х, А) без петель.
Выберем некоторое ребро а= (х, у)^А. Заменим вершину у во
всех ребрах Ье(Л\{а}), на вершину х и обозначим полученное
множество ребер через А'. Скажем, что граф 0'=(Х\{у}, А')
получен из графа О в результате стягивания ребра а в
вершину х. Граф О называется планарным, если он может быть
нарисован на плоскости таким образом, что произвольные два ребра
графа не пересекаются друг с другом. На рис. 5.10 изображены
полный граф Кь и полный
двудольный граф Дз,з, которые, как известно,
не являются планарными. Этих два
графа играют важную роль в теории
планарных графов и известны как
к5 Лз'3 графы Куратовского, поскольку
Кураре 5\1о товский впервые установил, что
неориентированный граф О непланарен
тогда и только тогда, когда он содержит пограф, стягиваемый к
графу Къ или графу Кг,ъ-
Матрица смежности. Пусть дан простой орграф С с
вершинами х\, Х2,...,хп- Его матрицей смежности называется квадратная
матрица В = ||Ь^|| порядка п, где
Г 1, если в О существует дуга (хс, х.-);
" | 0, если в С нет дуги (хс, X/).
Таким образом, матрица смежности графа, изображенного на
#
138

рис. 5.8, имеет вид:
Хл Хл Хо Хл ЛЬ Ха
Ч
Ч
х3
х4
Ч
хв
1 1
0
0
0
0
1о
1
0
1
1
0
0
1
0
0
0
0
0
1
0
0
1
1
0
0
0
1
0
0
1
П
0
0
0
0
0}
в
Матрица смежности полностью определяет структуру графа.
Например, сумма всех элементов строки Х{ матрицы В дает число
дуг, которые имеют вершину х,- своей начальной вершиной, а
сумма элементов столбца х* — число дуг, которые имеют x^ своей
конечной вершиной. Множество столбцов, имеющих 1 в строке
Хг, есть множество Г(хг), а множество строк, которые имеют 1 в
• столбце х,-, совпадает с множеством Г ! (х,).
Возведем матрицу смежности в квадрат. Пусть Ь,ь(2) — эле-
п
мент матрицы В2, тогда Ь$ = V Ьп-Ь{к. Слагаемое ЪцЪ^ равно 1
тогда и только тогда, когда оба числа Ь^ и Ь^ равны 1, в
противном случае оно равно 0. Из равенства Ь^=Ь^ следует
существование 'пути длины 2 из вершины х,- к вершине х&,
проходящего через вершину х3-. Следовательно, Ь,ь(2) в матрице В2 равно
числу путей длины 2, идущих из х,- в дс&.
Аналогично элемент Ъ^) матрицы Вр равен числу путей (не
обязательно простых) длины р из х,- в х&.
Матрица смежности неориентированного графа строится
аналогично.
Матрица инциденций. Пусть дан орграф О с вершинами
хь Х2,—,хп и дугами аи а2,-..,ат. Матрицей инциденций графа С
называется матрица Л = ||а,-3-|| размера пХт, строки которой
соответствуют вершинам, а столбцы — дугам, и
а-ц
1, если вершина х; является началом дуги а;-;
1, если вершина х; является концом дуги а;-;
0, если вершина х(- не инцидентна дуге а;- или если
дуга а;- является петлей.
Например, для графа, приведенного на рис. 5.8, матрица
инциденций имеет вид:
аг
х^О
х2
Хз
х4
Ч
Ч
0
0
0
0
10
аг
1
— 1
0
0
0
0
а3
0
— 1
1
0
0
0
а4
1
0
— 1
0
0
0
а-ъ
0
— 1
0
1
0
0
ав
1
0
0
— 1
0
0
а7
0
0
1
0
— 1
0
а8
0
0
0
— 1
1
0
а»
0
0
0
0
0
0
<*ю
0
0
0
0
—1
1
Оц
П
0
0
0
0
-1.
139

Поскольку каждая дуга инцидентна двум различным вершинам,
за- исключением того случая, когда одна дуга образует петлю, то
каждый столбец содержит либо один элемент, равный 1, и один,
равный —1, либо все элементы, равные 0.
Если О является неориентированным графом, то его матрица
инциденции определяется так же, как и выше, за исключением
того, что все элементы, равные —1, заменяются на + 1.
Матрица циклов (контуров). Пусть С — неориентированный
граф. Занумеруем его ребра а\, ач,...,ат и простые циклы с\,
С2,.--,ср. Матрицей циклов графа О называется матрица С = ||с^-||
размера рХт, где
_ [ 1, если простой цикл с1 графа С содержит ребро а,-;
( 0—в противном случае.
Таким образом, строки матрицы циклов соответствуют простым
циклам, а столбцы — его ребрам.
Если О — орграф, то занумеруем его дуги аи а2,...,ат и
простые контуры с\, С2,...,ср; матрица контуров С=\\с^^\
определяется аналогично:
1, если контур с( содержит дугу а,- и они
с . _ одинаково ориентированы;
" —1, если контур с( содержит дугу, обратную а,;
0—в остальных случаях.
Замечание. Выбор одинаковых символов для обозначения
матриц ориентированного и неориентированного графов
определяется тем, что основные свойства структуры этих матриц
одинаковы у ориентированных и неориентированных графов.
Поэтому при введении таких символов путаницы не произойдет.
Кроме того, свойства матриц орграфов и способы доказательства их
такие Же, как и для матриц неориентированных графов.
Упражнения. Убедитесь в справедливости следующих утверждений.
1. В любом конечном неориентированном графе число вершин нечетной
степени четно.
2. Пусть А — матрица инциденции простого неориентированного графа
без петель. Тогда матрица смежности В получается из ААТ (где Ат —
матрица, получаемая транспонированием матрицы А) путем замены всех элементов
на диагонали нулями.
3. Граф О является двудольным тогда и только тогда, когда для любого
нечетного числа п все диагональные элементы матрицы Ап равны нулю.
4. Если графы 0| и 0% изоморфны, то
II « • • матрицы смежности этих графов имеют
N. / одинаковые собственные значения.
N. / Замечание. Обратное утверждение
Ъ^ в общем случае не имеет места. Напрп-
I I / N. мер, два графа, изображенные на рис. 5.11,
/ >ч имеют одинаковые собственные значения
' * (Я==Ь2, 0, 0, 0), но, очевидно, не
являются изоморфными.
Рис 5.11 5. Любой минор матрицы инциденции
графа О равен +1,-1 или 0.
140

6. Ранг матрицы инциденций А связного графа (ориентированного и
неориентированного) Осп вершинами равен п—1.
7. Ранг матрицы циклов С связного графа Ост ребрами и п вершинами
равен т—п + 1.
8. Матрица инциденций А ортогональна матрице СТ, транспонированной
к матрице циклов С и полученной при таком же порядке нумерации ребер,
как и^в матрице инциденций А, т. е., другими словами, ЛСт = 0(мос12).
Эйлеровым графом называется неориентированный граф,
обладающий свойством: существует цикл, проходящий ровно один
раз по каждому из ребер графа. Цикл" в определении эйлерова
графа называется эйлеровым.
Теорема 8. Конечный неориентированный граф О является
эйлеровым тогда и только тогда, когда он связный и все его
вершины четной степени.
Доказательство. Очевидно, наши условия необходимы,
поскольку каждый раз, когда эйлеров цикл проходит через
какую-то вершину, он должен войти в нее по одному ребру и
выйти по другому.
Обратно, предположим теперь, что О связный и все его
вершины четной степени. Начнем цепь Р в произвольной вершине х
графа О и будем продолжать ее, насколько возможно, все
время через новые ребра. Так как в каждой вершине число ребер
четно, этот процесс может закончиться только в х. Если Р
содержит не все ребра графа О, то удалим из С часть Р,
состоящую из ребер этого цикла.
Графы Р и О имеют четные степени вершин; то же должно
быть справедливо и для оставшегося графа Р. Так как граф С
связный, в Р должна найтись вершина у, инцидентная также
ребрам из Р. Из у_ можно построить новую цепь Р', содержащую
ребра только из Р. Снова такая цепь может закончиться
только при возвращении в у. Но тогда из Р и Р' можно составить
новый цикл:
Р1 = Р{х, У)[}Р'\}Р{У, х),
который возвращается в х и содержит больше ребер, чем Р. Если
Р\ не является эйлеровым циклом, то это построение
повторяется. Когда этот процесс закончится, эйлеров цикл будет
построен.
Гамильтоновым циклом (гамильтоновыя контуром)
называется простой цикл (простой контур), проходящий через все
вершины графа. Граф называется гамильтоновым, если он
содержит гамильтонов цикл.
В применениях графов к играм вершины соответствует разным
позициям. Таким образом, существование гамильтонова цикла
равносильно существованию циклической последовательности ходов,
содержащей каждую позицию по одному разу. Примером является
известная задача о шахматном»коне: можно ли, начиная из
произвольного поля на доске, ходить конем в такой последовательности,
чтобы пройти через каждое из шестидесяти четырех полей и
вернуться на исходное поле? На рис. 5.12 указано одно из возможных
решений.
141

56
47
42
45
20
29
6
1
41
44
57
48
5
64
19
28
58
55
46
43
30
21
2
7
35
40
49
54
63
4
27
18
50
59
36
31
22
17
8
3
39
34
53
62
11
14
23
26
60
51
32
37
16
25
12
9
33
38
61
52
13
10
15
24
Рис. 5.12
На рис. 5.13 приведен пример эйлерова, но не гамильтонова
графа, а на рис. 5.14 — гамильтонова, но не эйлерова графа.
Несмотря на сходство в
определениях для эйлеровых и гамильтоновых
циклов, соответствующие теории для
этих понятий имеют мало общего.
Критерий существования эйлеровых
циклов прост (см. теорему 8); для
Рис. 5.13 Рис. 5.14 гамильтоновых циклов никакого
общего правила не известно. Более
того, иногда даже для конкретных графов бывает трудно решить,
можно ли найти такой цикл. Некоторые условия, при которых в
графе существует гамильтонов цикл, все же найдены и приведены
в различных книгах по теории графов. Желающим ознакомиться
с этими результатами рекомендуем книги [24], [25].
Деревом называется связной неориентированный граф без
циклов. Лесом называется неориентированный граф, каждая
компонента которого является деревом.
Теорема 9. Следующие утверждения эквивалентны:
а) неориентированный граф О — дерево;
б) любые две вершины в О связаны единственной цепью;
в) граф С является связным, но удаление любого его ребра
делает его несвязным;
г) добавление любого нового ребра к графу О приводит к
появлению в точности одного цикла.
Доказательство этой теоремы ввиду его тривиальности
опускаем.
Следующий результат о деревьях принадлежит Кэли, который
исследовал эти графы в связи с химическими структурными
формулами.
Теорема 10. Число различных деревьев, которые можно
построить на п данных вершинах, равно гап-2.
Доказательство. Пронумеруем все вершины дерева Т
натуральными числами от 1 до п. Обозначим через Ь4 висячую
вершину (т. е. вершину степени 1) с наименьшим номером, а через
и= (Ь, ау) — соответствующее висячее ребро. Удалив из Т ребро 1%
и вершину Ь{, получим новое дерево Ту. Для Ту найдем висячую
^
142

вершину с наименьшим номером; обозначим ее через Ьг, а
соответствующее ребро — через к= (Ьг, аг). Эта редукция повторяется,
пока после удаления ребра 1п-г= Фп-г, а„_2) не останется
единственное ребро /„_!= (Ьп_1, а„_1), соединяющее две оставшиеся
вершины. Тогда следующий набор в скобках
(аи а.2,..., а„_2),
называемый кодом Прюфера, однозначно определяется деревом Т
и двум различным деревьям Т и Т', очевидно, соответствуют
различные коды Прюфера.
Кроме того, коды Прюфера определяют деревья Т с помощью
обратного построения. Если дан код, то находится первая
вершина Ьи в нем не содержащаяся. Это определяет ребро /1=(61, 0,1).
Далее удаляем вершины а4 из кода и Ь4 из последовательности 1,
2, ..., п и продолжаем построение для оставшихся чисел.
Получившийся в результате граф является деревом, что может быть
установлено, например, по индукции. После удаления а4 код будет
содержать п—3 числа. Если они соответствуют дереву 7\, то граф
Т, получаемый из него добавлением ребра /1=(61, 01), также
является деревом, так как вершина Ъ\ не принадлежит 7\. Таким
образом, мы установили, что между кодами Прюфера и
деревьями имеется взаимно-однозначное соответствие. Но в коде Прюфера
каждый элемент может принимать любое из п возможных
значений. Все они соответствуют различным деревьям. Всего кодов
Прюфера может быть гс"-2, отсюда и следует наша теорема.
Если С — неориентированный граф с множеством вершин X,
\Х\=п, то остовным деревом (или просто остовом) графа С
называется всякий остовный подграф графа С, являющийся
деревом. Ребра графа, принадлежащие остову, называются ветвями,
а все остальные — хордами.
В некоторых ситуациях возникает необходимость в построении
полного списка остовов графа С (например, в том случае, когда
надо отобрать «наилучшее» дерево, а критерий, позволяющий
осуществить такой отбор, является очень сложным, так что
непосредственное решение задачи оптимизации оказывается
невыполнимым). В других ситуациях, например при нахождении
передаточных функций системы или при вычислении определителей
некоторых матриц в макроэкономической теории, с помощью всех
остовов соответствующего графа можно добиться упрощения
вычислительных процедур.
Число различных остовов полного связного неориентированного
помеченного графа на п вершинах дает нам теорема 10. Формулы
для числа остовов в более общих графах можно найти в книге
[14]. Приведем один из результатов.
Теорема 11. Пусть С — ориентированный граф без петель на
п вершинах и Л0 — его матрица инциденций с одной удаленной
строкой (т. е. матрица с п—1 независимыми строками). Пусть
А0Т — транспонированная матрица к Ао. Тогда определитель
143

Рис. 5.15
произведения АоА0т_равен числу
различных остовов графа О,
неориентированного двойника С.
Доказательство этой теоремы можно
найти в [78]. Алгоритмы же
порождения всех остовных деревьев графа
подробно разобраны в [24].
Все остовные деревья графа,
изображенного на рис. 5.15,, а их 21,
приведены на рис. 5.16. Матрица инциденций
графа имеет здесь следующий вид:
а2 а3 а4
1 0 0
0 1 1
1 —1 0
0 0—1
аъ аа
0 0
1 0
0 1
0 —1
а
0
0
0
1
1
— 1
0
0
0 0 0 0—1 0—1
Здесь мы считаем, что каждое ребро ориентировано от его
концевой вершины с меньшим индексом к вершине с большим
индексом.
АЛА
,А А
Рис. 5.16
Удаляя, например, строку х%, получаем матрицу Ао.
Произведение матриц А0Аот выглядит тогда так:
АИо ~"
/2—1 0
| —1 3—1
10—13
V 0 0—1
0
0
2
Определитель произведения равен 21. Следовательно, на рис. 5.16
приведен полный список остовов графа О, изображенного на
рис. 5.15.
144

Многие полученные остовы, очевидно, изоморфны, и возникает
вопрос о числе неизоморфных среди них. Это более трудная за-,
дача, но она очень важна для многих приложений. Поэтому и по
аналогичным вопросам, связанным с перечислением всех
неизоморфных графов частных типов, существует обширная
литература. Большинство этих работ опирается на теорию Редфилда —
Пойа (см. § 2.5).
Ориентированным деревом с корнем хо называется связный
орграф, где из вершины х0 в каждую другую вершину ведет путь, и
притом единственный.
Пусть С — неориентированный граф с п вершинами, т
ребрами и р связными компонентами. Число р(С)=п—р называется ко-
цикломатическим. Число V(С)=т—р(С)=т—п-\-р называется
цикломатическим.
В теории электрических цепей числа р(О) и V(0) имеют
прямой физический смысл. Так, цикломатическое число равно
наибольшему числу независимых контуров в графе электрической
цепи, т. е. наибольшему числу независимых круговых токов,
которые могут протекать в цепи. Коцикломатическое число равно
наибольшему числу независимых разностей потенциалов между
узлами электрической цепи.
Упражнения. 9. Приведите примеры ориентированных деревьев с
корнем.
10. Докажите, что цикломатическое число дерева равно 0.
11. Докажите, что каждое дерево является двудольным графом.
Пусть Т — остов графа С. В общем случае V(0) циклов,
получаемых добавлением какой-либо хорды из О к ветвям Т,
называются фундаментальными циклами.
Следует заметить, что хотя число фундаментальных циклов
равно V(0), сами эти циклы определены неоднозначно и зависят
от первоначально выбранного остова Т. Другими словами,
фундаментальный цикл (относительно остова Т) — это цикл,
получающийся добавлением к остову Т хорды. Например, для графа С я
его остова Т, изображенных на рис. 5.17, фундаментальными
циклами будут:
Ф1={а4, аю}; ф2=:{а2, а42, а10}; Фз={аз, сщ, а!3, аа, «к);
Ф4 = :{а4, «и, ац}; Ф5={а5, а41}; Ф6={а6, а15, а13, а!4};
Рис. 5.17
145.

Ф7={а7, Я1з, аи}; Ф8= {а8, а12, а^}; Ф9={а9, а12}.
Если семейство всех фундаментальных циклов обозначить через
Ф (в нашем примере Ф= {ф4,..., Ф9}), то любой другой цикл
графа, не принадлежащий к Ф, может быть выражен в виде линейной
комбинации циклов из Ф, если принять следующие соглашения.
Пусть каждый фундаментальный цикл ¢,-.1=1, 2,...^(0),
представлен т-мерным вектором, в котором /-я компонента
равна 1 или 0 в зависимости от того, принадлежит ли /-е ребро
данному циклу. Тогда любой цикл С графа С можно представить как
сумму по модулю 2 фундаментальных циклов. Так, цикл С{ =
= {аз, ац, ац, а6, а8, а4} нашего графа может быть представлен в
виде
С -^ Фх + Ф3 + Ф6 + Ф8 (той 2) =
100000000100000
001000000111100
000001000000111
000000010001001
(той 2).
- 101001010010010
'Отметим, что обращение вышеприведенного утверждения неверно,,
а именно некоторая сумма по модулю 2 фундаментальных циклов
не обязательно дает единственный цикл, но может представлять
два и более циклов. Например, сумма Ф2+Фз + Фб+Ф7(тос12)
соответствует двум простым циклам {а2, а3, ац, а^} и {ав, а7, а^}.
Таким образом, для порождения всех простых циклов графа О не
надо брать все 2^в)—1 комбинаций фундаментальных циклов и
складывать их по модулю 2: некоторые из этих сумм на самом
деле не будут циклами. Более того, если данная сумма не
порождает цикла, то нельзя отбрасывать другие суммы, ее содержащие,
так как, складывая по модулю 2 ее с другой суммой, мы можем
получить простой цикл.
Отметим также, что в графе О можно найти множество из
\(С) независимых простых циклов, которые нельзя получить
добавлением ребер к дереву, как это делалось выше. О таком
множестве не следует говорить что оно фундаментальное. На рис. 5.18
показано множество из \(С}=4
независимых простых циклов графа О,
которое не может быть получено
добавлением ребер ни к какому остову
графа С и которое поэтому не является
фундаментальным множеством.
Разрезом графа называется
минимальное множество ребер, удаление
которых увеличивает число компонент
графа.
Фундаментальный разрез (относительно остова Т) — это
разрез, содержащий точно одно ребро остова Т. Таким образом, в
1
0
»— :
' 1
(Л)
\ С)
Рис. 5.18
146

связном графе можно выделить п—1 фундаментальных разрезов..
Следующая теорема устанавливает связь между
фундаментальными разрезами и фундаментальными циклами и дает способ-
построения фундаментальных разрезов.
Теорема 12. Если Т — остов неориентированного графа О, то
фундаментальный разрез, определяемый ветвью щ из Т,
образован (ц и теми хордами из О, которые после добавления к Т дают
фундаментальные циклы, содержащие а^,
Доказательство. Если из остова Т удалить ребро а;, то
Т распадается на два поддерева: Т^ и Т2. Любое ребро, одна
концевая вершина которого лежит в Ти а другая в Т2, должно
принадлежать фундаментальному разрезу, так как добавление любого
такого ребра к ребрам из Т1 и Т2 приводит к образованию другого
остова графа О, и, следовательно, любое множество, не
содержащее таких ребер, не будет разрезом. Множество таких ребер-
вместе с ребром щ является разрезом, так как их удаление
разбивает граф на два подграфа, один из которых имеет множество
своих вершин 7\, а другой — Т2. Значит, этот разрез является
фундаментальным разрезом. Более того, поскольку ребро а^
является единственным ребром, через которое проходят цепи остова-
Т, начинающиеся в вершинах из Т± и оканчивающиеся в вершинах
из Т2. то единственными ребрами, замыкающими
фундаментальные циклы, содержащие ребро щ, будут те, одна концевая
вершина которых лежит в Ти а другая в Т2. Это доказывает теорему.
Пусть Т — остов неориентированного графа С. Матрицей
фундаментальных циклов Ф называется подматрица матрицы циклов
С, строки которой соответствуют простым циклам, определяемым
хордами, связанными с данным остовом Т. Другими словами, если
Т — остов, то матрицей фундаментальных циклов графа О
называется матрица Ф = ||ф;/11> состоящая из V(С) строк и пг
столбцов, в которой
(1, если ребро а! принадлежит фундаментальному циклу фг;
О — в противном случае.
Если хорды графа О пронумеровать последовательно ог 1 до*
V(0), а ветви — от ^(0)+1) до пг, то матрица фундаментальных,
циклов будет иметь вид:
Ф = ||^|Ф12||,
где Е — единичная матрица порядка у(С), а Ф12 — матрица
размера VX(т—V). Это объясняется тем, что каждый цикл Ф;
содержит одну и только одну хорду и циклы всегда можно
пронумеровать по числу хорд, вследствие чего все единицы в первой
(VXV) -подматрице матрицы Ф лежат на диагонали.
Матрица фундаментальных разрезов /С=||А<;|| определяется
как матрица с п—1 строками и пг столбцами, где
, _ ( 1, если ребро а,- принадлежит фундаментальному разрезу к(;
10 — в противном случае.
147

При той же нумерации ребер, что и в матрице фундаментальных
циклов Ф, матрица К имеет вид:
К=\\Ки/Е\\,
так как теперь каждый фундаментальный разрез содержит одну
и только одну ветвь из Т.
Пусть граф С и его остов Т изображены на рис. 5.19. Тогда
аг
Рис. 5.19
матрица фундаментальных циклов Ф равна
аг а2 аг а4 аь ае а7 а8 а9 а10 ап а12 а13
•10000001 10000
010000001 1 100
001000000001 1
1110 10 0 1
1110 0 0 0 0
0 0 0 10
0 0 0 0 1
а матрица фундаментальных разрезов К равна
аг а., а3 о, аъ ав а. а8 а9 а10 аи а12 а13
0 0 0 1 1 1 0 0 0 0 0 0 0
0001 101000000
1001 100100000
1 100000010000
0101000001000
0100000000100
0010000000010
0 011000000001
*5
I,
тде разрезы ки соответствующие ребрам остова, имеют номера
V(С) +1 = 5 + 1; 1 = 1, 2,...,8.
Существует несколько интересных соотношений между
матрицами фундаментальных циклов, фундаментальных разрезов и ин-
циденций неориентированных графов без петель.
Теорема 13. Матрица инциденций А0 (с одной вычеркнутой
строкой) и транспонированная матрица фундаментальных циклов
Фт ортогональны, т. е. Л0Фт = 0(тос1 2).
Теорема 14. Матрица фундаментальных циклов Ф и
транспонированная матрица фундаментальных разрезов Кт ортогональны,
т. е. Ф-Кт = 0(той2).
148

Теоремы 13 и 14 являются следствием двух очевидных фактов:
1) каждая вершина в цикле инцидентна четному числу ребер
этого цикла, а в случае простого цикла — двум ребрам;
2) каждый разрез цикла, индуцированный некоторым
разрезом, имеет четное число ребер, общих с этим разрезом.
Теорема 13 следует из факта 1), а теорема 14 — из факта 2),
если вспомнить, что все операции рассматриваются по модулю 2.
По теореме 14 можно написать:
Ф-/Г ==!!^|Ф12!|1! *»
Я[, ! Ф12 = 0(тос12).
Поэтому К\\т =—Ф12 = Ф12(тос12). Другими словами, матрица
фундаментальных разрезов может быть получена, как только
известна матрица фундаментальных циклов, и наоборот.
Упражнения. Убедитесь в справедливости следующих утверждений.
12. Квадратная подматрица размера (я—1)Х(л—1) матрицы инциденций
А связного графа является невырожденной, если столбцы этой подматрицы
соответствуют ветвям некоторого дерева.
13. Пусть матрица циклов С связного графа имеет ранг я—гп+1.
Ее квадратная подматрица В порядка п—т+\ является невырожденной тогда
и только тогда, когда столбцы этой подматрицы соответствуют множеству
хорд относительно некоторого остовлого дерева данного графа.
14. Невырожденная подматрица размера (п—1)Х(л—1) матрицы
инциденций А находится во взаимно-однозначном соответствии с остовами графа.
15. Невырожденная подматрица размера (п—от+1)Х(я—т-\-\) матрицы
циклов С находится во взаимно-однозначном соответствии с дополнениями к
остовам графа.
16. Если столбцы матриц Ао, Ф и К записать с использованием одного и
того же порядка ребер относительно некоторого остовного дерева, по которому
•образованы фундаментальные циклы и разрезы, а затем представить их в виде
Аа=\\Ап \А\2\\, где Л12 — невырожденная квадратная матрица порядка п—1,
Ф = ||Я|Ф12|| и К=\\Кц\Е\\, то
Кп = Ф12т=А12-1-Ап-
На этом мы вынуждены закончить введение в теорию графов.
Последняя накопила огромный фактический материал. Ее
изложению посвящено множество сочинений. Некоторые из книг мы
уже упомянули в тексте. Необходимо, впрочем, обратить внимание
читателей на интересную (и, по-видимому, единственную в своем
роде) книгу [79] о формировании и развитии теории графов.

Глава 6
МЕТОДЫ РЕШЕНИЯ
ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
6.1. ЭКСТРЕМАЛЬНЫЕ КОМБИНАТОРНЫЕ ЗАДАЧИ И
ПОДХОДЫ К ИХ РЕШЕНИЮ
Как было сказано в гл. 1, существуют три типа комбинаторных
задач: в одних решают вопрос о существовании или
несуществовании решений; в других подсчитывают число решений задачи; в
третьих из совокупности всех решений выделяют то, которое
обладает некоторым свойством в максимальной или минимальной
степени. Задачи этого последнего типа и называются экстремальными.
Приведем несколько примеров экстремальных комбинаторных
задач.
1. Задача о назначениях. Имеется п вакантных должностей и
столько же кандидатов на них. Назначение 1-го кандидата на
/-ю должность влечет выплату заработной платы сц : {, /= 1, 2 п.
Каждого кандидата можно назначить только на одну должность,
и на каждую должность может быть назначен лишь один
кандидат. Иными словами, совместительство и дробление должностей не
допускается. Задача состоит в проведении назначений при
максимальной экономии фонда зарплаты, т. е. в нахождении
п
т1п I с11{,
1=1
где /; — место, на которое назначается 1-й кандидат, а
(/ь /2, ..-, }п) — подстановка, соответствующая назначениям: I-*-/».
Если сц интерпретировать как производительность, задача будет
состоять в отыскании максимума, а не минимума. Задачи о
назначениях в зависимости от условий имеют много разновидностей.
•Например, для выполнения п независимых операций выделены т
рабочих; задана матрица 11^-Ц, где 1ц — время, затрачиваемое
1-м рабочим на /-ю операцию. Величина, минимум которой
разыскивают, есть время исполнения всей работы:
Р = тахЕс; Р1 --= ^ 1Ф
где Я{ — множество операций, выполняемых 1-ым рабочим.
В частном случае может быть задано число операций щ для
1-го рабочего: ^п1=п. При щ=\ (1=1, 2,...,«; п=т) полу-
150

чается задача о назначении с критерием минимакса. Наконец,
приведем такую формулировку задачи о назначениях, когда
учитывается время перехода рабочего с одной операции на другую.
Пусть заданы п операций и т рабочих. Составляют матрицы:
^=11^11. где 1ц есть время выполнения 1-м рабочим /-й операции,
и Ь = \\1ц\\, где /;3- — время перехода любого рабочего с 1-й
операции на /-ю. Требуется распределить операции среди рабочих и так
учесть время перехода, чтобы время выполнения всего комплекса
операций было минимальным.
2. Задача о коммивояжере. Коммивояжеру необходимо посетить
несколько городов. Он должен выбрать кратчайший маршрут,
чтобы, начав двигаться из своего города, побывать по одному разу в
других городах и вернуться назад. Попарные расстояния между
городами заданы в виде матрицы С = \\сц\\, I, /=1, 2 п, где п —
число городов.
3. Задача о ранце. Имеется п предметов, веса которых
аи а%, ..., а„, а ценность — 5Ь $2, ..., 5„. Требуется заполнить ранец,
способный вместить вес не более Я, таким набором предметов,
который обладал бы наибольшей ценностью.
Составим вектор Х=(хи Х2,...,хп), где л;, = 1, если 1-й предмет
должен быть помещен в ранец, и я; = 0 — в противном случае:
1=1, 2 п. Задача будет формулироваться как задача об
отыскании
п
тах^ з(х1
{=1
'(максимальной ценности вложенных предметов) при условии, что
п
^ х{ас < Я.
1 = 1
4. Минимизация времени выполнения набора операций. Пусть
требуется выполнить п операций. Поставим в соответствие каждой
операции вершину графа С, где от вершины г к вершине /
проведена дуга, если по технологическим условиям операция г
предшествует операции /. Все операции разбиты на т классов, причем
в данный момент можно выполнять только одну операцию
каждого класса. Известно время выполнения операций (г3- для /-й
операции). Требуется определить порядок выполнения всех операций,
приводящий к минимальному времени Т. Например, дана сеть
(схема) из 6 операций; А\, А%, Аз, Л4 — операции первого класса,
Ви В2 — операции второго класса; время выполнения каждой
операции указано в квадратиках на рис. 6.1. Пусть #4 и #2 —
последовательности выполнения операций для каждого класса
соответственно. Например, при #1=(2, 1, 3, 4); #2= (2, 1)
получим: Т = 36. Очевидно, что число допустимых комбинаций
существенно зависит от структуры сети.
151

5. Минимизация среднего времени обработки партии.
Рассматривается орграф О с вершинами 1, 2,.,., п, где вершина I
соответствует 1-му виду обрабатываемых деталей. Для каждой душ
(£, /) задана ее длина Ц^, которая интерпретируется как период от
обработки деталей 1-го вида до обработки деталей /-го вида. По-
А,
и
К
1 /
2
А
*\
*Л
6\
л
*\
»/
\/
_=►
-
^
^
12
I I
I I
! !
11
4
Рис. 6.1
Рис. 6.2
следовательность вершин 1*1, 1ъ...,1к, 1к+и где £^+1 = 11, задает цикл
обработки. Требуется минимизировать среднее время обработки
к
I <«..».■
/=1
т. е, найти в орграфе О контур с минимальной средней длиной.
6. Минимизация простоя сборочной линии. Пусть п операций
проделываются на конвейере из т участков. Чтобы конвейер
двигался непрерывно, время работы оператора не должно превышать
длительности цикла. Пусть на 1-м участке исполняют множество
операций #;. Тогда время занятости на 1-м участке равно Рь =
= V* 1/, а простой на нем равен й1. = С — V 1^ где С — общая
/ей,- /ек,-
длительность цикла операций. Суммарная величина простоя
т
й= V й{ должна быть сделана минимальной за счет распреде-
1=1
ления операций по участкам. Кроме того, можно поставить вопрос:
а) о минимуме длительности цикла С = тах р{ при заданном чис-
I
ле т участков; б) о минимуме числа т при заданной длине
цикла С. На рис. 6.2 введено 9 операций (в скобках указано число
единиц времени, затрачиваемых на выполнение соответствующей
операции) и 3 участка:
Я= (Яь #2, #з) = (1, 2, 3; 4, 5, 6; 7, 8, 9);
имеем
Л = 21; /^=16-, /^3=14,
152

Общее время простоя
й = Л^ =тС — Т = 3-21 —51 = 12 .
7. Задача о покрытии. Для данного неориентированного
графа О найти минимальное покрытие, т. е. минимальный набор
ребер, такой, чтобы любая вершина оказалась инцидентной
некоторому ребру из этого набора. Формализуем постановку этой задачи.
Занумеруем вершины графа числами 1, 2,..., гп, а ребра числами
1, 2 п. Пусть ||а,-3|| — матрица инциденции графа С. С ребрами
свяжем переменные х2- (/=1, 2 п) такие, что лс;-=1, если ребро/
входит в покрытие; х, = Ь — в противном случае. Нахождение МИ-
нимального покрытия эквивалентно отысканию тш V */ с допол-
нительными требованиями:
п
^ а0-х/> 1; I = 1,2, .. . , т.
Общий вид экстремальной комбинаторной задачи таков.
Имеется «-множество элементов. На нем задается множество (как
правило, конечное) комбинаций
Р= (Ль Л2, ..-, Яг) .
Под комбинациями ль яг, ••-, яг можно понимать перестановки,
сочетания, различные последовательности и т. п. На множестве
Р задается функция Р. Требуется отыскать экстремум Р
(максимум или минимум) или элементы множества Р, которые этот
экстремум доставляют.
Сама формулировка экстремальных комбинаторных задач
диктует выбор операций, применяемых для их решения. Во-первых,
надо располагать множеством значений функции Р, уметь делать
их перебор. Во-вторых, надо развить методику сравнения этих
значений и выделения из них максимального или минимального.
Первая же операция перебора практически редко оказывается
осуществимой, так как число возможных комбинаций может быть
слишком велико. В самом деле, в первом примере число всех
комбинаций равно п\, во втором (п—1)!, в третьем 2", в четвертом'
п
(п\)т, в пятом V (") (к — 1)! и т. д.
Не меньше трудностей доставляет операция сравнения. В
общем случае трудно судить, имеет место Р(щ)>Р(я?) или,
наоборот, Р(т) <Р(л;), без непосредственного вычисления. Кроме
того, само определение значения функции Р(т) представляет
собой, как правило, нелегкую задачу.
Трудности, связанные с перебором вариантов и сравнением
153

значений, весьма значительные. Именно они и являлись
препятствием для развития этой части комбинаторного анализа, несмотря1
на ее очевидную актуальность. Лишь около 30 лет назад введение
в математическую практику быстродействующих вычислительных
машин создало возможности для решения ряда экстремальных
задач.
Общая схема связи экстремальных комбинаторных задач с
методами линейного программирования выглядит примерно так:
элементы я,- интерпретируют как точки евклидова пространства»
чтобы «целевая» функция Р стала линейной формой.
Рассматривается задача нахождения экстремума этой функции на выпуклой
оболочке заданных точек (т. е. на выпуклом многограннике). В
самом деле, экстремум линейной формы на многограннике
достигается в одной из вершин, которые входят в множество
рассматриваемых элементов. Задача же нахождения экстремума линейной
формы и есть задача линейного программирования. Особенностью
комбинаторных задач при таком сведении останется то, что при
нахождении решения следует ограничиваться лишь точками с
целочисленными координатами.
Покажем на примерах, как ставятся задачи
программирования для комбинаторных экстремальных задач. Решение задачи о>
назначениях (пример 1) представляет собой перестановку
(рь /?2 рп) чисел 1, 2 п, полученную в результате
назначений вида I—*-рг-: 1=1, 2, ..., п. Целью является нахождение
п
Ш'ПХ< р' на конечном множестве указанных перестановок.
1 = 1
Каждая перестановка может быть интерпретирована как точка в
гг2-мерном евклидовом пространстве; при этом ее удобнее
представить в виде (пХп)-матрицы Х=||х^-||, где хц=1 в случае
назначения 1-го кандидата на /-ю должность и хц = 0 — в противном
случае. Заменим это условие другим: Хы3>0, чтобы не
воспрепятствовать применению программирования. Требования
недопустимости совместительства и дробления должностей запишутся как
условия:
п
^ % = 1; I ^= 1,2, ... , п;
п
]^ хч -=\; ]'---= 1, 2, ... , п.
1 = 1
Суммарные затраты, минимум которых разыскивают,
записываются как
п п
2^ 2, счха-
.=--1 /=1
154

В задаче о коммивояжере (пример 2) ищут, как известно,
п п
1=0 /=0
при условиях:
п
2] %= 1; /= 1, 2, . . . , п
(=0
(из каждого города коммивояжер уезжает лишь 1 раз),
п
^хС! = 1; 1 = 1,2, ... ,п
/=о
(в каждый город коммивояжер въезжает лишь 1 раз) и
щ—щ + пхц^.п—1; I, / = 1, 2,...,«; 1ф\.
Последнее условие введено, чтобы обеспечить единственность
цикла в пути коммивояжера. В самом деле, если бы
существовало решение, содержащее два или более циклов, то нашелся бы
подцикл хек звеньями, не проходящий через исходный пункт.
Сложение последних условий для х привело бы к противоречию:
пк*с (п—1)к.
Мы не определили и,- и щ в последнем условии. Они могут быть
найдены для любого цикла, начинающегося в исходной точке.
Если пункт I посещается на р-м этапе объезда (р=1, 2 п), то
положим иг = р. Для всех I и / отсюда следует, что «,-—щ<.п—1.
Последнее условие выполняется для всех хц = 0. Если же Хц=1,
то эти условия записываются как равенства:
и,-—щ + п-хц=р—(р+1) +п = п—1.
Задача о покрытии (пример 7) уже сформулирована так, что
позволяет ставить соответствующую задачу линейного
программирования. Ее более общая постановка состоит в том, чтобы для
данного конечного множества 5={5Ь 8г, ..., 8п) и некоторой
конечной совокупности его подмножеств 5,(/=1, 2 т) найти
минимальное покрытие множества 5, т. е. минимальный набор
подмножеств 53, в котором любой элемент 5е5 принадлежит хотя
бы одному из подмножеств.
Для этой общей задачи применяется аналогичный подход:
составляют матрицу инцидентности \\ац\\, в которой а13 = 1, если
8;е5;, и а^ = 0 — в противном случае. Определим Хц, которые
равны 1, если 53 войдет в покрытие, и 0, если не войдет. Тем
самым к задаче оказывается применимым линейное
программирование. Вопрос о минимальных покрытиях играет большую роль в
исследованиях, относящихся к комбинаторным геометриям, и
потому последние замечания могут быть полезными для
комбинаторно-геометрических исследовании.
155

Для решения экстремальных комбинаторных задач были
разработаны различные вычислительные методы. Наиболее
перспективные из них выделились в отдельную область комбинаторного-
программирования (см. [80]). Общая идея этих методов состоит
в замене полного перебора всех вариантов частичными
переборами меньших объемов. Для осуществления такой идеи отыскивают
некоторые подмножества, заведомо не содержащие искомого
экстремума, и сужают область перспективных вариантов. Методы
при этом получаются весьма разнородными, определяемые
структурой соответствующих конечных множеств. Ниже описывается
несколько методов, наиболее широко применяемых в настоящее
время.
6.2. МЕТОД ВЕТВЛЕНИЙ И ОГРАНИЧЕНИЙ*
Согласно этому методу множество всех допустимых
комбинаций ¢) разбивают на подмножества ¢^,(^, ...,(2,,. Каждое из
последних затем разбивают на подмножества фп. (?12> ■ ■ ■ > Яш*
(1=1, 2,...,81) и т. д., пока не дойдут до отдельных комбинаций.
Этот процесс ветвления удобно изображать в виде дерева. На
каждом подмножестве ^^1,^2...,I определяют функцию
предпочтения ф(С?1„(, 15). Начиная с вершины ¢), передвигаются с этапа на
этап, выбирая каждый раз подмножество с минимальным
значением этой функции (или максимальным, если этого требует
условие задачи). Полученное дерево будет деревом решений.
Задача состоит в подходящем выборе функции предпочтения,
чтобы получить хорошее решение. Иногда выбор подмножества
производится случайным образом: при этом вероятность выбора
данного подмножества тем больше, чем меньше значение его
функции предпочтения (рандомизированные функции
предпочтения).
Основная проблема в этом методе — выбор способа
определения нижней (или верхней) границы. Получить достаточно точное
ее значение не всегда легко, но зато число рассматриваемых
ветвей на дереве решений в общем случае сокращается. Это
получается потому, что если значение нижней границы для какого-
либо подмножества больше или равно (в случае минимизации;
меньше или равно — в противном случае) значению
минимизируемой функции одного из уже полученных решений, то
соответствующую ветвь дерева решений исключают из рассмотрения.
Пусть ¢) — множество всех допустимых решений некоторой
задачи: 0={дь д2, -.-. </«}; на множестве этих решений задана
функция /. Требуется найти подмножество С2пС1С}, на котором
функция / достигает минимума (или максимума).
Предположим, что мы знаем некоторую нижнюю границу Ь0
для функции / на множестве ¢). Пусть с помощью некоторого
* Известен также под названиями: метод прогрессивных разделений и
оценок, метод ветвей и границ.
156

приема нам удалось разбить (2 на множество А и его дополнение
Л, и после этого уточнить нижние границы / на множествах А и
Л, которые равны й4 и 6/ соответственно. Причем &1>Ьо; Ь/»^.
Пусть с помощью_других_приемов также удается разбивать С? на
две части: В я В; С а С, ... Рассмотрим множества А[\В; А[\В,
АГ\В\ А{\В и уточненные нижние границы / на этих множествах
Ь2, Ь2, Ь2" и Ь2" соответственно. При этом
Ь2>Ь1^>Ь0; Ь2">Ь/>Ьо;
&2'>&1>&о; Ь2'">Ь^Ъ0.
Таким образом можно образовать ориентированное дерево с
корнем (? (иначе прадерево) (рис. 6.3). Причем это дерево нет/
А п В пС...п N
Рис. 6.3
необходимости строить полностью. Предположим, что мы построили::
часть дерева, разбив множество ¢) на некоторые подмножества,,
и нашли нижние границы для вершин, соответствующих этим под-,
множествам. Выбираем из всех висячих вершин ту, у которой
наименьшая граница, и затем, разбивая соответствующее
подмножество, получаем две новые вершины, на которых уточняем
нижние границы функции /.
157"

Выскажем следующее простое утверждение: на любом этапе
объединение подмножеств, соответствующих висячим вершинам,
дает все (?. Поэтому, если в результате данного процесса мы
получим вершину из одноэлементного множества {¢,-} и нижняя
граница функции / на ней будет меньше, чем на остальных
висячих вершинах, то / принимает на ц\ свое наименьшее значение.
Процесс закончен.
С помощью аналогичных рассуждений можно описать алгоритм
нахождения максимального решения, если оно существует.
К сожалению, рассматриваемый метод не дает конструктивного
ответа на поставленную задачу. В каждой конкретной задаче надо
придумывать алгоритмы разбиения множества С? и наилучшие
способы уточнения нижних границ Ъ в висячих вершинах.
Рассмотрим пример применения метода к задаче о
коммивояжере. На языке теории графов в ней речь идет об отыскании
оптимальных гамильтоновых контуров. В 1963 г. Литтл нашел строгий
метод оптимизации для задач данного типа.
Пусть задан ориентированный граф С=(Х, II), где |Х|=гс и
каждой дуге (х{, я3-)е<7 приписано значение с,3 = с(л:{, х^). Мы
будем предполагать, что все сц>-0. Если дуга (Х{, х,)^11, то
С\]= оо.
Алгоритм нахождения минимального гамильтонова контура
будет состоять в построении прадерева, описанного в методе
ветвлений и ограничений.
А) С? — корень прадерева — множество всех гамильтоновых
контуров. Нижней границей для Е является, очевидно, нуль, но
мы_ найдем большую границу в процессе выявления множеств А
и А прадерева. Поступаем следующим образом. Находим в
каждой строке матрицы ||с^|| минимальный элемент и вычитаем его
из всех элементов этой строки. Если в полученной матрице
окажутся столбцы без нулевых элементов, то в каждом из них
находим минимальный элемент и вычитаем его из всех элементов
столбца. Получим в результате новую матрицу ||с',-;-||, в каждой
строке и в каждом столбце которой содержится хотя бы один
нуль.
Б) Просуммируем все элементы, которые мы вычитали в А).
Их сумма Ь и будет нижней границей для ¢). Действительно,
возьмем произвольный контур Ь с суммой значений дуг на нем /.
В пункте А) при преобразовании матрицы ||с,-;-|| в Цс'^Ц мы
вычитали некоторые числа из всех элементов соответствующих строк и
некоторых столбцов. При этом из величины / каждый раз эти
числа тоже вычитались и в конце концов длина контура Ь в
матрице Цс'^-Ц также неотрицательная. Следовательно, /з>6.
В) Перейдем к построению вершин прадерева следующего
уровня. Пусть с'11 = 0. Определим у^ как сумму наименьшего
элемента 1-й строки и наименьшего элемента /-го столбца (исключая
с,-и который равен нулю) и найдем
% = Уы= тах у,./.
158

Рассмотрим свойство рц\ «контур недодержит дуги (*,-, *,-)».-
которое будет применяться к дугам с с',-,- = 0.
Если гамильтонов контур не содержит дугу (хи X)), то он
осязательно использует некоторые две дуги (л;,-, х>); зф] и (л;,, х^,.
Г) Докажем, что Ь'^Ъ + уы является нижней границей для
множества контуров, удовлетворяющих свойству рьг.
Действительно рассмотрим произвольный гамильтонов контур ^ь не
содержащий дугу (хк, XI). Тогда после преобразования А) длина этого
контура в обновленной матрице будет не меньше ^нуля. 1ем
самым мы построим вершину прадерева Ёы с нижней границей
Ь' = Ь+®.
Д) Строим вершину Еы, определяемую свойством ры: «контур
использует дугу (хк, «)»• Удаляем ^из матрицы к-ю строку и-
1-й столбец и заменим на оо значение с'ш-
Е) Действуем как в А) с матрицей, получающейся в
результате Д).
Ж) Действуем, как в Б), с матрицей, получающейся в
результате Е) Прибавляя полученную сумму к границе для предыдущей-
вершины (в первом случае для (?), получаем границу для верши-
3) Если в результате Д) получают матрицу порядка 1, то
процесс заканчивается. Если нет, то переходим к И).
И) Среди всех висячих вершин уже построенного прадерева
выбираем вершину с наименьшей границей.
К) Если выбранная в И) вершина при построении
соответствовала свойству рц, то переходим к В). Если нет, то переходим к Л).
Л) Пусть выбранная вершина соответствовала при построении,
свойству ри. Заменяем значение в клетке (I, /) соответствующей
матрицы на оо. В 1-й строке, а также в /-м столбце находим
наименьший элемент и вычитаем его из всех элементов этой строки
(столбца). Затем переходим к В).
Рассмотрим теперь числовой пример, показывающий, как.
применяется алгоритм Литтла для
отыскания минимального гамильто-
нова контура графа. Пусть граф С
есть граф с 5 вершинами х\, хъ хз,
А, хъ, каждой дуге которого _ (Хг,
х,) приписано число сц: и /=1.
2,..., 5. Эти значения выписаны в
виде матрицы стоимостей на рис. 6.4.
Построим прадерево, описанное
в методе ветвления и ограничения,
для этого числового примера.
А) Из элементов строк х\, х%,
Хг, хА, хъ вычитаем соответственно
их наименьшие элементы 2, 3, 1, 2,
4; кроме того, из столбца х5
вычитаем 1 (см. рис. 6.6).
159
щ
XI,
оо
3
1
5
7
2
оо
7
7
6
3
7
ОО
г-
4
2
В
3
оо
в
7
7
7
3
оо
Рис. 6.4

Ц21п(]31пЦ,гп Цгь п Я
45
| 16
Цг. п Ол п цп п Цг1, п Ц„>,
/о
!1,.пО..Г11)1?пГ},, :,1),,,, !, и„
Рис. 6.5
ОСI ЗСп ЗС-1 X/, л*
хи хь
оо
0
0
3
3
0
оо
в
5
2
1
4
оо
0
0
0
3
2
оо
2
4
3
5
0
оо
х*
оо
Б
5
2
1
со
0
0
0
2
оо
2
4
5
0
оо
Рис. 6.6
Рис. 6.7

Б) Вычисляем сумму 2 + 3+1+2 + 4+1 = 13. Таким образом,
для вершины О (множество всех гамильтоновых контуров)
получаем границу: Ь = 13.
В) Переходим к рассмотрению всех нулевых элементов
матрицы:
У (XI, Дй)=2, у(хи х4)=2; у(х2, х4)=3; у(х3, да) =2;
V (*4, хз) = 0; у {х,, хъ) = 3; у(хь, х3) = 2..
Следовательно, @=у(х2, ^) = 3.
Г) Изображаем вершину <321 прадерева с нижней границей,
равной 13 + 3=16.
Д) Изображаем вершину <221, определяемую свойством:
«контур содержит дугу (х2, х{)». Исключаем вторую строку и первый
столбец. В клетку (1, 2) помещаем оо (см. рис. 6.7).
Е) Сначала из всех элементов строки х3 вычитаем 2, а затем
из первого столбца вычитаем 2 (см. рис. 6.8).
ССо СС>т х^ зс§
%
х2
х5
оо
г
3
0
1
оо
0
0
0
0
оо
2
4
3
0
оо
хг
хз
хи
оо
оо
0
3
3
0
оо
Б
5
2
1
4
оо
0
.0
0
3
г
оо
?.
4
3
'5
0
ОО
Рис. 6.8
Рис. 6.9
Ж) Сумма элементов, вычтенных из строк и столбцов по Е),
здесь равна 4. Следовательно, для вершины (221, имеем границу
13 + 4=17.
3) Здесь была получена матрица порядка 4. Переходим к
следующей операции И).
И) Висячая вершина с наименьшим значением 16 есть <321.
К) Вершина (221 получена с помощью свойства р24.
Переходим к Л).
Л) В клетку (х2, Хх) матрицы на рис. 6.6 помещаем оо.
Получаем матрицу, изображенную на рис. 6.9. Затем вычитаем 3 из
всех элементов строки х2. Результат см. на рис. 6.10.
В) Для матрицы на рис. 6.10 вычисляем: у(хи *2) = 2;
у(хи х4)=0; у(х2, х4)=0; у(х2, х5)=0; у(х3, лп) = 5; у(хь, х3)_=0\
у(хь, Хь)=0; у(х5, х3)=2. Получаем &=у(х3, *4)=5.
Г) Строим вершину 0.и[\С1зи которой отвечает граница:
16+5 = 21.
Д) Строим вершину <221П<2з1. Вычеркиваем строку х3 и
столбец XI. В клетку (*!, Хз) матрицы на рис. 6.10 помещаем оо. Ре-
6 К. А. Рыбников
161

X,
х2
х3
*4
%
X,
оо
со
0
3
3
хг
0
оо
6
5
2
х3
1
1
оо
0
0
я<<
0
0
2
оо
2
х5
4
0
5
3
ОО
хг
0
Оо
5
2
хз
©о
;
п
0
х*
0
0
оо
2
*5
4
0
0
оо
Рис. 6.10
Рис. 6.11
зультат см. на рис. 6.11.
Е) Все строки и все столбцы матрицы на рис. 6.11 содержат
нули.
Ж) Следовательно, для вершины С^ПФз! имеем границу,
равную 16.
3) Была получена матрица порядка 4. Переходим к И).
И) Висячая вершина с наименьшим значением 16 есть <221П(?31.
К) Вершина <221ПС?з1 получена с помощью свойства рз1.
Переходим к В).
В) Вычисляем у для всех нулевых элементов матрицы на
рис. 6.11.
у(*1, х2)=2; у{хи х4)=0; у(х2, *4)=0;
у(х2, *5)=0; у(хь, *з)=0; у(хь, х5)=0; у(х5, Хг)=%
&=у(Х1,_х2)=2.
Г) Строим вершину Оы[\0.ъ\[\(±и., граница для которой будет
16+2=18.
Д) Строим вершину <221ПС?з1ПС?12- Вычеркиваем строку х^ и
столбец хг матрицы на рис. 6.11. Получаем матрицу на рис. 6.12.
Е) В каждой строке и каждом столбце матрицы на рис. 6.12
содержатся нули.
Рис. 6.12
Рис. 6.13
х2
X/,
х5
х3
/
0
0
Хц
а
оо
2
х5
0
0
оо
ЛГ4
х5
*3
0
0
х4
0
оо
х5
х3
0
Рис. 6.14
Ж) Нижняя граница для вершины (Э21П<Эз1П<Э12^ 16.
3) Получили матрицу порядка 3. Переходим к И).
И) Висячая вершина с наименьшим значением 16 есть 0,'2\{)
П<Э31П<212-
162

К) Вершина ^ГКМЪ получена с помощью свойства р12. По-
ЭТОйГвиечи°сГм%В)для всех нулевых элементов матрицы на
РИС-6Л2: у{х2,х<)=2; Т(Ч^УМ^
Г) Строим вершину <Ы1<М1<г«Пй4, граница которой будет
РЭВШ СтеоЙм^вершину С&ПОиГКЬГК?*. Вычеркиваем строку дь
и сйпб^ матрицы на рис 6.12. Получаем матрицу ^на
РИСЕ)' В матрице на рис. 6.13 в каждой строке и в каждом столбце
С0Д1ТаГТрСаЯницЛаИдля вершины &ДММ» будет равна 16.
3) Имеем матрицу порядка 2, поэтому переходим кИ.
И) Висячая вершина с наименьшим значением 16 есть &4П
ЛР К^Э^вершина была получена с помощью свойства Р24. Пере-
Х°АВ) Вычисляем у для трех нулевых элементов матрицы на
рис. 6.13: .
Т(*4, *з)=0; у(*4, Х5)=°°; ?(*»• *3) = °о;
0 = 7(^4, *5) = оо.^
Г) Строим вершину фнГ^ГКЬПСмП^Б. Граница для нее
пяяня оо
Д) Строим вершину ^ПСмГКЬПСиГ^ Вычеркиваем строку
х4 и столбец *5. Получаем матрицу на рис. 6.14.
Е) Очевидно, что в полученной матрице ничего вычитать не
требуется. _ч |С . П_|К
Ж) Нижняя граница для вершины в Д) равна 1Ь+0-ш.
3) Имеем матрицу порядка 1 с минимальной границей среди
всех висячих вершин. Добавляя дугу (хъ, х3), получаем искомый
х1
хг
хз
х^
х5
X,
ОО
3
га
5
7
х2
2
оо
7 '
7
В
хз
3
7
8
2
и
я 4
2
ш
3
оо
в
■%
7
7
7
га
оо
Рис. 6.15
163

гамильтонов контур со значением 16: (х3, хи хг, Хь, хъ). Найденное
решение представлено на рис. 6.15 и 6.16.
Полученный алгоритм позволил найти решение поставленной
задачи. Однако могут существовать другие гамильтоновы контуры
с таким же значением. Это получается из-за того, что выбор
вершин в некоторых случаях был не однозначен.
Нетрудно видоизменить алгоритм Литтла для решения задачи
о нахождении гамильтонова контура с максимальным значением.
Мы, однако, несколько изменив условия, сведем задачу к уже
исследованной.
Припишем символ (—оо) всем парам вершин (л;,-, X}), для
которых в графе 0= (X, И) нет дуги (хх, х,). Пусть ||сг;|| — матрица
стоимостей графа С=(Х, V), |Х|=гс. Построим новую матрицу,
элементы которой определим по формуле
с'.. = С —сс/ (1,7= 1,2, ... , п), где С ^ тпяхсц.
Применим теперь к матрице ||с';,-|| алгоритм Литтла отыскания
минимальных гамильтоновых контуров. Полученное минимальное
решение дает максимальное для матрицы \\сц\\.
6.3. ЭВРИСТИЧЕСКИЕ МЕТОДЫ
Точные методы оптимизации, о которых мы упоминали выше,
треб; ют, как правило, очень большого объема вычислений.
Поэтому имеет большое практическое значение создание простых
методов, дающих решения, достаточно близкие к оптимальным.
Методы, в которых не оценивается близость полученных решений к
оптимальным, принято называть эвристическими. Если же можно
оценить отклонение решений от оптимальных, то такой метод
называют приближенным. Естественно, эвристический метод после
его успешного теоретического исследования может перейти в
разряд приближенных.
Наиболее часто в эвристических методах применяют локальную
оптимизацию.
Пусть у нас имеется множество Р—{т, яг, ..., яд-} комбинаций;
ставится задача вычисления минимума функции Р, определенной
на этом множестве, и отыскания комбинаций, на которых этот
минимум достигается. Метод локальной оптимизации состоит в
следующем.
Для каждой комбинации щ^Р определим множество (?;
комбинаций, которые будем называть соседними с щ- В терминах
теории графов это будет означать следующее: каждой
комбинации щ поставим в соответствие некоторую вершину графа О.
Соседние вершины щ и л, графа О соединим дугой (I, /) (я^С?,).
Полученный граф будем называть графом соседства комбинаций.
В графе С может существовать совокупность 1 его вершин, в
которой
Р(Пг)=Р(Л]), еСЛИ Яг, Щ^2\
164

Р{щ)<Р{щ), если я;е2; щ^2.\ (г, /)^^,
где II — множество дуг графа соседства. Такое множество 2
назовем изолированным. Это множество, разумеется, может состоять
и из одной вершины.
Первый шаг локального подхода, о котором идет речь, состоит
в том, чтобы, выбрав произвольную комбинацию я,-, определить
для нее граф'соседства, после чего на этом графе для всех П}<=()1
определить значения Р(л,).
Второй этап состоит в операции, которую принято называть
спуском. Находим п/ое(3, так, чтобы
Р(п1о) = тш ^(я/),
и если Р(п^)<.Р(л1), то переходим к комбинации п!е.
Так за конечное число шагов придем к изолированному
множеству. Однако даже попадание на изолированное множество не
дает уверенности, что достигнут не локальный экстремум (в
данном случае, минимум), а общий. Поэтому локальные «пробы»
приходится продолжать. Одним из способов продолжения поисков
может являться выбор новой допустимой комбинации и
повторение операции спуска в старом графе соседства. Возможны и
другие способы. Определим, например, последовательность графов
соседства Оь Ог. •••, Ов (графы 1-, 2-,... 5-соседства). После
попадания в С?1 на изолированное множество вершин 2 переходим к
графу Ог из произвольной вершины щ^2. Если 7. и в 02 остается
изолированным, перейдем к 03 и т. д. Если же из вершины я,
возможен спуск в изолированное множество 1\, то, перейдя в какую-
либо вершину я.^21, возвратимся к графу С\ и повторим процесс
уже из вершины я3-.
В описанном подходе имеется много неопределенного. В
особенности неясно, как строить графы соседства и чем это
построение будет лучше случайного выбора комбинаций. Однако опыт
подсказывает, что получать соседние комбинации иногда легче,
чем строить случайные последовательности. Анализ конкретной
задачи часто приводит к способу определения соседних
комбинаций, обеспечивающему эффективный спуск к оптимальному или
достаточно хорошему решению.
Рассмотрим некоторые примеры определения соседства.
1. Если комбинации суть просто перестановки, то соседние
комбинации часто определяют как такие, которые получаются
перестановкой близких элементов. Назовем 1-соседними комбинации,
получаемые перестановкой двух соседних элементов; 2-соседни-
ми — комбинации, получаемые перестановкой двух элементов,
расположенных через один, и т. д. Например, перестановка Я1 =
= (1, 2, 3, 4) имеет четыре 1-соседних комбинации: я2= (2, 1, 3. 4),
я3=(1, 3, 2, 4), Я4=(1, 2, 4, 3) и я5= (4, 2, 3, 1) (элементы Г и 4
также считаем соседними) и две 2-соседних комбинации: Яб =
= (3, 2, 1, 4), Я7=(1, 4, 3, 2). При таком определении 3-соседние
и 1-соседние комбинации совпадают.
165

В общем случае 2-соседние комбинации определяются
следующим образом: щ является 2-соседней для щ, если существует лк
такая, что щ есть 1-соседняя для ли, а ли есть 1-соседняя для я>
Аналогично вводятся 3-соседние комбинации и т. д.
2. В задачах 1 и 6 в § 6.1 рассматривался вопрос об
оптимальном назначении и о минимальном простое сборочной линии. В них
значение Р было определено как та х/^- для каждого участка
конвейера. Участки, для которых Р{ = тахР}, назовем критическими.
В таком случае представляется естественным определять соседние
комбинации следующим образом: комбинация л; является
1-соседней для л,, если она может быть получена из щ перестановкой
двух операций, одна из которых назначена на критический
участок, а другая нет.
Рассмотрим, например, схему задачи 6 (рис. 6.2) еще раз. Для
решения Я°= (1, 2, 3; 4, 5, 6; 7, 8, 9) получим: ^1 = 21; ,Г2= 16;
Р3=\4; Р = 21. Критическим оказался первый участок.
Перестановки допустимы только между операциями первого и второго
участков. Имеем:
#'=(1, 2, 4; 3, 5, 6; 7, 8, 9); Л=17; ^2=20; Р3 = 14; Р=20;
#^=(1, 3, 4; 2, 5, 6; 7, 8, 9); Л=19; ^2= 18; Р3= 14; Р=19;
Л3=(1, 3, 6; 2, 4, 5; 7, 8, 9); ^ = 22; ^2= 15; Р3 = 14; Р = 22;
Я*=(2, 3, 6; 1,4,5; 7, 8, 9); Л = 21; ,Р2= 16; ,Р3= 14; ^ = 21.
В решении Я2 первый участок остался критическим, но
рассмотрение соседних решений не дает улучшения, так как допустимы
перестановки операций только первых двух участков, а второй
участок имеет время работы /^=18, близкое к критическому
Р=19. Чтобы уменьшить Рг, рассмотрим допустимые перестановки
операций, назначенных на второй и третий участки.
Имеем две допустимые перестановки операций 6, 7 и
операций 5, 7. Соответствующие комбинации:
Я5=(1, 3,'4; 2, 5, 7; 6, 8, 9); Л=19; 7^2=14; Р3= 18; 7^=19;
Я6=(1,3, 4; 2, 6, 7; 5,8,9); Л=19; Рг= 16; ^з=16; ^=19.
В обоих решениях Я5 и #6 значение Р2 уменьшилось. Сделаем
следующий этап спуска, взяв, например, решение Я6. Соседние с ним
решения:
Я7=(1, 2, 3; 4, 6, 7; 5, 8, 9); Л = 21; ^2=14; ^3=16; ^=21;
Я8=(1, 2, 4; 3, 6, 7; 5, 8, 9); Л=17; ^2=18; ^з=16; Р=\8;
Я9=(1, 3, 6; 2, 4, 7; 5, 8, 9); ^1 = 22; Р2=13; Р3=\6; Р = 22.
Докажем оптимальность решения Я8. Для этого рассмотрим
применение метода ветвлений и ограничений к задаче 66 из § 6.1.
Определим процесс ветвлений следующим образом. Пусть у нас
сделаны назначения операций на к участков, т. е. определены
множества Яи Яг , Яи- Будем называть множество Як+1
допустимым, если: 1) назначение множества операций Яи+1 на
(&+1)-й участок не нарушает последовательности сборки;
166

2)5"* '/<С (С —заданная длительность цикла) ;3) не суще-
<е«*+1
ствует множества Я' такого, что Яь+1<Я'> удовлетворяющего
условиям 1 и 2. Оценка снизу числа участков для любого подмножества
решений имеет следующий вид: 9(^, • . . . Як) = & + ~"~ /_1 ^'
где £(£) есть множество еще не назначенных операций.
В нашем примере возьмем С=П. Для назначения на первый
участок имеется пять возможностей:
37 3
£1 = (1,4,7): Ф(Л!)=1+ —= 3—;
£2 = (1,2,4): ф(^)= 14-~ = 3;
/?? = (1,3)
Я} = (3, 6)
Я? = (2, 3)
9(^) = 14-^- = 3-^,
ф^> = 1:+-^ = 3-^-.
Выбираем /?1В=(1, 2, 4). Допустимы следующие назначения на
второй участок:
Я\ = (3,5,7); ф(Я*,Я') = 2 + -^- = 3
#1=(3,6); ¢(£2,^2) = 2 + -^- = 3
18 р 1
17 ~ 17
— = 3 —
17 17 '
Отсюда заключаем, что при С = 17 трех участков недостаточно,
что и доказывает оптимальность выбранного нами решения Я8
задачи 6а.
Упражнение. Показать, что при С=17 в задаче 66 оптимальным
является назначение операций на 4 участка, и найти эти назначения.
Рассмотрим применение локальных оптимизаций к задаче
о коммивояжере. Мы имеем множество А = {аи ..., ап} городов и
матрицу С = ||сг/|| стоимостей переезда от города а, до города а;.
На каждом шаге алгоритма будем строить маршрут Ат= (ак, ..., а1г)
по г-подмножеству множества А; г=1, 2, .... п. При этом
считаем, Что происходит переезд из города а, в щ , к=\, 2,...,
г—1, и из щ в а^. Берем для г=\: Ах = (а{) (маршрут состоит
из одного произвольно выбранного города щ). Если Ат построен,
то на следующем шаге ищем город а,г^(А\Аг) такой, что
р(а<,А)= т'п р(°/,А-)> где через р(аи АЛ мы обозначим
«расстояние» от а{ до Ат\ р(аи АГ) =тт{сг,\щ^.Аг}. При этом, если
р(а{, х2) = С1_1к для щк<= Аг, то беремЛ,+1 = (аи,. . ., сик, щ, сц . . .,
а, ).
167

Построенный алгоритм называется алгоритмом включения
ближайшего города.
Упражнение. Показать, что алгоритм включения ближайшего города
можно реализовать числом операций, пропорциональным я2.
Теорема. Пусть (пХп)-матрица С стоимостей в задаче о
коммивояжере симметрична и удовлетворяет неравенству
треугольника: С{к + сн}>>сц {и /, к=\,...п). Тогда
где /„ есть маршрут, даваемый алгоритмом включения
ближайшего города, Оп — оптимальный маршрут, |/п| и \Оп\ — их
суммарные стоимости.
Доказательство. Пусть города а^ аг ап
перенумерованы так, что на 1-м шаге алгоритма добавляется в маршрут
город аг-. Теорему будем доказывать установлением
взаимно-однозначного соответствия между городами а2, ..., ап и всеми ребрами
в Оп, за исключением наибольшего, таким образом, чтобы
стоимость включения города а& между щ и а,-, т. е. с-1к + ск!—сц (берем
с,; = 0 для корректности первого шага), не превышала удвоенной
стоимости ребра в Оп, соответствующего а%. На самом деле мы
получим несколько более сильную оценку, чем указанную в
формулировке: |/„|<2(|0„| — |/Шах|), где /тах — ребро в Оп,
обладающее наибольшей длиной.
На каждом шаге алгоритма будем рассматривать не только
текущий маршрут ^ а(, 1^<гг, но и некоторые дополнительные
ребра из Оп\{/тах}, соединяющие города щ+и а,+2, ..., ап с
текущим маршрутом. На 1-м шаге маршрут состоит из города а1 и
включает все ребра Оп кроме /Шах (рис. 6.17):
Рис. 6.17 Рис. 6.18
Пусть на {к—1)-м шаге мы имеем маршрут аи ..., ак-1 (показан
на рис. 6.18 жирной линией) с присоединен' мьлп к нему городами
аи ап при помощи «ног» (ребер, очерченных нежирной линией);
такую конструкцию будем называть паукообразной.
Пусть город аи, который должен быть включен в маршрут на
к-м шаге, является ближайшим к городу ат из маршрута (см.
рис. 6.18). Стоимость включения аи между ат и следующим за
168

ним городом ах равна С1к+скт—С1т. Пусть ах есть точка
маршрута, к которой присоединяется нога, включающая ак, и пусть
(ах, ау) — первое ребро этой ноги (может быть, ау = ак).
Поскольку ак — ближайший к маршруту, то имеем
Стк<ССху. (1)
По неравВнству треугольника имеем
(2)'
Из (1) и (2) получаем
С1к<СС1т + Сху (3)
Слбжив (1) и (3) и использовав симметричность матрицы С,
получаем
Сш + Сйтп-< С\т + 2сХу,
что эквивалентно неравенству
т. е. включение ак между щ и ат стоит самое большее 2сху- После
включения ак ребро (а*, ау) из конфигурации удаляем
(конструкция при этом остается паукообразной). Городу ак поставим в
соответствие ребро (ах, Оу). После прохода алгоритма по всем городам
а2 ап требуемое соответствие между {а2 ап} и 0„\{/тах}
устанавливается, что и доказывает теорему.
Покажем теперь, что имеется задача коммивояжера с п
городами (гс>6), для которой алгоритм включения ближайшего
города дает маршрут, почти вдвое больший оптимального.
Рассмотрим следующую матрицу стоимостей С : Сц = с^ = т\п(]—I, п—/ + 0>
т. е. а, есть длина кратчайшего пути из ! в /, следующего по
ребрам типа (к, (к+1) {тоАп)). Для гс = 8 эта конфигурация
изображена на рис. 6.19.
Рис. 6.20
Покажем, что маршрут Тп, состоящий из ребер (1, 2), (я—1, п)
и (I, 1 + 2) для 1<1<:гг—2 (на рис. 6.20 показан маршрут Т8),
может быть получен в результате применения алгоритма
включения ближайшего города. Заметим, что алгоритм может начать
работу с города 1, затем добавить к нему город 2, затем — город 3
и так далее. Пусть Тк, 3<&<:гг, — маршрут, полученный этим
алгоритмом после включения города к. Покажем по индукции, что
169

Тк состоит из ребер (1, 2), (к—1, к) и (£, 1+2) для 1-<1'-«:&—2.
Это очевидно для к = 3. Полагая, что это верно для 3<:1<&,
заметим, что Ти+1 получается из Тк включением города к+1 между
городами к—1 и к.
Длина маршрута Тп равна 2п—2, а оптимальный маршрут Оп,
состоящий из ребер (1, п) и (£, £+1), 1<1-<гг—1, имеет длину п.
Поэтому имеем
■1^ = 2(1-1).
\0„\ \ п )
Это отношение является наибольшим, допускаемым теоремой,
поскольку |/Шах| = 1.
Теоретическое исследование локальных оптимизаций проводят
и теоретико-вероятностными методами. Для этого на множестве
задач, решаемых данным локальным алгоритмом, вводится
вероятностная мера и показывается, что с ростом размерности задачи
мера задач, решения которых отклоняются от оптимального
больше чем на е, стремится к 0, когда размерность задачи растет.
Такое поведение решений называется асимптотической
оптимальностью. Асимптотическая оптимальность доказана для многих
алгоритмов решения задачи коммивояжера, в частности для
простейшего из них, когда на каждом шаге предлагается идти в
город, ближайший к тому, в котором коммивояжер находится в
данный момент. Более полные сведения читатель может найти в
обзоре [26].
Еще один вид эвристических алгоритмов оптимизации связан
со случайным выбором комбинаций в соответствии с некоторым
вероятностным распределением, которое подбирается из
соображений более вероятного получения желательных комбинаций. За
подробными сведениями и ссылками рекомендуем обратиться к
обзору [81].
6.4. ОПТИМИЗАЦИЯ НА ГРАФАХ
В предыдущих параграфах этой главы мы уже рассматривали
экстремальные комбинаторные задачи, связанные с оптимизацией
на графах (см. задачу о коммивояжере). В данном параграфе мы
рассмотрим еще ряд задач того же типа.
Будем рассматривать вначале ориентированные графы 0 =
= (X, Г) не имеющие контуров. Введем для них понятие
порядковой функции. Так называется функция О(хг), определенная на
множестве вершин Х= {хг} и принимающая целочисленные
значения. При этом, если ^ёГ(^), то 0(х,) >0(Хг). Иными словами,
если вершина х3- следует за х,, то значение порядковой функции
в ней больше, чем в хг-. Величину 0(хг) мы будем называть
уровнем ВерШИНЫ Хг.
Порядковые функции для конкретного графа 0=(Х, Г) можно
строить разными способами. Укажем один из них. Рассмотрим
170

подмножества вершин М0, Ми..,Мг, определенные следующим об-
РЭ30М: Мо={ъ\х^Е;Г-ЧхЛ=0Г-
Легко видеть, что множества^, К .. ££^£^%^
а функция О, принимающая значение к на множестве «л I»
= 01,.,"). является порядковой функцией графа О. На рис. 6.21
Г(Мг)'=0- '
Рис. 6.21 Рис- 622
изображен граф, множество вершин которого разбито на
подмножества #о, #1, ..., №т.
Помимо порядковой функции на множестве вершин графа
задают числовую функцию Ф. Через эту функцию определяют
численные характеристики задач, подлежащие оптимизации. Пусть
(хи х2,..., хп) — путь в графе С, т. е. хи х2,..., х„еА; Хг+1е:1 (х0
(1=1, 2, ..., га—1). Значением этого пути назовем число Л=ф(*1) +
+<р(х2) + - + ф(*п)-
Иногда числовая функция ф задается не на вершинах, а на
дугах. В таком случае значением пути (хи х2, ■ ■-, хп) называется
число Я = ф(Х1, Х2) + ф(*2, Хз) + .- +<((Хп-1, Хп).
Многие задачи оптимизации имеют следующую формулировку:
отыскать.среди некоторого множества путей Р минимальный (или
максимальный), т. е. путь, обладающий минимальным (или
максимальным) значением Я. В качестве множества Р может ^быть
выбрано, например, множество всех гамильтоновых путей. В этом
разделе мы рассмотрим задачу нахождения минимального и
максимального пути среди всех простых путей, соединяющих две
фиксированные вершины.
Теорема оптимальности. Пусть некоторый путь, соединяющий
вершину х уровня тп и вершину х' уровня 5, является
минимальным (максимальным). Тогда его подпуть между вершиной у
уровня к и вершиной у' уровня р (т*ск<р<з) также является
минимальным (максимальным).
171

Доказательство. Пусть путь (х, ..., у, ...,у' х')
является минимальным. Если его подпуть (у у') минимальным не
является, то существует другой путь из у в у' с меньшим
значением. Заменим прежний подпуть в пути (х,..., х/) на новый и
получим в результате новый путь из х в х' с меньшим .значением,
что приводит к противоречию.
Приведенная теорема лежит в основе метода отыскания
максимальных путей в графе без контуров. Этот способ был
предложен Беллманом и получил название метода динамического
программирования.
Разъясним сущность этого метода на примере. Пусть задан
граф 0=(Х, II) (рис. 6.22); числовая функция задана на дугах.
Будем искать путь из М в А с минимальным значением.
Порядковая функция О(х) принимает следующие значения:
О(М)=0; 0(Я)=0(/С) = 1; О(В) =0(С) =2; 0(Л)=3.
Начиная с А, рассматриваем последовательно все вершины графа
в порядке убывания его порядковой функции и приписываем
каждой вершине число, равное минимальному значению пути от этой
вершины до А.
Для отыскания минимальных путей в графах, имеющих
контуры, также существуют различные методы. Максимальных путей
в таких графах может не существовать.
Алгоритм Форда. Пусть числовая функция / задана на дугах
графа О, не имеющего контуров. Можно считать, что /
принимает только положительные значения (в противном случае этого
легко добиться, прибавляя достаточно большое положительное
число ко всем /(х,, х3)). Требуется найти минимальный путь из
х0 в хп. Каждой вершине Хг будем приписывать символы по
следующему алгоритму:
1) положим Яг = оо в каждой вершине хг- кроме Яо=0;
2) ищем дугу (хи X]) такую, что к]—Кг>1(хи х3), и заменяем
Я3- на Кг-\-1(хг, X]) <Ку, поступаем так до тех пор, пока возможно
найти дугу, уменьшающую хотя бы одно значение.
Докажем, что число -кп, найденное по указанному правилу,
будет значением минимального пути из хо в хп (если Яп = оо, то
такого пути нет).
Можно указать вершину хТ1 такую, что с помощью дуги
(Хг,, хп) в последний раз уменьшали значение Кп, и
^п ~ V, + ' {Хг> Хп).
Аналогично существует вершина хТг такая, что
V, = Кг, + ЦхГг, хГ1),
и так далее. Последовательность Хп, ХГ1, Кг, ■ ■ ■ строго убывающая.
Следовательно, при некотором к получим Кг — 0, т. е. хг =х0.
Докажем, что путь(х0, хГ1, хГг хп)— минимальный (его
значение равно %п)- Возьмем произвольный путь из хо в хп:
(хд, х0%, х01 х0/п, ап). Справедливы следующие соотношения:
172

Ли, — 0 -¾¾. / (х0, ха,);
Хп — Аит "С / (Х«т, Х„).
Сложив почленно эти неравенства, получим
Хп < / (х0, Хг,,) + I (хщ, хщ) + ...+/ (х0т, хп),
ч. т. д.
Заметим, что алгоритм Форда может быть использован для
отыскания максимального пути в графах без контуров. При этом
надо положить Хг = 0 для всех без исключения вершин, а затем
менять X] на Х'з = Х{-\-1(Х{, х;), если Х']>Х), до тех пор, пока можно
увеличивать Х}-.
Упомянем, наконец, алгоритм Беллмана — Калаба. Этот
алгоритм использует так называемый принцип оптимальности: «любой
подпуть минимального пути является минимальным путем между
соответствующими вершинами».
Пусть рассматривается орграф С=(Х, <7); |Я|=л+1.
Пронумеруем все вершины от 0 до п.
Пусть 1ц — значение, приписываемое дуге (х%, х3) (/« = со,
если (хи х/)^Ц; 1:/ = 0, если !=/). Будем искать путь
(х0, х!о .. . , Х;к, хп) такой, что значение пути 10,с1 + 11и12 + ... , 11к,п —
минимально.
Рассмотрим систему уравнений
у( = т!п (V,- -Ь /,■/); I ^= 0, 1, 2, .. . , п —1.
/*'
/ = 0, 1, 2, . .. , п
Тогда решения у* этой системы являются значениями
минимальных путей от хг до Хп'- 1 = 0, 1, ..., п—1. То, что значения
минимальных путей удовлетворяют указанной системе, следует из
принципа оптимальности. Обратное утверждение о том, что
решения системы являются значениями оптимальных путей, будет
следовать из алгоритма нахождения VI.
Положим
^(0) = /«п; 1 = 0, 1, 2,..., п— 1; о„<°)=0.
Вычисляем последовательно:
о<1> = пип (о<°> + /«•/); I, / = 0, 1, 2, ... , п — 1;
о<*> = тт(у<*-!> -г /,,);
!,(*) = 0.
Вычисление проводим до тех пор, пока не будет выполнена
система равенств
у(.*) = у<*-1); I = 0, 1, 2, . .. , п.
173

Из способа вычислений следует, что г^<т> есть минимальный путь
из вершины Х{ в вершину хп среди всех путей, которые проходят
не более чем через т дуг. Следовательно, для нахождения
решения системы достаточно п—1 итераций.
Заметим, что алгоритм Беллмана — Калаба может быть
применен для отыскания максимального пути в графе без контуров. Для
этого надо только во всех соотношениях заменить ггпп на тах и
положить 1ц равным — со,, если дуга (х\, х}) не содержится в
графе.
6.5. ПОТОКИ В СЕТЯХ
При решении экстремальных задач нередко используется их
интерпретация в терминах потоков в сетях. Сетью называют
ориентированный связный граф 0= (X, I]) с множеством вершин X и
множеством дуг II, где каждой дуге (х,, х3)е<7 придается
неотрицательная числовая характеристика с(х,, х3-), называемая
пропускной способностью. В О выделяются две фиксированные
вершины — 5 и ^; 5 называется источником, I — стоком, а остальные
вершины — промежуточными.
Стационарным потоком величины V из 5 в I сети 0= (X, 11) =
= (X, Г) назовем числовую функцию /, определенную на
множестве дуг V и удовлетворяющую следующим линейным уравнениям
и неравенствам:
Е П*.У)~ Ц Пу>х)=-\ о, х^',г; (1>
уеЦх) *ег"1(*> ! -а, х = 1;
0*С}(х, у)*ас(х, у), для всех (х, у)<^11. (2)
Для упрощения записи потоковых соотношений введем
следующие обозначения.
Пусть X, У — некоторые множества, тогда под (X, У) будем
понимать множество всех пар (х, у); х^Х, уеУ.
Положим для некоторой функции §(х, у) и п(х):
ё(Х,У)= ^ 8(х,у);
к(Х)= ^Р п{х).
хех
Задача о стационарном максимальном потоке есть задача
максимизации переменной V, подчиняющейся потоковым ограничениям
(1) и (2).
Разрезом Ь в сети (X, I]), отделяющим вершины 5 и I,
называется множество дуг (У, У), где У^Х, ?=Х—У, з^У, (еУ.
Число с (У, V) называется пропускной способностью разреза
(У, у).
Отметим, что любой путь из 5 в I содержит по крайней мере
174

одну дугу разреза (У, У). Поэтому, если из сети исключить дуги
какого-либо разреза, то в новой сети не останется ни одного пути
из 5 в ( и величина максимального потока по этой сети будет
равна нулю. Интуитивно становится понятно, что величина V
произвольного потока / не превосходит пропускной способности
любого разреза. Докажем справедливость этого утверждения.
Лемма 1. Пусть / — поток из 5 в I в сети (X, Г) величины V,
(У, У) — некоторый разрез, отделяющий 5 и (. Тогда
0=!(У, у)-!(у, У)<с(У, 7).
Доказательство. Перепишем соотношения (1) в более
компактном виде:
Д*. х) —1(х, з)=а;
[(х, X) —!(Х, х)=0; хфз, (■
Ц{, Х)-ЦХ, () = -а.
Сложим почленно те из них, которые относятся к хеУ.
Учитывая, что «еУ, а /еУ, получаем
. 0 = !(У,Х)-!(Х,Г);
используя соотношение Х=У\]У, получаем
«=!(у, у\]у)-!(Уи?, у) =
=!(У, У)+!(У, у)-!(У, У)-!(у, У) =
=!(У, ?)-!(?, У).
Остается заметить, что /(У, У) >0; /(У, У)<с(У, У). Тем самым
утверждение леммы доказано.
Следующая теорема о максимальном потоке й минимальном
разрезе является основным результатом относительно
максимального стационарного потока в сети.
Теорема 1. В любой сети максимальная величина потока из 5
в I равна минимальной пропускной способности разреза,
отделяющего 5И/.
Доказательство. Из леммы 1 следует, что достаточно
показать существование потока / и разреза (У, У), для которых
величина потока и пропускная способность разреза равны. Тогда
этот поток будет максимальным, а разрез — минимальным.
Возьмем максимальный поток / (такой поток, очевидно,
существует, хотя их может быть несколько) и определим некоторый
разрез (У, У) рекуррентно следующим образом:
а) 5еУ;
б) Если хеУ и 1(х, у)<с(х, у), то уеУ; если хеУ и }(у, х)>
>0, то уеУ.
Докажем, что полученное множество (У, У) является разрезом
в сети 0=(Х, II). Для этого достаточно доказать, что (еУ.
Предположим, что это не так. Тогда из определения множества
У следует, что существует путь изо! (5, хъ х2, ..., хп> (),
обладающий тем свойством, что для всех дуг (х,-, х,+!) этого пути либо
175

?(Х1, Х1+\)<С(Х1, ДСж), (3>
либо
!(хс+и х()>0. (4)
Пусть б! — минимум разности с—/, взятой по тем дугам пути
(5, х\, ... , х„, I), для которых выполняется неравенство (3), а
е2 — минимум I на всех обратных дугах, на которых выполняется
неравенство (4). Положим е = тт{б1, ег}>0. Изменим теперь поток
/ следующим образом: увеличим / на величину е на дугах пути
(5, XI, ..., хп, I), на которых выполняется (3), и уменьшим / на
величину е на обратных дугах, на которых выполняется (4). Так,
определенная функция, очевидно, является потоком в сети из 5 в /
величины о + е. Но это противоречит предположению
максимальности потока /. Следовательно, 1^У и множество (У 7) есть
разрез, отделяющий 5 и I.
Из определения У следует:
$(х, х)=с(х, х) для (х, *)е(У, У);
!(х, х)=0 для (х, х)е(У, У).
Следовательно,
0 = 1(У, У)-! (У,У)=с(У, У).
Теорема доказана.
Из доказанной леммы 1 и теоремы 1 можно вывести несколько
следствий.
Скажем, что некоторый путь из 5 в I увеличивает поток /, если
для каждой дуги V либо ^{Ь)<с(1]), либо />0 на дуге,
обратной к V.
Следствие 1. Поток / является максимальным тогда и только
тогда, когда нет ни одного пути, увеличивающего поток /.
Дуга (х, у) будет называться насыщенной потоком /, если
/(х, у)=с(х, у), и свободной от потока, если /(к, у) = 0.
Следствие 2. Разрез (У, У) минимален в том и только в том
случае, если_каждый максимальный поток / насыщает все дуги
разреза (У, У) и оставляет свободными все дуги, принадлежащие
(У, У)-
Следующая теорема показывает, что минимальный разрез
(У, У), построенный в теореме 1, в действительности не зависит от
выбора максимального потока /.
Теорема 2. Пусть (2, 2) —произвольный_минимальный разрез,
/ — некоторый максимальный поток и (У, У)—разрез,
построенный по потоку I в теореме 1. Тогда
У<=2.
Доказательство. Пусть У $~ 2, тогда У(\2аУ. Докажем
следующее утверждение:: {У[\2, У[\2) — также минимальный
разрез. Для доказательства воспользуемся следствием 2. Пусть
х^У[\2 и х^.У[\2. Следовательно, хеУ; д:е2; х^2~[]У, и
следовательно,^, х) принадлежит хотя бы одному разрезу, либо (У, У),
либо {2, 2), и по следствию 2 максимальный поток насыщает дугу
176

(л, х). Аналогично можно доказать, что произвольный
максимальный поток / оставляет свободной дугу (х, х). Следовательно, {У{\2,
У[\1)—минимальный разрез.
Пусть вершина хеУ и х^У{\2. Тогда хфз и существует путь
из х в х, скажем (5 = хи х2 хп = х) такой, что каждая его дуга
либо насыщена потоком /, либо обратная дуга не свободна от
потока. Поскольку 8^У(]2 и х^У[\2, то найдется пара (х;, хж), у
которой Хё^У(]2 и Х1+1^У(]2. Так как мы доказали, что (У(\2У
У[\Ъ) является минимальным разрезом, то по следствию 2 все ега
прямые дуги насыщены потоком /, а все его обратные дуги
свободны от потока /. Тем самым мы пришли к противоречию, а
следовательно, У^2. Теорема доказана.
Несколько источников и стоков. Предположим, что множество,
узлов х сети (X, {/) разбито на три множества:
5 — множество источников,
Т — множество стоков,
Я — множество промежуточных узлов.
Под потоком из 5 в Т понимается числовая функция I,
определенная на V и удовлетворяющая условиям:
Пх,Х)-!(Х,х)=0; хеЯ;
!(5,Х)-1(Х, 5)=V■>
!(Т,х)-!(Х, 7-)=-1/:
0</(х, у)^с(х, у).
Расширим сеть (X, £/), добавив два узла 5* и I* и все дуги;
(х*, 5) и (Т, I*). Получим новую сеть (X*, Ц*). Доопределим
функцию пропускной способности с на II*, положив
с*(5*, х)=оо; хе5; '
с*(х, г*)=оо; х<=Т;
с*(х, у)=с(х, у); (х, «/)€=г/.
Легко видеть, что сужение } любого потока /* из 5* в (* в сети
(X*, {/*) является потоком из 5 в Г в сети (X, II). И наоборот,
любой поток / из 5 в Т в сети (X, II) продолжается в поток Р из
5* в I* в сети (X*, <У*):
1*(5*,х)=!(х,Х)-!(Х,х); хе5;
!*(х, П=!(Х,х)-!(х,Х); хеГ; .
/* (х, у)=Цх, у) — в остальных случаях.
Следовательно, задача о максимальном потоке из 5 в Г в сети:
(X, Ц) равносильна задаче о максимальном потоке в расширенной
сети с одним источником и одним стоком.
Метод расстановки пометок для решения задачи о
максимальном потоке. Существует много алгоритмов нахождения
максимального потока. Однако в основе большинства из них лежит так
называемый «метод расстановки пометок». Опираясь на
доказательство теоремы 1 и ее следствий, мы приведем этот эффективный
метод построения максимального потока и минимального разреза.
177'

Для обеспечения окончания процесса будем считать, что
функция пропускной способности с принимает лишь целочисленные
значения. На практике это не является существенным
ограничением, так как рациональные пропускные способности за счет
изменения масштаба могут быть сведены к целочисленным.
Пусть дан некоторый целочисленный поток / в сети (X, I]).
(В начальный момент поток / может быть нулевым). Припишем
^вершинам данной сети пометки, которые будут иметь вид (х+, е)
или (х~, е), где х^Х, а е — натуральное число или оо. Во время
операции А возможны три состояния вершины: а) не помечена;
б) помечена, но не просмотрена; в) помечена и просмотрена.
Операция А (расстановка пометок). Источник 5 получает
пометку (—, оо), т. е. е(5) = оо. Теперь источник помечен, но не
просмотрен, а все остальные вершины не помечены. Вообще,
выберем любую помеченную, но не просмотренную вершину х. Пусть
она имеет пометку (г±, г(х)). Тогда всем вершинам у, которые не
помечены и для которых 1(х, у)<с(х, у), приписываем пометку
>(х+, е ((/)), где
е(у)=т1п[е(х), с(х, у)—?(х, у)].
Теперь вершины у помечены, но не просмотрены. Тем
вершинам у, которые после этого не помечены, но для которых $(у, х) >0,
приписываем пометку (х~, е(у)), где
в(у)=т'т[е(х), {(у, х)].
Такие вершины у теперь помечены и не просмотрены, а
вершина х помечена и просмотрена. Эту операцию повторяем до тех пор,
пока не окажется помеченным сток (, или же до тех пор, пока
нельзя будет больше пометить ни одну вершину, а сток останется при
этом не помеченным. В последнем случае процесс построения I
закончен. В первом же — переходим к операции В.
Операция В (изменение потока). Пусть сток I имеет пометку
(У+, е(0); тогда /(у, I) заменяем на /(у, 1)+ъ{1); если же I имеет
пометку (у, е(0). то 1(1, у) заменяем на }((, у)—е(^).
Затем в любом из этих случаев переходим к вершине у.
Вообще, если у имеет пометку (х+, е(у)), то }(х, у)
заменяем на /(х, у)+г(1), а если вершина у имеет пометку (х~~,
е(у)), то /(у, х) заменяем на /(у, х)—е(() и переходим к узлу х.
При достижении источника х изменение потока прекращается.
Стираются все пометки и вновь переходят к операции А для
нового увеличения потока.
В процессе расстановки пометок, если мы от операции А
перешли к операции В, то* следовательно, мы нашли путь от 5 к I,
увеличивающий поток /. Если же операция А закончилась, а сток
остался непомеченным, то поток был максимальным, а множество
дуг, связывающих помеченные вершины с непомеченными,
образуют минимальный разрез.
Из алгоритма расстановки пометок следует, что если
первоначальный поток был целочисленный (т. е. }(и) суть целые числа
для всех ие<7), то и все последующие после увеличений потоки
окажутся целочисленными. Следовательно, справедлива
178

Теорема 3 (теорема о целочисленности). Если функция
пропускной способности с целочисленна, то существует максимальный
поток, который также целочислен.
Нижние ограничения дуговых потоков. В определении потока,
вместо неравенства (2) можно положить
1(х, у)<!(х, у)<с(х, у), (5)
где 1(х, у) —действительная функция, определенная на дугах
множества Ь и 0</(х, у)<с(х, у).
Процесс расстановки пометок непосредственно переносится на
этот случай с небольшими изменениями. При ограничениях (5)
легко доказывается аналог основной теоремы 1.
Теорема 4. Если существует функция /, удовлетворяющая при
некотором V неравенствам (5) и уравнениям (1), то максимальная:
величина потока из 5 в I равна минимуму разности с(У, У)—
—/(У, У), взятому по всем разрезам (У, У) сети.
Далее будут доказаны теоремы, дающие необходимые и
достаточные условия существования потоков в сетях, удовлетворяющих
различным линейным неравенствам.
Теорема о спросе и предложении. Пусть 0=(Х, II)
•—произвольная сеть с пропускной способностью с = с(х, у), где (х, у)^1!
и X разбито на три множества: Х = 5[]К[]Т: 5 — источники, ^ —
промежуточные вершины, Т — стоки. Каждой вершине хе5
приписано число а(х), а каждой вершине (/еГ приписано число Ь(у);.
а(х)>0, хе5; Ь(у)>0, уеТ. а(х) можно понимать, как
предложение товара в источнике х, Ь(у) —спрос на товар в стоке у.
Возникает следующая задача: каковы необходимые и достаточные
условия, при которых спрос в стоках можно удовлетворить
предложением в источниках? Алгебраически это можно записать так:
[(х,Х)-[(Х,х)^а(х); хе5;
1(х,Х)-Т(Х,х)=0; хеЯ;
1(Х, х)-}(х, Х)^Ь(х); хеГ; (6)
0<}(х, у)<.с(х, у).
Теорема 5. Ограничения (6), где а(х)>0 и Ь(х)>0, допустимы;
в том и только в том случае, когда для каждого подмножества
У!=Х:
Ь(Т(]У)-а{5[\У)<с(У,У). (7)
Доказательство. Сперва докажем необходимость
неравенства (7). Пусть существует поток /, удовлетворяющий условиям
(6). Сложив эти неравенства по всем вершинам хеУ, получаем
неравенство:
Ь(Т(\У)-а(5П?)<?(Х, ?)-?(?, ^). (8)
Х=У[)У, поэтому (8) можно преобразовать:
&(7ПУ)-а(5ПР)<да У)-1(У, У).
Используя результат леммы 1, доказываем необходимость
условия (7).
Докажем теперь достаточность условия (7). Расширим сеть
С— (X, II), присоединив фиктивный источник 5, сток I и дуги (5,5)
и (Т, I). Получим новую сеть (X*, II*). Функцию пропускной спо-
179'

•собности на и* определим по формулам:
с*(5, х) = а(х); д:е5;
с*(х, I) = Ь(х); х<=Т;
с*(х, у)=с(х, у); (х, у)е= II.
Справедливость неравенства (7) означает, что разрез (Т, I) в
-сети (X*, <7*) является минимальным. Докажем это. Пусть (У*,
У*)—произвольный разрез, отделяющий 5 и I. Положим У =
= У*\5, Х = А:*\^, тогда
с*(У*, У*У—с*(Т, 0=с*(У, 1)+с*(з, ?) +
+С*(У, у)-сЦТ, 1)=Ь(ТГ)У)+а(5№+с<У, 7)-Ь(Т) =
= -Ь(Т[\У)+а(5[\Г) + с(У, У).
Применяя теорему о максимальном потоке и минимальном
'разрезе, получаем, что выполнение условия (7) влечет
существование потока /* из 5 в I в сети (X*, II*), насыщающего все дуги
разреза (Т, {). Тогда поток /, являющийся сужением потока /* в
сети (X, II), удовлетворяет условиям (6), так как
а(х)>!*(8, х)=[*(х,.Х)-!ЧХ, х)=1(х, Х)-ЦХ, х); хе5;
Ь(х)=!*(х, *)=/*(*, х)-!*(х, Х)=ЦХ, х)-[(х, X); х^Т.
Теорема доказана.
Теорема о циркуляции. Мы докажем еще одну теорему, в
которой идет речь о существовании циркуляции, т. е. потоков,
свободных от источников и стоков и ограниченных на дугах
заданными нижними и верхними границами.
Пусть для сети (X, I]) заданы / и с — соответственно нижняя
и верхняя граничные функции на II. Допустимая циркуляция в
сети (X, I!) есть /, определенная на V и удовлетворяющая
условиям:
1(х,Х)-1(Х,х)=0; х<=Х; (9)
0</(*, У)<[(х, у)<с(х, у); (х, у)е=г/. (Ю)
Теорема 6. Для того чтобы ограничения (9) и (10) были
допустимы, необходимо и достаточно, чтобы для всех У^Х
выполнялось неравенство:
с(У, Г)>1(У, У).
Доказательство. Расширим сеть (X, I]), добавив два узла
5 и I и множество дуг (5, X) и (X, I). В новой сети (X*, II*)
зададим функцию пропускной способности по формулам:
с*(х, у)=с(х, у) —I(х, у); (х, у)е= V;
с*(8,х)=1(Х,х); х^Х;
с*(х, {)=1(х, X); *е=Х
Если в сети (X, II) существует допустимая циркуляция /, то
юна порождает поток /* из 5 в ( в сети (X*, <7*):
1*(х, у)=1(х, у)—1(х, у); (х, у)е=Ц;
Г(5, х)=1(Х, х); х<=Х;
/*(*, ()=1(х, X); х<=Х.
180

Глава 7
ВЕРОЯТНОСТНЫЕ МЕТОДЫ
В КОМБИНАТОРНОМ АНАЛИЗЕ
7.1. ПРИМЕРЫ ПРИМЕНЕНИЯ ВЕРОЯТНОСТНЫХ
МЕТОДОВ
В § 2.4 рассматривались приложения комбинаторного
аппарата производящих функций к задачам теории вероятностей (для
подробного знакомства с последней рекомендуется книга [82]).
В настоящей главе постановка вопроса будет обратной. Мы
продемонстрируем метод (или группу методов) решения комбинаторных
задач средствами вероятностного характера. Существо метода
состоит в том, что исследуемые комбинаторные объекты
интерпретируются как события в некотором дискретном вероятностном
пространстве. Доказывается, что в этом пространстве вероятность
реализации объекта, обладающего заданными свойствами,
положительна. Тем самым доказывается существование такого объекта,
хотя сам объект в явном виде не строится. Неконструктивность
метода является недостатком, однако во многих комбинаторных
задачах достаточно установить сам факт существования объекта.
Описываемый метод использует развитый аппарат теории
вероятностей, что позволяет упростить громоздкие выкладки.
Разъясним существо метода на конкретных примерах.
Оценки чисел Рамсея. Сформулируем теорему Рамсея из § 3.3
для частного случая г=1—2, Ц\ = щ2^к.
Теорема 1. Существует такое наименьшее натуральное число
п = Я(к), что при любой раскраске в 2 цвета ребер полного
неориентированного гс-вершинного графа найдется полный ^-вершинный
подграф, все ребра которого раскрашены в один и тот же цвет.
Мы докажем вероятностным методом нижнюю оценку для
чисел Рамсея Н(к).
Теорема 2.
Н{к)^к-2к>2 ■ {-~-+ о{\)\ при6->°о.
Доказательство. Рассмотрим полный граф с множеством
вершин X, где \Х\ =п. В качестве вероятностного пространства
выберем множество всех раскрасок его ребер в 2 цвета — красный и
синий. Все раскраски равновероятны, т. е. каждое ребро
независимо от других окрашивается с вероятностью 1/2 в красный цвет
и с вероятностью 1/2 — в синий. Рассмотрим ^-подмножество
У<=Х. Вероятность того, что все ребра подграфа, порожденного
183

Обратно, если в сети (X*, <7*) существует поток [*(х, у), то в
сети (X, II) можно определить циркуляцию {(х, у), положив:
?(х,у)=!*(х,у)+1{х,у) для (х,4г)е=г/.
Легко проверяется выполнение соотношений (9) и (10).
Итак, задача сведена к вопросу о существовании потока из 5
в I в сети (X*, II*) величины 1(Х, X). Необходимое и достаточное
условие существования потока из х в I величины 1(Х, X) состоит
в том, чтобы пропускные способности всех разрезов были не
меньше 1{Х, X).
Пусть (У*, У*) —некоторый разрез, отделяющий « и I в сети
(А"*, Ь*). Определим множество У^Х следующим образом:
У = У*\х; Г = У*\г.
Тогда
с*(У*, У*)=с*(У1>, у{]()=с*(У, У)+с*($, у)+с*(У, 0 =
= с(У, У)-1(У, У)+1(Х, у) +1(У, X) =С(У, у) +
+ /(У, У)+1(У, Х)=с(У, У)+1(Х, Ху-1(У, У).
Следовательно, с*(У*, У*)>/(А", X) тогда и только тогда, когда
с(У, ?)>1(У, У).
Тем самым теорема доказана.
Наконец, докажем аналог теоремы Кенига (см. § 4.1),
продемонстрировав тем самым ее связь с теоремой о максимальном
потоке и минимальном разрезе.
Через 0 = [5, Т, 0] будем обозначать двудольный граф с
множеством вершин 5Щ1, все дуги в котором ведут из 5 в Г.
Теорема 7. Максимальное число дуг двудольного графа 0 =
= [5, Т, Щ, попарно не имеющих общих вершин, равно
минимальному числу узлов в некотором (5, Г)-рассекающем множестве
узлов.
((5, Г)-рассекающее множество узлов есть множество узлов,
блокирующее все пути из 5 в Т).
Доказательство. Присоединим к рассматриваемой сети
две вершины 5и/и дуги («, 5) и (Т, I). Для расширенной сети
определим функцию пропускной способности:
с(5, х) = 1; д:е5;
с(х, 0=1; х^Т; (11)
с(х, у)=оо; (х, у)е<7.
Пусть / — произвольный целочисленный максимальный поток
из 5 в I; (У, У) —некоторый минимальный разрез, отделяющий 5
и I. Учитывая (11), заключаем, что дуги множества 1 = {(х, у)<^11;
Дх> #)_=1} попарно не имеют общих вершии. Множество Б —
= (5ПУ) 11(7Т|У) является (5, Т) -рассекающим. Причем Б
находится во взаимио-однозначном соответствии с дугами
минимального разреза (У, У). Используя теорему о максимальном потоке
181

и минимальном разрезе, получаем, что если V — величина
максимального потока I, то |/| = |/?|=у. С другой стороны,
максимальное число дуг графа О, попарно не имеющих общих вершин, оче*
видно не больше минимального числа вершин в любом (5,
Г)-рассекающем множестве. Теорема доказана.
К связям теоремы о максимальном потоке и минимальном
разрезе с другими экстремальными комбинаторными задачами мы
вернемся еще в § 8.1.
Область экстремальных задач дискретного характера огромна.
Усилия многих математиков направлены на их решение.
Разработаны алгоритмы для решения отдельных классов задач. Единой,
цельной теории этой области еще не существует.

У, окрашены в красный цвет, равна 2~Ы. Для синего цвета эта
вероятность такая же. Поэтому вероятность того, что данное
подмножество вершин У порождает одноцветный подграф, равна
2-2^2^ =2!— \2К Подмножество У можно выбрать (?)
способами. Поэтому вероятность существования «-подмножества У, по-
/П\ 1-{к)
рождающего одноцветный подграф, не выше (ь)-2 '2-\ Следо-
П\ п1-("
вательно, если числа п и « таковы, что I к I -2 ^2^ < 1, то с
положительной вероятностью р = 1 — [А -2 \2' реализуется событие,
когда ни один порожденный «-вершинный подграф не является
одноцветным. В силу конечности множества раскрасок это
означает, что существует раскраска, при которой полных одноцветных
«-вершинных подграфов нет. Итак, из 1?)<2^2''"_! вытекает::
п<К(к). Следовательно,
Используя разложение Стирлинга «1 =_-&*е-*-У2я&-(1 + о(1)>
при «->оо, получим
Я(*)\ '*'
Я(«)*^«!.р^;у15г«].212
—!
Щк)^(к«е-ьу2лк.2 2 )* -(1+0(1))= * -(1+0(1)),
у 2. е
ч. т. д. ц
Свойство $1 (см. определение .в § 1.5). Обозначим через т(к)
наименьшее число членов в системе «-подмножеств, не
обладающей свойством $. Легко видеть, что система всех «-подмножеств.
(2«—1)-множества свойством <Ё не обладает, поэтому
'2« —Г
■"<*><(*)
Оценку снизу для т(«) мы получим методом первых моментов.
Теорема 3.
т(«)>2*-!.
Доказательство. Рассмотрим множество V и систему
А = {5и 52, ..., 5т} его «-подмножеств, не обладающую свойством
Д где т = т(к). Пусть С=(УЬ 1/2) —разбиение множества V, т.е.
^=^1111/2, 1/1П1/2=0. Положим
1 1 0, если 3Г&У(,
184

где 1=1, 2; /=1, 2, ..., т. Тогда
т 2
есть число членов системы Л, целиком содержащихся в одной из
частей разбиения С.
Пусть теперь С — случайное разбиение, где каждый элемент
множества V независимо от других с вероятностью 1/2
принадлежит первой части разбиения и с вероятностью 1/2 — второй части.
Тогда при 1=1, 2 для любого ^-элементного подмножества 5;:
ММС)=Р{/,7(С)=1} = 2-*.
Подсчитаем математическое ожидание Р(С):
т 2 т 2
МР(С> =И Е м/<-/(с) =Е I 2-* =т.2'-*.
Поскольку А не обладает свойством 3$, то р(С)>1 для любого
разбиения С, и следовательно
Мр(С)>1.
Таким образом, т-21-6>1, ч. т. д.
Задача о наибольшем количестве чисел, все суммы которых
различны. Обозначим через §(п) наибольшее количество к
натуральных чисел а,\, ..., аъ, не превосходящих п, у которых все
суммы \» сц при различных 5^={1, ..., к) различны. Ясно, что числа
1, 2, 4, ..., 26~! удовлетворяют этому условию при &<1+1о§2гс,
поэтому
ё(п)>-\+[\о&п].
С другой стороны, любая из сумм не превосходит кп. Если к = §(п),
то всего имеется 2г(п) различных сумм, и все они заключены между
О и п§(п), откуда 2е{п)<п§(п). Следовательно,
§{п) <.\оё2П + \о§2§(п) <\о%2 п + \оё2(1о%2п + \о%2 8 (п)) =
= 1оё2гс + 1оё2(1оё2гс) +о(1).
Эту верхнюю оценку можно улучшить, воспользовавшись
теоретико-вероятностным методом вторых моментов.
Теорема 4.
#(гг)<1о§2л + — 1о§2(1о§2л) +о(1) при га-^-оо.
Доказательство. Пусть числа ем, ..., аи удовлетворяют
условиям задачи. Рассмотрим случайную величину Е = Е о*. . где
8 — случайно выбранное подмножество множества {1, ..., к}.
Каждый из элементов этого множества входит в 8 независимо от
других с вероятностью 1/2. Поэтому
185

Каждая пара элементов 0', /}, где 1 <!</«:&, входит в
подмножество 8 с вероятностью 1/4. Поэтому
1-€8 /=1 |<К/<*
=т2«+т Е ^/--1-1:1+4-(14•
1=1 1<*</<6 ( = ! 1 = 1
0^/ЛЕ3-(Ж)2 = -^о2.
1 = 1
Воспользуемся неравенством Чебышева (с7>0):
Р{\1-М1\<о}^ 1--^ = 1--1^0^1--^.
1=1
Поскольку все суммы Уо,- различны, то число подмножеств
Зе={1, ..., к), удовлетворяющих условию IV а,-—МЪ, I < ст, не
165
превосходит 2а. Следовательно,
Я{|Е-М||<а}<2а- [-1]*
1—— <а-2!~*.
4а2
О
Положив а -■ ;г ]/к , получим 2к < п]^к , откуда находим:
о
&<1о§2гг + —- 1о§2 (10¾ '0 -\-о(1) при /г->-оо, ч. т.д.
7.2. ЗАДАЧИ ПЛАНИРОВАНИЯ ЭКСПЕРИМЕНТА
Рассмотрим следующую математическую модель задачи
отсеивающих экспериментов. В множестве Х~{х\, ..., хп}, состоящем из
а элементов, надо найти 5 фиксированных, но заранее не известных
элементов (назовем их дефектными). Конкретно это могут быть
следующие задачи: поиск фальшивых монет, нахождение
неисправности в телевизоре, прозванивание телефонного кабеля, выявле-
186

ние больного человека в большой группе людей с помощью
анализа крови и т. д.
^ Эксперименты проводятся следующим образом. Берется
некоторое подмножество У^Х. В результате теста (испытания)
получаем информацию, трактуемую в зависимости от постановки
задачи. Например, мы можем узнать, принадлежит ли множеству У
хотя бы один из 5 дефектных элементов, либо сколько именно
дефектных элементов находится в У.
Набор множеств У,- (£=1, 2, ..., Ы) называется планом
экспериментов. По результатам N экспериментов требуется однозначно
найти все 5 дефектных элементов. Причем на выбор У^Х
(£=1, 2, ..., Ы) могут накладываться некоторые ограничения.
Задачи планирования экспериментов естественно разбить на
два класса. К первому относится статическое планирование, где
выбор !--го множества У,- не зависит от результатов предыдущих
I—1 экспериментов. Второй класс — это последовательное
планирование, при котором результаты предыдущих проверок влияют на
постановку следующего эксперимента. Рассмотрим сначала
задачу об отыскании одного дефектного элемента.
Пусть 5=1, т. е. среди элементов множества Х = {х\, ..., хп}
находится в точности один дефектный. Пусть задан также
статический план экспериментов, т. е. набор множеств Уг^Х, £=1, ..., АЛ
По этому набору строим матрицу Л = ||аг/|| размера Л/Хгс:
_ ( 1, если х; е У;,
а'1' ~ \ О, если х, =*■ Кг (1< / < п; 1< I < .V).
Обратно, по такой матрице однозначно восстанавливаются
множества У; (£=1, 2, ..., Ы).
Лемма 1. Пусть 5=1. Эксперименты, построенные по матрице
^4 = 11^11 однозначно восстанавливают дефектный элемент тогда и
только тогда, когда все столбцы у матрицы А различны.
Доказательство. Пусть в матрице А к-й столбец равен
/-му столбцу. В этом случае мы не сможем отличить, какой из
элементов дефектный: Хк или хи — так как эти элементы
одновременно либо принадлежат множеству Ут (1<т<Л^), либо не
принадлежат. Следовательно, все столбцы у матрицы А должны быть
различны.
Обратно, пусть е; — результат £^ проверки, т. е. е,-=1, если
дефектный элемент принадлежит множеству У; из плана
экспериментов, построенного по матрице Л = ||а;/11, и е,- = 0 — в противном
случае. Таким образом, после N проверок мы получим вектор
результатов е=(еи е2, ..., е^)т (Т — операция транспонирования).
Если элемент х& дефектный, то е совпадает с к-ы столбцом
матрицы А = 110,-/11. Следовательно, если все столбцы матрицы А
различны, то по вектору результатов мы однозначно восстановим
дефектный элемент. Доказательство закончено.
Таким образом, задача статического планирования состоит в
187

нахождении матрицы А, состоящей из нулей и единиц, такой, что
все ее п столбцов попарно различны, а число строк минимально.
Это число будем обозначать А^.т
Теорема 5. В случае одного дефектного элемента
Доказательство. Если все п столбцов (0, 1)-матрицы А,
составленной из N строк, попарно различны, то их количество не
превосходит количества всех двоичных слов длины Ы, т. е. ^^2^.
Учитывая, что N — целое число, и полагая N = Л^т, получим:
Ыст > ~11о§, п | ".
ОПТ '^ I Ь2 I
Справедливость обратного неравенства следует из того, что
(О, 1)-матрица, столбцы которой представляют собой запись
натуральных чисел 1, 2, ..., п в двоичной системе счисления, содержит
|1о^2«Г строк. Теорема доказана.
Рассмотрим теперь случай, когда речь идет о двух дефектных
элементах. Если при 5=1 для ЛЛ^т найдена точная формула, то
при 5 = 2 полученные верхняя и нижняя оценки не совпадают. Уже
в этом случае проявляются трудности поисковых задач
планирования эксперимента для больших 5.
Как и при 5=1, статическому плану однозначно будет
соответствовать матрица Л = ||а,71|.
В линейной модели статического планирования в результате
1-го эксперимента мы будем получать информацию о количестве
дефектных элементов, содержащихся в множестве У,. Таким
образом, вектор результатов будет являться словом длины N над
алфавитом {0, 1, 2}.
Лемма 2. Матрица Л=||а,-;|| является статическим планом при;
5 = 2, т. е. однозначно восстанавливает пару дефектных элементов
тогда и только тогда, когда все ее попарные суммы столбцов
различны.
Суммы столбцов понимаются как покомпонентные, а сложение
будет обычным:
.0 + 0 = 0, 0+1 = 1+0=1, 1 + 1 = 2.
Доказательство леммы 2 проводится аналогично
доказательству леммы 1. Разница лишь в том, что теперь вектор результатов
есть сумма 1-го и /-го столбцов, если (х,, х,) —пара дефектных
элементов.
Теорема 6. В случае двух дефектных элементов
И" >1ое, ^,. (1)
опт ^ ьл , Г) \ V '
Доказательство. Пусть (0, 1)-матрица А такова, что все
ее попарные суммы столбцов различны. Так как всего можно
составить \Л\ попарных сумм столбцов и каждая такая сумма
является словом длины N над алфавитом {0, 1, 2}, где N — число
строк в А, то справедливо неравенство:
188

%)<&■
Положив N = Л^т, получим утверждение теоремы.
Позднее мы докажем более сильную нижнюю оценку для Л^т,
а пока перейдем к верхним оценкам для Л^,т.
Для получения верхних оценок воспользуемся методом
случайного конструирования матрицы статического плана.
Пусть матрица Л = ||а;/|| построена следующим образом:
Р{а,7=1} = р>0, Р{а,7 = 0} = <7>0, р + </=1;
(1=1, ..., Ы; /=1, ..., п),
и все случайные величины а,ц независимы в совокупности.
Рассмотрим вектор-столбец г=(ги ..., гп)т длины п, состоящий/
из 2 единиц и п—2 нулей. Этот вектор будет называться вектором
неисправности. В терминах векторов неисправности лемму 2
можно сформулировать следующим образом.
Лемма 2'. Матрица Л = ||аг/|| является статическим планом тогда,
и только тогда, когда для любой пары различных векторов неис-
-е- -е- -е- —>
правности г и V справедливо неравенство: АгфАь.
Матрица А умножается на вектор обычным способом.
Рассмотрим два вектора неисправности г и V такие, что обе
единицы вектора г и единицы вектора V стоят на четырех разных.
местах. Подсчитаем вероятность того, что Аг = А^. Предваритель-
но подсчитаем вероятность того, что г-е компоненты столбцов Аг
и Аь равны (1= 1, ..., Щ.
Перебором всех возможных случаев получаем
Р{ (Л?) г = (Ло),-} = Р4 + 4р V + <Л
Так как элементы матрицы суть независимые случайные
величины, то
Р{Аг=/Ь}= (р4 + 4р2^2 + ^)л'.
-е- —>
Рассмотрим теперь пару векторов неисправности и и до, у которых
одна единичная компонента совпадает, а вторые — различные.
Аналогично первому случаю получаем
Р{Аи=Аю)={р2 + ф)ы.
Оценим теперь вероятность существования векторов г\ и г2 таких...
что Аг1 = Аг2:
Р{Яги 5:Л^ = Л22}<М, (р4 + 4р2^2 + ^)^+М2(р2 + ^2)^,
где Мх — число пар векторов первого типа, а М2 — число пар
векторов второго типа.
Простые комбинаторные рассуждения приводят к следующим
равенствам:
189

л*!-з-(2), м2 = з^).
Таким образом,
Р (3 г,, 72: а7, = а72} < 3 (2) (р* + 4рУ+ (7Т + 3 (£) (р2 + </*)"•
Пусть для некоторых р и </ (р, д>0, р + д = 1) число Я = М(п)
таково, что
3 (^ (р* + 4Ру +9*^+3 (5) (р2 + ?Т < 1- (2)
Из этого будет следовать, что с вероятностью большей нуля
существует матрица А размера $Хп, для которой неравенство
АгфАь
выполняется для любых двух различных векторов неисправности
-*■ —»
г и V. Таким образом, матрица А будет соответствовать
статическому плану.
Следовательно, А^т < N.
В качестве вероятностей р и ц мы можем выбрать любые
неотрицательные числа, такие, что р + д=1. Однако выгоднее брать
такие р й</, чтобы выражения р4 + 4р2д2+д4 и р2 + д2 были как
можно меньше. Несложные поиски экстремальных значений
приводят к следующим результатам:
3 !
тш (р4 + 4р2^2 + ^^) = — и достигается при р = п = —,
р.я^й, 8 2
ппп (р2 + д2) =.— и достигается при р = ц = —.
р. я>й, 2 2
Поэтому положим р = д = — и перепишем соотношение (2):
мгдт)+з(;.)(т) "<■■ <з>
Если одновременно будут выполняться два неравенства:
и) [ 8) < 2 •
8<3)(тГ<т
(4)
то (3) также будет выполнено. Нетрудно проверить, что
неравенства (4) справедливы при #= ~]31о§2"Г • Таким образом, нами
доказана следующая теорема.
Теорема 7. В случае двух дефектных элементов
190

Замечание. Данный результат получен неконструктивно, &,
именно мы не построили конкретную матрицу статического плана
размера ~\Ъ\о&2п[~ Хп, а лишь доказали ее существование.
Отметим, что в этой задаче победа все-таки остается на
стороне «конструктивистов». Построенный с использованием кодов Боу-
за статический план с числом строк 2-~]1о§2гсГ (см- [83]) дает
сценку:
Л/«т<2П1оё^Г-
Однако для больших 5 метод случайного конструирования-
матрицы статического плана дает результаты существенно лучшие,
чем у «конструктивистов» (см. [84]).
Аналогичными методами можно получить верхние оценки
длины статического плана и для так называемой дизъюнктивной
модели, в которой в результате 1-й проверки мы имеем лишь
информацию о наличии хотя бы одного дефектного элемента в
множестве У,-.
7.3. ЭНТРОПИЙНЫЙ МЕТОД
Данный метод позволяет улучшить оценку (1), полученную в-
теореме 6. Предварительно напомним определение и основные
свойства энтропии.
Пусть имеется конечное распределение вероятностей 3* =
т
= {рь •••, рт}, $]р, = 1 , р;>0, 1=1, ..., т. Энтропией распреде-
1 — 1
т
леиия 3 назовем величину Н (?Р) = — V Рс 1о§2р,-. При этом, если
1 = 1
какое-нибудь из р; равняется нулю, то вместо неопределенного
слагаемого —р/1о§2р1 в сумму подставляется нуль (это естественно,,
так как Нт х1о§2х = 0). Рассмотрим основные свойства введенно-
го понятия.
Свойство 1. Справедливо неравенство:
Я(^)>0,
где равенство достигается тогда и только тогда, когда одна из
вероятностей р,- равна единице, а остальные равны нулю.
Свойство 2. Справедливо неравенство:
, Н(3>)^\оё2т, (5)-
в котором равенство достигается тогда и только тогда, когда р\—
= ... =рт=1/т.
т
Действительно, Я (&>) — 1о§2 т = ^ р11о§2 (1/р;т) <
!=1
191.

1ое„е » Р{ ( П == 0. Здесь мы воспользовались неравен-
1=1
ством 1о§2я<г:(я—1)1о§2е, в котором знак равенства достигается
лишь при х=1. Следовательно, равенство в (5) имеет место тогда
и только тогда, когда р\ = ... =рт=1/т.
Рассмотрим вопрос об энтропии сложного распределения
вероятностей & = {рц}, 1=1, ..., тх; /=1, ..., т2; рц^0, 2ткрц = \.
1.1
Образуем два простых распределения вероятностей &\ и ^2
следующим образом:
&1 = Ш, Р,(1)=Е>/, 1=1,...,/^5
т,
^2 = {р<-2)}- Р<-2)=2>/, /=Г, ...,т2.
1 = 1
Ясно, что &\ и ^2 действительно являются распределениями веро-
ятностей, т. е. р^'^0, р;<2)>0, 1=1, ..., т\\ /=1, ..., "V, ^] рР = 1,
1 = 1
т2
у р(2) = 1. Следующее свойство касается связи между
величинами Я (^), Я(^0 иЯ(^2).
Свойство 3 (субаддитивность энтропии). Справедливо
неравенство:
Н{&)<.Н{&Х)+Н{&2),
где равенство достигается тогда и только тогда, когда
распределения &\ и 0>2 независимы, т. е. для всех I, / выполняется
соотношение: рц=рср).
Рп1°ё2——'—■
Ре;
1.1
Применяя неравенство 1о§2ж(я—1)1о§2^, получим для каждого
члена суммы в правой части следующую оценку:
Ра 1°¾ — < Ри 1 1о§2е,
РЦ \ Рч ' I
причем равенство достигается тогда и только тогда, когда рц=
= р*(!)-р;(2). Следовательно,
Я (Р) - Я (^) - Я (<У>3)< 1о§2 е (- % й/ + Е^%}2))= 0, ч. т. д.
Отметим, что свойство субаддитивности энтропии может быть
192

легко распространено на произвольное число распределений 0>и
0>ь ..., &п.
Пример. Пусть 1<&<я/2, Н(р) = —р1од2р— (1—р)1оёг(1— р) •
*
Покажем, что ^] (?) < 2""<*/">.
£=0
Положим р = к/п. Имеем ("7" )(1+1) = —й— ^РПР11
*—1 Ч ' й
1 = 0, ..., й—1. Следовательно, р= (^] (" Т ')) (^ (?))"'< Р-
1=0 1=0
Пусть 1;е{0, 1}, /= 1, ..., п,
0 , если Т* '"/ > К
Р'. <п= { *
| (Е(?)) '-«ЛИ Е <;<*,
Р. ,,<>
Р.
Воспользовавшись
Ье2
ГС
/=1
2»; \1* /
1=0
Я ({Р. ,-,,
1 £=0
Ч-
1*1^1* *
1
свойством
- ц Р.,
''' 'л
р , если I;
— р , если 1/
11 '/-1'';+1'--
/=1
= 1
= 0,
Р1,
субаддитивности
,...,(,, 1о§2Рч,.
, .}) = пк(р)<пп(р)
..,'„ -
/
1 (так
так что
> 1п-
энтропии,
= Я ({д.,..
получим
.<■„» <
как р<р<—),
ч. т. д.
Вернемся к задаче отсеивающих экспериментов. Будем
рассматривать случай линейной модели статического плана, когда
имеются два дефектных элемента.
Теорема 8.
Л/«т> (1 + 0(1))- -^-Ь§2п.
Доказательство. Пусть г — вектор-столбец неисправности,
—>
содержащий две единицы и (п—2) нулей, е — столбец результатов
экспериментов, А — матрица статического плана. Тогда
е=Аг.
7 К. А. Рыбников 193

Введем на множестве ^ векторов неисправности равномерное
|\-1
распределение &: Р (г) = (" I . Так как отображение А:
2
:(д-^-А(<д) взаимно-однозначно, то на множестве А^)
индуцируется равномерное распределение вероятностей (2:
п\-1 „ н/п\ — и<<ъ\ _1™ (п
Р(е)==[^) иЯ((2) = Я(<У»)-1обМ2Г
Пусть в 1-й строке матрицы А имеется гао' нулей и щ1 единиц.
Распределение & индуцирует на множестве {0, 1,2}//
распределений С};, определяемых следующим образом:
яР = /><« = о> = (2°Д2)
/ \2/ п-(п — !)
"о'Л М°\ /"'Г' 2п<0;).п</>
я.(л-1)
Ясно, что /^ = Л] Р{е). Воспользовавшись свойством субадди-
7бЛ(й):е,=г
N
тивности энтропии, получим: 1о§2(^| = #(¢) < 2,#(ф,). Непосред-
ственно убеждаемся, что #(¢,) = ф (я,)(1 + о (1)), где х,- = -—?—.
га->- оо, и ф (л:) = — х21о§2 х2 —
- 2х'(1 -х) 1о§2х(1 - х)- (1 -*)* 1о& (1 — х)2.
Поскольку
тах ф(х) = ФШ = ±. и \]Я(<2,)<(1 +о(1))# тах <р (х),
ТО
1п\
^^-^^--0 + ^)) = (1+0(1)).^108^
*6[0,!]
Теорема доказана.
Используя аналогичные идеи (но на другом математическом
языке) и применяя дополнительно более тонкие комбинаторные
рассуждения, Линдстрем [85] получил более сильную оценку:
#опт>(1 +о(1))' — Ь§2га.
194

7.4. МЕТОД СЛУЧАЙНОГО БАЛАНСА
В предыдущих параграфах рассматривалась математическая
модель задачи отсеивающих экспериментов, в которой требовалось
найти 5 фиксированных, но заранее неизвестных элементов в
множестве X, состоящем из п элементов. Теперь мы предположим, что
каждому элементу хеХ поставлено в соответствие некоторое
действительное число ш(х), называемое его весом, и среди элементов
множества X лишь некоторые, заранее неизвестные элементы,
количество которых равно $>2, обладают ненулевым весом.
Требуется выделить эти 5 элементов из множества X и определить их
веса. В каждом эксперименте разрешается выбрать некоторое
подмножество У<=Х и определить сумму весов элементов из У (т. е.
«взвесить» элементы из У). Задача состоит в планировании
экспериментов таким образом, чтобы по их результатам можно было
определить веса и; = о)(х/) элементов из X (/=1, 2, ..., п).
В дальнейшем будем придерживаться следующей терминологии:
веса соь ..., со„ элементов хи ..., хп назовем факторами; фактор
<о;- назовем значимым, если соу^О. Число 5 значимых факторов
предполагается малым по сравнению с общим числом факторов п.
По набору подмножеств У1<=.Х (1=1 АО построим (ЙХп)-
матрицу экспериментов Л = ||а,/||, где ац=\, если х-^Ус, и а,/ = 0 в
противном случае. Таким образом, в каждом 1-м эксперименте
п
(1=1, ..., А') определяется величина е( ~ 2л а'1ыг Матрица экс-
периментов Л = ||а,-;1| называется также планом экспериментов.
К плану предъявляются следующие основные требования:
простота реализации и экономичность. Выполнение этих условий
приводит к необходимости минимизировать число N экспериментов в
плане.
В предыдущем параграфе был рассмотрен случай, когда 5 = 2
и все значимые факторы равны 1. Если же число 5 значимых
факторов произвольно, то нетрудно показать, что для их однозначного
выделения из общего числа п факторов потребуется провести не
менее 1о§8+1 I га) ' —1о§2 п экспериментов (5<гс). Л. Д. Ме-
шалкин был первым, кто обратил внимание на то, что на
практике значимые факторы различны и даже обладают некоторым
условием несоизмеримости (см. [86]). Это позволяет строить планы,
эффективно определяющие эти факторы примерно за 1о§2гс
экспериментов, что значительно меньше приведенной нижней оценки.
Определение. Факторы иь ..., со„ называются несоизмеримы-
п
ми над множеством Ле2 (где ОеЛ), если из условия X 11а1 = О,
где Я;€ЕЛ, следует, что Я;со; = 0 для всех /=1 п, т. е. Л; = 0 при
всех значимых факторах со;.
Поставленную задачу будем решать для Л=2 методом
случайного баланса. Схема рассуждений при этом следующая. Разраба-
7*
195

тывается алгоритм, исходными данными которого служат (0, 1)-
матрица Л = ||а(7||, содержащая N строк и п столбцов, и вектор-
столбец е=(еи ..., еу)геКя (Т — операция транспонирования).
Если матрица и вектор е обладают определенными свойствами, о
которых будет сказано ниже, алгоритм вырабатывает вектор
и'еК"; в противном случае алгоритм ничего не вырабатывает.
Этот алгоритм оказывается таким, что из е~Аа вытекает: 0)'=©.
Доказывается, что для всякого ре]0; 1[ можно указать такое
число Ы=Ы(п, з, р), что построенная случайным образом матрица А
и вектор е=Аы будут обладать нужными свойствами с
вероятностью не менее 1—р.
Отметим, что число я значимых факторов может быть
неизвестно заранее и определится в ходе экспериментов.
Теорема 9. Пусть факторы соь ..., соп несоизмеримы над
множеством 2, а план экспериментов Л = ||а,7Н строится случайным
образом:
Р{ап = 0} = Р{ач = 1} = -Ь I - 1, ... , #; / = 1 п.
Тогда, если 5 — неизвестное число значимых факторов, а р —
некоторое действительное число, причем 0<р<1, то при
#>8 + 1оё2(га—5+1) — 1о&>Р
с вероятностью не меньшей 1—р можно определить все значимые
факторы и их число 5. Ошибка в определении факторов при этом
исключена.
Отметим, что если количество 5 значимых факторов не
превосходит некоторого наперед известного числа к : 5<&<С«, то
приведенная теорема дает границу для числа экспериментов, которое
следует провести для того, чтобы построенный случайный план с
вероятностью не менее заданной определял значимые факторы.
Доказательству теоремы предпошлем следующую лемму
Л. Д. Мешалкина.
Лемма 3. Любая /-мерная плоскость в «-мерном
действительном пространстве (2<га; /<«) содержит не более 2' вершин
«-мерного куба.
Доказательство будем вести индукцией по п. При« = 2 / может
равняться 1 или 2 и утверждение леммы очевидно. Пусть оно уже
доказано для всех чисел п'<п, где «>3. Докажем его и для п' = п.
Выберем систему координат в пространстве К" таким образом,
чтобы данный «-мерный куб стал единичным, т. е. чтобы
координаты его вершин равнялись 0 или 1. Ясно, что если / = «, то всякая
/-мерная плоскость может содержать не более 2' вершин куба —
—>
общего количества всех его вершин. Если /=1, то прямая х(1) =
= а+ (Ь—а)1, проходящая через различные вершины а =
= (аь... ,ап)т и Ь=(Ьи ..., Ъ„)т(а1, 6,е{0, 1}, 1=1, ..., п), не может
196

содержать более ни одной другой вершины. Действительно, пусть
; такое, что а-фЬи Тогда х,(0)^=х,(1) и х,(0), х,-(1)е={0, 1}.
Следовательно, при всех 1ф0, 1:
Х1{1) =щ+ {Ь:—щ)1*${1д, 1}.
—>
Пусть теперь / такое, что 1 <1<п. Обозначим К;" = {хеК" : хп = 1},
1 = 0, 1. Если /-мерная плоскость Ь параллельна Ко" или К1П и не
лежит в них, то она не содержит ни одной вершины куба. Если же
Ь лежит в одной из гиперплоскостей Ко" или КЛ то утверждение
леммы будет выполнено по предположению индукции. Остается
рассмотреть случай, когда Ь пересекает обе гиперплоскости.
Обозначим Ь1 = ЩК.1п, 1 = 0, 1. Ясно, что размерности плоскостей
Ьй и Ь\ равны /—1. Вершины куба, лежащие в каждой из
гиперплоскостей К;" (1 = 0, 1), образуют (п—1)-мерный куб и,
следовательно, по предположению индукции плоскость £,- содержит не
более 2'~! таких вершин. Поэтому плоскость Ь содержит не более
2'"! + 2'"! = 2' вершин данного «-мерного куба. Лемма доказана.
Доказательство теоремы 9. Введем обозначения:
а;—у'-й столбец матрицы Л = ||а,-;||, Ь(а;1, • • • . а-1п) —линейная обо-
—> ' —*-
лочка векторов а-и, . . . , а/ . Будем говорить, что матрица А и век-
—>
тор е обладают свойством 5, если в А найдутся линейно-независи-
мые столбцы а;,, . . . , а-, , линейная оболочка которых не
содержит ни одного другого столбца, и система уравнений
-» т
—>
имеет единственное решение. Если матрица А и вектор е обладают
—>
свойством 5, то, решив систему (6), образуем вектор со' =
= (со'., ..., Со'п)Г, положив
<о'. = ( *г ПрИ 1 = 1'(г= !• ■■• •"»)•
| 0 при ]Ер{]\, ... ,/т},
где (хи ..., хт) — решение системы (6). Отметим, что если набор
номеров столбцов /ь ..., }т в свойстве 5 определяется
неоднозначно, то его можно выбрать произвольно. Таким образом, построен-
ныи вектор со' является искомым вектором со, если е = Лсо. Для
того чтобы доказать это, достаточно проверить, что номера всех
значимых факторов со/ принадлежат множеству {/ь ..., /т}.
Действительно, если это не так, то найдется набор {си, ... , си} номеров
столбцов, не содержащийся целиком в указанном множестве и
удовлетворяющий системе равенств:
е = ^ °Ч °ч •
197

где ©а,. • • • > йЦ — все значимые факторы.
Рассмотрим систему уравнений
^ а,х,-% аагуг = 0 (7)
с неизвестными х\, ..., дст, г/1, ..., г//. Из определения свойства 5 и
выбора набора {си, ..., а;} $£{/1, ..., /т} следует, что ее ранг не
меньше т+\. Следовательно, воспользовавшись процедурой
Гаусса, из этой системы уравнений можно исключить переменные
хи ..., хт и получить хотя бы одно уравнение, содержащее только
переменные уг (^=1, •••, I)'
В силу того что коэффициенты при неизвестных в системе (7)
были целыми, следует, что коэффициенты Ьг в (8) также можно
считать целыми. Система уравнений (7) имеет решение хТ = хг,
г= 1, ..., т; уг = аа , /-=1,...,/. Поэтому набор ша,, . . . , «оц
образует решение уравнения (8), что противоречит условию
несоизмеримости значимых факторов о)а,, . . . , осц.
—>
Итак, мы показали, что если матрица А и вектор е обладают
свойством 5, то неизвестный вектор ш однозначно определяется.
Оценим вероятность Р того, что при случайном построении плана
—>
с числом экспериментов Ы>8 + 1од2(га—5+1)—1о§2 Р пара (А, е)
-^- -^-
будет обладать свойством 5, где е=Аы.
Обозначим через /1, ..., /5 неизвестные номера значимых
факторов. Рассмотрим события:
X = {(Ит/.(а/,, ... , ад = я},
У; = (а, & Ь (с/,, . .. , а/5)}> У ^ {А. • • • . /,}>
у= |>> 2 = Х(]У.
—>
Ясно, что наступление события 2 влечет за собой, что пара (А, е),
где е—Аы, обладает свойством 5. Следовательно, />>Р(2).
Оценим вероятность события Ъ. Имеем
Р{1) = Р{Х(\У) =Р(Х) -Р(У\Х).
Несложные комбинаторные рассуждения с применением леммы 3
приводят к неравенству:
Р(У\Х)> (1—2-»+*)»-*.
Для того чтобы оценить вероятность события X, рассмотрим
следующие события:
198

Хг = {й\т Ь (а/,) = 1}, Х2 = {<Ит Ь (а,-,, а,,) = 2}, .. . ,
Х5_1 = {(Ит ^ (ал, . . . , а/51) = 5 — 1},
Хх = {а/, ф /. (а/,)}, Хг = {а,, $ Ь (ал, а/,)}, . . . ,
— —> —> -*■
Х5_1 = {а/з <ЕЁЦаи, ... , а1$1)}.
Воспользовавшись леммой 3, нетрудно заметить, что
Р{Х1) = 1—2~Н, Р(Хг\Хг)-&\ — 2-ы+', г = 1, ... ,5-1.
Поэтому Р(Х) = Р (X,) П Я (Хг I Хг) > П (1 - 2-*+') ^ 1 - 2-"+5
при 5>2. Доказательство последнего неравенства в этой цепочке
можно легко получить индукцией по 5. Итак, Р(2)>
»(1—2-Л,+8)п-5+!>1 — (я—5+1) 2-"+» при Л^>5, так как при
0<а<1 справедливо неравенство: (1—а)т>1—та.
Следовательно, при Л^>5 + 1о§2(гс—5+1) — 1о§2 Р выполняется неравенство:
Р(2)>1 — (п.—5 + 1)2"Л'+5>1—р, что и завершает доказательство
теоремы.
М. Б. Малютов и М. С. Пинскер [87] рассмотрели приведенную
выше задачу при более общих условиях, когда факторы ол, ... , <лп
предполагаются несоизмеримыми над множеством Л={—1, 0 ,1}
(эксперименты при этом проводятся не случайным образом, а
последовательно, т. е. с учетом предыдущих результатов). Ими
доказана следующая теорема.
Теорема 10. Пусть факторы оси, ..., ып несоизмеримы над
множеством Л={—1, 0, 1}; 5 — неизвестное число значимых факторов.
Тогда существует неслучайный способ проведения экспериментов,
позволяющий достоверно определить все факторы не более чем
за 5 10^2 5 + 10¾^ экспериментов. При этом число 5 определяется
в ходе экспериментов.
Доказательство. С помощью первого эксперимента опре-
п
делим е±= Гш,. Дальнейшие эксперименты проводим индуктив-
1=1
но. Предположим, что после некоторого количества экспериментов
множество всех факторов оказалось разбитым на гт+1
подмножеств 0(т, 1 = 0, 1, ..., гт (1<гт<:5), причем О0т не содержит
значимых факторов, а все остальные 0;т содержат хотя бы по одному
значимому, и известны суммы ^Г=У* а/, I — \, .. . ,гт. В следу-
0);-еот
ющем эксперименте разобьем каждое из подмножеств 0;т (1 =
= 1,..., гт) примерно поровну: 0^ = 0^1)0^,0^^0^ = 0,
1^Го1—1^иП"^1и определим сумму
199

с =^ 2] шу. Если ее |Л 6^16^^(0, 1}|, то, воспользовав-
шись условием несоизмеримости факторов, приходим к
заключению, что каждое из подмножеств СцВ/ содержит только
незначимые факторы. Тогда, выбрав сГ+! =°7Е.' а«т+1 = а1-т (/=1 /-т),
гт+1 = гт, 0^+1=( \] С™ )1}6%, где е;= (ег+1) той 2, продолжим
проводить эксперименты по указанной схеме до тех пор, пока не
определим все значимые факторы, т. е. до тех пор, пока/-т не станет
равным 5, а каждое из подмножеств 0;т будет состоять из единст-
венного значимого фактора. Если же е^[У 8,-071 |е,е {0, 1}},
1 = 1
то придется провести цикл экспериментов для определения сумм
(С = V ш/ значимых факторов во всех половинках 01е"\ £ =
= 1, ..., гт; е = 0, 1. Для этой цели проведем эксперимент и опреде-
Ет
ст»о' Выясним, принадлежит ли она множеству
1=1
[г„/2]
{ }Ь его71|е(е{0, 1}|- В случае положительного ответа приходим
£=1
к выводу, что каждое из подмножеств Сц,., £=1,...,-
' ! 2
содержит только незначимые факторы. В противном случае про-
водим еще один эксперимент и определяем сумму Т"4 ат- и так
1 = 1
далее. Отметим, что при этом дополнительные суммы, такие как
гт
]|[] °ш> определяются автоматически и с ними в дальней-
*=От/2]+!
шем следует поступать аналогично, деля, если необходимо,
множество, на котором определен индекс суммирования, примерно
пополам. Итак, в результате такого цикла экспериментов мы опре-
делим все суммы ст/е — ^ до,-, 1=1, ..., гт; 8 = 0, 1, и выясним,
какие из подмножеств Си"1 состоят целиком только из незначимых
факторов. Отнеся все эти подмножества заодно с подмножеством
Со"1 к подмножеству О0т+! и переобозначив все остальные под-
200

множества заново симвЪлами 6\т+х, ..., Ог^. гДе гт+\>гт,
придем к той ситуации, в которой мы находились вначале.
Оценим число экспериментов построенного последовательно
плана. Нетрудно заметить, что в каждом цикле число
экспериментов не превосходит (гт+1—/-т) (1 + 1о§2 гт). Каждый из остальных
экспериментов, которые не входят в циклы, уменьшает число
факторов, подозреваемых на значимость, вдвое (с очевидной поправкой
из-за того, что это число может не делиться на 2). Следовательно,
общее число N экспериментов плана не превосходит 5 \о§28 + \о§2п:
N < 1 + 1о§2 п + ^ (г„+1 — /•„) (1 + 1о§2гт) < 1 +
т
3-1
+ \о§2п + % ]Г (1 + 1о&0 = 1 + 1о%2п+ £(1 + Ь§2 О
т 1:гт<1<Гт+1 *=1
(так как 1 = Г1<г2< ... <гт<гт+1< ... <гр=з). Следовательно,
8 + 1 5
^<8т 1од2/г+ ^Г 1о§21<5 + \о&2п + \1о§2хс1х<.8\о&28-\- \о§2п.
1=2 2
Теорема доказана.
7.5. РАЗДЕЛЯЮЩИЕ СИСТЕМЫ ПОДМНОЖЕСТВ
Напомним, что система подмножеств {Уи У2, ..., У^ конечного
множества X называется разделяющей, если в ней для любых
двух различных элементов из X существует У-, (1«:1«:А^),
содержащее только один из этих элементов (см. § 1.5). Положим п =
= \Х\. В этом параграфе рассматривается задача нахождения
минимальной разделяющей системы, т. е. системы, состоящей из
возможно меньшего числа Ы=Ы(п, к) подмножеств, при условии,
что каждое подмножество содержит в точности к элементов. Нас
будут интересовать также минимальная разделяющая система,
каждое подмножество которой состоит не более чем из к
элементов. Количество подмножеств такой системы обозначим через
N(4, <:*).
К понятию разделяющей системы приводят некоторые задачи
планирования отсеивающих экспериментов (см. § 7.2).
Предположим, что в нашем распоряжении имеются аналитические весы,
с помощью которых можно определять веса подмножеств из
множества X, содержащего п монет. Известно, что за один
эксперимент можно взвешивать одновременно не более к монет. Все
монеты из X одинаковые, за исключением одной, фальшивой,
отличающейся от остальных по весу. Требуется предложить
статический алгоритм поиска, выявляющий за наименьшее возможное
количество экспериментов фальшивую монету.
Для определенности будем считать, что Веса настоящих монет
равны 0, а вес фальшивой монеты равен I. Пусть в 1-м экспери-
201

менте (1=1, ..., Ю определяется суммарный вес подмножества
монет У^Х, |У,-К*. Ясно, что система {Уь ..., у^} подмножеств
из X является статической стратегией поиска тогда и только тогда,
когда она — разделяющая. Задача, таким образом, свелась к
построению минимальной разделяющей системы, каждое
подмножество которой содержит не более к элементов.
Будем обозначать одним и тем же символом х\ у'-ю монету
и ее вес; / = 1, ..., п. Как и прежде, по набору подмножеств
{Уь ..., Ум) построим (ЫХп)-матрицу экспериментов Л = ||аг/Ц,
положив а;/=1, если Я/еУ,-, и а,-/ = 0 — в противном случае.
Заметим, что каждая строка матрицы А содержит не более к единиц.
При этом система {Уь ..., Ум} является разделяющей тогда и
только тогда, когда все столбцы матрицы А различны. Такая (0, 1)-
матрица А называется Р(п, ^&)-планом. Если при этом все
строки из А содержат ровно к единиц, то матрица А называется
Р(п, к)-планом. Нетрудно видеть, что минимальные количества
строк у Р(п, к)- и соответственно Р(п, ^к)-планов равны N{п, к)
и Ы{п, <*).
Приступим к изучению этих величин и построению
соответствующих планов.
Теорема 11. Справедливы следующие утверждения:
1) N{4, к)=Ы(п, п—к),
2) Ы(п, к) =Ы{п, <*) при п^Чк.
Доказательство. Справедливость первого утверждения
следует из того, что всякий Р(п, &)-нлан инверсированием 0 и 1
превращается в Р(п, п—&)-план. Докажем 2). Так как всякий
Р(п, &)-план является в то же время и Р(п, ^^)-планом, то
Ы{п, ^.к)^Ы{п, к). Обратное неравенство при п^2к следует из
алгоритма, превращающего Р(п, ^&)-план в р(п, &)-план.
Действительно, рассмотрим произвольную строку Р(п, ^.к)-плана и
обозначим через т количество единиц в ней. Рассмотрим столбцы
плана, которые в выделенной строке содержат нуль. Понятно, что
из этих п—т столбцов можно выбрать не менее (п—т)—т —
= п—2т столбцов таких, что замена у них выделенного нулевого
элемента на единицу сохранит свойство различимости столбцов
плана. Пользуясь этим, дополним недостающее до к число единиц
Р(п, 5¾^)-плана в каждой строке и превратим его тем самым
в Р(п, &)-ллан.
Результаты следующих двух теорем получил венгерский
математик Катона [37].
Теорема 12.
2(я-1)
2(я- 1)
<#(га, <&)<тах (
Доказательство. По определению Р(п, ^к)-плана общее
количество единиц в плане не превосходит Ык. Пусть П; —
количество столбцов плана, содержащих I единиц. Так как По^1, п^
^УУ, то
202

N
Ык^^т1^п1 + 2^п1 = п1 + 2(п~п1 — п0)^2(п—\)—Ы,
ДОК)
1=0
откуда и
следует нижняя оценка.
2(л
оценки положим
N = тах
Для
-О
к + \
доказательства верхней
и покажем, что
существует Р(п, «:&)-план размера ЫХп.
Будем рассматривать различные двоичные столбцы высоты N.
Два таких столбца а= (а0, ..., ая-хУ и Ь=(Ьо, ..., Ъц-\)т назовем
подобными, если а* = Ь(г+/)то<1 ^ при некотором натуральном у для
всех 1 = 0 N—1. Множество всех столбцов разбивается на
классы эквивалентности по отношению подобия. Ясно, что мощность
каждого такого класса является делителем числа N. Любые два
подобных столбца содержат одинаковое количество единиц.
Матрицу, состоящую из всех столбцов одного класса
эквивалентности, назовем блоком.
Рассмотрим блок размера ЫхМ, порожденный столбцом, на
первых тп<Ы местах которого стоят единицы, а остальные
числа — нули. Нетрудно заметить, что для любого натурального
числа г, 0<г<М, можно выбрать г столбцов этого блока так, что
число единиц в двух любых строках образованной ими матрицы будет
отличаться не более чем на 1. Матрицу, образованную этими г
столбцами, будем называть неполным блоком.
Р(п, ^&)-план строится теперь следующим образом. Он
содержит столбец, состоящий из одних нулей, N столбцов, содержащих
по одному единичному элементу. Остальные столбцы содержат по
два единичных элемента. Они располагаются в плане блоками.
Последний блок может быть неполным. Общее количество
столбцов, содержащих не более двух единиц, не меньше п:
1 + Ы +
Ы(Ы -I)
1 +
N(N + 1) _ 2(л —1) к+\
>
= п.
2 2 А + 1 2
Следовательно, при построении плана мы действительно можем
обойтись только такими столбцами. В построенном плане
количество единиц в каждой строке не превосходит к. В самом деле,
общее количество единиц в плане равно 2п—./V—2. Так как
количество единиц в любых двух строках отличается не более чем
~" 2(п — 1)—Ы
на 1, то каждая строка содержит не более
единиц. Теорема доказана.
Следствие. N (п, к) =
2(я-1)
к + 1
при п ^
N
к(к + 1)
<к
"V
+ 1.
Теорема 13. Справедливо неравенство:
М(п,к)>-
1о§2п
к(к1п)
где Н(р)=—р\оё2р—(1—р)1оё2(1—р).
Доказательство. Воспользуемся свойством субаддитивно-
203

сти энтропии для получения нижней оценки величины Ы(п, к).
Предположим, что (ЫХп)-матрица Л=||а//||, где N = N(11, к),
а,7е{0, 1}, является Р(п, к)-планом. Тогда А отображает
множество Вп1 всех последовательностей длины п, состоящих из одной
единицы и нулей, взаимно-однозначно на некоторое подмножество
множества Вы всех (0, ^-последовательностей длины АЛ
е = А х, х =(х1, ... ,хп) ^В\, е = (е1г ... , еы) ^ Вы.
Введем на множестве В„1 равномерное распределение 9 : Р(х) =
= \/п, хеВ„'. Тем самым на множестве А(Вп1)^Вц индуцируется
равномерное распределение, которое будем обозначать той же
—»■ —>
буквой 9 : Р(е) = 1/п, где ееЛ(В„!). Энтропия Н(&)
распределения вероятностей &, как нетрудно заметить, равна 1о§2". С другой
стороны, распределение вероятностей & на А(Вп1) образует N
простых распределений вероятностей ^,-, заданных на
координатах векторов из Вы : Р{е1=1} = к/п, Р{е, = 0}=1—к/п, 1=1, ..., N.
При подсчете последних вероятностей использовался тот факт,
что каждая строка матрицы А содержит ровно к единиц. Применяя
свойство субаддитивности энтропии, получим: 1о§2я = #(сРХ
N
< 2Я(«^,.) = М(р),где р = к1п, /г(р)=-р1оё2р-(1-р)1оё2(1-
(=1
1о§2 п ^. д. д. . , .
—р) — энтропия Шеннона. Следовательно, . . V /V — /V (п, к).
Следствие. Пусть п—>-оо,к = к(п) = |ргг| , где число р не
зависит от п и 0<р<1/2. Тогда справедлива асимптотическая формула:
*(«,*) = -^(1+0(1)).
Чр)
Доказательство. Построим конкретный Р(п, &)-плап
длины N = (1 +о(1)).хак как каждый Р(п, ^к)-плян
может быть преобразован при ти^2к в Р(п, &)-план той же длины,
то достаточно построить соответствующий Р(п, =^&)-план.
Выберем минимальное натуральное АЛ, для которого справедливо
неравенство ( . .) >гс. Логарифмируя это неравенство н
используя формулу Стирлинга для факториалов, нетрудно
заключить, что для такого N справедлива асимптотическая формула:
N = —— (1 +о(1)). План строим из столбцов высоты АЛ каж-
Нр)
дый из которых содержит ровно [рЩ единиц. Расположение
столбцов в плане производится блоками, с использованием в
случае необходимости в конце неполного блока. Этим мы обеспечим
различие количества единиц в строках плана не более чем на 1.
Неравенство / ^^«гарантирует, что при построении плана
204

нам хватит запаса столбцов с указанным количеством единиц
в каждом из них. Так как доля единиц в каждом столбце плана
не больше р, а количество единиц в любых двух строках
отличается не более чем на 1, то каждая строка содержит не более
к=~~\рп\~ единиц, т. е. план действительно является Р(п, >&)-пла-
ном. Теорема доказана.
Приведем одну верхнюю оценку для величины Ы{п, ^к),
которая близка к нижней оценке, полученной в предыдущей теореме
энтропийным методом (см. [88, 89]). Отметим, что она несколько
лучше верхней оценки Д. Катоны из [37].
Теорема 14. Справедливо неравенство:
~~ 1о§2л .1 —
Ы(п, <к)<
1о&
— 1
Доказательство основано на построении Ы(п, ^&)-плана,
исходя из двоичного кода Радемахера. Так мы будем называть
(О, 1 )-матрицу размера ~\\о§2п\~ Хп, все столбцы которой
различны. Для получения какого-либо кода Радемахера достаточно взять
ближайшую сверху к п степень числа 2 и, выбрав любые п чисел,
меньшие этой степени, записать их в столбцы в системе счисления
по основанию 2.
Пусть п = 3. Построим все эквивалентные с точностью до
перестановки столбцов коды Радемахера для этого случая:
001 001 011 101
010 011 001 011
Нам потребуется следующее простое тождество, справедливое
для любого действительного числа х и натурального п:
| X г
(9)
Доказательство теоремы. Пусть К = Я(к) —
произвольный код Радемахера длины к, I — натуральное число, 50, ...
..., 81-1 — произвольные числа из множества {0, 1}. Исходя из #,
построим другой код Радемахера #5„ з,_х следующим образом.
Возьмем каждую строку с номером !'е{1, ..., ~~|1о§2^|~} и заменим
в ней каждое число /е{0, 1} на число (/ + зу-.1)тоа)той2.
Выпишем в произвольном порядке один за другим все 21 кода
#з0 8/_, и получим матрицу М размера ]1о§2&[Х2г&. Эта
матрица разбивается на Хо = ]1~1]\оё2к\[=:]^11о§2к\ подматриц
Мм Я=1, ..., Яо (см. (9)). Подматрицы М^ при КФК0 образованы I
строками матрицы М с номерами 1 = 1(Х—1) + 1, 1{к—1)+2, ..., IX.
Подматрица М\0 образована строками с номерами 1 = 1(Х0—1) +
+ 1, 1(Хо—1)+2, ..., ]1о§2&[ и может иметь менее I строк.
Нетрудно заметить, что любая подматрица МК при ХфХц
содержит каждый из 2{ двоичных столбцов высоты I ровно к раз.
Обозначим количество строк подматрицы М\0 через т. Аналогично,
Мх„ содержит каждый из 2х двоичных столбцов высоты т ровно
2*--к раз.

Обозначим через Ь^ матрицу, составленную из к одинаковых
столбцов высоты I, представляющих собой запись в столбец числа
це{0, 1, ..., 21—1} в двоичной системе счисления. Выпишем
последовательно одну за другой все 21 матриц /.„ и полученную
матрицу обозначим через Мо. Припишем сверху к матрице М матрицу
Мо и результат обозначим через Л?.
Матрица М содержит ^+~\^о£2к\~ строк и 21-к столбцов,
которые попарно различны. Следовательно, М является кодом Раде-
махера.
Доказательство теоремы основано на построении Р(пу ^к)-
плана, исходя из кода М, где натуральное число I однозначно
определяется из условия 2''-!<гг/^^2'. Для каждого А,= 0, ..., Яо—1
построим матрицу М\, составленную из п столбцов высоты
— 1. В каждом столбце все элементы нулевые, за
исключением, быть может, одного, равного 1, и в М\ каждый ненулевой
столбец входит не более к раз. При этом два столбца в М\ равны
тогда и только тогда, когда равны столбцы с соответствующими
номерами в МК. Отметим, что указанными свойствами матрица
М\ определяется неоднозначно. Для нас важно, что такая
матрица всегда найдется. Понятно, что каждая строка М\ содержит
не более к единиц.
Аналогичным/ образом построим матрицу М'% . Она состоит
из п столбцов высоты
■ 21"г. Каждый из этих столбцов
либо целиком нулевой, либо содержит только одну единицу.
Каждый ненулевой столбец входит в М'х не более к раз, а нулевой
столбец—не более 2г~х-к раз. Столбцы в М'К располагаются
таким образом, что из условия равенства двух столбцов в М'к
следует равенство соответствующих столбцов в Мк . Каждая
строка МК„ также содержит не более к единиц.
Выпишем последовательно одну под другой матрицы М0',
М[> • • • > М'^ и обозначим результат через &'. Все столбцы вМ', а
значит и в М' попарно различны. Каждая строка М' содержит
не более к единиц. Следовательно, М' является Р(п, ^.к) -планом.
Оценим его длину Ы:
N
•Г
1 +
п
к
1о&
1
'А
"')
т
+(
п
~к
п
к
— 1
— 2<-
<
+ 1
10¾ к
— 1
к*,т
1о§2п
1о& —
А
п — к
Теорема доказана.
206

Проиллюстрируем построение Р(п, <&)-плана на примере д=
= 20, к = Ъ. Имеем: I
махера # длины 5:
Определим Я00, Я01, ^
1110 0
#оо : 1 1 0 1 0 ; #01
10 110
.00000
0 ' 0 0 0 0 0
1««', 4
2. Рассмотрим код Раде-
1110 0
#'- 1 1 0 1 О
10 110
#11> М>1 *-1> ^2> ^3
и
1110 0
о о 1 о 1; #ю
10 110
0 0 0 0 0
11111
0 0 0 11 0 0 0 11
1 1 0 1 0 '. #11 : 0 0 1 0 1 ;
0 10 0 1 0 10 0 1
11111
0 0 0 0 0
11111
11111
Дальнейшие построения кода М и Р(20, 5)-плана видны из
следующей диаграммы.
КодМ:
М0:
00000 00000 11111
11111 0 0 0 0 0
11100 11100 00011
11010 00101 ПОЮ
0 0 0 0 0
М :
М2
[10110 10110 01001
Р (20,5)-план:
11111
11111
00011
00101
01001
м:
м:
м:
Из теорем 13 и 14 вытекает
Следствие. Пусть п-*-оо,
асимптотическая формула:
N (п, к) =
11111
00000
00000
11000
00100
00010
10110
00000
екает
г-»-оо,
00000
11111
00000
00100
11000
00001
10100
00010
к = к(п)
00000
00000
11111
00010
00001
11000
00000
01001
= о(п)
00000
00000
00000
00001
00010
00100
00000
О1001
Тогда справедлива
"п 1о§2 "
п
*1о§2 —
(1 +0(1)).

Глава 8
КОМБИНАТОРНЫЙ АНАЛИЗ
НА ЧАСТИЧНО УПОРЯДОЧЕННЫХ
МНОЖЕСТВАХ
В главах 2—7 настоящей книги систематически описаны
методы решения комбинаторных задач. Однако становится все более1
очевидной (в особенности при попытках решения задач
экстремального типа) настоятельная необходимость более глубокого
исследования структуры дискретных множеств. От этого
непосредственно зависит возможность как дальнейшего развития общей
комбинаторной теории, так и (в особенности) ее приложений.
Цель настоящей главы: ввести читателя в область современных
попыток распространения комбинаторного анализа на множества
возможно более общей природы. Главными из структурных
свойств множеств, которые мы будем здесь рассматривать, — это
свойства упорядоченности и независимости.
Глава начинается общим описанием дискретных множеств
с определенными на них частичными упорядочениями. Затем более
подробно рассматриваются решетки — более узкий, но для
комбинаторного анализа весьма важный класс множеств. Для
оперирования с частично упорядоченными множествами вводятся алгебры
инцидентности. При этом особое внимание уделяется операции
обращения и связанной с ней функции Мебиуса. Наконец, в главу
включены начала теории матроидов — широких обобщений,
позволяющих связывать основы комбинаторной теории с рядом
разделов математики, в первую очередь современной алгебры и
топологии.
8.1. ЧАСТИЧНО УПОРЯДОЧЕННЫЕ МНОЖЕСТВА
Пусть (А, ^) — частично упорядоченное множество. Если
|Л|<оо, то частично упорядоченное множество называется
конечным. Если а и Ь — элементы частично упорядоченного множества
А, причем а^Ь, то множество
[а, Ь] ^{х\а^.х^.Ь}
называется интервалом. Частично упорядоченное множество
(А, ^) является локально конечным, если \ [а, Ь] |<оо для всех
а, Ь^А. Частично упорядоченные множества (А, < ) и (В, <)
называются изоморфными и обозначаются (А, <)^(В, <), если
существует взаимно-однозначное отображение ф множества А на
208

множество В такое, что а^а2 имеет место тогда и только тогда,
когда ф(а!)^ф(а2). Заметим, что взаимная однозначность
отображения ф может быть выведена из последнего условия.
Напомним, что элементы а и Ь называются сравнимыми, если
а^Ь или &^а. В противном случае а и Ъ называются
несравнимыми и обозначаются: а\\Ь. Таким образом, цепь \— это частично
упорядоченное множество, в котором нет несравнимых элементов.
Антицепью называется частично упорядоченное множество, в
котором а\\Ъ для всех афЪ.
Пусть (А, ^) — частично упорядоченное множество и В — его
непустое подмножество. Тогда на В существует естественный
частичный порядок ^в, индуцированный отношением ^. Назовем
(В, ^в) частично упорядоченным подмножеством множества
(А <).
Прежде чем вводить новые определения, рассмотрим ряд
важных примеров частично упорядоченных множеств, которые^ нам
понадобятся при дальнейшем изложении материала.
Пример 1. Тривиальное частично упорядоченное множество
(или антицепь), т. е. множество, в котором а^Ь тогда и только
тогда, когда а = Ь.
Пример 2. Множество N всех натуральных чисел с обычным
порядком, т. е. п^пг тогда и только тогда, когда пг—п
неотрицательно. Множество (Ы, =¾) линейно упорядочено и локально
конечно.
Пример 3. Множество действительных чисел с обычным
порядком. Оно линейно упорядочено, но не является локально
конечным частично упорядоченным множеством.
Пример 4. Множество ^(3) всех подмножеств множества
5, упорядоченное по включению, т. е. если А, Ве^(5), то А^.В
в ^Р(З) тогда и только тогда, когда А^В(А — подмножество
множества В). Множество (^(5), г) не является линейно
упорядоченным; например, произвольные одноэлементные подмножества
несравнимы. Если |5|<оо, то (^(5), Е) также конечно. В
противном случае (^(5), Е) не является даже локально конечным.
Пример 5. Множество 7. целых чисел, упорядоченных по
делимости, т. е. а^Ь тогда и только тогда, когда а\Ь (а делит Ь).
Множество (2., |) локально конечно, ио не является линейно
упорядоченным.
Пример 6. Множество О(п) всех делителей целого числа
п, упорядоченное по делимости. Это множество является частично
упорядоченным подмножеством множества (Т., |).
Пример 7. Множество Р(п) разбиений натурального числа
п (разбиением натурального числа п называется всякая конечная
невозрастающая последовательность натуральных чисел Хи к-г, ...
г
■ ■■, Кг, для которой 5^ Хс = п; числа Л; принято называть частями
1=1
разбиения), упорядоченных таким образом, что если %, цеР(гг),
то Я^ц тогда и только тогда, когда сложением отдельных частей
209-

разбиения Я можно получить разбиение ц. Например, 3+1 + 1 =
= (12, 3); 4+1 = (1, 4); 3 + 2=(2, 3) суть разбиения числа 5, при
этом (I2, 3)<(1, 4) и (I2, 3)<(2, 3), а (1, 4) и (2, 3) несравнимы
в Р (5).
Пример 8. Неупорядоченным разбиением конечного
множества 5 называется совокупность л = {ль лг, •••} непустых попарно-
непересекающихся его подмножеств, объединение которых равно 5;
подмножества л,- называются при этом блоками разбиения.
Рассмотрим множество В(5„) всех неупорядоченных разбиений
«-элементного множества 5„, упорядоченных по объединению блоков,
т. е. л^т тогда и только тогда, когда каждый блок л,- из л
содержится в некотором блоке т, из т (или, иначе говоря, каждый блок
Т/ получается «склеиванием» некоторых блоков из л).
Пример 9. Множество всех подпространств из «-мерного
векторного пространства У„(д) над полем из д элементов,
упорядоченное по включению, т. е. если V и V — подпространства У„(д),
то 2У^К тогда и только тогда, когда V — подпространство из V.
Пример 10. Множество всех граней ^-мерного выпуклого
многогранника (под ^-мерным выпуклым многогранником
понимаем ограниченное с?-мерное множество точек евклидова
пространства, которое можно представить как пересечение конечного
числа полупространств), упорядоченных по включению.
Частично упорядоченные множества примеров 6—10 являются
конечными.
Цепью С в частично упорядоченном множестве (А, ^)
называется его непустое подмножество, которое как частично
упорядоченное подмножество является цепью. Антицепью в частично
упорядоченном множестве называется его непустое подмножество,
которое как частично упорядоченное подмножество является
антицепью. Длина 1(С) конечной цепи С — это число, равное \С\ — 1.
Говорят, что частично упорядоченное множество А имеет длину п
(обозначение 1(А)=п), если в А существует цепь длины п и все
остальные цепи в А имеют длину не более п. Будем говорить, что
частично упорядоченное множество А имеет конечную длину, если
его длина равна п и пфоо. Скажем, что ширина частично
упорядоченного множества А равна п, если существует антицепь в А,
состоящая из п элементов, а все остальные антицепи из А
содержат не более п элементов. Заметим, что длина линейно
упорядоченного множества А равна \А\ — 1, а ширина — 1.
Пусть 5 — множество из п элементов. Найдем ширину булеа-
на ^(5), т. е. частично упорядоченного множества из примера 4.
Ответ на этот вопрос дает следующая теорема, принадлежащая
Шпернеру.
Теорема I. Пусть ^(5) — булеан, |5|=я. Тогда ширина
.^(5) равна I Г_2_1 ) где [х] — целая часть от х.
Доказательство теоремы непосредственно следует из
следующей леммы.
210

Лемма. Пусть (Ль Л2, ..., Ат) — произвольная антицепь,
в ^"(5), где |5| =гс. Тогда имеет место неравенство
<1.
(=1 (|А|)
Доказательство леммы. Рассмотрим в ^(5) цепи
0=ВосВ1с2...С2Вп = 5 такие, что \Вк\ =к для к = \, 2, ..., п. Число-
всех таких цепей в ^(5) равно п\. Среди этих цепей рассмотрим
те из них, которые «проходят» через подмножество Л,-, 1 = 1, 2, ...
..., т. Пусть |Л,-| = г Тогда эти цепи имеют следующий вид:
ВйаВхС1...С1Вг-\С1А1С1Вг+хС1...С1Вп.
Число подцепей В0аВхС1...аВг^1 равно |Д«-| ! = /•!, а число
подцепей ВгМа...с1Вп равно (п—|Л,-|)!=(л—г)! Следовательно, общее
число цепей длины п, проходящих через Л,-, равно |Л,|!(я—|Л,|)!.
При 1ф] цепи, проходящие через Л,- и Л/, различны. В самом
деле, пусть Л,-, Л; {1Ф\) принадлежат одной цепи. Тогда найдутся
такие элементы Вк и В/ цепи, что Л,=В* и Л; = В/. Но тогда либо-
А^аА/, либо А^А/, что противоречит предположению о
несравнимости Л« и А].
Отсюда общее число цепей длины п, проходящих через все
подмножества антицепи, равно
т
2|А|!(/г-|4|)!
1=1
Но эта величина не превосходит общего числа всех цепей длины.
п, поэтому
2 |А|!(л-1А|)!<я!
(=1
Отсюда следует неравенство**
2
1
<1.
' ЧАР
Что и требовалось доказать.
Доказательство теоремы 1. Пусть (Ви ..., Вь) —
семейство всех — - элементных подмножеств множества 5. Тогда
очевидно, что это семейство как подмножество из ^(5) является
антицепью
-Чин)-
Докажем теперь, что все остальные ан-
*) Часто в литературе это неравенство называют неравенством Любеля,
который доказал его в 1966 г., однако еще ранее его независимо получили-
Ямамото (1954) и Л. Д. Мешалкнн (1963).
211

тицепи в &(5) не превосходят по мощности к. В самом деле,
пусть (Аи ..., Ат) — произвольная антицепь из ^(5). Тогда
в силу доказанной леммы и очевидного неравенства
имеем
А,
<№
Ж)
<У
1 = 1
\А{\
<1.
Следовательно, /п-<| "
к, что и требовалось доказать.
Следующий принцип, относящийся к конечным частично
упорядоченным множествам, играет важную роль. Он утверждает
существование согласованной (с порядком) нумерации.
Теорема 2. Пусть (А, <) — конечное частично упорядоченное
множество. Тогда элементы А можно занумеровать таким
образом: Л = {аь аг, ..., ап}, что из щ<а, будет следовать 1<у.
Доказательство. Положим Хт='{Ъ\, Ь2, ..., Ьт), где
первоначальная нумерация А~ {Ьг, Ь2, ..., Ьп} выбрана каким угодно
способом. Построим последовательность взаимно-однозначных
отображений фт множеств {1, 2, ..., т) на себя, такую, что каждое
подмножество Хт, перенумерованное посредством Фт:^т={о™,
... , а™}, где а™ = Ьу (1-), будет удовлетворять
сформулированному в теореме утверждению: из (цт<щт следует, что /</.
При т = \ взаимно-однозначное отображение ф! строится
однозначно. Предположим, что взаимно-однозначное отображение
фл_, : {1, 2, .... п—1}-*{1, 2, ..., п—1}
с требуемым свойством уже построено. Обозначим через к
наименьшее из чисел I, обладающих свойством Ьп<щп~1. Построим
взаимно-однозначное отображение фП:{1,..., п—1,п}-*-{1, ...,п—1, га}
следующим образом:
Ф« (О
Иными словами, вставим Ь„ между а^-| и а^-!. Проверим, что
Ф„ обладает требуемыми свойствами. Если асп<а/п и {а?, а?} с= Х„_1,
то К] по предположению индукции. Если Ъп = аьп<а,1п, то к<]
по построению. Наконец, если шп<акп = Ь„, то а1} < а% < а^+!)
откуда $ < а^+! в силу транзитивности отношения порядка, и
п
1
+
»
1,
если
если
если
К к;
1 — &;
I >й.
212

наконец, Кк + 1 по предположению индукции, так как {а", а*+1} с:
аХп-1. Следовательно, и здесь Кк (случай 1 = к невозможен);
доказательство теоремы завершено.
В частично упорядоченных множествах полезно выделять
элементы некоторых специальных видов. Элемент М частично
упорядоченного множества А называется максимальным, если в А нет
элемента а, «большего», чем М, т. е. а^М не выполняется ни для
какого а&4, отличного от М. Аналогично элемент т^А
называют минимальным, если в А нет элемента а^А, отличного от т, и
такого, что а^т. Элемент оеЛ называется наибольшим, если
для всех с^А : с^а. Элемент Ь^А называется наименьшим, если
для всех сеЛ : о&. Для наибольшего и наименьшего элементов
частично упорядоченного множества будем использовать также
обозначения 1 (единица) и 0 (нуль) соответственно. Легко
проверяется, что всякий наибольший элемент является максимальным,
а всякий наименьший — минимальным. Обратное, вообще говоря,
места не имеет. Так, например, в тривиальном частично
упорядоченном множестве всякий элемент является как максимальным,
так и минимальным. Другой пример минимальных, но не
наименьших элементов доставляют простые числа во множестве целых
положительных чисел {2, 3, 4, 5, 6, ...}, упорядоченном по
делимости как в примере 5. Нулем 0 во множестве Р(п) из примера 7
является (1"), в булеане ^(5) — пустое множество 0 и в беллнане:
В(5«) — разбиение {а^, {а2}, ..., {ап}. Единицы в этих частично
упорядоченных множествах также существуют и равны
соответственно п, 8 и 5«.
Заметим, что определение наименьшего элемента получается
из определения наибольшего элемента простой заменой символа
^ на ^. Точно таким же образом связаны понятия минимального
и максимального элементов. Вообще, имея какое-либо
высказывание о частично упорядоченном множестве и заменяя ^ на 2э.
получаем новое высказывание. Высказывания, связанные таким
образом, называются двойственными.
Пусть (А, ^) — частично упорядоченное множество.
Отношение ^ (где а^Ь означает, что Ь^а) также является отношением
частичного порядка на А. Таким образом, (А, ^) также является
частично упорядоченным множеством, которое называется
двойственным частично упорядоченному множеству (А, ^). Далее, если
Ф — утверждение о частично упорядоченных множествах, то,
заменяя все вхождения < на >, получаем утверждение,
двойственное утверждению ф.
Принцип двойственности. Если утверждение Ф верно для всех
частично упорядоченных множеств, то двойственное ему
утверждение также верно для всех частично упорядоченных множеств.
Этот принцип справедлив просто потому, что Ф имеет место
в частично упорядоченном множестве (А, ^) тогда и только
тогда, когда двойственное ему утверждение имеет место в частично
.упорядоченном множестве (А, ^).
Пусть (А, О — частично упорядоченное множество. Скажем
213

что элемент а^А покрывает элемент Ь^А или Ь покрывается
элементом а (обозначение: а^Ь или 6-=>а), если а>Ь и не
существует с^А такого, что а>с>Ь. Элемент а называется атомом,
если а^О, и коатомом, если а—^ 1. Для случая, когда а покрывает
Ь или совпадает с ним, введем также обозначение а^-Ь.
Диаграммой Хассе частично упорядоченного множества А
называется ориентированный граф, вершинами которого являются
элементы множества Л, а дуга (а, Ь) наличествует тогда и только
тогда, когда а покрывает Ь в частично упорядоченном множестве
А. Дуги в этом графе принято изображать направленными вниз.
На рис. 8.1 изображена диаграмма Хассе частично
упорядоченного множества Р (5) из примера 7.
Рис. 8.1 Рис. 8.2 Рис. 8.3
Коатомами в Р (5) являются (1, 4) и (2, 3) и атомом — (I3, 2)-
Всего в Р (5) имеется 7 элементов. Значения \Р(п) | растут очень
быстро с ростом п; например: |Р(6)|=11, |Р(10)|=42, |Р(20)1 =
= 627, |Р(50) |=204 226, | Р (100) | =190 569 292.
Диаграммы Хассе булеана &{$), где 5 = {1, 2, 3, 4}, и частично
упорядоченного множества 1)(20) из примера 6 приведены
соответственно на рис. 8.2 и 8.3. В первом множестве атомами
являются все одноэлементные подмножества, а именно {1}, {2}, {3}, {4},
а во втором — числа 2 и 5.
Пусть А — конечное частично упорядоченное множество. Тогда
его диаграмма Хассе является орграфом без контуров. По
аналогии с теорией графов, матрицей смежности диаграммы Хассе
частично упорядоченного множества А назовем квадратную матрицу
НЛуЦ порядка \А\, у которой &;/ = 1, если (щ, а/) — дуга на
диаграмме Хассе (или, что эквивалентно, О/—$0* в А), и &/ = 0 —
в противном случае. Эта матрица совпадает с матрицей функции
покрытия из стандартной алгебры инцидентности 5 (Л) (см. ниже
§8.3).
Остановимся кратко на способах нумерации, согласованной
с порядком, существование которой гарантирует теорема 2. Ска-
214

жем, что элемент а есть предок элемента Ь или Ъ — потомок а,
если а>Ь в А.
Рассмотрим следующую важную в приложениях задачу:
Разбить все элементы частично упорядоченного множества А
на слои так, что-.
а) все элементы данного слоя не имеют потомков в следующем
слое;
б) элементы первого слоя не имеют потомков, а элементы пос-
ледного — предков;
в) каждый слой является антицепью в А.
Приведем один из методов решения этой задачи. Пусть К —
матрица смежности диаграммы Хассе частично упорядоченного
множества А. Обозначим через_а, В, ... вектор-столбцы этой
матрицы. Вычислим вектор аг= V а и припишем его справа к матри-
це К- Обозначим через А\ подмножество множества А, элементам
которого в вектор-столбце а\ соответствуют нули. Эти нули
означают, что элементы множества А\ не имеют потомков. Поэтому
множество А\ образует первый слой.
Вычислим теперь вектор а2 = аг — V а. Нулям этого век-
тор-столбца аг соответствуют элементы множества Л2, которые
образуют второй слой. Вычислим вектор а8 — а2— V а и элемен-
аел2
ты множества Л3, соответствующие нулям вектор-столбца,
отнесем к третьему слою. Будем продолжать вычисления до тех пор,
пока не получим вектор-столбец, состоящий из одних нулей.
Отнесем оставшиеся элементы множества А к последнему слою. Для
доказательства, что получившееся разбиение является искомым,
заметим, что на каждом этапе вычисления мы находим элементы
множества без потомков.
Проиллюстрируем этот метод на конкретном примере. Пусть
А — частично упорядоченное множество, диаграмма Хассе
которого приведена на рис. 8.4. Все вычисления для решения задачи
приведены в таблице. Диаграмма Хассе приведена на рис. 8.5.
215

а
Ъ
с
а
е
1
ё
к
1
]
к
а
0
0
0
0
0
0
0
0
1
1
0
Ь
0
0
0
1
0
0
0
1
0
0
0
с
0
0
0
0
0
0
0
0
0
0
1
а
1
0
0
0
0
0
0
0
1
0
0
е ! В
0 1 0
0 0 0
0 0 1
0 0 0
0 0 0
0 0 1
0 0 0
0 0 0
0 0 0
0 0 0
0 0 0
к
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
У
0
0
0
0
0
0
0
0
0
0
0
к
0
0
0
0
1
0
0
0
1
0
0
Слой
Элементы
Л
2
0
1
1
1
1
0
1
3
1
2
1
Ь,8
А2
2
X
0
0
1
0
X
0
3
1
2
2
с, й, /,
Л
Л
0
X
X
X
1
X
X
X
2
1
0
3
а, к
Л
X
X
X
X
0
X
X
X
0
0
X
4
е, 1, /
Замечание. При реализации рассмотренного метода
разбиения на слои на ЭВМ необходимо к матрице К прибавить матрицу
< I 0 0 ... 0 >
0 1 0 ... 0
0 0 1 ... 0
0 0 0 .
1
чтобы различать нули (0) и пустые места (X). Тогда нули станут
единицами и X — нулями.
Пронумеровав элементы частично упорядоченного множества
А произвольным образом внутри слоя 1, затем внутри слоя 2.
и т. д., получим нумерацию, согласованную с порядком
множества А. Например, элементы частично упорядоченного множества,
диаграмма Хассе которого изображена на рис. 8.4, можно
занумеровать Ь§НЫ1кае1]',илп§Ьсс1Щаке]1, или Ьд,\ЛсЬ,ак\1е и т. д.
Заметим, что при такой нумерации элементов К будет верхней
треугольной матрицей.
Перечислить все перестановки элементов частично
упорядоченного множества А, согласованные с его порядком, приведенным
методом, вообще говоря, невозможно. Поэтому в качестве
упражнения предлагаем читателю самостоятельно разработать метод
перечисления перестановок элементов конечного частично
упорядоченного множества, согласованных с его порядком, но
рекомендуем сделать это после изучения материала § 8.3.
Цепь, каждое непустое подмножество которой обладает
минимальным элементом, называется вполне упорядоченной. Вполне
упорядоченным множеством является конечная цепь. Естествен-
216

яым образом упорядоченное множество натуральных чисел также
вполне упорядочено. Множество всех целых чисел не является
вполне упорядоченным относительно естественного порядка, так
как оно не имеет наименьшего элемента. Однако оно становится
вполне упорядоченным, если установить порядок следующим
образом:
1<2<3<4<...<0<—К—2<—3<—4<...,
где, все положительные числа предшествуют остальным. Другим
примером не вполне упорядоченной цепи служит отрезок [0, 1],
ибо, например, интервал (—, 1] не содержит минимального
элемента.
Важность вполне упорядоченных множеств состоит в
возможности применения метода индукции, так называемой
трансфинитной индукции, известного нам по конечным и счетным множествам
в случае вполне упорядоченных множеств. Суть этого метода
заключается в следующем: пусть Р — некоторое утверждение об
элементах вполне упорядоченного множества А. Если Р
выполняется для минимального (или «первого») элемента Л и из
справедливости утверждения Р для всех х<а следует его справедливость
для элемента а, то утверждение Р выполняется для всех
элементов вполне упорядоченного множества А-
В самом деле, пусть выполнены посылки условия
индуктивности. Рассмотрим подмножество В всех элементов из А, для которых
не выполняется утверждение Р. Если заключение индукции не
имеет места, то В непусто. Поскольку А вполне упорядочено, в В
имеется минимальный элемент а. По условию этот элемент не
может быть минимальным элементом множества А. Если х<а, то
х&В к, следовательно, для х справедливо утверждение Р по
условию. Но тогда для а справедливо утверждение Р. Получили
противоречие. Значит, множество Б пусто, и утверждение Р
справедливо для всех &еА
Говорят, что частично упорядоченное множество А
удовлетворяет условию минимальности (соответственно максимальности),
если каждое непустое подмножество множества Л является
частично упорядоченным множеством, содержащим минимальные
(соответственно максимальные) элементы.
Любое вполне упорядоченное множество А удовлетворяет
условию минимальности, а двойственное ему А* удовлетворяет условию
максимальности. Примером такого множества является
множество натуральных чисел с обычным порядком, которое
удовлетворяет условию минимальности, но не удовлетворяет условию
максимальности.
Скажем, что частично упорядоченное множество удовлетворяет
условию обрыва убывающих цепей (соответственно условию
обрыва возрастающих цепей), если для произвольной счетной
последовательности {ап\п=\, 2, ...} элементов из А, такой, что а{^а2~^
Ж..^ап^... (соответственно а1^а2^...^а„^...), существует число
к такое, что ап = йк для всех п^к.
217

Теорема 3. В частично упорядоченном множестве А условие
минимальности (соответственно максимальности) эквивалентно
условию обрыва убывающих (соответственно возрастающих)
цепей.
Доказательство. Предположим, что выполняется условие
минимальности и а{^а{^...~^а,С^... — счетная цепь элементов из
А. Пусть а — минимальный элемент в подмножестве {ап\п =
= 1, 2, ...} множества А. Тогда а — аи для некоторого к и,
следовательно, ап=а = ак для всех п^к.
Обратно, пусть выполняется условие обрыва убывающих цепей
и В — непустое подмножество множества А. Тогда В содержит
.элемент а.\, и если й\ не является минимальным в В, то
существует элемент й2ёВ такой, что а{>а2. Предположим, что существуют
аи ..., ап^В такие, что а{>а2> ...>ап. Тогда либо ап является
минимальным в В, либо существует элемент ап+\^.В такой, что
ап>ап+\. Отсюда заключаем, что либо В имеет минимальный
элемент, либо существует бесконечная цепь а1>а2>...>ап>...
элементов из В. По предположению, возможен лишь первый случай.
Двойственным образом устанавливается справедливость
оставшейся части теоремы. Тем самым теорема доказана.
•Упражнения. Докажите, что
1. Если цепь С и двойственная ей цепь в двойственном частично
упорядоченном множестве вполне упорядочены, то С содержит конечное число
элементов.
2. Если частично упорядоченное множество не содержит ни бесконечных
цепей, ии бесконечных антицепей, то оно конечно.
3. Конечное множество удовлетворяет условиям минимальности и
максимальности. х
4. Если цепь не вполне упорядочена, то она содержит подцепь,
двойственную натуральному ряду.
5. Локально конечное частично упорядоченное множество удовлетворяет
условию минимальности.
Если А — частично упорядоченное множество, то множество
всех цепей само будет частично упорядоченным при помощи
теоретико-множественного включения. Максимальные элементы этого
последнего множества, если они существуют, называются
максимальными цепями множества А. Другими словами, цепь С
частично упорядоченного множества А называется максимальной цепью,
если для всякого элемента а из А, не принадлежащего С,
подмножество С11{а} уже не является цепью.
При изучении бесконечных множеств весьма часто приходится
использовать следующую аксиому выбора:
Если дано множество А, то существует функция ф,
сопоставляющая каждому непустому множеству В из А один определенный
элемент ф(В) этого подмножества.
Иными словами, функция ф помечает по одному элементу
в каждом из непустых подмножеств множества А.
Многочисленные математические исследования опираются на
аксиому выбора. Вопрос о логических основах этой аксиомы и
о законности ее использования принадлежит к числу самых
трудных и спорных вопросов обоснования теории множеств. Во всем
218

дальнейшем нашем изложении аксиома выбора будет
предполагаться справедливой. Для счетных множеств аксиома выбора
может быть легко доказана. В самом деле, если элементы
множества Л пронумерованы натуральными числами, то мы получаем
требуемую функцию, пометив в каждом подмножестве В из Л тот
его элемент, который имеет наименьший номер.
Пусть Л — множество, на котором заданы два отношения
частичного порядка < и =§. Будем говорить, что порядок =§ является
продолжением порядка ^, если для любых а, Ь^А соотношение
а<& влечет соотношение а=%Ь.
Теорема 4. Пусть А — частично упорядоченное множество,
удовлетворяющее условию минимальности. Тогда его частичный
порядок может быть продолжен до порядка, превращающего А во
вполне упорядоченное множество.
Прежде чем перейти к доказательству теоремы, дадим
несколько определений. Отрезком некоторого вполне упорядоченного
множества А назовем всякое его подмножество В, содержащее
вместе с любым своим элементом Ь все такие хеЛ, что х^Ь.
Множество элементов, строго предшествующих некоторому
элементу а из А, является истинным отрезком множества А, т. е.
отрезком, отличным от самого А, и этим исчерпываются все
истинные отрезки: если В — такой отрезок, то В состоит из всех
элементов, строго предшествующих минимальному элементу
дополнения Л\В, т. е. определяется этим элементом. Пустое
подмножество будем также считать истинным отрезком множества А; он
определяется минимальным элементом этого множества.
Доказательство теоремы 4. Пусть А — частично
упорядоченное множество, удовлетворяющее условию минимальности.
Отметим в каждом его непустом подмножестве В по одному
элементу ф(В), положив ф(В) равным одному из его минимальных
элементов. Это всегда можно сделать в силу условия
минимальности и аксиомы выбора. Будем называть непустое подмножество
В из А отмеченным, если его индуцированный порядок может
быть продолжен до порядка, превращающего его во вполне
упорядоченное множество, причем так, что для всякого оеВ : а =
= ф(Л\В'), где В' — отрезок множества В в указанной полной
упорядоченности, определяемой элементом а. Отмеченные
множества в А существуют; таково, например, подмножество (ф(Л)},
так как {ф(Л)}' = 0 и ф(Л) =ф(Л\0).
Пусть В и С — два отмеченных подмножества, для которых
выбраны полные упорядоченности, обладающие свойством,
указанным в предыдущем абзаце. Тогда оба эти подмножества
имеют ф(Л) в качестве первого элемента и поэтому обладают
непустыми совпадающими отрезками. Объединение О всех
совпадающих отрезков этих двух подмножеств будет, очевидно, отрезком
в каждом из них; это наибольший среди совпадающих отрезков.
Если бы отрезок И был отличен и от В, и от С, то по определению
отмеченного подмножества отрезок Б определялся бы и в В, и
в С элементом ф(Л\1>), а тогда-В и С обладали бы большим, чем
219

£), совпадающим отрезком, состоящим из О и элемента ф(Л\1>).
Это противоречие с определением О показывает, что одно из двух
отмеченных подмножеств В и С является отрезком другого.
Отсюда следует, что объединение 5 всех отмеченных
подмножеств из А само будет отмеченным. Действительно, если Ь и с
из 5 принадлежат соответственно к отмеченным подмножествам
В и С, то они оба лежат в большем из этих подмножеств,
например в В. Полагая Ь^с в 5, если Ь^с в этом А, мы получим в 5
линейную упорядоченность, которая будет даже полной
упорядоченностью: всякая убывающая цепь элементов в 5 целиком
содержится в некотором отмеченном подмножестве В и поэтому
должна обрываться. Наконец, если &е5, то Ъ содержится в некотором
отмеченном подмножестве В и определяет в 5 и в В один
и тот же отрезок В', причем Ь=ср(Л\В'). Этим доказана
отмеченность множества 5.
Для окончания доказательства теоремы остается указать, что
если бы 5 было отлично от А, то в противоречии с определением 5
мы получили бы большее, чем 5, отмеченное подмножество,
присоединяя к 5 элемент ф(Л\5) и считая этот элемент следующим
за всеми элементами из 5. Теорема доказана.
Из теоремы 4 немедленно следует
Теорема Цермело. На всяком непустом множестве можно
задать порядок, превращающий его зо вполне упорядоченное
множество.
Более того, из теоремы Цермело следует аксиома выбора.
В самом деле, если А — некоторое непустое множество, то,
согласно теореме Цермело, его можно считать вполне
упорядоченным. Если В — непустое подмножество множества А, то,
обозначив через ф(В) наименьший элемент множества В, убедимся, что
ф(В) удовлетворяет аксиоме выбора. Таким образом, мы доказали
эквивалентность теоремы 4, аксиомы выбора и теоремы Цермело-
Для более детального знакомства с аксиомой выбора и
эквивалентными ей теоремами (см. [33, 90, 91]).
Рассмотрим систему {Аа\а^Ь} частично упорядоченных
множеств, предполагая, что множество Ь также является частично
упорядоченным. Будем считать, что различные множества
рассматриваемой системы не имеют общих точек. Это, впрочем, не
мешает некоторым из них являться различными экземплярами
одного и того же множества. Обозначим через А
теоретико-множественное объединение множеств этой системы и через Р — прямое
произведение множеств системы {Аа\ае^Ь}, т. е. множество
функций а, ставящих в соответствие каждому множеству Аа элемент
аа^Аа. Функции а можно воспринимать как строку (аа), где а
пробегает множество Ь. Существование таких функций вытекает
из применения аксиомы выбора к \) Аа. Следовательно, прямое
СС € /-
произведение любой системы непустых множеств непусто.
Зададим на Р отношение <^, положив а<С,Ь тогда и только тогда, когда
при любом аб! из ааФЬа существует такое р<а, что а$<Ь$.
220

Теорема 5. Если частично упорядоченное множество Ь
удовлетворяет условию минимальности, то отношение =< на Р,
задаваемое условием:
а<6, если а = Ь или а<^Ь,
является порядком.
Доказательство. Рефлексивность отношения =<
очевидна. Пусть а<;Ь_и Ь <; а, но афЬ. Тогда найдется такой индекс
ае1, что аа ^Ьа и ар<Ьр для некоторого р<а. Но Ьр^ёар и 6<^а.
Следовательно, найдется Р1<а такой, что&р^ар,. Отсюда
ар.гё&р, и а^Ь. Поэтому найдется Рг<Р1 такой, что ар.,<Ьрг.
Продолжая этот процесс, получим бесконечную убывающую
последов ательносхь
а>р>р,>р2>...
элементов из Ь, но это противоречит условию минимальности Ь
(см. теорему 3). Значит, а=Ъ и антисимметричность отношения
<; доказана.
Проверим теперь транзитивность нашего отношения. Пусть
а =^Ь и Ь^с. Если а=Ъ или Ь = с, то транзитивность очевидна.
Если же а-^Ь и 6<^с, но не а<^с, то найдется такой индекс а^Ь,
что аа<^са и ар<);ср для всех р<а. Отсюда следует, что аа<);Ьа,
или Ьа<^са. Положим а! = а и допустим, что выбраны индексы
(11>(12>...>а,1
так, что для каждого а,- (1 = 1, 2, ..., п) имеет место аа[ < Ьа.
или Ьа. ' са . Если, например, аап < Ьап, то для некоторого р<а„
должно быть ар<Ьр. Если Ьр^ср, то ар<сР. Поскольку р<а,г<а,
это противоречит выбор а. Следовательно, Ьр<^с.з, что позволяет
положить ап+1 = р. Таким образом, мы получили вновь бесконечную
убывающую последовательность: (11>а2>...>ап>... элементов
из Ь, что противоречит условию минимальности Ь. Следовательно,
транзитивность отношения <^ доказана и доказательство теоремы
завершено.
Прямое произведение Р, снабженное порядком, описанным
в теореме 5, называется упорядоченным произведением частично
упорядоченных множеств Аа,
На множестве А также определим отношение <; положив
а^Ь тогда и только тогда, когда а, Ь^Аа и а^Ь в Ла или же
аеЛа, ЬеЛц и а<р в Ь. Проверим, что отношение <; является
порядком на "■ — У А*- В самом деле, очевидно, что ^ — РеФ"
лексивное отношение. Если а<;6 и Ь^а, то очевидно, что а, &е
еД, для некоторого ае! и, следовательно, а=Ъ. Если а<;6 и
Ь <;с, то а^Аа, ЬеЛр, сеЛ7 и неравенство а^с устанавливается^
несложным рассмотрением следующих четырех случаев:
1)а = р, Р=г; 2) а = р, ?,<у; 3) а<р, р<7; 4) а<р, р = Т.
Так что (Л, <;) действительно является частично упорядоченным
множеством, которое называется упорядоченной суммой частично
упорядоченных множеств Аа-
Если Ь — антицепь, то упорядоченная сумма называется кар--
221

Финальной суммой, а упорядоченное произведение — прямым
произведением. В случае прямого произведения, очевидно, а =<Ь тогда
и только тогда, когда аа^Ьа в Аа для всех ае1. Если Ь — Цепь,
то упорядоченная сумма частично упорядоченных множеств
называется ординальной суммой. Упорядоченное произведение в
случае, когда Ь — вполне упорядоченное множество, называется
лексикографическим.
Упорядоченная сумма А естественным образом содержит свои
слагаемые в качестве подмножеств. Это позволяет говорить, что
А разлагается в упорядоченную сумму своих подмножеств.
Частично упорядоченное множество, не представимое в виде
ординальной (соответственно кардинальной) суммы своих собственных
подмножеств, называется ординально (соответственно
кардинально) неразложимым.
Напротив, сомножители Аа упорядоченных произведений Р
не допускают столь естественного истолкования как его
подмножества. Правда, Аа вкладываются в упорядоченное произведение
Р, но таких вложений много.
Более подробно об упорядоченных суммах и произведениях
можно прочитать в [33]. Мы же сформулируем в виде упражнений
ряд их свойств.
Упражнения. Покажите, что
6. Всякое частично упорядоченное множество является кардинальной
(соответственно ординальной) суммой своих кардинально (соответственно
ординально) неразложимых подмножеств.
7. Каждое частично упорядоченное множество является упорядоченной
суммой одноэлементных множеств. '
8. Частично упорядоченное множество является кардинальной
(соответственно ординальной) суммой одноэлементных множеств тогда и только тогда,
когда оно является антицепью (соответственно цепью).
9. Ординальное сложение не коммутативно.
10. Упорядоченная сумма вполне упорядоченных множеств {Аа\а^^}
вполне упорядочена тогда и только тогда, когда Ь — вполне упорядоченное
множество.
11. Упорядоченная сумма частично упорядоченных множеств {Ла|ае^}
удовлетворяет условию минимальности тогда и только тогда, когда условию
минимальности удовлетворяют Ь и все Аа.
12. Упорядоченное произведение конечного семейства частично
упорядоченных множеств Ла удовлетворяет условию минимальности тогда и только
тогда, когда условию минимальности удовлетворяет все Аа.
13. Лексикографическое произведение цепей является цепью.
14. Лексикографическое произведение конечного семейства вполне
упорядоченных множеств вполне упорядочено.
В заключение этого параграфа остановимся на некоторых
результатах о частично упорядоченных множествах, где основное
внимание оказывается обращенным на цепи и антицепи. Типичной
для такого рассмотрения является задача о нахождении
минимального числа цепей, на которое можно разбить конечное
частично упорядоченное множество. Ответ дает следующая теорема,
принадлежащая Дилуорсу.
Теорема 6. Пусть Р — конечное частично упорядоченное
множество. Наименьшее число непересекающихся цепей, содержащих
все элементы Р, равно ширине Р.
222

Доказательство. Пусть й{Р) — минимальное число
непересекающихся цепей, содержащих все элементы частично
упорядоченного множества Р, Ц(Р) — семейство всех антицепей в Р
и 5(Р) — ширина частично упорядоченного множества Р, то есть
5( ' =,?)?,п' I" Тогда теорема утверждает, что й(Р)=з(Р).
Докажем это.
Очевидно, с1(Р)^з(Р), так как никакая цепь не содержит
более одного элемента из антицепи. Обратное неравенство докажем
индукцией по числу элементов частично упорядоченного
множества Р, т. е. \Р\. Если |Р| = 1, то утверждение очевидно. Пусть
оно верно для всех частично упорядоченных множеств С? таких,
что |(2|<|.Р|. Положим з(Р)=п и рассмотрим два случая:
Случай 1. Пусть существует антицепь Ле(/(Р), |/4|=га, не
содержащая ни антицепь Ат1п всех минимальных элементов Р,
ни антицепь Атах всех максимальных элементов Р. Определим,
два множества:
Р+ = {х<=Р\ ЭаеЛ : х>а};
Р- = {х<=Р\'3.а<=А : х<а}.
Из предположений относительно антицепи А имеем: Р+[\Р~ = А,.
Р+ЦР~ = Р, Р+ФР и р-фР. Следовательно, \Р~\<\Р\ и \Р+\<
<\Р\- Тогда по индуктивному предположению й(Р~) =0(Р~) = я
и с?(Р+)=0(Р+) —п, т. е. каждое из двух частично упорядоченных
множеств Р~ и Р+ представимо в виде объединения п
непересекающихся цепей:
1 = 1 1=1
Каждый элемент а антицепи А является одновременно
минимальным в Р+ и максимальным в Р~. Склеивая цепи СУ!) и Су(2),
содержащие элемент а, получаем цепь Са. Поскольку каждый
элемент а антицепи А, будучи минимальным в Р+ и максимальным
в Р~, является наибольшим для одной из цепей СУ!) и
наименьшим для одной из цепей С/2), то склеиванием покрывающих цепей
из Р~ и Р+ по общим элементам антицепи А получаем, что
Р— Р~[)Р+ = [} Са; \А | = п, т.е. существует покрытие частично
упорядоченного множества Р п цепями.
Случай 2. Каждая антицепь мощности п частично
упорядоченного множества Р содержит либо все его максимальные элементы,
либо все его минимальные элементы. Отсюда существует самое
большее две такие антицепи; одна — содержащая все
максимальные, а другая — все минимальные элементы. Возьмем
произвольный элемент а^Ат-ш и выберем Ь^Атах так, что Ь^а (Ь может
быть равным а). Пусть (2 = .Р\{а, Ь}. Очевидно, |(2|<|Р|.
Следовательно, по предположению индукции С? может быть разложено
на 5((2) цепей, но 5((2) =п—1 в силу предположения. Отсюда,
добавив к этим цепям еще цепь {а, Ь}, получим разложение Р на п
223»

цепей. Значит, и в этом случае ^(/^)0 = 5(/5). Доказательство
теоремы завершено.
Справедливо и двойственное утверждение.
Теорема 7. Пусть Р — конечное частично упорядоченное
множество. Тогда наибольшее число элементов в цепи из Р равно
минимальному числу непересекающихся антицепей, содержащих все
элементы множества Р.
Доказательство. Пусть 1{Р) — минимальное число
непересекающихся антицепей, покрывающих все элементы конечного
частично упорядоченного множества Р; С(Р) — семейство всех
цепей в Р и т(Р) = тах \С\. Требуется доказать, что ' 1(Р) =
С6С(Р)
= т(Р) для всякого Р.
Очевидно, что т(Р)^(Р), так как никакая антицепь не
содержит более одного элемента цепи. Индукцией по т~т(Р)
докажем обратное неравенство. Для т=1, очевидно, оно
выполняется. Пусть ^((2)^^((2) для всех частично упорядоченных
множеств (? таких, что т~т((2)<п. Тогда, если т(Р)=п,
рассмотрим антицепь А, включающую все максимальные элементы из Р.
Ясно, что АФ0, так как максимальный элемент каждой
максимальной цепи содержится в А. Рассмотрим частично
упорядоченное множество Р\Л. Легко показать, что т(Р\А) =п—1. В
самом деле, пусть х1<х2<...<хп — цепь мощности п в (Я\Л).
Поскольку т(Р)=п, то эта цепь максимальна и, следовательно,
Хп^А, что противоречит предположению: х„е(Р\Л). Значит,
в (Р\Л) нет цепей с п элементами и по предположению индукции
имеем, что ((Р\Д)<т(Р\Л) = п — 1. Отсюда ^(Р)^.т(Р) и
теорема доказана.
Теорема 6 была впервые сформулирована Дилуорсом [92]
в 1950 г. и доказана в связи с рассмотрением дистрибутивных
решеток (см. § 8.2). Однако весьма быстро было осознано, что эта
теорема имеет широкую область применения. Более того, она
оказалась эквивалентной многим минимаксным теоремам
комбинаторного анализа, например теореме Ф. Холла о системе различных
представителей (§ 3.2), Форда и Фалкерсона о максимальном
целочисленном потоке и минимальном разрезе (§ 6.4), Менгера
о вершинном разделении и другим. Ввиду многочисленных
интерпретаций перечисленные выше утверждения занимают в
комбинаторном анализе одно из центральных мест.
Теперь сформулируем ряд теорем, а затем, давая различные
их интерпретации, докажем эквивалентность некоторых из них.
Напомним, что двудольным графом называется граф 0 =
= С(У, £), в котором множество вершин V=511/ распадается на
два непересекающихся множества 5 и / так, что каждое ребро
(а, Ъ) соединяет некоторую вершину ае5 с вершиной Ье/. Граф
О является двудольным тогда и только тогда, когда все простые
циклы в кем имеют четную длину.
Любое бинарное отношение &е5Х/ на конечных множествах
5 и / можно рассматривать как ориентированный двудольный
224

граф С(8[}1, К), в котором все ребра ориентированы из 5 в /,
причем (а, Ь) — дуга в С тогда и только тогда, когда ае5,^Ье/
и (а, Ь)е#, и наоборот. Поэтому мы не будем в дальнейшем
различать бинарное отношение #е5Х/ и соответствующий
двудольный граф 0(5[}1, #), используя их как взаимозаменяемые
объекты. Любое семейство {Л^с'е/} подмножеств множества 5
порождает бинарное отношение #^5Х/, а именно (а, 1)<=К тогда и
только тогда, когда а^Аг, и любое бинарное отношение, очевидно,
можно рассматривать в этом смысле как систему множеств.
Пусть С(5[]1, К) — двудольный граф. Паросочетанием в графе
С называется множество Е ребер, никакие два из которых не
имеют общих вершин. Обозначим через 5(Е) и / (Е) множества
вершин паросочетания Е, лежащих соответственно в множествах 5
и /. Подмножество Л^5 называется частичной трансверсалью в 5,
если существует паросочетание Е такое, что Л=5(Е). Аналогично
определяется частичная трансверсаль и для В^1.
Другими словами, множество Л^5 является частичной
трансверсалью графа О (5[}1, Я) тогда и только тогда, когда
существует вложение ф : А-*-1 такое, что (а, ф(а))е# для всех а^А.
Теорему Ф. Холла о системе различных представителей
(см. § 3.2) можно теперь сформулировать в терминах двудольных
графов.
Теорема 8 (Ф. Холл). Пусть С(5[}1, К) — двудольный граф
с конечными множествами вершин 5 и /. Тогда Л^5 есть
частичная трансверсаль в том и только в том случае, когда |В[^|^(В) |
для всех В^А, где
Я(В) = [) {у]е=1\(а, у)=Я).
а€В
В самом деле, пусть {Л,|1'е/} — конечное семейство
подмножеств множества 5; здесь подмножества Л; не обязательно
различны. Определим бинарное отношение:
(£, а) е^, если а^А[.
Тогда # (/) = [) А; для всех /^/, и из теоремы 8 получаем теоре-
му Ф. Холла (см. § 3.2), а именно:
Семейство множеств {Лф'е/} обладает трансверсалью (или
системой различных представителей) тогда и только тогда, когда
| Ы Л71 > |У| для всех /С/.
/С/
Пусть С(У, Е) — произвольный граф, 5, /д^и 5(У=0.
Множество вершин называется (5, /)-разделяющим, если удаление
из графа этих вершин вместе с инцидентными им ребрами разры--
вает все цепи, идущие из вершин множества 5 в вершины
множества /. Будем говорить, что две цепи из вершины а в вершину
Ь графа С не имеют общих вершин, если у них общие только
вершины а и Ь.
Теорема 9 (Кениг). Пусть С = С(5[)1, #) — двудольный граф.
8х/г к- А- Рыбников
225

Тогда максимальное число дуг паросочетания в графе С равно
минимальному числу вершин в (5, /)-разделяющем множестве.
Проинтерпретируем теперь эту теорему в терминах матриц.
Пусть /4 = ||а;/|| — произвольная прямоугольная матрица с
действительными элементами. Будем интересоваться лишь тем, равен
ли элемент матрицы нулю или нет. Линиями матрицы будем
называть как строки, так и столбцы. Множество элементов матрицы,
отличных от нуля, назовем трансверсалью матрицы, если никакие
два из них не лежат на одной линии. Скажем, что множествго
М линий покрывает все ненулевые элементы, если каждый
ненулевой элемент матрицы А лежит хотя бы на одной линии из М.
Сопоставим матрице А двудольный граф, взяв в качестве вершины
множество строк и множество столбцов матрицы А и положив
(Ь{, С/)е# тогда и только тогда, когда ацФ§. Здесь через 6,- и с,
обозначены соответственно 1-й столбец и /-я строка матрицы А.
Тогда из теоремы 9 получаем теорему Кенига из § 4.1, а именно:
Наибольшая мощность трансверсали в матрице равна
наименьшему числу линий, покрывающих все отличные от нуля элементы.
Теорема 10 (Менгер). Пусть С(V, Е) — произвольный граф и
5, /еУ. Тогда наименьшая мощность (5, /.)-разделяющего
множества вершин графа С равна наибольшему числу цепей из 5
в /, попарно не имеющих общих вершин.
Теорема 10 справедлива-как для ориентированных графов,
так и для неориентированных. Кроме того, ее можно
видоизменить. Положим, что 5 = а, 1 = Ь — одноэлементные множества, не
соединенные ребром. Тогда непосредственно из теоремы 10
получаем следующий результат:
Следствие 11. Пусть С (У, Е) — неориентированный граф,
афЬ; а, Ь^У и (а, Ь)^Е. Тогда наименьшая мощность (а,
Ь)-разделяющего множества вершин равна наибольшему числу цепей из
а в Ъ, попарно не имеющих общих вершин.
Существует аналог теоремы 10 о вершинном разбиении —
теорема о реберном разделении, а именно:
Пусть С(V, Е) — произвольный граф и 5, 1аУ. Тогда
наименьшая мощность (5, /)-разделяющего множества ребер графа
О равна наибольшему числу цепей из 5 в /, попарно не имеющих
общих ребер. Множество ребер называется (5, I)-разделяющим,
если их удаление из графа С разрывает все цепи, идущие из
вершин множества 5 в вершины множества /.
Доказательство этой теоремы полностью аналогично
доказательству теоремы 10, и поэтому мы его приводить не будем.
Напомним формулировку теоремы о максимальном потоке и
минимальном разрезе из гл. 6.
Теорема 12 (Форд, Фалкерсон). Для любой сети с
целочисленными пропускными способностями максимальная величина потока
из источника 5 в сток I равна минимальной пропускной
способности разреза, отделяющего 5 и /.
226

Теоремы 6, 8, 9 и 10 в книге [28] получены как следствия
теоремы 12.
Наконец, проинтерпретируем теорему 6 в терминах графов.
Напомним, что диаграмма Хассе любого конечного частично
упорядоченного множества является ориентированным графом без
контуров. Пусть С — ориентированный граф без контуров.
Разложение графа О на цепи есть такое разбиение множества вершин
и дуг графа О, что каждая вершина из О принадлежит одной и
только одной цепи. Разложение с минимальным числом цепей
называется минимальным. Скажем, что а больше, чем Ь, если
имеется цепь, ориентированная из а в Ъ. Две вершины
ориентированного графа без контуров называются несравнимыми (или
независимыми), если не выполняется ни а<Ь, ни Ь<а.
Теперь теорему 6 можно сформулировать следующим образом:
Максимальное число взаимно несравнимых вершин в
ориентированном графе без контуров равно числу цепей в минимальном
разложении графа.
Докажем эквивалентность теорем 6, 8, 9, 10, 12 и следствия 11.
Эквивалентность теорем 8 и 9 уже установлена нами в гл. 4.
Вывод теоремы 9 из теоремы 12 был дан в § 6.4.
Покажем, что из теоремы 9 следует теорема 6. Для конечного
частично упорядоченного множества Р определим двудольный
граф 0{Р[]Р', Р), где Р' совпадает с Р и (х, у')^Р тогда и
только тогда, когда х<у в Р. Пусть О — семейство непересекающихся
цепей, покрывающих все элементы Р. Тогда множество Е ребер
(х, у') графа О таких, что х<у в одной из цепей семейства Д
очевидно образует паросочетание з графе О. Верно и обратное:
каждому максимальному паросочетанию Е в графе С
соответствует некоторое разбиение О частично упорядоченного множества Р
на цепи такое, что \Е\ + \0\=п. Если длина 1-й цепи в И равна
/;, то
|я|=Е(/,+ 1)=Е/« + |Д| = !Я|-НЯ|-
1=1 1 = 1
Пусть С = {*1, .... хк, у\, .... ут'} есть (Р, Р')-разделяющее
множество вершин графа О. Проверим, что в С все элементы
различны. В самом деле, пусть х^у/. Тогда, поскольку С является
(Р, Р') -разделяющим множеством, найдутся такие х^С и у'^С,
что (х, ух')^Р и (хи /)€=/?. Но тогда в силу транзитивности
отношения порядка (х, у') е=#, а это противоречит тому, что С, есть
(Р, Р')-РазДеляюЩее множество. Таким образом, все элементы
в С различны и множество [/ = Р\С есть антицепь в Р. Кроме
того: |С| + |С/| = |Р|.
Пусть теперь выполняется теорема 9, т. е. \Ё\ = | С\, где Ё —
максимальное паросочетание в С, а С — минимальное (Р,
Я')-разделяющее множество. Тогда |25| = |Г?|, где 3 — некоторое
разбиение частично упорядоченного множества Р на цепи, а О —
некоторая антицепь в Р. Но |1/|<|Л| для всех И, ОсР, так как ни-
8Х/2*
227

какие два несравнимых элемента не могут лежать в одной цепи.
Следовательно,
тах|{/| = тш| Б\.
Для доказательства обратного утверждения, что теорема 6
влечет теорему 9, достаточно двудольному графу 0(511/, #)
сопоставить частично упорядоченное множество 5Ц|/ с отношением
частичного порядка: х<у тогда и только тогда, когда (х, г/)е/?.
Таким образом, эквивалентность теорем 6, 8 и 9 установлена.
Оставшиеся эквивалентности предлагаем читателю найти
самостоятельно. В случае затруднения рекомендуется обратиться к книге
[1], в которой эквивалентность рассматриваемых нами
утверждений доказана.
8.2. РЕШЕТКИ
Пусть (А, ^) — произвольное частично упорядоченное
множество, а В — его непустое подмножество. Элемент а^А
называется точной верхней гранью (супремумом) множества В, если
а^Ъ для всех ЬеВ и если из справедливости
соотношения о^Ь для всех ЬеВ вытекает, что о^а. Двойственным
образом определяется точная нижняя грань (инфинум)
множества В: элемент оеЛ называется точной нижней
гранью, если а^Ь для всех ЬеВ и если из условия и^Ь для всех
веВ вытекает, что н^а. Точные верхнюю и нижнюю грани
множества В в частично упорядоченном множестве (А, ^) будем
обозначать соответственно символами зирл В и т1д В. Впрочем,
индекс А часто будем опускать. Непосредственно из определений
вытекает справедливость следующих утверждений:
а) Если а^Ь, то зир{а, Ь} = Ь и \п1{а, 6} = а.
б) Пусть В<=С. Если существуют вир В и вир С
(соответственно 1п{ В и ШС), то вир В^зир С (соответственно ш!В^ш1С).
в) Если А<=Ф(8), то вир Л совпадает с объединением всех
подмножеств из семейства А, а т{ А — с их пересечением.
Справедливость этих утверждений предлагаем проверить
читателю самостоятельно.
Частично упорядоченное множество (А, ^) называется
решеткой (или структурой), если для всех а, Ь^А существуют зир{а, Ь}
и \п({а, Ь}. Решетка не обязана иметь 0 и 1. Решеткой являются
всякая цепь, множество всех подмножеств, упорядоченное по
включению (см. пример 4 из § 8.1) и некоторые другие частично
упорядоченные множества, примеры которых рассмотрим позднее.
Если частично упорядоченное множество (А, ^) — решетка,
то двойственное ему частично упорядоченное множество (А, ^) —
тоже решетка. Таким образом, принцип двойственности применим
к решеткам.
Мы будем использовать обозначения
а/\Ь = 'тЦа, Ь}, а\/Ь = 5ир{а, Ь}
и называть Д — пересечением, а V — объединением. В решетках
228

д и V являются бинарными операциями, обладающими
следующими свойствами:
а) а/\а=а, а\/а = а (идемпотентность);
б) а/\Ъ = Ь/\а, а\/Ь — Ъ\/а (коммутативность);
в) (аАЬ)Лс = а/\(ЬЛс),
(а\/Ь) Vс = а\/ (Ь\/с) (ассоциативность);
г) а/\{а\/Ь)^а, а\/(а/\Ь) = а (поглощение).
Отношение порядка ^ в решетках можно охарактеризовать с
помощью операций Л и V- А именно
а <Ь*эаЛЬ = а
или же
а-< &*=* а\/Ь = Ь.
Такие характеризации позволяют рассматривать решетки как
множества с двумя бинарными операциями Л и V, которые
удовлетворяют свойствам идемпотентности, коммутативности,
ассоциативности и поглощения.
Теорема 13. Пусть А — множество с двумя бинарными
операциями Л и V, которые идемпотентны, коммутативны,
ассоциативны и удовлетворяют свойствам поглощения. Пусть а^Ь означает,
что а\/Ъ = Ь. Тогда отношенне ^ является отношением частичного
порядка на множестве А, а возникающее частично упорядоченное
множество оказывается решеткой, причем
а\/Ь = &ир{а, Ь}
а/\Ь = \п\{а, Ъ}.
Доказательство. Рефлексивность отношения ^ вытекает
из идемпотентности объединения. Если а^Ь и Ь<л, т. е. а\/Ь = Ь
и Ь\/а = а, то в силу коммутативности а = Ь, т. е. отношение ^
оказывается антисимметричным. Если а\/Ъ = Ъ и Ъ\/с=с, то в
силу ассоциативности получаем
а\/с = а\/{Ь\/с) = (а\/Ь)\/с=Ь\/с = с,
что доказывает транзитивность отношения =¾^. Следовательно,
отношение ^ является отношением частичного порядка на
множестве А. Далее, а\/ (а\/Ь) = (а\/а) VЬ = а\/Ь (воспользовались
последовательно свойствами ассоциативности и идемпотентности) и
Ь\/(а\уЬ) = Ь\/(Ь\уа) = (Ь\/Ь)\/а=Ь\/а^а\/Ь
(воспользовались последовательно свойствами коммутативности,
ассоциативности, идемпотентности и снова коммутативности).
Отсюда а=^а\/& и Ь^.а\/Ь. Если а^о и Ь^о, то, используя
идемпотентность, коммутативность и ассоциативность операции
объединения, имеем: (а\/Ь) \/V = а\/ (Ь\/V) =а\/V~V, т. е. а\/Ь<у.
Вспоминая определение точной верхней грани, убеждаемся, что
а\/Ь = &ир{а, Ь}. Наконец, из свойств коммутативности и
поглощения имеем
(а/\Ь)\/а = а\' (а/\Ь) =а
8 К. А. Рыбников
229

{а/\Ь)\/Ь^Ьу(а/\Ь) =Ь\ДЬ/\а)=Ь,
т. е. а/\Ь^а и а/\Ь^.Ь. Если «<а и «<Ь, то в силу свойств
ассоциативности и поглощения, а также ' определения отношения ^
получаем
и/\(аЛЬ) = (и/\а)/\Ь=(и/\(и\/а))/\Ь = и/\Ъ = и/\(и\/Ь)=и.
Отсюда в силу свойств коммутативности и поглощения вытекает,
что
иУ(а/\Ъ)^(иА(аАЪ))У(а/\Ъ) = (аАЬ)У{(а/\Ь)/\и)^{а/\Ь),
т. е. аАЬ^и. Таким образом, аЛ& = 'пГ{а, Ь} и теорема доказана.
Заметим, что двойственные рассуждения позволяют прийти
к тем же самым выводам, если отношение =¾ определить
условием а^Ь, если аАЬ = а.
1
Рис. 8.7
Рис. 8.8
Таким образом, любую конечную решетку всегда можно
описать с помощью таблицы пересечений/объединений или
диаграммы Хассе. Например, пусть Л={0, а, Ь, 1} имеет диаграмму Хассе,
изображенную на рис. 8.6, тогда решетка А полностью
определяется следующей таблицей пересечений/объединений:
Л
0
а
Ъ
1
Л
0
а
Ь
1
а
0
1
1
Ь
0
0
1
1
0
а
Ь
Значения на диагонали в этой таблице опущены, поскольку
х\/х = х и хАх = х для всех дсеЛ. Кроме того, в силу
коммутативности операций Л и V эта таблица полностью определяет
решетку. Для проверки этого достаточно проверить лишь тождества
ассоциативности и поглощения. Представляем возможность
сделать это читателю самостоятельно.
Мы будем использовать способы описания решеток, которые
сочетают в себе оба описанных нами способа. Опишем для приме-
230

ра две решетки на множестве из пяти элементов 0, а, в, с, 1,
диаграммы Хассе которых изображены соответственно на рис. 8.7 и
8.8. Решетка, изображенная на рис. 8.7, Ъ<а, с\/Ь=\ и аЛс = 0
называется Пентагоном. Описание Пентагона, приведенное нами,
полное, поскольку все другие соотношения Пентагона следуют из
приведенных. Решетка, изображенная на рис. 8.8, с а^\Ъ = а/\с=
= Ь/\с = 0 и а\уЬ = а\/с=Ь\/с=\, называется диамантом.
Подмножество В решетки А будем также называть Пентагоном или
диамантом, если оно является подрешеткой, изоморфной как частично
упорядоченное множество Пентагону или диаманту соответственно.
Таким образом, утверждая, что В = {ЪЪ Ь2, Ь3, Ь4, Ьъ} есть Пентагон
(соответственно диамант), мы предполагаем, что отображение
Ф : &1-Э-0, Ь2-+а, Ьъ-^-Ь, Ъ^с, Ъь-+\ есть изоморфизм решетки В
на решетку, изображенную на рис. 8.7 (соответственно на
рис. 8.8).
Уточним понятие изоморфизма решеток. Обычно для решеток
вводится два эквивалентных понятия изоморфизма.
1. Решетки (Ь0, ^) и (Ьи =¾) называются изоморфными, если
они изоморфны как частично упорядоченные множества. Этим
определением изоморфное™ решеток мы уже пользовались.
2. Решетки (Ь0; /\, V) и (Ьй /\, V) называются
изоморфными, если существует изоморфизм ф множества Ь0 на множество
Ьх такой, что для всех а, Ь^Ь0:
ф(аЛЬ)=ф(а)Лф(Ь);
ф(<Л/Ь)=Ф(а)Уф(Ь)-
Несмотря на эквивалентность этих определений, в дальнейшем
будем различать эти два понятия изоморфизма решеток во
избежание путаницы при их обобщениях.
Далее мы также откажемся от обозначений (Ь; /\, V) и
(Ь, ^) для решеток и частично упорядоченных множеств и будем
просто писать прописные буквы, указывая основные множества,
за исключением тех случаев, когда это понадобится для лучшего
понимания текста.
Изоморфизм частично упорядоченных множеств обобщается
следующим образом.
Отображение у\Ао-+А\ — называется изотопным (или
сохраняющим порядок) отображением частично упорядоченного
множества А0 в частично упорядоченное множество Аи если а^Ь в Ао
влечет за собой ф(а)^ф(Ь) в А\. Пример изотонного отображения
Ф : /,о->/-1 приведен на рис. 8.9, где ф(0)=0, ф(а)=ф(Ь)=с,
ер(1)=1.
Гомоморфизмом решетки (Ьо) Л, V) в решетку (Ьи Л, V)
называется отображение ф : Ь0-+Ьи удовлетворяющее для всех
а, Ь^Ьц условиям:
ф(а\/Ь)=ф(а)\/ф(Ь)'.
ф(аЛЬ)=ф(а)Лф(Ь)-
На рис. 8.10 приведен пример гомоморфизма ф : Ь^-^-Ь^
8*
231

Рнс. 8.9 Рнс. 8.10
Всякий гомоморфизм решеток является изотонным
отображением. В самом деле, если ф : Ьй-^Ь\ — гомоморфизм, то ф(а\/Ь) =
=ф(а)\/ф(^) Для всех а> Ь^Ьа. Пусть х, у^Ьа и л^г/ в Ьа. Тогда
у = х\/у и, следовательно, ф(г/) =у(х\/у) =ф(х)\/ф(г/), т. е.
ф(х)^ф(г/) в Ь\. Таким образом, гомоморфизм ф является также
изотонным отображением.
Обратное неверно. Например, изотонное отображение ф : Ьо-*-
->^1, изображенное на рис. 8.9, не является гомоморфизмом, так
как
Ф(а\/Ь)=ф(1) =1^=с = с\/с=ф(а)\/ф(Ь).
Частично упорядоченное множество А называется полной
решеткой, если всякое его непустое подмножество В имеет зирл В и
1П1л В. Полными решетками являются: отрезок [0, 1] с обычным
порядком; множество всех подмножеств некоторого множества,
упорядоченное по включению; всякая конечная цепь. Полную
решетку образует также частично упорядоченное множество В(Зп)
всех неупорядоченных разбиений конечного множества 5„ (см.
пример 8 из § 8.1). Ясно, что любая полная решетка должна иметь
0 и 1. Поэтому, например, решетка целых чисел с обычным
порядком не является полной решеткой.
Упражнения. Проверьте, что
1. Множество всех разбиений множества Л, упорядоченное по объединению
блоков, является полной решеткой.
2. Упорядоченная сумма полных решеток {Ла|ае/,}, где Ь — полная
решетка, является полной решеткой.
3. Прямое произведение полных решеток является полной решеткой.
4. Упорядоченное произведение полных решеток {Ла|ае/,}, где Ь —
полная решетка, удовлетворяющая условию минимальности, является полной
решеткой.
По данному разбиению л можно определить отношение
эквивалентности р, полагая арЬ тогда и только тогда, когда а и Ь
содержатся в одном и том же блоке разбиения я. Обратно, если
р — отношение эквивалентности, то семейство смежных классов
эквивалентности р на множестве А (смежным классом
эквивалентности р, определяемым элементом а^А, называется
подмножество {х^А\хра}) является разбиением множества А. Таким
образом, существует взаимно-однозначное соответствие между
разбиениями и отношениями эквивалентности. Стало быть, множество
всех отношений эквивалентности, определенных на множестве А,
упорядоченное следующим образом: р^т, если арЬ, влечет за
собой а%Ь, образует полную решетку.
232

Решетка, удовлетворяющая тождеству
(аЛЬ) V (аАс) = аЛ (Ь\/ (аАс))
или (что эквивалентно) следующему условию: а^-Ь влечет за
собой (аАс)\/Ь = аА(Ь\/с), называется модулярной. Важнейшим
примером модулярных решеток является решетка подпространств
линейного пространства (см. пример 9 из § 8.1). Действительно,
если А, В, С — подпространства и А^.В, то, очевидно, (В + С)ГИ —
^В+(ЛПС). Наоборот, если вектор а лежит в (В + С)[\А, то а =
= Ь + с, где Ь<=В, с<=С. Отсюда с= (а— Ь) <= (С(]А), т. е. а<=(В +
+ (ЛПС))и, следовательно, (В + С)[\А^В + (А(]С). Аналогично
проверяется, что модулярными являются решетки нормальных
делителей произвольной группы, идеалов кольца, подмодулей
модуля. Типичным примером немодулярной решетки является
решетка, диаграмма которой изображена на рис. 8.7.
Дадим теперь интуитивное представление о «самой общей
решетке», порожденной некоторым множеством элементов и
удовлетворяющей некоторым соотношениям. «Самые общие решетки»
далее будем называть свободными. Эти решетки будем строить
последовательным образованием «новых» элементов с помощью
операций объединения и пересечения до тех пор, пока не получим
решетку. Причем «новые» элементы будем отождествлять со
«старыми» в том и только в том случае, когда их равенства могут быть
выведены либо из тождеств решетки, либо из заданных
соотношений. Проиллюстрируем сказанное на примере построения «самой
общей решетки», порожденной элементами а, Ъ, с и
удовлетворяющей соотношению Ь<а. Прежде всего образуем объединения и
пересечения а\/с, Ь\/с, аАс, Ь/\с- Заметим, что а\/Ь\/с —
= (а\/Ь)\/с = а\/с, так как а\/Ь = а; аналогично аАЬАс = ЬАс.
Покажем теперь, что семь элементов а, Ь, с, а\/с, Ь\/с, а/\с, ЬАс,
которые мы уже имеем, являются попарно различными.
Напомним, что два из них были бы равны, если бы их равенство
следовало из соотношения Ь<а и аксиом решетки. Поэтому, чтобы
показать, что какие-либо два из этих элементов различны,
достаточно найти решетку с элементами а, Ь, с, удовлетворяющую
соотношению Ъ<а, в которой эти два элемента различны. Например,
чтобы показать, что афа\/с, возьмем решетку: {0, 1, 2}, где
0<1<2, и положим: 6 = 0, а=1, с=2, 6 = 0<1=а. Тогда а=1ф
Ф2 = \\/2 = а\/с. Следующий шаг состоит в образовании из этих
элементов новых объединений и пересечений таких, как Ь\/(аАс),
(Ь\/с)Аа- Легко заметить, что все остальные объединения и
пересечения равны одному из уже введенных элементов, например,
ЬА(аАс) =ЬАс, а\/ (аАс) =а. Докажем теперь, что девять
элементов а, Ь, с, а\/с, Ъ\/с, аАс, Ь/\с, Ь\/(аАс), аА(Ь\/с)
образуют решетку. Для этого надо доказать, что из этих девяти
элементов с помощью операций объединения и пересечения мы уже
не получим новых элементов. Все ( ) = 36 объединений и
столько же пересечений, которые мы должны проверить, вычисляются
233

тривиально. Например, а\/ (Ь\/ (а/\с)) = (а\/Ь) V (а/\с) =а в
силу свойства поглощения и так как а\/Ь = а; аналогично с/\(аЛ
Л(Ь\А)) = (сЛа)Л(ЬЛс) =аДс, так как сДа<Ь\/с.
Полученная «самая общая решетка» изображена на рис. 8.11.
Многообразием решеток будем называть класс всех решеток,
каждая из которых удовлетворяет некоторому заданному набору
тождеств. Класс всех решеток или класс всех модулярных
решеток являются примерами многообразий решеток.
Дадим теперь строгое определение «самой общей решетки»
или свободной решетки относительно некоторого многообразия
решеток.
Пусть А — частично упорядоченное множество и К —
некоторое многообразие решеток. Решетка Рк(А) называется свободной
решеткой в многообразии К, порожденной частично упррядочен-
ным множеством А, если выполнены следующие условия: 1
а) Рк(А)е=К;
б) А^РК(А) и для любых а, Ь,
с^А : ША{а, Ь}=с (зирл{а, Ь}=с)
тогда и только тогда, когда а/\Ь = с в
Рк(А) (соответственно а\/Ь = с в
Гк(А));
в) А — порождающее множество
решетки РК(А);
г) Пусть Ь^К и ф : А-^-Ь— изо-
тонное отображение такое, что если
а, Ь, с^.А и Ш1д{а, Ь} = с
(соответственно зирА{а, Ь) = с), то ф (а)Лф (Ь) =
= ф(с) в Ь (соответственно ф(а)\/
\/ф(6) =ф(с) в Ь). Тогда отображение
Ф можно продолжить до решеточного
гомоморфизма Ч*: Рк(А)-+Ь, т. е. такого гомоморфизма, что
ф(а) =4^(а) для всех а^А.
Решетка Рк(А) называется также /(-свободной решеткой над
частично упорядоченным множеством А.
В случае, когда К совпадает с многообразием всех решеток,
будем опускать индекс К и называть Р(А) свободной решеткой
над А. Если А — антицепь и |Л|=л, то будем обозначать Рк{п)
или Р(п) и называть эту решетку /(-свободной или просто
свободной решеткой от п порождающих. Дедекинд в 1900 г. показал,
что свободная модулярная решетка /гм(3) от трех порождающих
имеет 28 элементов и ее диаграмма имеет вид, изображенный на
рис. 8.12, где порождающие элементы мы обозначили через
х, у, г, а
а= (XVУ) Л (уУг) /\ (х\/г), Ь=(х/\у) V (у/\г) V (х/\г),
х, = (х/\а)\/Ь, ух = {у/\а)\/Ь, 2, = (г/\а) уЬ.
В следующей теореме дается очень полезная характеризация
модулярных решеток.
234

Рнс. 8.12
Теорема 14. Решетка Ь модулярна тогда и только тогда, когда
она не содержит пентагонов.
Доказательство. Если Ь — модулярная решетка, то
всякая ее подрешетка также модулярна. Поскольку Пентагон не
является модулярной решеткой, то его нельзя вложить в Ь.
Необходимость доказана.
Обратно, пусть Ь — немодулярная решетка. Тогда существуют
элементы а, Ь, с^Ь такие, что Ь^а и (а/\с)\/Ьфа/\(с/\Ъ).
Свободная решетка, порожденная элементами а, Ъ, с и
удовлетворяющая соотношению Ь<а, изображена на рис. 8.11. Подрешетка
в Ь, порожденная элементами а, Ъ, с, должна быть гомоморфным
образом этой свободной решетки. Следующие 5 элементов
свободной решетки: а/\с, Ь\/(а/\с), а/\(Ь\/с), с, Ь\ус образуют
Пентагон, и они не могут отождествляться при соответствующем
гомоморфизме, поскольку при отождествлении любых двух из этих
элементов будут отождествляться также элементы Ь\/(а/\с) и
а/\(с\/Ь), а это противоречит нашему предположению. Теорема
доказана.
Решетка, удовлетворяющая одному из следующих
равносильных тождеств:
235

(а\уЬ)А(а\/с)^а\/(ЬАс),
называется дистрибутивной. Очевидно, решетка, двойственная
дистрибутивной решетке, также дистрибутивна. Важнейшим
примером дистрибутивной решетки является булеан, т. е. решетка
№(3) всех подмножеств произвольного множества 5.
Дистрибутивной решеткой является также всякая цепь. Заметим, что всякая
дистрибутивная решетка является модулярной. Однако не всякая
модулярная решетка является дистрибутивной. Например,
модулярная решетка всех подпространств линейного пространства не
является дистрибутивной. Решетки, диаграммы которых приведены
на рис. 8.7 и 8.8, не являются дистрибутивными. Семейство всех
дистрибутивных решеток образует многообразие решеток.
Свободная дистрибутивная решетка /в(3) от трех порождающих имеет
18 элементов, и ее диаграмма изображена на рис. 8.13. Нетрудно
заметить, что диаграмма /^(3) получается из диаграммы Рм(3)
(см. рис. 8.12) «склеиванием»:
х\'(уЛг) с (х\'у)А(х\уг);
уУ(хАг) с (хуУ)А(у\/г);
г\/(х/\у) с (х\/г)А(у\/г);
хА(уУг) с (хАу)У(хАг);
уА(хУг) с (хАу)\У(уАг);
гЛ(х\Уу) с (хАг)\/(уАг)
(эти пары элементов совпадают в силу дистрибутивности). При
таком «склеивании» элементы а, х\, у\, ги Ь свободной
модулярной решетки также «склеиваются» в один элемент. Таким
образом, в дистрибутивной решетке
(х\/у) А (хуг) А (уУг) = (хАу) V (*Лг) V (уЛг) ■
Читатель может убедиться в этом самостоятельно.
Теорема 15. Модулярная решетка Ь дистрибутивна тогда и
только тогда, когда она не содержит диамантов.
Доказательство. Если Ь — дистрибутивная решетка, го
всякая ее подрешетка также дистрибутивна. Поскольку диамант
не является дистрибутивной решеткой, то его нельзя вложить в Ь.
Необходимость тем самым доказана.
Обратно, пусть Ь — модулярная, но не дистрибутивная
решетка. Тогда найдутся такие элементы х, у, ге1, что хА{у\/г)ф
ф(хАу) V (хА?)- Свободная модулярная решетка, порожденная
х, у, г, изображена на рис. 8.12. Из диаграммы этой решетки
видно, что ее элементы а, Ъ, х\, у\, гх образуют диамант. Поэтому
в любой модулярной решетке эти пять элементов образуют подре-
шетку, изоморфную гомоморфному образу диаманта. Но диамант
имеет лишь два гомоморфных образа: сам диамант и
одноэлементную решетку. В первом случае достаточность теоремы дока-
236

Рис. 8.13
зана. Во втором случае заметим, что при склеивании элементов
а и Ь склеиваются также элементы х/\(у\/г) и (х/\у) V (х/\г),
но это противоречит нашему предположению. Значит, всякая
недистрибутивная решетка содержит диамант и теорема доказана.
Из теорем 14 и 15 получаем следующую полезную характери-
зацию дистрибутивных решеток:
Теорема 16. Решетка Ь дистрибутивна тогда и только тогда,,
когда она не содержит ни пентагонов, ни диамантов.
Частично упорядоченное множество называется
ограниченным, если оно имеет 0 и 1. В ограниченной решетке Ь элемент а
называется дополнением элемента Ь, если а/\Ь = 0 и а\/Ь = \.
Ограниченная решетка, в которой каждый элемент имеет дополнение,,
называется решеткой с дополнениями.
Булевой решеткой называется дистрибутивная решетка с
дополнениями. Ее называют также булевой алгеброй, рассматривая
как алгебраическую систему с основными операциями Л. V и -
(операция дополнения) и двумя отмеченными элементами: 0, 1.
Упражнения. Докажите, что
5. Множество неотрицательных целых чисел, упорядоченное по делимости
(см. пример 5 из § 8.1), является дистрибутивной решеткой (считаем, что О-
237

делит 0; здесь вир {а, Ь} — наименьшее общее кратное чисел а и 6,
Ш {а, Ь) — наибольший общий делитель числа а и Ь),
6. Конечная булева решетка изоморфна решетке всех подмножеств
некоторого конечного множества.
7. Любая дистрибутивная решетка вложима в некоторую булеву решетку.
8. Всякая модулярная решетка с единственными дополнениями является
булевой решеткой.
Важнейшее свойство модулярности выражается следующим
утверждением.
Теорема 17. Если а и Ь — элементы модулярной решетки Ь, то
интервалы [а/\Ь, а] и [Ь, а\/Ь] изоморфны. При этом изоморфизм
осуществляется отображениями:
у(х) = х\/Ь (а/\Ь<ё.х*са)
и ;
Ъ(У) = а/\У (Ь^у^ауЬ).
Доказательство. Ясно, что ф и г|з — изотонные
отображения, причем -ф (ф (х)) = а/\ (х\/Ь)=х\/ (а/\Ь)=х (в силу
тождества модулярности и условия х>-а/\Ь) и ф(о|з(г/))= {а/\у)\/Ь =
= {а\/Ь)\/у = у (в силу тождества модулярности и условия г/<:
<:а\/&). Следовательно, ф и г|з — изоморфизмы, что и требовалось
.доказать.
Говорят, что решетка Ь удовлетворяет условию покрываемости
•сверху, если для любых ее элементов а, Ъ (афЬ) условия а/\Ь-^Ь
и а/\Ь-^а влекут за собой а-^а\/Ь и Ь-$а\/Ь. Двойственным
образом определяется условие покрываемости снизу: решетка Ь
удовлетворяет условию покрываемости снизу, если для любых а, Ь&Ь
(аФЬ) условия сц-^а\/Ь и Ь-^а\/Ъ влекут за собой а/\Ь-^а и
.а/\Ь--^Ь. Из теоремы 17 вытекает, что модулярная решетка
обладает условиями покрываемости как сверху, так и снизу.
Решетка Ь называется полумодулярной, если она
удовлетворяет условию покрываемости сверху, или, что эквивалентно, если для
любых а, Ъ, с^Ь условие а-~$Ь влечет за собой а\/с^Ь\/с
или а\/с=Ь\/с. Примерами полумодулярных решеток являются
модулярные решетки и некоторые важные решетки, возникающие
в геометриях (см. § 8.4). Еще два примера полумодулярных
решеток приведены на рис. 8.14.
Пусть А — частично
упорядоченное множество с 0. Определим на нем
функцию высоты (или ранга)
следующим образом: г (а) равняется длине
самой длинной цепи в интервале [0, а]
(если такая цепь не существует,
полагаем г(а) = оо). Если А —
частично упорядоченное множество конечной
длины Ы, то 0<:г(а)<:Л[ для любого элемента а^А. В
полумодулярной решетке конечной длины ранг г(а) совпадает с длиной
произвольной максимальной цепи в интервале [0, а]. Это
вытекает из следующей очень важной теоремы.
Теорема 18. (условие Жордана — Гёльдера). В полумодуляр-
:238

ной решетке Ь конечной длины любые две максимальные цепи
между произвольными а, Ъ^Ь такими, что а«:Ь, имеют
одинаковую длину.
Доказательство. Пусть 0,=0,(,-^^-^, ...-=^ ап = Ь —
максимально цепь длины п в [а, Ь]. Докажем индукцией по п, что всякая
другая максимальная цепь имеет длину п. При п = 0 утверждение
очевидно. Если п=\, то а-^Ь и, следовательно, максимальная
цепь в [а, Ь] единственна. Предположим, что наша теорема
справедлива для всех подрешеток [а, Ь] длины меньше га, где га>2.
Пусть а=Ь1-^Ь2-^...-^йт = Ь — другая максимальная цепь в
[а, Ь]. Если а\ = Ъ\, то в полумодулярной решетке [аи Ь]
максимальная цепь а\-^...-^ап = Ь имеет длину га—1; следовательно,
максимальная цепь а1-^Ь2-^...-=>Ьт = Ь должна иметь длину
га—1; поэтому п = т. Если а\ФЪ\ (см. рис. 8.15), то рассмотрим
максимальную цепь длины к в \а\\/Ъ\, Ъ]. В силу
полумодулярности имеем (ахУЬ^^-ох и (а^Ьг) ^~ЬЬ Следовательно, сц -^
-^){а.х\/Ь1)-^с1-^>с2-^>...-^ск = Ь — максимальная цепь длины к+\
в [аи Ь], а а!-^а2-^...-^а„ = Ь также максимальная цепь, но
длины п—1 в [а.\, Ь]. Таким образом, в силу индуктивного
предположения к+1=п—1. Аналогично к+\ = т—1, поэтому га = т.
Теорема доказана.
Двойственным образом
доказывается, что в любой решетке Ь конечной Ь=а„=ьт-=оК
длины, удовлетворяющей условию по-
крываемостп снизу, любые две
максимальные цепи между произвольными
элементами а, Ь^Ь имеют одинаковую
длину, т. е. выполняется условие Жор-
дана—Гёльдера для цепей.
Упражнения. Докажите, что
9. Если в частично упорядоченном
множестве А с О выполняется условие
Жордана—Гёльдера для цепей, то его ранговая функция г (а),
определенная для всех а^А, удовлетворяет еле
дующим условиям:
а) /-(0)=0:
б) из а^Ь следует: г(6)=г(а)+1|
10. Если на частично упорядоченном
множестве А определена функция г такая, что /-(0)=0
и из а -=?& следует г(Ь) = г(а) + 1, то А
удовлетворяет условию Жордана—Гёльдера для цепей и Рис. 8.15
эта функция совпадает с его ранговой функцией.
Модулярность и полумодулярность можно охарактеризовать в
терминах ранговой функции.
Теорема 19. Пусть Ь — решетка конечной длины с 0. Решетка
Ь является полумодулярной тогда и только тогда, когда она
удовлетворяет условию Жордана— Гёльдера для цепей и для всех а,
Ь^Ь имеет место неравенство:
Ощ-1
ит-2
где г-
г{а) +г{Ь) ^г(аЛЬ) +г(а\/Ь),
-ранговая функция решетки Ь.
239

Доказательство. В силу полумодулярности в решетке Ь
выполнено условие Жордана — Гёльдера для цепей. Пусть а/\Ь =
= сс-^с1-^...-^с^ = й — максимальная цепь в интервале [а/\Ь, Ъ].
Согласно условию Жордана — Гёльдера, длина этой цепи равна
г(Ь)—г(а/\Ъ). Из условия покрываемое™ сверху для
полумодулярных решеток для Ь имеем, что
а\/ (а/\Ь) = а= (а\/с0)*4(а\/й) =^---=¾ {а\/а)=а\/Ь
также является максимальной цепью, но в интервале [а, а\/Ь].
Длина этой цепи не превосходит длины первой цепи (некоторые
элементы могут совпадать), т. е. не превосходит числа: г(Ь) —
—г(а/\Ъ). С другой стороны, согласно условию Жордана —
Гёльдера, длина этой цепи равна г(а\/Ь)—г (а). Поэтому г(Ъ) —
—г(а/\Ь)>г(а\/Ь)—г(а) и необходимость доказана.
Докажем теперь достаточность. Пусть а, Ь^Ь такие, что
а$~- (а/\Ь), Ь$~- (а/\Ь) и афЬ. Тогда в силу условия Жордана-
Гёльдера (см. упражнение 9): г(а) =г(Ь) =г(а/\Ъ) + 1. Подставим
эти равенства в неравенство из условия теоремы и получим:
г(а\/Ь) <^г(а) + 1, г{а\'Ъ) <г(Ь) + 1. Отсюда непосредственно
следует, что (а\/Ь)^=а и (а\/Ь)^=Ь. Покажем, что а\/Ъфа. От
противного: пусть а\/Ь = а. Тогда а>Ь и а/\Ь = Ь, но это
противоречит тому, что Ь ^~(а/\Ь). Следовательно, (а\/Ь)^~а. Аналогично
проверяется, что (а\/Ь)^~ Ь. Теорема доказана.
Из теоремы 19 и из двойственности условий покрываемое™
сверху и снизу получаем следующий результат.
Следствие 20. Если в решетке Ь конечной длины с 0
выполняется условие покрываемое™ снизу, то для всех а, Ь^Ь имеет место
неравенство: г(а) +г(Ъ) <г(а/\Ь) +г(а\/Ь).
Другим приложением теоремы 19 является следующее
утверждение:
Следствие 21. Для решетки Ь конечной длины следующие
утверждения равносильны:
а) Ь— модулярная решетка;
б) решетка Ь удовлетворяет условиям покрываемости как
сверху, так и снизу;
в) Ь не содержит пентагонов;
г) для всех а, Ъ^Ь имеет место равенство
г(а)+г{Ь)=г{а/\Ъ)+г{аУЪ).
Доказательство. Мы уже установили, что а) влечет за
собой б). Теорема 19 и следствие 20 устанавливают, что из б)
вытекает г). Равносильность а) и в) доказана в теореме 14. Для
завершения дсхазательства следствия покажем, что из г) следует
в). От противного: пусть решетка Ь содержит Пентагон {0, а, Ь, с, 1}
(см. рис. 8.7) и для нее выполняется условие г). Тогда
г(а)+г(с) = г(аус)+г(аЛс)=г(1)+г(0) =
= г(Ь\/с)+г(Ь/\с)=г{Ь)+г{с).
Откуда г(а)=г(Ь), что невозможно, так как Ь<а. Доказательств©
следствия завершено.
240

Пусть Ь — решетка с 0. Подмножество / множества ^\{0}
называется независимым, если для любых его конечных
подмножеств А п В справедливо равенство
т{{зирЛ, зирВ}=зир(ЛПВ).
Теорема 22. Конечное подмножество / решетки Ь независимо
тогда и только тогда/ когда отображение ср: Л-*-зирЛ,
определенное для всех А^&>(1), является изоморфизмом между решеткой
булеана 1?(1) и подрешеткой решетки Ь, порожденной
множеством /.
Доказательство. Имеем зир {зир Л, зир В}=зир {Луй}, и'
поэтому, если множество / независимо (т. е. т{{зирЛ, зир В}=
= зир{Л(~|В}), то ф — гомоморфизм решеток. Если отображение ф
не взаимно-однозначно, то зирЛ = зирВ для некоторых
подмножеств А^1, В^1, АфВ. Пусть, например А с,В и ае(Л\В).
Тогда а<зирВ, афВ; поэтому а=т{{а, зир В} = т{ {вир {а},
зир В}=5ир({а}Г)В) =зир 0 = 0, что невозможно. Следовательно,
Ф — изоморфизм.
Доказательство обратного утверждения оставляем читателю.
Очевидно, что одноэлементное подмножество {а} всегда
независимо. Подмножество {а, Ь} независимо тогда и только тогда,
когда аЛ^ = 0(а,6е(/,\{0}), афЬ). Для независимости
подмножества {а, Ъ, с}, где а, Ь, се(^\{0}), все элементы а, Ъ, с попарно
различны, необходимо потребовать выполнения следующих
равенств:
аЛ(Ь\/с)=0; (а\/Ь)Л(а\/с)=а;
&Л(<Л/с)=0; (6ус)Л(6\/о)=6;
сД(а\/&)=0; {с\/а)А(с\/Ь)=с.
В полумодулярных решетках можно ограничиться меньшим
числом соотношений. Если Ь — полумодулярная решетка с 0, то
определение независимости эквивалентно следующему:
множество {аи ■■■ , ап) независимо, когда (а\\/ ... \/сц) Ла«-м = 0
для всех 1 = 1, 2, ... , п—1.
Упражнение 11. Докажите эквивалентность определений независимости
для полумодулярных решеток с 0.
Теорема 23. Пусть Ь — полумодулярная решетка с 0 и
ранговой функцией г. Множество атомов /={аь аг, ..., ап} решетки
Ь независимо тогда и только тогда, когда
г(а{\/ ... \уап)=п
Доказательство. Пусть (а\\/ ... \/сц) Л««+1 = 0 Для всех
1=1, 2, ..., п—1. Докажем индукцией по I, что г(а,1\/ ... \/сц) —I.
Для 1=1 утверждение верно. Если г(а{\/ ... \/щ) =1, то в силу
полумодулярности имеем (а\\/ ... V*) Н(о1\/ — \/а;\Мж) и
поэтому г(а{\/ ...\М;\Мт) =г{а{\/ ...Ут) + 1 = 1+1. Тем самым
необходимость доказана.
Для доказательства достаточности покажем, что множество
атомов / удовлетворяет условию теоремы 22. Из условия
241

г{ах\/ ... \/ап) = п имеем, что г(зирЛ) = |Л| для любого
подмножества А<=1, так что отображение ф:Л-^зирЛ
взаимно-однозначно. Отображение ф, очевидно, сохраняет объединения. Возьмем
теперь А, В^1, и пусть а = \п!{&ир А, вир В}, Ь = &ир {А[\В}. Тогда
а>Ь и из условия полумодулярности имеем
г(зир А) +г(зир В) >-г(а) +г{&ир {А[}В}),
так что \А | + |В| >-г(а) + \А[}В\. Отсюда делаем вывод, что
г(а)^\А\ + \В\-\АЦВ\ = \А[\В\.
С другой стороны, г(а)^г(Ь)= \А(]В\, следовательно, г(а)=г(Ь)-
и а = 6, т. е. ш!{зирЛ, вир В}=зир(ЛПВ). Отсюда следует, что
Ф—изоморфизм и в силу теоремы 22 множество атомов /
независимо. Теорема доказана.
Полная атомная (т. е. любой элемент представим в виде
объединения атомов) полумодулярная решетка без бесконечных цепей
называется геометрической или матроидной.
Дадим несколько определений.
Пусть ^(8)—множество всех подмножеств 5. Скажем, что
на множестве 5 задан оператор замыкания, если каждому
элементу Ле^(5) сопоставлен однозначно определенный элемент
4е#(5), называемый замыканием А, причем это сопоставление
для всех А, Ве^(5) удовлетворяет следующим условиям:
1. А<=А;
2. Если А<=В, то А^В (свойство сохранения порядка);
3. А = А (идемпотентность).
Множество А назовем замкнутым, если оно совпадает со своим
замыканием.
Пред геометрией (или матроидом) 0(5) называется множества
5 с оператором замыкания ~, удовлетворяющее свойствам:
а) замены: для любых р, ^<=8 и всякого Ле^(5) из
р^А\\{а} и р^А следует, что д^А[){р};
б) конечного базиса: для всякого Ле^(5) существует
конечное подмножество А^А такое, что А;=А.
Комбинаторной геометрией (далее всюду—геометрией)
называется предгеометрия, у которой все одноэлементные
подмножества, а также пустое множество являются замкнутыми.
Задание геометрии на множестве 5 отличается от задания _то-
пологии на 5 тем, что не требуется выполнения условия А[]В =
= А[]В для всех А, В^^(8), но имеет место свойство замены,
которое, вообще говоря, может не выполняться для замыкания
топологии.
Всякое замкнутое множество геометрии назовем поверхностью^
Поверхности геометрии О, упорядоченные по включению,
образуют полную решетку Ь(С) с бинарными операциями V и /\:
А/\В=А[\В, А\/В=А[]В, где А, В — поверхности геометрии О.
Теорема 24. Пусть 0 = (5, -) — геометрия. Тогда решетка
£(0) является геометрической. Обратно, если Ь —
геометрическая решетка, 5 — множество атомов решетки Ь и замыканием А
242

любого подмножества Л^5 является множество {ае5|а^зир А},.
то 0= (5, ~) — геометрия и решетка Ь изоморфна Ь(С)-
Доказательство. Пусть 0=(5, ~) — геометрия. То, что
решетка Ь{0) — полная, без бесконечных цепей и атомная,
проверить не представляет особого труда. Поэтому представляем это>
сделать читателю самостоятельно в виде упражнений. Докажем,,
что Ь(0) — полумодулярная решетка. Пусть А, В^Ь(О), Д =
= А[}{р} и р^А. Мы утверждаем, что тогда А-^В. Действительно;
если С^Ь(О) и АаС<=В, то существует элемент 9е(С\^) и
д^С^В=А[]{р); поэтому, согласно свойству замены, р^А[]{д}'=С^
Следовательно, В=А[]{р}^С. Получаем, что В = С; отсюда А -=^В-
Пусть теперь В<^Ь{С). Тогда В\/И = В\]й = А[}0[]{р} и А\'й =
=А[]П; отсюда либо р^А[}0 и поэтому А\/Б=В\/П, либо рф
^А[]П и в этом случае А\/0-^В\/0. В одну сторону теорема;
доказана.
Обратно, пусть Ь — геометрическая решетка, 5 — множество?
атомов в Ь и Л = {ае5|а^зир А) для всех Лд=5. Ясно, что Л-МГ
является оператором замыкания. В самом деле,_пусть оеЛ._Для
каждого А<=3 выполнено а^зир Л. Значит, А^А. Если А^В для
Л, В^5 и а^А, то а^зир В. Отсюда зирЛ^зирВ и, значит,
А^В.
Определение геометрической решетки обеспечивает выполнение
условий конечного базиса и замкнутости одноэлементных
подмножеств и пустого множества. Проверим выполнение свойства
замены. Пусть р^А[]{д) и р^А. Так как {д} является атомом, то в си-
лу полумодулярности А[]{д}={А\/{д})-^А, поэтому из АаА[]{р}^
-^11(^} следует Л[Др}=Л []{<?}; таким образом, д^А[}{р}. Тем
самым нами установлено, что (5, -) — геометрия. Обозначим ее
через С.
Докажем теперь изоморфность решеток. Обозначим через ф
отображение Л->зир Л, где Л;=5, А^Ь(С). Тогда оно отображает
Ь(С) в Ь. Так как каждый элемент решетки Ь является
объединением атомов, то включение ЛеВ равносильно неравенству
зир Л^зир В. Поэтому ф является взаимно-однозначным
отображением «на» и оба отображения ф и ф~! монотонны.
Следовательно, ф — изоморфизм. Теорема доказана.
Таким образом, решетка подпространств полностью определяет
геометрию, и наоборот. Диаграммы геометрических решеток
являются, как правило, слишком громоздкими, чтобы их можно было
как-то использовать. Тем не менее часто мы можем нарисовать
картинку геометрии, ассоциированной с решеткой. Элементы
ранга к (к^О) будем называть ^-поверхностями. При этом
1-поверхности будем называть точками, 2-поверхности — прямыми, 3-по-
верхности — плоскостями и т. п. Заметим, что плоскость является
решеточным объединением любой ее прямой с ее точкой, не
лежащей на этой прямой и т. п. Последнее можно кратко
сформулировать так:
243.

(*) всякая ^-поверхность и 1-поверхность, не лежащая на ней,
лежат на единственной (к+ 1) -поверхности.
При изображении геометрии прямые будем рисовать отрезка-
•д ми (или кривыми). При этом будем
изображать лишь те ^-поверхности,
которые не могут быть однозначно
восстановлены по рисунку, применяя лишь
свойство (*). Поясним это на примере. На
рис. 8.16 изображена геометрия ранга 3
с множеством точек {а, Ь, с, й, е, /, §},
причем прямые ай, ае, а§, Ъй, Ье, Щ, Ь§,
с/, с§, с?/, йд,, е§ и плоскости аЬс§, а}§,
сЛеё. 4ё, а<*8. ае§, Ьйц, Ье§, Ь}§, с$ё,
>*!}§ не проведены, поскольку они могут быть получены с помощью
•свойства (*).
Рис. 8.16
аЬсйе
аЪсв,
Рнс. 8.17
На рис. 8.17 а), 8.18 а), 8.19 а) и 8.20 а) представлены
геометрии, а на рис. 8.17 б), 8.18 б), 8.19 б) и 8.20 б) соответственно
диаграммы их решеток. Отметим простоту изображений геометрий
по сравнению с запутанностью диаграмм их решеток.
.аЪсйе
аЬс
Рис. 8.18
Матроиды (или геометрии) возникают в большом количестве,
-особенно в алгебре, теории графов, геометрии, теории трансвер-
салей, комбинаторике и т. д. Изучение же их началось со знамени-
244

Рис. 8.19
той задачи о семи кенигсбергских мостах, решенной около 200 лет
тому назад Эйлером. Изложение теории матроидов мы продолжим
в § 8.4, где приведем также другие примеры матроидов и их
приложений.
5
Рис. 8.20
Остановимся кратко на результатах о ширине геометрических
решеток, сформулированных в духе теоремы 1 (Шперпера).
Пусть Ь — конечная геометрическая решетка. Обозначим через
Е(1) множество всех элементов решетки Ь ранга I, и пусть
^ = 1^(01.
Заметим, что множество £(1) является антицепью решетки Ь.
Теорема 25. Пусть Ь — конечная геометрическая решетка, в
которой любой элемент а ранга I покрывается к; элементами и
покрывает т; элементов (числа 1ц и т.; зависят лишь от ранга I).
Тогда ширина Ь равна тах И^.
Доказательство. Пусть п — г(Ь) и тах №,г = Ц7А. Тогда
0<Г<п
£(£) — антицепь с Ц7А элементами. Нам осталось доказать, что
если А — произвольная антицепь в Ь, то |Л|^Ц7А. Для любого
а^Ь обозначим через 8 (а) число всех максимальных цепей,
проходящих через а. Очевидно, что если г(а)=1, то 8(а)=т\т2 ...
245

... т;&; ... кп-\- Следовательно, 8 (а) зависит только от ранга Г.
Поскольку каждая максимальная цепь имеет в точности один
элемент ранга I, то число 5 всех максимальных цепей в Ь равно
81а) №>. Отсюда из неравенства 1^г<^* имеем: 5(а) = — - >—-.
Наконец, каждая максимальная цепь проходит не более чем через
один элемент антицепи А. Следовательно,
т. е. [Л^ИРд., что и требовалось доказать.
Конечная геометрическая решетка Ь ранга п называется
унимодальной, если для некоторого числа к справедливы неравенства
^1<...<^*-1<^* и Ц7..г>^+!>...>1У„_,. Пусть А, В —
подмножества решетки Ь. Скажем, что между А и В существует
равнение, если существует взаимно-однозначное отображение го : А->В
(или ф : В->А, если |Л|^)В|) такое, что для всех сеЛ
(соответственно для всех а^В) элементы а. и го(а) сравнимы.
Теорема 26. Пусть Ь — конечная геометрическая решетка
ранга п. Если решетка Ь унимодальна и существует равнение между
£(1) и £(1+1) для всех Кп, то ширина Ь равна Ц7А) где
Доказательство. Для любого подмножества Ая=Ь число
й(А)== тах {г (а) - г (Ь))
а, Ь€А
назовем диаметром подмножества А. Пусть А — антицепь
решетки Е. Неравенство |Л|^и7й докажем индукцией по диаметру
а'(А). Если й(Л)=0, то А^Е(1) для некоторого I. Отсюда |Л|<;
^1^,:^¾7¾. Пусть теперь а'(А)>0 и неравенство справедливо для
антицепей меньшего диаметра. Так как а1(А)>0, то в антицепи А
всегда найдется такой элемент а, что г{а)Фк\ допустим для
определенности: г(а)<к. Пусть 1 = гаюг(й) и А=--А0[)Аи где А\ =
аеА
= А(]Е(() и А0 = А\А1. По предположению, Кк, поэтому (£(1)1^
^£(1+1)1 и. следовательно, существует равнение ц>:Е(1)-+
->Е(1+1). Положим А'=--Ай\}ц(А\). Множества А0 и <р(Л;) не
пересекаются. Действительно, если ое (Л0Пф(^1)). т. е. а = го(о) для
некоторого ЬееЛь то а, Ь^А, афЪ и а, Ь — сравнимы, что
невозможно, так как А — антицепь. Следовательно, |Л'| = |Л|. К тому
же Л' — антицепь. В самом деле, если а, Ь^А\, афЬ и а, Ь —
сравнимы, то аеЛ0 и Ь = ц(А{), т. е. Ь = го(с) для некоторого с^А\.
Так как г(Ъ) =1+1, то г(Ь) <г(а). Следовательно, Ь<а, но "это
противоречит условию, что с^Ь и с\\а. Значит, А' — антицепь. Но
а1(А') = а'(А) — 1, поэтому в силу предположения индукции \А\ =
= \А'\^.№к. Теорема доказана.
Приведем без доказательства еще несколько результатов о
числах IVк в геометрических решетках.
246

Теорема 27. Пусть Ь — конечная геометрическая решетка
ранга п. Тогда
№1<И^ для 1 = 2, 3, ..., п—\
и
№, + ...+ №*<№„_*+...+№„_1 для А=1, 2, .... л—2.
Теорема 28. Пусть /, — конечная геометрическая решетка
ранга п. Тогда при любом к=\, ..., п—2 равенство
^1+...+ №*= №„-* + ...+ №*-!
имеет место тогда и только тогда, когда решетка Ь модулярна.
Теорема 29. Пусть Ь — конечная модулярная геометрическая
решетка ранга п. Тогда для всех 0<&<я справедливо равенство:
1*7А = №„_,..
Упражнения 12. Докажите теорему 1, используя: а) теорему 25;.
6) теорему 26.
13. Обобщите теорему 25 на частично упорядоченные множества.
В главе 5 мы рассмотрели проективное пространство как пару
{А, Ь), где А — множество точек, а I — семейство прямых, для
которой выполняются следующие условия:
а) прямая /е! имеет не менее двух точек;
б) для любых двух точек а, Ьег:А существует только одна
прямая /е! такая, что а, Ь^1;
в) для любых точек а, Ъ, с, й, е^А и прямых 1\, Ъ^Ь,
удовлетворяющих условиям: а, Ь, д.<=1\ и Ь, с, е^12 существуют точка
/еЛ и прямые /3, и^Ь такие, что а, с, /е/3 и А, е, /е/4.
Остановимся теперь кратко на описании проективного
пространства его линейными подпространствами. Для любых а, Ь^А
(где афЪ) через а+Ъ обозначим прямую, содержащую точки а и
Ъ. Подмножество В^.А называется линейным подпространством
проективного пространства, если вместе со всякими двумя
точками из В ему принадлежит и прямая, определяемая этими точками.
Другими словами, В — линейное пространство, если а, Ь^В
влечет за собой а+Ь^В. Пусть В, С — линейные подпространства.
Положим В + С равным объединению всех прямых Ъ+с таких, что
Ь^В, с^С. Легко проверяется, что В + С также является
линейным подпространством. Пересечение любого числа линейных
подпространств снова является линейным подпространством. Отсюда
нетрудно получить следующий результат.
Теорема 30. Линейные подпространства проективного
пространства образуют модулярную геометрическую решетку.
Доказательство этой теоремы в качестве упражнения
предоставляем читателю.
Более того, существует взаимно-однозначное соответствие
между проективными пространствами, определяемыми точками и
прямыми, и модулярными геометрическими решетками. При этом
соответствии линейные подпространства проективного
пространства отображаются в элементы модулярной геометрической
решетки, т. е. в поверхности ассоциированной с ней геометрии.
247

Решетки Ь, удовлетворяющие для всех а0, аи а2, Ь0, Ь\, Ъ2&.Ъ
следующему неравенству:
{а0\/Ьо) Л («1 N/60 Л (а2\уЬ2) < ((с\/а0 Л До) V ((с\/^) ЛМ,
где с=((а0уа1)Л(&оУЬ1))Л(((аоУа2)Л(ЬоУЬ2))У((а1Уа2)Л
Л (Ь\\/Ь2))), называются арговыми. Это неравенство является
теоретико-решеточной формой теоремы Дезарга (см. теорему
в гл. 5). В самом деле, имеет место следующий результат:
Теорема 31. Модулярная геометрическая решетка Ь является
арговой тогда и только тогда, когда в ассоциированной с ней
проективной геометрии верна теорема Дезарга.
Доказательство этой теоремы технически несложно, поэтому
мы его опускаем. Желающие могут найти его в [32]. Там же
можно найти и доказательство следующего результата, который
является хорошо известной теоремой геометрии.
Теорема 32. Пусть Ь — модулярная геометрическая решетка,
и ассоциированная с ней проективная геометрия является
невырожденной (т. е. каждая прямая имеет не менее трех точек). Если
ранг решетки Ь не меньше 4, то она" аргова.
Упражнения. Докажите, что
14. Из арговости решетки следует ее модулярность.
15. Частично упорядоченное множество В(8п) (см. пример 8 из § 8.1)
всех неупорядоченных разбиений л-множества 5„ является геометрической
решеткой. Эту решетку часто называют беллианом.
16. Беллиан В(8п) модулярен тогда и только тогда,-когда п^З.
17. Любая конечная дистрибутивная решетка вложима в беллиан.
Представлением решетки Ь называется вложение этой
решетки в некоторый беллиан. Представление конечных решеток —
одна из старейших открытых проблем теории решеток.
Найдены ответы на нее лишь для частных классов решеток.
В этом параграфе мы осветили лишь немногие аспекты теории
решеток, останавливаясь в основном на комбинаторных примерах.
Для дальнейшего изучения теории решеток рекомендуем книги
[31—33].
8.3. ФУНКЦИИ ИНЦИДЕНТНОСТИ И ОБРАЩЕНИЕ
МЕБИУСА
Пусть Р — локально конечное частично упорядоченное
множество, а К — поле характеристики 0 (обычно поле
действительных чисел). Рассмотрим класс А(Р) функций /(х, у),
принимающих значения в поле К и определенных для всех х, у^Р.
Потребуем, чтобы /(х, 1/)=0, если не выполняется условие х^г/. Сумму
двух таких функций, а также умножение на скаляры определим
следующим образом:
(/ + 2)(*. У) = !(х, У) + §{х> У)\
{<*••!)(*, 30 = «•/(*. У)'
а произведение (или свертку*) /*§ — следующим образом:
248

(?*8){х, у) = 2 /(*, г) § (г, у).
г: дс^г<(/
Это произведение определено корректно, так как в силу локальной
конечности множества Р в правой части число слагаемых конечно
и (!*§) (х, у) =0 всякий раз, когда х ^у-
Множество А(Р) с операциями сложения, умножения (или
свертки) и умножения на скаляры называется алгеброй
инцидентности частично упорядоченного множества Р над К, а его
элементы — функциями инцидентности множества Р.
Нетрудно заметить, что умножение функций инцидентности
ассоциативно и дистрибутивно, а нейтральным элементом
относительно умножения (свертки) является функция Кронекера (или
дельта-функция):
{1, если х = у;
о(х, у) = \г>
4 *' (0 — в противном случае.
Докажем, к примеру, что операция умножения (свертки)
ассоциативна. Пусть /, §, Н^А(Р). Тогда
(Т*(В*Ь)) =
= Е /(*. г)(ё*Н){г, «/)= Е Цх, 2)(^ ё{г, ЦН{1, у)) =
= Е ( Е /(*. г) В (г, О) Л С </)= Е (!*В) (*.0 Ч*, У) =
Г- *<«(/ г: *<г« (: х<1<у
= Ш*в)*Щх, У)-
В силу сделанных замечаний видно, что алгебра инцидентности
действительно является ассоциативной алгеброй над полем К-
Причем А(Р) коммутативна тогда и только тогда, когда частично
упорядоченное множество Р является антицепью, т. е. тривиально
упорядочено.
Теорема 33. Функция инцидентности / в А(Р) имеет как левую,
так и правую обратные функции тогда и только тогда, когда
/(х, х)Ф0 для всех х^Р. Более того, правая и левая обратные
функции совпадают.
Доказательство. Пусть Ч
Е /(*• г)ё(г, У) = &(х, У).
г. х<г<(/
Поскольку 1=б(х, х)=1(х, х)§(х, х) при каждом х из Р, то
условие /(*, х)ф0 для всех хеР, очевидно, является необходимым.
Обратно, пусть [(х, х)Ф0 для каждого хеР. Тогда
§ (х, х) = для всех хеР. Найдем теперь §(х, у) при х<у.
Без ограничения общности предположим, что уже нашли §(г, у)
для всех г таких, что х<г<у. Для х<у имеем
в К. А. Рыбников
249

У*8)(х,у) = Ь(х,у) = 0= Е Г (х, г) в (г, у),
и, следовательно,
— 1(х,х)8(х,у)= Л !{х,г)§{г,у).
г:х<г<у
Отсюда можно найти §(х, у), так как /(х, х)Ф® и все слагаемые
конечной суммы в правой части последнего равенства известны.
Таким образом, мы не только доказали, что / имеет правую
обратную функцию, но и получили рекуррентную формулу для ее
вычисления.
Аналогично из соотношения (§*!) (х, г/)=б(х, у) получаем
рекуррентную формулу для определения левой обратной функции
для /.
Пусть теперь §\— правая, а §2—левая обратные функции к /
из Л(Р), т. е. /*#1 = §2*/=б. В силу ассоциативности
умножения фуНКЦИЙ ИНЦИДеНТНОсТИ §2 = §2*6 = #2*(/*&1) = (§2*!)*§1 =
— 6*1*1=1*1, т. е. левая и правая обратные функции совпадают.
Доказательство завершено.
Функцию, обратную к /, обозначим через /-1. Обозначим также
/°=б, р=1 Р=!*1, /3=М2. -, ^=!*!к~К ■- и гй= (Г1)*-
Помимо уже рассмотренной функции Кронекера 8(х, у) часто
среди прочих функций инцидентности в А (Р) выделяют
следующие:
дзета-функцию г [ 1, если х -< у,
ь [х, у) -
лямбда-функцию
К (х, у)
О — в противном случае;
1, если х = у
или у покрывает х;
О — в противном случае;
функцию цепей (эта-функцию)
Л (х, у) = Ъ (х, у) — Ь (х, у);
функцию покрытия (каппа-функцию)
х(х, у)=к(х, у)—6(х, у);
мебиус-функцию (мю-функцию)
И*> у)=Ъ~Чх> у);
функцию длины (ро-функцию)
р(х, у) =1(х, у), где 1(х, у) — длина интервала [х, у] в Р.
Причины выделения этих функций и их названия станут
понятными после рассмотрения свойств этих функций инцидентности.
Определение мебиус-функции р(х, у), как обратной к
дзета-функции 5(-х, у) из А(Р), корректно. В самом деле, 1,(х, х) = 1=^=0 для
всех хеР. Поэтому в силу теоремы 33 I, имеет обратную
функцию ц, которая является для нее как левой обратной, так и
правой обратной. Более того, в силу теоремы 33, мебиус-функция
\ь(х, у) локально конечного частично упорядоченного множества Р
250

может быть вычислена для фиксированных х, у^Р таких, что
х<у рекуррентным образом с помощью формул
И*.У) = - Е Ц(*,2) = - ^ Ц(2,4Г) (1)
с учетом условий, что ц(х, х) = 1 для всех хеР.
Пусть Р* — двойственное к Р частично упорядоченное
множество. Тогда, если Цх, у)евА(Р), а 1*{х, у)<=А{Р*), то I* (х, у) =
= С(#, х) для всех х, г/ из Р. Очевидно, аналогичные равенства
имеют место для лямбда-функции, функций Кронекера, цепей,
покрытия и длины, а в силу теоремы 33 и аналогичного свойства
дзета-функции и для мебиус-функции. Таким образом,
приведенные выше функции инцидентности не меняются, если вместо Р мы
будем рассматривать Р*.
Чтобы легче было понять смысл введенных определений,
рассмотрим матричные представления функций инцидентности. Для
этого сперва продолжим отношение частичного порядка < на
локально конечно упорядоченном множестве Р до отношения
порядка ^ , превращающего Р во вполне упорядоченное множество
(это всегда можно сделать в силу теоремы 4), а затем
воспользуемся этим вполне упорядоченным множеством для индексации
элементов множества Р. При этом получим, что если ха<%, то
а =<р. Теперь каждой функции инцидентности /(х, у) из А(Р)
сопоставим матрицу /^ = 11/^11 с элементами из поля К, в которой
строки и столбцы согласованы с индексацией множества Р,
а именно /ац = /(Ха, %). Вообще говоря, полученная матрица
может быть и бесконечного порядка. В случае конечного частично
упорядоченного множества Р матрицы функций инцидентности
будут порядка |Р|, а в качестве индексирующего множества в
этом случае можно взять натуральные числа от 1 до \Р\ (см.
теорему 2).
Матрица функции инцидентности }(х, г/)еЛ(Р), полученная
таким способом, очевидно, является верхней треугольной
матрицей, т. е. матрицей, под главной диагональю которой стоят только
нули.
Рассмотрим несколько примеров. Пусть Ъ — матрица дзета-
функции из А(Р). Если Р=5Э(5), где 5 = {а, Ъ, с}, то
0
1 1
0
0
0
0
0
0
0
а
1
1
0
0
0
0
0
0
ъ
1
0
1
0
0
0
0
■0
с
1
0
0
1
0
0
0
0
аЪ
1
1
1
0
1
0
0
0
Ъс
1
0
1
1
0
1
0
0
ас
1
1
0
1
0
0
1
0
аЬс
1 *
1
1
1
1
1
1
1
0
а
Ь
с
аЬ
Ъс
ас
аЬс
5 элементов, то
2 =
Если Р —цепь из
9*
251

1111
0 111
0 0 11
0 0 0 1
^0 0 0 0
Если Р — антицепь из 5 элементов, то
10 0 0
0 10 0
0 0 10
0 0 0 1
\0 о о о
Пусть /^=11^11 и 0 = |||*о&11 — матрицы соответственно функций
инцидентности / и § из А(Р), индексами которых служат
элементы вполне упорядоченного множества (Р, ^). Тогда, если
Р = {*8, Цх, У)=?(х, у)+§{х, у) и 1{х, у)=а{{х, у), то Р = РО,
Н = Р+С и Т = аР, т. е. рар = Т!/от^Р- В самом деле,
7
^] /»7#гР "-= ^ / (х«> хт) 8 (ху *р) = Е ^ (Ха" Ху)§ (Ху' Х^ =
7 7 *;>:%< *у<*Р
=Р (Ха, *р) = р«з
(мы воспользовались тем, что ${ха, хт) =0 при у<[а и 8^, %) =0
при р-^у)- Отсюда, если Р — конечное частично упорядоченное
множество, то А(Р) можно рассматривать как подалгебру алгебры
всех верхних треугольных матриц порядка \Р\. Матричные
представления существенно облегчают изучение частично
упорядоченных множеств и понимание сущности введения алгебр
инцидентности над ними. Отметим, что алгебры инцидентности двух
частично упорядоченных множеств изоморфны как кольца тогда и только
тогда, когда изоморфны сами множества. Этот результат
получен Стенли, его доказательство мы опускаем.
Непосредственно из определений функций инцидентности
вытекают следующие тождества:
а) / = / * б = б * /; б) б*
к-\
в) №*) = 5](?)т1'(*.*); *Г{х,у) = ^(-\г-* (?)№*);
1 = 0 1=0
П П
г) Ья(х,у) = %(п.}*(х,уУ, к"(х, у)=%(-1Г~1 (п.^ V (х, у);
1=0 1=0
д) (к*Ъ)(х, г/)=числу всех атомов в интервале [х, у] из Р.
е) (1,*н)(х, у) = числу всех коатомов в интервале [х, у] из Р.
Для получения тождеств в) и г) необходимо воспользоваться
также биномом Ньютона:
252

(а + Ь)п= V (п. \ап-1Ы.
1=0
Проверим справедливость тождества д). Имеем (к*?) (х, у) =
= V к(х, г)I,(г, у) = (поскольку к(х, г)Ф0 только, если х -$ г)
= V и (ж, г) I (г, у) = (так как 1,(2, у) = 1 для всех 2-^.у)
= V «(^,г). Но если %(х, г)Ф0, то к(х, г) = 1. Тождест-
г:х— < г<(/
во д) доказано. Тождество е) получается из д) двойственным
образом.
Кроме того,
Р(х,у)=(Г*П(х,у)= 2] !(х,г1)!(г1,у);
/3(X, «/)=(/* Л (*,«/) = (/*(/*/))(*, У) = .
= ^ /(^)( 5] /^,2,)/(2,,^)) =
= 2 (/^.21)/(2^2,)/(2,,^).
Далее по индукции получаем тождество
Ж) /* (*, Г/) = ^ / (*, 2Х) / (21, 2,) . . . / (2*_,, «/).
'1,2 ,гА_1:х<г,<.. .<гА_1<(/
Непосредственно из ж) и определений функций инцидентности
£, т), и локально конечного частично упорядоченного множества Р
получаем тождества:
з) цк(х, у) = числу всех цепей длины к между х и у в Р
(поскольку Т) (*, 21) Т) (21, 22) ... Т) (2ь_1, у) = 1 ТОГДЭ И ТОЛЬКО ТОГДЭ, КОГДЭ
ДГ<21<22< ... <2к-1<У)\
и) ий(*, г/) = числу всех максимальных цепей длины к между х и
у в Р (поскольку %(х, 24) и(21, 2г) ...и(2/1-1, «/) = 1 тогда и только
тогда, когда х^г^гг^ •■■ 2й-1-=? У);
к) {?(х, У) = \[х, у]\ (так как 1(х, г) 1,(2, у) = \ тогда и только
тогда, когда *«:2<:г/).
Часто в приложениях рассматривают не целиком всю алгебру
инцидентности А(Р), а только определенные ее подалгебры, трез
буя от функций инцидентности либо постоянства значений на
изоморфных интервалах частично упорядоченного множества Р, либо
так называемой мультипликативности.
Пусть А(Р) — алгебра инцидентности локально конечного
частично упорядоченного множества Р. Рассмотрим
подмножество всех функций инцидентности /еЛ(Р), для которых из изо-
морфности любых интервалов [*, у] и [а, Ь] в Р следует: /(*, у) =
253

= /(а, Ь). Обозначим это подмножество через 5(Р). Очевидно, что
5(Р) — подалгебра алгебры инцидентности А(Р), которую
называют стандартной алгеброй частично упорядоченного множества Р.
В самом деле, если /, §^А(Р) и ср — некоторый изоморфизм
интервала [х, у] в [а, Ь], то:
(/ + 8)(х, у) = /(*, у) +8(х, у) = /(а, Ь) + §(а, 6)-(/ + §) (а, Ь);
(а/) (*,«/) = а/ (х, «/) = а/(а, 6) = (а/) (а, Ь);
и*е){х,у)= Е /(*.2)г(г,у)= 5] /(Ф(*).Ф(2))г(<р(2),Ф(у))=
X / (а = Ф (х), Ф (г)) § (Ф (г), 6 = Ф (у)) = (Г*е) (а, 6).
2:а=ф(х)«р(г)«р(»)=Ь
Непосредственно из теоремы 33 получаем следующий результат:
Следствие 34. Пусть 5(Р) — стандартная алгебра частично
упорядоченного множества Р. Если функция инцидентности
принадлежит 5(Р) и обратима в А(Р), то она обратима также и в 5(Р).
Легко проверить, что функции р, б, £, К, т), и, определенные
выше, лежат в 5(Р), и в силу следствия 34 мебиус-функция ц
также лежит в 5(Р).
Пусть Р — решетка. Функция инцидентности /еЛ(Р)
называется мультипликативной, если для всех х, у^Р из условия
[х/\У, хУу] г* [хЛу, х] X [хЛу, у]
следует, что
Т(хЛу, х\/у)=!(х/\у, х)-!(х/\у, у).
Примерами мультипликативных функций инцидентности для
решеток являются б, С и С2 (см. тождество к)).
Следствие 35. Пусть / — мультипликативная обратимая
функция из А(Р). Тогда 1(х, х) = \ для всех хеР.
Доказательство. Из [х/\х, х\/х] ^ [х/\х, х] X [х/\х, х]
имеем, что /(х, х)=/(х, х) ?(х, х). В силу обратимости /(х, х)фЬ
для всех хеР. Следовательно, /(х, х) = 1.
Теорема 36. Пусть Р — решетка. Тогда все мультипликативные
обратимые функции из 5(Р) образуют группу относительно
операции умножения (свертки).
Доказательство. Пусть | и §■ — мультипликативные
обратимые функции инцидентности из стандартной алгебры 5(Р)'.
Проверим, что функция }*д также будет мультипликативной.
Допустим, что
[х/\у, х\/у]^[х/\у, х]Х[х/\у, у].
Тогда (/ * 8) (х/\у, х\/у) = ^ / (х Л у, г) 8 (г, х V у) =
(так как [х/\у, г] з* [х/\у, г/\х] х [х/\у, г/\у], [г, хУу] &
= [г, г\/х] X [г, г\/у] и /, 8 — мультипликативные функции)
254

= 2 !{х/\у, гЛх)Нх/\у,гЛу)§(г,г\/х)8(г,г\/у) =
(так как [г, г\/х] з* {г Ах, х], [г, г\/у] е* [г/\у, ц]и/,ге5 (Р))
^ (НхЛу,гЛх)8(гЛх,х))У(хАу,гЛу)8(гЛу,у)) =
(обозначим через и и V соответственно г/\х и г/\у, тогда хЛ^
<:и<:л: и хАУ<-и<су, поскольку хА(хАУ) = хАу, уА(хАу)=хАУ,
хА (х\/у) =х, уА(х\/у) =у)
= ^ 1{хАу,и)§{и,х) ^ !(х/\у^)в(^У) =
и:х/\У<и<х «:хЛУ<г><У
= (/ * г) (*Л«/, *) (/ * г) (*Л«/, у),
т. е. /*§—мультипликативная функция.
Проверим, что /-1 также мультипликативная функция. Докажем
индукцией по /, что условие мультипликативности выполнено для
всех интервалов длины не более /. При 1 = 0 это очевидно. Пусть
данное утверждение справедливо для /—1, докажем его
справедливость для /. Рассмотрим некоторый интервал [хАу, х\/у]
длины /. Тогда
0=6(хАу>х\Уу) = (?-1*П(хЛу,х\/у)=:
Ё ?-1(хЛу,г)Нг,х\уу) =
Е ?~1(хЛу,г)Пг,х\/у) + Г1(хАу,х\уу)Пх\/у,х\/у) =
г:х^у^г<хУу
(в силу предположения индукции, и учитывая, что }(х\/у, х\/у) =
= 1)
= 2 1-'{хАу,гАх)1^{хАу,гАу)Цг,г\/х)1{г,г\/у) +
г:х кУ<г<х\/у
+ /-1 (хЛу, х\/у) =
(в силу [г,г\/х]^[гАх,х], [г, г\/у] =* [гЛу, у] и /,^е5(Р))
Ё !-х{х/\у,гАх)}{гАх,х)1-х{хАу,гАу)!{гАу,у) +
г:х/\у^г<х\/у
+ 1~1{хАу,хУу) =
(обозначим через и и у соответственно гАх и гАУ с учетом того,
что [хАу, х\/у]^[хАУ. х] X [хАУ, У] и {(х, х) = 1 для всех х<=Р\
= ^ Г1(хАу,и)Ни,х) % /-1 (*Лу.»)/(». у) +
":*ЛУ<а<* V■.X^у^V<у
+ ?~1(хЛу,х) ^ Г1{х/\у,ъ)!{ъу) +
+ !'х{хАу,у) ^ !-1{хАу,и)!{и,х) + 1-1{хАу,хуу) =
255

(в силу формул из теоремы 33 и равенства [(х, х) = 1 для всех
*е=Р)
= (-Г1 (хЛУ, х)) (-/"'(х/\У, У))+!~1 (ХЛУ, х) (-/-*(хАУ, У)) +
+!-' (хЛУ, У) С-/"1 (хЛУ, х)) +/-' {х/\у, х\уу).
Таким образом, получили, что
ГЧхЛу, хУу)-!~ЧхАУ, х)^{х/\у, у)=о.
Следовательно,
Г1(хЛУ, хУу)=!-^{х/\у, х)^{х/\у, у),
и доказательство теоремы завершено.
Вычислим функцию Мебиуса для некоторых частично
упорядоченных множеств, приведенных в § 8.1.
Пример 1. Пусть А — тривиальное частично упорядоченное
множество. Тогда, очевидно,
. ,. (1, если а = Ь;
(О— в противном случае.
Пример 2. Пусть #={0, 1, 2,..., к} — подмножество целых
чисел с обычным порядком. Тогда в силу следствия 35 ц(п, п) — \
для всех п^Ы. Воспользуемся формулами (1) и получим, что
ц(п, п+1) = -1 и \1(п, п+к)=0 для всех п, к<=Ы и к>-2. Таким
образом:
1, если п=т;
ц(п, т)= — 1, если т — п= 1;
0 — в остальных случаях.
Пример 3. Пусть $Р(5п) — булеан (см. пример 4 из § 8.1),
ГДе Оп — {«1, 52, ..., 5„}. Рассмотрим семейство всех га-мерных
двоичных векторов а= (а4, ..., а„) с отношением порядка: а-^Ь тогда и
только тогда, когда а,<:&,- для всех 1=1, 2,..., п. Обозначим это
частично упорядоченное множество через 2„. Нетрудно проверить,
что
^(5„)^2„.
В самом деле, если Х^5п, то определим <р(Х) = (х^..., хп), где
0, если 5,-^" X;
X) =,.
1, если 5г е X.
Легко видеть, что ср — изоморфизм. Более того,
2„ - 2Х х 2х X • • • X 2Х.
В силу примера 2 для 2] и у^>х имеем ^(х, у) = (—I)"-*, так
как существуют только две возможности: х=у или х=0, у = \.
Пусть Х^У^5п, ч(Х)=(х1,.~,Хп) и ч>(УУ = (уь-,Уп) при
изоморфизме ^<5П)^21Х - Х24. Тогда
256

ц(Х, 10==11((¾.
*п), (У1>
2 »г-2 *'
1=1
= (-1/=1 '=' = (_!)■
Пример 4. Пусть /)(га) — множество всех делителей
натурального числа п, упорядоченное по делимости (см. пример 6 из
§ 8.1). По теореме о единственности разложения числа на простые
множители,
В(л) = В(/>?') X0(/%•) X ... X О(/>?')•
Следовательно, достаточно вычислить мебиус-функцию для 0(ра),
где р — простое число, а а — целое число. Но частично
упорядоченное множество 0(ра) является цепью 1 |р|р2| ... \ра,
изоморфной подмножеству целых чисел {0, 1, 2,..., а} с обычным
порядком, мебиус-функцию которого мы вычислили в примере 2.
Поэтому
1, если I = у;
И(Р'\ Р')= —1> если у —1=1;
0 — в остальных случаях.
В силу теоремы 36
I
ц(1, т) =
(-
1, если / = т;
\у, если — ==
РгРг
р, где р1г р2,
.., р5 — попарно различные простые^числа;
0 — в остальных случаях.
Классический вид функции Мебиуса
1, если й — 1;
(— 1 )\ если й = рхр2 ... р$, где ръ р2, ..., 1
различные простые числа;
0, если й = гЧ, йф\,
найденный Мебиусом около 1832 г. и используемый в теории
чисел, связан с функцией Мебиуса частично упорядоченного
множества О(п) следующим образом
И(<9 =
попарно
ц(/, т)=ц(—у
где
, га ,.
Эта связь объясняет происхождение названия функции Мебиуса.
Продолжим изложение методов вычисления функций Мебиуса
для произвольных частично упорядоченных множеств. Пусть Р и
Ь — два частично упорядоченных множества с функциями
Мебиуса цР и ц/. соответственно и / : Р->-Ь — отображение множества Р
в множество Ь, сохраняющее порядок. Нас будет интересовать,
257

как с помощью известных \иР и / найти ць. При этом обсудим два
типа отображений — операторы замыкания и соответствия Галуа.
Обобщим на произвольное частично упорядоченное множество
Р понятие оператора замыкания, введенного для булеана в § 8.2.
Отображение ф : Р->-Р называется оператором замыкания на
множестве Р, если для любых элементов а, Ь^Р выполняются
следующие условия:
а) а«р(а); б) если а<Ь, то ф(а)^ф(&);
в) ф(ф(а)) =ф(а). Примеры операторов замыкания весьма
многочисленны. Так, в полной решетке подпространств
топологического пространства оператором замыкания будет отображение,
ставящее в соответствие каждому подпространству его замыкание.
В частично упорядоченном множестве Р с единицей 1 оператором
замыкания оказывается отображение ф(х)=1 для всех хеР.
Если ф ■— оператор замыкания, то ф(х) называется
^-замыканием элемента х. Элемент, совпадающий со своим ф-замыканием,
называется (^-замкнутым.
Теорема 37. Если ф оператор замыкания на частично
упорядоченном множестве Р, подмножество А^Р состоит из ф-замкнутых
элементов и а = т1 А существует, то а является также ф-замкну-
тым элементом.
Доказательство. Так как а<* для всех х^А, то ф(а)<
<ф(х)=д; для всех х^А, и, следовательно, ф(а)<а. Обратное
неравенство вытекает из определения оператора замыкания.
Теорема доказана.
Теорема 38. Если ф — оператор замыкания на полной решетке
Р, то частично упорядоченное множество С всех ф-замкнутых
элементов, рассматриваемое как подмножество частично
упорядоченного множества Р, также является полной решеткой. При этом
для всякого непустого подмножества А множества С? имеют место
соотношения:
ш!в А = ШРА и зирс/А = ф(зирРЛ).
Множество С называется фактором частично упорядоченного
множества относительно оператора замыкания ф.
Доказательство. Пусть 1 — единица полной решетки Р.
Поскольку ф(1 )>1>ф(1), то 1 принадлежит С и, очевидно,
является единицей этого частично упорядоченного множества. Если,
далее, А — непустое подмножество множества С}, то элемент
а = ШрА согласно теореме 37 ф-замкнут. Конечно, а^х для всех
хеЛ. Если V^^ и у^д: для всех х^А, то у^а. Так что, а = \п^А,
и значит, С — полная решетка. Пусть, далее, Ь = зирр А и 5 =
= 5ир<2 А. _Ясно,_что Ье(2 и 5^Ь, поскольку 5^х для всех дг^СЛ.
Отсюда: Ь = ф(Ь)^ф(Ь). Неравенство 5^ф(й) справедливо
потому, что ф(Ь)^ф(х)=х для всех хеА Поэтому 5 = ф(Ь), что и
требовалось доказать.
Пусть ф — оператор замыкания на Р и (? — фактор частично
упорядоченного множества относительно ф. Рассмотрим алгебру
258

инцидентности А (С}) как подмножество алгебры А(Р),
доопределяя для всех /еЛ((2):
}(х, у) = 0, если х&<д или у<^<3.
Обозначим через [1 и [1« функции Мебиуса для частично
упорядоченных множеств Р и (? соответственно. Определим аналогично £,
1я и б, 6«,.
Теорема 39 (Рота). Пусть Р — локально конечное частично
упорядоченное множество и пусть ср — оператор замыкания на Р
с фактором С. Тогда для всех х, у^Р имеет место соотношение:
Е а(х 2) = |Ив(ф(*)-Ф(У)). если * = ф(*);
26Р: <р(2)=ф(40 ' } 0, есЛИХ<ф(*).
Доказательство.
Е И*. 2) = 2ц(Х, 2)6(^(9(2),9(1/)) =
= I! И(*. 2)^(9(2), 9И)МфИ> Ф(У)) =
¢(2), 1(:(ш)
= Е И(*. г) С (2, Ф И) МфИ>Ф (*/)) =
2, ф(Ш)
= 5] 6(х, ф(ш))ц(}(ф(ш),ф(у))
Ч)(ш)6Р
(здесь воспользовались тем, что 2^ф(ш) тогда и только тогда,
когда 9(2)^9(ш))- Теорема доказана.
Упражнения.
1. Вычислить функции Мебиуса для частично упорядоченных множеств,
приведенных в примерах 7, 8, 9 и 10 в § 8.1.
2. Пусть (1 — функция Мебиуса конечной решетки Р и х, у, геР. Дока-
зать следующие утверждения;
а) (Ф. Холл). Если х^у н у не является объединением элементов,
покрывающих х, то |а(лс, у)=0.
б) (Вайснер). Если я^у^г, то
Ц(х, I) =\
и гу1=у К 0, если г^=х.
3. Доказать, что функция Мебиуса }х конечной дистрибутивной решетка
Р задается следующим образом:
(0, если у не является объединением элементов, покрывающих х.
(—1)", если у равен объединению п различных элементов,
покрывающих х.
4. Пусть ц — функция Мебиуса конечной геометрической решетки Р и х,
уеР, жу. Доказать, что \1{х, у)ф0. Показать также, что значение \1(х, у)
положительно, если число г (у)—г(х) четно, и отрицательно, если оно нечетно.
Здесь г — ранговая функция Р.
5. (Крапо). Пусть Р — конечная решетка, а^Р и а-*-— множество допол
нений к элементу а в Р. Доказать, что для всех аеР;
ц(0, !)= 2- ц(0, 6) ? (6, с)ц(с, !).
Ь, сеа-1
6. Пусть Р — конечная решетка. Доказать следующие утверждения:
259

а). Если Р — решетка без дополнений, то ц.(0, 1)=0.
б). Если Р — модулярная решетка, то ц.(0, 1) =ц(0, а) 2и Ц(0> г)
для всех аеР.
в). Если Р — полумодулярная решетка, то ц (0, 1)=ц.(0, а) ш ц(СК г)
для всех модулярных элементов аеР.
Рассмотрим теперь соответствия Галуа. Пусть Р и Ь —
частично упорядоченные множества. Пара (а, х) отображений а : Р^>*
-*-Ь. называется соответствием Галуа между Р и Ь, если для всех
х, у^Р и для всех а, Ь^Ь выполнены следующие условия:
а). Если хг^й/ в Р, то а(х)^а(у) в Ь;
б). Если аг^й в Ь, то х(а)^.х(Ь) в Р;
в), х^та(х) для всех д:еР и а^Зат(а) для всех а^Ь.
Нетрудно проверить, что та и ах являются операторами
замыкания на множествах Р и Ь соответственно.
Данное понятие берет свое начало от теории Галуа для
алгебраических уравнений, где рассматривается соответствие Галуа
между подполями алгебраического расширения К данного поля Ко
и подгруппами групп всех тех автоморфизмов расширения К,
которые оставляют Ко поэлементно фиксированным. Рота и его
ученики, используя соответствия Галуа, существенно продвинули
теорию функций Мебиуса (см., например, [1]).
Приведем без доказательства очень важный результат,
принадлежащий Рота.
Теорема 40. Пусть (а, т) — соответствие Галуа между
локально конечными частично упорядоченными множествами Р и Ь, и
пусть С? — фактор множества Р относительно оператора
замыкания га. Тогда для всех хеР, у^Ь:
г 6 Р: 0(2)=(/ иеЦт{и)=х
Главное преимущество понятия соответствия Галуа в том, что
можно вычислять функцию Мебиуса ц/, решетки Ь, рассматривая
произвольное подмножество Р и булеву алгебру ^(Р), которую
оно порождает.
Рассмотрим теперь некоторые комбинаторные задачи, при
решении которых применяются функции Мебиуса. Начнем с
изложения обращения Мебиуса. Обращение конечных рядов является
одним из наиболее полезных инструментов комбинаторного
анализа и теории вероятностей. Его частным случаем является
классический принцип включений-исключений (см. § 3.1). Хотя многие
задачи обращения могут быть выражены в терминах включений-
исключений, подобная процедура часто выглядит искусственной.
Обычно возможно некоторое «естественное» упорядочение
изучаемых объектов. Это представляет собой основу техники
обращения Мебиуса.
260

Теорема 41 (1-я формула обращения Мебиуса). Пусть § и / —
функции, определенные на конечном частично упорядоченном
множестве Р со значениями в множестве действительных чисел, и
Я(х) = Е НУ) для всех хе Р.
УУ<х
Тогда
/(*)= Е 8(У)р(У> х) Для ^^ хе=Р.
у.у<х
Доказательство. Зафиксируем х и рассмотрим сумму
5= Е 8(У)Р(У> *) = Е ( Е /(г)) И (У. *)■
у.у<х У-У<* г:г<У
Здесь вместо §(у) мы подставили его выражение через /(г).
Изменим теперь порядок суммирования и получим
5= Е /(г) I и</. *)-Е/(2)Е(г. у) Е И (у, *) =
= Е/(2) Е Б(2. </)и(</> *) = Е/(2)б(2> *) = /(*). •
г у;г^,у<х г
т. е. теорема доказана.
Замечания. 1, Предположение о вещественности функций
!§ и / в формулировке теоремы 41 можно опустить, но потребовать,
чтобы они принимали значения в поле характеристики 0.
2. Теорема 41 справедлива также и для локально конечных
частично упорядоченных множеств. В этом случае для гарантии
конечности сумм требуют существования такого элемента т^Р,
что §(у) = 0 для всех у^т. При этом функция § корректно
определена. В самом деле:
е(х)= Е Пу)= Е Ну),
у:у<х у:т<у<х
где число слагаемых конечно для всякого локального конечного
частично упорядоченного множества.
3. Условия, при которых были бы допустимы бесконечные
суммы, пока не найдены.
Теорема 42 (2-я формула обращения Мебиуса). Пусть § и / —
функции, определенные на конечном частично упорядоченном
множестве Р, со значениями в множестве действительных чисел, и
ё(х) = Е / (У) Для в0^ х <= р-
у.у>*
Тогда
/(*)'= Е И(*. У)ё(У) для всех х гн; Р.
Г-У>*
261

Доказательство полностью аналогично теореме 41, и поэтому
его опускаем.
Рассмотрим несколько примеров.
Пример 5. Пусть / — функция, определенная на множестве
целых положительных чисел с обычным порядком, и
8(п)= Е !(т).
т- т<п
Тогда в силу теоремы 41 и примера 2 имеем
!(п)=8(п)-д(п-1).
Пример 6. Пусть $>(5п) — булеан, В(Щ= Е !(А)
А.А^В
и А(В)= ][] /(Л), где В^^(3п). Тогда в силу теорем 41 и 42,
А:А2В
а также примера 3 имеем
/(Я)= Е (-1)'В-:Л12(Л)
а-.аЕв
и
ПВ)= Е (-1)|ВМЛ|МЛ).
А.А^В
Полагая |В|=гс и суммируя отдельно в правой части равенства
!(В)= Е <-1),в:-И1*И)
А-.А^В '
слагаемые с |Л|=я, п—1, ..., 1, 0, получаем:
НВ) = 8(В)- Е 8(А)+ Е е(А)-...+
А'.АаВ; \А\=п— 1 А:А^В; \А\=п—2
+ Е (-1)к8(А)+...+(-1Г Е 8 (А).
А-.АСВ; (Л|=п—к АхАаВ; |Л|=0
Из последней формулы могут быть получены различные
варианты метода включений-исключений. Эти варианты используютпо-
нятие меры конечного множества. На конечном множестве 5„
зададим весовую функцию ы(х), х&5„, принимающую значения из
некоторого коммутативного кольца К. Используя эту функцию
ш(х), определим функцию меры на булеане ^(5„), которую также
обозначим через ш. Для любого Ле^(5„) положим
[ 0, если А == 0;
<»И) = | ]Г а(х)г если Аф0.
Пусть К — поле действительных чисел. Тогда, если ш (х) = 1 для
всех х^8п, то а (А) = \А\, Ле^(5л.)„ т.. е.. мера совпадает с мощ-
262

цостью множества- Если ш(х)^0 для каждого х^5п и 2л а(х)—К
то мера называется вероятностным распределением. В этом
случае элементы булеана ^(5«) называются событиями и мы имеем:
<о(Л)+ш(Л)=о)(5„), где Л = 5„\Л, Ле^(5„).
Используя законы де Моргана, получаем
о)(Л[Щ = о)(ЛПё);
а(А(]В) = а(АЦВ).
ПустЪ теперь задано множество 5„ = {хь ..., хп}, элементы
которого могут обладать или не обладать каждым из свойств Еи Е2,...
..., Ей На булеане ^(5„) задана некоторая мера ш. Будем считать,
что элемент йё5„ обладает (^-свойством, если он обладает
свойствами, индексы которых принадлежат множеству ^^=N={\, 2, ...
..., I). Пусть 0,\}0. = Ы, ^П^ = 0^^ /((2) есть мера подмножества
элементов из 5„, обладающих ^-свойством, а §{0.) — мера
множества элементов из 5„, обладающих ^-свойством и, может быть,
другими свойствами, номера которых принадлежат С}. Тогда
очевидно следующее равенство:
8(0)= I иву
Применяя формулы обращения, получаем при <3 = Ы:
/(Л0= Ц (-1)т-ш§(В) = о(5п)- Е §{В) + ...+
В:ВСд, В.Вс№, |В|=<—1
+ (-!)* Е §(В)+...+(-1У Е 8(В)'
В:ВсЫ: \В\^—к В:В~№, \В[=0
Отметим, что ?(Ы) есть мера множества элементов из 5„, не
обладающих ни одним из свойств £1, Е2, ..., Еы; §(В) — мера
множества элементов, обладающих всеми свойствами с номерами из
^\5 и, возможно, некоторыми свойствами с номерами из В;
Я(Л0=<а(5„).
Множество элементов из 5„, обладающих свойством Е{, удобно
обозначать той же буквой £,-, £=1, 2, ..., /. Тогда можно записать
/(Л0 = <а(П Ё{),
Г ш(5„) , если В = Ы;
ёФ)= Ш( л £,), если ВфЫ.
I 1€Ы\В
Тогда
е»<П £,)--= Е (-1Г"1Я«>( П Ег).
263

Отсюда следует, что
О)
(П £,) = Е (-1)|В1со(П Е,).
Полагая М(0) = ш(П К), А0 = а(Зп),
Ак= Е о(П Е{), где к=1, 2, ..., (,
получаем формулу Сильвестра
л*(0)=;е (-1)мь
являющуюся одной из формул метода включений-исключений.
Мера множества элементов из 5«, обладающих хотя бы одним
из свойств Ей Е2, —,.Еи записывается тогда следующим образом:
М(1) = а([} £,),
В силу очевидного равенства М(\) =ш(5«)— М(0) и формулы
Сильвестра получаем
М(1)=^(-1)*~МЬ
*—1
и (V £,) = 2 (- 1)^-^( П Е,).
С&Ы В-.ВЕН; ВФ0 'бВ
Применяя к последнему соотношению формулу обращения,
находим
ю(П Е<)= Е (-1)^-^( [} £,).
Используя обозначения
А[к]= Е <а(У £,), где А=1, 2, .... г.
В-.вЕЫ ЦЗ|-=* 1&в
получаем
(П ^)=Г(-1)*-М[А].
6=1
Обозначим теперь через М(г) меру множества элементов из
5П, обладающих в точности г свойствами из совокупности £1, Е2г...
..., Е{. Используя обозначение Ег как множества элементов,
обладающих свойством £,, можно записать:
264

М(г)= V ш(Л Е( П £/),
с=ссТ|С|=г 1€С /её
где /-=0, 1, ..., / и С = #\С.
Полагая 5„ = П £,. из ранее полученной формулы
ш(П £,)= V (-1)1В,со(Л £,-)
'6Л/ вас* ''6В
получаем, что
ш( п Е1 п £/)= Е (- 1),В|со( п £,- Л £/).
>'ес /ес *■*_ гее /ев
Отсюда следует, что
ш ( п £,- П_ £/) = V (- 1)1°мс' со ( п £,).
'ес /ее олсКоэс гб"
Из последних трех формул имеем
ми= Е Е (-1)^-^( п £,).
Поменяем порядок суммирования в правой части последнего
равенства и получим
мо= I (-1)|0|_^(.п £,-) Е к
Отсюда следует, что
м- 5] (-"Г-'^'Кп^).
Полагая |Л>| =/г и используя те же обозначения, что в формуле-
Сильвестра, окончательно получаем, что
1
к=г
где /-=0, 1, ..., /.
Пример 7. Пусть /)(я) — множество всех делителей
натурального числа п, упорядоченных по делимости, и
2<")=Е Пк)'
к:к\п
где к\п означает, что к делит п. В силу теоремы 41 и примера 4'
/(") = 2 И*. п)г(А) = 2 I* (т) *(А)>
265".

т. е. получаем хорошо известную формулу обращения Мебиуса из
теории чисел.
Рассмотрим несколько приложений полученной формулы.
Функция Эйлера. Функция Эйлера ф(я) определяется как
число положительных целых чисел, меньших п и взаимно простых
с ним. Если каноническое разложение п имеет вид: п = р^« р«« .. . р«г,
то
Ф<п)=<«)(1—4(1—4...(1-4.
Получим эту формулу методом включений-исключений. В
качестве элементов возьмем числа 0, 1, 2, ..., п—1. Скажем, что
элемент обладает свойством £,-, если он делится на число р,, 1=1, 2,...
..., г. Очевидно, что <р(п) равно числу элементов, не обладающих
ни одним из свойств £1, Е2, ..., Ег. Число элементов, обладающих
заданными свойствами^, £,,, . .. , Е1к, I К ]1<С ■ ■ ■ К \и </". равно
Применяя формулу Сильвестра, получим
Х=1 1^:1<...<1к& « !=1
Откуда следует мультипликативность функции ф(я), а именно
если тип взаимно просты, то ф(тгг) = ф(т)ф(я).
Обозначим через фй(") число положительных целых чисел,
меньших п и имеющих с п наибольший общий делитель, равный й.
Тогда очевидно, что фХ (гг) =ср (гг).
Пусть й\, й2, ..., йк — все делители числа п, а й\, й2\ •••, йк—
«х дополнительные делители, т. е. такие, что й('е(, = гг, £=1, 2, ..., к.
Тогда
<р(4) = ф(т:) = (М").
Очевидно,
к к
Отсюда получаем формулу Гаусса:
п = Е ф (ф.
Л:й\Л
Применяя формулу обращения Мебиуса, получаем
Ф(и) = 5] ^(й,п)й = ^ <*|Х (-^-).
Л:Л\п дг.й'п
266

Подсчет ожерелий. Предположим, что имеется неограниченный
запас бусинок к различных цветов. Сколько можно построить,
ожерелий, состоящих из п бусинок? Мы будем считать
одинаковыми те ожерелья, которые получаются друг из друга циклическим
сдвигом бусинок.
Перемещая все п бусинок «по кругу», мы обнаружим, что'
после некоторого числа сдвигов, скажем, через й сдвигов,
первоначальная «цветовая конфигурация» повторится, при этом й
будет делителем числа п. Периодом назовем наименьшее число-
сдвигов, приводящее к исходной конфигурации. Так, например,
бскбск->-кбскбс->-скбскб->-бскбск,
т. е. эта цепочка имеет период 3. Предположим, что у нас есть
цепочка длины п и периода й. При сдвигах получаем й различных
цепочек, включая и первоначальную. Соединяя концы каждой
такой цепочки, имеем одно и то же ожерелье. Более того, только-
такие цепочки дают это ожерелье. Отсюда, если обозначить череа
М(п) число ожерелий длины п и через пг(с1) — число цепочек
периода й, получаем, что
<Ы|п
Поскольку используются бусинки к различных цветов, то числом
всех цепочек длины п равно к'1 и, следовательно,
й-Л\п
Используя обращение Мебиуса, получаем
х:х\ а
Отсюда находим, что
^Ет1>(т)*'=т5>(т)л
Л:й\п х:х\й й:й\п
где ф[— ) — функция Эйлера.
Пример 8. Раскраска карт. Карта — это конечная
совокупность связных областей на плоскости, ограниченных гладкими
кривыми. Две страны, разделенные некоторой кривой (более чем
одной точкой), называются смежными. Если страны раскрашены
так, что нет двух смежных стран, раскрашенных в один и тот же
цвет, то раскраска считается правильной. Пусть С — карта и
Ма(К) — число ее правильных раскрасок К цветами. Подкарта
С карты О получается из С путем стирания некоторых границ
между странами. Любая карта может быть раскрашена Я101 сио-
267

зобами, где \0\ — число стран на карте 0; Каждая такая рас-
жраска является правильной ровно для одной подкарты. (Нужно
стереть границы между странами, раскрашенными в один цвет.)
Отношение «С является подкартой С» превращает множество
всех подкарт карты О в частично упорядоченное множество, и
а'-.о'са
Применяя обращение Мебиуса, приходим к формуле
Ма(Ц= ^ Ью\(0',0).
с-.а'ср
По очевидным соображениям, МС(Х) называют хроматическим
многочленом карты С. Если мы не имеем простого способа
вычисления значений ц, то нахождение многочлена Ме(Я) становится
трудной задачей. Хроматические многочлены были введены Бирк-
гофом при исследовании проблемы четырех красок.
Пусть Р — конечное частично упорядоченное множество с
нулем 0, единицей 1 и ранговой функцией г. Многочлен
Х(Р;.г)-= ^ ц(0, а)х'Ы-гЫ
называется характеристическим многочленом частично
упорядоченного множества Р. Очевидно, что он является обобщением
характеристического многочлена для решетки подкарт.
Непосредственно из теоремы 36 можно вывести следующий
результат:
Теорема 43. Пусть Р — конечное частично упорядоченное
множество с 0 и 1, обладающее ранговой функцией. Если Р — Р1ХР2,
то
х(Р; х)=х(Рч х)%(Р2; х).
Упражнения 7. Проверить, что характеристический многочлен х(^(5п);
х) булеаиа ЗР(5п) равен (х—1)".
8. Найти характеристические многочлены для частично упорядоченных
.множеств из примеров 7, 8 и 9 в § 8.1.
Используя в качестве основного средства обращение Мебиуса,
Крапо и Рота показали, что проблема четырех красок и изучение
хроматических и характеристических многочленов являются
частными случаями более общей задачи, а именно критической
проблемы для комбинаторных геометрий. Эта задача, состоящая в
нахождении минимальных множеств разделяющих гиперплоскостей
для множества точек в конечных проективных пространствах,
включает как частные случаи некоторые задачи теории
кодирования и результаты Сегре, связанные с характеризацией
независимых множеств в проективном пространстве. Кроме того,
установлены связи между алгебрами инцидентности и производящими
функциями, которые позволяют от решения некоторых перечисленных
" 268

задач переходить к нахождению определенных функций
инцидентности.
Пусть 5(Р) — стандартная алгебра инцидентности частично
упорядоченного множества Р. Отношение эквивалентности ~,
определенное на сегментах локально конечного частично
упорядоченного множества Р, называется совместным, если из условия
?(х, у)=!(и, у); §(х, у)=§(и, V) для всех пар сегментов таких,
что [х, у] ~ [и, V], /, #е=5(Р), следует, что (?*§)(х,у) =
= (1*§)(и, V). Например, для любого частично упорядоченного
множества Р отношение изоморфизма, разумеется, совместимо.
Именно это доказано в теореме 34.
Зафиксируем некоторое совместимое отношение
эквивалентности. Классы эквивалентности сегментов будем называть типами.
Рассмотрим множество функций, определенных на множестве
типов а, р, у, ..., причем умножение функций !*§ = !г определим
следующим образом:
*(">-2[м
/(Р)г(у)-
Суммирование проводится по всем парам типов. Символ I _ \
I Р. VI
равен числу различных элементов г из сегмента [х, у] типа а
таких, что [х, г] — сегмент типа р, а [г, у] — типа V. Этот символ
называется коэффициентом инцидентности. Пусть Лве5(.Р) и
, . . 11, если \х, у] типа б;
[О — в противном случае;
тогда
(Ар * Ну) (и, V) -=
а
м.
Так как ~ есть совместимое отношение, то левая часть
последнего равенства не зависит от конкретного выбора интервала [и, ь]
типа а.
Множество всех функций, определенных на типах, образует
редуцированную алгебру инцидентности Я(Р). Редуцированная
алгебра инцидентности Я(Р) изоморфна алгебре формальных
степенных рядов.
Действительно, элемент из Я(Р) единственным образом
определяется последовательностью [ап] действительных чисел, если
положить /(I, /)=а/_,-, 1</.
Произведение элементов задается равенством:
п
■ Полагая г=к—{, п=\—I, получим А(», /) =■» V агЪп-г = с„. Отсю-
269

да следует, что отображение множества степенных рядов в Я(Р)Г
определяемое следующим образом:
СО
есть изоморфизм.
Мы лишь кратко остановились на основных комбинаторных
направлениях алгебр инцидентности. Для дальнейшего их
изучения рекомендуем работы [1, 3, 12, 93].
8.4. МАТРОИДЫ
Начало теории матроидов было положено в 30-е годы нашего»
столетия. В 1930 г. Б. Л. ван дер Варден рассмотрел в своей
книге «Современная алгебра» наряду с линейной зависимостью
алгебраическую зависимость. В 1935 г. X. Уитни, желая обобщить
понятие дуального графа, впервые ввел абстрактное понятие
матроида. В 1936 г. М. Маклейн дал интерпретацию матроида &
терминах проективной геометрии (это послужило основанием тому,,
что матроиды стали называть комбинаторными геометриями), а
Г.'Биркгоф ввел понятие М-структуры (матроидной решетки) и
заметил, что проективные геометрии являются таковыми (каждый,
элемент есть объединение точек).
В 1942 г. Р. Радо обобщил теорему Ф. Холла о системе
различных представителей и показал, что экстремальные
комбинаторные задачи могут быть выражены в терминах абстрактной
структуры независимости. В 1965 г. Эдмондс и Фалкерсон открыли, что
для заданной системы подмножеств конечного множества
совокупность всех частичных трансверсалей есть совокупность
независимых подмножеств некоторого матроида, называемого теперь транс-
версальным матроидом. Такая связь привлекла большое
внимание к системам представителей, так как вскоре обнаружилось, что
многие тщательно изучаемые пространства независимости можно
представлять в виде трансверсальных пространств.
Эти и полученные позднее результаты прояснили тесную связь
теории матроидов с алгебраической теорией решеток и позволили
перенести в теорию матроидов понятия и образы проективной
геометрии, в частности понятие размерности линейного
пространства. Благодаря этому обнаружились довольно неожиданные
сходства между результатами различных разделов дискретной
математики (теории графов, теории трансверсалей, теории
кодирования и др.).
Матроиды как геометрические решетки нами уже рассмотрены
в § 8.2. Поэтому лишь кратко напомним некоторые определения
матроида и соответствующей ему решетки.
Предгеометрией (или матроидом) С называется конечное
множество 5 с оператором замыкания (~), удовлетворяющим свойству
замены: для любых элементов р, ^е5 и для всякого подмноже-
270

■ства А<=5 из р^А[){д}, р^А вытекает д<=АЦ{р}. Предгеомётрия
называется геометрией, если пустое множество и все
одноэлементные подмножества являются замкнутыми.
В определении предгеометрии О условие конечности
множества 5 часто заменяют условием конечного базиса: для всякого
Л^5 существует конечное подмножество А^А такое, что А[ = А.
Замкнутые подмножества геометрии называются
поверхностями. Множество всех поверхностей геометрии, упорядоченное по
включению (в теоретико-множественном смысле), образует
геометрическую решетку, которая с точностью до изоморфизма
определяет геометрию С (см. теорему 24).
Пусть Ь{С) —решетка геометрии 0=(5, ~). Рангом г
поверхности А называется длина максимальной цепи от нулевого
элемента до I в Ь(О) (см. теорему 18), а рангом множества А'—
ранг его замыкания в Ь{С), т. е. г(А)=г(А) для всех Л=5.
Следовательно, в силу теоремы 19 для ранговой функции г для всех
А, В<=5 выполнено основное свойство:
г{А\]В) + г{А[\В)^г{А) + г{В),
которое обобщает соответствующее свойство функции
размерности линейных подпространств проективного пространства (там
имеет место равенство). Кроме того, /-(0)=0 и г(А) *сг(А\]{р}) <
<.г{А) + \ для всех А<=5 и р<=5. Если г(А) = \А\, где \А\—
мощность подмножества Л^5, то А является независимым (см.
теорему 23). В противном случае /•(Л)<|Л| и А зависимо.
Множество Л^5 называется порождающим для геометрии О, если
А = 5. Независимые порождающие множества геометрии
называются базисами. Минимальные (по включению) зависимые
множества геометрии называются циклами.
Термины «зависимые и независимые множества», «базисы» и
«порождающие множества» хорошо известны из линейной
алгебры. Название «цикл» взято из теории графов, в рамках которой,
как мы увидим, циклы матроида в точности соответствуют
циклам графа.
Дадим теперь ряд других определений матроида
соответственно через ранг, независимые множества, базисы и циклы, а затем
докажем их равносильность.
Пусть 5 — конечное множество и г — целочисленная функция
на множестве !?{5). Пара (5, г) называется матроидом М(3, г),
а г(А)—рангом Л^5, если для всех А, В=5 выполняются
следующие условия:
#1) 0<г(Л)<|Л|;
#2) если А<=В, то г (А) <г(В) (монотонность);
Щ г(А[)В)+г(А(]В)-<г(А)+г(В) (полумодулярность).
Пусть 5 — конечное множество и г — целочисленная функция
на множестве ^>(3). Пара (5, г) называется матроидом М'(3, г),
а г (А) —рангом А^З, если для любых А<=5 и а, Ь^З
справедливы следующие условия:
#4) г(0) = О;
#5) г(А)<г(А[}{а))<г(А) + и
271

Я6) если г Щ~ г (А[){а})= г (А[){Ь)), то г (А[]{а, Ь})= г (А).
Пусть (5, г)—матроид М(3, г) и 5' = {ае5|/-({а}) =0}. Тогда
Г(А) =г(А\5') для любого Л^5, а значит, (5\5', г) является
матроидом, имеющим по существу такое же строение как (5, г).
Для а, Ь^5 пусть а=Ъ в том и только том случае, когда
г ({а, Ь}) — 1. Тогда = есть отношение эквивалеитиости, и если.
[а\\, ..., [ап] смежные классы, то /"([а^... \Лап]) — г({а\, ... , а„}) не
зависит от выбора представителей. Следовательно, мы можем
отождествить соответствующие элементы без потери общности.
Предполагая, что мы произвели это отождествление, для любого
А*=5 положим
А = {ае=3\г(А[}{а})=г(А)}.
Получаем геометрию, причем ее ранг вполне определяется
заданием его на замкнутых множествах. Значит, строение матроида»
можно определить, исходя из решетки поверхностей геометрии,
ассоциированной с этим матроидом.
Пусть 5 — конечное множество и Р — непустое семейство
подмножеств множества 5. Тогда пара (5, Р) называется матроидом
М(5, р), а элементы семейства Р — независимыми множествами:
М(3, Р), если выполняются следующие условия:
Р\) 0<=Р;
Р2) если А^В, ВеаР, то А<=Р;
РЗ) если А\ и А2—максимальные независимые подмножества
множества А, то |Л1| = |Л2|.
Отметим, что аксиома Р\) в действительности следует из Р2) „
Пусть 5 — конечное множество и С — семейство его непустых
подмножеств (циклов). Тогда пара (5, С) называется матроидои
М(5, С), если выполнены следующие условия:
С1) ни один из циклов не является собственным
подмножеством другого цикла;
С2) если С\ и С2 — различные циклы и а^.Сх{\С2, то найдется
цикл Сз^С такой, что Сз= (С^Сг)4^^.
Пусть 5 — конечное множество и В — семейство его непустых
подмножеств (базисов). Тогда пара (5, В) называется матроидом
М{5, В), если выполнены следующие условия:
В\) для всех А, Вг^5, если А<=Ви АФВХ и В^В, то А^В;
В2) для любых базисов Ви В2 и любого а^Вх найдется такой
Ь^В2, что (В1\{а})1|{*}{=Я.
Два матроида, (5Ь ~) и (52, _), называются изоморфными,
если существует такое взаимно-однозначное отображение ср:
31-^2, что а^А тогда и только тогда, когда ф(а)еф(Л), где
Л=5Ь
Теорема 44. Пусть (5, ~) —матроид на конечном множестве
5, г — функция ранга, а Р, С и В — соответственно семейства
независимых множеств, циклов и базисов матроида (5, ~). Тогда в
(5, ~) выполняются:
а) условия #1)—#6) матроидов М(5, г) иМ'(Х,г));
б) условия Р1)—РЗ) матроида М(5, Р);
в) условия С\) и С2) матроида М(5, С);
272

г) условия В1) и В2) матроида М{3, В);
■или, что эквивалентно, каждый матроид (5, ~) является матрои-
дом М(3, г), М'(5, г), М(5, Р), М(3, С) и М(3, В) одновременно.
Доказательство. Справедливость условий #3), #4) и #5)
в (5, ~) нами уже проверена. Получим остальные условия из этих
трех путем цепочки более простых утверждений.
1. Условия Я4) и /?5) влекут /?1) и Я2). Докажем сначала
следующее утверждение.
Лемма 45. Для всех А, Ве5, если Л=В, то
0<г(В)—г(А) <\В\А\.
Доказательство леммы. Если А = В, то утверждение
леммы очевидно. Пусть АфВ и В\Л = {а1, .... а*}. Тогда в силу
•свойства 45) имеем:
0<г(Ли{а,}) —г (А) <1;
0<.г(А[}{аи а2} — г(А[}{а1}) <1;
0<.г(А\Лаи а2, а3}) —г(А[}{аи а2})<1;
0<г(В) -г(В\{а*})<1.
Сложим все эти неравенства и получим требуемое неравенство:
0<г(В)—г (А) <: |В\Л|. Лемма доказана.
Непосредственно из леммы следует справедливость условия
Я2) и условия #1), но в последнем случае необходимо в
неравенство подставить А = 0 и воспользоваться условием #4).
2. Условия #2) и #3) влекут условия 46). Пусть г(А) =
■=г(А[]{а}) =г(А[}{Ь}), где Л^5; а, &е5. Требуется доказать, что
г(А\]{а, Ь})=г(А). Если а=Ь, то утверждение очевидно. Если
афЬ, то в силу условия полумодулярности #3) можно записать
2г(А) =г(А\Ла}) + г(АЦ{Ь}) >г{А\]{а, Ь}) +г(А),
откуда имеем: г(А{\{а, 6})</-(Л). Но А^АЩа, Ь}, и в силу #2):
г(А).<.г(А[]{а, Ъ}). Значит, г(А[}{а, Ь})=г(А). Импликация
доказана и тем самым проверка условий пункта а) завершена.
Проверим справедливость в (5, ~) условий Р\)—^3).
Очевидно, условие #4) влечет Р\).
3. Условие #5) влечет условие Р2). Докажем от противного.
Пусть А^В и В<=Р, но Л —зависимо. Тогда г(А)<\А\. В силу
леммы 45 имеем
г(В)<г(А) + \В\А\<\А\ + \В^А\ = \В
273

Следовательно, В— зависимо и, значит, В^р. Получили
противоречие. Поэтому А^Р, что и требовалось доказать.
4. Условие #6) влечет условие ^3). Пусть А, В<=5.
Непосредственно из #6) имеем, что если г {А[](а}) = г (А) для всех аеВ, то>
г(А[]В) =г(А). Воспользуемся этим фактом для доказательства
нашей импликации. Пусть А\ и А2— максимальные независимые'
подмножества множества А. Очевидно, Ах^А2, т. е. Л1\Л2=т^0.
Более того, для всех а^(А\\А2) справедливо равенств»
г(А2[}{а})=г(А2). Следовательно,
г(А,[)А2)=г(А2[)(А1\А2))=г(А2).
Аналогично, г{Ах{\А2)=г{Ах). Отсюда, г{Ах)=г{А2), т. е. |Л1|=-
= |Л2| и справедливость условия РЗ) и вместе с ним пункта б)'
установлена.
5. Условия #1)—#3) влекут условия С\) н С2).
Непосредственно из определения цикла и условия монотонности #2) получаем,,
что подмножество А<=5 является циклом тогда и только тогда,,
когда для всех элементов оеЛ имеет место равенство
г(А\{а)) = \А\-1.
Отсюда вытекает справедливость условия С1), а именно, что ни
один цикл не является собственным подмножеством другого-
цикла.
Далее, пусть теперь С\, С2—произвольные циклы матроида
такие, что С\ФС2 и а^(С\[\С2). Тогда С\{\С2фСх и, следовательно,.
(С\[\С2)^.Р. В силу условий монотонности #2) и
полумодулярности #3) получаем
г{{С^С2)\{а}) ^г{СА}С.) <.г{Сх) +г{С2)-г{Сх[\С2) =
= (|С,|-1)+(|С2|-1)-|С,ПС2| =
= \Сх\]С2\-2^\{С^С2)\{а}\.
Следовательно, {{С\\]С2)\{а}) ^Р. Поэтому найдется такой цикл"
Сз, что Сз^((С1[}С2) \{а]. Справедливость условия С2)
установлена.
6. Условия Р2) и РЗ) влекут условия В\) и В2). Пусть В\ к
В2 — базисы матроида. Ясно, что В\ и В2^Р. Пусть В\^В2, но
ВХФВ2. Тогда в силу условия РЗ) в В2 найдется элемент а^Ву
такой, что Вх{]{а)^Р. Это противоречит тому, что В\ — базис
матроида. Значит, В2^В, и справедливость условия В\) установлена.
Пусть теперь аеВь Очевидно, (В1\{а})е/\ Известно, что-
\В{\ = \В2\. Отсюда \В2\= |В,\{а}| + 1. В силу условия ^3) в
В2 найдется элемент &^"(В1\{а}) такой, что ((В1\{а}) []{&}) е/\
Но так как | (В1\{аШЬ}| = |В1| = |В2|, то {{В^Ш{Ъ})^В и,.
значит, условие В2) выполняется. Теорема доказана.
Доказывая теорему 44, мы на самом деле установили и
справедливость следующих утверждений.
274

Следствие 46. Каждый матроид М(3, г) является матроидом
М(3, С). Каждый матроид ЛГ(5, г) является матроидом М(3, Р)
и М(3, В) одновременно. Каждый матроид М(3, Р) является
матроидом М(3, В).
Продолжим доказательство равносильности определений мат-
роида.
Предложение 47. Каждый матроид М(3, г) является
матроидом М'(3, г).
Доказательство. Нами уже доказано, что условия #2) и
ЯЗ) влекут #6). Условие #4) очевидным образом следует из #1).
Проверим, что условия #2) и #3) влекут #5) и тем самым
предложение будет доказано. В самом деле, если оеЛ, то г(А[){а}) =
= г(А). Если же ае(5\Л), то в силу условий #2) и #3)
г (А) + 1 >г(А) +г({а}) >г(АЦ{а}) +г(0) = г(А[Ца}) >г(А).
Следовательно, г{А) -<г(А\}{а}) <г(Л) + 1 для всех А<=5 и ое5,
что и требовалось доказать.
Теорема 48. Каждый матроид М(3, Р) является и матроидом
(5, -) с семейством Р независимых множеств.
Доказательство. Пусть дано семейство Р независимых
множеств, удовлетворяющих аксиомам Р\)—РЗ). Назовем общую
мощность максимальных независимых подмножеств множества А
рангом А и обозначим его через г (А). Определим отображение
А-*-А, положив аеЛ в том и только в том случае, когда аеЛ или
найдется подмножество В^А такое, что В^Р и (В[){а}) ^р.
Докажем, что так определенное отображение А-*-А является
оператором замыкания со свойством заменьь
Свойства «А^А» и «если А*=В, то А^В», очевидно,
выполняются. Для доказательства свойства идемпотентности А=А
покажем сначала, что г(А)=г(А) для всех Л^5. Предположим
противное. Пусть существуют такие множества Аи А2^Р, что А^А,
А2^А и \Ах\=г(А) <г(А) = \А2\. Тогда в силу условия РЗ) най-
дется_элемент оеЛ2, удовлетворяющий условию А\[]{а}е.Р, причем
<ае(Л\Л) ввиду максимальности множества А\. Выберем
максимальное подмножество А'^А такое, что А'^Р и (А'[]{а})<^Р.
Тогда г(Л) = |Л'|<|Л1Ц{а}|, откуда в силу РЗ) (А'[}{а})е=Р, что
невозможно. Значит, г(А)=г(А) для всех А^З.
Далее, пусть теперь АФА, или, что эквивалентно, Ь^(А\А).
Тогда (А1[}{Ь})^Р для всех А^Р, А{<=А, и мы получаем
г (Л) 2* тах \А1[}{Ь}\ = г(А)+1=г(А)+1,
что противоречит только что доказанному факту. Таким образом,
А\А = 0 и идемпотентность установлена.
Остается показать, что отображение А-*-А удовлетворяет
свойству замены. Пусть а, &е5, А<=3 и а^А, а^А[]{Ь}. Из
определения замыкания следует существование такого_множества А^Р,
А1^(А\]{Ь}), что (А1[}{а))<$Р. Так как а^А, то Ъ^АХ и Л2 =
= ((Л,\{ВД{а})е.Р. Отсюда
А2и{Ь}^((А1\{Ь})[}{а})[]{Ь} = (Аиа})^Р.
275

Следовательно, по определению отображения Л->-Л имеем:-
Ь^А[}{а}. Таким образом, аксиома замены доказана.
Наконец, очевидно, что Ле/7 тогда и только тогда, когда
а^А\{а} для всех ае.А, т. е. матроид (5, ~) имеет такую
совокупность независимых множеств, которая в точности совпадает с
семейством Р матроида М(3, Р). Теорема доказана.
Пусть М(5, С) —матроид. Подмножество Л=5 называется
независимым, если оно не содержит циклов. Обозначим через Р
семейство независимых множеств матроида М(5, С). Ясно, что
С\^С тогда и только тогда, когда С\^Р и если из А^Си АфС\,
следует, что Ле/\
Предложение 49. Пусть Ле5 и ое5. Тогда, если Ле/7 я
(А[}{а) )ф^Р, то найдется единственный цикл С\ матроида такой, что-
Сх^(А\]{а}). Причем, очевидно, а^С\.
Доказательство. Пусть существуют два цикла С\ и С2.
такие, что С\ФС2, а^Сх<=(А\}{а}) и а^С2<=(А\}{а} ). Тогда в силу
условия С2) найдется цикл С3, где С3^ ((С!иС2)\{а})еЛе/г, что-
невозможно. Следовательно, двух таких циклов не существует и
предложение доказано.
Теорема 50. Матроид М(3, С) является матроидом М(5, Р).
Доказательство. Очевидно, условия Р\) и Р2) выполнены.
Проверим условие РЗ). Пусть А\ и Л2— различные максимальные
независимые подмножества Л. Тогда Аг\А2Ф0 и А2\Аф0„
Пусть ае(Л2\Л1). Тогда (А{^{а))^Р и, следовательно, сущест"-
вуетцикл С\ такой, что а^С^ (А1\]{а}). Более того, С1(](А1\А2))ф
Ф0, иначе С,!=Л2. Пусть Ь^(С1[](А1\А2)) »А3=(А1\{Ь})и{а}.
Заметим, что |Л3| = |Л1|.
Докажем теперь, что Аг^Р. В самом деле, очевидно, что-
(Л1\{6} )е/\ Предположим, что АгфР. Тогда найдется цикл С2
такой, что а<=С2'=Аз1=(А11){а}). Причем С2фСи так как Ъ<фС2г
Получили противоречие с условием. Значит, А3^Р.
Множество Л3 является максимальным независимым
подмножеством множества Л. Докажем это. Предположим, что Л' —
максимальное независимое подмножество множества Л такое, что
\ Аг<=А' и |Л3 <|Л'|. Элемент Ь^А', так как в противном случае
А\<=А' и \А\ <[Л'[. Тогда (А'\]{Ь})ф.Р. Следовательно, найдется
цикл С такой, что Ь<=С<= (А'\}{Ъ}) и, более того, С'[\(А'\Ах)Ф0,
так как иначе С'<=А{. Пусть се (С"П(Л'\Л,)). Тогда ((Л'\(с})и
[} {Ь} )е/\ Это устанавливается от противного в точности так же,
как мы доказали, что Л3е/\ Но Л1^((Л'\{с}и{Ь}) и |Л1|<
< | (А'\{с})[){Ь}\ = | Л'|; получили противоречие. Следовательно,
Л3 — максимальное независимое подмножество множества Л.
Таким образом, Л3 и Л2 — максимальные независимые
подмножества множества А. Если А3 = А2, то |Л1| = |Л2|. Если АгфА2г
то заметим, что | Л3ДЛ2| < | Л1ДЛ2|.
Повторяя аналогично Л3 процесс построения независимых
множеств Л„(|Л„| = |Л1|, |Л„ДЛ2|< |Л„_1ДЛ2|; п = 4, 5, ...), мы за
конечное число шагов придем к максимальному независимому под-
276

множеству Ап множества А такому, что Ап = А2, и, следовательно,.
докажем, что |Л1| = |Л2|. Теорема доказана.
Пусть М(5, В)—матроид. Подмножество А=5 называется
независимым, если найдется такой базис Ви что А<=:В\. Обозначим
семейство независимых множеств матроида М(5, В) через Р-
Очевидно, базисы матроида М(5, В) есть максимальные
независимые множества матроида М(5, В).
Предложение 51. Для любых базисов Вх и В2 матроида
М(8, В) имеет место равенство |В1| = \В2\.
Доказательство. Предположим В\ФВ2. Тогда В\\В2Ф0
и В2\Вхф0 согласно аксиоме В\). Пусть а^(В\\В2). Тогда по-
аксиоме В2) найдется элемент Ь^(В2\В\) такой, что Вг =
= ((#1 \{а} )11{Ь})еВ. Заметим, что | Я3| = |В,|. Если В3<=#2, то-
ВЪ = В2 по В\). Если В3$ЁВ2, то заметим, что \ВгАВ2\ < \ВХАВ2\..
Повторяя процесс построения базисов, как мы делали выше, за
конечное число шагов придем к базису Вп такому, что Вп^В2г
т. е. Вп = В2, и, следовательно, получим |51| = \В2\.
Теорема 52. Каждый матроид М(3, В) является матроидом
Л (5, Р).
Доказательство. Условия Р\) и Р2), очевидно,
выполняются. Докажем справедливость условия РЗ). Пусть А\ и А2 —
различные максимальные независимые подмножества множества
А. Тогда найдется базис В, такой, что Л( = В<ПА где £=1, 2.
Предположим, что |Л1|<|Л2|. Заметим, что (В1\В2)\АФ0. В самом
деле, предположим, что это не так и В1^А[]В2. Тогда |Л2\Л1| =
= I (В2\^1)ГИ <: |В2\В11 = В1\В2| = (в силу предложения 51) =
= \(В1\В2)[)А = |А\А|, что противоречит предположению-
|Л1|<|Л2|. Значит, (В1\В2)\Аф0. Теперь используем условие
В2), заменяя поочередно каждый элемент из (В1\В2)\Л
элементами из в2\#1 и, таким образом, определяя базис В', где-
А^В'ПА и ВЩА2\А1)Ф0. Если |Л,|<|Л2|, то |(В,\В2)ПЛ| =
= |Л1\Л2|<|Л2\Л1| = |(В2\В1)П^|, откуда получаем:
|(В1\В2)\Л|>| (В2\Д)\Л|. Следовательно, АхфВ'[\А. Но это
противоречит факту, что А\ — максимальное независимое
подмножество множества А. Следовательно, |Л1| = |Л2| и теорема
доказана.
Теорема 52 завершила доказательство равносильности
определений матроида.
Рассмотрим теперь различные примеры матроидов. При этом
часто будем опускать проверку выполнимости аксиом матроида,.
оставляя это читателю.
Примеры матроидов. 1. Свободные матроиды. Матроид
без Циклов на «-множестве 5 называется свободным и
обозначается Р„. Очевидно, свободный матроид является матроидом, в
котором каждое множество замкнуто. Легко видеть, что решетка
поверхностей свободного матроида Рп изоморфна решетке всех
подмножеств «-множества. На рис. 8.21 изображены свободные
матроиды Р\, Р2, Р3 и Р4.
2. Однородные матроиды. Матроид на «-множестве 5, базисами
27Г

Рис. 8.21
которого являются все ^-подмножества, а циклами — все (к+1)-
подмножества, называется однородным матроидом и обозначается
3. «-разбиения множества. Назовем п-разбиением такое покрытие
множества, где каждое п-элементное подмножество содержится в
одном и только в одном подмножестве, входящем в покрытие.
Каждому «-разбиению соответствует матроид, замкнутыми
множествами в котором будут:
а) все подмножества, состоящие менее, чем из п элементов;
б) все члены покрытия;
в) само множество.
Для произвольного подмножества А^З замыкание А здесь
определено следующим образом;
А, если А содержит менее п элементов;
^ В, если А содержит не менее п элементов и А
" содержится в члене покрытия В;
5 — в противном случае.
4. Геометрия Уилла порядка п. Пусть множество точек 5 вместе
с множествами подмножеств К и Р — кривых и поверхностей
соответственно удовлетворяет условиям:
а) любые п+1 различные точки лежат на единственной
кривой, и каждая содержит не менее п+1 различных точек;
б) любые п + 2 различные точки, не лежащие на одной кривой,
лежат на единственной поверхности, и каждая поверхность
содержит по крайней мере п + 2 различные точки, не лежащие на
одной кривой;
в) вместе с любыми п+1 различными точками поверхности
принадлежит и вся кривая, задаваемая ими;
г) если две поверхности лежат в замыкании (п + 3)
-элементного подмножества 5, то их пересечение содержит по крайней мере
п+1 различную точку.
Данная геометрия называется геометрией Уилла порядка п.
Подмножество А<=5 замкнуто в этой геометрии тогда и только
тогда, когда оно содержит все кривые и все поверхности,
проходящие через ее точки. Отношение замыкания на 5 в этой
геометрии задается как А->-А, где А—пересечение всех замкнутых
подмножеств, содержащих А.
Если п=\, то геометрия Уилла представляет собой
классическую проективную геометрию.
5. Линейные матроиды. Пусть 5 — конечное подмножество век-
278

торного пространства V. Пусть множество векторов А =■
= {а-1, ..., Оь}—^ принадлежит Р тогда и только тогда, когда
векторы а\, ..., аи линейно независимы в V. Тогда легко проверяется,,
что Р— семейство независимых множеств некоторого матроида М.
Функция ранга г этого матроида совпадает с размерностью
подпространства, натянутого на эти вектора. Всякий матроид,
изоморфный вышеописанному матроиду Му называется линейным.
6. Алгебраические матроиды. Пусть Р — поле, а К — его
расширение. Скажем, что множество {а\у а2, ..., а%} элементов из К
является алгебраически зависимым, если элементы аь а2, ..., ак
удовлетворяют полиномиальному уравнению вида /(аь а2, ..., а*)=0,.
где коэффициенты / являются элементами поля Р. В противном
случае аь а2, ..., ак алгебраически независимы над полем Р.
Предложение 53. Пусть 5 — конечное подмножество
расширения поля Р, подмножество А*=5 принадлежит Р тогда и только*
тогда, когда элементы множества А алгебраически независимы
над полем Р. Тогда Р есть семейство независимых множеств
некоторого матроида на множестве 5.
Доказательство этого результата не представляет больших
трудностей, и поэтому мы его опускаем.
7. Циклические матроиды графов. Пусть С=(Х, 5)
—неориентированный граф без петель с множеством вершин X и
множеством ребер 5. Определим теперь на множестве 5 матроид.
М(О), называемый реберным (полигонным или циклическим)
матроидоы графа С, следующим образом. Если а, Ь^Х и А<=5Г.
то ребро (а, Ь)^А в том и только в том случае, когда вершины
а и Ь являются Л-связанными, т. е. когда существует
последовательность ребер (а0, а.\), (аь а2), ..., (а„_ь а„) из множества А.
такая, что ай = а и ап = Ь.
Теорема 54. Пара (5, ~), где 5 — множество ребер графа;
0= (X, 5), есть матроид.
Доказательство. Все свойства матроида очевидны кроме,,
быть может, свойства замены. Пусть вершины а и Ь являются
Л-связанными. Тогда существует связывающая
последовательность ребер (а0, а.\), ..., (а„_ь а„), для которой число п
минимально. Мы утверждаем, что ни одно ребро не встречается дважды в
этой последовательности. Действительно, пусть 0<1</<:«—1 ш
(О;, 0,+0 = (0/, а/+1). Теперь, если щ = а,- иа,-+1 = а,;то вычеркивая
ребра (а,+1, а,-+2), ..., (а/, а^+х) из последовательности, получаем
более короткую связывающую последовательность. Если а,- = а/+!;
и а,-+1 = а/, то можно вычеркнуть все ребра (щ, щ+\), ..., (а/, а/+1).
Докажем теперь свойство замены для оператора замыкания. Пусть.
р<=А\Лд},гд,ер=(а, Ь) и ц= (с, й). Пусть 50, ..., 8п-\^{А{\^}) —
кратчайшая последовательность ребер, связывающая а и Ь. Так
как р^А, то одно из ребер 50, ..., зп-\ должно совпадать с ц.
Согласно сделанному выше замечанию только одно из ребер 5о,-
5Ь ..., 5„-ь скажем 5,-, равно ребру ц. Но тогда последовательность-
5,-+1, ..., 5п-1, я, «о, ...,5,-1 будет связывать вершины с и й. Отсюда
д^А[}(р}. Теорема доказана.
279»

Матроид М на множестве 5 называется графическим, если он
изоморфен циклическому матроиду какого-либо графа.
Предложение 55. Пусть М(С)—циклический матроид графа
Х)=(Х, 5). Тогда справедливы следующие утверждения:
а) подмножество ребер А<=5 является независимым
множеством матроида М(О) тогда и только тогда, когда остовный подграф
0=(Х, А) —лес;
б) подмножество В^5 есть базис матроида М(О) тогда и
только тогда, когда остовный подграф С=(Х, А) является лесом
с тем же числом компонент связности, что и граф С=(Х, 5);
в) подмножество С^5 есть цикл матроида М(О) тогда и
только тогда, когда С — множество ребер простого цикла в графе
€=(Х,5);
г) г(А) = \Х\—к(А)у где к(А)—число компонент связности
в остовном подграфе С=(Х, А).
Доказательство. Множество ребер А любого
леса'—независимое множество в М(О), так как удаление любого ребра хеЛ
делит компоненту связности, содержащую 5, на две части, т. е.
«еЛ\{5}. С другой стороны, если подграф 0=(Х, А) содержит
цикл {50, 5Ь ..., 5*.}, то по определению замыкания 50е{5ь ..., зк};
отсюда следует, что А—зависимое множество. Это доказывает
утверждения а), б) ив). Более того, этот факт говорит о том, что
ранг множества А равен числу ребер в остовном лесе подграфа
0= (X, А) с числом компонент связности, равным числу
компонент связности подграфа 0=(Х, А). У каждого дерева число
ребер на единицу меньше числа вершин. Следовательно, если
Хи ... у Хк(А) — множества вершин компонент связности подграфа
С=(Х,А),то
к(А)
/■и) = Е(|х,|-1) = |х|-ад.
1 = 1
Доказательство предложения завершено.
8. Абелевы группы без кручения. Напомним, что если все
элементы группы А, кроме нуля, имеют бесконечный порядок, то А
называется группой без кручения. Пусть А — абелева группа без
кручения. Скажем, что элемент а^А зависим на множестве В^АУ
-если а принадлежит подгруппе группы А, порожденной
множеством В. Подмножество С^А независимо, если никакой элемент а
из С не является зависимым на С\{а}. Тогда, если В — конечное
подмножество абелевой группы А без кручения, то независимые
подмножества множества В образуют матроид М. Замкнутыми
множествами матроида М являются все подгруппы Н группы А,
для которых фактор-группа А/Н—группа без кручения.
9. Трансвереальные матроиды. Пусть даны множества А\, А2, ...
..., Ат. Напомним, что подмножество А^5 = А1\}Ач[]... [)Ат
называется частичной трансверсалью, если существует
взаимно-однозначное отображение ср: Л->-{1, 2,..., т} такое, что оеЛ,|0) для
всех оеЛ. Пусть Р — семейство всех частичных трансверсалеи
280

множества 5. Тогда пара (5, Р) образует матроид на множестве
5. Отсюда непосредственно следует, например, что все
максимальные частичные трансверсали имеют одинаковую мощность.
После введения математических объектов обычно
интересуются конструктивными методами, т. е. тем, как можно построить
новые объекты из заданных. Перейдем к изложению основных таких
конструкций.
Пусть (5, -) — матроид на конечном множестве 5 и А, В*=5.
Определим для всех С^В\Л отображение
11А,ву.С^(СйА\]В)\А.
Предложение 56. Отображение 1[а,в] является оператором
замыкания на множестве В\Л.
Доказательство. Очевидно, что С^1[А,в\{С) и что из
С<=0 следует 1[А,в](С) <=[А,В](0) для всех С, й^(В\А). Осталось
доказать идемпотентность: 1[а,в](1[а,в](С) ) = 1[а,в](С) для всех
С^(В\Л). В самом деле,
/[л,в] /[л,в] (С) = [[(СйА П В)\Л] IIЛ П Я]М =
- [(сцлпв)илп в]\л = [(сцлил)п(в1Щп в\а =
= (СйАП(В[}А)ПВ)\А.
Из соотношения С{} А[\(В\) А)С1С\}А следует
С\]А(\{В\)А) ^СЦЛ = СЩ.
Отсюда С\]А П (В [} А) П В С~ С\]А Л В. Следовательно,
Щ%~ П (В V А) П В)\ А С (СЦЛ П В)\Л = /[Л,В] (С),
т. е. получили Адв] (/[л,в] (С)) <~/[л.в] (С)- Но 1[а,в] {На,в\ (С)) 2
Э/[л,в](С). Отсюда 1[А.в)(1[А.в](С)) = 1[а.в)(С), что и требовалось
доказать.
Предложение 57. Пусть М=(5, -)—матроид на конечном
множестве 5 и В^5. Тогда множество В вместе с отображением
1в: С~+С[\В, определенным для всех С^В, образует матроид
(В, 1В).
Доказательство. Если в операторе замыкания 1[А,в\{С) из
предложения 56 положим А = 0, то получим: 1в(С) =1[0,в](С) =
= С[\В. Значит, отображение С~+1в(С) —оператор замыкания.
Свойство замены, очевидно, также имеет место. В самом деле,
пусть ае=/д(С1){Ь}), а^1в{С). Тогда а^{С\Щ[\В), но а^ (С[\В).
Значит, а^С[}{Ъ), но а<^С. Отсюда по свойству замены для мат-
роида М И1меем: &еС[|{4 Следовательно, Ь^С[]{а}(]В, так как
а, Ь^В. Предложение доказано.
Ю К. А. Рыбников
281

Матроид (В, 1в) будем обозначать через М\В и называть под-
матроидом матроида М. Очевидно, что если Р— семейство всех
независимых множеств матроида М, то {Л|ЛеВ, ЛеЛ есть
семейство независимых множеств подматроида М\В. Кроме того,
решетка Ь{В) поверхностей подматроида М\В матроида М
получается из решетки /-(5) поверхностей матроида М образованием
внутри £(5) супремумов всех подмножеств множества В,
рассматриваемого как множество атомов в £(5). При этом
супремумы в Ь{В) и в £(5) совпадают, что не всегда имеет место для
инфинумов. В частности, если В — поверхность матроида М, то
решетка Ь(В) изоморфна интервалу [О, В] в £(5).
Предложение 58. Пусть М—(5, -)—матроид и А^5. Тогда
множество 5\Л, снабженное для всех С^5\Л отображением
1м/а:С^С\]А\А,
образует матроид (5\Л, 1м/а)-
Доказательство. Если в операторе замыкания 1[а,в\{С) из
предложения 56 положить В=5, то получим 1м/а(С) = 1[а,в](С) =
= С[]А\А. Значит, что С-*-1м/а(С) является оператором
замыкания. Осталость проверить свойство замены, т. е. что для любых
а, Ь^(3\А) и для всякого С^(5\Л) из а<=1м/А(С\]{Ь})у
аёр1М/А{С) вытекает: Ь^1м/А(С[){а}). В самом деле, пусть
аеЕ(СЦ{&}ЦЛ\Л), д€Ё(С\]А\А). Очевидно, что а, Ь&А. Отсюда
а^С\]А\]{Ь}, а^С[]А. В силу свойства замены для матроида М
имеем: Ь^С[}А[}{а]. Н0 Ь^А. Следовательно, Ь^(С[}А[}{а}\А) =
= 1м/А(С[}{а}), что и требовалось доказать.
Матроид (5\Л, 1м/а) будем обозначать через М/А и называть
сжатием матроида М посредством множества А Заметим, что если
^5\Л) —решетка поверхностей матроида М/А, то она
изоморфна интервалу [Л, 1] в решетке поверхностей матроида М= (5, ~).
Сжатие матроида М= (5, ~) посредством множества 5\Л
обозначим через М.А. Ясно, что если Р — семейство независимых
множеств матроида М, то семейство подмножеств В^А, для
которых в М существуют максимальные независимые подмножества
С из 5\Л, где {В(\С)^Р, является в точности семейством
независимых множеств сжатия М.А.
В качестве легких упражнений предлагаем читателю доказать
следующие два предложения.
Предложение 59. Пусть М — матроид на конечном множестве
5, М\В — его подматроид, а г и гв — функции ранга
соответственно для М и М\В. Тогда для всех А^В справедливы следующие
утверждения:
а) А независимо в М\В тогда и только тогда, когда А
независимо в М;
б) А — базис матроида М\В в том и только в том случае,
когда А — максимальное независимое подмножество множества
В в М;
в) А — Цикл в М\В тогда и только тогда, когда А — цикл в М\.
282

г) гв(А)=г(А).
Предложение 60. Пусть М— матроид на конечном множестве
5, М/А — его сжатие посредством множества Л, а г и Г5\а —
функции ранга соответственно для М и М/А. Тогда для всех
В=5\Л справедливы следующие утверждения:
а) В независимо в М/А тогда и только тогда, когда В\]С
независимо в М для всех независимых подмножеств С^А\
б) В — базис матроида М/А в том и только в том случае, когда
В[]С — базис матроида Л1=(5, ~) для всех максимальных
независимых подмножеств С множества А;
в) В — цикл в М/А тогда и только тогда, когда В = С\Аф0,
где С — цикл в М, тл В является минимальным множеством с
таким свойством;
г) г5^а(В)=,г(ВцА)—г(А).
Пусть (5, -) —матроид и А,В<=8. Пара (5, 1[а,в))
называется минором матроида (5, ~). Легко видеть, что каждый минор
матроида в свою очередь является матроидом, поскольку может
быть получен как подматроид сжатия матроида или, что
эквивалентно, как сжатие подматроида матроида.
Пусть М=(3, ~) — матроид. Часто для удобства подматроид
М|(5\{а}), где ое5, обозначают через М—а и говорят, что он
получен из матроида М исключением элемента а. Аналогично,
подматроид М\ (5\А) матроида М=(3, ~) обозначают через
М—А. В этом случае естественно минором матроида называть
произвольную последовательность сжатий и исключений матроида.
Предложение 61. Пусть (5, ~) —матроид на конечном
множестве 5 и Л, В^5. Если А — максимальное независимое
подмножество множества В, то А =В.
Доказательство. Если А = В, то утверждение
предложения очевидно. Предположим, что Л=^=В, т. е. АаВ. Тогда в силу
свойств оператора замыкания А <=В. Пусть теперь ае(В\Л).
Тогда (А\]{а))ф.Р. Следовательно, существует элемент Ь^.{А{]{а})
такой, что Ъ^(А\]{а}) \{Ь). Если а = Ь, то аеЛ. Если же афЪ, то
&еЛ и Ь&А\{Ь), так как Ле/7. Поэтому Ь^Л\{6}, Ъф
ф{А\]{а)\\Ь}. Отсюда по свойству замены опять-таки оеЛ.
Таким образом, В^А и, следовательно, В<=А. Значит, А =В и
предложение доказано.
Непосредственно из предложения 61 следует, что каждый базис
матроида является одновременно и максимальным независимым
множеством, и минимальным порождающим множеством. Именно
это соотношение послужило источником для введения понятия
двойственного матроида. Идея двойственности является одним из
наиболее мощных инструментов в теории матроидов и имеет
важные приложения во многих областях комбинаторики, в частности
в теории графов.
Теорема 62. Пусть М=(5, ~) —матроид на конечном
множестве 5, в —семейство его базисов и В* = {Л^5|Л; = 5\В,-, где
Б;еВ}, т. е. В* — семейство дополнений базисов матроида М в 5.
Тогда пара (5, В*) удовлетворяет аксиомам В1) и В2) и
является, таким образом, матроидом М*=М(5, В*).
30* 283

Матроид М* называют двойственным к матроиду М, а
элементы семейства В* — кобазисами матроида М.
Доказательство. В матроиде М=(5, ~), для любого
А^З и для всякого В\^В имеет место следующая импликация:
если ВХ<=А и В\ФА, то А^В, или, что эквивалентно:
для любого Л^5 и всякого Л2еВ*, если АХ<=А2 и А\фАъ то
Ах^В*. Таким образом, пара (5, В*) удовлетворяет аксиоме В\).
Пусть теперь Аи А2<=В*, АХФА2 и а<=(А\\А2). Докажем, что
тогда существует элемент &еЛ2 такой, что ((Л1\{а}) []{Ь]) ей*.
Тем самым установим справедливость аксиомы В2). Поскольку
а<^ (5\А1)^В и а^(А1\А2), то в силу предложения 49
существует единственный цикл С\ матроида М такой, что ое^е
!=((5\Л,)Ы{а}). Очевидно, С1<=(5\Л2), так как (5\Л2)еВ.
Выберем &е(С1\(5\Л2)), тогда, очевидно, &е (Л2П(5\Л1)).
Проверим, что £)= ((5\Л[) \{&})'и{а} — базис матроида М. В
самом деле, пусть В — зависимо. Тогда существует цикл С2 такой,
что С2^1) и а^С2. В силу предложения 49 имеем С\ = С2. Но это
невозможно, так как йе^ и Ъ^С2. Значит, множество £) —
независимо. Кроме того, |Г>| = |5\Л1|, а (5\Л1)еВ. Следовательно,
0<=В. Отсюда (5\#)€Е#*. Но 5\#= (А^а^ЩЬ}. Что и
требовалось доказать.
Теорема 63. Пусть М — матроид на конечном множестве 5,
Л^5 и М*—двойственный к М матроид. Тогда справедливы
следующие утверждения:
а) А — независимое множество матроида М* в том и только
в том случае, когда 5\Л — порождающее множество матроида М;
б) г*(А) = \А\—г(5)+г(5\Л), где г* — функция ранга
матроида М*; в частности г(5) +г*(5) = |5|;
в) М** = М.
Доказательство, а) В силу теоремы 62 множество А
независимо в М* тогда и только тогда, когда А содержит базис
матроида М*, или, что эквивалентно, тогда и только тогда, когда
5\Л содержит базис матроида М, или же тогда и только тогда,
когда 5\Л порождает матроид М. Таким образом, если
Р*—семейство независимых множеств матроида М*, то
Р*= {А<^5\3\А — порождающее множество в М) = {А<=5\
найдется базис В\^В такой, что В1^5\Л} = {Л&5|г(5\Л) =
= г(5)}.
б) Для всех Л^5: г*(А) =тах {| А[\А'\ \А'е=Р*}. Выберем
А'^Р*, тогда в силу а) найдется такой базис В\ матроида М,
что В1^5\Л', т. е. Л'^5\В1. Таким образом, |ЛГИ'|<
<:|ЛП(5\В,)| = |Л|-|ЛПВ1|. Но г(5\Л )>/■( (5\Л )Г|Я, ) =
= |(5\Л)ПВ1| = |В1 —|ЛПВ1|. Следовательно, |ЛГИ'|-с|Л| —
— |В,|+г(5\Л) = \А |—г(5) +г(5\Л). Таким образом, г*(А)<.
<|Л|—г(5)+г(5\Л). С другой стороны, найдется базис В2
матроида М такой, что г(5\А) = | (5\Л)П52| = |б2\Л| и, очевидно,
(5X^2)^/^*. Следовательно, г* (А) > | ЛП(5\В2) | = | А | —
-\А(]В2\ = \А\-(\В2\-\В2\А\)^\А\-г(5)+г(5\А).
Значит, Г*(А) = \А\— г(5)+г(5\А).
•284

в) Очевидным образом следует из определения матроида М*.
Доказательство завершено.
Пусть С=(Х, 8) —неориентированный граф без петель с
множеством вершин X и множеством ребер 5, а М(О) —циклический
матроид графа С. Матроид М*(С) двойственный к М(О)
называется коциклическим матроидом графа С. Матроид называется
кографическим, если он изоморфен коциклическому матроиду
некоторого графа.
Для иллюстрации приложений двойственности приведем без
доказательства следующий известный результат.
Теорема 64 (Уитни). Граф планарен тогда и только тогда,
когда его циклический матроид кографичен, или, что
эквивалентно, когда его коциклический матроид графичен.
Принимая во внимание теорему 64, часто пленарным называют
матроид, который одновременно является как графическим, так и
кографическим.
Пусть М,= (5/, /,)—матроиды с операторами замыкания /г,
1=1, 2, ..., п; такие, что 5гП5; = 0 при 1ф]. Тогда пара (5, /), где
п п
5= у 5( и 1(А)= у (^0¾. для всех А^З, очевидно, образует
1=1 1 = 1
матроид, который называют произведением матроидов М; (£=1,
п
2, ..., п) и обозначают через Г~] М-ь.
1 = 1
Теорема 65. Для всех Л^5 справедливы следующие
утверждения:
п
а) А — независимое множество матроида {"] Мг тогда и толь-
1=1
ко тогда, когда (Л (15/) — независимое множество матроида Ми
для всех V,
п
б) А — базис матроида \\ Мь в том и только в том случае,
1 = 1
когда (ЛП5/) — базис матроида Мг для всех г,
п
в) А — цикл матроида [~[ Мх тогда и только тогда, когда
1 = 1
найдется индекс £ такой, что (А(]8с)=А и (ЛП5;)=0 для всех
П
г) г(Л) = V гг (Лр| 5,-), где г,- —функция ранга матроида Ми
1 = 1
Доказательство теоремы очевидно, поэтому предлагаем
читателю самостоятельно восстановить его.
п
Матроиды М{ в Л4 == |~I УИ; называются множителями матрои-
1=1
да М. Матроид, который не разлагается в произведение меньших
матроидов называется связным.
285

Предложение 66. Пусть {— целочисленная, монотонно возрас:
тающая и полумодулярная функция, определенная на множестве
^(5) всех подмножеств конечного множества 5, /(0) =0 и Р =
= {А^З\УВ^А: |Д|</(Д)}. Тогда пара (5, Р) есть матроид и
его функция ранга г для произвольного подмножества Л=5
вычисляется по формуле
г(А) = тт{ПЩ + \А\В\}.
вел
Доказательство. Рассмотрим семейство К = {А^З\[(А) <
<|Л|} и докажем, что его минимальные элементы являются
циклами некоторого матроида, т. е. удовлетворяют условиям С1) и
С2). Условие С1), очевидно, выполняется по построению.
Пусть С\ФС2 — минимальные множества семейства К и
а(=(С\[\С2). Тогда |С1|>2 и, следовательно, \С\\—1 = |С1\{а}| <:
<:/(С!\{а})</(С1)<|С1|,т. е. \{СХ) = 1С,|-1 и ЦВ) > \В\ для
всех ВаС\. Аналогично получаем, что /(С2) = |С2|— 1. В
частности, имеем | С1ПС21 <-${С\[\С2), и таким образом, в силу
монотонности и полумодулярности функции / получаем
Н{С^С2) \{а}) <1(Сх\}Сг) </(С) +/(С2)-/(С,ПС2) <:
<|С!|-1+|С2|-1-|С1ПС2|<|С,иС2|-2<|(С!иС2)\{а}|.
Множество {С\[]С2) \{о] принадлежит семейству К и,
следовательно, содержит его минимальное множество. Условие С2) проверено.
Семейство Р, таким образом, определяет матроид М. Остается
доказать, что функция
г(А) =тт {?(В)+\А\В\},
вЯА
определенная для всех Л^5, есть функция ранга матроида М.
Для этого достаточно проверить, что г удовлетворяет условиям
#1)—#3). Непосредственно из определения г следует, что
0</-(Л)<|Л| для всех Л^5 и что г(А)*сг(В) при А^В, т. е.
условия #1) и #2) выполнены. Далее, для всех подмножеств
А^А и В\^В справедливо равенство
| Л\Л | + | В\В, | = | (А[}В) М^В,) | + \А(\В) \ (Л1ПЯ1) |.
Следовательно, в силу полумодулярности функции / имеем
(/(Л,) + |Л\Л,|) + (/(б,) + 1545,1)3^(^01) +
+ | (АиВ)\(А1\]В1) | +/(Л,ПВ,) + | (А(\В) \(Л,ПВ1) |.
Таким образом,
г (А) + г(В)= тш {ПА,) + \А\А1\+ /(^) + \В\В1\}>
л,сл
В,СВ
> ппп {ПСг)+\ (А {) В) \С±\ +/(С2) + |(ЛПВ)\С,|} =
С.САЦВ
СгСАГ\В
= г(А{]В) + г(А[\В).
286

Тем самым справедливость #3) установлена, а вместе с этим
доказано предложение.
Теорема 67. Пусть Мс = (5, гг) — матроид на конечном
множестве 5, п—функция ранга, а Р'(М;) —семейство независимых
множеств матроида М; (1=1, 2,..., п). Тогда пара (5, Р), где
Р = {А^З\А = Ах[]А2\}...\}Ап; А-1^Р{М1)},
есть матроид, у которого функция ранга г определяется
соотношением
г(А)=<пт{Тг1(В) + \А\В\\.
п
Доказательство. Пусть /(^) = 2^^(^) для всех Л^5.
1 = 1
Тогда / — целочисленная, монотонно возрастающая и
полумодулярная функция, поскольку таковыми являются функции ранга п
матроидов М.1. Следовательно, в силу предложения 66 семейство
/?* = {Л=5|УЯ=Л: \В\^(В)}
определяет матроид М(5, г), где
п
г(А) = гтп{ПВ) + \А\В\} = т\п{Тг1(В)+\А\В\).
ВО А В£А I** >
я
Далее, пусть В^А, А<=Р и В=у Д., где Д^Лг для всех 1 =
1=1
= 1, 2 п. Тогда
|б| = | О Д1< 2 | Д I = ^ г(Д) < 2 ЩВ),
'=' 1=1 1=! 1=1
так как Де/^М;) для всех 1=1, 2, .... п. Следовательно, ЛеР.
Очевидно, верно и обратное утверждение, что если А^Р*, то
Ле/\ Значит, Р = Р* и теорема доказана.
Матроид (5, Р) из формулировки теоремы 67 называют объ-
п
единением матроидов Ми ..., Мп и обозначают у Мг
1 = 1
Одноточечным расширением матроида М= (5, ~) точкой р^З
называется такой матроид М={3\]{р), ~), где г{М')=г(М) и
М = М'—р.
Предложение 68. Каждый матроид имеет одноточечное
расширение.
Доказательство. Пусть М= (5, ~)—матроид. Построим
его одноточечное расширение М'=(5[){р}, /), взяв за оператор
замыкания отображение Л-»/(Л), где
287

/(Л)
А , если р ¢: А и А ф 5;
Л\{р} У {р}, если ревА и г (А\{р)) = г (5) — 1;
5II {р}, если Л = 5илиреЛи/' (Л\{р}) = г (5) — I.
Проверим свойство замены. Пусть ае/ (/111(6}); а, 6^/(Л).
Тогда возможны два случая: а=р<=1(А[]{Ь}) и афр, а<=1(А\]{Ь}).
В первом случае имеем либо Ь=р, либо /-(/1)=/-(5) — 1. Отсюда
Ъ^1(А\]{а}). Во втором случае, если р^А, то Ъ^1 (А\]{а})\ если
же реЛ, то ае=/(Л1|{&}) = (1\{р})Ши{р}, откуда аеЛ\{р}и{&},
и, следовательно, по свойству замены для матроида М имеем
Ь^(А\{р})[}{а}. Равенство г(М') =г(М) выполнено по
построению. Предложение доказано.
Говорят, что два множества А, В<=3 матроида М=(5, -)
образуют модулярную пару, если
г{А[\В) +г(А[)В) =г(А) +г(В).
Модулярным фильтром матроида М=(3, ~) называется
семейство Ф подмножеств множества 5 такое, что
а) если ЛбФ и ЛеВ, то ВеФ;
б) если Л, ВеФ и (А, В) —модулярная пара, то ЛПВеФ.
Предложение 69. Пусть М=(5[){р}, I) —матроид на
множестве 5у{р}, р^8 с оператором замыкания / и функцией ранга г.
Тогда множество Ф = {Л^5|ре/(Л)} есть модулярный фильтр
матроида М—р.
Доказательство. Очевидно, что Ф — фильтр. Условие
ЛеФ эквивалентно равенству г (А\]{р}) = г (А). Следовательно,
если А, Веф и (Л, В) — модулярная пара в М—р, то
г((А№)\}1р})<г(Аи[р})+г(Ви{р})-г(А[}В[}{р})=г(А)+г(В)-
—г(А[}В)=г(АГ\В). Таким образом, А[\В<=Ф. Предложение
доказано.
Предложение 70. Пусть Ф — модулярный фильтр матроида
М=(8, ~). Тогда существует единственное одноточечное
расширение М'=(3[]{р}, I) матроида М такое, что Ф = {Л^5|ре/(Л)}.
Доказательство. Пусть г—функция ранга матроида М.
Определим целочисленную функцию г* для всех подмножеств
А^8[){р} следующим образом:
г*(А) =г(А) , если Лд=5;
г*(А[}{р})=г(А) + 1, если Л;=5 и Л^гФ;
г*(А[}{р}=г(А) , если Л=5 и ЛеФ.
Проверим, что г* — функция ранга некоторого матроида. Для
этого покажем, что она удовлетворяет аксиомам #1)—#3), тем
самым установим и единственность расширения.
Ясно, что г* удовлетворяет аксиомам #1) и #2). Для
проверки #3) необходимо рассмотреть два случая: пару Лу{р}, В и пару
А\]{р}, В\]{р), где Л, 5^5, р&З. В первом случае для любых
Л, В<=5 имеем г*(А[}В\Лр})—г*(А[}В)<г*(А[}{р})~-г*(А).
Заметим, что левая часть неравенства всегда меньше или равна 1, при-
288

чем равна 1 лишь при А[}В^Ф. Таким образом, А^Ф, так как в
этом случае и г* (А[){р})—г* (А) должно быть равно 1. Отсюда
следует, что г* {А\]В\}{р})—г* {А\]{р}) <.г* {А\]В)—г* (А) =г{А\]В) —
—г(А)<г(В)—г(Ар\В)=г*(В)—г*(Ар\В), тем самым
полумодулярность функции в данном случае установлена. Во втором случае
покажем, что
г* ((ЛПВ) Ш) + г* (А[}В[}{р}) <г* (А[}{р)) + г* (ВШ) ■
Если А[}В^Ф, то А, В и А[\В также не лежат в Ф и,
следовательно, г*(Х\Лр})=г(Х) + 1 при Х = А, В, А[]В и А[\В. Таким образом,
наше неравенство имеет место, поскольку в этом случае
совпадает с условием полумодулярности для функции ранга г
матроида М. Если же А[}В^Ф, то это может быть лишь если ЛеФ и
ВеФ. Кроме того, (А, В) — модулярная пара в М. Легко
показать, что тогда (А, В) также модулярная пара и, следовательно,
А[\В={А[\В)<=Ф. Отсюда г* (Х[){р}) = г(X) при Х=А, В, А[)В и
А[\В. Таким образом, неравенство доказано, поскольку и в этом
случае оно в точности совпадает с условием полумодулярности для
г. Предложение доказано.
Непосредственно из предложения 70 следует следующий
результат Крапо:
Следствие 71. Пусть Ф — модулярный фильтр матроида М =
= (5, -), М'= (5[}[р), I) —расширение матроида М, построенное с
помощью Ф. Тогда поверхностями в Ш являются все
подмножества 5[]{р} следующих видов:
а) Л0{р}, если А — поверхность матроида М и ЛеФ;
б) А, если А — поверхность матроида М и Л^Ф;
в) ^11{р}, если А — поверхность матроида М, А не лежит в Ф
и не покрывается в М никакой поверхностью из Ф. Других
поверхностей в М' нет.
Следует также отметить, что одноточечные расширения
матроида М=(5, ~), упорядоченные по включению их модулярных
фильтров в М, образуют решетку.
Определим еще две конструкции: усечение и наращение.
Теорема 72. Пусть М—матроид на конечном множестве 5,
Р— семейство его независимых множеств, г—функция ранга,
к—целое положительное число такое, что &<г(5). Тогда
семейство
Рк={А=5\Ае=Р и \А\<к}
является семейством независимых множеств матроида Мк на
множестве 5 с функцией ранга гк(А)=т'т{к, г (А)}. Решетка
поверхностей матроида Мк получается из решетки Ь (М) поверхностей
матроида М стиранием всех поверхностей ранга >-к и заменой их
на новый наибольший элемент решетки.
Доказательство теоремы не вызывает особых трудностей и
предлагается в виде упражнения.
Матроид Мк из формулировки теоремы 72 называют к-усечени-
ем матроида М.
289

Если матроид М на множестве 5 изоморфен (г—1)-усечению
матроида Я на множестве 5, то говорят, что матроид Я есть «а-
ращение матроида М. Без ограничения общности можно считать,
что решетка матроида Я получается из решетки матроида М
включением уровня новых коатомов, лежащего выше
первоначальных коатомов и под единичным элементом решетки.
Не будем подробно останавливаться на конструкции
наращения, а лишь приведем без доказательства некоторые результаты.
Теорема 73 (Крапо). Семейство Я непустых подмножеств
множества 5 является множеством коатомов в решетке наращения
матроида М=(5, ~) тогда и только тогда, когда выполнены
следующие три условия:
а) Я—антицепь в булеане ^*(5); _
б) для всякого ЛеЯ, если В^А и \В\=г—1, то В^А;
в) для каждого базиса В\ существует единственный элемент
А\^Н такой, что В\<=:А\.
Пусть Я и Т — две антицепи из булеана ^(5); говорят, что
антицепь Я меньше антицепи Т, если для всякого ЛеЯ найдется
такой элемент В^Т, что А^В. В случае, когда такой элемент
В^Т единствен, то говорят, что Т разбивает антицепь Я.
Различные наращения (точнее, семейства коатомов в решетке
наращения) матроида М на конечном множестве 5, упорядоченные как
антицепи булеана !Р{3), образуют полную решетку, наименьший
элемент которой называется свободным наращением матроида М.
Если свободное наращение матроида М известно, то все другие
наращения этого матроида могут ^быть получены путем разбиения
свободного наращения.
Доказательство приведенных и других факторов о расширениях
и наращениях матроидов можно найти в работах [94, 95].
Конструкция свободного наращения приведена в [96, 97].
Упражнения. 1. Пусть М= (5, -)—матроид, В^А^З. Верны ли
следующие равенства:
а) {М\А)\В=М\В;
б) М.В^=(М.А).В;
в) (М\А).В=(М.(5\(А\В)))]В;
г) (МЛ)|В=(М\(5\(Л\В))).В;
Д) (М\А)*=М* /(5\А);
е) (М1А)*=М*\(8\А)1
2. Убедитесь в справедливости следующих утверждений:
а) всякий мииор графического матроида является графическим;
б) каждый подматроид трансверсального матроида траисверсален;
в) сумма трансверсальных матроидов есть трансверсальный матроид.
3. Могут ли у графического матроида М быть неграфические наращення
и й-усечения? Если да, приведите примеры.
Слабым отображением геометрической решетки Р в
геометрическую решетку Ь называется отображение о: Р-*-Ь, при котором
а) о(х) =зир (о(а) |хз*.а, а§=0};
б) г(а(х)) <.г(х).
Сильным отображением геометрической решетки Р в
геометрическую решетю/ Ь называется отображение о: Р-*~Ь, при котором
а) о (зир А) = зир {о (х) | хеЛ} для всех А^Р;
б) из у^=х в Р следует, что о(у)^=а(х) в Ь.
290

Сильным (соответственно слабым) отображением геометрии
0=(5, -) в геометрию Н=(Т, ~) называется инъективная
функция
/: 5[}{0}^Т[}{0),
где О — пустое множество, такая, что /(0)=0 и прообраз
произвольного замкнутого (соответственно независимого)
подмножества геометрии Я является замкнутым (соответственно
независимым) в О. Каждое сильное отображение является слабым, но
обратное неверно.
Ни сильные, ни слабые отображения в отдельности не
образуют достаточно хороших категорий, чтобы в полной мере
использовать идеи теории категорий. Однако при их совместном
рассмотрении получаются некоторые результаты канонического вида,
поскольку объекты в категории матроидов и сильных отображений
имеют тенденцию быть каноническими по отношению к объектам
категории матроидов и слабых отображений. Причина этого, по-
видимому, кроется в том, что сохраняющие ранг сильные
отображения являются изоморфизмами, однако часто имеется несколько
матроидов одного и того же ранга, которые удовлетворяют
некоторой заданной диаграмме сильных отображений, связанных
между собой как раз слабыми отображениями.
Для знакомства с основными результатами сильных и слабых
отображений матроидов рекомендуем обратиться к работам
[98—102].
В заключение нашего краткого введения в теорию матроидов
обсудим некоторые проблемы. Одной из самых старых и до сих
пор полностью нерешенных задач теории матроидов является
проблема представления данного матроида векторами с
координатами из поля (иначе называемая проблемой координатизации).
Матроид М= (5, ~) называется представимым над полем Р,
если существует линейное пространство V над Р и отображение
ф: 5->-У, при котором Л^5 независимо в М тогда и только тогда,
когда ф взаимно-однозначно на Л и ф(Л) линейно-независимо в V.
Очевидно, что представимый над Р матроид описывается
матрицей размера гХп, столбцами которой служат образы элементов
5 при отображении ф (если |5|=п и /-(5)=/-). Проблема
представления состоит в том, чтобы определить, представим ли
данный матроид М над заданным полем (телом) Р.
Например, матроиды, которые представимы над полем СР(2),
называются бинарными.
Отметим наиболее характерные результаты по проблеме
представления матроидов:
а) матроид М=(5, ~) бинарен тогда и только тогда, когда он
не имеет минора, изоморфного однородному матроиду 112 (4), или,
что эквивалентно, тогда и только тогда, когда симметрическая
разность любых двух различных циклов матроида М есть
объединение непересекающихся циклов;
б) матроид М тернарен, т. е. представим над полем 0Р(3),
291

в том и только в том случае, когда он не имеет миноров,
изоморфных однородному матроиду 1^(5), матроиду Фано (рис. 8.22)
или двойственным им матроидам;
в) если матроид М без петель и
перешейков представим над полем СР(2)
и некоторым другим полем
характеристики, отличной от 2, то М представим
над всеми полями одновременно с
помощью вполне унимодулярной матрицы
(т. е. матрицы, все миноры которой
равны 0, ±1).
Матроиды, представимые над любым
5 полем, называются регулярными.
Матроид М=(а, —) называется петлей, если
г(а)=0, и перешейком, если г*(а) =
= 0.
Наряду с проблемой представления большой практический
интерес представляют проблемы описания классов матроидов:
бинарных, графических, кографических, регулярных, трансверсаль-
ных и других матроидов;
г) матроид М является графическим тогда и только тогда,
когда он бинарен и не содержит миноров, изоморфных коцикли-
ческим матроидам графов Куратовского Кз,з и Кь, матроиду Фано
и ему двойственному;
д) матроид М является кографическим тогда и только тогда,
когда он бинарен и не содержит миноров, изоморфных
циклическим матроидам графов Куратовского /Сз,з и Кь, матроиду Фано
и ему двойственному;
е) бинарный матроид является регулярным в том и только в
том случае, когда он не содержит миноров, изоморфных
матроиду Фано и ему двойственному.
Для иллюстрации важности проблем характеризации отметим,
что почти все известные методы топологического синтеза
электрических цепей и комбинаторных переключающих схем основаны
^на использовании свойств циклического и коциклического
матроидов графа схемы, а также следующего замечательного свойства:
матрицу 'инцидентности коциклического матроида графа схемы
(матрицу разрезов электрической схемы) при помощи
элементарных строчных операций можно свести к матрице инцидентности
А электрической схемы (т. е., иначе говоря, матроид,
соответствующий матрице инцидентности А над СР(2), изоморфен
матроиду разрезов графа схемы). Каждый графический и каждый когра-
фический матроид является бинарным, но не каждый бинарный
матроид является графическим. Например, матроид Фано
бинарен, но не является графическим, более того, его матрица
представления над ОР(2):
292

/10 00 1 1 1\
0 10 10 11
\0 0 1 1 10 1/
не может быть приведена при помощи элементарных строчных
преобразований к матрице инцидентности никакого графа схемы.
Поэтому исключительно важную роль при топологическом
синтезе электрических схем играют перечисленные выше характериза-
ции графических и кографических матроидов, а также следующие
факты:
— при ориентации ребер графа циклический матроид графа
также становится ориентированным;
— из ориентируемости матроида следует ориентируемость
двойственного ему матроида;
— ориентированный матроид имеет линейное представление
над всеми полями, т. е. является регулярным, и представим уни-
модулярной матрицей.
Среди приведенных нами характеризаций практически
отсутствуют конструктивные, поскольку перебрать все миноры матроида
и тем более установить их изоморфностъ другим матроидам
затруднительно даже для «малых» матроидов. Тем ценнее
конструктивная характеризация регулярных матроидов, полученная
недавно Сеймуром [103]. Приведем без доказательства его
результат.
Пусть М1=(3и ~) и Мг= (5г, ~)—бинарные матроиды,
причем 51 и 5г могут пересекаться. Тогда матроид М1АМ2 на
множестве 51Д52= (51 \5г)II (52 450, циклами которого являются все
подмножества множества 51Д52 вида С1ДС2 (где С; — циклы
матроида М;, 1=1, 2), является бинарным. Пусть |51|, |5г|<
<|51Д52|. Тогда матроид М1АМ2 называется 1-суммой
(соответственно 2- и 3-суммой) матроидов М\ и М2, если 5^52 = 0
(соответственно |51П52| = 1 и 51П52 = {г}, где г не является ни петлей,
ни копетлей матроидов М\ и М2; |51П52|=3 и 5^52=2, где
2 — цикл, не содержащий никакого коцикла матроидов М\ и Мг).
В 1975 г. Брилавский доказал, что 1-, 2- и 3-суммы двух
регулярных матроидов являются регулярными.
Пусть дана матрица
10 0 0 0-
0 10 0 0
0 0 10 0
0 0 0 10
0 0 0 0 1
-1
1
0
0
1
1
— 1
1
0
0
0
1
—1
1
0
Обозначим, через ^ю матроид, элементами которого являются
столбцы матрицы, а базисами — их максимальные
линейно-независимые множества в линейном пространстве над ОР(2).
Теорема 74 (Сеймур). Каждый регулярный матроид М может
быть построен посредством 1-, 2- и 3-сумм матроидов, каждый из
которых изоморфен минорам матроида М и является либо
графическим, либо кографическим, либо изоморфным матроиду #!0.
293

Остановимся и на других приложениях матроидов. Правильной
раскраской графа С называется такое приписывание цветов его
вершинам, что никакие две смежные вершины не раскрашены
одинаковым цветом, к-раскраской графа О называется правильная
раскраска графа О, использующая к или меньше цветов. Две
я-раскраски графа С будем считать различными, если они по
крайней мере одной вершине приписывают различные цвета.
Хроматическое число %(0) графа О определяется как наименьшее к,
для которого граф С имеет ^-раскраску. Легко найти
хроматическое число для некоторых известных графов, например: %(Кп) =
— п\ х(Ят,п)=2 и %{Т)=2 для любого нетривиального дерева Т.
Пусть Р(С; Я) —число различных Я-раскрасок графа О. Если
Я<х(С), то, естественно, Р(С; Я)=0. Наименьшее из натуральных
чисел Я, для которого Р(С; Я)>0, есть очевидно, хроматическое
число графа. Известная гипотеза четырех красок (ее
справедливость доказана недавно) утверждает, что если О — планарный
граф, то Р(С; 4) >0.
Очевидно, что для любого полного графа Кп имеем
Р(Кп; 1)=1(1-1) ... (Я—гг + 1),
так как любую данную вершину полного графа Кп можно
окрасить Я способами, для второй вершины можно взять любой из
а» уо2 (Я—1) оставшихся цветов и т. д.; нако-
\. у/ нец, последняя вершина окрашивается
\^/^ (Я—л+1) способами. Центральную вер-
./\° шину а0 графа Кь4, изображенного (на
уг >^ рис. 8.23, можно окрасить Я спосо-
а3* »а4 бами, а любую из висячих вершин
р с 823 к—\ способами. Поэтому Р{К\,4> Я)=-
=Я(Я—I)4.
Теорема 75. Пусть С — граф без петель и кратных ребер и
а — ребро графа О. Тогда
Р(0; Я)=Р(0—а; Я)— Р(С/а; Я),
где О—а и С/а — графы, полученные из С соответственно
исключением и стягиванием ребра а.
Доказательство. Требуемое равенство непосредственно
следует из факта, что множество правильных Я-раскрасок графа
О—а можно разбить на два подмножества: раскраски, в которых
концевые вершины ребра а окрашены в разные цвета, и те, в
которых они окрашены одним цветом. Мощность первого
подмножества, очевидно, равна числу Я-раскрасок графа О, т. е. Р(С, Я), а
мощность второго — числу Я-раскрасок графа С/а, т. е. Р(С/а; Я).
Теорема доказана.
Во всех приведенных примерах Р(С; Я) есть многочлен от
переменной Я. Это всегда так, в чем мы сейчас убедимся.
Пусть О — произвольный неполный граф на п вершинах.
Очевидно, он может быть получен из полного графа Кп с помощью
последовательного исключения ребер, не принадлежащих графу
* 294

С. Обозначим эти ребра для определенности через а\, .... ак.
Введем следующие обозначения: С\ = Кп—ах; 02=0\—а2; ..., Ок =
= 0А_1—ак и 01 = Кп1сц\ С2 = 61/а2, ..., Ск = Ск-1/ак. Тогда в силу
теоремы 75 имеем: Р (Кп; А.) = Р (Ок\ ^)-% Р(&, *-)> но Ок = С.
1=1
Следовательно,
Р(0;К)=Р(Кп-Л) +%Р(&-Л).
1=1
Каждый из графов 0\ где 1 = 1, ..., к, содержит (п—1) вершин, и
его функцию Р(0'; К) можно выразить через функции полного
графа на (п—1) вершинах и графов на (я—2) вершинах.
Следовательно, Р(0; К) можно представить в виде суммы Р(/С», К),
поскольку стягиванием ребер всегда можно прийти к полным
графам, например К\. Но Р(Кг, к)=Х... (%—£+1) являются
многочленами. Следовательно, Р(0; К)— многочлен от переменной Л
для любого графа С.
По этим причинам функцию Р(С; X) называют хроматическим
многочленом графа С (см. пример 8 из § 8.3).
Проиллюстрируем вышесказанное на примере и найдем
хроматический многочлен графа С, изображенного на рис. 8.24, а.
Обозначим через аи а2 и аз ребра полного графа Кь, не принадле-
Рис. 8.24 Рис 8.25
жащие графу С (см. рис. 8.24, б). Тогда 01 = Ка', С2 = К4, а граф
С3, изображенный на рис. 8.25, а, получается из полного графа
/С4 исключением ребра Ъ (см. рис. 8.25, б). Кроме того, К*/Ь=Кз-
Отсюда
Р(Кь\ %)=Р{0; К)-2Р(К4\ К)—Р(С'\ Я);
Р(К4; К)=Р(С*\ 1)-Р(Кз, К).
Следовательно, Р(С; К) = Р(Къ\ Я) + ЗР(Кс К) + Р(Къ, К) =
= Л(Л—1) (Л—2) (1-3) (а,—4) +ЗЯ(Л—1) (Л—2) (1-3) +%(К—1) X
х (я—2) =>.5—7Я4+ 18Я3—20Я2+8Я.
В частности, граф С можно раскрасить тремя цветами, поскольку
Р(С; 3)=6>0.
Перечислим некоторые свойства хроматического многочлена
Р(0; 1), вытекающие непосредственно из теоремы 75.
295

Теорема 76. Пусть 0=(Х, 5) —граф без петель и кратных
ребер с множеством вершин X, множеством ребер 5 и к
компонентами связности О-,, С2, ..., Ок. Тогда
а) Р(0; Я)— многочлен от переменной Я степени \Х\;
б) коэффициент при }}х[ в Р(С; Я) равен 1;
в) коэффициент при Я1Х1~! в Р(0; Я) равен —15|;
г) свободный член многочлена Р(0, Я) равен 0;
п
д) Р(0;К)=\']Р(0!-Л);
1=1
е) наименьший показатель у степеней переменной Я, входящих
в Р(0, Я) с ненулевыми коэффициентами, равен к.
Теорема 77. Граф Осп вершинами является деревом тогда и
только тогда, когда Р(С; Я)=Я(Я—1)п~!.
Доказательство. Индукцией по числу вершин покажем,
что хроматический многочлен любого помеченного дерева с п
вершинами равен Я (Я—I)"-1. Для п = \ и п = 2 результат очевиден.
Предположим, что хроматический многочлен всех деревьев с п—1
вершинами имеет вид Я(Я—1)п~2. Пусть х— висячая вершина
дерева Т, а а — его ребро, инцидентное вершине х. По
предположению индукции хроматический многочлен дерева Т—а есть
Я (Я—1)п~2. Вершину х можно окрасить любым цветом, отличным
от цвета другой концевой вершины ребра а, так что х можно
окрасить Я—1 способами. Таким образом, Р(Т; Я) = (Я—1)Х
ХР(Г-о-Д)=М^-1)""'-
Обратно, пусть О — граф, у которого Р(0; Я)=Я(Я—1)п-!. Так
как коэффициент при Я в Р(С; Я) не равен 0, а при Я"~! равен
(п—1), то в силу теоремы 76 граф С связен и имеет (п—1)
ребер, т. е. на единицу меньше, чем вершин. Следовательно, О —
дерево. Теорема доказана.
Приведем без доказательства еще несколько результатов о
хроматических многочленах.
Теорема 78. Пусть Р(0; Я) = V а^1 — хроматический много-
1=1
член графа 0= (X, 8). Тогда
а) последовательность а\, а2, ..., ап-\, а„=1 —
знакочередующаяся;
б) если С — связный граф, то
|*|>('*1-7')-.
в) ак~\](—\у шк1, где ты — число порожденных подграфов
/=о
графа О с к компонентами связности и / ребрами.
Среди проблем о хроматических многочленах остаются
нерешенными задачи описания графов, имеющих один и тот же хрома-
296

тнческий многочлен, и нахождения необходимых и достаточных:
условий, чтобы многочлен был хроматическим.
Пусть О — граф без петель и кратных ребер и Ь —
геометрическая решетка, определенная его циклическим матроидом М(С).
Для всякой раскраски а вершин графа С обозначим через А (а)
множество тех ребер графа, у которых обе концевые вершины
одинаково раскрашены в а.
Предложение 79. Для любой раскраски а множество ребер
А (а) есть поверхность в М(С).
Доказательство. Предположим, что это не так. Пусть
Ъ<= (А (а) \Л (а)). 'Тогда найдется цикл [Ь, аи ■■, а*} графа С
такой, что [а.1 а*}=Л(а) и Ь^А(а). Но это невозможно.
Значит, две концевые вершины ребра Ь одинаково окрашены при а:
и, следовательно, Ь^А(а). Отсюда Л(а)\Л(а)=0 и Л(а) =
= Л(а). Предложение доказано.
Для произвольного целого положительного числа Я и любой
поверхности А циклического матроида М(С) графа О обозначим
соответственно через ¢) (Я; А) и /•'(Я; А) число раскрасок а в Я-
цветов графа О таких, что А(а)=А и Л(а)эЛ соответственно..
Тогда
В силу формулы обращения Мебиуса (см. теорему 42) имеем
<2(к;А)= ^ \1(А,В)Р(к;В).
в.в>Аеи
В частности, при Л = 0:
С1(К0)= ^ р(0,В)Р(Ь;В),
в-.в&о в и
где В — поверхности циклического матроида М(О). Но (${%; 0)>
совпадает с числом правильных раскрасок в Я цветов, т. е. с
числом Я-раскрасок графа С, которое равно Р(0; Я). С другой
стороны, для любой поверхности В^Ь, вернее для подграфа графа
О, определяемого множеством ребер В,
Р (Я; В) = КНВ) Я|Х|-т,
где т—число вершин, а к (В) —число связных компонент в
подграфе, определяемом В. Значит
^(Я; В) = Я|Х|-т+ад = Я|ХКг(В),
где г — функция ранга циклического матроида М(С), так как в
силу теоремы 55 г(В) = т—к (В).
Таким образом, мы доказали следующий результат:
Теорема 80. Для произвольного графа С=(Х, 5) с к
компонентами связности и любого целого положительного числа Я:
29Т

Р(0; I) = Кт ^ К'пв)ц(0, В) = %* ^ яг(5)~г(В) ц (О, В),
В61, вех.
тде ^ — функция Мебиуса геометрической решетки /,
циклического матроида М(0) графа С, и сумма берется по всем
поверхностям В матроида М(О).
Пусть М=(8, ~)—матроид иг — его функция ранга.
Характеристическим многочленом Р(М; К) матроида М называется
характеристический многочлен решетки поверхностей Ь, т. е.
Р(М; К) = £11(0, А)ХГ(8)'Г(А\
Таким образом, если С=(Х, 5) —граф без петель и кратных
ребер, то в силу теоремы 80
).кР(М(С);Х)=Р(С;1),
где М(О)—циклический матроид графа С. Хроматическое число
%(М) матроида М определяется как наименьшее натуральное К,
при котором Р(М\ X) >0. Поскольку Р(С; Я)>0 в том и только в
том случае, когда Р(М(С); Я)>0, то хроматические числа графа
О и его циклического матроида М(О) равны между собой. Более
того, отсюда немедленно следует, что если графы О1 и 02 имеют
изоморфные циклические матроиды, то их хроматические числа
равны.
Характеристический многочлен Р(М; К) матроида М= (5, ~)
имеет много общих свойств с хроматическим многочленом графа
О. Например:
а) если а не является ни петлей, ни перешейком, то
Р (М; 7.) = Р (М—а; К) —Р (М/а; К);
б) если М имеет петли, то Р(М; К) =0;
в) если М разлагается на компоненты Ми ..., Мк, то
к
р(мл) = Г\Р(МгЛ)\
1 = 1
г) последовательность коэффициентов Р(М; К) является
знакочередующейся.
Пусть Л' — класс матроидов, замкнутый относительно прямых
сумм (объединений) и миноров. Рассмотрим функции /,
определенные на элементах класса К, со значениями в коммутативном
кольце с единицей, принимающие одинаковые значения на
изоморфных матроидах, такие, что для всех М, М\ и М2^К:
а) !(МХ + М2) =7(Л*1ШМ2);
б) 1(М) = {(М—а) + {(М/а), если а не является ни петлей, ни
перешейком.
Функции / с этими свойствами называются инвариантами Татта —
Гротендика.
Пусть К — класс всех матроидов. Положим !\(М) и 12{Щ
равными соответственно числу базисов и числу независимых мно-
'298

жеств матроида М. Легко видеть, что /г и /2 — инварианты Татта—
Гротендика. Можно также показать, что если Р(М; Я) —
характеристический многочлен матроида М, то (—1)Г<М>Р(А1; Я)—также
инвариант Татта — Гротендика.
Обобщенной функцией ранга матроида М=(8, ~) называется
многочлен
Я(М, х, </) = ]Г /(5>-^> у^-гч^л) (
АС. 8
где гиг* — функции ранга соответственно матроидов М и М*_
Используя соотношения между г и г*, можем записать, что
Я(М; х, у) = % х<5)~г{А)уш~«А\
АС8
Непосредственно из определения получаем:
Я(М;х,у)=Я(М*;у,х);
Я (М; х, у) = 1 + у, если М — петля;
Н{М; х, г/) = 1 4-х, если М — перешеек.
В качестве упражнения предлагаем доказать следующую
теорему:
Теорема 81. Многочлен К(М; х, у) является инвариантом
Татта — Гротендика для любого класса матроидов К.
Многочлен Т(М; х, у)=Я.(М; х—1, у—1) для графических
матроидов изучался Таттом и поэтому носит название многочлена
Татта.
Оказалось, что все инварианты Татта — Гротендика
произвольного класса К могут быть получены из многочлена Татта.
Например:
а) Т(М; 2, 2)=2'«!;
б) Т(М; 1, 1) равно числу базисов матроида М;
в) Т(М; 2, 1) равно числу независимых множеств матроида М;
г) Т(М; 1, 2) равно числу порождающих множеств матроида М;
д) Т(М; 0, 0) = 0;
е) Т(М; 1, 0) = (—1)Г(8У(0, 1), где ц—функция Мебиуса решетки
поверхностей матроида М.
Более того, через многочлен Татта выражается
характеристический многочлен Р(М; К) матроида М:
Р(М; 1) = (—1)г(3)Т(М; 1-Я, 0).
Рис. 8.26
29»

Однако даже неизоморфные матроиды могут обладать одним
-н-^гем же многочленом Татта. Например, матроиды М\ и М2 ранга
3 на множестве 5 = {1, 2, 3, 4, 5, 6, 7}, изображенные на рис. 8.26,
-являются таковыми:
Т(МХ; х, у) = Т(М2; х, у) = х* + 3х2 + х2у + 2х+5ху + 2ху2+.
+ 2у + 4у2 + 3у*+у\
Однако М\ отличается от М2 разными числами циклов,
поверхностей и коатомов.
Многочлены Татта осуществляют связь матроидов с
линейными кодами и упаковками, благодаря чему ряд проблем теории
кодирования сводится к задачам теории матроидов. Рассмотрим,
например, задачу вычисления распределения весов кода.
Пусть А — матрица порядка кХп с коэффициентами из
СР{д). Свяжем с каждой такой матрицей ранга к следующие два
объекта: £/ — линейный код над СР(д), т. е. пространство строк
матрицы А; М — матроид столбцов матрицы А. Пусть «е!7.
Весом т(и) вектора и называется число его ненулевых
компонент. Многочлен
А(Ц,г)=1г^ =^ 4*
ибУ 1=1
где А{ — число векторов «е(/ с гш(и)=1 называется весовым
нумератором кода V'.
Теорема 82. Функция /, определенная для всех (&Хгс)-матриц
А над СР(д) посредством
ЦА) = ! АО); г),
является инвариантом Татта — Гротендика. Более того,
\ 1 — г г I
где Т (М, х, у) —многочлен Татта.
В качестве иллюстрации взаимной связи между кодами и мат-
роидами можно вывести формулу Маквильямса (которая
связывает весовой нумератор с весовым нумератором двойственного
ему кода) из соответствующей двойственности многочлена Татта.
Критическая проблема. Пусть У(п, д)—векторное
пространство размерности п над конечным полем СР(д), и пусть 5 —
подмножество пространства V(п, д), не содержащее нулевой вектор.
Подпространство из У(п, д) размерности п—1 называется
гиперплоскостью. Критическая проблема для множества 5 состоит в
отыскании такого наименьшего целого положительного числа к,
для которого найдутся к гиперплоскостей Н\, Н2, ..., Я* таких, что
Н\[\Н2[\...$\Нк(\& = 0\ иначе говоря, для каждого р^5 найдется
по крайней мере одна гиперплоскость Я, такая, что р^Н;.
:300

Поскольку для каждой гиперплоскости Я,- пространства У(п, д)
существует такой линейный функционал Ь; на У (п, д) со
значениями в ОР(д), что Я, = /,г'(0)> то критическую проблему можно
сформулировать иначе. Скажем, что последовательность (Ь\, Ь2, ••■
... , Ьк) линейных функционалов различает множество 5, если для
каждого ре5 найдется такой индекс I (1 = 1, 2, ..., к), что
Ь1(р)Ф0. Наименьшее целое положительное к, при котором
последовательность (Ь\, Ь2 1^к) линейных функционалов различает
подмножество 5 из У{п, д), называется критической экспонентои
множества 5. Тогда критическая проблема и заключается в
отыскании критической экспоненты.
Если 5 состоит из одного нулевого вектора, то его критическая
экспонента равна 1. В случае, когда 5 состоит из всех ненулевых
векторов пространства У{п, д), его критическая экспонента,
очевидно, равна п.
Теорема 83. Пусть М — линейный матроид, порожденный
подмножеством 5 из У(п, д) (см. пример 5 в § 8.4), и пусть Р(М;К) —
его характеристический многочлен. Тогда число упорядоченных
последовательностей (Ь\, ... , Ьк) линейных функционалов на
У{п, д), различающих подмножество 5, равно Р(М, дк).
Доказательство. Пусть Ле5, и пусть §ь(А) —число
упорядоченных последовательностей (Ьи Ь2, ..., Ьь) линейных функ-
* -1
ционалов на У(п, д) таких, что АС~ |"| /,, (0). Пусть }к(А) —
1 = 1
число последовательностей (Ьи Ь2 Ьи), для которых А в точ-
ности равно пересечению ядер, т. е. А = ("*| и (0). Тогда
1 = 1
§к (А) = V /*. (В) и в силу формулы обращения Мебиуса (см. тео-
В:Ас:В
рему 42) имеем
/А(А)= ^ р(А,В)8к(В).
В:АаВ
Пусть IVв — линейная оболочка векторов из В в V(п, д). Тогда
К'в— подпространство пространства У(п, д) и сНтВ = г(В), где
г — функция ранга матроида М. Заметим, что §к{В) равняется
числу упорядоченных последовательностей (Ь\, Ь2, ..., Ьь)
линейных функционалов на фактор-пространстве У(п, д)/МРв. Так как
сНт У{п, д)/№в = г(8)—г(В), то
ЫЯ)=<7(Г<8,-Г(В,)*-
Следовательно, /, (А) = ]Г ц (А, В) д(ПЗ)'г[В),к.
ВАС.В
Положив А = 0, имеем
/*(0)= % 11(0,В)д«5)-пВ))к = Р(М;д>),
в-.ваз
301

где 1к{0) и есть число упорядоченных последовательностей (Ь^
Ь%, ••• • ^к) линейных функционалов на V(п, д), различающих 5.
Теорема доказана.
Следствие 84. Пусть М — матроид, порожденный
подмножеством 5 ненулевых векторов пространства V {п, д) размерности п.
над полем ОР(д). Тогда характеристический многочлен Р (М; X)
матроида М обладает свойством:
Р(М;дк)=0 для А = 0, 1, ..., с— 1;
Р(М; <7*)>0 для к>-с,
где С'—критическая экспонента множества 5. При этом с<гс для:
всех подмножеств 5 из У(п, д).
Крапо и Рота полагают, что критическая проблема является
«центральной проблемой экстремальной комбинаторной теории»
(см. [104]). Действительно, целый ряд комбинаторных задач
хорошо формулируется в ее терминах. Например, упомянутая выше
гипотеза четырех красок выглядит так:, если М—циклический
матроид простого планарного графа, то -критические экспоненты'
с(М; 2)<2 и с(М; 4)<1. Однако получено очень мало общих
результатов по критической проблеме. Доказано, например, что
а) критическая экспонента конечной линейной геометрии над
ОР (д) равна 1 тогда и только тогда, когда эта геометрия
изоморфна подматроиду аффинной геометрии АС(п, д);
б) корни характеристического многочлена Р(С; К)
сверхразрешимой геометрии О есть положительные числа, равные |Л,-+!\Л(|
(комбинаторная геометрия 0=(5, _) называется
сверхразрешимой, если существуют модулярные поверхности А0^А^ ...^Ап=8
такие, что г{А{)=1. Поверхность А геометрии О называется
модулярной, если она образует модулярную пару со всеми другими
поверхностями геометрии С).
Мы лишь кратко остановились на основных направлениях
теории матроидов. Для дальнейшего изучения рекомендуем работы
[1, 34, 104—109].

ЗАКЛЮЧЕНИЕ
Настоящая книга была задумана и написана с таким
расчетом, чтобы всякий, кто поработает над ней и над сборником
«Комбинаторный анализ. Задачи и упражнения», достиг следующих
результатов:
1. Получил цельное представление о современном состоянии
старинной по своему происхождению и всегда актуальной части
математики, которую именуют в силу исторически сложившейся
традиции комбинаторным анализом.
2. Усвоил, что содержание комбинаторного анализа опирается
на единые теоретические основы, что его средствами решают
весьма широкие классы задач, для чего используют богатый арсенал
разнообразных методов и интерпретаций.
3. Приобрел некоторые навыки решения задач комбинаторного
характера и определил (хотя бы интуитивно), какие классы этих
задач ему оказываются нужными или просто интересными.
4. Получил тем самым достаточные основания, чтобы поставить
перед собой вопрос: как продолжать работу в этой своеобразной,
привлекательной и такой необходимой отрасли математики.
Естественно, что самым лучшим путем продолжения занятий
будут ориентировка в более широком круге современных
сочинений и ознакомление с нерешенными проблемами для
последующего их обдумывания. Кстати, сама работа (будь то работа
математика, инженера, экономиста или кого-либо еще) будет самым
активным поставщиком таких проблем.

ЛИТЕРА ТУРА
КНИГИ ОБЩЕГО НАЗНАЧЕНИЯ
1. Айгнер М. Комбинаторная теория. — М.: Мир, 1982.
2. Кофман А. Введение в прикладную комбинаторику. — М.: Наука, 1975-
3. С а ч к о в В. Н. Введение в комбинаторные методы дискретной
математики. — М.: Наука, 1982.
4. Холл М. Комбинаторика. — М.: Мир, 1970.
5. Яблонский С. В. Введение в дискретную математику. — М.: Наука,.
1979.
СБОРНИКИ ЗАДАЧ
6. Гаврилов Г. П., СапоженКоА. А. Сборник задач по дискретной
математике. — М.: Наука, 1977.
7. Комбинаторный анализ. Задачи и упражнения / Под ред. К. А. Рыбникова.—
М.: Наука, 1982.
8. Ьоуазг Ь, СотЫпа4опа] ргоЫетз апй ехегазез. — Вис1аре84: АкайеггНаг
Ю'айо, 1979.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
к главе 1
9. Биркгоф Г., Барти Т. Современная прикладная алгебра. — М.: Мир,
1976.
к главе 2
10. Брейн Н. Дж. де. Теория перечисления Пойа. — В кн.: Прикладная
комбинаторная математика/Под ред. Э. Беккенбаха. — М.: Мир, 1968, с. 61 —
106.
11. Егорычев Г. П. Интегральные представления и вычисление
комбинаторных сумм. — Новосибирск: Наука, 1977.
12. Перечислительные задачи комбинаторного анализа. Сборник переводов/
/Под ред. Г. П. Гаврилова. — М.: Мир, 1979.
13. Платонов М. Л. Комбинаторные числа класса отображений и их
приложения. — М.: Наука, 1979.
14. Риордан Дж. Введение в комбинаторный анализ. — М.: ИЛ, 1963.
к главе 3 '
15. Грэхем Р. Начала теории Рамсея. — М.: Мир, 1984.
16. Эндрю с Г. Теория разбиений. — М.: Наука, 1982.
304

к главе 4
17. Маркус М., М и н к X. Обзор по теории матриц и матричных неравенств.—
М.: Наука, 1972.
18. Мин к X. Перманенты. — М.: Мир, 1982.
19. Носов В. А., Сачков В. Н., Тараканов В. Е. Комбинаторный
анализ. — Итоги науки и техники, 1980, т. 18.
20. Т> ё п е 8 X, К е е А \у е 11 А. Т>. Ьа1ш з^иагез апс! 1Ье1г аррНсаМопз. — Ви-
(1арез1: Акас1ёгта1 КЫо, 1974.,
к главе 5
21. К а рте си Ф. Введение в конечные геометрии. — М.: Наука, 1980.
22. Камерон П., Линт Дж. ван. Теория графов, теория кодирования и блок-
схемы. — М.: Наука, 1980.
23. Басакер Р., Саати Т. Конечные графы и сети. — М.: Наука, 1974.
24. Кристофидес Н. Теория графов. Алгоритмический подход. — М.: Мир,
1978.
25. О ре О. Теория графов. — М.: Наука, 1968.
к главе 6
26. Леонтьев В. К. Дискретные экстремальные задачи. — Итоги науки и
техники, 1979, т. 16, с. 39—101.
27. Саати Т. Целочисленные методы оптимизации и связанные с ними
экстремальные проблемы. — М.: Мир, 1973.
28. Форд Л., Фалкерсон Д. Потоки в сетях. — М.: Мир, 1966.
к главе 7
29. Сачков В. Н. Вероятностные методы в комбинаторном анализе. — М.:
Наука, 1978.
30. Э р д е ш П., С п е и с е р Дж. Вероятностные методы в комбинаторике. —
М.: Мир, 1976.
к главе 8
31. Биркгоф Г. Теория структур. — М.: Мир, 1984.
.32. Гретцер Г. Общая теория решеток. — М.: Мир, 1982.
33. Скорняков Л. А. Элементы теории структур. — М.: Мир, 1982.
34. \Уе1зЬ В: 1. А. Ма4гоМ 1Ьеогу. — Ьопйоп: Асайегтс Ргезз, 1976.
ПРОЧАЯ ЛИТЕРАТУРА
35. О г а Ь а т К. Ь. Оп раг1Шопз о{ а ПпИе зе1. — Т. СотЫпа1опа1 ТЬеогу,
1966, V. 1, N 2, р. 215—223.
36. Кепу1 А. Оп а ргоЫет о{ ш{огта1юп {Ьеогу. — РиЫ. Ма1Ь. 1пз1. Нип-
&аг. Асас!. 5а., 1961, V. 6, р. 505—516.
37. К а I о п а О. Оп зерагаИп^ зуз4етз о{ а ПпМе зе4. — X СотЫпа1опа1
ТЬеогу, 1966, V. 1, N 2, р. 174—194.
38. Э р д е ш П., К л е й т м а н Д. Дж. Экстремальные задачи о подмножествах
конечного множества. — В кн.: Эрдеш П., Спенсер Дж. Вероятностные
методы в комбинаторике. — М.: Мнр, 1976, с. 115—130.
39. Егйбз Р., СЬао Ко, К а А о К. 1п4егзесЛоп 1Ьеогетз {ог зуз1етз о{ Пш1е
зе1з. — <Эиаг*. Т. МаШ., зег. 2, 1961, V. 12, N 48, р. 313—320.
40. Т и г а п Р. Е&у §га4е1те1еН 52ё1збёг4ек{е1ас1а4го1. — Ма1. ёз Р12. Ьарок,
1941, уо1. 48, N 3, р. 436—453.
41. Сидоренко А. Ф. О проблеме Турана для 3-графов. — В кн.:
Комбинаторный анализ. Вып. 6. — М.: Изд-во МГУ, 1983, с. 51—57.
42. Б о л ь ш а ко в В. И. (А^ ..., Л„)-перманенты и нх приложения в
комбинаторике. — Вестн. Моск. ун-та, сер. матем., мех. (в печати).
305

43. МиШп К., К о* а О. С. Оп 4Ье {оипсШюпз о{ сотЫпа4опа1 4Ьеогу III:
{Ьеогу о{ Ъшогта1 епитега^оп. — 1п: ОгарЬ Шеогу апс! Из аррНсаМопз,
N. У.: Асас1егтс Ргезз, 1970. р. 167—213.
44. О и 1 п а п й А. Р. ТЬе итЬга1 тейюс!: а зигуеу о{ е1етеп4агу тпетопк апс!
татриЫгуе ивез. — Атег. Май. МопгЫу, 1979, V. 86, N 3, р. 187—195.
45. К а т з е у Р. Р. Оп а ргоЫет о{ {огта1 1о§1с. — Ргос. Ьопаоп Ма{Ь. 8ос.,
8ег. 2, 1929, V. 30, N 4, р. 264—286.
46. К о п 1 § О. 1Лэег ОгарЬеп ипс1 Шге Апууепйип^еп аи!" Ве4егтшап4еп{Ьеопе
ипс! Меп^еШеЬге. — Ма*Ь. Апп., 1916, V. 77, N 4, р. 453—465.
47. Н е й а у а { А., XV а 1 П з XV. О. Нас1атагс1 таЫсез апс! Н\еп аррНсаНопз.—
Апп. 5Ы18*., 1978, V. 6, N 6, р. 1184—1238.
48. К1ог(1ап X ТЬгее-Нпе Ьа{ш гес{ап^1ез. — Атег. Ма{Ь. Моп{Ыу, 1944,
V. 51, р. 450—452.
49. Добровольский М. Н. О четырехстрочных латинских
прямоугольниках. — В кн.: Материалы межвузовской научной конференции педагогических
институтов центральной зоны. Тула, 1968, с. 72—75.
50. У а гп а гп о I о К. Оп 1Ье азутр4оНс питЬег о{ ЬаЛп гес{ап^1ез. — Лар. Л.
о! МаШ., 1951, V. 21, р. 113—119.
51. Таггу О. Ье ргоЫете с1ез 36 оШаегз. — С.—К. Аззос. Рг. Асас1. 8а., 1900,
V. 1, р. 122—123; 1901, V. 2, р. 170—203.
52. М а п п Н. В. ТЬе сопзггисНоп о{ ог1Ьо&опа1 ЬаНп 5яиаге5. — Апп. Ма1Ь.
54аН8Нс8, 1942, V. 13, N 4, р. 418—423.
53. Возе К. С, 8Ьг!кЬап(1е 8. 8., Рагкег Е. Т. РигШег гезиНз оп гЬе
сопкггисНоп о? ти{иа11у ог4Ьо^опа1 Ьа{ш зяиагез апс! {Ье ЫзИу о{ Еи1ег'&
соп^есгиге. — Сапаа1ап Л. о! МаШ., 1960, V. 12, N 2, р. 189—203.
54. 81е1пег Л. СотЪша{опзсЬе АиЕ^аЬе. — Л. Кеше ипс! Ап^е\у. Ма1Ь., 1853,
V. 45, р. 181—182.
55. К е 1 з з М. иЪет еше 81ешегзсЬе сотЬша{опзсЬе Аиг^аЪе \уе1сЬе ш 45-з1еп
Вапс1е сНезез Лоигпа1, зеНе 181, §ез4е1Н \уогс1еп Ы. — Л. КеЫе ипс! Ап§е\у.
Май., 1859, V. 56, р. 326—344.
56. К1 г к т а п Т. К. Оп а ргоЫет ш сотЪшаглоп. — СатЬгМ^е апс! ВиЬНп
МаШ. Л., 1847, V. 2, р. 191—204.
57. К1гктап Т. К. 1Чо1е оп ап ипапз\уегес1 рпге диезМоп. — СатЪпйёе апй
ОиЫш Май. Л., 1850, V. 5, р. 255—262.
58. \УПзоп К. ГчошзотогрЫс ЗШпег Мр1е зувгетз. — МаШ. 2., 1974. у. 135,
р. 303—313.
59. Мооге Е. Н. Сопсегпш^ Шр1е зуз4етз. — Ма(Ь. Апп., 1893, V. 43, р. 271 —
285.
60. КеИо Е. ЬеЬгЬисЬ с1ег СотЫпагопк. — Оз1о: 1927, р. 234.
61. ЫпЛпег С. С, Коза А. 84ешег яиас1гир1е зуз4етз. — Вг'зсге4е Ма1Ь.,
1978, V. 21, р. 147—181.
62. Райзер Г. Дж. Комбинаторная математика. — М.: Мир, 1966.
63. В 1 п е I Л. Р. М. Методе зиг ип зу54ёте с1е 1огти1ез апагугляиек, е{ 1еиг арр-
НсаНоп а с)ез сопзМёгаНопз ^еотеШдиез. — Л. Ёс. Ро1у1., 1812, V. 9,
СаЬ. 16, р. 280—302.
64. СаисЬу А. Ъ. Методе зиг 1е {опсЛопз дш пе реиуеп! оЫетг дие с)еих
уа1еигз ё^а1ез е4 с1е з^пез соп4га!гез раг зшге с1ез гхапзрозШопз орёгёез епгге
1ез уапаЫез ди'еИез гепгегтеп!. — Л. Ёс. Ро1у{., 1812, V. 10, саЬ. 17, р. 29—
112, Оеиугез (2)!.
65. М и I г Т. Оп а с1азз о{ регтапеп{ буттеМс ЕипсНопз. — Ргос. Коу. 8ос.
Её1пЬигеЬ, 1882, V. 11, р. 409—418.
66. М и 1 г Т. А ге1аНоп Ъе{\уееп регтапеп{з гпй сЫегггипап4з. — Ргос. Коу.
8ос, Е<НпЪитф, 1897, V. 22, р. 134—136.
67. Е г о р ы ч е в Г. П. Решение проблемы Ван дер Вардена для перманентов.—
Институт физики им. Л. В. Киреенского СО АН СССР, Препринт
ИФСО—13М. Красноярск, 1980.
68. Ф а л и к м а н Д. И. Доказательство гипотезы Ваи-дер-Вардеиа о
перманенте дважды стохастической матрицы. — Матем. заметки, 1981, т. 29, № 6,
с. 931—938.
•69. Кострикии А. И., Маиин Ю. И. Линейная алгебра и геометрия. —
М.: Изд-во МГУ, 1980.
306

70. Панов А. А. О сигнатуре и ядре билинейной формы, связанной с
перманентом. — Успехи матем. наук, 1984, т. 39, № 6, с. 201—202.
71. \Уаег(1еп В. Ь. уап Лет. Аи{еаЪе 45. — 1Ьег. Веи1зсЬ. Ма1Ь. Уегеш.,
1926, V. 35, р. 117.
72. М а с М а Ь о п Р. А. КезеагсЬез г'п Ше Шеогу оЕ с1е4егтшап4з. — Тгапз.
СатЪгМее РЬМоз. Зое., 1924, V. 23, N 5, р. 89—135.
73. Брэгман Л. М. Некоторые свойства неотрицательных матриц и нх
перманентов. — Докл. АН СССР, 1973, т. 211, № 1, с. 27—30.
74. ЗсЬг1]'уег А. А зЬог4 ргоо{ о{ Мг'пс'з соп]ес4иге. — X СотЫпа4оп'а1 ТЬео-
гу, зег. А, 1978, V. 25, N 1, р. 80—83.
75. Наттегз1еу X М. Ап г'тргоуес! 1о\уег Ъоипй {ог Ше тиШйг'тепзг'опа] И-
тег ргоЫет. — Ргос. СатЬпМ^е РЬМоз. Зое, 1968, V. 64, N 2, р. 455—463.
76. Скорняков Л. А. Проективные плоскости. — Успехи матем. наук, 1951,
т. 6, вып. 6, с. 112—154.
77. Хартсхорн Р. Основы проективной геометрии. — М.: Мир, 1970.
78. Берж К. Теория графов. — М.: ИЛ, 1962.
79. В геез N. Ь., Ь1оус1 Е. К., XV г'1 з о п К. X ОгарЬ ТЬеогу; 1736—1936. —
Ох{огс1: С1агепс1оп Ргезз, 1977.
80. К1 е е V. СотЪша1опа1 орНтг'гаЛоп: \уЬа1 13 1Ье зЫе о{ 1Ье аг4? — Ма1Ь.
Орег. КезеагсЬ, 1980, V. 5, N 1, р. 1—26.
81. Бурков В. Е., Ловецкий С. Е. Методы решения экстремальных
комбинаторных задач. — Изв. АН СССР, сер. техническая кибернетика, 1968, № 4,
с. 82—93.
^82. Феллер В. Введение в теорию вероятностей н ее приложения, т. 1. — М.:
Мир, 1964.
83. В о з е К. С, С Ь о \у 1 а 5. ТЬеогетз ш 1Ье аййНЫе Шеогу о{ питЬегз. —
Соттеп*. МаШ. Не]у., 1962, V. 37, N 2, р. 141—147.
84. Д ь я ч к о в А. Г., Рыков В. В. Об одной модели кодирования для
суммирующего канала с множественным доступом. — Проблемы передачи
информации, 1981, т. 17, № 2, с. 26—39.
85. Ы п с! з I г б т В. Оп В2-зе^иепсез о{ уесгогз. — ,1 о{ МитЪег ТЬеогу, 1972,
V. \, N 3, р. 261—265.
86. МешалкинЛ. Д. К обоснованию метода случайного баланса. —
Заводская лаборатория, 1970, т. 36, № 3, с. 18—27.
87. М а л ю т о в М. Б., П н н с к е р М. С. Замечание о простейшей модели
метода случайного баланса. — В кн.: Вероятностные методы исследования. —
М.: Изд-во МГУ, 1974.
88. Ше^епег I. Оп зерагаНпд зуз4етз \уЬозе е1етеп1з аге зе4з о{ а1 тоз1 к
е1етеп4з. — П!зсге4е Май., 1979, V. 28, N 2, р. 219—222.
89. Л у з г и и В. Н. Разделяющие системы разбиений конечного множества. —
В кн.: Комбинаторный анализ. Вып. 5. — М.: Изд-во МГУ, 1980, с. 39—45.
90. К у р о ш А. Г. Лекции по общей алгебре. — М.: Наука, 1973.
91. Келли Дж. Л. Общая топология. — М.: Наука, 1968.
92. В П V о г I Ь К. Р. А йесотрозШоп Шеогет {ог рагОаНу отйетей зе1з. — Апп.
о! МаШ., зег. 2, 1950, V. 51, N 1, р. 161—166.
93. Стечкин Б. С. Теоремы вложения для мебиус-функций, -г Докл. АН
СССР, 1980, т. 260, № 1, с. 40—43.
94. С г а р о Н. Н. 51П§1е-е1етеп1 ех1еп1г'оп о{ та4гог'(1з. — X Кез. Иаг. Виг.
§1ап(1аг(1з, 1969, V. 69В, р. 55—65.
95. Сгаро Н. Н. Агасгш^ ^еотегпез. — Апп. Кем Уогк Асас!. 5а., 1970,
V. 175, р. 89—92.
96. Ревякин А. М. О наращениях комбинаторных геометрий. — Вестн. Моск.
ун-та, сер. мат., мех., 1976, № 4, с. 59—62.
97. N е и е п Н. 0. Сопзггисгш^ 4Ье {гее агасНоп о{ а §еоте1гу. — X СотЬша-
1оп'а1 ТЬеогу, зег. В, 1979, V. 27, N 2, с. 216—224.
98. В г П а V/ з к у Т. Мос1и]аг сопз4гис1юп {ог сотЫпа1оп'а1 ^еотеМез. — Тгапз.
Атег. Ма1Ь. Зое, 1975, V. 203, р. 1—44.
99. Ш^з О- Зггоп^ тарз о{ ^еотеШез. — X СотЬш. ТЬеогу, 1968, V. 5,
N 2, р. 185—191.
307

100. Нг^дз Г). Марз о{ ^еотеМез. — ^. Ьопёоп МаШ. 5ос, 1966, V. 41, N 4,
р. 612—618.
101. 14§иеп Н. р. Рипсгогз о? Ше саге^огу о\ сотЫпа{оп°а] §-еоте!:гу агк!
зггопе тара. — 0!зсге4е ЛЫЬ., 1977, V. 20, N 2, р. 143—158.
102. Ъ и саз О. Шеак тарз о{ сотЫпагопа] ^еотегпез. — Тгапз Атег Ма1Ь.
5ос, 1975, V. 206, р. 247—279.
103. Зеутоиг Р. Е>. ВесотрозгЧюп о? ге^иЫг таггайз. — Л. СотЪ['па1оп'а1
ТЬеогу, зег. В, 1980, V. 28, N 3, р. 305—359.
104. Старо Н. Н., Ко4а О.-С. Оп 4Ье {оипёагюпз о( СотЫпагопа1 гЬеогу II:
СотЫпагогЫ §еоте4п'ез. — СатЪпй^е Мазз.: М1Т Ргезз, 1970.
105. Мейсон Дж. X. Изучение матроидов как геометрических конфигураций.—
В кн.: Проблемы комбинаторного анализа. — М.: Мир, 1980, с. 7—50.
106. Ь1П(1з{гбт В. Ьесгигез оп та4г01Й8. — 51оск. Шпг., 1974, N 7, р. 1—43.
107. АИгзку Ь. Тгапзуегза1 гЬеогу. — N. V.: Асаёетк Ргезз, 1971.
108. К а п й о \у К. 1п{гойис110п 4о 4Ье {Ьеогу о{ та{го[°с1з. — 11ес4. Могез 1П Есоп.
апс1 Ма№. 5уз1, 1975, V. 109, р. 1—110.
109. ТиНе Ш. Т. Ьесгигез оп тагго^з. — Л. Кез. №1. Виг. о{ Згапйагйз, 1965,
V. 69 В, р. 1—47.
ПО. Ш.е1зЬ О. 3. А. Со1оипп§, Ио\уз апй рго^есНуе §еоте4гу. — №еи\у. агсЬ.
шзк., 1980, V. 28, N 2, р. 159—176.
111. Алексеев В. М., Тихомиров В. М., Фомин С. В. Оптимальное
управление. — М.: Наука, 1979.

Константин.Алексеевич Рыбников
ВВЕДЕНИЕ В КОМБИНАТОРНЫЙ АНАЛИЗ
Зав. редакцией С. И. Зеленский
Редактор А. Ф. Сидоренко
Художественный редактор Л. В. Мухина
Технический редактор Г. Д. Колоскова
Корректоры В. П. Кададинская, С. Ф. Будаева,
Г. В. Зотова
ИБ № 1927
Сдано в набор 16.11.84.
Подписано к печати 21.05.85
Л-103014 Формат 60X90/16 Бумага тип. № 1
Гарнитура литературная Высокая печать
Усл. печ. л. 19,5. Уч.-изд. л. 22,37.
Тираж 4200 экз. Заказ 550
Цена 1 р. 10 к. Изд. № 3186
Ордена «Знак Почета»
издательство Московского университета.
103009, Москва, ул. Герцена, 5/7.
Типография ордена «Знак Почета»
изд-ва МГУ.
119899 Москва, Ленинские горы