Компактные группы Ли и их представления - Желебенко Д.П.

Автор: Желебенко Д.П.

Теги: физика

Год: 1970

Похожие

Основные структуры и методы теории представлений

Лекции по методу орбит. Университетская серия, том 10

Математические основы теории симметрии

Основы дифференциальной геометрии. Том 2

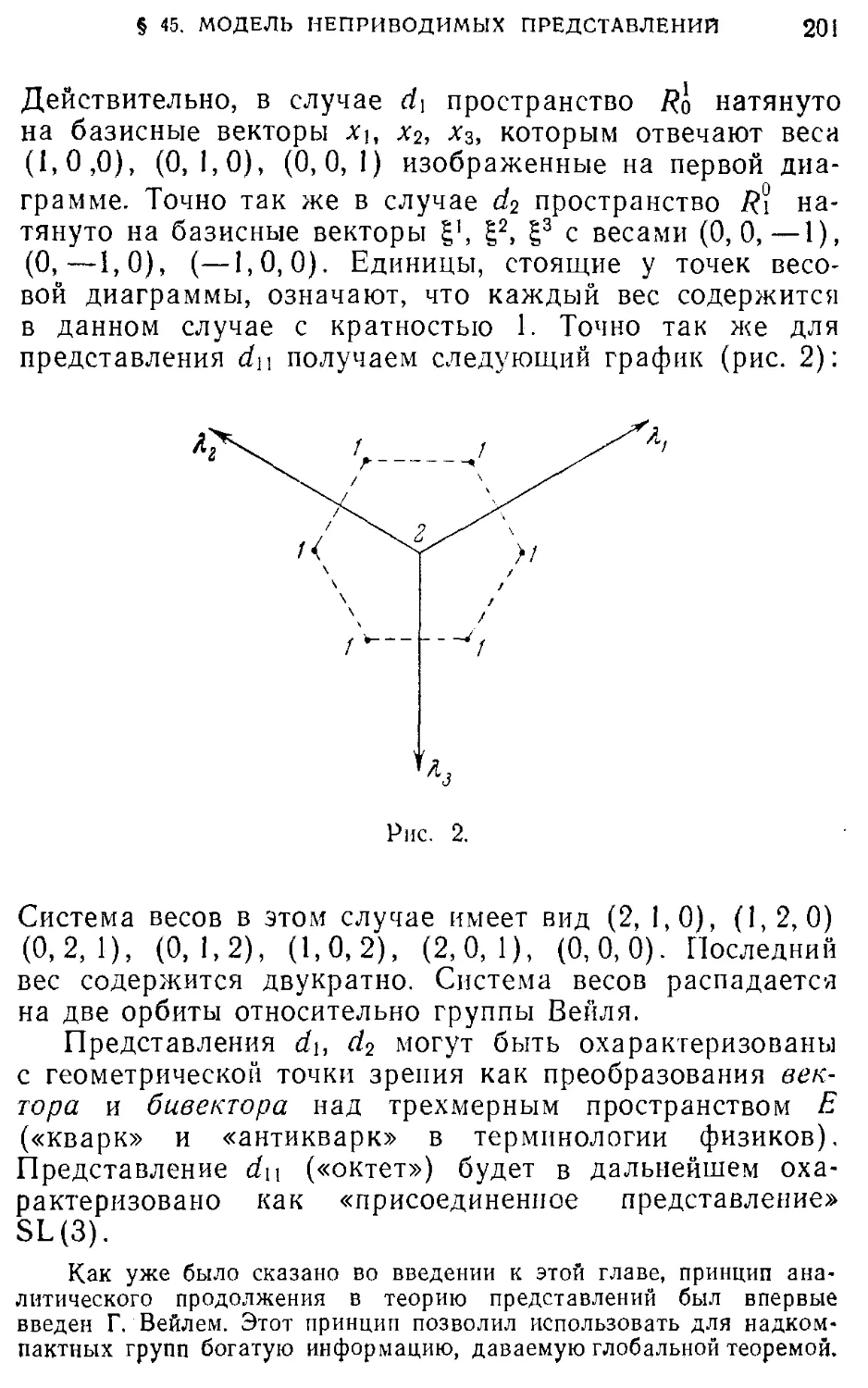
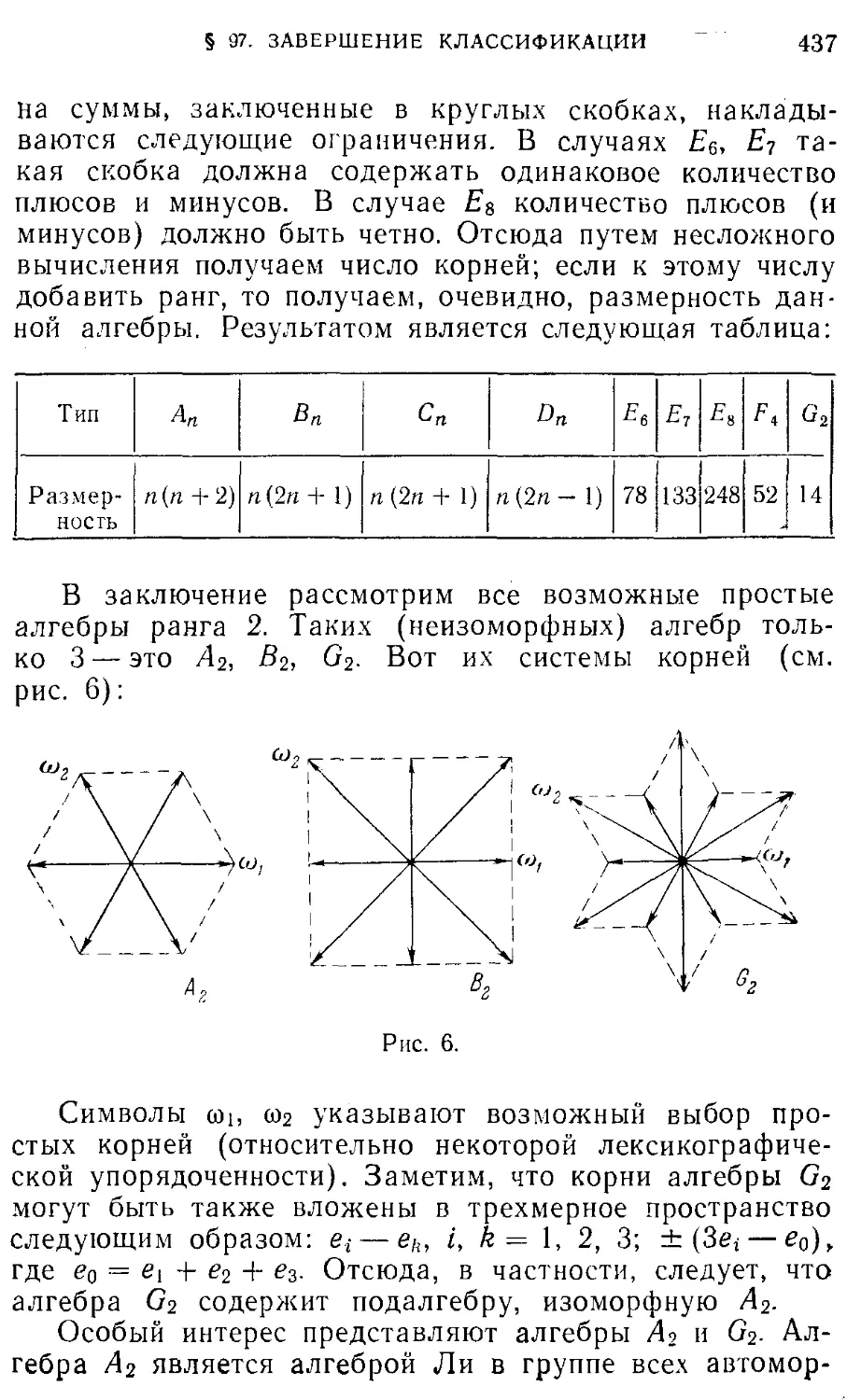
Текст

Д.П.Желобенко
КОМПАКТНЫЕ ГРУППЫ ЛИ И ИХ ПРЕДСТАВЛЕНИЯ
Имея в виду читателей-физиков, автор стремился сделать изложение по
возможности более элементарным. Это, в частности, привело к тому, что
пришлось опустить ряд интересных и глубоких вопросов, связанных с топологией
компактных групп Ли, а также с общей теорией соответствия между группами и
алгебрами Ли. В то же время сравнительно подробно рассматриваются вопросы,
имеющие приложение к современным задачам теоретической физики.
Содержание
Предисловие 3
ЧАСТЬ I. ВВЕДЕНИЕ
Глава I. Топологические группы. Группы Ли 15
§ 1. Определение группы 15
§ 2. Топологические группы 19
§ 3. Параметрические группы и группы Ли 25
§ 4. Теория Ли 28
§ 5. Локально изоморфные группы Ли 34
§ 6. Инвариантные формы на группе Ли 40
§ 7. Метрика. Мера Хаара 42
Глава II. Линейные группы 46
§ 8. Полная линейная группа. Экспоненциал 46
§ 9. Полная линейная группа. Основные разложения 48
§ 10. Линейные группы, связанные с формами второго порядка 53
§ 11. Кватернионы 57
§ 12. Вопросы односвязности 62
§ 13. Вопросы комплексификации 66
§ 14. Преобразования в классе тензоров 68
Глава III. Основные задачи теории представлений 74
§ 15. Функции на однородном пространстве 74
§ 16. Терминология теории представлений 78
§ 17. Редукция основной проблемы 84
§ 18. Элементарные гармоники 86
§ 19. Алгебры и группы, связанные с уравнением 91
§ 20. Лемма Шура 94
§ 21. Теорема Бернсайда 99
§ 22. Групповые алгебры и их представления 103
§ 23. Формулировка основных задач 106
ЧАСТЬ II. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
Глава IV. Компактные группы Ли. Глобальная теорема 111
§ 24. Определение компактной группы 111
§ 25. Формулировка глобальной теоремы 114
§ 26. Прием усреднения 116
§ 27. Свойство ортогональности 119
§ 28. Аппроксимационная лемма для линейной группы G 120

§ 29. Ряды Фурье на линейной группе G 122
§ 30. Завершение доказательства для линейной группы G 124
§ 31. Завершение доказательства в общем случае 12'/
§ 32. Гармонический анализ на однородном многообразии 129
§ 33. Характеры 132
§ 34. Теория представлений конечных групп 134
§ 35. Универсальность группы U(n) 139
Глава V. Инфинитезимальный метод в теории представлений 142
§ 36. Дифференциал представления 142
§ 37. Неприводимые представления группы SU(2) 147
§ 38. Матричные элементы группы SU(2) 157
§ 39. О некоторых группах, связанных с SU(2) 164
§ 40. О некоторых проблемах инфинитезимального метода 170
Глава VI. Аналитическое продолжение 176
§ 41. Общий принцип аналитического продолжения 176
§ 42. Надкомпактные группы Ли. «Унитарный трюк» Г. Вейля 182
§ 43. Бикомплексные группы и алгебры Ли 185
§ 44. Комплексная оболочка U(n). Веса и корни 191
§ 45. Модель неприводимых представлений группы SU(3) 196
Глава VII. Неприводимые представления группы U(n) 203
§ 46. Существование старшего веса 203
§ 47. Единственность старшего вектора 207
§ 48. Различные модели d(a) 210
§ 49. Индуктивные веса 213
§ 50. Произведение Юнга 216
Глава VIII. Тензоры и диаграммы Юнга 220
§ 51. Описание Z- инвариантов 220
§ 52. Диаграммы Юнга 224
§ 53. Симметризаторы Юнга 227
§ 54. Характеристика неприводимых тензоров в терминах симметрии 231
§ 55. Принцип взаимности 237
§ 56. Реализация d(a) на прямоугольных матрицах 241
§ 57. Гармонический осциллятор 244
Глава IX. Операторы Казимира 250
§ 58. Универсальная обертывающая алгебра 250
§ 59. Операторы Казимира для группы GL(n) 255
§ 60. Собственные значения операторов Ск 259
§ 61. Разделение точек спектра и алгебраическое доказательство полной 265
приводимости
§ 62. Полное описание центра для группы GL(n) 269
§ 63. Правило циклов 272
Глава X. Индикаторные системы и базис Гельфанда — Цейтлина 282
§ 64. Операторы левого сдвига на группе Z 282

§ 65. Индикаторные системы 287
§ 66. Алгебра Z-мультипликаторов и задача о сужении с группы на 293
подгруппу
§ 67. Базис Гельфанда — Цейтлина 300
§ 68. Понижающие операторы в инфинитезимальной форме 305
§ 69. Нормировка базисных векторов 315
§ 70. Дифференциал d(a) 320
§ 71. Матричные элементы d(a) 325
Глава XI. Характеры 331
§ 72. Инвариантная мера на группе U(n) 331
§ 73. Примитивные характеры U(n) 335
§ 74. Весовая диаграмма d(a) 338
§ 75. Вторая формула Вейля 345
§ 76. Заключительные замечания 349
Глава XII. Тензорное произведение двух неприводимых представлений 351
группы U(n)
§ 77. Метод характеров 351
§ 78. Метод Z-инвариантов 356
§ 79. Частные случаи 361
§ 80. Детерминанты Вейля 366
ЧАСТЬ III. ОБЩАЯ ТЕОРИЯ
Глава XIII. Основные типы алгебр и групп Ли 373
§ 81. Присоединенное представление алгебры Ли 373
§ 82. Идеал и нормальный делитель 375
§ 83. Основные типы алгебр Ли 377
§ 84. Разрешимые алгебры Ли 381
§ 85. Нильпотептные алгебры Ли 385
§ 86. Разложения Фиттинга 389
§ 87. Билинейная форма Киллинга — Картана 395
§ 88. Основные типы групп Ли 398
§ 89. Теорема Леви — Мальцева 402
Глава XIV. Классификация компактных и редуктивных алгебр Ли 406
§ 90. Компактные алгебры Ли 406
§ 91. Подалгебры Картана 410
§ 92. Базис Картана — Вейля 414
§ 93. Простые корни 417
§ 94. Структурная матрица Картана 421
§ 95. Простые комплексные алгебры Ли 425
§ 96. Вещественные формы полупростых комплексных алгебр Ли 431
§ 97. Завершение классификации 434
Глава XV. Компактные группы Ли в целом 439
§ 98. Инвариантные полиномы 439
§ 99. Алгебраические группы 442

§ 100. Разложение Гаусса 446
§ 101. Разложение Ивасавы 452
§ 102. Максимальные торы 456
§ 103. Фундаментальная группа и центр 462
§ 104. Теорема о линейности полупростой комплексной группы Ли 466
§ 105. Группа Вейля 469
§ 106. Существование комплексной оболочки 474
§ 107. Некоторые дополнительные результаты 480
Глава XVI. Описание неприводимых конечномерных представлений 486
§ 108. Основная теорема 486
§ 109. Старшие веса и сигнатуры 490
§ 110. Нормально вложенные подгруппы 494
§ 111. Полиномы на группе Z 496
§ 112. Завершение классификации 501
§ ИЗ. Симплектическая группа 506
§ 114. Ортогональная группа 514
§ 115. Теория спиноров 521
§ 116. Вещественные формы 526
§ 117. Произвольные связные группы Ли 529
§ 118. Несколько замечаний 532
Глава XVII. Инфинитезимальная теория (характеры, веса, операторы 539
Казимира)
§ 119. Разложение Картана — Вейля в универсальной обертывающей 539
алгебре
§ 120. Представления со старшим вектором 542
§ 121. Классификация конечномерных неприводимых представлений 546
алгебры X
§ 122. Формула Фрейденталя 550
§ 123. Формула Вейля для характеров 556
§ 124. Следствия из формулы Вейля 563
§ 125. Полиномы на картановской подалгебре, инвариантные относительно 565
группы Вейля
§ 126. Операторы Казимира 569
§ 127. О вычислении собственных значений операторов Казимира 573
Глава XVIII. Некоторые задачи спектрального анализа 579
конечномерных представлений
§ 128. Общая схема сужения с группы на подгруппу 579
§ 129. Сужение SO(n)/SO(n—1) 582
§ 130. Сужение Sp(n)/Sp(n—2) 587
§ 131. Тензорное произведение двух неприводимых представлений 590
§ 132. Сужения SU(m+n)/SU(m) X SU(n) и SU(mn)/SU(m) X SU(n) 592
§ 133. Сужение ^^(n)/SO(n) 596
§ 134. Сферические функции в п-мерном евклидовом пространстве 601
§ 135. О представлениях группы движений n-мерного евклидова 606

пространства
Добавление I. О бесконечномерных представлениях полупростой 611
комплексной группы Ли
§ 1. Элементарные представления 611
§ 2. Пространство элементарного представления 613
§ 3. Дифференциал элементарного представления 614
§ 4. Вопросы неприводимости 616
§ 5. Аналог формулы Планшереля 617
§ 6. Теоремы типа Пэли — Винера 619
§ 7. Минимальные представления 620
§ 8. Классификация неприводимых представлений 621
§ 9. О полуприводимых представлениях 622
Добавление II. Элементы обшей теории унитарных представлений локально 623
компактных групп
§ 1. Коммутативные группы 623
§ 2. Теорема Стоуна — фон Неймана 625
§ 3. Индуцированные представления 628
§ 4. Полупрямые произведения 631
§ 5. Нильпотентные группы Ли 633
§ 6. Разложение унитарных представлений на неприводимые 635
Добавление III. Унитарная симметрия в классе элементарных частиц 638
§ 1. Инвариантность и законы сохранения 638
§ 2. Элементарные частицы. Изотопический спин 641
§ 3. Унитарная симметрия в классе адронов 643
§ 4. Открытие Q-частицы 647
§ 5. Некоторые проблемы 648
Литература 650
Предметный указатель 660
Предметный указатель
линейная 48, 386
нильпотентная 380, 388
особая простая 435
полупростая 378, 397
простая 378
разрешимая 380, 381, 385, 395
редуктивная 377, 401
Базис Гельфанда—Цейтлина 302
— Картана—Вейля 415, 426
Блок-алгебра 481
Вектор аналитический 175
— вакуума 246
— дифференцируемый 145
— доминантный 353
Автоморфизм группы 17
внутренний 17
— зеркальный в S0(n) 515
— инволютивный 433
Алгебра (ассоциативная) 46
— групповая 105
— Клиффорда 65, 521
— коммутаторная 91, 96
— Ли 32
бикомплексная 186
классическая 435
коммутативная 34
компактная 406
комплексная 66

— инвариантный 79
— старший (младший) 151, 196, 487,
542
— строго доминантный 558
— целочисленный 557
Векторное поле на группе Ли 40
— — — — — ковариантное 40
Вес алгебры Ли 390
— индуктивный 213, 490
— инфинитезимальный 295, 492
— старший (младший) 151, 195, 205,
487, 542
Геодезические в группе Ли 44
компактной группе Ли 457, 459
Гомеоморфизм 63
Гомоморфизм 34
Группа 15
— абелева 16, 398, 399
— алгебраическая 442
— аналитическая 27
— вращений SO (3, R) 16,61, 164
— Вейля 194, 470
— дискретная 20
— коммутативная 16
— компактная 112
— комплексно ортогональная O(n, C)
55
— конечная 16
— Ли 27
бикомплексная 186
компактная 112
— — комплексная 66
локальная 174
— — надкомпактная 398
нильпотентная 182
полупростая 398, 401
простая 398, 401
разрешимая 398
редуктивная 398, 401
— — связная 27
— линейная 21
классическая 57
— локально евклидова 25
Группа локально связная 26
— матричная 21
— нильпотентная 399
— односвязная 38
— ортогональная О(п) 23, 55,112
— ортогонально-унитарная,
OU(n) 56
— параметрическая 25
— полная линейная GL(n) 21, 22, 46,
64
— псевдоортогональная O(p,q) 55,
112
— псевдоунитарная U(p,q) 56, 112
— Пуанкаре (фундаментальная) 39,
464
— разрешимая 399
— симметрии оператора -92
— симметрическая S(n) 136
— симплектическая Sp(n) 55, 506
— симплектически унитарная SpU(n)
57
— собственно ортогональная SO(n)
56, 514
унитарная SU(n) 56, 62, 63
— спинорная Spin (n) 66, 521
— унимодулярная SL(n) 48, 64
— унитарная U(n) 49, 56, 64, 112, 139
— циклическая 138
Делитель дискретный 39
— нормальный 18, 375
Детерминанты Вейля 366
Диаграмма весовая 194
— Юнга 226
Дифференциал представления 143
— d(a) 320
Дифференцирование в алгебре Ли
373, 398
— внутреннее 374
Идеал в алгебре Ли 375
ассоциативной алгебре 102, 440
Изоморфизм групп Ли 34
— локальный 36
SO(3,R), SU(2) 60, 374
Индикаторная система 287 357 496,
497, 581

Камера Вейля 470
Кватернион вещественный 60
— комплексный 57
— сопряженный 58
Класс смежности в группе 63
— сопряженных элементов 132
Коммутатор в алгебре Ли 32
ассоциативной алгебре 32, 48,
106, 251
— — группе 31
Комплексная оболочка
(комплексификация) алгебры
(группы) Ли 67
правильная 177
Компонента единицы связная 20
— представления 80
Корень в алгебре Ли 391
— простой 418
Корневая система полупростой
алгебры Ли 412, 420, 426
простой алгебры Ли 436
— — фундаментальная 474
Корневое подпространство 391
Коэффициенты Клебша — Гордана
108, 362
Критерий полупростоты 397
— разрешимости Картана 395
Лемма Больцано-Вейерштрасса 111
— Гейне — Бореля 111,
— Шура 94
Матрица 21
— Клебша — Гордана 351, 481
— положительно определенная 49
—, след 43, 48
— структурная Картана 421
— трансформационная 40
Матрицы Паули 58
Матричные элементы группы 87
, свойство ортогональности
119
SU(2) 157
— — представления 87
Мера (объем) множества 45
— на группе 45
Мера на группе право (лево-)
инвариантная 45
— Хаара 45
на компактной группе Ли 113
Метрика риманова 43
Множество (абстрактное) 15
— компактное в метрическом
пространстве 111
— матриц неприводимое 99
— — приводимое 99
Мультиплет группы Ли 531
Обмотка тора иррациональная 77,
140, 170
Оболочка ассоциативная алгебры Ли
106
— бикомплексная алгебры Ли 185
группы Ли 186
— комплексная группы Ли 67
правильная 177, 467, 480
Образующая тора иррациональная
140, 460
Образующие в группе 26
Оператор Гамильтона 92, 638
— инфинитезимальный 143
— Лапласа 92
— массы-энергии 247
— переплетающий 82
Операторы Бозе 245
— Казимира 147, 149, 254, 569
Орбита (траектория) точки 77, 86
Осциллятор гармонический 245
Параметры Кэли — Клейна 60
Подалгебра алгебры Ли 33
— Картана 410, 447, 461, 468
— —, автоморфизмы 424
Подгруппа 17
— аналитическая 33
— борелевская 611
— инвариантная 18
— Картана 451, 461, 468
— коммутаторная 401
— максимальная компактная 468
— нормально вложенная 494, 582
Подгруппа однопараметрическая 29

— однопараметрическая,
производящий оператор 143
— регулярно вложенная 582
— стационарная 84
Подпространство инвариантное 79
— неприводимое 80
— нетривиальное 79
Поливекторы 217
Полином гармонический 164
Полугруппа 218
Представление алгебры Ли 144, 374
— — — контрагредиентное 145
— аналитическое
(антианалитическое) 178, 188
— группы 76, 78
— — вполне приводимое 80
— — дуальное 96
— — квазирегулярное 85
— — контрагредиентное 81, 95
полуприводимое 169, 606, 622
— — приводимое 80
присоединенное 374
— —, размерность 79
регулярное 85
— — топологически неприводимое
89
унитарное 82
— индуцированное 629
— кратное 80
— полуприводимое 169
— спинорное 165, 518, 586
— точное (изоморфное) 108, 115, 467
— циклическое со старшим весом
542
Представления эквивалентные 79
Принцип аналитического
продолжения 181
— взаимности (для вполне
приводимых матричных
алгебр)102
— полной приводимости 115
Произведение локально прямое
(топологических групп) 186
— полупрямое 631
— прямое групп 24
Произведение прямое
топологических пространств 63
— тензорное операторов 70
представлений алгебры Ли 145
групп 81, 351, 590
— Юнга 218, 491
Пространство линейное 21
— — сопряженное (дуальное) 69
— — топологическое 89
— однородное 75
— — универсальное 84
— топологическое 19, 20
компактное 112
локально компактное 113
Радикал алгебры Ли 402
Разложение Гаусса в GL(n) 51
полу простой комплексной
группе Ли 450
обобщенное 451, 494
— Грама в GL(n) 52
— Ивасавы 456
— Картана 434
— Картана — Вейля 447, 540
— полярное в алгебре кватернионов
61
GL(n) 49
— Фиттинга в алгебре Ли 392, 411
Ряд Кемпбелла — Хаусдорфа 32
— Фурье на компактной группе Ли
115, 122
— — на однородном пространстве с
компактной группой движений
132
— — по характерам 133
Сигнатура 225, 492
Симметризаторы Юнга 227
центральные 230
Симметрия относительно точки 457
Соотношения Клебша — Гордана 476
Структурные константы 33
Схемы Дынкина 428, 435
Тело кватернионов 60
—— —, автоморфизмы 61

Тензор 43, 71
— ковариантный
(контравариантный) 71
— кососимметрический 44, 72
— метрический 43
— симметрический 72
— смешанный 71
Теорема Биркгофа — Витта 254
— Веддерберна 102
— глобальная (для компактной
группы Ли) 114
— Картана 468
— Кириллова 633
— Леви — Мальцева 402
— Ли 382, 384
— — глобальная 400
— Наймарка 625
— Петера — Вейля (основная
аппроксимационная) 115
— Стоуна — Вейерштрасса 121
— Стоуна —фон Неймана 625, 627
— Хана — Банаха 126
— Шевалле 566
— Энгеля 386
Теоремы Бернсайда 100, 135
Теория двойственности 108, 480
— представлений конечных групп
134
Тор двумерный 63
— максимальный 459
Универсальная линейная группа 529
— накрывающая 38
компактной группы Ли 140, 462
— обертывающая алгебра 106, 251
.центр 271, 569
Усреднение по Гурвицу 116
Фактор-алгебра 376
Фактор-группа 376 Фактор-
пространство 62
Фактор-топология 62
Форма билинейная 53
Киллинга — Картана 395, 397,
427
— вещественная алгебры (группы)
Ли 67, 431, 434
Форма дифференциальная 41
— — право (лево-) инвариантная 41
— ковариантная (контравариантная)
72
— кососимметрическая 72
— полилинейная 72
— симметрическая 72
— эрмитова (полуторалинейная) 53
Формула Костанта 564
— Фрейденталя 550
Формулы Вейля для характеров 338,
347, 561
Функции сферические 163, 601
— шаровые 163
Функция волновая 638
Характер абелевой группы 99
— представления 133, 331
— примитивный 335
Центр алгебры Ли 376
— группы 39, 376
— компактной группы Ли 140, 462
— универсальной обертывающей
алгебры 254, 271
Централизатор 172
Центральный ряд в алгебре Ли 388
группе Ли 399
— элемент группы 39
Экспоненциал 46
Экспоненциальное отображение (ехр)
31, 47, 456
Элемент регулярный в алгебре
(группе) Ли 463
Ядро гомоморфизма 34
Z-инвариантов метод 209, 221, 356,
580
Z-мультипликаторы 294
Содержание этой книги несколько отличается от традиционного понимания
темы «Компактные группы Ли и их представления». Прежде всего, имея в виду

читателей-физиков, автор стремился сделать изложение по возможности более
элементарным. Это, в частности, привело к тому, что пришлось опустить ряд
интересных и глубоких вопросов, связанных с топологией компактных групп Ли,
а также с общей теорией соответствия между группами и алгебрами Ли. В то же
время сравнительно подробно рассматриваются вопросы, имеющие приложение к
современным задачам теоретической физики. Стремление к элементарности
изложения сказалось также и в самом расположении материала (книга разбита на
три части, в значительной степени независимые друг от друга, с постепенным
возрастанием сложности изложения). С другой стороны, помимо компактных
групп Ли в этой книге рассматриваются также группы иной топологической
природы (которые связаны с компактными группами некоторым «соотношением
родства»). Это прежде всего редуктивные комплексные группы Ли (в том числе
полупростые), получаемые из компактных групп Ли путем аналитического
продолжения, а также их вещественные формы (редуктивные вещественные
группы Ли). Развивается теория конечномерных представлений для указанных
классов групп, причем повсюду, где возможно, автор стремится подчеркнуть
«компактную порожденность» этих представлений, т. е. их аналитические связи с
представлениями компактных групп Ли. Рассматриваются также
бесконечномерные представления полупростых комплексных алгебр Ли (гл.
XVII). Некоторые аспекты теории бесконечномерных представлений групп Ли
излагаются в виде краткого обзора в добавлениях I и II.
Указанный подход к изложению данной темы в то же время, конечно, не
является совершенно новым; он следует традициям известной монографии Г.
Вейля «Классические группы, их инварианты и представления» (в которой автор,
оставляя в стороне «горные массивы топологии», в значительной степени
ориентируется на проблемы развивающейся квантовой механики). Название
нашей книги выбрано не случайно; оно отражает преемственность и стремление
автора дать современные комментарии хотя бы к некоторым разделам
классической книги Вейля. Действительно, с момента выхода этой книги (1939 г.)
прошло уже около 30 лет. С тех пор достигнута известная завершенность как в
структурной теории компактных групп Ли, так и в общей теории их линейных
представлений. Это, в частности, позволяет подходить к теории представлений не
инфинитезимально, как это делалось в первоначальных работах Э. Картана и Г.
Вейля, а глобально, т. е. с точки зрения группы в целом.
Понятие группы существенно связано с понятием симметрии, будь то
симметрия фигуры относительно некоторых геометрических преобразований или
симметрия уравнений относительно функциональных преобразований в классе
переменных. Первоначально простейшие (конечные) группы были введены в
математику Эвари-стом Галуа (1832 г.) в связи с вопросами симметрии
алгебраического уравнения относительно подстановок его корней. Софус Ли
имел своей целью построение аналогичной теории для дифференциальных
уравнений с непрерывными группами преобразований; в результате возникла
специальная теория определенного класса непрерывных групп, называемых
теперь группами Ли. Геометрическим группам преобразований отводится

принципиальная роль в знаменитой «Эрлангенской программе» Ф. Клейна.
Известные работы Э. Картана и Г. Вейля посвящены классификации
геометрических объектов (тензоров, спиноров) относительно некоторых групп
преобразований; этими работами, по существу, завершается классический этап в
развитии теории групп Ли и их представлений. В дальнейших исследованиях, с
одной стороны, уделялось особое внимание топологии группового пространства
(Р. Брауэр, Г. Вейль, Л. С. Понтрягин, К. Шевалле, А. И. Мальцев и др.), что
позволило дать законченную классификацию важнейших типов групп Ли и их
конечномерных представлений. С другой стороны, с начала 50-х годов, после
известных работ И. М. Гельфанда и М. А. Наймарка, происходит интенсивное
развитие теории бесконечномерных представлений (не только групп Ли, но также
более широкого класса локально компактных групп). Эти вопросы в свою
очередь связаны с вопросами симметрии в современной квантовой теории поля.
Теория групп Ли в современном понимании в значительной степени связана с
теорией линейных представлений. Понятие представления, или «обобщенной
экспоненты», позволяет проследить глубокую связь между такими, казалось бы,
различными вопросами, как теория тензоров и гармонический анализ (ряды и
интегралы Фурье). Алгебраические основы этой теории были заложены Г.
Фробениусом на рубеже XX века; уже тогда было ясно, что эта теория имеет
тесную связь с теорией ассоциативных алгебр, которая постепенно занимает одно
из главнейших мест в современной математике. Современная теория
представлений в значительной степени может быть интерпретирована как
абстрактный гармонический анализ. Если ограничиться компактными группами
Ли, то мы получаем замечательное обобщение классической теории рядов Фурье,
где «обобщенные экспоненты» специального типа (неприводимые представления)
играют роль элементарных гармоник. В настоящее время хорошо известно, что
таким путем может быть получена универсальная теория специальных функций
математической физики. Дальнейшее развитие этой теории, несомненно, будет
происходить под влиянием квантовой теории поля.
Несмотря на то, что с момента создания теории относительности (А.
Эйнштейном) принципиальная роль теории групп в теоретической физике стала
очевидной, физики долгое время игнорировали общую теорию групп Ли,
ограничиваясь рассмотрением некоторых конечных групп (кристаллография),
группы движений трехмерного евклидова пространства и группы Лоренца.
Положение резко изменилось за последние годы благодаря замечательным
успехам теоретико-группового подхода в классификации элементарных частиц.
Классификация адронов и предсказание Q-частицы на основе этого подхода
показали, что методы теории групп позволяют установить определенные
закономерности в «хаосе» элементарных частиц, т. е. в той области, где даже
неизвестны уравнения динамики (но известны некоторые свойства симметрии).
Более подробному обзору этих результатов посвящается в нашей книге
добавление III.
Эта книга возникла из курса лекций, прочитанных автором для физиков-
теоретиков Объединенного института ядерных исследований (г. Дубна) в январе

— феврале 1965 г. (Однако идея написания книги появилась еще в 1961 г., когда
автору удалось предложить некоторое законченное описание для неприводимых
представлений связных групп Ли в конечномерных векторных пространствах, по
аналогии с индуцированными представлениями Гельфанда — Наймарка.) .Автор
отдает себе отчет в том, что лекционный характер изложения в значительной
степени сохранился в этой книге; соответственно эта книга ни в коей мере не
претендует на роль учебника или систематической монографии. Автор считал бы
свою задачу выполненной, если бы эта книга подготовила читателя к чтению
более специальной математической литературы.
Относительно вопросов, лишь частично затронутых в этой книге, мы
сошлемся на известные монографии Л. С. Понтрягина [38], К. Шевалле [46], Н.
Джекобсона [19], Ж.-П. Серра [40] по общей теории групп и алгебр Ли, на книгу
С. Хелгасона [42] по теории симметрических пространств, а также на недавно
вышедшую книгу Н. Я. Виленкина [14] по групповой теории специальных
функций. В нашем тексте мы почти не затрагиваем теорию специальных
функций; однако алгебраический аппарат, развиваемый в этой книге, может быть
положен в основу этой общей теории.
Несмотря на то, что физиков в первую очередь интересуют не доказательства,
а сводки результатов, автор всюду стремился проследить внутренние связи
развиваемой теории. Более того, местами мы используем «многоплановое»
изложение, т. е. получаем один и тот же результат различными способами. Здесь
сказалось убеждение автора в том, что для творческой работы с аппаратом теории
групп необходимо знакомство не только с результатами, но и с методами этой
теории.

ПРЕДИСЛОВИЕ
Содержание этой книги несколько отличается от тра¬
диционного понимания темы «Компактные группы Ли и
их представления». Прежде всего, имея в виду читате-
лей-физиков, автор стремился сделать изложение по воз¬
можности более элементарным. Это, в частности, при¬
вело к тому, что пришлось опустить ряд интересных и
глубоких вопросов, связанных с топологией компактных
групп Ли, а также с общей теорией соответствия между
группами и алгебрами Ли. В то же время сравнительно
подробно рассматриваются вопросы, имеющие приложе¬
ние к современным задачам теоретической физики.
Стремление к элементарности изложения сказалось так¬
же и в самом расположении материала (книга разбита
на три части, в значительной степени независимые друг
от друга, с постепенным возрастанием сложности изло¬
жения). С другой стороны, помимо компактных групп
Ли в этой книге рассматриваются также группы иной
топологической природы (которые связаны с компакт¬
ными группами некоторым «соотношением родства»).
Это прежде всего редуктивные комплексные группы Ли
(в том числе полупростые), получаемые из компактных
групп Ли путем аналитического продолжения, а также
их вещественные формы (редуктивные вещественные
группы Ли). Развивается теория конечномерных пред¬
ставлений для указанных классов групп, причем по¬
всюду, где возможно, автор стремится подчеркнуть
«компактную порожденность» этих представлений, т. е.
их аналитические связи с представлениями компактных
групп Ли. Рассматриваются также бесконечномерные
представления полупростых комплексных алгебр Ли
(гл. XVII). Некоторые аспекты теории бесконечномер-

ПРЕДИСЛОВИЕ
9
ных представлений групп Ли излагаются в виде краткого
обзора в добавлениях I и II.
Указанный подход к изложению данной темы в то же
время, конечно, не является совершенно новым; он сле¬
дует традициям известной монографии Г. Вейля «Клас¬
сические группы, их инварианты и представления» (в
которой автор, оставляя в стороне «горные массивы то¬
пологии», в значительной степени ориентируется на про¬
блемы развивающейся квантовой механики). Название
нашей книги выбрано не случайно; оно отражает преем¬
ственность и стремление автора дать современные ком¬
ментарии хотя бы к некоторым разделам классической
книги Вейля. Действительно, с момента выхода этой
книги (1939 г.) прошло уже около 30 лег. С тех пор до¬
стигнута известная завершенность как в структурной
теории компактных групп Ли, так и в общей теории их
линейных представлений. Это, в частности, позволяет
подходить к теории представлений не инфинитезимально,
как это делалось в первоначальных работах Э. Картана
и Г. Вейля, а глобально, т. е. с точки зрения группы в
целом.
Понятие группы существенно связано с понятием сим¬
метрии, будь то симметрия фигуры относительно неко¬
торых геометрических преобразований или симметрия
уравнений относительно функциональных преобразова¬
ний в классе переменных. Первоначально простейшие
(конечные) группы были введены в математику Эвари¬
стом Галуа (1832 г.) в связи с вопросами симметрии
алгебраического уравнения относительно подстановок
его корней. Софус Ли имел своей целью построение
аналогичной теории для дифференциальных уравнений
с непрерывными группами преобразований; в результате
возникла специальная теория определенного класса не¬
прерывных групп, называемых теперь группами Ли. Гео¬
метрическим группам преобразований отводится прин¬
ципиальная роль в знаменитой «Эрлангенской програм¬
ме» Ф. Клейна. Известные работы Э. Картана и Г. Вейля
посвящены классификации геометрических объектов
(тензоров, спиноров) относительно некоторых групп пре¬
образований; этими работами, по существу, завершается
классический этап в развитии теории групп Ли и их

10
ПРЕДИСЛОВИЕ
представлений. В дальнейших исследованиях, с одной
стороны, уделялось особое внимание топологии группо¬
вого пространства (Р. Брауэр, Г. Вейль, Л. С. Понтря-
гин, К. Шевалле, А. И. Мальцев и др.), что позволило
дать законченную классификацию важнейших типов
групп Ли и их конечномерных представлений. С другой
стороны, с начала 50-х годов, после известных работ
И. М. Гельфанда и М. А. Наймарка, происходит интен¬
сивное развитие теории бесконечномерных представле¬
ний (не только групп Ли, но также более широкого клас¬
са локально компактных групп). Эти вопросы в свою
очередь связаны с вопросами симметрии в современной
квантовой теории поля.
Теория групп Ли в современном понимании в значи¬
тельной степени связана с теорией линейных предста¬
влений. Понятие представления, или «обобщенной экспо¬
ненты», позволяет проследить глубокую связь между та¬
кими, казалось бы, различными вопросами, как теория
тензоров и гармонический анализ (ряды и интегралы
Фурье). Алгебраические основы этой теории были зало¬
жены Г. Фробениусом на рубеже XX века; уже тогда
было ясно, что эта теория имеет тесную связь с теорией
ассоциативных алгебр, которая постепенно занимает
одно из главнейших мест в современной математике. Со¬
временная теория представлений в значительной степени
может быть интерпретирована как абстрактный гармони¬
ческий анализ. Если ограничиться компактными груп¬
пами Ли, то мы получаем замечательное обобщение
классической теории рядов Фурье, где «обобщенные экс¬
поненты» специального типа (неприводимые предста¬
вления) играют роль элементарных гармоник. В настоя¬
щее время хорошо известно, что таким путем может быть
получена универсальная теория специальных функций
математической физики. Дальнейшее развитие этой тео¬
рии, несомненно, будет происходить под влиянием кван¬
товой теории поля.
Несмотря на то, что с момента создания теории отно¬
сительности (А. Эйнштейном) принципиальная роль тео¬
рии групп в теоретической физике стала очевидной, фи¬
зики долгое время игнорировали общую теорию групп
Ли, ограничиваясь рассмотрением некоторых конечных

ПРЕДИСЛОВИЕ
11
групп (кристаллография), группы движении трехмер¬
ного евклидова пространства и группы Лоренца. Поло¬
жение резко изменилось за последние годы благодаря
замечательным успехам теоретико-группового подхода в
классификации элементарных частиц. Классификация
адронов и предсказание Q-частицы на основе этого под¬
хода показали, что методы теории групп позволяют уста¬
новить определенные закономерности в «хаосе» элемен¬
тарных частиц, т. е. в той области, где даже неизвестны
уравнения динамики (но известны некоторые свойства
симметрии). Более подробному обзору этих результатов
посвящается в нашей книге добавление III.
Эта книга возникла из курса лекций,прочитанных ав¬
тором для физиков-теоретиков Объединенного института
ядерных исследований (г. Дубна) в январе — феврале
1965 г. (Однако идея написания книги появилась еще в
1961 г., когда автору удалось предложить некоторое за¬
конченное описание для неприводимых представлений
связных групп Ли в конечномерных векторных простран¬
ствах, по аналогии с индуцированными представлениями
Гельфанда — Напмарка.) .Автор отдает себе отчет в том,
что лекционный характер изложения в значительной сте¬
пени сохранился в этой книге; соответственно эта книга
ни в коей мере не претендует на роль учебника или си¬
стематической монографии. Автор считал бы свою за¬
дачу выполненной, если бы эта книга подготовила
читателя к чтению более специальной математической
литературы.
Относительно вопросов, лишь частично затронутых в
этой книге, мы сошлемся на известные монографии
Л. С. Понтрягина [38], К. Шевалле [46], Н. Д ж е-
кобсона [19], Ж.-П. Серра [40] по общей теории
групп и алгебр Ли, на книгу С. Хелгасона [42] по тео¬
рии симметрических пространств, а также на недавно
вышедшую книгу Н. Я. Виленкина [14] по групповой
теории специальных функций. В нашем тексте мы почти
не затрагиваем теорию специальных функций; однако
алгебраический аппарат, развиваемый в этой книге, мо¬
жет быть положен в основу этой общей теории.
Несмотря на то, что физиков в первую очередь инте¬
ресуют не доказательства, а сводки результатов, автор

12
ПРЕДИСЛОВИЕ
всюду стремился проследить внутренние связи развивае¬
мой теории. Более того, местами мы используем «много¬
плановое» изложение, т. е. получаем один и тот же
результат различными способами. Здесь сказалось убеж¬
дение автора в том, что для творческой работы с аппа¬
ратом теории групп необходимо знакомство не только
с результатами, но и с методами этой теории.
Автор пользуется случаем выразить благодарность
проф. М. А. Наймарку и А, И. Штерну, критические за¬
мечания которых значительно содействовали улучшению
рукописи этой книги.
Москва,
.1 марта 1968 г.
Д. Желобенко

ЧАСТЬ I
ВВЕДЕНИЕ

В этом введении, состоящем из трех глав, помимо
основных определений, соглашений о терминологии и т. д.
дается краткий обзор теории групп Ли, а также изла¬
гается сравнительно элементарный круг вопросов, свя¬
занный с линейными группами и линейными представле¬
ниями абстрактных групп. Читатель, знакомый с этими
вопросами, может непосредственно перейти к следующим
частям II и III («.Элементарная теория», «Общая тео¬
рия»).
Изложение могло бы выиграть в систематичности,
если начать его непосредственно с теории линейных
групп и линейных представлений, не затрагивая общей
теории групп Ли. Однако теория групп Ли (главным об¬
разом теория соответствия между группами и алгебрами
Ли) дает во многих случаях наиболее естественный под¬
ход к теории представлений. Поскольку теория групп
Ли систематически в этой книге не излагается, мы стре¬
мились пользоваться результатами этой теории по воз¬
можности иллюстративно. (Однако в части II теория
групп Ли существенно используется при доказательстве
линейности компактной группы Ли.) В то же время для
класса линейных групп важнейшие вопросы теории групп
Ли будут изложены с доказательствами в части III.
Большинство определений, касающихся общей топо¬
логии и общей теории групп Ли, излагаются в части I
также без соблюдения всех деталей «математической
строгости» (однако с таким расчетом, чтобы математи¬
чески образованный читатель мог без труда заменить их
«строгими» определениями). В конце каждой главы ука¬
зывается литература, где читатель при желании может
найти подробное изложение всех отмеченных здесь
вопросов.

ГЛАВА I
ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
Понятие группы первоначально возникло при изу¬
чении конкретных «операций», связанных законом
«умножения», или «композиции». Группа относится к
числу основных алгебраических структур (алгебра, по¬
ле, кольцо и т. д.), наделенных бинарной операцией
умножения. Частные случаи этого понятия — главным
образом группы преобразований — играют принципиаль¬
ную роль во многих задачах геометрии и физики.
§ 1. Определение группы
Абстрактное множество G называется группой, если:
(1) для любой пары его элементов g\, g2 определено
произведение g\g2, ассоциативное*) и, вообще говоря,
некоммутативное;
(2) существует единица е, т. е. элемент, обладающий
свойством eg = ge = g при любом g е G\
(3) для каждого g е G существует обратный эле¬
мент g~l:
gg= g~'g = е.
Нетрудно видеть, что единица е определяется аксио¬
мой (2) однозначно. Действительно, если в\, е2 — едини¬
цы, то их произведение должно совпадать как с eiy так
и с е2, откуда в\ = е2. Далее, поскольку умножение не¬
коммутативно, можно было бы вместо (3) отдельно вве¬
сти понятия левого и правого обратного элемента; одна¬
ко если уравнение xg — е разрешимо при любом g е G,
то, умножая его справа на х и слева на у, для кото¬
рого ух — е, находим gx = е\ следовательно, элемент х
*) То есть {ху)г — х(уг) для любых О.

16
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
является также и правым обратным для g. При том же
предположении легко проверить, что левая единица яв¬
ляется также и правой единицей, а также что g~l опре¬
деляется однозначно. Действительно, если xg = е, yg = е,
то также gy = е, откуда
* = xgy = У-
С конкретными примерами групп мы часто встре¬
чаемся в приложениях, особенно в геометрии. Обычно
элементами группы являются некоторые однотипные опе¬
рации, а произведение gig2 состоит в применении опера¬
ции g2 и затем операции gr, единица е соответствует со¬
стоянию неизменности.
Пример ы.
1. Группа вращений окружности. Каждое
вращение g(a) задается углом а, —л а < л; g(0) — е.
2. Группа сдвигов на прямой. Каждый сдвиг
g(t) задается вещественным числом t, —оо</<оо;
g( 0) = е.
3. Группа вращений сферы в трехмерном
евклидовом пространстве. Каждое вращение
может быть задано, например, тремя углами Эйлера.
В отличие от первых двух групп, эта группа некоммута¬
тивна (проверьте).
4. Группа всех унитарных операторов в
гильбертовом пространстве Я.
5. Группа всех подстановок над п эле¬
ментам и.
Последняя группа конечна, т. е. содержит лишь ко¬
нечное число элементов. Первые две группы коммута¬
тивны, или абелевы. Если dim Я = оо (размерность про¬
странства Я бесконечна), то группа в примере 4 не
может быть естественным образом параметризована с
помощью конечного числа вещественных параметров.
Подобные группы, как правило, мы в этой книге рас¬
сматривать не будем.
Становясь на абстрактную точку зрения, мы интуи¬
тивно интерпретируем группу как некое точечное мно¬
жество, конечное или бесконечное, иногда допускающее
аналитическое описание. Групповая операция умноже¬
ния дает нам при этом возможность рассматривать в

§ 1. ОПРЕДЕЛЕНИЕ ГРУППЫ
17
самой группе G естественные преобразования, порождае¬
мые элементами из G. Мы приводим ниже основные
типы таких преобразований; при этом, как уже было
сказано, группа G одновременно выступает в качестве
преобразуемого множества и также в качестве группы
преобразований.
I. Левый и правый сдвиги (трансляции):
g-^gog, g-^ggo-
Замечательным свойством группового сдвига (левого или
правого) является его транзитивность. Это означает, что
с помощью сдвига можно любую точку gieG перевести
в любую точку g2 е G. Действительно, это следует без
труда из аксиомы (3).
II. Инверсия: g-*-g_1. Заметим, что инверсия ме¬
няет местами левые и правые сдвиги. Действительно,
(.ab)-1 = Ь~'а~1.
III. Внутренние автоморфизмы:
8-*80880 1-
Автоморфизмом группы G называется всякое взаимно
однозначное преобразование множества G, сохраняющее
умножение. В частности, если положим a = g0ag~l, то
имеем ab = ab, т. е. преобразование а действительно яв¬
ляется автоморфизмом. Такой автоморфизм называется
внутренним, поскольку порождается элементом g0 s G.
Если группа G коммутативна, то в ней, очевидно, от¬
сутствует различие между левыми и правыми трансля¬
циями, а внутренние автоморфизмы вырождаются (т. е.
а = а для всякого aeG). Для записи закона умножения
в коммутативной группе иногда используется знак сло¬
жения ( + ); при этом символ единицы заменяется симво¬
лом 0. Примером является обычная группа действитель¬
ных чисел по сложению.
Всякое подмножество Я cz G, замкнутое относительно
умножения и взятия обратного элемента, называется
подгруппой в группе G. Иначе говоря, если g, а, b е Я,
то также g^1 е Я, ab е Я. Отсюда легко заключить, что
сеЯ. Следовательно, если рассматривать умножение

18
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
только в пределах множества Н, то это множество само
оказывается группой.
Если А, В — произвольные подмножества в G, то
условимся использовать обозначение АВ для множества
всех произведений вида ab, аеЛ, Jefl. Символом Л"1
обозначим инверсный образ множества Л, т. е. совокуп¬
ность всех элементов а~\ йеЛ. Наконец, если g0^G,
то символами gQA и Ago обозначим «левоконгруентное» и
«правоконгруентное» множества в G, получаемые из Л с
помощью левого и правого сдвига на go соответственно.
Подгруппа Н a G называется инвариантной, если она
инвариантна по отношению ко всем внутренним автомор¬
физмам в G, т. е. еслиg0Hg~l сг Н для всякого g0^G.
Умножая обе части слева на g^1 и справа на g0, полу¬
чаем обратное включение: g0Hg~l^H для всякого
G. В результате имеем*)
ёоИёо1 = 11 ■
Инвариантные подгруппы в G называются также нор¬
мальными делителями в G.
Замечание 1. В примерах 1 и 2, приведенных в
этом параграфе, группа G как множество идентична пре¬
образуемому пространству. В примере 3 это не так, по¬
скольку число углов Эйлера превосходит число пара¬
метров на сфере (широта и долгота); это является вы¬
ражением того обстоятельства, что каждая точка на
сфере может быть получена бесконечным (но однопара¬
метрическим) числом способов из некоторой фиксирован¬
ной точки, скажем из северного полюса е. Более подроб¬
ный анализ таких соотношений будет изложен ниже,
в § 17.
Замечание 2. Наличие трансляций позволяет нам
заключить, что группа как множество обладает важным
свойством «однородности». Это свойство, которое в даль¬
нейшем будет описано более точно, используется обычно
при внесении в группу G различных алгебраических или
аналитических конструкций (метрика, объем, понятие
*) В действительности мы используем то соображение, что (ле¬
вые и правые) сдвиги являются взаимно однозначными преобра¬
зованиями в G■

9 2. ТОПОЛОГИЧЕСКИЕ ГРУППЫ
19
производной). При этом, имея в виду трансляции, ока¬
зывается достаточным вести основные построения в ка¬
кой-либо одной фиксированной точке, скажем в единич¬
ной точке е.
Упражнения
1. Проверить, что определение подгруппы символически может
быть записано в виде НН Л = Н.
2. Пусть G — группа всех движений в евклидовом простран¬
стве Е и Н — подгруппа параллельных переносов. Проверить, что Н
является нормальным делителем в G.
§ 2. Топологические группы
Очень часто встречаются группы, в которых помимо
алгебраических операций определяется также естествен¬
ная топология, т. е. понятие близости (окрестность, пре¬
дельный переход)*). Группа G называется топологиче¬
ской, если в ней определена топология, относительно ко¬
торой элементы gig2 и непрерывно зависят от
(g ьДг) и g. Желая сделать это определение несколько
более строгим, мы рассматриваем функцию
f{gv £2) = Д,.?2_1,
определенную на множестве всех пар (£1,^2), т. е. на
квадрате G X G, и сочетающую в себе обе групповые
операции (уможение и взятие обратного элемента). Как
обычно, в G X G вводится естественная топология, опре¬
деляемая окрестностями вида U X V, где U и V — окре¬
стности в G. Тогда мы можем сказать, что группа G яв¬
ляется топологической, если функция f(gi,g2) непрерыв¬
на на G X G.
Существенно отметить, что трансляции (левые и пра¬
вые) переводят окрестность в окрестность (это следует
из свойства непрерывности умножения). Отсюда следует
также, что система окрестностей единичной точки е по¬
рождает после сдвига систему окрестностей произволь¬
ной точки go е G.
*) За основными понятиями общей топологии читатель отсы¬
лается к любому руководству по топологии, например к книге
Дж. Келли [27J. См. также [22'], [37'], [4], [46].

20
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
С топологической точки зрения в первую очередь
важно изучить вопросы дискретности и связности. Топо¬
логическое пространство называется связным, если лю¬
бые две его точки можно соединить непрерывной кривой,
целиком принадлежащей данному пространству*). То¬
пологическое пространство называется дискретным, если
все его точки изолированные.
Произвольное топологическое пространство распа¬
дается, очевидно, в теоретико-множественную сумму
своих связных «листов», называемых также связными
компонентами. Если каждый такой «лист» рассматривать
как отдельный элемент, то полученное множество листов
естественно топологизируется (см. стр. 62). При этом
во многих важных случаях оказывается, что все листы
изолированы друг от друга, т. е. пространство листов
оказывается дискретным.
Наличие групповой структуры позволяет сразу за¬
ключить о наличии простой и общей связи между связ¬
ными листами топологической группы; в частности, мы
увидим, что все эти листы конгруэнтны.
Теорема 1. Пусть G — произвольная топологиче¬
ская группа и Н — ее связная компонента, содержащая
единицу. Тогда множество Н является в G инвариант¬
ной подгруппой и всякий связный лист в группе G (лево-
и право-) конгруэнтен Н.
Доказательство. Если а и b непрерывно связаны
с е путями a(t), b(t), О-^Н-^1, то произведение ab так¬
же связано с е непрерывным путем a(t)b(t)\ точно так
же а-' связано с е непрерывным путем a(t)~l. Следова¬
тельно, Н является подгруппой. Нетрудно видеть, что Н
инвариантна (каждый путь a(t) заменяется путем
§оа (0 £о-1)- Первая часть теоремы доказана.
Далее, пусть Gx — связный лист, содержащий точ¬
ку х. Легко проверить, что имеет место равенство Gx =
= хН = Нх, т. е. что Gx получается (левой и правой)
трансляцией из множества Ge — Н. Следовательно, G*
конгруэнтно Н и все такие листы конгруэнтны между
собой.
*) Такие пространства обычно называют линейно связными. От¬
носительно другого понятия связности (по Хаусдорфу) см., напри¬
мер [4], [27], [38], [45]. В классе групп Ли оба понятия равносильны.

§ 2. ТОПОЛОГИЧЕСКИЕ ГРУППЫ
21
Замечание 1. Отдельные связные листы Gxcr.G
могут быть «занумерованы» точками х при условии, что
из каждого такого листа выбирается по единственной
точке. При этом, очевидно, только лист Ge = Н содер¬
жит единицу; следовательно, только этот лист является
подгруппой.
Замечание 2. Если точка е в группе G является
изолированной, то лист Ge = Н состоит из единственной
точки е. В этом случае каждый лист Gx состоит из един¬
ственной точки х и эта точка изолирована в G, т. е.
группа G дискретна.
Перейдем к рассмотрению примеров, иллюстрирую¬
щих теорему 1. Для этого нам будет удобно ввести в
рассмотрение важный класс групп, называемых линей¬
ными или матричными группами.
Пусть Е — линейное пространство размерности п над
фиксированным полем Ф. Обычно в. качестве Ф мы бу¬
дем рассматривать поле вещественных чисел R либо
поле комплексных чисел С. Символом
G = GL (п, Ф)
обозначается группа всех невырожденных аффинных
преобразований пространства Е. Группа G называется
полной линейной группой (general linear group). Всякая
подгруппа в группе G называется линейной или матрич¬
ной группой.
Последнее определение не вызовет неясностей у тех,
кому знакома теория матриц. Действительно, пусть
Re = {еь е2,.. ., е„) — фиксированный репер в простран¬
стве Е. Любое преобразование g е G вполне опреде¬
ляется репером Rg = {ge\, ge2, . . ., gen}, в который оно
переводит репер Re. Раскладывая каждый вектор ge* по
базису Re, мы получаем матрицу
Sn
g 12 ■
• gin
£ =
g>\
g» ■
■ gin
gn\
gn2 •
■ gun
где каждый столбец с номером / содержит координат¬
ную запись вектора ge, (в строке с номером i располо¬

22
ГЛ. 1. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
жена i-я координата вектора ge_,). При этом, как извест¬
но, обычное произведение двух матриц равносильно про¬
изведению соответствующих преобразований из груп¬
пы G.
Пусть М — совокупность всех квадратных матриц
п X п над полем Ф. Полная линейная группа G выде¬
ляется из М единственным условием невырожденности:
detg Ф 0.
Рассматривая М как евклидово пространство размер¬
ности п2, мы вносим в М обычную топологию и тем
определяем, в частности, топологию в группе G. Не¬
трудно видеть, что при этом G становится топологиче¬
ской группой.
Пример 1. Группа G = GL(1,0). Если Ф = R,
то эта группа совпадает с группой вещественных чисел
по умножению; если Ф = С, то эта группа совпадает с
группой комплексных чисел по умножению. В первом
случае имеем
G = G_ + G+
(теоретико-множественная сумма), где G_ содержит
только отрицательные и G+ — только положительные
числа. Точка 0 «выкалывается» из условия невырожден¬
ности. Ясно, что G_ и G+ — связные листы группы G.
Во втором случае группа G как множество предста¬
вляет собой комплексную плоскость с выколотой точ¬
кой 0. В этом случае группа связна.
Пример 2. Группа G = GL(rc, Ф) при произ¬
вольном п. Положим сначала Ф = R. Нетрудно про¬
верить, что два произвольных репера могут быть непре¬
рывно переведены друг в друга только в том случае,
когда они имеют одинаковую ориентацию. В частности,
репер Rg непрерывно связан с Re только при del g > 0.
В результате
G = G_ + G+,
где G_, G+ — связные листы, выделяемые условиями
detg<0, detg>0 соответственно. Лист G+ является
связной компонентой единицы. Лист G конгруэнтен Gщ
G_ = aG+ = G+a, где а — произвольное преобразование
с отрицательным детерминантом.

§ 2. ТОПОЛОГИЧЕСКИЕ ГРУППЫ
23
Если Ф = С, то группа G оказывается связной. Чи¬
тателю предлагается проверить это утверждение индук¬
цией по п.
Пример 3. Группа всех ортогональных
преобразований вещественного евклидо¬
ва пространства размерности п. Условие
ортогональности накладывает на матрицу g ограниче¬
ние g'g = е, где штрих означает транспонирование. От¬
сюда следует:
(det g)2 = 1, det g = ± 1.
Повторяя рассуждения предыдущего примера, заклю¬
чаем, что группа G по-прежнему распадается на два
связных листа, выделяемых условиями det g- — —1,
det g — + 1. Второй из этих листов содержит «собствен¬
но ортогональные» преобразования и является связной
компонентой единицы.
Пример 4. Группа всех ортогональных
преобразований псевдоевклидова прост¬
ранства с метрикой
х2=- х2 + х2 + ... +х2п.
Пусть Re = {е0, е,,..., еп} — фиксированный репер, по
отношению к которому числа xt являются координата¬
ми вектора х, и пусть Rg = {ge0, geь .. ., gen}. Если i =
= 1,2то векторы get имеют единичную длину,
т. е. скользят своими концами по поверхности связного
«однополостного» гиперболоида:
Г+: -х2 + х\+ ... +4=1.
В то же время вектор ge0 имеет квадратом длины чис¬
ло — 1, т. е. скользит своим концом по поверхности
«двуполостного» гиперболоида:
Г": -xl + x\+ ... +4= -1.
Гиперболоид Г- несвязен и распадается на два связ¬
ных листа соответственно условиям х0 <0, х0 > 0. Под¬
ставляя х = ge0, получим неравенства goo < 0, g00 > 0,
где gij — элемент матрицы g в репере Re. Даже если
репер Rg имеет одинаковую ориентацию с Re, он не мо¬
жет быть непрерывно совмещен с Re, если g0o < 0.

24
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
В результате заключаем, что группа G распадается на
четыре листа:
G = G ~ + Gt + G + + GX>
^&
где каждый лист Ge выделяется одной из возможны)!
комбинаций знаков e = sgndetgr, 6 = sgngr0o- Мы пре¬
доставляем читателю самостоятельно проверить (ин¬
дукцией по п), что лист G+ является связным. Следо¬
вательно, остальные листы G6B, когруэнтные G + , также
являются связными. Лист G+ является связной компо¬
нентой единицы.
Желая построить еще несколько более общий при¬
мер, введем предварительно следующее определение.
Пусть F и Я— произвольные группы. Рассмотрим мно¬
жество G = F X Я, состоящее из всевозможных пар
(/,/г), fef, АеЯ, и введем операцию умножения в
множестве G по правилу
(fi> hx)(/2, ^2) ~ (fif^1^2)-
Полученное множество G при этом становится группой,
которая называется прямым произведением F и Я. Если
F и Я — топологические группы, то множество G снаб¬
жается обычной топологией топологического произведе¬
ния. При этом, как нетрудно видеть, G является тополо¬
гической группой.
Пример 5. Если в предыдущем построении груп¬
па F является дискретной и группа Я связной, то мы
получаем топологическую группу G, в которой Я яв¬
ляется связной компонентой единицы.
Замечание. Элементы fef в примере 5 могут
быть использованы для нумерации связных листов груп¬
пы G. Соответствующие пары вида (/, е) образуют под¬
группу в группе G, изоморфную F; такие преобразова¬
ния условимся называть отражениями. Нетрудно видеть,
что некоторые примеры 1—4 являются частными слу¬
чаями примера 5 (так, в примере 1 отражения задаются
числами ±1).
Упражнение
Показать, что группа всех унитарных матриц порядка п яв¬
ляется связной.

§ 3. ПАРАМЕТРИЧЕСКИЕ ГРУППЫ И ГРУППЫ ЛИ
25
§ 3. Параметрические группы и группы Ли
Мы значительно приблизимся к обычной ситуации
анализа, если вместо общих топологических групп вве¬
дем специальное понятие параметрической группы. Груп¬
па G называется параметрической или локально евкли¬
довой, если она параметризуется (хотя бы локально, т. е.
в окрестности каждой точки) некоторой системой веще¬
ственных параметров
g = g(t) = g(tut2,. ■. ,tn)
и если при этом закон умножения и взятия обратного
элемента выражается непрерывной функцией от набора
параметров t. Записывая обе групповые операции в
виде gxg^x, мы имеем
g (t) g (s)'1 = g (f (t, s)),
где f(t,s) — непрерывная вектор-функция от совокуп¬
ности переменных / и s. Говоря о том, что множество G
параметризуется, мы имеем в виду, как обычно, что G
является топологическим или локально евклидовым
многообразием.
Таким образом, параметрическая группа предста¬
вляет собой топологическое многообразие, наделенное
групповой структурой, причем эта структура определен¬
ным образом согласована с топологией в множестве G
(непрерывность f(t,s)).
Если мы желаем охватить даже простейшие важные случаи не¬
коммутативных матричных групп, то нет никакой надежды, что
параметризация будет глобальной, т. е. единой на всей группе G.
Так, если группа G состоит из всех матриц второго порядка
I а Р I
S = А
I V о I
с определителем, равным единице, то многообразие G выделяется
из четырехмерного евклидова пространства уравнением аб — Ру = 1.
Выбирая а, Р, у в качестве независимых параметров, мы находим
e-^O + Pv),
откуда ясно, что полученная параметризация справедлива лишь в
тех областях группы G, где афО. Закон умножения в этом случае
задается рациональными функциями от а, Р,

2Й ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГГУППЫ. ГГУППЫ ли
Как увидим в дальнейшем, ситуация рассмотренного примера
является достаточно общей, т. е. в большинстве практически важ¬
ных случаев удается вложить группу G в объемлющее евклидово
пространство и записать закон умножения с помощью рациональ¬
ных функций. Тем не менее мы должны при развитии общей теории
иметь в виду обычные трудности, связанные с локальной парамет¬
ризацией, т. е. с наложением «евклидова атласа» на многообра¬
зие G.
Замечание 1. Если уже известно, что группа G яв¬
ляется параметрической, то наложение «евклидова ат¬
ласа» можно осуществить с помощью (левых или пра¬
вых) трансляций в группе G. Действительно, выбирая
независимые параметры в некоторой окрестности точ¬
ки е, мы разносим эту окрестность во все остальные
точки с помощью сдвигов. Нетрудно проверить, исходя
из определения параметрической группы, что мы полу¬
чаем таким путем непрерывное согласование парамет¬
ров в тех местах, где карты «атласа» взаимно пересе¬
каются.
Замечание 2. Согласно определению параметриче¬
ской группы всякая такая группа является локально
связной, т. е. любая ее точка обладает связной окрест¬
ностью. Отсюда следует, в частности, что группа G =
= GL (n,Q) над полем рациональных чисел Q не яв¬
ляется параметрической. Согласно общим концепциям
анализа мы придаем особое значение полю R веществен¬
ных чисел.
Сделаем теперь небольшое отступление в область
произвольных топологических групп. Множество 5 a G
называется системой образующих в группе G, если сте¬
пени Sn, п — 0,1,2,... (S° = {e}), покрывают всю груп¬
пу G. Следующая теорема подчеркивает роль окрест¬
ности в связной группе G.
Теорема 2. В связной группе G всякая окрестность
единичного элемента является системой образующих.
Доказательство. Фиксируем окрестность U точ¬
ки е, и пусть G0 — объединение всех степеней Um, т. е.
множество всех элементов, представимых (вообще го¬
воря, неоднозначно) в виде щи2.. . ит при некоторых
щ, «2, • • ■» ит е U и при сколь угодно высоком т. Оче¬
видно, Go — открытое связное множество в G. Мы по¬
кажем, что G0 = G.

§ 3. ПАРАМЕТРИЧЕСКИЕ ГРУППЫ И ГРУППЫ ЛИ
27
Действительно, пусть g0 — точка, лежащая на гра¬
нице G . Выберем точку h настолько близкой к единице,
чтобы h~]g0 содержалось в G0 и в то же время h содер¬
жалось в окрестности U. Тогда имеем h~lg0 — ихи2. . . ит,
откуда
go — huxu2 ... ит
при А, и,, и2, ..., um^U. Следовательно, fteG0
вопреки предположению о том, что go лежит на гра¬
нице G0. Полученное противоречие показывает, что
G0 = G. Теорема доказана.
Наконец, введем еще одно фундаментальное опреде¬
ление. Группа G называется группой Ли, если она пара¬
метрическая и если функция f, задающая закон умноже¬
ния, вещественно-аналитична *).
Можно было бы ввести понятие группы, несколько
раз дифференцируемой, однако существует следующая
замечательная теорема: всякая параметрическая груп¬
па в действительности является группой Ли. Эта теоре¬
ма является решением знаменитой V проблемы Гиль¬
берта. Мы не можем в рамках данной книги останавли¬
ваться на доказательстве этой теоремы (см. [36]). Смысл
ее состоит в том, что групповая структура позволяет по¬
лучить замечательные следствия в терминах анализа:
непрерывность функции f оказывается достаточной для
ее аналитичности.
Простейшим аналогом такой ситуации является решение функ¬
ционального уравнения
f(x + y) = f(x)f(y)
в классе непрерывных функций на числовой прямой. Как известно,
это уравнение имеет лишь экспоненциальные решения:
/ (х) = Сеах,
которые аналитичны. Аналогичный результат имеет место и в клас¬
се непрерывных матричных функций f(x).
Существенно важными объектами в теории групп Ли
являются, естественно, лишь связные группы Ли. Такие
группы называются также аналитическими группами.
*) Функция / называется вещественно-аналитической, если она
представима в виде локального степенного ряда (ряда Тейлора)
В окрестности каждой точки из области определения.

28 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
Аналитическая группа представляет собой аналитическое
многообразие, наделенное групповой структурой, при
условии известной согласованности этой структуры со
структурой аналитического многообразия (аналитич¬
ность f(t,s)). Более подробное определение аналити¬
ческой группы и группы Ли можно найти в моногра¬
фиях [38], [45], [46].
§ 4. Теория Ли
Как уже отмечалось во введении, первоначальные
результаты по теории групп Ли принадлежат норвеж¬
скому математику Софусу Ли. Однако в действитель¬
ности Софус Ли изучал лишь некоторые группы диффео¬
морфизмов (гладких точечных преобразований) и все
рассмотрения проводил локально. С современной точки
зрения результаты Ли естественно формулируются для
так называемых локальных групп Ли, определение ко¬
торых будет дано несколько ниже.
Не имея возможности сколько-нибудь подробно оста¬
новиться на систематическом изложении теории Ли, мы
ограничимся лишь кратким ее обзором и иллюстрацией
следующего основного положения: теория Ли устана¬
вливает замечательное соответствие между группами Ли
и значительно более простыми алгебраическими объек¬
тами— так называемыми алгебрами Ли.
Коль скоро в группе есть понятия дифференцируе¬
мости и даже аналитичности, мы можем изучать строе¬
ние группы локально, пренебрегая малыми величинами
того или иного порядка; при этом в силу свойства одно¬
родности достаточно рассматривать окрестность еди¬
ничного элемента е. Согласно общим принципам анали¬
за мы прежде всего осуществляем линеаризацию, т. е,
рассматриваем касательное пространство к многообра¬
зию G в точке е (конструкция касательного простран¬
ства становится особенно наглядной, если G является
гиперповерхностью в объемлющем евклидовом про¬
странстве)*). Полученное линейное пространство X яв¬
*) Относительно основных понятий дифференциальной геомет¬
рии см., например, [40], [39'].

§ 4. ТЕОРИЯ ЛИ
29
ляется объединением всевозможных касательных пря¬
мых в точке е. Его размерность равняется п, где п —
число параметров в группе G.
С каждым вектором мы связываем семейство
дифференцируемых кривых, проходящих в G через точ¬
ку е и имеющих х своим касательным вектором. Жела¬
тельно было бы выделить из этого семейства простейшую
линию — аналог прямой в евклидовом пространстве.
Естественно воспользоваться следующим эвристическим
рассуждением.
Для любой точки g е G существует серия gn,
п = 0, ± 1, ±2,. .. Если точка g допускает неограничен¬
ное извлечение квадратного корня (g'1*, g'u, .. .), то эта
серия включается в семейство вида gr, где г — произ¬
вольное двоично-рациональное число, причем имеем
gr'gu = gr'+r\ g° = e.
Если gr^e при г-»-0, то gr, gr' неограниченно сбли¬
жаются при | г — г' |—»-0. В этом случае возможно по¬
строить непрерывное однопараметрическое семейство
gl, где X— произвольное действительное число, причем
= g0==e-
Любое однопараметрическое семейство, удовлетворяю¬
щее этому мультипликативному соотношению и непре¬
рывно зависящее от вещественного параметра X, назы¬
вается однопараметрической подгруппой в группе G.
Мы будем считать однопараметрические подгруппы ана¬
логом прямых, проходящих через точку е. В теории
групп Ли доказывается следующее важное утверждение.
Теорема А. Единичная точка в группе Ли всегда
обладает окрестностью Q, через каждый элемент кото¬
рой проходит одна и только одна однопараметрическая
подгруппа gx, аналитически зависящая от X.
Проиллюстрируем эту теорему на примере матричной
группы G. Как известно, если матрица g достаточно
близка к единичной матрице е, то g представима в виде
матричной экспоненты:

30
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
Поскольку экспоненциальный ряд в свою очередь схо¬
дится всюду, т. е. для произвольной матрицы х, мы по¬
лучаем возможность заменить х на Ах В результате по¬
лучаем семейство
к кх , 1 , Мх2 , , кПХП Р
gk = еХх = е + 1х + __ -f . . . -| —
которое аналитически зависит от А, проходит через е
при А = 0, через g при А = 1 и для которого выполняется
мультипликативное соотношение
gtac . gH* 0СЛ.+|х) х 4
Замечание I. Пусть IWI — норма вектора х в «-мерном про¬
странстве Е, ilg|| — соответствующая норма матрицы g, определяе¬
мая по правилу
||g||= sup ||gx||.
11*11=1
Тогда мы имеем || gx || ^ || g || II х || и !| ab Ц ^ || а || Ц Ь || для произ¬
вольных двух матриц а и 6. Отсюда по индукции имеем 1!а’1|| ^
^ЦаЦ71. В частности, отсюда следует, что экспоненциальный ряд е1
мажорируется по норме числовым сходящимся рядом е'1 х l!, и мы
заключаем о сходимости е* при произвольном х. Далее, если
g = е — а, то мы положим
( а2 ап \
x = lng = ln(e —а) = — [а + — + ... + — + ... j.
Полученный ряд мажорируется рядом —1п(1—Ца|1) и, следова¬
тельно, сходится при ||а|| <1. Как легко проверить, eln“ = g. Мы
показали, что искомая окрестность Q в группе О может быть вы¬
делена условием ||е — g!l < 1.
Замечание 2. Покажем другим способом, исполь¬
зуя аналитичность по А, что всякая однопараметрическая
матричная группа имеет вид екх при некотором х. Дей¬
ствительно, из равенства gx+t = gxgB при малом е легко
находим
(gxY = xg\
где положено л: = (gx)[=n- Продолжая дифференцирова¬
ние, находим, что m-кратная производная функции gx
в точке А = 0 равняется хт. В результате
§х = е + Кх + л:2 + ... + хп + ... = еЧ

§ 4. ТЕОРИЯ ЛИ
31
Наряду с теоремой А справедлива также следующая
Теорема В. Пусть X — касательное пространство к
группе G в единичной точке е. Тогда для каждого
хе! существует единственная однопараметрическая
подгруппа, имеющая х своим касательным вектором.
Семейство этих подгрупп gk = g (А,, х) может быть вы¬
брано таким образом, чтобы
g(K x) = g(xf.
Полученная функция g(x) обозначается ехр х по ана¬
логии с матричной экспонентой. Векторы х е X опреде¬
ляют при этом систему параметров в некоторой окрест¬
ности Й точки е. Такие параметры называются канони¬
ческими.
Выясним теперь, как выражется закон умножения
при помощи канонических параметров в группе G. Если
ограничиться малыми первого порядка, то мы имеем для
случая матричной группы
= (е + Ах + .. .) (е + Аг/ + ...) = е + А (х + г/) + ...
Следовательно, кривая е*-хекУ имеет своим касательным
вектором х + у. То же верно и для произвольной группы
Ли. Однако мы теряем информацию о некоммутатив¬
ное™ (поскольку сложение векторов коммутативно). За¬
метим также, что
(eXx)m = еткх,
т. е. возведению е*1 в степень т соответствует (на этот
раз уже точно) m-кратное растяжение касательного век¬
тора х.
Для того чтобы восстановить утраченную информа¬
цию о некоммутативности, построим из произвольных
двух элементов g,h^G элемент
k = ghg~lh~\
называемый их коммутатором*). Если g = екх, h = eKy,
то мы находим, пренебрегая малыми выше второго
*) Если интерпретировать g, h как некоторые операции, то
операция k замыкает «кривой четырехугольник», составленный дви¬
жениями A-1, g'1, A, g в указанном порядке. Если А коммутирует
с g, то k = е.

32
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
порядка,
k = k (Я) = е + Я2 (ху — ух) + ...
Выражение [х,у] = ху — ух называется в алгебре ком¬
мутатором двух матриц х и у. Если рассматривать Я2 в
качестве параметра на кривой &(Я), то касательным
вектором к этой кривой оказывается вектор [х, у].
Введем аналогичное определение для произвольной
группы Ли. Тогда в касательном пространстве X возни¬
кает бинарная операция [х,у], по-прежнему называемая
коммутатором и обладающая следующими свойствами:
1° [у> А = — [х> у] (антикоммутативность);
2° [Кх + рг/, z] = 'K[x, z] + р [у, г] (линейность);
3° [ [*, у], г] + [ [у, г], х] + [ [г, х], у] = 0 (тождество
Якоби).
Произвольное линейное пространство, наделенное такой
структурой, называется алгеброй Ли. В частности, каса¬
тельное пространство к n-мерной группе Ли оказывается
n-мерной алгеброй Ли. Важнейшее значение этой связи
показывает следующая
Теорема С. Пусть g = exp х, h = exp у — два про¬
извольных элемента из группы G, выраженные через
канонические координаты. Если их произведение gh так¬
же может быть записано в виде ехр г, то вектор z выра¬
жается через векторы х и у с помощью операций сложе¬
ния и взятия кратного коммутатора.
Заметим, что г = In е*еу, где символ е* означает для
краткости групповую экспоненту. Известно даже явное
выражение функции z — f(x,y). Пусть скобка ...
... ап] означает кратный коммутатор вида [щ [аг ...
... [a„_i, ап]...]]. Тогда имеем
и \ , , г 1 , V (—1)т“‘ [х'7'/1 ... xPm/m]
f (х, у) = х + у + [х, у] + У. -— —- ,
11 i i
где суммирование ведется по всем неотрицательным це-
лым значениям pit qp i = 1, 2, ..., m\ m = 1, 2, 3, ...;
Pi + Чг =£ 0, за исключением простейших случаев при
т. = 0, 1, которые выписаны отдельно в виде первых трех
слагаемых. Полученный ряд называется рядом Кемп¬

§ 4. ТЕОРИЯ ЛИ
33
белла — Хаусдорфа (ввиду его сложности он редко ис¬
пользуется в приложениях).
Следствие. Операция коммутирования в алгебре
X определяет закон умножения в некоторой окрестности
группы G.
Пусть еи в2, ..., еп — произвольный базис в алгебре
X. Ввиду билинейности операции [х,у], для ее опреде¬
ления достаточно знания парных коммутаторов [е{, щ].
Поскольку каждый такой коммутатор снова является
элементом из Х% то мы имеем
(сумма по k от 1 до п), где Сц — коэффициенты разло¬
жения, называемые структурными константами. Ясно,
что эти константы удовлетворяют некоторым соотноше¬
ниям, вытекающим из антикоммутативности и тожде¬
ства Якоби. Знание этих констант вполне определяет за¬
кон коммутации в алгебре X.
Следовательно, структурные константы вполне опре¬
деляют также закон умножения в некоторой окрестности
группы G.
Завершая обзор теории Ли, остановимся кратко на
вопросе о связи между подгруппами в группе G и под¬
алгебрами в алгебре X. Множество У cz X называется
подалгеброй, если оно линейно и замкнуто относительно
операции коммутирования.
Пусть Н — замкнутая подгруппа в группе G. Тогда
легко проверить, что касательное пространство У к мно¬
гообразию Н в точке е является подалгеброй в алгебре
X. Обратно, всякой подалгебре У с X отвечает (однако,
вообще говоря, незамкнутая) подгруппа Н в группе G,
называемая аналитической подгруппой. Замыкание Н
может иметь размерность, большую размерности Н. Это
означает, что связь между подалгебрами в Л’ и под¬
группами в G не является взаимно однозначной*).
*) Очевидно, это обстоятельство значительно затрудняет изуче¬
ние группы Ли по ее алгебре Ли. Несколько более подробно мы
остановимся на этом в § 40.

34
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
Упражнения
1. Показать, что если алгебра Ли X коммутативна, то [х, у] = О
для всех х, у е X.
2. Показать, что трехмерное евклидово пространство является
алгеброй Ли относительно операции векторного произведения.
3. Показать, что операторы q = * (умножение на х),
г — 1 и их линейные комбинации образуют алгебру Ли.
4. Показать, что группа GL(n,R) является группой Ли.
5. Показать, что группа О(п) является группой Ли.
§ 5. Локально изоморфные группы Ли
В этом параграфе мы займемся вопросом о возмож¬
ности восстановления всей группы Ли по соответствую¬
щей алгебре Ли. Предварительно остановимся на неко¬
торых общих определениях.
Пусть А и В — две произвольные группы. Отображе¬
ние b = f [а), аеЛ, Ь^В, называется гомоморфизмом
группы А в группу В, если
/(а|а2) = /(о,)/(а2),
т. е. если f(a) «сохраняет умножение». Пусть е, е' — еди¬
ничные элементы в Л и Л соответственно. Покажем, что
f(e) = е'. Действительно,
f(e) = f(ee) = f(e)f{e)-,
умножая обе части на левый обратный элемент к f(e),
получаем f(e) — е'. Нетрудно также видеть, что
/(хг1) = f(x)-1 для всякого XG/1.
Если группы А, В топологические, то предполагается
также, что функция b = f(а) является непрерывной.
Если гомоморфизм f накрывает всю группу В, то гово¬
рят, что f является гомоморфизмом группы А на груп¬
пу В. Если при этом отображение f взаимно однознач¬
но и взаимно непрерывно, то оно называется изомор¬
физмом. Изморфные группы не считаются существенно
различными.
Остановимся несколько подробнее на алгебраиче¬
ских свойствах гомоморфизма. Пусть Е — множество
всех х еф для которых f(x) = е'\ множество Е назы¬
вается ядром гомоморфизма f. Покажем, что знание

§ 5. ЛОКАЛЬНО ИЗОМОРФНЫЕ ГРУППЫ ЛИ
35
ядра определяет «степень вырождения» гомоморфизма f
во всякой точке ае/1.
Теорема 3. Пусть f — гомоморфизм группы А в
группу В и Е — его ядро. Множество Е является инва¬
риантной подгруппой в А. Далее,
f~l (Ь) = аЕ = Еа
для всякой точки b е В, где а — произвольно фиксиро¬
ванный элемент, для которого f(a) = b.
Доказательство. Первое утверждение легко
проверяется. Далее, если а, а' — произвольные элементы
из f~x(b), то f(a~xa') = е', откуда пг’а'еД. Следова¬
тельно,
а' — ах,
где а фиксировано и х пробегает Е. Очевидно, эта фор¬
мула дает общий вид элементов а'е/-1(&). Точно так
же а' = уа, где у пробегает Е. Теорема доказана.
Следствие. Гомоморфизм / является изоморфиз¬
мом тогда и только тогда, когда его ядро состоит из еди¬
ницы.
Пример 1. Пусть А — аддитивная группа векторов
(х, у) на плоскости и В — аддитивная группа чисел на
прямой. Отображение
f(x, у) = х
является гомоморфизмом А на В. Ядро такого гомомор¬
физма определяется условием х = 0, т. е. совпадает с
осью Оу. Всякое множество f~l (х0) есть прямая линия,
параллельная Оу.
Пример 2. Пусть А — аддитивная группа чисел на
прямой и В — мультипликативная группа комплексных
чисел, лежащих на единичной окружности. Отображение
f(x) = е1'*
является гомоморфизмом А на В. Ядром такого гомо¬
морфизма является множество всех чисел вида 2пп, где
п — произвольное целое число.
Пример 3. Конструкция примера 2 легко обоб¬
щается на случай, когда группа А изоморфна произволь¬
ному векторному пространству конечной размерности.

36
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
В частности, пусть А двумерно и состоит из векторов
(х,у). Положим
II е‘х О I
f (х> У) ~ I q Qiy ■
Тогда отображение f является гомоморфизмом А на
группу В диагональных матриц второго порядка с соб¬
ственными значениями, по модулю равными единице.
Ядро гомоморфизма f составляют пары (2nnb 2яп2).
где Пи п2— произвольные целые числа.
Замечание 1. Группа В в примере 3 изоморфна
двумерному тору и как группа совпадает с группой дви¬
жений этого тора.
Замечание 2. Если группы А а В являются век¬
торными пространствами, то понятие гомоморфизма со¬
впадает в этом случае с понятием аддитивного опера¬
тора.
Вернемся теперь к теории групп Ли. Две топологи¬
ческие группы Л и В называются локально изоморф¬
ными, если существует взаимно однозначное отображе¬
ние / между окрестностями единичных элементов 11 cz А,
V сz В, которое переводит единицу в единицу и сохра¬
няет закон умножения внутри окрестностей U, V. По¬
следнее означает, что
f{aia2) = f(al)f(a2),
если «ь а2, а\а2 ё !i, и то же верно для обратного ото¬
бражения f~\ определенного на окрестности V. В част¬
ности, если группы А к В изоморфны, то они и локально
изоморфны, в то время как обратное, вообще говоря, не¬
верно. Две группы Ли, очевидно, могут быть локально
изоморфны только в том случае, когда они имеют оди¬
наковую размерность.
Примерами локально изоморфных групп являются
группы Л и В, рассмотренные в этом параграфе в при¬
мерах 2 и 3. Группы Л и В в примере 1 не могут быть
локально изоморфными, поскольку имеют разную раз¬
мерность.
Если две группы Ли локально изоморфны, то они
имеют, очевидно, одну и ту же алгебру Ли. Обратно,
если группы Л и В имеют одну и ту же алгебру Ли, то,

§ 5. ЛОКАЛЬНО ИЗОМОРФНЫЕ ГРУППЫ ЛИ
37
согласно теории Ли, они локально изоморфны. Следова¬
тельно, можно заключить, что алгебра Ли определяет
группу Ли с точностью до локального изоморфизма.
Замечание. Множество Й назовем локальной группой Ли,
если оно топологически отождествляется с некоторой окрестностью
я-мерного векторного пространства и если в нем введена групповая
операция ghr1, аналитическая в параметрах Й и определенная для
точек g и h, достаточно близких к единице. Вся теория Ли может
быть переформулирована для локальных групп Ли; при этом ло¬
кальная группа Й уже однозначно определяется своей алгеброй X.
В дальнейшем мы условимся рассматривать лишь
конечномерные алгебры Ли, опуская для краткости
слово «конечномерные». Если X — такая алгебра, то мы
введем обозначение оз(Х) для множества всех аналити¬
ческих групп, имеющих X своей алгеброй Ли. При этом
две группы считаются одинаковыми, если они изо¬
морфны. Согласно сказанному выше все группы класса
оз(X) локально изоморфны. Проблема состоит в описа¬
нии класса od(J).
Прежде всего, возникает вопрос, является ли класс
a)(X) непустым для произвольной алгебры X. Ответ яв¬
ляется положительным, но его доказательство слишком
сложно. Мы наметим идею доказательства в § 107. Да¬
лее, имеет место
Теорема D. В каждом классе со(X) существует
«максимальная» группа ©, определяемая однозначно.
Максимальность означает, что всякая группа Се со{X)
является гомоморфным образом
G = f(@).
Идея доказательства этой теоремы состоит в по¬
строении «накрывающего многообразия» для каждой
группы Сеи(Х). Понятие накрывающего многообра¬
зия в топологии основано на той же идее, что и понятие
римановой поверхности в теории функций комплексного
переменного. Мы не станем воспроизводить подробности
этого определения, отсылая читателя к руководствам по
общей топологии либо к книге Шевалле [46] (т. I,
стр. 61). Известно, что если G — связное многообразие,
каждая точка которого обладает базисной системой связ¬
ных окрестностей, то среди многообразий, накрывающих

38
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
G, существует максимальное многообразие © (см. [46]).
Максимальность означает при этом, что всякое накры¬
тие © гомеоморфно @. Если G — группа, то многообра¬
зие © также наделяется структурой группы, причем
группа G является гомоморфным образом @. Если груп¬
пы Gi, G2 локально изоморфны, то их накрывающие
оказываются изоморфными.
Указанное выше многообразие © может быть также
однозначно охарактеризовано свойством односвязности.
Это означает, что всякий замкнутый цикл в многооб¬
разии @ может быть стянут в точку непрерывной де¬
формацией в @. (В частности, прямая односвязна, а
окружность неодносвязна, причем прямая является на¬
крывающим многообразием для окружности.) Таким об¬
разом, группа @ из теоремы D является односвязной.
Она называется универсальной накрывающей класса
со(Х).
Следствие 1. Существует взаимно однозначное
соответствие между алгебрами Ли и односвязными груп¬
пами Ли.
Следствие 2. Две группы Ли локально изоморфны
тогда и только тогда, когда они имеют одну и ту же
универсальную накрывающую.
Рассмотрим в качестве простейшего примера тот слу¬
чай, когда алгебра X одномерна. Очевидно, в этом слу¬
чае X коммутативна. Роль универсальной накрывающей
класса со (У) играет аддитивная группа вещественных
чисел (группа сдвигов на прямой). Элементом класса
со (У) является также мультипликативная группа комп¬
лексных чисел ei(P (группа вращений окружности). Если
рассматривать каждую группу с точностью до изомор¬
физма, то легко показать (см. упражнение 2 в конце
параграфа), что указанными двумя группами исчерпы¬
вается в данном случае весь класс со (У).
Таким образом, теорема D в известном смысле за¬
вершает теорию групп Ли. Мы сделаем, однако, еще
одно простое замечание, которое позволит уяснить струк¬
туру формулы
G = /(©),

§ 5. локально Изоморфные группы ли
39
указанной в теореме D. Пусть @ — произвольная группа.
Всякий элемент ге®, перестановочный со всеми эле¬
ментами из &, называется центральным. Множество
всех центральных элементов называется центром
группы
Теорема 4. Ядро гомоморфизма /, указанного в
теореме D, является дискретным и содержится в центре
группы
Доказательство. Пусть Е — ядро гомоморфизма
/. Из непрерывности f следует замкнутость Е. Подгруппа
Е, как замкнутая подгруппа в группе Ли, сама является
группой Ли. Однако Е не может содержать ни одной
однопараметрической подгруппы, поскольку f взаимно
однозначно в окрестности точки е. Следовательно, Е
дискретно.
Далее, для каждого х е Е введем «орбиту» Ох как
совокупность всех элементов вида gxg~\ je®; тогда
Ох a Е, поскольку Е инвариантно относительно внутрен¬
них автоморфизмов. Всякая орбита является связной в
силу связности @ и в то же время дискретной ввиду
дискретности Е. Это может быть только тогда, когда Ох
состоит из единственной точки х. Следовательно,
gxg~x — х при всех и всякий элемент ie£ яв¬
ляется центральным. Теорема доказана.
Следствие. Для перечисления всех групп класса
(о(Х) достаточно перечислить подгруппы, лежащие в
центре группы @.
Дискретные подгруппы, лежащие в центре группы
мы будем также называть дискретными делителями
группы @. Если G = /(@), Д'(е) = 2, где @ — односвяз¬
ная подгруппа и Z — ее дискретный делитель, то Z на¬
зывается фундаментальной группой или группой Пуан¬
каре многообразия G. Фундаментальная группа показы¬
вает «степень неодносвязности» многообразия G.
Упражнения
1. Пусть S — векторное пространство размерности п. Показать,
что всякая дискретная подгруппа в группе S имеет вид дискретной
решетки ntei + л2е2 + ... + nheh, где e\, e2, ..., eh — линейно не¬
зависимые векторы (ft ^ n) и tii, tik — произвольные целые
числа.

40
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
2. Показать, что всякая коммутативная связная группа Ли изо¬
морфна прямому произведению /г-мерного тора на (п — к)-мерное
векторное пространство. (Указан и е: воспользуемся результатом
упражнения 1.)
§ 6. Инвариантные формы на группе Ли
Пусть G— группа Ли с локальными параметрами
t— (/', t2, ..., tn) в окрестности точки е. Мы будем
рассматривать правые сдвиги g-^gga как аналитиче¬
ские преобразования этих координат при условии, что
точки g, go, ggo достаточно близки к единице. Если
t, о, т — соответственно параметры этих точек, то мы
имеем т = ф (А ст), где ф — аналитическая функция от
/ист. Далее,
dx = А (т, t) dt,
где А (т, /) — матричная функция, составленная из част¬
ных производных д(р{ (/, ст) !dth\ при этом мы считаем т,
t независимыми переменными, подбирая ст из соотноше¬
ния между т, / и ст. Очевидно, матрица А (т, /) аналити¬
чески зависит от своих переменных. Далее, она невы¬
рождена, поскольку ее детерминант совпадает с якобиа¬
ном взаимно однозначного преобразования g-+ggo-
Повторное применение операции сдвига приводит нас к
формуле
А (t, т) А (т, t) = А (t, t),
справедливой при достаточно малых значениях входя¬
щих в нее параметров. Матрицу А (т, t) мы будем на¬
зывать трансформационной матрицей правого сдвига.
Аналогично можно было бы рассматривать левые сдвиги
на G.
Пусть a(t) = (<3i (/), a2{t) ап (/))— векторная
функция на группе G, т. е. векторное поле, выраженное
через локальные координаты. Векторное поле a(t) мы
будем называть ковариантным, если
а(т)Л (т, /) = a(t) (»)
для всякого правого сдвига на G. Хотя такое определе¬
ние является локальным, его нетрудно при помощи
атласа перенести на всю группу G. (Аналогично можно

§ 6. ИНВАРИАНТНЫЕ ФОРМЫ НА ГРУППЕ ЛИ
41
определить контравариантное векторное поле по пра¬
вилу А (т, t)b(t) = b{т).)
Пусть a(t)—произвольное векторное поле на G.
Записывая a(t) как вектор-строку и dt как вектор-стол¬
бец, мы рассмотрим свертку
со Д, dt) = a(t)dt,
которая дает нам общий вид линейной дифференциаль¬
ной формы на многообразии G. Форма co{t,dt) назы¬
вается правоинвариантной, если
со (т, dr) = со (t,dt),
где т —координаты новой точки, получаемой при сдвиге
ggo- Легко проверить, что форма ю инвариантна тогда и
только тогда, когда поле a(t) является ковариантным.
В результате мы приходим к эквивалентному опре¬
делению понятия ковариантности. Аналогично можно
было бы рассмотреть левые сдвиги на G. Докажем те¬
перь следующий основной результат:
Теорема 5. На группе Ли размерности п суще¬
ствует ровно п линейно независимых правоинвариант¬
ных и ровно п линейно независимых левоинвариантных
форм. Коэффициенты этих форм являются аналитиче¬
скими функциями на G.
Доказательство. Для определенности рассмо¬
трим правые сдвиги. Условимся, что / = О соответствует
единичной точке е. Согласно определению ковариант¬
ности имеем, в частности,
a(t) — а(0)Л (0, t).
Заменим множитель я(0) произвольным постоянным
вектором с и покажем, что полученное векторное поле
является ковариантным. Действительно, согласно свой¬
ствам трансформационной матрицы мы имеем
а(%)А (т, t) = сА (0, т) А (т, t) = с А (0, t) — a (t).
Мы показали, что общий вид ковариантного векторного
поля на группе G дается формулой
a{t) = с А (0, /),

42 ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
где с — произвольный постоянный вектор. Отсюда, в
частности, следует аналитичность функции a(t). По¬
скольку вектор с пробегает n-мерное пространство и ма¬
трица А (0, /) невырождена, мы действительно получаем
ровно п линейно независимых решений. Теорема дока¬
зана.
Замечание. Идея доказательства вкратце сводится
к тому, что произвольный фиксированный вектор с = о(0)
«разносится» определенным образом по группе G. В дей¬
ствительности наше доказательство требует большей
строгости при рассмотрении «атласа» на группе G.
Для иллюстрации рассмотрим случай матричной
группы и независимо получим в этом случае результат
теоремы 5. Если g — произвольная матрица, то симво¬
лом dg мы обозначим матрицу, составленную из диффе¬
ренциалов всех элементов матрицы g. Положим
м(Д dg) = dg-g-K
Рассматривая правый сдвиг, положим h = gg0. Тогда
dh = dg-g0, откуда dh ■ frl = dg ■ g~l. Следовательно,
матрица (£>(g,dg) является правоинвариантной. Заме¬
тим, что элементами этой матрицы являются дифферен¬
циальные формы на G. Число линейно независимых
среди этих форм, очевидно, равно числу параметров в
группе G.
Аналогично матрица 5>(g, dg) = g~*dg является лево¬
инвариантной и содержит нужное число линейно неза¬
висимых дифференциальных форм.
До сих пор мы рассматривали лишь дифференциаль¬
ные формы первого порядка, однако наши рассмотрения,
очевидно, без труда переносятся на формы любого по¬
рядка. Соответственно мы получаем описание ковариант-
ных и контравариантных тензорных полей на группе G.
§ 7. Метрика. Мера Хаара
Используя идеи предыдущего параграфа, мы полу¬
чаем, в частности, что справедлива следующая*)
*) По поводу терминологии теории римановых пространств см.,
например, [29], [39'].

s 7. МЕТРИКА. МЕРА ХААРА
43
Теорема 6. На группе Ли всегда существует поло¬
жительно определенная риманова метрит
[сумма по i, /), инвариантная относительно правых сдви¬
гов (то же верно для левых сдвигов). Метрический тен¬
зор a{j(t) аналитичен на G.
Доказательство строится по той же схеме, что
и доказательство теоремы 5. Если записывать исходный
тензор в виде матрицы a(t), то мы находим
где штрих означает транспонирование. При этом в ка¬
честве а(0) выбирается произвольная положительно
определенная матрица порядка п (где п — число пара¬
метров в группе G).
Следствие. Всякая группа Ли является римано-
вым пространством.
Если g и h — произвольные точки в группе G, то мы
определяем расстояние между ними по формуле
где inf берется по всем спрямляемым кривым, соединяю¬
щим g и h. Полученная метрика p(g,h) обладает сле¬
дующим свойством инвариантности:
т. е. не меняется при правых сдвигах в группе G. Точно
так же может быть построена метрика, инвариантная
при левых сдвигах.
Пример. На матричной группе G мы можем ис¬
пользовать форму to = сo(g,dg), построенную в преды¬
дущем параграфе, и положить
ds2 = atj (t)dtl dt1
a(t) = A'(0, г)а(0М(0, t),
p(ggo,hg0) = p(g,h),
где штрих означает транспонирование, sp — след и
сог'j — элемент матрицы со. Очевидно, эта форма является
положительно определенной.

44
ГЛ. I. ТОПОЛОГИЧЕСКИЕ ГРУППЫ. ГРУППЫ ли
Замечание. Связь между теорией групп Ли и гео¬
метрией римановых пространств впервые была плодо¬
творно использована Э. Картаном. В частности, важно
отметить, что однопараметрические подгруппы в группе
G оказываются геодезическими относительно введенной
римановой метрики*). Это свойство мы исследуем ниже
(§ 102) для отдельного частного случая групп Ли.
Точно так же, применяя «правило трансляции» к ко¬
сосимметрическому тензору ранга п (где п — число па¬
раметров в группе G), получаем следующий результат:
Теорема 7. На группе Ли размерности п суще¬
ствует элемент объема, инвариантный относительно пра¬
вых сдвигов и представимый в виде
dp (g) = £2 (t) dt1 dt2 ... dtn,
где Q (t) — аналитическая функция на группе G, опреде¬
ляемая однозначно с точностью до постоянного множи¬
теля.
Действительно, элемент объема задается в единич¬
ной точке е посредством обычного определителя, состав¬
ленного из линейно независимых касательных направле¬
ний. Этот элемент может быть записан также в виде
кососимметричной полилинейной формы порядка п. При¬
меняя правило трансляций, указанное в § 6, заметим
также, что кососимметрический тензор порядка п опре¬
деляется в «-мерном пространстве однозначно с точ¬
ностью до постоянного множителя.
Условие инвариантности элемента dpi(g) можно вы¬
разить формулой dp(ggo) = dp(g), понимая под заме¬
ной переменных обычное правило вычисления якобиана.
Иное выражение условия инвариантности дается фор¬
мулой
J f (ggo) dp (g) = J f (g) dp (g),
где f(g) —произвольная функция на группе G, интегри¬
руемая с весом dp(g'). Элемент dp(g) называется пра¬
*) Использование техники римановых пространств позволяет,
в частности, свести теоремы А и В в § 4 к соответствующим тео¬
ремам о геодезических. Отсюда следует, в частности, и естественный
способ доказательства указанных двух теорем.

§ 7. МЕТРИКА. МЕРА ХААРА
45
воинвариантной мерой на группе G. Аналогично строится
левоинвариантная мера.
Пусть А — произвольное измеримое множество в
группе G, т. е. такое, для которого интеграл
ц (Л) = J d\i (g)
А
существует. Полученный интеграл называется мерой
или объемом множества А. Инвариантность этого
объема относительно правых сдвигов выражается оче¬
видной формулой:
р04&о) = р(А)
для любого go^G. Функция р(А) называется также
мерой Хаара по имени математика, который доказал ее
существование (для класса групп более широкого, чем
группы Ли).
В этой главе был приведен лишь краткий обзор теории групп
Ли. Подробное изложение этой теории можно найти в монографиях
[38], [45], [46]. Оригинальное изложение первоначальной теории Ли
содержится в трактате Ли и Энгеля [32]. Связь с геометрией
римановых пространств приводится в [24], [47]; см. также [42]. Ре¬
шение пятой проблемы Гильберта — [36]*). Относительно инвариант¬
ного интегрирования на группе см. [9], [10], [35], [118], [134].
В следующей главе мы рассмотрим несколько более подробно
линейные (матричные) группы. Ряд результатов теории групп Ли
будет в дальнейшем изложен с доказательствами для этого част¬
ного класса групп.
*) См. также сборник «Проблемы Гильберта» (под ред.
П. С. Александрова), «Наука», 1969.

ГЛАВА II
ЛИНЕЙНЫЕ ГРУППЫ
Мы уже ввели понятие линейной группы в преды¬
дущей главе. Линейные группы являются важнейшим
объектом изучения в теории групп Ли. Они имеют
принципиальное значение также в геометрии и теоре¬
тической физике.
§ 8. Полная линейная группа. Экспоненциал
Абстрактное множество А называется алгеброй, если
оно является линейным пространством с ассоциативным
умножением, причем сложение и умножение связаны
обычным дистрибутивным законом. Говорят, что алгебра
А является алгеброй с единицей, если в ней существует
элемент е, для которого еа = ае = а при любом ае/1.
Множество всех обратимых элементов в алгебре А с
единицей, очевидно, является группой. Если, в частности,-
А — алгебра всех матриц п-то порядка, то таким путем
возникает полная линейная группа GL(n, Ф).
В качестве поля Ф мы обычно условимся рассма¬
тривать R или С. Если ясно, о каком поле идет речь, то
мы условимся для краткости обозначать полную линей¬
ную группу символом GL(n). Под топологией в GL(n)
мы будем всегда понимать топологию объемлющего ли¬
нейного пространства А.
Мы уже использовали в гл. I понятие матричной
экспоненты. Эту экспоненту условимся обозначать сим¬
волом ех или ехр х. Имеем
ехр х • ехр у = ехр (х + у),
если матрицы х, у перестановочны (в общем случае это
не так). Доказательство легко получить перемножением

§ 8. ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА. ЭКСПОНЕНЦИАЛ
47
двух рядов. Функция g = exp х доставляет нам кано¬
нические координаты в группе GL(n).
Теорема 1. Экспоненциальное отображение g =
= exp х, хе/1, накрывает всю группу GL(n) над комп¬
лексным полем С.
Доказательство. Воспользуемся нормальной
жордановой формой матрицы g. Согласно теории эле¬
ментарных делителей матрица g в некотором базисе мо¬
жет быть приведена к диагонально-блочному виду с
блоками вида
gi ~ i = I» 2, . . ., S,
где Ki — диагональная матрица с единственным соб¬
ственным значением и zt — треугольная матрица с еди¬
ницами на главной диагонали. Ограничившись отдель¬
ным блоком, мы запишем его в виде
g = Xz,
где матрица К кратна единице и матрица г описана
выше. Заметим, что г = е + £, где матрица | нульсте-
пенна (£т = 0 при достаточно большом пг). Отсюда сле¬
дует, что логарифм матрицы г может быть определен
в виде конечного степенного ряда. В результате
z = ехр т,
где матрица т нульстепенна. В то же время матрица %
также может быть записана в виде экспоненты exp h.
Поскольку матрица h кратна единичной, она переста¬
новочна с т. В результате имеем
g = exp h • ехр т = exp (h + т).
Мы показали, что всякая матрица g ^ GL(n, С) может
быть записана в виде экспоненты. Теорема доказана.
Замечание. Над вещественным полем подобная
теорема неверна, поскольку даже диагональная матрица
X с отрицательными собственными значениями, вообще
говоря, не может быть записана в виде экспоненты. Экс¬
поненциальное отображение накрывает лишь некоторую
область в GL(n,R).

48
ГЛ. П. ЛИНЕЙНЫЕ ГРУППЫ
В дальнейшем иногда мы будем использовать хо¬
рошо известную формулу Якоби:
det е* = esP *.
Здесь spx означает след матрицы х, т. е. сумму ее диа¬
гональных элементов. (Поскольку детерминант и след
не зависят от выбора базиса, то достаточно проверить
справедливость этой формулы в том базисе, где ма¬
трица л: треугольна. Существование такого базиса хо¬
рошо известно из теории матриц.) В частности, если
det екх = 1, —оо < % < оо, то мы имеем
sp х = 0.
Множество всех матриц порядка п с детерминантом,
равным единице, обозначается символом SL(n). Это
множество является группой и носит название унимо-
дулярной группы порядка п*).
Согласно общим конструкциям гл. I мы можем за¬
ключить, что алгебра Ли GL(n) совпадает по запасу
элементов со всей алгеброй А квадратных матриц
пхп Очевидно также, что алгебра Ли SL(n) выде¬
ляется единственным условием spx = 0. Мы обозначим
эти алгебры строчными символами gl(n), sl(n) соответ¬
ственно
Согласно общей теории групп Ли всякая замкнутая
подгруппа в GL(n) снова является группой Ли. Если
X — соответствующая алгебра Ли, то X а А и комму¬
татор в X выражается обычной формулой [х, у]=ху — ух.
Различные алгебры Ли отличаются в этом случае лишь
по запасу элементов. Такие алгебры иногда называются
также линейными алгебрами Ли.
§ 9. Полная линейная группа. Основные разложения
Мы отметим в этом параграфе некоторые способы
параметризации полной линейной группы G = GL (п,С).
Все они связаны с некоторыми мультипликативными
разложениями в группе G. С соответствующими изме¬
*) Расшифровка обозначения SL(rt)—«special linear group».

§ 9. ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА. ОСНОВНЫЕ РАЗЛОЖЕНИЯ 49
нениями результаты остаются верными также и для
вещественного поля.
А. Полярное разложение. Введем операцию
эрмитова сопряжения по формуле а* = а', где штрих
означает транспонирование матрицы а и черта — комп¬
лексное сопряжение. Заметим, что
(ab)* = Ь*а*.
Матрица h называется эрмитовой или самосопряжен¬
ной, если h* = h. Матрица и называется унитарной, если
и* = и~К Матрица р называется положительно опреде¬
ленной, если форма
Pit) = PijVh
положительно определена. Эрмитова матрица является
положительно определенной в том и только том случае,
когда все ее собственные значения положительны.
Теорема 2. G = RU, где R — множество всех поло¬
жительно определенных эрмитовых матриц и U = U(n) —
группа всех унитарных матриц порядка п. Индивидуаль¬
ное разложение g = ru, г е R, и е 11, однозначно.
Доказательство. Если матрица g обратима, то
матрицы g* и р = gg* также обратимы (ибо det^* =
= det^). Легко проверить, что р е R. Следовательно,
р = г2, где г е R (достаточно использовать тот базис,
в котором р диагональна). Полагая u = r~lg, находим
ии* = = е.
Следовательно, матрица и унитарна и g = ги. Если ма¬
трица g допускает какое-либо иное разложение такого
типа, скажем g = гхщ, то по-прежнему r2 = gg* = p, от
куда следует, что гх = г, ввиду однозначности извлече¬
ния корня в R. Следовательно, также щ = и. Теорема
доказана.
Разложение g = ru., г <= R, ц е U, называется поляр¬
ным разложением. Оно обобщает разложение комплекс¬
ного числа в произведение модуля на унитарное число
вида е1ф. При переходе к вещественному полю эрмито-
вость заменяется симметричностью и унитарность —
ортогональностью.

50
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
В. Разложение Гаусса. Пусть D = D(n) —
множество всех диагональных матриц из G (относи¬
тельно фиксированного базиса):
Пусть Z_ = Z_(«), Z+ = Z+(n) —соответственно множе¬
ства всех нижних и верхних треугольных матриц с еди¬
ницами на главной диагонали:
1 0 .
. 0
1 z12 .
• г1я
£21 1
. 0
. г =
0 1 .
• z-in
1 Zn2 •
. 1
0 0 .
. 1
Все эти множества являются группами. Далее, пусть
Аг — диагональный минор матрицы g, составленный из
первых I строк и первых i столбцов. Докажем, что имеет
место
Теорема 3. Если миноры A,-, i = 1, 2, , п, ма¬
трицы g отличны от нуля, то g разлагается, причем един¬
ственным образом, в произведение вида
g = ^eZ_, fie D, zgeZ+.
Элементы сомножителей £, 6, z выражаются рационально
через элементы матрицы g. Множество G0 = Z_DZ+ от¬
крыто и всюду плотно в группе G.
Доказательство. Умножим матрицу g справа
на х е Z+ и выпишем систему уравнений (gx)ij = 0 при
i < /:
/
2 £;***/ = О, К /</<«,
k= 1
которые выражают нижнюю треугольность матрицы gx.
Легко проверить, что детерминант такой системы при
фиксированном i совпадает с А,. Следовательно, эта си¬
стема разрешима, и, заменяя х на г-1, мы имеем
8 = Ьг\

§ 9. ПОЛНАЯ ЛИНЕЙНАЯ ГРУППА. ОСНОВНЫЕ РАЗЛОЖЕНИЯ 51
где матрица k является нижней треугольной. Очевидно,
всякая такая матрица может быть записана в виде £6,
где ?eZ.,
Далее, пусть g1'-2"' \р означает минор матрицы g,
Ч'2 *р
составленный из строк с номерами и, i2, ip и столб¬
цов с номерами /ь /г, /р. Легко находим по правилу
умножения миноров
р-1 2 ... р — 1 р Д ~
в 1 2 ... р-1 q р pq>
где Ар = k\ \k22 ■ • • kpp = 6162 . . . бр. Отсюда, в частности,
при р = q получается выражение для собственных зна¬
чений бр и при p<q — выражение для элементов гРч.
Обозначая минор, стоящий слева, через АР9, находим
Ар? ,
гря ~ др ’ Р
Аналогично вычисляя £, находим £И=Д' /А , где для
краткости положено Д'? = gj| р. Заметим также,
что
А р
бр ~ т , р 1, 2, .. ., п,
где положено До = 1.
Остается доказать единственность полученного раз¬
ложения. ЕСЛИ g = k\Z\ = k2Z2, TO k7lk-2 — , что воз¬
можно только в том случае, когда k\ — k2, z\ = z2. Впро¬
чем, единственность следует также из приведенного
выше явного вычисления параметров £, б, г.
Множество G0 = Z..DZ+ получается выбрасыванием
из G многообразия меньшей размерности (это многооб¬
разие определяется как объединение гиперповерхностей
А,- = 0, / = 1, 2, ..., п — 1). Следовательно, G0 открыто
и всюду плотно в G. Теорема доказана.
Разложение теоремы 3 мы будем называть разло¬
жением Гаусса (Гаусс использовал его для рекуррент¬
ного решения системы линейных уравнений). Заметим,
что G0 содержит единичную точку е, а потому и некото¬
рую окрестность точки е. Всякую точку geG0 мы бу¬
дем называть регулярной и множество G0 обозначать
также символом Greg.

52
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
С. Разложение Грама. Пусть Е означает сово¬
купность всех диагональных положительно определен¬
ных матриц. Докажем, что имеет место
Теорема 4. G = Z-EU. Индивидуальное разложе¬
ние g = £е«, ее£, £ е Z_, йе(/, однозначно.
Доказательство. Согласно критерию Сильвест¬
ра всякая положительно определенная матрица содер¬
жится в Greg. В частности, матрица р = gg* допускает
разложение Гаусса: р = £бг, причем из эрмитовости р
и единственности разложения Гаусса следуют равенства
l = z\ 6 = 6*, 2= S'-
Кроме того, матрица б является положительно опреде¬
ленной. Следовательно, б = е2, е ^ R. Полагая t = £е,
мы запишем матрицу р в виде tt* и положим и = t~lg.
Тогда имеем
ии* = t~'gg*i*~l = е,
откуда следует, что матрица и унитарна. В результате
g = tu = Sen. Единственность этого разложения уста¬
навливается таким же способом, как при доказательстве
теоремы 3. Теорема доказана.
Разложение теоремы 4 мы условимся называть раз¬
ложением Грама. Оно выражает процесс «ортогонализа-
ции» произвольной матрицы g е G при помощи тре¬
угольного сомножителя t = £е. Пусть Т — множество
всех таких треугольных матриц (с положительными соб¬
ственными значениями). Тогда мы имеем
GL (п) = Т-Щп)
Заметим также (это ясно из доказательства теоремы 4),
что соответствие между матрицей g и тройкой (£, е, и)
является взаимно непрерывным. Следовательно, группа
G как топологическое множество изоморфна прямому
произведению Z_ X Е X U.
Последнее замечание весьма существенно для уясне¬
ния топологической структуры группы G. Действитель¬
но, множество Т изоморфно евклидову пространству.
Следовательно, вся сложность топологической струк¬
туры «сосредоточена» в группе U (п).

§ 10. ЛИНЕЙНЫЕ ГРУППЫ, СВЯЗАННЫЕ С ФОРМАМИ
53
Упражнения
1. Показать, что GL(n, Ф) = Ф1 • SL(«, Ф), где группа Ф1 изо¬
морфна мультипликативной группе поля Ф. (У к а з а н ие: элементы
ф, диагональны с единственным собственным значением, отличным
от единицы.)
2. Показать, что U(п) — Ф0 • SU(n), где группа Ф0 изоморфна
окружности и группа SU(«) определяется как пересечение U(n)
с SL(п,С).
3. Показать, что GL(n)=UEU. (Указание: положить g = pu
(полярное разложение) и привести матрицу р к диагональному
виду.)
§ 10. Линейные группы, связанные с формами
второго порядка
В приложениях часто встречаются линейные группы,
которые выделяются из GL(«) условием сохранения не¬
которой формы второго порядка, подобно тому как
группа вращений сохраняет скалярный квадрат. Мы
займемся в этом параграфе классификацией и описа¬
нием простейших свойств таких линейных групп.
Пусть Е— исходное n-мерное пространство. Для
упрощения записей условимся рассматривать вектор
£ <= Е как координатный вектор-столбец и записывать
всякую билинейную форму над Е в виде
f(x,y) = x'fy, х,у<=Е,
где f — постоянная матрица, определяющая эту форму,
и штрих означает транспонирование. Заменяя транспо¬
нирование эрмитовым сопряжением, мы можем рассма¬
тривать также эрмитовы или полуторалинейные формы
вида x*fy (которые линейны по у и антилинейны по х).
В дальнейшем мы всегда предполагаем, что форма
f(x,y) невырождена, т. е. det / Ф 0. (В противном слу¬
чае форма / «содержит только часть переменных», опре¬
деляющих х и у.) Равенство
f{gx,gy) = f(x,y)
означает, что форма f остается инвариантной при преоб¬
разовании g. Множество Gf всех линейных преобразова¬
ний, оставляющих форму f инвариантной, как увидим,

54
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
образует группу. Действительно, имеем
x'g'fgy = x'fy.
Поскольку это равенство имеет место для всех значений
х, у е Е, то мы заключаем, что матрицы g'fg и f равны.
Равенство
g'fg = f (*)
необходимо и достаточно для инвариантности формы f.
В частности, это равенство является определяющим для
Gf. Вычисляя детерминанты обеих частей этого равен¬
ства, находим
(detg)2 det f = det Д
Поскольку мы условились, что det f ф 0, отсюда нахо¬
дим detg = ±l. В частности, матрицы g^Gf всегда
невырождены. Отсюда ясно, что Gf образует группу.
Отметим вначале простое правило для вычисления
алгебры Ли группы Gf. Записывая g в виде ехр tx, мы
подставляем эту экспоненту в (*). Дифференцируя по t
при t = 0, находим
x'f + fx — 0.
С другой стороны, предположим, что матрица х удовле¬
творяет этому условию. Дифференцируя функцию ф(0 =
= ехр tx' • f • ехр tx, с заменой х' на —fxf~l находим, что
ф'(г) =0. Следовательно, равенство
х' = —fxf~l (**)
необходимо и достаточно для того, чтобы матрица х
содержалась в алгебре Ли группы G}. Иными словами,
условие (•**) является определяющим для искомой ал¬
гебры Ли.
Замечание. В частности, мы получим ортогональ¬
ную группу О(п), если положим f = е. Условие (**)
принимает вид х' = —х, и мы заключаем, что всякая
матрица х, касательная к группе вращений, является
кососимметрической. Этот результат, в частности, хо¬
рошо известен в аналитической механике.
Перейдем к вопросу о классификации групп Gf. Огра¬
ничимся тем практически важным случаем, когда форма'
f симметрична или кососимметрична. За счет опреде¬

§ 10. ЛИНЕЙНЫЕ ГРУППЫ, СВЯЗАННЫЕ С ФОРМАМИ
55
ленного выбора базиса мы можем всегда привести
форму / к одному из принятых в алгебре «канониче¬
ских» видов. Особенно легко проводятся эти построения
над полем комплексных чисел.
I. Классификация групп Gf над полем С.
Если форма симметрична, то она, как известно, приво¬
дится в некотором базисе к виду
(х, у) = Х1у1 + Х2у2 + . . . + Хпуп.
Следовательно, в этом случае группа Gf изоморфна
ортогональной группе, обозначаемой 0(п,С) («ком¬
плексно ортогональная группа»). Если форма / кососим¬
метрична, то она, как известно, может быть невырожден¬
ной только в случае четной размерности п = 2v и при¬
водится к виду
[х, у] = ХхУп + Х2уп-1 + ■ • • +xvyv+1 — xv+i yv — —хпу ь
Полученная группа обозначается Sp(n, С) и называется
(комплексной) симплектической группой. Эта группа
встречается в геометрии при изучении комплексов пря¬
мых и в аналитической механике при изучении касатель¬
ных преобразований. Заметим, что в случае О (п, С)
форма / может быть также приведена к виду
{х, у} = XIуп + х2уп-\ + . .. + Хпуи
по записи сходному с [х, у]. Последний способ записи
действительно часто оказывается удобным при изучении
группы О (п, С).
II. Классификация групп Gf над полем R.
Над вещественным полем вместо формы (х, у) мы полу¬
чаем целую серию канонических форм:
(Х, У) pq ” Х\У\ -f- . . . -f- ХрУр Хр+\Ур+у . . . Xp+qPp+q,
р + q — п, которые отличаются друг от друга числом
коэффициентов, равных ±1. Группа Gf, сохраняющая
форму (x,y)pq, обозначается 0(p,q) и называется
псевдоортогональной группой. Форма
(х, у) = (х, у) п. о
определяет ортогональную группу 0(п) =0(n,R) над
полем вещественных чисел. В кососимметрическом

ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
случае мы по-прежнему получаем единственную группу
Sp (n,R), выделяемую из Sp(n, С) условием веществен¬
ности.
III. Классификация Gf для полуторали¬
нейной форм ы /. В полуторалинейном случае раз¬
личие между симметричными и кососимметричными
формами несущественно, поскольку умножение всех ко¬
ординат на / = V — 1 сводит эти случаи друг к другу.
Каноническая запись формы f(x,y) имеет вид
(-*■> y)pq ~ Х\У\ Т • • • + ХрУр -£р-нУр + 1 • • • ^p + qflp+qy
р + q = я. Линейная группа, сохраняющая эту форму,
обозначается U(р, q) и называется псевдоунитарной
группой. Если q = 0, то мы имеем форму
(х, у) = ххух + х2у2 + ... +хпуп.
Линейная группа U(я), сохраняющая эту форму, нам
уже известна. Группа U(«) состоит из всех унитарных
матриц порядка п и называется полной унитарной
группой.
IV. Пересечения сгруппой SL (я). Пусть Gf+ —
пересечение группы G, с унимодулярной группой SL(n).
Подгруппа Gf" выделяется из Gf условием detg=l.
Символ этой группы принято образовывать из символа
Gf приписыванием слева буквы S (special). Так возни¬
кают группы SU(«), SO (я), SO (p,q), SU (p,q). Группа
SO (я) называется иногда собственно ортогональной
группой.
V. Пересечения с группой и(я). Предста¬
вляют интерес линейные группы, получаемые из ком¬
плексной группы Gf пересечением с и(я). При этом
полученная группа сохраняет уже две формы второго
порядка, одна из которых билинейна, а вторая полутора¬
линейна.
Начнем с рассмотрения О (я) = О (я, С). В дальней¬
шем мы увидим, что если исходную билинейную форму
записывать в виде {х, у}, то пересечение О (я, С) с U (я)
дает новую группу, отличную от {е} и от обеих исходных
групп. Эта группа обозначается ОЩя) и называется
ортогонально-унитарной группой■

§ 11. КВАТЕРНИОНЫ
57
Аналогично, пересечение Sp(«, С) с унитарной груп¬
пой U(я) приводит к рассмотрению новой линейной
группы. Для этой группы мы введем обозначение
SpU(rt) и назовем ее симплектически-унитарной группой.
Символику, введенную для групп, дополним соответ¬
ствующей строчной символикой для алгебр Ли: so (п,С),
sp(я,/?) и т. д.
Упражнения
1. Согласно результатам этого параграфа матрицы
0
0
0
0
0
1
0
-1
0
“1 =
0
0
-1
, а2 =
0
0
0
, flj =
1
0
0
0
1
0
-1
0
0
0
0
0
образуют базис в алгебре so(3, R). Проверить, что закон коммута¬
ции в этом базисе имеет вид
[щ, а/] =ац,
где I, /, к — циклическая перестановка индексов 1, 2, 3. Полученная
алгебра называется алгеброй векторных произведений.
2. Найти закон коммутации для матриц
г
0 1
/
0 г
i
1 0
а\ = Y
1 0
. щ = т
-£ 0
0 -1
образующих базис в алгебре su(2).
3. Пусть pi, qi — линейно независимые символы в некоторой ас¬
социативной алгебре, подчиненные закону коммутации:
[Pv4i} = blp [Рр ?/]“[</,■ ?/] = 0’
где 6,-j — символ Кронекера. Проверить, что линейные комбинации
этих символов удовлетворяют таким же соотношениям коммутации
только в том случае, когда матрица преобразования симплектична.
§ 11. Кватернионы
Все линейные группы, рассмотренные в предыдущих
трех параграфах, принято называть классическими. Мы
покажем, что простейшие из этих групп тесно связаны
с геометрией кватернионов.
Пусть Е — четырехмерное пространство над полем
комплексных чисел с базисом е0, еи е2, е%. Введем в

58
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
пространстве Е следующую таблицу умножения:
е~0 = е0; е0ег- = = еь i = 1, 2, 3;
ei = —ео,
6i@j СjС
г= 1,2,3;
ей,
где I, /, k в последнем равенстве образуют циклическую
перестановку чисел 1,2,3. Тогда пространство Е пре¬
вращается в ассоциативную алгебру, называемую
алгеброй кватернионов.
Для каждого кватерниона х = х0е0 + ххв\ + х2е2 + х3е3
введем сопряженный кватернион по правилу х+ =
— х0е0 — Х\в\—х2в2-— хге3; тогда, как легко проверить,
(*)
хх+ = х+х = (х* + х\ + х\ + xfj е0.
Кватернионы вида Яе0 мы будем называть скалярами,
кватернионы, для которых х0 — 0, — векторами. Нетруд¬
но проверить, что закон умножения кватернионов соче¬
тается из скалярного и векторного произведений трех¬
мерных векторов.
Мы построим алгебру, изоморфную алгебре кватер¬
нионов, если рассмотрим систему матриц Паули:
0
Ml
0 i
III
0
0, =
а, =
-i 0
, 0ч =
||0
1
о|р
-1
которые удовлетворяют закону умножения щ = е,
OiOj = —iak, где множитель г (в отличие от индекса г)
означает умножение на’ У—1. Положим также о0 =
= —ie, где е — единичная матрица, и рассмотрим ли¬
нейные комбинации
х = i (х0о0 + *,0, + х2а2 + х3о3) =
х0 + ix3 xt + ix2
■Х\ + ix2 х0 — ixз!
Множество полученных матриц совпадает с алгеброй А
всех комплексных матриц 2X2. Формулы iak = eh, k =
= 0, 1,2,3, устанавливают изоморфизм между Е и А.
Заметим также, что
det х = xl + х\ + х22 + Ху

§ 11. КВАТЕРНИОНЫ
59
Пространство Е и алгебру А мы наделяем структу¬
рой комплексного евклидова пространства, считая сум¬
му квадратов координат скалярным квадратом век¬
тора х. Пусть а и b — произвольные унимодулярные
матрицы 2X2. Преобразование
т(a, b)x = axb~x
сохраняет det л:, т. е. сохраняет скалярный квадрат век¬
тора х. Следовательно, т(а, Ь) а О (4, С). Поскольку
матрицы а, b непрерывно связаны с единицей, то в дей¬
ствительности т {a, b) a SO (4, С).
Используя определение х(а, Ь), легко проверить, что
эта функция осуществляет гомоморфизм
© X ®-*G,
где положено для краткости @ = SL(2, С), G — SO(4, С).
Покажем, что имеет место
Теорема 5. Функция х{а,Ь) определяет гомомор¬
физм @ X © на всю группу G = SO(4, С). Ядром гомо¬
морфизма т являются пары (е,е) и (—е,—е), где е —
единичная матрица порядка 2.
Доказательство. Согласно результатам преды¬
дущего параграфа алгебра si (2, С) имеет размерность 3
и алгебра so (4, С) имеет размерность 6. Следовательно,
группы @ X © и G обе имеют размерность 6.
Далее, найдем ядро гомоморфизма т. Если axb~x — х,
то ах = xb для всех комплексных матриц х. Легко про¬
верить, что это возможно только при .а = b = Хе. Из
свойства унимодулярности матриц а и b следует X2 = 1.
В результате искомое ядро состоит из элементов (е, е) и
(—е, —е).
Поскольку ядро дискретно, размерность т(© X ©) по-
прежнему равна 6. Следовательно, мы имеем вложение
т(®Х®)сС двух связных групп одинаковой размер¬
ности. Согласно теореме 2 главы I мы можем заклю¬
чить, что эти группы совпадают. Теорема доказана.
Следствие 1. Группы @ X © и G локально изо¬
морфны, причем первая группа двукратно накрывает
вторую.

60
ГЛ. II. ЛИНЕИНЫЕ группы
При помощи теоремы 5 нетрудно получить еще не¬
сколько подобных следствий. В частности, положим
а — Ь\ тогда получим систему операторов
т (а) х — аха~\
которые сохраняют не только детерминант, но и след
матрицы х. Равенство х0 — 0 выделяет в алгебре Е под¬
пространство Ео, инвариантное относительно т(а). Ядром
гомоморфизма т(а) являются матрицы е и —е. Имеем
Следствие 2. Группа ® локально изоморфна
SO(3, С) и дважды накрывает ее.
С другой стороны, рассмотрим группу U==SU(2)
как подгруппу в группе @ и ограничим функцию т(а) на
значения well; поскольку «-1 = «*, то мы имеем
т(и) х = ихи*.
Условие вещественности координат хих2, х3 и равенство
Го = 0 делают матрицу х произвольной эрмитовой; трех¬
мерное пространство таких матриц инвариантно относи¬
тельно т(«). В результате имеем
Следствие 3. Группа U локально изоморфна
SO(3, R) и дважды накрывает ее.
Заметим, что функция т(ы) дает чрезвычайно удобную пара¬
метризацию группы SO(3,R), поскольку т(«|«2) = r(ui)r(u2). Пара¬
метры bgU называются параметрами Кзли — Клейна. В отличие
от углов Эйлера, эти параметры позволяют наиболее просто выра¬
зить закон умножения в SO(3, R).
Перейдем теперь к рассмотрению вещественных ква¬
тернионов. Полагая все координаты х0, хи х2, х3 веще¬
ственными, мы получаем з алгебре А подалгебру К, эле¬
менты которой называются вещественными кватернио-
мами.
Если х ф 0, то согласно формуле (*) х имеет обрат¬
ный в алгебре К■ Всякая алгебра, обладающая этим
свойством, называется телом. Следовательно, алгебра
вещественных кватернионов является телом.
Функция р = Yx+x — Ухх+ называется нормой
кватерниона х. Используя формулу (*), легко получаем,
что всякий кватернион х^К может быть представлен
в виде
х = ри, и SU (2),

§ 11. КВАТЕРНИОНЫ
61
Полученную формулу условимся называть полярным
разложением в алгебре К. Заметим также, что сопряже¬
ние в К совпадает с эрмитовым сопряжением в классе
матриц 2x2.
Всякое линейное преобразование в К, сохраняющее
умножение и сохраняющее норму, называется автомор¬
физмом тела К. Множество всех автоморфизмов тела К,
очевидно, образует группу.
Теорема 6. Всякий автоморфизм тела кватернио¬
нов задается формулой %(u)x = uxu~l, ueSU(2). Груп¬
па всех автоморфизмов тела К изоморфна SO(3, R).
Доказательство. Рассуждая, как при доказа¬
тельстве теоремы 5, заключаем, что всякое собственно
ортогональное преобразование тела К может быть за¬
писано в виде uxv~], «,BeSU(2)*). Если это преобра¬
зование сохраняет умножение, то имеем
uxv~luyv~l = uxyv~l
для произвольных х, у е К- Сокращая обратимые мно¬
жители и, ц-1, х, у, заключаем, что v~xu = е, откуда v = и.
Следовательно, наше преобразование сводится к т(и).
Далее, всякое несобственное ортогональное преоб¬
разование получается из собственного умножением на
единственное отражение в теле К, в качестве которого
мы выберем сопряжение х-ух+. Следовательно, искомое
преобразование имеет вид х -у их+v-1, и, ueSU(2). Как
и прежде, имеем
■ ux+v~'uy+v~1 = и (ху)+ v~l.
Заметим, что (ху)+= у+х+ согласно правилу эрмитова
сопряжения. Полагая, в частности, х = у, находим, как
и выше, что v = и. Однако подстановка v = и приводит
к противоречию: .х+у+ — у+х+. Следовательно, группа
автоморфизмов тела К содержит только собственные
преобразования. Теорема доказана.
В заключение рассмотрим векторное пространство
размерности v над телом кватернионов и для каждой
пары векторов а = (аи аг,. . •, яу)> b =(b\,bz,... ,bv)
*) Отсюда следует локальный изоморфизм между U X U и
SO(4, R), причем первая группа дважды накрывает вторую.

положим
a+b = a+bl + a+b2+ ... + a+6v.
Пусть G — группа всех линейных преобразований
at -v gijCij (сумма по /) над телом кватернионов, сохра¬
няющих форму а+Ь. Легко проверить, что группа G изо¬
морфна SpU(n) при п = 2v.
В частности, группа SpU(2), сохраняющая норму в
теле кватернионов, изоморфна SU(2).
Упражнение
Доказать локальный изоморфизм между SO(3, R), SU(2) путем
сравнения соответствующих алгебр Ли (см. упражнения 1 и 2
в конце предыдущего параграфа).
§ 12. Вопросы односвязности
В этом параграфе мы исследуем вопрос об одно¬
связности некоторых классических групп. Вначале на¬
помним некоторые простейшие сведения из общей топо¬
логии.
Пусть вначале М — произвольное множество, пред¬
ставимое в виде суммы непересекающихся подмножеств
Мр. В этом случае говорят, что семейство Мр образует
разбиение множества М, и множество В всех индексов р
называется фактор-пространством множества М отно¬
сительно этого разбиения. Переход от пространства М к
фактор-пространству В равносилен «склейке» всех то¬
чек, лежащих в одном и том- же подмножестве Mg. Если
все такие подмножества эквивалентны одному из них,
скажем А, то для обозначения фактор-пространства ис¬
пользуется символ
В = М/А.
Далее, пусть М — топологическое пространство. Мно¬
жество Р индексов р назовем открытым (замкнутым) в
В, если объединение всех подмножеств Мg, р еР, от¬
крыто (замкнуто) в М. Всякое открытое множество, со¬
держащее точку р, называется окрестностью этой точки.
Тем самым в В определяется топология, называемая
фактортопологией.

§ 12. ВОПРОСЫ ОДНОСВЯЗНОСТИ
63
Топологические множества Р и Q называются гомео-
морфными, если между ними существует взаимно одно¬
значное и взаимно непрерывное отображение. Если
В = М/Л
и если все слои Мр гомеоморфны слою А, то мы усло¬
вимся говорить, что пространство М является расслое¬
нием со слоем А и базой В.
Пример 1. Лист Мёбиуса является расслоением с
базой окружность и со слоем отрезок.
Пример 2. Двумерный тор является расслоением
с базой окружность и со слоем окружность.
Пример 3. Прямое произведение АхВ произволь¬
ных топологических пространств можно рассматривать
как расслоение со слоем А и базой В.
Далее, пусть G — произвольная группа и Н — ее под¬
группа. Каждому g е G поставим в соответствие слой
gH, называемый правым классом смежности по Н. Не¬
трудно видеть, что таким путем возникает разбиение с
фактор-пространством F = G/Н. Если G — топологиче¬
ская группа и Н — ее замкнутая подгруппа, то мы имеем
расслоение со слоем Н.
Понятие расслоения обычно используется для индук¬
тивного изучения топологических множеств и топологи¬
ческих групп. В частности, мы будем использовать сле¬
дующие общие утверждения (см., например, [46]):
1° Пусть G — связная группа Ли и Н — ее замкну¬
тая связная подгруппа. Если Н и G/Н односвязны, то
группа G также односвязна.
2° Пусть М = А X В, где А и В — топологические
пространства. Пространство М односвязно тогда и толь¬
ко тогда, когда односвязны А и В.
В дальнейшем мы условимся, что термин «односвяз¬
ность» будет применяться только к связному топологи¬
ческому множеству; иначе говоря, под этим термином
мы будем иметь в виду одновременно связность и одно¬
связность. Такое соглашение удобно, поскольку мы, как
правило, будем рассматривать только связные топологи¬
ческие группы. Изучение классических линейных групп
нам будет удобно начать с изучения группы SU(«).
Теорема 7. Группа SU(n) односвязна.

64
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
Доказательство. Связность SU(/z) легко выте¬
кает из рассмотрения соответствующего множества ре¬
перов. Для доказательства односвязности рассмотрим
единичную сферу S в исходном векторном пространстве
и фиксируем на ней произвольную точку, скажем
е = (0, 0,. . ., 0, 1). Пусть Я— стационарная подгруппа
точки е, т. е. множество всех преобразований, оставляю¬
щих е на месте. Положим
F = G/H,
где G = SU(/z). Нетрудно видеть, что группа Я изо¬
морфна SU(zz—1). В то же время фактор-простран¬
ство F гомеоморфно сфере S. Действительно, пусть G0—■
множество всех преобразований в G, переводящих ев о.
Если gu g2 е Ga, то g]lg2 е Я, откуда ясно, что
Ga = gH,
где g — произвольно фиксированный элемент из G0.
Если ел ф 02, то G0| ф Go,- Следовательно, мы получаем
взаимно однозначное соответствие между точками ае5
и правыми классами смежности, входящими в F. Не¬
трудно видеть также, что это соответствие взаимно
непрерывно.
Теперь мы можем применить критерий односвяз¬
ности 1°. Заметим, что единичная сфера х1х1 + х2х2 + ...
. .. + хпхп = 1 изоморфна вещественной сфере S2n-1 раз¬
мерности 2п— 1. Вещественная сфера Sh односвязна
при к^-2 (это утверждение легко проверяется по ин¬
дукции). Согласно 1° из односвязности SU(zz — 1) сле¬
дует односвязность SU(zz) при п^-2, и мы получаем
возможность индукции по п. Остается заметить, что
SU (1) состоит из единственной точки и потому одно¬
связна. Теорема доказана.
Теорема 8. Группа SL(zz, С) односвязна.
Доказательство. Согласно разложению Грама
(§ 9) группа SL(п,С) гомеоморфна прямому произведе¬
нию евклидова пространства на SU(zz). Согласно кри¬
терию 2° группа SL(zz, С) односвязна вместе с SU(/z).
Теорема доказана
Теорема 9. Группы U(n), GL(п,С) связны, но не¬
односвязны.

§ 12. ВОПРОСЫ ОДНОСВЯЗНОСТИ
65
Доказательство. Достаточно заметить (см.
упражнения 1 и 2 в конце § 9), что U(n), GL(n) гомео-
морфны соответственно прямым произведениям U(1)X
XSU(n), GL(l)XSL(n). Согласно критерию 2° груп¬
пы U(n) и GL(n) неодносвязны вместе с U(l), GL(1).
Теорема доказана.
Значительно более сложно исследуется случай орто¬
гональной группы SO (п). Группа SO (2) неодносвязна.
Оказывается также, что SO(n) неодносвязна при лю¬
бом п, п>2. Доказательство достигается путем непо¬
средственного построения универсальной накрывающей.
Изложим схему построения в общих чертах*). Пусть Е —
«-мерное пространство с базисом щ, е2, ..., еп. Пространство Е
включим в ассоциативную алгебру К, в которой парные произведе¬
ния е,-е3- связаны единственным условием:
e.e. + e.e. = 26./t (.)
где 6г, — символ Кронекера. Положим е0 = Г е, , , —е, е, ...
12 ‘п м h
... е. Пусть К — линейная оболочка таких одночленов. Согласно
1п'
(*) достаточно рассматривать лишь те одночлены, для которых
ii к ^ ^ *т! кроме того, если два индекса совпадают, то
возникающий множитель е? заменяется единицей. Следовательно,
одночлены
е, , , . /■</,<...< г' 0 < т < п,
12 "• 1т 1 1 т
образуют базис в алгебре К. В частности, К конечномерна. Полу¬
ченная алгебра К носит название алгебры Клиффорда.
Введем скалярный квадрат в пространстве Е как сумму квад¬
ратов координат относительно базиса elt е2, ..., е„. Если Е с: К, то
мы имеем
х2 = (х1е1+х2е2+ ... + хпеп)2 = х\ + х?2 + ••• + х2п.
Следовательно, квадрат элемента х е Е в алгебре К является ска¬
ляром и совпадает со скалярным квадратом в пространстве Е.
Рассмотрим в алгебре К преобразование вида х(у)х = уху~1,
где у — произвольный обратимый элемент из К. Пусть © — макси¬
мальное множество таких преобразований, сохраняющих Е и непре¬
рывно связанных с единицей. Если z — x(y)x, уев, то мы имеем
г2 = ухгу~1 = х2,
ибо х2 является скаляром. Следовательно, т(у) cz О(п). В силу
связности группы © имеем t(i/)cSO(/i). Дальнейшие действия мы
*) Более подробное изложение см. в § 115.

66
ГЛ. II. ЛИНЁИНЫЁ ГРУППЫ
излагаем сокращенно. Проверяется, что @ и SO(п) имеют одина¬
ковую размерность. Проверяется, что ядро гомоморфизма дискретно.
Следовательно,
т(©)= SO (я).
Более точно, ядро гомоморфизма т состоит из двух элементов: ±£о-
Это означает, что группа @ двукратно накрывает SO (п) *).
В дальнейшем мы увидим, что группа @ односвязна. Эта группа
называется спинорной группой и обозначается Spin (п).
Для каждого случая неодносвязной группы, рассма¬
триваемого в этом параграфе, нетрудно вычислить так¬
же соответствующую группу Пуанкаре. В частности,
группа Пуанкаре для SO(п) при п > 2 оказывается изо¬
морфной конечной группе, состоящей из чисел ±1 (по
умножению).
Упражнения
1. Проверить, что алгебра Клиффорда имеет размерность 2п.
2. Используя конструкцию предыдущего параграфа, показать,
что SU(2) является универсальной накрывающей для SO(3, R).
3. Доказать, что группы SpU(n), Sp(n, С) односвязны при про¬
извольном п.
§ 13. Вопросы комплексификации
Группа Ли называется комплексной, если она допу¬
скает комплексную параметризацию, относительно кото¬
рой закон умножения задается голоморфными (ком¬
плексно-аналитическими) функциями. Как следует из
этого определения, если ® — комплексная группа Ли, то
ее алгебра Ли допускает комплексную структуру, т. е.
является алгеброй Ли над полем комплексных чисел.
Комплексная структура сообщает алгебре Ли специфи¬
ческие свойства, обусловленные, как правило, тем об¬
стоятельством, что над комплексным полем всякое ли¬
нейное преобразование обладает собственным вектором.
Если J — комплексная алгебра Ли, то иногда в ней
удается выделить вещественную подалгебру X, имею¬
щую те же структурные константы, что и J. Очевидно,
это возможно тогда и только тогда, когда структурные
константы алгебры J в некотором базисе вещественны.
*) Очевидно, построение группы @ является обобщением кон¬
струкции предыдущего параграфа.

§ 13. ВОПРОСЫ КОМПЛЕКСИФИКАЦИИ
67
В этом случае имеем
Х = Х + IX
и вещественная размерность алгебры X совпадает с ком¬
плексной размерностью алгебры X. В этом случае гово¬
рят, что X является вещественной формой алгебры X, а
X — комплексной оболочкой алгебры X. Если ©— ком¬
плексная группа Ли с вещественной подгруппой G, то G
называется вещественной формой ©, при условии, что
алгебра Ли подгруппы G является вещественной формой
в алгебре Ли группы ©.
В последнем случае также говорят, что группа © яв¬
ляется комплексной оболочкой или комплексификацией
группы G. Поскольку всякая вещественная алгебра Ли
допускает комплексную оболочку и поскольку всякой
алгебре Ли соответствует хотя бы одна группа Ли, то
можно предположить, что и всякая вещественная груп¬
па Ли допускает комплексификацию. Однако в действи¬
тельности это не так. Противоречащий пример будет
указан в конце § 104. Тем не менее в данной книге ука¬
занная гипотеза будет проверена для класса компактных
групп Ли, которые являются основным объектом изуче¬
ния этой книги.
Поскольку комплексная алгебра Ли может допускать
вещественные структурные константы в различных бази¬
сах, то комплексная группа Ли может иметь несколько,
вообще говоря, неизоморфных вещественных форм. Про¬
стейшие примеры мы рассмотрим в этом параграфе.
Пример 1. Мультипликативная группа комплекс¬
ных чисел является комплексной оболочкой мультипли¬
кативной группы вещественных чисел и в то же время
комплексной оболочкой группы чисел е'ч, по модулю
равных единице.
Пример 2. Группа GL(n,C) является комплексной
оболочкой группы GL (n,R) и в то же время комплекс¬
ной оболочкой группы U(п). (Достаточно проверить, что
алгебра X антиэрмитовых матриц имеет размерность п2
и X + iX = X, где I — алгебра всех комплексных матриц
порядка п.)
Пример 3. Группа GL(п,С) является также ком¬
плексной оболочкой групп U(р, q), р + Я — п.

68
ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
Пример 4. Группы О (га, С), Sp (гг, С) являются со¬
ответственно комплексными оболочками О (ft,/?),
Sp(«, R). Они являются также комплексными оболоч¬
ками OU(ra), SpU(ra).
Пример 5. Группа SL(«, С) является комплексной
оболочкой SL(ra, Я) и также комплексной оболочкой
SU(^, q), р + q = п. В частности, SL(«, С) является ком¬
плексной оболочкой группы SU (га).
Пример 6. Группа SO (га, С) является комплексной
оболочкой SO (n,R).
Замечание. Подчеркнем, что группы U(n),
U (p,q), SU (p,q) не являются комплексными группами
Ли, хотя их определение и дается над полем комплекс¬
ных чисел. Например, алгебра и (га) состоит из всех
матриц а, для которых а* = —а. Это свойство нару¬
шается при умножении матрицы а на произвольный
комплексный множитель. Следовательно, и (га) не яв¬
ляется комплексной алгеброй Ли. В качестве другого
объяснения можно заметить, что закон умножения в
U (га) не задается голоморфными функциями, ибо эти
функции зависят не только от комплексных параметров
в U(га), но и от их комплексно сопряженных.
В дальнейшем мы увидим, что соотношения между
вещественными и комплексными группами Ли играют
существенную роль в общей теории.
§ 14. Преобразования в классе тензоров
С каждой линейной группой G тесно связана серия
геометрических преобразований, порождаемых этой
группой в классе тензоров. Для полноты изложения мы
напомним в этом параграфе основные свойства тензоров
и условимся в некоторой системе обозначений.
Пусть Е и Е' — два линейных пространства одина¬
ковой конечной размерности га; векторы из Е мы будем
обозначать латинскими буквами х, у, . . .; векторы из
Е' — греческими буквами g, rj,.. . Фиксируя в каждом
из пространств произвольный линейный базис, мы ото¬
ждествляем векторы х, у, g тр . . . с соответствующими
столбцами координат. Билинейная форма
fib х) = 1'х,

§ 14. ПРЕОБРАЗОВАНИЯ В КЛАССЕ ТЕНЗОРОВ
69
где штрих означает транспонирование, является одним
из важнейших объектов в линейной алгебре и геометрии.
Если рассматривать Е как основное векторное простран¬
ство, то функции 1'х являются линейными формами на Е
и уравнения \'х = 0 определяют всевозможные гипер¬
плоскости, проходящие через начало координат. Про¬
странства Е, Е' называют сопряженными, дуальными
или двойственными.
Пусть векторы х, | подвергаются линейным преобра¬
зованиям g, h (каждый в своем пространстве). Преобра¬
зования g, h называются дуальными или контрагре-
диентными, если их совместное применение не изменяет
формы f (|, х):
f(hl, gx) = / (|, х).
Поскольку то указанное правило сохранения
переписывается также следующим образом: I'h'gx = 1'х,
откуда ввиду произвольности | и х заключаем, что ма¬
трица h'g совпадает с единичной: h'g = е. В результате
имеем
h = g'~\
Эта формула дает явное выражение преобразования,
контрагредиентного к g. Заметим, что это преобразова¬
ние является автоморфизмом группы G при условии,
что G сохраняется при транспонировании.
Пусть х = хге; — координатная запись вектора ле£
в базисе е;. Преобразование g в пространстве Е можно
рассматривать как переход к новому базису е* с коорди¬
натами х\ Равенство х’е, = х1ёх показывает, что сим¬
волы е, преобразуются по тому же закону, что и ко¬
ординаты дуального вектора | е Е'. По этой причине
преобразование h = g'~l называется ковариантным (пре¬
образование по закону базиса).
В дальнейшем мы условимся использовать обозначе¬
ние g вместо g'~K Векторы £ е Е' будут называться ко-
вариантными, векторы х е Е — контравЪриантными.
Напомним определение тензорного произведения двух
линейных пространств X и У. Для каждой пары элемен¬
тов хеХ, у е У вводится формальное произведение
х ® у, которое предполагается дистрибутивным по обоим

70
гл. п. ЛИНЕИНЫЕ группы
сомножителям. Очевидно, имеем
X ® у = х1укеш,
где х{ — координаты х относительно базиса еи yh — коор¬
динаты у относительно базиса ей и eih = et <Z> е&. Про¬
странство Z = X X У определяется как линейная обо¬
лочка всевозможных векторов х®у, х^Х, у е У. Из
этого определения следует, что векторы eih образуют
базис в Z.
Согласно этому определению произвольный вектор
из Z имеет вид tiheih, где tih — произвольные числа. Сле¬
довательно, Z имеет размерность пт, где п = dimZ,
т = dim У. Векторы вида х ® у представляют собой
лишь частный случай элементов из Z. Действительно,
всякий минор матрицы xiyh равен нулю, за исключением
миноров порядка 1.
Пусть векторы х, у подвергаются линейным преобра¬
зованиям а, b (каждый в своем пространстве). Тогда
произведение х ® у также подвергается линейному пре¬
образованию, которое обозначается символом
с = а ® b
и называется тензорным произведением операторов а
и Ь. Если а = ||а*. |, 6 = 1^1 то легко проверить, что
матрица с имеет элементы с= ajbf относительно ба¬
зиса eih. Основное свойство тензорных произведений вы¬
ражается следующей формулой: если с, = at ® Ьи с2 =
= а2 ® Ь2, то
с^с2 === а^а2 b[Ь2'
Иначе говоря, композиция двух преобразований си с2
равносильна композиции компонент аи а2 в простран¬
стве X и одновременной композиции Ь\, Ь2 в простран¬
стве У.
В частности, пусть Ер— тензорное произведение р
экземпляров пространства Е. Каждому линейному пре¬
образованию g в пространстве Е отвечает преобразова¬
ние
о ig) = ё ® ё ® ® ё (Р сомножителей).

§ 14. ПРЕОБРАЗОВАНИЯ В КЛАССЕ ТЕНЗОРОВ
71
где кратное произведение определяется индуктивно. Как
следует из основного свойства тензорных произведений,
матрица a(g) удовлетворяет условию мультипликатив¬
ности: a(gig2) = a(gi)a(g2)\ кроме того, а(е) = ер, где
ер — единичный оператор в Ер. Следовательно, a(g) яв¬
ляется гомоморфизмом группы G в группу линейных
преобразований пространства Ер. Точно так же в про¬
странстве Е'ч мы имеем преобразование
b (§) ~ ё ® й ® ® й (я сомножителей),
которое является гомоморфным образом преобразова¬
ния g. Наконец, при произвольных р и q мы можем рас¬
сматривать гомоморфизм
c{g) = a{g)®b{g),
причем преобразование c(g) действует в Ерч = Ер X Е'ч.
Векторы пространства Ер называются контравари-
антными тензорами ранга р, векторы пространства Е'ч —
ковариантными тензорами ранга q. Наконец, векторы
пространства Ерч называются смешанными тензорами.
р раз контравариантными и q раз ковариантными.
Наряду с символикой «строка — столбец» мы будем
также пользоваться обычной символикой индексов. Ко¬
ординаты векторов из Ерч будут записываться в виде
t1.1)2" /. Закон преобразования при этом записывается
12 ‘q
следующим образом:
. 11 Ц ' ' ' Щ * 1 ^2 ~ ^ 1—^2 О ‘^ D
V,/,•••<,'
где g — g~l. Здесь мы считаем, что нижний индекс у
матрицы является индексом суммирования; поэтому
матрица g в действительности встречается в транспони¬
рованном виде.
Таким образом, с каждым преобразованием g^G
связана целая серия тензорных преобразований. Хорошо
известно, какую роль играют эти преобразования в гео¬
метрии и физике.
Вместо тензоров иногда практически удобно бывает
рассматривать полилинейные формы. Заметим вначале,

72 ГЛ. II. ЛИНЕЙНЫЕ ГРУППЫ
что если t ^ Ер, т^Е'р, то свертка
является инвариантом группы G. Если, в частности, тен¬
зор t является произведением векторов х, у,. .., w е Е,
то мы получаем общий вид ковариантной полилинейной
формы.
Ф(лг, у, ..., w) = ti^... ipxl'yl2 • • ■ w1p.
Нетрудно видеть, что коэффициенты этой формы могут
быть выражены в свою очередь как значения формы на
соответствующем наборе базисных векторов
%1\11 1р = e,V •••’ е‘Р)•
Допустим, что векторы х, у, . . ., w подвергаются пре¬
образованию g и тензор т подвергается соответствую¬
щему преобразованию b(g). Пусть B(g)ср — новая фор¬
ма с коэффициентами b(g) т. Свойство инвариантности
свертки может быть выражено формулой
В (я) Ф (gx, gy gw) = ф (х, у, . . ., w).
Отсюда в свою очередь следует явный вид преобразо¬
ванной формы:
B(g)q>(x, у, .... ш) = ф(§-!л:, g~xy, ...,
Очевидно, рассмотрение полилинейной формы с зако¬
ном преобразования B(g) равносильно рассмотрению
тензора т. Точно так же вместо контравариантного тен¬
зора t мы можем рассматривать контравариантную фор¬
му f(£, Л> •••> ш) с законом преобразования
A(g)f(l, Л, ®) = f(lg, ЛЯ. •••> “Я)-
Форма ф (лг, у,..,, w) называется симметричной (ко¬
сосимметричной) по паре аргументов, скажем х и у,
если она не меняется (меняет знак) при перестановке
этих аргументов. Соответствующий тензор также яв¬
ляется симметрическим (кососимметрическим) при пере¬
становке соответствующих тензорных индексов. Приме¬

§ 14. ПРЕОБРАЗОВАНИЯ В КЛАССЕ ТЕНЗОРОВ
73
ром формы, кососимметричной по всем переменным, яв¬
ляется детерминант:
Х\
У\ •
. W,
У, • •
., w) =
х2
У 2 ■
. w2
хп
Уп •
• wn
Более того, как известно, эта форма определяется усло¬
вием кососимметричности однозначно, с точностью до
числового множителя. Мы уже однажды воспользова¬
лись этим свойством в § 7.
Подобно тому как произвольный тензор ранга т мо¬
жет быть заменен полилинейной формой, произвольный
симметрический ковариантный тензор т, . . может
*1*2 1 m
быть заменен полиномом
p(x) = riii2...imxt'xt2 ... xtm
от единственного вектора х е Е. Действительно, число¬
вые значения полинома вполне определяют симметриче¬
ский тензор коэффициентов. Формула
T(g)p{x) = p{g~lx)
определяет соответствующее преобразование в классе
полиномов. Точно так же можно рассматривать поли¬
номы р(1) с законом преобразования T(g)p(l) = p(lg).
* *
Данное нами определение линейной группы исключает, согласно
традиции, «бесконечномерные линейные группы», т. е. группы линей¬
ных преобразований в бесконечномерных векторных пространствах.
Тем самым получаем специальный класс групп Ли, поддающийся
сравнительно простому описанию. Более подробно с некоторыми
свойствами классических групп и тензоров можно ознакомиться в
монографии Вейля [9].
Линейные группы, сохраняющие квадратичные формы, являются
частным случаем так называемых алгебраических групп. Теория
этих групп развита главным образом в работах Шевалле ([46],
т. 11); для этих групп удается независимо получить ряд глубоких
результатов, дублирующих «аналитическую» теорию. К этому во¬
просу мы еще вернемся в гл. XVI.

ГЛАВА III
ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
В предыдущей главе при рассмотрении тензоров мы
видели, что одна и та же линейная группа G допускает
гомоморфные отображения в полные линейные группы
других размерностей. Представляет интерес изучение
таких гомоморфизмов также и в том случае, когда G —
произвольная абстрактная группа; этим занимается тео¬
рия представлений. Прежде чем начать формальные
определения, мы рассмотрим один из важнейших при¬
меров линейного представления.
§ 15. Функции на однородном пространстве
Большинство прикладных задач, решаемых с по¬
мощью теории групп, может быть сведено к следующей
общей задаче.
Пусть дано некоторое множество X, называемое про¬
странством, в котором действует группа G как группа
преобразований. Результат преобразования точки хеХ
элементом g^G обозначим символом xg. Таким обра¬
зом, имеем:
1° Xglg2 = (Xgl)g2-
2° хе - х.
Изучение такой ситуации в общем виде является слиш¬
ком сложной задачей. Если мы желаем получить не¬
сколько большую аналогию с группой движений в ев¬
клидовом пространстве, то естественно наложить еще
одно дополнительное условие:
3° Условие транзитивности: всякая точка
.rel может быть переведена в любую другую точку
jel при помощи хотя бы одного преобразования
SeeG.

S 16. ФУНКЦИИ НА ОДНОРОДНОМ ПРОСТРАНСТВЕ
75
Если выполняется последнее условие, то говорят, что
X является однородным пространством с группой дви¬
жений G. Если группа G и пространство X топологиче¬
ские, то предполагают также, что xg непрерывно зави¬
сит от пары (х, g) е X X G.
Далее, пусть L — линейное пространство, составлен¬
ное из функций на множестве X. Допустим, что L вме¬
сте с каждой функцией f(x) содержит также функцию
fg W = f (xg)
при любом значении geG. Тогда преобразования точек
в пространстве X порождают семейство линейных пре¬
образований
Tgf = fg
в линейном пространстве L. Как следует из этого опре¬
деления, операторная функция Тg обладает мультипли¬
кативным свойством Tg>g, — Т StT g2, т. е. отображение
g-vTg является гомоморфизмом группы G*).
Естественно попытаться разложить пространство L
в геометрическую сумму «минимальных компонент», ин¬
вариантных относительно Тg, т. е. классифицировать
функции f(x) относительно преобразований группы G.
В дальнейшем такая постановка задачи будет уточнена.
При этом мы условимся говорить, что эта задача яв¬
ляется «основной проблемой» теории представлений.
Простейшим примером является классификация
функций на окружности по отношению к вращениям
окружности:
Т J (ф) = f (ф + а).
где а, ф — угловые параметры (сложение которых пони¬
мается по то(12я либо, что то же самое, функции f(q>)
считаются периодически продолженными, с периодом 2п,
на всю числовую ось). Приемами теории групп легко
удается установить, что единственными «минимальными
компонентами» являются «элементарные гармоники»
*) Необычная запись xg вместо gx выбрана именно с целью
получить гомоморфный закон умножения для операторов Тв. В слу¬
чае gx мы имели бы 7’g g2 = 7’g27’gi. Впрочем, мы опять получим желае¬
мый закон умножения, если положим Tsf (х) = / (g~'x).

76 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
еп (ф) = е‘гаф, п = 0, ± 1, ± 2,..., для которых
Таеп = Кп (а) еп,
где %п (а) = в1,па. Отсюда в свою очередь нетрудно полу¬
чить, что «всякая» функция /(ф) разлагается в ряд по
этим гармоникам. Мы приходим к известной теории
Фурье. Вопросы сходимости решаются обычными ана¬
литическими способами.
Изложенная схема построения теории рядов Фурье
в действительности может быть обобщена на многие
практически важные классы групп Ли. При этом роль
элементарных грамоник играют специальные функции,
простейшие из которых уже давно играют фундамен¬
тальную роль в математической физике. Теория групп
позволяет объединить разрозненные данные об этих спе¬
циальных функциях в единую общую теорию.
В этой книге, как правило, мы не будем заниматься
детальной разработкой конкретных вопросов, связанных
со специальными функциями*). Нашей целью является
проследить глубокие алгебраические закономерности,
лежащие в основе теории линейных представлений. Ли¬
нейным представлением (или просто представлением)
абстрактной группы G называется ее гомоморфное ото¬
бражение в группу обратимых линейных операторов
произвольного линейного пространства. Примерами яв¬
ляются преобразования в классе тензоров или построен¬
ные выше операторы Тё в классе функций на однород¬
ном пространстве.
Заметим, что с изложенной выше точки зрения тео¬
рия рядов Фурье есть спектральный анализ коммутатив¬
ного семейства операторов Та. В общем случае опера¬
торы Tg, как правило, некоммутативны, и это приводит
к установлению новых замечательных закономерностей.
Вместе с тем вскрываются алгебраические основы тео¬
рии рядов Фурье, обычных и «обобщенных»; оказывает¬
ся, что в значительной степени эта теория «алгебраична».
В заключение заметим, что иногда приходится рас¬
сматривать пространства, не являющиеся однородными
*) Этому посвящается недавно вышедшая монография Н. Я. В и-
ленкина [14].

§ 15. ФУНКЦИИ НА ОДНОРОДНОМ ПРОСТРАНСТВЕ
77
(преобразования в которых не транзитивны). Иногда
удается расслоить такое пространство на транзитивные
слои, подобно тому как евклидово пространство расслаи¬
вается на концентрические сферы под действием груп¬
пы вращений. Точнее, мы имеем в виду такое расслое¬
ние, при котором каждый слой является замкнутой ги¬
перповерхностью в X. Можно подумать, что такое
расслоение всегда возможно; однако в действительности
это не так. Примером являются так называемые «эрго-
дические движения», к числу которых относится «ирра¬
циональная обмотка тора».
Разворачивая тор на плоскость, мы получим прямо¬
угольник вида 0 ^Сх <а, 0 4/. у < b с отождествленными
противолежащими сторонами либо, что то же самое, всю
бесконечную плоскость с отождествлением по решетке
па + mb, где п, т — произвольные целые числа. (Два
вектора на плоскости отождествляются, если их разность
содержится в этой решетке.) Рассмотрим на плоскости
однопараметрическую группу преобразований
xt = x0 + tu, yt = yQ + tv,
где и, v — фиксированные числа, и затем перенесем ее
на тор. (Если точка (xt,yt) достигает границы выделен¬
ного прямоугольника, то она отождествляется с противо¬
лежащей точкой и движение продолжается.) Если чис¬
ла u/v, а/b несоизмеримы, то нетрудно показать, что
искомого расслоения не существует. В этом случае
траектория каждой точки (х0,у0) никогда не возвра¬
щается в эту точку и обматывает тор «всюду плотно»,
т. е. проходит в произвольной близости от любой на¬
перед заданной точки. Следовательно, замыкание этой
траектории совпадает со всем двумерным тором.
Описанная конструкция впервые была предложена,
по-видимому, Кронекером. Она легко переносится на
тор произвольной размерности. Соответствующая груп¬
па движений называется иррациональной обмоткой
тора.
Наиболее легко изучается тот случай, когда искомое
расслоение не только существует, но также порождает
«разделение переменных» в параметрическом много¬
образии X. Последнее означает, что пространство X

78 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
допускает такую параметризацию, при которой часть
переменных образует параметры внутри слоя и другая
часть переменных (непрерывно или гладко) параметри¬
зует семейство слоев. В этом случае задача, очевидно,
сводится к изучению однородного пространства, роль
которого играет каждый отдельный слой.
§ 16. Терминология теории представлений
1. Как уже было сказано, представлением группы G
в линейном пространстве V называется гомоморфное
отображение этой группы в группу обратимых линей¬
ных преобразований пространства V. Следовательно,
каждому элементу g е G ставится в соответствие ли¬
нейный оператор Tg, действующий в пространстве V,
причем
Tgig2= TglT g2,
Te = I,
где / — единичный оператор в V. Если группа G тополо¬
гическая, то при этом требуют также, чтобы оператор¬
ная функция Tg непрерывно зависела от g. Если V бес¬
конечномерно, то в этом определении необходимо уточ¬
нить, какая именно топология в пространстве операторов
имеется в виду. О важнейших примерах представлений
было сказано в предыдущем параграфе.
Заметим, что определение операторной функции Tg
естественно рассматривать как обобщение функциональ¬
ного уравнения для экспоненты. Некоторые группы об¬
ладают числовыми экспонентами, например, 7’g = detg'
для полной линейной группы GL(rt). Однако если в этой
группе рассмотреть подгруппу SL(n), для элементов
которой det g" = 1, то, как увидим, такая подгруппа уже
не имеет числовых экспонент, за исключением триви¬
ального случая Tg= 1. Однако у этой группы имеется
серия матричных экспонент (тензоры), с рассмотрения
которых исторически и началось развитие теории пред¬
ставлений. Кроме того, у этой группы имеется серия
бесконечномерных представлений, не сводящихся к тен¬
зорам.

§ 16. ТЕРМИНОЛОГИЯ ТЕОРИИ ПРЕДСТАВЛЕНИИ 79
Размерность пространства, в котором действует
представление, называется также размерностью этого
представления. Поскольку в этой книге мы преимуще¬
ственно будем рассматривать представления в прост¬
ранствах конечной размерности, то для краткости нам
будет удобно понимать под словом «представление»
только «конечномерное представление». Это соглаше¬
ние связано с традицией, но не всегда приемлемо в со¬
временной литературе, где часто рассматриваются бес¬
конечномерные представления. Все случаи бесконечно¬
мерных представлений нам придется оговаривать особо.
2. Два представления Tg, Sg считаются эквивалент¬
ными, если существует взаимно однозначное линейное
соответствие, переводящее Тв в Sg, т. е. если
Sg = ATgA~\
где А—линейный обратимый оператор, отображающий
пространство представления Tg на пространство пред¬
ставления Sg. Очевидно, эквивалентные представления
имеют одинаковую размерность. Если оба они опреде¬
лены в одном и том же пространстве, то матрицы Tg,
Sg переходят друг в друга при замене базиса.
3. Вектор е0 е В называется инвариантным, если
Tgeо = е0 для всех g е G. Подпространство В0 назы¬
вается инвариантным, если векторы из В0 переходят в
векторы из В0, т. е. если TgV(>cz В0. Заметим, что послед¬
нее условие можно также записывать в виде TgV0 = В0
(ввиду обратимости Tg). Подпространство Во назы¬
вается нетривиальным, если оно отлично от (0) и от про¬
странства В.
4. Если имеется инвариантное подпространство Bic:
с: В, то существенно выяснить, допускает ли оно инва¬
риантное дополнение, т. е. можно ли представить В
в виде прямой суммы
В = V, + V 2,
где В2 также инвариантно. В этом случае произвольная
матрица Tg может быть записана в виде двух независи¬
мых блоков:
Г11’ 0 I

80 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
если использовать базис, приуроченный к Vu V2. Опе-
™ (I) гр(2)
раторы Tg, lg определяют соответственно представле¬
ния в Vi, V2, называемые компонентами представления
Tg. Представление Tg называется в этом случае прямой
суммой представлений 7’g1), Tg\ В общем случае Tg мо¬
жет быть приведено только к квазитреугольному виду
относительно базиса, приуроченного к V\, V2, где V\ ин¬
вариантно и V = V\ + V2. При этом звездочка означает
прямоугольный матричный блок, элементы которого яв¬
ляются функциями от g.
Представление называется приводимым, если хотя
бы одно нетривиальное инвариантное подпространство
существует. Представление называется вполне приводи¬
мым, если всякое инвариантное подпространство имеет
инвариантное дополнение. Представление называется
неприводимым, если инвариантны только (0) и V.
Не представляет труда проверка следующих простых
утверждений. В пространстве всякого представления со¬
держится хотя бы одно неприводимое подпространство.
Отсюда заключаем (путем последовательной редукции),
что всякое представление может быть записано в квази-
треугольном виде с неприводимыми диагональными бло¬
ками. Представление вполне приводимо тогда и только
тогда, когда оно записывается в виде прямой суммы ко¬
нечного числа неприводимых представлений.
Представление Tg называется кратным представле¬
нию тg, если оно может быть записано в виде прямой
суммы конечного числа представлений, эквивалентных
тй. Символически пишем Т = kx, где k — кратность вхо¬
ждения т. Заметим, что это разложение существенно не¬
однозначно. В то же время, если Т = k\x\ + k2x2 + ...
...+knxn, где плюс означает прямую сумму, и если
г, — неприводимые взаимно неэквивалентные представ¬
ления, то такое разложение на компоненты й,т,- уже яв¬
ляется однозначным. Доказательство всех этих утвер¬
ждений предоставляется читателю,

§ 16. ТЕРМИНОЛОГИЯ ТЕОРИИ ПРЕДСТАВЛЕНИЙ 81
5. Два представления Tg, Tg, действующие в про¬
странствах V, V, называются контрагредиентными, если
существует невырожденная билинейная форма (х, |),
х ^ V, К, инвариантная по отношению к совмест¬
ному действию этих представлений:
(7>, 7^) = (*, |).
Невырожденность означает, что для любого а: ф 0 най¬
дется | е V такой, что (х, |) ф 0, и то же верно, если
поменять местами х и Пространства V и V имеют в
этом случае одинаковую размерность и их возможно
отождествить. При подходящем выборе базиса форма
(х, с) диагонализуется и условие контрагредиентности
принимает вид
Те = Т'е~\
Здесь штрих означает переход к транспонированной ма¬
трице по отношению к выбранному базису. Если интер¬
претировать V как пространство гиперплоскостей про¬
странства V (проходящих через начало координат), то
принадлежность вектора х гиперплоскости | ((х, |) =0)
равносильна принадлежности вектора Tgx гиперплоско¬
сти Tgl((Tgx, Tgl) = 0).
Примером контрагредиентных представлений являют¬
ся преобразования в классе ковариантных и в классе
контравариантных тензоров одного и того же ранга т.
6. Представление Tg называется тензорным произве¬
дением представлений Ag и Bg, если
Tg = A-g <S> Bg
для всех geG (определение символа <8> было дано в
§ 14). Заметим, что тензорное произведение двух линей¬
ных пространств X и У изоморфно пространству прямо¬
угольных матриц размерности пт, где п — dim X,
т = dim У. Если х и у — координатные столбцы из X и
У, то вместо х ® у мы можем формально писать г = ху',
где штрих означает транспонирование. Отсюда ясно, что
Т gz — AgzBg.

82 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
Полученная формула при произвольной матрице z раз¬
меров п X т дает явный вид представления Tg, который
часто оказывается удобным для вычислений.
7. В дополнение к введенным выше основным поня¬
тиям теории представлений мы введем еще некоторые
термины, которые будут иногда использоваться в даль¬
нейшем. Если представление Tg неприводимо в про¬
странстве V, то также говорят, что V неприводимо отно¬
сительно Tg. Если ATg — SgA, где Л—линейный опера¬
тор из пространства представления Tg в пространство
представления Sg, то А называется переплетающим опе¬
ратором для пары Tg, Sg. В частности, если А обратим,
то Sg = ATgA*1, и представления Tg, Sg эквивалентны.
Представление Tg называется унитарным, если опера¬
торы Тё унитарны при каждом g.
Следующее простое утверждение будет играть прин¬
ципиальную роль во многих дальнейших построениях.
Теорема 1. Всякое унитарное представление вполне
приводимо.
Доказательство. Пусть (х, у) — скалярное про¬
изведение, относительно которого Tg унитарно. Тогда
(тgX, у) = (х, Tgly) для всякой пары векторов х, у е V.
Покажем, что если V\ — инвариантное подпространство,
то его ортогональное дополнение У2 также инвариантно.
В самом деле, если х^У2, г/е V\, то имеем
(Tgx, у) = {х, Tgxy) = О,
ибо Tgxy содержится в V\ вместе с у. Мы видим, что
для всякого те Уг вектор Тgx также содержится в V2.
Следовательно, У2 инвариантно. Следовательно, всякое
инвариантное подпространство имеет инвариантное до¬
полнение. Теорема доказана.
Замечание. Теорема 1 (вместе с доказательством)
сохраняет силу также для бесконечномерного представ¬
ления Tg.
В заключение рассмотрим несколько простых при¬
меров приводимых представлений.
Пример Е Всякий тензор № однозначно записы¬
вается в виде суммы симметричного и антисимметрия-

s 16. ТЕРМИНОЛОГИЯ ТЕОРИИ ПРЕДСТАВЛЕНИИ 83
ного тензоров:
= у (*" + *"), alJ = -^(tiJ-tJi).
Подпространства этих тензоров инвариантны. Следова¬
тельно, g <S> g всегда разбивается в прямую сумму двух
представлений.
В дальнейшем мы увидим, что для группы GL(n) и
группы SL(n) такие два представления уже неприво¬
димы (для произвольной линейной группы это не так).
Пример 2. Смешанный тензор второго ранга пре¬
образуется по представлению g®g, которое может быть
записано с помощью явной формулы, указанной в этом
параграфе:
TgZ = gzg~l.
Здесь z — произвольная матрица п X п. Пространство
Z всех таких матриц запишем в виде суммы подпро¬
странства Z0, состоящего из матриц с нулевым следом,
и одномерного подпространства Zu натянутого на еди¬
ничную матрицу е:
Z — Zg + Zj .
Нетрудно видеть, что Z0, Zx инвариантны. Следователь¬
но, g® g также записывается всегда в виде суммы двух
представлений.
Заметим, что пространство Zx неприводимо (ибо од¬
номерно). Для группы GL(n) мы докажем в дальней¬
шем также неприводимость Z0.
Пример 3. Любопытно сравнить следующие два
представления аддитивной группы вещественных чисел
матрицами второго порядка:
cos t sin Л
ы(0 = . , , . 2(0 =
— sin г COS Л
1 t\ I
0 1
Первое из этих представлений неприводимо над полем
R, но распадается в прямую сумму двух представлений
над полем С:
"е-« 0

81 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
где тильда означает эквивалентность. В то же время
второе представление приводимо, но, как легко прове¬
рить, не вполне приводимо.
Для бесконечномерных представлений многие из
приведенных определений нуждаются в дополнениях и
уточнениях; в частности, для таких представлений су¬
ществует много различных определений неприводимо¬
сти и эквивалентности.
§ 17. Редукция основной проблемы
Поскольку правые (и левые) трансляции в группе
действуют транзитивно, группа G как множество сама
является однородным пространством. Нашей ближай¬
шей целью является показать, что это пространство яв¬
ляется в известном смысле универсальным в классе всех
однородных пространств с группой движений G.
Идея доказательства основана на свойстве транзи¬
тивности однородного пространства X. Действительно,
всякая фиксированная точка е е X может быть переве¬
дена в любую другую точку х е X путем хотя бы одного
преобразования geG. Следовательно, запас элементов
в группе G в известном смысле больше запаса точек в
пространстве X. Для более точного построения есте¬
ственно поступить следующим образом.
Пусть Я — совокупность всех преобразований, оста¬
вляющих точку е на месте; тогда, очевидно, Я является
подгруппой; такая подгруппа называется стационарной
подгруппой точки е.
Рассмотрим теперь произвольный класс смежности
Hg, где g — произвольный элемент из G. Нетрудно ви¬
деть, что все преобразования этого класса переводят
точку е в одну и ту же точку х = eg. Более того, ис¬
пользуя стандартные рассуждения, неоднократно при¬
менявшиеся выше, легко получаем, что множество Hg
содержит все преобразования, обладающие указанным
свойством. Следовательно, множество X находится во
взаимно однозначном соответствии с множеством всех
левых классов смежности, которое, как и в § 12, обо¬
значим GjH.

§ 17. РЕДУКЦИЯ ОСНОВНОЙ ПРОБЛЕМЫ
85
Перейдем к рассмотрению функций f(x), iel За¬
метим вначале, что всякая функция на G, постоянная на
каждом листе Hg, может рассматриваться как функция
на X. Обратно, всякую функцию на X мы можем рас¬
сматривать как функцию на G, постоянную на левых
классах смежности по Я.
Выясним закон преобразования пространства X в
терминах G/Я. Если множество Hg переводит е в л:, то
множество Hgg0 переводит е в точку у = xg0. Отсюда
очевидно, что в терминах G/Я мы получаем правые
сдвиги g -> ggo. В результате приходим к рассмотрению
операторов
Rj(g) = f{gg0)-
Представление g^Rg называется правым регулярным
представлением группы G. Более точное его определе¬
ние зависит от указания класса функций, в котором дей¬
ствуют операторы Rg. В частности, можно говорить о
всех, о всех непрерывных, о всех дифференцируемых
и т. д. функциях на G.
Представление Tgf(х) = f(xg) мы условимся назы¬
вать квазирегулярным представлением на однородном
пространстве X. Результаты нашего исследования мож¬
но выразить следующей теоремой.
Теорема 2. Всякое квазирегулярное представление
вкладывается в регулярное представление группы G.
При этом однородное пространство X отождествляется
с G/Н, где Я — стационарная подгруппа произвольной
точки eel
Замечание. Если вместо точки е рассматривать
точку ego, то подгруппа Я заменяется подгруппой
£“!Я£0. Отсюда следует, что все стационарные под¬
группы сопряжены между собой относительно внутрен¬
них автоморфизмов. Если вместо записи xg рассматри¬
вать запись g~lx, то мы получаем вложение в левое
регулярное представление группы G.
Примеры. 1. Пусть G = GL(n) и х — я-мерная
строка, умножаемая справа на матрицу geG. Фикси¬
руя в переменной матрице aeG какую-либо строку, мы
можем рассматривать ее вместо вектора л:. Очевидно,
преобразование x^xg заменяется преобразованием

86 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
a^>-ag. Вместо функций f(x) можно рассматривать
функции f(a), зависящие только от параметров выде¬
ленной строки.
2. Пусть G = SO(n) и х — «-мерная строка в евкли¬
довом пространстве В. Желая получить однородное про¬
странство, мы ограничиваемся в В рассмотрением еди¬
ничной сферы S. Если х пробегает S, то, рассуждая, как
в § 12, получаем, что S эквивалентно G/Н, где Н изо¬
морфно SO (л— 1).
3. Проиллюстрируем несколько иначе результат пре¬
дыдущего примера для случая п = 3. Используя углы
Эйлера, запишем произвольную матрицу из SO(3) в
виде g = h\uh2, где hu h2 — повороты вокруг оси Oz и
и — поворот вокруг оси Ох. Пусть е — северный полюс;
тогда подгруппа Н состоит из поворотов вокруг оси Oz.
Записывая вращение в виде gx, мы обнаруживаем, что
ge = к^иг. Параметры hi к и можно рассматривать как
параметры на сфере (широта и долгота).
В заключение заметим, что левое регулярное пред¬
ставление необходимо записывать в виде LgJ(g) =
— f{Sol§)' только при таком определении отображение
g->-Lg является гомоморфизмом. Подстановка g
в классе функций f(g) осуществляет, как легко прове¬
рить, эквивалентность Lg, Rg.
Упражнения
1. Пусть G — конечная группа и Н — ее подгруппа. Показать,
что порядок Н (число элементов в Н) является делителем по¬
рядка G.
2. Пусть G — конечная группа преобразований, Gx — стационар¬
ная подгруппа точки i и О, — орбита точки х. Показать, что число
элементов в О* равняется отношению порядков G и Gx.
3. Показать, что я! делится на яр пД ... nk\, если я = ti\ +
+ я2 + ... + nk и я, Я{ — натуральные числа.
§ 18. Элементарные гармоники
Согласно результатам предыдущего параграфа мы
можем ограничиться рассмотрением функций f(g) на
«универсальном однородном пространстве» G. Задача
состоит в классификации этих функций по отношению к

§ 18. ЭЛЕМЕНТАРНЫЕ ГАРМОНИКИ
87
правому сдвигу:
RJ (g) = f (ggo)-
Имея в виду аналогию с рядами Фурье, постараемся
прежде всего ответить на вопрос: какие функции f(g)
естественно считать «элементарными гармониками» на
G? Согласно той же аналогии мы можем исходить из
определяющего уравнения элементарных гармоник
RJ (g) = т (g0) f ig),
где функция t(g) является аналогом собственного зна¬
чения Xn — eina теории рядов Фурье. При этом, очевидно,
функция t(g') является гомоморфизмом, или «обобщен¬
ной экспонентой», на G.
Если считать t(g') числовой функцией, то мы далеко
не на всякой группе получим достаточно богатый запас
элементарных гармоник. Действительно, выше отмеча¬
лось, что некоторые группы вообще не имеют числовых
экспонент, кроме t(g) = 1. Поэтому естественно счи¬
тать, что r(g)—произвольное неприводимое конечно¬
мерное либо даже бесконечномерное представление
группы G.
Встав на эту точку зрения, мы можем сразу же отме¬
тить следующее очевидное обстоятельство. Согласно об¬
щей формуле
операторная функция t(g') сама является «собственной
функцией» оператора Rgl. Желая вместо операторной
функции рассматривать числовые, мы положим
Ф (g) = (r(g)x, у), (*)
где х — произвольный вектор из пространства представ¬
ления т(£), у — произвольный вектор из сопряженного
линейного пространства и скобка (х, у) означает били¬
нейную форму между этими пространствами.
Функции (*) называются матричными элементами
представления x(g). Матричные элементы всевозмож¬
ных неприводимых представлений группы G называются
для краткости также матричными элементами груп¬
пы G. Естественно ожидать, что всякая элементарная

88 гл. 111. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
гармоника является матричным элементом или линейной
комбинацией матричных элементов группы G.
Замечание. Пусть x(g)—конечномерное пред¬
ставление и в\, е2, еп — фиксированный базис в
пространстве представления. Тогда имеем
П
v{g)ej = 2
1 = 1
Если fi — линейный функционал, равный единице на е;
и нулю на всех остальных базисных векторах, то мы
имеем
тч/(&) = М£)е/, fi).
где скобка в правой части означает применение функ¬
ционала fi. Следовательно, функции X;j(g) являются
матричными элементами группы G.
Изложенная выше гипотеза о матричных элементах
легко доказывается в том случае, когда «собственное
значение» x(g) является конечномерным представле¬
нием. Действительно, пусть е, (g), e2{g), ..., en{g)—
базисная система элементарных гармоник, преобразую¬
щихся согласно x(g). Тогда имеем
П
е, (ggo) = 2 г„ {go) et {g),
i = 1
где tij(g)—соответствующая матрица оператора t(g).
Полагая, в частности, g = е и опуская индекс 0 у эле¬
мента go, мы находим
П
<?/(#)= 2 Тц/(£)С/.
i = 1
Здесь Ci = еДе). Согласно сделанному выше замечанию
функции хn(g) являются матричными элементами груп¬
пы G. Мы видим, что элементарные гармоники ej(g)
являются линейными комбинациями матричных эле¬
ментов.
С другой стороны, естественно предположить, что
всякое неприводимое представление содержится в регу¬
лярном. В частности, если x(g) =||тгД^) [| — конечномер¬
ное представление, то, полагая ej{g) =хij(g) при фик¬

§ 18. ЭЛЕМЕНТАРНЫЕ ГАРМОНИКИ
89
сированном г, мы имеем
п
e](ggo)= 2 ei(g)xil (g0).
i = 1
Следовательно, функции е, (g) преобразуются по закону
t(g), и для конечномерных представлений наше утвер¬
ждение доказано. Желая исследовать случай бесконеч¬
номерных представлений, мы вначале уточним опреде¬
ление неприводимости.
Представление Tg в линейном топологическом про¬
странстве V называется топологически неприводимым,
если в V не существует замкнутого инвариантного под¬
пространства, отличного от (0) и V. При этом мы пред¬
полагаем, что функция Tg непрерывна на V хотя бы
в смысле слабой топологии пространства V*).
Теорема 3. Всякое топологически неприводимое
представление группы G может быть вложено в правое
регулярное представление группы G, определенное в
классе непрерывных функций на G,
Доказательство. Фиксируем ненулевой линей¬
ный функционал f из сопряженного пространства V.
Каждому igF поставим в соответствие числовую функ¬
цию
X(g) = (TgX, f)
на группе G. Тогда элементу Tgax соответствует функ¬
ция x(gg0). Пусть L — множество всех получаемых та¬
ким образом функций x(g). Если -v0(g) = 0 на группе
G, то мы имеем
(v„, f) = 0.
Замыкание линейной оболочки векторов Tgx0 инва¬
риантно относительно Tg и отлично от V (поскольку
ортогонально f). Ввиду неприводимости Tg это замыка¬
ние содержит только вектор 0. Следовательно, хо = 0.
Мы показали, что отображение между V и L взаимно
однозначно. Кроме того, при этом отображении опера¬
ция Тпереходит в Rga. Теорема доказана.
*) По поводу всей терминологии, касающейся линейных топо¬
логических пространств, читатель отсылается к любому современ¬
ному руководству по функциональному анализу. См., например, [5].

90 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
Замечание. Для конечномерных представлений
рассуждения, изложенные выше, позволяют получить
следующий более точный результат. Неприводимое пред¬
ставление х (g) содержится в регулярном столько раз,
какова его размерность. Действительно, пусть Li — ли¬
нейная оболочка всех функций еДg) — Xij(g) при фик¬
сированном к Выше было показано, что всякая элемен¬
тарная гармоника, преобразующаяся согласно t(g),
содержится в геометрической сумме подпространств L,.
В конце этой главы будет показано, что подпростран¬
ства Li линейно независимы. Их число равно размер¬
ности t(g), и в каждом из них представление Rg сво¬
дится к t(g).
Все изложенные выше построения, разумеется, играют
роль наводящих рассуждений. Остается еще фундамен¬
тальный вопрос о разложимости Rg на неприводимые
представления. Мы опишем сейчас один из наиболее
естественных путей решения этого вопроса.
Пусть dp(g)—правоинвариантная мера Хаара на
группе G. Как мы видели в § 7, такая мера существует,
во всяком случае на произвольной группе Ли. Положим
Ш2= j\f(g) \2dn(g),
где интеграл понимается в смысле Лебега. Множество
Ж = L2 (G), состоящее из всех измеримых функций/^),
для которых |]f|| < оо, является гильбертовым простран¬
ством. Формула
(f, ф) = J f (g) Ч>Гё) d\i (g)
определяет скалярное произведение в этом простран¬
стве. Используя правую инвариантность меры dp(g),
сразу получаем, что (RgJ, Rg0q>) = (f, ф), т. е. правое
регулярное представление унитарно.
Согласно теореме 1 мы можем теперь заключить о
том, что представление R„ вполне приводимо. Отсюда
появляется надежда, что Rg разлагается на неприводи¬
мые представления.
Обращение к классическим примерам прямой и
окружности показывает, однако, что при этом могут

§ 19. АЛГЕБРЫ И ГРУППЫ. СВЯЗАННЫЕ С УРАВНЕНИЕМ 91
встретиться дополнительные аналитические трудности.
Действительно, на окружности элементарные гармоники
егпр содержатся в гильбертовом пространстве и обра¬
зуют его ортогональный базис. В то же время на пря¬
мой элементарные гармоники еа* неинтегрируемы с
квадратом модуля. Тем не менее хорошо известна про¬
цедура, приводящая к интегралам Фурье. В следующей
главе мы сумеем выделить группы, ситуация для кото¬
рых сходна с ситуацией окружности, и построить для
них обобщение гармонического анализа.
§ 19. Алгебры и группы, связанные с уравнением
Существует несколько иной аспект рассматриваемых
вопросов, особенно важный для приложений, но в на¬
стоящее время еще недостаточно разработанный. В ма¬
тематической физике, как известно, часто приходится
решать уравнения на собственные значения:
Еф = Еф, (*)
где L — линейный оператор, как правило, интегральный
или дифференциальный (оператор Лапласа, оператор
Гамильтона). Если F — оператор, перестановочный с L,
то его изучение дает обычно глубокую информацию о
собственных векторах оператора L. Мы рассмотрим в
этом параграфе лишь элементарную алгебраическую
схему такого подхода.
Если /Д Е2 перестановочны с L, то этим же свой¬
ством обладают их произведение и произвольные ли¬
нейные комбинации. Следовательно, множество всех
операторов, перестановочных с L, образует алгебру. Эта
алгебра носит название коммутаторной алгебры опера¬
тора L. Если Е — элемент коммутаторной алгебры и
ф — решение (*), то имеем
L (Еф) = ЕЕф = А (Еф).
Следовательно, вектор Еф является по-прежнему соб¬
ственным вектором относительно L, с тем же собствен¬
ным значением, что и ф. Иначе говоря, пространство 1Д
всех собственных векторов с собственным значением Е

92 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
инвариантно относительно F. Следовательно, оно инва¬
риантно также по отношению ко всей коммутаторной
алгебре оператора L.
Если Н — оператор Гамильтона в квантовой механике и F —
оператор физической величины, зависящей от времени, то эволюция
dF
оператора F описывается уравнением = FH — HF. Следователь-
dF
но, если F перестановочен с Н, то -^- = 0. Такие физические вели¬
чины играют роль сохраняющихся «интегралов движения» (энергия,
заряд, момент количества движения) и играют, как известно, прин¬
ципиальную роль в изучении физической системы.
В приложениях иногда встречаются случаи, когда
пространство Vy, конечномерно и операторы коммута¬
торной алгебры порождают полную алгебру матриц в
пространстве Vy,. Ясно, что в этом случае всякое реше¬
ние ф е Vy, может быть получено из единственного ре¬
шения ф0 ^ Vy,, фо Ф 0, при помощи преобразований
коммутаторной алгебры.
Примером является уравнение Аф = Хф, где А — оператор Ла¬
пласа, в классе функций на сфере в трехмерном евклидовом про¬
странстве. Решения такого уравнения существуют, как известно,
только при X = 1(1 + 1), где I — целое число, и являются линей¬
ными комбинациями сферических функций Ylm, т=—I, —I-1-1, ...
...,/, степени I. Число таких функций равно 21 + 1. Специалистам
по математической физике хорошо известны (см. [18]) дифферен¬
циальные операторы /_ и /+ такие, что
/ у1 = Y1
1 ±J т 1 т± 1
(правая часть заменяется нулем, если \т ± 1 | превосходит I). Опе¬
раторы /_, /+ содержатся в коммутаторной алгебре оператора А,
и их рассмотрение позволяет легко установить ряд замечательных
свойств сферических функций. Аналогичная ситуация имеет место
в теории системы л-мерных гармонических осцилляторов (в кван¬
товой механике). Эта задача будет рассмотрена нами в § 57.
Пусть G — множество всех обратимых преобразова¬
ний из коммутаторной алгебры оператора L. Множество
G образует группу, которую условимся называть полной
группой симметрии оператора L. Особенно интересен
тот случай, когда группа G является группой Ли, т. е.
зависит аналитическим образом от конечного числа па¬
раметров. Иногда удобно рассматривать G как пред¬

§ 19. АЛГЕБРЫ И ГРУППЫ. СВЯЗАННЫЕ С УРАВНЕНИЕМ 93
ставление некоторой абстрактной группы Элементы
из G записываются при этом в виде Tg, g е ©.
В приведенном выше примере с оператором Лапласа
роль группы © играет группа SO(3). Для системы п-
мерных гармонических осцилляторов в аналогичной роли
выступает GL(n).
С другой стороны, из элементов коммутаторной ал¬
гебры можно сконструировать алгебру Ли, ибо FXF2 —
— F2FX содержится в коммутаторной алгебре вместе с
Fx, F2. В рассмотренных выше примерах эта алгебра ко¬
нечномерна и совпадает с алгеброй Ли некоторой груп¬
пы симметрии G. В частности, описанные выше опера¬
торы /+ содержатся в алгебре Ли группы симметрии
оператора А, изоморфной so(3).
Если в уравнении (*) Я = О, то наряду с представлением Тg
можно рассматривать пару представлений Тв, Se, для которых L
играет роль переплетающего оператора: LTв = SgL. В этом случае,
если гр — решение (*), то, как легко проверить, вектор снова
является решением (*).
Мы уже отмечали в § 15, что теория представлений
групп является основой для общей теории специальных
функций. Напомним теперь, что специальные функции
обычно возникают как решения уравнений вида (*). На
связь теории представлений с теорией специальных
функций впервые обратил внимание еще Э. Картан.
В настоящее время известно (см. [14]), что все основные
классы специальных функций математической физики
могут быть получены в рамках групповой схемы; при
этом для них единообразным способом выводятся свой¬
ства ортогональности и нолноты, дифференциальные и
интегральные соотношения.
Рассмотрения, связанные с коммутаторными алгеб¬
рами, могут быть положены в основу самой теории
представлений; в частности, они позволяют раскрыть
основные закономерности, связанные с понятием непри¬
водимости. В следующем параграфе мы переходим к
рассмотрению таких закономерностей. Прежде всего мы
докажем так называемую лемму Шура, которая яв¬
ляется основным «ключом» к теории конечномерных
представлений.

94 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
§ 20. Лемма Шура
Условимся рассматривать линейные (конечномерные)
пространства только над полем комплексных чисел. Сле¬
дующая простая лемма принадлежит одному из осно¬
вателей теории представлений, немецкому алгебраисту
И. Шуру:
Лемма Шура. Допустим, что два неприводимых
представления Tg, Sg группы G связаны соотношением
ATg = (*)
где А — линейный оператор. Если эти представления не¬
эквивалентны, то А = 0; если они эквивалентны, то А
определяется однозначно с точностью до умножения на
число.
В частности, если Tg = Sg, то А = XI, где I — еди¬
ничный оператор.
Доказательство. Пусть X, Y — линейные про¬
странства, в которых действуют представления Т, S; то¬
гда мы имеем отображение
Л: X-+Y.
Пусть Х0, Yо — ядро и образ оператора А (т. е. сово¬
купность всех векторов rel, для которых Ах = 0, и
совокупность всех векторов Ах, xeJf). Ясно, что Ха
инвариантно в X и Y0 инвариантно в Y. Если А Ф 0, то
равенства Х0 = X и К0 = (0) исключаются. Следова¬
тельно,
%о ~ (0), К0=К
в силу неприводимости Т и 5. Полученные равенства
означают, что оператор А взаимно однозначно отобра¬
жает X на Y. Следовательно, Л-1 существует и
Sg=ATgA~',
т. е. представления Т, S эквивалентны. Докажем един¬
ственность оператора Л. Поскольку Т и S эквивалентны,
мы можем отождествить X и Y. Если Л и В удовлетво¬
ряют условию (*), то оператор С = В — ХА удовлетво¬
ряет этому условию при любом X. Как мы видели выше,
либо С — 0, либо С-1 существует. Но если X — корень
уравнения det (В—ХА) =0, то оператор С вырожден.

§ 20. ЛЕММА ШУРА
95
Следовательно, в этом случае С = 0 и В = %А. Лемма
доказана.
Последнее утверждение леммы самостоятельно фор¬
мулируется следующим образом:
Если линейный оператор А перестановочен со всеми
операторами неприводимого представления Tg, то он
кратен единичному *).
Отметим теперь несколько следствий из леммы Шура.
Следствие 1. Если группа коммутативна, то все
ее неприводимые представления (над полем комплекс¬
ных чисел) одномерны**).
Действительно, каждый оператор Tga перестаново¬
чен со всеми операторами Tg и потому кратен единич¬
ному. Следовательно, Tg — K(g)I. Но в этом случае вся¬
кое одномерное направление инвариантно. Следователь¬
но, размерность пространства равна 1.
Следствие 2. Пусть Tg, Sg — два неприводимых
представления группы G. Тензорное произведение
Тg ® Sg
содержит ненулевой инвариант только в том случае, ко¬
гда представления Tg, Sg контрагредиентны, и этот ин¬
вариант определяется однозначно с точностью до мно¬
жителя.
Действительно, как мы видели в § 16, тензорное про¬
изведение Ug = Tg<SiSg может быть реализовано фор¬
мулой
U gz = Т gZSg
в классе прямоугольных матриц г. Условие инвариант¬
ности (Ugz = г) может быть переписано в виде
TgZ = zSg,
где Sg = S'~' — представление, контрагредиентное Sg.
Следовательно, согласно лемме Шура либо 2 = 0, либо
*) Обычно именно это утверждение называют леммой Шура.
**) Над вещественным полем это неверно. Пример: пред¬
ставление
аддитивной группы вещественных чисел. Следовательно, лемма
Шура над вещественным полем также неверна (в приведенной
формулировке).

96 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
Tg, Sg эквивалентны, и искомый инвариант определяется
однозначно с точностью до множителя.
Замечание. Если отождествить Tg, Sg, то пред¬
ставление Ug записывается в виде
U gz = TgzTgl,
откуда ясно, что искомым инвариантом является ма¬
трица, кратная единичной. Если вместо Ug рассматри¬
вать дуальное представление, реализованное в классе
линейных форм /(г), то ясно, что искомым инвариантом
является форма
/о (г) = sp г,
определяемая с точностью до множителя.
Для формулировки очередного следствия введем вна¬
чале следующее определение. Пусть М — произвольное
множество матриц в векторном пространстве V. Сово¬
купность М', состоящая из матриц, каждая из которых
перестановочна со всеми матрицами из М, называется
коммутаторной алгеброй множества М (действительно,
как следует из этого определения, множество М' яв¬
ляется алгеброй).
Следствие 3. Пусть Tg — вполне приводимое пред¬
ставление в пространстве V, V = V\ + V2 +...+ Vm, где
Vi, i= 1,2, ..., m, — неприводимые подпространства.
Тогда коммутаторная алгебра представления Tg состоит
из всех операторов А, имеющих вид
m
А = 2 ТцСц,
i, / = 1
где оператор Сц обращается в нуль на всех подпро¬
странствах Vh, k Ф!, и отображает V,• на Viy а А,,-,
I, / = 1, 2, ..., т., — произвольные числа. При этом опе¬
ратор Сц осуществляет отображение эквивалентности
между неприводимыми представлениями в V, и Vj. Сле¬
довательно, если эти представления неэквивалентны, то
Сц = 0.
Для доказательства достаточно представить все опе¬
раторы {A, Tg) в блочном виде, соответствующем раз¬
биению Vi, V2, ..., Vm, и применить лемму Шура.

§ 20. ЛЕММА ШУРА
97
В частности, если представление Tg кратно неприво¬
димому представлению xg, то оно при подходящем вы¬
боре базиса может быть записано в виде
О
О
где tg — диагональные блоки матрицы Tg. Ясно, что в
этом случае все операторы C*j записываются в виде еди¬
ничных матриц (если У,- отождествляется с Vj) и опе¬
ратор А принимает вид
ЯцЦ ^12^ • • -
А =
где е — единичная матрица порядка п, п — размерность
представления т и Кц — произвольные числа. Заметим,
что после перенумерации базиса эта матрица становится
блочно-диагональной с п одинаковыми блоками Л =
= ll?Will. i, j = 1, 2, .... т. Коммутаторная алгебра имеет
в этом случае размерность т.2.
В общем случае мы группируем эквивалентные ком¬
поненты т(1), i=l, 2, s, и получаем запись опера¬
тора А в блочно-диагональном виде:
А
А =
Ао
О
О
Л.
где каждый блок Aiy t = 1, 2, s, имеет структуру,
описанную выше. Коммутаторная алгебра имеет в этом
случае размерность т\ +т\ + .. . + т2, где /п, — крат¬
ность, с которой встречается неприводимое представ¬
ление т<*>.

98 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
Сопоставляя полученные результаты, мы видим, что
коммутаторная алгебра М' несет в себе большую ин¬
формацию о структуре представления Тй. Зная М', мы
можем легко определить все подпространства, неприво¬
димые относительно Tg, найти их число и размерность.
В частности, коммутаторная алгебра М' диагонализуется
тогда и только тогда, когда представление Тg не содер¬
жит ни одной пары эквивалентных компонент; представ¬
ление Tg неприводимо тогда и только тогда, когда ком¬
мутаторная алгебра состоит из матриц, кратных единич¬
ной (обращение леммы Шура) *).
Анализируя проведенные рассуждения, мы видим,
что они нигде не опираются на специальные свойства
представления, а оперируют с понятиями приводимости
и полной приводимости, которые можно перенести на
произвольные множества матриц. Эта точка зрения бу¬
дет несколько подробнее изложена в следующем пара¬
графе.
Упражнения
1. Пусть неприводимое представление Tg сохраняет ненулевую
билинейную форму x'fy, где штрих означает транспонирование. По¬
казать при помощи леммы Шура, что: 1) матрица / невырождена;
2) матрица f симметрична или кососимметрична; 3) матрица / оп¬
ределена однозначно с точностью до скалярного множителя.
2. Пусть (а: т) означает кратность вхождения неприводимого
представления а во вполне приводимое представление т. Показать,
что (а : т) = (1 : а®т), где 1 означает единичное представление и а
означает представление, контрагредиентное а.
3. Показать, что (а: р 0 у) = (|3: у ® а) = (у: а ® Р), где а, р,
у — неприводимые представления и тензорные произведения Р®у>
Y®a, a®p предполагаются вполне приводимыми.
4. Показать, что всякое неприводимое (конечномерное) пред¬
ставление группы вращений окружности определяется формулой
emtp, где п — целое число и ср — угловой параметр в группе вра¬
щений с периодом 2я.
5. Показать, что всякое неприводимое (конечномерное) пред¬
ставление группы сдвигов на прямой определяется формулой е^*,
где % — произвольное комплексное число и х — аддитивный пара¬
метр группы (—оо < х < оо) **).
*) Напомним, что речь идет о вполне приводимых представ¬
лениях.
**) Одномерные представления абелевой группы G называют
также характерами этой группы.

§ 21. ТЕОРЕМА БЕРНСАЙДА
99
§ 21. Теорема Бернсайда
Результаты, связанные с коммутаторной алгеброй,
станут значительно более симметричными, если вместо
представления Tg рассматривать множество всех линей¬
ных комбинаций операторов Tg. Это множество замк¬
нуто относительно линейных операций и операции умно¬
жения, т. е. является матричной алгеброй. Мы приходим
к вопросу об изучении матричных алгебр и их комму¬
таторных алгебр в связи с вопросами приводимости и
полной приводимости.
Множество матриц в пространстве V называется
приводимым, если существует нетривиальное подпро¬
странство К0> инвариантное относительно всех этих ма¬
триц (т. е. относительно линейных операторов, опреде¬
ляемых этими матрицами). Соответственно вводятся по¬
нятия неприводимости и полной приводимости. Нашей
основной целью будет изучение неприводимых матрич¬
ных алгебр. Остановимся вначале на двух основных кри¬
териях неприводимости. Условимся рассматривать толь¬
ко алгебры с единицей.
1° Правило цикличности. Матричная ал¬
гебра А неприводима тогда и только тогда, когда каж¬
дый вектор ^eF, | ф 0, является циклическим в про¬
странстве V относительно А, т. е. если V совпадает с со¬
вокупностью векторов вида а\, вбА
Действительно, пусть V% = Al — циклическая оболоч¬
ка вектора £ относительно А, т. е. множество всех векто¬
ров вида а\, й£/1. Очевидно, 1Д всегда инвариантно от¬
носительно А. Следовательно, если А неприводима, то
V\= V для каждого \Ф 0. С другой стороны, если по¬
следнее условие выполняется, то ни один из векторов
| ф 0 не может содержаться в нетривиальном инвариант¬
ном подпространстве; следовательно, А неприводима.
2° Правило двойственности. Матричная ал¬
гебра неприводима тогда и только тогда, когда непри¬
водима алгебра А, составленная из всех транспониро¬
ванных (относительно некоторого базиса) матриц а',
aei
Действительно, операция транспонирования
где вектор | рассматривается как вектор-столбец, ото-

100 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
ждествляет V с пространством V всех линейных форм:
f(l) = х% леУ. Если Е0сгЕ — инвариантное
подпространство относительно А, то его ортогональное
дополнение Vo cz V' инвариантно относительно A (Vo
определяется как совокупность всех линейных форм,
равных нулю на Е0)- Для доказательства нашего утвер¬
ждения достаточно теперь заметить, что нетривиальность
V0 равносильна нетривиальности Vq.
Докажем теперь одну из основных теорем в теории
матричных алгебр*):
Теорема Бернсайда. Всякая неприводимая ма¬
тричная алгебра в комплексном векторном простран¬
стве представляет собой полную матричную алгебру,
(алгебру всех линейных операторов) в данном про¬
странстве.
Доказательство. Пусть аг- — i-й столбец матри¬
цы а. Если а пробегает А, то вектор at пробегает цикли¬
ческую оболочку Ле,-, где е* — i-й базисный вектор в про¬
странстве V. Следовательно, если А неприводима, то
каждый столбец а* пробегает все /г-мерное простран¬
ство V.
Пусть уже доказано, что прямоугольная матрица
[iа]р, составленная из первых р столбцов матрицы а, про¬
бегает ^/г-мерное пространство Vp, которое определяется
как прямая сумма р экземпляров пространства V. Рас¬
смотрим отдельно следующие две возможности:
а) Из равенства [а]р = 0 следует ар+1 = 0 для вся¬
кого элемента йё/4.
б) Существует хотя бы одна матрица деЛ, для
которой [а]р = 0, но йр+1 =h 0.
Если выполняется условие а), то др+1 является одно¬
значной функцией от вектора [д]р е Vp. Поскольку эта
функция является линейной, то мы имеем
Дрч-i С]Д] Ч- С2Д2 3“ ... Ч- СрДр,
где Си i=l, 2, ..., р, — линейные операторы в про¬
странстве V. Заменим а на ха, где х — произвольная ма¬
трица из Л; тогда каждый столбец дг заменяется на
*) Другой вариант доказательства см. в [10].

§ 21. ТЕОРЕМА БЕРНСАЙДА
101
хай и мы имеем
р р
х Ctat Ctxa,.
i=l (-1
Поскольку мы предполагаем, что матрица [а]р прини¬
мает произвольные значения из Vp, то, очевидно, имеем
отсюда
xCi = Cix.
(Действительно, все векторы, кроме ах, мы можем поло¬
жить равными 0; при этом а, пробегает пространство
V.) Следовательно, каждый оператор Ct перестаново¬
чен со всеми матрицами из А. Согласно лемме Шура за¬
ключаем отсюда, что С{ = kie, где е — единичная ма¬
трица в пространстве V. В результате получаем
Пр +1 = й\ + Х2а2 + . • • + hpCLp,
Полученное равенство означает, что ни одна из строк
матрицы а не пробегает n-мерного пространства (по¬
скольку между координатами строки существует линей¬
ная зависимость). Согласно правилу двойственности это
невозможно, ибо алгебра А неприводима. Полученное
противоречие показывает, что случай а) не может иметь
места.
Итак, мы показали, что выполняется условие б).
Пусть / — множество всех элементов из А, для которых
выполняется условие [а\р = 0. Тогда мы имеем Alai,
т. е. / инвариантно относительно левых умножений на
элементы ае<4*). Отсюда следует, что для каждого
| е V циклическая оболочка /| инвариантна относи¬
тельно А. Положим, в частности, V0 = Iep+i. Согласно
б) VоФ (0). Следовательно, V0 = V. Поэтому, если а
пробегает /, то вектор-столбец ар+х пробегает простран¬
ство V. Но это означает, что \а\р+х пробегает Vр+х.
В результате мы имеем возможность индукции по ин¬
дексу р — 1, 2, ..., п, и это доказывает теорему.
Следствие 1. Если Tg — неприводимое представле¬
ние группы G в комплексном пространстве V, то линей¬
ная оболочка операторов Tg совпадает с алгеброй всех
линейных операторов пространства V.
*) Всякое такое множество 1 называется левым идеалом в ал¬
гебре А.

102 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
Следствие 2. Матричные элементы непри¬
водимого представления Tg образуют систему линейно
независимых функций на группе G.
Действительно, условие линейной независимости мо¬
жет быть записано в виде sp CTg = 0, где С — постоян¬
ная матрица коэффициентов. Заменяя множество {Tg}
его линейной оболочкой, заключаем, что sp СХ = 0 для
всякой матрицы X. Отсюда С = 0.
Следствие 3 (принцип взаимности*)).
Если А — вполне приводимая алгебра с единицей, то
А' — также вполне приводимая алгебра с единицей, и
при этом
А" = А,
т. е. коммутаторная алгебра коммутаторной алгебры А’
совпадает с самой алгеброй А.
Несложное доказательство этого утверждения предо¬
ставляется читателю. Следствие 3 дает чрезвычайно цен¬
ную информацию о структуре вполне приводимой ал-
Г
гебры А. Действительно, пусть А = 2 (прямая
i=i
сумма), где А{ — неприводимая алгебра порядка щ,
входящая с кратностью т;. Тогда всякий элемент аеЛ
может быть записан следующим образом:
Г
а = 2 {at ® е{),
Z “ 1
где а* — произвольная матрица порядка П{ и — еди-
ничная матрица порядка т{. Согласно принципу взаим¬
ности всякая матрица 6еЛ' имеет следующий вид:
Г
Ь = 2 (ег <8> Ь{),
где е* — единичная матрица порядка щ и Ьг — произ¬
вольная матрица порядка яг*. В частности, мы видим,
Г
что алгебра А имеет размерность 2 п\ и алгебра А'
1
Г
имеет размерность 2 нг2. Если алгебра А неприводима,
*) Эта теорема принадлежит Веддербёрну (см. (10]}.

ГРУППОВЫЕ АЛГЕБРЫ И ИХ ПРЕДСТАВЛЕНИЯ
103
то она имеет размерность п? (п — размерность простран¬
ства V) и коммутаторная алгебра А' имеет размерность
1 (что уже известно нам из леммы Шура). Очевидно
также, что лемма Шура в свою очередь может быть
получена как следствие теоремы Бернсайда.
Упражнения
1. Пусть £2 — два вектора в пространстве представления Тg,
g е G, циклическая оболочка каждого из которых неприводима.
Положим | Выяснить условия, при которых цикличе¬
ская оболочка вектора £ также неприводима. (Указание: от¬
дельно рассмотреть те случаи, когда неприводимые представления,
содержащие |j, £2, эквивалентны и неэквивалентны.)
2. Пусть А — полная матричная алгебра п X п. Показать, что
всякое неприводимое (конечномерное) представление этой алгебры
имеет размерность п, т. е. изоморфно алгебре А. Показать, что это
представление может быть задано формулой f(x}=axa-\ х е А,
где а — фиксированный обратимый оператор.
3. Пусть А — вполне приводимая матричная алгебра и А' —
ее коммутант. Показать, что в А’ содержатся проекторы на все
подпространства, неприводимые относительно А. Показать, что в А'
содержатся все переплетающие операторы для неприводимых ком¬
понент алгебры А. Когда то же верно при перемене ролей А' и Л?
§ 22. Групповые алгебры и их представления
В предыдущих рассмотрениях настоятельно чувство¬
валась необходимость «расширения» группы до алгебры,
т. е. введения дополнительных линейных операций*).
Эта процедура может быть осуществлена весьма различ¬
ными способами.
1° Свободная линейная оболочка. Если
G — абстрактная группа, то мы можем рассматривать
формальные линейные комбинации
N
gi е G,
i = 1
где N — произвольное число (ограниченное, если группа
конечна). Это равносильно построению линейного про¬
странства С, в котором элементы группы G играют роль
(алгебраического) базиса. Избавляясь от индекса г, мы
можем записывать линейные комбинации х в виде
*) Эта процедура является естественной также с точки зрения
физики (принцип линейной суперпозиции).

104 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
суммы
х= 2 x(g)g,
g^O
где функция x(g) принимает ненулевые значения лишь
в конечном числе точек группы G. Если х = 2 х (g) g,
у = 2 У (g) g> т0 Для элементов х, у естественно рас¬
сматривать произведение
xy=1tx{g)y (/г) gh = 2 2 {g) g,
«.ft «
и линейное пространство С становится ассоциативной
алгеброй, которая называется свободной линейной обо¬
лочкой группы G. Если заменить под знаком двойной
суммы обозначение g обозначением gh~l, то g по-преж¬
нему пробегает группу G при каждом фиксированном
h. Приравнивая коэффициенты, находим
z(g) = 2 * у (/г).
h
Полученная формула может быть интерпретирована как
«свертка» функций на группе G и определяет закон
умножения в алгебре С. Заметим также, что
z{g) = 'Iix{h)y(h~1g).
h
Если § —Тg — представление группы G, то формула
Тх = ЪхШ-е
в
позволяет продолжить представление Tg до представле¬
ния Тх алгебры С. Эта конструкция часто оказывается
удобной. Если группа G конечна и имеет порядок п
(т. е. содержит п элементов), то алгебра С имеет раз¬
мерность п. В этом случае алгебра С называется груп¬
повой алгеброй группы G.
2° Групповые алгебры функций. Если груп¬
па G обладает мерой Хаара dp(g), то мы можем рас¬
сматривать свертку
ху (g) = / х (gh~l) у 0h) йц (/г)

ГРУППОВЫЕ АЛГЕБРЫ И ИХ ПРЕДСТАВЛЕНИЯ
105
двух произвольных функций x(g), y(g), для которых
такой интеграл существует. Если X — линейное простран¬
ство функций на G, для всех элементов которого свертка
существует и содержится в X, то X становится алгеброй,
которая также называется групповой алгеброй группы
G. Если g->Tg — представление группы G, то формула
Тх = J х (g) Tg dp (g)
позволяет перейти от представления Те к представле¬
нию Тх алгебры X. Действительно, как легко проверить,
Т —ТТ
1 ху 1 X1 у
при условии, что мы имеем право осуществлять пере¬
мену порядка интегрирования в данном классе функций.
Если G — группа Ли, то подобная конструкция воз¬
можна не только для обычных функций, но также для
мер и обобщенных функций на группе G, однако на
этом сейчас останавливаться не будем.
3° Ассоциативная оболочка алгебры Ли.
Алгебра Ли является по определению линейным про¬
странством, но не является ассоциативной алгеброй от¬
носительно умножения. Иногда чрезвычайно удобно бы¬
вает расширить ее до ассоциативной алгебры Я, вводя
умножение ху со следующим правилом коммутации:
ху-ух = [х, у],
где [х, у] — коммутатор в алгебре Ли. В частности, это
означает, что для каждого базиса е\, е2, еп в ал¬
гебре Ли выполняются тождества
где cktj — структурные константы алгебры Ли.
Если x^D(x) —некоторое представление алгебры
Ли, т. е. если отображение D(x) линейно и сохраняет
закон коммутации, то ясно, что функцию D(x) можно
продолжить по правилу
D(xy) = D(x)D(y}

106 гл. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИЙ
до представления всей ассоциативной оболочки Я. Ассо¬
циативная оболочка 31 называется также универсальной
обертывающей алгеброй алгебры Ли*).
Интересно отметить, что алгебра 31 оказывается изо¬
морфной алгебре обобщенных функций на группе G с но¬
сителем в точке е.
Все эти конструкции, чрезвычайно интересные для
теории представлений, мы вводим пока лишь формально,
в виде общих определений. Некоторые из них, например
групповая алгебра конечной группы и универсальная
обертывающая алгебра алгебры Ли, будут существенно
использованы в дальнейшем **).
§ 23. Формулировка основных задач
Из вышесказанного можно заключить, что основная
задача теории представлений состоит в их «спектраль¬
ном анализе», т. е. в разложении произвольных пред¬
ставлений на неприводимые. Однако в действительности
эта задача обладает более разнообразными аспектами.
Прежде всего, выделяются следующие самостоятельные
задачи:
1. Описать все неприводимые представления (с точ¬
ностью до эквивалентности) данной группы G.
2. Выяснить вопрос о возможности полной приво¬
димости (в том или ином классе групп и их предста¬
влений) .
3. Описать (если они существуют) представления
приводимые, но неразложимые, т. е. неразложимые в
прямую сумму хотя бы двух представлений.
Далее, если ограничиться более простым классом
вполне приводимых представлений, то естественно ожи¬
дать, что они разлагаются (в конечную сумму или аб¬
страктный интеграл) по неприводимым представлениям.
Это действительно так в конечномерном или унитарном
случае. Изучение вполне приводимых представлений
сводится при этом к спектральному анализу и изучению
*) Более подробное определение см. в § 58.
**) См. также [127].

§ 23. ФОРМУЛИРОВКА ОСНОВНЫХ ЗАДАЧ
107
отдельных неприводимых компонент. Здесь в свою оче¬
редь особо выделяются следующие задачи:
4. Разложение регулярного представления группы G.
5. Сужение неприводимых представлений с группы
на подгруппу (дано неприводимое представление группы
G, вполне приводимое относительно погруппы Н\ тре¬
буется разложить его на неприводимые по отноше¬
нию к Н).
6. Описание алгебры неприводимых представлений
по отношению к тензорному произведению.
В действительности некоторые из этих задач взаи¬
мосвязаны. В частности, поскольку регулярное пред¬
ставление является, как мы знаем, «вместилищем» всех
неприводимых представлений группы G (§ 18), спек¬
тральный анализ этого представления может явиться
источником для решения задачи 1. Далее, если перейти
к проблеме классификации функций на однородном мно¬
гообразии, то возникают следующие вопросы:
7. Аппроксимация функций на группе G и многооб¬
разии X «элементарными гармониками» группы G. Опи¬
сание специальных функций, связанных с этими гармо¬
никами.
8. Вопросы комплексификации (группы Ли, ее пред¬
ставлений, однородных многообразий).
9. Симметрия уравнений, в частности дифференциаль¬
ных и интегральных, по отношению к группам и алгеб¬
рам Ли. Аналоги операторов Лапласа для группы Ли.
Специально отметим также следующую классическую
задачу:
10. Разложение произвольных тензоров по отноше¬
нию к данной линейной группе G.
Гармонический анализ на группе тесно связан с изу¬
чением групповых алгебр относительно свертки на груп¬
пе G. Особый интерес представляет изучение «двойствен¬
ности» между группой G и множеством G, составленным
из элементарных гармоник на G. Если G — коммутативн
ная группа, то между G и G существует своеобразная
симметрия, которая проявляется, в частности, в анало¬
гии между прямым и обратным преобразованиями Фурье,
В общем случае ситуация является значительно более
сложной. Возникает задача:

108 ГЛ. III. ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ ПРЕДСТАВЛЕНИИ
11. Изучение групповых алгебр относительно свертки
на группе G. Построение общей теории двойственности *).
Заметим, что решение последней задачи, несомненно,
открыло бы ряд нобых закономерностей в теории пред¬
ставлений. Наконец, в общей теории групп важное зна¬
чение имеет следующая задача:
12. Выяснить, допускает ли данная абстрактная груп¬
па G точное линейное представление, т. е. возможна ли
ее изоморфная реализация в виде группы матриц.
В настоящее время известно (см., например, §§ 31,
104), что для «большого числа» важных классов групп
Ли проблема 12 решена положительно. Пример отрица¬
тельного решения приводится на стр. 469.
Более точная постановка и решение некоторых задач
для отдельных классов групп будут изложены в этой
книге.
* *
*
Доказанные в этой главе фундаментальные результаты теории
конечномерных представлений (лемма Шура, теорема Бернсайда)
сохраняют свой вид над произвольным алгебраически замкнутым
полем (заметим, что при доказательстве леммы Шура использова¬
лось существование корней векового уравнения det (В — ЯЛ)=0),
но требуют иной формулировки в общем случае, найти которую
можно, например, в книге Г. Вейля [10].
После того как эти результаты получены, можно наиболее
просто построить теорию представлений для произвольных конеч¬
ных групп. Однако в следующей главе мы сразу перейдем к рас¬
смотрению значительно более широкого класса групп, так называе¬
мых компактных групп Ли, изучение которых и является основным
предметом этой книги.
*) См. по этому поводу § 107. См, также замечание в [18] отно¬
сительно связи между матричными элементами и коэффициентами
Клебша — Г ордана,

ЧАСТЬ II
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ

В этом разделе, состоящем из девяти глав, дается
прежде всего доказательство классической «глобальной
теоремы» для произвольной компактной группы Ли. Гло¬
бальная теорема дает принципиальное решение всех
вопросов, касающихся линейных представлений для ука¬
занного класса групп. Доказывается, в частности, что
всякая компактная группа Ли может рассматриваться
(в смысле изоморфизма) как подгруппа в группе уни¬
тарных матриц U (я) при достаточно высоком п. Все
дальнейшее содержание этого раздела имеет приклад¬
ной характер и посвящается детальному изучению груп¬
пы U (я) и ее неприводимых представлений.
Читатель, желающий возможно быстрее получить ин¬
формацию о запасе неприводимых представлений Щя),
может пропустить гл. V и VI и приступить непосред¬
ственно к чтению гл. VII, изложение в которой, по су¬
ществу, независимо от всех предыдущих глав. Для
решения указанной задачи о классификации всех непри¬
водимых представлений U(я) достаточно вместо U(я)
рассматривать более широкую группу GL(n) и классифи¬
цировать все ее неприводимые комплексно-аналитические
представления. При решении этой задачи в свою очередь
существенно используется разложение Гаусса в GL(h),
которое доставляет систему параметров со специаль¬
ными алгебраическими свойствами. Однако за доказа¬
тельством того результата, что мы не пропустим при
этом ни одного неприводимого представления Щя),
придется вернуться к началу гл. VI.
Все дальнейшее изложение (гл. VIII-—XII) посвяща¬
ется более детальному изучению неприводимых пред¬
ставлений U(я), GL(я).

ГЛАВА IV
КОМПАКТНЫЕ ГРУППЫ ЛИ.
ГЛОБАЛЬНАЯ ТЕОРЕМА
В настоящей главе мы вводим основные объекты,
изучаемые в этой книге, — компактные группы Ли. При¬
менение специального метода «усреднения» позволяет
для данного класса групп получить замечательное обоб¬
щение теории классических рядов Фурье. Получаемая
теория имеет дело с «элементарными гармониками»,
т. е. неприводимыми представлениями группы G, и со¬
держит в себе основную информацию о строении этих
представлений.
§ 24. Определение компактной группы
В абстрактной топологии важную роль играет разли¬
чие между компактными и некомпактными множества¬
ми. Множество К в метрическом пространстве назы¬
вается компактным, если оно замкнуто и может быть
покрыто конечным числом шаров радиуса е при сколь
угодно малом е. По образному выражению Г. Вейля,
все «жители» области К находятся под охраной конеч¬
ного числа «милиционеров» (центры шаров) при усло¬
вии, что каждый милиционер имеет радиус действия е.
Оказывается, что условие компактности равносильно вы¬
полнению любого из следующих двух утверждений, ко¬
торые лежат в основе многих результатов классического
анализа.
Лемма Больцано — Вейерштрасса. Из вся¬
кого бесконечного подмножества множества К можно
извлечь подпоследовательность, сходящуюся в К-
Лемма Гейне — Б о р е л я. Из всякого бесконеч¬
ного покрытия множества К системой открытых мно¬
жеств можно выбрать конечное подпокрытие.

112 ГЛ. tV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
Поскольку эти утверждения не опираются на понятие
метрики, они используются для определения компактно¬
сти в топологических пространствах, более общих, чем
метрические. Наконец, как легко видеть, если множество
К расположено в евклидовом пространстве (с обычной
топологией), то требование компактности равносильно
замкнутости и ограниченности множества К.
Топологическая группа G называется компактной, ес¬
ли она компактна как топологическое пространство.
Примеры:
1. Ортогональная группа О (п) в вещественном про¬
странстве компактна. Действительно, элементы geO(ti)
выделяются среди «-мерных матриц условием
g'g =
которое равносильно ортогональности репера, соответ¬
ствующего матрице g. Следовательно,
S g], = n
1.1=1 1
и группа О (п) является подмножеством на сфере радиу¬
са уц в евклидовом пространстве размерности п2. Сле¬
довательно, множество 0(«) ограничено и, кроме того,
оно замкнуто, поскольку условие g'g = е сохраняется
при предельном переходе.
2. Унитарная группа U (п) компактна. Доказатель¬
ство аналогично предыдущему, с заменой прежнего ус¬
ловия условием g*g = е для матрицы geU(ti). Впро¬
чем, U(«)cO(2n) (замена комплексных координат ве¬
щественными) и О(п) cU(tt),
3. Группы О (п,С), О (p,q), U (p,q) при р, q ф 0 не¬
компактны. Действительно, все эти группы наряду с
обычными поворотами содержат также систему гипер¬
болических поворотов вида
ch t sh 11
sin chf ’
v(t) =
которые действуют в двумерных плоскостях. Поскольку
такая подгруппа v(t) гомеоморфна неограниченной пря¬

§ 24. ОПРЕДЕЛЕНИЕ КОМПАКТНОЙ ГРУППЫ ЦЗ
мой, то и каждая из данных групп неограничена как
множество.
Топологическое пространство называется локально
компактным, если каждая его точка обладает окрестно¬
стью с компактным замыканием. Соответственно вво¬
дится понятие локально компактной группы. Очевидно,
для локальной компактности группы достаточно, в силу
принципа однородности, существования окрестности с
компактным замыканием хотя бы для точки е.
Если ограничиться классом групп Ли, то в силу
их локальной евклидовости они всегда локально ком¬
пактны.
Наконец, если группа не компактна и даже не ло¬
кально компактна, то она может быть названа суще¬
ственно некомпактной. Группа унитарных операторов в
бесконечномерном гильбертовом пространстве является
примером такой группы*).
Одним из основных результатов теории групп яв¬
ляется установление принципиального различия между
представлениями компактных и некомпактных групп Ли.
В частности, мы увидим, что гармонический анализ на
компактной группе Ли сводится к рядам, в то время
как на локально компактной группе Ли — к обобщенным
интегралам Фурье. В основе этого различия лежит сле¬
дующее очевидное свойство:
1° Всякая компактная группа Ли имеет конечный
объем (относительно меры Хаара).
Мы предоставляем читателю детальное доказатель¬
ство этого утверждения. Отметим еще одно свойство
меры Хаара, которое является следствием свойства 1°:
2°. На компактной группе Ли всякая мера Хаара яв¬
ляется двусторонне инвариантной и инвариантной по от¬
ношению к инверсии.
Действительно, если du(g)— левоинвариантная мера
Хаара, то мера dy(gg0) снова является левоинвариантнон
и поэтому в силу принципа единственности отличается
*) Некомпактность единичной сферы в гильбертовом простран¬
стве является «первопричиной» принципиально новых закономерно¬
стей в теории линейных операторов. Если бы эта сфера была ком¬
пактной, то всякий непрерывный линейный оператор в гильбертовом
(и также в банаховом) пространстве имел бы дискретный спектр.

114 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
от dy(g) лишь умножением на константу:
dp (gg0) = с d]i (g)
(константа с зависит от go)- Интегрируя обе части этого
равенства по группе G, заметим, что точка h ='gg0 про¬
бегает (при фиксированном g0) также всю группу G,
откуда ясно, что J d\i(h)= J G?p,(g)=E, где V — конеч¬
ный объем группы G. Следовательно,
V = cV
и с= 1; но это и означает, что мера dp(g) является
правоинвариантной. Далее, мера t/p(g^1) снова яв¬
ляется инвариантной, откуда G?p(g-1) = k d\x (g), где k —
константа, и прежний прием позволяет заключить, что
k = 1.
Двусторонне инвариантную меру Хаара на группе G
мы условимся ради краткости обозначать просто симво¬
лом dg. Условие
J 1/(£) fdg< оо
выделяет гильбертово пространство числовых функций
на группе G, которое принято обозначать L2(G). Если
группа G компактна, то для меры Хаара мы будем
использовать нормировку
/ dg= 1,
которая означает, что полный объем всей группы пола¬
гается равным единице.
§ 25. Формулировка глобальной теоремы
Для компактной группы Ли удается в принципе ре¬
шить все основные проблемы, связанные с теорией пред¬
ставлений. Окончательный результат мы сформулируем
в виде перечня законов, называемого здесь «глобальной
теоремой».
Теорема 1 (глобальная теорема). Если
G — компактная группа Ли, то она обладает следую-
щими свойствами:

§ 25. ФОРМУЛИРОВКА ГЛОБАЛЬНОЙ ТЕОРЕМЫ
116
1. G имеет точное линейное представление.
2. Все неприводимые *) представления группы G
имеют конечную размерность и содержатся в классе
тензоров (над тем линейным пространством, где G
имеет точное представление).
3. Все конечномерные представления группы G экви¬
валентны унитарным и обладают свойством полной при¬
водимости **).
4. Число неприводимых представлений группы G
(определяемых с точностью до эквивалентности) конеч¬
но или счетно***), причем конечно только в случае,
когда группа G конечна.
5. Всякая непрерывная функция f(g) на группе G
может быть равномерно, с любой степенью точности,
аппроксимирована линейными комбинациями матричных
элементов
где индекс I означает нумерацию всевозможных непри¬
водимых представлений, а индексы /, / — обычные мат¬
ричные индексы относительно произвольного ба¬
зиса ****),
6. Если матрица xl (g) —1| xltj (g) || записана в ба¬
зисе, относительно которого она унитарна, то система
матричных элементов xltj (g) представляет собой полную
ортогональную систему в гильбертовом пространстве
H = L2(G). Все элементы %\j(g) при фиксированном I
имеют одинаковую норму, равную п~Ч\ где п = п(1)—■
размерность представления х1.
7. Если функция f(g) содержится в L2(G), то ее ряд
Фурье
fig)- 2 ^[ {g),
i, i, i 1
*) A priori бесконечномерные; при этом мы имеем в виду
понятие топологической неприводимости (см. стр. 89).
**) Это замечательное свойство называется принципом пол¬
ной приводимости.
***) Эта часть утверждения является очевидным следствием
свойства 2 (действительно, тензорная алгебра имеет счетный базис).
**'**) Эта часть теоремы носит название «основной аппроксима-
дионной теоремы» Петера — Вейля [124].

116 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
где c\s = п (/, т1.^, сходится к этой функции в среднем
квадратичном.
Замечание. В действительности мы увидим (до¬
бавление I, § 2), что ряд Фурье сходится равномерно,
если функция f(g) достаточное число раз дифференци¬
руема (по параметрам группы G), и тем быстрее, чем
выше степень гладкости функции f.
Напомним, что символ (f, ср), использованный в фор¬
мулировке теоремы, означает скалярное произведение
двух произвольных функций из И:
if, Ф)= J f(g)<f(g) би¬
ортогональность понимается также по отношению к это¬
му скалярному произведению. В § 32 мы опишем также
переход к произвольному однородному пространству с
группой движений G.
Доказательство теоремы будет разбито на несколько
частей.
§ 26. Прием усреднения *)
В основе доказательства глобальной теоремы лежит
операция усреднения произвольной непрерывной функ¬
ции— числовой, операторной или векторной — на груп¬
пе G. Этот прием в теорию представлений был введен,
по-видимому, Гурвицем. Если функция f(g) непрерывна
на компактном множестве К, то она ограничена (аналог
известной теоремы Вейерштрасса) **); следовательно,
среднее значение
Ш = / f(g)dg,
где | G j = j“ dg, существует. Используя нормировку
jG|=l, рассмотрим, в частности, произвольное линей¬
*) Здесь и в следующем параграфе роль группы G может
играть произвольная компактная группа с мерой Хаара (не обяза¬
тельно группа Ли).
**) Действительно, если функция f(g) принимает неограни¬
ченно возрастающие значения на последовательности точек gn, то,
выбирая подпоследовательность, сходящуюся к некоторому эле¬
менту go е/С, находим /(go)== что невозможно.

§ 26. ПРИЕМ УСРЕДНЕНИЯ
117
ное представление Tg группы G в векторном простран¬
стве V. Для каждого х е V мы получаем возможность
построить вектор
*о = [TgX],
который является «центром тяжести» множества всех
точек Tgx. Нетрудно видеть, что вектор Хо является
инвариантом группы G. Действительно, центр тяжести
множества точек Tgagx совпадает с центром тяжести
множества точек Tgx. Более формально,
Tgpco = [Т^х] = [Tgx] = хо
в силу левой инвариантности меры Хаара, и наше ут¬
верждение доказано*). Отсюда следуют:
Лемма 1. Если в пространстве V не содержится ни
одного ненулевого инварианта, то
[Тв] = о.
Лемма 2. В общем случае линейный оператор
Р = |Tg] является оператором проектирования на под¬
пространство V0 с V, состоящее из всех инвариантов
пространства V.
Доказательство леммы 1 очевидно. Для дока¬
зательства леммы 2 достаточно заметить, что постоян¬
ный вектор х можно вынести из-под знака интеграла,
откуда
Хо = IT**] = х = Рх,
где Р = [Tg] — постоянный линейный оператор. По¬
скольку
p2=llTe,M d83 =jdgjTghdh = jPdg = P,
то оператор Р действительно является проекционным и
область его значений совпадает с подпространством Vo
(в частности, Рх0 = Р2х = Рх — х0, т. е. преобразова¬
ние Р тождественно на Vo)- Леммы 1 и 2 доказаны.
*) В действительности здесь достаточно воспользоваться суще¬
ствованием центра тяжести у всякого ограниченного выпуклого
множества точек в векторном пространстве V [15].

118 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
Рассматривая, в частности, преобразование
Ugf (х, у) = f {Tgх, Tgy),
порожденное представлением Tg в классе билинейных
или в классе полуторалинейных форм f(x,y), и приме¬
няя к нему прием усреднения, находим форму fo(x,y) =
= [Vgf (х, у)], обладающую следующим свойством инва¬
риантности:
fo(Tgx, rgy) = f0(x, у)
для любого g^G и любых х, у. В частности, пусть
пространство V комплексно и форма f(x,y) положитель¬
но определена. Если квадратичная форма f(x,x) поло¬
жительно определена, то форма /0(х, х) также обладает
этим свойством; действительно, ясно, что /о (х, х) ^ 0;
кроме того, если
/о (х, х) = J / (Tgx, Tgx) dg = 0,
то в силу неотрицательности подынтегральной функции
она тождественно равна нулю, откуда, в частности,
при g = е находим f(x, х) = 0, что возможно только при
х = 0. Поскольку в конечномерном линейном простран¬
стве положительно определенная эрмитова форма f(x, у)
всегда существует, то мы получаем, что имеет место
Лемма 3 .В пространстве любого конечномерного
линейного представления компактной группы G всегда
существует инвариантная положительно определенная
эрмитова форма.
Выбирая эту форму в качестве скалярного произве¬
дения (х,у), находим, что представление Tg относитель¬
но (х, у) унитарно. Поскольку всякое скалярное произ¬
ведение диагонализуется в некотором базисе, то мат¬
рица
r*=iiTiyte)ii,
записанная по отношению к этому базису, унитарна.
Наконец, как мы видели в § 16, следствием унитарности
является полная приводимость. Следовательно, Tg впол¬
не приводимо, и мы доказали свойство 3 из глобальной
теоремы.

§ 27. СВОЙСТВО ОРТОГОНАЛЬНОСТИ Ц9
§ 27. Свойство ортогональности
Пусть Tg, Sg — два неприводимых представления
группы G, матрицы которых
Тв = IIШ (g) И, Sg = II oilv (g) И,
/,/=1,2, ..., /г; р, v = 1, 2, ..., m, записаны по отно¬
шению к тем базисам, в которых они унитарны. Рас¬
сматривая тензорное произведение
ug = Tg®sg,
где Sg = S'g ' — представление, контрагредиентное Sg,
напомним следствие 2 из леммы Шура, согласно кото¬
рому, если Tg и Sg неэквивалентны, то представление Ug
не содержит ненулевых инвариантов. Следовательно, в
этом случае
Wg] = o. (*)
Подставляя выражения отдельных матричных элементов
представления Ug через матричные элементы представ¬
лений Tg, Sg, заметим, что Sg = S'g = Sg, где черта
означает комплексное сопряжение каждого элемента
матрицы Sg. В результате матричное равенство (*) за¬
меняется системой числовых равенств
J ttiig)**»? (в) dg = 0,
которые в совокупности означают ортогональность меж¬
ду матричными элементами Tg, Sg.
Положим теперь Sg = Tg и реализуем представле¬
ние Tg в классе прямоугольных матриц (§ 20):
Ugz = ТgZTg .
Поскольку в классе этих матриц имеются лишь инва¬
рианты Хе, где X — произвольное число, то усредненная
матрица zQ = [Ugz] должна совпадать с одним из таких
инвариантов:
[Ugz] = Хе
для любого г. Для определения X = X(z) произведем вы¬
числение следа левой и правой части, учитывая, что

120 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
sp Ugz — sp z; в результате находим
sp z = К • sp е = Хп,
где п — размерность матрицы е. Следовательно,
А = sp z, и мы получаем окончательно
[^2] = ~(spz)e.
Полагая, в частности, z = вц, где матрица ец содержит
единицу на пересечении i-й строки с /-м столбцом и
нули на остальных местах, находим, что матрица
Ugz = TgzTgX = TgzTg состоит из элементов xpi {g)xqj (g),
p, </ = l, 2, ..., п. Следовательно,
J V (&) / (g) \ (SP ea) bpq = 4 bifipq,
где 6 ij, 6 pq — символы Кронекера (действительно,
ърец = бц, г, / = 1, 2, ..., п). В результате мы видим,
что имеет место
Лемма 4. Матричные элементы двух неприводимых
неэквивалентных представлений группы G взаимно орто¬
гональны. Матричные элементы каждого неприводимого
представления группы G ортогональны между собой и
все имеют одинаковую норму, равную п~'1\ где п — раз¬
мерность данного представления.
§ 28. Аппроксимационная лемма для линейной группы G
Мы желаем пока миновать самую сложную часть
теоремы, которая касается точной линейной представи¬
мости группы G. Поэтому будем считать, что группа G
линейна, и докажем все остальные утверждения теоремы.
Лемма 5. Пусть xl(g)—система всевозможных не¬
приводимых представлений, которые встречаются при
разложении тензоров, преобразуемых группой G. Тогда
всякая непрерывная функция f(g) может быть равно¬
мерно, с любой степенью точности, аппроксимирована
линейными комбинациями матричных элементов xllt(g).

§ 28. АЛПРОКСИМАЦИОННАЯ ЛЕММА
121
Наиболее просто лемма 5 может быть доказана с по¬
мощью теоремы Стоуна — Вейерштрасса, известной из
функционального анализа*). Утверждение этой теоремы
состоит в следующем. Допустим, что 91 — некоторое мно¬
жество непрерывных функций на компакте X, обладаю¬
щее свойствами:
1° 91 является алгеброй (по отношению к обычному
сложению и умножению функций);
2° 91 содержит единицу (т. е. функцию f0(x) = 1);
3° вместе с каждой функцией f(x) 91 содержит функ¬
цию f(x);
4° & «разделяет точки» компакта X в том смысле,
что для любой пары точек хи х2 найдется функция
/е!1, принимающая в Х\, х2 различные значения.
Тогда любая непрерывная функция ф(х) на компакте
X может быть равномерно аппроксимирована элемен¬
тами алгебры 91.
Предположим теперь, что множество 91 определяется,
согласно условиям леммы, как линейная оболочка ма¬
тричных элементов хк., и докажем, что в этом случае
свойства 1°—4° выполняются. Действительно, если пере¬
множить два матричных элемента, то мы получаем ма¬
тричный элемент представления тг <8> х1', которое снова
содержится в классе тензоров и, следовательно, разла¬
гается по некоторым неприводимым представлениям
х2, ..., х‘к (правило полной приводимости), но то¬
гда изучаемый матричный элемент является линейной
комбинацией матричных элементов этих неприводимых
представлений, т. е. содержится в множестве 91. Следо¬
вательно, 91 является алгеброй. Поскольку в число тен¬
зоров включаются и тензоры нулевого ранга (скаляры),
то 91 содержит единицу. Далее, функция х1ц (g) является
матричным элементом представления xl (g) = x!(g)'~\
которое контрагредиентно xl(g) и поэтому также содер¬
жится в классе тензоров. Наконец, поскольку группа
линейна, то сама матрица g (преобразующая тензоры
первого ранга, т. е. векторы) разделяет точки группы.
Лемма доказана.
*) См., например, [35], стр. 19.

122 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
Впрочем, поскольку G содержится в евклидовом про¬
странстве, при доказательстве этой леммы можно было
бы воспользоваться и классической теоремой Вейер-
штрасса.
§ 29. Ряды Фурье на линейной группе G
Каждой квадратично интегрируемой функции f(g)
на группе G поставим в соответствие набор ее «коэффи¬
циентов Фурье»:
с1ц = (/> «{/)>
где eltj — п'^х1^ — система нормированных матричных
элементов из леммы 5 (нормированных таким образом,
чтобы ЦеЕ||= 1, где \\f\\—норма в пространстве Я).
Упрощая обозначения, запишем это определение в виде
(/> *-v)>
где v означает сложный индекс, составленный из индек¬
сов /, г, /. Поскольку значения этого индекса пробегают
счетное множество, мы можем осуществить перенумера¬
цию таким образом, чтобы v = 1, 2, ... Пусть Ьп — ли¬
нейная оболочка векторов ev, v = 1, 2, ..., п. Выраже¬
ние ря = min II/ — т ]| представляет собой «среднее квад-
ts*n
ратичное отклонение» функции / от линейного подпро-
П
странства Ln. Если т = 2 ^vev> то мы имеем *)
V= 1
II / - Т II2 = II /1|2 - s - 2 avcv + 2 | av |2 =
v= 1 V= 1 V=1
= II/II2-2|cv|2+ 2|av-Cv|2.
V=1 v=I
Поскольку ll/ll и коэффициенты cv зависят только от
функции /, то ясно, что min ||/ — т|| достигается в точ¬
ности при av = cv, v = 1,2,откуда рп = II/ — «Л,
*) Здесь мы повторяем рассуждения, обычные при построении
рядов Фурье.

§ 29. РЯДЫ ФУРЬЕ НА ЛИНЕЙНОЙ ГРУППЕ G 123
п
где sn = 2 cvev — частичная сумма ряда Фурье, и,
V=»l
кроме того,
p„=m2-ikvi2. (*)
v=1
Допустим вначале, что функция f непрерывна, и выберем
п настолько большим, чтобы max|f(g) — тд(g)|<е при
о
некотором тп е Ln (возможность такого выбора следует
из аппроксимационной леммы); тогда мы имеем
р„= min ||f-T|K||f-T„||<e.
x^Ln
Следовательно, \\f — snll < в при найденном п и f =
= lim sn. Кроме того, переходя к пределу в (*), полу-
М-> оо
чаем равенство Парсеваля:
Ik, i2=nfii2.
v=1
Наконец, если f — произвольная функция из Я, то для
всякого е > 0 существует, как известно, непрерывная
функция ф, квадратичное отклонение которой от f не
превосходит е; следовательно,
II f ~ Т„ IKII f - ф II +1| ф - т„ || < 2е,
и все предыдущие рассуждения снова можно повторить.
В результате получена
Лемма 6. Если G — линейная компактная группа,
то для каждой функции f е L2(G) ее ряд Фурье сходит¬
ся к этой функции в среднем квадратичном:
оо
f — Субу,
V“ 1
и при этом выполняется равенство Парсеваля:
оо
II f II2 = 21 cv р.
V-l

124 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
В заключение заметим, что если /, ф — произвольные
элементы из Я, то из равенства Парсеваля следует
обычное равенство для скалярных произведений:
сю
(/> ф) = 2 cvYv,
v-l
где Yv — коэффициенты Фурье функции ф. Заметим так¬
же, что, как следует из проведенного построения, разло¬
жение в ряд Фурье определяется однозначно.
§ 30. Завершение доказательства
для линейной группы G
Возвращаясь к первоначальным обозначениям для
матричных элементов, получаем сокращенную запись
ряда Фурье:
f(g) = .2spcV(g),
I
где с1 = I с*.(.[| • п'1г — матрица, составленная из коэффи¬
циентов Фурье функции f с фиксированным номером I.
Непосредственное выражение для матрицы с1 дается,
очевидно, формулой
= Т'ten,
где штрих означает транспонирование. Если в группе G
происходит правый сдвиг g0, то каждое слагаемое в этой
сумме заменяется выражением
sp с V (gg0) = sp с V (g) xl (g0) = sp xl (g0) с V (g),
откуда ясно, что преобразованная функция f(g) = f(ggo)
имеет коэффициентами Фурье матрицы
cl = xl{gQ)cl.
Полученный результат естественно интерпретируется
как разложение правого регулярного представления на
неприводимые. Действительно,
Я = 2 Я*
i
(прямая ортогональная сумма), где каждое слагаемое
Н1 конечномерно и изоморфно пространству всех ма¬

§ 30. ДОКАЗАТЕЛЬСТВО ДЛЯ ЛИНЕИНОИ ГРУППЫ
125
триц сг\ поскольку каждый столбец такой матрицы пре¬
образуется по закону х1, мы заключаем, что представле¬
ние х1 содержится в Н1 с кратностью п(1)*).
Замечание. Нетрудно видеть, что из рассмотрения левых
сдвигов возникает то же самое разложение пространства Н. Далее,
если рассматривать Н как алгебру относительно свертки, то важно
отметить, что свертке двух функций из Н соответствует умножение
соответствующих блоков с1 при каждом фиксированном /; следова¬
тельно, алгебра Н изоморфна (дискретной) сумме полных матрич¬
ных блоков размерностей n(l) X п(1).
Поскольку, как мы видели в § 18, всякое неприво¬
димое представление группы G, конечномерное или бес¬
конечномерное, содержится в регулярном, интуитивно
ясно, что имеет место
Лемма 7. Линейная компактная группа G не имеет
иных топологически неприводимых **) представлений,
кроме представлений х1, действующих в классе тензоров.
Изложим строгое доказательство этой леммы. Пусть
Tg — топологически неприводимое представление груп¬
пы G в линейном топологическом пространстве V (про¬
извольной размерности), и пусть t(g') — одно из пред¬
ставлений х1, действующее в пространстве Е. Заметим,
что всякий линейный непрерывный оператор V-+-E
имеет следующий вид:
tl
Л*= 2 fi(x)eit
i=i
где — фиксированный базис в пространстве Е и fi(x) —
непрерывные линейные функционалы над V. Если опе¬
ратор А переплетает представления Tg, x(g), то мы на¬
ходим после несложных вычислений
ft (Tgx) = 2 f/(x) тtl(g),
i=i
где Ikij(g) II — матрица оператора t(g'). Это означает, что
в сопряженном линейном пространстве V' существует
*) Можно вместо матрицы с1 рассматривать набор гармоник
х\j, i, / = 1, 2, ..., п(1), которые образуют базис в Н1- при этом
каждая строка таких гармоник преобразуется по представлению х1.
**) См. стр. 89.

126 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
конечномерное инвариантное подпространство (относи¬
тельно представления Tg, контрагредиентного Tg).
Если V бесконечномерно и неприводимо, то отсюда за¬
ключаем, что А = 0. Если же А Ф 0, то V конечномерно
и, согласно лемме Шура, Tg эквивалентно т(§).
Допустим теперь, что А = 0 для всякого переплетаю¬
щего оператора А и всякого х1. Рассмотрим произволь¬
ный функционал f(x), xeF, и положим
Ax = f(x)l,
где £ — произвольный фиксированный вектор из Е. При¬
меняя к оператору А процесс усреднения по правилу*)
Ао= J *(£)“' ATgdg,
получаем переплетающий оператор AQ {A0Tg = т(ё')Л0);
следовательно, А0 = 0. Замечая, что T(g,)_I = r(g')*, на¬
ходим
А0х = J т (gY I ■ f(Tgx)dg = 0.
Полученное равенство означает, что числовая функция
q>(g) = f(Tgx) ортогональна всем матричным элементам
x\j{g).Следовательно, ср(£)=0 в силу полноты системы
этих элементов:
/(7» = 0, geC.
Поскольку f — произвольный элемент из V', это возмож¬
но (в силу теоремы Хана — Банаха [5]) только при усло¬
вии Tgx — 0. Поскольку х — произвольный вектор, мы
получаем противоречие. Лемма доказана.
Тем самым доказывается п. 2 глобальной теоремы,
откуда следует также и п. 4 (число элементарных гар¬
моник конечно только в том случае, когда простран¬
ство Н конечномерно, т. е. группа G конечна). В резуль¬
тате для случая линейной группы глобальная теорема
доказана полностью.
*) Существование этого интеграла вытекает из нижеследующей
формулы для AqX.

§ 31. ЗАВЕРШЕНИЕ ДОКАЗАТЕЛЬСТВА Ё ОБЩЕМ СЛУЧАЕ 127
§ 31. Завершение доказательства в общем случае
Имея дело с абстрактной группой G, мы вместо тен¬
зорных преобразований рассматриваем множество всех
(абстрактно определенных с точностью до эквивалент¬
ности) неприводимых конечномерных представлений
группы G. Пусть Ф — линейная оболочка матричных эле¬
ментов всех таких представлений. Повторяя рассужде¬
ния § 28, заключаем (из принципа полной приводи¬
мости), что множество Ф является алгеброй относитель¬
но обычного умножения.
Лемма 8. Алгебра Ф разделяет точки группы G*).
Доказательство. Пусть Ф — равномерное замы¬
кание алгебры Ф. Покажем, что Ф содержит произволь¬
ную непрерывную функцию x(g) на группе G, для ко¬
торой * (g”1) = *(§)• Действительно, сопоставим функ¬
ции *(g) интегральный оператор левой свертки
Xf(g)= j x(gh-')f{h)dh.
Как известно, такой оператор вполне непрерывен (это
следует из компактности множества G). Из условия
x(hg~l) = x(gh~l) следует также, что X — симметрич¬
ный оператор Гильберта — Шмидта. Согласно извест¬
ным результатам теории интегральных операторов ядро
x{gh~l) представимо в виде равномерно сходящегося
ряда с элементами вида As<ps (g) qps (/г), где cps — собствен¬
ные функции оператора X и As — соответствующие соб¬
ственные значения. Полагая, в частности, h = е, мы
находим
ОО
* (g) = 2 csф5 (g),
5=1
где сходимость ряда равномерная. Покажем теперь, что
собственные функции (ps(g) при Xs Ф 0 содержатся в
алгебре Ф. Действительно, пусть Н%— пространство
всех собственных функций с собственным значением
*) Здесь можно считать, что G — произвольная компактная
группа (не обязательно группа Ли).

128 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
X ф 0. Поскольку оператор X вполне непрерывен, про¬
странство Нь конечномерно. Поскольку оператор X по¬
рождается левыми сдвигами, пространство /Д. инва¬
риантно относительно правых сдвигов. Пусть в\ (g),...
...,en{g) — произвольный базис в пространстве Н%.
Рассуждая, как в § 18, получаем, что
П
е,- (ё) = 2 ctxtl (g),
i = l
где r(g') — конечномерное представление, действующее в
Н%. Следовательно, Ял а Ф, и отсюда следует, что
x(g)(= Ф.
Поскольку функции x(g-) указанного вида разделяют
точки группы G, то же верно и для алгебры Ф. Лемма
доказана.
Замечание. Всякая непрерывная функция (p(g)
на G может быть записана в виде x(g) + iy(g), где х и
у — функции такого же класса, как рассмотренные в до¬
казательстве леммы 8. Следовательно, Ф = С(С), где
C(G) — пространство всех непрерывных функций на G,
и мы получаем доказательство аппроксимационной тео¬
ремы для любой компактной группы G.
Заключающим элементом нашей конструкции яв¬
ляется
Лемма 9. Если алгебра Ф разделяет точки груп¬
пы G, где G — компактная группа Ли, то G допускает
точное линейное представление.
Доказательство. Если алгебра Ф разделяет точ¬
ки группы, то для каждой точки g фе найдется конечно¬
мерное представление 6 такое, что g не содержится в
его ядре. Следовательно, g ^ G6 = G — N&, где М6 —
ядро 6. Следовательно, система открытых множеств G6
покрывает группу G с выколотой точкой е. Следователь¬
но, эта система покрывает также всякое замкнутое мно¬
жество вида G — U, где U — окрестность точки е.
Согласно лемме Гейне — Бореля множество G — U
покрывается конечной системой множеств G6l, Св2,...
...,G4 . Но это означает, что подгруппа
N = N&lf\N6ir\ ... ПМт

§ 32. ГАРМОНИЧЕСКИЙ АНАЛИЗ
129
целиком содержится в окрестности U. Заметим, что N
является ядром представления 6о = 61 + 62 + .. . + 6m
(прямая сумма).
Предположим теперь, что окрестность U ограничена
и допускает канонические координаты. Если gl— произ¬
вольная однопараметрическая группа, то она гомеоморф-
на окружности либо прямой, в то время как пересечение
gl с U гомеоморфно ограниченному открытому множе¬
ству на прямой. Следовательно, gl целиком не содер¬
жится в U. Следовательно, U не содержит ни одной па¬
раметрической подгруппы, но тогда и вообще ни одной
подгруппы, кроме точки е. В этом случае N — {е} и пред¬
ставление 6о является точным. Лемма доказана.
Комбинируя леммы 8 и 9, получаем в результате,
что всякая компактная группа Ли допускает точное ли¬
нейное представление.
Глобальная теорема полностью доказана.
Упражнение
Пусть G — компактная группа Ли и Н—ее замкнутая под¬
группа. Показать, что если всякое неприводимое представление
группы G остается неприводимым при сужении на Н, то G = Н.
(Указание: проверить, что среднее значение всякой функции {(g)
по группе G совпадает со средним значением по под:руппе п.
В частности, если {(g)—расстояние от точки geG до подгруппы
Н, то отсюда следует, что {(g) = 0, т. е. G = Н.)
§ 32. Гармонический анализ на однородном многообразии
Теперь мы можем перейти к рассмотрению произ¬
вольного однородного многообразия X с компактной
группой движений G. Применяя конструкцию § 17, усло¬
вимся сразу рассматривать X в виде фактор-простран¬
ства G/Н, где Н — стационарная подгруппа некоторой
фиксированной точки из X. Напомним, что в этой кон¬
струкции каждая точка х^Х рассматривается как ги¬
перповерхность вида Hgx, где gx — фиксированный эле¬
мент из G. Всякую функцию f(x) на пространстве X мы
можем рассматривать как функцию f(g) на группе G,
инвариантную относительно левых сдвигов на элементы

130 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
из Н. Условие
J I / (g) I2 dg < 00
в этом классе функций выделяет гильбертово простран¬
ство функций f(x), которое мы обозначим L2(X) (можно
было бы также по мере Хаара dg построить соот¬
ветствующую меру dx на X*) и определить простран¬
ство L2(X) независимо). Следующее утверждение, по¬
лучаемое как следствие из глобальной теоремы, решает
задачу гармонического анализа в классе L2(X):
Теорема 2. Пусть x(g)— произвольное неприводи¬
мое представление группы G, унитарное в базисе еие^,...
..., еп, первые d элементов которого (d -С п) образуют
базис в подпространстве всех инвариантов относительно
подгруппы И. Определяя матричные элементы хu(g) =
— (x(g)ej,ei) относительно этого базиса, введем обозна¬
чение Sx для множества всех элементов
1ц (g), >■ = 1, 2, . .., d, j= 1, 2, .. ., n,
соответствующих первым d строкам матрицы x(g).
Пусть S — объединение всех St по всевозможным не¬
приводимым х (определяемым с точностью до эквива¬
лентности). Тогда система S является полной ортого¬
нальной системой в пространстве L2(X) и элементы из
ST имеют одинаковую норму, равную п~'^ (при условии,
что мера dg нормирована соотношением dg — 1).
Доказательство. Достаточно проверить, что
коэффициенты Фурье функции f(g):
получаемой как продолжение функции f(x) на группу G,
равны нулю при i = d + 1, d + 2, ..., п. В силу инва-
*) Попросту говоря, полагаем ф (*) dx = ф (g) dg для ЛЮ'
бой непрерывной функции ф(л) и для каждого множества А а X
определяем меру ц(Л)= J dx.
А

§ 32. ГАРМОНИЧЕСКИЙ АНАЛИЗ
131
риантности функции f(g) и меры dg относительно левых
сдвигов на элементы из Н имеем
П
сц = J f (g) т:ц (hg) dg = 2 J f (g) xik (h) xkj (g) dg.
k-\
Поскольку система e\, e2, . ■ ■, ed состоит из инвариан¬
тов группы Н, то линейная оболочка дополнительных
элементов ed+\, ed+2, ..., еп инвариантна относитель¬
но Н (инвариантность ортогонального дополнения); сле¬
довательно, в данном базисе матрица x(h) имеет вид
1
О
1
О
о
х (А) =
О
a (h)
где разбиение на блоки соответствует разбиению базиса
на элементы с номерами и ~>d. Следовательно, если
i = d + 1, d + 2, ..., п, то получаем
П П
сч= J f(g)*kl(g)dg = ^ Glk(h)Ckl,
k=d-\-1 k = dJr J
где am — матричные элементы представления o(h).
Интегрируя обе части полученного равенства по мере
Хаара на группе Н, замечаем, что
J aik (h) dh = О,
ибо представление a(h) не содержит инвариантов груп¬
пы Н (все такие инварианты относятся к базису в\,
е2, ..., ed). В результате Ci$ = 0.

132 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
Теорема доказана.
Таким образом, существует универсальная конструк¬
ция для классификации функций на произвольном одно¬
родном многообразии X с компактной группой движе¬
ний G (очевидно, X в этом случае также компактно).
В частности, всякая непрерывная функция на X допу¬
скает разложение в «ряд Фурье». Привлекая дополни¬
тельные построения (см. добавление I, § 2), нетрудно
также показать, что чем сильнее гладкость функции
f(x), тем быстрее сходится соответствующий ряд Фурье.
§ 33. Характеры
Если G — компактная группа, то для каждой пары
функций x(g), y(g)^L2(G) их свертка
z(g)= J х (gh~l) у {h) dh
снова квадратично интегрируема, т. е. 2(g)eL2(G).
Следовательно, пространство £ = L2(G) является алгеб¬
рой относительно этой свертки. То же самое можно ска¬
зать о пространстве C(G) всех непрерывных функций
на группе G. Представляет интерес, с точки зрения тео¬
рии представлений, найти центр 3 алгебры ф, т. е. со¬
вокупность всех функций, перестановочных (относитель¬
но свертки) с произвольными функциями из £. Произ¬
водя несложное вычисление, получаем, что условие
Z (go&So') = 2 (г). (*)
выполняемое при всех g0 е G, необходимо и достаточно
для принадлежности функции z(g) центру 3- Всевоз¬
можные точки gQggQl, получаемые внутренними авто¬
морфизмами из точки g, называются сопряженными
между собой; совокупность всех таких точек (при фик¬
сированном g) называется классом сопряженных эле¬
ментов. Таким образом, условие (-») можно выразить,
сказав, что функция z(g) постоянна на каждом классе
сопряженных элементов.
Примером функции такого типа является функция
z(g) = spTg,

§ 33. ХАРАКТЕРЫ
133
где Тя — произвольное (конечномерное) представление
группы G. В частности, если Tg — оператор неприводи¬
мого представления б, то для соответствующей функции
2(g) введем обозначение у.б(£)-
Функция Хб(ё) называется характером представле¬
ния 6. Следствием глобальной теоремы является
Теорема 3. Всякая функция z(g), постоянная на
классах сопряженных элементов, разлагается в ряд
Фурье по характерам неприводимых представлений
группы G.
Доказательство. Условие (*) мы можем пред¬
ставить в виде
где Lg и Rg — соответственно левое и правое регулярное
представление группы G. Применяя это условие, полу¬
чаем, что каждая матрица с1, состоящая из коэффи¬
циентов Фурье функици z(g), удовлетворяет тождеству
т. е. с1 перестановочна с операторами неприводимого
представления тг; но тогда по лемме Шура эта матрица
кратна единичной, и ряд Фурье для функции z(g) при¬
нимает вид
(см. общий вид такого ряда в § 30). Теорема доказана.
Кроме того, из ортогональности матричных элементов
получаем следствие:
т. е. система 2 всех характеров является ортонорми-
рованной системой.
Характеры играют замечательную роль в теории
представлений группы G. Действительно, как мы видели
в § 22, со всяким представлением Tg группы G связано
представление
LgJz (g) = Rgoz (g),
т7 (go) с1 = с1т1 (g0),
2(g) = 2ct;spT 4g)
j 0, если 6=^=6',
i 1, если 6 = 6',
Тх = J -г (g) Tg dg

134 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
групповой алгебры группы G, в частности алгебры $
(или C(G)). Если при этом геЗ, то ясно, что опера¬
тор Tz перестановочен со всеми операторами представ¬
ления Тх, а потому и со всеми операторами Тg. Следо¬
вательно, если Tg неприводимо, то оператор Тг кратен
единичному, а если Tg вполне приводимо, то Тг диаго-
нализуется в соответствующем базисе. В частности, если
положим
то операторы Р6, как легко проверить (доказательство
предоставляется читателю), являются проекционными
операторами, каждый из которых проектирует все про¬
странство V представления Tg на максимальное подпро¬
странство Vпредставление в котором кратно б. При
этом, очевидно, Р6Р&/ = 0 при б 4= 6' и
где / — единичный оператор в пространстве V. Следова¬
тельно, операторы Рв осуществляют разложение пред¬
ставления Тg на представления, кратные неприводимым.
Несмотря на то, что практическое вычисление про¬
екторов Р& далеко пе всегда является легким, мы полу¬
чаем (в сочетании с принципом полной приводимости)
универсальное решение проблемы спектрального ана¬
лиза.
§ 34. Теория представлений конечных групп
Всякая конечная группа, очевидно, является ком¬
пактной; следовательно, вся предыдущая теория при¬
менима к этому частному случаю. (Все доказательства,
лежащие в основе этой теории, можно было бы повто¬
рить применительно к этому случаю, заменяя интегралы
суммами.) Однако теория конечных групп и их представ¬
лений обладает и своими индивидуальными «арифмети¬
ческими» особенностями.
Прежде всего, из глобальной теоремы непосредст¬
венно вытекает
S/w,
б

§ 34. ТЕОРИЯ ПРЕДСТАВЛЕНИЙ КОНЕЧНЫХ ГРУПП 135
Теорема 4 («1-я теорема Бернсайда»).
Если конечная группа G имеет порядок N, то имеет ме¬
сто равенство
m
лг = 2 я*,
<•=1
где п{, £ = 1, 2, , ш, — размерности всех неприводи¬
мых (попарно неэквивалентных) представлений груп¬
пы G.
Действительно, групповая алгебра $ представляет
собою в этом случае линейное пространство размерно¬
сти N, и разложение
m
! = 1
дает искомое выражение для размерности, поскольку
dim $i = n2i (£; заменяет обозначение Н1 из § 30). В дей¬
ствительности это разложение содержит значительно
большую информацию об изоморфизме между группо¬
вой алгеброй ^ и вполне приводимой «блок-алгеброй»,
состоящей из полных матричных блоков размерностей
и,■ X п;. Далее следует
Теорема 5 («2-я теорема Бернсайда»),
Если m — число всевозможных попарно неэквивалент¬
ных неприводимых представлений группы G, то
m = х,
где х — число всевозможных классов сопряженных эле¬
ментов в группе G (G — конечная группа).
Для доказательства этой теоремы рассматривается
центр групповой алгебры В. который, как мы знаем, со¬
стоит из всевозможных функций, постоянных на клас¬
сах сопряженных элементов, т. е. представляет собой в
данном случае линейное пространство размерности х.
Поскольку всякая такая функция разлагается по харак¬
терам %i, £ = 1, 2, ..., m, то
пг
3= S3,,
/-1

136 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
где одномерное пространство 3* натянуто на характер
%i, и мы заключаем отсюда, что т = к. Теорема до¬
казана.
В дальнейшем мы увидим, что все такие «арифмети¬
ческие» закономерности сохраняются в известном смыс¬
ле и для произвольной компактной группы Ли, однако
при этом они приобретают «аналитическое» содержание
(вместо числа элементов группы или классов сопряжен¬
ных элементов рассматриваются размерности соответ¬
ствующих аналитических многообразий).
Пример. Симметрическая группа S(n).
Введенное обозначение мы будем использовать для груп¬
пы всех подстановок, производимых над п «предме¬
тами». Условимся считать, что данные предметы разме¬
щены на п занумерованных местах и символ
обозначает подстановку, которая состоит в перемещении
предмета с места ih на место jh (движение вниз); из
этого соглашения следует, что порядок расположения
пар (i^ /д) в символе s для нас не имеет значения,
а закон умножения в группе S (п)
напоминает закон умножения матриц (все индексы jh,
встречающиеся сверху и снизу, «сокращаются»). Извест¬
но, что всякая подстановка допускает разложение в
произведение циклов
S — (k 1, k-2, . • . , km{) (km-^l, • • • , kmj) ... ( . . . kn),
где каждый цикл (г'ь i2, ..., im) определяется как ча¬
стичная подстановка
(
h h • ■ • In
k\ k2 ... kn
h h • ■ ■ ln
ii /2 • ■ • in
l\ to ... Ifl
к | k2 ... kn
которая производится над предметами, стоящими на ме¬
стах i 1, г2, ..., im- Всякий внутренний автоморфизм

§ 34. ТЕОРИЯ ПРЕДСТАВЛЕНИИ КОНЕЧНЫХ ГРУПП 137
s—>-SoSS^! в группе S(п) перемещает, очевидно, номе¬
ра kh стоящие в отдельных циклах, но не меняет длину
циклов и их число. Условившись считать, что длины
циклов расположены в порядке убывания:
Щ\ ^ ^ mf, m.i + m2+ ... +mf = n
(f — число циклов), мы можем заключить, что всякий
набор таких чисел однозначно нумерует произвольный
класс сопряженных элементов 8т^т^,..т^ в группе S(n).
Следовательно, число таких классов совпадает с числом
всевозможных разбиений числа п в сумму невозрастаю¬
щих натуральных чисел. Следовательно, согласно второй
теореме Бернсайда, каждое неприводимое представление
группы S(n) может быть однозначно занумеровано ука¬
занным набором чисел Ш\, т2, ..., mf. К более подроб¬
ному рассмотрению таких представлений мы еще вер¬
немся в § 55.
Заметим, что группа S (п) допускает точное линей¬
ное представление с помощью преобразований хsx
в линейном пространстве размерности п, которые опре¬
деляются по правилу
seik = ejk> h' h = п'
в произвольном фиксированном базисе е2, е„
(здесь использовано одинаковое обозначение для под¬
становки
( t\ i2 . . . in
S = .
Vh к ■■■ 1п
и соответствующего ей линейного преобразования s).
Очевидно, при этом матрицы sseS(h) могут быть оха¬
рактеризованы как всевозможные матрицы, у которых
в каждой строке и в каждом столбце содержится по
единственному элементу, равному единице, а все осталь¬
ные элементы равны нулю.
Теорема о точном линейном представлении для конеч¬
ной группы доказывается тривиально, поскольку уже ре¬
гулярное представление этой группы (левое или правое)
является конечномерным и точным. Однако, анализируя

133 ГЛ. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
это представление, мы получаем в действительности бо¬
лее сильное утверждение:
Теорема 6. Всякая конечная группа изоморфна не¬
которой подгруппе в симметрической группе S (п).
Действительно, записывая элементы х ^ ф в виде
линейных комбинаций
х= 2 x(g)g,
ее а
мы рассматриваем точки g е G как базисные векторы
в пространстве Следовательно, правые сдвиги
g~*ggo
мы можем рассматривать как преобразование базиса в
пространстве £ и продолжить их до линейного преобра¬
зования
x->xgQ
во всем пространстве £. Поскольку точка h = gg0 пробе¬
гает (при фиксированном g0) все элементы группы G
точно по одному разу, то полученное линейное преобра¬
зование является оператором подстановки. Теорема до¬
казана.
Предлагается в качестве упражнений доказать само¬
стоятельно следующие утверждения:
1. Если все неприводимые представления конечной
группы G одномерны, то группа G коммутативна*).
(Указание: использовать вторую теорему Бернсайда.)
2. Всякая коммутативная конечная группа изоморф¬
на прямому произведению нескольких циклических
групп (циклическая группа порядка п определяется как
группа корней п-й степени из единицы).
В частности, первое из этих утверждений замеча¬
тельно в том отношении, что является примером инфор¬
мации, даваемой системой всех неприводимых представ¬
лений группы G относительно структуры самой груп¬
пы G (идея двойственности, см. § 23).
*) Обратное также верно согласно следствию 1 из леммы
Шура (§ 20).

§ 35. УНИВЕРСАЛЬНОСТЬ ГРУППЫ U(n)
139
§ 35. Универсальность группы U(n)
Подобно тому как симметрическая группа S (я) яв¬
ляется, согласно теореме 6, «универсальной» в классе
конечных групп, мы получаем (из глобальной теоремы),
что унитарная группа Щя) обладает аналогичным
свойством «универсальности» в классе компактных
групп Ли:
Теорема 7. Всякая компактная группа Ли изо¬
морфна некоторой подгруппе в группе U (п) (при до¬
статочно большом п).
Действительно, всякая компактная группа Ли обла¬
дает точным линейным представлением и всякое ее ли¬
нейное представление унитарно (свойства 1 и 3 из гло¬
бальной теоремы). Полученная теорема делает значи¬
тельно более доступной задачу о классификации
(с точностью до изоморфизма) всех компактных групп
Ли; действительно, для этого достаточно перечислить
все возможные замкнутые подгруппы в группе Щя).
Однако такая задача еще является достаточно сложной.
К вопросу о классификации мы перейдем только в
гл. XVI. В настоящее время нас в первую очередь будет
интересовать сама унитарная группа Щя), ее структура
и структура всех ее неприводимых представлений. (Огра¬
ничение этой задачей естественно не только с точки
зрения универсальности Щя), но и с точки зрения срав¬
нительной простоты в работе с этой группой.)
В заключение этой главы перечислим без доказа¬
тельства некоторые свойства компактных групп.
1° Всякая компактная топологическая группа имеет
лишь конечное число связных листов. В частности, вся¬
кая дискретная компактная группа конечна.
Доказательство этого утверждения предоставляется
читателю.
2° Всякая коммутативная связная компактная груп¬
па Ли изоморфна группе движений п-мерного тора.
В частности, всякая однопараметрическая замкнутая
подгруппа в любой компактной группе Ли изоморфна
группе вращений окружности.
См. по этому поводу более общее утверждение на
стр. 40.

140 гл. IV. КОМПАКТНЫЕ ГРУППЫ ЛИ. ГЛОБАЛЬНАЯ ТЕОРЕМА
Замечание. Существенно отметить, что компакт¬
ная группа Ли может содержать некомпактные под¬
группы. Типичным примером является иррациональная
обмотка тора (§ 15). Такая подгруппа является беско¬
нечной однопараметрической подгруппой g{t), —оо <
</< оо, в группе движений тора. Замыкание g(t)
совпадает со всей группой движений тора. Заметим, что
последнее верно также, если вместо g(t) рассматривать
дискретную подгруппу элементов g(n)=gn, где g = g(l).
Всякий элемент g е G, степени которого образуют всюду
плотное множество в G, мы условимся в дальнейшем
называть иррациональной образующей группы G. Со¬
гласно сказанному выше всякая коммутативная связная
компактная группа Ли обладает иррациональной обра¬
зующей. Однопараметрическая подгруппа g(t) в ком¬
пактной группе G является замкнутой только в том
случае, когда функция g(t) периодична с некоторым
периодом t0\ в этом случае группа g(t) изоморфна
окружности.
3° Универсальная накрывающая всякой компактной
группы Ли с дискретным центром снова является ком¬
пактной группой Ли. Центр этой группы конечен.
Это утверждение, принадлежащее Г. Вейлю [61],
доказывается наиболее сложно (см. § 103). Как след¬
ствие из 3° можно получить, что существует лишь конеч¬
ное число компактных связных групп Ли, локально изо¬
морфных между собой.
К перечисленным свойствам ограниченности и ко¬
нечности мы могли бы добавить еще замечательные
свойства конечности и дискретности, содержащиеся в
глобальной теореме. В ряде случаев из этих общих
свойств удается получить практический критерий ди¬
скретности спектра некоторых линейных операторов, до¬
пускающих компактную группу симметрии, а также
утверждение о конечной кратности их собственных зна¬
чений. В частности, унитарная группа U (п) как группа
симметрии встречается в некоторых важных задачах
теоретической физики.
Нашей ближайшей задачей является несколько бо¬
лее подробное изучение системы элементарных гармо¬
ник группы U (п).

§ 35. УНИВЕРСАЛЬНОСТЬ ГРУППЫ U(n)
Исторически первым классом групп, для которых была по¬
строена теория представлений, явились конечные группы. Перенос
этой теории на компактные группы Ли (в определенном смысле
«наиболее близкие к конечным») был осуществлен в работе Ф. П е-
тера и Г. Вейля [124]. Первоначальное доказательство «основной
аппроксимационной теоремы», данное этими авторами, существенно
использовало интегральный оператор свертки на компактной груп¬
пе G. В том варианте доказательства, который дается в этой главе,
мы используем такой оператор лишь однажды (§ 31), при доказа¬
тельстве линейности группы G. Более подробное изложение теории
конечных групп и их представлений можно найти в [3], [27], [31], [34],
[41]. Общие вопросы изложены в [9], [10], [46], [61].

ГЛАВА V
ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
В ТЕОРИИ ПРЕДСТАВЛЕНИЙ
С точки зрения глобальной теоремы представляет
особый интерес детальное изучение структуры непри¬
водимых представлений. Если речь идет о связной груп¬
пе Ли, то для решения этой задачи и других задач тео¬
рии представлений часто используется инфинитезималь-
ный метод. Этот метод сводит рассмотрение группы Ли
к рассмотрению соответствующей алгебры Ли.
Иллюстрацию метода мы изложим на примере
SU(2) и SO(3). Напомним, что эти группы локально
изоморфны, т. е. имеют одинаковую алгебру Ли.
В дальнейшем мы увидим, что всякая компактная
связная группа Ли содержит хотя бы одну подгруппу,
изоморфную SU(2) или SO(3). Поэтому изучение этих
групп интересно также с точки зрения общей теории.
§ 36. Дифференциал представления
Пусть G — группа Ли и g-+Tg — ее представление
в векторном пространстве V', вещественном или ком¬
плексном. Как правило, мы будем рассматривать только
конечномерные пространства. Все отступления от этого
правила будут специально оговариваться.
Рассмотрим вначале тот случай, когда группа G
представляет собой аддитивную вещественную группу
чисел t, —оо < t < 00. В этом случае речь идет о про¬
извольной однопараметрической матричной группе F(t),
непрерывно зависящей от t:
F(t + s) = F(t)F(s), F (0) = /,
где /—-единичная матрица в пространстве V. Пусть
ЦКЦ означает норму матрицы F в пространстве V и Q
означает окрестность единичной матрицы, выделяемую

§ 36. ДИФФЕРЕНЦИАЛ ПРЕДСТАВЛЕНИЯ
143
условием I.!/7 — /|) < 1. Изменяя, если нужно, нормировку
параметра t, мы можем считать, не ограничивая общ¬
ности, что F(l)eQ при |С^1- В частности, отсюда
следует, что /?(1) = ехрЛ при некотором А. Покажем,
что
F (t) = exp tA
для всех значений t, —оо < t < оо. Действительно, это
равенство должно иметь место для всех целых значе¬
ний t. Далее, F(l/2) совпадает с exp 1/2А, как единствен¬
ный квадратный корень в области Q из оператора F(l) =
= ехрЛ. Следовательно, наше равенство сохраняется
также для всех полуцелых значений t. Рассуждая индук¬
тивно, проверяем справедливость этого равенства для
всех двоично-рациональных чисел t. Но тогда оно спра¬
ведливо и на всей оси ввиду непрерывной зависимости
F(t) от t.
Полученный результат имеет принципиальное значе¬
ние во всей теории представлений групп Ли. Прежде
всего, мы видим, что функция F(t) аналитична. Заметим,
что оператор А может быть определен как касательный
вектор к кривой F(t)*). Этот оператор называется про¬
изводящим оператором или инфинитезимальным опера¬
тором однопараметрической группы F(t). Существенно,
что значение инфинитезимального оператора полностью
определяет всю группу F (t). Это замечание лежит в
основе излагаемого ниже общего «инфинитезимального
метода».
Пусть теперь G — произвольная группа Ли. Рассмат¬
ривая в пей произвольную однопараметрическую под¬
группу g(t) = exp tx, мы положим
F> {м) = -jp (техр tx)f^r
Здесь x — произвольный элемент в алгебре Ли X груп¬
пы G. Семейство операторов D(x) мы называем диффе¬
ренциалом представления Tg.

144
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
Теорема I. Пусть G — группа Ли, Tg — ее конеч¬
номерное представление и D(x) — его дифференциал.
Тогда D(x) является представлением алгебры Ли X
группы G. Если ^ = exрх, tgI, то Tg = expD(x).
Функция Tg является аналитической функцией на всей
группе G.
Дбказательство. Пусть х, у — произвольные
элементы из алгебры X. Напомним, что вектор z = Кх +
+ ру является касательным вектором к кривой
а (/) = exp tKx • exp tyy
в единичной точке е. Образом этой кривой в представ¬
лении ТЙ является A (t) = exp tXD (х) • exp ty,D(y). Каса¬
тельным вектором к A (t) в свою очередь служит
KD (х) + pD (у). Следовательно, D (z) = KD (х) + pD (у).
Аналогично рассматривается коммутатор z = [х, у] и
проверяется, что D (z) = [D (х), D (у)]. Следовательно,
отображение x-+D(x) является представлением алгеб¬
ры X. Далее, если х = Се, по отношению к некоторому
базису е{ в алгебре X, то мы имеем*)
Tg = exp D (х) = exp t‘E{,
где положено £,• = D (<?,). Следовательно, функция Tg
аналитична в той окрестности точки е, где определены
канонические координаты g = exp х.
Применяя сдвиги в группе G (левые или правые),
заключаем, что функция Т., аналитична также в окрест¬
ности каждой точки g0e^G. Теорема доказана.
Замечание 1. Подчеркнем, что в теореме 1 груп¬
па G рассматривается как вещественная и имеется в
виду вещественная аналитичность функции Tg. Если
группа G комплексна, то представление Tg аналитич-
но по вещественным параметрам в G. Однако если
функция Tg удовлетворяет условиям Коши — Римана
по отношению к этим параметрам, то функция Tg
является комплексно-аналитической на G. В этом слу¬
чае Tg = ехо ИЕи где И — комплексные параметры в
алгебре X.
*) Здесь и далее мы часто опускаем знак суммирования.

§ 36. ДИФФЕРЕНЦИАЛ ПРЕДСТАВЛЕНИЯ
145
Замечание 2. Пусть V бесконечномерно. Вектор £ назы¬
вается дифференцируемым, если вектор-функция Тдифференци¬
руема на G. В частности, если x(g)—дифференцируемая функция,
равная нулю вне компактного множества на G, то вектор
| = J х (g) Tg%0 dg является дифференцируемым для любого g0 е V
(проверьте). Пусть V0 — множество всех таких векторов |. Если функ¬
ционал f равен нулю на Во, то f(Tg%о) = 0 и, в частности, f(Sj0) = О
для любого |о е V. Следовательно, / = 0. Как следует из теории ли¬
нейных топологических пространств, в этом случае V0 всюду плотно
в V. Отсюда можем заключить, что дифференциал Ъ(х) допускает
определение на всюду плотном множестве в V.
Мы предоставляем читателю проверить следующие
свойства дифференциала:
Г Если g — инвариант представления Tg, то | анну¬
лируется всеми инфинитезимальными операторами D(x).
2° Если V0 — инвариантное подпространство относи¬
тельно Т„, то V’o инвариантно также относительно D (х).
3° Если два представления т'е, Tg эквивалентны, то
их дифференциалы D'(x), D"(x) также эквивалентны.
4° Если представление Tg является тензорным произ¬
ведением представлений Tg, Tg, то на векторах вида
|<8>т1 мы имеем
D (х) {I ® р) = D' {х) I ® т) +1 ® D" (х) г\.
5° Если представление Т„ контрагредиентно пред¬
ставлению Tg, то мы имеем
(D (х) £, т]) + (|, D (х) т)) = 0,
где D(x), D (х)—дифференциалы Те, Те, а скобка
(|, г|) означает билинейную форму, входящую в условие
контрагредиентности.
В частности, если Tg = Tg , то согласно 5° D(x) =
= —D(x)'. Такое представление в дальнейшем мы бу¬
дем называть представлением алгебры X, контрагре-
диентным D(x). Аналогично свойство 4° может быть
использовано для определения тензорного произведения
двух представлений алгебры X.
Если G — связная группа Ли, то согласно теореме 1
все эти утверждения допускают обращение. Действитель¬
но, в этом случае функция Tg порождается произведе¬
ниями операторов вида expZ)(x).

146
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
Далее, пусть е, — произвольно фиксированный базис
r алгебре X со структурными константами ckir Положим
Ei = D(ei). Тогда согласно теореме 1 имеем
[£„ £,]-с‘,£4 (.)
(сумма по к). Заметим, что между операторами Д* мо¬
гут существовать линейные соотношения.
Пример 1. Пусть X — алгебра Ли группы SU(2).
Согласно общим результатам § 10 алгебра Ли группы
su(2) состоит из всех антиэрмитовых матриц 2X2. Мат¬
рицы
0
1
/
0 i
i
1
0
1
0
’ а2=^\
-i 0
' a3=Y
0
-1
образуют базис в su(2). Несложное вычисление показы¬
вает, что элементы щ, а2, а3 подчиняются следующим
соотношениям коммутации:
\щ, Я/] &iik&ki
где Ецк — полностью антисимметрический тензор, для ко¬
торого 8123 = 1, и в правой части имеется в виду сум¬
мирование по k. Следовательно, если A4 = D(a;) для не¬
которого представления su(2),tomh по-прежнему имеем
[А{, Aj] = zijkAk.
Пр и м е р 2. Пусть G — группа всех треугольных
матриц 3 X 3 с единицами на главной диагонали. Не
ограничивая общности, будем говорить о верхних тре¬
угольных матрицах. Положим
0
1
0
0
0
0
0
0
1
P =
0
0
0
. q =
0
0
l
, r =
0
0
0
0
0
0
0
0
0
0
0
0
Тогда [р, q] = г и все остальные коммутаторы равняются
нулю. Элементы р, q, г образуют базис в алгебре Ли
группы G. Если Р, Q, R — образы р, q, г при некотором
представлении, то мы по-прежнему имеем
[Р, Q] = R-

§ 37. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ SU(2) 147
Легко проверить, что в условиях примера 1 опера¬
тор К = А\ + А\ + А\ перестановочен со всеми операто¬
рами Аи Л2,-Л3. Этот оператор мы в дальнейшем ис¬
пользуем при описании представления D(x). Условимся
называть его оператором Казимира представления D(x).
Упражнения
1. Показать, что если матрицы D(x) кососимметричны (или косо¬
эрмитовы), то представление D(x) вполне приводимо.
2. Пусть F(g)x = gxg~] для квадратных матриц х и g. Показать,
что всякий инфинитезимальный оператор группы F(g) имеет вид
Ах = [а, х].
д д
3. Положим 'S/P 1 — х/ з— — xk —— с циклической перестановкой
axk dxj
индексов i, j, k — 1, 2, 3. Показать, что линейные комбинации этих
операторов образуют представление алгебры su(2).
§ 37. Неприводимые представления группы SU(2)
В этом параграфе мы займемся частным вопросом
об описании неприводимых представлений алгебры
su(2). Мы не знаем пока, всякому ли представлению ал¬
гебры Ли отвечает представление соответствующей груп¬
пы Ли. Однако согласно результатам предыдущего па¬
раграфа, перечисляя неприводимые представления ал¬
гебры su(2), мы не пропустим, в частности, ни одного
неприводимого представления группы SU(2).
Согласно построениям предыдущего параграфа наша
задача сводится к рассмотрению всевозможных троек
линейных операторов Ль А2, Л3, удовлетворяющих соот¬
ношениям коммутации
[Д> Aj\ = Ah
с циклической перестановкой индексов г, k = \, 2, 3.
(Коммутаторы, взятые в обратном порядке, отличаются
знаком.) При этом данная тройка предполагается не¬
приводимой. Вместо базисных элементов Аи А2, Л3 удоб¬
но рассматривать их комплексные линейные комби¬
нации
E_ = i(Al-iA2), О0 = /Л3, £+ = i(Al + iA3),

148
ГЛ. V. ЙНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
которые удовлетворяют следующим соотношениям ком¬
мутации:
[£0> £+] = £+, [£0, £_]=-£_, [£+, £_] = 2£0-
Преимущество этих соотношений коммутации состоит,
формально говоря, в том, что операторы £+, £_ оказы¬
ваются «собственными векторами» относительно преоб¬
разования £0: /4->[£о, А]. Следствием этого условия яв¬
ляется
Лемма 1. Если вектор g является собственным век¬
тором в пространстве V относительно Е0 с собственным
значением Я, то векторы
£-g = g_, £+| = |+
также являются собственными относительно Е0 с соб¬
ственными значениями соответственно Я— 1, Я+1.
Доказательство. Заметим, что £0£+= £+£0+
+ [£0> £+] = £+(£о + !)• Отсюда имеем
Е<&+ ~ ДД+£ = (Е0 + 1) S = (^ + О £+•
Аналогично рассматривается вектор g_. Лемма доказана.
Поскольку пространство V предполагается конечно¬
мерным, то существует максимальное собственное зна¬
чение оператора £0, которое обозначим /. Пусть g0— со¬
ответствующий собственный вектор, тогда «повышаю¬
щий» оператор Е+ обращает этот вектор в нуль. В ре¬
зультате имеем
Е+^о “ 0, £0Ё,0 =/Ё,0.
Применяя к вектору |о «понижающий» оператор £_ и
его всевозможные степени, получаем цепочку элементов
gft = £Цо, k = 0, 1, 2, ..., каждый из которых является
собственным относительно £о с собственным значением
/ — £. Ввиду конечности числа собственных значений эта
цепочка должна оборваться:
£™+Ч 0 = 0.
Пусть Vo — линейная оболочка полученных векторов
go, £ь |т- Покажем, что V0 является циклической
оболочкой вектора go относительно алгебры 53 всех по¬
линомов от операторов £_, £0, £+. Действительно, ис¬

§ 37. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ SU(2) 149
пользуя соотношения коммутации, мы можем всякий
одночлен от этих операторов привести к виду
ЕР_Е^Е'+
с точностью до слагаемых, имеющих меньшую общую
степень. Этот одночлен может быть отличен от нуля на
векторе go только при условии г — 0. Операция Е0 сво¬
дится к растяжению вектора go, операция Е~ переводит
этот вектор в вектор, коллинеарный gp. Следовательно,
Vo = SPU Но тогда V0 = V ввиду неприводимости V.
Поскольку векторы g^ имеют различные собственные
значения, то они линейно независимы. Следовательно,
они образуют базис в пространстве V.
Нам уже известны правила действия операторов
£_, Е0 в выбранном базисе. Остается определить дей¬
ствие оператора £+. Для этого удобно использовать опе¬
ратор
А = ±(Е_Е++Е+Е_) + Е1,
который, как легко проверить, отличается лишь множи¬
телем — 1 от оператора Казимира К, введенного в конце
предыдущего параграфа. Отсюда следует, что А пере¬
становочен со всеми операторами ZL., Е0, Е+. Мы по-
прежнему будем называть оператор А оператором Кази¬
мира. Заметим, что
А = Е-Е+ + Е0{Е0 + 1) = £+£_ + Е0{Е0- 1)
в силу соотношений коммутации между операторами
Ео, Е+. Согласно первому из этих выражений мы имеем
= / (/ + 1) ёо-
Поскольку А коммутирует с Е_, мы, очевидно, имеем
также Agft =/(/+1)£й для каждого k = 0, 1, 2, ..., пг.
Следовательно, А является скалярным оператором на
всем пространстве V. (Это следует также из леммы Шу¬
ра.) Согласно второму из указанных выражений мы
имеем
Е+Е- = А — £0 (£0 — 1),

1Б0
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
и это тождество дает нам способ для вычисления опера¬
тора Е+. Действительно, применяя обе части этого тож¬
дества к вектору lh~\, находим
Е+\>и = (А — Е0 (Е0 —
Отсюда, заменяя каждый оператор в правой части со¬
ответствующим собственным значением, находим после
несложных вычислений, что имеет место
Лемма 2. Оператор Е+ в базисе = Ek_\v k =
= 0,1,2, ..., m, выражается следующей формулой:
E+lk = {2l-k+\)k\k^.
Между числами I и пг существует соотношение ш = 21,
т. е. I является целым или полу целым. Число —I являет¬
ся минимальным собственным значением оператора Еи.
Для доказательства последнего утверждения доста¬
точно рассмотреть вектор г| = \т, на котором Д_ обра¬
щается в нуль. Если вектор г| имеет собственное значе¬
ние V относительно Е0, то, согласно указанным выше
формулам для оператора Д, мы имеем
/(/ +1) = /'(/'-1).
Подставляя значение /'= /— т, мы находим после не¬
сложных вычислений (учитывая, что m 0) равенство
т — 21. Отсюда следует также равенство I' = —I.
Следствие. Спектр оператора Е0 симметричен от¬
носительно начала координат. Пространство V имеет
размерность 21 + 1.
Для окончательной записи полученного результата
удобно вместо нумерации k = m, m — 1, ..., 0 использо¬
вать нумерацию р =—/, —/+ 1, ..., /. Для этого мы
полагаем у = I + k и вводим обозначение для базис¬
ного вектора с собственным значением р.
Теорема 2. Всякое неприводимое представление
алгебры su (2) в пространстве конечной размерности оп¬
ределяется однозначно, с точностью до эквивалентности,
числом I, полуцелым или целым. Существует базис Хц,
р = —/, —I +1, . . . , /, относительно которого операторы
Е-, Е0, Е+ задаются формулами
Е0Хц = Р-Гц,
£_х^ = (/ + p)x_i, Е+х^ = {1-у)х^+1.

§ 37. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ SU(2) [51
Здесь операторы Е0, Е+ являются указанными выше
комплексными линейными комбинациями базисных опе¬
раторов A j, Л2, Л3. В частности, Е0 = iA3, и, следователь¬
но, в данном базисе оператор А3 диагонализуется. Про¬
странство представления имеет размерность 21 + 1.
Каждый из операторов А\, А2, А3 диагонализуется в не¬
котором базисе.
Доказательство. Формула Еах^ = рх^ следует
из определения вектора хц. Формула Е^х11 = (1+ц)л:д„1
равносильна нормировке базисного вектора хпри этом
автоматически учитывается условие E~X-i = 0. Формула
для Е+ легко вычисляется отсюда с помощью леммы 2.
Не представляет труда проверить, что полученное
представление действительно неприводимо. В самом
деле, если хФО — произвольный вектор в пространстве
представления, то, применяя к нему достаточно высокую
степень повышающего оператора Е+, получаем, с точ¬
ностью до множителя, базисный вектор xt. Применяя те¬
перь понижающий оператор Е-, получаем все остальные
базисные векторы хц, р = —I, —I + ], ..., I. Следова¬
тельно, циклическая оболочка SPx относительно алгебры
SP, порожденной Е0, Е+, совпадает со всем простран¬
ством V. Но это и означает, согласно правилу циклич¬
ности, неприводимость V.
Наконец, последнее замечание относительно диагона-
лизации операторов Аи А2, А3 вытекает непосредственно
из симметричности коммутационных соотношений по от¬
ношению к циклической перестановке таких операторов.
Теорема доказана.
Каждое собственное значение оператора Е0 принято
называть весом данного представления. Максимальный
вес I называется обычно старшим весом, а соответствую¬
щий базисный вектор Х[ — старшим вектором. (Аналогич¬
но вводятся понятия младшего веса и младшего вектора
представления — заменой I на —I.) Неприводимое пред¬
ставление со старшим весом I мы условимся обозначать
символом d(l).
Выясним теперь вопрос о возможности перехода к
группе SU(2). Поскольку каждое неприводимое пред¬
ставление этой группы реализуется в классе тензоров,
то естественно попробовать для каждого старшего веса I

162
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
отыскать соответствующее представление в классе тен¬
зоров. Исходя из нумерации т = 21, естественно иссле¬
довать в первую очередь симметрические тензоры. Дей¬
ствительно, симметрические тензоры ранга т над дву¬
мерным пространством имеют размерность т + 1 =
= 21 + 1.
Вместо симметрических тензоров tl дг--1т удоб¬
но рассматривать соответствующие полиномы
f(x) = tli‘2 tmxilXi2 . . . xifn, где индексы iu i2, . . . , im
пробегают значения 1, 2. Вводя обозначения х, у вместо
х,, х2 и располагая эти координаты в виде строки, при¬
ходим к рассмотрению следующих преобразований:
Действительно, указанная операция под знаком поли¬
нома равносильна умножению строки (х, у) справа на
матрицу
При этом f(x,y)—произвольный однородный полином
степени т, т. е. линейная комбинация одночленов
хт, хт~1у, . . . , ут. Используя свойство однородности, мы
можем положить / (х, у) = ymf (z), где положено z = х/у
и f(z) = f(z, 1). После несложного пересчета получаем
следующую формулу в классе функций f(z):
Здесь мы по-прежнему используем символ Tg для нового
закона преобразований в классе полиномов /(г). Очевид¬
но, /(г) является полиномом степени не выше т, т. е.
линейной комбинацией одночленов 1, г, г2, . . . , zm. Сле¬
довательно, пространство представления имеет размер¬
ность т + 1.
Теорема 3. Всякое неприводимое представление
группы SU (2) определяется однозначно с точностью до
эквивалентности числом I, полуцелым или целым. Это
представление может быть реализовано формулой (*)
Tgf(x, y) = f (ах + уу, р* + 6у).
(*)

§ 37. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ SU(2) 153
в классе однородных полиномов степени m = 21 либо
формулой (**) в классе полиномов f(z) степени *Ст.
Соответственно данное представление реализуется также
в классе ковариантных симметрических тензоров ран¬
га пг.
Доказательство. Найдем дифференциал пред¬
ставления (*). Строго говоря, мы должны построить в
SU(2) систему трех однопараметрических подгрупп с ка¬
сательными векторами ai, а2, аг и вычислить затем соот¬
ветствующие инфинитезимальные операторы Дь А2, А3
в пространстве представления (*). Однако удобнее вме¬
сто этого непосредственно отыскивать операторы Д_, До.
Е+. Для этого достаточно заметить, что формула (-?-)
задает представление не только группы SU(2), но так¬
же группы SL(2), которая является ее комплексной
оболочкой*). Очевидно, комплексные линейные комби¬
нации Д_, До, Д+ являются инфинитезимальными опера¬
торами по отношению к SL(2). При этом существенно
отметить, что формулы (*) задаются комплексно-ана¬
литическими функциями от параметров SL(2). Следова¬
тельно, при вычислении инфинитезимальных операторов
мы можем рассматривать однопараметрические подгруп¬
пы с комплексным аддитивным параметром. Положим
1 1
е-Ц2 о
1 0
g- (0 =
о 1 |г
£о(0 =
0 е-,/2
> g+ (0 =
t 1
где t—аддитивный параметр (комплексный или вещест¬
венный). Тогда мы получаем систему трех однопарамет¬
рических подгрупп с касательными векторами
е_
О
-72
о
о
‘/2
=
Непосредственной проверкой убеждаемся, что эти эле¬
менты удовлетворяют коммутационным соотношениям
[е0, е+]
-+>
[е0, еА\ = —е_., [е+, е_] = 2е0- Нетрудно так¬
же видеть, что е0 = ш3, е± — i(a\ ± ia2), где а\, а2, а3—
касательные векторы для SU(2). Переходя к операто¬
рам представления, положим Д± (t) = Tg ± т, Fo(t) = Те„у).
*) Определение комплексной оболочки см. в § 13.

154
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
В результате имеем
F-(t)f{x, y) = f{x, tx + y), F+ (t) f (x, y) = f(x + ty, y),
F0(t)f(x, y) = f(e-wX, e^y).
Производя дифференцирование по ( и полагая t = О, по¬
лучаем следующую систему инфинитезимальных опера¬
торов Ео, Е+:
с & г, 1 I д д \ п д
Е~~х д у • Е° ~ 2 \У ду Х ~дх) ’ Е+ ~ У ~дх '
Вычислим закон преобразования для элементов базиса
х^ = xl~v-yl+]i, р, = —I, —/+ 1, .. ., I. Имеем
F—Хр (I "Ь р) x^—i, Е_^х^ — (I р) •Vp.+ii
FqX)i = Р-^р,-
Следовательно, мы получаем те же основные формулы,
что и в теореме 2. Это означает, что для каждого пред¬
ставления d(l) алгебры su(2) найдено соответствующее
представление группы SU(2) (имеющее d(l) своим диф¬
ференциалом). Это означает также, что группа SU(2)
не имеет более (с точностью до эквивалентности) ника¬
ких иных неприводимых представлении. Действительно,
группа SU(2) является связной и всякое ее представле¬
ние определяется, с точностью до эквивалентности, сво¬
им дифференциалом.
Теорема доказана.
Неприводимое представление группы SU(2) со стар¬
шим весом / = т/2 мы условимся обозначать символом
dm. В результате получена полная классификация не¬
приводимых представлений этой группы.
Указанное выше построение является классическим
образцом применения инфинитезимальиого метода. От¬
метим несколько добавочных возможностей, заложенных
в этом построении.
Замечание 1. Пусть пространство V конечномер¬
но, но не обязательно неприводимо. Применяя указан¬
ный процесс построения, мы можем начать с рассмотре¬
ния старшего вектора | (Д+| = О, Я0Е = ^Е) и построить
шаг за шагом цепочки вида Ек-%, Ек-Х, ..., отвечаю¬
щие старшим весам Нетрудно видеть, что та¬

§ 37. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ SU(2) 155
ким путем удается построить базис в пространстве пред¬
ставления. Но это означает, что V вполне приводимо.
Таким путем мы получаем алгебраическое доказатель¬
ство принципа полной приводимости (для SU(2)).
Замечание 2. Если бы мы с самого начала использовали со¬
ответствие между представлениями su(2) и SU(2), то доказатель¬
ство теоремы 2 можно было бы несколько упростить. Действительно,
рассмотрим в SU(2) подгруппу диагональных матриц
e-iq) О I
V~ 0 еЧ|'
Соответствующее семейство операторов Т у унитарно и коммутативно;
следовательно, существует базис, в котором операторы Ту диагонали-
зуются. Но это приводит сразу к заключению о диагонализации опе¬
ратора £0, который является инфинитезимальным оператором однопа¬
раметрической группы Ту.
Далее, всякое собственное значение оператора Ту имеет вид
e‘nq), где п — целое число. Сравнивая с определением оператора Е0,
данным при доказательстве теоремы 3, заключаем, что собственные
значения Е0 могут быть только целыми или полуцелыми. Наконец,
полагая
О -1
S~ I 0 ’
замечаем, что преобразование sys-1 = Y’1 сводится к перестановке
собственных значений матрицы у. т- е. к замене ф на —ф. В то же
время TsTyT — Ту1, откуда легко заключить, что оператор Ts
переводит каждый собственный вектор Ту с собственным значением.
em(f в новый собственный вектор с собственным значением e_m<f
Отсюда следует симметрия в классе собственных значений опера¬
тора £о-
Замечание 3. Нетрудно видеть, что sgs~l = g'~l
для каждого g^SL(2). Отсюда следует, что всякое
представление SL(2) эквивалентно своему контрагре-
диентному. (Отсюда ясно также, почему все неприводи¬
мые представления SU(2) удалось реализовать в классе
только ковариантных тензоров.) Элемент s мы будем
иногда называть элементом Вейля.
Замечание 4. Отбросим условие конечномерности, но по¬
требуем взамен выполнения следующих двух условий: 1) существо¬
вания старшего вектора : £+£о = 0, £о?о = /|о; 2) цикличности
этого вектора по отношению к алгебре !Р, порожденной оператора¬
ми £ , £0, £+. Повторяя почти без изменения предыдущие

156
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
построения, получаем существование весового базиса |й = Ек__ |0,
k = 0, 1, 2, по отношению к которому операторы представления
имеют следующий вид:
E+\k = W-k+\)klk_v
Последняя формула аналогична указанной в лемме 2. Однако стар¬
ший вес / может быть теперь произвольным комплексным. Получен¬
ное представление неприводимо всегда, за исключением случая
21 = т при некотором целом неотрицательном т. Действительно, в
этом случае мы имеем
£-Лп-Н=0'
Следовательно, вектор £m+i снова является старшим по отношению
к Е+. Его циклическая оболочка V0 является инвариантным подпро¬
странством в пространстве V. Нетрудно видеть, что Va неприводимо.
В то же время фактор-пространство V/V0 конечномерно и в нем
действует уже известное нам конечномерное представление d(l).
В результате мы можем заключить, что алгебра su(2) допу¬
скает бесконечномерные неприводимые представления (которые, од¬
нако, не могут быть продолжены до представлений группы SU(2)).
Замечание 5. Неприводимое представление dm
группы SU(2) является симметризованной частью тен¬
зорного произведения d®m, где d = dl — двумерное пред¬
ставление (исходное представление Sll(2)) и <S>m озна¬
чает m-ю тензорную степень. В представлении d = dl
роль базисных векторов играют линейные функции х, у,
введенные выше. Если рассматривать х, у как неком¬
мутативные символы, то базисный вектор хп, построен¬
ный при доказательстве теоремы 3, возникает при
симметризации одночленов вида х, х. ... х. , х, = х, у,
1\ 12 1т 1
где л: встречается I — р раз и у встречается I + р раз.
Введем в пространство тензоров ранга т обычное ска¬
лярное произведение, при котором все одночлены
x.xt .. . xt взаимно ортогональны и имеют единичную
норму. Отсюда следует, что
(UJ|2 = c0(/-p)!(/ + p)!,
где Со — константа, не зависящая от р. Действительно,
(/—р)! (/ + р)! есть число одночленов указанного вида
и в то же время скалярный квадрат суммы таких одно¬
членов. В силу вышесказанного вектор х^ отличается

§ 38. МАТРИЧНЫЕ ЭЛЕМЕНТЫ ГРУППЫ SU(2)
157
лишь множителем с0 = 1/т! от этой суммы. Следова¬
тельно, если положим
то мы получим ортонормированный базис в простран¬
стве представления. Легко проверить, что
В реализации (-»*) следует заменить хц на одночлен
z1-^, р = —/, —/ + 1Операторы группы SU (2)
являются, очевидно, унитарными относительно выбран¬
ного базиса. Операторы АиА2,А3 антиэрмитовы, опера¬
торы £_, Е+ взаимно сопряжены, и оператор Е0 само¬
сопряжен.
На примере группы SU(2) в значительной степени
намечаются черты более общей теории*).
§ 38. Матричные элементы группы SU(2)
Для дальнейшего изучения неприводимых предста¬
влений группы SU(2) нам будет удобно записывать эти
представления с помощью дробно-линейной подстановки:
Здесь г — произвольное комплексное число, и подпро¬
странство 9?г, в котором действует представление dm,
I = m/2, натянуто на базисные векторы
Напомним, что I — полуцелое или целое число, т. е.
m = 21 является целым. При помощи указанной форму¬
лы нетрудно вычислить матричные элементы предста¬
вления dm. Действительно, матричные элементы t^v {§)
*) Главы VII, X, XVI, XVII.
Е-е» = VU + Р) (/ - Р + 1) <?ц-ь
Е+е» = /(/ - р) (/ + р - 1) е^+и
Ефр,
2^ = Zl~'i, [1= -I, -/+ 1, ..., /.

158
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
определяются следующей формулой:
Tgzv = (§)*»■
Следовательно, t^v (g) есть коэффициент полинома Tgzv
при степени z|i = zz-M'. Указанный коэффициент вычис¬
ляется с помощью обычной формулы Тейлора:
W + 6)'"(аг + vT’U-
Действительно, выражение в квадратной скобке есть
развернутая запись для полинома Tgzv. Полагая и =
= fiz + б, v = az + у, замечаем, что а и — ри = 1. Сле¬
довательно, если вместо переменной 2 ввести перемен¬
ную t = аи, то рv = t— 1, и после подстановок и = ~ t,
v = ——f), получаем следующий ре¬
зультат:
^(g) =10^a~"~V^+V{^[tl+V(1 ~
Действительно, t = ад при 2 = 0. Введем обозначение
Полиномы P(iv(0 отличаются лишь несущественными
множителями от хорошо известных полиномов Якоби.
В результате получаем
T4V (s) = (/ _ ^ t a P P\xv M).
До сих пор мы нигде не использовали унитарность ма¬
трицы g. Следовательно, полученный результат спра¬
ведлив для SL(2) (и даже для GL(2)). Предполагая
теперь унитарность (g*g = е) и унимодулярность
(det^=l), получаем следующую систему соотношений
на параметры матрицы g:
6 = а, у=-р, I a I2 + I Р Р = 1 •

§ 38. МАТРИЧНЫЕ ЭЛЕМЕНТЫ ГРУППЫ SU(2) 159
Следовательно, geSU(2) вполне определяется элемен¬
тами а, р, расположенными в первой строке, для кото¬
рых |а|2+|р|2 = 1 *). Мы положим | а |2 = /, argct =
= — Y (ф + Ф)> argP = у (ф ~ Ф)- В результате получаем
в SU(2) систему независимых параметров t, ф, ф, для ко¬
торых —2я^ф<2л;, 0^ф<2л**). В этих
параметрах имеем
<v (8) = е' М+ itl+V) (1 - t)~* (t).
Мы теперь имеем право рассматривать t под знаком
полинома Ply,v(t) как независимый параметр в нашей
группе (£ = 1<х|2 = а6). В результате получена следую¬
щая
Теорема 4. Матричные элементы т^(^) выра¬
жаются указанной выше формулой через полиномы
Якоби. Эти элементы нормированы условием т1 v(e) = 6vli.
Полагая
ai (g\ _ -if {I + й)1 б — йН i /g\
у (/ + v) ! (/ — v)!
получаем систему элементов, которые имеют одинако¬
вую норму в L2(G) при фиксированном старшем весе I:
| KMfdg= -~-х.
Последнее утверждение вытекает из замечания 5 в
конце предыдущего параграфа (переход к унитарному
базису в пространстве представления) и выражения для
нормы п~'12, л = 2/+1, даваемого глобальной теоремой.
Замечание 1. Мера Хаара в условиях теоремы 4
нормирована так, что мера всей группы SU(2) равна
единице. В параметрах t, ф, ф эта мера, как легко
*) Отсюда следует, что группа SU(2) как многообразие изо¬
морфна сфере 53 в четырехмерном евклидовом пространстве.
**) Нетрудно проверить, что указанное ограничение на пара¬
метры ф, ф равносильно условию —п ^ arg a, arg р < я. При / = О
и t = 1 параметры ф, ф определяются неоднозначно.

160
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
проверить, имеет следующий вид:
dg = -8\?dt dydty.
Замечание 2. Общая формула для (g) хороша
своей общностью и компактностью записи. Однако при
малых / = 0, ’/г, 1, . . . для нахождения матричных эле¬
ментов несравненно проще непосредственно вычислять
разложение полинома Tgzv по базисным элементам
Например, при / = 1 таким путем легко по¬
лучаем
а2
ар
р2
Т1 (g) =
2ау
аб + Ру
2ру
у2
уб
б2
Столбцы этой матрицы являются коэффициентами при
z2, z, 1 в разложении по степеням г полиномов (az + у)2,
(az + у) (рг + 6), (рг + б)2. Аналогично при / = 3/2 по¬
лучаем
а2р ар2 р3
а26 + 2а Ру 2арб + р2у Зр26
2ауб + Ру2 аб2 + 2руб Зрб2
у26 уб2 б3
Отсюда легко получить выражения матричных элементов
т Hg) =
а6
За2у
Зау2
■ (g)
через параметры t, ф, ф. Элементы
перенормировкой.
Замечание 3. Рассматривая матрицу s0 —
и вычисляя
получаются
0
1
1 0
ТSa на базисных элементах, легко находим
v(iV
(So) = <v(So) = V
uv означает символ Кронекера. Отсюда вытекают
где б
соотношения симметрии, которые имеют одинаковый вид
для матриц r'(g), o'(g). В частности, если условимся
записывать т'(а, р, у, 6) вместо xl(g), то мы найдем
(Y, Р) = v (а, р, у, б),
(Р, а, 6, у) = т?
v (а> P. Y. 6).

§ 38 МАТРИЧНЫЕ ЭЛЕМЕНТЫ ГРУППЫ SU(2) 161
Указанные равенства выражают в параметрах сс, р, у, 6
следующие соотношения: г1 {s0g) = xl (s0) xl (g), т1 (gs0) =
= х1 (g) г1 (s0). Аналогично, если вместо матрицы So
II - 1 О I
рассмотрим матрицу а = j , то получим
^v(a> “Р> Y. -6) = (-l)'~VT|iV(a, р, у, б).
Комбинируя полученные соотношения, можно выписать
еще другие свойства симметрии для матричных элемен¬
тов r^ig). Кроме того, представляет интерес рассмотре¬
ние элемента Вейля s = as0, для которого, как мы знаем,
sgs~x = g'~x. Вычисляя матрицу T;(g'-1), с одной сто¬
роны, как T'(g)'-1 и, с другой стороны, как
T;(s)T'(g)T;(s)_I, находим
^v(6> ~Р> -Y, «) = ( — l)tx+V'rLv, -ц(«> P. Y. б).
До сих пор мы не учитывали унитарности матрицы g.
Если g унитарна, то g'~l — g, где черта означает ком¬
плексное сопряжение. Следовательно,
^v(a, р, у, 5) = (-lf+VT'_v _д(а, р, у, д).
Если заметить, что t^v(g) = (g) (это очевидно из рас¬
смотрения тензоров), то последнее равенство можно за¬
писать также в следующей форме:
(§) = (-if+v<^Vi)-
Отсюда для geSU(2) получаем еще одну дифферен¬
циальную формулу*):
TBv(g) = TV^rQim+v<f)^ ("+V)(I д -At)-
Выясним теперь связь полученных функций с пред¬
ставлениями группы вращений SO(3). Заметим, что вве¬
денная нами параметризация группы SU(2) равносильна
*) Заметим, что Pl_^ _v (/) = -^г+— [tl~v (1 - f)'+v].

162
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
следующему разложению:
A(ip)go(0) А(ф),
где Л(ф) означает диагональную матрицу с собствен¬
ными значениями e-i(p/2, ei(p/2 и g0(6) означает матрицу
вида
Используя правило соответствия между SU(2), SO(3)
(§ 11), легко проверяем, что ф, 0, <р являются обычными
углами Эйлера. Условившись записывать трехмерные
векторы в виде строк, мы получаем преобразования
ge SO(3) в виде ig, где £— трехмерный вектор. По¬
лагая
мы можем, в частности, рассматривать сферу S: |2 = 1.
Как мы видели в § 17, эта сфера отождествляется с
фактор-пространством G/H, где G = SO (3) и Н — под¬
группа поворотов вокруг оси е3 = (0, 0, 1). Для перехода
от G к G/H достаточно положить ф = 0. Согласно тео¬
реме 2 гл. IV мы получаем следующий результат:
Следствие. Функции Y^ (g) можно рассма¬
тривать как функции на сфере S в трехмерном евклидо¬
вом пространстве. Эти функции образуют полную орто¬
гональную систему в гильбертовом пространстве L2(S).
Действительно, матричный элемент o^v(g) не зави¬
сит от параметра ф только при ц = 0. Заметим, что мера
Хаара dg может быть записана в виде
где do) = sin 0 rf0 rf<p — обычная (инвариантная) мера на
сфере S. Пространство L2(S) определяется по отноше¬
нию к этой мере. При этом согласно теореме 4 мы имеем
0 . 0
COS-s- Sin у
Ые) =
V2 0
/2= COS у,

§ 38. МАТРИЧНЫЕ ЭЛЕМЕНТЫ ГРУППЫ SU(2)
163
Этим однозначно, с точностью до множителя, по модулю
равного единице, определяется нормировка функций Y
Нетрудно видеть, что функции являются обычными
сферическими функциями.
Функции также бывают полезны при изуче¬
нии векторных полей на сфере S ([1], [71]). Эти функции
называются шаровыми функциями на S.
В заключение этого параграфа покажем, как при помощи тео¬
рии представлений можно непосредственно построить теорию сфе¬
рических функций на сфере S. Пусть Е — трехмерное вещественное
2 2 2 2
евклидово пространство с метрикой х = х1 + х2 + х3. Положим
G = SO(3,R) и рассмотрим представление
Tgf (x) = f(xg)
группы G в пространстве полиномов f(x) = f(xu х2, х3). Здесь, как
и выше, вектор х= (xt, х2, *з) записывается в виде строки и умно¬
жение xg означает умножение строки х на матрицу g. Выбирая в
группе G однопараметрические подгруппы, соответствующие враще¬
ниям вокруг осей Oxi, Ох2, Ох3, находим соответствующие инфини-
тезимальные операторы представления Те:
. !д д . д д . д д
А' = х*д^~х^' = А*“х'-дГл-х*Щ‘
Из этих операторов At, А2, А3 составим оператор Казимира:
>2-4
С = - А2, - А% - А%
который перестановочен со всеми операторами Аь А2, А3. Путем
несложных вычислений (учитывающих некоммутативность я,-, djdxt)
находим для этого оператора следующее выражение:
С = — х2 Л + L (L + 1).
/ д2 дг дг \
Здесь Л — оператор Лапласа — г Н у! и L означает
^ д4 дх23)
оператор Эйлера (xt —\-x2~S—|-х3 д—V символом х2 обозначен
\ иХ\ ОХ 2 ОХъ!
оператор умножения на х[ + х2 + х\. Покажем, как при помощи
оператора Казимира можно произвести спектральный анализ пред¬
ставления Tg.
Рассмотрим подпространство Pi всех однородных полиномов
степени I. Это пространство инвариантно относительно Те. Посколь¬
ку это подпространство конечномерно, то оно вполне приводимо
относительно Tg. На каждом неприводимом подпространстве опера¬
тор С, согласно лемме Шура, должен быть кратен единичному:
С — XI. С другой стороны, в силу однородности оператор Эйлера

164
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
тоже кратен единичному: L = II, где I — степень однородности. Сле¬
довательно,
Xf=~ х2 bf + l(l+\)f
для каждого вектора f, лежащего в неприводимом подпространстве.
Следовательно, каждый такой вектор f является собственным отно¬
сительно оператора х?Д.
В частности, пусть Hi — подпространство всех гармонических
полиномов степени однородности I. Если / е Ni, то Д/ = 0, и в этом
случае К = 1(1 + 1). Отсюда следует, что представление в Ht может
содержать неприводимые представления только со старшим весом I.
Поскольку, как легко проверить, dim Я; = 2/4-1, то Hi в действи¬
тельности неприводимо.
Замечание 4. Мы показали, что всякое неприводимое пред¬
ставление группы SU(2) с целым старшим весом 1 — 0, 1, 2, ... мо¬
жет быть реализовано в классе гармонических полиномов f(x) =
= /(*,, х2, Хз).
Далее, в пространстве Pi существуют подпространства вида
x2Hi-2, х4Я;_4, ... Нетрудно проверить, что все они по-прежнему не¬
приводимы и содержат старшие веса I — 2, / — 4, ... Из сравнения
размерностей получаем следующее тождество:
Pt — Hi + x2Ht-t + x1Hi-.t + ...
Это означает, что всякий однородный полином f е Pt разлагается
по гармоническим полиномам с коэффициентами, зависящими от х2.
Полагая х2 = I, заключаем, что всякий полином f(x) разлагается на
сфере S по гармоническим полиномам. Значение гармонического по¬
линома на сфере 5 называется сферической функцией.
Мы получили теорему полноты для сферических функций в
классе полиномов на 5. Отсюда обычным образом следует теорема
полноты в классе непрерывных функций на S, а также теорема пол¬
ноты в классе L2(S).
§ 39. О некоторых группах, связанных с SU(2)
Здесь имеются в виду следующие группы: SO(3),
SO (4), SL(2), U (2), GL(2). Все эти группы, за исклю¬
чением U (2), могут определяться как над комплексным,
так и над вещественным полем. Мы покажем, что суще¬
ствует определенное соответствие между представления¬
ми всех этих групп и группы SU(2).
I. SO(3, /?). Поскольку SU(2) является двукратным
накрытием SO(3, R) с ядром из матриц е, —е, то всякое
представление SO(3, R) можно также рассматривать
как представление SU(2), удовлетворяющее условию
четности: Т= Те. В этом случае также
Т =Т
~~ 1 s

§ 39. О НЕКОТОРЫХ ГРУППАХ. СВЯЗАННЫХ С SU(2) 165
для всякого geSU(2). Обратно, если представление Tg
удовлетворяет условию четности, то его можно рассма¬
тривать как однозначное представление SO(3, /?). Для
неприводимых представлений dm условие четности рав¬
носильно четности т, т. е. целочисленности I = т/2.
В предыдущем параграфе мы видели, что все такие
представления могут быть реализованы в классе гармо¬
нических полиномов (или, что то же самое, в классе сфе¬
рических функций) в трехмерном евклидовом простран¬
стве.
Если представление группы SU(2) не удовлетворяет
условию четности, то его по-прежнему можно рассма¬
тривать как «двузначное представление» S0(3,/?) . В ча¬
стности, двумерное представление SU(2) (I = 1f2) отно¬
сится к числу таких представлений. Это представление
обычно называется спинорным.
2. SL(2, С). Как мы видели при построении неприво¬
димых представлений SU(2), всякое такое представле¬
ние может быть продолжено до представления
TJ (г) = (pz + б Г ! (ЦД), е= SL (2, С),
операторы которого являются комплексно-аналитиче¬
скими функциями от параметров в SL(2, С). Заметим
теперь, что в группе SL(2, С) существует комплексное
сопряжение g-*g- (В SU(2) такая операция сводится
к g'~1-) Поскольку комплексное сопряжение является
автоморфизмом, то операторы TR = Tg по-прежнему
определяют представление группы G. Иначе говоря, мы
получаем новую серию неприводимых представлений:
Здесь по-прежнему мы пишем символ f(z), однако те¬
перь этот символ означает полином от комплексно со¬
пряженной переменной z. Операторная функция Tg яв¬
ляется теперь антианалитической и поэтому не может
быть эквивалентна ни одному из представлений dm (за
Исключением тривиального случая пг = 0). Полученное
представление обозначим символом dm. Обе серии

166
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫИ МЕТОД
представлений включаются в следующую общую серию:
ту (г) = (Pz + 6Г (^Тб)т' f '
В этом случае пространство представления зависит от
двух чисел т, tn' и определяется как множество всех
полиномов степени не выше т по г, не выше т' по I.
Обозначим это представление dmdm . Как следует из дан¬
ного определения, такое представление совпадает в то
же время с теазорным произведением dm ® dm.
Покажем, что такое представление в действитель¬
ности неприводимо. Для доказательства нам будет удоб¬
но воспользоваться формальными дифференциальными
операторами
_д_ _ J_ f_d_ __ . _д_\ _д_ _ J_ (_д_ , . _д_
дг 2 \ дх 1 ду ) ’ дг 2 \ дх 1 ду
Как известно, в классе полиномов (и даже в классе сте¬
пенных рядов) эти операторы действуют как обычные
частные дифференцирования по формально независи¬
мым переменным г, ъ. Нетрудно видеть, что операторы
д д ,
-^содержатся среди инфинитезимальных операто¬
ров группы SL(2, С). Действительно, полагая
1 ° II
t 1 II
+ (0=
с комплексным параметром t, мы получим две вещест¬
венные однопараметрические подгруппы при Im t = О,
Re t — 0. Операторы ■—, являются инфинитези-
мальными операторами этих подгрупп. Следовательно,
если © — класс комплексных линейных комбинаций
инфинитезимальных операторов dmdm , то -Jj , -jj е D.
Далее, полагая
1 t

I 39. О НЕКОТОРЫХ ГРУППАХ. СВЯЗАННЫХ С SU(3) 16?
мы получим следующее семейство операторов представ¬
ления:
F. (/) f (z) = (1 + tz)m (1 + Щт' f (-j^).
Если нас интересуют элементы класса Ф, то мы можем
непосредственно производить дифференцирование по
t, t, полагая затем t = 0. В результате получаем следую¬
щие два оператора:
п д р г — — д
E_ = mz — z-^—, E-^mz — z-^.
dz ’ dz
Вернемся теперь к поставленной выше задаче. Пусть
f(z) Ф0— произвольный полином из пространства пред¬
ставления. Применяя к нему нужное число раз опера-
д д
торы -gj-, получаем константу, отличную от нуля.
Следовательно, функция f0(z)=l содержится в цикли¬
ческой оболочке f(z). Далее, применяя к этой функции
нужное число раз операторы £_, £_, получаем все базис¬
ные одночлены zkzk', 0 0 Следова¬
тельно, dmdm неприводимо.
Замечание 1. Существенно отметить, что предста¬
вления dm ® dm , dm ® dm , как правило, приводимы. На¬
пример, d1 ® d1 означает преобразование в классе тен¬
зоров второго ранга, откуда легко получить, что
d1 ® d1 = d2 + d° (симметричные и антисимметричные
тензоры)*). _
Замечание 2. Представление dm, суженное на
подгруппу SU(2), совпадает с (dm)A (контрагредиент-
ное представление); но это представление, как мы знаем,
эквивалентно dm. Следовательно, сужение dm ® dm на
*) Индуктивно применяя указанную выше формулу, нетрудно
также получить следующий общий результат:
ll + li
d(/,)®d(/2)= 2
I U-h I
Более подробно о тензорных произведениях будет сказано в гл. XII.

168
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
подгруппу SU(2) эквивалентно тензорному произведе¬
нию dm ® dm . Такое представление неприводимо только
при т = О либо при т' = 0.
Замечание 3. Представления dm®dm при
т'ф 0 характеризуют, в сущности, группу SL (2, С) как
вещественную группу Ли удвоенной размерности. В то
же время dm сохраняет комплексную структуру этой
группы. Дифференциал такого представления линеен
над комплексным полем: D(Xx)=XD(x). Дифференциал
dm антилинеен над комплексным полем: D (Кх) = XD (х).
Более подробно о классификации таких представлений
будет сказано в гл. VII.
В гл. VII мы увидим, что серия dmdm исчерпывает
все (с точностью до эквивалентности) неприводимые
представления SL(2, С).
3. Группа Лоренца. Пусть L — связная компо¬
нента единицы в группе всех псевдоевклидовых враще¬
ний, сохраняющих форму — х% + х? + х\ + х% (координаты
Х{ вещественны). Как мы видели в § 11, L « SL(2, С)//V,
где N состоит из матриц вида е, — е. Представление
dmdm является однозначным представлением группы
Лоренца L тогда и только тогда, когда число m + т'
является четным.
4. SL(2, /?). Алгебра Ли этой группы имеет базис е_,
е0, е+ с соотношениями коммутации [е0, е+] = е+, [е0, е_] =
= —в-, [е+, е_] = 2е0. Следовательно, в данном случае
можно непосредственно использовать алгебраический
результат теоремы 2. Формула
Tgf(z) = (fr + 6)mf(lg±±),
где а, р, у. 6. г вещественны и {(г) —полином от г сте¬
пени не выше т, определяет все неприводимые представ¬
ления SL(2, R) с точностью до эквивалентности.
5. U(2). Как мы видели в § 9, U(2) « U(l) <8>SU(2).
Проекция на U(l) определяется отображением g -^-detg.
Поскольку операторы из U(l) перестановочны со всеми
операторами U(2), то они являются скалярами (соглас¬
но лемме Шура) в любом неприводимом представлении

§ 39. О НЕКОТОРЫХ ГРУППАХ. СВЯЗАННЫХ С SU(2) 169
U (2). Полагая detg = е,’ч>, замечаем, что указанное ска¬
лярное отображение должно с необходимостью иметь
вид ein4> = (detg)n, где п — целое число (это условие
вытекает из однородности представления). Формула
V(z) = (detgnp2 + 6rf(mj)
определяет общий вид неприводимого представления
группы U (2). Здесь т — неотрицательное целое число и
п — произвольное целое число. Если сделать п неце¬
лым, то соответствующая функция Tg станет неодно¬
значной.
6. GL(2, С). То же рассуждение можно повторить
и в данном случае. Поскольку det g = pe^, р > О,
то скалярный множитель в формуле для представ¬
ления может иметь вид (det g)n (det g)n > где разность
п— п' обязательно является целой. (Действительно,
/ j j \пТл 7 \п' п + п' i(n — n')($ \
(det g) (det g) =p e
Замечание 4, Отсюда очевидно существование не
вполне приводимых («полуприводимых») представлений
1 In р
GL(n). Примером является
О 1
где р = | det g \.
7. GL(2, R). Рассуждения остаются прежними. Если
ограничиться связной подгруппой G+, выделяемой усло¬
вием detg = p>0, то получаем всевозможные степени
(detg)\ где X — произвольное комплексное число. Если
же рассматривать всю группу G, то скалярный множи¬
тель в операторе представления может иметь либо вид
р\ либо рх sgn р, где р = det g ф 0. Соответственно полу¬
чаем две различные серии неприводимых представлений
группы G. Можно показать, что этими сериями исчер¬
пываются все неприводимые (конечномерные) представ¬
ления данной группы.
До сих пор мы рассматривали группу SO(3) только
над вещественным полем. Если поле становится ком¬
плексным, то все неприводимые представления SO(3,7?)
аналитически продолжаются на SO(3, С). Более под¬
робно процесс аналитического продолжения будет рас¬
смотрен в следующей главе.

170
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
§ 40. О некоторых проблемах инфинитезимального
метода
Желая исследовать структуру группы Ли или свой¬
ства ее линейных представлений при помощи инфините¬
зимального метода, мы должны постоянно иметь в виду
некоторые сложности, связанные с процессом «интегри¬
рования», т. е. с переходом от алгебры Ли к группе Ли.
Прежде всего, естественно возникают следующие во¬
просы:
Вопрос 1. Пусть G — группа Ли и X — ее алгебра
Ли. Верно ли, что всякому линейному представлению
алгебры X соответствует линейное представление груп¬
пы G (по отношению к которому данное представление
является дифференциалом) ?
Вопрос 2. Пусть G — группа Ли и X — ее алгебра
Ли. Верно ли, что всякой подалгебре Хйс^Х соответ¬
ствует замкнутая подгруппа G0cr G (имеющая Х0 своей
алгеброй Ли) ?
Ответ на первый вопрос является отрицательным,
даже если группа G является связной и представление
D(x) конечномерно. Действительно, операторная функ¬
ция Tg определяется посредством экспоненциального
отображения лишь на некоторой окрестности единицы
в группе G. Используя трансляции, можно продолжить
Tg и на всю группу G, но полученная функция Tg может
оказаться неоднозначной. (Пример: если G = {elx,
0^x<2jt}, то представление D(x) = Хх может быть
продолжено на группу G только при целом X.) Однако
если G односвязна, то функция Tg не может быть мно¬
гозначной. Действительно, в противном случае много¬
образие {Tg) накрывало бы группу G. Следовательно,
в этом случае первый вопрос решается положительно.
В дальнейшем мы для краткости условимся считать,
что термин «односвязность» включает в себя также и
предположение о связности. В частности, под термином
«односвязная группа» условимся понимать односвязную
связную группу.
Ответ на второй вопрос также является отрицатель¬
ным, как показывает иррациональная обмотка тора.
Действительно, пусть G — двумерный тор, порожденный

§ 40. О ПРОБЛЕМАХ МЕТОДА
171.
всеми унитарными диагональными матрицами второго
порядка. Положим
№ о. о I
eio ь |г
где отношение а/b иррационально и числа а, Ъ веще¬
ственны. Поскольку матрица е эрмитова, то матрица
ехр Не унитарна при всяком t, —оо <t< оо. Однопара¬
метрическая подгруппа
g(t) = ехр ite
является иррациональной обмоткой тора G (§ 15). Замы¬
кание этой подгруппы совпадает со всем тором G.
В этом случае одномерной подалгебре Х0 = {/е} не соот¬
ветствует замкнутая однопараметрическая подгруппа в
группе G.
В дальнейшем мы увидим тем не менее, что во мно¬
гих важных случаях ответ на второй вопрос все-таки
является положительным. Один из указанных частных
случаев описывается следующей теоремой:
Теорема 5. Пусть G — компактная группа Ли и
X — ее алгебра Ли. Тогда для всякой подалгебры A0c: X
с нулевым центром существует замкнутая подгруппа
G0 с G, для которой Х0 является алгеброй Ли.
Доказательство. Нам будет удобно использо¬
вать линейность группы G. Более того, согласно гло¬
бальной теореме можно считать, что GczO(n). По¬
скольку в условиях теоремы группа G играет роль объ¬
емлющей группы, мы можем также считать (хотя это и
не обязательно), что G = О(п). Все построения ведутся
над полем вещественных чисел. Алгебра X состоит в
этом случае из всех вещественных кососимметрических
матриц порядка п.
Пусть Х0 — фиксированная подалгебра в X. Мы по¬
лучим «первое приближение» к искомой группе G0, если
рассмотрим в О(п) подгруппу Gt, состоящую из всех
матриц gi, для которых = -^о *)• Согласно этому
определению группа Gx выделяется из О (п) некоторой
системой полиномиальных соотношений; как увидим
*) Эта группа называется нормализатором Х0.

172
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫЙ МЕТОД
в гл. XV (теорема 4), всякая такая группа является
группой Ли. Пусть X, — алгебра Ли группы G\. Тогда,
очевидно, Х0 а Хь
Нетрудно видеть, что билинейная форма (х, у) =
=—sp ху является скалярным произведением в обла¬
сти кососимметрических матриц (т. е. в алгебре Ли
О(п)). Пусть Y— ортогональное дополнение Х0 до Xi
относительно этого скалярного произведения. Заметим,
что
sp [х, y]z = sp [z, х]у.
В частности, если х, z е Х0 и у е Y, то мы заключаем,
что правая часть тождественно равна нулю (X0_LF).
Следовательно, вектор [х, у] одновременно содержится
в Х0 и ортогонален Х0- Следовательно, [х, у] = 0, и мы
заключаем, что элементы из Х0, Y взаимно перестано¬
вочны.
Далее, мы получим «второе приближение» к искомой
группе Gо, если рассмотрим в Gj подгруппу G2, состоя¬
щую из матриц g2, перестановочных с алгеброй Y '*):
g2yg~' = y для всякого у е Y. Рассуждая, как и
выше, заключаем, что G2 — группа Ли. Пусть Х2 — ее
алгебра Ли. Тогда, очевидно, X0azX2czXi. Пусть Z —
ортогональное дополнение Х0 до Х2.
Элементы множества Z перестановочны со всеми эле¬
ментами Х0 и в то же время со всеми элементами Y
(согласно определению G2). Следовательно, Z содер¬
жится в центре Х2. В то же время согласно условиям
теоремы центр подалгебры Х0 равен (0). Отсюда сле¬
дует, что Z является центром в Х2. В свою очередь Х0
может быть охарактеризована как фактор-алгебра X2/Z
либо как производная подалгебра в алгебре Х2.
Теперь естественно определить искомую группу G0
как производную подгруппу в группе G2. При этом груп¬
па Gо оказывается группой Ли с алгеброй Ли Х0. Тео¬
рема доказана.
Замечание. При доказательстве теоремы 5 мы считали оче¬
видным следующее утверждение: пусть Gi с G — две группы Ли
и Xi cz X — соответствующие алгебры Ли; тогда exp tx е G\ для
*) Эта группа называется централизатором Y.

§ 40. О ПРОБЛЕМАХ МЕТОДА
173
всякого х е Xi. Действительно, это утверждение доказывается в
общей теории групп Ли и составляет один из существенных момен¬
тов в соответствии между группами и алгебрами Ли. Приведем для
полноты изложения доказательство этого утверждения в линейном
случае G = GL(«).
Напомним, что алгебра -Yi определяется как касательное про¬
странство к многообразию Gi в точке е. Если g е Gb то gXi яв¬
ляется касательным пространством к многообразию Gj в точке g.
Иначе говоря, если |ь |2, ■ Е™— локальные параметры точки g
(достаточно близкой к е), то
т
i = 1
для всякого х е Хг, где функции ЫЕ. я) непрерывно зависят от
| = (!,■) и х е Xi. Заметим теперь, что однопараметрическая под¬
группа g(t)=exptx является решением дифференциального урав¬
нения
g'(t) = g(t)x, х^Хи
с начальным условием g(0) = е. Если функции E;=E;(0 опреде¬
лить как решения дифференциального уравнения (t) = ft (£ (t), х)
с начальным условием |г (0) =0, то функция g (t) = g (| (t)) будет
решением указанного выше уравнения (при достаточно малых t) с
начальным условием g (0) = е. В силу теоремы единственности
g (t) = g G)- Это показывает, что g(t) ей] при достаточно малых t.
Далее, пусть t0— точная верхняя грань тех I, для которых
g(t) е G1. Положим / (t) = g (ta + t). Тогда полученная функция
f(t) является решением дифференциального уравнения
r(t) = fV)x
с начальным условием / (0) = g (t0) е G[. Повторяя предыдущие
рассуждения, заключаем, что }(t) е G[ при достаточно малых t. Но
это противоречит определению to- Следовательно, g(t) е G, при
— оо < t < оо, и наше утверждение доказано.
Отсюда также легко получить, что если Хо — подалгебра в Х\
и Go — замкнутая связная подгруппа в G с алгеброй Ли Х0, то в
действительности Go cr Gi (это утверждение мы также считали оче¬
видным при доказательстве теоремы 5, полагая G = 0(n,R)).
В теории групп Ли доказывается следующая общая
теорема. Пусть G — группа Ли и X — ее алгебра Ли.
Тогда для каждой подалгебры X0czX существует ло¬
кально замкнутая подгруппа Go с: G, называемая анали¬
тической подгруппой. Таким образом, существует взаим¬
но однозначное соответствие между подалгебрами в ал¬
гебре Ли и аналитическими подгруппами в группе G.

174
ГЛ. V. ИНФИНИТЕЗИМАЛЬНЫИ МЕТОД
Если ограничиться некоторой достаточно малой
окрестностью единичной точки, то мы получаем мно¬
жество, называемое локальной группой Ли. Это множе¬
ство однозначно покрывается экспоненциальным отобра¬
жением, и в нем существует также взаимно однозначное
соответствие между подалгебрами Ли и локальными
подгруппами. Отметим еще один важный вопрос:
Вопрос 3. Пусть G — группа Ли и X — ее алгебра
Ли. Верно ли, что каждому разложению X =
= Х\ + Х2, где Х\, Х2— подалгебры, отвечает разложе¬
ние G = G\G2, где G\, G2 — соответствующие аналити¬
ческие подгруппы?
Если заменить группу G локальной группой Ли, то
ответ является положительным (см., например, [46],
т. III, стр. 180). Глобальное утверждение также имеет
место для некоторых частных случаев: а) группа G од¬
носвязна, G\ (или G2) инвариантно в G относительно
внутренних автоморфизмов; б) группа Gi является мак¬
симальной компактной подгруппой в G, и подгруппа G2
односвязна. См. по этому поводу, например, [108], [128].
Некоторые случаи таких разложений мы будем рассма¬
тривать далее (гл. XV). Там же будет рассмотрен при¬
мер разложения («разложения Гаусса»), когда множе¬
ство Gо = G\G2 не заполняет группы G, но всюду плот¬
но в G.
Хотя, как мы видим, ответ на последний вопрос яв¬
ляется отрицательным, существует несколько более сла¬
бая положительная формулировка. Напомним (§ 3), что
если группа G является связной, то всякая окрестность
единицы определяет в этой группе систему образующих.
Следовательно, если U — такая окрестность, то G яв¬
ляется объединением возрастающего семейства окрест¬
ностей Um, m = 0, 1, 2, ... Если U = U]U2, где Uи U2 —
локальные группы в G\, G2, то мы находим в результате,
что всякий элемент geG может быть представлен в
виде конечного произведения g\hig2h2 ... gmhm, где
gu S2> и hi, h2, ... e I/j.
В заключение вернемся к вопросу 1 в связи с теорией
бесконечномерных представлений. В этом случае проб¬
лема является еще более сложной, хотя бы потому, что
expD(x) не всегда существует. Более того, если даже

§ 40. О ПРОБЛЕМАХ МЕТОДА
175
представление Т8 определено, то оно не обязательно
аналитично. В частности, если g(t) = exp tx, то не обя¬
зательно Tg (f) = exp tD (x).
Каждый вектор £ e V, для которого вектор-функция 7g£ анали¬
тична, называется аналитическим. Если V—банахово пространство,
то множество всех аналитических векторов всюду плотно в V ([75],
[98], [100], [119]). В классе аналитических векторов соответствие
между представлением Tg и его дифференциалом взаимно одно¬
значно. В общем случае мы не можем даже утверждать, что из
неприводимости Tg следует неприводимость D(x) (и также что из
приводимости D(x) следует приводимость Tg). Действительно, воз¬
можно существование линейных многообразий, инвариантных отно¬
сительно D(x), замыкание которых не инвариантно относительно Tg
([98]).
Вместе с тем мы видим, что если ограничиться конеч¬
номерными представлениями и односвязными группами
Ли, то применение инфинитезимального метода не вызы¬
вает препятствий. Рассмотрение неодносвязной группы
также не вызывает особых сложностей ввиду наличия
универсальной накрывающей.
В первоначальных работах С. Ли рассматривались только ло¬
кальные группы Ли, причем, как правило, группы дифференцируе¬
мых преобразований в евклидовых пространствах. Глобальная тео¬
рия разработана значительно позже (см. по этому поводу, напри¬
мер, [38], [46], [128]). К локальным методам естественно приводит
рассмотрение многих вопросов классической и квантовой механики.
Как уже было сказано во введении к этой главе, мы рассматриваем
здесь лишь простейшие вопросы инфинитезимального метода.
Задача описания неприводимых представлений группы SU(2)
дает классический пример для иллюстрации инфинитезимального
метода. Глобальное решение этой задачи изложено в статье [84].
В этой же статье был предложен простой вывод формулы для мат¬
ричных элементов (теорема 4). По поводу иной методики см. также
значительно более подробное изложение в статье [71]. См. также
[18], [37], [66] и монографию [14], где дается значительно более об¬
щая теория специальных функций.

ГЛАВА VI
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
Идея аналитического продолжения, столь плодо¬
творная в общей теории функций комплексного пере¬
менного, играет принципиальную роль также и в общей
теории представлений. Этот метод в теорию представ¬
лений был впервые введен в работах Г. Вейля. В част¬
ности, он оказывается особенно эффективным при рас¬
смотрении компактной группы Ли и ее комплексной
оболочки.
Если G—компактная группа Ли ненулевой размер¬
ности, то ее комплексная оболочка всегда является не¬
компактной. Этот результат, который мы в дальнейшем
сумеем строго доказать, является следствием того про¬
стого замечания, что вместе с каждым «тригонометри¬
ческим поворотом» комплексная оболочка содержит
также и некоторый «гиперболический поворот». Следо¬
вательно, в наше рассмотрение включается существен¬
но новый класс некомпактных групп Ли, которые в
этой главе будут названы «надкомпактными».
Заметим, что метод аналитического продолжения
можно развивать локально и «в целом»; первый путь,
по существу, уже использовался нами при введении
«понижающих» и «повышающих» операторов для
SU(2). В этой главе мы изложим основы аналитиче¬
ского метода «в целом».
§ 41. Общий принцип аналитического продолжения
Метод аналитического продолжения состоит в про¬
должении операторной функции Tg (Tg — представление
группы G) на комплексные значения параметров группы,
т. е. на комплексную оболочку группы G. Разумеется,
при этом мы полагаем, что G — группа Ли и Tg — ee ве¬
щественно-аналитическое представление, которое за¬
дается локальными рядами Тейлора в окрестности каж¬
дой точки go е G. Прежде чем перейти к более точным

§ 41. ОБЩИЙ ПРИНЦИП АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ 177
определениям, мы рассмотрим следующие простые при¬
меры.
Пример 1. Комплексная плоскость с выколотой
точкой 0 является комплексной оболочкой группы чисел
е<ф. Всякое неприводимое представление einч> (п целое)
однозначно продолжается до представления г", где
z = ре»'Ф — произвольный элемент комплексной оболочки.
Пример 2. Та же комплексная плоскость является
комплексной оболочкой связной группы положительных
чисел р > 0. Всякое неприводимое представление рх
(к комплексное) продолжается до функции г1, которую
можно рассматривать как «многозначное представление»
комплексной оболочки. Эта функция однозначна только
при целом к.
Пример 3. Та же комплексная плоскость является
комплексной оболочкой несвязной группы всех веще¬
ственных чисел х ф 0. Существуют представления этой
группы, например sgn х, которые не продолжаются до
аналитических функций на комплексной оболочке. (Дей¬
ствительно, если аналитическая функция равна единице
при z — х > 0, то она тождественно равна единице.)
Анализ этих примеров показывает, что при форму¬
лировке метода аналитического продолжения прихо¬
дится соблюдать известные предосторожности. Прежде
всего, согласно примеру 3 естественно требовать, чтобы
различные связные листы исходной вещественной груп¬
пы G оставались изолированными друг от друга также
и в комплексной оболочке. (В противном случае локаль¬
ные ряды Тейлора, определенные на этих листах, могут
привести к различным аналитическим функциям.) В ре¬
зультате мы приходим к следующему определению:
Определение 1. Комплексную группу © мы бу¬
дем называть правильной комплексной оболочкой веще¬
ственной группы G, если © является комплексной обо¬
лочкой G и если в каждой связной компоненте © содер¬
жится лишь одна связная компонента группы G.
В частности, если © является связной, то и подгруппа
G согласно этому определению должна быть связной.
Таким' образом, группа комплексных чисел по умноже¬
нию является правильной комплексной оболочкой груп¬
пы положительных чисел по умножению, но это уже

178
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
неверно, если вместо последней группы рассматривать
группу всех вещественных чисел по умножению. Далее,
согласно примеру 2 естественно также обобщить само
понятие представления.
Определение 2. Пусть ® — комплексная группа
Ли. Операторная функция Tg будет называться аналити¬
ческим представлением группы @, если:
1) функция Tg является комплексно-аналитической
(возможно, многозначной) функцией на G;
2) для каждой пары значений Tgt, Tg, найдется та¬
кое значение Tglg2, что Tglg, = TglTg2-,
3) всякое значение Те обратимо, и одним из значе¬
ний Те является единичный оператор в пространстве
представления.
Аналогичное определение с заменой условия анали¬
тичности условием вещественной аналитичности (или
непрерывности) приводит также к понятию многознач¬
ного представления произвольной вещественной группы
Ли. Если представление Tg конечномерно, то условие
аналитичности функции Tg равносильно условию анали¬
тичности всех матричных элементов тa(g) (относительно
любого фиксированного базиса в пространстве представ¬
ления). Если представление бесконечномерно, то необ¬
ходимо указывать топологию в классе операторов, по
отношению к которой вводится понятие аналитичности.
Мы, однако, будем рассматривать, как правило, только
конечномерные представления.
Пример 4. Матричная функция
является аналитическим (счетнозначным) представле¬
нием мультипликативной группы комплексных чисел.
Прежде чем перейти к изложению общей теории, сде¬
лаем несколько простых замечаний.
Замечание 1. Поскольку аналитические функции
всегда являются комплекснознячными (за исключением
тривиального случая f(z)=l), то процесс аналитиче¬
ского продолжения может привести к окомплексиванию
пространства представления. Чтобы не заботиться об

s 41. ОБЩИИ ПРИНЦИП АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ 179
этом, мы условимся пространство V заранее предпола¬
гать комплексным. (Если исходное пространство V0 бы¬
ло вещественным, то всякий линейный оператор Л, и в
том числе Tg, переносится на V = V0 + iV0 по правилу
линейности: А(х + iy) = Ах + iAy.)
Замечание 2. Если комплексная группа @ являет¬
ся односвязной, то ее аналитическое представление Tg не
может быть многозначным. Это утверждение является
следствием известного принципа «монодромии» и может
быть легко доказано посредством «триангуляции» много¬
образия @. (Напомним, что согласно условию, принятому
в предыдущей главе, под термином «односвязность» под¬
разумевается также и связность.) Следовательно, в этом
случае аналитические представления группы @ являются
также ее представлениями в обычном смысле. Это заме¬
чание мы будем иногда использовать в дальнейшем.
Замечание 3. Пусть Tg — аналитическое предста¬
вление группы G и Tg — множество значений функции
Tg в точке g. Тогда очевидно, что множество Те является
группой. Согласно известным свойствам аналитических
функций все они не более чем счетнозначны. В частно¬
сти, Те является дискретной группой. Далее,
!Т\ _ rp ГГ\ ГГ\ rp
1 g ~~ 1 g1 e — 1 e1 g-1
т. e. множество Tg получается из группы Te путем умно¬
жения (слева или справа) на одно из значений Tg в
точке g. Следовательно, Те является инвариантной под¬
группой относительно отображения A—>TgATg\ Если
группа G является связной, то отсюда, как и в § 5,
легко получаем, что множество Те содержится в центре
представления Tg. Следовательно,
Т т —т Т
e g 1 g1 е
для каждой пары индивидуальных значений Те, Tg. Если
представление Tg неприводимо, то отсюда согласно лем¬
ме Шура следует скалярность операторов Те■ Заметим,
что в этом случае закон композиции в представлении Тй
может быть записан следующим образом:
TgiTg* ~ h (е) Tglg.,,
где к(е) — один из возможных скаляров, к которым

180
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
сводится оператор Те. Такие представления иногда
называют проективными. Множество (Я(е)} представляет
собой дискретную абелеву группу комплексных чисел.
В частности, если Tg конечнозначно, то множество {А(е)}
конечно и сводится к прямому произведению некоторого
числа циклических групп*).
Заметим также, что множество Те всегда определяет
степень многозначности данного представления (соглас¬
но формуле Tg = TgTe, отмеченной выше). В частности,
Tg однозначно тогда и только тогда, когда множество Те
состоит из оператора /.
После этих предварительных замечаний сформули¬
руем и докажем следующий общий результат:
Теорема 1. Пусть @ — правильная комплексная
оболочка вещественной группы G. Тогда всякое конечно¬
мерное представление группы G может быть продолжено
до аналитического (вообще говоря, многозначного) пред¬
ставления группы @.
Продолженное представление неприводимо, приво¬
димо или вполне приводимо тогда и только тогда, когда
соответствующим свойством обладает исходное предста¬
вление группы G.
Если группа @ односвязна, то продолженное предста¬
вление однозначно.
Доказательство. Пусть Tg — представление
группы G и тот же символ Tg означает аналитическое
продолжение этой функции иа комплексные значения
параметров в группе @. Существование такого продол¬
жения следует из вещественной аналитичности функции
Tg.. Прежде всего, локальный ряд Тейлора Текруе_ =
= exp t'Ei продолжается на некоторую окрестность
Ус® (параметры Р полагаются комплексными). Да¬
лее, поскольку степени окрестности U покрывают всю
группу @, то ясно, что функция Tg продолжается на всю
группу ©, т. е. ни одна из точек ge® не является осо¬
бой. Мультипликативное свойство функции Tg вытекает
из принципа сохранения алгебраических соотношений
(при аналитическом продолжении). Таким образом, пер¬
вая часть теоремы доказана.
*) См. упражнение 2 на стр. 140, а также [38], стр. 43.

§ 41. ОБЩИЙ ПРИНЦИП АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ 181
Далее заметим, что свойства приводимости и полной
приводимости могут быть выражены в терминах обра¬
щения в нуль некоторых матричных элементов Tij(g)
(при соответствующем выборе базиса). Если такой эле¬
мент обращается в нуль на @, то он, в частности, ра¬
вен нулю и на G. Обратно, в силу принципа единствен¬
ности аналитического продолжения, если этот элемент
равняется нулю на G, то он обращается в нуль также и
на всей группе @. Тем самым наше утверждение дока¬
зано для свойства приводимости и полной приводимости,
но тогда и для свойства неприводимости (как отрицания
приводимости).
Наконец, если @ односвязна, то согласно замеча¬
нию 2 («принцип монодромии») представление Тё дол¬
жно быть однозначным.
Теорема доказана.
Мы условимся называть теорему 1 общим принципом
аналитического продолжения. Разумеется, это название
условно, хотя бы потому, что в условиях теоремы 1 рас¬
сматриваются только конечномерные представления. Од¬
нако нетрудно обобщить эту теорему на случай, когда
представление Tg бесконечномерно и вещественно-ана-
литично. Отметим два очевидных следствия из этой тео¬
ремы:
Следствие 1. Существует взаимно однозначное
соответствие (определяемое сужением @->G) между не¬
приводимыми аналитическими представлениями группы @
и неприводимыми, вообще говоря, многозначными пред¬
ставлениями группы G.
Следствие 2. Спектральный анализ в классе
вполне приводимых представлений группы G равносилен
спектральному анализу в классе их аналитических про¬
должений.
В заключение заметим, что если группу ® рассмат¬
ривать как вещественную, то ее комплексно-аналитиче¬
ские представления далеко не исчерпывают всех веще¬
ственных представлений группы @.
Пример 5. Всякое неприводимое конечномерное
представление группы комплексных чисел по умножению
одномерно и задается формулой
f(z) = zpz\

182
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
где разность р— q является целой (условие однозначно¬
сти представления). Это представление аналитично толь¬
ко при q = 0.
Другие примеры мы видели в § 39 при рассмотрении
групп SL(2, С), GL(2, С). Более подробно о веществен¬
ных представлениях комплексной группы будет сказа¬
но в § 43.
Таким образом, мы видим, что аналитическое про¬
должение естественно приводит нас к изучению опреде¬
ленного класса многозначных представлений комплекс¬
ной группы ®.
Упражнение
Пусть g->Tg — неприводимое представление группы G в веще¬
ственном пространстве V и Те—линейное продолжение Tg на комп¬
лексное пространство V = V + iV. Показать, что представление Tg
либо неприводимо, либо распадается в прямую сумму двух неприво¬
димых представлений, комплексно сопряженных друг другу.
§ 42. Надкомпактные группы Ли.
«Унитарный трюк» Г. Вейля
Нам будет удобно использовать следующее опре¬
деление:
Определение 3. Правильная комплексная обо¬
лочка компактной группы Ли будет называться надком¬
пактной группой Ли.
Условимся рассматривать конечнозначные, но, вооб¬
ще говоря, бесконечномерные аналитические представле¬
ния надкомпактной группы Ли. Множество таких пред¬
ставлений обозначим символом К.
Теорема 2. Пусть К—совокупность всех конечно¬
значных аналитических представлений надкомпактной
группы Тогда всякое неприводимое представление
класса К неприводимо при сужении на вещественную
форму G с @. Всякое представление класса К вполне
приводимо. Всякое неприводимое представление клас¬
са К конечномерно.
Доказательство. Допустим вначале, что пред¬
ставление Tg однозначно. Пусть V0 — инвариантное
подпространство в пространстве представления V отно¬
сительно подгруппы G. Тогда для всякого линейного

§ 42. НАДКОМПАКТНЫЕ ГРУППЫ ЛИ
183
функционала /, равного нулю на V0, мы имеем
f(T£) = 0, t<=Vo, gf=G.
Ввиду аналитичности то же равенство верно и для вся¬
кого Но тогда линейная оболочка векторов
Tgl, g е @, I е Vo, не может быть шире V0. Действи¬
тельно, в силу теоремы Хана — Банаха [5] для всякого
г)фУ0 существует линейный функционал, равный нулю
на К0 и отличный от нуля в точке ту Следовательно,
V0 инвариантно также и относительно всей группы ®.
Следовательно, V0 = (0) или Vo = V ввиду неприводи¬
мости исходного представления группы @.
В частности, положим G = U, где U — компактная
вещественная форма в @. Поскольку всякое неприводи¬
мое представление Tg остается неприводимым при суже¬
нии на подгруппу U, то оно конечномерно.
Далее, используя предыдущие рассуждения при
G — U, получаем, что всякое представление класса К
вполне приводимо. (Более того, всякое подпространство,
неприводимое относительно ©, остается неприводимым
при сужении на U.)
Отбросим теперь условие однозначности; тогда Те —
конечнозначное представление группы U. Многообразие
{Tg} является конечным накрытием группы U и, следо¬
вательно, может рассматриваться как точное представ¬
ление группы U, которая является конечным накрытием
группы U. Как следует из этого определения, группа U
является компактной. Следовательно, для нее по-преж¬
нему верны использованные выше следствия глобальной
теоремы (принцип полной приводимости, конечномер¬
ность неприводимых представлений). Заменяя в пре¬
дыдущих рассуждениях группу U на U, получаем преж¬
ние результаты. Теорема доказана.
Замечание 1. Покажем, что ограничение конеч¬
нозначными представлениями для нашей цели сущест¬
венно. Действительно, представление

184
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
мультипликативной группы комплексных чисел не отно¬
сится к классу А’ и в то же время не является вполне
приводимым *).
Замечание 2. Если ограничиться классом конеч¬
номерных представлений, то теорема 2 является триви¬
альным следствием теоремы 1 (и глобальной теоремы
для компактных групп).
Следствие 1. Если группа @ односвязна, то суще¬
ствует взаимно однозначное соответствие между непри¬
водимыми аналитическими представлениями группы & и
неприводимыми представлениями ее компактной веще¬
ственной формы U.
Здесь предполагается, как и выше, что @ — правиль¬
ная комплексная оболочка группы U. Если @ неодно¬
связна, то же утверждение остается в силе для конечно¬
значных представлений группы @ (и подгруппы U).
Следствие 2. Если надкомпактная группа @ ли¬
нейна, то всякое ее неприводимое представление реали¬
зуется в классе тензоров**).
В дальнейшем мы увидим (гл. XV), что всякая над¬
компактная группа Ли (связная или несвязная) имеет
точное линейное представление. Таким образом, след¬
ствие 2 в действительности справедливо для произволь¬
ной надкомпактной группы Ли.
Таким образом, мы видим, что сужение @ -> U позво¬
ляет использовать для комплексной группы @ ряд след¬
ствий из глобальной теоремы. Этот замечательный прием
впервые был применен Г. Вейлем и носит название
«унитарного трюка» Вейля. Одним из основных след¬
ствий является принцип полной приводимости для груп¬
пы
*) В дальнейшем мы увидим, что условие надкомпактности яв¬
ляется решающим для принципа полной приводимости (см. § 61).
Пока заметим, что группа вещественных чисел по сложению, которая
не является надкомпактной группой, имеет даже однозначные не
вполне приводимые представления. Примером является жорданова
клетка
**) Это утверждение вытекает из аналогичного свойства ком¬
пактных групп. — Прим. ред.

§ 43. БИКОМПЛЕКСНЫЁ ГРУППЫ И АЛГЕБРЫ ЛИ 185
В дальнейшем мы увидим, однако, что комплексная
группа @ обладает, как правило, значительно более
простой алгебраической структурой, чем группа U. Это
позволяет использовать принцип Вейля «инверсным»
образом, получая для группы U информацию из рассмот¬
рения ее комплексной оболочки @. Можно было после¬
довательно провести эту точку зрения и даже полно¬
стью игнорировать глобальную теорему, развивая неза¬
висимую теорию для некоторого класса комплексных
групп Ли («редуктивные группы», § 88). Мы еще оста¬
новимся на этом в дальнейшем.
§ 43. Бикомплексные группы и алгебры Ли *)
В § 39 мы встретились с ситуацией (довольно обыч¬
ной в анализе), когда комплексные переменные z, z
(черта означает сопряжение) естественно рассматривать
как независимые. Логический анализ этой ситуации не¬
трудно провести для произвольной группы или алгебры
Ли. При этом мы получаем эффективное средство для
изучения вещественных представлений комплексной
группы (или алгебры) Ли.
Определение 4. Пусть X — вещественная алгеб¬
ра Ли, I — ее комплексная оболочка и I — комплексная
оболочка алгебры I, которая снова рассматривается над
вещественным полем (с удвоенным числом параметров).
Алгебру £ мы будем называть бикомплексной оболочкой
алгебры X.
Пусть е,- — произвольный базис в алгебре Х\ тогда
векторы eit, fk=V~ 1 £k образуют базис в веществен¬
ной алгебре I. Если с*. — структурные константы X, то
мы имеем
К-. ei\=ckuek’ К- е/] = £1Л> (*)
\fp ы= -^не¬
полученные формулы определяют также закон комму¬
тации в бикомплексной оболочке I при условии, что
*) При первом чтении этот параграф можно опустить.

Ш м. VI. АНАЛИДИЧеОкОЁ ПРОДОЛЖЕНИЕ
рассматриваются всевозможные комплексные линейные
комбинации независимых символов ek, fh-
Пример. Пусть X = su(2). Тогда формулы (*)
определяют закон коммутации в вещественной алгебре X,
которая является алгеброй Ли группы Лоренца. Пере¬
ход от X к X означает попросту, что допускаются ком¬
плексные линейные комбинации базисных элементов.
Всякую бикомплексную оболочку вещественной ал¬
гебры Ли мы будем называть бикомплексной алгеброй
Ли. Соответствующие определения будем использовать
для группы Ли.
Определение 5. Пусть G — вещественная группа
Ли, ©— ее комплексная оболочка и ©— комплексная
оболочка группы ©, рассматриваемой над полем веще¬
ственных чисел (с удвоенным числом параметров). Груп¬
пу © мы будем называть бикомплексной оболочкой
группы G.
Если © является правильной комплексной оболочкой
группы Си© является правильной комплексной обо¬
лочкой вещественной группы ©, то условимся также го¬
ворить, что © является правильной бикомплексной обо¬
лочкой группы G.
Условимся также в следующей терминологии. Ска¬
жем, что алгебра X является прямой суммой двух идеа¬
лов Хи Х2, если X = У, 4- Х2, где Х\, Х2 — две взаимно
перестановочные подалгебры в алгебре У*). Скажем,
что группа G является локально прямым произведением
двух подгрупп G\ и G2, если G локально изоморфна
прямому произведению G\XG2. Если G — группа Ли,
то очевидна связь между этими определениями, выте¬
кающая из общей связи между группами и алгеб¬
рами Ли.
Теорема 3. Пусть X — бикомплексная оболочка
вещественной алгебры X. Тогда I является прямой сум¬
мой двух идеалов, каждый из которых изоморфен ком¬
плексной оболочке X алгебры X.
Аналогично, если @ — бикомплексная оболочка веще¬
ственной группы G, то @ является локально прямым
*) Общее определение идеала будет дано в § 82.

§ 43. БИКОМПЛЕКСНЫЕ ГРУППЫ И АЛГЕБРЫ ЛИ
187
произведением двух подгрупп, каждая из которых изо¬
морфна комплексной оболочке @ группы G.
Доказательство. Вещественная алгебра X рас¬
падается в прямую сумму двух линейных подпространств
X и У, где Y = iX (умножение на i понимается в смысле
комплексной оболочки X). При этом, очевидно, суще¬
ствует изоморфное линейное отображение y = f(x), х е
еХ, у е У (заменяющее умножение на i=Y~ 1),
для которого
[хи f{x2)] = [f (*i), x2\ = f(x3), [f(*,), f(x2)\=~x з
при условии, что [х\, х2] = хз, Х\, а'2, х3е! Если вме¬
сто X рассматривать £, то в этом случае допускаются
всевозможные комплексные комбинации векторов хи
f(x2). Для каждого ге! положим
а(х) = ~(х — if (х)), a(x)=j(x + if (х)),
где символ f(x) продолжается на X по линейности
(f(Xx) = Xf(x) для любого комплексного X). Нетрудно
убедиться непосредственной проверкой, что элементы
afx^, а(х2) перестановочны при любых хи х2^Х, и
если [хих2] — х3, то мы имеем
[а(х,), а{х2)] = а{х3), [а(а:,), а{х2)] = а{х3).
Следовательно, множества А, А, состоящие из всевоз¬
можных элементов а(х), а(х), являются подалгебрами
в X. При этом, как нетрудно видеть, а (х,) + а (х2), хи
jt2el,пробегает всю алгебру X. Из сравнения размер¬
ностей следует также, что сумма X — А + А является
прямой. Следовательно, первая часть теоремы доказана.
Для доказательства второй части теоремы достаточ¬
но рассмотреть тот случай, когда группа @ односвязна.
Пусть Я, Я — односвязные группы Ли с алгебрами Ли
А, А соответственно. Группа ЯХЯ односвязна и по¬
тому изоморфна ®. Переход к общему случаю осуще¬
ствляется, как обычно, факторизацией по центральному
дискретному делителю. Теорема доказана.

188
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
Замечание. Запишем всякий элемент z еХ в виде
а (а:,) + а (х2) = у (х{ + *2) + у f(x{ — х2). Условимся также
отождествлять такой элемент с парой (х\,х2). Если хи
х2 вещественны, то мы получаем, очевидно, подалгеб¬
ру £0, изоморфную алгебре X. Если Х\ = х2, то также
получаем подалгебру, изоморфную X (которая может
быть определена как «диагональ» из элементов вида
(х,х)). Соответственно группа @ может быть реализо¬
вана как «диагональ» в группе © ~ © X @.
Идеалы А и А, построенные при доказательстве тео¬
ремы 3, мы будем называть соответственно аналитиче¬
ским и антианалитическим идеалами в X.
Пусть х-+х(х) — вещественное представление алгеб¬
ры X. Допуская комплексные комбинации операторов
х(х), мы можем продолжить это представление до пред¬
ставления алгебры I. Положим
D(x) = j (т (а) - ix (ix)), Ъ(х) = у (т (х) + ix (ix)).
Здесь мы используем символ ix вместо f(x), поскольку
это не может вызвать недоразумения. Как и в доказа¬
тельстве теоремы 3, легко проверить, что символы
D(x), D(x) осуществляют разбиение данного представ¬
ления в прямую сумму двух идеалов. Иначе говоря,
[D (х), D (г/)] = О
для всех х, у^Х, и каждый из символов D(x), D(x)
определяет представление алгебры X. Представление
алгебры X мы называем аналитическим (антианалитиче¬
ским)если D (х) =0 (D(x) = 0). Иначе говоря, в этих
случаях мы имеем соответственно
т (ix) = ix (х), т (ix) = — ix (х).
В первом случае х(Тх) = Хх(х) для любого комплексного
Я. Следовательно, х(х) является в этом случае комплекс¬
ным представлением алгебры X. Во втором случае мы
имеем т (Тх) = Ят (х).
Если х(х) возникает как дифференциал представле¬
ния Tg группы @, то операторы D(x), D(x) можно рас¬

§ 43. БИКОМПЛЕКСНЫЕ ГРУППЫ И АЛГЕБРЫ ЛИ
189
сматривать как инфинитезимальные операторы бикомп-
лексной группы Кроме того, эти операторы могут
быть определены с помощью формальных производных:
^ ^ = Ж ^ехр Хх ^=0» D (х) = Тех р \х |д_0,
где Я — произвольное комплексное число (и ехр ).х—■
однопараметрическая комплексная подгруппа в ком¬
плексной группе @). Следовательно, использование фор¬
мальных производных означает, по существу, переход к
бикомплексной группе
В заключение исследуем важный вопрос о структуре
неприводимых представлений группы Докажем вна¬
чале следующую общую лемму:
Лемма. Пусть алгебра X является прямой суммой
двух идеалов А и В. Тогда любое ее неприводимое пред¬
ставление является тензорным произведением неприво¬
димых представлений А и В, т. е. двух неприводимых
представлений алгебры X, одно из которых обращается
в нуль на В и второе обращается в нуль на А.
Доказательство. Пусть V—пространство пред¬
ставления и V\ — подпространство, неприводимое отно¬
сительно подалгебры А. Пусть |3 — произвольный поли¬
ном от инфинитезимальных операторов подалгебры В.
Тогда либо рУ] = (0), либо pVi инвариантно относи¬
тельно А, с представлением, эквивалентным представ¬
лению в V\. Действительно, из перестановочности р и А
следует, что р переплетает представления в V\, рУь
остается применить лемму Шура. Из цикличности V
по отношению к алгебре всех инфинитезимальных поли¬
номов следует, что У = 2рУн Ввиду конечномерности
V достаточно рассматривать лишь конечное число сла¬
гаемых. В результате
V = V1 + V 2 + V п
(прямая сумма), где Vi = РгУь i= 1, 2, ..., п. Мы ви¬
дим, что сужение данного представления на подалгеб¬
ру А распадается в прямую сумму п одинаковых

190
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
неприводимых представлений. Пусть е, — базис в под-
простанстве V\\ тогда векторы e,j = образуют базис
во всем пространстве V. (В частности, пространство V
имеет размерность пт, где т = dim VV) Легко прове¬
рить, что в найденном базисе представление алгебры X
имеет структуру тензорного произведения двух указан¬
ных в лемме неприводимых представлений. Лемма до¬
казана.
Применяя эту лемму к представлениям алгебры X
и группы @, получаем согласно теореме 3
Следствие 1. Пусть ©— комплексная оболочка
вещественной связной группы Ли. Тогда всякое непри¬
водимое конечномерное вещественное представление
группы ® является тензорным произведением двух не¬
приводимых представлений группы ®, одно из которых
аналитично, а другое антианалитично.
Действительно, достаточно проверить аналог этого
утверждения для представлений алгебры I, где I— ал¬
гебра Ли группы @. Каждое такое представление про¬
должается по линейности до представления комплекс¬
ной алгебры X = А + А, где А и А — аналитический и
антианалитический идеалы. Применяя лемму, получаем
нужное утверждение.
Замечание. Даже если исходное представление
группы ® было однозначно, его аналитическая и анти-
аналитическая компоненты могут оказаться неоднознач¬
ными (см. пример GL(2, С) в § 39).
Отметим еще одно важное следствие теоремы 3.
Следствие 2. Пусть ® — правильная комплексная
оболочка компактной группы Ли. Тогда для всех ее ве¬
щественных конечномерных {не обязательно комп¬
лексно-аналитических) представлений сохраняется прин¬
цип полной приводимости.
Мы докажем это утверждение только в том случае,
когда © односвязна. В этом случае © ~ © X ©. Вместо
представления группы © мы можем рассматривать его
аналитическое продолжение на @. Заметим, что если
U — компактная форма в ©, то U ~ И X И — компакт¬
ная форма в @. Следовательно, группа @ является над-

$ 44. комплексная оёолочка им веса и корни
191
компактной, и принцип полной приводимости выпол¬
няется для всех ее аналитических представлений.
Из результатов гл. XV в действительности будет сле¬
довать, что всякая бикомплексная оболочка компактной
группы Ли является надкомпактной. Отсюда вытекает
доказательство следствия 2 в общем случае.
§ 44. Комплексная оболочка U(n). Веса и корни
Проиллюстрируем метод аналитического продолже¬
ния на примере группы U(/i). Поскольку эта группа не¬
односвязна, нам будет удобно рассматривать вначале ее
подгруппу Go = SU(/i), которая получается удалением
всего лишь одного вещественного параметра. При этом
односвязная группа @0 = SL(/i, С) является правильной
комплексной оболочкой группы G0. Ввиду односвязно¬
сти все рассматриваемые ниже представления будут
однозначными. Мы также не оговариваем особо, что все
изучаемые представления являются конечномерными.
Из обоих результатов, полученных в этой главе, для
нашего случая вытекают следствия:
1° Все аналитические неприводимые представления
группы @о конечномерны (и однозначны).
2° Для описания всех неприводимых представлений
группы G0 достаточно перечислить все аналитические
неприводимые представления группы ®0.
Мы займемся решением последней задачи. В этом
параграфе будет дано лишь предварительное исследова¬
ние инфинитезимальной структуры представления. Мы
убедимся, что инфинитезимальный метод приводит в
данном случае к значительным трудностям*). Полное
решение задачи будет получено в следующей главе со¬
вершенно иначе (глобальным) путем. Тем не менее ин-
финитезимальная трактовка является чрезвычайно на¬
глядной, и это побуждает нас изложить ее достаточно
подробно.
Положим X = gl(n,C), Х0 = si (п,С). Напомним,
что X состоит из всех комплексных матриц п X п и
*) См., однако, общий результат в § 121.

192 гл. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
подалгебра выделяется условием sp х = 0. Элементы
/
еП
О ! О
о I о
образуют базис в алгебре X, элементы eih i ф j, h=
= еи — ei + u i + i образуют базис в подалгебре Х0. По¬
скольку вцвы = biketi, то мы имеем следующие соотноше¬
ния коммутации:
[&if> @kt\ £>ikeil ^il&kl"
Мы представим эти соотношения значительно более на¬
глядно, если выделим отдельно элементы е^, для кото¬
рых i > /, i = /, i < j. Получаемые системы элементов
обозначим символами е_, е0, е+.
Пусть Л_, Н, Х+ — линейные оболочки базисных век¬
торов из е_, е0, е+ соответственно. Как нетрудно ви¬
деть, для элементов системы е+ единственными нетри¬
виальными соотношениями коммутации являются соот¬
ношения
[Cf/, 6jk\ @ikt i< j < k.
Отсюда, в частности, следует, что Х+ является подалгеб¬
рой. Точно так же X_. является подалгеброй. Множе¬
ство Н является абелевой подалгеброй. Полагая й = дец,
мы имеем также
[.h, e{l] = {t‘-tJ)eil.
Это означает, что каждый вектор е,-,- является собствен¬
ным относительно линейного оператора Dhx — [h, х]. Соб¬
ственные значения ац = С — С мы условимся называть
корнями алгебры X. Все сказанное остается в силе так¬
же и для алгебры Х0, если положим tl + I2 + ... + ^п = 0.
Перейдем к изучению аналитических (конечномер¬
ных) представлений группы @ = GL(n, С) и ее подгруп¬
пы @o = SL(n, С). Пусть Tg — такое представление и

§ 44. КОМПЛЕКСНАЯ ОБОЛОЧКА U(n) ВЕСА И КОРНИ J93
D{x) — его дифференциал. Положим
Ец = 0{еи).
В частности, операторы Ei = Еи и их линейные комби¬
нации являются инфинитезимальными операторами ди¬
агональной подгруппы в @(@о). Используя принцип ана¬
литического продолжения, легко получаем отсюда:
I. Операторы Ei и их линейные комбинации одновре¬
менно диагонализуются в пространстве представления.
Действительно, пусть V — пространство представле¬
ния. Пространство V вполне приводимо относительно
подгруппы Г всех диагональных унитарных матриц, и
каждое неприводимое подпространство одномерно*).
Производя аналитическое продолжение, получаем то же
утверждение для подгруппы D всех диагональных мат¬
риц из в (во). Но тогда то же верно и для инфините-
зимальных операторов этой подгруппы. Наше утвержде¬
ние доказано.
II. Собственное значение оператора D(h) = ЕЕ{ яв¬
ляется линейной формой на алгебре Н: Х(1г)=ТХ{.
Доказательство очевидно (D (х) линейно зависит
от х). Каждое собственное значение X (h) называется
весом представления D(x). Иногда, если это не будет
вызывать недоразумений, мы будем называть весом на¬
бор коэффициентов Хц i = 1, 2, ..., п. Вектор %^V,
собственный относительно всех операторов D{h), назы¬
вается также весовым.
III. Если вектор | является весовым с собственным
значением X, то вектор = £гД также является весо¬
вым с собственным значением Хц = X 4- агц (где ац—
соответствующий корень).
Доказательство проводится так же, как и в случае
группы SU (2). Замечая, что D (Н) Ец = Ец{И (h) + a.ij),
получаем D(Н)1ц = (X(h) 4- аг-у (/г)) £Д,-. Заметим, что если
рассматривать ац как вектор коэффициентов формы
сXij(h), то мы имеем
*) Попросту говоря, коммутативное семейство унитарных матриц
диагонализуется.

191
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
где е{ означает ыт базисный вектор в д-мерном вектор¬
ном пространстве Н. При этом мы имеем aц(1г) = (ац,Н),
где в правой части имеется в виду обычное скалярное
произведение в пространстве Н\ (k,h) = кф* = k{h) *).
Мы получаем значительную информацию о спектре
представления D(h).
IV. Пусть s — произвольная матрица подстановки в
группе Если вектор | является весовым с собствен¬
ным значением к, то вектор %3 = Т3\ также является ве¬
совым с собственным значением ks = sk.
Действительно, если s — подстановка, то sh для
всякой диагональной матрицы /г, где Ъ означает также
диагональную матрицу с переставленными собственными
значениями. Следовательно, также SD (h) = D (Ti)S, где
положено S = Ts. Применяя это соотношение, легко по¬
лучаем нужное утверждение. Заметим, что оператор S
(в отличие от Ец) всегда является обратимым, и от¬
сюда вытекает, что собственные значения к, ks всегда
имеют одинаковую кратность. Действительно, отображе¬
ние S сохраняет размерность подпространства собствен¬
ных векторов с фиксированным собственным значением.
С учетом замечания о кратностях сформулируем по¬
лученный результат в несколько иной форме. Заметим,
что множество всех подстановок образует конечную под¬
группу © в группе @ (симметрическую группу поряд¬
ка п\). Эта группа будет называться группой Вейля.
С другой стороны, пусть /V — множество всех весов пред¬
ставления D (х) с соответствующими кратностями, т. е.
график функции пх, где пх — кратность веса к. Нами до¬
казано следующее утверждение:
V. Весовая диаграмма А инвариантна относительно
группы Вейля.
Следующий важный шаг состоит во введении лекси¬
кографической упорядоченности в множество весов. За¬
метим вначале, что всякий вес к = (Д, кг, кп) име¬
ет вещественные координаты. Действительно, если h со¬
держится в алгебре Ли унитарной подгруппы Г, то ко¬
*) Строго говоря, мы должны рассматривать к как элемент ду¬
ального пространства Н (составленного из линейных форм). Однако
введение скалярного произведения отождествляет Н и Н.

§ 44. КОМПЛЕКСНАЯ ОБОЛОЧКА U(п) ВЕСА И КОРНИ
195
ординаты Е в разложении h = Ееи должны быть чисто
мнимыми и показатели Я* в экспоненте ехр Я (ft) —
= ехр должны быть вещественными*). Для каждой
пары вещественных векторов Я, р полагаем X > р, если
либо Xi > pi, либо Я) = pi, но Я2 > р2 и т. д. Конечное
множество весов в диаграмме А становится при этом
вполне упорядоченным.
Заметим, что корни ац = е,— Sj также имеют веще¬
ственные координаты в базисе {е,}. Используя для этих
корней понятие лексикографической упорядоченности,
получаем следующий результат:
аг/<0 при />/, аг;>0 при г</.
Кроме того, a,j = 0 при г = /. Таким образом, разбиение
корней на отрицательные, нулевые и положительные со¬
ответствует разбиению базиса (е,Д на подсистемы е_,
е0, е+. Соответственно мы видим, что
Хц<Х при i >/, Яг/>Я при i</.
Здесь Хц = X + Иг; — собственное значение весового век¬
тора %ij = Eiil. Оператор £,j мы будем теперь называть
понижающим, если i > /, и повышающим, если i < /.
VI. Пусть а = (mi, m2, ..., m„) — максимальный из
весов в диаграмме А. Тогда > т2 >■... Соот¬
ветствующий вектор | обращается в нуль всеми повы¬
шающими операторами Ец.
Действительно, если бы вектор а не обладал указан¬
ным свойством упорядоченности, то, применяя преобра¬
зования группы Вейля, мы получили бы вес sa, удовлет¬
воряющий этим свойствам. При этом nsa — паф 0 и
sa > а, что противоречило бы условию максимальности
веса а. Очевидно, также, что = 0, г < /, так как по¬
вышение веса невозможно.
Полученный результат делает естественным следую¬
щее определение. Если D(x) неприводимо, то скажем,
что а является старшим весом и соответствующий
*) И даже целыми в случае GL(rc). В случае SL(n) парамет¬
ры Я; определяются с точностью до общего слагаемого (поскольку
= 0); однако и в этом случае мы можем условиться считать, что
Xi целые.

196
ГЛ VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
вектор 1 — старшим вектором этого представления.
В силу правила цикличности все пространство V яв¬
ляется циклической оболочкой вектора | относительно
полиномов от операторов E{j. Из соотношений комму¬
тации ясно также, что достаточно рассматривать поли¬
номы от понижающих операторов Ец (поскольку повы¬
шающие операторы аннулируют |). С помощью таких
операторов можно построить базис в пространстве V;
однако эта задача имеет нетривиальное решение.
В дальнейшем мы увидим, что старший вектор в не¬
приводимом представлении определяется однозначно с
точностью до множителя и старший вес а характери¬
зует это представление с точностью до эквивалентности.
§ 45. Модель неприводимых представлений SU(3)
В этом параграфе будет рассмотрена простая мо¬
дель неприводимого представления группы SU(n), ко¬
торая при и — 3 содержит все неприводимые представ¬
ления этой группы (определяемые с точностью до экви¬
валентности) .
Пусть Е — n-мерное пространство н Ф£ — простран¬
ство тензоров над Е, q раз ковариантных и р раз кон-
травариантных, т. е. тензоров вида/у|^ ... По анало¬
гии со случаем SU(2) мы можем ограничиться рассмо¬
трением тензоров, симметричных по ЙП2. • • •, iq и сим¬
метричных по /ь/2, .... jq. В этом случае вместо тензо¬
ров можно рассматривать полиномы
fix, i)=№:::iip\xi ... Х( ... s4
*1*2 *q l 2 p
где x = (Xj)—ковариантная строка и g = (gJ)—контра-
вариантный столбец. Очевидно, пространство этих тен¬
зоров все еще приводимо. Действительно, свертка по лю¬
бой паре индексов ih, jt перестановочна с преобразова¬
ниями в классе тензоров. В частности, тензоры, для ко¬
торых эта свертка дает нулевой результат, инвариантны
относительно любой аффинной группы G.
Пусть Rq — пространство тензоров из Ф£, симметрич¬
ных отдельно по нижним, отдельно по верхним индек¬

§ 45. МОДЕЛЬ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИИ 197
сам и таких, что свертка по индексам /ь /, обращается
в нуль. В силу условия симметричности свертка по
любой паре индексов ih, jt при этом также обращается
в нуль. Пусть dvq — представление группы G = GL(n)
в этом классе тензоров. Покажем, что dvq неприво¬
димо.
1. Найдем все элементы со е R°q, которые аннули¬
руются повышающими операторами. Заметим, что в
классе полиномов /(*,£) преобразования группы G за¬
даются следующей формулой*):
Tgf{x,l)-f{xg, gr'i).
Вместо повышающих операторов Ец мы можем рассмат¬
ривать соответствующие однопараметрические под¬
группы:
XI Xj + tX{, i<j-
(здесь имеется в виду, что все остальные координаты
Xu, k Ф /, %k, k Ф i, остаются неизменными.) Если и анну¬
лируется операторами Ец, i < /, то ы является инва¬
риантом относительно этих подгрупп. Полагая, в част¬
ности, i — 1, j = 2, 3, ..., п, подбираем параметры каж¬
дой ИЗ ЭТИХ подгрупп ИЗ УСЛОВИЯ Xj + tx\ = 0. Это воз¬
можно сделать при х\ ф 0. Поскольку и вполне опреде¬
ляется своими значениями при х\ Ф 0, то мы находим
из условия инвариантности
co(.v, ^) = co((yI, 0, 0 0); I),
где | отличается от | только первой координатой (кото¬
рая может быть найдена из условия инвариантности
свертки xl). Полагая, далее, i= 1, 2, ..., п—1, j — п,
мы добиваемся аналогично обращения в нуль всех ко¬
ординат вектора |, кроме последней координаты при
этом, как легко видеть, все координаты первого вектора
{хц 0, 0, ..., 0) остаются неизменными, за исключением
последней. В результате имеем
ю (*,£) = to ((*„ 0,0 0, т); (0, 0, ..., 0, |„)),
*) См. § 14 (стр. 73).

198
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
Значение т определяется из условия инвариантности
свертки х\. Следовательно, а(х, |) является полиномом
от х\, In и т = xl/ln. Поскольку в то же время со яв¬
ляется полиномом от х и то ясно, что (о является по¬
линомом от х\, \п и а = х\. В результате
со(х, 1) = Р{хи 1п, а),
где Р — полином.
2. До сих пор мы не использовали равенство нулю
всех сверток в пространстве Rp. Заметим, что взятие
свертки равносильно, с точностью до множителя, при¬
менению дифференциального оператора
Д = • -Дг (свертка по г).
дх{ *
Таким образом, Д/= 0 для всех элементов / е Rpq. Не¬
трудно проверить, что из всех полиномов от xi, а
этому условию удовлетворяют только те полиномы, ко¬
торые не зависят от а. Среди таких полиномов простран¬
ству Rp принадлежит лишь единственный (с точностью
до множителя) одночлен
со = x’lll.
3. Используем теперь принцип полной приводимости.
Как мы видели в § 44, каждое неприводимое представ¬
ление группы G обладает старшим вектором. Если бы
представление в Rp было приводимо, то решение со
определялось бы неоднозначно. Следовательно, dvq не¬
приводимо.
Замечание 1. Если использовать координаты
то свертка записывается в виде суммы квадратов этих (комп¬
лексных) координат. Соответственно оператор Д, введенный выше,
отождествляется с оператором Лапласа в комплексном евклидовом
пространстве размерности 2п. Следовательно, R£ отождествляется
с пространством гармонических полиномов степени однородности р
по х, степени однородности q по

§ 45. МОДЕЛЬ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ 199
Замечание 2. Можно показать, что все полиномы f е Rp
однозначно определяются своими значениями на конусе К'. х£ = 0.
Действительно, если / = 0 на К, то, заменяя векторы х, £ линейными
комбинациями вида Ух' + Ух" + ..., |i'£' + + ... и варьируя ко¬
эффициенты Я, |i, получаем, что полилинейная форма с коэффициен¬
тами их1У"\р обращается в нуль на всяком наборе векторов
М'2 ■ ■1 1Q
х’, х", . .., ..., попарные свертки между которыми равны
нулю. Фиксируя все переменные, кроме х = х\ | = приходим к
рассмотрению формы второго порядка:
ф (х, £) = x'jX^1,
для коэффициентов которой выполняется условие т- = 0 (свертка
по ()• Приравнивая нулю дифференциал этой формы и пользуясь
условием I+ X; = 0, легко находим, что xj = 0 при i ф j и
т‘-= const (не зависит от г). Согласно условию о свертке*) нахо¬
дим, что т\ = 0 при каждом (. Следовательно, Ту = 0. Применяя то
же рассуждение к форме тj по переменным х = х", £ = и про¬
должая этот процесс, получаем после конечного числа шагов равен¬
ство t)1]2 }р — 0.
м'2 "‘' д
Следовательно, dPQ может быть реализовано в классе полино¬
мов на конусе К. Это утверждение можно также получить как
тривиальное следствие результатов следующей главы.
Замечание 3. В приведенном выше построении
старший вектор со = Х\^чп представления dvq был най¬
ден явно. Для определения старшего веса введем диаго¬
нальную матрицу 6=diag{6b 62, 6Д и найдем соб¬
ственное значение 1(6) из условия Гасо = Я(б)со. По¬
скольку —> лг(-бг-, S,£- —> 6Д'g(-, то мы имеем
я (б) = б^бГ.
Полагая теперь 6,- = е1 и вычисляя производные по ti
при ti = 0, получаем искомый старший вес:
Я = (р, 0, 0, . . 0, - q).
Если рассматривать только подгруппу SL(n), то из
*) См. определение пространства Rp на стр. 196.

200
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
условия detg= 1 следует, что всякие два веса Я, Я + е,
е = (1,1,...,1), можно отождествить (они определяют
одно и то же собственное значение Я(б)). В частности,
при п = 3 вместо веса X можно рассматривать вес
а = (ти т2, т3), mi > m2 > т3,
где положено rri\ = р + k, т2 = k, тг = k — q с произ¬
вольным слагаемым k. Следовательно, при п = 3 в на¬
шей конструкции встречается произвольный старший вес
относительно подгруппы SL(3). Отсюда естественно
Рис. 1.
предположить, что данная конструкция содержит все
неприводимые представления SL(3). Действительно, это
будет следовать из результатов следующей главы.
В силу принципа аналитического продолжения то же
верно для подгруппы SU(3).
В заключение рассмотрим несколько более подробно
простейшие представления d\o, dou dn. Первые два из
этих представлений трехмерны, последнее восьмимерно.
Построим весовые диаграммы этих представлений. Усло¬
вимся рассматривать только подгруппу SL(3) (или
SU(3)). Тогда всякий вес X = (Яь Яг, Яз) определяется,
как мы видели выше, с точностью до общего слагаемого
у координат Яь Яг, Яз. Нормализуем этот вес условием
Я) + Яг + Яз = 0 и будем на этой плоскости рассматри¬
вать ортогональную проекцию трехмерной системы ко¬
ординат. Тогда для представлений d\ = dw, d2 = doi по¬
лучаем графики, изображенные на рис. 1.

§ 45. МОДЕЛЬ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ 201
Действительно, в случае d\ пространство Ro натянуто
на базисные векторы X], х2, х3, которым отвечают веса
(1,0,0), (0, 1,0), (0,0, 1) изображенные на первой диа¬
грамме. Точно так же в случае d2 пространство R°i на¬
тянуто на базисные векторы £', |2, |3 с весами (0,0,—1),
(0, —1,0), (—1,0,0). Единицы, стоящие у точек весо¬
вой диаграммы, означают, что каждый вес содержится
в данном случае с кратностью 1. Точно так же для
представления dn получаем следующий график (рис. 2):
Система весов в этом случае имеет вид (2, 1,0), (1,2,0)
(0,2,1), (0,1,2), (1,0,2), (2,0,1), (0,0,0). Последний
вес содержится двукратно. Система весов распадается
на две орбиты относительно группы Вейля.
Представления d\, d2 могут быть охарактеризованы
с геометрической точки зрения как преобразования век¬
тора и бивектора над трехмерным пространством В
(«кварк» и «антикварк» в терминологии физиков).
Представление dn («октет») будет в дальнейшем оха¬
рактеризовано как «присоединенное представление»
SL(3).
Как уже было сказано во введении к этой главе, принцип ана¬
литического продолжения в теорию представлений был впервые
введен Г. Вейлем. Этот принцип позволил использовать для надком-
пактных групп богатую информацию, даваемую глобальной теоремой.

202
ГЛ. VI. АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
В дальнейшем мы покажем, что комплексные группы допу¬
скают независимое изучение благодаря простой алгебраической
структуре. (Можно было бы провести эту точку зрения последова¬
тельно, но мы не ставили подобной цели в этой книге). Следова¬
тельно, принцип аналитического продолжения можно использовать
«в обратную сторону» — для получения информации о структуре
представлений компактной группы.
Примеры, приведенные в этой главе (представления SU(n),
SL(n)), следует рассматривать как иллюстративные. В них принцип
аналитического продолжения комбинируется с инфинитезимальным
методом. В дальнейшем, как уже было сказано, мы предпочтем
глобальный метод; однако инфинитезимальную конструкцию жела¬
тельно все время иметь в виду вследствие ее наглядности.

ГЛАВА VII
НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
ГРУППЫ U(n)
В этой главе будет получено полное описание не¬
приводимых представлений группы U(n). Следуя идее
аналитического продолжения, мы рассматриваем эти
представления аналитически продолженными на GL(n).
Тем самым возникает также полное описание неприво¬
димых аналитических представлений GL(n). Полагая
det g = 1, получаем те же результаты для SU(n),SL(n).
В действительности метод, применяемый при решении
этой задачи, позволяет столь же просто получить опи¬
сание и всех вещественных (конечномерных) неприво¬
димых представлений комплексной группы (SL(ra),
GL(n)). В дальнейшем условие конечномерности спе¬
циально не оговаривается.
Глобальный метод решения, предлагаемый в этой
главе, совершенно не зависит от всей предыдущей тео¬
рии. Иногда мы пользуемся инфинитезимальными по¬
строениями, но это делается лишь из соображений на¬
глядности. Что же касается теории компактных групп
Ли (глобальная теорема), то мы лишь однажды — при
описании пространства представления — пользуемся
принципом полной приводимости. В действительности
этот принцип может быть непосредственно доказан для
комплексной группы SL(h) (при помощи инфинитези-
мального метода).
Таким образом, теория конечномерных представле¬
ний комплексной группы может быть построена неза¬
висимо от теории компактных групп Ли. Мы будем ис¬
пользовать лишь элементарные методы линейной ал¬
гебры («разложение Гаусса», описанное в § 9).
§ 46. Существование старшего веса
Положим G = SL(n, С). Элементы группы G предпо¬
лагаются записанными в виде матриц относительно фик¬
сированного базиса eit е2, еп. Упорядоченность этого

204 ГЛ. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(n)
базиса позволяет выделить в группе G специальные под¬
группы, входящие в разложение Гаусса:
Greg = Z- DZ + .
Здесь Z-, D и Z+—подгруппы в группе G, составленные
соответственно из всех нижних треугольных с единица¬
ми на диагонали, диагональных и верхних треугольных
с единицами на диагонали матриц geC. Множество
Greg состоит из всех произведений
g = Z6z, ?€=Z_, 6eD, zeZ+.
Как известно из линейной алгебры (см. § 9), множе¬
ство Greg всюду плотно в G. Если Ар — главный диаго¬
нальный минор, составленный из первых р строк и пер¬
вых р столбцов матрицы g, то g <= Greg тогда и только
тогда, когда Др Ф 0, р = 1, 2, ..., п.
Пусть g —* Тg — представление группы G в векторном
пространстве V. Вектор V мы называем весовым,
если он является собственным относительно всех пре¬
образований подгруппы D:
. = Не¬
собственное значение р(б) называем весом (относитель¬
но подгруппы D). Очевидно, ц(б) является одномерным
представлением («характером») группы D. Если пред¬
ставление Tg аналитично, то ц(б) = б™>б™2 ... б™п, где
6; — собственные значения матрицы б е D.
Определение 1. Вектор | мы называем старшим
вектором представления Tg, если он является инвариан¬
том группы Z = Z+ и весовым относительно D.
Заметим, что группа G является односвязной; сле¬
довательно, все ее представления однозначны. Из усло¬
вия однозначности следует, в частности, что показатели
гп\, т.2, ..., тп всякого веса р(б) являются целыми*).
Вектор ц = (nii, т2, ..., тп) мы будем называть инфи-
нитезимальным весом представления Т g. Вес а (б), от¬
вечающий старшему вектору, будет называться старшим
*) См. сноску на стр. 195.

§ 46. СУЩЕСТВОВАНИЕ СТАРШЕГО ВЕСА
205
весом. Если в определении 1 рассматривать Z_ вместо
Zf, то аналогично вводятся понятия младшего вектора
и младшего веса.
Заметим также, что Z является связной (и одно¬
связной) подгруппой, алгеброй Ли для которой является
подалгебра Х+, введенная в § 44. Следовательно, стар¬
ший вектор | удовлетворяет системе уравнений
£,/| = 0, i<j.
Как мы видели в § 44, всякое аналитическое представ¬
ление группы G обладает таким вектором. Однако при
этом мы пользовались «унитарным трюком» Вейля (диа-
гонализация операторов подгруппы D). Здесь будет
предложено иное независимое доказательство, которое
пригодно также и для вещественных представлений груп¬
пы G.
Теорема 1. Всякое (конечномерное) представление
группы G — SL(я, С) (или G — GL(n, С)) обладает хотя
бы одним (ненулевым) старшим вектором.
Доказательство. Положим Т = DZ. Группа Т
состоит из всех треугольных невырожденных матриц
/eGL(n, С). Нижеследующая лемма является частным
случаем одной общей теоремы, принадлежащей Софусу
Ли. Эта лемма допускает глобальное доказательство
(§ 88), однако из соображений наглядности мы докажем
ее инфинитезимальным способом.
Лемм а. Всякое неприводимое представление группы Т в комп¬
лексном векторном пространстве одномерно.
Доказательство леммы. Вместо группы Т будем рас¬
сматривать ее алгебру Ли L = Н 4- А'+, где Н натянуто на диаго¬
нальные матрицы ец и Х+ натянуто на верхние треугольные мат¬
рицы ец, 1 < /. Пусть D(x) —неприводимое представление алгеб¬
ры L в пространстве V и Е^ — D (e.j), i<j.
Пусть Vo — подпространство, неприводимое относительно Х+.
Заметим, что оператор Ещ перестановочен со всеми операциями Х+.
Следовательно, согласно лемме Шура Е\п кратно единице на V0:
Etn = XI. Из соотношения [£i2, £2л] = Епри п > 2 заключаем, что
X = 0. Действительно, след коммутатора равен нулю. Заменяя опе¬
ратор Е\п нулем, замечаем, что теперь оператор £ь „_i перестаново¬
чен со всеми операциями алгебры Х+. Если п — 1 > 2, то, рассуж¬
дая, как и выше, получаем, что Ец n-i = 0. Продолжая это по¬
строение, заключаем, что все операторы Ец,, k > 2, обращаются в

206 ГЛ. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(п)
нуль на Vo и оператор ЕУ2 кратен единичному. Точно так же посту¬
паем с элементами Ё2к, k ^ 3, E3k, k ^ 4, п т. д. В результате
получаем, что операторы £),• = Eit j+b ( = 1, 2 п — 1, являются
скалярами на Ко и все остальные операторы Eij, j — i > 1, обра¬
щаются в нуль на Ко. Поскольку скаляры = Х21 взаимно пере¬
становочны, то отсюда заключаем, что Ко одномерно. Мы доказали
аналог нашей леммы для подалгебры Х+.
Далее, вернемся ко всему пространству К. Пусть е\ — собствен¬
ный вектор относительно Х± с собственным значением Х = Х(х),
iel+, Согласно сказанному выше такие векторы всегда суще¬
ствуют (и X = Х(х), очевидно, является линейной формой над Х+).
Цепочку векторов в\, е2, ..., ет назовем присоединенной к вектору
бь если
D (х) ek = X (х) ek (mod еу е2 е^),
т. е. если применение D(x) к вектору ек сводится к умножению на
Х(х) с точностью до некоторой линейной комбинации предшествую¬
щих векторов е\, е2, ..., еь-ь Пусть е\, е2, ..., ет — максимальная
присоединенная цепочка и Vt — линейная оболочка векторов
в\, е2, ..., ет. Очевидно, Ki инвариантна относительно Z+. Не¬
сложная проверка убеждает нас в том, что V\ инвариантна также
относительно всей алгебры L. Следовательно, К = Ki ввиду непри¬
водимости К.
Заметим теперь, что всякий оператор Ец, i < /, может быть за¬
писан в виде коммутатора [Ец,Ец]. Поскольку след коммутатора
равен нулю и след Ец пропорционален Х(е22) с ненулевым коэффи¬
циентом пропорциональности ( = dim К), то Х(ец) = 0 для всех зна¬
чений г < /. Следовательно, Х(х) = 0 на подалгебре ЙГ+. Наконец,
операторы А{ = D(en) перестановочны между собой, и согласно
лемме Шура пространство К одномерно. Лем.ма доказана.
Вернемся к доказательству теоремы. Пусть вектор §
определяет направление, неприводимо инвариантное от¬
носительно подгруппы Т. Тогда, как мы видели при до¬
казательстве леммы, Eijl = 0, г < /. Кроме того, век¬
тор Ц является собственным относительно всей подгруп¬
пы Т и, в частности, относительно подгруппы D. Следо¬
вательно, = g, 2eZ, 7’6g = |i(S)g, б eD.
Теорема доказана.
Замечание. При доказательстве теоремы 1 мы по¬
лучили также значительную информацию относительно
представлений треугольной группы Т. Мы видим, что
всякое неприводимое представление этой группы одно¬
мерно. Следовательно, в пространстве всякого представ¬
ления содержится вектор, собственный относительно всей
группы Т. Следовательно, также всякое представление
группы Т приводится в некотором базисе к треуголь¬

§ 47. ЕДИНСТВЕННОСТЬ СТАРШЕГО ВЕКТОРА 207
ному виду. Последнее утверждение легко доказывается
обычным методом индукции*).
Следовательно, свойство треуголыюсти восстанавли¬
вается в каждом (конечномерном, комплексном) пред¬
ставлении группы Т.
§ 47. Единственность старшего вектора
Покажем теперь, что из теоремы 1 вытекает чрезвы¬
чайно простое построение для каждого неприводимого
представления группы G.
Пусть g-+Tg — неприводимое представление груп¬
пы G в комплексном векторном пространстве V, и
пусть V — дуальное пространство, т. е. множество всех
линейных форм над V. Фиксируя линейную форму I, мы
можем каждому вектору хе1/ поставить в соответствие
функцию
f{g)=l(Tgx), g^G.
Таким путем, как мы видели в § 18, получается вложе¬
ние Tg в правое регулярное представление группы G.
Действительно, пусть Я — множество всех полученных
функций и Vo — множество всех векторов х е V, для ко¬
торых f(g) = 0. Очевидно, Vo инвариантно относитель¬
но Tg и VQd=V, откуда V0 = (0). Следовательно, 9? изо¬
морфно пространству V. Заменяя х на y—Tgax, полу¬
чаем новую функцию
RgJ (g) = f (ggo)•
Следовательно, представление Tg эквивалентно представ¬
лению Rg в классе SK. При этом в нашем распоряжении
имеется выбор линейной формы I.
Используя теорему 1, выберем вектор х0, кото¬
рый является старшим в пространстве V. Используя
*) Действительно, наличие собственного вектора означаетквази-
треугольность представления Tg с одномерным диагональным бло¬
ком и блоком Т 'g, размерность которого на единицу меньше размер¬
ности представления. Рассуждая индуктивно, можем считать, что
Tg треугольно, но тогда и Ts также треугольно.

208 ГЛ. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(л)
теорему 1 для контрагредиентного представления, вы¬
берем форму /о, которая является младшим вектором в
пространстве V. Тогда всякая функция f(g)^lЯ удов¬
летворяет следующим соотношениям:
f(£g) = f(g). f (68) = В (б) f (g),
где ?eZ_, SgD и p(6)— характер группы D. Функ¬
ция a(g) = lo(Tgx0) удовлетворяет, помимо этого, также
следующим соотношениям:
a (gz) = а (g), а (§6) = а (g) К (6),
где 2eZ+, вей и Я(б)— характер группы D. Полагая,
в частности, g = е, получаем, что а(£) = а(г) = а(е) и
а(б) = р(б)а(е) = а(в)Я(б). Равенство а(е) = 0 озна¬
чало бы, что а(6) = 0. Но тогда ввиду разложения
Гаусса функция
a (g) = а (£ 6z) = а (б) (*)
также равнялась бы нулю на всюду плотном множестве
Greg се G. Ввиду непрерывности отсюда вытекало бы,
что a(g) = 0; но это невозможно. Следовательно,
а(д)=£0. Нормируя векторы /о, х0 условием /0(дго) = 1,
получаем отсюда
a(£) = a(z)= 1, а (б) = р (б) = Я (б).
Второе из этих условий показывает, что старший вес
Я (б) определяется однозначно. Действительно, он совпа¬
дает с весом р.(б), который мы фиксировали в дуаль¬
ном пространстве V. Равенство (*) показывает также,
что функция a (g) определяется однозначно при усло¬
вии, что а(е)= 1. Но это означает также, что старший
вектор х0 е V определяется однозначно с точностью до
множителя, ибо равенство lo(Tgx0) = a(g) совместно с
условием /оМо)=1 определяет вектор х0 однозначно.
В результате получена следующая
Теорема 2. Если представление Tg неприводимо,
то его старший вектор определяется однозначно с точ¬
ностью до множителя. Соответствующий старший вес
a (б) определяет это представление однозначно с точ-

§ 47. ЕДИНСТВЕННОСТЬ СТАРШЕГО ВЕКТОРА 209
ностыо до эквивалентности. Положим
a (g) = « (£ М = « (б)
с непрерывным продолжением на всю группу G. Такое
продолжение действительно существует, и представле¬
ние Tg может быть реализовано с помощью правых
сдвигов в циклической оболочке SRa функции a{g).
Действительно, cc(g)<=9?a. В силу правила циклич¬
ности совпадает с линейной оболочкой функций
Rgfl (S) = « (ggo). G.
Неприводимое представление группы G со старшим
весом а мы условимся обозначать символом d(a). Если
использовать принцип полной приводимости, то из тео¬
рем 1 и 2 вытекает также практически важное
Следствие I. Представление Tg неприводимо тог¬
да и только тогда, когда оно обладает единственным,
с точностью до множителя, старшим вектором.
Действительно, если Тg содержит хотя бы две непри¬
водимые компоненты, то существует хотя бы два ли¬
нейно независимых старших вектора.
Следствие 2. Если Tg приводимо, то для его раз¬
ложения на неприводимые достаточно найти семейство
Q всех векторов, инвариантных относительно подгруп¬
пы Z, и выделить среди них весовые. При этом кратность
веса ц (6) совпадает с кратностью вхождения в Тн соот¬
ветствующего неприводимого представления d(p).
Мы видим, что следствие 2 дает непосредственный
практический метод спектрального анализа представле¬
ний группы G. Этот метод мы условимся в дальнейшем
называть методом Z-инвариантов. (Заметим, что прин¬
цип полной приводимости гарантирует также полную
приводимость Q относительно подгруппы D и содержа¬
ние в Q только тех весов, которые являются старшими
относительно всей группы G.)
Замечание. До сих пор мы полагали G = SL(n,C).
Однако теоремы 1 и 2 остаются верными ('вместе с до¬
казательствами) также для полной линейной группы
GL(n, С). В последнем случае необходимо соблюдать
известную осторожность в формулировках следствия 1
и следствия 2. Действительно, как мы видели в гл. Vi,
принцип полной приводимости выполняется, вообще

210 гл. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(п)
говоря, лишь для конечнозначных аналитических пред¬
ставлений группы GL(n, С)*). Во всяком случае, след¬
ствия 1 и 2 справедливы для вполне приводимых пред¬
ставлений этой группы.
§ 48. Различные модели d(cc)
Прежде чем завершить классификацию всех непри¬
водимых представлений группы G, остановимся на воп¬
росе о различных функциональных реализациях непри¬
водимого представления.
1. Реализация на группе Z. Поскольку все
функции из пространства удовлетворяют соотноше¬
ниям
f (£ 6z) = а (6) f (г),
то они вполне определяются своими значениями на Z.
Действительно, зная f(z), мы знаем значения f(g) на
множестве GTeg, но тогда по непрерывности также и на
всей группе G. Заменим f(g) на f (g) = f(ggo)', тогда мы
имеем
f {z) = f (zgQ) = f {I 61) = a (6) f (z),
где элементы 3, z определяются из разложения zg0 =
= £5z. Положим a (5) = a (z, gn) и z = zga. Заметим, что
a(z, go) совпадает со значением «производящей функ¬
ции» «(g) на элементе zg0. В результате получаем сле¬
дующее преобразование в классе функций f(z):
TJ(z) = a(z, g)f(zg).
При ti — 2 получаем, как легко проверить, известную
нам реализацию с помощью дробно-линейной подста¬
новки. Таким образом, преобразование z-*zg является
обобщением такой подстановки. Полученную нами мо¬
дель условимся называть реализацией на группе Z.
Мультипликативное свойство операторов представле¬
ния равносильно следующим тождествам (которые так-
*) Более подробно об условиях полной приводимости для
GL(п,С) см. конец § 61. Более общее утверждение см. также в
§ 118.

§ 48. РАЗЛИЧНЫЕ МОДЕЛИ d(a)
211
же легко проверить и непосредственно):
ze 1йг = (Zg,) g2>
a (z, gig2) = «(z, gi) • a (zgl, g2).
При этом очевидно также, что ze = z и a(z,e)=\.
Кроме того, a(z,Zo)= 1 для любого z0eZ и а (г, б) =
= а(б) для любого б еО. Следовательно, мы получаем
чрезвычайно простые формулы:
TJ (z) = / (zz0), Гб/ (z) = а (б) / (б-’гб).
Действительно, zZo = zz0 и za = б^'гб. Этими формулами
мы часто будем пользоваться в дальнейшем. Однако
при g^Z^ функция a(z,g) выглядит уже довольно
сложно.
Всякий старший вектор fo(z) должен удовлетворять
условию fo(zzo) = /о(z), z, z0eZ. Отсюда /0(z) = const,
и мы еще раз получаем единственность старшего век¬
тора. Кроме того, мы видим, что роль старшего вектора
в реализации на группе Z играет функция f0(z)== 1.
2. Реализация на группе Г. Вместо предыду¬
щих построений мы могли бы использовать разложение
g — 'Qt, ^eZ_, t^T, и заметить, что всякая функция
вполне определяется своими значениями на Г.
В результате получаем оператор
Rgf(t) = f(tg),
где точка tg определяется из разложения Гаусса tg = 'C,tg,
[eZ_, /гЕ Г. При этом функции из пространства пред¬
ставления удовлетворяют условию f{bt) = a(b)f(t). Роль
старшего вектора играет функция а(/). Это представле¬
ние мы называем реализацией на группе Т.
3. Реализация на группе U. Вместо разложе¬
ния Гаусса мы могли бы воспользоваться разложением
Грама: g = z'Qu (§ 9). Из этого разложения очевидно,
что всякая функция / е вполне определяется своими
значениями на унитарной подгруппе U = SU(/i). Фор¬
мула представления принимает следующий вид:
(и) = а (г') ф {ug).

212 ГЛ. VU. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ V(n)
Здесь матрицы г', ug определяются из разложения Гра-
ма ug = e%ug. Функции из пространства представления
удовлетворяют соотношению ср(уп) = а(у)ф(п), где у
пробегает «диагональную» подгруппу Г, состоящую из
всех диагональных матриц у е U. Роль старшего век¬
тора играет функция а (и). Заметим также, что
Т’иоф (ы) = ф (мм0), «0еИ,
т. е. действие элементов u0eU сводится к правому
сдвигу на U.
До сих пор мы рассматривали произвольные веще¬
ственные представления группы G. Если ограничиться
аналитическими представлениями, то они остаются не¬
приводимыми при сужении на унитарную подгруппу U.
В результате получаем описание всех таких представле¬
ний.
Теорема 3. Всякое неприводимое представление
группы U = U (п) определяется однозначно, с точностью
до эквивалентности, некоторым характером а (у) диаго¬
нальной подгруппы Г. Это представление может быть
реализовано с помощью правых сдвигов
ЯаЛ>(и) = ф(«ы0)
в конечномерном пространстве Фа, состоящем из функ¬
ций ф (и) на группе U. Пусть а (б)—аналитическое про¬
должение а (у) на группу D и а (g) — соответствующая
функция на группе G. Полагая а (и) — a(g) \g=u, мы мо¬
жем охарактеризовать пространство ©а как цикличе¬
скую оболочку функции а(и). То же верно для группы
SU (л).
Напомним, что матрица е, входящая в разложение
Грама, является диагональной положительно определен¬
ной матрицей. Отсюда следует, в частности, что
ugg*u-[ = е'Ц,*г' и а(е'2) = a(ugg*u-i). Извлекая квад¬
ратный корень, заключаем, что множитель а(е') может
быть записан следующим образом:
а(е') = {а(м/«“1)}’/\
где положено f = gg*. Практически реализация на груп¬
пе U является довольно сложной ввиду отсутствия про¬
стой параметризации для группы U. В то же время

§ 49. ИНДУКТИВНЫЕ ВЕСА
213
многообразие Z изоморфно евклидову пространству и
легко параметризуется. Поэтому неприводимое пред¬
ставление группы U обычно бывает удобно рассматри¬
вать также в реализации на группе Z.
Упражнение
Пусть диагональные матрицы s, s' связаны разложением Грама
us = 8’tp. Пусть /j, /г, •••, in, Тц Тг т„ —логарифмы собствен¬
ных значений матриц е, е', причем t\ ^ t2 ^ in- Показать, что
И + т2 + ... +tn = tl + t2+ ... + /„,
+ Т‘2 + **' **■ /г = 1, 2, ..., ц — 1,
при любом выборе матрицы usU(n). Здесь ц, ь h — произ¬
вольный набор индексов, принимающих значения 1, 2, .. ., л. Срав¬
нить с результатом упражнения 2 на стр. 345.
§ 49. Индуктивные веса
Для полного решения задачи классификации оста¬
лось перечислить все характеры а (6), которые являются
старшими весами неприводимых представлений груп¬
пы G. Такие характеры мы будем называть индуктив¬
ными.
Пусть Дь Д2, ..., Дп — главные диагональные ми¬
норы матрицы g ge G. Если g — 6, то эти миноры яв¬
ляются мультипликативными параметрами матрицы 6.
Следовательно, всякий характер ос(6) мы можем также
записывать в виде
а (6)= ПД?-
i=i
Здесь мы рассматриваем для простоты только комплекс¬
но-аналитические характеры. В общем случае необхо¬
димо добавить сомножители Д,- в некоторых степенях.
Заметим, что A„ = detgr=l для элементов группы
SL(n), однако мы сохраняем множитель Д„ для обоб¬
щения на GL(n). Существенно, что все миноры Д,- обла¬
дают следующим свойством: Д,-(£6z) = Д,-(6). Следова¬
тельно, имеет место также формула
<*(*) = Ид?,
»-1

214 ГЛ. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(n)
где А,- на этот раз означает главный диагональный ми¬
нор матрицы g. Заметим, что параметры г, связаны с
tl
параметрами в разложении а(б) = Цбт‘ следую-
« = 1
щими соотношениями:
ri = mi — mi+u i= 1, 2, ..n,
где положено для общности записи тп+\ = 0. Если пара¬
метры г* являются неотрицательными целыми числами,
то функция a{g) является полиномом на группе G. От¬
сюда следует, что в данном случае SRa конечномерно, и
мы получаем серию неприводимых представлений груп¬
пы G. Поскольку Дп является инвариантом, тот же ре¬
зультат получается при произвольном целом гп. Заме¬
тим, что полученные условия 0, г = 1, 2, ..., п—1,
равносильны следующему свойству упорядоченности:
/Л] ^ т2 ^ т3 ^ ... ^ тп.
Теорема 4. Характер а(6) является старшим ве¬
сом тогда и только тогда, когда для его показателей вы¬
полняется соотношение упорядоченности mj ^ т2 ^ . ..
... ^ шп. Иначе говоря, все разности гх = т^ — ь
I = 1, 2, . .. , п— 1, должны быть неотрицательными це¬
лыми.
Замечание!. Мы рассматриваем здесь только
аналитические характеры а (б). Отсюда непосредственно
вытекает целочисленность тг для GL(n) и целочислен-
ность разностей — тг+i для SL(n). Вещественные
характеры а (б) будут рассмотрены ниже.
Доказательство. Необходимость условий упо¬
рядоченности была уже доказана в § 44 путем рассмот¬
рения симметрии относительно группы Вейля. Если мы
желаем получить независимое доказательство, то можно
поступить следующим образом.
Заметим, что если G0 — подгруппа в группе G, сохра¬
няющая все базисные векторы, кроме еш, то G0 изо¬
морфна SL(2) и разложение Гаусса в группе G индуци¬
рует разложение Гаусса в G0. Если ^еСо, г е Z f 1 G0,
то формула
Tsf(z) = a(z,g)f(zg)

§ 49. ИНДУКТИВНЫЕ ВЕСА
215
определяет неприводимое представление SL(2) в цикли¬
ческой оболочке старшего вектора /о*). Следовательно,
если характер а(8) индуктивен по отношению к группе
G, то его сужение на подгруппу D0 = D П G0 является
индуктивным по отношению к Go- Заметим теперь, что
а (б0) = +
где А= бц — единственный мультипликативный параметр
в группе D0*'>!). Как следует из теории представлений
группы SL(2), показатель m, — mi+\ должен быть целым
неотрицательным ***). Следовательно, tn^m^ ...
Достаточность этих условий доказана в начале на¬
стоящего параграфа.
Теорема доказана.
Замечание 2. Если G = SL(«, С), то параметры
т\, т2, ..., тп определяются с точностью до общего
слагаемого (ибо det g = 1); следовательно, такие пара¬
метры могут быть и нецелыми. Они становятся целыми,
если ввести нормировку тп = 0 (вообще если хотя бы
одно из чисел т, выбрать целым).
Замечание 3. Если рассматривать вещественные
представления группы G, то общий вид характера а (б)
дается следующей формулой:
а (б) = И 6**5'/.
i = 1
Если мы желаем рассматривать только однозначные
представления, то разности /г;— необходимо выбрать
целыми для группы GL(«). Повторяя доказательство
теоремы 4, получаем следующие ограничения:
... >/„.
При этом числа kt — ki+\, /,• — li+l обязательно должны
быть целыми при i = 1, 2, ... , п— 1. Однако числа kn,
1п не обязаны быть целыми в случае GL(/j) и не обя¬
заны быть положительными.
*) Это следует из мультипликативной формулы для a(z,g).
**) Si+i, j+i Аг1 в силу условия detg= 1; = 1 при k Ф1
i+1.
***) Глобальное доказательство для SL(2) см. в [84], стр. 42,

216 гл. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(л)
Замечание 4. Всякое неприводимое представле¬
ние GL(rc) может быть построено по формуле неприво¬
димого представления SL(«) с добавочным скалярным
множителем вида (det g)t,l(det g)'n.
В дальнейшем мы, как правило, будем рассматривать
только аналитические представления GL(n). Всякий век¬
тор а = (т., т2, . . . , тп) с целочисленными координа¬
тами, удовлетворяющими условиям упорядоченности
nil ^ т2 ^ ^ тп, мы будем называть сигнатурой.
В случае SL(n) эта сигнатура определяется с точностью
до общего слагаемого у всех координат ти т2, . .., тп.
§ 50. Произведение Юнга
Условимся использовать наряду с обозначением
a = (/Jii, т2, ..., тп) также обозначение а — [гь г2, ...
..., /■„_,] для сигнатуры SL(n), где положено г,-—
= т., — mi+i. При этом все параметры rt, i = 1, 2, ...
..., п—1, являются целыми неотрицательными. Следо¬
вательно, множество всех сигнатур порождается векто¬
рами
а, = [0, 0, ... , 0, 1, 0, . .. , 0]
(с единицей на i-м месте) относительно сложения. Не¬
приводимые представления dt = d(a,i) мы условимся на¬
зывать базисными представлениями группы SL(«)*).
Выясним геометрическую структуру каждого из этих
представлений.
Пусть С1'2 1р — антисимметричный тензор ранга р.
В силу условия антисимметричности мы получим пол¬
ную систему независимых координат, если положим
ii < h < • • • < ip- Пусть е. . . — соответствующий ба-
12 р
зисный вектор (т. е. тензор, у которого отлична от нуля
только одна независимая координата i'1*2 1р = 1). Век¬
тор е. . . является весовым с весом
<,i2 1р
*) В статье [84] эти представления обозначались символами
Д,-, i = L, 2, ..., п — 1.

§ 50. произведение юнга
217
В силу условия i'i < i2 < . . . < ip все такие веса различ¬
ны. Следовательно, всякий старший вектор должен сов¬
падать с одним из элементов е, . , . Однако условию
М‘2 ‘р
упорядоченности сигнатуры удовлетворяет лишь един¬
ственный вес Др — pi 2... р'
Ар = 6j62 ... бр.
Соответствующая сигнатура определяется равенствами
гр = 1, Г), = 0 при к ф р, т. е. совпадает с символом Др,
определенным выше. Следовательно, тензор не.
приводим и соответствующая сигнатура совпадает с Др.
Антисимметричные тензоры ранга р называются по¬
ливекторами. Очевидно, поливектор ранга р определен
только при 1 р ^ п. (Если р > п, то тензор t‘
обращается тождественно в нуль в силу условий анти¬
симметрии.) Таким образом, базисное представление
dp отождествляется с поливектором ранга р*).
Из строения произвольной сигнатуры ясно, что вся¬
кое представление d(а) может быть определенным об¬
разом построено из базисных представлений du d2,
dn-\. Ясно, что искомая конструкция не сводится
к тензорному произведению, ибо тензоры, как правило,
приводимы. Для ответа на поставленный вопрос мы ис¬
пользуем операцию умножения в классе функций на
группе G (либо также на подгруппах Z, Т, U).
Пусть SKa — пространство неприводимого представле¬
ния в одной из функциональных реализаций, описанных
выше. Введем обозначение SRaSRp для линейной оболочки
всех произведений вида ф(л-)ф(.х), ф е SRa, ф е SRp. До¬
кажем, что имеет место
Теорема 5. SRa+p = SRaSRp.
Доказательство. Рассмотрим, например, реа¬
лизацию на группе G (во всех остальных случаях дока¬
зательство аналогично). Тогда пространство SRaSRp
*) В реализации на группе G базисный вектор г- отож¬
дествляется с минором gt j ^ j матрицы g, составленным из пер¬
вых р строк и столбцов с номерами ц, i2, ..., /р.

218 ГЛ. VII. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ ГРУППЫ U(n)
натянуто на функции
f*B, = а (gg\) Р (Sg-i), gu gi^G.
Отсюда очевидно, что оно инвариантно относительно
= fg<g«, g*gX Ясно также, что 3fafRp конечно¬
мерно. В то же время 9?а+р натянуто на функции
fg* = v(gg0)&(ggo)
и потому является подпространством в Осталось
доказать, что последнее пространство неприводимо. По¬
скольку все функции из этого пространства удовлетво¬
ряют соотношениям
f(Zg) = }(g), f (5g) = <* (6) р (6) f (g),
то они вполне определяются своими значениями на Z.
Поскольку операция /?,0 сводится к правому сдвигу на
Z, то единственной функцией f(z), удовлетворяющей ус¬
ловию RzJ(z) = f(z), является (с точностью до множи¬
теля) f0(z)= 1. Из единственности старшего вектора за¬
ключаем, что 9?а8?р неприводимо. Теорема доказана.
Полученный результат показывает, что операция ум¬
ножения в классе функций на группе G является иско¬
мой операцией, заменяющей тензорное произведение.
Определение 2. Представление d(а + Р) мы бу¬
дем называть произведением Юнга представлений d(а).
d(\3) и использовать для этого произведения символ
d(oc)d(P).
Абстрактное множество, удовлетворяющее всем ак¬
сиомам группы, кроме наличия обратного элемента, при¬
нято называть полугруппой. В терминах произведения
Юнга результат произведенной классификации можно
выразить следующим образом:
Следствие. Множество всех неприводимых анали¬
тических представлений группы G = SL(n, С) является
полугруппой с образующими d\, d2, ■ ■ ., dn-ь где dp —
поливектор ранга р:
d (а) = d\'drJ ... drn%'.
Заменяя SL(«) на GL(«), мы должны добавить две
образующие: dn и dn\ ибо показатель гп может быть
положительным и отрицательным. Если рассматривать

§ 50. ПРОИЗВЕДЕНИЕ ЮНГА
219
вещественные представления SL (п), то число образую¬
щих удваивается за счет добавления комплексно сопря¬
женных представлений du d2, .. ., dn~\. Если рассмат¬
ривать вещественные представления GL (л), то полу¬
группа представлений перестает быть дискретной, ибо
множители det g, det g входят необязательно с целыми
показателями.
В дальнейшем мы увидим, что представление d(а)
содержится в тензорном произведении d/ ® di ® ...
...<S>dim, где множитель встречается раз. При этом
d(а) содержится в таком произведении однократно и
сигнатура а является старшей среди всех остальных сиг¬
натур, входящих в это произведение (относительно лек¬
сикографической упорядоченности). Отсюда вытекает
возможность иного определения произведения Юнга.
Упражнение
Сформулировать результат классификации неприводимых пред¬
ставлений U (п) в «инвариантных» терминах (не зависящих от вы¬
бора базиса, в котором группа D диагональпа.) Указание: ис¬
пользовать орбиты в классе эрмитовых матриц п X п относительно
присоединенного представления U (п) (каждой такой орбите с цело¬
численными собственными значениями ставится в соответствие не¬
приводимое представление U(n)) *).
* *
*
Глобальный метод, которому мы следовали в этой главе, впер¬
вые был предложен Р. Г о д е м а н о м [74]. Однако функциональная
реализация представлений (на группе Z, на группе U) была вве¬
дена еще раньше в фундаментальной работе И. М. Гельфанда
и М. А. Наймарка [68] по теории бесконечномерных представле¬
ний. Изложение в этой главе следует статье автора [84], где разви¬
вается метод Р. Годемана. Свойство мультипликативности про¬
странств Э?а было впервые отмечено автором в работе [85].
В дальнейшем мы значительно уточним описание канонической
модели представления d(a) (гл. X) и обобщим эти результаты
на конечномерные представления произвольной связной группы Ли
(гл. XVI). В следующей главе будет изложена классическая кон¬
струкция представлений d(а) в классе тензоров; там же будут ука¬
заны еще и другие модели d(a).
*) Общий способ классификации неприводимых (бесконечно¬
мерных) представлений в терминах орбит предложен А. А. Кирил¬
ловым для класса групп, не содержащего U(n); однако этот способ
переносится также и на компактные группы Ли.

ГЛАВА V!IT
ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
Изучение тензоров является классической задачей
теории представлений. Речь идет о спектральном ана¬
лизе, т. е. о разложении тензоров на неприводимые
компоненты. Исторически решение этой задачи впервые
позволило Г. Вейлю [10] дать явную модель неприво¬
димых представлений группы GL(n) и других классиче¬
ских групп. Мы приступим к решению этой задачи, уже
имея информацию о запасе неприводимых представле¬
ний. Для простоты мы будем рассматривать только
контравариантные тензоры для группы G = GL(n).
В конце главы по аналогии с тензорами изложим
также две другие конструкции неприводимых представ¬
лений группы G.
§ 51. Описание Z-инвариантов
Вместо тензоров tl 1*2 •■■'m нам будет удобно
рассматривать соответствующие полилинейные формы
(р(х, у, = imXiiyi2 ••• wim, гд ex, у, w —
система m независимых ковариантных векторов-строк.
Согласно общим замечаниям, сделанным в конце § 14,
мы можем вместо тензорного закона преобразовании
рассматривать операторы
TgcpU, у ay) = cp(xg, yg, ..., wg),
определенные в классе полилинейных форм. Пусть Ф
означает полную алгебру (контравариантных) тензоров
и Фт — конечномерное подпространство тензоров ранга
т. Мы отождествляем тензоры с соответствующими фор¬
мами. Таким образом, операторы Tg образуют представ¬
ление группы G в пространстве Фт. Очевидно, это пред-

§ 51. ОПИСАНИЕ Z-ИНВАРИАНТОВ
221
ставление имеет вид
nm = d, ® d, <8> ... ® d,
(т сомножителей), т. е. совпадает с ш-й тензорной сте¬
пенью неприводимого представления т = db Поскольку
представление лт аналитично, оно вполне приводимо.
Следовательно, мы можем поставить задачу о разложе¬
нии ящ на неприводимые представления.
Следуя методу Z-инвариантов, мы решаем вначале
систему уравнений <р(xz,yz, ..., wz) = ф(х,у, w),
где г пробегает группу Z всех верхних треугольных мат¬
риц с единицами на главной диагонали. Отметим вна¬
чале следующее легко проверяемое утверждение-
1° Миноры
X,
Ху
... хр
Юр =
У1
Уг
• • • Ур
, 1 < р П
щ
и2
. . . Up
являются Z-инвариантами.
Далее, если ср и ф являются Z-инвариантами, то это
верно также для ?хр + рф, фф. Иначе говоря, имеет
место
2° Множество Q всех Z-инвариантов является под¬
алгеброй в алгебре Ф.
Заметим, что умножение в алгебре Ф некоммута¬
тивно. Действительно, в терминах полилинейных форм
умножение двух тензоров ф, ф задается равенством
фф (х,у, . . . , w, х', у', .. ., w') = ф (лг, у, .. ., w) ф (*', у',...
..., w') и произведение, взятое в другом порядке, отли¬
чается перестановкой аргументов. Для наших целей су¬
щественно также следующее замечание:
3° Алгебра Q инвариантна относительно всевозмож¬
ных подстановок s<p(x, у, ..., w) = ф (х\ у', ..., w'), где
х', у', ..., w' — подстановка х, у, ..., w.
Комбинируя 1° — 3°, мы получаем в алгебре £2 сле¬
дующий запас одночленов:
ю(а, s) — • • • юп">

222
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
где символ а отождествляется с набором неотрицатель¬
ных чисел г\, г2, ..., гп и символ s означает произволь¬
ную подстановку.
В теории инвариантов доказывается ([10]), что одно¬
члены вида со (a, s) образуют линейный базис в про¬
странстве й. Это утверждение сразу решает вопрос о
полном запасе Z-инвариантов. В действительности это
утверждение мы не будем использовать (и даже полу¬
чим его независимое доказательство из общих резуль¬
татов спектрального анализа). Тем не менее для более
удобного обзора ситуации мы можем вначале иметь в
виду этот общий результат, который сформулируем в
виде следующей леммы:
Лемма 1. Миноры соь а2, • • •, w„ являются обра¬
зующими в алгебре Й.
Выясним действие диагональной группы D на мино¬
ры ар. Если 6 = diag{61, б2, ..., 6„}, то положим Др =
= 6162... Sp. Очевидно, (Dp —* (ОрДр под действием опера¬
тора Т&. Следовательно, всякий одночлен со (a, s) яв¬
ляется весовым с весом
а (б) = ... б> - д;-д^ ... д;«.
Здесь числа rti\ >- т2 ^ тп неотрицательные целые
и числа Г\, г2, ..., гп связаны с ними обычными соотно¬
шениями гл. VII: = mi — mi+i, i= 1, 2, ..., п\
тп+1 = 0. Очевидно, числа rt совпадают с показателями
одночлена со (a, s). Заметим, что при этом
т = тх + т2+ ... + тп = г{ + 2г2+ ... + пгп,
где т—-ранг тензора со (a, s). Как и в гл. VII, мы пола¬
гаем а = {ти т2, .. ., тп) = [ги г2, . . ., гп\. Для крат¬
кости введем обозначение jct | для суммы тх + т2+...
... + тп. Из леммы 1 непосредственно находим
Следствие 1. Всякий старший вектор сигнатуры
а = (rri\, т2, ..., mn) содержится в линейной оболочке
одночленов со (a, s) с фиксированным а.
Указанную линейную оболочку обозначим символом
йа = Тогда Q = 2йа. Кроме того, йт = 2 йа,
1 2 п [ а I =*т
где Qm означает множество всех Z-инвариантов ранга пг.

§ 51. ОПИСАНИЕ Z ИНВАРИАНТОВ
223
Соответственно Фт = 2 Фа. где Фа — циклическая обо-
la |=т
лочка Qa относительно группы G.
Следствие 2. Кратность вхождения неприводи¬
мого представления d(a) совпадает с числом линейно
независимых одночленов среди со (a, s).
Результат нашего исследования может быть записан
в виде пт = 2 k(a)d(a), где k (a) — кратность вхож-
| а | =т
дения d(a) в Фш, а также и во всю алгебру Ф.
Пример 1. jti = d\. Представление т неприво¬
димо.
Пример 2. n2 = d'\ + d2. Действительно, при
т = 2 имеются только старшие векторы
= СО, (х) COj (у), со2 = со2(х, у)
и векторы, получаемые из них перестановками аргумен¬
тов х, у. Поскольку эти перестановки сохраняют со^ и
меняют знак со2, то мы получаем коллинеарные векторы.
Следовательно,
а — [2, 0, .... 0], р=[0, 1, 0, ..., 0]
являются единственно возможными сигнатурами и каж¬
дая из них встречается однократно.
Пример 3. л3 = <К\ + 2dld2 + d3. Действительно, в
данном случае имеются три вектора:
a3l = ai(x)al(y)ai(z), ш1со2 = (х) аз, (у, г), ©3 = со3 (х, у, г),
а также векторы, получаемые из них путем всевозмож¬
ных подстановок аргументов х, у, г. Эти подстановки не
меняют со^, сохраняют о>3 с точностью до знака и пере¬
водят форму со](02 с точностью до знака в три формы
т, т', т", для которых т + х' + х" = 0 (циклическая под¬
становка х, у, г). В то же время нетрудно видеть, что
формы т, х' линейно независимы; отсюда ясно, что did2
встречается двукратно.
В общем случае легко проверить, что имеют место
следующие закономерности:

224
ГЛ. vm. ТЕНЗОРЫ И ДИАГРАММЫ юнга
1. Представление d[n,tn = 0, 1, 2, встречается в
Ф однократно (симметричные тензоры ранга ш).
2. Представление dp, 1 р ■< п, встречается в Ф од¬
нократно (поливекторы ранга р).
Остальные представления требуют значительно более
глубокого изучения. В игру вступает симметрическая
группа S = S (пг) всех подстановок т аргументов х, у,...
. .., w. (На языке тензорных индексов это означает под¬
становку гь 1'г, im.) К рассмотрению группы S, дей¬
ствующей в пространстве Фт, мы сейчас и переходим.
§ 52. Диаграммы Юнга
Для более глубокого изучения симметрии в классе
тензоров мы займемся вначале более подробным изуче¬
нием симметрической группы S = S(m). Нам будет
удобно рассматривать эту группу как группу преобразо¬
ваний в классе чисел i = 1, 2, . . . , т. Каждый элемент
seS определяется при этом системой чисел si = si,
s2, . . . , sm, которые принимают те же значения в дру¬
гом порядке. Обычно в этом случае используется запись
1 2 ... т.
si s2 ... sm
причем порядок размещения каждой пары (k, sk) счи¬
тается несущественным. Закон композиции в группе оп¬
ределяется по правилу sai = s(ai). Обратное преобразо¬
вание s-1 мы также будем обозначать символом s'*).
Поскольку обратное преобразование сводится к инвер¬
сии пары (k, sk), то мы имеем
s'l s'2 ... s'm \
1 2 ... т / ’
Ясно, что операция s' удовлетворяет тождеству (sa)' =
= a's'. Допустим теперь, что Y = (ii, 12, ..., 1,,,} — упо¬
*) Если рассматривать t как базисный вектор в m-мерном ев¬
клидовом пространстве, то мы получаем точное линейное представ¬
ление группы S и штрих отождествляется с транспонированием
(поскольку все матрицы seS ортогональны).

§ 52. ДИАГРАММЫ ЮНГА
225
рядоченная схема, заполненная т «предметами» i\, k,. ..
. .., im (природа этих предметов несущественна*)). Мы
определяем действие подстановки s на схему Y по пра¬
вилу
{^11 iЪ • • 4n}s “ С'Ъ • • •» 4m}-
Иначе говоря, в схеме Ys на месте с номером k распо¬
лагается предмет, который в схеме Y был расположен
на месте с номером sk. При этом, как нетрудно видеть,
выполняется следующий закон композиции:
Ysc = (Ys)a-
Существенно заметить, что действие подстановки опре¬
деляется не номерами предметов, а номерами тех мест,
на которых они расположены**). Вслед за Г. Вейлем
мы можем повторить, что «весь этот на вид чрезмерный
педантизм оказывает серьезную помощь в уяснении по¬
рядка, в котором выполняется композиция подстановок».
Рассмотрим теперь произвольное разбиение m =
= mi + m2 + . . . + tnf числа m в сумму f невозрастаю¬
щих натуральных слагаемых: ni\ т2 ^ ^ mf. Вся¬
кому такому набору чисел сопоставим индекс а, назы¬
ваемый сигнатурой. Дополняя эти числа нулями, можем
считать, не ограничивая общности, что f = in. В классе
сигнатур мы будем использовать обычное определение
лексикографической упорядоченности. Рассмотрим кле¬
точную таблицу Y(а):
1
f4
2
f*2
3
f-3
it
I I
и 2 Ш-! /77
m,
СП р
й
/77,
*) В приложениях, которые нас интересуют, роль предметов
И, к, .... im будут играть тензорные индексы (принимающие зна¬
чения 1, 2 т) либо векторные аргументы х, у, w,
**) В то же время предмет с номером k располагается в схеме
И на месте с номером s'k.

226
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
Эта таблица содержит т,\ клеток в первой строке, тч
клеток во второй и т. д. Если положим — m,— mi+1,
i = l, 2, ..., f, nif+\ = 0, то rp означает число столбцов
длины р. На чертеже указана фиксированная нумерация
полей, которую условимся называть стандартной. Вся¬
кая таблица такого типа называется диаграммой Юнга.
Если эта таблица заполняется предметами i\, г'г, .. ., im,
причем предмет ih располагается на месте с номером k,
то такое заполнение будем называть стандартным и
обозначать тем же символом Е(а). Символом КДа)
будет обозначаться схема, получаемая из К(а) по ука¬
занному выше правилу подстановок.
С каждой сигнатурой а мы свяжем следующие под¬
группы в группе 5. Подгруппа Р состоит из всех «гори¬
зонтальных движений» в схеме Y (а) (движение внутри
строк). Подгруппа Q состоит из всех «вертикальных дви¬
жений» (движения внутри столбцов). Положим также
R = QP-
Элементы этого множества (которое, вообще говоря, не
является группой) условимся называть элементарными
подстановками. Если s = or, г е R, то условимся гово¬
рить, что s элементарно выражается через о. В заклю¬
чение этого параграфа докажем простую комбинаторную
лемму, которая будет играть принципиальную роль во
всех дальнейших построениях:
Лемма 2. Если а > а', то при любых подстановках
s, о существует пара предметов, расположенных в одной
и той же строке диаграммы Fs(a) и в одном и том же
столбце диаграммы Уа(а'). То же верно, если а = а',
но s не выражается элементарно через о.
Доказательство. Положим Y ~ Ks(a), Y' =
= Ya(a'). Условие означает, что число столб¬
цов диаграммы Y' не превосходит числа предметов, рас¬
положенных в первой строке диаграммы Y. Следова¬
тельно, если все такие предметы попадают в различные
столбцы диаграммы У, то обязательно тх = гп\. Отбра¬
сывая эти элементы, получаем то же заключение для всех
остальных строк. Следовательно, если все предметы, на¬
ходившиеся в одной строке диаграммы Y, попадают в

§ 53. СИММЕТРИЗАТОРЫ ЮНГА
227
разные столбцы диаграммы Y', то а = а'. Производя в
диаграмме Y' вертикальное движение q, мы можем по¬
ставить каждый предмет в ту строку, где он был распо¬
ложен в диаграмме Y. Производя затем горизонтальное
движение р, мы отождествляем У и Y'qp. Но это озна¬
чает, что s = or, где г = qp. Лемма доказана.
Очевидно, лемма 2 является качественным выраже¬
нием того обстоятельства, что с понижением сигнатуры
«повышается роль столбцов». Отсюда вытекает также
Следствие. Если а> а', то для любых подстано¬
вок s, о существуют горизонтальная транспозиция рй в
У(а) и вертикальная транспозиция qo в У(а/)> для ко¬
торых
spos-1 = ор0а~‘.
То же верно, если а = а', но s не выражается элемен¬
тарно через а. В частности, если s не элементарно, то
существуют транспозиции р0, Яо для которых
sPo — Pos-
Действительно, пусть г, / — номера предметов, ука¬
занных в лемме 2; тогда эти предметы расположены на
местах s'i, s'j в таблице Ys(а) и на местах оЧ, o'j в таб¬
лице Y0(a'). В качестве ро, qo мы выбираем транспози¬
ции этих пар. При этом равенства spos4 = /, oq0o4 = j
означают, что то = sp0s' = aqoO' есть транспозиция
пары (/,/).
§ 53. Симметризаторы Юнга
Мы будем рассматривать формальные линейные ком¬
бинации элементов seS, т. е. групповое кольцо, состоя¬
щее из элементов x = 2x(s)s. Каждой стандартной диа¬
грамме Юнга поставим в соответствие элемент
с = 2 ± ЧР,
называемый симметризатором Юнга. Здесь р пробегает
Р, q пробегает Q и знак определяется четностью или
нечетностью подстановки q. Если данная диаграмма со¬
стоит из одной строки, то оператор с определяет усред¬
нение по группе S; если диаграмма состоит из одного

228
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
столбца, то этот оператор определяет альтернирование
по группе S. Очевидны следующие тождества:
<70с=±с, ср0 = с, (*)
где знак ± определяется четностью или нечетностью
подстановки q0 (т. е. числом транспозиций в этой под¬
становке). Если вместо нумерации 1, 2, т считать
стандартной нумерацию si, s2, . . . , sm (нумерацию
предметов на полях диаграммы Ys), то вместо оператора
с получаем оператор
с' — scs~\
который будем называть эквивалентным оператору с.
Положим также с = c(Y), с' = с(Ys). Покажем, что сим-
метризаторы Юнга обладают рядом замечательных ком¬
мутационных соотношений.
Лемма 3. Положим с = с(У8(а)), с' = c(Ya(a')).
Тогда имеем:
1) с2 = рс, где константа р зависит от сигнатуры а
(но не зависит от s);
2) сс' = 0, если либо а> а', либо а = а', но s не
выражается элементарно через а;
3) сс' == ±p(sc0CT-1), если а = a', o~]s = qp\ при этом
Со = с (У (а)) и знак определяется как sgn q.
Доказательство. Положим х — с2, s — е. Как
следует из (•*), элемент х удовлетворяет тождествам
qx — ±х, хр = х. Записывая х в виде 2.x(s)s, находим
отсюда, что функция x(s) удовлетворяет следующему
тождеству:
х (qsp) =±х (s),
где знак определяется как sgn q. Если s не элементарно,
то, как мы знаем (следствие из леммы 2), существует
пара транспозиций р0, qo таких, что q0spo = s. Следова¬
тельно, в этом случае
x(s) = — x(s),
ибо транспозиция q0 нечетна. Следовательно, в этом слу¬
чае x(s) = 0 и функция x(s) может быть отлична от
нуля только при s элементарном, s = qp. Но тогда имеем
x(qp)= ±х(е),

§ 53. СИММЕТРИЗАТОРЫ ЮНГА
229
где по-прежнему знак определяется как sgn q. Полагая
р = х(е), мы находим, что х = рс. Свойство 1) доказано.
Для доказательства свойства 2) достаточно использо¬
вать транспозицию т0 = sp0s~l = aqост-1, для которой со¬
гласно мы имеем сто = с, то с' = —сЭлемент у= сс'
удовлетворяет при этом соотношению
сс' = ст0т0с' = — сс'.
В результате сс' = 0. Наконец, свойство 3) получается
непосредственной проверкой. Лемма доказана.
Докажем, что константа р отлична от нуля. Пусть
X — групповое кольцо группы S (т. е. линейное про¬
странство размерности т\). Всякий элемент аеХ, рас¬
сматриваемый как оператор левого умножения х-+ах,
ieX, задается квадратной матрицей [|a(sf-1)||, где s, t
пробегают S. Следовательно,
sp а = ml а (е),
где слева имеется в виду след оператора левого умноже¬
ния. Положим а = с = S ± qp, и пусть Х0 = сХ — область
значений оператора с. Поскольку след любого оператора
совпадает со следом на области значений, то для вы¬
числения sp с достаточно рассматривать подпростран¬
ство Х0. Но согласно 1) на Д оператор с сводится к
умножению на р. В результате sp с = рл0, «о = dim Х0,
и мы имеем
Р«0 = т\,
откуда р Ф 0. В результате получаем
Следствие. Всякий оператор d — -^-c является
проекционным (d2 = d), и два проектора d = ~-c,
d' = -^rc' взаимно ортогональны (dd'= 0), если выпол¬
няется условие 2) из леммы 3.
Если фиксировать симметризатор с0 = с(У(а)) и ус¬
реднить выражение scos-1 по группе S, то мы получаем
элемент, перестановочный со всеми элементами из S.
Положим
e = 7^S£:»rl'

230
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
где сумма берется по всем подстановкам seS. Полу¬
ченный элемент, зависящий только от сигнатуры а, мы
будем также обозначать символом в (а). Нетрудно про¬
верить, используя лемму 3, что
для всякого симметризатора с = sc0s_1, отвечающего
данной сигнатуре а. Оператор е мы будем называть
центральным симметризатором Юнга.
Лемма 4. Центральные симметризаторы е = е(а),
s' = е(а') являются взаимно ортогональными проек¬
ционными операторами:
Доказательство. Если использовать тождество
(**), то мы находим
Далее, поскольку операторы е, г' взаимно перестановоч¬
ны, то можем считать, не ограничивая общности, что
а > а'. Тогда согласно свойству 2) имеем
(здесь сумма берется по всем элементам c~scQs~l, с'—
= oc'o~l, s, сте5). Лемма доказана.
Лемма 5. Пусть е — единичный элемент в группе S
ив, е', . .. — совокупность всевозможных центральных
симметризаторов Юнга. Тогда е = е + в' + . .., т. е. про¬
екторы е, е', ... осуществляют разложение единицы в
групповом кольце группы S.
Доказательство. Пусть X—групповое кольцо и
3 — его центр. Элементы е, г', ... содержатся в 3 и ли¬
нейно независимы в силу свойства ортогональности.
Число таких элементов равно числу всевозможных сиг¬
натур mi > m2 > ... > mf, mi + m2 + ... + mf = m.
С другой стороны, если z = hz(s)s содержится в 3.
то функция г(«) должна удовлетворять следующему
се = вс = с
(**)
при а = а',
при афа'.
2
С = 8.

§ 54 СИММЕТРИЯ НЕПРИВОДИМЫХ ТЕНЗОРОВ 231
тождеству:
z(SoSSol)~z(s)
для всякого s0 е S. Следовательно, размерность линей¬
ного пространства 3 равняется числу классов сопряжен¬
ных элементов в группе 5. Как мы видели в § 34, число
таких классов также равняется числу сигнатур. Действи¬
тельно, если использовать преобразования s-*s0ss~1t то
всякая подстановка s может быть приведена к «нормаль¬
ной форме» вида
О = 0)02 ■ • • <Д,
где ой означает цикл длины mk, т.\ > т2 > ... > т.) и
числа 1,2, ..., т расположены под знаком этих циклов
в нормальном порядке. В результате мы видим, что эле¬
менты е, е', ... образуют базис в пространстве 3- По¬
скольку ееЗ, то мы имеем е = Хе + Х'г' + ... Умножая
последовательно на е, г', ..., получаем, что Х=Х'=...
...= 1. Лемма доказана.
В заключение заметим, что проекторы d, d', .... яв¬
ляются минимальными проекторами в X. Это означает,
что если d = d\ + d2, где d\, d2— взаимно ортогональные
проекторы, то либо d = d\, либо d = d2. Действительно,
согласно определению проекторов d{, i = 1,2, мы имеем
di = ddid. С другой стороны, повторяя доказательство
пункта 1) из леммы 3, получаем, что всякий элемент
Xq — dxd коллинеарен элементу d. В частности,
di — Xpd,
Поскольку di — проектор и d — ненулевой проектор, то
числа Xi могут принимать только значения 0 и 1. По¬
скольку также d — d\ + d2 = {Х\ + X2)d, то + Х2 = 1.
Следовательно, d — d\ либо d = d2.
§ 54. Характеристика неприводимых тензоров
в терминах симметрии
Вернемся теперь к рассмотрению тензоров для груп¬
пы G = GL(n). Роль симметрической группы в изучении
тензоров обусловлена тем очевидным фактом, что преоб¬
разования этой группы перестановочны с действием

232
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
группы G. Отсюда следует, что свойства симметрии по
отношению к группе S являются инвариантами по от¬
ношению к группе G и могут быть использованы для
характеристики инвариантных подпространств. Нашей
целью является показать, что этих свойств достаточно
также для характеристики неприводимых подпро¬
странств.
Условимся записывать ф(У) вместо ф(х, у, ..., да) и
tY вместо /г>г2" лт. Здесь У означает упорядоченную схе¬
му, которая заполнена в первом случае аргументами
к, у, . . . , да, а во втором случае — индексами ц, t2, ...
..., im. Для каждого seS положим
вф(У) = ф(Х5), stY = tY‘.
Нетрудно видеть, что эти определения эквивалентны, т.е.
stY является тензором коэффициентов преобразованной
формы «ф(А'). При этом мы используем одно и то же
обозначение для элемента seS и линейного оператора
в Фт. Соответственно положим
с0 = 2 ± <?р
для симметризатора с0 = с (У (а)). Здесь с0 уже является
линейным оператором в Фт. Операторы с = sc0s~1 назы¬
ваются эквивалентными симметризатору с0. Операторы
d, d', . . . ; е, е', ... вводятся так же, как и в § 53.
Докажем теперь, что имеет место следующая ос¬
новная
Теорема 1. Каждый симметризатор Юнга d—■
= — scQs~l проектирует пространство фт на неприводи-
№
мое подпространство со старшим вектором
П
со = «Дед*, а = [/-,, г2 гп],
где миноры со^ расположены в порядке убывания индек¬
сов k. Если сигнатура а = (mu т2, . . . , tnj) имеет бо¬
лее п ненулевых координат, то d<&m = (0). Подпростран¬
ство
Фа = е (а) Фт

§ 54. СИММЕТРИЯ НЕПРИВОДИМЫХ ТЕНЗОРОВ 233
является максимальным подпространством в Фт, пред¬
ставление в котором кратно d(а). Нормировочный мно¬
житель р = р(а) и кратность k(a), с которой d(a) со¬
держится в Фт, связаны следующим соотношением:
р. (а) • k (а) = т!.
Доказательство. Фиксируем сигнатуру а —
— (пг 1, т2, ..., m.f). Назовем такую сигнатуру допусти¬
мой, если f^Cn. Каждой допустимой сигнатуре а поста¬
вим в соответствие старший вектор
со0 = со...
где, как обычно, положено r{ = mt — mi+1, i= 1, 2, ..., п,
mn+i = 0 (если f < п, то числа mf+ь ..., шп заменя¬
ются нулями). Покажем, что вектор шо может быть за¬
писан в виде
= ^оФо.
где dQ = с0 = ± qp и ф0— некоторая форма из
пространства Фт. Для этого вычислим сначала тензор¬
ные коэффициенты формы о)0.
Напомним, что для всякой формы ф(х,у, ..., w)
коэффициенты Л'2'"*"* вычисляются по правилу
ЛРг ••• ‘т = т(е , е. , . .е; V Положим X = \е. , е. , ...
V 11 2 /Я/ 1 1 2
..., е, 1. Рассмотрим сначала следующую схему:
ех е, ех ... е, '
Х° =
е2 е2
еП'
где базисные орты е2, . .. , еп размещены в соответ¬
ствии со схемой Юнга (и где п'^Сп). Подставляя эти
аргументы в указанном порядке в форму а>о, находим,
что
со0(Х°)=1.
Если к схеме Х° применить подстановку типа р, то она
не изменится. Если к этой схеме применить подстановку

234
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
типа <7, то одночлен от0 умножается на sgn <7. В резуль¬
тате
%(X°M) = sgnq.
Нетрудно видеть, что во всех остальных случаях соо(Л') =
= 0. Действительно, если X = ^°-1,где подстановка s не
элементарна, то согласно лемме 2 схема X содержит
в некотором столбце два одинаковых орта и соответ¬
ствующий минор обращается в нуль. Тем более это вер¬
но, если X ф X°s ни при каком se5. В этом случае ко¬
личественное содержание ортов е\, е2, ■ . . , еп в схеме .V
отлично от случая Л-0 и непременно найдется хотя бы
один столбец, содержащий два одинаковых орта.
С другой стороны, рассмотрим вспомогательную фор¬
му <ро, определяемую равенствами фо(Л')= 1 при X = Х°,
фо(А') = 0 во всех остальных случаях. Применим к этой
форме симметризатор Юнга с0:
СоФо М = 2 ± Фо (Хдр).
Ясно, что полученная форма может быть отлична от
нуля только при ^ = где s — некоторая подста¬
новка на S. При этом
<w, F8 - 2 ± %«,»)■
Согласно определению формы фо в правой части может
встретиться отличное от нуля слагаемое только в слу¬
чае, когда X°sqp = .Y0. Но это означает, что sqp <= Р, т. е.
s = Po<7o. <7о = <7-1. Ро^Р-
(Действительно, только в этом случае схема Х° остается
инвариантной.) Наконец, в последнем случае отличны от
нуля только те слагаемые, для которых q~l = q0. Сум¬
мируя по группе Р, получаем в результате
соФо (X°pg) = Xsgnq,
где X— ненулевое число (порядок подгруппы Р). В ре¬
зультате имеем о)0 = — с0ф0. Выбирая другую норми¬
ровку для формы фо, получаем требуемое равенство:
(OQ = Нофр-

§ 54. СИММЕТРИЯ НЕПРИВОДИМЫХ ТЕНЗОРОВ 235
Теперь уже нетрудно завершить доказательство тео-
d = a^doa, а» = ог-'шо, получаем, что вектор ш неподви¬
жен относительно d. Далее, согласно пунктам 2) и 3) из
леммы 3 мы имеем
Но это означает, что проектор d0 проектирует все про¬
странство Qa на одномерное направление м0. Следова¬
тельно, также оператор d проектирует Qa на одномерное
направление и. Далее возможны следующие два вариан¬
та завершения доказательства.
1) Пусть в— центральный симметризатор Юнга, от¬
вечающий сигнатуре а. Поскольку еd = d, d& = а», то мы
имеем также есо = и. Но это означает, что в = в (а) яв¬
ляется единичным оператором на Qa. Если а Ф а', то мы
имеем согласно лемме 4
Следовательно, e(oc) является проектором на Qa во
всем пространстве Qm. Отсюда следует также, что d яв¬
ляется проектором на направление вектора и во всем
пространстве Qm. Действительно, при а Фа' имеем
Наконец, согласно свойству полноты, даваемому лем¬
мой 5, все пространство Qm является прямой суммой под¬
пространств Qa, отвечающих всевозможным сигнатурам
а = (ти т2, mf). Если f > п, то тензор гр = dq> дол¬
жен быть антисимметричен по набору индексов, боль¬
шему п, откуда гр = 0. Следовательно, в этом случае
Qct = (0). Наконец, из перестановочности d, вс опера¬
торами Tg следует, что d проектирует Ф,„ на цикличе¬
скую оболочку вектора ш и в(а) проектирует Фт на
циклическую оболочку Qa.
2) Вместо леммы 5 мы можем воспользоваться лем¬
мой 1, которая независимо дает условие полноты в
классе старших векторов. При этом автоматически
ремы. Поскольку do = d0, то dQco0 = d0<p0 = а»0. Полагая
0, если ст &R,
: со0, если o^R.
eQo' = ez'Qa' = (0).
dQ а/ = dsQa' = (0).

23 S
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
учитывается, что следует рассматривать лишь допусти¬
мые сигнатуры. Все остальные рассуждения остаются
неизменными.
Мы опустили пока соотношение между k(a), ц(а).
Заметим, что оператор с = sc0s~l имеет в пространстве
единственное отличное от нуля однократное собст¬
венное значение р, (на векторе ш). Следовательно,
spe(a) = V sp с = ml/ц. С другой стороны, посколь-
М-
ку е(а) — единичный оператор на Па, то spe(a) = £(a).
В результате p(a)&(a) = т\. Теорема доказана.
Замечание 1. Циклическая оболочка вектора щ
относительно группы G может быть определена как со¬
вокупность всех тензоров ф, для которых
dq> = ф,
j 1 1 -I
где а = — с = — sc0s 1 — соответствующий проектор
Юнга. (Соответственно сер = рф.) Этим свойством ха¬
рактеризуется неприводимое подпространство в Фт*).
Замечание 2. Циклическая оболочка подпрост¬
ранства Qa относительно группы G может быть охарак¬
теризована как совокупность всех тензоров ф, для кото¬
рых
е(а)ф = ф,
где е(а)—центральный проектор, отвечающий сигнату¬
ре а. Этим свойством характеризуется максимальное
подпространство Фа, представление в котором кратно
d(а).
Пр и м е р. Положим т = 3 и рассмотрим диаграмму
Юнга
1
3
2
*) Как следует из замечания 1, тензоры данного неприводи¬
мого подпространства обладают свойством антисимметричности:
qф= ±ф — по отношению к группе Q = sQoS~', где Q0 — подгруппа
вертикальных движений в У (а).

§ 55. ПРИНЦИП ВЗАИМНОСТИ
237
В этом случае подгруппы Р и Q содержат, кроме единич¬
ного элемента, лишь по одной транспозиции:
р = ( 1,3), </ = (1,2).
Множество R = QP состоит из четырех элементов: е, q,
р, qp, из которых первый и третий четны, а второй и чет¬
вертый нечетны. Оператор d0 имеет вид
do = -^r(e-q + p- qp).
Iх
Для вычисления ц напомним, что р/г = 3! = 6. В нашем
случае & = 2 (см. конец § 51). Следовательно, р = 3.
Применяя d0 к произвольному тензору t, получаем
тензор
хМ'Дз = -L (fhhh — fhiji -J. fl-J2«1 _ /ссь).
3
Заметим, что при вычислении qpt мы меняем местами
«предметы» i3, i2, стоящие на местах с номерами 1, 2
(q = (1,2)). Полученный тензор преобразуется по непри¬
водимому представлению с сигнатурой а = (2,1).
Мы оставили еще нерешенной задачу о явном вы¬
числении кратностей k — k(a). В гл. XII будет дана
простая рекуррентная формула для вычисления этой
кратности.
§ 55. Принцип взаимности
Аппарат симметризаторов Юнга позволил нам раз¬
ложить пространство Фт на подпространства, неприводи¬
мые относительно группы G. Тот же аппарат позволяет
решить аналогичную задачу и для самой симметриче¬
ской группы S, если вместо неприводимых подпро¬
странств рассматривать максимальные подпространства,
кратные неприводимым. Более глубокий анализ этой
ситуации позволяет установить замечательное свойство
взаимности, существующее между представлениями G
и 5.
Заметим вначале, что центральные симметризаторы
е(а), будучи перестановочны со всеми элементами груп¬
пы S, определяют в любом представлении этой группы
проекторы на инвариантные подпространства. Если

238
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
представление неприводимо, то лишь один из таких
проекторов может оказаться отличным от нуля и сво¬
дится в этом случае к единичному оператору в про¬
странстве представления. Если представление группы 5
обладает этим свойством по отношению к е(а), то ска¬
жем, что ему соответствует сигнатура а.
В частности, пусть, как и прежде, Фт — пространство
всех тензоров ранга пг над некоторым пространством
размерности п и Фа—область значений в Фт проекто¬
ра е(а):
Фа = г(а)Фт.
Как следует из теоремы 1, Фа является максимальным
подпространством, инвариантным относительно G =
= GL(rc), представление в котором кратно неприводи¬
мому представлению d(a). Докажем теперь, что имеет
место
Теорема 2. Пространство Фа является максималь¬
ным подпространством в Фт, в котором представление
группы S кратно неприводимому с сигнатурой а. Про¬
странство Фа изоморфно тензорному произведению
Фа ~ ® Qe,
где Qa — подпространство, натянутое на старшие век¬
торы группы G (с сигнатурой а), и 0?а — пространство
неприводимого представления d{a). Подпространство Qa
неприводимо относительно S. Пространство Фа неприво¬
димо относительно G X S.
Наконец, если @ и © — обертывающие алгебры опе¬
раторов Tg и s в пространстве Фт, то мы имеем
(Г = ©, ©' = @,
где штрих означает переход к коммутаторной алгебре.
Доказательство. Начнем с доказательства по¬
следнего утверждения. Согласно теореме 1 алгебра ©
содержит проекторы d, d', ... на подпространства, не¬
приводимые относительно @ и в сумме дающие Фт. До¬
статочно рассматривать только те проекторы, которые
линейно независимы. Кроме того, алгебра © содержит
переплетающие операторы (s е @) для эквивалентных
проекторов d, d', ... (d' = sds-1), т. е. для эквивалент¬

§ 55. ПРИНЦИП ВЗАИМНОСТИ
239
ных неприводимых представлений алгебры ®. Отсюда
согласно следствию 3 из леммы Шура заключаем, что
@ = Но тогда согласно принципу взаимности (§ 21),
который мы установили как следствие из теоремы Берн¬
сайда, мы также имеем @ = S'.
Перейдем к рассмотрению пространства Фа. Выбе¬
рем в Qa базис из векторов юь и2, ■ • • , «ц и натянем на
каждый из этих векторов циклическую оболочку 9?,-
относительно алгебры i = 1, 2, ..., г. Тогда 91г изо¬
морфно Ша и подпространства 9?,- линейно независимы.
Следовательно,
Фа ~ fRa ® Qa.
В каждом подпространстве 9?г выберем базис так, чтобы
действие алгебры @ было идентично в каждом из этих
базисов. При этом в силу единственности старшего век¬
тора мы можем считать, что и является одним из ба¬
зисных векторов в 9?г. Допустим, что Qa приводимо от¬
носительно S. Согласно равенству @ = 6' оператор про¬
ектирования на инвариантное подпространство является
элементом из Ввиду идентичности действия такого
оператора на векторы оц мы заключаем, что он рав¬
няется нулю или единице. Следовательно, Qa неприво¬
димо.
Теперь мы можем заключить, что представление груп¬
пы 5 в пространстве Фа кратно неприводимому пред¬
ставлению, действующему в Qa. Действительно, при
каждом geG пространство TgQa неприводимо инва¬
риантно относительно S (ввиду коммутативности G и S)
и оператор Tg переплетает представления в Qa, TgQa.
Отсюда очевидно также, что Фа неприводимо относи¬
тельно G X S.
Остается доказать свойство максимальности Фа. По¬
скольку Фт распадается в прямую сумму подпро¬
странств Фа, то достаточно проверить, что при а ф а1
неприводимое представление в Qa' неэквивалентно пред¬
ставлению в Qa. Но эквивалентность таких представле¬
ний противоречила бы равенствам е(а) = 0 на Qa',
e(a)= 1 на (действительно, e(a) является линейной
комбинацией операторов представления). Следовательно,
Фа есть максимальное подпространство, представление

240
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
в котором относительно S кратно неприводимому пред¬
ставлению с сигнатурой а. Теорема доказана.
Следствие 1. Среди линейных комбинаций опера¬
торов Tg содержатся все проекторы на подпространства,
неприводимые относительно S.
Следствие 2. Среди линейных комбинаций опе¬
раторов Та содержатся все переплетающие операторы
для эквивалентных подпредставлений группы S.
Аналоги этих утверждений при перемене ролей G и
S нам известны уже из предыдущих построений.
Замечание 1. Аппарат симметризаторов Юнга
позволяет также получить каноническую реализацию
всех неприводимых представлений группы S с помощью
(правых) сдвигов в классе функций на группе S. Дей¬
ствительно, полагая
e(a)x(s) = x(s),
где б(ос) интерпретируется как оператор, порожденный
левыми сдвигами в групповом кольце функций *(s), мы
получаем, как легко проверить, максимальное подпро¬
странство Ха, представление в котором кратно неприво¬
димому с сигнатурой а. Аналогично, полагая
dx(s) = х (s),
где d — симметризатор, «подчиненный» г (а), мы полу¬
чаем более дробное разбиение пространства Ха на под¬
пространства, неприводимые относительно правых сдви¬
гов. Из сравнения числа неприводимых представлений
(§ 34) с числом симметризаторов г (а) заключаем, что
таким путем получаются действительно все неприводи¬
мые представления группы S.
Подробности доказательства предоставляются чита¬
телю *).
Замечание 2. До сих пор мы рассматривали толь¬
ко контравариантные тензоры относительно G. Тем не
менее нам удалось получить сигнатуры, для которых
тх ^ т2 ^ ... ^ тп ^ 0.
*) Заметим также, что если т, то все неприводимые пред¬
ставления группы S = S(m) реализуются в классе Фт всех тензо¬
ров ранга т для группы G = GL(n).

§ 56. РЕАЛИЗАЦИЯ d(a) НА ПРЯМОУГОЛЬНЫХ МАТРИЦАХ 241
Для группы SL(tt) такие сигнатуры исчерпывают все
возможные сигнатуры. В случае группы GL(«) для по¬
лучения всех неприводимых представлений достаточно
использовать умножение на скалярные представления
(detg)”1. Заметим, что в классе смешанных тензоров
положение затрудняется наличием свертки
х% — xlV + х^ + • • • + *га|П>
где х— ковариантный и £ — контравариантный векторы.
Однако, в классе чисто ковариантных векторов все по¬
строения, по существу, ничем не отличаются от изучения
алгебры Ф.
§ 56. Реализация d(a) на прямоугольных матрицах
Опишем еще одну модель неприводимого представ¬
ления d(a), которая в некотором смысле является про¬
межуточной между реализацией в классе тензоров и
реализацией на группе G. Положим G = GL(«), Я =
= GL(m), где обе группы рассматриваются над полем
комплексных чисел. Пусть X — линейное пространство
всех комплексных матриц т X п и SF — пространство
всех полиномов f(x), i'el Положим
Tgnf ix) = f (h'xg),
где h пробегает Я и g пробегает G. Операторы Tgh оп¬
ределяют представление группы G X Я в пространстве
?Г. Поскольку однородные полиномы образуют инва¬
риантное подпространство относительно Tgh, то, в сущ¬
ности, нам приходится иметь дело с конечномерными
представлениями G X Я.
Заметим, что всякое неприводимое представление
группы G X Я определяется сдвоенной сигнатурой вида
(а| Р), где а — сигнатура G и |3 — сигнатура Я. Поставим
задачу о разложении Tgh на неприводимые представле¬
ния. Полагая f = max(n,m), мы условимся записывать
каждую сигнатуру в виде (нгьт2, ..., mf), дополняя,
если нужно, недостающие координаты нулями. Положим
также г (а) = т}. Докажем, что имеет место
Теорема 3. Представление в пространстве яв¬
ляется однократной суммой представлений G X Я

242
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
с сигнатурами вида (а|а), г(а)>Д. Вектор
f.w-П
i = i
хп .
•• хи
Хц .
• Хц
является старшим вектором, отвечающим сигнатуре
(а |а), а = (mi, т2, .... mh, 0, 0 0), k = min (n, т),
mi > т2 > . . . ^ mh ^ 0.
Доказательство. Заметим, что для матриц
имеет место следующий аналог разложения
Гаусса:
X = y'pz,
где yeZ(m), z^Z(n)—верхние треугольные матрицы
с единицами на главной диагонали и ц = diag{pb ц2> • • •
• ••, Ий} — диагональная прямоугольная матрица m X п.
Такое разложение справедливо, если
Мрф 0, р = 1, 2, . .., k,
где Мр — главный диагональный минор матрицы х, со¬
ставленный из первых р строк и первых р столбцов. До¬
казательство ничем не отличается от случая m = п,
рассмотренного в § 9. При этом имеем
мр
Ир Мр—\ ’ Р ^ ^ •
Найдем теперь все старшие векторы группы G X Н в
пространстве Если f(x)—-такой старший вектор, то
он является инвариантом Z(m)XZ(n) и мы имеем
f(x) = f (*/Vz) = f (и)-
Следовательно, f является полиномом от параметров
рр = Mp/Mp-i. Поскольку вектор f должен быть также
весовым относительно D(m)X D(n), то он является од¬
ночленом от Мь М2, ..., Mh:
f(x) = TlM^ г . = mi — m.+1,
i = l
где a = (mb m2, ..., mn) —сигнатура как относительно
левых, так и относительно правых сдвигов на элементы
б ^D(m), d^D(n). Согласно общим условиям, надо-

§ 56. РЕАЛИЗАЦИЯ d{a) НА ПРЯМОУГОЛЬНЫХ МАТРИЦАХ 243
женным на сигнатуру, в пространстве ЕГ содержатся
лишь такие одночлены, для которых л,- > 0, t = 1,2,...
..., k\ но тогда nil ^ т2 > ... > mf > 0 *). Теорема до¬
казана.
Пусть @~а — циклическая оболочка старшего вектора
fa(x), т. е. пространство неприводимого представления
группы G X Я. Согласно общей теории представлений
(см. § 43) мы имеем
F* - ШЦ ®
где 9ia, 9ia — пространства неприводимых представлений
Я и G, отвечающих сигнатуре а. Следовательно, @~а
может быть также составлено из прямоугольных мат¬
риц М X N, М = dim Sta, N = dim Ш%. Из полученной кон¬
струкции очевидно
Следствие 1. Пусть @ и $ —линейные оболочки
операторов Rg = Tge, Lh = Teh соответственно. Тогда мы
имеем ®' = £, ф' = @.
Отсюда, как и в предыдущем параграфе, мы можем
заключить, что в алгебре @ содержатся все проекторы
на неприводимые подпространства относительно 4? и в
алгебре $ содержатся все проекторы на неприводимые
подпространства относительно Аналогичные утвер¬
ждения верны и для переплетающих операторов.
Отсюда ясно, как произвести сужение на подгруппу,
изоморфную G (либо на подгруппу, изоморфную Я).
Пространство кратно неприводимому относительно
Я с кратностью N и кратно неприводимому относитель¬
но G с кратностью М. Здесь, как и выше М = dim ffia,
A=dim3[Ja. Рассмотрим специально случай m — п.
Следствие 2. Если m = п, то пространство @~а
может быть охарактеризовано как линейная оболочка
функций
iy / 1, 2, ..., Я,
где т“у (х) означает полином над X, совпадающий при
det х ф 0 с матричным элементом группы G сигнатуры а.
*) В действительности, если m — п, то из условий, наложенных
на сигнатуру, еще не вытекает неотрицательность гп (множитель
Мп = det х может входить в отрицательной степени); но ясно, что
f(x) является полиномом только при гп ^ 0.

244
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
8 п •
•• 8и
8п ■
■ 8и
г, = mi- тш
Действительно, матричные элементы неприводимого
представления T“(g) получаются левыми и правыми
сдвигами из производящей функции
г<
a (g) = Ц
i=i
(см. общую конструкцию таких представлений в гл. VII).
Вместе с функцией a(g) все эти матричные элементы про¬
должаются до полиномов над X. Ясно, что линейная обо¬
лочка этих элементов совпадает с пространством &"а.
Следствие 3. Матричные элементы аналитических
неприводимых представлений группы G образуют линей¬
ный базис в классе всех полиномов над X, где X — мно¬
жество всех матриц п X п.
Аналогичное утверждение нетрудно также получить
для полиномов от вещественных параметров в простран¬
стве X (т. е. полиномов от Хц, хц); однако при этом при¬
ходится рассматривать все вещественные неприводимые
представления группы G. Привлекая теорему Вейер-
штрасса, получаем также свойство полноты в классе не¬
прерывных функций над X: всякая непрерывная функция
над X может быть аппроксимирована линейными комби¬
нациями матричных элементов равномерно на каждом
компакте К с= X. В частности, поскольку U = U (л) яв¬
ляется компактом, то мы еще раз получаем аппроксима-
ционную теорему Петера — Вейля для U (п).
Если рассматривать полученную конструкцию как по¬
строение модели d(a), то ясно, что при т<п мы нахо¬
дим не все возможные представления группы G, при
т > п возникает избыток параметров, в то время как
случай т = п является оптимальным. Таким образом,
мы снова возвращаемся к реализации на группе G.
§ 57. Гармонический осциллятор
В заключение этой главы изложим еще одну замеча¬
тельную алгебраическую конструкцию, которая перво¬
начально возникла в теоретической физике. Вместо
группы G мы будем рассматривать ее алгебру Ли
X = gl(n,C).

§ 57. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
245
Пусть ау, а2, ап; а,+, а2+, а+ — образующие
в некоторой абстрактной алгебре 99 с соотношениями
коммутации
[а;,а;.] = [а+, а+] = 0, [а+, а;.] = 6;/,
где 6ц — символ Кронекера. Предполагается также, что
алгебра 99 содержит единицу. Коммутативные подалгеб¬
ры, порожденные элементами ар af, обозначим соот¬
ветственно 91 и 9Н.
Элементы at, at называют в теоретической фи¬
зике операторами Бозе. Операторы ai называются опе¬
раторами рождения, операторы а + —операторами унич¬
тожения*). Квадратичный элемент
К = а,а+ + а2а+ + ... + апа+
называется оператором числа частиц. Подобная система
операторов описывает квантовомеханическую модель,
называемую п-мерным гармоническим осциллятором.
Положим теперь
Ец , /, j — 1, 2, .,,, п.
Нетрудно проверить, что операторы Etj удовлетворяют
стандартным соотношениям коммутации алгебры X =
= gl (п,С). Таким образом, алгебра X может быть вло¬
жена в 99 **).
Далее, пусть §— бесконечномерное векторное про¬
странство, в котором действует циклическое представле¬
ние алгебры 99. При этом предполагается, что роль цик¬
лического вектора играет вектор f0, для которого
aff0 = 0, /=1,2,..., п.
Иначе говоря, вектор f0 аннулируется всеми операто¬
рами уничтожения. В физике вектор fo называется
*) Наши обозначения отличаются от общепринятых транспози¬
цией а,-, а*.
**) Полученная запись отвечает интуитивному представлению
об операторах как «операторах перехода из „состояния /“в„со¬
стояние i“». Очевидна также аналогия с представлением d\®dy
(шляпка означает контрагредиентное представление).

246
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
вектором вакуума (состоянием вакуума). Условие цик¬
личности записывается следующим образом:
5 = Щ0.
Нетрудно видеть, что 59 = 915В. Иначе говоря, при по¬
мощи соотношений коммутации можно каждый элемент
Ье 59 разложить по одночленам, у которых все множи¬
тели а,- сгруппированы слева и множители at сгруппи¬
рованы справа. Но тогда очевидно, что
5 = Що.
Следовательно, § является циклической оболочкой век¬
тора /о по отношению к полиномам а е Sf, содержащим
только операторы рождения. При этом существенно, что
алгебра 91 является коммутативной.
Как следует из последнего замечания, представления
указанного типа действительно существуют. В самом
деле, мы можем заранее положить 5 = &/0, предпола¬
гая, что между векторами
не существует никаких линейных зависимостей. Иначе
говоря, пространство S отождествляется с алгеброй Я
всех полиномов от коммутативных символов аи а2, ...
..., ап. Действие операторов ар af определяется оче¬
видным образом. В дальнейшем мы будем иметь в виду
именно указанные представления. Поскольку Хс8, то
получаем также представление алгебры X.
Займемся разложением этого представления на не¬
приводимые. Прежде всего, заметим, что каждый век¬
тор f.—fbb h является весовым:
Eiif k ' ' kitk•
Несложная проверка предоставляется читателю. Далее,
покажем, что вектор Д может быть старшим только при
условии k2 — k3 = ...=kn = 0. Действительно, если Д со¬
держит хотя бы один сомножитель ajt ]Ф 1, то он не
аннулируется оператором Etj = а<а+. С другой стороны,

§ 57. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
247
если положим
= а?/о>
то вектор (от аннулируется всяким повышающим опера¬
тором Eij, i< j. Далее, пусть — подпространство всех
векторов fh, для которых ki + k2 + • •. + kn = т. Нетруд¬
но видеть, что &т инвариантно относительно алгебры X.
Поскольку8т конечномерно,то оно вполне приводимо*).
Поскольку §т содержит лишь единственный (с точно¬
стью до множителя) старший вектор шт, то оно непри¬
водимо.
Таким образом, мы получаем, что в пространстве $
содержатся, причем однократно, все неприводимые пред¬
ставления алгебры X с сигнатурами (т, 0, 0, ..., 0),
m = 0, I, 2, ... Этим завершается спектральный анализ
пространства S- Заметим также, что оператор
К = Еп + Е22 + ... + Епп
сводится в подпространстве Sm к умножению на т. Опе¬
ратор К интерпретируется также как «массовый опера¬
тор» или «оператор массы — энергии».
Если сопоставить этот результат с рассмотрениями
предыдущего параграфа, то не должно показаться уди¬
вительным, что мы получили в спектре только представ¬
ления вида d?. Действительно, реализация в простран¬
стве $ равносильна реализации в классе полиномов от
одной числовой строки х = (х\, А'г, . . . , хп). Если мы же¬
лаем получить все остальные сигнатуры, то придется
рассматривать по крайней мере п строк (впрочем, для
получения сигнатур вида (т\, т2 .. . , mh, 0, 0, ..., 0)
достаточно рассматривать k строк).
Исходя из последнего замечания, мы приходим к
следующему обобщению нашей конструкции. Будем счи¬
тать, что алгебра Э содержит 2п2 образующих aip afj>
i, j = 1, 2, ..., тг, с соотношениями коммутации
[а1р аы\ = [а+, а+\ = 0, [а+, аи\ = Ь1кЬп.
*) Для применения принципа полной приводимости достаточно
заметить, что в 5,п существует скалярное произведение, относитель¬
но которого инфинитезимальные операторы подгруппы U(ti) анти-
эрмитовы. (См, упражнение 1 в конце § 36.) См. также § 61.

248
ГЛ. VIII. ТЕНЗОРЫ И ДИАГРАММЫ ЮНГА
Алгебра X состоит в этом случае из операторов
П
E.j = 2 aisa%- При этом, как и прежде, S3 = 9Ш+, где
Я и 91+ порождаются соответственно только элементами
a.j, а+. Массовый оператор определяется формулой
П
Ен.
i=1
Повторяя почти дословно предыдущие построения, полу¬
чаем бесконечномерное представление алгебры S3 в про¬
странстве % = Що с циклическим вектором f0, для ко¬
торого atjf0 = 0, г, /=1, 2, ..., п. Спектральный ана¬
лиз этого представления уже не производится столь эле¬
ментарно, однако достаточно воспользоваться результа¬
том теоремы 3.
В результате получаем новую реализацию всех не¬
приводимых представлений а = (ть т2, ..., тп),
mi >- т2 ... ^ тп ^ 0 (т*— целые числа). Хотя та¬
кая реализация вполне аналогична реализации преды¬
дущего параграфа, она в отдельных случаях может ока¬
заться более удобной для символической записи действия
инфинитезимальных операторов E{j. К этому вопросу мы
еще вернемся в гл. X.
Изложенная нами символическая конструкция до¬
пускает также весьма простую функциональную реали¬
зацию. Для этого достаточно положить
аи = аЪ = ~2 {ХП+~Ш^)'
где Хц, i, j = 1, 2, ..., п, — независимые вспомогатель¬
ные переменные. Определяя вектор вакуума по формуле
П
-2 А,
fo(x) = e ,
мы отождествляем пространство % с пространством всех
функций вида f(x) = p(x)f0(x), где р(х) —произвольный
полином от Xij*). При этом массовый оператор К ото-
*) Отсюда очевидна также связь с полиномами. Эрмита.

§ 57. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР
249
ждествляется с оператором Гамильтона
П
для системы из п «-мерных гармонических осцилляторов.
В заключение отметим, что массовый оператор пере¬
становочен со всеми операторами Ец и потому согласно
лемме Шура кратен единице в подпространстве каждого
неприводимого представления. Однако в общем случае
этот оператор уже «не разделяет точек спектра», т. е.
принимает одно и то же числовое значение на подпро¬
странствах с разными сигнатурами. Действительно, мож¬
но показать, что этот оператор сводится к умножению
на tn = т.\ + т-2 + ■ ■ ■ + тп во всем пространстве одно¬
родных полиномов степени т. Фундаментальным вопро¬
сом о разделении точек спектра мы займемся в следую¬
щей главе.
* *
's-
диаграммы Юнга первоначально возникли в связи с непосред¬
ственным изучением группы S ([148]). Г. Вейлем [10] показана
роль симметрнзаторов Юнга в изучении тензоров для GL(rc). При
этом существенно используется «принцип взаимности» между G
и S, при помощи которого получаются основные результаты (вклю¬
чая свойство полной приводимости для тензорных преобразований
GL(n)). flame изложение отличается явным использованием стар¬
ших векторов, что позволяет получить достаточно ясную картину
разложения без помощи группы S (§ 51); однако, лишь привлечение
группы S позволяет построить проекторы на неприводимые подпро¬
странства. Использование метода Z-инвариантов и доказательство
теоремы 3 излагаются согласно [84]. Алгебраическая схема с опера¬
торами Бозе была предложена в работах В. Б а р г м а н а и М. М о-
ш и некого [149], М. Мощи некого [155]. См. также [154].

ГЛАВА IX
ОПЕРАТОРЫ КАЗИМИРА
Мы уже не раз встречались с приложениями леммы
Шура к теории представлений. В этой главе исследуем
еще одну возможность такого приложения — в рамках
инфинитезимального метода. Речь будет идти о по¬
строении операторов, которые могут быть выражены
как полиномы от инфинитезимальных операторов Ец
группы GL(n) и которые перестановочны с каждым из
операторов Ei,. Пока изучим лишь простейшие свой¬
ства таких операторов. Предварительно рассмотрим об¬
щую алгебраическую схему для произвольной алгеб¬
ры Ли.
§ 58. Универсальная обертывающая алгебра
Пусть X — произвольная алгебра Ли с базисом
е\, еч, ..., е» и структурными константами
[<?., е,] = с*
Будем рассматривать символы еь вч, ..., еп как обра¬
зующие некоторой ассоциативной алгебры, в которой
eiej-eiei = ckilek (*)
и в которой между образующими нет иных соотношений,
независимых от (*). Иначе говоря, пусть Эс— линейная
оболочка всевозможных одночленов вида
i ... i ~ @1 • • • > eQ 1,
1 2 т 1 2 т
С ассоциативным умножением и пусть
0о = eiei ~ e,ei ~ 61'А-

§ 58. УНИВЕРСАЛЬНАЯ ОБЕРТЫВАЮЩАЯ АЛГЕБРА 251
Мы будем считать, что элемент ге! равен нулю тогда
и только тогда, когда его возможно представить как сум¬
му элементов вида авцЬ, где а и Ь — произвольные эле¬
менты из X. В частности, 0г-; = 0. Соответственно два
элемента х, у^Х считаются равными, если их разность
z = х — у есть нуль (иначе говоря, если они приводятся
друг к другу с помощью соотношений коммута¬
ции (*)).
Полученная алгебра X называется универсальной
обертывающей алгеброй или ассоциативной оболочкой
алгебры X. В алгебре X естественно использовать обыч¬
ное определение коммутатора:
[*, у] = ху- ух, х, уегЖ,
которое согласно (*) совпадает с определением комму¬
татора в X в том частном случае, когда х, у — линейные
комбинации в\, в2, • ■ • , еп. Следовательно, можем счи¬
тать, что X а X и коммутатор любых двух элементов
xjeX записывается в обычной альтернативной форме.
Положим также
D{x)y = [x,y], х, у<=Х.
Если х, у — два произвольных элемента из X и Я,
р— произвольные числа, то получаем следующие тож¬
дества:
1° D{Xx + \iy) = KD{x) + \iD{yy,
2° D{[x,y]) = [D{x),D(y)],
первое из которых очевидно, а второе является след¬
ствием тождества Якоби в алгебре X. Оба эти тожде¬
ства в частности означают, что отображение x-*-D(x)
является представлением алгебры X, действующим в са¬
мой алгебре X. Это представление принято называть
присоединенным представлением алгебры X.
Если х, а, b — произвольные элементы из X, то имеет
также место следующее тождество («правило дифферен¬
цирования») :
3° D{x)ab = {D(x)a)b + a{D{x)b),

252
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
которое, в частности, при позволяет заключить,
что D(x) удовлетворяет тождеству 2°, т. е. является пред¬
ставлением алгебры X во всей алгебре ЗЕ*).
Докажем теперь, что имеет место
Теорема 1. Всевозможные одночлены
е, . . = е. е. . . . е.
*1*2 гт 1\ г2 1тп
при i\ '<л2 -< . .. -</т образуют базис в алгебре ЗЕ. То же
верно для элементов
еп ,■ i \ = Р [е. . , /,</„<...< I.
(*г 2 lm) 1\гг"* ^ т
где символ Р означает симметризацию по индексам
1\, 12у • • • *
где s — произвольная подстановка индексов iь t2, .. . , im.
Доказательство. Пусть х — произвольная ли¬
нейная комбинация одночленов е. . . , k ^ т, и [х] —
12 lk
ее старший член, содержащий все слагаемые с k = т.
Положим
[х] = i,nei t
4 2 т
где предполагается свертка по i\, i2, . . ., im. Ясно, что
с помощью соотношений коммутации мы можем распо¬
ложить сомножители е, , е, , . . е. в произвольном
‘l 2 ‘т
порядке, изменяя лишь слагаемые с меньшей степенью
однородности. В частности, можем считать, что [х] раз¬
лагается лишь по одночленам е. , , при
12 ••• 1т 1 z
... ^ im. Но тогда по индукции то же верно и для
всего элемента х с заменой т на k^Cm.
Заметим, далее, что если тензор t антисимметричен
по отношению к хотя бы одной паре индексов, то суще¬
ствует (ввиду соотношений коммутации) такая запись
*) Действительно, используя соображения индукции, мы можем
считать, что а е X, b е S; но в этом случае 2° очевидно. Заметим,
что если iel, то отображение x->D(x) не мультипликативно, т. р.
не является представлением алгебры X.

§ 58. УНИВЕРСАЛЬНАЯ ОБЕРТЫВАЮЩАЯ АЛГЕБРА 253
полинома х, при которой [х] = 0. Действительно, не
ограничивая общности, можем считать, что этими индек¬
сами являются i 1, г2. Используя тождество
V<rT(V<,+V‘,)+iK' *<,]■
замечаем, что под знаком [х] второе слагаемое можно
отбросить (оно имеет меньшую степень однородности).
Следовательно [х] = 0, как свертка симметрического тен¬
зора с антисимметрическим.
Рассмотрим теперь оператор симметризации Р и по¬
ложим t0 = Pt. Используя диаграммы Юнга, мы можем
заключить, что
t — to — t\ + t2 + ... +t^j
где каждый тензор tj, / = 1, 2, ..., N, является анти¬
симметрическим по отношению хотя бы к одной транспо¬
зиции индексов г'ь г2, ..., /,„*). Согласно сделанному
выше замечанию все эти тензоры дают нулевой вклад в
[х], т. е.
[x] = tt/*-i'*et { , .
1 2 1т
Но в этой свертке, очевидно, можно заменить^. , , на
12 ‘т
е,. . ... То же верно и при k-<Cm.
(Ш h bn) F F
Теперь остается доказать, что элементы еп . , .
(Ч* 2’ 1т)
линейно независимы при i'i г2 г',п. Пусть х = 0;
тогда согласно определению алгебры X х представляется
как сумма элементов вида а$цЬ, a, b е X. Напомним,
что Q{j = etej — ejei — ck{iek. Заменяя в этом выражении
элементы е{, е3- вспомогательными числами заме¬
чаем, что [0гД обращается в нуль. Следовательно, и [х]
также обращается в нуль при подстановке вместо
В\, е2, . . . , еп коммутирующих символов |ь |2, .. .,
Но если
*) Это разложение нетрудно получить и непосредственно, без
обращения к диаграммам Юнга.

254
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
при всех числовых значениях gf, то симметрический тен¬
зор tQ также обращается в нуль. Следовательно, мы за¬
ключаем, что если у элемента х все тензоры коэффи¬
циентов записаны в симметричной форме, то равенство
х — 0 равносильно обращению всех этих тензоров в нуль.
Следовательно, элементы е,. , . /. <1L ... <1
(lV 12' ' ' ’ ’ lk) 1 1
-С 4, к-*Ст, образуют линейный базис в пространстве
Хт, составленном из всех полиномов степени k^Cm.
Наконец, поскольку наше утверждение доказано для
еп . . то оно также верно и для е. , . при
ГГ *2 гт) V2 1т
... ^ im (из соображений размерности).
Теорема доказана.
Следствие 1. Запись каждого элемента хе! в
симметризованной форме однозначна.
Следствие 2. Алгебра X как линейное простран¬
ство изоморфна алгебре всех полиномов от числовых пе¬
ременных gb g2 1п.
Последнее утверждение (равносильное теореме 1)
известно под названием теоремы Биркгофа — Витта*).
Замечание. Соответствие между алгеброй X и ал¬
геброй полиномов p(g), g = (gi, g2, . .. , g„), не является
мультипликативным, т. е. умножению двух таких поли¬
номов не соответствует умножение соответствующих эле¬
ментов xel. Однако нетрудно видеть, что этому умно¬
жению соответствует перемножение старших членов [дг],
введенных при доказательстве теоремы 1.
Следствие 3. Если X — алгебра Ли группы G, то
алгебра X изоморфна ( уже как алгебра) алгебре всех
дифференциальных операторов на G, порожденных ле¬
выми сдвигами на G. То же верно для правых сдвигов.
Доказательство предоставляется читателю.
В ближайшее время нас будет интересовать не вся
алгебра X, а только ее центр, который мы обозначим
символом 3- Множество 3 по определению состоит из
всевозможных элементов ге1, каждый из которых пе¬
рестановочен со всеми элементами из X. Такие элементы
называются центральными или операторами Казимира.
Условие центральности можно также выразить форму¬
*) См., например, [128].

§ 59. ОПЕРАТОРЫ КАЗИМИРА ДЛЯ ГРУППЫ GL(n)
255
лой D(x)z = 0 для всех элементов х е I. Множество 3,
очевидно, является подалгеброй в алгебре X.
Если х—*х{х) — представление алгебры X, то всякий
оператор т(х) является линейной комбинацией операто¬
ров £, = т(е*), i = 1, 2 п. Полагая для краткости
мы ставим в соответствие каждой линейной комбинации
элементов е, , . е $ линейную комбинацию операто-
12 * " /П
ров Ei i im с теми же коэффициентами. Получен¬
ное соответствие обозначим по-прежнему символом
х—>х(х),
где, однако, уже х^Х. Если геЗ, то оператор т(г)
условимся называть оператором Казимира представле¬
ния т(х); ясно, что всякий такой оператор перестаново¬
чен со всеми операторами х(х). Если х(х) неприводимо,
то в силу леммы Шура
т (z) = A, (z)l,
т. е. оператор Казимира кратен единичному. Это свой¬
ство операторов Казимира особенно существенно для
многих вопросов теории представлений.
§ 59. Операторы Казимира для группы GL(n)
Пусть, в частности, X — алгебра всех комплексных
матриц п-то порядка, т. е. алгебра Ли группы G =
= GL (п,С). Выбирая в X стандартный базис из эле¬
ментов ец, г, / = 1, 2, .. ., п, напомним прежде всего,
что оператор
ci =еп +е22+ ... +епп
является (как отмечалось в § 57) одним из операторов
Казимира. В этом случае С\ е X и оператор С\ является
(как легко проверить) единственным (с точностью до
множителя) оператором Казимира, принадлежащим са¬
мой алгебре X.
Для построения иных операторов Казимира допустим
вначале, что в X содержится некоторая система элемен¬

256
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
тов Хц, i, / = 1, 2, ..., п, которые преобразуются подоб¬
но элементам ец по отношению к присоединенному пред¬
ставлению D(x), т. е. таких, что
l^i/t xkl\ ^jkxil ^ilxkj'
Тогда, очевидно, сумма диагональных элементов Хц бу¬
дет оператором Казимира в X. Далее, пусть Хц, уц,
I, / = 1, 2, ..., я, — две такие системы элементов. По¬
ложим
%ц ~ xikUkj>
где предполагается суммирование по индексу k. Нетруд¬
но проверить, что гц снова образуют систему указанного
типа, и это позволяет нам построить целую серию по¬
добных систем, исходя из базиса системы ец:
eW = е.. е е. ..
ч п2 hH 1т>
Свертывая далее по индексам ;, /, получаем серию опе¬
раторов Казимира:
с = е. . е е. . .
т lil2 hh «ш'Г
где предполагается суммирование по каждому индексу
II, 12, .. ., im = 1, 2, . . . , п. Полученную формулу можно
рассматривать как формальное выражение следа для
матрицы ет, где е = j|e,j|| — матрица из (некоммутирую¬
щих) базисных элементов.
Заметим, что если бы матрица е была числовой, то
все степени еп+1, еп+2, . .. линейно выражались бы через
е°, е1, ..., еп с коэффициентами, полиномиально зави¬
сящими от с0, Ci, ..., с„ (следствие формулы Кэли —
Гамильтона). В этом случае мы могли бы заключить,
что с„+1,сп+2, ... полиномиально выражаются через
с о, сь . .., сп. Однако в нашем случае мы не можем
сразу заключить о выполнении подобного соотношения.
Отметим также очевидные обобщения использованного нами
приема для произвольной алгебры X с универсальной обертываю¬
щей алгеброй £. Прежде всего, имеет место
Правило 1. Пусть представление D(x) сводится в некоторых
инвариантных конечномерных подпространствах Vi, V2 с ЗЕ к кон-
трагредиентным друг другу представлениям д(х), д(х) Фоомула
с =

§ 59 ОПЕРАТОРЫ КАЗИМИРА ДЛЯ ГРУППЫ GL(n)
257
гдее^е V\, ейе V2— дуальные базисы по отношению к д, д, опре¬
деляет в этом случае оператор Казимира в алгебре £. Здесь предпо¬
лагается суммирование по ц от 1 до N, где N = dim V\ — dim V2.
Действительно, используя «правило дифференцирования», находим
D (х) с = (д (х) ец) ekl + ev {д (х) ev) = (<5V(i (х) + (х) ) е^1 — О
л
в силу равенства <5 = —д', выражающего контрагредиентность д и <3.
Следовательно, с — центральный элемент.
С другой стороны, согласно определению алгебры £ представ¬
ление D(х) является частью представления Яо + Я] + ... + яш + . . .,
где Яп (х) = 0 и
пт = я ® я ® ... ® я
(т сомножителей), причем Я! = я означает сужение D(x) на подпро¬
странство X. Следовательно, для описания всех операторов Казимира
достаточно перечислить все инфинитезимальпые инварианты в пред¬
ставлениях я™, т = 1,2, ... Отсюда, в частности, получаем
Правило 2. Если представление Я\ неприводимо, а ят вполне
приводимо при m — 2, 3, . . . , то всякий оператор Казимира в ал¬
гебре £ есть линейная комбинация операторов вида
с = Ekek
(сумма по k от 1 до п), где ен — произвольный базис в алгебре X
и гк — совокупность элементов, преобразующихся контрагредиентно
ek по отношению к D(x).
Действительно, ят = ят_[®Я1, и для перечисления всех инфини-
тезиыальпых инвариантов в ят достаточно выделить из Лт-i все не¬
приводимые компоненты, конграгредиентные Яь
В частности, если G = SL(n, С), то представление лй является
дифференциалом представления
х -> gxg~l
группы G, действующего в классе всех матриц с нулевым следом.
Предоставляем читателю доказать (используя, например, метод Z-ин¬
вариантов), что это представление неприводимо. Кроме того, лт
вполне приводимо (как аналитическое представление надкомпактной
группы). Следовательно, правило 2 в этом случае применимо. Если
G = GL(п, С), то, очевидно, в этом случае
Я1 = я0 + Y1 >
где я0 — сужение лй на подпространство матриц с нулевым следом.
Слагаемое yi соответствует найденному ранее оператору Казимира Си
Используя правило 2, можно было бы (для случая GL(n, С)) по¬
казать, что найденные выше операторы Казимира Си с2, ■ ■ ■, с„ яв¬
ляются образующими в центре алгебры £\ однако мы это сделаем
иным путем в § 61.
Рассмотрим теперь произвольное представление
алгебры X и продолжим его до представления всей

258
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
алгебры (см. конец § 58). Если оператор соответ¬
ствует базисному элементу e,-j, i, j — 1, 2, ..., п, то опе¬
ратор
Ck = Eixi2Ei2ib • •. Eikix
(суммирование по i\, i2, ■ ■ ■, ih) является оператором
Казимира, соответствующим центральному элементу
ck е 3- Если, в частности, рассматривать неприводимое
представление d( а) с сигнатурой а = (гп\, т2, ..., тп),
то находим в этом случае
Ck = ck{a)I,
где символом с* (а) обозначена константа, к умножению
на которую в данном случае сводится оператор Ch. Та¬
ким образом, каждому цеЗ ставится в соответствие
числовая функция ch(a) = ск(ти tn2, ..., тп).
Поскольку оператор Ch кратен единичному в d(а), то
для вычисления ch{а) достаточно применить Ch к лю¬
бому фиксированному вектору go из пространства пред¬
ставления d(а). Мы можем, в частности, в качестве go
выбрать старший вектор, для которого
Ец1о = т{10> г'= 1, 2, .. п,
Eltl0 = 0 при г < /, г, /= 1, 2, .. ., п.
Отсюда непосредственно получаем значение а(а) —
= т\ + т2 + ... + т,,. Для вычисления с2(а) запишем
оператор С2 в виде суммы трех слагаемых:
П
с2 = 2 Е% + 2 EijEa + 2 Е„Ец.
« = 1 i < j i > j
Последнее слагаемое этой суммы обращается в нуль на
векторе g0. Второе слагаемое с помощью соотношений
коммутации может быть приведено к тому же виду с
добавочным членом
2 [Еи, Ец\ = 2 (Еа - Еп).
I < ! < < /
Заменяя каждый оператор Ehh умножением на mk, полу¬
чаем следующий результат:
П
с2(а) = 2 т] + 2 (mi - т.).
i = 1 i<r и

§ 60. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ Ck
259
При помощи подобных построений легко находим, что
ср(а) является полиномом от ть /пг, пгп степени р
П
со старшим членом 2 однако остальные его коэф-
£ = 1
фициенты вычисляются сравнительно сложно.
Поставим теперь задачу о полном описании всех по¬
линомов ch(а). Заметим, что существенную роль в по¬
становке этой задачи играет то обстоятельство, что все
операторы Ck в различных представлениях имеют оди¬
наковую полиномиальную структуру, определяемую сим¬
волом ch es 3; следовательно, и ск{а) зависит только от
ск. Поэтому решение данной задачи дает нам также
информацию о возможных значениях спектра Ch в про¬
извольном конечномерном представлении алгебры X.
§ 60. Собственные значения операторов Ck
Пусть E{j — инфинитезимальные операторы представ¬
ления d(а). Вводя обозначение
X . U U р
1ц-Ьц -ЬцЬг21з •••
докажем вначале, что имеет место
Лемма 1. Если |0 — старший вектор представления
d(a), то
Тц10 = 0 при i < /, г, / = 1, 2, . .., п,
Т 1&0 = ^г|о> г'=1> 2, ..., П,
где константа зависит от сигнатуры а.
Доказательство. Напомним, что операторы Тц
обладают теми же трансформационными свойствами по
отношению к присоединенному представлению, что и
Отсюда следует, как и в § 44, то если \ — весовой век¬
тор с весом А, то Tij% — также весовой вектор с весом
А + а,],
где ccij — корень алгебры X, введенный в § 44. Посколь¬
ку ccij > 0 при i < /, то равенство 7^0 = 0 вытекает из
максимальности старшего веса *). Поскольку а,-,- = 0, то
*) Короче говоря, оператор 7Д является «повышающим» при
I < j (и «понижающим» при i > })■, отсюда Г^|р = 0 при i < j.

260
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
равенство Тц%0 = £t-g0 следует из единственности направ¬
ления старшего вектора. Лемма доказана.
П
Поскольку Ck = sp Т = 2 Tih то для вычисления
«=I
ch(а) достаточно вычислить все собственные значения t{
операторов Тц. Представим каждый такой оператор в
виде
Ти = ЯцЕц + 2 RijEji,
i ф i
где для краткости положено Яц = Если t> /, то
слагаемое этой суммы обращается в нуль на векторе £0-
Если t < /, то тот же эффект достигается (в силу лем¬
мы 1 для Rij) при перестановке сомножителей Ri3, Ец\
в результате этой перестановки возникает добавочный
член
2 [Rti,Eit]= 2 (Ru-Ru).
S=i+1 {=1+1
Следовательно, если каждый диагональный оператор
заменить соответствующим собственным значением, то
мы получим равенство
ti = rimi+ 2 (ri-rs),
i < i
которое выражает собственные значения операторов
Тц = Е(и через собственные значения г3 операторов
= £'(/у~"1). Проводя индукцию по k, сформулируем
окончательный результат в виде леммы:
Лемма 2. Если матрица а определяется равен¬
ством
alj = {ml + п - [)Ьи-^ц, i, /=1, 2, п,
[ 1 при i < /,
где 6,ч — символ Кронекера uQn = { _ _ . то соб-
13 г 1 [0 при t>],
етвенное значение t3 имеет вид
U = 2 (а%,
/=)

§ 60. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ СА 261
т. е. является суммой матричных элементов, расположен¬
ных в i-й строке матрицы ah.
Доказательство. Индуктивное соответствие ме¬
жду t. = t(-!l) и гI = ^-1) может быть переписано в виде
аиИ*-'\
где a =|l<2ijll, i, / = 1, 2, п, — матрица, определен¬
ная в условиях леммы. Мы можем использовать это со¬
ответствие также и при k = 1, считая, что tf = 1. Пони¬
жая степень k, выражаем tf через tf:
ДО).
(k)
S (а% tf,
i=i
что и совпадает с указанной выше формулой. Лемма
доказана.
П
С л е д ст в и е. cfe (а) = 2 (^)г/.
», /' = 1
Заметим, что матрица а является верхней треуголь¬
ной и имеет вид
lx -1 -1
0
-1
-1
-1
L
(*)
где собственные значения 1\, /2, 1п связаны с пара¬
метрами mt, m2, тп сигнатуры а формулой
/] = m, + {п — 1), /2 = т2 + {п — 2), ..., /п = тп.
Окончательное выражение для сДа) мы можем также
записывать в виде
cfe (а) = sp akE,
где Е — квадратная матрица, все элементы которой рав¬
ны единице.

262
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
Полученная формула дает уже достаточно простой
алгоритм для вычисления собственных значений ch(a).
При помощи этой формулы мы сумеем также получить
и несколько более явное выражение для ск(а).
Теорема 2. Собственное значение ch(а) оператора
Казимира Ск в представлении d(a) имеет вид
ck (а) = sp akE,
где матрица а задается формулой (-») и Е — постоянная
матрица, все элементы которой равны единице. Функция
ck(а) может быть также выражена через параметры
li = mi + (п — i), i = 1, 2, ..., п, с помощью формулы
где коэффициенты у,- выражаются рационально через
Доказательство. Первая часть теоремы нами
уже доказана. Далее, заметим, что матрица а имеет раз¬
личные собственные значения. Следовательно, она может
быть приведена к диагональному виду:
где диагональная матрица I имеет элементы U —
= т{ + (п — i). Положим у = хЕх~1\ тогда имеем
где у, = уц — диагональные элементы матрицы у. Для
явного вычисления этих коэффициентов достаточно вы¬
писать преобразующие матрицы х, х~1.
Запишем матрицу а в следующей блочной форме:
П
хах 1 = I,
П
ск (а) = sp lky = 2 Y Л>
. i = 1
Ь с
где b — аналогичная матрица порядка п—1с собствен¬
ней значениями 1\, Ц, 1п-й е — етрлбец из едина-

§ 60. СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ Ск 263
ковых чисел, равных —1, и X = 1п- Пусть матрица у при¬
водит b к диагональной форме:
yby~l — I',
где V — диагональная матрица с элементами l'a = U,
i=l, 2, п—1. Тогда нетрудно проверить, что ис¬
комая матрица х может быть представлена в виде
у {и-КУ'ус 1
0 1
где предполагается, что оператор (/' — к)~1у применяет¬
ся к вектору с*). В частности, если п = 2, то мы на¬
ходим
Х\<)
В общем случае замечаем, что результаты вычисления
при n = j—1 сохраняют силу также и при n = j для
столбцов с номерами 1, 2, . . . , / —1 (именно эти столб¬
цы входят в матрицу у). В то же время столбец с номе¬
ром / выражается через предыдущие столбцы по фор¬
муле
ХЦ = ~ 7“ ]. (1 + Х1, 1 + 1 + Х1, 1+2 + ••• +*/,/-i)>
где i = 1, 2, 1; хп = 1; xhj = 0 при k > /. Вводя
для краткости обозначение aij = (U — замечаем,
что сумма 1 + х,, ,+1 + . . . + Xj, j~2 отличается лишь мно¬
жителем от хг> Отсюда находим
xi, i-i
аИ
О-0г. i-\), *</•
Начиная с элемента x,-i<+i = —о», i+i и продвигаясь вдоль
строки направо, получаем в результате
/-1
хи = ~ <*ц П (1 ~ crfp), 1 </</< п.
p~i+1
При этом матрица х является верхней треугольной с
единицами на главной диагонали.
*) Достаточно проверить, что 1х — ха = 0, откуда хах ' = I.

264
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
Вычисление матрицы х~1 можно несколько упростить,
если заметить, что
— (b — I) 1 с
О 1
Теперь уже путем элементарных вычислений нетрудно
получить искомую формулу для коэффициентов у;.
Теорема доказана.
Из найденных формул для ch(а) первая непосред¬
ственно приводит к полиному, вторая — лишь к рацио¬
нальной функции от ти т2, . . . , тп. Однако вторая
формула содержит замечательную информацию о струк¬
туре функций си (а):
Следствие 1. Все собственные значения ch(a) яв¬
ляются симметрическими полиномами от /ь /2, . . . , /«.
Действительно, всякая перестановка этих чисел ве-
л
дет к одновременной перестановке степеней /; и соот¬
ветствующих коэффициентов у;- Отсюда в свою очередь
нетрудно получить
Следствие 2. В классе собственных значений опе¬
раторов Казимира для группы GL(n) содержатся все
симметрические полиномы от /ь /2, . . . , 1„.
Действительно, достаточно доказать это утвержде¬
ние для степенных сумм Ньютона
sfe (а) = 2 й,
i — \
через которые, как известно, всякий симметрический по-
лином выражается полиномиально. Записывая матрицу а
из теоремы 2 в виде I + р, где I — диагональная часть с
собственными значениями Д /2, 1п а р — постоянная
матрица, находим, что разность
Си (а) - Ч (а) = sp (/ + p)k Е - sp lkE
есть симметрический полином степени <ft. Следователь¬
но, рассуждая индуктивно, заключаем, что sft(a) выра¬
жается через ck(a) полиномиально (и рекуррентно).
Следовательно, sh{а) содержится в классе собственных
значений операторов Казимира.

§ 61. РАЗДЕЛЕНИЕ ТОЧЕК СПЕКТРА
265
Следствие 3. Если k > п, то оператор Казимира
ch выражается полиномиально через С\, с2, ..., с„.
Действительно, суммы Ньютона sk(a), k^.n, а вме¬
сте с ними и функции С/Да), k п, являются образую¬
щими в классе симметрических полиномов. Следователь¬
но, существует такой полином fh(zь 22, ..., zn), чтоопе-
ратор
б С/; / £ (С,, Со, . . ., Сд)
обращается в нуль на всех неприводимых представле¬
ниях d(а). Но тогда он обращается в нуль и в правом
регулярном представлении, определенном в классе поли¬
номов на G. Поскольку это представление является точ¬
ным для алгебры ЭЕ *), то 6 = 0.
В заключение отметим, что С/Да) есть коэффициент
при zh в разложении функции
П
c(-z’ =
по степеням вспомогательной переменной г. Вводя обо¬
значение
я(г, <х)=][ (l-т^Тд)
;= I
и разлагая это произведение в сумму простых дробей,
легко находим, что оно совпадает с выражением
1—zc(z, а). Следовательно,
c{z, а) = -^(1 -п(г, а)).
Из полученной формулы особенно отчетливо видна сим¬
метрия собственных значений по С, /2, ..., 1п-
§ 61. Разделение точек спектра и алгебраическое
доказательство полной приводимости
В предыдущем параграфе было показано, что функ¬
ции сДа), с2(а), ..., сп(а) образуют полиномиальный
*) Следствие 3 из теоремы 1. Очевидно при рассмотрении диф¬
ференциальных операторов на G достаточно ограничиться классом
полиномов.

266
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
базис в классе всех симметрических полиномов ог
U, h, ■ ■ ■, In- Отсюда легко вытекает следующее утвер¬
ждение:
Теорема 3. Собственные значения с i (а), с2 (а),...
сп( а) характеризуют сигнатуру а однозначно, т. е.
определяют неприводимое представление d(а) однознач¬
но с точностью до эквивалентности.
Доказательство. Если нам известны числа
А, = Ci (а), ... , Кп = сп (а), то известны также значе¬
ния всех симметрических полиномов от 1\, /2, ..., 1п.
Следовательно, числа Iь /2, ..., 1п определяются одно¬
значно с точностью до перестановок*). Однако, если
эти числа соответствуют сигнатуре а= {ть т2, . . ., /п„),
то между ними существует соотношение порядка
/] > 1-2~> ••• > 1п>
которое следует из их определения (/, = от,-+ (п — i),
i = 1, 2, . . . , п,) и неравенств т\ > /п2 > .. . > тп. Сле¬
довательно, в этом случае числа /ь /2, . .. , /„ опреде¬
ляются уже однозначно.
Теорема доказана.
Основное содержание теоремы 3 сводится к тому,
что если сигнатуры а, Р различны, то найдется хотя бы
одно значение k = 1,2, .. ., п, при котором ch(а) зАсДР).
Коротко можно сказать, что операторы Казимира «раз¬
деляют» неприводимые представления группы G.
До сих пор мы рассматривали только аналитические
представления группы GL(n); очевидно, те же резуль¬
таты имеют место и для всех неприводимых конечномер¬
ных представлений этой группы; однако набор операто¬
ров Казимира «удваивается», поскольку наряду с ана¬
литическими приходится рассматривать также и
антианалитические инфинитезимальные операторы. Пе¬
реход от GL(«) к SL(«) сводится к исключению линейно¬
го оператора Ci (вместе с ci в вещественном случае**));
*) Действительно, lu /2 In являются корнями алгебраиче¬
ского уравнения А71— sjA"-1 + s2A"~2— ...±sn=0, где si, s2, ...
..., sn — симметрические полиномы от h, k In-
**) Однако, используя известную связь с представлениями GL(n),
мы можем формально сохранить оператор сь рассматривая равен¬
ство С] (а) = т как условие нормировки отi + m2 -К , ,+тп = от. В ча¬
стности, можно считать, что т — 0.

S ei. РАЗДЕЛЕНИЕ ТОЧЕК СПЕКТРА
267
остальные операторы Казимира, очевидно, по-прежнему
разделяют неприводимые представления этой группы.
«Разделяющее свойство» операторов Казимира мо¬
жет быть использовано для алгебраического доказатель¬
ства полной приводимости, разумеется, в случае груп¬
пы SL (п). Сформулируем этот результат как следствие
теоремы 3:
Следствие. Всякое конечномерное представление
группы SL(«) вполне приводимо.
Мы наметим только схему доказательства этого
утверждения. Если в состав представления т входят два
неприводимых представления а и Ь, то матрицы т по от¬
ношению к некоторому базису принимают квазитре-
угольную форму:
II а с
Tio ь
Если а не эквивалентно Ь, то существует оператор Кази¬
мира А, разделяющий а и Ь; в данном базисе матрица
этого оператора имеет ту же квазитреугольную форму
с заменой а на А1Щ, b на Я2е2, где е\, е2— единичные мат¬
рицы соответствующего порядка. Поскольку Ai ф Я2,
оператор Д диагонализуется:
А,
О
О
(А,- = Кгви i = 1,2), причем замена базиса осуществляет¬
ся таким образом, что матрицы т имеют прежний ква-
зитреугольный вид. Поскольку
Ат — t/S,
= 0
и А| Ф А2, мы заключаем, что с = 0. Если а эквивалентно
Ь, то операторы Казимира не дают никакой информации;
однако, используя инфинигезимальную технику и един¬
ственность старшего веса, легко находим, что и в этом
случае представление т вполне приводимо. Переход к
произвольному количеству неприводимых компонент
осуществляется теперь без труда (по индукции).

268
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
Замечание 1. Для группы GL(n) подобное рас¬
суждение не проходит лишь в том случае, когда а экви¬
валентно Ь. Действительно, в этом случае представле¬
ние т может отличаться от а = b тензорным множителем
вида
[j 1 t II
0 A, t = In | det g I,
и свойство полной приводимости уже не выполняется.
Рассуждая индуктивно, разбиваем произвольное пред¬
ставление т в прямую сумму отдельных блоков, каждый
из которых отличается лишь тензорным множителем
вида
ехр/Д, &■
0
1
0
0 .
. 0
0
0
1
0 .
. 0
& =
0
0
0
1 .
. 0
0
0
0
0 .
. 0
t = ln| det g I,
от неприводимого представления GL(n)*). Иначе го¬
воря, все «жордановы клетки» группы GL(n) обуслов¬
лены наличием одномерных представлений g —> det g,
g—»detg', которые, в сущности, являются представле¬
ниями абелевой фактор-группы GL(n)/SL(n)**).
Замечание 2. Располагая инфинитезимальным
методом изучения полной приводимости, мы могли бы
вместо GL(n), SL(n) рассматривать их алгебры Ли
gl(n), si (я). При этом нет необходимости использовать
явную модель неприводимых представлений, достаточно
лишь знать***), что существует взаимно однозначное
соответствие между этими представлениями и сигнату¬
рами а = (tih, m2, ■■■, тп), mi ^ m2 5s- . . . > mn.
«Разделяющее свойство» операторов Казимира мо¬
жет быть, очевидно, использовано также для спектраль¬
*) Достаточно ограничиться преобразованием подгруппы D
в классе старших векторов и упорядочить эти векторы таким обра¬
зом, чтобы одинаковые старшие веса были соседними.
**) В § 118 мы получим гораздо более общую картину приво¬
димости для произвольной группы Ли.
***) См. § 121.

5 62. ПОЛНОЕ ОПИСАНИЕ ЦЕНТРА ДЛЯ ГРУППЫ GL(«) 269
ного анализа конечномерных представлений, точнее, для
перечисления всех неприводимых компонент, входящих
в данное представление. Однако практически этот ме¬
тод слишком сложен*).
§ 62. Полное описание центра для группы GL(/t)
Если нас интересует задача о полном описании цент¬
ра 3 в универсальной обертывающей алгебре X, то удоб¬
нее всего обратиться к симметризованной форме записи
элементов не!. Положим
е, °е; о ... »е, —Р[е;: , ],
И 2
где Р — оператор симметризации по индексам ц, г2, ...
... , im, введенный в § 58. Полученный символ уже не
зависит от порядка расположения индексов г'ь г2, . . . , im.
Напомним, что такие элементы образуют базис в X.
Умножение с кружочком можно по правилу дистри¬
бутивности продолжить также на любые элементы
геН!). Очевидно, это умножение коммутативно.
Если поставить в соответствие каждому элементу
ei,°eit° ... °eim числовое произведение ГДе
in i2, •••> In — вспомогательные независимые перемен¬
ные, то мы получаем взаимно однозначное соответствие
между X и алгеброй & всех полиномов от |2, • • •, in-
Для того чтобы это соответствие не зависело от выбора
базиса, достаточно предположить, что |ь £2, . .., \п —
ковариангные координаты в самой алгебре X. В этом
смысле будем писать = £Р(Х).
Заметим, что введенное соответствие между X и
!?(Х) является мультипликативным, если под умноже¬
нием в X понимать умножение с кружочком.
*) Однажды мы воспользовались этим методом в § 38.
**) При этом мы полагаем по определению
(е, °е,- о ... °е,- \°(е, °е, ° ... °е,Д
v li 2 т) Wi h !l>
Заметим, однако, что х ° у ф (ху + ух) для произвольных элемен¬
тов х, у eS.

270
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
Выясним теперь, какой подалгебре в @(Х) соответ¬
ствует центр 3 cr £. Для решения этого вопроса нам
будет удобно отказаться от чисто инфинитезимального
рассмотрения и считать, что X — алгебра Ли некоторой
группы G.
Если в группе G осуществляется внутренний автомор¬
физм h —* ghg~l, то этот автоморфизм вызывает также
преобразование х-> р{g)x в классе касательных векто¬
ров не! В частности, если G — матричная группа, то
р (g)x = gxg~l, не!
Подставляя в это выражение g = exp (у, у е X, и разла¬
гая правую часть в степенной ряд по /, получаем, что
р(ехр ty) = 1 +tD(y)+
т. е. представление D(y) является главной линейной ча¬
стью (дифференциалом) p(g). Представление p(g) на¬
зывается присоединенным представлением группы G.
Если I = {li} — ковариантные координаты в алгеб¬
ре X, то представление p(g) вызывает также преобразо¬
вание I—>%Й в классе этих координат. Формула
TgP(l) = p(lg)
определяет представление группы G в алгебре !Р(Х).
Если рассматривать только линейные формы р(£),
то они преобразуются контравариантно и представле¬
ние Tg совпадает в данном случае с представлением
p(g'). Следовательно, Tg продолжает p(g) на алгебру
&{Х).
Вычислим дифференциал представления Те. Если
р{1)—линейная форма, то, как мы знаем, этим диф¬
ференциалом является D(x). В общем случае мы вы¬
числяем инфинитезимальные операции представления Tg
по индукции как производные в точке g = е ог произ¬
ведения некоторого числа линейных форм. В силу «пра¬
вила дифференцирования», введенного в § 58, это приво¬
дит к тому же результату, что и определение D(x) в
алгебре £. Следовательно, D{x) в алгебре £ является
дифференциалом Tg.

§ 62. ПОЛНОЕ ОПИСАНИЕ ЦЕНТРА ДЛЯ ГРУППЫ GL(n) 271
Замечание. Из полученного результата, в частности, следует
что представление D(x) совпадает с представлением
я0 + я 1 + а (я2) + ... + а (ят) + ...,
где а(я,„) —симметризованная часть представления ят = я®я®...
... ®я (tn сомножителей). Эта запись уточняет замечание, сделанное
в § 59.
Напомним теперь, что 3 состоит по определению из
всех инфинитезимальных инвариантов D(x). Следова¬
тельно, 3 есть совокупность всех инвариантов представ¬
ления Tg. Сформулируем полученный результат в виде
следующей общей теоремы:
Теорема 4. Взаимно однозначное соответствие ме¬
жду алгеброй X и алгеброй SP{X) всех полиномов р(\)
от ковариантных координат в алгебре X приводит к со¬
ответствию между центром 3 и алгеброй всех полино¬
мов, инвариантных относительно присоединенного пред¬
ставления в X.
В частности, если X — алгебра Ли группы GL(n), то
всякий элемент записывается в виде х^вц, где
eij — стандартный базис, и всякая линейная форма
ре^(Х) записывается в виде р (|) = x'jEij = sp х%, где
матрица £ =И|ц11> Т / = 1, 2, . . . , п, составлена из вспо¬
могательных переменных, заменяющих базис е^. Преоб¬
разование х—*gxg~l контрагредиентно преобразованию
£,—>g~!%g в классе переменных Следовательно,
Тер &) = р (g~%g)
в классе всех полиномов р(|) от переменных |=||£п1!,
i, /= 1,2, ..., п. При этом рассматриваются только
«аналитические» полиномы р(1) (зависящие от gjj, но
не от lij).
Задача описания центра 3 сводится теперь к задаче
описания всех решений системы уравнений
P(g~llg) = Pit)
в классе полиномов /?(£). В частности, такими полино¬
мами являются элементы
M!) = spEm. m = 0, 1, 2,

272
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
Известно*), что любой инвариантный полином /?(£) яв¬
ляется в этом случае полиномом от k\, k2, . . . , kn. Ина¬
че говоря, k\, k2, ■ . ., kn являются образующими в ал¬
гебре 9>й всех инвариантных полиномов.
Возвращаясь от переменных |,-j снова к базисным
элементам получаем
Следствие 1. Операторы Казимира
km = sp em = et t ° e t t ° ... °e{ ,. , m = 1, 2, . . ., n,
12 2 3 ml
являются образующими центра 3 в случае группы
GL (п).
Заметим теперь, что полиномы km и сгп имеют оди¬
наковую старшую компоненту:
[^т] [Стг]>
где символ [х] был введен в § 58 для элементов х е $.
Действительно, оба эти полинома принимают одно и
то же значение при формальной подстановке g,j вместо
ец. Отсюда ясно, что системы km, cm, m = 0, 1, ..., п,
выражаются друг через друга полиномиально и рекур-
рентно. В результате получаем также
Следствие 2. Операторы Казимира ст, т= 1,
2, . .. , п, также являются образующими центра 3 в слу¬
чае группы GL(n).
Последнее утверждение представляет для нас инте¬
рес хотя бы в том отношении, что свойства симметрии,
найденные нами в § 60, переносятся теперь на произ¬
вольный оператор Казимира геЗ:
Следствие 3. Собственное значение z(a) всякого
оператора- Казимира геЗ является симметрическим по¬
линомом от параметров К, 12, .. ., 1п (К = + (п — г),
1=1,2, . . . , п).
§ 63. Правило циклов
В заключение этой главы предложим еще один метод
вычисления собственных значений операторов Казимира,
который, в отличие от метода теоремы 2, специально
*) См., например, [10]. В § 75 мы докажем это утверждение не¬
зависимо.

§ 63. ПРАВИЛО ЦИКЛОВ
273
приспособлен для работы с симметризованными опера¬
торами Казимира. Развитие нового метода представляет
интерес по той причине, что явная связь между изучен¬
ными ранее операторами сь с2, . . ., сп и симметризован¬
ными операторами k\, k2, . . . , kn практически является
довольно сложной. Впрочем, вместо операторов ku k2,. . .
. . ., kn нам будет удобнее рассматривать иную базис¬
ную систему операторов Казимира.
Используя снова вспомогательную числовую матрицу
I = lllijll, г, / = 1,2, . . ., п, мы рассмотрим ее характери¬
стический полином
j(X, S) = det(l—^)=1 — Л/, + Я2/2 -
Wn,
коэффициенты которого выражаются хорошо известны¬
ми формулами через диагональные миноры матрицы
in. (6) -
£
h t •
ч ч
’ ‘ Ч'/я
<‘т
1.
ml
•• h 1
т т
m= 1,2,..., п.
Полином j (X, |), а вместе с ним и его коэффициенты
/,п(Ю являются инвариантами относительно присоединен¬
ного представления более того, как известно,
полиномы /1 (g), /2(1), jm(l) являются образующими
в алгебре Ф0. Следовательно, мы получаем возможность
рассматривать новые операторы Казимира:
1т =
ei 1 •
" ei i
s 111
4 m
eW 1 •
■ j
■ Zs
т ■■
К 2,
п,
которые являются образующими в алгебре Кружочек
над знаком детерминанта означает при этом, что от¬
дельные одночлены, возникающие при раскрытии де¬
терминанта, вычисляются как коммутативные произве¬
дения с кружочком, например:
ец
е21
е12
е22
= е.
1 е22 ~ е12 ° е21-

274
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
В дальнейшем мы укажем простую явную связь между
образующими /1, /2, и образующими kx, k2,
..., kn. Наряду с операторами /ь /2, •••, /п мы можем
рассматривать также их линейную комбинацию
1 — Хехх
Хех2
• • ~Ъеы
m=
Хе2Х
1 — Хе22
.. Хе2п
.. 1 Хвпп
Полином /(X) будем называть производящим полиномом
операторов Казимира. Переходя от абстрактных опера¬
торов к операторам представления, заменяем символы
ен, im, j(X) соответствующими заглавными символами
Eij, Jт, J (А,) .
Полагая, в частности, т = п, мы рассмотрим опера¬
тор Казимира
£>,
Е\2 •
• Еы
Jn =
Е2\
Е22 •
■ Еы
ЕпХ
^■ni •
■■ Епп
от которого оператор J (X) отличается лишь несущест¬
венной заменой Ец на — ХЕц. Раскрывая этот детер¬
минант, замечаем, что каждое его слагаемое имеет вид
± Ец{ ° Ецг» ... о Егнп,
где (й, t2, in)—произвольная подстановка индек¬
сов 1,2, ..., п (знак определяется четностью или не¬
четностью этой подстановки). Поскольку умножение
коммутативно, мы можем сгруппировать сначала сомно¬
жители вида Ei/1E/i/2 ... Ejku затем сомножители вида
EsilEjlj2 ... Ejts, где s — один из индексов, не содержа¬
щихся в первой цепочке, и т. д., что равносильно разбие¬
нию исходной подстановки на отдельные циклы. Введем
теперь
Определение. Произведение вида
ZV2...,p = £V2°£V3° ... °£Vl,

S 63. ПРАВИЛО ЦИКЛОВ
275
где среди индексов i\, Д, ..., iv нет одинаковых, назо¬
вем циклом. Число р назовем длиной этого цикла*).
В частности, мы видим, что всякий детерминант Ка¬
зимира является полиномом от циклов по отношению к
умножению с кружочком; при этом перемножаемые цик¬
лы никогда не содержат общих индексов и потому вза¬
имно перестановочны. Для наших целей существенно,
что в произвольной ассоциативной алгебре X имеет ме¬
сто следующее
Правило умножения. Если базисные элемен¬
ты, входяище в два разных одночлена
*-vv "■
k = I, 2, ..., m, взаимно перестановочны, то эти одно¬
члены также перестановочны, причем
At ° Л2 о ... ° Am — AjA2 ... Ат.
Иначе говоря, для одночленов Ль Л2, ..., Ат умноже¬
ние с кружочками равносильно обычному умножению.
Действительно, согласно определению умножения с
кружочком имеем
W ... 0 Ат = lf + ...у
где f = fi + ?2 + • • • + fm и сумма распространяется на
все /! перестановок сомножителей et , et, е{ . Ус¬
ловимся считать два слагаемых в этой сумме эквива¬
лентными, если они получаются друг из друга переста¬
новкой лишь тех сомножителей, которые входят в один
и тот же одночлен Л^. Ясно, что каждый класс эквива¬
лентности имеет v = /i!/2! frA слагаемых и число раз¬
личных классов есть /!/v. При вычислении суммы сла¬
гаемых каждого класса мы можем воспользоваться пе¬
рестановочностью сомножителей, входящих в разные
одночлены Ah, и расположить на первых f 1 местах
*) Заметим, что цикл не меняется при циклической перестановке
индексов ц, i2, ..., i-p (ибо умножение с кружечками коммутативно).
Заметим также, что здесь, в отличие от записи § 59, не предпола¬
гается суммирование по индексам iu h Д.

276
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
сомножители из А\, на следующих f2 местах — сомножи¬
тели из А2 и т. д. При этом согласно определению экви¬
валентности на каждом из этих отрезков встречается по
одному разу всякая возможная перестановка сомножите¬
лей данной группы. Следовательно, искомая сумма 5
может быть записана в виде произведения SiS2 ■ ■ ■ S.,,,
где
s* = (e‘V2-%+ =
Следовательно, каждый класс эквивалентности дает
один и тот же вклад, равный S, и общая сумма вкла¬
дов есть f\/v-S = fl AiA2 ■ • • Ат. Производя деление на fl,
входящее в символ Ai°A2° . . °Ат, получаем нужный
результат. Отсюда, в частности, имеем
Следствие. Всякий детерминант Казимира яв¬
ляется полиномом от циклов по отношению к обычному
умножению.
Фиксируя некоторый цикл и применяя его к стар¬
шему вектору go, замечаем, что действие цикла добав¬
ляет к каждому весу слагаемое вида а, , + а, , + ... +
12 2*3
+ а,. , = 0. Следовательно, вес не изменяется и, в ча-
‘р л
стности,
Zlo = Цо
для каждого цикла Z. Покажем теперь, что собственное
значение А для каждого цикла Z может быть сравни¬
тельно просто выражено в явном виде
Условимся считать, что р = (г'ь i2, ..., iP)—цикли¬
ческая система индексов, т. е. такая, в которой номер р
считается предшествующим, номеру 1, и пусть р'— ли¬
нейная цепочка тех же индексов, распределенных в но¬
вом порядке. Фиксируем целое число k и будем исполь¬
зовать символы а, р для чисел и >k. Скажем, что
р' — инверсная цепочка порядка k, если
1° для каждой пары соседних индексов в р вида
(i, Р) индекс i встречается в р' ранее Р;
2° для каждой пары соседних индексов в р вида
(/, а) индекс а встречается в р' ранее /'.
При этом индексы t, / могут быть как типа а, так и
типа р. Из этого определения, в частности, следует, что

§ 63. ПРАВИЛО циклов
277
всякая цепочка из р вида (рь р2, •••, Р«) сохраняет свой
порядок следования в р', а цепочка вида (аь а2, ..., аt)
меняет порядок следования на обратный*). Пусть пк—
число всех инверсных цепочек порядка k.
Докажем теперь, что имеет место
Теорема 5. Собственное значение каждого цикла Z
на старшем векторе представления d(a) есть линейная
функция от сигнатуры а. Если Z = Zill2... / , то соб¬
ственное значение этого цикла имеет вид
г. , . =4-fm, -vm +v3m - ... ± m ),
11(2 1 ■ • lp p' 1 h h h lp‘
где ji, /2, ..., jP — расположение индексов i\, i2, ..., ip
в порядке возрастания, a = (mu m2, ..., mn), p-^n и
коэффициенты vk вычисляются no формуле
vk = nk_1 + nk,
где nh — число инверсных цепочек порядка k, построен¬
ных по системе (м, i2, ..., iP).
Доказательство. Пусть N — произвольное слагаемое в
цикле Z; докажем, что собственное значение N на старшем векторе |о
является линейной функцией от а. Действительно, это верно, если
цикл имеет длину 1. В общем случае заметим, что среди сомножите¬
лей одночлена N всегда содержится хотя бы один повышающий опе¬
ратор Е = Ец. Записывая N в виде N\EN2, где Nt, N2— дополнитель¬
ные сомножители, переставим местами Е и N2:
Л' =A/,JV2£ + JV, [Е, N2].
Очевидно, первое слагаемое этой суммы аннулирует старший век¬
тор £о- Далее, нетрудно видеть, что второе слагаемое всегда пред¬
ставляется в виде разности двух одночленов, имеющих степень одно¬
родности р — 1 и содержащихся в некоторых циклах длины р—I”*).
Следовательно, наше утверждение доказывается по индукции.
Ввиду доказанного свойства линейности мы можем для каждой
сигнатуры а = [гр г2, ..., г„] представить искомое собственное значе¬
ние в виде
п
*Ш2 ... SVk-
*) Однако индексы, соседние в р, не обязаны быть соседними
в р'. (В частности, в цепочке р' индексы аPj, i = 1, 2, ..., t, j =
= 1, 2, ..., s, могут чередоваться.)
**) Если Z — Z, ■ i , то эти циклы получаются вычеркива-
12 •••*/?
нием одного из индексов г, / в системе (ц, i2 ip).

278
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
где Zh — такое же собственное значение в базисном представлении
dh, k = 1, 2, ..., п. Реализуем представление dh в классе функций
от k векторов-строк x=(xt,x2, ..., хп), У=(У\,Уг, Уп) и усло¬
вимся использовать сокращенное обозначение
* Xik
[/,, k,..
ti
УЧ •
■ %
%
и1 ■
2
для произвольного минора fe-ro порядка, составленного из этих строк.
В частности, минор шь = [1, 2, ..., k\ является старшим вектором
представления dh. Поскольку преобразования группы О сводятся
к умножению векторов х, у, ..., и справа на geG, легко находим,
что в этом случае
с д л. д л. , д
Е,. = х, — + у, -= Ь ... +и, —■.
Ч ‘ dxj 1 dyj ‘ dtif
Применение такого оператора к минору [ft, t2, ..., <ч] равносильно
замене индекса / под знаком минора на индекс i (либо обращению
в нуль этого минора, если j не содержится среди индексов гь is, ...
..., ih). Мы получаем удобную схему для применения икфинитези-
мальных операторов Ец.
Рассмотрим теперь систему операторовГг = Et i , Г{ = Ei { , ...
.... Г,- = Е, , , входящих в определение цикла Z, и вычислим дей-
lP lpli
ствие на вектор шь произвольного одночлена вида
N = Т Г ... Г
* * 1 о 1 е ‘ • 1 о )
61 2 Ьр
где р' = (si, s2, ..., sP) — подстановка индексов р = (t'b i2, ..., ip)
Нетрудно видеть, что Д'ш.ч ф 0 только в том случае, когда р' — ин¬
версная цепочка порядка k. Действительно, допустим, что применение
операторов Ts в указанном порядке приводит после некоторого числа
шагов к ненулевому минору до. Пусть символы а, (3 относятся соот¬
ветственно к числам и >£. Дальнейшее применение оператора
Г. = Еj ; может привести к нулевому результату только в сле-
lm lmlm +1
дующих случаях: 1) пара (im, im + i) имеет вид (|3, (Г), и оператор Гр/
стоит левее Гр (т. е. индекс (3' еще не появился на схеме до); 2) пара
(im, im + j) имеет вид ((3, а), и оператор Га стоит правее Гр (т. е.
индекс а уже смещен со схемы до); 3) пара (im-ь im) имеет вид
(£, а), и оператор Г; стоит левее Га (в этом случае индекс а еще не
смещен со схемы w и применение Га приводит к появлению двух
одинаковых столбцов под знаком минора до). Но все эти случаи
исключаются, если р' — инверсная цепочка. Применение оператора
N к вектору ц>А приводит в этом случае к циклической перестановке

§ 63. ПРАВИЛО ЦИКЛОВ
279
всех индексов «ц а2, ... i а„ входящих как в цепочку (й, h, • ■, i?J.
так и в схему сол. Следовательно,
(-1)'7"1
Za>.= т, п. а.,
где функция Па и функция q = q(k) имеют, очевидно, скачки только
в точках (1, i2, ..., ip (причем q(k) меняется ровно на единицу). За¬
метим также, что rtm = пм-1 = 1, где т — min(и, i2,...,/р) и М =
= max («i, i2,..., ip), и также «м+в = 0 при 6^0; кроме того,
q(m) = 1. Располагая индексы й, (2,, ,.,/р в возрастающем порядке
/ь /г,..., ip, находим, что zili2 {р разлагается только по функциям
вида
r, + r,+ i+ ••• +г1.~чп1-тг,
где у = /д, /' = /*+ь ft *= 1, 2, .... р—1. Отсюда легко получается
формула, указанная в условиях теоремы. Теорема доказана.
Пример 1. Если р = 1, 2 и 3, то соответствующее
собственное значение не зависит, как легко проверить,от
порядка индексов и имеет вид zt = тр, ^ (mt — mj),
i</; zilk = (rtti -2ml + mk),i<j<k.
Пример 2. Если Z = Z!2... р+ь то числа 1, 2, .. ., k
относятся к типу а, a H 1, ..., + 1 — к типу р. Под¬
становка р' является инверсной, если k стоит на первом,
р + 1 — на последнем месте, а остальные р—1 чисел
распределяются между ними как угодно, но с убыванием
чисел типа а и с возрастанием чисел типа р. Ясно, что
в этом случае nk = Ckz\, где Clk — число сочетаний из k
по I, и мы находим
гы...р+1= (Р + 1)7— ptn2 + р{р~-^-т3-... ±mp+1}.
Полученное выражение есть конечная разность р-го по¬
рядка, построенная из чисел щь т2, • • •> тр+\.
Пример 3. Для вычисления собственного значения
/2(а) мы раскрываем миноры под знаком оператора /2:
■2
<</
Ец Е,
‘11
^ {ZtZj — Zij),
i <1

280
ГЛ. IX. ОПЕРАТОРЫ КАЗИМИРА
и заменяем каждый цикл Z,-, соответствующим соб¬
ственным значением (пример 1); в результате получим
к («) = ^ mimt -j 2 (,ni ~ mi)-
i < i i < i
Аналогично вычисляем также и функцию /з(а):
h («) = niinijiTik -j ^ | (тг - т;) +
i < j <k i</
I < j < к
В общем случае естественно сразу рассматривать Если п не
слишком велико, то «правило циклов», даваемое теоремой 5, позво¬
ляет легко подсчитать функцию j „(я). Если в операторе /п заме¬
нить каждый цикл Zi длины 1 оператором 1 — XZi и каждый цикл
Z, , , длины р > 1 — оператором (~X)PZ, , .• , то отсюда
12 ' /? г1*2 1р
непосредственно получаем собственное значение /(а, Л) производящего
полинома /(X). Отсюда разложением по X находим все остальные
функции jm, т — 1, 2 п.
В заключение заметим, что между характеристиче¬
ским полиномом числовой матрицы | и следами ее сте¬
пеней существует хорошо известное соотношение, пере¬
фразируя которое на язык операторов Казимира полу¬
чаем тождество *)
—/~(Я) = + .. • + 'K,mkm + . . .,
где j'(К)—производная по X и в правой части стоит
формальный степенной ряд. Отсюда, умножая на /(А,) =
= 1 —kj\ + ... ± Knjn, находим рекуррентные формулы
и = ьи
— 2/2 = — i\k\ + ^2>
З/3 = — k^i ~~ /1^2 Т ^з> • • •
*) См. [10], стр. 61. Поскольку все рассматриваемые величины
вполне определяются своими значениями на диагональных матри-
п
цах мы можем считать, что j (Я, £) =* JJ (1 — А|*), откуда легко по-
i = i
лучается нужное тождество.

§ 63. ПРАВИЛО циклов
281
Те же формулы имеют место при замене элементов /(Я),
jm, km соответствующими собственными значениями
/(аД), /»»(Я.), km(X). В частности, зная /(аД), мы нахо¬
дим значения km{a) как коэффициенты аналитической
функции — /'(а, Я.)//(а, Я).
Очевидно, величины /,„(а), т = 1, 2, . .., п, равно
как и km(a), т = 1, 2, . . . , п, «разделяют» систему не¬
приводимых представлений группы GL(h).
* *
*
Квадратичные операторы, перестановочные с элементами уни¬
версальной обертывающей алгебры X, были впервые введены К а-
з и м и р о м [93] для чисто алгебраического решения вопроса о пол¬
ной приводимости конечномерных представлений. В дальнейшем
подобные операторы, уже не обязательно квадратичные, стали на¬
зывать «операторами Казимира» или «операторами Лапласа». Об¬
щий метод описания алгебры этих операторов в терминах полино¬
мов, инвариантных относительно присоединенного представления,
был предложен И. М. Г ельфапдом [64]. Мы приводим все эти
конструкции в общем виде (с иллюстрацией на примере GL(п));
полученными результатами воспользуемся в дальнейшем при изу¬
чении произвольной компактной группы Ли.
При вычислении собственных значений операторов Казимира мы
используем традиционный метод (применение к старшему вектору),
который неоднократно применялся математиками и физиками. В из¬
ложении § 60 мы следовали результатам недавней работы А. М. П е-
реломова и В. С. Попова [122]; заметим, что эта работа была
стимулирована вниманием физиков-теоретиков к операторам Кази¬
мира. Симметрия относительно перестановок возникает при этом
несколько неожиданно (следствие 1 из теоремы 2). В дальнейшем
будет указано иное доказательство свойства симметрии (§ 126).
Рассмотрение детерминантов Казимира и «правило циклов» были
предложены (без доказательства) в лекциях автора [21]; здесь мы
излагаем этот метод несколько подробнее, с исправлением неточ¬
ностей, допущенных в [21]. В § 126 будет описан еще один общий
метод вычисления собственных значений операторов Казимира.

ГЛАВА X
ИНДИКАТОРНЫЕ СИСТЕМЫ И БАЗИС
ГЕЛЬФАНДА — ЦЕЙТЛИНА
В предыдущей главе мы слегка отклонились в сторону от за¬
дачи изучения неприводимых представлений d(а); вернемся теперь
к этому вопросу. Среди известных нам моделей d(a) мы отдаем
предпочтение реализации на группе Z, которая включает минималь¬
ное число независимых параметров; однако эта реализация страдает
пока существенным недостатком, поскольку для пространства пред¬
ставления мы имеем лишь малоэффективную характеристику (ци¬
клическая оболочка старшего вектора). Желательно было бы и в
этом случае построить аналог симметризаторов Юнга.
Решение этой задачи дается в § 65. В дальнейших параграфах
полученная информация используется для изучения «внутренней
структуры» и построения базиса в пространстве представления d(a).
При этом мы выписываем явную формулу для инфинитезимальных
операторов в найденном базисе. Дается также общая формула для
матричных элементов d(a).
§ 64. Операторы левого сдвига на группе Z*)
Нам будет удобно начать с реализации на группе G.
Напомним, что при выборе этой реализации мы осуще¬
ствили специальное вложение d(a) в правое регулярное
представление группы G; при этом векторы в простран¬
стве представления оказываются функциями на группе
G и, в частности, роль старшего вектора играет функ¬
ция
W gu ••• gu r‘
■<*)-Д
! = l gl\ • • • gii
*) В этом параграфе излагаются лишь эвристические сообра¬
жения и дается определение индикаторных систем. Основные ре¬
зультаты и доказательства собраны в § 65.

§ 64. ОПЕРАТОРЫ ЛЕВОГО СДВИГА НА ГРУППЕ Z
283
которую мы будем называть производящей функцией
представления d(a). Если к этой функции применять
только правые сдвиги, то мы получим (после взятия
линейных комбинаций) все векторы пространства пред¬
ставления. Если применять всевозможные левые и пра¬
вые сдвиги, то мы таким же путем получаем все мат¬
ричные элементы представления d(a).
Из перестановочности левых сдвигов с правыми есте¬
ственно ожидать, что при помощи операторов левого
сдвига можно получить описание пространства представ¬
ления d(a). В частности, соотношения
f(tg) = f(g), f(t>g) = a(t>)f(g), 6 gO,
справедливые для a(g), справедливы также и для всех
ее правых сдвигов, а отсюда и для всех f(g) из про¬
странства представления d(а). Нам будет удобно запи¬
сывать эти тождества в инфинитезимальной форме. Пре¬
жде всего имеем
1° L~f(g) = 0,
где L~—произвольный инфинитезимальный оператор
группы Z_, порожденный левыми сдвигами на группе G.
Очевидно, достаточно в этом равенстве рассматривать
операторы Ьц, отвечающие базисным элементам
i > /. Полагая для краткости Lt = 1ц, мы имеем также
равенство
2° Ьф(g) = mj(g), i = 1, 2, ..n- 1,
где m{ — координаты сигнатуры a = (mu m2, ..., mn)*).
Однако условия 1° и 2°, очевидно, не дают еще полной
характеристики пространства представления, поскольку
пространство всех совместных решений 1° и 2° бесконеч¬
номерно.
Если X — алгебра Ли группы G, то мы имеем для нее
стандартное разложение
Z = Z_+Z0 + Z+,
где Х_, Х0, Х+ соответственно натянуты на базисные век¬
торы e{j, i > j, i = /, i < j. Как легко проверить,
*) Напомним, что rt - т( — тц.1, i = j, 2',.,., л — 1, гп = т„.

284
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
элементы
являются образующими в алгебре AL. Действительно,
всякий базисный вектор из X- может быть представлен
в виде кратного коммутатора от еГ■ Точно так же эле¬
менты
являются образующими в алгебре Х+. Очевидно, усло¬
вие 1° равносильно системе условий
где Li — инфинитезимальный оператор, отвечающий
элементу ej• Выясним теперь, как действуют на функ¬
цию a(g) образующие алгебры Z+.
Пусть Lij — инфинитезимальный оператор левого
сдвига на группе G, отвечающий базисному вектору
е X. Вычисляя этот оператор по известному правилу,
находим
где в последней сокращенной записи имеется в виду
скалярное произведение векторов gi~(gn, g/2, •••, g/п)
и d/dgi = (d/dgih d/dgi2, d/dgia). Нестрого гово¬
ря, есть оператор подстановки /-й строки на место г'-й
строки. В частности,
где Lf = Li, 2+1 — инфинитезимальный оператор, отве¬
чающий элементу ef_ Применяя этот оператор к минору
2=1, 2, . . 22-1,
Li f(g) = 0, 2= 1, 2, . . п- 1,
П
2=1, 2, . . 22—1,

$ 64. ОПЕРАТОРЫ ЛЕВОГО СДВИГА НА ГРУППЕ Z
285
получаем следующий результат*):
/ 4.Л+1 ( 0 при i=£k,
(£,) Д„-0. где е,- = | , при
Иначе говоря, миноры Др при i ф р являются констан¬
тами по отношению к дифференцированию Lf и ми¬
нор Д(- ведет себя как линейная функция по отношению
к этому дифференцированию. Отсюда непосредственно
следует тождество
3° (Lt)ri+lf(g) = 0, i=l, 2, ..., п-1,
которое справедливо для a(g), а потому и для всякой
функции f(g) из пространства представления d(а).
Остальные операторы L+, отвечающие алгебре Х+, мы
пока рассматривать не будем. Введем обозначение ?Ra{G)
для пространства всех решений системы 1°—3°.
Переход к реализации на группе Z сводится к авто¬
матическому учету условий 1° и 2°. Вместо функции
a(g) мы рассматриваем теперь функцию «двух пере¬
менных»
a (z, g) = а (zg), ге Z, g^G,
где Z c= Z+. Оператор представления d(a) задается фор¬
мулой
Tgf(z) = a(z, g)f(zg),
и пространство представления 9Ja определяется как ли¬
нейная оболочка всевозможных функций fg{z)= a(z,g).
Существенно, что левые сдвиги на Z не перестановочны
со всеми преобразованиями Tg\ однако мы по-прежнему
рассмотрим операторы
@>i=zi+1-^7, <= 1, 2, . . ., п- 1,
и заметим, что функция a(z,g) удовлетворяет системе
дифференциальных уравнений
/а: №+'/(z) = 0, i= 1, 2 я— 1.
) Действительно, если i > р, то i-я строка не содержится в ми¬
норе ДР, если же i < р, то применение L* приводит к появлению
двух одинаковых строк под знаком минора Др; в обоих случаях
£,^., = 0. Равенство (1,^)2Д^ = 0 очевидно, поскольку Д* линейно
зависит от gf.

286
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Это вытекает непосредственно из формулы 3° для функ¬
ции a(g). Следовательно,
5Яа с Фа,
где Фа — пространство всех решений системы 1а. Есте¬
ственно исследовать связь между этими пространствами.
В частности, если га = 2, то Яа, как мы знаем, натянуто
на векторы 1,г, г2, ..., zm, т. е. совпадает с Фа.
В общем случае пока докажем, что имеет место
Лемма 1. Пространство Фа инвариантно относи¬
тельно операторов Tg.
Доказательство. Нетрудно видеть, что любая
матрица ге2 допускает однозначное представление в
виде
z = Zi(t)x,
где zt (t) = exp tef и матрица xgZ выделяется допол¬
нительным условием Xi, j+i = 0. Если рассматривать t
и х как параметры в группе Z, то имеем
х).
Следовательно, если Е*— совокупность всех решений
уравнения 2)гл+1 f (z) = 0 с фиксированным индексом i
(i = 1 2, ..., га—1), то Fi состоит из всевозможных
функций от t, х, которые являются полиномами от t
степени не выше г{.
Выразим теперь оператор Tg в параметрах (, х.
Используя транспонирование, запишем каждую матрицу
£eZ_ в виде Ш(т), где ii+i,t = 0 и (т) = ехртег.
Если матрица g допускает разложение Гаусса, то мат¬
рица при подходящем выборе сомножителей \
и х, очевидно, приводится к виду

§ 65. ИНДИКАТОРНЫЕ СИСТЕМЫ
287
где aeGL(2) преобразует базисные векторы с номе¬
рами i, i + 1. Заменяя в этом рассуждении матрицу g
произведением xg, получаем разложение
xg = lgtx,
где %i+\,i = Xi't+] = 0. Рассматривая теперь произволь¬
ную матрицу f = Zi(t)t,, замечаем, что / = Ггг(/), где по-
прежнему li+i, i = 0. Следовательно,
zg = I (zt (t) gt) x.
Поскольку функция a(g) не меняется при левых сдви¬
гах на £ и правых сдвигах на z, мы находим отсюда
a {z, g) = a{zt{t), gt) = p. (а„ + ta2l)r‘,
где коэффициенты ц и ац выражаются только через х
и g. Действительно, если Ар, Др — диагональные миноры
матриц gi = Zi(t)gi и g{, то Ар = Ар при р ф i, и Д,- =
= Д,-_1 (йп + ta2i), где dij — коэффициенты матрицы
agGL(2). Наконец, мы имеем
Tgf(t, x) = a(z, g)f(^±^-, х).
Действительно, разложение Гаусса элемента
приводит к дробно-линейной подстановке для пара¬
метра /.
Из полученной формулы очевидно, что пространство
Fj инвариантно относительно Тg. Но тогда это верно и
для пространства Фа, которое является пересечением
пространств FuF2, ..., /Д-ь Лемма доказана.
Операторы 2)\, ..., ZDn-i мы условимся назы¬
вать главными сдвигами на группе Z, а систему 1а —
индикаторной системой для сигнатуры а.
§ 65. Индикаторные системы
В предыдущем параграфе мы ввели понятие индика¬
торной системы лишь для аналитических представлений
d(a). Заменяя а двумя сигнатурами а, |3, мы рассмот¬
рим теперь более общую индикаторную систему Др:
®r/+lj(z) = 0, 0*»+1f(z) = 0, i=l,2 п 1,

288
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
где SDu SDi — аналитические и антианалитические опе¬
раторы левого сдвига на группе Z, отвечающие элемен¬
там ef — ei l+v i = l, 2, п—1. Неприводимое ве¬
щественное представление группы G, определяемое сиг¬
натурами а, р, мы условимся обозначать d(a, р):
d. (а, р) = d (a) <g> d (р).
Теорема 1. Пусть 8?ар — пространство полиномов
на группе Z, в котором действует неприводимое пред¬
ставление d(a, р). Тогда 9?а|з совпадает с совокупностью
всех решений индикаторной системы /ар.
Доказательство. Займемся сначала сравни¬
тельно простым алгебраическим вопросом. Линейный
оператор А называется нульстепенным, если Ап = 0 при
некотором натуральном п. Если А н В нульстепенны, то
это не обязательно имеет место для суммы А + В и
коммутатора [А, В]. Покажем, однако, что выпол¬
няется *)
Лемма 2. Пусть А, В — линейные операторы в век¬
торном пространстве V (без топологии) и операторы Л,
В являются нульстепенными на некотором подпростран¬
стве V0'-
Am = 0, Bn = 0.
Если коммутатор С = [А, В] перестановочен с А и В, то
он также является нульстепенным на V0- При этом вся¬
кая линейная комбинация операторов А, В, С также
является нульстепенной на W
Доказательство. Заметим, что по условию
леммы подпространство У0 не предполагается инвари¬
антным относительно А и В. Положим Vk = AhV0,
k = 0, 1, 2, тогда Vk = (0) при k > пг, и мы в дей¬
ствительности получаем конечное число подпространств.
Покажем, что оператор В по-прежнему является нуль¬
степенным на каждом из этих подпространств. Для это¬
го достаточно использовать следующее общее тожде¬
ство:
DnX= S CnX{k)Dn~k, (*)
*) В § 111 мы получим значительное обобщение леммы 2.

§ 65. ИНДИКАТОРНЫЕ СИСТЕМЫ
289
которое справедливо для любых двух операторов D, X
(и вообще для любых элементов абстрактной ассо¬
циативной алгебры). Здесь положено XW = [D, [D, ...
..., [D,X] ... ]] (коммутатор кратности k\ ЛГ<°) = 1), и
Сп — биномиальные коэффициенты. Полагая, в част¬
ности, X = A, D = В, получаем, что X" = X"' — ... = (0);
следовательно, в правой части (*) остается лишь два
слагаемых, содержащих Вп и Вп~К Следовательно,
Bn+lA V0 = 0, т. е. Bn+lV} = (0). Точно так же Bn+hVk =
= (0). Следовательно, оператор В является нульстепен-
ным также на геометрической сумме подпространств 1Д.
В этом случае определен также конечный степенной ряд
/2 02
В {t) = etB = 1 +tB + -Lf~+ ■ ■ ■
Рассмотрим теперь оператор XX = [А,Х]. Применяя этот
оператор к функции B(t) и пользуясь равенствами
ХВ = С, ХС = 0, легко получаем, что XB(t) = tB(t)C.
Для наших целей достаточно рассматривать случай г“=1.
Применяя оператор V повторно, получаем в результате
следующее равенство:
С = е V е , п — 0, 1, 2, ...
Применяя обе части этого равенства к векторам £ е Vo,
замечаем, что мы не выходим за пределы геометриче¬
ской суммы Vu (поскольку ХВ = АВ — ВА)\ следова¬
тельно, ев является полиномом от В и XNeB = 0 при
достаточно высоком N. Следовательно, CN = 0 на I/o.
Далее, используя соотношения коммутации между А,
В, С, легко проверить следующее тождество, в котором
каждая экспонента рассматривается как формальный
степенной ряд по переменной t*):
exp t (А + В) exp (— tA) = exp t (В — tC).
Это равенство следует понимать как равенство всех опе¬
раторных коэффициентов при степенях переменной t.
Поскольку В п С перестановочны, мы можем записы¬
вать правую часть также в виде ехр(—t2C)exptB.
*) Эта формула является частным случаем формулы Кемпбелла —
Хаусдорфа при [А, В] = С, [А, С] = [В, С] = 0.

290
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
В результате имеем
ехр t (А + В) = ехр (— t2C) ■ ехр tB ■ ехр М.
Применим обе части этого тождества к элементам
I е V0- Тогда, как и прежде, мы не выйдем за пределы
геометрической суммы подпространств Vk при действии
ехр М. Следовательно, ехр tB- ехр tA является полино¬
мом от t на V0• Поскольку С перестановочно с А и В,
то ехр(—ЕС) можно применять непосредственно к эле¬
менту | е V0. Следовательно, ехр/(Л + В) является по¬
линомом на V0. Но тогда (А + В)м = 0 при достаточно
высоком М. То же верно для ХА + рВ + хС. Лемма до¬
казана.
Следствие. Пусть х —*х(х)— представление ал¬
гебры Х+ в векторном пространстве V (без топологии)
и операторы
Ef = т(et, г+i), /=1,2 л-1,
нульстепенны на некотором подпространстве V0. Тогда
и все операторы т(х) нульстепенны на Н0 с показате¬
лями п(х), равномерно ограниченными по х.
Доказательство. Согласно лемме 2 из нуль-
степенности Eik, Ehj следует нульстепенность Bi;,
Z < k < /. Проводя индукцию по б = / — Z, заключаем,
что всякий оператор является нульстепечиым на V0.
Полагая, далее,
А, = а1 Ец
(сумма по / от 1 до j—1), замечаем, что все слагаемые
этой суммы взаимно перестановочны; следовательно, су¬
ществует показатель « = «(/), для которого А] = 0.
При фиксированном / операторы Aj и
В,- = Л/+1 -f Л/+2 + .. . + Ап
удовлетворяют условиям леммы 2 (проверку опускаем).
Следовательно, из нульстепенности В, вытекает нуль-
степенность Bj~\ = Aj + Bj. Понижая j от п до 1, полу¬
чаем наше утверждение. Следствие доказано.

i 85. ИНДИКАТОРНЫЕ СИСТЕМЫ
291
Докажем теперь, что имеет место
Лемма 3. Пространство всех решений системы /ар
конечномерно.
Доказательство. Пусть zh — произвольная мат¬
рица из Z, у которой над диагональю все элементы рав¬
ны нулю, кроме элементов tih, расположенных в k-м
столбце. Тогда, как легко проверить, произвольная мат¬
рица 2eZ может быть однозначно записана в виде
z = z2z3 ... zn.
Заметим, что множество Zh всех матриц вида zh яв¬
ляется абелевой подгруппой в Z и координаты tik яв¬
ляются аддитивными параметрами в Zh. Мы будем рас¬
сматривать числа tih, 1 ^Ci<k^Cn, как параметры во
всей группе Z. Фиксируем матрицу z0 ~ z2z3 ... zk-1 и
рассмотрим в группе Z однопараметрическую подгруппу
вида
z{t) = z0 (expteik)zo'1.
Пусть Lih — инфинитезимальный оператор левого сдвига
на Z, порожденный этой подгруппой. Пусть Lih — соот¬
ветствующий антианалитический оператор. Тогда, оче¬
видно,
/ -Л- 7~ д
№ J. ’ T-lk — =1 '
dtik dtik
Вводя обозначение Vo для совокупности всех решений
индикаторной системы 1ар, замечаем, что согласно след¬
ствию из леммы 2 любой инфинитезимальный оператор
левого сдвига является нульстепенным на V0: Lm = 0.
При этом можем считать, что показатель m не зависит
от L. В частности,
LTk = 0, 17Г = 0,
и это означает, очевидно, что всякая функция /(г)е V0
является полиномом по tih степени не выше т. Следо¬
вательно, V0 состоит из полиномов ограниченной сте¬
пени. Лемма доказана.
Теперь уже нетрудно завершить доказательство
теоремы 1. Мы имеем
с У о,

292
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
где V0 — совокупность всех решений индикаторной си¬
стемы /ар. Согласно лемме 3 Г0 конечномерно. Кроме
того, перефразируя лемму 1 на случай системы /ap, за¬
ключаем, что инвариантно относительно операто¬
ров Tg\
Tgf(z) = a(z, g)P(z, g)f(zg).
Поскольку эти операторы являются рациональными
функциями от g, нам надлежит еще показать, что они
не имеют полюсов на V0- Действительно, если элемен¬
ты z и g достаточно близки к единице, то zg е GTeg,
т. е. элемент zg допускает разложение Гаусса, и выра¬
жение Tgf(z) определено. Поскольку Tgf(z) удовлетво¬
ряет индикаторной системе /яр вместе с f(z), то Tgf(z)
является полиномом на Z и потому определено всюду
на Z. Следовательно, оператор Тg определен в V0 для g,
достаточно близких к е, но тогда в силу связности G
также и на всей группе G*). Следовательно, эти опера¬
торы определяют представление в К0.
Из единственности старшего вектора {f0{z)= 1)
следует, что представление Tg в пространстве К0 непри¬
водимо**). Следовательно, 9?яр = V0. Теорема доказана.
Замечание. До сих пор мы не уточняли, в каком
пространстве функций рассматривается система 1ар. Од¬
нако ясно, что допустима любая традиционная поста¬
новка задачи — либо в классе достаточное число раз
дифференцируемых функций f(z), либо даже в классе
обобщенных функций. При этом мы показываем, что все
решения в действительности являются полиномами на
группе Z ***).
Обращаясь к реализации на группе G, из теоремы 1
легко получаем
*) Можно также заметить, что инфннитезимальные операторы,
порожденные Т g, являются дифференциальными операторами с по¬
линомиальными коэффициентами на Z и, следовательно, дифферен¬
циал Tg определен всюду на V0-
**) В этом пункте мы неявно используем принцип полной при¬
водимости.
***) В чисто аналитических терминах можем сформулировать
теорему 1 следующим образом: единственными решениями системы
/ар являются функции а(г, §)р(г, g) и их линейные комбинации.

§ 66. АЛГЕБРА Z-МУЛЬТИПЛИКАТОРОВ
293
Следствие. В реализации на группе G простран¬
ство неприводимого представления d(а, Р) = d(a) ® d(fi)
совпадает с совокупностью всех решений системы 1°—3°
§ 64, дополненной аналогичными соотношениями для
антианалитических операторов.
Действительно, если f(g)^Vo, где Vo— множество
всех решений указанной системы, то f(z), очевидно,
удовлетворяет системе /ар, т. е. f(z)e9Jap. Поскольку
Vo инвариантно относительно правых сдвигов на G,
образ этого пространства при сужении на Z инвариан¬
тен относительно операторов Tg. Ввиду неприводимости
SRap этот образ совпадает с SRap.
Если нас интересуют только аналитические пред¬
ставления группы GL(n), то мы полагаем Si = S2 = ...
... = sn — 0 и получаем, что пространство Ша, в котором
действует представление d(a), выделяется индикаторной
системой 1а с дополнительными условиями
... =0„-,=О, (*)
которые означают, что полином f(z) зависит только
от 2fj, но не от гц. Иначе говоря, выделяется систе¬
мой 1а в классе всех аналитических функций на груп¬
пе Z. Система (*) может рассматриваться как аналог
уравнений Коши — Римана для группы Z.
§ 66. Алгебра Z-мультипликаторов и задача
о сужении с группы на подгруппу
Реализация на группе Z позволяет нам использо¬
вать новую алгебраическую операцию — умножение в
классе полиномов f(z) — для изучения структуры непри¬
водимого представления d(a). Так, в частности, еще
в гл. VII мы доказали следующее мультипликативное
свойство:
^a+|3 =
для пространств SRa, составленных из полиномов f(z),
в которых реализуются неприводимые представления
d(а). Здесь сигнатура а + Р вычисляется по правилу
сложения векторов аир. Линейные связи между

294
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
функциями из 9?а9?0 автоматически учитывают структуру
произведения Юнга.
Однако, даже если фиксировать сигнатуру а, опера¬
ция умножения на группе Z приводит к новому естест¬
венному методу изучения внутренней структуры d(a).
Действительно, напомним, что в 9fa всегда содержится
вектор /0(г)=1, который является старшим вектором
с весом а (б). Записывая всякий полином f(z)^9la фор¬
мально в виде
/ (г) = / (г) • /о (г),
мы получаем, что операция умножения на /(г) может
рассматриваться как «понижающая» операция. Действи¬
тельно, эта операция аналогична применению некоторого
полинома от инфинитезимальных операторов алгебры
Х-, понижающих вес. Оператор умножения на f(z) мы
условимся называть Z-мультипликатором.
Рассмотрим, в частности, мультипликатор Zjj, где
Zjj —один из матричных элементов матрицы ?eZ.
Пусть полином ф (г) имеет вес Х(б). Согласно общей
формуле для d(а) мы имеем
Т6ф (г) = а (6) ф (б“ z6) = К (б) ф (г).
Иначе говоря, функция ф(г) удовлетворяет следующему
тождеству:
Ф (б_1гб) = Ф (z). (*)
Заменим функцию ф(г) функцией ip(z) = г^ср(г). При
умножении матрицы z слева на б^1 и справа на б эле¬
мент заменяется элементом бГ'г^б/. Следовательно,
функция ф(г) также удовлетворяет тождеству (*) с
заменой веса К(6) весом
*(6) = 6rV(6).
Если записывать вес А, (б) в виде б^б*2 . .. б*л, то соот¬
ветствующий вектор показателей

§ 66. АЛГЕБРА Z-МУЛЬТИПЛИКАТОРОВ
295
мы будем называть инфинитезимальным весом. Умно¬
жение на бГ'б/ равносильно добавлению к этому век¬
тору хорошо известного нам «корня» алгебры X:
—ац = (0, О, -1, 0, О, 1, 0, 0) ~ ej — е{.
Полученный результат сформулируем в виде следую¬
щего правила:
Правило 1. Мультипликатор z{j в классе полино¬
мов f(z) приводит к добавлению корня
~ аи = е, - et
к каждому инфинитезимальному весу k — (/гь &2, . • •, kn),
т. е. к умножению веса Л (б) на множитель бГ'б/.
В общем случае мы условимся называть мульти¬
пликатор f(z) весовым, если /(б_1гб) = р(б)/(г); мно¬
житель р(6) условимся называть весом этого мульти¬
пликатора. В частности, согласно правилу 1 мульти¬
пликатор Zij является весовым с весом б,г,б/. Очевидно,
это определение не зависит от старшего веса а (б);
однако, если мы находимся в пространстве 9?а, надо
следить, чтобы умножение на f(z) не выводило за пре¬
делы этого пространства; в результате получаем
Правило 2. Границы действия мультипликаторов
Zij и полиномов от них в пространстве определяются
индикаторной системой 1а.
Так, в простейшем случае GL(2) мы имеем единственный муль¬
типликатор 2 = 212 (с весом и его применение к старшему
вектору /о = 1 приводит к базисной цепочке одночленов
1, 2, г2 zm,
которая ограничена индикаторной системой /а:
В общем случае, разумеется, не исключено, что применение мульти¬
пликатора гц или одночлена от этих мультипликаторов запрещает¬
ся, но возможно применение некоторых полиномов /(г). Так, если
d{a) = dk — базисное представление GL(n), то допустимыми

296
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
являются только мультипликаторы
гМх ' * * z\ik

zkit zkik
и их всевозможные линейные комбинации. Короче говоря, значение
всех допустимых мультипликаторов равносильно описанию простран¬
ства 9!а. Однако терминология Z-мультипликаторов оказывается
удобной при построении весового базиса в пространстве 9!а.
Прежде чем рассматривать весовые базисы, мы зай¬
мемся решением следующей более легкой задачи. Пусть
дано неприводимое представление d(a) с сигнатурой
а= (т.\, т2, тп), trii ^ т2 тп. Рассмотрим
в группе G = GL(ra) подгруппу G0, изоморфную
GL(n— 1) и составленную из матриц вида
а О
О 1
agGL (п- 1).
Если рассматривать операторы Тй только при g = g0,
то мы получим представление группы G0, которое обо¬
значим d (а) |0о и назовем сужением d(a) на подгруп¬
пу G0- Ясно, что это представление уже не обязано быть
неприводимым, и, естественно, возникает задача о его
разложении на неприводимые.
Для решения этой задачи мы используем стандарт¬
ный метод Z-инвариаптов. Пусть Z0 — пересечение Z
с Gо, т. е. совокупность всех матриц вида
л: О
О 1
Z(n-l).
Нетрудно видеть, что всякая матрица из Z единствен¬
ным образом записывается в виде произведения z'zQ,
где 20eZ0 и z'— матрица из Z, имеющая следующий
вид:
е t
О 1
где е — единичная матрица порядка п—1 и t—произ¬
вольный вектор-столбец с координатами t\, t2, ..., tn-

§ 66. АЛГЕБРА Z-МУЛЬТИПЛИКАТОРОВ
297
Мы можем рассматривать координаты t и х как пара¬
метры во всей группе Z.
Согласно общей схеме Z-инвариантов всякий стар¬
ший вектор для G0 является решением следующего
уравнения:
/ (zz0) = / (z),
где z0 пробегает подгруппу Z0. Используя введенную
параметризацию в группе Z, мы получаем отсюда
/ (z) = / (z'z0) = / (г'),
т. е. всякий Zo-инвариант зависит только от z'. Оче¬
видно, и обратно, всякая функция, зависящая только
от z', является Zo-инвариантом. Докажем теперь, что
имеет место
Лемма 4. Всякий старший вектор относительно Go
в пространстве 3Ja, а = [гь г2, ..., гп], шиеет выд
где vi, V2, ..., vn-i—произвольные неотрицательные
целые показатели, удовлетворяющие ограничениям
vh<rh, k = 1, 2, ..., я — 1.
Доказательство. Заметим, что = zin; следо¬
вательно, мультипликатор имеет вес
Pi = бГ’б/г-
Но тогда мультипликатор gv(/) имеет вес
a,v (в) = e~v*6"v*... •6^,+v2+-+^-!>
и все такие веса различны. Следовательно, всякий иско¬
мый старший вектор может отличаться лишь скаляр¬
ным множителем от одного из этих одночленов. Если
jt>i — главный сдвиг на группе Z, то мы, очевидно,
имеем
Поскольку умножение на ti+\ перестановочно с диф¬
ференцированием по tit индикаторная система /я

298
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
принимает вид
Если f(z) = £,v(t), то это равносильно ограничениям
для одночлена lv(t). Лемма доказана*).
Полагая 6n = 1 (случай группы G0) и умножая стар¬
ший вес а (6) = б^'б™2 ... 6™" на вес мультипликатора
gv, находим, что старший вектор |v имеет вес
av (6) = (х (6)KV (6) = 6”>-v‘d^-v* . . . 6
При доказательстве леммы 4 нам было удобно запи¬
сывать сигнатуру а в виде [г\,г2, ..., гп], где г* = m,—
— mi+i, тп+1 =0. Подставляя эти выражения в ограни¬
чения приходим к условиям
ttii ^ mi — V; ^ mt+u г = 1, 2 п— 1,
для показателей найденного веса av(6). Иначе говоря,
записывая этот вес в виде 6*!6*2 .. . б*"^1, мы прихо¬
дим к цепочке соотношений
Щ\ ^ k\ ^ т2k2^ ... /г„_! ^ тп.
Сформулируем окончательный результат в виде следую¬
щей теоремы:
Теорема 2. Сужение d (а) |0 содержит ровно по
одному разу все неприводимые представления группы
Gо с сигнатурами $~(kuk2, ..., где kt — произ¬
вольные целые числа, заключенные в пределах
my ^ k\ ^т2^ /г2^ • • ■ ^ ^п-1 ^ тп.
Подпространство jVp, в котором действует d(P), мо¬
жет быть определено как циклическая оболочка своего
*) Вместо индикаторной системы мы можем воспользоваться
критерием, даваемым теоремой 5 из § 50. Действительно, 9?а =
= Щ]1^2 ••• Ktn-il> ГДе 9G — пространство базисного представления
dj, i = 1, 2, ..., л — 1. Поскольку функции 1, ii содержатся в SR, при
V V V
фиксированном г, то одночлен V^22 *п-\ содержится в 9ta
При ЛЮбыХ Vj, 0 ^ Vi ^ rt.

5 66. АЛГЕБРА Z-МУЛЫИПЛИКАТОРОВ
299
т,-k,m„
zmn-l~kn-\
• ' * 1 и •
старшего вектора
Тk ~~ ‘'lrt ^2п • ■ • ~я-1, п
Если в 5Ra введено скалярное произведение, относитель¬
но которого представление d (а) |а (п) унитарно, то подпро¬
странства Nfi взаимно ортогональны относительно этого
скалярного произведения.
Доказательство. Первая часть теоремы уже
доказана. Для вычисления явного вида старшего век¬
тора вь{г) = %4{t) при v; = nii — ki достаточно заметить,
что
е t
х 0
л: t
г = z'z0 =
0 1
0 1
-—
0 1
т. е. что столбец параметров совпадает с последним
столбцом матрицы z. Наконец, если рассматривать ана¬
литическое представление d(а) только на компактной
подгруппе U(n), то оно унитарно, и из однократности
каждой неприводимой компоненты для U (п—1) следу¬
ет взаимная ортогональность подпространств N$*).
Теорема доказана.
Замечание. Если бы вместо подгруппы G0 мы
рассматривали подгруппу матриц вида
8 =
а
0
0
К
GL (п — 1), К О,
то, очевидно, результаты остались бы прежними, с тон
разницей, что каждому старшему вектору eh(z) припи¬
сывался бы вес вида
t-1
где Г (k) = (П1\ + т.2 + . . . + ПТп-1 + mn) — (k\ + &2 + • ■ •
п
... + kn.A) = s(m)~ s(k). Здесь s(m)=2mb s{k) =
«-1 ;=l
= 2 Это очевидно из предыдущих построений.
<-i
*) Иначе говоря, мы пользуемся инвариантностью ортогональ¬
ных дополнений для унитарного представления (§ 16) и однознач¬
ностью разложения на неприводимые в случае однократного («про¬
стого») спектра.

300
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Упражнения
1. Пусть а — эрмитова матрица с собственными значениями
си > а2 > - 5^ а„ > 0 и Ъ = рар, где р — произвольный ортого¬
нальный проектор размерности п—1. Показать, что собственные
значения ф, р2, •••> (G-i матрицы Ь в соответствующем простран¬
стве размерности п — 1 удовлетворяют неравенствам он ^ ф ^ а2 ^
й- р2 5= аз ^ > ап-i > Р„_, > а„.
2. Сформулировать правило сужения U(n)/U(n—1) в терми¬
нах орбит относительно присоединенного представления (см. упраж¬
нение в конце § 50).
§ 67. Базис Гельфанда — Цейтлина
Рассмотрим в G цепочку вложенных подгрупп
G„ => G„_, => G„_ 2гэ ... =)G,dG|,
где Gt изоморфна GL(;') и Gn= G. При этом нам будет
удобно считать, что Gi преобразует первые i базисных
векторов, оставляя остальные неподвижными. Следо¬
вательно, Gn_i состоит из матриц вида
II а ®
ё = 0 1
GL (п — 1),
и подобным образом G;_i вкладывается в Gi.
Как мы видели в § 66, если d(a.) — неприводимое
представление группы G = G„, то спектр сужения на
Gn-i является простым, т. е. каждое неприводимое пред¬
ставление G„._i содержится в d(а) однократно. Точно
так же, если б?(а,) — неприводимое представление под¬
группы Gi, то спектр сужения на G,-_i является простым.
Мы можем использовать это свойство для построения
базиса в пространстве fRa.
Действительно, сужая d(а) последовательно на G„ ■„
Gn-2, Gi, получаем на каждом шаге все более дроб¬
ное разбиение 0?а в ортогональную прямую сумму под¬
пространств, неприводимых относительно G,, причем
подпространства, получаемые на последнем шаге, одно¬
мерны (подгруппа Gi абелева). Выбирая в каждом из
этих одномерных подпространств по ненулевому век¬
тору, получаем ортогональный базис во всем простран¬
стве 0?а. Очевидно, каждый из этих векторов однозначно

§ 67. БАЗИС ГЕЛЬФАНДА - ЦЕИТЛИНА
301
определяется следующей таблицей целых чисел:
V- =
т.
тг
т
I, п-i
2 п
пг,
/г — 1, п
т„
2, /г-1
.. . т
п — 1, п-1
т12 т22
где каждая строка а,- = (тн, т2..., тц) означает сиг¬
натуру того неприводимого представления подгруппы
Gi, в пространстве которого данный вектор содержится.
При этом мы положили для общности записи ап = а,
т. е. заменили обозначение т-; на min (mi — параметры
сигнатуры а), т1п т2п Ж • тпп. Согласно тео¬
реме 2 mhi — произвольные целые числа, удовлетворяю¬
щие ограничениям
Следовательно, каждое из этих чисел в таблице ц из¬
меняется в пределах между двумя вышестоящими чис¬
лами*). Соответствующий базисный вектор обозначим
символом ev
Нетрудно видеть, что базисные векторы еи являются
весовыми относительно подгруппы D. Действительно,
вместо G„_ 1 мы могли бы рассматривать подгруппу мат¬
риц вида
а 0
0 б , а е GL (п — 1), 6„ Ф 0,
изоморфную G„-1 X Л, где Л = GL(1) —мультиплика¬
тивная группа комплексных чисел; при этом преобразо¬
вания подгруппы Л перестановочны с каждым d(an_i),
т. е. сводятся к умножению на число в пространстве
этого представления. Продолжая редукцию по размер¬
ности, получаем вместо G\ подгруппу, изоморфную Лп,
т. е. группу D. Вычисляя веса, получаем как следствие
теоремы 2 следующий результат:
*) Сигнатура си = (тц) понимается, естественно, как показа¬
тель одномерного представления Хт подгруппы Gj, где X = gu —
единственный параметр в Gь

302
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Теорема 3. В пространстве неприводимого пред¬
ставления d{a), а = (niu пг2, . .., пгп), существует орто¬
гональный базис ец, где ц означает описанную выше
таблицу целых чисел mife, 1
mik> тг,*_, > mi+Lk.
При этом каждый вектор е^ является весовым с весом
^(6) = 6st‘~4s/-s‘ ... б*»-5»-*,
k
где sk = 2 1nik — сумма чисел, расположенных в k-й
i = i
строке таблицы р, и s0 = 0.
Доказательство. Согласно замечанию, сделан¬
ному в конце § 66, старшему вектору представления
d(an-1) приписывается собственное значение 6,ln~Sn~l
относительно подгруппы Л; следовательно, то же соб¬
ственное значение имеют и все остальные векторы е^ с
фиксированной строкой ап-ь Аналогичную роль для
сигнатуры а* играет множитель 6si‘~Si~I (s0 = 0). Тео¬
рема доказана.
Полученный базис еп называется базисом Гельфан-
да — Цейтлина.
Замечание 1. Вектор ец является старшим век¬
тором относительно подгруппы G,-0 тогда и только тогда,
когда для каждого i *С i0 строка аг-1 получается из а,
вычеркиванием последнего параметра тц\ в этом случае
строки а„, а„-ь .. ., аг0 вполне характеризуют вектор
дц. В частности, старший вектор d(a) вполне характери¬
зуется исходной сигнатурой а.
Замечание 2. Нетрудно выписать явный вид базиса в
реализации на группе Z, хотя окончательные выражения получают¬
ся достаточно громоздкими. Мы рассмотрим для простоты только
случай п = 3, т. е. группу G3 = GL(3). В этом случае схема ц имеет
вид
/ Ш] т2 гпг
И “ I *i h
' s
где ть т2, т3 — параметры, задающие представление, и ^ kt ^
^ т2 ^ k2 ^ т3, Ji >s ^ k2. Напомним, что старшими векторами
относительно G2 являются в данном случае векторы <ps (г) =

§ 67. БАЗИС ГЕЛЬФАНДА - ЦЕЙТЛИНА
303
= г^1 , где k= (ki,k2). Применим к этим векторам пре¬
образование
7"g. = ехр т£_, — оо<т<оо,
где Е- = E2i — понижающий оператор группы G2, и заметим, что
Ер_ переводит вес б^'б^ в вес б[>~рб|!+р. Координата s, входящая
в схему р, должна совпадать с kt— р; следовательно, вектор е^
может быть получен (с точностью до множителя) как коэффициент
при %k'~s в разложении Tgq>k по степеням т. Положим
0 0
е =
■■ exp хе21;
х 1 0
0 0 1
тогда 7^ = ехр тСогласно общей формуле для d(а) мы имеем
гёф,(г) = дГ'-т^-т=(^) (-^l) ,
где Дк—диагональный минор матрицы zg, zeZ, g <= G2, и Д23—
минор этой матрицы, составленный из первых двух строк и столб¬
цов с номерами 1, 3*). В нашем случае Д| = 1 + xzt2, Д2 = 1,
Дгз = г2з + лги, где положено г13 = z12z23 — 2]3. Следовательно,
(г) = г1з‘ ‘ 0 + тг12)^' ‘ (г23 + тг13) ' кг'
Раскрывая произведения биномов и вычисляя суммарный коэффи¬
циент при приходим к следующему результату:
, „ е,-е, mj-ftj-e,
, ч 1 V 13 12 13 23
бм. (г) =
й iVp. ^ ер е2! (&! — т2 — еi)! (т2 — к2 — е2)!
ti~e2=kl — s
В общем случае подобная процедура позволяет получить рекуррент¬
ное соответствие между базисами Гельфанда — Цейтлина для Gn
и Gn~\- Однако мы в дальнейшем укажем эту связь в иной форме,
не зависящей от реализации на группе Z.
Из однократности спектра сужения вытекает еще
одно замечательное следствие, которое мы также сфор¬
мулируем в виде теоремы:
Теорема 4. Пусть Chi, — базисные
операторы Казимира для подгруппы G,-, изоморфной
GL(t')- Тогда операторы Chi одновременно диагонали-
*) Здесь мы впервые воспользовались общим видом операто¬
ров Tg в параметрах Гаусса (см. § 9).

304
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
зуются в базисе <?ц и каждый индекс р может быть од¬
нозначно занумерован совокупностью всех собственных
значений операторов См.
Доказательство. Операторы Chn являются ска¬
лярами на d(a), и их совокупные собственные значения
характеризуют, как мы знаем, сигнатуру а, т. е. пер¬
вую строку в схеме р. Точно так же Ch, п-\ являются
скалярами на d(an-1) и, следовательно, диагонализуют-
ся в базисе ец; при этом их собственные значения ха¬
рактеризуют вторую строку схемы р. Продолжая этот
процесс, приходим на последнем шаге к оператору С и,
который является единственным инфннитезимальным
оператором Gj и собственное значение которого совпа¬
дает с параметром тп, входящим в схему р. Теорема
доказана *).
Следствие. Всякий оператор, диагональный в ве¬
совом базисе ец, может быть представлен в виде поли¬
нома от операторов См.
Действительно, пусть ©— алгебра всех полиномов
от операторов Cki. Всякий оператор Се© диагоиали-
зуется в весовом базисе: Сец = с(р)ец, и функции с(р)
«разделяют» точки р, т. е. для каждой пары pi ф р2
найдется функция с(р) такая, что c(pi) ф с(р2). Заме¬
няя с(р) на ас(р)+ р, подбираем а, р таким образом,
чтобы полученная функция Сц,ц2 принимала значение 1
в точке pi и значение 0 в точке р2. Полагая ск(р) =
= II Gv (р), получаем символ Кронекера: сДр) =
V
Следовательно, в алгебре © содержится проектор на
каждый базисный вектор ех- Отсюда следует наше ут¬
верждение.
Пользуясь терминологией физиков, можем сказать,
что элементы алгебры © образуют «полную систему на¬
блюдаемых» в пространстве представления d{а).
Замечание. Если представление Т группы GL(п)
содержит неприводимые составляющие d(a) однократно,
i
*) Заметим, что суммы si = 2 пты, входящие в вес ец, яв-
k= 1
ляются собственными значениями линейных операторов Казимира
Си (/= 1, 2 п-1).

§ 68. ПОНИЖАЮЩИЕ ОПЕРАТОРЫ
305
то операторы С/,,- образуют «полную систему наблюдае¬
мых» также и в пространстве представления Т (дей¬
ствительно, подсистема Chn «разделяет» d{a)).
§ 68. Понижающие операторы
в инфинитезимальной форме
Мы установим в этом параграфе явную связь между
мультипликаторами zi3-, i < j, и понижающими операто¬
рами Ец, i > j, откуда, в частности, будет следовать
явное выражение для базисных векторов Гельфанда —
Цейтлина.
Условимся говорить, что линейный оператор F в
пространстве представления является весовым с весом
б^'б/, если он перестановочен со всеми диагональными
базисными операторами, кроме Ец, Ец, и если
[Е,„ F] = [F, Еа] = F;
очевидно, в этом случае оператор F переводит всякий
весовой вектор в весовой с умножением веса на бГ’б/.
В частности, этим свойством обладают операторы гц и
Ец, поэтому для достижения большего единообразия мы
условимся изменить обозначение гц на Ъц.
Лемма 5. В применении к старшему вектору /0
представления d{а) выполняется следующее тождество:
k-\
2 Efc jZц --- (nil ffik k i 1) Zhi, (*)
i=i
где /г > i и где положено Zu — I, i — 1, 2, .. ., n.
Доказательство. Рассмотрим вначале частный
случай i = l, k = п. Поскольку в реализации на группе
Z понижающие операторы действуют довольно сложно,
мы используем реализацию на группе G и положим
Ец ~ к ^ j , i, j 1, 2, . . ., п,
где х1 = {хи} — г-й столбец квадратной матрицы х и вы¬
ражение в правой части означает свертку векторов
х1, (при этом не обязательно считать, что
dxJ

306
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
det л: =?^= 0). Согласно общим формулам разложения Гаус¬
са мы имеем
где [('ь /2, iP] — минор, составленный из первых р
строк матрицы х и столбцов с номерами ii, ('г, . .., ip.
При этом старший вектор /о представления d(а) за¬
писывается в виде
Применяя к этому вектору операторы Enj-ZjU мы заме¬
тим, что Enj[1, 2, ..., г] = 0, если j > i и Eni[\, 2, ..., г] =
= [1,2, ..., /— 1, п, / + 1, ..., i], / ^ i; следовательно,
При этом мы воспользовались легко проверяемым тож¬
деством
которое означает, что определитель [1,2, ..., г], окай¬
мленный при помощи первой строки и последнего столб¬
ца матрицы х, равен нулю. Наконец, заметим, что
П— 1 П — 1
2 П = 2 («г ~ Щ+\) = *П\ - т.
В результате получаем

5 68. ПОНИЖАЮЩИЕ ОПЕРАТОРЫ
307
т. е. в нашем случае (*) доказано. В общем случае до¬
статочно заметить, что все операции, входящие в (*),
порождаются подгруппой Gih, которая преобразует толь¬
ко базисные векторы с номерами £, £ + 1, k. Стар¬
ший вектор fo имеет сигнатуру р = (пи, mi+ь ..., тк)
относительно этой подгруппы, и представление d(р)
естественно реализуется в классе квадратных матриц
п'Хп', где п' = k — £+ 1. Следовательно, мы получим
общий случай, если заменим т\, тп на т{, mh и п — 2
на п' — 2 = k — £ — 1. Лемма доказана.
Если вместо параметров т{, определяющих представ¬
ление, использовать параметры l{ = ш* + (п — £) *), то
h > h > ■ • ■ > 1п и (*) записывается в виде
2 = (**)
i=i
Полученное соотношение является соотношением рекур¬
рентного типа и может быть поэтому использовано для
вычисления мультипликаторов Zhi. Догажем, что имеет
место
Лемма 6. В применении к старшему вектору f0
представления d(a) мультипликатор Zhi может быть
представлен следующей формулой:
и
Zkt= Г1 (/, — // — I)-1 -VW( k>i,
j=i+1
где У*,- — полином от понижающих операторов Ejit ]>i,
и диагональных операторов Lj = Ejj + (п — /):
Vkt= .2 с/,/2 ••• lsEbiEl{li ... Elsi, k>i;Vu=l.
£ i > £ 2 >"‘>£j
Здесь сумма берется no всем возможным наборам ин¬
дексов j 1, /2, /а, расположенных между k, £ (т. е.
s = 1,2, . . ., k — /1— 1), и
с1д2 ••• Is = , П Ец, Ец — Li — Lj.
Я > J > I
I ф im
*) Мы уже встречались с этими параметрами в гл. IX при рас¬
смотрении операторов Казимира. Можно было бы с тем же успехом
положить li = rrii — i.

308
гл. х. индикаторные системы
Доказательство. Умножая обе части («) спра¬
ва на оператор *)
k-\ k-\ /
(^-1)= II а*-1)П {Lis-\) = NkjMn,
5=1+1 s=j+i s=i+i
k-\
замечаем, что ZnNkj = CkiZn, где Ck! = П Eis, и опе-
s=i+1
ратор Ckj перестановочен с Ekj. В то же время ZUM^ =
= Vji в применении к старшему вектору f0. Следова¬
тельно, («-*) переписывается в виде
к-1
^ X к Д /г ^ к i»
/= 1
где положено Xhj = CkjEkj. Поскольку это уравнение
имеет матричную структуру, введем формальные мат¬
рицы
0
0
0 .
0
0
Хп
0
0 .
0
0
х =
*з.
*32
0 .
0
0
Хпх
X п7
У «3 •
• • *га, /г-1
0
1
0
0 .
0
0
V21
1
0 .
0
0
У =
V31
V 32
1 .
0
0
v„,
У/г2
У «3 • •
• У/г, П--1
1
и запишем уравнение в виде
1 + JV = V,
где 1 — единичная матрица п X п. В действительности
следует рассматривать такое уравнение отдельно для
каждого столбца матрицы V (поскольку определение Xkj
зависит от индекса t), но вместо этого мы можем счи¬
тать, что вектор fо заменяется формальным столбцом из
*) Мы полагаем Ми = 1 (в этом случае нижний предел про¬
изведения превосходит верхний предел).

§ 68. ПОНИЖАЮЩИЕ ОПЕРАТОРЫ
309
элементов 0, . .., 0, /о, 0, ... , 0 с f0 на г-м месте. Оче¬
видно, матрица
v=i + x + xs + ... +Хп~1
является решением этого уравнения. Действительно,
Хп = 0, и мы имеем
l+XV=l + Z(l+Z+ ... +Хп~1) =
= 1 + Х + Х7+ . . . +Хп~' = V.
Расшифровывая каждый элемент полученной матрицы
V, получаем Vki. Лемма доказана.
Замечание 1. В процессе доказательства мы по¬
лучили следующее символическое выражение для мат¬
рицы V с элементами Vfli:
где Xhj = ChjEhj при k>j и Xkj — 0 при k < /. При
k-1
этом Ckl— JJ Lis и обе части равенства применяются
S-/+ I
к вектору (0, ..., /о, 0, .. ., 0) с f0 на г-м месте*).
Замечание 2. Условимся рассматривать E{j как
символическое произведение х'д>, где xi—«оператор
рождения» и д} — «оператор уничтожения»; тогда опера¬
торы Vftj мы можем записывать следующим образом:
^ki = x Bk-iBk-? Д + \dt, (***)
где В j = dj xi + Lfj и где величины Li, рассматриваются
как независимые коэффициенты, перестановочные с х1,
дi при I Ф i, I Ф /. Действительно, подставляя биномы
Д,- и раскрывая скобки, получаем сумму всевозможных
одночленов вида
xkd^xl'df2 ... x’sdi = ... Ejsi
*) Отсюда очевидно также рекуррентное соотношение V = 1 +
+ XV, т. е.
k-\
2 = vki.
i-t

310
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
с коэффициентами Нетрудно видеть также,
что биномы Bj в формуле (***) можно считать взаимно
перестановочными.
Мы будем теперь рассматривать операторы Vftl- .не
только на старшем векторе /о, но во всем пространстве
представления d(a).
Лем м а 7. Операторы Vhi взаимно перестановочны
при фиксированном k.
Доказательство. Заметим вначале, что всякий
операторный полином, содержащий только понижающие
(либо только повышающие) операторы Ец, можно запе¬
нить полиномом от х\ dj, располагая эти операторы в
произвольном порядке, но снабжая х\ dj, входящие в
один и тот же элемент Ец, каким-либо общим индексом,
скажем xi(s), dj(s). При этом мы используем соотноше¬
ние коммутации
[«Ms), x‘(t)} = 6(s, t),
где символ б(s,t) означает символ Кронекера пары s,t
(и операторы dj (s), x‘(t) взаимно перестановочны при
1 Ф}). Кроме того, выражение, полученное после пере¬
становки символов х\ dj, подлежит следующему правилу
расшифровки: оператор Ец располагается левее (пра¬
вее) Ejh, если dj стояло левее (правее) хК
Условимся также рассматривать E{j как независимые
символы, взаимно перестановочные между собой и удо¬
влетворяющие следующим соотношениям коммутации:
[Ец, d}] = [djt Lji\ = dh [Ец, х/] = [х/, Еп\ = - х1.
(Эти правила вытекают из прежнего определения Ец =
= Ец — Ejj + (] — /)*)•) Тогда операторы SJki мы можем
рассматривать как полиномы от понижающих операто¬
ров с коэффициентами, зависящими от Ец. При i > /
имеем
адг=(Д)2{ п п д.] д.
I/=(+1 J ls = Z+l J
*) Иначе говоря, [£<,-, л:1'] = х\ д,] = —и все остальные
коммутаторы равны нулю. Следовательно, оператору х‘ приписы¬
вается вес 6i и оператору dj — вес 6J1.

§ 68. ПОНИЖАЮЩИЕ ОПЕРАТОРЫ
311
Действительно, все сомножители взаимно перестановоч¬
ны, за исключением пар (Bj,Bj) и (dit Bj), где Bj =
= djX) + La, Bj = djxi + Ьц. Снабжая символы dj, х\
входящие в эти выражения, индексами 1, 2, 3, 4, мы
имеем
В/В; = д) (хО2 - б (2, 3) д, (1) х1 (4) +
где многоточие означает сумму членов, не зависящих от
порядка умножения Bj, Bj. В то же время
В,В, = д) (х'У - 6 (1, 4) д, (3) У (4) + ...
В первом случае расшифровка приводит к произведению
6(2,3)EPjEjg, где р > j > q\ во втором случае — к про¬
изведению 6(1,4) Ep'jEjq’, где p'>j>q'. Однако и в
первом и во втором случае под знаком WhiSJhi предпола¬
гается суммирование по р, q(p',q'). Следовательно, Bj
и Bj можно менять местами. Аналогично рассматривает¬
ся пара (ditBi) *). В результате VfeiVfei = Vkffki- Лемма
доказана.
Л е м м а 8. Между операторами Vfe, имеет место сле¬
дующее рекуррентное соотношение:
Уki — Ek. i^i, k~\ ~ Bit fc-iVfc-i, iEfti *_] • (****)
Доказательство. Вычисляя коммутатор
[EK ft_b V/i-i,,], где i определяется согласно лемме б
находим, что
[Ek.k-ъ ^А-1,/] ^ ^ ci\h ••• ' ‘ ' ^V"
Действительно, [Eh,u-ь Eh^u jt] = Ehjl и все осталь¬
ные коммутаторы равны нулю. Полученное выражение
отличается от Vfti, поскольку индексы /ь /г, ..., js при¬
нимают лишь значения г + 1, i + 2, . . . , k — 2. Однако,
умножая этот коммутатор слева на Liyk-\ и добавляя
Eh,и-lVfc-i.i, получаем Ущ. Следовательно,
^' ы h—I [E/t, k—\t V&—1, г] 3“ Ek' k—\^k—\, it
что является лишь другой формой записи (***-*).
*) При этом учитывается равенство 6iLn = Ltidi — ди

312 ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Лем м а 9. Операторы Vhi оставляют инвариантным
подпространство Vh-i, натянутое на старшие векторы от¬
носительно подгруппы Gfc-ь
Доказательство. Рассмотрим повышающий опе¬
ратор Pj = j и докажем вначале, что
Р,Чы = ХР„
где j=pk и X— полином от операторов Ерч, зависящий
от i, /, k. Не ограничивая общности, можем считать, что
i=l. Очевидно, Рj перестановочен с V;и при k = 1, 2,
..., / — 2, т. е. в этом случае наше тождество доказано
(X = V/ti). Остальные коммутаторы мы можем вычис¬
лить рекуррентно прн помощи тождества (****). При
этом [Pj, Vj_i, i] = 0, но при k = / имеем
P,Vn = ХР, + Lu4,-Ul.
Тем не менее при k = / + 1 наше тождество снова вос¬
станавливается (несложные преобразования мы опу¬
скаем), и дальше уже без труда проходит индукция
по k.
Пространство VV-i может быть охарактеризовано как
нуль-пространство операторов Pj при /= 2, 3, ..., k— 1.
Если 1Д_ь то мы имеем
Ej^kil — XP/l = О,
т. е. ^ Vk-л- Лемма доказана.
Следствие. Оператор
Vv-IKi. 0
1 = 1
отличается лишь скалярным множителем от Z-мульти-
пликатора
Zv = Uz:>, о < V, < гь
j = 1
в применении к старшему вектору f0 представления
d( а).

§ 68. ПОНИЖАЮЩИЕ ОПЕРАТОРЫ
313
Действительно, оба эти оператора являются весовыми
и имеют одинаковый вес; следовательно, оба они пере¬
водят /о в старшие векторы подгруппы Gn„, с одним и
тем же весом. Но тогда
VJ о ^v^vfo
ввиду единственности этого веса (теорема 2). Констан¬
ту %v нетрудно вычислить при помощи леммы 6.
Действительно, ввиду коммутативности операторов
Г = vj' мы можем применить их к вектору /0 в поряд¬
ке возрастания индексов г:
= ^'n-J'n-2 • • • ВДо.
При этом все возникающие множители вида
[ 1, 2, 1, я] . . п ,
Zin ~ [1, 2 г- 1, г] ’ 1 ~ ’ ’ • • •> п *>
являются константами по отношению к последующим
дифференцированиям Гр, р > t, которые согласно лем¬
ме 6 порождаются только операторами Ehj, k > / > i.
Следовательно, можно применять Гр непосредственно к
вектору /о, и мы получаем, что
К = ЪЪ ••• Yn-i)
где Yi — собственное значение Гг на /о- Для вычисления
Y; мы снова пользуемся леммой 6, согласно которой
П
Yi= S {h-h- !) ПРИ vi = !•
j = i+i
Поскольку минор, стоящий в числителе zin, является
константой по отношению к дифференцированию Vni,
дальнейшее применение этого оператора равносильно его
применению к вектору
гг _ [о
(1,2,...,/]’
который снова является старшим с сигнатурой
(т\,т2, ..., —1, mi+i, тп). Понижая

314
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
последовательно до rrii = mi — v*, заключаем, что
vi п
V -II П II
где Г,- = U — v,. Перемножая эти величины при < = 1,2,..,
.. ., п — 1, получаем окончательную формулу:
п-1
Я
(/<-//- 1)!
V
И П (ti-l,- 1)!
i=l /=1+1 w ' '
В частности, мы видим, что Xv Ф 0 при Сле¬
довательно, операторы Vv порождают (при действии на
[о) все подпространство 1;п-ь состоящее из собственных
векторов относительно Gn-\.
Теперь открывается возможность индукции по п, и
мы заключаем, что имеет место
Теорема 5. Всякий базисный вектор Гелъфанда —
Цейтлина может быть представлен в виде
еи = ~fj
1-1
где iV|i — нормирующий множитель и оператор яв¬
ляется полиномом от понижающих и диагональных опе¬
раторов Ец:
О = ТТ \mik~muk-x
Ы-Ц ±1 v ki у
где явный вид оператора Whi дается леммой 6 и где опе¬
ратор Vhi расположен левее V//, если k < / (при k = I
такие операторы перестановочны).
Замечание 1. Поскольку операторы Vhj колли-
неарны Zhh вообще говоря, лишь при k = п, нам остает¬
ся неизвестным явный вид полиномов ед(г) в реализа¬
ции на группе Z.
Замечание 2. При доказательстве теоремы 5 мы
пользовались явными моделями неприводимого пред¬
ставления d (а). Однако полученный результат выра¬
жается в терминах инфинитезимальных операций и, сле¬
довательно, универсален в том отношении, что не зави¬
сит от частной реализации d(а).

§ 69. НОРМИРОВКА БАЗИСНЫХ ВЕКТОРОВ 315
§ 69. Нормировка базисных векторов
Условившись считать, что старший вектор /о имеет
единичную норму, мы подберем коэффициенты jV^ та¬
ким образом, чтобы векторы
6^ = МГ ^ = 0
оказались ортонормальными (в частности, e0 = f0).
Иначе говоря, мы полагаем
К-У*
Для вычисления этих коэффициентов нам придется рас¬
сматривать операторы ViA, сопряженные V*, при k > i.
Напомним, что в пространстве представления d(a)
мы рассматриваем скалярное произведение, по отноше¬
нию к которому d(a)|U(n) унитарно*). Следовательно,
антиэрмитовым элементам алгебры X отвечают антиэр-
митовы операторы в пространстве представления. От¬
сюда легко получить, что
E*u==E/t> i, ]= I, 2, . п.
Действительно, ввиду аналитичности d(a) эрмитовым
элементам алгебры X отвечают также эрмитовы опера¬
торы в d(a). Условие e*lj = е/г означает, что сумма
ец + вц является эрмитовой, а разность вц— ец — анти-
эрмитовой; но тогда то же верно и при замене efj на Ец.
Докажем теперь, что имеет место
Лемма 10. Оператор V,ft, сопряженный Vhu & > t,
может быть записан следующим образом:
= . . 2 . , Chh ••• lsEiskEis-ds ■ • • EUhEiU>
^ 1 *2 " ' ' S
где условия суммирования и коэффициенты с/,/2.../ те
же, что и в лемме 6.
Доказательство. Мы получим нужные соотно¬
шения сопряжения для операторов Ец, если положим
*) Как легко получить из леммы Шура и неприводимости d(a),
это скалярное произведение определяется однозначно с точностью
до множителя.

316
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
по определению
(*')• = д/, Ш =
для операторов рождения и уничтожения. Используя
соотношения коммутации (ДД; = дДДj—1)), мы мо¬
жем представить оператор Yfti следующим образом:
^ki — dtBk-\Bk-2 ••• Bi + lxk,
где положено В, = djX1 + Lil — 1 = xldj + Ll{. Поскольку
каждый бином Bj является самосопряженным, мы имеем
отсюда
У ik ~ dkBi + \Bi+2 ... Bk-\X .
Окончательное выражение в терминах Д,-;- получается
отсюда по правилу расшифровки, указанному в § 68
(см. доказательство леммы 7). Лемма доказана.
Следствие. В применении к старшему вектору под¬
группы Gh~ 1 мы имеем
= ( П Lt,} Elk = Elk ( П (Ец + 1)} } •
К l=i+l J I/=i+l I
Действительно, в этом случае обращаются в нуль все
остальные слагаемые в У^. Положим теперь
vv = rKi.
i=»I
Лемма 11. В применении к старшему вектору |
подгруппы Gh мы имеем
V;Vv=PK_p aft),
где правая часть означает оператор умножения на
число:
ш \ ТТ Vt-h- О1 ТТ (/г-Т/-1)!
-1. ak) Ц (7 / 11 Qi-Tj)! ‘
1</</<4 1 К‘</<4-1 W '
k-1
*) Произведение полагается равным единице, если i
i +1
= 6—1.

§ 69. НОРМИРОВКА БАЗИСНЫХ ВЕКТОРОВ
317
Здесь U = nii — i, Г,- = га,- — г, a,h = (гаь га2> ..., mh) —
инфинитезимальный вес вектора | относительно под¬
группы Gh и a,h-\ = (mu m2, mh_x)— инфинитези¬
мальный вес вектора \ = Vvg относительно Gh-\-
Доказательство. Не ограничивая общности, мо¬
жем считать, что k = п. Используя коммутативность V,-,,.
расположим эти сомножители под знаком оператора:
П —1
V* = ГГ wvi
v J-J- in
« —1
в порядке убывания индексов i (при чтении слева на¬
право). Согласно следствию из леммы 10 индукцией по
степени находим, что
Vj‘=£j'n II (Lli + s).
5=1 /=*+1
Перемножая эти операторы, заметим, что Ец перестано¬
вочно со всеми сомножителями Ерп, расположенными
правее в Vv (P<i</); следовательно, все произведе¬
ния, содержащие Ьц, переносятся без изменения на¬
право. В результате имеем
п— 1 л-1 Vj л-1
К =11 ^11 П II (L{l + Si)
1 = 1 / = 1 5^=1 / = t+1
в применении к старшему вектору подгруппы Gn-i-
В частности, таким вектором является | = Vv^, и сомно¬
житель L{j в этом случае можно заменить на Г* — lj.
Заметим также, что Г,- + v* = /,-— 1. Следовательно,
V* = ТТ - J J • Ti EVJ
v 11 (//-//)! -Li in
!<«'</< л-l v ‘ / = 1
в применении к Реализуем теперь неприводимое пред¬
ставление d(a) на группе Z и напомним, что согласно
следствию из леммы 9 в этом случае

318
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
где константа Kv имеет вид
№-1,-1).
к,1)1
В то же время оператор Ein задается формулой
г- i д
‘-‘in Z g?n >
где гг означает i-й столбец матрицы г. Производя диф¬
ференцирование, находим, что
гг — 1 ( п— 1 ^ п — 1 гг—1
П I П гМ = П V;! = П (h - /<)!.
i = 1 I t = 1 ) I — 1 i = 1
Действительно, Е1п = -^-~, и применение этого опера-
UZ\n
тора *) в степени vi уничтожает множитель z[h, заменяя
его на vi!. Поскольку полученное выражение уже не за-
Е- д
висит от 2in, мы можем заменить Ь2п на — и т. д.
VZ2tl
Теперь остается перемножить все полученные кон¬
станты. Лемма доказана.
Следствие. II Vv|||2/||||[2 = Р (аь~и а*), где \ —
старший вектор подгруппы Gh с сигнатурой ak и Vvg —
старший вектор Gh-\ с сигнатурой a,h-\-
Действительно, (Vvg, Vvg) = (g, V^Vv|) = P(ak_v ak)(l, I)
Теперь уже без труда получаем окончательный резуль¬
тат:
Теорема 6. Базисный вектор /ф = ПДо имеет сле¬
дующую норму.
П— 1
«.-П! II
, (й, /г—1 — ijk~ О
ft=2 ll<( </<ft
X
(hk Oft 01
■ 0 * — 1
п
!<;</<ft-I
х
(Ни - и, ft-i)i V/.
(й, ft-i - lj, ft—i)I
где ||/oll = 1 u числа lih связаны с параметрами схемы ц
соотношениями
hk = mik - i.
Доказательство. Согласно определению векто¬
ра /д он является старшим относительно G\ с сигн.ату-
*) Здесь мы пользуемся перестановочностью операторов £(„,

§ 69. НОРМИРОВКА БАЗИСНЫХ ВЕКТОРОВ
319
рой а.\. = (ni\i). Кроме того, этот вектор получается по¬
нижающим оператором из вектора /у, старшего относи¬
тельно G2 с сигнатурой «2 = (т\2, т22) ■ Следовательно,
||/Д = Р(а„ а2)|[/И12.
Выражая аналогично /у через вектор /д> старший от¬
носительно G3, и т. д., мы приходим после конечного
числа' шагов к вектору f0, старшему относительно Gn.
В результате
1!/Д = П PWk, aft+i).
k=\
причем ал, k = 1, 2, . . . , n— 1, — строки схемы p. При¬
меняя лемму 11, заменяем обозначение U на и обо¬
значение и на Uj,_i. Теорема доказана.
Замечание. Поскольку в выражение для Л/ц вхо¬
дят только разности чисел 1цt, мы могли бы также по¬
ложить lih = mik + n — i. С другой стороны, если мы
желаем получить параметры, через которые в гл. IX
выражались собственные значения операторов Казими¬
ра для G],, то следует положить lik = mik + (k— /') с
соответствующей поправкой в формуле для Л/ц*).
В заключение отметим некоторые соотношения ме¬
жду функциями Р(ал-1, ak), которые легко проверяются
непосредственно:
aft + E/) __
p(aft-i. “*)
п — ! /? s / ~ !
= П ^ - 11 - !) I I ^ П {li - l> ~V~'\
i = I i = / +1 1 = 1
P(V,-cf afe) _
p(ra*-r a*)
Л-1 r-l
= Цаг-//-1) П d-h)II(h-h+ d-1-
/=1 /=/+i /=1
*) Разность Uh — lj.h-x заменяется на — lj, h-t + 1, и раз¬
ность /(, — Ijk — 1 заменяется на ^_! — Ijk.

320
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Здесь sj — (0, . .. , 0, 1, 0, . . . , 0) с единицей на /-м
месте и U, Г; определяются так же, как и в лемме 11.
Заменяя в 2° аи-\ на au-i + 6j, находим также
рК-1. %)
p(ak-i + е/, ak) ~
п п—1 /—I
= П - 7/> П (/'- - ~1> ~ 1> II- 7/Г’ •
i = I г = j +1 i - 1
В частности, Р(а, а) = 1, и мы имеем
3° Р(а, а+еу-) = Ц (// —/у) 11 (/г —^/+1)
( = / +1 i = у +1
где а = (т[, т2, . . ., т„), а + еу = (т1; т2, . . ., ту- +
+ 1, . . ., тп, 0).
§ 70. Дифференциал d(a)
Мы можем теперь установить явные формулы для
инфинитезимальных операторов Ец в базисе Гельфан-
да—-Цейтлина. Для диагональных операторов такая
формула дается уже теоремой 3:
Euevl (s/ $i—i)®u>
i
где st = 2 tn.ki ~ сумма чисел, расположениях в
k= I
i-й строке таблицы р (s0=0). Из сопряженности опера¬
торов Etj следует, что достаточно изучить, например,
подсистему повышающих операторов Ец, i < /', среди ко¬
торых в свою очередь достаточно выделить подсистему
образующих Eit y+i, i = 1, 2, . . . , п— 1. Наконец, из со¬
ображений индукции по цепочке G„ тэ Gn_i Gy
достаточно рассмотреть единственный оператор
Р =
Лемма 12. Оператор Р действует на базисный век¬
тор по формуле
п-I
Р/ц = 2 fl/W/n + e..
/ = 1 /

§ 70. ДИФФЕРЕНЦИАЛ d(a) 321
где в j означает вектор (0, ..., 0, 1, 0, ..., 0) с едини¬
цей на j-м месте, добавляемый к строке ап~\.
Доказательство. Согласно определению вектора
/и он содержится в подпространстве неприводи¬
мом относительно G/, с сигнатурой ан- Поскольку опе¬
ратор Р перестановочен со всеми преобразованиями
группы Gk при k^Cn — 2, он может отображать V{а/,)
только в себя (ввиду однократности аи в спектре й(а)).
Следовательно, строки ан при k ^ п — 2 остаются неиз¬
менными. Далее, положим
л-1
V = S ElnV (<*„_,) = Еп(8) V
i=1
где Е„_ 1 означает линейное пространство с базисом
Ein, i = 1, 2, . . ., п— 1. Вектор fu содержится в V. Фор¬
мула
ЕpqEin ^iqEpn “f" ЕinEpq, 1 ^ p,Q ^ tl 1,
показывает, что V инвариантно относительно Gn_j и
инфинитезимальные операции этой группы получаются
по правилу дифференцирования в тензорном произведе¬
нии d\ ®d(an_i), где d\ — преобразование (п—1)-мер-
ного вектора в Мы покажем в гл. XII, что
П— 1
с/j <8> d (a) = 2 d{a +е;), a = a„_,
/=i
(где в правой части допускаются лишь те слагаемые,
для которых a + gj является сигнатурой). Следователь¬
но, Pfy, разлагается по базисным векторам с сигнатурами
a„_i + gj, / = 1, 2, п — 1. Лемма доказана.
Мы можем теперь перейти к вычислению коэффи¬
циентов аДр). Представим вектор в виде
fp, ~ Rppjpv’
где понижающий оператор Дцщ содержит все операторы
Vi,-, k < п— 1, в соответствующих степенях и

322
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Согласно лемме 12 применение оператора Р к вектору
равносильно его применению к вектору /ц, *), т. е.
(И) = Я/ Ы-
Поскольку вектор /ц, является старшим относительно
подгруппы Gn-ь схема ро имеет вид
' т2 тъ ... т„_!
_ ihK т2
Ио — |
тх
где ntf = min, mi = mit n-\ и все остальные строки по¬
лучаются усечением из а.п-\. Следовательно, наша за¬
дача свелась к вычислению а;(ро). Используя снова
лемму 12, находим
а1 Ы ^Ро+6/ — ipn-\,n fи0> f\i0+е;.) —
= (fp0, E,n,n-\ f|i0 + Ey) = (fp0> V„;/^o).
Согласно лемме 8 мы имеем
Еп, / = у I^n, п-1 + 4j/)
в применении к весовому вектору / = где А,—
значение оператора Lit n_i на векторе f:
К = lj /rt-i 1>
и явный вид константы А/ нам не нужен. Поскольку
Еп, п—I = Vn, n-ь то первое слагаемое при умножении
на f дает вектор, ортогональный и его можно от¬
бросить. В результате
а1 (М’о) N10+Sj = X (W У = '
Следовательно,
а1 Ы = т
* К0+*, Р К-i, + <*/)' -Р (<*„-, + ву, а„)
*) При доказательстве леммы 9 мы видели, что Р перестаново¬
чен с Vfc( при k<n—1. Отсюда непосредственно можем заклю¬
чить, что Р перестановочен с Лцщ-

§ 70. ДИФФЕРЕНЦИАЛ d(a)
323
Пользуясь тождествами 2' и 3°, приведенными в конце
§ 69, находим окончательно, что
П
Ц (h-Ti)
а, Ы=й •
П &~h)
г = 1
Переходя к ортогональному базису имеем
п — 1
2 с/(и)<д+е/-
/=1
Для вычисления коэффициента сДц) достаточно умно¬
жить аДц) на отношение N/N, где N = Na и
N' — N^+e.. Согласно тождествам 1°, 2' имеем
У'2 _ Я (а,г-2, an-i + 6/) Я (ага-1 + е/, ап) _
N2 Я (art_2, ®n~i) Я (йп~~ь an)
л —2 _ n—!
II (Д-//-О П Oi-h)
_ + (=1
n — 1 n — \ *
ГГ (Д-7,)П (7,-7/ — I)
i = \ i = 1
где штрих означает, что исключается сомножитель при
i = /, и знак ± подбирается так, чтобы выражение
справа было положительно. Ввиду сопряженности
Еп, Еп, п-i имеем также
О (ц) (Еп— 1, п~ 1®и+в/)>
т. е. оператор Еп,п-1 имеет отличными от нуля лишь
коэффициенты
^га, л-1ец) = О (М1 ®/)-
Отсюда с помощью перенормировки можем также вы¬
числить действие Еп, n_i в базисе /ц. Результатом яв¬
ляется

324
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
Теорема 7. И нфинитезимальные операторы £р_ i, р,
Ер, р-1 действуют в базисе fp = QJ0 по формулам
Ш Vip— h< р->)
Ер-1,р/д = / , р—1 /д+Ёу(р —1)>
У“1 (к- р-\~ lj, р-\)
1 = 1
р-2
П р~2 —
Ер, p—ifp ~ р-i /д-еу (р—i)>
/“1
JJ (б, р-i ~ O', p-i)
г-1
где lip = mip — i и г,(р—1) означает добавление век¬
тора (0, ..., 0, 1, 0, 0) с единицей на j-м месте
к (р—1)-гг строке схемы р.. В ортонормальном базисе
е„ имеем
'Д
£
Р 11Р д
р-1
е„ =
-S
/=1
XJ (hp ~ lj, p-i) (б, p-г —■ 11, p-i — I)
г-i г—1
p-i p-i
(к, р—1 — lj, p-i — О (к, р—1 — lj, p—i)
г-i г-i
'-Д + Зу (Р —1)>
Ер,
р р-2
(hp ~ к, p-i + О (к, р—2— lj, p-i)
г-i г-i
p-i p-i
(к. p-i — h, p-i) XI (*г, p-\~lj, p-i +1 >
г-i г-t
?д-еу (p-i).
Во всех этих формулах штрих означает, что в произве¬
дении исключается нулевой сомножитель (г = /), 1^ = 0
при i > /, и фигурные скобки со знаком « + » заменяют
знак модуля.
Замечание. Обычно в литературе используются
только формулы для операторов Ец в ортонормальном
базисе. Между тем мы видим, что в базисе эти фор¬
мулы выглядят значительно проще.

§ 71. МАТРИЧНЫЕ ЭЛЕМЕНТЫ d{a)
325
§ 71. Матричные элементы а)
В заключение этой главы укажем простую общую
формулу для матричных элементов d(а). Мы опреде¬
ляем эти элементы из разложения
2 Vv (s')
в
где еи — ортонормальный базис Гельфанда — Цейтлина.
Нетрудно видеть, что производящая функция a{g) яв¬
ляется одним из таких элементов:
a{g) = {Tgeо, е0),
где индекс 0 нумерует старший вектор d(а). Действи¬
тельно, условие Eij=Eji означает, в частности *), что
эрмитово сопряжение переводит преобразования груп¬
пы Z_ в преобразования группы Z+; следовательно,
(Vo* eo) = (7eVo* Vo) = (Vo* ^q) = ct (6) = a (g). Условие
a (£gz) = a (g)
показывает, что функция a(g) является старшим век¬
тором относительно двусторонних сдвигов f (g)f (g'gg2)
на группе G. Поскольку линейная оболочка функций
Tuv(g) неприводима относительно этих сдвигов, то ясно,
что всякая такая функция может быть получена из
a(g) посредством понижающих операторов.
Нам будет удобно ввести несколько необычные обо¬
значения для инфинитезимальных операторов левого и
правого сдвигов на G. Условимся операторы левого
сдвига записывать слева, а операторы правого сдвига —
справа от функции f(g), полагая соответственно, что
в записи fAB оператор А действует раньше В. Поло¬
жим
Eikf (g) = gi-f~f (g)> f (g) Eki = f{g)~jgl,
dgk ogR
*) Для операторов Tg это условие означает, очевидно, что
Тg = Tgt, т. е. T'g = Тя„ где штрих означает транспонирование в
базисе Гельфанда — Цейтлина.

326
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
где gi означает г-ю строку и gi — г'-й столбец матрицы g
(элементы этой матрицы рассматриваются как незави¬
симые переменные). Тогда операторы Eih, Ehi являются,
образно говоря, «операторами подстановки» индекса i
вместо индекса k. Для выяснения вопроса, какие из
этих операторов являются повышающими и какие по¬
нижающими, удобнее всего использовать явный вид
а-функции:
а (fi) = П
i=i
fin
£;i
fi и
gu
откуда видно, что операторы E]k, Eki аннулируют эту
функцию при i < k. Следовательно, операторы, «пони¬
жающие индекс», нам приходится рассматривать как
повышающие*). Положим теперь
^ki= 2 c/i/2 ••• /g^b/Eii Eisi> k> i,
= i ^ EiliE'i^ ' ' ' E‘sk ' Chh ■■■ Is’ l<k’
*1*2 *’* * S
где коэффициенты с,- ,• в обеих формулах одни и те
же**):
с/,/2---/5= П *-Ч'
1 2 J KKk
Напомним, что L{j = L{ — Lj, где Е^ — Ец — i. Для
каждой схемы р = {ш/,г} рассмотрим всевозможные разно¬
сти ги = ты — i и положим
у гы
*) Это несколько неудобное соглашение вызвано желанием
конструировать a-функцию из диагональных миноров с индекса¬
ми 1, 2 р.
**) Напомним, что эти коэффициенты перестановочны со всеми
операторами Ejt, кроме Е,
‘s ~ ~
***) При этом операторы располагаются левее V(j, если
к <1, а для операторов имеется в виду обратный порядок сле¬
дования,

§ 71. МАТРИЧНЫЕ ЭЛЕМЕНТЫ d(а) 327
Теорема 8. Произвольный матричный элемент
Tuv(g) представления d(a) может быть выражен в виде
Tnv (§) = N^NV (§) Р\>
где a(g) —производящая функция d(a) и Nn, Nv — нор¬
мировочные множители, явный вид которых дается тео¬
ремой 6.
Доказательство. Формула
Tuv (gh) = 2 V {g) 4V (h)
к
показывает, что каждая строка матрицы ||тДу|| преобра¬
зуется согласно d(a) при правых сдвигах g -> gh. В ча¬
стности,
«(й = 2ч (g) т^о(Л),
н
откуда ясно, что функции ep(g) = Top(g) преобразуются
по закону ортонормального базиса в d{a). Следова¬
тельно,
iop(g) = j^a{g) Рп,
и функции тд0 {g) = т0д (g') *) выражаются аналогич¬
ным образом через операторы левого сдвига:
В свою очередь каждая из этих функций является стар¬
шим вектором для строки ruv(g). Следовательно,
тnv (г) = 7ГК Р»а № Pv
Ji, V
Теорема доказана.
Напомним, что согласно глобальной теореме функ¬
ции x[iv(gr) взаимно ортогональны по отношению к ска¬
лярному произведению
(f. Ф) = J /(ы)ф(м) du,
*) См. сноску на стр. 325.

328
ГЛ. X. ИНДИКАТОРНЫЕ СИСТЕМЫ
где интеграл берется только по подгруппе U(n). Опе¬
рации g-+u0g, g-*gu0, Uo^U(n), унитарны по отно¬
шению к этому скалярному произведению. Если счи¬
тать, что мера Хаара du нормирована условием
J du = 1, то
IKv(g)[|=ArV2,
где N = N (а)—размерность представления d( а). Од¬
нако при фиксированном а мы можем перенормировать
эту меру таким образом, чтобы llTUv(g)||= 1.
Полученная формула для T,*v(g) является дифферен¬
циальной формулой типа формулы Родрига для полино¬
мов Лежандра. Мы можем записывать эту формулу не¬
сколько иначе. Прежде всего, имеем
Следствие 1. Если выбрать в группе G парамет¬
ры (на всюду плотном множестве) при помощи «инверс¬
ного разложения Гаусса» g = z6£, то
(z6£) = P^a (z6£) P4,
где операторы Eh{, k Ф i, действуют только на параметры
z и операторы Eih, k Ф i, действуют только на парамет¬
ры I.
Действие диагональных операторов Lij = Ец — Ец +
+ (/ — г) проще всего учитывать, не выполняя диффе¬
ренцирования, но вычисляя вес вектора, к которому
они применяются. Если принять такое соглашение, то
мы получаем также
Следствие 2. Значение функции TUv(g) в произ¬
вольной точке g е G может быть вычислено следующим
образом:
Sv(g) = д Аг ^па Pv \z-l-e,
iV V
где Pw, Pv рассматриваются соответственно как диффе¬
ренциальные операторы по параметрам z и £.
Наконец, поскольку в этой формуле дифференциальные опера¬
торы применяются только в точке е, естественно попытаться заме¬
нить Eji, Ец на их значения в единичной точке, т. е. на ,

§ 71. МАТРИЧНЫЕ ЭЛЕМЕНТЫ d(a)
329
—— соответственно. Заметим, например, что оператор может
огц
быть переписан в виде
'ViV^'Va^'Va -Is
vki - _ S • • • Ei,uEk< г>
/,>/*> ->!s
S!\812 8ls8k dg,^ dg,^ dg,^ dgt Cl\l2---Is'
Такая запись была получена нами при доказательстве леммы 10
(через биномы Bj). Теперь, поскольку все операторы умножения
собраны слева, мы можем без труда положить g = е, т. е. заменить
gi на е,- = (0 0, 1, 0, ..., 0). В результате получаем оператор
уО = V д д _А_ с
и ** dg, { dg, , ' dgk, 1112 I,
jl>i2>...>ls ’s' ’s-1 >>s
который по-прежнему может быть переписан в виде
vo.= V . __д д д
kl ^ yi 'f'^dgk, dg,, ' dg, i’
/,>/2>••• >ls h ’s
Здесь коэффициенты с, , , легко вычисляются из «весовых»
соображений (они отличаются от с, , , заменой каждого мно-
‘VI ■1 • > S
жителя Lij на Lij + 1). Подобную операцию можно произвести и
над всем произведением Рц(Ру). Однако останавливаться на этом
подробно не будем.
Мы уже видели в гл. V, что функции ^(g) при
п — 2 выражаются через полиномы Якоби. Несомненно,
представляет интерес исследование этих функций при
произвольном п в терминах классической теории спе¬
циальных функций.
1 * , *
В этой главе мы собрали основную информацию о строении не¬
приводимого представления d{а). Ключом к получению этих ре¬
зультатов являются для нас индикаторные системы, построенные
автором в 1961 г. ([83], [84]). Однако выбор базиса в пространстве
d(a) и явные формулы для инфинитезимальных операторов в этом
базисе были предложены И. М. ГельфандомиМ. J1. Цейтли¬
ным [72] еще в 1950 г. Эти авторы предлагают готовый ответ на
задачу, справедливость которого может быть проверена, например,

330
гл. х. индикаторные системы
путем непосредственного вычисления соотношений коммутации. Ре¬
дукция с группы на подгруппу не указана в этой работе явно, но
достаточно очевидна из структуры параметров, определяющих ба¬
зисные векторы. Наш подход состоит в предварительном доказа¬
тельстве теоремы о редукции, откуда удается получить не только
матричные элементы инфинитезимальных операторов, но и струк¬
туру операторов понижения.
Понижающие операторы были найдены первоначально также
в статье [84]. Вслед за тем в работе [142] эти операторы были вы¬
ражены через операторы рождения и уничтожения, и также най¬
дена нормировка базисных векторов. Мы использовали символику,
предложенную в [142], при вычислении соотношений коммутации
между операторами Vs; и также частично следовали этой работе
при вычислении нормирующих множителей (§ 69). Близкие резуль¬
таты были получены в [155]. Формула типа Родрига для матричных
элементов была получена в [84]. Недавно И. М. Гельфанд и
М. И. Граев [66] получили выражение для матричных элементов
через обобщенные «бета-функции».
Заметим, что индикаторные системы действуют далеко не в пол¬
ную силу при доказательстве теоремы о редукции. В действитель¬
ности в этом доказательстве достаточно было бы использовать го¬
раздо более простой критерий (см. сноску на стр. 298). Однако в
следующих двух главах мы укажем дальнейшие приложения инди¬
каторных систем. В гл. XVI дается построение индикаторных систем
для каждой надкомпактной группы Ли.

ГЛАВА XI
ХАРАКТЕРЫ
Пусть G — произвольная группа. Каждому ее конечномерному
представлению Tg поставим в соответствие числовую функцию
% (g)^spTg.
Эта функция называется характером представления Тg; среди ли¬
нейных комбинаций матричных элементов Tg она играет особую
роль. Прежде всего, очевидно, что функция %(g) инвариантна отно¬
сительно внутренних автоморфизмов:
%(go'gg0) = X(g)- (*)
Иначе говоря, %(g) постоянна на классах сопряженных элементов
в группе G. Далее, если G — компактная группа Ли, то согласно
глобальной теореме множество всех характеров, отвечающих не¬
приводимым представлениям, образует полную ортогональную си¬
стему в классе функций, удовлетворяющих условию (*).
Характер обладает также и другими замечательными свой¬
ствами, некоторые из них мы отметим в конце главы. Основным
содержанием этой главы является прямое вычисление характеров
Ха(ё) неприводимых представлений d(а) группы \](п). С этой за¬
дачей тесно связана также еще одна задача, допускающая геомет¬
рическую интерпретацию,— построение весовой диаграммы пред¬
ставления d(a).
§ 72. Инвариантная мера на группе U(n)
Пусть du — инвариантная мера Хаара на группе
U(«), нормированная так, что объем всей группы равен
единице. Ввиду соотношения (*) нас будет интересовать
разложение
и = и~‘уи,
приводящее произвольную матрицу iieU(rt) к диаго¬
нальной матрице у. Выясним, можно ли рассматривать

332
ГЛ. XI. ХАРАКТЕРЫ
параметры о и ^ как параметры в U(n). Если это так,
то естественно будет записывать du в виде
du = a>dv dy,
где со — соответствующий якобиан.
Пусть Г — множество всех диагональных матриц в
группе G = U(n). Вводя угловые параметры, запишем
произвольную матрицу у е Г в виде
Если фиксировать у. т0 преобразующая матрица v в
искомом разложении определяется неоднозначно. Про¬
извол в определении этой матрицы выражается соотно¬
шением
уГ'уи1 = V2lyv2-
Иначе говоря, матрица w = у2у,-1 должна коммутиро¬
вать с матрицей у. Если у имеет различные собствен¬
ные значения, то это возможно только в случае w е Г.
Пусть Г0 — подмножество в Г, выделяемое условием
фг Ф фь i, / = 1, 2, .. . , п. Поскольку это подмножество
получается из Г выбрасыванием конечного числа поверх¬
ностей вида ф, — = 0, оно имеет полную размерность
в Г. Если у е Г0, то мы видим, что преобразующая мат¬
рица v определяется с точностью до произвольного ле¬
вого диагонального множителя:
V2 = wvu ®еГ,
Следовательно, можно считать, что множество преобра¬
зующих матриц отождествляется с множеством Q = G/r.
В дальнейшем ввиду произвольности диагонального мно¬
жителя мы определенным образом специализируем пре¬
образующую матрицу V.

§ 72. ИНВАРИАНТНАЯ МЕРА НА ГРУППЕ U(n)
333
Далее, если фиксировать ueG, то диагональная
матрица у определяется с точностью до перестановки
собственных значений. Следовательно, Г0 разбивается
на п\ областей, в каждой из которых имеется «предста¬
витель» у, отвечающий матрице и. Полагая
Го+={уеГ, ф]<ф2< ... <Ф„}>
мы получаем одну из таких областей. Все остальные
получаются из нее с помощью подстановки. Если у
пробегает Го" и v пробегает Q, то мы получаем, очевид¬
но, в группе G многообразие полной размерности. В этом
смысле можно говорить, что пара (у, v) параметризует
U (п). "
Найдем соотношения между дифференциалами всех
рассматриваемых матриц. Дифференцируя обе части ра¬
венства vu = yv, находим, что
dv • и + и ■ du = dy • v + у • dv.
Умножим полученное равенство справа на «-‘а-1 =
= о'1у“1 и для каждой матрицы х положим Ьх = dx- хгх\
в результате получим
би + и • бы • и-1 = бу + у • бо • у-1.
Заметим, что ввиду унитарности матрицы и матрица
дифференциалов du является косоэрмитовой: duik =
= —duki\ однако при вычислении якобиана перемен¬
ные uih, uih можно, как известно, считать формально
независимыми. При этом переход от матрицы б и к мат¬
рице бы = v • бы • v-1 имеет единичный якобиан. Следо¬
вательно, искомый якобиан со совпадает с якобианом
следующего преобразования:
бы = бу + у • би • у-1 — &V.
Запишем это преобразование в матричных элементах.
При этом используем произвол в выборе преобразую¬
щей матрицы и. Нетрудно видеть, что за счет подбора
диагонального (левого) множителя можно добиться вы¬
полнения условия bvu = 0 для всех диагональных эле¬
ментов матрицы V. Выписывая отдельно диагональные

334
ГЛ. XI. ХАРАКТЕРЫ
и недиагональные матричные элементы, получаем, что
наша система уравнений распадается:
6uii = 6\li = V-\d(fi, г= 1, 2, . . ., п\
= (Yi/Y/- 1)6»,/, г, /, = 1, 2, ..., п\ 1ф'\.
Для вычисления якобиана достаточно найти модуль
произведения всех выражений, стоящих в круглых скоб¬
ках. Заметим, что при транспозиции индексов i, / это
выражение заменяется сопряженным. Положим
А = II (Yi - Y/)-
i<i
При умножении круглых скобок \г/У)— 1 = (у'г — Yj) /Yj
знаменатели можно не учитывать, поскольку |ул1= '•
В результате получаем окончательное выражение для
якобиана со:
со = АА,
где черта означает комплексное сопряжение. Множи¬
тель dv мы нормируем таким образом, чтобы j du= 1.
Рассмотрим теперь произвольную функцию f(u), по¬
стоянную на классах сопряженных элементов, т. е. та¬
кую, что
f(u) = f(v~1\v) = f( y)-
Для краткости такие функции мы будем называть функ¬
циями классов. Имеем
j* / du = j* dv j* /со d<p = — j* /со dtp, dq> = d<p\d<p2 ... dq>n,
где A'o — нормирующий множитель. Для вычисления
этого множителя положим / = 1; тогда левая часть об¬
ращается в единицу ввиду условий нормировки, и, сле¬
довательно, М0= J сосйр. Заметим, что функция /(у)
симметрична относительно перестановки собственных
значений. Следовательно, оба интеграла по сйр можно
рассматривать (одновременно) либо по множеству Го",

S 73. ПРИМИТИВНЫЕ ХАРАКТЕРЫ U(n)
335
либо по всей группе Г. Окончательно имеем
J ДД/Лр
где оба интеграла берутся по «-мерному тору Г: 0<лрг-<
<2я, i = 1,2, . .., п.
§ 73. Примитивные характеры U(n)
Характеры неприводимых представлений принято
иногда называть примитивными характерами. В этом
параграфе мы найдем примитивные характеры группы
Для решения этой задачи достаточно использовать
соотношения ортогональности для примитивных харак¬
теров, даваемые глобальной теоремой*):
Здесь Ха — характер неприводимого представления d(a)
и ба|3 — символ Кронекера для пары сигнатур а, р. По¬
скольку подынтегральная функция есть функция клас¬
сов, мы можем использовать для нее полученную в пре¬
дыдущем параграфе формулу интегрирования. В резуль¬
тате получаем
где No — нормирующий множитель, равный ДДс?ф, и
Для нас существенно, что функция Xa(y) = sP^Y яв'
ляется полиномом от уь у2, ..., уп (как сумма весов),
кроме того, полином Ха симметричен относительно всех
подстановок (как функция классов). В то же время
функция Д является антисимметрическим полиномом.
*) В действительности мы используем только условие норми¬
ровки при a = р.
и («).
где положено

336
ГЛ. XI. ХАРАКТЕРЫ
Следовательно, и Ха является антисимметрическим по¬
линомом от Yi, Y2. • ■ • > Yn-
Расположим все одночлены, входящие в полином Ха,
в лексикографическом порядке и заметим, что Ха =
= АХа; где А — оператор антисимметризации. Следова¬
тельно, Ха разлагается в сумму однородных антисим-
метрических слагаемых вида
± Yf»Y|» • • • V>,
где сумма берется по группе подстановок (над элемен¬
тами yi. Y2. Yn) и знак ± выбирается в зависимо¬
сти от четности или нечетности подстановки. При этом
слагаемое Sk входит с целой кратностью с&. Действи¬
тельно, Ха и А имеют только целые коэффициенты; сле¬
довательно, то же верно и для функции Ха. Интегрируя
по группе Г, получаем, что функции Sh удовлетворяют
следующим соотношениям ортогональности:
| SkSi dq> = (2я)'г • п\Ьм,
где б ы — символ Кронекера для символов k =•--
= {k\,k2, ..., kn), I = (/j, k, ..., ln). Заметим, что, в
частности, Л является антисимметрической суммой вида
Sa„, где k0 = (ti—1 ,ti — 2, ..., 1, 0). Следовательно,
N0 = (2n)n-п\.
Далее, записывая функцию Ха в виде и ис¬
пользуя соотношения ортогональности, находим (сокра¬
щая на N о), что
ua=i.
Поскольку числа с& являются целыми, это возможно
лишь в том случае, когда все они равны нулю, за
исключением одного, который равен ±1.
Пусть у™‘Y™2 • • • Yпп ~ старший член характера Ха>
mi > т2 > ... ^ тп, где т\, т2, ..., тп — параметры
сигнатуры а. Тогда старшим членом Ха является
Y'pYl2 • • • Упп> гДе положено
h = тк + {п — k), k = 1, 2, ..., п.

§ 73 ПРИМИТИВНЫЕ ХАРАКТЕРЫ U(/i)
337
Поскольку этот старший член входит с положительным
коэффициентом, мы заключаем, что сг= +1, и оконча¬
тельно
В результате получена следующая
Теорема 1. Всякий примитивный характер груп¬
пы U (п) имеет вид
где Ха — антисимметрический полином от yi, у2, • • •> Уп,
который может быть записан в виде детерминанта:
и Л = Ха соответствует сигнатуре ао = (0, 0, ..., 0) *).
Параметры lh связаны с параметрами сигнатуры а со¬
отношениями
и уь уг, . •., уп — собственные значения матрицы
ueU (п).
Замечание. При доказательстве теоремы 1 мы
не пользовались классификацией, изложенной в гл. VII.
Более того, теорема 1 сама может быть использована
для классификации неприводимых представлений груп¬
пы U(«). Действительно, формула (*) показывает, что
функция x«(y) содержит старший вес
с кратностью 1. При этом т2^.. тп, и мы
снова приходим к понятию сигнатуры. Поскольку в
(*)
lk = tnk + {n- k), k = 1, 2, ..., n,
> n
n *
mk = lk + (« - *).
*) Напомним также, что Д (у ) = II {У1 — Y/)-
KJ

338
ГЛ. XI. ХАРАКТЕРЫ
силу глобальной теоремы различным представлениям
должны отвечать линейно независимые характеры, мы
получаем, что сигнатура определяет представления с точ¬
ностью до эквивалентности.
Все изложенное построение принадлежит Г. Вей-
л ю [10]. Формулу (*) мы будем называть первой фор¬
мулой Вейля для характеров.
В заключение заметим, что значение характера /(g)
позволяет также вычислить размерность представления
д/ = %(е). Подстановка 8 — е в первую формулу Вейля
приводит к неопределенности 0/0, для раскрытия кото¬
рой удобно ПОЛОЖИТЬ ф! = (п—1)ф, ф2 = (п — 2)ф, ...
..., Ф„ = 0-ф. При этом числитель (-*) превращается в
определитель Вандермонда чисел = который,
как известно, равен произведению разностей ер — еч,
p<q. Устремляя ф к нулю, замечаем, что ер — ед ~
~г'(/р— /9)ф. В результате
(Ip — lq)
at Кр<д<п
а 01112! ... (п- 1)! '
Действительно, выражение в знаменателе есть произведе¬
ние разностей l°p — lq’ p<q, где l°k = п — k, k= 1,2, . . ., п.
Полученная формула является одним из наиболее
важных следствий теории характеров. Действительно, зна¬
ние размерности обычно существенно для приложений.
§ 74. Весовая диаграмма d(a)
Мы уже отмечали при вычислении характеров, что
функция 5Са (у) = spTу представляет собой сумму всех
весов представления d(а), записанных мультиплика¬
тивно:
Xa (y) = Е п% • % (у).
Здесь Пу, — кратность вхождения веса К. Если К не со¬
держится в спектре d(а), то мы полагаем я*, = 0, По¬
ложим
X(y) = Yi*Y22 •• • Y*n-

§ 74. ВЕСОВАЯ ДИАГРАММА d(a)
339
Таким образом, n* = f(M.^2, .. ., Хп) есть неотрица¬
тельная целочисленная функция, отличная от нуля толь¬
ко в точках спектра d(а). Мы называем эту функцию
(см. § 44) весовой диаграммой d{а).
Вместо группы U(n) удобно рассматривать SU(n),
поскольку «геометрические свойства» спектра при этом,
в сущности, не меняются. Полагая Xi + Х2 + ... + Хп = с0,
мы получаем систему параллельных гиперплоскостей в
«-мерном пространстве. Для группы SU (п) весовая диа¬
грамма не зависит от с0 при условии параллельного пе¬
реноса
* ^-/г + С /г = 1, 2, ..., п.
В частности, мы можем положить со = 0 и рассмат¬
ривать весовую диаграмму только на этой гиперпло¬
скости.
Первая формула Вейля дает нам непосредственный
способ для вычисления весовой диаграммы, однако, к
сожалению, слишком сложный. Действительно, деление
в (*) § 73 практически легко производится в общем
виде лишь при п = 2. Полагая для группы SU(2) =
= у“‘ = у, мы имеем
= \l'~h ~ У1г~1'-
Заметим, что 1\ — 12 = т.\ — т2 + 1, где т\, т2 — пара¬
метры сигнатуры а. В гл. V мы положили т\ — т2 = 21,
где I — полуцелое или целое число. Следовательно,
/i — 12 — 21 + 1. Заметим также, что Д = у — у^1. В ре¬
зультате
_ V2i + 1 — у~(2г+1) _ sin (21 + 1) Ф
Y —Y_1 sincp ’
где положено у = ei(f. Для вычисления весовой диа¬
граммы достаточно заметить, что
Xa=V-2/+V-2(/-l,+ ... +V2(/-1, + Y2/.
Мы снова получаем хорошо известный результат (гл. V):
весовая диаграмма отлична от нуля только в точках
—I, —I + 1, ..., I (при соответствующем выборе мас¬
штаба), и в этих точках она равна единице. Очевидно,
что, и обратно, знание весовой диаграммы позволяет

340
ГЛ. ХГ. ХАРАКТЕРЫ
в данном случае получить выражение для характера
элементарным способом, без привлечения теории инте¬
грирования.
Рассмотрим теперь случай п = 3, т. е. G = SU(3).
Весовую диаграмму d(а), а — (mi, m2, m3), мы будем
рассматривать на плоскости Я1 + Я2 + Я3 = const. Спро¬
ектируем на эту плоскость оси
ОХь ОЯ2, ОХз так, чтобы их
положительные направления
расположились под углом 120°.
Тогда вся плоскость разбива¬
ется на шесть секторов с вер¬
шинами в начале координат и
с углами 60° (рис. 3).
Пусть еь е2, е3 — проекции
единичных векторов, направ¬
ленных вдоль ОХ1, ОЯ2, ОХз
соответственно. Всякий вес
изображается точкой вида
П\в\ + ^2^2 + где tl\, П-2,
пз — произвольные целые чис¬
ла. Действительно, всякий вес есть проекция на нашу
плоскость трехмерного вектора с целочисленными коор¬
динатами Хи Я2, Яз- Заштрихованный сектор выделяется
условием Х\ ^ Я2 Яз; только в этом секторе могут рас¬
полагаться старшие веса.
Напомним теперь, что всякий вес представления
2
d(a) может быть записан в виде а — 2 где
г = 1
со 1 = е\ — <?2 и со2 = е2— е3 — корни в алгебре si (3) и
k\, k2 — неотрицательные целые числа. Вычитанию век¬
тора ац соответствует горизонтальное движение налево
на нашей диаграмме, и вычитанию вектора ш2 соответ¬
ствует движение по направлению е3— е2.
Напомним также, что диаграмма весов должна быть
симметрична относительно группы Вейля. В нашем слу¬
чае группа Вейля порождается отражениями относи¬
тельно осей ОЯь ОХ2, ОХз-
Для построения весовой диаграммы мы используем
реализацию d(a) на группе Z. Согласно общим резуль-
Рис. 3.

§ 74. ВЕСОВАЯ ДИАГРАММА d(a)
341
тэтам гл. VII пространство представления натянуто на
векторы
a (z> g) = (a + bx + cy)p (a' + b'x' + c'y'f,
где p = m\ — m2, q = m2— m3, a, b, c, a', b' с' — неко¬
торые константы и x, у, x', у' — функции на группе Z,
связанные соотношением
у + хх' + у' = 0. (*)
Действительно, мы полагаем (в обозначениях
z=||zi;-||) х = Z12, у = 2i3, х' = —г23, г/' = — г13 + zl2z23.
Полином a (г, g) разлагается по одночленам от х, у,
х', у’\ при этом, учитывая формулу (*), мы можем по¬
нижать степени этих одночленов, заменяя хх' на —у—у'.
Следовательно, a(z,g) разлагается по одночленам вида
9ш = УкУ'гф± (s),
где положено qp+(s) = A:s, cp~(s) = A/s. Действительно,
указанная выше операция понижения приводит к од¬
ному из этих одночленов. Для одночленов 0“ мы имеем
следующие ограничения на показатели:
O^k^p, 0^1 + s^q.
Точно так же для одночленов 0+ мы имеем ограничения
O^k + s^p, Q-^l^q.
С другой стороны, используя индикаторную систему
(гл. X), легко проверяем, что все одночлены с такими
ограничениями сами содержатся в пространстве пред¬
ставления й(а). Поскольку эти одночлены линейно не¬
зависимы, мы получаем базис в пространстве представ¬
ления d( а).
Теперь остается найти веса всех базисных одночле¬
нов. Отнесем одночлен 0± к серии S0, если s = 0, и
введем для него в этом случае обозначение
/-кО k /1
Qki = y у ■
Одночлены 0~, s Ф 0, и 0+, s Ф 0, отнесем соответственно
к сериям и 5+ Заметим, что
0+ = rS0O ft- = v's0O
ukls Л vkls л

342
ГЛ. XI. ХАРАКТЕРЫ
Одночлены х, у, х', у' являются мультипликаторами на
группе Z в смысле гл. X. При этом первым двум из них
отвечают соответственно мультипликаторы \рЧ’2. Y~'Y3
в классе весов, а последним двум отвечает один и тот
же мультипликатор ур’Уз- Иначе говоря, умножению
на х, х' отвечает вычитание векторов соь сог (соответ¬
ственно), в то время как умножению на у, у’ отвечает
вычитание одного и того же
вектора coi + сог = £1 — е3.
Используя все эти правила
и ограничения на показатели
k. I, s, нетрудно завершить
наше построение. Фиксируем
точку а = (ти т2, т3) в за
штрихованном секторе на рис
3 и построим шесть точек sa
где s — элемент группы Вейля
Соединяя все эти точки пря
мыми линиями, получаем, как
показано на рис. 4, выпуклый
шестиугольник. Умножение на у, у' соответствует дви¬
жению вдоль пунктирной линии в направлении от а
к р. Умножение на 0^ равносильно вычитанию векто¬
ра т(е 1 — е3), где т = k + /. Полагая т = 0, 1, 2 ...,
подучаем соответствующие кратности весов:
1, 2, 3, ..., k0 1, &о, &о> ■ • • > *о> h 1, . . ., 3, 2, 1.
Действительно, для вычисления этих кратностей доста¬
точно найти число мультипликаторов 0^ с фиксирован¬
ной суммой т = k + I. При этом учитываются ограни¬
чения O^Ck^Cp, Отсюда легко получить, что
т0 = р + q (максимальное из чисел, для которых точка
Р = а — m0(ei — е3) еще является весом) и k0 =
= т\п(р, q) 4- 1. Аналогично производится вычисление
весов для всех остальных мультипликаторов 0±. При
этом сериям S+, S~ отвечают на рис. 4 точки лежащие
в областях /, // соответственно.
Окончательный результат выглядит следующим об¬
разом. Соединим вершины (а, р), (а', Р'), (а", р")>
объединенные попарно, отрезками прямых линий. Тогда

§ 74. ВЕСОВАЯ ДИАГРАММА d(a)
343
в пересечении образуется треугольник, который обозна¬
чим Д. Кратность пх равна единице на границе всего
шестиугольника, возрастает линейно (с шагом единица)
при движении к центру и принимает максимальное по¬
стоянное значение на треугольнике Д (внутри и на его
границе). Это максимальное значение есть
k0 = min (р, q) + 1.
Нетрудно также выделить линии уровня пх = const; они
представляют собой систему вложенных шестиугольни¬
ков, которые, начиная с некоторого момента, выро¬
ждаются в треугольники и (в некоторых случаях) даже
в точку. Для доказательства достаточно заметить, что
движение от а к а' осуществляется мультипликатором
х и движение от а к а" осуществляется мультиплика¬
тором х'. Применение таких мультипликаторов не изме¬
няет кратности.
На рис. 5 приводится весовая диаграмма в случае
а = (7, 2,0). В этом случае а' = (2,7,0), р" = (0, 7, 2),
Р = (0, 2, 7), |3'= (2, 0, 7), а"— (7,0,2). Кратности пх
указаны цифрами у линий постоянства. Эти кратности
равны 1 вдоль внешнего шестиугольника, 2 вдоль сле¬
дующего шестиугольника, 3 вдоль треугольника и 3 в
начале координат.
В общем случае нетрудно показать, что линии по¬
стоянства выделяются уравнениями вида ||х|| = const,
где положено
mi + т3 I
[ х И = шах
к г<з
- ■
для вектора х = х,е, + х2е2 + х3е3 *). В той части, где
кратность nx = fCk) меняется линейно, она задается
формулой
я>. = Ца||-Ш1+1.
Здесь а = (т\,П12,тз) — сигнатура представления. Мак¬
симальное значение кратности в области постоянства
было приведено ранее.
*) При этом должно соблюдаться условие дц + х2 + х3 =
= т\ + т2 + т3. В частности, || х || = шах | х* |, если сигнатура а
нормирована условием т\ + тг = 0.

344
ГЛ. XI. ХАРАКТЕРЫ
Предлагается в качестве упражнения получить опи¬
сание весовой диаграммы для SU (3) другим способом,
используя сужение на SU(2) (см. § 66).
Тем самым в случае п — 3 мы получаем окончатель¬
ный результат. Характер %а и кратности п% вычисляются
элементарным способом. Разумеется, и в общем слу¬
чае метод Z-мультипликаторов дает известную инфор¬
мацию о весовой диаграмме, но структура этой диа¬
граммы является значительно более сложной.
Мы вернемся к данному вопросу в гл. XVII. Пока
займемся описанием еще одного аналитического выра¬
жения для характера %а произвольной группы U(п).
Упражнения
1. Пусть А(а)—весовая диаграмма d(a). Показать, что Л(а)
содержится в выпуклом множестве, натянутом на точки sa, где s —
произвольная перестановка координат вектора а.

§ 75. ВТОРАЯ ФОРМУЛА ВЕЙЛЯ
345
2. Показать, что указанное выше выпуклое множество выде¬
ляется в «-мерном пространстве Еп следующей системой соотно¬
шений:
■И + %2 + ••• + хп = ах + а2 + ... + а.п,
xix + xi2+ ••• +*ift<ai+a2+ ... +aft, k = 1, 2, ..n - 1,
где i\, i2 ik — произвольная система индексов, принимающих зна¬
чения 1, 2, ..., п, и ai ^ а2 ^ ... ^ ап — параметры сигнатуры а.
Иначе говоря, если yt ^ у2 ^ ... ^ уп — перестановка чисел хи х2,
..., хп, то у\ 4- у2 4- ... 4- Уь ^ ai 4- а2 4- ... 4- аь со знаком равенства
при k = п.
§ 75. Вторая формула Вейля
Вернемся к общей формуле для примитивных харак¬
теров U(л). Введем систему вспомогательных чисел
22, ..., 2„ и заметим, что имеет место следующее тож¬
дество:
det
1
1 - YiZk
E*a(V)*a(z).
которое получается разложением слева каждого мат¬
ричного элемента в геометрическую прогрессию. Здесь
Ха задается тем же детерминантом, что и в условиях
теоремы 1, и суммирование ведется по всем сигнату¬
рам а = {nil, m2, ..., m„), для которых числа неот¬
рицательны. С другой стороны, в теории матриц из¬
вестно следующее тождество Коши*):
det
1
1 - Y14
А(у) а(г)
и (1 — Ylzk)
i, k
Здесь, как и в условиях теоремы 1, Д есть определитель
Вандермонда и произведение в знаменателе берется по
всем значениям t, k=\, 2, ..., п. Сравнивая оба тож¬
дества и вспоминая, что %а = XJA, получаем следую¬
щую формулу для характеров:
"zjj Ха (Y) /Са (^) ТТЛ Г *
~ llll-Yi**)
*) См., например, [10], стр. 276.

346
ГЛ. XI. ХАРАКТЕРЫ
Выражение, стоящее справа, можно было бы назвать
производящей функцией для характеров. Заметим, что
П (1 — \iz) = det (е — yz) есть характеристический поли¬
ном диагональной матрицы уеГ, При этом
—1—^00 + 00 + 0^+ ...,
где as есть сумма всевозможных одночленов вида
Y^'Yi2 • • • Yпп степени однородности k\ -\-k2 + ... +kn = k.
Иначе говоря, сц есть характер симметрического пред¬
ставления d\, где d\ — л-мерное представление груп¬
пы U(л) с сигнатурой (1,0,0, ..., 0). Полагая
z = Z\, z2, ..., гп и перемножая полученные ряды, мы
запишем производящую функцию в виде ряда, коэффи¬
циентами которого ЯВЛЯЮТСЯ ПОЛИНОМЫ ОТ СГ0, Сть 02, .
Умножая эту функцию на A(z), мы получим новый ряд,
коэффициенты которого должны совпадать, согласно
приведенной выше формуле, с характерами %а(у)- Пу¬
тем несложного вычисления получаем отсюда
Uh-(n-1)
atl-(n-2) •
■ 0/,
Xa(Y) =
ah-(n~ 1)
°h-(n- 2) ■
• au
%-(«-!)
Otn-{n-2) ■
..o,n
Полученная формула выражает характер произволь¬
ного представления d(a), а = (лгь т2,..., тп), Ш\ >
> т2 ^ ^ тп > 0, через характеры Oh, k = 0, 1,
2, ... При этом для общности записи мы полагаем
аи = 0 при k <0. Выражая параметры Ц через пара¬
метры m.i сигнатуры a (k = mi—(л — /)), получаем
следующий результат:
Теорема 2. Характер неприводимого представле¬
ния d(а), а = (mi, m2,..., mn), m\ > m2^ ... > m„ > 0,
может быть найден по следующей формуле:

§ 75. ВТОРАЯ ФОРМУЛА ВЕЙЛЯ
347
где ак, 6 = 0, 1, 2 — характер симметрического
представления dr.
ok = S Y*1 Y*2 • • • Yknn,
причем сумма берется no всевозможным показателям
ki > 0, для которых ki + 62 + • • • + kn = k. При этом
полагается ak = 0 при k < 0.
Полученную формулу (*) мы называем второй фор¬
мулой Вейля. Она представляет характер %а уже не¬
посредственно в виде полинома от уь у2, уп*)-
Вторая формула Вейля допускает замечательную ин¬
терпретацию в терминах спектрального анализа пред¬
ставлений. Для получения этой интерпретации напом¬
ним основные свойства матричного следа.
Поскольку след является аддитивной функцией по
отношению к сумме матриц, то он аддитивен также по
отношению к прямой сумме матриц разных размерно¬
стей. Кроме того, как известно, след является мульти¬
пликативной функцией по отношению к прямому про¬
изведению. В результате получаем
(Ь b ® Ь ^
где х<г. %ь — характеры представлений а, Ь, символ
афй означает прямую сумму и символ а <8> b — пря¬
мое (тензорное) произведение представлений а, Ь.
Если а = b ® с, то мы положим также с = aQb.
Тогда имеем
'X'aQb 'Х'Ь'
Полученные правила очевидным образом переносятся
на произвольные конечные системы представлений. При
этом сложению, вычитанию и умножению в классе
представлений отвечают такие же операции в классе
*) Из теоремы 2 и полноты системы характеров следует, в
частности, что всякий полином p(g), g е G, инвариантный относи¬
тельно внутренних автоморфизмов, разлагается по функциям Ok(g).
То же верно при замене о* (g) на Sh(g) = sp gk, k = 0, 1, 2, ... Од¬
нако это утверждение гораздо проще получить из теории симметри¬
ческих функций ([10]}.

348
ГЛ. XI. ХАРАКТЕРЫ
т I
характеров. Иначе говоря, если т= 2 aiQ 2 b,, то мы
i=i /=1
имеем
i
гх = 2 га.
1 1
' ХьГ
Далее, всякое конечномерное представление U (п) опре¬
деляется своим характером однозначно с точностью до
эквивалентности. Следовательно, указанные выше пра¬
вила допускают обращение, и мы заключаем, что вся¬
кое алгебраическое соотношение между характерами
равносильно соответствующему соотношению между
представлениями.
В частности, вторая формула Вейля равносильна
следующему тождеству:
*mi
d\
d?' + l
^m, + (n-l)
d( а) =
*m2-l
d\
dT-
,m. + {n—2)
. aj
dmn-(n-D
“l
,mn-(n-2)
1
При этом символ d\ заменяется нулем, если k < 0.
Знак тензорного произведения над детерминантом озна¬
чает, что этот символический детерминант раскрывается
по обычному правилу*), но каждое слагаемое пони¬
мается как тензорное произведение соответствующих
сомножителей:
d (а) = 2
d ‘'
“i
Здесь Bi принимает значения 0, 1, 2, ..., п—1, е2 при¬
нимает значения —1, 0, ..., п — 2 и т. д.
Пример. п = 3, а = (7, 2, 0).
d(a)
л8
ai
Л9
«1
00 —
*4
b- —
43
rfi
di
=
i 9
d\ d\
0
0
1
■■ d\ ® d\ - d\ ® d\.
*) Заметим, что а ® b — Ь ® а для любых представлений а, Ь.

§ 76. ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
349
§ 76. Заключительные замечания '
В заключение остановимся несколько подробнее на
общей теории характеров конечномерных представле¬
ний. Мы видели в § 73, что примитивный характер
группы U (л) определяет неприводимое представление
однозначно с точностью до эквивалентности. Покажем
теперь, что это свойство не связано со спецификой
группы U(га), а является универсальным.
Теорема 3. Пусть G произвольная группа и
X (ё) —ее примитивный характер. Тогда существует
лишь одно (с точностью до эквивалентности) неприво¬
димое (конечномерное) представление группы G, имею¬
щее своим характером %(g).
Доказательство. Пусть А — свободная груп¬
повая алгебра группы G, т. е. совокупность всех конеч¬
ных сумм вида a = ’^iaigi с произвольными комплекс¬
ными коэффициентами а*. Всякое представление Те
группы G мы продолжаем до представления алгебры А
по формуле Та = 2 aiTgr Соответственно всякий ха¬
рактер 5c(g')=sP^'g продолжается до характера х(а) =
= sp Та.
Пусть Л о — ядро представления Та, т. е. совокуп¬
ность всех элементов аеД, для которых Та = 0. Тогда
фактор-алгебра В = А/А0 изоморфна алгебре всех опе¬
раторов Та- Мы считаем, что представление Tg дейст¬
вует в конечномерном пространстве V. Допустим, что
Tg неприводимо. Тогда алгебра В, согласно теореме
Бернсайда (см. § 21), изоморфна полной матричной
алгебре в пространстве V.
Далее, пусть %(g)—характер представления Tg. По¬
кажем, что условие принадлежности элемента аеД
ядру Л0 можно выразить в терминах характера %(а).
Действительно, равенство
yv(ax) = sp ТаТх = 0
тождественно по геД означает в силу теоремы Берн¬
сайда, что sp ТаС = 0 для всякой матрицы С в про¬
странстве Е. Но это равносильно равенству Та = 0, т. е.
аеД0.

350
ГЛ. XI. ХАРАКТЕРЫ
Допустим теперь, что два неприводимых (конечно¬
мерных) представления группы G имеют одинаковые
характеры. Тогда согласно сказанному выше оба они
имеют одинаковое ядро А0. Следовательно, оба эти
представления можно рассматривать как точные пред¬
ставления полной матричной алгебры В. Как мы видели
в § 21, все такие представления эквивалентны между
собой. Теорема доказана.
Таким образом, общее свойство характеров, выра¬
жаемое теоремой 3, является следствием теоремы Берн¬
сайда.
Из последнего замечания следует также, что вместо
свободной групповой алгебры А мы могли бы рассматри¬
вать и другие алгебры, связанные с группой G, напри¬
мер универсальную обертывающую алгебру U (см.
§ 22). Характер каждого конечномерного представле¬
ния алгебры U определяется по-прежнему формулой
X (л:) = sp Т'х, x^U. Из доказательства теоремы 3 ясно,
что заключение этой теоремы остается в силе также и
для алгебры U.
* *
*
Понятие характера (для конечных групп) впервые было вве¬
дено Фробениусом [40'] в 1896 г. Вычисление примитивных'ха¬
рактеров группы U(n) мы приводим в этой главе по оригинальным
работам Г. Вейля [10], [61]. В гл. XVII мы укажем еще один ме¬
тод вычисления характеров. Весовая диаграмма для SU(3) («шести¬
угольник») была описана впервые, вероятно, Вигнером в 1937 г.
См. также [52]. Метод, принятый в этой книге, был предложен ав¬
тором в [21]. Свойства весовой диаграммы для U(n) и других ком¬
пактных групп мы будем еще рассматривать в дальнейшем
(гл. XVII). По поводу дальнейших свойств производящей функции
см. монографию Вейля [10] (гл. VII).

ГЛАВА XII.
ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ
НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
ГРУППЫ U(n)
Среди различных задач спектрального анализа для представле¬
ний группы О одной из основных является следующая задача. Даны
два неприводимых представления т и а группы О. Требуется разло¬
жить представление т ® а на неприводимые. Эта формулировка яв¬
ляется корректной, во всяком случае, если т®сг вполне приводимо.
В данной главе последнее условие всегда будет выполнено, посколь¬
ку в качестве G будет рассматриваться компактная группа U(n).
Первым шагом в решении указанной задачи является обычно
составление «списка» неприводимых представлений, входящих в
т ® а, т. е. перечисление соответствующих кратностей вхождения
(кратность является натуральным числом либо нулем). Более
сложной является задача описания инвариантных подпространств, в
которых действуют неприводимые компоненты*). Мы приводим ре¬
шение этой задачи для U (га) только в простейшем случае п — 2,
однако и для общего случая намечаем путь решения.
Для группы U (га) более подробная формулировка задачи при¬
водится в начале § 77. Мы приводим в этой главе несколько мето¬
дов отыскания спектральных кратностей: метод характеров (§ 77),
метод Z-инвариантов (§§ 78, 79) и сочетание последнего метода с
методом детерминантов Вейля (§ 80). Из этих методов лишь метод
Z-инвариантов может быть использован также для отыскания не¬
приводимых подпространств (см. § 79).
§ 77. Метод характеров
Положим G = U (п) и фиксируем два неприводимых
представления этой группы с сигнатурами аир. Пусть
ту — кратность, с которой встречается d(у) в тензорном
*) Матрица перехода от тензорного базиса в т ® ст к базису,
составленному из базисов неприводимых компонент, носит название
матрицы Клебша — Гордана. Хорошо известна роль этой матрицы
в некоторых задачах теоретической физики. См. по этому поводу
добавление III (§ 1).

352 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЯ
произведении d(<x) d(P). Тогда имеем спектральную
формулу
d (а) ® d (Р) = 21 (v)
v
(ту — 0, если d(у) не содержится в данном представ¬
лении). Требуется вычислить неотрицательную цело¬
численную функцию mY = mY(a, р). Для решения этой
задачи естественно попытаться использовать метод ха¬
рактеров. Действительно, вычисляя характеры обеих
частей спектральной формулы, мы находим
Xa(S)x3(6)= 2 ту%у (б)-
Поскольку характер есть функция классов, достаточно
рассматривать только диагональные матрицы fieU(n).
В результате получаем систему числовых уравнений для
определения кратности ту.
Поскольку для характеров /а(6) нам известна яв¬
ная формула (гл. XI), естественно попытаться найти
решение этой системы в явном виде. Положим 6 = ехр h
и запишем произвольный вес Ц6) в виде ехр(Х h),
где X— n-мерный вектор и (X, К)—скалярное произве¬
дение векторов X, h. Положим
Xa(S)=2Xexp (X, h).
Здесь пх — весовая кратность, или весовая диаграмма
в терминах гл. XI. Умножим обе части нашей системы
уравнений на полином Д(6); тогда /р, Ху заменятся со¬
ответственно полиномами Хр, XY, определенными в
§ 73. Левая часть спектральной формулы принимает
вид
2 пх exP (^> h) 2 (det s) exp (s (p + d), h).
К S
Здесь p — сигнатура, отвечающая второму сомножи¬
телю d(P), вектор d имеет координаты (п—1, п — 2,...
..., 1, 0); соответственно полином Хр выражается че¬
рез вектор I = р + d, для которого 1\ > 12 > ... > 1п,
и s означает произвольную подстановку координат

§ 77. МЕТОД ХАРАКТЕРОВ
353
U, h, Поменяем местами суммирование по К
и s. Поскольку «х = nsX, мы можем при каждом фикси¬
рованном s заменить ехр(Х, h) на exp (sK,h). В резуль¬
тате получаем
2 (det s) 2 «а exp (s (X + р + d), h). (*)
5 К
С другой стороны, правая часть спектральной формулы
имеет вид
2 (det а) 2 ту ехр (а (у + d), h). (**)
о Y
Здесь а — произвольная подстановка и у— произволь¬
ный «-мерный вектор; однако функция ту отлична от
нуля только в том случае, когда вектор у является сиг¬
натурой, входящей в произведение d(a)<8>d(p). При
этом имеем
(^*) — j.
Сравним обе части полученной формулы. Заметим
вначале, что вектор р — у +d удовлетворяет условию
Р\ > Р2 > • • • > Рп и ни один из векторов ор не удовлет¬
воряет этому условию. Назовем вектор х доминантным,
если Х\ > х2 ^ хп. Таким образом, можем сказать,
что показатель в (**) является доминантным только
при о = е.
С другой стороны, найдем все доминантные показа¬
тели в (*). Вектор g = A + p + d не обязан быть до¬
минантным. Однако при некоторой подстановке s мы
можем получить доминантный вектор р:
s(X + $ + d) = р. (***)
Если р не содержится в (**), то соответствующая экс¬
понента в (*) содержится с суммарным коэффициен¬
том 0, и этот случай нас интересовать не будет. С дру¬
гой стороны, если р содержится в (**), то р удовлет¬
воряет условию «строгой» доминантности р\> Р2> ...
... > рп, откуда очевидно, что подстановка s в (**•*)
определяется единственным образом. (Действительно,
*) Заметим, что dets = ±1 в соответствии с четностью или не¬
четностью подстановки s.

354 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
если Si, s2— две такие подстановки, то SiS2lp — p, от¬
куда 5^"' = ^ и Si = s2.) Для этой единственной под¬
становки введем обозначение sy(X). Она определяется
тем условием, что ее применение к вектору Я + р + d
переводит этот вектор в доминантный вектор, рав¬
ный у + d.
Соберем теперь все слагаемые в (*), которые при¬
водят указанным выше способом к одному и тому же
значению р. Тогда окончательно получаем, что
ту = 2 пк det sY (Я).
Действительно, экспоненты ехр(Я,h) при различных Я
линейно независимы, и равенство (*) = (*-») означает
равенство коэффициентов при каждой экспоненте.
Окончательный результат формулируется следующим
образом:
Теорема 1. Пусть пх — весовая диаграмма пред¬
ставления й(а) и ту — спектральная кратность пред¬
ставления d(a)<2>d(р). Тогда имеет место формула
Шу = det Sy (Я),
где подстановка зу(Я) определяется тем условием, что
она переводит вектор Я + р + d в вектор у + d. Здесь
d = (п — 1, п — 2, ..., 1,0) и det s = ±1 в зависимости
от четности или нечетности подстановки s.
Таким образом, вычисление кратности пгу можно
описать в геометрических терминах следующим обра¬
зом: 1) рассматривается орбита Oy+d точки y + d отно¬
сительно группы подстановок; 2) рассматривается мно¬
жество Sa + р + d, получаемое из спектра Sa представ¬
ления d(a) путем параллельного переноса на вектор
Р + d\ 3) определяется пересечение Ру этих двух мно¬
жеств, при этом искомая кратность /пу получается из
кратности пх знакопеременным суммированием по ко¬
нечному множеству Ру.
Пример. Даны две сигнатуры: а = (7,2,0),
р = (9,4,1) группы U(3). Положим у = (14, 7, 2). Тре¬
буется найти кратность вхождения d(у) в d(a)®d(P).
В нашем случае d = (2, 1,0), р + d = (1 Г, 5, 1),
у + d = (16, 8, 2). Орбита 0Y+d состоит из шести точек,

§ 77. МЕТОД ХАРАКТЕРОВ
355
получаемых из (16,8,2) перестановками координат.
Вместо вычисления Sa -Г р -Г d мы рассмотрим множе¬
ство 0Y+d — р — d. Оно состоит из следующих шести то¬
чек: (5,3,1), (-3,11,1), (-3,-3, 15), (-9,3,15),
(—9,11,7), (5,—3,7). С другой стороны, спектр Sa
приведен в § 74 (рис. 3). Из данных шести точек лишь
точка (5,3, 1) содержится в 5а, причем с кратностью 2.
Следовательно, искомая кратность равняется двум.
Упражнение
Найти (достаточные) условия на сигнатуры а, Р, при которых
пересечение орбиты 0Y+d с множеством Sa + (3 + d содержит лишь
единственную точку А,+ Р + й = у + й. Заметим, что в этом слу¬
чае ту = п /,, где у = X + р.
Сформулируем полученный результат в несколько
иной форме. Определим при фиксированном р функ¬
цию следующим образом. Назовем вектор х =
= (хь х2, • • •, хп) вырожденным, если хотя бы две его
координаты совпадают. Назовем вектор х четным (не¬
четным), если он невырожден и преобразуется к доми¬
нантному виду с помощью четной (нечетной) подста¬
новки. Положим
О, если вектор I + (3 + d вырожден,
+ 1, если вектор Л + р + с? четный,
— 1, если вектор Л+p + d нечетный.
Заметим, что всякий вектор х при помощи некоторой
подстановки может быть сделан доминантным; при
этом, если он невырожден, то такая подстановка s0
определяется единственным образом. Следовательно,
наше определение корректно и ^ = dets0. Покажем, что
имеет место
Теорема 2. Спектральная формула тензорного
произведения для группы U (п) может быть записана
в виде
d(a)®d(p) = Sn^d(Y(X)).
К
Здесь у(^) = so(^ + Р + d) — d, а функция и подста¬
новка so определяются, как выше. При этом = О, ±1

356 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЯ
в зависимости от вырожденности или невырожденности
вектора X + |3 + d.
Доказательство. Соберем в сумме (*) все
слагаемые с одинаковым доминантным показателем
р = s(X + р -f d). Соответствующий суммарный коэф¬
фициент есть 2 %0Ар, где сумма берется лишь по тем
а
значениям X, для которых справедливо указанное ра¬
венство, и
0Ар = S det s,
где сумма берется по множеству Nxp всех подстановок,
удовлетворяющих тому же равенству с фиксирован¬
ными X, р. Очевидно, N>mP = s0-Nx, где s0— произволь¬
ный элемент из и N% — группа всех подстановок,
сохраняющих вектор X -f р -f d. Соответственно
0^ = det s0 ■ 0Ъ
где 9\ = 2 del а, и последняя сумма берется по груп¬
пе 1Vv Если вектор X + р + d невырожден, то Nx со¬
стоит из единичного элемента и 0^ = 1. Если вектор
X + р + d вырожден, то группа Nx содержит хотя бы
одну транспозицию s (перестановка одинаковых коор¬
динат) . В этом случае
0а= 2 det so = det s • 0Х =—0а.
оеЛГА
ибо dets = —1. Следовательно, в этом случае 0*. = 0.
Полагая р = у(Х) -f й, — |х, получаем нужную фор¬
мулу. Теорема доказана.
§ 78. Метод Z-инвариантов
Попробуем теперь применить к решению нашей за¬
дачи метод Z-инвариантов. Если каждое из представ¬
лений d{a), cf(P) записывать в Z-реализации, то их
тензорное произведение запишется в классе полиномов
от двух матриц х, у е Z:
Tef(x, у) = а{х, g)P(y, g)f(xg, yg).

§ 78. МЕТОД 2-ИНВАРИАНТОВ
357
При этом пространство представления 9?ац выделяется
из пространства всех полиномов с помощью двух инди¬
каторных систем: системы 1а по переменным х (при
каждом фиксированном у) и системы /р по перемен¬
ным у (при каждом фиксированном я).
Следуя общей схеме метода, мы сужаем представ¬
ление на подгруппу Z и решаем задачу нахождения ин¬
вариантов операторов Tz, z s Z. Иначе говоря, решаем
систему уравнений
/ (xz, yz) = / (х, у), z<=Z.
(Напомним, что а(х, z) = а(у, z) = 1, xz = xz, yz = yz.)
Полагая z = y~l, находим, что
f(x, y) = f{xy~\ e),
где e — единичная матрица. Полагая f(z, e) =cp(z), мы
запишем полученное решение в виде
f(x, (/) = ф (ху~1). (*)
Следовательно, всякий Z-инвариант выражается через
функцию от одной матричной переменной. Обратно,
всякая функция вида (*), принадлежащая SRap, яв¬
ляется Z-инвариантом.
Теорема 3. Пусть а = [ги г2,..., r„], p=[sb s2,
Пусть Li — инфинитезимальный оператор левого сдвига
на группе Z, отвечающий элементу eiii+u i— 1, 2, ...
...,п — 1 *), и Ri — инфинитезимальный оператор пра¬
вого сдвига на Z, отвечающий тому же элементу. Обо¬
значим фар пространство всех решений системы урав¬
нений
Lrl+XФ = 0, Я?+'Ф = 0, t=l, 2, ..., п-1.
Формула f(x, у) = у(ху~1) осуществляет взаимно одно¬
значное отображение между старшими векторами SRap
и решениями ф(г) этой системы, для которых выпол¬
няется добавочное весовое условие
ф(б_|гб) = р (б) ф(г), 6 s D.
*) Матрица й;, 1 + 1 имеет единственный отличный от нуля и рав¬
ный единице элемент на пересечении i-й строки с ((+1)-м столб¬
цом.

358 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИИ
При этом старший вектор f(x,y) имеет вес
Y(6) = a(6)|3(6M6).
Доказательство. Согласно сделанному выше
построению достаточно выписать условия принадлеж¬
ности вектора (*) пространству 9Jap и выделить затем
среди таких векторов весовые. Согласно определению
индикаторных систем пространство выделяется сле¬
дующей системой уравнений:
Xr/+'f(x, у) = 0, Ys{‘+'f(x, t/) = 0.
Здесь Хи Yi — инфинитезимальные операторы левого
сдвига, действующие только на г и только на у (соот¬
ветственно) и отвечающие матрице ef = ei £+1. В приме¬
нении к вектору (*) оператор Х{ равносилен L,-. (Дей¬
ствительно, инфинитезимальные левые сдвиги переста¬
новочны с умножением справа на у-1.) В то же время
оператор
Yif(y) = ~f(exp(~te+)y)\ta0
при подстановке и = у-1 переходит в оператор Rt. Дей¬
ствительно, полагая f(y) = g(u), замечаем, что
ехр(—ta) * _у = ехр (—ta)- и~1 = (и • ехр следователь¬
но, Y{f(у) = Rig(u). Таким образом, мы действительно
получаем систему уравнений, указанных в условиях тео¬
ремы. Вектор a> = f(x,y) является весовым, если Гбю =
= Y(б) со. Вспоминая правило действия диагональных
операторов Т6, находим, что
а (б) р (б) ф (б-'лтг'б) = у (б) Ф (ху-1).
Заменяя ху~х на z, видим, что это условие равносиль¬
но соотношению
ф(б-‘2б) = ц(б)ф(2),
где р.(6) = у(б)/а(б)Р(б). Таким образом, старший вес
у(6) вычисляется по формуле у(й) = а(6)Р(б)ц(6). Тео¬
рема доказана.
Замечание 1. Пусть Zt — t-я строка матрицы г;
тогда оператор Li может быть сокращенно записан в

§ 78. МЕТОД Z-ИНВАРИАНТОВ
359
виде
Li %i+1 gz, i I 1 > 2, ..., n 1,
где имеется в виду формальная свертка векторов
zi+1 = (2,4.1, h) и d/dzi = (d/dzik). Точно так же
Ri=zl^~, i= 1, 2, п 1,
где zi означает i-й столбец матрицы 2.
Замечание 2. Запишем весовое условие в терми¬
нах показателей или «инфинитезимальных весов». Поло¬
жим а = (аи а2, сг„), Р = (Pi, Рг, Рп) и введем
вектор е = (еь е2, еп) такой, что р(8) = ехр(—е, h)
при б = exp h. Тогда сигнатура у = (уь у2, ..., уп) вы¬
числяется по формуле
у = а + р — е.
Знак минус, выбранный в этой формуле, соответствует
тому соображению, что мультипликаторы <p(z) должны
понижать веса (в терминах лексикографической упоря¬
доченности). Сигнатура а + Р является самой старшей
в 9?аР.
Полученный критерий дает нам способ описания
всех старших векторов, откуда непосредственно могут
быть найдены также все сигнатуры, входящие в
d(a)®d(P). Желая получить такую информацию в бо¬
лее явном виде, введем следующее определение. Пусть
V{а)—пространство неприводимого представления d(a)
и V\(a)—подпространство всех весовых векторов со
старшим весом X. Мы имеем
пх = dim V\(a)
в соответствии с обозначением § 77 для весовой диа¬
граммы d(a). Определим теперь в Vx(a) подпростран¬
ство V\(a, Р) с помощью следующей системы уравне¬
ний:
<р = 0, P = [s,, s2 s„]. (**)
Здесь S)i — инфинитезимальный оператор представле¬
ния d(а), отвечающий элементу е,-, i+] (&i = Eit i+i

360 гл. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
в обозначениях гл. VI). Заметим, что это определение
не зависит от реализации d{а).
Теорема 4. Кратность ту, с которой неприводи¬
мое представление d(y) содержится в d(a)®d(P), мо¬
жет быть выражена формулой
my = dim У Да, р),
где пространство УДа, р)сг УДа)сг У(а) определяется
выше и вес К, входящий в d(а), связан с сигнатурой у
соотношением у = % + р.
Доказательство. В реализации на группе 7.
пространство У(а) выделяется индикаторной системой
1а\ следовательно, согласно теореме 3 пространство
Фар можно рассматривать как подпространство в У (а).
При этом Фар выделяется в У (а) второй подсистемой
уравнений из теоремы 3, где оператор Ru как оператор
правого сдвига, может быть заменен на 2)i*). Следо¬
вательно, Фар выделяется в У (а) системой (**). Если
вектор ф&Фар имеет вес р(6), то это означает, что
в представлении d(a) он имеет вес /,(6) = а (б) и (6).
В то же время соответствующий старший вектор
a = f{x,y) имеет вес у(б) = а(б) Р (б) р (6). Сравнивая
эти формулы, находим, что у(б)= Д6)Р(6). В терминах
инфинитезимальных весов мы имеем у = X + р. Теорема
доказана.
Следствие 1. mY’-<%, где у = X + р.
Следствие 2. пгу = %, если условие (**) вы¬
полняется тождественно на УД а).
Заметим, что в реализации на группе Z все полиномы
из У (а) имеют старшую степень п + 2гг + ••• + пгп =
= o&i + о&2 + . • • + ап- Если Sj ^ ai + a2 + ... + а„,
i = I, 2, ..., п—1, то условие (**) выполняется тожде¬
ственно на всем У(cs), и в этом случае наша формула
принимает наиболее простой вид:
ту = п\, у = X + р,
для всех весов X из представления d(a).
*) Напомним, что сужение d(a) на подгруппу Z сводится к
правым сдвигам.

§ 79. ЧАСТНЫЕ СЛУЧАИ
361
§ 79. Частные случаи
Покажем, что критерий предыдущего параграфа, не¬
смотря на некоторую сложность формулировки, действи¬
тельно дает эффективный способ решения задачи.
В этом параграфе мы рассмотрим лишь простейшие ча¬
стные случаи.
Пример 1. Группа SU(2). Ввиду того, что обо¬
значения, принятые нами для группы SU(2), несколько
отличаются от общих обозначений для U(«), нам бу¬
дет удобно повторить все построение с самого начала.
Пусть /1,12 = 0, '/г- 1,3/2» ... — два произвольных стар¬
ших веса для SU(2). Формула
определяет тензорное произведение d{l\) ® d(12) при ус¬
ловии, что f(x, у) — произвольный полином степени не
выше 2/i по х и не выше 212 по у. Здесь х, у — произ¬
вольные комплексные числа и а, р, у, й — параметры
матрицы geSU(2) (см. § 37). Уравнение для Z-инва¬
риантов имеет вид
f(x + z, y + z) = f(x, у).
Очевидно, общее решение такого уравнения есть произ¬
вольный полином от х — у. Действительно, вводя обо¬
значение cp(z) = f(z, 0), находим f(x,y)=y(x — у). Сре¬
ди таких векторов весовыми являются только степени
Из условия принадлежности к пространству представле¬
ния вытекает, что k0 = min (2/ь 212). Остается вычис¬
лить сигнатуру, отвечающую вектору соа. Если g — диа¬
гональная матрица, у которой у = Р = 0. б = а-1 = Я,
то из формулы представления вытекает, что вектор ощ
имеет вес Следовательно, искомый спектр
содержит только старшие веса I = l\ + l2 — k, k =»
= 0, 1, 2, ..., k0. Минимальным весом является 10 =
= |h — к\- Окончательно
Щ = (х~У)к, k = 0, 1, 2, ..., kQ.
U+h
d(/i)®d(/2)= 2 d{l).
\h-h I

362 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
Мы получили для группы SU (2) хорошо известную
формулу. При этом, поскольку каждый старший вектор
данного веса определяется однозначно (с точностью до
множителя), каждое неприводимое представление d(l)
содержится в спектре однократно.
Замечание 1. Следуя этому методу, мы не толь¬
ко находим спектральную формулу, но легко получаем
и всю остальную информацию о структуре базиса в про¬
странстве представления (см. [84]), в том числе и ко¬
эффициенты Клебша — Гордана.
Пример 2. Положим d(a) = d\ (векторное пред¬
ставление группы U(л)), и пусть d(P)—произвольное
неприводимое представление U(«). Представление d\
реализуется в классе линейных форм от вектора-строки
х = (хи х2, ..., хп).
Действие диагональной группы: хг —+ xfii, где б,- — t'-e
собственное значение диагональной матрицы ieU(fi).
Следовательно, каждая координатная форма х,- являет¬
ся весовым мультипликатором с весом б;. Соответствую¬
щий инфинитезимальный вес есть ei = (0, ..., 0, 1,
О, . .., 0) с единицей на i-м месте. Следовательно,
di ® d(p) может содержать только сигнатуры
V = P + eft, /е = 0, 1, 2, п.
Пространство V\(a) всегда одномерно, если X — ек- Од¬
нако подпространство V\(a, (3) может быть нульмерно.
Действительно, пусть р = [sb s2, ■.. , sn]. Напомним
(§ 68), что оператор имеет вид xt-^—. В частности,
и X j
оператор 1 есть xt -3 . Если Sh Ф 0, то one-
QXi+i
ратор 3)skk+l аннулирует все линейные формы Xi, х2, ...
..., хп. Однако если Sh = 0, то форма хй+[ не аннули¬
руется. Следовательно, 1Д(а, Р) = 0, если X — e^+i и
Sh = 0.
Полученный результат станет гораздо яснее, если
мы запишем сигнатуру р с помощью круглых скобок:
р=(ть т2, ..., тп). При этом sh = mh — mh+1. Равен¬
ство sh = 0 означает, что mh = mA+1. Прибавление к сиг¬
натуре р вектора es+i = (0, .,., 0, 1, 0, 0) с еди¬

§ 79. ЧАСТНЫЕ СЛУЧАИ
363
ницей на (k + 1)-м месте нарушает в этом случае свой¬
ство доминантности ((&+ 1)-я координата становится
больше k-и). Естественно, что такие слагаемые в спек¬
тральной сумме должны отсутствовать. Окончательно
получаем следующий результат:
rf, <8> d (m,, т2, ..тп) =
= d(ml + \, т2, ..., тп) + d (ти т2 + 1, ..тп) + ...
... + d (m,, т2 тп + 1),
причем в правой части необходимо вычеркнуть те сла¬
гаемые, для которых нарушается условие доминантно¬
сти (т|>ш2>,..>тл). Если в исходной сигнатуре
все разности mk — mh+\ были отличны от нуля, то ни
одно из слагаемых не вычеркивается.
Замечание 2. Полученный результат позволяет
легко получить формулу для кратностей в тензорном
произведении пт = d\ 0 d{ 0 ... 0d{ (т сомножителей),
которое изучалось в гл. VIII. Действительно, мы имеем
пт= 2 /г (ти т2, .... тп) d {ти т2, ..., тп),
т1+т2+ ... + тп=т
где k(m\, т2, ..., тп)—искомая кратность. Заметим,
что пт = d\ 0 л,п_1. Разлагая представление nm_i на не¬
приводимые, мы умножаем каждое из них на dь поль¬
зуясь полученным выше правилом. В результате на¬
ходим рекуррентную формулу:
k{mu ть тп) =
= k(ml — 1, т2, mn) + k(mu т., — 1, ..., тп)+ ...
... +k(ml, т2 тп — 1).
Действительно, представление d(mu т2, ..., тп) мо¬
жет содержаться в лт лишь за счет того обстоятель¬
ства, что в dm-1 встречались представления
d(m.\ — 1, т2, ..., тп), ..., d(mu т2, ..., тп— 1) с со¬
ответствующими кратностями.
Пример 3. Положим d(a) — dp (поливектор ран¬
га р, 1^.р*Сп), и пусть d(p)—произвольное неприво¬
димое представление группы U(л). Пространство пред¬

364 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИИ
ставления dp мы можем считать натянутым на миноры
Щ Хи2
X2ii X2i2
Xpi] Xpi2
•. Xii .
, /( <1 i-2 ^ ... ipj
где xi = (xIA), x2 = {x2h) Xp = (xph) — независимые
векторные аргументы. Каждый такой минор является
весовым вектором с весом 6^6^ ... 6,у Соответствую¬
щий инфинитезимальный вес естьАу2... / =е/+е*2+...
... +ei. В силу условия упорядоченности ii<i2<...
... < ip все такие веса различны. Отсюда получаем воз¬
можные значения спектра:
Уу2... < =Чг2 — lp + Р-
различны, соответ-
Поскольку все веса = г ...
ствующие подпространства КДа) одномерны. Выясним,
когда V\(a, (3) нульмерно. Операторы £DU входящие в
индикаторную систему, в данном случае имеют вид
3)i = xi
дх
i +1 >
где xi означает i-й столбец прямоугольной матрицы х,
составленной из строк хь х2, ..., хр. Минор ... * не
аннулируется оператором ^*+1 только в том случае,
когда sft = 0, индекс k + 1 содержится среди индексов
М, г'г, • • •. ip, а индекс k среди этих индексов не содер¬
жится.
Как и в предыдущем примере, перейдем к обозначе¬
нию с помощью круглых скобок: р = (mi, т2, ..., тп).
Равенство sk = 0 означает, что т.и = mft+1. Добавление
вектора Kiii2... * = + е(-2 + ... + eip в этом случае не¬
возможно (нарушает условие доминантности), если
среди индексов i'i, i2, ..., ip содержится индекс k + I

§ 79. ЧАСТНЫЕ СЛУЧАИ
365
и отсутствует индекс k. В результате
йр 0 d(mu т2, .. тп) =
= S й(ти . . nti + 1 mi +l,...,mn)
11<1г< <‘р р
причем в правой части следует вычеркнуть все слагае¬
мые, не имеющие смысла (т. е. такие, для которых
вектор в круглых скобках не удовлетворяет условию до¬
минантности) .
Замечание 3. Может показаться, что для получе¬
ния спектра d(a)®d{|3) достаточно умножить характер
Ха (6) на старший вес |3(6) ив полученной сумме вы¬
черкнуть все слагаемые, для которых нарушается усло¬
вие доминантности. Следующий пример покажет, что
в действительности это не так.
Пример 4. Пусть d(a) — dT (симметрическая сте¬
пень векторного представления dt), и пусть d(j3)—про¬
извольное неприводимое представление U(n). Простран¬
ство представления dT натянуто на базисные одночлены
/v,v2 ... v„ = xi‘x22 • • • xln’ V, + V2 + ... + v„ = m.
Каждому такому одночлену отвечает инфинитезималь¬
ный вес Л = v|&i + v2e2 + .. . + vnen- Поскольку все та¬
кие веса различны, то соответствующие подпространства
V\(a) одномерны. Операторы Фи входящие в индика¬
торную систему, имеют тот же вид, что и в примере 2.
Условие
msk+'f ф п
'V*
возможно только в том случае, когда sh < vs+i. В ре¬
зультате получаем следующую спектральную формулу:
d?®d($)= S d(m,+vu m, + v2 тп + v„).
vl±?2 + +v„ = m
Здесь положено p = (mi, m2, ..., m„), sh = mh — mh+1,
k = 1, 2, . . . , n.
Замечание 4. В последней формуле индексы vi,
v2 vn оказываются недопустимыми, если хотя бы

366 гл. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИИ
один из векторов аи = {т\, т2, mh + Vh, .... и«)
не является сигнатурой.
Пример 5. Найдем произведение двух поливекто¬
ров dp, dq, \ р -^Сп. Заметим, что эта задача яв¬
ляется частным случаем задачи, рассмотренной в при¬
мере 3. Правило умножения, сформулированное в этом
примере, перефразируем следующим образом. Пусть
— характер представления dv:
£р= 2 6г,б/ ... 6, .
Умножим эту функцию на старший вес представления
dq, равный 6i62. •. 6д. Показатели каждого из получен¬
ных одночленов удовлетворяют условию доминантности
только в том случае, когда первые р — k индексов сре¬
ди I], /2, ip принимают значения 1,2, ..., р — k
(k-*Cp-^.q), а остальные принимают значения q + 1,
q + 2, ..,, q + k. В результате получаем
dp ® dg — 2 dp—kdq+k ip ^ q)'
k>0
При этом следует отбросить те слагаемые, для которых
р — k<0 или q + k>n. Индуктивно применяя эту
формулу, получаем также следующее простое тожде-'
ство:
! dn dp-i
^ \dq+l dq
для произведения Юнга двух базисных представлений
dp, dq *).
§ 80. Детерминанты Вейля
Все примеры, рассмотренные в предыдущем парагра¬
фе, относятся к случаю однократного спектра. Перейдем
*) Отсюда естественно напрашивается обобщение этого тожде¬
ства на случай произведения Юнга произвольного числа базисных
представлений dt , di , dt . Соответственно мы получили бы яв¬
ное выражение характера Ха произвольного представления d(a) че¬
рез элементарные симметрические функции |р—характеры базис¬
ных представлений dp, р = 1, 2, ..., п.

§ 80. ДЕТЕРМИНАНТЫ ВЕЙЛЯ 367
к рассмотрению общего случая. Мы предложим про¬
стой символический метод, основанный на второй фор¬
муле Вейля.
Для каждого т = 0, 1, 2, ... мы введем «мульти¬
пликатор» Гт, определяемый формально следующим
образом:
/2. •••,/«)= 2 d(fi+Vh /2 + V2 fn + Vn),
0s^v*+i<s*
Vl+V2+ ••• +Vn~m
где положено sh — fh — fh+u k = 1, 2, ..., n — 1. Как
мы видели в § 79, получаемая формула дает разложе¬
ние тензорного произведения dj" ® d{fv /2, ,.fn~j.
Далее, пусть сигнатура а имеет вид (mi, т2,..., тп).
Поставим в соответствие этой сигнатуре следующий
мультипликатор *):
Гт,
Гт, + 1
• Гт,+(„_1)
Гн =
Гт2-1
Г т,
• Гтг+(п~2)
Гл!п-(л-1)
Г/яп-(л-2) •
•• ч
Здесь элементы Гт рассматриваются как‘взаимно пере¬
становочные операторы и детерминант раскрывается по
обычному способу. Роль мультипликаторов Га объяс¬
няется следующей теоремой:
Теорема 5. Для вычисления спектра представле¬
ния d{a)® d($) достаточно применить мультипликатор
Га к символу d(.р). При этом мы имеем
Га^(Р) = 2"г/ (Y),
где ту — спектральная кратность d(a)<8>d(|3). Иначе
говоря, выражение rad((3) совпадает с правой частью
спектральной формулы для d(a) <8> d([3).
Доказательство. Достаточно напомнить (см.
конец § 75), что для представления d(а) имеет место
•) При этом мы считаем, что Гр = 1, Гт = 0 при m < 0.

368 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
формула
где показатели k\, k2, ... , kn распределяются в соот¬
ветствии со второй формулой Вейля. Умножение
d(a)®d(р) сводится, таким образом, к последователь-
док сомножителей не имеет значения, поскольку тензор¬
ное умножение двух представлений коммутативно.
Теорема доказана.
Пример. Положим а= (3,2,0), р=(9, 8, 7). Муль¬
типликатор Га имеет вид
Теперь построение спектральной формулы сводится к
следующей цепочке вычислений:
d (а) = 2 ± d\-1 ® й\'2 ® ... ® й\п,
ному умножению на dk\ d22, ..., dknn. При этом поря-
Г3 г4 г5
Г'а = ^1 ^2 Г'з
0 0 1
1) Г2(9, 8, 7) = (11, 8, 7)+(10, 9, 7) + (10, 8, 8) + (9,9, 8).
Г3(11, 8, 7) = (14, 8, 7)+ (13, 9, 7)+ (13, 8, 8) +
I.
+ (12, 10, 7)+ (12, 9, 8)+ (11, 11, 7)+ (11, 10, 8);
Г3(10, 9, 7) = (13, 9, 7) + (12, 10, 7) + (12, 9, 8) +
+ (11, 10, 8)+ (11, 9, 9)+ (10, 10, 9);
Г3(10, 8, 8) = (13, 8, 8) + (12, 9, 8) + (11, 10, 8);
Г3( 9, 9, 8) = (12, 9, 8)+ (11, 9, 9).
2) Г, (9, 8, 7) = (10, 8, 7) + (9, 9, 7) + (9, 8, 8).
Г4(Ю, 8, 7) = (14, 8, 7)+ (13, 9, 7)+ (13, 8, 8) +
II.
+ (12, 9, 8) + (12, 10, 7) + (11, 10, 8);
Г4( 9, 9, 7) = (13, 9, 7) + (12, 9, 8) + (11, 9, 9);
Г4( 9,8, 8) = (13, 8, 8) + (12, 9, 8).
Здесь мы опускаем символ d и действуем мульти¬
пликаторами Гт непосредственно на сигнатуру а. Сум¬

§ 80. ДЕТЕРМИНАНТЫ ВЕЙЛЯ
369
мируя правые части I, мы вычеркиваем все слагаемые,
входящие в правые части II. В результате получаем
(3,2, 0)0(9, 8, 7) = (12, 10, 7)+ (12, 9, 8)+ (11, 11,7)+’
+ 2(11, 10,8) + (11, 9, 9) + (10, 10, 9).
Заметим, что правило, даваемое теоремой 5, можно
выразить также следующим образом. Положим
Г = У 6V>6V2 bvn
1 т —1 • 1 • п >
vi + v2+ +vn~m
где символ бk рассматривается как оператор умножения
на 6й, заменяемый нулем в том случае, когда он нару¬
шает условие доминантности. Условимся также, что Га
выражается через Гт указанной выше формулой. Тогда,
как нетрудно проверить, имеем
ГаР(б) = 2
Действительно, достаточно проверить эту формулу при
d(a) = dГ; для этого в свою очередь достаточно вос¬
пользоваться примером 4 из § 79. При этом мульти¬
пликаторы 6й согласно их определению некоммута¬
тивны, однако операторы Гт оказываются коммутатив¬
ными.
Если Ф— ассоциативная алгебра, порождаемая
мультипликаторами 6&, k = 1, 2, . . ., п, то Га можно
рассматривать как «упорядоченный характер» %а, опре¬
деленным образом вложенный в эту алгебру. В этом
виде удобно сравнить первоначальный метод характе¬
ров (§ 77) с полученным методом детерминантов Вейля.
Если в первом случае нам приходилось перемножать два
характера %а и хр> то теперь ввиду условия «упорядо¬
ченности» достаточно умножить характер %а на старший
вес Р(6).
В заключение напомним, что метод Z-инвариантов
позволил также найти все старшие векторы представ¬
ления d(a)®d(|i). Знание понижающих операторов
(§ 68) позволяет получить из этих векторов все осталь¬
ные базисные векторы в компонентах d(y). Поэтому

370 ГЛ. XII. ПРОИЗВЕДЕНИЕ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ
можно надеяться, что на этом пути удастся получить
общие формулы для коэффициентов Клебша — Гор-
дана.
* *
*
Метод характеров принадлежит Р. Брауэру и Г. Вейлю [10].
Формулировка результата с помощью функции !;/. (теорема 2) была
предложена А. У. Климыком [104]. Метод Z-инвариантов приме¬
нялся автором [84]; в этой же статье было предложено правило де¬
терминантов (теорема 5). Первый метод обладает тем преимуще¬
ством, что он легко переносится на произвольные компактные группы
Ли. Второй метод может быть перенесен на классические группы О (п),
Sp(«). При этом практически он, по-видимому, более удобен. См.
также [2], [33], где рассматриваются модификации метода харак¬
теров. См. [18], [34], [84] по поводу вычисления коэффициентов
Клебша — Гордана для SU(2).

ЧАСТЬ 111
ОБЩАЯ ТЕОРИЯ

В этом разделе, состоящем из шести глав, излагается
общая теория компактных групп Ли, которая осно¬
вана на детальном изучении их алгебр Ли (компактных
алгебр Ли). Мы изложим картановскую теорию клас¬
сификации всех компактных алгебр Ли и их комплекс¬
ных оболочек (редуктивных комплексных алгебр Ли).
Отсюда в свою очередь в гл. XV будет получена клас¬
сификация всех компактных групп Ли и классификация
их комплексных оболочек.
Читатель-физик может при желании опустить гл. XV,
где собраны наиболее специальные математические по¬
строения, касающиеся компактных групп Ли «в целом».
Однако следует иметь в виду, что результаты этой гла¬
вы используются в гл. XVI при глобальной классифи¬
кации всех неприводимых представлений.
Картановская теория устанавливает замечательное
соответствие между классами компактных групп Ли и
комплексных редуктивных групп Ли. Это соответствие,
осуществляемое путем аналитического продолжения, пе¬
реносится также на неприводимые представления в ко¬
нечномерных векторных пространствах. Кроме того, ана¬
литическое продолжение позволяет классифицировать
полу простые вещественные алгебры и группы Ли, а так¬
же их неприводимые конечномерные представления.
Отсюда в свою очередь может быть получена классифи¬
кация неприводимых конечномерных представлений про¬
извольной связной группы Ли (гл. XVI).
В гл. XVII мы приводим чисто алгебраическое по¬
строение теории неприводимых (не обязательно конеч¬
номерных) представлений полупростой комплексной
алгебры Ли. В гл. XVIII решаются некоторые задачи
спектрального анализа конечномерных представлений.

ГЛАВА X!!!
ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
От рассмотрения группы U(rc) мы переходим теперь к произ¬
вольным компактным группам Ли. Однако прежде чем сделать это,
займемся в данной главе еще более общим вопросом. Постараемся
уяснить местоположение компактных групп среди произвольных
групп Ли. С этой целью мы займемся вначале инфинитезимальной
характеристикой, т. е. рассмотрением произвольных алгебр Ли.
Ключом к первоначальной классификации является рассмотре¬
ние присоединенного представления, с которым мы уже встречались
в гл. IX. Напомним, что алгебра Ли есть касательное пространство
к группе G в единичной точке е. Внутренний автоморфизм g0ggoi
переводит всякую однопараметрическую подгруппу g = g(t) в но¬
вую однопараметрическую подгруппу g = g(t). Соответствующее
преобразование касательных векторов есть линейное представление
группы G, действующее в алгебре Ли этой группы. Такое представ¬
ление называется присоединенным.
При рассмотрении алгебр Ли достаточно рассматривать диффе¬
ренциал такого представления, т. е. представление алгебры Ли, дей¬
ствующее в самой алгебре Ли (§ 81). Первоначальная классифика¬
ция алгебр Ли основана на простейших свойствах такого представ¬
ления.
§ 81. Присоединенное представление алгебры Ли
Пусть X — алгебра Ли. Линейный оператор D в про¬
странстве X называется дифференцированием, если
D[x, y] = [Dx, у] + [х, Dy].
Если D1, D2— дифференцирования, то всякая их линей¬
ная комбинация и коммутатор D=[DUD2] также явля¬
ются дифференцированиями. Следовательно, множество
Ф всех дифференцирований в алгебре X также образует
алгебру Ли.

374
ГЛ. XIII. ОСНОВНЫЕ типы алгебр и групп ли
Каждому элементу ае X отнесем линейный опера¬
тор а в пространстве X следующим образом:
ах = [а, х].
Как следует из тождества Якоби, оператор Da = а есть
дифференцирование. При этом
[Da, Db\ = D(a> Ь].
Операторы Da называются внутренними дифференциро¬
ваниями*). Как показывает последнее тождество, ото¬
бражение a-*Da является представлением алгебры X.
Пример. Как мы знаем, в алгебре Ли su(2) суще¬
ствует базис аь а2, Аз, относительно которого выпол¬
няются следующие соотношения коммутации: [а,, a2] =
= а3, [а2, аз] = аь [а3, ai] = а2, причем все остальные
коммутаторы либо равны нулю, либо получаются из
указанных изменением знака. Если рассматривать опе¬
раторы й\, a2, а3 в базисе аь а2, а3, то мы получаем
0
0
0
0
0
1
0
-1
0
d] =
0
0
-1
, й2 —
0
0
0
, а.з =
1
0
0
0
1
0
-1
0
0
0
0
0
Нетрудно проверить непосредственно, что эти операторы
образуют базис трехмерного представления алгебры
su(2). Если рассматривать su(2) как алгебру Ли SU(2),
то данное представление может быть продолжено до
трехмерного представления группы SU(2). Очевидно,
это представление задается ортогональными матрицами.
В результате получаем известный нам локальный изо¬
морфизм SU(2)-» SO(3).
Если X — алгебра Ли связной группы G, то пред¬
ставление Da всегда может быть продолжено до пред¬
ставления группы G, действующего в X как в линейном
пространстве. Это представление мы обозначаем Jt(g)
и называем присоединенным представлением группы G.
Исходя из общей теории групп Ли, легко проверить, что
я (go) совпадает с преобразованием касательных векто¬
*) Обычно в литературе для операторов St «= Dx используется
символ ad х (adjoint).

§ 82. ИДЕАЛ И НОРМАЛЬНЫЙ ДЕЛИТЕЛЬ
375
ров х^.Х относительно внутренних автоморфизмов
goggo”1 • Следовательно, всякое внутреннее дифференци¬
рование есть главная линейная часть внутреннего авто¬
морфизма в группе G.
§ 82. Идеал и нормальный делитель
Теперь мы можем ввести одно из самых основных
понятий в теории алгебр Ли (имеющее также аналог и
в теории ассоциативных алгебр *))— понятие идеала.
Идеалом в X называется всякое линейное подпро¬
странство, инвариантное относительно присоединенного
представления в X.
Иначе говоря, линейное подпространство У с= X яв¬
ляется идеалом, если для всякого аеХ и всякого
у е У мы имеем [а, у\ е У. Поскольку это условие вы¬
полняется, в частности, при аеУ, то всякий идеал яв¬
ляется подалгеброй в алгебре X. Поэтому можно опре¬
делить идеал как инвариантную подалгебру.
Аналогом этого понятия в теории групп (не обяза¬
тельно групп Ли) является понятие нормального дели¬
теля. Подгруппа Н с= G называется нормальным делите¬
лем, если она инвариантна относительно внутренних
автоморфизмов. Иначе говоря, если h е Н и geG, то
ghg-1 е= Я.
Если G — группа Ли и Я — ее нормальный делитель,
то алгебра Ли подгруппы Я является, очевидно, идеалом
в алгебре Ли группы G. Обратное также верно: всякому
идеалу в алгебре Ли отвечает аналитическая подгруппа
в группе G, которая является нормальным делителем в
G. Однако такое соответствие взаимно однозначно лишь
для связных подгрупп в группе G. В общем случае число
нормальных делителей в группе G «превышает» число
идеалов в алгебре X, поскольку связные нормальные
делители могут быть иногда расширены до несвязных.
В частности, группа G может содержать дискретные нор¬
мальные делители, для которых алгебра Ли состоит из
единственного элемента 0.
*) См. стр. 102,

376
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
1 0
-
У ^ II
о
1
0 1
О
I
Пример 1. Пусть X — трехмерная алгебра Ли, со¬
стоящая из матриц
О ас
0 0 b
ООО
где а, Ь, с — действительные (или комплексные) числа.
Показать, что подалгебра У, выделяемая условием а — 0,
является идеалом в алгебре X.
Пример 2. Показать, что алгебра A' = su(2) не со¬
держит ни одного идеала, кроме (0) и всей алгебры X.
Однако группа SU(2) содержит дискретный нормальный
делитель, состоящий из матриц
е =
Если У — идеал, то линейное фактор-пространство
Х/Y наделяется структурой алгебры Ли. Действительно,
если k(x)—класс эквивалентности (mod У), то мы по¬
лагаем по определению
[/?(*,), k(x2)\ = k([xu х2]).
Если У — идеал, то легко проверить, что это определе¬
ние корректно, т. е. коммутатор [zь z2] содержится в
единственном классе, если г, пробегает k(x\) и z2 про¬
бегает k(x2).
Точно так же, если Н — нормальный делитель в груп¬
пе G (не обязательно группе Ли), то фактор-простран¬
ство G/Н наделяется структурой группы. В этих случаях
Х/Y и G/Н называются соответственно фактор-алгеброй
и фактор-группой.
Предлагается в качестве упражнения найти фактор-
алгебру и фактор-группу в примерах 1 и 2.
Одним из наиболее важных частных случаев идеала
является центр алгебры X. Центром Z называется мно¬
жество всех элементов ге1, каждый из которых пере¬
становочен со всеми элементами из X.
Точно так же множество С называется центром груп¬
пы G, если оно состоит из всех элементов сей, каждый
из которых перестановочен со всеми элементами из G.

§ 83. ОСНОВНЫЕ ТИПЫ АЛГЕБР ЛИ
377
Если G — группа Ли и С — ее центр, то алгебра Ли
подгруппы С совпадает с центром Z с= А (где А—ал¬
гебра Ли группы G). Однако по алгебре Z непосред¬
ственно восстанавливается лишь связная компонента
единицы Сеа С, в то время как весь центр может быть
значительно шире. В частности, может случиться, что
Z — (0), в то время как С — дискретная подгруппа в
группе G.
Пример 3. Группа G = SL(n, С). Элементами
центра могут быть только матрицы Хе, кратные единице.
Условие det Хе — 1 означает, что Хп = 1, т. е. X является
произвольным корнем п-й степени из 1. Следовательно,
центром является циклическая группа порядка п.
С точки зрения присоединенного представления ал¬
гебра Z есть максимальное подпространство в X, на ко¬
тором все операторы в, не X, обращаются в нуль. Сле¬
довательно, Z является идеалом в X.
Предлагается в качестве упражнения найти центр в
алгебре 2(3), т. е. в алгебре X из примера 1.
§ 83. Основные типы алгебр Ли
Рассмотрение присоединенного представления есте¬
ственно приводит к основной классификации групп и
алгебр Ли. Мы начнем с рассмотрения алгебр Ли.
Определение 1. Алгебра X называется редуктив-
ной, если ее присоединенное представление вполне при¬
водимо.
Если алгебра X редуктивна, то X — Аг+А2 + ... + Хт
(прямая сумма), где Xh — неприводимые подпростран¬
ства относительно присоединенного представления. Усло¬
вие инвариантности Xh может быть выражено следую¬
щим образом:
[A, Xk] cz Xk,
где символ [А, В] означает линейную оболочку всех ком¬
мутаторов вида [а, Ь], а, Ь^А. Но это означает, что
As — идеал. Следовательно, все подпространства Xh яв¬
ляются идеалами в алгебре А.
Условие редуктивности значительно упрощает изу¬
чение алгебры А. Действительно, заметим, что [Aft, А;]

378 гл- XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
содержится одновременно в Xh и в Xt. Следовательно,
[Хк, А;] = 0 при k ф I
и в то же время [Хк, Xh] cz Xh. Отсюда заключаем, что
закон коммутации в алгебре X вполне определяется
структурными законами в подалгебрах Хк, k = 1, 2, ...
..., п. Иначе говоря, прямое разложение
А = А,+А2 + ... +Хт
является в то же время разложением алгебры X в пря¬
мую сумму (минимальных) идеалов.
Каждый идеал Xh обладает тем свойством, что его
присоединенное представление неприводимо. Следова¬
тельно, изучение алгебры X сводится к рассмотрению та¬
ких идеалов.
В дальнейшем мы увидим, что целесообразно спе¬
циально выделить тот случай, когда подалгебра Xh ком¬
мутативна. Поскольку Хк — идеал, то мы имеем также
[X,Xh] = [Xh,Xh] = (0). Но это означает, что Xk содер¬
жится в центре алгебры X. (Следовательно, в редуктив-
ной алгебре всякий коммутативный идеал является цен¬
тральным.) Из минимальности Xh получаем в этом слу¬
чае, что dim = 1. Желая исключить подобные слагае¬
мые, приходим к следующему определению:
Определение 2. Алгебра X называется полупро-
стой, если она редуктивна и центр ее равен (0).
Если алгебра X полупроста, то она не содержит ни
одного коммутативного идеала (кроме (0)). В частности,
алгебра X не содержит ни одного одномерного идеала.
Обратно, если выполняется хотя бы одно из этих условий,
то алгебра X не содержит центральных элементов (кро¬
ме 0); следовательно, алгебра X полупроста *). Если
алгебра X полупроста, то все ее неприводимые идеалы
удовлетворяют условию dimXft> 1.
Определение 3. Алгебра X называется простой,
если ее присоединенное представление неприводимо и,
кроме того, dim А >1.
*) Здесь все время предполагается, что алгебра X редуктивна.

§ 83. ОСНОВНЫЕ ТИПЫ АЛГЕБР ЛИ
379
Таким образом, коммутативные (абелевы) алгебры
Ли выделяются в особый класс. Отметим очевидные
связи между выделенными классами алгебр Ли:
1° Всякая редуктивная алгебра Ли есть прямая сум¬
ма своего центра и полупростой подалгебры.
2° Всякая полупростая алгебра Ли есть прямая
сумма простых идеалов.
Пример 1. Алгебра gl (п, С) является редуктивной
с одномерным центром.
Пример 2. Алгебра sl(n, С) является простой, если
п > 1.
Пример 3. Алгебра sl(ni,C) +sl(«2, С) является
полупростой, если пх ф 1, п2 ф 1.
До сих пор мы рассматривали только редуктивные
алгебры. В общем случае мы можем привести присоеди¬
ненное представление только к квазитреугольному виду.
Это означает, что алгебра X по-прежнему разлагается в
прямую сумму подпространств Xh, k = 1, 2, ..., m, но
мы имеем
[A, *, + А2+ ... +Afe.
Все операторы Da, а^Х, задаются в этом разложении
квазитреугольными матрицами с диагональными бло¬
ками пк X пк, где nh = dim Xh:
Da —
D<0
Df
0
D?>
Эти диагональные блоки D(ak\ k = 1, 2, .
ваем компонентами присоединенного
Разложение
А = А] + А2+ ... + Хт
называется максимальным, если все диагональные блоки
D(k) являются неприводимыми представлениями ал¬
гебры X. Очевидно, максимальное разложение всегда
возможно. Компоненты мы называем в этом случае
., т, мы назы-
представления.

380 гл. ХШ. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
неприводимыми компонентами присоединенного пред¬
ставления.
Заметим, что пространства Yk = Х\ + Х% +...+Х^
являются идеалами. Максимальность разложения ал¬
гебры X означает, что фактор-пространство Kft/Kft_i не¬
приводимо при каждом k = 1, 2, ..., m, где положено
Ко = (0), Ym = X. Подпространства Xh, вообще говоря,
не являются идеалами. Если это так для всех k = 1,
2, ..., m, то алгебра X является редуктивной. С другой
стороны, представляет интерес выделение следующего
частного случая:
Определение 4. Алгебра X называется разреши¬
мой, если все неприводимые компоненты DT, k=\,
2, ..., m, коммутативны*).
Если алгебра X рассматривается над комплексным
полем, то в силу леммы Шура все неприводимые ком¬
поненты в этом случае одномерны, т. е. A\mXh = К
(В вещественном случае dimXft-<2.) Следовательно, в
комплексном случае все операторы Da одновременно
приводятся к треугольной форме.
Среди разрешимых алгебр Ли специально выделяется
еще один подкласс.
Определение 5. Алгебра X называется нильпа-
тентной, если 0^ = 0, k — 1, 2, ..., m.
В этом случае все операторы Da одновременно при¬
водятся к треугольному виду с нулями на главной диа¬
гонали.
В последующих параграфах мы рассмотрим несколь¬
ко подробнее соотношения коммутации во всех указан¬
ных типах алгебр Ли и сформулируем для этих типов
иные определения, эквивалентные вышеизложенным.
Упражнения
1. Положим q — x, г = 1, где q рассматривается как
оператор умножения на независимую переменную х в некотором
классе функций f(x). Показать, что р, q, г и их линейные комбина¬
*) То есть операторы D(£\ а е X, перестановочны при каждом
фиксированном k.

§ 84. РАЗРЕШИМЫЕ АЛГЕБРЫ ЛИ
381
ции образуют нильпотентную алгебру Ли. Выписать операторы Dp,
Dg, Dr в базисе р, q, г.
2. Сделать то же самое по отношению к операторам р — д/дх,
qm = хт, т — 1,2 п, г = 1, с некоторым фиксированным п ^ 1.
3. Положим р = h ~ еХ- Показать, что операторы р, ft и
их линейные комбинации образуют разрешимую алгебру Ли.
4. Положим 0 = —^—, <7 = 1 — х -гг—, г = 2х — х2-^—. Пока-
идх дх дх
зать, что операторы р, q, г и их линейные комбинации образуют
простую алгебру Ли. Выписать операторы Dv, Dq, DT в базисе
Р. Q, г.
д2
5. Показать, что операторы ^ = Р — х< г= \ и их линей¬
ные комбинации не образуют алгебры Ли. Каким оператором необ¬
ходимо дополнить эту систему для получения алгебры Ли?
§ 84. Разрешимые алгебры Ли
Пусть X — алгебра Ли. Введем обозначение X' для
множества [X, X], составленного из коммутаторов [а, b],
a, b ^ X, и их всевозможных линейных комбинаций. Не¬
трудно видеть, что X' является подалгеброй и даже идеа¬
лом в алгебре X. Алгебра X' называется производной
подалгеброй алгебры X. По индукции вводятся также
определения:
X" = (ху, х'" = (Х"у, х<*> = (х<-к~»у.
В этом параграфе мы примем за основу следующие два
определения:
Определение 4'. Алгебра X называется разреши¬
мой, если цепочка ее последовательных производных об¬
рывается после конечного числа шагов, т. е. если
А(р) = (0) при некотором р.
Определение 4". Алгебра X называется разре¬
шимой, если в ней существует .цепочка вложенных под¬
алгебр
(0) = А0 с= Л, с= А2 с= ... с= Лт_, с= Ат = X
таких, что Aft_i является идеалом в Ah и фактор-алгебра
Ah/Ah-i коммутативна.
Докажем, что эти определения эквивалентны. Дей¬
ствительно, как следует из определения производной

382
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
подалгебры X', фактор-алгебра Х/Х' коммутативна. Сле¬
довательно, цепочка
(0) = Х{р) cz Х(р~>] cz ... cz X' cz Xl0) = X
удовлетворяет условиям определения 4", если А'’(р'=(0).
С другой стороны, если выполняются условия опреде¬
ления 4", то X' cz Ат-1, X" a A'm-i а Ат-2 и т. д., от¬
куда Х<р) = (0) при некотором р.
Заметим также, что в силу условия коммутативности
цепочку подалгебр Ak в определении 4" можно при же¬
лании считать максимальной, т. е. такой, что
dim Ak/Ak-i = 1. Предлагается самостоятельно доказать
следующие утверждения:
1. Всякая подалгебра разрешимой алгебры Ли раз¬
решима.
2. Всякая фактор-алгебра разрешимой алгебры Ли
разрешима.
3. Если идеал Y и фактор-алгебра Х/Y разрешимы, то
алгебра X также разрешима.
Принимая указанные в этом параграфе определения
разрешимости, мы докажем теперь следующую фунда¬
ментальную теорему, принадлежащую Софусу Ли.
Теорема Ли. Пусть X — разрешимая алгебра Ли.
Тогда всякое неприводимое представление алгебры X
коммутативно.
Доказательство. Условимся вначале рассматри¬
вать представления только в комплексных простран¬
ствах. Если dim A1 = 1, то алгебра X коммутативна, и
утверждение теоремы вытекает из леммы Шура, причем
в данном случае пространство представления одномер¬
но. В общем случае согласно определению разреши¬
мости мы имеем
* = *о + {е},
где А'о — разрешимый идеал в алгебре X и {е} — одно¬
мерное направление, натянутое на элемент е Ф 0. Пусть
р(х)—неприводимое представление алгебры X в про¬
странстве V и Vo — подпространство, неприводимое отно¬
сительно подалгебры Х0. Поскольку dim А'о < dim X, то
можем считать по допущению индукции, что для ал¬

§ 84. РАЗРЕШИМЫЕ АЛГЕБРЫ ЛИ
383
гебры Х0 теорема уже доказана; но тогда dim Vq = 1, и
мы имеем
р(х) 1о = К(х) g0
для всякого jg Jo и всякого g0 е Vo. (Здесь к(х) —ли¬
нейная форма над алгеброй Х0.) Далее, рассмотрим
оператор р(е) и положим gi — p(e)g0, Ъ = p(e)gi... Пусть
Ve — линейная оболочка этих векторов; тогда подпро¬
странство Ve инвариантно относительно р(е). Покажем,
что Ve инвариантно также относительно р(х), геД
Действительно, имеем
Р (х) U = Р (х) р (е) U-1 = Р (е) р (х) gfe_, + р (z) g4_,, (*)
где положено г = [i,e]e4 Если k = 1, то р(х) и р(г)
в правой части (*) мы можем заменить числовыми мно¬
жителями к (.г), k(z). В общем случае индукцией по k
получаем следующее равенство:
Р (*) I* = М*) I* + ■ • • >
где многоточие означает линейную комбинацию векторов
go, £1, •••, Ik-1- Инвариантность V£ доказана. Но тогда
мы имеем Ve = V ввиду неприводимости V. Если k0 —
максимальный из номеров, для которых векторы g0, gi,
g2, ..., Ik линейно независимы, то векторы go, gb g2, ...
..., gs0 образуют базис в пространстве V. Относительно
этого базиса матрица р(х), является треугольной
с одинаковыми диагональными элементами к(х). Сле¬
довательно,
sp р (х) = тк (х),
где т = dim V( = k0 + 1). Если у = [хи х2], то sp р(у) = О
(след коммутатора равен нулю). Следовательно, в этом
случае к (у) = 0. В частности, если х <= Х0 и z = [х, е], то
к (г) = 0. Возвращаясь к формуле (*), мы можем уточ¬
нить получаемый результат:
Р(*)£* = М*)£ь k = 0, 1, 2 k0.
Но это означает, что оператор р(я), х^Х0, является
скалярным оператором на V. Если ц — собственный

384
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
вектор оператора р(е), то направление г| инвариантно
относительно всей алгебры X. Следовательно, V = (т)},
и V одномерно.
Итак, для комплексного случая теорема доказана.
В вещественном случае полагаем V = V + iV и продол¬
жаем р(х) на V по правилу р(х) (| + гт)) = р (х) | + (р (х)т).
Согласно доказанному выше всякое неприводимое под¬
пространство в V одномерно. Если вектор £0 + гпо опре¬
деляет такое одномерное направление, то линейная обо¬
лочка векторов £о, Ло в пространстве V инвариантна
относительно р(х). Следовательно, diml/^2, и пред¬
ставление в пространстве V коммутативно*). Теорема
доказана.
Как уже отмечалось при доказательстве теоремы,
привлечение леммы Шура позволяет получить дополни¬
тельные ограничения: dim V = 1 в комплексном случае,
dim V -С 2 в вещественном случае. Если ограничиться
комплексными пространствами, то теорема Ли допус¬
кает одну из следующих трех эквивалентных формули¬
ровок:
1° Всякое неприводимое представление алгебры X од¬
номерно.
2° В пространстве любого представления алгебры X
существует хотя бы один вектор, собственный относи¬
тельно всей алгебры X.
3° Всякое представление алгебры X приводится в не¬
котором базисе к треугольной форме.
Подчеркнем, что речь идет о конечномерных пред¬
ставлениях. Для доказательства эквивалентности заме¬
тим, что среди логических следствий 1°г=> 2°=^> 3°г=> 1°
требует проверки только 2°г=> 3°. Но выполнение 2° озна¬
чает приводимость р(х) к блочному виду:
[I X (х) *
р(х) = 1 0 р'(*)
*) Действительно, если g0, »1о коллинеарны, то dim V — 1, и
наше утверждение доказано. Если же go, Но линейно независимы,
то мы имеем р (х) (g0 + /%) = X (к) (g0 + trio), откуда р (х) (g0 - Що) =
“ Р М (go + Шо) = я (х) (go - Що)> И представление р(*) в базисе g0,
т]о коммутативно.

§ 85. НИЛЬПОТЁНТНЫЁ АЛГЕБРЫ ЛИ
385
где Афх)—собственное значение и р'(х)—представле¬
ние алгебры X в пространстве меньшей размерности.
Применяя индукцию по размерности, получаем 3°.
Для произвольного поля (вещественного или комп¬
лексного) получаем из теоремы Ли
Следствие 1. Если p(x) —неприводимое представ¬
ление разрешимой алгебры X, то р(х) тривиально на
производной подалгебре X': р(г) =0 при геГ,
С другой стороны, применяя теорему Ли к присоеди¬
ненному представлению алгебры X, получаем дополни¬
тельную информацию о структуре этого представления:
Следствие 2. Алгебра X разрешима тогда и толь¬
ко тогда, когда существует цепочка вложенных идеалов
(0) = У0 с: а У, с: ... с= Ут_, czYm = X,
где Yh — идеал во всей алгебре X и фактор-алгебра
Yh/Yk-i коммутативна для всех k = 1, 2, ..., m.
Действительно, если X — комплексная алгебра, то
указанная цепочка возникает при приведении Da к тре¬
угольному виду, причем dim У*/Уй_1 = 1. В веществен¬
ном случае доказательство предоставляется читателю.
Наличие цепочки идеалов, указанной в следствии 2,
равносильно определению 4, данному в § 83*). Таким
образом, условия этого определения являются формаль¬
но более сильными, чем условия определения 4". Однако
мы видим, что в действительности эти условия эквива¬
лентны.
В результате получаем, что определения 4, 4', 4”
взаимно эквивалентны. В комплексном случае опреде¬
ление разрешимости может быть также сформулировано
следующим образом. Алгебра X называется разрешимой,
если в ней существует максимальная цепочка вложен¬
ных идеалов с возрастанием размерностей на единицу.
§ 85. Нильпотентные алгебры Ли
В этом параграфе мы намерены исследовать различ¬
ные определения нильпотентной алгебры Ли. Предвари¬
тельно докажем следующую классическую теорему.
*) Yh = + Х2 + ... + Xh в обозначениях § 83.

386
ГЛ. xili. ОСНОВНЫЕ ТИПЫ АЛГЁБР И ГРУПП ЛИ
Теорема Энгеля. Пусть X— линейная алгебра
Ли*), для каждого элемента которой выполняется усло¬
вие нульстепенности (хт = 0). Тогда все матрицы гё!
приводятся в некотором базисе к треугольной форме с
нулями на главной диагонали.
Доказательство. Если dim A' = I, то теорема
Энгеля верна. Мы будем вести доказательство индукцией
по dim А’, т. е. по числу линейно независимых элементов
в алгебре X. Допустим, что теорема Энгеля уже дока¬
зана для всякой линейной алгебры Y такой, что dim Y <
< dim X, и покажем, что в этом случае имеет место
Лемма. Всякая собственная подалгебра Y cr X мо¬
жет быть расширена до подалгебры Z cr X такой, что
Y — идеал в Z и dim Z/Y = 1.
Доказательство леммы. Заметим вначале,
что для линейной алгебры X оператор Da может быть
записан в виде Dax = ах — ха, ге! Рассуждая индук¬
тивно, получаем отсюда следующую формулу**):
Dpax = 2 (— 1)‘ С1раП~‘ха1,
i = 0
где Ср — биномиальные коэффициенты. Если ат = 0 и
р > 2т, то либо i > т, либо р — / > т, откуда D°a — 0.
Следовательно, алгебра S5 операторов Da также удовле¬
творяет условиям теоремы Энгеля.
Пусть у еУ, тогда DyY cr Y, откуда следует, что
при всяком разложении X = У + S (S — дополнительное
подпространство) оператор Dv может быть записан в
блочном виде:
где Ау — преобразование в У и Ву — преобразование в
S. Из нульстепенности Dy следует также нульстепен-
ность Ау и Ву.
*) Т. е. алгебра Ли, составленная из матриц n X п при неко¬
тором п.
**) Можно рассуждать и так: Da = L — R, где L — оператор
левого умножения на а и R — оператор правого умножения на а.
Поскольку эти операторы перестановочны, то Dpn= (— l)lClpLp~‘Rl.
А
у
О Вп

§ 85. НИЛЬПОТЕНТНЫЕ АЛГЕБРЫ ЛИ
387
Заметим теперь, что размерность алгебры {Ву} не
превосходит размерности алгебры У*). Используя до¬
пущение индукции, мы можем считать, что теорема Эн¬
геля верна для алгебры {В'у}. В частности, существует
вектор So <= S такой, что Bys0 = 0. Иначе говоря,
[г/, s0]^ Y для всех у е Y. Положим Z — Y + [s0}. Тогда
имеем
[Y,Z\<=Y, [Z,Z\czZ.
Следовательно, Z — подалгебра в X и У — идеал в под¬
алгебре Z. Лемма доказана.
Если а\—произвольный элемент подалгебры X, то
пространство {а^ = А\ является одномерной подалгеб¬
рой в X. Расширяя эту подалгебру до двумерной под¬
алгебры А2, затем расширяя А2 до трехмерной подал¬
гебры А о и т. д., получаем в X цепочку вложенных под¬
алгебр
(0)= Л0 с: Л; с: Л, сг ... сг Атс:Ат = Х
таких, что Л;,_j является идеалом в Ah. Следовательно,
алгебра X разрешима. Применяя теорему Ли, заклю¬
чаем, что все операторы х е X одновременно приводятся
к треугольному виду. Нульстепенность х означает, что
все его собственные значения равны нулю. Теорема до¬
казана.
В нижеследующих утверждениях мы предполагаем,
что алгебра X удовлетворяет условиям теоремы Энгеля.
Тогда из этой теоремы получаем
Следствие 1. Алгебра X содержит нетривиальный
центр.
Действительно, пусть 2 — такой элемент из X, кото¬
рый является собственным вектором с собственным зна¬
чением 0 относительно всех операторов Da, ае X. Тогда
[г, а]= 0, ael, и г содержится в центре алгебры X.
Следствие 2. Существует натуральное число р,
для которого х\х2---хр = 0, где хи х2, ..., хр — произ¬
вольные элементы из X.
Этот результат непосредственно следует из треуголь¬
ной структуры операторов хи х2, xv (с нулями на
*) Напомним, что размерность понимается как число линейно
независимых элементов.

388
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
диагонали). Указанное равенство, во всяком случае,
верно, если р — размерность линейного пространства,
в котором действует X.
Исходя из полученных результатов, мы естественно
приходим к следующим двум определениям.
Определение 5'. Алгебра X называется нильпо-
тентной, если хп = 0 для всякого х е X (при некотором
натуральном п, которое можно считать не зависящим
от х).
Определение 5". Алгебра X называется нилыю-
тентной, если [xi[x2, ..., [xq, xq+l] ...]] = О для всякого
набора элементов хи х2, .. ., xq+\ е X (при некотором
натуральном q, которое можно считать не зависящим
от х{).
Заметим, что последнее условие можно также запи¬
сывать в виде ххх2 ... xq = 0. Применяя следствие 2 к
линейной алгебре операторов х = Dx, заключаем, что
условия определения 5" могут быть получены как след¬
ствие из условий определения 5'. С другой стороны,
условия определения 5' представляют собой частный
случай условий определения 5". Следовательно, оба эти
определения равносильны.
Далее, согласно теореме Энгеля условия определе¬
ния 5 (§ 83) могут быть получены как следствие из
условий определения 5'. В то же время обратное утвер¬
ждение очевидно. В результате получаем, что все опре¬
деления 5, 5', Ъ" эквивалентны.
Определение нильпотентности может быть сформули¬
ровано также следующим образом. Пусть X — произ¬
вольная алгебра Ли. Положим
Zkn = [X,Zk], Z0 = X.
Тогда Zk+\ при любом значении k является идеалом не
только в Zh, но и во всей алгебре X. Цепочка идеалов
Zh называется центральным рядом в алгебре X. Опре¬
деление 5" формулируется теперь следующим образом:
Алгебра X называется нильпотентной, если ее цент¬
ральный ряд сходится к нулю, т. е. Zh = (0) при неко¬
тором /г.
В заключение отметим связь между центральным ря¬
дом алгебры X' и рядом последовательных производных

§ 86. РАЗЛОЖЕНИЯ ФИТТИНГА
389
алгебры X. Пусть Z'k — центральный ряд алгебры X' =*
= [X, X]. Тогда имеем
X' = [X, X] = Z'Q,
Х" = [Х', Х'] = [Х', Z'] = Z',
X'" = \Х", X"] с= [X', X"] = [X', Z[] = Z', ...
Рассуждая индуктивно, заключаем, что Xik) a Zi-i-
Если, в частности, алгебра X' = Z' нильпотентна, то
Х(р) = (0) при некотором р, т. е. алгебра X разрешима.
Обратно, если X разрешима, то все неприводимые ком¬
поненты D[a ' коммутативны (§ 83) и потому обращаются
в нуль для а е X'. Следовательно, если а е X', то
Da — нульстепенный оператор. Следовательно, алгебра
X' нильпотентна. В результате получаем следующий
важный результат:
Алгебра X разрешима тогда и только тогда, когда
ее производная подалгебра X' нильпотентна.
Упражнения
1. Показать, что всякая нильпотентная алгебра Ли размерности
2 коммутативна.
2. Показать, что всякая нильпотентная алгебра Ли размерности
3 либо коммутативна, либо задается единственным нетривиальным
соотношением коммутации [р, q] = г между базисными элементами
р, q, г (алгебра Ли группы Z(3)).
3. Пусть X — нильпотентная алгебра Ли размерности п. Пока¬
зать, что всякая ее подалгебра размерности п — 1, содержащая
центр, является идеалом в X. (Указание: рассмотреть присоеди¬
ненное представление как фактор по центру и воспользоваться лем¬
мой на стр. 386.)
§ 86. Разложения Фиттинга
В этом параграфе мы изложим один из общих ме¬
тодов изучения законов коммутации в произвольной
алгебре Ли. Этот метод допускает формулировку как
в комплексном, так и в вещественном случае. Однако
ради простоты мы будем рассматривать только алгебры
Ли над полем комплексных чисел.
Пусть а — линейный оператор в пространстве Е и
Е% — максимальное подпространство, натянутое на соб¬
ственные и присоединенные векторы этого оператора q

390 гл. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
собственным значением А:
ЕК = Ц: l^E, (а-\)п1 = 0, п = 0, 1,2,...}.
Тогда, как известно (из теории элементарных делите¬
лей), пространство Е может быть представлено в виде
прямой суммы подпространств Ex'.
Е = ЪЕх,
к
где суммирование ведется лишь по конечному множе¬
ству чисел А, которые являются собственными значения¬
ми оператора а. Оказывается, что этот результат пере¬
носится также на нильпотентные алгебры линейных опе¬
раторов в пространстве Е.
Пусть X — линейная алгебра Ли, определенная в
пространстве Е. Функция Х = Х(х), х^Х, называется
собственным значением или весом алгебры X, если
х| = А(х)| для некоторого вектора £ е Д, \Ф0\ оче¬
видно, Х(х) является линейной формой от хе! Про¬
странство
Ex = tt: |е£, (* - А (*) П = 0, п = 1, 2, ..., * е= X}
называется весовым пространством алгебры X, отвечаю
щим весу X. Иначе говоря, Ех есть пересечение всех
собственных пространств ЕХ(Х), определенных для от¬
дельных операторов те! При этом мы считаем, что
Ех = (0), если X не является весом алгебры X.
Докажем, что имеет место
Теорема 1. Если X — нильпотентная алгебра Ли,
то пространство Е разлагается в прямую сумму
Е = ЪЕх,
к
где суммирование ведется лишь по конечному множе¬
ству линейных форм X = А (я), которые являются весами
алгебры X.
Доказательство. Используя индукцию по п,
легко проверяем тождество
П
п . ’i L 1 k) 61 — k
a b = t'nb a ,
*-o

§ 86. РАЗЛОЖЕНИЯ ФИТТИНГА
391
где blk) = akb, справедливое для .любых линейных опера¬
торов а, b в пространстве Е (С* — биномиальные коэф¬
фициенты). Если а, /)еХ, то &(*>= 0 при достаточно
большом значении k. Заменяя а на а — К (а), применяем
обе части этого равенства к вектору £ е E%w. Поскольку
среди чисел k, п — k хотя бы одно превосходит я/2, то
при достаточно высоком п мы получаем
(а - Я (а) )" Ь\ = 0.
Но это означает, что Ех(а) инвариантно относительно b
при любых а, 6е/(.
Пусть е\, е2, ..., е„ — базис в алгебре X. Простран¬
ство Е есть прямая сумма подпространств Е1{, где Xi —
произвольное собственное значение оператора в\. В свою
очередь будучи инвариантно относительно е2, есть
прямая сумма подпространств = (Е\,)к, весовых от¬
носительно е2, и т. д. Следовательно,
Е- 2 Ehh...K
л,, А2, Кп
(прямая сумма), где каждое из слагаемых инвариант¬
но относительно всей алгебры X. Поскольку алгебра X
нильпотентна, то в силу теоремы Ли все матрицы х в
подпространстве ... %п одновременно приводятся
к треугольной форме. Отсюда ясно, что единственным
собственным значением в этом подпространстве являет¬
ся линейная форма Х(х) = Х,-х', и ... \п = Е\. Тео¬
рема доказана.
Теперь предположим, что X — произвольная алгебра
Ли и N — ее нильпотентная подалгебра. Применяя тео¬
рему 1 к линейной алгебре N = {i; х е N}, получаем раз¬
ложение алгебры X в прямую сумму весовых подпро¬
странств:
* = (*)
а
где а = а(х)—произвольный вес, определенный на ли¬
нейной алгебре N. Такие веса называются корнями, и
пространство Ха называется корневым подпростран¬
ством в алгебре X.

392 ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
Разложение (*) называется разложением Фиттинга
алгебры X (по отношению к нильпотентной подалгебре
N). Мы исследуем в этом параграфе основные свойства
такого разложения.
1° [Ха, *р] <= ха+ь.
Для доказательства этого утверждения достаточно
проверить (индукцией по п) справедливость следующего
тождества *):
(D — а — ру* [х, у]=ЪСкп [(£> - a)ft *, (D - ?,)п~ку],
ft-=o
где D — произвольное дифференцирование в алгебре X.
Полагая, в частности, D — Dz, z^N, ос = ос (г), (3 = р(г),
получаем в правой части нуль при достаточно высоком
п, если х е Ха, у е Х$.
2° [Х0, Ха} с Ха, [Х0, *0] с *„■
Эти равенства являются частным случаем 1°. Они
показывают, что корневое пространство Х0, отвечающее
корню 0, само является подалгеброй в алгебре X и каж¬
дое пространство Ха инвариантно относительно Х0.
3° N с=Х0.
Действительно, если z е N, то г имеет только нуле¬
вое собственное значение на N ввиду нильпотентности
М. Следовательно, N cz Х0. В частности, мы видим, что
нуль всегда содержится среди корней алгебры X (это
следует также из равенства [z, г]= 0).
Для получения более дробного разложения в алгеб¬
ре X естественно N выбирать по возможности макси¬
мальной. Особенно интересен случай N = X0. В этом
случае разложение Фиттинга называется регулярным.
Выясним, когда возможно регулярное разложение.
Элемент х ^ X назовем регулярным, если оператор к
имеет минимально возможную кратность нулевого соб¬
ственного значения в пространстве X. Очевидно, такие
элементы всегда существуют. Пусть h — регулярный
элемент п N — максимальная нильпотентная подалгеб¬
*) При а = р = 0 это тождество превращается в известное пра¬
вило Лейбница для кратной производной.

§ 86. РАЗЛОЖЕНИЯ ФИТТИНГА
393
ра, содержащая этот элемент. Условимся в этом слу¬
чае говорить, что алгебра N является регулярной.
Теорема 2. Если N — регулярная подалгебра, то
разложение Фиттинга является регулярным.
Доказательство. Рассмотрим вначале разложе¬
ние Фиттинга по отношению к единственному оператору
h, где h — регулярный элемент:
Х = Х0 + Х.
Здесь X— прямая сумма подпространств с ненулевыми
собственными значениями. Согласно свойству 2° полу¬
ченное разложение инвариантно относительно всех опе¬
раторов к, х е *0. Положим х — h + ех0, и пусть Р(е) —
детерминант преобразования х на подпространстве X:
Р(е) = detjf (7z + ei0).
Тогда Р(г)—полином от е и Р(0)=А0; поэтому
Р(г)ф 0 при достаточно малых значениях е. Следова¬
тельно, в этом случае все нулевые собственные значения
оператора к содержатся в подпространстве Х0. Посколь¬
ку их число не может быть меньше размерности Х0
(согласно определению регулярного элемента), то х —
нульстепенное преобразование в Х0. Пусть
Р0 {I, в) = detx, (I - х)
— характеристический детерминант оператора х в под¬
пространстве Х0. Тогда Pq(%, е) является полиномом от
% и е и Р0(к, г) = 'кп°, rto = dimX0, для достаточно малых
значений е. Следовательно, Р0(е) = /\.га\ и это означает,
что для любого JceX0 преобразование х нульстепенно
в Х0. Следовательно, Х0 — нильпотентная подалгебра.
Далее, пусть N — максимальная нильпотентная под¬
алгебра, содержащая h. Равенство hmN = (0) (при доста¬
точно большом пг) означает, что N а Х0. Ввиду макси¬
мальности N в классе нильпотентных подалгебр мы
имеем N = Х0. Алгебра N не может иметь нулевых кор¬
ней в X (поскольку h е N); следовательно, подпрост¬
ранство Х0 совпадает также с нулевым подпростран¬

394
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
ством в разложении Фиттинга относительно N. Теорема
доказана.
Следствие. В произвольной алгебре Ли сущест¬
вует регулярное разложение Фиттинга:
X = N+ 2 ха.
о Ф и
В дальнейшем мы будем рассматривать только та¬
кие разложения.
В заключение этого параграфа рассмотрим специаль¬
ные элементы вида z = \ха, ха^Ха, r_ael_t,
которые, как следует из регулярности, содержатся в ал¬
гебре N. Следовательно, для г определено понятие кор-
со
няЯ = Я(г). Подпространство 7= 2 XK+ka инвариан-
k=* — со
тно относительно %-а, а потому и относительно z.
Поскольку след коммутатора равен нулю, то мы полу¬
чаем соотношение
оо
2 пк {Я (z) -h ka (z)} = 0.
k— —oo
Здесь nh — размерность корневого подпространства
Xx+ha.’ отличная от нуля лишь для конечного числа зна¬
чений k = 0, ±1, ±2, ... , и выражение слева, очевидно,
равно sp^z для треугольной матрицы г. Поскольку
оо
2 пк ф 0, то это уравнение можно разрешить отно-
k= — СО
сительно X(z), откуда получаем A(z) = ra(z), где г —
рациональное число (зависящее от Я и а). Суммируя по
всем корням, мы получаем также равенство
sp £m = pma (z)m
с рациональным коэффициентом pm = 2 rf, где r% =
К
= — 2 fen. fc/2ttfc Для каждого корня Я. Если а ф 0, то
существует хотя бы один корень Я (например, Я = 0),
для которого Я' = Я + а также является корнем. Равен¬
ства гК = гх, — 0 приводят к противоречию, ибогл,—гк=\.
Следовательно, гк Ф 0, и отсюда рт ф 0 при чет¬
ном т.

§ 87. БИЛИНЕЙНАЯ ФОРМА КИЛЛИНГА - КАРТАНА 395
§ 87. Билинейная форма Киллинга — Картана
Пусть X — произвольная алгебра Ли, комплексная
или вещественная. Для любых элементов ijeX поло¬
жим
(х, у) = sp DxDy.
Полученная билинейная форма называется формой
Киллинга — Картана. Она обладает следующими свой¬
ствами:
1° (*, у) = (у, *);
2° ([х, у], г) = (х, [у, г]);
3° (х, у)х^ = (х, у)х, если Х0 — идеал в X и х, у е Хй
Мы не станем останавливаться на несложной про¬
верке этих соотношений. Заметим, что свойство 2° мо¬
жет быть также записано в виде
2' (Dyx, z) + (х, Dyz) = 0.
Следовательно, операторы Dv являются кососимметрич¬
ными относительно этой формы.
Пусть X1 — пространство всех векторов, ортогональ¬
ных к каждому вектору из X. Если вектор х обладает
этим свойством, то согласно 2' тем же свойством обла¬
дает Dyx. Следовательно, X1 является идеалом в X.
Особый интерес представляют два крайних случая:
X1 = X и Z1 = (0). В первом случае (х, у) = 0 тожде¬
ственно на всей алгебре X, и это условие равносильно
более частному условию (х, х) = 0, хе! Во втором
случае форма называется невырожденной*). Докажем
вначале, что имеет место
Теорема 3 (Критерий Картана). Если
(х, х) = 0 на всей алгебре X, то алгебра X является раз¬
решимой.
Доказательство. Ввиду возможности комплек¬
сного расширения (X -> X + iX) мы можем считать, не
ограничивая общности, что алгебра X является комплек¬
сной. Докажем вначале, что X' ф X.
*) Если (х, у) — ацх'у’ относительно некоторого базиса в X,
то условие невырожденности можно выразить формулой
det || atj || Ф 0.

396
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
Действительно, если X = X' = [X, X], то для всякого
разложения Фиттинга мы имеем ^о = 2[^а> ^-ol* Сле-
а
довательно, подалгебра Х0 является линейной оболоч¬
кой коммутаторов вида z = [ха, х_а]. Согласно замеча¬
нию, сделанному в конце § 86, мы имеем
(z, z) = sp 22 = р2а (;г)2 = О,
где рг Ф 0. Следовательно, a(z) — 0 для всех коммута¬
торов z, а потому и для всех элементов из А'о. Но это
означает, что все корни относительно Х0 нулевые, т. е.
X— Х0. Следовательно, алгебра X нильпотентна и Х'ФХ
вопреки допущению.
Итак, X' Ф X. В силу свойства 3° формы Киллинга —
Картана (х, х) = 0 также на подалгебре X'. Следова¬
тельно, X" ф X' ит. д. Следовательно, X(?) = (0) при
достаточно высоком р, т. е. алгебра X разрешима. Тео¬
рема доказана.
Как легко убедиться на простых примерах, обратное
утверждение неверно, т. е. (х, х) не обязательно равно
нулю для всякой разрешимой алгебры .Y*). Однако име¬
ет место
Теорема 4. Алгебра X разрешима тогда и только
тогда, когда (X, X') = 0 для производной подалгебры X'.
Доказательство. Если (х, у) — 0 для х е X',
у е X, то, в частности, (х, х) = 0 для х е X'. Следова¬
тельно, алгебра X' разрешима. Поскольку фактор-алгеб¬
ра Х/Х' коммутативна, то она также разрешима. Следо¬
вательно (см. § 84), алгебра X также разрешима.
С другой стороны, если алгебра X разрешима, то
подалгебра X' нильпотентна (§ 85). Приводя операторы
Da, ael, к треугольной форме (в вещественном слу¬
чае— к квазитреугольной), замечаем, что собственные
значения (диагональные блоки) оператора Dx равны
нулю, если х е X'. Следовательно, (a, х) = sp DaDx — 0.
Теорема доказана.
Покажем теперь, что в терминах билинейной формы
Киллинга — Картана можно также дать независимую
характеристику полупростых алгебр Ли.
*) Однако если алгебра X нильпотентна, то оператор Dx нуль,-
степенен, откуда (х, х) е= 0.

§ 87. БИЛИНЕЙНАЯ ФОРМА КИЛЛИНГА - КАРТАНА 397
Теорема 5. Алгебра X является, полупростой то¬
гда и только тогда, когда билинейная форма (х, у) не¬
вырождена.
Доказательство. Если алгебра X проста, то X
не содержит ни одного идеала, кроме (0) и А"; в частно¬
сти, [А", X] — X, и алгебра X не может быть разреши¬
мой. Если алгебра X полупроста, то всякий ее идеал
является суммой простых подалгебр. Следовательно,
алгебра X не содержит ни одного разрешимого идеала,
кроме (0). В то же время, если положим У = X1, то
на Y форма Киллинга — Картана обращается в нуль,
откуда следует, что Y — разрешимый идеал (теорема 3).
Следовательно, У = (0), и форма Киллинга — Картана
невырождена.
С другой стороны, предположим, что билинейная фор¬
ма (х, у) невырождена, и покажем, что присоединенное
представление в алгебре X вполне приводимо. Если К —
идеал, то его ортогональное дополнение У1 в виду 2'
также является идеалом. Следовательно, Z = Y П У1
также является идеалом. Полагая a, b е Z, получаем из
тождества Якоби, что [a,b]LX, откуда [а, 6] = 0, т. е. Z —
абелев идеал. Если zgZ, леА, то оператор DXDZ пере¬
водит X в Z, Z в (0), откуда следует, что (х, z) =
= sp DXDZ = 0, т. е. ZLX. В результате Z = (0). Отсюда
X — Y + У1 (прямая сумма). Действительно, если век¬
тор z ортогонален У + У1, то zeZ, откуда 2 = 0. Мы
показали, что алгебра X редуктивна. Если Z — центр
алгебры X, то Ог = 0, г е Z, откуда, как и выше, заклю¬
чаем, что Z = (0). Следовательно, алгебра X полупроста.
Теорема доказана.
Следствие 1. Алгебра X полупроста тогда и
только тогда, когда она не содержит ни одного разреши¬
мого идеала, кроме (0).
Следствие 2. Алгебра X полупроста тогда и
только тогда, когда она не содержит ни одного комму¬
тативного идеала, кроме (0).
Следствие 3. Условие полупростоты можно так¬
же записывать в виде [X, Z] = X.
Доказательства (несложные) предоставляются чита¬
телю. Каждое из приведенных условий может быть вы¬
брано в качестве независимого определения полупростой

398
ГЛ. ХШ. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
алгебры Ли. В заключение этого параграфа получим
еще один результат как следствие теоремы 5:
Теорема 6. Если алгебра X полупроста, то всякое
ее дифференцирование является внутренним.
Доказательство. Пусть ©— алгебра всех диф¬
ференцирований и £ — подалгебра, образованная внут¬
ренними дифференцированиями Dx, хе! Поскольку
алгебра X имеет нулевой центр, то представление Dx
является точным, и алгебра if полупроста. Далее, если
D — дифференцирование и у — Dx, то легко проверить
формулу
[О, Dх] = Dy,
из которой следует, что X является идеалом в Ф. Но
тогда ортогональное дополнение J1 к идеалу X относи¬
тельно скалярного произведения (Л,В)=зрЛВ также
является идеалом в ©. Из невырожденности формы в
идеале Ж следует, что уравнение d — аХЖ разрешимо
относительно аеУ для любого rfeS. Следовательно,
© = Ж -f Ж1 . Пересечение 3 = £ П Ж -1 ортогонально к Ж
во всей алгебре ©, но тогда и в идеале У (свойство 3°
формы Киллинга — Картана); следовательно, 3 = (0)
(ибо Ж полупроста). Оператор DV = [D,DX] содержится
как в идеале Ж, так и в идеале У-1, если Del1; следо¬
вательно, D;/ е 3 и Dy = 0. Но тогда также у = Dx — 0
для всякого х е X, откуда D = 0. В результате У1 = (0)
и © = У. Теорема доказана.
Упражнение
Выразить условие полупростоты алгебры Ли в терминах струк¬
турных констант Cq.
§ 88. Основные типы групп Ли
Если рассматривать только связные группы Ли, то
для получения их классификации можно непосредствен¬
но воспользоваться результатами классификации для
алгебр Ли. Связная группа Ли называется редуктивной,
полупростой, простой, разрешимой, нильпотентной или
абелевой, если ее алгебра Ли относится к одному из
перечисленных типов. Однако в случае несвязных групп
такой подход уже нежелателен, поскольку свойства

§ 88. ОСНОВНЫЕ ТИПЫ ГРУПП ЛИ
399
дискретной фактор-группы G/Ge, где Ge — компонента
единицы, при этом совершенно не учитываются. Так, в
предельном случае, когда группа G сама дискретна (т. е.
алгебра Ли равна (0)), мы вообще не получаем инфор¬
мации о структуре группы G. Кроме того, определения
разрешимости, нильпотентности и коммутативности есте¬
ственно формулируются не только для групп Ли, но во¬
обще для произвольных групп.
Пусть G — произвольная группа. Множество К с= G
называется коммутаторной подгруппой, если К состоит
из всевозможных коммутаторов вида k = aba~lb~l, а,
b е G, и их произведений в любом (конечном) числе.
Если G — топологическая группа, то вместо К рассмат¬
ривают обычно замыкание этого множества в топологии
G. Полученное множество снова является группой; оно
обозначается G' и называется производной подгруппой
в группе G.
Определение 1. Группа G называется разреши¬
мой, если G^pI = {е} при некотором р.
Здесь — кратная производная группы G, опреде¬
ляемая рекуррентно: G69 = [G^_1), G(p4)], где квадрат¬
ные скобки заменяют обозначение производной. Анало¬
гично можно ввести понятие центрального ряда группы
G. Мы полагаем G0 = G, G\ = G'. Далее, подгруппа
Gp определяется как [G, Gp„i], т. е. как замкнутая под¬
группа в Gp_i, порожденная коммутаторами вида k =
= aba~[b~{, aeG, J e Gp-i, Нетрудно видеть, что Gp
является нормальным делителем не только в Gp_i, но и
во всей группе G.
Определение 2. Группа G называется нильпо
тентной, если Gp = {е} при некотором р.
В частности, группа G является абелевой, если
G\ = G' = {е}, т. е. если ab = Ьа для всех a, b <= G.
Следовательно, определения нильпотентности и разре¬
шимости являются естественными обобщениями понятия
коммутативности. Как следует из данных определений,
№>c(G')p-i. Отсюда нетрудно получить следующее
утверждение: группа G разрешима тогда и только то¬
гда, когда ее производная подгруппа нильпотентна.
Для разрешимой связной группы имеет место также
аналог фундаментальной теоремы Ли:

400
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
Теорема Ли. Если G — разрешимая связная груп¬
па, то всякое ее неприводимое представление в комплек¬
сном пространстве одномерно *).
Доказательство. Минимальное из чисел р, для
которых (Цр) = {е}, назовем рангом группы. Если ранг
равен единице, то теорема верна. Далее будем вести
индукцию по рангу.
Пусть У— пространство представления Tg группы G
и У0— подпространство, неприводимое относительно Тg.
Нетрудно видеть, что G' вместе с G является разреши¬
мой связной группой. Поскольку ранг G' меньше ран¬
га G, мы можем считать по допущению индукции, что
У о одномерно. Следовательно,
Th\0 = MA)So
для /i g G' и |о G Уо- Применим к вектору £о произволь¬
ный оператор Tg и выясним действие оператора Th на
каждый элемент орбиты = Tgc,. Поскольку G' являет¬
ся нормальным делителем в G, то мы имеем hg =
= g{g~lhg) = g%, где ieW. Следовательно,
Thls = TgT~hl0 = X(h)lg.
Следовательно, всякий вектор lg снова является соб¬
ственным вектором относительно Th с собственным зна¬
чением Xg{h) = %(g~lhg). Далее существенно исполь¬
зуется конечномерность У и связность группы G. Из
первого условия следует, что функция Kg(h) при пере¬
менном g может принимать значения лишь из конеч¬
ного множества А, где А = {р(/г)}— множество всех
«весов» представления Th. Из второго условия следует,
что %g непрерывно зависит от g. Сопоставляя эти утвер¬
ждения, заключаем, что Ag не зависит от g, т. е.
l(g~lhg) = \(h) для всех g^G. Положим
Ул^еУ, 7-а1 = МАШ,
где К = K(h) фиксировано. Мы видим, что Ух инвариант¬
но в У относительно всей группы G; следовательно,
*) В вещественном пространстве — не более чем двумерно и
коммутативно. Мы для простоты рассматриваем комплексный случай.

§ 88. ОСНОВНЫЕ ТИПЫ ГРУПП ЛИ
401
Г*, = V. Если h является коммутатором, h. = aba~lb~\
то del Th = 1, откуда заключаем, что
К (h)n =1, п = dirn V,
для всех коммутаторов h е G', но тогда и для всех эле¬
ментов из G'. Из связности G' и непрерывности K{h)
заключаем, что k(h) = 1. Следовательно, Тп = I, где
/ — единичный оператор в V, и представление Tg ком¬
мутативно. Но тогда по лемме Шура V одномерно. Тео¬
рема доказана.
Нетрудно видеть, что для связных групп Ли опреде¬
ления 1 и 2 равносильны определениям в терминах
алгебры Ли. В то же время определения простоты, по¬
лупростоты и редуктивности, данные в начале этого
параграфа, принято переносить на произвольные (не
обязательно связные) группы Ли. Мы сформулируем
эти определения также в глобальной форме.
Определение 3. Группа Ли называется простой,
если она не содержит ни одного замкнутого связного
нормального делителя.
Определение 4. Группа Ли называется полу-
простой, если она не содержит ни одного замкнутого
связного разрешимого нормального делителя.
Определение 5. Группа Ли называется редук-
тивной, если ее фактор-группа по центру полупроста.
Эквивалентность этих определений определениям,
данным в начале параграфа, не очевидна. Действитель¬
но, мы видели в § 40, что некоторым подалгебрам в ал¬
гебре Ли не соответствуют замкнутые подгруппы в со¬
ответствующей группе Ли. Однако можно показать,
используя некоторые результаты А. И. Мальцева
[109], что в определениях 3, 4 вместо слов «замкнутый
нормальный делитель» можно использовать термин
«локально замкнутый нормальный делитель» (замкну¬
тый хотя бы в окрестности единицы). В такой формули¬
ровке определения 3, 4, очевидно, эквивалентны опреде¬
лениям, данным в начале параграфа. Это следует из
взаимно однозначного соответствия между локально
замкнутыми подгруппами и подалгебрами в алгебре Ли.
Заметим, что в определении 4 вместо разрешимого
нормального делителя можно ограничиться коммутатив¬

402
ГЛ. XIII. ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
ными нормальными делителями (см. следствие 2 из
теоремы 5). Заметим также, что всякий нормальный де¬
литель в простой связной группе Ли является дискрет¬
ным и центральным. Действительно, дискретность сле¬
дует из определения 3; в то же время мы видели в § 5,
что в связной группе G всякий дискретный нормальный
делитель централен.
Ясно также, что простые и полупростые группы Ли
могут иметь только дискретный центр.
§ 89. Теорема Леви — Мальцева
Проведенная выше классификация не является пол¬
ной в том смысле, что существуют группы (алгебры)
Ли, которые не относятся ни к одному из выделенных
классов. В частности, это верно даже для такой класси¬
ческой группы, как группа движений евклидова про¬
странства (включающая повороты и трансляции). Ока¬
зывается, однако, что любая группа (или алгебра) Ли
может быть (в известном смысле) составлена из от¬
дельных подгрупп, каждая из которых уже относится
к перечисленным выше классам.
Рассмотрим вначале алгебры Ли. Пусть X — такая
алгебра и R— ее максимальный разрешимый идеал.
Подалгебра R называется радикалом в алгебре X*).
Очевидно, фактор-алгебра Х/R уже не содержит разре¬
шимых нормальных делителей. Следовательно, алгебра
Х/R полупроста.
Теорема 7 (Леви — Мальцев). Всякая алгеб¬
ра Ли может быть разложена (как линейное простран¬
ство) в прямую сумму своего радикала R и полупростой
подалгебры S\
X = R + S.
Подалгебра S является максимальной полупростой под¬
алгеброй в алгебре X. Она определяется однозначно с
точностью до автоморфизма.
Мы не будем приводить доказательства этой теоре¬
мы, поскольку оно является достаточно сложным и это
*) Можно показать, что R определяется в X однозначно.

§ 89. ТЕОРЕМА ЛЕВИ — МАЛЬЦЕВА
403
увело бы нас в сторону от основного направления дан¬
ной книги. Отметим только соотношения коммутации:
[S, S] сг S, [/?, R] a R, [R, S] сг R.
Последнее соотношение является следствием того, что
алгебра R является идеалом. Таким образом, вообще
говоря, [Я, S] Ф (0), т. е. разложение Леви — Мальцева
не является прямой суммой двух идеалов.
Таким образом, основным содержанием теоремы 7
является результат о существовании в X подалгебры S,
дополнительной к радикалу R (отсюда уже вытекает,
что алгебра S является максимальной полупростой).
Отсюда, очевидно, вытекают аналогичные результаты
для произвольной связной группы Ли.
Пусть G — связная группа Ли, X = R + S — разло¬
жение Леви — Мальцева для ее алгебры Ли, Я и @ —
аналитические подгруппы, отвечающие подалгебрам R
и S. Тогда мы имеем
G = Я©.
При этом Я является нормальным делителем в G и груп¬
па © является максимальной в классе полупростых
связных подгрупп в группе G. Кроме того, Я и © яв¬
ляются замкнутыми подгруппами.
Полученное разложение, вообще говоря, неодно¬
значно; однако ЯП©, очевидно, дискретно (действи¬
тельно, алгеброй Ли такой подгруппы является (0)).
Если G — односвязная группа Ли, то полученное разло¬
жение однозначно и подгруппы Я, © являются одно¬
связными ([108]).
Пример. Пусть G — группа движений «-мерного
евклидова пространства. Если g^G и х— произволь¬
ный вектор этого пространства, то действие группы оп¬
ределяется по формуле
gx = ах +1,
где а — поворот и t — трансляция. Вместо вектора х
удобно рассматривать (п + 1)-мерный вектор т = (х, 1),
(я+1)-я координата которого равна единице. Тогда

404 гл- хш' ОСНОВНЫЕ ТИПЫ АЛГЕБР И ГРУПП ЛИ
группа G может быть записана как группа матриц:
a t
ё:
0 1
а ^ О (п).
Подгруппа поворотов ® выделяется условием t = 0; под¬
группа трансляций SR выделяется условием а = е, где
е — единичная матрица порядка п. Нетрудно пока¬
зать*), что всякая ортогональная группа является полу¬
простой. Следовательно, SR является радикалом в груп¬
пе G. Разложение G = SR® в данном случае очевидно.
Замечание 1. Группа G из этого примера не яв¬
ляется связной. Однако мы получим связную группу,
если ограничимся связной компонентой единицы. (Для
этого достаточно наложить ограничение deta=l.)
Замечание 2. Если группа G допускает одно¬
значное разложение в произведение двух подгрупп,
G = АВ, причем одна из этих подгрупп является нор¬
мальным делителем в G, то говорят, что G является
полупрямым произведением А, В. В частности, группа
движений является полупрямым произведением своих
подгрупп 9?и®.
Таким образом, теорема Леви — Мальцева показы¬
вает, что всякая связная группа Ли конструируется из
разрешимой и полупростой примерно по тому же пра¬
вилу, как группа движений евклидова пространства со¬
ставляется из трансляций и вращений.
* *
Как мы видели в этой главе, существует много вариантов есте¬
ственного определения для основных типов алгебр Ли. Мы попыта¬
лись унифицировать эти определения, прибегая к терминам присое¬
диненного представления. Однако получаемые таким путем опре¬
деления иногда недостаточно эффективны для проверки. Например,
теорема Энгеля дает гораздо более простой критерий нильпотент¬
ности алгебры X. В литературе наиболее употребительными яв¬
ляются определения простоты и полупростоты, заключенные в
следствиях 1 и 2 из теоремы 5. С. Хелгасон [42] принимает в
качестве определения полупростоты непосредственно условие не¬
вырожденности формы Киллинга — Картана (теорема 5). Для раз¬
решимости и нильпотентности наиболее употребительными являются
*) См., например, [77].

§ 89. ТЕОРЕМА ЛЕВИ - МАЛЬЦЕВА
405
определения в терминах последовательных производных и централь¬
ных рядов.
Невырожденность формы Киллинга — Картава является, по-
видимому, наиболее существенной информацией, необходимой для
дальнейшего изучения простых и полупростых алгебр Ли. Напом¬
ним, что этот результат в свою очередь является следствием кри¬
терия разрешимости Э. Картана (теорема 3). При доказательстве
этого критерия мы воспользовались, следуя [77], разложением Фит¬
тинга в алгебре X. Однако существует еще и другой вариант дока¬
зательства — при помощи так называемых «реплик» линейного опе¬
ратора ([128]). Доказательство теоремы о дифференцированиях (тео¬
рема 6) мы заимствуем из книги С. X с л г а с о н а [42]. Теорема Ли
в глобальной формулировке, по-видимому, впервые была доказана
Р. Г о д е м а н о м [74].
Существование разложения X = R + S для произвольной алгеб¬
ры Ли было впервые доказано Э. Леви [106]. Единственность полу¬
простой подалгебры S доказана А. И. Мальцевым [110] и также
независимо Хариш-Чандрой [136]. Доказательства см., напри¬
мер, в [19], [46], [113], [125].

ГЛАВА XIV
КЛАССИФИКАЦИЯ КОМПАКТНЫХ
И РЕДУКТИВНЫХ АЛГЕБР ЛИ
Теперь мы возвращаемся к первоначально постав¬
ленной задаче об описании всех компактных групп Ли.
Классификация, изложенная в предыдущей главе, име¬
ла своей исходной точкой чисто алгебраические сооб¬
ражения и потому, естественно, не включала компакт¬
ных групп, ибо понятие компактности существенно
топологическое. Тем не менее (и это является любопыт¬
ной особенностью групп Ли), как увидим в начале дан¬
ной главы, существует возможность дать характеристи¬
ку класса компактных групп Ли в терминах алгебры Ли.
Если G — компактная группа Ли, то ввиду глобаль¬
ной теоремы ее присоединенное представление вполне
приводимо. Следовательно, всякая компактная группа
Ли редуктивна. Поэтому ее комплексная оболочка так¬
же редуктивна. Поскольку над комплексным полем
задача классификации решается технически проще
(примеры этого мы видели в предыдущей главе), есте¬
ственно начать с классификации комплексных редуктив¬
ных алгебр Ли. Отбрасывая центр, мы можем также
ограничиться рассмотрением полупростых комплексных
алгебр Ли. Во всяком случае таким путем мы не про¬
пустим ни одной «компактной» алгебры Ли.
Задачу можно было бы несколько упростить, если
заранее воспользоваться условием компактности. Од¬
нако интересно выяснить также местоположение ком¬
пактных групп Ли среди редуктивных, и поэтому есте¬
ственно решать сразу более общую задачу. При этом
мы увидим (a posteriori), что все редуктивные группы
(алгебры) Ли в известном смысле «порождаются» ком¬
пактными.
§ 90. Компактные алгебры Ли
Начнем с алгебраической характеристики компакт¬
ной группы Ли.
Определение 1. Вещественная алгебра Ли X на¬
зывается компактной, если на X существует скалярное

§ 90. КОМПАКТНЫЕ АЛГЕБРЫ ЛИ
407
произведение {х, у), относительно которого операторы
Da кососимметричны:
{Dax, у) + {х, Day} = 0, а, х, у<=Х.
Напомним, что скалярное произведение есть симмет¬
ричная билинейная форма, которая является строго по¬
ложительно определенной, т. е. {х, х} > 0 при х ф 0. Ис¬
следуем связь введенного определения с понятием ком¬
пактной группы Ли.
Пусть X — компактная алгебра Ли и Z— ее центр.
Нетрудно видеть, что алгебра X редуктивна (действи¬
тельно, всякое инвариантное подпространство имеет ин¬
вариантное ортогональное дополнение); следовательно,
Х = F0Z,
где алгебра У полупроста (см. § 83). Пусть GY — группа
всех невырожденных линейных преобразований в про¬
странстве Y, для которых
1° {gx, gy} = {x, у}, х, у^Х\
2° [gx, gy] = [x, у], х, у<=Х.
Здесь {х, у} — скалярное произведение и [х, у] — комму¬
татор в алгебре Y. Как следует из условия Is, группа
Gy является подгруппой в группе 0(F) всех ортого¬
нальных преобразований пространства У. Как следует
из 1° и 2°, группа Gу является замкнутой подгруппой
в О(У).
Найдем алгебру Ли группы Gy. Согласно условию 2°
всякое инфинитезимальное преобразование этой группы
является дифференцированием в F. Согласно теореме
6 (§ 87) это дифференцирование является внутренним.
Следовательно, алгеброй Ли группы Gy является У, где
У — множество всех операторов у = Dv, y^Y. По¬
скольку алгебра У полупроста, ее представление Dv яв¬
ляется точным. Следовательно, У изоморфно У.
Заметим теперь, что Gy является компактной груп¬
пой Ли (как замкнутая подгруппа компактной группы
О (У) *)). Следовательно, мы показали, что существует
*) См. по этому поводу теоремы 3, 4 § 99,

408 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
компактная группа Ли, алгебра Ли которой изоморфна
алгебре У.
Далее, пусть т — размерность центра Z и Gz —
m-мерный тор, т. е. прямое произведение т экземпляров
группы вращений окружности. Тогда коммутативную ал¬
гебру Z мы можем рассматривать как алгебру Ли груп¬
пы Gz- Положим, наконец,
Gх — GY X Gz-
Группа Gx является компактной группой Ли, алгеброй
Ли которой является Y + Z, причем как У, так и Z яв¬
ляются идеалами в этой алгебре. Следовательно, алгеб¬
ра Ли группы Gx изоморфна алгебре X.
С другой стороны, пусть G — произвольная компакт¬
ная группа Ли и X — ее алгебра Ли. В силу глобальной
теоремы алгебра X редуктивна. Положим снова
X=Y + Z,
где Z — центр алгебры X и алгебра У полупроста. Пусть
(х,у)— билинейная форма Киллинга — Картана на под¬
алгебре У, (х, у) = sp DxDy. Положим для краткости
А = Dx при фиксированном х. Тогда мы имеем
(х, х) = sp А2 = 2 АиАц = - 2 А2ц < 0.
I, /' I, /
Здесь Ац—матрица оператора А относительно некото¬
рого фиксированного базиса в У; Ац = —Ац в силу ко¬
сосимметричности оператора A=DX. Равенство (х, х) =0
возможно в алгебре У только при х = 0 *). Следовательно,
форма Киллинга — Картана является отрицательно оп¬
ределенной в У. Положим {х, у}0= — (х, у) и дополним
скалярное произведение {х, у}0 до скалярного произведе¬
ния {х, у} во всей алгебре X, добавляя к {х, у}0 произ¬
вольную симметричную положительно определенную
билинейную форму на алгебре Z. В результате получим,
что алгебра X является компактной. Суммируя вышеска¬
занное, мы приходим к следующему утверждению:
*) Достаточно проверить это свойство для простой алгебры Y.
В этом случае (х, х) = кР(х,х)0, %ф 0, где Р — оператор усреднения
(см. стр. 118 и упражнение 1 на стр. 99) и (х, х)о — фиксированное
скалярное произведение в Y.

§ 90. КОМПАКТНЫЕ АЛГЕБРЫ ЛИ
409
Алгебра X является компактной тогда и только то¬
гда, когда она является алгеброй Ли некоторой компакт¬
ной группы Ли.
Таким образом, определение 1 действительно дает
искомую алгебраическую характеристику компактной
группы Ли.
Замечание. Термин «компактность», примененный
в определении 1, разумеется, должен пониматься в со¬
вершенно независимом смысле по отношению к обычной
топологической терминологии. (Во всяком случае, ал¬
гебра X как линейное пространство не является ком¬
пактной.)
В заключение этого параграфа заметим, что если ал¬
гебра проста, то скалярное произведение {х,у} опреде¬
ляется однозначно с точностью до множителя. Действи¬
тельно, мы видели в § 20, что скалярное произведение,
инвариантное по отношению к некоторому представле¬
нию (в нашем случае expDx), определяется однозначно
с точностью до множителя, если представление непри¬
водимо. Следовательно, в этом случае
{X, у} = k {х, у),
где k отрицательно (действительно, если алгебра X ком¬
пактна и полупроста, то, как мы видели выше, форма
Киллинга — Картана является отрицательно определен¬
ной). Следовательно, если алгебра X полупроста, то ска¬
лярное произведение {х, у] определяется однозначно
(с точностью до множителя) на каждой простой компо¬
ненте в X.
Теперь мы можем поставить задачу о дальнейшей
классификации компактных алгебр Ли. Как отмечалось
в начале главы, вместо этой задачи естественно рассма¬
тривать задачу о классификации всех полупростых (или
даже простых) комплексных алгебр Ли. К решению этой
задачи мы теперь переходим.
Упражнение
Показать, что алгебра X является компактной тогда и только
тогда, когда при некотором выборе базиса структурные константы
кососимметричны по всем трем индексам г, /, k = 1, 2 п

410 гл. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
§ 91. Подалгебры Картана
Решающим шагом в нашем построении является диа-
гонализация некоторого семейства операторов Dx для
полупростой комплексной алгебры X. Введем вначале
следующее.
Определение 2. Пусть X — полупростая алгебра
Ли и h0 — регулярный элемент *) в этой алгебре. Пусть
Я — максимальная коммутативная подалгебра, содержа¬
щая h0- Алгебра Я называется картановской подалгеб¬
рой в алгебре X.
Теорема 1. Если X — полупростая комплексная ал¬
гебра Ли и Н — ее картановская подалгебра, то все опе¬
раторы Dh, h е Я, одновременно диагонализуются в не¬
котором базисе алгебры X.
Доказательство. Рассмотрим разложение Фит¬
тинга алгебры X по отношению к подалгебре Я:
А = А0+ 2 Ха, Я с А0,
а Ф 0
где Ха — корневое подпространство, на котором все опе¬
раторы Dh, /г се Я, одновременно приводятся к треуголь¬
ной форме с единственным собственным значением на-
диагонали, равным a(h). Положим
D/i = Ah + Nh,
где Ah — диагональная часть оператора Dh (Ahx = a(h)x
для всякого Jtelj. Заметим, что для всякой пары век¬
торов iGla, i/eAp имеет место равенство
Ah [х, у] = [Ahx, у] + [х, Ahy].
Следовательно, Ah является дифференцированием на
всей алгебре X. Согласно теореме 6 (§ 87) это диффе¬
ренцирование является внутренним, т. е. Ah = Dz при
некотором zgI Поскольку Dz коммутирует с Dx, хеЯ
(это вытекает непосредственно из определения Ah), и
*) Напомним, что элемент h0 называется регулярным (§ 87),
если x(hts) =minvc(x), где х(х) означает кратность нулевого соб¬
ственного значения (вместе с присоединенными векторами) опера¬
тора X, действующего в X.

§ 91. ПОДАЛГЕБРЫ КАРТАНА
411
поскольку представление Dx является точным, то г ком¬
мутирует с Н в алгебре X. Следовательно, геЯ ввиду
максимальности Н. Элемент г — h имеет только нулевые
корни. Следовательно,
{х, z — h) = sp D xDz_h = 2 nua (a) a (z — h) = 0
для каждого x e H. (Здесь na = dim Xa.) Следователь¬
но, 2 — h = 0. Отсюда в свою очередь Nh = 0, и опера¬
торы Dh одновременно диагонализуются. Теорема дока¬
зана.
Замечание. Если бы мы предполагали дополнительно, что
X — комплексная оболочка компактной алгебры Ли, то утверждение
теоремы 1 можно было бы получить из унитарности присоединен¬
ного представления в X для компактной группы Gx, построенной
в §90*). -
В дальнейшем мы будем постоянно иметь дело с
разложением Фиттинга в алгебре X по отношению к кар-
тановской подалгебре Н. Заметим, что ввиду теоремы 1
операторы Dh обращаются в нуль на подпространстве
Х0. Следовательно, [/г, х0] = 0 для всех h е Я, х0 е Х0.
Следовательно, Я = Х0 ввиду максимальности алгебры
Я. Разложение Фиттинга мы будем теперь записывать
в виде
х = я + 2 ха. (*)
a =5^ 0
Докажем, что полученное разложение обладает следую¬
щими замечательными свойствами:
1° Если |3 Ф —а, то Ха ± Хр.
2° Форма Киллинга — Картана невырождена на паре
{X-*, Ха).
Для доказательства этих утверждений достаточно на¬
помнить соотношение [Ха, XJ cz Хх+а, доказанное в § 86.
Следовательно, DxX^cc Хх+а, если х е Ха. Следователь¬
но, также
Dх&уХ), •'^X+a+fJi
если х е Ха, у е Хр. Если |5 + а Ф 0, то все диагональ¬
ные блоки оператора DxDy нулевые (по отношению
*) С подобной ситуацией мы имели дело в гл. V при изучении
Неприводимых представлений группы SU(2).

412 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
к разложению (*)). Следовательно, в этом случае
(х, у) = sp DXDV — 0, и 1° доказано.
Свойство 2° непосредственно. вытекает из 1° и невы¬
рожденности формы Киллинга — Картана на паре
(Х,Х). Действительно, если вектор х^Ха ортогонален
к Л_а, то согласно 1° он ортогонален ко всей алгебре X,
откуда следует, что х = 0. Согласно известным резуль¬
татам линейной алгебры из свойства 2° мы получаем
также следующее утверждение:
3°. Пространства Ха, Х-а имеют одинаковую размер¬
ность.
Следовательно, вместе с корнем а обязательно встре¬
чается также корень —а, причем оба эти корня встре¬
чаются с одинаковой кратностью.
Из результатов 1° и 2° мы заключаем также, что ал¬
гебра Х0 = Н ортогональна ко всем подпространствам
Ха, а ф 0, и форма Киллинга — Картана невырож¬
дена в Я.
Поскольку система корней допускает симметрию по
отношению к замене а на —а, нам будет удобно выде¬
лить среди этих корней «положительные» и «отрицатель¬
ные». Для этого выберем в Я произвольный веществен¬
ный базис и положим
a(h) = a\t\ +а2^2 + . • . +
где /п/2 — комплексная размерность Я и t\, (2, •••, tm —
вещественные координаты элемента АеЯ. Назовем ко¬
рень а положительным, а > 0, если первая из ненулевых
координат аг, •••, ат положительна. Соответствен¬
но мы считаем, что а > р, если а — р > 0. Следова¬
тельно, мы ввели в систему корней лексикографическое
упорядочение. В результате
Х = Х_ + Н + Х+,
где X ЛХ+)—прямая сумма всех корневых подпрост¬
ранств Ха, для которых а < 0 (а>0). Подпространство
Я = Х0 соответствует нулевому корню.
Пример. .А = gl(n, С). Докажите, что элемент h0
является регулярным тогда и только тогда, когда все

§ 91. ПОДАЛГЕБРЫ КАРТАНА
413
его собственные значения различны*). Следовательно,
ho диагонализуется в некотором базисе и Н состоит из
всех матриц, диагональных в этом базисе. Положим
Х = Х_ + Н + Х+,
где Х_(Х+)—совокупность всех нижних (верхних) тре¬
угольных матриц с нулевыми элементами на диагонали.
Пусть вц — стандартный базисный элемент в алгебре Х\
тогда мы имеем
[h, 6,-/] = (Яг- Яу)е(-у,
где Я, — собственные значения матрицы h. Следователь¬
но, всякий ненулевой корень имеет вид ац = К — Xj,
i ф /, и соответствующее корневое подпространство од¬
номерно. Запишем всякий корень в виде a(h) = ailC +
+ a2ta + ■ • . + апХп\ тогда коэффициенты а* являются це¬
лыми числами (=0, ±1) и мы имеем
а;/<0, если г>/, аг/>0, если i<j.
Следовательно, указанное выше разложение совпадает
с тем стандартным разложением, которым мы постоянно
пользовались при изучении алгебры gl(n, С). Налагая
дополнительное условие spx = 0, мы получаем тот же
результат для X = s\(n, С).
Заметим теперь, что если X = si (п,С), то [X, X] — X,
и алгебра X является полупростой. (Действительно,
содержит все элементы etj — a~' |/i, eij\, i ф /, а
следовательно, и элементы вц — = [ец, вц].) Кроме
того, представление X неприводимо, т. е. алгебра X яв¬
ляется простой. Сопоставляя этот пример с общим
*) Достаточно проверить, что если hi = Я,ег + 8;, ( = 1, 2, ...
..., т — жордановы клетки оператора h с проекторами eit то спектр
оператора h содержит собственное значение Яг — Я,- с кратностью
tiitij, rih = dim eft. Формула
П
*='£4+ 2 nini
определяет суммарную кратность нулевого собственного значения
оператора h. Эта сумма минимизируется только в том случае, ко¬
гда rti = п2 = ... = п„, = 1 (откуда п = т) и Яг фкj для всех зна¬
чений i,j —1,2 т.

414 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
построением данного параграфа, мы отметим следую¬
щую специфику этого частного случая:
1. Все ненулевые корни различны, т. е. соответствую¬
щие корневые подпространства одномерны.
2. Корни coi = a,, i+i, i = 1, 2 n — 1, порождают
путем сложения все остальные положительные корни ац.
3. Корневые векторы е, = eiji+1, i = 1, 2, ..., п—1,
порождают при коммутировании всю алгебру Х+.
Важно заметить также, что корни имеют целые
координаты относительно некоторого базиса. В следую¬
щем параграфе мы исследуем аналогичные вопросы в
общем случае.
§ 92. Базис Картана — Вейля
Если выбрать базис в алгебре Я и корневых подпро¬
странствах Ха, а Я 0, то мы получим базис во всей ал¬
гебре X. Найдем соотношения коммутации между эле¬
ментами этого базиса. Прежде всего докажем, что имеет
место
Теорема 2. Пусть X — полупростая комплексная
алгебра Ли. Тогда:
1° Все корневые подпространства Ха, а Ф 0, одно¬
мерны.
2° Линейная оболочка 0 трех векторов ееТа, /еХ_а,
k = [£>/]. (e,f) =5^0, образует в алгебре X трехмерную
подалгебру, изоморфную si (2).
3° Если нормировать векторы е, / условием (е,/)=1,
то a (h) = (k, h) для всякого h е Н.
Доказательство. Поскольку форма Киллинга —
Картана невырождена на паре (Ха,Х^а), то существует
пара векторов е<=Ха, /е Х_а, для которых (e,f) Ф 0.
Нормируем эти векторы условием (е, /) = 1 и положим
k = [e,f].
Докажем, что k Ф 0. Для этого рассмотрим произволь¬
ный элемент АеЯ и заметим, что (в силу теоремы 1)
[h,e] = a(h)e. Следовательно,
(.h, k) = (h, Def) = - (Deh, f) = a (h) (e, f) = a (h).

§ 92. БАЗИС КАРТАНА - ВЕЙЛЯ
41б
Поскольку корень а ненулевой, то существует вектор
h^H, для которого a (h) ф 0. Следовательно, k ф 0.
Далее, в силу теоремы 1 векторы е, f являются собствен¬
ными относительно k:
[k, е] = ре, [k, f]= - [if,
где р = а (к) —значение корня а на векторе к. Если
р = 0, то согласно общей формуле, полученной в конце
§ 86, мы имеем Л(&) =0 для каждого корня Л. Отсюда,
как и на стр. 394, следовало бы, что k = 0. В результате
р ф 0. Полагая
_ е k f
e+~7W' е°~7’ e~~vW'
получаем, как легко проверить, закон коммутации в ал¬
гебре si (2). Следовательно, алгебра 0 = [e,f, k) изо¬
морфна si (2). Далее, рассмотрим линейное пространство
Z = Q-\-Xa-3rX2aJrXzaJr
где Ха — дополнение в Ха к направлению вектора
е е Ха. Подпространство Z инвариантно относительно k,
и след оператора k в этом подпространстве есть
рК + л2а + "за+ ■••)> ГДО na = dim^a> Пр = dim
С другой стороны, след коммутатора равен нулю,
откуда ti'a = п2а = п3а= ... =0. В частности,
dim Ха = 1,
и если а ф 0 является корнем, то 2а, За, ... уже не яв¬
ляются корнями алгебры X. Теорема доказана.
Замечание 1. Помимо утверждений, включенных
в формулировку теоремы, мы доказали еще следующее
утверждение:
4° Единственными кратными корня а в алгебре X
являются корни 0, ±а. Если а ф 0, то (а, а) ф 0.
Следствие. В алгебре X существует базис из эле¬
ментов h е Н и корневых векторов еа, а ф 0, где еа —
произвольный ненулевой вектор из Ха.
Полученный базис называется базисом Картана —
Вейля. В нем мы можем непосредственно выписать все
соотношения коммутации. Коммутатор ka = [еа, е_а], для

416 гл. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
которого имеет место тождество а (/г) = (h,ka), мы усло¬
вимся отождествлять с корнем а и обозначим тем же
символом а. Тогда имеем
[еа, б—а] rt, [h, еа] = (h, о) еа,
[ба, бр] = Аарба+р.
Последнее равенство вытекает из общего правила ком¬
мутации между Ха, Ар с учетом одномерности Ха+$.
При этом, разумеется, Na$ = 0, если а + р не является
корнем. Для окончательного описания законов комму¬
тации достаточно найти коэффициенты Na$. Мы дока¬
жем пока только следующее утверждение:
5° Если а + р является корнем, то NФ 0.
Для доказательства достаточно заметить, что Na$
является матричным элементом трехчленной алгебры
0 = {е_а, а, еа}. Точнее, пусть р и q — минимальное и
максимальное из целых чисел п, для которых р Ф па
является корнем, и Y — линейная оболочка корневых
векторов бр+ла, p^Cn^Cq. Тогда подпространство У ин¬
вариантно относительно Дх, хеб, и вектор е$+Па являет¬
ся собственным вектором относительно Da с собствен¬
ным значением (р, а) +п (а, а). Заменяя, как при доказа¬
тельстве теоремы 2, а на е0 = а/ (а, а), получаем цепоч¬
ку собственных значений вида с + п, p^n^Cq, с =
= (р, а)/(а, а). Согласно теории представлений алгебры
si(2) это возможно только в том случае, когда такая
цепочка симметрична относительно нуля и представление
в пространстве У неприводимо. При этом все веса с + п
должны встречаться без пропусков и «повышающий»
оператор ёа должен быть отличен от нуля на каждом ве¬
совом базисном векторе, за исключением старшего. По¬
скольку еяер = /Vapea+0, мы получаем нужное утверж¬
дение.
Замечание 2. Отметим некоторые свойства сим¬
метрии коэффициентов /Vap. Прежде всего N$a = —Na$
за счет антисимметричности коммутатора [еа,ер]. Далее,
пусть а, р, у — ненулевые корни, для которых а + р + у =
=0; тогда из тождества Якоби для элементов еа, ер, еу
находим
Npva + NvaP "У NapY = о•

§ 93. ПРОСТЫЕ КОРНИ
417
С другой стороны, а + р + у = 0, т. е. корни а, р, у лежат
в пересечении двух плоскостей. Если эти плоскости не
совпадают, то корни сс, р, у коллинеарны, откуда ввиду
условия а + р + у = О и свойства 4° заключаем, что хотя
бы один из корней обращается в нуль. Поскольку этот
случай исключен, то jVpY = Nya = Na$.
Замечание 3. Из свойства симметрии для цепочки
с + п, построенной при доказательстве утверждения 5°,
заключаем, в частности, что с + р = —(с + q), т. е.
, 2 (а, Р) , ,
р + я = --((*)
Здесь р и q — минимальное и максимальное из целых
чисел, для которых р + па является корнем. Мы суще¬
ственно воспользуемся этим замечанием в дальнейшем.
§ 93. Простые корни
Пусть г—размерность картановской подалгебры Н.
Как следует из определения этой подалгебры, число г
является инвариантной характеристикой алгебры X (не
зависящей от выбора Н). Это число называется рангом
алгебры X. Покажем вначале, что имеет место следую¬
щее утверждение:
1° Среди корней подалгебры Н имеется ровно г ли¬
нейно независимых.
Действительно, если zla для всех значений а и
геЯ, то а (г) = (а, г) = 0 для всякого корня а, откуда
(г, h) = 0, /г еЯ, т. е. г = 0 (поскольку форма Кил-
линга — Картана невырождена на подалгебре Я). Сле¬
довательно, линейная оболочка всех корней аеЯ со¬
впадает со всей алгеброй. Н.
Исследуем несколько подробнее геометрические свой¬
ства системы корней.
2° Пусть Н0 — вещественная линейная оболочка си¬
стемы всех корней. Тогда форма Киллинга — Картана
является (строго) положительно определенной на Н0 и
(а, Р) рационально для каждой пары корней а, р.
Действительно, если а Ф 0, то а — [еа, е_J и скаляр¬
ный квадрат элемента а может быть вычислен по

418 ГЛ. XIV. КОМПАКТНЫЕ И РЁДУКТИВНЫЕ АЛГЕБРЫ ЛИ
общему правилу, указанному в конце § 86:
(а, а) = sp D2a = р2 (a, af.
Здесь в правой части этого равенства скалярное произ¬
ведение (а, а) рассматривается как значение линейной
формы а на векторе а ей. Поскольку (а, а) ф 0, то
мы имеем
К а) = 4~>0-
Р2
Следовательно, (а, а) есть положительное рациональ¬
ное число. Далее, если (3 — корень, то (р,а) = р(а) =
= г-а(а) = г(а,а), где г-—рациональное число (см.
конец § 86). Следовательно, значение (а,р) является
рациональным для каждой пары корней а, р. Отсюда
также заключаем, что форма Киллинга — Картана яв¬
ляется вещественной на Н0. Наконец, если геЯо, то
мы имеем
{х, х) = sp D2X = 2 (a, xf Д 0.
а
Равенство (х,х) =0 возможно только при х = 0. Сле¬
довательно, форма Киллинга — Картана является (стро¬
го) положительно определенной на Я0.
Введем теперь следующее
Определение 3. Положительный корень со назы¬
вается простым, если его невозможно представить в
виде суммы двух положительных корней.
Теорема 3. Простые корни образуют базис в кар-
тановской подалгебре Н, Всякий корень а однозначно
Г
записывается в виде 2 где со, — простые корни и
г=1
пг{ — целые числа одинакового знака.
Доказательство. Если а — положительный ко¬
рень, то возможность его представления в виде суммы
простых корней с неотрицательными целыми коэффи¬
циентами очевидна. Действительно, если корень а не
простой, то а = р + у, где р и у — положительные кор¬
ни, причем, очевидно, р < а, у < а (относительно лекси¬
кографической упорядоченности в Я). Следовательно,
наше утверждение доказывается путем конечной индук¬

§ 93. ПРОСТЫЕ КОРНИ 419
ции. Остается проверить, что простые корни линейно не¬
зависимы.
Согласно замечанию, сделанному в конце § 92, для
каждой пары корней а, |3 имеет место следующая фор¬
мула:
2 («, (3) , ,
где р и q — минимальное и максимальное из целых чи¬
сел п, для которых р + па является корнем. Допустим,
в частности, что а, |3 — простые корни. Тогда их разность
Р — а — у не может быть ни положительным, ни отри¬
цательным корнем (в противном случае один из данных
корней оказался бы непростым). Следовательно, в этом
случае р = 0 и мы получаем
(а, Р)= - -j(а, а)<0.
Следовательно, если оц, (ог, wr — простые корни, то
их попарные скалярные произведения либо равны нулю,
либо отрицательны. Рассмотрим теперь произвольное
линейное соотношение между этими корнями:
Гсог = 0.
Здесь А*— произвольные комплексные числа. Умножая
скалярно на toполучаем систему числовых уравнений
для определения коэффициентов Аг':
г! (со,, со,) = 0.
Поскольку матрица этой системы действительна, то вме¬
сте с числами АТ числа Re Ат, ImAT также являются ре¬
шениями этой системы. Следовательно, можем рассма¬
тривать только решения в классе действительных чисел.
Запишем исходное уравнение в виде
а'со,- = Ь;со;-,
где числа а\ Ъ> неотрицательны и корни, входящие сле¬
ва и справа с ненулевыми коэффициентами, различны.
Пусть х — общее значение обеих частей этого урав¬
нения. Поскольку х^Н0, то мы имеем (х, х) >0.

420 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
С другой стороны, (о),-, (Dj)^0 при агТПХ),
а}Ъг’ = 0, откуда имеем
(х, х) = а’ЬЦыи <bj) < 0.
В результате х = 0. Поскольку > 0, заключаем от¬
сюда, что а{ = Ь* = 0. Следовательно, наша система до¬
пускает только нулевые решения. Теорема доказана.
Специально отметим важное геометрическое свой¬
ство простых корней, полученное при доказательстве
этой теоремы:
3° Все простые корни алгебры X расположены в ве¬
щественном евклидовом пространстве Н0 попарно под
прямым или тупым углом', (а, р)<^0 при аФ$.
Для всех элементов из Н0 и, в частности, для всех
корней понятие лексикографической упорядоченности
можно рассматривать по отношению к базису ац, i — 1,
2, .... г*).
4° Всякий положительный корень либо является про¬
стым, либо может быть представлен в виде суммы по¬
ложительного и простого корней.
Действительно, пусть р— положительный корень,
Г
Р = 2 Если (Р, 0)г) <0 для всех простых
i = 1
г
корней со,, то (р, р) = 2 mi (P. ®i) ^ 0, откуда р = 0.
< = I
Следовательно, если р не простой корень, то (р, а) > 0
хотя бы для одного простого корня а = со;. Тогда из ра¬
венства (*) § 92 находим, что p + q<Q. Поскольку q
не может быть отрицательно, то р < 0. Следовательно,
вектор у = Р— Wj является корнем. Так как корень ац
простой, то корень у не может быть отрицательным.
Следовательно, р = у + со,, у > 0.
1 5° Если известна система П всех простых корней, то
по ней однозначно может быть восстановлена система Д
всех ненулевых корней алгебры X.
Действительно, рассмотрим вначале систему Д+ всех
положительных корней. Запишем всякий корень а е Д+
*) Иногда вместо базиса С0( удобно рассматривать «дуальный
базис», состоящий из векторов д\ i = 1, 2,..., г, для которых
(д\ oij) = X,6ij, где 6ij — символ Кронекера.

§ 94. СТРУКТУРНАЯ МАТРИЦА КАРТАНА
421
в виде а = S Щю; и назовем число поряд-
i=1 г=1
ком этого корня. Множество всех корней порядка 1 сов¬
падает с системой П. Пусть Пт — множество всех кор¬
ней порядка т. Если система Пт уже описана, то для
описания Пт+] достаточно, согласно свойству 4°, пере¬
числить все пары |3 е П)п, а = сог е II, для которых век¬
тор у = |3 + а. является корнем. Отбросим тривиальный
случай (3 = а. Тогда мы имеем (3 = 2 яг/со,- + яггсоh где
/ ф i
хотя бы одно из чисел nij положительно. Следовательно,
вектор |3 + па является корнем только при яг, + я 0.
Если п 0, то корень (3 + па имеет порядок т + п ^ т,
и такие корни нам уже известны. Следовательно, нам
известно число р = min(n), где min берется по тем зна¬
чениям я, для которых р + па является корнем. Тогда
из равенства («) § 92 находим q = max (я). Вектор р + а
является корнем только при q Е
§ 94. Структурная матрица Картана
Пусть П = {со 1, сог, , сог} — система простых корней
алгебры X. Множество целых чисел
2(со., со.)
(“г “/)
(*)
несет в себе информацию о геометрии системы П.
Матрица с = ||сг-,|| называется структурной матрицей
Картана.
Теорема 4. Если две полупростые комплексные
алгебры Ли имеют одну и ту же структурную матрицу
Картана, то они изоморфны.
Доказательство. Пусть X, Y—две полупростые
комплексные алгебры Ли. Из совпадения структурных
матриц Картана следует, в частности, что эти алгебры
имеют одинаковый ранг. Кроме того, существует взаимно
однозначное соответствие между подсистемами простых
корней в X и Y. Заметим, что знание чисел (■::•) позво¬
ляет определить длины векторов м, с точностью до об¬
щего множителя К > 0. Далее, согласно свойству 5° из

422 гл XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
предыдущего параграфа существует также взаимно одно¬
значное соответствие между системами корней в X и Y.
Очевидно, это соответствие является изометрией с точ¬
ностью до множителя X. Пусть а, р— произвольные кор¬
ни алгебры X. Тогда имеем
(а, р) = sp DaD„ = 2 (а, Y) (y. Р)-
у
Такое же соотношение должно выполняться для алгеб¬
ры Y. Нетрудно видеть, что это возможно только при
Х = 1. Теперь мы попросту можем отождествить систе¬
мы корней в X и Y. Используя базис Картана — Вейля,
заключаем, что X и Y изоморфны как линейные про¬
странства. Далее, условимся, что корневые векторы
eteX, fa е Y нормированы одним и тем же соотноше¬
нием (еа, е_а) = (fa, /_а) = 1; тогда [еа, e_J = [fa, = а,
и остается исследовать соотношения коммутации вида
[= ^aflea+fl> [/а> ^[з] = ^ар^а+р-
Покажем, что за счет перенормировки базиса fa мо¬
жно добиться выполнения равенства АДр = Яар для всех
а, р g i. Заметим, что множество А вполне упорядочено.
Введем обозначение Др для множества всех ненулевых
корней а, для которых —р < а < р, реД+. Если ко¬
рень о непосредственно следует за р, то мы имеем
— {~ р}+ Ар + {р}-
Следовательно, в нашем распоряжении имеется возмож¬
ность конечной индукции по возрастающему индексу р.
Допустим, что равенство Na р = N ар уже доказано для
всех корней а, р таких, что а, р, а + ре Др. Добавляя
корень р, мы приходим к рассмотрению троек а, р,
а + р е Др, у которых хотя бы один из элементов сов¬
падает с ±р. Полагая а + Р = —у, приходим к рассмо¬
трению троек а, р, у е Да, а + р + у = 0, у которых хотя
бы один из элементов совпадает с ±р. Ясно, что этим
свойством может обладать лишь один из элементов
а, р, у. Рассмотрим отдельно следующие возможные
случаи.
1. Корень р невозможно представить в
виде суммы а + р, а, р е Др. В этом случае корень р
вообще невозможно представить в виде суммы двух по¬

§ 94. СТРУКТУРНАЯ МАТРИЦА КАРТАНА
423
ложительных корней (т. е. он является простым), и для
векторов Др, /р мы выбираем произвольную нормиров¬
ку с учетом равенства (fp,f-p) = 1.
2. Существует единственная пара векто¬
ров а, |ЗеДр, для которых а + р = р. Ввиду соот¬
ношений симметрии АДр = TVpY = Nya при у = —р, до¬
казанных в § 92, мы можем ограничиться рассмотрением
констант Nae, АДр- Вычисляя коммутатор [Д, fp], мы
нормируем вектор fp так, чтобы выполнялось равенство
[fa, fp] = Napfp-
Следовательно, в этом случае АДр = А^р. Нормируем те¬
перь /_р, исходя из условия (fp, f_p) = 1, и покажем, что
при этом выполняется также равенство N~a, -e = N-a, -р-
Для этого заметим, что
Д—a> Да, ®р] ] ^а$^—а, — у^р ^ар^—а. — р^р>
где —у = а + |3. Действительно, в силу условия а + р +
+ Y = 0 мы имеем АСа, = АДр, _а = —АПа_р. Разде¬
лим обе части этого равенства на (a, а)/2; тогда элемен¬
ты e_a, еа мы можем заменить нормированными элемен¬
тами е_, е+, введенными при доказательстве теоремы 2.
Тогда полученное равенство запишется в виде e_e+f = Xf,
где f = ер. Собственное значение X не зависит от
нормировки вектора f и определяется только законами
представлений трехчленной алгебры si (2). Следова¬
тельно,
АДрА^-а, -р = АДрА?_а1 -р’
и отсюда вытекает наше утверждение. В результате по¬
лучаем равенства АДр = АДр, АДа,-р = АДа,-р.
3. Наряду с рассмотренной парой корней
а, р существует также другая пара а', р',
для которой а' + р' = р, а', р'е Др. Нормировку век¬
торов f_р, fp производим, как и выше (по отношению к
паре a, Р). Положим у = —а', б = —р'. Тогда a + р +
+ у + б = 0, и ни одна из попарных сумм этих корней
не обращается в нуль. Применяя тождество Якоби к

424 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
элементам еа, ер, еу, легко получаем равенство
NafiN^6 "Ь N yaN 0.
Т акое же равенство должно иметь место для N ар, Ny6, ...
Заметим, что |3 + у> а + 6, у + а, р + 6 е Ар. Следова¬
тельно, в последних двух членах получаемой суммы
ШТРИХИ МОЖНО ОПУСТИТЬ. В результате Na&Ny6 = NaflNyd
(напомним, что Nag, = Naр), и отсюда Nye = Nye. Анало¬
гично, N-у, -б = N-у, -б.
Теорема доказана.
Следствие. Всякий автоморфизм*) подалгебры Н,
сохраняющий систему корней, может быть продолжен
до автоморфизма всей алгебры X, т. е. до линейного ото¬
бражения f(x), при котором [/(ли), f(y)] = f([x,y]).
Замечание 1. Пусть М = || (а, (3) || — матрица ска¬
лярных произведений всех корней а, р е Д, Как мы ви¬
дели при доказательстве теоремы 4,
М = М'М,
где штрих означает транспонирование (и также М = М2,
поскольку М = М'). Поскольку М вещественно, то от¬
сюда вытекает, что матрица М является положительно
определенной.
Замечание 2. Применим следствие из теоремы 4
к автоморфизму f(h) =—h в алгебре Н. Пусть f (х) —
продолжение этого автоморфизма на алгебру X; тогда,
очевидно, f (еа) = сае^а. Поскольку форма Киллинга —
Картана должна сохраняться при автоморфизме, то мы
имеем
(/ Ya), /" а)) (^-а* ^—а)>
откуда сас-а = 1. Полагая ea=Yca$a> получаем новые
корневые векторы ёа, для которых f(ea) = ё~а. Следова¬
тельно, векторы еа можно с самого начала считать нор¬
мированными так, чтобы отображение
а —* —а, еа —* е^а
*) Заметим, что автоморфизм коммутативной алгебры Ли есть
произвольное линейное невырожденное преобразование в этой ал¬
гебре.

§ 95. ПРОСТЫЕ КОМПЛЕКСНЫЕ АЛГЕБРЫ ЛИ
425
определяло автоморфизм всей алгебры X. Иначе говоря,
при указанном выборе базиса мы имеем Na$ = _р.
Полагая еа = i У^аёа, мы можем также добиться выпол¬
нения равенства Na$ = —_р.
Замечание 3. При доказательстве теоремы 4 мы
видели, что NaaN^a, = — X , где К — собственное
значение оператора ё-ё+ на векторе ер. Обращаясь к
теории представлений алгебры si (2), легко находим, что
X = (I — v) (/ + v + 1), где / = v + q = —(v + p) —стар¬
ший вес неприводимого представления si (2) в базисе
ец+па, р^Сп-^Сд. Следовательно,
g*-(a, a),
если условиться считать, как выше, что jVap = —ALa,_p.
Поскольку р -гС 0, q ^ 0, то мы заключаем, что ^ О,
т. е. jV«|3 — рациональное вещественное число. Известно
также ([145]), что при некоторой нормировке базиса все
константы Na р могут быть сделаны целыми*).
§ 95. Простые комплексные алгебры Ли
Резюмируем вначале результаты проведенного ис¬
следования.
Теорема 5. Во всякой полупростой комплексной
алгебре X существует базис из элементов /г,-, еа, где
элементы /г;, i = 1, 2, ..., г, порождают максимальную
коммутативную подалгебру Н и остальные соотношения
коммутации имеют вид
[h, еа] = (h, а) еа,
[еа, б_а] a, [еа, ер] N
Здесь индексы а (корни алгебры X) отождествляются
с векторами аеИ, для которых a(h)= (h,a), и h про¬
бегает Н. /Vap ф 0 тогда и только тогда, когда а + р
является корнем. Базисные векторы еа можно нормиро¬
вать так, чтобы константы Naр были вещественными.
*) Отсюда вытекает важное заключение о возможности опре¬
деления алгебры X над произвольным полем.

426 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
Далее, пусть П = {соь «2, • • ■, ыг} — система всех про¬
стых корней алгебры X. Простые корни образуют базис
в картановской подалгебре Н, Система П определяет
алгебру X с точностью до автоморфизма.
Перечислим также некоторые дополнительные свой¬
ства алгебры X, не включенные в теорему 5.
1° Алгебра X может быть представлена в виде пря¬
мой суммы
Х = Х-+Н + Х+,
где Х-, Х+— нильпотентные подалгебры в X, натяну¬
тые соответственно на корневые векторы еа, а < О,
а > 0.
Действительно, [eaj, [е^,..., [e^^J ...]] = 0 при
некотором п, если все корни а.\, аг, . ■., ап отрицатель¬
ны или все положительны. Следовательно, X_ и Х+
нильпотентны.
2°. Всякий корень а однозначно представляется в
Г
виде 2 /ягсо;, где mi — целые числа одинакового знака.
Если а — корень, то (а,а)>0.
Далее, напомним, что картановская подалгебра Н
определялась нами как максимальная коммутативная
подалгебра, содержащая регулярный элемент hQ. Од¬
нако теперь нетрудно получить другую характеристику
этой подалгебры, более удобную для приложений:
3° Картановская подалгебра Н может быть охарак¬
теризована как максимальная коммутативная подал¬
гебра в X, все преобразования которой (Dhx = [h, х])
в алгебре X диагонализуются.
Действительно, если алгебра Н обладает указан¬
ными свойствами, то для нее возможно повторить по¬
строение базиса Картана — Вейля. Пусть /10еЯ обла¬
дает тем свойством, что (h, при i = 1, 2, ..., г
(очевидно, такой элемент существует). Тогда нетрудно
видеть, что h0 регулярен, т. е. Н является картановской
подалгеброй.
4° Если алгебра X проста, то для каждого ее линей¬
ного представления p(x) мы имеем
{х, у) = ср sp р (*) р (у),

§ 95. ПРОСТЫЕ КОМПЛЕКСНЫЕ АЛГЕБРЫ ЛИ
427
где (х, у) — sp DXDV — билинейная форма Киллинга —
Картана и коэффициент ср не зависит от х, у е X.
Действительно, билинейная форма f(x,y) =
= sp р(х)р(г/) обладает свойством f (Dax, у) + f (х, Day) =
= 0. Поскольку алгебра X проста, то ее присоединен¬
ное представление неприводимо. Отсюда в силу леммы
Шура следует, что форма f(x,y) определяется одно¬
значно с точностью до множителя. Следовательно,
f(x, у) = — (х, у), и мы полагаем с = ср.
Рассмотрим, наконец, систему Г1 всех простых кор¬
ней алгебры X. Скажем, что система П распадается,
если П = IT U П", где корни подсистемы П' ортого¬
нальны корням подсистемы П". В качестве неслож¬
ного упражнения предлагается доказать следующее
свойство, выделяющее класс простых комплексных
алгебр Ли:
5° Алгебра X является простой тогда и только тогда,
когда система П не распадается.
Рассмотрим теперь структурную матрицу Картана:
Сц = 2(со;, coj)/((Of, coi), где to,-, i=l, 2, ..., г, — простые
корни алгебры X. Заметим, что
4 (м., со .)2
' 1 А Л 2П
С; j С ц = 7 г-. г = 4 COS" tj,f)
11 “
где d,j — угол между векторами сог-, coj (которые рас¬
сматриваются в вещественном евклидовом простран¬
стве Я0 с базисом со,, i=l, 2, ..., г). Поскольку чис¬
ла сц являются целыми, то мы заключаем, что
сцсп = 0, 1, 2, 3
либо CijCji = 4, но тогда cos2 0i3- = 1, т. е. со, = сщ. Усло¬
вимся каждый корень символически изображать кру¬
жочком. Если со,, соj — два различных простых корня,
то соответствующие два кружочка мы соединяем одним,
двумя или тремя отрезками прямой линии в зависимости
от числа Пц = сцСц:
/j о о г) <=d 3)

428 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
Если tiij — 0, то кружочки вообще не соединяются.
В этом случае cos 0;j. = 0, т. е. со, _L coj. В случаях 1),
2), 3) мы имеем соответственно 0,j = 120°, 135°, 150°.
Действительно, угол между простыми корнями должен
быть тупым.
Полученный способ чрезвычайно удобен для симво¬
лического изображения структурной матрицы Картана.
Этот способ был предложен Е. Б. Дын к и н ы м [77].
Если все простые корни алгебры изобразить графиче¬
ски указанным способом, то в результате возникает ко¬
нечная схема, называемая схемой Дынкина.
Поскольку ортогональные корни не связываются ли¬
нией, то мы получаем наглядную характеристику про¬
стых алгебр Ли. Алгебра X является простой тогда и
только тогда, когда ее схема Дынкина не распадается
на две подсхемы. В этом случае каждые два кружочка
соединяются между собой хотя бы одной ломаной ли¬
нией, состоящей из отрезков схемы. Такая схема на¬
зывается связной.
Для классификации всех простых комплексных ал¬
гебр Ли достаточно теперь перечислить всевозможные
связные схемы Дынкина в г-мерном евклидовом про¬
странстве. Мы не станем заниматься решением этой
задачи. См. по этому поводу [128]. Ограничимся иллю¬
страцией полученных результатов на примере класси¬
ческих алгебр Ли.
Пример 1. Алгебра si (и). Мы видели в § 91,
что корнями этой алгебры являются линейные формы.
а«7 (h) = ((ei- еД h) = Kt — Kj,
где е{ = (0, ..., 0, 1, 0,..., 0) с единицей на г-м месте в
скобка (х,у) означает скалярное произведение в ев¬
клидовом пространстве Еп размерности п. Следователь¬
но, векторы ссц = е,- — еj мы можем отождествить с кор¬
нями si (я). Корень а,-; является положительным при
i < / и отрицательным при i > j. Корни
®; = ас,(+ъ »=1. 2, . . ., п- 1,
являются простыми. Число г = п — 1 является рангом
алгебры sl(«). Воспользуемся теперь замечанием 4°, со¬
гласно которому вместо формы Киллинга — Картана

§ 95. ПРОСТЫЕ КОМПЛЕКСНЫЕ АЛГЕБРЫ ЛИ
429
в Н мы можем рассматривать скалярное произведение
в Еп. Нетрудно видеть, что 0;, ,-+i = 120° и 0,j = 90° во
всех остальных случаях. Следовательно, схема Дынки-
на в данном случае имеет вид
/
Единицы, стоящие под кружочками, указывают относи¬
тельную длину (относительно некоторого масштаба)
всех простых векторов соi, сог, con-ь Действительно,
все эти векторы имеют одинаковую длину.
Пример 2. Алгебра so(n). Вместо суммы квад¬
ратов нам будет удобно рассматривать в Еп квадра¬
тичную форму (sac, ас), где скобка означает обычное ска¬
лярное произведение и
s =
0
1
1
0
s- = е.
Тогда элементы из X = so(n) выделяются условием
sx's = —х, т. е. являются кососимметричными относи¬
тельно второй диагонали. Положим п = 2v или n = 2v+l
в зависимости от четности или нечетности размерно¬
сти п и условимся, что базис нумеруется целыми чис¬
лами —v, —v +1, ..., v, причем индекс 0 пропускается,
если п четно. Тогда транспонирование х = sx's относи¬
тельно второй диагонали задается формулой лД --
= x—j—i для матрицы а; = ||ас^-|Д j=_v, .... v. Элементы
fil б;/ l< —ь 1 ^ T
где вц— стандартный базис в классе матриц п X п, об¬
разуют базис в алгебре X. Далее, пусть Н — совокуп¬
ность всех диагональных матриц из X. Полагая
V
h — 2 ^-ieu, замечаем, что %i = —k-i в силу условия

430 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
кососимметричности; следовательно, также h = 2 ^tht,
<■-1
где _j и собственные значения \и i = 1, 2, ...
..., v, независимы. Имеем
[Л, ft/] = (Яг —
Следовательно, вектор /,7 является собственным векто¬
ром относительно оператора h = Dh. Если / Ф i, / > —д
то линейные формы ац(Н) — к{ — Kj не обращаются
тождественно в нуль и попарно различны. Отсюда за¬
ключаем, что алгебра Н является максимальной ком¬
мутативной подалгеброй в X. Согласно 3° алгебра 11
является картановской подалгеброй в X.
Для вложения корней в картановскую подалгебру Н
достаточно выразить все корни*) через значения Ки X,
с положительными индексами /, / = 1, 2, ..., v. При
этом мы имеем ац = К — Я,- = ((еj — е3),/г), i < /;
ctj, -j = Я* + А,,- = ((fix + 6j), h), ai0 = = (ej, /г). Следо¬
вательно, корни разбиваются на следующие подгруппы:
щ} = et-e,, i < /; 0l7 = е; + е,-, i, j = 1, 2, ..., v;
<%, = ег, «'= 1, 2, .. ., v
(последнее в случае, когда имеется индекс 0). Согласно
замечанию 4° мы можем вместо билинейной формы Кил-
линга — Картана в Н воспользоваться обычным скаляр¬
ным произведением в Ev. Если п нечетно, то простыми
корнями ЯВЛЯЮТСЯ корни СО, = (Ot, i+l, t= 1, 2, ..., V— 1,
cov = covo. В этом случае схема Дынкина имеет вид
г г гг г г г /
Если п четно, то в качестве простых корней мы выби¬
раем (о* = он, ,+ь t = 1, 2, ..., v—1, cov = 0V. В резуль¬
тате получаем схему Дынкина
*) В силу соотношения —X-i = Xi\ здесь мы вписываем только
положительные корни.

§ 96. ВЕЩЕСТВЕННЫЕ ФОРМЫ
431
Из рассмотрения этих схем непосредственно очевидно,
что алгебра so (я), n = 2v + l, я = 2v, имеет ранг v и
является полупростой при я > 2. Если п = 3, то схема
Дынкина содержит единственный кружочек; отсюда
снова получаем, что алгебра so(3) изоморфна sl(2)*).
Если я = 4, то схема Дынкина распадается и
so (4) ~ si (2)® si (2). Следовательно, алгебра so (4) не
является простой. Если я > 4, то алгебра so (я) является
простой.
Пример 3. Алгебра sp(n). Эта алгебра состоит
из всех комплексных матриц я X я, кососимметрических
относительно билинейной формы (sx, у) с матрицей
S =
О а
■ а О
а =
О
1
1
О
я = 2v.
Полагая я = 2v и повторяя почти без изменения построе¬
ния предыдущего примера, получаем схему Дынкина
следующего вида:
§ 96. Вещественные формы полупростых комплексных
алгебр Ли
Прежде чем заканчивать классификацию, сделаем
небольшое отступление. До сих пор мы рассматривали
алгебры Ли только над полем комплексных чисел. Од¬
нако возможность комплексного продолжения позволяет
свести вещественный случай к комплексному. Следова¬
тельно, для перечисления всех вещественных полупро¬
стых алгебр Ли достаточно найти все вещественные
формы полупростых комплексных алгебр Ли.
Одна из таких вещественных форм определяется
наиболее просто в базисе Картана — Вейля. Действи¬
тельно, мы видели в § 94, что при некоторой нормировке
*) См. § 11.

432 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
этого базиса константы /Vap становятся вещественными.
Кроме того, (а, (3) вещественно для двух произвольных
корней а, р. Следовательно, в данном базисе все струк¬
турные константы вещественны. Пусть L\ — веществен¬
ная линейная оболочка векторов а, еа, где а пробегает
систему всех корней алгебры X. Тогда L\ является ал¬
геброй Ли над полем вещественных чисел. Поскольку
dim/; Lj = dime X, алгебра Lx является вещественной
формой алгебры X.
Однако в нашем распоряжении имеется еще один
универсальный способ выделения вещественной формы.
Идея этого способа состоит в аналогии с известным
включением su (я) с; si (я). Условимся нормировать ба¬
зис Картана — Вейля таким образом, чтобы константы
подчинялись соотношению Na$ = —ALa, _р (см.
Г
§ 94). Каждому вектору х = 2 ci®i + 2 саеа поставим
i = l a
в соответствие вектор
г
х' = 2 d/CD; + 2 due_a.
i = I a
Здесь со,, i = 1, 2, ..., r, — простые корни алгебры X и
черта означает комплексное сопряжение. Операцию
х~*х* назовем эрмитовым сопряжением в алгебре X.
Как нетрудно проверить, [х, у]* = [у*, х*] и (кх)* = Хх*,
т. е. эрмитово сопряжение является «антиинволюцией»
в алгебре X. Отсюда следует, что множество Z-о всех
косоэрмитовых элементов (х* = —х) из алгебры X яв¬
ляется вещественной подалгеброй в алгебре X. Эле¬
менты
KDk, i (еа “Ь е~a), е~а,
где i=Y~ 1, k—\, 2г, а > 0, образуют веще¬
ственный базис в алгебре L0. Отсюда следует, что
dim# L0 = dime X, т. е. алгебра L0 является веществен¬
ной формой в алгебре X.
Напомним, что Н J_ еа, еа J_ ер при а Ф —(3 и
(ea, е-а) = 1. Положим
^’а = ^ ^ (еа 4" е-а)> sa ~ ^ (еа е-а)

§ 96. ВЕЩЕСТВЕННЫЕ ФОРМЫ
433
и выберем среди вещественных линейных комбинации
корней ортогональную систему элементов hk, k = 1,
2, . . . , г. Тогда элементы ihk, ica, isa образуют ортого¬
нальную систему элементов, и норма каждого из этих
элементов равняется —1. Следовательно, форма Кил¬
линга — Картана является отрицательно определенной
на L0 .Отсюда заключаем, что алгебра L0 является ком¬
пактной.
В результате мы находим, что имеет место следую¬
щая замечательная
Теорема 6. Любая редуктивная комплексная ал¬
гебра Ли содержит компактную вещественную форму.
Действительно, это верно для случая полупростых
алгебр Ли, но также верно и для абелевых алгебр Ли
(комплексных векторных пространств).
Следовательно, при комплексном продолжении ком¬
пактных алгебр Ли мы получаем все комплексные ре¬
дуктивные алгебры Ли.
Мы находим замечательное соответствие между
классами компактных и комплексных редуктивных ал¬
гебр Ли. Алгебру L0 мы будем называть компактной
формой Вейля.
В заключение отметим (уже без доказательства),
как можно получить классификацию всех вещественных
редуктивных (главным образом простых или полупро¬
стых) алгебр Ли. Пусть X — комплексная полупростая
алгебра Ли и L0 — ее компактная форма Вейля. Пусть
0 — произвольный автоморфизм этой формы:
0 (Хх + |ху) = А,0х + ц0г/, 0 [х, у] = [0х, 0г/].
Автоморфизм 0 является инволютивным, если 02 = 1.
Заметим, что всякий автоморфизм сохраняет форму
Киллинга — Картана: (0х, Qy) = (х, у). Следовательно,
0 является ортогональным преобразованием в алгеб¬
ре L0. Из условия 02 = 1 следует, что 0 имеет только
собственные значения ±1. Следовательно, все линейное
пространство L0 может быть представлено в виде пря¬
мой ортогональной суммы
Aq — Lq + Lq ,

434 гл. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
где Lo {bo) — максимальное подпространство в L0, на
котором Qx = х (0% =—х). Изменяя обозначения, мы
положим K=Lo, Р = iLo . В результате
L0 = К + iP,
где пространство Р уже не содержится в L0. Нетрудно
видеть, что [К, К] сг К, [К, Р] сг Р, [Р, Р] сг К. Следова¬
тельно, если положим
L = К + Р,
то получим подалгебру L в алгебре X. Из веществен¬
ности структурных констант в L0 следует также (ввиду
указанных законов коммутации) вещественность струк¬
турных констант в алгебре L. Кроме того, dim/? L =
= dime К. Следовательно, алгебра L является вещест¬
венной формой в алгебре X.
Оказывается, что таким путем могут быть получены
все вещественные формы в алгебре X*). Разложение
L = К + Р называется разложением Картана. Таким
образом, знание Ь0 и перечисление всех возможных ин-
волютивных автоморфизмов в L0 позволяют также пе¬
речислить все вещественные формы в X. См. по этому
поводу, например, [96]. Более подробное исследование,
включающее полную классификацию вещественных
форм, содержится в работе Ф. Р. Г антмахера [63].
§ 97. Завершение классификации
Теперь мы вернемся к комплексному случаю. Как
мы видели в § 95, задача классификации всех простых
комплексных алгебр Ли свелась к задаче описания всех
допустимых связных схем Дынкина. Такая задача ре¬
шается путем несложной комбинаторики, которую за
недостатком места мы не будем сейчас воспроизводить.
См., например, [128], стр. 152—162 или [19], стр. 144—
152. Результатом является
*) Заметим, что вещественная форма может быть простой, даже
если X не проста (но полупроста). Примером является вложение
50 (4, R) a so (4, С).

§ 97. ЗАВЕРШЕНИЕ КЛАССИФИКАЦИИ
435
Теорема 7. Всякая простая комплексная алгебра
Ли определяется одной из следующих схем Дынкина:
°п ' ° / / Т~ / / / 2
При этом получаем все неизоморфные простые алгеб¬
ры, если условимся считать, что п^\ для серии Ан,
п 2 для серии Вп, я 3 для серии Сп, п >4 для се¬
рии Dn.
Алгебра Ап есть алгебра Ли группы SL(n + 1). Ал¬
гебры Вп, Dn являются алгебрами Ли группы SO (m)
при m = 2n+\, пг = 2п соответственно. Алгебра Сп
есть алгебра Ли группы Sp(2/i). Все эти алгебры носят
название классических.
Как видим, согласно теореме 7, кроме бесконечных
серий Ап — Dn классических простых алгебр Ли, суще¬
ствует еще лишь пять отдельных алгебр: Е6, Е7, Е&, К4)
Go. Эти алгебры носят название исключительных или
особых алгебр Картана.
В книге [19] можно найти эффективное построение
алгебр Ли G2, К4, Е6 и доказательство существования

436 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
£7, £8. Мы приведем лишь частичную инфрмацию об
этих алгебрах*). Начнем с таблицы корней.
Тип
Корни
Простые корни
Ап
е,- — е/г, /, k = 1, 2, . .п + 1
ei — ei + u 7=1, 2, ..n
Вп
±ei, ±ei±ek, I, k = 1, 2, ..., n
ei - e,- + I. i=l,2 /г-I; e„
Сп
±2ei, ±ei±ek, i,k = 1, 2 n
e,- — e(- + i, / = 1,2 n — 1; 2e„
Dn
±e-t±ek, i, k—\, 2, .... n
e/-e/+b 7=1, 2 n- 1;
еп-i +
Ее
ei — ek, i, k — 1,2,... 6;
ei — ei+i. 7=1, 2 5;
±)/Г2ет; y(±e,±e2±e3±
1 ,
y( — ej -e2-ej + e4 +
±е4±е5±е6)± —=■
+ e5 + ee) + y|r
£7
ei — eh, i, k = 1, 2 7;
e; - e; +1, i= 1. 2 6;
у {±e,±e2±e3±e4±e5±e±
— (— ex — e2 — e3 — e4 +
±e7±es)
+ e5 + e6 + e7 + e8)
Ее
±ei±eh, i, k = 1, 2 8;
ei — e:+I, 7=1, 2, ..., 7;
1 .
у (±е1±еа±ез±е4±е5±
1
у (—e\ — e7 — e3 — e4 +
±e6±e7±«e)
+ e3 + e6 + eT + e8)
±ei, ±ei±eh, i, k— 1, 2, 3, 4;
e\ ~ e2’> e2 — e3; e$',
У (±ei±e2±e3±e4)
— (— ej — e2 + e3 + e4)
02
±ег, ± Кз e2;
1 Кз
±yei±— e2;
3 FT
±Ye,± ~~2~ ®2
3 4. ^
ei; - y e‘ ^—2~62
Здесь е\, е2, ..., еп — ортонормированный базис
n-мерного евклидова пространства. В случаях £6, £7, £8
*) В качестве подробного справочного руководства по структу¬
ре простых алгебр Ли можно указать статью Дж. Тите а [131"]-

§ 97. ЗАВЕРШЕНИЕ КЛАССИФИКАЦИИ
437
на суммы, заключенные в круглых скобках, наклады¬
ваются следующие ограничения. В случаях Ев, Е1 та¬
кая скобка должна содержать одинаковое количество
плюсов и минусов. В случае Es количество плюсов (и
минусов) должно быть четно. Отсюда путем несложного
вычисления получаем число корней; если к этому числу
добавить ранг, то получаем, очевидно, размерность дан¬
ной алгебры. Результатом является следующая таблица:
Тип
Ап
Вп
Сп
Dn
Ее
е7
Еа
02
Размер¬
ность
п{п + 2)
п{2п + 1)
п (2ti + 1)
п (2п — 1)
78
133
248
52
14
В заключение рассмотрим все возможные простые
алгебры ранга 2. Таких (неизоморфных) алгебр толь¬
ко 3 — это Л2, В2, G2. Вот их системы корней (см.
рис. 6):
Рис. 6.
Символы со 1, (02 указывают возможный выбор про¬
стых корней (относительно некоторой лексикографиче¬
ской упорядоченности). Заметим, что корни алгебры G2
могут быть также вложены в трехмерное пространство
следующим образом: е,- — eh, i, k = 1, 2, 3; ± (Зе,- — е0),
где е0 = е{ + е2 + е3. Отсюда, в частности, следует, что
алгебра G2 содержит подалгебру, изоморфную Л2.
Особый интерес представляют алгебры Л2 и G2. Ал¬
гебра Л2 является алгеброй Ли в группе всех авгомор-

438 ГЛ. XIV. КОМПАКТНЫЕ И РЕДУКТИВНЫЕ АЛГЕБРЫ ЛИ
физмов тела кватернионов (см. § II). Алгебра G2 яв¬
ляется ([19]) алгеброй Ли в группе всех автоморфиз¬
мов чисел Кэли *).
* *
*
Существует несколько вариантов определения компактной ал¬
гебры Ли; однако все эти определения близки друг другу. Так, в
[128] рассматриваются только полупростые алгебры Ли и требуется,
чтобы форма Киллинга — Картана была отрицательно определена.
В книге [42] требуется, чтобы матрицы присоединенного представ¬
ления образовывали компактную группу. Наше определение сле¬
дует работе [38].
Классификация простых алгебр Ли над комплексным полем
была начата Киллингом и завершена Э. К а р т а н о м [94]. Ряд
существенных упрощений был внесен Г. Вейлем [61]. Окончатель¬
ная классификация корневых систем принадлежит Б. Л. Ван-дер-
Вардену [60] и Е. Б, Дынкину [77]. В частности, Е. Б. Дынкин
предложил общепринятую в настоящее время систему классифика¬
ции в терминах простых корней. Теорема о вещественных формах
была получена Э. Картаном. Доказательство, изложенное в тексте,
принадлежит Г. Вейлю [61].
Теорема 7 является кульминацией картановской теории. Вместе
с тем она принадлежит к числу наиболее удивительных открытий
в математике. Любопытно, в частности, что наряду с четырьмя
бесконечными «правильными» сериями существует всего лишь пять
исключительных алгебр Картана. В заключение заметим, что в клас¬
се разрешимых (и даже в классе нильпотентных) алгебр Ли до сих
пор не получена полная классификация.
*) Всякое число Кэли может быть записано в виде формаль-
II а а II
ной матрицы второго порядка , где а, Р — комплексные
II Ь р ||
числа и а, b — произвольные векторы из трехмерного комплексного
евклидова пространства. Закон умножения определяется формулой
II а а IIII у с || N ау — ad ас + аб + b X d ||
II b Р 11 d б I || b\ + prf + а X с — Ьс + рб Г
где pq, р X q — соответственно скалярное и векторное произведение
векторов р, q. Умножение чисел Кэли некоммутативно и неассоциа¬
тивно, но удовлетворяет следующему «альтернативному» закону:
хгу = х(ху), ух2 = (ух)х.

ГЛАВА XV
КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ*)
После детального изучения компактных алгебр
Ли естественно перейти к задаче описания компактной
группы «в целом». Мы опишем в этой главе некоторые
структурные свойства компактных групп Ли, вытекаю¬
щие из картановской теории. Кроме того, остановимся
несколько более подробно на общетеоретических вопро¬
сах, которые в начале книги намечались лишь конспек¬
тивно.
Одним из замечательных свойств компактной груп¬
пы Ли, позволяющим решать глобальные вопросы, яв¬
ляется ее линейность (§ 31). Иначе говоря, компактную
группу Ли мы можем рассматривать как замкнутую
подгруппу в О(«). Помимо линейности мы установим
в начале этой главы еще более сильное свойство ком¬
пактной группы — ее «алгебраичносгь».
Для доказательства этого свойства нам будут нуж¬
ны некоторые сведения из теории инвариантов.
§ 98. Инвариантные полиномы
Пусть G — линейная группа, действующая в вектор¬
ном пространстве V. Формула
Tgp М = р (xg),
где xg е V — вектор, получаемый из х преобразованием
geG, переносит действие группы на алгебру полино¬
мов р(х). Полином р(х) называется инвариантным,
если
Р (xg) = р (*)
*) Читатель-физик при желании может' опустить эту главу,
ограничившись формулировками основных результатов,

440
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
для всех geG. Множество / всех инвариантных поли¬
номов является подалгеброй в алгебре 3* полиномов
р(х). Докажем, что имеет место*)
Теорема 1. Если G — компактная группа, то ал¬
гебра / имеет конечное число образующих.
Доказательство. В основе доказательства ле¬
жит классическая теорема Гильберта об идеалах в ал¬
гебре полиномов. Множество Д сг 3 называется идеа¬
лом, если =Э, т. е. если р{х)](х)^.Р/ для всякого
р(х)^3 и всякого Согласно теореме Гиль¬
берта ([7], [22]) для всякого идеала Д существует ко¬
нечное число элементов jh(x)<=3f, k—\, 2, ..., m, та¬
ких, что всякий элемент /йеЗ' может быть записан
в виде
/ (х) = р, (х) /, (х) + р2 (*) /2 (х) + ... + рт (х) jm (х),
где ph(x)^3, k=\, 2, ..., т. Элементы ju /2, •••, im
называются образующими идеала 3.
В частности, пусть / — алгебра полиномов, инва¬
риантных относительно группы G. Пусть /р — множе¬
ство всех инвариантных полиномов степени р, р — 0, 1,
2, ... Положим
у = 3р+3>12+ ... +3Ik+ ...;
тогда, очевидно, 3 является идеалом в 3. Образующие
Гильберта j\, /2, ..., /,,, можно в данном случае, оче¬
видно, считать инвариантными и однородными.
Докажем, что элементы /ь /2, ..., jm являются так¬
же образующими в алгебре /. Пусть / — однородный
инвариантный полином, / е/Р; тогда мы имеем /еЗ',
и, следовательно,
/ (х) = Pi (х) /, (х) + р2 {х) /2 (х)+ ... + рт (х) jm (х),
где ph{x)<=3, k — 1, 2, ..., т. Применим к обеим ча¬
стям этого равенства оператор Tg. Ввиду инвариантно¬
сти j(x), jh(x) преобразование Tg сводится к замене
*) Дли доказательства алгебраичности компактной группы G
эта теорема не нужна. Однако она несколько проясняет ситуацию
при рассмотрении данного вопроса и, кроме того, представляет не¬
сомненный самостоятельный интерес.

§ 98. ИНВАРИАНТНЫЕ ПОЛИНОМЫ
441
каждого коэффициента Pk{x) на Ph(xg). Используем
теперь процесс усреднения по компактной группе G.
Интегрируя по G, получаем
/ (*) = ф, (*) /, (х) + Ф2 (х) /, (х) + ... + фт (*) jm (х),
где щ{х)— результат усреднения ри{х) по группе G.
Согласно свойству усреднения (§ 26) фДх) является
инвариантным полиномом относительно G, ср 1{(х)^1.
Заметим теперь, что степень каждого из полиномов
q>k(x), jh(x) должна быть строго меньше степени j(x)
(в противном случае либо jk{x) = 0, либо ph{x) = 0).
Применяя индукцию по степени, заключаем, что j (х)
является полиномом от ji(x), j2 (х), ..., jm(x):
■ i(x) = F (jiix), j2(x) jm(x)).
Теорема доказана.
Пусть x — фиксированная точка из V. Множество
xG, состоящие из всех элементов xg, g е G, называется
орбитой элемента х (относительно группы G). Орбиту
элемента х мы будем иногда обозначать Ох. Очевидно,
две орбиты Ох, Оу либо совпадают (у = xg), либо не
имеют общих точек. Докажем, что имеет место
Теорема 2. Если G — компактная группа, то для
каждой пары орбит Ох, Оу, Ох ф Оу, существует инва¬
риантный полином ф(г)е/, принимающий на этих орби¬
тах разные значения.
Доказательство. Из компактности группы G
следует также компактность каждой орбиты Ох *). Если
Ох Ф Ои, то функция
6(z) = p(z, Оу) — р (z, Ох),
где р {а, В)—расстояние от точки а до множества В,
положительна на Ох и отрицательна Оу. Из компакт¬
ности Ох, Оу следует, что | б (z) j > & > 0, где z е Ох,
Оу. Действительно, непрерывная функция на компакте
достигает своего минимального значения, следователь¬
но, равенство min|6(z,)| = 0 невозможно. Далее, по гео-
*) Непрерывный образ компактного множества компактен. См.,
например, [4], [20], [29].

44
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
реме Вейерштрасса существует полином р(х) такой, что
| б (z) - р (z) I < б
для г е Ох, Оу. Очевидно, р (z) > 0 при г <= О* и р (г) < О
при z<=Oy. Применяя к p(z) оператор усреднения по
группе G, получаем инвариантный полином ф(г), поло¬
жительный на Ох и отрицательный на Оу. Теорема до¬
казана.
Заметим, что инвариантный полином является кон¬
стантой на каждой орбите Ох. В то же рремя согласно
теореме 2 алгебра таких полиномов «разделяет» отдель¬
ные орбиты.
Пример. Алгебра полиномов в трехмерном евкли¬
довом пространстве, инвариантных относительно пово¬
ротов, содержит единственную образующую / (х) =
— х\Л- х\Л- х\. Каждая орбита Ох есть сфера радиуса
\х\ — У7(аг). Отсюда непосредственно видно, что j(x)
принимает различные значения на каждой паре раз¬
личных орбит. Иначе говоря, орбиты Ох, Оу совпадают
тогда и только тогда, когда j(x) = j{y).
§ 99. Алгебраические группы
Множество Z cz V называется алгебраическим мно¬
гообразием, если оно выделяется из V некоторой си¬
стемой полиномиальных соотношений
ра(х) = 0, <хе=Л.
Здесь А — произвольное множество индексов. Соответ¬
ствующее множество полиномов ра называют иногда
определяющей системой многообразия Z.
Пусть 3—совокупность всех полиномов р{х), об¬
ращающихся в нуль на многообразии Z. Тогда, очевид¬
но, У является идеалом и, следовательно (по теореме
Гильберта), порождается некоторым числом образую¬
щих j\(x), /2(л;), jm{x). Следовательно, можем счи¬
тать, не ограничивая общности, что определяющая си¬
стема является конечной.
Линейная группа G называется алгебраической, если
она выделяется из GL(n) некоторой системой полино¬

§ 99. АЛГЕБРАИЧЕСКИЕ ГРУППЫ
443
миальных соотношений
Pa(g) = о, а еА
Иначе говоря, если М(л)— множество всех матриц
п X п, то группа G является пересечением GL (п) с не¬
которым алгебраическим многообразием в М (п).
Докажем, что имеет место
Теорема 3. Всякая компактная линейная группа
является алгебраической.
Доказательство. Если рассматривать группу
G как группу преобразований a-^ag в линейном про¬
странстве М (п), то G совпадает, очевидно, с орбитой
единичной точки ееМ(л). Следовательно, G выделяет¬
ся из М (п) системой полиномиальных соотношений
p(g)~p (е) = О,
где р(а) — произвольный инвариантный полином (т. е.
такой, что p(ag) = p(a), geG). Действительно, груп¬
па G компактна, и поэтому к ней применима теорема 2:
две точки g и е лежат на одной орбите тогда и только
тогда, когда p(g) = p(e) для всех инвариантных поли¬
номов р(а). Теорема доказана.
Замечание. Как следует из доказательства тео¬
ремы, компактная группа G может быть непосредствен¬
но определена как алгебраическое многообразие в М (п)
без дополнительного ограничения о невырожденности
матрицы g. Впрочем, это ясно также из известного нам
включения GcrO(n).
Поскольку всякая компактная группа Ли изоморфна
линейной, то из теоремы 3 получаем также
Следствие. Всякая компактная группа Ли алгеб-
раична (с точностью до изоморфизма).
С другой стороны, оказывается, что в классе линейных групп
предположение о том, что компактная группа является группой Ли,
излишне. В Действительности имеет место
Теорема 4. Всякая алгебраическая группа является груп¬
пой Ли *).
*) В действительности имеет место также более общая теоре¬
ма: всякая замкнутая линейная группа является группой Ли ([46]);
однако на этом результате мы не будем останавливаться.

444
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Доказательство [15]. Пусть Д — идеал, составленный из по¬
линомов, равных нулю на G, и /i(v), j2(x) i«i(x) — система об¬
разующих в этом идеале. Рассмотрим матрицу F(x), составленную
из частных производных djh(x) /дхц, 6=1, 2, . . . , m; i, / = 1,2 «.
Если г —ранг этой матрицы в точке х = е, то мы условимся счи¬
тать (не ограничивая общности), что первые г строк этой матрицы
содержат минор А, отличный от нуля в точке е. Тогда Д=£0 также
в некоторой окрестности точки е. Систему уравнений jh (х) —\h,
k= 1, 2, .... г, можно разрешить в некоторой окрестности точки е
относительно тех переменных хц, индексы которых содержатся в
миноре А. При этом получаемые функции выражаются аналитически
через gfe, k = 1, 2, ... , г, и остальные d — п2 — г координат хц. Сле¬
довательно, мы получаем локальную систему координат
в некоторой окрестности точки е, где иь и2, ил — дополнитель¬
ные координаты, в качестве которых можно, например, взять коор¬
динаты хц, индексы которых не содержатся в миноре Д. Полагая
= g2 = • .. = %г 0, получаем в М(п) некоторое алгебраическое
многообразие ©, которое, очевидно, содержит группу G. Каждая
точка этого многообразия, достаточно близкая к е, допускает ана¬
литическую параметризацию
При этом, очевидно, если х, у, ху е ©, то параметры матрицы ху
аналитически выражаются через параметры х и у.
Покажем, что в действительности оба многообразия Си®
имеют общую окрестность точки е. Иначе говоря, существует окрест¬
ность U сМ (п) такая, что U f) G — U f| ®- Отсюда будет следо¬
вать, что G —группа Ли.
Заметим вначале, что при каждом geG множество j\(xg),
j2(xg), ..., jm(xg) также является системой образующих в идеале У,
Следовательно,
где aih{x)—некоторые полиномы от матрицы х. Поскольку ji(x)~О
на группе G, то мы имеем также
для каждой точки *eG. Отсюда заключаем, что ранг F(xg) не
превосходит ранга F(x). Заменяя х на xg~l, заключаем, что ранг
F(x) постоянен на всей группе G. Следовательно, если А — построен¬
ный выше минор, то всякий минор, окаймляющий А, обращается в
нуль тождественно на всей группе G. Следовательно, он содержит-
X X (Ер Ео’ - • *’ Ер ^р ^d)
т
k (•*<?)= 2 и м aik w-

§ 99. АЛГЕБРАИЧЕСКИЕ ГРУППЫ
445
dj.
ся в идеале &. Отсюда следует, что всякая производная
дхЦ
может быть выражена через первые г таких производных по фор¬
муле
djk{x) 1 yi djt(x)
дх., Д дх.,
Ч j Ч
blk (X) + . .
где bih(x) —полиномы от х и многоточие означает слагаемое, при¬
надлежащее идеалу Э. Далее, пусть x(t)—кривая в многообра¬
зии @, проходящая через точку е при t = 0. Поскольку вдоль этой
dj.
кривой переменные |2. I г постоянны, то = 0, /= 1, 2, ...
г, и мы имеем
dik (■*) 1 жл dh
b.k{x)+ ... = ...,
dt Д XJ dt ‘k
1= 1
где многоточие означает элемент из &. Следовательно,
т
djk (х)
dt
ибо полиномы ji{x), 1=1, 2, ..., т, являются образующими в Э.
При этом jk(0) = 0, ибо точка е содержится в группе G. Согласно
теореме единственности заключаем из полученного уравнения, что
jh(x) =0, k = 1, 2 т, в некоторой окрестности вида @ П U.
Следовательно, @ П U cr G, т. е. @ П U = G Л U. Теорема доказана.
Покажем теперь, что свойство алгебраичности сохра¬
няется при переходе от компактной группы G к ее (пра¬
вильной) комплексной оболочке.
Теорема 5. Пусть G — компактная линейная группа
и G— ее правильная*) комплексная оболочка. Тогда
G является алгебраической группой Ли над полем ком¬
плексных чисел.
Доказательство. Условимся считать, что G, G
действуют в одном и том же комплексном пространстве
V (если с самого начала это было не так, то G вы¬
деляется условием вещественности всех ее матриц в
*) См. определение в § 41. Существование комплексной оболоч¬
ки здесь предполагается; сам факт существования будет доказан
Далее, в § 106.

446
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
некотором базисе пространства V). Согласно принципу
аналитического продолжения группы G, G обладают оди¬
наковым запасом инвариантов в классе (аналитических)
полиномов. В то же время при переходе от G к G число
орбит может только уменьшиться. Следовательно, для
G имеет место аналог теоремы 2; но тогда и доказатель¬
ство теоремы 3 переносится без изменения. Теорема до¬
казана.
В заключение отметим без доказательства следующий
критерий связности алгебраической группы G над полем
комплексных чисел ([46], т. 2, стр. 239): группа G яв¬
ляется связной тогда и только тогда, когда из равенства
p(x)q(x) = 0 (для любых полиномов р, q) на группе G
следует, что либо р(х) = 0, либо q(x) = 0 на группе G.
Упражнения
1. Докажите, что группа вещественных диагональных матриц
с диагональными элементами Я, Ят, где Я > 0 и т — фиксированное
положительное число, не является алгебраической. Найдите мини¬
мальную алгебраическую группу, в которой эта группа содержится
(отдельно при m рациональном и m иррациональном).
2. Пусть Z = Z(n)—группа всех (верхних) треугольных ма¬
триц п X п с единицами на главной диагонали. Показать, что вся¬
кая замкнутая связная подгруппа в группе Z является алгебраиче¬
ской. (Указание: использовать экспоненциальное отображение;
проверить попутно, что указанная подгруппа является группой Ли.)
§ 100. Разложение Гаусса
При изучении структуры полупростой комплексной
алгебры Ли была обнаружена замечательная симметрия,
позволяющая выделить в этой алгебре, наряду с карта-
новской подалгеброй, также аналог «понижающих» и
«повышающих» операторов, т. е. нильпотентные под¬
алгебры Х_, Х+ с определенными соотношениями комму¬
тации. Выясним, как отражается эта информация на
структуре соответствующей группы Ли.
Вместо полупростой комплексной алгебры Ли мы мо¬
жем сразу рассматривать алгебру редуктивную, т. е.
произвольную комплексную оболочку компактной ал¬
гебры Ли. Пусть X — редуктивная комплексная алгебра,
X' — ее полупростая компонента и 3 — центр. Выделяя в

§ 100. РАЗЛОЖЕНИЕ ГАУССА
447
X' картановскую алгебру Н и подалгебры Z_, Z+, мы
находим также, что
Х = Х„ + Х0 + Х+ (*)
(прямая сумма), где Z0— прямая сумма Н и центра 3-
Подалгебру Z0 мы будем называть картановской под¬
алгеброй в алгебре X, подалгебры Х-, Х+ — корневыми
подалгебрами в X. Разложение (•*) назовем разложе¬
нием Картана — Вейля. Поставим целью выяснить во¬
прос об «интегрировании» этого разложения.
Докажем, что имеет место
Теорема 6. Пусть G — редуктивная связная ком¬
плексная группа Ли. Тогда, исключая подмногообразие
меньшей размерности, мы получаем множество Greg,
всюду плотное в G, для которого выполняется следую¬
щее однозначное разложение:
Greg = Z-DZ+. (**)
Здесь D — максимальная абелева подгруппа в G с ал¬
геброй Ли Х0, Z_ и Z+ — максимальные нильпотентные
односвязные подгруппы с алгебрами Ли Х-, Х+. Если
группа G является алгебраической связной группой, то
D, Z_, Z+ также алгебраичны и группа D является связ¬
ной *).
Доказательство. Достаточно провести доказа¬
тельство в том случае, когда группа G односвязна.
(Действительно, поскольку D — максимальная абелева
подгруппа, то D содержит центр группы G. Следователь¬
но, разложение («•*) в общем случае может быть полу¬
чено факторизацией D по центральному дискретному
делителю.) Далее, пусть G', С — односвязные группы Ли
с алгебрами Ли X', 3- Если G односвязна, то она изо¬
морфна G' X С (ввиду односвязности последней и одно¬
значности универсальной покрывающей). Отсюда заклю¬
чаем, что разложение (**) достаточно поверить в том
случае, когда группа G полупроста.
Итак, пусть алгебра X полупроста. Мы рассмотрим
вначале тот случай, когда группа G является связной
*) В § 102 будет дано иное доказательство этого последнего
утверждения, не использующее алгебраичность группы G.

448
гл. xv. Компактные группы ли в целом
компонентой единицы в группе всех автоморфизмов ал¬
гебры X. При этом существенно будет использована
алгебраичиость группы G.
Лемма. Пусть ©— алгебраическая связная подгруп¬
па в GL(n) и группы Z_, D, Z+ определяются как пере¬
сечения этой группы с D(п), Z+(n) соответствен¬
но, где Z-(n). D(n), Z+(n) — компоненты разложения
Гаусса в GL(n). Пусть @reg— множество всех элементов
из @, допускающих разложение Гаусса в GL(n). Пред¬
положим, что ©reg и Z^DZ+ имеют общую окрестность
единичного элемента в Тогда @rcg = Z_DZ+, и под¬
группы Z_, Z+ односвязны.
Доказательство леммы. Предположим, что
g1 е 8rcg, т. е. g допускает разложение Гаусса в объ¬
емлющей группе GL(n):
g = Z 6z, 5eZ_(n), 5eD(n), z(=Z+(n).
Покажем, что zgZ+. Пусть p(g) — один из полиномов
определяющей системы группы необходимо прове¬
рить, что p(z) = 0. Согласно общим формулам разложе¬
ния Гаусса (§ 9) элементы матрицы г рационально за¬
висят от элементов матрицы g, т. е. функция R(g) =
= p(z(g)) есть рациональная функция в линейном про¬
странстве М(п), определенная для всех «регулярных»
точек из М(п) (допускающих разложение Гаусса). По
условию леммы Z?(gr) = 0 в некоторой окрестности U0 на
многообразии @. Но тогда R(g) = 0 на © ввиду связ¬
ности @. Следовательно, /;(г) = 0 и z е @. Аналогично
доказывается, что t е @. Но тогда и 8е@, В результате
£ ^ Z6 Г), z ^ Z+.
Следовательно, @reg = Z-DZ+. Заметим теперь, что г =
= е + х, где матрица х нульстепенна (действительно, г —
треугольная матрица с единицами на главной диагона¬
ли). Отсюда следует, что г однозначно записывается в
виде ехр а, где матрица а также нульстепенна. Заметим
также, что группа Z = Z4 алгебраична (как пересечение
алгебраических групп © и Z+(n)). Если p(z) — один из
определяющих полиномов группы Z, то мы имеем
ф(0 = р(ехР ta) = 0 при ( = 0, ±1, ±2, ...

§ 100. РАЗЛОЖЕНИЕ ГАУССА
449
(поскольку z"eZ, п = 0, ± 1, ±2, . . .). Следовательно,
qj(t) = 0 и exp ta <= Z при любом комплексном t. Экспо¬
ненциальное отображение устанавливает взаимно одно¬
значное соответствие между группой Z и ее алгеброй
Ли. Следовательно, группа Z односвязна*). Следова¬
тельно, обе группы Z_, Z+ являются односвязными. Лем¬
ма доказана.
Если группа @ в условиях леммы несвязна, то ре¬
зультат остается прежним, с той разницей, что множе¬
ство @reg всюду плотно в связной компоненте единицы
G с @. В частности, применим это замечание к алгебраи¬
ческой группе @ всех автоморфизмов алгебры X. Со¬
гласно (*) и общему критерию, указанному на стр. 174,
разложение Гаусса имеет место в окрестности единицы
группы @. Следовательно, теорема 6 имеет место для
связной компоненты единицы G с; @.
Рассмотрим теперь общий случай, когда группа G яв¬
ляется связной полупростой; тогда разложение (*•»)
доказано для присоединенного представления л(С)
группы G. Следовательно, (**) выполняется также и для
самой группы G, где Z_, D, Z+ определяются как полные
прообразы соответствующих подгрупп в n(G). Посколь¬
ку ядром представления я(С) является дискретный
центр группы G, то группы Z_, D и Z+ являются накры¬
вающими для n(Z_), n{D), л (Z+). Но, как мы видели
выше, группы n(Z_), n(Z+) односвязны; следовательно,
они изоморфны Z_, Z+ и центр группы G содержится в
подгруппе D.
Наконец, рассмотрим тот случай, когда группа G
алгебраична. Как увидим в дальнейшем (§ 104), всякая
комплексная редуктивная связная группа Ли является
надкомпактной. Отсюда, в частности, следует, что пре¬
образования картановской подалгебры Н диагонали-
зуются в некотором базисе. Собственные значения ал¬
гебры Н суть линейные формы над Н. Вводя для этих
форм такое же лексикографическое упорядочение, как
и для корней над Н, мы можем заключить, что суще¬
ствует базис, в котором преобразования из Х-(Х+)
*) Всякая аналитическая подгруппа в Z(«) замкнута и одно-
связна (А. И. Мальцев [109], [114]).

450
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
являются нижними (верхними) треугольными. Подгруппы
Z_, D, Z+ могут быть в этом случае непосредственно
определены как пересечения группы G с Z_(n), D(n),
Z+(n) соответственно. Следовательно, они являются
алгебраическими.
Пусть р(6), q(6)— такие полиномы на группе D, что
р(6)<7(6) = 0 при йей Полагая g = £6z, замечаем, что
б = 6(g) является рациональной функцией на группе G.
Подставляя 6(g) вместо 6 в полином p(6)q(6), полу¬
чаем рациональную функцию, тождественно равную
нулю на группе G. Умножая эту функцию на некоторые
степени диагональных миноров Ai(g), A2(g), •••, Xn(g)
(см. § 9), получаем также равенство вида P(g)Q(g) —
— 0, где Р, Q — полиномы на всей группе G. Отсюда
следует (см. замечание в конце § 99), что либо Р — 0,
либо Q = 0, т. е. либо р = 0, либо q = 0 на группе D.
Отсюда в свою очередь следует, что группа D является
связной *).
Теорема доказана.
Разложение (**) мы будем называть разложением
Гаусса в группе G; индивидуальное разложение g =
= £6г — разложением Гаусса элемента g е Greg- Заме¬
тим, что элементы £, б, г являются аналитическими функ¬
циями от g-, следовательно, соответствие между g и
тройкой (£, б, г) является аналитическим гомеоморфиз¬
мом. Тройку (£, б,г) мы можем рассматривать как си¬
стему параметров в множестве Greg-
Разложение Гаусса может быть обобщено следую¬
щим образом. Пусть П° — произвольная подсистема про¬
стых корней алгебры X и Х° — линейная оболочка кар-
тановской подалгебры Хо и всех корневых векторов еа,
где со представимо в виде линейной комбинации корней
из П°. Тогда, как нетрудно видеть, Х° является редук-
тивной алгеброй, и алгебра X может быть записана в
виде прямой (ортогональной) суммы:
X — L^. + Х° + L+,
где L+ — ортогональные дополнения в Х-, Х+ до кор¬
невых подалгебр алгебры X°(L-,L+ натянуты на те кор-
*) См. сноску на стр. 447.

§ 100. РАЗЛОЖЕНИЕ ГАУССА
451
невые векторы еа, со < 0, со > 0, где со непредставимо в
виде линейной комбинации корней из П°). Нетрудно ви¬
деть, что Z— и L+ являются идеалами в Х-, Х+. Алгебру
Х° мы будем называть центральной редуктивной компо¬
нентой или треугольным усечением алгебры X. В частно¬
сти, если П° = 0, то Х° = А0; если П° = П, то Х° = X.
Пусть Н — линейная оболочка корней алгебры X и
Н°— линейная оболочка корней подалгебры Х°. Поло¬
жим Н = Н° ® Н' и введем в пространство Н «относи¬
тельное упорядочение (mod Я0)», т. е. будем считать,
что h\ относительно меньше 1ц, если ортогональная про¬
екция hi на Н' меньше ортогональной проекции h2 (от¬
носительно лексикографической упорядоченности во
всем пространстве Н). Заменяя в доказательстве теоре¬
мы 6 обычную упорядоченность относительной и рассма¬
тривая вместо упорядоченных матриц соответствующие
блок-матрицы, получаем следующее разложение:
Greg = N-G°egN+. (***)
Здесь N-, N+ — односвязные нильпотентные подгруппы
в группе G с алгебрами Ли L+ и G reg множество
всех регулярных элементов из замкнутой подгруппы G°
с алгеброй Ли Х° (существование этой подгруппы полу¬
чается в процессе доказательства, равно как и сущест¬
вование диагональной подгруппы D). При этом АП, N+
оказываются инвариантными подгруппами относительно
G0. Разложение (**-*) мы условимся называть обобщен¬
ным разложением Гаусса. Группу G0 мы будем называть
центральной компонентой или треугольным усечением
группы G. В частности, если П° = 0, то G° = D\ если
П° = П, то G° = G.
Группу D из теоремы 6 мы будем называть карта-
новской подгруппой в группе G; эта группа может быть
охарактеризована как максимальная абелева подгруппа
в G с алгеброй Ли Х0.
Пример. Рассмотрим в «-мерном пространстве про¬
извольную блочную запись матриц g<=M(n). Пусть АП,
G°, N+ — совокупность всех нижних треугольных блок-
матриц с единичными блоками, совокупность всех невы¬
рожденных блочно-диагональных матриц и совокупность

452
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
всех верхних треугольных блок-матриц с единичными
диагональными блоками. Тогда имеет место (*«) для
группы G = GL(n), и группа G0 является треугольным
усечением в GL(«).
Замечание. Если G — присоединенная группа по-
лупростой комплексной алгебры X, то подгруппа G0 в
(**-.:-) может быть охарактеризована как совокупность
всех преобразований из G, оставляющих неподвижным
ортогональное дополнение в картановской алгебре Ядо
линейной оболочки Я0 системы П°. (Соответственно ал¬
гебра Х° есть централизатор Я0Я°.)
Упражнение
Пусть G — редуктнвная связная комплексная группа Ли и
0Ш—подалгебра в алгебре Ли X группы G, натянутая на векторы
е_м, h, ею, где h пробегает картаповскую подалгебру Х0. Показать,
что в группе С существует замкнутая подгруппа 0м с алгеброй Лн
0“ и 0“8 = Л“ОА'“, где Nt, — однопараметрические подгруппы
с касательными векторами е_м, ем. (Указание: рассмотреть вна¬
чале тот случай, когда группа G является присоединенной группой
алгебры X, и воспользоваться приведенным выше замечанием для
определения 0ю.)
§ 101. Разложение Ивасавы
В этом параграфе мы опишем еще одно замечатель¬
ное разложение, которое является аналогом разложения
матрицы в произведение треугольного и унитарного со¬
множителей. Мы могли бы, как и в предыдущем пара¬
графе, рассматривать сразу общий случай редуктивной
связной группы Ли. Однако предпочтем отдельно иссле¬
довать тот случай, когда группа G полупроста.
Теорема 7. Пусть G — произвольная связная полу-
простая комплексная группа Ли. Тогда эта группа до¬
пускает однозначное разложение вида
G = т\х,
где U—максимальная компактная подгруппа в группе
G и Т — максимальная односвязная разрешимая под¬
группа в G.

§ 101. РАЗЛОЖЕНИЕ ИВАСАВЫ
453
Доказательство. Рассмотрим вначале тот слу¬
чай, когда группа G имеет тривиальный центр. Если
X — алгебра Ли группы G, то G в этом случае изоморф¬
на присоединенной группе алгебры X, т. е. связной ком¬
поненте единицы в группе всех автоморфизмов алгеб¬
ры X. Согласно теореме 6*) группа G допускает разло¬
жение Гаусса:
а = £ez, а ен Стев.
Мы условимся отождествлять группу G с присоединен¬
ной линейной группой, действующей в пространстве X.
Рассмотрим в X эрмитово сопряжение, введенное в § 96,
и определим компактную форму Вейля К<^Х, как со¬
вокупность всех косоэрмитовых матриц (х* = —х).
Заметим, что если а — произвольная положительно оп¬
ределенная матрица, то все ее диагональные главные
миноры положительны и, следовательно, а допускает
разложение Гаусса. Если матрица а эрмитова, то мы
имеем для нее
г*6*£* = £ 6г.
Поскольку эрмитово сопряжение меняет местами Z-,Z+
и поскольку разложение Гаусса единственно, мы нахо¬
дим отсюда г = £*, 6 = 6*. В частности, 6 является диа¬
гональной положительно определенной матрицей. Сле¬
довательно, все ее собственные значения положительны.
Множество всех диагональных положительно определен¬
ных матриц из G мы обозначим Е. Докажем, что Е яв¬
ляется односвязной абелевой группой с алгеброй Ли Н0,
где Но — вещественная оболочка всех корней а еЯ.
Заметим вначале, что матрица еб£ сохраняет соот¬
ношение коммутации [h, еа] — a (h)ea. Если к и р— соб¬
ственные значения е на элементах /г, еа соответственно,
то мы находим отсюда Я,р = р, т. е. к = 1 **). Следова¬
тельно, алгебра Н неподвижна относительно преобразо¬
вания е. Далее, пусть еа — собственное значение преоб¬
*) Здесь мы используем лишь первую часть теоремы 6 (без
связности группы G). Более того, нам нужен лишь тот частный
случай, с рассмотрения которого мы начали доказательство тео¬
ремы 6.
**) Напомним, что е рассматривается как автоморфизм алгебры
Х\ отсюда, в частности, следует, что р ф 0,

454
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
разования е на векторе еа. Тогда, используя соотношение
коммутации [еа, ер] = Яареа+р, находим eaep = еа+р. Сле¬
довательно, матрица е вполне определяется своими соб¬
ственными значениями еи, где w — произвольный про¬
стой корень. Положим ц<о = In еи; поскольку простые
корни образуют базис в Я0, то существует вектор h е Я0,
для которого ц<о = (/i, со). Следовательно, е<о = е<л' “) и
еа = е(л’ а> для всех корней а. Следовательно, е = ехр h,
и наше утверждение доказано.
Рассмотрим теперь произвольную матрицу jeG и
положим а = gg*\ тогда получаем эрмитову положи¬
тельно определенную матрицу а. Согласно сказанному
выше а = £6£*, где 6g£, £ е Z_. Далее, положим
-ц-i
« = е I g,
где е= Vb. Поскольку матрица б положительно опреде¬
лена, то радикал существует и е также является элемен¬
том подгруппы Е. Имеем
» — 1с. — 1 »«.*— 1 -1 -I . -I
ии = е £ gg £ е = е ое = е.
Следовательно, матрица и является унитарной. В ре¬
зультате мы имеем
g = £eu.
Искомое разложение получено. Положим Т = Z-Е и обо¬
значим символом U пересечение группы G с унитарной
группой U (п); тогда имеем
g = та,
причем индивидуальное разложение g = tu, t^T и
не U, однозначно. Таким образом, в нашем случае тео¬
рема доказана.
Заметим, что односвязная группа Т не содержит ни
одной унитарной матрицы, кроме единицы. Следователь¬
но, U является максимальной компактной подгруппой в
группе G*).
Перейдем к рассмотрению общего случая. Утвержде¬
ние теоремы доказано для группы G' = n(G), где л озна¬
чает присоединенное представление. Следовательно,
*) Детдли доказательства предоставляются читателю.

§ 101. РАЗЛОЖЕНИЕ ИВАСАВЫ
455
G'= T'W, где Т' — односвязная разрешимая подгруппа
и U' максимальная компактная подгруппа в G'. Следо¬
вательно, также
G = Г-я-ЧИ'),
где Т — связная компонента единицы в л~1(7'/). Действи¬
тельно, из дискретности центра С (ядра представления
л) следует л(Т) = Т' (в противном случае Т' несвязна);
далее, при n(g) — t'u', t'^T', u'ell', выбираем /еГ
из условия л(t) — t' и находим, что t~lg = «ел-1 (U').
Поскольку связная группа Т накрывает односвязную
группу Т, то Т гомеоморфно V. В частности, ГПС = {е},
разложение g — tu, t^T, ueU, однозначно и t = t(g)
аналитически зависит от g. Следовательно, также
и — u(g) аналитически зависит от g. Отсюда имеем
G = ТП,
где U — связная компонента единицы в л'Ди7) (действи¬
тельно, u(g) непрерывно стягивается к е). В частности,
CcU, U' = U/С. Отсюда следует (§ 103) компактность
U и конечность С. Наконец, поскольку Т не содержит
компактных подгрупп (кроме {е}), заключаем, что U —
максимальная компактная подгруппа в G. Теорема до¬
казана.
Следствие 1. Всякая редуктивная связная ком¬
плексная группа G допускает разложение вида TU, где
Т — разрешимая подгруппа и U — максимальная ком¬
пактная подгруппа в группе G.
Действительно, G = G'N, где G' — полупростая ком¬
понента и N — связная компонента центра группы G.
Следствие 2. Пусть X — полупростая комплексная
алгебра JIu, L_ — разрешимая вещественная подалгеб¬
ра, натянутая на векторы еа, iea, h0, а < 0, h0^H0, и
Lq — компактная форма Вейля. Тогда мы имеем
X = L_ + L0
(прямая сумма). Аналитическая подгруппа Т, порожден¬
ная подалгеброй L_, замкнута и односвязна. Аналити¬
ческая подгруппа U, порожденная подалгеброй Ь0, зам¬
кнута и является максимальной компактной подгруп¬
пой в G.

456
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Из прямого разложения X = L_ + L0 следует локаль¬
ная однозначность отображения (t,u)^>tu группы Г X И
на группу G в каждой точке ge G. Отсюда следует, что
сответствие между Т X U и группой G является анали¬
тическим гомеоморфизмом. Отсюда, в частности, полу¬
чаем
Следствие 3. Полупростая связная комплексная
группа Ли как топологическое пространство изоморфна
произведению Т X U, где Т — евклидово пространство и
U — компактная связная полупростая комплексная груп¬
па Ли.
Согласно следствию 3 топологическая структура груп¬
пы G сводится, по существу, к топологической структуре
группы U. В частности, G и U могут быть односвязными
только одновременно.
Разложение теоремы 7 носит название разложения
Ивасавы. Заметим, что группа G в этом разложении вы¬
ступает фактически как вещественная полупростая груп¬
па Ли (с удвоенным числом параметров). В действи¬
тельности теорема 7 легко обобщается ([85], [92], [128])
на произвольную полупростую вещественную связную
группу Ли.
§ 102. Максимальные торы
В этом параграфе мы рассмотрим некоторые свой¬
ства торов (коммутативных связных подгрупп) в про¬
извольной компактной связной группе Ли. Докажем вна¬
чале, что имеет место
Теорема 8. Всякий элемент компактной связной
группы Ли содержится в некоторой однопараметриче¬
ской подгруппе.
Следствие. Если G — компактная связная группа
Ли, то экспоненциальное отображение накрывает всю
группу G.
Доказательство. Ради сокращения текста вос¬
пользуемся некоторыми результатами из теории римано-
вых пространств. Рассмотрим группу G как замкнутую
подгруппу в U(«) и введем в линейное пространство
матриц п X п метрику
ds2 = sp dx • dx\

§ 102. МАКСИМАЛЬНЫЕ ТОРЫ
457
где dx означает дифференциал переменной матрицы
1еМ(л) и звездочка означает эрмитово сопряжение.
Если ueU(n), то мы имеем
sp (dx • и) (dx ■ и)* = sp dx • dx*,
и то же верно при умножении dx слева на и. Следова¬
тельно, метрика ds2 является двусторонне инвариантной
на U(n) и, в частности, на группе G. Поскольку груп¬
па G является вещественным дифференцируемым (и
даже аналитическим) многообразием в М(п), то G яв¬
ляется римановым пространством. Функция
р (a, b) — inf s (L),
где s(L) — длина спрямляемой линии L и inf берется по
всем таким линиям, соединяющим а, Ь, определяет мет¬
рику в пространстве G. G является относительно этой
метрики компактным метрическим пространством.
Как известно*), в компактном римановом простран¬
стве через любые две точки можно провести хотя бы
одну геодезическую. Если р(а, 6) <6 при достаточно
малом 6, то геодезическая, проходящая через а, Ь, опре¬
деляется однозначно. Рассмотрим теперь преобразование
а = а0а-1а0
с фиксированной точкой а0. Согласно свойству двусто¬
ронней инвариантности и равенству da~l = —a~ldaa~l
переход от а к а сохраняет метрику. В частности, точ¬
ка а0 остается неподвижной, откуда р (а, а0) = р (а0, а).
Преобразование а->~ а называется симметрией относи¬
тельно точки аа.
Если а достаточно близко к а0, то все три точки а,
а0, а лежат на одной геодезической.
Приступим теперь к доказательству теоремы. Фик¬
сируем точку g ф е и проведем геодезическую у, соеди¬
няющую g и е. Покажем вначале, что существует одно¬
параметрическая подгруппа g(t), содержащая все точки
отрезка у, достаточно близкие к е.
Пусть gi е у настолько близко к е, что через gi про¬
ходит однопараметрическая подгруппаg(t), и у является
*) См., например, [29], стр. 118.

458
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
единственной геодезической, соединяющей g\ и е. Если
уже доказано, что пара точек p — g(t 1), g = g{h)
содержится в у, то мы рассматриваем точку г =
= £ (~'~2 ) и замечаем, что имеет место формула
rgit)~x r = g(tx + t2-t).
Полагая, в частности, t — t\,t2, заключаем, что симмет¬
рия относительно г переставляет р и q. Следовательно,
г лежит на геодезической, проходящей через р и q. Сле¬
довательно, ге у. Нормируем теперь параметр t таким
образом, чтобы е = g'(O), gi=g(l). Применяя индук¬
тивнопредыдущее рассуждение, заключаем, что у содер¬
жит все точки g{t), О где t двоично-рациональ¬
но. Ввиду непрерывности у*) у содержит также весь
отрезок g(t), (Хл-^Л. Наше утверждение доказано.
Заметим, что точка gj"1 симметрична точке gi отно¬
сительно е. Продолжая кривую g(t) и геодезическую у
на отрицательные значения t, заключаем, что у содер¬
жит также отрезок вида g{t), —1 ЛД<Л.
Далее, рассмотрим множество всех точек, принадле¬
жащих одновременно у и g(t), 0^Ct<*CT, где Т — доста¬
точно большое число**). Поскольку это множество зам¬
кнуто (как пересечение двух замкнутых множеств), то
его связная компонента у*, содержащая точку е, имеет
вид отрезка g(t), О <Л<Л0, при некотором to. Положим
go = g(to)■ Если go = g, то теорема доказана. Если g0 Ф
Ф g, то мы осуществляем левую трансляцию g~l во
всей группе G. Поскольку всякая трансляция переводит
геодезическую в геодезическую, то, в частности, кривая
g~!y является геодезической, проходящей через точку е.
Выбирая на этой кривой точку hu достаточно близкую
к е, заключаем, как и выше, что g~lу содержит отрезок
некоторой однопараметрической подгруппы /г(т), —1
Л^т-^1. Поэтому у содержит отрезок кривой goh{x),
*) Согласно теории римановых пространств геодезические не
только непрерывны, но и дифференцируемы на G.
**) Достаточно выбрать Г настолько большим, чтобы расстоя¬
ние по кривой g(t) от точки е до точки g(T) было больше (или
равно) расстояния по у от точки е до точки g.

§ 102. МАКСИМАЛЬНЫЕ ТОРЫ
459
— 1 <т< 1. Следовательно,
g (t) = g0h (т)
при достаточно малых т, —1-^т-^О, и при некоторых
значениях t, t0 — В частности, gQ — g(t0), от¬
куда заключаем, что h(x) = g(t—10). Следовательно,
h(x) совпадает с g(t) с точностью до замены (аддитив¬
ного) параметра. Поэтому g0 не является крайней точкой
множества у*, что противоречит определению g0. В ре¬
зультате заключаем, что g0 = g. Теорема доказана.
Замечание 1. Из доказательства теоремы 8 мы
получаем также замечательное соответствие между гео¬
дезическими и однопараметрическими подгруппами в
группе G. Всякая однопараметрическая подгруппа есть
геодезическая, проходящая через точку е. Всякая гео¬
дезическая получается (левой или правой) трансляцией
из однопараметрической подгруппы в группе G.
Замечание 2. Теорема 8 может быть доказана не¬
посредственно, без использования свойств симметрии,
если показать, что длина кривой, соединяющей точки е
и у, минимизируется только на однопараметрической
подгруппе. См., например, [15].
Рассмотрим теперь произвольные торы в группе G.
Напомним, что тором называется всякая связная комму¬
тативная компактная группа Ли. Тор Г в группе G на¬
зывается максимальным, если он не содержится ни в
каком другом торе из G (отличном от Г). Докажем, что
имеет место
Теорема 9. Пусть G —компактная связная группа
Ли м Г — ее максимальный тор. Тогда для любого эле¬
мента g е G найдется элемент us G, для которого
u-'gu е Г.
Доказательство. Согласно теореме 8 g = ехр х,
где X — алгебра Ли группы G. Рассмотрим про¬
извольный элемент «еб и положим*) ф (и) = (х, иуи~1),
где у — фиксированный элемент из X и скобка означает
скалярное произведение в X, относительно которого
операторы Dax = [а, х] кососимметричны. Положим
*) Мы рассматриваем G как линейную группу, что позволяет
умножать элементы g е G на элементы «si

460
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
и = Uo exp tz и заметим, что
Ф (и) = (х0, exp tz ■ у • exp (- tz)),
где х0 = u~lxuQ. Действительно, операторы я(и)х = ихи~1
ортогональны относительно формы (х, у), и оператор
я(и0) можно перебросить налево, заменяя и0 на и~1.
Далее, имеем
(и)
dt
<= о
= (х0, [z, у]) = { [у, xQ\, z).
Заметим теперь, что функция ср(и) является дифферен¬
цируемой (и даже аналитической) на G. Поскольку груп¬
па G компактна, то <р{и), согласно теореме Вейерштрасса,
достигает максимума на G. Если «о — точка максимума,
то dcp(м) = 0 при и — «о- Следовательно, в этом случае
([у, х0], z) = 0 тождественно по геХ Следовательно,
[у, х0\ = 0.
Пока еще в нашем распоряжении имеется произвол в вы¬
боре элемента i/gI Выберем у таким образом, чтобы
однопараметрическая подгруппа exp ty = 0 была всюду
плотной в торе Г. Тогда мы имеем
у-1.*0у = х0
для всех уеГ. Следовательно, также [у, х0] = 0 для вся¬
кого г/е Я, где Я —алгебра Ли тора Г. Поскольку Г —
максимальный тор, алгебра Я является максимальной
коммутативной подалгеброй в X. Следовательно, х0 е Я.
Следовательно, также go ^ Г, где g0 = exp х0 = u~lgu0.
Теорема доказана.
Следствие 1. Любые два максимальных тора со¬
пряжены в группе G.
Действительно, пусть Го — максимальный тор и уо —
его иррациональная образующая *), т. е. элемент, степе¬
ни которого образуют всюду плотное множество в Го.
Тогда элемент и~1у0и является образующей в максималь¬
ном торе «_1Го«- Поскольку для всякого максимального
*) См. § 40 (стр. 171).

§ 102. МАКСИМАЛЬНЫЕ ТОРЫ
461
тора Г найдется такой элемент и, что и~1у0и е Г, то
н-1 Го« = Г, и любой максимальный тор сопряжен Го.
Следствие 2. Любые две максимальные комму¬
тативные подалгебры в компактной алгебре X сопря¬
жены относительно внутреннего автоморфизма.
Доказательство вытекает из очевидного соответст¬
вия между максимальными торами и максимальными
коммутативными подалгебрами в X. Всякая такая под¬
алгебра в компактной алгебре X называется подалгеб¬
рой Картана. Соответственно всякая максимальная
коммутативная (не обязательно связная) подгруппа в
компактной связной группе G называется подгруппой
Картана.
Следствие 3. Всякая подгруппа Картана являет¬
ся связной и определяется однозначно с точностью до
сопряженности.
Действительно, пусть Г — подгруппа Картана и Го—■
ее связная компонента единицы. Если уеГ, то у’! е Го
при некотором натуральном п (поскольку группа Г/Го
конечна). Если п — минимальное из таких чисел, то
элементы у, у2, ..., у" содержатся в различных связ¬
ных листах группы Г. Рассмотрим элемент
6о = ехр 20,
где г0 определяется тем условием, что упехр г0 яв¬
ляется иррациональной образующей в Го- Тогда нетруд¬
но видеть, что уЕо является образующей в группе Гь
порожденной элементами Г0 и у. Если Г — максималь¬
ный тор, содержащий уе0, то Г) сг Г. Следовательно,
Го с: I'i сг Г, откуда Го = П = Г ввиду максимальности
тора Г0. Следовательно, у е Го и Г0 = Г.
Замечание 3. Из связности картановской под¬
группы в компактной подгруппе 11 и разложения Ива-
савы G = 7Т1 мы получаем также связность картанов-
скоп подгруппы D в произвольной связной полупростой
(и также редуктивной) группе G. Действительно,
D = ЕГ, где Е — максимальная односвязная подгруппа
в Г с алгеброй Ли Н0 (см. § 101) и Г — максимальный
тор в подгруппе U. Следовательно, мы получаем иное
доказательство заключительной части теоремы 6.

462
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Заметим также, что всякая подгруппа Картана со¬
держит центр группы G; следовательно, центр содер¬
жится в любом максимальном торе.
§ 103. Фундаментальная группа и центр
В этом параграфе мы займемся вопросом об опи¬
сании класса со (А) всех локально изоморфных групп Ли
с данной алгеброй Ли А. Алгебра X предполагается
компактной. Рассмотрим вначале тот случай, когда ал¬
гебра X полупроста.
Пусть @— односвязная группа Ли с алгеброй Ли X.
Далее, пусть. @0— присоединенная группа, т. е. связная
компонента единицы в группе всех автоморфизмов ал¬
гебры X. Группа ©о компактна. Поскольку алгебра X
предполагается полупростой, то группа ©о имеет X
своей алгеброй Ли, т. е. @0есо(А). Группы © и ©о
являются «максимальной» и «минимальной» группами
в классе со (А'). Действительно, если 3 — центр группы
@, то ©о изоморфна @/3-
Основным результатом этого параграфа является
Теорема 10. Пусть X — полупростая компактная
алгебра Ли. Тогда односвязная группа ©с: со (А) ком¬
пактна и центр этой группы конечен.
Следствие 1. Существует лишь конечное число
локально изоморфных связных групп Ли с полупростой
компактной алгеброй Ли X.
Следствие 2. Универсальная накрывающая полу¬
простой компактной группы Ли компактна.
Следствие 3. Центр полупростой компактной
группы Ли конечен.
Прежде чем приступить к доказательству этой тео¬
ремы, сделаем следующее замечание. В комплексной
оболочке А + IX выберем базис Картана — Вейля а, еа,
где а — произвольный корень. Напомним, что алгеб¬
ра А натянута на векторы /со, ica, isa, где
С(х ~2 З- а)’ 2/ <Х 0
и со — произвольный простой корень. Линейную оболоч¬
ку векторов /со обозначим А0. А0 есть максимальная

§ 103. ФУНДАМЕНТАЛЬНАЯ ГРУППА И ЦЕНТР
463
коммутативная подалгебра в X. Далее, рассмотрим в
X + iX множество всех преобразований
Yt («) = a, у, {еа) = е(' <«• (>еа,
где t — произвольный вектор из H0 = iX0 (корень а
рассматривается также как вектор из Я0). Нетрудно
видеть, что эти преобразования сохраняют алгебру X.
Следовательно, мы получаем коммутативную связную
подгруппу Г cz @о, где @0 — присоединенная группа
для X.
Поскольку алгеброй Ли подгруппы Г является мак¬
симальная коммутативная подалгебра Х0, мы можем за¬
ключить, что Г является максимальным тором в ©о*)-
Применяя теорему 9, получаем, что всякий элемент
^ё®о может быть представлен в виде
g = u~1yu, yes Г.
Иначе говоря, всякая матрица из @0 может быть при¬
ведена в X + iX к диагональному виду с диагональной
матрицей у е Г. Очевидно, отображение (и, у)->•£■ яв¬
ляется аналитическим. Разложение irlyu можно в из¬
вестном смысле (§ 72) рассматривать как выбор пара¬
метров в группе @о-
Заметим, что собственными значениями матрицы у
являются 1, ег'<“’ 1\ где а — корень и t — набор канониче¬
ских координат элемента у е Го- Поскольку вектор
t е #0 вполне определяется своими проекциями на кор¬
ни а, то матрица у определяется собственными значе¬
ниями матрицы g однозначно с точностью до переста¬
новки этих собственных значений. Следовательно, при
фиксированном g мы получаем лишь конечное число
разложений с различными диагональными элементами у.
Это замечание будет существенно использовано при до¬
казательстве теоремы 10.
Напомним, что вектор t е Н0 называется регулярным
(§ 91), если оператор t имеет ровно г нулевых собст¬
венных значений, где г = rang @0 = dim Н0. Соответ¬
ственно элемент ge@o назовем регулярным, если мат¬
рица g имеет ровно г единичных собственных значений,
*) Следствие 3 из теоремы 9,

464
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦВЛОМ
Доказательство теоремы 10. Исходя из
группы ®о, мы можем непосредственно вычислить
центр 3 односвязной группы @. Действительно, согласно
общему определению односвязной накрывающей центр 3
изоморфен фундаментальной группе (группе Пуанкаре)
многообразия @0.
1. Пусть 5 — множество всех нерегулярных элемен¬
тов из @о- Покажем, что 8 является объединением конеч¬
ного числа многообразий размерности п — 3, где п—раз¬
мерность многообразия @0- Действительно, фиксируем
корень а и обозначим Га множество всех матриц у =
= ехр it, t^H0, для которых (а,/) = 0. Далее, пусть
8а — множество всех элементов вида и~1уи, где у пробе¬
гает Га. Ясно, что
dim 8а = dim Га + dim ©0/@оа,
где ©оа — подгруппа в группе ©о, перестановочная с Га.
Если (a, t) = 0, то элемент t перестановочен не только
с Но, но также и с са, sa. Отсюда ясно, что алгебра Ли
подгруппы ©0а натянута на Х0 = iHо, са, sa. Следова¬
тельно, dim ®0а = г + 2. В результате
dim 8а = (г — 1) + {п — (г + 2)} = п — 3.
(Действительно, dimFa = r—1.) 8 является объедине¬
нием всех 8а. а > 0.
2. Рассмотрим элемент у0 е Г, достаточно близкий
к единице и регулярный. Рассмотрим произвольный
замкнутый путь, проходящий через уо- В силу преды¬
дущего замечания мы можем рассматривать (за счет
небольшой деформации) только пути, обходящие син¬
гулярное множество 8. Используя разложение и~хуи
как параметризацию в ©о, запишем данный путь в виде
g(t) = u(t)~ly(i)u(t), 0<г<1.
Положим yi = y(l) и покажем, что возможно неравен¬
ство уо=£\’1> т- е- ПУТЬ y(0> 0<Д<Л, может оказаться
незамкнутым. Действительно, поскольку ^(0) = g"(l), то
элемент s = n(l)«(0)“1 удовлетворяет соотношению
sVos~1 = Yi-
Если s переставляет собственные значения матрицы уо,
то это равенство возможно. Следовательно, в этом слу¬

§ 103. ФУНДАМЕНТАЛЬНАЯ ГРУППА И ЦЕНТР
465
чае путь у(0 не может быть непрерывной деформацией
стянут в точку (при условии закрепления концов).
3 С другой стороны, если путь y(t) является зам¬
кнутым, то он может быть стянут в точку у0 внутри
тора Г. Действительно, матрица у(0 имеет собственные
значения чМ>, ср (1)ей0, где ф (t)—непрерывный
путь в Н0. Путь ф(/), может быть незамкну¬
тым в Но только в том случае, когда (сь, ф (0)) —
— {а, ф (1)) = 2kan, где ka=f= 0 хотя бы при одном зна¬
чении a (ka — целое число). Нетрудно видеть, что в
этом случае путь у(/) проходит через сингулярный эле¬
мент, что исключается. Следовательно, путь у(/) может
быть непрерывной деформацией переведен в путь
f(t) = u(t)~ly0u(t).
Положим теперь fK (t) = и (t)~l у\~ки (/) • и (О)”1 у^и (0),
К
где уо—одиопараметрическая подгруппа, проходящая
через у0, с аддитивным параметром К. Полагая К = 0, 1,
заключаем, что fo(t)=f(t), в то время как путь
fi(t) вырождается в точку ы(0)_1уо«(0) = g(0). Следо¬
вательно, путь f(t) непрерывной деформацией перево¬
дится в точку.
Сопоставляя пункты 2 и 3, мы видим, что в про¬
странстве @0 существует лишь конечное число классов
путей, где пути из каждого класса гомотопны между
собой (т. е. переводятся друг в друга непрерывной де¬
формацией). Следовательно, фундаментальная группа 3
конечна. Поэтому группа @ компактна. Теорема
доказана.
С другой стороны, если X — коммутативная алгебра
Ли, то односвязная группа изоморфна вектор¬
ному пространству. Следовательно, в этом случае ана¬
лог теоремы 10 не имеет места. В этом состоит одно из
основных различий между полупростыми и коммута¬
тивными алгебрами Ли*).
*) Напомним также, что на коммутативных алгебрах Ли фор¬
ма Киллинга — Картана вырождается. Это и является основной
причиной исключения коммутативных алгебр из класса полупростых
алгебр Ли.

466
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Теорема 11. Всякая компактная связная группа
Ли может быть записана следующим образом:
G*s(9'X А)/С,
где ®' — односвязная связная полупростая компактная
группа Ли, А — коммутативная связная компактная
группа Ли и С — конечный центральный делитель такой,
что А Г) С = {е}.
Доказательство. Пусть X — алгебра Ли груп¬
пы G, X = X' + Y, где Х' = [Х,Х] и Y — центр алгеб¬
ры X. Пусть ®' — односвязная компактная группа Ли
с алгеброй Ли X' и F есть m-мерное векторное простран¬
ство, где m = dim У. Группа &'X F является односвяз¬
ной группой с алгеброй Ли X. Всякая группа Geco(X)
может быть записана в виде
G = ф(@/ X F),
где ф — гомоморфизм, ядром которого является дискрет¬
ный центральный делитель N. Для каждого g е G мы
имеем
g = 4>(g', f) = 4>(g', e)q>{e, f),
где g' пробегает ®' и / пробегает F. Следовательно,
также £ = ф(я', а), где а = ф(е,/) и ф— гомоморфизм,
определяемый формулой ty(g', а) = q>(g', е)а. Множе¬
ство А элементов вида я = ф(е, /) изоморфно F/F Г) N
и потому является связной подгруппой в G. В резуль¬
тате
G = ф(<Г х А).
Если G компактна, то подгруппа А также должна быть
компактной. Кроме того, элемент ф(с, а) — а обра¬
щается в единицу только при а = е. Следовательно,
если С — ядро гомоморфизма ф, то С Г) А = {с}. Теорема
доказана.
§ 104. Теорема о линейности полупростой
комплексной группы Ли
Исходя из принципа аналитического продолжения,
естественно предположить, что для полупростых ком¬
плексных групп Ли сохраняется свойство линейности,
справедливое для компактных групп Ли. Покажем, что

$ 104. ТЕОРЕМА О ЛИНЕИНОСТИ
467
это действительно так. Отметим вначале следующее
свойство:
1° Полу простая комплексная связная группа G яв¬
ляется правильной комплексной оболочкой своей мак¬
симальной компактной подгруппы U.
Это утверждение вытекает из теоремы 7. Действи¬
тельно, алгеброй Ли группы U является компактная
форма Вейля в алгебре Ли группы G. Далее, имеем:
2° Центр группы G конечен и содержится в подгруп¬
пе U.
Действительно, мы видели при доказательстве тео¬
ремы 7, что центр содержится в подгруппе U. Следова¬
тельно, этот центр конечен. Теперь докажем, что
имеет место
Теорема 12. Всякая полупростая связная ком¬
плексная группа Ли допускает точное аналитическое
линейное представление.
Доказательство. Если G односвязна, то всякое
линейное представление группы U продолжается анали¬
тически (§ 41) до однозначного представления груп¬
пы G. Следовательно, в данном случае теорема дока¬
зана. Далее, пусть @ — односвязная группа и G^®/N.
где N — конечный центральный делитель в @. Тогда
максимальной компактной подгруппой в группе G яв¬
ляется U//V (напомним, что N содержится в U). Пусть
р — точное линейное представление U/7V. Мы можем
рассматривать это представление как представление
группы U, ядром которого является N. Продолжим пред¬
ставление р до однозначного представления группы
Тогда ядром такого представления по-прежнему яв¬
ляется N*), т. е. оно является точным для ®/N. Тео¬
рема доказана.
Следствие. Всякая связная полупростая ком¬
плексная группа Ли является алгебраической.
Это утверждение вытекает из теоремы 5.
Приведем (без доказательства) также некоторые
свойства сопряженности, имеющие аналоги в компакт¬
ном случае.
*) Действительно, точное представление алгебры Ли группы U
продолжается до точного представления ее комплексной оболочки.

468
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
3° Максимальная компактная подгруппа в полупро¬
стой комплексной связной группе G определяется одно¬
значно с точностью до сопряженности.
При доказательстве этой теоремы (см., например,
[42]) многообразие G/U рассматривается как односвяз¬
ное риманово пространство (отрицательной кривизны).
Используется теорема Э. Картана, согласно которой
всякая компактная подгруппа в группе движений та¬
кого пространства имеет неподвижную точку. Рассмот¬
рим в качестве такой подгруппы максимальную ком¬
пактную подгруппу U]. Пусть х — элемент из G, для ко¬
торого класс смежности хМ неподвижен относительно U).
Тогда имеем Uix'czxU, откуда лгЧ^хсдЯ. Из макси¬
мальности Ui следует, что Х-ЧМ = U.
Следовательно, всякая максимальная компактная
подгруппа в группе G является связной.
4° Любые две подалгебры Картана в полупростой
комплексной алгебре X сопряжены относительно при¬
соединенной группы @о-
Это утверждение можно получить как следствие 3°,
однако известно и независимое доказательство (см., на¬
пример, [128]). Более того, можно утверждать, что иско¬
мый автоморфизм из @0 может быть выбран в виде
exp Dz, где Dz — нульстепенный оператор в X.
Далее, скажем, что точка geG является регуляр¬
ной, если оператор присоединенного представления я(^)
содержит собственное значение 1 с кратностью г =
= rangG*). Максимальная коммутативная подгруппа
в G, содержащая регулярный элемент, называется под¬
группой Картана.
5° Любые две подгруппы Картана сопряжены в груп¬
пе G относительно внутреннего автоморфизма.
Отсюда, в частности, следует, что всякая подгруппа
Картана изоморфна подгруппе D из теоремы 6; следо¬
вательно, она является связной.
Можно также показать ([116]), что любые две мак¬
симальные разрешимые подалгебры сопряжены в ал¬
гебре X, соответственно любые две максимальные раз¬
решимые подгруппы сопряжены в группе G. Разложе-
*) См. стр. 463.

§ 105. ГРУППА ВЕЙЛЯ
469
ние Гаусса (теорема 6) и разложение Ивасавы
(теорема 7) определяются однозначно с точностью до
сопряжения ([85], [92], [113]).
Таким образом, любая полупростая комплексная
связная группа Ли имеет структуру, во многих отноше¬
ниях сходную со структурой группы SL(/z, С). Заметим,
что в случае классических групп все указанные выше
утверждения легко проверяются непосредственно. По¬
этому новая информация получена, в сущности, для осо¬
бых групп Картана с алгебрами Ли Gi— Е%. В частно¬
сти, все эти группы допускают точное линейное пред¬
ставление.
Существенно, что в классе вещественных полупро-
стых групп Ли аналог теоремы 12 не имеет места. Су¬
ществуют группы этого класса с бесконечным (дискрет¬
ным) центром; все такие группы не допускают точного
линейного представления. (Предлагается в качестве
упражнения показать, что этим свойством обладает
универсальная накрывающая группы SL(2, #)*).)
§ 105. Группа Вейля
При изучении структуры полупростой комплексной
алгебры Ли и ее линейных представлений важнейшую
роль играет симметрия в классе корней и корневых век¬
торов, существование которой было установлено в
гл. XIV. Более детальное изучение этой симметрии по¬
зволяет связать с каждой комплексной полупростой
алгеброй Ли некоторую конечную группу симметрий,
называемую группой Вейля. В случае алгебры si (л, С)
эта группа определяется как группа подстановок я ба¬
зисных векторов.
Пусть X — полупростая комплексная алгебра Ли и
Я— ее фиксированная картановская подалгебра. Для
каждой пары векторов a, h е Я преобразование
*) Следовательно, также эта универсальная накрывающая не
допускает комплексификадии.

470
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
является зеркальным отражением относительно гипер¬
плоскости На, ортогональной вектору а. Мы будем на¬
зывать такое преобразование отражением по направле¬
нию вектора а.
Введем обозначение ® для группы, порожденной от¬
ражениями sa, где а пробегает систему всех простых
корней алгебры X. Группа @ называется группой Вейля.
Теорема 13. Группа Вейля сохраняет систему кор¬
ней и содержит все отражения sa, где а — произвольный
корень алгебры X.
Доказательство. Если а, р — корни, то, как
мы видели в § 92, —2(а, (3)/(а, а) = р + q, где р и q —
минимальное и максимальное из целых чисел п, для
которых р + па является корнем. Следовательно, вектор
= Р + (Р + <7)“
является корнем (действительно, р 0, <7^0, откуда
р р + q q). Отсюда следует также, что группа
Вейля сохраняет вещественное подпространство Я0, на¬
тянутое на корни алгебры X.
Выбросим из Яо все гиперплоскости Яа, ортогональ¬
ные корням; тогда оставшееся множество распадается
на конечное число связных областей; каждая такая об¬
ласть называется камерой Вейля.
Положим, в частности,
Д+ = {/г <= Я о, (h, cot) > 0, /=1,2, . . ., г),
где to, — простые корни алгебры X. Очевидно, это мно¬
жество является связным. Если йфК+, то (h, сщ)^0
хотя бы при одном значении (=1, 2, ..., г. Это озна¬
чает, что либо h е Яи , либо h отделено от К.+ гипер¬
плоскостью Яи,. Следовательно, К+ является камерой
Вейля.
Лемма. Всякая камера Вейля может быть полу¬
чена из камеры К+ некоторым преобразованием группы
Вейля.
Доказательство леммы. Заметим вначале,
что группа @ является конечной (действительно, эта
группа состоит из перестановок корней, число которых
конечно). Фиксируем точки г е Л', z+ е К.+ и среди ко¬

§ 105. ГРУППА ВЕИЛЯ
471
нечного множества точек sz, se6, выберем точку г0,
ближайшую к z+. Заметим, что sz ф Ни,, ни при одном
значении i = 1, 2, . . ., г. Действительно,
(sz, со,) = 0 (z, s~4) = 0,
что невозможно, ибо s-'cd, является корнем. Следова¬
тельно, либо zQ е К+, либо zq отделяется от К+ хотя бы
одной гиперплоскостью #ю.. Но в последнем случае от¬
ражение sM. приближает z0 к z+. В силу выбора z0 это
невозможно, т. е. z0 е К+■ Следовательно, sK cz К+
при некотором se® (поскольку К связно). Из макси¬
мальности К следует равенство sK = К+. Лемма до¬
казана.
Рассмотрим теперь произвольный корень а и выбе¬
рем камеру К таким образом, чтобы ее граница пересе¬
калась с гиперплоскостью На по многообразию размер¬
ности На. Если sK = К+, то, очевидно, sHa = #и., при
некотором i=l, 2, ..., г. Отображение s~lSiS является
зеркальным отражением относительно гиперплоскости
На. Следовательно, s~lSiS = sa, и отсюда следует, что
sa е ®. Теорема доказана.
Следствие 1. Группа ® конечна.
Следствие 2. Каждый корень а может быть по¬
лучен некоторым преобразованием se® из простого
корня (0,.
Действительно, если sHa = Hai, то sa = ±со,- По¬
скольку sM;co, = — со,-, то одно из преобразований s, s^.s
переводит а в со,.
Заметим теперь, что всякий автоморфизм se® мо¬
жет быть продолжен (§ 94, следствие из теоремы 4) до
автоморфизма всей алгебры X. Уточнением этого утвер¬
ждения является
Теорема 14. Пусть Gо — присоединенная группа
для алгебры X и U0 — максимальная компактная под¬
группа в С0, порожденная компактной формой Вейля.
Тогда для каждого se® существует преобразование
i/(s)e Uo, совпадающее с s на картановской подалгеб¬
ре Н.
Доказательство. Достаточно рассмотреть слу¬
чай s = sa. Докажем, что в этом случае u(s)=exp^,

472
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
где положено
х = ■
У 2 (а, а)
(ба "Т б_а).
Действительно, если h е На, то [h, еа] = [h, е_а] = 0, и
отсюда следует, чтохЯа = (0), т е. u(s) оставляет ги¬
перплоскость На неподвижной. Остается применить
u(s) к элементу a J. На. Заметим, что трехмерное про¬
странство {а, еа, е~а} инвариантно относительно Л и опе¬
ратор х в этом пространстве может быть записан в виде
матрицы х— ра, где р = Ы и
0
1
У2
1
У 2
a =
i
~~ yf
0
0
l
V2
0
0
относительно базиса а, У (а, а) еа, У {а, а) е_а. Заметим,
что а3 = а; следовательно, ехрра = 1 + (sin л)а + (cosn —
— 1) а2 — 1 — 2а2, откуда
ехр ра =
-1 О
О О
О 1
В частности, отсюда следует, что u(s)a = —а. В резуль¬
тате u(s)= sa на картановской подалгебре Я. Остается
заметить, что х содержится в компактной форме Вейля.
Теорема доказана.
Рассмотрим более подробно некоторые свойства
группы Вейля, которые часто используются в приложе¬
ниях. Для краткости положим si = Всякий элемент
s е 6 запишем в виде
s = St,S,
1) i2
Цепочку s назовем несократимой, если s невозможно
представить в виде S/,s/2 ... Sft, где /ь /2, ..., /; — под¬
последовательность индексов i\, 12, ..., im и I -Cm.

§ 105. ГРУППА ВЕЙЛЯ
473
1° Рефлексия s,- переводит со, в —со,- и переставляет
все остальные положительные корни между собой.
Доказательство. Если а—положительный ко-
Г
рень, а = 2 ks(£)j, то все коэффициенты kj должны быть
l=1
неотрицательны (§ 93). Имеем
S;<X = 2 kid), + (ki — п) со,-.
!Ф1
Если хотя бы одно из чисел kj, / Ф i, отлично от нуля,
то все остальные коэффициенты неотрицательны и
sa > 0. Если же kf = 0 при j ф i, то а = со,- и Sja = —а.
2° Если элемент se8 переводит всякий положитель¬
ный корень в положительный, то s = е.
Доказательство. Положим s — s,s, .. . s.- и
‘1 2 lm
условимся рассматривать только несократимые цепочки.
Доказательство будем вести индукцией по т.
Если т= 1, то 2° непосредственно следует из 1°.
Если гп > 1, то положим
s = (Si S, . . . s, ) s, = s's, .
^ 1\ 12 1т-1/ Чп Чп
Очевидно (ввиду 1°), что s' переводит со,-т в отрицатель¬
ный корень (и переставляет все остальные положитель¬
ные корни между собой). Разобьем цепочку s' следую¬
щим образом:
s' = (s, Si . . . S.-, ,) Si, (si. , ... Si ,) ~ OS,. T.
V • 1 l2 lk — \) lk \ lk + \ Чп — I/ lk
Если k = \ (m=l), то полагаем o = e (x = e). Под¬
берем номер k таким образом, чтобы rco<m>0, HOs(-ATco,-m<
<0. В этом случае непременно xa>im —aik. Исходя из
определения рефлексий, находим отсюда, что
TS; Т-1 = Si .
1ГП lk
Следовательно, ts,- =s,-.t и s' = = ctts,- . Значит,
’ lm lk lk lm ’
s = s'sim = ox, и цепочка s сократима, вопреки предпо¬
ложению. Полученное противоречие показывает, что s = e.
Наше утверждение доказано. В иной формулировке
оно выглядит следующим образом:

474
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Теорема 15. Группа Вейля действует просто тран-
зитивно на совокупности камер Вейля.
(Говорят, что группа G действует просто транзитивно
на множестве М, если для каждой пары точек m\, m2^M
существует одно и только одно преобразование группы G,
переводящее в т2.)
Действительно, как мы видели при доказательстве
теоремы 13, группа Вейля действует транзитивно на со¬
вокупности камер Вейля. В частности, sK = К+ для
каждой камеры Вейля К■ Если s]K = K+ и s2K = K+, то
sis2]K+ ~ К+" Согласно 2° отсюда заключаем, что
V"1 = е, т. е. s, = s2.
Система Ф, состоящая из корней, называется фунда¬
ментальной, если каждый корень а однозначно предста¬
вляется в виде 2^/Ф/, ф/^Ф, где числа kj одновре-
/
менно либо положительны, либо отрицательны. Из тео¬
ремы 15 вытекает
Следствие. Группа Вейля просто транзитивна на
совокупности всех фундаментальных систем*).
Доказательство предоставляется читателю. (До¬
статочно установить соответствие между фундаменталь¬
ными системами и камерами Вейля; см. также [128].)
В заключение отметим еще одну замечательную харак¬
теристику группы Вейля:
3° Группа Вейля изоморфна А!Аа, где А— совокуп¬
ность всех внутренних автоморфизмов, сохраняющих
картановскую подалгебру Н, и А0 — подгруппа всех
автоморфизмов вида exp Dh, h е Н.
Доказательство см., например, в [128], стр. 182—
187.
§ 106. Существование комплексной оболочки
До сих пор мы откладывали решение принципиаль¬
ного вопроса о существовании комплексной оболочки у
произвольной компактной группы Ли. Теперь приступим
*) Отсюда, в частности, нетрудно получить, что всякий корень
«в может быть сделан простым относительно некоторого лексикогра¬
фического упорядочения.

§ 106. СУЩЕСТВОВАНИЕ КОМПЛЕКСНОЙ ОБОЛОЧКИ 475
к решению этого вопроса. При доказательстве будем
опираться только на глобальную теорему (гл. IV).
Пусть G — произвольная компактная группа Ли. По¬
скольку G допускает точное линейное унитарное предста¬
вление, мы будем считать, что G линейна, и записывать
каждый элемент g е G в виде унитарной матрицы
II 8ц II/. /=1,2,.... п0- Функцию f(g) мы назовем полиномом
на группе G, если она представима в виде полинома от
переменных gih gijt i, j = 1,2,..., n0.
Лемма 1. Функция f(g) является полиномом на
группе G тогда и только тогда, когда она представима
в виде линейной комбинации матричных элементов
группы G.
Доказательство. Напомним, что матричные эле¬
менты группы G суть матричные элементы ее неприво¬
димых представлений. Согласно глобальной теореме каж¬
дое такое представление содержится в классе тензоров;
следовательно, его матричные элементы являются поли¬
номами на G. С другой стороны, каждый одночлен от
gih ёц является матричным элементом тензорного про¬
изведения вида g ® g ® . . . <3* g<S) . . . <3> g, где g = g'~l =
= g—контрагредиентное представление G. В силу прин¬
ципа полной приводимости этот одночлен раскладывает¬
ся в сумму матричных элементов группы G. Лемма до¬
казана.
Условимся записывать каждое неприводимое пред¬
ставление группы G в виде матрицы
та (я) = II Та (я) II
где а — дискретный индекс, нумерующий представление,
и jV = dirnxa. Между матрицами t“(g) существуют сле¬
дующие соотношения:
та {g) <8> тр {g) = С-1 (та> {g) © ... ® т> {g)) С,
с постояными матрицами С (зависящими от a, Р). Дей¬
ствительно, каждое из этих соотношений выражает раз¬
ложение та ® на неприводимые компоненты. Для ма¬
тричных элементов соответственно имеем
тр, (£) хы № = 2 cv (a, Р; р, q\ k, I) (g).
V. m> n

476
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Мы условимся называть такие соотношения соотноше
ниями Клебша — Гордана. Если выразить каждый из
матричных элементов в виде полинома от gijt gi;-, то по¬
лучаем систему алгебраических соотношений
фм.ы(8ц> £;/) = 0> (*)
которым удовлетворяют все матрицы g е G. Условимся
называть такие соотношения фундаментальными соотно¬
шениями для группы G. Докажем, что имеет место
Л е м м а 2. Система чисел £,“ удовлетворяет соотно¬
шениям Клебша — Гордана
СД= 2 cln{a,bp,q\k,l)lln
Y. m> п
тогда и только тогда, когда эти числа могут быть пред¬
ставлены в виде '*)
«.а а / \
lPq = ^Pq{xiP У а)’
где числа xtj, y{j удовлетворяют фундаментальным со¬
отношениям (*) с заменой gtj на Хц, gtj на уц.
Доказательство. Заметим вначале, что если ис¬
ходное представление группы G неприводимо, то пара¬
метры gu, gij сами входят в число матричных элементов
группы G. В общем случае мы положим
gu = 2 («, р, q) (g), gt/ = 2 \iit (a, p, q) %apq (g).
Здесь суммирование ведется по а, р, q и обе суммы ко¬
нечны. Если числа удовлетворяют соотношениям
Клебша — Гордана, то мы положим
х„ = 2 ЪИ (а, р, q) fpq, уц = 2 Pti (а, р, q) lapq.
Тогда эти числа, очевидно, удовлетворяют соотноше¬
ниям (-*). Фиксируем теперь индекс а = ао и рассмотрим
представление в классе тензоров, содержащее т“°; тогда
*) В правой части имеется в виду подстановка чисел Хц, уц
в полином xpq (gij, gij)- Заметим, что полином xpq определяется
своими значениями на группе G неоднозначно; здесь мы имеем в
виду любое из таких представлений.

§ 106. СУЩЕСТВОВАНИЕ КОМПЛЕКСНОЙ ОБОЛОЧКИ
477
мы имеем
U~'(g<8) g <8> ... ® g <8> ... ® g) U = та'(§)® ...
Разлагая в свою очередь представления g и g на не¬
приводимые, получаем в левой части формальный поли¬
ном (относительно операций ®, ©). Соответствующие
соотношения между матричными элементами являются
следствием сотношений Клебша — Гордана. Следователь¬
но, они не изменятся, если вместо т“ (g) сделать под¬
становку чисел . В результате
С = У а)’
где числа Xij, г/,-j выражаются указанными выше форму¬
лами через С другой стороны, если числа хц, уц удо¬
влетворяют соотношениям (*), то для чисел gp4 авто¬
матически выполняются соотношения Клебша — Горда¬
на. Лемма доказана.
Замечание. Если матрицы х = Цлг^-Ц, у = Цг/jjll удо¬
влетворяют фундаментальным соотношениям, то ху' = е,
где штрих означает транспонирование.
Действительно, в число фундаментальных соотноше¬
ний для матрицы g е G входит условие унитарности:
gg* = е,
которое выражает тот факт, что в тензорном произведе¬
нии g ® g содержится единичное представление. Заме¬
няя g на х и g на у, получаем нужное соотношение.
Введем теперь обозначение s&(G) для множества
всех пар х, у, удовлетворяющих системе фундаменталь¬
ных соотношений
Ф (*> у) — о,
где Ф — один из полиномов системы (-*). Тогда s4-(G) яв¬
ляется алгебраическим многообразием в М(2п0). По¬
скольку у = х'~\ то s4-(G) мы можем рассматривать
вложенным в группу GL(«0, С):
(G) a GL (п0, С).
Лемма 3. Многобразие j&(G) является группой.

478
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Доказательство. В силу леммы 2 достаточно
проверить, что если два набора | = т| = удо¬
влетворяют соотношениям Клебша—Гордана, то «про¬
изведение» £=|т], составленное из чисел
/V
также удовлетворяет соотношениям Клебша — Гордана.
Положим !“ = \\lapq ||, if = |hpj|. £a = ||S“J; Т0ГДа £a = S,a-na,
и согласно известному правилу тензорных произведений
мы имеем
£0 ® = (|а ® |Р) (ла ® rf).
Используя соотношения Клебша — Гордана для наборов
г], заключаем, что £a <g> = С ~1 © t“2 ® ... ®£“П)С.
Кроме того, согласно замечанию на стр. 477 матрицы из
M(G) обратимы в s£(G). Лемма доказана.
Согласно построению группа G содержится в
s6(G). Следовательно, G содержится также в
s*(G)nU(n0).
Лемма 4. Группа G совпадает с совокупностью всех
унитарных матриц из s&(G).
Доказательство. Положим Gi =s& (G) П U(ra0) •
Поскольку группа G\ линейна, всякий ее матричный эле¬
мент является полиномом от Хц, Xij, i, j = 1,2, ..., п; по¬
следние переменные в свою очередь могут быть разло¬
жены по матричным элементам трЧ(хи, ) (см- Д°ка"
зательство леммы 2). Из равенства таких полиномов
нулю на группе G следует их равенство нулю на Gi *).
Следовательно, всякое неприводимое представление груп¬
пы G] остается неприводимым при сужении на G. Как
мы видели в § 31 **), отсюда следует равенство G\ = G.
Лемма доказана.
Лемма 5. Группа M(G) является правильной ком¬
плексной оболочкой группы G.
Доказательство. Заметим, что группа s&(G)
вместе с каждым элементом g содержит также g*. Дей¬
*) Действительно, матричные элементы линейно независимы на
С (теорема Бернсайда).
**) См. упражнение на стр. 129.

§ 106, СУЩЕСТВОВАНИЕ КОМПЛЕКСНОЙ ОБОЛОЧКИ 479
ствительно, матрица С в соотношениях Клебша — Гор-
дана унитарна, и это позволяет заменить каждый эле¬
мент на (£“)*. Следовательно, s&(G) содержит также
элемент р2 = gg*. Покажем, что sfi(G) содержит ма¬
трицу р.
Пусть р — произвольная положительно определенная
эрмитова матрица из s4-(G)\ положим р = х~1ех, где
матрица е диагональна. Если f(g)— один из определяю¬
щих полиномов для s&(G), то f(pm) = 0 для всех значе¬
ний т — 0, 1, 2,. . . Следовательно,
f {х~1гтх) = 0, т= 1, 2, ...
Поскольку левая часть является полиномом от собствен¬
ных значений матрицы е, то отсюда следует также, что
f(x~'ekx) = 0 для любого комплексного X. Следователь¬
но, матрица рк содержится в s&(G) при любом ком¬
плексном X. Полагая, в частности, р = р2, заключаем, что
р11 содержится в s£(G) при любом комплексном X. Сле¬
довательно, унитарная матрица и в полярном разло¬
жении
g = p«
также содержится в sT(G). Поскольку р и и непрерыв¬
но зависят от g, то отсюда получаем, что многообразие
sfi(G) изоморфно прямому произведению:
sT (G) 3? X G,
где S? — совокупность всех положительно определенных
матриц из $0-(G). Если рей1, то p^^s^(G) при всех
комплексных X; в частности, рир содержится в G при
всех вещественных <р. Следовательно, dim i? ^ dim G.
С другой стороны, если иеб, и = exp ih, то аналогич¬
ное рассуждение показывает, что exp th^s&{G) при
любом вещественном t. Следовательно, dim 3? = dim G.
В результате, если X — алгебра Ли группы G и М(Х) —
алгебра Ли s£(G), то мы имеем разложение в прямую
сумму:
£ф{Х) = Х + IX.
Следовательно, s£(G) является комплексной оболочкой
группы G. Кроме того, s4-{G)~2? X G, где 3? является

480
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
евклидовым пространством. Следовательно, каждая связ¬
ная компонента группы s£(G) содержит лишь одну
связную компоненту группы G. Лемма доказана.
В результате получена следующая фундаментальная
Теорема 16. Всякая компактная группа Ли имеет
правильную комплексную оболочку.
Нетрудно показать, что эта оболочка определяется
однозначно (с точностью до изоморфизма). С другой
стороны, как показано в § 101, всякая связная редуктив-
ная комплексная группа Ли содержит компактную веще¬
ственную форму. Комбинируя с теоремой 16, получаем
Следствие. Множество всех надкомпактных связ¬
ных групп Ли совпадает с множеством всех редуктив¬
ных связных комплексных групп Ли.
Заодно мы получили еще одно доказательство алге-
браичности компактной группы Ли. Кроме того, мы ви¬
дим, что ее комплексная оболочка также алгебраична.
Упражнение
Показать, что всякая полупростая комплексная связная груп¬
па G допускает разложение вида U£tl, где подгруппы 11 и £ те же,
что и в разложении Ивасавы. (Указание: привести положитель¬
но определенную матрицу а = gg * к диагональному виду с по¬
мощью унитарного преобразования «ей ,?).)
§ 107. Некоторые дополнительные результаты
Остановимся вкратце на некоторых вопросах, близких
к тем, которые рассматривались в этой главе. Прежде
всего, в предыдущем параграфе, помимо доказательства
основной теоремы, мы получили еще значительную ин¬
формацию о свойствах компактной группы Ли. Этот
круг идей известен под названием теории двойствен¬
ности.
Пусть G — компактная группа Ли и индекс а нуме¬
рует все ее неприводимые представления (рассматри¬
ваемые с точностью до эквивалентности). Введем линей¬
ное пространство В как линейную оболочку формальных
символов eapq, р, q=\, 2, Na, где Na — размер¬
*) См. доказательство леммы 5.

§ 107 НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ 4S1
ность представления с номером а. Тогда мы имеем
в = 2©ва,
а
где Ва — линейная оболочка символов ер„ с фиксиро¬
ванным индексом а (все эти элементы считаются ли¬
нейно независимыми). Введем в пространство В били¬
нейную операцию х*у следующим образом:
еа * ер = С -1 (еа‘ ф е“2 ® ... фА)С.
Здесь еа = ||еа II и матрица С является ма-
11 Р<п1р, <7=1, 2, Na ^
трицей Клебша — Гордана для группы G. Указанное
символическое правило расшифровывается следующим
образом:
eapq*eit= 2 с* „(а, р; р, q- k, /)е?„
V, т, n
с коэффициентами, введенными в § 106. Операция х*у
называется кронекеровским произведением в В. Алгеб¬
ра В называется блок-алгеброй, ассоциированной с груп¬
пой G. Иногда эту алгебру называют также дуальным
объектом или дуальной системой для группы G.
Определим инволюцию в алгебре В как эрмитово со¬
пряжение в каждом блоке Ва\ при этом
(еа )* = еа
Vpq) qp
Характером алгебры В назовем произвольный линей¬
ный функционал 1(b), обладающий свойством мульти¬
пликативности:
Ub^b.2) = i(bx)i(b2).
Унитарным характером алгебры В назовем произ¬
вольный характер, удовлетворяющий дополнительному
свойству унитарности:
Пусть X — множество всех характеров алгебры В. Заме¬
тим, что каждый характер g е X однозначно определяет¬
ся набором чисел = | (е“ ). Положим

482
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Как следует из определения характера, числа удо¬
влетворяют соотношениям Клебша— Гордана. Отсюда
следует (см. § 106), что матрица обратима. Кроме
того, если |, г| — два характера, то матрица
la = Eaila
также определяет характер Следовательно, мно¬
жество X является группой. Множество Х0 всех унитар¬
ных характеров является подгруппой в группе X.
Теорема 17. Множество Х0 всех унитарных харак¬
теров алгебры В изоморфно группе G. Множество X
всех характеров алгебры В изоморфно комплексной обо¬
лочке s&(G).
Доказательство. Согласно лемме 2 из § 106 си-
стема чисел \pq тогда и только тогда удовлетворяет со¬
отношениям Клебша — Гордана, когда
ра ^та
fep<7 pq V6'
для некоторой точки ge^(G). Согласно лемме 4
g е G тогда и только тогда, когда все матрицы уни¬
тарны. Но это равносильно унитарности характера |.
Теорема доказана.
Иногда вместо блок-алгебры В рассматривают си¬
стему А всех неприводимых представлений группы G.
Всякий характер алгебры В называют представлением
системы А. Тогда группа G отождествляется с сово¬
купностью всех унитарных представлений системы А.
Пример. Пусть G — группа вращений окружности;
тогда каждое ее неприводимое представление нумерует¬
ся целым числом п, —оо < п < оо (и имеет вид ein,v, где
Ф — угловой параметр в группе G). Алгебра В натянута
на базисные элементы еп с законом умножения
&п * ёщ &п + т•
Найдем характеры алгебры В. Положим |п = |(еп); то¬
гда мы имеем систему уравнений
En+m*
Отсюда, в частности, следует, что |0 = 1- Далее, если
= z, то In = zn для всех значений п. Здесь 2 —произ-

§ 107. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ 483
вольное комплексное число. Налагая условие унитарно¬
сти, получаем характер
Ini ф) = егпф, 0<ср<2л.
Отсюда очевиден результат теоремы 17 для группы G.
В частности, множество всех унитарных характеров изо¬
морфно группе G.
Аналогичная структура всегда имеет место для про¬
извольной коммутативной компактной группы G, В этом
случае система А также состоит из характеров группы G.
Теорема 17 в этом частном случае была впервые дока¬
зана Л. С. Понтрягиным и именуется понтрягинским
принципом двойственности.
Далее, вернемся к вопросам структуры самой группы
Ли. Если G — разрешимая связная группа Ли, то оказы¬
вается ([92], [113]), что она разлагается в произведение
своих однопараметрических подгрупп:
G = G,G2 ... Gm.
При этом существует такое разложение, при котором
каждая подгруппа Rh= GftGft+i . . . G„, является нормаль¬
ным делителем в Rk-i (Ro = G). Если G односвязна, то
указанное разложение g = g\g2 ... gm однозначно и
взаимно непрерывно*).
Далее, используя теорему Леви — Мальцева и разло¬
жение Ивасавы, получаем следующий результат:
Теорема 18. Всякая односвязная группа Ли может
быть разложена следующим образом:
G = Т-A- U,
где Т — разрешимая односвязная подгруппа, А — одно¬
связная абелева подгруппа и U — компактная подгруппа
в G. При этом индивидуальное разложение
g = tau, t<=T, at=A, ueU,
однозначно и взаимно непрерывно (т. е. элементы t, а, и
являются непрерывными функциями от g).
*) Частный случай этого утверждения мы получим в § 111 при
доказательстве теоремы об индикаторах.

484
ГЛ. XV. КОМПАКТНЫЕ ГРУППЫ ЛИ В ЦЕЛОМ
Этот результат был получен независимо А. И. Маль¬
цевым [113] и К. Ивасавой [92]. См. также [128]. От¬
сюда, в частности, следует, что G гомеоморфно 2? X U,
где 3? — евклидово пространство. Следовательно, топо¬
логия связных групп Ли сводится, по существу, к топо¬
логии компактных групп Ли.
Заметим, что конструкция группы G в теореме 18 мо¬
жет быть получена непосредственно из алгебры Ли этой
группы [128]. Иначе говоря, на этом пути получается до¬
казательство существования группы Ли с заданной ал¬
геброй Ли.
Отметим еще одно доказательство этого утверждения, пригод¬
ное в случае полупростой комплексной алгебры X. По алгебре X
определяется система всех ее неприводимых конечномерных пред¬
ставлений, затем соответствующая блок-алгебра В, по которой в
свою очередь строится двойственная группа G. Очевидно, G — груп¬
па Ли с алгеброй Ли X. Поскольку G и X обладают «одинаковым
запасом» неприводимых конечномерных представлений, то отсюда
нетрудно заключить, что группа G односвязна. Кроме того, из этой
конструкции непосредственно вытекает алгебраичность группы G.
Аналогичная конструкция пригодна в случае компактной алгебры X.
Наконец, остановимся на одном весьма частном во¬
просе из теории инвариантов. Следующая теорема при¬
надлежит К- Шевалле [144].
Теорема 19. Пусть G — конечная линейная группа,
порожденная рефлексиями в п-мерном евклидовом про¬
странстве. Тогда алгебра I всех полиномиальных инва¬
риантов содержит п независимых образующих.
Таким образом, в данном случае мы получаем значи¬
тельное уточнение теоремы 1 из § 98.
* *
Теорема 1 принадлежит Д. Гильберту (см. [10]) и является од¬
ной из классических теорем теории инвариантов. Обобщения этой
теоремы можно найти, например, в [128], стр. 91. См. также [76],
стр. 26. Доказательство свойства алгебраичности компактной груп¬
пы Ли (теорема 3) заимствовано автором из лекций Э. Б. В и н-
берга [15]. (Заметим, что в этих лекциях вместо усреднения по
группе используется усреднение по векторному пространству, в ко¬
тором действует группа.) Теория алгебраических групп разработана
главным образом в работах К. Шевалле [46] (том. 11); мы ка¬
саемся здесь лишь простейших вопросов этой теории.

§ 107. НЕКОТОРЫЕ ДОПОЛНИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ 485
Разложения Гаусса и Ивасавы (§§ 100, 101) относятся к важ¬
нейшим разложениям полупростой (и редуктивной) группы Ли, ис¬
пользуемым в теории представлений ([68], [85]). В этой книге мы
рассматриваем такие разложения только для комплексных групп
Ли. Разложение Гаусса было в общем виде, по-видимому, впервые
получено в работах Хариш-Чандры. Здесь мы приводим доказа¬
тельство, данное в статье [85], и получаем разложение Ивасавы из
разложения Гаусса (см. доказательство теоремы 7). Первоначаль¬
ное доказательство принадлежит К. Ивасаве [92] и А. И. Маль¬
цеву [113]. См. также [85], [92], [113] по поводу обобщения на ве¬
щественный случай.
Связь между геодезическими и однопараметрическими подгруп¬
пами была впервые отмечена Э. Картаном. Более подробно этот
вопрос был рассмотрен К. Номидзу [120]. См. также [42], [128].
Теорема о сопряженности максимальных торов принадлежит
Г. Вейлю [61]. Здесь изложено простое доказательство, предло¬
женное Дж. Хантом [135].
В этой главе мы впервые затронули «глубокие» вопросы топо¬
логии (§ 103, «Фундаментальная группа и центр»). Основная тео¬
рема о компактности универсальной накрывающей принадлежит
Г. Вейлю; в настоящее время известно несколько вариантов дока¬
зательства этой теоремы ([128]), из которых мы предпочли наиболее
непосредственное построение (Л. С. Понтрягин [38]). Теорема
о линейности полупростой комплексной связной группы Ли полу¬
чается отсюда как простое следствие (см. § 104). Группа Вейля
была введена Г. Вейлем [61] при изучении структуры полупро-
стых комплексных алгебр Ли. Более подробное изложение свойств
этой группы можно найти в [19], [128].
Существование правильной комплексной оболочки для произ¬
вольной компактной группы Ли является одним из основных ре¬
зультатов этой главы. Как отмечалось в тексте, этот результат
мог бы быть изложен непосредственно вслед за глобальной теоре¬
мой, т. е. он не опирается на классификационную теорию. Наше из¬
ложение является упрощенным вариантом изложения К. Шевал-
ле [46] (том I, стр. 273—293).
Теория двойственности была впервые построена Л. С. По н-
тр я г иным [38] для произвольных локально компактных абелевых
групп. Ее обобщение на произвольные компактные группы принад¬
лежит Т. Таннаке [131]. В работе М. Г. Крейна [105] дается
аксиоматическое описание блок-алгебр, т. е. объектов, двойственных
к компактным группам Ли. По поводу обобщения этой теории на
некомпактные группы Ли см. [131'].
Относительно более детального описания компактных групп Ли
в целом см. также [46], [81], [128].

ГЛАВА XVI
ОПИСАНИЕ НЕПРИВОДИМЫХ
КОНЕЧНОМЕРНЫХ ПРЕДСТАВЛЕНИЙ
В этой главе будет построена глобальная теория
неприводимых (конечномерных) представлений произ¬
вольной связной группы Ли. Мы увидим, что решение
этого вопроса сводится, по существу, к рассмотрению
компактных групп Ли. В свою очередь, если ограни¬
читься компактными группами Ли, то основная техни¬
ческая сложность приходится на долю полупростых
(в действительности на долю простых) связных групп
Ли. Используя аналитическое продолжение, мы можем
ограничиться рассмотрением полупростых комплексных
групп Ли.
Теория неприводимых представлений полупростой
комплексной группы Ли может быть построена с по¬
мощью инфинитезимального метода (подобно тому как
в гл. V мы рассматривали группу SU(2)). Однако гло¬
бальный подход обладает преимуществом большей за¬
вершенности, поскольку каждое представление строится
эффективно в виде чрезвычайно простой «канонической
модели». Некоторые вопросы икфинитезималькой мето¬
дики будут рассмотрены в следующей главе.
§ 108. Основная теорема
Мы будем рассматривать в этой главе произвольную
комплексную редуктивную связную группу G. Согласно
результатам гл. XV эта группа надкомпактна (и потому
алгебраична). Кроме того, она обладает разложением
Гаусса, которое мы будем записывать в виде
G = zZDZ+.
Здесь черта означает замыкание множества Greg =
= Z_Z)Z+. Напомним, что множество Greg получается уда¬
лением из G некоторого «сингулярного» подмногообра-

§ 108. ОСНОВНАЯ ТЕОРЕМА
487
зия, размерность которого меньше размерности G. Здесь
D — «диагональная» (картановская) подгруппа, Z_, Z+—■
«корневые» подгруппы, которые порождаются касатель¬
ными векторами е_т, еш, со > 0. Z_ и Z+ односвязны и
нильпотентны.
Мы условимся рассматривать представление груп¬
пы G только в комплексных векторных пространствах.
Если использовать замечание, сделанное в конце дока¬
зательства теоремы 6 в гл. XV, то нетрудно заключить,
что во всяком линейном представлении группы G суще¬
ствует базис, относительно которого элементы из Z„, D,
Z+ становятся нижними треугольными (с единицами на
диагонали), диагональными и верхними треугольными
(с единицами на диагонали). Однако этим замечанием
мы сейчас не будем пользоваться.
Займемся систематическим описанием всех неприво¬
димых представлений группы G.
Определение 1. Пусть g-+Tg — произвольное ко¬
нечномерное представление группы G в (комплексном)
векторном пространстве V. Вектор | е V мы называем
старшим вектором, этого представления, если
Tzl = I
для всех элементов zeZ+ и если, кроме того, вектор £
является собственным относительно картановской под¬
группы D:
Т& = а( 6)1 (Е^О),
где б ей. Функция а (б) (которая, очевидно, является
характером группы D) называется старшим весом дан¬
ного представления.
Заметим, что группа R+ = DZ+ является разрешимой
связной группой Ли и группа Z+ является ее производ¬
ной подгруппой. Согласно теореме Ли (§ 88) в любом
конечномерном представлении группы R+ существует
вектор, собственный относительно R+. Всякий такой век¬
тор автоматически является инвариантом подгруппы Z+.
Следовательно, всякое конечномерное представление
группы G обладает хотя бы одним старшим вектором.
Теорема 1. Всякое неприводимое представление
группы G обладает единственным (с точностью до

488
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
множителя) старшим вектором. Соответствующий стар¬
ший вес определяет данное неприводимое представление
с точностью до эквивалентности.
Пусть а (б)—старший вес данного представления и
a(g)— значение функции а (б) на диагональной компо¬
ненте 6 в разложении Гаусса g = £62, £ е Z-, б еД
2gZ+. Тогда a{g) — аналитическая фнукция на груп¬
пе G и представление может быть реализовано следую¬
щей формулой:
Tgf{z) = a(z, g)f(zg).
Здесь a (z,g) = a(zg) и элемент z6gZ+ определяется
как правая компонента z в разложении Гаусса zg =
= £62. Пространство представления состоит из полино¬
мов на группе Z = Z+*) и является линейной оболочкой
всевозможных функций fg(z) = a(z,g), g^G.
Старшим вектором в данной модели является функ¬
ция fe(z)== 1 на группе Z. Всякий матричный элемент
данного представления является линейной комбинацией
функций qj(g-) = oc(gigg2), где gu g2 пробегают G.
Доказательство. Пусть Т — неприводимое пред¬
ставление группы G и fo(g) = (Т gx0, у о)—его произволь¬
ный матричный элемент. Согласно теореме Ли мы мо¬
жем выбрать векторы х0, Уо таким образом, чтобы они
были собственными относительно DZ+, DZ_ соответствен¬
но. Тогда имеем
/о (£ 62) = a (б) (х0, у0) = р (б) (х0, у0),
где a (б) — собственное значение оператора Тй на век¬
торе х0 и р(б) — собственное значение сопряженного
оператора Ть на векторе у0. Если (х0, уо) = 0, то
(7>о, Уо) = 0 тождественно на группе G, и это означало
бы, что циклическая оболочка вектора х0 ортогональна
вектору уо. Из неприводимости Т вытекало бы в этом
случае, что либо х0 = 0, либо у0 = 0, что исключается
теоремой Ли. Следовательно, а(б)= Р(б), и мы имеем
/о (£ 62) = а (б),
*) То есть из полиномов от канонических координат в Z.

§ 108. ОСНОВНАЯ ТЕОРЕМА
489
если нормировать векторы х0, Уо таким образом, чтобы
(яо, Уо) — 1. Если х'0— какой-либо другой старший вектор
представления Т, то мы по-прежнему имеем а'(б)=Р(б),
и вектор я'можно нормировать так, чтобы (*', г/0) = 1.
Отсюда следует равенство а/(б) = а(б) и также
((л:о — л:о)’ У о) ~
Поскольку вектор xa — x'Q по-прежнему имеет собствен¬
ное значение а(б), то либо он равен нулю, либо также
является старшим вектором представления Т. Послед¬
нее, как мы видели выше, невозможно ввиду ортогональ¬
ности xQ~ х'0 и г/о- Следовательно, х'0 = х0. Единственность
старшего вектора доказана.
Пусть S’t — линейная оболочка всех матричных эле¬
ментов представления Т. Тогда ST инвариантно и не¬
приводимо относительно двусторонних сдвигов:
TglJ(g) = f{g^gg2)-
Следовательно, St является циклической оболочкой
функции a(g) = fa(g). Если два неприводимых предста¬
вления Т,Т’ имеют одинаковый старший вес а(6), то
St = Sr, откуда заключаем, что Т эквивалентно Т'.
Рассуждая, как в гл. VII при построении «канониче¬
ской модели», мы реализуем представление Tg в классе
функций на группе Z = Z+. При этом пространство пред¬
ставления состоит из всевозможных функций вида
f (2) = (Tzx, г/0),
где х пробегает исходное пространство представления Т.
Поскольку Z = Z+ — односвязная нильпотентная группа,
то всякий элемент zeZ однозначно записывается в виде
г = ехр а, где а — элемент алгебры Ли группы Z. Следо¬
вательно,
Тг — ехР А = 1 + A + • ■ •>
где А — инфинитезимальный оператор группы Z. По¬
скольку А — треугольная матрица с нулями на главной
диагонали, то Аш = 0 при некотором т. Полагая

490
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
А = 2 (относительно некоторого базиса в алгебре
i
Ли), заключаем, что Тг является полиномом относитель¬
но канонических координат Теорема доказана.
Реализацию неприводимого представления, указан¬
ную в теореме 1, мы будем называть канонической мо¬
делью или реализацией на группе Z.
Функцию a(g), введенную в условиях теоремы 1, мы
будем называть производящей функцией данного пред¬
ставления. Имеем:
1° a(£gz) = a(g);
2° а (бg) = а (g6) = а (g) • а (б)
для всех значений ^eZ_, 2eZ+, б ей, g^G. Соот¬
ветствующая функция двух переменных a(z,g) — <z{zg)
обладает следующими свойствами:
3° а (г, ё^2) = а(г, g1)a(zgi, g2);
4° а {г, Zq) = 1;
5° а (г, 6) = а (б).
Здесь, г, Zq пробегают группу Z = Z+ и б ей. Первое
условие очевидно ввиду соотношений мультипликатив¬
ности для операторов Tg. Из остальных двух условий мы
получаем в свою очередь чрезвычайно простые правила
действия для преобразований из D и Z:
ТZrf (г) = f {zz0), 'Г J (z) = а (б) f (б_12б).
Мы будем существенно использовать эти правила в даль¬
нейшем.
§ 109. Старшие веса и сигнатуры
Назовем характер а(6) группы D индуктивным, если
он является старшим весом одного из неприводимых
представлений группы G. Пространство канонической
модели обозначим и само неприводимое представле¬
ние со старшим весом а (б) обозначим символом d{a).
Для полного описания всех возможных неприводимых
представлений группы G осталось перечислить все ин¬
дуктивные характеры. Отметим пока только их простей¬
шие свойства.

s 109. СТАРШИЕ ВЕСА И СИГНАТУРЫ
491
1° Если характеры а'(б), а"(б) являются индуктив¬
ными, то характер а (б) = а' (б) а” (б) также является
индуктивным, причем
;){а = !1{а4На„,
где правая часть означает линейную оболочку всевоз¬
можных функций вида f(z) = f'(z)f"(z), f' е
/" е ilia".
Доказательство. Достаточно заметить, что про¬
странство SRa'^a" конечномерно и инвариантно относи¬
тельно системы операторов
Tgf(z) = a(z, g)f(zg),
где положено a (z, g) = a'{z, g)a"(z, g); кроме того,
единственным старшим вектором в этом пространстве
является функция /е(г)= 1. Используя принцип полной
приводимости, заключаем, что DV^a" неприводимо. Оче¬
видно, старшим весом в этом пространстве является
а(б) = а/(б)а//(б).
Следствие. Неприводимые представления груп¬
пы G образуют полугруппу относительно умножения
старших весов.
Неприводимое представление й(а), отвечающее ха¬
рактеру а = а'а”, назовем произведением Юнга пред¬
ставлений d(a'), d(a") и условимся писать
d(a) = d {a') d (а").
Замечание. Как видно из 1°, представление d(a)
содержится в тензорном произведении d (а') <8> d (а").
Как увидим в дальнейшем (§ 131), оно содержится в
этом произведении однократно и является «старшим»
относительно некоторой лексикографической упорядочен¬
ности. Отсюда вытекает возможность иного определения
произведения Юнга.
Условимся вначале рассматривать для простоты толь¬
ко (комплексно) аналитические представления группы G.
Запишем произвольный аналитический характер a (б)
в виде экспоненты:
a (б) = exp (I, h) = exp 1ф‘,

49?
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
где б = ехр h и П— координаты вектора h относительно
некоторого фиксированного базиса в картановской под¬
алгебре Н *). Если характер а (6) является индуктив¬
ным, то' вектор I е= Н мы называем сигнатурой, а линей¬
ную форму (I, h)—инфинитезимальным старшим весом
представления d(a).
Заметим, что (l,h) является собственным значением
(на старшем векторе х0) инфинитезимального операто¬
ра D(h), отвечающего произвольному вектору АеЯ.
Очевидно, умножению Юнга отвечает сложение соответ¬
ствующих сигнатур.
Пусть G0—редуктивная связная подгруппа в группе
G и разложение Гаусса в группе G индуцирует разло¬
жение Гаусса в подгруппе G0, т. е.
/~>0 г\0 /уО
V reg = Z—L/ Z + ,
где Z-, D°, Z+— пересечения группы G0 с подгруппами
Z_, D, Z+ соответственно. Сужение всякого характера
а (6) на подгруппу D°(a°(6) = а (б) при Sefl0) назо¬
вем проекцией характера а(6) на подгруппу D0.
2° Если характер а(б) индуктивен для группы G, то
его проекция а0(б) индуктивна для подгруппы G0, при¬
чем
*Ra. = ataUz„
где правая часть означает совокупность всех сужений
f°(z) = f(z) при zeZ°, /eMa(z° = Z°+).
Доказательство. Достаточно заметить, что про¬
странство 9ta“ инвариантно относительно G0 и единствен¬
ным старшим вектором в этом пространстве является
функция /e(z)= 1. Отсюда следует, что SRa° неприводи¬
мо. Очевидно, старшим весом в этом пространстве яв¬
ляется а0.
Представление d(a°) мы условимся называть проек¬
цией представления d(а) на подгруппу G0.
Замечание. Как видно из последнего доказатель¬
ства, d(a°) содержится в сужении d(а) на подгруппу G0.
*) Поскольку такая запись использует канонические коорди¬
наты, то она является локальной; однако в дальнейшем мы увидим,
что такая запись определяет характер а(6) на всей группе D.

§ 109. СТАРШИЕ ВЕСА И СИГНАТУРЫ
493
В дальнейшем мы увидим (§ 128), что d{a°) содержится
в d(a) однократно и является «старшим» в этом разло¬
жении относительно некоторой лексикографической упо¬
рядоченности. Отсюда вытекает возможность иного опре¬
деления проекции.
Определение проекции удобно сформулировать также
в терминах алгебры Ли. Пусть X— редуктивная ком¬
плексная алгебра Ли и К0— ее редуктивная подалгебра,
причем разложение Картана — Вейля в алгебре X инду¬
цирует разложение Картана — Вейля в подалгебре К0:
Х° = Х°~ + Я0 + Х°+, где Х°~, Я0, Х+—пересечения ал¬
гебры Х° с подалгебрами К_, Я, Х+ соответственно (Я
означает картановскую подалгебру).
3° Если вектор I является сигнатурой для алгебры X,
то его ортогональная проекция на Я0 является сигнату¬
рой для подалгебры К0.
Доказательство. Достаточно заметить, что стар¬
ший вектор £ представления d(a) является также стар¬
шим вектором относительно подалгебры Х° и при h° е= Я0
мы имеем (/, h°) = (1°, h°) где 1° — ортогональная проек¬
ция вектора I на подалгебру Я0. Пространство предста¬
вления d(a°) является циклической оболочкой вектора |
относительно инфинитезимальных операторов подал¬
гебры Х°.
В частности, пусть 0Ш — трехчленная подалгебра в
алгебре К, натянутая на векторы е_т, со, еш, где со —
произвольный положительный корень в алгебре X. Про¬
екция 1° в этом случае одномерна, и индуктивность 1° по
отношению к алгебре 0О накладывает определенные
ограничения на сигнатуру I.
Действительно, положим е0 = со/(со, со); тогда, как мы
видели в § 92, соответствующий инфинитезимальный опе¬
ратор D(e0) может принимать на старшем векторе толь¬
ко полуцелые неотрицательные значения. Отсюда полу¬
чаем:
4° Если вектор I является сигнатурой, то для любого
положительного корня со число 1а — 2(1, ш)/(со, со) должно
быть целым неотрицательным.
В частности, пусть со — один из простых корней
со], со2, ..., сог алгебры X. Проекции lt = /со. мы будем на¬
зывать числовыми отметками вектора I.

{94 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
5° Если вектор I является сигнатурой, то все его чис¬
ловые отметки должны быть целыми неотрицательными.
Если алгебра X полупроста, то числовые отметки
являются координатами вектора I относительно некото¬
рого базиса в алгебре Н (дуального к векторам со* =
= 2(о,-/ (ton Wi)). В этом случае, как увидим в дальней¬
шем, условие 5° является не только необходимым, но и
достаточным для индуктивности характера а(6).
§ 110. Нормально вложенные подгруппы
Прежде чем приступить к окончательному описанию
всех возможных сигнатур, остановимся несколько по¬
дробнее на некоторых свойствах канонической модели.
Пусть G0— треугольное усечение группы G, т. е. ре-
дуктивная подгруппа, алгебра Ли которой порождается
некоторым набором простых корней из алгебры Ли груп¬
пы G (см. § 100). Как мы видели в § 100, множество
Gregcr G может быть в этом случае записано в виде
Greg = N-G%gN + , (*)
где jV_, N+ — односвязные нильпотентные подгруппы, ин¬
вариантные по отношению к G0. В этом случае мы бу¬
дем также говорить, что группа G0 нормально вложена
в группу G. Соответствующее разложение (*) мы на¬
звали в § 100 обобщенным разложением Гаусса.
Теорема 2. Неприводимое представление d (а)
группы G может быть реализовано в классе вектор-
функций на подгруппе N = N+ следующей формулой:
Tgf(n) = AJ(ng).
Здесь Ag„ — оператор неприводимого представления
группы G0 со старшим весом а, элементы ng и go опре¬
деляются из обобщенного разложения Гаусса ng =
= ?еЛ1_, go^G0, пя еЛф. Функции f{n) яв¬
ляются полиномами на группе N и принимают значения
в пространстве представления Ago.
Доказательство. Положим Z = Z+, Z° = Z+, где
Z+ — корневая подгруппа в группе G и Z+ — ее пере¬
сечение с группой G0. Поскольку всякий элемент из Z

§ ПО. НОРМАЛЬНО ВЛОЖЕННЫЕ ПОДГРУППЫ
495
допускает обобщенное разложение Гаусса, то мы имеем
Z = Z°N,
и группы N, Z0 пересекаются только в единичной точке.
Условимся писать f(z) = f{z°n) = f(z°,n), т. е. будем
рассматривать элементы 2° е Z°, fiejV как параметры
во всей группе Z. Пусть элементы £, g0, ng определяются,
как в условиях теоремы. Тогда мы имеем
zg = zong = z%g0ng = I (z%) ng,
где I — z°Lz°~l e N- (действительно, группа Я_ инва¬
рианта относительно G°). В результате мы видим, что
z°g0 является центральной компонентой в разложении
Гаусса элемента zg. Следовательно, a(zg) ■= cc(z°g0), и
мы имеем
Тgf (z°, n)=a (z°, £0)/(z°„, ne)-
Если рассматривать f(z°,n) как вектор-функцию от п,
то мы получаем формулу, указанную в условиях теоре¬
мы. Теорема доказана.
Иногда говорят ввиду теоремы 2, что представление
d(a) индуцируется представлением Лг„ подгруппы G0.
Теорема 2 дает нам удобное правило индукции при
изучении канонической модели. Нам достаточно сейчас
рассмотреть тот случай, когда группа G0 имеет в каче¬
стве своей алгебры Ли подалгебру
еи = {е..и, Я, ej,
где со — произвольный простой корень алгебры X. В этом
случае G0 нормально вложена в G и подгруппа Z0 =
= Z П G0 совпадает с однопараметрической подгруппой
exp tea. Группа G0 является редуктивной связной*) груп¬
пой с полупростой компонентой ©ю, где 0Л имеет трех¬
членную алгебру Ли и потому изоморфна SL(2) либо
SL(2)/C, где С — центр в SL(2), состоящий из матриц
е, —е. Применяя теорему 2, получаем
Tj(n) = K(gt)W + b)mt{^,ne),
*) Связность G0 доказывается так же, как связность картанов¬
ской подгруппы D в теореме 6 § 100.

496
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
где t — аддитивный параметр в Z°, Z(go)— одномерное
представление редуктивной группы G0 и коэффициенты
а, (3, у, 6 зависят от параметров п, g, но не зависят от
параметра t. При этом нетрудно проверить, что т —
= /м = 2(1, w)/(w, со), т. е. т — числовая отметка сигна¬
туры / на простом корне со. Из полученной формулы вы¬
текает следующие важные следствия:
Следствие 1. Положим z = (exp tew)z', где со —
простой корень и z' пробегает подгруппу в группе Z, по¬
рожденную касательными векторами е«', со' > 0, а'ф со.
Тогда все функции f(z)^9la являются полиномами от t
степени не выше 1а.
Следствие 2. Пространство всех функций на
группе Z, которые являются полиномами от параметра t
степени не выше 1а, инвариантно относительно операто¬
ров Tg представления d(а).
Следствие 3. Пусть 2Di — аналитический инфини¬
тезимальный оператор левого сдвига на группе Z, отве¬
чающий корневому вектору еШ[, где со* — простой ко¬
рень, i = 1, 2, . .. , г. Пусть Sfta — пространство всех ре¬
шений системы дифференциальных уравнений
ф\Пф{г) = 0, /=1,2 г, (**)
в классе всех комплексно-аналитических функций на
группе Z. Здесь положено 1{ — 1аг с = 1, 2, . . ., г. Тогда
9ia инвариантно относительно операторов ТЙ представ¬
ления d(a).
Г
Действительно, SRa =
i = 1
Систему (**) мы будем называть индикаторной си¬
стемой на группе Z с сигнатурой / = (/*).
§ 111. Полиномы на группе Z
Как мы знаем *), все комплексно-аналитические не¬
приводимые представления надкомпактной группы ко¬
нечномерны. Этот критерий можно было бы взять за
*) См. § 42.

§111. ПОЛИНОМЫ НА ГРУППЕ I
497
основу при описании множества всех сигнатур. Очевид¬
но, характер а(6) индуктивен тогда и только тогда, ко¬
гда соответствующая функция а (<§■), первоначально
определенная на множестве Greg, может быть продол¬
жена до функции, аналитической (и однозначной) на
группе G. Однако непосредственное изучение такого
продолжения представляется затруднительным, и мы
предпочтем окольный путь.
В основу будет положено рассмотрение индикатор¬
ных систем на группе Z. При этом мы одновременно
будем рассматривать не только комплексно-аналитиче¬
ские, но также и вещественно-аналитические (т. е. все
конечномерные вещественные) неприводимые представ¬
ления группы G.
Пусть £Di, 3)i — аналитический и антианалитический
инфинитезимальные операторы левого сдвига на груп¬
пе Z, отвечающие вектору еар i = 1, 2, . .., г, где сщ—
простой корень. Систему уравнений вида
SD’/^f(z) = 0, ^+1/(z) = 0, i=l, 2,..., г,
мы будем называть индикаторной системой на группе Z.
В частном случае ki = 0, i = 1, 2, . .., г, мы получаем
равенство нулю не только операторов 3)и но и всех их
коммутаторов, т. е. всех антианалитических операторов
левого сдвига на Z. Отсюда, очевидно, следует, что
функция f(z) является комплексно-аналитической целой
функцией от канонических параметров в группе Z. Ос¬
тавшаяся система уравнений
3)!‘+lf(z) = 0, 1=1,2 г,
совпадает с индикаторной системой в классе аналити¬
ческих функций, введенной в предыдущем параграфе.
Удвоенную систему параметров I = (/,), k = (&,■) ki—
неотрицательные целые числа) мы по-прежнему будем
называть сигнатурой.
В основе всех дальнейших построений лежит следую¬
щая теорема:
Теорема 3. Пространство решений любой индика¬
торной системы конечномерно и состоит из полиномов
на группе Z.

498 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Доказательство. Докажем вначале самостоя¬
тельное утверждение, которое является обобщением лем¬
мы 2 из § 65. Пусть L — нильпотентная алгебра Ли,
L' — производная подалгебра и ец е2, •••, Si — система
элементов, дополняющих базис в L' до базиса в алгебре
L. Нетрудно видеть, что ец е2, ■ • • , ^ являются обра¬
зующими в алгебре L, т. е. их коммутаторы порождают
L'*). Элементы ец е2, ..., et назовем каноническими
образующими в L.
Основная лемма. Пусть L — нильпотентная ал¬
гебра Ли с каноническими образующими ец е2, ..., et.
Пусть x—*D(x) —представление алгебры L в простран¬
стве V (возможно, бесконечномерном) и Vq — подпро¬
странство, на котором
Д(еЛ+‘ = 0, /=1,2,...,/,
где ni\, пг2, ..., mL — неотрицательные целые числа. То¬
гда операторы D(x), jgL, нульстепенны в Vo с показа¬
телем нульстепенности, равномерно ограниченным по х:
D(x)m+l = 0, a;sL
Доказательство леммы. Пусть п — размер¬
ность алгебры. Доказательство будем вести индукцией
по п. Фиксируем одну из образующих, скажем в\, и
пусть Lj — линейная оболочка элементов е2, еъ, ..., е\
и коммутаторов всех элементов еи е2, . . . , ец тогда,
очевидно,
L = L0 + Lu
где Lq = {щ} и L\ является идеалом в L размерности
п— 1. Среди элементов вида
еИ = ё[ер / = 2, 3, / = 0, 1, 2
*) Действительно, пусть Щ = [L, L^-i] — центральный ряд в
алгебре L0 = L: э1гэ ... zd Ьр= (0), и пусть Ак— до¬
полнение Щ до Lji_i; тогда мы имеем [Ai,Aj]czLk, где k-
= max(i, /); отсюда легко получить, что всякий элемент из Lu запи¬
сывается в виде линейной комбинации элементов из [Л;, Aj],
i, j ^ k, с точностью до элементов из Lk+\. Применяя это правило
индуктивно, заключаем, что всякий элемент из Lh записывается в
виде линейной комбинации кратных коммутаторов элементов из А\
(с точностью до элементов из Lh+l). Полагая k — p,p—1, ..., 1,
получаем нужное утверждение: Ц = Ai + [А,, А:] + [Аи [Ль Ai]] +...

§111. ПОЛИНОМЫ НА ГРУППЕ Z
т
содержится система образующих подалгебры Д. (Здесь
а означает, как обычно, оператор ах = [а,х].) Соответ¬
ственно среди операторов 20ц — D ДД содержится си¬
стема образующих алгебры £)(Д). Далее, пусть А =
= £>(еi), S==£)(ef) при фиксированном i. Вместо эле¬
ментов 20ц нам будет удобно рассматривать их линей¬
ные комбинации
F (0 = etABe~tA = 1 + 2Da + -J 2Dn + ...
Оператор F(t) определен как конечный степенной ряд
на подпространстве V0• Действительно, рассуждая так
же, как при доказательстве леммы 2 в § 65, получаем,
что оператор А нульстепенен не только на V0, но также
на BV0. Аналогично, рассматривая BhV0, k = 0, 1, 2, . . . ,
получаем оператор
z? / v \ ^ ^ А г\!'1 ~~t А
F (/) = е В е ,
определенный всюду на V0• Если k достаточно велико,
то F(t)k~ 0 на Со (ввиду нульстепенности В на С0,
AVо, A2Vо, ...). Следовательно, оператор F(t) является
нульстепенным с показателем нульстепенности, равно¬
мерно ограниченным по t. Среди операторов F(t) содер¬
жится, очевидно, система образующих алгебры /)(Д)*).
Поскольку dim Д < dim L, мы получаем в результате,
что операторы D(x) нульстепенны на С0 для всякого
х е Д.
Наконец, используя формулу Кемпбелла — Хаусдор-
фа**), мы можем представить всякий элемент ехр х,
jeI, в виде ехр Д ■ ехр у, у е Д, причем если х =
= te 1 + 2, 2 е Д, то у выражается с помощью кратных
коммутаторов от 2, Д; следовательно, у является поли¬
номом от i. Соответственно имеем
ехр D (х) = ехр tD Д) • ехр D {у).
Оператор ехр D(y) является полиномом от D{y) на V0
и, следовательно, является полиномом от i. Далее,
*) Действительно, операторы 2Д можно выразить как линей¬
ные комбинации операторов F(t) при различных значениях t.
**) Поскольку алгебра X нильпотентна, то ряд Кемпбелла —
Хаусдорфа является конечным.

500 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
используя обычные рассуждения (§ 65), получаем, что
D(e 1) является нульстепенным не только на У0, но так¬
же на D(y)hV0, k = 0, 1, 2, ... Следовательно, expD(x)
является конечным рядом на V0. Заменяя х на Хх, по¬
лучаем, что ехр^О(х) является полиномом от X. Следо¬
вательно, D(x) нульстепенен на Vo- Очевидно также, что
показатель нульстепенности равномерно ограничен на
L. Лемма доказана. .
Напомним теперь, что в алгебре L существует це¬
почка вложенных идеалов L = L0 до L\ до ... до Ln = (0),
где dim Lj_i/L, = 1, i = 1, 2, . . . , n (cm. § 85). Отсюда
легко заключить, что односвязная группа Z с алгеброй
Ли L допускает однозначное разложение в произведение
односвязных однопараметрических подгрупп Z,-, / =
= 1,2, ..., п, причем Ri = ZiZi+\ ... Zn является нор¬
мальным делителем в i *). Полагая
z(t) = z, (t,)z2(t2) . .. zn(tn),
где {-z,(/)} = Zj, мы можем рассматривать t\, /2, ..., tn
как параметры в группе Z. Нетрудно видеть (из фор¬
мулы Кемпбелла — Хаусдорфа), что эти параметры свя¬
заны с каноническими параметрами в группе Z рекур-
рентно и полиномиально. Введенные параметры мы бу¬
дем называть нормальными параметрами в группе Z.
Используя нормальные параметры, из основной леммы
получаем
Следствие. Пусть S), = D(e,-)—инфинитезималь-
ный оператор левого сдвига на группе Z, и пусть Fm—
пространство всех решений системы дифференциальных
уравнений
2>™‘+'f(z) = 0, 1=1,2,...,/,
в классе (обычных или обобщеных) функций на груп¬
пе Z. Тогда для любого набора неотрицательных целых
чисел Ши /=1,2, . . ., /, пространство Fm конечномерно
и состоит из полиномов на группе Z **).
*) Достаточно проверить, что Z =• ZiR2; поскольку dim R2 =
= п — 1, где п — dim Z, то наше утверждение вытекает из индук¬
ции по п.
**) Здесь группа Z рассматривается как вещественная.

§ 112. ЗАВЕРШЕНИЕ КЛАССИФИКАЦИИ
501
Действительно, согласно основной лемме всякая
функция
Ф (t) = f(z(t)z), fezFm,
где z(t)—произвольная однопараметрическая подгруп¬
па, является полиномом от переменной t с равномерно
ограниченной степенью (по f, z и z(t)). В частности, по¬
ложим
z = aZi(ti)b, z(t) = azt (t) a~\
где a = Z\Z2 • • • b = zi+\Zi+2 ••• zn — фиксированные
элементы и t,— нормальный параметр в группе Z с но¬
мером тогда мы получаем, что функция ф(^) является
полиномом от параметра t. Следствие доказано.
Остается применить полученное следствие к корне¬
вой подгруппе Z = Z+. Поскольку эта группа должна
рассматриваться как вещественная, то мы рассматри¬
ваем «удвоенную» систему образующих S)it Тео¬
рема доказана.
В заключение заметим, что все построения преды¬
дущих двух параграфов повторяются почти дословно
для вещественного характера а(6) группы D. В частно¬
сти, мы видим, что пространство SKa всех решений ин¬
дикаторной системы инвариантно относительно Tg. Из
конечномерности и неприводимости Tg мы сможем
в дальнейшем заключить (§ 112), что Oin = Tla, т. е. про¬
странство представления совпадает с пространством
всех решений индикаторной системы.
§ 112. Завершение классификации
Теперь мы можем доказать следующую основную
теорему:
Теорема 4. Пусть G — односвязная полупростая
комплексная группа Ли. Тогда вектор 1^Н является
сигнатурой в том и только в том случае, когда все чис¬
ловые отметки lt, (=1, 2, ..., г, являются целыми не¬
отрицательными.
Доказательство. Необходимость условий уже
доказана (§ 109). Докажем достаточность. По данному
характеру а(8) определяем функцию a(g) с помощью

502 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
формулы
a (g) = а (С бг) = а (б)
в некоторой окрестности единицы группы G (где спра¬
ведливо разложение Гаусса). Далее определяем функ¬
цию двух переменных a(z,g) — a(zg). Эта функция пока
определена только на множестве вида Z\ X Gu где Z\ —
окрестность единицы в Z и G\—окрестность единицы
в G. Рассуждая, как при доказательстве теоремы 2, по¬
лучаем, что
а (г, g) = а (г°, g0) = (0* + 6)4
где z° — z°(t)—однопараметрическая подгруппа с на¬
правляющим вектором /ш, со = сог, i = 1, 2, . .. , г, и па¬
раметры |3, б не зависят от t. Если /щ — неотрицательное
целое число, то заключаем отсюда, что функция a(z,g)
удовлетворяет дифференциальному уравнению
^i+'a(z,g) = 0, /г = /и..
Если все числовые отметки /,, 1=1, 2, . . . , г, неотрица¬
тельны и целочисленны, то функция fg(z)=a(z,g) со¬
держится в конечномерном пространстве 91а, где 'Ла
определяется как совокупность всех решений индика¬
торной системы. Следовательно, fg(z) является полино¬
мом и потому однозначно определяется на всей груп¬
пе Z.
Далее, воспользуемся формулой 3° § 108, которая
вытекает из определения функции a(g) и справедлива
при значениях g\, g2, достаточно близких к единице.
Эта формула позволяет определить операторы
ТУ (г) = а (г, g) f (zg)
для достаточно малых g в линейной оболочке Ла функ¬
ций fg(z). Действительно, ввиду конечномерности
Ла сд Ла существует конечное число функций ft (2) =
= f (z), образующих базис в Ла, и оператор Tg опре-
деляется для всех элементов g таких, что все произве¬
дения ggi достаточно близки к единице:
ТУ«^ — !gg г

§ 112. ЗАВЕРШЕНИЕ КЛАССИФИКАЦИИ
603
Следовательно, в Ша определено представление локаль¬
ной группы Ли, соответствующей группе G. Ввиду одно¬
связности G это представление однозначно продолжает¬
ся на всю группу G. Следовательно, вектор I действи¬
тельно является сигнатурой. Теорема доказана.
Теорема 4 доставляет замечательные следствия не
только для описания неприводимых представлений бо¬
лее широкого класса групп Ли, но также и для изучения
структуры самой группы G.
Следствие 1. Пусть G — односвязная полупро¬
стая комплексная группа Ли. Тогда для каждого кор¬
ня ш в группе G существует односвязная подгруппа Ли
G“ с алгеброй Ли 0“ = {е^, со, е<0}.
Действительно, если корень со простой, то группа G®,
построенная в § 110, должна быть изоморфна SL(2)
(в противном случае проекция 1а оказалась бы четной).
Поскольку всякий корень со может быть сделан про¬
стым относительно некоторого упорядочения (§ 105), то
наше утверждение верно для любого со.
Следствие 2. Пусть G — односвязная полупро¬
стая комплексная группа Ли. Тогда ее картановская
подгруппа D разлагается в прямое произведение
D = D\D2 ... DT
однопараметрических замкнутых подгрупп Di =
= {exp GoJ, й = 2со/(со, со), где 0<Лт ^ < 2л. Полагая
6 = exp T&i, 0 Im В < 2л, получаем однозначную па¬
раметризацию группы D.
Действительно группа D{ является подгруппой Кар¬
тана в Ga‘, и потому ее параметр В должен норми¬
роваться условием 0^1тР^С2л. Разложение D =
= DiD2 . . . Dt вытекает из связности D и перестановоч¬
ности подгрупп Dy, очевидно также, что D, П Dj = {е}
при i ф j. Это следствие может быть также записано
следующим образом:
Следствие 3. В группе D существуют мультипли¬
кативные координаты Я; = ехр В. Всякий комплексно¬
аналитический характер группы D записывается в этих
координатах следующим образом-. % (6) = Я,"1!"2 ... Я”г,
где п\, п2, . .. , пг — целые числа.

504 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Перейдем теперь к рассмотрению редуктивных групп
Ли. Если G — односвязная комплексная редуктивная
группа Ли, то, очевидно, G разлагается в прямое про¬
изведение G'C, где G' — полупростая связная подгруппа
и С — связная компонента единицы в центре группы G *).
Поскольку С является комплексной оболочкой тора, то
в С существуют некоторые мультипликативные коорди¬
наты Яг+(Дг+2, ..., Ящ. Отсюда получаем
Следствие 4. Если G — односвязная комплексная
редуктивная группа Ли, то всякий ее старший вес имеет
вид Я^'Я"2 . .. Я""', где числа щ являются целыми неот¬
рицательными при i = 1, 2, . . . , г и произвольными це¬
лыми при I = г + 1, г + 2, . . . , т.
Переход к неодносвязной группе осуществляется, как
обычно, путем факторизации по центральному нормаль¬
ному делителю. Поскольку этот делитель N содержится
в D, то представление d(a) оказывается однозначным
на G/N тогда и только тогда, когда характер а(6) обра¬
щается в единицу на N. Особенно просто решается этот
вопрос в случае полупростой комплексной группы (см.
§ 118).
Следствие 5. Если G — полупростая комплексная
односвязная группа Ли, то полугруппа ее неприводимых
представлений имеет ровно г образующих d\, d2,.. ., dr
(где г — ранг группы G). Всякое представление d(а)
однозначно записывается в виде
d(а) = ... d1;,
где 1и 12, . . ., —числовые отметки сигнатуры (под ум¬
ножением имеется в виду произведение Юнга). Если G
редуктивна, то к образующим d\, d2, . . ., dr добавляют¬
ся еще 2(m — г) образующих dt, d7\ i = r + 1, ..., m
(в обозначениях следствия 4).
Далее, рассмотрим вещественные неприводимые
представления группы G. Очевидно, всякий веществен-
*) Это утверждение следует из аналогичного разложения в
классе алгебр Ли, односвязности G'C и однозначности односвязной
группы Ли с данной алгеброй Ли.

§ 112. ЗАВЕРШЕНИЕ КЛАССИФИКАЦИИ
505
нып характер сс(6) группы G может быть записан в виде
т
а (6) = П ф*',
i = 1
где /,-, ki — комплексные числа, для которых, однако,
разности /j — ki должны быть целыми. Как и прежде,
условимся считать, что параметры Яц Х2, .. ., К отно¬
сятся к полупростой компоненте (остальные — к центру
группы G).
Следствие 6. Вещественный характер а(Ь) ин¬
дуктивен тогда и только тогда, когда индуктивны от¬
дельно его аналитический и антианалитический сомно¬
жители, т. е. когда Т, ki — целые числа, неотрицатель¬
ные при i=l, 2, ..., г. Представление d(a) является
тензорным произведением аналитического и антианали-
тического неприводимых представлений.
Подчеркнем, что в этом следствии речь идет об одно¬
связной группе G. В общем случае следствие 6 в основ¬
ном сохраняет силу, но аналитический и антианалитиче¬
ский сомножители могут быть неоднозначны (даже если
а(6) однозначно, см. § 43). Наконец, уточним описание
канонической модели.
Теорема 5. Пусть G — односвязная комплексная
редуктивная группа Ли и а — ее старший вес. Тогда
пространство 9?а, в котором действует неприводимое
представление d(а), состоит из всех решений индикатор¬
ной системы
@l.i+lf(z) = 0, ^'+У(2) = 0.
Здесь liy ki, i = 1, 2, . . . , г, — неотрицательные целые
числа такие же, как в следствии 6. Пространство со¬
стоит из полиномов на группе Z. Тот же результат име¬
ет место, если группа G неодносвязна (но представление
d(a) может быть конечнозначным).
Доказательство ничем не отличается от част¬
ного случая SL(ra), рассмотренного в § 65 (стр. 291) *).
*) Действительно, мы уже знаем, что ЗД с 91^, где di'a — ко¬
нечномерное пространство всех решений индикаторной системы, ин¬
вариантное относительно Tg. Остается воспользоваться принципом
полной приводимости и единственностью старшего вектора
(/о(г) = В-

506 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
§ 113. Симплектическая группа
Рассмотрение классических групп можно было бы
провести независимо от изложенной выше общей теории
([84]). Тем не менее эта теория дает нам универсальный
подход и универсальную терминологию (корни, их мет¬
рические свойства и т. д.), что позволяет рассматривать
все частные случаи с единой точки зрения. Мы начнем
рассмотрения с симплектической группы G = Sp(«, С),
которая устроена несколько проще, чем ортогональная
п-мерная группа. Положим
[х, у\ МУп 4" %2Уп~\ 4" ... 4" xvyv+1 xv+iyv ... хпу\.
Напомним, что группа G состоит из всех линейных пре¬
образований комплексного векторного пространства раз¬
мерности п = 2v, сохраняющих кососимметрическую
форму [х, у]. Условие принадлежности матрицы g груп¬
пе G записывается в виде g'~l = cr^’go, где о — матрица
формы [х, у\.
0
1
0 - s
s 0
, S =
1
1
0
Отсюда, в частности, следует, что матрица g имеет де¬
терминант, равный ±1; в действительности можно пока¬
зать, что этот детерминант равен 4-1. В частности, груп¬
па Sp(2) изоморфна SL(2). Группа G связна и одно¬
связна*). Ранг этой группы равен v, и схема Дынкина
имеет вид
О о о О " ■ О
ill i i i г
Покажем, что при указанном выше определении
фундаментальной формы [х, у] (т. е. при определенном
*) Прямое доказательство односвязности см., например, в [46],
т. I. Косвенное доказательство (основанное на теории представле¬
ний) будет изложено в этом параграфе.

§ 113. СИМПЛЕКТИЧЕСКАЯ ГРУППА
507
выборе базиса в я-мерном пространстве) разложение
Гаусса в GL(n) индуцирует разложение Гаусса в груп¬
пе G. Действительно, пусть g = a~’g'a. Записывая мат¬
рицу g в блочной форме (n = v + v), находим, что
a b N
sd's
— sb's
с d Р1 =
/
f
— sc s
sa s
где штрих означает транспонирование. Отсюда следует,
что преобразование g сводится к транспонированию по
отношению ко второй диагонали с изменением знака
некоторых матричных элементов. Очевидно, такое пре¬
образование сохраняет подгруппы Z~(п), D(n), Z+{n).
Отсюда легко заключить, что разложение Гаусса эле¬
ментов g е G происходит внутри G. В результате
G = Z-DZ+,
где Z-, D, Z+— пересечения группы G с подгруппами
Z-(n), D(n), Z+(n) (и черта означает замыкание). Дей¬
ствительно, множество Greg = Z-DZ+ содержит окрест¬
ность единичной точки в группе G, и отсюда следует,
что множество «сингулярных» элементов является под¬
многообразием меньшей размерности в G. Следователь¬
но, Greg всюду плотно в G.
С другой стороны, заметим, что группа G содержит
подгруппу G0, изоморфную GL(v). Эта подгруппа со¬
стоит из всех диагонально-блочных матриц в
G(b = с = 0)*). Согласно условию g = g"1, мы находим
при этом, что 3 = а~\ а = сН, где тильда для блоков
порядка V означает преобразование a-+sa's. Следова¬
тельно, общий вид матрицы g0 е G0 есть
II а 0 I
Яо= I q 5_i , aeGL(v).
Отсюда, в частности, следует, что группа D состоит из
всех диагональных матриц 6 е G0. Заменяя в этом слу¬
чае произвольную матрицу а диагональной матрицей
*) Существование такой подгруппы очевидно также из схемы
Дынкина (алгебра Ли подгруппы 0° содержит первые v—1 про¬
стых корней).

508 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Я = diag {Яь Яг, ... , Я„}, замечаем, что Я 1 = Яv—1, . ..
ЯГ1}. Следовательно, если расположить в нормаль¬
ном порядке собственные значения матрицы б, то всякие
два числа, симметрично расположенные относительно
центра, являются взаимно обратными. Параметры
Яь Яг, . . . , kv являются независимыми мультипликатив¬
ными параметрами в картановской подгруппе D.
Условимся рассматривать только комплексно-анали¬
тические представления группы G. Записывая характер
а (б) группы D в виде Я^'Я™2 ... Я"Ч выясним условия
индуктивности этого характера. Очевидно, разложение
Гаусса в группе G индуцирует разложение Гаусса в под¬
группе G°. Следовательно, характер а (б) должен быть
индуктивен также при сужении на G°. Это немедленно
приводит к ограничениям
Щ т2 ^ rnv
на параметры сигнатуры а = (mbm2, ..., mv). Кроме
того, в группе G содержится подгруппа Hv, преобразова¬
ния которой сохраняют все базисные векторы, кроме
ev, ev+i, и сводятся к произвольным унимодулярным пре¬
образованиям координат xv, xv+i. Из индуктивности ха¬
рактера а (б) по отношению к Hv вытекает еще одно
ограничение: mv^0. При этом все параметры
mi, т2 ..., niv, очевидно, должны быть целыми. Пере¬
писывая характер а(б) в виде А^'Д}}2 .. . Л1}'’, где
Гг = Ш{ — mi+1 (mv+i=0), мы находим, что указанные
выше условия являются не только необходимыми, но
и достаточными. Действительно, при выполнении этих
условий все разности rp, р= 1, 2, ..., v, являются це¬
лыми неотрицательными и характер а (б) однозначно
продолжается до функции a(g), аналитической на всей
группе G:
a (g) = Ai (g)'1 А2 (g)'2 ... Av (gfv. (*)
Здесь Ap(g)—главный диагональный минор матрицы
g, составленный из первых р строк и первых р столбцов.
При этом, как нетрудно видеть, действительно выпол¬
няются условия a(t,gz) = a{g), £<=Z_, zeZ+. В резуль¬

§ 113. СИМПЛЕКТИЧЕСКАЯ ГРУППА
509
тате получаем полную классификацию неприводимых
представлений группы G:
Теорема 6. Всякое неприводимое аналитическое
представление группы G = Sp(n,C) однозначно опре¬
деляется (с точностью до эквивалентности) сигнатурой
а = (ти т2, .. ., mv) с целочисленными параметрами
ть т2, . .. , mv, для которых
Щ ^m2'^z .. . ^ mv ^ 0, v = п/2.
Производящая функция этого представления опреде¬
ляется формулой («). Реализация на группе Z опреде¬
ляется стандартной формулой, и индикаторная система
имеет вид
+lf(z) = 0, /= 1, 2 V,
где Ti = mi — mi+u i = 1, 2, . . v, mv+i = 0. При этом
оператор 3!)i является аналитическим оператором левого
сдвига на группе Z, порожденным однопараметрической
подгруппой
Zi(t)= 1 +j(eh ,Ч1 -е/-,. /), г= 1, 2, . . v- 1;
zv (0 1 Т- teVt v+ь
где eij — обычная «матричная единица» и j — дополни¬
тельный индекс: j = п — i + 1 *).
В этой теореме остается пока недоказанным лишь
последнее утверждение. Для доказательства достаточно
найти простые корни и соответствующие корневые век¬
торы (см. § 93). Однако гораздо проще убедиться в
том, что векторы Д = у (еи г+| — е,_ь ,■), fv = ev. v+i яв¬
ляются образующими в алгебре Ли группы Z = Z+ и
операторы 3)^ удовлетворяют следующим соотношениям:
. , , I 0 при i¥=k,
*,'* Д» (г, г) - о. где.„-{ , при i = k
Отсюда следует также, что функция a(z, g) содержится
в пространстве решений соответствующей индикаторной
*) Оператор 3)i отвечает простому корню со* на схеме Дыи-
;ина, f = I, 2, . •., v.

510
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
системы. Повторяя стандартные рассуждения (§ 49),
связанные с конечномерностью и инвариантностью про¬
странства решений, заключаем, что это пространство
совпадает с пространством канонической модели. Заме¬
тим также, что f\ — 0, откуда Zi(t) = exp tfi = 1 + tft.
Ввиду практической важности индикаторной системы
мы приведем выражения операторов в двух различ¬
ных системах параметров на группе Z (такие системы
представляются на первый взгляд наиболее естествен¬
ными). Операторы JZ>,- мы будем называть главными
сдвигами на группе Z.
Первый способ параметризации. Заме¬
тим, что группа Sp(«.) содержит нормально вложен¬
ную*) подгруппу, изоморфную Sp(ra — 2). Эта под¬
группа выделяется условием сохранения координат х\
и хп. Остальные координаты подвергаются произволь¬
ному симплектическому преобразованию на Sp(ra — 2).
В частности, группа Z содержит подгруппу Z0, состоя¬
щую из матриц •
1
0
0
Z0 =
0
X
0
0
0
1
где х — треугольная матрица (с единицами на главной
диагонали) из Sp(ra — 2). С другой стороны, рассмот¬
рим в группе Z подгруппу Z', состоящую из матриц вида
1
t
т
г' =
0
е
?
0
0
1
где е — единичная матрица порядка п — 2, t — произ¬
вольная строка из чисел 11, t2, ..., tn_2, т — произволь¬
ное число и t линейно выражается через t (t — столбец,
состоящий из чисел ^„_2, ..., £v+i, —tv, . .. , —tu в по¬
рядке нумерации сверху вниз). Перемножая z0 и г'
*) См. определение в § 100.

5 113. СИМПЛЕКТИЧЕСКАЯ ГРУППА
511
получаем матрицу
1
*
т
ZqZ' =
0
X
xl
0
0
1
Нетрудно видеть, что таким образом может быть одно¬
значно представлена произвольная матрица zeZ. Сле¬
довательно, t, т и параметры матрицы х составляют си¬
стему параметров в группе Z. Рассуждая индуктивно*),
получаем, что в качестве независимых параметров мож¬
но выбрать следующие элементы матрицы г:
1 Z\2 2)з 2И Zi_ „-з 2ь„_2 Zln
^ Z23 Z24 Z2, ГС-3 Z2, ГС-2 Z2, гс-1
1 234 z3, гс-3 23, гс-2
1 ^V. V+1
Здесь единицы (диагональные элементы матрицы г)
поставлены для сохранения симметрии в таблице пара¬
метров (параметры zV; v+1, ..., z2, п-ь Z\n расположены
на второй диагонали матрицы z). Все остальные эле¬
менты матрицы 2 могут быть записаны в виде полино¬
мов от этих независимых переменных. Вычисляя в этих
переменных инфинитезимальные операторы левого сдви¬
га 3)р, находим, что они имеют вид
= ЛщГ ~^223 + + 2<1пдгм’
®, = J-+Z д ■ ■ - 5
2 дг,3 дг,А ^ дг,
dzv, v+i
При этом, как видим, коэффициентами этих линейных
дифференциальных операторов являются независимые
*) Заметим, что индуктивное рассуждение приводит также к
разложению Z = Z]Z2 ... Zv, где Zv = Z', Zv_j аналогичным обра¬
зом определяется в Z0 и т. д. Каждая подгруппа Zp является абе¬
левой группой и нормальным делителем в ZiZ2... Zp.

512
ГЛ. XVI. неприводимые представления
пе ременные zfj, за исключением z2„, z3i п_ь ... Все та¬
кие элементы непосредственно примыкают снизу ко вто¬
рой диагонали. Пусть wp означает такой элемент, рас¬
положенный в р-й строке. Повторяя разложение Z0Z\
легко определяем w2\ отсюда, рассуждая индуктивно,
находим, что
W
= [Zp, Zp.
р = 2, 3, . . ., v.
Здесь Zp означает р-ю строку в таблице независимых
параметров, дополненную с двух сторон нулями, и скоб¬
ка [х, у] означает фундаментальную билинейную форму
для группы Sp(n). В частном случае п = 4 мы имеем
дг,.
+ 2,
1- W2—~
дг13 дги
SDn = ■
(52,
23
ДО2 — 212223 — 2)3.
Второй способ параметризации (бинарное раз¬
ложение). Рассмотрим в группе G подгруппы G._, G(), G+, со¬
ставленные из блочных матриц следующего вида:
О \ / а О
а~
0
Из условия принадлежности к группе G (,^ = ^ 1) заключае,м,
что т], у— произвольные квадратные матрицы (v X v), симметрич¬
ные относительно второй диагонали. Нетрудно видеть (исходя, на¬
пример, из разложения Гаусса), что всякая матрица g е G, у кото¬
рой Av(g)=?=0, однозначно записывается в виде
£ = g_g0?+-
Полученное разложение мы будем называть бинарным (ввиду
разбиения матриц на блоки порядка я/2). В частности, каждая
матрица из Z однозначно записывается в виде
0
2 = 2П2 , =
о
е у
0 е
ху
0
: 2 (V).
Вычислим главные сдвиги в параметрах х, у. Нетрудно видеть, что
первые v—1 из этих сдвигов в точности совпадают с главными
сдвигами на треугольной подгруппе Z(v):
/> +1
щ— , р = 1, 2, ..., v — 1,
<5х0
где хр означает р-ю строку в треугольной матрице neZ(v). Сле¬
довательно, явный вид таких операторов значительно упрощается.

§ ИЗ. СИМПЛЕКТИЧЕСКАЯ ГРУППА
513
Для вычисления оператора 3)v заметим вначале, что
zv (t) z0z+ = z0zv (t) z+, где zv (t) содержится в G+ вместе с
zv(/.) *). Отсюда вытекает, что параметры х остаются неизмен¬
ными, в то время как матрица у заменяется матрицей
где положено для краткости а = лг1, Ь = а = х 1. Следовательно,
оператор SDV имеет вид
где сумма берется только по тем элементам уц матрицы у (сим¬
метричной относительно второй диагонали), которые мы считаем
независимыми. Очевидно также, что a(-v, b\j являются минорами
матрицы х. В частном случае п = 4 имеем
Заметим, что бинарное разложение позволяет чрезвычайно прос¬
то реализовать неприводимое представление d(a) в классе вектор-
функций на подгруппе G+. Действительно, согласно теореме 2 пред¬
ставление d( а) индуцируется одноименным представлением под¬
группы G0. Для получения явной формулы достаточно найти явный
вид бинарного преобразования матрицы z+g. В результате не¬
сложных преобразований получаем
Здесь, как и выше, матрица g считается записанной через блоки
а, Ь, с, d\ матрица у симметрична относительно второй диагонали,
f — вектор-функция от у и оператор Agi) есть оператор неприводи¬
мого представления группы GL(v) с сигнатурой (т.\, т2, ..., mv).
Таким образом, d(a) реализуется с помощью матричной «дробно¬
линейной подстановки».
В заключение заметим, что все неприводимые пред¬
ставления оказались однозначными на G. Отсюда сле¬
дует, что G односвязна. Действительно, если © — одно¬
связная накрывающая группа G и © ф G, то точное ли¬
нейное представление группы © (которое существует
согласно теореме 12 гл. XV) было бы неоднозначным
на G.
о о ... о
х-1 = y + t [aivb\j)
i, / = 1,2
t 0 ... 0
Tgf (.'/) = A-a+ycf ((a + yc) 1 (b + yd)).
*) Действительно, G+ инвариантна относительно Go.

514 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
§ 114. Ортогональная группа
Перейдем к рассмотрению ортогональной группы
G — SO (га, С) *). Эта группа связна и является связной
компонентой единицы в группе линейных преобразова¬
ний, сохраняющих симметрическую билинейную форму
(х, у) = х,уп + х2уп„1 + ... +хп^у2 + хпух.
Мы естественно приходим к выбору этой формы, если
желаем записывать разложение Гаусса с помощью тре¬
угольных матриц. Действительно, повторяя почти до¬
словно рассуждения предыдущего параграфа, получаем,
что разложение Гаусса в группе G индуцируется разло¬
жением Гаусса в объемлющей группе GL(ra). В резуль¬
тате
где компоненты Z_, Д Z+ определяются как пересече¬
ния группы G с подгруппами Z_(ra), D(ra), Z+(ra).
В дальнейшем мы будем отдельно рассматривать слу¬
чай четной (га = 2v) и нечетной (re = 2v+l) размерно¬
сти. В обоих случаях ранг группы G равен v и схема
Дынкина имеет вид
Зеркальный автоморфизм. Напомним, что
полная ортогональная группа О (га) состоит из двух
связных листов: 0+(га), О-(га), первый из которых со¬
впадает с группой G = SO(ra). Поскольку эта группа
является нормальным делителем в О (га) (как связная
компонента единицы), то g0gg~l<^G для всякой пары
элементов g^G, g0^O(n). Положим, в частности,
где матрица о определяется как перестановка базисных
векторов с номерами v, v + 1 в случае четного га (п — 2v).
G = Z_DZ+,
2 2 2 2 2 1
g = °g° >
-i
*) Случай п = 2 исключается (в этом случае G абелева, т. е.
яе полупроста).

§ 114. ОРТОГОНАЛЬНАЯ ГРУППА
515
Переход от g к g мы будем называть зеркальным авто¬
морфизмом в группе G. Заметим, что оеО'(п), В даль¬
нейшем мы увидим, что зеркальный автоморфизм (при
четном п) действительно является внешним, т. е. не сво¬
дится к внутреннему автоморфизму в SO (п). В схеме
Дынкина этот автоморфизм осуществляет (при п — 2v)
перестановку двух последних корней.
После этого (существенного) замечания перейдем к
решению задачи об описании всех неприводимых пред¬
ставлений группы G.
I. Случай четного п, 11 = 2v. Рассуждая, как и
в предыдущем параграфе, замечаем, что независимыми
мультипликативными параметрами в картановской под¬
группе D являются первые v собственных значений мат¬
рицы б ей. Вводя для этих параметров обозначения Я,ь
%2 Xv, положим
a(6)=xfa^...
Как и в предыдущем параграфе, группа G содержит
подгруппу G0, изоморфную GL(v). Индуктивность харак¬
тера a (б) по отношению к этой подгруппе приводит к
ограничениям ni\ Д т2 Д ... Д mv. Следовательно, харак¬
тер a (б) может быть также записан в виде
а (б) = ДЗД* .. . A'v,
где числа г* = m, — mi+ь i = 1, 2, ..., v—1, неотрица¬
тельны и rv = mv. При этом Ар является диагональным
минором матрицы б, равным Х1Х2 ... Хр. Заменяя Др
на Ap(g), где AP(g)— соответствующий диагональный
минор матрицы g, получаем производящую функцию
a(g). Заметим теперь, что зеркальный автоморфизм
сохраняет разложение Гаусса в группе G:
Z_ = Z_, D = D, Z+ = Z+.
(Действительно, алгебра Ли группы G состоит из всех
матриц, кососимметричных относительно второй диаго¬
нали, и отсюда легко получить, что зеркальный авто¬
морфизм оставляет инвариантными алгебры Ли под¬
групп Z._, Д Z+.) Отсюда мы получим существенное
свойство симметрии в классе сигнатур.

616 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Каждому представлению Tg группы G поставим в
соответствие зеркально сопряженное представление
Ts=Tg. Это представление действует в том же про¬
странстве, что и Tg. Если I — старший вектор представ¬
ления Tg, то мы имеем
ТЛ=Т£ = 1, Гв|=Гв| = а(б)|.
Следовательно, вектор | является также старшим отно¬
сительно Tg. При этом представление Tg имеет старший
вес а (б) = а (6). Поскольку для матрицы б преобразо¬
вание б сводится к замене собственных значений
Av, Av *> то мы имеем
й(б) = ЛГ> ...СТ1-O'-
Отсюда заключаем, что если вектор а = (ши гп%,..., mv)
является сигнатурой, то вектор а = (ти ..., mv_b —mv)
также является сигнатурой. Отсюда в свою очередь по¬
лучаем добавочное ограничение на сигнатуру a: mv_i^
^ —mv. Сопоставляя с найденными ранее ограниче¬
ниями, получаем в результате
тк ^ т2 ^ ... ^ mv_i ^ I |.
Существование двузначных представ¬
лений. Покажем вначале, что отрицательные значе¬
ния параметра mv действительно допустимы. Для этого
заметим, что все диагональные миноры Ар, р— 1, 2, ...
..., v— 1, матрицы б совпадают с соответствующими ми¬
норами Др, в то время как
Поскольку зеркальный автоморфизм сохраняет разло¬
жение Гаусса, то эти же равенства сохраняются при
замене Др на ДP(g). Следовательно, Av-i(g) делится
без остатка на Av(g). В дальнейшем мы условимся ис¬
пользовать обозначение Др также для миноров мат¬
рицы g.
Введем в рассмотрение главные сдвиги на группе Z.
Легко проверить, что образующими в алгебре Ли груп¬

§ 114. ОРТОГОНАЛЬНАЯ ГРУППА 517
пы Z являются следующие матрицы:
fp ~2 (®р, р+1 1, ?)> f + ~2 (^v— I, v +1 ®v. v+г)-
Здесь /7=1, 2, ..., v — 1, q = п — р + 1. Условимся
также использовать обозначение /_ === /v—1:
f~2 (ev-1, v — ev+l, ^+2)-
При этом очевидно, что зеркальный автоморфизм пе¬
реставляет векторы /+. Пусть S5P, JZ5_, JZ5+ — соответ¬
ствующие главные сдвиги на группе Z.
Полагая Ap = Ap(zg), /7=1, 2, v—1, мы легко
проверяем, что имеют место следующие тождества:
4-1 (0 при рф1,
0ер»+1(Д#) = О, где е . = , ' .
р \ <■) Р‘ [ 1 при Р = 1.
Действительно, операторы 3)v порождаются подгруп¬
пой G0, изоморфной GL(v), и миноры Лр зависят толь¬
ко от центрального множителя g0 в обобщенном разло¬
жении Гаусса:
g = n..g0n+, /i-е!-, go^G0, /i+ef+.
(Это разложение вполне аналогично бинарному разло¬
жению Sp (/г), рассмотренному в предыдущем парагра¬
фе.) В частности, нас будет особенно интересовать сле¬
дующее тождество:
Действительно, минор Av является константой по отно¬
шению к дифференцированию ®_ = ^v-i» и
^L(Av-i) = 0- Применяя к этому тождеству зеркаль¬
ный автоморфизм, мы получаем
2D\{VTv) = 0.
В совокупности с равенствами £Dp(Y&v) = 0, р— 1,
2, ..., v—1, это равенство означает, что характер
а (6) = является индуктивным по отношению к
группе О. Действительно, функция 5+=*\^Av удовлет¬

618 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
воряет индикаторной системе и потому является поли¬
номом на группе Z.
Полученное представление мы обозначим s+ и на¬
зовем спинорным представлением первого рода. Оче¬
видно, это представление двузначно на группе G (т. е.
является однозначным представлением универсальной
накрывающей группы G).
С другой стороны, применяя к представлению зер¬
кальный автоморфизм, получаем представление s_, опре¬
деляемое характером а (б) = Av ._JY~Av- Это представле¬
ние назовем спинорным представлением второго рода.
Запишем теперь произвольный характер а (8) в виде
а (б) = А['АГ/ ... Ar^_-22SsSr+,
где положено 5_ = Av-i/]/~A^. Как легко проверить,
показатели mv_i, mv связаны с показателями г_, г+ сле¬
дующими соотношениями:
г+= mv_, + mv, r_=/nv_,— mv.
Очевидно, соответствующая функция a (zg) удовлетво¬
ряет некоторой индикаторной системе тогда и только
тогда, когда все показатели гь г2, ..., г_, г+ являются
целыми неотрицательными.
В результате доказана следующая
Теорема 7. Всякое неприводимое представление
группы. SO (п) при п = 2v однозначно определяется сиг¬
натурой a=(tnum2, ..., mv), где ^ m2 ^ mv-{^
^\mv\ и числа ть т2, ..., mv являются одновремен¬
но целыми или одновременно полуцелыми. Полугруппа
неприводимых представлений имеет образующие dp с
сигнатурами
ctp — (1, 1, 1, 0, 0, 0),
р
р = 1, 2, ..., V — 2, и двузначные (спинорные) обра¬
зующие s_, s+ с сигнатурами
_/± ± 1 _±\ =Ц ± _L _L\
а- у 2 ’ 2 ’ ' ‘ ’ 2 ’ 2 )’ а+ \ 2 ’ 2’ 2’ 2/'
Если использовать символику произведений Юнга,
го всякое неприводимое представление d(а) с сигнату¬

S 114. ОРТОГОНАЛЬНАЯ ГРУППА
519
рой а = {т\, m2,..., mv) можно также записывать в
виде
d (а) = d\xdr* ... drJs22sl“s++>
где положено rv = mp — mp+u r± = mv^ ± mv и числа
гр, г± являются произвольными целыми неотрицатель¬
ными. При этом иногда мы будем использовать симво¬
лику а = [ги г2,..., rv_2; г_, г+}.
II. Случай нечетного п, п = 2v + 1. Этот слу¬
чай мы можем получить редукцией из предыдущего,
рассматривая SO (л) как подгруппу в SO(«+l), пре¬
образования которой сохраняют xv+i + xv+2. Поскольку
для диагональных матриц 6eSO(«+l) последнее
условие выполняется только при Яч,+1 = Яу+2 = 1, то при
сужении на SO (л) мы получаем в качестве проекции
характер
а (б) = Я^Я™2 . . . Я^Ч ml > пг2 > ... > mv > 0.
При этом числа rri\, т2, ..., mv должны быть одновре¬
менно целыми или одновременно полуцелыми. С другой
стороны, нетрудно видеть, что других старших весов
группа SO (л) не имеет. Действительно, сужая на SO (л)
главные сдвиги группы SO (п. + 1), получаем все глав¬
ные сдвиги на SO (л). Вводя обозначение S0=V/4>">
запишем характер а (б) в виде
а(6) = ДрД? . .. AO-j.54
Тогда нетрудно видеть, что числа гь г2, ..., rv_b г0 яв¬
ляются произвольными целыми неотрицательными.
Представление s0 с характером S0 является проекцией
спинорных представлений s_, s+ группы SO(«+l).
Представление s0 мы называем спинорным представ¬
лением группы SO (л) при нечетном п = 2v + 1.
Теорема 8. Всякое неприводимое представление
группы SO (л), rt = 2v+l, однозначно определяется
сигнатурой а = (ти т2,..., mv), > т2 > ... > mv > 0,
где числа ти т2, ..,, mv являются одновременно

520
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
целыми или одновременно полуцелыми. Сигнатуры
определяют систему образующих в полугруппе непри¬
водимых представлений группы SO (п). При этом вся¬
кое представление d(a) с сигнатурой а может быть
записано в виде произведения Юнга:
где числа гр — mp — тр+и г0 = 2mv произвольные целые
неотрицательные.
Замечание. Наряду с существованием двузнач¬
ных представлений мы доказали приводимость некото¬
рых диагональных миноров для ортогональной группы
SO (га). Действительно, при га = 2v + 1 имеем
Отсюда, между прочим, следует, что поливектор dv со¬
держится в тензорном произведении s0 ® s0 (см. заме¬
чание в § 109). Точно также при га = 2v имеем
В свою очередь доказательство приводимости этих ми¬
норов (как полиномов на Z при Ap = Ap(zg)) равно¬
сильно построению спинорных представлений.
Специально отметим, частный случай га = 4. В этом
случае всякое неприводимое представление имеет вид
sr_^-sr+ и представления s_, s+ зеркально сопряжены.
Как следует из схемы Дынкина, SO (4) локально изо¬
морфна квадрату группы Лоренца. Спинорные пред¬
ставления s„, s+ можно в этом случае рассматривать
как однозначные представления группы Лоренца.
Итак, мы показали, в частности, что группа
G = SO(ra) при любом значении га допускает двузнач¬
ные представления. Покажем, что G двусвязна *) (слу¬
чай га = 2 исключается).
р
Av — So-
*) То есть ее группа Пуанкаре состоит из двух элементов.

§ 115. ТЕОРИЯ СПИНОРОВ 521
Действительно, положим © = s+ при четном п и
© = s0 при нечетном п. Представления sr~sr+ (s'0)
являются однозначными представлениями группы ©*).
Поскольку © накрывает G, то и все остальные представ¬
ления d(a) также однозначны на @. Следовательно, ©
односвязна. При этом @ двукратно накрывает группу G.
§ 115. Теория спиноров
В предыдущем параграфе было показано, что орто¬
гональная группа SO (п) двусвязна, и также была эф¬
фективно построена ее универсальная накрывающая ©.
Группа © обозначается Spin (я) и называется спинор-
ной группой. В этом параграфе приводится ее класси¬
ческое построение и рассматриваются симметрические
тензоры для этой группы (называемые спинтензорами).
Кроме того, в конце параграфа намечается еще одно
элементарное доказательство существования спинорных
представлений, основанное на общей формуле «канони¬
ческой модели».
1° Спинорная группа. Выберем в н-мерном
пространстве Е базис ех, е2 еп таким образом, что¬
бы скалярный квадрат вектора х = ххех + х2е2 + ...
... + хпеп задавался обычной формулой: (*, х) = х* +
х\ + ... + х2п. Будем рассматривать символы в\, е2, ...
..., еп как образующие некоторой ассоциативной ал¬
гебры ® с соотношениями
efij + е,ег = 2б//;
где дц — символ Кронекера. В частности, е{е^ = —е^еи
j ф i, и ef=l, 1=1, 2, ..., п. Тогда скалярный квад¬
рат (х, х) совпадает с квадратом элемента ге®:
(.х1в1 + х2е2+ ... +xnenf = x\ + xl+ ... + **.
Алгебра $ называется алгеброй Клиффорда. Ниже мы
укажем матричную реализацию алгебры k.
*) Напомним, что s_, s+ зеркально сопряжены.

522 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Рассмотрим теперь линейную оболочку X всех по¬
парных произведений е^- = —i ф /, и обозначим
символом ец оператор коммутирования с элемен¬
том е*еу.
e*,z = [e-fij, г].
Здесь z — произвольный элемент из алгебры Клиффор¬
да и коммутатор [а, Ь] означает ab — Ьа. Нетрудно про¬
верить, что X является алгеброй Ли относительно этого
коммутирования. Кроме того, мы имеем
10, если i=£k, j=/=k,
2в{, если j = k,
— 2е{, если i = k.
Отсюда заключаем, что 1) пространство Е инвариантно
относительно алгебры X; 2) операторы являются
кососимметрическими в пространстве Е; 3) операторы
ец образуют базис в алгебре всех кососимметрических
операторов пространства Е.
Пусть Ец означает оператор ец, рассматриваемый
только на пространстве Е. Отображение ец—яв¬
ляется точным линейным представлением алгебры X.
Отсюда, в частности, заключаем, что алгебра X изо¬
морфна so (и).
Покажем теперь, что алгебра Ш имеет конечную
размерность. Действительно, с помощью соотношений
коммутации мы можем каждый одночлен от образую¬
щих е,- записывать в упорядоченном виде:
ещ ... i = еце< ... ei , i\ ^ t’2 ^ ^ i .
12 т. 1 2 nv m
Если til > n, то среди сомножителей в этом одночлене
хотя бы один элемент ег встречается дважды; посколь¬
ку е\—1, то степень можно понизить. В результате
остаются только те одночлены е,у2... гт, для которых
h < 12 < • • • < im и О^Ст^п (во = 1). Число таких
одночленов равно
dim St — 1 4- ti 4- Сд 4- ... 4- Сп 4" ... 4-1=2.
Таким образом, алгебра Клиффорда имеет размер¬
ность 2п.

{ 115. ТЕОРИЯ СПИНОРОВ
523
Каждый элемент qeS мы можем рассматривать
как линейный оператор z-+az, zeS. С этой точки зре¬
ния а является матрицей 2п X 2п. Таким образом, ал¬
гебра $ имеет точное матричное представление. (Дей¬
ствительно, если az = bz для всех 2 е то, в частно¬
сти, ае0 = Ье0, откуда а = Ь.) Алгебру В мы будем
теперь отождествлять с указанным матричным представ¬
лением.
В частности, алгебра X с= Ш получает точное матрич¬
ное представление размерности 2п X 2п. Заметим, что
линейное пространство к можно рассматривать как
прямую сумму подпространств, составленных из все¬
возможных /i-векторов над Е, р = 0, 1,2, .,., я. Отсюда
следует, что скалярное произведение из Е продолжается
на всю алгебру Ш так, что элементы из X остаются ко¬
сосимметрическими. Согласно теореме 5 гл. V в группе
SO(2n) существует связная подгруппа @ с алгеброй
Ли А'. Мы полагаем @ = Spin(я).
Вернемся к «-мерному представлению алгебры X.
Поскольку оно задается формулой z-*[x,z], х^Х,
z ев Е, то соответствующее представление группы @ за¬
дается формулой внутреннего дифференцирования:
г—>ага~~\ а <= @.
Поскольку дифференциал такого представления состоит
из кососимметрических матриц, то само представление
ортогонально, т. е. матрицы представления содержатся
в SO (я). Мы получаем отображение группы Spin (я) на
группу SO (я).
Упражнение
Сравнить с отображением SL (2, С) -» SO (3, С), построенным
в § И.
Поскольку отображение алгебры X является точным,
то ядро отображения группы Spin (я) дискретно. Не¬
трудно проверить, что оно состоит только из матриц
±е0. Таким образом, Spin (я) является двукратным на¬
крытием группы SO (я).
Замечание 1. Предыдущее построение справедливо как над
вещественным, так и над комплексным полем; соответствующая

524 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
спинорная группа обозначается Spin(п, R) или Spin(п, С). Для группы
Spin(n, #) мы укажем еще одну матричную реализацию, основан¬
ную на рассмотрении матриц Паули:
II 0 1 II
0 l
1 0
Hi 0 II’
Q
If
О
!
Q
II
т
О
Пусть 1 означает единичную матрицу 2X2 и v = [п/2]. Положим
(ст3 ® ст3 ® ... ® ст3) ® щ ® (1 ® 1 ® ... ® 1) при нечетном /,
(ст3®<т3® ... ®ст3)®ст2® (1 ® 1 ® ... ® 1) при четном i.
et
Л
Здесь матрица щ или а2 встречается на месте с номером [//2] и
общее число сомножителей равняется v. (При п нечетном,
п — 2v + 1, мы полагаем еп = о3®сг3® . . . ®ст3.) Нетрудно прове¬
рить, что матрицы е,- удовлетворяют нужным коммутационным со¬
отношениям и косоэрмитовы.
Следовательно, группа Spin (n, R) допускает также точное уни¬
тарное представление размерности 2V, где v = [п/2]. Группа
Spin (п, С) является комплексификацией Spin (n,R).
2° Спингензоры. Вернемся теперь к стандарт¬
ной методике построения неприводимых представлений.
Метрический тензор мы выберем так же, как и в § 114.
Положим п = 2v и рассмотрим семейство сигнатур вида
а = (т, т,..., т); соответствующее представление d(a)
имеет вид
d(a) = sf,
т. е. является (в некотором смысле) симметрической
степенью спинорного представления s+. Если гп является
целым числом, то представление d(a) может быть реа¬
лизовано как представление, индуцированное одномер¬
ным представлением Л^0 = (det а)т подгруппы G0, состав¬
ленной из матриц.
О ,
aeGL (v).
8 о =
а
0
а
-I
Действительно, это утверждение является частным
случаем теоремы 2. Для указания явной формулы пред¬
ставления мы вводим в группу G «бинарное разложе¬
ние»:
= n-gtin+,
а р II I! е
0
а
0
е х
8 =
Y & || И
е
0
ь 1
0 е

§ 115. ТЕОРИЯ СПИНОРОВ
525
где go пробегает G0 и т), х— произвольные матрицы
v X v, кососимметричные относительно второй диагона¬
ли. (Подобное разложение с симметрическими матри¬
цами г), х мы рассматривали в § 113 для группы Sp(«).)
После несложных вычислений получаем следующую
формулу:
Tgf (У) = (Я, det (е + г/л) )т f ((а + г/у)-1 ((3 + г/6)).
Здесь у — произвольная матрица vXv, кососимметрич¬
ная относительно второй диагонали, и Я = det а. Соглас¬
но результатам § 114 эта формула сохраняет силу также
и при полуцелом т. Пространство представления s2+
есть линейная оболочка всевозможных функций вида
М*/) = (det (е + г/л) )т.
В частности, мы видим, что спинорное представление s+
может быть реализовано с помощью матричной «дроб¬
но-линейной подстановки» в линейной оболочке функ¬
ций
Мг/)= V det (е + г/л) . (*)
Следовательно, все эти функции являются полиномами
от элементов матрицы у.
Замечание 2. Если фундаментальный метриче¬
ский тензор выбрать в виде
О
(Т =
О
где е — единичная матрица vXv, то матрицы л> У в
формуле (■:;•) становятся кососимметричными относи¬
тельно главной диагонали.
Из полученной формулы вытекает возможность эле¬
ментарного доказательства существования представле¬
ния s+. Действительно, достаточно доказать, что для
всякой пары кососимметрических матриц у, л функция
(•::) является ПОЛИНОМОМ.
При м е р. Пусть v = 3. Положим
I 0
У\
У>
0
- Й1
- Й2
У =
- У\
0
Уз
, 11 =
Л1
0
- Лз
1 - У 2
- Уз
0
Л2
%
0

626 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Тогда при помощи несложных вычислений получим
det (е + уц) = (1 + у{цх + у2 ц, + у3ц3)2.
Следовательно, в этом случае представление s+ реали¬
зуется в четырехмерном пространстве, натянутом на ба¬
зис 1, у и У2, Уз-
В общем случае в пространстве представления s+ со¬
держатся полиномы более высоких степеней.
Замечание 3. Поскольку зеркально сопряже¬
но s+, то нетрудно изучить также симметрические сте¬
пени s2-. Кроме того, в § 129 мы увидим, что
s+ U = U = so
для подгруппы Go, изоморфной SO (п—1) (вложенной
в SO(n), как указано в § 114). В частности, s+ остается
неприводимым при сужении на G0, и отсюда получаем
также явную формулу для s0.
Продолжая редукцию с группы на подгруппу, мы
покажем в гл. XVIII, что
dim s_ = dim s+ = 2v_i, dims0 = 2v.
§ 116. Вещественные формы
В этой главе при изучении неприводимых представ¬
лений мы существенно пользовались принципом анали¬
тического продолжения (действительно, при помощи
этого принципа была изучена структура комплексных
групп). Однако наиболее эффективным оказывается ме¬
тод аналитического продолжения при изучении непри¬
водимых представлений вещественных полупростых
(редуктивных) групп Ли. Действительно, этот метод из¬
бавляет от необходимости исследовать структуру каж¬
дой вещественной формы в отдельности; все ее непри¬
водимые представления уже содержатся в классе ана¬
литических представлений комплексной оболочки.
Из общих результатов гл. VI непосредственно вы¬
текает
Теорема 9. Пусть G — полупростая вещественная
связная группа Ли и & — ее комплексная связная обо¬
лочка. Всякое неприводимое конечномерное представле¬

§ 116. ВЕЩЕСТВЕННЫЕ ФОРМЫ
527
ние группы G определяется однозначно (с точностью до
эквивалентности) одной из сигнатур группы © и может
быть реализовано с помощью формулы
Тgf (z) — a (z, g)f(zg)
в классе полиномов Ша на корневой подгруппе Z с ©.
Здесь a (z, g) — производящая функция неприводимого
представления d(а) и g является произвольным эле¬
ментом из G. При этом, однако, следует рассматривать
также неоднозначные представления группы © (т. е.
представления ее универсальной накрывающей).
Пример 1. G = SO (p,q). Преобразования груп¬
пы G сохраняют вещественную квадратичную форму
х\ + х\ + ... +xl-xl+l- ... -xl+q.
Если группа G несвязна, то обозначим символом G+
ее связную компоненту единицы. Если считать координа¬
ты xh комплексными, то мы получаем комплексную связ¬
ную группу @ = S0(п, С), п = р + q. (Действительно,
в комплексном поле допустима подстановка xh -* ixh, и
фундаментальная форма превращается в сумму квадра¬
тов.) Отсюда легко заключить, что группа @ является
комплексной оболочкой группы G. Следовательно, вся¬
кое неприводимое представление группы G+ задается
сигнатурой а = (ти т2,. . ., mv), v = [п/2], причем
т{ ^ т2 ... Дг tfiv-i ^ I mv |, если п = 2v,
... ^ mv О, если п = 2v + 1,
и числа ти т2,..., mv являются одновременно целыми
либо одновременно полуцелыми (в последнем случае по¬
лучаем двузначные представления группы G+).
Пример 2. G = Sp(n, /?). Комплексной оболочкой
группы G является © = Sp (/г, С). Отсюда непосредствен¬
но вытекает, что всякое неприводимое представление
группы G задается сигнатурой (mt, т2,... ,mv), v = п/2
(п четно), причем
т1 > т2 > ... ^ mv ^ О
и числа mi, т2,..., mv являются целыми. Формула пред¬
ставления группы G получается из формулы представле¬
ния группы @ сужением на G.

528 гл. xvr. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Пример 3. G = SpU(«). Группа G состоит из всех
унитарных матриц ueSp(«, С). Формулировка резуль¬
тата очевидна.
Примеры вещественных форм группы SL(«, С) при
п = 2 были рассмотрены в гл. V.
Замечание 1. Если группа G несвязна (как в при¬
мере 1), то ее неприводимые представления могут быть
получены, например, при помощи теоремы Клиффор¬
да ([10]).
Замечание 2. Вещественная форма может не
иметь разложения Гаусса (например, SO («,/?)). Макси¬
мальная диагональная подгруппа в линейной группе G
может быть несвязной (например, в SL(п,/?)).
В статье [85] предложен еще один метод изучения не¬
приводимых представлений вещественной группы G, не
использующий аналитического продолжения. Этот метод
основан на «обобщенном разложении Гаусса»*). Ока¬
зывается, что всякая вещественная связная полупростая
(и также редуктивная) группа Ли может быть записана
следующим образом:
G = N-FN+.
Здесь АО, N+ — односвязные нильпотентные веществен¬
ные подгруппы, F—редуктивная подгруппа, которая
локально изоморфна прямому произведению некоторой
компактной подгруппы Q и односвязной абелевой под¬
группы А; черта означает замыкание. При этом подгруп¬
пы AM, N+ являются инвариантными относительно F.
Всякое неприводимое представление группы G задается
формулой вида
Tgф (я) = Af(f (ng),
где ф (п)—вектор-функция на подгруппе N = N+ и эле¬
менты f, ng определяются из обобщенного разложения
Гаусса ng = t,fng, ^eiV_, /е/7, ng^N+. Существенно,
что этот метод применим даже в том случае, когда груп¬
па G не имеет точного линейного представления
(§ 104) **).
*) См. стр. 451 для случая комплексной группы G.
**) И также в том случае, когда группа G не допускает компле-
ксификации (см. замечание в конце § 104).

§ 117. ПРОИЗВОЛЬНЫЕ СВЯЗНЫЕ ГРУППЫ ЛИ
529
Если односвязная вещественная группа G не имеет
точного линейного представления, то вместо нее удобно
рассматривать так называемую универсальную линейную
группу, введенную А. И. Мальцевым [111]. Оказывает¬
ся, что в каждом классе со (А) всех локально изоморф¬
ных групп Ли с полупростой алгеброй А всегда суще¬
ствует максимальная группа 0, допускающая точное
линейное представление. Группа G накрывает всякую
линейную группу из класса со (А). Иначе говоря, если
Geco(A), то всякое линейное представление группы G
можно рассматривать также как представление G.
Линейная группа G допускает комплексную оболочку
и группа @ оказывается односвязной. Пусть U — мак¬
симальная компактная подгруппа в @. Тогда, как
мы знаем (§ 101), группа U является связной и односвяз¬
ной. В силу принципа аналитического продолжения мы
можем заключить, что существует взаимно однознач¬
ное соответствие между неприводимыми представления¬
ми всех трех групп G, @, U.
Таким образом, всякое неприводимое представление
вещественной связной редуктивной группы Ли является
в некотором смысле «компактно порожденным», т. е.
вполне определяется структурой компактной группы U.
§ 117. Произвольные связные группы Ли
Если использовать теорему Леви — Мальцева, то ре¬
зультаты предыдущего параграфа могут быть перенесе¬
ны на произвольную связную группу Ли (комплексную
или вещественную). Решающим шагом при этом являет¬
ся следующая
Теорема 10. Пусть G — вещественная связная груп¬
па Ли и S — ее полупростая (связная) компонента Леви.
Тогда любое неприводимое представление группы G
остается неприводимым при сужении на S.
Доказательство. Пусть R — радикал группы G,
т. е. максимальный связный разрешимый нормальный
делитель. Тогда по теореме Ли в пространстве предста¬
вления Tg группы G существует хотя бы один вектор

530 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
х0¥=0, собственный относительно подгруппы R:
Trx0 = X (г) х0, re Д.
Поскольку R является нормальным делителем, то вся¬
кий вектор вида xg = Tgx0 снова является собственным
для R:
Trxg = h{g-lrg)xg,
с собственным значением Xg(r) = ^(g^rg). Из непрерыв¬
ной зависимости Xg от g, связности группы G и конеч¬
ности множества собственных значений группы R выте¬
кает (как при доказательстве теоремы Ли), что %g(r) =
= Х(г), т. е. Xg не зависит от g. Следовательно,
h(g~'rg) = X{r).
Ввиду неприводимости Tg инвариантная линейная обо¬
лочка векторов Хо совпадает со всем пространством V.
Следовательно, операторы Тт, г е R, являются скаляра¬
ми на всем пространстве V. Следовательно, если по¬
ложим
X(g)^X(sr) = X(r),
то получим одномерное представление всей группы
G — SR. Представление Tg = X(g)~1Tg тривиально на
радикале R(Tr= 1) и, следовательно, является непри¬
водимым при сужении на подгруппу S. Теорема дока¬
зана.
Следствие 1. Всякое неприводимое представление
группы G может быть записано следующим образом:
Tg = X (g) Tg,
где X(g) — одномерное представление группы G и Tg-
неприводимое представление группы G, тривиальное на
радикале R.
Заметим, что если группа G односвязна, то предста¬
вление X(g) тривиально на полупростой компоненте S.
Действительно, в этом случае S П R = {е}, и нагие утвер¬
ждение вытекает из конструкции характера X{g), дан¬
ного при доказательстве теоремы 10. В общем случае,
если G неодносвязна, то представления X(g), Tg могут
быть неоднозначны на G (даже если Tg однозначно).

S 117. ПРОИЗВОЛЬНЫЕ СВЯЗНЫЕ ГРУППЫ ЛИ
531
Следствие 2. Для всякой связной группы Ли су¬
ществует универсальное комплексное евклидово про¬
странство Z (корневая подгруппа, построенная по ком¬
плексной оболочке алгебры Ли группы S) такое, что
всякое неприводимое представление группы G реали¬
зуется в классе полиномов над Z.
Действительно, это верно для представления Tg, от
которого представление Тg отличается лишь одномерным
множителем X(g). Заметим, что при этом представление
Tg задается стандартной формулой
Tgf(z) = a(z, g)f(zg),
где функция a(z,g) отличается лишь множителем X(g)
от соответствующей функции a (z,g), определенной для
подгруппы S. Таким образом, форма индуцированного
представления оказывается универсальной.
Следствие 3. Для перечисления всех неприводи¬
мых представлений произвольной связной группы G до¬
статочно перечислить все неприводимые (возможно,
многозначные) представления ее полупростой компо¬
ненты S.
Последняя задача решена в этой главе. Таким обра¬
зом, можно считать, что мы описали неприводимые пред¬
ставления произвольной связной группы Ли.
В заключение введем понятие мультиплета. Мульти-
плетом мы будем называть всякое неприводимое — воз¬
можно, конечнозначное — представление связной группы
Ли в комплексном векторном пространстве V. При этом,
если данное представление остается неприводимым при
сужении с группы G на подгруппу Gb то условимся го¬
ворить, что G и G) имеют один и тот же мультиплет. Та¬
ким образом, понятие мультиплета относится к целому
классу групп, замкнутому относительно аналитического
продолжения, вещественного ограничения и факториза¬
ции по радикалу.
Поскольку мы рассматриваем также многозначные
представления, то фактически речь идет о представле¬
ниях алгебры Ли или о представлениях одиосвязной на¬
крывающей для некоторого класса групп Ли. Поэтому
условимся говорить, что мультиплет относится к классу
X, если он является неприводимым представлением

832 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
некоторой алгебры Ли X. (Согласно нашему определе¬
нию разные алгебры Ли могут иметь один и тот же
мультиплет.)
В данной главе мы подробно изучили мультиплеты
типов А„, Вп, Сп, Dn, Е6, Е-,, Е8, Г4 и G2. Было показано,
что каждый из этих мультиплетов задается некоторым
набором числовых инвариантов, называемым сигнатурой.
(В теоретической физике эти числовые инварианты на¬
зывают иногда квантовыми числами.) Дискретность на¬
бора квантовых чисел связана, как мы видим, с «ком¬
пактной природой» мультиплетов.
Результаты нашего исследования можно в терминах
мультиплетов выразить следующим образом. Все конеч¬
номерные мультиплеты произвольной связной группы Ли
относятся к одному из классов Ап — G2.
§ 118. Несколько замечаний
В заключение этой главы остановимся вкратце на не¬
которых вопросах, опущенных в основном тексте.
1° Обобщение теоремы Вейля о полной
приводимости. Чрезвычайно простой результат, да¬
ваемый теоремой 10, объясняется тем, что мы ограничи¬
лись рассмотрением неприводимых представлений. Дей¬
ствительно, в классе разрешимых связных групп Ли та¬
кие представления попросту одномерны. Однако тот же
пример разрешимой группы показывает, что может суще¬
ствовать чрезвычайно много «полуприводимых» предста¬
влений, устроенных по типу «жордановой клетки». При¬
рода таких представлений, очевидно, всегда заключается
в наличии радикала. Действительно, имеет место
Теорема 11. Представление связной группы Ли
вполне приводимо тогда и только тогда, когда вполне
приводимо его сужение на радикал.
За доказательством этой теоремы (хотя оно совсем
несложно) мы отсылаем к статье [85], стр. 63. Заметим
также, что в классе бесконечномерных представлений
теряют силу как теорема 10, так и теорема 11. Действи¬
тельно, разрешимые (и даже нильпотентные) группы
имеют неприводимые бесконечномерные представления
([102]). С другой стороны, в классе бесконечномерных

§ 118. НЕСКОЛЬКО ЗАМЕЧАНИЙ
533
представлений полупростой группы Ли теряет силу прин¬
цип полной приводимости. «Неразложимость» некоторых
приводимых бесконечномерных представлений была
впервые обнаружена автором на примере группы Ло¬
ренца (см. по этому поводу § 9 добавления I).
2° Различные реализации мультиплетов.
Для группы SL(«) мы рассматривали подробно различ¬
ные реализации мультиплетов в классе полиномов и тен¬
зоров (гл. VII, гл. VIII). Все эти построения могут быть
почти без изменений перенесены на произвольную полу-
простую комплексную связную группу G.
В частности, для группы G нетрудно построить реа¬
лизацию d(a) на группе G, на подгруппе U (где U—
максимальная компактная подгруппа в G)*). Последняя
реализация задается следующей формулой:
Tgф (и) = а (s') ф (ug),
где элементы s', ug определяются из разложения Ива-
савы: ug = s%ug, б'е£, £ е Z_, ug е U, где Е — макси¬
мальная односвязная подгруппа в картановской под¬
группе группы G. Такая реализация особенно удобна
(см. добавление I, § 2) для перехода к бесконечномер¬
ным представлениям группы G.
Заметим, что переход от реализации на группе Z к
реализации на группе U осуществляется следующей фор¬
мулой:
<р(ы) = а(ы)/(2),
где матрицы well, 2eZ связаны разложением Иваса-
вы: г = е£и, (е Z_. Для вычисления функции а (и)
заметим, что гг* = е£?’е, откуда а(гг) = а(е)2. Далее,
а(и) = а(£_1е_1г) = а(е)-1. В результате
а (и) = ■=' .
Yа (гг*)
Эта формула в свою очередь может быть использована
для обратного перехода от реализации на группе U к реа¬
лизации на группе Z. Далее, если г = sXju, то, как
*) Относительно реализации в классе тензоров для SO (nj,
Sp («) см. также [10].

634
ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
нетрудно показать, меры Хаара на Z и на U связаны
следующим соотношением:
Здесь P(g’) = Р(£6г) = Р(6), и Р(6)—характер картаыов-
ской подгруппы D, сигнатура которого является суммой
всех положительных корней группы G. Если для функ¬
ций ср(м) рассматривать метрику L2(U), то для функций
f(z) мы получаем метрику, определяемую нормой*):
Соответственно вводится скалярное произведение в клас¬
се функций на группе Z. Это скалярное произведение об¬
ладает тем замечательным свойством, что по отношению
к нему сужение d(а)[„ унитарно. (Действительно, то
же верно в L2(U).)
Пример. G = SL(2, С). Ортогонализация треуголь¬
ной матрицы 2gZ, очевидно, должна иметь следующий
вид:
где многоточием обозначены те члены, которые вполне
определяются из унитарности последнего множителя.
Используя параметры для группы SU(2), введенные в
§ 38, мы находим
Полагая dz = dx dy — р dp Дер, где p=|z|, получаем
меру Хаара на комплексной плоскости Z. В результате
где множитель Со подбирается в зависимости от норми¬
ровки мер Хаара на И и Z. Скалярный квадрат функ¬
*) Действительно, | q> (u) |2 du = | / (г) |21 а (и) |21 Р (и) |2 dz.
du = | Р(«) |2dz.
1 г|_, (1+|2рГ'/2 2(1 +|Z|2)~,/2
О 1 ее
t =
1+|2|2 ’ М (1 + |2|2)2 '
1 ., _ 2| г [ d \г\

§ 118. НЕСКОЛЬКО ЗАМЕЧАНИЙ
535
ции f{z) задается формулой
ИЛР= Jl/(z)p
dz
(l + [zl2)m+2 ’
где т — показатель характера а(6) = бГ (сигнатура
этого характера имеет вид (т, 0)). Действительно,
zz =
1
0
1
2
1 +1 ^ I2
Z
и a(zz*) = (l + \z\2)m. В то же время сигнатура харак¬
тера р имеет вид (1, —1) ~ (2, 0), т. е. р(6) = б1б^-1 = 6?.
3° Общий метод отыскания центра. Суще¬
ствует простой общий метод отыскания центра односвяз¬
ной полупростой комплексной группы G. Как мы виде¬
ли в § 112, картановская подгруппа D с: G параметри¬
зуется следующим образом:
б = ехр 2ш (ф А + ф2А2 + ... + фА),
где 0 < Re фь < 1, As = 2сщ/(соь, сой); соь — простой корень,
k = 1,2Искомый центр С содержится в подгруп¬
пе D и является ядром присоединенного представления
группы G. Если На—оператор присоединенного пред¬
ставления, отвечающий вектору 2а/(а, а), то мы имеем
Н е = 2 е
Пав$ (а, а)
Достаточно рассматривать только простые корни а, р,
так как все остальные собственные значения опреде¬
ляются по ним однозначно. Для отыскания центра С до¬
статочно найти все значения параметров фй, 0 АЯефь <
< 1, для которых оператор Тд = ехр2яг(ф!# +ф2#2+ • ■ .
... + фгЯг), где Н{ = На., обращается в единицу на
векторах coj, / = 1,2, ..., г. В результате получаем си¬
стему уравнений вида

536 ГЛ. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
где Cij = 2(со,, cOj)/(cO{, со,) — структурная матрица Кар¬
тана и N означает аддитивную группу всех целых чисел.
Исследуя такую систему, получаем ([85]), что число ли¬
нейно независимых решений (0^Recpft<l) в точности
равно детерминанту структурной матрицы Картана
® =11 сц II,-, /=1, 2 г Очевидно также, что все эти реше¬
ния вещественны. (Действительно, матрица © веществен¬
на и det©=£0, откуда следует, что числа Imcpk удовле¬
творяют однородному уравнению с невырожденной ма¬
трицей коэффициентов.) Это еще раз показывает, что С
содержится в максимальном торе Гсг£>. В результате
получаем, что имеет место
Теорема 12. Пусть G — односвязная комплексная
полупростая группа Ли и С— ее центр. Тогда порядок С
равняется детерминанту структурной матрицы Картана.
Группа С является циклической всегда, за исключением
случая G = Spin (2m), когда эта группа изоморфна
Z2 X Z2.
Более подробное доказательство см. в [81], [85]. Вы¬
числяя центр для каждой простой односвязной группы
Ли, получаем следующую таблицу:
Алгебра
Ап
вп
Сп
°п
Е7
Е8
F4
°2
det (5
п + 1
2
2
4
3
2
1
1
1
N (ш)
с (п + 1)
2
2
4
2
2
1
1
1
Здесь N (со) означает число неизоморфных групп в
классе со (А) всех связных групп Ли с данной алгеброй
Ли А, а с(р) — число различных делителей целого чис¬
ла р, включая 1 и р. (Действительно, с(р) есть число
различных подгрупп в циклической группе Zp.) Класси¬
ческие линейные группы, разумеется, могут быть рас¬
смотрены и независимо (хотя приведенное рассуждение
доставляет новое доказательство односвязности SL(n, С),
Sp {п,С), Spin (л, С)). Для особых групп Картана по¬
лучаем следующие элементы центра в канонических ко¬

§ 118. НЕСКОЛЬКО ЗАМЕЧАНИЙ
537
ординатах ф^:
£6: е, а, Ь, где а = , ~, 0, 0, -j , | j,
4 = (т'7.0.°-4-7)-
Е7: е, а, где а = (у, 0, у, 0, у, О, о).
Нумерация базиса определяется при этом следующей
нумерацией простых корней:
Еб' ° г Jf~5 g Е? ° г j t~6 7
В то же время мы видим, что алгебрам Ли Е&, <?2
отвечает лишь единственная (с точностью до изомор¬
физма) связная группа Ли.
Упражнения
1. Сформулировать результат классификации неприводимых
представлений компактной группы G в «инвариантных» терминах,
не зависящих от выбора картановской подгруппы.
2. Пусть До — преобразование из группы Вейля, переводящее
все положительные корни в отрицательные. Показать, что операция
I = —s0l
переводит сигнатуру I в сигнатуру I, отвечающую контрагредиент-
ному представлению группы G. Выписать условия контрагредиент-
ности для алгебр Ли Ап, Вп, Сп, Dn.
3. Показать, что все неприводимые представления алгебр Ли
Вп, Сп, D2hl Ет, Е$, F4, G2 самоконтрагредиентны. Показать, что
условием самоконтрагредиентности для Ап, D2i, + u Ее является сле¬
дующее симметричное расположение числовых отметок на схеме
Дынкина:
А Я-t A? А А? А А

538 гл. XVI. НЕПРИВОДИМЫЕ ПРЕДСТАВЛЕНИЯ
Содержание этой главы в основном соответствует статье [85]
(см. также [83]). Основным результатом является не только вло¬
жение неприводимого представления d(а) в класс полиномов на
группе Z (теорема 1), но, главным образом, описание индикаторной
системы, т. е. описание класса полиномов, в котором действует
d(a) (теорема 5). «Каноническая модель» d(а), получаемая таким
образом, универсальна в том отношении, что она описывает все
представления не только самой группы G, но также и ее универ¬
сальной накрывающей.
Спинорные представления группы SO (и) были впервые открыты
Э. Картаном (см. [25]). Все представления полупростой комплекс¬
ной алгебры Ли были также впервые классифицированы Э. Кар¬
таном [94]. См. по этому поводу замечания к следующей главе.
Глобальная теория, изложенная в этой главе, представляет ин¬
терес еще и в том отношении, что она совершенно элементарно мо¬
жет быть построена для классических групп Ли. Этим вопросам
посвящается другая статья автора [84]. В частности, такой подход
позволяет единообразно получить не только тензорные, но также
спинорные и спинтензорные представления.
В § 117 мы показываем, как при помощи теоремы Леви—
Мальцева получить обобщение всех этих результатов на произволь¬
ную связную группу Ли. Такое обобщение может показаться не¬
сколько неожиданным, но оно вполне объясняется тем, что действие
радикала, по существу, тривиально (теорема 10). Доказательство
этой теоремы основано на той же идее, что и глобальное до¬
казательство теоремы Ли, предложенное Р. Годеманом (§ 88); ип-
финитезимальное доказательство здесь, по-видимому, было бы зна¬
чительно сложней. Из теоремы 10 естественно вытекает также тео¬
рема 11, которая является обобщением теоремы Вейля о полной
приводимости.
Описание центра полупростой односвязной комплексной группы
Ли является хорошо известным результатом ([81], [128]). Здесь при¬
водится формулировка, включающая детерминант матрицы Картана
([85]).

ГЛАВА XVII
ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
(ХАРАКТЕРЫ, ВЕСА, ОПЕРАТОРЫ КАЗИМИРА)
Если ограничиться изучением представлений полу-
простой комплексной алгебры Ли, то все основные ре¬
зультаты, касающиеся классификации неприводимых
представлений, их внутренней структуры (в том числе
симметрии относительно группы Вейля), собственных
значений операторов Казимира и т. д., могут быть
получены чисто алгебраически. На этом пути удается
также получить независимое доказательство принципа
полной приводимости (§61) и чисто алгебраический
вывод формулы Вейля для характеров неприводимых
представлений. Помимо вычисления характеров удается
также получить некоторую (далеко не полную) инфор¬
мацию о весовой диаграмме неприводимого представ¬
ления.
Естественно, что при решении этих задач основным
инструментом является универсальная обертывающая
алгебра, т. е. ассоциативная оболочка изучаемой ал¬
гебры Ли.
§ 119. Разложение Картана—Вейля в универсальной
обертывающей алгебре
Всюду на протяжении этой главы символом X будет
обозначаться полупростая комплексная алгебра Ли и
символом U — ее универсальная обертывающая алгебра
(§ 58), т. е. ассоциативная оболочка над полем ком¬
плексных чисел. В алгебре X раз навсегда фиксируются
картановская подалгебра Н и корневые векторы еа с за¬
коном коммутации
[h, еа] = (h, а) еа,
[еа, б—а] [ба> 6jj] ^ajj^a+0*

540
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
В алгебре Я фиксируется лексикографическая упоря¬
доченность и выделяются простые корни со*, £ = 1, 2, ...
.г (которые образуют базис в Я). Линейные обо¬
лочки векторов е_а, еа, а > 0, обозначаются соответст¬
венно символами Х_, Х+. Напомним, что Х_, Х+ — ниль-
потентные алгебры Ли с образующими еа., где
ы, — простой корень, £=1,2, ..., г.
Разложение алгебры X в прямую сумму трех под¬
алгебр Я, Х+ мы называли в гл. XV разложением
Картана — Вейля в алгебре X. Следующая теорема об¬
общает это разложение на универсальную обертываю¬
щую алгебру Ж:
Теорема 1. Универсальная обертывающая алгеб¬
ра Ж полупростой комплексной алгебры Ли может быть
записана в виде
Ж =
где Ж-, ф, Х+ — ассоциативные оболочки подалгебр Х_,
Я, Х+ и произведение ассоциативных подалгебр пони¬
мается как линейная оболочка всевозможных произве¬
дений элементов этих подалгебр (в указанном порядке
умножения).
Доказательство. Достаточно проверить, что
каждый одночлен от элементов h, еа, расположенных в
произвольном порядке, может быть приведен с помощью
соотношений коммутации к виду
• • • e-%K+i4+2 • • • вап>
где ар > 0 и () е £, с точностью до слагаемых меньшей
степени однородности. Если базисные элементы h, еа
считать занумерованными в некотором порядке, то все
одночлены от этих элементов также снабжаются есте¬
ственной упорядоченностью, и наше утверждение легко
доказывается методом конечной индукции путем пони¬
жения степени одночлена.
Теорема доказана.
Полученное разложение мы будем называть разло¬
жением Картана — Вейля в алгебре Ж. Очевидно, это
разложение является аналогом разложения Гаусса в
группе G.

§ 119. РАЗЛОЖЕНИЕ КАРТАНА - ВЕЙЛЯ
541
Замечание. Напомним, что алгебры X_, Х+ ин¬
вариантны относительно картановской подалгебры Н.
Отсюда также нетрудно заключить, что алгебры I_, J+
инвариантны относительно подалгебры £, т. е.
П), х-] <ее I_, ft, х+] се 1+
для каждой пары элементов r.eL, л+е1+ ($е£).
Следовательно, разложение Картана — Вейля мы мо¬
жем также записывать в одном из следующих видов:
I = £1-1+ = !_£!+ = 1_1+£.
Вместо элементов h, еа мы будем рассматривать
иногда образующие алгебры X, которые определяются
следующим образом. Положим, прежде всего,
где со и f=l, 2, ..., г,— простые корни алгебры X. Да¬
лее, заменим векторы е~а., еш. коллинеарными векто¬
рами fi, е{ так, чтобы выполнялись соотношения комму¬
тации
[еь ft] = hi-
Заметим, что если а, р— простые корни, то вектор
а — р не может быть корнем (см. § 93). Отсюда сле¬
дует, что [eit fj] = 0 при i ф /. Векторы fi, е, являются
образующими в подалгебрах А_, Х+. Далее, имеем
[hlt в]] = Сцв/,
где Cij — структурная матрица Картана. Аналогичное
соотношение выполняется для пары hi, fj с заменой ctj
на —c{j. В результате получаем следующую систему со¬
отношений для элементов hi, е{, fi.
[е1, //] = бijhi,
[hi, в/\ = Сцв], [hlt fj] = — Cijfj,
[hh h,\ = 0.
Заметим, что эти соотношения вполне определяют струк¬
туру алгебры X (поскольку они содержат структурную

542 ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
матрицу Картана). Элементы hu eit (и даже еи /,).
являются образующими во всей алгебре X. Эти обра¬
зующие мы будем называть каноническими.
Заметим, что элементы /у (а,) являются образую¬
щими в ассоциативной алгебре (I+). Кроме того, эле¬
менты hi являются образующими в алгебре
Вещественную линейную оболочку всех векторов
hj ^ Н, i = 1,2, ..., г, мы будем иногда обозначать сим¬
волом Я о.
§ 120. Представления со старшим вектором
В этом параграфе будут исследованы представления
алгебры X, не обязательно конечномерные, которые об¬
ладают следующими свойствами:
1° В пространстве представления существует век¬
тор £, который аннулируется всеми преобразованиями
подалгебры X_ и является собственным относительно
подалгебры Я.
2° Вектор i является циклическим в пространстве
представления (т. е. все это пространство получается
из Е, преобразованиями ассоциативной алгебры I).
Пусть V — пространство представления и р(х) —
оператор представления, отвечающий элементу х е I.
Тогда определение вектора g выглядит следующим об¬
разом:
Р (ег) 1. = 0, г= 1, 2, ..г, р (Л) £, = Я (Л) h^H.
Вектор Е, называется старшим вектором, и линейная
форма Я(/г)—старшим весом данного представления.
Числа Ki = К (hi) в этом определении могут быть про¬
извольными комплексными.
Представление р(х), обладающее свойствами 1° и 2°,
мы будем называть циклическим представлением со
старшим весом X. Иногда такое представление назы¬
вают также представлением со старшим вектором.
Теорема 2. Пусть р(х)—циклическое представле¬
ние алгебры X со старшим весом X. Тогда старший век¬
тор определяется однозначно (с точностью до норми¬
ровки) и преобразования р(Л), ЛеЯ, диагонализуются
в пространстве представления. Всякий вес р(Н) подал¬

§ 120. ПРЕДСТАВЛЕНИЯ СО СТАРШИМ ВЕКТОРОМ 543
гебры Н при этом имеет вид
Г
ц (h) = Я (h) - 2 (h),
<=i
где a,(ft) = (a,, h) — значение простого корня аг- на век¬
торе h и Hi — неотрицательные целые числа. Каждый
вес встречается в пространстве представления с конеч¬
ной кратностью. Наконец, для каждой линейной формы
Я (h) над алгеброй Н существует единственное (с точ¬
ностью до эквивалентности) неприводимое представле¬
ние со старшим весом Я.
Доказательство. Согласно свойству циклично¬
сти пространство V представления р(х) может быть за¬
писано в виде
V = *l,
где символ означает множество всех векторов вида
р(х)|, xe3f, Согласно разложению Картана — Вейля
мы получаем также
V = Х.&+1 =
поскольку = {Я^} и = {Я|}. Иначе говоря, про¬
странство V является циклическим также относительно
подалгебры
Пусть fi — канонические образующие в подалгеб¬
ре тогда элементы вида f. f. ... f. образуют ба-
Г 1\ 2 lm
зис в X- (вместе с элементом f0 = 1) и соответственно
элементы вида
h i .../ =Р(ft ft
12 m \ li *2 lm)
порождают пространство V. Очевидно, каждый такой
элемент является весовым с весом
и = Я — а, — а, — ... —а. .
1 2
Следовательно, операторы р(/г), h е Н, диагонализуют-
ся в пространстве V, и каждое собственное значение ц
имеет конечную кратность (поскольку существует лишь
конечное число одночленов от /,■ с постоянной суммой
6 = а, + а,. + ... + а, С Первая часть теоремы до-
1\ 12 1т/
казана.

544
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
Далее, пусть X— произвольная линейная форма на
алгебре Н и Яг = Я(/гг), г = 1, 2, г. Определим про¬
странство & как свободную ассоциативную алгебру с
единицей и с образующими zu z2, ..., zr. Положим
p(h)\ = X(h)l,
р (h)z. z. ... z. =
l 2 m
= (X{h)-al^(h)-ai^h)- ... - ct^ (й))2г д
р(ег)1=0, p (fi) 1 = zh
P (fi)Z,Z. ...2, =2,2,2. ...2. ,
*1 <2 ‘m г г1 гг гт
Р (*,) • • ■ zim = (e,) z,a .. . 2,m + 6{ii p (А,) 2г.г
2,
В последнем соотношении мы исходим из равенства
P(ei)p(fi) — p(fj)p(ei)+SiiP(hi)> которое должно выпол¬
няться для всякого представления алгебры X. Это со¬
отношение позволяет определить оператор р(е,) индук¬
тивно для всех одночленов z, z, ... z, . В результате,
Ч 12 т
как легко проверить, мы получаем представление ал¬
гебры X во всем пространстве iS.
Всякий одночлен z, z, ... 2является весовым век-
Ч 2 т
тором относительно алгебры Н с весом Я —а. —а. — ...
1\ 12
... —а. . Следовательно, среди таких весов вес X
1т
является старшим и содержится однократно в про-
странстве 3L. Кроме того, согласно определению опера¬
тора p(fi) вектор 1 является циклическим относительно
алгебры Следовательно, р(х) является циклическим
представлением со старшим весом X.
Пусть Si'— произвольное инвариантное подпростран¬
ство в Si и х = 2 хц — разложение произвольного век¬
тора по весовым векторам хц с различными ве¬
сами р. Принадлежность х ^ Si' можно рассматривать
как линейную зависимость (modSJ')- Поскольку векторы
с различными весами не могут быть линейно зависимы,
то Хц ^ Si' при каждом р. Следовательно, преобразова¬

§ 120. ПРЕДСТАВЛЕНИЯ СО СТАРШИМ ВЕКТОРОМ
545
ния р(й), h^H, диагонализуются в Z'*). Пусть А'—
максимальный из весов, содержащихся в Z'. Мы исклю¬
чаем случай А' = А, когда Z' = Z. Следовательно,
А' < А. Пусть Z+— геометрическая сумма всех инва¬
риантных подпространств с максимальными весами
А' < А; тогда Z+ есть максимальное инвариантное
подпространство в Z, отличное от Z. Следовательно,
Z/Z+ неприводимо. Мы доказали существование не¬
приводимого представления со старшим весом А.
Докажем теперь единственность такого представле¬
ния. Пусть рх — неприводимое представление со стар¬
шим весом А и старшим вектором |. Положим
•••
Тогда, как легко проверить, операторы рх(х) действуют
на векторы £г { _ { по тем же формулам, что и опера¬
торы р(х) в пространстве Z на векторы г, г. ... z, .
L\ 2 т
Однако между £, . , могут существовать нетриви-
4*2 т
альные линейные соотношения. Следовательно, про¬
странство представления рх можно отождествить с фак¬
тор-пространством Z/Zq, где Zq— инвариантное под¬
пространство, определяемое этими соотношениями**).
Ввиду неприводимости р^, Zq должно быть максималь¬
ным инвариантным подпространством, отличным от Z.
Но, как мы видели выше, такое подпространство опре¬
деляется однозначно. Теорема доказана.
Замечание 1. Вместо свободной ассоциативной алгебры 3Z
в доказательстве этой теоремы мы могли бы рассматривать алгеб¬
ру Z, с образующими zi} z2, ..., zr, для которых выполняются соот¬
ношения
[z£, Z/J-o^Zfc,
*) Очевидно, это рассуждение справедливо для любого диаго¬
нального представления. В частности, в условиях теоремы 2 пре¬
образования p(h), h^H, диагонализуются не только в простран¬
стве V, но и в любом инвариантном подпространстве V0 cz V.
**) Подпространство 3Z0 состоит из тех линейных комбинаций
базисных одночленов г; zi ... , которые обращаются в нуль
1 V ТП
при замене г; z; ••- на I, ,■ , .
r ‘1 2 12 т

546
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
ъ „ !
где числа ац определяются из соотношении коммутации для эле¬
ментов et, ей (или fk). Алгебра 3Z изоморфна, таким образом,
алгебрам X- и ЗЦ.
Замечание 2. Циклическое представление р(х) со стар¬
шим весом X может быть построено также при помощи левых сдви¬
гов в алгебре .V. Действительно, положим
Г Т
н = S * (hi - и) + 2
<=1 i=i
Множество ЭЦ является левым идеалом в X (ХХк = Хк), и отсюда
следует, что левые сдвиги в X индуцируют некоторое представление
в фактор-алгебре Х/Хк= Zk. Нетрудно проверить, что SL% изоморф¬
на алгебре S из предыдущего замечания и представление в
задается теми же формулами, что ивЖ.
§ 121. Классификация конечномерных неприводимых
представлений алгебры .X
В предыдущем параграфе мы получили классифика¬
цию всех неприводимых представлений алгебры X, обла¬
дающих старшими векторами и не обязательно конеч¬
номерных. Каждое такое представление определяется
с точностью до эквивалентности своим старшим весом
X = X(h). Выясним, когда такое представление конеч¬
номерно.
1° Если представление рх со старшим весом X ко¬
нечномерно, то числа Ki — X(h{) должны быть целыми
неотрицательными.
Доказательство. Если представление рх конеч¬
номерно, то циклическая оболочка старшего вектора |
относительно трехчленной подалгебры 0, = {/,, А,, так¬
же конечномерна*). Поскольку вектор | является стар¬
шим относительно 0,-, то проекция Я,- = А,(А,-) должна
быть целой неотрицательной.
2° Если представление рк со старшим весом X конеч¬
номерно, то множество всех его весов инвариантно от¬
носительно группы Вейля.
*) Точнее говоря, мы имеем в виду циклическую оболочку от¬
носительно ассоциативной оболочки алгебры 0(.

§ 121. КЛАССИФИКАЦИЯ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИИ 547
Доказательство. Пусть р,— произвольный вес
представления pv Положим
оо
Ец 2 V ц + ка> И = И/,
k= —оо
где Vv означает подпространство всех весовых векторов
веса v. Тогда в действительности эта сумма является
конечной и инвариантно относительно трехчленной
алгебры 0г- = {fi, h{, ег). Согласно теории представлений
такой алгебры вместе с весом (р, h{) пространство Е^
должно содержать также вес — (р, hi) относительно эле¬
мента hi. Следовательно, среди весов v = р + kai дол¬
жен содержаться такой вес р', что сумма р + р' орто¬
гональна корню щ. Но тогда рефлексия s,- из группы
Вейля переводит р в р':
s,p = p'.
Следовательно, множество всех весов представления р*
инвариантно относительно s*, i — 1, 2 г, но тогда
и относительно всей группы Вейля @.
Отбросим теперь условие конечномерности и взамен
предположим, что числа Aj = A(/ij), г = 1, 2, ..., г, все
являются целыми неотрицательными. Покажем, что по-
прежнему имеет место аналог утверждения 2°.
3° Если числа Aj = A(/ij) являются целыми неотри¬
цательными, то множество всех весов представления о*
инвариантно относительно группы Вейля.
Доказательство. Пусть Li — циклическая обо¬
лочка старшего вектора | относительно трехчленной под¬
алгебры 0,- = {fi, hi, ег}. Поскольку А* = А (/г,) — целое не¬
отрицательное число, то согласно результатам § 37 мы
можем утверждать, что пространство Li конечномерно и
неприводимо.
Далее, пусть L — произвольное конечномерное под¬
пространство, инвариантное относительно 0*. Положим
L = XL. Если ге 0j, то мы имеем
Р (z) р (х) Т] = р ([Z, х}) Т] + Р (*) Р (2) Х\
для каждого вектора це! и каждого элемента j:eI
Следовательно, L также является конечномерным под¬
пространством, инвариантным относительно 0*.

548
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
Пусть W — линейная оболочка всех конечномерных
подпространств, инвариантных относительно 0г. Тогда
мы видим, что W инвариантно относительно всей ал¬
гебры X. Поскольку W содержит L,-, то W содержит так¬
же и старший вектор £. Следовательно, W = V ввиду
неприводимости пространства V представления рх.
Рассмотрим теперь произвольный вес р, и пусть р—
весовой вектор веса р. Согласно сказанному выше мы
можем положить
где каждый вектор гр содержится в конечномерном под¬
пространстве, инвариантном относительно 0*. Следова¬
тельно, вектор г] также содержится в одном из таких
подпространств. Повторяя те же рассуждения, что и в
доказательстве утверждения 2°, получаем, что вес р/ =
= sfp содержится в пространстве V. Утверждение 3° до¬
казано.
Теперь уже нетрудно получить окончательный ре¬
зультат:
Теорема 3. Неприводимое представление рх со
старшим весом к конечномерно тогда и только тогда,
когда все проекции М = k (hi) являются целыми неотри¬
цательными. Множество всех весов в этом случае инва¬
риантно относительно группы Вейля, и для каждого ве¬
са р число 2(р, а)/(а, а) является целым, где а — ко¬
рень.
Доказательство. Согласно теореме 2 всякий вес
Г
представления рх имеет вид к — 2 niai> гДе числа
i = i
п{ неотрицательные целые. Если числа М = k(ht) веще¬
ственны, то это же верно для чисел рг-= р(Ы)\ следо¬
вательно, в этом случае все веса представления рх со¬
держатся в вещественном пространстве Но (веществен¬
ной линейной оболочке всех корней). Покажем, что при
этом (р, р) ^ (л, к).
Действительно, согласно 3° множество всех весов
инвариантно относительно группы Вейля. Поскольку
преобразования группы Вейля ортогональны, то они не
изменяют скалярного квадрата (р,р). Согласно резуль¬
татам § 105 мы можем подобрать преобразование Вей-

§ 121. КЛАССИФИКАЦИЯ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ 549
ля таким образом, чтобы полученный вектор был доми¬
нантным, т. е. числа ц* = были неотрицательны.
Тогда при fi = 2 ntаг имеем
г = 1
г
О*. Р) = S Щ (ц, аг) > 0.
г = 1
Следовательно, угол между векторами ц и |3 не может
быть тупым. Но тогда скалярный квадрат вектора
К = ц + р не может быть меньше скалярного квадрата
вектора ц. Наше утверждение доказано.
Пусть R— дискретная решетка всех векторов вида
Г
X — 2 п-М, где числа п* неотрицательные целые. Мы
г=1
видим, что множество всех весов представления рх со¬
держится в пересечении решетки R со сферой радиуса
У^, К). Следовательно, это множество конечно. По¬
скольку
у = 2^,
ч
где Vy — весовое подпространство с весом ц и
dim Уд < оо (теорема 2), то пространство V также ко¬
нечномерно. Теорема доказана.
Поскольку каждое конечномерное представление ал¬
гебры содержит (в силу теоремы Ли) хотя бы один
старший вектор, то теорема 3 дает нам полную класси¬
фикацию всех неприводимых представлений алгебры К.
Замечание 1. Из доказательства пункта 2° не¬
трудно заключить, что подпространства Vц, IV, где
|/ = ДгЦ, имеют одинаковую размерность. Следователь¬
но, если рх конечномерно, то весовая диаграмма этого
представления инвариантна относительно группы Вейля.
Замечание 2. Можно показать ([121]), что не¬
приводимое конечномерное представление рх алгебры X
может быть реализовано с помощью левых сдвигов
в фактор-алгебре = £/®ix, где — максимальный
левый идеал, определяемый следующим образом:
гг Г
= + 2iXtti+> (ср. с замечанием 2

550
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
в § 120). Этот результат имеет очевидную аналогию с
индикаторными системами, построенными в гл. XVI.
Замечание 3. Назовем представление алгебры X
экстремальным, если в пространстве этого представле¬
ния существует вектор g такой, что
Р (еа) Е = 0> p(h)l = X{h)%
для некоторой фундаментальной системы корней а =
= оч, а2, • • •, а г (определение фундаментальной си¬
стемы см. в § 105). Для экстремальных представлений,
очевидно, имеет место аналог теоремы 2.
Конечномерное неприводимое представление экстре¬
мально относительно всякой фундаментальной системы
корней (ввиду симметрии относительно группы Вейля).
Более того, лишь конечномерные представления обла¬
дают этим свойством. Мы видим также, сколь «малую»
часть занимают конечномерные представления в классе
всех неприводимых (и даже в классе всех экстремаль¬
ных) представлений алгебры X.
§ 122. Формула Фрейденталя
Начиная с этого параграфа, мы будем рассматри¬
вать только конечномерные представления. Займемся ис¬
следованием весовой диаграммы неприводимого пред¬
ставления р>,. В этом параграфе будет установлена
рекуррентная формула для кратностей весов в представ¬
лении рх, принадлежащая Фрейденталю.
Теорема 4. Пусть пп — кратность веса р в непри¬
водимом представлении со старшим весом X. Тогда
оо
= 110) 2 X n*+ka ^ + ka>
а> 0 k=\
Здесь каждый вес рассматривается как элемент из Н
и скобка (х,у) означает билинейную форму Киллинга —
Картана. Множитель с(р) отличен от нуля для каждого
веса р и вычисляется по формуле
с(р) = ||Я + б|Р-||р+б|р,
где ||х|| = (х, х) и б означает полусумму всех положи¬
тельных корней в алгебре X.

§ 122. ФОРМУЛА ФРЕЙДЕНТАЛЯ
551
Доказательство этой теоремы основано на рас¬
смотрении в рх квадратичного оператора Казимира
д = 2ягяг- 2 £аЕ-а.
г = 1 а ф о
Здесь положено Я,- = р?,(/г;), Я* = р*.(/г2'), Еа = р(еа), и
базисные векторы /г*, еа выбраны с таким расчетом, что¬
бы ковариантные числовые переменные образовывали
квадратичный инвариант относительно присоединенного
представления. Для этого, как обычно, достаточно поло¬
жить
(еа, в—а) 1
и выбрать векторы h{ таким образом, чтобы они образо¬
вывали базис, дуальный к /г;, т. е. (hi, №) = 6,-j, где 6ц —
символ Кронекера. Тогда, как нетрудно видеть, опера¬
тор А перестановочен со всеми операторами представле¬
ния р^. Заметим, далее, что
ДЕ = VI,
где собственное значение у зависит от старшего веса X.
Поскольку А перестановочен со всеми понижающими
операторами px(fi), то Ар = ут| для всякого вектора
р 6 V, где V — пространство представления р*,. Следова¬
тельно, А является скаляром на К*). С другой стороны,
положим
к = 2IV
ч
где Vц означает весовое подпространство размерности
отвечающее весу р. Очевидно, инвариантно отно¬
сительно ЕаЕ-а. Вычисляя на этом подпространстве след
оператора А, находим
Г
Y«n = Пц 2 В (hi) р (h‘) - 2 sp
i = l афО
Займемся вычислением отдельных слагаемых, входящих
в правую часть.
*) Это можно получить также из леммы Шура. Однако прове¬
денное рассуждение показывает, что Д является скаляром для лю¬
бого экстремального (не обязательно конечномерного) представле¬
ния алгебры X.

552
ГЛ. xvn. ИНФННИТЕЗИМАЛЬНАЯ ТЕОРИЯ
1° Разлагая вес р. по базису /г4 и дуальному базису
’ Г
h\ находим р = 2 Р (^‘)^г = 2 Р (^;) откуда (р, р) =
1 = 1
Г
— 2 р(Л*)р(/*0- Следовательно, первая сумма в нашей
i—1
формуле может быть заменена скалярным квадратом
(р, р).
2° Фиксируем корень а и найдем выражение
sp ЕаЕ-а, где след берется только по весовому подпро¬
странству Уд. Рассмотрим вначале тот случай, когда
число
/ = О’ а)
0 (а, а)
является неотрицательным. Тогда 1п является одним из
возможных старших весов для трехчленной подалгебры
операторов
Р _ Е-а р _ Hg р _ Eg
Y(а. а)/2 ’ 0 (а, а) ’ + К(а, а)/2 ’
где положено На = рх(а). Кроме того, если Уд, то S
разлагается по базисным векторам с весами /0, содержа¬
щимся в неприводимых подпространствах относительно
{£_, Ко, К+} со старшими весами 10, К + У У + 2, . .. Сле¬
довательно,
Яд = х (/о) "Ь х (У + 1) У к (К + 2^ + .. .,
где х(/) означает кратность вхождения старшего веса I в
оо
подпространство 2 Уц+/сг Отсюда также следует,
что
х (/о + /) = Яц+/а — Яд+(/+ 1)а.
Теперь мы воспользуемся явными формулами для непри¬
водимых представлений трехчленной подалгебры si (2),
найденными в § 37. Согласно этим формулам, если | яв¬
ляется базисным вектором веса /о в неприводимом под¬
пространстве со старшим весом /, то мы имеем
E+E-l = + /0 + 1)&.

§ 122. ФОРМУЛА ФРЕПДЕНТАЛЯ
553
Полагая в этой формуле / — 10 + / и умножая каждое
собственное значение на x(l0 + j), получаем вклад не¬
приводимого подпространства со старшим весом / в сум¬
му sp Е+ЕВ результате
оо
sp Е + Е- = 2| (гец+/а — % + (/ + 1) а) (21J + /) (/ + 1) =
1 = 0
оо оо
^ 2 п\1 + 1а№0 + /)(/ + 0 ~ 2 (2^0 + I — 1) inn + la-
1=0 I-1
Вторая сумма не изменится, если распространить сумми¬
рование также на j = 0. Приводя подобные члены, по¬
лучаем
оо
sp£+£- = 2 2 Яц+/0(/о + /)-
у-о
Если умножить теперь обе части полученного равенства
на —(а, а)/2, то мы найдем искомую формулу для
sp ЕаЕ^а. Напомним, что /0 = (р, а)/(а, а), откуда
(/0 + /) (а, а) = (р + /а, а). В результате
оо
sp ЕаЕ.- а = - 2 «ц+/а (и + /а, а). (*)
1=о
3° Рассмотрим теперь тот случай, когда (р, а)<0.
Пусть s = su — отражение из группы Вейля по направле¬
нию корня а и р' = sp. Положим
, _ (р', а) (р, а)
0 (а, а) (а, а)
и заметим, что всякий вектор | е У(1 имеет вес — /0 отно¬
сительно оператора Е0. Все предыдущие построения
остаются в силе, если заменить р на р' и вес /0 на вес
— /0. В результате получаем следующую формулу:
оо
sp ЕаЕ^а = - 2 /V+уа (р' + /а, а), р' = sp,
/ = 1
где след по-прежнему берется только по весовому под¬
пространству Ец. Заметим, что р/= р + та, где т =
= — 2(р, а)(а, а)>0. Следовательно, эга формула может

554
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
быть также записана в виде
оо
sp ЕаЕ-а = — 2 «ц+уа(Р + /а, а)-
/=т + 1
Покажем, что суммирование можно распространить на
значения |л от 0 до оо. Действительно, если i + j = т, то
сумма векторов р + га, р + /а ортогональна корню а и
эти векторы сопряжены друг другу относительно ре¬
флексии s. Поскольку в этом случае Пц+га = Пц+5(Х (весо¬
вая диаграмма инвариантна относительно группы Вей¬
ля), то мы имеем также
«и+/а (Р +/«> а) + «ц+гн(р+га, а) = 0.
Отсюда, очевидно, следует, что сумма слагаемых
яи+;'а(р + /а> а) по / от 0 до т обращается в нуль. Сле¬
довательно, формула (*) сохраняет силу для любого
веса р и любого корня а ф 0.
Суммируя результаты 1°, 2°, 3°, получаем следующее
тождество:
00
Y«^ = rt^(p, р)+ 2 2 «ц,+ /а(Р + /«. а)- (**)
а^о /=о
Преобразуем полученную формулу. Прежде всего, заме¬
тим, что слагаемые пДр, а), яДр,—а) взаимно уничто¬
жаются, так что суммирование в можно вести по
/ от 1 до оо. Далее, из приведенных выше рассуждений
относительно рефлексии sa следует, что сумма слагае¬
мых ft(j,+ja(p +/а, а) по j от —оо до оо всегда обра¬
щается в нуль. Следовательно,
оо оо
2 «ц-га(р-/а, а) = ГСц(Р> а)+ 2 »n+;a(p + ia> а)-
/=1 ^ У= 1
Используя это тождество, мы можем исключить в фор¬
муле (-») все слагаемые с a < 0. В результате имеем
оо
Y«|i = «n(p. Р)+ 2 %{\1, а)+ 2 2 2«а+уа(р + /а. а).
а > 0 а > 0 у=-г

§ 122. ФОРМУЛА ФРЕЙДЕНТАЛЯ
555
Если использовать обозначение б = у ^ а, то эта фор-
а > О
мула переписывается в виде
оо
Y% = (р, р + 26) + 2 2 2 «ц+/а (в + /а, “)•
а > 0 / = 1
Наконец, для нахождения множителя у достаточно в ка¬
честве р взять старший вес Я. Тогда п% = 1, nx+ja = 0 при
/ > 0, и мы находим, что у = (Я, Я + 26) = ||Я + 6||2 —
■— ||б[|2. Подставляя это выражение снова в общую фор¬
мулу, получаем окончательно
оо
(IIЯ + б II2 - II р + б II2) Лц = 2 2 2 «ц+/а (н + /а, «)•
а > 0 / = I
Осталось показать, что коэффициент при пц отличен от
нуля. Для этого установим следующие два предложения,
имеющие также самостоятельную ценность:
4° Пусть б — полусумма положительных корней. То¬
гда все числовые отметки вектора б равны единице*)-.
6 =6(/гг) = |(б’ = 1 /=1,2,..., г.
‘ V и ((01, щ) ’ ’ ’ ’
Если s — элемент из группы Вейля, отличный от еди¬
ницы, то б > s6 (относительно лексикографической упо¬
рядоченности в Н).
Действительно, пусть s,-— отражение относительно
простого корня а4. Тогда, как мы видели в § 105, для
каждого положительного корня а Ф со,- корень sta также
положителен. Следовательно,
s>'6 = \ s‘a = ~ Т а‘ + Т S “ = 6 ~ “*•
a > 0 а Ф
а > 0
В то же время s,6 = б — бга, согласно общей формуле
для рефлексий. Следовательно, б, = 1, /= 1,2, ..., г.
Аналогично, если s — произвольный элемент из группы
Вейля, то
s6 = б — 2 а,
*) Иначе говоря, если А4 — базис, дуальный hi, то все коорди¬
наты вектора б в этом базисе равны единице.

ГЛ. XVII. ИНФПППТЕЗИМАЛЬНАЯ ТЕОРИЯ
где сумма берется по тем а > 0, для которых sa < О,
Если таких а нет, то преобразование 5 сохраняет до¬
минантную камеру Вейля, откуда 5 = е (§ 105). Следо¬
вательно, 56 — 6 < 0.
5° Если р— произвольный вес представления ръ от¬
личный от старшего веса X, то ||р + 6||<||Я + 6||.
Действительно, если р ф X, то р < ?., и мы имеем
[| Я + 6 |р —1| р + б ||2 = || К |р -1| р |р + 2 (X - р, б).
Как мы видели в § 121, ||Я||>||'р||. Далее, поскольку век¬
тор X — р является линейной комбинацией простых кор¬
ней с неотрицательными коэффициентами, не равными
тождественно нулю, и (а,, 6) >0, то ||Я + 6||2—||р + б||2>0.
Теорема доказана.
Поскольку все веса в правой части формулы Фрей-
денталя выше р (относительно лексикографической упо¬
рядоченности), то эта формула действительно позволяет
найти все кратности пц, исходя из кратности пх = 1.
§ 123. Формула Вейля для характеров
В этом параграфе мы приводим чисто алгебраическое
доказательство формулы Вейля, принадлежащее Фрей-
денталю, для характеров неприводимых конечномерных
представлений алгебры X. Если встать на алгебраиче¬
скую точку зрения, то характер % представления рх мо¬
жет быть определен с помощью формулы
г = Ъ <he (м-),
в
где е(р)—формальный символ, определенный в классе
весов и удовлетворяющий мультипликативному соотно¬
шению
е(Х)е(ц) = е(Х + р).
Иначе говоря, мы можем рассматривать % как элемент
ассоциативной алгебры с единицей 1 = е(0) и образую¬
щими уг = е(/г‘). уя1 ~е( — hl), где /Е — дуальные векто¬
ры для h{ = 2coj/(to;, (Oj), t=l, 2, ..., г. Действитель¬
но, всякий вес имеет целые координаты в дуальном ба¬
зисе (каждая из этих координат является «числовой

§ 123. ФОРМУЛА ВЕЙЛЯ ДЛЯ ХАРАКТЕРОВ
557
отметкой» (§ 109) на одном из простых корней со*). Над
полем комплексных чисел мы можем также положить
е(р) = ехр(р, /г),
где положено р = рцИ,\ h = tlhi и (р, h) — щС. Однако
алгебраическое определение удобно в том отношении,
что «формальная экспонента» е(р) может быть опреде¬
лена над произвольным полем.
Веса конечномерных представлений алгебры X мы
будем также иногда называть целочисленными векто¬
рами. Заметим, что каждый корень является весом (ве¬
сом присоединенного представления алгебры X). Поло¬
жим
Q — И (е (а/2)-е (-а/2)).
а> 0
Здесь мы нарушили предыдущие соглашения, поскольку
а/2, вообще говоря, не является весом. Однако нетруд¬
но видеть, что определение элемента Q может быть так¬
же дано в следующей корректной форме:
Q = е (— 6) П (е(а)~ 1) = е(6) П (1 -<?(-а»,
а > 0 а > 0
где б —полусумма положительных корней. Первое опре¬
деление обладает тем преимуществом, что из него не¬
посредственно очевидна кососимметричность по отно¬
шению к группе Вейля. Действительно, положим
se (р) = e(sp)
для каждого s из группы Вейля @ и распространим оп¬
ределение оператора s по линейности на все линейные
комбинации экспонент. Если s = s{ — рефлексия по на¬
правлению простого корня сог-, то оператор s меняет
знак у скобки e(aJ2)—е(—a.i/2) и переставляет все
остальные скобки между собой. Следовательно, s{Q —
= —Q, и отсюда sQ — (det s)Q для всякого se®, Мы
условимся записывать характер % в виде отношения
F/Q, т. е. вместо % введем новую искомую функцию
F = %Q-
Из симметричности весовой диаграммы по отношению к
группе Вейля следует симметричность характера %. Из

558
ГЛ. XVIГ. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
симметричности % и антисимметричности Q следует так¬
же антисимметричность F.
Лемма 1. Q= 2 (dets)e(sS), где 6— полусумма
s е ®
положительных корней.
Доказательство. Рассмотрим вначале произ¬
вольную антисимметрическую функцию / = 2 (р)-
Скажем, что функция / является элементарной, если ве¬
са, входящие в ее разложение, лежат на одной орбите
относительно группы Вейля. В этом случае среди таких
весов имеется лишь один доминантный вес ро и все
остальные веса получаются из него преобразованиями
группы Вейля. Очевидно, в этом случае
/ = с0Ае (р0), cQ = const,
где А означает оператор альтернирования: А =
~ ~w (det s) s (w — порядок группы Вейля)*). Заме-
SS®
тим, что оператор А удовлетворяет тождеству А<гг=—А
для всякой рефлексии по направлению корня сог-. Следо¬
вательно, если р0(Аг)=0 при некотором i, то Ле(р0) =
= Л5ге(р0)=—Ле(цо), откуда следует, что в этом слу¬
чае / = 0.
Вектор р е/f мы условимся называть строго доми¬
нантным, если все его числовые отметки рг = р (Лг)
положительны. В результате мы видим, что всякая
элементарная функция определяется (с точностью до
множителя) своим единственным строго доминантным
весом ро. Очевидно также, что всякая кососимметриче¬
ская функция / является линейной комбинацией элемен¬
тарных **).
Покажем теперь, что функция Q является элементар¬
ной. Действительно, все веса, входящие в разложение Q,
имеют вид р = 6—р, где |3 — сумма некоторых поло¬
*) Действительно, / = А[ и Ле(р) = ±Ле(ц0) для каждого
веса |х, лежащего на одной орбите с Цо. Следовательно, f может
отличаться лишь множителем от Ае(ро).
**) Для получения такого разложения достаточно выделить
в сумме / = 2 (и) все строго доминантные веса и применить
к соответствующим функциям оператор альтернирования.

§ 123. ФОРМУЛА ВЕЙЛЯ ДЛЯ ХАРАКТЕРОВ
559
жительных корней. Если вектор р является строго до¬
минантным, то
Рг < бг= 1
(числовые отметки вектора б равны единице). Как сле¬
дует из определения вектора р, его числовые отметки
Pi = 2(р, ы;)/(а>г, Иг) являются целыми. Следовательно,
Pi 0. С другой стороны, коэффициенты в разложении
Р по простым корням неотрицательны и отличаются
лишь положительными множителями от дуальных коор¬
динат рг'= (р,/Е). Следовательно, (р, р) = pjfP <<0, от¬
куда р = 0. Мы показали, что вектор б является един¬
ственным строго доминантным среди весов в разложе¬
нии Q. Разность R = Q— 2 (dets)e(s6) кососимметрична
и не содержит ни одного строго доминантного веса,
откуда R — 0. Лемма доказана.
Пусть Е — алгебра всех функций, которые являются
линейными комбинациями экспонент, и Е — множество
всех вектор-функций / = /'ft,, где R е Е и ht — фиксиро¬
ванный базис в каргановской алгебре Н. Мы определим
отображения £—►Д и £ —>Е, называемые соответствен¬
но градиентом и лапласианом в Е:
Уе (р) = <? (р) р, Де(р) = (р, р)е(р),
с линейным продолжением па всю алгебру Е. Из муль¬
типликативного соотношения для экспонент е(р) выте¬
кает обычное правило дифференцирования V(ab) —
= (Уа)б + а(\'Ь) и соотношение
* A (ab) = (Да) b + 2 (Уа, \!Ь) + а{АЬ),
где скалярное произведение двух элементов из Е опре¬
деляется так же, как и в картановской алгебре Н, с за¬
меной числовых коэффициентов коэффициентами из Е.
Докажем теперь еще одну лемму, которая является ос¬
новной для нашего изложения.
Лемма 2. Функция F = %Q удовлетворяет сле¬
дующему дифференциальному уравнению-.
ДF — {К + б, X + б) F.
Доказательство. Используем формулу (**), по¬
лученную в предыдущем параграфе при доказательстве

560 ГЛ. XVII. ИНФННИТЕЗИМАЛЬНАЯ ТЕОРИЯ
формулы Фрейденталя. Умножая обе части этой фор¬
мулы на экспоненту е(р) и суммируя по р, находим
оо
УХ = А% + 2 2 2 (ц + /а> а)е (р)-
Ь а Ф0 / —0
Умножим обе части этого равенства на функцию
Р= П (е(а)-1)= П Ра-
аФО о.Ф$
Заметим, что если фиксировать корень а и положить
Р = RaPa> гДе Ра ~ II (в (Р) — 1), то общий член под
6*з£а
знаком тройной суммы принимает вид
Рап»+ /а (р + /а. а) (е (р + а) - е (р)).
Суммируя по / от 0 до оо, заметим, что суммарный ко¬
эффициент при экспоненте е(р + а) равен
• со
Ра X 2 {rtn + /a(P + /«. a)-«n + (/-Da(P + (/- !)a, a)} =
i—o
= /?аЯд(р, a).
Суммируя теперь по аФО, замечаем, что выражение
2 RaP-e (а) совпадает с градиентом функции Р. С дру-
афо
гой стороны, суммируя по р, замечаем, что выражение
2 ПцЦе (р) совпадает с градиентом характера /. В ре-
ч
зультате имеем
УХ’ Р — (Ах) • Р + (Vx, VP).
Из определения функций Р, Q следует, что Р = ±Q2.
Следовательно, VP = ±2QVQ, и скалярный множитель
можно вынести за знак скалярного произведения. Со¬
кращая на ±2Q, получаем следующее тождество:
YX-Q = (Ax)Q + 2(V*, VQ).
Согласно отмеченному выше общему правилу для лап¬
ласиана выражение в правой части есть A(xQ)—x(AQ)-
11ола:ая f = %Q, находим
yF = AF — % AQ.

§ 123. ФОРМУЛА ВЕЙЛЯ ДЛЯ ХАРАКТЕРОВ
561
Остается заметить, что AQ = (6, 6)Q в силу леммы !.
Кроме того, в предыдущем параграфе было найдено сле¬
дующее выражение для множителя у: у = (А,+6, А,+ 6)—
— (б, б). Подставляя все эти выражения, получаем нуж¬
ный результат. Лемма доказана.
Теперь уже нетрудно найти явный вид элемента F.
Функция F = %Q является линейной комбинацией экспо¬
нент е(ц + s6), где ц — произвольный вес представления
Рх и SE®. Каждая из этих экспонент является собст¬
венным вектором лапласиана с собственным значением
(ц + s6, ц + s6). Ввиду линейной независимости соб¬
ственных подпространств оператора Д каждое слагаемое
должно иметь то же собственное значение, что и вся
функция F. Следовательно, l|s-lp + б|| = ||А, + б||. Как
мы видели в конце § 122, это возможно только в случае
s—1 ц = X, т. е. ц = sX. Следовательно, F является эле¬
ментарной функцией с единственным строго доминант¬
ным весом А,+ 6. Следовательно, F — с0 2 (dets)e(s(A, + б)).
seS
Сравнивая коэффициенты при е(Х), заключаем, что
с0 = 1. В результате доказана следующая
Теорема 5. Характер % неприводимого конечно¬
мерного представления рх может быть представлен в
виде отношения двух элементарных функций:
2 (det s) e{s{X + 6))
^ 2 (det s) е (sb) ’
ssj
где X — старший вес представления р* и б — полусумма
всех положительных корней. Преобразование s пробега¬
ет группу Вейля, и det s = ± 1.
Над комплексным полем мы можем заменить е(ц)
настоящей экспонентой ехр(ц, А). Осуществляя, как и
в § 73, предельный переход при h -* 0, получаем следую¬
щую формулу для размерности:
Л (а, X + 6)

562
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
Здесь Nj, — размерность представления р*,. Мы преобра¬
зуем эту формулу следующим образом. Каждый ко¬
рень а представим в виде суммы простых корней. Каж¬
дый вектор Я, б разложим по базису h\ дуальному к век¬
торам hi = 2а,7 (а,, аг):
Я = Я£/г‘, 6 = 6 ft.
Координаты Я,, б, являются числовыми отметками век¬
торов Я и 6: Я,-= 2(Я, аг)/(ссг-, a,), б£=1. Следователь¬
но, числа Я; являются целыми неотрицательными. Далее,
нормируем простые корни а, таким образом, чтобы чис¬
ла Wi = (а,-, аг) принимали значения 1, 2, 3. Поскольку
W,
ai=—2~hi и базисы hi} h* дуальны друг другу, то мы
имеем
N,
П
2 (яг+ l)wiki
(ki) ^ wiki
где числа &£ определяются из разложения а = ^ fe£a£ и
I=1
произведение берется по всем последовательностям /г,-,
/г,- ^ 0, для которых а является корнем.
Замечание. Имея дело с классическими группа¬
ми, гораздо удобнее пользоваться теми координатами
старшего веса а. = (//гь ш2, ..., mv), которые были вве¬
дены исходя из основного линейного представления этих
групп (v = я для SL(n), v = [я/2] для SO(n), Sp(w)).
Например, для Sp (я) мы имеем
Ха
ylil
Y,
Y,'2
Y,v-Yi v
i, -i,
Y2‘ ~ Y2 1
y22 - y2 2
y2v - y2
->v
1
-к,
V 1
IV
- y/1
Tv
y!?
Yv4
где lv = nip + (v — p), p = 1, 2, ..., v, и знаменатель Q
получается из числителя подстановкой тр = 0. Соответ¬
ствующая размерность имеет следующий простой

§ 124. СЛЕДСТВИЯ ИЗ ФОРМУЛЫ ВЕЙЛЯ
568
вид:
*=1 1<г<А<у
где Qо получается из числителя подстановкой тр = 0.
Более подробную информацию по всем этим вопросам
можно найти в книге Г. Вейля [10], где вычисление ха¬
рактеров производится интегрально и где для каждой
классической группы получается также аналог «второй
формулы Вейля», доказанной нами для группы SL(n-).
§ 124. Следствия из формулы Вейля
Отметим некоторые простые следствия из формулы
Вейля, которые относятся к нахождению кратностей ве¬
сов и описанию спектра тензорного произведения двух
неприводимых представлений.
1° Еще одна рекуррентная формула для
кратностей весов. Умножим обе части формулы
Вейля на знаменатель Q и приравняем полученные ли¬
нейные комбинации экспонент:
2 2 Пц ■ (det s) • е (р + s6) = 2 (det s) е (s (к + 6)).
S IX s
Рассмотрим произвольный вес р, отличный от старшего
веса к; тогда, как мы знаем, ||р + 6||<||А, + б||, и, следо¬
вательно, р + б не может совпадать ни с одним из зна¬
чений s(k + 6). Следовательно, суммарный коэффициент
в левой части при е(р + б) должен равняться нулю. Но
этот коэффициент получается суммированием по тем ве¬
сам р', для которых р' + s6 = р + б. В результате
2 «ix+б—s6 (det 5) 0.
seS
Поскольку, как мы знаем, б — s6 > 0 для всех значений
s Ф е, то эта формула является рекуррентной. Действи¬
тельно, она может быть переписана в виде
«м. = “ 2 (det s)«n+6_s6,
s-фе
где все веса, входящие в правую часть, строго больше р.
Эта формула значительно проще рекуррентной формулы

561
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
Фрейденталя. Эту формулу можно назвать рекуррентной
формулой по «звездочке» б — sб.
2° Формула Костанта. Попробуем разложить
1IQ в бесконечный (формальный) ряд по экспонентам
е(ц). Напомним, что Q = e(6)II (1—е(-а))- Отсюда
а > О
ясно, что искомое разложение сводится к перемножению
геометрических прогрессий:
П (1 -е(-а))_1= II (1 + е{а) + е (2а) + ...) =
а > 0 а > О
= 2 ^(вМр).
и
Здесь функция Р(ц) определяется следующим образом:
Р(0) = 1, Р(р) при р ф 0 есть число различных разбие¬
ний вектора р, в сумму положительных корней *). Функ¬
ция Р(ц) называется функцией разбиения. Подставляя
теперь полученное разложение в характер хх =
находим
2/V?(tO = 2 (det s)e(s(X + б)) 2 — — б).
\х \х'
Остается сравнить коэффициенты при каждом базисном
элементе е(р). Для каждого р подбираем р' из равен¬
ства р = 5(Я + б) — р' — б. В результате получаем сле¬
дующую формулу:
«и= 2 (det s) (Р (s (р + б) — (р + 6))).
Эта формула впервые была найдена Костантом ([19]),
однако значительно более сложным путем. Указанный
простой вывод был отмечен П. Картье [99] и
Р. Штейнбергом [147']. Практическое применение
этой формулы связано еще со значительными вычисле¬
ниями.
3° Тензорное произведение двух непри¬
водимых представлений. Вычисляя характер
тензорного произведения рА ® рА , с одной стороны, как
произведение характеров сомножителей и, с другой сто¬
*) Заметим, что указанное определение пригодно при любом
цеЯ, однако Р(ц)=0, если и не является целочисленным.

§ 125. ИНВАРИАНТЫ ГРУППЫ ВЕЙЛЯ
565
роны, как сумму характеров неприводимых компонент
Рх, входящих с кратностями тх, получаем следующее ра¬
венство:
2 2 «n(det s)e(p + s (Я2 + 6)) = 2 2 (det s)mke{s (Я+ 6)).
li s К s
Здесь мы предварительно умножили обе части на Q и
заменили характеры %А соответствующими альтер¬
нированными суммами FK, F%. Символ означает ве¬
совую диаграмму представления рА. Рассуждая, как
при выводе 1°, получаем следующее равенство:
тк = 2 (det s) nx+6_s(k2+&).
se3
Это равенство выражает искомую кратность тА через
весовую диаграмму пи представления рА. Путем не¬
сложных преобразований получаем отсюда, как и в
§ 77, спектральную формулу для рА <g> рАу
Рл, ® Ра2 = 2 пд?д+х2+бР| д+А;+б)-б-
Здесь суммирование ведется по всем весам представле¬
ния рА ; £v = 0, если существует такое преобразование
se®, для которого sv = v; = det sv, если такого s не
существует и sv переводит вектор v в доминантный век¬
тор, обозначаемый | v |.
Заметим, что вышеуказанная формула для кратно¬
сти тх была получена еще Г. Вейлем [10]. Г. Вейль
отметил также, что подобный прием пригоден всегда
при разложении некоторого представления р на непри¬
водимые при условии, что известен характер представ¬
ления р. В частности, аналогичная формула может быть
получена при исследовании сужений с группы на под¬
группу.
§ 125. Полиномы на картановской подалгебре,
инвариантные относительно группы Вейля
При изучении характеров нам пришлось иметь дело
с вопросами симметрии относительно группы Вей¬
ля. В этом параграфе будут рассмотрены близкие

566
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
вопросы, которые в свою очередь будут использованы в
дальнейшем изложении. Мы рассмотрим полиномы на
картановской подалгебре Я, инвариантные относитель¬
но группы Вейля, которым в дальнейшем будут постав¬
лены в соответствие операторы Казимира алгебры X.
Сделаем вначале одно небольшое замечание отно¬
сительно алгебры Е, рассмотренной в § 123 и состоя¬
щей из функций / = 2 1»е (ц), где ц — произвольный
в
вес. Как мы видели при построении характеров, всякий
кососимметрический элемент этой алгебры является ли¬
нейной комбинацией элементарных функций iy =
= 2 (dets) е (s (X + 6)), где к — старший вес представле¬
ния pv Соответственно всякий симметрический элемент
этой алгебры является линейной комбинацией примитив¬
ных характеров ух. Действительно, умножая данный
элемент на кососимметрическую функцию Q, мы разла¬
гаем полученную функцию по Fh, что равносильно раз¬
ложению исходной функции по хх-
В действительности все эти утверждения могут быть
сформулированы без привлечения алгебры Е, поскольку
речь идет о функциях каждая из которых отлична
от нуля лишь в конечном числе целочисленных точек
|1еЯ, В частности, мы видим, что всякая симметриче¬
ская функция (gS)x = gp.) является линейной комби¬
нацией конечного числа весовых диаграмм п , я',
отвечающих старшим весам к, к', ...
Докажем теперь следующую теорему, принадлежа¬
щую К- Шевалле:
Теорема 6. Всякий полином p(h) на картановской
подалгебре Н, инвариантный относительно группы Вей¬
ля, может быть продолжен до полинома р(х) на всей
алгебре X, инвариантного относительно присоединенного
представления.
Доказательство*). Пусть А+—множество всех
доминантных целочисленных векторов к е Я. Оче¬
видно, линейные комбинации элементов вида (k,h)k,
*) Здесь мы используем идею доказательства, предложенную в
препринте работы [121]. Другой вариант доказательства см. в [128],
стр. 221.

§ 125. ИНВАРИАНТЫ ГРУППЫ ВЕЙЛЯ
567
& = 0,1,2, ..., содержат все одночлены относи¬
тельно фиксированного базиса /г;еЯ и потому совпа¬
дают с алгеброй £Р(Н) всех полиномов над Н. Применяя
к таким элементам оператор усреднения по группе Вей¬
ля, получаем элементы вида
Ф* *(й) = 2]$Ми. hf, £ = 0,1,2,..., АеЛ+,
11
линейные комбинации которых порождают всю алгебру
1(H) полиномов, инвариантных относительно группы
Вейля. При этом, очевидно, каждая функция сим¬
метрична по индексу р. Используя замечание, сделан¬
ное в начале этого параграфа, мы разлагаем функцию
J-М по весовым диаграммам п^> со старшими весами
Я,, i = 1, 2, . .., N. Соответственно полином ср%,h(h) раз¬
лагается в линейную комбинацию полиномов
flk W = 2 (|х, hf = sp р,. (hf.
Но каждый из этих полиномов допускает продолжение
(с заменой ЛеЯ на геХ) до полиномов на алгебреX,
инвариантных относительно присоединенного представ¬
ления в X. Теорема доказана.
С другой стороны, если р(х) инвариантен относи¬
тельно присоединенного представления, то р(х) инва¬
риантен также относительно внутренних автоморфизмов,
отвечающих группе Вейля (см. § 105). Следовательно,
сужение р(К) на подалгебру Н инвариантно относитель¬
но группы Вейля в Я. В результате получаем
Следствие. Существует взаимно однозначное со¬
ответствие относительно сужения p(x)-*p(h) между ал¬
геброй всех полиномов над X, инвариантных относитель¬
но присоединенного представления, и алгеброй всех
полиномов над Н, инвариантных относительно группы
Вейля.
Согласно другой теореме Шевалле, приведенной на¬
ми без доказательства в § 107, алгебра 1(H) всех поли¬
номов над Н, инвариантных относительно группы Вейля,
имеет ровно г независимых образующих. Все образую¬
щие могут быть выбраны однородными. При этом, как
показано К- Шевалле [145], если pi, р%, ..., рт —

568 гл. XVII. ИНФИНИТЕЗИМЛЛЬНАЯ ТЕОРИЯ
степени однородности образующих, то р^р2... pr = ta,
где w — число элементов в группе Вейля. Иначе говоря,
произведение степеней всех образующих равно порядку
группы Вейля*).
Пример 1. Алгебра Ап. Картановская подал¬
гебра Н имеет размерность п, однако удобно вкладывать
ее в (л+ 1)-мерное пространство (пространство основ¬
ного линейного представления Лп). При этом элементы
из Н задаются наборами координат t\, t2, .. ., tn+\ та¬
ких, что ti + t2 + . . . + tn+1 = 0. Группа Вейля состоит
из всевозможных перестановок координат tu t2, .. ., tn hi
и имеет порядок (п-Ь1)!. Образующими алгебры 1(H)
являются элементарные симметрические функции
4>kU)— 2-j ti ti .,. ti , k = 1, 2, ., ., n 4- 1.
Степень такой образующей равняется k, и произведение
всех степеней есть \-2---(п+ 1) = (л-Ь 1)!. Вместо эле¬
ментарных симметрических функций можно рассматри¬
вать также суммы Ньютона
sk (0 = Ч + t2 + ... 4- tkn+v k = 1, 2, ..., п 4- 1.
Алгебра / (Н) состоит в этом случае от всех симметри¬
ческих полиномов от переменных t\, t2, . .., <n+[.
Пример 2. Алгебра Вп. Картановская подал¬
гебра Н имеет размерность п. Если воспользоваться
классическим базисом, который доставляется (2л 4-1)-
мерным представлением алгебры Вп, то группа Вейля
порождается всевозможными перестановками коорди¬
нат t\, t2, ..., t„ и зеркальными отражениями tt-*—tit
i — 1, 2, ..., л. Порядок группы Вейля есть 2" • л!. Об¬
разующие в алгебре /(Н) таковы:
= + tf+ ... +tf, k=\, 2, ..., л.
Степень такой образующей есть 2k, и произведение всех
степеней равно 2 • 4 • 6-• • 2л = 2п ■ л!.
ПримерЗ. Алгебра Сп. Результаты те же, что
и в примере 2. Заметим, что условием доминантности
*) См. по этому поводу также [39].

§ 126. ОПЕРАТОРЫ КАЗИМИРА
569
вектора (т\, гп2, . . . , тп) в указанном базисе является
Ш\ > m-i > ... > т„ > 0.
Пример 4. Алгебра D„. Исходя из 2л-мерного
представления алгебры Dn, вводим базис, относительно
которого группа Вейля порождается перестановками
координат 11, t2, . ■ ■ , tn и преобразованиями вида
ti —* —th при i ф k. В этом случае каждое преобразова¬
ние из группы Вейля допускает лишь четное число пере¬
мен знака. Порядок группы Вейля есть 271-1 •«!. Обра¬
зующие в алгебре /(/'/) таковы:
s2k(t), k = 1, 2, . . ., п- 1; n(t) = ttt2 ,. . tn.
Заметим, что в выбранном базисе условием доминантно¬
сти вектора (tnu т2, ..., тп) является пц ^ т2 > . ..
. .. > m„_i ^ j тп |. Во всех примерах 1—4 формула Кил-
линга — Картана (суженная на Н) диагонализуется в
выбранном базисе.
Пример 5. Алгебра С2. Порядок группы Вей¬
ля в этом случае равен 12 ([19]), стр. 258). Поскольку
среди образующих всегда имеется одна квадратичная
(квадрат Картана—Киллинга), то в данном случае сте¬
пени образующих равны 2 и 6.
Относительно остальных особых алгебр Картана см.,
например, [57]. См. также конец § 127.
§ 126. Операторы Казимира
Пусть X — полупростая комплексная алгебра Ли и
ЭЕ— ее универсальная обертывающая алгебра. Как мы
видели в гл. IX, центр 3 алгебры ЭЕ отождествляется с
алгеброй / (X) всех полиномов над алгеброй X, инва¬
риантных относительно присоединенного представления.
Согласно теореме Шевалле, доказанной в предыдущем
параграфе, мы можем также отождествить алгебру 3
с алгеброй 1(H) всех полиномов над //, инвариантных
относительно группы Вейля. (Оба эти соответствия ли¬
нейны, но не мультипликативны.) Элементы алгебры 3
мы будем называть центральными или операторами Ка¬
зимира алгебры X,
Если с — произвольный элемент из алгебры инварн
антов 1(H), то соответствующий оператор Казимира мы

570 гл. XVII. ИНФЙНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
обозначим символом С. Построение оператора С по дан¬
ному с производится следующим образом. Инвариант¬
ный полином c(h) продолжается (по теореме Шевалле)
до полинома с(х) на алгебре X, инвариантного относи¬
тельно присоединенного представления. Если еь е2,
..., еп — произвольный базис в алгебре X, то полином
с(х) выражается через ковариантные числовые коорди¬
наты: с(х) = с(х\, х2, х„), после чего полагается
С = с(еь е2, . . . , е„).
Пусть pj, — произвольное неприводимое конечномер¬
ное представление алгебры X и С — оператор Казимира
в этом представлении. Тогда, как мы знаем,
С = с(Я)/,
т. е. оператор Казимира сводится к умножению на чис¬
ло с (К). Функцию с(Я) мы называем собственным значе¬
нием оператора Казимира; согласно построению она
вполне определяется полиномом с (h), h^H.
Теорема 7. Собственное значение всякого опера¬
тора Казимира является полиномом от Я е Я. Функции
с (Я) и с (Я) имеют один и тот же однородный член стар¬
шей степени однородности:
с (Я) = с (Я) + Я еЯ,
где многоточие означает сумму слагаемых меньшей сте¬
пени однородности. Функция с (Я), как полином от Я + б
(б — полусумма положительных корней), инвариантна
относительно группы Вейля.
Доказательство. Воспользуемся разложением
Картана — Вейля в алгебре X (§119). Пусть m — стар¬
шая степень однородности в многочлене с(е) —
= с(еь е2, ..., еп) и f(e)—произвольный одночлен из
с(е), имеющий степень т. Используя для f(e) разложе¬
ние Картана — Вейля, мы можем записать (с точно¬
стью до слагаемых меньшей степени однородности)
f (е) = е-а/-а, • • • е-арср (h) ер е^ . . . е^,
где корни а,, Pj положительны и cp (h) —одночлен от ба¬
зисных векторов в Я. Поскольку с(х) является инва¬
риантом присоединенного представления, то, в частно¬

§ 126. ОПЕРАТОРЫ КАЗИМИРА
571
сти, он является весовым вектором веса нуль относи¬
тельно подалгебры Н. Следовательно,
<Xi+a2+ ... + ap = [3] + |32 + ... +Р4-
Рассмотрим теперь произвольное конечномерное
представление рЛ. Поскольку оператор С является ска¬
ляром в ръ то для вычисления с(Х) достаточно приме¬
нить оператор С к старшему вектору £. Пусть F — опе¬
ратор, отвечающий одночлену f(e). Тогда мы имеем
Fc, = 0, если q ф 0. Следовательно, ненулевой вклад вно¬
сят только те слагаемые f(e), для которых q = 0. Но
тогда и р = 0 (в силу соотношения между корнями, ука¬
занного выше). Следовательно, если ст(Х) —сумма соб¬
ственных значений всех одночленов f(e) степени одно¬
родности т на векторе |, то
С,п (А) = ст (X),
где ст(Х)—сумма собственных значений тех одночле¬
нов f(e), для которых р — q = 0. Для выделения этих
одночленов достаточно символы еа заменить нулями,
что равносильно (ввиду ортогональности еа, Н) суже¬
нию полинома с(х) на подалгебру Н. Наконец, очевид¬
но, что ст(Х) является полиномом от X, поскольку
Р= (X, h)^, где (X, h)—линейная форма над Н.
Продолжая эти рассуждения для всех остальных
однородных компонент, заключаем, что с (Л.) является
полиномом от X и полиномы с(Х), с(Х) имеют общий
старший член ст(Х) = ст(Х) *).
Для завершения доказательства осталось показать,
что с(Х) = ср(Х + 6), где полином ф(Л) инвариантен отно¬
сительно группы Вейля. Рассмотрим вместо соответ¬
ствующее представление d(a) односвязной группы G
с алгеброй Ли X. Реализуя d(a) в классе матричных
элементов на группе G, мы рассмотрим, в частности,
характер xa(g), который, как линейная комбинация мат¬
ричных элементов сигнатуры а, должен быть собствен¬
*) Точнее, мы рассматриваем с(Х), с(Х) как значения некото¬
рых полиномов на доминантных целочисленных векторах

572
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
ным вектором оператора С с собственным значением
с {к):
C%a(g) = 4:(v)Xa(g), где р = А + 6.
Нам будет удобно далее сделать унитарное ограничение,
т. е. считать, что gelt, где U — максимальная компакт¬
ная подгруппа в группе G. Полагая g = и~{уи, где у про¬
бегает максимальный тор, мы видим, что %a(g) зависит
только от у (действительно,%а является функцией клас¬
сов). Следовательно,
С%a (g) = С%а (g),
О
где С — дифференциальный оператор относительно ка¬
нонических координат it, tz, ..., tr элемента у*). Поло¬
жим согласно формуле Вейля %а = FJQ, где Fa и Q —
кососимметрические функции от t\, t%, ..., tr, и введем
обозначение А = QCQ~K Тогда мы имеем
Д/?а(0 = ф(р) Fa(t).
Здесь А — дифференциальный оператор по параметрам ?
и р = А + 6. Напомним, что Fa = 2 ± exp (sp, h). За¬
меняя р на sp, мы сохраняем функцию Fa с точностью
до знака. Следовательно, tp(sp) = ip(p). Теорема дока¬
зана.
Замечание 1. В формулировке теоремы предпо¬
лагалось, что С — симметризованный оператор Казими¬
ра, т. е. полином с(е) выражается через базис
еи е2, . . ., еп с помощью симметричных тензорных ко¬
эффициентов. Однако в действительности это ограниче¬
ние излишне. В самом деле, как мы видели в гл. IX,
всякий полином с(е) и его симметризованная форма
имеют одно и то же слагаемое старшей степени однород¬
ности.
Замечание 2. Если С — квадратичный оператор
Казимира, то, как легко проверить, соотношение
о
А = QCQ-’, использованное в доказательстве теоремы 7,
о
устанавливает связь между радиальной частью С опе¬
ратора С и формальным лапласианом А, введенным в
*) Оператор С называется радиальной частью оператора С.

§ 127. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИИ 573
§ 123. Оказывается также, что в общем случае опера¬
тор Д является дифференциальным оператором с по¬
стоянными коэффициентами по t\, ..., tr, инвариант¬
ным относительно группы Вейля. Это позволило
Ф. А. Березину [49] дать полное описание радиаль¬
ных частей операторов Казимира*).
Следствие 1. Алгебра собственных значений с (к)
изоморфна алгебре 1(H) всех полиномов над Н, инва¬
риантных относительно группы Вейля.
В свою очередь отсюда получаем
Следствие 2. Алгебра 3 операторов Казимира
изоморфна алгебре 1(H). В частности, алгебра 3 имеет
ровно г независимых образующих.
Действительно, соответствие между оператором С и
собственным значением с (к) является линейным и муль¬
типликативным. Кроме того, если с(л) = 0, то с(Я) = 0
(согласно теореме 7), и отсюда С = 0. Следовательно,
это соответствие взаимно однозначно. Заметим, что об¬
разующие можно выбрать однородными, и для их степе¬
ней по-прежнему выполняется условие р\р% • • • Pr = w,
где w — порядок группы Вейля. Отсюда легко получаем
также **)
Следствие 3. Собственные значения операторов
Казимира определяют представление однозначно с
точностью до эквивалентности.
Примеры, связанные с алгеброй si (я), мы уже рас¬
сматривали в гл. IX. В следующем параграфе остано¬
вимся на алгебрах so(п), sp(«).
§ 127. О .вычислении собственных значений
операторов Казимира
В гл. IX мы воспользовались «-мерным представле¬
нием алгебры si (я) для вычисления собственных значе¬
ний ее операторов Казимира. Аналогичное построение не¬
трудно провести и для других классических алгебр Ли.
*) Отсюда вытекает еще один способ вычисления характера хл
(поскольку Xl~FllQ: где F^ — собственная функция квадратичного
оператора к = д2jdtf + д2/dt% + ... +d’jdt2y
**) См. по этому поводу [39], стр. 47,

574
ГЛ. XVII. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
Условимся записывать фундаментальную билиней¬
ную форму для so(я), sp(re) в том же виде, как и
в гл. XVI, и занумеруем все координаты числами
—v, —v + 1, ..., v—1, v, где v = [п/2], с пропуском
нуля при четном п. Тогда соотношения коммутации в
алгебре Ли записываются следующим образом:
[Хц, Хы] — (bjkXu — 6itXkj) + (е;-, ~[Xkt -i — efe] -Д-/, i),
при соответствующем выборе базисных операторов Хц,
где положено
бtj для so (я),
Е<; I е,-еj 6и для sp (я),
причем eft = sgn k (0 при k = 0, 1 при k > 0, —1 при
6<0). Нетрудно проверить, что при этом выборе ба¬
зиса следующие операторы являются операторами Ка¬
зимира:
С„ = . 2. Xiltixlils р = О, 1,2, ...
‘ll2 ••'V
Из рассмотрений предыдущего параграфа нетрудно за¬
ключить, что среди таких операторов содержится систе¬
ма образующих центра для sp(n) и для so (я) при нечет¬
ном я. В последнем случае при четном я достаточно до¬
бавить еще один оператор Казимира:
с; - 2± х,
где сумма берется по всем наборам индексов t'i, t‘2, ...
..., tv и их перестановкам /ь /2, . . ., /у; при этом знак
± отвечает четности или нечетности перестановки. Не
останавливаясь на вычислениях, приведем окончатель¬
ные результаты ([123]).
Условимся записывать старший вес в виде сигнатуры
а = (тц т2 mv) с соотношениями порядка, указан¬
ными в гл. XVI. Введем в рассмотрение треугольную
матрицу с элементами
au = (h + Р) б// ~~ 0»/ + -j Yfit. -/>
где = tni + 1\ — линейные формы от nzj и все коэффи¬
циенты даются следующей таблицей:

§ 127. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИИ
Алгебра
13
V,-
«S
so (2v + 1)
sp (2v)
so (2v)
v - Ч2
V
V — 1
1 + ei
-(1 +*i)
1 + 8/
(n + Ч2) 8/ - i
(tl -b 1)8; — i
net — i
Кроме того, матрица ||0,-,|| определяется следующим об¬
разом: 0,-j = 1 при t > /, 0,-j = 0 при / </. Нетрудно ви¬
деть, что если индексы г, / расположены в порядке воз¬
растания (от —v до v), то матрица ||а,-;|| является ниж¬
ней треугольной.
Пусть 0Р(а) означает собственное значение операто¬
ра Ср в неприводимом представлении с?(а). Тогда имеет
место следующая формула:
gp (а) = sp арЕ, р = 0, 1, 2,
где av — р-я степень матрицы a =\\a,ij\\ и Е—постоян¬
ная матрица, у которой все матричные элементы равны
единице. Для собственного значения о'(а) оператора Cv
получается следующий результат:
V (V— 1)
<т'(а) = ( —1) 2 •2v-v!/i/2 .. .lv.
Из полученных результатов (за исключением послед¬
него) не видна непосредственно симметрия собственных
значений относительно группы Вейля. Одиако по анало¬
гии с § 60 можно получить следующий результат:
где hi = /,•+ (5 — собственное значение мат-
Р i 1
рицы а и где положено
ь-
1
п
1*1
1 +
ац + “ц
1.-1.
! I
при
при
i = 0.
I Ф- 0.
При этом полагается также /о = 0, откуда h0 = Р + 7г
(для алгебры so(2v+l)). Умножая каждый оператор
Ср на степень г? вспомогательной переменной z и сум¬
мируя по р от 0 до оо, получаем «производящую

576
ГЛ XVII ИНФИНИТЕЗММАЛЬНАЯ ТЕОРИЯ
функцию» операторов Ср:
оо
Р — 0 i
Путем несложных преобразований можно привести эту
функцию также к виду C(z) = (l—П(г))/г, где поло¬
жено
Из этих выражений становится уже очевидной симмет¬
рия собственных значений относительно группы Вейля.
Замечание 1. Замечательной особенностью «-мер¬
ных линейных представлений, использованных при по¬
лучении указанных результатов, является простота
весового спектра. Иначе говоря, каждый вес в таком
представлении встречается с кратностью единица. По¬
добными представлениями обладают также алгебры G2,
Е6 и Е7. Если взять за основу такое линейное предста¬
вление иолупростой комплексной алгебры X, то все ука¬
занные выше результаты легко обобщаются на этот
случай.
Замечание 2. Как мы видели в предыдущем па¬
раграфе, каждому оператору Казимира отвечают два
полинома на алгебре Я: с (к), с(Х). Первый из этих по¬
линомов непосредственно определяет структуру опера¬
тора С, второй означает его собственное значение в р^.
Ф. А. Березину [51] удалось установить непосред¬
ственную связь между этими полиномами. Тем самым
возникает еще один метод явного вычисления собствен¬
ных значений.
В заключение этой главы приведем без доказатель¬
ства (см. [57], [143]) порядки образующих операторов
Казимира для исключительных алгебр Картана:
G2: 2, 6.
F4: 2, 6, 8, 12.
Е6: 2, 5, 6, 8, 9, 12.
Е7: 2, 6, 8, 10, 12, 14, 18.
Е8: 2, 8, 12, 14, 18, 20, 24, 30.

§ 12?. ВЫЧИСЛЕНИЕ СОБСТВЕННЫХ ЗНАЧЕНИЙ 57?
Отсюда легко вычисляется также порядок группы Вей¬
ля: w — p\p2...pr, где рг — порядок i-й образующей.
Числа Pi тесно связаны ([143]) с важнейшими топологи¬
ческими характеристиками соответствующей группы Ли
(числа Бетти, полином Пуанкаре).
Упражнения
1. Пусть Я — строго доминантный вектор из картановской под¬
алгебры Н. Показать, что число точек на орбите Oi — © • Я равно
порядку группы Вейля @.
2. Пусть Я — доминантный вектор из Я и ®i—подгруппа в
группе Вейля, состоящая из всех элементов s, для которых sX = Я.
Показать, что группа ©^ порождается рефлексиями st относительно
тех простых корней со,-, для которых (Я, он) = 0.
3. Показать, что группа ©я, из упражнения 2 изоморфна группе
Вейля для полупростой подалгебры Xi, порожденной образующими
е-а> > шг> еа>1’ для к°торых (Я, (О,) = 0.
4. Пусть Я — доминантный вектор из Н. Показать, что число
точек на орбите 0^=©-Я равно отношению порядков группы ©
и подгруппы ©х,— стационарной подгруппы точки Я." (Указание:
использовать упражнение 2 на стр. 86.)
5. Пусть di — базисное представление алгебры £7 с числовыми
отметками
/
(отсутствие цифры у простого корня toi означает равенство нулю
соответствующей отметки Я;). Показать, что множество всех весов
такого представления состоит из единственной орбиты относительно
группы Вейля. (Указание: воспользоваться упражнением 4 и
проверить по формуле Вейля, что размерность данного представле¬
ния равняется 56.)
6. Пусть di — базисное представление алгебры Ее с числовыми
отметками
Показать, что множество весов такого представления распадается
на две орбиты относительно группы Вейля.
Независимое рассмотрение полупростой комплексной алгебры
Ли позволяет, как мы видим, получать простые алгебраические до¬
казательства многих фактов глобальной теории. Классификация

578
ГЛ. XVtl. ИНФИНИТЕЗИМАЛЬНАЯ ТЕОРИЯ
неприводимых представлений была впервые получена Э. К а р-
таном [97] путем пересмотра в отдельности каждого типа простых
алгебр Ли (Ап — G2). Общее доказательство было получено почти
одновременно Хариш-Чандрой [138] и Шевалле (доказатель¬
ство Шевалле не опубликовано). Здесь мы излагаем упрощенный
вариант доказательства Хариш-Чандры, принадлежащий Н. Д ж е-
кобсону [19]. Одним из преимуществ алгебраического доказатель¬
ства является возможность рассмотрения также некоторых беско¬
нечномерных (экстремальных) представлений алгебры Ли. Кроме
того, на этом пути возникает также доказательство существования
особых алгебр Картана ([19]). Остальные библиографические
ссылки были сделаны непосредственно в тексте. Результаты упраж¬
нений 5 и 6 сообщены автору Э. Б. Винбергом.

ГЛАВА XVIII
НЕКОТОРЫЕ ЗАДАЧИ СПЕКТРАЛЬНОГО
АНАЛИЗА КОНЕЧНОМЕРНЫХ ПРЕДСТАВЛЕНИЙ
В этой главе будут рассмотрены несложные спек¬
тральные задачи, связанные с классическими линейны¬
ми группами. Для группы SL(га) такие задачи были
уже рассмотрены ранее. В общем случае компактных
и надкомпактных групп Ли мы вправе рассчитывать
на значительную аналогию со случаем SL(ra) ввиду из¬
вестной общности структуры. Однако сказываются так¬
же и различия в устройстве корневых систем. Практи¬
чески для SO (га), Sp(ra) и особых картановских групп
конкретные вопросы спектрального анализа еще недо¬
статочно разработаны.
Мы остановимся главным образом на задаче су¬
жения с группы на подгруппу. Эта задача, по суще¬
ству, является основной в спектральном анализе ко¬
нечномерных представлений. К ней, формально говоря,
сводится также и задача о тензорном произведении
двух неприводимых представлений («диагональ» в
G X G). К этой задаче сводится также и описание ве¬
совых диаграмм (сужение в d( а) на картановскую
подгруппу). Особенно существенную роль играет за¬
дача о сужении в теории специальных функций. Дей¬
ствительно, мы видели в гл. X (на примере базиса
Гельфанда — Цейтлина), что сужение с группы на под¬
группу доставляет нам систему «квантовых чисел», ну¬
мерующих базисные элементы в пространстве неприво¬
димого представления.
§ 128. Общая схема сужения с группы на подгруппу
Пусть G — редуктивная связная группа Ли и G0 — ее
редуктивная связная подгруппа. Неприводимое пред¬
ставление d(a) группы G всегда является вполне при¬
водимым относительно G0:
d (а) 1С„ = 2 ту d (у),

580
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
где d{у) означает неприводимое представление G0 со
старшим весом y- (Действительно, d(a) вполне приво¬
димо по отношению к центру G0, который содержится
в картановской подгруппе группы G, и также вполне
приводимо относительно полупростой компоненты в Go.)
Следовательно, возникает задача о вычислении кратно¬
стей ту.
Мы будем рассматривать в этой главе только ком¬
плексные группы G, G0. (Вещественный случай сводится
к комплексному с помощью аналитического продол¬
жения.) В комплексном случае мы можем непосред¬
ственно использовать метод Z-инвариантов, общая фор¬
мулировка которого очевидна из частного случая груп¬
пы SL(«).
Следующая теорема является формулировкой ме¬
тода Z-инвариантов применительно к задаче сужения.
Мы предполагаем, что разложение Гаусса в группе G
индуцирует разложение Гаусса в подгруппе G0. Симво¬
лом Z обозначается фиксированная корневая подгруппа
в группе G, символом Z0 — ее пересечение с G0. Тогда
Z0 является корневой подгруппой в G0. Ради определен¬
ности мы считаем, что подгруппа Z порождается каса¬
тельными векторами е(а), а > 0. Представление d(а)
реализуется в канонической модели на группе Z. Про¬
странство представления обозначается 9?а.
Теорема 1. Пусть Qa — совокупность всех функ¬
ций из Ша, которые являются инвариантами подгруп¬
пы Z0:
/(22°) = /(2).
Тогда Qa вполне приводимо относительно картановской
подгруппы D° cz G0 и каждый собственный вектор
f (b~lzb) = у (d)f(z), 6 eD°,
является старшим вектором подгруппы G0. Кратность
собственного значения ц = у/а равняется кратности
вхождения d(у) в d(а).
Доказательство. Достаточно напомнить, что
d(а) вполне приводимо относительно G0 и каждое не¬
приводимое подпространство содержит лишь одно одно¬
мерное направление, неподвижное относительно Z0 (на¬

§ 128. ОБЩАЯ СХЕМА СУЖЕНИЯ С ГРУППЫ НА ПОДГРУППУ 581
правление старшего вектора). Это направление инва¬
риантно также относительно D0, и собственное значе¬
ние у(б) определяет сигнатуру данного неприводимого
представления. Теорема доказана.
Следовательно, задача спектрального анализа в d(а)
относительно G0 сводится к задаче спектрального ана¬
лиза в относительно абелевой подгруппы D0. Обыч¬
но решение этой задачи не представляет никаких за¬
труднений. Значительно большая трудность состоит в
описании самого пространства £2а. Действительно, для
описания элементов этого пространства приходится ис¬
пользовать довольно сложную индикаторную систему.
Заметим, что искомые 2°-инварианты являются фак¬
тически функциями на Z/Z0. Естественно выбрать в
этом фактор-пространстве достаточно удобные пара¬
метры и выразить в этих параметрах главные сдвиги,
входящие в индикаторную систему. Так, в большинстве
практически важных случаев удается представить груп¬
пу Z в виде
Z = Z'Z°,
где Z' — некоторое многообразие в Z, изоморфное ев¬
клидову пространству и такое, что Z' [) Z0 = {е). В этом
случае индивидуальное разложение z = z'z°, z'^.Z',
Zq e Z°, дает нам систему параметров в группе Z и
пространство состоит из всех решений индикаторной
системы, зависящих только от z'. Очевидно, индикатор¬
ную систему в этом случае также естественно выразить
через параметры г'*).
Упрощение индикаторной системы получается реаль¬
но лишь в тех случаях, когда многообразие Z/Z0 имеет
сравнительно небольшое число параметров (примерно
того же порядка, что и ранг группы G). Это, во всяком
случае, имеет место, если подгруппа 6ю «не слишком»
отличается от группы G. Отсюда естественно приходим
к идее постепенного сужения с группы на подгруппу,
т. е. к рассмотрению цепочки вложенных подгрупп.
*) Главные сдвиги 3)i в классе функций от г' являются диф¬
ференциальными операторами первого порядка на Z' с коэффициен¬
тами, зависящими от г е 2.

682
ГЛ. XVIII. спектральный анализ
Упражнение
Показать, что при сужении rf(a)|G" неприводимая компонента
со старшим весом а(б), {ей0, входит однократно и является стар¬
шей относительно лексикографического упорядочения весов. (У к а-
з а н и е: проверить, что единственным весовым мультипликатором
веса а является функция fo(z) = 1.)
Если корни подгруппы G0 являются также корнями
группы G, то такое вложение называется регулярным.
Если то же имеет место для простых корней, то такое
вложение называется нормальным (см. § 110). В дей¬
ствительности первый случай можно свести ко второму
внутренним автоморфизмом, однако на этом мы здесь
останавливаться не будем. Если вложение нормальное,
то, как мы видели в § 110, корневая группа Z всегда
допускает указанное выше разложение, причем Z' яв¬
ляется нормальным делителем в Z. В этом случае реше¬
ние задачи значительно упрощается.
Очевидно, метод Z-инвариантов позволяет не только
найти спектральную формулу, но также и определить
все неприводимые подпространства (как циклические
оболочки старших векторов).
После всех этих общих замечаний перейдем к рас¬
смотрению отдельных примеров.
§ 129. Сужение SO(n)/SO(n — 1)
Рассмотрим вначале тот случай, когда размерностьп
является нечетной, п = 2v + 1. Подгруппу G0 мы выде¬
ляем условием сохранения базисного вектора с номе¬
ром v + 1. Тогда в силу ортогональности координата
xv+i — (х, ev+i) также остается инвариантной. Здесь ска¬
лярное произведение выбирается в том же виде, что и
в § 114. Все матрицы из G0 записываются с помощью
четырех квадратных блоков v X v, разделенных нулями,
с единицей на пересечении (v + 1)-й строки и (v-f-l)-ro
столбца. В частности, матрицы из Z0 имеют следующий
общий вид:
?п 0 Z12
z0= 10
Z22

§ 129. СУЖЕНИЕ S0(rt)/S0(rt-1)
583
где Zij — квадратные блоки vXv, под диагональю стоят
нули и блоки связаны также условиями принадлеж¬
ности группе Z. Дополнительное многообразие Z' можно
в этом случае составить из матриц
1
z =
где е — единичная матрица порядка v, а — произволь¬
ный столбец и р — строка, линейно выражающаяся
через а: р' = —sa, где s — специальная матрица по¬
рядка v, введенная в § 113. Действительно, легко про¬
верить, что матрица z’ содержится в группе Z и про¬
изведение z = z'z0 пробегает по одному разу все эле¬
менты из группы Z*). При этом z имеет вид
Z = 2 2П =
2] 2
Р
Z22
где явное выражение блока z 12 через а, 212, 222 нам не
будет нужно. Искомые 2°-инварианты являются функ¬
циями только от чисел ось аг, •••, ау> входящих в стол¬
бец а.
Найдем индикаторную систему в классе функций,
зависящих только от а. Применяя к матрице 2 левый
сдвиг, отвечающий i-му корневому вектору, i = 1, 2, ...
..., v, находим, что это преобразование в классе пара¬
метров а сводится к замене aj на otj + tai+\, где t —
параметр сдвига и av+i = 1. В результате получаем ин-
финитезимальные главные сдвиги
% = ai
д
+1 да,
i= 1, 2,
V.
*) Умножая произвольную матрицу zeZ на подходяще вы¬
бранный множитель zj"1, мы можем сделать диагональные блоки
единичными; тогда полученная матрица необходимо имеет вид г'.
Кроме того, Z' П -Z0 — {е}, и отсюда следует, что полученное раз¬
ложение z = z'z0 однозначно.

S84
ГЛ. Xvtll. СПЕКТРАЛЬНЫЙ АНАЛИЗ
Выписывая индикаторную систему в классе функций
/(а) = / (а 1, а2, • • •. аУ)> находим, что искомое простран¬
ство 2°-инвариантов натянуто на следующий базис:
fk = ai'а22 • • • atv> 0 < < rv
где г,- = т,- — т*+1 — неотрицательные целые параметры
исходной сигнатуры а = (ти т2,..., mv), mi^m2>...
... ^ mv > 0, mv+j = 0. Применяя к такому вектору пре¬
образование Т6, б е D0, находим, что этот вектор яв¬
ляется весовым с весом
ук{1) = 1™'~к'1'"2~к2 ... l™v~kv.
Введем обозначение pi = m, — kp тогда в силу указан¬
ных выше ограничений на параметры ki получаем си¬
стему ограничений на параметры pp. ni\^- pi^ m2^
>-/?2 ^ ^ pv >—mv. В результате доказана сле¬
дующая
Теорема 2. Сужение SO(2v + 1 )/SO(2v) опреде¬
ляется при указанном выше выборе базиса следующей
спектральной формулой-.
d{mu m2, ..., mv)|G0= 2 d(pu p2, ..., pv),
аде mv+i заменяется на —mv. Здесь параметры pt при¬
нимают одновременно целые или одновременно полу-
целые значения в зависимости от целости или полуце-
лости параметров пг{.
Следствие. Каждое неприводимое представление
подгруппы SO(2v) содержится в указанном сужении
однократно.
Рассмотрим теперь тот случай, когда размерность п
является четной, п = 2v. Подгруппа G0 выделяется усло¬
вием инвариантности двух базисных векторов: ev, ev+1.
Ввиду ортогональности при этом сохраняются также ко¬
ординаты xv = {х, ev+l), av+1 = (x,ev). Многообразие Z'
составляется из матриц
е а а аВ

i 129. СУЖЕНИЕ SO(rt)/SO(rt-l)
585
где e — единичная матрица порядка v—1, а — столбец,
состоящий из независимых переменных, р —строка, ко¬
торая линейно выражается через а. При этом перемен¬
ные аи t = l, 2, ..., v — 1, выражаются в разложении
г — z'Zq следующими формулами:
°г = ту(zivZj,v+i)> i 1» 2, * • ■ > v 1,
через параметры исходной матрицы 2. Заменяя пару
переменных 2iv, ziiV+l их полусуммой а; и полуразно-
стью б,, легко получаем, что главные сдвиги в классе
функций, зависящих только от имеют следующий
вид:
®1 = ам~Щ' Z'=I>2 v-2, 2)- = 2D+ = -^—-.
В этом случае старшими векторами относительно G0
по-прежнему являются одночлены, и несложный подсчет
сигнатур показывает, что в искомое разложение вхо¬
дят только сигнатуры {qu q2,..., qv~i), для которых
т\ ••• <7v-i I mv I- Результатом
является
Теорема 3. Сужение SO(2v)/SO(2v—1) опреде¬
ляется при указанном выше выборе базиса следующей
спектральной формулой:
(тИ т2, mv)\G = 2 (Чи Чг, •••> <7v-i).
где mv заменяется на \mv\. Здесь параметры q( прини¬
мают одновременно целые или одновременно полу целые
значения в зависимости от целости или полуцелости па¬
раметров m-i.
Следствие. Каждое неприводимое представление
SO (2v — 1) содержится в указанном сужении одно¬
кратно.
Теоремы 2 и 3 в совокупности позволяют получить
в пространстве 9?а естественный базис из старших
векторов цепочки вложенных подгрупп: SO («)=)
zd SO (л — 1) SO(3) SO (2). Каждый вектор ба¬
зиса нумеруется системой чисел т^, t, k = 2, 3, ..., п,
min = m{, с определенной системой ограничений. При

586
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
нечетном п имеем
Щп> "*i,n-i>"*2n>"*2.n-i> >"*vn>"*v,n-i>~"*vn>
"*1, л —1 ^ "*1, л —2 ^ "*2, л —I ^ ^ Ш\ — 1 > л —2 ^ I "*v, л_ ] |,
"*1, л-2 "*1, „_з ^ ГПо, л-2^ • • • "*v-l, л-3 ^ — "*v-l, л-2>
"*i5 > m14 > m25 > т24 > - /П25,
"*U>"*13^I"*24 I.
"*13 >"*12 >-т13.
При четном п аналогичную систему можно получить,
отбрасывая первую строку. Такое определение базиса
было впервые предложено И. М. Гельфандом и
М. Л. Цейтлиным [73]. При этом, как и в случае
SL(«), были указаны явные формулы для инфините¬
зимальных операторов SO (п) в этом базисе. Однако
внутренняя структура d(a) в этом случае еще плохо
изучена. В частности, неизвестны «понижающие» и
«повышающие» операторы.
Интересную информацию дают также теоремы 2 и 3
при рассмотрении спинорных представлений. Пусть
sо — спинорное представление SO(2v + l) с сигнатурой
(!/г, ’/г, • • •, 7г)• Согласно теореме 2 сужение s0 на под¬
группу SO(2v) распадается в прямую сумму двух неприво¬
димых представлений с сигнатурами ('/г, '/г- •••> —'/г).
(‘/2, 72 7г):
s010. = «- +S+.
Иначе говоря, при сужении на G° ~ S0(2v) мы получаем
два зеркально сопряженных спинора первого и второго
рода. С другой стороны, сужая эти представления на
подгруппу G00f»SO(2v — 1), получаем согласно тео¬
реме 3, что оба они остаются неприводимыми и совпа¬
дают с представлением типа s0. Из соображений индук¬
ции отсюда, в частности, следует
dims0 = 2v, dims_ = dims+ = 2V_I.
Заметим также, что зеркально сопряженные пред¬
ставления S0(2v) становятся эквивалентными для под¬

§ 130. СУЖЕНИЕ Sp(n)/Sp(n—2)
587
группы SO(2v—1). В свою очередь при сужении
SO(2v + l)/SO(2v) вместе с каждым неприводимым
представлением встречается также зеркально сопря¬
женное.
§ 130. Сужение Sp(«)/Sp(« — 2)
В данном случае редукция нетривиальна ввиду того,
что размерность приходится понижать сразу на две еди¬
ницы. Правда, вместо подгруппы, изоморфной Sp (/г — 2),
можно рассматривать подгруппу, изоморфную
Sp (п — 2) XSp(2) (о чем мы скажем ниже). Вместо
этого мы рассмотрим сейчас несколько более легкую
задачу, выделяя в Sp(2) ее диагональную часть.
Группа G = Sp(«) реализуется так же, как и в
§ 113. Напомним, что п четно, п = 2v. Подгруппа G0
определяется как совокупность всех преобразований
из Sp (/г), которые диагональны на координатах с но¬
мерами v, v + 1. При этом из условия симметричности
вытекает, что мы вправе рассматривать только преобра¬
зования xv-*Xxv, xv+i —» ^-i.£v+i. Полагая Я=1, полу¬
чаем подгруппу, изоморфную Sp (/г — 2). Ясно также,
что G0 изоморфна Sp (/г — 2) X А, где А — мультиплика¬
тивная группа комплексных чисел. Сигнатуру этой
группы мы будем записывать в виде
(^1> ^2> • • • > Qv— 1 1^)>
где qi, <72, •••. Qv-1 — сигнатура подгруппы Sp (/г — 2) и
s — целочисленный параметр, определяющий характер
Xs подгруппы А.
Теорема 4. Сужение d(a) = d(mu т2,..., mv) на
подгруппу G0 содержит в спектре все сигнатуры вида
Ypq (^7l> Q'2j •••> Qv— llSpg)»
где положено
V V—1 V
sp? == 2 2 Pi 4i 2 Щ-k
t = 1 /-1 A-l

538
ГЛ. XVIII. спектральный анализ
и где целочисленные индексы q$, р; принимают всевоз¬
можные значения в пределах
Щ ^Р\ ... >pv_,>mv>pv> О,
P\>qi>P2>q2> ••• > pv-i>qv-i>Pv
Если v = 1, то символы q отсутствуют и m\^-pi'^>0.
Доказательство. Искомое пространство Z°-hh-
вариантов состоит из полиномов, которые зависят толь¬
ко от элементов следующих двух столбцов:
Zlv v+l
^2v ^2, v+I
1 Zv. v+l
при условии, что параметры в группе Z выбираются
так же, как и в § 113 (первый способ). Индикаторная
система в пространстве имеет вид
0?+7 = (zl4i,v1|-+Zm,v+> V + 1 f= °-
\ iv "г, v+l I
Здесь положено zvv = zv+u v+lt = 1, zv+i> v = 0 и пара¬
метры Ti выражаются через параметры обычными
формулами: г{ = пг{ — mi+l, mv+l = 0. Решение такой
системы довольно сложно, однако мы можем восполь¬
зоваться аналогией с полной линейной группой
GL(v+ 1). Действительно, точно такой же вид имеет
индикаторная система при сужении GL(v+l)/GL(v— 1).
В этом случае мы можем производить сужение не сразу,
а в два этапа, вставляя между данными группами еще
одну подгруппу, изоморфную GL(v).
Для того чтобы получить соответствие с нашей за¬
дачей, мы рассматриваем неприводимое представление
группы GL(v+l) с сигнатурой (mu т2,. ■., тч, 0),
Ш\ > m2 ^ ^ mv > 0, где лг, — целые числа. Вместо
GL(v—1) рассматриваем подгруппу, изоморфную
GL(v—1) X А2. Применяя результаты, полученные в
§ 66, находим следующий спектр сужения:
(hTj, Н12> ' * • > mv> 0) !о ^ ^ (Д> q2* • • • > <7v-l 1
mt>Pi >mi+l

§ 130. СУЖЕНИЕ Sp(n)/Sp(n-2)
589
где индекс 0 означает сужение на указанную подгруппу
и Si, s2 — целые числа, входящие в определение харак¬
тера группы Л2. При этом мы имеем
V V V V—1
Sp = 2 mk - 2 Pi, Sr2p.-2 Pi
ft=l i = 1 i = 1 / = 1
согласно замечанию, сделанному в конце § 66. Теперь
для перехода к нашему случаю достаточно положить
= К, %2 = Я-1, после чего характер переходит
в Xs'~s\ В результате получаем набор сигнатур, ука¬
занный в условиях теоремы. Теорема доказана.
Пользуясь полученным результатом, можно выписать
в пространстве 0Ц естественный базис, аналогичный ба¬
зису Гельфанда — Цейтлина. Этот базис состоит из век¬
торов epq, где
Plv
Plv Plv
Pvv
Рь
т
<
i
Pv-1, v-l
р=|
Pll
1
<7iv
Q2v Qiv
Qvv
я =
Я\,
'-1 Q2, v-l
9v— I. V—I
Q ii
и где целочисленные параметры pih, qjh подчиняются
следующим ограничениям: p{h > qit h-\ Pi+1, h, Qu ^
^ pi, Qi+i, i, причем для общности записи положено
qiv — mv и символ qi,i+i заменяется нулем. Интерпрета¬
ция этих векторов как старших векторов цепочки вло¬
женных подгрупп очевидна.
Замечание 1. Как видно из теоремы 4, спектр
сужения Sp(n)/Sp(n — 2) не простой, т. е. возможны
кратности, большие единицы. То же верно при замене
Sp(n — 2) на Sp(n — 2) х Л.
Замечание 2. Положение не улучшится, если
вместо Sp(« — 2) рассматривать подгруппу, изоморф¬
ную Sp(« — 2)XSp(2). В этом случае к индикаторной

590
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
системе добавится еще одно уравнение:
/ д д , ,
(Zlvdг l"Z2v5z ^
V У I.V+1 у 2. V+1
(‘
V, V + I
д
Такая же система уравнений встречается при рассмот¬
рении тензорного произведения df ® d (Р), где d2 — би¬
вектор и р— произвольная сигнатура группы GL(v + l).
Нетрудно видеть, что и в этом случае встречаются крат¬
ные точки спектра.
В этом случае, в отличие от SL(n), SO(n), мы уже
не можем разделить векторы базиса с помощью соб¬
ственных значений операторов Казимира вложенных
подгрупп.
§ 131. Тензорное произведение двух неприводимых
представлений .
Эта задача уже была рассмотрена нами для груп¬
пы SL(n). Ее обобщение на произвольную комплекс¬
ную полупростую (или редуктивную) группу Ли рас¬
сматривается почти буквально так же.
Рассмотрим группу G X G, составляемую из всех
матриц вида
Всякое неприводимое представление этой группы за¬
дается сдвоенной сигнатурой (а, Р), где а, р— сигна¬
туры группы G. Реализуем группу G как «диагональ-»
в G X G, состоящую из матриц
Тогда сужение d(a, P)|g совпадает с тензорным произ¬
ведением d(a)<S>d( р).
Реализуя данное представление в классе функций
на Z X Z, мы используем следующее очевидное разло¬
жение:
х 0 I II 2 0 АЦ у 0 j
0 у {j I 0 е || 0 у | ’
г = ху~\

§ 131. ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ ПРЕДСТАВЛЕНИЙ 591
для введения параметров в эту группу. Здесь х, у, z—■
произвольные матрицы из Z и е— единица в группе Z.
Искомые Z-инварианты зависят только от z. Заметим,
что умножение слева на матрицу с компонентами х0, уо
приводит к преобразованию
^ —* X0zy0 , -VQ, 1/q s Z,
в классе параметров z. Отсюда следует, что искомая
индикаторная система в классе функций f(z) имеет вид
объединения двух индикаторных систем 1а, /р, где 1а—
индикаторная система пространства 9?а и /р получается
из индикаторной системы /р заменой z на z~K
Сформулируем полученный результат более подроб¬
но. Пусть Qap — пространство всех Z-инвариантов,
имеющих вид f(x,y) = f(z), т. е. зависящих только от
z = ху~К Тогда мы имеем:
1) Qa(,c SRa,
2) Qap с Яр.
Здесь шляпка означает замену каждой функции f(z)
на f(z~'). Условие 2) удобнее сформулировать следую¬
щим образом. Выпишем индикаторную систему /р:
^/+7(z) = 0.
Замена z на z_1 равносильна тому, что операторы ле¬
вого сдвига заменяются (с точностью до знака)
операторами правого сдвига, которые обозначим Хр
Xl/+lf(z) = 0.
Но операторы правого сдвига являются инфинитези-
мальными операторами самого представления d( а).
В результате получаем, что имеет место
Теорема 5. Пусть G — полупростая связная ком¬
плексная группа Ли и d(a), d(р)— два ее неприводи¬
мых представления. Пусть У£ — весовое подпростран¬
ство в d(а) с весом ц и УЦ (|3) —подпространство
в У^> состоящее из всех решений системы уравнений
Х;.‘- + 7 = 0, /=1,2,..., г,

592 гл. XVIII. спектральный анализ
где Xi — инфинитезимальный оператор d(а), отвечаю¬
щий корневому вектору еф. с простым корнем «и,
i = 1, 2, г, и U — параметры сигнатуры р:
U = 2(р, сог)/(сог, ац). Тогда имеет место тождество
my (а, р) = dim (р), ц = y - Р,
для кратности my(а,р), с которой неприводимое пред¬
ставление d(y) содержится в тензорном произведении
d(a) ® d(p).
Доказательство. Вектор feQap как элемент
пространства Яа имеет вес р, определяемый из уравне¬
ния
a (б) f (б-12гб) = ц (6) / (г).
Тот же вектор как элемент пространства Ша <8> Яр имеет
вес у, определяемый из уравнения
a (б) Р (6) f (б- гб) = у (6) / (z).
Переходя к аддитивной записи, получаем, что р + р=у-
Теорема доказана.
Следствие. my(a, Р)^«^а1р, где — кратность
веса р в представлении d(а).
Если G — классическая группа, то при помощи тео¬
ремы 5 нетрудно, как и в случае SL(rt), рассмотренном
выше, получить простой алгоритм для вычисления спек¬
тральной формулы. При этом, как и в случае SL(n),
удобно использовать для характера %а аналог второй
формулы Вейля [10].
§ 132. Сужения SU(m + n)/S\J(m) X SU(«)
и SU(m«)/SU(m) X SU(re)
Заменяя каждую группу SU(r) ее комплексной обо¬
лочкой SL(r), мы можем использовать обычную схему
Z-инвариантов.
Заметим, что индикаторные системы в этих задачах
выписываются легко, но найти их общее решение до¬
вольно сложно. Поэтому мы рассмотрим подробно лишь
представление d(a) = du которое является симметризо-
ванной степенью вектора. Используя вторую формулу

§ 132. ГРУППЫ SU(mfn) и SU(mrt) 633
Вейля (§ 75), мы можем свести общий случай к этому
частному случаю.
1° Сужение SL(m + n)/SL(m) X SL(«). Запишем
(т + п)-мерный вектор-строку в виде х = (х',х"), где
х' — m-мерная строка и л:" —«-мерная строка. Преоб¬
разования группы G° « SL(m) X SL(«) сводятся к не¬
зависимым унимодулярным преобразованиям векторов
х', х". Рассматривая только преобразования корневой
подгруппы Z°f^Z(m) X Z(n), мы можем привести век¬
тор х к виду *) х° = (х\е[, х"егде х', х'( — первые ко¬
ординаты векторов х', х" и е[, е" — соответствующие
базисные векторы. Отсюда ясно, что в представлении
d\ старшими векторами являются только одночлены:
<*p'P" = (xif\x"Y"’ Р' + Р" = Р-
Здесь р', р" — неотрицательные целые числа. Если А/,
X" — диагональные преобразования из SL(m), SL(«) со¬
ответственно, то вектору сор'р" соответствует вес
„ ; /р\ //р" \/Г>'
ар'р" ~ 'S 'ч — •
Здесь Х\, А" — первые собственные значения матриц
А/, %" и Аь АГ — соответствующие диагональные ми¬
норы первого порядка. Заменяя каждый минор Ai, Af
,/ ,//
соответствующим символом представления й\, й\ , по¬
лучаем следующую спектральную формулу:
«nw-i d’r'if. (.)
U ft=0
Здесь d\P — симметризованная степень вектора для
SL(m) (сигнатура {р', 0, 0,..., 0)) и d['P — симметри¬
зованная степень вектора для SL(«) (сигнатура
(//', 0, 0,..., 0)). Иначе говоря,
(р, 0, 0, ..., 0) |Q0 = 2 (//,0,0, 0\р", 0, 0, ...,0).
р'+р"“Р
*) При условии, что х\ ф 0, х" Ф 0; однако это условие в
классе полиномов несущественно.

594
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
Здесь вертикальная черта в правой части разделяет
сигнатуры SL(т) и SL(n) в сигнатуре группы G0.
2° Сужение SL(mn)/SL(m) X SL(n). Условимся
считать, что т ^ п. Разобьем вектор-строку х размер¬
ности тп на п частей размерности т: х = (х([\ х<2>,...
...,х<")). Подгруппа, изоморфная SL(m), подвергает
все эти строки х^\ х<-2\ ..., Дп> одному и тому же уни-
модулярному преобразованию. Назовем эту группу
внутренней группой и обозначим Gm• Подгруппа, изо¬
морфная SL (/г), подвергает унимодулярному преобра¬
зованию символы ДД Д2>, ..., х
П
х^‘] —> 2 QijX^K
Назовем эту группу внешней группой и обозначим Gn-
Подгруппа G0 является прямым произведением
Gm X G". Расположим теперь строки х^\ Д2>, ..., Дп)
в виде следующей прямоугольной матрицы:
4[>
4» ..
• лт~ 1
хт
X =
X®
42> .
х^21
' лт~ 1
v(2)
т
х\п)
4п) ■
■ лт-1
х(п)
т
Пам будет удобно считать, что повышающие преобразо¬
вания внутренней группы Gm задаются верхними тре¬
угольными матрицами, а повышающие преобразования
внешней группы Gn — нижними треугольными матри¬
цами. Тогда всевозможные повышающие операторы
группы G0 действуют по правилу
где zn — произвольная матрица из Z (п), zm — произволь¬
ная матрица из Z(m) и штрих означает транспониро¬
вание. Дополняя матрицу х произвольными строками
до квадратной матрицы m X m, мы можем использо¬
вать разложение Гаусса, из которого очевидно, что вся¬
кий искомый 2°-инвариант является линейной комбина¬

§ 132. ГРУППЫ SU (m+n) и SU(mn)
595
цией одночленов
где Wi — i-й главный диагональный минор матрицы х,
составленный из первых i строк и первых i столбцов,
i— 1, 2, п. Пусть X', X" — диагональные преобразо¬
вания из внутренней и внешней группы соответственно.
Тогда, очевидно, одночлен а>Р1р2... Рп является весовым
с весом
„ _(Урч/Р2 > ,РА(\ ,"V\
apip2 ■■■ рп ~ ' 1 2 ■ ■ ■ п )' 1 2 • • • /'
Для того чтобы такой вес являлся старшим весом груп¬
пы G0, необходимо, чтобы числа pi, i = 1, 2, ..., п—1,
были целыми неотрицательными. Расширяя SL (/?) до
CiL(/j) и учитывая, что все рассматриваемые представ¬
ления реализуются в классе контравариантных тензо¬
ров, получаем также, что рп является целым неотрица¬
тельным числом*). В результате получаем следующую
спектральную формулу:
d\ |Go = 2 {л'№' ... d'nPn) {df'df* ... dfn).
P,+2p2+ ... +npn=p
(**)
Здесь d't, d'i — обычные образующие (Рвекторы) в по¬
лугруппе неприводимых представлений G'm, G" соот¬
ветственно. Условие р\ + 2р2 + ... + прп = р вытекает из
вычисления степени однородности одночлена Шр,р2 ... рп
(эта степень должна равняться р). Иная форма записи:
d(p, 0, 0, . . ., 0)|с„ =
= 2 d(quq2, .. qn,0,0, ..0\quq2, .. .,qn).
<7j + <72+ ••• +qn—P
ql>q2>--- >qn> 0
Здесь вертикальная черта разделяет сигнатуры G'm, Gn.
Числа <72, должны быть целыми.
*) Все эти результаты очевидны также, если заметить, что
<й_ _ „ является полиномом только при условии, что числа р.,
р\рг рп
р.2, ..., рп являются целыми неотрицательными. (Это следует хотя
бы из рассмотрения тензоров для GL(n), § 51.)

696
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
В заключение напомним вторую формулу Вейля:
d?1
d?l+l
. й\
d(mu т2, .
• > тп) =
а 1
d?'
.m,+(n-2)
. d i
d?*-(n~i)
d?»-{n-2) .
. d?n
Для применения этой формулы к нашим задачам заме¬
няем п на т + п и подставляем в правую часть вместо
каждого члена d\ его сужение на G0, даваемое форму¬
лой (*) или (**).
Заметим, что если mk+\ = mh+2 = ...■= тп = 0, то
этот детерминант (в правой части формулы Вейля)
можно заменить его усечением, составленным из пер¬
вых k строк и первых k столбцов.
Пример, а = (2, 1, 0, 0, 0, 0) для группы SU (6).
Полагая G° ~ SU(3)X SU(2), находим
d (а) |0„ = d[3d[f + d[d'2df + d[d'2d” + d".
§ 133. Сужение SU(n)/SO(n)
В этом параграфе будет рассмотрен лишь частный
случай п = 3*). Другой частный случай (d{a) = dT с
произвольным п) будет рассмотрен в следующем пара¬
графе**). Заметим, что задача, которая здесь рассмат¬
ривается, относится к классу «нерегулярных» вложений.
Используя аналитическое продолжение, мы прихо¬
дим к задаче сужения GIG0, где G = SL(n,C) и G° =
= SO (п,С). В дальнейшем полагается п = 3. Ортого¬
нальная группа G0 сохраняет квадратичную форму
2x_jX+l + х2, Подгруппа Z0 состоит из матриц
1 t —t2/2
Z0 =
0 1
0 0
*) При изложении этого материала в лекциях [21] была допу¬
щена ошибка. Автор пользуется случаем выразить благодарность
И. А. Малкину, отметившему эту ошибку.
**) Отсюда ввиду второй формулы Вейля будет следовать так¬
же и общий случай.

§ 133. СУЖЕНИЕ SU(n)ISO(n)
697
Дополнительное многообразие Z' нам будет удобно па-
раметризировать следующим образом:
1 ар — а2/2
zr — О 1 а
0 0 1
Перемножая эти матрицы, получаем произвольный эле¬
мент группы Z:
1 a + t р-.(а + <)2
'ZZn =
2
a — t
1
Следовательно, а, р, t являются параметрами в группе Z.
1 1
Формулы а = у (zI2 + z23), p = zI3 + -J-, t = у(г12-2:2з)
выражают эти параметры через элементы матрицы z.
Напомним, что группа Z = Z(3) имеет два главных
сдвига. Первый из них задается формулами
■ Z19 + е,
-2П + EZo;.
“23
“23»
откуда (с точностью до малых второго порядка по е)
мы имеем в параметрах а, р, t
Отсюда
2D, = — — 4- 2а— 4- — —
2 За <3р 2 dt
возникает
д , 1
2 ’ 1 11 ’ 1 2 '
инфинитезимальный оператор
Точно так же, рассматривая
второй главный сдвиг, получаем оператор = —
~Y’W‘ Заметим теперь, что искомые 2°-инварианты
не зависят от t. Следовательно, в классе этих полиномов
мы имеем следующие два оператора:
2 да ”^2а ар ’
1 д
2 да
В частности, второе индикаторное уравнение сводится
к ограничению на степень а.

598
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
Замечание. Может показаться странным, что на¬
рушена симметрия между вектором и бивектором. Од¬
нако замена переменных у = Р— 2а2 приводит наши
операторы к виду
1 2 да 1 2 да ду
Первое индикаторное уравнение сводится теперь при
новом выборе переменных к ограничению на старшую
степень а.
Мы можем упростить решение индикаторной систе¬
мы, если сразу будем искать только весовые решения.
Заметим, что группа D0 содержит лишь один мульти¬
пликативный параметр X: 6ц = X, 622=1, бзз = Я-1.
Произвольный вес мы запишем в виде Xh. Переменные
а, р условимся рассматривать как мультипликаторы в
пространстве представления. Иначе говоря, всякий иско¬
мый старший вектор запишем в виде
f = f(a, P)f°,
где f°(z)^=l — старший вектор исходного представле¬
ния группы G. Нетрудно видеть*), что мультиплика¬
тору а отвечает вес Я-1 и мультипликатору |3 — вес Х~2.
Отсюда следует, что всякий весовой мультипликатор
/(a, р) имеет вес Хк, где k неположительно. Условимся
такой мультипликатор называть четным или нечетным
в зависимости от четности или нечетности k.
Исходное представление группы G запишем в виде
dr\dr<2 (d 1 — вектор, d2 — бивектор). Рассмотрим отдель¬
но четные и нечетные мультипликаторы.
1° Четные мультипликаторы. Всякий чет¬
ный мультипликатор разлагается только по р, а2 и, сле¬
довательно, может быть записан как полином от р, у,
где у — введенная выше вспомогательная переменная.
Пусть п\, п2 — старшие степени этого полинома по пе¬
ременным р, у. Поскольку р = у + 2а2 и первое инди¬
каторное уравнение в переменных а, у имеет вид
*) Напомним (§ 128), что вес р, мультипликатора /(г) опреде¬
ляется по формуле / (б- *гб) = р (6) / (г).

§ 133. СУЖЕНИЕ SU(га)/SO(га)
599
f = О, то мы получаем ограничения 2л)-<г1.
Точно так же соотношение у = (3 — 2а2 и второе инди¬
каторное уравнение в переменных а, Р приводят к огра¬
ничению 2п2 -С г2. В результате получаем
Правило 1. Всякий четный мультипликатор яв¬
ляется полиномом от переменных
где Zi3 = zi3 — zi2z23, степени не выше [п/2] по р и сте¬
пени не выше [г2/2] по у.
2° Нечетные мультипликаторы. Всякий не¬
четный мультипликатор мы можем представить в виде
f (а, р) —afi(a, р), где /Да, р)— четный мультипликатор.
Повторяя предыдущие рассуждения, заключаем, что
имеет место
Правило 2. Всякий нечетный мультипликатор мо¬
жет быть получен умножением переменной
Для вычисления кратности n(k), с которой входит
мультипликатор веса \~к, достаточно найти число одно¬
членов вида an = PV, i + / = fe/2 (при четном k) или
число одночленов вида вц = аа>ц, i + / = (k— 1)/2 (при
нечетном k). Здесь i, /— неотрицательные целые числа,
ограниченные сверху значениями imax = [и/2], /max =
= [г2/2] (при четном k) ИЛИ Imax = [ (И — 1)/2], /max =
= [(г2—1) /2] (при нечетном k). Искомая кратность
n{k) равняется числу целочисленных точек (обе коор¬
динаты целочисленны), лежащих на линии i + j = k/2
или i + / = (k—1)/2 внутри и на границе прямоуголь¬
ника О"4 imax, О <*С/ /шах- Так, при четном k гра¬
фик кратностей имеет вид, изображенный на рис. 7.
Параметры этой трапеции легко вычисляются из ука¬
занного выше прямоугольника. Точно так же при не¬
четном k график имеет вид трапеции с вертикальной
о 212 „ 223
P = Zi3 + -2-, Y = Дз 2~ >
г12 + 223
2
на полином от р, у степени не выше
по $ и
степени не выше
степени не выше по у.

600
ГЛ. XVIII. спектральный анализ
осью симметрии. При этом общий график кратностей
получается наложением двух указанных трапеций.
Символически удобно использовать «суммарный
мультипликатор» М = 2 п (k) К~к. Искомая спектраль¬
ная формула получается применением этого мультипли¬
катора к исходному старшему весу Ад'Аг3 = АГ‘+Г2:
d?dr22 |fl0= Шг,+г*.
Здесь в правой части каждое слагаемое А,п рассматри¬
вается как символ неприводимого представления груп¬
пы SO(3) со старшим весом т = г{ + г2 — к. Выраже¬
ние в правой части означает прямую сумму таких не¬
приводимых представлений.
Рис. 7.
Пр и мер 1. Положим г\ = 0, г2 — 5. В этом случае
имеется три четных мультипликатора соц'- сооо, ©оь <о02-
Нечетные мультипликаторы отсутствуют. В результате
d\ |G0 = (l + А,-2 + AT4) А,5 = А5 + А3 + А.
Пр имер 2. Положим гх = 1, г2 = 5. В этом случае
имеются те же четные мультипликаторы, что и в пре¬
дыдущем примере, и, кроме того, три нечетных мульти¬
пликатора 0J3 = асоif. 0оо, 0оь 002- В результате
did% |сь = А + А + А + а" + А + А.
Пример 3. Положим г\ = 4, г2 = 4. Четные муль¬
типликаторы СОоо’, СО ю, СОоГ, С020, СОц, ©02! ©21, ©12! ©22-
Нечетные мультипликаторы: 0Оо! 0до, Эоь 0и- В резуль¬
тате
d\dt lot = (А8 + 2А6 + ЗА4 + 2А2 + А0) + (А7 + 2А5 + А3).

$ 134. СФЁРИЧЁСКИЁ ФУНКЦИЙ
Нетрудно выписать также и общую формулу для крат¬
ностей. Однако результат гораздо более нагляден из
графика и рассмотренных примеров.
§ 134. Сферические функции в л-мерном
евклидовом пространстве
Как известно, теория сферических функций в трех¬
мерном вещественном евклидовом пространстве тесно
связана с гармоническими полиномами от трех пере¬
менных. Мы опишем краткую схему перенесения этой
теории на произвольное число переменных*). Выбирая
квадратичную форму в виде суммы квадратов, рассмот¬
рим соответствующий оператор Лапласа:
а д2 . д2 , , д2
А 2" Ч <г + ... Н 5“.
дх{ дх\ дхп
Полином р(х) = р (*i, х2,..., хп) называется гармониче¬
ским, если Ар(х) = 0.
Теорема 6. Всякий полином р(х) = р (х\, х2,..., хп)
может быть однозначно представлен в виде
р = h0 + r2hx + r4h2 + ...
(конечная сумма), где г2 = х\ + х\ + ... + х\ и h0,
hb h2, ... — гармонические полиномы. Линейное про¬
странство Нгп всех однородных гармонических полино¬
мов степени пг является циклической оболочкой един¬
ственного полинома
и>™ — {х + iy)m
относительно группы вращений SO (л). Здесь х, у —
проекции вектора х на два произвольных взаимно орто¬
гональных направления.
Доказательство. Не ограничивая общности, мо¬
жем считать, что х = xlt у = х2. Введем в рассматри¬
ваемое л-мерное пространство Е «картановские» коор¬
динаты х± k = (xtk ± ixik), Xq = у~2 xh, где (ih, jh) — раз¬
биение индексов 1, 2, ..., л на пары (при четном л) с
*) При изложении этой схемы мы не пользуемся результатами
общей теории, однако имеем в виду идею старшего вектора.

602
ГЛ. XVtll. СПЕКТРАЛЬНЫЙ анализ
дополнительным индексом i0 (при нечетном п). Тогда
скалярное произведение в Е принимает вид
(*, У) = + *-v+l#v-l + • • • + *v+l#v-l + *v^-v)>
Аналогично может быть записан и оператор Лапласа
(через формальные операторы дифференцирования по
х+и, *о). Отсюда, в частности, очевидно, что всякий по¬
лином вида x±k~(xlk — z'x/*)m является гармоническим.
Заметим, что всякий полином р(х) может быть одно¬
значно продолжен на комплексные значения хи хг, ...
..., хп- Переменные x±h (*о) мы можем при этом счи¬
тать независимыми.
Расположим переменные x±ft(xo) в порядке убыва¬
ния индексов от +v до —v (с пропуском нуля при чет¬
ном п). Не ограничивая общности, можем считать, что
x±v = х ± iy. Рассмотрим в группе комплексных пово¬
ротов SO (п,С) однопараметрические преобразования
Xa'+Xa+tX+v, X_V->X_V— tX-a,
где а принимает одно из значений —v + 1, ..., v—1.
Если х+уФ 0, то с помощью таких преобразований мы
можем обратить в нуль все координаты вектора х, кро¬
ме x±v. При этом координата x+v остается неизменной,
а новая координата x_v определяется из условия
x+vx_v= (лг, х) = г2. Если применить все указанные пре¬
образования к произвольному полиному £(.*), то полу¬
чаем в результате полином от двух переменных x+v,
xLv. Поскольку г2 не делится на x+v, то полученный по¬
лином является также полиномом от x+v, г2.
Пусть Рт — линейное пространство всех однородных
полиномов р(х) степени т. Каково бы ни было инва¬
риантное подпространство в Рт, мы видим, что оно со¬
держит полином, зависящий только от х+л?, г2. В частно¬
сти, всякое неприводимое подпространство является цик¬
лической оболочкой такого полинома. Воспользовав¬
шись теперь принципом полной приводимости, мы мо¬
жем заключить, что Рт есть прямая сумма неприводи¬

5 134. СФЕРИЧЕСКИЕ ФУНКЦИИ
603
мых подпространств, каждое из которых является цик¬
лической оболочкой некоторого одночлена от x+v, г2.
Пусть Ртк— циклическая оболочка одночлена
x™~2kr2k. Мы видим, что Рт распадается в прямую (ко¬
нечную) сумму:
Pm = РтО + Рт\ + Рm2 “Ь ...
В частности, Рто является циклической оболочкой одно¬
члена = x™v. Из гармоничности этого одночлена и
перестановочности оператора Лапласа с поворотами вы¬
текает гармоничность всякого элемента h е Рт0. С дру¬
гой стороны, если f е Ртк, k > 0, то f = г2р, где р —
однородный полином степени <т; нетрудно видеть, что
такой полином является гармоническим только при
f = 0*). Если f — h + r2p гармоничен, то р = 0, и мы
заключаем, что Рто = Нт. Отсюда также
Pmk = r2Hm-2k, k = 0, 1, 2, ...
Сопоставляя с найденным выше разложением, мы по¬
лучаем оба утверждения теоремы. Теорема доказана.
Следствие 1. Рт = Нт + г2Рт-2-
Следствие 2. Сужение всякого полинома р(х)
на единичную сферу S (г2 = 1) разлагается по суже¬
ниям однородных гармонических полиномов.
Сужение однородного гармонического полинома на
сферу S называется сферической функцией.
Следствие 3. Всякая непрерывная функция на
сфере S может быть равномерно аппроксимирована ли¬
нейными комбинациями сферических функций.
Действительно, согласно теореме Вейерштрасса вся¬
кая непрерывная функция на S аппроксимируется суже¬
ниями полиномов р(х) на S. Остается воспользоваться
следствием 2.
Пусть Lm — пространство всех сужений h(о), о е S,
h <= Нт. Сферические функции из Lm назовем сфери¬
*) Действительно, пусть / = r2sq, где s > 0 и q не делится
на г2. Вычисляя Д/, получаем после несложных преобразований вы¬
ражение Kr2l-S~l>q +r2s Д9, где X ф 0. Если Д/ — 0. то q = — г2 (Дq)
вопреки предположению, что q не делится на г2. Следовательно,
Д/ = 0 =^> / == 0.

604
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
ческими функциями степени т. В пространстве функций
на 5 рассмотрим обычное скалярное произведение
(f> <Р)= J f(a)<p(<r)d<r,
где da— инвариантная мера (относительно поворотов)
ка сфере 5. Заметим, что da = dx/rn-2dr, где dx — эле¬
мент объема в пространстве Е. В каждом конечномер¬
ном пространстве Lm выберем некоторый ортогональный
базис.
Теорема 7. Сферические функции всевозможных
степеней образуют ортогональный базис в гильбертовом
пространстве L2(S).
Доказательство. Рассмотрим вначале две сфе¬
рические функции со,п, co'm , m > m', где со = х + iy,
о/ = х' + iy', при произвольном выборе проекций х, х',
у, у'. Выражая х', у' через х, у и некоторые добавочные
ортогональные координаты, мы получаем
о/ = Ха + I + рй,
где черта означает комплексное сопряжение и | — линей¬
ная комбинация добавочных координат. Подставляя эти
выражения в скалярное произведение А = (со"1, ю/Ш ),
произведем поворот на угол а в плоскости (х,у). Тогда
со —> собга, <в —► ae~ia, откуда
т'
А —> е‘ша 2 Ckeika.
k = -m'
С другой стороны, скалярное произведение в L2(S) не
изменяется при поворотах, т. е. правая часть должна
совпадать со своим значением при а = 0. Поскольку
т > т', то показатель т + k не принимает нулевого
значения, откуда заключаем, что Ch = 0 и А = 0.
Мы показали, что com _L со,т при т ф т'. Отсюда,
очевидно, следует, что Lm _L Lm’, т ф т'. Остается
заметить, что согласно следствию 3 сферические функ¬
ции образуют в L2(S) полную систему. Теорема до¬
казана.
Доказанная выше теорема 6 позволяет также без
труда вычислить все сферические функции степени т.

§ 134. СФЕРИЧЕСКИЕ ФУНКЦИИ
605
Действительно, рассмотрим в комплексной группе
SO(rt) всевозможные однопараметрические преобразо¬
вания вида
Xk~*xk + ixh x-i~>x-i-tx-k, k>-l.
Такие преобразования вместе с диагональными преоб¬
разованиями Xh-+bhXh (которые для наших целей не¬
существенны) порождают всю группу SO(«). Нетрудно
видеть, что все указанные преобразования оставляют со™
неподвижным, за исключением случаев, когда k = v,
1 = —v + 1, ..., v—1. Все эти преобразования пере¬
становочны между собой. Применяя их к вектору со™,
получаем функцию
Qm = \xv+ 2 tixi — p2x-v
\ i = -v +1
Величина p2 определяется из условия ортогональности
матрицы поворота, первая строка которой имеет эле¬
менты 1, f_v+1, ..., £у_], —р2. Напомним, что ортого¬
нальность записывается по отношению к картановскому
базису x±h(x0). Отсюда получаем, что р2 = у (i-v+i^v-i+
+ t-v+2tv-2 + ... + Д'-Д-v+i) — скалярный квадрат
вектора t. Заменяя нумерацию от v—-1 до —v+ 1 ну¬
мерацией 1, 2, ..., п — 2, положим
I dm I
Ymim2 ••• тп~ 2==С"п ..т т Л_. Q Uo>
dh dt2 ... dtn*2 2
где m = mi +' m2 + ... + /nn-2- Очевидно, среди этих
функций содержится базис пространства Д. Для даль¬
нейшего изучения базисных функций естественно ис¬
пользовать редукцию SO(n)=>SO(n—1) SO (2).
При этом возникает ортогональный базис пространства
L2(S). Дальнейшие вычисления предоставляются чита¬
телю.
Функцию Q' естественно назвать производящей функ¬
цией степени I. Формула, определяющая Утхт2 ... тп_ 2,
является формулой типа формулы Родрига для по¬
линомов Якоби. Из этой формулы легко получить

606
ГЛ. XVIII. спектральный анализ
выражения сферических функций через полиномы Геген-
бауэра. Такое выражение найдено иным путем в [14].
Замечание I. Результаты ортогональности и пол¬
ноты могут быть получены также как следствие гло¬
бальной теоремы, если использовать отображение SO(«)
на S, описанное в § 17.
Замечание 2. Поскольку в пространстве Рт дей¬
ствует представление dT группы SU(«), то вся теория,
изложенная в этом параграфе, может быть интерпрети¬
рована как сужение dT lG„. где G° = SO (я) *).
§ 135. О представлениях группы движений «-мерного
евклидова пространства
В этом параграфе мы рассмотрим нетривиальные
примеры полуприводимых представлений. Если расши¬
рить ортогональную группу S = SO(n) до группы дви¬
жений «-мерного евклидова пространства Е, то такие
представления естественно возникают в классе полино¬
мов над Е. Мы покажем, что метод старших векторов
дает и в этом случае эффективный способ исследования
представлений.
Определим группу G как совокупность всевозмож¬
ных пар (s,t), seS, t^T, где S = SO(n, С) и Т изо¬
морфно Е. Преобразования группы G в пространстве Е
определяются формулой
gx = sx + t.
Элементам вида (s, 0) отвечают повороты вокруг на¬
чала координат, элементам вида (e,t)—трансляции
в Е. Соответствующие подгруппы мы отождествляем
с S и Г. Закон умножения в G определяется очевидным
образом. Группа G есть связная компонента единицы
в группе всех движений пространства Е.
Условимся рассматривать х как вектор-строку и за¬
писывать матрицу g справа от х. Пусть & — простран¬
ство всех полиномов от х. Формула
Ggp(x) = p(xg)
*) Относительно обобщения этого результата см. сноску на
стр. 596.

§ 1,15. ПРЕДСТАВЛЕНИЯ ГРУППЫ ДВИЖЕНИЙ
607
определяет в SP представление группы G. Подпростран¬
ство Рт всех однородных полиномов степени т. не ин¬
вариантно относительно этого представления. Однако
подпространство ТРт всех полиномов степени *Ст уже
инвариантно относительно Ug.
Покажем, что представление в пространстве 9>т не
является вполне приводимым. Для примера рассмотрим
случай т = 1. Имеем 5Р\ = Р0 + Р\, где Р0 — одномер¬
ное подпространство, натянутое на вектор р0(х)=\,
и Р\ есть д-мерное подпространство линейных форм,
которое мы можем отождествить с пространством Е.
Оба эти подпространства инвариантны и неприводимы
относительно S. В то же время для группы Т имеем
Utp(x) = р(х + t).
Если р(х) — линейная форма, то p(x + t) = p(x) +
+ p{t)p0(x). Преобразования группы Т в двумерном
подпространстве {р(х), р0(х)} задаются неразложимой
жордановой клеткой
1 0
Pit) 1
Отсюда ясно, что представление группы G в простран¬
стве 5^1 также неразложимо, т. е. не может быть пред¬
ставлено в виде прямой суммы двух представлений.
Действительно, каждое из этих представлений должно
быть также представлением подгруппы S, т. е. совпа¬
дать с одним из представлений в Р0 и Р\. Но подгруппа
трансляций действует неразложимо в паре {До. Р\}.
Перейдем к рассмотрению общего случая. Заметим,
что Рт инвариантно относительно S. Согласно рассмот¬
рениям предыдущего параграфа единственными стар¬
шими векторами в Рт являются векторы вида х\ {х, х)1,
k + 21 = т, где Х\ — координата вектора х относительно
некоторого фиксированного базиса. Введем обозначение
Pik для циклической оболочки (я, х)1 х\ относительно
подгруппы S. Докажем, что имеет место
Теорема 8. Условимся для подпространств Рш
использовать лексикографическую упорядоченность от¬
носительно пары (l,k). Тогда циклическая оболочка

608
ГЛ. Xvrtl. СПЕКТРАЛЬНЫЙ АНАЛИЗ
подпространства Р;и относительно группы G содержит
все подпространства Рту, подчиненные Рш.
Доказательство. Пусть PQ означает линейную
оболочку всех полиномов вида pq, р е Р, q е Q. Дока¬
жем вначале, что имеет место
Лемма. Подпространства Р\Рщ неприводимы отно¬
сительно подгруппы S, за исключением Р\Рп = Рп +
+ Рг+i, о-
Доказательство леммы. Достаточно заме¬
тить, что умножение на Рi отображает Рт на Рт+\:
Р\Рщ = Рт+ь и при четном т число неприводимых сла¬
гаемых не повышается, а при нечетном — повышается на
единицу. При этом расщепляется именно Р\Рц, посколь¬
ку среди линейных комбинаций р(х)х{(х, х)1, где р(х) —
линейная форма, содержится старший вектор (х, х)г+1.
Лемма доказана.
Теперь перейдем к доказательству теоремы. Фикси¬
руем старший вектор ?0 = (х, х)1 х\ и разложим Ut\0 по
степеням параметров t. При этом степень однородно¬
сти т—1 (т = k + 21) имеют только члены, линейные
по t. Таких слагаемых только два:
kt\x 1-1 (*, x)‘ + 2lxi(t, х)(х, х)/_1-
Здесь первое слагаемое является старшим вектором в
Pi,h-1, в то время как второе слагаемое содержится в
подпространстве P\Pi-\tli, которое согласно лемме либо
совпадает с Pi-1, ь+i, либо распадается в сумму Pi-\,h+\ +
+ Pi,k-1 (гаоб^т-г). Следовательно, циклическая оболоч¬
ка о относительно группы G имеет вид
Gt,o = Pi-\,k+\ + Pi, k-\ (mod^m_2).
Заменяя (/, k) на (/—1,&+1) или (/, &—1), мы полу¬
чаем шаг за шагом все подпространства Puk', для кото¬
рых (/', k')jC(l, k). Теорема доказана.
Результат теоремы 8 удобно выразить графически.
Пусть Tih — представление подгруппы S в подпростран¬
стве Piu. Условимся, что стрелки, исходящие от симво¬
ла Гиг, направлены в сторону тех подпространств Pw,
которые содержатся в циклической оболочке GPm■ Тогда,

§ 135. ПРЕДСТАВЛЕНИЯ ГРУППЫ ДВИЖЕНИИ
60»
например, для представлений, содержащихся в ^5, мы
имеем
т = 5 /7?=4 /77 - с? т = 2 т = / т- О
Здесь номер т для каждого столбца (т = k + 21) озна¬
чает степень однородности. Циклическая оболочка каж¬
дого подпространства P[h содержит все подпространства
Pi'k’, символы которых расположены правее и выше сим¬
вола Гiilt если движение «выше» понимать в смысле на¬
клонных стрелок. В заключение докажем, что имеет ме¬
сто
Теорема 9. Всякое инвариантное подпространство
в пространстве является циклической оболочкой не¬
которого набора подпространств Pih.
Доказательство. Пусть Q — инвариантное под¬
пространство в 5Рт и Q0 — его неприводимое инвариант¬
ное подпространство относительно S. Старший вектор
в Q0 обязательно имеет вид
£о = А {ай°1 + а1а'~' + ... + ар0) = x\f (а),
где а = (х, х). Действительно, о является инвариантом
группы S, и потому сигнатура определяется только по¬
казателем k. Докажем, что Q содержит все векторы
т]г = х\а1~1, для которых а* ф 0 (i — 0, 1, 2,..., /). В са¬
мом деле, циклическая оболочка Г£0 содержит вектор
■Sir = ?™0 Т % (х + Tei) - So (*)} = 2А+Т (а).
Здесь в\ — первый базисный вектор в разложении
х — Х\в\ + ... + хпеп. Наше утверждение доказывается
теперь индукцией по степени полинома f(a), поскольку
f'(o) — полином меньшей степени. Следовательно, Q со¬
держит вместе с каждым старшим вектором go также все

610
ГЛ. XVIII. СПЕКТРАЛЬНЫЙ АНАЛИЗ
его компоненты (х, х)1 х*, входящие с ненулевыми коэф¬
фициентами. Но тогда, очевидно, Q содержит также со¬
ответствующие подпространства P[h и является их цикли¬
ческой оболочкой. Теорема доказана.
Напомним, что согласно теореме 10 гл. XVI непри¬
водимые представления группы G, по существу, не отли¬
чаются от неприводимых представлений подгруппы S.
В то же время, как видно из рассмотрений этого пара¬
графа, группа G имеет совершенно иные, «ступенчатые»,
структуры в классе приводимых представлений.
Как уже отмечено во введении к этой главе, здесь содержатся
лишь фрагменты спектрального анализа конечномерных представле¬
ний. Одним из нерешенных в общем случае вопросов является во¬
прос о возможности разделения кратных точек весового спектра
с помощью цепочки вложенных подгрупп. Представляет также не¬
сомненный практический интерес описание «понижающих» операто¬
ров неприводимого представления (см. § 68 для SL(n)) и более
подробное изучение тензорных произведений d(a) <8 d(fi).
Базис неприводимого представления SO(rt) был построен
И. М. Г е л ь ф а н д о м и М. Л. Цейтлиным [73] в виде фор¬
мальных схем с явным определением инфинитезимальных операто¬
ров на этих схемах. Аналогичный базис для Sp(ft) был указан в
статье [84]. Отдельные примеры §§ 132—134 рассматривались в курсе
лекций [21]. Общая схема Z-инвариантов и теорема о тензорных
произведениях излагаются согласно [84]; в этой же статье были рас¬
смотрены полуприводимые представления группы движений «-мер¬
ного евклидова пространства.

ДОБАВЛЕНИЕ I
О БЕСКОНЕЧНОМЕРНЫХ ПРЕДСТАВЛЕНИЯХ
ПОЛУПРОСТОЙ КОМПЛЕКСНОЙ ГРУППЫ ЛИ
В 1943 г. И. М. Гельфанд и Д. А. Райков [70] показали,
что всякая локально компактная группа (с мерой Хаара) обладает
достаточно «богатым» запасом неприводимых унитарных представ¬
лений в гильбертовых пространствах. Если группа О некомпактна,
то эти представления, как правило, бесконечномерны. С работы [70],
по существу, берет свое начало теория бесконечномерных представ¬
лений группы G. С 50-х годов развивается также теория неунитар¬
ных представлений*). В этом добавлении приводится краткий об¬
зор такой теории для случая полупростой комплексной связной
группы Ли. Рассматриваются также некоторые вопросы гармониче¬
ского анализа функций па G.
§ 1. Элементарные представления
Пусть G — полупростая связная комплексная группа Ли и А —
ее алгебра Ли. Под дифференцируемостью функции f(g) на груп¬
пе G мы будем понимать применимость инфинитезимальных опера¬
торов левого и правого сдвига на G. Пусть Е — пространство всех
бесконечно дифференцируемых функций на G. Операторы правого
сдвига
Rgf(x)= f(xg), x,ge=G,
образуют представление группы G в пространстве Е. Разумеется,
это представление приводимо. В частности, как мы видели в нашей
книге, всякое неприводимое конечномерное представление группы G
содержится в инвариантном подпространстве пространства Е. По¬
пробуем, по аналогии с этой конструкцией, использовать представ¬
ление Rg для построения всех неприводимых представлений груп¬
пы G.
Пусть Z_, D, Z+— компоненты разложения Гаусса в группе G.
Максимальная разрешимая подгруппа В — Z-D называется так¬
же иногда борелевской подгруппой в группе G **). Пусть
*) Более подробно об этом см., например, [107], [117].
**) Как мы знаем из основного текста, группа В определяется
однозначно с точностью до внутреннего автоморфизма в G.

612
ДОБАВЛЕНИЕ Г
а — произвольный характер (одномерное представление) группы В и
Еа — совокупность всех функций из Е, удовлетворяющих уравнению
f (bx) = a(b) f (х), b <= В, х е G.
В пространстве Е мы будем рассматривать топологию равномерной
сходимости функций и их производных на каждом компакте в G.
Тогда Еа—замкнутое подпространство в Е. Очевидно, Еа инва¬
риантно относительно Re.
Определение. Сужение Rg на Еа называется элементарным
представлением группы G с сигнатурой а.
Введем обозначение е(а) для элементарного представления
группы G с сигнатурой а. Выясним, какими параметрами задается
это представление. Прежде всего, a(z)= 1, zeZ. (поскольку Z_ —
производная подгруппа в группе В); следовательно, для вычисления
а(Ь) достаточно вычислить а(6), 6 eD. Далее, а (б) = а (е) а (у)
при б = еу, ееЕ, у е Г, где Г — максимальный тор и Е — од¬
носвязная подгруппа (изоморфная векторному пространству). Если
г — ранг группы G, то dim Е = dim Г = г. Характер а(у) задается л
целыми числами, характер а(е) —произвольными г комплексными
числами. Следовательно, всякое элементарное представление груп¬
пы G задается набором 2г чисел, г из которых являются целыми
и г комплексными.
Рассмотрим подробнее тот случай, когда группа G является
односвязной. Пусть 6;, i=l, 2, ..., г,— мультипликативные коор¬
динаты в группе D (§ 112). Тогда характер а(6) можно также за¬
писывать в виде
а (б) = JJ 6^5^,
г'=]
где К,, Цг — произвольные комплексные числа, разность которых
целочисленна. Нетрудно видеть, что это условие необходимо и до¬
статочно для однозначности функции а(6) на группе D. Напомним,
что б,- = exp Р, где Р — координаты в картановской алгебре Н от¬
носительно базиса е,-= 2ct)i/(o)i, Wt), (=1, 2, ..., г. Следовательно,
также
In а (б) = (Л, х) + (р, х), б = ехрх,
где положено К = К,е(, р = р,е’ (сумма по /), е1 — дуальный базис
для е,-, и черта означает комплексное сопряжение координат Р.
Следовательно, характер а(б) задается иарой векторов К, р ef/,
разность которых целочисленна в базисе е* *).
Нам будет удобно несколько изменить введенные параметры.
Положим К = р — d, р = ? — d, где d — полусумма положительных
корней в алгебре Н. Это равносильно подстановке Ki = pi — 1, р, =
= <7i — 1 для всех i — 1, 2,..., г. Пару векторов а = (р, q), р, q е Н,
*) В общем случае (если G неодносвязна) вместо последнего
условия надо требовать, чтобы разность К — р была весом груп¬
пы Г.

§ 2. ПРОСТРАНСТВО ЭЛЕМЕНТАРНОГО ПРЕДСТАВЛЕНИЯ 613
разность которых целочисленна, мы будем называть сигнату¬
рой. Таким образом, е(а) = e(p,q).
Как и в основном тексте (в случае конечномерных представле¬
ний), мы можем использовать разложения Гаусса и Ивасавы для
получения иных моделей представления е(а). В частности, пусть
U — максимальная компактная подгруппа в группе G, порожденная
компактной формой Вейля К с X. Пусть Ф— пространство всех бес¬
конечно дифференцируемых функций на U. Условие
Ф (ум) = а (у) ф (и), уеГ, вэ11,
выделяет замкнутое подпространство в пространстве 2). Поскольку
характер а(у), a=(p,q), зависит только от целочисленной разно¬
сти v = р — q, мы обозначим это подпространство символом Sv.
Вектор v мы будем называть индексом сигнатуры а. Представление
е(а) может быть реализовано в пространстве ®v с помощью из¬
вестной формулы:
Tgф (и) = а (е') ф (ug), е' е£, ug э U,
где элементы е', ug определяются из разложения Ивасавы ug —
= &%ug, £ е Z-. Заметим, что характер а(е) зависит только от
суммы р = р + q. Вектор р мы будем называть показателем сигна¬
туры а. Вектор р является произвольным вектором из Я.
В несколько ином варианте определения элементарные пред¬
ставления были впервые введены в работе И. М. Гельфанда и
М. А. Н а й марка [68]. Наше определение следует статье [88].
§ 2. Пространство элементарного представления
Пространство Ф является топологическим векторным простран¬
ством относительно топологии равномерной сходимости на U функ¬
ций со всеми производными. Нетрудно видеть, что Ф является мет-
ризуемым полным пространством, т. е. пространством Фреше. Более
глубокую информацию о топологической природе Ф мы получим,
если разложим представление е(а) на мультиплеты относительно
компактной подгруппы U.
Заметим, что сужение е(а) на U сводится к правым сдвигам
Ruф(х) = ц>(хи) на группе U. Разложение этого представления на
неприводимые хорошо известно и сводится к разложению функции
Ф(и) в ряд Фурье по матричным элементам группы U. Однако су¬
щественно учесть бесконечную дифференцируемость функций ф(а).
Пусть А — квадратичный оператор Казимира, порожденный
правыми сдвигами па U (оператор Лапласа-—Бельтрами на U).
Матричные элементы старшего веса Я являются собственными век¬
торами оператора А с собственным значением /г(Я), причем /г(Я)
является полиномом степени 2 относительно Я:
k (Я) = Я,-Яг + с (Я)
(сумма по i от 1 до г), где ЯЯ* — взаимно дуальные координаты
в алгебре Н и с(Я) —линейная форма от Я (см. § 126). Таким об¬
разом, й(Я) С||Я!| для достаточно больших значений Я.

614
ДОБАВЛЕНИЕ I
Из бесконечной дифференцируемости функции ф (и) следует, что ее
ряд Фурье сходится в среднем квадратичном с любым весом
(й(А))", п = 0, 1, 2, ....
W )"|с}/|2ш(*)<«>,
A i,l
где c\j — коэффициенты Фурье — Петера — Вейля функции ф(«)
и со (А,)—квадрат нормы матричного элемента. Отсюда, как и в
обычном анализе Фурье, следует, что ряд Фурье функции ср(ц) схо¬
дится к этой функции в топологии пространства ©, т. е. равно¬
мерно вместе со всеми производными. Коэффициенты Фурье функ¬
ции ф(ц) убывают быстрее любой степени k(X)\
| скц | < Ап (ИЯ) )п, я = 0,1,2,...
Отсюда следует, что пространство © изоморфно пространству Кёте
быстро убывающих последовательностей ([115']). Согласно оценкам
статьи [115'] легко находим, что пространство Ф является монте-
левским и ядерным.
Как мы знаем, мультиплет dx группы U со старшим весом А
содержится в пространстве Ф с кратностью п% = dimdx. При этом
нетрудно видеть, что на долю ©v приходится nx(v) таких мульти-
плетов, где nx(v)—кратность веса v в представлении d\. Тем са¬
мым определяется кратность вхождения d\ в представление е(<х).
В частности, минимальным из весов А, для которых dx содер¬
жится в ©V, является вес Ао = ! v I, где | дс I—доминантный вектор
на орбите вектора х относительно группы Вейля (см. § 105). При
этом «j^(v)=l, т. е. d^codepotcuTCH в ©v однократно.
§ 3. Дифференциал элементарного представления
Как следует из определения элементарного представления (§ 1),
инфинитезимальные операторы группы G применимы к любому век¬
тору из пространства представления е(а). Пусть е(а, х)—инфини¬
тезимальный оператор представления е(а), отвечающий элементу
геХ, Полагая е(а, ху) = е(а, х)е(а, у), продолжаем дифферен¬
циал е(а,х) до представления универсальной обертывающей ал¬
гебры S. Элементы е(а,х), х е 3F, являются полиномами от инфини-
тезимальных операторов группы G.
Поскольку при дифференцировании оператора ТЙ (§2) прихо¬
дится дифференцировать экспоненту a(s) = ехр(р — 2d, t), е = exp t,
инфинитезимальные операторы е(а,х), деХ, линейно зависят от
показателя р сигнатуры а. Следовательно, также операторы
е(а,х), х е 3F, являются полиномами от вектора р.
Пусть S’— линейная оболочка (множество конечных линейных
комбинаций) матричных элементов группы U. Пусть S'v — пересе¬
чение S’ с ©V- Векторное пространство S’v мы будем называть
основным линеалом в пространстве ©v. Покажем, что основной ли¬
неал инвариантен относительно дифференциала е(а,х), х е X. Для
этого достаточно рассматривать только элементы де!

£ 3. ДИФФЕРЕНЦИАЛ ЭЛЕМЕНТАРНОГО ПРЕДСТАВЛЕНИЯ 615
Действительно, пусть V^ — линейная оболочка всех матрич¬
ных элементов нз S’v с фиксированным старшим весом X. Пусть К —
алгебра Ли подгруппы U. Если гбК, то е(а, х) V*" с: Vя" по опреде¬
лению С другой стороны, рассмотрим билинейную функцию
f(x, \)= е(а, х)%, как элемент тензорного произведе¬
ния А®к\ Формула е(сх, z)f(x, |) = /([г, х], |) + {(х, е(а, г) |),
геК, показывает, что f(x, g) преобразуется алгеброй К по за¬
кону тензорного произведения Л , где Л — представление ал¬
гебры К, в пространстве А, порожденное присоединенным представ¬
лением. Следовательно, е (а, х) с где X' пробегает
конечное семейство неприводимых компонент из тензорного произ¬
ведения л ® dx-
При определении семейства элементарных представлений е(а)
мы видели, формально говоря, что это семейство получается «ана¬
литическим продолжением» (по сигнатуре) из семейства неприводи¬
мых конечномерных представлений dxц группы G. Теперь мы мо¬
жем придать этому утверждению более точный смысл. Рассматри¬
вая индикаторные системы представлений нетрудно показать
(см. [88]), что пространство такого представления выделяется
следующей системой уравнений:
А^.(+1ф = 0> Х^г+1<р = 0, 1 = 1, 2 г,
где X±i — инфинитезимальные операторы левого сдвига на U, отве¬
чающие корневым векторам со = ±И;, г = 1, 2, ..., г, в комп¬
лексной оболочке алгебры К- При этом d%^ действует в .2\, только
при X — (я = v. Отсюда следует, что каждое j?v является объеди¬
нением возрастающего семейства своих подпространств К>41:
X-H = v
Фиксируем два произвольных матричных элемента е, е' е S’v
и рассмотрим функцию /(а) = (е(а, х)е, е'), где (ф, ф')—скаляр¬
ное произведение в L2(U). Поскольку /(а) является полиномом, /(а)
вполне определяется своими значениями на дискретном семействе
представлений dj^, X—ц = V. В этом смысле дифференциал е(а;
является аналитическим продолжением семейства дифференциа¬
лов dx^i-
Отметим простое, но важное следствие относительно операто¬
ров Казимира е(а, г), г е 3, где 3 — центр алгебры ЗЕ. Если е,е' —
два матричных элемента из S?v, то (е(а, г)е, е') = с(а)6(е, е'), где
6(е, е')—символ Кронекера для пары е,е' и с(а)—числовой поли¬
ном от а. Действительно, эта формула верна для семейства d^, но
тогда и для произвольных е(а). Следовательно, оператор Казимира
е(а.г) кратен единичному оператору для любого элементарного
представления е(а).

616
ДОБАВЛЕНИЕ I
§ 4. Вопросы неприводимости
Исследование элементарных представлений на неприводимость
проводилось многими авторами, начиная с первоначальных работ
И. М. Гельфанда и М. А. Найм арка [68], в которых иссле¬
довались унитарные представления «основной серии» для классиче¬
ских групп. Окончательное решение вопроса было получено в ра¬
боте автора [88]. Поскольку в доказательстве используется сложная
полиномиальная техника, мы ограничимся только формулировкой
результатов.
Скажем, что сигнатура а = (р, q) имеет вырождение по на¬
правлению корня со, если числа ри) = 2(р, со)/(со, со), qa —
= 2(q, со)/(со, со) являются целыми ненулевыми одинакового знака
(т. е. рО1Ра>>0)- Скажем, что сигнатура а вырождена, если она
имеет вырождение по направлению хотя бы одного корня. Резуль¬
тат исследования е(а) на неприводимость выражается следующей
теоремой:
Элементарное представление е(а) топологически неприводимо
тогда и только тогда, когда сигнатура а невырождена.
Оказывается также, что топологическая неприводимость е(а.)
равносильна алгебраической неприводимости дифференциала е(а, к),
tel, в линеале Z?v- Кроме того, для неприводимых представле¬
ний е(а) выполняется следующий аналог теоремы Бернсайда: вся¬
кий непрерывный линейный оператор в пространстве $>v может быть
слабо аппроксимирован линейными комбинациями операторов Тв =
— е(а, g), g^G. Всякое представление, обладающее таким свой¬
ством, принято называть вполне неприводимым [88]. Следователь¬
но, е(а) вполне неприводимо тогда и только тогда, когда сигна¬
тура а невырождепа.
Пусть W — группа Вейля алгебры X. Определим действие груп¬
пы Вейля па сигнатуру а = (р, q) по правилу аа =■- (sp,sq), sett7.
Оказывается, что если сигнатура а невырождена *), то представ¬
ления е(а), е(а,) эквивалентны. В общем случае между е(а), e(as)
существуют некоторые соотношения «частичной эквивалентности».
Рассмотрим для примера группу Лоренца, т. е. группу G =
= SL(2, С). В этом случае сигнатура имеет вид а= (р, q), где р
и q — комплексные числа с целой разностью v = p — q. Представле¬
ние е(а) в реализации на группе Z имеет вид
Tgf (г) = фг + б)*3-1 (PF+S) 4~lf ).
Здесь г — комплексное число. Класс функций f(z) описан в книге
[16]. Представление е(а) неприводимо тогда и только тогда, когда
числа р, q не являются одновременно целыми ненулевыми одинако¬
вого знака. Представления е(а), е(—а) в этом случае эквива¬
лентны.
Назовем для краткости вырожденную сигнатуру а целой точ¬
кой. Точку а будем называть положительной (отрицательной), если
*) В этом случае сигнатура а, также невырождена.

§ 5. АНАЛОГ ФОРМУЛЫ ПЛАНШЕРЕЛЯ
617
р > 0, q > 0 (р < 0, q < 0). Если точка а является целой положи¬
тельной, то е(а) содержит в инвариантном подпространстве конеч¬
номерное неприводимое представление d(a). При этом оказывается,
что оператор D— осуществляет «частичную эквивалент¬
ность» между е(а) и е(Р), р = (—р, q):
De(a, g) = е(р, g)D.
При этом оператор D аннулирует конечномерное подпространство
представления d(a) и осуществляет эквивалентность фактор-пред¬
ставления e(a)/d(a) с представлением е((5). Точно так же оператор
е(Р) и е(—а), причем оказывается, что е(Р) действует в инвариант¬
ном подпространстве е(—а), а е(—а)/е(Р) эквивалентно d(а).
Соотношения эквивалентности такого типа были впервые обна¬
ружены автором [86]. См. также [16], [82].
Естественно предположить по аналогии с теорией Петера —
Вейля, что элементарные представления е(а) должны играть роль
«элементарных гармоник» в гармоническом анализе функций на G.
Принципиальный результат в этом направлении был получен
И. М. Г е л ь ф а н д о м и М. А. Н а й марком [68], которые по¬
строили для классической группы G аналог 72-теории преобразова¬
ний Фурье*). Обобщение этих результатов на произвольную полу-
простую комплексную связную группу Ли было сделано в работе
Хариш-Чандры [140].
Заметим прежде всего ([88]), что операторы Ts--e{a,g) огра¬
ничены относительно нормы в гильбертовом пространстве Ж — /.2(U).
Следовательно, представление е(а) можно продолжить также до
представления в гильбертовом пространстве 3ffv> где Ж-$— попол¬
нение ®v. в метрике Ж. Далее, для каждой сигнатуры а = (р, q)
положим а* = (—q,—p). Оказывается ([88]), что для каждой пары
функций ф, ф е Жч выполняется тождество
где (ф, ф)—скалярное произведение в Жч (заметим, что сигна¬
тура а* имеет тот же индекс, что и а). В частности, если
р = р + q — чисто мнимое число, то а* = а. В этом случае опера¬
торы е(а, g) унитарны. Пусть А0—множество всех таких сигнатур.
Соответствующее семейство унитарных представлений е(а) назы¬
вается основной серией. Именно с рассмотрения основной серии на¬
чалось развитие теории бесконечномерных представлений группы G.
Перейдем теперь к рассмотрению функций на группе G. Если
функция x(g) локально интегрируема относительно меры Хаара dg
*) Более простой вариант изложения был предложен в работе
И. М. ГельфандаиМ. И. Граева [66'].
осуществляет «частичную эквивалентность» между
§ 5. Аналог формулы Планшереля
(е (a, g) ф, е (а*, g) ф) = (<р, ф),

618
ДОБАВЛЕНИЕ I
и достаточно быстро убывает на бесконечности (например, финит¬
на), то имеет смысл операторный интеграл
X (а) = | * (g) е (a, g) dg. (1)
Здесь Х(а), как и е(а, g),— линейный оператор в гильбертовом
пространстве Операторную функцию Х(а) мы будем называть
преобразованием Фурье функции x(g). Если функция x(g) финитна
и бесконечно дифференцируема, то рассуждения, аналогичные про¬
веденным в § 2, показывают, что матричные элементы оператора
Х(а) являются быстро убывающими в базисе Петера — Вейля. Это
убывание является настолько быстрым, что имеет смысл выражение
для следа spA'(a), где след выражается в виде абсолютно сходя¬
щегося ряда из диагональных матричных элементов. Оказывается,
что (1) допускает формулу обращения, которая имеет вид
*(g)= j sp{X(a)e(a, g)*}dp(a), (2)
О
где звездочка означает эрмитово сопряжение и d\i(oc)—некоторая
мера на множестве сигнатур А0, называемая мерой Планшереля.
Таким образом, формула обращения содержит только представле¬
ния е(а) основной серии. Для описания меры й|д(а) положим
а= (р,а). Интеграл по мере rf|r(a) означает суммирование по ин¬
дексу v и интегрирование по чисто мнимым значениям р с плот¬
ностью
! \ _ ТТ (Р> “) (?■ ®)
т (р) с0 ^ ш)2 ,
И>0
где со — произвольный положительный корень и d — полусумма всех
таких корней (константа с0 не зависит от сигнатуры а).
Положим, в частности, в формуле (2) g = е и заменим в полу¬
ченном интеграле функцию x(g) сверткой вида J х (а) у (ag) da.
Нетрудно проверить, что Х(а) заменяется при этом на X(a)Y(rx)*,
где У(а) —преобразование Фурье функции y(g). В результате
имеем
J х (g) у (g) dg = | sp [X (a) Y (a,)*} d\i (a).
•4 о
В частности, при x(g)=g(g) получаем выражение для квадрата
нормы функции x(g) в пространстве L2{G) через интеграл по А0 от
следа spA"(a)X(a)* с мерой rfp(a). Полученная формула имеет
смысл уже для произвольных функций из L2(G). Эта формула яв¬
ляется аналогом классической формулы Планшереля из гармониче¬
ского анализа на прямой.

S в. ТЕОРЕМЫ ТИПА ПЭЛИ - ВИНЕРА
619
Заметим теперь, что согласно результатам § 4 элементарные
представления основной серии неприводимы*). Формула (2) может
быть интерпретирована как разложение регулярного представления
в L2(G) на неприводимые унитарные представления.
§ 6. Теоремы типа Пэли — Винера
Пусть N — пространство всех бесконечно дифференцируемых
финитных функций x(g) на группе G. Особый интерес представляет
описание образа 91 пространства N при преобразовании Фурье
x(g)->A(a). Заметим, что N является алгеброй относительно
свертки на группе G. Преобразование Фурье переводит свертку
функций на G в умножение их образов Х(а). Таким образом, мно¬
жество 91 является алгеброй относительно произведения оператор¬
ных функций А (а).
Для каждого линейного оператора А в пространстве Жу поло¬
жим || А || = {sp АА*} Оператор А называется оператором Гиль¬
берта— Шмидта, если || А || < оо. В частности, все операторы
Х(а) е 91 являются операторами Гильберта — Шмидта. При этом
Х(а) является слабо аналитической операторной функцией с оцен¬
ками вида
1° || р V* (а) л' || < С (п, k, I) еа 1 Re р ', п, k, I = 0, 1,2,...,
где р — показатель сигнатуры а и Д — оператор Лапласа — Бельт-
рами на группе U, Кроме того, А(а), как и e(a,g), удовлетворяет
соотношениям «частичной эквивалентности», о которых упоминалось
в § 4. Если г — ранг группы G, то существует 2г операторов Wi, Si,
i'=l, 2 г, зависящих от сигнатуры а, для которых выпол¬
няются следующие «соотношения симметрии»:
2° WtX {а) = Х (a;)U7(., StX (а) = X (a,) S,-; 1=1, 2 г.
При этом операторы W{ являются интегральными, а S,-—диффе¬
ренциальными операторами в £>v- Все остальные соотношения экви¬
валентности и «частичной эквивалентности» между операторами
Х(а) являются следствиями соотношений 2°.
Оказывается, что все перечисленные выше свойства описывают
общий вид операторной функции Х(а) е 91. Этот результат принад¬
лежит автору [89]. Полученные свойства позволяют описывать фи-
нитность и бесконечную дифференцируемость функции x(g) в тер¬
минах ее преобразования Фурье.
Аналогичное описание удается получить ([89]) для квадратич¬
но интегрируемых финитных функций x(g), для «быстро убывающих
функций» x(g) **) и даже для всех обобщенных функций *(g)
*) Для случая классической группы G этот результат был полу*
чен еще И. М. Гельфандом и М. А. Наймарком [68].
**) Для «быстро убывающих» функций близкий результат был
также анонсирован И. М. Гельфандом и М. И. Граев ым [67].

620
ДОБАВЛЕНИЕ I
с компактными носителями на G. Особый интерес представляет се¬
мейство обобщенных функций, сосредоточенных в единичной точке
группы G. Это семейство изоморфно универсальной обертывающей
алгебре X, построенной по алгебре Ли группы G.
Все перечисленные здесь результаты являются аналогами клас¬
сических теорем типа Пэли — Винера на прямой (см., например,
[15']). Эти результаты имеют принципиальное значение в теории
бесконечномерных представлений группы G.
§ 7. Минимальные представления
Элементарные представления группы G с невырожденными
сигнатурами а являются важнейшим примером неприводимых бес¬
конечномерных (не обязательно унитарных) представлений груп¬
пы G. Другие примеры таких представлений мы можем получить,
исследуя структуру инвариантных подпространств для представле¬
ний е(а) в вырожденных точках.
Фиксируем какой-либо ненулевой вектор eQ s V^\ где Яо—ми¬
нимальный из старших весов компактной формы Вейля в линеале
З'у, (§ 2). Назовем вектор во минимальным вектором класса v.
Пусть S’(а)—циклическая оболочка вектора еа относительно
е(а,х), х^Х (здесь а — произвольная сигнатура с индексом v).
Если сигнатура а невырождена, то S(а) = Sv. В общем слу¬
чае представляет интерес исследование циклической оболочки
S(a).
Заметим вначале, что если р = as, s е If, то пиклические обо¬
лочки JS (а), (Р) связаны соотношением вида J? (Р) =
= А (р, a) (а), где /1(р, а) —некоторый «оператор симметрии»,
порожденный операторами Wi, i = 1, 2, ..., г, из § 6 (см. по этому
поводу [87]). Оказывается, что на орбите {as, as \V) всегда можно
найти две точки а_ и а+ со следующими свойствами: 1) S(aJ) =
= SV\ 2) S(a+) неприводимо. Представление в пространстве
S(a+) назовем минимальным представлением алгебры X с сигна¬
турой а+.
Пусть Ф(а)—замыкание S(а) в топологии пространства Ф.
Тогда Ф(сс) инвариантно относительно е(а, g). Положим а = а+.
Сужение е(а, g) на Ф(а) обозначим р(а) и назовем минимальным
представлением группы G с сигнатурой а. Если а = (ад)„ то по¬
ложим, по определению, р(а) = р(йд).
Заметим, что если векторы 7, = р — d, р = <7 — d являются стар¬
шими весами группы G, то минимальное представление р(а), а =
= (p,q), совпадает с конечномерным представлением dtai, рассмот¬
ренным в § 3. В этом случае, как мы видели в § 3, пространство
представления d\(1 выделяется из Ф некоторой системой урав¬
нений, содержащих инфинитезимальные операторы левого сдвига на
группе U.
В общем случае до сих пор неизвестно достаточно эффективное
описание пространств Ф(сс) минимальных представлений р(а). Из¬
вестно только, что Ф(а+) является образом Фу> где v — индекс а_,

§ 8. КЛАССИФИКАЦИЯ НЕПРИВОДИМЫХ ПРЕДСТАВЛЕНИЙ 621
относительно оператора симметрии А0 = А (а+, а_). Весьма ве¬
роятно, что »(<*). подобно Vх^х, также выделяется из Ф с помощью
инфинитезимальных операторов левого сдвига. (Эта гипотеза про¬
верена авторомвслучае v = 0.)
§ 8. Классификация неприводимых представлений
Вопросы классификации бесконечномерных неприводимых пред¬
ставлений группы G существенно зависят от аксиоматики в классе
таких представлений. Действительно, даже если вместо группы G
рассматривать аддитивную группу R вещественных чисел, то про¬
блема классификации ее топологически неприводимых представле¬
ний равносильна до сих пор нерешенной проблеме классификации
линейных непрерывных операторов (с точностью до эквивалентно¬
сти) в топологическом векторном пространстве. Положение значи¬
тельно упрощается, если вместо топологически неприводимых пред¬
ставлений группы R рассматривать ее вполне неприводимые пред¬
ставления (см. § 4). В этом случае ввиду выполнения теоремы
Бернсайда можно утверждать ([88]), что вполне неприводимое
представление группы R одномерно. Следовательно, оно имеет вид
экспоненты е}'х, teR.
Однако при переходе от группы R к группе G возникает еще
одна трудность. Действительно, как мы видели выше, операторы
представления е(а) могут быть определены как в гильбертовом
пространстве 5^v, так и в монтелевском пространстве Фу. При этом
Фу всюду плотно в Жм, и представление е(а) в обоих пространствах
вполне неприводимо. Естественно считать такие представления в не¬
котором роде одинаковыми, т. е. использовать соответствующее
определение эквивалентности. Такое определение было предложено
М. А. На й марком [117]. Мы приведем несколько видоизменен¬
ный вариант такого определения.
Пусть Тй — представление группы G в топологическом вектор¬
ном пространстве L, и пусть L0—инвариантное векторное подпро¬
странство в L. Скажем, что представление Тg в L0 является уплот¬
нением представления Тв в L, если в L0 существует более сильная
топология, по отношению к которой То полно и операторы Те не¬
прерывны. Скажем, что два представления группы G слабо экви¬
валентны, если они имеют эквивалентные уплотнения.
Теперь мы можем сформулировать один из вариантов поста¬
новки задачи о классификации неприводимых представлений груп¬
пы G. Требуется классифицировать все вполне неприводимые пред¬
ставления этой группы с точностью до слабой эквивалентности.
Окончательное решение этой задачи было получено в недавней
работе М. А. Наймарка и автора [91] (см. также [90]) *). Оказалось,
что всякое вполне неприводимое представление группы G слабо
эквивалентно одному из ее минимальных представлений р(а).
*) Близкий (но более слабый) результат был получен в более
ранней работе Ф. А. Березина [49].

622
ДОБАВЛЕНИЕ I
§ 9. О полуприводимых представлениях
При исследовании элементарных представлений обнаружилась
еще одна любопытная особенность бесконечномерных неунитарных
представлений группы G. Оказалось, что в классе этих представле¬
ний теряет силу теорема Г. Вейля о полной приводимости.
Действительно, мы видели в § 4, что представление е(а) груп¬
пы Лоренца с положительной целой точкой а содержит инвариант¬
ным образом конечномерное представление d(а) и фактор-представ¬
ление e(a)/d(a) эквивалентно е(Р) при некотором р. Оказывается,
что е(а) невозможно представить в виде прямой суммы представ¬
лений d(a) и е(р). Этот результат является частным следствием
теоремы типа Пэли — Винера, впервые полученной автором [86] для
группы Лоренца (см. также [82], [87]).
Точно так же и в случае произвольной полупростой комплекс¬
ной группы G элементарное представление е(а) в вырожденных
точках имеет довольно сложную «ступенчатую» структуру. В про¬
странстве такого представления существует лишь конечное число
инвариантных подпространств. Если (0) = L0 Т.! cz ... сzL„=L —
максимальная цепочка таких подпространств (определяемая, вообще
говоря, неоднозначно), то представление в каждом фактор-про¬
странстве LklLu-i эквивалентно одному из минимальных представ¬
лений группы G.
В статье [87] была предпринята попытка исследовать все полу¬
приводимые представления группы Лоренца, имеющие «конечную
ступенчатую структуру», т. е. содержащие лишь конечное число не¬
приводимых компонент. С помощью теоремы Пэли — Винера эта
задача была сведена к некоторой задаче линейной алгебры, окон¬
чательное решение которой было получено в недавней работе
И. М. Гельфанда и В. А. Пономарева [69].
Значительно более сложной является теория бесконечномерных
представлений (даже унитарных) для полупростой вещественной
группы Ли. Мы не имеем возможности в рамках данной книги
остановиться сколько-нибудь подробно на обзоре этой теории.

ДОБАВЛЕНИЕ II
ЭЛЕМЕНТЫ ОБЩЕЙ ТЕОРИИ УНИТАРНЫХ
ПРЕДСТАВЛЕНИЙ ЛОКАЛЬНО КОМПАКТНЫХ
ГРУПП
В классе общих локально компактных групп существенно
усложняются задачи теории представлений и, в частности, задача
гармонического анализа на группе. Действительно, мы видели в до¬
бавлении I на примере полупростых комплексных групп, что не¬
приводимые представления локально компактной группы не обяза¬
тельно конечномерны. Вместо обобщенной теории рядов Фурье (тео¬
рии Петера — Вейля) возникает обобщенная теория интегралов
Фурье (вообще говоря, не числовых, а операторных). В настоящее
время в теории представлений локально компактных групп суще¬
ственно разработана только теория унитарных представлений (при
построении которой важнейшую роль играет основная спектральная
теорема функционального анализа). Краткий обзор этой теории яв¬
ляется целью настоящего добавления.
§ 1. Коммутативные группы
Рассмотрим вначале аддитивную группу R всех действитель¬
ных чисел. Унитарное представление этой группы есть произволь¬
ная однопараметрическая группа Ut, —оо < t < оо, унитарных опе¬
раторов в гильбертовом пространстве Н*). Согласно известной тео¬
реме Стоуна (см., например, [22']) семейство операторов Ut может
быть записано в виде
Ut—eitA, — оо < t < оо,
где А—самосопряженный оператор в пространстве Н. Оператор А
называется производящим оператором однопараметрической группы
Ut. Применение к этому оператору классической спектральной тео¬
ремы функционального анализа ([39"], [22'], [37']) позволяет получить
дальнейшую информацию о строении представления Ut. Прежде
*) Согласно определению представления операторная функция
предполагается непрерывной по t. См., однако, по этому поводу за¬
мечание на стр. 636.

624
ДОБАВЛЕНИЕ И
всего, операторная функция Ut может быть записана в виде
интеграла:
ОО
и, = J ет dP (X), (•)
где Р(Х)—семейство проекционных операторов, называемое разло¬
жением единицы и обладающее следующими свойствами:
1) Р(Х)Р(\х) — Р(Х) при X ^ р; 2) Р(Х) перестановочно со всяким
непрерывным линейным оператором, перестановочным с А; 3) Р(Х)\
непрерывно слева по X при любом £ е Н; lim Р(Х)Ъ, = 0, lim Р(Х)% =
— ОО + 00
= | для всякого | е Н.
Формула (*) дает наиболее существенную информацию о пред¬
ставлении Ut. Очевидно, Ut неприводимо только в том случае, ко¬
гда спектральная мера dP(X) сосредоточена в единственной точке
Хо и пространство Н одномерно. В этом случае Ut — eil^° *). Фор¬
мула (*) означает, следовательно, разложение Ut на неприводимые
представления.
Из формулы (*) можно получить также другую интерпретацию
спектральной теоремы для Ut. Предположим вначале, что в прост¬
ранстве Н существует вектор £0, циклический относительно произ¬
водящего оператора А (т. е. такой, что Н есть замыкание линейной
оболочки векторов /4"|0, п = 0, 1, 2, ...). Положим о(7.) =
= (Р{Х) Ё,о, So) • Тогда пространство Н изоморфно гильбертову про¬
странству числовых вектор-функций f(X), — оо < X < оо, с квадра-
ОО
том нормы J | f (X) |2 da (X) < оо Операторная функция U, за-
— ОО
дается при такой реализации формулой
UJ(X)=eitKf(X), (*.)
в то время как оператор А сводится к умножению на X: Af(X) =
= Xf(X)**). Действие проектора Р(р) сводится в этом случае к
умножению на характеристическую функцию полуоси —оо < X < р.
В общем случае представление Ut разлагается на циклические (т. е.
такие, для которых циклический вектор |0 существует). Формула
(**) по-прежнему сохраняет силу, с той разницей, что f{X) теперь
*) Следовательно, всякое унитарное неприводимое представле¬
ние группы R одномерно (что может быть доказано и независимо).
Для неунитарных топологических неприводимых представлений
группы R вопрос остается открытым (см. по этому поводу, напри¬
мер, [74]). Однако тот же результат остается справедливым для
вполне неприводимых представлений группы R.
**) Заметим, что оператор А, вообще говоря, неограничен, Его
область определения всюду плотна в Н,

§ 2. ТЕОРЕМА СТОУНА - ФОН НЕЙМАНА
625
является (вообще говоря, бесконечномерной) вектор-функцией
от к*).
Заметим, что в реализации (»*) каждая б-функция 6(Л — Я0)
является, формально говоря, собственным вектором семейства Ut с
собственным значением ег<\ Хотя б-функция и не является эле¬
ментом Н, такому утверждению можно придать строгий смысл, если
воспользоваться аппаратом обобщенных собственных векторов по
Г ельфанду [17] и Костюченко.
Наконец, перейдем к случаю произвольной коммутативной ло¬
кально компактной группы G. В этом случае имеет место теорема
Наймарка [37']**), обобщающая формулу (*). Пусть Ug — унитар¬
ное представление группы G в гильбертовом пространстве Н, X —
группа всех унитарных характеров группы G, т. е. одномерных
унитарных представлений %'-g-+%(g). Тогда согласно теореме Най-
ыарка
ug= | у. (g)dP (г)’
где интеграл берется по группе X и dP(%) —- спектральная мера,
определенная на борелевских множествах в X. Подробности см. в
[37'], сгр. 487. Отсюда нетрудно получить также и обобщение фор¬
мулы (**)• Пространство Н изоморфно реализуется в виде гильбер¬
това пространства вектор-фупкций fix), Х^Х, квадратично инте¬
грируемых относительно некоторой меры. Представление Ug за¬
дается явной формулой
Ugf (%) = x(g)f (х)-
Как и прежде, в частном случае группы R, эти результаты озна¬
чают разложение Ug на неприводимые представления. В частности,
всякое неприводимое унитарное представление группы G одномерно
и задается одним из характеров %(g).
Гармонический анализ на коммутативной локально компактной
группе G является наиболее развитым в настоящее время обобще¬
нием обычного анализа Фурье. (Из гармонического анализа на G
вытекает, в частности, теория двойственности Понтрягина, о кото¬
рой мы упоминали в § 107.) На более подробном обзоре этой тео¬
рии мы сейчас не имеем возможности останавливаться. Отдельные
вопросы рассмотрены в монографиях [18'], [35], [37'].
§ 2. Теорема Стоуна — фон Неймана
До сих пор мы имели дело только с коммутирующими семей¬
ствами унитарных или эрмитовых операторов в гильбертовом
*) Векторная размерность функции f(k), вообще говоря, зави¬
сит от X. См. по этому поводу общее определение прямого интегра¬
ла гильбертовых пространств (стр. 636). См. также [37'].
**) Эта теорема независимо и несколько позднее доказывалась
также другими авторами (Стоун, Эмброз, фон Нейман).

626
ДОБАВЛЕНИИ II
пространстве Н. Одним из простейших примеров некоммутирующей
системы является система эрмитовых операторов Я, Q, для которых
[я, Q] = и,
где 1 = У— 1 и / — единичный оператор в пространстве Н (опе¬
раторы координаты и импульса в квантовой механике). Рассмотре¬
ние этого примера играет существенную роль также в развитии об¬
щей теории. Заметим вначале, что {Pn,Q\ = in Рп~1 для всех нату¬
ральных п, откуда следует общая формула
[f(P),Q] = if'(P) (•)
для произвольных полиномов /(г) с заменой г на Р, где штрих в
правой части означает дифференцирование по г. Естественно пред¬
положить, что (*) сохраняет силу также для более широкого класса
функций f(z). В частности, рассмотрим резольвенту R\ = (Р — XI)'1
в тех точках, где она определена. Имеем
[*л> Q] = Kji [Q> Р - Щ = - iR\,
что совпадает с формулой (*) при f (г) = (г — Х)~1. Но тогда фор¬
мула (*) сохраняет силу также для всевозможных полиномов от
Р, Ri и также для сильных пределов таких полиномов (при усло¬
вии, что /'(Я) имеет смысл). К последнему классу функций отно¬
сится, в частности ([22']), однопараметрическая группа операторов
Ut = eitp *). Следовательно, [U,, Q] = —tUt, откуда имеем **)
UfxQUt=Q + tI. (.*)
Из формулы (**) следует, что спектр оператора Q заполняет всю
действительную ось. Воспользуемся для Q спектральной теоремой,
т. е. реализуем этот оператор как оператор умножения на х в клас¬
се вектор-функций f(x), интегрируемых с квадратом по мере da(x):
Qf(x) =xf(x).
Из формулы (**) следует, что вектор-функция f(x) имеет одинако¬
вую размерность во всех точках х и мера d<x(x) совпадает с обычной
лебеговой мерой. Следовательно, можно считать, что f(x) при¬
нимает значения в некотором фиксированном гильбертовом про¬
странстве Н0. Пространство Н состоит при этом из всех таких функ-
*) Существование унитарной группы Ut следует из спектраль¬
ной теоремы для оператора Я. Если бы оператор Я был ограничен¬
ным, то мы могли бы непосредственно выразить Ut в виде степен¬
ного ряда по степеням оператора Я.
**) Эта формула может быть получена значительно проще, если
заметить, что функция Ut дифференцируема по t, причем U't=iPUt.
Полагая F (t) = UfxQUt, имеем отсюда F(t)' = — i[P, Q] = /. Следо¬
вательно, F(t)" = 0, и в результате F(t) = F(0) + ti = Q + ti.

§ 2. ТЕОРЕМА СТОУНА - ФОН НЕЙМАНА
627
оо
ций 1(х), для которых J || f (х) ||g da (х) < оо, где || / ||0 означает
— ОО
норму в пространстве Н0. Рассмотрим в Н оператор дифференци¬
рования
(определенный на всюду плотном множестве в Н). Тогда, как легко
проверить, [Я, Q] = И, т. е. операторы Р, Q удовлетворяют тем же
коммутационным соотношениям, что и пара Р, Q. Следовательно,
оператор Р — Р перестановочен с Q. Но тогда, как известно из
спектральной теории, Р — Р есть оператор умножения на некоторую
функцию от переменной х; следовательно,
Р = Р + ф (х) = i + ф (х).
В силу эрмитовости Р и Р функция ф(х) действительна. В резуль-
i-k n . d
тате мы находим явное выражение для оператора Р: +
+ Ф (лт). Рассмотрим унитарный оператор s=e~l№x’>tix. Имеем SQS~[ =
= Q, SPS~t = Следовательно, после унитарного преобразова¬
ния S в пространстве Н мы получаем из пары Р, Q пару операторов
р*-14г' Q°=x-
Следовательно, с точностью до унитарной эквивалентности всякие
два эрмитовых оператора Р, Q, удовлетворяющие соотношению
коммутации [P,Q] = i, сводятся к паре Я0, Qo- Эго и составляет
содержание известной теоремы Стоуна — фон Неймана. Разумеется,
мы привели доказательство этой теоремы с некоторыми сокраще¬
ниями *).
Замечание. Нетрудно видеть, что уравнение [P,Q\ = U не
имеет никаких (эрмитовых или неэрмитовых) решений в классе ко¬
нечномерных линейных операторов. Действительно, след левой части
этого соотношения равен нулю, в то время как след правой части
отличен от нуля.
Рассмотрим теперь группу Z(3) всех треугольных матриц 3X3
с единицами на главной диагонали. Легко видеть, что алгебра Ли
этой группы натянута на три базисных элемента р, q, г с единствен¬
ным нетривиальным соотношением коммутации [р, q] = г. Элемент г
является центральным. Пусть теперь Р, Q, R — образы элементов
р, q, г в некотором унитарном представлении Z(3). В силу унитар¬
ности этого представления можно считать (за счет умножения на
*) См. также [130'], [118], [102].

628
ДОБАВЛЕНИЕ II
i = Y~ 0, что операторы Р, Q эрмитовы. Если представление не¬
приводимо, то оператор R оказывается кратным единичному, и мы
получаем соотношение коммутации
[A Q] = А/,
где I — единичный оператор в Н. Если X = 0, то [Р, Q] = 0, и пред¬
ставление коммутативно. (При этом в силу неприводимости оно
одномерно.) Если же ХфО, то мы имеем, как и выше, =
Q — Хх с точностью до унитарной эквивалентности. Для соответ¬
ствующих однопараметрических подгрупп Ut=eitP, \7t = eit(^ по¬
лучаем следующие формулы:
Utf (*) = f (х - 0, Vtf(x) = ettKxHx). (...)
Таким образом, теорема Стоуна — фон Неймана позволяет получить
описание всех, с точностью до унитарной эквивалентности, непри¬
водимых унитарных представлений группы Z(3). (Действительно,
однопараметрические подгруппы Ut, Vt порождают эти представле¬
ния.) Мы видим, что всякое такое представление либо одномерно,
либо бесконечномерно.
В первом случае представление задается двумя действитель¬
ными скалярами а и |3, к умножению на которые сводятся опера¬
торы Р и Q (R = 0). В этом случае Ut = etta, Vt = Во втором
случае представление задается явными формулами (***), причем
результат классификации зависит от действительного числа ХфО.
Нетрудно проверить, что представления с различными X при этом
попарно неэквивалентны.
Геометрически множество всех неприводимых унитарных пред¬
ставлений группы Z(3) можно отождествить с множеством всех пло¬
скостей ?i = constat0 и множеством всех точек на плоскости X = Q
в трехмерном евклидовом пространстве с координатами X, а, р.
§ 3. Индуцированные представления
Прежде чем приступить к дальнейшему изложению теории,
остановимся на рассмотрении специального типа представлений, на¬
зываемых индуцированными. Пусть X — однородное пространство с
группой движений G, причем действие элемента g s G на точку
ге]( обозначается символом xg. Рассмотрим линейный оператор
Тв, действующий в пространстве функций на X по формуле
Tgf(x)=a(x, g)f(xg).
Для того чтобы семейство операторов Tg являлось представлением
группы G, необходимо и достаточно выполнение следующих условий:
а(*. gig2) = «(*. gi)a(xgu g2), а(х,е) = \. (*)
Найдем общее решение этого функционального уравнения. Фиксируем
некоторую точку XjeJT и положим для краткости a(g) =а(х0, g).

§ 3. ИНДУЦИРОВАННЫЕ ПРЕДСТАВЛЕНИЯ
629
Тогда согласно (*) функция a{g) удовлетворяет функциональному
уравнению
a (gog) = « (go) a (g), а (<?) = !, (**)
для произвольных элементов go е Go, geG, где Go — стационар¬
ная подгруппа точки х0. Далее, выберем для каждой точки
элемент gx s G, переводящий х0 в х. Тогда всякий элемент geG
однозначно запишется в виде gogx, go s G, и мы имеем в силу (*)
а (х0, gxg) = а (х0, gx) а (х, g).
Отсюда видно, что функция а(х, g) может быть выражена через
функцию a(g):
а (х, g) = a (gx)~1 a (gxg).
Представим элемент gxg в виде gogy, где g« е G0, у^Х. Тогда из
последнего соотношения имеем также *)
а (х, g) = а {gx)~X a (g0) a (§„)•
Полученная формула дает общий вид решения а(х, g). Используя
преобразование эквивалентности Af(x) = a(gx)f(x), мы можем за¬
менить представление Tg эквивалентным представлением Tg —
= ATgA'K При этом
Tgf (*) = а (х, g) f (xg),
и функция a(x,g) удовлетворяет условию a(gx) =1. Следователь¬
но, в этом случае мы имеем а(х, g) — a(gо), где go, как и прежде,
определяется разложением gxg = gogv.
Функция a(g0) является, согласно (**), представлением груп¬
пы G0. Принято говорить, что представление Те группы G инду¬
цируется представлением a(g'c) подгруппы Go**). Все изложенные
выше построения сохраняют силу также в том случае, когда f(x) —
вектор-функции со значениями в некотором векторном пространстве
L и а(х, g) —линейные операторы в L. Представление Tg при этом
по-прежнему называется индуцированным. Если dim L = 1, то та¬
кое представление иногда называют мономиальным.
Условие неприводимости a (go) необходимо, но недостаточно
для неприводимости Tg. Действительно, в добавлении / мы имели
дело с элементарными представлениями полупростой комплексной
группы G. Все они мономиальны, т. е. представление a(g0) одно¬
мерно и потому неприводимо. Однако мы видели, что элементарное
представление может быть приводимым. Заметим, кстати, что роль
группы G0 играет в этом случае максимальная разрешимая под¬
группа в G.
*) Здесь мы используем функциональное уравнение (**).
**) Напомним, что Go — стационарная подгруппа произвольно
фиксированной точки х0 е X. Если заменить Хо на x0g, то подгруп¬
па Go заменяется сопряженной подгруппой g~lG0g.

630
ДОБАВЛЕНИЕ II
Как мы знаем из основного текста (§ 17), однородное простран¬
ство X можно отождествить с фактор-пространством G/Gо, где G0—
стационарная подгруппа фиксированной точки Хо е X. Можно также
отождествить пространство X с множеством точек-представителей
gx, х е X. Используя разложение g = gogx, будем вместо функций
/(х) рассматривать функции f(g) = f(gogx) = a(g0)f(x). Все эти
функции, очевидно, удовлетворяют соотношению
f(gog) = a(g0)f(g)
при любых значениях g0 е G0, ge С. Пусть Fa—множество всех
таких функций на группе G. Преобразование правого сдвига
Rgf(a) — 1(аё) образует представление в Fa, которое, как легко
проверить, эквивалентно исходному представлению Tg. Следователь¬
но, мы получаем еще одну реализацию индуцированных представ¬
лений (которой уже неоднократно пользовались в основном тексте).
До сих пор мы не накладывали никаких ограничений на про¬
странство функций, в котором действует индуцированное представ¬
ление. Однако в приложениях это постоянно приходится делать,
причем произвол в определении такого пространства довольно ши¬
рок (например, дифференцируемые функции или функции класса IX
в условиях добавления 1). Если на X существует мера dx такая,
что d(xg) =сt>(x,g)dx с конечным якобианом <о(х, g) (такая мера
называется квазиинвариантной), то условие
а (*, g) а(х, g) = ю (х, g), (***)
где черта означает комплексное сопряжение, позволяет построить
унитарное представление группы G с помощью формулы индуциро¬
ванного представления. Для этого надо ограничиться классом всех
функций f(x), интегрируемых с квадратом по мере dx. (Несложная
проверка предоставляется читателю.) Здесь мы предполагаем, что
f(x) —числовая функция, однако если L — гильбертово простран¬
ство, то условие (*** ) этого добавления сохраняется, с заменой
черты на эрмитово сопряжение. В этом случае
a (go) = и (go) Р (go),
где fi(go)—нормирующий множитель и представление «(go) груп¬
пы Gо унитарно. Обычно, имея дело с унитарными представлениями,
говорят, что представление ТЙ индуцируется представлением «(go)
(а не a(go), как принято в нашем тексте). Однако если мера dx
инвариантна (d(xg) — dx), то fi(go) = 1.
Конструкция индуцированных представлений часто используется
для построения явных моделей неприводимых представлений той
или иной группы G *). Большинство известных математикам непри¬
водимых представлений классических групп Ли являются индуци¬
рованными и даже мономиальными.
*) Теория индуцированных представлений восходит к Фробе-
ниусу, рассматривавшему конечные группы. Современное развитие
этой теории начинается с работы И, М. Г е л ь ф а н д а и М. А. Н а ft-
мар к а [68] н систематизируется в работах Г. Макки [107'], [107"],
Ф. Б р ю а [59].

§ 4. ПОЛУПРЯМЫЕ ПРОИЗВЕДЕНИЯ
631
§ 4. Полупрямые произведения *
Рассмотрим практически важный случай, когда группа G мо¬
жет быть представлена в виде G = ST (однозначное разложение),
где S — подгруппа и Т — нормальный делитель. Такое произведение
двух подгрупп называется полупрямым. (Пример: группа дви¬
жений G с подгруппой вращений S и подгруппой трансляций Т.)
В этом параграфе мы ограничимся частным случаем, когда под¬
группа Т коммутативна. Покажем, что знание неприводимых уни¬
тарных представлений подгруппы S позволяет перечислить также
все неприводимые унитарные представления группы Т.
Пусть Ug — неприводимое унитарное представление группы G
в гильбертовом пространстве Н. Согласно результатам §1 суже¬
ние этого представления на подгруппу Т может быть записано в
виде прямого интеграла одномерных представлений по множеству
X, где X — группа всех унитарных характеров группы G. Иначе го¬
воря, пространство Н мы можем реализовать в виде пространства
вектор-функций f(x), х е X, причем
Utf(x)-x(t)f(x), (.)
где x(t)—значение характера teJi на элементе teT. Напомним,
что функции j(х) интегрируемы в квадрате по некоторой мере dci(x).
Знание этой меры существенно для описания представления.
Рассмотрим теперь преобразование U„ seS. Поскольку Т яв¬
ляется нормальным делителем в G, то, в частности, s~xts е Т. По¬
ложим t(s) — s~lts. Тогда имеем
utus — USU((X).
С другой стороны, рассмотрим в пространстве Н преобразование
V.f(x) =f(x„), где характер xs определяется по формуле xs(t(s)) =
— x(t). Тогда, как легко проверить, имеет место тождество
U(V $ — V SU KSy
Сопоставляя последние две формулы, мы видим, что преобразова¬
ние USV~* перестановочно со всеми операторами U,, t^T. Но вся¬
кое такое преобразование, как известно ([37']), является оператором
умножения на некоторую функцию от х. В результате =
= а (х, s), откуда имеем
Usf(x)'=a(x,s)f(xs). (**)
Полученные формулы (*), (**) вполне определяют представление
группы G. Мы видим, что такое представление может быть записа¬
но по формуле индуцированного представления в некотором классе
функций f(x), Однако мы не можем, вообще говоря, утвер¬
ждать, что пространство X является однородным *).
До сих пор мы не пользовались условием неприводимости пред¬
ставления Ug. Очевидно, свойство приводимости существенно зависит
*) То есть что преобразование x->xs транзитивно.

632
ДОБАВЛЕНИЕ И
от структуры преобразования в пространстве X, а также
от меры do(x). Может случиться, что преобразование ,*->х8 яв¬
ляется эргодическим (§ 17). Этот случай особенно сложен для изу¬
чения, и мы его исключим. Иначе говоря, предположим, что про¬
странство X расслаивается на однородные. При этом можно пока¬
зать, что в силу неприводимости Uе мера da(x) сосредоточена лишь
на одной однородной компоненте X a X.
Условимся теперь рассматривать функции f(x) только при
х е X. Тогда согласно (*), (**) мы получаем формулу индуциро¬
ванного представления в классе функций f(x) на однородном про¬
странстве X. Согласно результатам предыдущего параграфа пред¬
ставление Ug индуцируется некоторым представлением a(go) под¬
группы Gо cz G, причем можно считать, что
Ugf (х) = a (g0) f (xg),
где точка go определяется из разложения gxg = g«gv- Подгруппа Go
есть стационарная подгруппа некоторой фиксированной точки х0 е X.
Отсюда следует, что G0 содержит Т (ввиду коммутативности Т).
Следовательно, мы имеем
О0 = S0T,
где S0 — некоторая подгруппа группы S. Очевидно также, что
a(go) = a(s0t) = a(s0)xo(t), поскольку a(l) = x0(t). Допуская воль¬
ность речи, иногда говорят, что представление Ug индуцируется
представлением a(s0) подгруппы S0 *). Однако в действительности
представление Ug характеризуется следующими данными: 1) непри¬
водимое представление a(s0) подгруппы S0; 2) характер x0(t) под¬
группы Т такой, что xo(t{s)) = хо(0> 3) мера da(x) на орбите
x0(t(s)), s s= S **).
Пример. Пусть G — группа движений n-мерного евклидова
пространства с подгруппой вращений S и подгруппой трансляций Т.
Символически удобно записывать элементы g е G в виде матриц
порядка п + 1 следующего вида:
|] s t I
s =! о 1 г
где seS и t — n-мерный вектор, отвечающий трансляции (еГ.
При этом мы отождествляем элементы seS, feT с матрицами
Is 0 II
t =
е t
[о 1 [Г
0 1
*) Физики называют такую подгруппу «малой группой» (small
group).
**) При этом можно показать, что мера da(х) должна быть
квазиинвариантна относительно преобразования x->xs. Если меры
da(x), dx(x) эквивалентны (т. е. da(x) = сй(х)Л(х) с невырожден¬
ным якобианом со (я)), то соответствующие представления также
эквивалентны.

5 5. НИЛЬПОТЕНТНЫЕ ГРУППЫ ЛИ
633
где е — единичная матрица п X п. Вычисляя s~4s, находим, что это
преобразование сводится к замене вектора t на s~lt. Далее, всякий
характер x(t) запишем в виде x(t) — exp i(a,t), где скобка означает
скалярное произведение re-мерных векторов a, t. Отсюда следует,
что преобразование x->xs сводится к замене вектора а на s-1a.
Действительно,
Xs U (s)) = exp i (s_1a, s~'t) = exp i (a, t) = x (t).
Всякая орбита преобразования a-»s-1a есть сфера в n-мерном про¬
странстве некоторого радиуса г. Рассмотрим такую сферу X; тогда
на ней существует мера dx, инвариантная относительно поворотов
x->sx. Искомое пространство функций f(x) составим из функции
f(x), ieX, квадратично интегрируемых относительно dx.
Остается определить подгруппу Go. Фиксируем произвольную
точку х0 е X. Подгруппа поворотов S0, сохраняющих эту точку,
очевидно, изоморфна 0(я—1). В результате О0 = S0T, где Т — под¬
группа трансляций. Согласно изложенной выше общей теории не¬
трудно получить, что всякое неприводимое унитарное представление
группы G задается следующими данными: 1) неприводимым (ко¬
нечномерным) представлением группы 0(ra—1); 2) неотрицатель¬
ным числом г ^ 0 (радиус орбиты). Мера dx при этом определяется
однозначно с точностью до множителя*).
Результаты, изложенные в этом параграфе, принадлежат
Г. Макки [107'], [107"]. Мы опустили все сложные вопросы, свя¬
занные с теорией меры, в том числе рассмотрение эргодических
движений.
§ 5. Нильпотентные группы Ли
Пусть теперь G — нильпотентная связная группа Ли. В этом
параграфе мы докажем следующую теорему А. А. Кириллова: вся¬
кое неприводимое унитарное представление группы G мономиально.
Доказательство будем вести индукцией по размерности груп¬
пы G, т. е. по размерности соответствующей алгебры Ли, которую
обозначим А. Этот метод позволяет считать, не ограничивая общ¬
ности, что представление алгебры А является точным. (Действитель¬
но, в противном случае мы имеем дело с представлением некоторой
фактор-алгебры, имеющей меньшую размерность.) Далее, пусть Z —
центр алгебры А. Ввиду неприводимости операторы центра являют¬
ся скалярами**). Ввиду предположения о точности мы можем от¬
сюда заключить, что dim Z = 1. (Действительно, всякая нильпотент¬
ная алгебра содержит нетривиальный центр (§ 85); следовательно,
dim Z =£0; в то же время поле скаляров имеет размерность 1.)
*) Действительно, всякая мера, квазиинвариантная относитель¬
но компактной группы (в нашем случае О(п— 1)), эквивалентна ин¬
вариантной. Доказательство предоставляется читателю.
**) Это следует из обобщенной леммы Шура [37'], о которой
подробнее будет сказано в § 6.

634
ДОБАВЛЕНИЕ II
Следовательно, можем считать, что алгебра А имеет одномерный
центр.
Если dim А = 1, 2, то в этом случае алгебра А коммутативна
(упражнение 1 на стр. 389) и теорема верна (всякое неприводимое
представление одномерно, а потому мономиально). Если dim/4 = 3,
то, исключая коммутативный случай, имеем лишь единственную
алгебру Ли — алгебру Ли группы Z(3) (упражнение 2 на стр. 389).
В этом случае утверждение теоремы следует из результатов § 2
этого добавления. Итак, при dim/4 = 1, 2, 3 теорема доказана.
В дальнейшем мы предполагаем, что dim А > 3. Остальное доказа¬
тельство разобьем на несколько шагов.
1. Согласно структурной теории нильпотентных алгебр Ли (§85)
мы можем расширить Z до двумерной подалгебры Y такой, что
[A, Y] с Z. Пусть у, z — базис в Y, причем ге/. Тогда имеем
[а, у] = у (а) г (*)
для всех аеЛ (ввиду одномерности Z). Здесь ф(а)—линейный
функционал над алгеброй Л, отличный от тождественного нуля, по¬
скольку элемент у нецентрален. Следовательно, существует элемент
* е Л, для которого ф(лг) = 1. Отсюда имеем
[х, у] = z.
Мы показали, что в алгебре А существует трехмерная подалгебра С,
изоморфная алгебре Ли группы 2(3), причем ее центр совпадает с
центром всей алгебры А.
2. Введем обозначение Аа для гиперплоскости в Л, выделяемой
условием ф(а) = 0. Покажем, что Л0 является идеалом в Л. Дей¬
ствительно, Л0 состоит из всех элементов аеЛ, для которых
Day = 0, где положено Day = [о, у]. В частности,
D\a. Ь]У ~ \^а’ Db]y = 0
согласно (•) и центральности элемента г. Следовательно, всякий
коммутатор содержится в Л о. В частности, [Л, Л0] с: Л о, т. е. Л0 яв¬
ляется идеалом. Очевидно, Л = Ло + {*}. Поскольку Л0 — идеал, то
отсюда в свою очередь получаем разложение для группы:
G = G0T
(полупрямое произведение), где положено Оо = ехрЛо, Т = {ехр tx}.
Теперь можно было бы воспользоваться результатами предыдущего
параграфа, однако мы предпочтем видоизмененное построение, кото¬
рое покажет, что представление группы G индуцируется представ¬
лением подгруппы О0.
3. Итак, пусть Tg — неприводимое унитарное представление
группы G в гильбертовом пространстве Н. Согласно теореме Стоу¬
на — фон Неймана мы можем реализовать пространство Н в виде
пространства вектор-функций /(/), —с» < t < оо, интегрируемых с
квадратом по мере Лебега, так, чтобы образы Тх, Ту, Tz элементов
х, у, z задавались формулами
d

§ 6. РАЗЛОЖЕНИЕ УНИТАРНЫХ ПРЕДСТАВЛЕНИИ 635
При этом Хф 0, поскольку представление является точным. Далее,
пусть go s G0. Согласно определению Go оператор rg() перестано¬
вочен с Ту. Следовательно, этот оператор при каждом g0 сводится
к умножению на некоторую функцию от переменной t:
TgJ (0 = Л (t, g0)f(t).
В то же время TexV,xf(t) = f(t + х). Отсюда следует, что прямая
Х0 = {— оо < t < с»} является однородным пространством для G.
Согласно разложению G = G0T формулы для Tgt> и Гехр $х вполне
определяют представление Tg. Мы видим, что это представление
индуцировано представлением
Ggri = A (t0, g0)
подгруппы Go (здесь t0 — произвольно фиксированная точка в До) ■
4. Остается воспользоваться следующим «правилом транзитив¬
ности» из теории индуцированных представлений ([102]): пусть G2 а
cfficG — цепочка вложенных подгрупп; если представление т
группы G индуцировано представлением ti подгруппы Gb которое
в свою очередь индуцировано представлением т2 подгруппы G2, то
представление т индуцировано также представлением т2. Это откры¬
вает возможность для индукции. Постепенно понижая размерность,
приходим к случаю dim А = 3, рассмотренному выше. Теорема до¬
казана.
В статье А. Кириллова [102] дается дальнейшее уточнение
изложенной конструкции. Мономиальное представление задается,
очевидно, некоторым линейным функционалом f над алгеброй А
(алгеброй Ли группы G). Оказывается, что представления, инду¬
цированные функционалами /а и /2, эквивалентны тогда и только
тогда, когда имеет место равенство
f\ — Р (8) /2. S s G,
где p(g)—представление группы G, сопряженное присоединенному
представлению этой группы в алгебре А. Таким образом, возникает
взаимно однозначное соответствие между орбитами p(g) и непри¬
водимыми унитарными представлениями группы G. Различные опе¬
рации тензорной алгебры (тензорное произведение, сужение с груп¬
пы на подгруппу) также получают замечательную интерпретацию в
терминах орбит. Заслуживает особого внимания то обстоятельство,
что «язык орбит» не зависит от структурной теории (которая для
нильпотентных групп фактически не развита). Можно надеяться, что
этот язык в известной степени окажется универсальным также в
классе произвольных групп Ли (при описании всех неприводимых
унитарных представлений).
§ 6. Разложение унитарных представлений
на неприводимые
До сих пор мы рассматривали лишь отдельные типы групп и,
главным образом, их неприводимые представления. Остановимся
теперь na некоторых общих результатах в предположении, что G —
произвольная локально компактная группа со счетной базой окрест¬

636
ДОБАВЛЕНИЕ II
ностей единицы. (Этому условию удовлетворяет, в частности, всякая
группа Ли.)
Пусть Ug — унитарное представление группы G в сепарабель¬
ном гильбертовом пространстве Н. Заметим, что в классе таких
представлений для сильной непрерывности операторной функции Ug
достаточна ее слабая непрерывность ([37'], стр. 443). Мы уже от¬
мечали в основном тексте, что для унитарных представлений имеет
место принцип полной приводимости. Последовательное применение
этого принципа позволяет заключить о разложимости представления
Ug на неприводимые. Однако число неприводимых компонент мо¬
жет быть несчетно, и потому для строгого описания полученной си¬
туации приходится использовать специальное понятие прямого ин¬
теграла.
Пусть Л — компактное пространство с мерой do (к). Предполо¬
жим, что почти каждой точке X е Л поставлено в соответствие гиль¬
бертово пространство Hi размерности п(к) = 1, 2, ..., оо. Предпо¬
ложим, что функция п(к) измерима по мере da(k). Так как функ¬
ция п(к) принимает лишь счетное число значений, то пространство
Л разбивается в счетную теоретико-множественную сумму непере-
секающихся подпространств Л&, на каждом из которых п(к) — const.
Следовательно, при 1еЛ(, все пространства H-L можно отожде¬
ствить с некоторым фиксированным пространством Нх. Вектор-
функцию f(k) еЯ(, к е Л*, мы называем измеримой, если число¬
вые функции (f(k), ф) измеримы при каждом tp еЯ(. Вектор-функ¬
цию f(к) ЕЙь ).еЛ, назовем измеримой, если она измерима на
всех подпространствах Hi. Определим пространство Н как множе¬
ство всех измеримых функций /(7) еЯь для которых
Соответствующим образом вводится скалярное произведение двух
функций f [k), g(k) е Н. Функции f(k), для которых [| / || =0, ото¬
ждествляются с нулем. В результате пространство Н становится
гильбертовым пространством. Это пространство называется прямым
интегралом пространств Hi и обозначается символом
Заметим, что Hi, вообще говоря, не является подпространст¬
вом в пространстве Н (исключение составляет тот случай, когда
мера точки к конечна). Если почти в каждом пространстве Hi задан
оператор Ai, то оператор Af(k) = Aif(k) называется прямым инте¬
гралом операторов Ai.
Вернемся к рассмотрению унитарного представления Ug группы
G. Основной результат формулируется следующим образом: пред¬
ставление Ug есть прямой интеграл неприводимых унитарных пред¬
ставлений Ug(k) по некоторой мере do(к).
i/г = [ шл)р*тах«>.
Л
Л

§ 6. РАЗЛОЖЕНИЕ УНИТАРНЫХ ПРЕДСТАВЛЕНИИ 637
Существенно, что полученное разложение, вообще говоря, не яв¬
ляется однозначным. Более того, существуют такие группы, для ко¬
торых неоднозначным является также спектр, т. е. «список» непри¬
водимых представлений, входящих в разложение ([37']). Положение
упрощается, если вместо неприводимых представлений рассматри¬
вать представления, «кратные неприводимым», точнее, так назы¬
ваемые «фактор-представления».
Представление Ug есть прямой интеграл взаимно неэквивалент¬
ных фактор-представлений ([37']). Такое разложение определяется
однозначно. Известны условия, при которых всякий ограниченный
оператор в Н, перестановочный с Ug, есть прямой интеграл скаляр¬
ных операторов р (Я)/^, где />.—единичный оператор на // и
р(Я) —число (континуальный аналог леммы Шура ([37'], стр. 413)).
В частности, всякий ограниченный оператор, перестановочный
со всеми операторами неприводимого унитарного представления,
кратен единичному (однако этот результат, конечно, доказывается
независимо и значительно проще).
Если Uе — регулярное (правое или левое) представление груп¬
пы G, то указанное выше разложение приводит к так называемой
«абстрактной формуле Планшереля» (И. Сигал [129]). Однако для
каждого конкретного класса групп проблема состоит в описании
явного вида меры, входящей в разложение (так называемой меры
Планшереля).
К значительно большим сложностям приводит рассмотрение не¬
унитарных представлений. Ввиду отсутствия принципа полной при¬
водимости здесь не существует даже корректной постановки задачи
о разложении. Неприводимые представления сравнительно подробно
изучены только в случае полупростой комплексной группы Ли.

ДОБАВЛЕНИЕ III
УНИТАРНАЯ СИММЕТРИЯ
В КЛАССЕ ЭЛЕМЕНТАРНЫХ ЧАСТИЦ
Мы уже упоминали во введении, что методы теории линейных
представлений групп Ли позволили в последнее время получить
значительные успехи в некоторых разделах теоретической физики,
главным образом в вопросах классификации элементарных частиц.
Целью этого добавления является вкратце проследить основные
этапы логического развития идей, приведших к упомянутым ре¬
зультатам.
§ 1. Инвариантность и законы сохранения
Напомним вначале основные постулаты квантовой механики, ко¬
торые в известной степени сохраняются также и в квантовой тео¬
рии поля.
1. Волновая функция. Согласно основным положениям
нерелятивистской квантовой механики эволюция всякой физической
системы во времени определяется уравнением Шредингера =■
= г'Гф, где Г — оператор энергии (гамильтониан, массовый опера¬
тор). Здесь ф является элементом некоторого гильбертова простран¬
ства Н, называемого пространством состояний. Вся информация
о физической системе содержится в векторе ф, который называется
вектором состояния или волновой функцией. Важнейшую роль в
теории играют квадратичные формы вида (Лф, ф), где Л—линей¬
ный оператор в Я. Обычно рассматриваются только эрмитовы опе¬
раторы, которые соотносятся той или иной физической величине
(импульс, координата, момент импульса, энергия, заряд). Выраже¬
ние (Лф, ф) означает при этом среднее значение физической вели¬
чины Л в состоянии ф.
Обычно используется та или иная функциональная реализация
пространства Я. Всякая такая реализация связана с выбором неко¬
торой системы коммутирующих эрмитовых операторов Ль Л2, ...
..., Ат, которые «диагонализуются» в общем базисе в смысле § 1
добавления II. Иначе говоря, пространство Я реализуется в виде
пространства вектор-функций f(x)=f(xь х2, ..., хт), квадратично
интегрируемых относительно некоторой меры da{x), причем опера-

§ 1. ИНВАРИАНТНОСТЬ И ЗАКОНЫ СОХРАНЕНИЯ
639
торы Ai действуют по формуле Atf(x)=Xif(x), i = 1, 2, т.
В качестве таких операторов иногда выбирают операторы коорди¬
нат, которые характеризуют пространственное положение отдельных
частиц системы. В этом случае, если Лц,— оператор умножения на
характеристическую функцию некоторой области <о m-мерного про¬
странства векторов х, то форма (Лш/,/) определяет вероятность
локализации системы в области ш.
Особую роль играют состояния с фиксированной энергией А.
Для таких состояний Гф = Аф. Точно так же, если вектор ф яв¬
ляется собственным относительно некоторого эрмитова оператора А:
Лф = цф, то состоянию ф соответствует определенное значение ц
физической величины Л.
2. Законы сохранения. Предположим, что оператор Л
перестановочен с гамильтонианом. Тогда соотношение Лф = цф не
нарушается при эволюции вектора ф во времени. Действительно,
ф = eltr фо, где ф0 — значение ф при t = 0, в предположении, что Г
не зависит от времени (впрочем, это предположение несуществен¬
но). Следовательно, физическая величина Л является в этом слу¬
чае интегралом движения. Иначе говоря, значение этой величины
сохраняется со временем.
Законы сохранения играют в квантовой механике, пожалуй, еще
большую роль, чем в механике классической. Действительно, они
порождают «правила запрета», согласно которым система не мо¬
жет переходить из состояния {Л = рц} в состояние {Л = ц2} при
р, ф р2. Таков закон сохранения энергии (действительно, Г комму¬
тирует с Г), закон сохранения полного момента импульса (в неко¬
торых случаях спина), закон сохранения заряда, четности и т. д.
Поскольку законы сохранения связаны, как мы видим, с инва¬
риантностью уравнения Шредингера относительно той или иной си¬
стемы операторов, то естественно возникают алгебры и группы та¬
ких операторов (см. § 19), оставляющих это уравнение инвариант¬
ным*). Здесь физики невольно сталкиваются с тем фактом, что
структурные законы данной алгебры или группы играют суще¬
ственную роль в классификации решений волнового уравнения.
3. Аддитивные квантовые числа. Если имеются две
физические системы с состояниями ф и ф, то смешанная система
определяется тензорным произведением векторов ф и ф. Физическая
величина называется аддитивной, если ее значение в смешанной си¬
стеме равняется сумме значений в состояниях ф и ф. Используя
произвол в выборе физической величины (состоящий в том, что
вместо Л можно рассматривать некоторые функции /(Л)), физики
обычно стараются выявить аддитивные величины, как наиболее
простые. Такими величинами являются, например, энергия и заряд.
Однако полный момент импульса L, связанный с законами инва¬
риантности относительно группы вращений SO(3), не является
*) Любопытно отметить, что законы сохранения заряда свя¬
заны с инвариантностью волнового уравнения относительно преоб¬
разований ф -> е£аф, где 0 ^ а < 2я. Здесь существенно, что вол¬
новая функция является комплексной.

640
ДОБАВЛЕНИЕ III
аддитивным. Его сложение подчиняется закону спектра старших ве¬
сов при тензорном умножении неприводимых представлений SO(3),
т. е. сложение Li и L2 приводит к возможным значениям вида
L\ + L^, L\ + L2—1, I Li—L2 |. См., например, [31']*).
Здесь мы сталкиваемся с приложением в теоретической физике
понятия тензорного произведения двух представлений некоторой
группы G (например, группы вращений). Если волновые функции
фиф преобразуются соответственно по неприводимым представле¬
ниям аир этой группы, то тензорное произведение фф преобра¬
зуется по правилу а ® р = yi + у2+• • • + Vm, где правая часть
означает прямую сумму неприводимых представлений. Это озна¬
чает, что смешанная система может с той или иной вероятностью
находиться в состояниях фь ф2, ... , фт, преобразующихся согласно
Yn V2 У То' Соответствующие вероятности по определенному
правилу вычисляются с помощью коэффициентов Клебша — Горда-
на. Таким образом, групповая структура здесь играет существен¬
ную роль.
Если физическая величина А является аддитивной, то ее соб¬
ственные значения называются обычно аддитивными квантовыми
числами.
4. Нарушение симметрии. Существенно отметить, что
всякая симметрия в квантовой механике, как правило, является
приближенной либо выполняется только в идеальных условиях. Так,
симметрия относительно группы SO(3) возможна лишь в централь¬
но-симметричном силовом поле. Пространственная симметрия моле¬
кул идеального газа возможна только при отсутствии силового
поля. Наложение продольного магнитного поля изменяет форму
гамильтониана и нарушает эту симметрию (сохраняя лишь симмет¬
рию поворота относительно выделенной оси).
Остановимся на последнем примере несколько подробнее. В от¬
сутствие поля состояния молекулы газа могут характеризоваться
неприводимым представлением группы SO(3) со старшим весом L.
Всего, как мы знаем, имеется 2L + 1 таких состояний. Все эти со¬
стояния отвечают одному и тому же собственному значению опера¬
тора Г, который в данном случае совпадает с оператором Казимира
группы SO(3). Поскольку оператор Г является оператором массы-
энергии**), то это означает также, что все 2L + 1 состояний имеют
один и тот же энергетический уровень (одну и ту же массу). Фи¬
зики говорят в этом случае о «вырождении» (т. е. о кратности) соб¬
ственного значения. Наложение магнитного поля приводит к тому,
что все 2L + 1 состояний уже становятся существенно различными.
В частности, они находятся на разных энергетических уровнях. (Фи¬
зики говорят в подобных случаях о «снятии вырождения».)
Описанный эффект известен под названием эффекта Зеемана
и допускает наглядную иллюстрацию (расщепление спектральных
линий в магнитном поле).
*) Однако проекция момента на некоторую фиксированную
ось является аддитивной (сложение весов при тензорном произве¬
дении) .
**) В силу эквивалентности (по Эйнштейну) массы и энергии.

§ 2. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ. ИЗОТОПИЧЕСКИЙ СПИН 641
§ 2. Элементарные частицы. Изотопический спин
Теория элементарных частиц имеет дело с простейшими из из¬
вестных в настоящее время состояниями материи, из которых со¬
ставляются более сложные образования (атомное ядро, атом, моле¬
кула). Некоторые из этих частиц существуют стабильно (протон,
нейтрон), некоторые обладают ничтожной продолжительностью жиз¬
ни. В природе происходят постоянные изменения в состояниях эле¬
ментарных частиц, причем эти частицы при столкновениях друг
с другом уничтожаются и рождают новые частицы.
1. Основные типы элементарных частиц. Извест¬
ные в настоящее время элементарные частицы распределяются по
следующим основным типам в зависимости от их массы покоя.
1) Фотоны (частицы света) с нулевой массой покоя. 2) Пептоны
(легкие частицы), к которым относятся электрон, мюоны (ц-ме-
зоны), нейтрино и соответствующие античастицы. 3) Мезоны (сред¬
ние частицы). При классификации мезонов существенную роль иг¬
рает аддитивная физическая величина S, называемая странностью.
Известно, что эта величина (при определенной нормировке) прини¬
мает лишь целые значения, причем для мезонов S = 0, ±1. Значе¬
нию S = 0 отвечают я-мезоны, тумезоны, р-мезоны, /°-мезон и т. д.
Значению S = 1 отвечает /С-мезон. 4) Барионы (тяжелые частицы).
Для барионов S = 0, —1, —2. К барионам относятся нуклоны (про¬
тон р и нейтрон п), Л-гиперон, S-гипероны, 3-гипероны и т. д.
5) Античастицы барионов.
Существует также множество неустойчивых частиц, называемых
резонансами, которые трактуются обычно как возбужденные состоя¬
ния стабильных частиц. Эти частицы пока недостаточно исследо¬
ваны даже экспериментально.
2. Основные типы взаимодействий. Наряду с мас¬
сой покоя существенную роль играет распределение частиц по тем
типам взаимодействий (ядерных реакций); в которых они могут
принимать участие. Физики различают электромагнитное, слабое и
сильное взаимодействия. При электромагнитных взаимодействиях
непременно участвуют фотоны. Слабые взаимодействия характери¬
зуются наличием хотя бы одного из следующих двух признаков:
а) участие нейтрино; б) несохранение странности (нарушение S-сим¬
метрии). Все остальные взаимодействия называются сильными. Эти
взаимодействия характерны главным образом для процессов в атом¬
ном ядре. Указанные типы взаимодействий различаются также
по степени интенсивности (что отражается в их названиях, при¬
чем электромагнитное взаимодействие является наименее интен¬
сивным) .
Среди указанных типов взаимодействий наиболее хорошо ис¬
следовано электромагнитное. Этому разделу соответствует класси¬
ческая часть квантовой теории поля (включая теорию расходимо¬
стей). Наименее исследовано слабое взаимодействие. (К этой об¬
ласти относятся известные работы Ферми, а также работы Ли и
Янга по несохранению четности.) В теории ядерных сил (сильные
взаимодействия) роль переносчика энергии вместо фотона играют
обычно я-мезоны или другие частицы.

642
ДОБАВЛЕНИЕ III
В дальнейшем изложении мы будем рассматривать только ча¬
стицы, принимающие участие в сильных взаимодействиях. Такие
частицы называются адронами.
3. Изотопический спин. В теории ядра существенную
роль играет так называемая изотопическая инвариантность между
основными составляющими этого ядра — протонами и нейтронами.
Обе частицы имеют одинаковый спин (по отношению к простран¬
ственной группе вращений) и почти одинаковую массу. Если от¬
влечься от электромагнитных взаимодействий, в которых играет
роль электрический заряд ( + 1 для протона, 0 для нейтрона), то
обе частицы по существу оказываются идентичными. Возникает
симметрия по отношению к перестановкам (протон — ней¬
трон) *).
Вместо симметрии по отношению к перестановкам мы можем
рассматривать также более общие унитарные преобразования в
двумерном пространстве со степенями свободы «протон» — «ней¬
трон». Пусть р — волновая функция состояния «протон» и п — вол¬
новая функция состояния «нейтрон». Рассмотрим волновую функ¬
цию
ф = <р(р)р + Ф(л)я, (•)
где ф(р), ф(п)—числовые коэффициенты. В квантовой теории су¬
щественную роль играют соотношения нормировки (II р II = 1,
|| га || = 1) и соотношения ортогональности ((р,п)= 0). Поэтому из
векторов ф мы также условимся выделять два ортогональных нор¬
мированных вектора:
Ф = ар + уп, ф = р/7 + б п.
В силу условий ортогональности и нормировки матрица этого пре¬
образования оказывается унитарной. Отбрасывая несущественные
преобразования вида р -> etap, п->е‘ап**)’ мы приходим к груп¬
пе SU(2), т. е. к группе всех матриц
^ , и*и = е, det и = 1.
V б II
Согласно общим принципам симметрии (§ 1) состояния (*) обла¬
дают теми же энергетическими свойствами, что и пара протон —
нейтрон. При этом мы получаем простейшее (двумерное) представ¬
ление группы SU(2).
В действительности в теории ядра приходится иметь дело со
многими нуклонами (т. е. протонами и нейтронами). Рассматривая
соответствующие волновые функции как тензорные произведения
нужного числа сомножителей р, п (снабженных индексами), мы
получаем приводимые представления группы SU(2). Разлагая их
*) Два ядра, получаемые друг из друга такой перестановкой,
действительно близки по своим энергетическим свойствам. Такие
ядра называются зеркальными или зеркально сопряженными.
**) Эти преобразования связаны с принципом сохранения за¬
ряда (см. сноску на стр. 639).

§ 3. УНИТАРНАЯ СИММЕТРИЯ В КЛАССЕ АДРОНОВ 643
на неприводимые, получаем волновые функции неприводимых ком¬
понент, которые характеризуются, с точки зрения SU(2), своим
старшим весом и весом базисного вектора по отношению к диаго¬
нальной подгруппе в SU(2). Эти характеристики называются пол¬
ным изотопическим спином и его проекцией. В частности, проекция
является аддитивным квантовым числом.
Заметим, что антинуклоны (антипротон р и антинейтрон п)
преобразуются по дуальному представлению изотопической группы
SU(2). Однако мы знаем из теории представлений SU(2), что оба
эти представления эквивалентны.
Излагаемая теория становится содержательной лишь после того,
как понятие изотопического спина приписывается всем остальным
адронам (мезонам и барионам). После этого можно сформулиро¬
вать принцип полного изотопического спина *) при сильном взаимо¬
действии. Это дает реальные правила запрета при ядерных реак¬
циях. Кроме того, коэффициенты Клебша — Гордана изотопической
группы SU(2) определяют вероятности тех или иных процессов
в ядерных реакциях.
Наряду с изотопическим спином существует еще ряд дискрет¬
ных характеристик элементарных частиц. К их числу относится
странность S (уже упоминавшаяся выше) и барионный заряд В,
который попросту означает число барионов в системе. Очевидно, В
является аддитивной величиной. При сильных взаимодействиях обе
величины В и S сохраняются. Их сумма У = В + S называется
гиперзарядом.
Заметим, что наличие дискретных инвариантов движения позво¬
ляет объяснить стабильность адронов при сильных взаимодействиях.
Например, из закона сохранения гиперзаряда следует невозмож¬
ность превращения протона в позитрон с излучением фотона.
Открытие изотопического спина явилось исторически первым
шагом по установлению более сложных законов симметрии в классе
элементарных частиц. К рассмотрению этих обобщений мы перехо¬
дим в следующем параграфе.
§ 3. Унитарная симметрия в классе адронов
После многочисленных попыток обобщения понятия изотопиче¬
ского спина М. Гелл-Манном и независимо И. Нейманом в 1961 г.
была предложена, по-видимому, наиболее удовлетворительная мо¬
дель, основанная на рассмотрении унитарной группы SU(3). В этой
модели аддитивными квантовыми числами являются проекция изо¬
топического спина и гиперзаряд. Кроме того, рассматриваются пол¬
ный изотопический спин (старший вес подгруппы SU(2)) и так
*) Как видно из определения, изотопический спин не имеет ни¬
какого отношения к пространственному спину. Однако между ними
имеется формальная аналогия, поскольку эти величины связаны
с локально изоморфными группами SO(3) и SU(2). Оператор абсо¬
лютной величины изотопического спина есть оператор Казимира
группы SU(2) (отсюда видно, что эта величина не аддитивна).

644
ДОБАВЛЕНИЕ III
называемый унитарный спин, задаваемый двумя целыми числами
(старший вес группы SU(3)).
1. Начнем с рассмотрения барионов. Среди барионов выде¬
ляются следующие подсистемы частиц: 1) Л-гиперон (инвариант
изотопической группы); 2) нуклоны pan (изотопический спин 1/2);
Н-частицы 5~ и Е° (изотопический спин 1/2); 3) 2-частицы 2", 2°
и 2+ (изотопический спин 1). По терминологии, принятой у физиков,
мы имеем синглет, 2 дублета и один триплет. Иначе говоря, мы
имеем следующее представление группы SU(2):
a = d(0) + 2d (Va) + d(О,
(•)
где d(l) означает неприводимое представление со старшим весом I.
Все указанные частицы обладают той замечательной особенностью,
что их массы имеют близкое значение (но не равны). Внутри каж¬
дого неприводимого представления массы можно считать приблизи¬
тельно равными (в рамках сильного взаимодействия). Приближен¬
но мы имеем следующее:
т (Л) =1115, т (N) — 939, ш(Е)=1318, т (2) -1193
(в некоторых единицах), причем символ N отвечает подсистеме ну¬
клонов.
Сделаем теперь следующее важное допущение. Предположим,
что существует некоторое идеализированное «ультрасильное взаи¬
модействие» ([150]), при котором массы всех указанных восьми ча¬
стиц являются равными. Тогда представление а принадлежит од¬
ному и тому же собственному значению некоторого гипотетического
гамильтониана Жо- Заметим теперь, что формула (*) совпадает
с сужением на SU(2) неприводимого представления did2 группй
SU(3), т. е. присоединенного представления этой группы. Нельзя
ли отсюда сделать вывод, что указанный октет (восьмерка) частиц
обладает свойством SU(3)-симметрии?
2. Займемся формальным анализом представления did2. Это
представление естественно реализовать в классе матриц х —
= || Xij ll»j = i, 2, з со следом, равным нулю. Формула (х, у) = Sp ху*
определяет скалярное произведение векторов (матриц) х, у, инва¬
риантное относительно SU(3)*). При сужении на SU(2), с дей¬
ствием на индексы £, / = 1, 2, получаем следующие инвариантные
подпространства:
X 0 0
1) матрицы вида
2) матрицы вида
0 X 0
0 0 -2Х
ООО
ООО
а Ъ 0
— синглет;
0
0
а
и вида
0
0
Р
— два дублета;
0
0
0
*) Преобразование ueSU(3) действует на матрицы х по фор¬
муле х -> ихиг1.

§ 3. УНИТАРНАЯ СИММЕТРИЯ В КЛАССЕ АДРОНОВ 645
3) матрицы вида
х у О
г — х О
О 0 0
— триплет.
Все эти подпространства взазимно ортогональны. Кроме того,
если все указанные координаты (А,, а, Ь, а, р, х, у, г), кроме одной,
положить равными нулю, то мы получаем ортогональный базис во
всем пространстве представления. Этот базис станет ортонормиро-
ванным (как легко проверить), если положить Х = ■ а,
У 6
1 о
х = - т, а все остальные координаты оставить прежними. В ре-
V ^
зультате получаем следующую параметризацию произвольной мат-
рицы х *):
У
а Ь ■=■ а
/6
Рассмотрим теперь инфинитезимальные операции группы SU(3).
Расширяя эту группу до U(3), имеем 9 «генераторов» Eij, i,j =
= 1, 2, 3 (базисные инфинитезимальные операторы, введенные в
гл. VI). Особую роль играют диагональные операторы Ец, i =>
= 1, 2, 3, образующие базис в картановской подалгебре. Вместо
этих операторов нам будет удобно рассматривать следующие их
линейные комбинации:
С = -д- (Ец + Е22 + £зз)> Та = — (Е22 —• Ец)
Y-Е,.- С.
Используя тензорный аппарат для SU(3) (см. § 45), читатель без
труда найдет веса всех базисных функций в пространстве матриц х,
т. е. собственные значения операторов С, То, Y. В частности, опера¬
тор Т0 определяет веса для подгруппы SU(2), преобразующей ин¬
дексы 1, 2. Оператор С является скаляром (оператор Казимира для
L'(3)). Оператор Y принимает значение 0 для синглета и триплета
и значения ±1 соответственно на первом и втором дублетах.
*) Если волновая функция октета записывается в виде
2<Р(в)е, где е — базисная функция элементарной частицы, то ко-
е
ординаты а, а, Ь, а, р, т, у, г отождествляются соответственно с
ф(Л), —<р(р), <р(п), Ф(2“), Ф(Н°), ф(2°), ф(2"), ф(2+). См., на-

646
ДОБАВЛЕНИЕ III
3. Теперь мы получили формальную схему, при помощи которой
волновую функцию октета можно отождествить с вектором х. Опе¬
ратор То отождествляется с проекцией изотопического спина. Опе¬
ратор Y отождествляется с гиперзарядом (что соответствует экспе¬
риментальным данным). Оператор Q = C — Еп отождествляется
с электрическим зарядом частицы. Мы получаем интерпретацию
важнейших аддитивных физических величин в рамках группы SU(3).
Теперь принимается гипотеза об SU(3)-инвариантности (в дей¬
ствительности даже U (3)-инвариантности, но это различие несуще¬
ственно). Эта гипотеза приводит, в частности, к законам сохранения
операторов Казимира группы SU(3). В частности, квадратичный
оператор Казимира отождествляется (при некоторой нормировке)
с гамильтонианом Г0. Существенно, однако, что величина Г0 яв¬
ляется инвариантом только в рамках SU.(3)-симметрии, т. е. при
идеализированном «ультрасильном» взаимодействии.
4. Мы переходим к важнейшему вопросу о «снятии вырожде¬
ния» по массе, т. е. к объяснению реальной разницы между массами
барионов. Будем искать реальный гамильтониан в виде Г = Г0 + ДГ.
Подбор ДГ осуществляется по формуле
лг “ е 2 *зЛз+ 6 2 *зЛз> <*•)
i-i i=i
где черта означает комплексное сопряжение. Таким образом, пред¬
полагается, что сильное взаимодействие, по сравнению с ультра-
сильным, особым образом действует на индекс / = 3. Полагая в мат¬
рице х все координаты равными нулю, кроме одной, мы получаем
для каждой элементарной частицы соответствующее приращение
массы Дт. Несложное вычисление приводит к следующим резуль¬
татам *):
Дт (Л) = (е + б), Дт (N) = е, Дт (Е) = б, Дт (2) = 0.
О
Мы получили так называемую «массовую формулу Гелл-Манна —
Окубо». Используя приведенную выше таблицу для масс, читатель
легко проверит, что эта формула выполняется в хорошем прибли¬
жении, если положить е = 125, б = —254.
Мы изложили классификацию октета барионов (Л, N, Е, 2)
с точки зрения группы SU(3). Наряду с этим октетом мы имеем
также соответствующий октет античастиц. Оба октета эквивалентны
с точки зрения группы SU(3) **).
5. Совершенно аналогично классифицируются мезоны. Здесь
выделяются два октета. I. Октет псевдоскалярных мезонов. С точки
зрения изотопической группы SU(2) этот октет разбивается на сле¬
*) Коэффициент 2/3 есть квадрат нормировочного множителя
в равенстве х33 = — 2/V6 о.
**) Ввиду особой роли октета (присоединенное представление
SU(3)) вся теория унитарной симметрии была названа Гелл-Ман¬
ном «восьмеричным путем» (8 приближений Будды к совершенству).

5 4. ОТКРЫТИЕ П ЧАСТИЦЫ
647
дующие подсистемы: 1) трмезон (синглет), 2) tf-мезоны и их анти¬
частицы (2 дублета), 3) л-мезоны (триплет). II. Октет векторных
мезонов. С точки зрения SU(2) этот октет разбивается на следую¬
щие подсистемы: 1) ф-мезон (синглет), 2) К*-мезоны и их анти¬
частицы (2 дублета), 3) р-мезоны (триплет) *).
Для мезонов по-прежнему выполняется формула Гелл-Манна —
Окубо, с той разницей, что выражение вида (*») дает теперь по¬
правку для квадрата массы, т. е. А(Г2). Заметим, что мезонные
октеты симметричны относительно перехода к античастицам. Отсюда
следует, что е = б. Формула Гелл-Манна — Окубо дает хорошее со¬
гласие с экспериментом.
§ 4. Открытие fi-частицы
Помимо описанных выше октетов физикам были известны сле¬
дующие подсистемы барионов, классифицируемые с помощью изо¬
топической группы SU(2): 1) Е*-гипероны (дублет), 2) 2*-гипероны
(триплет), 3) Д-гипероны (квадруплет). Все они образуют приводи¬
мое представление SU (2):
6' = d(V2) + d(l)-M(3/2).
Попытка вложить это представление в рамки группы SU (3) при¬
вела к рассмотрению неприводимого представления этой группы
6 — (симметризованный куб вектора d\). Однако сужение б на
SU(2) не совпадает с б':
6 = d(0) + d('/,)+d(l)-M(3/2).
Естественно было предположить, что синглет d(0) является неот¬
крытой частицей. Изложенная выше схема соответствия между фи¬
зическими величинами и генераторами группы SU(3) позволила вы¬
сказать предположения об изотопическом спине, заряде и гиперза¬
ряде этой неизвестной частицы П. Кроме того, была предпринята
попытка предсказания массы П. На этом расчете мы остановимся
несколько подробнее.
Декуплет б имеет чрезвычайно простую структуру как симмет¬
ризованный тензор третьего ранга для SU(3). Пусть е\, е2, еъ —
ортонормальный базис в трехмерном унитарном пространстве. То¬
гда символы (ijk) = eiejeh, I, j, k = 1, 2, 3, где сомножители ег счи¬
таются перестановочными, образуют базис в пространстве представ¬
ления б. Расположим эти символы в виде следующей схемы, назы¬
ваемой «египетской пирамидой»:
(333)
(332) (331)
(322) (321) (311)
(222) (221) (211) (111)
*) Октет векторных мезонов обычно дополняется до нонета
с помощью присоединения со-мезона (см., например, [157]).

648
ДОБАВЛЕНИЕ 111
Строки этой схемы отвечают неприводимым представлениям под¬
группы SU(2). Вершина египетской пирамиды соответствует син-
глету, который обозначается символом Q. Поправка для массы
з
ищется по формуле ДГ = 3d 2 I *г/з I2, где Xiih—координаты
U 1=1
симметрического тензора в базисе (ijk). Отсюда вытекают следую-,
щие формулы:
Дт(Д) = 0. Дт (2‘) = й, Дт(3*)=2d, Am (Q) = 3d,
т. е. «закон эквидистантности» для строк египетской пирамиды.
Иначе говоря, поправка к массе пропорциональна числу индексов,
равных 3, в символе (ijk).
Для известных ранее частиц закон эквидистантности выпол¬
няется с хорошим приближением. Экспериментальное открытие
Q-гиперона в 1964 г. ([162]) также подтвердило все теоретические
предположения. Таким образом, систематика элементарных частиц
с точки зрения SU(3) сыграла здесь ту же роль, что и таблица
Менделеева при открытии новых элементов.
Гипотеза SU (3)-симметрии позволила также объяснить ряд дру¬
гих закономерностей для адронов (соотношения между магнитными
моментами барионов, интенсивность взаимодействия мезонов с ба-
рионами, вероятности ядерных реакций). За подробностями мы от¬
сылаем читателя к специальной литературе. См., например, [150],
[156], [157], [160].
§ 5. Некоторые проблемы
SU (3)-симметрия не позволяет учитывать такие важные харак¬
теристики частицы, как барионное число (определяется только
Y = В + S), пространственный спин (группа SO(3, R)) и реляти¬
вистская инвариантность (неоднородная группа Лоренца). Все эти
соображения привели к поискам более широких групп симметрии*).
Рассматривались, в частности, компактная группа SU(6) и неком¬
пактная группа SL(2, С) X SL(2, С). О трудностях, возникающих на
этом пути, см., например, [156]. Однако и в рамках SU(3) имеются
некоторые неясности.
Тензорная алгебра группы SU(3) имеет две образующих — d,
и d2 (вектор и бивектор). Имеют ли эти представления реальный
физический смысл? Если это так, то возникает гипотеза «прамате-
рии», из элементов которой (по законам тензорных произведений)
составляются известные элементарные частицы. Физики называют
d 1 и d2 соответственно «кварком» и «антикварком». Согласно об¬
щим формулам § 3 (этого добавления) эти частицы должны иметь
дробные заряды и гиперзаряды (со знаменателем 3) по отношению
к нуклонам. Экспериментально такие частицы до сих пор не обна¬
*) Наряду с SU(3), т. е. с алгеброй Ли А2, рассматривались
также алгебры В2 и G2 ([156]). Однако рассмотрение А2 приводит
к лучшим результатам.

§ 5. НЕКОТОРЫЕ ПРОБЛЕМЫ
649
ружены. С математической точки зрения принятие SU(3) неизбеж¬
но влечет принятие d\, di, однако возможно, что физический смысл
имеет только группа SU(3)/Z, где Z — центр SU(3). Тогда пред¬
ставления d\, di автоматически исключаются *).
Теория унитарной симметрии возникла на базе незначительных
экспериментальных данных, которые не позволяют пока судить
о законах динамики элементарных частиц. Однако даже эти «неяс¬
ные знаки» удалось подвергнуть расшифровке, основываясь на ме¬
тодах теории групп и их представлений. Это дает убедительный
повод считать, что законы теории групп имеют глубокую связь с за¬
конами строения материи.
*) Аргументом в пользу реального существования кварков и
антикварков является особая роль третьего тензорного индекса, на
которой основан вывод формул Гелл-Манна — Окубо. Создается
впечатление, что d\, di— реальные векторные поля, компоненты ко¬
торых испытывают неодинаковое возмущение при переходе от уль-
трасильного к сильному взаимодействию. Заметим также, что гене¬
раторы Ец группы SU(3) могут быть выражены в терминах опера¬
торов рождения и уничтожения для кварков и антикварков
(см. § 57).

ЛИТЕРАТУРА *)
А. Монографии
Ахиезер А. И., Берестецкий В. Б.
[1] Квантовая электродинамика, Гостехиздат, 1953.
Бернер (ВоегпегН.)
[2] Group Representations, Berlin, 1955.
Бернсайд (Burnside W.)
[3] The Theory of Groups of Finite Order, Cambridge, 1911.
Бурбаки (BourbakiN.)
[4] Общая топология (основные структуры), Физматгиз, 1958.
[5] Топологические векторные пространства, ИЛ, 1959.
[6] Elements de mathematique, XXVI: Groupes et algebres de
Lie, Paris, 1960.
Ван - дер-Варден (WaerdenB. L., van der)
[7] Современная алгебра, тт. I, II, Гостехиздат, 1947.
[8] Методы теории групп в квантовой механике, Харьков, 1939.
В е й л ь A. (Weil А.)
[9] Интегрирование в топологических группах и его примене¬
ния, ИЛ, 1950.
Вейль Г. (Weyl Н.)
[10] Классические группы, их инварианты и представления, ИЛ,
1947.
[11] Gruppentheorie und Quantenmechanik, 1931.
[12] Raum, Zeit, Materie, 5-е изд., Berlin, 1923.
Вигнер (W i g n e r E.)
[13] Теория групп и ее приложения к квантовомеханическон тео¬
рии атомных спектров, ИЛ, 1961.
Виленкин Н. Я.
[14] Специальные функции и теория представлений групп, «На¬
ука», 1965.
ВинбергЭ. Б.
[15] Компактные группы Ли (учебное пособие), Изд-во МГУ,
1967.
Винер иПэли (Wiener N., Р а 1 е у R.)
ЦБД Преобразование Фурье в комплексной области, «Наука»,
1964.
*) Звездочкой отмечена литература по теории бесконечномер¬
ных представлений.

ЛИТЕРАТУРА
651
Г е л ь ф а н д И. М., Граев М. И., Виленкин Н. Я.
[16] Интегральная геометрия и связанные с ней вопросы теории
представлений, «Обобщенные функции», вып. 5, Физматгиз,
1962.
ГельфандИ. М., Виленкин Н. Я.
[17] Некоторые применения гармонического анализа: оснащенные
гильбертовы пространства, «Обобщенные функции», вып. 4,
Физматгиз, 1961.
ГельфандИ. М., М и н л о с Р. А., Шапиро 3. Я.
[18] Представления группы вращений и группы Лоренца, Физ¬
матгиз, 1958.
ГельфандИ. М., Р а й к о в Д. А., Шилов Г. Е.
[18'] Коммутативные нормированные кольца, Физматгиз, 1960.
Джекобсон (Jacobson N.)
[19] Алгебры Ли, «Мир», 1964.
Дьедонне (DieudonneJ.)
[20] Основы современного анализа, «Мир», 1964.
ЖелобенкоД. П.
[21] Лекции по теории групп Ли, Дубна, 1965.
Зарисский, Самюэль (Zariski О., Samuel Р.)
[22] Коммутативная алгебра, ИЛ, 1963.
Иосида (YosidaK.)
[22'] Функциональный анализ, «Мир», 1967.
Картан (CartanE.)
[23] Oeuvres completes, ■ partie 1, v. 1, 2, Gauthier-Villars, 1952.
[24] Геометрия групп Ли и симметрические пространства, HJl, 1949.
[25] Теория спиноров, ИЛ, 1947.
[26] Геометрия римановых пространств, ОНТИ, 1936.
Келли (Kelley J.).
[27] Общая топология, «Наука», 1968.
Кириллов А. А.
[27''] Элементы теории представлений групп: I, II (учебное посо¬
бие), Изд-во МГУ, 1966.
Клейн (Klein F.)
[28] Развитие математики в XIX веке, т. I, Физматгиз, 1958.
Колмогоров А. Н., Фомин С. В.
[29] Элементы теории функций и функционального анализа, «На¬
ука», 1968.
К у р о ш А. Г.
[30] Теория групп, «Наука», 1967.
Кэртис и Райнер (Curtis Ch. and Reiner I.)
[31] Теория представлений конечных групп и ассоциативных
алгебр, «Наука», 1968.
Л а и д а у Л. Д., Л и ф ш и ц Е. М.
[ЗГ] Квантовая механика, Физматгиз, 1963.
Л и и Э н г е л ь (L i е S., Е n g е 1 F.)
[32] Theorie der Transformationsgruppen, Leipzig, Bd. 1, 2, 3, 1893.
Литлвуд (Littlewood D.)
[33] The Theory of Group Characters, Oxford, 1950.
Любарский Т. Я.
[34] Теория групп и ее применение к физике, Гостехиздат, 1957.

652
ЛИТЕРАТУРА
Л ю м и с (Loomis L.)
[35] Введение в абстрактный гармонический анализ, ИЛ, 1956.
Монтгомери, Циппин (Montgomery D., Zip pin L.)
[36] Topological Transformations Groups, Interscience, New York,
1955.
НаймаркМ. A.
[37] Линейные представления группы Лоренца, Физматгиз, 1958.
[37'] Нормированные кольца, «Наука», 1969.
Понтрягин Л. С.
[38] Непрерывные группы, Гостехиздат, 1954.
Рака (R а с a h G.)
[39] Group Theory and Spectroscopy, Reprint of the lectures deli¬
vered at the Inst, for Advanced Study, Princeton, 1951.
РашевскийП. K.
[39'] Введение в риманову геометрию и тензорный анализ, «На¬
ука», 1968.
Рисс и Секефальви Надь (Riesz F., Nagy В. von Sz.)
[39"] Лекции по функциональному анализу, ИЛ, 1954.
Серр (Serre J.-P.)
[40] Алгебры Ли и группы Ли, «Мир», 1969.
Фробениус (FrobeniusG.)
[40'] Теория характеров и представлений групп, Харьков, 1937.
Хамермеш (Н amermesh М.)
[41] Теория групп и ее применение к физическим проблемам,
«Мир», 1966.
Хелгасон (HelgasonS.)
[42] Дифференциальная геометрия и симметрические простран¬
ства, «Мир», 1964.
Хейне (Heine W.)
[43] Теория групп в квантовой механике, ИЛ, 1963.
Хуа Ло-ген (Н u a Lo-gen)
[44] Гармонический анализ функций многих комплексных пере¬
менных в классических областях, ИЛ, 1959.
Чеботарев Н. Г.
[45] Теория групп Ли, Гостехиздат, 1940.
Шевалле (ChevalleyC.)
[46] Теория групп Ли, т. 1, ИЛ, 1948; тт. 2, 3, ИЛ, 1958.
Эйзенхарт (EisenchartL. F.)
[47] Непрерывные группы преобразований, ИЛ, 1948.
Б. Журнальные статьи по теории групп
и их представлений
А д о И. Д.
[48] О представлении конечных непрерывных групп с помощью
линейных подстановок, Изв. физ.-матем. о-ва, Казань 7
(1934/1935), 3—43.
Березин Ф. А.
[49]* Операторы Лапласа на полупростых группах Ли, Тр. Моск.
матем. о-ва 6 (1957), 371—463.

ЛИТЕРАТУРА
6БЗ
[50] Письмо в редакцию, Труды Моск. матем. о-ва 12 (1963),
453—466.
[51] Несколько замечаний об ассоциативной оболочке алгебры
Ли, Функциональный анализ и его приложения 1, № 2
(1967), 1—14.
Березин Ф. А., Гельфанд И. М.
[52] Несколько замечаний к теории , сферических функций на
симметрических римановых многообразиях, Тр. Моск. ма¬
тем. о-ва 5 (1956), 311—356.
Березин Ф. А., Гельфанд И. М., Граев М. И., Н а й-
м а р к М. А.
[53] Представления групп, УМН 11 (1956), 13—40.
Б и р к г о ф (В i г k h о f f G.)
[54] Analytical groups, Trans. Amer. Math. Soc. 43 (1938),
61—101.
[55] Representability of Lie algebras and Lie groups by matrices,
Ann. Math. 38 (1937), 526—533.
[56] Lie groups simply isomorphic with no linear group, Bull.
Amer. Math. Soc. 42 (1936), 833—888.
Б'орель, Шевалле (Borel A., Chevalley C.)
[57] The Betti numbers of the exceptional groups, Mem. Amer.
Math. Soc. 14 (1955), 1—9.
Брюа (BruhatF.)
[58]* Работы Хариш-Чандры по теории представлений групп Ли,
Математика (сб. переводов) 6:5 (1962), 43—50.
[59]* Sur les representations induites ’des groupes de Lie, Bull.
Soc. Math. France 84 (1956), 97—205.
Ван-дер-Варден (WaerdenB. L., van der)
[60] Die Klassifikation der einfachen Lieschen Gruppen, Math. Z.
37 (1922), 446—462. (Русский перевод: УМН 4 (1937),
201—274.)
Вейль Г. (W е у 1 Н.)
[61] Theorie der Darstellungen kontinuierlicher halbeinfacher
Gruppen durch linear Transformationen, 1, Math. Z. 23 (1924),
271—304; П, там же 24 (1925), 328—395 (неполный русский
перевод: УМН 4 (1937), 201—246).
Г а п т м а х е р Ф. Р.
[62] Canonical representation of automorphisms of a complex
semisimple Lie group, Матем. сб. 5, № 1 (1939), 101 —144.
[63] On the classification of real simple Lie groups, Матем. сб.
5, № 2 (1939), 217—250.
Гельфанд И. М.
[64] Центр инфинитезимального группового кольца, Матем. сб.
26 (1950), 103—112.
[65]*0 структуре кольца быстро убывающих функций на группе
Ли, ДАН СССР 124, № 1 (1959), 19—21.
Гельфанд И. М., Г р а е в М. И.
[66] Конечномерные неприводимые представления унитарной
и полной линейной группы и связанные с ними специальные
функции, ИАН СССР, сер. матем. 29, № 6 (1965),
1329—1356.

654
ЛИТЕРАТУРА
[66']* Аналог формулы Планшереля для классических групп,
УМН 17, № 1 (1963), 27—76.
[67]* Преобразование Фурье быстро убывающих функций на комп¬
лексных полупростых группах Ли, ДАН СССР 131, № 3
(1960), 496—499.
ГельфандИ. М., НаймаркМ. А.
[68]* Унитарные представления классических групп, Тр. Матем.
ин-та АН СССР им. В. А. Стеклова, XXXVI, Изд-во АН
СССР, 1950.
ГельфандИ. М., Пономарев В. А.
[69]* Представления группы Лоренца, УМН 23, №2 (1968), 3—60.
ГельфандИ. М., Райков Д. А.
[70]* Неприводимые унитарные представления локально биком¬
пактных групп, Матем. сб. 13 (1943), 301—346.
Г ельфанд И. М., Шапиро 3. Я.
[71] Представления группы вращений в трехмерном простран¬
стве и их применения, УМН 7, № 1 (1952), 3—117.
Г ельфанд И. М., Цейтлин М. Л.
[72] Конечномерные представления группы унимодулярных мат¬
риц, ДАН СССР 71, № 5 (1950), 825—828.
[73] Конечномерные представления группы ортогональных мат¬
риц, ДАН СССР 71, № 6 (1950), 1017—1020.
Годеман (GodementR.)
[74]* A theory of spherical functions, I, Trans. Amer. Math. Soc.
73 (1952), 496—556 (неполный русский перевод в сб. «Ма¬
тематика», 5 : 5 (1961), 55—87).
Гординг (GardingL.)
[75]* Vecteurs analitiques dans les representations des groupes de
Lie, Bull. Soc. Math. France 88 (1960), 73—93. (Русский
перевод: «Математика» (сб. переводов) 9:5 (1965), 78—94.)
Диксмье (DixmierJ.)
[76]* Некоторые результаты Хариш-Чандры, «Математика» (сб.
переводов) 6:5 (1962), 23—32.
Д ы н к и и Е. Б.
[77] Структура полупростых алгебр Ли, УМН 2, № 4 (1947),
59—127.
[78] О представлении ряда log (exev) для некоммутирующих х, у
через коммутаторы, Матем. сб. 25 (1949), 155—162.
[79] Нормированные алгебры Ли и аналитические группы, УМН
5, № 1 (1950), 135—186.
[80] Максимальные подгруппы классических групп, Тр. Моск.
матем. о-ва 1 (1952), 349—466.
Д ы н к и н Е. Б., О н и щ и к А. Л.
[81] Компактные группы Ли в целом, УМН 10 (1955), 3—74.
Желобенко Д. П.
[82]* О гармоническом анализе функций на полупростых груп¬
пах Ли, I, ИАН СССР, сер. матем. 27, № 6 (1963),
1343—1396.
[83] Описание всех неприводимых (конечномерных) представле¬
ний произвольной связной группы Ли, ДАН СССР 139.
№ 6 (1961), 1291—1294.

ЛИТЕРАТУРА
655
[84] Классические группы. Спектральный анализ конечномерных
представлений, УМН 17, № 1 (1962), 27—120.
[85] К теории линейных представлений комплексных и веществен¬
ных групп Ли, Тр. Моск. матем. о-ва 12 (1963), 53—98.
[86]* Описание некоторого класса линейных представлений груп¬
пы Лоренца, ДАН СССР 121, № 4 (1958), 586—589.
[87]* Линейные представления группы Лоренца, ДАН СССР 126,
№ 5 (1959), 935—938.
[87']* Симметрия в классе элементарных представлений полупро¬
стой комплексной группы Ли, Функциональный анализ и его
приложения 1, № 2 (1967), 15—38.
[88]* Анализ неприводимости в классе элементарных представле¬
ний полупростой комплексной группы Ли, ИАН СССР, сер.
матем. 32, № 1 (1968), 108—133.
[89]* Операционное исчисление и теоремы типа Пэли — Винера
для полупростой комплексной группы Ли, ДАН СССР 170,
№ 6 (1967), 1243—1246.
[90]* Аналог теории Картана — Вейля для бесконечномерных
представлений полупростой комплексной группы Ли, ДАН
СССР 171, № 5 (1967), 24—27.
Ж е л о б е н к о Д. П., Н а й м а р к М. А.
[91]* Описание вполне неприводимых представлений полупростой
комплексной группы Ли, ДАН СССР 171, № 1 (1967), 25—28.
Ивасава (Iwasawa К)
[92] On some types of topological groups, Ann. Math. 50 (1949),
507—558.
Казимир, Ван-дер-Варден (Casimir H., Waer-
den B. L„ van der)
[93] Algebraischer Beweis der vollstandigen Reduzibilitat der
Darstellungen halbeinfacher Lieschen Gruppen, Math. Ann. 11
(1935), 1—12.
Картан (Cartan E.)
[94] Sur la structure des groupes de transformations finis et con¬
tinue, These, Paris, Nony, 1894; 2-е изд., Vuibert, 1933.
[95] Les groupes projectives qui ne laissent invariante aucune mul¬
tiple plane, Bull. Soc. Math. France 41 (1931), 53—96.
[96] Les groupes reels simples et continus, Ann. Sci. Ecole Norm.
Sur. 31 (1914), 263—355.
[97] Les tenseurs irreductibles et les groupes simples et semi¬
simples, Bull. Sci. Math. 49 (1925), 130—152.
Картье (Cartier P.)
[98]* Представления групп Ли (по Хариш-Чандре), «Математи¬
ка» (сб. переводов) 6:5 (1962), 33—41.
[99] О формуле характера Г. Вейля, «Математика» (сб. перево¬
дов) 6:5 (1962), 139—141.
К а р т ь е, Д и к с м ь е (Cartier P., D i х m i е г J.)
[100]* Vecteurs analytiques dans les representations des groupes
de Lie, Amer. J. Math. 80 (1958), 131—145.
Киллинг (Killing W.)
[101] Die Zusammensetzung der stetigen endlichen Transformation
gruppen, I, Math. Ann. 32 (1888), 252—290; II, там же 33

656
ЛИТЕРАТУРА
(1889), 1—48; 111, там же 34 (1889), 57—122; IV, там же
36 (1890), 161 — 189.
Кириллов А. А.
[102]* Унитарные представления нильпотентных групп Ли, УМН
17, № 4 (1962).
К л е й н (С 1 е i n F.)
[103] Сравнительное обозрение новейших геометрических иссле¬
дований («Эрлангенская программа»), Казань, 1896.
К л и м ы к А. У.
[104] О кратностях весов неприводимых представлений полупро¬
стой комплексной группы Ли, ДАН СССР 177, № 5 (1967),
1001 — 1004.
К р е й н М. Г.
[105] Принцип двойственности для бикомпактной группы и квад¬
ратной блок-алгебры, ДАН СССР 69, № 6 (1949), 725—729.
Леви (Levi Е.)
[106] Sulla struttura dei gruppi finiti e continui, Atti Accad. Torino
40 (1905), 3—17.
Макки (MackeyG. W.)
[107]* Бесконечномерные представления групп, «Математика» (сб.
переводов) 6:6 (1962), 57—103.
[107']* Induced represetations of locally compact groups, Ann. Math.
55, No. 1. (1952), 101 — 139.
[107"] Imprimitivity for representations of locally compact groups,
Proc. Nat. Acad. Sci. USA 35, No. 4 (1949), 537—545.
Мальцев А. И.
[108] Об односвязности нормальных делителей группы Ли, ДАН
СССР 34, № 1 (1942), 12-151.
[109] Подгруппы групп Ли в целом, ДАН СССР 36, № 1 (1942).
[110] О разложении алгебры Ли в прямую сумму радикала и по¬
лупростой подалгебры, ДАН СССР 36, № 2 (1942), 46—50.
[111] О линейных связных локально замкнутых группах, ДАН
СССР 40, № 3 (1943), 108—110.
[112] О полупростых подгруппах групп Ли, ИАН СССР, сер. ма-
тем. 8 (1944), 143—174.
[113] On the theory of the Lie groups in the large, Матем. сб. 16
(1945), 163—190.
[114] О разрешимых алгебрах Ли, ИАН СССР, сер. матем. 9
(1945), 329—356.
[115] Коммутативные подалгебры полупростых алгебр Ли, ИАН
СССР, сер. матем. 9 (1946), 291—300.
Митягин Б. С.
[115'] Аппроксимативная размерность и базисы в ядерных про¬
странствах, УМН 16, № 4 (1961), 63—132.
Морозов В. В.
[116] О нильпотентном элементе в полупростой алгебре Ли, ДАН
СССР 36, № 3 (1942), 91—94.
Наймарк М. А.
[117]* Бесконечномерные представления групп и смежные вопросы,
серия «Итоги науки»: Математический анализ, Теория вь
роятностей, Регулирование, ВИНИТИ, 1964.

ЛИТЕРАТУРА
657
Нейман (Neumann J.)
[118] Zum Haarischen Mass in topologishen Gruppen, Comp. Math.
1. Nr. 1 (1934), 106—114. (Русский перевод: УМН 2 (1936),
168—176.)
H e й м а н, ф о н (Neumann J. von).
[118'] Die Eidentigkeit der Schrodingerschen Operatoren, Math. Ann
104, Nr. 3 (1931), 570.
Нельсон (Nelson E.).
[119]* Analytic vectors, Ann. Math. 70 (1959), 572—615. (Русский
перевод: «Математика» (сб. переводов) 6-3 (19621
89—132.)
Н о м и д з у (N о m i d z u К.)
[120] Invariant affine connections on homogeneous spaces, Amer.
J. Math. 76 (1954), 33—65.
Партасарати, Ранга Pa о, Варадараджан (Partasa-
rathy К. P., Ranga Rao V. S., V a г a d a r a j a n)
[121]* Representations of complex semisimple Lie groups and Lie
algebras, Ann. Math. 85, No. 3 (1967), 383—429.
Переломов А. М., П о п о в В. С.
[122] Операторы Казимира для групп Щя) и SU(n), Ядерная
физика 3, № 5 (1966), 924—931.
[123] Операторы Казимира для ортогональной и симплектиче-
ской групп, Ядерная физика 3, № 6 (1966), 1127—1134.
Петер, Вейль Г. (Peter F., W е у 1 Н.)
[124] Die Voilstandigkeit der primitiven Darstellungen einer ge-
schiossenen kontinuierlichen Gruppe, Math. Ann. 97 (1927),
737—755. (Русский перевод: УМН 2 (1936), 144—160.)
P а ш e в с к и й П. К.
[125] О некоторых основных теоремах теории групп Ли, УМН 8,
№ 1 (1953).
[126] Теория спиноров, УМН 10, № 2 (1954).
[127] Ассоциативная сверхоболочка алгебры Ли, ее регулярное
представление и идеалы, Тр. Моск. матем. о-ва 15 (1966),
3—54.
Семинар «С о ф у с Л и»
[128] Теория алгебр Ли. Топология групп Ли. ИЛ, 1962.
Сигал (Segal I.)
[129]* On extension of Plancherel formula to separable unimodular
groups, Ann. Math. 52, No. 2 (1950), 272—292.
Сирота А. И., Солодовников A. C.
[130] Некомпактные полупростые группы Ли, УМН 18 (1963),
87—144.
Стоун (S t о n е М. Н.)
[130'] Linear transformations in Hilbert space, III, Operational
methods and group theory, Proc. Nat. Acad. Sci. USA 16,
No. 1 (1930).
[130"] On one-parameter unitary group in Hilbert space, Ann. Math.
33, No. 4 (1932), 643—648.
Таннака (Tannaka T.)
[131] Ober Dualitatsatz der nichtkommutativen topologischen Grup¬
pen, Tohoku Math. 53 (1938), 1—12.

658
ЛИТЕРАТУРА
Тацуума (Tatsuuma Nobuhiko)
[131'] A duality theorem for locally compact groups, Math. Kyoto
Univ. 6, No. 2 (1967), 187-293.
T и т с (T i t s J.)
[131"] Классификация полупростых алгебраических групп, «Ма¬
тематика» (сб. переводов) 12:2 (1968), 110—143.
Фрейденталь (Freudenthal Н.)
[132] Zur Berechnung der Charakler der halbeinfachen Lieschen
Gruppen, 1, 11, 111, Indag Math. 16 (1954), 369—376,487—492;
18 (1956), 511—514.
[133] Октавные особые группы и октавная геометрия, «Матема¬
тика» (сб. переводов) 1 : 1 (1957), 117—133.
Хаар (Нааг А.)
[134] Der Massbegriff in der Theorie der Kontinuierlichen Gruppen,
Ann. Math. 34 (1933), 147—169.
Хант (H u n t G. A.)
[135] A theorem of Elie Cartan, Proc. Amer. Math. Soc. 7 (1956),
307—308.
Хариш-Чандра (Harish-Chandra)
[136] On the radical on Lie algebra, Proc. Amer. Math. Soc. 1
(1950), 14-17.
[137] Lie algebras and the Tannaka duality theorems, Ann. Math.
51 (1950), 299—330.
[138] On some applications of the universal enveloping algebra of
a semi-simple Lie algebra, Trans. Amer. Math. Soc. 70 (1951),
28—96.
[139]* Plancherel formula for the 2X2 real unimodular group, Proc.
Nat. Acad. Sci. USA 38 (1952), 337—34,2.
[140]* The Plancherel formula for complex semi-simple Lie groups,
Trans. Amer. Math. Soc. 76 (1954), 485—528.
Хелгасон (Helgason S.)
[141] Some results on invariant theory, Bull. Amer. Math. Soc. 68
(1962).
ХуПи-ю (HouPei-yu)
[142] Orthonormal bases and infinitesimal operators of the irre¬
ducible representations of group U„, Scientia sinica 15, No. 6
(1966), 763.
Шевалле (ChevalleyC.)
[143] The Betti numbers of the exceptional Lie groups, Proc. Intern.
Congr. of Math., Harvard, II (1950), 21—24.
[144] Invariants of finite groups, generated by reflections, Amer.
J. Math. 77 (1955), 778—782.
[145] Sur certains groupes simples, Tohoku Math. J. 7, No. 1
(1955), 14—66.
Шевалле, Эйленберг (Chevalley С., Eilenberg S).
[146] Cohomology theory of Lie groups and Lie algebras, Trans.
Amer. Math. Soc. 63 (1948), 85—124.
Шрайер (SchreierO.)
[147] Abstrakte kontinuierliche Gruppen, Abh. Math. Sem. Univ.
Hamburg 4 (1925), 15—32,

ЛИТЕРАТУРА
659
Штейнберг (Steinberg R.)
[147'] A general Clebsh-Gordan theorem. Bull. Amer. Math. Soc.
67 (1961), 406 407. (Русский перевод: «Математика» (сб.
переводов) 6:5 (1962), 142—143.)
Юнг (Joung А.)
[148] On the quantitative substitutional analysis, Proc. Lond. Math.
Soc. 33 (1900), стр. 97; 34 (1902), стр. 361.
В. Журнальные статьи по приложениям
теории групп в теоретической физике
Баргман, Мошинский (Bargmann V., Moshinsky М.)
[149] Group theory of harmonic oscillators, I, II, Nuclear Physics
18 (I960), 697; 23 (1961), 177.
Берестецкий В. Б.
[150] Динамические симметрии сильно взаимодействующих частиц,
УФН 85, № 3 (1965), 393—444.
Вигнер (W i g п е г Е.)
[151] Симметрия и законы сохранения, УФН 83, № 4 (1964),
729—736. '
Виленкин Н. Я., С м о р о д и н с к и й Я. А.
[152] Инвариантные разложения релятивистских амплитуд, ЖЭТФ
46, № 5 (1964), 1793.
Дайсон (DysonF.)
[153] Математика и физика, УФН 85, № 2 (1965), 351—364.
Малкин И. А., М а н ь к о В. И.
[154] Симметрия атома водорода, Ядерная физика 3, вып. 2
(1966), 372—382.
Мошинский (Moshinsky М.)
[155] Bases for irreducible representations of the unitary group and
some applications, J. Math. Phys. 4, No. 9 (1962), 1128.
Сборники статей
[156] Теория групп и элементарные частицы (сб. статей под ред.
Д. Иваненко), «Мир», 1967.
[157] Физика высоких энергий и теория элементарных частиц, сб.
статей, изд-во «Наукова думка», Киев, 1967.
[158] Элементарные частицы и компенсирующие поля, Сб. перево¬
дов под ред. Д. Иваненко, «Мир», 1964.
Д е С в а р т (S w а г t J. d е)
[159] Октетная модель элементарных частиц, УФН 84, № 4 (1964),
651—692.
С м о р о д и и с к и й Я. А.
[160] Унитарная симметрия элементарных частиц, УФН 84, № 1
(1964), 3—36.
Фок В. А.
[161] Zur Theorie des Wasserstoffatoms, Zeitschr. fur Phys. 98,
Nr. 1 (1935), 145.
Фаулер, Сеймиос (Fowler W., S a m i о s N.)
[162] Открытие омега-минус-частицы, УФН 85, № 3 (1965), 523

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоморфизм группы 17
— — внутренний 17
— зеркальный в S0(я) 515
— инволютивный 433
Алгебра (ассоциативная) 46
— групповая 105
— Клиффорда 65, 521
— коммутаторная 91, 96
— Ли 32
бикомплексная 186
— — классическая 435
— — коммутативная 34
—■ — компактная 406
комплексная 66
— — линейная 48, 386
— — нильпотентная 380, 388
— — особая простая 435
полупростая 378, 397
простая 378
разрешимая 380, 381, 385,
395
редуктиниая 377, 401
Базис Гельфанда—Цейтлина 302
— Картана—Вейля 415, 426
Блок-алгебра 481
Вектор аналитический 175
— вакуума 246
— дифференцируемый 145
— доминантный 353
■— инвариантный 79
■— старший (младший) 151, 196,
487, 542
— строго доминантный 558
— целочисленный 557
Векторное поле на группе Ли 40
ковариантное 40
Вес алгебры Ли 390
— индуктивный 213, 490
— инфииитезимальный 295, 492
-- старший (младший) 151, 195,
205, 487, 542
Геодезические в группе Ли 44
компактной группе Ли
457, 459
Гомеоморфизм 63
Гомоморфизм 34
Группа 15
—■ абелева 16, 398, 399
— алгебраическая 442
— аналитическая 27
— вращений SO (3, R) 16,61, 164
— Вейля 194, 470
— дискретная 20
— коммутативная 16
— компактная 112
— комплексно ортогональная
О (я, С) 55
—• конечная 16
— Ли 27
бикомплексная 186
— — компактная 112
— — комплексная 66
— — локальная 174
— — надкомпактная 398
— — нильпотентная 182
— — полупростая 398, 401
— — простая 398, 401
— — разрешимая 398
редуктивная 398, 401
— — связная 27
— линейная 21
— — классическая 57
— локально евклидова 25

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
661
Группа локально связная 26
— матричная 21
— нильпотентная 399
— односвязная 38
— ортогональная О (л) 23, 55,
112
— ортогонально-унитарная,
ОЩя) 56
— параметрическая 25
— полная линейная GL(rz) 21,
22, 46, 64
— псевдоортогональная О (p,q)
55, 112
— псевдоунитарная U (p,q) 56,
112
— Пуанкаре (фундаментальная)
39, 464
— разрешимая 399
— симметрии оператора -92
— симметрическая S (я) 136
— симплектическая Sp (я) 55,
506
— симплектически унитарная
SpU (я) 57
— собственно ортогональная
SO(n) 56, 514
унитарная SU(«) 56, 62,
63
— спинорная Spin (я) 66, 521
— унимодулярная SL(rc) 48, 64
— унитарная Щя) 49, 56, 64,
112, 139
— циклическая 138
Делитель дискретный 39
— нормальный 18, 375
Детерминанты Вейля 366
Диаграмма весовая 194
— Юнга 226
Дифференциал представления 143
— d(а) 320
Дифференцирование в алгебре
Ли 373, 398
— внутреннее 374
Идеал в алгебре Ли 375
ассоциативной алгебре
102, 440
Изоморфизм групп Ли 34
— локальный 36
SO(3, /?), SU (2) 60, 374
Индикаторная система 287 357
496, 497, 581
Камера Вейля 470
Кватернион вещественный 60
— комплексный 57
— сопряженный 58
Класс смежности в группе 63
— сопряженных элементов 132
Коммутатор в алгебре Ли 32
— — ассоциативной алгебре 32,
48, 106, 251
группе 31
Комплексная оболочка (ком-
плексификация) алгебры
(группы) Ли 67
— — правильная 177
Компонента единицы связная 20
— представления 80
Корень в алгебре Ли 391
— простой 418
Корневая система полупростой
алгебры Ли 412, 420, 426
простой алгебры Ли 436
фундаментальная 474
Корневое подпространство 391
Коэффициенты Клебша — Гор¬
дана 108, 362
Критерий полупростоты 397
— разрешимости Картана 395
Лемма Больцано-Вейерштрасса
111
— Гейне — Бореля 111,
— Шура 94
Матрица 21
— Клебша — Гордана 351, 481
— положительно определенная
49
—, след 43, 48
— структурная Картана 421
— трансформационная 40
Матрицы Паули 58
Матричные элементы группы 87
— — —,свойство ортогонально¬
сти 119
SU(2) 157
■ представления 87
Мера (объем) множества 45
— на группе 45

662
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Мера на группе право (ле¬
во-) инвариантная 45
— Хаара 45
— — на компактной группе Ли
113
Метрика риманова 43
Множество (абстрактное) 15
— компактное в метрическом
пространстве 111
— матриц неприводимое 99
приводимое 99
Мультиплет группы Ли 531
Обмотка тора иррациональная
77, 140, 170
Оболочка ассоциативная алгеб¬
ры Ли 106
— бикомплексная алгебры Ли
185
— — группы Ли 186
— комплексная группы Ли 67
правильная 177, 467, 480
Образующая тора иррациональ¬
ная 140, 460
Образующие в группе 26
Оператор Гамильтона 92, 638
— инфинитезимальный 143
— Лапласа 92
— массы-энергии 247
— переплетающий 82
Операторы Бозе 245
— Казимира 147, 149, 254, 569
Орбита (траектория) точки 77,
86
Осциллятор гармонический 245
Параметры Кэли — Клейна 60
Подалгебра алгебры Ли 33
— Картана 410, 447, 461, 468
—■ —, автоморфизмы 424
Подгруппа 17
— аналитическая 33
— борелевская 611
— инвариантная 18
— Картана 451, 461, 468
— коммутаторная 40!
— максимальная компактная
468
— нормально вложенная 494,
582
Подгруппа однопараметрическая
29
— однопараметрическая, произ¬
водящий оператор 143
— регулярно вложенная 582
— стационарная 84
Подпространство инвариантное
79
— неприводимое 80
— нетривиальное 79
Поливекторы 217
Полином гармонический 164
Полугруппа 218
Представление алгебры Ли 144,
374
— контрагредиентное 145
— аналитическое (антианалити-
ческое) 178, 188
— группы 76, 78
вполне приводимое 80
дуальное 96
— — квазирегулярное 85
контрагредиентов 81, 95
полуприводимое 169, 606,
622
приводимое 80
— — присоединенное 374
— —, размерность 79
регулярное 85
— — топологически непригодл
мое 89
— — унитарное 82
— индуцированное 629
— кратное 80
— полуприводимое 169
— спинорное 165, 518, 586
— точное (изоморфное) 108,
115, 467
— циклическое со старшим ве¬
сом 542
Представления эквивалентные 79
Принцип аналитического про¬
должения 181
— взаимности (для вполне при¬
водимых матричных алгебр)
102
— полной приводимости 115
Произведение локально прямое
(топологических групп) 186
— полупрямое 631
— прямое групп 24

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Произведение прямое топологи-
• ческих пространств 63
— тензорное операторов 70
представлений алгебры Лн
145
— — — групп 81, 351, 590
— Юнга 218, 491
Пространство линейное 21
— — сопряженное (дуальное)
69
— — топологическое 89
— однородное 75
— — универсальное 84
— топологическое 19, 20
— — компактное 112
— — локально компактное 113
Радикал алгебры Ли 402
Разложение Гаусса в GL(n) 51
■ — полупростой комплекс¬
ной группе Ли 450
— — обобщенное 451, 494
— Грама в GL(n) 52
— Ивасавы 456
— Картана 434
-— Картана — Вейля 447, 540
— полярное в алгебре кватер¬
нионов 61
— GL{«) 49
— Фиттинга в алгебре Ли 392,
411
Ряд Кемпбелла — Хаусдорфа 32
— Фурье на компактной группе
Ли 115, 122
на однородном простран¬
стве с компактной группой
движений 132
— по характерам 133
Сигнатура 225, 492
Симметризаторы Юнга 227
— — центральные 230
Симметрия относительно точки
457
Соотношения Клебша — Горда-
на 476
Структурные константы 33
Схемы Дынкина 428, 435
Тело кватернионов 60
— —, автоморфизмы 61
Тензор 43, 71
— ковариантный (контравари-
антный) 71
— кососимметрический 44, 72
— метрический 43
— симметрический 72
— смешанный 71
Теорема Биркгофа — Витта 254
— Веддерберна 102
— глобальная (для компактной
группы Ли) 114
— Картана 468
— Кириллова 633
— Леви — Мальцева 402
— Ли 382, 384
— — глобальная 400
— Наймарка 625
— Петера — Вейля (основная
аппроксимационная) 115
— Стоуна — Вейерштрасса 121
— Стоуна — фон Неймана 625,
627
— Хана — Банаха 126
— Шевалле 566
— Энгеля 386
Теоремы Бернсайда 100, 135
Теория двойственности 108, 480
— представлений конечных
групп 134
Тор двумерный 63
— максимальный 459
Универсальная линейная группа
529
— накрывающая 38
— — компактной группы Лн
140, 462
— обертывающая алгебра 106,
251
—.центр 271, 569
Усреднение по Гурвицу 116
Фактор-алгебра 376
Фактор-группа 376
Фактор-пространство 62
Фактор-топология 62
Форма билинейная 53
Киллинга —- Картана 395,
397, 427
— вещественная алгебры (груп¬
пы) Ли 67, 431, 434

664
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Форма дифференциальная 41
— — право (лево-) инвариант¬
ная 41
— ковариантная (контравари-
антная) 72
— кососимметрическая 72
— полилинейная 72
— симметрическая /2
— эрмитова (полуторалинейная)
53
Формула Костанта 564
— Фрейденталя 550
Формулы Вейля для характеров
338, 347, 561
Функции сферические 163, 601
— шаровые 163
Функция волновая 638
Характер абелевой группы 99
— представления 133, 331
— примитивный 335
Центр алгебры Ли 376
— группы 39, 376
— компактной группы Ли 140,
462
— универсальной обертывающей
алгебры 254, 271
Централизатор 172
Центральный ряд в алгебре Ли
388
— группе Ли 399
— элемент группы 39
Экспоненциал 46
Экспоненциальное отображение
(ехр) 31, 47, 456
Элемент регулярный в алгебре
(группе) Ли 463
Ядро гомоморфизма 34
2-инвариантов метод 209, 221,
356, 580
2-мультипликаторы 294

ОГЛАВЛЕНИЕ
Предисловие 8
ЧАСТЬ 1
ВВЕДЕНИЕ
Глава I. Топологические группы. Группы Ли 15
§ I. Определение группы 15
§ 2. Топологические группы 19
§ 3. Параметрические группы и группы Ли 25
§ 4. Теория Ли 28
§ 5. Локально изоморфные группы Ли 34
§ 6. Инвариантные формы на группе Ли 40
§ 7. Метрика. Мера Хаара 42
Глава II. Линейные группы 48
§ 8. Полная линейная группа. Экспоненциал .... 46
§ 9. Полная линейная группа. Основные разложения 48
§ 10. Линейные группы, связанные с формами второго по¬
рядка 53
§ 11. Кватернионы 57
§ 12. Вопросы односвязности 62
§ 13. Вопросы комплексификации 66
§ 14. Преобразования в классе тензоров 68
Глава III. Основные задачи теории представлений .... 74
§ 15. Функции на однородном пространстве 74
§ 16. Терминология теории представлений 78
§ 17. Редукция основной проблемы 84
§ 18. Элементарные гармоники 86
§ 19. Алгебры и группы, связанные с уравнением ... 91
§ 20. Лемма Шура 94
§ 21. Теорема Бернсайда 99
§ 22. Групповые алгебры и их представления 103
§ 23. Формулировка основных задач 106

4
ОГЛАВЛЕНИЕ
ЧАСТЬ II
ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
Глава IV. Компактные группы Ли. Глобальная теорема . .111
§ 24. Определение компактной группы 111
§ 25. Формулировка глобальной теоремы 114
§ 26. Прием усреднения 116
§ 27. Свойство ортогональности 119
§ 28. Аппроксимациопная лемма для линейной группы G 120
§ 29. Ряды Фурье на линейной группе G 122
§ 30. Завершение доказательства для линейной группы G 124
§ 31. Завершение доказательства в общем случае . . .127
§ 32. Гармонический анализ на однородном многообразии 129
§ 33. Характеры 132
§ 34. Теория представлений конечных групп 134
§ 35. Универсальность группы U(ra) 139
Глава V. Инфинитезимальный метод в теории представлений 142
§ 36. Дифференциал представления 142
§ 37. Неприводимые представления группы SU(2) . . .147
§ 38. Матричные элементы группы SU(2) 157
§ 39. О некоторых группах, связанных с SU (2) .... 164
§ 40. О некоторых проблемах инфинитезимального метода 170
Глава VI. Аналитическое продолжение 176
§ 41. Общий принцип аналитического продолжения . . 176
& 42. Надкомпактпые группы Ли. «Унитарный трюк»
Г. Вейля .182
§ 43. Бикомплексные группы и алгебры Ли 185
§ 44. Комплексная оболочка U(ra). Веса и корни . . .191
§ 45. Модель неприводимых представлений группы SU(3) 196
Глава VII. Неприводимые представления группы L (га) . , . 203
§ 46. Существование старшего веса 203
§ 47. Единственность старшего вектора 207
§ 48. Различные модели d(а) 210
§ 49. Индуктивные веса 213
§ 50. Произведение Юнга 216
Глава VIII. Тензоры и диаграммы Юнга 220
§ 51. Описание Z-инвариантов 220
§ 52. Диаграммы Юнга 224
§ 53. Симметризаторы Юнга 227
§ 54. Характеристика неприводимых тензоров н терминах
симметрии 231
§ 55. Припцип взаимности 237
§ 56. Реализация d(а) на прямоугольных матрицах . . 241
§ 57. Гармонический осциллятор 244

ОГЛАВЛЕНИЕ
5
Глава IX Операторы Казимира 250
§ 58. Универсальная обертывающая алгебра 250
§ 59. Операторы Казимира для группы QL (я) .... 255
§ 60. Собственные значения операторов С* ..... . 259
§ 61. Разделение точек спектра и алгебраическое доказа¬
тельство полной приводимости 265
§ 62. Полное описание центра для группы GL(n) . . . 269
§ 63. Правило циклов 272
Глава X. Индикаторные системы и базис Гельфанда — Цейт¬
лина 282
§ 64. Операторы левого сдвига на группе Z 282
§ 65. Индикаторные системы 287
§ 66. Алгебра Z-мультипликаторов и задача о сужении с
группы на подгруппу 293
§ 67. Базис Гельфанда — Цейтлина 300
§ 68. Понижающие операторы в инфинитезимальной форме 305
§ 69. Нормировка базисных векторов ........ 315
§ 70. Дифференциал rf(a) 320
§ 71. Матричные элементы d(a) 325
Глава XI. Характеры 331
§ 72. Инвариантная мера на группе U(n) 331
§ 73. Примитивные характеры 0 (гг) 335
§ 74. Весовая диаграмма d{a) 338
§ 75. Вторая формула Вейля 345
§ 76. Заключительные замечания 349
•Глава XII. Тензорное произведение двух неприводимых пред¬
ставлений группы U (я) 351
§ 77. Метод характеров 351
§ 78. Метод Z-инвариантов . 356
§ 79. Частные случаи 361
§ 80. Детерминанты Вейля 366
ЧАСТЬ ill
ОБЩАЯ ТЕОРИЯ
Глава XIII. Основные типы алгебр и групп Ли ...... 373
§ 81. Присоединенное представление алгебры Ли . . . 373
§ 82. Идеал и нормальный делитель 375
§ 83. Основные типы алгебр Ли 377
§ 84. Разрешимые алгебры Ли 381
§ 85. Нильпотептные алгебры Ли 385
§ 86. Разложения Фиттинга 389
§ 87. Билинейная форма Киллинга — Картана 395
§ 88. Основные типы групп Ли 398
§ 89. Теорема Леви — Мальцева 402

6
ОГЛАВЛЕНИЕ
Глава XIV. Классификация компактных и редуктивных ал¬
гебр Ли 406
§ 90. Компактные алгебры Ли 406
§ 91. Подалгебры Картана 410
§ 92. Базис Картана — Вейля 414
§ 93. Простые корни 417
§ 94. Структурная матрица Картана 421
§ 95. Простые комплексные алгебры Ли 425
§ 96. Вещественные формы полупростых комплексных
алгебр Ли 431
§ 97. Завершение классификации 434
Глава XV. Компактные группы Ли в целом 439
§ 98. Инвариантные полиномы . 439
§ 99. Алгебраические группы 442
§ 100. Разложение Гаусса 446
§ 101. Разложение Ивасавы 452
§ 102. Максимальные торы 456
§ 103. Фундаментальная группа и центр 462
§ 104. Теорема о линейности полупростой комплексной
группы Ли 466
§ 105. Группа Вейля 469
§ 106. Существование комплексной оболочки 474
§ 107. Некоторые дополнительные результаты .... 480
Глава XVI. Описание неприводимых конечномерных пред¬
ставлений 486
§ 108. Основная теорема 486
§ 109. Старшие веса и сигнатуры 490
§ 110. Нормально вложенные подгруппы 494
§111. Полиномы на группе Z 496
§ 112. Завершение классификации 501
§ 113. Симплектическая группа 506
§ 114. Ортогональная группа 514
§ 115. Теория спиноров 521
§ 116. Вещественные формы 526
§ 117. Произвольные связные группы Ли 529
§ 118. Несколько замечаний 532
Глава XVII. Инфинитезимальная теория (характеры, веса,
операторы Казимира) 539
§ 119. Разложение Картана — Вейля в универсальной
обертывающей алгебре 539
§ 120. Представления со старшим вектором 542
§ 121. Классификация конечномерных неприводимых
представлений алгебры X 540
§ 122. Формула Фрейденталя 550
§ 123. Формула Вейля для характеров 556
§ 124. Следствия из формулы Вейля 563
§ 125. Полиномы на картановской подалгебре, инвариант¬
ные относительно группы Вейля 565

ОГЛАВЛЕНИЕ
§ 126. Операторы Казимира 569
§ 127. О вычислении собственных значений операторов
Казимира 573
Глава XV111. Некоторые задачи спектрального анализа ко¬
нечномерных представлений 579
§ 128. Общая схема сужения с группы на подгруппу . . 579
§ 129. Сужение SO (гг) /SO (п — 1) 582
§ 130. Сужение Sp(n)/Sp(n — 2) 587
§ 131. Тензорное произведение двух неприводимых пред¬
ставлений 590
§ 132. Сужения SU(m + rt)/SU(m) X SU(/i) и
SU(m«)/SU(m) X SU(rc) 592
§ 133. Сужение SU(n)/SO(«) 596
§ 134. Сферические функции в n-мерном евклидовом про¬
странстве 601
§ 135. О представлениях группы движений п-мерного ев¬
клидова пространства 606
Добавление 1. О бесконечномерных представлениях полу¬
простой комплексной группы Ли . . . .611
§ 1. Элементарные представления 611
§ 2. Пространство элементарного представления . . . 613
§ 3. Дифференциал элементарного представления . . .614
§ 4. Вопросы неприводимости 616
§ 5. Аналог формулы Планшереля 617
§ 6. Теоремы типа Пэли—Винера 619
§ 7. Минимальные представления 620
§ 8. Классификация неприводимых представлений . . . 621
§ 9. О полуприводимых представлениях 622
Добавление II. Элементы общей теории унитарных пред¬
ставлений локально компактных групп . . 623
§ 1. Коммутативные группы 623
§ 2. Теорема Стоуна — фон Неймана 625
§ 3. Индуцированные представления 628
§ 4. Полупрямые произведения 631
§ 5. Нильпотентные группы Ли 633
§ 6. Разложение унитарных представлений на неприво¬
димые 635
Добавление III. Унитарная симметрия в классе элементар¬
ных частиц 638
§ 1. Инвариантность и законы сохранения 638
§ 2. Элементарные частицы. Изотопический спин . . 641
§ 3. Унитарная симметрия в классе адронов 643
§ 4. Открытие Q-частицы 647
§ 5. Некоторые проблемы 648
Литература 650
Предметный указатель 660