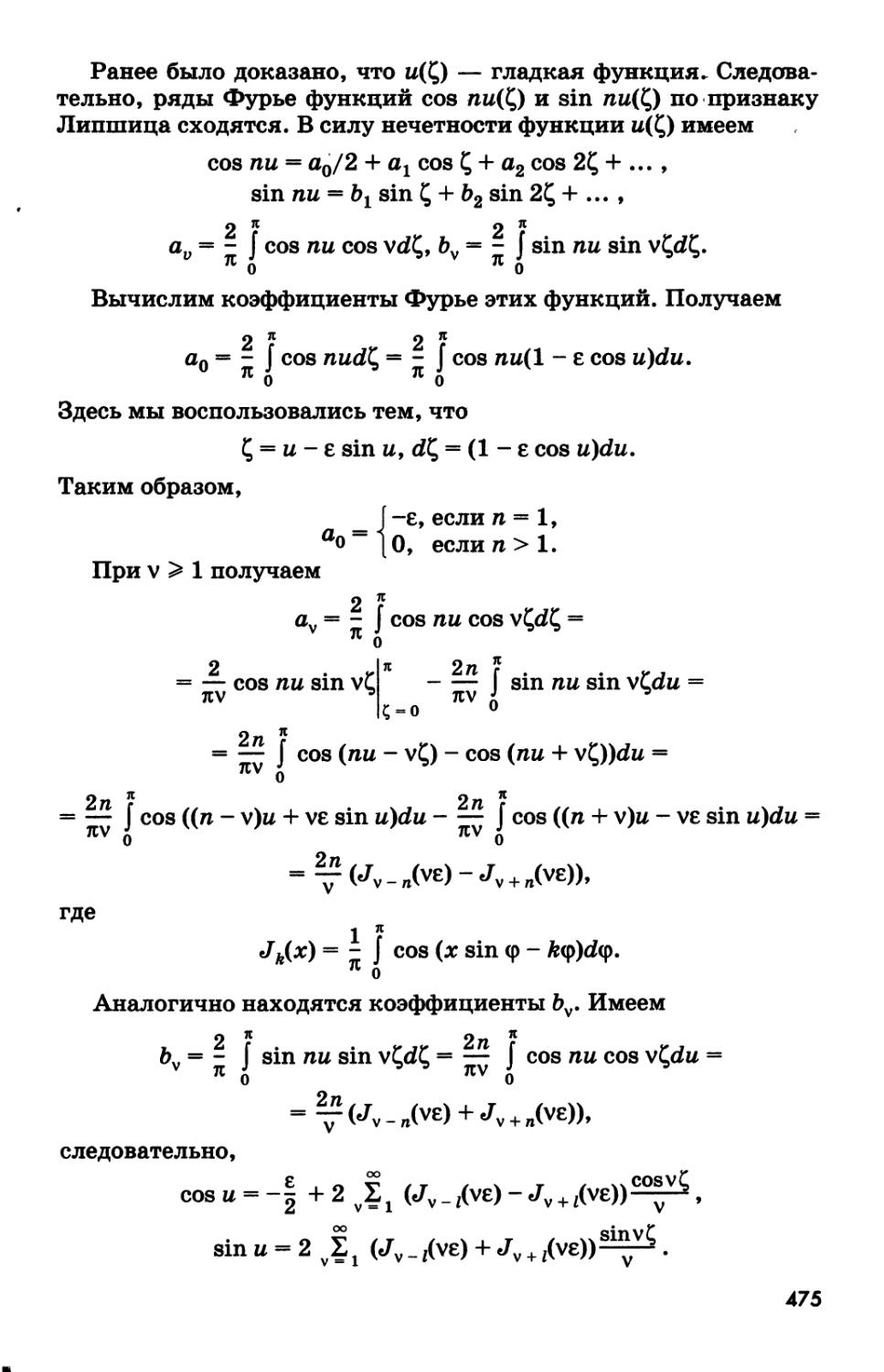Московский государственный университет имени М, В. Ломоносова КЛАССИЧЕСКИЙ УНИВЕРСИТЕТСКИЙ УЧЕБНИК
 е
Г, И. Архипов, В, А. Садовничий, В, Н. Чубариков
ЛЕКЦИИ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Серия КЛАССИЧЕСКИЙ УНИВЕРСИТЕТСКИЙ УЧЕБНИК
основана в 2002 году по инициативе ректора МГУ им. М.В. Ломоносова академика РАН В.А. Садовничего
и посвящена
250-летию
Московского университета
КЛАССИЧЕСКИЙ УНИВЕРСИТЕТСКИЙ УЧЕБНИК
Редакционный совет серии:
Председатель совета ректор Московского университета В.А. Садовничий
Члены совета:
Виханский О.С., Голиченков А.К., Гусев М.В., Добренькое В.И., Доннов А.И., Засурский Я.Н., Зинченко Ю.П. (ответственный секретарь), Камзолов А.И. (ответственный секретарь), Карпов С.П., Касимов Н.С., Колесов В.П., Лободанов А.П., Лунин В.В., Лупанов О.Б., Мейер М.С., Миронов В.В. (заместитель председателя), Михалев А.В., Моисеев Е.И., Пушаровский Д.Ю., Раевская О.В., Ремнева М.Л., Розов Н.Х., Салеикий А.М. (заместитель председателя), Сурин А.В., Тер-Минасова С.Г., Ткачук В.А., Третьяков Ю.Д., Трухин В.И., Трофимов В.Т. (заместитель председателя), Шоба С.А.
Московский государственный университет имени М.В. Ломоносова
Г.И. Архипов, В.А. Садовничий, В.Н. Чубариков
ЛЕКЦИИ
ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Рекомендовано Министерством образования Российской Федерации в качестве учебника для студентов высших учебных заведений, обучающихся по направлениям и специальностям физико-математического профиля
5-е издание, исправленное
Издательство Московского университета Издательство «Дрофа»
Москва 2004
УДК 517.1(075.8)
ББК 22.161я73
А87
Печатается по решению Ученого совета Московского университета
Серия «Классический университетский учебник»
Рецензент академик РАН С. М. Никольский
Архипов, Г. И.
А87 Лекции по математическому анализу : учеб, для вузов / Г. И. Архипов, В. А. Садовничий, В. Н. Чубариков ; под ред.
В. А. Садовничего. — 5-е изд., испр. — М. : Дрофа, 2004. — 640 с. — (Классический университетский учебник).
ISBN 5-7107-8900-3
Книга является учебником по курсу математического анализа, посвящена дифференциальному и интегральному исчислениям функций одной и нескольких переменных и соответствует программе для высших учебных заведений, рекомендованной Министерством образования РФ. В ее основу положены лекций, прочитанные авторами на механико-математическом факультете МГУ им. М. В. Ломоносова.
В учебнике предложен новый подход к изложению ряда понятий и теорем анализа, а также и к самому содержанию курса,
Для студентов университетов, педагогических вузов и вузов с углубленным изучением математику,
УДК 517.1(075.8)
ББК 22.161я73
ISBN 5-7107-8900-3
© ООО «Дрофа», 2003
© МГУ им. М. В. Ломоносова, художественное оформление, 2003
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Вы открыли одну из замечательных книг, изданных в серии «Классический университетский учебник», посвященной 250-ле-тию Московского университета. Серия включает свыше 150 учебников и учебных пособий, рекомендованных к изданию учеными советами факультетов, редакционным советом серии и издаваемых к юбилею по решению Ученого совета МГУ.
Московский университет всегда славился своими профессорами и преподавателями, воспитавшими не одно поколение студентов, впоследствии внесших заметный вклад в развитие нашей страны, составивших гордость отечественной и мировой науки, культуры и образования.
Высокий уровень образования, которое дает Московский университет, в первую очередь обеспечивается высоким уровнем написанных выдающимися учеными и педагогами учебников и учебных пособий, в которых сочетаются как глубина, так и доступность излагаемого материала. В этих книгах аккумулируется бесценный опыт методики и методологии преподавания, который становится достоянием не только Московского университета, но и других университетов России и всего мира.
Издание серии «Классический университетский учебник» наглядно демонстрирует тот вклад, который вносит Московский университет в классическое университетское образование в нашей стране, и, несомненно, служит его развитию.
Решение этой благородной задачи было бы невозможным без активной помощи со стороны издательств, принявших участие в издании книг серии «Классический университетский учебник». Мы расцениваем это как поддержку ими позиции, которую занимает Московский университет в вопросах науки и образования. Это служит также свидетельством того, что 250-летний юбилей Московского университета — выдающееся событие в жизни всей нашей страны, мирового образовательного сообщества.
Ректор Московского университета
академик РАН, профессор	Л . вллл & А* Садовничий
ПРЕДИСЛОВИЕ
Курс лекций по математическому анализу представляет собой учебник, охватывающий программу по данному предмету на механико-математических факультетах университетов и педагогических вузов. Как показала практика, он может быть с успехом использован студентами технических вузов с углубленным изучением математики.
В учебнике среди прочих решается и задача выделения необходимого минимума сопутствующего материала, обеспечивающего усвоение основного содержания. Авторы стремились соединить доступность изложения, свойственную учебнику, с краткостью конспекта. С математического анализа как учебной дисциплины начинается процесс обучения высшей математике в вузе. Обилие и сложность новых понятий при этом часто подавляют творческое восприятие содержания курса. Для того чтобы правильно сориентировать читателя, мы сознательно допускаем определенную категоричность суждений — в процессе обучения он сам разберется во всем многообразии связей между различными аспектами предмета.
Авторы стремились прежде всего облегчить процесс усвоения знаний за счет доступного изложения и упрощения доказательств. Следует заметить, что краткость доказательства не всегда говорит о его простоте. Иногда более короткие доказательства бывают малодоступны и, по существу, затрудняют усвоение материала. В то же время мы исходим из того, что доказательство утверждений и примеры должны отличаться живостью, интересом, убедительностью и особенно краткостью. Для более краткой записи рассуждений и утверждений часто используют символику кванторов, что, однако, затрудняет непосредственное восприятие материала и ограничивает возможность следить за логикой рассуждений. Мы стараемся не злоупотреблять этой символикой, чтобы упростить сопоставление отвлеченных понятий со сходными явлениями из внешнего, доступного нашим чувствам мира, сделать понятия более наглядными.
В учебнике, по-видимому, впервые предлагаются такие аспекты, как общее понятие предела функции в смысле Гейне, простое излбже-ние формул суммирования Эйлера, Абеля и Пуассона, теоремы о связи измеримости по Жордану и интегрируемости по Риману, теоремы о связи кратных и последовательных пределов, критерий Маркова—Гордона о равенстве двух повторных пределов по базам множеств, теорема Пуанкаре о бесконечных определителях, изложения доказательства общей формулы Стокса на основе классического подхода, обобщающего классические теоремы трехмерного векторного анализа, и ряд других тем.
В заключение авторы выражают глубокую благодарность М. 3. Гараеву, Ф. М. Малышеву, А. М. Полосуеву, Е. А. Ширяеву и всем нашим коллегам за многочисленные полезные замечания по содержанию предыдущих изданий книги.
6
Дифференциальное исчисление функций одной переменной
В основу данной части книги положены лекции первого из четырех семестров основного курса математического анализа, читаемого авторами в течение последних лет на механико-математическом факультете Московского государственного университета им. М. В. Ломоносова. Ее содержание охватывает дифференциальное исчисление функций одной переменной.
Следует обратить внимание на существенное различие между стилем изложения, принятым в учебнике и в конспекте лекций. Дело в том, что в учебнике, как правило, доказательство утверждений подготавливается предварительными разъяснениями и примерами, в то время как конспект в основном включает в себя формулировки и доказательства.
Понятие предела — основное в первой части книги. На нем, в частности, основано изучение теории непрерывных и дифференцируемых функций одной переменной.
Обратим внимание еще на одно обстоятельство. Первые лекции по каждому из предметов, с которых начинается преподавание высшей математики (как правило, это математический анализ, алгебра и аналитическая геометрия), бывают посвящены изложению основ теории множеств. Подобный параллелизм создает у части студентов неверное впечатление о предмете «Математика» в целом и затрудняет восприятие материала. Положение усугубляется непривычной абстрактностью этих новых понятий. Выделение их в рамки одного предмета представляется нецелесообразным, поскольку в каждой дисциплине факты из теории множеств приводятся в расчете на излагаемый материал. Обычно в той или иной форме на эту особенность обращается внимание.
ГЛАВА 1
Введение
Лекция 1
$ 1. МНОЖЕСТВА. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ. ДЕКАРТОВО ПРОИЗВЕДЕНИЕ МНОЖЕСТВ.
ОТОБРАЖЕНИЯ И ФУНКЦИИ
Под термином «математический анализ» подразумевается прежде всего дифференциальное и интегральное исчисление, созданное Ньютоном и Лейбницем в XVII в., хотя некоторые основные понятия анализа сформировались гораздо раньше. Сейчас его в значительной степени рассматривают как устоявшуюся учебную дисциплину. Однако из сказанного не следует делать вывод, что в математическом анализе не осталось тем для научных исследований и глубоких открытий. Дело в том, что составные части математического анализа настолько разрослись, что давно превратились в отдельные математические дисциплины, такие, как теория функций действительного переменного (ТФДП), теория функций комплексного переменного (ТФКП), теория вероятностей, дифференциальные уравнения, математическая статистика, уравнения в частных производных, уравнения математической физики, вычислительная математика и т. д. В шйроком смысле математический анализ включает в себя все эти области, т. е. йочти нею математику.
В узком же смысле, как учебная дисциплина, математический анализ представляет собой составную и, пожалуй, большую долю той части математического знания, которая в настоящее время является общей для всех современных математических дисциплин. Поэтому приятна совершенно исключительная роль, которую играет математический анализ в математическом образовании. Он, по существу, является фундаментом математических знаний.
Не будет преувеличением сказать, что номинальным и стержневым понятием курса анализа является понятие предела во всевозможных его проявлениях. В общих чертах вы с ним уже знакомы из школьной математики. Тем не менее, получить ясное и
9
отчетливое представление о пределе — самая большая трудность при изучении курса анализа и самый важный его момент.
Каждый должен и может овладеть этим понятием, так как далее понятие используется в различных ситуациях. Тому, кто сумеет это сделать, в дальнейшем при изучении основного курса потребуется в большей степени усердие, чем способности.
Понятие предела является главным, но не единственным понятием анализа. Оно само опирается на понятия множества, отображения и функции.
Определение 1. Множество — это совокупность объектов любой природы.
На первый взгляд, это определение никуда не годится, поскольку вводимое понятие, т. е. «множество», определяется через четыре (!) других понятия, никак нами не определенных. Однако это не совсем так. Дело в том, что назначение определений — это вовсе не наведение логической строгости как таковой. Устанавливать логическую строгость требуется только там, где нестрого введенные понятия приводят к недоразумениям.
Как решить, что приводит к недоразумениям, а что нет? У современной математики есть для этого только такие средства: логический анализ, практика и интуиция.
Имеется два типа определений: логически строгое сведение определяемого объекта к уже введенным понятиям; описательное определение с помощью слов разговорного языка.
Определение множества является определением второго типа. В математике предпочитают, конечно, первый тип определений, но начальные понятия, к которым и относится понятие множества, приходится вводить описательно. Это плохо по многим причинам, и прежде всего потому, что приводит к противоречиям (есть так называемые парадоксы теории множеств). Однако иного подхода не найдено и приходится доверяться интуиции. Здравый смысл подсказывает, что по-другому и вообще нельзя сделать [19].
Определение 2. Объекты, образующие в своей совокупности данное множество, называются его элементами или точками.
Для обозначения различных множеств чаще всего будем использовать заглавные (прописные) буквы латинского алфавита, а для обозначения элементов этих множеств — малые (строчные) буквы.
Определение 3. Два множества X и Y называются равными, если они состоят из одних и тех же элементов.
10
Это записывают так:
Х = УилиУ = Х.
Если элемент а принадлежит множеству А, то пишут
а е А (или А эа).
Если а не принадлежит А, то этот факт записывают в виде
ае А (или а ё А).
Определение 4. Если все элементы множества В принадлежат множеству А, то В называется подмножеством множества А и пишут9.
В с А (или A z> В).
Очевидно, что если В а А и А с В, то А = В.
Обычно удобнее рассматривать все множества, участвующие в каком-либо рассуждении, как подмножества некоторого фиксированного множества В, которое будем называть универсальным. Таким образом,
А с В для любого множества А.
Для того чтобы с определенностью говорить о каком-либо множестве А (являющемся, как мы условились, подмножеством В), нужно иметь четкий критерий, правило, условие, свойство, которое дает возможность установить, какие именно элементы входят в А. Если обозначить это условие через а, то факт, что условие а порождает множество А, будем записывать следующим образом:
А « {a g В|а}.
Читается это так: множество А совпадает с множеством тех элементов (из множества В), которые удовлетворяют условию а.
Может оказаться, что для некоторого свойства а во всем множестве В вообще нет элементов, ему удовлетворяющих. Для единообразия считают, что и в этом случае запись А = {а е В (а} определяет особое множество, называемое пустым множеством. Пустое множество не содержит ни одного элемента. Оно обозначается символом 0. В наших обозначениях можно записать, например, так:
0 = {а е Е\а а}.
Здесь а — это свойство, что а и а.
краткости вместо некоторых часто употребляемых выражений общепринято использовать особые математические Знаки, называемые кванторами:
11
3 — «существует»;
3! — «существует строго один элемент» или «существует единственный элемент»;
V — «для всякого», «для всех»;
=> — «справедливо», «следует», «имеет место».
В качестве примера в этих обозначениях запишем следующее утверждение: VAcE=>0ciA. Здесь утверждается, что пустое множество является подмножеством любого множества из Е. Это утверждение следует из наших определений, так как означает, что если элемент принадлежит 0, то он принадлежит А, что действительно так, поскольку в пустом множестве 0 вообще нет ни одного элемента и для* доказательства справедливости этого утверждения его не надо проверять ни для одного элемента.
Определение 5. Множество С называется объединением (или суммой) множеств А и В, если оно состоит из тех и только тех элементов, которые принадлежат хотя бы одному из указанных множеств.
Объединение С множеств А и В обозначается так:
C=AUB.
Свойства объединения множеств
1°,AUB = BUA.
2°. A U (В U С) = (A U В) U С.
Определение 6. Пересечением множеств А и В называется множество С9 состоящее из всех элементов, принадлежащих одновременно и А, и В, т. е. элементов, общих для этих множеств.
Свойства пересечения множеств
1°.ААВ = В А А.
2°. А А (В А С) = (А А В) А С.
Доказать равенство двух множеств — значит доказать^ что всякий элемент х, принадлежащий правой части равенства, принадлежит и левой, и наоборот.
Для произвольной совокупности множеств Аа, где а пробегает все элементы некоторого множества I, пишут
С= UA=UA, ael « a a если С — объединение всех множеств Aa, а е I.
Аналогично,
c = QAx’
если С — пересечение всех множеств Аа.
12
Определение 7. Разностью С = А \ В двух множеств А и В называется множество, состоящее из всех элементов А, не принадлежащих В.
Множество А' = Е \ А называется дополнением А или дополнением до Е множества А. Если множество индексов I есть просто множество натуральных чисел, т. е. натуральный ряд 1, 2, 3, ... , то его обозначают I = N, а вместо U Аа и А Аа пишут оо	оо
U А и П А„.
Определение 8. Симметрической разностью С = А/\В двух множеств А и В назовем множество
С = (A U В) \ (А Л В).
Свойства операций над множествами
1°.АсА.'
2°. А а В, В а А => А = В.
3°.АсВ,ВсС^АсС.
4°. 0сАХ/А.
5«. (уАа)ПВ = у(АаПВ).
6». (ЛАа) U В = Л(Аа U В).
7°. А с В => A U B = В, А А В = А,
8°. A U А’ - Е, АЛ А' = 0.
9°. 0' = Е,Е' = 0.
10°. (UAJ'-ЛА'.
v<x а/	а а
11°. (AAa)' = UA'.
v а а'	а а
12°. АДВ = (А \ В) U (В \ А).
Все эти свойства доказываются весьма просто. Покажем для примера, каким образам доказывается последнее свойство. Надо доказать, что если Сх = (A U В) \ (А А В) и С2 = (А \ В) U (А \ В), то (\ = С2. Это значит, что надо доказать следующие утверждения:
1) Va е Сг => а е С2, откуда С\ а С2;
2) Va е С2 => a g С19 т. е. С2 a Cv
Ограничимся только доказательством утверждения 1, т. е. что Cr с С2. Пусть a g Сх; тогда а е A U В, но а ё А А В. Но если a G A U Ё, то или а е А, Или а ё В. Рассмотрим первый случай, т. е. a g А. В этом случае а ё В, так как иначе было бы a g А А В, что неверно. Тогда a g А \ В, откуда a g С2 = (А \ В) U (В \ А), что и требовалось доказать. В первом случае справедливость соотношения а. С2 мы доказали. Второй случай разбирается точно так же, только А и В меняются местами. Поэтому всегда Сг с С2.
Следующим после множества и тоже важнейшим понятием математики является понятие отображения, а также эквивалентное ему понятие функции. Но сначала дадим определение декартова произведения множеств.
13
Определение 9. Декартовым произведением С - Ах В множества А и В называют множество всех возможных пар (х, у), где первый элемент х каждой пары принадлежит А, а второй ее элемент у принадлежит В.
Определение 10. Подмножество F декартова произведения двух множеств Ах В называется отображением множества А в множество В, если выполнено следующее условие:
Vx € А 3! пара (х, у) е F.
ПРИМЕР. Пусть А = {1, 2, 3}, В = {2, 3, 4, 5}. Тогда подмножество F = {(1, 3), (2, 2), (3, 3)} множества А х В является отображением, а подмножество Ф = {(2, 2), (2, 3), (3, 3), (3, 4)} не является отображением.
Понятия «отображение» и «функция» — синонимы. Они несколько отличаются только буквенной символикой и сферами употребления. Мы будем гораздо чаще употреблять термин «функция». Тот факт, что F является отображением А в В, записывают так:
F : А—> В или А Д В.
Определение 11. Пусть отображение F : А —> В определяется следующим образом: V х g А3\ у g В такое, что (х, у) g F. Тогда элемент у g В называется образом х при отображении F и это записывается так:
у = F(x).
Элемент х называется прообразом (одним из возможных) элемента у.
Множество F(A) всех элементов F(x) Vx g А называется образом множества А при отображении F, т. е.
F(A) = {у е В|у = Г(х), х е А}.
Для множества С = F(A) само множество А при отображении F называется (полным) прообразом множества С.
Как уже отмечалось, термины «отображение» и «функция» — синонимы, но при употреблении слова «функция» вся терминология обычно меняется. Множество А называется областью определения, а множество F(A) с В — множеством (или областью) значений. Каждый элемент х g А называется значением аргумента (или просто аргументом), а элемент у = F(x) — значением функции в точке х.
Для того чтобы конкретно задать какое-либо отображение, т. е. функцию, надо, вообще говоря, определить способ (правило), как из всего декартова произведения А х В выбрать множество F с нужными свойствами. Указание этого способа, по существу,
14
и задает функцию. Поэтому для функции очень часто дается следующее определение.
Определение 12. Функцией F называется правило, по которому каждому элементу х е А ставится в соответствие строго один элемент у множества В. При этом пишут у « В(х).
Недостатком этого определения является то обстоятельство, что функцией оказывается правило, а не множество, как в предыдущем случае, что неестественно, так как из школьного курса математики известно, что функции можно складывать, умножать и выполнять с ними другие арифметические операции.
Считается, что употребление термина «отображение» больше свойственно геометрическому стилю изложения, а термина «функция» — аналитическому стилю.
Рассмотрим некоторые типы отображений, обратную функцию и взаимно однозначное соответствие.
Отображение F называется сюръективным, или отображением «на» (т. е. отображением А на В), или накрытием, если F(A) = В.
Отображение F называется инъективным, или вложением, если у каждой точки у = F(x) существует строго один прообраз, т. е. из условия у = F(xx) - В(х2) следует, что хх = х2.
Отображение F называется биективным, или взаимно однозначным, если оно является накрытием и вложением одновременно. В этом случае отображению F : А —> В можно поставить в соответствие обратное отображение F"1: В —> А по правилу: вместо пар (х, у) в декартовом произведении А х В надо рассмотреть соответствующие пары (у, х) из В х А, поменяв х и у местами. Очевидно, что В-1 — это также отображение. Кроме того,
В’ЧЛх)) = х V х € А и F(F~\y)) = yV у е В.
Биективное отображение называется еще взаимно однозначным соответствием или биективным соответствием.
Лекция 2
§ 2. ЭКВИВАЛЕНТНЫЕ МНОЖЕСТВА. СЧЕТНЫЕ И НЕСЧЕТНЫЕ МНОЖЕСТВА.
МОЩНОСТЬ КОНТИНУУМА
Понятие взаимно однозначного соответствия играет большую роль при перенесении представления о «количестве» элементов множества с конечных множеств на бесконечные. Это необходимо, поскольку мы постоянно имеем дело с бесконечными множествами. Приведем некоторые из них:
N — множество всех чисел натурального ряда;
Z — множество всех целых чисел (положительные, отрицательные целые числа и нуль);
R — множество вещественных чисел на прямой;
RxR — множество точек на координатной плоскости.
О количестве точек множества можно говорить только для конечных множеств, а для бесконечных — нельзя. В этом случае говорят о мощности множества. Таким образом, мощность множества — это понятие, которое обобщает понятие «количество элементов» на случай бесконечных множеств. Если же множество конечно, то термины «мощность множества» и «количество элементов множества» — синонимы.
Определение 13. Множества А и В называются эквивалентными или равномощными, если между ними можно установить взаимно однозначное соответствие. Это обозначается так*. А- В.
Свойства множеств
1°.А~А.
2°.А~В=>В~А.
3°.А~В,В~С=>А~С.
Другими словами, можно биективно отобразить одно множество на другое. Если А и В эквивалентны, то еще говорят, что они имеют одинаковую мощность.
Приведем важный пример эквивалентности бесконечных множеств.
УТВЕРЖДЕНИЕ 1. Множество N (натуральных чисел) и множество Q (рациональных чисел, т. е. всех дробей ^,те Z,ne N, (т, п) = 1), эквивалентны.
Здесь символом (т, п) обозначен наибольший общий делитель чисел тип.
16
► Достаточно показать, как присвоить собственный номер каждому рациональному числу. Для этого представим каждое рациональное число в виде несократимой дроби:
^ = Р/<Ь Р е qe N, (р, <?)= 1.
Такое представление единственно. Высотой рационального числа г = p/q назовем величину \р | + q = h. Эта высота сама является натуральным числом, т. е. принимает значения 1, 2, 3, ... и т. д. При фиксированном А > 1 существует не более 2А различных несократимых дробей, так как тогда знаменатель q может принимать значения 1,2, ... , h - 1 (число которых равно h - 1), а для данного q числитель р числа г может принимать не более двух значений: ±(й - q) (точнее* либо два, если дробь p/q получается несократимой, либо нуль, если она — сократима, так как тогда она имеет другое значение q в представлении в виде несократимой дроби). Таким образом, с данной высотой h число рациональных чисел не более 2(й - 1) < 2Л.
Будем нумеровать дроби в порядке возрастания А; при фиксированном й в порядке возрастания д, а при фиксированных hnq — в порядке возрастания р. Тогда получим
гг = 0/1 = 0 г2 = -1/1 = -1, г4 = -2/1 = -2, гв = -1/2, г8 = -3/1 = -3, Г1о = “1/3,	(Л = 1), г3 = 1/1 = 1 (Л = 2), г6 = 2/1 = 21 г7 = 1/2, J (А 3)’ г, = 3/1 = 31 „ -1/0 г(Л = 4)ит. д. ги-1/3, ]
Ясно, что каждое рациональное число когда-нибудь получит свой порядковый номер. При этом все номера 1, 2, 3,... будут использованы и разные рациональные числа получат разные номера. Тем самым построено взаимно однозначное соответствие множеств QulN. ◄
Определение 14. Всякое множество, эквивалентное (равномощное) множеству натуральных- чисел, называется счетным множеством.
Таким является, как было показано, множество рациональных чисел.
УТВЕРЖДЕНИЕ 2. Всякое непустое подмножество счетного множества конечно или счетно.
► Занумеруем элементы счетного множества и перенумеруем затем элементы подмножества в порядке возрастания этих номеров. Если мы исчерпаем все подмножество на койечном шаге, то оно конечно, иначе — счетно. ◄
7
УТВЕРЖДЕНИЕ 3. Сумма конечного или счетного числа счетных множеств — счетное множество.
► Занумеруем элементы суммы множеств по следующей схеме:
Aj =	•••)>
А& = (а31» а32»	а339
......................ИТ.	д.
(при этом пропускаем уже встречавшиеся элементы). За 2г2 шагов будут заведомо занумерованы все элементы ak9l9 k 4-1 < г. ◄ Обратим внимание, что бесконечные множества, рассмотренные в утверждениях 1—3, оказались равномощными, точнее, счетными. Но не все бесконечные множества равномощны. Имеет место следующее утверждение.
ТЕОРЕМА 1. Совокупность Z = Q(X) всех подмножеств любого множества X сама образует множество, не эквивалентное X.
Эта теорема (точнее, ее модификация: N ~ R) была доказана Г. Кантором (1845—1918) в 1874 г.
► Воспользуемся методом от противного. Пусть Z ~ X. Значит, имеется биективное соответствие X 4 Z. Тогда, если а е Х9 то ему однозначно соответствует А € Z9 т. е. F(a) = A, F~X(A) = а. Теперь всякую точку a g X назовем правильной, если она принадлежит своему образу, т. е., если а е F(a). В противном случае эту точку а мы будем называть особой точкой. Назовем дефектом множество D с Х9 состоящее из всех особых точек а е X. Тогда ясно, что D является элементом множества Z. В силу наличия взаимно однозначного соответствия F между X и Z найдется такая точка d g X, что F(d) = D. При этом сама точка d обязана быть либо правильной, либо особой. Но первое не имеет места, поскольку тогда по определению правильной точки она принадлежала бы D = F(d), что невозможно, так как ко множеству D по построению отнесены только особые точки. Но второй случай приводит к противоречию, так как тогда, с одной стороны, по определению особой точки d е F(d) = D, с другой стороны, тогда точка d, как особая точка, должна войти в дефект D по его построению.
Таким образом, предположение о существовании биекции между Z и X во всех случаях ведет к противоречию, т. ё. Z~X. ◄
18
Следует отметить, что как результат, так и доказательство теоремы 1 справедливы и в частном случае, когда X — пустое множество 0. Тогда мощность множества X равна 0, а множество Z = £2(Х) состоит ровно из одного элемента, т. е. самого X и поэтому его мощность равна 1 = 2°. Заметим еще, что для конечного множества Х9 состоящего из k элементов, мощность множества Z = £2(Х) равна в точности 2*.
Определение 15. Бесконечное множество называется несчетным, если оно не эквивалентно N.
По теореме 1 несчетным множеством, например, является множество подмножеств N, значит, и множество последовательностей, составленных из 0 и 1 (fe-й член последовательности равен 1 или 0, в зависимости от того, принадлежит или не принадлежит число k подмножеству).
Прием, с помощью которого мы доказали теорему 1, называется канторов диагональный процесс. Впервые он был применен Г. Кантором в 1874 г. при доказательстве несчетности точек на отрезке. Этот процесс называется диагональным, потому что если в теореме 1 в качестве X взять натуральный ряд N, то получится, что множество подмножеств, т. е. совокупность последовательностей, составленных из нулей и единиц, не эквивалентно X. Доказательству теоремы 1 в этом случае можно придать следующий вид.
► Предположим, что N ~ Z = £2(ЛГ). Тогда имеем взаимно однозначное соответствие
1	= (Лц, й12, ^13» •••)>
2 <->	= (^21» Л22» ^23’ •••)»
и т. д. (здесь символами Н19 Н29 ... обозначены некоторые различные последовательности из нулей и единиц).
Возьмем последовательность, составленную из «диагональных» элементов: (Л22, й12, h339 ...), и поменяем все разряды на противоположные, т. е. единицы заменим нулями, а нули — единицами. Получим: Н = (h119 й22, Л33, ...). Этот элемент не совпадает ни с одним из Нт9 т. е. он не занумерован. Имеет место противоречие. ◄
Определение 16. Мощность множеств, эквивалентных множеству всех последовательностей, составленных из нулей и единиц, называется мощностью континуума.
УТВЕРЖДЕНИЕ 4. Множество I точек отрезка [0, 1] имеет мощность континуума.
19
► В двоичной записи каждая точка единичного отрезка [0,1] может быть записана в виде О, Ах Л2 А3 ... , hk = | k = 1, 2, 3, ... . Такая запись единственна, за исключением чисел вида п/2Л, ft, п е Числам такого вида соответствуют в точности две запйси (у одной, начиная с некоторого номера, все цифры равны нулю, а у другой — все единицы). Для всех точек, за исключением точек вида п/2Л, установим соответствие следующим образом:
х = (хр х2, ...) <-> 0, ххх2 ... .
Так как множество точек вида n/2k счетно, то счетным множеством является также множество последовательностей, им соответствующих. Следовательно, между ними можно установить взаимно однозначное соответствие и тем самым будет установлено взаимно однозначное соответствие между точками отрезка [0, 1] и множеством последовательностей, составленных из нулей и единиц, т. е. множество точек отрезка имеет мощность континуума. ◄
Лекция 3
$ 3. ВЕЩЕСТВЕННЫЕ ЧИСЛА
Предметом изучения в курсе математического анализа преимущественно будут числовые функции, областью определения и множеством значений которых являются числовая ось, отрезки, интервалы, промежутки на этой оси или какие-нибудь другие ее подмножества. При этом требуется более глубокое представление о вещественных числах, чем то, с которым имеет дело школьная программа по математике. Подчеркнем, однако, что мы будем целиком на нее опираться и уточним только то, что действительно требует большей ясности.
В отношении рациональных чисел мы ничего уточнять не будем. Рациональные числа — это обыкновенные дроби. Вещественные числа, которые рациональными не являются, как известно, называются иррациональными.
Следует отметить, что вещественные числа, как рациональные, так и иррациональные, в природе не существуют. Они — абстракция и придуманы для практических нужд, о чем говорит здравый смысл. Можно сказать, что они «породили саму математику», а в дальнейшем она предъявила к числам свои требования. И оказалось, в частности, что одни только рациональные числа этим требованиям не отвечают.
Самое простое и естественное назначение чисел в математике — измерение длин отрезков. Это означает, что длина каждого отрезка должна измеряться вещественным числом. С другой стороны, заметим, например, что диагональ единичного квадрата на координатной плоскости не может измеряться рациональным числом а.
Действительно, если это число рациональное, то а = т/п, (тп, п) = 1, и по теореме Пифагора имеем а2 = т2/п2 = 2. Следовательно, т2 = 2п2. Рассмотрим возможные случаи: 1) т нечетно; 2) т четно.
1)	Если т нечетно, то т = 2k + 1, т2 = 4fe2 + 4Л + 1 нечетно и потому равенство т2 = 2п2 невозможно.
2)	Если т четно, то т = 2Л, т2 = 4fe2 и 2k2 = п2. Но тогда, рассуждая аналогично, получаем, что п тоже четно. А это значит, что оба числа /пип делятся на 2, откуда (тп, п) > 2, что противоречит условию. Значит, а — не рациональное число, что и требовалось доказать.
Задача измерения длины отрезка (относительно заранее заданного «эталонного» единичного отрезка) полностью решается
21
с помощью бесконечных десятичных дробей. Их-то мы и будем называть вещественными (действительными) числами.
Итак, вещественное число — это бесконечная десятичная дробь, взятая со знаком «плюс» или «минус».
Замечания. 1. Знак «плюс» в записи можно опустить.
2.	Десятично-рациональные числа, т. е. числа вида h/lQk имеют при этом два представления, которые нами отождествляются, и можно считать, что нет десятичных дробей, имеющих цифру 9 на всех местах, начиная с некоторого.
3.	Мы отождествляем вещественные числа и точки вещественной числовой оси, служащей изображением множества вещественных чисел.
4.	Множество всех вещественных чисел обозначается буквой А.
Основные свойства вещественных чисел
1°. Для а, Ъ имеем: или а = b9 b = а, или а > Ь, Ь < а, или а <Ь, Ь> а.
2°. Если а> Ь, Ь> с, то а> с. Если а = Ъ, Ъ = с, то а = с.
3°. Для а, Ь g R 3! число се R такое, что а + Ь = с.
4°. Для a9be R имеем (а + Ь) + с = а + (Ь + с).
5°. Для a9b е R имеем а + Ъ = Ь + а.
6°. 3! число 0 е R такое, что а + О = О + а = а.
7°. Для ае Я 3! (-а) е R такое, что а + (-а) = 0.
8°. Для а,Ь е RB\c е R такое, что аЬ = с.
9°. Для а,Ъ,се R имеем (ab)c = а(Ьс).
10°. Для a9be R имеем ab = Ьа.
11°. 3! число 1^0 такое, что а • 1 = 1 • а = а.
12°. Для а 5* 0 3! а-1 такое, что аа-1 = 1.
13°. (а 4- Ь)с = ас + Ъс.
14°. Если а> Ь, то а + с > Ъ + с.
15°. Если а> Ъ, с > 0, то ас > Ьс.
Указанные свойства призваны отражать количественные характеристики простейших математических объектов, таких, например, как длины отрезков, площади прямоугольников и объемы прямоугольных параллелепипедов, а также изменения этих величин при различных преобразованиях.
Запись числа в виде бесконечной дроби, которую мы отождествили с самим числом, можно было бы рассматривать как одно из подобных свойств. С другой стороны, свойствам 1°—15° обязаны отвечать рекуррентные процедуры определения последовательности десятичных знаков для результатов арифметических операций над двумя вещественными числами, заданными бесконечными десятичными дробями.
22
Эти процедуры могут быть заданы на основе правила сравнения величин бесконечных десятичных дробей, которое будет рассмотрено далее при доказательстве полноты множества вещественных чисел.
Априорность свойств вещественных чисел, т. е. тот факт, что они рассматриваются в качестве исходных для построения дальнейшей теории, наводят на мысль считать их аксиомами, которые определяют (вместе с двумя другими свойствами) само множество вещественных чисел. Однако подобный подход нас не вполне устраивает, поскольку понятие натурального числа неявно присутствует в законах логики, на которые мы опираемся в своих рассуждениях [19].
Подчеркнем, однако, исключительную плодотворность аксиоматического метода для обоснования исходных принципов в других областях математики. Прекрасным примером этого является идущая от Евклида аксиоматика элементарной геометрии.
Есть еще несколько важных свойств вещественных чисел. К ним прежде всего относится аксиома Архимеда (287—212 гг. до н. э.), он сформулировал ее для отрезков:
16°. Для любого вещественного положительного числа а существует натуральное число п такое, что ап > 1.
► Если а > 1, то можно взять п = 1 и доказывать больше нечего. Если же 0 < а < 1, то
а = 0, 0 ... аЛаЛ+1...,	= ... = ak_x = 0, ak 0.
Тогда имеем
10*a = aft,aft+1...
т. е. свойство 16° имеет место при п = 10Л. ◄
Свойство 17° сформулируем и докажем позже.
Рассмотрим теперь только неотрицательные числа. Договоримся, что для десятично-рациональных чисел рассматривается только запись, заканчивающаяся нулями. Число, стоящее перед запятой в десятичной записи числа х, будет целым, и оно называется целой частью х или антье от х. Таким образом, целой частью числа х называется целое число п, удовлетворяющее неравенствам п < х < п 4- 1. Будем использовать стандартное обозначение: п = [х]. Тогда предыдущее неравенство можно записать в виде
[х] < х < [х] + 1 или х - 1 < [х] < х.
Число, стоящее после запятой в десятичной записи числа х, называется дробной частью х. Пишется так: {х}. Очевидно,
23
[х] + {х} = х. Итак, величина [х] есть наибольшее целое, не превосходящее х. Это свойство берется в качестве определения значения символа [х] при отрицательных х.
Примеры: [1, 5] = 1; [0, 3] = 0; [-0, 7] = -1; [-3, 5] = -4.
Далее, при х < 0 символу {х} дробной части числа х мы приписываем значение: {х} = х - [х]. Таким образом, при всех х значение символа {х} удовлетворяет условию 0 < {х} < 1.
Определим моду ль, или абсолютную величину числа х:
. I [ х, если х > 0, Iх I ~ ] -х, если х < 0
(|х| выражает расстояние от нуля до точки х на вещественной оси); Имеет место следующее неравенство (неравенство треугольника):
\а 4- &| < \а| 4- |Ь|.
Докажем это неравенство. Имеем:
1) если аЬ > 0, то а + & | = |а| +1&|;
2) если аЬ < 0, то а 4- &| < |а| 4- |&|.
В качестве приложения введенных выше понятий докажем три утверждения.
УТВЕРЖДЕНИЕ 5. Для любого целого числа а и любого натурального числа Ь существует единственная пара целых чисел q, г такая, что
a = bq + г, 0<г<Ь.
►	Действительно, неравенству q < | < g + 1, т. е. неравенству qb < а < (q 4-1)& удовлетворяет единственное число 9 я [|]* Тогда величина г определяется однозначно равенством г = а - bq и удовлетворяет неравенствам
0 < г = а -	< а - b^ - 1) =Ь. ◄
Отметим, что рассмотренное выше число г называется остатком от деления целого числа а на натуральное число Ь. Целое число q называется неполным частным.
УТВЕРЖДЕНИЕ 6. Любое натуральное число а при некотором натуральном п единственным способом представляется в виде
а = а0 + 10ах 4-... + 10иап,
где ат, тп = 0,..., и — целые числа с условиями 0 < ат < 9, ап > 1.
►	Заметим, что а < 10а. Действительно,
а= Е Г т = 0 m = 0
10е-1 9
< 10а.
10т =
24
Следовательно, найдется единственное неотрицательное целое число птакое, что
10" < а < 10n+1.
При 0 < т < п положим
а =Г-2-"|-10Г—-—1.
т LiomJ Li0'n +
Заметим, что все числа ат целые и справедливы неравенства
-1 = -£--1-10- —2— <ат< -£--10*(—2— -1) =10, 10m	10m + 1	10m kJQm + 1 J
т. e. 0 < am < 9;
так как 10n < а < 10n+1 и Г—-—| = 0. Далее имеем
L10» +1J
S 10-а = S 10m(T—l-iol—П = m-0 т т = 0	VL10mJ L10m + 1J^
= [a] - 10п+1Г—1 =а.
1 J Lion + 1J
Докажем единственность указанного в утверждении представления числа а. Пусть кроме представления а = ^Е 0 10т ат имеется k
другое представление а = ^Е 10w bm. Тогда при некотором з, не превосходящем максимума из чисел пик, справедливо равенство
0 = a - a = S _ Ютст, m = 0 m
s-l где ст = ат - 6m, |cj < 9, с, * 0. Отсюда имеем 108cs =	110mcm
и, следовательно,
10е < |с. • 10sI = I-	10mc J <	9•10m = 9• 10<,~l =
1 8	1 I m - 0 m| m = 0	10 “1
= 10s - 1 < 10s, что невозможно. ◄
Приведенное в утверждении 6 представление называется представлением числа в десятичной (позиционной) системе счисления. Числа ат называются цифрами данного числа. Число а записывается в виде а = ап ... а0. Число десять называется основанием данной позиционной системы счисления. Заметим,
25
что в качестве основания позиционной системы счисления можно взять любое натуральное число, большее единицы. В частности, в § 2 мы уже использовали двоичную систему счисления.
Определение 17. Будем говорить, что число а представимо в виде бесконечной десятичной дроби а0,	... ап ..., где
а0 = IaL 0<аЛ<9, А>1 — целые, если для любого натурального п справедливо неравенство
О < а - $л(а) < 10-п, где sn(a) называется округлением числа а до п-го знака после запятой.
УТВЕРЖДЕНИЕ 7. Для каждого вещественного числа а > 0 существует единственная запись в виде бесконечной десятичной дроби
а = а0,а1а2... аЛ..., удовлетворяющих при всех натуральных п условиям зп(а) = а0,а1а2 ...ап.
► Предположим противное, т. е. существует другое представление а = р, р0 ... Рп .... В силу того, что эти два представления различны, при некотором п имеет место неравенство
Ап = Од, ага2 ... ап * Ва = 0, 0О ... р„.
Из определения конечных десятичных дробей получим, что числа 10ЛАЛ и 10"ВЛ — целые. Кроме того, числа Ап и Вп представляют собой округление числа а до n-го знака, поэтому
О < a - Ап < 10"", 0 < a - Вп < 10"",
0 < 10"(a - Ап) < 1, 0 < 10"(а - Вп) < 1.
Из последних двух неравенств имеем, что целое число 10"(Ап - Вп) удовлетворяет неравенствам -1 < 10п(Ап - Bn) < 1. Следовательно, Ап = Вп, т. е. имеет место противоречие.
Теперь установим, что для каждого вещественного числа существует представление в виде бесконечной десятичной дроби. Опишем алгоритм нахождения десятичной записи вещественного числа а, удовлетворяющей условиям утверждения 7.
Положим а0 = [а], аЛ = [10na] - ЮЦО""1»]. В силу неравенства Р - 1 < [р] < Р при п > 1 имеем
-1 = (10"a - 1) - 10"а < ап < 10"а - ХОЦО""1» - 1) = 10,
т. е. 0 < ап < 9. Рассмотрим бесконечную десятичную дробь а0, а1а2 ... ал ... . Покажем, что она является представлением
26
числа а. Для этого достаточно показать, что при любом натуральном п число Ап = а0, аха2 ... ап является округлением числа а до n-го знака. Преобразуя Ап, получаем
= а + -^
" а0 + 10 + 102
ап = r„i . у [10"»а] -10(10”»-1а] =
Ю»	m -1	Ю
= Га1 + Е f[10OTa] _	[Ю”а]
1 J m-lk 10"»	10"»-1 '	10"
Отсюда
a - 10~" = —~1 < A <	= a, t. e. a - 10" < An < a.
10* n 10й	n
Последнее неравенство и означает, что Ап является округлением числа а до n-го знака. ◄
Заметим, что для чисел a =
, где а и А — натуральные (та-
кие а называются десятично-рацональными числами), условию утверждения отвечают только конечные десятичные дроби.
Далее понадобятся следующие понятия и обозначения. Множество М точек х, удовлетворяющих неравенствам: а < х < Ь, называют интервалом (пишут: М = (а, Ь));
а < х < Ь клы а < х < Ь — полуинтервалом (М = (а, Ь] или М = [а, &));
а < х < Ь — отрезком или сегментом (М = [а, &]). Каждое из этих множеств называется промежутком. Множество L точек х, определяемое соответствующим усло-
вием, называют:
х < а или х > а — открытым лучом (обозначения: L = (-°°, а) или L = (а, +°°));
х < а или х > а — замкнутым лучом (обозначения: L = (-°°, а] или L = [а, +°°)); а — вершина луча.
Здесь символ +°° читается плюс бесконечность, а символ -оо — минус бесконечность.
Множество всех точек х на вещественной оси, удовлетворяющих условию |х - а| < е, где а > 0 и а — некоторые фиксированные вещественные числа, называется ^-окрестностью (или просто окрестностью) точки а.
Множество всех точек х с условием |х| > е, где е > 0, называется ^-окрестностью (или просто окрестностью) бесконечности.
Множество всех точек х с условием х > е, где е > 0, называется ^-окрестностью (или просто окрестностью) плюс бесконечности.
Множество всех точек х с условием х < -£, где е > 0, называется ^-окрестностью (или просто окрестностью) минус бесконечности.
В заключение отметим, что утверждения 5—7 имеют характер некоторых пояснений и уточнений.
27
Лекция 4
§ 4. ПОЛНОТА МНОЖЕСТВА ВЕЩЕСТВЕННЫХ ЧИСЕЛ
Определение 18. Непустое множество А на вещественной оси R называется ограниченным сверху, если существует число b е R такое, что для всех а е А выполняется неравенство а < Ь. Другими словами,
V ае А=> а< Ь.
Число Ъ называется верхней гранью множества А. У ограниченного сверху множества существует бесконечно много верхних граней, например Ь+1,Ь + 2ит. д.
Аналогично определяем нижнюю грань d непустого множества А:
V ае А => d < а.
Непустое множество А называется ограниченным, если существует Ь > 0 такое, что для всех а е А имеем |а| < Ь.
Множество В всех верхних граней Ъ непустого ограниченного сверху множества А является ограниченным снизу.
► Действительно, каждая верхняя грань Ь е В удовлетворяет неравенству а < Ь при любом фиксированном а из множества А. Это и означает, что а есть нижняя грань для В. ◄
Сформулируем теперь свойство полноты множества вещественных чисел R (свойство, упомянутое в лекции 3).
17°. Для всякого непустого ограниченного сверху множества А множество В его верхних граней Ь содержит минимальный элемент Ь', т. е. существует единственный элемент &' е В такой, что:
1) V — верхняя грань множества А, т. е. для всех ае А имеем Ъ' > а;
2) Ь' — наименьший элемент множества В, т. е. для всех be В справедливо неравенство Ь' < Ъ.
Элемент Ь' называется точной верхней гранью или супремумом множества А. (Обозначение: &' = sup А.)
Прежде чем доказывать это свойство, отметим, что точно так же обстоит дело и с множеством нижних граней D ограниченного снизу множества А, а именно: существует единственный элемент d' е D такой, что:
1) V а е А=> d' < а;
2) V d е D => d' > d; d' = inf А (читается: точная нижняя грань, или инфимум).
Докажем теперь свойство 17°.
28
► Построим число &' конструктивно. Можно считать 0 е А, и тогда для всех Ъ е В имеем Ъ > О. Действительно, возьмем какое-нибудь ах € А. Заметим, что для любой верхней грани Ъ е В выполнено неравенство Ь > а19 откуда Ь - аг > 0.
Теперь вместо множества А рассмотрим множество А' чисел вида а - av Если нам удастся доказать, что существует число &i = sup А', то тогда очевидно, что существует и число &' = sup А, причем &' = &х + ах и наоборот. Справедливо следующее правило.
Правило сравнения вещественных чисел
Если а > Ь > 0 и десятичная запись этих чисел имеет вид а ^q, ^1^2 ••• *** Ь &0, ^1^2 ”* *** * пъо либо aQ > либо найдется номер k такой, что а0, аха2 ... > &0, Ьх&2 •••
Договоримся далее все десятично-рациональные числа из множества А записывать только с нулями на бесконечности.
В множестве А возьмем подмножество Ад, состоящее из всех а е Ас условием а > 0, т. е. Aq = {a g А|а > 0}. Для каждого из чисел а е Ад рассмотрим его целую часть [а] = п0(а).
Так как 0 < [а] < а < Ь, то функция [а] при a g Ад принимает лишь конечное число значений. Наибольшее из этих значений обозначим через х0. Рассмотрим множество At с Ад, состоящее только из тех чисел a g Ад, для которых [а] = х0. Заметим, что для всех а ё Ах имеем неравенство а < х0.
На множестве Аг определим функцию пх(а), равную числовому значению первого десятичного знака после запятой у числа а. Всего она принимает не более десяти значений. Наибольшее из них обозначим через xv Образуем множество А2, состоящее из чисел, принадлежащих Ар у которых п^а) = xv Обозначим через $х(а) число, получаемое из а заменой всех, начиная со второго, десятичных знаков числа а нулями, т. е. если а = nQ, пг..., то sx(a) = Пд, nv Тогда для любого a g А2 имеем $х(а) = х0, хр но при всех а £ А2 выполнено неравенство а < х0, хх. Для всех a g А2 определим функцию n2(a), равную значению ее второго десятичного знака. Наибольшее его значение выразим через х2. Образуем множество А3 с: А2 такое, что для любого a g А3 n2(a) = х2. Тогда для s2(a), т. е. для числа, полученного заменой всех, начиная с третьего, десятичных знаков числа а нулями, справедливы соотношения s2(a) = Хд, ххх2 для любого a G А3; а < х0, ххх2 для любого а е А3. Продолжая этот процесс далее, на Л-м шаге, имеем
**(«) = *о> ЭД — X* V a е Ak+l;
а < х0, ххх2 ... xk V а £ Ak+1.
29
Таким образом, получена последовательность знаков, которые определяют число Ь'9 имеющее десятичную запись вида &' = х0, хгх2 ... .
Докажем теперь, что V является точной верхней гранью множества А, т. е. что V = sup А. Для этого надо проверить следующие условия:
1) У — верхняя грань, т. е. для всех ае А имеем а < Ъ'*
2) V — наименьшая из всех верхних граней, т. е. если Ъ < Ь'9 то существует ае А такое, что а > Ь.
Докажем условие 1). Допустим противное, т. е. что существует а е А такое, что а > V. Тогда из правила сравнения чисел имеем, что существует номер k такой, что
Ма) >х0,х1...хк = sk(b'),
8l это противоречит построению числа Ь'.
Докажем условие 2). Если b < Ь', то по правилу сравнения вещественных чисел существует номер ke N такой, что
Ьо> ... Ьк = sk(b) < sk(b') = xQ, хг... хк.
Будем считать, что в случае десятично-рационального числа Ь здесь использована запись с нулями на бесконечности. Но по построению найдется элемент а е АЛ+1 такой, что зл(а) = sk(b'). Отсюда имеем sk(b) < sk(a), b <а. ◄
Заметим, что число b' = sup А может принадлежать А, а может и не принадлежать.
В качестве примера рассмотрим множество А рациональных чисел а с условием а < 0 или а2 < 2 и множество В = Q \ А, составленное из положительных рациональных чисел b с условием Ь2>2.
В силу того, что не существует рационального числа, квадрат которого равен двум, имеем: 1) A U В = Q; 2) А А В = 0; 3) А и 0, В 5^ 0; 4) для любых чисел а е А и любых чисел b е В справедливо неравенство а < Ь.
Определение 19. Любое разбиение рациональных чисел на два множества со свойствами 1)—4) называется сечением (дедекиндовым сечением).
Множество В «ограничивает сверху» множество А, т. е. при любом фиксированном Ъ е В выполняется условие 4), и множество В исчерпывает все множество верхних граней множества А.
Покажем, что множество В не имеет наименьшего элемента, а множество А, являющееся множеством всех нижних граней для множества В, не имеет наибольшего элемента. Это означает, 30
что множество Q рациональных чисел не является «полным», т. е. для него не выполнено свойство 17°.
Действительно, предположим противное, т. е. что существует минимальное число bQ в множестве В. Рассмотрим число Ьо - й, &2 — 2 k е Q такое, что 0 < k < -2--- Тогда имеем
2&0
(Ь0-й)2 = Ь2 + Л(Л-2Ь0)>Ь§-й.2&0>&§- Ц^-2Ь0 = 2.
Следовательно, bQ - k е В, что противоречит минимальности числа Йд.
Допустим теперь, что а0 — максимальное число множества А. та	,	.	, 2-ag
Рассмотрим неотрицательное число h < 1 с условием h < -—
Тогда имеем
(а0 + й)2 = а% + й(2а0 + й)<	+ й(2а0 + 1) <	+ (2 - а2) = 2.
Таким образом, число о0 + й е А, что противоречит предположению о максимальности числа а0 в множестве А.
Понятие сечений в множестве рациональных чисел было введено Ю. В. Р. Дедекиндом (1831—1916) для* построения теории вещественных чисел (в его подходе вещественные числа отождествляются с сечениями). Хотя в данном курсе эта же задача решается с помощью бесконечных десятичных дробей, следует отметить, что дедекиндовы сечения оказываются полезными и в других вопросах. В частности, на них фактически опирается строгое определение степенной и показательной функций при произвольных значениях показателя степени и аргумента.
Свойство точной верхней грани
Если b = sup А, то для любого е > 0 существует элемент а из А такой, что а>Ь- е.
► Воспользуемся методом от противного. Предположим, что найдется е > 0 такое, что для всех а е А выполняется неравенство Ъ - а > е. Но тогда й' = й - е является верхней гранью множества А, которая меньше, чем й, а это невозможно, поскольку Ъ — наименьшая из верхних граней. 4
Докажем еще одно свойство вещественных чисел.
ЛЕММА 1. Для любых вещественных х, у е R с условием х < у существует рациональное число т/п е Q такое, что х < т/п < у.
►	В силу аксиомы Архимеда (свойство 16°) для положительного вещественного числа у - х существует натуральное число п та-
31
кое, что справедливо неравенство п(у - х) > 2. Отсюда следует, что интервал (лх, пу) имеет длину, превосходящую 2. Следовательно, на этом интервале найдется целое число т такое, что пх < т < пу (например, т = [п#] - 1). Согласно свойству 15° из последнего неравенства получим искомое неравенство. ◄
Замечание. Так же просто показывается, что между любыми числами 0 < х < у найдется иррациональное число. Действительно, в силу леммы 1 между числами x/j2 и y/j2 лежит некоторое рациональное число т/п. Но тогда иррациональное число mj2/n находится на интервале (х, у).
В заключение, опираясь на правило сравнения вещественных чисел между собой, сформулируем лемму 2, которая по существу дает способ последовательного вычисления десятичных знаков при выполнении арифметических операций над вещественными числами.
ЛЕММА 2. Пусть а, Ь > 0 — вещественные числа, с = sup (s„(a) ± Sn(b)), d = sup (s„(a)sn(b)), f = 8up	J, если sn(b) > 0.
Тогда имеем с = a±b9 d = ab, f при b > 0.
►	Доказательство этой леммы основано на следующих соображениях. 1) Очевидно, что во всех трех случаях точные верхние грани существуют. 2) Далее прямыми вычислениями проверяется выполнение свойств 1°—17°. ◄
§ 5. ЛЕММЫ ОБ ОТДЕЛИМОСТИ МНОЖЕСТВ, О СИСТЕМЕ ВЛОЖЕННЫХ ОТРЕЗКОВ
И ПОСЛЕДОВАТЕЛЬНОСТИ СТЯГИВАЮЩИХСЯ ОТРЕЗКОВ
ЛЕММА 3 (об отделимости множеств). Пусть АиВ - непустые множества на вещественной прямой, т. е. 0, В # 0, А с Я, В с Я. Пусть также для любых а € А и для любых be В выполнено неравенство а < Ь.
Тогда существует число х такое, что для всех а е А и для всех be В справедливо неравенство a < х < &.
► Из определения множества В следует, что каждая его точка является верхней гранью множества А. Положим х = sup А. Тогда, поскольку х — это верхняя грань, для всех а е А имеем неравенство а < х, и так как х — точная верхняя грань А, то х < b для любого Ъ е В, т. е. для всех а е А и для всех b е В имеем а < х < Ь. ◄
32
Определение 20. Системой вложенных отрезков называется множество М, элементами которого являются отрезки, причем для любых Др А2 g М выполнено одно из условий: Ах а. Л2 или Д2 с Др т. et все точки одного отрезка принадлежат другому отрезку.
Л EMMA 4 (о системе вложенных отрезков). Пусть М — система вложенных отрезков. Тогда существует число х такое, что для любого отрезка Ле М имеем, что х g Д. Это значит, что все отрезки А из множества М имеют общую точку х.
►	Пусть А — множество левых концов отрезков, принадлежащих М, В — множество их правых концов. Тогда для всех a g А и для всех Ь g В имеем а < Ь. Действительно, пусть а — левый конец отрезка [а, &'] g М и Ь — правый конец другого отрезка [a', b] g М.
Возможны два случая: 1) [а', &] с [а, &']; 2) [а', &] => [а, &']. В случае 1) имеем а < а' <&<&', а в случае 2) имеем а' < а < Ь' < Ь. Тогда в силу леммы об отделимости существует число х такое, что для любого отрезка [a, ft] g М справедливо неравенство а < х < Ь. ◄
Замечание. С помощью леммы 4 (о системе вложенных отрезков) можно доказать несчетность множества точек отрезка. (Указание. Предполагаем, что все точки пересчитаны. Отрезок делим на три части. Тогда точка с номером один не принадлежит одному из этих отрезков. Делим его на три части. Точка с номером два не принадлежит одному из получившихся отрезков деления и т. д. По лемме 4 существует точках, принадлежащая сразу всем отрезкам, но эта точка не занумерована.) Определение 21. Система М вложенных отрезков называется последовательностью вложенных отрезков, если все эти отрезки занумерованы, причем любой отрезок с большим номером содержится в любом отрезке с меньшим номером.
Определение 22. Последовательность вложенных отрезков называется стягивающейся, если среди отрезков, в нее входящих, имеются отрезки сколь угодно малой длины. Другими словами, каково бы ни было положительное число е, в последовательности стягивающихся отрезков содержится и такой отрезок, длина которого меньше е.
ЛЕММА 5. Последовательность стягивающихся отрезков содержит общую точку и притом только одну.
►	Первая часть утверждения следует из леммы 4.
Докажем вторую часть этого утверждения. Если бы все отрезки содержали одновременно две различные точки а и Ь (а < Ь), то тогда длина каждого отрезка из М была бы больше, чем b - а > 0, но это не так, поскольку по определению в М есть отрезки и меньшей длины. ◄
33
2 - 4953
ГЛАВА 2
Предел последовательности
Лекция 5
§ 1.	МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ.
БИНОМ НЬЮТОНА И НЕРАВЕНСТВО БЕРНУЛЛИ
Для обоснования метода математической индукции будем использовать следующее свойство натуральных чисел: в любом непустом подмножестве множества натуральных чисел существует наименьшее число.
Убедимся в том, что данное свойство действительно имеет место. Для этого возьмем какой-нибудь его элемент (это можно сделать, так как данное подмножество не пусто). Если окажется, что выбранный элемент минимален, то свойство доказано. В противном случае число натуральных чисел, меньших данного числа, конечно. Рассматривая их последовательно, мы найдем требуемый минимальный элемент.
Метод математической индукции состоит в следующем: для справедливости любого утверждения, высказанного для всех натуральных чисел п > 1, достаточно:
1)	доказать это утверждение для п = 1;
2)	предположить его справедливость при п = k и k > 1;
3)	основываясь на утверждении 1) и предположении, доказать, что оно верно при п = k + 1.
Действительно, отсюда следует, что высказанное утверждение верно для всех натуральных п. Допустим противное. Тогдд множество тех п, для которых утверждение неверно, содержит наименьший элемент т. Число т и 1, поскольку утверждение верно для п = 1. Число т не может быть больше 1, так как в этом случае утверждение верно для т - 1 и в силу п. 3 оно справедливо и для т, что противоречит выбору числа т.
Замечание. Методом математической индукции можно доказывать утверждения, справедливые и при п > тп, где т > 1. В ходе доказательства надо заменить первый шаг: доказать утверждение при и = т, а все остальное оставить, как и прежде, при необходимости использовать то, что п > тп.
34
Рассмотрим формулу бинома Ньютона. Определим величину n! = n(n - 1)... 2 • 1, 0! = 1 (л! читается: эн-факториал). В частности, имеем 1! = 1, 2! = 2 • 1 = 2, 3! = 3 • 2 • 1 = 6 и т. д.
ТЕОРЕМА 1. Имеет место следующее равенство [формула бинома Ньютона):
(1 + х)п = С° + С\х + ... + Cknxk + ... 4- С”хп.
Коротко эту формулу можно записать так:
(1 + х)*= Д0С*х*,
( п п\ где С" =	==----------биномиальный коэффициент.
\ к J kl(n — k)l
► Воспользуемся методом математической индукции.
1.	При п = 1 формула верна: 1 4- х = 1 4- х, поскольку
Р
Р
Г Р 10)
= 1.
2.	Пусть формула бинома Ньютона справедлива при п = ty t > 1.
3.	Докажем, что она верна при п = t 4- 1. Сначала докажем вспомогательное утверждение о биномиальном коэффициенте: при 0 < k < п - 1 имеем
Г п 1
Л 4- 1 ч k 4- 1 J Действительно, и! п\ = k\(n-k)\ (k 4- l)!(n - k - 1)! = ra! f 1 + 1 ) = f n +1 М(в-Ы)Дп-* k + 1' l* + P Далее имеем
(1 + x)t+1 = (1 + x)*(l + x) =
t + i | + 0 J
t 4- 1 Lt _|_
t J V
t + 1 x#+1. t + 1)
35
2‘
Замечание. Аналогично доказывается и формула для полинома Ньютона от s неизвестных вида
(х + у + ... + zy -	Е _	х>>1 ук2 •” г*‘ ’
где ... , k8 — целые неотрицательные числа.
При изложении теории предела последовательности нам потребуется приводимое далее неравенство Бернулли.
ТЕОРЕМА 2. При х > -1, х * 0 и при целом п> 2 справедливо неравенство (неравенство Бернулли)
(1 + х)п > 1 + хп.
► Доказательство проведем по индукции. Сначала убедимся, что при п = 2 оно верно. Действительно,
(1 + х)2 = 1 + 2х + х2 > 1 + 2х.
Предположим, что для номера п = k оказалось, что утверждение справедливо:
(1 + х)* > 1 + fex, где k > 2. Докажем его при п = k + 1. Имеем
(1 + х)* +1 = (1 + x)k(l + х) > (1 + kx)(l + х) =
= 1 + (k + 1)х + kx2 > 1 + (k + l)x. ◄
Отметим, что метод математической индукции допускает многочисленные, иногда неожиданные, модификации. В качестве примера приведем доказательство одной теоремы из книги известного норвежского математика Т. Нагелля [34].
Под методом мультипликативной индукции будем понимать доказательство, которое проводится по следующей схеме.
1.	Опытным или каким-либо другим путем выдвигается гипотеза о том, что для каждого номера п (>1) выполнено свойство Е.
2.	Проверяется, что свойством Е обладают все простые числа р.
3.	Предполагается, что некоторое натуральное число т обладает свойством Е.
4.	Исходя из предположения индукции доказывается, что числа вида тр тоже обладают этим свойством.
5.	Отсюда по теореме об однозначности разложения на простые сомножители натуральных чисел, больших единицы, вытекает, что свойством Е обладают все натуральные числа, и тем самым установлена справедливость гипотезы из пункта 1 [34].
► Докажем методом мультипликативной индукции свойство мультипликативности функции Мёбиуса, определяемой на множестве натуральных чисел следующим образом:
36
)1, если n = 1, , О, если р2 делит и, (-1)г, если п=р1 ...pr9pk *pl9 k l91 < k9 К г.
Будем говорить, что функция f(n) натурального аргумента является мультипликативной^ если для любых взаимно простых чисел тип справедливо равенство f{mn) = f(m)f(n).
Достаточно доказать утверждение о мультипликативности функции Мёбиуса только для чисел т и п9 не делящихся на квадрат простого числа, т. е. бесквадратных чисел. Зафиксируем произвольное т. Покажем, что утверждение имеет место для п = р, где р — произвольное простое число. Действительно, так как (m,p) = 1, то ц(тпр) = (-1)г+1, если т =	... рг ир19 ... 9рг —
различные простые числа. Следовательно, ц(тпр) = ц(т)ц(р).
Пусть утверждение верно для п = k. Докажем его для п = kp9 где р — произвольное простое число. Так как и — бесквадратное число, то (fe, р) = 1. По условию (тп, n) = 1, поэтому (mk9 р) = 1. Тогда согласно доказанному утверждению для простых чисел и предположению индукции имеем цепочку равенств
ц(тпи) = p(mfep) = p(mfe)p(p) = p(m)p(fe)p(p) =
= и(тп)и(М = p(m)p(n). ◄
Заметим, что функция Мёбиуса встречается во многих областях математики, играя важную роль при изучении ее дискретных объектов.
$ 2. ЧИСЛОВЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. БЕСКОНЕЧНО МАЛЫЕ И БЕСКОНЕЧНО БОЛЬШИЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ИХ СВОЙСТВА
Определение 1. Функция9 определенная на множестве натуральных чисел N и принимающая числовые значения9 называется числовой последовательностью или просто последовательностью.
Обозначения: х19 х2, х39 ... , или, коротко, {хп}9 или, если это не вносит путаницы, просто хп. При каждом значении п число хп называется n-м членом последовательности.
ПРИМЕРЫ. 1. Последовательность 8П длин вложенных отрезков (см. определение 2 § 5) {Дп}, Дис Я, &n+i^nVne N.
2. хп — с при всех натуральных п (постоянная последовательность).
37
Определение 2. Если {хп} и {уп} — две числовые последовательности , то {хп + i/n} называется суммой двух числовых последовательностей, {хп - уп} — разностью двух числовых последовательностей, {хпуп} — произведением двух числовых последовательностей, при уп и 0 последовательность {хп/уп} называется частным двух числовых последовательностей.
Замечание. Обычно мы подразумеваем, что запись а/b сама по себе предполагает выполнение условия Ь 0.
Последовательности бывают:
1)	ограниченными сверху, если найдется а такое, что для всех членов последовательности выполняется хп < а;
2)	ограниченными снизу, если существует Ь такое, что хп> Ъ при всех п € N;
3)	ограниченными, если существует с такое, что для каждого номера п € N имеем |хп | < с.
Определение 3. Последовательность {хп} называется бесконечно большой, если для любого с > 0 множество тех членов последовательности, которые удовлетворяют неравенству |хп| < с, конечно.
Другими словами, это значит, что для всякого с > 0 существует номер и0 = п0(с) такой, что все члены последовательности {хп} с номерами, большими чем п0, удовлетворяют неравенству | хд| > с.
Коротко это определение записывается так:
V с > 0 3 п0 = nQ (с) такое, что V п > nQ имеем |хп| > с.
ПРИМЕР. Последовательности {уп = и} и {zn = -п} — бесконечно большие последовательности.
Определение 4. Последовательность {хд} называется бесконечно малой, если для всякого е > 0 множество членов последовательности {хд}, удовлетворяющих неравенству |хд| > е, конечно.
Коротко это определение записывается так:
V е > 0 3 nQ = nQ (е) такое, что V п > nQ => |хд| < е.
ПРИМЕРЫ. 1. Длины отрезков из последовательности стягивающихся отрезков (см. определение 3 § 5) образуют бесконечно малую последовательность.
2. хп = 1/п — бесконечно малая последовательность.
► Чтобы это доказать, надо для всякого е > 0 найти хотя бы одно натуральное число п0 = п0(е) такое, что для любого п > п0 име-38
ем |хд| < е. В качестве такого п0 = п0(е) возьмем число [1/е] + 1. Тогда для каждого п с условием
п > п0(е) = [1/е] +1 > 1/е имеем 1/п < е. ◄
Вообще, если надо доказать, что {хп} — бесконечно малая последовательность, то, по существу, надо найти хотя бы одно п0(е) с нужными свойствами, т. е. такое, что если п > п0(е), то выполняется неравенство |хд| < е, или хотя бы каким-либо образом доказать его существование.
ТЕОРЕМА 3. Бесконечно малая последовательность ограничена. ► Пусть {хд} — бесконечно малая последовательность. Тогда, например, неравенству |хд| > 1 удовлетворяет лишь конечное множество ее членов. Сумму модулей таких членов обозначим через с0. При этом считаем, что с0 = 0, если таких членов вообще нет. Очевидно, тогда для каждого члена хп имеем неравенство |xj < с = с0 + 1. Следовательно, бесконечно малая последовательность {хд} ограничена. ◄
ТЕОРЕМА 4. Если {хп} — бесконечно большая последовательность и хп^ 0, то {1/хд} — бесконечно малая последовательность , и наоборот, если {хд} — бесконечно малая последовательность и хп^ 0, то {1/хд} — бесконечно большая последовательность.
► Ограничимся рассмотрением только прямого утверждения. В этом случае при любом е > О неравенство 11 /хп | > е равносильно неравенству |хд| < с = 1/е, которому, в свою очередь, удовлетворяет лишь конечное множество членов, поскольку {хд} — бесконечно большая последовательность. Это значит, что {1/хд} — бесконечно малая последовательность. ◄
ТЕОРЕМА 5. 1. Если {хп} — бесконечно малая последовательность , то {|хд|} — бесконечно малая последовательность, и наоборот.
2. Сумма (разность) двух бесконечно малых последовательностей есть бесконечно малая последовательность.
► Первое утверждение теоремы непосредственно следует из определения бесконечно малой последовательности.
Докажем второе утверждение. Пусть {хд} и {уп} — бесконечно малая последовательность. Тогда для любого е > О существуют номера пг (е/2) и п2 (е/2) такие, что
v п > пг (е/2): |хп| < е/2 и V п > п2 (е/2): |у„| < е/2.
39
Тогда, полагая п0 = max (nt (е/2), п2 (е/2)), имеем
V n > ге0: |х„ ± j/n| < |хп| + |j/J < е/2 + е/2 = е.
Следовательно, {хп ± уп} — бесконечно малая последовательность. ◄
СЛЕДСТВИЕ. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство следствия очевидно.
ТЕОРЕМА 6. Произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.
► Пусть {xk} — бесконечно малая последовательность, а последовательность {yk} ограничена. Тогда при некотором с > 0 имеем \уп\ < с для всех п € N. Далее, так как {xk} — бесконечно малая последовательность, то для всякого е > 0 найдется номер
с условием, что |хп| <	= г/с для всех п > п^г^). Поэтому, пола-
гая п0(е) = п^г/с), имеем
Vn>n0(e): |х„-г/п| < |хп|-с < |-с = е.
Другими словами, {хп уп} — бесконечно малая последовательность. ◄
СЛЕДСТВИЕ 1. Произведение двух бесконечно малых последовательностей есть бесконечно малая последовательность.
• ► Согласно теореме 3, одну из двух бесконечно малых последовательностей мы можем рассматривать как ограниченную последовательность. Тогда их произведение будет бесконечно малой последовательностью в силу теоремы 6. ◄
СЛЕДСТВИЕ 2. Произведение любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Доказательство следствия получается очевидным последовательным применением предыдущего утверждения.
ТЕОРЕМА 7. Если {хп} — постоянная и бесконечно малая последовательность, то хп = 0.
► Действительно, если хп = с и 0, то в |с|/2-окрестности нуля нет ни одной точки нашей последовательности, и это значит, что {хп} не является бесконечно малой последовательностью. ◄
40
ПРИМЕРЫ. 1. {<?"} — бесконечно малая последовательность при 1,1 <1.
► Действительно, если 0 < q < 1, то q = 1/(1 + Л), где h > 0. В силу неравенства Бернулли,
(1 + Л)л > 1 + nh при п > 2.
Отсюда
qn < 1/(1 + nh) < 1/nh.
Зададим теперь е > 0. Нам надо выбрать п0 = п0 (е) так, чтобы для каждого п > п0 выполнялось неравенство qn < е. Для этого достаточно, чтобы была справедлива следующая цепочка неравенств:
1/nh <E^nh> 1/е <=> п > 1/Ле.
Положим
п0 = п0 (£) = [1/*е] + 1-Покажем, что для всех п > nQ имеем qn < е. Это следует из цепочки неравенств
„ 1 1^1
4 nh + 1 noh следовательно, {qn} — бесконечно малая последовательность. ◄
2.	nqn — бесконечно малая последовательность при |g| < 1.
► Рассмотрим случай 0 < q < 1. Тогда q = . 1 . , где h > 0. Из п + 1
формулы бинома Ньютона имеем
(1 + Л)” > "( V^h? при п > 2.
Отсюда получаем , » п	2	..2	2	.,
4	(1+Л)	(п-1)Л2	еЛ2 еЛ2
Положим п0 = [2/ей2] + 2. Тогда для всех п > п0 имеем nqn < е. ◄
Лекция 6
$ 3. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение 5. Последовательность {ап} называется сходящейся, если существует число I е R такое, что последовательность ап = ап - I является бесконечно малой последовательностью.
В этом случае говорят, что {ап} сходится или что {ап} имеет предел и этот предел равен I. Записывают это так:
lim а=1 или а„ -» I при п -» сю.
Это определение на «е-языке» можно записать следующим образом:
V е> 03 п0 = п0(е) такое, что V п > nQ имеем \ап - 1\ <е.
Будем говорить также, что последовательность {ап} расходится к «плюс бесконечности», если для любого с > 0 лишь для конечного числа членов ее выполняется неравенство ап< с. Обозначается это так:
lim а = + ею или а„ —> + оо при п —> оо. П —> ОО п	п
Последовательность {ап} расходится к «минус бесконечности», если для любого Ъ < 0 лишь для конечного числа членов ее выполняется неравенство ап > Ь. Обозначается это так:
lim а„ = -оо или а„ —> -оо при п —> оо. П->оо п	п	г
И, наконец, последовательность {ап} расходится к «бесконечности», если для любого с > 0 лишь для конечного числа членов ее выполняется неравенство |ад| < с. Обозначается это так:
lim а„ = оо или а„ —> °° при п —> оо. п —> оо п	п
УТВЕРЖДЕНИЕ 1. Если последовательность {ап} сходится, то она имеет единственный предел.
►	Пусть это не так. Тогда существуют числа 1Х и 12 такие, что последовательности ап = ап - и Рд = ап - 12 являются бесконечно малыми последовательностями. Отсюда ап + = ап = Рп + 12, поэтому Zi - 12 = Рл -	— бесконечно малая последовательность.
Но тогда по теореме 7 § 2 имеем 1Х - 12 = 0, т. е. 1Х = 12. ◄
УТВЕРЖДЕНИЕ 2. Если {ап} — бесконечно малая последовательность, то lim а„ = 0.
42
►	Действительно, при I « О имеем: ап - 0 = ап есть бесконечно малая последовательность, т. е. предел {ап} при и —> оо равен нулю. ◄
УТВЕРЖДЕНИЕ 3. Если последовательность {ап} сходится, то она ограничена.
►	Если последовательность {ап} сходится, то найдется число I такое, что аЛ = ап - I — бесконечно малая последовательность. Значит, существует с > 0 такое, что при всех натуральных п имеем |ап| < с. Но ап = I + ап, откуда
l°nl = R + а„| < и + |ап| < И + с = Ср
т. е. {ап} — ограниченная последовательность. ◄
УТВЕРЖДЕНИЕ 4. Если Шп^ ап = I и ап и О, I 0, то существует пое N такое, что при всех п> п0 имеем |an| > |Z|/2 [или, что то 1	2 ч
же самое,:—: < пг • |«n| RI >
Это означает, что последовательность {1/ал}, составленная из обратных величин, ограничена.
►	В силу условия имеем, что ссл = ап - I — бесконечно малая последовательность. Тогда вне |/|/2-окрестности нуля лежит только конечное число членов последовательности {ал}. Пусть п0 — самое большое значение номера таких членов; тогда при всех п > п0 имеем |ал| < |1|/2. Отсюда при этих п получаем (Z = ап - ссл):
И =1«п - а„| < |а„1 + |-а„| = |а„| + |а„|.
Следовательно, |ал| > |Z| - |а„| > |Z| -\11/2 = |Z|/2. 4
УТВЕРЖДЕНИЕ 5. Если ап-> lv Ьп-> 12 при п -> <», то сп = ал ± Ьл -> -> 1г ± 12 при п-^оо. Другими словами, для сходящихся последовательностей предел их суммы равен сумме их пределов.
►	Из условия имеем а„ = ап - 1Х,	= Ьп -12 — бесконечно малые
последовательности. Следовательно,
cn-(Z1±Z2) = (an±bn)-(Z1±Z2) = a„±Pn = Yn
— бесконечно малая последовательность. Значит, из определения предела имеем Итп^ сп = 1Г ± 12. ◄
УТВЕРЖДЕНИЕ 6. Если an^>lr,bn^> 12 при п^^,тосп = апЬп -»1±12 при п->°° (предел произведения равен произведению пределов).
43
►	Имеем an = ll + ап, bn = l2 + р„, сп = anbn = 1г12 +	+
+ алРл = 1г12 + уп. Но уп — бесконечно малая последовательность, так как она является суммой трех последовательностей, каждая из которых есть бесконечно малая последовательность. Отсюда lim сп~1Л9. ◄
УТВЕРЖДЕНИЕ 7. Пусть lim а_ = L, lim b„ = I. 0. Тогда (an/bn) = lr/l29 тп. e. если предел знаменателя не равен ну-люг то предел отношения равен отношению пределов.
►	Рассмотрим последовательности
Сп ьп
и
Z-i	li anl9 b„l-t
Уп = Сп~ Т = Т ~ Г = Ц > <*п = ап~ 11> Рп = Ьп ~ 12'
Из условия вытекает, что ап, Рп — бесконечно малые последовательности. Достаточно доказать, что величина уп тоже является бесконечно малой последовательностью. Для этого запишем уп в виде
__ (Zj + 0Сп)^2 ~ (^2 +	~ Ml 1
1п ' ЬЛ	h К
Теперь заметим, что последовательность (awZ2 “ М1)/^2 является бесконечно малой в силу утверждений 5 и 6, а последовательность 1/Ьп ограничена в силу утверждения 4. Но тогда по теореме 6 § 2 последовательность уп является бесконечно малой. Таким образом, сп = lr/l2. ◄
ПРИМЕР. Сумма членов бесконечно убывающей геометрической прогрессии.
► Пусть зп = а 4- aq + ... 4- aqn~x. Тогда qsn = aq + ... 4- aqn~x 4- aqn, sn = (a- aqn)/(l - q). Так как при |g| < 1 имеем {qn} — бесконечно малая последовательность, то
s = sn= a/(1 -	”
Величину s можно представить в виде
8 = 8п + гп = а/(1 - ?).
где sn =	ад*-1 называется п-й частичной суммой ряда,
а величина rn = s - sn — остатком ряда.
44
$ 4. ПРЕДЕЛЬНЫЙ ПЕРЕХОД В НЕРАВЕНСТВАХ
УТВЕРЖДЕНИЕ 8. Пусть Ип^ ап = Z; тогда, если для всякого п имеет место неравенство ап> с (или ап > с), то I > с.
►	Из условия имеем, что ап = ап-1 — бесконечно малая последовательность, причем ад = ап -1 > с -I. Если допустить, что с -1 > О, то тогда при е = (с - 1)/2 получим, что е-окрестность нуля вообще не содержит ни одной точки последовательности {ад}. Это противоречит тому, что {ад} — бесконечно малая последовательность. Значит, с - Z < О, Z > с. ◄
УТВЕРЖДЕНИЕ 9. Пусть Шп^ ап = Z; тогда, если ап< с (или ап < с) при всех пе N, то I < с.
►	Если Ьп = -ап, то bn —> -Z при п -» 00, Ьп > -с (или Ьп > -с). Тогда из утверждения 8 имеем, что - I > -с, т. е. Z < с. ◄
УТВЕРЖДЕНИЕ 10. Пусть Jim^ ап = 119 Нп^ Ьп = 12. Тогда:
1)	если ап < Ьп, то Z2 < 12;
2)	если ап < Ьп, то lt < 12.
►	Рассмотрим последовательность сп = Ьп- ап. По условию сп > 0 (или сп > 0) при всех п и ch —> 8 = 12 - при п —> оо.
Согласно утверждению 8 в обоих случаях имеем 8 > 0, т. е. /2 1\» ◄
УТВЕРЖДЕНИЕ И. Если {ад} — бесконечно малая последовательность и при всех натуральных п имеем |РД| < ад, то Рд — тоже бесконечно малая последовательность.
►	Из условия следует, что любая е-окрестность нуля вместе с точкой ад содержит и точку Рд, так что вне этой е-окрестности могут находиться Рд только с такими номерами, для которых |ад| > е. Но так как {ад} — бесконечно малая последовательность, то их число конечно, и поэтому {Рд} — тоже бесконечно малая последовательность. ◄
УТВЕРЖДЕНИЕ 12. Пусть ап < сп < Ьп для всех п g N и пусть Jirn ап = Z, bn = I. Тогда предел сп существует и равен I. ► Из условия следует, что 0 < сп ~ ап < Ъп - ап. Но справедливо соотношение (Ьп - ад) —> 0, т. е. Ьп - ап — бесконечно малая последовательность. Но тогда по утверждению 4 имеем, что (сп - ап) — тоже бесконечно малая последовательность, т. е. (сп - ап) —» 0. Следовательно, с„ = (с„ ~ а„) + а„ -» 0 + I = I при п —> оо. ◄
ГА х г*	**
45
ПРИМЕРЫ. 1. Если а > 1, то lim nJa = 1.
П -> ОО
► Действительно, nJa = 1 + а„, ав > 0. Тогда
а = (1 + а„)" > 1 + па„, 0 < ап < (а - 1)/га.
По утверждению 5 имеем lim а_ = 0, откуда следует, что lim nJa =1. •«
П —> оо
2.	lim l/n = 1.
П —> ОО
► Действительно, положим nJn = 1 + аЛ. Тогда
- .	. п(п - 1) 9 п(п -1) о Л	/ 2~
n = 1 + па„ + Л~2	а„2 + ... > g- а*, 0 < а„ < J —.
По утверждению 5 имеем lim ага = 0, откуда следует, что lim'i/n = l. ◄ п —> оо
+ ... + ап
3.	Пусть lim ап = а. Тогда lim------------ а.
J п-^оо п	* п->оо п
► Действительно, пусть Ьп = ап - а. Тогда Шп^ Ьп = 0, и достаточ-
но доказать, что Jim^ ——~ = 0. Так как {Ьп} — бесконечно малая последовательность, то существует с > 0 такое, что при всех п имеем |&Л| < с. Кроме того, для любого е > 0 существует п0 = п0 (е) такое, что при всех п > nQ справедливо неравенство | Ьп | < е. Следовательно,
b-t + ... + b„ + Ь . 1 + ••• + Ьп
1	по п0 +1	п
п
cnQ + (п - п0)е п п
если только сп^/п <г,п> cnQ/t9 т. е. п > max {п0, сп0/е}. Отсюда уже легко следует требуемый результат. ◄
ТЕОРЕМА 8 (теорема Штольца). Пусты
i) Уп+i >Уп>0’>
2) lim уп = +оо;
X . - хп
3) существует lim -------2— = Тогда существует предел
П”>°° У п + 1 _ У п
М <хм=* 1-
Хп + 1 ~ хп
► Из условия теоремы вытекает, что-------— = + ап» гДе ап —
Уп +1 Уп
бесконечно малая последовательность. Поэтому для всякого е > О существует N = N(e) такое, что при всех п > N имеем |ап| < е/2.
46
Полагая значение номера равным последовательно ЛГ, ... , п9 получаем следующую систему равенств:
хп+1 - 1Уп+1 = хп~ 1уп + а» (Уп+1 - Уп)-
xn+i IVn+i~xn ^Ух + ах(Ух+1 Vn)‘
Сложим эти равенства
«п+1 - *Уп+1 = XN - lyN + «п (Уп+1 - Уп) + - + «X (Ух+1 " Vn>-Заметим, что все разности вида yk+1 - yk9 k = 1, ... N, в этом pa? венстве положительны. Поэтому, выполняя очевидные арифметические преобразования и переходя к неравенствам, получим
1«п+1 - 1Уп+1\ < 1«х - 1Vn\ + 1«п II Уп+1 - Уп1 + - + 1«х(Ух+1 - Ух)’ 1«п+1 - 1Уп+1 < 1*х + 1Vn\ + (£/2) (Уп+1 - Уп) + - + (£/2) (Ух+i " Ух)’
Хп + 1 _ / < Iх* ~*Ух| + £ Уп + 1 ~ Ух
Уп + 1	Уп +1	2 Уп +1
Поскольку уп = +оо, существует пг = пх(е) такое, что для I xn ~	. е
всех п > пх справедлива оценка 11	.
Положим nQ = max {п19 N}. Тогда для любого п > п0 имеем
Xn + l^J
Уп + 1
< е. Следовательно, xnfyn -» I при п —> °о. ◄
Лекция 7
§ 5. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ТЕОРЕМА ВЕЙЕРШТРАССА.
ЧИСЛО «е» И ПОСТОЯННАЯ ЭЙЛЕРА
Определение 6. Последовательность называется:
невозрастающей, если хп+1 < хп для всех п е N (обозначение: хлФ);
неубывающей, если хп+1 > хп для всех натуральных п (обозначение: хлТ);
убывающей, если хп+1 < хп для всех п g N (обозначение: хп 44);
возрастающей, если хп+1 > хп (обозначение: хдТТ).
ТЕОРЕМА 9 (теорема Вейерштрасса). Пусть {ап} — неубывающая и ограниченная сверху последовательность. Тогда {ап} сходится и lim аи = sup {а„}.
П—>ОО п	п
► Так как последовательность {ап} ограничена сверху, то существует sup {ад}. Пусть I = sup {ап}. Покажем, что ап = L
Другими словами, требуется доказать, что ап = ап - I — бесконечно малая последовательность, т. е. что для любого £ > 0 существует номер п0 = п0 (б) такой, что при всех п > nQ имеем |ад | < < е. Но sup {ад} = 0. Это значит, что:
1) ад < 0 для любого п е N;
2) для любого £ > 0 найдется число k такое, что -£ < ak < 0. Но последовательность ak не убывает, поэтому при всех п > k имеем
-с < ак < а„ < 0, |а„| < |аА| < е.
Таким образом, в качестве п0 = п0 (е) можно взять указанное выше число k. ◄
ТЕОРЕМА 10. Невозрастающая, ограниченная снизу последовательность имеет предел, равный inf {ап}.
► Вместо {ад} рассмотрим последовательность {Ьп}, Ъп = -ап. Тогда inf {ап} = -sup {Ьп} и теорема 10 следует из теоремы 9. ◄
ПРИМЕР. Итерационная формула Герона. Пусть
Ж»+1= |(Х»+
48
где а — фиксированное положительное число, хг — любое положительное число. Докажем, что {хп} — убывающая последовательность при п > 2, ограниченная снизу величиной Та, и что lim x=Ja. п->°о п
Действительно, имеем:
2) х - х +1 = х - \(х 4- — 1	> 0.
f п n+1 п 2V п хп; 2хп
Из предыдущих формул получаем х2 > ... > хп > Ja. Далее, в силу теоремы Вейерштрасса, для монотонной последовательности существует lim х_ = х > Ja > 0. Тогда справедливо равенство П —> оо '*
lim хпЧг1 = if lim хп 4-	—),
П^оо п+1 2Vn->oo п lim х J
П-><х> п
т. е. х = (х 4- а1х}12\ х= <Ja.
При вычислении квадратного корня из положительного числа по итерационной формуле Герона число верных десятичных знаков быстро растет. Важно отметить, что если в процессе вычислений допущена ошибка, то в дальнейшем она будет автоматически исправлена (саморегулирующийся итерационный процесс).
Приведем другое доказательство того, что xn -> Ja при п -» оо. Из равенства
г (хл±7а)2
имеем
Положим —------р = q. При хх > 0 имеем |g| < 1. Далее получаем
хх 4- Ja Х
ХП ~	_ д2л~1
xn + Ja
1 + 02"*
откуда хп-------,
49
Заметим, что Дл определяет скорость сходимости данного итерационного процесса. Далее, так как д2"’1 — бесконечно малая последовательность, то хЛ = Ja.
Перейдем к определению числа е.
ТЕОРЕМА 11. Последовательность ап = (1 + 1/п)п имеет предел.
► Сначала заметим, что при k > 1
fe! =	- 1)... 2 • 1 > 2fe~x.
По формуле бинома Ньютона получаем
п
1
п
п
1
п
± п
п21 2
п 1 П
= 2 + k =СТ;
I п
_ _ а I у 1 П П 1
П ~ fe + 1 п
но тогда
а„< 2+ JL — = 3-п	k = 2 2* -1
1
2п -1
Кроме того, в выражении о при k > 2 с ростом п возрастает fe-й член суммы и число членов всякий раз увеличивается на единицу, т. е. ап не убывает и последовательность {ап} ограничена. По теореме Вейерштрасса последовательность {ап} сходится. ◄
Следуя Эйлеру, предел этой последовательности обозначают через е. Известно, что е = 2,7 1828 1828 4590 45 ... . Постоянную е называют неперовым числом или числом Д. Непера (1550— 1617). Логарифм числа а по основанию е называется натуральным логарифмом числа а и обозначается символом In а.
(	п+1
Рассмотрим далее последовательность i+e . Имеем
lim Ь„ = lim f 1 +	• lim f 1 +	= e.
n->oo n n-t<x> \ Д/ n->OO \ Л/
Последовательность {bn} убывает. Действительно, из неравенства
Бернулли при п > 1 имеем
.	(1+1ГХ
Ьа = У п) /	1 у + 1 е п + 1
6п + 1 fi I 1 У + 2	п2 + 2п' п + 2
v п + 1'
п + 1 А е п + 1 = (п2 + Зп + 1)(п + 1) _ п3 4- 4п2 + 4п + 1 > п(п + 2)' п + 2 п(п + 2)2	п3+4п2 + 4п
50
Следовательно, bn > е. Так как Ьп> е> ап, то

Величина гп характеризует скорость сходимости последовательности {ап}.
Поскольку число е играет важную роль в анализе, приведем для него другое выражение.
ТЕОРЕМА 12. Пусть с„ = 1 4- Д + Д + ... + Д. Тогда lim с„ = е. 1! 2!	п\	п-юо п
► Последовательность {сЛ} является монотонно возрастающей и ограниченной. Действительно,
и +	4" ••• + —-— = 3 — —-— < 3.
2	22	2п~1	2Л-1
Следовательно, существует предел lim с„ = е*. Далее, так как
п —> оо	х
п

то е < ev При фиксированном з < п имеем
Отсюда
е = lim а„ > lim cL (п) = ся, т. е. е — верхняя грань для {с8}. Но так как Ит ca = sup {с,} =
то е > ех. Следовательно, е = ех. ◄
Заметим, что если е = сп 4- гп, то
0<r = S 1 <	1	Г1+ 1	4-	1	4- 1 =
п * = n+ifc! (n + i)| V	п + 2 (п + 2)2
=	1________1	= п + 2	< 1
(п + 1)! 1-1/(п + 2) (п + 1)(п + 1)!	п*п!*
ТЕОРЕМА 13. Число е — иррациональное.
► Допустим противное. Тогда е = p/q9 (р, q) = 1 и с учетом сделанного выше замечания имеем
51
Домножая обе части этого неравенства на д!, получаем, что А = ql(e - cq) — целое число и, в то же время, 0 < А < 1/д, что невозможно. ◄
Определим еще одну известную константу, играющую важную роль в математическом анализе.
ТЕОРЕМА 14. Пусть yn = 1 4- | 4-... 4- i - In п. Тогда существует предел у = уп.
► Последовательность {уп} монотонно убывает. Действительно,
Yn+1-Yn=TT7-^(ra + D + lnn=-|7 -1п(1 + 1)<0, так как /	п+1	/	1 \ n + 1
1 < In |^1 4- -J , поскольку е < |^1 + -J = 6П, что было уже доказано выше.
Далее покажем, что последовательность {уп} ограничена снизу числом 0. Из доказательства теоремы 11 имеем
1п(1 + 1Г<1,т.е.1„1±1 <1, V П/	п п
поэтому
Yn = 1 + z +...+ - — In П > In Y 4" In 5 4-... 4-In П 1 — In n = 1n 2 n	12	n
Следовательно, по теореме Вейерштрасса последовательность {yn} имеет предел. ◄
Этот предел называется постоянной Л. Эйлера и обычно обозначается буквой у или буквой С. Для этой константы Эйлер вычислил 15 десятичных знаков после запятой, а именно, у = 0,5 7721 5664 9015 32... .
С арифметической природой постоянной Эйлера связан ряд «старых» математических проблем. В частности, до сих пор неизвестно, является ли константа у алгебраическим или трансцендентным числом. Попытки выразить эту константу через известные величины, например через л, е или логарифмы алгебр раических чисел, пока тоже не имели успеха. Число называется алгебраическим 9 если оно является корнем алгебраического многочлена с целыми коэффициентами. Если у этого многочлена коэффициент при старшей степени неизвестной равен единице, то данное число называется целым алгебраическим числом.
52
Очевидно, что к алгебраическим числам относятся все рациональные числа. Если же число не является алгебраическим, то оно называется трансцендентным.
В качестве еще одного приложения теоремы Вецерштрасса о пределе монотонной последовательности приведем пример последовательности, задаваемой с помощью простой формулы и принимающей только значения простых чисел.
ТЕОРЕМА 15 (теорема Миллера). Существует такое вещественное число а > 1, что если а = а0, 2а° = ар ..., 2а" = ап+1,... , то [осЛ] — простое число при всех n > 1. Другими словами, существует вещественное число а > 1 такое, что при всех и > 1
Г -,а“1
натуральные числа рп = 22‘ являются простыми числами при всех п > 1.
► Доказательство теоремы 15 опирается на знаменитую теорему П. Л. Чебышёва, известную так же как «постулат Бертрана» (см., например, [18]): для любого х > 1 существует простое число р такое, что х < р < 2х.
Построим последовательность рп = [ап] по индукции. Положим рг = 3. По теореме П. Л. Чебышёва существует простое число рп+19 удовлетворяющее условиям
2P"<Pn+i<Pn+i + l<2p» + 1.
Если pn+1 + 1 = 2Рп +1, то рп+1 = 2Р" +1 - 1 не может быть простым, так как оно имеет делитель 2(Рл +1)/2 - 1. Следовательно, 2Р"<Рп+1<Р„+1 + 1<2Рл + 1.
Положим
u„ = log2...log2p„, vn = log2...log2 (pn+1). и	n
Очевидно, из неравенств
Р» < log2P„+i < log2 (рл+1 + 1) <рп+1
имеем ип < ип+1 < vn+1 < vn, так что ип, vn — монотонные последовательности. Следовательно, по теореме Вейерштрасса существует предел ип == а и ип < а < vn. Положим
а = log2 ... log2 а„. п
Тогда в силу монотонности функции у = log2 * получаем Рп<а„<Рп + 1»т. е.рп = [а„].	«
53
Лекция 8
§ 6. ТЕОРЕМА БОЛЬЦАНО—ВЕЙЕРШТРАССА О СУЩЕСТВОВАНИИ ЧАСТИЧНОГО ПРЕДЕЛА У ОГРАНИЧЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение 7. Пусть {ап} — некоторая последовательность и пусть {fen} — некоторая строго возрастающая последовательность, состоящая из натуральных чисел. Тогда последовательность Ь„ = аь называется подпоследовательностью по-следовательности ап.
Определение 8. Если существует предел Ъп = 19 то I называется частичным пределом или предельной точкой последовательности {ап}.
Образно говоря, каждая подпоследовательность получается из последовательности {ап} путем отбрасывания части ее членов с сохранением порядка следования оставшихся членов.
ТЕОРЕМА 16 (теорема Больцано—Вейерштрасса). Из всякой ограниченной последовательности {ап} можно выбрать сходящуюся подпоследовательность.
► По условию имеем, что найдется с > 0 такое, что |ап| < с для всех п. Разделим отрезок IQ = [-с, с] пополам. Один из получившихся отрезков содержит бесконечное число членов последовательности. Назовем его и в качестве первого члена в искомой подпоследовательности возьмем какой-либо элемент ап^ е 119 т. е. положим Ьг = аП1. Затем отрезок снова разобьем на два и обозначим через 12 ту его половину, которая содержит бесконечно много членов последовательности {ап}. Среди них выберем такой член аЛг, номер которого п2 превосходит число п19 и. положим &2 = O'nz* Повторяя описанную процедуру применительно к отрезку 129 получаем отрезок 13 а. 12 и. член Ь3 — аЛд с условием п3 > п2. Далее таким же образом найдем b4 = ап* еЦс I3, b5 = ап* е 15с:14 и т. д. В результате получим числовую последовательность {bk} и последовательность вложенных отрезков {Ik}9 причем bk е Ik9 bk = ап*9 nk < nk+1 при всех k g N. Другими словами, {bk} будет подпоследовательностью для {ak}.
Осталось показать, что последовательность {bk} сходится. Для этого заметим, что длина 8k отрезка Ik равна с • 2"fe+1, откуда 8fe —> О
54
при k —> 00• Это значит, что последовательность вложенных отрезков {Ik} стягивающаяся и все отрезки Ik имеют единственную общую точку I. Именно это число I и будет пределом для {bk}. Действительно, если Ik = [зЛ, fj, то sk < I < tk9 tk- 8k = 8fe, аЛ = = l - sk < 8fe, = tk -1 < 8Л. Но так как 8fe -> 0 при k —> 00, To ak —> 0 и _> 0, откуда sk = I - ak I, tk = I 4-	—> Z, и так как bk = an^
sk < аПк < tk, to bk = аПк -» l при k —> 00, что и требовалось доказать. «
Определение 9. Наибольший из частичных пределов последовательности называется ее верхним пределом, а наименьший — ее нижним пределом.
Заметим, что если последовательность ограничена, то она имеет верхний и нижний пределы. Рассмотрим, например, случай верхнего предела. В силу теоремы 16 множество L всех частичных пределов данной последовательности {ап} непусто. Кроме того, каждая ее подпоследовательность лежит в тех же границах, что и сама последовательность {ап}.
Таким образом, если при всех п справедливо неравенство т < ап < М, то для всякого I g L имеем т < I < М. Это значит, что множество L ограничено. Пусть X = sup L. Тогда для всякого натурального числа k на промежутке вида £-Х -	, Х] лежит по
крайней мере один из частичных пределов I = lk последовательности {ап}9 и, следовательно, неравенству lk -	< bk = удов-
летворяет некоторый член последовательности {ап}. При этом можно считать, что номера nk строго возрастают с ростом параметра k. Тогда числа bk образуют некоторую подпоследовательность, удовлетворяющую неравенствам X - | < bk < М.
Так как {bk} ограниченная последовательность, то по теореме 16 из нее тоже можно выбрать сходящуюся подпоследовательность {bk }. Если lQ — ее предел, то имеют место неравенства
J™-£>'«
Но {bk } одновременно является подпоследовательностью для {ап}9 т. е. lQ g L. Но тогда lQ < X = sup L. Итак, X < Zo < X, т. е. X = lQ является частичным пределом для {ап}9 что и утверждалось выше.
55
§ 7. КРИТЕРИЙ КОШИ ДЛЯ СХОДИМОСТИ ПОСЛЕДОВАТЕЛЬНОСТИ
Очевидно, что из теоремы 16 § 6 непосредственно вытекает следующее необходимое и достаточное условие сходимости последовательности .
Определение 10. Последовательность {ад} называется фундаментальной или последовательностью Коши, если выполнено условие:
V е > 0 3 п0 = п0 (е) такое, что V т, п > nQ имеем \ат - ап| < е.
ТЕОРЕМА 17 (критерий Коши). Для того чтобы последовательность {ап} сходилась, необходимо и достаточно, чтобы она была фундаментальной.
► Необходимость. Если ап = I, то для любого е > 0 существует и0 = п0 (е) такое, что для всякого п > nQ имеем \ап - 1\ < е/2. Следовательно, для любых т, п > п0
l«n - «ml = 1(«в - 0 - («т " 01 < |в„ - П + 1«т “ *1 < е/2 + е/2 = S.
Поэтому {ап} — фундаментальная последовательность.
Достаточность. По условию последовательность {ап} является фундаментальной.
1. Докажем, что {ап} ограничена. В самом деле, возьмем е = 1. Тогда найдется n0 = nQ (1) такое, что для всех п > п0 имеем \ап - ап^\ < 1. Но в этом случае
|aJ < \ап - ап | + |ап | < 1 + |ап | = h.
1 №	। л ”о’	।
Отсюда
|a„| CmaxdaJ,..., |а„о|, h) = с.
2. В силу теоремы Больцано—Вейерштрасса существует сходящаяся подпоследовательность an^, ... , ап*, ... —> а при k —> оо.
Условие ее сходимости можно записать так:
V е > 0 3 kr e kr (е) такое, что V k > kr имеем \ап* - а| < е/2.
Пусть Nr = nk^ = max (п0 (е/2), Д^). Тогда для всех п > N и пк> N имеем
\ап - а| = \ап - ап + ап - а| < |а_ - ап | + \ап - а| < е/2 + е/2 = е, т. е. последовательность {ап} сходится. ◄
Важно отметить, что теорема 1 допускает следующую переформулировку, полезную для доказательства расходимости конкретных последовательностей.
56
ТЕОРЕМА 18. Для расходимости последовательности {ап} необходимо и достаточно, чтобыf она не была фундаментальной, т. е. существовало число е > О такое, что для каждого н0 g N нашлись бы номера т > nQ и п > п0, для которых выполнялось неравенство
\ат~ап\ >£-
ПРИМЕРЫ. 1. ап = 1 + | + ... + i . Возьмем е = 1/2. Тогда при любом т имеем неравенство
_	=	1	4-	4- — > — = 1
х2т хт m 4.1	2т ' 2т 2'
Последовательность {ап} расходится (здесь мы полагаем, что т = = n0, п = 2т).
2. Для решения уравнения Кеплера
х - a sin х = у (0 < а < 1) используют метод последовательных приближений:
хо =!/, xi = У + « sin х0,..., хп = у + а sin xn_v
Докажем, что существует £ = lim^ хп и что х = £ является единственным корнем уравнения Кеплера.
Согласно критерию Коши для любого е > 0 существует число п0 = по (£) такое, что при всех п > п0 и при всех р > 1 имеем |хЛ +р - хп| < е. Оценим модуль разности |хЛ +р - хп |. В силу неравенства |sin у\ < |z/| имеем
1«п+р " «nl = « lsin «п+р-1 - Sin «п-11 < « 1«п+р-1 - «п-11 < < а2 |х„+р_2 - х„_2| < а" 1«р ~ «01 = ап +1 |sin xp_J < ап+1.
Далее, поскольку |а| < 1, последовательность {ап+1} является бесконечно малой последовательностью. Поэтому для любого е > О существует « пг (е) такое, что при всех п > пг имеем |ап+1| < е.
Теперь в теореме 17 положим nQ = nv В результате получим, что последовательность является фундаментальной и, следовательно, сходится к некоторому числу £. Поэтому, переходя к пределу при п —> оо в равенстве хп = у + a sin хп_19 получаем £ ==у + a sin£, т. е. х = £ — решение уравнения Кеплера. Далее, если — другое его решение, то - £| = a |sin - sin £| < а - £|, и если то отсюда имеем 1 < а, что не так по условию. Другими словами, х = — единственный корень уравнения, что и требовалось доказать. Уравнение Кеплера ввел в рассмотрение И. Кеплер (1571—1630) при изучении движения планет по эллиптической орбите (задача двух тел).
57
ГЛАВА 3
Предел функции в точке
Лекция 9
§ 1.	ПОНЯТИЕ ПРЕДЕЛА ЧИСЛОВОЙ ФУНКЦИИ
Мы познакомились с понятием предела числовой последовательности. Последовательность — это функция, определенная на множестве натуральных чисел. Но еще большую роль в анализе играет понятие предела функции, определенной на всей числовой оси или на каком-либо ее промежутке либо луче. В дальнейшем будет рассмотрен ряд понятий подобного рода. Эти понятия близки как между собой, так и с уже рассмотренным понятием предела последовательности. Перечислим наиболее важные из них:
1)	I = Jim f(x) — предел функции f(x) в точке х0;
2)	I = Jim + Дх) — правый предел функции Дх) в точке х0;
3)	I = Jim Дх) — левый предел функции Дх) в точке х0;
4)	I = Jim Дх) — предел функции Дх) при х -> °о;
5)	I = Jim^ Дх) — предел функции Дх) при х ±°°.
Считаем, что функция Дх), о пределе которой будем говорить, определена на всей числовой прямой R или на некотором множестве А, являющемся его подмножеством, т. е. А с: R. Этим множеством А, например, может быть интервал, отрезок, совокупность промежутков и вообще какое угодно бесконечное множество. Важно только, чтобы точка х0, к которой устремляется аргумент функции f (х) (т. е. х —> х0), являлась предельной точкой множества А, а именно: чтобы в любой 8-окрестности точки х0 содержалось бесконечно много точек из множества А. В случае х —> или х —> ± оо это означает, что множество А должно быть: не ограничено, если х —> сю; не ограничено сверху, если х -l-оо; не ограничено снизу, если х —> - сю.
В дальнейшем понадобится следующее определение.
Определение 1. Множество точек х, принадлежащих А и удовлетворяющих неравенству 0 < |х - х0| < 8, Называется проколотой ^-окрестностью точки х0 (относительно множества А).
58
При А = R проколотая 8-окрестность точки х0 состоит из двух интервалов: (Xq ~ 8, Xq) U (Xq, Xq + 8).
Определение предела	
По Коши	По Гейне
Число 1 называется пределом V е > 0 3 8 = 3(e) > 0 такое, что Vx: (х е А, 0 < |х - х0| < 8) => => 1ft*) — г| < е. Обозначение: 1 e lim Дх) х->х0	функции Дх) при х -» х0, если: для любой последовательности {*„}= Хп * Х0 V П 6 N Хп € А И хп —> х0 при п-><х> имеем f(xn) —>1. или f(x) -> 1 при х —> х0
Число 1 называется правым преде V е > 0 3 8 = 3(e) > 0 такое, что Vx: (х е А, 0 < х - х0 < 8) => => Iftx) - z| < е. Обозначение: 1 == lim f(x\ x->x0+'v	лом функции f(x) при х -» х0, если: для любой последовательности {х„}: хл > х0 V л е	€ А и хл —> х0 при п->°° имеем f(xn) -> 1. I или Дх) -> 1 при х -> х0+
Число 1 называется левым предел V е > 0 3 8 = 8(e) > 0 такое, что Vx: (х е А, -8 < х - х0 < 0) => => |ftx) - z| < е. Обозначение: 1 = lim fix] х->х0-	юм функции Дх) при х —»х0, если: для любой последовательности {*„}: х„ < х0 V п е N хп е А и хл -> х0 при п^оо имеем f(xn) -> 1. ) или Дх) -> 1 при х -» х0 -
Число 1 называется пределом V е > 0 3 с = с(е) > 0 такое, что Vx: (х е А, |х| > с) => | Дх) - l\ < е. Обозначение: 1 = lim Дх) X -» ОО	функции Дх) при х —> оо, если: для любой бесконечно большой последовательности {хл}: хп е А, при п-^<х) имеем f(xn) —> 1. или Дх) —> 1 при х —> оо
Число 1 называется пределом с V е > 0 3 с = с(е) > 0 такое, что Vx: (х е А, х > с) => | Дх) -1\ < е. Обозначение: 1 = lim fix] 	 Х-»+ОО	рункции Дх) при х -» +°о, если: для любой бесконечно большой последовательности хп > 0: хп е А, при п -> оо имеем fix*) -> L . 1 или Дх) -> 1 при х -> +оо
59
Окончание табл.
По Коши	По Гейне
Число 1 называется пределом ( V е > 0 3 с = с(е) < 0 такое, что Vx: (х е А, х < с) => |/(х) -1\ < £. Обозначение: 1 = lim f(x] X —> -ОО	рункции /(х) при х -» -оо, если: для любой бесконечно большой последовательности хп < 0: хп е А, при п->°° имеем f(xn) —> 1. I или /(х) —> 1 при X —> -ОО
Для всех этих видов пределов справедливы теоремы, аналогичные теоремам о пределах последовательности. Например, если /х(х) Zp f2(x) -» Z2 (при одном и том же виде стремления аргумента х), то:
1)Г1(х)±/2(х)^/1±/2;
3) fi(x)/f2(x) -> 1г/12, при 12 * 0.
Если с(х) — постоянная, т. е. с(х) = I для любого х е А, то с(х) -> I.
Доказательства этих теорем, по существу, повторяют доказательство утверждений для сходящихся последовательностей. Тем не менее, их надо провести, а это достаточно трудоемко. Поэтому дадим общее определение предела, под которое подходят все рассмотренные выше пределы, в том числе и предел последовательности. Речь идет о пределе по базе множеств.
§ 2. БАЗА МНОЖЕСТВ. ПРЕДЕЛ ФУНКЦИИ ПО БАЗЕ
Определение 2. Пусть А есть область определения функции /(х). Тогда совокупность множеств {&} = В, где Ь а А, называется базой множеств или просто базой для множества А, если для ее элементов выполняются следующие условия:
1) В состоит из бесконечного числа непустых множеств {&};
2) V &р Ь2 е В 3 &3 g В такое, что Ъ3аЬ1П Ъ2.
(Здесь &х, Ъ2, Ь3 — подмножества множества А.) Элементы множества В называются окончаниями базы В. Само множество А будем называть основным множеством базы В. Далее для любых двух окончаний Ьх и Ь2 базы В с условием Ь2 а. Ьг будем говорить, что &2 следует за Ь19 а Ьг предшествует Ь2.
Определение 3. Число I называется пределом функции f(x) по базе В, если для любого е > 0 существует окончание Ь е В такое, что для всех х е & имеем неравенство |/(х) - 1\ < е.
60
Обозначение:
lim f(x) = l или f(x) —> l (по базе В). s'
В этом случае еще говорят, что f(x) сходится к Z по базе В. Аналогично определяются следующие пределы: lim f(x) = оо(±оо).
Заметим, что с точки зрения формальной корректности определения 3 предела функции по базе В требование бесконечности множества окончаний в базе В является избыточным. В случае конечного количества окончаний данное определение малосодержательно и не отражает в достаточной степени существа понятия предела.
Важно отметить, что если вместо основного множества А базы В взять любое ее окончание &0, то совокупность В' окончаний базы В, следующих за &0, с учетом сделанного выше замечания, тоже образует базу множеств. При этом из существования предела Inn f(x) = I следует, что существует предел lun f(x) = I и наоборот. В силу этого свойства на практике между базами В и В' фактически не делается различия.
ПРИМЕРЫ БАЗ.
1.	А = N. База Во (обозначение: п —> оо) состоит из множеств Ъ = Ns, s > 1, где Ns — множество натуральных чисел {$, s 4- 1, з 4- 2, ...}.
Тогда предел по базе Во — это предел последовательности {ап}:
х = п9 f(x) = апп Пт Дх) = Jim ап.
2.	А = R. База Вг состоит из всех проколотых 8-окрестностей точки х0, 8 > 0 (обозначение: х -> х0). Тогда lim Дх) — это предел при х -» х0, т. е.	, ,	,
limftx) = lim f(x).
By	X —» Xo
3.	A = R. База B2 (x —> x04-) состоит из всех интервалов вида (х0, х0 + 3), где 8 > О,
lim ftx) = lim Дх).
В2	Xх0+
4.	А = R. База В3 (х —> х0~) состоит из всех интервалов вида (х0 - 3, х0), где 8 > О,
lim ftx) = lim Дх).
Bg	X -» х0
5.	А = R. База В4 (х —> 00) состоит из всех множеств {&}, где Ъ есть объединение двух лучей: (-°°, -с) U (с, +°°), с > О,
lun ftx) = Jim ftx).
61
6.	A = R. База В5 (х -> 4-оо) состоит из всех лучей вида (с, +°о), где с > О,
Hm f(x) = hjn^ /(х).
7.	А = R. База Вб (х —> -оо) состоит из всех лучей вида (-°°, с), где с < О,
lim Дх) = lim Дх).
Легко убедиться в том, что все эти совокупности множеств Во, Вр В2, ...» Bq действительно удовлетворяют определению базы. Проверка всех этих множеств на соответствие определению базы однотипна. Поэтому ограничимся рассмотрением только множества В2.
1) В2 состоит из окончаний Ь = вида (х0 - 8, х0) U (х0, х0 + 8) и 0, где 8 — произвольное положительное число. Следовательно, В2 является бесконечным множеством, и каждое его окончание не пусто.
2) При всех 8Х < 82 имеем П &§2 =	, т. е. и второе условие
базы выполнено.
Таким образом, множество В2 является базой множеств.
Определение 4. Пусть множество D с А (где А — область определения Дх)) и пусть существует с > 0 такое, что |Дх)| < с при всех х е D. Тогда функция Дх) называется ограниченной (числом с) на множестве D.
Аналогично определяется ограниченность функции Дх) на множестве D сверху и снизу.
Определение 5. Функция, ограниченная (ограниченная сверху, снизу) на каком-либо окончании базы В, называется финально ограниченной (финально ограниченной сверху, снизу) относительно этой базы.
УТВЕРЖДЕНИЕ 1. а) Пусть Дх) = с при всех х е Ъ, где Ъ — некоторое окончание базы В. Тогда lim Дх) = с.
б)	Если предел функции по базе В существует, то он единствен.
► а) Для любого е > 0 возьмем окончание Ъ g В. Тогда при всех х g Ь имеем |Дх) - с| = 0 < е.
б) Допустим противное, т. е. что существуют и 12 такие, что lim Дх) = Zp lim Дх) = 12.
Возьмем е = |ZX - Z2|/2. Тогда:
62
3 &i =* &х(е) е В такое, что V х е Ъх имеем |Дх) - ZJ < е;
3 Ь2 = Ь2(г) е В такое, что V х g Ь2 имеем |Дх) - Z2| < £•
По определению базы, существует окончание базы Ь3 такое, что b3 а. br А Ь2. Выберем какое-нибудь х g Ь3. Тогда
1*1 - *21 = 1(Я«) - У - (Л*) -*1) I < 1Я*) - *г1 + 1ЯХ) - *11 < 2е =
= R1 “ ^г1»
что невозможно. ◄
УТВЕРЖДЕНИЕ 2. а) Если lim f(x) = Z, то функция f(x) финально ограничена числом |/| + 1.
б) Если lim Дх) = I и I 0, то функция g(x) = 1/Дх) финально ограничена числом 2/\1\ на окончании Ъ(\1\/2), а функция Дх) на том же окончании имеет знак, совпадающий со знаком I.
Докажем это утверждение.
Для базы Вх (х —> х0)	В общем случае
► а) Возьмем е = 1. Тогда найдется 8 = 8(1) такое, что при всех х из проколотой 8-окрестности имеем | Дх) -1\ <1. Отсюда при всех х: 0 < |х - х0| <8 имеем |/(х)| =|(Г(Х)- 0 + Z| < |(flx) - Z| + + И < i + |z|.	► а) Возьмем е = 1. Тогда найдется Ъ = Ь(1) — окончание базы В такое, что при всех х g Ь имеем | Дх) - Z| <1. Отсюда при всех х g g Ъ получим |Дх)| = |(Дх) - Z) + Z| < < |(f(x)-Z| +|Z| < 1 + |Z|.
б) Разберем только случай Z > 0 (второй случай аналогичен). Возьмем е = Z/2. Тогда найдется 8 « 8(e) > 0 такое, что при всех х: 0 < |х - х0| < 8 имеем |Дх) - Z| < е = Z/2. Следовательно, справедливы следующие неравенства: Дх) -Z > - Z/2, Дх) > Z/2 > 0, 0 < #(х) = 1/Дх) < 2/Z.	◄	б) Разберем только случай Z > 0 (второй случай аналогичен). Возьмем е = Z/2. Тогда найдется b == &(е) — окончание базы В такое, что при всех х g Ъ имеем | Дх) - Z| < е = Z/2. Следовательно, справедливы следующие неравенства: Дх) - Z > -1/2, Дх) > Z/2 > 0, 0 < #(х) = 1/Дх) < 2/Z.	◄
УТВЕРЖДЕНИЕ 3. Пусть существуют пределы lim Дх) = и lim g(x) = 12. Тогда справедливо равенство
lim (Дх) + g(x)) = + l2.
Не вполне строго можно сказать, что предел суммы двух функций равен сумме их пределов.
63
* -» *0	В общем случае
► В качестве радиуса искомой 8-окрестности возьмем 8 = min(81(e/2),82(e/2)), где 8х(е/2) — это радиус проколотой 8г-окрестности точки х0, в которой |f(x) - / J < 6/2, а 82 — это радиус проколотой 82-окрестности точки х0, где |g(x) - Z2| < 6/2. Тогда проколотая 8-окрестность точки х0 содержится и в 8гок-рестности, и в 82-окрестности точки х0 с условием 0 < |х - х0| < < 8. Поэтому для х имеем: |(/(x) + g(x))-(Z1 + Z2)|< <|ftx)-zj+|g(x)-z2|<e. ◄	► В качестве окончания Ь(е) возьмем одно какое-либо окончание Ь3 такое, что Ь3^Ь1(е/2)ПЬ2(е/2), где Ь1(е/2) — окончание, на кото-ром I ftx) - zj < е/2, а Ь2 (е/2) — это окончание, на котором |g(x) - Z21 < е/2. Тогда V х е Ь3 имеем |(ftx) + g(x))-(Z1 + Z2)| < < Ift*)-*il +|g(x)-Z2| <е. ◄
УТВЕРЖДЕНИЕ 4. Пусть f(x) = g(x) при всех xeb, где b — некоторое окончание базы В и lim f(x) = I. Тогда
В
lim g(x) = I.
15
►	Имеем g(x) = f(x) + (g(x) - f(x)). Так как g(x) - f(x) = 0 при всех x e b, то по утверждению 1 а) получим lim (g(x) - ftx)) = 0. Отсюда
lim g(x) = lim ftx) + lim (g(x) - ftx)) = I + 0 = I. 4 В	В	В
Определение 6. Если lim а(х) = 0, то функция а(х) называется бесконечно малой функцией по базе В.
Замечание. Из утверждений 1 а) и 3 следует, что условие существования предела lim f(x) = I эквивалентно условию, что функция
а(х) « f(x) - I
есть бесконечно малая по базе В.
УТВЕРЖДЕНИЕ 5. Пусть функция а(х) является бесконечно малой по базе В, f(x) финально ограничена по той же базе,
IP(x)| < |a(x)ftx)|.
Тогда функция Р(х) будет бесконечно малой по базе В.
Докажем это утверждение.
64
* ->*о	В общем случае
► Для любого £ > 0 надо указать число 8 = 8(e) > 0 такое, что Vx: 0 < |х - х0| < 8 => |Р(х)| < £. В силу финальной ограниченности функции Дх) существует 8г > 0 такое, что V х: 0 < |х - х0| < 8г \fM\<c. Найдется 82 = 82(е/С) > 0 такое, что Vx: 0 < |х - х0| < 82 имеем |а(х)| < е/с. Положим 8 = min(81, 82(е/с)). Тогда Vx: о <1* - *ol < 8 имеем |Р(Х)| < |а(х)| • |/(х)| < < Е/С • С = £. ◄	► Для любого £ > 0 надо указать окончание Ъ = Ь(е) базы В такое, что при всех х е b => |р(х)| < е. В силу финальной ограниченности функции Дх) окончание Ьг такое, что при всех хе	| Дх)| < < С. Найдется Ь2 = Ь2(г/С) е В такое, что при всех хе Ъ2=$ => |а(х)| < е/С. Возьмем окончание &3 из условия Ь3 с. Ьг А &2(е/С). Тогда при всех хе Ъ3 имеем 1Р(х)| < |а(х)| • |/(х)| < < е/С • С - е. <
УТВЕРЖДЕНИЕ 6. Пусть lim f(x) = llt lim g(x) = l2. Тогда В	в
lim f(x)g(x) = 1г12. О
►	Имеем f(x) = + a(x), g(x) = l2 + P(x), где a(x), P(x) — бесконечно малые функции по базе В. Тогда получим
f(x)g(x) -1^2 - a(x)/2 + P(x)Zx + a(x)p(x)
— бесконечно малая. ◄
УТВЕРЖДЕНИЕ 7. Пусть lim f(x) = llt lim g(x) = l2, l2 и 0. Тогда
в g(x) l2
► Имеем
/(x) _ h = Zi +a(x) _ Zj = a(x)Z2 - P(x)Zx . 1 =
g(x) l2 i2 + P(x) l2	h	’ S(x)
Здесь (a(x)Z2 ~ Р(х)/х)//2 — бесконечно малая функция по базе В, 1/£(х) — финально ограниченная функция по той же базе, поэтому 7(х) есть бесконечно малая функция по базе В. ◄
3 - 4953
Лекция 10
$ 3. ПЕРЕХОД К ПРЕДЕЛУ В НЕРАВЕНСТВАХ
УТВЕРЖДЕНИЕ 8. Пусть с е R, lim f(x) = I и, кроме того, f(x) > с (или f(x) > с) на некотором окончании b базы В. Тогда 1> с.
►	По условию а(х) = f(x) -I — бесконечно малая функция, причем для всех х е Ь
а(х) = f(x) - 1> с-1.
с — I
Допустим, что с - I > 0. Тогда для е = найдется окончание Ьх g В такое, что при всех х е имеет место неравенство |а(х)| < е. Заметим, что найдутся окончание Ь2 с b A Ьг и. точка х g &2» Для которой выполнены неравенства
е > |а(х)| > а(х) > с - I = 2е > 0.
Отсюда вытекает, что 0 < 2е < е, а это невозможно. ◄
УТВЕРЖДЕНИЕ 9. Пусть lim Дх) = l19 lim g(x) = /2» /(х) < на некотором окончании b базы В. Тогда < 12.
►	Рассмотрим й(х) = g(x) - Дх). По условию й(х) > 0, lim й(х) = I = = l2 - lv Из утверждения 1 имеем I > 0, т. е. l2 > lv ◄
УТВЕРЖДЕНИЕ 10. Пусть Дх) < g(x) < Л(х) на некотором окончании базы В, lim Дх) = I, lim й(х) = I.
в	в
Тогда существует lim g(x) = I.
►	Из условия имеем
0 < g(x )-ftx) < й(х) - ftx), а(х) = h(x) - f(x) -> 0 (по базе В), т. е. а(х) — бесконечно малая функция по базе В.
Но так как |g(x) - /(х)| < а(х), то по утверждению 5 § 2 функция g(x) - f(x) — бесконечно малая функция по базе В. Тогда
lim g(x) = lim (g(x) - f(x)) + lim f(x) = 0 + 1 = 1. < В	В	в
§4. КРИТЕРИЙ КОШИ
СУЩЕСТВОВАНИЯ ПРЕДЕЛА ФУНКЦИИ ПО БАЗЕ
ТЕОРЕМА 1 (критерий Коши). Для существования предела функции f(x) по базе В необходимо и достаточно, чтобы для любого е > 0 существовало окончание Ь = &(е) такое, что при всех х, у g Ь справедливо неравенство |Дх) - f(y)\ < е.
66
► Необходимость. Пусть lim f(x) = L Тогда для любого е > 0 существует окончание Ьг = Ь1(е/2) е В такое, что при всех х, у е Ьг имеем
1Дх) - (|< е/2,\f(y) -1|< е/2.
Отсюда при всех х, у е Ьг
|Дх) - Ду)\ <\f(x) -l\ + \f(y) - 1\ < е/2 + е/2 - е.
Достаточность. Докажем, что Дх) финально ограничена. Действительно, возьмем е = 1. Тогда существует 6(1) € В такое, что при всех х, у е 6(1) имеем |Дх) - Ду)| < 1. Зафиксируем у. Тогда при всех х е 6(1)
1Дх)| < |Дх) - /<у)| + |Ду)| < 1 +|Ду)|.
В силу условия Коши для любого е > 0 существует 6(e) е В такое, что при всех х, у е 6(e) имеем |Дх) - Ду)| < е. Но это значит, что е — верхняя грань значений величины |Дх) - Ду)| для всех х, у е 6(e). Используя также финальную ограниченность Дх), получаем
тп(е) = inf Дх) е R, ЛГ(е) = sup Дх) е R, хе &(е)	х€
е > sup |Дх) - Ду)| = sup (Дх) - Ду)) = sup Дх) - inf Ду) = x,ye&(E)	x,ye&(e)	xeb(e)	0€О(е)
= М(е) - тп(е).
Положим е — гп = 1/п. Тогда можно считать, что 6(1/п2) с Ь(1/7гх) при всех п2 > nv Действительно, если, например, Ь(1/2) <7 6(1), то вместо 6(1/2) можно взять Ь3 из условия Ь3 а. 6(1) А 6(1/2) и т. д. В силу этого имеем
771(1/71!) < ТП(1/П2), M(l/nJ > М(1/П2).
Кроме того, при всех х е 6(e) справедливо неравенство
тп(е) < /(х) < М(е).
Каждому е = еп > 0 соответствует свой отрезок 1п = (тп(1/п), М(1/п)]. Вся совокупность отрезков 1п образует последовательность стягивающихся отрезков, так как при гп > е8
тп(еЛ)<тп(е8)<М(ев)<М(еЛ),
т. е. 18 а 1п. По лемме о последовательности стягивающихся отрезков существует точка I такая, что для любого номера п имеем I е 1п.
Докажем, что lim ftx) = I. Для этого надо доказать, что для любого е0 > 0 существует 6х(е0) е В такое, что при всех х е 6х(е0) справедливо неравенство |ftx) - 1\ < е0.
з*
67
В качестве ^(Eq) возьмем Ь(1/п), где п > Зе^1. Тогда при всех х, у е Ь1(е0) по условию Коши выполняется неравенство |ftx)-fty)| <1/п<е0/2
и при всех х е Ь1(е0) имеем
тп(1/п) < /(х) < М(1/п).
Кроме того, I е 1(1/п). Это значит, что
т(1/п) < I < М(1/п).
Отсюда
|/(х) - 1\ < М(1/п) - т(1/п) < е0/2 < е0. ◄
Определение 7. Две базы Вг и В2 называются эквивалентными, если любое окончание базы Вг содержится в некотором окончании базы В2 и наоборот.
Заметим, что для эквивалентных баз утверждения о пределах выполняются одновременно.
Лекция 11
$ 5. ЭКВИВАЛЕНТНОСТЬ ОПРЕДЕЛЕНИЙ СХОДИМОСТИ ПО КОШИ И ПО ГЕЙНЕ
ТЕОРЕМА 2. Сходимости функции f(x) по Коши и по Гейне при х —> х0 эквивалентны. Другими словами, существование предела функции по Коши при х —> х0 влечет за собой существование предела функции по Гейне по той же базе и наоборот, причем в обоих случаях значения пределов совпадают.
► 1. Пусть существует Jim Дх) по Коши. Докажем, что существует соответствующий предел по Гейне.
Действительно, из условия имеем, что
V е > 0 3 8 = 8(e) > 0 такое, что V х: 0 < |х -> х0| < 8 выполняется неравенство |Дх) - 1\ < е.
Пусть {хп} — произвольная последовательность, стремящаяся к х0 при п —> оо и хп и х0 при всех п € N. Тогда для любого 8 > О существует = АГХ(8) такое, что при всех п > Nr
о < |х„ - ХО1 < 8-
Так как 8 можно взять любым, то и для 8 = 8(e) справедливо то же утверждение.
Надо доказать, что для любого е > 0 найдется номер N(e) такой, что
V п > АГ(е) имеем | Дхп) - 1\ < е.
Положим АГ(е) = Nx(8(e)). Тогда, в силу того, что 0 < |хд - х0| < 8(e), имеем | Дхд) - 1\ < е.
2.	Докажем теперь обратное утверждение. Пусть для любой последовательности {хп} с условиями хп х0 и хп и х0 имеем f(xn) -> I при п -» оо.
Далее будем рассуждать от противного. Пусть I не является пределом функции Дх) по Коши. Это значит, что найдется е > О такое, что
V 8 > 0 3 х: 0 < |х - х0| < 8, для которого выполняется неравенство | Дх) - 1\ > е.
Рассмотрим последовательность 8П = 1/п. Тогда для любого п найдется число хп такое, что: 1) хп и х0; 2) |хл - х0| < 1/п, но 3) 1/(хл) - 1| > е. Числа {хп} образуют последовательность, сходящуюся к х0, следовательно, в силу сходимости по Гейне при п —> оо
69
существует предел Jirn^ /(хл) = I. Но тогда, переходя к пределу в неравенстве | f(xn) - 1\ > е, имеем 0 = \1 - 1\ > е. Полученное противоречие устанавливает справедливость второго утверждения теоремы. ◄
$ 6. ТЕОРЕМЫ О ПРЕДЕЛЕ СЛОЖНОЙ ФУНКЦИИ
Напомним, что сложной функцией h(x) называют функцию вида
ft(x) = /(g(x)),
где f(y) и g(x) — некоторые функции такие, что область определения f(y) содержит все множество значений, принимаемых функцией g(x). Функцию h(x) еще называют композицией (или суперпозицией) функций / и g. Символически это записывается так: h = f ° g.
Следовало бы ожидать, что справедлива следующая теорема: Пусть lim g(x) = yQ9 lim f(y) = l; тогда
x -> x0	у —> Уо
Jim f(g(x)) = l.
Это утверждение справедливо, например, для непрерывных функций. Однако в общем случае данная теорема неверна.
ПРИМЕР.
.. . f О, если х и 0, . v _ — j J, если х = о, g(x) — 0.
Тогда
lim g(x) = 0, lim Дх) = 0,	= 1 V х е R, lim f(g(x)) = 1.
X —> О	X —> О	X —> и
Тем не менее, справедливы следующие утверждения.
ТЕОРЕМА 3. Пусть lim g(x) = у0, lim f(y) = Др0). Тогда
lim f(g(x)) = f(y0).
x —» Xo
► Надо доказать, что для любого е > 0 существует 8 = 8(e) > 0 такое, что при всех х с условием 0 < |х - х0| < 8 имеем
lf(g(x)) - Др0)1 < £•
Далее, для любого заданного е > 0 существует 8Х = 8j(e) > 0 такое, что при всех у: |р - р0| < 8Х имеем |Др) - Ду0)| < е. Для этого 8Х существует 3 = 3(81) > 0 такое, что при всех х с условием 0 < |х - х0| < 3 имеем
1#(х) - Уо1 < 5Г
70
Полученное S и требовалось найти. Теперь при всех х с условием О < |х - х0| < 8 имеем |g(x) - yQ\ < 8V Следовательно, имеем |Г(£(х)>-Я!/о)1 <«• *
ТЕОРЕМА 4. Пусть lim х„ = a, lim f(y) = f(a). Тогда п —ь оо '1	у —> а
м	=/(а)-
► Надо доказать, что для любого е > 0 существует га0 = п0(е) такое, что при всех п > п0 выполняется неравенство
lft*n) - fta)l < £•
По условию имеем:
1) для любого е > 0 существует 8Х = 8х(е) > 0 такое, что при всех у с условием \у - а\ < 8Х выполняется неравенство
1ftУ) - fta)| < е;
2) существует п0 = п^б^ такое, что при всех п > п0 выполняется неравенство
|хп - а| < 5Р
Положим n0 = n^S^e)). Тогда при всех и > п0
|хп - а| < 8г и |ftxn) - fta)| < е. ◄
ТЕОРЕМА 5. Пусть Jim g(x) = у0, причем для всех х из некоторой проколотой окрестности точки х0 имеем g(x) и у0, и пусть lim f(y) = I. Тогда
lim ft#(x)) = Z. x -»x0
► Надо доказать, что для любого е > 0 существует 8 = 8(e) > 0 такое, что при всех х с условием 0 < |х - х0| <8 выполняется неравенство
|/U(x))-Z|<e.
По условию имеем, что для любого е > 0 существует такое 8t = = 8х(е) > 0, что при всех у с условием 0 < \у - ^/0| < 8Х выполняется неравенство \f(y) - l\ < е. Для заданного 8Х > 0 имеем также, что существует S2 = SCSjj > 0 такое, что при всех х с условием 0 < |х -- х0| < 82 выполняется неравенство |g(x) - у0| < 8Р Кроме того, согласно условию существует 83 > 0 такое, что при всех х с условием 0 < |х - х0| < 83 справедливо неравенство g(x) yQ. Тогда возьмем
8 = mln (83, 82(81(е))).
Получаем, что при этой величине 8 выполняется требуемое неравенство. ◄
71
Пусть теперь f(x) имеет предел по базе В. В каком случае сложная функция h(t) = f(g(t)) по некоторой другой базе D имеет тот же предел? Другими словами, когда в функции,, стоящей под знаком предела, разрешается делать замену переменной х на новую переменную (с соответствующей заменой базы В на новую базу D) так, чтобы значение предела сохранялось? Здесь имеет место следующая теорема.
ТЕОРЕМА 6. Пусть lim f(x) = I. Тогда для того чтобы суще-ствовал предел
lim = I, достаточно, чтобы при отображении х = g(t) каждое окончание Ь базы В содержало (целиком!) образ некоторого окончания d базы D.
► В силу определения предела функции по базе В имеем, что для всякого е > 0 существует окончание b « Ь(б) е В такое, что при всех х е Ь имеем |/(х) - 1\ < е.
Из условия теоремы следует, что существует окончание de D такое, что g(d) с b, следовательно, для любого ted
1ЯМО)-*|<е, что и означает справедливость утверждения теоремы. ◄ ПРИМЕРЫ. 1. Пусть
lim f(x) = l,x = 1/t.
Тогда	* 00
lim f (= I.
t->o \t)
Действительно, любое окончание b = {x ||x| > с} базы В (x -» oo) содержит целиком образ окончания d = {t ||t| < 1/c} базы D (t —> 0).
2.	Пусть
.	= J1, если x = 0,
~ 10, если x 0, и g(t) = 0. Тогда
lira f(x) = 0, но lim = 1,
т. e. сложная функция имеет другой предел. В этом случае окончания Ь8 е В (х —> 0) имеют вид 0 < |х| < S, но образ любого окончания d е D, d = {t | 0 <|11 < 8Г}, имеет вид х = 0, т. е. в окончаний Ь8 базы В не содержится образ ни одного окончания базы D, т. е. не выполнены условия теоремы 1.
3.	Пусть /(х) -> I при х —> а и g(t) -» а при t -> Ь, причем g(t) * а в некоторой проколотой окрестности точки Ь. Тогда для сложной функции h(t) имеем h(t) = f(g(t)) -> I при t —> b.
72
Действительно, каждое окончание базы х -> а представляет собой некоторую проколотую окрестность точки х — а< Но в силу условия g(t) -> а и g(t) а при t —> Ъ эта окрестность содержит образ некоторой проколотой окрестности точки t — b при отображении х = g(t). Таким образом, здесь выполнены условия теоремы 6, и поэтому ft(t) -> I при t -> b, что и требовалось доказать.
Доказанные теоремы применяются при вычислении пределов функций.
4.	При х О
.. \ = *2 + 2х + 1 О2+ 2<0 + 1 = .. х3 + х + 1 О3+ 0 + 1
5.	При х —> 2
.	22 + 2<2 + 1 = _9_
/W -> 23 + 2 + 1	11 ’
6.	При х —>
.. . 1 l + 2/x + l/x2	_
- х  l +	+	°-
$ 7. ПОРЯДОК БЕСКОНЕЧНО МАЛОЙ ФУНКЦИИ
Определение 8. Пусть а(х), Р(х), т(х) — бесконечно малые функции по базе В, причем Р(х) # 0 на некотором окончании базы. Тогда, если а(х) представлена в виде
а(х) = р(х)у(х), то говорят, что а(х) имеет больший (или более высокий) порядок малости, чем Р(х).
Определение 9. Бесконечно малые функции а(х) и р(х) называются эквивалентными (по базе В), если разность
8(х) - а(х) - р(х) имеет более высокий порядок малости, чем а(х) (или Р(х)). В этом случае пишут: а ~ р (по базе В).
УТВЕРЖДЕНИЕ 11. Следующие утверждения эквивалентны: 1) а ~ Р (по базе В): 2) p/а - 1 (по базе В), а/Р - 1 (по базе В).
► 1) По условию 8 = а - р имеет более высокий порядок малости, чем а, т. е. 8 = осу, где у — бесконечно малая функция. Следовательно, Р = а - 8,
р/а = (а - 8)/а = а(1 - у)/а = 1 - у —> 1.
2) Обратное утверждение доказывается аналогично. ◄
73
Определение 10. Пусть функция g(x) не обращается в нуль на некотором окончании базы В.
1.	Если функция Л(х) = f(x)/g(x) финально ограничена (по базе В), то пишут:	>
f(x) = O(g(x)) (по базе В).
Читают: f есть О большое от g по базе В и пишут:
f(x) < g(x) (по базе В).
В случае, когда f(x) g(x) Дх), говорят, что функции f(x) и g(x) имеют одинаковый порядок по базе В.
2.	Если функция Л(х) — бесконечно малая, то пишут: Дх) = = o(g(x)) и читают: f есть о малое от g.
3.	Если существуют число 8 > 0 такое, что для любого окончания Ь базы В найдется хе b условием |й(х)| > 8 > 0, то пишут:
Дх) = £2(g(x)) (по базе В).
Читают: f есть омега от g (по базе В).
4.	Функция Дх) = О(хт) при х —> 0 называется бесконечно малой порядка т.
Знаки O(g), o(g), £2(g) предложены Э. Ландау, а знак <К ввел И. М. Виноградов.
ПРИМЕРЫ. 1. При х -> оо имеем
(х + 1)/(х + 2) = О(1).
2.	При х —> °о имеем
sin х/х = о(1), sin х/х « 0(1/х), sin х/х e Q(l/x).
3.	При х —> 0+ имеем Jx - х ~ Jx.
4.	При х —> +°° имеем Jx - х —х.
ГЛАВА 4
Непрерывность функции в точке
Лекция 12
$ 1. СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ В ТОЧКЕ
Определение 1. Функция f(x) называется непрерывной в точке х0, если выполнено одно из следующих эквивалентных условий:
1)V е>038 = 8(e) > 0 V х: |х - х0| < 8 => |/(х) - Дх0)| < е;
2)	Нт ftx) = /(х0);
3)	Нт /(х) = ft Нт х);
4)	f(x) = ftx0) + а(х), где а(х) — бесконечно малая функция при х —> х0, а(х0) = 0;
5)	для любого е > 0 имеем: г-окрестностъ точки ftx0) содержит образ (при отображении f) некоторой окрестности точки х0.
Эквивалентность этих определений следует из доказанных ранее теорем о пределах.
Определение 2. Функция называется непрерывной справа, если
f(x0+) = lim f(x) = f(x0);
X —? XqT
непрерывной слева, если
Лхо_) = Л“ f(x) = f(x0).
УТВЕРЖДЕНИЕ 1. Для того чтобы функция f(x) была непрерывной в точке х0, необходимо и достаточно, чтобы она была одновременно непрерывна и справа, и слева.
► Необходимость. Если f(x) непрерывна, то f(x) -> ftx0) при х -» -> х0. Это значит, что для любого е > 0 существует 8 = 8(e) > 0 такое, что при всех х: |х - х0| <8 справедливо неравенство Iftx) - ftx0)| < е. Но тогда при всех х: -8 < х - х0 < 0 имеем Iftx) “ ft*0)l < е» т* е* Ях) непрерывна слева. Непрерывность справа устанавливается аналогично.
75
Достаточность. Функция /(х) непрерывна справа и слева при х —> х0. Тогда
V е > О Э 8Х = 8х(е) > О V х: 0 < х - х0 < 8Х => |/(х) - f(x0)\ < е;
3 62 = 32(е) > О V х: -32 < х - х0 < 0 =» |/(х) - f(x0)| < е.
Возьмем 8 = min (8Х, 32). Тогда для любого е > 0 существует 8 > О такое, что при всех х: |х - х0| < 8 имеем |Дх) - /(х0)| < е, т. е. функция Дх) непрерывна в точке х0. ◄
ПРИМЕР. Пусть функция Дх) непрерывна в каждой точке отрезка [а, &]. Тогда функция
тоже непрерывна в каждой точке отрезка [а, Ь] (непрерывность в концевых точках отрезка понимается как непрерывность справа или слева).
Действительно, имеем: функция F(x) непрерывна при х = х0, где х0 — нецелое число, поскольку в некоторой окрестности этой точки С(х) ?= cnf(ri)9 А(х) = *	* сп — постоянные. Пусть
х0 — целое число. Тогда
F(x0+) - Um + F(x) = а жоcnf(n) - f(x0) а<^х<сп = F(x0), F(x0-) = Um . F(x) = a < Jxo_ x cnf(n) - f(x0) * < cn = F(x0). В силу предыдущего утверждения функция F(x) непрерывна в точке х = х0.
Свойства непрерывных функций вытекают из соответствующих свойств пределов.
Пусть функции f и g непрерывны в точке х0. Тогда в точке х0 имеем:
а)	функция crf + c2g непрерывна для всех ср с2 е R;
б)	функция fg непрерывна;
в)	функция f/g непрерывна, если £(х0) и 0;
г)	если функция Дх0) и 0, то существует 8 > 0 такое, что
f(x)f(x0) > О V х е (х0 - 8, х0 + 8)
(т. е. функция Дх) сохраняет знак);
д)	функция Дх) ограничена в некоторой окрестности точки х0;
е)	если Дх) непрерывна в точке х0, g(y) непрерывна в точке j/0 = Лхо)’ то ^(х) = £(Д*)) непрерывна в точке х0.
76
$ 2. НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИИ
Перечислим элементарные функции.
1.	Р(х) — многочлен, Р(х) = aQxn + ... + ап.
2.	Рациональная функция f(x) = Q(x)/P(x), где Р(х), Q(x) — многочлены.
3.	Показательная функция /(х) = ах9 а > 0, а 1.
4.	Степенная функция Дх) = ха = еа1п х.
5.	Логарифмическая функция Дх) = loga х, а > 0, а # 1.
6.	Все тригонометрические функции.
7.	Всевозможные суперпозиции всех этих функций.
Эти функции называют элементарными потому, что только их рассматривают в рамках элементарной математики. Описание функциональных свойств этих функций существенным образом опирается на определение понятий показательной, степенной и логарифмической функций, а также на определения функций синус и косинус от вещественного аргумента. Следует сказать, что в элементарной математике свойства перечисленных функций устанавливаются, в основном, описательно, исходя из наглядных арифметических и геометрических соображений. В курсе математического анализа эти функции используют главным образом в качестве материала для применения общей теории, и мы могли бы оставаться на данной «наивной» точке зрения. Однако средства математического анализа позволяют дать вполне строгое определение всех основных элементарных функций. Для показательной, логарифмической и степенной функций это будет сделано сразу после изучения свойств монотонных функций. Несколько сложнее ситуация с тригонометрическими функциями, поскольку их определение должно опираться на понятие длины дуги окружности или на понятие степенного ряда. Пока же, отвлекаясь от строгих определений и опираясь на основные функциональные свойства, докажем непрерывность показательной функции у = ах и функции у = sin х.
УТВЕРЖДЕНИЕ 2. При любом х0 g R функция у = ах непрерывна.
► Пусть а > 1. Тогда надо доказать, что для любого е > О существует 8 = 8(e) > 0 такое, что при всех х с условием |х - х0| < 8 имеем |ах - ахо| < е, или, что то же самое, |а* " *<> - 11 < еа~х° = еР Заметим, что можно ограничиться случаем ех < 1. В качестве 8(e) возьмем число 8Х = 8х(ех) > 0 такое, что из неравенства |х - х0| < 8Х следует неравенство |а*“*о - 1| < еР Далее положим 8(e) = 81(е1) = ^/(а-1).
77
Имеем -8Х < х - х0 < 8Х. Так как а > 1, то а"81 < ах~х° < а81, а-81 -1<ах~х° -1 < а81 -1.
Сначала докажем, что а81 - 1 < ех. Положим
Тогда 1/8х > N, т. е. 8Х < 1/N. Так как
(1 + ех)х> 1 + exN> 1 + ех^ >а, ТО
1 + ех > a1/N > а81. Отсюда следует, что
Окончательно имеем
-ех < a"5i - 1 < ах-хо- 1 < a5i - 1 < ер следовательно, |ах-х<> - 1| < ер Тем самым доказана непрерывность f(x) = ах в точке х0. ◄ УТВЕРЖДЕНИЕ 3. Функция f(x) = sin х непрерывна в точке х0. ► Вспомним, что |sin х| < |х|. Тогда имеем
.	х-х0 х-х0
|sm х - sin х0| = 2sm—— cos——
=|х - х0|.
< 2
х-х0 2
Таким образом, для любого е > О положим 8(e) = е, и получим |sin. х - sin х0| < е V х: |х - х0| < е.
Следовательно, функция Дх) = sin х непрерывна. ◄ Эти утверждения можно записать так:
sin х = sin х0 + а(х), ах = а*0 + 0(х), где а(х), р(х) — бесконечно малые функции.
Оказывается, что при х -> 0, т. е. при х0 = 0, имеют место более точные соотношения, которые называются замечательными пределами:
sinx J ех -1	1
х ~ ’ х
Эти пределы используются далее для изучения дифференциальных свойств элементарных функций.
78
Лекция 13
$ 3. ЗАМЕЧАТЕЛЬНЫЕ ПРЕДЕЛЫ
УТВЕРЖДЕНИЕ 4. Имеют место следующие соотношения:
a)	lim (1 + 1/х)х = е;	в) lim
б)	lim (1 + х)1/х = е;	г) lim -—- = 1.
’ х-»0'	’	' х-*0 X
► а) Рассмотрим сначала случай х —> +°о. в силу свойства монотонности показательной функции справедливы неравенства
/	1	\[х]	/	1 \*	/	1 \ [х] + 1
(1 + ятг) +	
Но мы знаем, что
п
= е.
Отсюда
п
п + 1)	*
= е*
т. е. справедливы утверждения
Ve>03^»N1(e): Vn
3N2 = N2(e):Vn>N2^
1 \п
1 + —Ч) п + 1)
1 \ п + 1
Тогда при п > max (Nt, N2) имеем
1 \n + l
Если х > 1 + max (N19 N2) = N, то [x] > max (N19 N2) = N - 1. Следовательно, при x> N справедливы неравенства
/	1	/ I \x /	1 \i*] +1
e-e<(l + —-]	< 11 +	- I	< l +	Al	<e + e.
k [x] + l/ I	x) k	M)
Таким образом, получаем
Это значит, что (1 + 1/х)х —> е при х —> +°°.
79
Рассмотрим теперь случай х -> Положим у = -х. Тогда, используя теорему 6 гл. III о пределе сложной функции, имеем
(	1 XV	( и \У	/	1 Vs
е = lim 11 4----- | = lim I ] = lim 11 — | =
у -> 4-00 у	у - 1 ) У-^+со \у — 1 J У -++°° V у J
= lim fl + -1 • х —» —оо \	х )
Объединяя случаи х —> 4-оо и х —> -°°, приходим к соотношению
( IV
lim | 1 + - I = е.
Х->оо у	X )
Утверждение а) доказано.
б)	Для доказательства соотношения Jim (14- х)1/х = е воспользуемся той же теоремой 6 гл. III. Полагая х = 1/у, получаем
(1 V
14-- = lim (1 4- х)1/*. у) х->о v '
в)	Так как
(1 4- Х)1/х = gln(l+x)/x е ПрИ х —> О, то из непрерывности и монотонности функции у = ех следует, что
lim 1ПЦ+-5Е2 .1. х-»0 X
г)	Вновь воспользуемся теоремой о пределе сложной функции, полагая
g(x) = ех -1 -> 0 при х —> О,
/(y)=111-a"±iL) —>1приг/~>0, У
и, кроме того, /(0) = 1. Тогда имеем f(g(x)) = хЦех - 1) -> 1 при х —> 0. Отсюда следует утверждение г). <
УТВЕРЖДЕНИЕ 5. lim = 1.
х-»0 X
► При 0 < х < л/2 рассмотрим сектор единичного круга, отвечающего дуге длины х, и два треугольника, один из которых вписан в сектор, а второй, прямоугольный, содержит его, имея с ним общий угол и сторону на оси абсцисс. Сравнивая площади этих фигур, имеем sin х/2 < х/2 < tgx/2. Отсюда получаем cos х < sin х/х < 1. Последние неравенства связывают четные функции, поэтому они имеют место при 0 < |х| < л/2. Так как cos х — непрерывная функция, то по теореме о переходе к пределу в неравенствах
sinx -hm------ = 1.
80
Рассмотрим примеры вычисления пределов.
fl +	- 1
ПРИМЕРЫ. 1. lim ------------а.
х-»0 X
(1 + х)а- 1 = galnd+x)-! = еах + о(х)-1 = 1 + дХ + о(х) - 1
= а + о(1) -> а при х —> 0.
Этот прием называется заменой бесконечно малой функции на эквивалентную ей.
Л ..	1 - cosx 1
2.	hm -----5— = о-
х->0 х2 2
1 - cosx	= 2sin2(x/2)	2(х/2 + о(х))2	_ х2/2 + о(х2)	_ 1
х2	х2	х2	х2	2	1 '*
Таким образом:
1)	(1 + х)а = 1 + ах + о(х) при х -> 0;
х2
2)	cos х = 1 - -у + о(х2) при х —> 0;
3)	Jirn^ (1 + xln}n = ех. Положим хп = х/п —> 0 при п —>	Тог-
да по теореме о пределе сложной функции имеем
X Um ln(1 + *>Л
lim (1 + х/п)п = lim ((1 + х_)1/ж» F = е п^°° *»	= ех.
П —> оо	и —> оо	п'	'
§ 4.	НЕПРЕРЫВНОСТЬ ФУНКЦИИ НА МНОЖЕСТВЕ
Определение 3. Функция Дх) называется непрерывной на множестве А9 если она непрерывна во всякой точке х е А.
Если не все точки множества А входят в него с некоторой окрестностью, то это определение немного меняется.
Определение 3'. Функция Дх) называется непрерывной на отрезке [а, &], если она непрерывна при всех х0 с условием а < xQ<b, непрерывна справа в точке а и непрерывна слева в точке Ь.
Определение 4, Функция Дх) на множестве А называется: а) неубывающей (f Т на А), если f(a) < f(b) при всех значениях а, b е А9 а < Ь;
б)	невозрастающей (fl на А), если f(a) > f(b) при всех значениях а9Ье А9 а <Ь;
в)	(строго) возрастающей (/??), если f(a) < f(b) при всех значениях а9 b е А9 а < Ь;
г)	(строго) убывающей если f(a) > f(b) при всех значениях а9 be А9 а <Ь.
Если функция Дх) неубывающая, или невозрастающая9 или возрастающая9 или убывающая на А, то она называется монотонной функцией на А.
81
Определение 5. Если в своей области определения функция f(x) не является непрерывной в точке х0, то она называется разрывной в точке х0. Точка х0 называется точкой разрыва f(x).
Определение 6. Точка х0 называется точкой разрыва первого рода функции f(x), если существуют конечные пределы Jim + f(x) и Jim __ Дх). В противном случае точка разрыва функции f(x) называется точкой разрыва второго рода.
ПРИМЕРЫ. 1. у = {х} имеет разрывы первого рода в целых точках.
2. у = sin (1/х) в точке х0, = 0 имеет разрыв второго рода. ^Рассмотреть две последовательности: х_ = — , уп =----.)
КП тс/2 + пп '
Определение 7. Разрыв первого рода в точке х0 называется устранимым, если существует lim Дх) = I, но I * f(xQ).
Этот разрыв устраняется, если по-новому определить (или, возможно, доопределить) Дх) в точке х = х0, положив Дх0) = = Jim Дх). Если функция Дх) -> I при х -> х0, но Дх) не определена при х = х0, то говорят также, что имеет место устранимый разрыв. В противном случае разрыв первого рода называется неустранимым.
ТЕОРЕМА 1 (о точках разрыва монотонной функции на отрезке). Пусть функция Дх) — монотонная на отрезке [а, &]. Тогда она может иметь на этом отрезке разрывы только первого рода. Более того, при всех х0 е [а, &] имеем
lim Дх) = inf Дх) = 1г, lim f(x) = sup Дх) = l2, l2<f(XQ)<lv
если f(x) не убывает. Если же функция f(x) не возрастает, то
lim Дх) = sup Дх) = 11г lim Дх) = inf Дх) = 12,
х -> Хо+	х > хо	X -> х0-	х < х0
Z1 < Дх0) < 12.
► Рассмотрим только один случай, когда функция Дх) не убывает (ft) на [а, &]. Остальные случаи рассматриваются аналогично. Докажем теорему в этом случае. Имеем
lim Дх)= inf Дх) = 1Р
х —> Х0Т	х > х0
Аналогично доказывается, что
lim Дх) = sup Дх) = 12.
X х0-	X < х0
82
Так как — точная нижняя грань множества значений Дх)при х > х0, то:
l)7(x)>Z1Vx>x0;
2) V е > 0 3 хг > х0 такое, что Дхх) +
В силу того, что Дх) — неубывающая функция, имеем
Vx: х0 < х < хх => 1г < Дх) < 1г + е, следовательно, = Jim + Дх). Имеем еще, что число Дх0) — нижняя грань для {Дх)} при х > х0, откуда Дх0) < lv
Аналогично Дх0) > Z2, откуда 12 < Дх0) < lv ◄
ТЕОРЕМА! (критерий непрерывности монотонной функции). Пусть функция Дх) определена и монотонна на отрезке [а, &]. Тогда для непрерывности ее на этом отрезке необходимо и достаточно, чтобы для любого I е [Да), Д&)1 нашлась точка х0 g [а, &] такая, что Дх0) = I.
► Рассмотрим только случай неубывающей функции Дх) на отрезке [а, &].
Необходимость. Возьмем любое число I g [Да), Д&)]. Рассмотрим множество X = {х} cz [а, &], для которых Дх) > I, и пусть х0 = inf X. Тогда, поскольку Дх) неубывающая функция, имеем
lim Дх) = inf Дх) = lx > I.
При х < х0 (если х0 а) Дх) < I. Отсюда lim f(x) = l2<l, X —» х0
т. е. l2 < I < lv
Если функция Дх) непрерывна на [а, &], то она непрерывна в точке х0, т. е. 12 = = Дх0). Следовательно, I = 12 = 1г = Дх0).
Если же х0 = а, то Да) < I < 1Х, то из непрерывности функции Дх) в точке а слева следует, что Да) = Zp значит, I = Да) = lv
Достаточность. Будем рассуждать от противного. Пусть функция Дх) имеет разрыв в точке х0 и Дх) не убывает на [а, &]. Тогда для значений 1г = lim + Дх), l2 = lim _ Дх) выполняются неравенства l2 < Zi и 12 < Дх0) < lv
Возьмем I g (l2, IJnl?* Дх0). Имеем:
I > Дх) при х < х0, I < Дх) при х > х0, l^f(x) при х = х0, т. е. функция не принимает значение I на [а, &]• Таким образом, мы пришли к противоречию. «
83
ТЕОРЕМА 3 (об обратной функции). Пусть функция у = /(х) строго возрастает и непрерывна на отрезке [а, Ь]. Тогда существует функция х = g(y), строго возрастающая, определенная на отрезке [/(а), /(&)] и непрерывная на нем, такая, что
= x9m.e.g = Л1.
► 1. Отображение [а, &]	[/(а), /(&)] инъективно, где [а, &] = 119
[/(а), /(&)] = 129 т. е. является вложением. Другими словами, для любых точек хг х2 имеем неравенство ftxj f(x2).
2. Отображение / сюръективно, т. е. является накрытием. Это имеет место по теореме 2, утверждающей, что для любого числа I е [/(а), /(&)] найдется точка х0 g [а, &] такая, что /(х0) = I. Следовательно, f есть биекция, т. е. f устанавливает взаимно однозначное соответствие между и 12. Тогда существует обратное отображение g9 т. е. обратная функция х = g(y).
1. Эта функция монотонно возрастает, так как если уг > у29 то gtyj = хх и g(y2) = х2, причем /(xj = угн f(x2) = у2. Отсюда хх > х2, поскольку /(х) монотонно возрастает.
2. Эта функция g(y) принимает все значения из [а, &], так как для каждого х существует у такое, что g(y) = х, и этим у является число /(х). Отсюда в силу теоремы 2 имеем, что функция g(y) непрерывна на отрезке 12. ◄
Используя доказанные выше теоремы о монотонных функциях, снова обратимся к изучению элементарных функций. Прежде всего, заметим, что при натуральном т функция Дх) = хт -= х ... х является непрерывной и строго возрастающей при х >0.
т раз
Действительно, если а > Ь > 0, то
ат > am~rb > ат~2Ъ2 > ... > аЬ"1"1 > Ьт.
Непрерывность же функции Дх) = хт следует из того, что она является произведением т непрерывных функций вида у = х.
По теореме 3 при всех х > 0 для нее существует обратная функция g(x), которая тоже непрерывна и строго возрастает. Для нее, как известно из курса элементарной математики, используется обозначение g(x) = mJx и она называется операцией извлечения корня тп-й степени. Зафиксируем теперь число х > 0 и натуральное т и рассмотрим числа у = mJx9 z = mJx^. Тогда ут = х, утп = хп, zm = хп* откуда имеем (уп)т = zm иуп = z9 т. е. (mJx)n = = "л/х". Это значит, что операция извлечения корня и возведе
84
ния в целую степень перестановочны, и для числа z возможно использовать обозначения вида z = xn/m и z~x *= x-n/m.
Пусть теперь г *= а/& и гх *= а1/Ь1 — рациональные числа, при? чем а, аг — целые числа, а &, Ьг — натуральные числа. Полагая d = имеем
xrxri =	=	+ «1* = х(аЬ1+а1Ь)/ЬЬ1 =	.
Аналогично получаем
(хг)Г1 = (da&i)ai/6i = daai = xaai^bbi) = xrri.
Таким образом, для рациональной степени фиксированного числа х выполняются те же функциональные соотношения, что и для целой степени того же числа %.
Далее, используя прежние обозначения, допустим, что г>т\ и х > 1. Тогда d > 1, abr > агЬ и dabi > daib, xr > xri.
Следовательно, при возрастании рационального числа г при х > 1 значение хг возрастают. Далее положим х — е. Ранее для любого натурального Ь были получены неравенства
(1+ l/b)b < е < (1 + 1/&)&+1.
Отсюда следует, что
е1/(&+1)<1 + 1/&<е1/&>
Выполняя очевидные преобразования, получаем
ei/(6+D < 1 + 1 = t	> 1 - 1/(& + 1).
Далее, пусть |r| < 1 и г = m/п. Тогда |т\ < п. Применяя неравенство Бернулли, приходим к неравенству
(е±1/Л)|т| > (1 ± |тп|/п), ет/п = > 1 + г.
Отсюда в случае 0 < г < 1 имеем
e~r> 1 - г, ег< 1/(1 - г) = 1 + г/(1 - г).
Пусть теперь а — иррациональное число и рациональные числа и г2 удовлетворяют неравенствам < а < г2. Тогда если {rj — множество всех рациональных чисел, определяемых условием т\ < а, то соответствующее ему множество чисел Mr = {eri} ограничено сверху числом егк Следовательно, существует число уг = sup {eri}. В силу аналогичных соображений относительно множества ЛГ2 = {еГ2} существует число у2 = inf {erz}.
Покажем, что на самом деле имеет место равенство yt = у2. Для этого сначала заметим, что каждое из чисел егг является верхней гранью множества М19 в то время как ух — точная верх
85
няя граць этого множества. Следовательно, для любого г2 > а выполнено неравенство ух < ег2. Это значит, что ух — нижняя грань множества М2. Но так как у2 — это точная нижняя грань данного множества, то ух < у2.
Выберем теперь некоторые значения т\ и г2 с условием
[а] < т\ < а < г2 < [а] + 1.
Тогда справедливы неравенства
О < Yo - у, < егз - eri = ег>(еГ2' r' ~ 1) < еМ+1—Гг ~ Г1— . '2	1	1-(г2-гх)
Но поскольку число у2 - ух — фиксировано, а число г2 - гх > О может быть сколь угодно малым (например, в качестве гх и г2 можно выбрать любые округления числа а с избытком и недостатком), отсюда следует, что у2 - ух = 0, т. е. у2 = ух. Указанную величину ух = у2 = у возьмем в качестве значения степени еа, т. е. по определению полагаем у = ух = у2 = еа. Тем самым мы определили функцию у = ех для всех возможных вещественных значений х.
Осталось показать, что эта функция строго возрастает и удовлетворяет функциональному уравнению вида	= e*i + *2.
Прежде всего следует отметить, что из ее определения вытекает, что если гх < а < г2, где гх и г2 — рациональные числа, то имеет место неравенство eri < еа < еЪ Но тогда, если а < 0, то на интервале (а, 0) найдется рациональное число г3 такое, что имеет место неравенство еа < егз <
Таким образом, строгая монотонность функции у = ех установлена. Пусть теперь ц = ос + 0. Заметим, что если ц — рациональное число, то и в этом случае при рациональных гх и г2 имеем
& = sup eri = inf егк П < И г2>ц
Доказательство последнего равенства по существу повторяет рассуждения, проведенные выше для иррационального числа ц.
Представим теперь число гх в виде rx = rj + /х', где /х < а и < 0, а число г2 — в виде г2 = г2 + г^, где > а и г2 > 0. Тогда будем иметь
eri —	+ г'{ <	< вг'2 + г2 — еГ2, егх < gg < er2e
Отсюда следует, что h = |е^ - еаеР| < егг -
Но ранее уже было показано, что данное неравенство при произвольных рациональных значениях гх и г2 с условием гх < Ц < г2 влечет за собой равенство Л = 0. Другими словами, это означает, что eg = ea + p = eaep>
86
и тем самым все требуемые свойства функции у = ех9 определенной ранее на всей вещественной оси доказаны полностью.
Тогда у функции /(х) = ех, отображающей вещественную ось R на луч (0, +°°), существует обратная функция g(x), отображающая луч (0, +°°) на всю вещественную ось Я. Эта функция называется натуральным логарифмом и обозначается так: g(x) = = In х. Она всюду непрерывна, строго возрастает и удовлетворяет условию: х = е1п х. Отсюда имеем
gin xy =	= gin Xgln у = gin x+ln у.
Поэтому справедливо равенство In xy = In х + In у. Тем самым установлено основное свойство функции у = In х.
Рассмотрим степенную функцию у = ха, где х > 0. Для рациональных значений а ее свойства уже описаны при определении показательной функции. Если же а — иррациональное число, то тогда эту функцию можно определить равенством ха = еа1пх. В этом случае все ее элементарные свойства следуют из уже рассмотренных свойств показательной и логарифмической функций.
Здесь снова уместно подчеркнуть, что строгое обоснование свойств тригонометрических функций в этой части курса проводиться не будет.
Рассмотрим несколько примеров на применение доказанных выше теорем.
ПРИМЕРЫ. 1. Функции у = arcsin х, у = arccos х, у = arctg х — непрерывные на всей области их определения. Это утверждение является прямым следствием доказанных выше теорем.
2. Существует единственная функция х = х(у) (-°° < у < +°°), удовлетворяющая уравнению Кеплера
х - е sin х = у (0 < е < 1).
Действительно:
1) функция у(х) монотонно возрастает, так как при хх > х2
У1 - У 2 = Х1 “ Х2 ~ £(sin Х1 ~ sin Х2> =
Х1 ~ х2 Х1 + Х2
= «1 - х2 - 2е sin—g— cos ——
Xt - X, X, + Хп	X. - Хп
2esin—Ц5—- cos \ 2 < 2е-Ц—2 a	&	и
= £(*! - Х2),
У1 - у2 > (1 - £X*i - х2) > 0;
2) у(х) = х - е sin х — функция непрерывная.
По теореме 3 отсюда следует, что на любом отрезке а < у < b существует единственная непрерывная функция х(у), удовлетворяющая уравнению Кеплера.
Лекция 14
§ 5. ОБЩИЕ СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ
ТЕОРЕМА 4 (об обращении функции в нуль). Пусть функция f(x) определена и непрерывна на [а, Ь] и на концах этого отрезка она принимает значения разных знаков, т. е. f(a)f(b) < 0. Тогда существует с g (а, Ь) такое, что f(c) = 0.
►	Воспользуемся методом Больцано. Отрезок Jo = [а, Ь] разделим пополам точкой хх = (а + Ь)/2. Если Дхх) = 0, то все доказано. Если нет, то f(x^j имеет знак, отличный либо от Да), либо от /(&). Обозначим через тот из двух отрезков [а, или [хх, &], на концах которого Дх) принимает значения разных знаков. Теперь разделим Jx пополам точкой х2 и выберем отрезок J2 так, чтобы на концах его функция Дх) имела значения разных знаков. Поступая так и далее, получим последовательность вложенных отрезков Jq3 J2j ... . Это последовательность стягивающихся отрезков, так как длина Jn равна 8П = 8О/2П —> 0 при и -» оо. Пусть х0 — общая точка всех отрезков. Тогда если Jn = = [ап, Ьп], то ап -> х0 и Ьп -> х0 при п -> оо, и отсюда
/(«„) -> Лхо) и Л&п) -> f(xo) при п ОО.
Так как /(а„)/(Ь„) < 0, то Jim f(an)f(bn) = /2(х0) < 0. Следова-тельно, Дх0) = 0. ◄
ТЕОРЕМА 5 (о промежуточном значении непрерывной функции). Пусть функция Дх) непрерывна на [а, &], Да) = а, ДЬ) = 0 и пусть с — любое число, удовлетворяющее условию
а < с < р, если а < Р, Р < с < а, если р < а.
Тогда существует точка х0 g [а, Ь] такая, что Дх0) = с.
►	Рассмотрим функцию £(х) = Дх) - с. Если g(a) или g(b) = 0, то тогда х0 = а или х0 = Ь. Если же g(a)g(b) * 0, то g(a) и g(b) имеют значения разных знаков. По теореме 4 существует точка х0 g [а, Ь] такая, что £(х0) = 0, откуда Дх0) = с. ◄
ТЕОРЕМА 6 (об ограниченности непрерывной функции). Функция, непрерывная на [а, Ь], ограничена на этом отрезке.
►	Проведем доказательство методом Больцано. Предположим противное, т. е. пусть функция Дх) не ограничена. Тогда разде
88
лим отрезок JQ = [л, &J пополам. В качестве J\ выберем ту половину отрезка, где f(x) не ограничена. Снова делим пополам и выбираем в качестве J2 ту его половину, на которой Дх) не ограничена. Имеем JQ Z) J\ z> J2 Z)... Z) Jn z> ... . Получена последовательность стягивающихся отрезков. Пусть х0 — их общая точка. В ней функция Дх) непрерывна. Возьмем S(l) — окрестность точки х0, в которой |Дх) - Дх0)| < 1. Тогда
|Д*)1 = |(Дх) - Дх0)) + Дх0)| < |Дх) - /(х0)| +1 Дх0)| < 1 + | Дх0)|
и функция Дх) ограничена в 5(1)-окрестности точки х0. Поскольку 8(1) > 0, то в ней целиком содержится всякий отрезок Jn, если только его длина 8Л = (Ь - а}/2п < 8(1). Но тогда Дх) ограничена и на отрезке Jn, это противоречит построению {Jn}. ◄
ТЕОРЕМА 7 (о достижении непрерывной функцией точной верхней и нижней граней). Функция, непрерывная на отрезке, достигает своей точной верхней грани и точной нижней грани, т. е.
хг е [а, &] такое, что sup Дх) = ДхЛ, х € [а, ft]
х2 е [а, Ь] такое, что inf =
Докажем теорему только для sup Дх), так как для случая inf Дх) можно рассмотреть функцию Д(х) = -Дх).
► Воспользуемся методом от противного. Пусть А = sup Дх), А 5^ Дх) при всех х g [а, &]. Тогда А > f(x) для любого х. Но тогда А - Дх) — непрерывная функция и А - Дх) > 0 при всех х g [а, &].
Следовательно, функция g(x) = 1/(А - Дх)) тоже непрерывна. Поэтому функция g(x) ограничена по теореме 3 и, значит, найдется В > 0 такое, что
А - f(x)
Отсюда
А - Дх) > 1/В, Дх) < А - 1/В,
т. е. число А - 1/В есть верхняя грань, которая меньше, чем А, но это противоречит тому, что А — наименьшая верхняя грань. ◄
Так как для непрерывной функции Дх) на отрезке точная верхняя грань и точная нижняя грань достижимы, то А = sup Дх) называют максимальным значением f(x), а В = inf Дх) — минимальным значением Дх) и пишут:
А = max Дх), В = min Дх).
хе[а, ft]	хе [a, ft]
89
ПРИМЕР. Пусть функция Дх) непрерывна на отрезке [а, &] и пусть а = хг < х2 < ... < хп = Ь. Тогда существует точка £ е [л, Ь] такая, что выполняется равенство
= f(x1) + f(x2) + ...+f(xn)
Действительно, пусть
т = min (/(хх), Дх2)...ftxj), М = max (/(xj, ftx2),, f(xn)).
Тогда, очевидно, справедливо неравенство
/(ХХ) + Лх2) + ... + ftxn)
т <---------------------- = А < М.
п
Следовательно, в силу теоремы 5 о промежуточном значении непрерывной функции, отрезок [m, М] принадлежит области значений функции Дх), и поэтому существует точка £ е [а, &] такая, что Д£) = А. Это и есть искомая точка.
Лекция 15
§ 6. ПОНЯТИЕ РАВНОМЕРНОЙ НЕПРЕРЫВНОСТИ
Запишем определение функции, заданной на множестве X и непрерывной в точке х0 е X: для любого е > 0 существует такое 8 = 8(e) > 0, что при всех хе X и |х - х0| < 8 имеем | Дх) - Дх0)| < е.
Вообще говоря, при фиксированных е > 0 у каждой точки х0 будет свое значение величины 8(e), т. е. 8(e) зависит от х0 и это можно символически записать так: 8(e) = 8(е, х0).
Если оказалось, что для любого е > 0 и всякой точки х0 е X величина 8(e) не зависит от х0, то функция Дх) называется равномерно непрерывной на множестве X.
Запишем это определение более четко в эквивалентной форме. Определение 8. Функция Дх) называется равномерно непрерывной на X, если V е > 0 3 8 = 8(e) > 0 такое, что
V хр х2 е X : |xt - х2| < 5 => Iftxj) - ftx2)| < е.
ТЕОРЕМА 8 (теорема Гейне—Кантора). Функция, непрерывная на отрезке, равномерно непрерывна на нем.
► Для доказательства воспользуемся методом от противного. Пусть функция Дх) непрерывна, но не является равномерно непрерывной на [а, &]. Тогда
3 е > О V 8 > 0 : Va, р е X : |а-Р| < 8 и |Да) - ДР)| > е.
Рассмотрим последовательность 8 = 8Л = 1/п. Каждому п тогда соответствует пара точек ад, Рп такая, что
|а„ - р„| < 1/п, |/(ап) -/(рл)| > е.
Последовательности {ап} и {р„} являются ограниченными. По теореме Больцано—Вейерштрасса из а„ можно выбрать сходящуюся подпоследовательность {а,,*}, т. е. an* -> х0 е X при k -»оо. Далее,
1% ~ < 1/га*’
следовательно,	- Рп* — бесконечно малая последовательность и Рп* х0 при ft -> оо. Но тогда yk =	Л*о)> ** =
= /(РП(к) Дх0) при ft оо, т. е. tk = \yk - 2 J -> О при ft -> оо. Но это противоречит тому, что tk — |yk - zk\ > е, так как, переходя в этом неравенстве к пределу при k —> оо, получаем 0 > е, что неверно. ◄
91
Доказательство теоремы Кантора аналогично и для множества X, которое не обязательно является отрезком. Достаточно, чтобы множество X было ограниченным и содержало все свои предельные точки.
$ 7. СВОЙСТВА ЗАМКНУТЫХ И ОТКРЫТЫХ МНОЖЕСТВ.
КОМПАКТ. ФУНКЦИИ, НЕПРЕРЫВНЫЕ НА КОМПАКТЕ
Определение 9. Множество точек (на вещественной прямой) называется замкнутым, если оно содержит все свои предельные точки.
Напомним, что х0 — предельная точка множества А, если во всякой окрестности точки х0 находится бесконечно много точек, принадлежащих А (сама точка х0 может принадлежать или не принадлежать А).
Определение 10. Множество называется открытым, если каждая его точка содержится в ее 8-окрестности, целиком состоящей из точек этого множества.
ПРИМЕР. Ийтервал — открытое множество, а отрезок — замкнутое множество.
Определение 11. Ограниченное замкнутое множество (на вещественной прямой) называется компактом.
УТВЕРЖДЕНИЕ 6. а) Если А — замкнутое множество, тоАг = R\ А открыто.
б) Если В открыто, то Br = R\ В замкнуто.
► а) Воспользуемся методом доказательства от противного. Если существует a g Ар у которой нет окрестности, целиком состоящей из точек множества Ар то во всякой S-окрестности точки а есть хотя бы одна точка из А, отличная от а, следовательно, и бесконечно много точек из А. Но тогда а — предельная точка множества А, и в силу замкнутости А имеем, что а е А, но а е АР Имеет место противоречие.
б) Пусть р — предельная точка для Вг и Р g В. Тогда в любой ее окрестности есть точки Вр а это противоречит тому, что у любой точки множества В есть окрестность, состоящая из одних только точек множества В. Это значит, что Р ё В, т. е. р g Вр следовательно, Вг замкнуто. ◄
УТВЕРЖДЕНИЕ 7. о) Любое объединение открытых множеств открыто, конечное пересечение открытых множеств — тоже открытое множество.
92
б)	Любое пересечение замкнутых множеств замкнуто, конечное объединение замкнутых множеств замкнуто.
►	Пусть а е у Аа. Тогда существует номер а0 такой, что а е А^, и существует 8-окрестность точки а, целиком принадлежащая Аао- Обозначим ее О8(а). Тогда О8(а) с U Аа, т. е. U Аа открыто.
Пусть теперь а g . Ah. Тогда 3 Оя (а) cz Ат V т п при 8 = = min (8Р ...» 8т) имеем
°8<а> = *61 °з/а) С Л61А-
Таким образом, утверждение а) доказано, а утверждение б) следует из утверждения а). ◄
Определение 12. Пусть заданы множество А и система множеств {В}. Будем говорить, что В есть цокрытие А, если для любого а е А существует В е {В} такое, что а е В.
Следующее утверждение обычно считают определением компакта.
УТВЕРЖДЕНИЕ 8 (лемма Боре л я). Из любого покрытия компакта открытыми множествами можно выбрать конечное подпокрытие.
► Используем метод доказательства от противного. Пусть А — компакт, тогда существует отрезок Jo такой, что А с Jo (поскольку А ограничено). Делением отрезка пополам строим систему стягивающихся отрезков Jo b z> ... Jk о ... с условием, что множества А П Jk не допускают конечного покрытия для любого k. Пусть xQ — их общая точка.
Поскольку Jk А А не допускает конечного покрытия, в каждом отрезке Jk есть точки из А. Это значит, что точка х0 е А, так как А замкнуто. Всякая точка множества А покрыта некоторым множеством из системы множеств {В}, т. е. существует множество В такое, что х0 е В. Далее, существует номер k такой, что JkczB, поскольку длина Jk -> 0, а множество В открыто. Тем самым В покрывает Jk и A A Jk допускает конечное покрытие. Имеет место противоречие. ◄
ТЕОРЕМА 9 (обобщение теоремы Гейне—Кантора). Функция, непрерывная на компакте, равномерно непрерывна на нем.
►	Возьмем любое е > 0 и зафиксируем его. Каждую точку х0 е К накроем 8'-окрестностью радиуса 8' = |8^|, х0), где 8^|, х0) = 8 определяется из условия, что для любого х е К с условием
93
|х - х0| < 8 имеем |/(х) - /(х0)| < е/2. Каждая такая З'-окрест-ность — это открытое множество. По лемме Бореля выберем конечное подпокрытие для К. Пусть оно состоит из интервалов J\, ... , Jk с длинами соответственно 81, ... , 8fe и центрами аг, ... , ак. Положим 3(e) = min (8Р ..., 8к). Если теперь точки хх и х2 таковы, что |х2 - xj < 8(e), то при некотором а = ав имеем, что точка хх принадлежит |з(|, а j-окрестности точки а, т. е. |хх - а| < |	°)* Но < I а)’ ПОЭТОМУ
1*2 ~ а1 = 1(*2 “ xi) + <*1 ” а)1 < 1*2 “ *il +1xi “ °1 <	а).
Отсюда |/(х2) - /(а)| < е/2. Но так как |/(хх) - /(а)| < е/2, то
l/(*i) - /(х2)| = |(/(хх) - /(а)) + (/(а) - Дх2))| < <1Г(*1)-Г(а)| + |/(х2)-/(а)|<е.
Это и означает, что /(х) равномерно непрерывна на К. <
ПРИМЕРЫ. 1. Функция у = Jx равномерно непрерывна при х > 1. Действительно, для любых хр х2 > 1 имеем неравенство
। ГТ _ ГТ I = Iх! хг| < Iх! ~ хг| ( 8 = Ч 1д/х1 vx21 Г— , Г- 2 ^2 е/
Отсюда для любого е > 0 получим, что при 8 = 2е
V хр х2е (1, +оо) :|х1-х2| <8=> |7*i ~ 7*^1 <е.
2. Функция у = х2 не является равномерно непрерывной на R, поскольку при е = 1 справедливо неравенство для разности
у(п 4- 1/п) - у(п) = (п + 1/п)2 - п2 = 2 4- 1/n2 > 1 = е
при всех натуральных п, а это означает, что не существует числа 8(1) > 0 такого, что для любых двух точек, находящихся на расстоянии, меньшем 8(1), модуль разности значений функции х2 в этих точках был меньше 1.
Ради полноты приведем позитивную формулировку свойства функции f(x) не быть равномерно непрерывной на множестве А.
ТЕОРЕМА 10. Функция f(x) не является равномерно непрерывной на множестве А, если можно указать такое е > 0, что при всяком 8 > 0 найдутся числа ах = ах(8) g А и а2 = а2(8) G А с условием |ах - а21 < 5» которых [/(ах) - /(а2)1 е*
94
Замечания. 1. В данном определении вместо всех 8 > 0 достаточно ограничиться только числами 8 вида 8 — 8П — 1/п.
2. Непрерывность функции в некоторой точке х0 предполагает, что функция f(x) определена в некоторой 8-окрестности этой точки. Доказанная выше теорема 1 справедлива в несколько более общей ситуации. Приведем соответствующее определение.
Определение 14. Функция /(х), определенная на множестве А, называется непрерывной в точке х0 относительно данного множества А, если для любого г > 0 найдется 8 = 8(e) > 0 такое, что при всех хе Ас условием |х - х0| < 8 выполнено неравенство |/(х) - /(х0)| < е.
С учетом сделанных ранее замечаний, данное определение непрерывности можно записать через предел функции по некоторой базе.
Рассуждения, проведенные при доказательстве теоремы 9, остаются полностью справедливыми и в том случае, когда условие непрерывности функции в точке заменяется сформулированным выше определением непрерывности относительно множества А, если только множество А = К является компактом. ч
L
ГЛАВА 5
Дифференцирование функций одной переменной
Лекция 16
$ 1. ПРИРАЩЕНИЕ ФУНКЦИИ.
ДИФФЕРЕНЦИАЛ И ПРОИЗВОДНАЯ ФУНКЦИИ
Свойство функции Дх) быть непрерывной в точке х = а равносильно тому, что разность а(х) = Дх) - Да) является бесконечно малой при х —> а. Другими словами, это означает, что
Дх) = Да) + а(х), где а(х) — бесконечно малая функция при х -> а.
Таким образом, для всякой непрерывной функции в точке х = а имеет смысл рассматривать аналитическое выражение (т. е. формулу)	а(х) = Дх) - Да).
Это выражение называется приращением функции f(x) в точке х = а. Обозначение а(х) = А/(х). Данное обозначение используется даже и в том случае, когда f(x) не является непрерывной функцией в точке х = а.
Итак, если А/(х) -> 0 при х -> а, то функция f(x) непрерывна в точке х = а, и наоборот. Для простейшей функции f(x) = х ее приращение а(х) = х - а называется приращением аргумента, поскольку при Дх) = х значение функции /(х) равно значению аргумента. Это выражение имеет специальное обозначение: а(х) = Ах. Имеем, что Ах -» 0 при х -> а.
Аргумент х можно выразить через его приращение Ах. Действительно, х = а + (х-а) = а + Ах. Следовательно, при фиксированном а приращение АДх) можно рассматривать как некоторую функцию от Ах, т. е.
а(х) = А/(х) = f(x) - f(a) = f(a + Ах) - f(a) = Р(Ах).
Когда хотят подчеркнуть, что значение А/(х) равно А при х = а и Ах = Ь, то пишут
Аь/(а)=А или А/(х)|	=А.
Ах = Ъ
ПРИМЕР. Если Дх) = х2, х = 1, Ах = 2, то
ДхН^Л = ((х + Ах)2 - х2)| х = 9 - 1 - 8.
Ах = 2
96
Теперь рассмотрим более подробно приращение ДДх) как функцию от приращения аргумента Дх. Очень важным для построения ’Курса математического анализа является случай, когда ДДх) бесконечно мала и при этом еще и эквивалентна линейной функции вида сДх, где с — некоторая вещественная постоянная. В этом случае говорят, что приращение ДДх) имеет линейную часть, называемую дифференциалом функции f(x) в точке х = а, а функцию Дх) называют дифференцируемой в точке х = а.
Другими словами, мы приходим к следующему определению. Пусть Дх) определена в некоторой 8-окрестности точки х = а.
Определение 1. Линейная функция £(Дх) = сДх называется дифференциалом приращения ДДх) (или дифференциалом самой функции Дх) в точке х = а), если
ДДх) ~ сДх при О, т. е.
ДДх) = сДх + т(Дх)Дх,
где се Ru у(Дх) 0 при &х —> 0.
Дифференциал функции Дх) обозначают df(x) или просто df. Из определения вытекает, что
Если при этом с 0, то
-С 1 при Дх -» 0.
Отметим, что функция у(Дх) определена в некоторой проколотой окрестности точки х = а, функция ДДх) определена в некоторой 8-окрестности этой точки, а функция df(x) = сДх определена для всех х е R. Нам удобно определить функцию т(Дх), полагая 7(0) = О. В результате в равенстве
ДДх) = df(x) + т(Дх)Дх, определяющем дифференциал df(x)9 все функции определены и непрерывна в^ненЬТорой окрестности точки Дх = 0. Далее, легко видеть, что Д*х^= dx.
Определение 2. Число с =	— называется производной
функции Дх) в точке х = а. Для производной используют следующие общепринятые обозначения:
c^f(a)=a-^ x = a = DfM\x__
4-4953
97
Если df(x) существует, то, исходя из определений 1 и 2, мы также можем написать
f'(a) = lim	=с,
х^а х-а т. е.
f(x) - f(a) ~ f'(a)(x - а) при х -> а.
Введенные выше понятия дифференциала и производной функции имеют не только глубокий аналитический смысл, но вполне определенный физический, точнее, механический, а также геометрический смысл.
Определение 3. Касательная, точнее, наклонная касательная к кривой у = f(x) в точке координатной плоскости с координатами х = а, у = f(a) — это такая прямая, которая проходит через точку (а, Да)), и ее угловой коэффициент k, т. е. тангенс угла ее наклона, равен пределу углового коэффициента А(Дх) «секущей» прямой, проходящей через точки (а, /(а)) и (а 4- Дх, f(a 4- Дх)) при Дх 0.
Поэтому говорят, что касательная — это предельное положение секущей.
Геометрический смысл производной раскрывается следующим ее свойством: число f’(d) есть "тангенс угла наклона касательной к кривой, задаваемой уравнением у = Дх), на координатной плоскости хОу в точке (a, f(a)).
Механическая интерпретация: если t — текущее время; s(t) — путь, пройденный телом за отрезок времени t - tQ, где tQ — начало отсчета, то Ав(011 = а — путь, пройденный телом за время от t = а до t = а 4- М, т. е. Дз(£) = s(a 4- М) - з(а).
Отношение	есть средняя скорость на отрезке време-
t-a
ни [а, а 4- Де], а предел этой скорости при Де -> 0 — мгновенная скорость тела в момент времени t = а. Именно эту величину показывает спидометр автомобиля при его движении.
УТВЕРЖДЕНИЕ 1. Если функция f(x) дифференцируема в точке х = а, то она непрерывна в этой точке.
Действительно, тогда ~ df = сДх, поэтому Д/ бесконечно мала при Дх -> 0, значит, Дх) непрерывна в точке х = а.
ПРИМЕРЫ. 1. Пусть Дх) = х2, а = 2,5. Тогда
ДДх) = (а 4- Дх)2 - а2 = 2аДх 4- (Дх)2, Д/(2,5) = 5Дх 4- (Дх)2, Дх = dx, df(x) = 2adx, df(2, 5) = 5dx.
2. Пусть Дх) = Зх - 1, a = 2. Тогда
ДДх)|х = 2 = Д2 + Дх) - Д2) = ЗДх = df(2) = 3dx.
98
Дифференциал функции, если он существует, является линейной функцией приращения аргумента, поэтому его называют линейной частью приращения аргумента. Если f (а)	0, то
дифференциал в точке х = а называют еще главной частью приращения. Это название отражает свойство разности вида 0(Ах) = = А/ - df, которая есть о(Дх), следовательно, и o(df), т. е. = = o(df). Таким образом, эта разность является бесконечно малой более высокого порядка, чем А/, и поэтому дифференциал df вносит при малых Ах главный вклад в значение приращения АД
Легко привести пример функции Дх), непрерывной в точке х = 0, но не дифференцируемой в этой точке (т. е. Дх) не» имеет дифференциала и производной в этой точке). Действительно, для функции
J х, если х > О, Дх) = IхI = । если х < О, имеем А(|х|) = |х + Ах| - |х|. Отсюда при х = 0 получаем
Д(1х1)1х-0 = l^l-Тогда
|Ах|/Ах -> 1 при Ах	0+, |Ах|/Ах -1 при Ах -> 0-,
т. е. JHm (|Ах|/Ах) не существует.
Но все же правый и левый пределы в этом случае существуют. Они называются правой и левой производной функции.
Приведенный пример показывает, что непрерывная функция может и не иметь дифференциала. Для некоторого класса таких функций вводится более общее понятие односторонних производных.
Определение 4. Конечные пределы (если они существуют)
lim = lim	и Um = lim
Дх -> 0+ Дх х -» а+ X ~ а	Дх -> 0- Дх -> о-	х - а
называются соответственно правой и левой производной функции Дх) в точке х = а.
В рассмотренном выше случае у = |х| односторонние производные в точке х = 0 существуют, при этом правая производная в этой точке равна +1, а левая -1. Связь понятий односторонних и обычной производных между собой выражается следующим очевидным утверждением.
УТВЕРЖДЕНИЕ 2. Функция Дх) имеет производную в точке х = а тогда и только тогда, когда существуют левая и правая производные и они равны между собой.
99
4*
Лекция 17
$ 2. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
ТЕОРЕМА 1. Пусть функция <p(t) дифференцируема в точке t — а, причем <р(а) = Ъ, <р'(а) = а. Далее, пусть функция fix) дифференцируема в точке х = Ь, причем f'(b) = 0. Тогда сложная функция g(t) = /(<p(t)) дифференцируема в точке t = а, причем g(t) = 0 • а.
► В силу дифференцируемости функций <p(t) и fix) имеем
Д<р(О = аД< + а^ДОД*, 04(G) = 0;
Д/(х) = рДх + Рх(Дх)Дх, Рх(0) = 0.
Здесь функции ах(Д<) и p/At) определены в некоторых окрестностях точек At = 0 и Дх = 0 соответственно и стремятся к нулю при At -> 0 и при Дх -> 0. Возьмем во втором равенстве величину Дх равной A<p(t). Тогда получим
Д/(х) = рДф(О + ДфСОРДДчКО) = = раД£ + Д^аР^ДфСО + ах(Д0Р1(Дф(0 + Рах(Д0).
Кроме того, имеем, что Д/(х) = Д£(0, т. е.
Д£(0 = РаДД + Д/т(ДО, где
7(Д0 = ар^ДфСО) + ах(Д0Р1(Дф(0) + ра^ДО-
Но Дф(0 0 как функция Д£ при Д£ -> 0, поскольку функция ф(£) дифференцируема в точке t = а. Отсюда по теореме о пределе сложной функции имеем, что Рх(Дф(О) и «1(Д0 есть бесконечно малые при At —> 0. Следовательно, функция у(Д^) — тоже бесконечно малая при Д£ —> 0, а это означает, что РаД£ — дифференциал функции g(t) в точке t = а, т. е.
dg(t) = РаД£ = Padf, = Ра. ◄
Замечание. Область определения функций ах(Д^) и рг(Дх)
Дф = аД* + ах(Д0Д*» Д/ = рДх + Рх(Дх)Дх целиком содержит некоторые окрестности точек Д£ = 0 и Дх = 0, поскольку при определении дифференциала мы доопределили эти функции в нуле по непрерывности, положив ах(0) = рх(0) « 0. Если этого не сделать, то рассуждения при доказательстве теоремы о дифференцируемости сложной функции будут ошибочны, так как аг(Д£) может принимать значение, равное нулю, даже тогда, когда Д^ 0 для некоторых Д£, принадлежащих той окрестности точки 0, в которой была определена функция.
100
Отметим также, что мы говорим о производной функции f(x) в точке х = а только в том случае, когда эта точка — внутренняя точка области определения Дх). Если же говорится только о правой производной /Л(а+), то область определения Дх). должна содержать промежуток (а, а + 8), а если о левой — то (-8 + а, а).
Дифференциал df(x) функции Дх) в любой точке х « хд отрезка [а, Ь] является линейной функцией сДх от аргумента Дх. Здесь для каждого значения производная f '(х0) = с имеет свое собственное значение. Таким образом, процедура взятий дифференциала порождает отображение отрезка [а, Ь] в множество линейных функций. Это отображение не является числовой функцией, так как его образ состоит не из чисел, а из функций. За такими отображениями утвердилось название «оператор», в данном случае — дифференциальный оператор. Сама процедура отыскания дифференциала или производной функции в точке, как уже говорилось, называется операцией дифференцирования или просто дифференцированием. Напомним также, что функция, для которой существует производная в точке х0, называется дифференцируемой в этой точке.
ПРИМЕР. Пусть Дх) = х2 при 0 < х < 1. Тогда имеем
f(x) = 2х при 0 < х < 1, /'(0+) = 0, Д(1-) = 2.
Докажем теперь теорему о производной обратной функции. Вообще говоря, правило дифференцирования обратной функции следует из теоремы о производной сложной функции, но мы докажем его при более слабых предположениях, не требуя заранее существования производной обратной функции.
ТЕОРЕМА 2 (о производной обратной функции). Пусть функция Дх), определенная и непрерывная на отрезке [а, &], имеет обратную функцию g(y), определенную на отрезке I, концами которого являются точки f(a) и f(b). Пусть х0 — внутренняя точка отрезка [а, &], a yQ — внутренняя точка отрезка /, причем Дх0) = yQ и g(yQ) = х0. Пусть в точке х = х0 функция f(x) имеет производную, отличную от нуля, т. е. f'(xQ) 0. Тогда в точке yQ функция g(y) имеет производную g'(yQ), причем
► Если известно, что g'(y0) существует, то, воспользовавшись предыдущей теоремой, получаем g(f(x)) = х, (g(f(x)))'x = 1, но
(g(f(x))yx = g'(.yQ)f'(x0), следовательно, g'(y0) =	.
101
Если существование производной заранее не предполагается, то доказательство проведем так. Заметим, что Дх) строго монотонна на [а, 6], следовательно, g(y) непрерывна на I и строго монотонна на нем. По определению производной,
„ ч V S(y)-g(yQ) g(y0) = lim----------,
У-^УО y-yQ
если этот предел существует.
В силу непрерывности Дх) в точке х = х0 и теоремы о пределе обратной функции имеем, что g(y) -> g(yQ) = х0 при у -> yQ.
Определим на [а, &] функцию F(x), полагая 2Дх0) = 1/Д(х0) и
х - х0
Тогда F(x) непрерывна в точке х — х0, поскольку
™ ч 1- х“хо	1	1
Х0 xl^of(X)-f(Xo) X^of(x)-f(xo)
х-х0
Сделаем замену переменной вида х = g(y)‘.
р . .. = g(y) ~ g(y0)	= g(y) ~ g(y0)
У	- f(g(.y0>) y~y0
Применяя теорему о пределе сложной функции, получаем, что
существует предел

X = <(1/0)
Но, с другой стороны,
1- и/ / V g(y)-g(go) ,, , lim F(g(y)) = lim --------------g (y0). ◄
У-^Уо	У-^Уо у Уо
ТЕОРЕМА 3 (об инвариантности формы первого дифференциала). Если вместо дифференциала независимой переменной х в формулу для дифференциала df(x) функции Дх) подставить дифференциал некоторой функции х = ф(£), то полученное выражение окажется дифференциалом сложной функции g(t) = Д(р(О)«
Другими словами, пусть df = cxdx — дифференциал функции Дх) в точке х = a, dcp = cxdt — дифференциал <р(£) в точке t = а, причем (р(а) = а. Тогда функция = cxc2dt — дифференциал функции g(t) = Дф(О)в точке t = а.
102
► Эта теорема является прямым следствием теоремы о дифференцируемости сложной функции, так как согласно последней dg(t) = g'(t)dt = c1c2dt = c^cpO).
Смысл этой очень простой и, казалось бы, «пустой» теоремы станет понятным позже, когда мы увидим, что дифференциалы высших порядков уже не обладают свойством инвариантности.
ПРИМЕР. Решение уравнения Кеплера х — х(у): х - е sin х = у, О < Е < 1 — дифференцируемая функция в силу теоремы о производной обратной функции, причем
х 1 - ecosx(y)'
$3. ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ
Рассмотрим правила дифференцирования.
Пусть функции f(x), g(x) дифференцируемы, се R. Тогда'.
1.	(cftx))' = cf\x).
2.	Если f(x) = const, то f'(x) = 0.
3.	(/(x) + g(x))' = f(x) + g'(x).
Эти утверждения следуют из определения производной. Докажем, например, утверждение 3. Имеем: А(/ + g) = &f + Ag. Откуда
A^.+	-> f + g' при Ax —> 0.
Ax Ax Ax '
4.	(ftx)g(x))' = /'(x)g(x) + ftx)g'(x).
► Имеем
A(/g) = f(x + Ax)g(x + Ax) - /(x)g(x) =
Ax	Ax
f(x + Ax)g(x + Ax) - f(x)g(x + Ax) + f(x)g(x + Ax) - /(x)g(x) Ax

-> g{x)f\x) + f(x)g'(x) при Ax -> 0, так как
g(x + Ax) -> g(x),	g'(x) при Дх —> 0. ◄
1 Y g(x))	g2(x)'
► Имеем
1_______1
A(l/g) = g(x + Ax) g(x) = g(x) - g(x + Ax)
Ax	Ax	Ax *g(x)g(x + Ax) g2
103
поскольку
g', ----------> при Дх -> 0.	<
Дх g(x + Дх) g(x)
СЛЕДСТВИЯ.
1. (gi-...’gny = J jSi • ... 'g'b- - ‘gn-
‘	g2
Производные элементарных функций х' — 1;
(хп)' = пхл-1;
, г>х + Дх_ рх	, лДх _ I
(ехУ = lim -— ------ = ех lun — = ех;
Дх -► 0 Дх	Дх -> 0 Дх
(sin xy = lim sin(* + A*)-sinx = '	Дх-»0	Дх
= lim 8in(A*/2) . cos (х +	) - cos х;
д*->о Дх/2 V 2 / (cos х)' = -sin х, так как cos х = sin (тг/2 - х);
(Inх)' =	, f(x) = Inx,
g’(f(x)) efM eXnx x g(x) = ex — обратная функция;
у = x“, a 0 — степенная функция, (xa)' = (ea to*)' = (oln x)' • ealn* = ax01"1;
(tgx)' e f sin*Y = cosx * cosx 4- sinx * sinx = 1	_ 2 x + 1*
\COSX/	cos2x	cos2x	9
(ctgx)' = ftgf - x)Y = —-— -----------f ~ - xY = ~  *- ;
v V2 J J cos2(n/2 - x) 2	/ sm2x
(arcsin x)' = ——i-;—- = ,	1.	= . * ;
cos(arcsinx) _ 8ina(arcsinx) 71 x2
(arccos x)' = f- arcsin x)' = - , 1	;
V2	7	71 -x2
(arctg x)' = —------------- = ——-;
tg2(arctgx) + 1	1 + x2
(arcctg x)' =	1— .
1 + X2
104
Из теоремы 2 о дифференцировании сложной функции и из правил дифференцирования следует:
(ахУ = (ех 1п аУ *= ех ln а(х In а)' = ах 1п а;
/1 w flnxY 1	1
( Oga %)	[ 1па J 1па х 9
<1п
(и0)' = (еоЪ1иУ = euln“(v In и)' = u^v'ln и + v j.
Замечание. Если Л(х) = f(g(x)), то символы f^.(g(x)) и /^(g(x)) определяются равенствами f'x(g(x)) = h'(x), f'^g(x)) = /х(г(х)), где f/x) = f(x).
Лекция 18
$ 4. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ
Пусть функция f(x) дифференцируема в каждой точке интервала (а, &). Тогда каждой точке х е (а, &) можно поставить в соответствие число — производную f'(x) в этой точке. Полученная функция называется функцией, производной от данной, и. обозначается f\x). Может случиться, что она сама имеет производную. Тогда эта производная называется второй производной функции f(x). Обозначение: f'\x) — {f'(x})'.
Подобным образом определяются третья, четвертая и все последующие производные: f"'(x) = (f"(x)Y, fln\x) = (f(n-1)(x))'.
ПРИМЕР, (x3)" = ((x3)')' = (3x2)' = 6x.
ТЕОРЕМА 4 (формула Лейбница). Пусть и, v имеют п-е производные. Тогда справедлива формула
(uv)^ = U(n)l> + nu(n-1)v' +
n(rao 1) u<n-2>v" + ... + HV(n) = 4U
)
где u<°> = u, i/°> = u.
► Воспользуемся методом индукции. При п = 1 утверждение теоремы справедливо. Предположим, что оно верно при п = s > 1. Докажем его при п = s + 1. Имеем
8 ( 8 А (uu)<s+1) = ((iw)<s>)' = X \ т	=
771 ”v| f/v I
8 А	з ( 8
u(m+l)v(s-m)+ V Ш	m = 0	771
7	\
u(m)v(s-m+l) =
8 t ~ 1
u(0u(3-t+l) + V t = О I f'
ц(0)у(8+1) -|-
u(t)u(»-t+l) =
106
поскольку
Имеется еще одно обозначение для n-й производной:
и X
Последнее обозначение связано с понятием дифференциала высшего порядка, к определению которого мы приступаем.
Пусть функция f(x) дифференцируема на (а, &). Тогда существует ее дифференциал df(x) = f (x)dx.
Зафиксируем значение приращения аргумента dx = Дх = й. Тогда df(x) можно рассматривать как функцию от х, заданную на том же интервале (а, Ь). Если она дифференцируема, то дифференциал имеет вид
d(/'(x)ft) = Г '(х)йДх.
Если в этом случае значение Дх взять снова равным й, то получим
d(f'(x)h) = Г(х)й2 = f"(x)dx2.
Это выражение называется вторым дифференциалом и обозначается d2/(x), т. е.
d2/(x) = /"(x)dx2.
Аналогично определим:
d3f(x) = d(d2/(x)) = f "(x)dx3, dnf(x) = d(dn~ V(x)) = fn\x)dxn.
Очевидно, в силу такого определения можно записать:
’ 1 ’ dxn
Целесообразность введения понятия n-го дифференциала будет ясна позднее. Например, будет показано, что приращение Д/(х) во многих случаях можно представить в виде
(формула Бернулли). Смысл этого равенства будет уточнен при его доказательстве.
107
Заметим, что уже второй дифференциал не обладает свойством инвариантности. Действительно, если
f\x) = ^(х) и /"(х) = /2(х), то при х = g(t) имеем
(Лесо»» = (w)te'(o); = f2(g(t) • (gw+л(^о)г"(о-
Отсюда получаем
d2f(g(t)) = Wt)dt2 = Q(g(x))(dg(x))2 + f'g(g(x))d2g(x), в то время как второй дифференциал функции /(х) равен d2f(x) = f'xx(x)dx2,
и при подстановке в правую часть равенства функции g(t) получим выражение fgg(g(x))(dg(x))29 которое, как видим, отличается от правой части равенства для d2f(g(x)). Следовательно, свойство инвариантности для второго дифференциала не имеет места.
Для того чтобы глубже прояснить сущность свойства инвариантности дифференциала, рассмотрим несколько более общие понятия.
Будем называть дифференциальным мономом Dk порядка k от п функций /(х), g(x)9 ... , й(х), п < k9 одной переменной х следующее выражение:
Dk = сЛ«)(х)^Р)(х)... №\x)dxk9
где а + 0 + ...+у=й, причем а, 0, ... , у — натуральные числа и с — некоторая вещественная постоянная.
Всякая линейная комбинация дифференциальных мономов фиксированного порядка от одного и того же набора функций f9 g9 ... , h называется однородным дифференциальным выражением порядка k.
Неоднородным дифференциальным выражением называется линейная комбинация конечного числа мономов разного порядка, но от тех же функций f9 g9 ... , h.
Отметим, что любое дифференциальное выражение можно рассматривать как функцию двух независимых переменных, а именно: х и dx. Но в данный момент нас будет интересовать не функциональная, а алгебраическая сторона вопроса, точнее, свойство дифференциального выражения сохранять свою форму при замене независимой переменной х на функцию <р(0 и, соответственно, dx на dq(t) = y\t)dt. Поясним более четко, что конкретно имеется в виду. Бели подставить в однородное дифференциальное выражение D порядка k вместо х функцию ф(£), то вме-
108
сто дифференциала dxk будем иметь выражение (4ф(£))* = = (ф'(0)*(<^)Л, а вместо производных Ла)(*),	, hf$(x) —
выражения /^(9(0)» £^(ф(0)» ••• ,	(<№))> т. е. получим не-
которое дифференциальное выражение В19 зависящее от t и от dt. Другое дифференциальное выражение В2, зависящее от тех же величин t и dt9 получим, если то же однородное выражение D применим к функциям Д<р(О)> #(ф(0), ••• > Л(ф(О), т. е. вместо /*а)(х), g®\x)9 ... , №(х) рассмотрим /$р(ф(0),	(ф(0), ••• ,
(ф(0), а вместо (dx)k — выражение (dt)k. Если при этом оказывается, что вне зависимости от вида функции ф(£) имеет место равенство Вх — В2, то мы говорим, что дифференциальное выражение D обладает свойством инвариантности, или инвариантно относительно замены переменной. В противном случае считаем, что оно указанным свойством не обладает. Иными словами, инвариантность В означает возможность перестановки порядка выполнения операции замены переменной и операции вычисления этого дифференциального выражения, т. е. коммутативности этих двух операций.
В смысле введенных понятий дифференциалы первого и высших порядков являются однородными дифференциальными выражениями, причем первый дифференциал обладает свойством инвариантности (относительно любой замены переменной), а дифференциалы порядка, большего единицы, этим свойством не обладают. Заметим, однако, что в случае линейной замены переменной инвариантность все же имеет место.
Возникает вопрос, существуют ли дифференциальные выражения порядка, большего единицы, обладающие свойством инвариантности. Известно, что, вообще говоря, инвариантные дифференциальные выражения от нескольких функций существуют. Единственным инвариантным дифференциальным выражением, зависящим от одной функции, является первый дифференциал. Для двух функций f и g все инвариантные выражения порождаются двумя однородными дифференциальными выражениями Вг и. В2 вида Br = fg'dx29 В2 = (f"g' - f'g")dx3. Ф. М. Малышев в 1978 г. доказал общую теорему о конечности количества N(n) «образующих» однородных дифференциальных выражений от п функций и получил оценку N(n) < п\. Кроме того, для степени инвариантного дифференциального выражения имеет ме<?то неравенство k < п(п + 1)/2 [21].
Приведем еще одну теорему, которая касается производных высших порядков от сложной функции.
109
ТЕОРЕМА 5 (теорема Фаа ди Бруно). Пусть функции F(x) и и(х) имеют п-е производные. Тогда для п-й производной функции G(x) = F(u(x)) имеет место следующая формулах
G<»)(X)= X ^“+₽+ir+-Wa+₽+7+... >
а + 2р + Зу +... - п
п! (и'Х* (и"^ (и"у
Лх+р+у+... ccipiy! V1! J 12! J I 3! J
Суммирование в правой части ведется по всем целым неотрицательным числам а, р, у, ... , удовлетворяющим равенству а + 2р + Зу + ... = п.
► Последовательно применяя правило дифференцирования сложной функции, приходим к равенству вида
G^\x)= ki1Ck(x)^Ku)9
где ck(x) — некоторые выражения, вид которых не зависит от конкретного задания функций у = F(u), и = f(x). Поэтому для определения точного выражения ck(x) через функцию и(х) можно использовать любые удобные функции. В силу этого будем считать, что F(u) и и(х) — многочлены n-й степени, записанные в виде
F'(u0)
F(u) = F(u0) + z-^
F^(u0) и!
u'(x0)	w(n)(*o)
u(x) = u(x0 + 0 = u(x0) +	+ ... +	.
Здесь мы полагаем, что переменные znt определены равенствами г = и - u0, uQ = u(x0), t = х - х0. В этом случае функция G(x) представляет собой многочлен степени п2, который можно запи-
сать в виде
G'(x0)
G(x) = G(x0)+4^ + ...+
Gn(x0)	G(n2)(*0)	2
—tn + — + "7-2u tn n\	(n2)!
а также в виде
F'(n0) / u'(Xq)	u^(Xq) \
G(x) = F(u0) +	(4^ t + ... + -^4t* J +
F^Huq) (u'(x0)	и(л)(*о) .n\n
+ n! Ul f n\ J
Раскрывая скобки в последнем равенстве с помощью полинома Ньютона (см. замечание к § 1 гл. 2) и сравнивая коэффициенты при tn в получившемся выражении с первым равенством, приходим к утверждению теоремы. ◄
110
§ 5.	ВОЗРАСТАНИЕ И УБЫВАНИЕ ФУНКЦИИ В ТОЧКЕ
Пусть х0 — внутренняя точка области определения f(x).
Определение 5. Функция Дх) возрастает в точке х = х0, если существует некоторая окрестность этой точки, в которой:
a)	f(x) > f(x0) при х > х0;
б)	/(х) < Дх0) при х < х0.
Ясно, что точка х = х0 является точкой возрастания функции Дх), если > 0 при Дх 0 в некоторой окрестности точки х = х0.
Определение 6. Функция f(x) убывает в точке х = х0, если существует некоторая окрестность этой точки, в которой:
а)	Дх) < Дх0) при х > х0;
б)	Дх) > Дх0) при х < х0.
Точка х = х0 является точкой убывания функции Дх), если в некоторой окрестности этой точки выполняется неравенство
< 0 при Дх 0. Дх *
Определение 7. Функция имеет в точке локальный максимум (локальный минимум), если в некоторой проколотой окрестности этой точки выполняется неравенство f(xQ) > Дх) (соответственно f(xQ) < Дх)).
Определение 8. Функция Дх) имеет локальный экстремум в точке х = х0, если в этой точке она имеет или локальный максимум, или локальный минимум.
ТЕОРЕМА 6 (достаточное условие возрастания или убывания функции в точке).
1. Если f'(xQ) = с > 0, то точка х = х0 — точка возрастания функции f(x).
2. Если f'(xQ) = с < 0, то функция Дх) убывает в точке х = х0.
► 1. Так как
Г(*о) =
* * *0
Дх) - Дх0) х-х0
то существует число 8 = 8(с/2) > 0 такое, что неравенство
Дх) - Дх0)	с
х-х0	2
111
выполняется для всех точек проколотой 8-окрёстности точки х = х0. В этой окрестности имеем
с Дх) - Дх0) Зс < 2 < X - Xq 2
Следовательно, А/ имеет тот же знак, что и Ах, т. е. х0 — точка возрастания. Случай 2 сводится к случаю 1 заменой Дх) на -Дх). ◄
Эта теорема называется леммой Дарбу.
Докажем несколько более общую теорему, а именно, теорему Ферма. Пусть, как и ранее, Дх) непрерывна на [а, Ь].
Определение 9. 1) Внутренняя точка х0 называется точкой несобственного локального максимума (или локального максимума в широком смысле), если существует проколотая 8-ок-рестностъ точки х0, в которой
АДх0) = Дх) - Дх0) < 0.
По аналогии определим, что такое точка несобственного локального минимума.
2) Функция Дх) имеет несобственный локальный минимум (локальный минимум в широком смысле) в точке х0, если существует проколотая Ъ-окрестность, в которой
ДДхо) = Дх)-Дхо)>О.
3) Точки несобственного локального минимума и максимума называются точками несобственного локального экстремума.
Ясно, что экстремальные точки можно рассматривать и как несобственные экстремальные точки, но не наоборот.
ТЕОРЕМА 9 (теорема Ферма). Пусть внутренняя точка х0 отрезка [а, &], на котором определена и непрерывна функция Дх), является точкой экстремума (в широком смысле) этой функции и пусть существует f'(xQ). Тогда имеем f'(x^) = 0.
► Точка х0 не может быть точкой возрастания (убывания), так как тогда в некоторой проколотой 8-окрестности этой точки АДх0) л /АДх0) л	\	.
> 0 I - д — < 0 соответственно 1. Но тогда неравенства Д(х0) > 0 (Г(хо) < 0) невозможны. Остается принять, что Д(х0) = = 0. ◄
Лекция 19
§ 6. ТЕОРЕМЫ РОЛЛЯ, КОШИ И ЛАГРАНЖА
ТЕОРЕМА 8 (теорема Ролля). Пусть функция /(х) непрерывна на [а, Ь] и дифференцируема во внутренних точках этого отрезка. Пусть также f(a) = /(&). Тогда на интервале (а, Ь) существует точка £ такая, что /'(£) = 0.
► Функция f(x) непрерывна на [а, &]. Следовательно, на этом отрезке найдется точка х19 в которой /(х) имеет максимум, а также точка х2, являющаяся точкой минимума для Дх). Если хх = х2, то Дх) постоянна на отрезке [а, &] и f'(x) = 0 всюду на [а, &]. Если же хг х2, то либо Дхх), либо Дх2) не равна Да) = f(b). И та точка из них, для которой равенство не имеет места, является внутренней точкой отрезка [а, &] и одновременно точкой локального экстремума. Обозначив ее через £, имеем по теореме 9 § 5 /'(£) = 0. ◄ ТЕОРЕМА 9 (теорема Коши). Пусть функции f(x) и g(x) непрерывны на отрезке [а, Ь] и дифференцируемы внутри него. Пусть g'(x) * 0 при всех х е (а, Ь). Тогда на интервале, (а, Ь) найдется точка с такая, что
fW-f(b) . Щ g(a)-g(b) g\cY
► Преобразуя эквивалентным образом требуемое равенство с учетом того, что g'(c) и 0, имеем
(Да) - f(b))g\c) - (g(a) - g(b))f(c) = 0.
Заметим, что слева в последнем равенстве стоит значение производной функции Н(х) в точке х = с, где
Н(х) = MxW) - ЛЬ)) - Г(х)&(а) - g(fe)).
Таким образом, достаточно доказать существование точки с, в которой Н'(с) = 0. Но функция Н(х) дифференцируема во внутренних точках отрезка [а, Ь] и
Н(а) = ЩЬ) = -g(a)f(b) + f(a)g(b).
Поэтому по теореме Ролля существует точка се (а, Ъ) такая, что Н\с) = 0. ◄
СЛЕДСТВИЕ (теорема Лагранжа). Пусть функция f(x) непрерывна на отрезке [а, &] и дифференцируема на интервале (а, Ь). Тогда имеет место формула
Да)-ДЬ) = Г(с)(а-&),
где с — некоторая внутренняя точка этого отрезка.
113
Утверждение следствия является частным случаем теоремы Коши при g(x) = х. Это следствие называется также формулой конечных приращений.
Замечания. 1. (О схеме доказательства леммы Дарбу.) Эта лемма утверждает, что если f(xQ) > 0, то в точке х0 функция f(x) возрастает. С другой стороны, ее возрастание означает, что приращение функции Д/(х) w f(x) - /(х0) и приращение аргумента Дх = х - х0 имеют одинаковый знак и Д/(х) И 0 при Дх * 0 в некоторой окрестности точки х0. Доказательство этого факта, по существу, основано на свойстве функции, имеющей положительный предел, быть положительной на некотором окончании базы. В данном случае
f(х0) = lim — г —»х0	X Xq
и поэтому в некоторой проколотой окрестности точки х0 имеем неравенство
Лх) - Дх0) х -х0
>0.
Это и означает, что в данной проколотой окрестности точки х0 значения ДДх) и Дх имеют одинаковый знак и Д/(х) И 0 при Дх 0.
2. а) (По поводу теоремы Коши.) Для справедливости утверждения теоремы, в частности, требуется, чтобы g'(x) И 0 для любого х, принадлежащего отрезку [а, Ь]. Отсюда следует, что g(a) - g(b) И 0, т. е. в знаменателе отношения в формулировке теоремы стоит ненулевое число. Действительно, если предположить, что g(a) = g(b), то по теореме Ролля существует число с такое, что g'(c) = 0, но по условию теоремы это не так.
б) (Геометрическая интерпретация теоремы Коши.) Пусть при а < t < b имеем
(х = /(0,
Тогда в некоторой точке с тангенс угла наклона касательной к этой кривой равен тангенсу угла наклона хорды:
Т g(c) g(a)-g(b)
3. (По поводу теоремы Ролля.) Эта теорема, по существу, утверждает, что при некоторых дополнительных условиях между двумя «нулями» функции всегда лежит «нуль» ее производной. Доказательство теоремы основано на том, что если точка глобального экстремума является внутренней, то она не может быть точкой возрастания или убывания, а отсюда уже следует, что производная в этой точке обращается в нуль.
Докажем еще одну теорему об обращении в нуль производной.
114
ТЕОРЕМА 10. Пусть функция f(x) дифференцируема На (а, Ь), а < ах < Ъх < Ъ и f'(bj) < 0. Тогда существует такая точка е (alr bt), что /'(£) = 0.	'
►	Рассмотрим сначала случай f'(at) > 0. Пусть % — точка максимума на отрезке [ар &х]. Тогда она является внутренней для этого отрезка, так как ах — точка возрастания, а Ьх — точка убывания. Но в этом случае имеем /'(£) = 0. Случай /'(ах) < 0 сводится к первому с помощью замены функции f(x) на g(x) = -f(x). ◄ СЛЕДСТВИЕ (теоремаДарбу). Пусть функция f(x) дифференцируема на (а, Ь) и для некоторых ах, Ьг е (а, Ь):
/'(ах) = а, f(61) = p.
Тогда для всякого числа %, лежащего между а и 0, найдется точка х0 е [ах, Ьх] такая, что f'(x0) =
►	Рассмотрим функцию g(x) = f(x) - х£. Имеем
Я'(ах) = а - g\bx) = р -
Но так как £ лежит между а и 0, тоа-£ир-£ имеют разные знаки. Тогда по теореме 10 существует точка х0 такая, что g\x$) = 0. Отсюда следует, что
f'(x0) - £ = 0, т. е. f'(x0) -	◄
ТЕОРЕМА 11. Функция g(x) « f'(x) не может иметь разрывов первого рода, т. е. если в некоторой окрестности точки х0 существует f\x) их^ — точка разрыва f\x), то х0 является точкой разрыва второго ряда.
►	Пусть f\x) -> а при х -ь х0+, f\x) -> Ь при х -> х0~. Докажем, что а = Ь. Предположим, что это не так. Тогда а и 6. Пусть
х„ = х0 + 1/п -> х0+, уп = х0 + 1/п -> х0—, тогда
Г(хп) а при п -> оо, f'(yn) -> Ъ при п -> оо.
Так как а и Ь, то или а и f'(xQ), или b и /'(х0).
Допустим, что имеет место случай а f'(xQ). Так как число (f(xn) 4- f'(x0))/2 находится между f'(xn) и f'(xQ), то, в силу теоремы Дарбу, существует сп с условием хп < сп < х0, кроме того,
Г'(сп) = (/'(хп) + /'(х0))/2.
Поскольку сп -» х0, согласно определению правого предела по Гейне имеем f(cn) -> а. Отсюда а = (а 4- f'(xn)/2, т. е. а = Г(х0), а это
115
противоречит тому, что /'(х0) # а. Следовательно, предположение, что а * Ь, неверно и а = Ь. Это значит, что функция f'(x) не может иметь разрывов первого рода.
Попутно мы доказали, что если f(x) -> г0 при х -> х0+ (или X ->Х0-), Т0 20 = /'(х0).	*
Рассмотрим пример точки разрыва производной.
ПРИМЕР. Положим
J х2 cos (1/х), если х и О, ’	— 10, если х = 0.
При х 0
f'(x) = 2х cos (1/х) + sin (1/х), а при х = 0 по определению производной
Г(0) _ lim	_ Um (A*)’eos(l/Ax) _
7 Дх-»0 Дх	Дх—>0	Дх
В точке х = 0 не существует ни правого, ни левого предела f\x). Определение 10. Если (Дх) - Дх0)/(х - х0) —>	оо при х -> х0,
то говорят, что Дх) в точке х0 имеет бесконечную производную, и пишут:
f'(x0) = (+оо.
То же самое говорят и пишут о правой и левой производных.
ПРИМЕР. f(x) = Jx. При х и 0 имеем f(x) = 1/(2 Jx). Тогда /'(0+) = lim ^*~° = +оо.
7 v 7 Дх-»О Дх
Лекция 20	< ।
§7. СЛЕДСТВИЯ ИЗ ТЕОРЕМЫ ЛАГРАНЖА
ТЕОРЕМА 12. Пусть f'(x) = 0 для всех х € (а, Ь). Тогда f(x) * = const =
►	По теореме Лагранжа имеем ../а + ЬА .. . .(аЛ-Ьу .( а+Ь\ п
= /(«)-/[ —2~) = f<c\x-2> = 0-
Отсюда
.. .	.(а + Ь\
ТЕОРЕМА 13. Пусть функция f(x) дифференцируема на интервале (а, Ъ). Тогда для того чтобы f(x) не убывала на (а, Ь), необходимо и достаточно, чтобы
f'(x) > 0 V х е (а, Ь).	‘	‘ ‘
►	Необходимость. Условие неубывания функции f(x) эквивалентно тому, что > 0- Переходя к пределу в неравенствах, получаем
Достаточность. Если f\x) > 0, то по теореме Лагранжа
=7'(с)>0
при некотором с е (а, Ь), т. е. функция Дх) не убывает на (а, &). ◄ ТЕОРЕМА 14. Если f\x) > 0 на интервале (а, &), то функция Дх) монотонно возрастает на (а, &).
►	По теореме Лагранжа имеем
АДх) = Д(с)Ах > 0 при Ах > 0. ◄
ТЕОРЕМА 15. Пусть функция Дх) дифференцируема на отрезке [а, &]. Тогда для того чтобы функция Дх) строго возрастала на нем, необходимо и достаточно, чтобы f\x) > 0 на интервале (а, Ь) и Д(х) не обращалась в нуль тождественно ни на каком отрезке [ар &J, лежащем внутри отрезка [а, &].
►	Необходимость. Воспользуемся методом доказательства от противного. Если условие теоремы не выполнено, то или Д(х0) < 0
117
I
для некоторой точки х0 е (а, &), или f\x) = 0 при всех х е [ар Ьг]. | Тогда в первом случае х0 — точка убывания функции Дх), а во I втором случае — Дх) = const на [ар 6J. Это противоречит уело- I вию возрастания функции Дх).	I
Достаточность. Так как по условию Д(х) > 0, то при любых I ai<b19 где a19b1e [а, Ь], имеем	:
Д&1)-Да1) = Г(с)(&1-а1)>0,
т. е. функция Дх) не убывает.	t
Докажем, что Дх) возрастает. Пусть это не так, и Дах) = Д&х)
при br > аг. Но тогда, в силу неубывания Дх) на отрезке [ар Ьх],	|
имеем, что Дх) = const на нем, и, следовательно, f(x) = 0 на (ар & J, | что противоречит условию теоремы. ◄
$ 8. НЕКОТОРЫЕ НЕРАВЕНСТВА
ТЕОРЕМА 16 (неравенствоЮнга). Пусть а, Р > 0, а + Р = 1. Тогда при х > 0 имеем	*
ха < ах + р.
► Рассмотрим функцию Дх) = ха - ах - р. Заметим, что /(1) =
= 1- а- р = 0. Далее, поскольку
f'(x) = а(ха-1 - 1) < 0 при х > 1,
при х > 1 функция Дх) убывает. Следовательно, при х > 1 выпол-
нено неравенство Дх) < Д1) = 0.	<
Если же 0 < х < 1, то
f\x) = а(ха-1 - 1) > 0.
Отсюда получаем, что Дх) < Д1) = 0 при 0 < х < 1. Таким образом, для всех х > 0 выполнено неравенство ха - ах - Р < 0, откуда следует справедливость теоремы. ◄
Положим х = а/Ъ > 0. Из неравенства Юнга имеем неравенство ааЬР < аа + Р&. Это неравенство справедливо при любых а, b > 0. Теперь положим
° x;=1uv1/a’ b и просуммируем по v от 1 до п. Получим У f	У ( Uv/P V-1 1лл=1“Г“) 118	uv, vv > 0, Л2 5 J <1, J
т. е.
Это неравенство называется неравенством Гельдера.
Пусть теперь выполняются следующие условия: р > 1; av,.&v > О, v = 1,... , и. Тогда
► Введем обозначение 1/р + 1/q = 1. Используя неравенство Гельдера, имеем
А = 1 х (av + bv)P = 1х av(av + b^1 + 1x &v(av + bv)P~l = B + C, В = av(av + bv)P-' < (Д x a₽)v₽	+ bjM -
С = Дх bv(av + &v)₽-i < (Д ft?XvSx(av +
Так как q(p - 1) = p9 to
откуда, поскольку 1 - 1/q = 1/р, имеем
,»;)« + ( <
Это неравенство называется неравенством Минковского.
§ 9. ПРОИЗВОДНАЯ ФУНКЦИИ, ЗАДАННОЙ ПАРАМЕТРИЧЕСКИ
Пусть <р(0 и у(£) — две функции, заданные и дифференцируемые на [0,1], и для всех t е [0,1] имеет место неравенство <p'(t) > О (или <р'(0 < 0). Тогда <p(t) строго возрастает (<p(t) строго убывает при <р' < 0) и эта функция имеет обратную функцию t = g(x). Совокупности пар (q>(t), ф(<)) задают функцию у = Дх) такую, что
(х, у) = (х, /(х)) = (<p(t), ф(0).
где х = ф(0, t = g(x), Дх) = y(g(x)).
Найдем производную этой функции. Имеем
поскольку
8	v^(z(z))'
119
Равенство для f\x) можно записать в следующем виде: 
что дает правило нахождения производной функции, заданной параметрически. Таким же образом можно вычислить производные любого порядка. Найдем, например, формулу для второй производной. Имеем
Их) = /^(Ф(О).
С одной стороны, справедливо равенство
(/'ф(ф(О));=г^(ф(О) • фчо,
с другой стороны,
Следовательно,
Лекция 2*1
$ 10. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
0
ТЕОРЕМА 17 (первое правило Лопиталя; неопределенность вида g при х а—). Пусты	’
1)	Дх) и g(x) определены и дифференцируемы в некотором интервале вида (а - 8Р а), 5Х > 0;
2)	Jim_ Дх) = Jim_ g(x) = 0;
3)	g'(x) 0 при всех х е (а - 82, а) при некотором 82 > 0;
4)	существует конечный или бесконечный предел при х —> а-f'(x)	г Г(х)
отношения , т. е. существует hm ЧтЛ.
g(X)	*	x-*a-g(X)
_ _	_	f(x)
Тогда существует предел отношения - и имеет место g\X)
равенство
и™ aa-umga. х-»а- g(x) x-*a-g(x)
► Можно считать, что предел f\x)/g\x) при х -» а- является конечным числом и равен I, поскольку если это не так, можно рассмотреть отношение g(x)/f(x).
Доопределим Дх) и g(x) в точке х в а, полагая /(а) = g(a) = 0. Тогда функции 7(х) и g(x) непрерывны в точке а слева. Поскольку t\x)/gfah при х -» а-, для любого е > 0 существует 83 = 83(е) > 0 такое, что при всех х е /(83) = (а - 83, а) имеем
ЙЦ-ке.
g<X)
Положим 8 = min(8p 82, 83). Тогда для каждого хе (а - 8, 8), используя теорему Коши, получим
/(х) - Да) = g(x) - g(a)
где с е (х, а) с (а - 8, а).	.
Таким образом, по определению предела Jim. = I-
СЛЕДСТВИЕ 1.В теореме 17 можно заменить условие х —> а-и интервал (а - 8, а) на условие х -> а+ и интервал (а, а + 8).
► Докажем этот факт. Достаточно сделать замену переменной у = 2a - х и применить теорему 17 к функциям Д(у) = Дх) и g^y) = = g(x). Очевидно, эти функции удовлетворяют условиям теоремы, причем у = 2a - х —> а- при х -> а+. ◄
Г(с) g'(c)
g(x)
121
СЛЕДСТВИЕ 2 (первое правило Лопиталя; неопределенность ви-
да q при х -> а I. Пусты
1)	f(x) и g(x) определены на некотором интервале (а - 8, а 4- 8) и дифференцируемы на нем, за исключением,, быть может, точки х = а;
2)	lim /(х) = lim g(x) = 0;
3)	f'(x), g'(x) * 0 при хе (а - 8, а + 8), х -> а;
4)	существует конечный или бесконечный предел*, lira •
Тогда существует предел lim и имеет место равенство
lim —rr = lim .
x^ag(x) x->ag'(x)
Доказательство непосредственно вытекает из теоремы 17 и следствия 1.
тт	/(*)
Похожая теорема имеет место для предела отношения и
5\Х)
в том случае, когда функции f(x) и g(x) стремятся к оо при х —> а (неопределенность вида j. Однако доказательство в этом случае усложняется по причине, которая будет ясна дальше. Справедлива следующая теорема.
ТЕОРЕМА 18 (второе правило Лопиталя; неопределенность вида ~ при х а-). Пусты.
1)	f(x) и g(x) дифференцируемы в интервале вида (а - h, а), й>0;
2)	f\x), g\x) # 0 при всех хе (a-h, а);
3)	f(x) -> оо, g(x) -> оо при х —> а-;
4)	существует конечный или бесконечный предел Jimp—.
Тогда предел отношения функций также существует и имеет место равенство
lim - Um 0*1.
x-+a-g(x) x->a-g (х) ► Очевидно, что можно считать lim е Я.
т. е. предел конечен. Действительно, если	= оо, то
lim 7^7 = 0.
122
f(x)
И вместо того чтобы доказывать, что lim -т-т — °° ^достаточно х->а g\X)
£г(х)
показать, что Jim_ = 0. Одновременно это будет означать,
/(х)
что Jim= сю. Как и при доказательстве теоремы 17, будем
использовать формулу Коши. Но здесь ситуация сложнее, так как мы не можем сразу отношение f(x)/g(x) заменить отношением ДДх)/Д£(х). Тем не менее, это можно сделать с малой погрешностью, которая, по существу, стремится к нулю. Будем считать, что в некоторой полуокрестности (а - h19 а) точки а выполняется неравенство Дх) 0 и g(x) # 0. Это возможно, поскольку Дх) —> оо, g(x) -> оо при х —> а-.
Пусть ех — любое число, 0 < ех < 1/2. Возьмем 8Х = 81(е1) > 0 такое, чтобы неравенство
-1 < ev 8r < min (Л, hj)
выполнялось для всех х из интервала (а - 8Р а). Это возможно, так как	>
Нт = I е R
*^>a-g (X)
существует по условию. Пусть х0 — некоторая точка из этой окрестности. Поскольку Jim f(x) = оо, то найдется 82 = SgCeJ > 0 такое, что
|ДХ)| > V х е (а - 52, а).
Аналогично найдется 83 = 83(е) > 0 такое, что
|<(х)| > ^7^ v х € (а - 83, а).
С1
Пусть 84 = min (8Р 82, 83), 14 = {х| х е (а - 84, а)}. Тогда для любого х е 14 в силу теоремы Коши имеем
ДД*о) 4g(x0)
f(x) - ftx0) _ = f(C). g(x) - g(x0)	g'(c)
где c g (x, x0) с I4. Отсюда получим
Af(x0)
Д£(х0)
Д/(х0)
Д£(х0)
+ 1 <E1 + |Z| < 1 + |Z|.

123
Далее для тех же значений х будем иметь цепочку неравенств:
	/(х). g(x) S Д((хо)	, Г(х) _ Д/(х0 g(x) Ag(xc U) _ дАх0)	)	Д«х0) ,) Ag(x0) Д/(х0) _	-1 < < А + ег
< Но так как		г(х) Д£(х0) Ag(x0)/g(x)	1 Дд	
	Д£(х0)	Д/(х0)/Лх)		
Дя	.	£(*о)	‘	। ।
7 = 1“7^у = 1 + а’где 1а1 ei’
Д/	1	ЛХ0)	Ч	।	Q IQI
f	1	f(x)	1	+	Р’ гДе 1Р1 <	^1»
то
1 + а _ 1 = а - Р
1+р	1+р
2ei
<d=4£i-
Следовательно, получаем
-1 < (И + 1)4е1 + £i = e1(4|Z| + 5) = е.
Положим

Тогда для любого е = (О, (4|Z| 4- 5)/2) найдено 8 = 8(e) =
>4\4|Z| +5
такое, что для любого хе (а - 8, а) выполняется не-
равенство
f(x) 7	- ~
-у-- - I < е. Это значит, что g(x)
lim = I. x^a-g(x)
С Л Е ДСТВИ Е 1. Если в теореме 18 условия х а- и х е [a - h,a) заменить условиями х а+ и х е (а, а 4- Л), то утверждение теоремы остается в силе.
► Достаточно применить теорему 18 к функциям
Л(</) = Л(2а - X) = /(х), gr(y) = gi(2a - х) = g(x). ◄
СЛЕДСТВИЕ 2 ^второе правило Лопиталя; неопределенность вида
00	А „
— при х al. Пусть:
124
1)	/(x), g(x) определены и дифференцируемы в проколотой h-окрестности точки а;
2)	f'(x)9 g'(x) и 0 в той же окрестности точки а;
3)	f(x) -> °°, g(x) -> оо при х^а\
f'( х)
4)	существует предел отношения производных lim'Л х и g \Х)
f(x}
Тогда предел отношения функций -т— существует и равен g\X)
v /(*) г f(x) lim = lim . x-^ag(x) x^ag(x)
Доказательство этого утверждения непосредственно следует из утверждений теоремы 18 и следствия 1.
Замечания. 1. В теоремах 17 и 18 условие х -» а- можно заменить условием х —> +°° или х —> а во вторых следствиях теорем 17 и 18 — условием х -» сю.
Доказательство проводится посредством подходящей замены пере-
менной. Например, в случае lim 37— надо положить х =	.
Х-»+оо g\X)	t
Тогда
= r;(-i/o/(i/^) =	= г; со
хав_1/е ^(-l/t)/d/t2)	g[W
f(x) g'M
Отсюда следует существование предела
lim -7-77- = I, t —»о— gi \Ч
и затем по теореме 17 имеем
Г	, Г Кх)
lim —7-т = I = lim 37-4 . х-»0- Я1(^)	х-»+оо g(x)*
2. Применение теоремы Штольца о пределе отношения двух последовательностей позволяет существенно упростить довольно громоздкий вывод второго правила Лопиталя. Далее мы приведем еще один вариант доказательства теоремы 18, основанный на указанной выше идее.
► Докажем теорему 18. В силу определения предела по Гейне, /(*)/#(*) -> I при х -» а- означает выполнение условия f(xn)/g(xn) -> I для любой возрастающей последовательности {хп}, сходящейся к а, хп ** а. Но так как по условию теоремы g(x) —> 00 при х а-9 то и g(xn) —> сю при п —> оо, а это значит, что к отношению /(xn)/g(xn) можно применить теорему Штольца. Поэтому, используя еще и теорему Коши, имеем
r Кхп> = К*п + 1) -К*»)- Г(сп) g(xn) g(xn + Р - g(xn) п™ Я'(СЛ) ’
если только последний предел существует. Но для чисел сп здесь справедливы неравенства хп < сп < хп+19 откуда следует, что сп —> а при п —> сю, поэтому последний предел существует и равен Z.
125
Следует иметь в виду, что монотонность последовательности gtxn)9 необходимая для применения теоремы Штольца, обеспечивается условием g'(x) И 0 в некоторой левой полуокрестности точки х = а. ◄
i
ПРИМЕРЫ. 1. lim Xх = 1. По второму правилу Лопиталя имеем х-> 0+
In Xх = х In х — 77^ , 1/х’
lim 77^ = lim = Hm (~х) = 0, х-»0+1/Х	х->0+-1/Х2	х->0+	'
lim Xх = lim elnx* = eJ™o+xlnx = e° = 1. x -> 0+	x —» 0+
2. Используя первое правило Лопиталя, получаем х - sinx .. 1 - cosx	.. sinx	1
---з— = lim—т—о— = hm= £ .
X3	х-»0 3xz	хчО ОХ	О
lim x-»0
i
Лекция 22
§11. ЛОКАЛЬНАЯ ФОРМУЛА ТЕЙЛОРА
В качестве приложения докажем формулу Тейлора с остаточным членом в форме Пеано или, как ее еще называют, локальную формулу Тейлора.
Мы видим, что дифференциал df приближает приращение А/ с точностью до бесконечно малой порядка, большего 1. Это означает также, что ДДа) - df(x)\х = а = о(Дх), т. е.
f(x) - /(а) - f'(a)(x - а) = о(|х - а|) при х -> а.
Правило Лопиталя позволяет обобщить это утверждение.
Рассмотрим многочлен Тейлора степени п:
д(х) = /„(а, х) = /(а) + М Ах + М (Дх)2 + ... +	(Дх)«,
где Дх = х - а.
ТЕОРЕМА 19 (формула Тейлора с остаточным членом в форме Пеано). Пусть Дх) дифференцируема п - 1 раз в некоторой окрестности точки х = а и существует f(n\a). Тогда
г(х) = Дх) - fn(a9 х) = о((Дх)п) при Дх -> 0.
► Первое доказательство локальной формулы Тейлора. Применяем первое правило Лопиталя п - 1 раз при х -> а к отношению
а(х) “	» получаем
lim _да_ = lim —да-----------... = lim =
Х~*а(х-а)п Х^ап(х-а)п~1	Х~>ап!(х-а)
= J. цт	-q(n~1)(x) .
п! *-><» х-а
Далее имеем
5<п-1>(х) = /(п-1)(а) + /(п)(а)(х _ а).
Отсюда
lim а(х) = lim —r(n	=
х^а	х-»а ((x-a)n)(n-D
= 1 lim	_ /(п)(а)) = 1 (/(„)(а) _ /(«)(а))=о.
П\ х->а \	х — а	' п\
Другими словами, а(х) — бесконечно малая функция при х -> а. Следовательно, Да) = (х - а)па(х), где а(х) — бесконечно малая,
г(х) = о((х - а)»). ◄
127
Формулу Тейлора с остаточным членом в форме Пеано удобно использовать для вычисления пределов. Действительно, при х —> О имеем, например,
sin х = х - gj- +	+ о(х5).
Отсюда
v sinx-x + x3/6	.. х5/120 + о(х5)	1
х->0 х5	х—>0	х5	120
Важно отметить, что локальная формула Тейлора имеет и глубокий содержательный смысл. В частности, она обобщает понятие дифференцируемости функции в точке, поскольку при п = 1 мы получаем из нее данное выше определение дифференциала функции.
Будем говорить, что при некотором п g N функции Дх) и g(x) имеют касание п-го порядка в точке х0, если при х —> х0 выполняется соотношение Дх) - g(x) = о((х - х0)Л). Тогда локальная формула Тейлора утверждает, что многочлен Тейлрра fn(x) имеет касание n-го порядка с функцией Дх).
Заметим, что если два многочлена n-й степени Рл(х) и Qn(x) имеют касание порядка п в некоторой точке х0 с какой-либо функцией £(х), то их коэффициенты совпадают и Рп(х) = Q„(x). Действительно, тогда
An(x) = Pn(x) - Qn(x) = (Рп(х) - £(х)) + (g(x) - Qn(x)) = о((х - х0)").
Но так как многочлен hn (х) имеет степень п, то, устремляя х х0, получаем, что все коэффициенты Лл(х) равны нулю. Это и означает, что Рп(х) и Qw(x) представляют собой один и тот же многочлен. Отсюда также следует, что многочлен Тейлора fn(x) = fn(a, х), из доказанной выше теоремы, определен однозначно. Производные функции Дх) в точке а выражаются через его коэффициенты ck по формулам
Д(а) = k\ck, k = 1, ... , n.
Интересно, что возможна ситуация, когда в точке а у функции Дх) вторая производная f"(a) уже не существует, и в то же время в этой точке имеет место касание порядка п > 2 этой функции и многочлена Рп(х) степени п. Тогда при k > 2 величины
= ^ck>
п
где ck — коэффициенты многочлена Pfe(x) = ck(x - a)A, можно рассматривать как обобщение понятия производной соответствующего порядка функции Дх) в точке х = а. Будем называть
128
эти числа метками k-го порядка функции Дх) в точке х = а и обозначать их через ЭЛ = dk(f(a)).
ПРИМЕР; Функция Дх) на отрезке [а, &] «почти всюду» разрывна, но в то же время она на «всюду плотном множестве» имеет не только производную первого порядка, но и метки ЭЛ(Дх)) любого порядка (точный смысл слов, взятых в кавычки, станет ясным ниже). Эта функция задается так:
J0, если х — иррациональное, д ~ [ и"п, если х = т/п9 (тп, п) = 1.
Ограничимся доказательством утверждения существования только первой производной данной функции.
Очевидно, что если х0 — рациональное число из отрезка [0, 1], то Дх) разрывна в точке х0. Если х0 — иррациональное число, то для любого е > 0 существует лишь конечное число дробей со знаменателями, не превосходящими N = [1/е] + 1, а именно, г19..., rk.
Пусть 8 = min|x0 - rj. Тогда для любого х с условием |х - х0| < 8 имеем
IГ(х) - Дх0)| -1Дх)| < N~N < АГ* < е.
Далее нам потребуются следующие определение и теорема.
Определение. Число а называется алгебраическим, если оно удовлетворяет алгебраическому уравнению с целыми коэффициентами. Оно будет иррациональным9 если любой многочлен первой степени с целыми коэффициентами не обращается в нуль.
Приведем без доказательств следующую теорему.
ТЕОРЕМА 20 (теорема Рота). Пусть £ — иррациональное алгебраическое число и р > 2 — произвольная постоянная. Тогда существует конечное число пар (р9 q) целых чисел9 q > 1, (р, д) = = 1 таких, что |£ - p/q\ < \/q~?
Пусть х0 — любое алгебраическое иррациональное число. По теореме Рота при р > 2 неравенство
\x~p/ql <l/qp.
имеет лишь конечное число решений. Обозначим эти решения черезPi/q19 ... , pr/qr* Зададимся произвольным е > 0 и положим
N = max (gp ..., gr, р, [1/е] + 1), 5 = min|x0 -рг/д4|.
Тогда, если |х - х0| < 5, то при х = т/п, (m, n) = 1, имеем
п > N, |тп/п - х0| > 1/гер, |/(х) - /(х0)| = 1/пв.
129
5 - 4953
Следовательно,
t(x) - f(x0)
n~P
х-х0
11
п <N
Если же х — иррациональное число, то
/(х) - /(х0) х -х0
= 0 < Е. ◄
Таким образом установлено, что при алгебраическом иррациональном числе х0 функция Дх) имеет производную, равную нулю.
Назовем множество А всюду плотным на отрезке [а, Ь], если для любой точки х е [а, Ь] в каждом интервале, содержащем х, находится хотя бы одна точка множества А.
Тогда указанная выше функция: 1) разрывна на всюду плотном множестве отрезка [0, 1]; 2) непрерывна на всюду плотном множестве в [0, 1]; 3) имеет производную на всюду плотном множестве в [0, 1] [34].
В связи с рассмотренным примером может возникнуть вопрос: будет ли функция g(x) на отрезке [а, Ь] дифференцируема п раз, если в каждой точке этого отрезка у функции g(x) существует метка dng(x)? Пример функции у = е-1/*2 sine1/*2 дает отрицательный ответ.
В заключение приведем другое доказательство локальной формулы Тейлора, допускающее простое обобщение на случай функций от нескольких переменных.
► Второе доказательство локальной теоремы Тейлора. Воспользуемся методом математической индукции по параметру п. При п = 1 утверждение теоремы следует из определения дифференциала функции. Предположим теперь, что п > 1. Из условия теоре- i мы вытекает, что функция г(х) дифференцируема (и - 1) раз | в некоторой окрестности U точки х = а, и в самой точке диффе- « ренцируема п раз. Кроме того, в точке а сама функция и все ее 1 производные до n-го порядка включительно равны нулю.	|
Далее, пусть хе U и Ах = х - а. Обозначим через g(Z) функцию | вида g(t) = г(а + £Дх). Тогда имеем	|
r(x) = г(х) - r(a) = r(a + Ах) - r(a) = g(l) - £(0).	|
Отсюда, применяя формулу Лагранжа к функции g(t), при неко- I тором £, 0 < £ < 1, получаем	|
r(x) =	= г'х(а + £Дх)Дх.	I
130
Заметим, что точка а + ^Дх е U. Поэтому к производным в правой части последнего равенства можно применить предположение индукции с заменой значения параметра п на п - 1. Тогда
будем иметь
г'х(а + £Дх) = о(|х - а|Л~х).
Отсюда следует, что Дх) = о(|х - а|п). ◄
$ 12. ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ОБЩЕЙ ФОРМЕ
Согласно формуле Тейлора с остаточным членом в форме Пеано, в окрестности точки можно записать приближенное равенство Дх) ~ /п(а, х). Оказывается, что многочлен /п(а, х) может хорошо приближать Дх) и в некоторой, иногда весьма большой, окрестности точки а. Более того, знание всех чисел fn\a)9 соответствующих только одной точке а, часто позволяет вычислить Дх) при любом х с любой требуемой степенью точности. Этот факт важен не столько для вычислений, сколько для построения теории. Точнее, мы сейчас докажем одну из важнейших теорем анализа, а именно, формулу Тейлора с остаточным членом в общей форме (или в форме Шлемильха—Роша).
ТЕОРЕМА 21 (формула Тейлора). Пусть Дх) - (л + 1) раз дифференцируемая функция на интервале (х0, хх). Пусть а < Ъ — любые две точки из этого интервала. Тогда для любого положительного а > 0 существует точка с9 лежащая между а и Ь такая, что
r.w - № - f.(a, ») -	•«, - е)"«.	.
Напомним, что
4(а, b) = f(a) + 0^ (Ь - а) + ... +	(6 - а)».
► Определим число Н равенством
f(b)-fn(a9b) И (Ь- а)а ’
По существу, надо доказать, что на интервале (а, Ъ) найдется точка с такая, что
Докажем это, опираясь на теорему Ролля. Равенство, определяющее число Н9 можно записать так:
Д&)-4(а, &)-Н(Ь-а)а = 0.
131
5*
Рассмотрим функцию ф(£), определенную на [а, 6] соотношением Ф(0 = /(&)-/„ (О b)-H(b-ty.
Тогда, очевидно, <р(а) = 0. Кроме того, имеем, что ф(0 дифференцируема на (а, Ь) и непрерывна на [а, Ь]. Далее, так как справедливо равенство fn(b, b) = f(b), то
<Р(Ь) = Г(Ь) - f(b) - ЩЬ - by = 0.
Следовательно, по теореме Ролля на интервале (а, Ь) производная ф'(0 обращается в нуль в некоторой точке с, т. е. <pz(t) = 0 при t = с, с е (а, 6). Запишем <р'(0 в развернутой форме:
ф'(о--г„(о &)+ан(б-оа-1 =
= ’(7(0 + Ф (Ь - о + ... + (b - tyj + аН(Ь - О”’1.
Так как при s = 1, ... , п имеем
то
Ф'(0 = аН(Ь - 0“-1 - (Ъ - 0".
Отсюда при t = с получаем
ф'(с) = аЯ(Ь - сГ’1 - /(в+1)(с)(г> ~ с)" = 0.
Следовательно,
Н= ^±1(6-с)"+1-а. f(n + 1)<c) a v 7 (га + 1)!
СЛЕДСТВИЕ. Формула Тейлора с остаточным членом в форме Шлемильха—Роша верна и при а > Ь.
► 1. Если & = а, то fn(a9 Ь) = /(а), гп(Ь) = 0 и формула имеет место.
2. Если & < а, то применим теорему к функции g(x) = f(2a - х), &х = 2а - &. Тогда Ьг > а и справедливо равенство
£(&i) = Sn(a, 6Х) + RM.
Но легко убедиться в том, что gfbj) = /(&), gn(a, &х) = fn(a, 6), Яп(&х) = rn(b). Действительно, имеем
(Ьх - а)» = (а - ЬУ = (-l)s(& - а)®; 0 < s < п;
gn(a, &х) = g(a) +	(6Х - а) + ... +	(6Х - а)" =
= f(a) +	(& - а) + ... + (Ь - аУ = /„(а, &).
132
Далее, при некотором с19 а < сх < Ь, справедливо равенство.

71 + 1 а
Положим с = 2а - ср тогда b < с < а,
п + 1 а
ад)=

Таким образом, формула Тейлора с остаточным членом в форме Шлемильха—Роша в случае а > Ь имеет тот же вид, что и при а < Ь. ◄
Частные случаи формулы Тейлора
1. Остаточный член в форме Лагранжа (а = п + 1). В этом случае
-r+i/(n + 1)(c) _Г(в + 1)(с)
1	’ (п + 1)! (П +1)!
2. Остаток в форме Коши (а = 1):
с = а + 0(& - а), 0 < 0 < 1,1 - 0 =	,
о - а
гп(Ь) = (Ь- д)п+1(1 - 0)»/<П + 1)(а *е(& а)).
Замечания. 1. Формула Тейлора (с остаточным членом в любой форме) в частном случае а = 0 обычно называется формулой Маклорена.
2. Сравнивая формулы Тейлора с остаточными членами в общей форме и в форме Пеано, видим, что в первом случае имеем более точный результат, однако достигается это за счет более жестких требований к функции. В самом деле, в первом случае в окрестности точки, в кдторой рассматривается разложение, требуется существование (п + 1)-й производной данной функции, а во втором случае — только (п - 1)-й производной, т. е. на две производные меньше.
Лекция 23
$ 13. ПРИМЕНЕНИЕ ФОРМУЛЫ ТЕЙЛОРА К НЕКОТОРЫМ ФУНКЦИЯМ
1.	Показательная функция: Дх) = е*. Имеем
ДО) = /'(0) = ... = Дл)(0) = 1, /<л+1>(х) = ех.
Формула Тейлора с остаточным членом в форме Лагранжа принимает вид
у»	-у«2	<у»п	уП +1
^=1+^+^+... + ^ + ---• <ч,еЧ О < 0 < 1.
1!	2!	п! (п + 1)!
При любом фиксированном х остаток в ней стремится к нулю, поскольку
Хп + 1
2.	Функция Дх) — sin х. Имеем
Дл)(х) = sin (х + пл/2),
/(2*+1)(fbc) “ sin (Ox + {2k + 1)л/2) = (-1)* cos Ox.
Формула Тейлора с остаточным членом в форме Лагранжа дает
-у»3	-у«5	v2k ~ 1	<у»2Д? +1
sin х - х -	+ й - ... + (-!>*-cos te.
3.	Функция Дх) = cos х. Имеем
Лп)(х) = cos (х + пл/2), /<2*)(0х) = cos (Ох + 2йл/2) = (-1)* cos 0х.
Тогда у2	v2k — 2	^2k
cos х _ ! _ £. + i_ .... +	+ (-ц.^ соа ex.
4.	Функция Дх) = In (1 + х). Имеем
Следовательно, у-2	-у»3
ln(l+x) = x- у+у - ...+(-l)n-1^- +Rn>
134
Заметим, что если |х| < 1, то Rn —> 0 при п —> ею. Кроме того:
а) если 0 < х < 1, то |ЯП | <
б) если -1 < -г < х < 0, то \Rn | <
рП + 1
^й’где
д = <~1)пx”+1 f1 ~9 V " П 1+0x11+0x7
(остаток в форме Коши).
5.	Функция f(x) = (1 + х)“. Имеем
Дп)(х) = а(а - 1)... (а - п + 1)(1 + х)а-п, поэтому л ।	-1 ,	. а(а-1) , , а(а-1)(а-2) , ,
(1+ х)а = 1 + ах + -*-=—х2 + —-st------ х8 + ...
Z	о!
а(а-1) ... (а-га + 1) ... т	х -ГЛИ,
где
= а(а~Д)-1(«~п) х»+1(1 + 01х)“-"-\ 0 < ^ < 1
(остаток в форме Лагранжа),
д = а(а-1)...(а-п) +1(1 + 0 )а-/ J_Z М 0 < 02 < 1
п (п + 1)!	2	[1 +02xj	2
(остаток в форме Коши). Если |х| < 1, то Rn -> 0 при п -> °о.
Видим, что во всех этих случаях Rn —> 0 при п —> °©. Другими словами,
Ъ <0’ х>=
Это предельное выражение символически записывается так:
Г(х) = Да) + Q^(x - а) + ... +	- а)п + ...
и называется рядом Тейлора функций f(x) в точке х = а.
Заметим, что при всех п е N для n-го члена ряда имеет место равенство
fW(a)(x aV-dnfM - dnf(x) п\ '	' n! п\
х = а Дх = х - а
135
Поэтому ряд Тейлора можно переписать в следующем виде:
. , df +d2f 4-	4-	4-
AZ=1! +-2!" +- + ^ +--
Тем самым определен точный смысл равенства, приведенного ранее в лекции 18, § 4.
Замечание. Ряд Тейлора не всегда сходится к породившей его функции.
ПРИМЕР.
f/x\ = I е“1/х2, если х# О, 10,	если х = 0.
Тогда при любом натуральном k имеем = 0.
Таким образом, видим, что ряд Тейлора нулевой, а породившая его функция отлична от тождественного нуля.
Лекция 24
§ 14.	ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ. ЭКСТРЕМАЛЬНЫЕ ТОЧКИ. ВЫПУКЛОСТЬ
Наша дальнейшая цель — применение построенной теории к решению задач, связанных с изучением поведения функций. Одна из них — задача отыскания локальных и глобальных экстремумов функций. Напомним некоторые уже доказанные утверждения подобного типа и приведем понятия, которые потребуются далее.
1.	Точки х, в которых f'(x) = 0, называются стационарными.
2.	Для того чтобы функция Дх) не убывала на (а, &), необходимо и достаточно, чтобы f(x) >0 на (а, Ь) (критерий возрастания в широком смысле на интервале (а, Ь) дифференцируемой функции).
3.	Для того чтобы функция f(x) строго возрастала на (а, &), необходимо и достаточно, чтобы f'(x) > 0 на (а, &) и, кроме того, f(x) & 0 ни на каком интервале (а19 Ьг) зэ (а, Ь) (критерий возрастания в строгом смысле).
Отсюда имеем: для того чтобы Дх) строго возрастала, достаточно, чтобы f'(x) > 0 при всех х g (а, Ъ) (достаточное условие строгого возрастания).
4.	Если в точке х0 g (а, Ь) имеется несобственный локальный экстремум функции Дх), то х0 — стационарная точка (теорема Ферма).
Далее мы выведем несколько достаточных условий достижения функцией локального экстремума в заданной точке.
ТЕОРЕМА 22. Пусть функция Дх) дифференцируема в некоторой окрестности стационарной точки х0 (т. е. в этой точке Д(х0) = 0). Тогда'.
1а) если f'(x) > 0 слева от х0 и f(x) < 0 справа от х0, то х0 — точка строгого локального максимума функции Дх);
16) если f'(x) < 0 слева от х0 и Дх) > 0 справа от х0, то х0 — точка строгого локального минимума Дх);
2) если f'(x) имеет справа и слева от точки х0 один и тот же знак, то х0 не является точкой экстремума ни в широком, ни в строгом смысле.
► 1а) По теореме Лагранжа имеем
f{x) = ftx0) + Л(с)(х - х0),
где точка с находится на интервале с концами х0 и х.
137
Из условия следует, что f'(c)(x - х0) < 0. Действительно, если х - х0 > 0, то с > х0 и, значит, f'(c) < 0, (х - х0)Д(с) < 0; если же х - х0 < 0, то f'(c) > 0 и (х - х0)Д(с) < 0. Отсюда получим, что Дх) < Дх0), что и требовалось доказать. Доказательство п. 16) проводится аналогично.
2. Если f'(x) > 0 справа и слева от х0, то f'(c)(x - х0) < 0 слева и больше нуля справа. Отсюда имеем Дхх) < Дх0) < Дх2) при хх < Xq < х2, что и требовалось доказать. Случаи f'(x) < 0 рассматривается аналогично. ◄
Доказанная теорема позволяет сформулировать следующее правило исследования стационарной точки на экстремум:
Если при переходе через стационарную точку слева направо производная меняет знак + на знак то функция имеет локальный максимум в этой точке, если знак - меняется на знак +, то функция имеет локальный минимум, и если производная не меняет знак, то локального экстремума нет.
ТЕОРЕМА 22'. Пусть функция Дх) непрерывна в некоторой окрестности точки и дифференцируема в проколотой окрестности этой точки. Если f(x) меняет знак + на знак - при переходе через точку х0 слева направо, то Дх) имеет локальный максимум, если знак - на знак +, то локальный минимум, и если не меняет знак, то локального экстремума нет.
Доказательство этой теоремы совершенно аналогично доказательству теоремы 22, так как там мы нигде не использовали существование производной функции Дх) в точке х = х0.
Приведем общее правило отыскания (локального и глобального) экстремума функции Дх) на отрезке в случае, когда Дх) непрерывна и кусочно-дифференцируема (т. е. дифференцируема всюду, за исключением, быть может, конечного числа точек):
находим все стационарные точки и точки, в которых Г(х) не существует, и проверяем их на экстремальность. Затем, добавляя концевые точки и выбирая наибольшее и наименьшее из значений функции в этих точках, находим ее глобальные экстремумы.
ТЕОРЕМА 23 (второе достаточное условие экстремума). Пусть Д(х0) = 0 и существует f"(x^). Тогда:
1) если /"(х0) < 0, то точка х0 — точка (строгого) локального максимума;
2) если f"(xQ) > 0, то точка х0 — точка (строгого) локального минимума.
138
► 1. Так как f"(xQ) < 0, то f'(x) убывает в точке х == х0, и поскольку f'(xQ) = 0, то f'(x) меняет знак с + на - при переходе через xQ слева направо. Поэтому по теореме 22' точка х0 является локальным максимумом.
2. f"(xQ) > 0, поэтому f\x) возрастает в точке х = х0.
Из теоремы 22' тогда следует, что х0 — точка локального минимума. ◄
ТЕОРЕМА 24 (третье достаточное условие экстремума). Пусть
f\x0) =... =	= О, Л2*’(х0) и 0.
Тогда".
1)	если Л2Л)(х0) < 0’ то хо — точка локального максимума;
2)	если fl2k4x0) > 0, то х0 — точка локального минимума.
►	1. При k = 1 утверждение следует из теоремы 23. Пусть k > 1. Выразим f'(x) по формуле Тейлора:
f (х) = f (х0)+—j^—(х-х0) + ... + (2fe_3), (х-х0)2* 3 +
/(2*-!)(с) . _ -2Й-2 (2fe-2)!(* Х°}	•
Отсюда
Так как /(2ft)(x0) < 0, то /(2fc-1)(x) убывает и, следовательно, /(2*_1)(x) меняет знак + на - при переходе через точку х0, значит, и 1\х} меняет знак + на -. Поэтому х0 — точка локального максимума. Случай 2 рассматривается аналогично. ◄
Определение 11. Дифференцируемая в точке х = х0 функция f(x) называется выпуклой вверх в этой точке, если вспомогательная функция
g(x) = f(x) - f'(x0)(x - х0) имеет в ней локальный максимум.
При этом в случае строгого максимума выпуклость считается строгой, а для нестрогого максимума — нестрогой. Говорят еще, что функция у = Дх) в точке х = х0 имеет выпуклый график. Геометрически это означает, что график функции у = Дх) лежит «под касательной», т. е. что в некоторой проколотой окрестности точки х0 в строгом случае имеет место неравенство
/(х) < ftx0) - f\x0)(x - х0) < 0 или Af(x)|x _ Xq - df(x)|x - Х() < °,
139
а в нестрогом — неравенство
f(x) < f(x0) - f'(x^x - x0) < О или ДДх)|х _ Xq - </Дх)|х _ х<) < О, поскольку уравнение касательной к графику функции у = Дх) в точке х = х0 имеет вид у = Дх0) + f'(x0)(x - х0).
Аналогично определяются строгая и нестрогая выпуклость вниз в точке х = х0. Просто здесь знаки неравенств в определений 11 заменяются на противоположные. Выпуклая вверх или вниз функция в точке х = х0 называется просто выпуклой в этой точке соответственно в строгом или нестрогом смысле. Если без дополнительных оговорок употребляется термин «выпуклая функция», точнее, например, «функция, выпуклая вверх», то обычно имеется в виду строгая выпуклость.
Определение 12. Функция f(x) называется выпуклой вверх на множестве М a. R, если она выпукла вверх в каждой точке этого множества, как в строгом, так и в нестрогом смысле.
Точно также определяется и выпуклость вниз на множестве.
ТЕОРЕМА 25. Если f\x) строго убывает в точке х = х0, то функция Дх) строго выпукла вверх в этой точке.
►	В силу строгого убывания производной f\x) в точке х = х0 в некоторой проколотой окрестности слева от х0 имеем: g\x) = f\x) -- /'(*о) > 0, а справа f\x) - f'(xQ) < 0. Но тогда по теореме 22 функция g(x) = Дх) - f'(xQ)(x - х0) имеет в точке х = х0 строгий локальЦый максимум, поскольку ^(х) = f'(x) - f'(xQ) меняет знак в точке х0. ◄
СЛЕДСТВИЕ. Если f\x) строго возрастает в точке х = х0, то функция Дх) строго выпукла вниз в этой точке.
►	Достаточно вместо функции Дх) рассмотреть функцию Д(х) = = -Дх). ◄
ТЕОРЕМА 25'. 1) Если f"(x0) > 0, то функция f(x) выпукла вверх в точке х = х0.
2) Если f"(x0) < 0, то функция Дх) выпукла вниз в точке х = х0. ► Для функции g(x) = Дх) - f '(х0)(х - х0) имеем g\xQ) = 0, g'(х) = = £'(х0) + g’\xQ)(x - х0) + о((х - х0)2).
Следовательно, в некоторой окрестности точки х0 функция g\x) меняет знак в случае 1) с плюса на минус при переходе через точку х0, что согласно теореме 22 отвечает локальному максимуму функции g(x) в точке х0, и тем самым Дх) выпукла вверх в точке х0. Случай 2) рассматривается аналогично. ◄
140
Замечание 1. Нестрогая выпуклость функции Дх) в точке х х0 выводится из нестрогой монотонности ее производной в этой точке.
Замечание 2. Свойство функции Дх) быть выпуклой в точке х =*= х0 не изменится при замене f(x) на любую функцию вида f2(x) = f(x) + ax + b, где a, b е R, поскольку
Д(ах + b) = d(ax + b).
ТЕОРЕМА 26. Пусть Дх) непрерывна на отрезке Е = [а, 6], нестрого выпукла вверх на интервале (а, Ь) и f(a) = f(b) = 0. Тогда f(x) > 0 всюду на отрезке [а, &].
► Достаточно доказать неравенство Дх) > 0 на интервале (а, Ь). Проведем доказательство методом от противного. Допустим, что найдется точка d g (л, b) такая, что f(d) < 0. Тогда т = min Дх) < < f(d) < 0. В силу непрерывности Дх) на Е по теореме Вейерштрасса существует точка х0 g Е такая, что Дх0) = т < 0. При этом х0 а nxQ^b, так как Да) = Д&) = 0. Заметим, что множество М с: Е состоит из всех точек х, удовлетворяющих условию Дх) = т < 0.
Пусть с = inf М. Далее, если оказалось, что с е М, то Де) = = т < 0. Покажем, что соотношение сё М невозможно. Действительно, тогда можно выбрать последовательность точек {xn} g М такую, что хп -»с при п -» оо. Следовательно, так как с g Е и Дх) непрерывна в точке х = с, то
lim f(xn) = ftlim г) = ft с).
Но f(xn) = т при всех п, поэтому Де) = тп, и тем самым с е М. Итак, Де) = т = min/(x), откуда f(c) = 0. А так как функция Дх) выпукла вверх при с g (а, Ь), то
Дх) < Де) - Д(с)(х - с) = тп < 0
в некоторой 8-окрестности (с) точки х = с.
Величина т является минимумом функции Дх) на отрезке Е. Отсюда следует, что в данной окрестности выполнены неравенства т < Дх) < тп, т. е. Дх) = тп, но это невозможно, поскольку с = = inf М, т. е. иъ(с) сМ. ◄
СЛЕДСТВИЕ. Если Дх) непрерывна на отрезке Е = [а, &] и выпукла вверх на интервале (а, &), то график функции у = Дх) лежит над «хордой», т. е. над отрезком, соединяющим точки (a, f(a)) и (b, f(b)) на плоскости хОу.
Другими словами, если данная хорда есть график функции у = Дх), заданной на отрезке Е, то g(x) = Дх) — 1(х) > 0 на этом отрезке.
►	Действительно, функция g(x) удовлетворяет условиям теоремы 26. «
141
ТЕОРЕМА 26' Пусть f(x) удовлетворяет условиям предыдущей теоремы. Тогда для любых точек хг < х2 из интервала (л, Ь) выполнено неравенство f\x^) > f'(x2), т. е. f(x) не возрастает на интервале (а, Ь).
►	Соединим точки А = (хх, Дхх)) и В = (х2, f(x2)) на плоскости хОу хордой L. Тогда по следствию теоремы 26 на отрезке [хх, х2] хорда L лежит «под кривой» у = Дх), а тем самым и под касательными к графику функции у = f(x) is. точках х = хг и х = х2. Если k — угловой коэффициент линейной функции у = 1(х)9 частью графика которой является хорда L, то
f\xr) >k> f\x2). ◄
Замечание. Из теоремы 27 следует, что всякая хорда, соединяющая две различные точки графика функции, выпуклой вверх, лежит под ее графиком, а для функции, выпуклой вниз, она лежит над графиком. Это свойство часто берут в качестве исходного определения выпуклости функции (вверх или вниз соответственно).
Рассмотрим свойство подробнее на примере функции, выпуклой вверх. Запишем свойство выпуклости вверх функции в аналитической форме с помощью неравенств. Значения координат точки (х, у), находящейся на хорде с концами в точках (хх, ух), ух - Дхх) и (х2, у2)’ У2 = при хх и х2, принадлежащих интервалу (а, &), с условием хх < х2 можно записать в виде
X = ХхХх + Х2х2, у == ^1У1 + ^2^2’ где 1Х > О, Х2 > 0 и 1х + Х2 = 1. Поскольку величина у в этом случае не должна превосходить Дх), условие выпуклости вверх выражается следующим соотношением
ДХххх + Х2х2) у = ^1У1 + ^<2^2 = ^1Я^1) + ^г/(х2)«
В этом случае функция Дх) непрерывна на интервале (а, Ъ) и имеет на нем правую и левую производную. Далее мы докажем непрерывность функции и ограничимся рассмотрением только правой производной.
Сначала докажем непрерывность справа функции Дх) в любой точке х0 интервала (а, Ь). Прежде всего отметим следующий геометрический факт, состоящий в том, что всякая прямая пересекает график функции Дх) либо по некоторому отрезку, либо не более чем в двух точках. Действительно, если бы нашлись три такие точки А = (хх, ух), В = (х2, у2) и С = (х3, у3), хг < х2 < х3, то на интервале (хр х2) или на интервале (х2, х3) существовала бы точка х4, для которой точка D = (х4, Дх4)) не лежит на хорде с концами А и С. Но тогда при хе (хх, х2) точка D обязана лежать выше хорды АВ и хорда DC лежит выше точки В, что противоречит выпуклости вверх функции Дх). Если бы точка х4 лежала на интервале (х2, х3), то выше точки В проходила бы хорда AD.
Отсюда следует, что если точка х5 е (а, Ъ) лежит левее точки х0, то часть графика функции Дх), отвечающая точкам х > х0, лежит под про
142
должением хорды lv соединяющей точки (х5, Дх5)) и (х0, Дх0)). Это значит, что если kr — угловой коэффициент хорды 119 то при всех х > х0 имеем ДДх0) < fexAx, где Ах = х - г0. Следовательно, при Дх > 0 заключаем, что Д/(х0) = О(Дх) -» 0 при Дх —> 0+, т. е. функция Дх) непрерывна справа в точке х0 € (а, &). Подобным же образом можно установить, что функция Дх) в точке х0 непрерывна слева. Таким образом, во всех точках интервала (а, Ъ) эта функция является непрерывной.
Переходя к доказательству существования правой производной функции Дх) в точке х « х0, заметим, что для любых точек х6 и х7 с условием х0 < х6 < х7 хорда, соединяющая точки (х0, Дх0)) и (хб, Дх6)), лежит не ниже хорды, соединяющей точки (х0, Дх0)) и (х7, Дх7)), поэтому для угловых коэффициентов kQ и k7 этих хорд справедливо неравенство > ^7’ т*
, ДД*о) йв--дГ"
>
Ах = х6 - х0
Aftxp) Дас
-*7.
Ах =» х7 - х0
Таким образом, отношение ДДх0)/Дх не убывает при монотонном стремлении величины Лх к нулю справа. С другой стороны, это отношение ограничено величиной k19 рассмотренной выше при доказательстве непрерывности справа функции Дх) в точке х — х0. Следовательно, согласно свойству монотонных функций существует предел отношения Нт (ДДх0)/Дх), который по определению и называется правой производной функции Дх) в точке х0. Случай левой производной аналогичен.
Итак, мы доказали, что у выпуклой вверх функции правая и левая производные в любой внутренней точке отрезка [а, &] существуют, хотя они и не обязаны быть равными.
С другой стороны, мы установили, что правая производная функции Дх) в точке х0 не превосходит углового коэффициента k7. Но предел величины k7 при х7 —> х0 есть левая производная f'(xQ~) функции Дх) в точке х = х0, откуда следует, что в любой точке интервала правая производная не превосходит левой производной. Если же рассмотреть две различные точки х0 < х19 то угловой коэффициент k хорды, соединяющей точки (х0, Дх0)) и (xn f(x1))9 «разделяет» значения правой производной Дх0+) в точке х0 и левой производной /'(^i“)в точке х19 т. е.
f'(xQ+) > k >
Отсюда следует, что f'(x+) не возрастает на (а, &). То же справедливо и для левой производной. Поскольку обе эти функции монотонны, каждая из них имеет не более чем счетное множество точек разрыва первого рода. Все остальные точки интервала (а, Ь) являются точками непрерывности обеих функций. Но в этом случае в силу последнего неравенства их значения совпадают, и тогда функция Дх) имеет обычную производную
Г(х0) = f (х0+) = /'(«о-)» которая к тому же будет непрерывной и невозрастающей функцией в этой точке.
143
Лекция 25
§15. ТОЧКИ ПЕРЕГИБА
Определение 13. Точку х0 из интервала (а, Ь) будем называть точкой перегиба дифференцируемой функции f(x) (или ее графика), если существует проколотая 8-окрестность точки х0 такая, что и в правой, и в левой ее полуокрестностях функция f(x) имеет выпуклый график, но направление выпуклости справа и слева разное.
ТЕОРЕМА 27 (необходимоеусловие перегиба). Если функция f(x) в точке х = х0 имеет вторую производную и точка х0 — точка перегиба, то
№о) = о.
►	По условию в точке х0 существует вторая производная f"(x^), поэтому f'(x) непрерывна в этой точке. Для определенности будем считать, что в правой полуокрестности точки х0 функция Дх) выпукла вверх, а в левой — выпукла вниз. Тогда по теореме 26' § 14 производная f'(x) правее точки х0 не возрастает, а левее ее — не убывает. Это значит, что в точке х0 она имеет локальный минимум. Применяя принцип Ферма, отсюда заключаем, что
(Г(Ж-^-Г(хо)-о. «
Далее будем говорить о точках перегиба только в строгом смысле, имея в виду, что в определении точки перегиба имеет место строгая выпуклость в обеих полуокрестностях.
ТЕОРЕМА 28 (первое достаточное условие строгого перегиба). Пусть функция Дх) дважды дифференцируема в проколотой окрестности точки х = х0 и f'(x) имеет в ней разные знаки при х < х0 и х > х0. Тогда, если f"(xv) = 0 или f"(xv) не существует, то х0 — точка строгого перегиба графика функции Дх).
►	Так как f"(x) сохраняет знак при х < х0 и х > х0 в некоторой проколотой 8-окрестности, то Дх) имеет разные направления строгой выпуклости в этих частях 8-окрестности. По определению это означает, что х0 — точка строгого перегиба. ◄
Эту теорему можно сформулировать так: если f"(xQ) = 0 и f"(x) строго возрастает в точке х0, то х0 — точка строгого перегиба (то же и в случае Д'(х0) = 0, Д'(х) строго убывает).
ТЕОРЕМА 29 (второе достаточное условие строгого перегиба). Пусть функция Дх) дважды дифференцируема на (а, Ъ), f"(xQ) = 0 и существует f"'(xQ) и 0. Тогда х0 — точка строгого перегиба.
144
►	Так как Д3)(х0) 5^ 0, то либо Д3Х*о) > либо Д3)(х0) < 0. В первом случае f"(x) строго возрастает в точке х0, а во втором f"(x) строго убывает в этой точке. Поэтому из теоремы 2 в обоих случаях следует, что х0 — точка строгого перегиба. ◄
ТЕОРЕМА 30 (третьеусловие строгого перегиба). Пусть х0 е (а', Ъ) и пусть функция f(x) дифференцируема 2k раз на [а, 6]. Пусть существует Л2Л+1)(^о) * 0 и А2)(хо) = Л3)(хо) = - = fl2k)(xo) = °-Тогда х0 — точка строгого перегиба.
►	Заметим, что х0 в силу условия Д2*+1)(х0) # ® является точкой возрастания или убывания для f2k\x). Рассмотрим проколотую 5-окрестность U точки х0, в которой f2k\x) меняет знак при переходе через х0 и сохраняет знак внутри каждой из двух ее полуокрестностей.
Далее можно считать, что k > 2, так как при k = 1 теорема 30 следует из теоремы 29. Пусть х е U. По формуле Тейлора имеем
Л2)(х) = Л2)(х0) + ... + f((2fe (X - х0)2*-3 +	- *о)2*"2 =
f2*)(c) (2fe —2)!
(х - X0)2fe’2,
где с - с(х) е U и (х - х0)(с - х0) > 0. Но (х - x0)2fe"2 сохраняет знак при х е 17, a f2k\c) меняет знак. Поэтому и Д2)(х) меняет знак, следовательно, по теореме 28 точка х0 — точка строгого перегиба. ◄
ПРИМЕРЫ. 1. у = х3: точка х = 0 — точка Перегиба (строгого).
2. у = x2fe+1: точка х = 0 — точка перегиба (строгого).
Определение 14. Прямая х = а на плоскости хОу называется вертикальной асимптотой функции Дх), если один из пределов Jim Дх) или Jim+ Дх) равен ±оо.
ПРИМЕР, у = 1/х. Здесь прямая х = 0 — это вертикальная асимптота.
Определение 15. Прямая у = kx + Ь называется наклонной асимптотой функции Дх) (точнее^ графика функции у = Дх)) при х +оо, если
а(х) = Дх) - kx - Ь -» 0 при х -> +°°.
Аналогично определяется асимптота при х -оо.
ТЕОРЕМА 31. Для существования наклонной асимптоты у = kx + Ь при х +оо у функции Дх) необходимо и достаточ
145
но, чтобы при х —> +оо (одновременно) выполнялись следующие два условиях
1) Нт — = /г, /г е Я;
' х->+оо X
2) Нт (Дх) - kx) = b,be R.
X —> +оо
► Необходимость. Пусть y = kx + b — асимптота, тогда
а(х) = Дх) - kx - b —> 0 при х —> +оо.
Следовательно,
Дх) - kx - Ь А
-^-L--------> 0 при X -> +°°,
откуда
lim — = /г. х-»+оо X
Далее,
Wx) “ ftx) =	~kx~b) + b) = b.
Первая часть теоремы доказана.
Достаточность. Так как Jim^ (f(x) - kx) = 6, то
Jirn^ ot(x) = Jim^ (Дх) - kx - b) = Hrn^ ((f(x) - kx) - b) = b - b = 0.
Теорема доказана полностью. ◄
Если для функции f(x) выполнено условие 1 теоремы 31, то мы будем говорить, что прямая у = kx задает асимптотическое направление.
Приведем пример нахождения наклонных асимптот в случае функции, заданной неявно.
ПРИМЕР. Рассмотрим уравнение кривой
х3 + у3 - Заху = 0.
Зададим ее параметризацию, полагая у = tx. Тогда получим
х3(1 + t3) - ЗахН = 0, 1 . л За* Л 3at ! + <-— -О,
Отсюда имеем: у/х = t = t(x) — ограниченная величина при х -> 00 и Дх) —> -1. Следовательно, t = -1, т. е. прямая у = -х задает асимптотическое направление. Найдем теперь значение параметра b в уравнении касательной у = -х + Ь. Имеем
у = -х + b + о(1), х3 + (-х + Ь)3 - Зах(-х + Ь) = о(х2), откуда
Зх2(Ь + а) + Зх(аЬ - Ь2) + Ь3 = о(х2), , ^ab-b2 Ь3 ... b + а Ч--------+ т—5 = о (1).
х Зх2 ' '
146
Переходя в последнем равенстве к пределу при х -» оо для постоянного Ь, получаем равенство b + а = 0, откуда Ь = -а, и, следовательно, искомое уравнение асимптоты при х —> оо имеет вид у = -х - а.
Краевой экстремум. Пусть функция Дх) задана на отрезке [а, &].
Определение 16. Точка а называется точкой краевого локального максимума (минимума), если существует интервал (а, а + 8) g [а, Ь], для всех точек х которого справедливо неравенство f(a) > Дх) (соответственно Дх) > Да)).
При Да) > Дх) имеет место несобственный (локальный) максимум; при Да) < Дх) — несобственный (локальный) минимум.
То же самое можно определить и для точки Ь9 только интервал (а, а + 8) надо заменить на интервал (Ь - 8, &).
Краевые максимум и минимум называются краевыми экстремумами.
ЛЕММА 1. Для существования (собственного) краевого экстремума в точке а (или Ь) достаточно, чтобы в этой точке существовала отличная от нуля односторонняя производная функции Дх).
► Доказательство аналогично доказательству леммы Дарбу.
Например, если f'(x) > 0 при хе (а, а + 8), то а — краевой минимум, поскольку при х е (а, а + 8) существует се (а, а + 8) такое, что Дх) - Да) = f'(c)(x - а) > 0, т. е. Дх) > Да). ◄
Общая схема построения графика функции Дх)
1.	Найти область определения функции Дх).
2.	Учесть особенности функции (четность, периодичность, знакопеременность). Найти пересечения графика с осями координат.
3.	Отметить значения функции на границе области определения и в точках разрыва. Найти вертикальные асимптоты.
4.	Найти наклонные асимптоты.
5.	Определить участки монотонности. Определить локальные и краевые экстремумы.
6.	Найти промежутки выпуклости и точки перегиба.
7.	Отобразить перечисленные особенности функции при построении ее графика.
Лекция 26
§ 16. ИНТЕРПОЛИРОВАНИЕ
Целью интерполирования, или интерполяции, является приближенное нахождение функции по известным значениям этой функции и ее производных в некоторых заданных точках области ее определения. Эта задача становится определенной, если задан вид функции и число неизвестных параметров не превышает количества заданных значений функции и ее производных. Так, например, многочлен n-й степени имеет и + 1 параметров (его коэффициенты) и может быть определен по значениям его в п + 1 различных точках.
Пусть в точках хр ... , хп многочлен Р(х) принимает соответственно значения /(хх), ... , /(хп).
ТЕОРЕМА 32. Существует единственный многочлен Р(х) степени п - 1 такой, что P(xk) = /(xfe), k = 1, ... , n.
► Имеем
Q zx)= /1’еСЛИХ = Х*’
**’ ’	10, еслих = хх, ...,xk_u xk + 1,... ,xn,
где
Q = (* ~ *i) -ix-xk_ x)(x - xft + x)... (x - x„) " (xk - xx)... (xft - xk _ x)(xfc - Xk + x)... (xk - x„) 
Тогда P(x) можно записать в виде
Р(х) = ftxJQ^x) + ... + /(xn)Qw(x).
Докажем, что многочлен Р(х) единствен. Действительно, допустим, что существует еще один многочлен с указанными свойствами, т. е. Q(xk) = f(xk). Отсюда получаем, что многочлен (п - 1)-й степени Р(х) = Р(х) - Q(x) имеет п корней, а именно, F(xfe) = О, k = 1, ... , п. Следовательно, F(x) = 0, т. е. многочлены Р(х) и Q(x) тождественно совпадают. ◄
Формула, задающая многочлен Р(х), называется интерполяционной формулой Лагранжа. При этом точки хр ... , хп называют узлами интерполяции.
Пусть Дх) — некоторая функция. Обозначим через Pfe(x) многочлен степени k - 1, принимающий в точках хр... , xk значения /(х1), ... , f(xk). Тогда интерполяционную формулу можно записать в виде
Р(х) = Рх(х) + ki2 (Pk(x) - Рк_г(х)) = Р„(х).
148
Многочлен РА(х) - P^-iC*) степени k - 1 в силу определения обращается в нуль в точках хр ... , xk_v Следовательно, он имеет вид Ak(x - х0) ... (х - xk_j). Коэффициент Ak совпадает со старшим коэффициентом многочлена Pk(x) и в силу интерполяционной формулы Лагранжа равен
А =__________________+
* (Xi -х2)... (Xj -Xk)
+__________f(x2)_________ +	+_________f(Xk)____
(х2-Х1)(х2-х3)... (х2-Xft) “	(xk-x1)... (xk-xk_1)‘
Таким образом, коэффициент Ak является некоторой функцией отГр ..., xk. Обозначим ее через Ak = fk(x19 ..., хл). Тогда интерполяционный многочлен Р(х) можно записать в виде
Р(х) = /1(х1) +
+ (X - х^/^Хр х2) + ... + (х - хх)... (х - Хл_1)/л(х1, ..., хп), где, очевидно, полагая х = хр имеем f^x^ = /(xj. Эта формула называется интерполяционной формулой Ньютона. Функции fk(x19 ..., xk)9 k = 1, ..., п, называются интерполирующими функциями.
Полагая в формуле Ньютона х = хп, получаем
/(x„) = P(x„) = /(x1) +
+ (х„ - х^Хр х2) + ... + (х„ - хх)... (х„ - Хд.^/Дхр ... , хл).
Здесь узел интерполяции хп — произвольное число, поэтому, заменяя хп на х, имеем
Г(х) =
= f(Xj) + (х - Х^Хр х2) + ... + (х - хр ... (х - Хп_1)/п(х1,..., х). Уменьшим количество узлов интерполяции на один, исключив точку хп_19 запишем эту формулу для узлов интерполяции хр..., хп_2, х и вычтем получившееся тождество из предыдущего. Тогда получим
...Xn-2’X)~fn-l<Xl....ХП-1>
4(Хр - , Х„_р X)---------------——------------------•
Х Хп -1
Таким образом, при п = 2, 3, ... имеют место соотношения
№.. *> -	. №.. Ъ	,
которые позволяют с помощью простого алгоритма вычислить интерполирующие функции. Для определения всех коэффици
149
ентов интерполяционного многочлена Ньютона (и - 1)-й степени 1 достаточно вычислить значения интерполирующих функций I в п(п - 1)/2 точках (с учетом кратности)* Здесь существенно, что I при добавлении новой точки интерполяции интерполирующие 1 функции, вычисленные ранее, сохраняются и надо только доба- I вить к ним значения интерполирующих функций в этой точке. |
ТЕОРЕМА 33. Пусть функция f(x) имеет п-ю производную на | отрезке [а, &], а < хг < х2 < ... < хп < Ь. Тогда имеет место формула /(б) = р„(&) + ад,
где R(b) =	~ (Ь- хх)... (Ь - хЛ), причем с — некоторая точка,
принадлежащая (а, &).
► Рассмотрим вспомогательную функцию
Я(х) = f(x) - Рп(х) - (х -Xj).. .(х - хп)Н, где Н — некоторое число, значение которого выберем ниже.	>
Имеем
Я(х1) = ...=В(хп) = О.
Величину Н найдем из соотношения R(b) = 0. Отсюда по теореме Ролля, примененной п раз, получаем, что существует число с е (а, 6), для которого Rtn\c) = 0, откуда
- п!Н = 0.
Следовательно,
Н-1^. <	!
п\
Лекция 27
§ 17. МЕТОД ХОРД И МЕТОД КАСАТЕЛЬНЫХ (МЕТОД НЬЮТОНА). БЫСТРЫЕ ВЫЧИСЛЕНИЯ
Пусть функция f(x) дифференцируема на отрезке [а, 6]. Тогда функция f(x) непрерывна на [л, Ь] и по теореме Коши о промежуточном значении для любого а е Я, лежащего между числами f(d) и f(b)9 внутри отрезка [а, Ь] найдется точка с такая, что f(c) = = а. Естественной и важной задачей и в теоретическом, и в практическом смысле является задача вычисления приближенного значения числа с с наперед заданной точностью. Например, можно поставить вопрос о нахождении корня уравнения х2 = 2 с точностью до десяти знаков после запятой, т. е. для л/2 найти приближенное значение с0 такое, чтобы имело место неравенство 172 - с0| < 1О"10 и т. п.
Рассмотрим два естественных метода нахождения таких приближенных значений, а именно: метод хорд и метод касательных, который еще называют методом Ньютона, поскольку он первым его применил. Эти методы важны не столько сами по себе, сколько тем, что они являются простейшей моделью многих вычислительных процессов, применяемых в гораздо более сложных ситуациях. Оба метода итерационные, т. е. они состоят в последовательном вычислении некоторых чисел х19 х29 ••• 9 хп9 . При этом разность |с - хп| —> О при п —> оо, и поэтому, начиная с некоторого номера п0, она должна стать меньше наперед заданного значения, называемого заданной точностью или погрешностью вычисления.
Метод хорд. Число хг определим как абсциссу точки пересечения горизонтальной прямой у = а с «хордой* графика функции у = ftx), т. е. с отрезком, соединяющим точки (а, /(а)) и (Ь, ftb)). Обозначим отрезок [а, Ь] через /0. Полагая А = f(a) и В = ftb), исходя из подобия соответствующих треугольников для нахождения величины хг имеем уравнения:
а -А = В - а = а-В хг- a Ъ - хг хх - b ’
Отсюда находим
хх(а - А) - Ь(а - А) = хг(а - В) - а(а - В),
_ -а(а - В) + Ь(а -А)
В-А
151
Затем в качестве берем один из отрезков [л, xj или [хр &] так, чтобы число а вновь находилось между значениями f(x) на его концах, т. е. на концах отрезка функция Дх) - а имеет значения разных знаков. По тому же правилу находим 12 и т. д. Получим систему вложенных отрезков: IQ о о ... z) In z> ... Как известно, они содержат общую точку с.
Если, например, f'(x) > 0, то Дх) не убывает, и тогда из непрерывности Дх) следует, что Де) = а, поскольку на концах каждого из отрезков 1п функция g(x) = f(x) - а имеет значения разных знаков.
Метод касательных. Этот метод состоит в следующем. Пусть для простоты а = 0. (Если это не так, то вместо уравнения Дх) = а рассмотрим уравнение g(x) = 0, где g(x) = Дх) - а.) Величину хх определим из соотношения
f(b) =	. т r v f(b)
b - х, f (Ь)’ Тф е‘ X1 b f\b) •
При n > 1 имеем
Л*п) Х« f(x„)•
В обоих методах надо еще уметь определить момент, когда следует оборвать процесс вычислений. Чтобы упростить решение этого вопроса и сократить объем вычислений, применяют следующий комбинированный метод.
Метод хорд и касательных. Сущность этого метода состоит в нахождении пар точек xn, i/n, подчиненных следующему условию хп < с < уп. Схема вычисления величин хп и уп такова. Пусть f'\x) > 0 на IQ = [а, Ь]. Определим хх по методу хорд, а уг — по методу касательных. Тогда имеем хх < с < у19 и далее за принимаем отрезок [хр pj. Точно так же, находя х2 методом хорд, а у2 методом касательных, получаем отрезок 12 = [х2, у2] и т. д. Как только окажется, что |хЛ - уп\ < 8, на этом процесс вычисления с с точностью до 8 обрывают.
ПРИМЕР. Пусть Дх) = х2 - а, а = 0, а = 2. Применим метод касательных. Для определенности положим х0 = 1. Величина хп+1 находится по формуле
*п+1 Хп Г(Хп) Хп
= хп д 1
2х„	"	2 2хп 2
Для того чтобы выяснить, как быстро сходится этот вычислительный процесс, проведем оценку погрешности на (п 4- 1)-м шаге. Для этого обозначим через гп величину rn = \Ja - хп|. Тогда
г2п = (л/а - х„)2 = а - 2xnJa + х2,
152
откуда
Из неравенства -•* > Jab получаем, что при п > 1 &
хп+1 = 2	’
4 хп 7
следовательно, так как а = 2,
Отсюда можем заключить, что если хп приближает Ja с точностью до k десятичных знаков после запятой, т. е. rn < 10"fe, то хп+1 приближает Ja уже с точностью до 2k знаков, т. е. rw+1 < 10~2k. Если за х0 возьмем, например, число 1,4, которое, как известно, приближает J2 с точностью до одного знака, т. е. |Т2 - 1,4| < 10"1, то получим < 10”2, г2 < 10~4, ... , гп < 10~2", .... Видим, что за п шагов точность составит величину, не меньшую чем k знаков, где k = 2п. Так что для вычисления числа J2 с заданной точностью в k знаков достаточно выполнить п итераций, где п « [log2 А] + 1.
Такого же типа оценки для метода Ньютона имеют место и в общем случае решения уравнения f(x) = 0, если начальное приближение взято достаточно «хорошим». Доказательство этого утверждения основано на применении формулы Тейлора с разложением до второго члена.
Обратим внимание на следующий факт: при оценке эффект тивности вычислительного алгоритма надо обращать внимание не только на количество итераций, но и на количество арифметических операций в каждой итерации. Например, при вычислении Ja количество арифметических операций в каждой итерации равно 3: одно деление, одно сложение и одно умножение. Следовательно, для вычисления Ja с точностью до k знаков надо выполнить 3 [log2 &] + 3 арифметических операций. Но и это еще не все. Во-первых, надо иметь в виду, что нет необходимости в начальных итерациях учитывать все k знаков, так как точность приближения от этого не возрастает; во-вторых, проводить деление в столбик гораздо труднее, чем умножать числа, а умножать труднее, чем складывать.
153
Отметим, что метод Ньютона дает возможность заменить деление умножением. Действительно, f(x) = 1/х - а, х0 = 1. Тогда
f(x„)	1/х„-а
Хп+1 Хп f(xa) Хп -1/Х2 %Хп ^Хп"
Как и раньше, имеем 1 --------------------х„, г а п 9 1
•2 = 1/а2 - 2х„/а + х2,
п
аг2 = 1/а - (2хп + ах2) = г„+1.
Теперь, например, при а < 1 и г0 < 10 1 для величины п (количества итераций) при вычислении с точностью до k десятичных знаков после запятой имеем: п < [log2 А] + 1.
Еще более строгий подход к вопросу об эффективности вычислительного алгоритма состоит в учете операций над цифрами, с помощью которых записывается число. Тогда можно сказать, что, например, сложение двух n-значных натуральных чисел требует не более Зп операций, а «школьный» способ умножения чисел в столбик требует порядка п2 поразрядных умножений и порядка п2 сложений. Поэтому кажется естественным, что быстрее чем за О(п2) операций умножить два n-значных числа нельзя. В 50-х годах академик А. Н. Колмогоров поставил задачу доказать это, на первый взгляд, правильное утверждение. Но оказалось, что это не так.
В 1961 г. А. А. Карацуба доказал замечательную теорему, которая положила начало совершенно новому направлению в вычислительной математике — теории быстрых вычислений. Он доказал, что два n-значных числа можно умножить не за О(п2), аза О(п1ов23) операций.
ТЕОРЕМА 34 (теорема А. А. Карацубы). Существует алгоритм, позволяющий умножить два n-значных числа за О(г№2*) операций.
► Представим числа в двоичной записи: а = ап ... а19 Ь = Ъп ... рх. Заметим, что
аЬ = ((а + Ъ)2 - (а - &)2)/4.
Для деления числа на 4 достаточно сдвинуть его на 2 разряда вправо, это займет только О(п) операций. Так что достаточно доказать, что возведение в квадрат n-значного числа потребует указанного числа операций. Доказательство проведем по индукции. Пусть для простоты п = 2k и пусть
а = 2Л/2 • а + Р,
154
где а и Р — n/2-значные числа. Тогда имеет место тождество а2 = а2(2п - 2Л/2) + (а + р)22"/2 - р2(2"/2 - 1).
Если число операций для возведения в квадрат n-значного числа обозначить через К(п), то
К(п) < ЗК(п/2) + сп, К(п/2) < ЗЛГ(п/4) + сп/2,
, К(2) < 32С(1) + с,
К(п) < 3* + с(п + (Зп/2 + 32п/4 + ... + 3fe), где k = log2 п. Отсюда имеем
К(п) < 3Л(Зс + 1). ◄
В заключение укажем на соображение общего характера, лежащее в основе многих итерационных вычислительных алгоритмов. Пусть требуется найти значение функции в точке х0, т. е. вычислить /0 = /(х0). Обозначим через fn приближение к /0 с точностью Дп (до п десятичных знаков):
Дп = 14-Го1-
Допустим, что известна функция G(x) со следующим свойством: Gifo)-fo,G'(x)\x = frO.
Тогда имеем
G(fn) = ВД + G'( Wn - /о) + (fn ~ /о)2.
откуда |/0 - G(fn)| < сД2, где с = max —	. Теперь, полагая fn+1 =
= G(/n), получаем приближение к fQ с точностью порядка 2п десятичных знаков после запятой. Тем самым мы имеем быстро-сходящийся алгоритм для приближенного вычисления значения /0. Заметим, что рассмотренный выше алгоритм вычисления корня квадратного из числа х0 является частным случаем приведенного при /(х0) = и =	+ хо//"п)/2-
ГЛАВА 6
Неопределенный интеграл
Лекция 28
$ 1. ТОЧНАЯ ПЕРВООБРАЗНАЯ. ИНТЕГРИРУЕМЫЕ ФУНКЦИИ
Определение 1. Функция F(x) называется точной первообразной для функции f(x) на (а, Ь), если при любом х е (а, Ь) имеем F\x) = f(x), т. е. в каждой точке х интервала (а, Ь) значение функции f(x) является производной функции F(x).
ТЕОРЕМА 1. Пусть f(x) определена на (а, Ь) и Fr(x), F2(x) — две ее точные первообразные. Тогда существует число с е R такое, что при любом х е (а, Ь)
Fj(x) - F2(x) = с.
► Пусть функция
G(x) = F1(x)-F2(x).
Тогда G(x) — дифференцируемая функция, причем всюду на (а, Ь)
G'(x) = F'^x) - F'2(x) = Дх) - /(х) = 0.
Положим х0 = (а + 6)/2. Тогда по формуле Лагранжа конечных приращений имеем
G(x) - G(x0) = G'(^)(x - х0) = 0, т. е.
(?(х) = G(x0) V х е (а, &).
Но, полагая с = G(x0), получаем, что G(x) = с для всех точек х интервала (а, &).	◄
Замечание. Из теоремы 1 следует такое утверждение: любые две первообразные F(x) и G(x) функций /(х) и g(x) отличаются на константу тогда и только тогда, когда их производные совпадают, т. е. когдаF' = f = g = G'. Ранее было показано, что далеко не все функции, заданные на каком-либо интервале (а, &), имеют производную.
Аналогично обстоит дело и с первообразной, т. е. не все функции имеют производную. Но если функция /(х), определенная на (а, Ь), имеет первообразную, то она называется интегрируемой.
156
Прежде чем перейти к изучению класса интегрируемых функций, несколько обобщим понятие точной первообразной.
Определение 2. Непрерывная функция F(x) называется первообразной функции f(x) на интервале (а, Ь), если в каждой его точке х за исключением, быть может, конечного их числа, выполняется равенство F'(x) = f(x).
ТЕОРЕМА 2. Пусть Fr(x) и F2(x) — первообразные функции f(x) на (а, Ь). Тогда найдется число с такое, что всюду на этом интервале
F^x) - F2(x) = с.
► Пусть xv ... , хп — конечное множество точек, на котором не существует Fj(x) или F2(x). Тогда множество (а, Ь) состоит из конечного числа интервалов Ik, на которых производные обеих функций существуют. Следовательно, по теореме 1 их разность постоянна на каждом таком интервале. Кроме того, эта разность является непрерывной функцией на всей области определения. Отсюда следует, что в общей граничной точке любых двух смежных интервалов ее значение равно одновременно пределу справа и слева. Эти значения, в свою очередь, совпадают с ее значениями на смежных интервалах. А это значит, что функция на смежных интервалах, включая точку их общей границы, постоянна. Следовательно, она постоянна на всем интервале (а, Ь). ◄
Определение 3. Совокупность всех первообразных функций для какой-либо одной функции f(x) на интервале называется неопределенным интегралом от функции f(x). Эта совокупность обозначается символом J f(x)dx (читается*, интеграл от f(x)dx).
Из теоремы 2 следует, что все функции этой совокупности отличаются друг от друга на постоянную. Поэтому, если F(x) какая-нибудь одна первообразная, то можно записать равенство
$ f(x)dx = F(x) + с,	(1)
где с — произвольное число. Это равенство надо понимать как равенство двух множеств, состоящих из функций, определенных на (а, Ъ), причем слева стоит совокупность, образующая неопределенный интеграл от f(x), а справа — совокупность функций, отличающаяся от функции F(x) на функцию, значение которой равно числу с для всех точек х этого интервала. (
ПРИМЕРЫ.
1.	J 1 • dx = х + с, так как х' = 1.
2.	J 0 • dx = с.
3.	J cos xdx = sin х + с, так как (sin х)' = cos х.
157
Для доказательства этих равенств надо продифференцировать правую часть и убедиться, что ее производная равна функции, записанной слева между знаком J и символом dx. Она называется подынтегральной функцией. Знак J называется знаком интеграла, а выражение, записываемое справа от него, — подынтегральным выражением.
Легко видеть, что подынтегральное выражение есть не что иное, как дифференциал любой первообразной функции для Дх). Действительно, если F(x) — первообразная Дх), т. е. F\x) = = Дх), то по определению дифференциала dF(x) = f(x)dx. А так как
J f(x)dx - F(x) + с, d(F(x) + с) = dF(x),	(1)
то можно записать равенства
J dF(x) = F(x) + с, d(I f(x)dx) = dF(x) = f(x)dx, (2) причем знак равенства в последнем соотношении означает, что все функции, входящие в совокупность J f(x)dx, имеют один и тот же дифференциал dF(x). Также имеем
(J/(x)dx)' = f(x).	(3)
Определение 4. Нахождение неопределенного интеграла от функции Дх), заданной на (а, &), называется интегрированием этой функции. Саму задачу нахождения неопределенного интеграла можно рассматривать как обратную к задаче нахождения дифференциала функции.
Лекция 29
§ 2. СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Из правил дифференцирования функции и теоремы 2 следует ряд свойств неопределенного интеграла. Приведем некоторые из них, которые задаются равенствами и доказываются с помощью дифференцирования обеих частей этих равенств. Прежде всего докажем, что равенство точных первообразных
J f(x)dx = J g(x)dx	(4)
эквивалентно одному из следующих четырех равенств:
(J f(x)dx)' = (J g(x)dx)';
d(J f(x)dx) = d(J g(x)dx);
/(x) = g(x);
f(x)dx = g(x)dx,
которые имеют место при всех х е (а, Ъ).
В самом деле, в силу приведенных выше свойств (1)—(3) (см. лекцию 28) эти равенства действительно эквивалентны.; А равенство (4) означает лишь то, что любые две первообразные F, G для функций fug отличаются между собой на константу. Но согласно замечанию к теореме 1 для этого необходимо и достаточно, чтобы f = g.
Замечание. Свойство (4) дает критерий равенства двух неопределенных интегралов: они совпадают тогда и только тогда, когда совпадают их производные или дифференциалы. Докажем теперь следующее свойство:
J (/(х) + g(x))dx = J f(x)dx + J g(x)dx,	(5)
f a/(x)dx = a J f(x)dx V a* 0.	(5')
Эти равенства надо понимать как совпадение двух совокупностей функций, стоящих в этих равенствах справа и слева. (Напомним, что два множества равны, когда они состоят из одних и тех же элементов.) Поясним, что совокупность
J f(x)dx -F J g(x)dx состоит из всевозможных функций, образованных суммами функций F(x) + G(x), где F(x) е J /(x)dx, G(x) е J g(x)dx, т. e.
J f(x)dx + J g(x)dx = {F(x) + G(x)}, где {F(x)} «J /(x)dx, {G(x)} = J g(x)dx.
Теперь для доказательства (5) в силу свойства (4) достаточно продифференцировать эти равенства. Доказательство закончено.
Отметим, что для простоты применения на символы / f(x)dx и J g(x)dx Удобно смотреть, как на обычные функции, подразумевая под ними некоторые первообразные функций f(x) и g(x) соответственно, а равенство
159
между выражениями, в которые они входят линейно, понимать с «точностью до постоянной», имея в виду, что правая и левая его части отличаются на функцию, постоянную на (а, Ь).
С помощью свойства (4) можно легко установить еще два свойства неопределенных интегралов, важных для непосредственного интегрирования.
Правило интегрирования по частям
u(x)v(x) - J u(x)dv(x) = J v(x)du(x)9	(6)
Правило замены переменной
Mx)dx = f/((p(O)<p'(O<ft,	(7)
где х = <р(0 — дифференцируемая функция от t9 определенная на интервале (а, Р), причем множество значений {<р(0} принадлежит интервалу (а, &). Мы предполагаем, что в обоих равенствах интегралы в левых частях действительно существуют; из этого следует существование интегралов и в правых частях этих равенств.
► Докажем свойство (6). Так как по условию интеграл в левой части равенства существует, то ее дифференциал равен
d(uv - J udv) = udv + vdu - udv = vdu.
Отсюда в силу свойства (4) следует справедливость свойства (6).
Для доказательства свойства (7) заметим, что по правилу дифференцирования сложной функции и согласно свойству (3) при х = <р(0 имеем
d f(x)dx)'t = d ftxydxyj&p = f(x)\x . *t) • ф' = Г(Ф«)Ф'(О).
Следовательно, согласно свойству (4) интеграл f f(x)dx при х = = ф(£) есть в то же время и неопределенный интеграл от функции /'(ф(О)ф'(О» Т. е.
J f(x)dx = J /((p(t)d(p(t)) = f /(<p(<))(p'(i)di. ◄
С помощью дифференцирования легко убедиться в том, что справедливы следующие равенства для неопределенных интегралов от простейших элементарных функций:
1) J xndx = —-+1 + с9 п * -1; 3) f  = arctg х 4- с;
п + 1	1 + х2
2)f	=1п|х| +с;
4)f-^4 =1п
1-х1 2
1 + X 1-х
160
5)	J . dX— = arcsin x 4- c; 9) J cos xdx = sin x + c;
Jl-x2
6)	J . dx _ = ln|x 4- Jx2 ± 11 4- c; 10) J  dx  = -ctg x 4- c; sin2x
7)	J axdx = £—I- c, a > 0,	11) J = tg x 4- c;
7 J	Ina ’	9	J cos2x
a 1, J exdx = ex 4- c;	12) J In xdx = x In x - x 4- c.
8)	J sin xdx = - cos x 4- c;
Как уже было отмечено, не всякая функция имеет точную первообразную, так как не всякая функция является производной от другой функции. Рассмотрим, например, функцию
Л*)=
1,	если х g (0,1),
2,	если х = 1,
3,	если х g (1, 2).
Эта функция определена на (0, 2) и не может являться производной какой-либо функции F(x) на (0,2), так как по теореме Дарбу производная принимает все свои промежуточные значения, а функция f(x) — всего три значения: 1,2,3.
Далее будет доказана формула Ньютона—Лейбница, из которой следует, что функция, непрерывная на интервале, имеет первообразную, т. е. интегрируема. Поэтому все элементарные функции интегрируемы на всех интервалах, входящих в их области определения. Однако в результате интегрирования далеко не всегда получаются снова элементарные функции, как это имеет место при дифференцировании. Например, можно доказать, что функции
г dx
li х = J (интегральный логарифм),
f sinx , z	о ч
si х = J-- dx (интегральный синус)
не являются элементарными.
Фуйкции, сами не являющиеся элементарными, но определяемый через них с помощью аналитических соотношений типа интегрирования и дифференцирования, обычно называют специальными функциями. Однако следует отдавать себе отчет в том, что, например, с вычислительной точки зрения специальные функции, вообще говоря, «ничуть не хуже», чем элементарные, а иногда и «лучше». Но все же простейшие элементарные Функции имеют преимущество, состоящее в простоте тех функциональных соотношений, которым они удовлетворяют.
161
6 - 4953
Еще раз подчеркнем, что единого метода интегрирования элементарных функций существовать не может, так как первообразная может и не быть элементарной функцией. Но для нахождения первообразной в явном виде имеется несколько приемов. Говоря о методах интегрирования, снова напомним, что для выяснения того, является ли известная нам функция F(x) первообразной Дх), нет необходимости «брать интеграл*, т. е. вычислять J f(x)dx, надо просто найти F\x) и сравнить ее с f(x).
ПРИМЕР. 1. Пусть функция Дх) имеет непрерывную производную на (а, &), С(х) = о х с„. Тогда
F(x)= о <Z< х cnf(n) - C(x)f(x) = -J C(x)f'(x)dx.
Действительно, если х — не целое число, то, поскольку С(х) и а х сп f(n) кусочно-постоянны на интервалах, не содержащих целых точек,
F'(x) = -С(х)Д(х).
Ранее мы убедились, что F(x) непрерывна на (а, Ь), так что F(x) есть первообразная функции C(x)f'(x).
2. Пусть функция Дх) имеет непрерывную производную на (а, &), р(х) =5 - {х}. Тогда имеет место формула
F(x) = а <Z< х f(n) - p(x)f(x) + p(a)f(a) = J (f(x) - p(x)f'(x))dx.
Действительно, если x — не целое число, то
F'(x) = (-p(x)ftx))' = f(x) - p(x)f'(x).
Далее, так как F(x) — непрерывная функция, то F(x) — первообразная функции Дх) - p(x)f'(x).
Иногда дифференцирование ответа оказывается очень громоздкой процедурой, так что целесообразно с помощью различных приемов сводить процесс вычисления к табличным интегралам. Для того чтобы уверенно и быстро вычислять интегралы, необходим определенный навык применения стандартных приемов интегрирования. Самые простые и самые общие из этих приемов — это метод замены переменной и метод интегрирования по частям [см. свойства (5) и (6)].
Подробнее с различными методами интегрирования можно познакомиться, например, в [4, 7, 15, 16].
Лекция 30
ДОПОЛНЕНИЕ. ОБОБЩЕНИЕ ПОНЯТИЯ ПРЕДЕЛА ПО ГЕЙНЕ НА ФУНКЦИИ, СХОДЯЩИЕСЯ ПО БАЗЕ МНОЖЕСТВ
Предметом настоящей лекции является распространение классического понятия предела функции по Гейне на общий случай сходимости по базе множеств. Как известно, построение курса математического анализа основано на двух эквивалентных понятиях сходимости: пределах по Коши и по Гейне. Одновременное использование обоих понятий в курсе мотивируется его содержанием. В частности, это позволяет унифицировать и сделать ясным использование пределов во всем их разнообразии, включая теорию интегрирования, функции многих переменных и др.
Необходимо отметить, что понятие сходимости по базе множеств впервые было сформулировано А. Крыжановским [22] (в несколько отличающейся терминологии). В 1937 г. В. И. Гли-венко [23] использовал это понятие для общего определения интеграла. Позже, как отмечал А. Н. Колмогоров, французская математическая школа пришла к тому же понятию в рамках теории фильтров.
В связи с успешным развитием теории сходимости по Коши возникла неотложная необходимость в соответствующем обобщении понятия предела функции по Гейне [24], [25]. Здесь мы решаем эту задачу. Введем понятие Н-предела по базе, которое совпадает с классическим определением предела по Гейне в простейших конкретных случаях. Затем установим эквивалентность понятия Н-предела по базе, введенного нами, и общепринятого определения предела функции по Коши. Наконец, как нетривиальный пример введенного понятия Н-сходимости по базе, продемонстрируем новый подход к определению и исследованию верхнего и нижнего пределов функции по базе.
1. Пусть А — основное множество элементов х, А = {х}, и В — база его подмножеств, которая состоит из бесконечного числа окончаний Ь, т. е. b а А, Ь g В, удовлетворяющих следующим условиям:
1)	каждое окончание является непустым множеством;
2)	для любых двух окончаний Ь19 Ь2 существует окончание Ь3 такое, что b3 с br П b2.
Определение 1. Назовем последовательность {хп}> хп g А, фундаментальной по базе В, если для любого окончания Ь существует только лишь конечное число членов последовательности, которые не принадлежат Ь.
163
Определение 2. Фундаментальная последовательность называется монотонной (по базе В)9 если условие хп е Ъ влечет условие хд+1 g Ъ для каждого окончания Ь.
Далее ограничимся базами В, удовлетворяющими также следующим условиям:
3)	для любых двух окончаний Ь19 Ь2 имеем, что либо Ьг с 62, либо Ь2 с &р
4)	существует по крайней мере одна монотонная последовательность по базе множеств В;
5)	А & = 0.
2. Докажем несколько свойств монотонных последовательностей по базе.
ЛЕММА 1. Любая подпоследовательность {yk = хп*} монотонной последовательности {хп} сама является монотонной последовательностью.
► Пусть Ь — произвольное окончание из базы В. Тогда вне его лежит не более конечного числа членов последовательности {хд}. Следовательно, {yk = хд*}, не входящих в окончание &, также конечно. Выберем среди них член yk с максимальным значением
номера k = kQ. Тогда yk^ + 1е Ь. А если kx > kQ + 1, то nk^ > п^ + р откуда, в силу монотонности исходной последовательности {хд}, имеем yk^ = хПь g &, т. е. последовательность {yk} — монотонна. ◄
nk.
Л Е М М А 2. Пусть {хд} — монотонная последовательность по базе В. Тогда существуют ее подпоследовательность {yk}9 yk = хп*9 и последовательность окончаний Ьп g В, зависящая от {yk}9 такие, что хп* g bk9 но хп* £ bk^19 bk+1 с bk.
► В качестве выберем произвольное окончание из В. Существует только конечное число членов последовательности, которые не принадлежат Пусть хп^ g Ьр тогда для любого k > 0 имеем хп + k е Ъг (согласно свойству монотонности {хд}). В качестве Ь2 выберем некоторое окончание, которому не принадлежит хп^. Такое Ь2 существует, поскольку Нв = Аь € в Ъ = 0. Действительно, если хП1 g b для любого окончания 6, то хп^ е Нв. Но тогда Нв не будет пустым множеством. В качестве хп^ выберем член последовательности с минимальным индексом, начиная с которого все последующие члены последовательности принадлежат &2, и т* Д-
164
Таким образом, получаем две последовательности: элементов ys = хп и окончаний {68}, Ь8 е В таких, что хп g 6g, хп t b8+1 и b8+1 cz Ь8 для каждого s > 1. ◄
Последовательность {Ьп} назовем основной последовательностью окончаний.
ЛЕММА 3. Пусть {Ъп} — основная последовательность окончаний. Тогда для каждого окончания Ь g В существует окончание Ъп е В такое, что Ъп с Ь.
►	Пусть Ь — произвольное окончание из базы В. Вне этого окончания лежит не более конечного количества членов yk, т. е. найдется хотя бы одно значение k = kQ, при котором ykQ g Ь. Рассмотрим также окончание Ь^о+1 из основной последовательности окончаний.
По условиям, наложенным на базу В, имеет место одно из двух включений: 1) & с ЬЛо+1 или 2) Ь э ЬЛо+1. Однако первый случай невозможен, поскольку тогда имеют место соотношения yko 6 ba ЬЛо+1, или ykQ g ЬЛо+1, что невозможно, так как yk^ е bkQ, но уЛо ё ЬЛо+1 по построению последовательностей {ук} и {bk}. Следовательно, имеет место именно второй случай, т. е. Ъ о => Ч+1- <
Л Е М М А 4. Справедливо соотношение kQl bk = 0.
►	Предположим противное, т. е. что существует z g bk при всех натуральных k. Поскольку £ b = 0, найдется окончание Ъ, не содержащее z.
По лемме 3 существует bk^ такое, что bk^ а Ь. Отсюда следует, что z не входит и в окончание bk^, откуда z g k П J>k, что противоречит сделанному выше предложению. 4
Заметим, что в силу доказанных лемм основная последовательность окончаний сама образует некоторую базу Bk^ эквивалентную исходной базе В. Эквивалентные базы иногда называют еще конфинальными.
3. Пусть f(x) — вещественная функция, определенная на А. Мы называем число I С-пределом функции f(x) по базе В, если для всякого е > 0 существует окончание Ъ = &(е) такое, что для всех х g b имеем |/(х) - 1\ < е.
Обозначение: I = С-lim f(x) или просто I = lim f(x). в	в
У 65
Это соответствует определению предела функции по Коши. Дадим теперь аналогичное определение предела по Гейне.
Число I будем называть Hm-пределом функции f(x) по базе В, если для каждой монотонной последовательности {хп} по базе В
nh“oAxn) = t
Обозначение: I = Нт-lim f(x).
ТЕОРЕМА 1. Для того чтобы существовал C-lim f(x), необходимо и достаточно, чтобы существовал Hm-lim /(х); более того, Hm-lim f(x) = C-lim f(x).
В	в
Другими словами, понятия Нт-тгредела и С-предела функции по базе В являются эквивалентными.
► Необходимость. Пусть С-предел существует, т. е.
C-lim f(x) = I.
Тогда по определению для любого е > 0 существует Ь = &(е) такое, что при всех х g b справедливо неравенство \f(x) - 1\ < е.
Рассмотрим произвольную последовательность {хп}, монотонную по базе В. Из условия монотонности следует, что существует п0 такое, что для всех п > п0 имеет место соотношение хп е Ъ. Следовательно,
|Л*„) - z| < е V п > п0, т. е.
Достаточность. Предположим противное. Пусть Hm-lim f(x) = = Z, но С-предел не существует или не равен I. Это означает, что существует е > 0 такое, что для каждого окончания Ь g В найдется х g &, для которого |Дх) - 1\ > е.
Рассмотрим основную последовательность окончаний {Ьп}. Пусть g Ьг и |/(2х) -1\ > е. Так как Нв = П Ъ = 0, то существует окончание &(1) g В такое, что zx £ &(1). В силу леммы 3, при некотором пх имеем &Л1 с: &(1). Следовательно, zx £ Ьп^
Далее, существует точка z2 е Ьп^ такая, что |/(х2) - 1\ > е. Как и выше, находим окончание Ъп^ удовлетворяющее условию z2 £ <£ Ъп^. Затем выбираем z3 g Ъп^ такое, что |f(z3) - 1\ > £, и т. д. Таким образом, получаем последовательность {zn}, которая удов-
166
летворяет условиям zk g Ьп , zk £ Ьп , и последовательность k — 1	ь
окончаний = bn^ Z) Ьп^:э ... .
Покажем, что последовательность {zn} является фундаментальной и монотонной по базе В.
Фундаментальность. Возьмем любое окончание Ь* е В. По лемме 3 существует окончание bk такое, что bk а. Ъ*. Если п8 > k, то bn* <^bka b*. Окончанию Ьп* не принадлежат только элементы z19 ... , z8 последовательности {zn}9 и для любого п> з имеем zn е е Ьп с Ъ*. Значит, последовательность {znj является фундаментальной.
Монотонность. Воспользуемся методом от противного. Предположим, что существует окончание ft* g В такое, что для некоторого номера k имеем zk е b*9 zk+1 ё Ъ*. Из построения последовательности {zn} получаем, что ё Ьп^. Следовательно, bn* z> Ъ* (согласно свойству 3 базы). Так как zk g Ь*, то zk g Ъп*. Однако это противоречит тому факту, что по построению последовательности {zk} справедливо условие zk<£ bn . Таким образом, последовательность {zk} является монотонной.
Далее, из того, что Hm-lim f(x) = Z, имеем f(zn) = l. Следовательно, можно перейти к пределу в неравенстве
|Дгп) - Z| > е > 0.
Получим 0 > е > 0, что невозможно. ◄
Будем говорить, что число I называется Н-пределом функции f(x) по базе В9 если для любой фундаментальной последовательности {хп} по базе В выполнено условие
lim f(xn) = I.
Обозначение: I = Д’-lim f(x).
ТЕОРЕМА 2. Следующие три понятия предела эквивалентны".
1)	lim Дх) = I;
2)	Н-1пл Дх) = Z;
3)	Hm-lim Дх) = I.
В
► Имеет место следующая цепочка утверждений: 1 => 2 => 3 =$ 1. Первые два из них очевидны, третье утверждение следует из теоремы 1. ◄
167
4. Докажем несколько свойств верхнего и нижнего предела по базе. Пусть {хЛ} — монотонная последовательность по базе В и пусть существует ДхЛ) = I* Тогда I называется частичным пределом по базе В. Наибольший из частичных пределов (если он существует) называется верхним пределом функции f(x) по базе В и обозначается lim Дх); подобным образом наименьший частичный предел называется нижним пределом по базе В и обозначается lim Дх).
в
Число 1Г называется верхним предельным числом, если
li = inf sup f(x), хе Ь
а число 12 — нижним предельным числом, если
L = sup inf Дх).
ЬеВ хеЬ
ТЕОРЕМА 3. Пусть функция Дх) финально ограничена. Тогда верхний и нижний пределы f(x) по базе В существуют и
lim Дх) = inf sup Дх), lim Дх) = sup inf Дх).
В	ЬеВ хеь	&	xeb
► Для любых двух окончаний Ь19 Ь2 базы В имеем
inf Дх) < sup Дх).
хе bi	хе Ьг
Действительно, существует окончание Ь3 базы В с условием Ь3 а с П Ь2. Тогда
inf Дх) < inf Дх) < sup Дх) < sup Дх).
хе&1	хе^з	хеЬ3	хе&2
Следовательно, в силу финальной ограниченности Дх) по базе В существует такое число X, что
А, = inf sup Дх).
ЬеВ
Докажем, что
lim Дх) = X.
Шаг 1. Можно найти окончание b* g В, для которого Дх) < < X + 1 для любых х g &*. Из леммы 3 следует, что существует окончание Ьп^ е В с условием Ьп^ а Ь*. Покажем, что можно найти элемент xr g Ьп^ с условием X + 1 > Дхх) > X - 1. Достаточно показать, что
sup Дх) > ДхЛ > X - 1.
168
Если бы такого элемента хх не было, то V х е Ьп^ выполнялось неравенство f(x) < X - 1. Следовательно,
sup f(x) < X - 1, ^ьП1
откуда
X = inf sup f(x) < X - 1.
beB xeb
Имеет место противоречие.
Далее можно найти окончание такое, что хг ё Ь$\ (Такое окончание существует, поскольку Нв = ^ & = 0.)
Ш а г 2. Выберем окончание &(2) е В, подчиненное условию
f(x) < X + 1/2 V х g &<2).
Рассмотрим окончание Ц2) с Ь<2) П Ь$\ Окончанию Ц2) g В не принадлежит xv Далее, как и в шаге 1, существует окончание Ъп^ а Ь[2\ которое содержит точку х2 хг такую, что
X - 1/2 < f(x2) < X + 1/2,
и т. д. Наконец получаем последовательность {х8}, которая удовлетворяет условиям
xs е xs « \ _ 1’ Х “ 1/3 <	Х + 1/»-
Как и при доказательстве теоремы 1, устанавливаем, что {хп} — монотонная последовательность по базе В. Кроме того, при п оо справедливо равенство lim Дхп) = X, т. е. X — частичный предел по базе В.
Шаг 3. Покажем, что любой частичный предел функции Дх) по базе В не превосходит X. Из определения величины X имеем, что для любого £ > 0 существует окончание Ь с условием
sup Дх) < X + е.
xeb
Пусть {хЛ} — произвольная монотонная последовательность по базе В, для которой существует Шп^ f(xn). В силу фундаментальности последовательности {хп} только конечное число ее членов не принадлежат Ь, т. е. существует номер п0 такой, что для всех номеров п, больших п0, имеем Дхп) < X + £. Переходя к пределу при п -» °°, получаем
lim Дхи) < X + е.
В силу произвольности е > 0 имеем liir^ Дхп) < X. ◄
169
Пусть и 12, как и прежде, верхнее и нижнее предельные числа соответственно. Назовем число 12 -	> 0 колебанием функ-
ции f(x) по базе В и обозначим
osc f(x) = l2-lv
Критерий Коши в этих обозначениях формулируется следующим образом.
Для существования предела функции f(x) по базе В необходимо и достаточно, чтобы osc f(x) = 0.
В
Отметим, что из теоремы 3, в частности, имеем:
и щл =м sup л*);
х-Я-оо	Т > 0 х > Т
2) lim f(x) = inf sup f(x);
^°°	T>0 |x|>T
3) lim f(x) = inf sup f(x).
x—^Xq	5>0 0<|x-x0|<5
Замечания. 1. Теорема 1 даже в простейших случаях несколько сильнее, чем классическая теорема, утверждающая эквивалентность поточечной сходимости по Коши и Гейне, поскольку требуются только монотонные последовательности. Это, в свою очередь, иногда удобно в приложениях.
С другой стороны, можно рассматривать базы, для которых каждая фундаментальная последовательность не является монотонной. В этом случае, конечно, Hm-сходимость не определена, тем не менее, теорема 2, утверждающая эквивалентность Н- и С-сходимости, остается справедливой, так как ее доказательство, по существу, тождественно с выводом теоремы 1 при очевидной подстановке просто фундаментальной последовательности вместо монотонной.
2.	Необходимо подчеркнуть, что понятия Нт-, Н-сходимости могут быть определены в том случае, если существует по крайней мере одна монотонная фундаментальная последовательность по базе. Кроме того, как показано в лемме 2, для такой базы всегда существует основная последовательность окончаний, которая сама является счетной базой, кофинальной к первоначальной. На языке теории фильтров это означает, что проблема обобщения теоремы Гейне об эквивалентности Н- и С-сходимости может рассматриваться только для фильтров со счетной базой.
3.	Мы ограничиваемся рассмотрением понятия сходимости только для числовых функций. Однако результат теоремы 2 без труда может быть распространен на общий случай отображений двух баз тогда и только тогда, когда они допускают существование монотонных или просто фундаментальных последовательностей.
4.	Условие 3, налагаемое на базу В, иногда оказывается невыполненным. Обычно в этих случаях можно вместо базы В рассматривать базу D, удовлетворяющую этому условию, заданную на том же основном множестве и эквивалентную базе В в том смысле, что сходимость любой функции по одной из этих баз влечет за собой ее сходимость и по другой базе к тому же самому значению.
Примером эквивалентных баз являются база В и основная последовательность окончаний {Ьп} из леммы 2.
170
Интеграл Римана. Дифференциальное исчисление функций многих переменных
Эта часть курса математического анализа включает основы интегрального исчисления функций одной переменной и дифференциального исчисления в пространстве нескольких измерений. Обе темы объединяет появление в них геометрических понятий как главного объекта изучения.
Источником основных понятий математического анализа во многом являются представления о простейших свойствах геометрических объектов в реальном пространстве. В качестве примера можно привести метод вычисления площадей у Архимеда или метод «исчерпывания» Евдокса. Устанавливается взаимосвязь понятия интегрируемости функции по Риману и вопроса о существовании площади криволинейной трапеции, т. е. ее измеримости по Жордану.
Еще один источник понятий математического анализа — арифметика. Поэтому мы стремились к раскрытию арифметических аспектов математического анализа, понимая под этим, скорее, их обусловленность дискретными элементами, имеющими арифметическую природу, связанную, в конечном счете, со свойствами натуральных чисел. Сюда можно отнести доказываемые формулы суммирования Эйлера и Абеля, метод интегральных сумм, равномерные разбиения в теории интеграла Римана, критерий Г. Вейля для равномерного распределения последовательности по модулю единица, признак алгебраичности функций, данный А. Эйзенштейном. Отметим, что вывод формулы длины дуги кривой приведен в упрощенном варианте.
Рассмотрен ряд понятий, которые в дальнейшем более подробно изучаются в рамках других предметов. О них дается первое и в то же время достаточно отчетливое представление с тем, чтобы облегчить усвоение соответствующего материала в будущем, и, может быть, обеспечить понимание специальных курсов естественнонаучного содержания.
ГЛАВА 7
Определенный интеграл
Лекция 1
§1. ВВЕДЕНИЕ
Пусть функция /(х) определена на интервале (а, Р), содержащем отрезок [а, Ь]. Определенным интегралом от функции /(х) на этом отрезке [а9 Ь] называется число, равное площади криволинейной трапеции, т. е. фигуры, заключенной между прямыми х = а, х = &, I/ = 0 и кривой у = /(х), причем площадь той части, которая лежит выше оси абсцисс, берется со знаком + и ниже ее — со знаком -. Интеграл обозначается так:
f f(x) dx, а
где число а называется нижним 9 а число b — верхним пределами интегрирования.
В связи с данным определением интеграла возникает ряд вопросов.
1)	Что такое площадь? (Этому принципиальному вопросу далее уделяется много внимания.)
2)	Почему эта площадь обозначается почти так же, как и неопределенный интеграл?
3)	Какая связь существует между неопределенным и определенным интегралами?
Забегая вперед, ответим на последние вопросы.
Прежде всего, заметим, что определенный интеграл можно рассматривать как функцию верхнего (или нижнего) предела интегрирования, считая другой предел интегрирования фиксированным, т. е., если зафиксируем, скажем, число а, то при любом Ь g (а, Р) мы будем получать свои величины, равные значению интеграла на отрезке [а, &]. Тем самым, определяется некоторая функция F(&), заданная на интервале (а, Р). Оказывается, что если функция /(х) непрерывна на (а, Р), то из теоремы Ньютона—Лейбница, о которой будем говорить далее, следует, что функция F(x) является дифференцируемой, и, более того, она
173
является первообразной функции Дх), т. е. имеем F'(x) = Дх), и, кроме того, справедливо равенство
ъ
/ f(x)dx = F(b)-F(a). а
Пусть J\(x) — другая первообразная Дх). Тогда, поскольку Fr(x) = = F(x) + с, где с — некоторая постоянная,
ъ
F^b) - Ft(a) = F(b) + с - F(a) -с = F(b) - F(a) = J ftx) dx.
a
Другими словами, это равенство имеет место для любой первообразной из семейства, образующего неопределенный интеграл, т. е. теорема Ньютона—Лейбница указывает на то обстоятельство, что неопределенный и определенный интегралы — это тесно связанные между собой понятия. И для того чтобы их далее изучать, надо разобраться, какой же смысл вкладывается в понятие площадь криволинейной трапеции. К этому вопросу можно подходить по-разному, и в зависимости от этого у одной и той же трапеции площадь может существовать или не существовать. Но если в двух различных смыслах она существует, то всегда в обоих случаях она должна быть одной и той же величиной.
$ 2. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА РИМАНА
Уже отмечалось, что понятие «определенный интеграл» по существу сводится к определению понятия «площадь криволинейной трапеции», т. е. площадь фигуры, лежащей в полосе а < х < Ъ и заключенной между графиком функции у = Дх) и осью абсцисс. Другими словами, эта фигура образована множеством А точек вида
{(х, 1/)| а < х < Ь, 0 < у < Дх)}, и множеством В
{(х, у)| а < х < b, f(x) < у < 0}.
Площадь всякой плоской фигуры D будем обозначать через ц(В). Заметим, что площадь любой фигуры на плоскости — это неотрицательное число. Определенный интеграл отличается от площади тем, что равен разности площадей фигур А и В, т. е.
ь
J Дх)</х = ц(А)-ц(В), а
а не их сумме, как можно было бы ожидать.
Из школьного курса геометрии известны следующие простейшие свойства фигур, имеющих площадь:
1)	Если Dx a D29 то ц(Вх) < р(В2).
174
2)	Если Dr A D2 = 0, то 11(1^ U D2) = p(Bx) + p(Z>2)’
3)	Площадь прямоугольника равна произведению длин двух соседних его сторон.
Фигуры, составленные из прямоугольников со сторонами, параллельными осям координат, имеют площадь. Такие фигуры назовем простейшими.
Теперь можно определить понятие площади криволинейной трапеции D, значит, и понятие определенного интеграла I от функции f(x) на отрезке [а, &] следующим образом. Для простоты рассуждений рассмотрим только случай, когда функция Дх) неотрицательна.
Впишем в фигуру D и опишем вокруг нее простейшие фигуры — соответственно Dr и D2. Для наглядности можно положить, что функция Дх) является непрерывной. Очевидно, Dr с D a. D2. Отметим также, что некоторые части границ фигур Dr и D2 являются. ступенчатыми функциями на отрезке [а, Ь]. Напомним, что функция Л(х) называется ступенчатой, если на каждом промежутке (х-_ р xf), i = 0, 1, ... , и, а = х0 < хх < ... < хп = Ь, она принимает постоянное значение ht. Пусть фигуре Dr отвечает ступенчатая функция Л(х), а фигуре D2 — ступенчатая функция g(x). Тогда имеем Л(х) < Дх) < g(x).
Интегралом от ступенчатой функции h(x) назовем величину
ДЙ)=.Е1 Мхг
Справедливо неравенство 1(h) < 1(g).
Рассмотрим два числовых множества А = {1(h)} и В = {№)}. В силу леммы об отделимости этих множеств найдется число I, их разделяющее. Если оно единственно, то назовем его интегралом от функции Дх) на отрезке [а, &], а саму функцию — интегрируемой на этом отрезке.
Известно, что если числа inf 1(g) я sup 1(h) совпадают, то их D2 z> D	Dxa. D
общее значение равно I. Поэтому справедлив следующий критерий интегрируемости ограниченной функции Дх) на [а, &].
ТЕОРЕМА 1. Для того чтобы ограниченная на отрезке функция Дх) была интегрируема на нем, необходимо и достаточно, чтобы для любого е > 0 существовали ступенчатые функции Л(х) и g(x) с условием h(x) < Дх) < g(x), и такие, что
1(g) - 1(h) < е.
Эту теорему доказывать сейчас не будем, поскольку построим теорию интеграла Римана, основываясь на более традиционном подходе, и в рамках этого подхода критерий интегрируемости
175
будет доказан. Тем самым покажем, что оба подхода к построению интеграла Римана дают один и тот же класс интегрируемых функций.
Отметим также, что рассмотренный выше подход дает возможность определить понятие площади фигуры D через вписанные и описанные простейшие фигуры. Подобным образом далее определим фигуры, измеримые по Жордану, и докажем, что для измеримости по Жордану криволинейной трапеции, отвечающей функции Дх), необходимо и достаточно, чтобы Дх) была интегрируема по Риману.
Существуют и другие конструкции, с помощью которых можно ввести понятие и площади, и определенного интеграла, интересующего нас в первую очередь. Смысл этих конструкций состоит в том, чтобы поставить в соответствие каждой функции из некоторого класса свое число таким образом, чтобы при этом выполнялся ряд естественных свойств, которыми обладает площадь простейших фигур. Заметим, что чем сложнее конструкция, тем шире становится класс функций, для которых понятие «определенный интеграл» приобретает смысл. Будем рассматривать конструкцию, предложенную немецким математиком Б. Риманом, и поэтому соответствующий интеграл назовем интегралом Римана. Также познакомимся и с интегралом более общего вида: интегралом Лебега, но, в основном, будем заниматься интегралом Римана. Изложение оригинальной конструкции Б. Римана можно найти в статье «О возможности представления функции посредством тригонометрического ряда», написанной Риманом в 1853 г. Впервые эта статья была опубликована в 1867 г. На русском языке она была напечатана в 1914 г.
Например, интеграл Лебега является более общим, чем интеграл Римана, на том основании, что все функции, интегрируемые по Риману, также являются интегрируемыми по Лебегу, но не наоборот. Подчеркнем, что если функция интегрируема двумя разными способами, то значения интеграла всегда обязаны совпадать. Так что задача расширения понятия интеграла может состоять только в том, чтобы, приписать числовые значения определенным интегралам от все более широких классов функций, не меняя при этом значений интегралов для тех функций, у которых это значение установлено.
Переходим к изложению конструкции интеграла Римана. Будем считать, что функция Дх) определена на интервале (а, Р), содержащем отрезок [а, &].
Определение 1. Конечное множество Т точек х0, хр ... , хп называется (неразмеченным) разбиением отрезка [а, &], если п > 1 и а = х0 < хх < ... < хп = Ь.
V76
Определение 2. Будем говорить, что разбиение Т\ предшествует разбиению Т2 (или разбиение Т2 следует за разбиением 7\), если имеет место теоретико-множественное включение а Т2 (или Т\ =) Т2)* Разбиение Т2 называется измельчением разбиения Tv
Очевидно, справедливы следующие свойства.
1°. Всякое разбиение есть измельчение самого себя.
2°. Если Т3 = U Т2, то разбиение Т3 есть измельчение и разбиения Т1, и разбиения Т2.
Для любого разбиения Т = {х0, хр ... , хп} через АЛ обозначим отрезок вида [хЛ_р xj. Длину этого отрезка обозначим так:
Ах» = xk - x„_v
Определение 3. Величина Аг = ^ах^ Axfe называется диаметром разбиения Т.
На каждом из отрезков Afe выберем точку k = 1, ... , п, т. е.
**-!<£*<**♦
Определение4. Совокупность точек {х0, ... , хп, £р ..., ^п} называется размеченным разбиением отрезка [а, &].
Обозначим его через V, а соответствующее ему неразмеченное разбиение — через Т = T(V).
Определение 5. Сумма
G(V) = f(^X1 + ... + f(QAxn = kt1 f(^)bxk называется интегральной суммой функции Дх), соответствующей размеченному разбиению V.
Определение 6. Число I называется определенным интегралом (Римана) от функции Дх) на отрезке [а, &], если для всякого е > О существует 8 = 8(e) > 0 такое, что для любого размеченного разбиения V отрезка [а, &] с условием AF < 8 справедливо неравенство
\1-<5(У)\<г, т. е.
\I-ki1f(^k\<e.
Для интеграла I используют обозначение
ь
I = J f(x)dx.
177
Определение 7. Функция f(x), для которой существует интеграл Римана, называется интегрируемой (по Риману) на отрезке [а, &].
Легко доказать следующее утверждение: если существуют два числа 1Х и 12, удовлетворяющие определению интеграла Римана от функции f(x) на отрезке [а, Ь], то они совпадают, т. е. 1Г = 12.
► Действительно, если, например, 1Г < 12, то в качестве величины £ возьмем число, равное (12 -1^/2. Тогда в силу определения интеграла существует число 5 = 8(e) > 0 такое, что для любого размеченного разбиения V с условием Дг < 8 имеем
|gf“/1I<£, |Оу~ /21 < следовательно,
Ц -11 = IA - Al < IA - <*vl + l<V- Al < 2е = А - А-
Отсюда получаем 12 - 1Г < 12 -1г, что невозможно, так что имеем А = А- «
ъ
Определенный интеграл J f(x)dx можно рассматривать как а
предел по некоторой базе. Определим эту базу, т. е. опишем множество окончаний, из которых она состоит.
Напомним определение базы В подмножеств Ь основного множества А. Окончания Ь с: А базы В, т. е. ее элементы, удовлетворяют следующим условиям:
1) пустое множество не является окончанием базы;
2) для любых двух окончаний Ь19 Ь2 базы В найдется окончание Ь3 € В с условием Ь3 с: П Ь2.
В качестве основного множества А возьмем множество всех размеченных разбиений отрезка [а, &]. Для каждого 8 > 0 рассмотрим множество Ь3 а А, состоящее изо всех размеченных разбиений с диаметром Дг меньшим, чем 8, т. е. Дг < 8. Совокупность множеств {&§} и будет искомой базой. Интегральная сумма g(V) является функцией, определенной на множестве А размеченных разбиений V. Тогда определенный интеграл от функции f(x) на отрезке [а, Ь] оказывается не чем иным, как пределом интегральных сумм g(V) по базе В, т. е.
ь
I = J f(x)dx = lim g(V).
Это равенство означает следующее: для всякого числа е > 0 существует окончание = Ь3(г) базы В такое, что для любого размеченного разбиения V е bs(e) имеет место неравенство |g(V) —1\ < е.
178
В предыдущем определении интеграла в качестве 8 — 8(e) > О надо взять величину 8, которая порождает окончание &§(е).
Так как интеграл — это предел интегральных сумм по базе В, то к нему применимы теоремы о пределе функции по базе множеств.
Докажем следующее важное свойство интегрируемых функций.
ТЕОРЕМА 2. Пусть функция f(x) интегрируема на отрезке [а, &]. Тогда она ограничена на нем.
► Предположим, что функция f(x) не ограничена на отрезке [а, &]. Возьмем любое разбиение Т: а = х0 < xt < ... < хп = Ь этого отрезка такое, что Дг < 8. Тогда существует отрезок Дг = [хг_р хг], на котором функция f(x) не ограничена. Покажем, что функция g(V) не ограничена. Возьмем любое число М > 0. Построим раз-метку V разбиения Т такую, что |g(V)I > М. С этой целью точки £р ... , £г_р £г+р ... , возьмем произвольно. Положим
А=
к в 1, к * г
Поскольку функция Дх) не ограничена на отрезке Дг, существует точка е Дг такая, что
Отсюда имеем
п	М + А
|o(V)| >|дидхг|- 2 ЯЦДх» > ^±*Дхг-А = М,
следовательно, o(V) не ограничена, т. е. функция f(x) — не интегрируема. ◄
Лекция 2
§3. КРИТЕРИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
Установим критерий интегрируемости по Риману функции, ограниченной на отрезке.
Определение 8. Верхней суммой Дарбу функции f(x) на отрезке [а, Ы, отвечающей разбиению Т = {х0,	, хп}9 называется
сумма
где Mk = sup f(x)9	— отрезок [хл-1, xfe], а Axfe — его длина.
хе А*
Нижней суммой Дарбу называется сумма
s(T)=kii где mh = inf Дх). хе А*
Определение 9. Число Г = inf, S(T) называется верхним ин-тегралом9 а число I* = sup з(Т) — нижним интегралом от Те А'
функции Дх) на отрезке [а, &], где А' — множество всех разбиений [а, &].
ТЕОРЕМА 1 (критерий Римана интегрируемости функции на отрезке). Для того чтобы ограниченная функция была интегрируема на отрезке9 необходимо и достаточно9 чтобы выполнялось условие
lim (S(T)-s(T)) = O. дг —»о
Для доказательства этого критерия потребуются следующие свойства верхних и нижних сумм Дарбу.
ЛЕММА 1. Для любого размеченного разбиения V имеем s(T(V)) < a(V) < S(T(V)).
ЛЕММА 2. Пусть TQ — любое фиксированное разбиение и а(Т0) — множество разметок этого разбиения. Тогда
s(T0) - inf a(V), S(T0) = sup o(V).
V'eafTo)	Vea(T0)
Л E MM A 3. Для любых неразмеченных разбиений Тг и Т2 имеем з^КЖТг).
180
ЛЕММА 4. Для ограниченной функции верхний и нижний интегралы I* и Z* существуют, причем для любого разбиения Т справедливы неравенства
s(T)<Z*<Z*<S(T).
Л EMMA 5. Диаметры размеченного разбиения V и отвечающего ему неразмеченного разбиения Т = T(V) совпадают, поэтому если V е Ь§, то T(V) е &8. Здесь — окончание базы размеченных разбиений и &8 — окончание базы неразмеченных разбиений, отвечающие числу 8.
ЛЕММА 6. Для любого разбиения Т имеем
Z*-Z*< S(T) - s(T) = Q(T).
►	Доказательство этих утверждений не представляет большого труда. Поэтому докажем только леммы 3, 4 и 6.
Начнем с доказательства леммы 3. Отметим, что при измельчении разбиения Т нижняя сумма Дарбу з(Т) может разве что возрасти, а верхняя сумма S(T) разве что уменьшиться, поэтому возьмем разбиение Т3 = Тг U Т2 и получим, что
Лемма 3 доказана.
Доказательство леммы 4 по существу вытекает из леммы 3. Если мы образуем числовое множество Мг всех значений вели-чин з(Т) и множество М2 всех значений S(T), то утверждение леммы 3 означает, что любой элемент а е М2 есть верхняя грань для множества Mv Но тогда наименьшая верхняя грань множества Мр т. е. величина Z*, не превосходит а. Это означает, что Z* — нижняя грань множества М2, а по своему определению Г — точная нижняя грань множества М2, поэтому имеем
з(Т) </*</*< S(T).
Утверждение леммы 6 следует из цепочки неравенств
S(T) - з(Т) >Г- з(Т) >Г -Z*.
Утверждение лемм 1, 2 и 5 непосредственно следуют из определений. ◄
Теперь можно перейти к доказательству критерия интегрируемости функции по Риману.
►	Необходимость. Пусть Jim o(V) = I. Это значит, что для любого числа ет > О найдется число 8Х =	> 0 такое, что для любого
181
размеченного разбиения V с диаметром Дг < 8Х имеем |g(V) - Z| < ер т. е.
Z-e1<o(V)<Z + e1.	(1)
Рассмотрим произвольное неразмеченное разбиение Т с условием Дт < 5Р Имеем
s(T) = inf о(У), S(D = sup g(V).
Vea(T)	Vea(T)
Тогда из (1) вытекает, что
I - ех < з(Т) < I + ер I - ех < S(T) < I + Ер следовательно, числа з(Т) и S(T) лежат на одном и том же отрезке [I - Ер I 4- eJ длины 2ер т. е.
|S(T) - s(T)| < 2ег
Если взять ех = е/3 и 5 = 81(е/3), то получим, ЧТО ДЛЯ ВСЯКОГО Е > О существует 8 = 8(e) > 0 такое, что для всякого разбиения Т с условием Дт < 8(e) имеем неравенство |S(T) - з(Т)| < е, т. е.
lim (S(T)-s(T)) = O. дг —> о
Достаточность. Докажем, что из условия lim (S(T) - s(T)) = 0 дт —> о
следует существование предела lim g(V)-
Ду —»о
Сначала убедимся, что верхний и нижний интегралы Г и I* равны между собой. В силу леммы 6 имеем
0 < Z* - Z* < S(T) - з(Т).
Следовательно, при Дг —> 0 получаем h = Г - Z* —> 0, т. е. h = 0 и Z* = Z* = Z.
Осталось доказать, что lim g(V) = I. Зададимся произволь-Ду —> о
ным е > 0. Тогда существует 8 = 8(e) > 0 такое, что для любого разбиения Т с условием Дг < 8 выполняется неравенство
S(T) - з(Т) < е.
Но тогда для любого размеченного разбиения V с условием Ду < 8 имеем
S(T(V)) - s(T(V)) < Е, и, кроме того, s(T(V)) < g(V) < S(T(V)), s(T(V)) < I < S(T(V)), т. e. обе точки g(V) и I лежат на отрезке [s(T(V))> S(T(V))], длина которого меньше е, но это значит, что расстояние между любыми точками его меньше, чем е. Другими словами, для любого раз
182
биения V с условием Ду < 8 справедливо неравенство | q(V) -1\ < е, т. е. имеем lim g(V) = I. ◄
Av-> о
Замечание. При доказательстве достаточности в критерии интегрируемости установлена справедливость следующего утверждения.
Пусть для ограниченной функции выполняется условие
lim (S(T) - s(T)) = 0.
Ду —> и
Тогда имеет место равенство Г = /*.
ПРИМЕРЫ. 1. Функция Дирихле
/1,еслих — рациональное число, W । о, если х — иррациональное число,
не является интегрируемой по Риману на отрезке [а, &].
Действительно, возьмем любое разбиение Т этого отрезка. На любом промежутке Д* разбиения Т содержатся как рациональные точки, так и иррациональные, поэтому колебание функции на этом промежутке равно 1. Следовательно,
Й(Т) = S(T) - s(T) = цДх, = Д &x( = b- а.
Но согласно критерию интегрируемости функции по Риману должно выполняться условие
lim (S(T)~ s(T)) = 0.
—> о
Значит, функция Дирихле D(x) неинтегрируема по Риману.
2. Функция Римана
J 1/п, если х = m/п, (тп, п) = 1, W [ 0, если х — иррациональное число, интегрируема по Риману на отрезке [0,1].
Зададимся произвольным числом е > 0. Положим число N равным величине N = [2/е] + 1 и возьмем число 8 из условия 0 < 8 < е/2ДГ2. Возьмем теперь любое разбиение Т с условием Дг < 8. Колебание функции R(x) на любом промежутке Д* удовлетворяет условию 0 < о). < 1. Представим сумму £2(Т) = S(T) - s(T) в виде суммы двух слагаемых и О2 в соответствии с тем, что выполняется неравенство 0 < со. < 1/N и 1/N < со- < 1. В сумму Q2 входят промежутки Др содержащие рациональные точки со знаменателем, меньшим, чем N. Количество таких точек не превосходит N2. Поэтому получаем
Q(T) = Qj + Q2 <	+ 8№ < | + | = е,
183
где штрих и два штриха в знаке суммы означают, что промежутки Дх^ входят соответственно в суммы и Q2- Следовательно, функция Римана Я(х) интегрируема.
Замечание. Введенная в рассмотренных выше примерах величина п	п
£2(Т) = S(T) - s(T) SMk *	“ J
называется омега-суммой, соответствующей данному разбиению Т от* резка [а, Ь]. При этом величина cofc = Mk - mk называется колебанием функции f(x) на отрезке Д* == [хь-р XJ- Бели в определении величин Mk, mk cofc вместо отрезка ДЛ взять интервалы (xk_v xfe), то получим числа M'k = sup f(t)9 m'k = inf f(t) и (o'k = M'k - m'k, а также величину t e (x*-i» xk)	t € (xfc_p xk)
Q (T), которую тоже будем называть омега-суммой.
Лекция 3
$ 4. ЭКВИВАЛЕНТНОСТЬ ТРЕХ УСЛОВИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
Докажем критерий интегрируемости функции по Риману в трех эквивалентных формах.
ТЕОРЕМА 4. Для интегрируемости ограниченной на отрезке функции необходимо и достаточно, чтобы выполнялось хотя бы одно из трех эквивалентных условий: l)lim(S(T)-s(T)) = O;
Zlj, —> и
2)/* = /*;
3) inf (S(T) - 8(Т)) = 0. т
► Докажем, что имеет место следующая цепочка заключений: 1) => 2) => 3) => 1), откуда и следует искомая эквивалентность.
В силу замечания к теореме 1 § 3 получаем, что из 1) => 2). Докажем, что из 2) => 3). Справедливо следующее соотношение:
inf (S(T) - s(T))- h -1* - Д. T
а)	Сначала покажем, что h являемся нижней гранью множества S(T) - з(Т). Имеем
Г < S(T), -1* < -з(Т), следовательно, S(T) - s(T) >Г- Ц.
б)	Докажем теперь, что величина h является точной нижней гранью множества S(T) - з(Т), т. е. что для любого е > 0 число й + е не является нижней гранью. Из определения верхнего и нижнего интегралов следует, что найдутся разбиения 7\ я Т2 такие, что
S(7\) < Г + е/2, з(Т2) > Г - е/2.
Отсюда для разбиения Т3 = 7\ U Т2 имеем
S(T3) < S(Ti) < Г + е/2, з(Т3) > з(Т2) > Г - е/2, следовательно,
S(T3) - з(Т3) < Г -1* + е = й + е, т. е. й + е действительно не является нижней гранью множества значений S(T) - з(Т).
Так как утверждение 2) состоит в том, что й = 0, то из доказанного выше имеем inf (S(T) - s(T)) = 0. Таким образом, из утверждения 2) мы вывели утверждение 3).
185
Докажем теперь, что из 3) => 1). В силу условия 3) имеем, что для любого е > 0 существует разбиение 7\ такое, что S(TX) - 8(ТГ) < < е/2. Обозначим через п число точек разбиения Tv В силу ограниченности на отрезке функции Дх) существует число М > 0 такое, что для всех точек х из этого отрезка имеем | Дх) | < М. Положим 8 = e/(4nAf). Далее возьмем любое разбиение Т с условием Дг < 8. Тогда для разбиения Т2 = Т U Тг имеем
S(T2) - а(Т2) < S(7\) - з(Т\) < е/2,
или, что то же самое, £1(Т2) < Q(7\) < е/2. Аналогично, имеем Q(T2) < Q(T).
Оценим сверху величину Q(T). Поскольку
Q(T) = Q(T2) + (Q(T)-Q(T2)),
достаточно оценить Q(T) - £1(Т2). Разбиение Т2 является измельчением разбиения Т и получается из него так, что на некоторые промежутки разбиения Т добавляются точки разбиения Tv Количество таких промежутков не превосходит п, длина каждого из них меньше 8, а колебание функции Дх) на этих промежутках не превосходит 2М. Следовательно, Q(T) - Q(T2) 2Мп8.
Таким образом, получаем
Q(T) < е/2 + 2Мп8 = е.
Это означает, что для любого е > 0 существует 8 = е/4Мп такое, что для любого разбиения Т с условием Дг < 8 выполняется неравенство £2(Т) < е, т. е.
lim (S(T)-s(T)) = 0. ◄
—> о
§ 5. СПЕЦИАЛЬНЫЙ КРИТЕРИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
Верхнюю (соответственно нижнюю) сумму Дарбу функции Дх) на отрезке [а, &], отвечающую разбиению Тп отрезка [а, &] на п равных частей, обозначим через Sn (соответственно sn).
Докажем следующий специальный критерий интегрируемости функции по Риману.
ТЕОРЕМА 5. Для интегрируемости ограниченной функции Дх) на отрезке [а, Ь] необходимо и достаточно, чтобы выполнялось условие

186
► Необходимость следует из критерия Римана (теорема 1 § 4). Достаточность. Пусть
Z*=inf S(T), Z*=sup s(T).
Тогда для любого разбиения Т имеем
з(Т)	S(T).
Следовательно,
sn<h<r<Sn.
Отсюда получаем
Sn-sn> Г - !*> 0.
Но поскольку (Sn - sn) = 0, то Z* == Z* = Z, и в силу теоремы 2 § 4 (условие 2) функция f(x) интегрируема на отрезке [а, &]. ◄
СЛЕДСТВИЕ. Для интегрируемости ограниченной функции на отрезке необходимо и достаточно, чтобы выполнялось одно из следующих эквивалентных условий:
4)M(sn-sB) = °;
5) inf(Sn-8n) = O.
Очевидно, имеем цепочку заключений 5) => 3) =❖ 1) => 4) => 5). Следствие доказано.
Условия 4) и 5) дополняют условия 1), 2) и 3) теоремы 2 § 4.
ПРИМЕР. Рассмотрим последовательность {хп}9 0 < хп < 1. Пусть а и Р — любые числа с условием 0 < а < Р < 1. Обозначим через Nq количество членов последовательности {xk}9 1 < k < Q, попадающих на отрезок [а, р], т. е. а < xk < р, 1 < k < Q.
Будем говорить, что последовательность {хл} равномерно распределена по модулю единица (p.p. (mod 1)), если выполняется соотношение
Докажем следующий критерий равномерной распределенности, принадлежащий Г. Вейлю.
ТЕОРЕМА 6 (критерий Г. Вейля). Для того чтобы последовательность {хп} была равномерно распределена по модулю единица9 необходимо и достаточно9 чтобы для любой интегрируемой по Риману функции f(x) имело место равенство
1 Q	I
lim 5 Е f(xr) = J f(x) dx.	(1)
Q->oo r - 1	J
187
► Достаточность. Периодическая функция /(х) с периодом 1 „	[ 1, если а < х < Р,
/	= <PW “ [ 0 — в противном случае,
интегрируема на отрезке [0, 1]. Кроме того, имеем
Q	1
Nq = Е фСх,), J <p(x)dx = Р - а,
О следовательно,
N lim -77 = В - а, Q-4OO Q Г
т. е. последовательность {хп} равномерно распределена по моду* лю единица.
Необходимость. Пусть f(x) — произвольная интегрируемая по Риману функция на отрезке [0, 1]. Тогда в силу критерия интегрируемости для любого е > 0 существует разбиение Т такое, что
Q(T) - S(T) - s(T) < |, s(T) = /Е1 т{Дх(, S(T) =	М^.
Очевидно, справедливо неравенство
1 в(Т) < J f(x)dx < S(T).
О
Положим
[ 1, если х g Ф/(х)	[ 0, если х £ Др
ф(х) = .Ej mz(p;(x), Ф(х) = <si Мг(р;(х).
Заметим, что если равенство (1) выполняется для некоторых функций /\(х), f2(x), ...» fr(x)9 то оно справедливо и для функции g(x) = c{fx(x) + c2f2(x) + ... + crfr(x). Поэтому, исходя из определения равномерной распределенности, получаем
lim f ф(хг) = J (p(x)dx = s(T), W -»00	' a	q
lim i 1 Ф(хг) = J Ф(х)</х = S(T).
Q -» ооЦЛ г - 1	Q
Следовательно, для всякого е > О существует Qo = Q0(e) такое, что для всех Q > Qo имеем
8(T)-i Д,ф<хг)<£,
1	F
S(T)-1 Х,Ф(хг)<|.
188
Далее, поскольку имеет место неравенство <р(х) < ftx) < Ф(х), । । rl 1	। J1 । Л1 ф(*г) < S(T) +1.
1 Q	1
Следовательно, как g /(хг)> так и значение интеграла J f(x)dx ** г~	о
принадлежат отрезку [s(T) - е/3, S(T) + е/3]. Поэтому
1 Q	I	Ол
1 Q	}	Ос
± rE/(xr) - J f(x)dx < Q(T) + у < e.
Замечание. Легко видеть, что условия 1)—5) интегрируемости функции можно дополнить еще одним эквивалентным условием еле* дующего вида:
6)	inf О'( Л = 0. т
► Действительно, при всех х справедливы оценки < cofe, откуда Я'(Г) < Q(T). С другой стороны, очевидно, что при любом е > 0 к заданному разбиению можно добавить несколько новых точек так, чтобы для нового разбиения выполнялось неравенство П(7\) < Q'(T) + е, а это значит, что если inf Q'(T) = 0, то и inf Q(T1) = 0.	◄
Т	Т,
§ 6.	МЕТОД ИНТЕГРАЛЬНЫХ СУММ
Метод интегральных сумм основан на следующей лемме.
Л EMMA 7. Пусть функция f(x) интегрируема на отрезке [а, &], и пусть {Vn} — любая последовательность размеченных разбиений с условием, что последовательность диаметров разбиений {Дг} —> 0 при п —> сю. Тогда при п —> °о имеем
a)Sn = S(T(V„))^I; Ъ) sn = S(T(Vn)) Ц в) а„ = о(И„) I.
► По определению интеграла и по критерию интегрируемости функции по Риману для всякого числа е > 0 существует число 8 = 8(e) > 0 такое, что если Д^ = &т<уп) < 5» то
|<т„ - /| < е/2, |$„ - /| < е/2 < е, |а„ -1| < е/2 < е.
Но так как последовательность {Дг} стремится к нулю при п —> то вне соответствующей 8-окрестности нуля лежит не более конечного числа п0(8) значений Дг. Поэтому вне 8-окрестности числа I тоже лежит не более, чем п0(8) значений величин on, Sn, 8п. Следовательно,
I = lim о„ = lim S„ = lim s„. ◄ n —> ОО	n OO rl nOO
189
b	1
ПРИМЕРЫ. 1. Имеем J exdx = eb-e°.	I
a	I
Поскольку функция ex непрерывна на отрезке [a, b], она ин- I тегрируема на нем. Для того чтобы найти значение интеграла, I остается только выбрать последовательность {Уп} и вычислить I предел lim a„.	|
п _> оо ri	I
Положим при k = 0,	, п	>
xk = а +	» ^>k = Л*-1’	= ~~ = Д, хк = а +	;
отсюда
= "Ё * ев+*д • Д = Де“(1 + е4 + ... +	=
= Aga1 ~е"А----Д_ (еЬ _ ga).
1	- ед	ед - 1
Так как при п -> °о справедливо равенство lim —-— = 1, то
П->ооеД _ |
Ъ lim ои = eb - еа = [ exdx. п^оо п	*
2.	Пусть 0 < а < Ь. Тогда имеем [	- т •
а х2 а Ъ
Возьмем произвольное разбиение отрезка [а, Ь], а именно
а = х0 < ... < хп = Ь и положим = Jxk _1xfe, k = 1, ... , n. Тогда для соответствующей интегральной суммы сгЛ имеем
СТп =
fe=e 1	xk^ a b
следовательно,
К Ja х2 а
1 b
3.	Найти предел lim f—— + —— 4-... + —1 = I. + 1 п + 2	п + п^
Очевидно, имеем
Z=lim t 1
n^oo * = 11+^ n Jl+x n
Отсюда по формуле Ньютона—Лейбница, которая будет доказана чуть позже, получим I = 1п 2.
190
В частности, используя это, найдем сумму ряда
s/-1)*'1 - lim (Д . lim {1 - 1 + 1 - ... - 1 1-
fe=l k	n —> oo \fe = 1	fa / n->oo\ 2	3	2п /
= lim f —+ —— + ... + —1— ) = In 2.
n->oo4n + i n + 2	n + n.'
4.	Справедливо следующее равенство:
fi zi о .	[2я1п|а|,если а >1,
J In (1 - 2acos x + a2)dx -	a < k
Положим xk = Tik/n9 %k = xk9 k = 19... 9 n; тогда имеем Axfe = л/п. Следовательно,
an = i Ml “ 2a cos xk + a2)^ = kL1 ln|(a - eixk)(a - e~Zx*)l =
= - In fenj(a - eixb)(a -	= я ln|a2n - 1| i .
Переходя к пределу при n -> сю, получаем искомое значение интеграла.
5.	Пусть /(х) не убывает и ограничена на отрезке [а, &]. Тогда для величины
справедливы неравенства
О < 8 < (f(b)-f(a))(b-a). п	п
Очевидно, имеем
£(Ь-а)
X..+;(6 ’ " «*>) dx *
±-(b - а)
* .t +>-“>)- +- “ф* -
	. (?(“ + ;(»-«))- f(a + V» -“)))- ^ т» - Л“».
а это и доказывает требуемое неравенство.
6.	Пусть функция /(х) имеет на отрезке [а, Ь] ограниченную и интегрируемую производную, и пусть символ 8П обозначает то же, что и в примере 5. Тогда
11m „8_ _ (>-«)</<»-/<»» .
п -> оо п	2
191
В силу теоремы Лагранжа о конечных приращениях, на каждом отрезке Afe = [xfe_p xj, k = 1, ... , n, для любой точки х е А* существует точка принадлежащая интервалу (xfe_1, xfe) такая, что f(a + | (Ь - а)) - /(х) = f | (Ь - а) - х} .
Пусть тк, Мк — соответственно нижняя и верхняя грани производной f'(x) на отрезке ДА. Тогда тк < /'(£*) <Мк.
Из определения 8Л имеем
£(Ь - а) + а
Sn = JL f (a+^(b-a)-x)№)dx.
* 1 A(6-a) + av	п	7
Отсюда следуют неравенства
HLi®)2 £	<5 < VLi®)2 £ м*.
2 \ п / k = 1 К п 2 v д 7 fc = i К
Домножая обе части неравенства на п и переходя к пределу, получаем требуемое предельное соотношение. Отсюда, в частности, для последовательности примера 3 имеем
lim п(—— 4- 1 4-... 4- —-— - In 21 = -7 .
П^°° чП4-1 п 4- 2	п 4- п '	4
7.	Пусть функция р(х) непрерывна и положительна на отрезке [О, 1]. Тогда справедливы неравенства
1
Jlnp(x)dx х
—-— < е°	< J p(x)dx.
f	0
k
Положим xk = - , k = 0,... , n. Тогда для соответствующих интегральных сумм в силу неравенств между средними гармоническим, геометрическим и арифметическим имеем
_—”—— <	+;
—— + ...+—— п
Р(^1)	Р(*п)
Переходя в этих неравенствах к пределу при и ^ °°, получаем искомое неравенство.
Лекция 4
$ 7. СВОЙСТВА ИНТЕГРАЛА РИМАНА КАК ПРЕДЕЛА ПО БАЗЕ
Напомним данное в конце § 1 определение интеграла Римана как предела по некоторой базе.
Пусть А — совокупность всех размеченных разбиений отрезки [а, Ь]. Множество А будет основным множеством базы В. При всяком 8 > 0 окончаниями Ь — Ь8 е А этой базы В являются множества, состоящие изо всех размеченных разбиений V е А с диаметром разбиения Дг, меньшим 8. Другими словами, окончание &8 задается так:
&s = {Vg А|ДГ< 8}.
Пусть, как и ранее, g(V) — интегральная сумма, отвечающая размеченному разбиению V = {х0, хр ... , хп; ... , £п}, т. е.
всю-Ляцд*».
Тогда число I называется интегралом Римана от функции Дх) на отрезке [а, Ь], если I = lim a(V).
Другими словами, число I — интеграл от функции Дх) на от^ резке [а, 6], если для всякого е > 0 существует число 8 = 8(e) > О такое, что для любого размеченного разбиения V отрезка [а, 6] с условием Дг < 8 имеем \l - o(V)l < е.
Пусть теперь А' — совокупность неразмеченных разбиений отрезка [а, Ь]. Это множество А' является основным множеством базы В', состоящей из окончаний &§, причем состоит изо всех неразмеченных разбиений Т с диаметром Дг < 8.
Определение верхнего и нижнего интегралов Дарбу. Пусть S(T) и s(T) — соответственно верхняя и нижняя суммы Дарбу, отвечающие неразмеченному разбиению Т и Q(T) = S(T) - s(T). Тогда число Г = inf, S(T) называется верхним пределом Дарбу, а число I* = sup s(T) — нижним пределом Дарбу от функции ТеА'
Дх) на отрезке [а, &].
Возьмем любое фиксированное неразмеченное разбиение То. Обозначим через а(Т0) множество всех тех размеченных разбиений V, которым соответствует одно и то же неразмеченное разбиение То, т. е. множество всех его разметок. Тогда, исходя из леммы 2 § 3, определение верхнего и нижнего интегралов Дарбу можно записать и так:
Г = inf sup g(V), I* = sup inf g(V).
ТеА'Уеа(Т)	TeA' Vea(T)
Приведем несколько свойств введенных выше понятий.
193
7 - 4953
Л E M M A 8. Пусть размеченное разбиение V есть разметка разбиения То, т. e.V е а(Т0). Тогда, если V е 68, то:
1)	а(Т0) а Ь8;
► Действительно, имеем ДГо = Дг. Следовательно, для любого размеченного разбиения V\ е а(Т0) получаем = Дг < 8, поэтому а(Т0) с &§. Свойство 2) проверяется аналогично. ◄
Отметим теперь несколько свойств базы В. Кроме указанных ранее двух свойств:
1)	любое окончание базы — непустое множество;
2)	для любых окончаний Ьх и Ь2 существует окончание &3 с условием Ь3 с U Ь2> выполняются следующие три свойства:
3)	для любых окончаний и Ь2 выполняется одно из условий: либо а Ь29 либо Ь2 <z bv
4)	напомним определение фундаментальной и монотонной последовательности по базе множеств (см. лекцию 30, ч. I). Последовательность разбиений {Vn} называется фундаментальной по базе В9 если для любого окончания be В существует только конечное множество членов последовательности, не принадлежащих Ь. Фундаментальная последовательность {Vn} называется монотонной по базе В9 если для любого окончания b из условия Vn е b следует, что Vn+1 е Ь. В качестве монотонной последовательности по базе В можно взять последовательность {Vn} размеченных разбиений отрезка [а, Ь] таких, что Тп = T(Vn) является разбиением его на п равных частей;
5)Д6-0.
Введем следующие обозначения для верхнего и нижнего пределов по базе В:
J* = lim o(V), J* = limo(V).
в	в
Справедливо следующее утверждение.
ТЕОРЕМА 7. Имеют место неравенства:
J* < I* < Г < J*.
Отсюда в силу критерия Коши получаем следующий критерий интегрируемости функции по Риману.
ТЕОРЕМА 8. Для того чтобы функция была интегрируема по Риману, необходимо и достаточно9 чтобы выполнялось равенство
194
► Из определения верхних интегралов Г и J* и свойств верхнего предела по базе множеств (теорема 3, лекция 30, ч. I) имеем
Г = inf S(T) = inf sup o(V) = inf inf sup a(V) <
T	T Уеа(Т)	5 > 0 AT < 6 Kg<x(T)
< inf inf sup o(V) * inf sup o(V) = Um o(V) = J*, 5 > 0 Ar < 5 Veb8	b8eB Veb6	В
т. e. I* < J*. Аналогично, получаем, что J* < /♦. ◄
Замечания. 1. Итак, критерий Римана для существования интеграла в форме Г = I* на языке понятия предела по базе, в сущности, эквивалентен критерию Коши существования предела по базе —> 0.
2.	Из эквивалентности понятий предела по Коши и по Гейне для базы Дт -» 0 вытекает, что функция интегрируема тогда и только тогда, когда для любой последовательности разбиений {Уп} с условием Ду -» 0 при п -> оо последовательность интегральных сумм {о(Уп)} является сходящейся последовательностью. С другой стороны, специальный критерий интегрируемости, который был доказан ранее» говорит о том, что здесь можно ограничиться лишь одной последовательностью равномерных разбиений отрезка интегрирования. В этом проявляется специфика рассматриваемой базы Дг -> 0.
Уточним теорему 7, а именно, покажем, что верхний предел по базе В интегральных сумм совпадает с верхним интегралом Дарбу. Для этого нам будут необходимы несколько лемм.
Л EMMA 9. Пусть модуль функции f(x) ограничен на отрезке Е = [а, &] числом М. Пусть Т — разбиение этого отрезка с диаметром 8 > 0. Пусть также разбиение Тг получается из Т добавлением к нему одной точки. Тогда для разности верхних сумм Дарбу S(T) и S(T^) имеем оценку
|8(7\) - S(T)| < 2М8.
►	Рассмотрим отрезок Ео = [а0, &0], являющийся отрезком разбиения Т и содержащий точку t е Т19 не входящую в разбиение Т. Тогда наборы точек т = {а0 < &0} и = {а0 < t < &0} можно рассматривать как неразмеченное разбиение отрезка Ео. Пусть при этом S(t) и SCq) — верхние суммы Дарбу на этом отрезке. Тогда из определения следует, что
S(T1)-S(T) = S(t1)-S(t).
Отсюда
|S(TX) - S(T)| = I S(Tj) - S(T)| < I Step I +1 S(T)| < Af5 + AfS = 2M8. ◄ ЛЕММА 10. Если в условиях леммы 9 разбиение Тг получается из разбиения Т добавлением не более, чем п точек, то имеет место оценка
|S(TX) - S(T)| < 2M5n.
195
7*
Справедливость леммы 3 устанавливается п кратным применением леммы 2.
ЛЕММА 11. Пусть разбиение Т отрезка Е = [а, д] удовлетворяет условию леммы 9, а разбиение Тг того же отрезка содержит не более п внутренних точек. Тогда справедливо неравенство
S(T) < S(Ti) + 2М5п.
►	Рассмотрим разбиение Т2 = Т U Tv Тогда, в силу основного свойства верхних сумм Дарбу, справедливы неравенства
S(T2)<S(T), stfycs^).
Далее, применяя лемму 10 к суммам S(T) и S(T2), получаем
S(T) - S(T2) < 2М8п.
Отсюда следует, что
S(T) < S(T2) + 2М5п < S(7\) + 2М8п. ◄
ТЕОРЕМА 9. Пусть модуль функции f(x) ограничен на отрезке Е = [а, &] числом М > 0. Пусть, далее, Г — верхний интеграл Дарбу от функции f(x), a g(V) — интегральная сумма, отвечающая размеченному разбиению V отрезка Е. Пусть также J* = Пт g(V). Тогда имеет место равенство J* = Z*.
Av —> 0
Замечание. В силу ограниченности функции f(x) числа Г и J* существуют.
►	Обозначим через T(V) неразмеченное разбиение отрезка Е, полученное из размеченного разбиения V отбрасыванием точек разметки, а через а(Т0) — множество всех размеченных разбиений V с условием T(V) = То.
Тогда непосредственно ий определений и свойств верхнего предела по базе и из леммы 8 вытекает, что
S(T0)= inf sup (g(V), Г = inf S(T) = inf inf S(T), Ar < 8 VeafT)	T	8>OAT<8
J* = lim g(V) = inf sup g(V) = Ay —> 0	5 > 0 Ar < 5
= inf sup sup g(V) = inf sup S(T).
8>0 Ar < 5 Vea(T)	8>OAr<8
Таким образом, всегда имеет место неравенство
Г = inf inf S(T) < inf sup S(T) = J*.
8 > 0 Ar < 8	8 > 0 A,, < 8
Нам надо доказать, что I* = J*. Заметим, что для любого числа е > 0 число I* + е уже не является нижней гранью множества значений S(T), поэтому существует разбиение То такое, что
Г < S(T0) < /* + е.
196
Далее заметим, что величина sup S(T) как функция от 8 являет-
Дг < 5
ся неубывающей. Поэтому существует 80 > 0 такое, что для всякого 8 с условием 0 < 8 < 80 имеем
J* < sup S(T) < J* + е.
Ду < 5
Отсюда, в частности, следует, что существует разбиение Тг с условием ДГ1 < 8 такое, что
J* - е < S(7\) < J* + е.
Обозначим через п количество внутренних точек разбиения То. Тогда по лемме 11 справедлива оценка
S(7\) < S(T0) + 2М8п.
Следовательно,
J* - е < S(7\) < S(T0) + 2М8п < Г + е + 2М5п.
Поэтому справедливо неравенство
О < J* - Г < 2е + 2М8п.
Но так как числа е>0и0<8<80 можно выбрать сколь угодно малыми, то J* - Г = О, J* = Г. ◄
СЛЕДСТВИЕ ТЕОРЕМЫ 9. Справедливо равенство J* = I*.
► Рассмотрим функцию g(x) = ~/(х). Тогда по теореме 3 имеем, что J\g) = /*(£), но J*(g) = и I*(g) = Отсюда получим J*(f) = Л(Г). «
§8. КЛАССЫ ФУНКЦИЙ, ИНТЕГРИРУЕМЫХ ПО РИМАНУ
Докажем, что любая непрерывная на отрезке функция и любая монотонная на отрезке функция являются интегрируемыми на этом отрезке.
ТЕОРЕМА 10. Всякая функция, непрерывная на отрезке, интегрируема на нем.
► В силу теоремы Кантора функция f(x), непрерывная на отрезке [а, Ь], является равномерно непрерывной на нем. Поэтому для любого числа е > 0 найдется 8 = 8(e) > 0 такое, что для любых точек х, у е [а, &] с условием |х - у\ <8 выполняется неравенство
197
Возьмем любое разбиение Т отрезка [а, Ь] с диаметром Дт < 8. Тогда имеем
(йк - sup (ftx) - f(y)) <	6	.
х,уеДЛ	2(о — а)
Отсюда получаем
П(Т) = . S, окЛх, < —5— Axt = I < s. fc-i *	*	2(6-a)*"1	*	2
Следовательно, для всякого e > 0 мы нашли число 8 = 8(e) > О такое, что для любого разбиения Т с диаметром Дт < 8 выполняется неравенство Q(T) < 8, т. е. Jimo Q(T) = 0. Отсюда в силу критерия интегрируемости следует, что функция f(x) интегрируема на отрезке [а, &]. ◄
ТЕОРЕМА 11. Всякая функция Дх), ограниченная и монотонная на отрезке [а, &], интегрируема на нем.
► Без ограничения общности можно рассмотреть только случай неубывающей на отрезке [а, Ь] функции Дх). Зададимся произвольным числом е > 0 и положим
8=-------------------,
f(b - О) - f(a + 0) + 1
<ak = sup (Дх) - f(y)) = f{xk - 0) - ftxft_x + 0). x, yeAfe
Тогда для любого разбиения Т : а = х0 < ... < хп = b с диаметром Дг < 8 имеем п	п
Q(T) = kZ1 wk\xk < 8 ю* < (Д& - 0) - Да + 0))8 < 8, т. e. получаем, что дИшо Q(T) = 0, и, значит, в силу критерия интегрируемости функция Дх) интегрируема на отрезке [а, &]. ◄ ТЕОРЕМА 12. Всякая ограниченная на отрезке [а, Ь] функция, непрерывная всюду, за исключением конечного числа разрывов, интегрируема на этом отрезке.
► В силу критерия интегрируемости функции Дх), в форме inf Q(T) = 0 достаточно для любого 8 > 0 построить разбиение Т с условием Q(T) < 8.
Пусть количество точек разрыва Дх) равно т и М = sup | Дх)|. хе[а, Ь] Каждую точку разрыва ds, s = 1, ... , т, окружим окрестностью вида А. = (d - ? -, d, + А ). Тогда в каждом из отрезков
s Vs 8Мт 8 8Мт )
198
[£ € “1
^-i + 8Mm ’ dr ~ 8MmJ’ r=1> — >m + 1’do = a> dm+i ~ b
функция f(x) непрерывна, значит, по теореме Кантора она является равномерно непрерывной на каждом из этих отрезков. Поэтому можно выбрать число 5 = 8(e) > 0 такое, что для любых точек х, у, принадлежащих этим отрезкам, и |х - у\ <8, выпол-
няется неравенство |/(х) - f(y)\ <
е
2(Ь-а)’
Построим теперь про-
извольное разбиение То указанных отрезков так, чтобы выполнялось условие ДГо < 8. Объединяя это разбиение То с построенными ранее окрестностями точек разрыва, получаем разбиение Т отрезка [а, &]. Далее имеем
Q(T) =	+ Q2,
= £ co^<2Mm-= I, 1 k = 1 »	«	4Mm 2
m	p	e
- A.&. M*4x* < № - °) •	 2 •
Следовательно, Я(Т) < e. ◄
Лекция 5
§ 9. СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА
Рассмотрим свойства интеграла, связанные с интегрируемостью на заданном фиксированном отрезке. Множество всех интегрируемых функций на отрезке [а, Ь] будем обозначать символом Я[а, Ь] или просто IR.
УТВЕРЖДЕНИЕ 1. Пусть функция f(x) отлична от нуля только в I точках. Тогда f е IR и
ь
J f(x)dx = 0.
а
► Пусть М = ^ах J/(x)|. Возьмем произвольное число е > 0 и положим 8 = г/(2М1). Тогда для любого размеченного разбиения V с условием Дг < 8 имеем
<е.
Мы воспользовались тем, что сумма <j(V) содержит не более I слагаемых, отличных от нуля, и тем, что Ахк < 8. В силу произвольности выбора числа е > 0, получаем, что
lim <j(V) = 0.	◄
Ду —> о
УТВЕРЖДЕНИЕ 2. Пусть функции f(x) и £(х) интегрируемы на отрезке [а, &]. Тогда*.
1) функция f(x) 4- g(x) g Л[а, Ь] и
ь	ь	ь
J (/(*) + g(x))dx = f f(x)dx + J g(x)dx*.
a	a	a
2) для любого вещественного числа k функция kf(x) g Я[а, Ь] и ь	ь
J kf(x)dx = k J f(x)dx.
► 1) Поскольку f(x) и g(x) интегрируемы на отрезке [а, &] и для любого размеченного разбиения V: а = х0 < < хг < ... < < хп = Ь справедливы равенства
Переходя к пределу при Ду —> 0, видим, что предел левой части равенства существует, следовательно, существует и предел правой части, т. е. функция Дх) 4- g(x) интегрируема на отрезке [а, &], и, кроме того, имеет место равенство
ъ	ь	ь
J (ft*) + g(x))dx = J f(x)dx + f g(x)dx.
a	a	a
200
В случае 2) имеем: о^ДК) = fccfy(V). Из этого следует интегрируемость функции Дх) и выполнение равенства
ь	ъ
J kf(x)dx = k J f(x)dx. ◄ a	a
УТВЕРЖДЕНИЕ 3. 1) Пусть функция Дх) интегрируема и неотрицательна на отрезке [а, &]. Тогда
ъ
f f(x)dx >0.
а
2) Пусть функция Дх) интегрируема и неотрицательна на отрезке [а, &], и пусть в точке х = х0 непрерывности Дх) выполнено неравенство f(xQ) > 0. Тогда
ь
J f(x)dx > 0.
а
► 1) Составим для любого размеченного разбиения V интегральную сумму o(V). Она неотрицательна, и, следовательно, интеграл как предел интегральных сумм будет величиной неотрицательной.
2) Поскольку х0 — точка непрерывности и Дх0) > 0, существует число 8 > 0 такое, что для всех х с условием |х - х0| < 8 имеет Дх) > Дх0)/2. Возьмем любое размеченное разбиение V с диаметром Af < 80/2. Тогда на интервале (х0 - 8, х0 + 8) будут содержаться полностью некоторые отрезки разбиения V с суммой длин не меньшей, чем 80. Отсюда получаем
80Дх0)
а(У)>-0М_^>0 Л
УТВЕРЖДЕНИЕ 4. Пусть функция Дх) непрерывна и неотрица-ь
тельна на отрезке [а, Ь] и J f(x)dx = 0. Тогда для всех точек а
х е [а, &] имеем Дх) = 0.
► Воспользуемся методом от противного. Допустим, что существует точка х0 g [а, Ь] такая, что f(xQ) > 0. Тогда из утвержде-
ъ
ния 3 имеем, что J f(x)dx > 0. Это противоречит условию, что а
Ь
$f(x)dx = 0.	◄
а
УТВЕРЖДЕНИЕ 5. Пусть а<Ьи на отрезке [а, Ь] справедливо неравенство f(x) > g(x). Тогда имеем
ь	ь
f f(x)dx > J g<x)dx. а	a
201
►	Рассмотрим функцию Л(х) = f(x) - g(x) > 0. Из утверждения 3 ь
следует, что J h(x)dx >0, а из утверждения 2 имеем а
Ъ	Ь	Ь	Ь	Ь
J f(x)dx = J (й(х) + g(x))dx = J h(x)dx + J g(x)dx > f g(x)dx. ◄ a	a	a	a	a
УТВЕРЖДЕНИЕ 6. Пусть а<Ьи на отрезке [а, Ь] справедливо неравенство т < f(x) < М. Тогда имеем
ь т(Ъ - а) < J f(x)dx < М(Ь - а), а
Утверждение 6 является простым следствием утверждения 5.
УТВЕРЖДЕНИЕ 7. Пусть функция f(x) интегрируема на отрезке [а, &]. Тогда функция [/(х)| интегрируема на нем и имеет место неравенство
ь	ь
J f(x)dx < J |ftx)|dx. а	а
►	Поскольку Iftx) - f(y)\ > |ftx)| - |fty)|,
sup Iftx) - ftj/)| > sup (|ftx)| - |ftj/)|), X, уеДЛ	x, уеДА
и, следовательно, соЛ(/) > cofe(|/|). Отсюда для любого разбиения Т имеем, что
QZ(T)>Q1Z|(T)
По условию функция Дх) интегрируема на отрезке [а, Ь], следовательно, существует разбиение Т такое, что ОДТ) < е. Отсюда имеем £2|f|(T) < е. А это согласно критерию интегрируемости означает, что функция |Дх)| интегрируема на отрезке [а, &].
Так как справедливо неравенство
-Ш < ft£)<
то для любого размеченного разбиения V получаем
-о|И(У) <	< <Т|И(К>-
Переходя в последнем неравенстве к пределу,
-J lftx)ld* с J ftx)dx < f |ftx)|dx, а	а	а
т. е.
ь	ь
J f(x)dx < f|ftx)|dx. а	а
◄
202
УТВЕРЖДЕНИЕ 8. Пусть f(x) е Я[а, Ь]. Тогда f\x) е В[а, &].
► Обозначим через М супремум функции | f(x)| на отрезке [а, Ь]. Тогда справедливо неравенство
\f2(x)-f^(y)\<2M\f(x)-f(y)\,
и, следовательно, со^С/2) < 2Mok(f). Отсюда получаем
af^T) < 2MQf(T), значит, согласно критерию интегрируемости функция ^(х) интегрируема на отрезке [а, Ь]. ◄
УТВЕРЖДЕНИЕ 9. Пусть функции f(x) и g(x) интегрируемы на отрезке [а, Ь]. Тогда их произведение f(x)g(x) также интегрируемо на отрезке [а, 6].
► Имеем
fe = ((f + £)2-(f-£)2)/4.
Тогда из утверждений 8 и 2 следует, что произведение функций f(x) и g(x) интегрируемо на отрезке [а, &]. ◄
ТЕОРЕМА 13 (об интегрируемости сложной функции). Пусть функция f(x) интегрируема на отрезке [а, &], т = inf f(x)9
х е [а, Ь]
М = sup Дх), и пусть <р(х) непрерывна на отрезке [т, М]. х е [а, Ь]
Тогда сложная функция h(x) = <р(/(х)) интегрируема на [а, &].
► Возьмем произвольное е > 0. В силу равномерной непрерывности функции <р(х) на отрезке [т, М] имеем, что существует число S = 8(e) > 0 такое, что для любых хи х2 е [m, Af] с условием |хх - х2| < 8 выполняется неравенство |<р(хх) - ср(х2)| < е. Далее, в силу критерия интегрируемости функции Дх) на отрезке [а, Ь] найдется разбиение Т этого отрезка такое, что
п
ЩТ) = *£1Й)л(/)Дх*<е8, где <i»k(f) — колебание функции Дх) на отрезке ДА разбиения Т.
Разобьем все отрезки ДЛ, k = 1,..., п, разбиения Т на два класса. К первому классу отнесем те ДА, для которых справедливо неравенство соА(/) < 8. На этих отрезках также имеет место неравенство <s>k(h) < е. Ко второму классу отнесем все остальные отрезки разбиения Т, т. е. те, для которых соА(/) > 8. В связи с этим сумму ЙЛ(7Э представим в виде ЙА(Т) = Qx + П2, где
Qx = Е' шА(Л)ДхА, йх = Е" <оА(Л)ДхА, причем штрих в сумме означает, что суммирование ведется по k9 отвечающим отрезкам разбиения Т, относящимся к пер
203
вому классу, а два штриха в сумме £12 показывают, что суммирование ведется по числам k, отвечающим отрезкам ДЛ из второго класса.
Из определения суммы Qx имеем
Qi = 2' <оА(Л)Дхь < е Е' Дх* < е(& - а). k	k
Оценим сверху сумму длин отрезков Axfe, принадлежащих второму классу. Имеем
5Z" ДхЛ < S" o>ft(/)Axft < X <М/)Дх* = ЩГ) < 5е. К	к	к	'
Следовательно, Е" Axfe < е.
Пусть С — max |ф(х)|. Тогда для суммы получим оценку xe[m, М]
Q2 = Е" cofe(ft)Axfe < 2С Е" Дх* < 2Се. k	k
Таким образом, £lh(T) < е(Ь - а + 2С), т. е. в силу произвольности выбора числа е > О получим соотношение inf Q>h(T) = О, а это, в силу критерия интегрируемости, означает, что функция Л(х) = ср(Дх)) интегрируема на отрезке [а, &]. ◄
§ 10. АДДИТИВНОСТЬ ИНТЕГРАЛА РИМАНА
Свойство аддитивности интеграла выражается следующим утверждением.
ТЕОРЕМА 14. Пусть функция Дх) интегрируема на отрезке [а, Ь]. Тогда для любой точки с е [а, 6] она интегрируема на отрезках [а, с] и [с, &]. И наоборот, если f(x) интегрируема на [а, с] и [с, &], то она интегрируема на [а, &], причем
ebb
J f(x)dx + J f(x)dx = J f(x)dx.	(1)
аса
► Пусть функция Дх) интегрируема на отрезке [а, Ь]. Тогда в силу критерия интегрируемости имеем, что inf Q(T) = 0, т. е. для любого е > 0 существует разбиение Т такое, что О(Т) < е. Рассмотрим разбиение То = Т U {с} отрезка [а, Ь]. Получим £2(Т0) < £2(Т) < е. Разбиение То можно представить как объединение разбиений Тг отрезка [а, с] и Т2 отрезка [с, Ь]. Поэтому
n(T1) + Q(T2) = Q(T0)<e.
Следовательно,
Q(T1)<e, Я(Т2)<е.
204
В силу инфимум-критерия интегрируемости функции Дх) отсюда имеем, что Дх) интегрируема на отрезках [a, с] и [с, Ь].
Пусть теперь функция Дх) интегрируема на отрезках [а, с] и [с, Ь]. Тогда для любого е > 0 существует разбиение Тг отрезка [а, с] и разбиение Т2 отрезка [с, &] такие, что < е/2, Q(T2) < е/2* Следовательно, для разбиения Т = Тг U Т2 отрезка [а, &] имеем
Q(T) = Q(7\) + Q(T2) < е/2 + е/2 = е.
Отсюда, в силу инфимум-критерия интегрируемости функции Дх), следует, что Дх) является интегрируемой на [а, Ь]. Возьмем произвольные размеченные разбиения отрезка V\ отрезка [а, с} иУ2 отрезка [с, &], V « V\ U V2 отрезка [а, Ь]. Имеем равенство
a(V) = a(F1) + G(V2).
Переходя в последнем равенстве к пределу при Дг —> 0, получаем равенство (1). ◄
По определению, положим, а	Ь
J f(x)dx = | f(x)dx = 0. а	ь
Пусть функция Дх) интегрируема на отрезке [с, а]. Тогда при с < а, по определению, полагают
J f(x)dx = -f f(x)dx. а	с
В силу этого определения утверждение теоремы можно переформулировать так.
СЛЕДСТВИЕ. Пусть х0 < хр а, b, с е [х0, xj и функция /($) интегрируема на отрезке [х0, xj. Тогда
J f(x)dx + J f(x)dx + J f(x)dx = 0. а	с	ь
Здесь утверждается также, что интегралы на указанных отрезках с концами а, Ь, с существует.
Для доказательства справедливости равенства в силу симметричности равенства относительно точек а, &, с достаточно рассмотреть один случай а < с < Ь. Но это точно совпадает с утверждением теоремы.
ГЛАВА 8
Основные теоремы теории интеграла Римана
Лекция 6
$ 1. ИНТЕГРАЛ РИМАНА КАК ФУНКЦИЯ ОТ ЕГО ВЕРХНЕГО (НИЖНЕГО) ПРЕДЕЛА ИНТЕГРИРОВАНИЯ. ПРОИЗВОДНАЯ ИНТЕГРАЛА
В 7 главе доказано, что если функция /(х) интегрируема на отрезке [а, Ь], то для любого х е [а, Ь] она интегрируема на отрезке [а, х], т. е. существует функция
F(x)= J f(u)du.
а
Докажем несколько свойств этой функции.
ТЕОРЕМА 1. Пусть функция f(x) интегрируема на отрезке
X
[а, &]. Тогда F(x) = J f(u)du является непрерывной функцией на а
этом отрезке.
► Из интегрируемости функции f(x) следует, что она ограничена на отрезке [а, &], т. е. найдется постоянная М > 0 такая, что для всех х е [а, &] выполняется неравенство |f(x)| < М. Возьмем любые точки х, х + Дх g [а, Ь]. Имеем
| AF(x)| =|F(x + Дх) - F(x)| =
f(u)du <
f |/(u)|du <М|Дх|.
Зададимся произвольным числом е > 0. Тогда для любой величины Дх с условием |Дх| < t/М имеем |ДГ(х)| < е. Следовательно, функция ДГ(х) является бесконечно малой при Дх —> 0, т. е. функция F(x) непрерывна на отрезке [а, Ь]. ◄
ТЕОРЕМА 2. Пусть функция f(x) интегрируема на отрезке [а, &] и непрерывна во внутренней точке х0 этого отрез-X
ка. Тогда F(x) = jf(u)du дифференцируема в точке х = х0 и а
Р'(х0) = ftx0).
206
► В силу непрерывности функции Дх) в точке (х0) для всякого числа е > 0 существует 5 = 8(e) > 0 такое, что для всех и с условием \и - х0| <8 справедливы неравенства
v Дх0) - е < f(u) < Дх0) + е.
Возьмем любое |Дх| < 8 так, чтобы отрезок с концами х0 и х0 + Дх содержался бы в отрезке [а, &]. Интегрируя неравенства, получаем
1 *%+Ах л	Г(х0 + Дх) - F(x0)	1 *о + Д*
£ /	(f(x0)-e)du<	0	'---— f (f(x0) + e)du,
XQ	*0
т. е. при любом Дх с условием |Дх| <8 выполняются неравенства
/(х0)-е<	</(х0) + е.
Отсюда имеем
Г(х0)= Пт =/(х0).	«
$ 2. ТЕОРЕМА НЬЮТОНА—ЛЕЙБНИЦА.
ФОРМУЛЫ СУММИРОВАНИЯ ЭЙЛЕРА И АБЕЛЯ
Формулу Ньютона—Лейбница называют основной теоремой интегрального исчисления, поскольку она связывает понятия определенного и неопределенного интегралов.
ТЕОРЕМА 3. (Формула Ньютона—Лейбница.) Пусть функция Дх) ограничена на отрезке [а, &] и имеет не более конечного числа
X
точек разрыва. Тогда функция F(x) = J f(u)du является перво-а
образной для функции Дх) на отрезке [а, &] и для любой первообразной Ф(х) справедлива формула
ь
J /(u)du = Ф(&) - Ф(а). а
► Из теорем 1 и 2 предыдущего параграфа следует, что функция X
F(x) = J f(u)du является непрерывной на отрезке [а, 6] и во всех а
точках непрерывности функции f(x) существует производная от F(x) и она равна f(x). Следовательно, функция F(x) является первообразной для функции f(x), кроме того, имеет место формула
Ь	а
J f{u)du = F(b) = F(b) - F(a), F(a) = J f(u)du = 0. a	a
207
Пусть Ф(х) — любая другая первообразная функция для Дх), Тогда согласно свойству первообразной функции существует такое число с, что Ф(х) = F(x) + с. Следовательно, имеет место равенство
ь
Ф(6) - Ф(а) = F(b) - F(d) = J f{u)du. ◄
a
В качестве приложения формулы Ньютона—Лейбница выведем формулы суммирования Эйлера и Абеля.
ТЕОРЕМА4 (формула суммирования Эйлера). Пусть функция f(x) имеет непрерывную производную на отрезке [а, &], р(х) = = 1/2 - {х}. Тогда при любом х, принадлежащем отрезку [а, &], справедлива формула
Е f(n) - р(х)/(х) = f f(u)du - f p(u)f(u)du - р(а)Да).
a < n < x	а
► Обозначим левую часть последнего равенства через G(x). Легко видеть, что функция G(x) непрерывна на отрезке [а, &]. Действительно, если число х — нецелое, то она будет даже дифференцируема, а если число х = п — целое, то сумма в выражении для G(x) возрастает на величину Дп), а функция р(х)Дх) убывает ровно на Ди) при переходе через точку х = п, так что скачок суммы гасится скачком функции р(х)Дх). Следовательно, можно применить формулу Ньютона—Лейбница. Но тогда при нецелом х имеем
G(x) = G(a) + j G'(u)du = -p(a)f(a) + j (-p(u)f(u))'d« = a	a
= -p(a)f(a) + J f(u)du - J p(u)f'(u)du. ◄ a	a
Важность этой формулы состоит в том, что она позволяет приближенно заменить сумму на интеграл. Заметим, что часто удобно в качестве пределов суммирования брать полуцелые числа.
ПРИМЕР (упрощенная формула Стирлинга). При п > 2 справедливы неравенства
1 < п!е” < к
5 С	с 5-
Действительно, из формулы суммирования Эйлера получаем
In n! = In 1 + In 2 + ... + In п — X In т =
0,5 < т < п + 0,5 п + 0,5	п + 0,5 , ,ч
= J In t dt - J dt =
0,5	0,5 Г
= (n + 0,5) In (n + 0,5) - n - 0,5 - 0,51n 0,5 + 0,5 - r(n).
208
t
Оценим величину r(n). Полагая о(£) = J p(u) du, |о (t)| < о
|, имеем
n 4-0,5	4	n 4- 0,5
4»>- J 0,5	1	(
V’5 do(Q = 0(0 n+0,5 +n+f0’5 0(0 dt 0,5	*	*	0,5	°’5 t2
Следовательно, справедлива оценка |r(n)| < 2*2* 1/8 = 1/2. Таким образом, находим
1п п\ = (п + 0,5) 1п п - п + (и + 0,5) In f 1 + --1 + 0,5 In 2 - r(n),
|ln ra! - (n + 0,5) In n + n| < (n + 0,5) In (1 + JL) + 0,5 In 2 + |r(n)| <
< 0,5 In 2 + | < In 5. О
Потенцируя это неравенство, получаем сформулированную оценку. Заметим, что в случае, когда пределы суммирования в теореме 4 — целые числа, то ее можно переписать в несколько иной форме.
ТЕОРЕМА 5. Пусть а и Ъ — целые числа и функция f(x) имеет непрерывную производную на отрезке [а, 6]< Тогда справедлива следующая формула*.
ь	ъ	ь
S f(n) - f(a) + f f(x) dx + J {x} f(x) dx. a	a
► Так как а и Ь — целые числа, то р(а) = р(Ь) = 1/2. Кроме того, имеем
J р(х) f '(х) dx = i f(b) - i f(a) - f {x} f (x) dx. a	"	a
Подставляя полученные выражения в формулу теоремы 4, приходим к утверждению теоремы 5. ◄
ПРИМЕР. При целом N > 1 имеет место соотношение
Jil=lnn + T+A.+ lA^+o(±).
В силу теоремы 5 получим
209
oo J- ,
Обозначим через у следующее выражение: у = 1 - J dx.
1 х Имеем
1 аг .	. 1 F dx Г Р(*) л 1 хг .	, 1 Г <*(*)
sN = In + у + J - J ‘тг dx = In N + У + 2N - [ “У ’
1 х
где р(х) = - - {х}, g (х) = J р (i) dt. Интегрируя последний интег-о
рал по частям, получаем
1 АТ _1_	.	1 О(ЛГ) ,of° °(Х) Л
sN = \nN + y+^	+ 2J dx.
1	х
И наконец, положим а0 (х) = о (х) - т? ,	(х) = J о0 (t) dt. Оче-
1Z	о
N
видно, имеем (N) = J о0 (О dt = 0. Интегрируем в последней о
формуле для sN интеграл по частям, находим
sN lnN + y+ 2N + 6 J x3 + 2 J t3 •
Отсюда получаем требуемую формулу для sN.
Докажем теперь формулу суммирования Абеля.
ТЕОРЕМА 6. Пусть функция Дх) имеет непрерывную производную на отрезке [а, &] и пусть А(х) = Е ат. Тогда при любом х е [а, &] имеем
„ х а„ f(n) - А(х) /(х) = -f A(t) f (0 dt.
► Обозначим через G(x) левую часть последнего равенства. Аналогично доказательству теоремы 2 функция G(x) имеет непрерывную производную в нецелых точках, а при целых значениях она является непрерывной функцией. Заметим также, что при нецелых значениях х имеет место равенство А'(х) = 0. Следовательно, продифференцировав G(x) при нецелых х, получим G'(x) = -А(х) f\x). Но и производная правой части рассматриваемого равенства равна той же функции. Тогда из формулы Ньютона—Лейбница имеем искомое равенство. ◄
Лекция 7
§ 3. ФОРМУЛЫ ЗАМЕНЫ ПЕРЕМЕННОЙ И ИНТЕГРИРОВАНИЯ ПО ЧАСТЯМ В ОПРЕДЕЛЕННОМ ИНТЕГРАЛЕ
Важную роль при вычислении интегралов играют формулы замены переменной и интегрирования по частям. Они являются следствием формулы Ньютона—Лейбница. Имеет место следующее утверждение.
ТЕОРЕМА 7 (теорема о замене переменной). Пусть функция /(х) непрерывна на некотором отрезке [х0, xj. Пусть также точки а9 b е [х0, хх], а < Ь9 ф (а) = а, ф (0) = b и множество значений функции ф (t) при а < t < 0 является подмножеством отрезка [х0, хх]. Пустъ9 кроме того, производная ф' (t) непрерывна на отрезке [а, 0]. Тогда справедлива формула
ь	Р
f f(x) dx = f Дф(О) ф' (О dt. а	а
► Так как функция /(х) непрерывна на отрезке [а, &], то по теореме Ньютона—Лейбница существует ее первообразная F(x) ь
и F'(x) - f(x), Jftx) dx = F(b) - F(a). a
При всех t e [a, P] по условию теоремы определена функция G(t) = Г(фСО)> которая на этом отрезке имеет производную, причем
<?'(*) = F't (ф(0) = F; (ф(0) • Ф'(О = /(Ф(О) <₽'(*)•
Это значит, что функция G(t) является первообразной функции Дф(О) • ф'(0* Следовательно, имеет место равенство
Р	ъ
j Г(Ф(О)Ф'(О dt = F(<p(0)) - F(<p(a)) = F(b) - F(a) = J f(x)dx. ◄ a	a
TEOPEMA8 (формула интегрирования по частям). Пусть на отрезке [а, Ь] заданы гладкие функции f(x) и £(х). Тогда имеем
f /(X)g' (х) dx = f(x)g(x)\ba - f f'(x)g(x)dx, a	a
где символ й(х)|^ означает разность h(b) - h(a).
► Пусть й(х) = f(x) g(x). Тогда
Л'(х) = f'(x) g(x) + f(x) g'(x).
Следовательно, ь	b	b
J h'(x) dx= f f'(x) g(x) dx+ J f(x) g'(x) dx.
211
По теореме Ньютона—Лейбница имеем ъ J h'(x)dx = й(&) - Л(а) = f(x)g(x)\ba. а
Подставляя последнюю формулу в предыдущую, получим искомую формулу. ◄
§ 4. ПЕРВАЯ И ВТОРАЯ ТЕОРЕМЫ О СРЕДНЕМ ЗНАЧЕНИИ ИНТЕГРАЛА
ТЕОРЕМА 9 (первая теорема о среднем значении). Пусть функции f(x) и g(x) интегрируемы на отрезке [а, &]. Пусть также на этом отрезке функция g(x) неотрицательна, а для функции f(x) при некоторых вещественных числах т и М имеют место неравенства т < /(х) < М. Тогда найдется вещественное число ц с условием т < ц < М такое, что
ь	ь
J ftx) g(x) dx — ^if g(x)dx. а	а
► Поскольку неравенства
тп£(х) < f(x)g(x) < Mg(x)
Справедливы, интегрируя их, получим
b	ь	ь
m\g(x)dx < f f(x)g(x)dx < М\g(x)dx.	(1)
а	а	а
Ъ	Ь
Заметим, что f g(x)dx > 0, так как g(x) > 0. Тогда если \g(x)dx = 0, а	а
то из неравенства (1) имеем ь	ь
f f(x)g(x)dx = 0 = f g(x)dx а	а
и число ц можно положить равным т.
ь
Если f g(x)dx > 0, то получим а
Ь
J ftx)g(x)dx
т < ---------- < М.
ь jg(x)dx а
Положим отношение интегралов равным ц. Тогда имеем
ь	ь
f f(x)g(x)dx = ц f g(x)dx, а	а
где т < ц < М. ◄
212
СЛЕДСТВИЕ 1. Пусть функции f(x) и g(x) интегрируемы на отрезке [а, &]. Пусть также на этом отрезке функция g(x) неположительна, а для функции f(x) при некоторых вещественных т и М имеют место неравенства т < f(x) < М. Тогда найдется вещественное число ц с условием т < р < М такое, что
ь	ь
/ f(x)g(x)dx = pf g(x)dx. a	a
► Положим
£1(х) = -g(x).	' , . ; '
Тогда функции f(x) и gt(x) удовлетворяют условиям теоремы 1 й мы имеем равенство
ь	ь
/ f(x>^i(x)dx = pf gx(x)dx, а	а
где т < ц < М. Подставляя в это равенство £х(х) = -g(x), получим утверждение следствия. ◄
СЛЕДСТВИЕ 2. Пусть функция f(x) непрерывна на отрезке [а, Ь] и функция g(x) интегрируема на этом отрезке, причем для всех точек х е [а, &] функция g(x) неотрицательна. Тогда существует точка с е [а, &] такая, что
ь	ь
J f(x)g(x)dx = f(c)J g(x)dx. а	а
►	По теореме Коши о промежуточном значении непрерывной функции на отрезке существует точка с, а < с < Ь9 такая, что ц = = /(с), т < ц < М. Отсюда, в силу теоремы 1» получаем утверждение следствия. ◄
СЛЕДСТВИЕ 3. Пусть функция f(x) непрерывна на отрезке [а, Ь]. Тогда на отрезке [а, &] найдется точка с такая, что
f f(x)dx = f(c)(b - а), а
►	Данное утверждение получается из следствия 2 при g(x) = 1. ◄
Замечание. Среднее арифметическое значений функций на отрезке [а, &] стремится к величине ъ
-i- J f(x)dx, ь -а а
поэтому говорят, что интеграл — это среднее значение функции /(х) на отрезке [а, &]. ◄
213
ТЕОРЕМА 10 (вторая теорема о среднем значении). Пусть функции f(x) и g(x) интегрируемы на отрезке [а, Ь]. Пусть, далее, функция g(x) на этом отрезке неотрицательна и не убывает. Тогда на отрезке [а, &] найдется точка с такая, что
ь	ь
J f(x)g(x)dx = g(b) J f(x)dx. a	c
► Рассмотрим последовательность разбиений Tn : а = х0 < ... < < хп = Ь с условием, что диаметр Тп, равный 8П, стремится к нулю при п —> (Например, всегда можно считать, что разбиение Тп отрезка [а, &] есть разбиение на п равных частей и тогда 8П = = 1/п.) Положим
п	Xk
Qn = Z g(xk) J f(x)dx, M = sup |/(x)|, K ~ 1	x	xe[a, b]
= sup |g(x') - g(x")| = g(xk - 0) - g(.xk_i + 0). x', xg ДЛ
Имеем
(g(xk) - g(x))f(x)dx\ <
n	Xk	n
< x wk(g) J |f(x)|dx < M8n x wk(g) < M8ng(b). . xk-i
b
Следовательно, an = J f(x)g(x)dx.
Поскольку интеграл как функция нижнего предела есть непре-ь
рывная функция, функция F(x) = J f(t)dt является непрерывной х
и достигает своего минимального и максимального значений на отрезке [а, &], соответственно, в точках аир.
Теперь преобразуем сумму оЛ. Имеем
СТП =	f f(x)dx - f ftx)dx) =
Xk-1	xk
= Xrt**^**-!) - Jirt**)^**) =
= J ^xk+i)F(xk) - g(xk)F(xk) =
= gtxJFta) + x (g(xfe+1) - g(x))F(xk).
Так как для любого х е [а, &] справедливы неравенства
F(a) < F(&) < F(p), g(b) > 0, и функция g(x) не убывает, то из последнего неравенства для оЛ получим
F(a)g(b)<o„<F(P)g(&).
214
Переходя к пределу при п —> +оо, имеем
F(a) g(b) < J f(x)g(x)dx < F(P) g(b). a
Поскольку функция f(x) непрерывна на отрезке [a, &], по теореме Коши о промежуточном значении найдется точка с е [а, Ь] такая, что 1 ь
Лс) - J f(x)g{x)dx или	а
b	ь
J f(x)g(x)dx = g(b) J f(x)dx. ◄ a	c
ТЕОРЕМА 11. Пусть функции f(x) и g(x) интегрируемы' на отрезке [a, Ь]. Пусть, далее, функция g(x) на этом отрезке неотрицательна и не возрастает. Тогда на отрезке [а, Ь] найдется точка с такая, что ь
J f(x)g(x)dx - g(a) J f(x)dx. a	a
►	Положим xt = -x, f^xj = f(-x), g1(x1) = g(-x). Тогда в силу того что g(x) не возрастает на отрезке [а, &], то функция ^(xj не убывает на отрезке [-&, -а]. Поэтому к функциям fx(x^) и ^(xj можно применить теорему 10. Отсюда следует, что на отрезке [-&, -а] найдется точка -с такая, что
J /i(xi)^i(«i)dxi = ^i(-a) J AOQdXi. -b	~c
В интегралах последнего равенства сделаем замену переменной вида х = -xv Получим
Ь	с
J f(x)g(x)dx = g(a) J f(x)dx. ◄ a	a
СЛЕДСТВИЕ. Пусть функции f(x) и g(x) интегрируемы на отрезке [a, Ь]. Пусть, далее, функция g(x) монотонна на этом отрезке. Тогда на отрезке [а, &] найдется точка с такая, что
J f(x)g(x)dx = g(a) J f(x)dx + g(b) J f(x)dx. a	a	c
►	Пусть сначала функция g(x) не убывает на отрезке [а, Ь]. Тогда функция gi(x) = g(x) - g(a) будет неотрицательной и неубывающей на этом отрезке. Следовательно, по теореме 10 имеем
ь	ь
j /(x)gi(x)dx - g^b) J f(x)dx.
Подставляя в последнее равенство выражение для g^x), получаем утверждение следствия.
215
Пусть теперь функция g(x) не возрастает на отрезке [а, Ь]. Тогда положим g±(x) = g(x) - g(b). Функция £х(х) — неотрицательная и невозрастающая. Поэтому к функциям f(x) и £х(х) применима теорема 11. Отсюда и следует искомая формула. ◄
ПРИМЕР. Пусть Ь > а > 0. Тогда справедливо неравенство
?sinx .	2
I---- dx < - .
i х а
Действительно, функция 1/х — положительная и невозрастающая на отрезке [а, Ь]. Тогда по теореме 3 найдется такая точка с g [а, &], что
rsinx , If.	> Icosc-cosal	2
I---- dx = - I sin xdx = 1--------1 < - .
i x	a>a	a	a
Приведем теперь вариант доказательства второй теоремы о среднем для гладких функций.
ТЕОРЕМА 12. Пусть функция Дх) непрерывна и функция g(x) дифференцируема на отрезке [а, &], причем производная g'(x) на этом отрезке неотрицательна и непрерывна. Тогда на отрезке [а, &] найдется точка с такая, что
J f(xjg(x)dx = g(a) J f(x)dx + g(b) J f(x)dx. a	a	• c
► Пусть
F(t) = jf(x)dx. a
Тогда функция F(t) как функция верхнего предела является дифференцируемой, поскольку подынтегральная функция /(х) — непрерывна. Следовательно, имеем
ь	ъ
I = J f(x)g(x)dx = J g(x)dF(x). а	а
Интеграл I проинтегрируем по частям. Получим
ъ
I = g(x)dF(x)\ba~ $ F(x)dg(x). а
Но так как производная g'(x) неотрицательна, F(x) и g'(x) непрерывны на отрезке [а, Ь], то по первой теореме о среднем значении интеграла, имеем ъ	ь
J F(x)g'(x)dx = F(c) J g\x)dx = F(c)(g{b) - q(a)). a	a
Следовательно,
c	b
I = g(b)F(b) - g(b)F(c) + g(a)F(c) = g(a) j f(x)dx + g(b) j f(x)dx. « a	c
216
Лекция 8
§ 5. ФОРМУЛА ТЕЙЛОРА С ОСТАТОЧНЫМ ЧЛЕНОМ В ИНТЕГРАЛЬНОЙ ФОРМЕ
Равенство, которое доказывается в следующей теореме, называется формулой Тейлора с остаточным членом в интегральной форме.
ТЕОРЕМА 13. Пусть п> 0 — целое число и пусть функция f(x) имеет (п + 1)-ю непрерывную производную на отрезке [а9 &]. Тогда имеет место формула
f(b)-fn(a9 &) + Яп(а, Ь), где fn(a9 b) — многочлен Тейлора, т. е.
fn(a, b) - f(d) +	(& - а) + ... + (Ь - а)",
а остаточный член Rn(a9 &) имеет вид
I Ь	Ч	К X	V ,
Я„(а, &) = ± J f<n+1W - Ondt./ . . ' ;
а <
► Воспользуемся методом математической индукции. При п « О должно иметь место равенство
f(b) = f(a)+^j fXt)dt = f(a) + j f'(t)dt.	‘
u- а	а
Это есть формула Ньютона—Лейбница. Так что при п = 0 теорема доказана.	.	'
Пусть при п = k утверждение теоремы уже доказано, т. е. справедливо равенство
/(&) = 4(а, Ь) + Я,(а, 6).
Докажем его при п = k + 1. Для этого проинтегрируем Rk(a9 b) по частям. Получаем
&) = А / Г(*+1)(О(Ь - t^dt = J f(k+1W(b - f)*+1 -а	{В JJ! а
=	/<fc+1)(0(b - 0*+1l* + J /(ft+2)(О<Ь - ty+'dt =
- 7ГИ7 '’ o)‘+1 + ЙГ? J ~
Подставляя это выражение в равенство, справедливое по предположению индукции при п = k9 имеем
/(&) = fk+1 (a, b) + Rh+1 (а, Ь). ◄
217
Замечания. 1. В результате замены переменной интегрирования ви-да t = а + и (Ь - а) остаточный член в формуле Тейлора можно представить в виде
Rn (a, b) = (b-y + 1 J Л"+1>(а + и (b - а))(1 - га)Ми.
О
2. Если применить к остатку Rn (а, Ъ) теорему о среднем, то можно получить формулу Тейлора с остаточным членом в форме Шлемильха— Роша, но, правда, при более жестких условиях на функцию /(х). Действительно, при любом а > 0 имеем
1 ъ
Rn (а, Ь) = J /<л+1>(0(«’ - 0п+1-“(& -	-
П' а
=	Ля+1)(с)(& - c)»+1-“(fe - а)“,
где с — некоторая точка интервала (а, Ь).
В качестве примеров получим формулу Тейлора с остаточным членом в интегральной форме для некоторых элементарных функций при а = 0 и Ь = х. В двух первых примерах воспользуемся формулой Тейлора из доказанной выше теоремы, а в остальных упростим ее вывод, применяя специальные приемы.
1.	Показательная функция. Из теоремы следует, что
уи
е* = 1 + х + 2[ +	+ п? +
где	i
Rn = Rn (0, х) = J е-(1 - и)п du.
2.	Тригонометрические функции. Имеем
(2*-1)!
n-1 (_]xkx2k
+ -R„, cos x =	^2k~y.	r"’
где
= (~l)»X2n + 1
" (2га + 1)!
п (2га)!
J (1 - u)2n~l cos их du, о
\Пх2п |
J (1 - u)2n cos их du. о
3.	Логарифмическая функция. Пусть f(x) = In (1 + x). Тогда no формуле суммы геометрической прогрессии получаем
Интегрируя это равенство пределах от 0 до х, найдем .
1(х) = 1П (1 + X) = J1 + Rn> Rn = (-1)" f fn • n i «	q 1 ~г Г
218
4.	Арктангенс. Пусть f(x) = arctg х. Тогда
Проинтегрируем это равенство в пределах от 0 до х. Получаем
Из теоремы о среднем следует, что существует величина 0 = 0(х) такая, что 0 < 0 < 1 и
р = С"1)” х2п + 1 п 14- 0х22п 4-1 ’
Отсюда имеем, что при |х| < 1 предел Rn равен 0 при п -> оо, т. е.
при |х| < 1 ряд	x2k+1 сходится и он равен arctg х.
л = о 2к 4- 1
5.	Формула бинома. Пусть Дх) = (14- х)а. Было доказано (ч. I, лекция 23, пример 5), что многочлен Тейлора g(x) = gn_1 (х), п > 2, этой функции в окрестности точки х = 0 имеет вид
х ч	, а(а - 1)... (а - п 4- 2) „ t л^1 ь
g(x) = 1 + ах + ... +	------>- x-~l = ak x*,
и, более того, ряд Тейлора fcZoaAx* сходится при |х| < 1 и равен (14- х)а. Далее, функция Дх) удовлетворяет следующему дифференциальному уравнению:
аДх)-(14-х) Д(х) = 0.
Подставляя в это уравнение вместо функции Дх) ее ряд Тейлора и приравнивая к нулю коэффициенты при степенях аргумента х, получаем равенства
kak - (а - k + 1) ak_x = 0, k > 1,
справедливость которых можно проверить непосредственно. Найдем формулу для выражения Л(х) = ag(x) - (1 + х) g'(x).
Имеем
Л(х) = a £oak х* - (1 + х) "?ойа* х*-1 =
= Ж“ ak x* ~	+ a*+i ** ~ х* =
п-2
= (aa0 - аг) + к?0((а - k) ak - (k + l)aft+1)x* + + («лп_1 - (n - l)a„_1)xn’1 = (a - n + l)a„_! x”"1 = nan x"’1. Следовательно, остаточный член R = Rn(x) = Дх) - g(x) формулы Тейлора удовлетворяет уравнению
aR - (1 4- х)Я' = пап хп-1,
219
т. е. справедливо равенство
/ R у пОдХ”-1 1(1+х)“;	(1+х)“ + 1’
интегрируя которое в пределах от 0 до х, получаем
R = RAx) = naAl + х)“ Г —--.
п	пУ > J (1 +t)a + l
Таким образом, доказано, что имеет место формула
, а(а - 1)... (а - п + 2) _ , ,
(1 + х)а = 1 + ах + ... + —--------------- хп 1 + г,
(п-1)!
а(а-1) ... (а-п + 1)	f un~ldu
(п-1)! U +Х) Х J(l+xn)« + i-
6.	Арксинус. Пусть /(х) = arcsin х. Тогда f'(x) = (1 - х2)-1/2. Отсюда по формуле бинома получаем
Г(х) - 1 -	+ ... +	х2п-2 + г,
г = (-1/2)(-1/2-1)...(-1/2-п + 1)	_ ~_1/2„2п | и»-Чи
 (п-1)!	*	’	J(l-x2w)“ + 1‘
Далее имеем
(-1/2)(-1/2-1)... (-1/2-fe + l) fc(2fe-l)!! fe(2/g - 1)!! k\	1 2kk\ 1 ' (2fe)!!
следовательно, । । < l(2n - 1)!! x2ra r1 un~xdu 2(2n - 2)11	- x2 0 Ji _u
Используя формулу понижения, получаем
j1 и* \du = 2 f ц _ t2y-idt = 2(2уг.2)!! .
6	о	(2п-1)!!
Отсюда имеем
Интегрируя формулу для f'(x)9 при некотором 0 = 0(х), |0| < 1 получаем
"v1 (2^-1)!! x2* + i
arcsin х = х + kL1	+ 0Я„,
где
220
Заметим, что предел последовательности {Вл} при п -> оо равен нулю, если |х| < 1. Следовательно, при |х| < 1 ряд Тейлора
х+ у (2fe-l)!! х2* + 1
к~1 (2*)!! 2k +1 сходится к функции arcsin х.
X .
7.	Интегральный синус. Пусть функция Дх) = J dt. Тогда Л	о *
из примера 2 имеем
Пх) = ^=
X	(2* -1)!
где
г = rn(x) = (g*)"*2” f (1 - «)2n+1 cos(ux)du.
Интегрируя равенство для f'(x) в пределах от 0 до х, получаем
Дх) = f dt = f	+
О t * = 1 (2* - 1)(2* -1)! к
где
|Я| < j\r(t)\dt <--------.
о	(2п + 1)!(2п + 1)(2п + 2)
Отсюда следует, что для любого х е R выражение R стремится к нулю при и Следовательно, для любого х е R имеет место разложение в ряд Тейлора
f sint _ у (~1)*~1х2ж~1
о t *“ Х(2Л - 1)(2А - 1)! ’
$ 6. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ИНТЕГРАЛЫ
ТЕОРЕМА 14 (неравенствоГельдера). Пустьр, q> 0, 1/р + 1/q = 1 и пусть Дх), g(x) интегрируемы на отрезке [а, Ь]. Тогда справедливо неравенство
f f(x)g(x)dx < QlAx^dx^QlgCx^dx)17’
► Функции |Дх)|^, |g(x)|? интегрируемы на отрезке [а, Ь] по теореме об интегрируемости сложной функции (теорема § 9 гл. 7). >
Рассмотрим разбиение Тп : а = х0 < ... < хп = Ь отрезка [а, &] на п равных частей. Тогда искомое неравенство получается предельным переходом в неравенстве для их интегральных сумм

221
или эквивалентном неравенстве

Последнее неравенство есть неравенство Гельдера для сумм (см. § 8 гл. 5). ◄
При р = q = 2 приведенное выше неравенство называется неравенством Коши—Буняковского.
ТЕОРЕМА 15 (неравенство Минковского — обобщенное неравенство треугольника). Пусть р > 1, и пусть /(х), g(x) интегрируемы на отрезке [а, Ь]. Тогда справедливо неравенство
( J|/(x) + g(x)\Pdxy/p < Q|f(x)|₽)dxy/₽ + Q|g(x)|₽dx j1/₽.
► Случай p = 1 очевиден. Возьмем, как и в предыдущей теореме 14, разбиение Тп отрезка [а, &] на п равных частей. Тогда достаточно доказать неравенство для соответствующих интегральных сумм
(,?Ж>+У" < (. ? Ж>1'^ У"+ у/р или
(.?>«=,) +	< (.£ J Л«)1')‘" + (,? >=01'У"-
Последнее же неравенство есть неравенство Минковского для сумм (см. § 8 гл. 5). ◄
ТЕОРЕМА 16. Пусть функция /^(х), ... , fm(x) интегрируемы на отрезке [а, &]. Тогда справедливо неравенство
(Ъ	\2	/&	\2	ь
\f^x)dx +... + Jfm(x)dx < ]jfl(x) + ... + /2(x)dxdx.
a	7	V	)	a
► Разделим отрезок [a, ft] на n равных частей и положим xk = = а + -—- /?,/? = 0,1,... , п. Для соответствующих интегральных
сумм должно иметь место неравенство
f v* £ / \b ।	। (	а \2
< (.?, л2(».>+•+№.) 4^ У-
222
Действительно, это неравенство выводится из следующей цепочки соотношений:
т z п	\о ш z и	\ z п	\
Ji (*5i	= ,5i Q,51	=
n n z m	\
= 1 1C - 1
Д Д I m	~	n f I m - \o
Заметим, что неравенство в этой цепочке соотношений следует из неравенства Коши. ◄
Лекция 9
§ 7.	КРИТЕРИЙ ЛЕБЕГА ИНТЕГРИРУЕМОСТИ ФУНКЦИИ ПО РИМАНУ
Ранее мы уже доказали и неоднократно использовали критерий интегрируемости функции на отрезке, принадлежащий Риману. Этот критерий имеет следующий вид: ограниченная на отрезке функция интегрируема тогда и только тогда, когда имеет место одно из эквивалентных соотношений:
a) Hm Q(T) = 0 или б) inf Q(T) = О,
где понятие омега-суммы определено ранее (лемма 6 § 3 главы 7).
Как видим, этот критерий непосредственно ничего не говорит о том, какие именно функции интегрируемы по Риману, а какие — нет. На данный вопрос и отвечает критерий Лебега.
Для его формулировки определим понятие множества, имеющего нулевую меру Лебега.
Определение 1. Множество А точек на числовой прямой имеет лебегову меру нуль, если для всякого числа е > О существует конечное или счетное покрытие А интервалами с общей длиной, не превосходящей е. Другими словами, для всякого е > О найдутся интервалы 119 ... , 1п, ... с длинами их соответственно 5Р ... , 8Л, ... такие, что А а ух 1п и для любого натурального п имеет место неравенство sn = 8г + ... + 8П < е.
Обозначение*. ц(А) = 0.
УТВЕРЖДЕНИЕ 1. Любое не более чем счетное множество точек {хп} на числовой прямой имеет лебегову меру нуль.
Действительно, можно взять интервалы с центрами в этих точках и длинами 8Х = е/2,..., 8П = е/2л, .... Тогда имеем
sn = е/2 + ... + е/2п = е(1 - 1/2") < е.
УТВЕРЖДЕНИЕ 2. Пусть ВсАи ц(А) = 0. Тогда и ц(В) = 0.
► Утверждение следует из того, что всякое покрытие множества А интервалами является и покрытием для множества В. ◄
Теперь сформулируем критерий Лебега.
ТЕОРЕМА 17. Для того чтобы ограниченная на отрезке [а, &] функция Дх) была интегрируема на нем, необходимо и достаточно, чтобы множество А — точек разрыва этой функции имело лебегову меру нуль, т. е. ц(А) = 0.
Прежде чем доказывать этот критерий, рассмотрим его применения.
224
ТЕОРЕМА 18. Пусть функция g(x) интегрируема на отрезке [а, Ь] и т = inf g(x), М = sup g(x), и пусть функция f(t) не-хе [а, 8]	хе [а, Ь]
прерывна на отрезке [т, М]. Тогда функция f(g(x)) интегрируема на [а, &].
► Пусть х0 — точка непрерывности функции g(x), тогда по теореме о непрерывности сложной функции Л(х) = f(g(x)) является непрерывной функцией в точке х0. Следовательно, точками разрыва функции Л(х) могут быть только точки разрыва функции g(x). Пусть А — множество точек разрыва g(x), а, В — множество точек разрыва Л(х). Тогда имеем В с А.
Поскольку функция g(x) интегрируема на отрезке [а, Ь], по критерию Лебега получаем, что ц(А) = 0. Отсюда в силу утверждения 2 имеем ц(В) = 0. Таким образом, по тому же критерию Лебега, функция Л(х) = f(g(x)) является интегрируемой на отрезке [а, &]. ◄
ТЕОРЕМА 19. Пусть функция Дх) монотонна на отрезке [а, Ь]. Тогда она интегрируема на отрезке [а, Ь].
► Покажем, что множество точек разрыва функции Дх) является счетным. В гл. 4 § 4 (теорема 1) доказано, что Дх) имеет разрывы только первого рода. Пусть х0 — точка разрыва, тогда в этой точке существуют левосторонний и правосторонний пределы: Jim Дх) = l19 Jim + Дх) = 12, причем 1± # 12. На интервале с концами в точках и 12 можно выбрать рациональное число г, и это рациональное число поставить в соответствие данной точке х0. Множество всех выбранных таким образом рациональных чисел г, как подмножество всех рациональных чисел, является не более чем счетным. Согласно утверждению 1, не более чем счетное множество имеет лебегову меру, равную нулю. Следовательно, согласно критерию Лебега, монотонная на отрезке функция интегрируема на этом отрезке. 4
§ 8. ДОКАЗАТЕЛЬСТВО КРИТЕРИЯ ЛЕБЕГА
Пусть функция Дх) ограничена на отрезке [а, &]. Обозначим через I = Д8, х0) промежуток (х0 - 8, х0 + 8) П [а, &], если х0 — внутренняя точка отрезка [а, &], и, соответственно, промежуток [а, а + 8) или (Ь - 8, &], если х0 = а или х0 = 6.
Определение 2. Колебанием функции Дх) в точке х0 назовем величину
со(х0) = аь(х0) = inf sup (Дх)-Дг/)),
8> 0 х,уе/(8)
225
8-4953
другими словами, величина со(хо) определяется равенством w(x0) = inf (ЛГ8(х0) - т8(х0)), где
Ms(xQ) = sup f(x), m8(x0) = inf Дх). xe/(8)	xeZ(8)
Имеет место следующий критерий непрерывности функции в точке.
ЛЕММА 1. Функция f(x) непрерывна в точке х0 тогда и только тогда, когда колебание шДх0) функции Дх) в точке х0 равно нулю. ► Необходимость. Предположим противное, т. е. что имеет место равенство со/хо) = а > 0. Рассмотрим последовательность 8В = 1/п, п = 1, 2, ... . Пусть I = /(1/п). В силу определения инфимума имеем
sup (Дх) - Ду)) = ЛГ1/п(х0) - пг1/в(х0) > а. х, уе!
Далее, в силу определения супремума, получим, что существуют точки хп, уп е /(1/п) такие, что Дхв) - /(i/„) > СС/2 > 0. Но так как длина промежутка /(1/п) стремится к нулю при п, стремящемся к бесконечности, то имеем lim х_ = lim у„ = ха.
Переходя в последнем неравенстве к пределу, используя непрерывность функции f(x) в точке х0, получаем 0 > а/2 > 0. Имеет место противоречие. Следовательно, соДхо) = 0.
Достаточность. Дано, что со/хо) = 0. Но тогда для всякого е > 0 существует 8 = 8(e) > 0 такое, что для любых х, у е 1(8) имеем | Дх) - f(y)\ < е. Положим здесь у = х0. Тогда получим условие непрерывности функции Дх) в точке х0. ◄
Пусть В(а) обозначает множество точек отрезка (а, &], для которых выполнено неравенство ш(х) > а.
Л EMMA 2. Множество точек В(а) является замкнутым.
► Пусть х0 — предельная точка множества D(a). Тогда существует последовательность {хп}9 сходящаяся к х0 при п -» °°, причем колебание функции Дх) в точках хп не меньше, чем а, т. е. со/(хл) > а. Заметим, что каково бы ни было число 8 > 0, найдется член последовательности хп е I^xQ). Положим
Si = min (хв - х0 + 5, х0 + 5 - хв), т. е. величина 8j равна расстоянию от точки хв до границ интер-вала 16(х0). Тогда получим, что Г61(хп) a. I§(xQ). Отсюда
М5(х0) - т&(хо> >	- m8i(xn) > <0z(x„) > a.
226
Так как при произвольном числе 8 > 0 имеем неравенство М8(х0) “ я^о) > то
inf (М5(х0) - тп5(х0)) = <ty(x0) > а.
Следовательно, всякая предельная точка множества D(a) принадлежит ему самому, т. е. Р(а) — замкнуто. ◄
Докажем теперь критерий Лебега.
Необходимость. Дано, что функция f(x) интегрируема на отрезке [а,. &]. Надо доказать, что множество D точек разрыва функции f(x) имеет лебегову меру нуль.
Предположим противное, т. е. что множество D не является множеством нулевой меры. Так как D = U D(l/n), то найдется а — 1/тп такое, что D(l/m) не будет множеством нулевой меры. Тогда существует число е0 > 0 такое, что для любого множества интервалов, покрывающих множество D(a), В(а) а найдется натуральное число п0 с условием 8Х + ... + 8По > е0. Отметим, что число п0 зависит от последовательности интервалов {1п}.
Рассмотрим теперь любое разбиение Т отрезка [а, &]. Среди отрезков [Xfc-p xj разбиения Т выделим те, внутри которых содержится хотя бы одна точка множества Z)(a). На каждом таком отрезке [хл_р xk] колебание функции Дх) не меньше, чем а. Сумма длин этих отрезков будет не меньше, чем е0, поскольку множество D содержится в них, за исключением, быть может, конечного числа точек, попадающих в точки xk разбиения Т. (Если бы оказалось, что сумма длин указанных отрезков^-р хл] была бы меньше, чем е0, то, покрывая точки xk е D(d) конечным числом интервалов так, чтобы общая сумма длин всех интервалов, покрывающих D(a), оказалась меньше, чем е0, получим систему интервалов, покрывающих D(a) и имеющих общую длину, меньшую, чем е0, что невозможно.)
Таким образом, для любого разбиения Т отрезка [а, 8] имеем
Q(T) > ае0.
Следовательно, inf П(Т) > ае0 > 0, а это в силу критерия интегри-т
руемости функции по Риману означает, что функция Дх) не является интегрируемой. Имеет место противоречие. Необходимость доказана.
Достаточность. Для любого е > 0 построим разбиение Т такое, что П(Т) < е. Пусть М — max |Дх)|. Положим 8 = е/(4М), а = е/(2(Ь-а)).
227
8*
Так как множество Z)(a) с D и D имеет лебегову меру нуль, то П(а) также имеет лебегову меру нуль и его можно покрыть системой интервалов I, имеющих сумму длин меньшую, чем 5. В каждой точке xQ множества К = [а, Ь]\/ колебание функции f(x) равно 0, поэтому существует интервал, покрывающий эту точку х0, на котором колебание функции будет меньше, чем а. Итак, получим систему интервалов J, покрывающих множество К. Из системы интервалов I U J, покрывающих отрезок [а, &], можно выделить конечное покрытие [а, Ь]. В качестве точек xk разбиения Т возьмем концы интервалов этого конечного покрытия.
Сумму £1'(Т) представим в виде	+ Q2, где и Q2
представляют собой суммы слагаемых вида причем в первой сумме переменная суммирования k пробегает значения, удовлетворяющие условию [xfe_p xk] al, а все оставшиеся значения k входят во вторую сумму £12.
Тогда для £1'(Т) получим оценку вида
£1'(Т) =	+ Q2 < 2М8 + а(& - а) = е/2 + е/2 = е.
Отсюда в силу того, что inf Q'(T) = 0, следует интегрируемость т
функции f(x). Теорема доказана полностью. ◄
При использовании критерия Лебега (в частности, для доказательства неинтегрируемости функции по Риману) иногда бывает полезна другая его формулировка в виде приведенной ниже теоремы.
ТЕОРЕМА 20. Для того чтобы ограниченная на отрезке [а, Ь] функция была интегрируема по Риману, необходимо и достаточно, чтобы для любого а > 0 множество П(а) имело лебегову меру нуль.
► Необходимость. Поскольку f(x) интегрируема по Риману, по доказанному выше критерию Лебега мера множества точек разрыва ее равна нулю, ц(Р) = 0. Но для любого а > 0 имеет место следующее включение: В(а) a D. Следовательно, ц(В(а)) = 0.
Достаточность. Очевидно, D =	D(l/n). По условию тео-
ремы для любого натурального числа п имеем ц(П(1/п)) = 0. Следовательно, ц(П) = 0, и по критерию Лебега функция f(x) интегрируема. ◄
ГЛАВА 9
Несобственные интегралы
Лекция 10
§ 1. ОПРЕДЕЛЕНИЕ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
Дальнейшая цель состоит в распространении понятия интегрируемости функции по Риману на новые классы функций, а именно:
1) на функции, заданные на бесконечном промежутке;
2) на неограниченные функции.
Понятие предела, которым мы владеем, позволяет достичь этой цели без особого труда, а обобщение понятия интеграла Римана при этом называется несобственным интегралом.
Для первого случая интегралы типа
J f(x)dx, J f(x) dx, J f(x) dx a	-oo	-oo
называются несобственными интегралами первого рода, во втором случае, когда функция f(x) является неограниченной на ь
конечном отрезке [а, &], интеграл J f(x)dx называется несобст-а
венным интегралом второго рода.
Случай, когда и промежуток интегрирования, и сама функция не ограничены, не вносит ничего нового в эту проблематику, так как его можно свести к случаю несобственных интегралов первого и второго родов простым разбиением промежутка интегрирования на части, и потому отдельно мы его рассматривать не будем. Остановимся более подробно на понятии несобственного интеграла первого рода, при этом ограничимся только случаем оо
интегралов вида J f(x)dx.
а
Определение 1. Пусть а — вещественное число и пусть для любого А > а функция /(х) интегрируема по Риману на отрезке [а, А] и
F(A)= A\f{x)dx.
а
229
Если при. А —> +°о существует предел I =	F(A), то этот
предел называется несобственным интегралом первого рода от функции f(x) на промежутке [а, +°о].
Для интеграла I используется следующее обозначение:
I = f f(x)dx (= J /*(x)dx). о	a
Если предел I существует, то говорят, что несобственный интеграл сходится. Если же этот предел не существует, то выра-оо
жение J f(x)dx понимают как некий символ, который тоже на* а
зывают несобственным интегралом, но говорят про него, что он расходится.
Аналогично определяется несобственный интеграл вида f f(x)dx= lim f f(x)dx, A^-oo
+OO а несобственный интеграл J f(x)dx понимают как сумму двух несобственных интегралов
J f(x)dx= J Дх)с/х4- J f(x)dx. -оо	-оо	о
Замечания. 1. В отличие от несобственных интегралов обычный интеграл Римана по конечному промежутку называется собственным.
2. Из свойств собственного интёграла и определения несобственного интеграла для любых вещественных а и Ь тривиально имеем
J f(x)dx + J f(x)dx - J f(x)dx. а	ъ	a
ПРИМЕРЫ. 1. При a > 0 справедливо равенство
00 , lim —— (А1" a - a1" a), если a # 1, J = M->+oo x_av
a xCL Jim^ (In A - In a), если a = 1.
Отсюда следует, что этот интеграл сходится при a > 1 и равен ..1— а1"01, и расходится при a < 1. a - 1
2. При натуральном числе п интегрированием по частям получаем
4-оо
J ^e^dt = и!.
о
230
$ 2. КРИТЕРИЙ КОШИ И ДОСТАТОЧНЫЕ УСЛОВИЯ СХОДИМОСТИ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
Из критерия Коши существования предела функции при А -> оо непосредственно получается следующая теорема.
ТЕОРЕМА 1 (критерийсходимости несобственного интеграла перво* +ОО
го рода). Для сходимости интеграла J f(x)dx необходимо и до-а
статочно, чтобы выполнялось условие Коши, т. е. чтобы для всякого е > 0 существовало число В = В(е) > А такое, что для всех чисел Аг, А2, больших В, выполнялось неравенство
J f(x)dx
А
<£.
Символически это условие Коши можно записать так:
V е > 0 3 В = В(е) > 0 : V А19 А2 > В =>
^2
J f(x)dx
А
ТЕОРЕМА2 (общий признак сравнения). Пусть для всех х е [а, +°°)
4-ос
справедливо неравенство |Дх)| < g(x) и пусть интеграл J g(x)dx а
4-оо
сходится. Тогда будет сходиться интеграл J f(x)dx.
а
► Докажем, что выполнено условие Коши для сходимости несобственного интеграла от функции f(x). В силу сходимости интеграла от функции g(x) имеем, что для любого е > 0 существует В = В(е) > 0 такое, что при любых А2, АГ>А2> В справедливо А
неравенство J g(x)dx < е. Но поскольку Ai
Ag	А2	А2
f f(x)dx < J |/(x)|dx < J g(x)dx < £,
условие Коши выполняется и для интеграла от функции /(х) с тем же самым В = В(е). ◄
ПРИМЕР. Пусть при некотором а > 1 и при х —> оо выполняется неравенство
|/(х)| « 1/ха, т. е. существуют с > 0 и х0 = х0(с) > 0 такие, что |/(х)| < сх-апри х > х0. Тогда интеграл J f(x)dx сходится.
231
Действительно, имеем
J f(x)dx = J f(x)dx + J f(x)dx. a	a	x0
Первый из интегралов суммы является собственным, а второй +ОО
интеграл f f(x)dx сходится по признаку сравнения, поскольку
*о
Тdx	1
J — сходится при а > 1.
х
$ 3. АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИМОСТЬ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ.
ПРИЗНАКИ АБЕЛЯ И ДИРИХЛЕ
Сначала дадим определения понятий абсолютной и условной сходимости несобственных интегралов.
Определение 2. Несобственный интеграл J f(x)dx называет-
а
4-ос
ся абсолютно сходящимся, если сходится интеграл J |/(x)|dx.
а
Определение 3. Несобственный интеграл J f(x)dx называет-
1 а
4-оо
ся условно сходящимся, если интеграл J f(x)dx сходится, а 4-оо	а
интеграл J |/(x)|dx расходится, а
Из общего признака сравнения непосредственно следует, что абсолютная сходимость интеграла влечет за собой его условную сходимость. Обратное неверно.
Как и ранее, будем считать, что функция /(х) интегрируема на отрезке [а, А] при любом А > а.
ТЕОРЕМА 3 (признак Дирихле). Пусть при любом х е [а,+°о) X
функция F(x) = J f(u)du ограничена, и пусть функция g(x) не-а
отрицательна, и, не возрастая, стремится к нулю при х —> +о°. 4-оо
Тогда интеграл I = J f(x)g(x)dx сходится, а
► Поскольку функция g(x) на плюс бесконечности не возрастает и стремится к нулю, для всякого ех > 0 существует В = В(е) > а такое, что для всех х > В имеем неравенство 0 < g(x) < ег Пусть,
232
далее, М = sup |F(x)|. Тогда по второй теореме о среднем для лю-х > а
бых А19 А2, А2> Ах> В найдется такое число А3, Аг<А3< А2, что
J f(x)g(x)dx
Al
g(Ai) J8 f(x)dx A
A
J f(x)dx
= 81
J f(x)dx-j f(x)dx
< 2егМ.
Если теперь мы зададимся произвольным е > О, то, взяв ех = e/(2Af), получим, что для любых Ар А2, А2 > Аг > выполнено неравенство
А
J f(x)g(x)dx
Al
< Е,
т. е. выполняется условие Коши, поэтому интеграл I сходится. ◄
4-оо
ТЕОРЕМА 4 (признак Абеля). Пусть интеграл J f(x)dx сходится а
и функция g(x) неотрицательна, монотонна и ограничена свер-4-00
ху на промежутке [а, +оо). Тогда интеграл I = J f(x)g(x)dx а
сходится.
4-оо
► Поскольку интеграл J f(x) dx сходится, в силу критерия Kott
ши имеем: для всякого ег > О существует В = B(eJ такое, что для всех Ар А2, А2 > Аг > В справедливо неравенство
А
J f{x)dx
Al
<еР
Далее, по второй теореме о среднем, существует такое число А3, Ах < А3 < А2, что
J /(х) g{x) dx = giAJ f ftx) dx + g(A2) J f(x) dx.
Ai	Ai	A3
Положим M = sup g(x). Но так как
x > a
то получим
j’f(x)dx
Ai
<ep
^2
f f(x) dx
^3
<ep
J2f(x)g(x) dx
A
<2Mer
233
Поэтому, взяв ех = e/(2Af), будем иметь, что для любых чисел Аг А2, А2> Ах> В (е/(2ЛГ)) справедливо неравенство
f f(x)g(x)dx
Ai
< е.
Следовательно, по критерию Коши интеграл I сходится. ◄
ПРИМЕРЫ. 1. Согласно признаку Дирихле при а > 0 сходится интег-4-оо .	А
рал J —— dx, так как для любого А > 1 функция F(A) = J sin х dx i х	1
ограничена, а при а > 0 и при х —> +°о функция х-01, монотонно убывая, стремится к нулю.
2. Пусть f(x) — многочлен степени большей, чем 1. Тогда схо-4-оо
дится интеграл J sin Дх) dx. о
Без ограничения общности можно считать, что старший коэффициент многочлена Дх) положителен. Тогда, начиная с некоторого А > 0, производная его f'(x) будет положительна и монотонно возрастать к плюс бесконечности. Достаточно доказать, 4-оо
что сходится интеграл J sin Дх) dx. Для любого В > А в интегра в	А
ле J sin Дх) dx сделаем замену переменной интегрирования у = Дх), А
х = Л1 (у)- Получим интеграл
sin у
dy.
По второй теореме о среднем он ограничен величиной 2/Д(А) и при А —> +°о будет стремиться к нулю, а это и доказывает сходимость исходного интеграла.
Лекция 11
8 4. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА
Определение 4. Пусты
1)	функция f(x) задана на промежутке [а, Ъ) и не ограничена на нем;
2)	для любого а, а < а < &, функция f(x) ограничена и интегрируема на отрезке [а, а]; а
3)	существует предел I = lim J /(х) dx. а
Тогда этот предел I называется несобственным интегралом второго рода от функции f(x) на отрезке [а, &]. При этом для предела I используется обозначение
ь
I = ]f(x)dx. а
Замечания. 1. Точка Ь называется особой точкой интеграла I,
2.	Если предел / е R существует, то говорят, что несобственный ин-ъ
теграл J f(x) dx сходится, в противном случае говорят, что этот интеграл а
расходится. ъ
3.	Если особой точкой интеграла J f(x)dx является нижний предел а
интегрирования, то несобственный интеграл второго рода определяется аналогично.
4.	Если особая точка с лежит внутри отрезка [а, Ь], то несобст-ъ
венный интеграл J f(x) dx определяется как сумма двух несобственных а
интегралов: ь	ь	ь
J f(x) dx = f f(x) dx + J f(x) dx. a	a	c
ПРИМЕР. Справедливы следующие равенства:
г dx .. f dx J — = lim I — 5 xa a-»0+ i xa
lim „ 1 (1 - a1 ~ a), если a 1, a->o+ 1 - a
lim (-In a),	если a = 1.
i
Отсюда следует, что интеграл J о
1
& и расходится при a > 1.
— сходится при a < 1, равен
Рассмотрим основные свойства несобственного интеграла вто-ь
рого рода на примере интеграла J f(x) dx с единственной особой а
235
точкой b. Эти свойства аналогичны свойствам несобственных ин
тегралов первого рода.
1°. Критерий Коши сходимости несобственного интеграла второго рода.	ь
Для сходимости интеграла J f(x)dx необходимо и достаточно, а
чтобы имело место условие Коши: для всякого 8 > 0 найдется число 8 = 8(8) > 0 такое, что при любых <хр а2 с условиями ар а2 е (Ь - 8, Ь) выполняется неравенство
f f(x)dx
а1
< 8.
2°. Общий признак сравнения.
Пусть для всех х е [а, Ъ) справедливо неравенство |/(х)| < g(x) ъ
и несобственный интеграл \g(x)dx сходится. Тогда сходится ИН-fl
Ь
теграл J f(x)dx. а	ь
3°. Несобственный интеграл второго рода J f(x)dx называем
ь
ется абсолютно сходящимся, если сходится интеграл J |Дх)| dx, и условно сходящимся, если он сходится, но не абсолютно, т. е. ь
интеграл J |Дх)| dx расходится, а
Можно сформулировать признаки, аналогичные признакам Абеля и Дирихле для интегралов первого рода.
И наконец, любой интеграл с бесконечными пределами интегрирования (или одним бесконечным пределом интегрирования) и конечным числом особых точек можно рассматривать как сумму несобственных интегралов, каждый из которых имеет одну особую точку, являющуюся границей отрезка интегрирования (точки +оо и -оо также можно считать особыми), т. е. исследование любого несобственного интеграла сводится к несобственным
интегралам первого и второго рода.
§ 5.	ЗАМЕНА ПЕРЕМЕННОЙ И ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ В НЕСОБСТВЕННОМ ИНТЕГРАЛЕ
ТЕОРЕМА 5. Пусть производная <р'(0 непрерывна на отрезке [а, Р] и отлична от нуля на интервале (а, Р), и пусть функция f(x) непрерывна на интервале (ф(а), <р(Р)). Тогда имеет место формула
* * и ф(Р)	р
f Дх) dx = f ft<p(f)) <р'(*) dt
<р(а)	а
как для собственных, так и для несобственных интегралов.
236

► Пусть сначала точки аир являются конечными. Тогда особыми точками функций f(x) и /(<р(^)) могут быть концы соответствующих отрезков. В силу монотонности функции х = ф(0 каждое значение х принимается лишь один раз, когда переменная t изменяется на интервале (а, Р). Тогда для любых 8Х > 0 и е2 > 0 по теореме о замене переменной для собственного интеграла имеем
ф(Р - е2)	0 - е2
/ f(x)dx= f Дф(О) ф'(0
ф(а + Ej)	а + £j
Переходя к пределу в этом равенстве при 0 и s2 -> 0, получим искомую формулу.
Если же аир — бесконечны, то, взяв ар Рх g R и используя вновь теорему о замене переменной для собственного интеграла, получаем
Ф(Р1)	Pi
J f(x) dx = f /(ф(0) Ф'(0 dt.
фС«1)	ai
Отсюда, переходя к пределу при ах -оо и рх -> +°о, получаем искомое равенство. ◄
ТЕОРЕМА 6. Пусты
1) функции f'(x) и g'(x) — непрерывны на промежутке (а, +°°); 2) сходится хотя бы один из несобственных интегралов
f f(x) g'(x) dx и J f'(x) g(x) dx; a	a
3) существует предел	f(x) g(x), а в случае если a —
особая точка, то существует предел l2 = lun f(x)g(x).
Тогда существуют оба интеграла и имеет место равенство
4-оо	4-оо
J Дх) g'(x) dx = f(x) g(x)|+°° - J f'(x) g(x) dx. a	a
► Рассмотрим собственные интегралы на отрезке [a + £, &]. По теореме об интегрировании по частям в собственном интеграле имеем
ь	ь
J f(x)g'(x)dx = f(x)g(x)\ba+s- f f'(x)g(x)dx. а + е	а + е
Устремив в этом равенстве е к нулю, а Ь — к плюс бесконечности, получим искомую формулу. ◄
Иногда полезными оказываются следующие специальные определения несобственного интеграла.
237
4-А
Определение 5. Вещественное число I — lim J f(x)dx называ-
А->+0° -А +ОО ется главным значением (по Коши) интеграла j f(x) dx и обо-
значается так:
4-оо I = v.p. J f(x) dx. —оо
Определение 6. Если с — особая точка несобственного интеграла второго рода от функции f(x) исе (а, Ь)9 то главное значение интеграла определяется так:
,с - 8	Ь
*1= lim ( J ftx)dx + f f(x)dx].
б->0 V а	с 4-8	/
ГЛАВА 10
Длина дуги кривой
Лекция 12
$ 1. КРИВЫЕ В МНОГОМЕРНОМ ПРОСТРАНСТВЕ
Определение 1. Кривой L в пространстве Rm (пространственной кривой в т-мерном пространстве) называется множество точек М a Rm, состоящее из всех значений (фх(0, ••• > Фт(0) нс-которой вектор-функции хх = фх(0, ... , хт = фт(£), причем функции фх(^), ... , Фт(0 заданы на некотором промежутке I cR и непрерывны в каждой его точке.
Под промежутком мы понимаем либо конечные отрезки, интервалы и полуинтервалы, либо бесконечные интервалы и полуинтервалы.
Для простоты в дальнейшем будем рассматривать случаи I = [а, &]. Напомним, что в концах отрезка непрерывность понимается как односторонняя непрерывность.
Определение2. Точка с = (cv ..., ст) е L называется кратной точкой кривой L, если имеются по крайней мере две различные точки * t2 промежутка I такие, что ф1(^1) = ФхС^г) = =	...,	= <pTO(t2) = ст.
Точки кривой, не являющиеся кратными, называются простыми точками кривой.
Кривая L, имеющая только конечное число кратных точек, называется параметризуемой кривой.
Кривая L, не имеющая кратных точек, за исключением, быть может, концевых точек промежутка I, называется простой кривой.
Если только в концевых точках tr и t2 отрезка I значения функций фх(0> •••» Фт(0 совпадают, то простая кривая называется простой замкнутой кривой.
ЛЕММА 1. Всякую параметризуемую кривую можно представить в виде объединения конечного числа простых кривых.
Для доказательства достаточно отрезок I разбить на конечное число отрезков с концами в кратных точках исходной кривой.
239
Определение 3. Функция f(t), непрерывная на отрезке [а, &], называется кусочно-линейной [а, &], если для любого значения t е [а, &], за исключением конечного их числа: t19 ..., tn_19 имеем: f'(t) равна постоянному значению на каждом отрезке [£fe, tk + J, k = 0, ... , п. Это означает также, что на любом отрезке [Zfe, ZA+1] имеет вид f(t) = akt + bk (здесь tQ = a, tn = Ь).
Определение 4. Простая кривая L называется ломаной линией, если <рх(0» ••• > являются кусочно-линейными функциями.
Очевидно, что каждая ломаная состоит из отдельных отрезков, которые называются ее звеньями, а концы этих отрезков — точки Ар ... , Ап, называются ее узлами. Точки tQ, ... , tn, которым соответствуют эти узлы, образуют разбиение отрезка [а, &].
Рассмотрим одно звено ломаной с начальной точкой Аг (хх, ... , хт) и конечной точкой А2 (у19 ... , ут). По теореме Пифагора его длина |Z| равна величине
И = J(yi-X!)2 + ...+(ym-Xm)2 .
Если же точки Д) (хь 0, ..., хт , 0),..., Ап (хъ	хт „) являются
последовательными узлами ломаной I, то длина этой ломаной обозначается символом |Z| и, очевидно, она равна
п -----------------------------------
И = J(Xl,k ~Х1,\-1)2 + •” + (Xm,k	‘
Определение 5. Ломаная I, соответствующая разбиению Т отрезка [а, 6], называется вписанной в кривую L, задаваемую уравнениями хг = фх(0» ••• , хт = <pm(t), t е [а, &], если начальная точка звена совпадает с концом предыдущего и узлы ломаной I лежат на кривой L. При этом узлам ломаной и соответствующим точкам кривой отвечают одни и те же значения параметра.
Определение 6. Простая кривая L называется спрямляемой, если длины |Z| всех ломаных I, вписанных в кривую L, образуют ограниченное сверху множество.
Определение 7. Длиной \L| спрямляемой кривой L называется число, равное точной верхней грани длин всех ломаных, вписанных в данную кривую.
Замечания. 1. Очевидно, что если мы хотим правильно определить понятие длины кривой, то мы должны требовать, чтобы вписанная ломаная была короче самой кривой. В данном случае это так, поскольку кратчайшее расстояние между двумя точками, как известно, достигается на отрезке прямой, проходящей через эти точки.
2. Бывают неспрямляемые кривые, но они задаются очень сложно, и поэтому примеры таких кривых мы приводить не будем.
240
§ 2. ТЕОРЕМА О ДЛИНЕ ДУГИ КРИВОЙ
ТЕОРЕМА 1. Пусть функции фДО, ••• * Фш(0» задающие простую кривую L, имеют непрерывные производные на отрезке [а, Ь]. Тогда кривая L — спрямляема и ее длина |L| выражается формулой
ь __________________________
|l| = J 7(ф'1(о)2 + -+ (<p;(o)2 dt. а
► Покажем сначала, что длина любой ломаной не превосходит величины
ь ___________________________
А= J V^t))2 +... + (q>;(t))2dt. а
Пусть узлы ломаной I соответствуют точкам tQ, t19 ... , tn разбиения Т отрезка [а, &]: а =	< ... < tn = b. Тогда имеем
И = ,51	- I»2 + - +	- I»2 =
= J	+ ... + J <p'm(t)dt
Далее, в силу неравенства (см. гл. 8, § 6, теорема 16)
jfittydt + ... + jfm(t)dt < j Jfl(t) + ... + /2 (t) dt
«	7
получаем
И < t j’ 7((pi(o)2 +... + (ф;(о)2^=а.
Таким образом доказано, что A — верхняя грань длин всех ломаных Z, вписанных в кривую L, т. е. кривая L является спрямляемой.
Покажем, что А — точная верхняя грань длин таких ломаных, т. е. длина кривой L равна А.
Поскольку функции ч4(0, А = 1, ... , т, непрерывны на отрезке [а, Ь], по теореме Гейне—Кантора они являются равномерно непрерывными на этом отрезке.
Следовательно, при всех k = 1, ... , т для всякого е > О существует число 8 = 8(e) > 0 такое, что для всех f, t" е [а, &]: \t' - t"\ <8 выполняется неравенство
1<Р*(#Э - ф'*(*")| <	= е1-
*jm{b а)
241
Возьмем любое разбиение Т отрезка [а, Ь] с диаметром Дт < 8, Т: а = tG < tr ... < tn = Ь9 и пусть ломаная I соответствует этому разбиению Т.
Оценим теперь сверху разность А - |Z| >0. Имеем
А - |Z| = J VCcp'iCO)2 + ... 4- dt -а
п I иг
- л ~	=
П /в | / ТП ~ I тп гДф*(*„1Н2 1 .
Гв-1\	I	V	8-1	'	)
где Д <р* (Zg-i) = <pft (*8) - Фк (<8-i), Д *8-i = ts - te_v
Далее применим неравенство треугольника в следующем виде. Пусть заданы вершины О (0, ..., 0), А (ар ..., am)9 B(bv ..., Ьт) треугольника ОАВ. Тогда имеет место неравенство треугольника (неравенство Минковского при р = 2):
I / zn ~	/ тп ~I / т	~
Ш ? % - №. л21 *=	
Следовательно, получаем
I.	л. Л	i) \2
А - и с,?., ул (”«'’ --ХСГ-)
Л е8 I ТП	л	f8 Г~~
= ,?i I 7Л?1(<Р*(*)_	f ex7mdf =
= 6j Jm (b - a) = e,
где T|A, s — некоторая точка отрезка [£8_р tj. «
СЛЕДСТВИЕ. Пусть s = s(u) — длина дуги кривой L, задаваемой уравнениями хх = хг(<), ... , хт = xm(t), а < t < и. Тогда для дифференциала длины дуги кривой ds справедлива формула
(ds)2 = (dXj)2 + ... + (dxm)2.
► Из теоремы о длине дуги кривой имеем
s(u) = J7(х'1(О)2 + — + (X'n(t))2 dt. а
Дифференцируя это выражение, найдем
ds(u) = 7(«i(u))2 + ... +(x'2(u))2 du, или
ds = 7(dxx)2 + ... +(dxm)2 . ◄
242
Таким образом, квадрат дифференциала длины дуги плоской кривой (т = 2) в полярных координатах (г, <р) равен
ds2 = dr2 + г?</ф2, где координаты г и ф определяются по формулам х — rcos ф, у = г sin ф, г > 0, 0 < ф < 2л. Действительно, dx = cos ф</г - г sin qx/ф, dy = sin фйг + г cos ф</ф. Следовательно, получаем
ds2 = dx2 + dy2 = dr2 + т^скр2.
В частности, если уравнение эллипса задано в параметрической форме
г = г(ф) = (a cos ф, b sin ф), а > b > О, и угол ф между осью Ох и радиусом-вектором г изменяется от нуля до 2л, то для дифференциала длины дуги эллипса имеем ds = 7а28ш2ф + &2соз2ф dtp.
ПРИМЕР. Найти длину дуги кривой (циклоиды)
J х = R (t - sin t), [у = R (1 - cos t), где 0 < t < 2л. Имеем: ds2 = dx2 + dy2, ds2 = 4R2 sin2 ^(dt)2, вл
ds = 2R sin 5 dt. Следовательно,
s = s(0) = 4Я(1 - cos 0/2). Эта кривая задает траекторию движения точки на ободе катящегося колеса радиуса R.
ГЛАВА 11
Мера Жордана
Лекция 13
§ 1.	ПЛОЩАДЬ ПЛОСКОЙ ФИГУРЫ И ОБЪЕМ ТЕЛА. ОПРЕДЕЛЕНИЕ МЕРЫ ЖОРДАНА
О площади плоской фигуры уже говорилось, когда вводилось понятие определенного интеграла как площади криволинейной трапеции. Причем, давая точное определение этого понятия, мы исходили из основных свойств площади фигуры, справедливых для площадей простейших фигур, например таких, которые являются объединением конечного числа прямоугольников и треугольников.
Сформулируем эти свойства. Обозначим через ц(Р) площадь фигуры Р.
1°. Для каждой фигуры Р, имеющей площадь, функция ц(Р) неотрицательна и однозначно определена.
2°. Площадь квадрата со стороной, равной единице, также равна единице.
3°. Функция ц(Р) является аддитивной, т. е. если фигура Р разбита на две непересекающиеся фигуры Рг и Р2, Р = Рх U Р2, Pi А Р2 = 0, то
р(Р) = р(Р1) + р(Р2).
4°. Функция ц(Р) является инвариантной относительно всех движений плоскости.
Другими словами, если фигуры Рх и Р2 можно наложить одну на другую так, чтобы все их точки совпали, т. е. Рг и. Р2 можно совместить при помощи поворота плоскости вокруг некоторой неподвижной точки или параллельного переноса плоскости, то цСР^^цСР,).
5°. Функция ц(Р) является монотонной, т. е. если Рх с Р2, то [ДР^ < ц(Р2).
Эти свойства имеют место не только для площадей простых фигур, но и для объемов простых тел, а также для суммарных длин простейших множеств на прямой, т. е. множеств, составленных из конечного числа промежутков и отдельных точек.
244
В дальнейшем простейшей будем называть фигуру, являющуюся объединением конечного числа прямоугольников, стороны которых параллельны осям координат. Такие прямоугольники будем называть стандартными прямоугольниками.
Стандартный прямоугольник может включать в себя любое подмножество точек, лежащих на его сторонах. Как известно, каждый стандартный прямоугольник имеет площадь, равную произведению длин его смежных сторон.
При определении площади фигуры в общем случае, как и в случае криволинейной трапеции, можно действовать по аналогии с критерием Римана существования определенного интеграла.
Для этого естественно для плоской ограниченной фигуры Р ввести понятие верхней площади фигуры (по аналогии с верхней суммой Дарбу) как точной нижней грани площадей ц(Рх) всех простейших плоских фигур Рр описанных вокруг Р, т. е. Р с^Рг; а также нижнюю площадь этой фигуры как верхней грани площадей ц(Р2) всех простейших фигур Р2, вписанных в Р, т. е. Р2 с Р.
Обозначение: Ц*(Р) — верхняя площадь, Ц*(Р) — нижняя площадь.
Заметим, что для простейшей фигуры Р мр)=ц(р)=т.
Если для фигуры Р справедливо равенство р*(Р) = Ц*(Р), то эта величина называется площадью фигуры Р и обозначается через ц(Р). Точно так же обстоит дело и с объемом трехмерных фигур, т. е. аналогично определяются верхний и нижний объемы трехмерной фигуры. Для них используют те же обозначения: ц*(Р), ц*(Р) и ц(Р), где, по определению, для измеримой фигуры Р полагают ц(Р) = Ц*(Р) = Ц*(Р).
Введенное понятие площади фигуры называется мерой Жордана, а сами фигуры, которым с помощью этого определения приписывается значение площади (или объема в трехмерном пространстве) — квадрируемыми (или кубируемыми в случае объема) или измеримыми по Жордану. Для таких фигур вычисление площади (или объема) сводится к вычислению определенного интеграла Римана.
ПРИМЕРЫ. 1. Плоская мера Жордана отрезка I, параллельного одной из осей координат, равна нулю. Этот отрезок содержится внутри прямоугольника, одна из сторон которого имеет длину, равную нулю.
2.	Любой отрезок I имеет нулевую меру Жордана, так как этот отрезок можно поместить в простейшую фигуру сколь угодно малой площади.
245
3.	Пусть Р — простейшая фигура. Тогда мера Жордана ее границы ЭР равна нулю. Границей Р служат стороны прямоугольников, составляющих фигуру Р. Их конечное число, и каждый можно поместить в прямоугольник, одна сторона которого имеет длину, равную нулю.
4.	Объединение, пересечение и разность простейших фигур является простейшей фигурой.
Действительно, пересечение двух стандартных прямоугольников — стандартный прямоугольник. Поэтому для фигур А = U Pk и В = U Qt, состоящих из стандартных прямоугольников РЛ, Qz, их пересечение А П В = JJ* (Pk П Qz) — простейшей фигурой. Разность двух стандартных прямоугольников — простейшая фигура. Покажем, что разность А \ В двух простейших множеств А и В является простейшим множеством. Пусть Р — прямоугольник, содержащий A U В, тогда А \ В = А П (Р \ В).
§ 2. КРИТЕРИЙ ИЗМЕРИМОСТИ МНОЖЕСТВА ПО ЖОРДАНУ
Как и в случае интеграла Римана, можно сформулировать критерий квадрируемости фигуры, аналогичный критерию Римана с омега-суммами (по форме он напоминает критерий Лебега). Для этого введем понятие границы ЭР фигуры Р, которое, в свою очередь, использует следующие понятия.
1.	Пусть 8 > 0. Тогда 8-окрестностью точки xQ на плоскости назовем множество точек х, лежащих внутри круга радиуса 8 с центром в точке х0.
2.	Точка х0 называется внутренней точкой множества Р, если найдется 8-окрестность Е(х0, 8) точки х0, целиком принадлежащая Р, т. е. Е(х0, 8) а Р.
3.	Точка xt называется внешней точкой множества Р, если существует окрестность Е(х19 8) такая, что Е(хг, 8)(УР = 0.
4.	Если точка х не является ни внутренней, ни внешней точкой множества Р, то она называется граничной точкой множества Р.
5.	Множество всех граничных точек фигуры Р называется его границей и обозначается через ЭР. Назовем фигуру Р замкнутой, если ЭР с: Р, и открытой, если ЭР П Р = 0. Множество ЭР U Р обозначается символом р и называется замыканием Р.
ТЕОРЕМА (критерий квадрируемости фигуры). Фигура Р квадрируема тогда и только тогда, когда мера ее границы равна нулю, т. е. ц(ЭР) = 0.
246
► Необходимость. Надо доказать, что если Р — квадрируемая фигура, то ц(ЭР) =т 0. Для этого достаточно при любом е > 0 указать простейшую фигуру Н такую, что ЭР с Н и ц(Н) < е.
Поскольку фигура Р — квадрируема, существует величина ц(Р) = ц*(Р) = р*(Р). Следовательно, для всякого ех > 0 найдутся открытая простейшая фигура Рг и замкнутая простейшая фигура Р2 такие, что Р2 с Р с Рх и, кроме того, справедливы неравенства
ц(Р) = р*(Р)<Ц(Р1)<М(Р) + е1, р(Р)-е1<ц(Р2)<ц(Р) = МР).
Рассмотрим фигуру Р3 = Рх \ Р2. Она является простейшей. Пусть Н == Р3. Тогда вне этой фигуры Н содержатся только внешние или внутренние точки фигуры Р. Поэтому ЭР с: Н. Далее, имеем Pr = Р2 U Р3, Р2 П Р3 = 0, следовательно, ц(Рх) = ц(Р2) + + ц(Р3), откуда
ц(Р3) = ^(Pi) - ц(Р2) < ц(Р) + ех - ц(Р) + ех = 2ег
Заметим, что ц(Р3) = ц(Р3), так как граница простейшей фигуры имеет нулевую меру.
Возьмем ег = е/2; получаем, что ц(И) < е, ЭР с Н9 следовательно, ц(ЭР) = 0. Необходимость доказана.
Достаточность. Дано, что граница ЭР фигуры Р имеет нулевую меру. Надо доказать, что фигура Р измерима по Жордану, т. е. имеет место равенство Ц*(Р) = ц*(Р).
Для этого потребуется следующая лемма, полезная и сама по себе.
ЛЕММА 1 (о связности отрезка на плоскости). Пусть на плоскости заданы отрезок I с концами Аг и А2 и некоторое множество М, причем Аг е М, А2 <£ М. Тогда существует точка Aq е I такая, что Aq е дМ.
► Докажем эту лемму. Для каждой точки а е I рассмотрим функцию р(а), равную расстоянию от нее до точки Очевидно, что для любой точки а е I справедливо неравенство р(а) < \1\. Пусть В = IП М. Тогда множество В непусто, так как точка Аг принадлежит и отрезку Z, и множеству М. Пусть, далее, р0 = sup р(А).
Ае В
Рассмотрим точку (Xq, лежащую на расстоянии р0 от точки Любая точка а, удаленная от точки на расстояние р(а) > р0,,не принадлежит как В, так и М, поэтому а0 не может быть внутренней точкой множества М. С другой стороны, в любой окрестнос-
247
ти точки а0 на отрезке I найдется точка, принадлежащая В cz М. Поэтому точка а0 не является внешней точкой множества Af, следовательно, а0 е ЭМ. Лемма доказана.
Итак, пусть ц(ЭР) = 0. Это значит, что для любого е > 0 существует открытая простейшая фигура Р3 такая, что ЭР cz Р3, ц(Р3) < е. Граница ее ЭР3 состоит из конечного числа отрезков, параллельных осям координат. Заключим эти фигуры Р и Р3 в квадрат К со сторонами, параллельными осям координат. Далее, продолжим отрезки границы ЭР3, параллельные оси Ох, до пересечения со сторонами квадрата К. Тогда квадрат К и фигура Р3 разобьются на отдельные стандартные прямоугольники. Пусть это прямоугольники h19 ..., hm (каждый из них будем рассматривать без границы). Тогда прямоугольники Л8, s = 1, ..., тп, либо целиком принадлежат Р3, либо h8 А Р3 = 0.
Покажем, что если прямоугольник h8 не является подмножеством Р3, но имеет хотя бы одну общую точку с фигурой Р, то h8 а. Р. Действительно, если в этом прямоугольнике xr g Р, х2 g Р, то некоторые точки отрезка I, соединяющего эти точки (а он тоже целиком принадлежит прямоугольнику Л3), принадлежат Р, а некоторые точки не принадлежат Р. По лемме отрезок I содержит точку х0 g ЭР, т. е. точка х0 g hs9 х0 g ЭР с: Р3, а это значит, что hs cz Р3, что противоречит условию, что прямоугольник hs не является подмножеством Р3.
Таким образом, если hs П Р ё 0, то прямоугольник h8 целиком лежит в Р. Объединим все такие прямоугольники h8 во множество Р2. Очевидно, что Р2 с: Р.
Рассмотрим еще простейшую фигуру Рх = P2UP3. Докажем, что Р a. Pv Действительно, фигура Р, как и всякая фигура, состоит из внутренних точек, образующих множество Р \ ЭР, и некоторого подмножества Г cz ЭР, — множества своих граничных точек. Достаточно показать, что ЭР с Р19 Р \ ЭР с Pv
Включение ЭР с Рх следует из того, что ЭР с Р3 с Pv А всякая внутренняя точка множества Р по построению принадлежит: 1) либо Р3; 2) либо некоторому открытому прямоугольнику Л8; 3) либо его границе dh8. Но тогда в первом случае точка х g Р3 cz Р19 и, следовательно, она принадлежит Рх; во втором случае х g hs9 х g Р, а это значит, что h8 cz Р2 (по способу построения множества Р2), т. е. х g h8 cz Р2 cz Рх; в третьем случае имеем, что внутренняя точка множества Р лежит на границе открытого прямоуголь-248
ника hs. Но тогда некоторая е-окрестность этой точки целиком состоит из точек множества Р и в то же время в ней содержатся точки из прямоугольника hs. Тогда hs а. Р2, откуда dhs а Р2, поэтому х € ЭЛ8 cz Р2 с: Р. Отсюда имеем: Р cz Pv Далее имеем: Р2 А Р3 = 0, кроме того, Рр Р2 и Р3 — простейшие фигуры, поэтому
|Л(РХ) = р.(Р2) + ц(Р3) < ц(Р2) + е, следовательно,
ц(Р2) < щ(Р) < ц*(Р) < Ц(Р1) < Ц(Р2) + е-
Таким образом, получаем
О < ц*(Р) - щ(Р) < ц(Р2) + е - ц(Р2) = е.
Но так как е > 0 — произвольно, то, следовательно, р*(Р) = Ц*(Р),
т. е. фигура Р измерима по Жордану. <
Лекция 14
$ 3. СВОЙСТВА МЕРЫ ЖОРДАНА
Проверим, что неотрицательная функция ц(Р), определенная для измеримых фигур на плоскости, обладает свойствами монотонности, инвариантности относительно движений плоскости и аддитивности, имеющих место для простейших фигур.
Во-первых, покажем, что множество измеримых фигур замкнуто относительно теоретико-множественных операций: объединения, пересечения и разности множеств. Другими словами, если фигуры Рг и Р2 измеримы, то измеримыми по Жордану являются фигуры Рх U Р2, ?i П Р2, Pi \ Р2»
Докажем сначала измеримость объединения двух множеств. В силу критерия измеримости множества по Жордану достаточно показать, что U Р2)) = 0. Докажем, что
Э(РХ U Р2) с дРг U ЭР2.
Возьмем любое х е 9(Pt U Р2). Предположим, что х £ ЭРр х <£ дР2. Тогда точка х является либо внутренней точкой Р19 либо внутренней точкой Р2, либо внешней точкой и Рр и Р2. Отсюда следует, что точка х по отношению ко множеству Pr U Р2 является либо внутренней, либо внешней точкой. Но это противоречит тому факту, что точка х принадлежит границе множества Рх U Р2. Следовательно, граница объединения двух множеств является подмножеством объединения границ этих множеств.
Поместим измеримые множества Pt и Р2 в стандартный квадрат К. Тогда множества К \ Рг и К \ Р2 являются измеримыми по Жордану, так как их граница содержится в объединении границ множеств К9 Рг и Р2. Отсюда следует измеримость множеств
Pi\P29 P1AP2 = ^\(^\P1)U(^\P2).
Рассмотрим теперь свойства монотонности функции ц(Р). Если Pi а Р2, то всякая простейшая фигура, описанная вокруг Р2, содержит и Рр поэтому рЧ?!) < p*(P2)’ Но так как фигуры Рх и Р2 измеримы, то
ц(Р1) = ц*(Р1)<ц*(Р2) = И(Р2).
Это и означает, что функция ц(Р) является монотонной.
Инвариантность меры Жордана относительно параллельных переносов следует из того, что при параллельном переносе площадь простейшей фигуры не меняется, поэтому при сдвигах плоскости не меняется значение величин р*(Р) и ц*(Р).
250
Далее, по теореме Шаля все движения плоскости сводятся к симметриям, сдвигам и поворотам плоскости относительно некоторой неподвижной точки. Так что для завершения доказательства инвариантности меры Жордана относительно движений плоскости достаточно показать, что она инвариантна относительно поворотов плоскости вокруг некоторой неподвижной точки. Заметим, что при повороте плоскости площадь простейшей фигуры не меняется, но она уже перестает быть простейшей.
Итак, пусть задана измеримая по Жордану фигура Р. Тогда существуют простейшие фигуры Рр Р2 такие, что Рх с Р с Р2, причем
Ц(Л) < ЩР) < р(Рх) + е, ц(Р2) - е < |1(Р) < р(Р2),
и Рр Р2 можно представить в виде объединения конечного числа стандартных прямоугольников. При повороте плоскости вокруг неподвижной точки фигуры Р, Рх и Р2 перейдут соответственно в измеримые фигуры Q, Qx и Q2, причем Qx с Q с Q2. Очевидно, достаточно показать, что если стандартный прямоугольник при повороте переходит в прямоугольник П, то его можно заключить в открытую простейшую фигуру Пх и вписать в него замкнутую простейшую фигуру П2 такие, что П2 с П с Щ и разность ц(Пх) -- ц(П2) может быть сделана сколь угодно малой. Для этого обрамляем прямоугольник П прямоугольником По со сторонами, параллельными сторонам П и находящимися от них на достаточно малом расстоянии. Затем вписываем в По простейшую фигуру, которая содержит П. Она и будет искомой фигурой ПР Фигура П2 строится аналогично.
Докажем теперь свойство аддитивности меры Жордана. Заметим сначала, что для простейших фигур справедливо неравенство
g(A U В) < ц(А) + ц(В).
Далее, пусть фигуры Рх и Р2 измеримы по Жордану и пусть Р = Pr U Р2, Рг А Р2 = 0. Тогда по критерию измеримости множества фигура Р измерима, поскольку граница объединения двух множеств содержится в объединении границ самих множеств. Докажем, что имеет место равенство
р(Р) = ц(Р1) + ц(Р2).
В силу измеримости фигур Рг и Р2 для всякого е > 0 найдутся простейшие фигуры Qx и Q2, Rr и R2 такие, что
U(Qi) < H(-Pi) < g(Qi) + е, H(Q2) - е < u(Pi) < h(Q2)> и(7?1) < Ц(-Р2) < н(д1) + Е, |X(-R2) - е <	< Н(Я2)-
251
Кроме того, для простейших фигур Q1nR1c условием Qx П = 0 имеем p(Qx U Rj) = p(Qx) + а также |i(Q2 и ^2) < |XQ2)+ У-(Я2). Поэтому, учитывая теоретико-множественные включения
Q1UB1cP1UP2 = PgQ2UB2, получаем
g(Qi) +11(7?!) = p(Qx U RJ < ц(Р) < p(Q2 U Я2) < p(Q2) + ц(Я2) < < iXQj) + ii^) + 4 е.
Также очевидно, что
Ц(С1) + ц(^1) < Ц(Л) + н(р2) < H(Q1) + Н(Я1) + 2е.
Из последних неравенств найдем
|ц(Р)-ц(Р1)-р(Р2)|<4е.
В силу же произвольности выбора е > 0 имеем р(Р) = р(Р1) + р(Р2).
Это и доказывает свойство аддитивности меры Жордана.
§ 4. ИЗМЕРИМОСТЬ СПРЯМЛЯЕМОЙ КРИВОЙ
Покажем, что если L — спрямляемая кривая, то ее плоская мера Жордана равна нулю. Значит, в силу критерия измеримости фигуры по Жордану, будет измеримой фигура, ограниченная спрямляемой кривой.
В дальнейшем потребуется следующая лемма о спрямляемых кривых.
ЛЕММА 2. Пусть кривая L задается уравнениями вида х = ср(О, у = у(0, t € [а, &] и является спрямляемой кривой. Тогда длина s(t) части этой кривой, соответствующей отрезку [а, J], где t е [а, Ь] — непрерывная и монотонно возрастающая функция параметра t.
► Возрастание функции s(t) следует из свойства аддитивности длины дуги кривой. Действительно, при < t2 имеем s(t2) — = s(^1) + s0, где s0 — длина дуги кривой, находящейся между точками Аг = (<p(£x), V(^!)) и А2 = (<р(£2),	т* е* величина s0 поло-
жительна. Отсюда имеем: s(t2) > s(^x).
Докажем, что функция s(t) не имеет разрывов. В самом деле, пусть в точке t0 функция s(t) имеет разрыв. Тогда в силу монотонности з(0 точка t0 является точкой разрыва первого рода со скачком h > 0. Значит, для любого отрезка t2], содержащего эту точку t0, длина дуги кривой, отвечающей этому отрезку t2], превосходит h.
Далее, исходная кривая L является спрямляемой, поэтому для всякого числа е > 0 существует вписанная ломаная I такая, что 0 < s(L) - s(l) < е. Эта ломаная порождает неразмеченное разбиение Т : а = tQ < tx < ... < tn = Ь отрезка [а, &], и каждая точка Ak =	W*)) отвечает некоторому узлу ломаной I. Очевидно,
для любого наперед заданного положительного числа 8 можно считать, что Дг < 8. Ясно, что длина lk звена ломаной с номером k удовлетворяет условию
Пусть точка tQ принадлежит некоторому интервалу (tk_19 tk+1). В силу равномерной непрерывности функций ф(£) и \|/(£) на отрезке [а, &] существует положительное число 8 такое, что для всех t', t" с условием - t"\ <8 выполняются неравенства
|ф(Г) - ф(Г)| < I, |ф(t') - y(t")| < | • Следовательно, имеем
lk = 7(Ф(Г) - Ф(П)2 + W') - ф(П)2 < Л/4, lk+l <h/4.
Отсюда и из условия спрямляемости кривой получаем
Л/2 = h — 2Л/4 <	~	~ (lk + ^fe+i) ” s(0 <
Последнее неравенство справедливо при любом е > 0, но при £ = й/2 > 0 оно противоречиво. Следовательно, предположение о разрывности функции s(t) не имеет места. ◄
ТЕОРЕМА 2. Пусть L — спрямляемая кривая. Тогда она имеет плоскую меру Жордана, равную нулю.
► Разделим кривую L на п дуг, длина каждой из которых равна а = s(L)/n. Это возможно, поскольку функция s(t) является монотонной и непрерывной. Тогда k-я дуга кривой L при k = 1, ... , п целиком лежит внутри квадрата со сторонами, параллельными осям координат и равными 2а, и центром в А-й точке деления кривой L. Объединение всех квадратов образует простейшую фигуру Р9 целиком покрывающую L, причем
ц(Р) < п(2а)2 = 4п • =	.
Устремим п к бесконечности. Получаем ц*(Ь) = 0, значит, и p(L) = = 0. ◄
СЛЕДСТВИЕ. Пусть граница фигуры Р является спрямляемой кривой. Тогда Р измерима по Жордану.
► В силу критерия измеримости и предыдущей теоремы получаем измеримость фигуры Р. ◄
253
$ 5. СВЯЗЬ МЕЖДУ ИНТЕГРИРУЕМОСТЬЮ ФУНКЦИИ ПО РИМАНУ И ИЗМЕРИМОСТЬЮ ПО ЖОРДАНУ ЕЕ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ
Рассмотрим криволинейную трапецию Р, ограниченную кривыми у = Дх), у — 0, х = а, х = Ь. Имеет место следующий критерий интегрируемости функции по Риману.
ТЕОРЕМА 3. Пусть функция f(x) ограничена и неотрицательна на отрезке \а9 &]. Тогда для интегрируемости функции f(x) по Риману необходимо и достаточно, чтобы криволинейная трапеция Р9 отвечающая кривой у = f(x), была измерима по Жордану.
► Необходимость. Дано, что функция Дх) интегрируема по Риману. Тогда в силу критерия интегрируемости имеем, что для любого е > 0 найдется разбиение отрезка [а, Ь] такое, что S(T) -- з(Т) < е, где S(T), s(T) — соответственно верхняя и нижняя суммы Дарбу, отвечающие разбиению Т.
Замкнутая простейшая фигура Р19 соответствующая верхней сумме Дарбу S(T), объемлет криволинейную трапецию Р, а замкнутая простейшая фигура Р2, соответствующая нижней сумме Дарбу з(Т), вписана в нее, т. е. имеют место теоретико-множественные включения Р2 сР сРх и отвечающие им неравенства
з(Т) = ц(Р2) < МР) < И*(Р) < И(Р1) - S(T).
Так как справедливо неравенство S(T) - s(T) = pCPJ - ц(Р2) < e, то p*(P) - p*(P) < e. Отсюда в силу произвольности выбора числа е > 0 имеем, что р*(Р) = ц*(Р), т- е- криволинейная трапеция Р измерима по Жордану. Необходимость доказана.
Достаточность. В силу критерия измеримости граница ЭР криволинейной трапеции Р имеет плоскую жорданову меру нуль. Следовательно, плоская мера Жордана ее части: кривой L вида у = Дх), а < х < Ь равна нулю. Поэтому для всякого е > 0 существует простейшая фигура Q такая, что L с Q, p(Q) < е. Продолжим вертикальные отрезки сторон стандартных прямоугольников, составляющих фигуру Q, до пересечения с осью Ох. Эти точки пересечения дадут разбиение Т отрезка [а, &]. Обозначим через Qt простейшую фигуру, лежащую под фигурой Q в области у > 0, а через Q2 обозначим фигуру Q U Qv Тогда имеем
Qi <= Р cz Q2, p(Q2) - pCQi) = p(Q) < e.
Заметим, что фигуре Qx соответствует нижняя сумма Дарбу, а фигуре Q2 — верхняя сумма Дарбу. Следовательно, S(T) - s(T) < е, т. е.
inf (S(T) - s(T)) = О,
254
значит, по критерию интегрируемости функция Дх) является интегрируемой. ◄
ПРИМЕРЫ. 1. Соображения, использованные при доказательстве первой части предыдущей теоремы, показывают, что площадь криволинейной трапеции
Р : у - Дх) > 0, у = 0, х = а9 х - &, равна
ц(Р)= jf(x)dx. а
2. Площадь криволинейного сектора Р, граница которого задана в полярных координатах уравнениями г — Дф), ф = а, ф = 0, определяется по формуле
1 ₽ И(Р) - 5 J ^ФМФ-
а
Доказательство этой формулы опирается на свойство монотонности меры Жордана. Разобьем отрезок [а, р] на п равных частей точками а = ф0 < фх < ... < фл = р. Кривая г = Дф) точками АЛ(гЛ, фА), = ДфЛ), разбивается на п дуг, а сектор Р — на п малых секторов Pk. Пусть
/* = min Лф), Fk = max Дф). Фе(ф*~1» Ф*]	фе[ф*_1,Ф*]
Тогда площадь ft-го криволинейного сектора содержит круговой сектор радиуса fk и находится внутри сектора радиуса Fk. Используя формулу площади кругового сектора и свойство монотонности пЛощади, имеем
| /*Аф* < iW < | **ДФ*» дФл = Ф*+1 ~ Фь-
Отсюда получаем 1 п	1 п
*п = I Л 42дф*< н(Р) < I =<8„.
Суммы sn и Sn являются нижними и верхними суммами Дарбу для интеграла
1 р 1=И/2(фМф-
Л а
Поскольку функция Дф) — непрерывна, /2(ф) непрерывна и интегрируема, при п -» оо имеем sn —> Z, Sn —> Z. Отсюда получаем |i(P) = Z. Утверждение доказано.
Аналогично можно вычислять и объемы различных фигур, вписывая в них и описывая вокруг них простейшие фигуры, за-
255
висящие от некоторого параметра п, и устремляя затем его к бесконечности. Подобным образом находил площади и объемы еще Ацхимед, т. е. мы применили метод исчерпывания, принадлежащий Архимеду.
Итак, понятие измеримости по Жордану позволяет значительно расширить класс фигур Р на плоскости и в пространстве, которым можно приписать значение площади или объема ц(Р). Однако легко можно привести пример плоского множества Р, не измеримого по Жордану. Рассмотрим, например, функцию Дирихле %(х) на отрезке [0, 1]:
_ J 1, если х — рациональное число, лхх) [0, если х — иррациональное число.
Пусть Р — криволинейная трапеция, соответствующая этой функции, т. е. множество точек (х, у) на плоскости хОу9 определяемое для всякого х, принадлежащего отрезку [0, 1], условиями 0 < у < %(х).
Очевидно, что любая простая фигура, содержащая Р, должна содержать единичный квадрат, и поэтому верхняя мера ее р*(Р) равна единице. Но в то же время простые фигуры, вписанные в Р, могут, очевидно, состоять только из конечного числа отрезков, и они имеют поэтому нулевую площадь, следовательно, нижняя мера фигуры Р равна нулю. Значит, фигура Р неизмерима по Жордану. Здравый смысл показывает, что фигуре Р, тем не менее, разумно приписать меру нуль, по следующей причине.
Как известно, рациональные точки отрезка можно занумеровать, поэтому фигура Р состоит из счетного числа отрезков. Возьмем любое е > 0 и накроем первый отрезок прямоугольником, площадь которого равна е/2, второй отрезок — прямоугольником площадью е/22 и т. д. Тогда вся фигура покроется счетным количеством стандартных прямоугольников, а их общая площадь не превышает величины
е/2 + е/22 + е/23 + ... = е.
Так как фигура Р накрыта прямоугольниками, общая площадь которых не превышает е, то естественно считать, что и площадь фигуры Р тоже не превосходит е, а это может быть только в том случае, если она равна нулю.
Тем самым теперь можно определить понятие площади даже для фигур, которые неизмеримы по Жордану. Развивая этот подход, приходим к понятию меры Лебега, которое можно построить для пространства любой фиксированной размерности, в том числе и для прямой R.
ГЛАВА 12
Элементы теории меры и интеграла Лебега. Интеграл Стильтьеса
Лекция 15
§ 1. ОПРЕДЕЛЕНИЕ И СВОЙСТВА МЕРЫ ЛЕБЕГА
Рассмотрим случай плоской меры Лебега.
Определение 1. Пусть ограниченная плоская фигура Р покрыта конечным или счетным множеством стандартных открытых прямоугольников hn, п = 1, ... . Совокупность Н = {hn} всех этих прямоугольников назовем покрытием плоского множества Р (или фигуры Р). Величину
назовем мерой покрытия Н. Открытую простейшую фигуру Н будем называть простейшим множеством.
Заметим, что величина ця всегда неотрицательна.
Определение 2. Число ц*(Р) = inf ця, где инфимум берется по всем возможным покрытиям простейшими множествами фигуры Р9 называется верхней мерой Лебега фигуры Р.
Очевидно, имеем 0 < ц*(Р) < +°°, поскольку в силу ограниченности фигуры Р найдется стандартный квадрат К со стороной I такой, что Р cz К. Отсюда получаем, что ц*(Р) < I2.
Определение 3. Пусть СР = К \ Р, где К — стандартный квадрат, покрывающий фигуру Р. Нижней мерой Лебега плоского множества Р назовем число
МР) = ц(^)-ц*(СР).
Определение 4. Плоское множество Р называется измеримым по Лебегу, если
ц*(Р) = МР) = ц(РЬ
а число ц(Р) называется плоской мерой Лебега.
Докажем следующий критерий измеримости множества по Лебегу.
9-4953
257
ТЕОРЕМА 1. Пусть А — ограниченное множество. Тогда для измеримости по Лебегу множества А необходимо и достаток’ но9 чтобы выполнялось следующее условие*, для всякого е > О существует простейшее множество В = В(ё) такое, что справедливо неравенство
ц*(АДВ) < е.
Это значит, что любое измеримое по Лебегу множество с любой степенью точности может быть аппроксимировано простейшими множествами.
► Необходимость. В силу ограниченности множества А существует стандартный квадрат К, покрывающий А, т. е. А с К. Дано, что множество А — измеримо, следовательно, Ц*(А) = Ц*(А), т. е. Р*(А) + и*(^\А) = и(ЛГ).
Из определения верхней меры Лебега имеем, что для любого е > 0 существует последовательность открытых стандартных прямоугольников {Сл}, покрывающая множество А, т. е. А с С = д U х Сп, и такая, что
p*(A)< J1g(C„)<p*(A) + e/2.
Аналогично, найдется последовательность стандартных прямоугольников {Dn} такая, что
К \ А с пи х Dn = D,Y(K \ А) < J1 рЦ)„) < J1U \ А) + е/2.
Отметим, что множества С и D образуют покрытие квадрата К. Так как ряд Ъ ц(С„) сходится, то существует номер k = fe(e/2) та-
кой, что . Z,, ц(С„) < е/2.
Положим
Заметим, что множества В и Р образуют покрытие множества А, т. е. В U Р z> А, и, следовательно, множество Р содержит А \ В. Имеем также, что множество Q содержит В \ А. В самом деле,
© = ВПВз>ВП(К\А) = В\А.
Таким образом,
Р U Q э (А \ В) U (В \ А) = А АВ.
Оценим сверху величину ц(Р U Q). Поскольку для любых двух простейших множеств FtilG справедливо равенство
ц(Р U G) = p(F) + ц(С) - p(F П G),
258
получаем
И(Р U Q) = Ц(С П D) = Ц(С) + |i(D) - ц(С U D) < < Ц*(А) + е/2 + |i*(tf \ А) + е/2 -	= е.
Следовательно, для любого е > 0 найдено множество В — В(е) такое, что
ц(АДВ) < |i(P U Q) < е.
Достаточность. Дано, что для любого е > 0 существует простейшее множество В = В(е/2) такое, что |1*(АДВ) < е/2. Далее, поскольку В А (А \ В) = 0, А Л (В \ А) = 0, справедливы неравенства
ц(В) + И*(А \ В) > Ц*(А), Ц*(А) + Ц*(В \ А) > р(В).
Отсюда и из условия А \ В сАЛВ, В \ А 4AR имеем
Ц*(А) - Ц(В) < Ц*(А \ В) < Ц*(АДВ) < е/2, |1(В) - Ц*(А) < Ц*(В \ А) < Ц*(АДВ) < е/2, т. е. |р*(А) - Ц(В)| < е/2.
Далее, поскольку множество А ограничено, существует стандартный квадрат К такой, что К э А. Очевидно, имеем
(К\А)ЩК\В)=АДВ.
Поэтому, как и раньше,
|nU \A)-p(tf\B)| <е/2.
Используя равенство |1(В) +	\ В) = p.(iT), получаем
|ц*(А) + № \ А) - МК)\ < IpU) - Ц(В)I +1 ии \ А) - р(К \ В)| < е, т. е. |р*(А) + р*(^ \ А) - ц(ЛГ)| < е. В силу произвольности выбора числа е > 0 отсюда следует, что
ц*(А) + ц*(^\А)-ц(^)==О,
т. е. Ц*(А) = ц(ЛГ) -	\ А) = ц*(А). Последнее равенство и озна-
чает, что множество А измеримо. ◄
Исходя из доказанного критерия, очевидно, имеем, что для любых измеримых множеств А и В их объединение, пересечение, разность и симметрическая разность являются измеримыми множествами. Более того, если измеримые множества А и В не пересекаются, то
ц(А U В) = ц(А) + ц(В).
Мы не будем детально изучать свойства множеств, измеримых по Лебегу, однако отметим, что это ненамного сложнее, чем изучение измеримости по Жордану. Тем не менее, мера Лебега обладает существенным преимуществом перед мерой Жордана,
259
9*
так как помимо свойств инвариантности относительно движений плоскости и монотонности, она обладает свойством счетной аддитивности взамен свойства конечной аддитивности, которым обладала мера Жордана.
ТЕОРЕМА 2. Пусть Av ... , Ап, ... — бесконечная последовательность непересекающихся множеств, измеримых по Лебе-оо
гу. Пусть их объединение А = л U х Ап является ограниченным множеством. Тогда множество А измеримо по Лебегу, причем
Ц(^) =	(MU1) + ... + |i(An)) = £ t |1(А„).
► Так как множество А ограничено, то существует стандартный квадрат К, содержащий А. В силу этого и свойства конечной аддитивности для любого фиксированного числа k > 1 имеем соотношения
п?1ц(Ап) = ц(лУ1Ап]<И(^).
Отсюда следует, что ряд ц(Ап) сходится, поэтому для любого е > 0 существует /?0 = /?0(е) такое, что для любого числа k > kQ вы-
полняется неравенство ц(Ап) < е/2.
Зафиксируем какое-нибудь число k, большее kQ. Тогда множе-k
ство С = п U Ап — измеримо, следовательно, по критерию измеримости (теорема 1) для всякого е > 0 существует простейшее множество В = В(е/2) такое, что р*(САВ) < е/2.
Очевидно, справедливо следующее соотношение:
AABc(CAB)uf U АЛ1
v ' Kn=fe+1 п)
Используя неравенство
nXi(l(A.)<C/2,
получаем, что р*(АДВ) < е. Следовательно, множество А — измеримо. Аналогично доказывается, что и множество Ck = Ап является измеримым.
Далее, в силу свойства конечной аддитивности имеем
k
ц(А) = Д1И(Ай) + р(С*).
Кроме того, ранее было показано, что Jun |nCfe = 0, а это значит, что
оо
260
Важным следствием доказанного выше свойства счетной аддитивности меры Лебега является измеримость пересечения счетного числа измеримых множеств, а также измеримость объединения счётного или конечного числа измеримых множеств при условии ограниченности этого объединения.
В частности, отсюда имеем измеримость любого ограниченного открытого множества как объединения не более чем счетного числа открытых стандартных прямоугольников. Но тогда и любое замкнутое множество измеримо как дополнение до открытого множества, следовательно, будет измеримым по Лебегу и любое не более, чем счетное, объединение и пересечение открытых и замкнутых множеств.
Докажем еще одно полезное свойство меры Лебега: свойство непрерывности.
ТЕОРЕМА 3. Пусть Ар ... , Ап, ... — измеримые множества, и пусть А = лУ1 Ап — ограниченное множество. Кроме того, пусть At сА2а ... с Ап с ... . Тогда ц(А) = Ит^ ц(Ап).
► Имеем
Ап = Ах U (А2 \ AJ U ... U (Ад \ Ал_х), А = Ах J 2 (Ав \ Ав_х), причем для любых s, t > 2, s * t, справедливы соотношения
Ах П(А8 \ As_x) = 0, (Ag \ As_x) А (АД А,_х) = 0.
В силу свойства счетной аддитивности меры получаем
lim ц(Ап) = цОМ + Е |1(AS \ A J = ц(А). ◄ fl	О
Отметим, что не всякое множество на плоскости измеримо по Лебегу, но неизмеримые множества имеют «экзотический» вид.
Ответим на вопрос, как связаны между собой понятия измеримых множеств для разных размерностей. Например, если имеется измеримая плоская фигура Р и мы будем пересекать ее прямыми параллельными одной из осей координат. В этом случае в сечении будут получаться линейные ограниченные множества. Вопрос, измеримы ли они по Лебегу, имеет принципиально важное значение. За исключением некоторого множества прямых, которое в пересечении с другой осью координат образует множество линейной меры нуль, они будут измеримы.
Вообще, если какое-нибудь условие выполнено для всех точек множества М с R, за исключением множества точек М' а М, мера которого равна нулю, ц(М') = 0, то говорят, что это условие имеет место для почти всех точек множества М. Почти все в смысле меры Лебега означает, что некоторое свойство выполня
261
ется на всем множестве, за исключением, быть может, множества меры нуль.
Рассмотрим теперь линейную меру Лебега, т. е. меру Лебега для ограниченных множеств на числовой прямой R. Очевидно, что счетное множество имеет меру нуль. Возможен еще один вопрос: существуют ли несчетные множества меры нуль? Да, существуют, например, канторово совершенное множество М, являющееся подмножеством отрезка [0, 1] и состоящее из тех чисел, которые записываются в троичной системе счисления в виде бесконечной дроби, не содержащей цифры 1. Например, числа О, 2; 0,200202; 0,222...2... = 1 ит. д.
Очевидно, множество М имеет мощность континуума, в то же время его получают так: отрезок [0,1] делят на три равные части и выбрасывают средний интервал (1/3, 2/3), затем эту процедуру повторяют с каждым из двух отрезков, полученных после первого деления, и т. д.
Пусть Eq — исходный отрезок [0, 1], Ег — множество, которое осталось после первого шага, Е2 — множество, оставшееся после второго шага, и т. д. оо
Очевидно, Eq z> Ег z>... z> Еп id... и множество М равно 1 Еп. Тогда при любом n > 1 для верхней меры множества М справедливы оценки ц*(М) < ц(Еп). Очевидно, имеем
ц(Еп) = (2/3)2 ц(Е0) = (2/3)" -> 0 при п оо.
Следовательно, мера множества М равна нулю.
Заканчивая рассмотрение основ теории меры Лебега, заметим, что теорема 1 позволяет дать другое определение меры Лебега, не требующее введения понятия нижней меры и расширяющее класс измеримых множеств на неограниченные множества.
Лекция 16
§2. ИНТЕГРАЛ ЛЕБЕГА
Понятие линейной меры Лебега позволяет расширить класс интегрируемых функций с помощью введения понятия интеграла Лебега. Для того чтобы сказать, что это такое, сначала введем понятие измеримой функции.
Определение 5. Функция Дх), заданная на отрезке [а, Ь], называется измеримой на этом отрезке, если для всякого у е R множество Е точек х е [а, &], для которых выполняется неравенство Дх) < у, является измеримым множеством на отрезке [а, Ь] в смысле линейной меры Лебега.
Из свойств меры Лебега, доказанных в предыдущем параграфе, имеем, что вместе с множеством Е измеримыми являются множества точек х е [а, Ь], для которых справедливы соотноше-НИЯ fix) > у, fix) = y,Z< fix) < у.
В частности, любая непрерывная на отрезке [а, Ь] функция fix) измерима, поскольку множество Iy = {х € [а, 6]| fix) > у} будет замкнутым, а любое замкнутое множество является измеримым.
В качестве второго примера измеримой на отрезке I = [а, 6] функции Дх) рассмотрим ограниченную функцию, имеющую разрывы на множестве лебеговой меры нуль. В силу критерия Лебега она интегрируема по Риману. Покажем, что эта функция является измеримой.
Возьмем любое число у € R. Достаточно показать, что множество 1у = {х е /| Дх) > у} является измеримым. Предельные точки х0 множества 1у могут быть двух видов: точками непрерывности функции Дх) и ее точками разрыва. Если такая точка х0 — точка непрерывности, то она обязана принадлежать 1у. Действительно, поскольку х0 — предельная точка множества 1у, существует последовательность точек хп е 1у таких, что
Л™ хп = хо> f(xn)>y.
Отсюда в силу непрерывности Дх) в точке х0 имеем
у< Jin	w л Jin х»)=
т. е. точка х0 принадлежит 1у.
Если же предельная точка х0 множества 1у не принадлежит 1у, то она является точкой разрыва функции Дх). Обозначим множество всех таких точек х0 через F. Множество F имеет меру нуль как подмножество множества нулевой меры Лебега.
263
В силу того, что множество А = Iy U F — замкнуто, оно измеримо. Следовательно, множество 1у — измеримо, как разность измеримого множества и множества меры нуль. Тем самым установлена измеримость функции, имеющей множество точек разрыва нулевой меры Лебега.
Рассмотрим далее функцию /(х), заданную на отрезке [а, Ь], ограниченную и измеримую на нем. Тогда для некоторого М > О для всех точек х е [а, Ь] выполняется неравенство |/(х)| < М. Отрезок [-М, М] на оси ординат разобьем на п равных частей: -М = Ув<У1 ... < уп = М. Множество точек х, удовлетворяющих условию ys < /(х) < ys+19 обозначим через Es, s = 0, ... , п - 1. Заметим, что множество Es — измеримо и положим ц8 = |1(Е8).
п - 1
Определение 6. Сумма Sn = gL0 |i8z/8 называется интегральной суммой Лебега.
Можно доказать, что всегда существует предел I = Sn. Этот предел называется интегралом Лебега от функции /(х) по
ь
отрезку [а, &] и обозначается так: (L) J f(x)dx. Поскольку для лю-а
бой интегрируемой по Риману функции множество точек разрыва имеет меру нуль (критерий Лебега), в силу доказанного выше она измерима по Лебегу. Более того, интеграл Лебега от этой функции равен интегралу Римана. Действительно, пусть Т : а = = х0 < хх < ... < хп = Ь — произвольное разбиение отрезка [а, &], Аг = [хг — 1, xj, Ахг = х, - х£_р = inf ftx), Mt = sup ftx). Тогда xeA, для интеграла Лебега имеют место неравенства
xi mi^xi < (L) J f(x)dx < MzAxf. xi-i
Следовательно, в силу аддитивности интеграла Лебега, для верхней S(T) и нижней з(Т) сумм Дарбу получаем
s(T) < (L) j f(x)dx < S(T). a
Отсюда, переходя к пределу при диаметре Дг разбиения Т, стремящемся к нулю, имеем
ь lim s(T) = lim S(T) = (Я) J f(x) dx. дг -> о	дг -> о	д
Таким образом, мы доказали, что интеграл Лебега равен интегралу Римана, если последний существует. Заметим, что поэтому
264

для интеграла Лебега используется то же обозначение, что и для интеграла Римана.
Перейдем теперь к рассмотрению неограниченных измеримых функций на отрезке [а, Ь]. Рассмотрим сначала случай неотрицательной функции Дх). Для любого вещественного числа у определим функцию fy(x) следующим образом:
Дх), если Дх) < у, у, если Дх) > у.
Эта функция измерима. Тогда интегралом от функции Дх) на отрезке [а, Ь] называется предел
ь	ь
 J f(x)dx = lim J f(x)dx. a	a
Если этот предел конечен, то функция Дх) называется суммируемой. Очевидно, что суммируемая функция может обращаться в бесконечность лишь на множестве лебеговой меры нуль.
Пусть теперь функция Дх) принимает значения произвольного знака. Тогда определим функции
f+ (х) = тах(/(х), 0), f_ (х) = тах(-/(х), 0).
Будем говорить, что функция Дх) суммируема, если суммируемы обе функции Д_(х) и /_(х), и интеграл от функции Дх) равен разности интегралов от функций /+(х) и f_(x)*
Отметим, что в случае ограниченной функции Дх) на отрезке [а, &] понятия суммируемой и измеримой функций совпадают. Из определения суммируемой функции непосредственно следует, что:
1)	вместе с Дх) будет суммируемой функция |Дх)|, при этом модуль интеграла от подынтегральной функции Дх) не превосходит интеграла от модуля этой функции;
2)	если Дх) — измерима и |Дх)| — суммируема, то функция Дх) — суммируема;
3)	если Дх) — измерима и модуль ее не превосходит суммируемой функции g(x), то функция Дх) — суммируема;
4)	если Дх) — суммируема и g(x) — ограниченная измеримая функция, то их произведение является суммируемой функцией;
5)	если Дх) — суммируемая функция и g(x) не совпадает с ней на множестве меры нуль, то функция g(x) — суммируема, и интегралы от этих функций равны между собой.
Отметим еще, что для интеграла Лебега от суммируемой функции верны те же свойства, что и для интеграла Римана, но кроме этого добавляется еще одно важное свойство: свойство
265
счетной аддитивности интеграла Лебега; Его можно сформулировать так.	. .
Пусть на отрезке [а, &] задано счетное разбиение единицы, т. е. задано счетное множество измеримых функций gn(x)9 принимающих всего два значения 0 и 1, причем для любого х е [а, &] одна и только одна функция gn(x) отлична от нуля. Тогда для всякой суммируемой функции Дх) на отрезке [а, Ь] имеем
Ь	оо Ь
J f(x) dx = Z J Дх) gn(x) dx. a	a
Это свойство можно сформулировать и по-другому. Пусть отрезок [а9 Ь] разбит на непересекающееся семейство измеримых множеств Еп. Тогда интегралы от функции Дх) по множествам Еп существуют и имеет место равенство
J f(x)dx = Z J f(x)dx.
а	е„
Интеграл по множеству Еп можно записать и так:
J Дх) dx - f Дх) я„(х) dx,
Е.	а
где gn(x) — индикаторная функция множества Еп9 т. е.
z ч [1, если х € Еп9 j о, если х £ Д*.
В заключение отметим, что в случае интеграла Лебега упрощается по сравнению с интегралом Римана предельный переход под знаком интеграла. Приведем точную формулировку этого утверждения.
ТЕОРЕМА 4 (теорема Лебега). Пусть на отрезке [а, &] последовательность измеримых функций fn(x) сходится к функции Дх) и пусть для некоторой суммируемой функции g(x) на отрезке [а, Ь] выполнено неравенство |/л(х)| < g(x). Тогда предельная функция Дх) — суммируема и имеет место равенство ь	ь
Jim J fn(x) dx = J Дх) dx.
► По условию теоремы абсолютные величины функций /п(х), и > 1, не превосходят суммируемой функции <р(х). Следовательно, и абсолютная величина предельной функции Дх) не
266
превосходит <р(х), и, значит, она является суммируемой функцией.
&
Надо доказать, что Шп J gn(x) dx = 0, где gn(x) = f(x) - /п(х).
Зададимся произвольным числом е > 0. Для каждого п > 1 определим множество Ап тех точек х, для которых |gn(x)l > £1 = 7777^—г. 3(о ~ а)
Тогда в силу упомянутого выше свойства счетной аддитивности меры Лебега справедливо равенство ц(Ап) = 0. В противном случае нашлась бы точка х такая, что для бесконечного множества значений п выполнялось неравенство |gn(x)| > ер а это противоречит тому, что
lim gn(x) = 0. п -4 оо "
ft
Представим интеграл J = J gn(x) dx в виде а
** ~ 67 1 ' ^2’
где<7х= J g„(x)dx,J2 = f gn(x) dx, I = [a, 6]. /\А,	a.
По теореме о среднем имеем
1Л1 <ех (Ъ~а)~ |,
а для интеграла J2 справедлива оценка
| J2| < J |gn(x)| dx < 2 J g(x) dx.
Пусть Bm = {x e An|g(x) > тп}. Тогда в силу сходимости интеграла Ф = J (р(х) dx имеем
А.
lim J g(x)dx = O.
Вт
Следовательно, существует mQ е N такое, что для всех т > т0 имеет место неравенство J g(x)dx < е/3.
вм
Далее, представим интеграл Ф в виде Ф = Фх + Ф2, где
Фх = / g(x)dx, Ф2= J g(x)dx. в„	л,\вп
В силу теоремы о среднем имеем
|Ф2| < тц(Ап \ Вт) < Ш|Д.(АП).
267
Поскольку мера множества Ап стремится к нулю при п -> оо, при любом фиксированном т > тп0 можно указать n0 g N такое, что для всех п > п0 справедливо неравенство
|Ф2| < тц(Ап) < е/3.
Следовательно, для любого е > 0 мы нашли n0 е N такое, что для всех п > п0 выполняется неравенство
ь	ь
J gAx)dx < е, т. е. lim J gn(x)dx = 0. ◄
Отметим еще один факт, состоящий в том, что для ограниченной неотрицательной функции интегрируемость по Лебегу эквивалентна измеримости по Лебегу ее криволинейной трапеции.
Лекция 17
§ 3. ИНТЕГРАЛ СТИЛЬТЬЕСА
Имеется еще одно обобщение понятия интеграла Римана — это интеграл Стильтьеса. Он отражает другую особенность интеграла Римана по сравнению с интегралом Лебега. Если мера Лебега и интеграл Лебега вводились для того, чтобы расширить класс измеримых множеств и класс интегрируемых функций, то введением интеграла Стильтьеса решается другая задача. Суть ее состоит в следующем. На фиксированном отрезке [а, Ь] интеграл
I = J f(x)dx а
— это число, которое ставится в соответствие каждой интегрируемой функции. Тем самым интеграл Римана задает некоторую числовую функцию, определенную на множестве {/} всех функций, интегрируемых на отрезке [а, Ь]. Сузим класс функций и будем рассматривать непрерывные функции, определенные на отрезке [а, &]. Множество всех таких функций принято обозначать символом С[а, &], причем для каждой функции f е С[а, Ь] определяют величину ||f|| = max |Дх)|, называемую нормой х€[а, Ь]
функции f(x) в пространстве С[а, &]. Пусть f е С[а, Ь], тогда, как мы знаем, функция f интегрируема по Риману на отрезке [а, &] и
ь
1(f) = j f(x)dx.
а
1(f) — линейная числовая функция, т. е. для любых f,ge С\а, Ь] и любых а, р g R справедливо равенство
I(af + fig) = al(f) + $I(g).
Напомним, что числовые функции, определенные на множестве, элементами которого являются функции, во избежание путаницы называют функционалами. Более того, функционал Z, ставящий всякой функции f е С[а, Ь] в соответствие число 1(f), называется линейным функционалом, если выполняются следующие свойства:
1°. Аддитивность
ДА + А) = ДА) + ДА) V А, А * С[а, ь].
2°. Однородность
I(cf) = cl(f) V се R,Vfe С[а, Ь].
3°. Ограниченность: существует М > 0 такое, что для любой функции f е С[а, &] справедливо неравенство |Д/)| < мIlf ||. На-именыпее из таких чисел М называется нормой линейного функционала I и обозначается ||Z ||.
269
Таким образом, интеграл Римана 1(f) задает линейный функционал на пространстве С[а9 &]. С помощью интеграла Римана на пространстве С[а, 6] можно построить много других линейных функционалов. Например, для любой фиксированной интегрируемой по Риману функции g(x) на пространстве С[а9 Ь] можно задать линейный функционал
W = J f(x)g(x)dx. а
Заметим, что, если функция G(x) такова, что для всякого х е [а,Ь] справедливо равенство g(x) = G'(x)9 то Ig(f) можно представить в виде о
Ig(f)=]f(x)dG(x). а
Для развития теории интегрирования и для некоторых ее приложений, например для теории вероятностей, вариационного исчисления, теоретической механики, важно знать ответ на вопрос: любой ли линейный функционал ф(/) на пространстве С[а9 &] можно представить в таком виде, т. е. всегда ли найдется такая функция g(x)9 что ь	ь
Ф(/) = I/f) = j f(x)g(x)dx = J f(x)dG(x). a	a
Легко понять, что если мы имеем дело с обычным интегралом Римана, то ответ отрицательный, так как тогда, например, функционал (р(/) = f(xQ)9 где х0 — фиксированная точка отрезка [а, &] (в частности, х0 « (а + &)/2), в таком виде представить нельзя. Однако можно расширить понятие интеграла Римана таким образом, что уже любой линейный функционал ф(/) на пространстве С [а , &] можно будет представить в виде
<р(/) = /г(хмад. а
Расширение понятия интеграла Римана в указанном направлении и достигается введением понятия интеграла Стильтъе-са. Для этого потребуется определить новый класс функций.
Определение 7. Функция и(х) называется функцией с ограниченным изменением или9 что то же самое, функцией ограниченной вариации на отрезке [а, &], если существует вещественное число М > 0 такое9 что для любого разбиения
Т : а = tQ< t}<	< tn = Ь
выполняется неравенство
V(f;T) =
270
Величина, равная sup V(f; Т) = Vb(f), называется полным из-т
менением или полкой вариацией функции Дх) на отрезке [а, &]. Отметим следующие свойства функций с ограниченным изменением на отрезке.
1°. Сумма двух функций с ограниченным изменением есть функция с ограниченным изменением.
Действительно, пусть й(х) — Дх) 4- g(x). Тогда для любого разбиения Т отрезка [а, &] справедливо неравенство
V(h; Т) < У(/; Т) + V(g; Г).
Отсюда следует, что полное изменение V^(h) функции Л(х) не превосходит суммы полных изменений функций Дх) и g(x).
2°. Ограниченная монотонная функция на отрезке [а, Ь] — функция с ограниченным изменением.
Рассмотрим только случай неубывающей функции Дх) на отрезке [а, &]. Имеем vba(f) = f(b)-f(a).
3°. Пусть а <с <Ьи функция f(x) имеет ограниченное изменение на отрезке [а, 6]. Тогда имеет место равенство
Vb(f) = V‘a(f) + Vb(f).
Возьмем любые разбиения й Т2 отрезков [а, с] и [с, 6] и положим Т = Тг U Т2. Тогда V(f; Т) = V(/; TJ + У(/; Т2). Так как
sup V(f, 7\) = Vca(f), sup V(f, T2) = Vb(f), M	T2
то, переходя в предыдущем равенстве к супремумам по разбиениям Тг и Т2, получим
П(П + vb(f) = т su?j, V(f, Т) < Vb(f).
Возьмем теперь любое разбиение Т отрезка [а, &] и добавим к нему точку с. Получим разбиения отрезка [а, с] и Т2 отрезка [с, &]. Тогда
V(f9 Т)<У(А ТО + УСА Г2).
Переходя в этом неравенстве к супремумам по всем разбиениям Т, получаем
П(П < sup (У(Л Л) + У(А Г2)) < V%f) +
Вместе с ранее доказанным противоположным неравенством это дает
П(О = П(О + vb(f).
4°. Каждая функция с ограниченным изменением на отрезке [а, Ь] может быть представлена как разность двух ограниченных монотонно возрастающих функций.
271
Положим ф(х) = V*(f). Тогда функция <р(х) не убывает и неотрицательна на отрезке [а, &]. Далее положцм у(х) = ф(х) - Дх). При хг > х2 имеем
V(xx) - у(х2) = V£ - V* - ДХ1) + Дх2) = V% - (Дхх) - Дх2)) > О, так как
^2 = sup V(f9 Т) > sup \81± (f(as) - Да8_х))| = |Дх2) - ftx^.
5°. Функция с конечным числом максимумов и минимумов на отрезке [а, &] является функцией с ограниченным изменением.
Пусть отрезки [xs_x, xj, s = 1, ..., п, задают участки монотонности функции Дх) на отрезке [а, &]. Тогда
W < Д	t(f), где V*st(f) = |flxs) - Ях,_х)|.
ПРИМЕР. Найти полное изменение функции Дх) = sin х при х е [0, 2л].
Разобьем отрезок [0, 2л] на отрезки монотонности функции sin х: [0, л/2], [л/2, Зл/2], [Зл/2, 2л]. Тогда согласно свойствам 5° и 3° имеем:
yg(sin х) =
sin х, если 0 < х < л/2, 2 - sin х, если л/2 < х < Зл/2, 4 + sin х, если Зл/2 < х < 2л.
Пусть Дх) — непрерывная функция и и(х) — функция с ограниченным изменением на отрезке [а, &], и пусть V = {а = tQ < tr < ... < < tn = &,	... £n} — размеченное разбиение отрезка [а, &] и Т =
= T(V) — соответствующее*ему неразмеченное разбиение. Пусть, кроме того,
= и(*8) - w(*8-l)> <XV) - GU(V) = St1
Тогда g(V) называется интегральной суммой Стильтьеса. Если существует предел
то функция Дх) называется интегрируемой по функции и(х) на отрезке [а, Ь], а величина I = Iu(f) — интегралом Стильтьеса от функции Дх) до функции и(х) (или относительно функции и(х)) и обозначается так:
/ =	Kx)du(x).
а
Этот предел можно рассматривать как предел по базе В, окончаниями которой b = служат множества, состоящие из размеченных разбиений U с диаметром Д^ < S. Следовательно, предел I единствен.
272
Докажем теперь одно достаточное условие существования интеграла Стильтьеса.
ТЕОРЕМА 5 (достаточное условие интегрируемости). Пусть функция и(х) имеет ограниченное изменение на отрезке [а, 6]. Тог
да для существования интеграла Стильтьеса J /(x)du(x) до
статочно, чтобы функция f(x) была непрерывной на [а, &].
► Согласно критерию Коши, существование предела интегральных сумм Стильтьеса lim g((7) эквивалентно выполнению условия
Ajj -» О
Коши: для всякого е > 0 должно найтись число 8 = 8(e) > 0 такое, что для любых размеченных разбиений иг и U2 с условием Д^2 < 8, < 8, следует, что справедливо неравенство |с(С\) - g(L72)I < е-Обозначим через v полное изменение функции и(х) на отрезке [а, х]. Зададимся произвольным числом е > 0. Тогда в силу непрерывности функции /(х) существует число 8 = 8(e) > 0 такое, что для любых хр х2 с условием |хх - х2| <8 выполняется неравенство |/(хх) - Дх2)| < ех = е/(2р). Возьмем теперь любые размеченные разбиения Ur и U2 с диаметрами Д^ и Д^, меньшими 8. Пусть Тг = Т(иг) и Т2 = Т(С72) — соответствующие им неразмеченные разбиения отрезка [а, &]. Разбиение Т3 = Тг U Т2 является измельчением разбиений Тг и Т2, и пусть U3 — произвольное разбиение с условием Т3 = T(U3). Тогда
|о(С7х) - <т(С73)| = ,ЕХ ftxfou -
<e1v.
Аналогично доказывается, что |ст(С72) ~ g(C73)| < eiu- Следовательно, IctCCZO - g(U2)| < Ig^) - g(173)| + |g(Z73) - o(J72)| < 2e*i> = e. ◄
Приведем основные свойства интеграла Стильтьеса.
1°. Если функция и(х) дифференцируема, то имеет место
равенство
J /(x)du(x) = J f(x)u'(x)dx,
где последний интеграл понимается как интеграл Римана. 2°. Свойство линейности:
I (/1(х) + f2(x))du(x) = J fjixydutx) + J f2(x)du(x),
J af(x)du(x) = a j f(x)du(x) Va e R.
273
3°. Свойство аддитивности: при а<с <Ь имеем Ь	с	Ъ
J f(x)du(x) = f f(x)du(x) + J f(x)du(x). a	a	c
4°. Правило интегрирования no частям', если f'(x) и u(x) интегрируемы no Риману, то
b	b
J f(x)du(x) = f(x)u(x)|* - J f'(x)u(x)dx, a	a
где последний интеграл понимается как интеграл Римана.
5°. Если и(х) монотонно возрастает на отрезке [а, Ь] и f(x) > g(x) на этом отрезке, то
ь	ь
J f(x)du(x) > f g(x)du(x). а	а
Рассмотрим примеры вычисления интегралов Стильтьеса.
ПРИМЕРЫ 1. Пусть {х} — дробная часть числа х, т. е. {х} = х - [х], где [х] = т е Z — целая часть числа х, тп<х<?п+1. Найти зна-з
чение интеграла J xd{x}. о
Имеем
3	3
J xd{x} = jxdx+l'(-1) + 2• (-1) + 3• (-1)--1,5. О	о
2. Пусть f sin х, если 0 < х < л, и(х) — cojg х* если к < х < 2л.
2п
Вычислить интеграл I = J xdu(x).
ТТ	О
Имеем л	2л
I = J xdsin х + J xdcos х + (-1) • л = -2. О	л
В заключение приведем теорему об общем виде линейного функционала в пространстве С[а9 Ь].
ТЕОРЕМА 6. 1)Пусть функция и(х) имеет ограниченное изменение на отрезке [а, &]. Тогда интеграл Стильтьеса
ъ 1(f) = ] f(x)du(x) а является линейным функционалом в пространстве С[а, &].
2) Пусть 1(f) — любой линейный функционал в С[а, Ь]. Тогда существует функция и(х) с ограниченным изменением на отрезке [а, &] такая, что 1(f) представляется в виде
ь
1(f) = J f(x)du(x).
274
► Остановимся только на основных моментах доказательства этой теоремы.
1) Аддитивность и однородность 1(f) следует из линейности интегральных сумм Стильтьеса a(U)9 соответствующих размеченному разбиению U отрезка [а, Ь], Т = T(U). Для этой суммы справедливо неравенство
|о(С7)| < ||/||’У(и, Т) < ||f || •Vj’(u).
Переходя в этом неравенстве к пределу при Д v -> 0, получаем
f /(x)du(x) < ||/||УЬ(М). а
Тем самым доказана ограниченность /(/).
2) Пусть 1(f) — линейный функционал на пространстве С[а, &]. Этот функционал можно продолжить на пространство ступенчатых функций. Пусть отрезок [а, Р] содержится в отрезке [а, 8]. Тогда положим
(О, если х = а, р < х < Ь, Хр(х)— [ 1, если а < х < р.
Далее определим функцию /р(%) = и(Р). Эта функция и(р) имеет ограниченное изменение на отрезке [а, 6].
Зададимся произвольным е > 0. Тогда в силу равномерной непрерывности f(x) на отрезке [а, Ь] имеем, что существует число 5 = 8(e) > 0 такое, что для всех хр х2 с условием |хх - х2| < 8 выполняется неравенство - /'(;v2)| < е< Возьмем теперь размеченное разбиение U : {а = х0 < хг < ... < хп = Ь, ... , £п} с диаметром Дц, меньшим 8.
Рассмотрим функцию
Ф(*) = О,/*) + Д2 Г(^)(Хж/х) - Хх, _ /*))♦ Имеем
Дф) = /(^1)и(Х1) + Д2 Д£*)(и(хк) - u(xA_1)).
Далее, из определения функции <р(х) получаем, что для любого х е [а, 6] справедливо неравенство |/(х) - ф(х)| < е. Следовательно,
\If - 1ф| = |Д/ - <р)| < е ||Z ||.
Это означает, что при Дс, —> 0 величина If является пределом величин 1ф, но предел /<р представляет собой интеграл Стильтьеса
J f(x)du(x). ◄
275
ГЛАВА 13
Некоторые понятия общей топологии. Метрические пространства
Лекция 18
§ 1. ОПРЕДЕЛЕНИЯ И ОСНОВНЫЕ СВОЙСТВА ПРОСТРАНСТВ
В главе 12 было показано, что с помощью интеграла Стильтьеса можно выражать линейные функционалы, определенные на пространстве непрерывных функций С [а, Ь]. На примере пространства С[а, fe] мы познакомились с функциональным пространством. Может возникнуть вопрос: почему множество С[а, &] непрерывных на отрезке [а, &] функций называется пространством? Ответ достаточно прост. Дело в том, что термин «пространство» по существу эквивалентен термину «множество». Отличие состоит в том, что термин пространство «в чистом виде» употребляется редко, а чаще в сочетании с другими терминами, например: топологическое пространство, метрическое, линейное, нормированное пространства и т. д. Все эти понятия играют важную роль в математике вообще и в математическом анализе в частности. Познакомимся с некоторыми из них.
На следующей схеме показаны некоторые из рассматриваемых в математике пространств, определения которых будут даны. Стрелки имеют такой смысл: пространство, на которое указывает стрелка, является частным случаем того пространства, из которого она «выходит».
Полные----► Банаховы----► Гильбертовы---► Евклидовы
276
Определим пространства, указанные на схеме.
Пусть X — некоторое множество, Е = Ех — множество, состоящее из некоторых подмножеств множества X, т. е. X с Q(X), где £2(Х) — множество всех подмножеств X. Пусть Е обладает следующими свойствами:
1°. X g Е, 0 g Е.
2°. а) Если А и Be Е, то А А В g Е.
б) Объединение любого числа элементов из Е принадлежит Е.
Для того чтобы указать, что элементами Е являются некоторые подмножества множества X, говорят, что Е есть некоторая система подмножеств.
Определение 1. Каждая система подмножеств Е, удовлетворяющая свойствам 1° и 2°, называется топологией на множестве X.
Определение 2. Пара множеств (X, Е) называется топологическим пространством.
Часто говорят просто, что X — топологическое пространство, если на нем задана топология Е. Каждый элемент G g Е, т. е. каждое подмножество б с X, принадлежащее системе Е, называется открытым множеством (в топологии Е).
Любое подмножество А с X такое, что X \ A g Е, называется замкнутым множеством (в топологии Е).
Пусть х — некоторая точка, принадлежащая X. Тогда любой элемент g g Е, которому принадлежит точка х, называется окрестностью точки х, т. е. любое открытое множество, содержащее точку х, называется ее окрестностью. Фиксированные окрестности точки х часто обозначают символом gx.
Определение 3. Топологическое пространство Т = (X, Е) называется хаусдорфовым, если любые две различные точки х и у этого пространства имеют непересекающиеся окрестности G„ и g Е, т. е. Gt A G = 0.
ПРИМЕР. Рассмотрим пример хаусдорфова пространства (Я, Е). Пусть множество Е состоит из всевозможных подмножеств вещественной оси Я, образованных конечной или счетной совокупностью непересекающихся интервалов. Тогда пространство (Я, Е) является хаусдорфовым, поскольку любые две различные точки х и у можно окружить непересекающимися открытыми 8-ок-рестностями.
277
Изучение различных топологических пространств составляет предмет теоретико-множественной топологии.
Определение 4. Пусть задан декартов квадрат X2 = X х X некоторого множества X и пусть на множестве X2 определена числовая функция р(хр х2) со следующими свойствами*.
1)	для любых (хр х2) g X2 имеем р(хр х2) > 0, причем р(хр х2) = = 0, если хх = х2 и р(хр х2) > 0, если хх х2 (неотрицательность);
2)	для любых (хр х2) е X2 имеем р(хр х2) = р(х2, хх) (симметричность);
3)	для любых х9 у9 2 е X справедливо неравенство треугольника р(х, у) < р(х, z) + р(г9 у).
Тогда пара (Х9 р) или само множество X называется метрическим пространством9 а функция р(хр х2) называется метрикой этого пространства 9 или расстоянием от точки хх до точки х2 или функцией расстояния.
ПРИМЕРЫ. 1. Пусть X — произвольное множество и
[ О, если х = у9 Р(х’ ^11, если х у9
тогда пара (X, р) является метрическим пространством.
2. Пусть на множестве вещественных чисел расстояние задается по формуле р(х, у) = |х - у\9 тогда пара (Я, р) является метрическим пространством.
Метрику на одном и том же множестве X можно задавать по-разному. При этом получаются различные метрические пространства. Например, на плоскости R2 можно задать расстояние между точками х = (хр х2) и у = (у19 у2) как по формуле
Ро(я» у) = тах (lxi - !/11» 1*2 - г/г1>» так и по формуле
Р(*, У) = 7(х1 “ У1)2 + (х2 - Уг)2 •
Для всякого числа е > 0 определим открытые е-окрестности точек х е X в метрическом пространстве (X, р) (обозначим их через ох(е)) как множество точек, содержащееся в X и состоящее из всех точек у е X с условием р (х, у) < е. Множества о, являющиеся объединением любой совокупности, составленной из е-окрест-ностей различных точек х е X, назовем открытыми. Тогда можно показать, что система множеств Е = {<?} задает на множестве X топологию и превращает это множество в топологическое хаусдорфово пространство. Заданная топология называется топологией, порожденной метрикой р.
278
Определение 5. Последовательность точек хр х2, ... , хп, ... метрического пространства (X, р) называется последовательностью Коши или чаще фундаментальной последовательностью, если она удовлетворяет условию Коши, а именно: для всякого числа е > 0 найдется номер nQ = п0(е) такой, что для всех номеров п19 п2 > nQ имеем р(хп , х„2) < е.
Определение 6. Последовательность {хп е X} называется сходящейся к точке а е X, если числовая последовательность Рп = Р(хп» а) сходится к нулю при п, стремящемся к бесконечности.
Этот факт записывается следующим образом:	= л.
Из неравенства треугольника легко можно показать, что такая точка a g X единственна.
Определение 7. Метрическое пространство (X, р) называется полным, если всякая последовательность Коши сходится к некоторой точке а е X.
Обратимся теперь к линейным пространствам, которые рассматриваются в курсе высшей алгебры.
Определение 8. Множество X = {х} назовем линейным пространством, если выполнены следующие условия:
1)	для любых двух элементов х, у е X однозначно определен элемент г такой, что z = x + y, называемый их суммой, причем: а) х + (у + z) = (х + у) + z-, б) х + у “ у + х;
в)	существует нулевой элемент 0 такой, что для любого х g X имеем х + 0 = х;
г)	для всякого х g X существует обратный элемент (~х) такой, что х + (-х) « 0;
2)	для любого вещественного числа а и любого хе X определен элемент ах g X (произведение элемента х е X на число а g R), причем:
а)	а(Рх) = (аР)х;
б)	1 • х = х;
3)	операции сложения и умножения связаны свойством дистрибутивности:
а)	(а + Р)х = ах + Рх;
б)	а(х + у) = ах + ау.
Примерами линейных пространств являются n-мерное векторное пространство, пространство непрерывных функций С[а, &].
Элементы линейного пространства называются векторами.
279
Определение 9. Линейное пространство X называется нормированным, если для любого вектора х определена его норма ||х||, обладающая следующими свойствами:
1)||0|| = 0;
2)	для любого х # 0 имеем ||х|| > 0;
3)	для всякого вещественного числа а имеем ||ах|| = |а|||х||;
4)	для любых элементов х, у е X справедливо неравенство треугольника: ||х + у\\ < ||х|| 4- \\у\\.
Заметим, что пространство С[а, &] функций, непрерывных на отрезке [а, &], является нормированным пространством с нормой II/II = max |/(х)|.
хе[а, Ь]
УТВЕРЖДЕНИЕ 1. Функция р(х, у) = ||х - у\\, определенная на декартовом квадрате X2, где X — нормированное пространство, является метрикой на пространстве X.
► Покажем, что функция р(х, у) является метрикой. Для этого надо проверить, что функция р(х, у):
1)	неотрицательна; 2) симметрична и 3) удовлетворяет неравенству треугольника.
Действительно, имеем:
1)	р(х, у) = ||х - у\\ > 0 и р(х, у) = ||х - у\\ = 0 тогда и только тогда, когда х = у;
2)	р(х, у) = ||х - у|| =|- 1| • ||у - х|| = р(х, у);
3)	пусть а = х- z, Ь = z-y, тогда р(х, у) = 11а + Ь11 < ||а|| + ||&|| = = II* - *11 + II* ~ *11 = Р(*> z) + p(z, у). ◄
Определение 10. Полное нормированное пространство называется банаховым пространством.
Переходим к определению гильбертова пространства. Для этого потребуется определение скалярного произведения. Пусть на множестве X задана структура линейного пространства. Определим функцию f(a, &) на декартовом квадрате X2, т. е. на множестве пар (а, &), где а е X, Ъ е X. Пусть, далее, функция f(a, Ъ) обладает следующими свойствами.
1°. Свойство положительности: для любого элемента а е X имеем f(a, а) > 0 при а и 0.
2°. Свойство симметричности: для любых элементов a, be е X имеем f(a, b) = f(h, а).
3°. Свойство аддитивности: для любых элементов а, Ь, с е X имеем f(a, b + с) = f(a, b) + f(a, с).
4°. Свойство однородности: для любых элементов а, Ъ е X и любого вещественного числа X справедливо равенство f(ka, Ь) = = Да, \Ъ) = Л/(а, &).
280
Функцию /(а, Ь) со свойствами 1°~4° называют скалярным произведением. Обозначение (а9 Ь).
Оказывается, что функция J(a, а) = ||а|| является нормой, и само пространство X с этой нормой, таким образом, является нормированным. В самом деле, неотрицательность и однородность функции J(a, а) очевидна. Осталось проверить неравенство треугольника.
Докажем сначала неравенство Коши.
Неравенство Коши:
(х, у)2 < (х, х)(у, у).
Положим хх =
2L и =-*-
IMI ’У1 IWI •
Тогда последнее неравенство сле-
дует из того, что |(хр г/х)| < 1. Действительно, без ограничения
общности можно считать, что (хр уг) > 0. Тогда имеем
0 < Сч ~ !/Р	- yj = (хр хх) + (у19 yj - 2(Хр j/i) = 2 - 2(хр z/J,
откуда получаем: (хр уг) < 1, что и требовалось доказать. ◄
Неравенство треугольника:
л/(Х + Z/,X + Z/) < 7(Х,Х) + 7(1/,I/) .
► Используя неравенство Коши, имеем
||х + 1/П2 = (х + у9 х 4- у) = (х, х) + (у9 у) + 2(х, у) < < ||х||2 + ||z/||2 + 2||х|| • \\у\\ = (||х|| + ||z/||)2. «
Полное метрическое пространство X с метрикой р(х, у) = ||х - z/|| называется гильбертовым пространством. Следовательно, гильбертово пространство — частный случай банахова пространства X с нормой ||х|| = 7(х,х). Конечномерное гильбертово пространство называется евклидовым пространством. Ограничимся рассмотрением этих пространств и в дальнейшем более подробно будем изучать метрические пространства.
Лекция 19
§ 2.	ХАУСДОРФОВОСТЬ МЕТРИЧЕСКОГО ПРОСТРАНСТВА В ЕСТЕСТВЕННОЙ ТОПОЛОГИИ
Сначала введем понятие открытого множества в метрическом пространстве.
Определение 11. При любом е > 0 открытым шаром О(а9 е) радиуса е с центром в точке а в метрическом пространстве (X, р) называется множество, состоящее из всех точек х € X, удовлетворяющих условию р(а, х) < е.
Определение 12. Шар О(а, е) называется также г-окрестно-стью точки а.
Определение 13. Множество точек К (а, е), определяемое условием р(а, х) < е, называется замкнутым шаром радиуса е > О с центром в точке а.
Заметим, что при ех < е2 имеем
О(а, ех) с О(а, е2), К(а, ej с: К(а9 е2).
Определение 14. Точка a g М а X называется внутренней точкой множества М, если она имеет г-окрестность, целиком составленную из точек множества М.
Определение 15. Множество М называется открытым, если любая его точка является внутренней.
ПРИМЕР. Для всякой точки а е X любая ее е-окрестность будет открытым множеством.
Действительно, если точка у g О(а, е), то имеем р0 = р(а, у) < е. Возьмем ех — окрестность точки у, где ех = 0,5(е - р0). Тогда эта окрестность целиком принадлежит множеству О(а, е), так как для всякой точки х g О(у, ег) из неравенства треугольника имеем р(а, г) < р(а, у) + р(г/, z) < р0 + 0,5(е - р0) = 0,5е + О,5ро < е, т. е. р(а, г) < е, следовательно, точка 2 g О(а, е), что и требовалось доказать.
Докажем некоторые свойства открытых и замкнутых множеств.
УТВЕРЖДЕНИЕ 2. Пересечение двух открытых в X множеств Мг и М2 — открытое множество.
► Пусть х g Мг А М2, тогда х g М19 х g М2. Поскольку Мг и М2 — открытые множества, найдется ех-окрестность точки х, содержащаяся в М19 и найдется е2-окрестность точки х, содержащаяся 282
в М2. Возьмем е = min (ер е2). Тогда е-окрестность точки х принадлежит и множеству М19 и множеству ЛГ2, т. е. е-окрестность точки х содержится в Мх А М2. ◄
УТВЕРЖДЕНИЕ 3. Объединение V любого числа открытых множеств М является открытым множеством.
► Возьмем любую точку хе V. Тогда существует множество М с V такое, что х е М, и точка х — внутренняя точка множества М. Следовательно, существует е-окрестность точки х, целиком содержащаяся в М, значит, содержащаяся в V. ◄
Итак, введенные открытые множества образуют топологию, которую называют естественной топологией метрического пространства. Это пространство является и хаусдорфовым. Действительно, пусть х, у — любые точки метрического пространства V и х # у, р(х, у) = Ро > 0, тогда окрестности О(х, р0/3) и О(у, р0/3) этих точек, согласно неравенству треугольника, не пересекаются. Если бы существовал элемент х е О(х, р0/3) А О(у, р0/3), то Ро ~ Р(я» у) < р(х» + Р(*> у) < Ро/3 + Ро/3 = 2р0/3» т. е. р0 = 0, но это не так.
$ 3. ВНУТРЕННИЕ, ВНЕШНИЕ И ГРАНИЧНЫЕ ТОЧКИ МНОЖЕСТВА В МЕТРИЧЕСКОМ ПРОСТРАНСТВЕ
Определение 16. Любое открытое множество а, содержащее точку х, называется окрестностью точки х.
Определение 17. Всякое множество & метрического пространства х, дополнение которого о = X \ ж— открыто, называется замкнутым.
Определение 18. Внешней точкой множества А называется всякая внутренняя точка его дополнения В = X \ А.
Определение 19. Точка z называется граничной точкой множества А, если она не является ни внутренней, ни внешней точкой этого множества.
Множество {z} всех граничных точек А называется границей и обозначается через дА.	s
УТВЕРЖДЕНИЕ 4. Пусть В = Х\А. Тогда дА = ЭВ, т. е. множества АиВ имеют общую границу. Кроме того, д(дА) а. дА.
Действительно, если z — граничная точка множества А, то любая ее окрестность содержит как точки из множества А, так и точки из множества В, а потому z — граничная точка множест
283
ва В. И наоборот, если z g йВ, то z g йА. Следовательно, границы множеств А и В совпадают, т. е. йА = йВ. Свойство же й(йА) cz йА вытекает из того, что если х е й(йА), то всякая окрестность точки х содержит некоторую точку у из йА вместе с какой-то ее окрестностью, а в нее уже входят как точки из А, так и точки из В, и тем самым х е йА, т. е. й(йА) cz йА.
УТВЕРЖДЕНИЕ 5. Если множество А — замкнуто, то йА cz А, и если йА cz А, то А — замкнуто.
► Действительно, в первом случае, в силу того, что множество В = X \ А — открыто, точки его границы йВ не принадлежат В, значит, они принадлежат его дополнению, т. е. множеству А и йВ cz А, но так как йА = йВ, то йА cz А. С другой стороны, если йА = йВ с: А, то йВ не входит в В. Поэтому множество В открыто, а множество А = X \ В замкнуто. ◄
Определение 20. Точка а называется предельной точкой множества А, если в любой s-окрестности точки а содержится:
хотя бы одна точка х е А такая, что х^ а;
б) бесконечно много точек х е А;
в) точка а называется предельной точкой множества А, если существует последовательность точек {хп} сА,хп^а такая, что lim х„ = а.
УТВЕРЖДЕНИЕ 6. Определения а)—в) эквивалентны.
► Очевидно, что из б) следует а). Докажем, что из а) следует в). Для этого надо построить последовательность {хп}, сходящуюся к а, хп а. Строим ее следующим образом. Точку хг е А выбираем произвольно в 1-окрестности точки а, точку х2 — в 1/2-окрестности точки а и т. д. Тогда для любого числа в > 0 вне любой £-окрестности точки а содержится не более п0 = п0(е) = [1/е] + 1 точек последовательности {хп}, т. е. точка а является пределом последовательности {хп}.
Докажем теперь, что из в) следует б). Поскольку последовательность {хп} бесконечна и вне любой окрестности точки а лежит лишь конечное число членов последовательности, в ней содержится бесконечно много членов этой последовательности. ◄ Определение 21. Если точка х е А, но не является предельной точкой множества А, то она называется изолированной точкой множества А.
Теперь заметим, что в определении сходимости в полном метрическом пространстве последовательности {хп} к точке а не обязательно требовать, чтобы {хп} была фундаментальной, так как, если для любого £ > 0 существует п0 = п0(£) такое, что для любого
284
n> nQ выполнено неравенство р(хп, а) < е/2, то тогда для любых nv п2 > п0 имеем
Р(*П1, хп2) < Р(ХЛ1» «) + Р(хп2«а) < £/2 + £/2 = е> т. е. последовательность {хп} фундаментальна. ◄
Докажем еще одно простое утверждение.
УТВЕРЖДЕНИЕ 7. Если последовательность {хп} имеет предел, равный числу а, то а — единственная ее предельная точка.
► Действительно, пусть Ь — другая предельная точка. Тогда р(а, Ъ) = р0 > 0. Возьмем р0/2-окрестность точки а. Вне ее находится лишь конечное число точек последовательности. Тогда внутри р0/2-окрестности точки Ъ будет находиться лишь конечное число членов этой последовательности, быть может, ни одного. Имеет место противоречие. Следовательно, последовательность, имеющая предел, имеет единственную предельную точку, что и требовалось доказать. ◄
Докажем теперь критерий замкнутости множества.
ТЕОРЕМА 1. а)Множество является замкнутым тогда и только тогда, когда оно содержит все свои предельные точки.
б) Множество А замкнуто тогда и только тогда, когда его граница ЭА содержится в нем, т. е. дА а А.
► Докажем утверждение а).
Необходимость. Пусть хп == а, хпе А. Надо доказать, что а е А. Точка а не может быть внешней для множества А, так как в любой ее окрестности ость точки из А. Значит, она является либо внутренней, либо граничной, т. е. а е А или а е дА с А, и в обоих случаях точка а принадлежит множеству А. Необходимость доказана.
Достаточность. Пусть множество А содержит все свои предельные точки. Надо доказать, что его дополнение В = X \ А — открытое множество, т. е. любая точка х е В является внутренней точкой множества В. Если хе В, то точка х или внутренняя точка В, или граничная точка В. В первом случае доказывать нечего. Рассмотрим случай хе В и х е дВ, т. е. х — граничная точка множества В. Но, с одной стороны, эта точка не принадлежит А, так как х е В, с другой стороны, точка х е дВ = дА, т. е. в любой окрестности точки х есть точка из множества А, поэтому х е А по условию теоремы, но это невозможно, так как х е В. Согласно сделанному предположению, и А П В = 0. Следовательно, точка х ё ЭВ, т. е. имеет место только первый случай: х — внутренняя точка множества В, что и требовалось доказать.
Пункт б) уже доказан в утверждении 5.	◄
285
§ 4. ЛЕММА О ПОСЛЕДОВАТЕЛЬНОСТИ СТЯГИВАЮЩИХСЯ ШАРОВ.
ПРИНЦИП СЖИМАЮЩИХ ОТОБРАЖЕНИЙ
Рассмотрим два свойства полных метрических пространств. Первое из них — лемма о последовательности стягивающихся шаров.
ЛЕММА 1. Пусть К(хх, rj id Х(х2, r2) id ... — последовательность вложенных замкнутых шаров в полном метрическом пространстве X, причем lim^ гп = 0. Тогда существует единственная точка х0, принадлежащая всем шарам.
► Прежде всего заметим, что последовательность центров шаров {хп} является фундаментальной. Действительно, зададимся произвольным е > 0. Тогда существует и0 — тг0(е) такое, что для всякого п > nQ имеем гп < е, поэтому при любых пг > п2 > и0, согласно включению А?(хП1, rn^ К(хп^ гп ), имеем р(хИ1, rnJ < г < е, т. е. последовательность {хп} удовлетворяет определению фундаментальной последовательности.
Так как {хп} — фундаментальна, то в силу полноты пространства X, существует предел lim^ хп — х^ g X, причем х0 — предельная точка для каждого шара, а поскольку они замкнуты, для любого натурального числа п имеем х0 € Х(хп, гл).
Покажем, что точка х0 является единственной точкой, принадлежащей одновременно всем шарам. Пусть это не так, т. е. найдется точка уц е X(xn, rn), р(х0, yQ) = р. Очевидно, существует п такое, что гп < р/2. Из неравенства треугольника получим
Р = р(*0> Уо> < Р(*п» *о) + Po<x«> < Р/2 + Р/2 = Р-
Имеет место противоречие. Следовательно, х0 является единственной общей точкой для всех шаров. ◄
Определение 22. Пусть X — полное метрическое пространство, и пусть f : X X — отображение этого пространства в себя, причем существует вещественное число а с условием 0 < а < 1 такое, что для любых a, Ь g X имеем
р(/(а), /(&)) < ар(а, &).
Тогда отображение f называется сжимающим.
Докажем теперь принцип сжимающих отображений.
ТЕОРЕМА 2. Если f : X —> X — сжимающее отображение, то существует единственная точка х0 g X такая, что Дх0) = х0.
Точка х0 называется неподвижной точкой сжимающего отображения f.
286
► Пусть хх — любая точка, принадлежащая X, х2 — f(Xj), , ... , х„+х = Дх„). Докажем, что последовательность {хп} фундаментальная. Действительно, пустьрп = р(хп, хл+х). Тогда
Рп = Р(*п> xn+i) = Р(Я(«»-1). Ях»)) < ар(*п-1» хп) = арл_х.
Следовательно, рл < ап-1р1. Отсюда, используя неравенство треугольника, получаем
Р<Хп> Хп + т) < Рп + Рп+1 + - + pn + m-l<
< (ал-1 + а“ + ... + ап+те-2)рх < 7— р,.
Г1 1-аГ1
Поскольку 0 < а < 1, при п -> оо имеем ап-1 -4 0. Следовательно, для всякого £ > 0 найдется n0 в и0(е) такое, что при любом п > п0 и любом т > 1 выполняется неравенство р(хл, хп + т)< е, что и означает фундаментальность последовательности {хп}. Так как X — полное метрическое пространство, то существует точка х0 такая, что lim х„ =
Теперь докажем, что Дх0) = х0. Воспользуемся методом от противного. Пусть /(х0) = р0 и х0 и р(х0, р0) = h > 0. Возьмем число п0 — п0(й/2) такое, что для любого п > п0 имеем р(хп, х0) < Л/2. Тогда
Р(*п+1» Уо> “ Р(/(хп)> /(хо» < Р(хп» хо) < ^/2.
Следовательно,
Р(*о> Уо) < Р(*0» хп+1) + Р(хп+1> Уо) < h/2 + h/2 = h = р(х0, у0), что при h > 0 невозможно. Итак, х0 — неподвижная точка отображения f. Она является единственной неподвижной точкой, так как если а и Ь — неподвижные точки, т. е. /(а) = а, f(b) Ь, то р(а, Ь) = р(/(а), /(&)) < ар(а, Ь) < р(а, 6), что невозможно. ◄
Лекция 20
§ 5.	НЕПРЕРЫВНЫЕ ОТОБРАЖЕНИЯ МЕТРИЧЕСКИХ ПРОСТРАНСТВ
Определение 23. Пусть заданы два метрических пространства (X, рх) и (У, ру), и пусть определено отображение F : X -> У. Тогда отображение F называется непрерывным в точке х0, если для всякого е > 0 найдется 8 = 8(e) > 0 такое, что для любого х с условием рх(х, х0) < 8 имеет место неравенство Py(F(x), F(x0)) < е, т. е. в пространстве У любая г-окрестность Oy(F(x0), е) точки F(xQ) е У содержит целиком образ некоторой 8-окрестности этой точки при отображении F, а именно: F(Ox(x0, 8)) с Oy(F(x0), е).
Определение 24. Отображение F метрических пространств X в У называется непрерывным, если оно непрерывно в каждой точке хе X.
ПРИМЕР. Сжимающее отображение F : X —> X является непрерывным. В этом случае достаточно взять 8(e) = е.
Определим базу множеств х —> х0 для точек метрического пространства X как множество всех открытых 8-окрестностей точки х0. Тогда определение непрерывности выглядит так: lim F(x) = = F(x0), где х, х0 g X, F(x), F(x0) g У.
Заметим также, что определение предела по базе множеств В отображения F : X -> У метрического пространства X в метрическое пространство У имеет следующий вид: точка yoeY называется пределом отображения F : X ->Y по базе В, если для всякого е > 0 найдется окончание Ъ = Ь(е) g В такое, что для всякой точки х g b имеем py(F(x), yQ) < е. Для числовых функций остается прежнее определение предела функции f : X —> Я по базе В со всеми доказанными ранее свойствами предела.
Теоремы 3 и 4 являются следствием ранее установленных общих свойств предела функции по базе множеств в смысле Коши и Гейне. Тем не менее, приводим их прямое доказательство.
ТЕОРЕМА 3. Пусть отображения F'.X^YuGiY^Z таковы, что отображение F непрерывно в точке х0 g X, а отображение G непрерывно в точке yQ = F(x0) g У. Тогда композиция отображений F и G, т. е. отображение Н : X —> Z, где Н(х) = = G(F(x)), является непрерывной функцией в точке х0.
► Положим z0 = G(yQ). Тогда справедливы равенства Н(х0) = = G(F(x0)) = G(i/0) = Zq. Так как отображение G непрерывно в точ
288
ке z/0, то для любого числа £ > 0 найдется 8 = 8(e) > 0 такое, что при любом у € Oy(i/0, 8) имеем G(y) е О^(20, £).
Далее, в силу непрерывности отображения F в точке х0, найдется 8г = 8х(8(е)) > 0 такое, что для всякого х е Ох(х0, 8Х) имеем F(x) е Оу(1/0, 8) = Oy(i/0, 8(e)). Отсюда следует, что для всякого е > О нашлось 8Х = 8х(8(е)) > 0 такое, что при любом х g O^Xq, 8J имеем Н(х) = G(F(x)) g О^г09 е), т. е. отображение Н(х) непрерывно в точке х0, что и требовалось доказать. ◄
ТЕОРЕМА 4. Пусть последовательность {хп} в метрическом пространстве X сходится к точке х0, а отображение F : X —> У непрерывно в точке х0. Тогда имеем
№£F<xn) =	т-е- М *(*») =	хп>-
► В силу непрерывности отображения F для всякого е > 0 найдется 8 = 8(e) > 0 такое, что для любого х g Ох(8) имеем F(x) g g Oy(F(xo)9 e).
Далее, так как lim хп = х0, то можно указать п0 = п0(8) = = п0(8(е)) такое, что для любого п > п0 имеем хп g Ох(х0, 8). Отсюда следует утверждение теоремы. ◄
Отметим, что определение 2 понятия непрерывности отображения метрических пространств равносильно тому, что полный прообраз всякого открытого множества из У открыт в X. Обычно таким способом вводится понятие непрерывности отображения для хаусдорфовых пространств.
§ 6.	ПОНЯТИЕ КОМПАКТА.
КОМПАКТЫ В Rn И ПОЛНОТА ПРОСТРАНСТВА Rn.
СВОЙСТВА НЕПРЕРЫВНЫХ ФУНКЦИЙ НА КОМПАКТЕ
Определение 25. Множество К в метрическом пространстве X называется компактом9 если из любого покрытия открытыми множествами этого компакта можно выделить конечное подпокрытие.
Определение 26. Множество В в метрическом пространстве называется ограниченным^ если оно содержится в некотором шаре О(х0, г) с центром в точке х0 и радиуса г.
ЛЕММА 2. Компакт является ограниченным множеством.
► Пусть К — компакт. Возьмем любую точку х0 g К. Тогда шары Оп = О(х0, п) в совокупности покрывают все пространство X, в том
ОАО
10 - 4953
числе и К. В силу компактности К из них можно выделить конечное подпокрытие {Oti ... a Ot9 tr < t2 < ... < tB\К g_ Ot}, а это означает, что компакт К является ограниченным множеством. ◄
Л Е М М А 3. Пусть К — компакт. Тогда любая бесконечная последовательность {хп} а: К имеет хотя бы одну предельную точку, принадлежащую К.
► Будем рассуждать от противного. Пусть последовательность {хп} не имеет предельных точек, принадлежащих К. Тогда любую точку хе К можно окружить своей е-окрестностью О (х, е), внутри которой не будет точек из {хп}9 кроме, быть может, самой точки х. Получаем покрытие компакта К открытыми множествами. Выберем из него конечное подпокрытие. Но тогда имеем, что точками К9 принадлежащими последовательности {хп}9 могут быть только центры выбранных £-окрестностей, а их конечное число. Следовательно, множество точек последовательности {хл} — конечно. Имеет место противоречие. ◄
ЛЕММА 4. Компакт К является замкнутым множеством.
► Достаточно показать, что компакт К содержит все предельные точки. Действительно, пусть х0 — любая предельная точка К. Тогда можно указать последовательность {хп} с К такую, что при п и т имеем хл # хт и хл -> х0 при п —> оо. Отсюда по лемме 3 получаем, что х0 g К. ◄
ЛЕММА 5. Всякое замкнутое подмножество М компакта К само является компактом.
►	Множество В = Х\М открыто. Если к любому покрытию множества М добавить множество В, то получится покрытие для К. Из него можно выбрать конечное подпокрытие для К. Отбросив множество В, будем иметь конечное покрытие для М. 4
Опишем теперь компакт в n-мерном пространстве и докажем полноту пространства Rn.
ТЕОРЕМА 5. Любой замкнутый куб в евклидовом пространстве Rn9 т. е. множество точек х = (хр ..., хл) с условием ав< xg < а8 + l9 s = 1,..., п, является компактом.
►	Будем рассматривать только случай Я2, так как общий случай Rn принципиальных отличий не имеет. Итак, пусть h — замкнутый квадрат — покрыт бесконечной системой открытых множеств {U}. Надо доказать, что из этого покрытия можно выделить конечное подпокрытие. Докажем это утверждение от
290
противного. Разделим h на четыре равных квадрата прямыми, проходящими через середины его сторон, параллельно осям координат. Так как квадрат h не допускает конечного подпокрытия, то, по крайней мере, один из четырех новых замкнутых квадратов не допускает конечного подпокрытия. Тогда этот квадрат делим на четыре равных квадрата и т. д.
Мы получим систему вложенных квадратов. Их проекции на любую из двух осей образуют систему стягивающихся отрезков, которая имеет единственную общую точку, т. е. существует точка х0 на оси Ох, и аналогично, точка у0 на оси Оу такие, что х0 принадлежит проекциям всех вложенных квадратов на ось Ох, а i/0 — проекциям на ось Оу. Но тогда точка А = (х0, у0) принадлежит,всем квадратам. Кроме того, она покрыта каким-то открытым множеством UQ из покрытия {U}. Следовательно, найдется Е-окрестность О(А, е) с 170, целиком накрывающая некоторый квадрат из построенной системы вложенных квадратов. В частности, таким может быть квадрат KQ с длиной стороны меньшей, чем е/ 72 . Но тогда квадрат KQ будет покрыт всего лишь одним множеством UQ. Имеет место противоречие. ◄
Напомним, что метрика р(а, Ь) в Rn для любых двух точек а, b е е Rn задается с помощью скалярного произведения (а, Ь) равенством р(а, Ь) = 7(а - Ь, а - Ь).
ТЕОРЕМА 6. Метрическое пространство Rn является полным.
► Достаточно показать, что любая фундаментальная последовательность {хл} сходится к элементу этого пространства. Очевидно, что {хп} ограничена, поэтому ее можно покрыть замкнутым кубом К. Поскольку К — компакт, по лемме 3 существует предельная точка х0 е К последовательности {хл}. Следовательно, {хп} сходится к х0, так как фундаментальная последовательность не может иметь более одной предельной точки. ◄
Докажем теперь критерий компактности множества в Rn.
ТЕОРЕМА 7. Множество KcRn является компактом тогда и только тогда, когда К ограничено и замкнуто.
►	Необходимость. Если К — компакт, то по леммам 2 и 4 это множество ограничено и замкнуто.
Достаточность В силу ограниченности, множество К может быть помещено в некоторый замкнутый куб h. Поскольку h является компактом, а К с h замкнуто, по лемме 5 множество К тоже компакт. ◄
ю*
291
Напомним, что числовой функцией на множестве А называется отображение F : А -> R. Далее под термином «функция» мы будем понимать только числовые функции. Докажем несколько свойств функций, непрерывных на компакте.
ТЕОРЕМА 8. Пусть функция f(x) непрерывна на компакте К с: Rn. Тогда:
1) f{x) — ограничена на К;
2) существуют хр х2 е К такие, что Дхх) = М = sup Дх), /(х2) = т = inf f(x).
хеК
► 1) Для каждой точки х е К найдется окрестность О (х, 8(х)) этой точки, в которой функция Дх) ограничена. Эти окрестности образуют покрытие открытыми множествами. Выделяя из него конечное подпокрытие, получаем, что f(x) ограничена на всем компакте К.
2) Проведем доказательство методом от противного. Пусть ни в какой точке функция f(x) не принимает максимального значения. Тогда функция g(x) = l/(Af - Дх)) является непрерывной на компакте К. Следовательно, согласно утверждению 1) этой теоремы она ограничена. Отсюда имеем
0<HF^j <м" или /(х)<м"лЬ
т. е. число М - 1/Мг — верхняя грань значений функции Дх), меньшая, чем М. Это противоречит определению числа М. В случае нижней грани значений функции Дх) доказательство проводится аналогично. ◄
В заключение укажем на следующие важные свойства непрерывных отображений компактов в метрических пространствах.
1°. Непрерывный образ компакта является компактом.
2°. Пусть X и Y — метрические пространства, X — компакт и F — взаимно однозначное непрерывное отображение X в Y. ЕслиВсХ - произвольное открытое множество, то его образ F(B) открыт в У. При этом граница дВ переходит в границу, внутренние точки — во внутренние, внешние точки — во внешние, а обратное отображение непрерывно.
Докажем эти утверждения. 1°. Рассмотрим произвольное открытое покрытие образа F(K) компакта К. В силу непрерывности F, полный прообраз каждого элемента покрытия является открытым множеством. Такие множества в совокупности образуют покрытие компакта К. Из этого покрытия можно выбрать конеч-
292
ное подпокрытие для К. Тогда образ данного подпокрытия образует конечное подпокрытие для F(K).
2°. Положим К = В U ЭВ. Тогда К" и ЭВ — компакты, поскольку они замкнуты^ а X — компакт. Их образы тоже будут компактами. Следовательно, граница множества F(K) входит в F(K). Это значит, что образы точек р, внешних для К, не входят в F(K) или его границу, т. е. точки F(y) являются внешними для F(K). Повторяя это рассуждение для замкнутого множества Кх =Х \ В, получаем, что внутренние точки Ь множества В переходят во внутренние точки множества F(B). Пусть теперь точка х является граничной дляВиу = F(x) ее образ в У. Рассмотрим любую окрестность <зу точки у. В силу непрерывности F она содержит образ некоторой окрестности бх точки х. Но так как х g ЭВ, то в входят как точки из В, так из его дополнения Х\В. Поэтому бу включает в себя точки из F(B), а также точки из F(X \ В) = = F(X) \ F(B). Это значит, что у g ЭГ(В) и Г(ЭВ) a dF(B).
Рассматривая теперь обратное отображение F-1 пространства У в X, имеем, что прообраз F(B) a Y всякого открытого множества В открыт в У, так как оно состоит только из внутренних точек. Следовательно, отображение F-1 непрерывно.
Утверждения 1 и 2 доказаны полностью. 4
§ 7. СВЯЗНЫЕ МНОЖЕСТВА И НЕПРЕРЫВНОСТЬ
Определение 27. Множество А в метрическом пространстве X называется связным, если при любом его разбиении на два непустых непересекающихся подмножества и А2 они будут иметь общую граничную точку, принадлежащую А, т. е. точку а с условиями:
1) a g А;
2) в любой г-окрестности точки а есть как точки из множества Ар так и точки из множества А2, отличные от а.
Примерами связных множеств на плоскости являются отрезок, прямоугольник, круг.
Связное открытое множество называется областью, а связное множество, являющееся компактом, континуумом.
ТЕОРЕМА 9. Пусть А — связное множество в Rn, функция F(x) непрерывна на А, и пусть существуют точки х19 х2 g А, F(xx) = a, F(x2) = &, а < Ь. Тогда для любого числа с g (а, 6) существует точка х3 g А такая, что F(x3) « с.
293
► Рассмотрим множества Мх = {х е А| F(x) < с} и М2 = А \ Mv В силу связности множества А, существует точка х3, являющаяся граничной точкой как для множества М19 так и для множества М2. В каждой из окрестностей Оп = О(х3, t/h) есть точка ап е Мх и точка Ьп е М2. Последовательности {ап} и {Ьп} сходятся к х3. Тогда из непрерывности функции F(x) имеем
F(x3) = F( Нт ап) = Нт F(a„) < с, р(хз> =	=	> с'
т. е. в точке х3 функция F(x) равна с. ◄
ГЛАВА 14
Дифференциальное исчисление функций многих переменных
Лекция 21
$ 1. НЕПРЕРЫВНЫЕ ФУНКЦИИ В Rn
Еще раз обратим внимание на тот факт, что поскольку понятие непрерывности функции определяется как предел функции по базе, над непрерывными функциями п переменных в точке х = х0 можно совершать арифметические операции, сохраняя их непрерывность с обычной оговоркой о необращении в нуль знаме-натёля частного f(x)/g(x) в точке х = х0. Справедливы также теоремы о неравенствах для непрерывных функций в точке х = х0 типа таких: если Дх0) > g(x0), то в некоторой окрестности точки х = х0 имеем Дх) > £(х).
Будем, как и раньше, говорить, что функция Дх), заданная на множестве А с Ял, является непрерывной на множестве ВсА, если Дх) непрерывна для любой точки хе В. Напомним, что для функции, непрерывной на компакте, справедливы теоремы об ограниченности на нем функции, о достижении ею точной верхней и точной нижней граней и о равномерной непрерывности, а для непрерывной функции, заданной на связном множестве, справедлив аналог.теоремы о промежуточном значении.
Но кроме этих свойств имеются свои специфические особенности функций многих переменных.
Пусть а = (ар ... , ап) — некоторая точка из Rn и функция Дх) определена в некоторой окрестности точки а. Выделим одну из координат точки а. Пусть это координата с номером з, 1 < s < п, и обозначим через М с Rn множество всех тех точек, у которых все координаты, кроме з-й, совпадают с координатами точки а. Если в качестве аргумента х рассматривать точки х € М, то получим функцию ф(х8) одной переменной х8, ф(х8) = Дар ..., х8, ..., ап). Например, если Дхр х2) = х| + хх х2, то ср(х2) = af + ахх2.
Определение 1. Будем говорить, что функция Дх) непрерывна в точке а по переменной х8, если ф(х8) непрерывна в точке xs = а8.
295
Можно дать более общее определение непрерывности функции f(x) по любому направлению.
Определение 2. Направлением в Rn называется любой единичный вектор ё е Rn.
Определение 3. Множество всех точек х вида х = х + te называется:
а)	открытым лучом, выходящим из точки а в направлении ё, если t> 0;
б)	замкнутым лучом, если t>0;
в)	прямой, проходящей через точку а в направлении ё, если t — произвольное вещественное число.
Рассмотрим функцию у(0 = f(a + tё).
Определение 4. Будем говорить, что функция f(x) непрерывна в точке а по направлению ё, если у(£) непрерывна в точке t - 0.
Имеет место следующее очевидное свойство. Если f(x) непрерывна в точке х = а как функция п переменных, то она непрерывна в точке а по любому направлению ё. Обратное, вообще говоря, неверно.
ПРИМЕР. 1) Пусть функция f(x, у) задана следующим образом:
xi//(x2 + у2), если х2 4- у2 0, 0,	если х = у = 0.
Она непрерывна в нуле по х и по у, но разрывна в этой точке как функция двух переменных х, у.
2) Пусть функция f(x, у) задана соотношениями: ху2/(х2 + у2), если х2 + у2 5* 0, 0,	если х = у = 0.
Она является непрерывной по любому направлению, проходящему через точку х = 0, у = 0, но разрывна как функция двух переменных в этой точке.
Рассмотрим теперь отображение F : Rn —> Rm. Этому отображению однозначно соответствуют т функций ф^х), ... , фт(х), которые представляют собой координаты точки у = F(x) е Rm, т. е.
У = (Ф1(х)»... > Фт(х)), Уа = фД*)» в - 1,...» Щ.
УТВЕРЖДЕНИЕ. Для непрерывности отображения F : Rn -> Rm в точке х е Rn необходимо и достаточно, чтобы все функции ф8(х) были бы непрерывны в точке х = х0.
Т(х, у) =
f(x, у) = I
296
Доказательство утверждения непосредственно следует из определения непрерывного отображения, поскольку
п	п
Переформулируем теперь теорему о непрерывности сложного отображения метрических пространств на случай функций многих переменных.
ТЕОРЕМА 1. Пусть f : Rn -> Rm, g : Rm -> Я, и пусть отображение f(x) непрерывно в точке х = х09 а функция g(y) непрерывна в точке yQ = Дх0). Пусть также в некоторой окрестности точки xQ определена сложная функция h(x) = g(f(x)). Тогда функция h(x) непрерывна в точке х = х0.
Определение 5. Функция F : А R, A a Rn, называется равномерно непрерывной на множестве А, если для любого е > О существует число 5 = 8(e) > 0 такое, для любых х9 у е А с условием р(х, у) < 8 имеем |F(x) - F(i/)| < е.
ТЕОРЕМА 2. Функция F, непрерывная на компакте К9 является равномерно непрерывной на нем.
► Зададимся произвольным 8 > 0. Возьмем число ех = е/2 и для каждой точки х е К рассмотрим окрестность О(х, б-^)), состоящую из точек у с условием |Дх) - f(y)\ < еР Тогда «усеченные» окрестности о(х9 | 8-(8х)) покрывают компакт К. По определению компакта, из этого покрытия можно выделить конечное подпокрытие. В качестве 8 = 8(e) возьмем минимальный из конечного числа радиусов выбранных шаровых окрестностей. Рассмотрим любые две точки х9 у с условием р(х, у) < 8. Тогда найдется о(х0, | S-Jej), содержащая точку х. Далее, согласно неравенству треугольника, имеем
р(У, *о) с Р(У> *) + Р(*> *о) < б-
Следовательно,
1Г(х) - f(y)\ <|Г(х) - Дх0)| + | f(xQ) - f(y)\ < 2£1 = 8.
Таким образом, для любого числа 8 > 0 мы указали 8 = 8(s) такое, что для любых х9 у е К с условием р(х, у) < 8 выполнено неравенство \f(x) - f(y)\ < 8, следовательно, функция f(x) — равномерно непрерывна на компакте К. ◄
297
§2. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИИ В Rn	.
Пусть числовая функция f(x) определена в некоторой окрестности точки х = а е Rn.
Определение 6. Приращением ДДх) функции f(x) в точке х = а называется разность ДДх) = Дх) - Да). Разность Дх = х - а называется приращением аргумента х.	' 9
Длина вектора Дх обозначается через |Дх| и равна р(х, а).
УТВЕРЖДЕНИЕ 2. Если функция Дх) непрерывна в точке х = а, то ее приращение ДДх) стремится к нулю при Дх, стремящемся к нулю, т. е. ДДх) = о(1).
Доказательство очевидно следует из определения й свойств предела функции по базе множеств.
Определение 7. Линейная функция от приращения аргумента Дх называется дифференциалом df(x) функции Дх) в точке х = а, если приращение ДДх) при Дх —> О можно представить в виде
Af(x) = df(x) + о(|Дх|).
Будем говорить, что функция Дх) дифференцируема в точке х= а, если существует дифференциал df(x) функции в точке х = а.
УТВЕРЖДЕНИЕ 3. Если функция дифференцируема в точке х — а, то она непрерывна в этой точке.
Доказательство утверждения очевидно следует из того, что ДДх) —> 0 при Дх —> 0.
Подчеркнем еще раз, что дифференциалом df(x) функции Дх) в точке х = а называется линейная или главная часть приращения функции Дх) в точке х = а. Поскольку df(x) — линейная функция, ее можно записать в виде
df(x) = А^Х! - аг) + ... +Ап(хп - ап) = ДД>с„
где А, — некоторые вещественные числа и Ах, = х, - а,. Если f(x) = х,, то df(x) = dx, = Axg.
ТЕОРЕМА 3. Пусть f(x) дифференцируема в точке х = а, тогда все координатные функции (pe(xs) =	... , х,,... , ап) диф-
ференцируемы в точках х,— a,, s — 1, ..., п, причем А, = <p'(as). ► В формуле для приращения Д/(х) в точке х = а через его дифференциал положим хг = аг при г з. Получаем
А/(х) = ftx) - fta) = А,Ах, + о(|Дх,|).
298
Тогда, согласно определению функции <р8(х8), имеем /(х) - Ла) = ф,(х8) - Фв(ав) = ДДх8 + о(|Дх8|), т. е.
Определение 8. Производная q's(a^, когда она существует, называется частной производной функции f(x) в точке х = а по s-й переменной и обозначается так:
ф>,) =
Э/(а) _ Э/(х) дх8 дх8
СЛЕДСТВИЕ. Дифференциал функции f(x) в точке х = а однозначно записывается в виде
df(x)\x = a ^)дж1 + — + Эхп)ЛХп'
► Доказательство свойства очевидно. ◄
ПРИМЕР. Пусть f(x, у) = х2 + ху. Тогда
У) = 2х + у, у) = х, d/(x, у) = (2х + y)dx + xdy.
Итак, необходимым условием дифференцируемости функции в точке является существование всех ее частных производных в этой точке. Докажем теперь одно достаточное условие дифференцируемости функции в точке.
ТЕОРЕМА 4. Пусть в некоторой окрестности точки а су
ществуют все ее частные производные
s = i Эх. ’ 8 Х’ -
и, и
эти частные производные непрерывны в точке х = а. Тогда функция fix) является дифференцируемой в этой точке.
► Для краткости записи будем считать, что п = 2. Приращение ДДх, У) функции f(x, у) в точке (а, Ь) можно записать так:
Af(x, у) = f(a + Дх, Ь + Ду) - Да, &) =
= (Да + Дх, Ь + Ду) - Да, b + Ду)) + (Да, Ъ + Ду) - Да, &)).
К каждой из двух разностей в скобках можно применить формулу конечных приращений Лагранжа, поскольку в рассматриваемой окрестности точки (а, Ъ) функция Дх, у) имеет непрерывные частные производные по х и по у. Получаем
а//	\ ЭДа + %Дх, Ь 4-Ду) ЭДа, Ь +ч\Ьу) А
Д/(х, у) = ——--------------522 Дх + —ь* Дг/.
299
где Т| — некоторые постоянные, 0 < £, Т| < 1. Далее, в силу непрерывности частных производных при Дх —» О, имеем следующие соотношения:	;. '
ЭДд + %Дх, Ь + Ду) = ЭДа, Ь) + Эх	Эх '
ЭДа, fr+ W) ЭДа, Ь) + Эу	Эу v h
Отсюда имеем
&f(x, у) = df(“* Ь) Ах + д-(£’- Ду + 0(1 Дх| + | Ду|).
Поскольку
|Дх| < |Дх|, |Ду | < Дх |, Дх = (Дх, Ду), получаем
Af(x, у) = df(“* b) dx + df(“’ b) dy + о(|Дх|) = df(x) + o(|Дх|),
т. е. функция Дх, у) дифференцируема в точке (х, у) = (а, Ь). ◄
Приведем пример непрерывной функции, имеющей частные производные в окрестности точки (0, 0), но недифференцируемой в этой точке: z = 7 |ху|.
Частные производные этой функции, очевидно, существуют при х2 + у2 0. По определению, они существуют в точке (0, 0):
Дг(О,О) = 2(Дх,0) -2(0,0) =	Д?(0,0) =
Дх	Дх	’ Ду 9
следовательно, z'x(09 0) = 0, z'(0, 0) = 0.
Если же Дх = Ду > 0, то приращение функции z(x, у) в точке (О, 0) равно Дх, но, по определению дифференциала, оно должно быть о(Дх).
Таким образом, функция z = 7|ху| не является дифференцируемой в точке (0, 0).
Определение 9. Отображение ф(х) из Rn —> Rm, равное (фх(х),... , Фт(х)), называется дифференцируемым в точке х = = х0 е ЯЛ, если все функции фх(х), ... , фт(х) дифференцируемы в этой точке.
Лекция 22
$ 3. ДИФФЕРЕНЦИРОВАНИЕ СЛОЖНОЙ ФУНКЦИИ
ТЕОРЕМА 5. Пусть ф(х) = (фх(х),, фт(х)) есть отображение из Rn в Rm, определенное в некоторой окрестности точки х = = а и дифференцируемое в этой точке. Пусть, далее, для всякого е > 0 при отображении ф образ некоторой ^-окрестности О(а, 8) содержится в г-окрестности точки Ь = ф(а). Пусть, наконец, для любой точки у g О(Ь, е) определена числовая функция f(y), которая является дифференцируемой в точке Ь. Тогда сложная функция h(x) = /(ф(х)) является дифференцируемой в точке х = а, причем имеют место равенства
ЭЛ_=Эй_#Эф1	_ЭЛ_Эф^
Ъх8 дуг * дх8	дут ду8’ S 9 П‘
Здесь частные производные по переменной х8 рассматриваются в точке х = л, а частные производные по yl91 = 1, ... , т — в точке у = Ъ.
► В силу дифференцируемости функции f(y) в точке у = Ъ приращение функции Д/ при произвольном приращении аргумента Ду = у - Ь можно представить так:
ДГ=# + О(|Ду|), где v V А df ~ dyt ЬУг
Подставим вместо Ayz приращение Дф; функции фДх) соответствующее приращению Дх аргумента х. Тогда слева в этой формуле получаем ДЛ(х) и она принимает вид
ДЛ(х) = Д ДфДх) + 0(1 Дф(х)|).
В силу дифференцируемости функций ф^(х) имеем
Дф;(х) = ,5^ Дх, + 0(1 Дх|, I = 1, ..., т.
Частные производные функций фДх) в точке х = а — это конкретные вещественные числа. Поэтому существует число М > О такое, что они по абсолютной величине не превосходят М. Тогда имеем
|Д фДх)| < 2Мп|Дх|, |Д ф| < 2Мп2|Дх|.
301
Отсюда найдем
о(|Дф(х)|) = о(|Дх|).
Подставляя теперь значения АфДх) в формулу для АЛ(х), получаем утверждение теоремы. ◄
СЛЕДСТВИЕ 1 (инвариантность формы первого дифференциала). Если в выражение для первого дифференциала df(y) вместо независимого приращения &у8 подставить дифференциал функции у8 = фв(х), то полученное выражение будет дифференциалом сложной функции h(x) = /(ф(х)). Другими словами, форма первого дифференциала функции не изменится, если независимые переменные оказываются зависимыми функциями.
Утверждение следствия — простая переформулировка утверждения теоремы 5.
СЛЕДСТВИЕ 2.
Правила дифференцирования
Справедливы следующие формулы:
a) d(cu) — cdu Vc е Я; в) d(uv) = udv + vdu;
б)d(u ± и) = du + dv; г)d(-1	при v(x0)0.
► Докажем только свойство в). Пусть z = z{u9 v) = uv9 тогда
dz = du + dv = vdu + udv. du dv
В случае, если и и v — функции от других независимых переменных, то воспользуемся свойством инвариантности формы первого дифференциала (следствие 1). ◄
§ 4. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ. ГРАДИЕНТ
Пусть задано направление ё = (ер..., еп)9 |ё| = 1, и k19... , kn — направления векторов осей координат Ох19 ... , Охп. Тогда, очевидно, если а8 — угол между k8 и ё9 то
es = (ё, ks) = |ё| • |Л,| cos ag = cos as.
В силу этого определения, числа е19 ... , еп называются направляющими косинусами направления ё.
Пусть f(x) — дифференцируемая функция в точке х = й, и ё — некоторое направление. Рассмотрим сложную функцию Л(0 =*= = /(а + £ё). Она является функцией от одной переменной t9 и, в си-302
лу теоремы о дифференцируемости сложной функции, при t = О справедливо равенство
dh(t)-hWdt-i$l,dt.
Тогда имеем .,/лч Д df Я df МО)-	S^cosa*.
Определение 9. Эта величина h'(0) называется производной функции f(x) по направлению е в точке а.
Обозначение:
df df(x) де де
_ _ = й'(0). х = а
Определение 10. Вектор
п
называется градиентом функции f(x) в точке х — а. Обозначение:
^7f= grad/.
Таким образом,
= (ё, grad f) = (ё, V/), где	/ а	а ч
V = (—	— 1
(Эх!’•”*Эхп J — оператор «набла».
Приведем некоторые свойства производной по направлению.
1°. Максимальное значение производной функции f(x) по направлению равно длине вектора градиента и достигается при
2°. Производная по направлению равна нулю, если вектор градиента равен нулю или он ортогонален вектору направления.
3°. Минимальное значение производной функции f(x) по на-
правлению равно - |grad /|, если ё =	•
Отсюда видно, что скорость возрастания функции в направлении градиента — наибольшая.
$ 5. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА
Для простоты изложения будем рассматривать функции двух переменных.
Определение 11. Поверхностью Р в R3 называется график всякой непрерывной функции z = f(x, у), заданной в некото
303
рой области RQ. cz R2. Другими словами, поверхность Р — это множество точек (х, у, z) е Я3, где координата z е R и точка (х, у) g R2 связаны соотношением z = /(х, у).
Напомним, что под областью понимают связное открытое множество.
Определение 12. Говорят, что поверхности z = fx (х, у) и z = f2 (х, у) касаются друг друга в точке (а, Ь, с), если с = =	(a, b) = f2 (а, Ь) и разность
г(х9 у) = fr (х, у) - /2 (х, у)
является величиной о(|х - а|) при |х - а| —> 0.
График линейной функции z = kx + ly + т, k,I, m G R является плоскостью в R3.
ТЕОРЕМА 6. Пусть функция f(x), хе О (а, е) с R2 — дифференцируема в точке х = а = (av а2) и 20 = f(a). Тогда плоскость П, задаваемая линейным уравнением вида
__ Э/(а) , ч , Э/(а) , ч
2 20 дхх <Х1 а^+ Эх2 (Х2 а2>’
касается поверхности Р: z = f(x) в точке х = а.
► Рассмотрим плоскость П как график линейной функции g(x), где
g(x) = z0 + df(x).
Поскольку функция /(х) дифференцируема в точке х = а, имеем f(x) - g(x) - f(a) + df(x) + о(|Дх|) - z0 - df(x) = о(|Дх|).
Следовательно, исходя из определения касания поверхностей, плоскость П и поверхность Р касаются друг друга. ◄
В дальнейшем нам понадобится понятие нормали к поверхности.
Определение 13. Нормалью к поверхности Р : z = /(х, у) в точке (х0, р0, zQ) называется прямая, проходящая через точку (*о’ У& го) параллельно вектору (//,	“!)•
Лекция 23
$ 6. ЧАСТНЫЕ ПРОИЗВОДНЫЕ ВЫСШИХ ПОРЯДКОВ
Пусть функция f(x) имеет в некоторой 5-окрестности 0(а, е)
все первые частные производные
dftx) дх.
,3=1,
п. Эти частные
производные сами являются функциями от п переменных и могут иметь частные производные, т. е. можно определить следующие величины:
ЭхДэхв) ЭхгЭх8	s, г - 1, ... , re.
Эти величины называются частными производными второго порядка. Если s и г, то они называются смешанными производными.
Имеют место следующие теоремы о равенстве смешанных производных второго порядка.
ТЕОРЕМА 7 (теорема Шварца). Пусть функция f(xl9 х2) в некоторой окрестности точки х = а = (ар а2) имеет смешанные л	л d2f ^2f
частные производные второго порядка ^х ^х и ^х ^х , причем они непрерывны в точке х = а. Тогда в точке х — а эти производные равны между собой, т. е.
/'х'х(а) = Г;х(а).
►	Рассмотрим вторую разность Д2/ функции f(x) в точке х = а Д2/ = /(аг + йр а2 + й2) - /(ах + йр а2) - f(a19 а2 + й2) + Дар а2).
Положим ф(х) = /(х, а2 + й2) - /(х, а2). Дважды применяя формулу Лагранжа конечных приращений, получаем ф(ах + йх) - ф(ах) = h^\ax + 01й1) == = x^ai	а2 + ^2) — fx^ai +	=
= й1й2/?^Х2(а1 + 0хйх, а2 + 0£Й2).
В силу непрерывности функции f'x1X2(xi> хг) в точке х = а имеем ф(ах + йх) - ф(ах) =	а2) + о(1)).
С другой стороны,
фСах + йх) - ф(ах) = ф(а2 + й2) - у(а2), где у(х) = /(ах + йр х) - /(ар х).
305
Вновь применяя теорему Лагранжа, находим
v(#2 + ^2) V(a2) = Х^а1 + ^1» а2 +	~ f x^av а2 + ®$)) =
= hih2f'x^O’i + Д2 + ^2^2) = Мг(/дЦа1» а2) + °(1))-
Отсюда
А1А^л(<»Р «2) + <К1) = Wfvfa а2) + о(1)), т. е. равенство справедливо:
/xtx2(«P а2> = ^.(«Р «2>-	*
ТЕОРЕМА 8 (теорема Юнга). Пусть функции fX1(xvx2) и fX2(xv х2) определены в некоторой окрестности точки х = а = = (av а2) и дифференцируемы в точке а. Тогда
/х^/ор аг) = ^л(<»р аг)-
►	Рассмотрим функции
А2/ = /(<4 + й, а2 + Л) - Дах + й, а2) - /(ах, а2 + й) + /(ах, а2), <р(х) = f(x, a2 + h)~ f(x, а2).
Имеем
Д2/ = ф(а1 + Л) - (pC^).
Из теоремы Лагранжа следует, что
А2/ = Йф'(в1 + М) = Wx/Oi + е1А’ а2 + А) - f'xSai + е1А’ аг))-
В силу того что функция f'Xi(x19 х2) дифференцируема в точке х = а,
/х,(°1 + 01А’ а2 + А) - f'X1(aV а2> = е1А/'х1х1(о) + hf'x.x^ + °(А>» fx/Ol + 91А> а2> “ /’х/Ор °2> = 01А^Л(5> + °<А)’
следовательно,
Д2/ = А2Г"Ж2(а) + о(Л2).
С другой стороны,
Д2/ = ф(а2 + й) - <р(а2),
где \g(i/) = f(at + h9 у) - f(a19 у). Аналогично предыдущему получаем
А2/ = а2/"х1(о) + °(а2)-
Таким образом, «2> = ^Л(Лр а2)-	«
СЛЕДСТВИЕ. Теоремы Юнга и Шварца имеют место при п> 2.
Для доказательства надо зафиксировать все переменные, кроме xr9 xs, и применить доказанные теоремы к получившимся функциям.
306
Определение 14. Функция Дх) называется дважды дифференцируемой в точке, если все первые производные дифференцируемы. Вообще, функция Дх) называется п раз дифференцируема, если все частные производные (п - 1)-го порядка являются дифференцируемыми функциями.
ТЕОРЕМА 9 (достаточное условие дифференцируемости). Для того чтобы функция Дх) была п раз дифференцируема в точке, достаточно, чтобы все частные производные порядка п были непрерывны в этой точке.
Доказательство проводится по индукции.
СЛЕДСТВИЕ (из теоремы Юнга). Если функция f(x) является п раз дифференцируемой, то смешанные частные производные до порядка п не зависят от порядка, в котором производится дифференцирование.
Доказательство получается индукцией из теоремы Юнга.
$ 7. ДИФФЕРЕНЦИАЛЫ ВЫСШИХ ПОРЯДКОВ. ФОРМУЛА ТЕЙЛОРА
Пусть функция Дх) дважды дифференцируема в точке х = а. Зафиксируем приращение dx = h. Тогда получим новую функцию g(x) = g(x, h), определяемую выражением
g(x) = df(x) =
Это дифференцируемая функция в точке х = а, и ее дифференциал равен
-лхг, т. е.
Положим теперь hs = Axs = dxs. Тогда получим d2/(x) = f.	dxtdxr.
v ' г=и~\дхядхг 8 r
Это выражение называется вторым дифференциалом функции Дх) в точке х = а. Аналогично определяется дифференциал dkf(x) порядка k:
dkf(x) = t ... Е	dxs... dxr.
r= 1 e = 1 dx8 ... dxr 8 r
307
Очевидно, это выражение можно символически записать так: dkf(x) = (Д х dxs£- J f(a), где для получения развернутого выражения надо формально возвести выражение в скобках в степень как многочлен, считая символы dxs9 как бы независимыми переменными, а затем к ох8
числителю выражения -—— справа приписать Да). дх8... дхг
Отметим, что drf(x) при г > 2, вообще говоря, не обладает свойством инвариантности, т. е. если вместо dxs в выражение для d2f(x) подставить первые дифференциалы dys(t) функций xs = ф/Z), то получится выражение, которое уже не будет вторым дифференциалом.
Действительно, если h(t) = Дф( О), то
d2h(t) = Е 2/ Жр/йр 4- S е/2ф8.
з = 1 г = 1 дх8дхг v 8 = 1 дх8 Ys
Здесь мы воспользовались тем, что
d(^)d<p,+^<(4-
Но если ф8(О — линейные функции, т. е.
фДО = \), 8	^1, 8^1 +	8^П»
то </2ф8 = 0 и инвариантность второго дифференциала все же имеет место. Аналогичное утверждение справедливо и для третьего дифференциала и т. д. В силу этого, например, если х = а 4- te и g(t) = Да 4- te)9 то
d'f(a + te)|t.o = drg(Olf = о = 8<r)(0Xd0r, т. e. функция g(t) является г раз дифференцируемой. Воспользуемся последним замечанием для вывода формулы Тейлора для функции от п переменных.
ТЕОРЕМА 10 (формула Тейлора с остаточным членом в форме Пеано). Пусть функция Дх) дифференцируема k раз в точке х = а. Тогда при х, стремящемся к а9 справедлива следующая формулах f(x) = Р(х) + г(х), где
Р(х) = f(a) + d/(a)|di . 5_5 + 1 d^a)^ .	+ ...
... + idkf(a)\d- _ 5_5, г(х) = о(|х - а|*).
308
► Воспользуемся методом математической индукции по параметру k. При k = 1 утверждение теоремы следует из определения дифференциала функции. Предположим теперь, что k > 1.
Из условия теоремы вытекает, что функция г(х) в некоторой окрестности U точки х = а имеет все производные до порядка (fe - 1) включительно. Кроме того, в точке а сама функция и все ее частные производные до /г-го порядка включительно равны нулю.
Далее, пусть хе U и Дх = х - а. Тогда имеем
г(х) = г(х) - г(а) = г(а + Дх) - r(a) = D± 4- ... 4- Dn9
где при s = 1, ... , п величины Ds определены равенствами
Ds = ^а1 + Дх1 ’ - ’ as + as+l> ••• ♦ «») -
- г(ах + Ахх,... , а*-! + Дх8_р as,... , a„) = g(as + Дхв) - g(a8).
Отсюда, применяя формулу Лагранжа к каждой величине D89 при некоторых ^8 с условием 0 <	< 1 получаем
Ds = S'x,(a3 + ^Дх8)Дх8 = ГХ,(« +
где v8 = (Дхр ... , Дх8_р £8Дх8, 0, ... , 0). Следовательно,
r(x) = г'х(а 4- у1)Дх1 4- ... 4- г'х(а 4- ул)Дхп.
Заметим, что точка а 4- v8 е U для каждого s = 1, ... , п. Поэтому к частным производным в правой части последнего равенства можно применить предположение индукции с заменой значения параметра k на k - 1. Тогда при всех з от 1 до п будем иметь r'x (а + vg) = о(|* - al*-1).
Отсюда следует, что r(x) = о(|х - а|*). ◄
ТЕОРЕМА 11 (формула Тейлора с остаточным членом в форме Лагранжа). Пусть функция f(x) имеет (k 4- 1)-й дифференциал для любого х е О(а, е), где е — некоторое положительное число. Тогда для любой точки Ь е О(а9 е) существует такая точка с = а 4- 0(Ь - а), 0 < 0 < 1, что
/(&) = /(«) +JriF
, d* + 1/(c) dx = Ь - а (fe + 1)!
dx = Ь - а
► Пусть g(t) = f(a 4- t(b - а)). Тогда по формуле Тейлора для одной переменной с остаточным членом в форме Лагранжа имеем
rf1)=<r(o)+*ao)	^^>(0)
0!	k\ (£ + 1)! ’
309
где 0 < 0 < 1 — некоторая постоянная. Поскольку справедливы равенства
£(0) = Да), £'(0) = df(a)\d- = -..., ^>(0) -= dk(a)\d- ~-b--a> £(fe+1)(0) = d^f(c)\d-
подставляя их в предыдущее соотношение, получим утверждение теоремы.
Замечание. Отметим разницу в условиях существования формулы Тейлора с остаточными членами в форме Пеано и Лагранжа (теоремы 10 и 11). Она состоит в том, что в первом случае ^-кратная дифференцируемость функции f(x) предполагается только в точке х = а, в то время как во втором случае требуется (k + 1)-кратная дифференцируемость ее в окрестности О(а, е). Обратим внимание на то, что в случае функции одной переменной ^-кратная дифференцируемость ее в точке х = а обеспечивает (k - 1)-кратную дифференцируемость в окрестности, в кратном же случае это условие дает существование в этой окрестности только частных производных до (k - 1)-го порядка включительно.

Лекция 24
§ 8.	ПРИЛОЖЕНИЕ ФОРМУЛЫ ТЕЙЛОРА.
ЛОКАЛЬНЫЙ ЭКСТРЕМУМ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Определение точки локального экстремума для функции многих переменных дословно совпадает с аналогичным понятием для функции одной переменной, и, вообще, для функций, определенных в любом метрическом пространстве, только е-окрестность точки, в которой функция имеет экстремум, определяется соответствующей метрикой.
Определение 15. Точка а е Rn называется точкой строгого локального максимума функции f(x)9 если существует г-ок-рестностъ О(а9 е) точки а такая, что для любой точки х * а и х е О(а9 е) имеем неравенство f(x) < f(a): если f(x) < f(a)9 то а — точка нестрогого максимума; если f(x) > f(a)9 то а — точка строгого минимума; если f(x) > (а), то а — точка нестрогого минимума.
Строгие локальные максимумы и минимумы в точке называются локальными экстремумами в точке, а нестрогие — нестрогими локальными экстремумами в точке.
ТЕОРЕМА 12 (необходимоеусловие экстремума). Если а — точка локального экстремума (нестрогого) функции f(x) и существует дифференциал df(x) ее в этой точке, то для любого приращения Хх имеем
= °’ или Srad №\х-а = б-
► Очевидно, достаточно доказать, что при s = 1, ... , п выполняются равенства
д/(х) Эх8
Рассмотрим функцию g(t) = f(a 4- te8), где ё8 — направляющий вектор оси Ох8. Тогда ясно, что g(t) имеет в нуле точку локального экстремума, откуда £*'(0) = 0. Но так как ^-г-(0)-0,
то это доказывает утверждение теоремы. ◄
Определение 16. Точка а, в которой градиент функции f(x) обращается в б, называется стационарной точкой функции f(x).
= 0. х = а
311
Заметим, что второй дифференциал d2f(x) функции Дх) в точке х — а е Rn является квадратичной формой от п переменных dxp ... , dxn.
Определение 17. Стационарная точка а функции Дх) называется регулярной, если в этой точке существует второй дифференциал d2/(x) и он является невырожденной квадратичной формой от переменных dx19 ... , dxn, т. е. определитель матрицы этой квадратичной формы отличен от нуля.
Выведем теперь достаточное условие экстремума функции.
ТЕОРЕМА 13 (достаточное условие экстремума). Пусть а — регулярная стационарная точка функции Дх), т. е. дифференциал этой функции в точке а обращается в нуль и существует второй дифференциал в этой точке с невырожденной квадратичной формой от переменных dx19 ... , dxn. Тогда:
1)	если в этой точке d2f(x) — положительно определенная квадратичная форма, то в точке х = а функция Дх) имеет локальный минимум;
2)	если d2f(x) — отрицательно определена, то а — точка локального максимума;
3)	если d2f(x) является неопределенной формой, то точка а не является точкой локального экстремума.
► 1) Обозначим через А матрицу квадратичной формы d2/(x) от переменных Дх8, s = 1, ... , п, а через S(a) — множество точек х g Rn с условием |Дх| = 1.
Множество S(a) ограничено и является замкнутым, так как совпадает со своей границей dS(a), в поэтому содержит эту границу. Следовательно, S(a) — компакт, а потому на множестве S(a) второй дифференциал, как функция от приращения Дх, достигает своего минимума т, т. е. найдется вектор ё0, |ё0| = 1 такой, что
d2ftx)k-5Mx = eo=,n>0-
Заметим, что для любого вектора Дх = | Дх|е = 1, имеем
</2/(х)|; = 5>д5 = |Дх|2</2/(х)|- = -в.
По формуле Тейлора с остаточным членом в форме Пеано получаем
ДДх) = df(a) 4- I d2f(a) 4- о(|Дх|2) > | Дх|2тп(1 4- о(1)),
т. е. найдется е > 0 такое, что для любой точки х g О(а, е) выполняется неравенство ДДх) > 0.
312
Пункт 2) рассматривается аналогично.
3) В силу неопределенности квадратичной формы d2f(a), получаем тп < 0 < М, где
М = sup d2f(a), m = inf d2f(a), |Дх|=1	|Дх| = 1
причем величина М достигается на векторе ё19 а величина тп — на векторе ё2. Тогда функция gx(f) = f(a + te^) при t = 0 имеет локальный максимум, функция g2(t) = f(a 4- te2) — локальный минимум, а сама функция f(x) в любой окрестности точки а принимает значения, как большие /(а), так и меньшие /(а), т. е. точка а не является точкой локального экстремума. ◄
§9. НЕЯВНЫЕ ФУНКЦИИ
Пусть заданы точка (а, Ь) = (ах,... , ап-19 b) е Rn, некоторая ее е-окрестность и множество точек, принадлежащих этой е-ок-рестности и удовлетворяющих уравнению f(x, у) = 0.
Определение 18. Функция ф(х), зависящая от (п - 1)-й переменной х = (хх, ... , хЛ_х) и заданная в некоторой 8-окрестности точки а, называется неявной функцией, соответствующей уравнению f(x, у) = 0, если для любой точки х из этой 8-окрестности имеет место равенство f(x, ф(х)) = 0.
Определение 19. Функция f(x) называется гладкой в области Q a Rn, если для любой точки х е Q она является дифференцируемой и ее частные производные непрерывны.
Докажем теперь теорему о неявной функции.
ТЕОРЕМА 14 (теорема о неявной функции). Пусты
1)	функция f(x, у) непрерывна в некоторой ъ-окрестности Q точки (a, ft) е R2;
2)	f(a, Ь) = 0;
3)	для любой точки (х, у) е Q частные являются непрерывными функциями;
4)ЗДа1Щ>0
Тогда существует единственная функция у = <р(х), определенная в некоторой 8-окрестности точки а, такая, что;
1) ф(а) = Ь;
2) для любой точки х, принадлежащей 8-окрестности, имеет место равенство f(x, ф(х)) = 0. Более того, оказывается, что эта функция ф(х) является гладкой, причем
Л df df производные и &-
гх(^^\у^(х)
ф'(х) = -
313
► Так как f'y(x, у) — непрерывна на Q и /^(а, Ь) > 0, то существует замкнутый квадрат К с Q с центром в точке (а, Ь) и со сторонами, параллельными осям координат, длины 2й, внутри которого минимальное значение f'y(x9 у) равно т > 0. В силу того, что /^(х, у) > 0, функция /(а, у) возрастает. Далее, так как /(а, Ь) = 0, то /(а, Ь 4- й) > 0 и /(а, Ь - й) < 0. В силу непрерывности функции f(x9 у)9 существует число 8 > 0 такое, что для любого значения х g [а - 8, а 4- 8] имеем f(x9 b + й) > 0 и /(х, Ь - й) < 0.
Отсюда следует, что на отрезке, соединяющем точки Аг = = Ах(х) = (х, & - й) и А2 = А2(х) = (х, & + й), монотонная функция g(y) = f(x9 у) обращается в нуль только в одной точке ух.
Каждой точке х g [а - 8, а + 8] поставим в соответствие точку ух. Оно определяет функцию у = ф(х) = ух9 для которой
/(х, ф(х)) = Дх, ух) = 0,
при этом из равенства f(a9 &) = 0 имеем ф(а) = уа = Ь.
Фунзщяя ф(х) и является искомой. Надо только доказать, что функция у = ф(х) дифференцируема внутри интервала (а - 8, а 4- 8), причем
„ ч	/;(х,ф(х»
Ф(Л)	г;(х,<р(х))-
Докажем сначала непрерывность ф(х). Пусть точки х и х0 принадлежат интервалу (а - 8, а 4- 8). Покажем, что Дф(х0) = ф(х) -- ф(х0) -» 0 при Дх = х - х0 —> 0. Положим у = ф(х), yQ = ф(х0), Ау = Дф(х). Тогда f(x9y) = /(х0, у0) = 0. Следовательно, для функции g(t) = /(х0 4- £Дх, у0 4- tAy) справедливы равенства £(0) = = g(l) = 0. Функция g(t) при любом t g [0, 1] имеет производную
g\t) =	Уо + ^у)Ах 4- fy(xQ 4- tAx9 yQ +
По теореме Ролля, существует число 0 g (0, 1) такое, что £'(®)= О’ Отсюда получаем
Ду =	fx(^)
Ах fy(l) ’
где £ = (х0 4- 0Дх, у0 4- 0Ду). Следовательно,
It^I < rn ’ М =	Ю1. т =	у)| > 0,
|Дх| III'	К	К 9
т. е. величина ограничена. Поэтому Ду = Дх • —- —> 0 при Дх —> 0, т. е. ф(х) является непрерывной функцией. Кроме того, 314
так как при Дх —> О имеем, что Ду —> 0, тоД —» (х0, у0). Далее, в силу непрерывности частных производных f' та f' > 0, получаем Л у
ф'(х) =
Замечания. 1. Случай у) < О сводится к рассмотренному заме-ной функции f на £ =
2. График функции у = <р(х) является частью линии уровня 2 = 0 для поверхности г = Дх, у).
СЛЕДСТВИЕ (общая теорема о неявной функции). Пусты
1)	функция Дх, у) непрерывна в некоторой ^-окрестности Q точки (а, Ъ) = (а19 ... , ап_19 b) е Rn;
2)	Да, Ь) = 0;
df
3)	для любой точки (х, у) е й частные производные , ...
df
... , ч- и j- являются непрерывными функциями^
®Хп-1 °У
>0.
Тогда существует единственная функция у = ф(х), определенная в некоторой 8-окрестности точки а такая, что:
1)<р(а) = &;
2) для любой точки х, принадлежащей 8-окрестности, имеет место равенство Дх, (р(х)) = 0;
3) функция ф(х) является гладкой, причем
ф;,(х) - -
К*-|Ч-,й 
Доказательство, по существу, дословно совпадает с доказательством теоремы. Надо только вместо точек (а, Ь ± Л) рассмотреть точки (а, Ь + Л), а вместо интервала (а - 8, а + 8) — шар О(а9 8).
В качестве приложения предыдущей теоремы рассмотрим задачу об арифметических свойствах неявных функций, представимых степенными рядами. Приводимый здесь результат является частным случаем одной теоремы Эйзенштейна.
ТЕОРЕМА 15. Пусть задано алгебраическое уравнение F(x, у) = 0 с целыми коэффициентам^ причем F(0, 0) = 0 и F'y(09 0) * 0. Пусть также степенной ряд у = у(х) = л?0 аЛхп является решением этого уравнения9 т. е. у = у(х) — алгебраическая функ
315
ция. Пусть, далее, коэффициенты ak, k > 0, — рациональные числа. Тогда существует такое целое число I, что при замене х на 1х коэффициенты степенного ряда, получившегося из ряда у = у(х), будут целыми числами, за исключением, быть может, а0.
► В силу теоремы о неявной функции существует единственная функция у0 = у0(х), удовлетворяющая уравнению F(x, у) в 0 в некоторой окрестности точки (0, 0). Следовательно, эта функция совпадает со степенным рядом у = у(х).
Запишем многочлен F(x, у) в виде
F(x, у) = Ро + Pty + ... + Ртут,
где Ро = Р0(х), ... , Рт = Рт(х) — многочлены от переменной х. Так как F(0, 0) = 0, то Ро(О) = 0. Из условия F^(0, 0)^0 получим: Л(0) # 0. Представим многочлены Ро = Р0(х), ... , Рт ~ Рт(х) в следующей форме:
Р» = 8ох + М2 “*"•••>
Р1 = £1 + hrx + ..., gr # 0,
Р = g + h х + .... х т sm ' ..........
[ X = g2t
Положим теперь = ® где * и и — новые переменные. Сокращая равенство F(gfy, gx и) на g%, получаем
GQt + HQt2 + ... + (1 + Grt + Hrt2 + ...) и + (Gm + Hmt + .f.)um = 0, где Gq, Hq, ... , G19 H19... , Gm, Hm, ... — целые числа. Из последнего уравнения имеем
GQt + Hot2 + ...	Gm + Hmt + ...
и =-----2----2—-Л-------...----------—2-----ит. (*)
1 + Gi* + Н^2 + ...	1+ Grt + Н^2 + ...	v '
При |z| < 1 воспользуемся равенством
7^- - 1 - 2 + 2г -	+ (-1)" 2n + ... .
1 + z
Тогда выражение (*) принимает вид
и = (А^ + A2t2 + ...) + (Во +	+ ...)и2 + ... .
Будем искать функцию и = u(t) в следующей форме: и = m,it + m2t2 + m3t3 + ... .
316
Тогда коэффициенты т19 т2, т3,... определяются из равенств
7П1 = т2 = А2 + Вот*, т3=А3 + 2Вот1т2 + Вгт1,
Отсюда следует, что числа т19 т2, т39 ... — целые. ◄
В частности, из последней теоремы следует, что функции
00 Yk	00	Yk
не являются алгебраическими.
ЗАДАЧИ. 1. Пусть функция Дх, у) определена во всех точках квадрата К е R2 и для любого фиксированного у функция g(x) = = f(x> У) непрерывна для каждой точки х. Тогда внутри квадрата К найдется точка непрерывности Дх, у) как функции двух переменных.
2. Пусть функция Дх, у) определена на R2 и для каждого фиксированного значения одной переменной она является многочленом по другой переменной. Тогда функция Дх, у) является многочленом от двух переменных.
3. Построить замкнутое множество А, содержащееся внутри замкнутого единичного квадрата на плоскости хОу, которое обладает следующим свойством: для любого линейного замкнутого множества L на отрезке [0,1] а Ох найдется точка yL е [0,1] а Оу такая, что проекция на ось Ох множества точек плоскости, лежащих на пересечении с горизонтальной прямой у = yL, в точности совпадает с множеством L.
Лекция 25
$ 10. СИСТЕМА НЕЯВНЫХ ФУНКЦИЙ
Рассмотрим отображение
f: Rn Rm, f(x) = (Ых),..., Гт(х)).
Пусть все функции /х(х), ... , fm(x) являются гладкими в е-ок-рестности О(а, е) точки а. Тогда такое отображение называется гладким.
Определение 20. Пусть функции (fr(x), ..., fm(x) дифференцируемы в точке х е Rn. Тогда матрица
J = Jf ^2 ; fe = 1,..., тп, 8 = 1,..., п;
Эх,
имеющая т строк и п столбцов, называется матрицей Якоби отображения f(x) = (f^x),..., /щ(х)).
Строки матрицы Якоби представляют собой градиенты функций fk(x), k = 1,..., т.
Пусть т п. Рассмотрим какие-либо т различных столбцов матрицы J. Они образуют подматрицу J(klt..., fem) порядка т х т матрицы J, где klf... ,km — номера выбранных столбцов.
Определение21. Определитель Н матрицы J(kv ..., km) называется якобианом (одним из якобианов) отображения f(x) и обозначается так'.
D(fu - >fm) D(xki,... ,xkm) *
Определение 22. Дифференцируемое отображение f(x) называется невырожденным в точке х = а, если один из якобианов этого отображения отличен от нуля.
Это означает, что:
1) матрица J имеет максимальный ранг, или
2) градиенты функций /\(х), ... , линейно независимы в этой точке.
ТЕОРЕМА 16 (теорема о системе неявных функций). Пусть п = т + р, р> 0, кроме того:
1)	отображение f : Rn -> Rm — невырожденное в точке (а, 6), где а = (ар ... , ар) и Ь = (Ьр ..., Ьт), и гладкое в некоторой окрестности £1 = 0 ((а, Ь), е) точки (х, у) = (а, 6);
318
2)	f(a, b) = 0;
3)	H(y) =	...fm\ * 0.
’ В(у1г... ,yn)
Тогда в некоторой окрестности О(а, 8) = Qx с Rp точки а существует единственное гладкое, отображение ф(х) » (фх(х), ... ... , Фт(х)), где х = (хх, ... , хр), обладающее следующими свойствами*.
1)	Да, ф(а)) = 0;
2)	для всех хе имеем f(x9 ф(х)) = 0;
3)	(х) = -А"1 В, где А = Jf(y)9 В = Jf(x).
Здесь А и В — две части матрицы Якоби Jf9 отвечающие переменным у19... 9 ут и х19... , хр соответственно.
Другими словами, эта теорема утверждает, что система уравнений
4 (Хр ..., хр, уг,..., ут) = 0, k = 1,..., т, разрешима относительно переменных ух, ... , ут как функций от переменных (х19..., хр) таким образом, что функции уг = фх(х),..., ..., ут = фт(х) удовлетворяют тождествам
4(х, ф(х)) = 0 Vx g Qp
где Qx — некоторая окрестность точки а, причем:
а)	Да, ф(а)) = 0;
б)	Дх, у) является невырожденным гладким отображением в некоторой окрестности точки (а, Ь) с условием
^Уи... ,ут) и’
За	мечания. 1. Матричное равенство п. 3 определяет все частные производные вида
ЭфЛ(х) ,	.	1
—, k = 1, ... , т9 з = 1, ... 9р.
2. Если Дх) — линейное отображение, то утверждение теоремы есть простой факт из линейной алгебры о решениях системы линейных уравнений.
► Докажем теорему. Рассмотрим определитель Якоби Н(у) матрицы А. Разложим его по последнему столбцу. Получим
ЭД ЭЛ	ЭЛ
Я(й) = н. + я2 +... + нт .
1 ^Ут 2 дут	т дут
319
Так как Н(у) не обращается в нуль в точке (а, Ь), то, по крайней мере, один из миноров матрицы А не равен нулю. Без ограничения общности можно считать, что Нг ** 0.
Проведем доказательство методом математической индукции по чйслзгурявнений тп. При тп = 1 утверждение теоремы доказано в предыдущем параграфе. Предположим, что теорема верна для тп - 1 уравнения. Докажем ее для тп уравнений.
Так как Нг 0, применяя предположение индукции к функциям /2(х, у)9..., fm(x9 у)9 получаем, что существуют функции
У1 = Ут), ..., Ут-1 = Vm-1 (X, ут), удовлетворяющие условиям
fk (х, ¥1,... , vm_ v ут) = 0, k = 2,... , т, для любой точки (х, ут) в некоторой окрестности £20 точки (а, Ьт). Подставим теперь ... , в функцию /\(х, у). Имеем
/1 (X, ^(Х, ут), ... , Ym-1 (X, Ут)~Ф {х, ут).
Покажем, что	ЭФ >	0 в точке (а, Ьт). Действительно,	
ЭФ	^/1 t	! 9ft Эфст_1 + Э/х
дут '	9l/i ^Ут	9ут_1 дут дут9
п 		Э/г	-|-	^т-1 _|_ ^/2
и =	9j/i Ъут	9j/m_! дут дутг
л			+ 9fm 9у)П_1 Э/То
и —	9»i дут	9j/m-i 9t/m дут'
Домножим первое уравнение на Н19 второе — на Н2 и т. д. Сложим получившиеся выражения. В результате будем иметь
ЭФ
Нг = Н9 так как при k # тп справедливо равенство
ZH8^-= о, 8=1	8 ^yk
а при k = тп эта сумма равна Н.
ГТ	ТТ ТТ	^Ф Н	гл
Далее, поскольку Н и Нх не равны нулю,	0. Сле-
довательно, по теореме о неявной функции, существует единственная функция ут = <рт (х) такая, что (х, ф(х)) = 0 в некоторой окрестности Q точки а, где
Ф1(х) = Vl(x, Фт (*)). ... ♦ Фт-1(*) =	фт («)).
При k = 2,..., т в области Q имеем fk (х, <р(х)) = 0. 320
В силу инвариантности формы первого дифференциала при k = 1, ... , т имеем
О = dfk = dxi + ... + dx + dtpxO) + ... + ^ dtp (х).
1 дхр р dyi Т1	дуп vnt'
В векторном виде это можно записать так:
Bdx + Ad<p(x) = О,
где
8fi	3fi
8V1	8Ут
дхх
8fm ‘ дхр)
8fm dxY
Sfm Sfm 8У1'“ 8Ут )
d<p(x) =
Имеет место равенство
dq>!(x)
d<PmW>
dx =
dxx
dq>(x) = J/x) dx,
где
Jv(x) =
£<Pi g<Pi ' 5*1 ’ ’ ’ 8xp
8<?m	8<?m
dxY * * * dxp >
Таким образом, получаем
AJ^(x)dx + Bdx = 0, т. e. (J9(x) + A~rB)dx = 0.
Итак, линейное отображение переводит любой вектор dx е RP в нулевой вектор. Следовательно, это нулевое отображение и е7ф(х) + А~ГВ = б, т. е. J/x) = -Аг'В. ◄
СЛЕДСТВИЕ (теорема об обратном отображении). Пусть гладкое отображение <р: Rn —> Rn в окрестности точки х ая невырожденное в этой точке. Тогда существует обратное гладкое отображение \^(у) = определенное в некоторой ^окрестности точки Ь = ф(а), т. е. такое отображение, что \|/(ф(х)) = причем матрица Якоби	отображения у (у) равна
321
11 -4953
Теорема является прямым следствием теоремы о системе неявных функций. Надо только записать равенство у - ф(х) = 0 в виде системы неявных функций
fi(x, у) = фх(х) - z/j = О,
fn(x, у) = ф„(х) - уп = О, а затем по этой теореме выразить х через у.
811. УСЛОВНЫЙ ЭКСТРЕМУМ ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Определение 23. Пусть Q — область точек Rn9 на которой определены гладкие функции фп(х), , фш(х), т < п. Тогда множество Qx с й решений системы уравнений ф(х) = 0, k = 1, ..., т, называется многообразием, порожденным функциями фр ..., фт. Уравнение фА(х) = 0 называется уравнением связи для многообразия Qr
Определение 24. Точка а называется точкой условного локального максимума на многообразии £1, если в некоторой окрестности точки а для любой точки х, принадлежащей этой окрестности и многообразию Q, справедливо неравенство f(x) < f(a).
Аналогично определяются точки условного локального минимума и экстремума.
Замечание. Если связи отсутствуют, то условный локальный экстремум называется безусловным экстремумом.
Определение 25. Точка а функции f(x) называется особой, если grad f(a) = 0, и неособой, если grad f(a) # б.
Определение 26. Многообразие £2Х называется невырожденным, если для любой точки х е векторы градиентов Ф8 = = grad ф8(х) при з = 1,..., т являются линейно независимыми. ТЕОРЕМА 17 (необходимое условие условного экстремума). Для того чтобы неособая точка а функции f(x) была точкой условного экстремума функции f(x) на невырожденном многообразии Qp необходимо, чтобы вектор F = grad f(x) в точке х = а выражался в виде линейной комбинации градиентов
Фх = grad ф(х),..., Фт = grad фт(х)
322
в этой точке, т. е. чтобы существовали вещественные числа Хр , Хто такие, что
Г = А.1Ф1 + ... + ХтФт.
Утверждение этой теоремы допускает следующую переформулировку для практического нахождения условного экстремума. СЛЕДСТВИЕ (метод множителей Лагранжа). Пусть Хр ... ,	—
независимые вещественные переменные. Рассмотрим функцию Лагранжа
Цх, X) = ftx) - X^iCx) -... - Xm<pm(x).
Для того чтобы неособая точка а функции Дх) была точкой условного экстремума этой функции на невырожденном многообразии необходимо, чтобы при некотором X = Х0 имело место равенство
d£(x,X)|i_5.x-Io = 0’ т. е. чтобы все частные производные функции Цх, X) по переменным х8 и Хг обращались в нуль.
► Докажем следствие. Если приравнять к нулю частные производные по переменным Хг, то получим уравнение связи. А если продифференцировать по х8, s = 1,..., п, то имеем условие выражения градиента функции f(x) в виде линейной комбинации градиентов функций фг(х), что по теореме и является необходимым условием. Следствие доказано.
Идея доказательства теоремы состоит в том, чтобы найти п - т линейно независимых векторов aw+1, ... , ап g Rn таких, что каждый из этих векторов одновременно перпендикулярен вектору F и векторам Фр ... , Фт. Отсюда будет следовать, что линейное пространство L, состоящее из всевозможных линейных комбинаций этих векторов, обладает свойством F 1 L и Фй 1 L, k = = 1, ... , т. Ортогональное дополнение пространства т. е. пространство L1, состоящее из всех векторов х 6 Rn, ортогональных к L, содержит векторы F и Фх, ... , Фт. Размерность пространства 1Л равна п - т. Поскольку векторы Фх,... , Фт — линейно независимы, они образуют базис L. Следовательно, вектор F есть линейная комбинация векторов Фр ... , Фт.
Заметим, что на самом деле L состоит из всех векторов, лежащих в каждой из касательных плоскостей к поверхностям Ф8(х) = 0, з = 1,... , т, в точке х — а.
323
и*
Итак, осталось указать векторы йр ... , ал_т е IA. Будем их выбирать следующим образом. Без Ограничения общности можно считать, что
Р(Ф1,... ,Фт) #
D(xp ... ,xm)
По теореме о системе неявных функций, в некоторой 8-окрестности точки а е Rn существует т гладких функций уДЗ), ... , где z = (xm+1, ... , хп) таких, что
<P*(Vi(*)> — , z) = 0, а также
<P*(Vi(*o)’ • >	*о) = °’ (Vi(^o), - ’	*o) = 5-
Пусть ёг — направляющий вектор оси Oxr, г = т + 1, ... , п. Рассмотрим функции
Ч ДО = <P*(Vi(*o +	*о + ^г) = °,
где k = 1, ... , тп, а также функцию
й0, г(0 = /Ш*0 + ^г), • > Vm(*o +	*0 +
В точке t = 0 производные всех функций равны нулю: у первой, ... , тп-й — потому, что они тождественно равные нулю функции, а у функции hQ r(t) — потому, что точка t = 0 должна быть точкой локального экстремума этой функции.
Вычисляя h'k>г(0|е = о по теореме о производной сложной функции, получаем
Ь' ГА1 = дЧ1 ।	. дЧт I dy^k
= 0 дХ1 дХг + ••• + дХт дХг + дХг>
й' (rt|	+^L^ + ^L
«0,rWlt = 0 дХ1 дХг + ••• + дХт дХг + дХг>
где k = 1,... , т; г = т + 1,... , п, т. е. имеем
^,r(Olt = 0 = <ФЛ’ аг) = 0» *0,r(Olt-0 = аг) = 0 причем
^=.0..1
г V дхг
число 1 находится на т + r-м месте.
Таким образом, все векторы ат+1, ... , ап перпендикулярны каждому из векторов F, Фр ... , Фт, при этом, очевидно, векторы Фр ... , Фт, в силу невырожденности многообразия £2Х, будут линейно независимы. «
324
J
$ 12. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ. МАТРИЦА ЯКОБИ
Покажем, что матрица Якоби отображения f : Rn -> Rm обладает некоторым важным свойством, аналогичным свойству производной функции.
Определение 27. Пусть отображение а : Rn -» Rm определено в некоторой окрестности точки х = б. Тогда будем говорить, что а(х) есть о-малое от длины вектора х, и обозначать это так:
а(х) = о(|х|), если lim = 0. |х|
Определение 28. Линейное отображение /(Дх) из Rn в Rm называется дифференциалом отображения f(x) в точке х = а, если
Af(x) = /(Дх) + о(| Дх|).
Обозначение: l(tix) =
Если существует дифференциал отображения в точке, то оно называется дифференцируемым, в этой точке. Дифференциал отображения можно определить следующим равенством:
Um
Дх->0 |Дх|
УТВЕРЖДЕНИЕ 4. Если дифференциал отображения существует, то он определен однозначно.
►	Пусть ^(Дх) и /2(Дх) — дифференциалы отображения f(x) в точке х = а. Положим /(Дх) = /х(Дх) - /2(Дх).
Из неравенства треугольника имеем
|/(Дх)| <|Д/(х) - /х(Дх)| + | Д/(х) - /2(Дх)|.
В силу определения дифференциала отображения отсюда получаем
Г |ЦДх)1 А Inn Л-/1 =0.
Ах->0 |Дх|
Далее, поскольку отображение /(Дх) линейно, для любого приращения Дх имеем
|/(Дх)| _ |Z(tAx)| _
ПдгГ	"°*
Таким образом, отображение /(Дх) переводит все линейное пространство в нулевой вектор. Следовательно, отображение /(Дх) — нулевое, что и требовалось доказать. ◄
325
УТВЕРЖДЕНИЕ 5. Пусть Дх) — дифференцируемое отображение. Тогда имеет место равенство
ДДх) = е7Дар Дх + о(|Дх|Х
где выражение J^a)*^x понимается как умножение матрицы Якоби Jf(a) на вектор Дх.
►	Доказательство очевидно. ◄
Приведем еще несколько свойств дифференциала отображения, которые непосредственно выводятся из его определения.
1°. Дифференциал df(x) отображения Дх) существует тогда и только тогда, когда существуют все дифференциалы dfk(x) функций fk(x), f(x) =	..., fm(x)).
2°. Если отображение у = g(x) дифференцируемо в точке а, а отображение f(y) дифференцируемой в точке Ь — g(a), и образ некоторой окрестности точки а при отображении g содержится в некоторой окрестности точки Ъ, то отображение h(x) = f(g(x)) дифференцируемо и
3°. Отображение f : Rn -> Rm, которое является гладким в некотором шаре О(а, е), а е Rn, е > 0, заведомо дифференцируемо во всем шаре О(а, е).
Часть III
Функциональные ряды и параметрические интегралы
В последнее время в преподавании курса математики наметилась тенденция перехода от излишней абстрактности изложения к его содержательности. В известной степени это перекликается с представлениями математиков прошлого. Примером сочетания четкости изложения с конкретностью и идейной ясностью является учебник Ш. Ж. ла Валле-Пуссена «Курс анализа бесконечно малых», который во многом служит образцом. Авторы этого учебника предполагали сочетать краткость изложения, свойственную конспекту лекций, с доступностью и полнотой учебника. С другой стороны, концепция курса предполагает выделение роли понятия предельного перехода во всевозможных его проявлениях как фундаментальный принцип изложения предмета. Также отметим, что материал этой части отражает наиболее существенные элементы всего курса математического анализа, связанные с одновременным рассмотрением и перестановкой порядка выполнения нескольких предельных переходов в сочетании с понятием двойного предела.
Здесь рассмотрены такие приложения общей теории, как бесконечные произведения и бесконечные определители, основы теории эйлеровских интегралов, задача Кеплера о движении двух тел и функции Бесселя, формула Лагранжа для обратной функции, обобщающая формулу Тейлора, формула суммирования Пуассона и вычисление точного значения суммы Гаусса. Другое приложение теории — это изложение асимптотических методов Лапласа и стационарной фазы, являющихся, как известно, вещественной интерпретацией метода перевала в теории функций комплексного переменного. Обращаем внимание на то обстоятельство, что лекции, в которых излагается материал приложений, как правило, превосходят по объему отдельные лекции, содержащие теоретические основы курса. Заметим также, что выбор приложений обусловлен стремлением привить студентам математический вкус и любовь к предмету.
ГЛАВА 15
Числовые ряды
Лекция 1
§ 1. ОСНОВНЫЕ СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ. КРИТЕРИЙ КОШИ
Эта часть курса математического анализа охватывает три большие темы, а именно:
1)	числовые и функциональные ряды;
2)	интегралы, зависящие от параметра;
3)	ряды и интегралы Фурье.
Тему 3) при формальном подходе следует отнести к двум первым, однако ввиду особой важности и специфических особенностей ее традиционно выделяют в самостоятельный раздел.
Понятие числового ряда вскользь рассматривалось еще при изложении темы о числовых последовательностях. Теперь рассмотрим этот вопрос более детально.
Напомним основные определения.
Определение 1. Пусть {ап} — произвольная числовая последовательность. Числовым рядом или просто рядом называется формальная бесконечная сумма S вида
S = ах + а2 +	+ ••• •
Обычно используется сокращенная запись: S = Ъ ап, или просто Е ап. Здесь натуральный параметр п в знаке суммы определяет номер члена последовательности. При фиксированном п соответствующий ее член ап называется п-м членом ряда. В то же время символ ап, рассматриваемый как функция своего номера, называется общим членом ряда. Вместо буквы п можно использовать любую другую букву, обозначающую переменную, принимающую натуральные значения.
Рассмотрим теперь новую последовательность ал, задаваемую равенством
п s„ = аЛ + ... + а„ = Е аь. п 1	п k = 1 к
329
Определение 2. Последовательность зп называется последовательностью частичных (или частных) сумм ряда Ъ ап, а ее п-й член называется п-й частичной суммой этого ряда.
Определение 3. Если последовательность зп частичных сумм ряда Ъ ап сходится к числу з, т. е. если зп = з, то ряд Ъ ап называется сходящимся (к з), а число з — его суммой. В этом случае пишут:
Zon=»?io» = s-
Если же последовательность {зп} не имеет предела, то говорят, что ряд Ъ ап расходится.
В основном нас будут интересовать сходящиеся ряды.
Определение 4. Если ряд Ъ ап сходится к числу з, то последовательность гп = з - зп называется остаточным членом или остатком ряда.
Заметим, что так как зп -> з при п —> оо, то rn -> s - з = 0 при п оо.
Модифицируем введенные определения и обозначения. Если в числовой последовательности ап отбросить несколько начальных членов, например, в количестве т > 0, то оставшиеся члены ат+1, ат + 2» ••• в совокупности можно снова рассматривать как некую новую последовательность Ьп, задаваемую равенством Ьп ~	4- п*
Рассматривая Ъп как общий член ряда Ъ Ъп, для его частичных сумм з'п получаем равенство
~ ^1 +	^т+1 + ••• + ^т+п ^m+k ””	&т+п §п*
Кроме того, ряд как формальную бесконечную сумму, можно записать в виде
П?1 Ьп = Ь1 + Ь2 + ••• = ат+1 + ат + 2 + ••• k + 1
Таким образом, бесконечную сумму k eE+ ak можно рассматривать как ряд.
Далее будем рассматривать формальные ряды вида gZ1 ап , где п8 — какая-либо последовательность натуральных чисел, и исследовать их на сходимость.
330
УТВЕРЖДЕНИЕ 1. Остаточный член гп ряда можно представить в виде ряда k явЕ+ г ak в том смысле, что:
1)	его сумма равна гп, когда исходный ряд лЕх ап сходится;
2)	это представление понимается как формальное равенство, когда оба ряда расходятся;.
3)	другие случаи не имеют места.
► Доказательство начнем с п. 3). При k > 1 для частичных сумм s'k ряда я_Е+1 ап и зк+п ряда ^ап имеет место равенство s'k = sk+n - sn.
При фиксированном п сходимость и расходимость последовательностей и sft + п имеют место одновременно, что и означает справедливость утверждения п. 3).
В случае 1), т. е. когда оба ряда сходятся, можно перейти к пределу при k -> °° в равенстве s'k = sk+n - sn. Тогда получим
8 = fe 8* = fe (8fe+« " 8»> = 8 " 8» = г»;
тем самым утверждение п. 1) доказано.
Относительно утверждения п. 2) следует заметить, что формальное равенство
ОО	п	оо	оо
Ои	==	а,	du । .
k	k k=n+lk *=1	*+*
можно рассматривать как определение одной из возможных операций над формальными числовыми рядами. При введении подобных операций необходимо только требовать, чтобы правые и левые части равенств переходили в равенство между числами в случае наличия сходимости хотя бы для одной из частей равенства, что действительно имеет место в рассматриваемом случае. Доказательство утверждения 1 закончено. ◄
00 1
ПРИМЕРЫ 1. Ряд	j) сходится, и его сумма равна 1.
Действительно, имеем
8»=П2+2Ь+- + ^ТТ) = (1-1)+(Ы) + -+(п"Г
при п —» оо т. е. з = lim з„ == 1.
2. Сумма членов бесконечной геометрической прогрессии вида а + aq + ... + aqn + ... при а # 0.
331
В случае q = 1 имеем sn = па, и ряд расходится. При g # 1 справедливо равенство
sn = а + aq + ... 4- aqn~r = а (1 + q 4-... 4- g71"1) = = а(1 -qn) = a __ aqn 1-q	1-q	1-g’
Известно, что qn -> 0 при |g| < 1 и {qn} расходится при |g| > 1. Таким образом, указанный ряд сходится к сумме з = —— при |g| < 1 1 -q
и расходится при |g| > 1, а * 0.
3. Гармонический ряд Е 1/п = 1 4- 1/2 4-... 4- 1/п 4-... расходится, а ряд Е 1/па =14- 1/2а 4-... 4- 1/па 4-... сходится при а > 1. Заметим прежде всего, что расходимость ряда есть расходимость последовательности его частичных сумм, т. е. надо доказать, что последовательность sn = 1 4- ... 4- 1/п расходится. Для
этого достаточно показать, что эта последовательность не огра
ничена.
При п = 2* имеем
«п = «2‘=1 + | +(| +|) +
+(1 + 1 + 1 +11+•••+(—-— + ••• + —k \5	6	7	8'	'2fe-14-l 2k
>1 + 1+ 2«Д+...+ 2*-1 • Д = 1 + 2	22	2*	2	2
Отсюда следует, что, каково бы ни было число М > 0, всегда найдется номер п = 2* такой, что sn > k/2 > М. Для этого достаточно выбрать натуральное число k большим, чем 2М. Другими словами, подпоследовательность з2* не ограничена и поэтому она расходится, как и сам гармонический ряд.
Для доказательства сходимости ряда Е1/па по теореме Вейер-штрасса достаточно доказать ограниченность его частичных сумм tn= 1 4- 1/2а4- ... 4- 1/па, поскольку они монотонно возрастают. Рассмотрим какое-либо k с условием n < 2*. Тогда справедлива следующая оценка:
*<«,* = ! + —+ (—+—1 + п 2 2а ^За 4а'
332
Таким образом, частичные суммы {tn} ограничены в совокупности, что и означает сходимость искомого ряда.
Установим несколько простейших свойств сходящихся рядов.
УТВЕРЖДЕНИЕ 2. Отбрасывание любого конечного числа членов в бесконечной сумме или добавление к ней любого конечного числа новых слагаемых не влияет на сходимость ряда.
► Рассмотрим случай отбрасывания слагаемых, так как второй случай аналогичен. Итак, пусть мы отбросили члены ряда Еал с номерами пг < ... < nk. Оставшиеся слагаемые перенумеруем в порядке возрастания их прежних номеров. Общий член получившейся таким образом последовательности обозначим через Ьп. Тогда при любом т > nk имеем
т	т - k
= Ьп + ап + ••• + ап •
П = 1	“ П = 1	“	пк
Отсюда следует, что последовательности частичных сумм этих рядов зт = и з'т = "Ё* Ьп = зт - ап- ... - аПксходятся и расходятся одновременно. -4
УТВЕРЖДЕНИЕ 3. Если Ъап = з и с е R, то ^сап = сз.
УТВЕРЖДЕНИЕ 4. Если Zan = s и Zbn = t, то Цап + Ьп) = s + t.
Доказательство утверждений 3 и 4 — прямое следствие определения суммы ряда и арифметических свойств сходящихся последовательностей sn и tn как частичных сумм рядов Еал и ЕЬЛ.
УТВЕРЖДЕНИЕ 5 (необходимый признак сходимости ряда). Если ряд Ъап сходится, тоап->0 при п -» оо. Другими словами, ап — бесконечно малая последовательность.
Имеем ап = зп - Зд.р Отсюда при п -> оо получаем ап —> s - з = О, что и требовалось доказать;
ПРИМЕРЫ. 1. Ряд (-1)п-1 = 1 — 1 + 1 — 1+... расходится, так как ап = (-1)л-1 не стремится к нулю. Л. Эйлер приписывал этому ряду сумму, равную 1/2. И хотя в рамках наших определений это неверно, существует иной, более общий взгляд на проблему, и он позволяет придать утверждению Эйлера строгий математический смысл. Речь идет о корректной и продуктивной постановке задачи суммирования расходящихся рядов. Например, можно сумму расходящегося ряда рассматривать как значе
333
ние особого линейного функционала, определенного на последовательности {ап}, и т. п.
2. Ряд sin п расходится. Чтобы доказать это утверждение, достаточно установить, что равенство lim^ sin п = 0 не имеет места. Действительно, пусть sin и —» 0 при п -> оо. Тогда, так как
sin п = sin ((и - 1) + 1) = sin (и - l)cos 1 4- sin lcos (и - 1), sin 1 # 0, cos 1 # О,
то, переходя к пределу в предыдущем равенстве, получаем
О = lim sin п = cos 1 • lim sin (n - 1) + sin 1 • lim cos (n - 1) = = 0 + sin 1 • lim cos (n - 1).
71 —> OO
Отсюда имеем Jim^ cos(n - 1) = 0. Но в этом случае при п —> оо 1 = (sin и)2 + (cos п)2 —> 0 4- 0 = 0,
что невозможно. Следовательно, ряд Е sin п расходится, что и требовалось доказать.
Рассмотренные примеры показывают, что даже простейшие признаки сходимости ряда оказываются полезными при исследовании рядов на сходимость. С другой стороны, наличие общего критерия Коши для сходимости последовательности позволяет установить соответствующий критерий и для числового ряда.
ТЕОРЕМА 1 (критерий Коши). Для сходимости ряда ап необходимо и достаточно, чтобы для любого е > 0 существовал номер п0 = п0(е) такой, что при всяком натуральном р и всех п > п0(е) имело место неравенство

Ё а т=п+1 ™
Утверждение теоремы равносильно критерию Коши для сходимости последовательности sn частичных сумм ряда, что, согласно определению, и есть сходимость его самого.
Теорему 1 можно переформулировать таким образом, чтобы иметь критерий расходимости ряда Е ап в прямой форме.
ТЕОРЕМА 2 (критерий Коши для расходимости ряда). Для расходимости ряда Ъап необходимо и достаточно, чтобы существовало хотя бы одно £ > 0 с условием, что для любого nQ > 1 найдутся натуральные п > nQu р, для которых справедливо неравенство
Ё а 771 = П + 1	™
>Е.
334
Определение5. Всякое выражение вида sn+p ~ sn = т _Е₽+ Jam называется отрезком ряда S ап.
ПРИМЕРЫ. 1. Ряд Е, сходится.
п-1 п2
Для доказательства этого утверждения воспользуемся теоремой 1. Имеем
, । _ cos (га + 1)	соз(га + р) < — + ... + —<
(л +1)2	(л+р)2 (п + I)2	(л+р)2
< —-— + ... +------------=
п(п + 1)	(л +р - 1)(л + р)
1 - _J_)+...+(__1_ -	1 - -J- < 1.
п л 4-1 7	'п+р-1 п+р' п п+р п
Требуемое неравенство |sn+p - sn| < г выполняется, если, например, 1/п < 8, т. е. п > 1/е. Положим п0(е) = [1/е] + 1. Тогда п0(е) > 1/е и для любого натурального р и любого п > п0(е) выполняются не
равенства
1/п < 1/п0(е) < е, |s„ +р - sn| < е, следовательно, по теореме 1, ряд сходится.
2. Гармонический ряд 1 4- 1/2 4- 1/3 4- ... расходится. Применяя теорему 2, при всех п пр = п имеем
о о	1 _L _L 1	>	1 _L	1	1
2	л 4-1	2л 2л	2л 2
Таким образом, условия теоремы 2 будут выполнены, если положить 8 = 1/2 и при любом n0 > 1 в качестве пир взять числа п = р = п0. Тем самым расходимость ряда установлена.
3. Ряд
п-2л1пл 21п2	л1пл
расходится. Действительно, при любом натуральном k имеем
2£*	1	>	2*	=	1
n-2‘+i nlnn " 2* + 1(fc + 1)1п2	2(k + 1)1п2 ’
Следовательно, при k > 1 получаем з -з >	1	+	+	1	>	*	- 1
22Л	2* 2(£4-1)1п2	*”	4£1п2	4А?1п2	41п2‘
Положим 8 = 1/(4 In 2). Тогда, если в качестве п и п 4- р взять числа п = 2лип+р = 22\ то при любом k > 1 выполняются условия теоремы 2, и, значит, данный ряд расходится.
335
Обратим еще раз внимание на тесную связь между .теорией * сходимости рядов и последовательностей. Мы установили, что всякий ряд порождает последовательность частичных сумм, которая определяет его сходимость. Имеет место и обратный результат, а именно: всякую последовательность можно рассматривать как последовательность частичных сумм некоторого ряда. Действительно, если {Ьп} — некоторая последовательность, то с ней можно связать ряд Z ап, полагая аг = Ъх и ап+1 = &п+1 - Ьп при п > 1.
Лекция 2
$ 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
Определение 6. Ряд Ъап называется рядом с неотрицательными членами* если при всех п имеем ап > 0.
Ряды с неотрицательными членами — это простейший тип числовых рядов. Их свойства используют при изучении рядов общего вида, и поэтому изложение теории рядов обычно начинают именно с рядов с неотрицательными членами. Для общего члена такого ряда будем преимущественно использовать обозначение рп (вместо ап). В основном нас будут интересовать вопросы сходимости этих рядов.
ТЕОРЕМА 3. Для сходимости ряда Ърп, где рп> 0 при всех п, необходима и достаточна ограниченность последовательности его частичных сумм.
► Пусть sn — п-я частичная сумма ряда Е рп. Поскольку рп > 0, имеем, что последовательность {зп} не убывает. Теперь требуемый результат вытекает из критерия Вейерштрасса для сходимости монотонной последовательности. ◄
ПРИМЕР. Пусть Ъп -> +°° и {Ьп} не убывает и положительна. Тогда ряд X (Ьп+1 - Ьп) расходится, а ряд Z (—• - г—— 1 сходится.
Действительно, для частичных сумм sn и tn этих рядов имеем
8„ = ЬП+1-61^+ОО^П=^-^<^.
Теперь требуемый результат вытекает из теоремы 3.
ТЕОРЕМА 4 (признаксравнения). Пусть Ерп и Е qn — два ряда с неотрицательными членами и пусть, начиная с некоторого nQ, для всех п> п0 имеем 0 < qn< рп. Тогда:
а)	сходимость ряда Ъ рп влечет за собой сходимость ряда
б)	из расходимости ряда Ъ qn следует расходимость ряда Ърп-
► Без нарушения сходимости можно отбросить первые п0 членов каждого ряда. При всех п > nQ полагаем
п	п
8п=°	*п = гДя9"1'
337
Тогда для любого п > л0 имеем 0 < tn < sn. В случае а) последовательность {зп} ограничена, следовательно, и {Zn} тоже ограничена и ряд Е qn сходится. В случае б) последовательность tn +°о, поэтому sn -> +°°, т. е. ряд Е рп расходится. ◄
Определение 7. Ряд Е рп в теореме 4 называется мажорантой для ряда Ъ qn, а ряд Е qn -— минорантой для ряда Ъ рп. Говорят еще, что ряд Е рп мажорирует ряд Ъ qn, а последний, в свою очередь, его минорирует.
Аналогичное определение имеет место и для неотрицательных числовых последовательностей.
Схема применения признака сравнения состоит в подборе подходящей мажоранты для доказательства сходимости ряда или миноранты для доказательства его расходимости. Обычно в качестве мажоранты и миноранты используются ряды с общим членом более простого вида, чем у исходного ряда, либо ряды общеизвестные, например гармонический ряд, геометрическая прогрессия и т. д.
ПРИМЕР (признак разрежения Коши). Если последовательностьрп > О не возрастает, то ряды пЕг рп и nEt 2kp2k сходятся и расходятся одновременно.
► Поскольку рп > 0, последовательность частичных сумм ряда Е рп не убывает, а любая ее подпоследовательность зПк сходится и расходится одновременно с sn. Далее, для любого натурального п найдется целое число k с условием 2*"1 < п < 2*. Для таких п и k определим последовательность Ьп = р2к. Тогда, согласно условию, выполнены неравенства
<p2»-i+1 +... +р2* <
Следовательно, для частичных сумм и а2* ряда Е Ьп имеем
2*	k	2*
G2* = n?ibn = m?i2W 1P2'«^n?iPn = 2*-i	2*'1
= S2k 2П?1&Л = n^i^mP2m= 2a2fc_x.
Это значит, что а2* является минорантой, a 2a2ft_x — мажорантой для s2k. Таким образом, ряды Е рп и Е 2kp2k сходятся и расходятся одновременно, что и утверждалось выше. ◄
Идея, заложенная в признаке сравнения, позволяет вывести и некоторые другие полезные утверждения подобного рода. Следующая теорема относится к их числу.
338
ТЕОРЕМА5 (обобщенный признак сравнения). Если в условии теоремы 4 неравенство qn < рп заменить неравенством qn+1/qn < < рп+1/рп, пго ее утверждение также будет иметь место.
► Поскольку отбрасывание нескольких первых членов ряда не влияет на его сходимость, с самого начала можно считать, что nQ = 1. Перемножая все неравенства из условия теоремы до номера п включительно, приходим к неравенствам вида
I;
Применяя теорему 4, получаем требуемый результат относительно рядов pr n^1qnH qr Ъ х рп, а так как умножение всех членов ряда на одно и то же число, отличное от нуля, не влияет на сходимость, то тем самым теорема 5 доказана полностью. ◄ ТЕОРЕМА 6 (признак Даламбера). Пусть для членов ряда Ерп, начиная с некоторого номера п0, выполнены условия:
1)рл>0;
2) Dn =< g, где 0 < g < 1.
Рп
Тогда ряд Е рп сходится. Если же при всех п> nQ вместо неравенства 2 имеем рп+х/рп > 1, то ряд Е рп расходится, ► 1) Сравним ряд Ерп со сходящимся рядом Ebn, где Ьп = qn. При п > nQ имеем
Pn+i . _frn+i Рп " 9 ЬП ’
Поэтому первое утверждение теоремы 4 вытекает из теоремы 3.
2) Во втором случае надо положить bn = 1 для всех п. Тогда в силу расходимости ряда Е Ьп и неравенств
Рп +1	- ^п + 1
—
Из той же теоремы 5 следует расходимость ряда Е рп. ◄
ТЕОРЕМА 7 (признак Даламбера в предельной форме). Рассмот-
рим ряд Ърпс условием рп> 0 для всех п. Положим
Т* РП + 1	& п +1
q = lim ---, г = lim ---.
П —> оо Рп	П —> ОО Рп
Тогда при q < 1 ряд Ъ рп сходится, а при г > 1 — расходится.
339
Напомним, что
lim а„ = inf sup ап, lim ал = sup inf a„. П neN n n ------------ n	fr n n
И —> oo	ne7V "	П->оо
n m	n & m
► Рассмотрим сначала случай сходимости. Положим qr = q + |.
... р । х
Тогда q < qx < 1. Поскольку -------= g, при некотором п0 имеем
sup
п, п > п0
рп+1 Рп
.	_ g +1 _ 1 1 g ~ 1 -I
<91	2	*+ 2 < 1‘
Следовательно, ряд Ерл сходится в силу первого утверждения теоремы 6.
Рассмотрим случай расходимости. Положим гх в (г + 1)/2. Тогда имеем г > r\ > 1. Поскольку lim рп+1/рп = г, при некотором пг имеем оценку
г- 1 2
. п Рп + \ . г + inf ----- > гл = —
п, п > п0 рп	2
Тем самым ряд Е рп расходится согласно второму утверждению теоремы 6.	◄
Замечание. При q = 1 вопрос о сходимости рядаЕрп в теоремах 4 и 7 остается открытым. Примером являются ряды Е 1/п2 и Е 1/п, один из которых сходится, а второй — расходится, но в обоих случаях q « 1. Для исследования сходимости подобных рядов требуются более «тонкие» признаки, которые будут рассмотрены позже.
Более «тонкий» признак дает следующая теорема.
ТЕОРЕМА8 (признак Коши). Если для членов ряда Ърпс условием Рп 0, начиная с некоторого номера п0, имеет место неравенство pVn < q, где число q < 1 и фиксировано, то ряд Е рп сходится.
Если же для бесконечно многих п имеем р*/п > 1, то этот ряд расходится.
►	Рассмотрим сначала первый случай. Последовательно имеем Рпп ^<ЪРп^ 9п* и так как g < 1, то ряд Е рп сходится по признаку сравнения вместе с рядом Е gn.
Во втором случае для бесконечного количества значений п имеем рп > 1. Это значит, что рп 0 и ряд Е рп расходится, поскольку условие необходимого признака сходимости ряда (рп -> О при п -> оо) не выполняется. ◄
340
ТЕОРЕМА 9 (признак Коши в предельной форме). Пусть
lim рУп = а, поо п
где рп> 0 при всех п. Тогда при q < 1 ряд Ъ рп сходится, а при q > 1 — расходится.
►	Положим сначала qx = (q 4- 1)/2 и допустим, что q < 1. Тогда при некотором п0 > 1 имеем
sup Pl/n<ql<l.
п. п > п0
Поэтому, согласно первому случаю признака Коши, ряд Е рп сходится.
Если же q > 1, то при всех пг > 1 имеем оценку sup p\'n>qx>\.
п.п> п1
Это означает существование бесконечного множества значений п, для которых справедливо неравенство р^п > qx>l. Следовательно, ряд Е рп расходится по второму случаю признака Коши. ◄
Признак Коши, как и признак Даламбера, является довольно грубым. Он, например, тоже не позволяет решить вопрос о сходимости рядов Е 1/п и Е 1/п2. Однако он тоньше или, как еще говорят, сильнее признака Даламбера, поскольку можно указать ряд, к которому признак Коши применим, а признак Даламбера нет, но не наоборот. Точнее, можно доказать, что если для ряда Е рп выполнены условия признака Даламбера с некоторыми q и п0, то для него выполнены и условия признака Коши с тем же значением q и, возможно, иным значением п0.
Лекция 3
§ 3. ОСНОВНЫЕ ПРИЗНАКИ сходимости ДЛЯ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
Рассмотренные ранее признаки сходимости рядов относятся к числу простейших и являются исходными для построения основных признаков сходимости. Гораздо более тонким признаком сходимости ряда является, например, признак Раабе.
ТЕОРЕМА 10 (признак Раабе). 1. Ряд Ерп сходится, если для всех п, начиная с некоторого значения п0, и некоторого а > 1 имеет место неравенство
2. Ряд Ъ рп расходится, если, начиная с некоторого п19 выполнено неравенство
► 1. Воспользуемся теоремой 5. Рассмотрим вспомогательный ряд вида Е 1/п$, где р = (а + 1)/2, а > р > 1. Этот ряд сходится (см. пример 3 к утверждению 1 § 1). Обозначим его общий член через qn = 1/дР. Тогда при и —» оо имеем
Но так как а > р, то при достаточно больших п, т. е. при п > п19 где пг — некоторое число, имеем
Чп	п \п2)	п рп
Тем самым, для ряда Е рп выполнены условия теоремы 5 и поэтому он сходится.
2. При п > 2 положим bn = 1/(п - 1) и Ъг = 1. Неравенство п. 2 при п > 2 можно переписать в виде
^п + 1 > П-\ =	1/п	= &п + 1
Рп ”	1/(и-1) Ьп
Поскольку ряд Е Ъп расходится (это просто гармонический ряд), по второму утверждению теоремы 5 ряд Е рп тоже расходится. ◄
342
ТЕОРЕМА 11 (признак Раабе в предельной форме). Пусть рп> О для всех п и существует предел
lim Ьп = lim п (1 -	1 = I.
П —> оо " п->оо \	П 7
~ п
Тогда при I > 1 ряд S рп сходится, а при I < 1 — расходится.
Эта теорема выводится из теоремы 10 аналогично тому, как теорема 9 из теоремы 8 или теорема 7 из теоремы 6.
Замечание. Иногда вместо последовательности Ьп в формулировке теоремы 11 рассматривают последовательность
в =/_£»_ -1) = ПГ 1 -1).
^Pn + l	J	J
При этом в обоих случаях имеем соотношение Dn = рп+1 / рп-> 1 при п -> оо. А так как имеет место равенство Ьп = BnDn, то Ьп ~ Вп при п -> оо. Следовательно, в теореме 11 замена Ъп на Вп допустима. Из подобных соображений неравенство в условии 1) можно заменить на неравенство Вп > 1 + а, а неравенство в условии 2) этой теоремы — неравенством Вп < 1.
ТЕОРЕМА 12 (признак Куммера). Пусть {ап} и {сп} — две последовательности положительных чисел.
1) Если существует а > 0 и номер и0 такие, что для всех п> nQ имеем
сп - СВ+1	> а>
то ряд S ап сходится.
2) Если найдется число и0 такое, что при всех п> nQ выполнено равенство
с - с +1 — < 0
П	П~г 1 п
ип
и ряд S (1/сп) расходится, то и ряд S ап тоже расходится.
Прежде чем перейти к доказательству теоремы, обратим внимание на замечательную ее особенность, состоящую в том, что заключение о сходимости выводится относительно одного только ряда S ап, в то время как вторая последовательность {сп} не фиксируется, что позволяет выбирать ее в каждом случае применения признака Куммера для исследования сходимости конкретного числового ряда.
► Без ограничения общности будем считать, что n0 = 1, так как ясно, что члены с номерами п < nQ можно отбросить.
343
1) Имеем
Спап Сп+1ап+1
Суммируя это неравенство по п при всех п = 1, ... , т, получаем а1«1 ~ ст+1ат+1 > “(«I + ••• + откуда
Это означает, что все частичные суммы sm ряда Е ап ограничены в совокупности и по теореме 3 этот ряд сходится.
2) Неравенство можно переписать в виде
а„ + 1 > Vfn + 1 «п " 1/с. '
Но так как по условию ряд Е 1/сп расходится, то по теореме 5 расходится и ряд Е ап. ◄
Рассмотрим некоторые следствия из теоремы 12.
СЛЕДСТВИЕ 1. Положим сп = 1 для всех п. Условие сходимости ряда Е ап тогда запишется в виде
О _ I -|	О । -j
1-----> а или ------ < 1 - а.
ап	*	ап
Для расходимости в этом случае имеем
an + i	ап + 1	1
------1 >0 или ----- > 1.
Таким образом, мы получаем новое доказательство признака Да-ламбера.
СЛЕДСТВИЕ 2. Положим сп = п - 1. Тогда сходимость ряда Е ап имеет место при выполнении условия
Ряд Ъ ап расходится при условии
сп = п - 1, п---(п - 1) > 0, т. е.-- >1 — .
Другими словами, мы получаем признак Раабе.
344
СЛЕДСТВИЕ 3(признакБертрана).
1.	Ряд Ъ ап, ап > 0 сходится, если существует а> О и номер nQ такие, что при всех п> nQ выполнены неравенства
gn + i 1 _ 1 _ 1 +а ап	п nlnn *
2.	Данный ряд расходится, если при всех достаточно больших п имеет место неравенство
ап + 1	1_____1_
ап '	п п\пп ‘
► 1. В качестве сп в признаке Куммера положим
сп = (и - 1) In (п - 1).
Тогда условие сходимости в нем запишется так:
(п - 1) In (и - 1) - и In	а,
т. е.
ап + 1	х _ 1 + (п - 1) In (1 - 1/п) _ а .
ап	п	nlnn	ri\nn ’	1	" ''
Далее, поскольку
(п - 1) In (1 - 1/п) = In (1 - 1/пу-1 > -1, неравенство (*) вытекает из следующего неравенства:
an + i	х _ 1 _ 1 +а	с г _ 1	_ (п — 1)1п(1 — 1/п)_а
ап	п nlnn п	nlnn	nlnn	’
т. е. выполнение условия сходимости в признаке Бертрана обеспечивает справедливость условия сходимости в признаке Куммера.
Таким образом, признак Бертрана для сходимости ряда доказан.
2. Положим в признаке Куммера сп = (п - 2) In (п - 1). Тогда ряд Е ап расходится, если выполнено неравенство
(п - 1) In - (П-2) In (п - 1) > 0.
ап
Достаточно показать, что оно является следствием условия расходимости в признаке Бертрана вида
an + i >]L_1____L_
ап	п	nlnn ’
345
т. е. доказать при всех п, больших некоторого п0, неравенство
ап + 1	1 _ 1 _ 1	п — 2 е 1п(п - 1)
ап п nlnn	п-1 Inn
Оно, в свою очередь, вытекает из следующей цепочки неравенств (п > 3):
In (1 - 1/п) < -1/п,
1-1- 1	1 ъ
п nlnn \	п-1'^ ПШП/
>fl- 1 Y1 + ln(l-l/n)A n-2 Jn(n-l)
<	n-l'*< Inn ) n — 1 Inn •
Простым следствием признаков Даламбера, Раабе и Бертрана является признак Гаусса.
ТЕОРЕМА 13 (признак Гаусса). Если ап > 0 для всех натуральных п, £ > 0 — некоторая постоянная и
= X + Н 4- О(п~1~е),
ап + 1	п
то:
1)	ряд S ап сходится при X > 1 и расходится при X < 1;
2)	если X = 1, то ряд сходится при ц > 1 и расходится при ц < 1.
► 1) Имеем Dn = ап+1/ап -> 1/Х при п -> оо, поэтому по теореме 7 ряд S ап сходится при X > 1 и расходится при X < 1, что и утверждалось в п. 1).
2) Если X = 1 и ц # 1, то Вп = n(an/an+1 - 1) —> ц. Поэтому, согласно замечанию к теореме 2, ряд сходится при ц > 1 и расходится при ц < 1. Если же X = ц = 1, то при некотором г0 > 0 и п -* оо имеет место предельное соотношение
=1-1 +О(п'1-£°).
ап	п
Но поскольку In п = о(пе°), при всех достаточно больших п выполнено неравенство
=1-1 + О(га-1-е°) > 1 - 1 --1—.
ап	п	п nlnn
Таким образом, при X = ц = 1 ряд S ап расходится согласно признаку Бертрана. ◄
Комбинируя полученные выше результаты и снова привлекая, по существу, те же соображения, что и выше, можно получать все более и более тонкие и сложные признаки сходимости. 346
Однако на практике реально используется один гораздо более простой и более сильный признак сходимости рядов, а именно, интегральный признак Коши—Маклорена, к доказательству которого мы переходим.
ТЕОРЕМА 14 (интегральный признак Коши—Маклорена). Пусть функция f(x) определена на промежутке [1, +°о) и Дх) убывает на нем. Тогда:
1) если 0 < рп < f(n) при всех п> nQ и несобственный интег-оо
рал J f(x)dx сходится, то ряд S рп тоже сходится;
1
2) если рп > f(n) > 0 при всех п> п0 и несобственный интег-оо
рал f f(x)dx расходится, то расходится и ряд S рп. 1
► Как и выше, без ограничения общности будем считать, что n0 = 1. Далее, поскольку функция Дх) монотонно убывает, при всяком натуральном к и К х < & + 1 имеем
Дй)>Дх)>Дй + 1).
Интегрируя это неравенство по указанному промежутку, получаем
Л+1	k + 1	k + l
f(k) = f f(k)dx> J f(x)dx> J f(k + l)dx = f(k + 1>. k	k	k
При всяком n > 2 просуммируем эти неравенства по k от 1 до п - 1. Получаем
п-1	»	п-1	/П	\
вП-1 - *5 ! /(*) > f	, f(k +	x f(k)) - /(1) = S„ - ftl).
Рассмотрим каждый из двух случаев отдельно.
оо
1. В этом случае интеграл I = J f(x)dx сходится, поэтому при 1
всех п > 2 для частичных сумм sn ряда S Ди) имеет место единообразная оценка вида sn < I + Д1), и поскольку Ди) > 0 для всех натуральных п9 ряд S Ди) сходится, а вместе с ним сходится и мажорируемый им ряд S рп, что и требовалось доказать.
оо
2. Поскольку в этом случае интеграл J f(x)dx расходится,
1 п
f f(x)dx -> +°° при п -> оо. Но так как
1	п
«п > ®п-1 > f f(x)dx, 1
той зл-> +оо при п -> °°. А это означает, что ряд S Ди) расходится вместе с рядом S рп, для которого первый ряд по условию является минорантой. ◄
347
oo
Замечание. Очевидно, что в условии теоремы 5 интеграл J f(x)dx 1
оо
можно заменить интегралом J f(x) dx, где а > 1 — произвольное число.' а
Рассмотрим некоторые следствия, вытекающие из интегрального признака.
1.	Ранее было доказано, что при s > 1 ряд Ъ 1/п8 сходится. Его сумма обозначается символом £(з) и называется «дзета-функцией Римана». Приведем другое доказательство сходимости этого ряда. Действительно, при таких значениях з несоб-оо
ственный интеграл J x~sdx сходится и легко вычисляется. 1
Имеем
Г х~3 dx = х 8 + 1
1	-s +1
00 _ 1
1	8-1’
Следовательно, по теореме 14 ряд S п 8 тоже сходится, что и
оо
требовалось доказать. Если же з < 1, то интеграл J х~8 dx расхо-1
дится, а вместе с ним расходится и ряд Ъ 1/п8.
оо
Замечание. Ряд Ъ х 1/п8 при некоторых значениях з впервые рассматривал Л. Эйлер. Более того, при з, равном четному натуральному числу, он нашел точные значения для суммы £(з). Позднее Б. Риман определил функцию £(з) для всех значений аргумента з, исключая точку з=1, причем не только вещественных, но и комплексных. Он детально исследовал свойства этой функции, и поэтому она носит его имя. Дзета-функция Римана играет огромную роль в теории чисел. Относительно некоторых свойств этой функции Риман высказал ряд гипотез, которые давно уже доказаны, кроме одной. Это гипотеза Римана о нулях ^-функции. На сегодняшний день эта гипотеза является самой престижной математической проблемой.
2.	Валле Пуссен показал [35], что при s > 1 справедливо равенство
S - = 1 + f (1 + 1 (	1	- 1 Y) (*)
n = 1 ns s — 1	П==1<п8 s-lVn + 1)8’1 ns-1"9
причем ряд в правой части сходится при з > 0. Действительно, общий член рп последнего ряда можно представить в виде
0<р„=	.
п Зп Vns Xs' п» (п + 1)8
348
Следовательно, ряд S рп сходится при 8 > 0. Равенство (*) при 8 > 1 получаем, раскрывая скобки в правой его части и используя при тех же з равенство
_ 1	1 2 f 1	1 )
8-1	8-1	+	п8'1'
3.	Опираясь на интегральный признак, исследуем сходимость ряда Z гдер, -	+	ц • Имеем
Г_____*£___________Г df J-'l - J- ,
1 (х + l)ln2(x + 1) 2	1п2
т. е. несобственный интеграл сходится, поэтому ряд S рп тоже сходится.
Лекция 4
$ 4. АБСОЛЮТНАЯ И УСЛОВНАЯ СХОДИМОСТЬ РЯДОВ. РЯДЫ ЛЕЙБНИЦА
Продолжим рассмотрение числовых рядов общего вида.
Определение 8. Ряд Е ап называется абсолютно сходящимся, если сходится ряд Ъ |ал|.
Всякий сходящийся ряд с неотрицательными членами абсолютно сходится. В то же время, легко построить сходящийся ряд, который не является абсолютно сходящимся. В качестве примера можно привести следующий ряд:
1	2	2	3	3	4	4	— ’
Его сумма равна нулю, и в то же время ряд, составленный из модулей его членов, расходится в силу расходимости гармонического ряда.
Определение 9. Сходящийся ряд Е ап называется условно сходящимся, если ряд Е |ал| расходится.
Согласно этому определению, рассмотренный выше ряд является условно сходящимся. Заметим, что про абсолютно (или условно) сходящийся ряд говорят еще, что ряд сходится абсолютно (или условно). Целесообразность введенных понятий подтверждает следующая теорема.
ТЕОРЕМА 15. Если ряд Е ап абсолютно сходится, то он является сходящимся.
► Согласно критерию Коши, из сходимости ряда Е |ал| следует, что при любом £ > 0 найдется номер и0(е) такой, что при всех р > 1 и п > п0(е) имеем
п +р
тЛ+Х1<е’ откуда п+ р	п+р
z а < Е |а |<е. m = n + 1 m т = п +
Но это означает выполнение критерия Коши. 4
Определение 10. Числовой ряд Ъ ап называется знакочередующимся, если все его соседние члены имеют разные знаки.
Определение 11. Знакочередующийся ряд вида Ъ ап называется рядом Лейбница, если модуль его общего члена |ал| монотонно стремится к нулю.
350
ТЕОРЕМА 16. Всякий ряд Лейбница Z ап сходится.
► Покажем сначала, что всякий отрезок этого ряда мажориру-п+р
ется модулем его первого члена. Пусть х ат — некоторый отрезок ряда. Мы хотим доказать неравенство вида
тЛ + 1а™ С1ап+11-
Положим bk = | ak | при всех k е N. Тогда
I#* + afe+il = laJ ” lafe+iI = bk “ bk+1 < bk.
Кроме того, при всех k числа (bk - bk+1) имеют один и тот же знак. Следовательно, при четном р = 2г имеем
О lan+l + ап + 2 "*"••• + an+2r-l + ап+2г1 =
= (&! — &2) + ••• + (^2г-1 — ^2г) =
=	“ (Ь2 ~ Ьз) “ ••• ~ (&2г-2 “ ^2г-1) “ ^2г^ = lan+lI*
Если же р = 2r + 1 нечетное, то
О lan+l + ••• + an+2r+ll = (^1 “ fyz) + ••• + (^2r-l ~ ^2r)	^2r+l в
=	~ (Ь2 ~ Ь3) ~ ... - (&2r ~ &2r+l)	= fan+ll*
Таким образом, в обоих случаях
Т
* П,р
z
Но теперь, так как Ьп+1 —» 0, мы при любом наперед заданном е > О и достаточно большом п имеем Тп р < &п+1 < е, откуда в силу произвольности р9 исходя из критерия Коши, заключаем, что ряд Е ап сходится. ◄
ТЕОРЕМА 17 (оценка остатка ряда Лейбница). Для остатка гп ряда Лейбница Е ап справедлива оценка |rn| < |ап+1|.
► Согласно теореме 16, ряд Е ап сходится, поэтому
1Гп1= п.Л + 1ап-
Заметим, что при доказательстве теоремы 16 для тцобого;, нату, рального р получена оценка
тЛ+А cK+il-
Устремляя р -» оо, получаем требуемое неравенство.
351
$ 5. ПРИЗНАКИ АБЕЛЯ И ДИРИХЛЕ
Признаки Абеля и Дирихле применяются при доказательстве достаточно широкого класса числовых рядов общего вида. Доказательство обоих признаков основано на формуле дискретного преобразования Абеля.
k
ТЕОРЕМА 18. Пусть Ak = S Тогда при М > N имеют место формулы
М	М-1
k . 1 аА = Амьм + k _	. Ai№k “ fyfe+i);	(1)
М	М-1
kJ% + 1akbk==AMbM+i + fe=^ + 1 А№ъ ~ fyfe+i)*	(2)
► Прежде всего заметим, что правые части формул равны между собой, так как, вычитая правую часть формулы (2) из правой части формулы (1), получаем
AiAn “ AAf+i “	~ ^м+1) = о.
Следовательно, достаточно доказать только формулу (1). Преобразуя ее правую часть, имеем
М-1	М-1	М-1
АМЬМ + fe = +	“ bk+i)=AMbM + k = ^+1 Akbk ~	! Akbk+1 =
MM	M
= * Л + 1 А»Ьк ~ I ^N + 2Al~lbl= AN+lbN+l + k	+ /А “ Л-Л =
M	M
= ^¥+1^¥4.1 + S Uzbu =	аЗУи» ◄
JV + l 2V + 1 k = N + 2	* « k = N + l R R
Признаки Абеля и Дирихле применяются к рядам вида S апЬп.
ТЕОРЕМА 19. Справедливы следующие утверждения.
(А) (признак Абеля). Если последовательность Ъп монотонна и ограничена, а ряд S ап сходится, то ряд S апЬп также сходится.
(Д) (признак Дирихле). Если последовательность Ьп монотонна и Ьп-+ 0 при п-><х>, а последовательность sn частичных сумм ряда Ъ ап ограничена, то ряд Ъ апЬп сходится.
► Ограничимся рассмотрением случая, когда Ьп > 0 и Ъп убывает. Все прочие случаи легко сводятся к данному следующим образом. Если Ьп < 0, то надо изменить знаки у всех ап и Ьп. Если же Ьп1\ то Ьп надо представить в виде Ьп = b0 - dn, где Ьо = Jim^ Ъп, и свести теорему к исследованию ряда S andn. Здесь уже имеем
352
Доказательство теоремы проведем, применяя критерий Коши к ряду ап^П' Для этого применим формулу (1) преобразования Абеяя к отрезку этого ряда Тп р. Используя обозначение Ак = sk-sn и учитывая, что Ък - Ьк+1 > 0, получаем
|гп,р| =
< К-Л+р + nmax+p|Ak|ft _Ё+	- bk+l) < n<maxjAfe|b„+1.
X ukuk ' и + 1 к я
ak^k ^П+р^П+р п+р-1

Рассмотрим теперь случай (А). Так как последовательность Ьп ограничена, при некотором с > 0 для всех п имеем |Ьп+1| < с. Далее, так как ряд S ап сходится, то для любого е > О найдется номер п0(е) такой, что при всех п > п0(е) и k > п имеем
1А1 = „Л+1ат =18*“8л1<18*1 + 18п1<е-
Тогда при указанных п и любом р для величины Тп р справедлива оценка
п+р
|Т_ -| = . Е акЬк < се. 1	k = п 4-1 я К
Но так как е произвольно, а с фиксировано, то последнее неравенство означает, что ряд X апЬп удовлетворяет критерию Коши и поэтому сходится. Тем самым признак Абеля доказан.
В случае (Д) ограничены частные суммы Ak ряда X ап, и поэтому существует с, для которого \Ak| < с при всех k. Кроме того, Ьп 0. Следовательно, при произвольном е > 0, достаточно большом п > и0(е) и произвольном р > 1 имеем оценку
|гп>р| =
п + р . 2.., аЛк < се. k = п + 1 Я Я
Отсюда, как и в случае А, заключаем, что по критерию Коши ряд X апЬп сходится. ◄
12-4953
Лекция 5
§ 6. ПЕРЕСТАНОВКИ ЧЛЕНОВ РЯДА
Определение 12. Пусть а : N N •— взаимно однозначное отображение натурального ряда на самого себя. Тогда ряд Е Ьп, где Ьп = аа(п), называется перестановкой ряда Е ап.
ТЕОРЕМА 20. Любая перестановка Е Ъп абсолютно сходящегося ряда % ап = А абсолютно сходится к той же сумме А.
► Положим
оо	П	п	ОО	п
А = г£1ап’	=	= л?11алЬ ^n = jfe51lafel*
Зафиксируем некоторое £ > 0. Пусть пх настолько велико, что А' - А^ < е. Тогда при любом п > пг для остатка гп = А - Ап ряда Е ап имеем оценку
|г | = Е ak < Е |afe| =А'-А'П <е.
Пусть теперь п2 таково, что среди чисел о(1), о(га2) содержатся все целые числа отрезка [1, raj. Положим
т = max (о(1),..., о(га2)).
Тогда при всех п > п2 имеем п	п	П1	™
= Е Ьь = Е ал/ьч = Е аь + . 2 . ак.
Штрих в последней сумме означает, что некоторые слагаемые в ней опущены. Для этой суммы, очевидно, имеют место оценки
|В„-АЯ1| =
m
k -	+ X ak
т
<* S ,|а*| <A'm-A' <A'-A' <e. ft + 1 • w1 «*	«1
Отсюда следует, что при всех п > п2
|А - В„| <|А - AnJ + |В„ - A„J < (A'-A'ni) + (А' - А'п) < 2е.
В силу произвольности выбора £ > 0 это означает, что Вп -> А при и —> т. е. ряд Е Ъп сходится и Е bn = X ап. Отсюда, в частности, следует, что и ряд Е |6П| сходится к сумме А', т. е. ряд Е Ьп сходится абсолютно. ◄
Основное отличие в свойствах абсолютно и условно сходящихся рядов обнаруживается при перестановке их членов. Как показывает теорема 20, бесконечная сумма абсолютно сходяще
354
гося ряда в этом случае ведет себя точно так же, как и конечная сумма, т. е. при перестановке слагаемых сумма не изменяется. Гораздо более сложная, ситуация имеет место дляусловно сходящегося ряда. Тем не менее, она достаточно полно описывается следующей теоремой.
ТЕОРЕМА 21 (теорема Римана о перестановке членов условно сходящегося ряда). Каково бы ни было вещественное число А, найдется сходящаяся перестановка ЪЬп условно сходящегося ряда Е ап такая, что А.
► Для простоты будем считать, что ап 0 при всех п. Сначала в ряде Е ап выделяем все положительные слагаемые pk и отрицательные слагаемые -ql9 нумеруя их индексами k и I в порядке следования в ряде Е ап. Затем составляем перестановку Е Ьп ряда Е ап: в качестве Ьх берем р19 если А >0, и -q19 если А < 0. Подчеркнем, что все pk и gz положительны.
п ,
Далее мы добавляем в общую сумму ^Е гЬт очередные слагаемые по следующему правилу: если сумма не превышает А, то добавляем очередное положительное слагаемое Ьп+1 = pk^9 а если она превосходит А, то добавляем очередное отрицательное слагаемое 6n+1 e ~gz . В результате сумма все время колеблется вокруг значения А, причем размах колебаний постепенно убывает до нуля, и в пределе для суммы ряда Е Ьп получаем требуемое значение А.
Для того чтобы доказательство теоремы было полным, достаточно в приведенной схеме обосновать только некоторые ее моменты.
Докажем, что оба ряда Е pk и Е (~gz) расходятся. Действительно, если бы оба они сходились, то исходный ряд Е ап сходился бы абсолютно, а если бы один ряд расходился, а другой сходился, то частичная сумма ряда Е ап9 составленная из двух частичных сумм рядов Е pk и Е qt соответственно, тоже расходилась, что неверно. Далее заметим, что поскольку {pk} и {-gz} являются подпоследовательностями для {ап}9 pk-> 0 при k -> оо и -gz 0 при I -> оо.
Для определенности будем считать, что А > 0. Тогда по построению ряд Ьп имеет такую структуру:
S bn =Р1 + ...+р»1-91-...-9,1 +
Pi	Qi
+Рк1 +1 +;••+ qh +1 ~ ~	+ -
К
355
12*
Здесь Р19 Р2, ... , Qp Q2, ... — суммы подряд идущих слагаемых одного знака в ряде Е Ьп. Количество групп слагаемых одинакового знака в этой сумме бесконечно, так как в противном случае ряд Е Ьп отличался бы от Е pk или от Е (-gz) лишь конечным числом членов, и тогда он расходился бы к +оо или к -оо соответственно. Но это не имеет места, так как по построению величина частичной суммы sn ряда на каждом шаге изменяется в направлении приближения к числу А, если только зп А. В силу этого, в сумму Е Ьп войдут все числа pk и -ql9 а следовательно, и все ал, т. е. Е Ьп — действительно перестановка ряда Е ап.
Теперь оценим разность гп = зп~ А. При всяком п член ряда Ьп в зависимости от своего знака попадает в одну из сумм Рт или Qm. Следовательно, имеем одно из равенств: bn = pk или Ьп = -gz.
По построению ряда Е Ьп величина гп меняет знак в том случае, если Ьп = pkmили bn = -qtm. Тогда в обоих случаях имеет место оценка
Для всех прочих п при добавлении очередного слагаемого величина |гЛ|, т. е. расстояние значения частичной суммы sn до числа А убывает, и поэтому справедливо неравенство |гл| < |гп_х|. Следовательно, всегда имеем
|sn-A|<pfc +qt +qi . т т т-1
Здесь номер т можно рассматривать как монотонно стремящуюся к бесконечности функцию от и, и поэтому для последовательности dn, где dn = pk +qt + qt , в силу того, чтор* и gz 0 при k и I -» °°, имеем dn -» 0 при и —» оо. Отсюда при п -» оо окончательно получаем rn = sn - А 0 и sn —» А. ◄
Лекция 6
$ 7. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
Вы уже знакомы с некоторыми действиями над числовыми рядами такими, как почленное сложение, одновременное умножение всех членов ряда на одно и то же число, перестановки членов ряда. Все эти действия будем называть арифметическими операциями над рядами. Рассмотрим и другие математические операции, а именно: расстановку и раскрытие скобок, а также операцию умножения рядов.
УТВЕРЖДЕНИЕ 5. Если в сходящемся ряде Е ап некоторые группы слагаемых заключить в скобки, то его сходимость не нарушится и сумма не изменится.
► Любая формальная расстановка скобок в бесконечной сумме Е ап приводит к новой бесконечной сумме вида
(°1 + — + ak,) + (akt + i + — + %) + — = bi + b2 + — »
где при s = 0, 1, ... имеем b8 = ak + ... + ak и kQ = 0.
Очевидно, что последовательность {В8} частичных сумм ряда Е Ь8 не что иное, как подпоследовательность {Ak } частичных сумм ряда Е ап. Но так как всякая подпоследовательность сходится к тому же пределу, что и сама последовательность, то для Ak —> А имеем, что Bs=Ak А при s оо. <
Пример сходящегося ряда (1 - 1) + (1 - 1) + ... = 0 + 0 + ... = 0 показывает, что обратное утверждение не всегда справедливо. Однако имеет место, например, следующее утверждение.
УТВЕРЖДЕНИЕ 6. Пусть ряд, составленный из скобок, сходится к сумме В, точнее, пусть ЪЪп = В, где Ъп = (ап1 4- ... + ank), причем k фиксировано, и пусть каждая из k последовательностей является бесконечно малой, т. е. ап8 -» 0 при п -» оо и всех з = 1, ... , k. Тогда в ряде Ъ Ъп можно раскрыть скобки. Другими словами, ряд
аи + а12 + ••• + alk + а21 + ••• = dl + d2 + ••• + dk + dk+\ + •••’
где dk(n_1}+8 = an8, сходится, причем к той же самой сумме, что и ряд Е Ьп.
357
► Утверждение вытекает из свойств сходящихся последовательностей. Действительно, для частичных сумм Dn и Вт рядов Е dn и Е Ът при п = km имеем равенство
Ая. = -вт-^-ВпРиот-^о°-
Заметим, что разность ап = Dn - Dkm при т = [n/k] и s = п- km равна
— &кт + 1 + • • • + &Ът + 8 “ ат, 1 "*“••• + ат, а*
А так как ат 8 при любом s = 1, ..., k — бесконечно малая величина при тп —» оо, то поскольку тп —»оо при п —> °0, имеем
l«nl < К, 11 + ••• + \ат, .1 < К, 11 + - + l«m, J О, а„^0,Р„ = Втк + а„^В + 0 = В. ◄
Если в некоторых скобках содержится менее k слагаемых, то можно подразумевать вместо отсутствующих слагаемых нули. Другими словами, доказанное утверждение справедливо и в этом, несколько более общем случае.
Сложнее вопрос о произведении числовых рядов. Для этого потребуются новые определения.
Определение 13. Занумеруем каким-либо образом счетное множество тар (т, п) натуральных чисел т и п, т. е. поставим каждой паре в соответствие свой номер k. Тем самым получаем две последовательности: т = m(k) и п = n(fe), принимающие натуральные значения. Такую нумерацию будем называть линейной нумерацией пар. Если теперь 1апи1Ьп~ два числовых ряда и hk = am^bn(k), то ряд kL1 hk будем называть их произведением, отвечающим данной линейной нумерации пар индексов (тп, п) или данной перестановке попарных произведений атЬп.
ЗАДАЧА (теорема Штейница). Пусть {сп} — последовательность, составленная из векторов k-мерного пространства Rk, k > 2. Пусть для любого вектора f е Rk, f и 0, ряд Е ап, где ап = (сп, /п) — скалярное произведение векторов сп и f, условно сходятся.
Требуется доказать, что для всех Ъ g Rk существует пере-т	_
становка Е со(п) такая, что Ит^ сО(П) *= Ь.
Определение 14. Ряд пЕ1 hn, где hn = ^^k^n-k+v называется формальным произведением (или просто произведением) двух рядов Е ап и Е Ъп.
358
ТЕОРЕМА 22. Если оба ряда Е апи% Ьп абсолютно сходятся^ причем Е ап = А, л Е Ьц = В, то при любой перестановке попарных произведений их членов ряд £ hk абсолютно сходится к сумме АВ.
► Зафиксируем какую-либо перестановку попарных произведений k <-> (zn(fe), n(k)). Докажем сначала, что ряд S hk сходится абсолютно. Пусть H'k — последовательность частичных сумм ряда S |йЛ| и г — какой-либо номер. Тогда
H'r = fc?Jam(fe)bn(fe)l-
Положим т0 = max m{k), п0 = max n(k). В этом случае, очевидно, г	то	п0
Н'г = ilam(fe)l •	А'В',
где А'= S|an|, В'= S|&n|.
Таким образом, частичные суммы ряда Е|hk\ ограничены в совокупности, а это значит, что ряд % hk абсолютно сходится к некоторой своей сумме Н. Но тогда при любой перестановке его членов сходимость не нарушается и сумма не изменяется. Переставим эти члены так, чтобы при любом k = п2 частичная сумма Hk имела вид Hk = (ax + ... + ап) (Ъ1 + ... + 6П) = АпВп. Тогда при п -> оо имеем Нп2-> АВ. В силу сходимости ряда S hk последовательность Hk его частичных сумм сходится к Я, и так как Нп2 — подпоследовательность Hk, то Н = АВ.
Итак, если абсолютно сходятся оба ряда Е ап и Е Ъп, то сумма произведений рядов равна произведению их сумм. 4
В общем случае на такое равенство рассчитывать не приходится. Действительно, если ряд Е ап сходится условно, а в качестве Е Ьп взят простейший ряд вида Е Ьп = 1 + 0 + 0 + ..., то, исходя из определения, можно убедиться, что их произведение, отвечающее некоторой перестановке пар (тп, п), дает ряд Е сп, являющийся некоторой перестановкой ряда Е ап. Но, согласно теореме Римана, при перестановках такого ряда его сумма может измениться.
Естественно, что при определенных ограничениях утверждение предыдущей теоремы допускает различные обобщения. Например, справедлива следующая теорема.
359
ТЕОРЕМА 23 (теорема Мертенса). Пусть ряд X ап абсолютно сходятся к сумме А и ряд Ъ Ьп условно сходится к сумме В.
Тогда формальное произведение hn этих рядов сходится к сумме АВ.
► Пусть Нп — последовательность частичных сумм ряда X hn. Имеем
п	пт	п	n-k + 1
Н = Ёthm= ЁЛ.аД..м-1.1к Л, п т — 1 т т = Ik = 1 кт	fe = 1 R 1 = 1	1
Положим I = т - k + 1. Очевидно, имеем 1 < k < т < п, откуда получаем l<7n-fc + l = Z<n-fe + l. Следовательно,
п п - k +1	п
Нп = Л?! ak bl = ak&n-k+v
Здесь Bn_k+1 — соответствующая частичная сумма ряда X Ьп.
Поскольку ряд X Ьп сходится к сумме В, разность pz = В - Bt является его остатком Pz = * Х+ bk, который стремится к нулю с ростом I. Поэтому, обозначив через ап лАп остаток и частичную сумму ряда X ап, будем иметь
п	п
Нп — afrBn-k+l =	а)№ ~ Рл-fe+l) =
~	_ П?1 аЛ-*+1 = АВ - anB - >Ё1 a*Pn-ft+1.
Осталось показать, что если Rn = АВ - Нп, то Rn —» 0 при п —> Но а„ -> 0, поэтому Rn = а„В —> 0 при п —> оо. Рассмотрим теперь
суммуК'“»?1вЛ-*+1: п
I, Хг
= k Л/г'0*' ’ ।1 + „/2 Л < Ja*l * ।Рп-Л+11 = Z1 + Z2*
Так как -> 0, то при некотором с > 0 для всех k имеем неравенство |рй| < с, откуда
п/2 Л < J***' *	п/2 < Ja*'C Сп/2 <1к J*1*' = С^‘
Но ряд X |an| сходится, поэтому, согласно критерию Коши, при всяком е > 0 и достаточно большом п > п0(е) справедливо неравенство Т < £, откуда вытекает, что Х2 < се- С другой стороны,
360
так как рп -> 0, то при достаточно большом l=n-k+l> nfo) имеем |pz| < е. А это значит, что если п/2 > тг1(е) и k < п/2, то 10л-* +11 <е> откуда
^i = k А/г'0*! *	+ е* е"^'’
К n/Z	К Ч П/Л
где А' — сумма сходящегося ряда	Таким образом, при
п > 2пх(е) + п0(е) имеем
Я" < еА' + ес = е(А' + с).
В силу произвольности выбора числа е > 0 это означает, что Я" -> О при п —> оо. Но тогда и Rn = R'n + Я" -» 0, откуда Нп ->АВ. ◄
Лекция 7
§ 8.	ДВОЙНЫЕ И ПОВТОРНЫЕ РЯДЫ
Понятие произведения двух рядов можно рассматривать как пример более общего понятия двойных рядов, изучению которых посвящен этот параграф.
Определение 15. Числовая функция а(т, п) = ат,п = атп двух натуральных аргументов тип называется двойной последовательностью.
Для таких последовательностей также будем использовать обозначение {am J.
Определение 16. Двойным рядом оо оо
У У а = У а =
т = 1 П = 1 п т?п п	т, п
называется формальная бесконечная сумма S вида
S =	+ а12 4- О1з + ••• + а21 + а22 + а23 + ••• + аз1 а32 + азз 4" ••• •
Определение 17. Конечная двойная сумма
Ат, п = Л1Л1 аМ = «И + - + «1» + - + «ml + - + атп называется (прямоугольной) частичной суммой двойного ряда вида S ат п. Исходная последовательность ат п называется общим членом ряда.
Дадим определение сходимости двойного ряда как предела частичных сумм Ат п.
Определение 18. Число I называется пределом двойной последовательности {Вт п} (или двойным пределом), если для всякого е > 0 найдутся числа ти0(е) и п0(е) такие, что для всех пар (т, п) с условием т > тп0(е) и п > о0(е) выполнены неравенства
Понятие предела двойной последовательности полностью согласуется с общим определением предела функции по базе В. В данном случае база В представляет собой совокупность окончаний Ьт п , каждое из которых образовано множеством пар (т, п) натуральных чисел т и п с условием т > mQ, п > nQ. Предел А = = lim Ат п по этой базе и есть указанный выше двойной предел. Для самой базы В будем использовать обозначение т -» п оо. Также будем писать:
гп —> оо п -> оо
362
Для двойных пределов выполнены все свойства предела по базе множеств. Например, предел суммы равен сумме пределов, имеет место единственность предела. В частности, отсюда для сходящегося двойного ряда вытекает необходимый признак сходимости.
УТВЕРЖДЕНИЕ 17 (необходимый признак сходимости двойного ряда).
Если ряд 1ат „ сходится, то ат „ —> О при т п -» сю.
► Имеем am n=Am<n -Ат> п_г - Am_1( „ + Am_b n_v Так как по условию Ат п -> А, то
lim ат „ -А-А-А + А = 0. т —> оо п ~»оо
Исходя из общей формулировки критерия Коши для существования предела функции по базе множеств, можно сформулировать критерий Коши для двойных рядов.
ТЕОРЕМА 24 (критерий Коши). Для того чтобы двойной ряд Ъ ат п сходился, необходимо и достаточно, чтобы для любого £ > 0 существовали числа тп0(е) и п0(е) такие, что при всех т19 т2> Шц (е) и nv п2 > п0 (е) справедливо неравенство
~	„ I < е.
В важном случае двойных рядов с неотрицательным общим членом Рт п > 0 справедлива следующая теорема.
ТЕОРЕМА 25. Для сходимости двойного ряда п с условием рт, п > 0 необходимо и достаточно, чтобы его частичные суммы Рт, п были бы ограничены в совокупности, т. е. чтобы существовало число С > 0, для которого Рт* п< С при всех натуральных тип.
► Достаточность. Заметим, что если тг < т2, пг < п2, то Рт^ пх ?т2, п2 Далее из ограниченности частичных сумм Рт п следует, что существует число М такое, что М = sup Рт п. Тогда при любом е > 0 число М - е уже не является верхней гранью для {Рт п}, поэтому найдутся тп0(е) и и0(е) такие, что М - г < < ?т0, nQ Но в этом случае при всех т > т0 и п > nQ имеем
М-Е<Рт п <Ртп<М,
откуда \Рт, п~М\<г. Это значит, что Pm п М при т °°, п °°, Т‘ е‘ m	п = М•
Необходимость. Ограниченность последовательности Рт п в случае ее сходимости является следствием соответствующего общего свойства функции, имеющей предел по базе. «
363
Определение 19. Двойной ряд п называется абсолютно сходящимся, если сходится ряд	л|, составленный из
модулей его членов.
ТЕОРЕМА 26. Двойной абсолютно сходящийся ряд ^^ат^ п сходится.
► Положим
п = 1Д/П>П1 + а — 1Дт,п| + Дт,п
Рт. п	2	’ п	2
Тогда имеем |ат> „| = pm> л + qm, п и
^т, п ~ Рт, п 9т, п’ Рт, п 9т, п
Поскольку ряд Sn|am> л| сходится, найдется число С > 0 с условием т п
Ат, п = *5П?1 \ak,i\< с
при всех т и п. Но для частичных сумм Рт п и Qm п справедливы неравенства Pm п < л, п < A'mt п, поэтому по теореме 25 ряды п и п сходятся. Следовательно, ряд л, равный их разности, тоже сходится. ◄
Бесконечная сумма вида mSlnSx ат п позволяет рассматривать и иную важную конструкцию использования предельного перехода, которая приводит к понятию повторного ряда.
Определение 20. Пусть {ат> л} — двойная последовательность. Зафиксируем параметр т и рассмотрим формальный ряд Ъ ат п. Обозначим его символом Ьт. Тогда формальная бесконечная сумма
ОО	ОО/ОО	х
Z Ь =' S I X a 1
называется повторным рядом.
Очевидно, с одной и той же двойной последовательностью ат п можно связать еще один двойной ряд, а именно,
ОО	ООхОО	X
л? i Рп “* л? х (т? х ат, п)’
где рл = х л. Если в этом равенстве опустить скобки, то, вообще говоря, выражение	л можно рассматривать и как
двойной ряд, и как повторный ряд, и это может приводить к недоразумениям. Там, где эти недоразумения возможны, необхо
364
димо ставить скобки или специально оговаривать точный смысл выражения.
Введем понятие сходимости повторного ряда и рассмотрим связи между сходимостью двойного и повторного рядов.
Определение 21. Если при любом т ряд х ат п сходится к сумме Ьт и ряд Ът тоже сходится к некоторому числу А, то повторный ряд х Qs х называют сходящимся к сумме А и записывают в виде
ООхОО	х
S I S а	|— А.
т = 1 Vn = 1 nJ
Определение 22. Пусть (т (/?), n(k)) — некоторая линейная нумерация совокупности всех пар (тп, п). Тогда обычный числовой ряд kL1 dk9 где dk =	называется линейной пере-
становкой двойного ряда т^1 х ат п9 отвечающей данной нумерации его членов.
ТЕОРЕМА 27. Пусть ат, п > 0 для всех пар (тп, п) и пусть ряд S dk — некоторая его линейная перестановка. Тогда если сходится хотя бы один из трех рядов
ОО	ОО	ОО	X ОО	X	ОО
S	S а	,	X	I X а	I	и	Z
m = 1	п = 1	п*	т = 1	In = 1	”J	k = l
то два других ряда тоже сходятся к той же сумме.
► Обозначим через А, В и В сумму каждого из рассматриваемых рядов. Требуется доказать, что если существует хотя бы одно из этих трех чисел, то существуют и два других и все они равны между собой. Для этого достаточно доказать три утверждения: 1) если существует сумма А, то существует сумма В и В < А; 2) если существует сумма В, то существует сумма D и D < В; 3) если существует сумма В, то существует сумма А и А < D. Рассмотрим эти утверждения.
1)	Существование числа А означает сходимость частичных сумм Ат> п ряда t Y х ат п к его сумме А при тп -» оо, п _> оо. Ранее было доказано, что в этом случае А = sup Am> л, откуда Ат п < А при всех натуральных тп, п. Очевидно, что при этом справедливы неравенства
п	т п
Ьт (га) = Z?1 am,l г?1 ak,l=A-m, п
365
Следовательно, при любом т существуют числа
Ьт = SUP frm(n) =
Далее, так как т	т п
У Ь , (n) = S X аь ,=А	<А.
^ = 1^' ' fe = 1 / = 1 «> I m,n f то, устремляя п -> оо, при любом т имеем
т
fe?i bk = J3m-
Но Вт не убывает, поэтому при тп —» оо последовательность Вт сходится к некоторому числу В, причем В < А. Утверждение 1 доказано.
2)	Пусть В существует. Тогда для любой частичной суммы k
Dk= %! dk найдется пара чисел (тп0, п0) с условием, что тп(г) < тп0 и п(г) < п0 при всех г < k. Но тогда все слагаемые dr одновременно будут входить и в суммы причем
т0 л0	т0	оо	т0
А _ = Е Е	ак , <	Е	Е	ак , =	Е	Ък = Вт < В.
w0,n0 Л = 1 Z = 1	1	k = 1	I = 1	*	Л = 1	К mQ
Другими словами, все частичные суммы Dk ограничены сверху числом В и поэтому при некотором D имеем Dk —> D < В при fe —»оо. Утверждение 2 доказано.
3)	Пусть существует D. Тогда для любого Ат п можно найти номер kQ такой, что сумма Dk^ = dk содержит все слагаемые ak 19 входящие в сумму Ат, п. Но тогда при всех тп, п имеем Am п < Dk^ < D. Следовательно, существует А = sup Am> п и А < В, что и требовалось доказать. ◄
ТЕОРЕМА 28. Утверждение теоремы 27 останется в силе, ес-ли условие ат* п > 0 опустить, а сходимость рядов рассматривать как абсолютную.
► Числа ат, п представим в виде ат п=Рт,п~ qm, п, где
|am,n| amtn п	lam,n| “ ат,п Л
Рт, п = ---2---- > °’	*------2----- °*
Далее достаточно применить теорему 27 к рядам с общими членами рт nnqm пи рассмотреть их разность. ◄
ТЕОРЕМА 29. Любая перестановка членов двойного абсолютно сходящегося ряда не нарушает его сходимости и не изменяет его суммы.
366
►	Пусть ЕЕ Ът п — перестановка двойного абсолютно сходящегося ряда ЕЕ ат< п = А. Рассмотрим соответствующие рядам ЕЕ ат п и ЕЕ Ьт п однократные ряды ftE и Е dk из теоремы 27. Тогда ряд Е dk = А абсолютно сходится, а ряд *Е d'k является некоторой его перестановкой. Но тогда он тоже абсолютно сходится, а вместе с ним абсолютно сходится и ряд ЕЕ Ьт „, причем
А = ЕЕ а „ = Е d'k = Е dk = Е Ъ „. ◄ ТП, П	К	К	ТП, п
ТЕОРЕМА 30. В повторном абсолютно сходящемся ряде вида (Sn am> п) можно менять порядок суммирования. При этом ряд остается абсолютно сходящимся и его сумма не изменяется.
►	В силу теоремы 28 двойной ряд SS ат, п также абсолютно сходится, а вместе с ним по той же теореме абсолютно сходится и ряд S (S ат, п), причем суммы всех трех рядов совпадают. ◄
В заключение подчеркнем, что вообще свойство сохранять сумму при изменении порядка суммирования будет в дальнейшем представлять особый интерес. Теорема 30 дает пример возможности изменения последовательности выполнения предельных переходов.
ГЛАВА 16
Функциональные последовательности и ряды
Лекция 8
§ 1. СХОДИМОСТЬ ФУНКЦИОНАЛЬНОГО РЯДА
Понятия функциональной последовательности и функционального ряда связаны между собой так же тесно, как и в обычном числовом случае. С этими понятиями мы, по существу, ранее уже встречались. Примерами могут служить бесконечная геометрическая прогрессия
при |д|<1
или дзета-функция Римана
^) =	ПРИ8>1-
Если в первом случае зафиксировать д, а во втором з, то мы получаем обычные числовые ряды. Но эти же параметры можно рассматривать как аргументы числовых функций, и тогда суммы рядов тоже будут представлять собой некоторые числовые функции. Подобные соображения приводят нас к следующим определениям.
Определение 1. Функциональной последовательностью называется занумерованное множество функций {/п(х)}, имеющих одну и ту же область определения DcR. При этом множество D называется областью определения функциональной последовательности {fn(x)}.
Здесь термин «занумеровать» означает «поставить во взаимно однозначное соответствие с натуральным рядом АГ».
Определение 2. Пусть {ал(х)} — некоторая функциональная последовательность (ф. п.), определенная на множестве D. Формальная бесконечная сумма вида
ах(х) + а2(х) + а3(х) + ... = ап(х), или просто Е ап(х), называется функциональным рядом, определенным на D.
368
Фиксируя какое-либо значение х = х0 е D, получаем обычный числовой ряд S ап(хб)* Как и в числовом случае, определим понятие частичной суадмы функционального ряда.
Определение 3. При всех п е N функция
Ап(х) = ах(х) + а2(х) +... + а„(х) - ай(х)
называется п-й частичной суммой функционального ряда Е ал(х) и ап(х) — его общим членом.
В дальнейшем пусть D обозначает область определения функционального ряда Е ал(х), т. е. последовательности {Ал(х)}.
Определение 4. Если при фиксированном х = х0 е D сходится числовой ряд Е ал(х0), то говорят, что функциональный ряд Е ал(х) сходится в точке х = х0.
Определение 5. Множество DQ cz D, состоящее из тех точек х0, в которых ряд S ал(х) (или последовательность Ап(х)) сходится, называется областью сходимости этого ряда (или этой, последовательности).
Замечание. Область сходимости функционального ряда обычно бывает уже, чем область ее определения. Пример — бесконечная геомет-оо
рическая прогрессия —2— = Е qn.
1-Q n = 1
Определение 6. Пусть DQ — область сходимости функциональной последовательности {Ап (х)} и пусть А(х) есть предельное значение этой последовательности при фиксированном значении х е Во. Тогда множество пар (х, А(х)) при всех х е Dq задает некоторую функцию у = А(х), определенную на всем множестве Во. Эта функция называется предельной функцией функциональной последовательности {Ал(х)}. Если при этом Ап(х) — последовательность частичных сумм ряда Е ап(х), то функция А(х) называется суммой этого ряда.
Итак, сумма функционального ряда — это некоторая функция, определенная на его области сходимости. При х е DQ остаток ряда гп(х) тоже представляет собой некоторую функцию от х, гп(х) = А(х) - Ап(х), причем гп(х) 0 при п -> оо и при любом xeD0.
Многие свойства суммы А(х) такие, например, как непрерывность суммы ряда Е ап(х), связаны с поведением его остатка гп(х) при и оо. Для описания этого поведения далее введем важное
369
понятие равномерной сходимости функциональных рядов и функциональных последовательностей на множестве. Для того чтобы подчеркнуть отличие от него введенного выше понятия простой сходимости, последнюю называют еще поточечной сходимостью.
Важные примеры функциональных рядов возникают из разложения различных функций по формуле Тейлора. Например, разлагая в точке х0 = 0 функцию у = sin х при хе Я, имеем
х2п-1
уЗ	_
sin х = х - 3! + ... + (-1F-1	+ rn(x),
где rn(x) — остаточный член формулы. Записывая его в форме Лагранжа, получаем
у2п
Г"(Х)=(2^)! Sin(2">z
при некоторой точке z с условием, что она лежит между точками О и х. Отсюда
I . lxl2n
1гп(*)1 < (2га)!'
Но при п > х2 имеют место следующие неравенства:
т. е. гл(х) —» 0 при п —>
Таким образом, полагая z ч (-1)п-1х2п~1
при всех х g R имеем разложение sin х = ал(х).
00 fn(a)
Определение 7. Степенной ряд	 (х - а)п называется
рядом Тейлора функции /(х) в точке х = а,а также разложением функции /(х) в ряд Тейлора в этой точке.
Рассмотрим примеры рядов Тейлора для некоторых функций:
ПРИМЕРЫ. 1. е1 = Z .^(VxsB). n = on!v	'
2. ln(l + x) = nE1(-l)»-1^(-l <х< 1).
00	r2n-l
3,stax-
370
4.	cos x = Jo (-IF ^(Vxe Я).
5.	(1 + x)“ = 1 + BEi^Sc-^ -”!(a~n + 1) x»(-1 < x < 1).
6.	arctg x = Д/-1)"-1	< 1)-
,	.	. v (2n-1)!! x2n + 1 „ .
7.	arcsin x = x + Z, —7^ .1/ • --7 ( x < 1).
n = i (2n)!! 2n + 1	1	7
§ 2. РАВНОМЕРНАЯ СХОДИМОСТЬ
Определение 8. Пусть последовательность функций {гп(х)} сходится к нулю при всех хе М. Тогда говорят, что гп(х) сходится к нулю равномерно на множестве М9 если для любого £ > 0 найдется такой номер и0 = п0(е), что при всех п > nQ и одновременно при всех хеМ выполнено неравенство |гп(х)| < £.
Обозначение: гп(х) =► 0 при п->°°.
м
Замечание. Слово «одновременно» в этом определении, вообще говоря, является избыточным и его можно опустить, однако оно обращает внимание на главное отличие равномерной сходимости от поточечной, состоящее в том, что в первом случае число п0(е) в определении предела одно и то же для всех точек х е М, а во втором случае оно может зависеть еще и от х, т. е. л0(е) = тг0(е, х).
Определение 9. Если функция А(х) = Ап(х) + гп(х), где гп(х) => О при п —» оо, то последовательность Ап(х) называют равномерно сходящейся к функции А(х) на множестве М при п -> оо и это обозначают так:
Ап(х) =* А(х) при п->°°.
м
Символ М здесь можно опустить, если по смыслу понятно, о каком множестве идет речь. Далее, если при этом Ап(х) — последовательность частичных сумм ряда Е ап(х), то этот ряд называют равномерно сходящимся к А(х) на множестве М.
Важность введенного понятия равномерной сходимости видна на примере следующей теоремы.
ТЕОРЕМА 1. Пусть каждая из функций ап(х) непрерывна в точке х0 е R и ряд Ъ ап(х) равномерно сходится к функции А(х) на интервале I = (х0 - 8, х0 + 8), где 8 > 0 — некоторое фиксированное число. Тогда сумма А(х) является непрерывной функцией в точке х = х0.
371
►	По определению равномерной сходимости имеем А(х) = Ап(х) + гп<х)> Гп(Х)	0 0» ОО),
Ап<х) = *tx <»*(*)> гп<х> = k _f + 1
Используя обозначение Д/(х) = f(x) - f(x0), где f(x) — любая функция, получаем
АА(х) = ДА„(х) + Дг„(х) = ДА„(х) + г„(х) - гв(х0).
Отсюда
|ДА(х)| < |ДА„(х)| + |г„(х)| + |г„(х0)|.
Поскольку гв(х) у 0 (п -» оо), при любом Ех > 0 найдется номер n0 = п0(ех) такой, что для всех п > п0 и для всех хе I имеем
1гв(*)1 < еР |г„(*о)1 < £1*
Заметим, что функция Ап(х) непрерывна в точке х = х0, поэтому для любого ех > О найдется 8Х = SJeJ > 0 такое, что при всех х с условием |х — х0| < 8г выполняется неравенство
|ДА„(х)| = |Ав(х) - А„(х0)| < £х.
Теперь при заданном е > 0 можно взять ех = е/3; тогда при всех х с условием |х - х0| < 8(e) = и при п = n0(ex) + 1 = и0(е) получаем
|ДА(х)| < |ДА„(х)| +1 г„(х)| + I гв(х0)| < £х + Ех + Ех = Е.
Но это и означает, что функция А(х) непрерывна в точке х = х0. ◄
Рассмотрим некоторые простые свойства равномерно сходящихся функциональных последовательностей.
Определение 10. Последовательность функций {Ап(х)} называется равномерно ограниченной на множестве М, если существует такое число С, что при всех пе N и при всех хе М имеем
К(Х)|<С.
УТВЕРЖДЕНИЕ 1. Равномерно сходящаяся на множестве М последовательность Ап(х), состоящая из ограниченных на М функций, является равномерно ограниченной на М.
►	Пусть Вт = sup |Am(x)| для каждого натурального числа т. хеМ
В определении равномерной сходимости возьмем е = 1. Тогда при всех достаточно больших п > nQ и при всех хе М
|А(х) - А„(х)| < 1, |А(х)| < |А„(х)| + 1 < В„+1.
Это значит, что последовательность А(х) ограничена.
372
Далее, пусть Во = sup |А(х)|, В = max Bk. Положим С = В + 1.
Тогда при k < nQ справедлива оценка [АЛ(х)| < В < В + 1 = С, а при k > п0 имеем 1А(х)| < \А(х) - (А(х) - АДх))| < |А(х) | + |(А(х) - АЛ(х)| <
<В0 + 1<В + 1=С. ◄
Попутно доказано еще одно утверждение.
УТВЕРЖДЕНИЕ 2. Если функция А(х) ограничена на множестве М и Ап(х) =► А(х), то при некотором n0 е N функциональная последовательность Вп(х) = Ап +п(х) равномерно ограничена на М.
Следующие два утверждения приведем без доказательства, поскольку они доказываются точно так же, как и в аналогичных случаях для числовых рядов.
УТВЕРЖДЕНИЕ 3. Пусть при п —> 00 имеем ап(х) а (х), &„(х) =? Ь(х). м	м
Тогда:
1°. ал(х) + &л(х) =£ а(х) + &(х).
2°. Если |&(х)| < С при некотором С > 0 и всех х е М, то а„(х)-Ьл(х) =5а(х)-Ь(х).
м
3°.	=» £7^, если только 1/|Ь(х)| > С > 0 при всех х е М.
. Ь„(х) м Ь(х)’	/I v /I	г
УТВЕРЖДЕНИЕ 4. Если последовательность dn(x) является равномерно ограниченной и гл(х) 0 при п -» то dn(x)rn(x) О м	м
при п
Лекция 9
§ 3. КРИТЕРИЙ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Докажем теперь критерий Коши равномерной сходимости функциональной последовательности.
ТЕОРЕМА 2 (критерий Коши). Для того чтобы функциональная последовательность Ап(х) равномерно сходилась на множестве М, необходимо и достаточно, чтобы для любого е > 0 существовал номер и0 = п0(е) такой, что при всех т > nQ и п > nQ и всех х g М имело бы место неравенство |Ал(х) - Ат(х)| < е.
► Необходимость. В этом случае Ап(х) А(х). Таким образом, для любого е > О существует число п0 = л0(е) такое, что для всех п > nQ и для всех хе М имеем |Ал(х) - А(х)| < е/2. Но в этом случае при т > nQ и п > nQ имеем
\Ат(х) - Ал(х)| < |Ат(х) - А(х)| + |А(х) - Ал(х)| < е/2 + е/2 = е.
Достаточность. При каждом фиксированном хе Мфункциональная последовательность Ап(х) превращается в числовую и для нее выполняется критерий Коши. Это значит, что она имеет предел А(х), т. е. предельная функция существует на всем множестве М. Далее, каково бы ни было число е > 0, по условию найдется номер = п1(е/2) такой, что при всех т и п > пг имеем \Ап(х) - Ат(х)\ < г/2.
Снова произвольно зафиксируем хе М и устремим т к бесконечности. Получаем неравенство
|Ав(х)-А(х)| < е/2 < е.
Но тогда, полагая п0 = п0(е) — п1(е/2), при всех п > п0 и всех хе М имеем
|А„(х) - А(х)| < е, т. е. Ал(х) =* А(х). ◄
Если Ал(х) — последовательность частичных сумм функционального ряда X ал(х), то теорема 2 дает критерий Коши равномерной сходимости этого ряда. Сформулируем его в виде следующей теоремы.
ТЕОРЕМА 3. Для равномерной сходимости ряда Z ал(х) на множестве М необходимо и достаточно, чтобы для любого £ > О существовало п0 = п0(е) такое, что для каждого п > л0, и для каждого р е N, и для всех х е М выполнялось бы неравенство
п+р
. Е ,aJx) <е.
k = п + 1 я '
374
И наконец, исходя из теоремы 3, сформулируем в прямой форме критерий отсутствия равномерной сходимости ряда Е ап(х).
ТЕОРЕМА 4. Утверждение о том, что ряд Е ап(х) или последовательность Ап(х) не являются равномерно сходящимися на множестве М, означает, что существует е > 0 такое, что найдутся две последовательности {пт} и {рт} е N, причем пт+1 > пт* а также последовательность {хт} е М, для которых имеет место неравенство


Рассмотрим примеры неравномерно сходящихся рядов и последовательностей.
ПРИМЕРЫ. 1. Ряд А(х) = п50 х(1 - х)п сходится неравномерно на [0, 2). Действительно, сумма ряда А(х) при х # О равна
А(х) = х Е (1 - х)я = х-—77-- = - = 1
и А(0) = 0. Это значит, что х = 0 — точка разрыва функции А(х). Но если бы сходимость была равномерной, то функция А(х) была бы непрерывной в силу теоремы 1, поскольку ап(х) = х(1 - х)п непрерывна в нуле. Но это не так. Следовательно, равномерной сходимости нет.
2. Если Ап(х) = хп, то на множестве М = (0, 1) равномерная сходимость не имеет места.
Действительно, в теореме 4 положим е = 0, 1 и при каждом т > 1 возьмем пт = т, хт = 1 - 1/тп, рт = тп. Тогда будем иметь |Am(xw) - А2т(хт)\ = |(1 - 1/тГ - (1 ~ V™)2ml =
= (1 - 1/тп)™(1 - (1 - 1/т)т) > 1/3 • 2/3 > 0,1 = е.
Таким образом, по критерию Коши в форме теоремы 4 последовательность Ап(х) не является равномерно сходящейся.
ЗАДАЧА. Пусть функции fn(x) непрерывны на [0, 1] при всех п е N и fn(x) -» /0(х) при п оо. Докажите, что функция /0(х) имеет точку непрерывности на (0, 1).
$ 4. ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ
Докажем три признака равномерной сходимости функционального ряда, принадлежащие Вейерштрассу, Абелю и Дирихле. Эти признаки дают достаточные условия для равномерной сходимости, но они не являются необходимыми, т. е. ряд
375
Z an(x) может сходиться равномерно, но не, удовлетворять любому из них. Впрочем, та же ситуация имела место и для сходимости обычных числовых рядов. С другой стороны, отметим, что они соответствуют признакам сходимости числовых рядов того же названия и развивают заложенные в них принципы.
Рассмотрим сначала следующий критерий равномерной сходимости для бесконечно малой функциональной последовательности.
ТЕОРЕМА 5. Для того чтобы Ьп(х) 0 при п °°, необходимо и достаточно, чтобы существовала числовая последовательность с условием Рл —» 0 при п оо и |&п(х)| < рп для каждого п е N и для всех х е М.
► Достаточность. Пусть такая последовательность рп существует. Тогда для любого е > 0 существует номер п0 = п0(е) такой, что для каждого п > nQ справедлива оценка Рп < е. Но тогда при тех же п и всех хе М имеем |bn(x)| < РЛ < е, т. е.
Ьп(х) => 0 при д —> оо. м
Необходимость. Пусть Ьп(х) =* 0 при и —» оо. Положим Рл = л/
= sup | &„(*)!• Поскольку для любого е > 0 существует номер п0 = X G М
= п0(е) такой, что для каждого п > п0 справедливо неравенство |&„(х)| < £, при тех же п имеем Pn = sup |Ь„(х)| < е. Это значит, что х&М
Рп -> 0 при п -» ОО. «
Замечание. Последовательность рп в теореме 1 называется мажорантой для Ьп(х), и утверждение этой теоремы означает, что равномерная сходимость бесконечно малой функциональной последовательности равносильна существованию бесконечно малой ее мажоранты.
Рассмотрим теперь признак Вейерштрасса для равномерной сходимости функционального ряда.
Определение 11. Сходящийся числовой ряд Ърп с условием Рп 0 при всех п называется мажорантой функционального ряда Ъ ап(х) на множестве М, если для каждого п е N и всех х е М справедлива оценка |ал(х)| < рп. Говорят также, что ряд Е ал(х) мажорируется рядом Ъ рп на множестве М.
ТЕОРЕМА 6 (признак Вейерштрасса). Пусть функциональный ряд Ъ ап(х) на множестве М имеет мажоранту Ъ рп- Тогда он равномерно сходится на этом множестве.
376
► Достаточно установить, что остаток ряда гл(х) равномерно сходится к нулю на М. Заметим, что при любом фиксированном хе М числовой ряд X ал(х) сходится, поскольку имеет мажоранту = Р. Кроме того, при каждом фиксированном х имеем
kn(x)l = feЛ +1 о*<*) < kЛ+	< кЛ + rPk - рп.
где рл — остаток числового ряда Ерл и рл —» О при п —» оо. Но по теореме 5 это означает, что гл(х) имеет бесконечно малую мажоранту рл. Следовательно, гл(х) 0 при п —> оо, т. е. ряд Е ал(х) равномерно сходится. ◄
ТЕОРЕМА 7.
(А) (признак Абеля). Пусты
1)	Е а„(х) А(х);
м
2)	последовательность Ъп(х) равномерно ограничена на М;
3)	при всех фиксированных хе М числовая последовательность Ьп(х) монотонна. Тогда ряд Е йл(х), йл(х) = ал(х)&л(х), равномерно сходится на М.
(Д) (признак Дирихле). Пусть:
1)	частичные суммы Ал(х) равномерно ограничены на М;
2)	&л(х)	0 при п -» ОО;
3)	при всех фиксированных хе М числовая последовательность Ъп(х) монотонна. Тогда ряд Ъ hn(x), hn(x) = an(x)bn(x), равномерно сходится на М.
► Используем ту же схему, что и при доказательстве одноименных признаков для числовых рядов. Как и раньше, сначала будем считать, что последовательность 6л(х) убывает и 6л(х) > 0 для каждого п е N. Применяя преобразование Абеля к частичным суммам ряда Е йл(х) и используя обозначения
Н'(х) = п£\h(x), A'k(x) - Е , ат(х)
для отрезков рядов X йл(х) и Е ал(х), получаем
|я;(х).|- kiP+1ak(x)bk(x)
= А'п+р(х) bn+p(x) + k =S+ х А'к(х) «Ьк - Ьк^(х)) <
п +р - 1
< lAn+p(*)l&n +р(Х) + SUP l^k(*)l * Л + 1	“ ЬЛ+1<Х)) <
п<Л<п+р
SU₽ lAft(X)l-
n<k<n+p
377
Рассмотрим случай (А). В силу равномерной сходимости ряда Е ап(х) и согласно критерию Коши, для любого е > 0 существует номер п0 = п0(е) такой, что для каждого k > nQ справедливо неравенство
sup|A^(x)| < е.
х&М
Кроме того, в силу равномерной ограниченности Ъп(х) при некотором С > 0 для каждого п е N и для всех хе М имеем Ьп(х) < С. Следовательно, при п > nQ справедлива оценка |Н'р(х)| < Се.
В силу произвольности е > 0 это означает выполнение условия критерия Коши для равномерной сходимости ряда Е Лл(х), т. е. в случае (А) теорема доказана.
Рассмотрим теперь случай (Д). При этом в силу равцомерной ограниченности сумм Ak(x), а вместе с ними и А^(х) = Ak(x) -- Ап(х) найдется число С > 0 такое, что |А^(х)| < С при всех k е N и всех х е М. В силу п. 2 имеем bn(x) 0 при п -> оо. Тогда для любого е > 0 при достаточно большом п > и0(е) получим |Ьл+1(х)| < < е, откуда, как и раньше, имеем |7/р(х)| < Се. Тем самым утверждение (Д) тоже доказано.
Осталось освободиться от ограничений: 1) последовательность &л(х) убывает; 2) Ьп(х) > 0 при всех п. Для того чтобы снять ограничение 1), можно поменять знаки на противоположные у всех функций ал(х) и &л(х) одновременно. Тогда условие возрастания ЬАх) переходит в условие убывания Ьл(х), а все условия на ряд £ал(х) сохраняются. Чтобы освободиться от ограничения 2), рассмотрим функцию 60(х), где Ь0(х) = inf 6л(х) = Шг^ 6л(х). Тогда &л(х) = 60(х) + Рл(х), где рл(х) > 0 для всех х е М и Рл(х) убывает. Отсюда
X а„(х) &„(х) = &0(х) X а„(х) + X ап(х) р„(х).
В случае (Д) первое слагаемое равно нулю, а в случае (А) оно представляет собой равномерно сходящийся ряд. Второй же ряд удовлетворяет условиям теоремы и обоим сделанным выше допущениям. ◄
Докажем следующий изящный критерий равномерной сходимости синус-ряда ([36], [37]).
ТЕОРЕМА 8. (Критерий Чоунди—Джолиффе равномерной сходимости тригонометрического синус-ряда.) Пусть Ьп — положительная, монотонно убывающая последовательность. Тогда для равномерной сходимости ряда lbn sin пх на R необходимо и достаточно, чтобы
lim nbn = 0. п -> оо п
378
► Необходимость. Согласно критерию Коши имеем, что для любого £ > О найдется п0 = п0(е) такое, что при всех т > nQ, всех п > п0
и всех х е [0, л] справедливо неравенство
п
, Е bk sin kx
k = m + 1 Л
E.
Возьмем m = [n/2] и x = л/(4п). Тогда при m + 1 < k < n получим
sin kx > sin (л/4) = 72/2. Следовательно,
. E bk sin kx > (n - m) bnj2 /2 > nbnj2 /1. к=т+1 n	n	1
Таким образом, для любого £ > 0 нашлось число п0 = п0(е) такое,
что при всех п> nQ выполняется неравенство |л&л| < 4е/а/2 , т. е.
Jim, nbn = 0. Необходимость доказана.
Достаточность. Так как для любого натурального числа п функции sin пх — периодические с периодом 2л и нечетные, то
достаточно доказать равномерную сходимость рассматриваемого ряда только на отрезке [0, л]. Из условия теоремы имеем, что для любого е > 0 найдется п0 = п0(е) такое, что при всех п > nQ справедливо неравенство |и&п| < е. Возьмем любое п > nQ и любое р > 1
и оценим сумму
п + р
. Е , bk sin kx k - n + 1 «
где
sx=
[я/*]	n + p
ь E i t bh sin kx , E2 = ь E bk sin kx
Л = n +1 «	* k = [n/x] +1 *
При k < л/х имеем sin t < t9 поэтому
ln/x]
E< < E , T kx < £ Л. 1 k = n + 1 к
Для оценки суммы Е2 применим преобразование Абеля. Получим
п + q
Е2	ЬГя/л.1+1 max Е sin kx
2	[л/х]+1	Л = [я/х]
Е Л [л/х] 4-1 х
поскольку функция sin t/t монотонно убывает при 0 < t < л/2 и
n + g
Е sin kx k = [п/х]
cos(n + q - l/2)x - сое([л/х] 4- l/2)x 2sin(x/2)
_JL_<5
sin(x/2) x*
Следовательно, E < £ (л 4-1). Таким образом, для любого £ > 0 нашлось число п0 = и0(е) такое, что для всех п > п0, для всех р > 1 и для любого х е R выполняется неравенство Е < е (л 4- .1), что в силу критерия Коши равномерной сходимости ряда означает равномерную сходимость Е, bn sin пх. <
Отметим, что интересные обобщения этой теоремы даны Г. X. Харди [37].
Е =
Ej + E2,,
379
Лекция 10
§5. ТЕОРЕМА ДИНИ
Докажем теорему Дини» которая важна для прояснения сущности понятия равномерной сходимости.
ТЕОРЕМА 9 (признак Дини). Пусть последовательность неотрицательных функций рп(х), непрерывных на отрезке I = [а, 6], сходится поточечно к нулю на этом отрезке, причем рп(х) > > рп+1(х) при всех х g I и при всех п е N. Тогда эта сходимость равномерная на отрезке I, т. е. рп(х) у- 0 при п оо.
► В силу поточечной сходимости последовательности рп(х) к нулю для всякого е > 0 и для каждой точки хе Iможно указать номер п = п(е, х) такой, что рп(х) < е/2. Но так как функция рп(х) непрерывна, то у точки х найдется некоторая 8-окрестность, где 8 = 8(e) > 0, для всех точек у которой имеем рп(у) < е. Совокупность всех таких окрестностей полностью покрывает отрезок I, и в силу того, что он является компактом, из этого покрытия можно выбрать конечное подпокрытие О(8Р хг), ... , O(8fe, xk). По построению каждому из чисел хр ... , xk соответствуют свои номера ..., nk и функциирП1(у),... , pnk(y) такие, что 0 < p„g (у) < е при всех у е О (8S, xs). Положим n0 = max1 с 8 < k п8. Тогда 0 < pnQ(y) < Рп(уУ < е ПРИ любом у е О (8ng, хп) и s = 1,..., k. Каждая точка у из отрезка I входит в некоторую такую окрестность, поэтому в каждой из них выполняется неравенство 0 < PnQ(y) < £• Но тогда для всех п > nQ = и0(е) и одновременно для всех у е I имеем [рл(г/)| < е, т. е. рп(х) р 0 при и —» оо. ◄
Если в теореме 9 в качестве рп(х) рассматривать последовательность остатков гп(х) функционального ряда Е ап(х) с условием ап(х) > 0, то вместе с доказанной ранее теоремой о сохранении непрерывности суммы ряда при его равномерной сходимости получаем следующий критерий.
ТЕОРЕМА 10. Для того чтобы сумма ряда, составленного из непрерывных и неотрицательных функций на отрезке I = [а, &], была также непрерывна на I, необходимо и достаточно, чтобы ряд сходился равномерно на этом отрезке.
Замечание. Для справедливости утверждения теоремы 9 существенно, что отрезок I является компактом. Если, например, в ее условии отрезок I заменить интервалом, то она уже не будет верной. Это подтверждает разобранный ранее пример ряда Е х(1 - х)п, который не является равномерно сходящимся на интервале (0, 1).
380
§6. ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ РЯДА
Наша дальнейшая цель состоит в нахождении условий, обеспечивающих возможность почленного дифференцировайия и интегрирования функциональных рядов. Понятие равномерной сходимости ряда и здесь играет главную роль.
Теорема о непрерывности суммы равномерно сходящегося ряда означает, что
А(х0) - lim А(х) = lim (lim А„(х)) = lim Z а„(х) = X Xq	х Xq п ОО	X Xq
= Z а„(хп) = lim A„(xn) = lim (lim А„(х)).
Другими словами, эта теорема позволяет менять порядок выполнения двух последовательных предельных переходов вида х -» х0 и п -> оо. Далее докажем утверждение весьма общего вида, а пока отметим, что почленное дифференцирование, как и почленное интегрирование, тоже можно рассматривать как изменение порядка выполнения предельных переходов относительно двух баз множеств разного типа.
Рассмотрим вопрос о почленном интегрировании ряда.
ТЕОРЕМА 11. Сумма А(х) равномерно сходящегося на I = [а, р] ряда Ъ ап(х), составленного из функций, интегрируемых на [а, р] по Риману, тоже является интегрируемой по Риману функцией, причем
Р	оо Р	оо
в = jA(x)dx = nZ j a„(x)dx = Ъ tbn. a	a
► Согласно критерию Лебега, интегрируемости функции по Риману, мера множества Тп точек разрыва каждой из функций ап(х) равна нулю. Но тогда объединение Т всех таких множеств, Т = UTn, также имеет лебегову меру нуль. Все остальные точки промежутка I будут общими точками непрерывности одновременно для всех функций an(x). Поэтому, в силу равномерной сходимости ряда Z ап(х), сумма А(х) этого ряда ограничена и в этих точках непрерывна. Другими словами, тогда лебегова мера точек разрыва ограниченной функции А(х) тоже равна нулю и согласно критерию Лебега, А(х) интегрируема по Риману на [а, р]. Тогда при всех п е N имеем
Р	Р	Р
J A(x)dx = J An(x)dx 4- J rn(x)dx. a	a	a
381
Но так как гп(х) у 0 при п -> оо, то sup |гп(х)| = рп -»0 при и -»оо. Отсюда при 71 —> оо получим
0	0	0	0
J A(x)dx - J An(x)dx < J |r„(x)dx| < j pBdx = p„(P - a) -> 0, a	a	a	a
т. e. [в - kL1 0 при n -» оо и В = feEt bk. ◄
Полученный результат позволяет весьма просто доказать первое правило почленного дифференцирования ряда.
ТЕОРЕМА 12. Ряд Е ап(х) можно почленно дифференцировать, если:
1)	этот ряд сходится в некоторой точке х0 отрезка I = [a, Р];
2)	производные всех его слагаемых ап(х) существуют и непрерывны на I;
3)	ряд Е а'п(х), составленный из этих производных, равномерно сходится на отрезке I.
Точнее, имеем:
1)	Д х ak(x) = Ап(х) =: А(х);
2)A'(x) = Z<(x).
► Условия данной теоремы позволяют применить теорему 11 для почленного интегрирования ряда Е а'п(х) на отрезке с концами xQ и t при любом t е [а, р]. При этом с помощью формулы Ньютона—Лейбница получаем
A(t) - A(xq) = B(t) = J A'(x)dx = J E a'n(x)dx = *0	Xq
= nl x f a'n(x)dx = J x (a„(t) - a„(x0)> = J x ba(t).
xo
Это равенство означает, что A\t) = B'(t) = E a'n(t). Осталось показать, что ряд Е an(x) сходится равномерно на I. Имеем
Р»(0 "7 r'n(x)dx = f к _Е+ х a’k(x)dx -*о	*0
= fc =Е+ х	- afc(x0)) = к_Е+ х bk(t), ₽n(t) = B(t) - feEx bk(t).
Ho r'n(x) =► 0 при 7i —> поэтому существует последовательность pn с условиемpn —»0 и |т^(х)| < рп при всех достаточно больших п > п0 и всех хе I. Следовательно,
1Рл(0| < J k;(x)|dx < J pndx =pn(t - х0) < pn(a - Р). *0	хо
382	I
I
Это значит, что 0л(х) =t 0 при п -» °°, т. е. ряд £ &n(t) сходится равномерно на I, а вместе с ним и ряд £ ап(х) тоже равномерно сходится, так как
A(t) = Ea„(t) = Sbn(O + Sa„(xo), где Е а(х0) — сходящийся числовой ряд. •< ТЕОРЕМА 13. Пусть:
1) ряд Е ап(х) сходится в некоторой точке х0 е I = [а, 0];
2) ряд Е а„(х) равномерно сходится на I,
Тогда ряд Е ап(х) тоже равномерно сходится на I, причем его сумма А(х) имеет производную А'(х), равную сумме ряда а'п(х).
Заметим прежде всего, что здесь нельзя воспользоваться формулой Ньютона—Лейбница, поскольку функции а'п(х) могут уже не интегрироваться по Риману и необходимо действовать по-иному.
► Докажем сначала, что исходный ряд Е ав(х) равномерно сходится на I. Для этого проверим выполнение для этого ряда критерия Коши. Точнее, будем рассматривать разность
Е (а„(х) - а„(х0)) = Е Лп(х),
что допустимо, так как Е an(x) = Е Л„(х) + Е ап(х0), где числовой ряд Е ап(х0) сходится.
Применяя к отрезку ряда hn(x) формулу конечных приращений Лагранжа, при некотором t е (х0, х) имеем
п+р


Но тогда, согласно критерию Коши, для любого е > 0 и при достаточно большом п > nQ и любом ре N имеем
Т < |х - х0| •
<е|х-х0|.
Поскольку £ > 0 произвольно, это означает, что условие критерия Коши для ряда Е hn(x) тоже выполнено и он равномерно сходится вместе с рядом Е ап(х).
Теперь необходимо показать, что его сумму А(х) можно дифференцировать, причем производная суммы равна сумме производных во всякой точке хг отрезка I = [а, р]. Для этого рассмотрим отношение
ДА(х) _ А(х) - А(хх) _ ДАп(х) Дгп(х) _
Дх	х-хх " Дх + Дх
где п е N произвольно.
383
Снова применяя формулу конечных приращений, для Rn получаем оценку
l«nl =
гп(х) ~ rn(Xi) X - хг
Пт , р->°° fe = n + l X - Хг

< sup р
п£> gfe(x) -gfe(xx)
Л = n 4- 1 X — X*
< sup tel
p 6 N
n+p
„ E , a'k(t) = Tx. k = n + 1 д '	1
В силу равномерной сходимости ряда Z а'п(х), величина Тг при любом заданном значении е > 0 и достаточно большом п > становится меньше, чем е. Поэтому при таких п имеем |Ял| < е. Полагая D(x) = Е ал(х) и dn(x) = Л=Е+1а*(х) = D(x) - Ал(х), при тех же п и всех хе I, очевидно, имеем оценку |dn(x)| < 7\ < е.
Далее, функция Ап(х) дифференцируема при любом х, поэтому
&Ап(х)
Dn=^^ =А'П(Х1) + 1П(Х),
где ул(х) -> 0 при любом фиксированном п и х —» хР Зафиксируем теперь какое-либо п > п0(е), например п = n0(e) + 1, и выберем число 8(e) > 0 так, чтобы при данном п и всех х с условием О < |х - х0| < 8(e) выполнялось неравенство |ул(х)| < е. Тогда для всех таких х имеем
- D(xx) = |Z>n + Rn - D(xx)| = \A'n(Xl) + Yn(x) + Rn - D(xx)| = = It„(*) - d„(xx) + Я„| < Зе,
а это значит, что ДА(х)/Дх -> D(xx) при Дх -> 0 или А'(х) =
= „1,^(4 **
Лекция 11
. § 7. ДВОЙНЫЕ И ПОВТОРНЫЕ ПРЕДЕЛЫ ПО БАЗЕ МНОЖЕСТВ
Примеры равенства повторных пределов различных типов ясно подсказывают целесообразность выработки возможно более общего взгляда на этот вопрос. Здесь мы рассматриваем его в связи с еще одним понятием — понятием предела по совокупности двух баз. Нам потребуется ряд новых определений.
Определение 12. Пусть функция Дх, у) определена на декартовом произведении X х У двух множеств X и Y, т. е. на множестве всех пар (х, у), где х е X и у е У. Пусть на множестве X задана некоторая база В. Будем говорить, что функция Дх, у) сходится к функции g(y) по базе В равномерно на множестве У, если для всякого е > 0 найдется окончание Ь(е) g В такое, что при всех х g b(e) независимо от у е У справедливо неравенство \f(x, у) - g(i/)| < е. В этом случае будем писать:
в fix, у) =: g(y).
Рассмотрим теперь базу D = {d}, заданную на множестве У.
Определение 13. Если f(x, у) сходится к g(y) по базе В, а функция g(y) сходится к 1г по базе D, то число 1г назовем повторным пределом функции f(x, у) по базам В и D. Этот предел будем обозначать символом lim lim Дх, у) = lv
Изменяя порядок выполнения предельных переходов, можно рассматривать еще один повторный предел, lim lim Дх, у) = 12. Далее введем понятие двойного предела по базам В и D.
Определение 14. Рассмотрим в качестве основного множества декартово произведение X х У, состоящее из всевозможных пар (х, у), где xeXuyeY, и рассмотрим определенную на нем базу Н, составленную из всех возможных сочетаний h вида h = b X d, где Ь g В и d g D. Эту базу будем называть декартовым произведением баз В и D и обозначать: Н = В х D.
Легко убедиться в том, что множество Н действительно образует базу множеств. В самом деле: 1) каждый ее элемент h = Ъ х d, очевидно, не пуст и 2) пересечение любых двух ее элементов hr A h2 = (Ьх X di) А (Ь2 х d2) содержит некоторый третий элемент h3 = b3x d3, где окончания Ь3 е В и d3 е D удовлетворяют условиям Ъ3 cz Ьг А Ь2 и. d3 с dx A d2.
385
13-4953
ТЕОРЕМА 14 (теорема о двойном и повторных пределах по базам В
множеств). Пусть f(x, у) у Рг(у) и f(x> у) -» F2(x)* Тогда существуют оба повторных пределах
lim lim Дх, у) = Zp lim lim Дх, у) = 12
и двойной предел по базе Н = В X Dx
lim Дх, у) = Z3, причем Zx = Z2 = в
► Пусть е > О произвольно. Поскольку Дх, у) у F^y), существует окончание Ь = &(е) g В такое, что при всех х е Ь(е) и при всех у g Y справедливо условие |Дх, у) - Fx(y)| < е/3. Зафиксируем какое-либо х = х0 g &(е). В силу условия Дх0, у) F2(x0) на®“ дется окончание d = d(e) g D, для всех точек уг и у2 которого | Дх0, уг) - f(x0, у2)\ < е/3. Но тогда при тех же уг и у2 справедливо неравенство
1Л(»1)-Л(1/2)1 =
= 1(Л(У1) - Я*0’ У1)) +	У1) - f(xo> У 2>) + У г) ~ Л(»г))1 <
< 1Л(У1) “	Р1)1 +1 Я*о» У1) - f<x0> »г)1 +1 Лх0’ !/г) ~ Л(Уг)1 <
< Е/3 + Е/3 + Е/3 = £.
Согласно критерию Коши отсюда следует, что при некотором
I имеем FAy) Z, т. е. lim lim Дх, у) = I. Теперь покажем, что D В
f(x, у)^1,гдеН = В X D. Поскольку F^y) Z, для любого Е > О найдется окончание d = d(E) g D с условием |Fx(i/) - l\ < е/2 при в
всех у g d(e). Далее, в силу того, что Дх, у) у F^y), найдется окончание Ь(е) с условием |Дх, у) - FXG/)| < £/2 при всех х g &(е) и у g Y. Возьмем теперь в качестве h = Л(е) g Н окончание й(е) = Ь(е) ♦ d(E). Тогда для всех его элементов (х, у) имеем неравенство
|Г(х, у) - Z| < |/(х, у) - Л(у)| + |ГХ(1/) - Z| < е/2 + е/2 = е.
Это значит, что f(x, у) I.
Осталось доказать, что F2(x) -> I. Для этого в неравенстве \f(x, у) - F^-y)! < е/2,
справедливом при всех (х, у) е Л(е) = 6(e) х d(e), при каждом фиксированном х рассмотрим предел по базе D. Получаем
|F2(x)-Z|<e/2<e.
Это и означает, что F2(x) I. •<
386
Т. П. Лукашенко обратил внимание на критерий существования и равенства повторных пределов по совокупности двух баз В и D, доказанный Р. А. Гордоном [32] в 1995 г. Это утверждение обобщает соответствующий критерий А. А. Маркова для повторных рядов.
ТЕОРЕМА 15 (критерий существования повторных пределов по базам множеств). Пусть на множестве X = {х} задана база В9 а на множестве Y = {у} — база D. Рассмотрим функцию f(x9 у)9 определенную на декартовом произведении X X Y и удовлетворяющую следующим условиям:
Дх, у))	g(y), Дх, у) h(x).
Тогда для того чтобы оба повторных предела lim lim Дх, у) — = lim g(y) и lim lim Дх, y) = lim h(x) существовали и были равны между собой, необходимо и достаточно выполнения следующего условия: для любого е > 0 найдется окончание &(е) е В такое, что для каждой его точки х существует свое окончание d = dx(z) е D, для всех точек у которого выполнено неравенство |/(х, у) - g(p)| < е.
► Необходимость. Пусть оба повторных предела существуют и равны I. Тогда справедлива оценка
\Дх, у) - g(p)| = |(Дх, у) - й(х)) + (й(х) - Z) + (Z - Жр))| < <\Дх, у) - й(х)| + |й(х) - Z| + |Z - g(i/)|.
Так как оба повторных предела равны I, то для всякого е > 0 найдутся окончания Ъ е В и d е D такие, что при всех х е Ь и при всех yed имеем |й(х) -1\ < е/3 и \g(y) - Z| < е/3. Кроме того, при фиксированном х е Ь в силу условия Дх, у) h(x) найдется окончание dx е D, для всех точек у которого выполнено неравенство \f(x, у) - й(х)| < е/3. Теперь в качестве искомого окончания Ь(е) возьмем окончание Ь, а в качестве <Zx(e) — некоторый элемент d0 е D, принадлежащий пересечению d и cZx, т. е. dx(E) = d0 с a d П dx. Тогда для всех точек х е й(е) и всех у е </х(е) будут выполнены все три неравенства, откуда имеем |Дх, у) - g(p)| < е. Необходимость доказана.
Достаточность. Возьмем произвольное число е > 0 и рассмотрим окончание &(£) е В из условия теоремы. Проверим выполнение критерия Коши для сходимости g(y) по базе D. Для этого рассмотрим фиксированную вспомогательную точку х е Ь(е) и соответствующее ей окончание dx(E) базы D. В силу сходимости Дх, у) h(x), из критерия Коши следует, что при данном х найдется окончание de D такое, что для всех рх, у2 е d справедливо
387
13*
неравенство \f(x, уг) - /(х, у2)\ < е. Возьмем теперь окончание dQ с: d A dx(e). Для любых точек уг и у2, принадлежащих окончанию dQ е D, величина А =	- g(i/2)l оценивается так:
Л <	- f(x, j/j)! + |/(х, yj - f(x, J/2)| + \f(x, y2) - g(y2)\ < 3e.
Это и означает, что при некотором I имеет место сходимость
z v D , g(y) -»l-
Осталось показать, что h(x) I. Для этого снова возьмем про-извольное число е > 0 и соответствующее ему окончание Ь(е) g В, и для каждой фиксированной точки х 6 Ь(е) оценим величину Aj = |Л(х) - /|. Из условий /(х, у) й(х) и g(y) I следует, что существует окончание de D такое, что для всех у g d выполняется неравенство
|/(Х, у) - Л(х)| < £ И |g(p) - Z| < £.
Возьмем вспомогательную точку у g d A dx(e). Тогда справедлива оценка
Ai = |й(х) - Z| < |й(х) - Дх, у)\ + |/(х, у) - g(y)\ + |g(y) - Z| < Зе.
Другими словами, имеем й(х) I. ◄
Замечание. Если в формулировке теоремы 15 положить dx(s) = Y, то получится условие равномерной сходимости по базе В относительно множества Y. В этом случае утверждение теоремы является следствием теоремы 14. Таким образом, теорема 15 позволяет осуществлять перестановку предельных переходов при более слабых ограничениях. Однако при этом двойной предел в общем случае уже не существует, так что обе теоремы имеют свои сферы применения. Тем не менее, если в условии теоремы 15 считать, что в качестве dx(e) можно взять окончание </(е) одним и тем же вне зависимости от точки х G 5(e), то двойной предел существует и равен повторному.
Отметим также, что утверждение теоремы 15, являясь критерием существования и равенства повторных пределов, симметрично относительно двух рассматриваемых баз, в то время как в ее условие обе базы входят неравноправно. Это дает определенную свободу выбора при ее использовании.
Лекция 12
§8. СТЕПЕННЫЕ РЯДЫ
Напомним, что степенной ряд — это ряд вида ап(х - xQ)n = = А(х), где х0 — фиксированное вещественное число. Основные свойства степенных рядов практически не зависят от х0, и поэтому часто считают, что х0 = 0.
Примерами степенных рядов являются рассмотренные ранее ряды Тейлора. Оказывается, что всякий степенной ряд является рядом Тейлора своей суммы. Рассмотрим вопросы, связанные с определением области сходимости степенного ряда.
Определение 15. Число р называется радиусом сходимости степенного ряда Ъ ап(х - х0)п, если этот ряд сходится при всех х с условием |х - х0| < р и расходится при |х - х0| > р.
Корректность определения обеспечивается следующей теоремой.
ТЕОРЕМА 16 (теорема Коши—Адамара). Пусть задан степенной ряд Ъ fn(x) = Z ап(х - х0)п. Рассмотрим числовую последовательность Ьп = |ал|1/п. Тогда*.
1)	если Ьп является неограниченной последовательностью, то этот ряд расходится при всех х # х0;
2)	если Ьп ограничена ul = liir^ bn и 0, то р = 1/1;
3)	если lim Ьп = 0, то данный ряд сходится при всех хе R.
Напомним, что для всякой ограниченной последовательности существуют верхний и нижний пределы.
►	Для краткости записи будем, считать, что число х0 равно нулю. Для общего члена числового ряда имеем равенство
14(*)1= КИ =	= (&п1*1)л-
В случае 1) общий член /л(х) не стремится к нулю и поэтому ряд расходится. В случае 2) при фиксированном |х| < 1/Z и любом п > п0, применяя признак сходимости Коши в предельной форме к ряду Е|/Л(х)|, имеем
Нт |Л(х)|1/л = х lim Ь < 1/1 = 1.
Это значит, что все х < 1/1 принадлежат области сходимости ряда. Если же |х| > 1/7, то общий член ряда, как и в случае 1), не стремится к нулю и ряд тоже расходится.
В случае 3) снова согласно признаку Коши при всех х имеем lim |/L(x)|1/п =|х| lim b = 0 < 1, т. е. ряд сходится. ◄
389
Замечание. Если |х| = р, то .ряд X /п(х) в доказанной теореме может и сходиться, и расходиться. Примером служит ряд
для которого р = 1 и при х = -1 имеет место сходимость, а при х = 1 — расходимость.
ТЕОРЕМА 17. Пусть р > 0 — радиус сходимости степенного ряда Ъ апхп иг — произвольное число с условием 0 < г < р. Тогда на отрезке [-г, г] этот ряд сходится абсолютно и равномерно, а его сумма А(х) непрерывна на нем.
►	Точка т\ = (р + г)/2 < р принадлежит области сходимости ряда, поэтому при х = т\ его общий член апг% ограничен, т. е. |an|rj < с при некотором с > 0 и всех п. В силу того, что г < rv имеем
X а лгп= X а nkil“ I ^п(”| =	“ •
п = О’ Л’ п = О1 п1 1 Vr17 n = okr17 l-r/rx
Но тогда сходящийся ряд X|an|r" < оо будет мажорантой для X апхп на отрезке [~г, г]. Следовательно, на этом отрезке ряд сходится абсолютно и равномерно.
При тех же условиях сумма А(х) ряда X апхп является непрерывной функцией на отрезке [-г, г], поскольку он сходится там равномерно и его члены непрерывны. 4
ТЕОРЕМА 18. Если р > 0 — радиус сходимости степенного ряда Ъ апхп9 то на любом отрезке [-г, г] с (-р, р) этот ряд можно почленно дифференцировать и интегрировать.
► Формальное почленное дифференцирование степенного ряда £оа„хл дает ряд
х'1 Е, па„хп = х-1 Е Ь„хп, п = 1 п	П = 1 П
а интегрирование его приводит к ряду
~	~ апхп
х Х_ спхп = х Хп---------
п = О п	п = 0 П + 1
Для величин |ЬЛ|1/П и |сп|1/п в теореме Коши—Адамара имеем равенства
= ni/n|aJi/*, |cji/n = (n +
Но так как (и + l)"1/n -> 1 при п —» оо, то по этой теореме радиусы сходимости всех трех рядов равны и ряды сходятся равномерно на любом отрезке вида [-г, г], г < р. Но тогда их можно по
390
членно дифференцировать и интегрировать на этом интервале сходимости. ◄
ТЕОРЕМА 19 (теорема Абеля). Пусть ряд Ъап хп сходится в точке х = с > 0. Тогда его сумма А(х) непрерывна на отрезке I = [0, с]. Если же число с < 0, то функция А(х) непрерывна на отрезке [с, 0].
► Рассмотрим сначала случай с > 0. Представим общий член апхп этого ряда в виде апхп = ап(х)Рп(х), где ап(х) = апсп и Рп(х) = хп/сп. Тогда к этому ряду на отрезке 1 = [0, с] можно применить признак равномерной сходимости Абеля, так как:
1) ряд Хапсп не зависит от х и поэтому сходится равномерно на отрезке Z;
2) последовательность Рп(х) == хп1сп монотонна и равномерно ограничена наI, так как |xn/cn| < 1 при всех xg L
Но тогда сумма А(х) этого ряда непрерывна на I. Случай с < 0 сводится к рассмотренному заменой у = -х. ◄
ТЕОРЕМА 20 (выражение коэффициентов степенного ряда через значения производных его суммы в точке разложения). Пусть степенной
ряд Ъ ап(х - х0)п = А(х) имеет положительный радиус сходимости р. Тогда а0 = А (х0) и при всех п > 1 имеем равенства ап = А<л> (х0)/п!.
►	По теореме 18 равенство А(х) = пЕ0 ап (х - х0)в можно почлен-но дифференцировать. Поэтому при х = х0 имеем
А(х0) = nS0 а„(х0 - х0)в - а0,
А'(х0) - nE t ап • га(х0 - Хо)""1 = ах • 11,
А" <хо) = „5 2 ап * **(» " 1) (*о ~ хо)в”2 = а2 * 21,
А<*> (х0) = а„ • п(п - 1) •... • (п - k + 1) (х0 - х0)в~* = ак • й!.
Отсюда и следует требуемое утверждение. ◄
Таким образом, степенной ряд Z an(xQ - xQ)n с ненулевым радиусом сходимости всегда является разложением в точке х = х0 в ряд Тейлора своей суммы А(х). Представляет интерес вопрос, как связаны между собой радиусы сходимости двух тейлоровских разложений функции А(х), взятые в различных точках х0 и хг. Здесь имеет место, например, следующая теорема.
391
ТЕОРЕМА 21. Пусть RQ > 0 — радиус сходимости степенного ряда Z ап(х - х0)п. Рассмотрим другое разложение функции А(х) в ряд Тейлора в точке хр где |х0 - хх| = г < RQ. Тогда, если &0, Ьх, ... — его коэффициенты, a Rr — радиус сходимости, то Ri>R0~ru
А(х) = nS0 bh(x - xj*, если |х - хх| < Rv
►	Для простоты будем считать, что х0 = 0, и положим х - хх = у. Тогда х - х0 = х = у + xv |хх| = |хх - х0| = г. Если |у| < Ro - г, то
|</| + |хх| < Ro - г + г = Ro. Поэтому ряд „SJaJ (|у| + |хх|)в сходит-°° п ( п Л
ся абсолютно. Но тогда повторный ряд Z a Z . 1/*х£“*тоже абсолютно сходится и его члены можно переставить произвольным образом. В силу этого имеем
00 п ( пУ	00	00	( пУ	00
А(х) = Z	a Z , lukXi ~k =	Z	uk Z	a , x?“fe=	Z	ukbb,
00	( П \	-I / 00	\
W bk = k )x"~k = ^{nlkn(n-l)-...-(n-k+l)an xf*}
Тем самым мы установили, что разложение ^Lj)kyk функции А(х) в ряд Тейлора в точке хх с условием |хх - х0| = г < RQ сходится абсолютно к сумме А(х) при всех |i/| < RQ - г. ◄
Определение 16. Функция А(х) называется аналитической в точке х = х0, если в некоторой окрестности этой точки она может быть представлена степенным рядом, т. е. ее рядом Тейлора.
Теорема 21 показывает, что в каждой точке внутри области сходимости степенного ряда его сумма А(х) является аналитической функцией. Заметим еще, что внутренность области сходимости всегда является интервалом, возможно, бесконечного радиуса, так что говорят об интервале сходимости степенного ряда.
Возможно, что при разложении суммы А(х) степенного ряда Z ал(х - х0)л в какой-либо точке хг и х0 из его области сходимости новый степенной ряд Z Ьх(х - хх)л = А(х) будет иметь свой интервал сходимости, выходящий за пределы прежнего интервала. Рассмотрим, например, разложение вида
А(х) = —= 1 - X + х2 - ...  ----------5------------ -
1+х	2+(х-1)	2 1+(х-1)/2
= 1 - х~ 1 + (х~1)2 -
2	2-2	2-22
Здесь разложение по степеням х имеет радиус сходимости RQ = 1, а по степеням (х - 1) — радиус Вх = 2.
392
Определение 17. Метод распространения области определения аналитической функции путем ее разложения в степенной ряд в точке, не совпадающей с центром первоначальной области определения, называется принципом аналитического продолжения функции.
Особую ценность этот принцип приобретает при рассмотрении степенных рядов от комплексного аргумента. Дело в том, что формальная подстановка комплексного числа г = а + Ы вместо вещественного х в степенной ряд X ап(х - х0)п позволяет естественным образом распространить область определения функции А(х) на точки комплексной плоскости. Для этого достаточно ввести понятие сходимости ряда, составленного из комплексных чисел. Самый простой способ сделать это состоит в том, чтобы считать ряд Е (an + ibn) сходящимся к комплексному числу А + Bi, если одновременно Е ап сходится к А и Е Ьп сходится к В. Можно очень просто показать, что для сходимости рядов с комплексными членами верен мажорантный признак Вейерштрасса. Но тогда если, например, ряд Е апхп сходится при некотором х = х0 * О, то при всех г с условием г < |х0| ряд Е|ап| • г71 тоже сходится. А ес-ли г = а + Ы и |z| = г, то сходится и ряд Е anzn. Это значит, что область сходимости ряда Е anzn содержит на комплексной плоскости С круг радиуса R = |х0| с центром в нуле. Используя принцип аналитического продолжения, можно определить значения аналитической функции и в других точках комплексной плоскости. Важно, что указанная процедура, по существу, дает в некотором смысле однозначное продолжение. Такой способ позволяет однозначно продолжить на комплексную плоскость все элементарные функции. Например, оказывается, что при вещественных а и b имеем
еа + ib = еа (cos b + i sin b).
Аналитические функции на комплексной плоскости играют очень важную роль в математике. Связанные с ними проблемы составляют содержание ее обширной области — теории функций комплексного переменного, знакомство с которой входит в отдельный курс.
ЗАДАЧА. Пусть Дх) — бесконечно дифференцируемая на интервале (а, Ь) функция. Обозначим через kn число решений уравнения (х) = 0. Пусть kn < С при некотором С и всех п е N. Доказать, что функция f(x) является аналитической на интервале (а, Ь).
393
Лекция 13
§ 9. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
Определение 18. Рассмотрим числовую последовательность положительных чисел {Ьл}. Формальное бесконечное произведение всех ее членов
••• •••
называется бесконечным числовым произведением, или бесконечным произведением, или просто произведением.
Бесконечное произведение обозначается так:
bvb2...= П h = П&_.
Определение 19. Конечное произведение Пп вида Пп = Ъг ... Ъп называется п-м частичным произведением.
Определение 20. Если последовательность Пп сходится к числу П # 0 (т. е. П > 0), то бесконечное произведение называется сходящимся (к числу П). Если П = 0, то это бесконечное произведение называется расходящимся к нулю, а если П +оо, то оно называется расходящимся к бесконечности. Если пре? дела нет вообще, то оно называется просто расходящимся.
УТВЕРЖДЕНИЕ 5 (необходимый признак сходимости бесконечного произведения). Если П&л сходится, то Ьп 1 при п -» оо.
► Если Пп -> П 5* 0, то
п ПП	П 1
Ьп = п— -» й = 1 при и -> оо. «
УТВЕРЖДЕНИЕ 6. Сходимость бесконечного произведения ПЬЛ влечет за собой сходимость ряда In Ьп, и наоборот, причем
In П 6 = Е In Ъп.
► Имеем In Пл = In bk. Функция у = In х устанавливает непрерывное взаимно однозначное соответствие между лучом (0, +°о) и всей вещественной осью R = (-оо,+оо). Поэтому в силу положительности Ъп для всех п g N возможен переход к пределу в одной части равенства при сходимости другой его части, и при этом In П = kL1 In bk. Расходимость к нулю левой части равенства эквивалентна расходимости к -оо правой его части. ◄
394
Замечание. Очевидно, что отбрасывание или добавление любого конечного числа ненулевых сомножителей не влияет на сходимость бесконечного произведения. Поэтому можно считать, что конечное число членов этого произведения могут быть и отрицательными.
Определение 21. Бесконечное произведение называется абсолютно сходящимся, если абсолютно сходится ряд Ъ In bk. Это означает сходимость ряда Е|1п Ьп|. Сходящееся бесконечное произведение ПП1&П, не являющееся абсолютно сходящимся, называется условно сходящимся.
Из предыдущего утверждения и теоремы о сходимости абсолютно сходящегося ряда непосредственно вытекает следующая теорема.
ТЕОРЕМА 22. Абсолютно сходящееся произведение всегда сходится в обычном смысле.
Поскольку мы считаем, что Ъп > 0 при всех п, числа Ъп обычно представляют в виде Ъп = 1 + ап, где ап> -Л. Тогда имеем
П^- П (1+а„).
ТЕОРЕМА 23 (критерий абсолютной сходимости бесконечного произведения). Бесконечное произведение П (1 + ал) абсолютно сходится тогда и только тогда, когда сходится ряд Е |ал|.
► Так как 1 + ал —> 1 при п —> °о, то ал —>0. Однако
1п(1+х)	-	Л
—1 при х —> 0, поэтому при п -» оо имеем
1п(1+а„)	|1п(1+а„)|
Следовательно, при достаточно большом п > nQ выполняются неравенства
1	|1п(1 +а„)|	3
2	|а„|	2 *
Если, например, сходится ряд Е |ln (1 + ап)|, то он будет мажорантой для ряда Е |а„|/2, а если сходится ряд Е |ал|, то он является мажорантой для ряда Е 2|ln (1 + ап)|/3. Но это означает, что ряды Е |а„| и Е [In (1 + ап)| сходятся и расходятся одновременно. ◄ Следствием этой теоремы является следующее утверждение.
395
УТВЕРЖДЕНИЕ 7. Если при достаточно большом п > п0 все числа ап имеют один и тот же знак, то сходимость произведения П(1 + ап) эквивалентна сходимости ряда ^ап.
► Поскольку и сходимость ряда, и сходимость произведения влечет за собой соотношения
1п(1 + а_)
ап —> 0, In (1 + ап)	0,------- 1 при п оо,
ап
отсюда следует, что при достаточно большом п > nQ величина In (1 + ап) сохраняет знак вместе с ап. Это означает, что сходимость рядов Е ап, Е In (1 + ап) и произведения П(1 + ап) эквивалентна их абсолютной сходимости. Теперь, применяя теорему 23, получаем требуемое утверждение. ◄
Рассмотрим некоторые примеры бесконечных произведений.
ПРИМЕР 1. Гамма-функция Эйлера Г(з). По определению имеем
Пв)-А; П, (1 + -
sei8 п - 1 nJ
где « # 0, -1, -2, ... — любое вещественное число (или даже комплексное число, если определение 20 распространить на комплексные числа), у — постоянная Эйлера,
у = lim f 1 + | + ... + - - In nl = 0,577... . n -> oo	£	n	J
Бесконечное произведение, через которое определяется гамма-функция Эйлера, сходится абсолютно при любом з # 0, -1, -2, ..., так как при достаточно большом п > nQ в силу формулы Тейлора с остаточным членом в форме Лагранжа справедлива оценка
|In &л| = |In ((1 + s/n)‘‘1es/n)| = |s/n - In (1 + s/n)| < s2/n2,
и сходящийся ряд Е з2/п2 является мажорантой для ряда Е |1п Ьп\.
УТВЕРЖДЕНИЕ 8 (формула Эйлера). Имеет место следующая формула:
Г(з) = з1 пПх (1 4- l/n)s(l + s/n)"1.
► Уже доказано, что бесконечное произведение в определении гамма-функции сходится абсолютно в любой точке своей области определения. Поэтому из определения гамма-функции имеем
396
Г(«) = S’1 lim e-«d + V2 + ... + 1/m-ln m) iim П fl + i'l ^s/» =
= s-1 lim ma П(14-s/n)-1 = s-1 lim П (1 4-1/n)» П (14-s/n)-1 =
= s-1 lim (ft (1 + l/n)8(l + e/n)-‘)(l + 1/m)-» = m —> oo \n — 1	7
= S"1 eftx (1 + l/n)»(l + s/n)-1. ◄
УТВЕРЖДЕНИЕ 9 (функциональное уравнение для гамма-функции Эйле-
ра Г(з)). Справедлива следующая формула’.
Г(з + 1) = зГ(з), Г(1) - 1.
► По формуле Эйлера имеем, что Г(1) = 1, а также
Г(з 4- 1) = 8	(1 4- 1/п)»4-1	1 4-з/П	=
Г(з) S41"=1 (14-1/п)* 14-(з4-1)/п
00	I Ч	I
_	8	Я 4- s _
S 4- 1 п = 1 п П 4-3 4- 1
= $ lim ft 2*3 ... Qn 4-1) (1 4-з)... (т 4-з) =
3 4-1 т-*°о»=1	1.2... т (2 4- з)... {т 4-1 4- з)
= lim (s 4-1) m + 1	= s.
s 4-1	m 4-1 4- s
Отсюда следует, что Г(з 4-1) = зГ(з). ◄
Из утверждения 9 непосредственно получаем такое следствие.
СЛЕДСТВИЕ. Для натуральных чисел п имеем Г(п 4-1) == п!
Далее будет доказано, что при s > 0 имеет место формула интегрального представления для Г(з) вида
Г(з) = f x8~1e~xdx. о
ПРИМЕР 2. При всех вещественных х следующее бесконечное произведение сходится:
П (1-4^ ^)=
Это равенство будет доказано ниже, а сходимость вытекает из утверждения 3.
ПРИМЕР 3. Бесконечное произведение для дзета-функции Рима-
на. При s > 1 функция £(з) определена сходящимся рядом £(з) =
00 1
= х — . Пусть Pi = 2,р2 = З,р3 = 5, ..
— последовательно зану-
мерованные простые числа натурального ряда.
397
УТВЕРЖДЕНИЕ 10 (формула Эйлера бесконечного произведения дзета-функции Римана ^(s))- При s > 1 имеет место следующая формула1.
оо 1	°°	/	1 X 1
«•>- Л, ?-,0,(1-^)-.
► Имеем
ПЛ= nfi-±V= ft (1 + ±+ х А т = 11	Р8 J	m = 1 I	п8	I
4	яг т '	4	г т	'
Раскрывая скобки, согласно неравенству pk > k, справедливому при всех ke N, получаем fe 1
00 1
С другой стороны, очевидно, что IL = Е . —, где ат — неко-ж m = 1 д® т
торая подпоследовательность натуральных чисел, которая не содержит повторений в силу однозначности разложения натурального числа на простые сомножители. Отсюда имеем неравенства
ОО 1	со 1	k 1
$(s)= Е, - > Е, 4 =nfc> 2,-4
Переходя здесь к пределу при fe —» оо, получаем требуемый результат. ◄
При s = 1 справедлива оценка
= II (1 + — Ч-----т + ... 1 > 1 + + ... + г ,
k m==1V Рт Pl )	2 k
поэтому произведение П 11-----Г расходится к +оо, а вместе
« “ Pk J
оо
с ним расходятся ряды In
(л 1 v 1
11-----I и X, —-.
\ Pk )	~ 1 Pk
Лекция 14
$ 10. БЕСКОНЕЧНЫЕ ОПРЕДЕЛИТЕЛИ
Понятие определителя бесконечного порядка возникает в связи с изучением систем из бесконечного числа линейных уравнений от бесконечного количества неизвестных. Потребность в рассмотрении таких систем уравнений и таких определителей впервые возникла при исследовании задачи об определении движения перигелия лунной орбиты, которое провел Г. Хилл. В 1886 г. А. Пуанкаре дал строгое математическое обоснование метода Хилла. Еще одно приложение метода бесконечных определителей приведено в работах Е. Фредгольма (1903) при исследовании линейных интегральных уравнений.
Пусть Ътп — двойная последовательность вещественных чисел. Обозначим через Dm = ||Вт\\ определитель квадратной матрицы Вт = где индексы k и I пробегают значения от 1 до т. В этой матрице число bkl находится на пересечении строки с номером k и столбца с номером Z. Главную диагональ этой матрицы образуют числа bkk, где k = 1, ... , т. Обозначим через В бесконечную матрицу ||Ьдад||, где т, п = 1, 2, 3, ... .
Определение 22. Если последовательность определителей Dm сходится к числу D при т °°, то будем говорить, что бесконечный определитель D = ||В|| матрицы В сходится к числу D или что он равен D. Если последовательность Dm расходится, то этот определитель будем называть расходящимся.
Определители Dm будем называть частичными определителями бесконечного определителя D. Введем новые обозначения. Для диагональных элементов матрицы В положим bnn = 1 + апп. Если же т # п, то будем считать, что атп = bmn.
Определение 23. Мажорантой Пуанкаре бесконечного определителя D назовем бесконечное произведение Р вида
ОО ✓	ОО	X
? ~ JJ1 (1 + n? Ja/nn)
при условии, что все ряды n?1|amn| сходятся и само произведение Р тоже сходится.
Определение 24. Конечное произведение Рт вида
т z /п \ ?т =	+	\akl\ J
называется мажорантой Пуанкаре определителя Dm.
399
ТЕОРЕМА 24 (лемма Пуанкаре). При всех т е N справедливы следующие оценки:
V\om\<Pm;
2)	l^m+1 “ ^т\ ?т+1 ~
► 1. Определитель Dm состоит из т\ слагаемых вида
(-1)С(СТ)ЬП1 • ... -ът, . Здесь с(а) — функция четности подстановки *1	*тп
о = (Zp Zm), с(о) = 0 для четной и с(о) = 1 для нечетной подстановки о. Следовательно,
тп z тп х тп z т х
|лт| < ч1 <
Утверждение 1) доказано.
2. Разложим определитель по элементам последней строки. Получим
^т+1	ат+1, 1Ап+1,1 + ••• + ат+1, т^т+1, т +	+ ат+1, m+l^m*
Здесь Am+lj k — алгебраические дополнения в матрице Вт+1 к элементам ат+1 k ее последней строки
^m+1,z = (-l)m+1+z	1+Оц ...			ai,z+i	а1, т+1
	®m, 1	...	^т, 1-1	ат. Z+1	^т, т+1
Как и выше (при доказательстве п. 1), имеем
тп (т + 1 А т z т + 1 х lAn+l, zl** п?1|Ь*>л|	*51(1 + „?11Ч nlj ~^т'
Заметим, что Qm > Рт > 0 и Pw+1 = Qm(l + |am> j). Поэтому 1Лп+1 “ Dm\ < l^m+l, 11 * l^-zn+l, 11 + ... + I am+l, ml * l^m+l, ml + + I ®m+l, m+1 I * l^ml Qm (l^m+1, 11 + ••• I ^m+1, ml I ^m+1, m+11) = ^m+1 ~ ®m ^m+1 ~
ТЕОРЕМА 25 (теорема Пуанкаре). Бесконечный определитель сходится, если абсолютно сходятся бесконечное произведение его диагональных элементов и двойной ряд, составленный из его недиагональных элементов.
► Так как bm т = 1 + am т, то абсолютная сходимость тПхЬт т произведения диагональных элементов эквивалентна сходимости ряда x|am m|. Кроме этого, по условию, сходится и двойной ряд л|ат J. Но тогда сходится и бесконечное произведение Р, где
ОО X	ОО	х
Р= 11,11+ Е,|а „| ,
тп = 1\ п = I1 т» П1 у
400
так как его сходимость обеспечена сходимостью повторного ряда JE nE1|am J. Представим значение определителя D матрицы В в виде суммы ряда
D — Dx + (Z>2 «Di) + (O3 D2) + ... — dj + d2 + d2 + ... — n^i dn.
Согласно теореме 24, при всех пе N справедлива оценка KJ = 1Вп+1 “ »п\ ?п + 1 ~ РП=Рп+1>
где Рп — мажоранты Пуанкаре определителя Dn и Рп < Р. Отсюда следует, что сходящийся ряд „Е рп+1 = Р- Рг является мажорантой для ряда dn+1, и поэтому сходится последний ряд, а также и последовательность его частичных сумм Dn. Но это и означает сходимость бесконечного определителя D. ◄
Замечание. Аналогичная теорема имеет место и для бесконечного определителя D матрицы В вида В = (Ьт п), где -оо < т, п < +оо. Здесь частичные определители Dm и матрицы Вт имеют вид
Dm = HBmll. Вт = (bk, Z>» ~т <	1 < т‘
ЗАДАЧА. Доказать теорему Коха о том, что необходимым и достаточным условием абсолютной сходимости определителя D вида
п= lim /П -> ОО	1 Р1	«1 1	...	0 0	0 0
	0	0	...	1	am
	0	0	...	Pm	1
является абсолютная сходимость ряда Ъ ап рл. При этом абсолютная сходимость определителя D означает сходимость ря-да
В заключение дадим еще одно определение, обобщающее понятие мажоранты Пуанкаре.
Определение 25. Пусть Ап(х) — функциональная последовательность, а Вп — числовая последовательность, причем Вп В при п -» оо. Пусть также при всех п е N для каждого хе D справедливо неравенство |Ал+1 (х) - Ал(х)| < Вл+1 - Вп. Тогда числовая последовательность Вп называется мажорантой для последовательности функций Ап(х) на множестве D.
Очевидно, что последовательность Ал(х), имеющая на множестве D мажоранту Вп, равномерно сходится на этом множестве.
401
§11. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ И ТЕОРЕМА АРЦЕЛА
Докажем теорему Арцела, важную главным образом для приложений за пределами основного курса математического анализа.
Определение 26. Множество функций М называется равностепенно непрерывным на отрезке I = [а, &], если для всякого е > 0 найдется число 8 = 8(e) > 0 такое, что для любой функции f(x) g М и любых хги ХоС условием lar-L - х2| < 8 справедливо неравенство |/(х2) - f(x2)] < е.
ТЕОРЕМА 26 (теорема Арцела). Если бесконечное множество функций М равномерно ограничено на отрезке I и равностепенно непрерывно на нем, то из всякой последовательности функций fn(x) е М можно выбрать подпоследовательность fn (х), равномерно сходящуюся на I к некоторой непрерывной на I функции /0(х), не обязательно принадлежащей М.
► Будем для простоты считать, что I = [0, 1]. Идея доказательства состоит в замене с допустимой ошибкой произвольной точки х при использовании критерия Коши на близкую к ней двоично-рациональную точку с возможно меньшим знаменателем.
Занумеруем множество {хп} всех двоично-рациональных чисел a/2k этого отрезка в порядке возрастания показателя степени k при его различных значениях и в порядке возрастания числителя дроби а при равных значениях знаменателя дроби 2k. Таким образом, имеем хх = 0, х2 = 1, х3 = 1/2, х4 = 1/4, х5 = 3/4,..., х2*+1= (2k-l)/2k, x2k+2== l/2fc+1, ... . Рассмотрим теперь множество чисел Вг = {fk(Xy)}, где fn(x) — исходная последовательность функций, /п(х) е М. Множество Вг ограничено в силу условий, наложенных на М, и по теореме Больцано—Вейерштрасса из последовательности Вг можно выбрать сходящуюся подпоследовательность fn (хх).
Рассмотрим последовательность номеров пр ... , пт, ... получившейся последовательности и образуем первую вспомогательную подпоследовательность функций Gr = {glt m(x)}, полагая ^i, m(x) = fn (*)• Тогда имеем, что последовательность gx m(Xi) = = fn (хх) сходится к некоторому значению уг.
Далее образуем по тому же правилу подпоследовательность функций G2 = {g2 j(x), ... , g2 m (x), ...}, используя в предыдущих рассуждениях последовательность gx т (х) вместо /п(х) и точку х2 вместо хР В результате получаем, что g2im(x) — подпоследовательность для {#1>zn(x)} и g2,m(x^) у2 при тп -» оо. Многократно повторяя этот процесс, получаем подпоследовательности G3 = = {^з, m(x)}’ G4 =	и т- Д-’ причем тогда gk<m{xk) -> yk при
402
т -> оо и последовательность gk m(x) будет подпоследовательностью относительно gk_lf т(х) при всех k > 2.
Рассмотрим теперь «диагональную» последовательность функций {Лл(х)}, где Лп(х) = gn п(х). По построению, начиная с номера п = k9 все функции Лл(х) при п > k образуют подпоследовательность последовательности Gfe, поскольку
М«) = 9п,пМ е Gncz G„_x с ... с Gk.
Отсюда следует, что при любом k и п > k числовая последовательность hn(xk) является подпоследовательностью для gn(xk), и поэтому hn(xk) —>yk при п -»оо.
Покажем, наконец, что последовательность функций йп(х) удовлетворяет критерию Коши равномерной сходимости. Рассмотрим произвольное число е > 0 и покажём, что существует номер п0 = п0(е) такой, что при всех т и п > nQ одновременно для всех хе I выполнено неравенство |/т(х) - /л(х)| < е. Для этого, используя равностепенную непрерывность множества функций М9 найдем число 8 = 8(е/3) такое, что при всех хг и х2 е I с условием |х2 - xj < 8 и для любой функции f(x}e М имеем |/(х2) - /(*1)1 < £/3* Выберем число k из условия 8/2 < 2“* < 8 и перенумеруем все двоично-рациональные точки х19 ... , х2*+1 со знаменателями, не превосходящими 2*, в порядке возрастания их величин. Если zl9... , г2*+1 — их новая нумерация, то z8+1 - z8 = 2~k < 8 при всех а = 1, ..., 2*+1. По построению любая из числовых последовательностей {h(z8)} сходится, и поэтому для нее найдется номер п такой, что при всех п и т > п8 тлеем
|Лж(х.) -	< е/3.
Теперь в качестве п0(е) выберем номер тг0(е) = max п8 и показе 2Л »1
жем, что он удовлетворяет требуемым условиям. Действительно, пусть х е [0, 1] и zt — ближайшее к нему число из множества z19 ... , z2k + 1. Ясно, что |х - zt\ < 2~k < 8, откуда вытекает, что |йЛ(х) - hk(zt)l < е/3 при всех k е N.
Окончательно при всех т и п > n0(e) > nt имеем
|Лт(х) - Л„(х)| < |Лт(х) - hm(zt)\ +1 hm(zt) - ha(zt)\ + + |	- л„(х)| < Е/3 + Е/3 + Е/3 = £.
Это значит, что по критерию Коши последовательность йл(х) сходится равномерно на I. ◄
Замечание. Утверждение теоремы 1 можно рассматривать как достаточное условие компактности некоторого множества в пространстве С[0, 1] всех функций, непрерывных на отрезке I = [0, 1]. Можно показать, что это условие является и необходимым для замкнутого множества функций.
403
ГЛАВА 17
Интегралы, зависящие от параметра
Лекция 15
§ 1. СОБСТВЕННЫЕ ПАРАМЕТРИЧЕСКИЕ ИНТЕГРАЛЫ И ИХ НЕПРЕРЫВНОСТЬ
Изучение интегралов, зависящих от параметра, или параметрических интегралов, составляет большую тему, охватывающую элементарную теорию собственных и несобственных интегралов. Сначала рассмотрим собственные интегралы от функций, зависящих от одного числового параметра.
Пусть функция /(х, у) задана на прямоугольнике П = X /2, где Ij и 12 — отрезки вида = [а, &], I2 = [с, d]. Другими словами, П есть множество точек {(х, у)} координатной плоскости хОу, удовлетворяющее условиям а<х<&, c<i/<d.
Будем считать, что при любом фиксированном у е 12 функция g(x) = gy(x) = f(x, у) интегрируема по Риману на [а, Ь].
ь
Определение 1. Интеграл J /(х, y)dx = <p(i/) называется unmeet
гралом, зависящим от параметра у. Отрезок I2 = [с, d] в этом случае будем называть множеством значений параметра у.
Разумеется, вместо 12 в качестве множества значений параметра у может выступать любое подмножество М вещественной оси Оу, и в этом случае будем сохранять введенную выше терминологию. Помимо отрезка 12, чаще всего в качестве такого множества мы будем рассматривать интервалы, открытые и замкнутые лучи, проколотые окрестности точек или саму вещественную прямую R.
ТЕОРЕМА 1. Если f(x, у) непрерывна на прямоугольнике П = /j х Z2, где и 12 — отрезки, 1г = [а, Ь], 12 = [с, d], то функция
ъ ф(у) = J f(x, y)dx а
непрерывна на отрезке 12.
404
► Поскольку прямоугольник П является компактом, функция /(х, У)9 непрерывная на нем, является равномерно непрерывной на П. Следовательно, при любом 8 > 0 и (х2, у2) £ П с условием (хг - х2)2 4- (уг ~ у2)2 < 82 справедливо неравенство
Ух) - f(x2, j/2)l <е-
Зафиксируем произвольно некоторую точку у0 на 12. Тогда для любого у из ее проколотой 8-окрестности на оси Оу и любого х е = [а, Ь] для разности r(x) = r(x, у91/0) = f(x, у) - f(x, yQ) имеем оценку
Н*)1 = I/U, У) - f(x> Уо)1 < е>
поскольку расстояние р(А, В) между точками А = (х, у) и В = (х, i/0), равное \у - у0|, не превышает 8. Интегрируя г(х) по отрезку I, по-
лучаем
ь
ь
|ф(у) - <P(J/o)I “ I r(x)dx < J|r(x)|dx < г(& - а).
В силу произвольности выбора 8 > 0 отсюда следует, что ф(г/) -> -> <р(г/0) при у -» yQ, т. е. функция ф(г/) непрерывна в точке у = yQ,
и так как точка yQ выбрана произвольно, то <р(у) непрерывна на 12. ◄
Доказанная теорема допускает следующее простое обобщение.
ТЕОРЕМА 2. Пусть функции фх(1/) и ф2(г/) непрерывны на отрезке I2 = [с, d] и удовлетворяют неравенствам а < Фх(1/) < ф2(*/) Тогда в условиях теоремы 1 функция h(y), где
ф2(у)
h(y) = J f(x, y)dx,
Ф1(у) тоже непрерывна на 12.
Прежде чем доказывать эту теорему, заметим, что функцию h(y) тоже можно рассматривать как параметрический интеграл, поскольку	ъ
h(y)= f М*» y)dx> а
где /\(х, у) = Дх, у) при фх(1/) < х < ф2(г/) и /\(х, у) = 0 в противном случае.
► Снова рассмотрим произвольную точку у0 отрезка 12. Для приращения Aft(i/0) = h(y) - h(yQ) функции h(y) в этой точке имеем соотношения
Ф2(!/)	Ф2(!/о)
Л*(Уо) = J f(x> y)dx ~ J Л*» У№х = Ф1(р)	Ф1(Ро)
Ф2(У)	f Ф2(!/)	Ф2(!/о)	А
= f (f(x, у) - f(x, y0))dx + f f(x, y0)dx - J f(xt y0)dx =
Ф1(1/)	\Ф1(!/)	Ф1(!/о)	j
= My) + r2(i/).
405
Оценим величины т\(у) и г2(у) в предположении, что \у - yQ\ < 8(e), где 8(e) > 0 и е > 0 имеют тот же смысл, что и в теореме 1. Имеем
Ф2(</)
ki(F)l < J |ЯХ. У) ~ f(x, y0)\dx < е|ф2(у) - фх(у)| < e(& - a).
Ф1(у)
Далее, если M = sup |/(x, y)\, то для величины r2(y) получим оценки
Ф1(!/о)	Ф2(!/)
k20/)l < J Лх» y^dx + J Ях» Уо)^х < м
Ф1(0	Ф2(Ро)
Ф1(р)
J dx =
Ф2(Уо)
= М |Афх(у0)| + МI Аф2(у0)|.
Поскольку функции (p1(i/) и ф2(г/) непрерывны на 12, при достаточно малом |Аг/0| = \у ~ i/ol < $i(e) выполнены неравенства IАф1(у0)| < Е И IАф2(у0)| < Е. Положим
80(е) = min (5х(е), 82(е)).
Тогда при всех у с условием |у - г/0| < 80(е) имеем
|А/г(г/0)| < I гх(г/)| + | г2{у)\ < е(Ь - а) + 2еМ = е(& - а + 2М).
Но так как е > 0 произвольно, то отсюда, следует, что функция h(y) непрерывна в точке у = yQ е 12, а также и на всем отрезке 12. ◄
Следует заметить, что приведенное выше доказательство теоремы 1 фактически состоит из вывода следующих двух утверждений.
УТВЕРЖДЕНИЕ 1. Если функция f(x, у) непрерывна на П = X /2, где и 12 — отрезки вида = [а, Ь] и I2 = [с, d], и если функция g(x) = gy(x) = Дх, у), то при любом yQ е 12 имеем
gy(x) gyo(x) = f(x, y0) при у -> y0.
УТВЕРЖДЕНИЕ 2. Пусть для некоторого yQ е [с, d] при у yQ имеет место равномерная сходимость f(x, у) Дх, yQ). Кроме того, в некоторой окрестности точки yQ существует пара-ь
метрический интеграл вида J Дх, y)dx. Тогда при у у$ су-а
ществует предел ъ	ь
lim J f(x, y)dx = J f(x, y0)dx. У * Уо a	a
406
§ 2. ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ СОБСТВЕННЫХ,(1АРАМЕТРИЧЕСКИХ ИНТЕГРАЛОВ
ТЕОРЕМА 3 (правило Лейбница). Пусть функция /(х, у) непрерывна на П = х 12, где 11и12 — отрезки, = [а, b], I2 = [с, d]. Пусть частная производная fy(x, у) существует и непрерывна на П. Тогда функция g(y), где
ъ g(y) = J К*, y)dx, а
является дифференцируемой на 12, причем ъ
§'(У) = J y}dx.
а
►	Зафиксируем произвольно точку у е /2* При любом h и 0 с условием у + h е 12 можем записать равенство
g(y + h)-g(y) = г f(x,y + h)-f(x,y) dx h	[	h
Подынтегральная функция в правой части этого равенства непрерывна по х, и поэтому она интегрируема по Риману. Применяя к ней формулу конечных приращений Лагранжа, получаем
g(y + /o-g(y) = J ^(х> у + eA)dx> о < е < 1.
В силу непрерывности f'y(x, у) на П и на основании утверждения 1 § 1 имеем
f'y(x, y + eh)^ f'y(x, у) при h -> 0.
Наконец, используя утверждение 2 § 1, приходим к равенству lim g(y +	= g'(y) = J f'(Xt	◄
ТЕОРЕМА 4 (обобщенное правило Лейбница). В условиях теоремы 1 будем считать, что а(у) и Р(у) дифференцируемы на 12 и а < а(у), 3(1/) < Ь. Тогда имеет место формула
(М»)	у М»)
g'y = J f(x, y)dx L = J f'(x, y)dx + 7X3(1/), y) 3'(1/) - y) a'(y).
►	Пусть, как и выше, h # 0 и точки у, у + h е 12. Рассмотрим выражение d(h), где
d(h) =	= 1 ff+Л)Дх> у + ft)Lx _ f /(х> y)dxy
П	n{aXy+h)	J afc/)
407
Используя стандартные обозначения Да = а(г/ + й) - a(i/), ДР = p(i/ + h) - Р(у), Д/ = Дх, у + й) - Дх, у), его можно записать в виде
0
d(ft) = hr1 J (f(x, у + й) - f(x, y))dx + a a	p + Ap
+ h~l J f(x, у + h)dx + й-1 J fix, у + h)dx = Ax + A2 + A3.
a + Aa	p
Дословно повторяя рассуждения теоремы 3, для интеграла Аг при h -> 0 имеем
0
А -> J f (x, y)dx.
a
Далее, применяя теорему о среднем для интегралов А2 и А3 и используя непрерывность функции Дх, у), получаем
А2 = ~ fta + 01Да, у + й), А3 = flp + 02Д0, у + Л).
Отсюда при й —»О имеем
А2 -» -a'(y)/(a(y), у), А3 -> 0'(У)/(Р(!/). !/)• *
Пояснение к доказательству теоремы 3. Проведем более подробно обоснование возможности предельного перехода
ъ	ъ
lim J fy(x, у + Bh)dx = J f'y(x, y)dx, опираясь на условие равномерной сходимости
/у(х, у + 0й) 4 f'y(x, у) при й -»О, где = [а, й].
Как известно, интеграл по отрезку от функции F(x, й) = = У + 9Л) есть предел интегральных сумм
a(T) = oF(T) =	й)ДхЛ.
Здесь предел берется по базе Дг -> 0, определенной на основном множестве А, образованном всеми размеченными разбиениями {Т} отрезка Ir = [а, й]. При этом точки а = х0 < х2 < ... < хп = й образуют разбиение, а точки £х, £2, ... , лежат соответственно на отрезках [х0, xj, ... , [xn_j, хп] и образуют его разметку, величины же ДхЛ = xk - xk_t равны длинам соответствующих отрезков. Функция	определена на множестве А, а величина Д7 равна
max ДхЛ, и, наконец, окончания й§, 8 > 0, базы Дг —> 0 состоят из всех размеченных разбиений Т с условием Дт < 8.
408
Важно подчеркнуть, что если при некотором е > 0 и всех хе имеем
|F(x, й) - F(x, 0)| = \fy(x, у + 6Й) - fy(x, у)| < е, ’оЬдх,*)*2’) GF(x, 0)(Т)| < е(Ь - а).
Отсюда следует, что если при h -> 0 выполнено условие y + Qh)z$ f'y(x, у), то и при й —> 0 также имеем
CF(x, у)(^)	CF(x,
А
Но тогда оба повторных предела существуют и равны между собой, т. е. существует предел
I = lim lim	hAT) = lim lim hdT).
Л->0Дг->0	' Агч0/гч0 г(х, Лр '
При этом имеем ь
Д^о Л)(Т) = / У + 0Л)</Х’
Inn f’y{x, y + Qh) = f’y(x, у), откуда b	b
lim J f'y(x, у + Qh)dx = J fy(x, y)dx, что и утверждалось выше. С другой стороны, аналогичное утверждение прямо доказано в теореме 1 на основе использования равномерной непрерывности подынтегральной функции. Точно так же мы могли бы рассуждать и в данном случае.
ТЕОРЕМА 5. Если функция f(x9 у) непрерывна на прямоугольнике П = 1г х 12» г&е Л = [я, Ь], Л = Iе’ то °^а повторных интеграла b d	d b
н= f dx j f(x, y)dy и G= J dy J f(x, y)dx a c	c a
существуют и равны между собой.
► Рассмотрим вспомогательную функцию g(t9 у)9 где
t
g(t, у) = J f(x, y)dx, t e [a, ft], у e [c, d]. a
Покажем, что эта функция непрерывна на П по совокупности переменных (t9 у). Действительно,
|Ag| = |g(t + At, у + Ду) - g(t, у) =
t +At
J a
t
f(x, у + &y)dx - J f(x, y)dx a

409
< j (/(«» У + Ay) - ftx> y))dx + J f(x, у + Aj/)dx < a	t
< (b - a)max |Д /(x, y)| + c|At|, XG/j У
где с = max |Дх, y)|.
(x, у)€П
Поскольку функция Дх, у) непрерывна, max Au/(x, у) -» 0 при &у -» 0. Следовательно, Ag —» 0 при (Аг/, Af) -> (0, 0), т. е. g(x, t) непрерывна на П.
Далее, gj(*, у) = f(t, г/), поэтому по теореме 3 для функции d	d	t
(ДО = J g(t, y)dy = J dy J Дх, y)dx c	c	a
имеем d d	d	d
G'(t) = щ j g(t, y)dy = JtfXx, y)dy = J f(t, y)dy = h(t). c	c	c
d
С другой стороны, функция h(t) = J f(t, y)dy тоже непрерывна, с
поэтому по формуле Ньютона—Лейбница
b(t)=^h(x)dx = H'(0,
t	t	d
где H(t) = J A(x)dx = J dx J Дх, y)dy. Следовательно, h(t) = H'(t) = a	d	c
= G'(t). Кроме того, очевидно, что (ДО) = Н(0) = 0, поэтому при всех t е 12 имеет место равенство G(t) = H(f). В частности, при t = Ъ имеем G = (ДЬ) = Я(Ь) = Н. ◄
Лекция 16
$ 3. ТЕОРЕМА ЛАГРАНЖА
Дадим приложение обобщенного правила Лейбница (теорема 4) к выводу формулы Лагранжа с остаточным членом в интегральной форме. Этой формуле Лагранж посвятил две знаменитые работы, опубликованные в Me moires de VAcademic de Berlin (1768) и Note (1798, XI). Приведем ее доказательство, предложенное Е. И. Золотаревым.
ТЕОРЕМА 6 (формула Лагранжа). Пусть функция f(x) имеет п непрерывных производных для всех хе R. Пусть также некоторая функция х = x(u, t) является решением уравнения
и - х + tf(x) = 0.
Тогда для любой функции Р(у)9 имеющей п непрерывных производных, справедлива формула
v tkdk~4FXu)fk{u)) „
F(x(u, t) = F(u) +	+ Rn,
где
dn\ J F'(x)(u - х + tf(x))ndx
11	J
n n\	dun
X(u)
► Рассмотрим функцию Sk = Sk(u) = J F'(x)(u - x + tf(x))kdx.
Продифференцируем ее по параметру и. По теореме 2 получаем
dSb
- kSk_x - tkF'(u)fk(u), Т. е.
tk ,	1 dSk
Продифференцировав последнее равенство k - 1 раз, имеем
d" = & dk~1(F’{u)fk(u))	1 dkSk
duk~* k duk~^	duk
Переписывая это равенство при k = 1, ..., и, получаем
dS.
so - tF'(u)f(u) +	,
dSi =	£2 d(F'(u)f2(u))	1	d2S2
du	2 du	2	du2	’
da~lsn-i	= t_2 da~l(F'(u)fn(u))	1	dnSn
du*'1	n du*'1	dun
411
Подставим последнее выражение в предпоследнее и т. д. до первого выражения, имеем
Я - tF'(iAf(„\ 4- t2 d(F'(^f2W) ,	. t" dn~1(F'(u)fn(u)) ,
So - tF (u)f(u) + 2,	+ ... +	f---- +
! 1 dnSn n\ dun
Кроме того, для So справедливо равенство
So = Xf ’ F\x)dx = F(x(u)) - F(u). u
Подставим эту формулу в предыдущее выражение. Получим сформулированное в теореме утверждение
г./ Z чх ™ х , V tk dn-\F\u)fk(u)) , „
F(x(u)) = F(u) +	+ Rn,
где /x(u)	\
,nO d" / F\x)(u-x + tf(x))ndx\
1 dnSn	11	I
д __ x_____2 _ x \ и_____________________7
n n\ dun n\	dun
Приведем два частных случая формулы Лагранжа.
1. В случае когда выполнено тождественное равенство f(x) = 1, формула Лагранжа превращается в формулу Тейлора с остаточным членом в интегральной форме.
2. Пусть f(x) = sin х. Тогда функция х = х(и) является решением уравнения Кеплера х - t sin х = и, где t — эксцентриситет эллиптической орбиты в задаче двух тел.
Для функции Я(х) — 1 - t cos х Лаплас получил разложение в ряд Лагранжа
/ w 1	* lx v tk dfe-1(sinu)* + 1
jR(x(u)) = 1 - t cos и + t r?----H—r------
v v "	k = i k\ duk~x
и, по существу, установил его сходимость при t < 0,662... .
В заключение отметим, что о богатстве содержания понятия ряда Лагранжа позволяют судить исследования этого ряда, которые провели Л. Эйлер, И. Г. Ламберт, П. С. Лаплас, Бюрман, И. В. А. Пфафф, О. Шлемильх, Е. Гейне, О. Коши, К. Г. Якоби, П. Д. Г. дю Буа Раймон, Е. Руше, П. Л. Чебышёв, Е. И. Золотарев, Ю. В. Сохоцкий, П. А. Некрасов. Исследования по вопросам сходимости обобщений ряда Лагранжа актуальны и сегодня.
Лекция 17
§4. РАВНОМЕРНАЯ СХОДИМОСТЬ ПО ГЕЙНЕ
Понятие равномерной сходимости функции по базе множеств является обобщением классического понятия равномерной сходимости и опирается в своей основе на понятие предела функции по Коши. В математическом анализе используется и другой тип определения предела — предела по Гейне, как обычного, так и равномерного. Оба определения равномерной сходимости — по Коши и по Гейне — эквивалентны, и каждое из них оказывается более предпочтительным в своей сфере применения. Оба эти определения удобно использовать в различных ситуациях, поэтому мы докажем теорему об эквивалентности понятий равномерной сходимости по Кошй и по Гейне в общем случае сходимости по базе множеств.
Нам потребуется несколько новых определений.
Определение 2. Пусть В — некоторая база, определенная на основном множестве X, и для любых ее окончаний Ъх и Ь2 имеем или Ъх с Ь2, или с Назовем последовательность {хп}, хп е X, фундаментальной по базе В, если вне любого окончания Ь содержится лишь конечное число членов этой последовательности.
Определение 3. Фундаментальную последовательность {хп} мы будем называть монотонной по базе В, если для любого окончания Ь условие хпе Ь влечет за собой включение хп+1 е Ь.
Далее будем считать, что рассматриваемая база множеств В обладает хотя бы одной фундаментальной монотонной последовательностью. Кроме того, полагаем, что пересечение всех окончаний базы В пусто.
Рассмотрим, наконец, функцию f(x), определенную на некотором окончании Ь базы множеств В.
Определение 4. Число I называется пределом по Гейне функции f(x) по базе В, если для всякой монотонной по базе В последовательности {хп} имеем, что f(xn) = I.
В этом случае пишем: Нт-lim f(x) = I.
Имеет место теорема об эквивалентности определений предела по Гейне и в обычном смысле, т. е. по Коши. Приведем ее формулировку (см. ч. I, лекция 30).
413
ТЕОРЕМА 7. Для существования предела Hm-lim f(x) необходимо и достаточно существования lim f(x) по Коши. При этом имеем Hm-lim f(x) = lim f(x).
в	в
Для того чтобы подчеркнуть, что lim f(x) есть обобщение предела по Коши, будем также писать
lim f(x) = C-lim f(x). D	D
Доказательство этой теоремы опирается на две следующие леммы, имеющие самостоятельный интерес.
ЛЕММА 1. Пусть {хп} — монотонная последовательность по базе В. Тогда найдутся ее подпоследовательность yk = xnk и соответствующая ей последовательность окончаний {bk е В} такие, что при всех k е N имеем bk+1 с bk, yk е bk, *0 yk * bk+1.
Определение 5. Последовательность окончаний {bk} из леммы 1 будем называть основной последовательностью окончаний.
Ее члены обозначим символом bk.
Л Е М М А 2. Для любого окончания b е В найдется член bk последовательности основных окончаний, для которого имеем bk с Ь.
Введенные выше понятия позволяют по-новому подойти и к общему определению равномерной сходимости. Для этого определим на декартовом произведении X х Y множеств X и У функцию f(x, у) и будем считать, что на множестве X задана база В.
Определение 6. Функция f(x, у) сходится к функции g(y) по базе В равномерно на множестве Y, если для всякого е > 0 найдется окончание Ь(е) е В такое, что при всех х е Ь(е) независимо от у е Y справедливо неравенство \f(x, у) - g(i/)| < е.
В этом случае пишем f(x, у) => g(y).
Определение 7. Будем говорить, что функция f(x, у) сходится по Гейне к функции g(y) равномерно на Y, если для любой последовательности {хп}, монотонной по базе В, функциональная последовательность fn(y) = f(xn, у) сходится к g(y) равномерно на множестве Y.
В этом случае пишем f(x, у) =$Нт g(y).
414
$ 5. ЭКВИВАЛЕНТНОСТЬ ДВУХ ОПРЕДЕЛЕНИИ РАВНОМЕРНОЙ СХОДИМОСТИ
Теперь можно перейти к теореме об эквивалентности понятий равномерной сходимости по Коши и по Гейне.
ТЕОРЕМА 8. 1. Если функция f(x, у) сходится по Гейне к g(y) в
по базе В равномерно на множестве Y, то тогда f(x, у) g(y).
2.	Если f(x, у) =1 g(y), то f(x, у) =>и" g(y).
► Рассмотрим утверждение 1. Будем рассуждать от противного.
Допустим, что /(х, у) g(y) для любой монотонной по базе В по-в следовательности {хп}, но равномерная сходимость f(x, у) у g(y) не имеет места. Последнее условие означает, что найдется е > 0 такое, что для любого окончания be В найдутся точки xb е Ъ и уъ е Y такие, что |/(хь, yb) - g(yb) > е. Возьмем сначала в качестве такого Ъ окончание Ьг из основной последовательности окончаний и обозначим через хх и ух соответствующие ему точки х^ и у^. Точка хх не может принадлежать сразу всем окончаниям &, так как их пересечение пусто. Поэтому найдется Ъ е В с условием хх ё Ь. По лемме 2 найдется число kr такое, что bkicb,n ддя него также имеем xt ё bk. Теперь в качестве х2 и у2 возьмем точки х2 = х^ е bki м. у2 = yb* е Y и повторим указанную процедуру снова и снова. Таким образом мы получим последовательность точек хп и уп, для которых справедливо неравенство |/(хл, уп) - g(yn)\> е при всех п е N.
Покажем, что последовательность хп является монотонной по базе В. Для этого установим сначала ее фундаментальность. Заметим, что последовательность натуральных чисел kn монотонно возрастает. Но всякое окончание bQ е В по лемме 2 содержит некоторое bk°9 а при kn > kQ имеем хп+1 е bk° с boc 60, значит, вне Ьо лежит не более k0 точек из последовательности {хп}, т. е. она фундаментальна.
Чтобы доказать монотонность хл, заметим, что хпе bk^ я хп+1 е bkn> Но если для некоторого Ьо * Ьк* мы имеем условие хп е Ьо, то из двух допустимых включений Ьо с bk или b0 bk может иметь место именно второе, так как иначе хое Ьос т. е. хп е bk , что неверно. Но тогда хп+1 е bk с. 60, т. е. последовательность {хп} монотонна.
415
Итак, мы построили монотонную последовательность точек хп е X такую, что при соответствующих уп е Y справедливо неравенство |f(xn, уп) - g(i/n)| > е при всех п е N. Это значит, что равномерная сходимость функциональной последовательности fn(y) = f(xn, у) к функции g(y) при и —> не имеет места, что противоречит сделанному предположению. Таким образом, утверждение 1 теоремы доказано.	(В)
Рассмотрим утверждение 2. Поскольку f(x, у) ^Нт g(y), при любом е > 0 найдется окончание b = 6(e) е В такое, что при всех у g Y и при всех х е 6(e) имеем |/(х, у) - g(i/)| < е. Пусть теперь {хп} — любая монотонная последовательность по базе В. Тогда вне 6(e) лежит лишь конечное множество точек хп и при достаточно большом п > и0(е) имеем, что хп е 6(e), откуда при тех же п имеем |/(хп, у) - £(!/)| < Е, а это значит, что f(xn, у) =» g(y) при п -»<». ◄
Подчеркнем, что в теореме 8 на базу В накладываются следующие ограничения:
1)	каждое окончание Ь базы В непусто, но пересечение всех окончаний пусто;
2)	для любых двух окончаний 6Х и 62 имеем либо включение 6Х с 62, либо включение Ьг э 62;
3)	существует хотя бы одна монотонная по базе В последовательность.
На первый взгляд может показаться, что эти ограничения весьма обременительны, особенно условие 2, которое ужесточает обычное условие, указывающее на существование 63 с 6Х П 62. Но это не совсем так, поскольку вместо базы В практически всегда можно рассматривать базу Во, эквивалентную В в том смысле, что существование предела по базе В влечет за собой сходимость по Во, и наоборот. При этом все три сформулированных выше условия для базы BQ уже будут выполнены. Например, в случае прямого произведения баз Н = В X В, где В и D есть базы х 4-оо и у —> +оо, в качестве соответствующего Яо можно взять базу, составленную из окончаний вида h = {(х, у)\х > а9у> а}.	/
Для полноты изложения приведем обобщение критерия Коши равномерной сходимости функций по базе множеств.
ТЕОРЕМА9 (критерий Коши для равномерной сходимости функции). Для того чтобы функция f(x, у), определенная на множестве X X У, сходилась к некоторой функции g(y) по базе В, заданной на множестве X, равномерно на множестве У, необходимо и достаточно, чтобы для всякого е > О нашлось окончание b = 6(e) базы В такое, что для любых его точек х1их2и любого у е У выполнялось бы условие
|Л*1» у) - f(x2, у)| < £•
416
► Необходимость. Если /(х, у) у g(y)9 то для всякого е > О существует окончание 6(e) такое, что для всех у g Y справедливо неравенство |/(х, у) - g(y)\ < е/2. Тогда для любых хх и х2 g 6(e) и любого у g Y имеем
|/(хР у) - f(x2, J/)| < Iftxp у) - g(j/)| + |g(y) - f(x2, y)| < e/2 + e/2 = e.
Достаточность. Зафиксируем произвольную точку у g Y. Тогда функция Л(х) = hy(x) = /(х, у) удовлетворяет обычному критерию Коши для сходимости по базе. Следовательно, существует число g = g(y) такое, что Л(х) g, т. е. имеет место поточечная сходимость
Л(х) = hy(x) = f(x, у) g(y), где g(y) — некоторая функция, определенная на множестве Y. Покажем, что данная сходимость является равномерной на Y. Действительно, рассмотрим окончание 6(e) с условием, что при любых хх и х2 g 6(e) и при любом у g Y выполняется условие |Л*Р У) - f(x2, Z/)l < е/2.
В этом неравенстве при фиксированном у перейдем к пределу по базе В применительно к переменной х2. Тогда получаем
|Л*1. У) - £(*/)! < е/2 <е.
Последнее неравенство выполняется при любом xr е 6(e) и при любом у g Y. Это означает, что
/(х, у) => g(y). ◄
В качестве прямого следствия теоремы 9 приведем прямую формулировку критерия Коши отсутствия равномерной сходимости на множестве Y для функции /(х, у) по базе В, заданной на множестве X.
ТЕОРЕМА 10 (критерий отсутствия равномерной сходимости). Пусть (х, у) g X х Y. Для того чтобы равномерная сходимость функции f(x, у) на множестве Y по базе В, заданной на X, не имела места, необходимо и достаточно, чтобы при некотором е > 0 для любого окончания be В существовала пара точек хг е Ь и х2 е Ь и точка у е Y с условием
У) - f(x2, у)| > е.
Замечание. И в теореме 9, и в теореме 10 из двух возможных определений равномерной сходимости, по Коши и по Гейне, рассматривается первое определение. Если же опираться на второе определение^ которое, как было показано выше, ему эквивалентно, то тогда вопрос по существу сводится к критерию Коши равномерной сходимости функциональной последовательности, доказанному ранее в § 3 гл. 16.
417
14-4953
Лекция 18
§ 6. РАВНОМЕРНАЯ СХОДИМОСТЬ НЕСОБСТВЕННЫХ ПАРАМЕТРИЧЕСКИХ ИНТЕГРАЛОВ
Дальнейшее развитие теории интегралов, зависящих от пара* метра, приводит к рассмотрению несобственных интегралов, которые составляют ее наиболее существенную часть. Из двух типов таких интегралов сосредоточим свое внимание главным образом на интегралах первого рода. Интегралов второго рода коснемся лишь вскользь, поскольку их теория не имеет принципиальных отличий от интегралов первого рода.
Рассмотрим функцию Дх, у), заданную на множестве I х У, где I — промежуток вида [а, +°°), а У — некоторое множество вещественных чисел, т. е. У с R. Допустим, что при любом фиксированном у е У функция Дх, у) интегрируема по Риману на любом конечном отрезке вида [а, &] и существует несобственный интеграл первого рода от этой функции по переменной х е I = [а, +°°). Тогда этот интеграл сам представляет собой некоторую функцию от у, заданную на У равенством
g(y) = J y)dx.
а
Определение 8. Функция g(x), представленная в указанном выше виде, называется несобственным интегралом первого рода, зависящим от параметра у е Y.
Замечание. Вместо несобственных интегралов по промежутку вида [а, +оо) можно, разумеется, рассматривать интегралы по промежуткам вида (-со, Ь] или по всей вещественной прямой R ® (-со, +оо). Все эти случаи сводятся к рассмотренному точно так же, как это делалось при изучении обычных несобственных интегралов. Например, интеграл
J Дх, y)dx, yet,
—оо достаточно представить в виде суммы интегралов
4-оо	+ОО	Ч-оо
\f(x,y)dx = jf(x,y)dx+ jf(x,y)dx —оо	—со	—оо
и сходимость этой суммы понимать как сходимость каждого из двух ее слагаемых. Первое слагаемое сводится ко второму заменой переменной х на -х. Кроме того, можно, конечно, рассматривать и формальные несобственные параметрические интегралы и при этом ставить вопрос об области их сходимости У. Подобного рода вопросы разобраны при рассмотрении функциональных рядов, поэтому мы им много внимания уделять не будем, иногда, однако, будем пользоваться аналогичной терминологией.
418
ПРИМЕРЫ. 1. При у > 1 справедливо равенство Г— - lim f г - lim ‘ = { х»	J ху <->+=° i х
2. При у > 0 имеем
JSM dx = J-Ш d(xj,) = J Ж dx. 0 х о XV	0 х
1 »-1’
Определение 9. Интеграл J f(x, y)dx называется равномерно а
сходящимся по параметру у на множестве Y, {у} = Y, если t
j Дх, y)dx - F(y, t) у g(y) при t -> +°°. a
Другими словами, это значит, что для любого е > 0 существует t0 = #0(е) такое, что при всех t > t0(e) и всех yeY имеем
j Дх, y)dx - g(y) <e
оо
где g(y) = J Дх, y)dx.
Исходя из общей теоремы, сформулируем критерий Коши конкретно для равномерной сходимости несобственных интегралов первого рода.
ТЕОРЕМА 11. Необходимое и достаточное условие равномерной оо
сходимости несобственного интеграла первого рода J /(х, y)dx а
на множестве Y состоит в том, чтобы для любого е > 0 существовало Т = Т(е) такое, что при всех t2> t{> Т и любом у е Y выполнялось бы неравенство
J f(x,y)dx <e.
Приведем также прямую формулировку критерия отсутствия равномерной сходимости несобственного параметрического интеграла.
ТЕОРЕМА IV. Равномерная сходимость несобственного интеграла
J f(x, y)dx
на множестве Y не имеет места, если найдется е > О такое, что для любого Те R найдутся числа t1ut2> Т и у е Y такие, что
/ f(x,y)dx >e.
419
14*
oo
Определение 10. Если интеграл J g(x)dx сходится и при всех I	I	а
х > а и у е Y имеем |/(х, i/)| < g(x), то функция g(x) называется мажорантой для f(x, у) на П = I х У.
ТЕОРЕМА 12 (признак Вейерштрасса равномерной сходимости не-оо
собственных интегралов первого рода). Интеграл J = J /(х, y)dx а
сходится равномерно на Y, если функция f(x, у) имеет мажоранту g(x) на П = X х У, где X = [а, +«>).
оо
► Воспользуемся критерием Коши. Поскольку интеграл J g(x)dx а
сходится, при любом е > 0 найдется число Т = Т(е) такое, что при г2
всех t2 >	> Т выполнено неравенство J g(x)dx < е. Но тогда при
всех у е У имеем
J ftx, y)dx < J |/(х, y)\dx < J g[x)dx < e.
Отсюда согласно критерию Коши заключаем, что интеграл J сходится равномерно на У. ◄
оо
ПРИМЕР. При з > s0 > 1 интеграл J x~8dx сходится равномерно на 1
множестве s > з0, поскольку он имеет мажоранту g(x) = х"в°.
ТЕОРЕМА 13 (признаки Абеля и Дирихле для равномерной сходимости параметрических несобственных интегралов первого рода). Пусть функция /(х, у) определена на множестве П = X х У, где X = [а, +°°), У = [с, d] и f(x, у) = а(х, z/)P(x, у). Пусть Р(х, у) монотонна по х при любом фиксированном у е У.
(А) (признак Абеля). Пусть, кроме того: оо
1) интеграл J а(х, y)dx сходится равномерно по у на У;
2) функция р(х, у) ограничена на П = X XY, т. е. |р(х, у)\ < с при некотором вещественном числе с>0и всех (х, у) е П.
оо
Тогда интеграл J = J f(x, y)dx сходится равномерно на У.
(Д) (признак Дирихле)Пусть вместо условий (А) имеем:
1) при некотором О 0 а всех t > а, у е Y, имеет место нера
венство
J а(х, y)dx < с; а
2) функция Р(х, у)равномерно на У сходится к нулю при х —»оо. Тогда, как и в случае (А), интеграл J сходится равномерно на У.
420
► Эта теорема как по своей формулировке, так и по доказательству похожа на соответствующие утверждения из теории рядов. По существу, все отличие сводится к замене использования преобразования Абеля на применение второй теоремы о среднем значении интеграла.
Для доказательства снова воспользуемся критерием Коши. Применяя вторую теорему о среднем, имеем
*2	*3	*2
J а(х, у)Р(х, y)dx = P(tv у) J а(х, y)dx + p(t2, у) J а(х, y)dx,
где t3 — некоторая точка отрезка [fx, t^\.
Теперь в случае (А) в силу равномерной сходимости интеграла
J а(х, y)dx при любом е > 0 и всех достаточно больших t2 > tx > f0(e)
имеем J а(х, y)dx < е и J а(х, y)dx < е, откуда h	*з
®2	*8
J а(х, y)P(x, y)dx < P(tpj/)J а(х, y)dx +
*2
+1 p(f2, iz)| • J a(x, y)dx <ce + cE = 2ce,
поскольку |P(x, i/) | < с при всех x и у. В силу произвольности числа £ > О это влечет за собой равномерную сходимость интеграла J и справедливость утверждения (А).
В случае (Д) интегралы от функции а(х, у) ограничены числом с и Р(х, у) стремится к нулю равномерно по у9 поэтому при всяком е > 0 и достаточно больших t2 >	> ?0(е) выполнено неравенство
|Р(х, у)\ < Е, откуда с учетом предыдущей формулы имеем
J а(х, i/)p(x, y)dx < се + се = 2се,
что влечет за собой справедливость утверждения (Д). ◄
Лекция 19
$ 7. НЕПРЕРЫВНОСТЬ, ДИФФЕРЕНЦИРУЕМОСТЬ И ИНТЕГРИРУЕМОСТЬ ПО ПАРАМЕТРУ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
Докажем теорему о переходе к пределу функции в точке под знаком несобственного интеграла.
ТЕОРЕМА 14. Пусть функция f(x, у) задана на множестве Р = X х Y, где X = [а, +°°), Y = [&, с]. Пусть, далее, выполнены следующие условия:
1) при некотором уое Y и при любом t € X на промежутке Е =Et = [a, t] имеет место равномерная сходимость
Л*, при У Уо>
оо
2) несобственный интеграл h(y) = J /(х, y)dx сходится рав-а
номерно на Y.
Тогда:
а)	функция g(x) интегрируема по Риману на любом отрезке Et; оо
б)	интеграл J = J g(x)dx сходится;
а
в)	существует предел I = lim h(y);
г)	имеет место равенство
оо	оо	оо
I = lim h(y) — lim J f(x, y)dx = J lim f(x, y)dx = J g(x)dx = J.
У Уо	У Уо д	а У	a
► Рассмотрим произвольную монотонную числовую последовательность уп е Y с условием уп у0. Тогда в силу условия 1) для функциональной последовательности gn(x) = Дх, i/n) при и -> оо справедливо соотношение gn{x) =► g(x), где Et = [а, £] и t > а — любое фиксированное •число. Далее, из теоремы 1 § 6 гл. 16 об интеграле от функциональной последовательности вытекает, что функция g(x) = lim gn(x) интегрируема на Е„ причем
п —> оо	1
t	t	t
J fix, yn)dx = J gn(x)dx = Qf, „ Qf = J g(x)dx, a	a	a
где величины Qt n и Qt определяются последним равенством.
В силу условия 2) при t —» +оо имеем Qt п Л(у0), поскольку для любого е > 0 существует tQ == t(e) > а такое, что при всех t > tQ и при всех натуральных п справедливо неравенство п - A(i/n)| < е.
422
Следовательно, по теореме о двойном н повторном пределах по базам (§ 6 гл. 16) существуют и равны оба повторных предела, т. е.
lim lim Qt п = lim lim Qt П —> OO t-t+oo.	f-»+oon->oo n
Но тогда
lim lim Qt = lim J f(x, yMx = lim Л(у_) = I, n-^OO t -> +OO г» л nCO Ja	n	n-*OO
а также	,
lim lim Q, = lim f g(x)dx = J,
откуда I = J. В силу произвольности выбора последовательности уп отсюда вытекает утверждение теоремы. ◄
Из этой теоремы вытекает следующее свойство непрерывности несобственных параметрических интегралов.
ТЕОРЕМА 15. Пусть функция Дх, у) непрерывна на множестве Р = X х У, где X = (а, +°°), Y = [&, с], и пусть интеграл
h(y) - J f(x, y)dx а
равномерно сходится на У. Тогда функция h(y) непрерывна на У.
► Непрерывность h(y) в каждой фиксированной точке yQ е У означает, что h(y) h(yQ) при у yQ. Для доказательства этого соотношения воспользуемся теоремой 14. Очевидно, ее условие 2) выполнено. Далее, из непрерывности Дх, у) на Р следует ее равномерная непрерывность на Pt = [a, f] х [с, d] при любом t > а. В свою очередь, отсюда имеем, что
Я*. у) [3] Кх> Уо) ПРИ У Уо’
т. е. условие 1) теоремы 14 выполнено, а это означает, что при У~*Уо
Л(У) -> j f(x, y0)dx = й(у0). ◄
а
ТЕОРЕМА 16 (условие интегрируемости несобственных интегралов по параметру). Пусть функция Дх, у) непрерывна на Р = X X У, оо
где X = (а, +°°), У = [&, с], и пусть интеграл g(y) = J Дх, y)dx а
существует и равномерно сходится на Y. Тогда функция g(y) С
будет интегрируема на У, а функция h(x) — J f(x, y)dy будет ь
интегрируема на X = [а, +°°), причем
J gW)dy - J h(x)dx, b	а
423
т. е. равны повторные интегралы
J dyj f(x, y)dx = J dx j f(x, y)dy. ba	a b
► Рассмотрим произвольную монотонную последовательность tn е X с условием tn -> +°о. Тогда функциональная последова-
tn
тельность gn(y)9 где gn(y) = J f(x9 y)dx9 равномерно сходится к а
функции g(y) на множестве У. Каждая из функций gn(y) непрерывна на У, потому при фиксированном п по теореме об интегрировании собственных интегралов по параметру (теор>ема 16 § 4) имеем
f dy J fix, y)dx = j gn(y)dy = J dx J f(x, y)dy.	(*)
ft a	ft	a ь
По теореме 11 гл. 16 возможен переход к пределу при п —»оо под знаком интеграла и существует число А такое, что
А = JiPL hn^dy = / Jim gn(y)dy = fg(y)dy - jdyff(x, y)dx. ft	ft	ft	ft a
Переходя в равенстве (*) к пределу при п -> оо, получаем, что предел его правой части существует и равен А,
tn с
А = lim f dx J Дх, y)dy.
n“>o° а ь
Но поскольку последовательность tn — произвольная, последний предел равен интегралу
JdxJf(x, y)dy. ◄ а b
Теперь докажем теорему о дифференцировании несобственного интеграла по параметру.
ТЕОРЕМА 17 (правилоЛейбница). Пусть'.
1)	функция Дх, у) непрерывна на Р = X X У, где X = (а, +°°), У = [с, d];
2)	частная производная fy(x9 у) существует и непрерывна на Р;
оо
3)	интеграл g(y) = J Дх, y)dx сходится при всех у е У; оо	а
4)	интеграл J f'y(x9 y)dx равномерно сходится на У. а
Тогда функция g(y) дифференцируема на У и имеет место равенство
g'(y) Jf'/X, y)dx.
а
424
► В силу непрерывности функции Дх, у) при всех п > а существует непрерывная на Y функция gn(y) вида
Sn(y) = ]f(x, y)dx. а
Применяя правило Лейбница для собственных интегралов, получаем
g'n(y) = J fy(x> у№х-а
Заметим, что для функциональной последовательности gn(y) при п -» °° имеют место соотношения
ёп(у) Му) = / f(x, y)dx и g'n(y)" =£ J f'(x, y)dx. п	* л
Следовательно, по правилу дифференцирования функциональной последовательности имеем
(8^У =	£'п(У), Т. е. g'(y) - J f'y(x, y)dx. ◄
а
Докажем еще две теоремы о несобственных повторных интегралах, которые потребуются в дальнейшем.
ТЕОРЕМА 18. Пусть f(x9 у) задана и непрерывна на Р = X X У, где X = [а, +°°), У = [Ь, +°°) и Дх, у) > 0 на Р. Пусть при всех
у е У интеграл J Дх, y)dx сходится к функции g(x), непрерыв-а
оо
ной на У, и при всех х е X интеграл J Дх, y)dy сходится к
функции й(х), непрерывной на X.
Тогда если сходится интеграл Jr = J g(y)dy9 то сходится и оо	Ь
интеграл J2 = \ h(x)dx, и наоборот, причем = J2> т- е-
J dy J f(x, y)dx = J dx J f(x, y)dy.
► Будем считать, что существует интеграл J19 так как второй случай рассматривается аналогично. Рассмотрим произвольную монотонную числовую последовательность tm9 подчиненную требованиям tm > а и tm -» +°°, и натуральные числа п > Ъ. Символом п обозначим повторный интеграл вида
Jm,n=J dx]f(x,y)dy.
а ь
425
Положим еще
gm(y)= J Кх> у№ и hn(x> = J Кх> у№у-a	b
По теореме об интегрируемости собственного параметрического интеграла имеем
п	tm	п
Jm,n= I dyJ f(x> У)dx = J gm(y)dy-b	a	b
Далее, так как Дх, у) > 0, то 0 < gm(y) < g(y)* Поэтому справедливо неравенство
dm, п < J gtlMy < J g<3My = dv b	b
С другой стороны, rm 7 Jm,n = J dx J ft*, M = J *»(*#*• a b	a
При этом Лп(х) > 0 и при каждом фиксированном х эта последовательность является неубывающей; кроме того, она составлена из непрерывных функций и ее предел, т. е. функция Л(х), также непрерывен. Следовательно, по теореме Дини, при п -» оо имеем
м*) [Я„]Л(х)>
Но тогда при п -» оо выполнены равенства
J(m) = Jim Jm n = Jim J ft„(x)dx = J (Jim hn(x))dx = J h(x)dx.
Поэтому, переходя к пределу при п -» оо в неравенстве п < J19 получаем соотношение
J(m) = J A(x)dx < Jv а
Но так как Л(х) >0, то с ростом т последовательность J(m) монотонно возрастает и ограничена. Следовательно, по теореме Вейерштрасса величина J(m) имеет предел Z, причем I < Jv В силу произвольности выбора последовательности tm отсюда вытекает, что I одновременно является пределом величины
t	оо
lim J h(x)dx = J A(x)dx = J2. t a	a
Таким образом, J2 существует и J2 = К Jv Но тогда, меняя в проведенных выше рассуждениях величины J\ и J2 местами, одновременно получаем неравенство < J2. Следовательно, = J2. ◄
426
Приведем некоторое обобщение теоремы 18.
ТЕОРЕМА 19» Пусть функция f(x, у) удовлетворяет условиям теоремы 18, кроме условия Дх, у) > 0; но функция F(x9 у) > |Дх, у)\ удовлетворяет всем ее условиям. Тогда утверждение теоремы 18 имеет место не только для функции F(x, у), но и для функции Дх, у).
► Заметим, что функции
Ф,<х, 0 -	„ ф2(х, „) -
удовлетворяют условиям теоремы 18, но тогда функция ф^х, у) -- Фг(х» У)= f(x> У) тоже ей удовлетворяет. ◄
Вообще говоря, условия теорем 18 и 19 являются избыточными. Далее будет доказано значительно более общее утверждение.
В заключение приведем пример, указанный Коши, в котором при перемене порядка интегрирования получаются различные значения повторных интегралов. Это связано с тем, что подынтегральная функция
f(X у) = *2~У2 = А (_____А = 1 ( У-. "I
’У (х2 + у2)2 дх V х2-у2)	ду\х2+у2)
имеет разрыв в точке (0, 0), в частности, при подходе к этой точке по прямым у = kx. При |Л| > 1 имеем lim Дх, kx) = +оо, а при |fe| < 1 имеем lim Дх, kx) = ~°°. Но для двух повторных интегралов от этой функции справедливы равенства
J Л/J ftx, i/)dx = - J ^-2
J dx J ftx, y)dy = J = I. 0	0	о 1 х
Отметим, что данный пример относится к несобственным интегралам второго рода, которые будут рассмотрены в следующем параграфе.
Лекция 20
§ 8. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА
Сформулируем основные понятия элементарной теории несобственных параметрических интегралов второго рода и приведем формулировки некоторых утверждений, соответствующих доказанным нами теоремам об интегралах первого рода.
Рассмотрим множество Р = X X У, где X = (а, &], YeR, Пусть функция f(x, у) задана на Р и не ограничена как функция от х хотя бы при одном фиксированном у е У. Далее, пусть при любых у g У и 8 > 0, 8 g (0, Ь - а) функция Дх, у) интегрируема по Риману на отрезке [а 4- 8, Ь] как функция от х.
Определение 11 • Введенное выше формальное выражение вида ь
J f(x> y)dx называется несобственным параметрическим интегралом второго рода с одной особой точкой х = а.
Определение 12. Если при любом фиксированном значении у е У этот интеграл сходится, то множество У называется ь
областью сходимости интеграла и его значения g(y) = J Дх, y)dx порождают функцию, определенную на множестве У.
Подобные определения имеют место и в случае, когда особая точка находится на правом конце промежутка интегрирования X = [а, Ь], т. е. в точке Ь. В случае когда особая точка х = х0 лежит внутри отрезка X, его можно разбить на две части этой точкой х0 и рассматривать каждую часть отрезка отдельно.
Аналогичные рассуждения позволяют рассматривать несобственные интегралы с переменной особой точкой х0 = x0(i/), но здесь мы входить в детали не будем.
ПРИМЕР. Интеграл J = J - -i сходится на У = [0, 1] и его мож-0 J\x - у\
но вычислить.
Действительно, имеем
g{y) =	+ ^2(у) = J 7== + J 7== = 2л/у + 271 ~У-
о 4у -X у цх- у
Определение 13. Несобственный интеграл второго рода ъ g(y) = J f(x, y)dx а
называется равномерно сходящимся по у на множестве У, если для функции	ь
g(F>,y) = J f(x, y)dx,
а + 6
428
при 8 —»0+ выполнено условие
8$, у) у 2(0, у) = g(i/).
Исходя из общей формулировки критерия Коши, можно сформулировать его для равномерной сходимости несобственного параметрического интеграла второго рода. Ограничимся формулировкой одной сводной теоремы, содержащей утверждения, важные для практических применений.
Т Е О Р Е М А 20. Пусть функция f(x9 у) непрерывна на Р = X X У, где X = (а, &], У = [с, </]. Пусть также а — особая точка несобственного параметрического интеграла
ь g(.y) = J f(x, y)dx. а
Тогда справедливы следующие утверждения.
ь
1.	Если интеграл J /(х, y)dx сходится равномерно на У, то а
функция g(y) непрерывна при всех yeY.
2.	В этом случае
d	b d
J £{y)dy = jdx J/(x, y)dy. c	a c
b
3.	Если интеграл jf(x9 y)dx сходится, частная производная a
Ь f'y(x9 У) существует и непрерывна на Р, а интеграл J f'y(x9 y)dx сходится равномерно на У, то существует g'(y)9 причем
ь g'(y) = f fy(.x, y)dx. a
Если особая точка х0 является внутренней точкой отрезка X = [а, Ь], то, как было отмечено выше, необходимо отрезок X разбить этой точкой на две части и рассматривать каждый из двух получившихся интегралов отдельно. Тот же подход можно применить и в случае, когда бесконечный промежуток интегрирования X = [а, +оо) содержит конечное число особых точек х19 ... , хп. Тогда этот промежуток можно разбить на 2п промежутков точками < t2 < ... < t2n таким образом, чтобы на каждом отрезке вида [fs, ^8+1], где s = 1, ... , 2п - 1, лежала бы ровно одна особая точка, а на промежутке [t2n9 +°о) особых точек не было. В результате получаем 2п - 1 несобственных интегралов второго рода и еще один — первого.
На этом заканчиваем изложение теории несобственных параметрических интегралов и рассмотрим ее приложения.
429
$ 9. ПРИМЕНЕНИЕ ТЕОРИИ ПАРАМЕТРИЧЕСКИХ ИНТЕГРАЛОВ
Вычислим интеграл Дирихле В(а), называемый еще разрывным множителем Дирихле. По определению,
ч Гsinax , Л(а) = J dx.
О
Прежде всего заметим, что точка х = 0 не является особой, так как подынтегральная функция ограничена. Очевидно, что Р(0) = 0. Далее, если a > 0, то интеграл сходится по признаку Дирихле, поскольку
г .	,	1 - cosat 2
J sm a xdx = ------- < -.
о	a a
В этом случае возможна линейнця замена переменной интегрирования вида ах = t, и тогда имеем
D(a) = I d(«x)= J ~ dt = D(\) = D. 0	0
Если же a < 0, то a = -|a|, sin ax == -sin|a|x, откуда
4	?° sinax , r° sin|a|x ,	~
B(a) = J —— dx = -J —dx = -D.
о	0
Таким образом,
D(a)H
D при a > 0, 0 при a = 0,
-D при a < 0.
Вычислим теперь значение D.
ТЕОРЕМА 21. Справедливо равенство D = п/2.
► Рассмотрим параметрический интеграл g(y), где у е Y = [0, N], Ne Rn
/ \ г°e~yxsinx , 8<У) = J -T-- dx’
0
Подынтегральная функция f(x, у) = e~yx sin x/x непрерывна всюду на P = X x У, где X = [0, +°°), У = [0, АГ], если положить ДО, у) = 1.
Убедимся, что интеграл g(y) ско^пися равномерно на У. Для этого воспользуемся признаком Абеля. Положим а(х, у)= sin x/x, ₽(Х, у) = е ху. Тогда функция Р(х, у) монотонна и 0 < Р(х, у) < 1, оо
а интеграл J a(x, y)dx сходился равномерно на У, поскольку а(х, у) о
не зависит от у.
430
Равномерную сходимость g(y) можно установить и непосредственно из определения с помощью интегрирования по частям.
Возьмем теперь на отрезке Y произвольную точку J/o 0 и окружим ее некоторым отрезком У5 = [yQ -$,yQ + 5], целиком принадлежащим множеству У. На этом отрезке интеграл
оо	оо
J f'y(x, У)йх = -J е~Ух sin xdx о	о
сходится равномерно. Это следует из признака Вейерштрасса, оо
поскольку |е-х^ sin х| <	а интеграл / e^o^dx сходится,
о
Кроме того, подынтегральная функция sin х непрерывна на Р8 = Х X У§. Поэтому по правилу Лейбница для несобственных интегралов имеем
g'{y) = “J е~ух sin xdx. о
Последний интеграл можно вычислить интегрированием по частям. При этом g'(y) = 1/(1 + у2). Итак, мы показали, что функция g{y) непрерывна на У = [О, N], а ее производная g'(y) существует при всех у # 0 и равна -1/(1 + у2). Отсюда по формуле Ньютона—Лейбница при всех у е (О, N] вытекает равенство
у dt
g(y) = g(N) - J = g(N) + arctg N - arctg y.
Используя непрерывность функции g(j/) в точке у — 0, получаем
g(0) = lim g(y) = lim (g(N) + arctg N - arctg y) =
У -> o+	у -> 0+
= g(N) + arctg N.
Теперь, устремляя N к +<», приходим к соотношениям arctg N -» ->я/2,
|g(N)| < J	dx < J e~Nxdx =	0.
0	0
Отсюда следует, что
D = g(0) = lim {g(N) + arctg N) = л/2. ◄ ДГ-» oo
Непосредственно из теоремы 21 вытекает справедливость следующего утверждения.
СЛЕДСТВИЕ. При всех a е R имеет место равенство
D(a) = {п/2) sign a.
431
Лекция 21
§ 10. ИНТЕГРАЛЫ ЭЙЛЕРА ПЕРВОГО И ВТОРОГО РОДА
Гамма-функция Эйлера, которая была определена ранее, и бета-функция, определение которой будет дано ниже, называются соответственно интегралами Эйлера второго и первого рода.
Продолжим изучать свойства гамма-функции.
ТЕОРЕМА 22 (формула Эйлера—Гаусса). При s * 0, -1, -2, ... имеет место равенство
Г(8)= lim Pm(s), где р (8) = (m-iy.m» т s(s + l) ... (s + m-1)*
► Применяя формулу Эйлера, получаем выражение для Г(а):
1 п(1 +	1П1	+ £Г=Ит	1	П(1 + 1Г.(1+‘Г-
8 п = 1 х	П / х	Пу т-юо	s	п = 1 х Пу	х И /
= Ит 1 (1	+ 1Y	... (1 + -I- Y(	1	+ £ Г ... [1	+ -L- Г =
т -^оо § к J	к т — 1 '	х	1 у х	т — 1 '
= 1Ч“ооРт(«)-	<
ТЕОРЕМА 23 (формула Гаусса). При з > 0 в обозначениях теоремы 22 справедливо равенство
► С помощью замены переменной и интегрирования по частям получаем
(1 +	)8J (i - ^t^dt = (т + l)sf (1 - x)mx8~xdx =
0	i	0
= (тп + I)3 - J(1 - x)m~1xsdx = ...
8 0 1
... = (тп + l)8-----—---------J xs+^dx =
s(s 4-1) ... (s 4- m - 1) о
= (тп + I)8----—-------- = Pm+i(s). ◄
s(s 4-1) ... (s 4- m)
Имеет место следующее представление гамма-функции в виде несобственного интеграла.
ТЕОРЕМА 24 (интегральное представление для гамма-функции Эйлера). При s > 0 справедливо равенство
Г(з) = J xs-1e-xdx.
о
432
► Прежде всего заметим, чта при s > 1 рассматриваемый параметрический интеграл является несобственным интегралом первого ро<ца, а при О < s < 1 он имеет особую точку х = 0. Но в обоих случаях он сходится, поскольку в окрестности нуля подынтегральное выражение мажорируется функцией Xs-1, а на бесконечности — функцией е"х/2.
Рассмотрим разность Ят(з), где
Ят(«) =	- Рж+1(«)(1 + 1
т .	,	ч ч
S
В силу выпуклости графика функции g(y) = еу - 1 - у, при всех у имеем 1 4- у < еу, поэтому неравенства
И
-х
1 - - < е~х/п, п
справедливы при всех вещественных х и натуральных и. Кроме того, заметим, что из неравенства Бернулли при 0 < у < 1 следует, что (1 - у)т > 1 - тш/, т. е. 1 - (1 - у)т < ту. Отсюда при 0 < х < т иу = х2/т2 получаем оценки
Г = е~х( 1 - X1 - -"П < е~х( 1 - (1 +	1 -	=
0<е"х
= е~х
e~xxi m
Но в этом случае величина Rm(s) оценивается так:
т j _	оо
О < я_(8) < j -—— dx < - f x^le~xdx.
m q m	mJ0
Здесь s 4- 1 > 1, поэтому последний интеграл сходится, откуда
О < Rm(s) <	, где As — некоторая величина, зависящая только
от параметра з. Следовательно, Rm(s) -> 0 при m -> °о. Окончательно имеем
f x*~re~xdx = lim f x8-1e_*dx =
0	m->ooJ
= lim + Pm+i(s)(l + » - 0 + Hs) • 1 = Г(8).
433
Замечания. 1. Идея изложенного доказательства теоремы 24 высказана Шлемильхом (1879).
2. С помощью интегрирования по частям из теоремы 24 выводится следующая формула Коши, справедливая при всех значениях 8 вида -(т 4-1) < s < -т, где т € N:
r(s) = jtf-'te-1' - <pm(r))dx, О
где q>m(x) =	. Здесь условия, наложенные на з, обеспечивают схо-
димость несобственного интеграла, имеющего две особые точки: х - О и х = 4-оо. Действительно, в окрестности особой точки х = 0 подынтегральная функция эквивалентна величине х8 +	1, а в окрестности
(т 4-1)!
точки х = 4-оо является величиной порядка 0(r8+m l). Отсюда по признаку сравнения следует сходимость интеграла.
Далее потребуется представление функции sin тез в виде бесконечного произведения. Приведем его в качестве следующей леммы, которая будет доказана при изучении рядов Фурье.
ЛЕММА 3 (лемма Эйлера). При всех вещественных нецелых з имеет место формула
sin its = ns П (1 - ~ \ П - 1 К П2 '
ТЕОРЕМА 25 (формула дополнения Эйлера). При всех нецелых з справедливо равенство
Г(1-8)Г(8)=-" зшлз
В частности, Г(1/2) = Тл.
► Из формулы Эйлера и леммы 3 имеем
Г(1 - .)Ц.) -	- 1 П (1 - ! )-(1 + £ У -
= 1 п Г =5----------------------------2Е-.
8П	П Л8 П (1 -82/п2) 8ЮЯ8
п = 1
Второе утверждение теоремы прямо следует из первого. ◄
ТЕОРЕМА 26 (формула удвоения Лежандра). Справедливо равенство
Г(2з)Г(1/2) = 22в“1Г(з)Г(а + 1/2).
► Составим произведение Fm(s), где
F ,._22*-iPm(S)Pm(S + l/2)
P2m(2s)Pm(l/2)	•
434
Запишем явное выражение для Fm(s). Имеем
= 22,-1(m-l)!m*(/n-l)!m,+1/2 «28...(28 + 2т-1) • 1/2...(т-1/2) (2m-l)!(2m)28-1(7n-l)!m1/2s...(s + 7n- 1)(8 + 1/2)...(з + тп--1/2) *
При т -» 4-оо приходим к равенству
228 - хГ(з)Г(з + 1/2) = Г(2з)Г(1/2)
Рассмотрим теперь интеграл Эйлера первого рода, т. е. бе-
та-функцию Эйлера.
Определение 14. При а > 0 и р > 0 бета-функция Эйлера В(а, р)
задается равенством
1
В(а, р) = J- x^~ldx.
о
ТЕОРЕМА 27. При а > 1 и Р > 1 справедлива формула
в(а,В.г<2)Ш>. ' 1	Г(« + Р)
► В интеграле, определяющем функцию В(а, Р), выполним за-
мену переменной вида х = у/(1 + у). Тогда имеем
dx = ——— х“-1 — ——— (1 - х)₽-1 ------------------
ах (1+у)2’	(1+у)“-₽’и Х) (l+y)^1’
В(а R1 = Г Уа'1аУ ( ,Р) J а+у)®-1’ Отсюда следует, что
Н = В(а, р)Г(а + Р) = Г	.
Далее, если у > 0, то
Г(а + р) = Jx“+₽-1e"xdx = (1 + у)«+Р Jx“+₽-4r*J' + «dx. О	о
Поэтому
Я = +у)а + р fjxa+P-ie-xCy + Ddxldy» О (l+y)a р %	'
= jQ(x|/)<x"1xPe"x^ + 1)dxjdi/.
В последнем интеграле получаем
Н = J (J(ху)а~ге~хУхду \fi~re~xdx = Г(а) Jx^~xe~xdx = Г(а)Г(р). о %	*	о
435
Остается только обосновать перестановку порядка интегрирования. Подынтегральная ФУНКЦИЯ /(х, у) = Z/a“1Xa+P-1e"x^+1) всюду положительна и непрерывна. Кроме того, каждая из функций, т. е. интегралов
g(y) = J f(x, у) dx =	Р, Л(х) = J f(x, y)dy =
о	(1 + У) р	о
непрерывна и неотрицательна на [0, +оо) х [0, +°°), а несобствен-оо	оо
ные интегралы J g(y)dy и J h(x)dx сходятся. Следовательно, по-о	о
рядок интегрирования действительно можно изменить. ◄
Замечание. Поскольку гамма-функция Г(з) определена при всех s # 5^ 0, -1, -2, ... , формула теоремы 6 позволяет распространить определение функции B(a, Р) на все множество вещественных значений (а, 0), за исключением точек (a, Р), где либо величина а, либо величина В равна О,-1,-2,... .
Лекция 22
§11. ФОРМУЛА СТИРЛИНГА
Изучение эйлеровских интегралов завершим доказательством важной для приложений формулы Стирлинга, дающей приближенное значение для гамма-функции или для функции и!
ТЕОРЕМА 28 (формула Стирлинга). При з > 2 имеет место равенство
In Г(з) = (з + 1/2) In (з + 1/2) - (з-F 1/2) - In з + с0 + В, где cQ = In J2n, а для величины остатка R выполняются неравенства
► Воспользуемся равенством
Нт Р„(8) = Г(8).
Далее имеем п - 1 In Рп(б) = S In n - In 8 + ^Xjln Л - In (A? + s)).
Применяя формулу суммирования Эйлера, получаем
In Pn (s) =А - В, где
А = J (In х - In (х + s))dx + s In n - In s, В = J p(jc)f |-2“ Vх-
Сначала рассмотрим величину А. Имеем n-0,5	n-0,5	n-0,5	n+8-0,5
J In xdx - J In (x + s)dx = J In xdx - J In xdx = 0,5	0,5	0,5	«+0,5
8+0,5	n+e—0,5
= J In xdx - J In xdx = Аг - A2. 0,5	n-0,5
Интегрируя, находим
= (x In x - x)|^50’5 = (8 + 1/2) In (s + 1/2) - s + In 2/2.
Далее будем считать, что п > 2s. Тогда, применяя формулу In (1 + х/п) = О(х/п), получим п+8-0,5	8-0,5
з In п - А2 = J (In п - In x)dx = -J ln(l + x/n)dx = n-0,5	-0,5
s-0,5
= J O(x/n)dx = O(s2/n). -0,5
437
Таким образом, приходим к соотношению
А = (а + 1/2) In (s + 1/2) - в + In s + сх + O(s2/n),
где сх — постоянная.
Рассмотрим теперь величину В. Заметим, что неравенство
"5 < / P(x)dx < 0 8	0,5
справедливо при всех t > 0,5. Поэтому, согласно признаку Ди-оо . .
рихле, интеграл J dx сходится. Следовательно, 0,5 *
f ^dx = c2 + o(l).
0,5 Х ,+f°’5p(x) .
J r dx применим вторую теоре-0,5 X + S
п 4- 0,5
Для оценки величины В2 = му о среднем. Тогда получаем
Вг- 1
откуда- 1	< В2 < 0. Но по определению В = В1~ В2. Следова-
8s “Ь 4
тельно, из равенства In Pn(s) =А- В вытекает соотношение
In Pn(s) = (s + 1/2) In (s + 1/2) - (s + 1/2) - In s + c0 + B2 + O(s2/n), где c0 — некоторая абсолютная постоянная. Устремляя п к бесконечности, приходим к равенству
In Г(з) = (з + 1/2) In (s + 1/2) - (s + 1/2) - In 8 + с0 - 0/(8s + 4), где 0 = 0(з) — некоторая функция с условием 0 < 0 < 1. Осталось вычислить значение константы с0. Для этого воспользуемся формулой Лежандра. Тогда при з -» +°° имеем
(2з - 1) In 2 + In Г(з) + In Г(з + 1/2) =
= In Г(2з) + In Г(1/2), (s + 1/2) In (s + 1/2) - (s + 1/2) - In s +
+ co + (S + 1) In (s + 1) — (s + 1) - In (8 + 1/2) + Cq + + 0(1/8) + (2s - 1) In 2 = (2s + 1/2) In (2s + 1/2) -- (2s + 1/2) - In (2s) + c0 + In Jit + O(l/s).
Воспользовавшись соотношением
In (s + a) = In s + a/s + O(l/s2), получим
(s + 1/2) In s + 1/2 + O(l/s) - (s + 1/2) + c0 - In s +
+ (s + 1) In s + 1 + O(l/s) - (s + 1) + c0 - In s + (2s - 1) In 2 = = (2s + 1/2) In 2 + (2s + 1/2) In s + 1/2 + O(l/s) -<
- (2s + 1/2) - In 2 - In s + c0 + Jit.
438
Приводя подобные членьь приходим к равенству с0 = In 72л + O(l/s)9
откуда имеем с0 = 1п 72л. ◄
Отметим, что если снова воспользоваться соотношением
In (з 4- а) = In з 4- a/s + O(l/s2), то из теоремы 1 можно получить еще один вариант формулы Стирлинга вида
In Г(з) = (з - 1/2) In з - з 4- In72л 4- О(1/з).
В частности, при s = п + 1 отсюда имеем
In Г(п 4-1) = In и! = (п 4- 1/2) In п + 1 - (п 4-1) 4- 1п72л 4- О(1/п) = = п In п - п 4- In 72 л и 4- О(1/п).
Следовательно, справедлива асимптотическая формула
и! = 72лп ео(1/л) = J2nn (1 4- О(1/п)), которая тоже называется формулой Стирлинга.
Более тщательные вычисления позволяют получить оценку вида 0 > R > -1/(24з 4-12) для остатка R в асимптотической формуле теоремы 28. Этот результат был установлен Гауссом. Он же доказал, что величину в асимптотической формуле для и! можно заменить на ее", где 0 < 0П < 1/(12п).
Разумеется, теория эйлеровских интегралов не исчерпывается доказанными здесь утверждениями, однако рамки данного курса требуют ограничиться рассмотренными вопросами.
ГЛАВА 18
Ряды и интегралы Фурье
Лекция 23
§ !• ПРЕДСТАВЛЕНИЕ ДРОБНОЙ ДОЛИ ВЕЩЕСТВЕННОГО ЧИСЛА ТРИГОНОМЕТРИЧЕСКИМ РЯДОМ. ФОРМУЛА СУММИРОВАНИЯ ПУАССОНА. СУММЫ ГАУССА
Эта глава в основном посвящена изучению тригонометрических рядов Фурье. Важность рассматриваемой темы обусловлена той большой ролью, которую играют ее приложения не только в математике, но и в механике, физике и других научных дисциплинах. Во многом это обусловлено тем, что тригонометрические ряды Фурье соединяют в себе особенности как тригонометрических рядов, так и общих рядов Фурье. Заметим, что при знакомстве с очередным утверждением полезно отмечать для себя, какую из двух указанных сторон теории оно по преимуществу отражает;
Обширность темы не позволяет сколько-нибудь полно охватить в курсе лекций даже классические ее аспекты, поэтому ограничимся наиболее простыми теоремами, отражающими общую ситуацию. В конце главы коснемся некоторых вопросов элементарной теории интеграла Фурье. Сначала дадим основные определения.
Определение 1. Функция Рп(х) вида
а0 £
Рп(х) =~2 + cos kx + Ьь sin fex) называется тригонометрическим многочленом степени п или порядка п.
Поясним, почему при определении одночлена «нулевой степени» а0/2 коэффициент а0 берется с числовым множителем 1/2. Дело в том, что указанная запись позволяет единообразно представить коэффициенты а0, ар ... , ап и Ьр ..., Ъп в следующем виде:
а* = i J Рл(х) cos kxdx, bk = i J Pn(x) sin kxdx, 71 0	71 0
где k = 0, 1, ... , n.
440
Определение 2. Функциональный ряд вида
aQ 00
Z/n(x) = у + kL1(ak cos kx + bk sin kx) называется тригонометрическим рядом, точнее, формальным тригонометрическим рядом.
Замечание. В определениях 1 и 2 аргумент х может принимать любые числовые значения. Поэтому вместо независимой переменной х можно рассматривать любую функцию х = (p(f). Полученный таким образом формальный функциональный ряд будем также называть тригонометрическим рядом.
Определение 3. Если существует функция g(x) такая, что все коэффициенты ak и bk тригонометрического ряда Е /л(х) могут быть выражены по формулам Эйлера—Фурье вида
1 2п	1 2п
ak = - J g(x) cos kxdx и bk = - J g(x) sin kxdx, k = 0, 1, ...,
то этот ряд называется тригонометрическим рядом Фурье функции g(x). При этом интегралы во всех формулах могут быть и несобственными.
При изучении тригонометрических рядов возникают, в основном, те же вопросы, что и в случае любых функциональных рядов. Например, для конкретного ряда можно ставить задачу определения области сходимости и функциональных свойств его суммы. Можно также рассматривать вопросы о представлении данной функции в виде тригонометрического ряда, о единственности такого представления, о специальных признаках сходимости ряда в точке и на некотором множестве, о правилах почленного интегрирования и дифференцирования ряда и т. д.
С другой стороны, будут доказаны неравенство Бесселя, равенство Парсеваля и другие утверждения, отражающие свойства общих рядов Фурье. Следует отметить, что коэффициенты ряда Фурье конкретной функции несут полезную информацию о ней даже и тогда, когда ряд расходится. В этом случае существуют различные способы ее извлечения. В частности, большую роль здесь играют методы суммирования расходящихся рядов, о которых упоминалось ранее.
Но сначала разберем пример, важный для дальнейших приложений. Рассмотрим тригонометрический ряд f(x) вида
ч v sin2nfcx
Его n-ю частичную сумму обозначим через зл(х). Определим функции р(х) и р0(х), полагая р(х) = | - {х} и
441
J p(x), если x — нецелое число, Po'x) ~ [ 0, если x — целое число.
Функция р0(х) называется функцией Бернулли.
ТЕОРЕМА 1. При натуральном п справедливы формулы р(х) = sn(x) 4- оп(х), р0(х) = зп(х) + гп(х), причем
|п„(х)| < В„(х), Iг„(х)| < Я„(х),
4
a)	s^(x) = Tn(x) - 1;
6)	|Tn(x)| < 2n 4-1;
где Rn(x) =	=.
71 4- n2 * * sin2 nx
Доказательство теоремы опирается на следующие две леммы и проведено ниже.
Введем еще одно обозначение. Положим
п
Т„(х) = Е cos 2лЛх =1 + 2 cos 2 лх + ... + 2 cos 2лпх. ' k = -п
ЛЕММА 1. Имеют место соотношения:
B)J T„(x)dx = l;
г) Т (X) = sin7t*(2ft 4-1) 7	7 sinrcx
► Утверждения а)—в) очевидны. Рассмотрим утверждение г). Имеем 2 cos ax sin ₽х = sin (a 4- p)x - sin (a - p)x, откуда следует, что
1 n
Т-(х) =	, E 2 cos 2лЛх sin лх =
n ’ 2smnx
1 n
= k ?-n (8*п	+	“ s *in - l)x) =
_ sinjt(2n + l)x - sinn(-2n - l)x _ sin7t(2ra + l)x
2sinnx	sinnx
ЛЕММА 2. При 0 < 8 < 1/2 справедлива оценка
/ Tn(x)dx = 8
► Функция Тп(х) — периодическая с периодом 1 и четная, поэтому
1/2	-8	1-8
J T„(x)dx= / T„(x)dx= J T„(x)dx=A
8	-1/2	1/2
Положим a = тс(2и 4-1), тогда
== 1Г 5 sinax f/2 sinrcx = _1 fcosaxli -s a \ sinKX|i/2
1-8
J Tn(x)dx < 1/2
4
71 + (2n + I)2sin7t5
dx = _l1r’8dcosax = a f/2 sinrcx
- f cos axd\ -Д— 1).
1/2	VsinitX//
442
На участке интегрирования функция sin пх монотонно убывает, а функция ф(х) = 1/sin тех монотонно возрастает, поэтому ф'(х) > 0. Кроме того, |cos ах\ < 1, и при х = 1/2 имеем cos ах =
= cos (2n + 1) = 0. Следовательно,
1-5 f COS 1/2
axd\ -Д— кзшлх
ч	1 -«	1-5
I = J созахф'(х)</х < J y'(x)dx =
7	1/2	1/2
1 зтлб
Отсюда, учитывая, что
cosoxli - s Sin7tX|l/2
< —-, имеем зшлЗ
|A|<
2 азтлЗ *
Далее, так как функция у = sin х/х убывает на промежутке (0, л/2) и лЗ < л/2, то имеем
зшлЗ	зш(л/2) = 2 лЗ	л 1	1
лЗ л/2 л ’ sin л 8	2 ’ sin л 8	28 ’
Следовательно,
IAK-2--V---------1----.
11 а-28 а8 к(2п +1)8
Если теперь---------- < 8 < 1, то lAl < 1, а если 0 < 8.<---,
л(2п +1)	2	11	я(2п +1)
то в силу оценки |Tn(x)| < 2n + 1 имеем
|А| = 78 Tn(x)dx ?= | - J Tn(x)dx < 1 + 8(2n + 1) < 1 + 1 < 1.
Таким образом, справедлива оценка
|А| < min fl, —Д—-1 < 2 min f 1, —Д—- 1 < ----*------ ,
V айшлЗУ	V азшлЗ /	+ a2sin2n6
так как при любых х > 0 и у > 0 имеет место очевидное неравенство
Докажем теперь теорему 1. Значения функций р(х) и р0(х) отличаются только в точках вида х = z, где z — целое число. Проверим сначала справедливость утверждения теоремы для этих точек. Действительно, имеем
on(z) = оп(0) = р(0) - зп(0) = 1/2 < 4 = Вп(0), Tn(z} = гп(0) = ро(О) - зп(0) = 0 < 4 = Яп(0).
443
Если же х нецелое, то ал(х) = гп(х) и достаточно ограничиться рассмотрением одной только функции стл(х). Поскольку обе функции |ол(х)| и Rn(x) четные и периодические с периодом 1, можно считать, что 0 < х < 1/2. В этом случае
[ Tn(y)dy = f (1 + 2 J 1Cos 2nky}ly = x + J	= x + sn(x).
Но так как 0 < x < 1/2, то {x} = x и p(x) = 1/2 - {x} = 1/2 - x, x = 1/2 - p(x). Следовательно,
I Tn(y)dy = 1/2 - p(x) + s„(x) = 1/2 - o„(x), 0 откуда
x	1/2	1/2	1/2
o„(x) = 1/2- Jr„(y)d!/ = 1/2- j Tn(y)dy + f Tn(y)dy = j Tn(y)dy.
0	0	x	x
Теперь для оценки ал(х) применим лемму 2. Получим
1/2
|ол(х)| = I Tn(y)dy <
__________4___________
71 + (2л + l)2sin2Ttx
4
71 + n2sin2Ttx
=ад.
Теорема 1 доказана. ◄
В качестве простого следствия теоремы 1 докажем еще одну теорему.
ТЕОРЕМА 2. При п -> 0 имеем:
а)	зл(х) -+ р0(х);
б)	если 8 > ОI = [8, 1 - 8], то sn(x) р(х) и зп(х) р0(х).
► Утверждение а) эквивалентно тому, что последовательность гл(х) -> 0 при п -> оо. Это действительно так, поскольку гл(0) = О при всех и, а если х — нецелое число, то |ал(х)| < /?л(х) -> 0. Утверждение б) следует из признака Вейерштрасса, поскольку величина |зл(х)| мажорируется на I бесконечно малой числовой по-
следовательностью Ял(х) = z -- -------. ◄
71 + n2sin2rcx
ТЕОРЕМА 3 (формула суммирования Пуассона). Пусть а < Ь — полуцелые числа, т. е. числа вида г + 1/2, где г — целое число. Пусть функция /(х) имеет производную f'(x), непрерывную на X = [а, &], |/'(*)l < М. Тогда при любом натуральном N справедлива формула
N ье
S = Е J(n) = S J /(х) cos 2nnxdx + R„, а < n < b' v n =	™
где
ip I < 8M(b-a)\nN
444
В частности, при N -> оо
S = S , f(ri) = S' ( f[x) cos 2nnxdx. а < n^b ' v ' n = -oo J 1 ' '
oo
Здесь символ n 27^ означает, что сумма ряда берется в смысле главного значения по Коши.
► Применим к сумме S формулу суммирования Эйлера. Получим
ь	ь
S = J f(x)dx - J p(x)f'(x)dx. а	а
По теореме 1 имеем р(х) = sN(x) = cv(x). Следовательно,
ъ	ь
S = f f(x)dx - f S/^xyf'ixydx + RN, a	a
b
где RN = - f oN(x)ff(x)dx. Интегрируя по частям и учитывая, что а
s^a) = Sj^b) = 0, получаем ь	ь	ь	ь	
J f(x)dx - J s^xjf '(x)dx = f f(x)dx - f(x) 8^х)|*+ J s^(x)f(x)dx = a	a	a	a
f	f f N	\	N bt
= J f(x)dx 4- J f(x)lk %_N cos 2nkx - 1 \dx = k S J f(x) cos 2nkxdx. a	a 4	•'a
Осталось оценить остаток RN. Применяя теорему 1 и учитывая, что |Л(я)} < М, получаем оценку
b	.
________dx_______ а л/1 + N2sin27tx
l-Bj= I vN(x)f'(x)dx < 4М f а
Подынтегральная функция в последнем интеграле периодичная с периодом 1 и четная, поэтому
1/2 я	/1/ЛГ	1/2 я \
|E„|<8M(b-a) |	.. dx ^<8W-a)(J dx + j ^-J =
о 71+№sin2nx	ko
= 8M(&-a)(l +
1I1N/2V SM(b-a)hiN 2N ) W
Изящное приложение формулы суммирование Пуассона дал
Дирихле. Он нашел точное значение сумм Гаусса вида Z, cos ——, п “1 N
х sin . Упомянем еще об одном красивом применении формулы Пуассона, данном в 1903 г. Г. Ф. Вороным, к задаче
445
о нахождении асимптотического выражения для количества целых точек под гиперболой (эта задача называется проблемой делителей Дирихле). Остановимся на вычислении значений сумм Гаусса. Гаусс в своих «Арифметических исследованиях» предложил несколько разных способов их вычисления, но мы будем основываться на методе Дирихле.
ТЕОРЕМА 4. При натуральном N справедлива следующая формулах
G(N) = Е, е2яи2/х = 1+Г^ "-1	1 + Г1
► Напомним формулу Эйлера:
= cos ф 4- I sin ф,
где ф — действительное число. Записывая формулу суммирования Пуассона в комплексной форме, при k -> оо получаем
2k
G(N) = ml._2kI(m) + R, где
Дт) = J e } dx,B = OI^S^l.
0,5	V k '
Преобразуем интеграл Дт). Имеем
N + 0,5
1(тп) = J e2ni((x+0,5znN)2/N-m2N/4)dx =
0,5
-2ni^ M0,5m + 1) + 0,5 2jt<£
= e 4 J e Ndy.
0,5mN + 0,5
Суммируя величины Дт) отдельно по четным числам тп (тп = 21) и отдельно по нечетным числам тп (тп = 2Z - 1), получаем

W(i + l) + 0,5	k -*£!L W +0,5)+ 0,5 2ni^
J e Ndy+ Y e 2 f e Ndy + R =
Nl + 0,5	=	N(l - 0,5) + 0,5
JV(* + l) + 0,5 2nil£	W(fc + 0,5) + 0,5 2)t^
J e N dy + i~N f e N dy + R =
-Nk + 0,5	N(k - 0,5) + 0,5
= JN(1 + i~N) f e2nl*2dz + OtN-^k-1/2) + R,
—oo
так как при | a | < Jn имеет место неравенство
+| e2*lz2dz
k JN + a

446
Переходя к пределу при k —> оо в последней формуле для G(N), получаем	.х
G(N) - 7^(1 + i~N) J e2*ilc2dz.
—oo
В частности, при N = 1	*
1 = G<1) = (1 + H) J e2*iz2dz.
Следовательно,	~°°
1 + i-N —
Далее потребуется выражение характеристической функции ф(х) = ф/х) промежутка I = [а, Ь], где 0 < а < Ь < 1, через функцию р0(х).
Определение 4. Функция ф(х) = Ф/х), заданная на отрезке [О, 1],
ф(х) =
1, еслиа<х<Ь,
1/2, если х = а или х = Ь, О, если х < а или х > &,
называется характеристической функцией промежутка I.
Л EMMA 3. При х е [0, 1] справедливо равенства
ф/х) = (Ь - а) + р0(х - а) - р0(х - &).
► Обозначим через Дх) правую часть доказываемого равенства. Очевидно, при всех х * а или Ь имеем
/'(х) = Ро(х - а) - Pq(x - Ь) = -1 + 1 = 0.
Следовательно, f\x) — кусочно-постоянная функция, как и функция ф/х). При этом точки их разрыва совпадают. Кроме того,
f(a) = Ь - а + ро(О) - р0(а - Ь) = Ъ - а + р0(Ь - а) = = Ь - а + 1/2 - (Ь - а) = 1/2.
Аналогично проверяется равенство ДЬ) =1/2. Также имеем
Ла + Ъ\ .	,	(Ь-а\	(а-Ь\
Ч 2 J “& а + ро[ 2 J р4 2 J “
,	, о (Ъ-а\	,	, - лЪ-а . (а + Ъ\
= b-a+ 2р0^~=Ь- a + l-2-у = 1 = ф^—g-J.
В точке х = а обе функции имеют скачок, равный +1, а в точке Ъ этот скачок равен -1. Это значит, что обе функции совпадают во всех точках отрезка [0, 1]. ◄
Из леммы 3 и теоремы 1 непосредственно вытекает справедливость следующей леммы.
447
ЛЕММА 4. При всех п > 1 справедлива формула фДх) = (b - а) + sn(x -a)- sn(x -b) + Еп(х), где
|Е„(х)| < -===== + .	4	=.
71 4- n2sin2n(x - а) 71 + n2sin2n(x - Ъ)
Аналогичное утверждение имеет место и для любой кусочнопостоянной функции, периодической с периодом единица и равной полусумме своих предельных значений слева и справа в точках разрыва.
Лекция 24
§ 2. НЕРАВЕНСТВО БЕССЕЛЯ. ЗАМКНУТОСТЬ И ПОЛНОТА ОРТОНОРМИРОВАННОЙ СИСТЕМЫ ФУНКЦИЙ
Начнем рассмотрение со следующего определения, предложенного Лебегом.
Определение 5. Точка х0 называется регулярной точкой функции f(x), если существуют ее левый и правый предел^ при х, стремящемся к х0, а ее значение f(x0) в этой точке равно их полусумме. В этом случае говорят, что функция f(x) регулярна в точке х. = х0.
Очевидно, что каждая точка непрерывности данной функции является ее регулярной точкой.
Определение 6. Функция f(x), регулярная в каждой точке промежутка I, называется регулярной на этом промежутке.
Определение 7. Периодическая функция, имеющая.конечное число точек разрыва на каждом отрезке вещественной прямой и регулярная в этих точках, называется строго регулярной функцией.
Определение 8. $сли периодическую функцию g(x) можно представить в виде	। ,s
g(x) = f f(f)dt + g(a),
где /(t) — строго регулярная функция, то функция g(x) называется строго кусочно-гладкой функцией.
Эти определения мы будем использовать при изучении тригонометрических рядов Фурье.
Множеством = Wt всех строго регулярных функций, имеющих один^и тот же период I > 0, образует линейное пространство. Справедливости этогр утверждения легко проверяется.
Для каждой пары функций /(х) и g(x) из этого множества W зададим функционал Т(Д g) по формуле
T(f, g) = xj f(x)g(x)dx.
О
Здесь х > О — произвольное фиксированное число, которое назовем весовым коэффициентом*
Приведем ряд свойств функционала Т(Д g).
1°. Симметричность, т. е. T(f, g) = T(g, f).
449
15-4953
2°. Билинейность, т. е. при любых aufieRuf9g9heW T(f, ag + $h) = aT(f9 g) + рТ(Д h).
3°. Положительная определенность, m. e.\
а)	Т(Д П > 0 при всех feW;
б)	Т(Л f) > О, если только f(x) отлична от нуля хотя бы в одной точке.
Последнее неравенство следует из того, что если /(х0) = yQ # О, то либо левый предел 119 либо правый предел 12 этой функции в точке xQ отличен от нуля, и тогда при некоторых е > 0 и 5 > О для всех точек левой или правой 5-полуокрестности точки х0 справедливо неравенство | f(x)\ > е. Следовательно,
1
Т(Д /) = xj ^(х)дх > хбе2 > О, о
что и означает справедливость утверждения 36).
Другими словами, билинейный функционал Т = Tt х, заданный на декартовом произведении Н = W х W9 можно рассматривать как скалярное произведение, определенное на пространстве W. Поэтому вместо символа Т(/, g) можно писать просто (/, £).
Определение 9. Функциональная последовательность fn(x) е W называется ортогональной системой функций9 если при всех тп # п имеем (fn9 fm) = 0, тп. е. fm и fn ортогональны между собой.
Если при этом для всех пе Nвыполнено условие J(fn9fn) = 1, то эта последовательность называется ортонормированной системой функций.
Напомним, что величина 7(Л/) = ||/|| называется нормой функции f(x) относительно введенного нами скалярного произведения. Заметим, что одновременно это число является нормой функции f(x) в пространстве Ь2 всех функций, заданных на отрезке [О, Z], квадрат которых интегрируем по Лебегу на этом отрезке. Известно, что функциональное пространство Ь2 удовлетворяет аксиомам гильбертова пространства. Однако, так как систематическое изучение теории интегрируемости по Лебегу осталось за пределами нашего курса, этого вопроса далее мы касаться не будем.
Итак, ортонормированная система функций — это такая функциональная последовательность fn(x) е W9 все члены которой взаимно ортогональны и норма каждого члена равна единице.
Определение 10. Число сп »= cn(g) = (/n, g) называется коэффициентом Фурье функции g(x) е W по ортонормированной системе функций F = {fn}. Функциональный ряд IL^cJ^x) называется рядом Фурье функции g(x) по ортонормированной системе функций F.
450
Введенное понятие, и есть общее определение ряда Фурье по ортонормированной системе функций. <
Коэффициенты Фурье сп можно вычислить и для функций g(x), не обязательно входящих в W. Например, для интегрируемых на I = [О, Z] в собственном или даже в несобственном смыс-i
ле, если только все интегралы J fn(x)g(x)dx существуют. И в этом о
случае ряд Е cnfn(x) можно назвать рядом Фурье функции g(x) по системе F. Однако такой подход вполне оправдан лишь в том случае, когда функция g(x) принадлежит области определения введенного нами ранее скалярного произведения. В частности, это означает, что для этой функции существует ее скалярный 1
квадрат (g, g) = х J g2(x)dx. Именно это условие будет положено * ь \ .о
в основу определения общего понятия ряда Фурье по ортонормированной системе функций F.
Определение 11. Пусть функция g(x) удовлетворяет условию
z
'	(g, g) = xj g2(x)dx < +°°. ;
< о
Тогда функциональный ряд Z cnfn(x), где fn(x) e F и cn = (g, fn), называется «стандартным» рядом Фурье по ортонормированной системе F = {fn}. В случае, когда скалярный квадрат (£, g) расходится, но все коэффициенты сп = (g, fn) существуют, соответствующий ряд lLcnfn(x) будем называть «нестандартным» рядом Фурье по системе функций F.
Важным примером ортонормированной системы на отрезке [0, 2л] относительно скалярного произведения с весовым коэффициентом х = 1 является система функций
{1 cosx sinx cos их sinnx
—— -    е ф е ——  — —— е е е >в
а/2л’ л/п ’ а/л	л/л л/л * J
Если же положить х =? 1/п, то ортонормированной системой является система функций
„ [ 1 • «1
F9 = < —, cos х, sm х, ... , cos nx, sin пх, ... k
2 [72’	J
В этом случае ряд Фурье можно записать в следующем виде:
s fn(x) =	j (an cos пх + bn sin пх).
451
15*
По существу, мы получаем определенный ранее тригонометрический ряд Фурье. Легко убедиться, что и рассмотренный выше
тригонометрический ряд S,	является рядом Фурье
п “ 1 лсп
функции рв(х) по ортонормированной системе функций
F3 = {1, л/2 cos 2лх, л/2 sin 2лх,..., «/2 cos 2ппх, J2 sin 2ппх,...}
на отрезке [0,1] со значением х = 1.	>
Аналогично, на отрезке [О, Z] при х = 1 ортонормированной
является система функций
F4 = {1/a/Z, а/2/Z cos 2лх//, J2/1 sin2nx/Z,...
... , J2/1 cos 2nnx/l, -J2/1 sin 2nnx/l,...}.
Ряд Фурье по системе функций F4 будем называть тригонометрическим рядом Фурье по отрезку [0, /].
Для коэффициентов Фурье сп функции g(x) справедлива следующая теорема.
ТЕОРЕМА5 (неравенство Бесселя). Для любой ортонормированной системы F = {ДД и любой функции g(x) с условием (g, g) < +°° при произвольном т е N справедливо неравенство
< (g, g), где ck = (g, fk), k = 1,..., m.
► Рассмотрим функцию
8m = gmM =
Положим h = hm(x) = g(x) gm(x)- Тогда получаем
(a f i= S c(f = JC"GpHn<zn’
V&zn» fn* k - 1'	' n* I Q ПрИ n >
у. ч (Сд ПрЙ 71 > TH, ("m’ In) ~ cn (gm’ In> ~ j о при n < m
Отсюда имеем (m	m \ m m	m
*?	Л fnfn) = *5 ln5 ic*cn(4» 4) “ *5 Xе*-
Следовательно, m (gm, A) = (A,gm) = fe51Cfe(ft,4) = 0.
Поэтому
(g, g) = (gm + h,gm + h) = (gm, gm) + 2(gm, h) + (й, Л) =
= (gm, gm) + (Л, Л) > (gm, gm) = J ч
452
Заметим, что попутно доказано равенство
ТП	'	,
(Я,^) = кХ1с2 + (й,й).
Определение 12. Функцию gm(x) теоремы 1 будем называть т-м многочленом Фурье по ортонормированной системе F.
Из теоремы 5 непосредственно следует справедливость двух утверждений, которые мы сформулируем в виде Следующей теоремы. ТЕОРЕМА 6. Ft условиях теоремы 5:
а)	справедливо неравенство	, 
JS/i <1И1а - (*» <);
б)	сп = сп№) 0 при п^оо.,
Определение 13. 1. Ортонормированная система F = {fn} называется замкнутой в линейном пространстве V, если
Это равенство называется равенством Парсеваля.
' 2. Ортонормированная система F — {fn} называется полной в линейном пространстве V9 если для любой функции g£ V с условием (g, fk) = 0 при всех k е N выполняется равенство (g, g) *= 0.
УТВЕР)КДЕНИЕ 1. Всякая замкнутая ортонормированная система функций является полной.	-
► Предположим прЬтйвное, т. е. будем считать,) что (g, g) > 0, но
= ck(S) = 0 при всех k е Nt Тогда 6 силу замкнутости ортонормированной системы функций имеем
о < (g, g) = Ec^fe) = b, что невозможно. ◄
ТЕОРЕМА 7 (свойство экстремальности коэффициентов Фурье). При любых вещественных ар t... , Qtm справедливо неравенство
g~ ’
где ср ..., ст — коэффициенты Фурье по системе функций F = {fk}. ► Снова воспользуемся равенством (hm, fk) = (g - g^, fk) = 0, справедливым при всех k < т. Получим
т 2 II	' т	2
т	I 2
= II«-*JI2.+ »?1(c*-afc)4| =
Im | 2	| m ||2
g— X cbfb + S — ab)2 > g— Z cjd . ◄
453
Лекция 25
$ 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ ФУНКЦИЙ
Нашей целью является доказательство равенства Парсеваля для ортогональной тригонометрической системы функций
Fo ~ {4(х)} = {1/2, cos х, sin х,..., cos пх, sin пх, .v}.
ТЕОРЕМА 8 (теорема Ляпунова). Тригонометрическая система Fo замкнута в пространстве W2jt. Другими словами, для любой строго регулярной и 2п-периодической функции g(x) имеет место равенство Парсеваля вида
i J g2(x)dx - у + t (а| + bl),
где коэффициенты ak и bk определяются через g(x) по формулам Эйлера—Фурье.	*
Прежде чем доказывать эту теорему, заметим, что если функцию /х(х) = 1/2 в системе Fo заменить на h^x) = 1/72, то система Fq преобразуется в систему F29 ортонррмированную относительно весового коэффициента х = 1/л. Точнее, получаем систему функций F2 = {hk(x)}9 причем если k = 1, то йх(х) = 1/72, если же k = 2п, то hk(x) = h2n(x) = cos пх; а если к = 2п + 1, то hk(x) = = й2л+1(х) = sin пх* Коэффициенты Фурье, ck функции g(x) по системе F2 при k = 1, 2, ... связаны с величинами ak и bk следующими равенствами:
а0 ^72, ak-=т с2к9 Ьк = с2Л + 1, k = 1, 2,... , поэтому равенство Парсеваля можно записать в виде
1 2л	оо
(g, g) = £ j g2(x)dx = х cl,
что согласуется с определением замкнутости о^тонормирован-ной системы, данным ранее.
Доказательство теоремы 8 опирается на следующие две леммы.
Л EMMA 5. Для каждой строго регулярной функции g(x)9 периодической с периодом 2л, и любого е > 0 найдется тригонометрический многочлен Рт(х), удовлетворяющий условию
||g(x) - Рт(х) |[ < Е.
454
В терминологии гильбертовых пространств это означает, что тригонометрические многочлены {Рт(х)} являются всюду плотным множеством в4 линейном пространстве W = W2n по норме гильбертова пространства Ь2-
► Рассмотрим функцию gr(x) — g(2nx). Она имеет период I = 1 и тоже является строго регулярной. Точки разрыва х19 ... , хп этой функции разбивают отрезок I = [0,1] на интервалы 119..., 1п. На каждом из них функция g^x) непрерывна и имеет левый и правый пределы. Следовательно, на каждом интервале 1к функция gx(x) равномерно непрерывна. Это значит, что при любом ех > О интервал Ik можно разбить на конечное количество непересе-кающихся промежутков так, чтобы колебание функции gx(x) на каждом* из последних не превышало ех. Теперь рассмотрим функцию g2(x), которая является непрерывной на любом из указанных промежутков и равна на нем значению функции gx(x) в его центре. Будем также считать, что в смежных точках этих промежутков g2{x) равна полусумме сво'йк пределов слева и справа. Тогда очевидно, что g2(x) — кусочно-постоянная и строго регулярная функция, причем при всех вещественных х справедливо неравенство
tel(*) - £2(х)| < е1-
Отсюда имеем
fl	li
||£1(я) - g2(*) II = !(#1(х) - g2(x))2dx < fefdx = ех.
У О	N о
Пусть теперь 0 —	< tr < .•. < tk < 1 — все возможные точки
разрыва функции g2(x) на промежутке [0,1). При п = 1,..., k определим функции <рп(х), периодические с периодом 1 и задаваемые на отрезке [0, 1] условиями »
<М*) =
1
1/2 при х
О в остальных случаях.
Тогда, очевидно, при некоторых постоянных <хх, ... , аЛ имеет место равенство
£2(Х) = Ж<М>П(*)-
Но ранее было установлено, что
Фп(*) = tn - t„-i + Р0(* - *„-1) - Ро(* - tn).
455
L
Поэтому при некоторых Ро, Рр ...., Pfc имеем
Кроме того, выше было доказано, что
IРо(* - М - sm(x - t„)| < Rm(x - tn),
где m > 4 и
Sm(x) = kf1^^,Rm(x) =
Следовательно, справедлива оценка
4
71 + /n2sin2nx
l^(x)-Qm(x)|< £ JPjBJx-Q,
где Qm(x) = p0 + Ъ P„8OT(x - t„). Применяя неравенство Коши, отсюда получаем , .
1г2(*) - <U*)I2 < („? J₽A(x - и)2 < „? A? хМ<х -1„). Интегрируя это неравенство по отрезку [О, 1J, в силу периодичности функции Rm(x) находим
||g2(x) - Qm(x) ||2 = j(g2(x) - Qn(x))2dx < О k	k 1	k №	1
< „5, P.2.?,!W - «JI* - s*.?, p2 I /*	<
о	о 71 + m2sm2rtx
< 8fe S, p2 1 J2 - m<ix  < 3* f R2f < d, m J i+m2x2	1+^2 m
где A — некоторая величина, не зависящая от тп. Далее, используя неравенство треугольника, получаем Q (^i(x) - Qn(x))2dx]i/2 = ||g^x) - Qm(x)|| = “ 8m < ll^i(x) - g2(x) || + ||g2(x) - Qm(x) || < ex 4- (A/m)V2.
Но тогда, производя замену переменной интегрирования вида х = </(2л) и полагая Pm(t\ = Qm(#/(2x)), имеем
- К;	illsw-p.mll2-
Следовательно,
||g(t) - Pm(t)) II < 72 (ех + (A/m)V2).
456
Очевидно, что функция Pm(t) является тригонометрическим многочленом порядка т. Кроме того, при gj = е/4 и т > 8А/е1 2 * имеет место неравенство
, + ...
откуда окончательно получаем ||g(t) - Pm(t) || < е.
ЛЕММА 6. В условиях теоремы 5 для т-го многочлена Фурье функции gm(x) функции g(x) справедливо соотношение
ll*m II = ||<(х) - gm(x) || при т оо.
► Согласно свойству ? экстремальности коэффициентов Фурье, для любого тригонометрического многочлена рп(х) порядка п имеет место неравенство
И*) - gn(x) II < IИх) -р„(х) ||.
В силу того же свойства при всех натуральных k
И*) - gk+l(x) II < И*) - gk(x) II,
поскольку при п = k + 1 многочлен Фурье gk(x) можно рассматривать в качестве тригонометрического многочлейа рп(х).
Теперь при произвольном е > 0 рассмотрим многочлен Рт(х) из леммы 5. Тогда, полагая п0(е) — т; при всех'л > т = п0(е) получаем неравенство
И*) - g„(x) || < Их) - Яя^х)!! < Их) - Мх)|| ,< И*) - -Pm(*)ll < Е-
Это означает, что при и -»оо имеем \\h„ 11 —» О. ◄ 4 * * *
Докажем теперь теорему 1. Как было показано ранее, достаточно доказать, что
1 2л
где ck = (g, fk) = - J g(x)fk(x)dx, f^x) = 1/^2, а при k > 1 имеем к о
f2k = COS fzk + l(x) = 8*п
Кроме того, при доказательстве леммы 5 было установлено, что при любом п е N справедливо равенство
(g, g) - (gn, gn) = (g - g„, g ~ gn) = (*n, *n).
По лемме 6 имеем (Лп, Лп) 0 при п оо. Поэтому, переходя к пределу в последнем равенстве, получаем
п	оо
= М =Л
Тем самым теорема 8 доказана.
457
В заключение заметим, что для того, чтобы любая полная ор-тонормированная система функций в линейном пространстве V со скалярным произведением была замкнутой, необходимо и достаточно, чтобы пространство V было полным относительно нормы, определяемой этим скалярным произведением. Другими словами, V должно быть гильбертовым пространством. Доказательство последнего утверждения не слишком сложно, но оно выходит за рамки данного курса.
§ 4. ПРОСТЕЙШИЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ РЯДОВ ФУРЬЕ
Уже отмечалось, что не всякий тригонометрический ряд вида
~ ао S >
Z fn(x) « -=• + L Аап cos пх + Ьп sin пх)
обязан быть рядом Фурье некоторой функции даже в том случае, если он сходится при всех вещественных значениях х. В качестве примера можно указать ряд
n?o^x^_n?i inen •
Согласно признаку Дирихле, он сходится во всех точках х вещественной оси, но можно доказать, что он не является рядом Фурье какой-либо функции.
С другой стороны, теорема Рисса—Фишера утверждает, что если сходится числовой ряд
то существует функция g(x), коэффициентами Фурье которой являются числа ап и Ьп. Кроме того, тогда по теореме Карлесона сумма ее ряда Фурье существует «почти всюду» и равна g(x). Докажем следующие утверждения.
ТЕОРЕМА 9. Если коэффициенты cn(f) и cn(g) рядов Фурье строго регулярных функций Дх) е W2n и g(x) е W2k совпадают, то f(x) = g(x) при всех вещественных значениях х.
► Коэффициенты Фурье ck(h) разности этих функций, й(х) = = f(x) - g(x) е W2k удовлетворяют соотношению tk{h) = ck(f) -- ck(g) = 0. Поэтому, в силу равенства Парсеваля, справедливо равенство
(й,й) = Jxc2(A) = 0,
а отсюда следует, что й(х) = 0 или f(x) = g(x) при всех х. ◄
458
ТЕОРЕМА 10. Если тригонометрический ряд «
а0 °°
Е ckfk(x) = у + j (ап cos пх + bn sin пх)
сходится равномерно на отрезке I = [0, 2л], то его сумма g(x) является непрерывной функцией на I и данный ряд является ее рядом Фурье и он допускает почленное интегрирование.
► Все функции sin пх и cos пх непрерывны на I, и, в силу равномерной сходимости ряда Е ck fk(x), его сумма g(x) является непрерывной функцией. Отсюда вытекает, что равенство
f„(x)g(x) = 4(х) J jC J„(x)
можно проинтегрировать по отрезку I и при этом, в силу равномерной сходимости ряда на Z, в правой части равенства возможно почленное интегрирование. В результате приходим к равенствам
ck(g) - (/*, g) - n? ^„(4, fn) = ck,
поскольку (4, fn) = о при k * n и (4, fk) = 1.
Таким образом, установлено, что числа ck.одновременно являются коэффициентами Фурье функции g(x). ◄
ТЕОРЕМА 11. Тригонометрический ряд Фурье Е cnfn(x) строго кусочно-гладкой 2п-периодической функции g(x) сходится к ней равномерно на отрезке I = [0,2 л].
► Покажем, что тригонометрический ряд
а0 00
Е ck fk(x) =-g + nEx (ап cos пх + &nsin пх)
сходится равномерно на I. Для этого достаточно показать, что числовой ряд Е (|ak\ 4-1 bk[) сходится и тем самым является мажорантой для S ck fk(x).
Прежде всего заметим, что функция й = h(x) = g'(x) е W2n, поэтому (Л, й) < 4-оо, й для'функции й(х) справедливо равенство Парс ев ал я, т. е.
< ' °°
(Л,Л)=У +	+
где
•| 2л	2л
ай = - Г ft(x)cos kx dx —J g'(x)cosfex dx,
n о	 к о
। 2л	। 2л
= - J ft(x)sin kx dx = - J g'(*)sinfcx dx.
я о	n о
459
Далее, поскольку g'(x) :— строго регулярная функция, то при всех k е N в этих интегралах допустимо интегрирование по частям. Выполняя интегрирование, получаем
1 г’	k г”
ak = - J g'(x) cos kx dx = -- J g(x) sin kx dx = -kbk,
1 2it	k 2it
= - J g'(x) sin kx dx = - J g(x) cos kx dx = kak, n о	яо
т. e. ak = bh = -ak/k. Но тогда
|a*l =IPJA < Pi + I/*2» IM - N/* < &k + I/*2-
Отсюда следует, что
Лам+1 p*D < Д/at+Pi)+2 Д .i/k2 < GO	1
Итак, мы доказали, что ряд Е ckfh(x) сходится равномерно на I к некоторой сумме <р(х). Но по теоремам 9 и 10 функция ф(х) должна быть непрерывной и совпадать с g(x). ◄
ТЕОРЕМА 12. Если 2ппериодическая функция g(x) дифференцируема п раз, где п > 1, и ее п-я производная является строго кусочно-гладкой функцией, то:
1) ряд Е kn(|ak| 4-1 bk\) сходится;
2) ряд Фурье функции g(x) можно почленно дифференциро* вать п раз. Здесь числа ak и bk являются коэффициентами Эйлера—Фурье для функции g(x).
► На основании теоремы 11 заключаем, что функция <рп(х) = = gtn\x) равна сумме своего ряда Фурье, который равномерно сходится на отрезке I = [0, 2л]. Кроме того, если аЛ и (3fe — ее коэффициенты Эйлера—Фурье, то ряд Е (|aj + IPJ) сходится, Отсюда последовательным интегрированием по частям, как и при доказательстве теоремы 11, приходим к равенствам
|aj = knlakl, |pfe| = fen|6j, если n — четное, |aj = iPfel = если n — нечетное.
Тем самым утверждение 1 доказано.
Справедливость утверждения 2 следует теперь из общей теоремы о почленном дифференцировании функционального ряда, так как тогда каждый из числовых рядов Eft™ (|aft| 4- |6Л|) сходится при любом тп = 1,...,п-1и является мажорантой для по-460
следовательных производных суммы тригонометрического ряда Фурье, т. е. функций <pm(x) = АтЦх) на отрезке I = [0, 2л]. «
Заметим, что вместе с теоремами 11 и 12 попутно доказана следующая теорема.
ТЕОРЕМА 13. 1. 'Если сходится числовой ряд Е|а„| + |&„|, то тригонометрический ряд ай/2 + Еап cos пх + bnsin пх.сходится равномерно на отрезке [0,2я] к некоторой непрерывной функции g(x), являясь ее рядом Фурье. .
2. Если при этом сходится ряд En*(|dn| + |Ь„|), где k > 1, то ряд Фурье функции g(x) можно почленно дифференцировать k раз.
Лекция 26
$ 5. ИНТЕГРАЛЬНОЕ ПРЕДСТАВЛЕНИЕ ДЛЯ ЧАСТИЧНОЙ СУММЫ РЯДА ФУРЬЕ.
ПРИНЦИП ЛОКАЛИЗАЦИИ РИМАНА	?
Одной из важных задач теории тригонометрических рядов Фурье является нахождение условий, обеспечивающих сходимость данного ряда в фиксированной точке к значению породившей его функции. Возникающая здесь ситуация достаточно сложна. Оказывается, что ряд Фурье функции, непрерывной в данной точке, может в ней расходиться. В то же время пример функции р0(х) показывает, что разрывность функции, вообще говоря, не препятствует сходимости ее ряда Фурье к ней самой во всех точках вещественной оси. Далее мы рассмотрим простейшие признаки поточечной сходимости тригонометрических рядов Фурье. Для этого потребуется вывести интегральное представление для их частичных сумм.
Введем следующее обозначение. Будем писать
а0 ~
£(х) ~ у + feZ1ajfecos kx + Z^sin kx,
если все числа ak и bk выражаются через g(x) по формулам Эйлера—Фурье. Другими словами, тригонометрический ряд в правой части последнего соотношения является рядом Фурье функции g(x). Если он сходится в точке х0 к значению g(x0), то можно записать равенство
а0 00
g(x0) = ~2 + fe?iafecos kxo + Min kxo-
Преобразуем ряд Фурье функции g(x) с помощью формулы Эйлера
eix = cos х + isin х, где i — мнимая единица, i2 = -1. Для простоты можно эту формулу рассматривать как определение функции ех при мнимых значениях аргумента. Легко доказать, что тогда основное функциональное свойство экспоненты в этом случае сохраняется на всей комплексной плоскости, т. е. если г = а + Ы (а, b е Я), и мы считаем, что ег = еа+ы = еа • ew, то
e*i+*2 =^i .е*г9
где zr и z2 — комплексные числа. Далее, поскольку cos kx = (eikx + e~ikx)/2, sin kx = (eikx - e~ikx)/(2i),
462
имеет место равенство
\= ? + Л i(a*cos кх+ъ*sin кх) - k
где
d0 = а0/2 и dk = (aw -	Ьщ)/2' = (aw - »wsign k)/2 при k * 0.
Заметим, что для величин dk при целом k выполнены соотношения
- 2л	.j 2л
dk — — ( g(x) e~lkxdx = — J g(x) (cos kx - i sin kx)dx = ля о	2л 0
i /1 2®	i 2л	\	i
= 5 ( - J S(x) cos kx	dx	- — f g(x).sin kxdxj =	i (ai*| -	ibi*i sign k).
2 v л q	in q	/	2	• •	1 1
Введем теперь	для	Комплекснозначных 2л-‘периодйческих
функций f(x) и g(x) скалярное произведение (Д g) по формуле
(A g) = Л J f(x)g(x) dx. <	о
Как обычно, черта над знаком функции означает операцию комплексного сопряжения. Тогда имеем (A g) = (g, /)>	=	,
откуда следует, что dk = (g(x), е‘*х) = 1 и (eikx9 eikx) = 1.
Таким образом, совокупность функций {eikx}9 где k принимает все целые значения, образует ортонормированную систему функций относительно введенного выше скалярного произведения^ Заметим еще, что весовой коэффициент к равен здесь 1/(2л).
Эту комплексную форму записи ряда Фурье мы используем при выводе удобной для применения формулы для частичной суммы Sn ряда Фурье функции g(x). Имеем
n	1 п	2л
S _=S	Е е»™] g(t)e~iklfdt =
п k = -п К 2 л k = ~п	о
- 2л	п	1 2л
= i J g(t\ S	dt = J g(t) Dn (x - o dt,
^Л о «	« 5	0
где функция Dn(y) определяется равенством
D.w-
Определение 14. Функция Dn(y) называется ядром Дирихле порядка п.
Установим связь между введенной ранее функцией Тп(у) и ядром Дирихле Dn(y). Имеем
Т (у) = sinn(2n + 1)у = х + 2 f „os 2л ky = ь S cos 2л ky =
= . S_ (cos 2nky + i sin 2л ky) = . Z e2nikv = 2nD (2ny). Й Л	к e Л
463
Полагая у = х/2л, отсюда получаем равенство
п 1 т = 1 sin(” + V2)*
2тс "UnJ 2л sin(x/2) ’
Свойства функции Dn(x)
2к
1°. J Dn(x) dx = 1.
Л о
2<>.Dn(x) = Dn(-x).
пП ТЛ / \	1 sin(n + l/2)x	1 ( . X .	.	Л
3°. Dn(x) =	(ctg 2 sin пх + cos пх )•
Поскольку функции g(x) и Dn(x) являются 2л-периодически-ми, с помощью замены переменной вида t = х + у частичная сумма Еп преобразуется к следующему выражению:
К =	(g(x)) = j”g(t)Dn(x - t)dt = Гg(t)Dn(t -x)dt =
+ 2	°	°
= J g(x + y) Dn (y) dy= j g(t + y) Dn (y) dy = X	-П
1 5	< sin(n + l/2)y ,
= I + sin(y/2) dy =
Iя	JJ	1	71
= 2rc f £(x + У) ctg f sin пУ dy + 2ic J ^X + У) cos пУ ЛУ'
Определение 15. Эту цепочку равенств назовем интегральным представлением частичной суммы Ъп ряда Фурье.
Справедливо следующее утверждение.
ЛЕММА 7 (лемма Римана). Пусть g(x) е ТУ2л и при некотором 8 > О имеем равенство g(x) = 0 при всех хе (xQ- 8, х0 4- 8). Тогда ряд Фурье функции g(x) в точке х = х0 сходится к нулю.
► Пусть функции f^y) и f2(y) определены равенствами 2/^у) = = g(x0 + у) ctg (у/2) и f2(y) = | g(x0 + у). Тогда f^y) и f2(y) е W2k, поскольку функция ctg (у/2) непрерывна вне лтйбой 8-окрестности каждой точки вида у = 2лй, где k — произвольное целое чис-лб, а внутри этой окрестности функция f^y) равна нулю. Поэтому при х = х0 имеем
= E„(g(x0)) = f g(x0 + y)Dn(y)dy =
= я J 1 ^xo + y)ctg 2 sin nydy + я J 1	+ y)cOS nydy =
-Ш) + аж(/Х
где ЬдС/х) и an(f2) — коэффициенты Эйлера—Фурье функций /г(у) И соответственно. Поскольку для этих функций справедли
464
во равенство Парсеваля, Ьл(/Х> О и ал(/2) -» 0 при п -» сю, откуда и следует, что Ел -> О. ◄
Из леммы Римана вытекает справедливость следующего утверждения.
ТЕОРЕМА 14 (принцип локализации Римана). Поведение ряда Фурье в точке х = х0 полностью определяется значениями функции g(x) е W2n в произвольно выбранной 6-окрестности этой точки.
► По существу, надо доказать, что если функцию g(x) изменить произвольным образом вне любой фиксированной 3-окрестности точки xQ9 то сходимость ряда Фурье не нарушится и его сумма в этой точке не изменится. Другими словами, если частичная сумма En(g(x0)) ряда Фурье функции g(x) е W2n в точке х = х0 сходится к числу а и функция й(х) g W2n совпадает с g(x) внутри некоторой 3-окрестности точки х0, то и Ел(й(х0)) а при п -» оо.
Рассмотрим разность r(x) = g(x) - й(х) g W2n. Функция г(х) в точке х == х0 удовлетворяет условию леммы Римана, поскольку г(х) = 0 при всех х е (х0 - 8, х0 + 8). Следовательно, при п -» оо
Ел(г(х0)) = ЗД(х0)) - Ел(й(х0))	0.
Но так как En(g(x0)) а при п -» оо, то и Ел(й(х0)) -» а при и-»оо. <
Требование принадлежности функции g(x) классу W2n можно значительно ослабить. Действительно, анализ доказательства леммы Римана и теоремы 14 показывает, что для их справедливости, по существу, достаточно, чтобы коэффициенты Эйлера—Фурье разности г(х) = g(x) - Л(х), а также функции <р(х) = r(x) ctg (х/2) стремились к нулю с возрастанием их номера к бесконечности. Для этого, вообще говоря, достаточно интегрируемости по Риману модулей этих функций на отрезке [0, 2к] как несобственных интегралов второго рода. Доказательство последнего утверждения мало чем отличается от уже рассмотренных случаев.
Метод, использованный в лемме 7, позволяет доказать еще одну лемму, которая потребуется при выводе признаков поточечной сходимости рядов Фурье.
ЛЕММА 8. Пусть f(x) е VF2n. Положим
ь	ь	ь
ап = j f(y)cosnydy, Р„= $f(y)ctg(y/2)sinnydy, уп = $ f(y)Dn(y)dy. а	а	а
Тогда если 0 < а < Ь < 2л, то ап —> 0 при п если же выполнено более строгое условие 0 < а < Ь < 2л, то Рп —> 0 и у„ -> 0 при п —> оо.
465
► Величину ал можно рассматривать как коэффициент Фурье функции g(x) е ТИ2я, которая совпадает с /(х) на интервале (а, Ь) и обращается в нуль для точек х отрезка [0, 2я], не принадлежащих отрезку [а, Ь], т. е. для точек множества Е = [0, 2я] \ [а, 6]. Отсюда согласно свойству коэффициентов Фурье имеем ап -» О при п —> оо. Подобным образом величину рл можно рассматривать в качестве коэффициентов Фурье Ъп другой функции Л(х) е W2n, которая на интервале (а, Ь) совпадает с функцией f(y) ctg у/29 а для точек множества Е обращается в нуль. Поэтому рл —»О при п -» оо. а так как уп = (ал + рл)/2п, то и ул -> 0 при п —>	«
§ 6. ПРИЗНАКИ ПОТОЧЕЧНОЙ сходимости РЯДОВ ФУРЬЕ
Снова рассмотрим функцию g(x) из класса 1У2я. Используя интегральное представление для частичной суммы ряда Фурье, найдем выражение для разности гп между значением функции g(x) в точке х = х0 и значением ее частичной суммы Ел в этой точке. Имеем
r„ = Zn - g(x0) = J (g(x0 + у) - g(x0))Dn(y)dy = J + ... + j ... =
n( g(.x0 + y)+g(x0-y)-2g(x0)	«
= 2 J ----------5-----------Dn(y)dy - 2 J <p(y)Dn(y)dy =
0	*	0
= | J Ф<У)81П(8”пу/22)У dy = я j	у/2 sin ny + cos ny)dy,
где
. . /х g(x0 + у) + g(x0 - у) - 2g(x0) ф(Ю = Фх0(У) -----------2------------*
Здесь величина <p(j/) как функция от у принадлежит пространству W2n9 (КО) = 0 и функция <p(z/) непрерывна в точке у = 0.
ТЕОРЕМА 15 (признак Дини). Пусть при некотором 8 > 0 существует следующий несобственный интеграл второго рода:
о *
Тогда ряд Фурье Е функции g(x) в точке х = х0 сходится к значению g(x0).
► В силу произвольности 3, можно считать, что 8 < я. Поскольку интеграл
о *
466
сходится, при любом е > О найдется число h = Л(е) > 0 с условием
О *
Л&лее из интегрального представления для разности гп =	- g(x0)
имеем равенство rn = rnl + rn2 + гп3, где
1 п
г„ = - J <p(!/)(ctg у/2 sin пу + cos ny)dy,
71 о
1 h rni = - J Ф(У) ctg у/2 sin nydy, 71 0
1 n
rn2 = Z J Ф<У) cts У/2 sin nydy, П h я
Гп3 = И <KlO COS nydy.
n 0
По лемме 8 имеем rn2 0 и rn3 -> 0 при п °°, т. е. при всех достаточно больших п получаем гп2 < е и гп3 < е. Относительно величины гп1 заметим, что если 0 < у < h < тс, то поскольку на указанном выше промежутке справедливо неравенство sin (у/2) > у/п. Отсюда следует, что
Iгп11 = М fi(y) sin nydy < i J l/^jOlcty < J dy < e. /Lo	7L о	0
Поэтому при всех n > и0(е) имеем оценку |rn|< Зе. В силу произвольности выбора числа е > 0 это означает, что гп 0, т. е. в точке х = х0 ряд Фурье Z сходится к значению g(x0). ◄
Определение 16. Будем говорить, что функция g(x) удовлетворяет условию Липшица с параметром а, где 0 < а < 1, если в некоторой 8-окрестности точки х0 выполняется неравенство
IM*) - g(x0)| < £|х - х0|“, где L> 0 — некоторая постоянная.
В случае когда это условие выполнено во всех точках отрезка [х0, xj, говорят, что функция g(x) принадлежит «классу Липшица а». ЧислоL называется константой Липшица. При а = 1 просто говорят, что g(x) удовлетворяет условию Липшица.
ТЕОРЕМА 16. Если в точке х0 для функции g(x) выполнено условие Липшица с параметром а, то ее ряд Фурье в данной точке сходится к значению g(xQ).
467
► Покажем, что в данном случае к функции g(x) можно применить признак Дини. Действительно, при |у| < 5 имеем
1^)1 <	+	+	£|
&
откуда следует, что
Bg= jfe)l	<+оо.
О у	о
Это значит, что условия признака Дини выполнены и ряд Фурье функции g(x) сходится к значению g(x0).	◄
Докажем еще два признака сходимости рядов Фурье.
ТЕОРЕМА 17. (Признак Дирихле.) Если 2п-периодическая и строго регулярная функция g(x) является кусочно-монотонной на отрезке [0, 2л], то ее ряд Фурье сходится всюду к значению g(x).
Замечание. Кусочная монотонность функции g(x) означает, что весь отрезок [0, 2л] можно разбить на конечное число промежутков, на каждом из которых g(x) монотонна. В частности, кусочно-монотонная ограниченная функция будет функцией ограниченной вариации.
Доказательство теоремы 17 является простым следствием еще одного признака, заключенного в следующей теореме.
ТЕОРЕМА 18. (ПризнакЖордана.) Пусть функция g(x) е W2n и О < 8 < л. Пусть, далее, в некоторой 8-окрестности точки х0 функция g(x) имеет ограниченную вариацию. Тогда ряд Фурье этой функции сходится в точке х0 к значению g(xQ).
► Поскольку <p(z/) — функция ограниченной вариации, ее можно представить в виде ф(у) = (р^у) - <р2(*/)» где Ф^г/) и ф2(у) — неубывающие неотрицательные функции. Можно считать, что фх(0) = ф2(0) = 0 и функций фх(1/) и ф2(г/) непрерывны в точке у — О, так как этими свойствами обладает функция ф(у). Действительно, монотонные функции имеют в каждой точке односторонние пределы. Тогда правосторонние пределы в точке у = 0 для обеих функций совпадают. Вычитая из каждой функции это общее предельное значение, получаем две новые функции, которые удовлетворяют всем указанным выше условиям, если только их значения в нуле взять равными нулю. Следовательно, для любого е > О существует значение h = Л(е) > 0 такое, что 0 < фх(Л) < е и 0 < ф2(Л) < е. Можно считать, что h < 8.
Для остатка ряда Фурье функции g(x) в точке х0 справедливо представление п
ГП = 2 i ^y)Dn(y)dy = rn> 1 + Гп> 2, где	h °
rn,1 = 2j(^y)Dn(y)dy, rn 2 = 2j<p(y)Dn(y)dy. 0	h
468
Без ограничения общности будем считать, что <p(i/) = 1ч е. <р(у) — неубывающая неотрицательная функция. По лемме 2 § 5, величина гп 2 -> 0 при п —> оо. Поэтому достаточно показать, что гп, 1 < се> гДе с > 0 — некоторая постоянная. Заметим, что <р(Л) < е. Применяя к интегралу гп> х вторую теорему о среднем, получаем
h	h/2n
Гп, 1 = 2<р(Л) J Dn(y)dy = 4гар(Л) J Tn(x)dx,
где функция Tn(x) определена в § 1. Далее, 0 < Л/2л < 8/2л < 1/2, поскольку 8 < л. Поэтому, применяя к последнёму интегралу оценку леммы 2 § 1, имеем гп х < 2ф(Л) • 4 < 8е. ◄
Замечание. Использование леммы 2 в доказательстве теоремы связано с тем, что величина £ « в зависимости от п может изменяться, поэтому прямое применение леммы 8 невозможно.
Лекция 27
§ 7.	ПОВЕДЕНИЕ КОЭФФИЦИЕНТОВ ФУРЬЕ
Приведем несколько утверждений о поведении коэффициентов Фурье для некоторых классов функций.
1.	Пусть g(x) g W — четная функция. Тогда из формул Эйлера—Фурье имеем, что все коэффициенты Фурье Ьп = 0, т. е. ряд Фурье функции g(x) представляет собой тригонометрический ряд по косинусам.
Пусть теперь g(x) е W — нечетная функция. Тогда ап = 0 для всех натуральных чисел и, т. е. функция g(x) разлагается в ряд Фурье по синусам.
ПРИМЕР. На интервале (0, л) имеет место равенство
л - х = у sin&x 2	k ’
которое является простым следствием разложения функции Бернулли р0(х) в ряд Фурье.
Если на интервале (0, л) задана функция g(x) g W, причем g(0) = lim^ g(x), £(л) = Jim g(x), то ее можем распространить на всю вещественную ось, как 2л-периодическую и четную или нечетную функцию. В случае четной функции ей соответствует ряд Фурье по косинусам, а в случае нечетной — ряд Фурье по синусам.
2.	Пусть g(x) g 1¥. Тогда ее коэффициенты Фурье стремятся к нулю при возрастании их номеров к бесконечности. Действительно, из неравенства Бесселя имеем, что ряд Е (а% 4- Ь^) сходится. Поэтому из необходимого признака сходимости ряда получаем
lim а„ = lim b„ = 0. П -> оо " п -> ОО «
Это свойство коэффициентов Фурье мы уже неоднократно использовали.
Замечание. Если ап и Ьп таковы, что ряд я2 оо сходится, то а0 -=• + Е (ап cos пх 4- Ьп sin пх) Z л = 1 ' *	п
— ряд Фурье некоторой функции f(x) из класса L2 — функций, интегрируемых в квадрате (теорема Ф. Рисса—Фишера). В этом случае гово-
470
рят, что ряд Фурье сходится в среднем квадратичном. Более точно это означает, что при п -> оо имеет место соотношение
2л
J (f(x) - Sn(x}^dx -> 0. о
Покажем, как теорема Ф. Рисса—Фишера сведется к свойству полноты класса функций L2. Пусть
ап Д зл (х) = у 4- t (aftcos kx 4- &fesin kx)
— п-я частичная сумма тригонометрического ряда. Тогда при п > т, т -> оо в силу сходимости ряда S (а% 4- Ь%) имеем
2л	2л , п	ч2
J (8„(*> - sm(x№dx = J (jk-£ + l akcoakx + bksinkx) dx =
Следовательно, в силу полноты класса функций L2 последовательность частичных сумм {зл(х)} ряда Фурье сходится в среднем квадратичном к некоторой функции из этого класса.
3.	Пусть функция f(x) удовлетворяет условию Липшица, т. е.
|/(х 4-й) - Дх)| < L|ft|a, где L > 0 и a > 0 — некоторые постоянные. Тогда справедливы следующие неравенства:
|ал| < 1/Л°7па, |ЬЛ| < Lna/na.
Из определения коэффициентов Фурье и периодичности f(x) и cos пх имеем
2л - л/п f(x) cos nxdx = -- f f n 0	71 -Я/П
= - A J 2 + у I cos nydy.
Л Q 4 n /
Отсюда получаем
an=jz I (Ax) -	+ x) ) cos nxdx,
ait q v	Tl ' '
следовательно,
|a _|<	+x)dx<—.
' nl 2л 5 v ' vra / n“
Аналогично доказывается оценка и для Ьп.
4.	Пусть f(x) — функция ограниченной вариации на периоде. Тогда имеем ап = О(1/п), Ьп = О(1/га).
( - + у ) cos nydy = ЧП, 7

471
Из определения функции ограниченной вариации на [0, 2л] получаем, что Дх) = /\(х) - f2(x), причем функция /^(х) и f2(x) положительны и не убывают,. Применим вторую теорему о среднем для оценки следующего интеграла. При некотором 0 < £ < я, имеем
2гс	2п	dnnF
J fx(x) cos nxdx = /1(2тс) J cos nxdx = -^(2^)^-- = 0(1/n).
о	$	n
Следовательно, an = Q(l/n), bn = O(l/n).
5.	Ряд Фурье для 2/-периодической функции g(x) е W при I * # л. Рассмотрим функцию h(y) = g(ly/n)9 которая имеет период 2л. Поскольку h(y) е W9 то так как
а0 “
h(y) ~ у + (ak cos kU + bk sin M-
Если теперь выразить у через х : у = хк/19 то получаем
g(x) = й(х) - у + Д ak cos — + bk sin — J, при этом
1 f LZ \ I- J	1 f Z X kxn 7
ak = - J h(y) cos kydy = у J g(x) cos -y— dx.
-7C	-I
Аналогично имеем
,	1 г z ч • kxn ,
bk= j J g(x) sin — dx.
Другими словами, вся построенная нами теория рядов Фурье для функций, имеющих период 2л, с помощью линейной замены переменной переносится на случай 2/-периодических функций.
§ 8. РАЗЛОЖЕНИЕ КОТАНГЕНСА
НА ПРОСТЕЙШИЕ ДРОБИ И ПРЕДСТАВЛЕНИЕ СИНУСА В ВИДЕ БЕСКОНЕЧНОГО ПРОИЗВЕДЕНИЯ
Развитый выше аппарат теории разложения функции в тригонометрический ряд Фурье позволяет, наконец, достаточно просто вывести формулу, представляющую синус в виде бесконечного произведения. Для этого сначала докажем не менее известную формулу разложения котангенса на простейшие дроби.
На отрезке [-л, л] рассмотрим функцию g(x) = cos ах, где |а| < 1/2 — некоторое фиксированное число. Продолжим ее на всю числовую ось как периодическую с периодом 2л. Тогда функция g(x) будет четной и непрерывной на всей вещественной оси R. Так как g(x) является непрерывной и кусочно-гладкой 472
функцией на I, ее ряд Фурье равномерно сходится на I к g(x). Поэтому для всех хе I имеем разложение
gw = у + Л 1(лcos ~ +b*81П “Г )’
где ак и bk — коэффициенты Эйлера—Фурье.
Далее, в силу четности функции g(x), все bk равны нулю, а для коэффициентов ak при а О имеют место равенства
ао 1 г .	sin ал
- = - jcosaxdx=—,
—я
1 ?	> >	/ 2а sinax
ak = я Jcos ах cos kxdx = (-l)fc^Tp •
Таким образом,
, ч	sin an fl , £ , «и. 2a . А
g{x) = cos ax =	(- + ^ (-1)* cos kx ).
Отсюда при x = -л получаем
cos ал	,	1 , р 2а	Д 1
п—---- = л ctg ал = - +	;—-z = lim L X ----- .
sin ал	® а л = i a2 — fe2 n-»oo/? = -n - k
Последняя формула дает классическое разложение котангенса на простейшие дроби. Отсюда легко получить представление синуса в виде бесконечного произведения. Для этого заметим, что ряд справа сходится равномерно относительно параметра а при О < |а| < 1/2, поскольку имеет мажоранту вида Z 2/k2. Более того, поэтому он является производной своей первообразной.
С другой стороны, имеем
A sinna Y ,	- ,
I In —L = л ctg ла - 1/а,
1 (1 _ а2 Y = 2а = 1	1
\ k2 )	a2 -k2 a-k	aik'
Следовательно, в силу непрерывности функции 1п х при некотором се R справедливо равенство
-с + Um - g )-с + Нт 1пД(1 - g )-
Это значит, что при всех а с условием 0 < |а| < 1/2 имеет место формула
зтла гт f-i а2 Ч
-— - Л (1 - *5 }
где сх = ес.
473
Бесконечное произведение в правой части данного равенства сходится равномерно по а при |а| < 1/2. Поэтому, переходя к пределу при а —»О, находим сх:
Окончательно имеем
sin ла = fj f 1	а2 Л
па ~ /А к1 h2 /
Таким образом, формула представления синуса в виде бесконечного произведения доказана.
§ 9. ЗАДАЧА КЕПЛЕРА И РЯДЫ БЕССЕЛЯ
Предположим, что планета М движется по эллипсу, в фокусе которого находится неподвижная планета F. Полуоси эллипса соответственно равны а и Ь, а > Ь. Пусть Т — время полного оборота планеты М вокруг планеты F, a t — текущее время, отсчитываемое от положения планеты в точке А, находящейся на большой полуоси. Обозначим через SAFM площадь сектора эллипса АРМ. По закону Кеплера имеем
Т- е- SAFM = ™bt/T.
Рассмотрим окружность с центром в точке О, находящейся в центре эллипса, и радиусом, равным О А = а, и обозначим через Мг точку на окружности, являющуюся образом точки М при проекции на большую ось эллипса параллельно малой его оси. Положим также £ = OF/ОА, и = Z. AOMV Из геометрических соображений найдем площадь сектора эллипса AFM. Поскольку эллипс получается аффинным преобразованием из окружности сжатием по оси Оу в Ь/а раз, имеем SAFM = (b/a)SAFM.
Далее находим SAFMi = SAOM} - SFOMi = а2и/2 - а2е sin (u/2). Следовательно, SAFM = db(u - Е sin и)/2. Мы приходим к уравнению Кеплера
и - Е sin и = 2nt/T = £ = Z. АОМ.
Величина £ называется средней аномалией планеты, и — эксцентрической аномалией. Если £ увеличивается на 2л, то и и увеличивается на 2л. Поэтому cos пи, sin пи являются 2л-пе-риодическими функциями от £, т. е.
cos (пи(^ 4- 2л)) = cos (nu(t)).
474
Ранее было доказано, что u(Q — гладкая функция. Следовательно, ряды Фурье функций cos nu(Q и sin nu(Q по признаку Липшица сходятся. В силу нечетности функции имеем
cos пи = а0/2 + ах cos £ + а2 cos %* + ••• > sin пи = br sin £ + Ь2 8*п	+ ... »
2 я	2 я
av = - J cos пи cos vd£, bv = - J sin nu sin
71 0	71 0
Вычислим коэффициенты Фурье этих функций. Получаем
а0 = ~ j cos nudC, = - J cos nu(l - e cos u)du. 71 о	71 0
Здесь мы воспользовались тем, что
£ = и - £ sin u, d^ = (1 - £ cos u)du.
Таким образом,
_ [“£, если п = 1, а°— [О, если и >1. При v > 1 получаем
2 71
av = - J cos пи cos = 71 о
2	. г
— COS пи Sin VL rcv	*
я 2п ? .	г.
- — J sin пи Sin NLfiu =
£ = 0	0
2 д я
= — J cos (пи - vQ - cos (пи + vQ)du = 7CV ’
= — j cos ((n - v)u + ve sin u)du —- J cos ((n + v)u - ve sin u)du = о	nv о
= V<Jv-n(VE)-^v + n(VE)),
где 1 n Jk(x) = - J cos (x sin <p - fc<p)d(p. n 0
Аналогично находятся коэффициенты bv. Имеем
bv = - J sin пи sin v^dC, = — J cos nu cos vfylu = л о	KV о
= V(Jv-n(ve) + A + n(vE)), следовательно,
cos и = -1 +2vEj (jv_z(ve)-Jv + Z(ve))^^,
sin и = 2 vE t (Jv _ z(ve) + Jv + z(ve))^^.
475
Значение угла и9 0 < и < 2л, однозначно определяется по его синусу и косинусу. Поэтому указанные разложения этих функций решают задачу об определении движения двух планет. Они были найдены В. Берселем. Эти ряды сходятся при всех значениях и любом значении эксцентриситета эллипса е. До Бесселя задачу двух тел решал Лаплас с помощью разложения в степенные ряды по малому параметру е, сходимость которых была доказана при е < 0,66274....
Функции Jk(x) называются функциями Бесселя.
Лекция 28
$ 10. ЯДРО ФЕЙЕРА
И АППРОКСИМАЦИОННАЯ ТЕОРЕМА ВЕЙЕРШТРАССА
Наряду с тригонометрическими многочленами Фурье, которыми, согласно определению, являются частичные суммы ряда Фурье, большую роль в теории тригонометрических рядов играют многочлены Фейера. В качестве примера использования свойств этих многочленов докажем теорему Вейерштрасса о равномерном приближении функции, непрерывной на отрезке, последовательностью тригонометрических и алгебраических многочленов. Определение 17. Тригонометрическим многочленом Фейера порядка п для функции g(x) называется функция Рп(х) вида
Рп^ = л т? 0
где gm(x) — многочлен Фурье порядка т для функции g(x), т. е. частичная сумма ряда Фурье вида
gm(x) = у + Д i (ak cos kx + bk sin kx), причем числа ak и bk при всех k = 0, 1, ... , m являются коэффициентами Эйлера—Фурье функции g(x).
Из определения, очевидно, имеем
Р„(х) = 7	(1 - £ ) («* C°s kx + bk Sin kx)‘
Используя интегральное представление для gm(x), приходим к равенству
1 п - 1 у	у
Рп(х)= - _?0 J g(x + y)Dm(y)dy = J g(x + y)Fn(y)dy, п —п	-к ‘
где
р 1 "у1 Sin(m + 1/2>У
2пп т-0 sin(y/2)
Определение 18. Функция Fn(y), определенная последним равенством, называется ядром Фейера порядка п.
Установим некоторые свойства функции Гл(х). Справедливы следующие утверждения.
Л ЕМ МА 9. При п > 1 справедливо равенство т?	1 (sin(rar/2)\2
2пп t sin(x/2) ) '
Отсюда, в частности, следует, что Fn(x) > 0 при всех х.
477
► Суммируя по тп, с помощью известных тригонометрических формул получаем
_ ( . = 1	"у1 sin(m + 1/2)х =
'nW 2пп m = o	sin(x/2)
1	п-1
= й—, . , ,ОЧЧ2 nsin	+ 1 /2)х sin (*/2) =
2лп(81П(х/2))2 m»0 v ' '	\ / /
________1______ "у1 cosznx - cos(zn 4- l)x _ 2nn(sin(x/2))2 m = o	2
=	* ~cosnx = 1 /sin(nx/2)A2
” 2лп • 2(sin(x/2))2 ” 2nn V sin(x/2) J '
ЛЕММА 10. При n > 1 имеем
Jn = J F„(x) dx = 2 J F„(x) dx = 1. —л	0
► Так как при всех т справедливо равенство
jDm(x)dx = l,
1 п- 1	л
то J=- S 1 = 1. ◄ п п m = 0
ЛЕММА 11. Для любой функции g(x) g W2K справедлива формула
Рп(х) -	= J (g(x + у) - g(x)) Fn(y) dy.
-л
Это утверждение непосредственно следует из леммы 10 и из формулы интегрального представления для Рп(х).
ТЕОРЕМА 19 (теорема Фейера). Если функция g(x) непрерывна на отрезке I = [-л, л] и g(-ic) = g(ic), то последовательность ее многочленов Фейера Рп(х) сходится к g(x) равномерно на I.
► Функцию g(x), как 2л-периодическую, продолжим на всю вещественную ось. Она будет непрерывна на Я, следовательно, и равномерно непрерывна на I. Это значит, что при любом е > 0 найдется число 8 = 8(e) > 0 такое, что при всех у с условием |у\ < 8 и всех хе I выполнено неравенство
|g(x + у) - £(х)| < е/2.
Кроме того, в силу ограниченности g(x) на отрезке I при некотором С > 0 и всех х и у е I имеем \g(x 4- у) - g(x)| < С. Но тогда справедливы оценки
л	6	л
Ito - Pn(x)| < JFn(y)\g(x + у) - g(x)|dy < J Fn(y) I dy + 2 J Fn(y)Cdy < -Я	-8	8
. e ? „ . . , , C f sin(nu/2)2 , . e , С 1
C 2 №№№ + nn j sin(j//2)2 dy " 2 + n (sin(8/2))2 E’
478
xx	20	и-	r» / \ ►
если только n > n0 (e) = — £- 9. Но это и означает, что Р„(х) и e(sino/2)z	*	7
=> g(x). В силу 2л-периодичности Рп(х) и g(x), отсюда при п -> оо также имеем Рп(х) =* g(x). ◄
R
Из этой теоремы немедленно вытекает справедливость следующей аппроксимационной теоремы Вейерштрасса для алгебраических многочленов.
ТЕОРЕМА 20. Пусть функция g(x) непрерывна на отрезке /0 = [0, я]. Тогда существует последовательность алгебраических многочленов Qn(x), равномерно сходящаяся к g(x) на этом отрезке.
► Доопределим четным образом функцию g(x) на отрезке [-л, 0] и затем периодически продолжим ее на всю числовую ось R с периодом 2л. Тогда функция g(x) будет удовлетворять условиям теоремы 19. Поэтому при е = 1/п найдется номер тп, для которого многочлен Фейера Рт(х) приближает g(x) с точностью до е/2. Но сам многочлен Рт(х) можно разложить в ряд Тейлора, который сходится равномерно на IQ = [0, л] к g(x). Теперь в качестве Qn(x) возьмем многочлен Тейлора, приближающий Рт(х) с точностью до е/2. Тогда всюду на IQ многочлен Qn(x) будет приближать £(х) с точностью до е.
Обратим внимание на то обстоятельство, что степень многочлена Qn(x) вовсе не обязательно будет равна номеру п, но этого нам и не требуется.
Итак, при всех хе IQ имеет место неравенство
\g(x) - Q„(x)| < е = 1/п.
Отсюда следует, что Qn(x) g(x) при п -> оо. «
А)
§11. ИНТЕГРАЛ ДИРИХЛЕ И РАЗЛОЖЕНИЕ НА ПРОСТЕЙШИЕ ДРОБИ
Используя свойства ядра Фейера, вычислим значение интеграла Дирихле. Очевидно, имеем
°?	°?	/1 х
I- ! ( =
О V sin2x +°°
X
о 0
о 2sinxcosx ,	7 sinx ,
dx= J ----- dx.
о x
X
479
Далее, выполняя замену переменной интегрирования х = Ny9 N > О, получаем
Я/2
J sin2Nx о
= 1 *(2 (sintfxA2 ,	1
N J I sinx J ах+ N
1 Л,	0 7 dx
sin2x ГХ	N }/2х2
где |0| < 1. Поскольку справедливы следующие формулы для ядра Фейера:
И^)!-2”Г"(2хЧВД</*-5’
из предыдущего равенства имеем
л V2 х2 - sin2x 2 + N J x2sin2x
dx + ^jejci.
Функция (х2 - sin2x)/(x2 sin2x) интегрируема по Риману на [0, л/2], следовательно,
I = л/2 + O(l/N).
Устремляя N к плюс бесконечности, получим, что I = л/2.
Докажем еще две формулы, дающие представления для функций л/sin пх и п ctg тех в виде простейших дробей. Для второй из этих функций такое разложение было получено ранее с помощью разложения функции sin ах в ряд Фурье. Здесь мы используем интегральное представление некоторой тригонометрической суммы и свойство коэффициентов Фурье строго регулярной функции стремиться к нулю с возрастанием их номера к бесконечности.
Имеют место следующие две формулы:
k
1) л/sin лх = lim Е и (-1)п / (х - и);
к —> ОО П = — К k
2) л ctg лх = Jim n E_fe 1/(х - п).
Докажем формулу 1. Для этого рассмотрим функцию
Имеем
z ч Л (-l)rtsinxx
_ £	_ £ л i e„„x-.t<lx _
й ' n = -k х - n n — ~k 2 Д
= 5 / е*и* ( £ . e-^tn) dt = 5 j e^tx shint(.k
2 Д \n~-k J 2	sin(xt/2)
i
J cos ntx
sinxf(fe + 1/2) sin(xt/2)
dt.
л
2
480
Так как имеет место соотношение
f	J 2, если n = 0,
A	[ 0, если n и 0, n g Z,
то
А/2)	— f f У fi-nitn
2 at \\n^-ke
( 8*пл*(& + 1
-4 sinTU/2
Отсюда получаем
” - «W - ! J (1 - СОЗ ЖХ) + dt -a -i	. simcr/z
= л J sin2 «£* gisffy + y2> dt =
4	. 2 sin(Ttt/2)
= 2л J sin2 (ctgsin (nkt) + cos (nkt)] di =
= 2nbk (sin2 212 ctg у ) + 2nak (sin2 ).
Следовательно, при k -> oo имеем л - gk(x) -> 0, т. e. при x £ Z получаем
-JS-.Um S* tlE,
SIIIKX fe-^oo n = -k x _ n или, в другой форме записи, = 1
+ £
п ~ 1 п2 - X2
Л sinrcx
Формула 1 доказана. Заметим, в частности, выражение для числа л:
л = 2 + 4 п = 1 / °
что при х = 1/2 получаем следующее
4п2 - 1 Докажем теперь формулу 2. Для этого рассмотрим функцию 4(Х)= f 8Ш2ЯХ
Найдем интегральное представление суммы fk(x). Имеем
; (х) = S ь	= i J e2mt(x-n)dt =
""* х-п »--* 4
г1 „ Г Д „.А	е о . fi-2nitk _ ЛпЩк +1)
= Л J е2я,<х( Е . e~2mtn I dt = п f e2n‘tx ----------dt =
= n J Sin^(2fe + D dt = 2лfcos2ntx ^(2^ +D dt =
2!	smrct	J	sinrcf
481
16-4953
1/2	1
= 2л J cos 2ntx sinit*(2fe + P dt + 2л J cos 2ntx + df =
5	SinTtt	f/2	SinTtt
= 2л f cos 2л*х81пя*(2* + 1>dt + 2л f cos 2nx(u + \)*™™£k + Vdu.
5	Sinnt	-f/2	sin ли
Кроме того,
1/2	,	1/2 k
f	f f S e2*itn\dt = 1.
-1/2 sinitf	-i/2^n~~k J
Аналогично выводу формулы 1 получаем, что функция fk(x) -- л(1 + cos 2пх) выражается в виде линейной комбинации коэффициентов Фурье bfe(sin2 ntx ctg nt), bk(sin nxu sin nx(u + 2) ctg nu), bk(sin nxu sin nx(u - 2) ctg пи) и коэффициентов ak от тех же функций, но не содержащих множителей ctg nt и ctg пи. Эти коэффициенты стремятся к нулю с возрастанием их номеров к бесконечности. Следовательно,
lim = lim I t -±- = тс<1 + СО082**) - к ctg кх.
81п2лх Л->оо w = -fe X - п sin2rcx <
Формула 2 доказана.
Лекция 29
$ 12. ПРЕОБРАЗОВАНИЕ ФУРЬЕ И ИНТЕГРАЛ ФУРЬЕ
Пусть /(х) — периодическая функция с периодом 2п1 и разлагается в сходящийся ряд Фурье. Тогда имеем
/(«)•“ й2_соС*еЙХ//' где
1 nl
Обозначим через yk величину ЪЦъ. пусть
л/
—nl
Тогда функцию f(x) можно представить в следующем виде:
Последняя сумма представляет собой формальную бесконечную интегральную сумму Римана с шагом ДА = 1/1 для интеграла
Г Zi(y)eixydy, где	™
8i(y) = / fitye-^dt.
—nl
Если в интеграле Ft(x) формально перейти к пределу при /-><», то получится повторный несобственный интеграл вида
F(x) = i Г «ЧТ fWe-VdtXiy. £»П -оо Ч-ОО	7
Определение 19. Функция F(x) называется интегралом Фурье или интегральной формулой Фурье.
Если строго регулярная функция |/(х)| интегрируема по Риману (в несобственном смысле) на всей числовой оси, то интеграл gt(y) сходится равномерно на (-оо, +°°) по признаку Вейерштрасса и можно доказать возможность предельного перехода при I -> +оо. Исходя из этого дадим следующее определение.
Определение 20. Функция
g(y) = J fttye-iy'dt
-оо
называется преобразованием Фурье функции f(x)9 причем интеграл g(y) понимается в смысле главного значения по Коши.
483
16*
Функцию же F(x) называют обратным преобразованием Фурье функции g(x).
Как правило, имеет место равенство F(x) = f(x). Кроме того, часто вместо «весовых» коэффициентов 1 и 1/(2л) в функциях прямого и обратного преобразований Фурье берут коэффициент 1/ л/2тс. Ясно, что от этого вид интеграла Фурье не меняется.
В качестве примера найдем преобразование Фурье функции
Имеем
1/(2/), если -I < х < I, f(x) = 1/(4/), если х = -/, х = I, в остальных случаях.
О —
g(y) = Г f(t)e~lytdt = j e-Mdt =	.
-ОО	-I	ly
Для обратного преобразования Фурье отсюда получаем:
F(x) = J e,yxdy = f(x).
-oo ly
В частности, при x = О
^4	— oo *У
Приведем наиболее часто встречающиеся прямые и обратные преобразования Фурье [31].
Функция Дх), область ее определения	Функция g(y)
-1- e“*2/2, -оо < х < 4-оо, J2n нормальное распределение	е-»г/2
ll/а, если х е [0, а], ]0, если х £ [0, а],	i равномерное распределение	eia* -1 lay
11/(2а), если х е [-а, а], ]0,	если х £ [-а, а], равномерное распределение ; 	sin а у ау
J1 (1 - !*! ] если х е [-а, а], 10,	если х g f-а, а], треугольное распределение	pl - cosay а2у2
1 1-_соаах , _оо < х < +оо л ах2	11 -	, если у е [-а, а], (О,	если у с [-а, а]
484
Окончание. щабл.
Функция f(x), область ее определения	Функция g(y)
>.о, t > 0, гамма-плотность	
1 е-|х|? -оо < х < +°°, А	х двустороннее показательное распределение	1 1 +у2
_ ,2 , 2 ’ °°<^< +°°» * > 0, я tz + X2 распределение Коши	
е~х • j Jt(x), х > 0, t > 0, Бесселева плотность	(l-iy-Vd-ij/2)-!)4
—4-, °° < * <+°°,	j ’ nchx ’	’ гиперболический косинус	1 ch(ity/2)
В правом столбце таблицы 'указаны плотности f(x) распределения вероятностей, т. е. функции /(х) с условиями f(x) > О,
J/?(x)dx = l.
Преобразование Фурье от функции распределения вероятностей называется характеристической функцией. Класс характеристических функций среди всех преобразований Фурье выделяется тем, что различным распределениям вероятностей соответствуют различные характеристические, функции (теорема единственности), а также тем, что последовательность распределений вероятностей {Fn} сходится к распределению вероятностей F тогда и только тогда, когда последовательность соответствующих характеристических функций сходится к непрерывной предельной функции (теорема непрерывности). Эти важные теоремы теории вероятностей мы доказывать не будем.
Сформулируем и выведем достаточные условия цредстави-мости функции в виде интеграла Фурье. Эти условия аналогичны соответствующим условиям Дини и Дирихле—Жордана для рядов Фурье. При их доказательстве будем опираться на свойство непрерывности преобразования Фурье g(x) п его стремление к нулю при у од.
Обозначим через L' = L'(""°°, + °°) класс функций, абсолютно интегрируемых по Риману на (—оо, +оо) и являющихся строго регулярными на любом конечном отрезке.
485
ЛЕММА 12. Пусть функция f е L'. Тогда ее преобразование Фурье g(x) является непрерывной функцией на всей числовой оси R.
► Интеграл g(y) равномерно сходится на R по признаку Вейерштрасса, так как функция |/(х)| является мажорантой для его подынтегральной функции е^х/(х).
Рассмотрим сначала случай, когда /(х) непрерывна на R. Тогда функция ф(х, у) = е^х/(х) является непрерывной для всех точек (х, у) е R2. По теореме о непрерывности равномерно сходящегося несобственного интеграла функция g(y) в этом случае является непрерывной.
В общем случае для строго регулярной функции /(х) можно указать непрерывную функцию й(х), отличающуюся от /(х) только в некоторых малых 8п-окрестностях точек х = хп разрыва функции /(х), причем й(х) представляет собой линейную функцию с условием
J \f(x)-h(x)\dx<-^~. |х-х„|<8	3 • 2п
Следовательно,
J |/(х) - h(x)\dx < |.
-оо	о
Положим
<1(у)= Г h(x)e‘vxdx.
-оо
По доказанному выше g^y) является непрерывной для всех у eR, Поэтому существует число 8 > 0 такое, что для любого h с условием |й| < 8 справедливо неравенство
|Д£1 = 1#х(г/ + h>- <i(y)l < I • О
Оценим сверху модуль величины Ag = g(y + й) - g(y). Имеем
|Ag| < |AgJ + 2 jj/(x) - A(x)|dx < | + 2 • | = £.
Следовательно, функция g(y) непрерывна для всех у eR. ◄
ЛЕММА 13 (леммаРимана). Пусть f(x) е L'[a, Ь]. Тогда при у °о имеем
ъ
g(y) = f /(x)e^xdx 0. а
► Выполняя замену переменной интегрирования х = t + л/у, получаем
£<!/) = - J f(t+^)eVdt.
а - п/у	У '
486
Следовательно, ь	ь-п/у
g(y) = 1	- оХ"/(х + j Уухах) =
= lb~f/y(f(x)-f(x + 7,]yyxdx+l I f(x№xdx-± J ftx)e^dx =
2 a	У''	*b - n/y	2 a - K/y
=	+ A2 + A3.
Поскольку f(x) — строго регулярная функция, отрезок [a, &] можно разбить на промежутки непрерывности функции Дх). И если на каждом промежутке непрерывности утверждение леммы будет доказано, то в силу того, что их число конечно, это утверждение будет справедливым и для всего отрезка [а, &]. Поэтому можно считать, что функция Дх) непрерывна на [а, Ь].
В силу непрерывности Дх) имеем, что для любого £ > 0 существует С > 0 такое, что для всех у с условием |у| > С выполняется неравенство
Дх)-/(х+5]
4 У ' Ь - а
Так как непрерывная функция на отрезке ограничена на нем, то существует такое число М > 0, что |/(х)| < М для всех х е [а, 6]. Следовательно, |А2| + |А3| < яМ/1у].
Отсюда получаем, что при |у| > max (С, 2лЛГ/б) имеет место неравенство |g(i/)| < £. А это и означает стремление к нулю функции g(y) при у -> 0. ◄
ЛЕММА 14. Пусть функция Дх) е L' (-оо, +оо). Тогда ее преобразование Фурье g(y) стремится к нулю при у ею.
► Зафиксируем произвольное с > 0. В силу абсолютной интегрируемости функции Дх) имеем, что существует число А > 0 такое, что
j |/(x)|dx + f |f(x)|dx < |. -oo	oo	&
В силу леммы Римана существует У > 0 такое, что при | г/| > У
f /(x)e^dx < |.
-4	&
Следовательно, |g(i/)| < е при |i/| > У, т. е. g(y) -» 0 при у -> ею. < ТЕОРЕМА 21. Пусть функция |Дх)| является интегрируемой на (-°°, +°°) и на любом конечном отрезке функция Дх) строго регулярна. Пусть также при некотором 8 > 0 существует несобственный интеграл второго рода
о У	*
Тогда интеграл Фурье функции Дх) сходится в точке х0 к значению Дх0).
487
-oo
► Рассмотрим функцию
/л(х) = Jg(y)e~iyxdy = Je-^dx Je^faydt.
В последнем интеграле поменяем порядок интегрирования. Это возможно сделать, так как подынтегральная функция является непрерывной и несобственный интеграл равномерно сходится на всем множестве значений параметров. Получаем
Л ~°°	-А
- 2i Lm-----------------Л - i L,,u + x)— du -
- ; J (Л» + *) + f(* - U^“ du. п о	u
Докажем, что Jim^ /А(х0) = Дх0). Для этого сначала вспомним, r° sinAu , л
что I----- du = 5 , поэтому
о u	z
» , ч v 2 7sinAu z ч , fA(xo) - Яхо) = й I “7“ ^du-
В силу сходимости интеграла В5 имеем, что для любого е > 0
существует h > 0 такое, что J dy < - . Из леммы Римана следует, что существует Y > 0 такое, что для всех А > У справедливо неравенство
( <P(U) Л u
sin Audu < x. 22
Отсюда имеем, что lim /,(х0) = Дх0). ◄
ТЕОРЕМА 22. Пусть /(х) е LX”00, °°) и пусть также в некоторой Ь-окрестности точки х0 функция /(х) имеет ограниченную вариацию, 8 > 0. Тогда ее интеграл Фурье сходится в этой точке к значению Дх0).
► Из доказательства предыдущей теоремы получаем, что
Za(xo) - Яхо) = I Гdu-
Поскольку последний интеграл сходится,’для любого е > 0 существует число В > 0 такое, что
2 7 / ч sinAu , е - |ф(и)-----du < о*
л '	7 и	2
О
В силу условия теоремы функция ф(х) имеет ограниченную вариацию на интервале (-8, 8) и, кроме того, ф(г/)	0 при у 0.
488
Следовательно, эту функцию можно представить в виде разности положительных неубывающих ограниченных функций фг(х) и Ф2(х), причем каждая из них стремится к нулю при у 0.
Достаточно доказать, что интеграл
о 2 ? z ч sinAu , z J — du
0
стремится к нулю при А -» оо.
Сначала из условия lim ^(и) = 0 имеем, что существует число h > 0 такое, что при всех |u| < h справедливо неравенство ф^и) < < е/8. Представим R в виде R = Rx + В2, гДе Bi и Я2 — интегралы от той же подынтегральной функции, что и интеграл Я, но переменные интегрирования у них изменяются в других пределах: у Rx они изменяются от 0 до Л, а у R2 — от h до В. По второй теореме о среднем при некотором k9 0 < k < Л, имеем
1т> ।	2 z,4 ? sinAu ,	2 z,4 Arh sinu ,	.
1Д11= л<Р1(Л) J —— du = „Ф1(ЛН ~du <
2 z,. ?° sinu , z, 4	£
< J ~du = <Pi(ft)<
Далее, при фиксированных k и В в силу интегрируемости функции Ф1(м)/и из леммы Римана следует, что Я2 —> 0 при. А -» оо. Поэтому существует число Ао такое, что при А > Ао
1дг1 = | J Vi<u)^£du < л
Таким образом, получаем
1/а(*о) - Я*о)1 = I J du < е,
следовательно, lim Л(х0) = /(х0). ◄
Замечание. Пусть f(x) G £'. Тогда из теоремы 21, в частности, следует, что если, кроме того, функция f(x) является кусочно-гладкой в некоторой 8-окрестности точки х0, то выполняется условие Дини, поэтому интеграл В8 существует, следовательно, интеграл Фурье функции f(x) в точке х0 сходится к f(xQ). Из теоремы 22 следует сходимость интеграла Фурье в точке х0 к /(х0), если абсолютно интегрируемая функция f(x) в некоторой окрестности точки х0 Является не только абсолютно интегрируемой, но и кусочно-монотонной.
Л С ММ А 15. Пусть (1 + |x|V)(*) G L'(-°°, +оо). Тогда преобразование Фурье k раз дифференцируемо.
► Поскольку имеют место неравенства
|/(x)(ix)V^| < (1 + |x|n)|/(x)|, п = 1,..., k,
4 ЙО
в силу признака Вейерштрасса интегралы J f(x)(ix)neixydx равномерно сходятся на всей числовой оси соответственно к функциям п = 1, ... , k. ◄
ЛЕММА 16. Пусть функция Дх), ... , е L'(~°°, +°°) и пусть при х справедливы соотношения Дх) -> 0,... , fk~x\x) -> 0. Тогда имеем |g(i/)| = о(Ы“*).
► Интегрируя по частям, при любом А > 0 имеем
А
f fk\x)eixydx = (fjfe’1)(x)e/xOl-A + -А
+ J fk~2\x)(-iy)eixy)\^A + ... + (~iy)k J f(x)eixydx. -A	-A
Устремляя A -> получаем
J fk\x)eixvdx = (~iy)k f f(x)eixvdx = (~iy)kg(y). -oo	-oo
По лемме Римана имеем
lim J f^xj^dx = 0,
У 00 — oo
поэтому |g(y)| = o(|y|-*).	◄
ТЕОРЕМА 23 (равенство Планшереля). Пусть
/(X), /'(X), /"(X), Ф(Х) 6	-оо)
и при х -» оо имеем Дх) -> 0, f(x) -> 0. Пусть g(y) и \р(у) — преобразования Фурье соответственно f(x) и <р(х). Тогда справедливо равенство
J f(x)^(x)dx = J g(y)v(y)dy, —оо	"Н —оо
где черта над функцией \|/(i/) обозначает операцию комплексного сопряжения.
► Пусть А >0 — любое число. Преобразуем интеграл
J f(x)q>(x)dx = J ср(х)(£ gtyye-^dyyix =
= Г (f (p(x)e^dxjg(y)dy = f F(x,y)dy.
Перемена порядка интегрирования в последнем несобственном интеграле обосновывается тем, что при некотором с > 0 имеют место неравенства
|g(y)| < с(1 + Ij/I2)-1, \F(x, у)| < с J |<p(x)|dx
1 + Ij/I2 -оо
490
и, следовательно, несобственный интеграл сходится равномерно на отрезке [-А, А]. Более того, в силу признака Вейерштрасса имеет место и равномерная, сходимость по параметру А при , его изменении на всей числовой оси. Поэтому возможно перейти к пределу под знаком несобственного интеграла, и мы получаем равенство, утверждаемое в теореме. ◄
Наконец, в качестве приложения теории интегралов Фурье докажем важную формулу Котельникова.
Назовем функцию f(x) сигналом, а ее преобразование Фурье g(y) спектром сигнала. Возникает задача восстановления сигнала по его спектру, т. е. функции по ее преобразованию Фурье. Часто известен спектр на конечном промежутке, т. е. финитный спектр, и мы хотим восстановить сигнал, отвечающий этому спектру, по некоторому дискретному множеству значений сигнала. Это и позволяет сделать формула Котельникова.
Пусть существуют следующие интегралы
g(y) = f(y) = -4= J f(x)0xvdx, fa(x) = -4= f g(y)e-ixydy.
-CO	л/2л -a
Разложим функцию g(y), определенную на [-a, a] и периодически продолженную на всю числовую ось с периодом 2a, в ряд Фурье. Имеем
+°° iyn-
«(y) = *J-ooCBe a>
где
—q	LiU v (I '
Следовательно, получаем
fa(x) =

«/2Й -а
1 +s f f е lyn~adu- Т # fnjtAsin(ax-nn) У	ax-nit •
Если ряд Фурье функции g(y) при |р| < а сходится равномерно, то его можно почленно проинтегрировать. Поэтому получаем
4(*) =
у5 f ^sin(ax - пп)
Л “ -°0 a / ах - mt
Эта формула называется формулой Котельникова.
Лекция 30
$ 13. МЕТОД ЛАПЛАСА И МЕТОД СТАЦИОНАРНОЙ ФАЗЫ
Лаплас разработал метод для изучения асимптотического поведения при п —>	интегралов вида
ь
J(n) = J /(x)<pn(x)dx,
а
где функция ф(х) положительна при всех х е [а,Ь].
Суть его метода состоит в следующем. Пусть Дх) и ф(х) — гладкие функции и ф(х) имеет только один строгий максимум в точке х = с. Тогда при п -> оо этот интеграл с большой точностью можно заменить интегралом от этой же подынтегральной функции в некоторой достаточно малой окрестности точки х = с. Но в ней можно воспользоваться разложениями Тейлора функций Дх) и ф(х) и затем достаточно точно вычислить последний интеграл.
Изложим метод Лапласа в нетрадиционной форме.
ТЕОРЕМА 24. Пусть А, Х2,	— некоторые положительные
постоянные, F(x) — вещественная функция, непрерывная со своими производными до третьего порядка, на отрезке [а, Ь], и при всех х е [а, Ь] справедливы неравенства
О < Х2 = -F"(x) < АХ2, |F"(X)| < А13.
Пусть также существует точка с, а с Ъ, такая, что F'(c) = 0. Тогда справедлива формула
Ь	N |F"(C)|V2
R <	Х24/5Ц/5 + fifmin f, №1/21 +
2	3 д v|f"(a)|	2	)
где В — некоторая абсолютная постоянная.
► Из условия теоремы следует, что функция F'(x) является монотонной и, следовательно, обращается в нуль не более чем в одной точке. Это и есть точка х = с. Положим 8 = (Х2Х3)“1/5. Пусть сначала для точки с выполняется условие а + 5<е<Ь-5. Тогда
Ъ	»с-8 с + 8 fe
fe^>dx= I + f + f =Л+'2 + /з-a	a	c - 8 c - 8
Интегралы и I3 оцениваются одинаково. По второй теореме о среднем имеем
492
и.! - Т у'!й<“М <
1 11 i F'(x)
1
|F'(c-S)|
c-8
J de™ < ^с-8) a
1
|F'(c-8)|’
]Z | = J F'l^ ~ dX < ^+8)
3	?+8 F<x>
1 |F'(c-6)l’
Кроме того, справедливы неравенства
|F'(c + 3)| =
с + 8
J F’’(x)dx
V(e-8)
= T|F"(x)|d* > 8X2, 3X2.
Следовательно,
O/v2	O/l2
Используем разложение Тейлора функции F(x) на (с - 8, с + 8).
При некотором % е (с - 8, с + 8) получаем
с + 8	8	8 Лс) + О£}„2+^^„3
I2 = J eF^dx = J ef<c+»)dp = J е 2	6 , dy =
с - 8	-5	-8
8 f^2	8 03,2,™^	.
= e^)f e 2 У dy + e^f e 2 V (e 6 V -1}^-
-8	-8	V	'
+oo
----eFW_ +r°° 2/2 _	e^(c) Дс)|1/1 2/2 |F"(c)|V2 X *	\F"(c)\V2	У
8 ^”'(С)Ц2	,(,x	, ,	ч
+ B^> J е	- JTn + B2^>(X + V<) -

где В, Bx, B2 — некоторые абсолютные постоянные.
Если а < с < а + 3, то интеграл 1Г оценивается так:
1Л1< f с-8	с - 8	\^)
с-8
1 eF(a) \F'(a)\e
Аналогично, если 8-8<с< 6, то
11,1 <	1	ef<8)
1 з1 |Г(Ь)|
Отметим, что всегда имеет место оценка
b
|	J e
a
b M* ~ c>2 dx < f e 2
dx 1^,
ь F"(l;)(*-c)2 2
a
493
поэтому
|Д| < min (eF«’>|F'(a)l"1, Ля eF^k~W), |Г3| < min (e^lF'GOl’1, Лле*^1/2). ◄
ПРИМЕР. Найти асимптотическую формулу при 1 —> +°о для
Г(Х + 1) = Т txe~*dt.
О
Приводя подынтегральное выражение к виду, данному в условии теоремы 24, получаем
F(t) = X In t- t, F(t) = X/t - 1, F"(0 = -X/f2, F"'(0 « 2Х/Я
В точке t = X функция F(t) имеет максимум. Представим интеграл для Г(Х + 1) в виде суммы трех интегралов:
X/2 2Х оо
г(Х + 1)= J + J + J = /1 + /2 + /3.
О X/2 2Х
Интегралы на промежутках (О, X/2), (2Х, +оо) оценим исходя из второй теоремы о среднем. Получим
Х/2
= J t^e^dt < о
ер(1/2)	/X?
Г(Х/2) и; UJUJ ’
eF(2X)
Гз< |F'(2X)|

На промежутке [X/2, 2Х] применим теорему 24. Имеем
16Х2 = £ > -F"(t) > ^ = к2,	- I? < Ц - 16*3,
2^	___ /1 \Х zl \Х
J t^dt =	+ bQJ V/б*-2/5.
Таким образом, при X -» +°° получаем
Г(Х+1)= л/2ЙХ(;)Х + b(j)\2/5, т. е. при X -> +оо имеет место асимптотическая формула
Г(Х + 1) = ЛЙХ + BX-V10).
Видим, что доказательство теоремы 24 основано на принципе локализации, т. е. на получении асимптотики интеграла в окрестности особой точки. Аналогичное применение принципа локализации к интегралам от тригонометрических функций называется методом стационарной фазы.
494
Приведем формулировку этого метода в виде теоремьг. Следует отметить, что доказательство ее в основных чертах повторяет доказательство теоремы 24.
ТЕОРЕМА 25. Пусть А, Х2, Х3 — некоторые положительные постоянные, F(x) — вещественная функция, непрерывная со своими производными до третьего порядка на отрезке [а, Ь], и при всех х е [а, &] справедливы неравенства
О < Х2 < F"(x) < АХ2, |F"'(x)| < АХ3.
Пусть также существует точка с, а < с < Ь, такая, что F\c) = 0. Тогда справедлива формула
{	.__ piK/4+F(c)
/ elF^dx = л/2л !/2 + К*
я < в(х-/»ч/‘ + (йя  )+ mln (irbi ’ ^I/2 ))
где В — некоторая абсолютная постоянная.
Заметим, что если при всех х е [а, Ь] справедливы неравенства 0 < Х2 < -F"(x) < Ak2, то из теоремы 25 следует формула для функции G(x) = -F(x), т. е. мы получаем соответствующую фор-ь мулу для интеграла вида J e~iF{^dx. а
► Функция F'Cx) обращается в нуль только в точке х = с, поскольку F'(x) является монотонной функцией в силу положительности F"(x) на отрезке [а, &]. Положим 8 = (Х2Х3)~1/5. Пусть сначала для точки с выполняется условие а + 8<с<Ь-8. Тогда
Ъ	с -5 с + 5 Ъ
Оценим сверху интегралы |1г| и |/3|. По второй теореме о среднем
имеем
6Г(х)созЛх) . c78F(x)sinP(x) F(x) ах + J F(x)
1
|F'(c - 8)|
с-8
J F'(x) cos F(x)dx +
с — 8
J F'(x) sin F(x)dx <
<	4___________4
"|Г(с-8)| le
J F"(x)dx e-8
c 6X2-
Такая же оценка имеет место и для величины |13|.
495
По формуле Тейлора при некотором £ е (с - 8, с + 8) получаем
с+ 8	6	8	+^-Юи2 +——^«з)
I2 = J eiF(x)dx = J eiF(c+^dy = Je'- 2	6 dy =
с “ 8	—8	—8	•
8 iF"(c) 9	8 '
= e™ f e 2 dy + e™ J e -8	-5
2 y (e 6 v ~\\ly =
piF(c) +°°	1	+°°	5
= (F"(c))1/2 Leiy /2dy ~ 20	^Дс))1/2е,у2/2 dy + B1 {l*y3dy =
=	(F"(c))1/2 +B2(j^8 +^4)= '•/2™ (F"(c))1/2 +B^2 4/5^з/5’
где В, Bv B2, 0, 0 < 0 < 1, — некоторые абсолютные постоянные.
Если а < с < а + 8, то интеграл 1Г оценивается по второй теореме о среднем. Имеем
j	
e}-s F(x)
2 |Г(а)|
еГ(а)#
Аналогично* если Ъ - 8 < с < Ь, то |I3| < jp^j[ • Н° так как всегДа имеет место оценка
ь
то
1Л1 < min (4\F'(a)\-\ вХ^2), |/3| < min (4|F'(a)|~1, 8X^/2).
Для завершения доказательства теоремы 25 осталось показать, что
J e^dx < 2	.
Положим 8 = 2Xj1/2. Будем считать, что Ь - а > 48, так как в противном случае тривиальная оценка интеграла, имеющая вид b - а, является достаточной. Представим интеграл в виде
Ь	с-6 с+6 Ь
je^dx^ J + J + J -Ir + I2 + I3. а	а »с-6 с + 8
Если а < с < а + 8 или b - 8 < с < Ь, то будем рассматривать только сумму двух интегралов:
с + 8	Ь	с — 8 Ъ
J + J или J + J . а с + 8	л с - 8
496
Так как для х е (а, с - 8) или х е (с + 8, &) имеем
j F"(t)dt
|F'(*)h
> Х2|х - с| > Х28,
то 1Л1 < 4/(Х28); |Г3| < 4/(Х28). Кроме того, тривиально получаем |/2| < 28. Следовательно,
ь
J eiF^dx а
<	+ 28 < 8X2V2. «
ПРИМЕР. Найдем асимптотику функции Бесселя
1 я
Jk(x) = - J cos (х sin ф - Лф)Жр при х -» 4-оо. к о
Рассмотрим интеграл
1 п
- J е^^с/ф, Р(ф) = Лф - х sin ф.
п о
Имеем Г'(ф) = k - х cos ф, F"^) = х sin ф, Г'"(ф) = х cos ф. Определим точку ф0 из условия F'^o) = 0» т. е. cos ф0 = Л/х. Тогда F"^o) = ^х2	• Так как х +°°, то ПРИ достаточно больших
значениях х имеем л/4 < ф0 < Зл/4. Поэтому
л	л/4 Зл/4 л
| е^(ф)</ф = J 4- J 4- j . О	0 я/4 Зя/4
Оценивая первый и третий интегралы, из второй теоремы о среднем получаем
я/4
j е^(<р)йф о
4	=	4	< В
1^"(л:/4)|	|х/2/2 -х
В х ’
J e‘F№d(p Зя/4
где В — некоторая положительная постоянная. Для точек ф а/2
из промежутка [тс/4, Зтс/4] имеем х > |F"^)| = |х sin ф| > х--, а
|F"'(<p)| < х. Следовательно, из теоремы 25 находим
3У4	___ ^«(л/4 + Г(ф0))
т. е.
т/ /2 соз(тс/4 4- Лагссов(Л/х) - 7х2 - Л2) , J*(X) “ k	(X2-*2)V4	+
или
J (х\~ /2 соз(я/4 +nfe/2 -х)
Ji
497
В заключение заметим, что соединение методов Лапласа и стационарной фазы в теории функций комплексного переменного приводит к методу перевала. Важный вклад в разработку его внесли О. Коши, Б. Риман, П. А. Некрасов, П. Дебай. Современное изложение метода перевала можно найти в монографиях Э. Т. Копсона, М. А. Евграфова, Н. Г. Брейна, Г. Джеффриса, Б. Свирлса.
История вопроса обсуждается в статье С. С. Петровой и А. Д. Соловьева (Об истории создания метода перевала. Историко-математические исследования. 1994. Вып. 35).
Кратный интеграл Римана. Поверхностные интегралы
Заключительные главы курса математического анализа касаются разделов математики, общих как для математического анализа, так и для специальных дисциплин — таких, как теория функций действительного и комплексного переменного, дифференциальная геометрия, функциональный анализ.
Эта часть курса, в основном, посвящена теории кратного интеграла Римана, а также криволинейным и поверхностным интегралам в пространстве произвольного числа измерений. На взгляд авторов учебника, современная теория интегрирования на поверхностях опирается на понятие интеграла Римана, что предполагает систематическое его изучение в курсе анализа. Здесь доказаны классические теоремы Грина, Стокса и Гаусса—Остроградского с их стандартной интерпретацией в виде формул векторного анализа. Чтобы показать возможности предложенного подхода к построению теории поверхностных интегралов, приведено доказательство формулы Стокса для кусочно-гладкой ориентированной поверхности произвольной размерности в многомерном пространстве. Параллельно строится элементарная теория дифференциальных форм и теория объема многомерной поверхности.
Ряд важных теорем рассмотрен в курсе в «модельной» ситуации, т. е. в частном случае, принципиально сохраняющем все наиболее трудные аспекты общего случая, но позволяющем упростить изложение. К их числу относятся формула замены переменных в кратном интеграле, а также некоторые формулы и теоремы о криволинейных и поверхностных интегралах.
ГЛАВА 19
Кратные интегралы
Лекция 1
$ 1. ДВОЙНОЙ ИНТЕГРАЛ РИМАНА КАК ПРЕДЕЛ ПО БАЗЕ
Двойной интеграл — это интеграл от функции двух переменных, взятый по обеим переменным одновременно. Это не определение, мы только указываем, как намерены вводить обобщение понятия определенного интеграла на случай функции двух переменных.
Чтобы получить такое обобщение, вспомним определение интеграла в одномерном случае, т. е. в случае функции jy = /(#) от одной переменной х, определенной на отрезке I = £а, Ь] и интегрируемой на нем по Риману. Одно из эквивалентных определений данного понятия можно сформулировать так.
ъ
Определение 1. Интегралом J f(x)dx от ограниченной функ-а
ции f(x) называется, число* равное алгебраической, сумме площадей криволинейных трапеций* образованных кривой у = t(x) при х g [а, Ь]. При этом в данную сумму входят площади криволинейных трапеций* расположенных над осью абсцисс со знаком «+», а под ней — со знаком
Если обобщить понятие криволинейной трапеции на случай функции двух переменных z = g(x* у)* заданной на прямоугольнике Р = Ir X 12 =< [ах, bj X [а2, Ь2Ъ то и получим одно из возможных определений двойного интеграла от функции g(x* у) по прямоугольнику Р. Этот интеграл обозначается символом
&1 ь2
Л g(x, y)dxdy = J J g(x, y)dxdy. P	al a2
Допустим сначала, что g(x* у) > 0 для всех (х, у) е Р. Вмёсто криволинейной трапеции рассмотрим пространственную фигуру Н* заключенную между поверхностью z = g(x* у) и. плоскостью 2 = 0 при (х, у) е Р. Другими словами, фигура Н состоит из всех тех точек (х, у* z)* для которых х е 119 у е 12* а третья координата z удовлетворяет условию 0 < z < g{x* у).
501
Определение 2. Фигуру Н будем называть цилиндрической криволинейной фигурой, порожденной поверхностью z = g(x, у).
Если окажется, что эта фигура измерима каким-либо способом (по Жордану, по Лебегу или еще как-нибудь), то ее меру ц(Н) можно взять в качестве искомого определения значения двойного интеграла
I = JJ ё(х, у) dx dy = ц(Я). р
Если ц — мера Жордана, то данное выше определение двойного интеграла эквивалентно определению двойного интеграла Римана, которое дано ниже. Можно таким же образом разобрать общий случай, когда функция g(x, у) принимает как положительные, так и отрицательные значения, что и сделано в дальнейшем при доказательстве критерия измеримости по Жордану цилиндрической криволинейной фигуры.
Перейдем к построению теории двойного интеграла Римана по прямоугольнику Р. Сначала определим понятие цилиндрической фигуры в общем случае.
Определение 3. Фигура Н с R3 называется цилиндрической криволинейной фигурой, порожденной поверхностью z = g(x, у), заданной на Р, если Н состоит изо всех таких точек (х, у, z), для которых (х, у) е Р, а координата z заключена между числами 0 и g(x, у), то есть при g(x, у) > 0 имеем 0 < z < &(*, у), а при g(x, у) < 0 имеем g(x, у) < z < 0.
Разобьем прямоугольник Р на меньшие прямоугольники с помощью прямых, параллельных осям Ох и Оу и проходящих через точки ах = х0 < хг < ... < хт = разбиения Тх на оси Ох и а2 = У о < Уг < ••• < Уп = ^2 разбиения Ту на оси Оу.
Прямоугольник Pk* t cz Р, точки (х, у) которого удовлетворяют условиям
х е Д*> = [xft_p xj, у е Д|»> = [yz_p yj,
где Д^ есть А-й отрезок разбиения Тх и Д|у) - Z-й отрезок разбиения Ту, будем называть элементом разбиения Т прямоугольника Р с индексом (k, I), а множество всех прямоугольников Pkl, k-1, ... , m, I = 1, ... , п — разбиением Т прямоугольника Р.
В каждом прямоугольнике z возьмем точку Ak> t с координатами t, Qk z). Множество прямоугольников Pk t и точек z будем называть размеченным разбиением прямоугольника Р и обозначать его через V.
Очевидно, что каждому размеченному разбиению V однозначно соответствует неразмеченное разбиение Т прямоугольника Р, 502
получаемое из V отбрасыванием точек «разметки» (£fc> t, 0fe г). Другими словами, Т = Т(У).
Отметим, что площадь элемента разбиения Г, т. е. площадь прямоугольника Рк t, равна A xft A j/z = (xfc - хй-1> (у{ - yz_x).
Определение 4. Сумма m п = *?11?1 р е*.z)д х»д У1
называется интегральной суммой Римана функции g(x9 у), соответствующей (отвечающей) размеченному разбиению V стандартного прямоугольника Р.
Длину 7д«л + Ду/2 диагонали прямоугольника Pk> t будем называть его диаметром.
Определение 5. Диаметром разбиения (размеченного V и неразмеченного Т) прямоугольника Р будем называть максимальное значение диаметров элементов разбиения {Pk J и обозначать символом (соответственно Дг).
Определение 6. Число I называется (двойным) интегралом Римана от ограниченной функции g(x9 у) по прямоугольнику Р9 если для всякого числа е > 0 существует число 8 = 8(e) > 0 такое, что для любого размеченного разбиения V прямоугольника Р с условием Дг < 8 справедливо неравенство
|g(V)- 1| <е.
Здесь 0(V) — интегральная сумма для функции g(x, у), которая соответствует размеченному разбиению V. Поэтому последнее неравенство можно записать еще и так:
Im п	I
z» е*. z)д хи д Vi - *| < е.
В этом случае будем говорить, что g(x9 у) является интегрируемой по Риману на прямоугольнике Р.
Рассмотрим следующие вопросы:
1)	убедимся, что интеграл I есть предел по некоторой базе;
2)	определим верхние и нижние суммы Дарбу и докажем критерий Римана интегрируемости функции от двух переменных;
3)	установим свойства двойного интеграла, аналогичные свойствам однократного интеграла.
Начнем с определения баз множеств В и В'. Множество всех неразмеченных разбиений прямоугольника обозначим через Ар9 а размеченных — через А'р. В качестве окончаний Ь'ь базы В' возьмем множество {У|Ду < 8}, т. е. множество разбиений, состоящее из тех Vg А'р9 ддя которых диаметр Дк меньше, чем 8 > 0.
503
Так как o(V) определена всюду на Ар, то, очевидно, определение двойного интеграла, данное выше, эквивалентно определению предела Ит o(V) по базе В'. Проверка справедливости этого утверждения состоит в том, что надо формально записать определение предела по базе и сравнить его с данным выше определением. Далее базу В' будем обозначать символом —> 0.
Аналогично определяем базу Дт —» 0 для всех неразмеченных разбиений Ар.
Итак, двойной интеграл есть предел по некоторой базе. Поэтому уже можно говорить о единственности двойного интеграла, применять теорему о переходе к пределу в неравенствах и т. д., получая отсюда различные утверждения о двойном интеграле типа его линейности, монотонности и другие. Некоторые такие естественные свойства будут приведены ниже.
Отметим, что неразмеченное разбиение Т прямоугольника Р можно определить и как пару (Тх, Ту), состоящую из неразмеченного разбиения Тх : аг = х0 < хг < ... < хт = Ьг отрезка [ах, &г] на оси Ох и неразмеченного разбиения Ту : а2 = yQ < уг... < уп = Ъ2 отрезка [а2, &2]на оси Оу- Это разбиение Т получается проведением m + 1 вертикальных прямых х = хЛ, k = 0, ... , m, и п -I-1 горизонтальных прямых у = yt,1 = 0,..., и. Снова заметим, что если у размеченного разбиения V отбросить разметку точками z, Qk l) g Pk то, очевидно, возникает неразмеченное разбиение, которое будем обозначать символом Т = T(V).
Определение 7. Множество всех размеченных разбиений {V}, которым отвечает одно и то же неразмеченное разбиение TQ, будем называть множество разметок TQ и обозначать символом Ар (То). Если V е Ар (То), то будем говорить, что V является разметкой То или, что то же самое, T(V) = То.
§ 2. СУММЫ ДАРБУ И ИХ СВОЙСТВА
Переходим теперь к построению теории Дарбу для двойного интеграла Римана по прямоугольнику.
Обозначим для некоторого неразмеченного разбиения Т прямоугольника Р через Mk, t n тк t величины
Mk,i= SUP g(x,y), mk l= inf g(x, y).
K’1 (x,y)ePkJ	’l
Тогда верхней суммой Дарбу функции g(x, у), соответствующей (отвечающей) разбиению Т, называется сумма S(T), где
т п
S(T) =
504
а сумма
называется нижней суммой Дарбу.
Омега-суммой Q(T), отвечающей разбиению Т, назовем величину
Й(Т) = S(T) - s(T) = ДП?1(ОК ,ДхАДУ/, где<оЛ>/ = Мк>/-/пй>/.
Определение 8. Число I* = inf S(T) называется верхним ин-ТеАр
тегралом Дарбу от функции g(x, у) по прямоугольнику Р, а число Ц = sups(T) — нижним интегралом Дарбу от функции ТеАР
g(x, у).
Ддлее потребуются следующие свойства сумм Дарбу.
ЛЕММА 1. Для любого размеченного разбиения V е А р имеем s(T(V))<o(V)<S(T(V)).
ЛЕММА 2. Зафиксируем некоторое разбиение То е Ар. Имеем следующие соотношения:
з(Т0) = inf G(V), S(T0) = sup o(V).
FeAj>(To)	VeAp^j
ЛЕММА 3. Для любых неразмеченных разбиений Т\ и Т2
8(Т\) < S(T2).
ЛЕММА 4. Для ограниченной на прямоугольнике Р функции верхний Г и нижний I* интегралы Дарбу существуют, причем для любого разбиения Т е Ар справедливы неравенства
з(Т) < Л < I* < S(T).
ЛЕММА 5. Размеченное разбиение V принадлежит окончанию Ь'ъ е В' тогда и только тогда, когда T(V) е bs.
Доказательство лемм аналогично доказательству соответствующих утверждений в одномерном случае и не представляет большого труда. Стоит лишь сказать о лемме 3, поскольку там участвуют два разных разбиения. Здесь, как и в одномерном случае, введем понятие измельчения разбиения.
Определение 9. Неразмеченное разбиение Т2 называется измельчением разбиения Тг, если разбиение Т2 получается из Тг добавлением конечного числа новых точек разбиения на оси Ох и на оси Оу. Говорят еще, что Т2 следует за Тг и пишут Т2 z> Тг или Tr cz Т2.
505
В частности, любое неразмеченное разбиение Т есть измельчение самого себя. Далее, очевидно, что при измельчении разбиения Т нижняя сумма Дарбу з(Т) не может уменьшиться, а верхняя сумма Дарбу S(T) не может увеличиться. Поэтому для доказательства утверждения леммы 3 надо на каждой оси Ох к Оу взять разбиение Т3, объединяющее разбиения и Т2. Тогда получаем
з(Тх) < а(Т3) < S(T3) < S(T2).
Отсюда имеем sfTJ < S(T2), что и доказывает утверждение леммы 3.
Отметим также, что утверждение леммы 4 по существу вытекает из леммы 3. Действительно, если образуем числовое множество М19 состоящее изо всех значений величин з(Т), и множество М2 значений величин S(T), то утверждение леммы 3 означает, что любой элемент а е М2 есть верхняя грань множества М19 a потому наименьшая верхняя грань множества М19 т. е. I* не превосходит этого элемента а е Mv Отсюда для любого числа а е Мх имеем Д < а. Это значит, что Д является нижней гранью множества М2. Но величина I*, по своему определению, есть точная нижняя грань множества М2, и поэтому для любого разбиения Т е Ар
з(Т) < Д < Г < S(T).
Лемма 4 доказана.
ЛЕММА 6. Для любого разбиения Т имеем £1(Т) > Г - Ц.
Действительно, из леммы 4 получаем
Q(T) = S(T) - s(T) s(T) >1*- Ц.
*
Лекция 2
$ 3. КРИТЕРИЙ РИМАНА ИНТЕГРИРУЕМОСТИ ФУНКЦИИ НА ПРЯМОУГОЛЬНИКЕ
ТЕОРЕМА 1 (критерий Римана интегрируемости функции на прямоугольнике). Для того чтобы ограниченная функция g(x, у) была интегрируема на Р = [ар х [а2, &2], необходимо и достаточно, чтобы выполнялось одно из эквивалентных условий:
1)	Um Q(T) = O;
—> О
2)Г = Л;
3)	inf Q(T) = 0. т
► Докажем сначала эквивалентность условия интегрируемости функции условию 1.
Необходимость. Пусть Jim g(V) = I. Это значит, что для любого ех > О найдется Зх = SjXe!) > 0 такое, что для любого размеченного разбиения V с условием Дг < 8Х имеем |o(V) -1\ < ер т. е.
/-ex<o(V)<I + ex.	(*)
Рассмотрим произвольное неразмеченное разбиение Т с условием Дг < 8Х. Для него получаем
s(T) = inf g(V), S(T) = sup o(V). FeAp(T)	VeAp(T)
Тогда из неравенства (*) вытекает, что
/ - ех < s(T) < I + £р I - £х < S(T) < I + Ер
Следовательно, значения з(Т) и S(T) лежат на одном отрезке [/ - Ер Z + ех] длины 2ех, т. е. имеет место неравенство
Q(T) = S(T) - s(T) < 2ех.
Если взять £х = е/3, 8(e) = 81(е1), то получаем, что для любого е > 0 существует число 8 = 8(e) > 0 такое, что при любом разбиении Т с условием Дт < 8 имеем £2(Т) < е, т. е. справедливо соотно-
шение lim Й(Т) = 0. Необходимость доказана. дт —> о
Достаточность. Надо доказать, что из условия JimQ Q(T) = 0
следует существование предела Jiin g(V).
Сначала убедимся, что 1* = Г. Из леммы 6 для любого разбие
ния Те Ар имеем
0 < I* - Г < Й(Т),
и, следовательно, й = /*-/*—» 0 при Дг —> 0. Так как й — постоянное число, то й = 0 и I* = Г = I. Осталось доказать, что g(V) I
507
при Дк —> 0. Возьмем произвольное положительное число ер Из условия существования предела lim Q(T) можно найти число
81 = 81(е1) > 0 такое, что для всех разбиений Т с условием Дг < 8Х выполняется неравенство £2(Т) < ер Но тогда для любой разметки V этого разбиения имеем
s(T(V)) < G(V) < S(T(V)), з(Т(У)) < Z* = I = Г < S(T(V)), S(T(V)) - s(T(V)) = Q(T) < e,
т. e. обе точки o(V) и I лежяп на отрезке [s(T(V)), S(T(V))], длина которого не превосходит ер Это значит, что расстояние между этими точками тоже не превосходит ех, поэтому для любого размеченного разбиения V с условием Ду < 8Х имеем |o(V) - l\ < ер Следовательно, lim o(V) = I. Достаточность доказана.	<
Av—> 0
Итак, условие 1 теоремы 1 эквивалентно условию интегрируемости функции по Риману.
Докажем теперь эквивалентность условий 1, 2 и 3. Для этого убедимся в справедливости цепочки утверждений:
1) =» 2) => 3) => 1).
а) б) в)
а)	Нам следует доказать, что если lim Й(Т) = 0, то Z* = Z*. Но дг —> о
этот факт уже установлен при доказательстве достаточности условия 1.
б)	Сначала докажем, что
inf Q(T) = h = Z* - Z*. т
Число h = I* - Z* — нижняя грань Q(T), поскольку из леммы 6 имеем
Q(T) > Z* - Z* = h.
Докажем, что h — точная нижняя грань множества {Q(T)}. Для этого возьмем произвольное Е > 0. Тогда в силу определения сумм Дарбу имеем, что существуют разбиения Тг и Т2 такие, что
S(7\) < Z* + е/2, s(T2) > Z* - е/2.
Возьмем разбиение Т3 = 7\ U Т2. Получим
S(T3) < S(TJ < Z* + е/2, s(T3) > s(T2) >1*- e/2.
Отсюда следует, что Q(T) < Г - Z* + е = h + е, т. е. h = inf Q(T). Та-т
ким образом, из доказанного и условия 2 имеем
inf Q(T) = Z* - Z* = 0. т
Тем самым утверждение б) доказано.
508
в)	Надо доказать, что если inf Q(T) = 0, то lim Q(T) = 0.
Т	Дт->0
Для любого е > 0 существует разбиение Т1 такое, что Q(TX) < < е/2. Разбиению соответствует пара разбиений Т^у)) по осям Ох и Оу. Количество точек разбиений Т^х), Тг(у) обозначим через q.
Далее, поскольку g(x, у) ограничена на Р, существует М > 0 такое, что \g(x, у)\ < М для всех (х, у) е Р. Обозначим через d длину наибольшей стороны прямоугольника Р. Положим теперь 8 = &/(4qdM).
Возьмем любое разбиение Т = (Т(х), Т(у)) с условием Дг < 5. Тогда для разбиения Т2 = Т U Тг имеем
Q(T2)<Q(T1)<8/2,
поскольку Т2 — измельчение разбиения Т19 т. е. Т2 о Tv Перейдем к оценке сверху величины Q(T). Имеем
Q(T) = Q(T2) + а(Т, 7\).
Здесь а(Т, Тг) > 0, поскольку Т2 о Tv Кроме того,
а(Т, Тг) = SS (<»мДхЛДуг - <й’к ... - (о^Дх^Дг/^) < ES
причем символ ЕЕ означает, что суммирование ведется по тем парам (fe, Z), Для которых прямоугольник Pk z разбиения Т разлагается на меньшие прямоугольники с индексами ', ... ,(г) посредством разбиения Тг (илй Т2). Другими словами, пара (k, I) тако-
ва, что внутри отрезков Д^х) или Д^ лежит по крайней мере одна точка разбиения 7\(х) или разбиения Т1(у).
Достаточно оценить сверху величину а(Т, 7\). Будем считать,
что символ ЕЕ означает, что суммирование ведется по тем парам (fe, Z), для которых внутри отрезка Д^ находится по крайней мере одна точка разбиения Т1(х), а переменная I принимает все воз-
можные значения, определяемые разбиением Т. Аналогично оп-
ределяется символ ЕЕ. При оценивании воспользуемся следую-(Z)fe
щими неравенствами:
(ok z < 2М, Дх* < 8, Дг/; < 8, S Дх* < d, Z &yt < d, Тогда имеем
а(Т, 7\) < SS (ok< t^x^yt < SS <oft> fix^ +
+ SS i^x^yt < 2M8 (s(e Д^) +	Дх*)) <
< 2M8d (j 1 + S 1) < 2M5dq < e/2.
509
Следовательно,
Q(T) = Q(T2) + a(T, TJ < e/2 + e/2 = e.
Утверждение в) доказано, и тем самым теорема 1 доказана полностью. ◄
$4. СПЕЦИАЛЬНЫЙ КРИТЕРИЙ ИНТЕГРИРУЕМОСТИ ФУНКЦИИ НА ПРЯМОУГОЛЬНИКЕ
Рассмотрим последовательность разбиений Тп прямоугольника Р, отвечающую разбиениям каждого из отрезков [ах, Ьх], [а2, на п Равных частей, т. е. разбиение Тп будет состоять из и2 равных между собой прямоугольников. Соответствующие разбиению Тп верхнюю и нижнюю суммы Дарбу обозначим через Sn и sn, а омега-сумму — через £1п.
ТЕОРЕМА 2. Для интегрируемости функции, ограниченной на прямоугольнике, необходимо и достаточно, чтобы выполнялось условие
lim Q_ = 0. n -> ОО п
► Необходимость утверждения следует из теоремы 1 предыдущего параграфа, поскольку из условия lim Q(T) = 0 получаем, дт —> о
что lim Qn = 0.
Достаточность. Для любого разбиения Т s(T) < I. < Г < S(T), следовательно,
Sn<i*<r<sn.
Отсюда получаем, что
Qn^Sn-sn>r-h>0.
Но так как предел Jim^ Qn = 0, то /* = /* = /. В силу условия 2 теоремы 1 § 2, отсюда следует интегрируемость рассматриваемой функции по Риману. ◄
Следующая теорема является дополнением и уточнением теоремы 1 предыдущего параграфа.
ТЕОРЕМА 3. Для интегрируемости ограниченной функции на прямоугольнике необходимо и достаточно, чтобы выполнялось одно из следующих эквивалентных условий:
4)	lim Q_ = 0;
5)	inf Q„ = 0.
510
► В силу теоремы 1 и теоремы 2 имеем цепочку заключений:
5) =» 3) =» 1) =» 4) =* 5). ◄
Утверждения этого параграфа представляют интерес для вычислительных целей. Из них следует, что достаточно рассмотреть лишь одну последовательность разбиений Тп.
В силу теоремы 3 для любой последовательности {Vn} разметок, соответствующих последовательности неразмеченных разбиений Тп, имеем lim^ о(Уп) = 19 причем ошибка при замене I на а(Уп) не превосходит Qn, т. е. |о(Уп) -1\ < £2П.
На самом деле справедливо более общее утверждение: для любого размеченного разбиения V и для Т = T(V) имеем
|g(V) - /| < Q(T(V)).
Действительно, справедливы неравенства
s(T(V)) < a(V) < S(T(V))> s(T(V)) < I < S(T(V)).
Это означает, что отрезку [s(T(V))> S(T(V))], длина которого равна S(T(V)) ~ з(Т(У)) = Q(T(V)), принадлежат оба числа о(У) и I, откуда
|c(V)-/|<Q(T(V)), что и утверждалось выше.
Лекция 3
§ 5. ИЗМЕРИМОСТЬ ПО ЖОРДАНУ ЦИЛИНДРИЧЕСКОЙ КРИВОЛИНЕЙНОЙ ФИГУРЫ
Напомним определения, связанные с понятием измеримости по Жордану трехмерной фигуры.
Определение 10. Фигура Р называется простейшей, если она является объединением конечного числа параллелепипедов, стороны которых параллельны осям координат. Такие параллелепипеды назовем стандартными.
Обозначим через П = П3 множество всех простейших фигур в пространстве Я3.
Очевидно, что мера (или объем) Жордана простой фигуры — это сумма объемов открытых непересекающихся стандартных параллелепипедов, на которые эту фигуру можно разбить.
Определение 11. Верхней мерой Жордана p*(F) ограниченной фигуры F называется величина inf ц(Р), т. е. точная ниж-Ре П, FcP
няя грань объемов всех простых фигур, содержащих F.
Аналогично, нижней мерой Жордана p*(F) фигуры F называется величина
p*(F) = sup ц(Р).
Ре П, PcF
Если p*(F) = p*(F), то фигура F называется измеримой по Жордану и ее мера (объем) Жордана равна p(F) = p*(F) = p*(F).
Заметим, что объем любой ограниченной части плоскости всегда равен нулю.
Напомним критерий измеримости фигуры F по Жордану. Обозначим через 3F границу фигуры F, т. е. множество точек в Я3, не являющихся ни внутренними, ни внешними для фигуры F.
ТЕОРЕМА 4. Для измеримости фигуры F по Жордану необходимо и достаточно, чтобы мера ее границы p(dF) была равна нулю.
Доказательство этого критерия проводить не будем, поскольку оно ничем не отличается от его доказательства в двумерном случае. Отметим только следующие четыре свойства величины p(F).
1°. Если F uG измеримы, то фигуры FUGuF AG измеримы.
2°. Если F и G не пересекаются, то p(F U G) = p(F) 4- H(G) (свойство аддитивности).
3°. Если F a G, то p(F) < p(G) (свойство монотонности).
4°. Сдвиги и повороты фигуры F не изменяют значения меры этой фигуры (свойство инвариантности).
512
Т Е О P E M A 5; Для интегрируемости ограниченной функции g(x, у) на прямоугольнике Р необходимо и достаточно, чтобы цилиндрическая криволинейная фигура F, отвечающая поверхности z = g(x, у), была измерима по Жордану.
► Необходимость. Пусть функция g(x9 у) интегрируема на Р. Надо доказать» что фигура F измерима. Граница dF этой фигуры состоит из шести поверхностей:
3F = H1UH2U... ияб,
где Н19 ... , Н5 — часть границы фигуры F, состоящая из частей плоскостей, параллельных координатным плоскостям, и Н$ — поверхность
z ~ g(x, у), (х, у) 6 Р.
Заметим, что |х(Э7Ух) = ... = р(ЭН5) = 0, так как всякий прямоугольник или его часть имеют нулевой объем.
Из критерия интегрируемости по Риману функции g(x, у) имеем, что inf £2(Т) = 0. Следовательно, для всякого е > 0 существует разбиение Т такое, что справедливо неравенство Й(Т) < е. Для этого разбиения Т рассмотрим простую фигуру D, которая является объединением замкнутых параллелепипедов (брусов) Dk t, соответствующих разбиению Т прямоугольника Р. Каждый брус Dk, t состоит из точек (х, у, г) таких, что для всех (х, у) € Pk t имеем mk 2 < Mk t (напомним, что mk t = inf g(x, y), Mk t ==
= sup g(x,y)).
(X, y)€ pk I
Тогда, очевидно, фигура D содержит все точки поверхности Н6. Далее, имеем p(Z>) = Q(T) < е. Поскольку HQ с D, получим, что ц*(Н6) < е. В силу произвольности е > 0 это значит, что Ц(Н6) == 0. Отсюда следует, что |i(3F) = 0, и тогда, согласно критерию измеримости, фигура F измерима по Жордану. Необходимость доказана.
Достаточность. Имеем, что фигура F измерима. Из критерия измеримости получим |1(3F) = 0. Это значит, что для любого е > 0 существует фигура D е П такая, что Н6 с D и p(D) < е. Фигура D есть объединение нескольких замкнутых брусов Dr, г = 1, ... , t.
Можно считать, что проекция фигуры D на плоскость г = 0 совпадает с Р. Если это не так, то можно вместо D взять ее пересечение с бесконечным цилиндром, состоящим из точек (х, у, г) с условием (х, у) е Р.
Проекции всех брусов Dr, г = 1, ... , t, на плоскость 2 = 0 дают разбиение прямоугольника Р на прямоугольники Qr.
513
17-4953
Продолжая стороны каждого прямоугольника Qr до пересечения со сторонами прямоугольника Р, получаем некоторое разбиение Т прямоугольника Р на прямоугольники Pk t.
Для любой точки (х, у) е Pk l имеем
(х, у, mkl) е Dn(x, у, Mk>t) е D, где mk , = inf g(x, у), Mk , = sup g(x, у). Это утверждение ’	(х.»)еР»_,	’	(х,у)ё Р„л
имеет место, поскольку Н6 с D.
Обозначим через Dk t брус с условием
(X, у)еРк1,
Пусть Dq — объединение всех таких брусов Dk t. Тогда получим: DocD и ц(£>0) < ЦСО) < £• Отсюда имеем, что Ц(ЬО) = Г1(Т) < е. Следовательно, inf Q(T) = 0, т. е. g(x9 у) интегрируема на Р. ◄ т
$ 6. ПОНЯТИЕ ДВОЙНОГО ИНТЕГРАЛА РИМАНА
ПО ОГРАНИЧЕННОЙ ОБЛАСТИ, ИЗМЕРИМОЙ ПО ЖОРДАНУ
Для дальнейшего рассмотрения нам потребуется ввести понятие предела еще по одной базе множеств.
Рассмотрим функцию g(x, у), определенную на ограниченной области D, измеримой по Жордану. .
Определение 12. Разбиением т области D будем называть конечный набор измеримых по Жордану множеств Dx, ... , Dt с условиями:
1) U ... UDt = D;
2) при всех т, п < t, т* п, имеем ц.(2>т Л Dn) = 0.
Совокупность всех разбиений т обозначим через AD.
Определение 13. Диаметром d = d(D) множества D называется величина sup р(а, 6).
а, ЬбВ
Диаметром \ разбиения т области D будем называть величину Дх = max d(Dn).
Точки ар ..., ар а8 g Ds, 1 < s < f, будем называть разметкой данного разбиения т и обозначать символом р = pD, а разбиение р будем называть размеченным разбиением.
Множество всех размеченных разбиений множества D обозначим через Ар.
Определение 14. Интегральной суммой размеченного разбиения р будем называть величину
°(Р) = „?	ап = (хл, уп).
514
Определение 15. Число I называется обобщенным' двойным интегралом Римана функции g(x, у) по ограниченной области D9 измеримой по Жордану, если для любого е > 0 найдется число 8 = 8(e) > 0 такое 9 что для любого разбиения Р = с условием Др < 8 имеем |о(Р) - 1\ < е.
Обобщенный двойной интеграл можно рассматривать как предел по базе. Обозначим эту базу символом Др 0; она будет состоять из окончаний Ь'ь с A'D9 определяемых условием
~ {Р = Рр|Др < 8}.
t
Очевидно, что функция о(р) = JE xg(an)p(Z>n) определена на множестве A'D9 а ее предел по базе Др 0 и есть обобщенный двойной интеграл по области D.
Пусть тп = inf g(a), Мп = sup g(a), о = М - тп. Тогда опре-абВп	aeZ)„
делим верхнюю и нижнюю суммы Дарбу соответственно следующими выражениями:
S(t) = „?#„№), «(T) = J1mBg(Dn),
t
и омега-сумму — выражением Q(t) = Е eyi(D„).
Дадим еще одно определение кратного интеграла от ограниченной функции g(x, у) по ограниченной, измеримой по Жордану, области D.
Пусть для некоторого прямоугольника Р имеем D с Р. ределим функцию g(x, у) на весь прямоугольник Р, полагая
g(x, у), если (х, у) е D, 0, если (х, у) е Р \ D.
Определение 16. Если функция g9(x, у) интегрируема по Риману на прямоугольнике Р, то двойной интеграл J от ёй{х, у) по Р называется двойным интегралом Римана по множеству D от функции g(x, у), т. е. по определению имеем
JJ g(x, y)dxdy = J = fl g0(x, y)dxdy. D	P
На первый взгляд может показаться, что понятие обобщенного интеграла I расширяет класс интегрируемых функций по сравнению с понятием интеграла J, но на самом деле это не так.
ТЕОРЕМА 6. Для существования обобщенного двойного интеграла I необходимо и достаточно9 чтобы существовал интеграл J9 причем тогда I = J.
g0(x, у) =
515
17*
► Заметим, что теорию Дарбу и критерии интегрируемости можно перенести на случай обобщенного двойного интеграла.
1. Пусть существует интеграл J по прямоугольнику Р. Тогда в силу критерия интегрируемости (inf Q(T) = 0) имеем, что для т
всякого е > 0 найдется разбиение Т такое, что П(Т) < е, причем Т состоит из прямоугольников Pk t. Возьмем в качестве Dk t = D A Pk t. Тогда получаем разбиение т множества D. Колебание функции g(x, у) на множестве Dk t не превосходит ее колебания на Pk z, поэтому имеем Q(t) < Q(T) < е, т. е. согласно критерию интегрируемости существует обобщенный интеграл I.
Аналогично можно получить неравенство S(t) < S(T), поэтому Г < S(T), Г < J*, I = Г < J* = J, I < J. Из подобного неравенства для нижних сумм Дарбу имеем з(т) > з(Т), / = /* > J* = J. Из этих неравенств следует, что I = J. Необходимость доказана.
2. Пусть существует обобщенный интеграл / по ограниченному измеримому множеству D. Надо доказать, что существует интеграл J от функции gQ(x9 у) по прямоугольнику Р, содержащему D. Из критерия интегрируемости имеем, что существует разбиение т = {D19 ..., Dt) такое, что О(т) < е. Для каждого г = 1, ... , t множество Dr измеримо, поэтому |1(Э/)Г) =г 0. Следовательно, найдется простейшая фигура F, состоящая из прямоугольников Pk t и такая, что суммарная площадь всех Pk l9 содержащих хотя бы одну точку границы dDr9 г = 1, ...,£, не превосходит е, т. е. p(F) < е.
Продолжим прямолинейные* отрезки границы F до пересечения со сторонами прямоугольника Р. Получим разбиение Т этого прямоугольника. Вклад <ох в омега-сумму Q(T) тех прямоугольников, которые принадлежат Р \ F, не превосходит П(т) < е. Вклад же со2 в тех прямоугольников, которые принадлежат F, не превосходит
со2 < 2M|i(F) < 2Мг.
Следовательно,
Q(T) = (Dj + со2 < (2М + 1)е.
Отсюда в силу критерия интегрируемости функции по прямоугольнику следует, что существует интеграл J.
Рассуждая аналогично для верхних сумм Дарбу, получим неравенство
S(T) - 2Мг < S(t).
516
i л
Следовательно, J < I + 2Me. В силу произвольности выбора положительного числа £ отсюда имеем J < I. Из оценок для нижних сумм Дарбу получаем противоположное неравенство J > I. Таким образом, I = J. ◄
Из эквивалентности определений интеграла Римана видно, что при построении теории можно было бы ограничиться квадратами К :□ D и разбиениями их на и2 равных квадратов, и при этом класс интегрируемых функций был тем же самым, что и при определении обобщенного интеграла. Но при таком построении теории есть одно неудобство, связанное с тем, что в пересечении двух квадратов не обязательно получится квадрат, поэтому мы и ограничились рассмотрением прямоугольников.
Лекция 4
§ 7.	ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
Рассмотрим свойства двойного интеграла, а в случае существенного отличия их от свойств однократного интеграла приведем их доказательства.
Пусть D9 Dv D29 ... — измеримые по Жордану множества, и функции g(x, у)9 gx(x9 у)9 g2(x9 у) интегрируемы по Риману на рассматриваемых множествах. Тогда имеют место следующие свойства.
1°. Справедливы равенства:
a)	JJ (ё1(х, у) + g2(x, y))dxdy = JJ g^x, y)dxdy + JJ g2(x, y)dxdy; D	D	D
6)	JJ cg(x9 y)dxdy = c JJ g(x9 y)dxdy V ce R (свойство линейности). D	D
2°. Пусть функции gx и g2 интегрируемы на D9 тогда gxg2 интегрируема на D.
3°. Пусть на D справедливо неравенство gr(x9 у) < g2(x, у)-В этом случае:
a)	JJ g^x, y)dxdy < JJ g2(x9 y)dxdy (свойство монотонности).
d	\ D \
б)	Пусть также \g(x9 y)\ интегрируема на D. Тогда
JJ g(x, y)dxdy < JJ|g(x, y)\dxdy. D	D
в)	Пусть f(x9 i/) >0, m = inf g(x9 y)9 M = sup g(x9 у). Тогда cy-D	D
ществует число c9m<c < M9 такое, что JJ f(x, y)g(x9 y)dxdy =
D
= c JJ f(x, y)dxdy (теорема о среднем).
D
4°. JJ 1 • dxdy = p(D). D
Это утверждение следует из эквивалентности определения меры Жордана и определения обобщенного двойного интеграла.
5°. Если |х(В) = 0, то JJ g(x, y)dxdy = 0 для любой ограничен-D
ной на D функции g(x, у).
► Так как функция g(x, у) ограничена на множестве D, то найдется число М > 0 такое, что для всех точек (х, у) g D выполняется неравенство \g(x, у)\ < М. Из свойств 3°, 1° и 4° имеем
JJ g(x, y)dxdy < JJ|g(x, y)\dxdy < M JJ dxdy = M p(D) = 0. ◄
D	D	D
518
6°. Пусть области Dx и D2 не имеют общих внутренних точек. Тогда
JJg(x, y)dxdy + JJ g(x, y)dxdy = JJ g(x, y)dxdy ®i	o2	DjUDg
(свойство аддитивности интеграла как функционала от области интегрирования).
► Пусть стандартный прямоугольник Р содержит Dx и D2. Тогда по определению
tfg(x, y)dyc - JJ gx(x, y)dxdy, JJg(x, y)dp = JJ g2(x, y)dxdy, Dj	p	d2	p
где
six u\ = J	еслИ y) e	D1>
S1' ,y’	10,	если(х,у)е	P\DX,
(	„1 = Ых,у),если(х, y)e D2,
,y' lO,	если (x, y)e	P\D2,
Отсюда и из свойства линейности интеграла получаем
JJ g(x, y)dy. + JJ g(x, у)ф =
О1	ог
= JJ gi(x, y)dxdy + JJ g2(x, y)dxdy = p	p
= JJ (Si(x, y) + g2(x, y)dxdy - JJ gdy. « P	DjUD,
7°. Если значения функций g^x, у) и g2(x, у) отличаются только на множестве Dx, причем	= 0,D1a D, то
JJ gi(x, y)dxdy = JJ g2(x, y)dxdy. D	D
► Действительно, имеем
JJ gl(x, y)dll = JJ g^X, y)d\L =
= JJ gi(x, y)dy. + JJ g^x, y)dy. = 0 + JJ g2(x, у)ф = Dt	D\Dy	D\Dt
= JJ g2(x, y)d[i + JJ g2(x, y)dp = JJ g2(x, y)dp. ◄ Dj	D\Dt	D
$ 8. ПЕРЕХОД ОТ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ
Сформулируем теорему о равенстве двойного и повторного интегралов.
ТЕОРЕМА 7. Пусть функция g(x, у) интегрируема на прямоугольнике Р = Тх х 12,1г — [ар &J, 12 = [а2, &2]. Пусть также для
519
любого фиксированного значения х е 1г функция f(y) = fx(y) = = g(x9 у) от одной переменной у является интегрируемой по у
t2
на отрезке 12 и Л(х) = J f(y)dy. Тогда имеет место формула
«2
Ь1
А = JJ g(x, y)dxdy = J h(x)dx =
P
^lz ^2	^1	^2
“ / (J fx(y)dy dx = J dx J g{x, y)dy, al	al	a2
m. e. двойной интеграл равен повторному интегралу.
► Для любого разбиения Т = Тр прямоугольника Р имеем неравенства mk, t < g(x, у) < Mkt 19 где (x, у) e Pk tn величины mk t и Mk z, A = 1, ... , m91 = 1, ... у n имеют обычный смысл.
При фиксированном х = это неравенство можно проинтегрировать по у в пределах от yt_x до уг. Получаем
Vi
тк,АУ1< J g&k’ y)dy <
У1-1
Просуммируем это неравенство по I. Имеем П	&2	п
< J «(5*. у№у =
а2
Умножая последнее неравенство на Axk и суммируя его по k9 получаем
т п	т
8(Т) = Ли^1т^хь^У1 <	= o(V(x)) <
т п
где V(x) — разметка разбиения Т отрезка Iv Кроме того, имеем s(T)<A<S(T).
Так как функция g(x, у) интегрируема на Р, то для любого числа е > 0 найдется число 8 = 8(e) > 0 такое, что для всякого разбиения Т с условием Дг < 8 имеем S(T) - з(Т) < е.
Разбиение Т = (Т(х), Т(у)) образовано парой разбиений: Т(х) — по оси Ох, Т(у) — по оси Оу. В качестве разбиения Т(х) можно взять любое разбиение с условием ДТ(х) < 8. Возьмем любую раз-метку разбиения Т(х). Получим размеченное разбиение V = V(x) отрезка Iv
Далее, в силу того, что оба ^исла А и o(V) лежат на одном отрезке длины е, имеем |o(V) - А| < е. Это неравенство справедливо для любого размеченного разбиения с условием Дг < 8. Следовательно, имеет место равенство
А = lim o(V) = J h(x)dx. ◄
520
Случай интегрирования по любому измеримому множеству D мало чем отличается от рассмотренного. Пусть прямоугольник Р содержит D. Тогда по определению имеем
А = JJ g(x, y)dxdy = JJ gQ(x, y)dxdy, D	P
где g0 совпадает с функцией g на множестве D и g0 = 0 вне D.
Обозначим через Е(х) множество точек у9 для которых (х, у) е D. Пусть множество Е(х) состоит из конечного числа отрезков
г2
[<Р1(х), фх(х)],...,[ф((х), ф((х)]. Тогда если Л(х) - J gQdy, то а2
f1 А = J Л(х)</х, а1
где
г2	Л
h{x) = J g0(x, y)dy = £ J g(x, y)dy.
<h.	ФДх)
Следовательно, имеет место формула
t	уДх)
А= Е J dx J g(x,y)dy, ai <pr(x)
которая обобщает утверждение теоремы 7.
§ 9. ИНТЕГРИРУЕМОСТЬ НЕПРЕРЫВНОЙ ФУНКЦИИ НА ИЗМЕРИМОМ МНОЖЕСТВЕ
Имеют место следующие утверждения.
ТЕОРЕМА 8. Пусть функция g(x9 у) непрерывна на прямоугольнике Р. Тогда g(x, у) интегрируема на нем.
►	Прямоугольник Р — компакт. Поэтому функция g(x9 у) равномерно непрерывна на нем. Другими словами, для любого ех > О найдется число 8Х = 8х(е) > 0 такое, что для любого разбиения Т с условием Ат < 8Х имеем z = z - mk, z < ex. Следовательно,
m n	m n
Q(T) <	t ЩР*.z) < ex	z) = exp(P).
Возьмем любое e > 0 и положим ех = е/ц(Р). Тогда для любого разбиения Т с условием Дт < 8х(е/ц(Р)) получим, что Q(T) < е. Это означает, что lim Q(T) = 0, т. е. функция Р(х, и) интегрируема Дг —> О наР. ◄
ТЕОРЕМА 9. Пусть функция g(x9 у) ограничена и непрерывна на измеримом множестве D. Тогда g(x9 у) интегрируема на D.
521
Докажем более общую теорему, из которой следует теорема 9.
ТЕОРЕМА 10. Пусть функция g(x, у) ограничена на замкнутом измеримом множестве D и непрерывна во всех точках множества D, за исключением множества D19 причем pCPi) = 0. Тогда g(x, у) интегрируема на D.
►	Зафиксируем произвольное число ех > 0. Так как множество D измеримо, то существует замкнутая простая фигураFcD такая, что p(D \ F) < еР Кроме того, существует открытая простая фигура Fr такая, что Dr е Fr и pCFx) < еР Тогда простая фигура F2 = F \ Fx замкнута и ц(2> \ F2) < 2еР
Функция g(x, у) непрерывна в каждой точке фигуры F2, поэтому из теоремы 1 следует ее интегрируемость на F2. Следовательно, существует разбиение Т = TF^ такое, что Q(T) < еР
Дополним это разбиение Т до разбиения т множества D, добавив к нему фигуру Dq = D \ F2. Тогда в сумму Q(t) добавится слагаемое (М0 - 7И0)ц(1>0), где mQ = inf g(x, у), MQ = sup g(x, у). Следовательно, имеем
Q(t) < ex + (MQ - m^Ze^ = e1(2Af0 - 2m0 + 1) = e,
t. e. inf Q(t) = 0. Это и означает, что функция g(x, у) интегрируема на D. ◄
Лекция 5
§ 10. МНОГОКРАТНЫЕ ИНТЕГРАЛЫ
Ранее двукратный интеграл был определен как предел по базе 0 (или Др —> 0 на множестве D), где V и — размеченные разбиения соответственно прямоугольника Р и множества D.
Это определение можно дословно перенести на случай функций от большего числа переменных. Другими словами, если, например, в определении интеграла I функцию g(x, у) заменить функцией g(x) = g(xp ... , хп) при п > 2, а области D, D19 ... , Dt считать n-мерными, то поскольку измеримость по Жордану была определена при любом п> 1, тем самым будет получено определение л-кратного интеграла по области D a Rn9 измеримой по Жордану. Для этого интеграла введем следующее обозначение:
I = I... J , xn)dx1... dxn = J... J g(x)d[L. D	D
Точные определения для общего случая приводить не будем. Нас будут интересовать случаи п = 2, 3, для которых интеграл I обычно записывают так:
I = fj Жх, y)dS, I = flj g(x, у, z)dV. D	D
Все факты, доказанные для случая п = 2, без принципиальных изменений в доказательстве переносятся на общий случай п > 2. Укажем, что к ним относятся и критерий интегрируемости функции в разных формах, и свойства 1°—7° двойного интеграла.
Приведем теорему о сведении n-кратного интеграла к (п - 1)-кратному интегралу. Ограничимся случаем п » 3.
ТЕОРЕМА 11. а) Пусть существует тройной интеграл А от функции g(x9 у9 г) по параллелепипеду Р = х I2 х 73. Пусть также существует двойной интеграл h(x) по прямоугольнику Q = 12 х /3, тп. е. интеграл Л(х) = JJ g(x9 у9 z)dydz. Тогда функ-
Q
ция h(x) является интегрируемой на отрезке и справедливо равенство
А = J h(x)dx.
Л
б)ПустьD с Р = х /2 х /3 и пусть при фиксированном хе символ D(x) обозначает собой измеримую по Жордану область точек (у9 z)el2xi3c условием (х, у9 z) е D (тп. е. D(x) является пересечением множества D с плоскостью, состоящей из то
523
чек, у которых первая координата фиксирована и равна х). Пусть также при всяком таком х существует интеграл
h(x) = JJ g(x, у, z)dydz.
Тогда имеем
А = J h(x)dx.
Л
При фиксированном х, применяя аналогичную теорему к двойному интегралу h(x), получаем
Л(х) = J dy J g(x, у, z)dz, «2 D(X,y)
где множество D(x, у) является пересечением множества D с плоскостью х = const, у = const.
ПРИМЕР 1. Найти значение интеграла
I = J... J /(«1) — Kx^dx-L... dxn, D
где область D определяется условиями
D = {(хх, ..., х„)|0 < хх < ... < хп < 1}.
Обозначим через область
~ {(xi> ••• > xn)|0 < хо(1) < ••• < хо(п) < отвечающую перестановке о чисел 1, ... , п.
Для различных перестановок пит области и Dx не Пересе* каются. Далее, интеграл /(о), отвечающий области интегрирования 2)а, от той же самой функции Дхх)... (хп) равен I. Количество перестановок п чисел равно и!, следовательно,
пМ = ЕIa = J ... J /(*х)... f(xn)dxx... dxn = ( J ftx)dx 1". 0	0	vo	7
Таким образом мы свели вычисление n-кратного интеграла к однократному и получили формулу
ПРИМЕР 2. Докажем следующую формулу Дирихле—Лиувилля. Пусть Дх) непрерывна на отрезке [0, 1] и пусть S — симплекс в n-мерном пространстве, определяемый условиями хх + ... + хп < 1, хх >0, ... , хл > 0. Тогда имеем
J = Jn(plt..., рп) = J... J Г(хх + ... + х^хр-1... xp-1dxx ... dxn -S
Г(рх)... Г(р„)
Г(рх + ...+р„)
J /'(u)u*+-+p-~1du. о
524
Действительно, положим X = хг + ... + хп_2. Расставим пределы интегрирования в интеграле J. Тогда два последних интеграла по переменным хп_1ихп принимают вид
н = J dxn-i f ”"/'(X + x„_x + xn)x^-*-1x^-*dxn. О	о
Сделаем во внутреннем интеграле замену переменной вида
Тогда v =---, ахп =	— и интеграл Н принимает вид
Хп-1+хп	у2
1-Х	1	»'
Н = J dxn_1 J f(k +	” v)Pn~1v~Pn~1dv.
о	*B.-L	4	v 7
1-X
Поменяв порядок интегрирования в Н9 получаем
Н = J dv J f(k +	- )x£ri1+Pn-1(l “
о о 4 v '
Сделаем еще одну замену переменной вида хп_х = vt. Имеем
1	i-x
Н = f (1 - vy^vP^dv J ДХ + 0^B1+Pn" dt = о	о
= B(pn_19pn)j 7(X + t)tp^p^dt. о
Отсюда получаем следующую рекуррентную формулу:
d = ^n(Pv - >Рп) = В(РП-1’РПУП-1(Р1> •” >Pn-2’Pn-l+Pn)’ из которой имеем
J = B (Рп-1>Рп) В(Рп-2> Рп-1 + Pj — В(Р1> Рг + ”• +Рп) х
X Jx(px + ... +рп) =	J/(U)uA+...+₽-ldu.
Г(р1 4- ... +рд) о
Таким образом, формула Дирихле—Лиувилля доказана.
В частности, следствием этой формулы является выражение для объема n-мерного шара, заданного соотношением xf 4-... + х% < а2. В силу симметрии шара относительно гиперплоскостей xk = О, k = 1, ... , и, можно ограничиться вычислением объема области К9 части шара, определяемой так:
4-... + г** < а2, хг > 0,... , хп > О, при этом объем ее будет в 2п раз меньше объема шара V. Имеем
^=2nJ... Jdxx... dxn.
К
525
После замены переменных аиг = xf,..., аип = х% область К перейдет в симплекс S, который определен выше, и поскольку dxk = = aduk/(2jiTk), k = 1, ... , п, получим
.	. du* ... du„
s ... un
Последний интеграл есть интеграл Дирихле—Лиувилля при
f(uv ..., ип) = 1, Pi = ... =р„ = 1/2.
Итак, объем n-мерного шара радиуса а равен пп/2ап/Г(п/2 + 1).
§11. СВОЙСТВА ГЛАДКОГО ОТОБРАЖЕНИЯ НА ВЫПУКЛОМ МНОЖЕСТВЕ
Известно, какую большую роль в построении теории однократных интегралов играет метод замены переменной. В случае кратных интегралов роль этого метода не меньше (а быть может, и больше). Для его обоснования понадобятся некоторые свойства гладких отображений.
Пусть функция g(y), у = (ур ... , уп), определена на компактной измеримой области D с Rn и интегрируема на D. Пусть I обозначает интеграл
I = f... j g(y)dyi... dyn.
D
Рассмотрим отображение у = ф(х) измеримого компакта Во с с Rn на множество В, которое устанавливает взаимно однозначное соответствие между внутренними точками множеств D и Do. Напомним, что отображение у = ф(х) задается системой п функ-ций уг = фх (хр ... , хп), ... , уп = Фв (Хр ... , х„), определенных на Во.
Будем считать, что каждая из этих функций имеет все непрерывные частные производные на Во.
Замечания. 1. Функции (рДх) называются криволинейными координатами, определенными на Во.
2. Условие взаимной однозначности отображения ф : Do —» D для внутренних точек области Во обеспечивается требованием отличия от нуля якобиана этого отображения в каждой точке области Во (теорема об обратном отображении).
Сформулируем и докажем утверждения о гладких отображениях на областях.
526
ТЕОРЕМА 12. Пусть Do выпуклое и замкнутое множество и ф(х) гладкая функция на множестве Do. Пусть также точки х и х + Дх принадлежат D& Тогда существует точка | = х + 0Дх, О < 0 < 1, такая, что Дф = (Дх, grad <р(О).
►	Рассмотрим функцию h(t) одной переменной t, 0 < t < 1, h(t) = ф(х + £Дх).
Ясно, что h(t) — гладкая функция на отрезке [0,1]. Следовательно, к ней можно применить формулу Лагранжа конечных приращений. Тогда существует число 0, 0 < 0 < 1, такое, что
Дф = Дй = Л(1) - Л(0) = h'(0)(1 - 0) = Л'(в)-
Функция h(t) является сложной функцией от t и по правилу дифференцирования сложной функции получаем
Л'(0) =	+ _ + Дх„ = (Дх, grad ф(|)),
где = х + 0Дх. ◄
ТЕОРЕМА 13. Пусть ф(х) — гладкое отображение выпуклого компакта DQ на область D. Тогда существует число с > 0 такое, что для любых точек а19 а2е Во справедливо неравенство ПфСох) - ф(а2)|| < c||ax - а2||, где ||х|| — длина вектора в евклидовой метрике.
►	Из теоремы 12 при k = 1, ... , п имеем
Ф*(«1) ~ Ф*(й2) = ДФ* = (й2 ” SV Srad Ф/Лл))’
где = аг + 0Л(а2 - ах) и 0fe — некоторое число из интервала (0,1). Далее воспользуемся неравенством Коши |(а, Ь)| < 11а || • ||Ь ||. Получаем
I ДфЛ1 < ll«2 -“«ill* II grad фЛ(У ||.
Поскольку Dq компакт и функция 11 grad фЛ(х) || непрерывна на Do, она ограничена на этом компакте некоторой постоянной ck > 0. Используя это и числовое неравенство
л/а1 + ••• +аП ^ll + ••• + 1апЬ имеем
||Аср|| < |Афх| + ... + | Афп| < (сх 4-... + сп) ||Дх || = с ||Дх ||,
где Ах = а2- av ◄
Обозначим через Аф(х) матрицу Якоби отображения ф: Rn -» Rn в точке х.
527
Определение 17. Линейное отображение Ду = Аф(х)* Дх приращения Дх вектора х называется дифференциалом отображения ф и обозначается символом d<p(x).
Очевидно, что </ф(х) — вектор с координатами
dqk(x) = (Дх, grad ф*(х)).
ТЕОРЕМА 14. Пусть ф — гладкое отображение выпуклого компакта DQ и г(х, Дх) = Дф - dtp. Тогда имеет место следующий равномерный предел
Цг(х,Дх)|| п |. и п ||дх|| Б*0 р Лх °’
Другими словами, существует числовая функция а(Дх) 0 при Дх -»О такая, что для всех хе DQ справедливо неравенство
||г(х, Дх)|| < а(Дх)||Дх||.
► Рассмотрим fe-e координаты векторов Дф и сйр. По определению имеем </фЛ = (Дх, grad фЛ(х)), а по теореме 12 при некотором £ получим
Дф* = ф*(х + Дх) - Ф*(х) = (Дх, grad Ф*(^)),
следовательно,
Дф* - </ф* = (Дх, grad ф*(£) - grad ф*(х)).
Далее, так как частные производные отображения ф непрерывны на компакте DQ, то в силу их равномерной непрерывности на Dq будем иметь
d<pfe(£) _ Эф^(х) дх8 дх8
< а*(Дх),
где аЛ(Дх) зависит только от Дх и аЛ(Дх) —> 0 при Дх -> 0. Отсюда, используя неравенство Коши, получаем
|Дф* - </ф*I < IIДх II • л/n а*(Дх),
следовательно, п	г— П
||г(х, Дх)|| <	1|Дф* - с?ф*| < IIДх II • Jn £ ^(Дх) = а(Дх) ||Дх||,
причем а(Дх) —> 0 при Дх -» 0. ◄
Лекция 6
§ 12. ОБЪЕМ ОБЛАСТИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ.
ТЕОРЕМА О ЗАМЕНЕ ПЕРЕМЕННЫХ В КРАТНОМ ИНТЕГРАЛЕ
Докажем теорему об объеме области в криволинейных координатах.
ТЕОРЕМА 15. Пусть Q — выпуклый измеримый по Жордану компакт и S — образ его при гладком взаимно однозначном отображении <р. Тогда:
1) множество S измеримо по Жордану;	*
2) р($) < J... гДе J — определитель матрицы Якоби
Q	_
(якобиан) отображения ф.
Напомним, что определение матрицы Якоби и дифференциала отображения дано в конце предыдущего параграфа.
► Ограничимся рассмотрением случая плоских областей Q с В2. Заметим сразу, что так как модуль якобиана отображения ф является непрерывной функцией на Q, то эта функция интегрируема на Q.
Пусть Р — некоторый стандартный квадрат, содержащий компакт Q. Пусть, далее, квадраты г со стороной h составляют разбиение квадрата Р. Тогда множества Qk t = Q П Pk t образуют разбиение т компакта Q на выпуклые измеримые множества. Зафиксируем произвольное ех > 0 и возьмем величину h столь малой, чтобы общая площадь всех квадратов Pk l9 содержащих хотя бы одну точку границы 3Q компакта Q, была бы меньше еР Назовем такие пары (k,I) особыми, а остальные — обычными.
Диаметр dk t каждого множества Qk t, отвечающего особым (fe, I) при отображении ф, по теореме 13 возрастает не более, чем в с раз, т. е. его образ z можно накрыть кругом, радиус которого не превосходит ch, или квадратом со стороной, не превосходящей 2ch. Его площадь не превосходит 4с2й2. Обозначим через щ сумму по особым парам (А, I) площадей Sk, t = ф((?л> z). Имеем
цх = Г n(Sfc> а < Г 4С2ц(Р г) < 4с2ер
Поскольку 9S принадлежит объединению этих Sk, t, |1(3S) < < 4с2е1. В силу произвольности выбора числа ех > О отсюда имеем, что ц(Эв) = 0, т. е. множество S измеримо по Жордану.
Обозначим через p(S) меру Жордана области S. Тогда имеем |i(S) = цх +112» гДе величина рх определена выше и ц2 =	/),
(Л, Z) *
529
где символ Е" означает, что суммирование ведется по обычным парам (A, I).
Рассмотрим теперь какой-либо квадрат Pk l9 целиком лежащий внутри Q. Тогда имеем Qk t « Pk t. Обозначим его вершины через х0, х0 + а19 х0 + а2, х0 + ах + а2, причем Haji = ||а2|| = Л. Очевидно, что для любого хе Pk l имеем || х - х01| = ||Лх || < 2h. Пусть А — матрица Якоби отображения ф. Тогда при линейном отображении с этой матрицей квадрат Pk t перейдет в параллелограмм К с вершинами у0 = ф(х0), ух = ф(х0) + Аах = у0 + Ь19 у2 = ф(х0) + + Ла2 = у0 + Ъ2> Уз = Ф(*о) + А(й1 + йг) = У о + (&i + М-
Пусть а(Дх) — функция, определенная в утверждении теоремы 14. Заключим стороны параллелограмма в «рамку» К19 образованную точками, отстоящими во внешнюю сторону от параллелограмма на расстояние, не превосходящее р = а(2й) • 2й. Тогда# с Kv
Докажем, что z с К19 т. е. что для любой точки хе Pk l ее образ у = ф(х) g Kv Действительно, так как х е Pk 19 то у0 + <2ф(х) g К. Поэтому
||ф(х) - Ф(хо) - d<p(x) II = II г(х0, Дх) II < 2йа(2Л) = р,
т. е. ф(х)е #Р
Теперь заметим, что множество Sk, t измеримо по Жордану по тем же причинам, что и S. Периметр параллелограмма К не превосходит с* Ah. Поэтому, исходя из построения фигуры К19 будем иметь
ц(#х) < ц(#) + р • с • 4й + 4лр2.
Поскольку t с К19 величина |X(Sfe z) удовлетворяет неравенству z) < p(#i). Используя эти неравенства, приходим к оценке
i) < №) <	+ Р ’ с • 8й + 4лр2 = р(#) + Д(й).
Из линейной алгебры известно, что для линейного отображения с матрицей А, определитель которой равен J, и при котором квадрат Pk , переходит в параллелограмм К9 справедливо равенство ц(#) = I J\[i(Pk z). Используя это равенство, получаем
Н(«м) < lJ<p(^,Z)lH(Qfe,z) + А(й).
Далее, для каждой особой пары (й, Z) выберем произвольным образом точку xk, te Qktin образуем сумму
Qi = Z	1)9
где 27 означает, что суммирование ведется по особым парам (А, I).
530
Так как функция | е7ф(х)| непрерывна на компакте Q, то по теореме Вейерштрасса она ограничена некоторой постоянной с2 > 0. Поэтому
|O1I < с2 Г n(Qfe> 1) = с2цх < с2ех.
Пусть ст = ох + ст2, где ст2 = Е"|	z)|z), причем в послед-
ней сумме суммирование распространено на обычные пары (k, I). Оценим разность между интегральной суммой ст и величиной ц(5). Имеем
|n(S) - а| -|Е"(и(8.,,) Лисе»,,) + ЕЖ.,) - а,| < < |Е"| +|Г| + |а,|.
Воспользовавшись ранее доказанными неравенствами, получим
|S"I <	S"*2 = z) < n(Q),
|Е'| < 4с2ех, |стх| < c^v
Сумма о представляет собой интегральную сумму для функции |е7ф(х)| по множеству Q. При h -» 0 эта сумма сходится к интегралу
J- JJ 1^(х)|ф.
Q
Поскольку &(h)/h2 стремится к нулю при h -» 0, из полученных выше оценок при й —»0 находим
p(S) < J + | p(S) - J\ < J + e1(4c2 + c2).
В силу произвольности выбора числа ех отсюда получаем, что р(В) < J. ◄
ТЕОРЕМА 16. Пусть Q — измеримый по Жордану компакт в пространстве RnuS образ его при гладком взаимно однозначном отображении <р. Тогда*.
1) множество S измеримо по Жордану,
2)ЩЗ) < J ... г&е J =	— якобиан отображения ф.
Q
► Покажем, что в условии теоремы 15 можно отказаться от требования выпуклости множества Q. Для этого, как и в теореме 15, рассмотрим разбиение Q на обычные и особые множества Qk полагая при этом, что мера (1(D) объединения D всех стандартных квадратов, содержащих особые множества Qk 19 не превышает ер где ех > 0 — любое наперед заданное число. При доказательстве теоремы 1 показано, что мера р(ТУ) образа W множества D при отображении ф не превосходит 4с2еР Далее, каждое обычное
531
множество Qk t*= Pkl является стандартным квадратом, и тем самым удовлетворяет условиям теоремы 15, поэтому для каждого из них справедливо неравенство
Pk,l
Здесь, как и ранее, z = <jj(Qfe z) =	/)• Суммируя по всем па-
рам (ft, О, мы приходим к неравенству
И(5) = S а < 4с261 + f ... f Иф. («, О	Q
В силу произвольности выбора 8Х > О оно влечет за собой справедливость неравенства
Q
ТЕОРЕМА 17. Пусть условия теоремы 16 выполнены и, кроме того, при всех х е Q имеет место неравенство |J-| > 5, где 8 > 0 — некоторое фиксированное число. Тогда справедлива формула
M(S)=
Q
► Рассмотрим отображение у, определенное на множестве S и обратное к отображению ф. Тогда у является гладким отображением, его якобиан непрерывен и
кн^в-1.
По теореме 16 имеет место оценка
Н(-8) < f f iJjdM = sup s(T),
где s(T) — нижняя сумма Дарбу по неразмеченному разбиению Т множества Q.
Имеем з(Т) =	где Qk — элемент разбиения Т мно-
жества Q на области Qx, ... , Qn, измеримые по Жордану, mk = inf | J-1,	(Qk) nQk= w(Sk). По теореме 16 при всех k
от 1 до п справедлива оценка
и (Qk) < J...
sk
Применяя к последнему интегралу теорему о среднем, получаем
Rk
532
где Mk = sup|«7^1. Теперь заметим, что	= J^1, поэтому mk = М*1.
Но тогда приходим к неравенству
з(Т) <	= Jх g(Sft) = g(S).
Тем самым получены неравенства g(S) < J... f К1Ф < И($), кото-
Q
рые равносильны равенству p(S) = J ... J|еЛ |с?|Л. ◄
Q v
ТЕОРЕМА 18» Утверждение теоремы 17 остается в силе и без ограничения на значение якобиана
► Рассмотрим множество К точек х е Q, в которых якобиан J(x) = = Jy(x) обращается в нуль. Покажем, что множество точек К замкнуто. Действительно, если х0 — предельная точка для К9 то найдется последовательность хп е К такая, что хп —> х0 при п -» оо. Тогда J(xn) = 0 и в силу непрерывности функции J(x) справедливы равенства
J(x0) = J( lim хп) = lim J(xn) = О,
следовательно, x0 g K.
Зафиксируем произвольное число 8 > 0. Каждую точку х е К окружим окрестностью, в которой функция J(x) удовлетворяет неравенству | J(x)| < 8. Поскольку К — компакт, то из всей совокупности окрестностей можно выделить конечное подпокрытие. Обозначим выделенные окрестности через KQ и разобьем множество Q на два множества Qo и Q19 полагая Qo = A’0AQhQx = Q\ Qo.
Тогда Q = Qq U Qx и Qo A Qx = 0. Оба множества Qo и Q19 очевидно, измеримы по Жордану. Кроме того, множество Qo открыто, a Q замкнуто, поэтому множество Qx тоже замкнуто. Тогда по теореме Вейерштрасса функция | J(x)| достигает на Qx своего минимального значения т в некоторой точке хое QP Число т больше нуля, так как х0 не входит в К с Qo, поскольку множества Qo и Qx не пересекаются, следовательно, к образу Sx множества Qx при отображении ф можно применить теорему 17, а к образам S и SQ множеств Q и Qo — теорему 16. Тогда, используя еще и теорему о среднем, получаем
g(S) = g(S0) + №), mso = J ... J|J^| dg,
Q
0 < g(S0) < J ... J|JJ dg < 5g (Qo) < 5g (Q),
Qo
533
следовательно,
о< J...J|J<p|dg-H(S) =
Q
= (f... /|^|ф - mSi)) + J... Jl^lФ - U(SO) < J... /иФ|ф < W).
v Qi	' Q«	<?o
В силу произвольности выбора 5 > 0 это означает, что
/..Ж1Ф = Н(5). <
Q
ТЕОРЕМА 19 (формула замены переменных в кратном интеграле). Пусть Dq — измеримый по Жордану компакт и ф — гладкое взаимно однозначное отображение компакта DQ на D. Пусть также функция g(y) интегрируема на D, а функция f(x) = = g((p(x))|J^(x)| интегрируема на DQ. Тогда
f ... Му) ... dyn = J... J/(x) dx!... dxn.
D	D„
► Возьмем произвольное разбиение T области D на измеримые области Sp ... , Sf, и пусть ф(<?8) = S8, s = 1, ... , t. Обозначим через т8 = inf g(y)9 Ms = sup g(y). По теореме о среднем
^8	R8
ms J ... f Иф < J... M<p(x))|J<p(x) < Ma J... J|J| ф.
Q.	«.	0.
Из теоремы 18 следует, что p(Sg) = J J |J| dy.. Поэтому, просум-e.
мировав предыдущие неравенства по s от 1 до t, получим
t тп8ц (Ss) < J ... Мф(х))|«7ф(х)|</х <
Do
т. е. справедливы следующие неравенства для верхних и нижних сумм Дарбу от функции g(y) по области D, отвечающих разбиению Т:
s(T) < J ... /^<р(х))|еЛф(х)|сгх < S(T).
А)
В силу интегрируемости функции g(y) получим s(T)—>A, S(T) —>А при Дт -> 0, где А = J ... Jg(y) dy, следовательно,
D
J ... J§(У) dy< J... J£(<p(x))|J^(x)\dx. D	Dq
Замечание. В теоремах 18 и 19 в качестве отображения ф можно взять любое ортогональное отображение. Якобиан этого отображения равен 1. Следовательно, мера Жордана и интеграл Римана инвариантны относительно движений пространства и их определение не зависит от выбора прямоугольной системы координат. Отметим, что инвариантность меры Жордана ранее была получена нами из геометрических соображений.
534
ПРИМЕРЫ. 1. Переход к полярным координатам от прямоугольных координат производится по формулам
х = г cos ф, у = г sin ф, г > О, О < ф < 2л.
Якобиан отображения (х, у) —»(г, ф) равен г. Формула замены переменных имеет вид
JJ g(x, у) dxdy = JJ g(r cos ф, x sin ф) rdrdq.
D	Do
2. Переход к сферическим координатам от декартовых прямоугольных координат выполняется по формулам
х = г cos ф cos 0, у = г sin ф cos 0, z = г sin 0, где г — длина радиуса-вектора текущей точки М от начала координат, 0 — величина угла между радиусом-вектором ОМ и его проекцией на плоскость хОу, ф — величина угла между осью Ох и ОМ, и, кроме того, г > 0, 0 < ф < 2л, |0| < л/2.
Якобиан этого отображения равен г2 cos 0. Таким образом, для дифференциального выражения элемента объема dV получаем следующую формулу:
dV = dxdydz = г2 cos 0 drdydti.
Лекция 7
§13. КРИТЕРИЙ ЛЕБЕГА
Начнем с определения множества нулевой меры Лебега. Открытый параллелепипед назовем стандартным, если его ребра параллельны осям прямоугольной системы координат. Объединение не более чем счетного числа стандартных параллелепипедов назовем простейшей фигурой.
Определение 18. Множество А точек в пространстве Rn имеет лебегову меру нуль, если для любого £ > 0 существует конечное или счетное множество открытых стандартных параллелепипедов Щ, k = 1, ... , с объемом ц(Щ) — 8k, покрываю-oo	00
щих А, А с k U х Щ, и таких, что £ 8k < £.
ЛЕММА 7. Конечное или счетное объединение множеств лебеговой меры нуль является множеством лебеговой меры нуль.
► Дано p(Afe) = 0, k = 1, ... . Докажем, что ц(А) = pl U Ak 1 = 0. Действительно, по определению, для любого £ > 0 существует простейшая фигура Пл такая, что Ak cz Щиц(Щ)<8/2*.
Кроме того, имеем А = U х Ak cz k U JI* и pQ U хП* j <	хц(П*) <
< £. Следовательно, множество А имеет лебегову меру нуль. ◄ ЛЕММА 8. Пусть В cz А, ц(А) = 0. Тогда ц(В) = 0.
►	Поскольку любая простейшая фигура, покрывающая множество А, покрывает и множество В, утверждение леммы сразу следует из определения множества лебеговой меры нуль. ◄
ЛЕММА 9. Компакт A cz Rn, п > 1, лебеговой меры нуль измерим по Жордану и его мера Жордана равна нулю.
►	Так как лебегова мера компакта А равна нулю, то для любого £ > 0 существует простейшая фигура, состоящая не более чем из счетного множества открытых стандартных параллелепипедов, покрывающая А и имеющая объем, меньший £.
Из этого покрытия можно выделить в силу компактности конечное подпокрытие с объемом, меньшим £. Следовательно, множество А измеримо по Жордану и его мера Жордана равна нулю. ◄
Далее, пусть функция g(x, у) ограничена на параллелепипеде Р. Обозначим через П = П(8) = П(х0, 5) куб, состоящий из точек (хр ... , хп) с условием х0 s - 8 < xs < х0 s + 5, s = 1, ... , п, где хо=(хОЛ...,хОп).
536
Определение 19. Колебанием функции g(x) в точке х0 назовем величину
®(х0) = ®г(*о) = W SUP (g(x) - g(y)), тп. е.
<о(Хо) = inf (М5 (х0) - m8 (So)), где
М5 (х0) - sup g(x), m8 (х0) = inf g(x). ЗгеП	хеП
Имеет место следующий критерий непрерывности функции в точке в терминах колебания функции в точке.
ЛЕММА 10. Функция g(x) непрерывна в точке х0 тогда и только тогда, когда со* (х0) = 0.
►	Необходимость. Пусть функция g(x) непрерывна в точке х0. Предположим, что (£)g (х0) = а > 0. Рассмотрим куб П1/п. Из определения величины <о*(хо) имеем М1/п (х0) - т1/п (х0) > а. Отсюда получим, что существуют точки хп и уп такие/что
g(xn) - g(yn) > а/2 > 0.
Кроме того, Jim^ хп = уп = Жо. Но тогда, переходя в предыдущем неравенстве к пределу при и оо и используя непрерывность функции g(x) в точке х0, получаем 0 > а/2 > 0. Это противоречивое неравенство показывает, что сделанное предположение неверно, следовательно, <og(x0) = 0. Необходимость доказана.
Достаточность. Поскольку cog (х0) = 0, для любого е > 0 существует 8 = 8(e) > 0 такое, что для любых х, у е П(8) имеем |g(x) “ £(17)| < £• Положим у = х0. Тогда последнее условие является условием непрерывности функции g(x) в точке х0.	◄
Обозначим через D(d) множество точек х g Р, удовлетворяющих условию <og(x) > а > 0.
ЛЕММА 11. Множество D(a) замкнуто.
►	Пусть х0 — предельная точка множества D(a). Докажем, что она принадлежит Р(а). Поскольку х0 предельная точка Z>(a), существует последовательность хл g D(a), сходящаяся к х0.
Для любого 8 > 0 найдется хп е П§(х0). В силу того, что П§(х0) — открытое множество, существует 8Х > 0 такое, что
П81(хп) с П8 (х0).
537
Отсюда имеем
М& (х0) - zn8 (х0) > М81(х„) - тп81 (х„) > &g (х„) > а.
Следовательно, cog(x0) = inf (Afs(x0) - тп5(х0)) > а, т. е. х0 g D(a). ◄
ТЕОРЕМА 20. Ограниченная на прямоугольнике функция интегрируема по Риману тогда и только тогда, когда для любого а > 0 множество D(a) имеет лебегову меру нуль.
►	Необходимость. Предположим, что существует а > 0 такое, что множество Р(а) не является множеством лебеговой меры нуль, т. е. найдется £0 > 0 такое, что для любой простейшей фигуры, содержащей D(a), ее объем не меньше е0.
Рассмотрим любое разбиение Т прямоугольника Р на прямоугольники Pk t. Пусть По — множество всех тех прямоугольников Pk 19 внутри которых находится хотя бы одна точка множества D(a). Площадь простейшей фигуры По не меньше £0. Если это не так, т. е. площадь ц(П0) =	< е0. Покроем границу ЭП0 стан-
дартными прямоугольниками общей площадью, не превосходящей (е0 + е1)/2. Тем самым множество D(a) покрыто открытой простейшей фигурой площади, не превосходящей £х + (Ч - е1)/2 " = (е0 + ех)/2 < £0. Это противоречит нашему предположению, следовательно, ц(П0) > £0.
Для любого стандартного прямоугольника из По колебание функции на этом прямоугольнике не меньше, чем а. Поэтому для любого разбиения Т имеем Q(T) > а £0 > 0. Отсюда получаем, что inf Q(T) > a е0 > 0. Но это означает, что рассматриваемая функция не интегрируема на прямоугольнике, что противоречит условию теоремы. Следовательно, сделанное предположение не имеет места, и, значит, для любого a > 0 лебегова мера ц(1)(а)) = 0. Необходимость доказана.
Достаточность. Положим a = е/(4ц(Р)), 8 = е/(4М), М = = max|g(x)|. Так как множество Р(а) имеет лебегову меру нуль, ХбР то его можно покрыть простейшей фигурой с общей площадью, меньшей, чем 8. Множество D(a) замкнуто и ограничено, следовательно, оно компакт. Выделим из системы стандартных прямоугольников, из которых состоит эта простейшая фигура, конечное подпокрытие I. Рассмотрим множество К = Р \ I. Оно является компактом. Для любой точки хое К имеем, что <о^(х) < а. Из определения со^(х) получаем, что существует квадрат П^х), у > 0 такой, что колебание функции g(x) на нем меньше, чем 2a. Квадраты Пу/2(х) образуют покрытие множества К. Выделим из 538
него конечное подпокрытие V. Продолжим стороны прямоугольников, составляющих I и V, до пересечения со сторонами Р. Получим разбиение Т прямоугольника Р.,
Сумму Й(Т) представим в виде
= 22 соЛ i bxk	+ ЕЕ (ok t \xk = Ex + E2,
v»» if	if
где в сумму ЕЕ' входят слагаемые, для которых элемент разбиения Рн с /, а в сумму ЕЕ" — слагаемые, для которых Pk t cz V. Имеем	^1)
Ех < 2М bxk < 2М8, Е2 < 2а ЕЕ" < 2ац(Р),
следовательно,
Q(T) = Ех + Е2 < 2М8 + 2ар(Р) = е/2 4- е/2 = е.
Таким образом, имеем inf Q(T) = 0, т. е. функция g(x) интегрируема на прямоугольнике Р. ◄
ТЕОРЕМА 21 (критерий Лебега). Ограниченная функция g(x) интегрируема по Риману на прямоугольнике Р тогда и только тогда, когда множество D точек разрыва ее имеет лебегову меру нуль.
►	Необходимость. По теореме 20 для любого натурального числа п множества D(l/n) имеют лебегову меру нуль. Отсюда полу-
чаем, что лебегова мера D = D(l/n) равна нулю.
Достаточность. Для любого а > 0 имеем D(a) cz D. Поэтому, если мера ц(П) = 0, то ц(В(а)) = 0. Из теоремы 20 следует интегрируемость функции g(x) на прямоугольнике Р. ◄
ТЕОРЕМА 22. Пусть функция g(x) интегрируема на прямоугольнике, т = inf g(x), М = sup g{x) и пусть функция f(t) непрерывна на отрезке [т, М]\ Тогда функция f(g(x)) интегрируема на прямоугольнике Р.
►	Точка непрерывности функции g(x) будет точкой непрерывности функции f(g(x)). Следовательно, точками разрыва f о g могут быть точки разрыва функции g. Поэтому множество точек разрыва fog имеет лебегову меру нуль как подмножество множества меры нуль (по критерию Лебега мера множества точек разрыва g(x) равна нулю). 4
Лекция 8
$ 14. НЕСОБСТВЕННЫЕ КРАТНЫЕ ИНТЕГРАЛЫ
Для обычных однократных интегралов мы определили два вида несобственных интегралов. Аналогично в случае кратных интегралов назовем:
1) несобственным кратным интегралом первого рода — интеграл по неограниченной области D от ограниченной функции g(x);
2) несобственным кратным интегралом второго рода — интеграл по ограниченной измеримой по Жордану области D от функции g(x)9 имеющей конечное число особых точек х19 ... , xk таких, что в любой окрестности каждой из этих точек функция g(x) не ограничена (точки х19 ... , xk не обязаны принадлежать области D).
ПРИМЕР. Функция g(x9 у) = 1/(х2 + у2) в области D = {(х, у)\ х > О, у > 0} имеет особую точку х = 0, у ?= 0.
Для несобственных интегралов используется то же обозначение, что и для собственных интегралов:
I - JJ ё(х, у) dxdy.
D
Для простоты будем рассматривать только двойные интегралы и сначала случай несобственных интегралов второго рода с одной особой точкой а. Проще всего этот интеграл как предел при г -> 0 интегралов Ir = JJg(x, y)dxdy9 где Dr = D\O(a9 г) — шар радиуса г Dr
с центром в точке а, т. е. по определению имеем
I = JJ S(x, у) dxdy = lim /г.
D	'->0
Это значение I будем называть главным значением в смысле Коши несобственного интеграла от функции g(x9 у) по области D.
Аналогично для несобственного интеграла первого рода главным значением в смысле Коши назовем величину I = lim IR9 где Я-> оо л
ir = Jf &х, у) dxdy, DR = DC\ 0(0, R).
D„
Перейдем к общему определению несобственного интеграла.
Определение 20. 1) Число I называется несобственным двойным интегралом первого рода от функции g(x9 у) по неограниченной области D9 если для любой последовательности областей Dn9 являющихся ограниченными, открытыми, связными, 540
измеримыми по Жордану, и удовлетворяющих следующим условиям:
а)	для любого натурального числа п имеем Dn с Dn+1 с D (условие монотонности);
б)	дУ х = D (условие исчерпывания), имеет место соотношение Jim^ In = I, где In = JJ q(x, y)d\L.
2) Число I называется несобственным двойным интегралом второго рода от неограниченной функции g(x, у) по ограниченной измеримой по Жордану области D со множеством особых точек L cz D (D — замыкание D), если для любой последовательности областей Dn, являющихся открытыми, связными, измеримыми по Жордану, и удовлетворяющих следующим условиям:
а)	для любого натурального числа п имеем Dn с •°п+1 с D (условие монотонности);
б)	nU Dn = D (условие исчерпывания);
B)Lr\D=<Z>, имеет место соотношение lim In = I, где
ГП = JJ s(x> №
D.
Последовательность {Dn} в определении несобственных интегралов первого и второго рода будем называть допустимыми (или D-допустимыми).
Замечания. 1. Ясно, что для существования несобственного интеграла второго рода необходимо, чтобы ц(£) = 0.
2. В обоих случаях несобственного интеграла первого и второго рода сохранено стандартное обозначение / = ffg(x, y)d\L.
D
3. Точно такое же определение несобственного кратного интеграла имеет место и в случае кратности, большей двух.
ТЕОРЕМА 23. Пусть g(x, у) > 0. Тогда для сходимости несобственного интеграла I = fjg(x, y)dy. необходимо и достаточно, D
чтобы числовое множество <1 п = JJ g(x, y)d\L ► было ограничено
I Dn
хотя бы для одной последовательности D-допустимых множеств Dn.
► Необходимость. Если интеграл I существует, то последовательность интегралов 1п сходится к I. Следовательно, последовательность {1п} ограничена. Необходимость доказана.
541
Достаточность. Пусть последовательность {/„} ограничена. Тогда по теореме Вейерштрасса существует предел In = lim 1„, где 70 = sup 1п.
Пусть {D'n} — другая В-допустимая последовательность и Гп = = JJ g(x, y)dxdy — соответствующая ей последовательность ин-
тегралов. Зафиксируем теперь некоторое множество D'm и рассмотрим последовательность D" = D'm П Dn.
Очевидно, последовательность {D"} является D'm-допустимой. В частности, для любого п имеем D" с Пл+1, У = -0^» и все множества D'^ являются открытыми, связными и измеримыми по Жордану. ◄
В дальнейшем будет необходима следующая лемма, имеющая и самостоятельный интерес.
ЛЕММА 12 (лемма об исчерпывании). Справедливы следующие соотношения*.
Мн(Ю = №), lim IKW-O-
► Последовательность = ц(£>") неубывающая и ограничена сверху числом р(Р^). Следовательно, существует число ц0 = Шп^, причем |10 < И (В'т).	__
Надо доказать, |10 = Рассмотрим замыкание D'm множества D'm, т. е. множество D'm = D'm U dD'm. Так как множество D'm измеримо, то = 0. Следовательно, для любого е > 0 существует открытое простейшее множество W = W£ е П такое, что
Множество D'm — компакт, а множества {D$, п = 1, 2,..., и W образуют его покрытие открытыми множествами. Из этого покрытия можно выделить конечное подпокрытие множества D'm: D" с ... с D"* и W. Отсюда имеем D" U W о D'm. Следовательно,
№>п) + Н(Ю > №'т),	+ е > g(D'm),
т. е. для любого е > 0 справедливо неравенство
ц0 + е >	+ е > gCDJn).
Поэтому имеем ц0 > Но мы уже показали, что |10 < Таким образом, получаем, что Цо = |1(В^).
Далее, в силу того что (D'm \ D") U D" = D'm и (D’m \ D") U D" = = 0, из свойства аддитивности меры имеем
ц(п;\ п") + цта = №).
Следовательно, Пп^ g(O'm \ D'^) = 0. ◄ 542
СЛЕДСТВИЕ. Пусть выполнены условия леммы 12. Пусть также функция g(x, у) интегрируема на D'm. Тогда имеет место равенство
Jin JJ y>dxdy = JJ S(x, y)dxdy = I'm.
П^&’п 1Ут
► В силу свойства аддитивности интеграла, имеем g(x,y)dxdy = JJ g(x,y)dxdy. d"
Поскольку функция g(x, у) ограничена на D'm, т. е. существует число с > О такое, что для любой точки (х, у) е 1Ут имеем \g(x, у)| < с, при п —> оо получаем
~ JJ S{x, y)dxdy <	\ D") -> 0.
К
Завершим теперь доказательство теоремы 23. Так как .D" с Dn, то справедливо неравенство
JJ g(x, уЩ<.1я<1й.
Перейдем в этом неравенстве к пределу при п —» оо. Используя следствие, получаем
Гт = ЛП JJ С h-
Отсюда имеем, что существует Г = Ит^ 1'т9 причем I' < /0. Но если теперь в приведенных рассуждениях последовательности Dn и D'n поменять местами, то получаем противоположное неравенство IQ < Г. Следовательно, IQ = Теорема 23 доказана. ◄
ТЕОРЕМА 24. Пусть функции g(x, у) и gQ(x, у) интегрируемы на любом измеримом по Жордану компакте, содержащемся в множестве D, и пусть на этом множестве D справедливы неравенства 0 < gQ(x, у) < g(x, у). Тогда имеем:
1) если несобственный интеграл JJ g(x, y)dp = I сходится, D
то сходится интеграл JJgQ(x, y)dp, = Io;
D
2) если же несобственный интеграл JJg0(x, i/)dp расходится, D
то будет расходиться и интеграл JJg(x, y)dp.
D
► Так как интеграл I сходится, то существует В-допустимая последовательность {Вп} такая, что при п —> оо имеем
/п= $jg(x, y)dp-+I.
Dn
543
Но тогда справедливы неравенства
Вп
и, кроме того, последовательность Гп является неубывающей. Следовательно, существует предел Гп = Zo < I. По теореме 23 существует несобственный интеграл IQ = JJ gQ(x9 y)d\L.
D
2) В силу расходимости интеграла JJ g0(x, i/)d|Li для любой П-до-D
пустимой последовательности Dn при и —» оо имеем
Л = ff +°°-о.
Следовательно, при и —» оо или -> +ОО, поскольку 1п> Гп. ◄
СЛЕДСТВИЕ. Пусть несобственный интеграл JJ|g(x, £/)|d|Liexo-
D дится. Тогда сходится интеграл JJ g(x, y)d\i.
D
► Рассмотрим функции
Поскольку 0 < g_ < |g| и 0 < g+ < |g|, по теореме 24 сходятся интегралы JJ g_d|LL, JJ Но тогда сходится интеграл от функции D	D
g = g+~g_- ◄
Определение 21. Если сходится интеграл JJ \g(x9 z/)|d|Li, то го-
D
ворят, что интеграл JJ g(x9 y)d\i сходится абсолютно.
D
Последнее следствие можно сформулировать так: если несобственный интеграл сходится абсолютно, то он сходится.
Утверждения, аналогичные теоремам 23 и 24, имеют место и для несобственных интегралов второго рода. Оказывается, что в случае несобственных кратных интегралов обычная сходимость влечет за собой и абсолютную сходимость. В случае однократных интегралов это не так.
Приведем только формулировки двух теорем, полезных для приложений.
ТЕОРЕМА 25. Если интеграл JJ g(x9 y)d[i сходится и сущест-D
вует повторный интеграл от функции g(x9 у) по области D9 то двойной интеграл равен повторному.
544
ТЕОРЕМА 26. Если интеграл JJ g(y)dp сходится и у = <р(х) —
D
гладкое отображение области DQ в D, взаимно однозначное для внутренних точек Do, то справедлива следующая формула замены переменных:
, П = JJ g($(x))| J=(x)dx. D	D„
ПРИМЕРЫ. 1. Интеграл J ... гДе II* II ~ Jxi + ••• + *2 ’ схо‘
дится при а > и и расходится при а < п.
Рассмотрим множество SA точек х, удовлетворяющих неравенствам А < ||х || < 2А. Полагая А = Ak = 2*, k = 0, 1, 2, ... , получаем
и/
Последний ряд сходится при -а 4- и < 0, т. е. при а > и. Пусть КА — множество точек х вида ||х || < А. Тогда
p(SA) =	= А»(№) - №)).
Отсюда
U/i> =>.<o5sb2‘W-№».
Последний ряд представляет собой геометрическую прогрессию со знаменателем, равным 2п-а. Следовательно, по признаку сравнения интеграл расходится при а < и.
2. Интеграл
J J------dx----
где ар ..., ал > О, сходится при 1/ах 4-... 4- 1/ал < 1 и расходится при I/04 4-... 4- 1/ал > 1.
Пусть SA — множество точек, для которых справедливо неравенство
А<|х1|«1 + ... + |хл|ал<2А.
Тогда для любой точки х е SA имеем |xs| < (2А)1/а«, а = 1, ... , и.
Следовательно,
g(SA) <	2" • 21/<Х1 + •" + 1/а"
2Л(1/<хх +... +1/ал)
545
18-4953
Отсюда получаем, что интеграл сходится при
1/ах + ... 4- 1/ап - 1 <0.
Пусть КА — множество точек х с условием ||4-... 4- | хп|а» < < А и SA =	\ КА. Очевидно, имеем
g(SA) =	- ц(*Л) = А1/а1+ - + 1/а» (№) - №)).
Таким образом, интеграл
U/ WO1 + ... + Ha” *	>
те *(± + ... + ±)
расходится при 1/ах 4-... 4- 1/ап - 1 >0.
На этом мы завершаем рассмотрение теории несобственных кратных интегралов.
Лекция 9
$ 15. ПЛОЩАДЬ ПОВЕРХНОСТИ
Задача состоит в том, чтобы распространить понятие измеримости на множества, расположенные на двумерных поверхностях в пространствах размерности три и выше. Для этого необходимо ответить на следующие вопросы. Что такое поверхность? И какие поверхности мы будем рассматривать?
Мы называли поверхностью Q множество точек (х, у9 z)9 удовлетворяющих уравнению z = g(x9 у) для некоторой функции g(x9 у) от двух переменных х и у9 причем точка (х, у) принадлежит некоторому множеству на плоскости хОу. Обычно от функции g(x9 у) требуют непрерывности всюду, за исключением, быть может, множества L нулевой меры Жордана. Проекцией црверх-ности Q на плоскость хОу является область D. Предположим, что область D — измеримый по Жордану компакт. Пусть измеримые множества D19 ... , Dt образуют его разбиение т. Возьмем точки Afp ..., Mt на границе соответственно каждой из областей Dv ..., Dt. Этим точкам при проекции на плоскость соответствуют точки Nv ... , Nt на поверхности Q. Пусть ур ... , yt — углы между нормалью к поверхности Q в точке N89 s e 1, ... , t9 и осью Oz. Рассмотрим части касательных плоскостей Qe, s = = 1, ... , t9 проходящих через точки N8 и имеющих своей проекцией на плоскость хОу область Z>8. Получаем «чешуйчатую» поверхность. Из линейной алгебры известно, что ее площадь |x(Qs) равна
“ |cosye| > « -
Назовем площадью поверхности Q величину г v	ff dxdy
Поскольку уравнение поверхности имеет вид z = g(x9 у)9 нормаль ее в точке N поверхности Q можно представить в виде
п = n(N) = -====^===.
71 +(£)2 + ($;)2
Следовательно, имеем
1
cos V = -=======.
71 +(£)2 + te;)2
547
18*
Отсюда получаем
M-(Q) = JJ71 +	)2 + (Sy У2 dxdy.
D ‘
Итак, из не вполне строгих геометрических соображений мы получили формулу площади поверхности в трехмерном пространстве. Далее мы дадим некоторое уточнение и обобщение этого понятия.
Определение 22. Поверхностью Q в п-мерном пространстве Rn называется множество точек {г}, г = (гр ... , гп), таки^, что г = г(х), где х = (хх, х2) € Л, причем область D является ограниченной и измеримой по Жордану и г = г(х) есть взаимно однозначное отображение внутренних точек множества D на точки множества Q, непрерывно всюду, за исключением множества L, имеющего нулевую меру Жордана.
Напомним, что отображение г = г(х) = (гр ... , гп) непрерывно в точке х, если непрерывны функции rk = rk(x), k = 1,..., п.
Назовем отображение г(х) = (гх(х), ... , гп(х)) гладким, если для любой точки хе D функции rA(x), k = 1, ... , п, имеют непре* рывные частные производные (на границе 3D рассматриваются односторонние производные).
Замечание. Поверхность Q можно задать различными способами. Указанное выше задание поверхности Q называется параметрическим (или параметризацией множества Q). Выбор параметризации также может быть разным. При любых фиксированных значениях сх и с2 кривые на Q вида г « г(хр с2) и г = г(ср х2) называются криволинейными координатами на поверхности Q. Каждой точке f е Q соответствует пара (сх, с2) криволинейных координат.
Определение 23. Поверхность Q называется гладкой, если задающее ее отображение г = г(х) является гладким. Гладкая поверхность называется невырожденной, если ранг матрицы Якоби отображения г = г(х) максимален, а именно: он равен двум.
Мы стремимся определить меру, т. е. понятие площади множеств на невырожденных поверхностях. Для этого сначала уясним, какими свойствами должна обладать площадь или мера множества. Кроме обычных свойств меры (монотонность, аддитивность, инвариантность относительно ортогональных преобразований пространства, независимость от параметризации) необходимо, чтобы в случае r3 s 0, ..., гп = 0, т. е. «плоского» отображения г = г(х), мы имели формулу
U(Q) = JJI J-^x^dx^x^
D
548
где«/-(х)— якобиан отображения г — r(x),
Эгх Эг2
J;W- 3X13X1.
Г	ЭГ1 ЭГ2
Эх2 Эх2
Для простоты рассуждений предположим, что плоское множество D — замкнутый квадрат. Тогда в этом случае мера p(Q) образа D — предел при Дт —> 0 интегральных сумм о(Т) для разбиения Т квадрата D на равные квадраты Dk z = 1, ... , и, со стороной h z) = ft2),
п п
G(T) = fcZHZ1|J?(xft>z)|g(Dk(Z),
где xkt t — левая ниясняя вершина крадрата Dk4.
При выводе формулы площади фигуры Q мы видели, что число z) равно площади параллелограмма, в который переходит квадрат Dk t при замене отображения Дг = г(х) - r(xfe z) на линейное отображение р вида
р = р(х) =5 A(xk> z)(x - Xki z) = dr(xft> z),
где A(xk j) — матрица Якоби отображения г = г(х) в точке х = xk, t.
Итак, при вычислении ц(О мы берем разбиение D на квадраты Dk l9 а затем для каждого квадрата Dk t заменяем отображение Дг линейным отображением dr(xk При такой замене можно сказать, чему равна площадь образа. Сумма же полученных площадей по всем парам (й, Z), Л, Z s 1,	, п, дает интегральную
сумму а(Т).
Естественно ту же самую схему положить в основу определения площади поверхности Q и в общем случае, т. е. надо взять разбиение Т квадрата D на равные квадраты Dk l9 k91 = 1, ... , п. Далее, заменить отображение Дг линейным отображением р,
Р = Р*,Д) = </^,г)’
и просуммировать меры Rk t = р(1\ г). Тогда получаем
Определение 24. Если существует предел при Дт —> Q, то этот предел мы и будем называть площадью поверхности Q.
549
Осталось провести явное вычисление величины с(Г) и найти ее предел p(Q). Для этого заметим, что векторы ёг = (Л, 0) и ё2 = (0, Л) при отображении р = dr(xk z) переходят в векторы
_	/dri	Эг_\
«1 = р(«1) =
_	/dri	дг„\
а2 = р(е2) =	, ...»
Теперь надо найти площадь параллелограмма, образованного векторами ах и а2. Для этого воспользуемся формулой линейной алгебры, которая утверждает следующее:
Л2= (EG - F2)*2.
Приведем простой вывод этой формулы. Очевидно, формула площади параллелограмма, составленного из векторов аг и а19
имеет вид
и “НМ*
2-_KiF
Преобразуем эту формулу. Получаем
||ах ||2|12 = (а2 ||ах ||2 -	а2), а2 ||ах ||2 - ах(ах, а2)) =
= ll^i II4 ll®2 II2 ~ 11^1 ll2(®i» ^г)2 "* Н®1 Н2(®1» ®г)2. Следовательно,
Р2 = 1|ах II2 ||а2 II2 - (ах, а2)2 = (EG - F2)h2 = Г(х)й2. Таким образом, имеем
С(Т) = ДДУГ(^)И(ПМ).
Функция а/Г(х) непрерывна на D, поэтому существует предел
Jun о(Т) = JJ 7Г(х) dxxdx2 = p(Q).
Другими словами, p(Q) = JJ JEG - F2 dxxdx2.
D
Заметим, что последний интеграл может оказаться как собственным, так и несобственным. Площадь параллелограмма, образованного сторонами ах = hr'Xv а2 = Лг£2, равна
№./)=л211[г;1, г;2]||.
Отсюда получаем еще одну формулу для площади поверхности: P(Q)= ПНКр r;2]||dxxdx2.
550
ПРИМЕРЫ. 1 . Площадь поверхности верхней полусферы х2 + у2 + г2 = = 1» г > 0 равна 2л.
Имеем
dxdy cos(n,e3) *
где п = (х, у, 2), г = 71 - х2 - у2, cos (и, ё3) = г. Следовательно, получаем	, ,
dxdy
H(Q)= JJ X2 + у2 < 1
«е)- я ,, , ,•
х2 + у2< 1 71 ~ X2 - у2
Переходя к полярным координатам, имеем ? rdr } dr2 Idt n we) - /	 *1 7, = 2"-
2. Площадь двумерного тора Q e R3, задаваемого уравнением г = г(ф, в) = ((Ь + a cos 0) cos ф, (6 + a cos 0) sin ф, a sin 0), Ь > а, на области D изменения параметров,
D = {(ф, 0)|О < ф < 2л, 0 < 0 < 2л}.
Имеем
= (—(Ь + a cos 0) sin ф, (& + a cos 0) cos ф, 0),
Гд = (-a sin 0 cos ф, - a sin 0 sin ф, a cos 0), Е = (г'г г^)«(Ь + a cos 0)2, F = (г^, г^) = 0, G = (г'в,г’6) = а2, JEG - F2 = а\Ь + a cos 0| = а(Ь + а cos 0).
Отсюда получаем
p(Q) = JJ JEG - F2 <fcpd0 = j”сГф j”a(b + a cos 0)d0 = 4л2аЬ. D	0	0
§ 16. ПЛОЩАДЬ m-МЕРНОЙ ПОВЕРХНОСТИ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ П ИЗМЕРЕНИЙ
Пусть тп, п — натуральные числа, 1 < т < п.
Назовем т-мерной поверхностью Q в Rn множество точек {г}, г = (гр ... , гп), таких, что г = г(х), где х = (хр ... , хт) е Z>, причем множество D ограничено и измеримо по Жордану, а отображение г взаимно-однозначно отображает D на Q и оно непрерывно всюду на D, за исключением множества L, имеющего нулевую меру Жордана.
Будем говорить, что гладкая поверхность Q невырождена, если ранг матрицы Якоби отображения г = г(х) максимален, т. е. равен тп.
551
Пусть, для простоты, множество D — куб и пусть Т — разбиение его на равные кубы D- со стороной Л. Пусть, также, — левая нижняя вершина куба D-.
Положим р = р-(Зс) = dr(x^),	= р(Р-) и определим интег-
ральную сумму
о(Т) = k к
Определение 25. Площадью поверхности Q назовем величину |1(Q) = liraо(Т).
Лг —> о
Для вычисления о(Т) необходимо найти объем параллелепипеда R&, образованного векторами аг = hf'x9 ... , ат = hr'x .
Из линейной алгебры известно, что
ц(^)=7Г(й1,...,ат)=Ут,
где Гт = Г(ар ... , ат) — определитель матрицы Грама
... (a1(am)
Г(О1,.. .,ат) =
(am,ai) ... (ат,ат)
Выведем формулу для Vm. При т = 1, 2, очевидно, имеем = = Haji = V19 Jr2 = V\ • h2 = V2. Следовательно, й| = Г2/ГР Докажем, что = Гт/Гт_р где hm — расстояние вектора ат до т - 1-мерного пространства с базисом а19 ... , am_v
Представим ат в виде ат = Ьт + Лт, где bm е {ар ..., ат_х} = L, hmLL. По условию, существуют некоторые вещественные числа ср ... , cm_x такие, что Ьт = сх ах + ... + cm_x am_v Тогда справед
лива следующая цепочка равенств: ,
552
так как определитель в числителе первого слагаемого равен нулю (последняя строка в нем является, л инейной комбинацией предыдущих).
Таким образом, объем Vm =* ц(й-) параллелепипеда R* равен
Заметим, что Гт > 0. Это следует из равенств
тД-=Л2>0, Гх = ||а11|2 > 0.
1 т-1
Таким образом,
С(Т) - Z	......И(О£).
Переходя в этом равенстве к пределу при Дг —> 0, получаем формулу для вычисления площади m-мерной поверхности в n-мерном пространстве:
H(Q) = J J ^Пг'^х), ... r'Xm(x)) dxi ...dxm.
При т = 1 получаем формулу длины дуги гладкой кривой
Ц(О == J 11 r\t) \\dt, а при т =*= п приходим к формуле замены пере-
D
менных в n-кратном интеграле:
H(Q) = f... J dx1... dxn = J...	... dxm,
где Jr(x) — якобиан отображения г = r(x).
Замечания. 1. ПустьА = (ах, ... , ат) — матрица из т векто-ров-столбцов в n-мерном пространстве и А* — транспонированная к ней матрица. Тогда из формулы Бине—Коши имеем
г = v2 = Z
т т 1 < ii <„. < im < п
aix,l ain2 • • • ailtm
aim,l aim,2 • • • aim,m
Это равенство означает следующее: квадрат объема параллелепипеда равен сумме квадратов объемов его проекций на все координатные тп-мер-ные подпространства (обобщение теоремы Пифагора).
2. Справедливо неравенство Адамара Г (ар ..., ат) < Г(ах)... Г(ат), причем равенство достигается только, если векторы at и a;, i * j9 ортогональны для всех 1 < i, j < т.
3. В силу определения, величина площади m-мерной поверхности не зависит от выбора параметризации.
553
ГЛАВА 20
Поверхностные интегралы
Лекция 10
$ 1. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Криволинейные интегралы — это интегралы по кривой L в n-мерном пространстве. Рассмотрим два вида таких интегралов: интегралы первого и второго рода.
Сделаем некоторые допущения. Пространство, в котором задана кривая L, для простоты считаем двумерным. Саму кривую L будем считать кусочно-гладкой, т. е. ее можно разбить на конечное число гладких кусков (участков). Рассмотрим только один такой кусок.
Как известно, кривая L является образом некоторого отрезка [а, Ь] при отображении г = r(f), t е [а, &], где r(t) = (x(f), y(t))9 причем x(t) и y(t) — гладкие функции на отрезке [а, Ь]. Кром^ того, внутренние точки отрезка переходят во «внутренние» точки кривой, а концы отрезка — точки а и & — переходят в граничные точки кривой А и В, т. е. г(а) = А, г(Ъ) = В. Будем предполагать, что кривая L невырождена, т. е. не содержит особых точек. Другими словами, для любого t е [а, Ь] вектор г'(0 отличен от нуля.
Пусть Т — размеченное разбиение отрезка [а, Ь]: а «tQ < tr < ... ... < tm = b, ... ,	— точки разметки, xk - x(^), yk =
k = 1, ... , m; Д lk — длина части кривой L, которая является образом отрезка Дл = tj. Длина рассматриваемой кривой L выражается формулой
Д** = /‘7(x’(t))2 + («/’(O)2 dt.
Пусть функция g(x9 у) определена на кривой L.
Определение 1. Если существует предел при Дг —> 0 интегральных сумм
т
О1(Т) = kl.g(xk, уk)Mk,
то он называется интегралом первого рода от функции g(x9 у) по кривой L.
554
Этот интеграл обозначается так:
= J g(x, y)dl.
L
Рассмотрим интегральную сумму гДе
°2(Т) = Д У») &Хк, &Xk = X(tk) ~ Х(^_х).
Определение 2. Если существует предел 12 интегральных сумм <з2(Т) при Дг 0, то он называется интегралом второго рода от функции g(x9 у) в направлении от А к В.
Обозначение:
12 = J g(x, У№х-АВ
Аналогично определяется еще один интеграл второго рода
I3 = J Six* y>dV‘
АВ
Для интегралов 12 и 13 обычно используют следующие обозначения:
Л = J р(х> y^dx’ h = J у№у-AB	AB
Выражение
I = J P(X, y)dx + Q(x, y)dy
AB
называется общим криволинейным интегралом второго рода по кривой L = АВ от линейной дифференциальной формы Pdx + + Qdy (здесь кривая обозначается своими начальной и конечной точками).
§ 2. СВОЙСТВА КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
Пусть х = x(t) — постоянная величина. Тогда
I2= jP(x,y)dx = O.
АВ
Действительно, так как для любого разбиения Т величина Дхй = 0, то а2(Т) = 0. Отсюда следует, что 12 = 0.
ТЕОРЕМА 1 (выражение значения криволинейного интеграла через интеграл Римана). Пусть функция g(x, у) непрерывна на L. Тогда криволинейные интегралы 119 129 13 существуют и равны соответственно
11 = f g(x(t), y(t))J(x'(t))2 + (y'(t))2dt, I2 = J g(x(t), y{t))x\t)dt, a	a
b
I3 = J g(x(t), y(t)y\t)dt.
a
555
► Рассмотрим сначала интеграл Iv Интегральная сумма Е1(71) для интеграла
ъ	_______________
f g(x(t), j/(t))7(x'(t))2 + (y'(t))2dt a
отличается от интегральной суммы о1(Т) криволинейного интеграла тем, что вместо &lk там должна стоять величина 7(x'(^fc))2 + (y'(^fe))2 А** при некотором ^к е Дй, т. е. дифференци-ал длины дуги кривой, взятый в точке и отвечающий приращению \tk переменной t. Далее можно сослаться на определение интеграла Стильтьеса
ь,
1г = J g(x(0, а
t ________________
где l(t) =	и тем самым завершить доказа-
ла
тельство равенства интегралов. Но мы дадим прямое доказательство этого факта.
В силу непрерывности производной l'(t) на отрезке [а, &] имеем равномерную непрерывность ее на нем. Тогда для любых точек t, е [£л_р tk] имеем - Г(£л)| < причем Hmco(z) = 0.
Отсюда получаем
Д/, = J* l'(t)dt =	/ (*'(0 -	=
= l'&k)btk + О(®(Д^)Д#Й).
Поскольку g(x9 у) непрерывна на компакте L, она ограничена на нем, т. е. найдется М >0 такое, что для любых (х, у) е Ъ имеем \g(x, j/)| < М.
Преобразуем интегральную сумму сг1(Т). Получаем
СТ1(Т) = Е g(xk, ук)Мк = Е g(xk, ук)1'Ък)Ык + о[ЕМД^®(Д^)) =
= Е1(Т) = О(В), где
Ж М тахсо(Д<А)Е < M(b - а)тах<£>(Д?А). k	k	k л
Так как R -> 0 при Дт -> 0, то это значит, что ах(Т) и Sj(T) одновременно сходятся и имеют один и тот же предел. ◄
Теорема 1 дает универсальный метод вычисления значений криволинейных интегралов. Следующйе следствия из этой теоремы получаются простым переходом от криволинейных интегралов к интегралам Римана.
556
1°. Справедливо следующее равенство:
J Pdx + Qdy = J(P cos ax + Q cos a2)dZ, AB	L
где
x
cos 04 = (t, ej =
cos a2 = (t, e2) ~
y'
7(х')2 + (Ю2’
V(x')2 + (J/')2’
т = (x', y') — касательный вектор к кривой L в точке (х, у); ё1 и ё2 — единичные орты, направленные по осям координат Ох и Оу.
2°. Если для любых точек (х, у) е L справедливо неравенство gx(x, у) < g2(x, у), то имеем \grdl < J g2dl.
L	L
3°. Выполняется неравенство J gdl < J|g|dL L	L
4°. Если функция g непрерывна на кривой L, то существу-
ет точка £ е L такая, что J gdl = £(£)|ll(L), где |1(L) — длина L
кривой L.
Значения криволинейных интегралов первого и второго рода не зависят от выбора параметризации, так как от нее не зависят интегральные суммы в их определении. ,
В частности, интеграл не зависит от того, какую точку А или В считать началом, а какую — концом кривой L (параметризации в этом случае можно определить, например, соотношением t = а 4- Ъ - и).
В то же время, ймеет место равенство J Pdx= - J Qdy, т. е. вела	АВ
личина интеграла зависит от выбора направления обхода кривой L.
Рассмотрим две параметризации кривой L : г = г(0, * €	Ь],
и = т\(и), и е [ях, Ьх]. Пусть t = t(u) — гладкое отображение отрезка [ях, bj на отрезок [а, Ь]. Тогда имеем гг = г\(и) = r(t(u)), xt = x(t(u)).
Отметим, что производная t\u) имеет один и тот же знак на всем отрезке [ях, Ьх]. В противном случае по теореме Вейершт-расса существовала бы точка u0 е [ях, bj такая, что f(u0) = 0. Но тогда r't(u0) = г J(f(u0)) • t'(uQ) = 0, и кривая L имеет особую точку, т. е. она является вырожденной, что на самом деле не так.
Поскольку при отображении t = t(u) концевые точки отрезка [ях, bj переходят в концевые точки отрезка [я, Ь], при t'(u) > 0 имеем £(ях) = a, f(bx) = b. Действительно, из теоремы Лагранжа
557
при некотором £ g [ар bj имеем - t(a^) =	~ ai)* Следо-
вательно, t(by) > а это и означает, что t(ax) = a, t(b^) = Ь.
Далее воспользуемся теоремой 1 и теоремой о замене переменной в интеграле Римана. Получаем цепочку равенств
ь
J g(r)dx = J g(f(t))x'(t)dt = L	а
= J g(r(t(u)))x'(t(u))t'(u)du = J gir^uyyx’/uydu = J glr^dx^ fli	ai	L
В случае t\u) < 0 имеем f(ax) = 6, t(b^) = a. Повторяя предыдущие рассуждения, получим, что при переходе в этом случае от одной параметризации к другой параметризации справедливо равенство
jg(r)dx = -J gtrJdXi. L	L
Аналогичные свойства для криволинейных интегралов имеют место в пространствах размерности большей двух. Например, в трехмерном случае
ь	___________________________
J g{x, у, z)dl = J g(x(t), y(t), z(t))J(x'(t))2 + (j/'(t))2 + (z'(t))2dt, L	o,
b
J Pdx + Qdy + Rdz = J (Px'(t) + Qy'(t) + Rz'(t))dt =
AB	a
= J (P cos 04 + Q cos a2 + R cos a3)dZ,
L
где т = г' /| f z|, cos ak = (t, ek), k = 1, 2, 3.
На этом мы завершаем изучение общих свойств криволинейных интегралов.
Лекция 11
в 3> КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ ВТОРОГО РОДА ПО ЗАМКНУТОМУ КОНТУРУ. ФОРМУЛА ГРИНА
В силу аддитивности интеграла второго рода для любых кривых Lx =АВ и Ь2 = ВС в случае, когда кривая L = Lr U L2 не имеет кратных точек, получаем
J gdx + J gdx = J gdx. AB	ВС	AC
По этой же формуле определяется и понятие интеграла по кривой L в том случае, когда точки А и С совпадают. В этом случае объединение кривых L « Lr U L2 называется замкнутой кривой.
Определение 3. Кривая называется замкнутой кусочно-гладкой кривой (без кратных точек), если
1)	L = Lr U Ь2;
2)	LxuL2 — кусочно-гладкие кривые, концы которых совпадают;
3)	других общих точек кривые Lr и L2 не имеют.
Если на кривой Lr задано направление обхода, т. е. заданы начальная точка А п концевая точка В, и если на кривой L2 за начальную точку принять В, а за концевую — точку А, то на кривой L будет задано направление обхода в том смысле, что для любых трех различных точек А19 А2,А3е L всегда будет иметь место один из следующих порядков следования точек: At А2 А3 Аг или Ai А3 А2 Ах.
Поскольку на любой замкнутой кривой L имеется точно два направления обхода, одно из них естественно считать положительным, а другое — отрицательным.
Заметим, что при этом для интеграла I от дифференциальной формы Pdx + Qdy по замкнутой кривой L, взятому в положительном направлении, используется обозначение
I = f Pdx + Qdy.
L
Определим, как следует выбирать положительное направление обхода замкнутой кривой. Сначала рассмотрим важный пример окружности L: хI 2 + у2 = 1. За положительное направление обхода окружности берется «направление обхода против часовой стрелки». Оно определяется так. Разобьем окружность на верхнюю полуокружность Lr: х2 + у2 = 1, у > 0, и нижнюю полуокружность L2. На верхней полуокружности за начало отсчета
559
возьмем точку А с координатами (1* 0) и будем считать точку В концевой точкой, для нижней полуокружности Ь2 в качестве на* чальной точки возьмем В, а концевой точкой будем считать точку А.
На окружности L можно однозначно задать направление обхода, указав в любой произвольно взятой на ней точке А Касательный вектор т.
Будем рассматривать окружность L hsl плоскости хОу в пространстве Я3. Пусть в каждой точке ее заданы п — вектор внешней нормали к окружности, лежащий в плоскости хОу, т — касательный вектор к ней. Если орт ё3, направленный по оси Oz, совпадает с векторным произведением [п, т], то будем говорить, что вектор т задает положительное направление обхода окружности L.
Это свойство окружности положим в основу определения положительного направления обхода общей крйвой L.’
Определение 4. Пусть замкнутая кусочно-гладкая кривая L без кратных точек является границей выпуклого множества D на плоскости хОу. Пусть ё3 — орт, направленный по оси Oz. В каждой точке кривой L зададим касательный вектор т и вектор внешней нормали п. Будем говорить, что на кривой L задано положительное направление обхода, если вектор ё3 совпадает с векторным произведением [п, т].
Ближайшая цель — доказать формулу Грина, которая устанавливает связь между криволинейным интегралом по замкнутой кривой L = Э£>, являющейся границей области D, й двойным интегралом по этой области. Для простоты рассмотрим случай выпуклой области D.
ТЕОРЕМА 2 (формула Грина). Пусть D — выпуклый, измеримый по Жордану, компакт, граница L = 3D которого является замкнутой невырожденной кусочно-гладкой кривой. Пусть также функции Р(х, у) и Q(x, у) непрерывны на D и имеют
л ЭР Э(?	~
там же непрерывные частные производные и Тогда
справедлива формула
f Pdx + Qdy = Л (jf ~ dxdy,
где кривая L обходится в положительном направлении. ► Докажем только равенство
f Pdx = -^^dxdy.
560
Аналогично доказывается равенство.
f Qdy = JJ j^dxdy.
L	D
Пусть отрезок [а, b] является проекцией области D на ось Ох. Через точки (а, 0) и (6, 0) проведем вертикальные прямые х = а и х = Ь. В силу выпуклости множества D граница его L = 3D разбивается на четыре участка: отрезки Lr и L3, лежащие на прямых х = а и х = b (каждый из них может состоять только из одной точки), и кривые L2 и £4, лежащие в полосе между этими кривыми.
На кривых и L3 величина х постоянна, поэтому
J Pdx = J Pdx = 0.
Li	L3
Всякая прямая х = х0 при х0 е (а, Ъ) пересекает (в силу выпуклости D) каждую из кривых L2 я Ь4 строго в одной точке, которые обозначим соответственно фх(х0) и ф2(х0), т. е. кривая L2 является графиком функции у = ф4(х), а кривая L4 — графиком функции у = ф2(х).
Заметим, что из кусочной гладкости кривой L следует кусочная гладкость функций ф4(х) и ф2(х).
Из теоремы о выражении криволинейного интеграла через интеграл Римана имеем
ь	ь
J Р(х, y)dx = J Р(х, ф1(х))с?х, J Р(х, y)dx = - J Р(х, ф2(х))</х.
Ь2	ь4	*
Отсюда получаем
ъ
J Р(х, y)dx = J (Р(х, <рх(х)) - Р(х, <p2(x)))dx = Н.
l2ui4	а
эр
Поскольку функция непрерывна на В, по теореме Ньютона—Лейбница имеем
ф2(*)
Р(х, фх(х)) - Р(х, <р2(х)) = - J	3- dy.
Ф1(Х) °У Следовательно,
„	? . ЭР . ff ЭР . .
н = -J dx J djdy = -JJ fodxdV-
a <Pi(x)	D
В силу того, что j Pdx = J Pdx = 0,
L
справедлива формула H = jPdx. ◄
L
56У
Заметим, что в силу аддитивности интеграла формула Грина верна для областей, являющихся конечным объединением выпуклых областей.
ПРИМЕРЫ. 1. Площадь области D выражается согласно формуле Грина через криволинейный интеграл в следующем виде:
ц(£>) = f xdy = -f ydx = i f xdy - ydx.
L	L	£ L
2. Пусть ф : Dq -> D — гладкое взаимно однозначное отображение двух плоских областей. Пусть также якобиан отображения
1= В(х,у)
D(u9v)
не меняет знак в области Do и <p(5D0) = 8D. Кроме того,
пусть непрерывна на Do. Тогда, исходя из формулы приме-ouov
pa 1, проведем вычисление меры области D. Имеем
H(D) = f xdy.
dD
Далее, пусть задана параметризация вида и « u(t)9 и = v(t), а < t < b, кривой 8DQ. Тогда соответствующая параметризация кривой 8D задается уравнениями х = x(u(t)9 v(t))9 у = y(u(t)9
Из выражения криволинейного интеграла через интеграл Римана получаем
И(Р) - i xdy - f x(t)i^dt - f	dt.
dD a dtt и du Clt uV dt'
Но последний интеграл можно представить как интеграл по кривой 8Dq. Имеем
ц(П) = £ f х(du + dv9 dD ^ди	dv'
где £ = 4-1, если кривые 8DQ n 8D имеют одинаковое направление обхода, £ = -1 — в противном случае.
Преобразуя последний интеграл, используя формулу Грина, получаем
М<С) ‘	+	" я; (ха9) d“‘to *
^0	^0
Поскольку якобиан I не меняет знака и величина ц(П) неотрицательна, то е! = |1|. Поэтому имеем
J1CD) = ff |I| dudv.
Таким образом, получена формула для вычисления в криволинейных координатах площади плоской области.
562
Лекция 12
§4. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Рассмотрим гладкую поверхность D в Я3. Будем считать, что она невырождена во всех своих точках, т. е. при ее параметрическом задании г = r(u, v), где г = (х, у, z)9 (и9 v) е DQ ранг ее матрицы Якоби максимален и равен двум.
Допустим сначала, что область DQ является квадратом. Возьмем его размеченное разбиение V на равные квадраты Pk t с разметкой (uk l9 vktl)9 k91 = 1, ... , и. Здесь точка (uk l9 vk, z) — вершина левого нижнего угла квадрата Pk z со стороной 8. Рассмотрим область Dk t — элемент поверхности D9 соответствующий квадрату Pk l9 т. е. Dk г = r(Pkt z). Рассмотрим также множество точек Rk z — часть касательной плоскости к поверхности D в точке rk t = r(uk l9 vkt z), отвечающую квадрату Pk t.
На поверхности D в точке f = r(u9 v)9 (u9 v) e Do, определены два касательных к ней вектора гх и г2, являющихся соответственно первым и вторым столбцами матрицы Якоби J-(n, и), т. е.
гг = r'u(u9 v) ==
Эх ди
ди дг ди
г2 = г'и(и, V) =
Эх Эи Эу dv дг dv
В силу условия невырожденности матрицы Якоби, имеем, что для любой точки (u, v) g D векторное произведение [гр г2] отлично от нуля. Заметим, что особыми точками поверхности называются такие ее точки, в которых ранг ее матрицы Якоби меньше двух.
Рассмотрим вектор
[Г1,Г2]
1Р..МГ
Определение 5. Вектор п =* п(г) будем называть нормалью к поверхности D9 отвечающей параметризации г = r(u9 и).
Такое название вызвано тем, что вектор п перпендикулярен касательным векторам гх и г2. В частности, при (и9 v) = (uk l9 vk* z) получаем, что вектор п перпендикулярен к касательной плоское-
563
Если 8 — длина стороны квадрата Pk 19 то Rk t представляет собой параллелограмм и его площадь z) равна ||[гр г2] ||82, где касательные к поверхности D векторы гх и г2 взяты в точке
Если задана другая параметризация р поверхности D9 то всегда выполнено одно из равенств, й(г) = и(р) или п(г) = ~й(р), Следовательно, функция f(u9 v)9 равная скалярному произведению векторов п(г) и п (р), принимает всего два значения +1 и -1. Но эта функция является непрерывной на Ро. Отсюда имеем, что она либо тождественно равна 4-1, либо тождественно равна -1. Это означает, что при замене параметризации определенная нами нормаль к поверхности D либо не меняется во всех точках D, либо меняет свое направление сразу во всех точках D. Поэтому говорят, что нормаль к поверхности, отвечающая некоторой параметризации этой гладкой поверхности без особых точек, выделяет на ней ее сторону. Поверхность с выделенной стороной называется двусторонней поверхностью.
Определение 6. Выделение одной из сторон поверхности D с помощью параметризации называется ориентацией поверхности D.
Далее, пусть на поверхности D задана функция й(г) трех переменных г = (х, у, z). Рассмотрим следующие четыре интегральные суммы, отвечающие размеченному разбиению V:
o0(V)= Е ft(rfc>z)|i(Bfc>z);
«, I
g8(V) = Е h(rk z)(n, ё8), 8 = 1,2, 3. к, I
Отсюда, в частности, имеем следующие выражения:
ox(V) = Е h(rk г)ц(В* z) cos X = Е Л(гй i)A(uk vk z)82, к, l	H, I
где
cos X = (n, ex), A(u, v) =
Аналогично можно записать выражения для q2(V), за-меняя cos X на cos Y = (п, ё2), cos Z = (п, ё3) и А = А(и, v) на
У'и *'и y'v *'v
В == B(u, v) =
*и Хи
Zv Xv
, С = С(и9 v) =
Хи Уи xv y'v
Вектор нормали п можно представить в следующем виде: n = (A/Jf,B/JT,C/JV), V=A2 + B2 + C2 = EG-F2.
564
Определение 7. Если существует предел IQ при —> О интегральной суммы <\)(V), то он называется поверхностным интегралом первого рода от функции h(f) по поверхности D. Этот интеграл обозначается так:
Io = jj h(r)dS.
D
Определение 8. Если существуют пределы 11912> пРи Ду —> О интегральных сумм c2(V)9 o3(V), то они называются поверхностными интегралами второго рода от функции Л(х, у9 г) по стороне поверхности D9 отвечающей параметризации г = = r(u9 v).
Для интеграла второго рода введем следующие обозначения: /1 = JJ h(r)dy Л dz9I2 = JJ h(r)dz Л dx913 = JJ h(r)dx Л dy.
D	D	D
Здесь знак Л позволяет отличить поверхностный интеграл второго рода от обычного двойного интеграла по плоскому множеству D. Часто этот знак опускается (в тех случаях, когда это не ведет к двусмысленности).
Отметим, что вместо дифференциальных форм в интегралах 1\9129 h можно ввести форму
со = Pdy Л dz + Qdz Л dx + Rdx A dy и рассмотреть интеграл второго рода от этой дифференциальной формы I = JJ со.
D
Приведем два свойства введенных интегралов первого и второго рода, которые непосредственно вытекают из их определений.
1°. Справедливо равенство
I^jjPdy /\dz + Qdz Л dx 4- Rdx /\dy = D
= JJ (P cos X 4- Q cos Y 4- R cos Z)dS9 D
где cos X = (n9 e^)9 cos Y = (n, e2), cos Z = (n, e3).
2°. T E О P E M A 3 (о сведении поверхностного интеграла к двойному интегралу). Пусть функция h(f) непрерывна на гладкой9 невырожденной (без особых точек)9 измеримой по Жордану, компактной поверхности D. Тогда имеют место следующие равенства:
/0 = JJ h(r)dS = JJй(г(и, v))Jf dudv, Г = EG- F2;
D	Do
I = JJ Pdy /\dz + Qdz A dx 4- Rdx Ady =
D
= JJ (P cos X 4- Q cos Y + R cos Z)dS = JJ (PA + QB + RC)dudv. D	D
565
► В отличие от криволинейных интегралов здесь; по существу, нечего доказывать, так как функции под знаками интегралов являются интегрируемыми, в силу их непрерывности на компакте D. Поэтому при —> 0 соответствующие интегральные суммы o0(V), ... , o3(V) обязаны сходиться к значениям этих интегралов. ◄
Замечание. Определения поверхностных интегралов в п-мерном пространстве, несколько сложнее (в основном, из-за понятия ориентации). К ним мы вернемся позже.
ПРИМЕР 1. Рассмотрим поверхность D — «внешность» верхней полусферы х2 + у2 + z2 = 1. Ее можно представить как образ круга Do = {(х, у)\х2 + у2 < 1} при отображении
х = х, у = у, 2 = 71 -(х2 + у2).
Покажем, что п = й(г) = г. Действительно, для параметризации г = г(х, у) имеем
-т'х = fi, о, -	У г' = (о, 1, - ,.-У—.. 1,
'	- X2 - у2 / X	- х2 - у2 '
—	। —	у	। —
= вл .	+ Со 1 .........  +	во<
71 - х2 - у2 л/1 “ X2 - у2
Следовательно, “**’*'’2)-f'
Вычислим теперь интеграл I = JJ zdx Л dy. Применяя теорему 3, получаем	D
I = Цг cos ZdS =	Цг	cos Z?xty	-
Do	Do	ICOSZI	>
= JJ *(*, y)dxdy = J dtp J 71 ~ r2 rdr = -2л | (1 - r2)3/2^ =	.
Z)o	0	0	°
ПРИМЕР 2. Пусть поверхность D задается уравнением z = ф(х, у), где ф(х, у) — гладкая функция, (х, у) е Do, и интегрирование ведется по верхней стороне поверхности D, т. е. в этом случае cos Z > 0. Обозначим эту сторону через D+. Тогда
JJ Л(х, I/, z}dx /\dy= JJ Л(х, у, ф(х, y))dxdy. d+	d0
566
$ 5. СОГЛАСОВАНИЕ ОРИЕНТАЦИИ ПОВЕРХНОСТИ И ЕЕ ГРАНИЦЫ
По существу мы дали определение поверхностных интегралов только в случае, когда область DQ является квадратом. Для интегралов первого рода это определение тривиально распространяется на случай поверхностей, составленных из отдельных частей, каждая из которых есть гладкий образ некоторого квадрата, и соприкасающихся между собой по общим участкам границ. Тогда поверхностный интеграл первого рода понимается как сумма интегралов по составляющим ее частям. Рассуждая стандартно, мы переходим от специального случая к определению поверхностного интеграла для произвольного измеримого по Жордану компакта DQ. Более того, таким образом можно рассмотреть интеграл первого рода по поверхностям, которые являются границей пространственных тел, например, по поверхности куба или шара в трехмерном пространстве. Во всех этих случаях будем считать, что понятие интеграла по таким поверхностям уже определено и верна теорема о его сведении к двойному интегралу.
Определение 9. Поверхность D называется кусочно-гладкой, если она связна и является объединением конечного числа гладких поверхностей, каждая из которых есть образ выпуклого плоского множества, имеющего кусочно-гладкую границу. При этом общие точки у любых двух поверхностей (если они есть) обязательно принадлежат образам границ указанных выше плоских множеств.
Определение 10. Интеграл первого рода по кусочно-гладкой поверхности равен сумме интегралов по ее гладким частям.
Более сложная ситуация имеет место в случае интегралов второго рода по кусочно-гладкой поверхности, так как здесь необходимо согласовывать ориентацию ее частей. Рассмотрим этот случай.
Выведем ряд новых определений.
Определение 11 • Границей L — 3D гладкой поверхности D называется образ границы А = Э1)о множества DQ, которое отображается в D при ее параметризации г. При этом считаем, что А — кусочно-гладкая замкнутая кривая без кратных точек, а множество DQ выпукло.
Замечание. Очевидно, что поверхность D может быть плоской, и при этом не обязательно быть выпуклым множеством. Так что выпуклость не является существенным ограничением. Поэтому можно считать множество Dq образом выпуклого множества.
567
1
Определение 12. Будем говорить, что параметризация г поверхности D отвечает ориентации ее границы L = dD (или «согласована» с ориентацией ее границы), если при этой параметризации г ориентация кривой L порождается положительной ориентацией ее прообраза Л (границы множества DQ — прообраза поверхности D).
Замечание. Если т = rj/|r'| — касательный вектор к кривой L в точке А, отвечающий ее параметризации, и п = й(г) — вектор нормали к поверхности D в точке А, то согласованность ориентации кривой L и ориентации, отвечающей параметризации г, означает, что «обход» кривой L относительно векторай совершается «против часовой стрелки». Другими словами, вектор b = [Т, п] является нормалью кривой L, лежащей в касательной плоскости к поверхности D и «внешней» по отношению к проекции D на эту касательную плоскость. Это полностью отвечает определению согласованности ориентации в плоском случае.
Определение 13. Будем говорить, что кусочно-гладкая поверхность D является двусторонней поверхностью с выделенной стороной, если параметризации ее разных кусков выбраны так, что общие участки границ этих кусков при указанных параметризациях ориентированы в противоположных направлениях.
ПРИМЕР. Пусть поверхность D является плоской и лежит на плоскости хОу. Рассмотрим верхнюю сторону D и пусть D = Dr U D2. Тогда ориентация поверхностей D, Dlf D2 будут согласованы с ориентацией их границ L,LVL2, если все эти кривые «обходятся против часовой стрелки». При этом ясно, что общий кусок границ и L2 ориентирован в противоположных направлениях для каждой из них.
Поясним определение «согласования» ориентации поверхности D и ее границы L = dD. Пусть задана параметризация г поверхности D, являющейся образом плоского множества DQ. Пусть также параметризация и = u(t), v = v(t) задает границу Л = ЭВ0 и порождает положительную ориентацию. Тогда параметризация границы L : г = r(t) = f(u(t), v(t)) задает с помощью вектора т направление обхода контура (кривой) L, которое мы называем согласованным со стороной поверхности D. Пусть задана любая другая параметризация р(£х) кривой L. Тогда вектор = pj/lp^l задает обход контура L. Если векторы т и совпадают, то мы говорим, что ориентация поверхности D и ориентация кривой L, заданная параметризацией p(fx), согласованы или отвечают параметризации г.
Определение 14. Поверхностным интегралом второго рода от функции h(r) по выделенной стороне двусторонней кусочно-гладкой поверхности D называется сумма соответствующих поверхностных интегралов по всем, составляющим поверхность D, гладким кускам.
568
Это определение распространяет цонятие поверхностного интеграла второго рода на случай поверхностей, являющихся образами при гладком отображении квадрируемых (т. е. измеримых по Жордану) плоских фигур. Вместе с тем, в этом случае оказывается верной теорема о выражении поверхностного интеграла второго рода через двойной интеграл Римана.
Замечание. (Важное для теоремы Стокса.) Указанная выше теорема позволяет рассматривать интегралы типа
JJ Pdx Л dx, JJ Qdy Л dy, JJ Rdz A dz.
D	D	D
Сводя с ее помощью эти интегралы к обычным двойным интегралам, получаем, что для любых функций Р, Q, R справедливо равенство
JJ Pdx /\dx= JJ Qdy Л dy “ JJ Rdz A dz ~~~ 0.
D	D	D
Это замечание позволяет, например, записать формулу Грина в следующей компактной и удобной форме:
j Pdx 4- Qdy = JJ (dP) A dx 4- (dQ) A dy.
D
Здесь D — выпуклая область, Л — ее кусочно-гладкая граница, ориентированная в положительном направлении, dP и dQ — дифференциалы функций Р и Q. При этом интеграл JJ понимает-
r	D
ся не как двойной, а как поверхностный интеграл второго рода по верхней стороне плоской поверхности D. Действительно, тогда имеем
JJ (dP) Л dx = JJ (Р'х dx 4- P' dy) /\dx =
D	D
= JJ Px dx A dx+ JJ P' dy A dx = - JJ P' dx A dy.
D	D	D
Аналогично получаем
JJ (dQ) Ady= JJ Q'x dx A dy.
D	D
Выбирая тривиальную параметризацию x = x, у = у, последние интегралы можно рассматривать как обычные двойные интегралы. Поэтому мы получаем формулу Грина в доказанном ранее виде.
Замечание. Отметим, что поверхности, задаваемые с помощью достаточно простых формул, не всегда являются кусочно-гладкими. К ним относится, например, поверхность конуса с вершиной. Тем не менее, построенная выше система определений позволяет рассматривать интегралы и для поверхностей такого рода. Для этого можно использовать конструкцию, родственную теории несобственных интегралов. В указанном выше случае значение поверхностного интеграла определяется как предел интегралов по поверхностям конуса без некоторых окрестностей его вершины, при условии, что радиусы данных окрестностей стремятся к нулю.
569
Лекция 13
$6. ФОРМУЛА СТОКСА
В указанной выше форме формула Грина справедлива не только в плоском случае, но и в трехмерном пространстве, где она называется формулой Стокса.
ТЕОРЕМА4 (формула Стокса). Пусть D — гладкая невырожденная (без особых точек) поверхность в Я3, которая является образом плоского выпуклого множества DQ при отображении г = r(u, и), причем его координаты являются дважды непрерывно дифференцируемыми функциями. Пусть кривая L — кусочно-гладкая граница поверхности D, являющаяся образом кусочно-гладкой границы А множества Dq. Ориентация границы L отвечает параметризации г. Пусть также Р, Q, R — гладкие функции на D.
Тогда справедлива формула
f Pdx + Qdy + Rdz = JJ (dP) A dx + (dQ) Ady + (dR) Adz =
L	D
= JJ(™	dy^dz+{d/	-d^\
£ \dy	dz)	* \dz	dx)	<dx dy) y
► В силу линейности поверхностного интеграла достаточно рассмотреть случай интеграла К = f Pdx, т. е. доказать формулу
L
К = f Pdx = JJ (dP) A dx = JJ P'z dz A dx- P' dx Ady = S. L	D	D
Пусть f(u9 v) = (x(u, v), y(u9 v)9 z(u9 v)) — параметризация поверхности D, причем (u9 v) g Dq. Кроме того, на границе А области Dq задана кусочно-гладкая параметризация
(и9 v) = (u(t)9 v(t))91 g I = [0, 1], (u(0), i?(0)) = (u(l), t>(l)),
которая определяет на кривой L параметризацию r(u(t)9 u(f))«
В силу теоремы о выражении криволинейного интеграла через определенный интеграл имеем
1
К = f Pdx = J P{r(u(t),v(t))) dx i>(0). L	0
По этой же теореме последний интеграл равен
К = f P(r(u, v)) dx (u9 v) = f P(r(u9 v)) (x'u du + x'v dv). A	A
Применим к интегралу К формулу Грина. Для этого воспользуемся инвариантностью формы первого дифференциала и не
570
прерывностью вторых частных производных функций х(и, и), у (и, u), z(u, v). Имеем
dP(r(u, v)) = Р'х dx (u, v) + P' dy (u, v) + P' dz (u, v), К = j P(r(u, u)) dx (u, v) = JJ (dP(r(u, v)) A dx (u, v),
A	Do
следовательно,
K= ftp? dz (u, v) A dx (u, v) - P' dx (u, v) A dy (u, u) — Sx.
A,
Здесь Sx рассматривается как поверхностный интеграл второго рода по верхней стороне плоской области Do. Но при параметризации г = г (и, р) оба интеграла S и Sx дают одно и то же выражение. Для того чтобы убедиться в этом, достаточно раскрыть скобки в выражениях dz (u, р) Л dx (и, р) и dx (u, р) Л dy (и, р), считая, что dx (u, р) = x'udu 4- x'vdv и т. д.
Окончательно имеем, что S и 8Х сводятся к одному и тому же двойному интегралу
S = Sx = JJ (Р^В - р;с) dudv, гдр	D<>
2f	X.'	2f	X.'
U	U Q _ U	U
2»	XV	ZV	XV
Тем самым доказано равенство К = S. ◄
Замечание. Применяя формулу Стокса к плоской поверхности D, распространим формулу Грина на случай областей, которые являются образами выпуклых множеств, а затем, используя это утверждение при доказательстве формулы Стокса, можно в теореме 4 считать, что область Do — образ выпуклого измеримого множества.
$ 7. ФОРМУЛА ГАУССА—ОСТРОГРАДСКОГО
Эта формула является аналогом формулы Грина в трехмерном пространстве.
ТЕОРЕМА 5 (формула Гаусса—Остроградского). Пусты
1)	множество V с Я3 — выпуклый, измеримый по Жордану, компакт;
2)	граница S множества V — невырожденная (без особых точек) кусочно-гладкая поверхность;
3)	заданы гладкие функции Р = Р(х, у, z), Q = Q (х, у, z), R = = R (х, у, z) на множестве V.
Тогда имеет место формула
$Pdy /\dz + Qdz Л dx 4- Rdx /\dy = JJJ(P* 4- Q' 4- R^) dxdydz.
s+	v
571
Здесь интеграл в левой части равенства является интегралом второго рода, который берется по внешней стороне поверхности S+, а в правой части равенства — обычный тройной интеграл по множеству V.
► Как и при доказательстве формулы Грина, рассмотрим только случай Р = О, Q = 0. Спроектируем поверхность S на плоскость хОу и обозначим эту проекцию через D. В силу выпуклости V9 всякая прямая, параллельная оси Oz и пересекающая D, пересекает V по отрезку. Пусть (х, у) g В, тогда нижний конец этого отрезка имеет координаты (х, у, (х, у)), а верхний конец отрезка — координаты (х, у, ф2 (х, у)). Пусть, далее, Л = dD обозначает границу множества D. Тогда поверхность D разбивается на три кусочно-гладких части:
Si = {(х, у, z)|(x, у) е D, 2 - <рг (х, у)},
S2 = {(х, у, z)|(x, у) е D, г = ф2 (х, у)}, «з = {(х, у, z)|(x, у) е Л, (х, у, z) й Sx U S2}.
Здесь для поверхности интегрирование ведется по ее нижней стороне, для поверхности S2 — по верхней стороне, и, наконец, для поверхности S3, представляющей боковую часть поверхности S, — по стороне, нормаль к которой перпендикулярна оси Oz и является внешней нормалью по отношению к D.
По теореме о сведении поверхностного интеграла к двойному интегралу Римана имеем
JJ Rdx Л dy = JJ R cos (n, ё3) dS = 0, $з	s3
поскольку cos (n, e3) = 0. Далее,
JJ Rdx Ady=j$R cos (n, e3) dS = - JJ 2?(x, y, фх (x, y)) dxdy9
Sj	Si	D
JJ Rdx A dy = JJ R cos (n, ё3) dS = JJ Я(х, у, ф2 (x, y)) dxdy.
s2	S2	D
По формуле Ньютона—Лейбница при фиксированных (х, у) получаем
R (х, у, ф2 (х, у)), - R(x, у, фх (х, у)) = J -dz.
Ф1(х> у) Следовательно,
JJ Rdxdy = JJ Rdxdy - JJ Rdxdy =
S	s2	S'
cc i i	dR(x,y,z) fff dR(x, y, z)
= JJ dxdy J —dz = JJ J \ y dxdydz. ◄
572
Замечания. 1. Тем же способом, что и в случае формулы Грина» эту формулу можно распространить на случай областей V, которые, являются образом выпуклой области при некотором гладком отображении.
2.	Ясно, что если 7 = ^0 У2, где области Vx и V2 удовлетворяют условиям теоремы 1 и соприкасаются по кусочно-гладкой границе, то и для V теорема 1 тоже верна.
3.	Формуле Гаусса—Остроградского можно придать вид, аналогичный формулам Грина и Стокса, т. е.
$ Pdy /\dz + Qdz Л dx 4- Rdx Ady = s
= JJJ (dP) Ady A dz + (dQ) Adz A dx + (dR) Adx Ady.
v
Но это требует введения некоторых новых понятий. Доказательство общей формулы указанного выше вида для пространства п измерений и поверхности размерности k < п, которая называется общей формулой Стокса, по существу такое же, что и для формулы Гаусса—Остроградского. Правда, при этом в связи с согласованием ориентации поверхности и ее границы возникают некоторые новые сложности.
4.	Определим «внешнюю нормаль» к кусочно-гладкой поверхности S, которая является границей выпуклого пространственного тела V.
Если в точке г е S существует вектор п, то из геометрических соображений ясно, что п = (лх, п2, п3) — внешняя нормаль для верхней части S2 поверхности S, если выполняется условие тг3 > 0, а для нижней части 8Х поверхности S имеем условие п3 < 0.
Для нормали, отвечающей параметризации г = (р(х, у), имеем
По —	v.
Ji + (<p'x )2 + «р; )2
Следовательно, параметризации г = ф(х, у) всегда отвечает «верхняя» сторона поверхности, поэтому при переходе к двойному интегралу в случае поверхности S2 мы берем перед интегралом знак +, а в случае поверхности Sx берем знак -.
ПРИМЕР 1. Из теоремы 1 имеем следующее выражение для объема тела V через поверхностный интеграл по поверхности S = dV:
V = ffxdy Adz = ffydz Adx = fjzdx A dy. s+	s+	s+
Здесь поверхностные интегралы берутся по внешней стороне поверхности.
Для определения внешней стороны поверхности S следует через точку, на поверхности провести нормальную прямую к ней и в качестве направления внешней нормали к поверхности S выпуклого тела V взять то направление луча этой прямой с вершиной в данной точке, на котором не содержится других точек тела V.
ПРИМЕР 2 (интеграл Гаусса). Пусть S — кусочно-гладкая, невырожденная, измеримая по Жордану, компактная поверхность. Пусть Р — некоторая фиксированная точка, М — переменная точка на поверхности S, г = r(P, М) — радиус-вектор с началь-
573
ной точкой Р и концевой точкой М, п — внешняя нормаль к поверхности в точке М, Тогда имеем
G= Jfcos^n) dS = < s+ r
4л, если Р е V \ S, 2л, если Р е S, О, если Р &V.
Рассмотрим сначала случай, когда точка Р £ V \ S. Пусть точка М имеет координаты (х, у, г), а точка Р — координаты (а, &, с). Тогда г = (х - а, у - &, г - с), вектор нормали к поверхности в точке М равен п = (cos a, cos 0, cos у).
Следовательно,
cos (г, и) = (\п) = (х ~ e)cosa + (У ~ b)cosp + (г - c)cosy
Используя формулу Гаусса—Остроградского, получаем
<?=ш
V
Далее имеем
dxdydz.
х~а}	У ~~
< г3 ' =	3(х-а)г; г3 J = _1 _ З(у-Ь)г;
дх г3 г4 ’ ду г3 г4 ’
* ~с>1
к г3 ' _ 1 _ 3(z - c)f г х - а . __ у ~b , _ г - с дг г3 г4 ’ х г ’ у г ’ 2 г
Следовательно,
С - Ш( ’ -	^d2 _0
Если точка Р е V \ S, то окружим ее шаром Ve, целиком лежащим внутри V \ S. Поверхность этого шара обозначим через Sg. В силу предыдущего имеем
0= Я dS= JJJOdF. s\se r	v\ve
Но так как имеет место равенство, которое символически можно записать следующим образом:
л =л-п, то, в силу равенства
rjcos(^n) dS = 4 s; г2
имеем, что значение G интеграла в случае Р g V \ S равно 4л.
Случай, когда Р е S, рассматривается аналогично.
574
ПРИМЕР 3 (формула Грина). Замечательным следствием формулы Гаусса—Остроградского является еще одна формула Грина, имеющая важные приложения в математической физике.
Пусть и и и — гладкие функции, имеющие непрерывные вторые частные производные и”х, иуу9 и^г. Пусть также V — выпуклый, измеримый по Жордану, компакт с границей 9V, являющейся кусочно-гладкой ориентированной поверхностью. Пусть, а д2и । д2и . д2и	тг	ди
кроме того, Ди = — + —^ +	— оператор Лапласа, —
дх2 ду2 дг2	дп
производная по направлению внешней нормали к поверхности dV. Тогда справедлива следующая формула Грина:
Л (“й " °й)ds = Ш <vAu -
Qy дТ1 иТ1 '	у
Действительно, по формуле Гаусса—Остроградского получаем

dz
ду
у I дх
- Jf (и^ cos (п, ё,) + cos (п, ё2) + и соз(п, ё3)^</5 = ff и^- dS.
Qy дх	ду	dz	/ ду дп
Далее, имеем
д
дх
_ ди dv , цд2и	= —— + u^Zv
дх дх дх2 ’ ду ду ду ду2 *
дг' _ ди dv . ud2v дг dz dz dz2 ’
Используя полученную для А формулу, найдем
+ dudv +du^yv= ffuf£dS_fff u^vdV.
\dx dx dy dy dz dz /	dn у
Поменяем в последней формуле функции и и v местами. Левая часть равенства при такой замене не изменится, следовательно, не изменится и значение выражения, стоящего в правой части, а это дает следующее равенство:
Л «Й dS “ Ш ^dV = Д vg dS - JfJ v&udV, dV on	у	ду СП	у
т. е.
Последняя формула называется формулой Грина; она весьма полезна при исследовании гармонических функций, т< е. функций, удовлетворяющих уравнению Лапласа Ди = 0.
575
Лекция 14
§ 8. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ТОЛЬКО ОТ ПРЕДЕЛОВ ИНТЕГРИРОВАНИЯ
Будем считать, что Р, Q, R — гладкие функции, заданные в выпуклой области. Сформулируем и докажем теорему о независимости криволинейного интеграла от пути интегрирования, имеющего фиксированные начальную и концевую точки.
ТЕОРЕМА 6. Пусть L — кусочно-гладкая невырожденная кривая. Тогда для того чтобы интеграл
I = J Pdx + Qdy 4- Rdz
L
не зависел от пути интегрирования (а зависел только от начальной и концевой точек кривой L), необходимо и достаточно, чтобы существовала функция h(x, у, z) такая, что
dh = Pdx 4- Qdy 4- Rdz.
Мы считаем, что Р, Q, R, L определены внутри некоторого шара Q g Я3.
► Необходимость. Пусть интеграл I не зависит от пути интегрирования. Обозначим через г0 центр шара Q и через г, гг — произвольные точки шара Q. Поскольку интеграл I зависит только от начальной и концевой точек кривой L, интеграл J-^pCO, со = Pdx 4- Qdy 4- Rdz, есть функция от г. Обозначим ее через й(г). Пусть точки и г лежат на прямой, параллельной оси Ох. Тогда
й(г) - й(гх) = J Pdx = j P(t, yr, zr)dt.
L	«1
Дифференцируя это равенство по первой переменной х, получаем
ЦР -PCrJ. дх v 17
Аналогично имеем = Q, || = R. Следовательно, дифференциальная форма со есть полный дифференциал.
Достаточность. Пусть гх и г2 — любые точки, принадлежащие Q, и L — кусочно-гладкая невырожденная кривая, имеющая своими концами точки гх и г2. Пусть г = f(t), t е [0, 1], — параметризация этой кривой. Тогда, переходя от криволинейного интеграла к определенному интегралу от одной переменной, получаем
1
J dh = J h't(f(t))dt = Л(г2) - й(гх). L О
576
Это означает, что интеграл от полного дифференциала зависит от начальной и концевой точек пути интегрирования, но не зависит от самого этого пути. ◄
Выясним теперь условия, при которых дифференциальная форма со есть полный дифференциал от некоторой функции й(г). Для простоты рассмотрим только двумерный случай.
ТЕОРЕМА 7. Пусть.Л — выпуклая область в R2. Для того чтобы дифференциальная форма со = Pdx + Qdy на Q была полным дифференциалом, необходимо и достаточно, чтобы для
~	ЭР dQ
всех точек Q выполнялось равенство	.
► Необходимость. Если дифференциальная форма со является полным дифференциалом, то есть со = dh, то равенство означает равенство смешанных производных. Необходимость доказана.	эр
Достаточность. Пусть выполняется равенство у- =	.
Рассмотрим функцию	v
х	У
h{x, у) = J P(t, y)dt + J Q(x0, v)dv, *o,	Уо
где (х0, yQ) — некоторая фиксированная точка области £2. Тогда имеем

По правилу Лейбница получаем
U = Q(x0, У) +'J dt = Q(x0, у) + J dt = = Q(x0, у) + Q(x, у) - Q(x0, у) = Q(x, у).
Таким образом, дифференциал функции h(x, у) совпадает с дифференциальной формой со. ◄
Аналогично доказывается следующее утверждение.
ТЕОРЕМА 8. Пусть Q — выпуклая область. Дифференциальная форма а) = Pdx + Qdy 4- Rdz тогда и только тогда является полным дифференциалом, когда для всех точек области Q выполняются равенства
ЭР = 3Q ЭР = ЭЯ 3Q = ЭЯ Эу Эх ’ Эг Эх ’ dz ду '
И вообще, в выпуклой области Q с Rn условие, что дифференциальная форма со является полным дифференциалом некоторой функции h, т. е. со * dh, эквивалентно условию dco = 0.
577
19-4953
ПРИМЕР. Пусть f(z) — функция комплексного переменного z = = х + iy9 х, у е В, принимающая комплексные значения
f(z) = и(х9 у) + iv(x9 у) = и + iv9
где и9 v — вещественнозначные функции и f(z) — однозначная в некоторой области Q комплексной плоскости С. Пусть L — простая спрямляемая ориентированная кривая, L е Q.
Определим криволинейный интеграл I от функции f(z) по кривой L:
I = J f(z)dz = J (и + tv)(dx + idy) = L	L
= J (udx - vdy) + i J (vdx + udy). L	L
Пусть функции и = u(x9 у) И v = v(x9 у) являются гладкими в области Q. Далее потребуем, чтобы интеграл I не зависел от кривой интегрирования L, а зависел только от начальной ее точки Zq и концевой точки z. В силу теорем 6 и 7 в этом случае имеем
Эи _ Эи Эи _ Эи
Эх Эу9 ду Эх *
Эти условия называются условиями Коши—Римана. Отметим, что при наличии гладкости функций и и и в области Q они являются необходимыми и достаточными условиями дифференцируемости функции комплексного переменного.
Итак, пусть функции и и v являются гладкими. Рассмотрим интеграл
F(z) = J f(z)dz = J f(z)dz = U(x, у) + iV(x, у), L	Zq
где 2	2
U = U(x, y) = J udx - vdy, V = V(x, y) = J vdx + udy.
2o	2o
Отсюда получаем
dU = dV	_dU = dV =
Эх ду	ду дх
Следовательно, функция F(z) является дифференцируемой и
ч ди ,dV	.
F(z^^+l^c	+	=
Таким образом, функция F(z) является первообразной функции f(z)9 и для интеграла от функции f(z) имеет место теорема Ньютона—Лейбница.
Простым следствием теорем 6 и 7 является следующая теорема. 578
ТЕОРЕМА 9. Пусть функция f(z) однозначна и непрерывна в области П, принадлежащей комплексной плоскости С. Тогда для любого простого спрямляемого ориентированного замкнутого контура L е Q справедливо равенство
f f(z) dz = 0.
L
Полученная теорема называется основной теоремой Коши в теории функций одного комплексного переменного.
§ 9. ЭЛЕМЕНТЫ ВЕКТОРНОГО АНАЛИЗА
Рассмотрим выпуклую область V в трехмерном пространстве R3. Пусть на этой области задана скалярная функция Л(й), и g V и отображение ф(и) области V в трехмерное пространство.
Традиционно в приложениях анализа к математической физике и механике ряд вопросов, связанных с изучением функций й(и) и ф(и), выделяется в отдельный раздел, который называется векторным анализом или теорией (векторного) поля. По существу, этот раздел ничего нового, кроме обозначений, не содержит, но язык этих обозначений надо знать.
Определение 15. Функция h(u) называется скалярным полем, а отображение ф(й) — векторным полем на области V. Если функции h(u) и ф(и) гладкие, то соответствующие поля тоже называются гладкими.
Далее будем считать, что h(u) и ф(и) — гладкие функции на V.
Определение 16. Векторное поле А(й) =	|“) = Srad ^(й)
называется градиентом скалярного поля h(u).
Определение 17. Производной по направлению I скалярного поля h(u) в точке и0 называется величина
Ит й(й0 + te) - h(u0) = Qh t-Jo	t	dl ’
где ё — вектор, определяющий направление I.
Известно, что
чт = (grad Л(й), ё).
01
ПРИМЕР 1. Множество всех точек и, удовлетворяющих условию h(u), равно некоторой постоянной величине а, называется множеством уровня функции h(u). Пусть множество уровня
579
19*
h(u) * Л(и0) — а представляет собой гладкую поверхность П = Па в окрестности точки й = и0. Тогда в любом направлении I для кривой L е П, имеющей это направление, т. е. касательный вектор к кривой L в точке и0 совпадает с вектором направления Z,
справедливо равенство =0, поскольку для точек кривой L ol
имеем АЛ(и0) = Л(их) - Л(и0) = 0. Отсюда
U = (grad Л(й), ё) = 0.
Следовательно, если вектор grad Л(и0) и 0, то вектор градиента функции Л(и) в точке и0 ортогонален вектору ё, касательному к поверхности уровня П.
ПРИМЕР 2. Рассмотрим функцию й(й) = /(г), где г = ||u - и0||. Поверхностью уровня П = Па этой функции является сфера с центром в точке й0 и радиусом, равным а. Тогда вектор градиента функции f(r) направлен по нормали к сфере, т. е. по ее радиусу г = й - й0. Следовательно, grad f(r) = f'(r)(r/r). В частности, имеем grad (-1/г) = г/г3.
ПРИМЕР 3. Пусть в точке и0 помещена пробная единичная точечная масса, а в точках йг — масса т19 ... , uk - масса mk. Пусть
г1 = й1-й0, ... , rk = uk~uQ.
Тогда сила притяжения, действующая на пробную массу, равна
F(u0) =	+ ... +	.
Из примера 2 получаем
Р(й0) = grad
' в
ПРИМЕР 4. Пусть на измеримом по Жордану компакте V е R3 задана кусочно-непрерывная функция распределения р(М), М е V, массы тела V. Положим р(М) = 0, если М £ V. Пусть Р — некоторая фиксированная точка, М — любая переменная точка и пусть г = г(М) = r(P, М). Тогда сила, действующая на пробную точечную единичную массу, помещенную в точке Р, по аналогии с дискретным случаем равна
р(Р)= jjj	dV(M),
у г*(М)
где dV(M) = dx(M) dy(M) dz(M).
580
Силовую функцию F(P) можно представить в следующем виде:
Р(Р) = grad <р(Р), где
ф(Р) = ~$7(ё) dV(M)‘
Действительно,
grad <р (Р) = JJJp(M) grad	) dV{M) =
V	4 туг, ivi) у
Определение 18. Пусть ф(г) = (Р, Q, R) — гладкое векторное поле. Тогда величина
+^+^=div<p дх ду дг
называется дивергенцией векторного поля, а вектор
(dR_dQ dP_dR aq v ду	дг 9 дг дх9 дх ду)
— ротором векторного поля <р.
Если введем в рассмотрение оператор «набла» V, полагая
v = fA, А,
\дх ду дг)
то предыдущие определения можно формально записать в виде div ф = ,(V, ф), rot ф = [V, ф], grad h = V h,
где символические выражения (V, ф), [V, ф] обозначают соответственно скалярное и векторное произведения.
Можно также определить div ф и rot ф из тождества для дифференциальных. форм:
dco2 = (dP) Ady A dz + (dQ) A dz A dx + (dR) AdxAdy =
** (div ф) dx dy dz, do^ = (dP) A dx 4- (dQ) A dy + (dR) Adz = = vxdy Adz + v2 dz A dx + v3 dx A dy, где rot ф = (up v2, u3), dh(u) = (grad h(u), du).
Отсюда, используя соотношения dx A dx = 0, dx Ady = -dy A dx и т. д., получаем соответственно выражения для div ф и rot qj.
Приведем два полезных тождества:
rot grad й(и) = 0, div rot <р(й) = О, которые доказываются прямыми вычислениями и являются следствием того, что для дифференциальной формы со справедливо равенство d2co = 0.
581
Действительно, первое из тождеств следует из формулы d(dh(u)) = d2h(u) = О,
а второе тождество — из формулы
d2®! = d(dP Л dx + dQ Ady + dR A dz) = 0.
Определение 19. Криволинейный интеграл IQ второго рода
Iq = f Pdx + Qdy + Rdz
L
no кусочно-гладкой ориентированной замкнутой кривой L называется циркуляцией вектора ф = (Р, Q, R) по замкнутому контуру L.
Если т — единичный касательный вектор в положительном направлении обхода контура L, то интеграл IQ можно записать в виде
Io = f (ф. t)dZ,
L
где dl — элемент длины дуги кривой L.
Определение 20. Поверхностный интеграл второго рода по выделенной стороне двусторонней кусочно-гладкой измеримой поверхности S вида
I = JJ Pdy Adz + Qdz Л dx + Rdx A dy s
называется потоком вектора ф = (Р, Q, R) через поверхность S. Если через п обозначить нормаль к поверхности, соответствующую выбранной стороне поверхности, то поток I через поверхность S можно записать в виде
I = JJ (ф, n)dS.
S
Переформулируем в векторном виде теоремы Стокса и Гаусса—Остроградского.
Пусть сторона поверхности S, отвечающая вектору нормали п, согласована с направлением обхода контура, отвечающим вектору т, единичному касательному вектору к кривой L. Это можно сделать, например, так. По непрерывности определим вектор нормали на кривой L, а затем вектор т направим в ту сторону, чтобы относительно п обход контура совершался «против часовой стрелки».
ТЕОРЕМА 10 (формула Стокса). Циркуляция вектора ф по кусочно-гладкой границе L кусочно-гладкой поверхности S равна потоку rot ф через эту поверхность, т. е.
j (ф, x)dl = JJ (rot ф, n)dS.
l	s
582
ТЕОРЕМА 11 (формула Гаусса—Остроградского). Поток вектора ф через кусочно-гладкую границу S выпуклой трехмерной области V равен тройному интегралу от дивергенции вектора ф по множеству V, т. е.
JJ (ф, n)dS = JJJ div cpdV, S	V	'	,	< , ' .
где п — внешняя нормаль к поверхности S.
Отметим три интересных следствия формулы Гаусса—Остроградского. Справедливы следующие равенства:
Jf (n,<p)dS = JJJ(V,<p)dy,	(1)
s	V
П (п, 4>)dS = ДО (V, <p)dv,	(2)
s	V
fj nhdS = JJJ VAdK	(3)
S	V
Действительно, рассмотрим, например, формулу (2). В ней первая координата векторного равенства имеет вид
П (В cos р - Q cos Y)dS - flf (g - g )dV.
Для векторного поля фх = (О, Я, -Q) предыдущее равенство представляет собой обычную формулу Гаусса—Остроградского. Аналогично устанавливается равенство вторых, третьих координат равенства (2).
Равенство (3) следует из формулы Гаусса—Остроградского для векторных полей (Л, 0, 0), (0, й, 0), (0, 0, й). Обозначим через d диаметр области V, а через p(V) ее объем. Тогда, используя теорему о среднем для каждой компоненты векторных полей rot ф = = [V, ф] и grad й = \7й в равенствах (1)—(3), а затем, переходя к пределу при d -> 0, получаем:
div ф = pmn Я	(4)
rot ф =	^7) Я фМ5»	<б>
grad Л = lim -1^ ff nh dS.	(6)
Интеграл в равенстве (4) представляет собой поток векторного поля ф через замкнутую поверхность S, являющуюся границей тела V. По аналогии с этим интегралы в равенствах (5) и (6) назовем векторными потоками соответственно векторного поля ф и скалярного поля й через поверхность S.
Эти формулы дают инвариантное относительно выбора прямоугольной системы координат определение градиента, дивергенции и ротора.
583
Лекция 15
$ 10. ПОТЕНЦИАЛЬНОЕ И СОЛЕНОИДАЛЬНОЕ ВЕКТОРНЫЕ ПОЛЯ
Определение 21. Векторное поле F(M), М eV, называется потенциальным в области V, если найдется скалярная функция h(M) такая, что F(M) = grad h(M), сама функция h(M) тогда называется потенциалом векторного поля F(M).
Если величину F(M) рассматривать в качестве силы, действующей в точке М на пробную точечную единичную массу, то потенциал h(M) будет иметь смысл работы по перемещению этой точечной массы из бесконечности в точку М.
Действительно, пусть задана кривая L с начальной точкой А и переменной точкой М. Обозначим через 1(М) длину дуги AM этой кривой, а через т(М) — единичный касательный вектор к ней в точке М. Тогда работа W(P) силы F(M) по перемещению пробной массы по пути АР равна
W(P) = J (F{M), т(М)) dl(M) = f (grad h(M), т(М)) dl (M) = АР	AP
= J dl{M) "	- h{A}-
ap dl
Определение 22. Циркуляцией векторного поля F(M) по замкнутому контуру L назовем величину f (F(M), T(Af))
L
Из предыдущего выражения для работы W(P) силы F(M) по контуру L имеем, что циркуляция потенциального поля по любому замкнутому спрямляемому контуру равна нулю.
В теоремах 6, 7 и 8 были получены необходимое и достаточное условия потенциальности поля. Сформулируем эти условия, используя новую терминологию.
ТЕОРЕМА 12. Для того чтобы гладкое векторное поле было потенциальным в выпуклой области Q, необходимо и достаточно, чтобы выполнялось одно из эквивалентных условий:
1) для любой кусочно-гладкой замкнутой кривой LeQ.
f х(М)) dl = 0;
2) rot F(M) = 0.	1
Напомним, что для отображения F(M) = (P(Af), Q(M), R(M)) в силу определения имеет место равенство
rotF(M) = (^ -д/,д/ -д*д£ -д/\
V ду dz dz дх дх ду /
584
Определение 23. Векторное поле ф(и) называется соленоидальным (или трубчатым), если существует векторное поле ф(й) такое, чтоу(й) = rot ф(м), а векторное поле ф(й) называется векторным потенциалом поля ф(й).
ТЕОРЕМА 13. Пусть Q — выпуклый компакт. Для того чтобы векторное поле ф было соленоидальным, необходимо и достаточно, чтобы для всех точек Q выполнялось равенство div ф = 0.
► Необходимость. Поле ф является соленоидальным, следовательно, ф(й) = rot ф(и). Но поскольку для любого векторного поля ф справедливо равенство div rot ф = 0, имеем div ф = 0 на области Q. Необходимость доказана.
Достаточность. Пусть теперь div ф = 0 на области Q. Докажем, что существует векторное поле ф такое, что rot ф = ф. Поставим в соответствие векторному полю ф = (Р, Q, R) дифференциальную форму
cd = cd (г, dr) = Pdy Adz + Qdz A dx 4- Rdx A dy, r = (x, y, z), dr = (dx, dy, dz).
Тогда условие div ф = 0 на Q эквивалентно тому, что dco = 0 на Q. А условие существования векторного поля ф = (А, В, С), удовлетворяющего равенству rot ф = ф, означает, что найдется дифференциальная форма а = Adx 4- Bdy 4- Cdz такая, что da = cd.
Рассмотрим форму а вида
а = f J (Qz - Ry)t dt) dx + (j (Rx - Pz)t dt\dy 4- Q (Py - Qx)t dt) dz. vo	J vo	7 vo	7
Докажем, что da = со. Будем ^исходить из равенства
J	dt = a(-rt d-ry
o dt
В силу линейности формы, достаточно рассмотреть Только одно слагаемое со0 = R dx Л dy. Имеем
д = d(t2P(tr)) =	+ t2 dR е
и dt	dt
Полагая u = tx,v = ty,w = tz, получаем
+»¥ +	+ И +и|«).
и \ ди dv dw /	\ ди dv dw /
Далее воспользуемся тем, что dco = 0, т. е.
^Р + dQ	dR = о
ди dv	dw
585
Получаем
d(t2R(tr)) _ t(d(Ru) d(Rv) _ dP _wdQ} = dt I du dv du dv)
_ Jd(Ru - Pw) + d(Rv - Qw) A
v du	dv )*
Отсюда
Qo = |d(^R(tr)) dtdxAdy =
= (j (Ru ~ ^“Ot di) + (f (Rv ~ Qw)t dt)) dx A dy.
Пусть da = Ady /\dz + Bdz A dx + Cdx A dy. Достаточно доказать, что R = С. Из определения формы а имеем
С =	(/ (Qz - Ry)t di) +	(j (Rx - Pz)t dt) =
^f(^w-R-^v)tdt + j(^u + R-^w)tdt = dv / J Уди	du J
= (f (Ru ~ Pw)tdi) + Q (Rv - Qw)t di). ◄
Замечание. Теорема 13 — частный случай теоремы Пуанкаре о множестве замкнутых и точных дифференциальных форм. Форму а в доказательстве достаточности этой теоремы можно выбрать разными способами. Например, условию теоремы удовлетворяет любая форма вида a + сф. Отметим также, что любое векторное поле можно представить в виде суммы потенциального и соленоидального полей.
ПРИМЕР. Пусть V — некоторый выпуклый измеримый по Жордану компакт, V cz Я3. Для любой фиксированной точки Р g R3 и любой точки MeV определим радиус-вектор
г = r(M) = (x(Af), у(М), z(M)), г = Jx2(M) + у2(М) + z2(M)
и элемент объема dV области V в виде dV == dx(M) dy(M) dz(M). Пусть на области V задано векторное поле j = j(M).
Тогда силовое поле Н = ЩР) векторного поля j(M) можно определить по следующей формуле:
Н = Н(Р) = Ш dV.
В любой точке Р е R3 определено силовое поле Н(Р). В случае Р е R3 \ V интеграл, задающий поле Н9 представляет собой обычный тройной интеграл Римана от гладкой функции. Если же Р е V, то этот интеграл является несобственным и его сходимость следует из признака сравнения (для этого область V можно разбить на шаровые слои с центром в точке Р и радиусом г с условием е < г < 2е, е = 2~k9 k е N).
536
Покажем, что для любой точки Р £ V имеет место равенство div Н = 0, т. е. в силу теоремы 13 поле Н является соленоидаль-ным в области Я3 \ V.
Действительно, если ё19 ё2, ё3 — орты, направленные по осям координат Ох9 Оу9 Ог прямоугольной системы координат, ] = = 01» /2» /з)» г = (*> У» 2)» т0
[LZl =
*3
Cj ё2 h >2 /з х У 3 НУ -j2* е3
_ъ ]2г~}зУ .3 h*~h* ~ е1—— + е2——
Отсюда
= О'зУ -J22)|f»	= 01« ~i2x)^,
Следовательно,
r3
>3
= Рё} + (?ё2 + Яе3.
si  °2* 71У)Т5 •
1
z
= 0,
div Н = dx dy dz
т. е. поле Н является соленоидальным в области Я3 \ V.
__ Покажем теперь, что при Р V векторным потенциалом поля Н является векторное поле
V Г
т. е. поле Н представляется в виде Н = rot J.
В силу гладкости подынтегральной функции можно поменять порядок следования оператора rot и тройного интеграла. Тогда достаточно доказать, что
Действительно, имеем
rot i
«1 d dx
ё2 d dy /2
d dz h
61 7з ду 72 дг
-ГЛУ А? Л в2171"5Г 7з“эГ
= -Рёх - Qe2 - Re3,
+ ^3 72 дх h ду
где функции Р, Q и R определены выше. На этом заканчиваем рассмотрение вопросов, связанных с векторным анализом.
587
ГЛАВА 21
Общая формула Стокса
Лекция 16
§ 1. ПОНЯТИЕ ОРИЕНТИРОВАННОЙ МНОГОМЕРНОЙ ПОВЕРХНОСТИ
Общая формула Стокса является естественным многомерным обобщением теоремы Ньютона—Лейбница о выражении определенного интеграла через первообразную функцию. Впервые эта формула была опубликована А. Пуанкаре в 1899 г. в знаменитом мему аре «Новые методы небесной механики». Чтобы подчеркнуть возможность использования найденной формулы при интегрирований по поверхности любой размерности, он назвал ее обобщением теоремы Стокса, имея в виду фбрмулу Стокса, связывающую поток векторного поля через поверхность и его циркуляцию вдоль границы поверхности.
Современное изложение доказательства различных вариантов общей формулы Стокса, как правило, опирается на применение достаточно развитой теории внешних дифференциальных форм и интегралов от них по поверхностям. Эта причина, по-ви-димому, является определенным препятствием для полного изложения ее доказательства в курсах анализа.
Приведем новый вариант доказательства общей формулы Стокса, использующий, по существу, те же средства, что и в классическом трехмерном случае. Сначала с помощью параметризации поверхности определяем понятие интеграла от дифференциальной формы. При этом показываем, что его значение с точностью до знака не зависит от выбора параметризации. Далее обосновываем связь между выбором параметризации, определяющей ориентацию поверхности, и знаком интеграла. Следующий шаг — введение правила согласования ориентации поверхности и ориентации ее границы, что одновременно используем для конструирования поверхности путем «склейки» образов выпуклых множеств по общим частям их границ, имеющих противоположную ориентацию. Использование выпуклости прообразов этих множеств позволит упростить доказательство основной теоремы без существенного ограничения общности.
588
Отметим еще раз важность проблемы согласования ориентации поверхности и ориентации ее границы, которая возникает неоднократно в процессе изложения. Уже на примере самой формулы Ньютона—Лейбница эта особенность выявляется как зависимость знака интеграла от направления интегрирования, т. е. изменение знака интеграла при перестановке пределов интегрирования. Наиболее просто вопрос о согласовании ориентации поверхности и ее границы решается в случае поверхностей размерности 1 (кривые) и коразмерности 0. Данное обстоятельство лежит в основе индуктивного определения ориентации поверхности и ее границы. При этом Согласование ориентации проводится с использованием выпуклости прообраза поверхности.
В заключение отметим, что основная трудность при выводе общей формулы Стокса как раз и состоит в построении необходимой системы понятий, в то время как само доказательство очень простое.
Пусть k и п — натуральные числа, 1 < k < п. Определим кусочно-гладкую ориентированную поверхность размерности k в пространстве п измерений индукцией по ее размерности k.
При k = 1 эта поверхность представляет собой кусочно-гладкую кривую без кратных точек, на которой задано направление обхода, т. е. начало следующего гладкого куска кривой совпадает с концом предыдущего. При этом под гладким куском кривой мы понимаем образ направленного отрезка числовой оси при гладком взаимно однозначном отображении, имеющем ранг, равный единице.
Пусть k > 2. Тогда поверхность (точнее, гладкий кусок поверхности) размерности k определяется как образ В выпуклого ^-мерного множества А в Л-мерном пространстве, имеющего кусочно-гладкую границу ЭА, при гладком взаимно однозначном невырожденном (т. е. ранга k) отображении ф, т. е. В = ф(А).
В этом случае ЭВ — граница поверхности В — является поверхностью размерности k - 1 > 1(ЭВ = ф(ЭА)). Прообраз А отображения ф называется картой гладкого куска поверхности В. Само отображение ф назовем параметризацией данного куска поверхности.
Пусть заданы две параметризации ф и ф поверхности В. Будем говорить, что они определяют одинаковую ориентацию поверхности В, если замена параметров является диффеоморфизмом X с положительным якобианом Если же якобиан отрицателен, то параметризации ф и ф задают противоположные ориентации.
Если якобиан отображения X положителен хотя бы в одной точке, то он положителен и для всех точек множества А. Этот
589
факт следует из того, что отображения ф и ф не вырождены, т. е. матрицы Якоби и отображений ф и ф имеют максимальный ранг, равный А, и	Таким образом, ориентируемая по-
верхность допускает в точности две ориентации.
Для того чтобы определить понятие ориентированной поверхности, состоящей из многих гладких кусков, прежде всего потребуется «согласовать» ориентацию поверхности и ее границы.
$ 2. СОГЛАСОВАНИЕ ОРИЕНТАЦИЙ ПОВЕРХНОСТИ И ЕЕ ГРАНИЦЫ В ОБЩЕМ СЛУЧАЕ
Определим сначала внешнюю сторону границы ЭА с Rk. Так как она является кусочно-гладкой поверхностью размерности k - 1, то в каждой точке ее гладкости можно задать вектор нормали к ней (этот вектор ортогонален касательному подпространству размерности k - 1). Прямая, проходящая через рассматриваемую точку х0 е ЭА и коллинеарная вектору нормали, пересекает множество А по некоторому отрезку в силу выпуклости А. Тогда направляющий вектор п луча этой прямой с началом в точке х0, не пересекающий множество А, называется внешней нормалью к границе ЭА в точке х0, а вектор (~п) — внутренней нормалью.
Пусть параметризация % = %(j), х = (Xv — * Хл)» * = (t19..., задает данный гладкий кусок границы множества А. Будем говорить, что эта параметризация отвечает (соответствует) внешней стороне границы ЭА, если матрица Якоби этого отображения, дополненная слева вектором внешней нормали и, т. е.
Эх Эх А
матрица \п9	... , J имеет положительный определи-
тель. Тем самым на прообразе А мы согласовали ориентацию множества А и ориентации его границы ЭА.
Далее пусть, как и раньше, ф : Rk Rn задает параметризацию поверхности В = ф(А) и пусть х • Я*”1 —> Rk задает параметризацию границы ЭА. Тогда отображение ф • х задает параметризацию границы ЭВ поверхности В.
Будем говорить, что ориентация поверхности В и ориентация ее границы, ЭВ согласованы, если ЭВ есть образ границы ЭА, параметризация которой отвечает ее внешней стороне.
ПРИМЕР. Пусть множество ЭВ задается уравнением xk = f(x19 ... ..., xk_r) на границе ЭА выпуклого множества А в k - 1-мерном пространстве, где f — кусочно-гладкая функция на А. Тогда
590
множество дВ является кусочно-гладкой поверхностью размерности k - 1 и ее параметризацию <р можно задать следующими уравнениями: Xj — ..., хк_г = tk_v xk = f(tlt...,
Матрица Якоби этого отображения имеет ранг, равный k - 1, поскольку она содержит единичную подматрицу размерности k - 1. Внешняя нормаль п к поверхности В коллинеарна вектору
df _д£
Э^2

h h’
а матрица п,
а' I может быть записана в виде
(A 2L h atj
Л dt2
О
о
Л dtk_x
1 h
1
dtk-i >
ее определитель равен

df\2 	 ( W У Y/2
dt2J + J
Следовательно, ориентация поверхности В и ориентация ее границы ЭВ в данном случае согласованы, если k — нечетное число. В случае четного числа k для того, чтобы согласовать ориентации поверхности В и ее границы, следует ориентацию границы ЭВ заменить на противоположную.
Определим теперь кусочно-гладкую ^-мерную ориентированную поверхность в n-мерном пространстве, состоящую из нескольких связанных между собой гладких ориентированных кусков с согласованно ориентированными границами.
Пусть два таких куска фх: Ах —»Вх и ф2 : А2 ->В2 соприкасаются по участку (Ь) их границ ЭВХ и ЭВ2, причем Вх П В2 = (Ь) с с ЭВХ А ЭВ2. Если при этом: 1) участок (Ь) является кусочно-гладкой поверхностью размерности k - 1 и 2) две ориентации поверхности (&), порождаемые фх и ф2, являются противоположными, то объединение поверхностей В = Вх U В2 мы будем рассматривать как одну кусочно-гладкую ориентированную поверхность В
591
(состоящую из двух кусков поверхности Вг и В^). Аналогично поступаем и для случая любого конечного количества связанных между собою подобным образом гладких кусков поверхности.
При разбиении гладкого куска ориентированной поверхности на две кусочно-гладкие ориентированные поверхности с помощью кусочно-гладкой ориентированной граничной поверхности эта граничная поверхность относительно каждого из получившихся ориентированных кусков приобретет противоположные ориентации.
Совокупность карт, отвечающих всем кускам данной поверхности, будем называть ее атласом.
$ 3. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Определение 1. Пусть 1 < k < п. Тогда дифференциальной формой k-го порядка, определенной на открытом множестве U с Ял, будем называть следующее выражение (канонический вид дифференциальной формы):
со = со(х, dx) =
= Е • • -Е F т (x)dx А ..., A dx ,
причем операция А внешнего произведения дифференциалов (формальная) удовлетворяет условиям:
a)	(dx A dy) /\dz = dx A (dy A dz) (ассоциативность);
6)	dx /\dy = -dy A dx (антисимметричность);
в)	d(axx + bx2) A dy A ... A dz = a dxr A dy A ... A dz + + b dx2 dy Л ... /\ dzY a, b e R (полилинейность).
Дифференциальную форму coo вида со = F(x) dxm^/\ ... А Лхт* назовем базисной дифференциальной k-формой.
Заметим, что условия а)—в) позволяют любую дифференциальную форму о привести к каноническому виду. Кроме того, отсюда очевидным образом определяется внешнее прдизведение со1 А со2 дифференциальных форм сох и со2.
ПРИМЕРЫ. 1. Пусть k = 1. Тогда форму первого порядка можно представить в виде
со(х, dx) = Д^/х^х,.
2. Пусть k = п. Тогда сумма в определении дифференциальной формы со состоит из одного слагаемого, и форма со имеет вид
со(х, dx) = F(x)dxx A ... A dxn.
592
§ 4. ЗАМЕНА ПЕРЕМЕННЫХ В ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
Определение понятия замены переменных в дифференциальной форме нужно в основном для того, чтобы ввести понятие поверхностного интеграла по ориентированной кусочно-гладкой поверхности, размерность которой меньше размерности основного пространства. Но оно имеет место и в случае, когда эти размерности совпадают. По существу, данное определение достигается заменой х на <р(£) и dxt на dtp^t).
Определение 2. Пусть со — дифференциальная k-форма и ср — гладкое отображение, ф : Rn -> Rn. Тогда имеет место следующее правило замены переменных х = ср(£):
<о(х, dx) = <»!(?, dt), где
©1 = co1(Z, dt) =
= 1 < Л*..........«/фсп а... л d^ty,
= rt^r dtr.
Приведем форму <ох к каноническому виду
co1(?,d?)=	E---S Ф_	л... л dt .
'	1<Г1< ... <rk^n rl’-’rk' rl	rk
Для этого сначала преобразуем к каноническому виду элементарную форму со0, где
®0 = d<Pmi(0 А — л
Имеем
( Д 5<р, а?
( п дф.
А ... A
Vг* “ 1 dt,

п
S • •
Д ^Фи»! dt.
д(от
-£pdtrA...Adt,
5<Pmt
... ---------I dtr А ... A dt
8 У
= Е-
1 < п< •
v ^((р	.....<р )
• 2	-----1---------—
 <r„<n D{tre ... , trk)
dtr А ... A dt.. rl	rk
593
Здесь ео равно +1 или -1 в зависимости от четности подстановки а, составленной из чисел а(гх), a(rfe). Подставляя последнее выражение в равенство, определяющее форму cdx , найдем В(фт » ••• » Фг» ) к : :£ < Ли -.	—гт •
*	»	1 ч • • • < п *	®	-и \ j • • • , v j
Форму (Ох обычно обозначают символом (Ох = ф*(0 и называют формой, индуцированной отображением <р, или просто индуцированной формой.
ПРИМЕРЫ. 1. Пусть k = 1. Тогда
п	п	Эф«.
<р*(0 = г?1 ФД t)dtr, ФД t) = Ъ х Гт(ф(«))-^.
2. При k = п имеем D((o,.....................
<р*<о = ЛФ(О)д(^  J") dti Л ... л dtn.
Лекция 17
§ 5. ИНТЕГРАЛ ОТ ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЫ
Сначала рассмотрим интеграл от дифференциальной п-формы по n-мерной ориентированной поверхности В в пространстве п । измерений. Канонический вид формы со в этом случае можно записать так:
со = F(x) dxr A ... A dxn.
Определим интеграл от со по поверхности В (ориентированной естественным образом) как n-кратный интеграл Римана, т. е.
J со = J F(x) dxx... dxn.
|	в в
Так как после замены переменных х = ф(£)> которая связана с параметризацией поверхности В = ф(А), отвечающей ее ориента-!	ции, то мы приходим к дифференциальной 6-форме ср* со, опреде-
1	ленной на 6-мерном множестве А в пространстве k измерений
и имеющей канонический вид
сох = ср* со = Ф(£р ... , tk) dtx A ... A dtk,
по аналогии co случаем k = n получаем правило, выражающее 6-кратный поверхностный интеграл от 6-формы сох через обычный 6-кратный интеграл Римана.
Это обстоятельство позволяет дать следующее определение ’ поверхностного интеграла от дифференциальной формы.
Определение 3. Поверхностным интегралом I по кусочногладкой ориентированной поверхности В от гладкой дифференциальной k-формы со (т. е. формы с гладкими коэффициентами) называется выражение
I = J со = J ср* со, В А
где множество А есть k-мерное выпуклое компактное измеримое по Жордану множество в пространстве k измерений, В = ср(А).
При этом интеграл по множеству А, как и в случае k = п, <	выражается через обычный k-кратный интеграл Римана с по-
I	мощью формальной замены выражения dtx А ... A dtk на выра-
жение dtr... dtk.
Заметим, что если параметризация ср поверхности В опреде-I ляет на В ориентацию, противоположную заданной, то согласно данному выше определению
I = J со = -Jcp* со. В А
595
।
J
ПРИМЕР. Пусть В = L — окружность с центром в нуле радиуса 1 на плоскости хОу, пробегаемая против часовой стрелки. Зада* дим эту ориентацию с помощью отображения ф : [О, 2л] —> В равенствами х = cos t, у = sin t, 0 < t < 2л. Рассмотрим дифференциальную 1-форму
Тогда имеем ф* со = dt. Отсюда следует, что
2я J со = J ф*со = J dt = 2л. L А	О
Для проверки корректности определения интеграла J со надо до-в _ казать, что его величина не зависит от параметризации ф, сохраняющей ориентацию. Напомним, что любые две такие параметризации ф и ф связаны между собой соотношением ф = ф • X : А Ах — некоторый диффеоморфизм с положительным якобианом.
ТЕОРЕМА 1. Пусть параметризации ф : А В и ф : Аг —> В задают одну и ту же ориентацию поверхности В. Тогда
J Ф*со = J у*со. А	А
► Дифференциальная форма ф*со является ^-формой в пространстве Rk той же размерности поэтому канонический вид ее таков: ф*со = Ф(1) dtr Л ... Л dtk.
Воспользовавшись теперь формулой замены переменных ф(й) = (ф • X) (u), t = Х(и), получим
ф*со = (ф • X)* cd = Ф(Х(и) dXx(u) Л ... Л dXfe(u) =
= Ф (X(u)) dur Л ... Л duk.
Так как > 0 (из условия сохранения ориентации), то по Р(и)
формуле замены переменных в кратном интеграле имеем
Jф*со = J(ф • Х)*со = Jф(Х(и))	dur Л ... Л duk =
А А	А	Т>(и)
= J Ф (Х(й)) dUi... duk = J Ф(«) dtx... dtk =
A	V(U)	A
= J Ф(1) dtr A ... A dtk = J Ф* CD. ◄ A	A
596
Следующая теорема является весьма полезной в различных приложениях поверхностных интегралов. В случае интеграла Римана она решает задачу нахождения подынтегральной функции по её первообразной.
ТЕОРЕМА 2. Пусть U — выпуклый измеримый компакт в Rn. Пусть также для любой ориентированной кусочно-гладкой k-мерной поверхности В cz U существует интеграл второго рода 1(B) от непрерывной дифференциальной k-формы со. Тогда форма со однозначно определяется по значениям интегралов 1(B).
► Пусть форма со имеет вид
со =	Е---Е at i(x)dxai Л... Adxat.
1 С ij< • • ♦ < С л 1*	’ л	1	k
Пусть а(х) = а^.ik (х) — любой коэффициент формы со. Найдем
его значение в точке х0 = (х10,..., хл0) е СЛ Для этого на 6-мерной плоскости xt = хю, i^i19... 9ik9 возьмем е-окрестность S£ точки х0. Это будет ориентируемая поверхность в Rn. В качестве ее параметризации возьмем переменные t = (tp ... , tk)9 tx = x^, ... , tk = xif. Тогда интеграл I(Se) равен
j co = j a(x109..., t^9... 9 хл0) dt}... dtk9 Se Se
где последний интеграл является обычным 6-кратным интегралом Римана. Отсюда по теореме о среднем имеем
$ 6. ОПЕРАЦИЯ ВНЕШНЕГО ДИФФЕРЕНЦИРОВАНИЯ
В дальнейшем всюду будем использовать то, что дифференциальную форму dF(x), записанную в каноническом виде, можно рассматривать и как обычный дифференциал функции F(x). Приведем теперь определение внешнего дифференциала.
Определение 4. Дифференциалом (точнее, внешним дифференциалом) дифференциальной k-формы со называется k + 1-форма <ох = d<o вида
du)= Е • • -Е dFm т (х) л dx Л ... Л dxm . с /»!< • • • < mk п	«	1	•
ПРИМЕРЫ. 1. Пусть k = 1. Тогда
ЭР dfr Л</Х- =
= 1 < Л п(э^ “ Эх^) dxrAdxm.
597
2. Пусть k - п - 1 = 2, а = (Р, Q, R), со = Pdy /\dz + Qdz Л dx + + Rdx A dy. Тогда
ЭР	ЭО	ЭР
d(a= j^dx A dy Л dz + dy Л dz A dx + dz A dx A dy =
=	j dx /\dy f\dz = (div a}dx f\dy A dz.
ЛЕММА 1. Пусть заданы C0j — дифференциальная k^-форма, ... ... , азг — дифференциальная кг-форма. Тогда имеет место равенство
dm = <2(а>! Л ... Л сог) =	+ - + *•-! а>х л ... л dcos л ... <ог.
► Очевидно, можно ограничиться рассмотрением базисных дифференциальных форм вида
©1 = F^xydx^ Л ... Л dxo(ftl) = Fr(x)©x> 0, ...
... , ©r = Fr(x)dxT(X) Л ... Л dxo(M = Fr(x)wr>0, где о, т — некоторые подстановки п чисел. По определению
dm = d(Fx(x)... Fr(x)) Л й10Л ... Лшг 0 =
= (Fx(x)... Fs(x)... Fr(x)) Л сох>0 Л ... Л cor 0 =
= eEx + - + л ... л dms Л ... сог. ◄
Л Е М М А 2. Справедливо равенство d2m = 0.
► Действительно, имеем
d2<o = d(dm) = n n 92Fm m (x) = E - • -E E E ----------V *— dx. Adx_Adx_ Adxm =
1< »»!<••• <m,< ns = 1 r- 1 OXgdxr	* r mx mk
= E- • *E EE fd2•••	_ d2^!....x
1 C m1< • • • < C n 1 C s < r C n I	Эх8Эхг	ЭхгЭх, I
x dx. л dx. л dxm л ... л dx_ = 0.
Здесь мы воспользовались теоремой Шварца о равенстве вторых смешанных производных при условии их непрерывности. ◄
ТЕОРЕМА 3. Пусть ф : Rn Rn — дважды непрерывно дифференцируемое отображение и со — гладкая дифференциальная форма. Тогда справедливо равенство <p*(dco) = с?(ф*со).
► Очевидно, достаточно доказать утверждение теоремы только для дифференциальной формы
со = F(x)dxm Л ... Л dxm .
598
Из определения дифференциала формы со и леммы 1 имеем
сГ(ф*<о) = d(F($(t)dq>mi(i) Л ... Л dcpmJi)) = = dF(q(t)) Л d<pOTi(t) Л ... Л dq>m/i) +
+ F(9(t) Л d(d<pm (t) Л ... Л <%,/£)) = А + В.
Вновь воспользовавшись леммой 1, а затем леммой 2, получим k
В = Л - Л Л - Л = °*
Далее по определению индуцированной формы имеем
А = <p*(dF(x) Л dxmi Л ... Л dxm^ = cp*(dco). ◄
§ 7. ДОКАЗАТЕЛЬСТВО ОБЩЕЙ ФОРМУЛЫ СТОКСА
Имеет место следующая теорема.
ТЕОРЕМА4 (общая формула Стокса). Пусть В — кусочно-гладкая невырожденная ориентированная поверхность размерности k, которая является образом выпуклого множества А при отображении ср, причем его координаты являются дважды непрерывно дифференцируемыми функциями, и ориентация ее границы дВ согласована с ориентацией самой поверхности В, со — гладкая k - 1-форма. Тогда справедливо равенство
J со = J dco.
ЭВ в
► Пусть поверхность В задается отображением ср : А —» В. Тогда из следующей цепочки равенств получаем утверждение теоремы:
f (1) f _*	(2) г	ч (3) ,	ч (4) f
J со = J ср со = J d(cp со) = J ср (dco) = J dco.
ЭВ ЭА	А	А	В
В доказательстве нуждается только равенство (2):
/ф*<0= р(ф*со).
ЭА	А
так как равенства (1) и (4) следуют из определения поверхностного интеграла второго рода, а третье — из справедливости соотношения cp*(dco) = d(cp*co).
Согласно определению k - 1-формы в ^-мерном пространстве и операции дифференцирования, имеем
ф*со= Е---Е Фт m(t19..., tk)dtm A ... Adtm ,
Y К т,< • • • <тл_1< ft ...	ft/
</(ф co) = E • • • E ------1--Ч----------dt8 A dtm A ... A dtm ,
V ' 1 < тг< • • • <	<k	0t8	8 mi	mk-i9
где 1 < s < k9 s # m19 ... , mk_v
599
Из этого представления в силу линейности интеграла следует, что достаточно доказать равенство t =	... ,
г	-	ГЭФ(£, tk)
J Ф(^, tk)dt^ л ... л dtk_i = J чт dtk Л di\ Л ... Л dtk_v
ЭА	а °т*
Обозначим через D проекцию множества А на гиперплоскость tk = 0. В силу выпуклости множества А его можно представить в виде
A = {(Mft): teD, ftf) < tk < f2(t)}9
где ffo}, ... , ffc-x), f2(tv ••• ’ tk-i) — некоторые функции, определенные на множестве D.
Границу множества D можно разбить на следующие три множества:
Пх = {(I, tk): t g D, tk =	••• ,
П2 = {(t, tk): t g D, tk = f2(£p ... ,
П3 = {(*, U : t e 3D, f^t) <tk<
Ограничимся рассмотрением случая, когда поверхность П3 является кусочно-гладкой ориентированной поверхностью. Она также является цилиндрической, а поверхности Пх и П2 можно представлять себе как «нижнюю» и «верхнюю» крышки этой цилиндрической поверхности.
Следует отметить, что множество П3 может быть и пустым, что, например, имеет место в случае, когда А есть ft-мерный шар вида 4- ... + t% < 1. Тогда, очевидно, поверхности П-j^ и П2 являются полусферами вида t\ + ... 4-t2k = 1 с условием tk < 0 и tk > 0 соответственно.
Покажем, что интеграл по поверхности П3 равен нулю. Действительно, поскольку П3 есть k - 1-мерная поверхность в пространстве k измерений, то ее можно параметризовать
t\ =	... , tk-i = tk-i ы = (Мр ••• 9 uk-i) е л3, £(я3) = П3.
Заметим, что t(u) является диффеоморфизмом.
Предположйм, что якобиан отображения t : л3 П3 в точке й = й0 не равен нулю, т. е.
..., tk _ р
---------—— 5^ 0.
D(uv
Тогда в силу непрерывности функции J(u) в некоторой окрестности точки й = й0 она отлична от нуля. Далее, согласно теореме
600
об обратном отображении, точка t(u$) будет внутренней точкой множества D (проекции множествах на гиперплоскость tk = 0). Но точка t(uQ) — граничная точка множества D, что невозможно. Следовательно, в любой точке й е л3 имеет место равенство
••• > uk -1)
используя которое, после замены переменных I = 1(й) в поверхностном интеграле получаем
J Ф(/, tk) dt. Л ... Л dtk_. = J Ф(*(й), t^J(u) du. Л ... Л duk_. = 0. П8	*8
Рассмотрим теперь интегралы по поверхностям Пх и П2. В силу определения ориентации поверхности (см. пример § 12) имеем
J Ф(£, dt. Л ... Л dtk_. = (—l)fe 1 J Ф(1, tk9 /2(f)) dt. ••• dtk_.9 п2	D
J Ф(£, tk) dt. A ... A dtk_. — (—1)* J Ф(tk9 f.(t)) dt.... dtk_..
nx	D
Следовательно, справедлива цепочка равенств
£ф(«Л*)Л1Л...АЛ*_1-| +f =
= (-1)*1 J (Ф(«, r2(i)) - ф(*. fi (tyv'dt! dt^ =
D
= (-1)^ 1 J ( J — dtk^ dt.... dtk_. =
D V /2C0 dtk 7
= (-1)*’1 f dt. ... dtk = (-!)*-! f A ... A dtk =
A ctk	A Ctk
= J dtk л dt. л ... л dtk_., ◄
A otk
Замечание. Ограничение на множество П3, наложенное при доказательстве последней теоремы, на самом деле не является существенным. Дело в том, что любое выпуклое тело D в пространстве Rn можно рассматривать как бесконечно-гладкий образ другого выпуклого тела Do е Rn9 граница dDQ которого не содержит отрезков прямой, а для такого тела множество П3 пусто.
Легко построить бесконечно-гладкое в обе стороны отображение ср такое, что <p(Z>0) - D и \|/(В) = Во, причем <р(\|/(х)) = X для всех х е Rn. В качестве соответствующего примера рассмотрим отображение у(х), задаваемое равенством
v(x) = х0 + (х - х0) (1 + e-Ф -«<J2).
601
Здесь х0 — некоторая фиксированная внутренняя точка тела D е Rn, 6 > 0 — вещественная постоянная. Тогда тело Do получается как образ D при отображении у. Обратное отображение ф всегда существует, причем как ф, так и ф являются бесконечно-гладкими.
С другой стороны, с помощью стандартных вычислений можно показать, что при достаточно малом (в зависимости от отношения минимального и максимального расстояний от точки х0 до границы 3D тела D) значении параметра 5 дело DQ будет выпуклым и его граница dZ>0 не содержит отрезков прямой. Учитывая достаточную громоздкость этих выкладок и большой произвол в выборе отображения у, ограничимся сделанным замечанием.
Лекция 18
§ 1. ПОНЯТИЕ РАВНОМЕРНОГО РАСПРЕДЕЛЕНИЯ. ЛЕММА ОБ ОЦЕНКЕ КОЭФФИЦИЕНТОВ ФУРЬЕ
Понятие равномерного распределения значений числовых последовательностей на отрезке ввел в математику Г. Вейль. Он заложил основы теории равномерного распределения, которая получила дальнейшее развитие в теории чисел, теории функций, классической механике. Здесь мы докажем критерий равномерного распределения значений числовой последовательности на отрезке, принадлежащий Г. Вейлю.
Пусть ..., хя,... — последовательность вещественных чисел. Построим последовательность дробных частей {xj, ... , {хп}, ... . Для простоты изложения в дальнейшем будем считать, что все члены последовательности {хп} находятся на полуинтервале [0, 1). Пусть F(N) = F(N, а, р) обозначает количество членов последовательности {хп} таких, что п < N и а < {хп} < р, причем 0 < а < Р < 1.
Положим
D(N) = sup IN"1 F(N, а, p) - (P - а)|.
О < а<р< 1
Величина D(N) называется отклонением первых N членов последовательности {хп}.
Определение 1. Последовательность {хп} называется равномерно распределенной по модулю, равному единице (p.p. mod 1 или просто р.р.), если ^lim D(N) = 0.
В дальнейшем понадобится следующая лемма об оценке сверху абсолютной величины коэффициентов Фурье одной функции.
ЛЕММА 1. Пусть задано разложение функции
1
в ряд Фурье
V(x) = ЧЧ<*) = м2 . .
л/1 + АГ2 sin2 л х
Y(X)=m?-ooCme2’ti'nX-
Тогда при N > 1 и т> 0 справедлива оценка ы -ы < ЧЧ
► Очевидно, для коэффициентов Фурье имеет место равенство
V2	1/2 p2nimt
с-т = f	dt = е J ,	dt = eKm,
-1/2	-1/2 л/£2 + Sin2ltt
где е = 1/N.
603
Рассмотрим в полуполосе П = {z|S г > О, 1^| < 1/2} функцию комплексного переменного f(z) = -==z==. Знаменатель ее л/е2 + sin27tz
-	. .ln(e + J1 + е2) - * ч
обращается в нуль в точке z = га = 1— ---------. Функция f(z)
будет однозначной функцией в области П с разрезом по лучу (ia, +/ОО).
Рассмотрим произвольное число Ь > а > 0 и построим контур L, состоящий из следующих промежутков вида Lr = [-1/2, 1/2], L2 = [1/2, 1/2 + ib]9 L3 = [1/2 4- ib9 ib]9 L4 == [ib9 id]9 Lb = [ia9 ib], L6 = [ib9 -1/2 + ib]9 L7 = [-1/2 + ib9 -1/2], т. e. построим замкну-7
тый контур L = 8 U L89 который обходится в положительном набирав лении («против часовой стрелки»).
Согласно основной теореме Коши (пример к § 8), J f(z) dz = 0.
L Следовательно, справедливо равенство
crn = J f(z)dz = -j f(z)dz-...-j f(z)dz. Li	L2	L7
В силу периодичности подынтегральной функции (f(z + 1) = f(z))9 имеем
J f(z)dz = -\ f(z)dz. l2	l7
Далее, так как по разным берегам разреза значения квадратного корня от аналитической функции отличаются только знаком, а направления обхода по отрезкам L4 и Ь5 — противоположны, то J f(z)dz = J f(z)dz.
Пусть z = x + ib9 x e Lv Тогда при b -» 4-oo имеет место равномерный предел
/(2) = т	4 °-
7е2 4- sin27CZ s
Здесь мы воспользовались теоремой Вейерштрасса, поскольку для некоторой постоянной с > 0 справедливо неравенство
\f(z)\ =|/(х 4- ib)\ < се-яЬ(2,п+1).
Следовательно, по теореме о переходе к пределу под знаком собственного интеграла от функции, зависящей от параметра, получим
J f(z)dz = J f(z)dz = 0.
Ьз
404
g-27tmi 7е2 - sh2Kt
+?° fi-2nmt dt = 2 f -=?== dt.
a 7sh2TCt “E2
Таким образом	.
К = J f(z) dz = 2 lim J f(z) dz = 2 J f(z) dz. L,	^+°°L4	ш
Заметим, что sin (nit) = ish (nt). Поэтому интеграл KE преобразуется к виду
#e = 2i
Очевидно, что па = In (е + 71 + е2), е™ = е 4- 71 4-е2 , в~™ = -Е + 71 + Е2 , sh па = £.
Выполняя в последнем выражении для интеграла Ке замену переменных вида х = t - а, получаем +?°	р-2пт(х + а)
К? = 2 J . ......... dx.
о 7sh2rc(x 4- а) - sh2Tta
Используя формулы
sn и 4- sh v = 2sh o ch 	, sh и - sh v = 2ch o sh o ,
&	a	a	* a
найдем
sh2 tc(x 4- a) - sh2 na = sh л(х 4- 2a) • sh nx.
Следовательно, интеграл Кг принимает вид
+?°	р-2птх
Kt = 2е.-2пат J	----- dx = 2e~2mmGa.
о Vshjt(x + 2a)shnx
Так как при х > О функция sh х — монотонная и sh лх > лх, то справедливы неравенства 2® л-2птх	+?°	1
(?„<!,+ Д,1. = f ... -......= dx, Io = J -F— dx.
О 7лхз11л(х + 2a)	2a shnx
Далее имеем (sh 2na = 2e71 + e2 ):
T <	1	[“ dx = / 8a	2
1" 7лзЬ2ла ! Jx N nsh2na	n ’
Воспользовавшись заменой переменной t — елх, получаем
! _ ? Т _dt_
2 лД»*2-1’
605
В результате замены переменной и = 1/t находим
Т dt	du _1. 1+е-2я«_11 chira _ 1 . 71 + е2
eL t2 -1 Jo 1 - и2 2т1-е-2яа	2 1П shira 21П е
Таким образом, справедливо неравенство
Наконец, получаем оценку для коэффициента Фурье
I I Л (% . 1 1 71 + Е2 А _тр £ (л I 1	1 А тс 4 4- 1пЛГ т/А7
ст < 2е - + - 1п---- 1е т£ < - 4 + 1п - е~т£ =-— e~m^N.
1 т \лл е ) к у е )	nN
Далее можно использовать более слабые оценки коэффициентов Фурье функции но приведенная оценка имеет самостоятельный интерес. ◄
§2. КРИТЕРИЙ Г. ВЕЙЛЯ
Докажем теперь следующую теорему, которая называется критерием Г. Вейля равномерного распределения значений последовательности по модулю, равному единице.
ТЕОРЕМА 1. Эквивалентны следующие утверждения*.
(1)	последовательность {хп} равномерно распределена по модулю единица;
(2)	при любых фиксированных аир, 0 < а < Р < 1, имеет место соотношение
.. Жа,р)	Q
lim •’	 = р - а;
ДТ —» оо N	г
(3)	для любой интегрируемой по Риману функции /(х), определенной на отрезке [0, 1], справедливо соотношение
N	J
Л if(xJ = f f^dx>
(4)	для любой непрерывной функции f(x)
N	J
N~' Л1/(Хл) = jf(x)dx;
(5)	при любом целом числе тп # О
lim ЛГ1 Е, e2nimXn =0.
► Очевидно, из определения имеем, что из первого утверждения теоремы следует второе утверждение. Кроме того, из утвержде
606
ния (3) следует утверждение (4), а из него следует утверждение (5). Остается только доказать, что справедливы импликации: (2) => (3) и(5)=>(1).
Докажем, что из утверждения (2) следует утверждение (3). Определим периодическую функцию g(x) с периодом 1 равенством
, 1 = J1’ если а х < Р’
'	[0 — в противном случае.
Тогда утверждение (2) можно представить в виде
n	J
^сЛ"1 Л = J
Заметим, что если последнее равенство выполняется для нескольких функций gx(x), ..., gk(x), то оно выполняется для любой их линейной комбинации с1^1(х) + ... + c^k(x) с вещественными коэффициентами сх, ... , ck. Следовательно, это равенство имеет место для любой кусочно-постоянной функции.
Возьмем теперь любую интегрируемую функцию /(х). Тогда для всякого £ > 0 существует разбиение Т:О = хо<...<хг=1 отрезка [0, 1] такое, что выполняются неравенства
8(Г) < j f(x)dx < S(T), S(T) - s(T) < |, 0	*
где s(T) и S(T) — соответственно нижняя и верхняя суммы Дарбу, s(T) == tх m,Axp S(T) =
mt = inf f(x), Mt = sup /(x).
Суммы Дарбу s(T) и S(T) можно представить также в виде
1	1
s(T) = J h(x)dx, S(T) = J H(x)dx, О	о
где
й(х) = mt, Н(х) = М(, если xg = [xf_p xf), t = 1, ... , г.
Так как Л(х) и Н(х) — кусочно-постоянные функции, то существует число Nq такое, что для всех N > NQ выполняются неравенства
N-1 n^!1h(xn) - J h(x)dx < |,
N	1	P
N-i Z'HtxJ- j H(x)dx <|, следовательно,
P	N	N	P
s(T) - | < N’1 J t h(xn) < АГ-* вЕ x Я(х„) < S(T) + |.
607
Но поскольку для всех точек хе [0, 1] выполняется неравенство Л(х) < f(x) < Н(х), имеем
N	N	N
N-i Л(х„) < N-i вЕ1 f(xn) < tf-i Д t H(x„).
Поэтому из предыдущего неравенства получаем
8(Г) - | < ЛГ-1 J t Г(Х„) < S(T) + |,
следовательно,
N	J	2₽
N-1 Д /(х„) - / f(x)dx < S(T) - 8(Т) + у < £, о	°
а это и означает, что выполняется утверждение (3).
Докажем теперь, что из (5) следует (1). Надо доказать, что
lim D(Q) = 0. Q -> оо
Для этого преобразуем функцию
F(Q,a,p)= Е g(x„), п С Q где
( 1 = J1’ если a х < Р’ ®'	[0 в противном случае.
Заметим, что функцию g(x) можно представить в виде g(x) = Р(р -X) - р(а - х) + (р - а), где р(х) = 1/2 - {х}. Рассмотрим далее периодическую функцию g0(x), с периодом 1,
&о<х) =
1, еслиа<х<р,
1/2, если х = а, х = р, 0, если 0<х<а, р<х<1.
Она совпадает с функцией g(x) во всех точках, кроме точек х = a и х = р, в которых она принимает значение, равное 1/2. Эту функцию можно представить в виде
F0(x) = Ро(р -х) - p0(a - X) + р - а, где
( _ J1/2 - {х}, если х — нецелое число, PoW [0, если х — целое число.
Ранее (см. лекцию 23, ч. III) для любого N > 1 мы получили неравенство
z ч Д sin2n/ix ч
Тв............. С^(х)’
608
где Wn(x) = 4/71 + N2 sin2 тех. Заметим, что последнее неравенство остается справедливым, если значение функции р0 в целых точках, равнбе нулю, заменить на значение 1/2 функции р(х) = = 1/2 - {х} в тех же точках.
Разложим функцию УдДх) в ряд Фурье. По лемме его коэффициенты Фурье ст оцениваются следующим образом:
|с J < (лЛГ)“1(4 + In N)e~M/N. Таким образом,
N J g(x) = р - а + JS j — (sin 2ли(р - х) - sin 2яп(а - х)) + RN, где
1дх1 < УлХР - X) + ЧМ« - х).
Положим М = [W In N] + 1. Тогда функцию у^х) можно представить в виде
у^х) = Е с е2Мтх + of \
Преобразуя функцию F(Q; а, Р), исходя из соотношений для функции g(x), получаем
IQ-W; а, р) - (₽ - а)| = IQ’1 Е g(xn) - (Р - а)| < п С Q
+ вд +| r-wll+d?’ где А >0 — некоторая постоянная, т (Р) = Е еЫп&-*п)'
Для любого вещественного числа р справедливо равенство |Тте(Р)| = |Т„(О)| = Тт.
* Возьмем любое число е > 0. Выберем наименьшее число N из условия
Alntf е N 2’ т. е.
Х7 г2А . 2Ап . .
Мт1пт.|+1'
Так как Jim Q~1Tm = 0, то существует число Qo такое, что для всех Q > Qq и для всех тп, 1 < т < М = [N log N] + 1 выполняется неравенство
609
20 - 4953
|Q-1T I <------—---------.
1 ml 4(1 +1 +
Следовательно, для всякого e > 0 найдено число Qo такое, что для всех Q > Qo справедливо неравенство
D(Q) - sup |Q-1F(Q; а, р) - (р - а)| < е. 0<а<₽<1
Это означает, что lim D(Q) = 0. ◄
N-> оо
ПРИМЕР 1. Пусть аир — вещественные числа и а — иррациональное число. Тогда последовательность {ап + р} равномерно распределена по модулю 1.
Действительно, при любом фиксированном целом числе тп, отличном от нуля, имеем
n	1
Так как а — иррациональное число, то sin тспга и 0. Поэтому Одг -> 0 при N оо. Следовательно, согласно критерию Г. Вейля, последовательность {ап + р} равномерно распределена по модулю 1.
ПРИМЕР 2. Пусть а — иррациональное число и Дхп = хл+1 - хп -> а при п оо. Тогда последовательность {хп} равномерно распределена по модулю 1. В частности, последовательность хп = an + Jn равномерно распределена по модулю 1.
Положим хп+1 - хп = а + уп, уп = 0. Рассмотрим тригонометрическую сумму
N
sn = n-1 z e2”im4 n « 1
Имеем
= N-l f e2jcim<xn +1 ’ »n> = N-1 f e2*lmxn +1 + r n = 1	1
где
rN = N~l J x (e2"m(x" * 1 -- e2*imXn -1).
Отсюда получаем
S^l - e2iama) = rN + N-\e2nimXN +1 - e2nimxi).
Правая часть последнего равенства стремится к нулю при N -> оо. Действительно, имеем
N	о N
IrvI <N~' n?i k2”"’4"’ -1| = jy n5JsinптУп\с зяН#-1 |у„|.
610
Воспользуемся тем, что HmJуп\ = 0. Получаем
N lim N~r Ё Ji/J = 0,
поэтому имеем: ^lim rN = 0.
Так как 1 - e2nima # 0 (в силу иррациональности числа а), то ^lim SN = 0, а это и означает, что последовательность {хп} равномерно распределена по модулю 1.
ПРИМЕР 3. Пусть {Fn} — последовательность чисел Фибоначчи: Fr = 1, F2 = 1,	= Fn + Fn_x при n > 2. Тогда последователь-
ность {In Fn} равномерно распределена по модулю 1.
Действительно, для Fn имеет место формула
Отсюда получаем
Следовательно, при п -» оо имеем, что In Fn+1 - In Fn -» In a, поскольку число In a является иррациональным. Значит, в силу утверждения примера 2, последовательность {In Fn} равномерно распределена по модулю 1.
ПРИМЕР 4. Пусть f'(x) = a — иррациональное число. Тогда последовательность {f(n)} равномерно распределена по модулю 1.
В самом деле, из теоремы Лагранжа о конечных приращениях имеем Jirn^ A/(n) = а. Отсюда, используя утверждение примера 2, получаем, что последовательность {/(п)} равномерно распределена по модулю 1.
Прежде чем рассматривать следующий пример, докажем неравенство Г. Вейля—Ван дер Корпута.
ЛЕММА 2. Пусть и19	, uN — любые комплексные числа, Н —
натуральное число, 1 < Н < N. Тогда справедливо неравенство
о
Я2 S ип <Я(Я + Я-1) Е |и |2+
+ 2(W + H-1)“?
Здесь и — число, комплексно сопряженное к числу и.
611
20*
► Для удобства рассуждений определим числа ип для всех целых значений п следующим образом: ип = 0 при п < 0 и при п > N. Тогда имеет место равенство
N	N + H-1Н-1
н S и = Ё Ей п = 1 л n = 1 т = 0 л-W
Возводя обе части этого равенства в квадрат и используя неравенство Коши
|ZavM2<E|avl2l|M2,
получаем
N
Н2 Ъип п = 1 л
< (N + Н - 1)ТУ,
2
где
Л
W =
Я-1
X U т = о л-т
2
Преобразуем сумму W. Для этого выделим сумму «диагональных» членов и сумму «недиагональных» членов W2. Имеем
Я-1 Я-1 N + H-1
W = Е Е Е, Un_mun_k =	+ W2,
m = 0 k = 0 n = 1 n m n к i z7 где
Я-1 Я + Я-1	2
Wl~ m?o n?i un-m ’
N + H-1
1 Л1 + ичи<йчл_1 '* A
Очевидно, справедливо равенство
N+H-1	N
n?i Un-m “ n?i Un>
так как un = 0 при и < 0 и при п > N. Поэтому
N 2
= »[„?! “л •
Преобразуем сумму W2. Для этого введем следующие обозначения п- т = l9 п - k = I + h. Получаем
Я-1 Н-т-1 N-h
^2 = о Л? Г Z?1 ^UlUl+h + UlUl+h^
Меняя порядок суммирования по h и по т в сумме W2 и переходя к неравенствам, имеем
612
ПРИМЕР 5. Пусть для любого фиксированного натурального числа h последовательность {хп+Л - хп} равномерно распределена по модулю 1. Тогда последовательность {хп} равномерно распределена по модулю 1.
Зафиксируем целое число т9 отличное от нуля, и натуральное число Н. Согласно неравенству Г. Вейля—Ван дер Корпута, имеем
1 у
N 1
2
2nimxn
H + N-1 UN
Л = I	H2N	N п«1 е
При любом фиксированном й > 1 последовательность {хп + h - хп} равномерно распределена по модулю 1, следовательно, по критерию Г. Вейля при N —» оо
1	e2nim(Xn+h~xn) . Q
N n-i e
Устремляя N к бесконечности в предыдущем неравенстве, по-
лучаем
lim
N оо
1 v 2nimx„ т-Т X. е п
N п »1
2<± < н
В силу того, что последнее неравенство имеет место для сколь угодно больших Н, имеем
lim 1	=0,
N->oo N п = 1
а это и означает, что {хп} p.p. mod 1.
ПРИМЕР 6. Пусть й > 1 — некоторое фиксированное число. Пусть также предел Jim^= а является иррациональным числом. Тогда последовательность {хп} равномерно распределена по модулю 1.
Доказательство утверждения получаем по индукции по параметру й. При k = 1 оно совпадает с утверждением примера 2. Предположим, что это утверждение верно при й = т. Докажем его при й = т + 1. Имеем
Ah(^xn)~W(xn + ll)-^xn = = Дт+1 хп + Am+1 хп+1 + ... + Дт+1 хп + h _ р
Отсюда при фиксированном Л > 1 и при п <х> получаем ДА(Дт хп) -* Ла, причем Аа — также иррациональное число.
613
Заметим теперь, что Дл (Дт хп) = Дт (ДА хп). В силу предположения индукции, примененного к последовательности {ДЛ хп}, имеем, что последовательность {ДЛ хп} равномерно распределена по модулю 1 при любом фиксированном Л > 1.
Следовательно, из утверждения примера 5 имеем, что последовательность {хп} равномерно распределена по модулю 1. В частности, отсюда следует, что последовательность значений многочлена /(и) со старшим коэффициентом, являющимся иррациональным числом, будет равномерно распределена по модулю 1.
ПРИМЕРНЫЕ ВОПРОСЫ И ЗАДАЧИ К КОЛЛОКВИУМАМ И ЭКЗАМЕНАМ
Семестр I
КОЛЛОКВИУМ 1
1.	Множества. Операции над множествами. Декартово произведение. Отображения, функции. Взаимно-однозначное соответствие. Обратная функция.
2.	Эквивалентность множеств. Счетные множества. Счетность множества рациональных чисел.
3.	Теорема Г. Кантора о неэквивалентности множества и множества всех его подмножеств.
4.	Множество мощности континуум. Несчетность континуума.
5.	Иррациональность квадратного корня из двух. Десятичная запись вещественного числа. Свойства вещественных чисел. Аксиома Архимеда.
6.	Теорема о существовании точной верхней грани у ограниченного сверху числового множества.
7.	Лемма об отделимости множеств. Лемма о системе вложенных отрезков. Лемма о последовательности стягивающихся отрезков.
8.	Бесконечно большие и бесконечно малые последовательности и их свойства.
9.	Неравенство Бернулли и бином Ньютона.
10.	Сходящиеся последовательности и их арифметические свойства.
11.	Предельный переход в неравенствах.
12.	Монотонные последовательности. Теорема Вейерштрасса.
13.	Число е и его иррациональность. Постоянная Эйлера.
14.	Теорема Больцано—Вейерштрасса о существовании частичного предела ограниченной числовой последовательности. Верхний и нижний пределы последовательности.
15.	Критерий Коши сходимости последовательности.
16.	Теорема Штольца. Предел последовательности средних арифметических членов сходящейся последовательности. Существование решения уравнения И. Кеплера.
17.	Сумма членов бесконечной геометрической прогрессии. Итерационная формула Герона. Предельные соотношения:
lim a1/n = 1, а > 0; lim п1/п « 1. п —> оо	п —> оо
615
Задач и
1.	Докажите, что: [а, Ь] ~ (а9 Ь)9 [а, Ь] ~ [а, Ь).
2.	sup А = - inf(-A), sup A U В = max (sup A, sup В). Д Л
3.	a) lim — = 0, где k — постоянная;
' п—>оо 2п
б)	lim п(а1/п - 1) = 1п а, а > 0.
п —> оо
4.	Пусть lim х„ = +°°. Тогда lim *х +	+	= +°о.
5.	Пустьрп > 0 для всех п е N и lim рп = р. Тогда lim (рх... рп)1/п s р.
6.	Исходя из Jun (1 + 1/п)71 = е, докажите, что Jim = е.
7.	Докажите, что последовательность ап = (1 + 1/п)п+р строго убывает тогда и только тогда, когдар > 1/2.
8.	Для любого рационального числа г с условием |r| < 1 справедливо равенство 1 + г<ег<1+	•
9.	lim f—Ц- Ч---Ц- + ... + Л-1 = In 2.
\п 4 1 п 4 2	2n)
10.	Пусть хп — последовательность с ограниченным изменением, т. е. существует С > 0 такое, что для всех п е N имеем XjZ	~ xj < С.
Тогда последовательность хп сходится.
11.	Пусть 0 < хт+п < хт 4- хп. Тогда существует предел Jim^ .
12.	a) lim (а„ 4- b„) < lim а„ 4- lim Ъ„, если последние пределы сущест-п —> оо "	п -> оо " л -> ОО "
вуют.
б)	Если существует предел lim а = а и lim b„ = Ь9 то lim anb„ = аЬ. I—> оо Л	П —> оо '*	п-^оо п п
в)	lima =-lim(-а ).
л —» оо п	П -> ОО п
13.	Пусть lim а„ = 4-оо. Тогда существует min а„. л —» оо п	neN п
14.	Пусть lima„ = а. Тогда последовательность {аи} имеет либо на-Л —> оо "	"
иболыпий, либо наименьший элемент, либо и тот, и другой.
15.	Пусть sn = аг 4- ... 4- ап -> 4-оо, ak > 0, liman = 0. Тогда множество предельных точек дробных частей {зд} совпадает с отрезком [0, 1].
16.	Пусть lim(s_., - s„) = 0 и не существует ни конечного, ни беско-
нечного предела lim s„9 и пусть I = lim s„9 L = lim s„. Тогда после-Л —> oo п	n-too п	П-^ОО п
довательность sn расположена всюду плотно на отрезке [Z, L].
17.	а) Пусть ап > 0 и lim ап = 0. Тогда существует бесконечно много номеров п таких, что ап > max (an+i> an 4- 2, an + 3, ...).
б) Пусть о > 0 и lim ап = 0. Тогда существует бесконечно много номеров п таких, что ап < min (а19 а2,... , ап_1).
616
КОЛЛОКВИУМ 2
1.	Предел функции в точке. Функции, бесконечно малые в точке. Финальная ограниченность функций, имеющих предел в точке. Арифметические операции над функциями, имеющими предел. Свойство монотонности предела функции.
2.	Критерий Коши существования предела функции по базе множеств.
3.	Эквивалентность определений предела функции по Коши и по Гейне.
4.	Теоремы о пределе сложной функции по базам множеств.
5.	Непрерывность функции в точке. Односторонняя непрерывность. Арифметические операции над непрерывными функциями. Непрерывность синуса и показательной функции.
6.	Замечательные пределы.
7.	Разрывы функции в точке и их классификация. Разрывы монотонных функций.
8.	Критерий непрерывности монотонной функции. Теорема о непрерывности обратной функции. Непрерывность элементарных функций. Непрерывность уравнения Кеплера.
9.	Теоремы Коши о промежуточных значениях функций, непрерывных на отрезке. Теоремы Вейерштрасса об ограниченности и о достижении экстремальных значений функциями, непрерывными на отрезке.
10.	Теорема Кантора о равномерной непрерывности функции на отрезке. Свойства открытых и замкнутых множеств на числовой оси.
11.	Лемма Бореля о конечном покрытии компакта открытыми множествами. Теорема Кантора о равномерной непрерывности функции на компакте.
12.	Понятия дифференциала и производной функции. Геометрический смысл производной и дифференциала. Односторонние производные. Связь дифференцируемости и непрерывности функции.
13.	Производная сложной и обратной функций. Инвариантность формы первого дифференциала. Дифференцируемость решения уравнения Кеплера.
14.	Производная суммы, произведения и частного двух функций. Производные элементарных функций.
15.	Производные и дифференциалы высших, порядков. Формулы Лейбница и Фаа ди Бруно.
16.	Теорема Дарбу о возрастании функции в точке. Теорема Ролля о нуле производной. Теоремы Коши и Лагранжа о конечных приращениях.
17.	Теорема Ферма об экстремуме функции. Теорема Дарбу о промежуточном значении производной. Теорема о точках разрыва производной на интервале.
Задачи
1.	Докажите, что: a) lim = 0 (а > 1, п > 0);
X —>4-00 Д*
б)	lim =0(а> 1,е>0).
' Х-4+ОО Х6
617
2.	Пусть функция f(x) ограничена на любом интервале (1, &), Ь > 1. Тогда:
б)	xlim (/(x))Vx = Jim (f(x) >0 0).
3.	Пусть функция f(x) ограничена на любом интервале (1, Ь), b > 1,
и пусть lim (Дх 4-1) - Дх)) = оо. Тогда lim = оо. X ->+ОО	X ->+оо X
4.	Пусть при х > 1 задана последовательность вещественнозначных функций Д(х), /2(х), ••• , ЛХ*)» ••• • Тогда найдется функция Дх), растущая быстрее любой из этих функций при х —» +оо.
5.	Пусть функция Дх) непрерывна на отрезке [а, д]. Тогда функции
-с, если f(x) < -Су
fc(x) = 1 Аж)» если |ftx)| < с, с, если Дх) > с9
где с > 0 — любое вещественное число, также непрерывны.
6.	Пусть функция Дх) непрерывна и ограничена на интервале (а, +оо). Тогда для любого числа Т найдется последовательность хп +оо такая, что Дип^ (Дхп 4- Т) - f(xn)) = 0.
7.	Пусть функция Дх) непрерывна на отрезке [а, Ь] и а = х0 < хх < ... ... < хп = Ь. Тогда существует точка £ G (а, Ь) такая, что
8.	Для того чтобы функцию Дх), непрерывную на конечном интервале (а, Ъ)у можно было продолжить непрерывным образом на отрезок [а, Ь], необходимо и достаточно, чтобы функция Дх) была равномерно непрерывна на интервале (а, Ь).
9.	Пусть функция Дх) определена на всей числовой оси, непрерывна хотя бы в одной точке, периодична и отлична от постоянной. Тогда эта функция имеет наименьший положительный период.
10.	Пусть функция Дх) непрерывна на всей числовой оси, отлична от постоянной и удовлетворяет функциональному уравнению Дх + у) = = /(х)Д^). Тогда Дх) = аху где а = Д1). В этой задаче условие непрерывности можно заменить условием ограниченности функции на любом интервале (0, а).
11.	Докажите, что функция
J е-1/*2, если х 5й О, f(x) =10, если х = О, бесконечно дифференцируема при х = 0.
12.	Приведите пример функции, определенной на всей числовой оси, непрерывной и разрывной на всюду плотном ее множестве.
13.	Пусть уравнение х3 4- рх 4- q = 0, р, q е R имеет три различных вещественных корня. Тогда р < 0.
618
14.	Пусть функция Дх) имеет производную (п - 1)-го порядка на интервале (а, &), п раз дифференцируема на отрезке [а, Ь] и справедливы равенства Дх0) = fix^) = ... = f(xn) (а = х0 < хг < ... < хп = Ь). Тогда существует точка £ G (а, Ъ) такая, что Лп)(£) = 0.
15.	Пусть функция Дх) дифференцируема на отрезке [1, +<*>) и •fi
lim f\x) = 0. Тогда lim = 0. И наоборот, если Дх) = о(х), то X —>4-00	X—>4-00 X
Ит |/'(х)| =0.
16.	Пусть функция Дх) непрерывна на отрезке [а, +°°), f(a) < О, и при некотором положительном k для всех х > а выполняется неравенство f'(x) > k. Тогда уравнение Дх) = 0 имеет единственный корень в интервале (а, а - f(d)/k).
17.	Пусть функции Дх) и g(x) дифференцируемы п раз при х > х0, пусть также Дх0) = g(x0), /(Л)(х0) = £(Л)(х0) при k » 1, ... , л - 1 и Дп)(х) > g^n\x) при всех х > х0. Тогда при х > х0 справедливо неравенство Дх) > g(x).
Семестр II
КОЛЛОКВИУМ 3
1.	Критерий Римана интегрируемости функции на отрезке.
2.	Эквивалентность трех условий интегрируемости функции по Риману. Специальный критерий интегрируемости функции по Риману.
3.	Интеграл Римана как предел по базе. Классы интегрируемых функций.
4.	Основные свойства определенного интеграла. Аддитивность интеграла.
5.	Интеграл как функция верхнего (нижнего) предела интегрирования. Производная интеграла.
6.	Теорема Ньютона—Лейбница. Формулы суммирования Эйлера и Абеля.
7.	Формулы замены переменной и интегрирования по частям в определенном интеграле.
8.	Первая и вторая теоремы о среднем значении.
9.	Формула Тейлора с остаточным членом в интегральной форме.
10.	Неравенства, содержащие интегралы.
11.	Критерий Лебега интегрируемости функции по Риману.
12.	Определение несобственного интеграла. Критерий Коши и достаточное условие сходимости несобственных интегралов.
13.	Абсолютная и условная сходимость несобственных интегралов. Специальные признаки сходимости.
14.	Формулы замены переменной и интегрирования по частям в несобственном интеграле.
15.	Кривые в многомерном пространстве. Теорема о длине дуги кривой.
16.	Площадь плоской фигуры и объем пространственного тела. Определение меры Жордана.
619
17.	Критерий измеримости множества по Жордану.
18.	Свойства меры Жордана. Измеримость спрямляемой кривой.
19.	Связь между интегрируемостью функции по Риману и измеримостью по Жордану ее криволинейной трапеции.
20.	Определение и свойства меры Лебега. Интеграл Лебега. Интеграл Стильтьеса.
Задач и
1.	Пусть f(x) е Я[а, Ь]. Тогда точки непрерывности функции f(x) на отрезке [а, Ь] образуют всюду плотное множество.
2.	Пусть f(x) G Я[а, Ь]. Тогда для выполнения равенства J f2(x)dx = 0 необходимо и достаточно, чтобы f(x) = 0 во всех точках непрерывности функции f(x) на отрезке [а, &].
3.	Пусть f(x) G В[а, &]. Тогда функция f(x) удовлетворяет условию ь
lim J \f(x + h) - flx)|dx = 0.
4.	Найдите предел lim- (sin - + sin — 4- ... 4- sin —— n-»oo/l \ П	П	П
5.	Пусть f(x) g [0, +°°), lim f(x) « А. Найдите предел lim J f(nx)dx. X—>4-00	n—>oo
6.	Пусть f(x) — непрерывная периодическая функция с периодом Т. х
Тогда функцию F(x) = J f(x)dx можно представить в виде суммы хо
линейной функции и периодической функции с периодом Г.
7.	Пусть f(x) — многочлен степени, большей 1. Тогда интеграл
J sin (f(x))dx сходится, о
8.	Пусть f\x) монотонна и |f'W| > А на [а, &]. Тогда
f
sin(/(x))dx <
2
А9
9. Пусть f'\x) непрерывна и |/"(х) > А на [а, &]. Тогда
ь
J sin (f(x))dx
Л’
4
10.	Пусть функция f(x) монотонна на интервале (0, а) и существует
интеграл
а
f x?f(x)dx. Тогда lim xP+1f(x) = 0.
о	х->+о°
ь
11.	Пусть Дх) g R[a, &]. Тогда lim J Дх) sin nxdx = 0.
П-»00 *
ь	2 Ь
12.	Пусть Дх) g R[a, Ь]. Тогда lim f f(x)|sin nx|dx = - J f(x)dx.
n —> °° д	7C
n [л/2] zOv _ -j \ J
13.	Пусть Дх) G B[0, 1]. Тогда lim - S f\ ---------] = J f(x)dx.
n—»oo7lv™l у П J *.
620
14.	Пусть f(x) е Я[0,1]. Тогда:
lim /(1/n) ~ /(2/rt) -F ...'+ (-l)"/((n - l)/n) = 0
15.	lim ((SX1X5)... («))2/^+1» « e.
16.	Докажите формулу Валлиса it = lim f 1	, интегрируя no
n->oo V(2n - 1)!! J n
отрезку [0, л/2] неравенство sin2rt+1 x < sin2n x < sin2"-1 x.
17.	Пусть функция Дх) ограничена. Для того чтобы fe В[а, &] необходимо и достаточно, чтобы для любого е > 0 и любого 5 > 0 множество точек отрезка [а, &], в которых Дх) имеет колебание больше чем е, можно покрыть конечным числом интервалов, сумма длин которых меньше 8 (критерий Дюбуа—Реймона).
18.	Пусть f,ge В[а, 5]. Тогда max (Д g) G В[а, &] и min (/, g) е Й[а, Ь].
19.	Пусть а(0, Ь(0 е С[а, Ъ] и J (a(t)x'(O + b(t)x(t))dt = 0 Vx(0 g CJ[a, ft], x(a) = x(6) = 0. Тогда функция a(t) дифференцируема и a\t) = b(t).
20.	При s > 1 имеем
= kn'S = ^77 dx + TTi + 1 ’ P<*> “ 1 ” W-
21.	lim («8)-^)= y.
22.	Пусть Дх) > 0 и не убывает на [1, +°°), и пусть при х Ч-оо справедливо соотношение J du ~ х. Тогда Дх) ~ х при х —» +©о.
1 и
23.	Пусть Дх) >0 на [0, +°о), и при 8 -» 0+ справедливо равенство +ОО	т
J f(t)e~btdt ~ о . Тогда при Т -> имеем J f(t)dt ~ Т.
1	0	о
24.	Пусть Дх) > 0 на [а, &] и fe С[а, 5]. Тогда справедливо равенство lim f Г/’n(x)dxY/" = sup Дх).
n->o° \a	J xe[a,d]
ЭКЗАМЕН
1.	Критерий Римана интегрируемости функции на отрезке.
2.	Эквивалентность трех условий интегрируемости функции по Риману. Специальный критерий интегрируемости функции по Риману.
3.	Интеграл Римана как предел по базе. Классы интегрируемых функций.
4.	Основные свойства определенного интеграла. Аддитивность интеграла.
5.	Интеграл как функция верхнего (нижнего) предела интегрирования. Производная интеграла.
6.	Теорема Ньютона—Лейбница. Формулы суммирования Эйлера и Абеля.
7.	Формулы замены переменной и интегрирования по частям в определенном интеграле.
621
8.	Первая и вторая теоремы о среднем значении.
9.	Формула Тейлора с остаточным членом в интегральной форме.
10.	Неравенства, содержащие интегралы.
11.	Критерий Лебега интегрируемости функции но Риману.
12.	Определение несобственного интеграла. Критерий Коши и достаточное условие сходимости несобственных интегралов.
13.	Абсолютная и условная сходимость несобственных интегралов. Специальные признаки сходимости.
14.	Формулы замены переменной и интегрирования по частям в несобственном интеграле.
15.	Кривые в многомерном пространстве. Теорема о длине дуги кривой.
16.	Площадь плоской фигуры и объем пространственного тела. Определение меры Жордана.
17.	Критерий измеримости множества по Жордану.
18.	Свойства меры Жордана. Измеримость спрямляемой кривой.
19.	Связь между интегрируемостью функции по Риману и измеримостью по Жордану ее криволинейной трапеции.
20.	Непрерывные функции в Rn. Дифференцируемые функции в Rn, Достаточное условие дифференцируемости функции в точке.
21.	Теорема о дифференцировании сложной функции. Инвариантность формы первого дифференциала. Правила дифференцирования. Производная по направлению. Градиент. Геометрический смысл дифференциала.
22.	Частные производные высших порядков. Теоремы о равенстве смешанных производных второго порядка.
23.	Дифференциалы высших порядков. Достаточное условие дифференцируемости. Формулы Тейлора с остаточным членом в форме Пеано и Лагранжа.
24.	Приложение формулы Тейлора. Локальный экстремум функции многих переменных. Достаточное условие экстремума.
25.	Неявные функции. Теорема о неявной функции.
26.	Система неявных функций. Теорема о системе неявных функций. Теорема об обратном отображении.
27.	Условный экстремум функции многих переменных. Необходимое условие условного экстремума. Метод множителей Лагранжа.
Семестр III
КОЛЛОКВИУМ 4
1.	Сходимость числового ряда. Гармонический ряд. Формулировка критерия Коши. Общий член и остаток ряда.
2.	Признаки сходимости рядов (признаки сравнения, Даламбера, Коши, Куммера и Раабе). Интегральный признак Коши—Макло-рена. Сходимость ряда дзета-функции Римана.
3.	Признаки сходимости Лейбница, Абеля и Дирихле для произвольных числовых рядов.
622
4.	Абсолютная и условная сходимость рядов. Перестановки членов абсолютно сходящегося ряда.
5.	Теорема Римана о перестановках членов в условно сходящихся рядах.
6.	Теорема о произведении абсолютно сходящихся рядов. Теорема Мертенса о произведении рядов.
7.	Теоремы о сходимости двойного и повторных числовых рядов.
8.	Равномерная сходимость функциональных рядов. Непрерывность суммы равномерно сходящегося функционального ряда. Критерий Коши и признак Вейерштрасса для равномерной сходимости функционального ряда.
9.	Признаки Абеля и Дирихле равномерной сходимости ряда.
10.	Теорема Дини о равномерной сходимости функционального ряда.
11.	Почленное интегрирование и дифференцирование функциональных рядов.
12.	Теорема о двойном и повторных пределах по базам множеств.
13.	Степенные ряды. Радиус сходимости. Теорема Коши—Адамара. Теорема Абеля о непрерывности суммы ряда на отрезке.
14.	Бесконечные произведения. Признак абсолютной сходимости. Выражение гамма-функции в виде бесконечного произведения, формула Эйлера и функциональное уравнение для гамма-функции.
15.	Непрерывность собственных интегралов, зависящих от параметра. Правило Лейбница. Теорема о равенстве повторных интегралов.
16.	Признаки Вейерштрасса, Абеля и Дирихле для равномерной сходимости несобственных интегралов.
17.	Теоремы о непрерывности, дифференцируемости и интегрируемости несобственных интегралов.
18.	Теорема о повторных интегралах с бесконечными пределами. Вычисление интеграла Дирихле.
19.	Интегральное представление для гамма-функции Эйлера. Формула дополнения. Формула Стирлинга.
Задачи
. _. S cos Inn)	-
1.	Ряд X —*------ расходится при любом вещественном числе t.
ne2 П
2.	Пустьрп > 0 и ряд Ерп сходится. Тогда ряды Ер£ и Е—сходятся.
3.	Пусть рп > 0, ряд Ерп сходится и rn = *_Е J рк. Тогда ряд Еуг рас-
ходится, а ряды Е и Е -77- (а > 0) сходятся.
А ГП
п	р
4.	Пусть р > 0, ряд Е ра расходится и sn = Е рк. Тогда ряд Е-2 рас-8п
ходится, а ряды Е и Е (а > 0) сходятся.
8п	8П
5.	а) Пустьрп > 0, рп не возрастает и ряд Ерп сходится. Тогда lim прп = = 0.
623
б)	Пусть рп > О,рп а(а> 0) не возрастает и ряд S рп сходится. Тогда lim пр„ = 0.
П->оо "
в)	Пусть рп > 0, прп не возрастает и ряд Ерл сходится. Тогда lim (n 1п п)рп = 0.
6.	Пусть {рп } — последовательность всех простых чисел. Тогда ряд (Ininn)a СХ°ДИТСЯ п₽и а > 1 и расходится при а < 1.
7.	Пусть 0 < ад < С Уп е N, ai +- tа" < ап+1, ряд S ип сходится и \пип\ < (\Уп е. N, где С, Сх > 0 — некоторые постоянные. Тогда ряд S алил сходится.
8.	Ряд S	—----------— сходится при а > г/2 и расходится
mi..mr=1 (mf + ... + т;)а
при а < г/2.
00 1 11
9.	Ряд S ------------------ сходится при — +... + — < 1 и расхо-
...m'=1	+ + m“;	<*i са-
дится при — + ... + — >1.
(Х1	аг
10.	Пусть г > 0, s = S ("Л”—,1. Тогда ряд Е а_, а = Е —(“В” .2— , являющийся квадратом исходного ряда, сходится к з2 при г > 1/2 и расходится при г < 1/2.
11.	Ряд ------——сходится неравномерно в любой фик-
сированной окрестности точки х = 0.
°°
12.	Исследовать на равномерную сходимость ряд f(x, у) = JE в области:
а) 8 < х < 2л - 8, у > 0; б) у > 0.
13.	Доказать, что ряды Тейлора для функций ех, sin х сходятся неравномерно на R.
14.	Пусть
J х, если 0 < х < 1,
Ф(х) - j 2 - х, если 1 < х < 2;
“ /о\п
ф(х + 2) = ф(х) Vx g R. Тогда функция f(x) • X Н ф(4п х) непре-рывна и нигде не дифференцируема на R.
15.	а) Пусть Дх) определена Vx е [а, &], fAx) =	. Тогда Zn(x) zj
П	[а, Ь]
zt Дх) (П _> оо).
[а, ft]
б)	/я(х) » п(Дх + 1/п) — Z(^))> fix) имеет непрерывную производную на [а, Ь]. Тогда fAx) zt Д(х) (п -> оо).
[а, ft]
в)	fa(x) = 1 i,f(x + И. Тогда fn(x) =: J/(x) (n -► oo).
n fe-0 k n J	[a, ft] a
624
16.	Пусть ряд X ап п а сходится при некотором а > 0. Тогда при N -» оо имеем ах + ... 4- aN = o(N+a).
1	QO
17.	\х~х dx = Е п~п.
I________«-1
18.	J1 4- 71 + 71 4- ... = 1 + -Ц— .
1 +—=—
ЭКЗАМЕН
1.	Сходимость числового ряда. Гармонический ряд. Формулировка критерия Коши. Общий член и остаток ряда.
2.	Признаки сходимости рядов (признаки сравнения, Даламбера, Коши, Куммера и Раабе). Интегральный признак Коши—Макло-рена. Сходимость ряда дзета-функции Римана.
3.	Признаки сходимости Лейбница, Абеля и Дирихле для произвольных числовых рядов.
4.	Абсолютная и условная сходимость рядов. Перестановки членов абсолютно сходящегося ряда.
5.	Теорема Римана о перестановках членов в условно сходящихся рядах.
6.	Теорема о произведении абсолютно сходящихся рядов. Теорема Мертенса о произведении рядов.
7.	Теоремы о сходимости двойного и повторных числовых рядов.
8.	Равномерная сходимость функциональных рядов. Непрерывность суммы равномерно сходящегося функционального ряда. Критерий Коши и признак Вейерштрасса для равномерной сходимости функционального ряда.
9.	Признаки Абеля и Дирихле равномерной сходимости ряда.
10.	Теорема Дини о равномерной сходимости функционального ряда.
11.	Почленное интегрирование и дифференцирование функциональных рядов.
12.	Теорема о двойном и повторных пределах по базам множеств.
13.	Степенные ряды. Радиус сходимости. Теорема Коши—Адамара. Теорема Абеля о непрерывности суммы ряда на отрезке.
14.	Бесконечные произведения. Признак абсолютной сходимости. Выражение гамма-функции в виде бесконечного произведения, формула Эйлера и функциональное уравнение для гамма-функции.
15.	Непрерывность собственных интегралов, зависящих от параметра. Правило Лейбница. Теорема о равенстве повторных интегралов.
16.	Признаки Вейерштрасса, Абеля и Дирихле для равномерной сходимости несобственных интегралов.
17.	Теоремы о непрерывности, дифференцируемости и интегрируемости несобственных интегралов.
18.	Теорема о повторных интегралах с бесконечными пределами. Вычисление интеграла Дирихле.
625
19.	Интегральное представление для гамма-функции Эйлера. Формула дополнения. Формула Стирлинга.
20.	Теорема о приближении функции Бернулли тригонометрическим многочленом.
21.	Неравенство Бесселя для строго регулярной функции. Полнота замкнутой ортонормированной системы.
22.	Теорема о замкнутости тригонометрической системы функций.
23.	Теорема о равномерной сходимости ряда Фурье для строго кусочно-гладкой функции.
24.	Ядро Дирихле и интегральное представление частичной суммы ряда Фурье. Принцип локализации Римана.
25.	Признак Дини для сходимости ряда Фурье. Признаки Липшица, Жордана и Дирихле.
26.	Разложение котангенса на простейшие дроби. Представление синуса в виде бесконечного произведения.
27.	Ядро Фейера. Аппроксимационная теорема Вейерштрасса для тригонометрических и алгебраических многочленов.
28.	Методы Лапласа и стационарной фазы.
Семестр IV
ЭКЗАМЕН
1.	Двойной интеграл Римана как предел по базе. Критерий Римана интегрируемости функции от двух переменных по прямоугольнику.
2.	Эквивалентность трех формулировок критерия существования двойного интеграла по прямоугольнику. Специальный критерий интегрируемости функции двух переменных по прямоугольнику, связанный с равномерными разбиениями.
3.	Критерий измеримости по Жордану цилиндрической криволинейной фигуры.
4.	Эквивалентность двух определений — обобщенного и через характеристическую функцию множества, — двойного интеграла по ограниченной области, измеримой по Жордану.
5.	Критерий измеримости по Жордану плоского множества.
6.	Основные свойства двойного интеграла (линейность, интегрирование неравенств, теорема о среднем, аддитивность). Сведение двойного интеграла к повторному.
7.	Интегрируемость функции двух переменных: а) непрерывной на прямоугольнике; б) непрерывной и ограниченной на множестве, измеримом по Жордану.
8.	Теорема об оценке погрешности при замене приращения гладкого отображения на его дифференциал на компактном выпуклом множестве.
9.	Лемма о площади образа выпуклого множества при гладком отображении. Замена переменных в двойном интеграле.
10.	Критерий Лебега интегрируемости функции двух переменных по Риману.
626
11.	Несобственные интегралы первого и второго рода. Критерий сходимости и признак сравнения для несобственного интеграла .первого рода от неотрицательной функции.
12.	Площадь поверхности. Выражение площади поверхности через двойной интеграл.
13.	Свойства криволинейных интегралов первого и второго рода. Сведение криволинейного интеграла к определенному интегралу.
14.	Криволинейный интеграл второго рода по замкнутой кривой. Формула Грина.
15.	Поверхностные интегралы первого и второго рода. Ориентация кусочно-гладких поверхностей.
16.	Формула Стокса.
17.	Формула Гаусса—Остроградского.
18.	Замена переменных в дифференциальной форме. Интеграл от дифференциальной формы по ориентированной поверхности.
19.	Общая формула Стокса.
20.	Потенциальное и соленоидальное векторные поля. Условия независимости криволинейного интеграла от пути интегрирования.
21.	Дивергенция и ротор векторного поля. Основные формулы векторного анализа.
ЛИТЕРАТУРА
1.	Ильин В. А.9 Садовничий В. А, Сендов Б. X. Математический анализ. Т. I, II. М.: Изд-во Моск, ун-та, 1985.
2.	Валле Пуссен Ш. Курс анализа бесконечно малых. Т. I, II. Л.; М.: ГТТИ, 1933.
3.	Уиттекер Е. Г., Ватсон Г. Н. Курс современного анализа. Т. I, II. Л.; М.: ГТТИ, 1933.
4.	Фихтенгольц Г. М. Курс математического анализа. Т. I—III. М.: Физматгиз, 1962.
5.	Рудин У. Основы математического анализа. М.: Мир, 1976.
6.	Дьедонне Ж. Основы математического анализа. М.: Мир, 1964.
7.	Никольский С. М. Курс математического анализа. Т. I, II. М.: Наука, 1990.
8.	Кудрявцев Л. Д. Курс математического анализа. Т. I—III. М.: Дрофа, 2003.
9.	Виноградов И. М. Дифференциальное исчисление. М.: Наука, 1985.
10.	Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. I. Изд. 4-е, перераб. и доп., 1982; Ч. II. М.: Наука, 1980.
11.	Камынин Л. И. Курс математического анализа. Ч. I, II. 1993, 1995. М.: Изд-во Моск, ун-та.
12.	Зорич В. А. Математический анализ. Ч. I. М.: Фазис, 1997. Ч. II. М.: Наука, 1990.
13.	Садовничий В. А. Теория операторов. М.: Дрофа, 2001.
14.	Ландау Э. Основы анализа. М.: ИЛ, 1947.
15.	Демидович Б. П. Сборник задач и упражнений по математическому анализу. М.: Наука, 1990.
16.	Виноградова И. А, Олехник С. Н.9 Садовничий В. А. Задачи и упражнения по математическому анализу. М.: Дрофа, 2001.
17.	Полиа Г.9 Сеге Г. Задачи и теоремы из анализа. Ч. I, II. Изд. 3-е. М.: Наука, 1978.
18.	Гелбаум Б., Олмстед Дж. Контрпримеры в анализе. М.: Мир, 1967.
19.	Пуанкаре А О науке. М.: Наука, 1983.
20.	Архипов Г. И.9 Карацуба А. А.9 Чубариков В. Н. Теория кратных тригонометрических сумм. М.: Наука, 1987.
21.	Малышев Ф. М. Симплециальные системы линейных уравнений. В кн.: Алгебра. М.: Изд-во Моск, ун-та, 1980. С. 53—56.
22.	Крыжановский Д. A. Sur les differentes dёfinitions de limite. Одеса. Наукови записки науково-дослидчих катедр. 1924. Т. 1 (№ 8—9), с. 1—10.
628
23.	Гливенко В. И. Опыт общего определения интеграла. Докл. АН СССР, 1937. Т. 4, № 2, с. 61—63.
24.	Arkhipov G. 1.9 Sadovnichii V.A., Chubarikov V. N. A generalisation of the Heine limit for functions which converge on a base. Analysis Math. 1993, 30, № 4, p. 161—171.
25.	Архипов Г. И., Садовничий В. А., Чубариков В. Н. Об эквивалентности двух типов сходимости по базе множеств. Докл. РАН 1993, т. 330, № 6, с. 677—679.
26.	Архипов Г. И.9 Садовничий В. А, Чубариков В. Н. О сходимости по декартову произведению баз и о последовательных пределах. Докл. РАН. 1994, т. 339, № 4, с. 437—438.
27.	Архипов Г. И., Садовничий В. А., Чубариков В. Н. Об общей формуле Стокса. Вестник МГУ. Сер. Мат., Мех. 1995, № 2, с. 34—44.
28.	Архипов Г. И.9 Садовничий В. А., Чубариков В. Н. О двойных и повторных пределах по базе. Вестник МГУ. Сер. Мат., Мех. 1995, №5, с. 31.
29.	Архипов Г. И., Садовничий В. А., Чубариков В. Н. О равномерной сходимости функций в смысле Гейне. ДАН. 1996, т. 347, № 3, с. 298—299.
30.	Архипов Г. И.9 Садовничий В. А., Чубариков В. Н. О равномерной поточечной сходимости по базе множеств. Вестник МГУ. Сер. Мат., Мех. 1997, № 1, с. 70—72.
31.	Феллер В. Введение в теорию вероятностей и ее приложения. М, 1967.
32.	Gordon R. A. An iterated limits theorem applied to the Henstok integral. Real analysis Exchange. 1995/96, v. 21(2) p. 774—781.
33.	Lyche R. T. Sur les fonctions d’une variable reelle. Det Kongelige Norske Videnskabers Selskab Forhandliger.—1938, Bd. XI, № 2, S. 4—6.
34.	Nagell T. Introduction to Number Theory. Stockholm.: Wiley & Sons, 1951.
35.	De la Vallee Poussin Ch.-J. Mem. de 1’Acad. de Belgique. 1896, v. LIII, № 6.
36.	Chaundy T. W., Joliffe A. E. The uniform convergence of a certain class of trigonometrical series. Proc. London Math. Soc.(2), 1916, v. 15, p. 214—216.
37.	Hardy G. H, Some theorems concerning trigonometrical series of a special type. Proc. London Math. Soc.(2), 1930, v. 32, p. 441—448.
СОДЕРЖАНИЕ
Предисловие.......................................... 5
ЧАСТЬ I
Дифференциальное исчисление функций одной переменной
Глава 1. ВВЕДЕНИЕ
ЛЕКЦИЯ 1 § 1. Множества. Операции над множествами. Декартово произведение. Отображения и функции.................... 9
ЛЕКЦИЯ 2
§ 2.	Эквивалентные множества. Счетные и несчетные множества. Мощность континуума..................... 16
ЛЕКЦИЯ 3 § 3. Вещественные числа............................. 21
ЛЕКЦИЯ 4 § 4. Полнота множества вещественных чисел........... 28
§ 5.	Леммы об отделимости множеств, о системе вложенных отрезков и последовательности стягивающихся отрезков............................. 32
Глава 2. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ
ЛЕКЦИЯ 5
§ 1.	Метод математической индукции. Бином Ньютона и неравенство Бернулли............................. 34
§ 2.	Числовые последовательности. Бесконечно малые и бесконечно большие последовательности и их свойства...................................... 37
ЛЕКЦИЯ 6 § 3. Предел последовательности...................... 42
§ 4.	Предельный переход в неравенствах.............. 45
ЛЕКЦИЯ 7
§ 5.	Монотонные последовательности. Теорема Вейерштрасса. Число е и постоянная Эйлера.......... 48
630
ЛЕКЦИЯ 8
§ 6.	Теорема Больцано—Вейерштрасса о существовании частичного предела у ограниченной последовательности............................... 54
§ 7.	Критерий Коши для сходимости последовательности ...	56
Глава 3. ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ
ЛЕКЦИЯ 9
§ 1.	Понятие предела числовой функции............. 58
§ 2.	База множеств. Предел функции по базе........ 60
ЛЕКЦИЯ 10
§ 3.	Переход к пределу в неравенствах............. 66
§ 4.	Критерий Коши существования предела функции по базе.......................... 66
ЛЕКЦИЯ 11
§ 5.	Эквивалентность определений сходимости по Коши и по Гейне............................... 69
§ 6.	Теоремы о пределе сложной функции............ 70
§ 7.	Порядок бесконечно малой функции............. 73
Глава 4. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
ЛЕКЦИЯ 12
§ 1.	Свойства функций, непрерывных в точке........ 75
§ 2.	Непрерывность элементарных функций........... 77
ЛЕКЦИЯ 13
§ 3.	Замечательные пределы........................ 79
§ 4.	Непрерывность функции на множестве........... 81
ЛЕКЦИЯ 14
§ 5.	Общие свойства функций, непрерывных на отрезке ....	88
ЛЕКЦИЯ 15
§ 6.	Понятие равномерной непрерывности............ 91
§ 7.	Свойства замкнутых и открытых множеств. Компакт. Функции, непрерывные на компакте..................... 92
Глава 5. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
ЛЕКЦИЯ 16
§ 1.	Приращение функции. Дифференциал и производная функции............................ 96
ЛЕКЦИЯ 17
§ 2.	Дифференцирование сложной функции........... 100
§ 3.	Правила дифференцирования................... 103
ЛЕКЦИЯ 18
§ 4.	Производные и дифференциалы высших порядков.. 106
§ 5.	Возрастание и убывание функции в точке...... 111
631
ЛЕКЦИЯ 19 § 6. Теоремы Ролля, Коши и Лагранжа............... 113
ЛЕКЦИЯ 20 § 7. Следствия из теоремы Лагранжа................ 117
§ 8.	Некоторые неравенства........................ 118
§ 9.	Производная функции, заданной параметрически. 119
ЛЕКЦИЯ 21 § 10. Раскрытие неопределенностей................. 121
ЛЕКЦИЯ 22 § 11. Локальная формула Тейлора................... 127
§ 12.	Формула Тейлора с остаточным членом
в общей форме................................ 131
ЛЕКЦИЯ 23
§ 13.	Применение формулы Тейлора к некоторым функциям.............................. 134
ЛЕКЦИЯ 24
§ 14.	Исследование функций с помощью производных. Экстремальные точки. Выпуклость................... 137
ЛЕКЦИЯ 25 § 15. Точки перегиба.............................. 144
ЛЕКЦИЯ 26
§ 16.	Интерполирование............................ 148
ЛЕКЦИЯ 27
§ 17.	Метод хорд и метод касательных (метод Ньютона). Быстрые вычисления................................ 151
Глава 6. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ЛЕКЦИЯ 28 § 1. Точная первообразная. Интегрируемые функции.. 156
ЛЕКЦИЯ 29 § 2. Свойства неопределенного интеграла........... 159
ЛЕКЦИЯ 30
Дополнение. Обобщение понятия предала по Гейне на функции, сходящиеся по базе множеств........... 163
ЧАСТЬ II
Интеграл Римана. Дифференциальное исчисление функций многих переменных
Глава 7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
ЛЕКЦИЯ 1 § 1. Введение....................................... 173
§ 2.	Определение интеграла Римана................. 175
632
ЛЕКЦИЯ 2
§ 3.	Критерий интегрируемости функции по Риману.... 180
ЛЕКЦИЯ 3
§ 4.	Эквивалентность трех условий интегрируемости функции по Риману.................. 185
§ 5.	Специальный критерий интегрируемости функции по Риману ......................................... 186
§ 6.	Метод интегральных сумм....................... 189
ЛЕКЦИЯ 4
§ 7.	Свойства интеграла Римана как предела по базе. 193
§ 8.	Классы функций, интегрируемых по Риману....... 197
ЛЕКЦИЯ 5
§ 9.	Свойства определенного интеграла.............. 200
§ 10.	Аддитивность интеграла Римана................ 204
Глава 8. ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ ИНТЕГРАЛА РИМАНА .
ЛЕКЦИЯ 6
§ 1.	Интеграл Римана как функция от его верхнего (нижнего) предела интегрирования. Производная интеграла.......................................... 206
§ 2.	Теорема Ньютона—Лейбница. Формулы суммирования Эйлера и Абеля................ 207
ЛЕКЦИЯ 7
§ 3.	Формулы замены переменной и интегрирования по частям в определенном интеграле................. 211
§ 4.	Первая и вторая теоремы о среднем значении интеграла.......................................... 212
ЛЕКЦИЯ 8
§ 5.	Формула Тейлора с остаточным членом в интегральной форме............................... 217
§ 6.	Неравенства, содержащие интегралы............. 221
ЛЕКЦИЯ 9
§ 7.	Критерий Лебега интегрируемости функции по Риману.......................................... 224
§ 8.	Доказательство критерия Лебега................ 225
Глава 9. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
ЛЕКЦИЯ 10
§ 1.	Определение несобственных интегралов первого и второго рода..................................... 229
§ 2.	Критерий Коши и достаточные условия сходимости несобственных интегралов........................... 231
§ 3.	Абсолютная и условная сходимость несобственных интегралов. Признаки Абеля и Дирихле............... 232
633
................и.........I......Illlllllllllll.....Hill.....I.......I.......Il....Illlllllllllllll......111111111111111111]1111111111111111111111111111111111111111111111111111111111111111111111111111П1111111111Н111111111111111111111111111111111ПН|||||Н||Ш1111111|1111)ШЦ
ЛЕКЦИЯ 11
§ 4.	Несобственные интегралы второго рода......... 235
§ 5.	Формулы замены переменной и интегрирование по частям в несобственном интеграле.............. 236
Глава 10, ДЛИНА ДУГИ КРИВОЙ
ЛЕКЦИЯ 12
§ 1.	Кривые в многомерном пространстве ........... 239
§ 2.	Теорема о длине дуги кривой.................. 241
Глава 11. МЕРА ЖОРДАНА
ЛЕКЦИЯ 13
§ 1.	Площадь плоской фигуры и объем тела. Определение меры Жордана......................... 244
§ 2.	Критерий измеримости множества по Жордану.... 246
ЛЕКЦИЯ 14
§ 3.	Свойства меры Жордана........................ 250
§ 4.	Измеримость спрямляемой кривой............... 252
§ 5.	Связь между интегрируемостью функции по Риману и измеримостью по Жордану ее криволинейной трапеции ........................................ 254
Глава 12. ЭЛЕМЕНТЫ ТЕОРИИ МЕРЫ И ИНТЕГРАЛА ЛЕБЕГА.
ИНТЕГРАЛ СТИЛЬТЬЕСА
ЛЕКЦИЯ 15
§ 1.	Определение и свойства меры Лебега........... 257
ЛЕКЦИЯ 16
§ 2.	Интеграл Лебега.............................. 263
ЛЕКЦИЯ 17 § 3. Интеграл Стильтьеса.......................... 269
Глава 13. НЕКОТОРЫЕ ПОНЯТИЯ ОБЩЕЙ ТОПОЛОГИИ. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
ЛЕКЦИЯ 18
§ 1.	Определения и основные свойств пространств... 276
ЛЕКЦИЯ 19
§ 2.	Хаусдорфовость метрического пространства в естественной топологии......................... 282
§ 3.	Внутренние, внешние и граничные точки множества в метрическом пространстве....................... 283
§ 4.	Лемма о последовательности стягивающихся шаров. Принцип сжимающих отображений............................ 286
ЛЕКЦИЯ 20
§ 5.	Непрерывные отображения метрических пространств.......................... 288
634
§ 6.	Понятие компакта. Компакты в Rn и полнота пространства Rn. Свойства непрерывных функций на компакте......................................	289
§ 7.	Связные множества и непрерывность.......... 293
Глава 14. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
ЛЕКЦИЯ 21
§ 1.	Непрерывные функции в Rn................... 295
§ 2.	Дифференцируемые функции в Rn.............. 298
ЛЕКЦИЯ 22
§ 3.	Дифференцирование сложной функции ......... 301
§ 4.	Производная по направлению. Градиент....... 302
§ 5.	Геометрический смысл дифференциала ........ 303
ЛЕКЦИЯ 23 § 6. Частные производные высших порядков........ 305
§ 7.	Дифференциалы высших порядков. Формула Тейлора................................. 307
ЛЕКЦИЯ 24
§ 8.	Приложение формулы Тейлора. Локальный экстремум функции многих переменных............................... 311
§ 9.	Неявные функции............................ 313
ЛЕКЦИЯ 25 § 10. Система неявных функций................... 318
§11. Условный экстремум функции многих переменных........................... 322
§ 12. Дифференцируемые отображения. Матрица Якоби............................... 325
ЧАСТЬ III
Функциональные ряды и параметрические интегралы
Глава 15. ЧИСЛОВЫЕ РЯДЫ
ЛЕКЦИЯ 1
§ 1. Основные свойства сходящихся рядов. Критерий Коши............................... 329
ЛЕКЦИЯ 2 § 2. Ряды с неотрицательными членами............ 337
ЛЕКЦИЯ 3
§ 3. Основные признаки сходимости для рядов с неотрицательными членами.................. 342
635
ЛЕКЦИЯ 4 § 4. Абсолютная и условная сходимость рядов.	<
Ряды Лейбница.................................. 350
§ 5. Признаки Абеля и Дирихле...................... 352
ЛЕКЦИЯ 5 § 6. Перестановки членов ряда...........?.......... 354
ЛЕКЦИЯ 6
§ 7. Арифметические операции над сходящимися рядами.......................... 357
ЛЕКЦИЯ 7 § 8. Двойные и повторные ряды...................... 362
Глава 16. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
ЛЕКЦИЯ 8
§ 1.	Сходимость функционального ряда............... 368
§ 2.	Равномерная сходимость........................ 371
ЛЕКЦИЯ 9
§ 3.	Критерий равномерной сходимости функциональной последовательности................. 374
§ 4.	Признаки равномерной сходимости............... 375
ЛЕКЦИЯ 10 § 5. Теорема Дини.................................. 380
§ 6.	Почленное дифференцирование и интегрирование ряда............................. 381
ЛЕКЦИЯ 11 § 7. Двойные и повторные пределы по базе множеств.. 385
ЛЕКЦИЯ 12 § 8. Степенные ряды................................ 389
ЛЕКЦИЯ 13 § 9. Бесконечные произведения...................... 394
ЛЕКЦИЯ 14 § 10. Бесконечные определители...................   399
§ 11.	Равностепенная непрерывность
и теорема Арцела.............................. 402
Глава 17. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
ЛЕКЦИЯ 15
§ 1.	Собственные параметрические интегралы и их непрерывность................................ 404
§ 2.	Дифференцирование и интегрирование собственных параметрических интегралов............ 407
ЛЕКЦИЯ 16 § 3. Теорема Лагранжа.............................. 411
636
ЛЕКЦИЯ 17
§ 4.	Равномерная сходимость по Гейне.......... .<	413
§ 5.	Эквивалентность двух определений равномерной сходимости.........................	.. 415
ЛЕКЦИЯ 18
§ 6.	Равномерная сходимость несобственных параметрических интегралов........ 418
ЛЕКЦИЯ 19
§ 7.	Непрерывность, дифференцируемость и интегрируемость по параметру несобственных интегралов.... 422
ЛЕКЦИЯ 20
§ 8.	Несобственные интегралы второго рода.......... 428
§ 9.	Применение теории параметрических интегралов . 430
ЛЕКЦИЯ 21
§ 10.	Интегралы Эйлера первого и второго рода...... 432
ЛЕКЦИЯ 22
§ 11.	Формула Стирлинга............................ 437
Глава 18. РЯДЫ И ИНТЕГРАЛЫ ФУРЬЕ
ЛЕКЦИЯ 23
§ 1. Представление дробной доли вещественного числа тригонометрическим рядом. Формула суммирования
Пуассона. Суммы Гаусса......................... 440
ЛЕКЦИЯ 24
§ 2.	Неравенство Бесселя. Замкнутость и полнота ортонормированной системы функций.................. 449
ЛЕКЦИЯ 25
§ 3.	Замкнутость тригонометрической системы функций . . . 454
§ 4.	Простейшие свойства тригонометрических рядов Фурье..................... 458
ЛЕКЦИЯ 26
§ 5.	Интегральное представление для частичной суммы ряда Фурье. Принцип локализации Римана............. 462
§ 6.	Признаки поточечной сходимости рядов Фурье .. 466
ЛЕКЦИЯ 27 § 7. Поведение коэффициентов Фурье................. 470
§ 8.	Разложение котангенса на простейшие дроби и представление синуса в виде бесконечного произведения....................................... 472
§ 9.	Задача Кеплера и ряды Бесселя................ 474
ЛЕКЦИЯ 28
§ 10.	Ядро Фейера и аппроксимационная теорема Вейерштрасса....................................... 477
§ 11.	Интеграл Дирихле и разложение на простейшие дроби................................ 479
637
ЛЕКЦИЯ 29 § 12. Преобразование Фурье и интеграл Фурье.......... 483
ЛЕКЦИЯ 30 § 13. Метод Лапласа и метод стационарной фазы........ 492
ЧАСТЬ IV
Кратный интеграл Римана. Поверхностные интегралы
Глава 19. КРАТНЫЕ ИНТЕГРАЛЫ
ЛЕКЦИЯ 1
§ 1.	Двойной интеграл Римана как предел по базе... 501
§ 2.	Суммы Дарбу и их свойства.................... 504
ЛЕКЦИЯ 2
§ 3.	Критерий Римана интегрируемости функции на прямоугольнике ................................. 507
§ 4.	Специальный критерий интегрируемости функции на прямоугольнике.......................... 510
ЛЕКЦИЯ 3
§ 5.	Измеримость по Жордану цилиндрической криволинейной фигуры................ 512
§ 6.	Понятие двойного интеграла Римана по ограниченной области, измеримой по Жордану...... 514
ЛЕКЦИЯ 4 § 7. Основные свойства двойного интеграла......... 518
§ 8.	Переход от двойного интеграла к повторному... 519
§ 9.	Интегрируемость непрерывной функции на измеримом множестве............................. 521
ЛЕКЦИЯ 5 § 10. Многократные интегралы ..................... 523
§ 11.	Свойства гладкого отображения на выпуклом множестве.......................................... 526
ЛЕКЦИЯ 6 § 12. Объем области в криволинейных координатах. Теорема о замене переменных в кратном интеграле ................................. 529
ЛЕКЦИЯ 7 § 13. Критерий Лебега ............................ 536
ЛЕКЦИЯ 8 § 14. Несобственные кратные интегралы............. 540
ЛЕКЦИЯ 9 § 15. Площадь поверхности ........................ 547
§ 16.	Площадь m-мерной поверхности в евклидовом пространстве п измерений.............. 551
638
Глава 20. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
ЛЕКЦИЯ 10
§ 1.	Криволинейные интегралы.................... 554
§ 2.	Свойства криволинейных интегралов.......... 555
ЛЕКЦИЯ 11
§ 3.	Криволинейные интегралы второго рода по замкнутому контуру. Формула Грина............. 559
ЛЕКЦИЯ 12
§ 4.	Поверхностные интегралы.................... 563
§ 5.	Согласование ориентации поверхности и ее границы ... 567
ЛЕКЦИЯ 13
§ 6.	Формула Стокса............................. 570
§ 7.	Формула Гаусса—Остроградского.............. 571
ЛЕКЦИЯ 14
§ 8.	Криволинейные интегралы, зависящие только от пределов интегрирования....................... 576
§ 9.	Элементы векторного анализа................ 579
ЛЕКЦИЯ 15
§ 10.	Потенциальное и соленоидальное векторные поля .... 584
Глава 21. ОБЩАЯ ФОРМУЛА СТОКСА
ЛЕКЦИЯ 16
§ 1. Понятие ориентированной
многомерной поверхности....................... 588
§ 2.	Согласование ориентаций поверхности и ее границы в общем случае.................................... 590
§ 3.	Дифференциальные формы...................... 592
§ 4.	Замена переменных в дифференциальной форме . 593
ЛЕКЦИЯ 17
§ 5.	Интеграл от дифференциальной формы.......... 595
§ 6.	Операция внешнего дифференцирования ........ 597
§ 7.	Доказательство общей формулы Стокса ........ 599
ЛЕКЦИЯ 18
§ 1. Понятие равномерного распределения. Лемма об оценке коэффициентов Фурье........... 603
§ 2. Критерий Г. Вейля........................... 606
Примерные вопросы и задачи к коллоквиумам и экзаменам................................... 615
Литература....................................... 628
Учебное издание
Архипов Геннадий Иванович Садовничий Виктор Антонович Чубариков Владимир Николаевич
ЛЕКЦИИ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Учебник для вузов
Зав. редакцией Б. В. Панкратов Ответственный редактор Ж. И. Яковлева Технический редактор Н. И. Герасимова Компьютерная верстка Г. М. Татаринова Корректор Г, И. Мосякина
Художественное оформление серии выполнено Издательством Московского государственного университета им. М. В. Ломоносова и издательством «Проспект» по заказу Московского университета
Художники В. А. Чернецов, Н. С. Шувалова
Санитарно-эпидемиологическое заключение № 77.99.02.953.Д.006315.08.03 от 28.08.2003.
Подписано к печати 08.09.04. Формат бОЭО1/^. Бумага офсетная. Гарнитура «Школьная». Печать офсетная.
Усл. печ. л. 40,0. Тираж 1000 экз. Заказ № 4953.
ООО «Дрофа».
127018, Москва, Сущевский вал, 49.
По вопросам приобретения продукции издательства «Дрофа» обращаться по адресу: 127018, Москва, Сущевский вал, 49.
Тел.: (095) 795-05-50, 795-05-51. Факс: (095) 795-05-52.
Торговый дом «Школьник».
109172, Москва, ул. Малые Каменщики, д. 6, стр. 1А. Тел.: (095) 911-70-24, 912-15-16, 912-45-76.
Магазины «Переплетные птицы»: 127018, Москва, ул. Октябрьская, д. 89, стр. 1. Тел.: (095) 912-45-76;
140408, Московская обл., г. Коломна, Голутвин, ул. Октябрьской революции, 366/2.
Тел.: (095) 741-59-76.
Отпечатано в полном соответствии с качеством предоставленных диапозитивов в ОАО «Можайский полиграфический комбинат».
143200, г. Можайск, ул. Мира, 93.
Московский государственный университет имен КЛАССИЧЕСКИЙ УНИВЕРСИТЕТСКИЙ УЧЕБНИК