Релятивистские квантовые поля. Том 1 - Дрелл С.Д., Бьёркен Дж.Д.

Автор: Дрелл С.Д. Бьёркен Дж.Д.

Теги: физика квантовая физика

Год: 1978

Похожие

Введение в релятивистскую квантовую теорию поля

Элементарная квантовая теория поля

Квантовая теория поля. Том 1. Общая теория

Этюды о симметрии

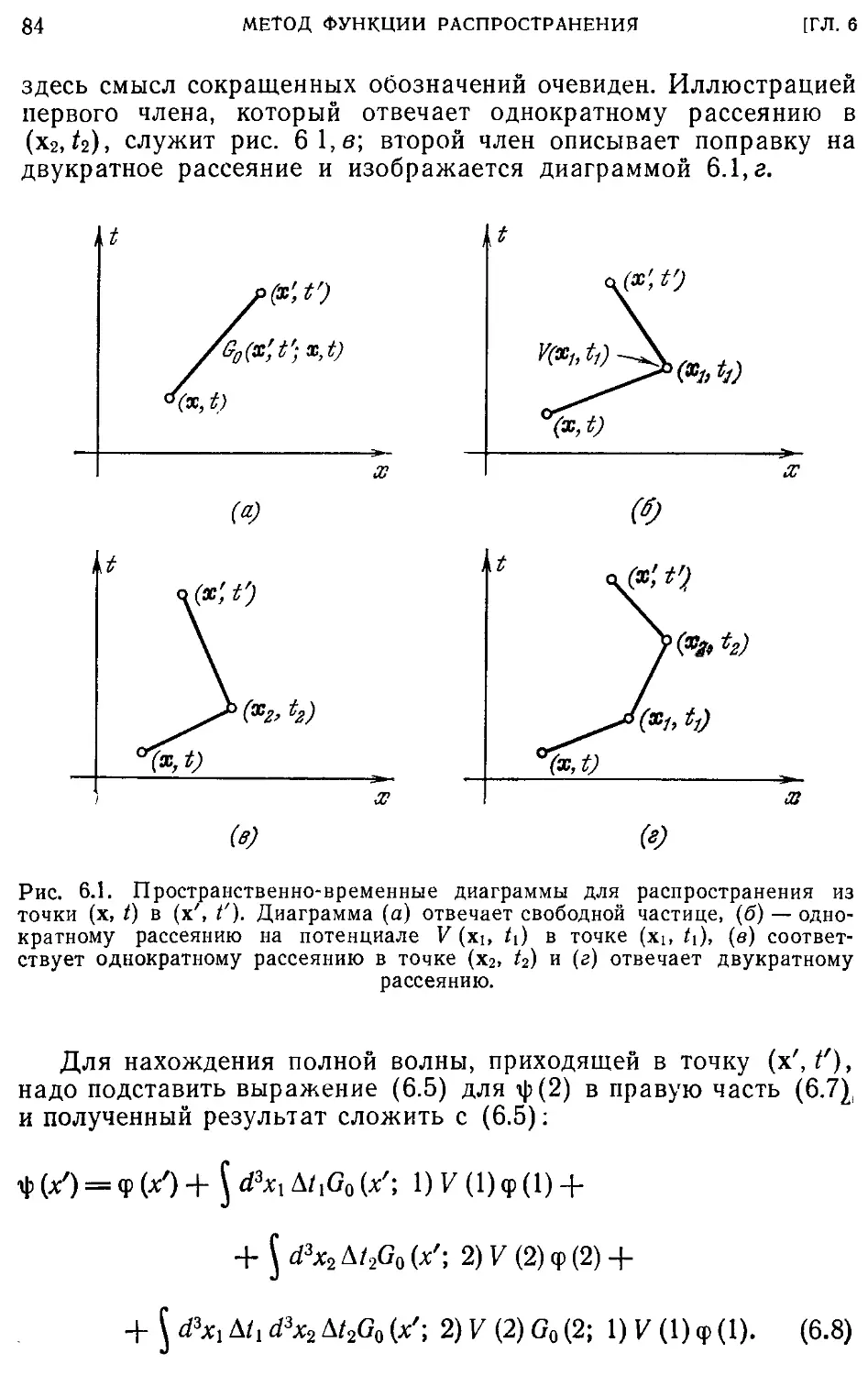
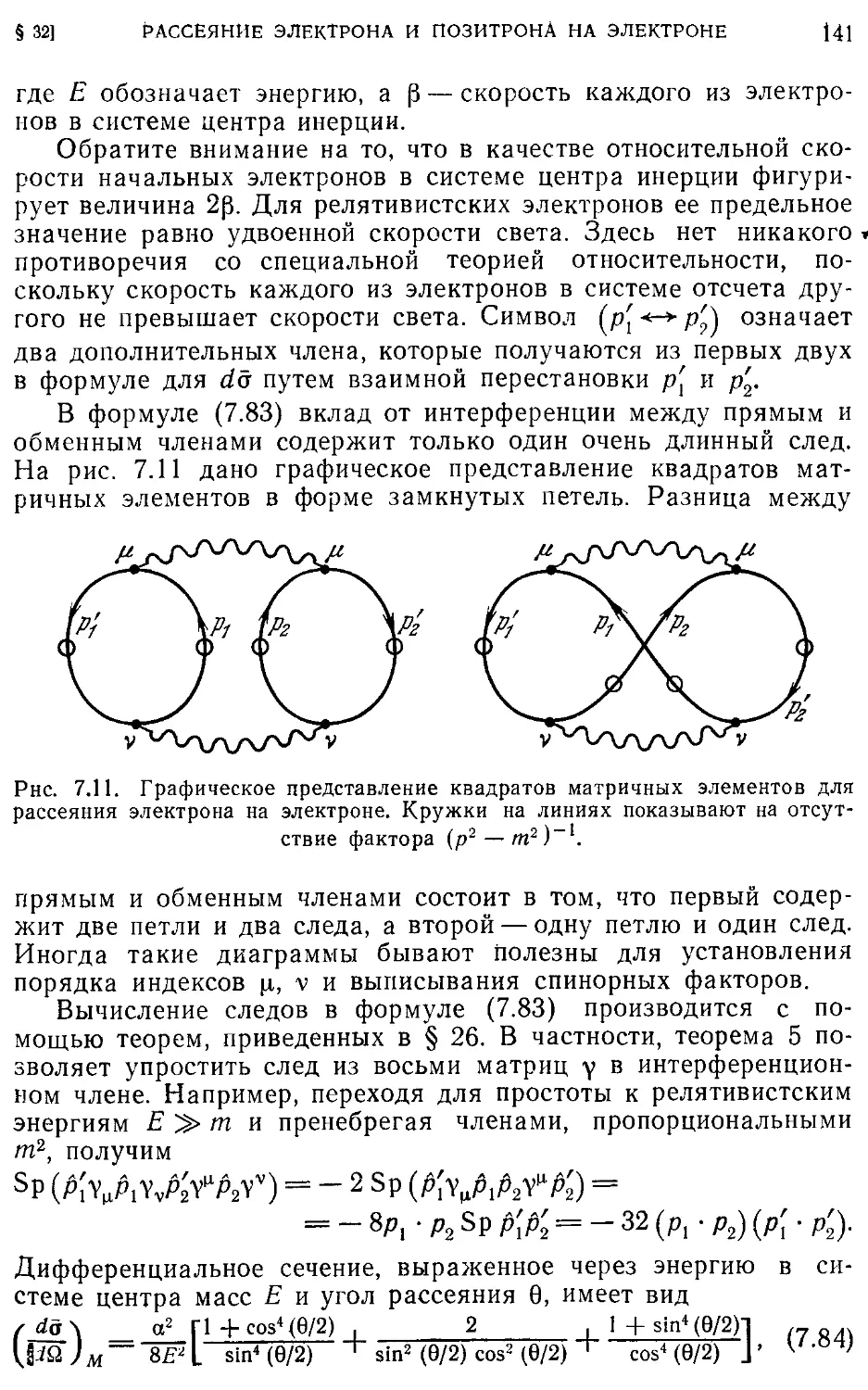
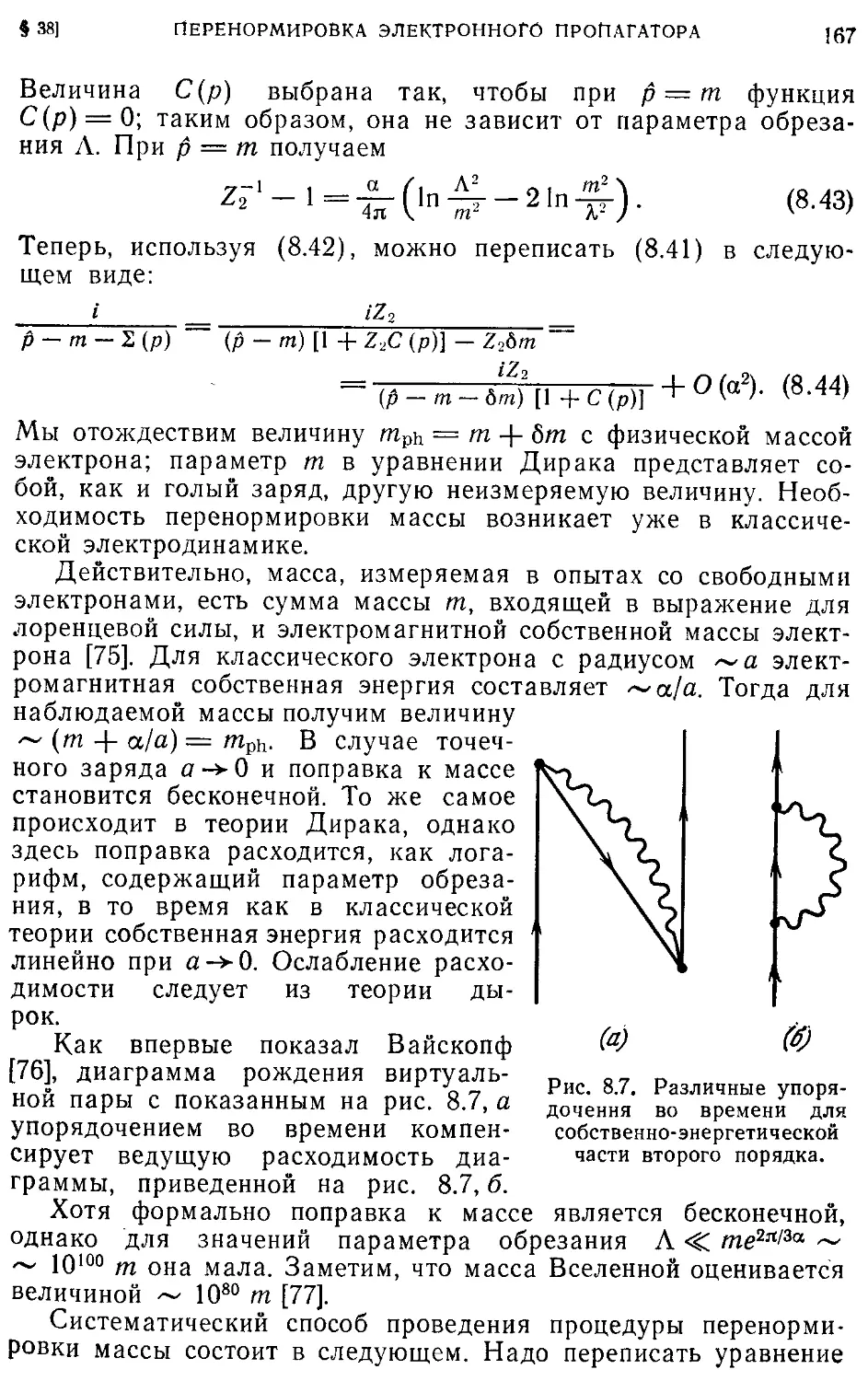
Текст

Дж.Д.Бьёркен, С.Д.Дрелл
РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ ТЕОРИЯ
т. 1. Релятивистская квантовая механика
Книга, написанная известными американскими физиками-теоретиками,
представляет собой систематический курс квантовой электродинамики.
Рассмотрение всех вопросов проводится на основе метода функции
распространения, что позволяет сделать изложение наглядным и доступным. В
книге подробно обсуждаются уравнение Дирака и свойства его решений, метод
функции распространения, проблема перенормировок и электродинамика частиц
с нулевым спином и др. Развитые методы применяются к неэлектромагнитным
взаимодействиям элементарных частиц.
ОГЛАВЛЕНИЕ
От редактора перевода 6
Предисловие 8
Глава 1. Уравнение Дирака 11
§ 1. Формулировка релятивистской квантовой теории 11
§ 2. Предварительные замечания 13
§ 3. Уравнение Дирака 16
§ 4. Переход к нерелятивистской теории 19
Задачи 23
Глава 2. Лоренцева инвариантность уравнения Дирака 24
§ 5. Уравнение в ковариантной форме 24
§ 6. Доказательство ковариантности 26
§ 7. Пространственное отражение 33
§ 8. Ковариантные билинейные формы 33
Задачи 35
Глава 3. Решения уравнения Дирака для свободной частицы 36
§ 9. Плоские волны 36
§ 10. Проекционные операторы для энергии и спина 41
§11. Физический смысл решений в виде плоских волн и волновых
пакетов 44
Задачи 51
Глава 4. Преобразование Фолди — Ваутхайзена 52
§ 12. Введение 52
§ 13. Преобразование для свободной частицы 53
§ 14. Общее преобразование 54
§ 15. Атом водорода 68
Задачи 66
Глава 5. Теория дырок 68
§ 16. Проблема решений с отрицательной энергией 68
§ 17. Зарядовое сопряжение 71
§ 18. Поляризация вакуума 74
§ 19. Обращение времени и другие симметрии 75

Задачи 79
Глава 6. Метод функции распространения 81
§ 20. Введение 81
§ 21. Нерелятивистский пропагатор 81
§ 22. Формальное определение и свойства функции Грим 88
§ 23. Функция распространения в теории позитрона 94
Задачи 103
Глава 7. Приложение теории к описанию основных 104
электродинамических явлений
§ 24. Рассеяние электронов в кулоновском поле 104
§ 25. Теоремы о вычислении следов; усредненное по спинам сечение 108
рассеяния в кулоновском потенциале
§ 26. Кулоновское рассеяние позитронов 110
§ 27. Рассеяние электрона на дираковском протоне 112
§ 28. Поправки высших порядков к рассеянию электронов протонами 120
§ 29. Тормозное излучение 124
§ 30. Комптоновское рассеяние 131
§31. Аннигиляция электронной пары в гамма-лучи 135
§ 32. Рассеяние электрона и позитрона на электроне 139
§ 33. Поляризационные эффекты при рассеянии электронов 143
Задачи 148
Глава 8. Поправки высших порядков к матрице рассеяния 150
§ 34. Рассеяние электрона позитроном в четвертом порядке • 150
§ 35. Поляризация вакуума 156
§ 36. Перенормировка внешних фотонных линий 163
§ 37. Собственная масса электрона 164
§ 38. Перенормировка электронного пропагатора 166
§ 39. Поправки к вершине 169
§ 40. Лэмбовский сдвиг 179
Задачи 183
Глава 9. Уравнение Клейна — Гордона 184
§41. Введение 184
§ 42. Пропагатор для уравнения Клейна — Гордона 186
§ 43. Введение электромагнитных потенциалов 188
§ 44. Амплитуды рассеяния 190
§ 45. Процессы рассеяния низшего порядка 192
§ 46. Процессы высшего порядка 195
§ 47. Нерелятивистский предельный переход в уравнения Клейна — 199
Гордона
Задачи 207
Глава 10. Неэлектромагнитные взаимодействия 208
§ 48. Введение 208
§ 49. Сильные взаимодействия 209

§ 50. Формализм изотопического спина 220
§ 51. Сохраняющиеся токи 224
§ 52. Приближенные методы; нуклон-нукломное рассеяние 225
§ 53. Мезон-нуклонное рассеяние 229
§ 54. Проекционные операторы для изоспина и углового момента 232
§ 55. Сечения рассеяния пионов на нуклоне 234
§ 56 Электромагнитная структура мезонов и нуклонов 238
§ 57. Слабые взаимодействия 244
§ 58 Бета-распад 245
§ 59. Теория лвухкомпонентного нейтрино 255
§ 60. Распад (i-мезона 258
§ 61. Распад л-мезона 261
§ 62. Два типа нейтрино 266
§ 63 Гипотеза о сохраняющемся векторном токе 267
§ 64. Частично сохраняющийся аксиальный ток 271
Задачи 276
Приложение А Обозначения 278
Приложение Б. Правила Фейнмана 282
Дополнения редактора перевода 288
Литература 291

ОТ РЕДАКТОРА ПЕРЕВОДА
Эта книга написана двумя выдающимися физиками-теоретиками из Стен-
фордского центра физики высоких энергий, внесших своими исследованиями
существенный вклад в развитие физики элементарных частиц. Вышедшая в
1964 году, эта книга широко используется, и ссылки на нее постоянно и часто
встречаются в мировой научной литературе. Уже это оправдывает появление
книги на русском языке, несмотря на то, что наша литература по квантовой
теории поля достаточно богата как оригинальными, тгк и переводными моно-
монографиями.
Книга состоит из двух частей, существенно различающихся по характеру
изложения и рассчитанных на различный контингент читателей. Первая часть
носит более элементарный характер, ее цель объяснить и научить читателя
методам, которыми практически пользуются для получения практических ре-
результатов в квантовой электродинамике, теории слабых взаимодействий, а
также некоторых качественных результатов в теории сильных взаимодействий.
Основой для этого является метод, восходящий к первым работам Фейнма-
на, — метод функций распространения Для наглядности авторы исходят из
определения функций распространения в пространстве и времени и применяют
их к решению конкретных задач. Порой это приводит к более длинным вы-
выкладкам, чем если бы раз и навсегда сформулировать общее правило напи-
написания амплитуд рассеяния по диаграммам Фейнмана, но авторы предпочи-
предпочитают прагматическим правилам детальное прослеживание пространственно-
временной картины процесса.
Во второй части авторы исходят из формального гамильтонова метода
квантования. Ради его четкости они предпочитают в случае электродинамики
пользоваться методом, явно-неинвариантным относительно лоренцевых и кали-
калибровочных преобразований. Инвариантность оправдывается на другом этапе.
Затем строится теория возмущений и подробно исследуется схема перенорми-
перенормировок с использованием метода Вейнберга. Подробно исследуются: аналити-
аналитические свойства амплитуд, особенности Ландау, метод дисперсионных соотно-
соотношений. В общем, вторая часть книги достаточно полно отражает состояние
квантовой теории поля к моменту написания книги.
За истекшие с момента написания книги десять с лишним лег в физике
элементарных частиц и теории поля произошел существенный прогресс. Он
практически не затронул квантовую электродинамику, поэтому в этой своей

ОТ РЕДАКТОРА ПЕРЕВОДА 7
части книга не устарела. В области же слабых и сильных взаимодействий
возникли существенно новые теоретические идеи и методы (в их разработке
активное участие принимали и авторы этой книги). Учесть «на ходу» эти
изменения невозможно — они требуют отдельной монографии. Эта же моно-
монография не теряет своей ценности и, помимо ее уже не меняющихся от вре-
времени разделов, останется введением к будущей, так же как ее первая часть,—
ко второй. Поэтому мы ограничились небольшим количеством дополнений,
идейно непосредственно примыкающих к содержанию книги, относящихся к
взаимодействию электронов с адронами и мюонами.
В. Б. Берестецкий

ПРЕДИСЛОВИЕ
Предложенный в 1949 г. Р. Фейнманом подход к релятиви-
релятивистской квантовой теории, основанный на методе функции рас-
распространения, позволил сформулировать квантовую электроди-
электродинамику в интуитивно привлекательной и практически удобной
форме и в то же время оказался весьма плодотворным для ши-
широкого класса задач в теории элементарных частиц. Процедура
перенормировок, на которой основана вера теоретиков в пред-
предсказания квантовой электродинамики, зависит на самом деле от
анализа диаграмм Фейнмана. То же относится и к значитель-
значительному прогрессу, достигнутому в доказательстве аналитических
свойств, необходимых для написания дисперсионных соотноше-
соотношений. Можно, наконец, пойти еще дальше и принять крайнюю
точку зрения, согласно которой набор всех диаграмм Фейнмана
и есть теория.
В этой книге и в следующем томе «Релятивистские кванто-
квантовые поля» мы не выступаем в защиту этой точки зрения, как,
впрочем, вообще не пытаемся отстоять какую-либо единствен-
единственную точку зрения в ущерб всем остальным. Сейчас никто не
может позволить себе подобной роскоши ввиду неудовлетвори-
неудовлетворительного положения, сложившегося в физике элементарных час-
частиц. В особенности нам не хотелось бы приуменьшить значение
прогресса, достигнутого в формальной теории поля и диспер-
дисперсионной теории мезон-нуклонного взаимодействия при низких
энергиях. Тем не менее основное ударение мы делаем на раз-
развитие правил Фейнмана, которые следуют непосредственно из
волнового уравнения для дираковского электрона, если это урав-
уравнение проинтегрировать с граничными условиями, вытекающими
из теории дырок.
Взяться за написание книги (превратившейся затем в целых
две), излагающей именно такой подход, нас побудили три ос-
основные причины:
1. Фейнмановские диаграммы и правила вычислений выра-
выражают результаты квантовой теории поля в форме, удобной для
анализа экспериментальных данных. Хотя формулировка теории
в терминах диаграмм может означать использование теории воз-

ПРЕДИСЛОВИЕ 9
мущений, пример проблемы многих тел показывает, что графи-
графические методы пригодны для описания явлений, не поддающихся
анализу с помощью теории возмущений (как, например, сверх-
сверхпроводимость и бозе-газ, состоящий из твердых сфер).
2. Вполне может случиться, что правила Фейнмана в некой
видоизмененной форме окажутся долговечнее, чем сложная ма-
математическая конструкция локальной квантовой теории поля, ос-
основанная на таком идеализированном понятии, как поле, задан-
заданное в фиксированных точках пространства-времени. Поэтому мы
будем в первую очередь развивать фейнмановские правила не-
независимо от формализма теории поля. С течением времени мо-
может выясниться, что формализм этот есть скорее надстройка,
чем фундамент теории.
3. Такой путь построения — более прямой и менее формаль-
формальный и, возможно, не столь трудный для понимания, как дедук-
дедуктивный теоретико-полевой подход. Он должен вооружить мето-
методами вычисления и анализа фейнмановских диаграмм круг фи-
физиков, значительно более широкий, чем круг теоретиков, вла-
владеющих методом вторичного квантования. В особенности мы
имели в виду наших коллег экспериментаторов и студентов, ин-
интересующихся физикой элементарных частиц. Мы полагаем, что
такое изложение предмета окажется полезным.
Первоначально мы намеревались написать одну книгу, но
со временем она превратилась в два тома. В первом томе «Ре-
«Релятивистская квантовая механика» мы излагаем метод функ-
функции распространения для дираковских частиц, фотонов и подчи-
подчиняющихся уравнению Клейна — Гордона мезонов, и проводим
ряд вычислений для иллюстрации разнообразной полезной тех-
техники и приемов, используемых в теории электромагнитного, сла-
слабого и сильного взаимодействий. Сюда относятся определение
и проведение процедуры перенормировок и вычисление радиа-
радиационных поправок, таких как лэмбовское смещение в низшем
приближении. Для чтения этой книги достаточно владеть кур-
курсом нерелятивистской квантовой механики, например, в объеме
книги Л. Шиффа «Квантовая механика» (Москва, ИЛ, 1957).
Во втором томе «Релятивистские квантовые поля» мы изла-
излагаем каноническую теорию поля и затем, построив с помощью
техники Лемана — Шиманчика — Циммермана (LSZ) замкну-
замкнутые выражения для функций распространения и амплитуд рас-
рассеяния, вновь возвращаемся к диаграммам Фейнмана. Пока-
Показано, что разложение амплитуды рассеяния в ряд теории воз-
возмущений, полученное в рамках канонической теории поля, совпа-
совпадает с рассмотренным в первом томе разложением по правилам
Фейнмана. Путем дальнейшего анализа диаграмм мы исследуем
аналитические свойства фейнмановских амплитуд в любом по-
порядке по константе связи и разъясняем дисперсионные методы.

10 ПРЕДИСЛОВИЕ
В заключение мы доказываем перенормируемость квантовой
электродинамики в любом порядке по взаимодействию.
Не останавливаясь более подробно на материале, изложен-
изложенном в курсе, перечислим основные вопросы, которые в нем не
освещены. Полностью отсутствует изложение принципа действия
и предложенная Швингером формулировка квантовой теории
поля, основанная на вариационном подходе. Мы прибегаем к
вариации действия только при исследовании свойств симметрии.
Опущено подробное обсуждение еще двух вопросов: существен-
существенного прогресса, достигнутого в аксиоматической квантовой тео-
теории поля, с одной стороны, и не связанного с теорией поля S-
матричного подхода — с другой. За исключением содержащегося
в первом томе обсуждения лэмбовского сдвига и спектра атома
водорода, проблема связанных состояний не рассматривается.
Дисперсионные соотношения лишь в минимальной степени
используются в динамических вопросах. Не приводится форму-
формулировка квантовой теории поля для массивных векторных мезо-
мезонов, так же как и теории поля, содержащей связи с производ-
производными. Кроме того, мы не подготовили библиографию всех су-
существенных оригинальных работ по рассмотренным в нашем
труде вопросам. Отмеченные пробелы могут быть восполнены
с помощью изданных в последнее время монографий и учеб-
учебников [1 —20].
В заключение мы обязаны поблагодарить многих студентов
и наших коллег, которые были чуткими слушателями и неоце-
неоценимыми критиками в тот период, когда наши лекции превраща-
превращались в написанные главы, профессора Леонарда Шиффа, вооду-
воодушевившего нас на написание этих книг и оказавшего затем
поддержку, а также Розмари Стэмпфель и Элен Манн за бле-
блестящую оформительскую работу.
Джеймс Д. Бьеркен
Сидней Д. Дрелд

ГЛАВА 1
УРАВНЕНИЕ ДИРАКА
§ 1. Формулировка релятивистской квантовой теории
Поскольку принципы специальной теории относительности
являются в настоящее время общепринятыми, правильно по-
построенная квантовая теория должна удовлетворять релятивист-
релятивистским требованиям: законы движения, справедливые в одной инер-
циальной системе, должны быть справедливы во всех инерци-
альных системах. На математическом языке это означает, что
релятивистская квантовая теория должна быть сформулирована
в ковариантной относительно преобразований Лоренца форме.
Переходя от нерелятивистской к релятивистской квантовой
механике, мы попытаемся сохранить принципы, лежащие в ос-
основе нерелятивистской теории. Ниже мы кратко напоминаем эти
принципы '):
1. Для заданной физической системы существует вектор со-
состояния Ф, который содержит всю информацию о рассматривае-
рассматриваемой системе. Излагая на первых порах одночастичную релятиви-
релятивистскую теорию, мы обычно будем иметь дело с координатным
представлением вектора состояния, т. е. с волновой функцией
¦ф(<7ь ..., <?п; si sn; t). Волновая функция ^(q,s,t) яв-
является комплексной функцией от всех классических степеней
свободы <7ь ..., <?п, времени t и дополнительных степеней сво-
свободы, таких как спин s*, имеющих квантовомеханическую при-
природу. Сама волновая функция не имеет прямой физической ин-
интерпретации, однако квадрат ее модуля, \ty(qu .., qn\ s\, ¦¦¦
..., sn; t)\2 ^ 0, интерпретируется как вероятность того, что в
момент времени t система характеризуется набором переменных
<?ь ..., <7„; Si, ..., sn. Из вероятностной интерпретации очевид-
очевидным образом следует, что для физически допустимых волновых
функций ty величина \ty\2 должна быть конечной для любых зна-
значений <7ь ..., <7„; Si, ..., sn в любой момент времени t.
2. Любой наблюдаемой физической величине соответствует
линейный эрмитов оператор. В частности, канонической
') Подробнее см. курсы [21—24].

12 УРАВНЕНИЕ ДИРАКА (ГЛ. 1
переменной импульса pi отвечает в координатном пространстве
следующий оператор:
h д
3. Физическая система является собственным состоянием опе-
оператора Q, если
ЙФ„ = со„Ф„, A.1)
где Ф„ — п-е собственное состояние, отвечающее собственному
значению а>п. Для эрмитова оператора шп — действительная ве-
величина. В координатном представлении уравнение A.1) имеет
вид
й (q, s, t) -фп (q, s, t) = со„г|)я (q, s, t).
4. Постулат о разложении гласит, что произвольная волно-
волновая функция, или вектор состояния, физической системы может
быть разложена по полной ортонормированной системе собствен-
собственных функций tyn полного набора коммутирующих операторов.
Следовательно, мы можем записать
Ф = Z ОпУп,
п
а условие ортонормированности имеет вид
-. О *»(*/. ••¦• Sl •••> () = 6пт-
Величина |ап|2 есть вероятность того, что система находится
в и-м собственном состоянии.
5. Результатом измерения наблюдаемой физической величины
является одно из ее собственных значений. В частности, если
физическая система описывается волновой функцией ф=2 «п^ге,
где Q^n = a>ni>n, измерение наблюдаемой физической вели-
величины Q дает собственное значение шГ1 с вероятностью |ап|2.
Среднее значение наблюдаемой Q по большому числу измере-
измерений, проведенных в одинаково приготовленных системах, дается
выражением
)*( )Q{ .... s, .... /) =
6. Развитие физической системы во времени описывается
уравнением Шредингера
|f A.2)

§ 2| ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 13
в котором гамильтониан Н является линейным эрмитовым опе-
оператором. Для замкнутой физической системы гамильтониан не
зависит явно от времени, т. е. dH/dt = 0, и в этом случае его
собственные состояния являются возможными стационарными
состояниями системы. Принцип суперпозиции следует из линей-
линейности гамильтониана Н, а сохранение вероятности из свойства
эрмитовости Н:
Х15 = о. A.3)
Мы постараемся сохранить перечисленные шесть известных
принципов в качестве фундамента релятивистской квантовой
теории.
§ 2. Предварительные замечания
Простейшей физической системой является свободная изо-
изолированная частица, нерелятивистский гамильтониан которой
имеет вид
Переход к квантовой механике осуществляется путем замены
H-ythjf, p-^yV, A.5)
которая приводит к нерелятивистскому уравнению Шредингера
<А^ = ^-1>(*,0. A.6)
Уравнения A.4) и A.6) нековариантны и потому не могут быть
признаны удовлетворительными. Их левые и правые части по-
разному преобразуются при лоренцевых преобразованиях. Со-
Согласно специальной теории относительности полная энергия Е
и импульс (рх, ру, Pz) преобразуются как компоненты четырех-
четырехмерного вектора')
квадрат длины которого равен
з
ц-0
) При этом Рц=Г—, — pj, xli = (ct, — х). (Прим. ред.)

\4 УРАВНЕНИЕ ДИРАКА [ГЛ. 1
где т — масса покоя частицы, ас — скорость света в вакууме.
Более подробное обсуждение используемых в книге ковариант-
ных обозначений содержится в приложении А. Отметим, что со-
соответствие A.5) между классическими величинами и операто-
операторами ковариантно относительно преобразований Лоренца, ибо
оно устанавливает связь между двумя контравариантными 4-
векторами1) p^-»-ifi д/дх^.
Рассуждая подобным образом, естественно в качестве га-
гамильтониана релятивистской свободной частицы взять выраже-
выражение
Н = Vp2c2 + m2c4; A.8)
тогда релятивистский аналог A.6) будет выглядеть так:
mJtL = у_ ft2c2V2 + mV ifr. A.9)
Тут мы сразу сталкиваемся с проблемой интерпретации квадрат-
квадратного корня из оператора в правой части A.9). Если разложить
корень в ряд, мы получим уравнение, содержащее все степени
оператора дифференцирования; следовательно, теория нело-
нелокальна. В таких теориях имеются серьезные трудности и они
представляют собой весьма непривлекательный вариант уравне-
уравнения Шредингера, в которое пространственные координаты и
время входят несимметричным образом.
В целях математической простоты (а возможно, за неиме-
неимением убедительной физической картины) мы избавимся от квад-
квадратного корня из оператора в уравнении A.9), записав
Я2 = р2с2 + т*с\ A.10)
Другой, эквивалентный способ — дважды подействовать опера-
операторами, входящими в A.9). Тогда, пользуясь тем2), что при
[Л,Б] = 0 из Лф = Bty следует A2ty = B2ty, мы получаем урав-
уравнение
_ ft2 -^г у = (- h2V2c2 + т2с4) Ц,
в котором нетрудно узнать классическое волновое уравнение
где
дх*
') Согласно нашим определениям xa — (ct, x) и V11 =
дхи '
2) Мы будем всюду использовать обозначение [Л, б] &= АВ — ВА для ком-
коммутатора и {А, В) == АВ -\- ВА — для антикоммутатора.

§ 2J ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ 15
Прежде чем продолжить исследование уравнения A.11), за-
заметим, что, возводя в квадрат выражение для энергии, мы ввели
добавочный корень, отвечающий отрицательной энергии:
Н = - л/У с2 + т2с4 .
Для того чтобы получить простое уравнение, мы пожертвовали
положительно определенной энергией, и возникла трудность,
связанная с существованием «лишних» решений с отрицатель-
отрицательной энергией. Трудность эта оказывается преодолимой (мы уз-
узнаем об этом из гл. 5), и решениям с отрицательной энергией
можно дать физическую интерпретацию. Эти решения связаны
с античастицами, существование которых в природе является
сильным экспериментальным подтверждением обсуждаемой схе-
схемы. Поэтому будем пока рассматривать соотношение A.10) и
вытекающее из него уравнение A.11).
Наша первая задача состоит в построении сохраняющегося
потока, поскольку уравнение A.11) есть уравнение второго
порядка и отличается от уравнения Шредингера A.2), которое
является основой для вероятностной интерпретации нерелятиви-
нерелятивистской теории. Аналогично тому, как находится сохраняющийся
поток для уравнения Шредингера, помножим A.11) на ф*, за-
затем сопряженное уравнение помножим на г|з и результаты выч-
вычтем один из другого:
или
Величине 1-^—г I I ty -тт—^~1п) хотелось бы придать
смысл плотности вероятности р. Это, однако, невозможно, по-
поскольку она не является положительно определенной. Поэтому,
следуя историческому пути развития [25], мы на время отка-
откажемся от уравнения A.11) в надежде найти уравнение, содер-
содержащее первую производную по времени и допускающее, как и
уравнение Шредингера, непосредственную вероятностную трак-
трактовку. Мы еще вернемся к уравнению A.11). Хотя в дальней-
дальнейшем нам удастся найти уравнение первого порядка, окажется
все же невозможным сохранить положительно определенную од-
ночасгичную плотность вероятности и одновременно придать
физический смысл отрицательному корню A.10). Поэтому урав-

16 УРАВНЕНИЕ ДИРАКА (ГЛ. 1
нение A.11), которое часто называют уравнением Клейна— Гор-
Гордона, претендует на роль релятивистского квантового уравнения
ничуть не меньше, чем уравнение, к изучению которого мы сей-
сейчас приступаем.
§ 3. Уравнение Дирака
Наше изложение будет следовать историческим работам Ди
рака 1928 г. [26, 23] по поиску релятивистски-ковариантного
уравнения вида A.2) с положительно определенной плотностью
вероятности. Поскольку такое уравнение содержит производную
по времени первого порядка, естественно попытаться построить
гамильтониан, содержащий первые производные по пространст-
пространственным координатам. Подобное уравнение может выглядеть так:
^. A.13)
Входящие сюда коэффициенты а,- не могут быть просто чис-
числами, так как тогда уравнение не будет инвариантно даже от-
относительно обычных пространственных вращений. Кроме того,
если мы хотим оставаться в рамках сформулированных в § 1
общих требований, волновая функция гр не может быть скаля-
скаляром. Действительно, для того чтобы в фиксированный момент
времени / интеграл по всему пространству от плотности вероят-
вероятности р — г|з*1|5 был инвариантом, величина р должна быть вре-
временной компонентой сохраняющегося 4-вектора.
Чтобы избавить уравнение A.13) от этих недостатков, Ди-
Дирак предложил рассматривать его как матричное уравнение.
По аналогии со спиновыми волновыми функциями в нерелятиви-
нерелятивистской квантовой механике волновая функция ty задается в виде
столбца с N компонентами
а постоянные коэффициенты а,- и р — в виде матриц размерно-
размерности N X N. В итоге уравнение A.13) заменяется на систему N
уравнений первого порядка
.f. dibn he V"* ( & i d i д \ , , V a •> ¦
lh дГ = T L lttl ^ + a2 a^" + a3 aFjot ^+ L^mc

§ 3] УРАВНЕНИЕ ДИРАКА 17
Мы далее всюду используем матричные обозначения и опу-
опускаем индексы суммирования. Тогда система A.14) внешне вы-
выглядит как уравнение A.13), но теперь A.13) следует понимать
как матричное уравнение.
Для того чтобы можно было считать уравнение A.13) от-
отправным пунктом для дальнейшего построения теории, оно
должно удовлетворять трем условиям. Во-первых, оно должно
приводить к правильной связи между энергией и импульсом
свободной частицы
?2 = р2с2 _|_ т2с4>
во-вторых, допускать уравнение непрерывности и вероятностную
интерпретацию волновой функции г|з и, в-третьих, быть лоренц-
ковариантным. Сейчас мы рассмотрим первые два из этих тре-
требований.
Правильное соотношение между энергией и импульсом сле-
следует из уравнения A.13) в том случае, если каждая из компо-
компонент ty0 волновой функции ty удовлетворяет уравнению второго
порядка Клейна — Гордона
-К2^ = (-П2с2У2 + т*с*)%. A.15)
Квадрируя уравнение A.13), находим
aiai+aiai дч
fa 2 дх'дх'
о I о \ <5Ф I O2 2 4 i
Х;й -+- ра,) —-Ц 4- В m с гЬ.
Мы можем привести это уравнение к виду A.15), если матрицы
а( и р подчиняются следующей алгебре:
Какими еще свойствами должны обладать матрицы а,- и р, и
можем ли мы построить эти четыре матрицы в явном виде? Мат-
Матрицы а, и р должны быть эрмитовыми, тогда входящий в урав-
уравнение A.14) гамильтониан Нах будет эрмитовым оператором,
как того требуют сформулированные в § 1 постулаты. Поскольку
согласно A.16) а2 = 62=1, собственные значения щ и 8 равны
±1. Из соотношений антикоммутации вытекает, что след, т. е.
сумма диагональных элементов, каждой из матриц ее, и В ра-
равен нулю. Например,

18 УРАВНЕНИЕ ДИРАКЛ [ГЛ. 1
Под знаком Sp матрицы можно циклически переставлять,
Sp АВ = Sp В А; отсюда получаем
Sp щ = + Sp р2а< = + Sp 0агр = — Sp at = 0.
Поскольку след есть сумма собственных значений, число соб-
собственных значений, равных -|-1, должно совпадать с числом
собственных значений, равных —1, и, следовательно, матрицы
а; и р четной размерности. Наименьшая четная размерность,
iV = 2, не подходит, так как ей отвечает набор лишь из трех
антикоммутирующих друг с другом матриц Паули а, и единич-
единичной матрицы. Минимальная размерность N, допускающая по-
построение матриц a.i и р, равна четырем, и именно случай М = 4
мы будем изучать. В одном из конкретных представлений мат-
матрицы а.{ и р имеют вид
¦ ч°1 ° )' P~U -l ;•
где о, — известные матрицы Паули размерности 2X2, а 1 в
матрице р означает единичную матрицу 2>B
Для получения закона сохранения тока в дифференциальной
форме мы, во-первых, вводим эрмитово-сопряженную волновую
функцию ^+ = (^j ... г|L) и умножаем A.13) слева на г|>+:
AЛ8)
Затем построим уравнение, эрмитово-сопряженное к A.13), и
умножим его справа на ф:
4
dt i dx
здесь а+ = аг, р+ = р. Вычитая A.19) из A.18), находим
з
fie d , + .
ИЛИ
^rp + divj = O. A.20)
В этом уравнении мы отождествили с плотностью вероят-
вероятности и с трехмерным вектором плотности тока вероятности

$ 4] ПЕРЕХОД К НЕРЕЛЯТИВИСТСКОЙ ТЕОРИИ |Q
следующие величины:
4
р = ф+1|)=Е*>0, A-21)
0=1
ik = cV+atf. A-22)
Интегрируя A.20) по всему пространству и используя теорему
Грина 1), получаем
|$Лг|Л|) = 0. A.23)
Это равенство поддерживает нашу интуитивную интерпретацию
величины р = г|)+г|; как положительно определенной плотности
вероятности.
Обозначения в уравнении A.20) подчеркивают, что плотность
тока вероятности j является вектором, если равенство A.22) ин-
инвариантно по отношению к поворотам трехмерной системы ко-
координат. На самом деле нам нужно доказать справедливость
гораздо более общего утверждения.
Чтобы обеспечить ковариантность уравнения непрерывности
и возможность вероятностной интерпретации, плотность веро-
вероятности и плотность тока вероятности в уравнении A.20) долж-
должны образовывать четырехмерный вектор по отношению к пре-
преобразованиям Лоренца. Кроме того, прежде чем признать урав-
уравнение Дирака A.13) удовлетворяющим нашим требованиям, мы
должны показать его лоренцеву ковариантность.
§ 4. Переход к нерелятивистской теории
Прежде чем углубляться в проблему лоренцевой инвариант-
инвариантности уравнения Дирака, полезно убедиться в том, что это урав-
уравнение имеет физический смысл.
Можно начать просто с рассмотрения свободного электрона
и подсчитать число решений для электрона в покое. В этом слу-
случае уравнение A.13) упрощается и принимает вид
поскольку де-бройлевская длина волны бесконечно велика и
волновая функция постоянна во всем пространстве. В частном
представлении A.17) для матрицы р нетрудно выписать четыре
') Равенство \ divAdy=(T>AdS в отечественной литературе принято
v ?
называть теоремой Остроградского — Гаусса. (Прим. перев.)

20 УРАВНЕНИЕ ДИРАКА [ГЛ. 1
решения этого уравнения:
0
|, гр' = ехр< W~'\\ n I'
A.24)
из которых первые два отвечают положительной энергии, а два
других — отрицательной.
Посторонние решения с отрицательной энергией, к которым
приводит квадратичная форма Н2 — р2с2 + т2с4, являются ос-
основной трудностью, однако преодоление этой трудности приво-
приводит к такому важному триумфу теории, как античастицы. Мы
вернемся к этому вопросу в гл. 5 Пока же ограничимся «допу-
«допустимыми» решениями с положительной энергией. В частности,
покажем, что для них имеется разумный переход к двухкомпо-
нентной теории спина Паули. Для этой цели мы введем взаимо-
взаимодействие с внешним электромагнитным полем, описываемым
4-потенциалом,
Лм: (Ф, А).
Взаимодействие проще всего ввести путем калибровочно-инва-
риантной замены
р^/-|Л>\ A.25)
которая производится в классической релятивистской механике
при описании взаимодействия точечной частицы, обладающей
зарядом е, с внешним полем. В нашем случае замена согласно
A.5)
и A.25) приводят уравнение Дирака A.13) к виду
ih |f = (са • (р —i А) + рте2 + еф) ф. A.26)
Уравнение A.26) описывает «минимальное» взаимодействие ди-
раковской частицы, рассматриваемой как точечный заряд, с
внешним электромагнитным полем. Чтобы подчеркнуть анало-
аналогию с классикой, мы записали гамильтониан в A.26) в виде
И = //0 + И', где Н' = —еа-А + еФ. Матрица са является опе-
операторным аналогом скорости в классическом выражении для

§ 4] ПЕРЕХОД К НЕРЕЛЯТИВИСТСКОЙ ТЕОРИИ 2t
энергии взаимодействия точечного заряда:
//класс = — 7 v • А + еФ.
Это операторное соответствие vonep = са легко прослеживается
и в выражении A.22) для тока вероятности Оно следует также
из релятивистского обобщения соотношений Эренфеста [21—23]
\H r] ca v
4^ = 4E + 7vonepXB]( A.27)
где я = р — (е/с) А— оператор, соответствующий импульсу, и
E = --4?--V<I>, B = rotA
с at '
—напряженности электрического и магнитного полей.
Уравнение A.27) есть операторное уравнение для движения
точечного заряда е. Введение более общего взаимодействия в
уравнение A.26) привело бы, по аналогии с классической тео-
теорией, к появлению магнитного дипольного члена и членов более
высокой мультнпольности.
Переходя в уравнении A.26) к нерелятивистскому пределу,
удобно воспользоваться представлением A.17) и выразить вол-
волновую функцию через двухкомпонентные столбцы ф и %:
-(f).
A.И)
Тогда уравнение A.26) примет вид
В нерелятивистском пределе наибольшей из фигурирующих
в задаче энергий является энергия покоя тс2. Поэтому мы запи-
запишем
где функции ф и % медленно меняются со временем и удовлет-
удовлетворяют паре матричных уравнений

22 УРАВНЕНИЕ ДИРАКА [ГЛ. 1
Если кинетическая энергия и энергия взаимодействия малы по
сравнению с тс2, второе из уравнений A.30) приводится к виду
^- A.31)
Уравнение A.31) позволяет говорить о х как о «малой» компо-
компоненте волновой функции г|з по сравнению с «большой» компонен-
компонентой ф. В нерелятивистском приближении % имеет по отношению
к ф малость порядка и/с<§;1. Подставляя A.31) в первое из
уравнений A.30), мы получаем двухкомпонентное спинорное
уравнение
Преобразуем это уравнение, используя следующее тождество
для спиновых матриц Паули:
а • а о • b = а • b + ш • а X Ь,
или, в нашем случае,
в к а-« = я2+ io -пХк = п2 — ~а ¦ В. A.33)
Тогда мы получаем уравнение
В + еФ ф, A.34)
в котором легко узнать уравнение Паули [21—23].
Уравнение A.34) дает нам уверенность в том, что мы пошли
по верному пути, приняв уравнения A.13) и A.26) за отправную
точку для построения теории релятивистского электрона. Две
компоненты ф соответствуют двум степеням свободы электрона
со спином половина; правильное значение магнитного момента
электрона, отвечающее гиромагнитному отношению g = 2, по-
получается автоматически. Чтобы явно убедиться в этом, преобра-
преобразуем уравнение A.34), сохранив в нем только члены первого
порядка по взаимодействию со слабым однородным магнитным
полем В = rot А, А^'/гВХг:
Здесь L = rXP—орбитальный угловой момент, S = ]/2h(f —
оператор спина электрона с собственными значениями ±fi/2, a
множитель при члене, описывающем взаимодействие спина с по-
полем В, дает правильное значение магнитного момента элек-
электрона, отвечающее значению g, равному 2.

ЗАДАЧИ 23
Вдохновленные успешным переходом к нерелятивистскому
пределу в уравнении Дирака, мы двинемся дальше и установим
лоренцеву ковариантность теории Дирака. Затем мы должны
исследовать дальнейшие физические следствия этой теории; в
первую очередь надо дать физическую интерпретацию решениям
с «отрицательной энергией».
ЗАДАЧИ
1. Запишите уравнения Максвелла в дираковской форме A.13), используя
шестикомпонентные амплитуды поля. Какие матрицы соответствуют матрицам
а и Р? (См. [27, 4*].)
2. Проверьте, что матрицы A.17) удовлетворяют алгебре A.16)
3. Проверьте соотношение A.33).
4. Проверьте соотношение A.27).

ГЛАВА 2
ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ
УРАВНЕНИЯ ДИРАКА
§ 5. Уравнение Дирака в ковариантной форме
Уравнение Дирака и лежащее в основе его физической ин-
интерпретации уравнение непрерывности должны быть ковариант-
ными относительно преобразований Лоренца. Напомним сна-
сначала, что мы подразумеваем под преобразованием Лоренца Г28].
Два наблюдателя О и О', находящиеся в разных инерциаль-
ных системах отсчета, приписывают одному и тому же физи-
физическому событию разные пространственные координаты и время.
Соответствие между координатами *>\ которыми описывает со-
событие наблюдатель О, и координатами (х11)'. которыми поль-
пользуется для описания того же события наблюдатель О', задается
преобразованием Лоренца
з
М'==1ау = аУ- B.1)
Это линейное однородное преобразование и коэффициенты а?
зависят только от относительных скоростей и ориентации двух
систем отсчета О и О'. Основным инвариантом по отношению к
преобразованиям Лоренца является интервал собственного вре-
времени
ds2 = ^v dx» dxv = dx» dx^. B.2)
Инвариантность этой величины следует из физического наблю-
наблюдения, состоящего в том, что скорость света в вакууме одна и
та же во всех лоренцевых системах отсчета Равенства B.1) и
B.2) приводят к следующему соотношению для коэффициентов
преобразования:
<а" = 6*. B.3)
Соотношения B.!) и B.3) служат определением как соб-
собственного, так и несобственного преобразований Лоренца. В пер-

§ 5| УРАВНЕНИЕ ДИРАКА В КОВАРИАНТНОЙ ФОРМЕ 25
вом случае определитель, составленный из коэффициентов пре-
преобразования, удовлетворяет условию
deta = + 1.
Собственное преобразование Лоренца может быть представлено
как бесконечная последовательность инфинитезимальных преоб-
преобразований. Собственные преобразования Лоренца включают в
себя переходы между различными инерциальными системами
координат, движущимися в произвольных направлениях, и обыч-
обычные трехмерные вращения. Несобственные преобразования Ло-
Лоренца— это дискретные преобразования пространственного от-
отражения и обращения времени. Их нельзя представить как
последовательность инфинитезимальных преобразований. Мат-
Матрицы несобственных преобразований удовлетворяют условию
deta = - 1,
справедливому как для пространственного отражения, так и для
обращения времени.
Наша задача — установить соответствие между заданной се-
серией наблюдений, произведенных над дираковской частицей на-
наблюдателем О, и теми же наблюдениями, осуществленными на-
наблюдателем О', находящимся в другой системе отсчета. Иначе
говоря, мы ищем закон преобразования, связывающий волновые
функции гК*) и ty'(x')< относящиеся к наблюдателям О и О' со-
соответственно. Этот закон преобразования позволяет наблюда-
наблюдателю О' найти г|)'' (х') по известной функции ty(x). Согласно тре-
требованию лоренцевои ковариантности этот закон преобразования
должен приводить к волновым функциям, которые являются ре-
решениями уравнения Дирака, имеющего один и тот же вид во
всех системах отсчета. Неизменная форма уравнения Дирака
есть выражение лоренцевои инвариантности лежащего в его
основе соотношения между энергией и импульсом
РцРи = т2с2,
на которое опирались приведенные в гл. 1 рассуждения.
Для обсуждения свойств ковариантности желательно запи-
записать уравнение Дирака в четырехмерных обозначениях, обеспе-
обеспечивающих симметрию между ct и хк С этой целью умножим
A.13) на р/с и введем обозначения
Y° = P, Y' = Pa<, /=1, 2, 3.
Тогда получаем
I| 8|J)-0. B.4)

2fi ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА |ГЛ. 2
Вновь введенные матрицы уй позволяют придать изящную
форму коммутационным соотношениям A.16):
B.5)
где 1 означает единичную матрицу размерности 4X4; в даль-
дальнейшем мы не будем каждый раз это оговаривать. Из опреде-
определения этих матриц ясно, что у' антиэрмитова, причем (у'J =
= —1, а у0 эрмитова. В представлении A.17) они имеют вид
v=U «')• Mi -?)• м
Удобно ввести обозначения с «крышкой» '):
и, в частности,
дх» с dt
Тогда уравнение B.4) в сокращенном виде выглядит так:
(zTzV - тс) г|) = 0, B.7)
или, вводя р^ = ih ——,
(р — тс) г|з = 0. B.8)
Введение электромагнитного взаимодействия путем «минималь-
«минимальной» замены A.25) дает
(р - ¦—¦ - тс} Мр = 0.
Такая замена никак не влияет на свойства ковариантности, по-
поскольку р^ и Л", а следовательно, и их разность являются 4-век-
торами.
§ 6. Доказательство ковариантности
Для доказательства ковариантности уравнения Дирака от-
относительно преобразований Лоренца мы должны установить, что
выполняются следующие два условия. Во-первых, должно су-
существовать явное правило, по которому наблюдатель О' мог
') Авторы используют «перечеркнутые» обозначения:
однако мы сочли возможным заменить их обозначениями, принятыми с оте-
отечественной литературе. (Прим. перев.)

% 6] ДОКАЗАТЕЛЬСТВО КОВАРИАНТНОСТИ 27
бы, зная волновую функцию ty(x), относящуюся к наблюдателю
О, найти волновую функцию ty'(x')> описывающую то же самое
состояние и относящуюся к наблюдателю О'. Во-вторых, в со-
соответствии с принципом относительности, ty'(х') должна быть
решением уравнения, которое имеет вид B.7) в штрихованной
системе координат:
Матрицы у11 удовлетворяют условиям антикоммутации B.5),
поэтому из эрмитовости гамильтониана следует, 4to(y°)+ = y° и
(у')+ = — y'. Длинное алгебраическое доказательство [29]
приводит к тому, что все такие матрицы yu размерности 4X4
эквивалентны с точностью до унитарного преобразования U:
поэтому мы не будем делать различия между у'' и уд и за-
запишем
''(*') = 0, B.9)
где
Мы потребуем, чтобы преобразование между гр и гр' было
линейным, так как и уравнение Дирака, и преобразование Ло-
ренца для координат B.1) являются линейными. Введем это
преобразование в следующем виде:
г|/ (*') = л|/ (ах) = S (а) г|> (х) = S (а) ф (а~ U"'), B.10)
где S(а)—матрица размерности 4X4, действующая на четы-
рехкомпонентный вектор гр (х). Она зависит от относительных
скоростей и пространственных ориентации систем О и О'. Мат-
Матрица S должна иметь обратную матрицу, так чтобы наблюда-
наблюдатель О, зная функцию г|/(л:'), которую наблюдатель О'исполь-
О'использует для описания заданного физического состояния, мог по-
построить свою волновую функцию гр (л:):
^(x) = S^(a)^(x') = S-[(a)^(ax). B.11)
Столь же правильно будет, воспользовавшись B.10), предста-
представить гр(х) в виде
Отсюда следует равенство

28 ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА 1( П. 2
Главная задача — найти S. Матрица S должна удовлетворять
равенствам B.10) и B.11). Если такая матрица S существует,
наблюдатель О' по заданному значению ty(x) сможет найти
гр'(х'), воспользовавшись B.10).
Равенство B.11) позволяет наблюдателю О' переписать для
функции ip'(x') уравнение Дирака B.7), относящееся к наблю-
наблюдателю О. Затем О' может проверить, удовлетворяет ли i|/(x1)
его собственному уравнению B.9). После умножения слева на
S(a) он получит
\ihS (a) v^S"' (а) -^- - тс] ф' (х') = 0.
L дх» J
Используя B.1), можно записать
д dx'v д „ д
dx'v °» дхч
Следовательно, уравнение в «штрихованных» координатах имеет
вид
\ihS (a) y^S'1 (а) с? -4- - тс] ф' {/) = 0.
L dxv J
Это уравнение имеет инвариантную форму, т. е. совпадает
с B.9), если можно найти матрицу S, обладающую следующим
свойством:
или, что то же самое,
^ 1 B.12)
Уравнение B.12) есть основное соотношение, определяющее S.
Если мы покажем, что уравнение B.12) имеет решение, и най-
найдем это решение, ковариантность уравнения Дирака будет до-
доказана. По существующей терминологии волновую функцию,
преобразующуюся согласно B.10) и B.12), называют четырех-
четырехмерным лоренцевым спинором1). Мы подчеркиваем, что S бу-
будет иметь новые свойства, не описываемые обычным тензорным
исчислением, поскольку можно ожидать, что билинейные формы,
которые можно составить из гр, такие, например, как ток вероят-
вероятности A.20), окажутся 4-векторами.
Сначала мы построим 5 для инфинитезимального собствен-
собственного преобразования Лоренца
а1 = el + Н, а^ = g*» + Аш^, B.1 За)
где
Aojvm. _ _ A(oM.v> B.136)
») Или биспинором. (Прим. перев.)

§ 6) ДОКАЗАТЕЛЬСТВО КОВАРИАНТНОСТИ 29
Последнее равенство следует из условия B.3) для интервала
собственного времени. Каждый из шести отличных от нуля неза-
независимых матричных элементов матрицы Аи генерирует инфини-
тезимальное преобразование Лоренца; например, элемент
Дш01 = Да/с
отвечает переходу к системе координат, движущейся со ско-
скоростью Аи вдоль оси х, а
АЦ = — Дсо12 = Aqp
отвечает повороту на угол Дф вокруг оси г, и т. д.
Разлагая S по степеням Ди^' и сохраняя только линейные
по инфинитезимальным генераторам члены, получаем
S=l-4<vAu»|iV и S"' = l + 4^vA(o^v, B.14)
где согласно B.136)
Каждый из шести коэффициентов cruV есть матрица той же раз-
размерности 4X4, что и оператор S и единичная матрица 1. Под-
Подставляя B.13) и B.14) в B.12) и удерживая только члены
первого порядка по Д©^, находим
Отсюда, учитывая антисимметрию генераторов Дш^, получаем
2/toe-^Ye) = [Yv, <таВ]. B.15)
Теперь задача об установлении ковариантности уравнения
Дирака относительно собственных преобразований Лоренца све-
сведена к нахождению шести матриц оаз, удовлетворяющих усло-
условию B.15). Самое простое предположение относительно aag со-
состоит в том, что они являются антисимметризованными произ-
произведениями двух матриц. Используя B.5), мы находим, что
V> = 4-[VYv] B.16)
и есть искомая матрица. Согласно B.14) матрица S для инфи-
нитезимального преобразования имеет вид
5=1 + jfYu, Yv] A«a"v= I --f^vAffl^- B.17)
Завершая решение нашей задачи, получим конечное соб-
собственное преобразование Лоренца как последователь-
последовательность инфинитечнмальных преобразований. Сначала построим

30 ПОРЕНЦЕВА ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА (ГЛ. 2
преобразование B.1) из B.13). Запишем
V. B18)
Здесь Дсо— бесконечно малый параметр, или «угол поворота»
вокруг оси с направлением п, а величина 1п представляет собой
матрицу 4X4, действующую на пространственные координаты
и время и отвечающую повороту на единичный угол вокруг оси
п. Индексы v и \х нумеруют соответственнно строки и столбцы
этой матрицы. Так, например, для перехода к штрихованной си-
системе координат, движущейся вдоль оси х с бесконечно малой
скоростью, сАсо = Aw, имеем
При этом
Используя следующее алгебраическое свойство;
A 0 0 0ч
0 0 0 0 Г 1 =~т *>
оооо/
мы можем представить конечное преобразование к системе от-
отсчета, равномерно движущейся вдоль оси х, в виде
0
—1
0
0
—1
0
0
0
0
0
0
0
0
0
0
0
= (е«>Х & = (ch со/ + sh <о/? х» = A - /2 + Р ch со + /
откуда для отдельных компонент получаем
ch со — sh со 0 0'
— sh со ch со 0 0
0 0 10
0 0 0
ИЛИ
& = (ch со) (х° - th со*1), х1' = (ch со) (х1 - th со х°),
X
—; v2 y^ ; уЗ
B.21)
Связь угла лоренцева поворота со с относительной скоростью v
дается равенствами
th со = —, ch со = —. .

§ 6] ДОКАЗАТЕЛЬСТВО КОВАРИАНТНОСТИ 31
Этот результат можно обобщить на случай движения вдоль
любого направления или пространственного вращения вокруг
любой оси. Шесть матриц /^, генерирующих шесть независи-
независимых лоренцевых поворотов, являются четырехмерными обобще-
обобщениями поворотов трехмерного пространства, хорошо известными
из нерелятивистской теории.
Перейдем теперь к построению матрицы S, определяющей
конечное преобразование спинора г|з(*).Из B.14) и B.18) имеем
(х) = lim A - 4 -? a
V V * W
JV-»°o
B.22)
Если вновь обратиться к преобразованию частного вида B.19),
получим
^'{x') = e-w™^(x), B.23)
где х' я х связаны друг с другом равенствами B.21).
Аналогично для поворота на угол <р вокруг оси z имеем
/12 = _ /21 = _ !
и
ty'{x') = e«l2)<*°"^{x), B.24)
где в представлении A.17)
-"-(I- :,)¦
а сг3 есть обычная матрица Паули размерности 2X2
Мы замечаем сходство преобразования B.24) с поворотом двух-
компонентного спинора Паули у(х):
Входящие в B.18) ковариантные «угловые» переменные
играют в преобразовании Лоренца ту же роль, что угол пово-
поворота и направление ю в трехмерном вращении. Появление
в B.24) половинного угла, фигурирующего и в B.25), есть отра-
отражение двузначного характера закона преобразования спиноров
при вращении; нужно совершить поворот на 4я, чтобы значение
спинора вернулось к начальному. Поэтому все наблюдаемые
величины в теории Дирака должны быть либо билинейными по
ip(x), либо выражаться через другие четные степени г|)(х).
Для пространственных вращений матрица S = Sr унитарна,
поскольку матрица огз- эрмитова и

32 ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА [ГЛ. 2
Это несправедливо для матрицы 5 = SL, осуществляющей пере-
переход к движущейся системе координат. Например, для преобра-
преобразования B.23)
с -(i/2)WGo! -(щ/2) а, г.+ , o-i
oz. = е =е = oi =т==с>/ .
Однако SL обладает следующим свойством:
которое можно установить, разлагая SL в степенной ряд. По-
Поскольку [уо, оЩ = О, это свойство можно обобщить на вращения
и записать
'+Yo- B-26)
Уравнение непрерывности также ковариантно. Вектор плот-
плотности тока вероятности A.21) и A.22) в обозначениях B.4) вы-
выглядит так:
Под действием B.1) он переходит в
f = сг|/+ {/) y°y4' (х') = пр+ (х) S+Yoy'5^ (x) -
= с^+ (х) YoS-VStf W = са^+ (ж) Yoy4 M = flv/v (x). B.27)
Очевидно, что /д(х) является лоренцевым 4-вектором и урав-
уравнение непрерывности
дГ (х) п
инвариантно. Кроме того, плотность вероятности /°(х) = ср(х)
преобразуется как временная компонента сохраняющегося 4-век-
тора. Мы уже упоминали об этом свойстве в § 3 как о желае-
желаемом. Оно необходимо для того, чтобы интеграл
\ г|з+ (х) т|) (х) (Рх
представлял собой релятивистский инвариант.
Поскольку входящая в B.27) комбинация гр+Yo встречается
очень часто, введем для нее специальное обозначение
гр(х) = г1,+Уо. B.28)
Функцию ^(х) называют сопряженным спинором1). Преобразо-
Преобразование Лоренца для \j> (x) задается равенством
B.29)
') Или дираковски-сопряженным. (Прим. ред.)

§ 8] КОВАРИАНТНЫЕ БИЛИНЕЙНЫЕ ФОРМЫ 33
§ 7. Пространственное отражение
Теперь пора расширить наше изложение и принять во внима-
внимание существование несобственного преобразования Лоренца —
пространственного отражения:
х' = -х, f = /.
Для ковариантности вновь необходимо, чтобы уравнение
B.12) имело решение, однако в данном случае его нельзя по-
построить из инфинитезимальных преобразований. Но оказывает-
оказывается, что уравнение B.12) легко решить непосредственно. Матрица
преобразования имеет вид
A 0 0 0
0 -1 °
о о-1 о
0 0 0—1
Если ввести для оператора инверсии координат обозначение
S = Р, то уравнение B.12) будет выглядеть так1):
p-lyvP = gvY. B.31)
Ему можно удовлетворить, положив
Р = е«*уо- B.32)
Фазовый множитель не представляет физического интереса, и
его значения сводятся либо к ±1, либо к ±i. К такому выбору
мы приходим, потребовав, чтобы при четырехкратной инверсии
спинор переходил сам в себя по аналогии с вращением на угол
4л. Очевидно, что задаваемый равенством B.32) оператор Р
унитарен, Р~1 = Р+, и, кроме того, он удовлетворяет уравнению
B.26). Равенство B.32) означает, что
г|/ (/) = ф' (- х, /) = e"»Yo4> (x, /)• B.33)
В нерелятивистском пределе г|з стремится к собственному со-
состоянию Р и из A.24) и B.6) видно, что в покое состояния с по-
положительной и отрицательной энергией имеют разные собствен-
собственные значения Р, или, как говорят, разные внутренние четности.
Рассмотрение других несобственных преобразований, таких
как обращение времени, более сложно; оно приводится в гл. 5.
§ 8. Ковариантные билинейные формы
Составляя произведения из матриц у, можно построить 16 ли-
линейно независимых матриц Г^в, которые часто встречаются в
') Здесь суммирование по v не подразумевается. (Прим. ред.}

34 ЛОРЕНЦЕВА ИНВАРИАНТНОСТЬ УРАВНЕНИЯ ДИРАКА ГГЛ. 2
приложениях теории Дирака. Эти матрицы имеют вид
rp = /YVY2Y3 = Y5^Y5, r^YsY^. B.34)
Используя соотношения антикоммутации B.5), нетрудно до-
доказать линейную независимость матриц Г. Будем рассуждать
следующим образом:
1. Каждая из матриц Г" удовлетворяет условию (ГпJ =
= ±1.
2. Для каждой из матриц Гп, за исключением Ts, существует
другая матрица Гт такая, что
Отсюда следует, что след матрицы Г" равен нулю:
Sp Г" = Sp Г" (ГтJ = — Sp ГтГ"Гт = - Sp Г" (ГтJ = 0.
3. Для заданных матриц Га и Г6, а Ф Ь, существует матрица
Гп ф Гя такая, что
Это свойство можно установить непосредственной проверкой.
4. Предположим, что существует набор чисел ап такой, что
Умножим это равенство на Гт ф Г8 и вычислим след; используя
свойство 3, мы получим, что ат = 0. Если Гт = Гя, то as = 0
и все коэффициенты, таким образом, обращаются в нуль. Тем
самым линейная независимость Гп установлена. Отсюда сле-
следует, что любую матрицу размерности 4X4 можно представить
в виде комбинации матриц Г".
Теперь мы можем записать преобразование Лоренца для би-
билинейных форм г^(х) Гпар (х), построенных из 16 матриц Гп. За-
Заметим прежде, что
Y^Ys+YsY^O B.35)
и поэтому
[Y6, <*|iv] = 0,
или
[S, Ye] = 0, B.36)
что справедливо для всех собственных преобразований Ло-
Лоренца. Частным случаем B.35) является равенство
B.37)

ЗАДАЧИ 35
С помощью вычислений, схожих с B.27), находим
ф' (*') г|/ {/) = тр (л:) г|з (*) — скаляр,
*' (*0 У5? (*') = ф (*) ^"VsS^ (*) = det | а | ф (х) у5^> (х) - псевдо-
псевдоскаляр,
*' (*') Vv? {/) = ^ (х) y4 W - вектор,
¦ф' (л:') y5Yv^' (*') = det | а | а^ (х) у5У^Ф W — псевдовектор,
гр'(л;') (Т^уг|з'(л;') = а^а^ (х) ааег(з (л:) — тензор второго ранга. B.38)
ЗАДАЧИ
1. Проверьте равенство B.26).
2. Проверьте законы преобразования B.38).
3. Задан спинор и(р) для свободной частицы. С помощью преобразова-
преобразования Лоренца выразить через и(р) спинор и(р + q) в случае, когда д^ -> 0 и
4. Показать, что существуют четыре матрицы Г41 размерности 4X4 та-
такие, что
Re Г?р = 0. {1> Tv} = 2g|lv, [lTpd/дХь - m] * (л) = 0,
т. е. уравнение Дирака не содержит мнимых коэффициентов.

ГЛАВА 3
РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА
ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ
§ 9. Плоские волны
Мы убедились в том, что дираковская теория лоренц-кова-
риантна и для решений с положительной энергией имеется ра-
разумный переход к нерелятивистскому пределу.
Для более глубокого понимания физической природы реше-
решений уравнения Дирака надо рассмотреть уравнение для сво-
свободной частицы. Четыре решения для частицы в покое даются
формулами A.24), которые можно переписать в следующем
виде:
г|)г (*) = wr @) е-("гиг1/*) \ г = 1, 2, 3, 4, C.1)
где
+ 1, г= 1, 2,
j j- —— з ^
В представлении A.17) для матриц Дирака входящие сюда спи-
спиноры равны
A\ /°\ /°\ /°Л
Ч ш*@) = М, , шЗ@)= J , w40) = [ll C.2)
Первая пара решений описывает две спиновые степени свободы
электрона, подчиняющегося уравнению Паули. Другой паре ре-
решений (г = 3, 4) с отрицательной энергией еще предстоит дать
физическую интерпретацию. Все четыре решения являются соб-
собственными функциями оператора az — С12 с собственными зна-
значениями + 1 и —1. Решения для свободной частицы с произ-
произвольной скоростью можно получить с помощью преобразования
Лоренца B.10). Переходя к системе координат, движущейся
со скоростью —v относительно системы, в которой электрон по-

§9J
ПЛОСКИЕ ВОЛНЫ
37
коится, мы получим волновую функцию свободного электрона,
движущегося со скоростью +v.
Для того чтобы явно выразить зависимость от 4-радиус-век-
тора частицы, надо записать входящую в C.1) экспоненту в
инвариантной форме:
(
ехр ^—
= ехр
ier
(
= exp ^—
C.3)
где уУ-' = a^xv и р^ = a^pvm = а^тс; мы будем везде пользо-
пользоваться обозначением р° = Е/с =-\-л/р2-{• т2с2 > 0. При соб-
собственных преобразованиях Лоренца и пространственном отра-
отражении решения с положительной и отрицательной энергией пре-
преобразуются независимо, не перепутываясь друг с другом. Это
видно из выражения C.3), поскольку 4-импульс свободной ча-
частицы времениподобен, р^рп = тс2 > 0. Следовательно, 4-век-
тор р^ лежит внутри светового конуса в /7-пространстве. Преоб-
Преобразования Лоренца, дополненные пространственной инверсией,
не переводят ось р° из одной полости светового конуса в дру-
другую, поэтому сохраняется разделение решений на решения с по-
положительной и отрицательной энергией.
Согласно B.23) спиноры преобразуются с помощью опера-
оператора
S = e-('/2)«w«, C.4)
где для простоты мы выбрали направление скорости вдоль оси
Л'. Входящий в C.4) лоренцев угол со равен
со
-arcth(-i) —arcth(i)
и отличается по знаку от B.21), так как мы производим преоб-
преобразование к системе координат, движущейся вдоль оси х со
скоростью —v.
Применяя преобразование C.4) к спинорам C.2), получаем
г (о) = (ch -^— ct! sh-^-) wr @)
-th-2-
0 -thf-
1 -thf
-th-f- 1
wT @). C.5)
Из формул C.2) для шг@) ясно, что спинор wr(p) есть просто
столбец с номером г этой матрицы преобразования. Используя

38
РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
тригонометрические формулы
,. ш — th со
— th — = , —
2 1 + VI - th2co
v/c
рс
1 + Vl - v2lc2
E + тс2
И
E + me2
2mc2
C.6)
можно выразить wv(p) через энергию и импульс частицы.
Можно обобщить C.5) для произвольного направления ско-
скорости v. Для этого в B.19) следует заменить матрицу / на
О — cos a — cos p — cos у
— cos а О О О
— cos р О О О
• — cos у О О О
где cos а, cos р и cosy — направляющие косинусы скорости v.
Тогда
<7nv/«v = 2 @oi cos а + 002 cos р + 0ОЗ cos у) — — 2/ У .
Используя C.6), получаем отсюда
-V-
Е-\-тс2
Чтс2
1
0
Е+ тс2
Р+с
0
1
Е + тс2
-ргс
Р-С
Е + тс2
Р+с
Е + тс2 Е + тс2
Е + тс2 Е+тс2
1
0
C.7)
здесь р+ = рх± ipv. Общий вид решения для свободной ча-
частицы есть
tf(*) = rcr(p)<r"'-(V|1/*), C.8)
где в представлении A.17) для матрицу спинор wr(p) есть стол-
столбец с номером г в матрице C.7).
Спиноры wr(p) удовлетворяют следующим полезным соот-
соотношениям:
(р - ermc) wr (p) = 0, C.9а)
wr (р) wr' (р) = 6ГГ'ег, C.96)
I]er^(p)^(p) = 6af}. C.9в)

§ 9] ПЛОСКИЕ ВОЛНЫ 39
Уравнение C.9а), получаемое применением дираковского опе-
оператора (iV — m) к функциям C.8), есть уравнение Дирака для
свободной частицы в импульсном пространстве. Для г = I, 2
имеем 8г=+1 и (р — тс)wr(р) = 0. Это уравнение для двух
решений с положительной энергией, задаваемых двумя первыми
столбцами матрицы C.7). В нерелятивистском пределе их третьи
,и четвертые компоненты являются «малыми» и в отсутствие
внешнего поля эти решения переходят в A.29) и A.31). Для
решений с отрицательной энергией «большие» и «малые» ком-
компоненты меняются местами. Мы ввели также сопряженный спи-
спинор согласно определению B.28):
wr(p) = W+ (p)Yo-
Он удовлетворяет сопряженному уравнению
wr (р) (р - егтс) = 0, C.10)
которое получается, если взять эрмитово-сопряженное от урав-
уравнения C.9а), умножить его справа на y° и воспользоваться ра-
равенствами (y°J= + 1 и yV^Y0 = У^1-
Соотношение C.96) является ковариантным условием нор-
нормировки. Как было показано в предыдущей главе, билинейная
форма wr(p)wr'{p) представляет собой лоренцев скаляр (см.
B.39)), поэтому достаточно проверить выполнимость C.96) для
решений C.2), описывающих покоящуюся частицу. Плотность
вероятности wr+ (p)W (р) не является инвариантом, а преоб-
преобразуется как временная компонента 4-вектора (см. B.27)).
Пользуясь для вычислений столбцами матрицы C.7), находим
Wr + (8ГР) WT' (8r,p) = -Лг ЬГГ'. C.11)
Отсюда видно, что нужно ввести в плотность вероятности нор-
нормировочный фактор тс2/Е для компенсации лоренцева сжатия
элемента объема вдоль направления движения и обеспечения
инвариантной нормировки 4-вектора плотности тока. Обратим
внимание на то, что C.96) есть соотношение ортогональности
между спинором и сопряженным спинором с одними и теми же
значениями импульса р, в то время как согласно C.11) спинор
с положительной энергией ортогонален эрмитово-сопряженному
спинору с отрицательной энергией и противоположным импуль-
импульсом. Таким образом, две плоские волны с одним и тем же им-
импульсом р, но противоположными энергиями, ортогональны, т. е.
¦фг + (х) грг' (х) = 0, если г=\, 2, а г' = 3, 4, либо наоборот.
Соотношение C.9в) есть условие полноты для четырех ди-
раковских спиноров при заданном значении импульса. Для сво-
свободной покоящейся частицы оно очевидно. Чтобы доказать его
Для произвольного значения импульса, сделаем преобразование

40 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
Лоренца к системе покоя, а затем воспользуемся спинорами
C.2):
4 4
rw'a (p) а$ (р) = ? e,Sav (- ?) а/, @) wi @) S«' (-"?) =
r-1
To обстоятельство, что в соотношении полноты фигурирует w, а
не w+, есть следствие равенства
S+ = yS y.
которое в свою очередь отражает тот факт, что преобразование
Лоренца не является унитарным.
Действуя на решения C.2), которые описывают покоящийся
электрон, поляризованный в направлении г, операторами пово-
поворота
5 = e(</2)<ra-s
можно получить состояния, поляризованные в произвольном на-
направлении s. Такие состояния определяются равенством
о • sw — w,
где спинор w описывает частицу, поляризованную вдоль на-
направления единичного вектора s. Благодаря структуре входящей
в B.24) матрицы а конкретный вид спиноров близок к виду
двухкомпонентных спиноров Паули.
Для дальнейшего изложения удобно ввести несколько иные
обозначения. Обозначим посредством u(p,s) спинор, являю-
являющийся решением уравнения Дирака с положительной энергией,
импульсом р» и спином s». Спинор u(p,s) удовлетворяет урав-
уравнению
(р-тс)а^{р, s) = 0. C.12)
Четырехмерный вектор спина s^ определяется с помощью трех-
трехмерного вектора поляризации s<°> в системе покоя следующим
образом:
здесь sl0)v = @, s°), а a|J — коэффициенты преобразования к си-
системе покоя, т. е. р» = а»р{0) v, где /7<0)v = (mc, 0). Заметим, что
s^ = — 1, р@)*sm * = 0 и, следовательно, p^sH = 0. В системе
покоя спинор и удовлетворяет уравнению
о • s<% (рю, si°>) = и (р;0), s<°>). C.13)

§ 10! ПРОЕКЦИОННЫЕ ОПЕРАТОРЫ ДЛЯ ЭНЕРГИИ И СПИНА 41
Аналогично обозначим посредством v(p, s) решение с отрица-
отрицательной энергией
(P + )v(p, s) = 0 C.14)
и поляризацией в системе покоя, равной —s<°>. В системе покоя
для v имеем
а • s<°>o (p@>, s<°>) = - v {p'°\ s<°>). C.15)
Спиноры и(р, s) и v(p, s) связаны со спинорами о/(р) следую-
следующим образом:
да1 (р) = и(р, uz), w3(р) = v(р, — uz),
= u(p, — иг), w4(p) = v(p, uz)\
здесь uv — 4-вектор, который в системе покоя имеет вид
ы«Пи = @, ы<г0)) = @, 0, 0, 1).
Таким образом, любой спинор характеризуется импульсом
ри, знаком энергии и поляризацией в системе покоя s'?\
§ 10. Проекционные операторы для энергии и спина
Для практических вычислений удобно иметь операторы, ко-
которые осуществляют проектирование на спинор с заданным зна-
знаком энергии и поляризацией. Эти проекционные операторы яв-
являются четырехмерными аналогами нерелятивистских двумер-
двумерных операторов
проектирующих произвольное состояние на состояния со спином
вверх и спином вниз.
Пусть задано некоторое решение уравнения Дирака в виде
плоской волны с импульсом р. Мы ищем четыре оператора, ко-
которые выделяют из этого решения четыре независимых реше-
решения, отвечающих положительной и отрицательной энергии и
двум значениям проекции спина на заданное направление. Же-
Желательно, чтобы эти операторы были записаны в ковариантной
форме; тогда мы сможем без труда переходить из одной лорен-
цевой системы в другую, что очень важно в практических рас-
расчетах.
Четыре проекционных оператора обозначаются символами
Рг(р) = Р(Рц, uz, s) и по определению обладают следующими
свойствами:
Pr(p)wr'(p) = 6rr'Wr'(p),
или, что то же самое,
prto)Pr'(p) = t>rr'Prto)- C.17)

42 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
Оператор, проектирующий на состояния с положительной и
отрицательной энергией и данным импульсом р, можно получить
сразу в ковариантной форме непосредственно из уравнения
C.9а). Обозначим его посредством
либо
^4^- C.18)
Используя равенство рр = р2 = тс2, можно убедиться в том, что
тс2 A + егег,) + тер (ег + ег,) ( 1 + егег,
Лг (р) Лг- (р) = ^v = ^
т. е.
Л2+(р) = Л+(р), Л+(р)Л_(р
Отметим также равенство
Аналогичные спиновые операторы проще всего получить в
системе покоя, а затем попытаться придать им ковариантный
вид. В качестве оператора проектирования на состояние со спи-
спином вверх естественно взять A + ctz)/2. Для того чтобы в дву-
двумерном спиновом операторе (l+az)/2 избавиться от явной за-
зависимости от направления z, его переписывают в виде следую-
следующего скаляра:
1+a-uf
2 "
Для придания дираковскому спиновому проекционному опера-
оператору скалярной формы используем 4-вектор u^v и запишем
1 ' 40) Ч ' + У54О)Уо
Это выражение можно преобразовать к ковариантному виду,
исключив матрицу у0. В системе покоя действие матрицы у0 на
дираковский спинор сводится к умножению на ±1. Принимая
во внимание C.14) и C.15), получаем следующее выражение
для дираковского инвариантного спинового проекционного опе-
оператора:
1
или, для произвольного 4-вектора спина sv, удовлетворяющего
условию s^pp := О,
2(s) = -LLv5i. C.19)

§ 10J ПРОЕКЦИОННЫЕ ОПЕРАТОРЫ ДЛЯ ЭНЕРГИИ И СПИНА 43
В системе покоя имеем
1 4- V й@' 1 4- о
2 (««») w1 @) = 25 * ш1 @) = 2 * ш1 @) = ш1 @) C.20)
и
Аналогично для спиноров с отрицательной энергией
@)=ш;3@) C.21)
Для спиноров и и v, определенных согласно C.16), эти равен-
равенства выглядят так:
2(uz)u(p, иг) = и(р, иг),
2 (иг) v (р, иг) = v (р, иг),
2 (- иг) и (р, иг) = S (- иг) v (р, иг) = 0.
Вследствие ковариантности проекционного оператора 2 для лю-
любого вектора поляризации s^ (s^p^ = 0) можно записать
2(s)u{p, s) = u(p, s),
2(s)v(p,s) = v(p,s), C.22)
2(-s)u(p, s) = Z(-s)v(p, s) = 0.
Имея в своем распоряжении четыре проекционных оператора
А±(р) и S(±s), мы можем полностью характеризовать движе-
движение свободной частицы ее 4-импульсом р^, знаком энергии е и
поляризацией s^, причем s^p^ = 0. Для этого мы построим из
C.18) и C.19) четыре проекционных оператора:
Р, (р) = Л+ (р) 2 (иг), Р3 (р) = Л_ (р) 2 (- иг),
Р2 (Р) = Л+ (р) 2 (- иг), Р4 (р) = Л_ (р) 2 (uz).
Заметим, что для векторов, удовлетворяющих условию siipVt = 0,
[S(s), Л± (/?)]= 0,
поскольку р антикоммутирует как с ув, так и с s. Следова-
Следовательно, построенные операторы Рг(р) удовлетворяют опреде-
определению C.17).
Мы будем очень часто обращаться к этим операторам для
получения приемов быстрого и эффективного счета. Они позво-
позволяют пользоваться свойствами полноты и тем самым избавляют

44 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
нас от необходимости явно выписывать все матрицы и компо-
компоненты спиноров.
Чтобы получить релятивистски-инвариантную теорию, мы
ввели решения с отрицательной энергией и импульсом р, кото-
которые, согласно C.8), являются собственными функциями опера-
оператора импульса р с собственным значением —р. Подобным же
образом, согласно C.19) и C.21), решения с отрицательной
энергией, описывающие состояния со спином вверх и спином
вниз, переходят в системе покоя в собственные функции опера-
оператора а2 с собственными значениями, равными •—1 и +1 соответ-
соответственно. Физическая причина такого «соответствия наоборот»
для решений с отрицательной энергией станет ясной, когда мы
в гл. 5 рассмотрим теорию дырок.
§ 11. Физический смысл решений в виде плоских волн
и волновых пакетов
Теперь мы можем построить локализованные волновые па-
пакеты путем суперпозиции решений в виде плоских волн. В силу
принципа суперпозиции эти пакеты также будут решениями
уравнения Дирака для свободной частицы, поскольку уравне-
уравнение Дирака линейно. Займемся изучением пакетов, чтобы до-
достичь более глубокого понимания физического смысла решений
для свободной частицы.
Начнем с того, что построим пакет только из решений с по-
положительной энергией:
~TiT Д/ ^ Yi b (p> s) u ^' s) e~iP*x4h- C-23)
± s
Для нормировки коэффициентов разложения b(p,s) на единич-
единичную вероятность обратимся к соотношениям ортогональности
C.11). Получим1)
I j3 (+)*^" / \ D-)
= \
о, s)u+(p, s')u{p, s) =
±s, ± s'
~~\b(p, s)|2=l. C.24)
±S
') Приведем известные свойства б-функции Дирака, используемые при
выводе C.24),
dx el (s"a) х = 2яб (s - а), \ ds б (s - a) / (s) = / (a),

§ П) ФИЗИЧЕСКИЙ СМЫСЛ РЕШЕНИЙ 45
Средний ток для такого волнового пакета дается средним
значением оператора скорости
+)+V+)^ C.25)
Вычислим JK+), воспользовавшись следующим важным соотно-
соотношением между тремя 4-векторами, которые можно построить из
решений для свободной частицы:
если tyi(x) и г|J(х) есть два любых решения уравнения Ди-
Дирака
(р - тс) \р (х) = О,
то
U ^ fe Р* (*2O"*v*i). C-26)
Чтобы доказать C.26), заметим, что для любых двух 4-векторов
а»- и Ь^ справедливо равенство
йЬ = а„Ьу [~ (W + Г Г) + у (У^Г - YVY^)] =
= cPb» — ictbva^. C.27)
Далее, исходя из уравнения Дирака, напишем
О = 'Фг (— Р — tnc) й$1 + 'Фг^ (Р ~ тс) ti =
где 'фр = Рц'фу'1- Отсюда C.26) получается приравниванием
коэффициентов при произвольном векторе а^.
Равенство C.26) известно как разложение Гордона [31]. Оно
выражает дираковский ток как сумму тока переноса, аналогич-
аналогичного нерелятивистскому, и спинового тока.
где интегрирование проводится по интервалу, включающему точку s = а, и
предполагается, что в этом интервале функция f(s) не имеет особенностей;
±"| = 1 с | б (s), | с | Ф 0.
Понятие б-функции является математически строгим; оно обосновывается в
теории обобщенных функций; см., например, [30].

46 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
Используя C.26) при г|:г = ty\ = if> и C.23), для тока C.25)
находим
± s, ± s'
X -щ-п
или, учитывая нормировку C.24),
J(+> = <ca)+ = (^)+ = (vrpynn}+, C.29)
где символ ( )+ означает среднее значение по пакету с положи-
положительной энергией. Таким образом, средний ток для произволь-
произвольного пакета, построенного только из решений с положительной
энергией, есть просто классическая групповая скорость. Подоб-
Подобное утверждение хорошо известно из нерелятивистской шре-
дингеровской теории.
Теперь мы перейдем к важному отличию, присущему реля-
релятивистской теории. В шредингеровской теории в выражение для
тока входит оператор р/пг, который является константой для
свободного движения. В теории Дирака, однако, ток не пропор-
пропорционален импульсу и, в то время как из соотношений Эрен-
феста A.27) следует, что для свободного движения dp/dt = O,
оператор скорости са не является константой, поскольку
[а, Я] ф 0. Действительно, собственные функции оператора са
должны строиться из решений как с положительной, так и с от-
отрицательной энергией, так как собственные значения са1 равны
±с, тогда как согласно C.29) |(са*)+| < с.
Включим в наше рассмотрение решения с отрицательной
энергией и построим волновой пакет из полного набора реше-
решений для свободной частицы. Обобщением C.23) будет
\_b (p, s)ui
+ d*(p, s)u(p, s)e+*|1V*]. C.30)
Нормировка снова производится на единичную вероятность.
В результате несложных вычислений получаем
3x^+ (х, 0 4>(х, 0=S d3p ?[| b(p, s) f + \d(p, s) |2]= 1.

§ 11] ФИЗИЧЕСКИЙ СМЫСЛ РЕШЕНИЙ 47
Поток для такого пакета равен')
|&(P, s)\2 + \d(p, s)f\-^f +
b*(—p, s') d* (p, s) ё>Лх^Ч (- p, s') aftow {p, s) —
± s, ± s'
b(-p, s')d(p, s)e~2ix'P'i4(p, s')okou{-p, s)\. C.31)
Кроме независящей от времени групповой скорости, в этом вы-
выражении появились перекрестные члены между решениями с по-
положительной и отрицательной энергией, которые быстро осцил-
осциллируют во времени с частотой
= 2. 1021 сек-1.
Эти быстрые осцилляции, или «дрожание» («zitter-bewegung»
[32]), пропорциональны амплитуде, с которой входит в пакет ре-
решение с отрицательной энергией. Пока в нашем изложении мы
еще не выяснили физический смысл этих решений, однако мож-
можно задаться вопросом, когда следует ожидать присутствия этих
решений в пакете со значительной амплитудой. Из общего вида
решения для свободной частицы видно, что поскольку величины
b(p,s) не зависят от времени, то в отсутствие внешнего воздей-
воздействия в волновом пакете, первоначально построенном только из
решений с положительной энергией, не появятся компоненты
с отрицательной энергией. Однако пакет, описывающий элек-
электрон, так или иначе локализованный в конечной области в на-
начальный момент времени, содержит, вообще говоря, решения
с обоими знаками энергии.
Рассмотрим, например, решение
Ч,(г,О, s) = (ndT%e-ihr!ldW{0), C.32)
которое отвечает гауссовскому распределению плотности вокруг
начала координат с полушириной ~d в момент времени t = 0.
В любой последующий момент времени i это решение может
быть представлено в виде пакета C.30) с коэффициентами Ь и
') Несмотря на некоторую непоследовательность, мы везде будем поль-
пользоваться обозначением
и (Vp2 + т2 , — р, s) = и(— р, s)
и аналогичными обозначениями для коэффициентов разложения Ь, d* и т. д.

48 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
d*, задаваемыми своими начальными значениями при t = 0, т.е.
Е ^
~+ d* (p, s) v (p, s) е-*г1к] = {nd2Y% е-*"""*,1 @).
Производя преобразование Фурье и используя
f d3r e-r2l2dVl-rlh = BndT e-lkl44h\
— oo
получаем
f& ^s')" 0». s') + d* (- p. s')y (- p. s')l =
Из соотношений ортогональности C.11) находим
й (/>, «) = д/^F1 (iS-O' e-pl'"/!!fc'«+ (P, s) ш' @),

Таким образом, амплитуда решения с отрицательной энергией
d* в пакете C.32) отлична от нуля. По отношению к амплитуде
решения с положительной энергией b она подавлена как верх-
верхняя, или «малая», компонента v по отношению к верхней, или
«большой», компоненте и, т. е. по порядку величины в pc/(E-\-i
+ тс2) раз. Отсюда ясно, что амплитуды решений с отрица-
отрицательной энергией существенны при значениях импульса ~ тс.
Однако из C.33) видно, что пакет сформирован в основном из
состояний с импульсом р\<. Ь/d. Поэтому для того, чтобы вклад
состояний с отрицательной энергией стал существен, пакет дол-
должен быть локализован в области с размерами, сравнимыми с
комптоновской длиной волны электрона, т. е.') с d ~ Ь/тс.
Этот результат можно получить из размерных соображений
с помощью соотношения Ар Ах ~ Ь, не пользуясь гауссовской
формой распределения. Когда речь идет о задачах, где электрон
«размазан» по области, много большей его комптоновской
длины волны, можно вообще не принимать во внимание суще-
существование решений с отрицательной энергией и тем не менее
надеяться получить обладающие физическим смыслом и доволь-
довольно точные результаты. Такое приближение становится непри-
') Понятие пространственной координаты дираковского электрона с по-
положительной энергией обсуждается в работе [33].

§ И)
ФИЗИЧЕСКИЙ СМЫСЛ РЕШЕНИЙ
49
менимым, если электрон локализован в области с размерами по-
порядка Ь/тс. При этом амплитуды решений с отрицательной
энергией делаются существенными, в токе возникают «дрожа-
«дрожащие» члены и мы сталкиваемся с такими парадоксами и дилем-
дилеммами, разрешить которые в рамках развитой нами теории ди-
раковского электрона оказывается невозможным. Знаменитым
да
Рис. 3.1. Потенциальный барьер, удерживающий электрон с энергией Е
в области / слева.
Л А А
\J\J \j
i
V(z)
-E
Рис. 3.2. Электростатический потенциал, представленный для простоты стенкой
с резким краем, на которую из области / падает движущаяся вправо сво-
свободная электронная волна с энергией Е. При Vo > Е + тс2 отраженный от
потенциала поток превосходит падающий; это один из примеров парадокса
Клейна.
примером такого рода трудности является парадокс Клейна [34],
который можно пояснить на следующем примере.
Чтобы локализовать электроны, мы должны создать сильное
внешнее поле, удерживающее их в заданной области. Предполо-
Предположим, например, что мы хотим удержать свободный электрон
с энергией Е в области / слева от точки начала координат
г — 0 в одномерном потенциале, изображенном на рис. 3.1.
Если мы потребуем, чтобы электрон не проникал в область //,
лежащую правее точки 2 = 0, глубже, чем на расстояние d, то
потенциал V должен на интервале г .<: d быстро возрастать до
значения Vo > Е; тогда решение будет в области // спадать
с характерной длиной ^.d. Все будет происходить так, как в
шредингеровской теории, до тех пор, пока интервал, на котором

50 РЕШЕНИЯ УРАВНЕНИЯ ДИРАКА ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ [ГЛ. 3
мы хотим удержать электрон, не сожмется до размеров ~Ъ\тс,
а разность Vo — ? не превысит величины тс2.
Чтобы понять, что произойдет далее, рассмотрим потенциал
с резким краем, изображенный на рис. 3.2, и вычислим отражен-
отраженный и прошедший поток для электрона (с волновым вектором
k\ и спином, направленным по оси z), налетающего слева на
область действия этого потенциала. Решения с положительной
энергией для падающей и отраженной волн в области / имеют
вид
1
о
C.34)
( ' ^
•ф = Ье~'*¦* I _ ckjh I + Ь'е-ik>* 0
\ Е + тс2 ) \ ckjh
Е + тс2
Прошедшая волна представляет собой решение уравнения Ди-
Дирака в постоянном внешнем потенциале еф = Vo. Оно отли-
отличается от решения для свободной частицы лишь заменой ро =
= A/с) (Е— Vo), поэтому в области // имеем
h2k\c2 = (Е— Vof — тс = (Е - тс2 - Vo) (Е + тс2 — Vo).
Следовательно, прошедшую волну с положительной энергией
Е > 0 можно записать как
Амплитуды d и d' определяются из условия непрерывности ре-
решения на границе потенциала, которое в свою очередь следует
из сохранения потока. Имеем
а + Ь = й,
„ и k2 Е + тс2 , , .„ „„.
аЪ d rd C36)
Ь' = d' = 0 (переворота спина не происходит).
При Уо>0 \
чисто мнимый: k2 = -\-i
и \Е—
й: k2 =
< тс2 волновой вектор в области //
k2\ и решение в этой области представ-
ляет собой затухающую экспоненту с характерной длиной за-
затухания d > Ь/тс. Если мы, однако, захотим уменьшить глубину

ЗАДАЧИ 61
проникновения электрона в область // и увеличим высоту потен-
потенциального барьера, сделав его выше, чем Vo = Е + тс2, прошед-
прошедшая волна станет осциллирующей. Нетрудно вычислить прошед-
прошедший и отраженный ток. Получаем
/trans 4r /ref A ~ ГУ . Arans /о оу\
/,„с A +г)* ' /,пс A + гУ /,пс • V-a/>
Хотя по форме эти результаты напоминают предсказания нере-
нерелятивистской теории, следует заметить, что поскольку Vo > Е +
+ тс2, то, согласно C.36), г < 0.
Мы получили результат, противоречащий нашим обычным
представлениям: прошедший поток оказался отрицательным, а
отраженный поток больше падающего. Что представляет собой
поток в области //, который на рис. 3.2 направлен справа на-
налево из области // в область /?
В надежде локализовать решение внутри интервала, равного
комптоновской длине волны электрона h/mc, мы сделали потен-
потенциальный барьер выше, чем Е + тс2, но в итоге получили не за-
затухающее, а осциллирующее решение. Как следует понимать это
явление? Его можно понять, только выяснив физический смысл
решений с отрицательной энергией. Из рассмотрения волновых
пакетов ясно, что решения с отрицательной энергией существен-
существенны, когда частица локализована в области размером Ь/тс.
С другой стороны, из приведенного примера видно, что именно
на таких растояниях наша физическая картина перестает соот-
соответствовать действительности.
Мы займемся разрешением этих вопросов, начиная с гл. 5.
Прежде обратимся к широкой (хотя и ограниченной) области
физических явлений, в которых приложенные поля являются сла-
слабыми и медленно меняются в масштабе, где единицей длины
служит величина Ь/тс2, а единицей энергии — величина тс2.
Мы надеемся найти здесь множество разнообразных примене-
применений уравнения Дирака и теории электрона с положительной
энергией.
ЗАДАЧИ
1. Получить C.11) непосредственно из уравнения Дирака.
2. Доказать, что равенство C.9) справедливо независимо от конкретного
представления для дираковских спиноров.
3. Получить выражение для потока C.31).
4. Показать, что C.36) есть следствие сохранения потока.
5. Найти уровни энергии дираковской частицы в одномерной прямо-
прямоугольной потенциальной яме глубиной Fo и шириной а.
6. Проверьте следующее условие полноты:
г-1

ГЛАВА 4
ПРЕОБРАЗОВАНИЕ ФОЛДИ - ВАУТХАЙЗЕНА
§ 12. Введение
Если не принимать в расчет проблему отрицательных энер-
энергий, то уравнение Дирака дает вполне удовлетворительное опи-
описание электрона. Оно имеет разумный нерелятивистский предел
и приводит к правильному значению магнитного момента. Те-
Теперь мы займемся исследованием взаимодействия дираковского
электрона с заданным внешним потенциалом. В первую очередь
нас будет интересовать область низких энергий, свободная от
трудностей, связанных с решениями с отрицательной энергией.
При рассмотрении волновых пакетов в предыдущей главе мы
подчеркивали, что роль этих решений практически очень мала
в таких вопросах, как, например, задача об атоме водорода,
когда электрон локализован на боровской орбите с радиусом ')
I/am > Mm.
Мы убедимся в том, что стационарные уровни энергии ато-
атома водорода, полученные с помощью уравнения Дирака, чрез-
чрезвычайно близки к наблюдаемым. Однако, прежде чем присту-
приступить к поиску собственных значений в кулоновском потенциале,
будет весьма поучительно сформулировать дираковскую теорию
в такой форме, когда взаимодействие электрона с внешним по-
полем представлено суммой членов, каждый из которых имеет на-
наглядный нерелятивистский смысл.
Рассмотрим поэтому последовательный метод, предложенный
Фолди и Ваутхайзеном [35], а именно каноническое преобразо-
преобразование, при котором уравнение Дирака превращается в пару
двухкомпонентных уравнений. Одно из них в нерелятивистском
пределе переходит в уравнение Паули, другое описывает состоя-
состояния с отрицательной энергией.
') Ниже мы везде будем полагать ft = с = 1. Комптоновская длина вол-
волны электрона равна \/т = 3,86- 10~и см, а его энергия покоя т = 0,511 Мэв.
Постоянная тонкой структуры a = е2/4п ?? 1/137 В этих единицах
10" 1021
0,511 M '1

§ 13J ПРЕОБРАЗОВАНИЕ ДЛЯ СВОБОДНОЙ ЧАСТИЦЫ 53
§ 13. Преобразование для свободной частицы
В качестве первого примера проделаем преобразование
Фолди — Ваутхайзена над уравнением Дирака для свободной
частицы. Для этой цели удобнее записать уравнение Дирака в
гамильтоновой форме, используя для матриц а представление
A.17). Мы ищем унитарное преобразование UF, которое освобо-
освободит уравнение от всех операторов типа а, связывающих между
собой «большие» и «малые» компоненты. Любой такой оператор
будем называть нечетным; те же операторы, которые не связы-
связывают между собой «большие» и «малые» компоненты, назовем
четными. Согласно этому определению операторы а, \, ув и т. д.
являются нечетными, а операторы 1, р, о и т. д. — четными.
Записывая UF в виде
UP = e+iS,
где оператор 5 эрмитов и не зависит от времени, получаем сле-
следующее унитарное преобразование:
i Л?- = e+isHMp =
Мы требуем, чтобы Н' не содержал нечетных операторов.
Поскольку Я = а-р + рт, причем {а, р} = О, наша задача
совершенно эквивалентна задаче о нахождении унитарного пре-
преобразования, которое приводит двухкомпонентный спиновый
гамильтониан Ж = вхВх + ozBz к виду, содержащему лишь чет-
четные операторы (такие, как 1 ио,). Как известно, такое преобра-
преобразование есть просто поворот вокруг оси у, и ему отвечает опера-
оператор е('72HА = е'/2СТг0хео) где tg90 = Bx/B2. Поэтому можно пред-
предположить, что в нашем случае искомый оператор имеет вид
eis = ейа-р9(Р) =: cos | р 10 + i^P- sin | р 10;
здесь правая часть равенства получена разложением экспонен-
экспоненты в ряд по степеням 0. При таком выборе преобразования
имеем
X (cos | р I e — -^е- sin i р | е) =
= (а • р + Рт) ехр (— 20а • рв) =
a-p(cos2|p|0--~ sin2|p|6) +
(т cos 21 p 19 + | p | sin 21 p 10).

54
ПРЕОБРАЗОВАНИЕ ФОЛДИ - ВАУТХАИЗЕНА
[ГЛ. 4
Чтобы избавиться от нечетного оператора, положим
tg2|p|9 =
_ IPI
т
Тогда преобразованный гамильтониан
2 + P2, D.1)
в чем легко убедиться, глядя на изображенный на рис. 4.1 тре-
треугольник. Мы получили тот самый гамильтониан, который был
Рис. 4.1. Треугольник, отвечающий преобразованию Фолди — Ваутхайзена.
отвергнут в гл. 1, с той, однако, существенной разницей, что те-
теперь в наше рассмотрение включены решения с отрицательной
энергией.
§ 14. Общее преобразование
Обратимся теперь к общему случаю, когда электрон нахо-
находится в заданном внешнем электромагнитном поле, и найдем
соответствующий оператор S. Гамильтониан имеет вид
Я = а • (р - ек) + ?>т + еФ = рт + О + S\
D.2)
здесь О = а ¦ (р — ек), & = еФ и $0 = —0$, $& = +р
Входящие в D.2) внешние поля, а следовательно, и сам га-
гамильтониан могут зависеть от времени. Преобразование S тоже,
вообще говоря, зависит от времени, поэтому невозможно по-
построить оператор 5, который удалял бы из гамильтониана
нечетные операторы во всех порядках, как в D.1). Мы довольст-
довольствуемся разложением преобразованного гамильтониана в степен-
степенной ряд по 1/т, сохранив в разложении члены вплоть до имею-
имеющих порядок (кинетическая энергия/mK и (кинетическая энер-
энергия) (энергия поля)/т2.
Преобразование, как и прежде, вводится равенством

§ 14| ОБЩЕЕ ПРЕОБРАЗОВАНИЕ 55
Далее имеем
Таким образом,
Оператор S разлагается в ряд по степеням 1/т, следовательно,
в нерелятивистском пределе он «мал». Поэтому выражение, стоя-
стоящее в квадратных скобках, можно разложить в ряд, построен-
построенный из многократных коммутаторов, используя для этого сле-
следующее соотношение'):
e+iSHe~is = н + i [Sf щ + М?_ [Sf [s> щ]+ ^
Поскольку S = О (l/m), то с требуемой точностью имеем
H' = H + i [S, Я] -1 [5, [S, Я]] - ± [S, [S, [S, Я]]] +
+ -& P. [s, [s, [s, я]]]] - s - 4 is, s] + {[s, [s, s]].
Начнем построение S с рассмотрения членов нулевого порядка
малости по 1/т:
Н' = pm + S + О + I [S, р] т. D.3)
Мы требуем, чтобы выражение D.3) не содержало нечетных
операторов. Руководствуясь результатом, полученным для сво-
свободной частицы, положим S = —i$0/2m. Тогда с требуемой
') Чтобы убедиться в справедливости этого разложения, рассмотрим
оо
Отсюда последовательно получаем
¦Ц5—*'win[S, [S,...,[S,H]...]]e-tKs.
Результат подставляем снова в (а) и полагаем Я, = 1.

56 ПРЕОБРАЗОВАНИЕ ФОЛДИ — ВАУТХАПЗЕНА [ГЛ. 4
точностью получим
I- [5, [S, Щ] = - ig - ^ {О, [О,
о = |
Собирая вместе все члены, имеем
D.4)
Члены с нечетными операторами (они обозначены посредством
О') имеют в D.4) порядок 1/т. Чтобы еще повысить их поря-
порядок малости, проделаем второе преобразование Фолди — Ваут-
хайзена, пользуясь тем же самым рецептом:
Л ~ 2т U — 2т { 2т [U' ® 1 Ът? + ~2т~
В результате преобразования получим
Н" = е*' (Н' - »-|-) e-«' =Pm + #' + ^[tf', S'l + ML^
^$т + &' + 0",
где <7" — величина порядка О A/т2). Наконец, с помощью
третьего канонического преобразования
° ~ 2т
можно избавиться и от О'. Окончательно получаем
Н"' = ets" (я" - / -J-) e-'s" = Pm + «" =

§ 14J ОБЩЕЕ ПРЕОБРАЗОВАНИЕ 57
Вычисляя произведения операторов с нужной нам точностью,
находим
О* _ (а ¦ (р - М)J . _ р - еА)г е_
2т 2т 2т 2т *'
i.i
Таким образом, в рассматриваемом приближении гамильтониан
имеет вид
D.5)
Каждый отдельный член в D.5) имеет четкий физический
смысл. Выражение в квадратных скобках является разложе-
разложением
V(P - eXf + m2
с требуемой точностью; этот член учитывает релятивистскую за-
зависимость массы от импульса. Следующие два члена дают энер-
энергию электрического заряда и магнитного диполя во внешнем
поле. Четвертый и пятый члены, взятые вместе, являются эрми-
эрмитовыми; их можно отождествить с энергией спин-орбитального
взаимодействия. Они имеют привычный вид, если электрическое
поле центрально-симметричное. Тогда rot E=0 и
Таким образом, эти два члена сводятся к
е I dV
^spin-orbit =-4^2" — ~дГ° ' L" D>6^
Этот результат согласуется с классическим. Действительно, если
перейти в систему, в которой частица покоится, возникает маг-
магнитное поле В' = — v X Е. в котором энергия взаимодействия
будет равна

58 ПРЕОБРАЗОВАНИЕ ФОЛДИ — ВАУТХАЙЗЕНА (ГЛ. 4
Однако соответствующий член в D.5) имеет лишний множитель
7г («томасовская половинка»). Появление этого множителя
указывает на то, что гиромагнитное отношение для магнитного
момента электрона, связанного с орбитальным движением,
имеет обычное значение g=l.
Наконец, последний член, известный под названием дарви-
дарвиновского, можно связать со шредингеровским «дрожанием». По-
Поскольку координата электрона испытывает флуктуации на рас-
стояних порядка 8гс^1/т, электрон «чувствует» несколько
«размазанный» кулоновский потенциал; поправка составляет
FF) = (V (г + 6г)) - (V (г)) = /fir f- + ^ ? fir, fir, ^
~ — br2V2V л; — V21/ (А 7\
что качественно совпадает с дарвиновским членом.
§ 15. Атом водорода ')
Перейдем к рассмотрению решений уравнения Дирака, отве-
отвечающих связанным состояниям, и в первую очередь найдем
уровни энергии электрона в кулоновском поле. Уравнение Ди-
Дирака для электрона в кулоновском поле имеет вид
#ф = [« • р + Рт + V (г)] ф = Е$, D.8)
где V(r)=—Za/r. Для разделения переменных воспользуемся
тем, что угловой момент частицы в центральном поле сохра-
сохраняется. Действительно, оператор J = L + S = rXp + V20 ком-
коммутирует с гамильтонианом D.8), и поэтому можно построить
собственные функции, отвечающие определенным собственным
значениям Н, J2 и Jz. Для нахождения этих функций обратимся
к нашему опыту работы с матрицами Паули и вспомним, что
в представлении, использованном в гл. 3, матрица
диагональна при условии, что ее элементами считаются матри-
матрицы Паули размерности 2X2. Поэтому, если выразить \|з через
двухкомпонентные спиноры
¦-(!)¦
') Задача о движении электрона в кулоновском поле была впервые ре-
решена, в работах [36].. Подробное рассмотрение применений уравнения Дирака
в атомной физике и соответствующие ссылки можно найти в книгах [37, 38].

§ 151
ATOM ВОДОРОДА
59
то угловые переменные в ф и % отделяются точно так же, как
в двухкомпонентной теории Паули. Угловая часть двухкомпо-
нентных решений является собственной функцией /2, /г, L2 и
S2 и может быть двух типов.
При/=/+72
При j=l — 7
V
l + Чг + т
21 + 1
I + '/2 — m
21+1
21+ 1
~yl+2l'++\
D.9а)
D.96)
где фаза шаровых функций задана условием Y] т = (—1)тУЛ _т,
а решения ф(-) существуют только при / > 0. Оба эти решения
удовлетворяют следующим уравнениям на собственные значе-
значения:
L • oq>?> = (Р - U - 3/4) Ф(±) = - A + к) Ф<±>,
где
«Ч
= + (/ + 72), i = i-lk.
При заданном / решения ф^+' и ф'.~> обладают противополож-
противоположной четностью, поскольку отличаются на единицу по /. Они мо-
могут быть получены друг из друга с помощью нечетного скаляр-
скалярного оператора. Этот оператор должен быть линейной комбина-
комбинацией функций У Г (9, ф), так как он меняет значение / на 1 и
потому должен быть пропорциональным г. В нашем распоряже-
распоряжении имеется единственный псевдовектор а, и, пользуясь им, мы
строим псевдоскаляр а-т/r. Далее находим
a -r
т/т
= -^Ф'
7т-
D.10)
Общее решение для центрального поля при заданных / и m
можно представить в виде

€0
ПРЕОБРАЗОВАНИЕ ФОЛДИ — ВАУТХАЙЗЕНА
[ГЛ. 4
Это решение можно разбить на два, каждое с определенной чет-
четностью. Поскольку потенциал V(r) инвариантен по отношению
к пространственной инверсии, собственным функциям можно
наряду с определенными значениями / и т приписать также
определенную четность. Пользуясь этим свойством, мы построим
четные и нечетные решения; при преобразовании х' =—х они
ведут себя следующим образом:
!1/(х') = (Жх) = ±Ф(х'). D.11)
Эти решения даются формулой
где введены обозначения
G1
г г чп
D.12)
Fn = s
<. / = '+725
и использовано равенство D.10). В соответствии с D.11) чет-
четность этих решений равна (—1)'. Для получения из D.8) урав-
уравнений для радиальных функций воспользуемся следующими
тождествами:
43
В итоге имеем следующие уравнения для радиальных функций:
D.13)
Решения этих уравнений, отвечающие связанным состояниям,
можно найти обычными методами [36—38]. Мы приведем лишь
некоторые результаты.
Уровни энергии даются выражением
4.14)

15]
АТОМ ВОДОРОДА
61
в котором квантовое число п = 1, 2, ..., оо пробегает целые
положительные значения, а угловой момент изменяется в пре-
пределах от 0 до / -+- У2 ^ п, причем должно быть выполнено усло-
условие 0^/^п —1. Разлагая D.14) в ряд по степеням (ZaJ,
мы убеждаемся в том, что число п соответствует главному
квантовому числу в нерелятивистской теории
3
3 N1 , _.
D.15)
Положив в D.14) я=1 и /=72, получим энергию основного
уровня
c0 — my i — za~m —
Выпишем также отвечающие этому уровню нормированные вол-
волновые функции со спином вверх и спином вниз
1
У
2ГA+2у)
BmZarL-[ e~mZar
0
~ V)
Za
cos 8
Za
е)Ф) =
/
v
i+y
2ГA+2у)
Za
• cos 9
I Za
где Y = V 1—Z2a2. В нерелятивистском пределе у~*'>
A—y)/Za-*-0 и эти функции переходят в шредингеровские
волновые функции, умноженные на двухкомпонентные спиноры.
В релятивистском случае при г—>0 функции имеют слабую син-
сингулярность вида BmZar)~iZ2a*)!~,
ной лишь на расстояниях
которая становится существен-
существен2mZa
p-2/Z'a'
Если Za^l, то величина у мнимая и решения при г->-0
осциллируют; это явление напоминает нам о парадоксе Клейна.
При этом исчезает «щель» между решениями с положительной
и отрицательной энергией и мы снова не можем придать реше-
решению физический смысл.

62
ПРЕОБРАЗОВАНИЕ ФОЛДИ - ВАУТХАЙЗЕНА
[ГЛ. 4
Уровни энергии, задаваемые формулой D.14), принято обо-
обозначать, как в нерелятивистском случае, т. е. посредством орби-
орбитального момента /, фигурирующего в i|^m, и полного момента /.
В таблице мы приводим несколько первых уровней.
Уровни
п
1
2
СМ С^1
1
0
0
1
1
1
'/2
'/г
'/2
72
mVl -Z2a2
m / 1 -f Vl -Z2a2
m / 1 + Vl — Z2a2
V 2
^V4-Z2a2
Уровни 2Si/2 и 2Pi/2 вырождены, будучи собственными со-
состояниями с противоположной четностью, отвечающими
одному и тому же значению п и /. Уровень 2Р=/, расположен
выше, чем 2Pij2; разность энергий между ними, равная
[m(ZaL/32](l -f- O((Z<xJ) -f .-¦). представляет собой энергию
тонкой структуры. Тонкая структура есть следствие спин-орби-
спин-орбитального взаимодействия D.6). Из формулы D.15) видно, что
чем больше / при заданном п, тем выше лежит уровень.
Как согласуются эти предсказания с наблюдаемым на опыте
спектром атома водорода? До 1947 г. согласие с опытом было
вполне удовлетворительным (с учетом сверхтонкого расщепле-
расщепления, обусловленного взаимодействием спина электрона со спи-
спином протона). Однако в 1947 г. измерение тонкой структуры
атома водорода, произведенное Лэмбом и Резерфордом'), под-
подтвердило возникшее еще раньше подозрение в том, что уровень
2Si/2 сдвинут вверх относительно уровня 2А/2 (рис. 4.2). Это так
называемое смещение Лэмба, которое снимает вырождение уров-
уровней с одинаковыми значениями / и п, но разными /, происходит
благодаря взаимодействию электронов с флуктуациями кванто-
квантованного поля излучения. Имеются очень точные измерения и
расчеты как сверхтонкого расщепления, так и лэмбовского сме-
смещения; согласие теории с экспериментом хорошее [41].
Сверхтонкая структура возникает благодаря взаимодействию
протона с магнитным моментом электрона [42] (см. также [37]).
В результате каждый уровень расщепляется на две компоненты
Ссылки на последующие работы можно найтн в [37, 40].

15]
АТОМ ВОДОРОДА
63
в соответствии с двумя возможными значениями полного мо-
момента атома. Этот момент складывается из полного момента
электрона / и полуцелого спина протона. Найдем энергию сверх-
сверхтонкого расщепления для S-состояний. Для этой цели оказы-
оказывается достаточным нерелятивистское описание электрона.
Взаимодействие имеет вид
2т
где
В ="
1
4я | г - г'
здесь I —оператор спина протона (Iz = ±lk), a p(r')—плот-
p(r')—плотность магнитного момента протона (мы не считаем протон
Е
2S®
,3В*
LМалоерасщепление (mcvem
лэмбовскога сдвига)
Тонкая структура (спин-орбиталше
азаимадействие)
-(триштшф-
-(синглетм/й)
I— Сверхтонкое расщепление
Рис. 4.2. Нижние уровни энергии атома водорода. Схема изображена без
соблюдения масштаба.
точечной частицей). Используя тождество V ХA X V) =
= IV2—(I-V)V и тот факт, что для сферически-симметричной
волновой функции
получаем
в = 4
ИIV2

64 ПРЕОБРАЗОВАНИЕ ФОЛДИ - ВАУТХАЙЗЕНА [ГЛ. 4
Тогда для сдвига уровня по нерелятивистской теории имеем
АЕп = «.„ЯЧд = 4 & о ¦ I S dh < (г) р (г) <,„ (г)
'p
•4
~ 6 тМр " ¦ i *
Далее
Г + 7г Для триплетных состояний,
о • I = s о,
(, — /2 для синглетных состоянии.
Таким образом, расщепление б„ «-го уровня равно
Л — tvtn^
По сравнению с тонкой структурой оно в пг/Мр раз меньше.
Велтон [43] предложил простое качественное описание сме-
смещения Лэмба, основанное на рассмотрении взаимодействия
нерелятивистского электрона с вакуумными флуктуациями элек-
электромагнитного поля. Поскольку динамика нормального колеба-
колебания электромагнитного поля эквивалентна динамике гармониче-
гармонического осциллятора, то после квантования каждое нормальное
колебание приобретает «нулевую энергию», равную ю/2. В ре-
результате этого квантового эффекта флуктуирующие электромаг-
электромагнитные поля имеются, даже если внешнее поле отсутствует.
Хотя средние значения напряженностей поля равны нулю, их
среднеквадратичные значения отличны от нуля. Взаимодействие
электрона с этим полем приводит к среднеквадратичным флук-
туациям координаты электрона. Нам надо оценить амплитуду
таких «качаний» связанного электрона. Как мы выяснили при
рассмотрении дарвиновского члена D.7), они приводят к появ-
появлению у электрона добавочной энергии взаимодействия. Эта
энергия возникает за счет «размазывания» действующего на
электрон кулоновского поля и равна Уб((бгJ) V2V. В наиниз-
наинизшем порядке соответствующий сдвиг уровня электрона есть
Д rrLamb = .Д. ((бгJ) J ^ ^ у2у (г) % = _*L Za {{brf) j ^ (Q) |2> D Д 6)
Чтобы оценить (FгJ), будем считать электрон классической
нерелятивистской заряженной частицей. Уравнение движения
для колебаний электрона вокруг равновесного положения имеет
вид
бг = — Е,
m '
где Е — флуктуирующее электромагнитное поле. Для фурье-ком-
понент имеем

§ 15) АТОМ ВОДОРОДА 65
Отсюда для среднеквадратичных значений получаем
^(^). D.17)
Для определения среднеквадратичной напряженности рассмот-
рассмотрим полную энергию вакуумного поля
А.-1 ft
где два значения Я отвечают двум поперечно-поляризованным
состояниям, а сумма по & распространяется на все колебания
в некотором большом объеме пространства
Поскольку для свободных электромагнитных волн \d3xE2 =
= \d3xB2 и (o = |k|, среднеквадратичная напряженность поля
в вакууме равна
Подстановкой последнего звена этой цепочки равенств в D.17)
находим
где интегрирование производится от 0 до со. Вследствие того,
что наше рассмотрение электрона является слишком грубым,
интеграл расходится на обоих пределах. Этого не происходит
при правильном релятивистском описании электрона, локали-
локализованного в атоме водорода. Волны, длина которых больше бо-
ровского радиуса (Zam)~l, оказываются несущественными, так
как имеется минимальная частота вынужденных колебаний
(Omin ~ mZa, отвечающая характерным атомным размерам.
Происходит также высокочастотное обрезание на расстояниях
порядка комптоновской длины волны электрона 1/т, обуслов-
обусловленное релятивистской структурой электрона. Эта структура,
которой отвечает уже знакомая нам амплитуда «дрожания»,
приводит к тому, что частоты выше, чем сотах ~ т, несуществен-
несущественны для рассматриваемого процесса. Поэтому в качестве оценки

66 ПРЕОБРАЗОВАНИЕ ФОЛДИ — ВАУТХАЙЗЕНА fTJl. 4
мы примем
и из D.18) получим для среднеквадратичной амплитуды коле-
колебаний электрона в поле вакуума
Окончательное выражение для сдвига уровня, получаемое из
D16) имеет вид
D.16), имеет вид
Г 8 Z4a3 /, 1 41 / 1 о \ .
~ 1000 Мгц для п = 2, Z = 1, / = 0.
В итоге мы объяснили почти весь наблюдаемый на опыте
сдвиг уровня 2Si/2 атома водорода; сдвиги уровней с / ф 0 хотя
и не равны нулю, однако значительно меньше из-за обращения
в нуль волновой функции в начале координат.
ЗАДАЧИ
1. Получите соотношение D.10).
2. В уравнении Дирака, описывающем взаимодействие протона или ней-
нейтрона с внешним электромагнитным полем, имеется дополнительный член,
отвечающий тому, что эти частицы обладают аномальным магнитным момен-
моментом:
где F^v — тензор электромагнитного поля
а) Для протона i = р, еР — |е|; для нейтрона t = п, е„ = 0. Проверьте,
что значения кр = 1,79 и к„ = —1,91 отвечают наблюдаемым магнитным мо-
моментам этих частиц, а также то, что уравнение с добавочным взаимодей-
взаимодействием по-прежнему лоренц-ковариантно. Убедитесь в том, что гамильтониан
эрмитов и вероятность сохраняется.
б) Проделайте преобразование Фолди — Ваутхайзена для нейтрона, со-
сохранив члены того же порядка, что в D.5). Укажите физический смысл каж-
каждого отдельного члена. Найдите сечение рассеяния нейтронов в электростати-
электростатическом поле. Как можно измерить это сечение? (См. [44].)
3. Найдите точные уровни энергии и волновые функции для дираковского
электрона в однородном статическом магнитном поле (см. [45]).
4. Рассчитайте в наинизшем по а2 приближении линейный эффект Зеема-
на для электрона в атоме водорода. Как изменятся зеемановские уровни,
если гиромагнитное отношение для электрона станет отличным от значения
g = 2 (дать ответ в первом порядке по разности g — 2)?

ЗАДАЧИ в7
5. Обсудите прецессию спина заряженной дираковской частицы с ано-
аномальным магнитным моментом к в статическом магнитном поле. В частности,
покажите, что разность между частотами прецессии спина частицы и ее век-
вектора скорости пропорциональна (g — 2) или к. Как этот результат зависит
от массы частицы? (См. работы [46].)
6. Постройте добавочный член в гамильтониане, отвечающий аномально-
аномальному электрическому дипольному моменту дираковской частицы. Что произой-
произойдет с этим членом при пространственной инверсии? Как он повлияет на
уровни атома водорода? (См. [47].)
7. За счет мезонных эффектов (обсуждаемых в гл. 10) заряд протона
распределен по области с линейными размерами 10~13 см. Найдите влияние
такого распределения заряда на уровни энергии водородного атома, считая
среднеквадратичный радиус распределения равным г « 0,8- Ю-13 см. Сравни-
Сравните результат с лэмбовским сдвигом.

ГЛАВА 5
ТЕОРИЯ ДЫРОК
§ 16. Проблема решений с отрицательной энергией
В нашем изложении мы уже не раз касались решений урав-
уравнения Дирака с отрицательной энергией. Например, была най-
найдена доля таких решений в локализованном волновом пакете.
Однако до сих пор мы старались избегать вопроса об их физи-
физическом смысле [48, 49]. Теперь наступила пора заняться этой
проблемой.
Сам факт существования решений с отрицательной энергией
требует существенного пересмотра дираковской теории, по-
поскольку надо запретить радиационные переходы электронов
с атомных уровней в состояния с отрицательной энергией
и дальнейший ничем не ограниченный каскад. Эта трудность
отсутствует, если полностью пренебречь взаимодействием элек-
электронов с полем излучения. В этом случае можно найти стацио-
стационарные решения, как было сделано в предыдущей главе; опре-
определить уровни энергии и вероятности перехода, которые в целом
хорошо согласуются с экспериментом. Однако вопрос о том, как
удержать электрон от скатывания в состояние с отрицательной
энергией, остается принципиальным как для теории, так и для
практических вычислений, если их надо выполнить с точностью,
требующей учета взаимодействия с излучением. Вероятность пе-
перехода электрона из основного состояния атома водорода в со-
состояние с отрицательной энергией может быть найдена с по-
помощью полуклассической теории излучения с использованием
полученных в гл. 4 волновых функций. Вероятность перехода
в энергетический интервал от —тс2 до —2тс2 приближенно
равна
2^^
и становится бесконечной для переходов на все состояния с от-
отрицательной энергией. Но это явный абсурд!

16J
ПРОБЛЕМА РЕШЕНИЙ С ОТРИЦАТЕЛЬНОЙ ЭНЕРГИЕЙ
Чтобы спасти уравнение Дирака, мы должны найти интер-
интерпретацию состояний с отрицательной энергией, отличную от той,
которую предлагает одночастичная шредингеровская теория. Эта
задача была решена Дираком в 1930 г. Он сформулировал так
называемую «теорию дырок», в которой дилемма, поставленная
существованием решений с отрицательной энергией, разре-
разрешается просто путем заполнения электронами всех состояний
с отрицательной энергией в соответствии с принципом запрета
Паули. Тогда состояние вакуума есть состояние, в котором все
уровни с отрицательной энергией заполнены электронами, а все
уровни с положительной энергией свободны. Тем самым, напри-
например, обеспечивается стабильность основного состояния атома
водорода, поскольку согласно принципу Паули ни один доба-
добавочный электрон не можег попасть в «море» с отрицательной
энергией.
Из предположения о заполненном электронами море с отри-
отрицательной энергией вытекает множество следствий. Электрон
с отрицательной энергией может поглотить излучение и перейти
в состояние с положительной энергией, как схематически пока-
показано на рис. 5.1. В результате мы будем наблюдать электрон
Незанятые
состояния
Занятые
состояния
Е
-0
-тсг
1
• Злектр
I
1 f/s/iyve/tue
1
'Дырка
О
-тс?
Е
Электрон
Излучение
Рис. 5.1. Рождение пары: элек-
электрон с отрицательной энергией
поглощает излучение и по-
попадает в состояние с положи-
положительной энергией.
У////ШШ/.
Рис. 5.2. Аннигиляция пары:
электрон с положительной
энергией опускается в состоя-
состояние с отрицательной энергией
с испусканием излучения.
с зарядом —\е\ и энергией +? и дырку в море с отрицательной
энергией. Дырка означает отсутствие электрона с зарядом —\е\
и энергией —Е, и, сравнив это состояние с вакуумным, наблю-
наблюдатель скажет, что имеется частица с зарядом -\-\e\ и энергией
+?; эта частица называется позитроном. Такова основа объяс-
объяснения процесса рождения пар в теории дырок.
Соответственно дырка в море с отрицательной энергией, или
позитрон, является ловушкой для электрона с положительной

70 ТЕОРИЯ ДЫРОК [ГЛ. 5
энергией, и в этом состоит объяснение процесса аннигиляции
электрон-позитронной пары с испусканием излучения, который
изображен на рис. 5.2.
Следует понимать, что, приняв теорию дырок, мы совершили
переход к многочастичной теории, описывающей частицы обоих
знаков заряда. Теперь волновая функция уже не имеет простой
вероятностной интерпретации, как в одночастичной теории, по-
поскольку она должна описывать процессы рождения и уничтоже-
уничтожения электрон-позитронных пар.
Вспомним, однако, что мы отвергли уравнение Клейна — Гор-
Гордона и перешли к уравнению Дирака потому, что хотели по-
построить одночастичную теорию. Поэтому законно будет спро-
спросить, а почему бы нам не отказаться и от уравнения Дирака?
Наше нежелание поступить подобным образом имеет ту простую
причину, что с помощью уравнения Дирака мы уже получили
впечатляющее количество «правильных» результатов, к которым
относятся спектр атома водорода и гиромагнитное отношение
для электрона. Более того, позитроны, предсказываемые теорией
Дирака, наблюдаются на опыте.
Таким образом, мы строили теорию так, как в свое время
было намечено Дираком, и сначала получили желаемое урав-
уравнение, а теперь подвергли теорию пересмотру и отказались от
тех предположений, которые послужили первоначальным толч-
толчком к ее развитию. История физики знает множество примеров
такого пути развития. Поэтому мы сохраним уравнение Дирака
и его интерпретацию, основанную на теории дырок, но отка-
откажемся от одночастичной трактовки вероятности, к которой мы
так стремились. Заметим, что теперь можно вновь вернуться
к уравнению второго порядка Клейна — Гордона и спасти его,
придав новый физический смысл волновой функции.
По сравнению с уравнением Клейна — Гордона преимуще-
преимущество уравнения Дирака состоит в том, что оно правильно описы-
описывает электрон со спином '/г и гиромагнитным отношением g = 2.
Уравнение Клейна — Гордона, как будет показано в гл. 9, при-
применимо для бесспиновых частиц, таких как пионы. Инвариантом
для обоих уравнений является квадратичное соотношение между
энергией и импульсом свободной частицы p^pv- = пг2. В обоих
случаях требуется дать такое толкование решений с отрица-
отрицательной энергией, которое обеспечивает стабильность основных
состояний. Отсюда с неизбежностью следует существование ан-
античастиц. Частицы (для уравнения Дирака электроны с мас-
массой пг и зарядом —\е\) описываются решениями с положи-
положительной энергией, а античастицы (позитроны с массой m и за-
зарядом + 1е1) описываются заново истолкованными решениями
С отрицательной энергией.

§ 17] ЗАРЯДОВОЕ СОПРЯЖЕНИЕ 71
§ 17. Зарядовое сопряжение
Следствием теории дырок является новая фундаментальная
симметрия в природе: каждая частица имеет античастицу, в ча-
частности, из существования электронов вытекает существование
позитронов. Теперь нам надо найти для этой симметрии фор-
формальное выражение, которое можно было бы использовать для
получения в явном виде волновой функции позитрона из вол-
волновой функции соответствующего электрона с отрицательной
энергией.
Согласно нашей физической картине дырка в море с отрица-
отрицательной энергией, означающая отсутствие энергии —Е (Е > 0)
и заряда -\-е (для электрона е<0), эквивалентна присутствию
позитрона с энергией -\-Е и зарядом —е. Поэтому имеется одно-
однозначное соответствие между решениями с отрицательной энер-
энергией уравнения Дирака
(/V — еА — пг) ф = 0 E.1)
и собственными функциями позитрона. Поскольку по своему фи-
физическому смыслу позитроны вводятся как положительно заря-
заряженные электроны, волновая функция позитрона \рс должна
быть решением с положительной энергией уравнения
(iV + еА-пг)^с = 0. E.2)
Можно пойти обратным путем, более близким к историче-
историческому, и начать с уравнения E.2) для позитронов. Нигде в на-
наших рассуждениях знак заряда е не играл существенной роли.
В этом случае отсутствие решений уравнения E.2) с отрица-
отрицательной энергией будет означать существование электронов.
Итак, имеется однозначное соответствие между решениями урав-
уравнений E.1) и E.2) для обоих значений знака заряда, и тем са-
самым мы приходим к необходимости построения оператора, пе-
переводящего эти уравнения друг в друга.
Прежде всего мы замечаем, что для перехода от E.1) к E.2)
необходимо изменить относительный знак членов iV и А. Этого
проще всего добиться путем операции комплексного сопряжения:
id/dx^ = — (id/dx1)* и Д1=-|-Лд. В результате уравнение E.1)
переходит в
[О ~Ь+еА»)г*+т] ^=0> E-3)
Если бы теперь мы смогли найти несингулярную матрицу, обо-
обозначаемую Су0, подчиняющуюся алгебре
' = -У11, E.4)

72 ТЕОРИЯ ДЫРОК [ГЛ. 5
то уравнение приобрело бы желаемый вид
(tV + еА - т) (Су°ф*) = О,
где функция
СуЦ* = Сф = фг E.5)
есть волновая функция позитрона Существование матрицы С
может быть установлено прямым построением. Покажем это
в представлении B.6), в котором yV1 Y° — У^т> так что равен-
равенство E.4) превращается в Су^С-1 = —у11» или
В этом представлении матрица С должна коммутировать с yi
и уз и антикоммутировать с у0 и у2. Подходящей является мат-
матрица
С = гуУ=- С~' = -С+ = -С7'. E.6)
Этого достаточно для построения матрицы С в любом заданном
представлении; матрица С в новом представлении получается из
E.6) с помощью унитарного преобразования, осуществляющего
переход от одного представления к другому. Заметим, что опе-
оператор С E.6) определен с точностью до фазового множителя,
подобно рассмотренному ранее оператору пространственной ин-
инверсии. Для нашего рассмотрения фаза волновой функции не
представляет физического интереса и мы не будем заниматься
этим вопросом.
Теперь мы подробно остановимся на действии введенного
оператора я|эс = Сфг = iy2^* на собственные функции свободной
частицы с отрицательной энергией. Волновая функция покоя-
покоящегося электрона с отрицательной энергией и спином вниз
имеет вид
°\
\e+imt
N
Соответствующее решение для позитрона есть
E.7)

§ I7J ЗАРЯДОВОЕ СОПРЯЖЕНИЕ 73
Таким образом, отсутствие покоящегося электрона с отрицатель-
отрицательной энергией и спином вниз эквивалентно присутствию покоя-
покоящегося позитрона с положительной энергией и спином вверх.
Если внешнего поля нет, то нет и никакой разницы между элек-
электроном и позитроном и из E.7) мы видим, что путем преобра-
преобразования E.5) просто получается другое электронное решение.
Применяя то же преобразование к собственному состоянию
с произвольными спином и импульсом и используя условия
[С, Y5] = 0 и y? = Y5 = Y5, находим
=. с*' = erf - с» (у (Ц)
?)(^{±-)(idIi)i. E.8)
Снова мы видим, что произведение операций комплексного со-
сопряжения и матричного умножения на Суо = 'Y2 переводит ре-
решение с отрицательной энергией, 4-импульсом р^ и поляриза-
поляризацией s^ в решение с положительной энергией и теми же са-
самыми /?ц и Sp,. Для спиноров, отвечающих свободным частицам,
равенства E.5) имеют вид
, s),
<?**<p.%(/?, s) = CvT(p, s).
Отсюда видно, что v(p,s) и u(p,s) являются зарядово-сопря-
женными спинорами (с точностью до фазы <t>(p,s)).
Напомним, что мы строили решения так, что
Заметим также, что s не меняет знак при зарядовом сопряже-
сопряжении, а спин меняет знак, в чем мы убедились на примере E.7).
Как уже говорилось в § 10, эта разница связана с тем, что спи-
спиновый проекционный оператор имеет в системе покоя вид
A + Yo o-s/2), где s** =@, s) и изменение знака происходит за
счет матрицы уо-
Оператор в равенстве E.5) осуществляет явное построение
волновой функции позитрона. С его помощью можно ввести та-
такую операцию, относительно которой уравнение Дирака инва-
инвариантно. Для этого требуется определить добавочный оператор,
изменяющий знак электромагнитного поля. Тогда формально
дираковская теория будет инвариантна относительно следующей
последовательности операций: 1) комплексное сопряжение,
2) умножение на Су0 и 3) замена -\-А^ на —А^. При этом урав-
уравнение E.1) (E.2)) для электрона (позитрона) переходит в то
же самое уравнение для позитрона (электрона). Это преобра-
преобразование называется зарядовым сопряжением и обозначается С.

74 ТЕОРИЯ ДЫРОК ГГЛ. 5
Физический смысл зарядового сопряжения состоит в том, что
каждому физически реализуемому состоянию электрона в поле
Ац(х) отвечает физически реализуемое состояние позитрона
в поле —Ау,(х). Таким образом, операция С заменяет электроны
с положительной энергией и спином вверх на позитроны с по-
положительной энергией и спином вверх. Это достигается путем
преобразования решений с положительной энергией уравнения
E.1) в решения с отрицательной энергией этого же уравнения,
что согласно теории дырок означает переход к позитрону.
То, что динамика позитрона в поле — А^ в точности такая
же, как электрона в поле -\-А^, неудивительно из классических
соображений. Новый и удивительный результат теории дырок
состоит в том, что из существования электронов с массой т
и зарядом е с необходимостью следует существование позитро-
позитронов с той же массой m и зарядом —е.
Существование в природе электронов с двумя знаками за-
заряда и одной и той же массой есть один из самых сильных
доводов в пользу по крайней мере частичной правильности ре-
релятивистской квантовой теории.
§ 18. Поляризация вакуума
Теория дырок, устраняя трудности, связанные с отрицатель-
отрицательной энергией, приводит, однако, к новым принципиальным пре-
препятствиям, которые приходится преодолевать, и новым физиче-
физическим предсказаниям, требующим экспериментальной проверки.
Рассмотрим, к примеру, влияние вакуума на определение за-
заряда электрона и взаимодействие между двумя зарядами.
Между электроном с положительной энергией и электронами
из моря с отрицательной энергией имеется электростатическое
отталкивание. Поэтому электрон поляризует вакуум вокруг себя.
Суммарная плотность заряда электрона ро(г) и поляризованного
вакуума рР(г), измеренная относительно вакуума, схематически
изображена на рис. 5.3.
Заряд электрона, измеренный с помощью макроскопического
внешнего поля или удаленного пробного заряда, равен
\ d3r [рс (г) + рр (г)] = е0 и представляет собой «физический» за-
заряд. Однако, если проводить измерения с помощью пробного
заряда, находящегося на расстояниях г0 < R, то измеренное
значение заряда будет становиться все более отрицательным до
тех пор, пока в пределе г0 —*0 не станет равным \ d3r р0 (г) = е0,
т. е. значению «голого» заряда, причем |ео|>|е|.
Это явление наблюдается в спектре атома водорода. Элек-
Электронные s-уровни расположены ниже, чем уровни с I. =?= О, так

§ 19]
ОБРАЩЕНИЕ ВРЕМЕНИ И ДРУГИЕ СИММЕТРИИ
75
как в состояниях с / = 0 электрон находится ближе к протону.
Этот эффект поляризации вакуума, вычисление которого будет
проведено в гл. 8, слегка уменьшает смещение Лэмба. В той же
главе мы рассмотрим вопрос о связи «голого» заряда изолиро-
изолированного электрона со значением заряда, наблюдаемым на боль-
больших расстояниях.
В связи с теорией дырок возникает еще один вопрос: какой
смысл имеет введенный нами бесконечный отрицательный пол-
полный заряд вакуума? Пока мы оставим этот вопрос в стороне,
Ро
Рр
R
R
Рис. 5.3. Влияние поляризации вакуума на плотность заряда электрона.
Величина р0 представляет собой плотность заряда «голого» электрона,
а рр есть плотность заряда поляризационного облака, образованного вир-
виртуальными электрон-позитронными парами.
заметив лишь, что электрическое поле от этого распределен-
распределенного заряда не имеет выделенного направления. Наблюдаемыми
являются только неоднородности в распределении, обусловлен-
обусловленные поляризацией вакуума1).
§ 19. Обращение времени и другие симметрии
Рассмотрим теперь преобразования пространственной инвер-
инверсии и обращения времени. Кроме них, имеется еще одна операция
симметрии, также не относящаяся к собственным преобра-
преобразованиям Лоренца, — это калибровочная инвариантность элек-
электромагнитного взаимодействия. Однако инвариантность относи-
относительно калибровочных преобразований автоматически обеспечи-
обеспечивается введением взаимодействия в виде рц — еЛц. Проверка
этого утверждения производится в точности, как в шредингеров-
ской теории.
') Этот вопрос рассматривается в книге авторов [50], русский перевод
которой выходит в издательстве «Наука». (Прим. перев.)

76 ТЕОРИЯ ДЫРОК [ГЛ. 5
Напомним, что, как было установлено в § 7, операцию про-
пространственной инверсии можно записать следующим образом:
Ря(з (х, 0 = г|/ (х', /) = е^уЧ (х, t), где х' = — х. E.9)
Для решений в виде плоских волн пространственная инверсия
состоит в изменении знаков импульсов при неизменных значе-
значениях спинов, т. е. происходит гак, как следует ожидать из клас-
классических соображений. Такое преобразование волновой функции
в сочетании со следующим хорошо известным преобразованием
над 4-потенциалом электромагнитного поля:
РФ (х, /) = Ф' (х', 0 = Ф (х, t),
0 A'(x'/) A(x /) Где х--х' <5Л°)
оставляет неизменными уравнение Дирака и значения всех на-
наблюдаемых физических величин. Физическое содержание инва-
инвариантности дираковской теории относительно пространственной
инверсии можно пояснить следующим образом.
Рассмотрим некоторую серию наблюдений над состоянием,
описываемым волновой функцией \(з (х, /). Заснимем наши на-
наблюдения на кинопленку, причем съемочную камеру направим
на плоское зеркало, в котором отражается экспериментальная
установка. Тогда мы сможем сказать, что динамика явления,
которое мы наблюдаем, инвариантна относительно простран-
пространственной инверсии, если в заснятом в зеркале кинофильме по-
показана физически возможная последовательность явлений, т. е.
если, смотря этот фильм, невозможно установить, видим ли мы
зеркальное отражение или само явление. Поэтому вместо про-
пространственной инверсии достаточно рассматривать зеркальное
отражение, хотя эти операции и не тождественны. При зеркаль-
зеркальном отражении меняется знак только у координат, направление
которых перпендикулярно к плоскости зеркала; чтобы получить
преобразование инверсии, надо еще произвести поворот на
угол я вокруг нормали к поверхности зеркала. Однако такой
поворот уже включен в собственные преобразования Лоренца.
Переходя к обсуждению симметрии относительно обращения
времени, мы для выяснения ее физического содержания опять
воспользуемся мысленной киносъемкой последовательности на-
наблюдений над состоянием, описываемым волновой функцией
•ф(дс). Просмотрим теперь отснятый кинофильм в обратном на-
направлении, от конца к началу. Можно утверждать, что динамика
наблюдаемого явления инвариантна относительно обращения
времени, если показанный в обратном порядке фильм изобра-
изображает физически возможную последовательность наблюдений.
Эта инвариантность будет обеспечена при условии, что мы мо-
можем заменить t на F = —t и проделать такое преобразование,

§ 19] ОБРАЩЕНИЕ ВРЕМЕНИ И ДРУГИЕ СИММЕТРИИ 77
которое приводит уравнение Дирака к прежнему виду с преж-
прежней физической интерпретацией. Преобразованная волновая
функция будет описывать первоначальный электрон, движу-
движущийся назад во времени, и она будет физически возможной,
поскольку будет удовлетворять уравнению Дирака.
Для построения искомого преобразования обращения вре-
времени запишем уравнение Дирака в гамильтоновой форме
а^х, t) = ^ = [а . (_ г-у - еА) + N + еФ] \р (х, t) E.11)
и определим преобразование S такое, что при /' = —t
= 2/ф@- Тогда E.11) переходит в 1)
Инвариантность относительно обращения времени означает, что
%Н {t)Z~l = -H{t'), либо ZiZ~x = — i.
Для выяснения поведения Н при действии оператора % мы
должны сперва установить закон преобразования 4-потенциала
электромагнитного поля А^ при замене ? = —t. Поскольку А
обусловлен токами, которые меняют знак при обращении вре-
времени, мы потребуем
А'(О = -А@
и аналогично
Ф'(/0 = + Ф@ E.13)
вследствие того, что Ф обусловлен зарядами; кроме того,
V=-f-V, так как х' = +х. Теперь ясно, что для приведения
уравнения E.12) к первоначальному виду необходимо, чтобы
преобразование ? ... ?-' заменяло i на —i; следовательно,
? можно представить в виде оператора комплексного сопряже-
сопряжения, умноженного слева на некоторую постоянную матрицу
размерности 4X4:
1)'(О = 7У(/). E.14)
Тогда имеем
В представлении A.17), которым мы обычно пользуемся, это
означает, что матрица Т должна коммутировать с а2 и р и ан-
тикоммутировать с ai и аз- Таким образом, нашим требованиям
') Мы опускаем несущественную здесь зависимость от х.

78 ТЕОРИЯ ДЫРОК [ГЛ. 5
удовлетворяет матрица
Г = -/<z,a3 = + ivV, E.15)
где фазовый множитель выбран произвольно.
Чтобы показать, что преобразование ? соответствует тому,
что мы подразумеваем под обращением времени в классической
физике, применим E.14) и E.15) к решению в виде плоской
волны для свободной частицы с положительной энергией:
(Чг) ("
(x) О, E.16)
где р' = (/?о,—р) и s' = (so,—s) и, следовательно, проектиро-
проектирование производится на решение, отвечающее свободной частице
с измененными на обратные значениями трехмерных векторов
импульса р и спина s. Эта операция, известная как вигнеровское
обращение времени, была впервые введена в 1932 г. [51].
Поскольку теория инвари-антна относительно операций про-
пространственной инверсии и обращения времени, мы, если поже-
пожелаем, можем использовать эти операции при построении волно-
волновой функции позитрона. Объединяя E.9), E.14) и E.15) с E.5),
находим простое соответствие между волновой функцией по-
позитрона
Ърст W) ^ РС\о С&|> (*))* = РСЩ (х) =
=/e'^W, где *? = -*,,, E.17)
и волновой функцией электрона, умноженной на iVys и описы-
описывающей электрон, движущийся в обратном направлении в про-
пространстве и времени.
Для собственного состояния свободной частицы ty(x), ха-
характеризующегося определенными значениями импульса и
спина (/?•*, si*) и е = —1 имеем
E.18)
Уравнение E.18) отличается от E.8) только направлением
спина, и поэтому мы можем представить волновую функцию по-
позитрона с положительной энергией как волновую функцию элек-
электрона с отрицательной энергией, умноженную на ie^ys и отве-
отвечающую движению в обратном направлении в пространстве-
времени.
Чтобы убедиться в справедливости высказанного утвержде-
утверждения для произвольного решения во внешнем электромагнитном

ЗАДАЧИ 79
поле, надо вернуться к уравнению для отрицательных собствен-
собственных значений энергии
[а • (- iV - ек) + рт + еФ] я|з = - ?Ч|> E.19)
и произвести преобразование E.17). Из E.10) и E.13) можно
видеть, что при комбинированной операции инверсии простран-
пространства и обращения времени А'^{х') — + А^(х) и х'^—— х^, следо-
следовательно, E.19) приобретает желаемый вид
[а . (_ /у' + ек' (*')) + N - еФ' (хг)] Ърст (*') = + Е^рст (*')•
Интерпретация позитронов как электронов с отрицательной
энергией, движущихся в обратном направлении в пространстве-
времени, составляет основу теории позитронов Штюкельберга —
Фейнмана [52—54]. Мы будем часто пользоваться этой теорией
в последующих главах для построения теории рассеяния.
В заключение обратим внимание на то, что выбранный нами
вид взаимодействия электронов с электромагнитным полем был
продиктован опытом, накопленным нами в классической элек-
электродинамике и в нерелятивистской электродинамике электро-
электронов. С другой стороны, существование рассмотренных нами
принципов симметрии зависит от вида взаимодействия. Напри-
Например, введенное в задачах к гл. 4 взаимодействие аномального
магнитного момента протонов и нейтронов добавляет в уравне-
уравнение Дирака член вида o^vF^ty. Его присутствие не влияет ни на
одну из рассмотренных симметрии. Распространяя дираковскую
теорию на другие частицы со спином '/г. такие как ц-мезон
и нуклоны, весьма естественно предположить, что инвариант-
инвариантность относительно преобразований ?, С и Р справедлива
и для них.
Большая заслуга Ли и Янга [55] состоит в осознании того,
что это и в самом деле всего лишь предположение, которое надо
проверять на опыте. Они высказали гипотезу, что во взаимодей-
взаимодействиях типа р-распада нарушается инвариантность Р и С. Од-
Однако инвариантность относительно операции ?СР обеспечи-
обеспечивается гораздо более слабыми предположениями об инвариант-
инвариантности относительно собственных преобразований Лоренца и
правильной связи спина со статистикой.
ЗАДАЧИ
1. В борновском приближении покажите, что скорость радиационного пе-
перехода электрона из основного состояния атома водорода в незаполненные
состояния с отрицательной энергией, лежащие в интервале от —шсг до
—2пгс2, составляет приблизительно 2а6тс2/яй « 108 cen~i.
2. Разрешите парадокс Клейиа, изложенный в гл. 3, с помощью теории
дырок-

80 ТЕОРИЯ ДЫРОК [ГЛ. 5
3. Покажите, что если Уц и у^ являются двумя представлениями мат-
матриц у. связанными между собой унитарным преобразованием \^ = UyuU~ , то
С = {U ) CU, где С и С есть соответствующие матрицы зарядового со-
сопряжения. Справедливы ли для С соотношения E.6)?
Аналогичным образом устраните зависимость преобразования E.15) от
конкретного представления матриц у.
4. Для того чтобы оператор % был оператором симметрии в дираковской
теории, правила интерпретации волновых функций г|/(^') и г|)(/) должны быть
одними и теми же. Это означает, что наблюдаемые величины, построенные из
билинейных форм, составленных из i|/ и i|/+, должны иметь тот же самый
смысл, что и наблюдаемые, построенные из г|) (иногда имеется различие в
знаке).
а) Проверьте это утверждение для тока
и для
<<•>' = (О, <р') = -<Р>.
б) Повторите эти выкладки для зарядового сопряжения С. В частности,
покажите, что
(х),
и объясните это равенство, исходя из теории дырок.

ГЛАВА 6
МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ
§ 20. Введение
Мы переходим к общему рассмотрению процессов рассеяния.
Наша цель — иметь возможность вычислять, в принципе точно,
вероятности переходов и сечения в дираковской теории элек-
электронов и позитронов; на практике вычисления обычно прово-
проводятся в низших порядках по параметрам взаимодействия. Воз-
Возможность изменения числа частиц в таких процессах, как
рождение электрон-позитронных пар или аннигиляция, выводит
нас за рамки применимости нерелятивистской теории. Тем не
менее мы будем как можно дольше откладывать решение гран-
грандиозной задачи построения формализма квантовой теории поля
для описания процессов рождения и аннигиляции.
С этой целью мы, следуя Фейнману [53, 54], воспользуемся
методом функции распространения (пропагатора). В этом ме-
методе процесс рассеяния описывается интегральными уравне-
уравнениями. Граничные условия, которым удовлетворяют их решения,
включают в себя согласно Штюкельбергу — Фейнману интерпре-
интерпретацию позитронов как электронов с отрицательной энергией,
движущихся назад во времени. Такой подход позволяет сфор-
сформулировать однозначные правила для расчета любого физиче-
физического процесса1). Начнем с напоминания о методе функции рас-
распространения для нерелятивистского уравнения Шредингера.
§ 21. Нерелятивистский пропагатор
В задачах рассеяния наше внимание больше сосредоточено
на нестационарных решениях, которые развиваются во времени
из заданных в отдаленный момент начальных значений, чем
на стационарных решениях, т. е. плоских волнах. Характерная
постановка задачи такова: по заданному в отдаленный началь-
начальный момент времени волновому пакету, описывающему
Теоретико-полевое обоснование этих правил содержится в [50].

82 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. 6
приближающуюся к источнику потенциала частицу, определить,
как будет выглядеть волна в далеком будущем.
При рассмотрении процессов рассеяния удобно пользоваться
принципом Гюйгенса. Если волновая функция я|э(х, t) известна
в некоторый определенный момент времени t, то в любой более
поздний момент времени V ее можно найти, считая, что в мо-
момент t каждая точка х является источником сферических волн.
Амплитуда волны, пришедшей в точку х' в момент времени f
из точки х, будет пропорциональна исходной амплитуде я|э(х, t).
Если обозначить коэффициент пропорциональности посредством
iG{\',tr\x,t), то согласно принципу Гюйгенса в точку х' в мо-
момент времени f придет волна ')
ф (х', Г) = i \ d4 G (х', t'\ х, t) ф (x, t), t' > t, F.1)
где функция G(x', t';x, t) называется функцией Грина, или про-
пагатором. Согласно принципу Гюйгенса G(x',/';x, t) характе-
характеризует влияние функции я|э(х, t) на г|)(х', f). Знание G дает нам
возможность построить физическое состояние, которое полу-
получается развитием во времени из любого наперед заданного на-
начального состояния. Таким образом, нахождение функции Грина
эквивалентно полному решению уравнения Шредингера.
Мы, однако, должны еще дать функции G формальное опре-
определение. Пока мы лишь провозгласили ее существование, исходя
из физических соображений. Остановимся на этих соображениях
подробнее, чтобы уяснить суть метода функции распростра-
распространения.
Рассмотрим сначала решение в виде свободной волны. Дви-
Движение свободной частицы полностью известно, поэтому нет ни-
ничего удивительного в том, что соответствующую функцию Грина
Go для свободного движения можно получить в замкнутом виде.
Если теперь ввести потенциал, G,o видоизменится. Пусть V(xi,/i)
представляет собой потенциал, который в момент t\ «вклю-
«включается» на очень короткий промежуток времени Д/j. До мо-
момента t\ мы будем иметь волновую функцию свободной час-
частицы ф, а соответствующим пропагатором будет Go. Согласно
уравнению Шредингера V(\\,t\) действует как источник новых
волн
(^)(х,, /,) = V(xb f,)i|>(Xb U). F.2)
') Поскольку уравнение Шредингера является уравнением первого по-
порядка по времени, принцип Гюйгенса применим к нему без модификации,
данной Кирхгофом.

§ 21] .НЕРЕЛЯТИВИСТСКИЙ ПРОПАГАТОР 83
Правая часть отлична от нуля в течение времени At\ и в это
время она вызывает дополнительное изменение \|з по сравнению
с тем, которое происходит в отсутствие V. Эту добавочную
волну Д\|)(хь^) находим интегрированием F.2) с точностью
до первого порядка по Д^:
Дф (хь /,) = - iV (х,, tt) Ф (хь /,) Д*,. F.3)
Согласно принципу Гюйгенса и F.1) найденная добавочная
волна приводит в свою очередь в более поздний момент времени
/' к новой добавке к г|з (х7, t'), равной
х', П = J d% Go (x', V; х,, h) V (хь f,) q> (хь /,) Д*,. F.4)
Таким образом, результатом развития во времени произвольного
пакета ф, заданного в отдаленном прошлом, является волна
ф (х', О = ф (х', П + J dhx Go (x', f\ хь h) V (х,, if,) ф (хь tt) Д/, =
= i\d3x[G0(x', f; x, 0 +
+ J d3x, A/,G0 (x', t'\ x,, /,) F (xlf f,) Go (xi, /,; x, /)] Ф (x, /)• F-5)
Сравнивая это выражение с F.1), находим
G(x', f; x,O = Go(x/>^; x, t) +
d3*, Af,G0 (x', tr; x,, <,) F (xb /,) Go (x,, /,; x, /)• F.6)
Иллюстрацией этого равенства могут служить изображенные
на рис. 6.1 пространственно-временные диаграммы. Первому
члену, который описывает распространение свободной частицы
из точки (х, t) в (x',tf), отвечает рис. 6.1, а. Диаграмма 6.1,6
изображает свободное движение из (х, t) в (xi,^i), рассеяние
в точке (xi.^i) и свободное движение из {x\,t{) в (х', V).
В момент времени t2 > t\ мы можем на время At2 включить
другой потенциал V(x2,t2). Тогда по аналогии с F.4) У(х2, t2)
дает при t' > t2 добавочный вклад в г|)(х', V), равный
х') = J d% Go (/; 2) V B) ф B) At2 =
= i J d?x d% At2G0 (*'; 2) V B) [g0 B; x) +
(х); F.7)

84
МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ
[ГЛ. 6
здесь смысл сокращенных обозначений очевиден. Иллюстрацией
первого члена, который отвечает однократному рассеянию в
(х2, ^2), служит рис. 6 1, в; второй член описывает поправку на
двукратное рассеяние и изображается диаграммой 6.1, г.
(*',t'J
(в)
(г)
Рис. 6.1. Пространственно-временные диаграммы для распространения из
точки (х, f) в (х', f )• Диаграмма (а) отвечает свободной частице, (б) — одно-
однократному рассеянию на потенциале V (хь fi) в точке (xi.fi), (в) соответ-
соответствует однократному рассеянию в точке (х2, t2) и (г) отвечает двукратному
рассеянию.
Для нахождения полной волны, приходящей в точку (х', t'),
надо подставить выражение F.5) для г|)B) в правую часть F.7^
и полученный результат сложить с F.5):
ф (хО = Ф (*') + \ d% Д/.Go (*'; 1) V A) ф A) +
i Д/i d% At2G0 {x'; 2) V B) Go B; 1) V A) q> A). F.8)

§ 21] НЕРЕЛЯТИВИСТСКИЙ ПРОПАГАТОР 85
Не проводя дальнейших выкладок, нетрудно записать ответ для
волны, приходящей в точку (\',?), в случае, когда потенциал V
был включен в течение п подобных интервалов:
(х') = Ф (х') + ? [ d% Д/;С0 (*'; Xi) V (х,) Ф (х,) +
i
Л, Д/, d3xy Д/уО0 (*'; xt) F (х,) Go (*,; х,) F (х,) Ф (х,)
i/fe
(tt>tj>tk)
X Go (x'\ xt) V {xi) Go (xr, Xj) V (Xj) Go (x,-; xk) V {xk) ф {xk) + ... F.9)
Сравнивая F.9) с F.5) и F.6), получаем соответствующее вы-
выражение для функции Грина G:
G{x'; x) = G0(x'; x)+ У\ d3XiAliG0(x'; x,, t,)V{xt, t,)G0(xt, U\ x) +
,Д//О0(х/; х,, ^)K(x/t/,)X
i
X Go (xb /f; X/, /y) V (x/f f,) Go (X/) f,; x) + ... F.10)
Мы можем снять ограничения, связанные с упорядочением
времени (t{ >tj и т. д.), если условимся считать G0(x', t'\ x, /) =0
при ? < t. Такое граничное условие означает, что волны распро-
распространяются только вперед во времени. Соответствующий пропа-
гатор Go принято называть запаздывающим. Физически это озна-
означает, что гюйгенсовское возмущение Д\|з от г-й итерации
(в момент времени t\) начинает распространяться только с мо-
момента tu
В пределе, когда взаимодействия происходят непрерывно,
суммы по временным интервалам могут быть заменены инте-
интегралами по dt и мы получаем
G (*'; х) = Go (/; х) + J d% Go (*'; Xl) V (jc,) Go (*,; x) +
d*xx d*x2 Go {x'\ xd V (x,) Go (x,; x2) К (jc2) Go (x2; x) + ..., F.
где
dh = d3x dx0 = d3x dt.

86 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. в
Предполагается, что ряд F.11), отвечающий многократному рас-
рассеянию, сходится ') и тогда результат его суммирования можно
представить в виде уравнения
G (*'; х) = Go (х'; х) + J d% Go (xf; x,) V (*,) G (x,; x). F.12)
Заметим, что не только G0(x';x), но также и G(x';x) обра-
обращается в нуль при f <. t в соответствии с нашим простейшим
принципом причинности.
Уравнение F.12) позволяет методом итераций выразить G
через V и Go и тем самым построить волновую функцию г|)(х', t'),
если она известна в более ранний момент времени. В частности,
для решения задачи рассеяния мы должны найти волну в отда-
отдаленном будущем по заданному волновому пакету ф(х, t), опи-
описывающему частицу, которая в отдаленном прошлом прибли-
приближается к области взаимодействия. Чтобы задача рассеяния была
поставлена правильно, взаимодействие в начальный момент
должно отсутствовать; тогда ф будет решением уравнения для
свободной частицы и требуемые начальные условия удовле-
удовлетворены.
Математически такую постановку задачи удобно осуществить
путем локализации взаимодействия во времени2), адиабати-
адиабатически включая V(x, t) при t—*—оо; тогда в отдаленном про-
прошлом точное решение \|з приближается к ф и рассеянная волна
отсутствует. В более поздний момент времени г|з (х', /') дается
выражением F.1):
,|,(х', /')== lim / ( d?xG{x', /'; х, /)<р(х, t). F.13)
Выражая G через Go согласно F.12), находим
гКх', О = lim i \ d'x \G0 (x't f\ x, t) +
0(x', f\ \)V{\)G{\; x,
= Ф(х', n+\d%G0(x',t'; x,,/,)K(x,,/,)ф(х,, /,)• F-14)
В действительности не получено никакого решения, поскольку
неизвестная функция -ф фигурирует под знаком интеграла в пра-
правой части. Мы, однако, имеем такую формулировку задачи, ко-
') Здесь мы пренебрегаем возможностью существования в потенциале V
связанных состояний.
2) С таким же успехом можно строить волновые пакеты, локализованные
в пространстве и удаленные в начальный момент времени от области взаимо-
взаимодействия.

§ 21] НЕРЕЛЯТИВИСТСКИЙ ПРОПАГАТОР 87
торая включает требуемые граничные условия и позволяет не-
немедленно получить приближенное решение, если возмущающий
потенциал V мал.
Мы в первую очередь интересуемся видом рассеянной волны
при f -> оо. В этом предельном случае частица покидает область
взаимодействия и \|з снова становится решением уравнения для
свободной частицы. Чтобы эго условие выполнялось, мы, как
и прежде, адиабатически выключаем взаимодействие при
/'->+ оо. Вся информация о рассеянной волне заключена в ам-
амплитудах перехода при t'-*--\-oo в различные конечные свобод-
свободные состояния
^ FЛ5)
из заданной падающей волны фг-; в частности, мы можем поль-
пользоваться плоскими волнами1). Амплитуда перехода для задан-
заданных (/, i) является элементом матрицы рассеяния и дается вы-
выражением
Sfl = Jirn^ J q>; (х', П
= lim
+ J d'x Go (%', f\ х, О V (х, /) ф<+) (х, t)] =
= 63(к.-к.)+ lim (А;ЙФ;(х' t')G0(x', f; x, t)X
X V (x, 0 ^<+> (x, 0, F.16,
где г^.+Чх, t) есть такое решение волнового уравнения F.14),
которое при t-+—оо переходит в плоскую волну с импульсом kj.
Под сокращенной записью /->±оо мы подразумеваем, что /
стремится к такому большому конечному значению, когда час-
частицы находятся вне области взаимодействия (иначе говоря,
') В F.15) решение в виде плоской волны нормировано на б-функцию.
Иногда пользуются нормировкой в ящике; при этом
где V — объем ящика, в котором заключено физическое взаимодействие. Если
пользоваться нормировкой в ящике, то б-функция в F.16) заменяется б-сим-
волом Кронекера
I при к. = к,,
бь.ь =< „ /'
О при к, фк..

МЕТОЛ ФУНКЦИИ РАСПРОСТРАНЕНИЯ
[ГЛ. 6
когда V выключается). В частности, t—>±°° может означать
времена, когда частицы рождаются и регистрируются.
Путем итерации уравнения F.14) мы можем разложить ф<+>
в ряд многократного рассеяния, члены которого будут отвечать
диаграммам, изображенным на рис. 6.1.
§ 22. Формальное определение и свойства функции Грина
С физической точки зрения мы подготовили все необходимое
для решения задачи рассеяния. Теперь мы построим формаль-
формальный математический аппарат, позволяющий получать эти реше-
решения. Наша цель —исследовать дифференциальное уравнение,
определяющее G, и, в частности, получить явное решение для
Go. Тогда можно будет произвести разложение G, о котором
говорилось выше. Начнем с уравнения F.1), справедливого при
I' > t, и перепишем его в виде, справедливом при любых f и /:
6 {f - t) г|з (*') = i J d3x G (x'; x
; F.17)
здесь Q(t' — t) — единичная ступенчатая функция, определенная
согласно
\: t><t. <бл8)
Она имеет следующее очень полезное интегральное представ-
представление:
]
Расположение контура интегрирования в комплексной плоско-
плоскости со показано на рис. 6.2.
\
t<0
-is
Рис. 6.2. Контур интегрирования в комплексной плоскости для единичной
функции-ступеньки G (т).
При т > 0 контур замыкается бесконечной полуокружностью
в нижней полуплоскости, чтобы обеспечить экспоненциальное
затухание подынтегрального выражения, и значение интеграла

§ 22] ФУНКЦИЯ ГРИНА gg
равно 1 согласно теореме К.оши. При т < 0 контур замыкается
в верхней полуплоскости и значение интеграла равно нулю, по-
поскольку полюс в точке —ie оказывается вне контура. Вследствие
того, что 0(т) испытывает единичный скачок при т = 0, ее про-
производная есть б-функция
Теперь, пользуясь F.17), мы попытаемся получить для
функции G (х'\ х) дифференциальное уравнение и исследовать
ее формальные свойства. Как известно, г|)(л/) удовлетворяет
уравнению Шредингера, поэтому применим к F.17) оператор
е (С - о ч> (/) = /б (/' - о * (*') =
= i \ dH [i -jp- - Н (*')] G {х'\ х) ф (х). F.21)
Поскольку это равенство справедливо для любого решения \|з,
из него можно получить уравнение для шредингеровской функ-
функции Грина
\i-§p--H (x')] G (х'\ х) = б3 (х' - х) б (/' - i) = б4 {х' - х). F.22)
Это уравнение вместе с граничным условием, отвечающим рас-
распространению вперед во времени,
G (*'; Х) = О при f < t, F.23)
определяет запаздывающую функцию Грина, или пропагатор,
соответствующий уравнению F.17).
Для свободной частицы, когда гамильтониан есть Н0(х') =
= —5—^х'. уравнение для функции Грина может быть ре-
решено явно. В этом случае Gq{x'\x) зависит только от разности
координат точек (х', f) и (х, t). Это связано с тем, что волна
в (х\ f) от единичного источника, расположенного в х и вклю-
включаемого в момент /, зависит лишь от интервала (х' — х; У — t),
а функция Go(x';x) есть не что иное, как амплитуда этой волны.
Рассмотрим фурье-преобразование
G0(x'; jc) = GoU'-jc)= J-^^-e'P-(«'-«)-'«P'-«G0(p, со). F.24)

90 Метод функции распространения [гл. 6
Уравнение F.22), записанное для GQ(p, со), имеет вид
= \ &$¦ (со - ?) Go (p, со)
Следовательно, для со Ф р2/2т
G0(p, m) = ю_р2/2т- F.25)
Это выражение необходимо дополнить правилом обращения
с особенностью в нуле знаменателя. Оно вытекает из граничного
условия запаздывания F.23).
Вспоминая сказанное по поводу представления 0-функции
в виде F.19), введем в знаменатель бесконечно малую положи-
положительную мнимую добавку и проведем интегрирование в F.24).
I Ш@
Рис. 6.3. Особенность функции Go (p, со).
Особенность лежит ниже действительной оси, как показано на
рис. 6.3, и мы получаем
оо
dco e-ie>(t'-t)
2я со — (р2/2т) + ie
Фр (х', /') Ф; (х, /), F.26)
где в последней форме записи использовано обозначение F.15).
Полученное равенство — один из примеров (для случая пло-
плоских волн) выражения функции Грина в виде суммы по пол-
полному набору собственных функций соответствующего дифферен-
дифференциального уравнения1). В общем случае, если мы можем по-
') Функцию Грина для свободной частицы можно записать в замкнутой
форме

§ 22] ФУНКЦИЯ ГРИНА 91
строить полный набор нормированных решений уравнения Шре-
Шредингера, который удовлетворяет условию полноты
Е % (х', /) Ч>; (х, /) = б3 (х - х'), F.27)
п
где 2 обозначает как сумму, так и интеграл по непрерывному
п
спектру, то функция
G (*'; х) = - /0 (/' - t) Z Ч>„ (х') ф; (х) F.28)
удовлетворяет уравнению F.22) с требуемым граничным усло-
условием. Выражение F.26) для Go получается отсюда как частный
случай, если учесть, что для непрерывного спектра V —*¦ \ d3p.
п
Из вида выражений F.26) и F.28) следует, что та же са-
самая функция Грина, которая описывает развитие решения урав-
уравнения Шредингера в прямом направлении во времени, описы-
описывает развитие комплексно-сопряженного решения в обратной
временной последовательности. Умножая F.28) на \|>т(х), ин-
интегрируя по х и используя ортонормированность собственных
функций, мы вновь приходим к уравнению F.17):
* \ d3x G (х'; х) 4>m (х) = 6 (? - О J] ч>„ (*') J dh ч,; (х) ^т (х) =
Проделаем ту же операцию, но только умножая на ty*m{x') и ин-
интегрируя по х'. Получим
/ \ d3/ ф; {/) g {/¦, х) = е (/' - о ч>; (Х). F.29)
Мы используем эти соотношения для получения различных по-
полезных представлений S-магрицы.
Из F.17) и определения F.16) можно получить компактное
выражение для S-матрицы через точный пропагатор:
SH = Mim lim \ d3x' d3x ф! {х') G {х'\ х) ф. (х). F.30)
Однако такая запись еще не приносит пользы, поскольку мы,
вообще говоря, не умеем находить точный пропагатор. Из F.28)
Эта формула напоминает выражение, получаемое в теории броуновского дви-
движения для вероятности того, что частица, находившаяся в точке х в момент
времени t, под влиянием случайных воздействий достигнет точки х' в мо-
момент времени /'. Единственное отличие состоит в замене (t, t') иа (—it, —it').
Та же самая замена переводит уравнение Шредингера в уравнение диффузии-

92 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. 6
ясно, какая богатая информация заключена в G(x';x).
В G{x'\x) с равными весами входят все решения уравнения
Шредингера, включая те, которые отвечают связанным состоя-
состояниям. Поэтому нет ничего удивительного в том, что найти G
очень трудно.
Поступим так же, как мы действовали, когда из интуитив-
интуитивных соображений получали равенство F.11). Тогда мы восполь-
воспользовались методом итераций, начав с функции Грина для свобод-
свободной частицы.
Записав Н в виде Н = Но + V, перегруппируем члены в урав-
уравнении F.22):
[/ -?г - Но {/)] G (*'; х) = б4 (*' -x) + V {/) G (/; х) =
= J dKx" б (/ - х") [б4 {х" — x) + V (x") G (х"\ х)\. F.31)
В правой части в член, содержащий взаимодействие, мы ввели
б-источник. Тогда интеграл в F.31) можно выразить через сво-
свободный пропагатор и в итоге мы получим
G (/; х) = \ d*x" Go (/¦ х") [б4 {к" -x) + V (x") G (х"; х)] =
= Go (*'; х) + J d4x" Go (х'\ х") V (х") G (х"\ х), F.32)
что согласуется с F.12). Подставляя F.32) в F.30) и используя
равенства F.17) и F.29) для свободных частиц, имеем
Sfl = \ d3x Ф; (х) ф. (х) + 1 im \ d\ dhФ; (х,) V (х,) G (*,; х) Фг (jc) =
- I \ d\ d%qrt(l) V A) G0(l, 2) V B)ср. B) -
-i\d\d%d%<p;(l)V(l)G0(l,2)VB)G0B,3)V(S)<t>lC)+...F.33)
Этот ряд многократного рассеяния почленно совпадает с рядом,
получаемым из F.16). Как и F.16), его можно просуммировать,
воспользовавшись решением точного уравнения Шредингера.
Для этого заметим, что в первом звене равенств F.33) можно,
обратившись к F.17) и выключив взаимодействие, записать
lim \ d3x G {х"; х) % (х) = Iim \ dh G {x"\ x) ifo (jc) = - 1% (**).
<-»-<v

§ 22] ФУНКЦИЯ ГРИНА 93
Тогда уравнение F.33) переходит в
Sf. = 6f. - i \ d*x" Ф; (х") V (*") Ч><+> (х"), F.34)
где \р\+)(х") есть решение, которое при t" —*—оо переходит
в свободную волну (см. F.14)):
$(+) {х") = ф. (Х") + $ d4 Go (x"; х) V (х)
Уравнения F.34) вместе с F.14) и F.30) вместе с F.32) яв-
являются эквивалентными формами записи S-матрицы; оба эти
представления приводят к ряду многократного рассеяния F.33).
В практических вычислениях мы будем обычно сохранять
только первый или два первых неисчезающих для данного взаи-
взаимодействия члена в выражении F.33) для S-матрицы. На-
Насколько это правомерно, зависит от малости взаимодействия V
и быстроты сходимости данного ряда по степеням константы
взаимодействия.
Общим свойством S-матрицы, которое следует из сохране-
сохранения вероятности, является унитарность. Из вводных замечаний
к гл. 1 мы помним, что из эрмитовости гамильтониана вытекает
сохранение вероятности. Поэтому скалярное произведение не
зависит от времени и мы имеем
)*{x)V+){x)= lim [ d3xЧ><+>*(х) г|Л+> (*) =
= {Игт^ J d3x q>; (x) Ф/ (х) = 6„. F.35)
В частности, для плоских волн
Мы также можем вычислить это скалярное произведение в да-
далеком будущем, и тогда, согласно F.16) и условию полноты
F.27) для функций ф, решения \)з((+) допускают разложение по
плоским волнам с элементами S-матрицы в качестве коэффи-
коэффициентов разложения:
lim iM+)(*')=Zcpn(x')Sni) F.36)
t'-^ + oo n
| где V = \ d3p для представления плоских волн j.
Подставляя F.36) в левую часть F.35), находим
Z SniSl,- = в/( F.37)
п
или, в матричных обозначениях, S+S = 1.

94
МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ
[ГЛ. 6
Если, подобно ф„ в F.36), функции г|з'.+)(л;) образуют полный
набор, то S+ = ?-' и мы приходим к выводу об унитарности
S-матрицы ').
§ 23. Функция распространения в теории позитрона
Теперь мы обобщим рассмотренный в рамках нерелятиви-
нерелятивистской теории метод функции распространения на случай реля-
релятивистской теории электрона. Отправным пунктом нам послу-
послужит представление о нерелятиви-
нерелятивистском пропагаторе G(x';x) как
амплитуде вероятности распро-
распространения волны-частицы из х в
х'. Эта амплитуда, определяемая
выражением F.11), является
суммой амплитуд, n-й член кото-
которой есть произведение величин,
изображенных на диаграмме
рис. 6.4. На этом рисунке каждая
линия соответствует амплитуде
G0(X{, Xi-i) свободного распро-
х странения волны, испущенной в
точке х,-_| до точки xt. В точке xt
(обозначаемой кружками) эта
волна рассеивается с амплитудой
вероятности V(xt) на единицу
объема в четырехмерном про-
пространстве-времени и превращает-
превращается в новую волну, распространяю-
распространяющуюся с амплитудой Go(x,+i; х,)
вперед во времени до следующего взаимодействия. Затем по-
полученная таким способом амплитуда суммируется по всем точ-
точкам в пространстве-времени, в которых может произойти
взаимодействие. Можно сказать, что взаимодействие в г-й точке,
или вершине, уничтожает частицу, дошедшую до точки х{, и
создает частицу, которая распространяется до точки Xi+\, где
Такую картину мы сохраним и в дираковской теории дырок.
Она хорошо соответствует релятивистской теории, поскольку
описывает процесс одновременно в пространстве и во времени,
в противоположность гамильтонову формализму, в котором упор
делается на временном ходе процесса. Наша цель состоит
в том, чтобы по аналогии с нерелятивистским методом функции
Рис. 6.4.
Вклад га-го
в О(х,х').
порядка
') Если имеются связанные состояния, то сумма в F.27) должна вклю-
включать дискретный спектр. Это никак не влияет на доказательство унитарности.

9 23]
ФУНКЦИЯ РАСПРОСТРАНЕНИЯ В ТЕОРИИ ПОЗИТРОНА
распространения получить правила расчета различных процес-
процессов в дираковской теории дырок. Однако задача осложняется
существованием процессов рождения и аннигиляции, которые
также должны быть включены в описание. Основное правило,
которым мы будем руководствоваться в такой ситуации, состоит
просто в том, что вычисления с пропагатором должны согласо-
согласовываться с динамикой уравнения Дирака, общими постулатами,
сформулированными в гл. 1, и поправками, внесенными в них
при обсуждении позитронов в гл. 5. В этой и последующих гла-
главах мы будем полагаться больше на интуитивные соображения,
чем строгие выводы1).
X
X
{а)
(б)
00
Рис. 6.5. Примеры пространственно-временных диаграмм в теории позитрона.
Диаграмма (а) отвечает рождению пары, (б) — рассеянию и (в) — замкнутой
петле.
Посмотрим на картинки типичных процессов, описываемых
в теории позитронов. Помимо процессов рассеяния типа изобра-
изображенного на рис. 6.4, имеется еще рождение пар и аннигиляция,
иллюстрацией которых служит рис. 6.5. Диаграмма 6.5, а
') Строгий вывод этих правил дается в систематическом, но слож-
сложном изложении формальной квантовой теории поля в цитированной выше
книге [50].

% мет од Функции распространения [гл. 6
изображает рождение электрон-позитронных пар в потенциале,
действующем в точке 1; две частицы затем распространяются до
точек х и х' соответственно. Диаграмма 6.5,6 изображает элек-
электрон, распространение которого начинается в точке х и закан-
заканчивается в х'. Между этими точками потенциал в точке / рож-
рождает пару; позитрон из этой пары аннигилирует с первоначаль-
первоначальным электроном в поле, действующем в точке 3; электрон из
пары распространяется до точки 2, где он разрушается потен-
потенциалом. Этот потенциал рождает электрон, достигающий х'. На
диаграмме 6.5, в показано рождение пары в точке 1 и рас-
распространение ее до точки 3, где происходит аннигиляция
в поле.
Из этих диаграмм видно, что нам надо иметь не только
амплитуду рождения электрона, скажем в точке 1, распростра-
распространения его из / в 2 и уничтожения в точке 2, как в нереляти-
нерелятивистском случае, но также и амплитуду рождения, распростра-
распространения и уничтожения позитрона. Если эти амплитуды для пози-
позитронов будут найдены, можно попытаться сопоставить каждому
из изображенных на рис. 6.5 процессов свою амплитуду вероят-
вероятности и построить полную амплитуду любого заданного про-
процесса путем суммирования или интегрирования по всем проме-
промежуточным траекториям, которые дают вклад в этот процесс.
Так, например, в рассеяние дают вклад траектории двух типов,
изображенные на рис. 6.4 и 6.5,6.
Мы должны определить позитронную амплитуду в соответ-
соответствии со сформулированной в предыдущей главе теорией дырок.
Поскольку существование позитрона рассматривается как от-
отсутствие электрона с отрицательной энергией из заполненного
моря, мы можем считать уничтожение позитрона в точке 3 на
рис. 6.5 эквивалентным рождению в этой точке электрона с от-
отрицательной энергией. Отсюда следует возможность того, что
амплитуда рождения позитрона в / и уничтожения его в 3 свя-
связана с амплитудой рождения электрона с отрицательной энер-
энергией в 3 и уничтожения его в 1. Тогда диаграммы рис. 6.5 соот-
соответствуют распространению вперед во времени электронов с
положительной энергией и назад во времени электронов с отри-
отрицательной энергией. Диаграмму 6.5, а, которая описывает рожде-
рождение пары, можно рассматривать как рождение в точке х' элек-
электрона с отрицательной энергией, распространение его назад во
времени до точки /, где он уничтожается, и распространение
вперед во времени электрона с положительной энергией до
точки х. В процессе рассеяния электрон, распространившийся
до точки 3, может либо рассеяться на потенциале в положитель-
положительном направлении в пространстве-времени, как па рис. 6.4, и рас-
распространяться далее с положительной энергией, либо рассеяться
с отрицательной энергией назад в точке /, как на рис. 6.5, б.

§ 23) ФУНКЦИЯ РАСПРОСТРАНЕНИЯ В ТЕОРИИ ПОЗИТРОНА 97
Вдобавок к электронным траекториям в виде зигзагов вперед
и назад во времени имеются еще траектории в форме замкну-
замкнутых петель типа показанной на рис. 6.5, в. В теории дырок этой
траектории отвечает следующий процесс: в точке / электрон из
моря с отрицательной энергией рассеивается на потенциале
и попадает в состояние с положительной энергией, а затем
в точке 3 он рассеивается обратно в море. На языке функции
распространения мы скажем, что электрон, родившийся в /,
рассеивается назад во времени в 3 и уничтожается в /. Процес-
Процессами такого типа нельзя пренебрегать. Их требует формализм
теории, а эксперимент, как мы в дальнейшем убедимся, под-
подтверждает их существование.
Начнем осуществление намеченной программы с построения
функции Грина для описания распространения электронов и по-
позитронов. Будем руководствоваться результатами рассмотрения
позитронов в гл. 5 и итогами исследования метода функции рас-
распространения в нерелятивистской теории в настоящей главе.
Нерелятивистский пропагатор определялся уравнением
F.22). По аналогии определим релятивистский пропагатор
S'F (x'\ х) как решение уравнения
4
? [v* 0 ~ir ~еА* (*°) ~ Л s^p(х''х)=баеб4 (*' ~х)'F-38)
Определенный таким образом пропагатор есть матрица той же
размерности 4X4, что и матрицы у. Перепишем F.38) в мат-
матричных обозначениях, опуская индексы:
(tV' - еА' - т) Sfp (х', х) = б4 (*' - *). F.39)
Другое отличие от F.22) состоит в том, что в F.38) оператор
i-qP И (*') умножается на у0, чтобы получить ковариантный
оператор (/V' — еА' — т).
Пропагатор для свободной частицы
(tV' - т) SF {/, х) = б4 (*' - х) F.40)
можно найти путем фурье-преобразования к импульсному про-
пространству. Как и в нерелятивистском случае F.24), он зависит
только от разности (х' — х), поэтому1)
SF (х', х) = SP (x' -х) = \ -^ e-*-*-*SP (p). F.41)
') Здесь и далее мы пользуемся четырехмерным обозначением
р ¦ х = р^ — ро1 — р • х.

98 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. 8
Подстановка в F.40) дает
4
.? (р — т)аХ Sp^ (р) = 6ар.
Разрешая это уравнение относительно SF(p) и вновь возвра-
возвращаясь к матричным обозначениям, имеем
SF (р) = Р + т2 == -^J— , если р2 ф т2. F.42)
Для полноты определения необходимо указать, как поступать
с сингулярностью при р2 = т2, т. е. при /?0 = ± Vpz + m2 = ± ?•
Из нерелятивистской теории мы помним, что ответ на этот во-
вопрос следует из граничных условий, налагаемых на SP(x' — х)
при интегрировании F.41).
По своему физическому смыслу SF(x'— х) есть волна, вы-
вызываемая в точке х' единичным источником, расположенным
в точке х. Значительная часть фурье-компонент такого локали-
локализованного точечного источника содержит значения импульса,
большие, чем т, обратная комптоновская длина волны элек-
электрона. Следует поэтому ожидать, что наряду с электронами
такой источник будет создавать позитроны. Однако в теории
дырок имеется необходимое физическое условие, состоящее
в том, что волна, распространяющаяся из точки х в будущее,
содержит электронные и позитронные компоненты только с по-
положительной энергией. Позитроны и электроны с положитель-
положительной энергией описываются волновыми функциями с положи-
положительно-частотной зависимостью от времени. Например,
есть соответственно (ненормированные) волновые функции по-
позитронов и электронов с импульсом р& и р° > 0. Поэтому
SF(x' — х) может содержать в будущем, при х'й > х0, только
положительно-частотные компоненты.
Чтобы обеспечить это, вернемся к фурье-разложению
SF(x' — х) F.41) и F.42) и проведем интегрирование по dpo
вдоль изображенного на рис. 6.6 контура в комплексной плос-
плоскости ро- При t' > t контур замыкается в нижней полуплоско-
полуплоскости и содержит только положительно-частотный полюс при
Ро=+ Vp2 + tn2=E. В результате имеем
t'>t. F.44)

i 23]
ФУНКЦИЯ РАСПРОСТРАНЕНИЯ В ТЕОРИИ ПОЗИТРОНА
99
Отсюда видно, что волна в точке (х', t') содержит только поло-
положительно-частотные компоненты. При t' <Ct контур можно
замкнуть сверху, захватив полюс в точке Ро = — Vp2 + w2- Это
дает
SP{xf-x) =
d3P ,-p.,v'-vi 4.,-и «'-<) (~ gVo - P • V + от)
BitK e e 2?
(/' < /). F.45)
Следовательно, при V <t пропагагор содержит волны только
с отрицательными частотами.
Такие волны с отрицательной энергией, отсутствующие в не-
нерелятивистской теории, оказываются здесь неизбежными. Лю-
Любой другой выбор контура С в F.44) приводит либо к распро-
распространяющимся в будущее волнам с отрицательной энергией,
либо к волнам с положительной энергией, распространяющимся
в прошлое. Более того, появление волн с отрицательной энер-
энергией, распространяющихся в прошлое, является достоинством;
они представляют собой позитроны с положительной энергией.
Рис. 6.6. Расположение особенностей относительно контура интегрирования
для величины SF (p).
Это станет более очевидным, когда мы применим метод функ-
функции распространения к задачам рассеяния. Причиной появления
волн с отрицательной энергией является полюс при
р0 = — Vp? + т2, который отсутствовал в нерелятивистской
теории.
Выбор контура С можно фиксировать введением в знамена-
знаменатель F.42) малой положительной комплексной добавки или про-
просто заменой пг2—*т2 — is, подразумевая предел при е->0+:
о»
Формулы F.44) и F.45) можно объединить путем вве-
введения проекционных операторов C.18) и замены р на —р

100 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. 6
в отрицательно-частотной части:
SF (х'~х) = -1\-0р (if) [Л+ (р) е-'»-*-» 6 (/' -t) +
+ Л- (р) е+'р-с*'-*) 0 (/ -1% F.47)
где ро = Е > 0. Другую, эквивалентную форму записи мы по-
получим, если воспользуемся нормированными решениями в виде
плоских волн
Тогда для SF {%' — х) находим
2
sF (х' -Х) = - /в (/' - /) \ d3P
/6 (/ - /') J с?р J] ^ (хО г^гр (х) F.48)
'=3
и с помощью C.11) убеждаемся в том, что SF(x' — х) описывает
развитие решения с положительной энергией т|з<+) от прошед-
прошедшего к будущему и решения с отрицательной энергией в обрат-
обратном направлении:
9 (/' _ /) ф(+) {Х') = i^SF {/ - х) YoV+) (x) d\ F.49)
6 (/ - I') 4^ {х') = - i \ SF (х' - х) YoV"' (x) dh. F.50)
Определенную таким образом функцию SF(x' — x) принято
называть фейнмановским пропагатором. Он был впервые введен
в теорию позитронов в 1942 г. Штюкельбергом и, независимо,
в 1948 г. — Фейнманом, который использовал его во многих рас-
расчетах.
С помощью свободного пропагатора SF(x' — х) мы можем
формально построить полную функцию Грина и элементы S-мат-
рицы, т. е. амплитуды различных процессов рассеяния с уча-
участием электронов и позитронов в присутствии внешних полей.
Для этого надо проделать такие же выкладки, как в нереляти-
нерелятивистском случае.
Точный феинмановскии пропагатор SF(x' — х) удовлетворяет
уравнению F.39) и по аналогии с F.31) и F.32) может быть
представлен в виде суперпозиции свободных фейнмановских
пропагаторов. Имеем
(iVx, - т) S't. (х'; х) = \ d'y б4 (*' _ у) [б4 (у-х) + еА (у) S'F(у; х)].

§ 23] ФУНКЦИЯ РАСПРОСТРАНЕНИЯ В ТЕОРИИ ПОЗИТРОНА \Q\
Интегрируя это уравнение, получаем
S'f {%'; х) = SP{x'-x) + e\ d'y SF {/ -у) А (у) S'P (у, х). F.51)
Подобно F.14), точное решение уравнения Дирака
(iWx - т) XV (x) = eAW (x) F.52)
с фейнмановскими граничными условиями имеет вид
W (х) = ф (х) + е J d*y SF (х-у) А (у) Ч (у). F.53)
Рассеянная волна в F.53) содержит только положительные час-
частоты в будущем и отрицательные в прошлом в соответствии
с F.48):
2
W (х) -*(*)->$ ®Р ? ^ (х) [- ie J Л & (у) А (у) W (у)]
при /~> + оо, F.54)
4
W (х) - ф (х) - J 3 2 [
г=3
при /-> — оо. F.55)
Таким образом, полученная нами формулировка задачи рас-
рассеяния F.54) согласуется с тем требованием теории дырок, что
электроны не могут после рассеяния во внешнем поле А^(у)
попасть в море с отрицательной энергией; доступными для них
оказываются только незаполненные состояния с положительной
энергией. Уравнение F.55) показывает, что волны, рассеянные
назад, от будущего к прошедшему, имеют отрицательные
энергии.
Из F.54) и F.55) следует, что элементы S-матрицы можно
отождествить с коэффициентами при свободных решениях г|)г(х),
т. е.
Sfl = 6f/ - leef J d*y % (у) А (у) V, (у). F.56)
Здесь я|)/(г/) представляет собой конечную свободную волну
с квантовыми числами /; е/ = +1 Для решения, положительно-
частотного в будущем, и е/ — —1 для отрицательно-частотного
в прошлом решения. В соответствии с налагаемым на решение
F.53) фейнмановским граничным условием Wi(y) это падаю-
падающая волна, которая при г/о-*-— °° переходит в tyi(y), падающую
волну с квантовыми числами i и положительной частотой, или
при г/о->+°° —в отрицательно-частотную волну, распростра-
распространяющуюся из будущего в прошедшее.
В уравнениях F.56) и F.53) заключены правила вычисле-
вычисления амплитуд рождения пар и аннигиляции (см. рис. 6.5), так

J02 МЕТОД ФУНКЦИИ РАСПРОСТРАНЕНИЯ [ГЛ. 6
же как и амплитуды — «обычного» процесса рассеяния
(см. рис. 6.4).
Рассмотрим сначала обычный процесс рассеяния электрона.
Тогда ^г(у) при уо->—°о переходит в падающую плоскую
волну с положительной энергией i|)<+) (у) и вклад «-го порядка
в F.56) равен
- ien \ \
(уп) А(Уп) SP (уп -уп_{)А (*„_,) .. .
¦¦¦SF(y2-yl)A(y1)i^(yl). F.57)
Ряд F.57) содержит как диаграммы типа изображенной на
рис. 6.4, так и такие, как на рис. 6.5, б.
Для расчета рождения пары мы подставляем в F.56) вместо
4ri(y) решение, которое при t—»+oo переходит в плоскую
волну с отрицательной энергией. В частности, в случае рожде-
рождения электрон-позитронной пары с квантовыми числами (р_, s_)
и (р+, s+) соответственно (где/?0±>0), мы подставляем в F.56)
вместо Ч*г(у) решение уравнения F.53), которое при /-у+оо
переходит в плоскую волну с отрицательной энергией и кванто-
квантовыми числами (+р+, +s+, е = —1), т. е.
=VI
e+ip+'
В качестве -фу мы возьмем решение с положительной энергией,
характеризуемое (р-, s_, e= 1). Согласно тем основным прави-
правилам, к которым мы пришли при обсуждении теории дырок, от-
отсутствие электрона с отрицательной энергией, 4-импульсом —/?+
и спином —s+ воспринимается как присутствие позитрона
с 4-импульсам р+ и поляризацией s+. В методе функции рас-
распространения мы отождествили амплитуду рождения позитрона
в точке х, распространения его вперед в пространстве-времени
из области взаимодействия и достижения им точки х', куда он
попадает в виде плоской волны, характеризуемой (р+, s+), с ам-
амплитудой распространения электрона с отрицательной энергией,
4-импульсом —р+ и спином —s+ из точки х' назад в область
взаимодействия, где он уничтожается в точке х. Таким образом,
чтобы связать с процессом рождения пары амплитуды перехода,
надо проследить за путем электрона с отрицательной энергией
назад во времени в область взаимодействия; там он рассеи-
рассеивается в поле и испускается с положительной энергией, распро-
распространяясь вперед во времени. Соответствующие фейнмановские
диаграммы в двух низших порядках изображены на рис. 6.7,
причем амплитуда во втором порядке в свою очередь разла-
разлагается на две, отличающиеся временнбй последовательностью
двух актов рассеяния.

Задачи
103
Аналогичным образом для нахождения амплитуды анниги-
аннигиляции пары мы подставляем место Wi(y) решение уравнения
F.53), которое при у-*оо переходит в ^+)(у)- Оно отвечает
электрону с положительной энергией, который распростра-
распространяется до взаимодействия вперед во времени, а затем рассеи-
рассеивается назад и испускается в состоянии с отрицательной энер-
энергией. В п-и приближении амплитуда того, что электрон рас-
рассеется в заданное «конечное» состояние Ц~\ характеризуемое
квантовыми числами (р+, s+, е = —1), равна
F.58)
На языке теории дырок это амплитуда «-го порядка рассея-
рассеяния электрона в конечное состояние с отрицательной энергией,
4-импульсом —р+ и спином —s+. Это состояние при t = —оо
должно быть пустым, т. е. должна быть дырка, или позитрон,
с 4-импульсом р+ и спином, или поляризацией s+.
it
X
Рис. 6.7. Пространственно-временные фейнмановские диаграммы для рожде-
рождения пары в первом и во втором порядках. Вклад второго порядка в свою
очередь разлагается на две части в соответствии с временной последова-
последовательностью двух актов рассеяния.
Наконец, для описания рассеяния позитрона «падающая»
волна с положительной частотой в F.56) и F.58) должна быть
заменена решением с отрицательной частотой и квантовыми
числами (р'+, s'+, е = —1). Оно отвечает испускаемому по-
позитрону с импульсом и спином (р' s\
ЗАДАЧИ
1. Покажите, что в нерелятивистском пределе SF(x',x) сводится к шре-
дингеровскому запаздывающему пропагатору для свободной частицы.
2. Непосредственной проверкой убедитесь в справедливости F.48).
3. Проверьте равенства F.49) и F.50) и получите аналогичные формулы
для сопряженных спиноров ф' и ф*~\
4. Получите явиое выражение для SF(x). Выясните поведение этой функ-
функции при х -*¦ оо, х ->- 0 и на световом конусе.
5. Пусть в нашем формализме вакуум заменяется на ферми-газ ферми-
евским импульсом kF. Как при этом изменится фейимановский пропагатор?
Найдите изменение SF в пределе малой плотности.

ГЛАВА 7
ПРИЛОЖЕНИЕ ТЕОРИИ К ОПИСАНИЮ
ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ
§ 24. Рассеяние электронов в кулоновском поле
В этой главе мы используем метод функции распростране-
распространения для проведения различных практических вычислений. Когда
у нас накопится достаточный опыт работы с амплитудами рас-
распространения, мы путем естественного и правдоподобного об-
обобщения перейдем к амплитудам, описывающим взаимодействие
между несколькими частицами. Наш план изложения такой
же, как в оригинальных работах Фейнмана [53]: сначала будут
получены правила для нахождения вероятностей перехода и се-
сечений основных процессов, представляющих физический инте-
интерес, а затем мы обратимся к некоторым формальным операциям
квантовой теории поля.
Мы начнем с задачи о рассеянии электрона в заданном ку-
кулоновском поле. Матричный элемент перехода, отвечающий
этому процессу, дается выражением F.56):
Sfi = - ie \ d'xф, (д) А(х) V, (х), \Ф i; G.1)
здесь е < О— заряд электрона. Мы должны привести S/t- к бо-
более конкретному и явному виду. В низшем порядке Ч^*) сво-
сводится к падающей плоской волне tyi(x), описывающей электрон
с импульсом Pi и спином s;:
u(Pi>
где функция гр(л:) нормирована на единичную вероятность в
ящике объемом V. Аналогично
G.3)

§ 241 РАССЕЯНИЕ ЭЛЕКТРОНОВ В КУЛОНОВСКОМ ПОЛЕ 1 05
Кулоновский потенциал точечного заряда —Ze > 0 задается
выражением
А>М = -4^тг. А(*) = о.
Таким образом,
V"( s>Y°«f s)J-|7Te {f •
Интегрирование по времени дает 2яб(?/— ?,), что выражает
равенство энергий начального и конечного состояний в статиче-
статическом потенциале. Интеграл по пространственным координатам
есть хорошо известное фурье-преобразование кулоновского по-
потенциала
где q = p/ — р,. Наш матричный элемент принимает вид
Число конечных состояний в интервале импульсов d3p/ есть
Vdzpfj{2п)г, и, таким образом, отнесенная к одной частице ве-
вероятность перехода в эти состояния равна
BяK —
Квадрат б-функции требует некоторых пояснений. Если бы мы
рассматривали переходы, происходящие в течение заданного
промежутка времени (—Т/2, Т/2), то б-функция по энергии ока-
оказалась бы размазанной; это означает, что
Г/2
f f \t sin (Г/2) (Ef — ЕЛ
ЕгвЛ' = 2 2 ^ 1±
2_ ^. G.7)
-Г/2
Из G.7) видно, что для большого, но конечного Т
Если последнее выражение рассматривать как функцию Ef, то
площадь под кривой, изображающей эту функцию, равна 2пТ;
поэтому можно отождествить
[2яб (Ef - Et)? = [2яб @)] 2яб (Ef - Et) = 2пТЬ (Ef - Et). G.8)

106 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Или, еще проще'),
2яб @) = Т. G.9)
Эвристически этот результат можно получить прямо из опреде-
определения
Г/2
2nb{Ef-Ei) = \
-Г,2
Следовательно,
Г/2
2я6@) = \ dt — T.
>-Г/2
Возвращаясь к G.6) и деля обе части этого равенства на
время, получаем, что число переходов R за единицу времени в
интервал импульсов dzpt равно
4ZW \й(р{, sf)Vo«(p.,s.)P d>pf
Сечение определяется как скорость перехода R, отнесенная к по-
потоку падающих частиц /fnc = tyt (х) yatyt (x), где а обозначает
компоненту вектора вдоль направления скорости падающих ча-
частиц v, = Pi/E{. Согласно принятому в G.2) условию норми-
нормировки поток равен |/щс| = |Vf|/V. Таким образом, дифферен-
дифференциальное сечение рассеяния do, приходящееся на единичный те-
телесный угол ofQ, есть
do Г AZWm* \u(pf.sj)i»u{Pi.st)\* Pjdp,
^J~KR7 Г^Т -^-HEf-Ei). G.10)
Пользуясь равенством
Pi dpf = Ef dEf,
окончательно получаем
da 4Z2a2m2
°«(p;, s{)\2, G.11)
что в нерелятивистском пределе согласуется с формулой Резер-
форда.
Обычно поляризация конечных частиц не регистрируется, а
поляризация начальных частиц не задается. Если падающий
пучок имеет остаточную поляризацию, то для этого, как пра-
правило, имеются веские причины и экспериментатор в конечном
') Если падающие и рассеянные частицы описывать волновыми пакета-
пакетами, то удается избежать появления не вполне корректно определенных ква-
квадратов б-функцич. Тогда равенству G.9) можно дать строгое обоснование
(см. [56]).

§24] РАССЕЯНИЕ ЭЛЕКТРОНОВ В КУЛОНОВСКОМ ПОЛЕ Ю7
итоге их обнаружит, как это произошло в случае с поляризован-
поляризованными электронами от р-распада. Когда подобная информация
отсутствует, различным начальным поляризационным состоя-
состояниям априорно приписывается равная вероятность. Это означает,
что наблюдаемое сечение представляет собой сечение G.11),
просуммированное по конечным спиновым состояниям и усред-
усредненное по начальным, т. е.
do 4Z2a2m2 V~> , _ , , n , ч l9 ,_ , -ч
Ча^Т^Г Ij 1"^/. sf)Y°«(Pt, s*)I2. G.12)
± sf, st
Сумму, по спинам можно переписать в виде
2 й„(р,, sf)\°a&ua(Pi, st)u+(Pl, s()\l+y°6+u0(pf, sf) =
±sf,si
= I ua(Pf, sf)Y>6(^, s.)«6(p., st)i&a(pf, Sf),
+ Sf, S(.
где, как обычно, подразумевается суммирование по повторяю-
повторяющимся индексам. Это частный случай общего соотношения, ко-
которым мы будем часто пользоваться:
| п {f) Ги (О Р = [й (f) Tu (/)] [п (i)Yu (/)]; G.13)
здесь Г = Y°^+Y°- Например,
= /у5,
abc • • • р = р • • • cbd.
Суммирование по спинам можно заменить вычислением следов,
если воспользоваться проекционными операторами C.18):
4
"з (Р^ sd Ч (Р^ st) = Е в№ (Pi) *>у (Р«)
Тогда сумма по спинам в G.12) переходит в
а, В ±Sf
a, B

108 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
где мы применили тот же самый прием. Последнее выражение
представляет собой след, т. е. сумму диагональных элементов
матрицы
(fit + m) (pf + m)
Yo 2m Yo 2m ¦
Поэтому G.12) можно записать в виде
da 4Z2a2m2 (p. + т) (df + m)
lF=^HF-SPVoi^riVoi^ri. G-14)
§ 25. Теоремы о вычислении следов; усредненное
по спинам сечение рассеяния в кулоновском потенциале
Теперь мы сделаем некоторое отступление и установим ряд
полезных свойств матриц Дирака. Эти свойства позволяют вы-
вычислять сечения, не производя никаких действий с матрицами
Дирака. Они выводятся из коммутационных соотношений для
матриц у и справедливы независимо от выбора конкретного
представления для этих матриц. Мы перечислим эти свойства
в виде ряда теорем.
Теорема 1.
След нечетного числа матриц у равен нулю.
Доказательство. Для нечетного п
Sp й, • • • йп = Sp di • • • dnyby5 = Sp Ys^i • • • dny5;
здесь мы воспользовались тем, что след не меняется при цикли-
циклической перестановке, в частности, Sp АВ = Sp В А. Последова-
Последовательно переставляя первую из матриц у5 направо, мы п раз
получим знак минус, возникающий из свойства антикоммутации
+ Y5Yn = 0' В итоге для нечетного п имеем
0. G.15)
Теорема 2.
Sp 1 =4,
Sp db = Sp hd = '/2 Sp {fib + hd) = a ¦ b Sp 1 = 4a ¦ b.
Теорема 3.
Sp di • • • dn = «i • a2 Sp d3 - • • dn — a, • a3 Sp d2d4 • • • dn +
••• -fa, ¦anSpd2 ••- un-i. G.17)
В частности,
Sp didzdidi = A [ax • a2flj • aA + «i • aAa2 ¦ a, — at ¦ a3a2 • a4].
Доказательство. Пользуясь равенством d\d2 = —d2di-\-2axa2>
мы переставим d{ вправо по отношению к а2, т. е.
Sp dxd2 -•• dn = 2fl, • a2 Sp ds • • • dn — Sp d2d{d3 ••• dn.

§ 25] ТЕОРЕМЫ О ВЫЧИСЛЕНИИ СЛЕДОВ Ю9
Действуя далее аналогичным образом, получим
Spd, ••• й„ = 2а, -a2Spd3 ••• dn — ... + 2а, • anSpd2 • •• dn_,-
-Spd2 ¦•• йпйх.
Наконец, воспользовавшись свойством цикличности следа, мы
вновь переставим й\ влево относительно других матриц у; тем
самым теорема доказана.
Эта теорема в особенности полезна для упрощения сложно-
сложного следа, хотя при п > 6 следует, если это возможно, прибегать
к более изощренным приемам, чтобы избежать лавинообразного
роста числа членов.
Теорема 4.
0, G.18)
Sp Ш &\
где eapYfl === + 1, если перестановка (a, {3, у, б) получается из
(О, 1,2, 3) в результате четного числа транспозиций, eafiy6 = — 1,
если число транспозиций нечетно; еару6 = 0, если среди индек-
индексов имеются совпадающие.
Доказательство. Первые два равенства немедленно следуют
из того, что Y5 = jy°y'y2Y3- Для получения третьего надо рас-
рассмотреть отдельные компоненты. Чтобы данный член вносил не-
ненулевой вклад, все компоненты векторов а, Ь, с, d должны быть
различны, а полный вклад представляет собой сумму по различ-
различным комбинациям компонент, причем знак каждого из слагае-
слагаемых определяется знаком перестановки. Общий знак задается из
SP YsYoYiY^ W = feol23ao6'C2d3 Sp Y§ = 4/eol23a°fr W.
Теорема 5 ').
n = 4,
» = - 2d,
y^1 = 4a ¦ b, G.19)
^^ = - 2cbd,
yjLbcdy» = 2 [dak + cbud].
Теорема 6.
Sp й42 - • • d2n = Sp аы • • • a,. G.20)
') Хотя соотношения 5 не относятся непосредственно к следам, но ими
приходится пользоваться в тех же расчетах, где необходимо вычислять следы.
Поэтому мы для удобства их здесь приводим. Их доказательство предла-
предлагается в качестве полезного упражнения

110 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Доказательство. При рассмотрении зарядового сопряжения
в гл. 5 было показано, что существует матрица С, обладающая
свойством CyC~l =— Yn- Далее
~l =— Yn- Далее
Sp di ¦¦¦ а2п = Sp Cd{CxCa2C~x ¦ ¦ ¦ Ca2nC~x =
Jn
= (- lJn Sp aUl ¦ ¦ ¦ aT:n = Sp [a2n ¦ ¦ ¦ af = Sp
2n
Возвращаясь к задаче о кулоновском рассеянии и используя
теорему 1, получаем из G.14)
-Ж = Щг fSP ^'Y°P/ + "i* Sp (y0J].
Применяя теоремы З и 2, находим окончательное выражение
для дифференциального сечения рассеяния
Ж = W (8f*?f - 4P/ • />f + 4m2). G.21)
Можно выразить дифференциальное сечение через энергию рас-
рассеиваемой частицы Ё = Ei — Ef и угол рассеяния Э. Для этого
воспользуемся кинематическими соотношениями
p.. Pf = E2- р2 cos 9 = ш2 + 2Р2?2 sin2 -|
Тогда
da Z2a2 /. fi2 2 9\
Это так называемое сечение Мотта [57]; оно переходит в резер-
фордовское при р->0.
§ 26. Кулоновское рассеяние позитронов
Переходя к рассмотрению рассеяния позитронов в кулонов-
кулоновском поле, мы прежде всего заметим, что в низшем порядке по
а сечение рассеяния такое же, как для электронов. В этом
проще всего убедиться, записав матричный элемент. Из фор-
формулы F.56) и сопровождающих ее пояснений следует
Sft = ie J d4x ф, (х) А {х) ?^ (x). G.23)
Здесь начальное состояние относится к будущему и должно ин-
интерпретироваться как электрон с отрицательной энергией и
4-импульсом —Pf, движущийся назад во времени (см. рис. 7.1).

261
КУЛОНОВСКОЕ РАССЕЯНИЕ ПОЗИТРОНОВ
111
В низшем порядке в качестве волновой функции подстав-
подставляем плоскую волну:
/(pf,sl)e+ir'rx. G.24)
Аналогично конечное состояние в G.23) представляет собой
электрон с отрицательной энергией, распространяющийся в
прошлое. Его волновая функция есть
n-v(PhSi)e+!pi-x. G.25)
Она описывает налетающий позитрон, который до рассеяния
имеет импульс р, и поляризацию st. Подставляя G.24) и G.25)
в выражение для S-матрицы, имеем
iZe2 I
i (р.-р.)-х
e f ¦
Полученное выражение аналогично G.4).
Вследствие инвариантности относительно зарядового сопря-
сопряжения можно в том же порядке по е вместо G.23) записать
Sft = + ie\ d'x ^ci (x) A^cf (x) = - ie J d*x Щ (*) С
что приводит к прежнему результату. При таком описании по-
позитрон распространяется вперед во времени и \pcf (л:) = C\°ty* (x)
есть волновая функция начального по-
позитрона.
Повторяя вычисления, посредством
которых была получена формула
G.12), находим выражение для диф-
дифференциального сечения
da)e+
2Z2a2m2
|q[4
± Sf. S,
I V (Pi, St) y°V (pf, sf) |2.
G.26)
Рис. 7.1. Кулоновское рас-
рассеяние позитронов.
Сумму по спинам, как и прежде, можно привести к следу, ис-
используя следующее соотношение для позитронных спиноров
(см. C.9)):

П2 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Таким образом,
что совпадает с G.14) с точностью до замены т на —т.
Поскольку полученное нами выражение для сечения рассея-
рассеяния электронов было четным по т, мы убеждаемся в том, что
в низшем порядке по а сечения рассеяния для позитронов и
электронов равны друг другу. Мы могли получить этот резуль-
результат из инвариантности относительно зарядового сопряжения.
В гл. 5 было показано, что каждому решению для электрона
в потенциале Ап отвечает решение для позитрона в потенциале
—Лц, т. е. рассеяние электрона в потенциале —е/4кг есть то же
самое, что рассеяние позитрона в потенциале +е/4яг; однако,
поскольку вычисленное сечение зависит только от е4, знак Л^
не играет роли.
Для поправок порядка е6, которые возникают как произведе-
произведение амплитуд первого и второго порядка, изображенных на
рис. 7.2, это заключение несправедливо. Такие поправки имеют
разные знаки для электронов и позитронов.
Pi, Si
Рис. 7.2. Кулоновское рассеяние электронов.
Нетрудно также заметить, что сечение для позитронов полу-
получается из сечения для электронов путем замены /?; ¦*—>¦ —р;; это
общее свойство теории позитронов, именуемое «правилом под-
подстановки» («substitution rule»). Оно тесно связано с методом
функции распространения. Примеры применения этого правила
еще не раз встретятся нам в дальнейшем.
§ 27. Рассеяние электрона на дираковском протоне
Рассмотрим теперь рассеяние электрона не в фиксирован-
фиксированном кулоновском поле, а на протоне (пока мы будем считать
протон бесструктурной дираковской частицей). Как изменится
полученный нами результат?

§27| РАССЕЯНИЕ ЭЛЕКТРОНА НА ДИРАКОВСКОМ ПРОТОНЕ ИЗ
Зная протонный ток /"¦(*), можно с помощью уравнении
Максвелла найти создаваемое им поле. Амплитуда рассеяния
электрона в этом поле дается S-матрицей G.1). Повторив пре-
предыдущие рассуждения, мы получим скорость перехода и сече-
сечение рассеяния в низшем порядке по а.
Итак, сначала найдем создаваемое протоном электромагнит-
электромагнитное поле. Потенциал определяется из уравнения
ОАи(х) = Г(х), G.27)
где для удобства мы выбрали лоренцеву калибровку. Чтобы про-
проинтегрировать это уравнение и найти Ап(х), мы, как и для слу-
случая электрона, вводим функцию Грина, или пропагатор. Пропа-
Пропагатор DF(x — у) определяется уравнением
иОР{х-у) = Ь'{х-у). G.28)
Его фурье-преобразование имеет вид
где DF (q2) = - \/q2 для q2 Ф 0.
Как и для фермионов, необходимо задать поведение в полюсе
при q2 = 0. По аналогии с дираковским пропагатором, рассмот-
рассмотренным в гл. 6, мы добавляем к q2 бесконечно малую положи-
положительную мнимую часть; это эквивалентно введению малой от-
отрицательной мнимой массы (см. F.46)):
Такой способ обращения с полюсной особенностью означает вы-
выделение излучения с положительной частотой или энергией, рас-
распространяющегося вперед во времени. Когда мы рассматриваем
рассеяние излучения веществом, например, преломление света
при прохождении пузырьковой камеры, мы должны позаботить-
позаботиться о том, чтобы волны с положительной частотой, отвечающие
квантам с положительной энергией, испускались без отрица-
отрицательно-частотного сопровождения. Соответствующий фейнма-
новский пропагатор задается формулой
Ы* - У) =
а определяемый из G.27) потенциал имеет вид
Ах (х) = J d*y DF {x - у) Г (у). G.31)

114 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ.7
Подстановка этого выражения вместе с решениями в виде пло-
плоских волн для электронов в элемент S-матрицы G.1) дает
S,, = -i\ d*x d'y [в*, (х) y^i (x)] DF (x - у) 7й (у). G.32)
Теперь мы должны решить, какое выражение следует вы-
выбрать в качестве протонного тока Jn(y). Естественный с физи-
физической точки зрения выбор вытекает из принципа соответствия.
В качестве тока перехода берется матричный элемент
J*(y) = e$(y)Vatf(y), G-33)
где ер = — е > 0 — заряд протона, а \|з° (у) и \jj° {у) представ-
представляют собой решения в виде плоских волн для начального
и конечного свободных протонов. Они имеют тот же вид,
что G.2) и G.3), с той разницей, что масса протона есть М,
а его начальные и конечные импульс и энергия — Ри Pf и <§Г,,
ё>] соответственно. Тогда для тока имеем
Iй (У) = - VipT Т е'(РгР
Потенциал А*(х), определяемый уравнениями G.31) и G.33),
принято называть потенциалом Мёллера [58] для дираковского
протона. В нерелятивистском приближении такой выбор тока
перехода в качестве источника А<х(х) был принят Гайзенбергом
и применен им к переходам электрона при расчете излучения
атомов с помощью матричной механики (см., например, [22, 59]).
Подставляя G.34) в G.32) и используя G.30), мы без труда
вычисляем интегралы и получаем для элемента S-матрицы
Sfl = ^4е- Bя)« 6< (Р, - Р, + р, - Pt)
X \п (р,, sf) Yll« (pt, st)] ( '<J+7Г [п (Pf, Sf) y»u (Pu St)]. G.35)
Симметрия полученного результата по переменным электрона
и протона подтверждает правильность выбора тока в форме
G.33). Если бы мы в качестве исходного пункта наших вычи-
вычислений взяли выражение G.1) для амплитуды рассеяния про-
протона в поле, создаваемом током электрона, и выбрали G.33) в
качестве тока электрона, то мы должны были бы прийти к тому
же самому результату.
Сравнение с выражением G.5) показывает, что различие ме-
между рассеянием электрона в кулоновском поле и на протоне
сводится к замене выражения ZY°/|q|2 на

§ 27) РАССЕЯНИЕ ЭЛЕКТРОНА НА ЛИРАКОВСКОМ ПРОТОНЕ Ц5
и V — на BлK б3 (Р f — Рi-\-pf — р;), что выражает сохранение
импульса.
Формула G.35) дает амплитуду электрон-протонного рассея-
рассеяния в наинизшем порядке по а; она не учитывает эффектов бо-
более высокого порядка, которые приводят к искажению плоских
волн в выражении для тока. Выраже-
Выражению G.35) удобно сопоставить фейн-
мановскую диаграмму, изображенную
на рис. 7.3.
Одинарная сплошная линия со
стрелкой, указывающей направление
времени, отвечает электрону, а двой-
двойная— протону. Волнистая линия опи-
описывает электромагнитное взаимодей-
взаимодействие, которому в матричном элемен-
элементе отвечает величина, обратная квад-
квадрату переданного импульса или об-
обратная оператору Даламбера (см. Рис 73 Рассеяние элек.
G.27)) в импульсном представлении. трона на протоне.
Мы будем говорить, что эта линия опи-
описывает «виртуальный фотон», посред-
посредством которого электрон и протон обмениваются 4-импуль-
сом q = Pj —pi = Pi — Pf. Амплитуда распространения вирту-
виртуального фотона между двумя токами есть— (q2 + ie)~'. Точкам
или вершинам, из которых исходит и в которые входит фотон,
сопоставляется фактор еу^, который стоит в обкладках из спи-
спиноров л/т/Е и(р, s), отвечающих свободным реальным началь-
начальным и конечным частицам. Каждой линии и каждому пересе-
пересечению линий на диаграмме отвечает свой единственный член
в выражении для S-матрицы. Кроме того, S-матрица всегда со-
содержит четырехмерную б-функцию, выражающую общий для
всего процесса закон сохранения энергии-импульса.
Для вычисления сечения вернемся к рис. 7.3 и формуле G.35)
и прежде всего путем деления |S/,|2 на время наблюдения Т и
пространственный объем области взаимодействия найдем ско-
скорость перехода, отнесенную к единичному объему. Получаем
^Pt-Pi- Pi)! % Z I Щ 2
G.36)
где величина
t, st)]-r^[u{Pf, S,)ru{P,, S,)]
представляет собой лоренц-инвариантный матричный элемент
и будет в дальнейшем именоваться инвариантной амплитудой.

116 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ.7
Переходя от G.35) к G.36), мы представили квадрат б-функ-
ции в виде, аналогичном, но несколько более общем, чем G.8),
а именно
[Bя)« б< (Р, + р,- Рг - Pl)f = Bя)« б* @) Bя)« X
X б4 (Р, + Pf-P,- Рд + VT Bа)* б4 (Pf + Pf- P, - Pt). G.37)
Далее разделим скорость перехода, отнесенную к единичному
объему, на поток падающих частиц |/щс| и на плотность частиц
мишени, которая согласно использованной в G.2) нормировке
равна 1/V.
Наконец, чтобы получить физическое сечение, необходимо
просуммировать по заданному набору конечных состояний элек-
электрона и протона, отвечающему условиям наблюдения. Число
конечных состояний с заданным спином, приходящееся на ин-
интервал импульсов d%pi d3Pf, есть
Таким образом, сечение перехода в конечное состояние, лежа-
лежащее в интервале т, равно
V
BлK
t
d3pf d3Pf тМ тМ BяL б4 (Pf + pf — Pt — р()
BлK BлK '
Можно еще просуммировать это выражение по спиновым со-
состояниям конечных частиц и усреднить по начальным спинам
для случая, когда поляризация отсутствует.
Теперь мы можем отметить некоторые общие для всех про-
процессов рассеяния черты. Физика явления заключена в квадрате
инвариантной амплитуды |STO/j|2. Каждой из внешних фермион-
ных линий, т. е. каждой падающей или испускаемой дираков-
ской частице, отвечает фактор т/Е. Фазовый объем каждой из
конечных частиц дается фактором d3pf/BnK. Таким образом,
мы видим, что за счет каждой из конечных частиц появляется
выражение (т/Е) [ерр/BлK]. Оно представляет собой лоренц-
инвариантный объем в импульсном пространстве, в чем нетрудно
убедиться из следующего равенства:
^ - m2) d3p = J d*P б (р^ - т2) 0 Ы, G.40)
Ро>О,
Ро<О.

§27] РАССЕЯНИЕ ЭЛЕКТРОНА НА ДИРАКОВСКОМ ПРОТОНЕ Ц7
Здесь в(ро) — введенная в F.18) функция-ступенька; она ло-
ренц-инвариантна, если 4-вектор pv- времениподобен, как в на-
нашем случае. Общий для всего процесса закон сохранения энер-
энергии-импульса выражается б-функцией BяLб4(Р/+ р*— Pi—pt).
Наконец, имеется фактор 1/V [ Ущс |; поток |/inc| для коллинеар-
ных пучков есть число частиц на единицу площади, пересекаю-
пересекающихся друг с другом за единицу времени, т. е.
| v, - Г..
¦Мпс I
if I i '< ' i
•Mnr- Г7
В сочетании с нормировочными множителями для обеих нале-
налетающих частиц величина К|/шс| образует лоренц-инвариантное
выражение
тМ тМ тМ ,_ ,.<
*Л I *, - Г, | ~ | р, |ff, + | Р, | Е, ~ У(Р(- ¦ Ptf -^Ш "
Отсюда видно, что полное сечение инвариантно относительно
преобразования Лоренца, совершаемого вдоль направления на-
налетающих пучков. Таким образом, можно записать равенство
G.39) в инвариантной форме
da = [ . тМ ==г | ай„ |2 BяL б4 (P. -Pi + p,- pt) X
P{f -
m d3pf M d3Pf
Полученное выражение содержит величины самой общей при-
природы; в дальнейшем мы будем опускать детали их появления.
Нормировочный объем V не вошел в конечный ответ. Тот же
ответ был бы получен и при других нормировочных условиях,
не содержащих объем V.
Если сталкивающиеся пучки не коллинеарны, удобнее рас-
рассматривать непосредственно число событий в единицу времени
dN/dt, которое находится из G.36) и оказывается равным
Здесь ре(х, 0 и рР(х, t) — число электронов и протонов в еди-
единице объема; эти величины появились взамен двух факторов
A/1/), которые нормируют выражение G.36) на единичную ве-
вероятность в объеме V.
Как уже говорилось, выражение G.42) отвечает переходу из
заданного начального спинового состояния электрона и протона
в заданное конечное. Если поляризации не регистрируются, мы

118 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
должны провести усреднение по начальным спиновым состоя-
состояниям и суммирование по конечным. В результате получим
v=
Sl,Si,sf,sl
ел
2m Y 2m V Ър 2M Y^ 2M
Вычисление первого следа с использованием теорем, приведен-
приведенных в § 25, дает
(pf + т) (р. + т) 1
SP Т V [2т У" = -Ш
= W [PfPl + P'tPf ~ ^ (P, ¦ Pi - m2)].
Второй след имеет тот же вид, и после некоторых алгебраиче-
алгебраических преобразований получаем следующий конечный ответ:
- т2 (Pf ¦ Р^ - М2 (р} ¦ Pl) + 2М2т% G.43)
Сечение рассеяния неполяризованных частиц получается под-
подстановкой этого выражения в формулу G.42). Полезно вычис-
вычислить da в лабораторной системе, в которой начальный протон
покоится. В этой системе имеем р, — (?', р'), Pi = (Е, р) и
Рг = (М,0).
Чтобы найти дифференциальное сечение рассеяния электрона
в элемент телесного угла dQ' в направлении, задаваемом по-
полярным углом 6, проведем интегрирование по фазовому про-
пространству, воспользовавшись равенством G.40). Записав йгр' =
= р'2 dp' dQ. = p'E' dE' du', получим
M+E
p'dE'\3Rn\2b Bm2 - 2 (?" - E) M - 2E'E + 2pp' cos 9) ==
м _
G.44)
m2M p' \mfi\
4я2 p M + E- (pE'lp') cos 9 '
причем условие сохранения энергии, выражаемое б-функцией,
имеет вид
Е' (М + Е) - р'р cos 0 = ЕМ + т2, G.45)

§27] РАССЕЯНИЕ ЭЛЕКТРОНА НА ДИРАКОВСКОМ ПРОТОНЕ 119
и для получения конечного ответа мы воспользовались форму-
формулой jj dx б (f (хУ) = | df (x)/dx Г1 •
Если энергия электрона много меньше массы протона, ?<М,
мы, пренебрегая Е/М <С 1, вновь приходим к прежнему резуль-
результату для рассеяния в статическом кулоновском поле. В этом
предельном случае G.44) переходит в формулу Мотта G.21):
Л- — Л?-\т I2 — «Г 1
а условие G.45) дает Е' = Е.
Из G.43) имеем
Если отдача протона становится существенной, электрон
можно рассматривать как ультрарелятивистский и пренебрегать
поправками по массе электрона. Из G.43) и G.44) видно, что
линейные (и вообще нечетные) члены по т/Е отсутствуют, так
что поправки имеют порядок (т/ЕJ. Пренебрегая этими по-
поправками, имеем
dQ' 4я2 1 + BЕ/М) sin2 (9/2) ' fl ' ' Е ^ 1-
Вычисляя в этом предельном случае |2ГС/г|2, удобно записать
в виде Pf = Pi + Pi — Pf, что Дает
I2 =
r [2P, • Pf Pi ¦ Pi + Pi ¦ P; (Pi • Pi - Pi ¦ Pf - M2)] =
8л2а2??"
m216?2?" sin4 (9/2) L 2
я2а2
q2
m2??"sin4(9/2)
где ?2= (/7/-/7iJ =
Таким образом, дифференциальное сечение равно
rfq ^_ a2 cos2 F/2) - (?2/2AF) sin2 (9/2) jn . .
dQ' 4?2 sin4F/2)[l + B?/M) sin2 (9/2)] ' E <^1' W-^
Здесь мы воспользовались соотношением G.45) в пределе
т2->0:
?"?A - cos 6) = М(Е-Е').
Формула G.45) получена в предположении, что по своим
свойствам протон представляет собой тяжелый электрон с мас-
массой М Однако такое описание является неполным, поскольку
оно не учитывает структуру протона и его аномальный магнит-
магнитный момент, т. е. свойства, имеющие мезонную природу. Более

120 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
полное описание протона требует изменений в формуле G.46),
которые становятся существенными при высоких энергиях, пре-
превышающих несколько сотен Мэв. Мы еще вернемся к этому
вопросу в гл. 10.
§ 28. Поправки высших порядков
к рассеянию электронов протонами
Проведенное рассмотрение рассеяния электронов протонами
справедливо только в наинизшем неисчезающем порядке по е2.
Чтобы получить поправки следующего, более высокого порядка
по е2, мы должны вернуться к выражению F.57) и рассмотреть
амплитуду второго порядка по взаимодействию между электро-
электроном и протоном. Она дается выражением
S$ = - ii \ d*x d'y $f (x) A (x) SP (x-y)A (у) Ь (у), G.47)
где, как и прежде, электромагнитный потенциал создается то-
током протона. Чтобы установить форму этого тока, посмотрим,
каков вид тока электрона во втором порядке. Формула G.47)
описывает взаимодействие этого тока с А11(х) и Av(y). Как и
в первом порядке (см. 7.35)), амплитуда Sff должна быть сим-
симметричной по току электрона и протона. Ток электрона во вто-
втором порядке имеет вид
(X — у) Yv^? (У) = ty (X) У Л Z 9 (*0 — Уо) Фп (X) Ф„ (У) —
In; ро>О
- Е
п: ро<О
Множитель i необходим для того, чтобы ток во втором порядке
можно было представить как линейную комбинацию произве-
произведений двух токов перехода. Опираясь на подобные наводящие
соображения, запишем, следуя G.31),
Лц (х) Av (у) = ё\ \ d*w d4z DF (x - w) DP (у - z) ty (w) y^ X
I n: po>
I o>O
n\ P0<0
= ie% \ d*wd*zDF(x - zv) Dp (y - z) tf (w) Y(lS? (w - z) Yv^f (z). G.48)
Здесь DF(x — w)DF(y — г) представляют собой фейнмановские
пропагаторы для двух внешних фотонных линий, изображенных
на рис. 7.4, а.

i 28]
ПОПРАВКИ K РАССЕЯНИЮ ЭЛЕКТРОНОВ ПРОТОНАМИ
121
Фотоны распространяются между электронной и протонной
вершинами, изображенными в виде точек, которым отвечают
факторы еух и еруа соответственно. Внутренним электронной и
протонной линиям соответствуют фермионные пропагаторы
X f\/\/\/VVV\A/\fl iv
Hr(x-w)
/V Pi
(a)
Pf-fi
1 wwyww
Pi, si
Pf,Sf
Pi,
Pf, Sf
'Pt, ^
Pf,Sf
Рис. 7.4. Вклад четвертого порядка в электрон-протонное рассеяние.
Sf(x — у) и Sf(w — z). Таким образом, мы имеем пример соот-
соответствия между диаграммами Фейнмана и элементами S-мат-
рицы, записанными в координатном представлении. Чтобы по-
получить полное выражение для Sjf, необходимо добавить в про-
протонный ток еще один член, отражающий неразличимость двух
фотонов. Электрон, взаимодействующий с фотоном в точке х, не
различает, испустился ли этот фотон из точки w или г, и наряду
с процессом, изображенным на рис. 7.4, а следует учитывать
процесс, показанный на рис. 7.4, б.

122 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ.1
Фотонные фейнмановские пропагаторы обеспечивают распро-
распространение вперед во времени только положительных частот. Од-
Однако взаимодействие содержит все различные упорядочения че-
четырех точек х, у, w и z во времени, и фотон в точке w может
быть как первым, так и вторым испущенным или поглощенным
электроном.
Для симметризации переменных двух неразличимых фотонов,
которыми обмениваются электрон и протон, мы добавим к G.48)
член
ie\ \
d'z DF (x - z) DF (у - w) tf (w) yvSpF (w - z) y^p B).
Тогда G.47) принимает вид
Sf? = ee\ J d*x d'y d*w d*z ty (x)yv,SF (x - y) y4fy (y) X
X {Dp (x - w) DF (y - z) tf (w) y»SpF (w - z) Yvttf (z) +
+ DF(x- z) DF (y - w) Ц (ш) y"SpF (w - z) Y4f (z)}. G.49)
Оба члена в G.49) удовлетворяют одним и тем же правилам
получения элементов S-матрицы в координатном представлении
из соответствующих диаграмм Фейнмана.
Заметим, что сформулированные нами правила содержат
пока неясность1) в отношении множителей i. Мы сопоставляли
б'-матрице общий множитель (—i) и, кроме того, записывали
протонный пропагатор Sp с множителем L В высших порядках
всем протонным пропагаторам S? будет приписываться множи-
множитель i по тем же причинам, что и в разобранном примере. Мож-
Можно ввести единое правило для всех фермионных пропагаторов,
если сопоставлять iSp каждой электронной линии, а каждой ве-
величине А приписывать множитель (—г), т. е.
— ieASFeASp ... еА = (— leA) iSF (— ieA) ... (— ieA).
Тогда общий множитель (—i) войдет в лишнюю (по сравне-
сравнению с SF) величину А. Таким образом, каждой вершине у^ на
электронной линии мы приписываем фактор (—/)• Можно также
сопоставить (—i) каждой протонной вершине, если компенсиро-
компенсировать этот множитель фактором i перед каждым фотонным про-
пагатором DF. Тогда мы получаем единое правило относительно
множителей i: (—i) отвечает каждой вершине, a i — каждой ли-
линии на диаграмме. В дальнейшем мы будем следовать этому
правилу.
Для практических вычислений удобно перейти к импульсному
представлению. Для этого применим преобразование Фурье ко
всем фигурирующим в формуле G.49) величинам. Предпола-
') Для устранения возможных сомнений относительно общего множителя,
равного 2, рекомендуется решить задачу 2 в конце этой главы.

§ 28] ПОПРАВКИ К РАССЕЯНИЮ ЭЛЕКТРОНОВ ПРОТОНАМИ 123
гается, что волновые функции внешних частиц (т. е. начальных
и конечных электронов и протонов) являются плоскими вол-
волнами, как в G.2), G.3) и G.34). Тогда, например, первый член
в G.49) перейдет в
еА \ ач а*у d*z d*w л/л/ т: Г 4 T
V J Л/ EfEl Л/ SjSi BяL BяL BяL BлL q\ + ie
q_ + te L ^ p — m + ie J
x
Проведем интегрирование по всем пространственным координа-
координатам. Интегрирование по каждой из пространственных координат
дает множитель BяL и б-функцию, выражающую сохранение
энергии-импульса в вершине, отвечающей этой координате. Да-
Далее можно проинтегрировать по импульсам; в результате G.50)
примет вид
r
— M + ie
ieyvu(Pi, st)]x
yvu(Pi, S,)], G.51)
J
где, как и прежде, q = pf — pt.
Обратите внимание на б-функцию, отражающую общий закон
сохранения энергии-импульса, и на интегрирование по 4-им-
пульсу <7ь текущему вдоль замкнутой петли фейнмановской ди-
диаграммы в импульсном представлении, изображенной на
рис. 7.4, в. Множители BпL сократились, за исключением од-
одного, стоящего при четырехмерной 6-функции, и компенсирую-
компенсирующего его множителя Bя)-4, входящего в интеграл по d*qi.
Можно установить соответствие между всеми остальными вы-
выражениями, входящими в G.51), и фейнмановской диаграммой
подобно тому, как это было сделано для диаграммы низшего по-
порядка, показанной на рис. 7.3. Каждая вершина вносит множи-
множитель—1?уц, а каждая внешняя частица — множитель +Jт\Е. Но-
Новым здесь является фактор i[p — т + i'e]-', который в матрич-
матричном порядке ставится между вершинами и представляет собой
пропагатор, относящийся к виртуальному промежуточному фер-
миону.
Достаточно небольшого опыта, чтобы научиться, глядя на
заданную диаграмму Фейнмана, сопоставить ей выражение типа

124 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
G.51). Амплитуда диаграммы Фейнмана, изображенной на
рис. 7.4, г, отличается от G.51) заменой блока, относящегося
к протону, на
l
Окончательное вычисление амплитуд G.51) и G.52) не
является тривиальным; оно требует проведения сложного четы-
четырехмерного интегрирования. В статическом пределе, когда про-
протон рассматривается как точечный кулоновский источник, инте-
интеграл был вычислен Далицем [60]. В этом случае возникают
трудности, связанные с бесконечным радиусом кулоновского
взаимодействия. Мы не будем проводить дальнейших вычислений.
§ 29. Тормозное излучение
Может оказаться, что один из двух квантов, участвующих
в обмене, изображенном на рис. 7.4, в и г, удовлетворяет усло-
условию Эйнштейна q2 = 0. Тогда он может быть испущен в виде
свободного излучения, называемого тормозным. Для изучения
влияния, оказываемого таким взаимодействием с полем излуче-
излучения на процесс рассеяния, мы вновь воспользуемся эвристиче-
эвристическими соображениями, близкими к приведенным в книге Шиф-
фа [22]. Это позволит без большого труда получить полезные
результаты, совпадающие с теми, которые получаются на основе
строгого квантового рассмотрения излучения, излагаемого в [50].
Четырехмерный потенциал «фотона» с 4-импульсом k^ и по-
поляризацией е11 записывается в виде плоской волны
Л11 (х, к) = -^Lr (е-'*-* + *'*•*), G.53)
где kykv- = 0. е** является единичным 4-вектором поляризации,
удовлетворяющим условию поперечности
е»к» = 0. G.54)
Существует лоренцева система отсчета, в которой е^ является
чистым пространственноподобным вектором, т. е. е»1 = @, е),
?-е=1; в произвольной лоренцевой системе 4-вектор е*1 про-
странственноподобен и нормирован условием
eue|i = —1. G.55)
Нормировочная постоянная в G.53) выбрана так, что энергия
волны А& равна <о = &о = |к|. Чтобы убедиться в этом, вы-
вычислим

§29]
ТОРМОЗНОЕ ИЗЛУЧЕНИЕ
125
Поскольку
В = rot А = / л/Щ7ке X е (e~ikx - eikx) = л/Щ7ке X е sin k ¦ x
и, согласно G.54) и G.55),
ке X « • кв X » = s • в - (кв • еJ = 8 ¦ 8 - (е0J = + 1,
имеем
?/ = -y- J d3xsin2(w/ - к • х) = k = <d.
Рассмотрим амплитуду рассеяния, описывающую излучение
такого «фотона» во время рассеяния. Для простоты вернемся
к статическому приближению, заменив протон статическим ку-
лоновским полем, как в G.4), и найдем S/, в наинизшем неис-
чезающем порядке по е.
Диаграммы Фейнмана для этого процесса, изображенные на
рис. 7.5, отвечают процессу второго порядка. Одна вершина со-
соответствует взаимодействию электрона с кулоновским полем, а
\Pi, Si \pt}
Рис. 7.5. Тормозное излучение электрона в кулоновском поле.
другая — испусканию тормозного кванта. Испускание излучения
в первом порядке в отсутствие внешнего поля запрещено зако-
законом сохранения энергии и импульса: k2 = О ф (р/— ргJ <С 0.
Во втором порядке элемент S-матрицы имеет вид
fi = e2\ d\d'y ^f (x){- iA (x, k)iSF{x-y){- iy°)
+ (- /Y°) Акул (x) iSF (x - y) [- iA (y, k)]} ф, [у), G.56)
где
а два члена соответствуют различному порядку расположения
вершин, как показано на рис. 7.5.
Как обычно, удобно перейти в G.56) к импульсному пред-
представлению, произведя фурье-преобразование всех входящих в

126 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ |ГЛ. 7
эту формулу величин и проинтегрировав по пространственным
координатам. В результате этой, теперь уже привычной нам
операции получаем
Sfi = =Щ- 2я6 {El + k- Et) j= V^TTF * <Р" S* X
X [ jj Yo> ^^Ь^ ]
G.57)
где q = pf -\- k — pi. Имеется еще дополнительный вклад от пер-
первого члена в G.53), содержащий б-функцию Ь(Ег-\-k — Es).
Этот член описывает поглощение энергии в процессе рассеяния
и не дает вклада в рассматриваемый нами процесс, в котором
налетающий электрон передает энергию полю излучения и испу-
испускается с энергией Е/ = Et — k < ?,•. Отметим новую черту,
появившуюся в G.57), которая пополняет наши растущие зна-
знания о фейнмановских амплитудах: вершине испускания свобод-
свободного фотона с поляризацией е^ соответствует множитель (—1г)
и фактор \j-\j2kV возникает как нормировочный множитель фо-
фотонной «волновой функции».
Сечение тормозного излучения можно получить из S-мат-
рицы G.57). Мы ограничимся предельным случаем ?->0, т. е.
испусканием очень мягкого фотона. Более общий результат, из-
известный под названием формулы Бете — Гайтлера, можно найти
в большинстве других учебников. В нашем предельном случае
выражение в квадратных скобках в формуле G.57) принимает
вид
-ш{ри sf) [г {pf + kK __ от2 + Vo {pt _ky_mz\u (Pi,
[2e • Pf ~ {Pf ~ m)
— Ш (pf, sf)
, Y0[2e-/>,-
и (p{, st) =
- 2^ • Pi
= — iii(pf, sf)you(pi,
где мы пренебрегли величиной k->0 в знаменателе и на послед-
последнем этапе воспользовались свойствами C.9) дираковских спи-
спиноров. В пределе k-*-Q матричный элемент тормозного излуче-
излучения содержит амплитуду упругого рассеяния в качестве сомно-
сомножителя. Чтобы вычислить сечение, мы берем из G.57) и G.58)
квадрат модуля Sfi, делим его на поток \v\/V и на 2л6@) и по-

5 29] ТОРМОЗНОЕ ИЗЛУЧЕНИЕ \27
лучаем скорость перехода, а затем производим суммирование
по конечным состояниям (V2 d3k d3pf)/BлN, лежащим в инте-
интересующей нас области фазового пространства. Для неполяризо-
ванных электронов требуется также просуммировать по конеч-
конечным и усреднить по начальным спиновым состояниям электрона.
В итоге получаем
e-Pf e-PjY
k.pf k-pj
I « (Pf sf) Yo" [Pp *t) Г
I.N X
Выделяя члены, соответствующие упругому рассеянию G.11),
находим
da / da
G.59)
Это сечение соответствует тому, что электрон окажется в телес-
телесном угле flffi/, а фотон с поляризацией е будет испущен с им-
импульсом к, лежащим в интервале dQkdk. Таким образом, сече-
сечение рассеяния с испусканием мягкого фотона разбивается на
два множителя, один из которых есть сечение упругого рассея-
рассеяния электрона при той же энергии и в тот же телесный угол.
Из G.59) видно, что энергетический спектр фотона имеет вид
dk/k, поэтому вероятность испускания фотона с нулевой энер-
энергией бесконечно велика. Это явление называется «инфракрасной
катастрофой». Для преодоления возникшей трудности необхо-
необходим тщательный анализ экспериментальных условий, в которых
наблюдается тормозное излучение. Суть дела состоит в том, что
любой регистрирующий прибор имеет конечное разрешение по
энергии, поэтому если он детектирует неупруго рассеянные элек-
электроны в некотором конечном интервале энергии, включающем
точку k — 0, то он регистрирует также и упруго рассеянные
электроны.
Для корректного сравнения с экспериментом необходимо
учесть как упругое так и неупругое сечения, вычисленные в од-
одном и том же порядке по е2. Поскольку вклад тормозного излу-
излучения G.59) имеет порядок е2 по отношению к вкладу упругого
рассеяния, необходимо учесть в том же порядке по е2 радиа-
радиационные поправки к (doldQf)ei- Последние содержат члены двух
типов. Во-первых это члены, описывающие кулоновское рассея-
рассеяние электрона во втором порядке; соответствующие диаграммы
Фейнмана изображены на рис. 7.4, а, б. Во-вторых, необходимо

128
ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. ?
учесть взаимодействие электрона с самим собой через поле из-
излучения.
Фейнмановские диаграммы для этого процесса, приведенные
на рис. 7.6, изображают виртуальный фотон, испускаемый элек-
электроном и вновь поглощаемый им же, вместо того, чтобы про-
взаимодействовать с кулоновским источником (или протоном),
как на рис. 7.4, о. Отвечающая этим диаграммам амплитуда со-
содержит расходящийся член, который в точности компенсирует
расходимость в G.59) при
k = 0. Нам необходимо
накопить достаточно опы-
опыта, прежде чем браться за
решение столь тонкого во-
Zs проса, как вычисление
этой амплитуды.
Прежде чем закончить
обсуждение формулы
G.59), найдем еще сече-
сечение испускания Мягкого
тормозного кванта в ин-
интервал энергии Д?, кото-
который не содержит в себе
точку, соответствующую
упругому процессу. Начнем с суммирования по поляриза-
поляризациям фотона, для чего воспользуемся весьма удобной техникой,
предложенной Фейнманом [54]. Заметим, что точное выражение
G.57) для матрицы рассеяния обращается в нуль, если заменить
поляризацию фотона е^ на его 4-импульс №. Это свойство со-
сохраняется также и в приближении мягких фотонов G.59). Оно
является следствием сохранения тока djtl(x)/dxil = 0, которое
в импульсном представлении выглядит как k^(k) = 0. Сохра-
Сохранение тока тесно связано с калибровочной инвариантностью элек-
электродинамики, поскольку в импульсном пространстве калибро-
калибровочное преобразование имеет вид A^{k)—*A^(k)-{- №A(k) и до-
добавочный член, пропорциональный №, не должен менять
конечный результат.
Чтобы воспользоваться этим свойством, запишем
Рис. 7.6. Радиационные поправки к куло-
новскому рассеянию.
s 6 J 7-rr"
G.60)
и выберем систему координат, в которой № = (k°, k\ 0, 0), где
?1 = k° = k. Так как величина G.60) является скаляром, ее
можно вычислять в произвольной лоренцевой системе отсчета;
в частности, мы выберем такую систему, в которой скалярный
потенциал в G.53) обращается в нуль, Л°(л;) = 0. В этой си-

§ 29] ТОРМОЗНОЕ ИЗЛУЧЕНИЕ |29
стеме потенциал А(х) поперечен и в соответствии с G.54) и
G.55) можно задать две поперечные поляризации в виде
в(') = (о, 0, 1,0),
8<2> = @, 0, 0, 1).
Суммируя G.60) по поляризациям, имеем
Z e,ev/^ = /22 + /33 = У00 - /" - t /Ц.
pol ц = 0
Поскольку, как отмечалось выше, k^J^ = kvJ^v = 0, то /ov = /lv,
Jv0 = Jvl и, следовательно, /00 = /п. Отсюда получаем
pol
где мы вновь вернулись к принятому ранее соглашению о сум-
суммировании. Сумма по поляризациям приобрела явно ковариант-
ный вид. Полученная форма записи является весьма общей; она
основана только на сохранении тока. Таким образом, если а&
и Ь^ — сохраняющиеся токи, т. е. k-a(k) = k-b(k)— 0, то сум-
суммирование по поляризациям дает
Z e, (k) а* (*)] [ev (k) bv (k)] = - a • b. G.61)
pol
Применяя G.61) к G.59), получаем сечение тормозного из-
излучения, просуммированное по поляризациям. Интегрируя по
всем углам вылета фотона и энергиям в интервале 0 < fe
^ k ^ &max -С Е{, получаем
do
fema
а Г
f )
*„,.„
где рг и р/ — начальная и конечная скорости электрона, причем
р,= Р| = р в предельном случае мягкого фотона и рг-р/ =
= р2 cos 6/ для рассеяния на угол б/. Интегрирование двух по-
последних членов в G.62) производится элементарно:
1
m2 _ m2 f J_ . 1 = .
2 ~ ?2 J2fl2f(I-PzJ
4я ?2A-Р-ке)

130 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 1
Первый интеграл легко берется с помощью другого приема,
также введенного Фейнманом [54]. Он состоит в параметризации
подынтегрального выражения путем дополнительного интегри-
интегрирования согласно формуле
i
= \ *1 . G.63)
J [ах + Ь A — х)]2 '
ab
о
Применение этого приема дает
Ф = (Pf - PiJ« - 4?2 sin2 у.
Таким образом, сечение тормозного излучения мягких квантов
равно
здесь первое выражение справедливо для нерелятивистских
(NR), а второе для ультрарелятивистских (ER) электронов.
Чтобы получить конечный результат при &min -> 0, формулу
G.64) необходимо объединить с формулой для радиационных
поправок к (-з§-

30]
КОМПТОНОВСКОЕ РАССЕЯНИЕ
131
§ 30. Комптоновское рассеяние
Теперь мы можем рассмотреть взаимодействие с полем пло-
плоской волны G.53) во втором порядке. Пусть G.53) описывает
начальный падающий фотон, который поглощается электроном
в одной вершине, а
А'^х' a'^-^JL^e^e-'*'-*'+ *<*'¦*') G.65)
описывает конечный фотон, испускаемый в другой вершине.
Этот процесс называется комптоновским рассеянием. Он проис-
происходит на свободном электроне с сохранением энергии и импульса
k + Pi = k' + pf. ¦ G.66)
Амплитуда комптоновского рассеяния во втором порядке отли-
отличается от G.56) тем, что она содержит y^A^(Z, k') вместо
•уо<4оУЛ- Подставляя G.53) и G.65) в 5-матрицу второго по-
порядка и переходя с помощью преобразования Фурье к импульс-
импульсному представлению, получим
х [(- й#>
<*, st).
G.67)
Соответствующие диаграммы Феинмана изображены на рис. 7.7.
В G.67) опущены три добавочных члена, которые отличаются
Pi,
Pi, Si
Рис. 7.7. Комптоновское рассеяние.
либо знаком k, либо k', либо, наконец, знаками k и k'. Два из
них обращаются в нуль, поскольку содержат четырехмерную
6-функцию, налагающую следующие условия на 4-импульсы:
Pi = Pf + k + k', pj = pi + k + k',
которым невозможно удовлетворить. Эти условия соответствуют
кинематически запрещенному процессу распада свободного

132 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
электрона на свободный электрон и два фотона. В третьем члене
с переставленными k и k' требуется выполнение условия k' +
-)- рх = k + Pu которое отвечает переходу фотона в результате
рассеяния из начального состояния с 4-импульсом k' в конечное
с 4-импульсом k. Это кинематическое условие не может быть
выполнено совместно с G.66), поэтому данный член также дол-
должен быть отброшен. Оставленный в G.67) член возникает из
слагаемого e~ik'x в G.53), которое отвечает поглощению в
точке х фотона с 4-импульсом №, и из слагаемого e+ik''x в
G.65), соответствующего испусканию в х' фотона с 4-импуль-
4-импульсом k'.
Заметим, что выражение G.67) для Sf°unr симметрично от-
относительно перестановки
Это свойство известно как кросс-симметрия. Данная симмет-
симметрия является точной во всех порядках по взаимодействию [50].
Она играет важную роль в физике элементарных частиц.
Вычисление сечения комптоновского рассеяния производится
по уже знакомой нам схеме; единственная серьезная трудность
заключается в спинорной алгебре. Сечение рассеяния do полу-
получается возведением амплитуды G.67) в квадрат, делением ее на
BяLб4@), в результате чего получается скорость перехода, де-
делением на поток падающих частиц |v|/F и на число частиц в
единице объема мишени 1/V и, наконец, суммированием по фа-
фазовому объему [V2/BnN]d3pfd3k':
d3k'
X
u(pf, s^)(i' —— e+ e- rr г'\и{ри st)
\ p + k m p k' m )
2
G.68)
В лабораторной системе, в которой электрон покоится, вели-
величина m/kEi\v\ есть просто l/k. Интеграл по импульсу электрона
отдачи и по телесному углу рассеянного фотона dQk', в направ-
направлении угла рассеяния б, в лабораторной системе вычисляется
с помощью равенства G.40):
k'2dk' md3pf
~W EL
ft- J k' dk' 6 [(k + pi — k'f -ffl2]8(H«- k') =
о
k+m
\^cosQ)] = ^dQk', G.69)

§ 30] КОМПТОНОВСКОЕ РАССЕЯНИЕ 133
где k' и k связаны условием Комптона, налагаемым б-функцией
в G.69):
к 1 +(k/m)(\ -cos9) I + {2k/m) sin2 (9/2) ' yl'lv)
Формула G.68) принимает теперь следующий вид:
da ofk'X2
dQ \ k )
-,
p. + k —
m
r,
p.-k -
и (pi, st)
2
G.71)
Она дает дифференциальное сечение для случая, когда элек-
электроны и фотоны поляризованы как в начальном, так и в конеч-
конечном состояниях. Спинорную структуру матричного элемента
можно упростить выбором специальной калибровки, в которой
начальный и конечный фотоны поперечно поляризованы в ла-
лабораторной системе отсчета, т. е.
еи = @, е), 8 ¦ к = 0,
еи' = @ • е'), в' • к' = 0.
При таком выборе е-рг = е'-pi = 0 и спинорная часть матрич-
матричного элемента сводится к
2fe.p. е + е -2У-р
= -u(ph
где мы переставили ей е' справа налево и, как и прежде, вос-
воспользовались следующим свойством дираковских спиноров:
(pi + т) ей (pi, Si) = е (—pi + т) и (/?,-, st) = 0.
Подставляя полученный результат в G.71), суммируя по
спиновым состояниям Sf конечного электрона и усредняя по на-
начальным спиновым состояниям slt получаем с помощью G.13)
сечение для неполяризованного электрона
da 1 V"* da
2
±st, sf
ъ'гк ее'k' \ pt + т / ке
""" )
а2/й'\2 pf+m/ ъ'гк ее'k' \ pt + т / кее'
=Т \Т) SP 1m \2k-Pi """ 2k' ¦ Pi ) 2m \2k-pt
2k' ¦ p{
G.72)
В этой формуле мы сталкиваемся со следами от произведений
большого числа матриц у, вплоть до восьми. Имеются три от-
отличных друг от друга следа, которые необходимо вычислить;
из циклической симметрии следа и теоремы 6 § 26 следует, что

134 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
два перекрестных члена, имеющие в знаменателе (k-pi) (k'-pt),
равны друг другу. Для упрощения сложных следов, содержа-
содержащих один и тот же вектор более одного раза, обычно бывает
целесообразно переставить сомножители таким образом, чтобы
одинаковые векторы оказались рядом; тогда, пользуясь равен-
равенством ad = а2, можно избавиться от двух матриц у.
С помощью этого приема вычисление следов в G.72) произ-
производится следующим образом:
Тх = Sp (pf + m) г'гк {pi + m) Ш' =
= Sp pfi
(члены, пропорциональные m2, выпадают, поскольку k2 = 0)
= Sp 2k ¦ pipfs'skee' = 2k ¦ pt Sp pfe'ke' =
= 8k ¦ Pi{k ¦ pf + 2k ¦ z'pf ¦ e') =
(здесь мы воспользовались теоремой 3)
Sk-Pi[k'-Pi + 2{k.z'f].
Здесь был учтен закон сохранения энергии-импульса k + Pi =
= k' + ps, откуда
k' ¦ pi = k ¦ pf и е' • pf = e'k. G.73)
Подобным же образом вычисляем след
Т2 = Sp (Pf + m) ee'fe' (p,- + m) k'e's,
который отличается от Г] только заменой е, k <-> е', — k', по-
поэтому
Ta = 8k' ¦ pt[k ¦ pt-2{k' ¦ е)*\.
Для последнего следа с помощью тех же приемов находим
Т3 = Sp (pf + m) e'efe (pt + m) k'z'z =
= Sp (pi + m) s'ek (pi + m) k'&'& + Sp (k - k') г'екр^'&'г =
= Sp (pi + m)k (р{ + m) &'ё'ёе'ё + 2k ¦ e' Sp (-1) kpik'z' —
Sp pik'e'Ws — 8(k- e'J k' ¦ Pi + 8 (k' •zfk-pi =
i)(k' ¦ Pi)\2(z' ¦ eJ - l]-8(fe • e'J k'¦pi + 8(k'-zf k-Pi.
Подставляя результаты вычислений следов в G.72), получаем
формулу К^лейна. — Нишины [61] для сечения, комптоновского

§ 31] АННИГИЛЯЦИЯ ЭЛЕКТРОННОЙ ПАРЫ В ГАММА-ЛУЧИ C5
рассеяния
где k' и k связаны друг с другом углом рассеяния согласно G.70).
В низкоэнергетическом пределе ?-$-0 получаем классическое
томсоновское сечение
«2 (г г'\2
m2 ^ *>'
а __ е о 8 . 1 л~13
т Аптсг '
где величина
есть классический радиус электрона.
Если угол рассеяния 0->О, то k->k' и из формулы G.74) мы
видим, что для рассеяния вперед сечение оказывается томсонов-
ским при всех энергиях. Наконец, для неполяризованных фотонов
сечение получается суммированием по конечным поляриза-
поляризациям е' и усреднением по начальным поляризациям г. Это про-
производится в точности так же, как в классической электродина-
электродинамике, и мы можем позаимствовать оттуда конечный результат
Полное сечение нетрудно получить интегрированием по телес-
телесному углу фотона. Вводя z = cos б и используя G.70), находим
J [ (klm)(\-z)f +
-l
+ [1 + (k/tn) A - z)] ~ [1 + (k/m) A - z)Y } • S7'75^
При низких энергиях сечение вновь переходит в томсоновское
8я a2 k n
а при °
[, Ik . 1 , „ / т . k
При высоких энергиях полное сечение равно
Jta2
aWTm-
Доминирующим является логарифмический член, возникающий
от второго слагаемого в G.75).
§31. Аннигиляция электронной пары в гамма-лучи
Если повернуть диаграммы Фейнмана для комптоновского
рассеяния и расположить их, как показано на рис. 7.8, то мы
получим другой интересный физический процесс. Это двухфо^
тонная аннигиляция электрон-позитронной пары. .

136 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Соответствующий матричный элемент в импульсном про-
пространстве с указанными на рис. 7.8 обозначениями имеет вид
+ К - Р+ - P.)v{p+, s+) X
X [(- ih)~ 1 (- i&i) +
](р_, s). G.76)
— kx> — tn
Он симметричен относительно перестановки двух фотонов, что
согласуется с требованиями статистики Бозе. Этот процесс имеет
'%г> ?г
Рис. 7.8. Аннигиляция пары.
следующую интерпретацию на языке фейнмановских пропага-
торов: родившийся в прошлом электрон переходит в результате
рассеяния в состояние с отрицательной энергией —р+ и распро-
распространяется назад в прошлое. По пути он испускает два фотона,
т. е. дважды отдает энергию полю излучения. Это наинизший
по е2 порядок, в котором может происходить данный процесс, по-
поскольку при однофотонной аннигиляции пары нарушается за-
закон сохранения энергии-импульса. Чтобы обеспечить симметрию
S$air) относительно перестановки двух фотонов, необходимо учи-
учитывать обе изображенные на рис. 7.8 диаграммы:
Возвращаясь к амплитуде комптоновского рассеяния, мы
замечаем большое сходство между G.76) и G.67). Действи-
Действительно, при замене
е, &«->еь — ku
е', k' <-*¦ е2, + &2>
G.77)
Pt, st*-*p_, s_,
РР sf+-* — P+, +s+
эти амплитуды переходят друг в друга. Мы имеем в данном
случае пример общего правила [50], справедливого во всех

§ 31] АННИГИЛЯЦИЯ ЭЛЕКТРОННОЙ ПАРЫ В ГАММА-ЛУЧИ 137
порядках теории возмущений, которое связывает между собой
процесс
А + В-+С + D
и, например, процесс
A + C-+B + D,
где В означает античастицу по отношению к В и т. д.
Другой пример применения этого правила, называемого
кросс-симметрией, относится к связи между амплитудой тормоз-
тормозного излучения G.56), которой соответствуют диаграммы на
рис. 7.5, и амплитудой рождения пары в кулоновском поле, изо-
изображенной на рис. 7.9.
Рис. 7.9. Рождение пары в кулоновском поле.
Дифференциальное сечение получается из матричного эле-
элемента G.76) уже знакомым нам способом. Для неполяризован-
ного позитрона, сталкивающегося с покоящимся в лабораторной
системе неполяризованным электроном, оно имеет вид
_
da =
Р+ ( ?i?
\2p_-
^ 2т \2р_.^ ' 2p_.k2J 2т ^
Б~ТГ ) ~2Й~ ~2Й~ 6 (ki + k2-P--P+)' G-78)
"— В2 / 1 2
¦}_¦ kx ' 2р.
где р+ = Р+/Е+ есть скорость налетающего позитрона, множи-
множитель '/4 возник в результате усреднения по начальным спиновым
состояниям электрона и позитрона, а знак минус возник за счет
принятой нами нормировки волновой функции позитрона (см.
формулы C.9)). Матричный элемент упростился благодаря вы-
выбору поперечной калибровки, согласно которой в лабораторной
системе имеем
В силу кросс-симметрии эта калибровка совпадает с использо-
использованной нами при расчете эффекта Комптона. Таким образом.

138 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
нет необходимости заново вычислять следы, можно воспользо-
воспользоваться G.72) и G.73), произведя замену G.77). Остается только
избавиться от б-функции, учтя при этом кинематические соотно-
соотношения в лабораторной системе отсчета:
E++m
б [2m2 + 2m?+ — 2k{ (m + E+ — p+ cos 6)] =
= T (от + E+ - p++cos 6J dQfel< GJ9^
Подставляя результаты вычисления следов и интегрирования
по фазовому пространству в G.78), получаем сечение анниги-
аннигиляции пары, выраженное через энергии и углы в лабораторной
системе:
™9 / ... I ?7 \ Г" U U
а2 (от + ?+)
8p+(m + ?+-p+cos9J ^
G.80)
где в соответствии с налагаемыми в G.78) и G.79) кинематиче-
кинематическими ограничениями
1 т + Е+ — р+ cos 9
Е , — р cos 9
Полное сечение получается суммированием da/dQ^ по поля-
поляризациям конечных фотонов и интегрированием по телесному
углу dQfcj. Последнее требует определенной осторожности, по-
поскольку конечное состояние содержит две тождественные час-
частицы. Формула G.80) означает, что один из фотонов испускается
в элемент телесного угла dQft,; вследствие их неразличимо-
неразличимости это может быть любой из двух фотонов. Если бы мы проин-
проинтегрировали da/dQfe, по всему телесному углу 4я, мы учли бы

§ 32] РАССЕЯНИЕ ЭЛЕКТРОНА И ПОЗИТРОНА НА ЭЛЕКТРОНЕ 139
каждое различимое состояние дважды. Поэтому при вычисле-
вычислении полного сечения мы возьмем половину этого интеграла
§-dukl- G.81)
Из G.81) и G.80) нетрудно получить полное сечение в пределе
низких и высоких энергий: если р+->0, то к] ->—к2 и усредне-
усреднение по поляризациям дает (ei • е2J —> 1/2; следовательно1),
В ультрарелятивистском случае имеем
...1,
J
где в ведущий член вносят равные вклады первые два члена
в G.80), а сумма двух других членов в G.80) имеет фактор ма-
малости т/Е+. Впервые этот результат был получен Дираком
в 1930 г. [62].
§ 32. Рассеяние электрона и позитрона на электроне
Рассеяние электрона электроном описывается почти так же,
как рассеяние электрона протоном. Однако в первом случае
имеется дополнительная диаграмма, возникающая вследствие
тождественности электронов. Две диаграммы для рассеяния
электрона электроном изображены на рис. 7.10, там же ука-
указана необходимая кинематика. Соответствующая амплитуда
рассеяния, аналогичная амплитуде G.35) для электрон-протон-
электрон-протонного рассеяния, имеет следующий вид (спиновые индексы
опущены):
, »(рО(-%)
+p,_P|_
G.82)
Разные относительные знаки первого и второго членов обуслов-
обусловлены статистикой Ферми, согласно которой амплитуда должна
быть антисимметричной относительно перестановки двух конеч-
конечных электронов. Она, кроме того, антисимметрична относительно
') При р+ -*• 0 это приближение для а является плохим. Плоские волны
для электрона и позитрона следует заменить кулоиовскими волновыми
Функциями.

140
ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Pi
перестановки начальных электронов, что также соответствует
требованиям статистики.
В силу аналогичных аргументов амплитуда рассеяния двух
тождественных бозонов должна быть симметричной относитель-
относительно перестановок как начальных, так и конечных частиц. При-
Примером может служить изображенная на рис. 7.8 амплитуда ан-
аннигиляции электрон-позитроннои пары, которая, как мы видели,
симметрична относительно двух фотонов.
Мы не ввели в формулу G.82) никакого добавочного нор-
нормировочного множителя типа 1/д/2 или 2, связанного с появле-
появлением обменного члена. Присутствие тождественных частиц в на-
начальном или конечном состоянии
не влияет на правила получения
дифференциального сечения из
амплитуды Sfi. Надо, однако, по-
помнить о множителе 1/2 в формуле
G.81). Если в конечном состоя-
состоянии имеются две тождественные
частицы, этот множитель должен
быть включен в интегрирование
по углам при получении полного
сечения. Для тождественных ча-
частиц в начальном состоянии ни-
никаких дополнительных множите-
множителей не появляется, поскольку начальный поток не меняется.
Рассеяние электрона на электроне дает нам простой и ясный
пример справедливости этого правила. Для рассеяния вперед
с малой передачей импульса (/?, — /?[J можно пренебречь вто-
вторым, обменным членом в G.82). В этом предельном случае ам-
амплитуда сводится к комптоновской — результат, который не за-
зависит от статистики.
Выражение для дифференциального сечения рассеяния не-
поляризованных электронов получается из G.82) обычным спо-
способом. В системе центра инерции дифференциальное сечение
равно
Pt-Pf
Pi
Pi
'Рг
Pr-Рг
Pt
Рг
Рис. 7.10. Рассеяние электрона на
электроне.
da =
e'm*
BяJ ?4 Bр)
XSp(^
XS
H{[(^Wsp(-
+ in p, + m
2ot
•)
X
1m
2m
PiJ(Pa —PiJ
) ..„. (p, + «
X
v
2m У" 2m У
г) } 64 (Pi + P2 -Pi- P2
2т
G.83)

32]
РАССЕЯНИЕ ЭЛЕКТРОНА И ПОЗИТРОНА НА ЭЛЕКТРОНЕ
141
где Е обозначает энергию, а |5 — скорость каждого из электро-
электронов в системе центра инерции.
Обратите внимание на то, что в качестве относительной ско-
скорости начальных электронов в системе центра инерции фигури-
фигурирует величина 2р\ Для релятивистских электронов ее предельное
значение равно удвоенной скорости света. Здесь нет никакого
противоречия со специальной теорией относительности, по-
поскольку скорость каждого из электронов в системе отсчета дру-
другого не превышает скорости света. Символ (/?[-*->/??) означает
два дополнительных члена, которые получаются из первых двух
в формуле для da путем взаимной перестановки р\ и р'г
В формуле G.83) вклад от интерференции между прямым и
обменным членами содержит только один очень длинный след.
На рис. 7.11 дано графическое представление квадратов мат-
матричных элементов в форме замкнутых петель. Разница между
Рнс. 7.11. Графическое представление квадратов матричных элементов для
рассеяния электрона на электроне. Кружки на линиях показывают на отсут-
отсутствие фактора (р2 — ш2)~1.
прямым и обменным членами состоит в том, что первый содер-
содержит две петли и два следа, а второй — одну петлю и один след.
Иногда такие диаграммы бывают полезны для установления
порядка индексов |л, v и выписывания спинорных факторов.
Вычисление следов в формуле G.83) производится с по-
помощью теорем, приведенных в § 26. В частности, теорема 5 по-
позволяет упростить след из восьми матриц у в интерференцион-
интерференционном члене. Например, переходя для простоты к релятивистским
энергиям Е ~^> т и пренебрегая членами, пропорциональными
т2, получим
^Р {р[ч P1Yvp2^^2'Vv) = — 2 Sp (р[у PiP2y^p2) =
= - 8p, • p2 Sp p[p'2 = - 32 (p, ¦ p2) {p[ ¦ p'2).
Дифференциальное сечение, выраженное через энергию в си-
системе центра масс Е и угол рассеяния б, имеет вид
/ da \ _ а2 N + cos4 F/2) . 2 . 1 + sin4 (9/2I
\Ш)м~ 8?Ч sin4 (9/2) "*" sin2 (9/2) cos2 (9/2) "*" cos4 (9/2) J'

142
ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
где первое и третье слагаемые представляют собой квадраты
матричных элементов для двух диаграмм, изображенных на
рис. 7.10, а второе слагаемое дает вклад от интерференции этих
диаграмм.
При получении этого результата были использованы следую-
следующие кинематические соотношения: рх- р2 = р[ш Р2 = 2?2, р\р2 =
= Р] . р'2 = 2?2 cos2 (9/2) и рх ¦ р\ = р2 ¦ р2 = 2Е' sin2 F/2), которые
справедливы, если пренебрегать членами порядка т2. Выраже-
Выражение G.84) есть ультрарелятивистский предел формулы Мёллера
[58] в системе центра инерции.
Обратимся теперь к рассеянию позитронов на электронах.
В силу кросс-инвариантности можно получить сечение из фор-
формулы Мёллера заменой, анало-
¦_,,-/ гичной G.77). Диаграммы Фейн-
мана для этого процесса, изве-
известного как рассеяние Баба [63],
изображены на рис. 7.12.
Путем замены
-9,
p-p,
Рис. 7.12. Рассеяние электрона
на позитроне.
Pi-
p\-
p%-
¦Р\,
¦р\.
G.85)
и изменения общего знака в соот-
соответствии с F.56) получаем ам-
амплитуду рассеяния позитрона на электроне
Sfi=-
1
V1 {Е Е ,Е Е
A'^
(~ %) » {Pi) б {Яд (~ 'УЦ) °(q'i)
'\2
(p. ~ p\)
1
. й (pi)(~ %) ° Wi) р {id (~ 'У")»
1
G.86)
Первый член описывает прямое рассеяние; он аналогичен пер-
первому члену в амплитуде рассеяния электрона на электроне
G.82). Аннигиляционный член соответствует второму, обмен-
обменному члену в G.82). Знак минус между двумя членами возни-
возникает вследствие перехода из G.82) заменой согласно свойству
кросс-симметрии.
Антисимметрия амплитуды G.82) по отношению к переста-
перестановке двух начальных либо двух конечных электронов превра-
превращается в G.86) в антисимметрию между входящим электроном

§ 33] ПОЛЯРИЗАЦИОННЫЕ ЭФФЕКТЫ 143
с положительной энергией (р\) и «входящим электроном» с от-
отрицательной энергией (— q[), движущимся назад во времени,
либо между выходящими электронами р\ и —q{. Чтобы дать
интерпретацию этой антисимметрии в терминах теории дырок,
заметим, что до взаимодействия начальное состояние содержит
электрон р{ с положительной энергией и море состояний с от-
отрицательной энергией, заполненное, за исключением дырки, в со-
состоянии с отрицательной энергией —q\. В частности, это море
содержит электрон с отрицательной энергией в состоянии — q[,
поэтому согласно статистике Ферми начальное состояние должно
быть антисимметричным по отношению к перестановкер1 ¦«-»¦—q'x\
подобные рассуждения применимы и к конечному состоянию.
Антисимметризация должна быть произведена также по всем
остальным частицам из моря, но, поскольку они не фигурируют
в G.86), форма этого выражения никак не меняется от такой
антисимметризации.
Сечение рассеяния позитрона на электроне в системе центра
инерции получается из G.83) заменой G.85) и вычислением сле-
следов, производимым так же, как для мёллеровского рассеяния.
В ультрарелятивистском случае это дает
( do\ __ _cf_ rl+cos<(8/2) _ 2 cos4 (8/2) , 1 + cos2 9 1 . _ .
\ dQ )в~~ 8Е* I sin4 F/2) sin2 (8/2) "*" 2 Jp K'-°n
§ 33. Поляризационные эффекты
при рассеянии электронов
В качестве примера практического применения введенных
в гл. 3 спиновых проекционных операторов вернемся к рассмот-
рассмотренному в § 26 сечению Мотта и проведем вычисления для слу-
случая поляризованного пучка падающих электронов. В гл. 10 мы
увидим, что электроны, возникающие от распада (г-мезонов, по-
поляризованы, причем их спины антипараллельны направлению
движения.
Сечение кулоновского рассеяния электронов, имеющих им-
импульс р^ и спин su причем s^pi = 0, просуммированное по ко-
конечным спиновым состояниям ±s/, определяется формулой (см.
G.11))
da 4Z2a2m2
±sf
4Z2a2m2 V . _ , \ n / \ j? /т пп\
= —j-^-p— 2, I «(Pf > sf) Y°« (Pi, st) |2. G.88)
Для того чтобы при получении сечения по формуле G.88) вос-
воспользоваться методом взятия следов, введем согласно C,19) и

144 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ |ГЛ. 7
C.22) спиновые проекционные операторы
ВДы(Р/, st) = u(ph st),
2(Si)«(p,, -s,) = 0.
Повторяя переход от G.13) к G.14), получим1)
da 4Z2a2m2
. G,0)
Из G.15) и G.18) следует, что след, содержащий вектор спина,
равен нулю и мы вновь тем самым возвращаемся к формуле
Мотта G.22). Полученный нами результат о совпадении сечений
для поляризованного и неполяризованного начальных пучков
справедлив только в наинизшем порядке теории возмущений, но
в общем случае он неверен [64].
Приведем пример наблюдаемого поляризационного эффекта.
Рассмотрим снова налетающий электрон, спин которого ориенти-
ориентирован вдоль направления движения, и вычислим поляризацию
рассеянного электрона как функцию угла рассеяния. Начальный
вектор поляризации st удовлетворяет условиям
s? = -l=(s?J-srSi G.91)
и
sr pt = 0 или s\ = s. • Р;,
где
Ь=Т1- G-92)
Объединяя G.91) и G.92), имеем
|st| = -7====; G.93)
здесь s? обозначает единичный вектор в направлении st. Элек-
Электрон, спин которого направлен вдоль вектора рь называют пра-
вополяризованным с поляризацией siR. Для такого электрона
имеем
К*1==7^еГ=^' s?« = Pl's'«l< G'94)
') Можно, конечно, ввести 2(s) дважды — как в матричный элемент, так
И в сопряженный к нему, но в этом нет необходимости.

§ 33] ПОЛЯРИЗАЦИОННЫЕ ЭФФЕКТЫ 145
Аналогично, электрон со спином, антипараллельным вектору рь
называют левополяризованным с поляризацией siL = —s,h, и
для него
и
Такие же соотношения справедливы и для рассеянного элек-
электрона с той разницей, что всюду индекс i следует заменить на
/. Векторы siR = —siL с правой и левой поляризацией образуют
очень удобный базис, которым мы в дальнейшем будем часто
пользоваться. Собственные состояния оператора E(s) G.89), от-
отвечающие собственным значениям s — +sH = +sL, называют
состояниями с положительной и отрицательной спиральностя-
ми [65].
Поляризация рассеянных электронов характеризуется вели-
величиной
где NR означает число рассеянных частиц с положительной спи-
ральностью (или с правой поляризацией), a NL — с отрицатель-
отрицательной спиральностью (левой поляризацией). Величины NR, NL и
Р являются, вообще говоря, функциями энергии и угла рас-
рассеяния.
Поляризация рассеянных электронов при кулоновском рас-
рассеянии правополяризованного пучка определяется согласно
G.11) и G.95):
р _\u(Pj S!R) Vo" (Pi- stn) f ~ 1 « (Pp sfL) Vo» (Pt- siR) I2 _
R I " (Pf- sm) Vo" [Pi sit<) I2 + I " (Pf sfL) Vo» (Pi sir) f
i Qn L С + У'*) У' + т) С + vs^r) (Pf + m) 1
= \ Ь P LYo 2 2^~ Yo 2 2^~J -
cn Г.
Г.. С
[Yo
v
Yo
2ffl
. G.96)
Мы снабдили поляризацию PR индексом, который указывает на
То, что начальный пучок был полностью правополяризован.

146 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
Как и в G.90), все члены, линейные по siR либо по s/н, исче-
исчезают. След в знаменателе уже вычислялся ранее и дается
выражением G.21); числитель упрощается путем «протаскива-
«протаскивания» матриц Y5 друг к другу и применения G.17). После про-
простых преобразований и подстановки G.94) получаем следующий
результат:
Р - 1 _ Г 2«2 sin2 (9/2) и
rR— l IE2 cos2 (9/2) + т2 sin2 (9/2) J ' K -У/'
В ультрарелятивистском пределе, когда т/Е->0, или Р-> 1,
имеем PR -> 1, т. е. в пределе высоких энергий кулоновское рас-
рассеяние не приводит к деполяризации начальных электронов.
Если начальный пучок был не полностью, а лишь частично
поляризован вдоль направления движения, можно ожидать, что
результат G.97) перейдет в
Р = pPR. G.98)
Здесь р означает поляризацию начальных электронов, т. е.
где pR есть доля электронов с положительной спиральностью,
a pL = 1—Pr — доля частиц с отрицательной спиральностью.
Чтобы убедиться в справедливости G.98), заметим, что выраже-
выражение G.96) линейно по спиновым проекционным операторам
начального и конечного электронов. Поэтому с помощью ра-
равенства
„ 1+У<* i - * ~ У <я _ *
Pr г h Pl 2 ~
получаем требуемый результат
Г 2m2 sin2 (9/2) I
г — Р L ?2 cos2 (9/2) + т2 sin2 (9/2) J * <-' •
В частном случае р = 0 формула G.99) показывает, что непо-
ляризованный начальный пучок остается неполяризованным в
результате кулоновского рассеяния.
Полученным результатам можно сопоставить наглядную гео-
геометрическую картину. Определим следующим образом угол а
между направлением спина движущегося электрона, описывае-
описываемого спинором u(p,s), и произвольным направлением, задавае-
задаваемым единичным вектором п^ = @, п):
, ч и+ (р, s)a ¦ п и (р, s)
(a-n)= и?(р's)u(p;Ps) ' =
-Vl-P2«(P, s)y5nu(p, s), G.100)
где р = p/E.

§ 33) ПОЛЯРИЗАЦИОННЫЕ ЭФФЕКТЫ 147
Для вычисления матричного элемента G.100) мы вновь вве-
введем проекционные операторы и воспользуемся методом взятия
следов. Тогда с помощью G.93) получим
cos a = VT^T2 SP (^) ()
= Л/Г^158-п=д/т4^? s'-n. G.101)
Отсюда видно, что если se и р перпендикулярны, то |cosa|^
^д/l — Р2- Следовательно, в состоянии со спином, перпендику-
перпендикулярным скорости, среднее значение спина, определяемое выра-
выражением G.100), обращается в нуль при р->1. С другой сто-
стороны, для случая, когда спин s направлен вдоль скорости, т. е.
для спиральных состояний, получаем
cosa = se-n G.102)
и проекция спина на направление п, параллельное либо анти-
антипараллельное s, равна ±1. Обозначая в этом случае a = 6,
имеем
cos6=±l. G.103)
Среднее значение cos a для пучка рассеянных электронов
дается выражением
(cosa)= X w{p, s)cosa, G.104)
±s
где w(p,s) есть вероятность перехода в заданное конечное
состояние с импульсом р и спином s. Сумму в G.104) проще
всего вычислить, просуммировав по двум спиральным состоя-
состояниям. Для проекции спина на направление движения из G.103),
G.104) и G.95) находим
(cos 6) = w (sR, p)-w (sL, p) = P. G.105)
Таким образом, поляризация определяет косинус угла между
векторами спина и импульса. Для кулоновского рассеяния по-
поляризованного начального пучка электронов с р = 1 из G.105)
и G.99) получаем в пределе больших энергий, Е >• т, или ма-
малых углов рассеяния, 0 >С 1,
<6>~fe, G.Ю6)
т. е. угол между векторами спина и импульса рассеянного пучка
составляет равную т/Е долю от угла рассеяния [66].
Расчеты поляризационных эффектов в ультрарелятивистском
случае проще всего проводить, предварительно упростив поля-
поляризационные проекционные операторы в пределе т/Е -+ 0.
Покажем, как упрощается в этом предельном случае

148 ОПИСАНИЕ ОСНОВНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ ЯВЛЕНИЙ [ГЛ. 7
поляризационный проекционный оператор для продольно-поля-
продольно-поляризованных электронов со спином s, параллельным импульсу р.
Из G.93) и G.94) имеем
при р->1. Отсюда для проекционного оператора получаем
/1 ±y5sR\/
V 2 Д
2т )^\ 2 Д 2т
Аналогично
Дальнейшее упрощение в G.107) достигается путем перехода
к ультрарелятивистскому пределу в энергетическом проекцион-
проекционном операторе. Ранее из формулы G.99) мы заключили, что
в пределе т/Е-*~0 кулоновское рассеяние не приводит к депо-
деполяризации электронов. Теперь этот результат может быть по-
получен совсем просто. Найдем амплитуду рассеяния для случая,
когда начальный релятивистский электрон имеет правую поля-
поляризацию
u(pt, sl)= {1+2Уъ и(р1г s^,
а конечный — левую
u(Pf, sf)= A"~2Y6) u(pf, sf).
Для взаимодействия вида у11 амплитуда пропорциональна
(р1, st) =
= «(Pf, sf) у,
ЗАДАЧИ
1. Покажите, что решения в виде плоских волн, нормированные согласно
G.2) и G.3), обладают требуемыми трансформационными свойствами отно-
относительно преобразований Лоренца. В частности, учтя преобразование Лоренца
нормировочного объема V, покажите, что величина ф (х) ф (х) является скаля-
скаляром, а величина г|)+(х)г|)(л:)—временной компонентой 4-вектора.
2. Постройте амплитуду рассеяния электрона на протоне, отвечающую
изображенному на диаграммах рис. 7.4, г и в обмену двумя фотонами. Пока-
Покажите, что в статическом пределе при бесконечной массе протона она совпа-
совпадает с изображенным на диаграмме рис. 7.2 вторым борновским приближе-
приближением для рассеяния электрона в кулоновском поле.
3. Постройте амплитуду тормозного излучения при рассеянии электрона
на протоне и покажите, что в статическом пределе она переходит в ампли-
амплитуду G.57) тормозного излучения в кулоновеком поле. Убедитесь в том, что

ЗАДАЧИ 149
между этими двумя амплитудами имеется такое же соответствие, как между
амплитудами G.5) и G.35) для упругого рассеяния.
4. Получите формулу Бете — Гайтлера для сечения тормозного излучения
протона при произвольной энергии [67].
5. Выведите формулу Бете — Гайтлера для сечения образования элек-
трон-позитронной пары фотоном в кулоновском поле. Покажите, что ампли-
амплитуда этого процесса связана с амплитудой тормозного излучения кросс-сим-
кросс-симметрией.
6. Из формулы G.80) найдите полное сечение процесса е+ + е~ -*¦ у + у
при произвольной энергии и покажите, что ответ согласуется с приведенными
в тексте предельными значениями для G.81) при низких и высоких энергиях.
7. Выразите дифференциальное сечение электрон-электронного рассеяния
в наинизшем борновском приближении через энергии и углы в лабораторной
системе.
8. Вычислите сечение поглощения света связанным атомным электроном
для атомов с таким небольшим Z, что Za = Z/137 <С 1 и ?Связ ^ тс2. Счи-
Считать, что частота света удовлетворяет условию Йсо 3> ?Связ ¦ В этих упро-
упрощающих предположениях найдите дифференциальное сечение для двух пре-
предельных случаев:
а) нерелятивистский предел, ?связ < Йсо < тс2;
б) ультрарелятивистский предел, Йсо ;§> тс2.
9. Суммы по спинам в G.99) и G.105) были вычислены путем сложения
вкладов состояний с положительной и отрицательной спиральностями. В ка-
качестве базиса можно было использовать любую другую пару независимых
спиновых состояний. Покажите, что конечный результат не зависит от выбора
базиса.
10. Проверьте формулу G.97) для поляризации при рассеянии в кулонов-
кулоновском поле.

ГЛАВА 8
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ
К МАТРИЦЕ РАССЕЯНИЯ
§ 34. Рассеяние электрона позитроном
в четвертом порядке
Рассмотренные в предыдущих примерах правила построения
элементов 5-матрицы можно распространить и на более высо-
высокие порядки теории возмущений по константе связи, однако тут
возникает ряд новых проблем. Рассмотрим, например, вклады
порядка е4 в электрон-позитронное рассеяние. Для построения
соответствующей амплитуды нарисуем все возможные диаграм-
диаграммы Фейнмана с четырьмя электромагнитными вершинами, отве-
отвечающие данному процессу. Затем выпишем матричный элемент,
следуя изложенным ранее правилам.
Некоторые из этих диаграмм (всего их 18) изображены на
рис. 8.1. Диаграмма (а) описывает двухфотонныи обмен между
электроном и позитроном и вносит в амплитуду вклад, анало-
аналогичный выражениям G.47) и G.48) для электрон-протонного
рассеяния:
SlT> = - (- ief \ d'w d4x d*y d'z [Ц» (X) yjSF (x - y) Yv^+) (y)] X
X IDP (x - w) iDF {у - z) [$7> (Z) yviSF (z - w) yWf~] (w)l (8.1)
где индексы i и f, i' и f' означают соответственно квантовые
числа электрона и позитрона. Диаграмма (б) отвечает анниги-
ляционному члену и имеет знак минус по отношению к (8.1):
ЯГ = f (- ief \ d'w d\ d'y d'z [Ц+) (х) yJS, (x - у) у^ (у)] X
X iDp (x - w) iDp (y - z) 01:' (z) yviSF (z - w) y41+> (w)]. (8.2)
Происхождение знака минус между двумя амплитудами здесь
такое же, как в низшем порядке G.82); он возникает за счет
антисимметризации волновых функций по начальным электрон-
электронным состояниям с положительной и отрицательной энергией.

*34]
РАССЕЯНИЕ ЭЛЕКТРОНА ПОЗИТРОНОМ
151
Диаграмма (рис. 8.1, в) отвечает такому процессу, когда воз-
возникший при аннигиляции фотон рождает пару, которая перед
переходом в конечное состояние перерассеивается. Амплитуду
(Ф
f /fr
Рис. 8.1. Некоторые диаграммы четвертого порядка для рассеяния элек-
электрона на позитроне.
этого процесса запишем по известным нам правилам: каждой
вершине сопоставляется величина —ieyu и инвариантное интег-
интегрирование \ d4x, каждой внутренней линии отвечает пропага-
тор iSF(x — у), свободным начальным и конечным частицам со-
соответствуют волновые функции. Таким образом, получаем
(8.3)
$e) = +(- ief J d'w dAx d*y d'z iDF (x - w) iDF {y-z)X
X [Ц+) (x) yJSF (x - y) yJSp (y - w) v VfT' И] X
В пояснениях нуждается только выбор общего знака перед
амплитудой (8.3). Он определяется требованием статистики

152
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ
[ГЛ. 8
Ферми—Дирака, согласно которой два электронных состояния
должны быть антисимметричными по отношению к перестановке
электронов. Один из возможных способов упорядочения во вре-
времени четырех вершин диаграммы (а) показан на рис. 8.2 вместе
с соответствующим вариантом для диаграммы (в).
Рис. 8.2. Возникновение, благодаря статистике Ферми, относительного знака
минус между диаграммами рис. 8.1, а и 8.1, в.
Эти две диаграммы отличаются перестановкой электронных
линий / и //. Относительный знак минус между (8.1) и (8.3)
обеспечивает требуемую антисимметрию полного матричного
элемента относительно перестановки двух тождественных фер-
мионов. Член (8.3) имеет такой же знак, какой вносил в выра-
выражение G.86) вклад аннигиляционной диаграммы (рис. 7.15,6)
в низшем порядке.
Когда мы симметризуем амплитуду относительно переста-
перестановки двух фотонов, то оказывается необходимым включить так-
также диаграмму вида (г); действительно, фотоны, входящие в
вершины w и у на рис. 8.1, б, могли быть испущены и из вершин
z и х соответственно. Это приводит к следующему члену 4-го
порядка в 5-матрице:
= + (- ief
d*w
X
(*)
d'y dAz iDF (x - y) iDF {w-z)X
{x - y) v»iSF (y - w) y^ (w)] X
(8.4)
который имеет такой же знак, что и (8.3).
Диаграмма (д) на рис. 8.1 отвечает такому процессу, когда
рождающийся при аннигиляции фотон образует пару, которая,

§34]
РАССЕЯНИЕ ЭЛЕКТРОНА ПОЗИТРОНОМ
153
прежде чем перейти в конечное состояние, вновь взаимодей-
взаимодействует аннигиляционным образом. Те блоки диаграмм (в) и (д)
на рис. 8.1, которые расположены выше вершины у, связаны
между собой так же, как диаграммы рассеяния электрона на
позитроне во втором порядке, изображенные на рис. 8.1. По-
Поэтому естественно ожидать, что, как и в G.86), вклады в S-мат-
рицу диаграмм (в) и (д) имеют противоположные знаки. Тогда
для вклада диаграммы (д) можно записать
™ = _ (_
X iDp (w - x) \yl,iSp (y - x\k y^iSF (x - y)%a] X
X iDp (y - z) [^ (z) y^\+) (z)]. (8.5)
Независимый способ выбора общего знака в (8.5) состоит в за-
задании соответствующего упорядочения во времени, как было
сделано на рис. 8.2.
Требования симметрии и антисимметрии, которыми мы до
сих пор руководствовались, приводят к дополнительному клас-
классу диаграмм; пример такой диаграммы приведен на рис. 8.3. Она
возникает из диаграммы рис. 8.\,д в
результате симметризации по двум фо-
фотонам. Действительно, фотон, входя-
входящий в вершину w, мог быть испущен
как в z, так и в х. Такие несвязные ди-
диаграммы, т. е. диаграммы, содержа-
содержащие полностью изолированную часть,
которая не связана ни с одной из на-
начальных или конечных частиц, не при-
принималась во внимание в наших расче-
расчетах. Диаграмма на рис. 8.3 изобра-
изображает электрон, распространяющийся
до точки х; там он испускает фотон и
рассеивается обратно в точку у, где
он уничтожает и себя, и испущенный
фотон. Пользуясь языком теории дырок, можно сказать, что та-
такой процесс представляет собой флуктуацию, когда электрон, на-
находящийся в море с отрицательной энергией, испускает виртуаль-
виртуальный фотон и переходит в незанятое состояние с положительной
энергией, а затем вновь поглощает испущенный фотон и возвра-
возвращается в море с отрицательной энергией. Такие флуктуации
происходят постоянно; происходящие в вакууме процессы слу-
служат фоном, по отношению к которому определяется амплитуда
рассеяния. Мы отделяем вклад всех несвязанных «пузырей», ко-
которые вносят лишь некий фазовый множитель во все интересую-
интересующие нас диаграммы.
Рис. 8.3. Пример несвязной
диаграммы.

154 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. S
Дадим следующую сводку правил построения амплитуд про-
процессов высших порядков:
1. Нарисовать все связные диаграммы.
2. Каждой диаграмме сопоставить амплитуду, причем каж-
каждой вершине сопоставить фактор
- iey» \ d*x.
3. Каждой внутренней линии с концами в вершинах хну
сопоставить пропагатор iSF(x — у) или iDF(x — у) для фермиона
и фотона соответственно. Для фотона ввести еще дополнитель-
дополнительный множитель g^, связывающий матрицы f и yv в вершинах,
соединяемых фотонной линией.
4. Ввести волновые функции для каждой внешней линии,
т. е. линии, отвечающей падающей или рассеянной частице.
Эти правила совпадают с полученными ранее при рассмотре-
рассмотрении низших порядков теории возмущений. Новым является лишь
условие, согласно которому учитываются только связные диа-
диаграммы. Наконец, добавим еще правила относительно знаков:
5. Два члена, которые отличаются друг от друга переста-
перестановкой двух тождественных фермионов, имеют относительный
знак минус. Для двух электронов с положительной энергией
примером служит амплитуда G.82), которой соответствуют изо-
изображенные на рис. 7.10 диаграммы, а для одного электрона с
положительной и другого с отрицательной энергиями примером
является амплитуда G.86), которой отвечают диаграммы на
рис. 7.12. Это правило приводит к дополнительному знаку минус
в амплитуде (8.5), которой соответствует диаграмма с замкну-
замкнутой петлей, изображенная на рис. 8Л,д. В общем случае множи-
множитель (—1) привносится в амплитуду каждой замкнутой фер-
мионной петлей на диаграмме Фейнмана.
6. В соответствии с F.56) амплитуда имеет общий множи-
множитель (—1)", где п — число позитронов в начальном состоянии.
Прежде чем сравнивать теорию с экспериментом, остается
решить еще существенный вопрос о вычислении интегралов, в
особенности для диаграмм четвертого порядка. Диаграммы (а)
и (б) на рис. 8.1 вместе с двумя диаграммами с перекрестными
фотонными линиями, получаемыми из (а) и (б) перестановкой
вершин хну, приводят к трудному для вычисления четырехмер-
четырехмерному интегралу типа G.51). Мы не будем заниматься вычисле-
вычислением таких интегралов.
При рассмотрении диаграмм (в) и (д) на рис. 8.1 удобно
перейти к импульсному представлению и связать эти диаграммы
с соответствующей диаграммой низшего порядка, изображенной
на рис. 7.12,6, которая дает вклад во второй член амплитуды
G.86). Переходя к импульсному представлению, находим, что

34] РАССЕЯНИЕ ЭЛЕКТРОНА ПОЗИТРОНОМ
ff отличается от второго члена в G.8G) заменой тока
E5
п (р\) ey^v (<?)
X ,
п
<- ie^ X
(8.6)
t ГЦ «r ? i . '
— к — m-\- is — <7i — k — m -\- is
a Sff отличается тем, что в качестве волновой функции конеч-
конечного электрона подставляется выражение
70
~ /eYv) X
Х-7-
i
— т + ie
(8-7)
и, наконец, амплитуда Sfi отличается подстановкой вместо фо-
фотонного пропагатора следующего выражения:
(-0
S
k — pi — i?i — m + te
(8>8)
Блоки диаграмм, которым соответствуют выписанные выраже-
выражения, приведены на рис. 8.4.
(в) (г)
Рис. 8.4. Диаграммы Фейнмана, иллюстрирующие: (в) — поправку к вершине
(см. рис. 8.1, в); (г) — электрогшую собственно-энергетическую часть (рис. 8.1, г);
(д) — поляризацию вакуума (рис. 8.1, д).
Все остальные диаграммы четвертого порядка содержат
вклады диаграмм трех рассмотренных типов. К сожалению, та-
такие замкнутые петли приводят к выражениям, которые расхо-
расходятся при й-уоо. Перейдем теперь к последовательному иссле-
исследованию и вычислению этих диаграмм.

156
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ
[ГЛ. 8
§ 35. Поляризация вакуума
Самую сильную расходимость содержит выражение (8.8),
которое отвечает замкнутой электронной петле, изображенной на
рис. 8.4,E. Вклад этой диаграммы называют фотонной собствен-
собственно-энергетической частью второго порядка. Соответствующий
интеграл содержит два электронных пропагатора, поэтому в чис-
числителе остается вторая степень k и интеграл квадратично рас-
расходится.
Достаточно правдоподобный способ устранения квадратичной
расходимости основан на использовании условия калибровоч-
калибровочной инвариантности. Подобные рассуждения уже приводились
ранее перед формулой G.60). Калибровочное преобразование
Лц (i?) ~* А^ (q) + q^\ (q) не должно изменять конечного резуль-
результата вычисления физической амплитуды. Посмотрим, к каким
следствиям для интеграла (8.8)
приводит это требование.
Пусть фотон на диаграмме
рис. 8.4, д является реальным, т. е.
имеет <72 = 0, как, например, тор-
тормозной фотон, или фотон, уча-
участвующий в комптон-эффекте.
Как изображено на рис. 8.5, элек-
электронная петля дает поправки по-
порядка е2 к току, текущему через
блок, взаимодействующий с
/1Д(<7) (на рисунке этот блок обо-
обозначен вопросительным знаком).
Калибровочная инвариантность
требует, чтобы произведение <7Ц на ток обращалось в нуль. Та-
Таким образом, для (8.8) имеем
<7^nv (?) = 0 (8.9)
при условии
<72 = 0.
Произведение q^I{iv{q) можно записать следующим образом:
Рис. 8.5. Поправка к электромаг-
электромагнитному процессу за счет поляри-
поляризации вакуума.
— 6 Р
Bя)< k-q~
(k-q-m + ie)]
т—VvT— — =
— т + ie k — $ — m + te
— [(k — m + ie) —
k-
_ 1 [ йЧг с ( * 1 \
~ ~ 6 J Bя)< ЬР 1 к - q - m + /8 k - m + 1г ) Yv>
(8.10)

§ 35] ПОЛЯРИЗАЦИЯ ВАКУУМА 157
Если бы интеграл сходился, мы могли бы в первом члене поло-
положить k' = k — q и в результате вычитания двух одинаковых ин-
интегралов получить нуль. Однако интеграл расходится, и выраже-
выражение (8.10) оказывается неопределенным. Чтобы продвинуться
дальше, обрежем выражение (8.8) на высоких частотах путем
замены ')
= /,v (q, nv) + Z C. (Mj) I (q, Aff) ^ I c;/,v (<?, mj), (8.11)
где М? — большие массы, а постоянные Ci выбраны так, чтобы
интегралы сходились. Такой способ обрезания не является един-
единственным и выбран лишь для математической определенности.
Если какие-либо физические наблюдаемые величины окажутся
зависящими от параметров обрезания, теорию придется при-
признать несостоятельной. Во всяком случае, существование расхо-
расходящихся выражений наводит на подозрения о существовании
при больших импульсах (или, что то же самое, на малых рас-
расстояниях) трудностей в теории.
Обратим внимание на следующее важное преимущество ме-
метода обрезания (8.11): он обеспечивает выполнение условия
калибровки (8.9). Если бы мы произвели обрезание в каждом
отдельном пропагаторе, условие калибровочной инвариантности
не было бы соблюдено.
Вычисление величины I^viq), удовлетворяющей условию
(8.9), проще всего производится путем представления знамена-
знаменателя пропагатора в экспоненциальной форме с помощью тож-
тождества
оо
т'+1°К (8.12)
k — т + ге k2 — т2 -\- /е
Это дает
оо оо
Ли* (Я) = - 4 (- ief J dZl \ dz2 J -|^ X
о о
X [^(k - q)v + kv(k- q\ - guV(k2~k ¦ q-m*)] X
X exp {/z, [k2 - m2 + ге] + iz2 [(k — qJ - m2 + it]}, (8.13)
где было произведено взятие следа и изменен порядок интегри-
интегрирования. Дополняя показатель экспоненты до полного квадрата
') См. [54, 68]. Альтернативный метод преобразования расходящихся ин-
интегралов, который впервые привел к калибровочна-инвариантному результату.
Развит в работе [69].

158 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
путем замены переменной интегрирования согласно
l=k m— = k-q+-^-. (8.14)
z\ + z2 ^ ' zi + гг v '
производим интегрирование по импульсу с помощью равенства ')
f [l, 0,2lffij ¦ (8.15)
В результате получаем
(8.16)
Член, пропорциональный (g^q2 — <?ц^), автоматически удовле-
удовлетворяет условию калибровки (8.9), в то время как последние
три члена, пропорциональные g^V) этому условию не удовлетво-
удовлетворяют. Однако можно показать, что они уничтожаются, т. е.
оо оо
f f rfz, dz2 у Г 2 _ __i, q2zlZ2 1
J J (z, + z2f L Ci \mi (г, + z2) (г, + z2f J
0 0 i
(
0 0 i
X { exp г'
f f dzx dz2 у Г ___^ «?гг,гг 1
J J (г, + г2J Z-. 6' L7™' Я (г, + г2) (г, + z2Y J
0 0 i
0 0
О 0 i
(8.17)
') Это равенство проще всего выводится в прямоугольной системе коор-
координат. Если повернуть контур интегрирования на 45°, каждый из интегралов
превращается в гауссовский, например,
Г di0
J 2я
2я 2 V:
ita

§ 35] ПОЛЯРИЗАЦИЯ ВАКУУМА 159
Здесь по ходу выкладок мы сделали замену 2,—>-Яг,-. Полагая
далее в подынтегральном выражении Kz,—*zit убеждаемся, что
интеграл не зависит от Я,; следовательно, (8.17) есть тождествен-
тождественный нуль.
Оставшийся вклад в 1^ вычисляется с помощью того же
самого приема, состоящего во введении масштабного множи-
множителя. Воспользуемся тождеством
о
Тогда
оо оо оо
Г.,(,)-^(ад,-t*ft j j \ "\tZT X
j j \
оо
\ dzx dz^zfab A — zx — 22) X
0 0 0
X J] с. ехр [Л [<? V2 - m? + г'е)]> (8-19)
где мы опять сделали замену z, -> ^2;.
К сожалению, интеграл по X логарифмически расходится, и
мы вычислим его с помощью процедуры обрезания. Выбирая в
(8.11) Сх = —I, Ci = 0 (t > 1), находим
2ia , 2ч f , ,, ч . М2
^^ g?2) J dz z A - z) In ^_^г(
0
(8.20)
Чтобы понять физический смысл результата (8.20), рассмотрим
вклад замкнутой петли, изображенной на рис. 8.1,C, в рассея-
рассеяние. Включение этого вклада в амплитуду второго порядка
G.86) дает согласно (8.8) фотонный пропагатор, который мо-
может быть записан в виде суммы двух членов
^ ^ЛФ^-. (8.21)

160 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ (ГЛ. 8
Подставляя сюда (8.20) и опуская члены, пропорциональные
qn и <7v, которые равны нулю вследствие сохранения тока в элек-
электронных вершинах, находим
—'guv Г а , М2 . 2а Г , ,, ч , /. q2z{\ — z)\\ ,0 ооч
г,— 1 — -5—In—j- -\ \ dzz(\—z) In I 1 — —i—г-1) . (8.22)
o-| Ззт т2 л J v ' V. m2 - IE Л
L о J
Мы получили фотонный пропагатор, включающий поправки
порядка а. Выражение (8.22) описывает вклад электронной
петли в амплитуду для любой диаграммы Фейнмана с обменом
фотоном между двумя сохраняющимися токами. В предельном
случае q2—»-0 изменение в пропагаторе сводится к умножению
его на величину Z3, определенную согласно
Поэтому, например, амплитуда кулоновского рассеяния прини-
принимает при малых переданных импульсах вид
^_>fe»iwi(i _ - lni?)ei^. (824)
q- qz \ Зл т.* J ql v '
Отсюда мы заключаем, что параметр е2, фигурирующий в
уравнении Дирака, на самом деле больше, чем 4я/137, посколь-
поскольку измеряемая величина е\ должна равняться 4л/137. Заряд eR
называется перенормированным, а е — голым зарядом. В любом
процессе с обменом фотоном независимо от переданного им-
импульса присутствует перенормировочная константа
(8-25)
Следовательно, перенормировка заряда электрона происходит
также и за счет статической поляризуемости вакуума. Поэтому
расходимости в вычислениях вплоть до порядка е2 исчезают,
если сечения выражать через наблюдаемые заряды е\. Наблю-
Наблюдаемые, зависящие от импульса поправки возникают за счет
второго члена в (8.22), который исчезает в статическом пределе
при <7~«-О. Вклад этого члена конечен и не зависит от выбран-
выбранного способа обрезания. От способа обрезания зависит только
соотношение между голым и физическим зарядом. Например,
при малых переданных импульсах, |<?2/т2|<1, зависящая от
импульса поправка к амплитуде кулоновского рассеяния (8.24)
имеет вид
Зл тг 15зт т2 )
(8.26)

§ 35] ПОЛЯРИЗАЦИЯ ВАКУУМА ]6]
Она может быть следующим образом выражена в виде дополни-
дополнительного взаимодействия в координатном пространстве:
-ra?V04 = 4 + lSJ-6C)W- (8.27)
Такое взаимодействие приводит в первом порядке к следующему
сдвигу АЕп1 атомных уровней водородоподобного атома с заря-
зарядом Z:
(о) I2« - (т
Для п = 2, I = 0 и Z = } имеем
v = ~- = — 27
Знаки выражений (8.26) и (8.27) именно такие, какие следовало
ожидать из изложенного в гл. 5. Для рассеяния электронов с ма-
малой передачей импульса, \q2\<^ т2, и соответственно большим
прицельным параметром взаимодействие пропорционально пол-
полному заряду. При рассеянии с малым прицельным параметром
и большим переданным импульсом, q2 = —|q|2, электрон про-
проникает в глубь поляризационного облака и сила взаимодей-
взаимодействия возрастает.
Вычисления возникающего при этом изменения в законе
Кулона впервые были проведены в 1935 г. [70]. Полученные пред-
предсказания проверялись в опытах по измерению лэмбовского
сдвига уровней 25/2 и 2Ру2 атома водорода. Вместо ожидавшейся
разности уровней 2Su2 и 2Рч2, равной 27 Мгц, в 1947 г. было
получено значение порядка 1000 Мгц; такое расхождение свя-
связано в первую очередь с вакуумными флуктуациями поля излу-
излучения, обсуждавшимися в гл. 4.
Проведенные в течение последних десяти лет весьма точные
измерения и вычисления лэмбовского смещения уровней атома
водорода с п = 0 согласуются с точностью до 0,2 Мгц, что под-
подтверждает существование сдвига в 27 Мгц за счет поляриза-
поляризации вакуума. Это является убедительным свидетельством как
в пользу теории дырок для уравнения Дирака, которая приво-
приводит к вкладам диаграмм в виде замкнутых петель, так и в
пользу принятого нами простого выбора вершины взаимодей-
взаимодействия электрона с фотоном.
Проверка теории при больших q2, которые соответствуют ма-
малым расстояниям, остается пока задачей эксперимента, который
должен указать на необходимость внесения изменений в теорию
при больших q2. При рассеянии с большим переданным им-
импульсом,
ll 22

162 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 3
поправки в (8.22) логарифмически возрастают и фотонный про-
пагатор в первом порядке по неперенормированному заряду а
принимает вид
^(f !«?)(» ^l) (8.29)
Когда переданный импульс достигает предела обрезания АР,
поправка компенсирует перенормировочную константу для за-
заряда и можно предположить, что в пределе бесконечных энер-
энергий взаимодействие определяется голым зарядом, как изобра-
изображено на рис. 5.3. Это интересное, но недоказанное предположе-
предположение ').
Если импульс q виртуального фотона является временипо-
добным и <72 превышает Am2, как для диаграммы рождения
пары, изображенной на рис. 8.1, д, поправка в пропагаторе
(8.22) оказывается комплексной с мнимой частью, равной [54]
Чтобы понять природу мнимой части, вспомним об унитарно-
унитарности шредингеровской S-матрицы. Мы уже обсуждали это свой-
свойство в гл. 6, когда рассматривали нерелятивистский пропагатор.
Условие унитарности, которое записывается в виде
S+5=l, т. е. ZSnfSni = bft, (8.31)
позволяет дать вероятностную интерпретацию решениям задачи
рассеяния. Согласно условию унитарности сумма всех вероят-
вероятностей переходов из заданного начального состояния равна
единице. В теории, включающей позитроны, частицы могут рож-
рождаться и уничтожаться и сумма по состояниям п должна вклю-
включать все электронные, позитронные и фотонные конечные со-
состояния, в которые может перейти данное начальное состояние.
При этом сохраняется смысл (8.31) как условия сохранения
вероятности. Поскольку (8.31) является тождеством по е,
S-матрица должна удовлетворять условию (8.31) в каждом
порядке теории возмущений по константе взаимодействия. Если
') См. замечаний в § 18. Подробное обсуждение оснований для такого
предположения и вытекающих из него следствий содержится в работах [71,
72, 3].

§ 36] ПЕРЕНОРМИРОВКА ВНЕШНИХ ФОТОННЫХ ЛИНИЯ 153
мы произведем разложение
5f(-==6f(-+5(f!-) + S(f1)+ .... (8.32)
то условие унитарности примет вид
Sfi + sVf* = 0, (8.33а)
Si? + S$jT=-i:s«, (8.336)
п
оC> , оC)* у ГоA)*оB) , оB)*сAЛ
<bfi + bif = — 2j LAif •Ьпг + onf 5n(J, (8.33в)
n
oD) , qD)* у ГоA)*оC) j_ qB)*~B) . QOr^dn
n
Если начальное состояние i представляет собой свободные элект-
электрон и позитрон, то Sf'j) = O, поскольку реакция е- + е+->1у
запрещена законом сохранения энергии-импульса. Соотношению
(8.336) удовлетворяет амплитуда G.86), которая обладает тре-
требуемым свойством антиэрмитовости. Равенство (8.33г) выражает
отличную от нуля эрмитову часть амплитуды четвертого порядка
через вклады второго порядка. Именно этому вкладу четвер-
четвертого порядка отвечает формула (8.30); вследствие действитель-
действительности (8.30) соответствующая часть амплитуды эрмитова. При-
Присутствие в (8.30) ступенчатой функции 0A — 4m2/q2) указы-
указывает, что это выражение отлично от нуля только при таких
значениях импульса, при которых, помимо виртуальных пар в
виде замкнутых петель, в конечном состоянии может рождаться
реальная пара '). Наилучшее доказательство унитарности S-мат-
рицы в любом порядке теории возмущений дается в квантовой
теории поля [50].
§ 36. Перенормировка внешних фотонных линий
До сих пор мы обсуждали вклад замкнутой петли (8.8) в
пропагатор виртуального фотона. Замкнутые электронные петли
внесут поправки также и во внешние фотонные линии. В этом
случае фотон можно представлять себе как испущенный некото-
некоторым удаленным источником; соответствующая диаграмма изо-
изображена на рис. 8.6.
Вакуумный пузырь, включенный в эту диаграмму, приводит
в соответствии с (8.23) и (8,24) к появлению перенормировочной
константы Z3 в матричном элементе, записанном без учета по-
*) Величина мнимой части (8.30) как раз такая, что полная вероятность
всех переходов из начального состояния равна единице с точностью до а2.
Подробнее см. [73].

164
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ
[ГЛ. S
правок. Однако при этом ток источника остается неперенормн-
рованным. Если фактор д/^з сопоставить с источником, а дру-
другой фактор д/^з — с интересующим нас блоком, то голый за-
заряд е в каждой вершине заменит-
заменится на V Z3<? = eR. Таким образом,
правило обращения с реальными
внешними фотонами состоит в
том, чтобы пренебрегать поправ-
поправками ко всем внешним линиям
и заменять е на еп в каждой
внешней вершине. Это эквива-
эквивалентно вычислению всех попра-
поправочных диаграмм к внешним ли-
линиям, включая замкнутые по-
поляризационные петли, и после-
последующему делению на V Z3 для
каждой внешней фотонной
линии.
В дальнейшем при записи
Рис. 8.6. Обмен реальным фотоном
между двумя токами, макроско-
макроскопически разделенными в про- формул мы будем предполагать,
странстве. что перенормировка уже произве-
произведена: е2/4л будет обозначать
1/137, а голый заряд, если он нам потребуется, обозначим
как е0.
§ 37. Собственная масса электрона
Диаграмму рис. 8.4, г называют электронной собственно-
энергетической частью порядка е2. Соответствующая амплитуда
дается интегралом (8.7), а именно
S^4? / Л
^V-V + i
- (8.34)
Выражение (8.34) расходится, поскольку знаменатель содержит
/г лишь в третьей степени (k во второй степени из фотонного
пропагатора и k из электронного). Величина к представляет
собой малую массу фотона, введенную для предотвращения
инфракрасных расходимостеи.
Пользуясь представлением (8.12) и проводя вычисления, ана-
аналогичные (8.16), получаем
о о
(8-35)

§ 37] СОБСТВЕННАЯ МАССА ЭЛЕКТРОНА Jg5
Выражение (8.35) для Б(р) пригодно как для внутренних элект-
электронных линий с произвольными р2 и р на диаграммах Фейнма-
на, так и для внешних линий. В последнем случае р2 = т2 и,
кроме того, р располагается после спинора для свободной ча-
частицы, как в (8.7). Тогда можно воспользоваться уравнением
Дирака и положить р = т. Далее, как и при расчете поляриза-
поляризации вакуума, применяем тождество (8.18), заменяем г,-->уг» и
получаем
z[2m- /3A - z)]J-^-exp {iy[p2z(l - z) -
о
- m2z - К2 A - z) + is]). (8.36)
Интеграл
/ (р, т,к)=\^- exp {/Y [р2г A - г) - m2z - к2 A - z) + /e]}
о
расходится логарифмически; мы произведем обрезание, вычтя
из него интеграл J(p,m,A), где Л — большая масса.
Применим тождество
^L(e'«_e«*) = lni. (8.37)
о
Тогда пропагатор после обрезания примет вид
m2z + Я2 A - z) — p2z A - 2) — ie
1
1
a f , m л ,. ,,, m222 + Я2 A — z)
¦ -5- \dz [2m - p A - z)] In Я2П_2)_ргг ._
0
/>^ .111 9 . _ V Л/ l/i/ HI „a 1^
2)
1
" ^2 [2/ .A „л||п т2г2 + ЯA-г)

166 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
Вся зависимость от обрезания содержится в первых двух чле-
членах, от которых мы освободимся путем перенормировки1). При
р2 — т2 >• тХ интеграл легко вычисляется и мы получаем
р
'+С^I"^]- <8-39>
Вблизи «массовой поверхности», т. е. когда р2 « т2 (однако
р2 — т2 3> тХ) и когда 2 стоит рядом со спинором для свобод-
свободной частицы (р = т), имеем
{^ ^A) (8.40)
Обратим внимание на логарифмическую особенность при
р2-*т2. При р2~>т2 величина 2 становится комплексной, что
отвечает существованию процесса распада виртуального элект-
электрона на электрон и фотон. С аналогичным явлением для фотон-
фотонного пропагатора мы уже знакомы. При р2 — т2 <С тХ послед-
последний логарифм в (8.40) заменяется на \п(Х/т). В этом можно
убедиться путем прямого вычисления2) интеграла в (8.38) в
пределе р2 —¦ т2.
§ 38. Перенормировка электронного пропагатора
Изменение, внесенное в предыдущем параграфе в электрон-
электронный пропагатор, состоит, согласно (8.34), в замене
(8.41)
Из (8.40) имеем
2 (р) = дт - [Z2""' - 1 + С (/?)] (р — т), (8.42)
где
. Зага , Л-'
m2.
1) Выделенный в (8.38) конечный член однозначно определяется из усло-
условия обращения его в нуль на массовой поверхности при р2 = тг.
2) Вычисление полного вклада второго порядка в электронную собствен-
собственно-энергетическую часть содержится в работах [2, 741.

§38]
Перенормировка электронного проПагатора
167
Величина С(р) выбрана так, чтобы при р = т функция
С(р) = 0; таким образом, она не зависит от параметра обреза-
обрезания Л. При р = т получаем
(^^) (8-43)
Теперь, используя (8.42), можно переписать (8.41) в следую-
следующем виде:
г iZ2
р — т — 2 (р) ~ (р - т) [1 + Z2C (р)] — Z2bm ~~
Мы отождествим величину тръ. = /п + 8т с физической массой
электрона; параметр т в уравнении Дирака представляет со-
собой, как и голый заряд, другую неизмеряемую величину. Необ-
Необходимость перенормировки массы возникает уже в классиче-
классической электродинамике.
Действительно, масса, измеряемая в опытах со свободными
электронами, есть сумма массы т, входящей в выражение для
лоренцевой силы, и электромагнитной собственной массы элект-
электрона [75]. Для классического электрона с радиусом ~а элект-
электромагнитная собственная энергия составляет ~а/а. Тогда для
наблюдаемой массы получим величину
~ (т + а/а) — /пр11. В случае точеч-
точечного заряда й->-Ои поправка к массе
становится бесконечной. То же самое
происходит в теории Дирака, однако
здесь поправка расходится, как лога-
логарифм, содержащий параметр обреза-
обрезания, в то время как в классической
теории собственная энергия расходится
линейно при а->0. Ослабление расхо-
расходимости следует из теории ды-
дырок.
Как впервые показал Вайскопф
(а)
(Ф
[76], диаграмма рождения виртуаль- рис Различные упоря.
ной пары с показанным на рис. 8.7, а Д0Чення во времени для
собственно-энергетической
части второго порядка.
упорядочением во времени компен-
сирует ведущую расходимость диа-
диаграммы, приведенной на рис. 8.7, б.
Хотя формально поправка к массе является бесконечной,
однако для значений параметра обрезания Л <С пге2я/3а ~
~ 10100 т она мала. Заметим, что масса Вселенной оценивается
величиной ~ 1080 т [77].
Систематический способ проведения процедуры перенорми-
перенормировки массы состоит в следующем. Надо переписать уравнение

168 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
Дирака в терминах физической массы и рассматривать разность
между голой, или затравочной, массой и физической массой как
дополнительное взаимодействие. Таким образом, запишем
(/V — mPh) ¦ф = еАф + (т — mph) г|з = еЛг|> — дт$. (8.45)
Дополнительному взаимодействию отвечает диаграмма на
рис. 8.8. Этот член сокращается с первым членом в (8.40), и при
р -> тръ пропагатор приводится к виду,
*—$т содержащему свободный пропагатор в
* X J качестве сомножителя.
Рис. 8.8. Массовый контр- в Дальнейшем мы всегда будем пред-
член, полагать, что перенормировка массы уже
произведена, т. е. считать включенной
диаграмму, изображенную на рис, 8.8. Обозначение т мы со-
сохраним за физической массой электрона.
Остается еще поправка к пропагатору, заключенная в Z2 и в
функции С(р), выбранной так, что при р = т функция С{р) = 0.
В частности, при р » т пропагатор имеет вид
iZi (8.46)
р — т р — т '
т. е. отличается фактором Z2, который в этом смысле аналогичен
фактору Z3 в фотонном пропагаторе. В данном случае Z2 также
можно включить в заряд е0, входящий в обе вершины на концах
электронной линии; однако в этом нет необходимости, по-
поскольку, как мы увидим, поправки к самим вершинам сокра-
сокращаются с Z2. Вряд ли можно ожидать, что величина Z2 имеет
глубокое физическое содержание, так как согласно (8.43) она
зависит от массы фотона.
Требуется определенная осторожность, чтобы не внести по-
поправки во внешние линии дважды; с подобной ситуацией мы
уже сталкивались в случае фотонов. Пропагатор есть величина
билинейная по амплитудам поля, это видно, например, из выра-
выражения F.48). Однако внешняя линия соответствует амплитуде
поля, поэтому она перенормируется множителем V'Z2. Таким
образом, если вычисления проведены с учетом всех диаграмм,
дающих поправки к внешним линиям, результат следует разде-
разделить на -уfZ2 в степени, равной числу внешних электронных
линий.
Нерелятивистская теория возмущений дает хорошо известный
пример аналогичного явления, а именно
2^- (8.47)

§39]
ПОПРАВКИ К ВЕРШИНЕ
169
где
Zn = l-
I (Фт. V*n) 12
(8.48)
тфп
Здесь также Z находится, по сути дела, из функции Грина, а
волновая функция перенормируется величиной VZ .
§ 39. Поправки к вершине
Нам осталось рассмотреть только диаграмму, изображенную
на рис. 8.4,6, которая отвечает поправке за счет обмена фотоном
между электронными концами вершины уд- Такую диаграмму
называют вершинной частью второго порядка. Чтобы вычислить
ее вклад в физические процессы, рассмотрим интеграл
р) = (- геУ \ — „\,
p — k — m + ie
X
(8.49)
где р' означает импульс электрона, а —р — импульс физического
позитрона, рожденного виртуальным фотоном, как показано на
рис. 8.4,6. То же самое выражение (8.49)
отвечает и вершинной радиационной по-
поправке к изображенному на рис. 8.9 рассея-
рассеянию электрона на внешнем потенциале. В
этом случае р' вновь является импульсом
конечного электрона, однако р теперь пред-
представляет собой импульс начального элек-
электрона. Таким образом, одна и та же функ-
функция (8.49) описывает поправки к различ-
различным физическим процессам.
Амплитуда (8.49) расходится, поскольку
знаменатель подынтегрального выражения
содержит k лишь в четвертой степени. Кро-
Кроме того, мы вновь сталкиваемся с инфра-
инфракрасной расходимостью и поэтому припи-
приписываем фотону малую массу, чтобы изба-
избавиться от вклада мягких фотонов. Рассмотрим Av(p', p) при
Рис. 8.9. Вершинная
поправка к рассея-
рассеянию во внешнем элек-
электромагнитном поле.
считая бесконечную часть выделенной. Начальный и конечный
электроны будем считать свободными, т. е. р = т, р' = т.
В этом случае
п(р) Л^ {р, р) и (/,) = (Zf' - 1) й(р) у»и(р),
(8.50)

170
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ
[ГЛ. 8
где Z\ является константой, зависящей от масс т2 = р2, X2 и от
обрезания, которое необходимо сделать, чтобы эта константа
была конечной. Соотношение (8.50) является самым общим, по-
поскольку единственный входящий в него 4-вектор pv есть то же
самое, что величина myv, стоящая в обкладках (sandwiched) из
спиноров п(р) и и{р).
Рис. 8.10. Радиационные поправки второго порядка к^рассеянию во внешнем
электромагнитном поле.
Нет необходимости вычислять Z\, так как прямое сравнение
(8.49) при р' = р с пропагатором 21 (р), задаваемым формулой
(8.34), показывает, что
Л,(р,р) = --^. (8.51)
Здесь мы использовали следующее важное тождество:
д 1 11
о^ р — т
> — т
(8.52)
Оно означает, что дифференцирование свободного пропагатора
по импульсу эквивалентно введению в соответствующую линию
фотона с нулевой энергией. Вычисляя производную dl>(p)jdp»

§ 391 ПОПРАВКИ К ВЕРШИНЕ G1
непосредственно из (8.42), получаем
п (р) Л,» (р, р) и (р) = (Z2"' - 1) и (р) у» и (р), (8.53)
или, согласно (8.50),
Z, = Z2 (8.54)
с точностью до е2.
Следовательно, в этом порядке поправка к вершине равна
Л„ (р', р) = (Z2"' - 1) Yn + Л? (р\ р). (8.55)
Вся зависимость от обрезания содержится в Zb Величина
ScVi{p\p) является конечной при условии, что инфракрасная ка-
катастрофа устранена введением массы фотона X > 0. Кроме того,
она удовлетворяет условию
й(р)Л?(р,р)м(р) = 0 (8.56)
и определена однозначно.
Можно считать, что Z, либо перенормирует заряд е в вер-
вершине, либо просто сокращает -у'Z2 в перенормировке внешних
линий. В этом проще всего убедиться путем рассмотрения всех
диаграмм порядка не выше е2, дающих вклад в процесс рас-
рассеяния электрона вперед на внешнем потенциале. Эти диа-
диаграммы приведены на рис. 8.10.
Ниже перечислены вклады каждой из них в пределе q-±0:
(а) — iey^,
F)-ieyil(ZTi-l),
(в) + Ьт j^ (- feYlx) - (Z2-' - 1) (- /eYJ, (8-57)
(г) — Ьт р-т (— Иц).
(д) - I(—/еуц) -^^-^т = - г'еУц(Z3 - 1).
Как было показано ранее, надо еще поделить эти выражения
на V^2 Для каждой внешней электронной линии и на V^.i Для
каждой внешней фотонной линии. Сумма всех этих вкладов с
точностью до порядка е2 равна
(8.58)
где при последнем преобразовании мы использовали (8.25) и
(8.54). Таким образом, перенормировочные константы в вер-

172 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
шинной части и в пропагаторе полностью сократились. Перенор-
Перенормировка заряда целиком обусловлена поляризацией вакуума.
Целесообразность сложных обозначений, принятых при вы-
выводе (8.58), оправдывается при рассмотрении более высоких
порядков. В частности, (8.51) и соотношение (8.54), согласно
которому Z\ = Z2, справедливы во всех порядках (так назы-
называемое тождество Уорда). То же относится и к утверждению
о том, что все расходящиеся интегралы можно включить в пере-
перенормировочные константы Z\, Z2 и Z3 [50].
Мы уже указывали на наблюдаемый физический эффект,
обусловленный конечной частью диаграммы поляризации ва-
вакуума. Обращаясь к конечным вкладам от вершинной и элект-
электронной собственно-энергетической частей, мы также получим
интересные физические предсказания.
Рассмотрим вершинную часть А^(р',р), задаваемую инте-
интегралом (8.49). Его вычисление требует довольно громоздких
выкладок. Прежде всего придадим электронным пропагаторам
вид, содержащий в знаменателе квадраты импульсов, а затем
объединим знаменатели, пользуясь либо экспоненциальным
представлением, как в (8.12), и масштабным преобразованием
(8.18), либо непосредственно по формуле1)
V • (8'59)
') С помощью этого интеграла Фейнмана [54] вычисления проводятся
следующим образом:
К2 + ie (p' — kJ — т2 + ie {p — kf — т2 + ie
оо оо оо
: 2 \ \ \ dz\ dz2 dz3 Ь A — z\ — z2 — Z3) X
000
d<kf(k)
X
\
_i [k2 - 2k ¦ p'z2 - 2k ¦ pz3 - X2zi + (p[2 - m2) z2 + {p2- m2) z3 + ief
0 0 0

§ 39] ПОПРАВКИ К ВЕРШИНЕ 173
После интегрирования no k и обрезания расходящегося
интеграла путем введения параметра Л2 находим
оо оо оо
0 0
0 0 0
m2 A — ZiJ + X2zi — q2z2z3 — ie
CO « ОО у о
0 0 0
[/)' A - г2) - ^гз + т] Y|1 [р A - г,) - р'г2 + от] yv
т2 A - г,J + Л2г, - <?2z223 - ie
^ '
В знаменателе последнего числа перенесем, с помощью пра-
правила антикоммутации, р и р' на края, где они могут действовать
на электронные спиноры, в обкладках из которых стоит Лд. Да-
Далее воспользуемся соотношением Гордона C.26). Тогда знаме-
знаменатель последнего члена принимает вид
- у, [2т2 A - 4г, + z2) + 2q> (I - z2) (I - «,)] - 2mzlz2 [f, YJ.
(8.61)
где
С s (p'z2 + P23) • (p'Z2 + PZ3) + A.2Z] — (p'2 — ОТ2) Z2 — (p2 — ОТ2) 23 =
= — p'2z2 A — z2) — p223 A — 23) + 2p • р'г223 + от2 A — Zi) + A.2zi =
= — (p'2 — ОТ2) Z2 A — Z2) — (p2 — ОТ2) 23 A — Z3) — <72222з -f
B интеграле \ d*k сначала проводим интегрирование по dka. Полюсы по dk0
расположены в точках ± л/\ к \2 + с . С помощью добавки =F ie сместим их
с контура интегрирования следующим образом:
k*-c + ie = {k0 - V|k|2 + c + ie) {k0 + л/\к\*+с - ie).
Это дает
\
Для произвольной степени знаменателя п > 3 ответ получается дифференци-
дифференцированием этого равенства по с. Поскольку знаменатель зависит только от к1,
нетрудно учесть зависимость от k^ в знаменателе: все нечетные степени
6ц -> 0, k^kv -> 'hgnvk2 и т. д.

174 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
Интегрирование по переменным zt в общем случае сопряжено
с трудностями, хотя его все же удалось провести аналитиче-
аналитически1). Мы ограничимся двумя предельными случаями, когда
\q\2<^m2 и \q\2'S>m2. В первом случае с точностью до членов
порядка q2 включительно имеем
При |<7|2 5?> т2 получаем только члены, зависящие от X:
(8.63)
Складывая эти результаты с вкладом от поляризации ва-
вакуума, мы получаем радиационную поправку порядка а к рас-
рассеянию электрона во внешнем поле, которое является источни-
источником фотона q. Из (8.26) заключаем, что в пределе малых пере-
переданных импульсов поляризация вакуума добавляет постоянную
— 7б к —3/8 в (8.62) и не влияет на члены, содержащие инфра-
инфракрасную расходимость и магнитный момент.
Последний член в (8.62) приводит к добавке к магнитному
моменту электрона, равной а/2я. Действительно, в статическом
пределе он следующим образом видоизменяет взаимодействие
электрона с внешним полем:
- М (/) (у, + ? А?г-) " (Р) А' (?) =
[Ч^+0 + ?)*?¦]«w * <* (8-м)
Поправочный фактор A + а/2я) к магнитному моменту элект-
электрона был впервые получен Швингером [78] в 1948 г. и его суще-
существование было подтверждено экспериментально [79].
Затем появилась возможность экспериментально наблюдать
поправку порядка а2 к магнитному моменту. Ее теоретическое
значение [80] равно —(а2/я2) @,328), что согласуется с совре-
современными экспериментальными данными2). Теоретический ре-
результат был получен из рассмотрения вершинных диаграмм с
двумя виртуальными фотонами3).
') См. [54]. Для случая, когда электроны находятся вне массовой по-
верхности р2 ф т2. р' ф т2, см. [74].
2) Последнее экспериментальное значение для ц равно [81]
ц = 1 + а/2я — [0,327 ± 0 005] а2/я2.
3) После издания английского оригинала книги для аномального магнит^
ного момента электрона были получены значительно более точные экспери-
экспериментальные и теоретические значения. Экспериментальное значение в иастоя-

§ 39] ПОПРАВКИ К ВЕРШИНЕ 175
Другие члены в (8.62) и (8.63) приводят к появлению инфра-
инфракрасной расходимости в сечении рассеяния электрона. Однако
эта расходимость исчезает, если учесть вклад, вносимый в сече-
сечение тормозным излучением мягких фотонов. Любая экспери-
экспериментальная установка имеет конечное разрешение по энергии,
поэтому, если детектируются электроны, имеющие разброс по
энергии АЕ, то число зарегистрированных событий отвечает
сумме упругого сечения и сечения тормозного излучения, при-
приводящего к электронам с энергией, отличающейся от энергии
упруго рассеянных электронов не более чем на Д?.
Проверим с точностью до членов порядка е2 утверждение
о том, что такая сумма упругого и неупругого сечений конечна
и свободна от инфракрасной расходимости. Для этого сопоста-
сопоставим выражения G.64), (8.62) и (8.63). С точностью до порядка
е2 «инфракрасная» часть упругого сечения имеет вид
где
I 1 ч2
(_02) „г (8-66)
inJ_JLL_i _ J— •*> 1
Здесь (do!dQ),Q представляет собой вклад наинизшего порядка
в упругое сечение. Сечение тормозного излучения согласно
G.64) равно
(*°) (*?)? Ь (8.67)
торм
Мы видим, однако, что выражения (8.65) и (8.67) нельзя скла-
складывать непосредственно, поскольку обрезание по фотонам с ма-
малой энергией введено в них различным способом.
Для преодоления этой трудности необходимо либо вновь
получить сечение тормозного излучения, введя конечную массу
фотона, либо заново вычислить поправки к вершине, наложив
запрет на излучение фотонов с энергией меньше kmin. Мы выбе-
выберем вторую возможность, чтобы избежать трудностей, связан-
связанных с появлением реальных продольных квантов при отличной
от нуля массе фотона X. Следует, однако, иметь в виду, что обре-
обрезание с помощью параметра km\n является нековариантной опе-
операцией, поэтому, проводя перенормировку вершины таким спо-
способом, необходимо соблюдать осторожность в выделении пере-
перенормированных частей. Именно по этой причине мы ранее про-
Щее время принимается равным A159656,7 ± 0,5) • 10~9, а разность между
экспериментальным значением и теоретическим с учетом второго порядка по а
составляет (см. [81]) A,68 ±0,33) (а/яK. (Прим. перев.)

176
ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
вели перенормировку с помощью инвариантной массы фотона X.
Для упрощения математических выкладок положим kmin ^> X.
Итак, вернемся к выражению (8.49) и преобразуем фотонный
Рис. 8.11. Области в импульсном пространстве, в которых пропагаторы под-
подвергаются изменению благодаря инфракрасному обрезанию.
пропагатор таким образом, чтобы при k < kmin амплитуда обра-
обращалась в нуль. Это означает, что задаваемый формулой G.30)
фотонный пропагатор DF(x — у,Х),
DP(x-y, x) = i
мы преобразуем к виду
Dp{x — y, kmln) = i
Г d*q
~" J B)
„-iq-(x-y)
BяL q2 — X2 + ie
(8.68)
BяK 2 | q Г
d3q
2яK 2 |
. giq-(x-y)-( \qa 1 \ xa-ya! __
= DF{x-y,
где
BяK
I4l<*nrin
——.
q2 — X2 + (8
. ,(8.69)
2 + (8 v '
(8.70)

§ 39]
ПОПРАВКИ К ВЕРШИНЕ
177
Области в импульсном пространстве, в которых обрезание из-
изменяет пропагаторы, изображены на рис. 8.11.
Соответствующее изменение 6ЛД(//, р) в вершине (8.49)
равно
-Лй(р', р, kmta) =
= Лй(р', р,
d4
dku
2л
X
X
-k + m)
(k2 - к2 + ie) \(p' - kJ - nr + ie] [(p - kf - in2 + ie] '
(8.71)
Это выражение не содержит ультрафиолетовой расходимости
благодаря ограниченности области интегрирования.
Для вычисления (8.71) проведем сначала интегрирование по
k0. Выберем контур интегрирования в комплексной плоскости
ko, как показано на рис. 8.12, и воспользуемся теоремой Коши.
Re A,
Рис. 8.12. Особенности на плоскости k0, учитываемые при вычислении
6Л (' )
Контур охватывает три простых полюса, которые указаны на
том же рисунке. В предельном случае kmin <g; m в интеграл
дает вклад только вычет в полюсе, расположенном в точке
ко = -\/к2 -\-12. Выражение для бЛм,(р',р) принимает вид
d3k yv (p' + т) Уц (р + т) yv
6Л
BjtK 2 Vk2 + к2
Bk ¦ р) Bk ¦ р')
Р-Р
(8.72)
BзтK 2 Vk2 + Я2 (k-p)(k-p')
Подчеркнем еще раз, что бЛ^ ставится в обкладки из спиноров.

178 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ.8
Перенормировка оказывается теперь весьма тонкой опера-
операцией, поскольку обрезание проведено нековариантным способом.
Благодаря тому, что равенство (8.51) по-прежнему справедливо,
можно вновь воспользоваться утверждением о том, что если
собственно-энергетические части корректно учтены, то прово-
проводить перенормировку Лд не требуется (Zi = Z2). Однако из-за
изменения и фотонном пропагаторе величина 2 тоже меняется.
Действительно,
со
¦Vй
BяK J 2я Г11 p-k-m-
(8.73)
Поскольку мы ищем изменение перенормировочной константы
Z2 (в 8т не содержится инфракрасной расходимости), выраже-
выражение (8.73) должно быть вычислено с точностью до членов по-
порядка р2 — т2 включительно.
Сначала, как и для вершины, проведем интегрирование по
&о в первом порядке1) по р2 — т2:
... J
IK i<.«m,-n
= 2
Таким образом, с учетом изменений в фотонном пропагаторе
вершина меняется на величину
BяK 2 Vk2 + Я2
:min
L
2(p-kf
') Члрн O(ftmln) вносит в 6m пренебрежимо малое изменение,,

§ 40] ЛЭМБОВСКИЙ СДВИГ 179
Мы взяли половину вклада собственно-энергетических частей,
изображенных на рис. 8.10, в и 8.10, г, так как поправка
V^2 ~ 1 + 7г(^2— 1) относится к волновым функциям внешних
частиц.
Вычисление (8.75) в нерелятивистском пределе \q2/m2\<gi 1
дает
^^4) (8-76)
Таким образом, из (8.62) и (8.71) имеем
5 з
й (р , р, kmla) = -^ |_ г^Г" + 1^ Y^ Vln 2ft~ +
(8.77)
При \q2/m2\^$> 1 для членов с инфракрасной расходимостью по-
получаем
6Л; (//, р) = - у, ? [Ш (^) - 1] (in -J - In -A_) (8.78)
и, следовательно, из (8.63) и (8.71) находим
ЛЖ р, ^in) = -Y^ln1^[ln(^fl)- 1]. (8.79)
Отсюда мы видим, что при обрезании с помощью kmia для инфра-
инфракрасной части сечения упругого рассеяния вместо (8.65) имеем
Добавляя сюда сечение тормозного излучения (8.67), получаем
инфракрасную часть сечения рассеяния с учетом излучения фо-
фотонов с энергией меньше, чем kmax:
Результат не зависит от kmin и К [82, 83].
§ 40. Лэмбовский сдвиг
Можно считать, что поправка к рассеянию (8.77) возникает
благодаря добавочному «эффективному потенциалу», который
действует между электроном и источником фотонов. В качестве
последнего возьмем ядро с зарядом Ze. Изменение энергии
атомных уровней за счет этого добавочного взаимодействия
представляет собой лэмбовский сдвиг, который мы можем те-
теперь обсудить более подробно, чем в гл, 4, где были приведены
простые физические соображения.

180 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ [ГЛ. 8
Эффективное взаимодействие в импульсном пространстве ме-
между электроном и источником тока eA»(q) складывается из
(8.77) и вклада от поляризации вакуума (8.26):
«>- <8'82>
Выражение (8.82) описывает поправки порядка а к оператору
тока электрона п{р')у[Хи(р), обусловленные фотонами с им-
импульсами, большими, чем kmia. Оно справедливо при малых пе-
переданных импульсах QVu = p'—Р> удовлетворяющих условию
\q2/m2\ <С 1. Для электрона в кулоновском поле ядра с зарядом
Ze источник тока есть eA^(q) =—(Ze2/|q|,0) и (8.82) прини-
принимает вид
(ri. (8.83)
Первый член не зависит от спина и является фурье-преобразова-
нием эффективного потенциала, имеющего вид
Za , 4а Z
В водородонодобном атоме он приводит к сдвигу энергии уров-
уровней, который в первом порядке теории возмущений равен
4a Za /rv4 а (л i
I *'@) Ч1п ^Г +14
Этот сдвиг обусловлен фотонами с импульсами, большими, чем
&min- К нему надо еще добавить вклад от мягких фотонов с им-
импульсами меньше ?mln.
Естественно ожидать, что параметр обрезания имеет порядок
?тш<; (Zee)m, т. е. соответствующая длина волны фотона велика
по сравнению с атомными размерами. Нельзя выбрать &mln про-
произвольно малым, так как при р2 — т2 ~ (ZaJm2 пронагатор
связанного электрона отличается по виду от пропагатора сво-
свободной частицы. Для электрона в атоме имеем
p»~{m + V, p),
где
V ~ {ZaJ т и | р | ~ Zam.
В проведенном ранее вычислении собственно-энергетической ча-
части 2(р), так же как и вершины Лц (см. (8.74)), мы предпола-
предполагаем
k ¦ р да kmlam > р2 — m2 ~ (ZaJ пг2.

§ 40] ЛЭМБОВСКИЙ СДВИГ 181
Для фотонов с импульсами меньше kmia релятивистские поправ-
поправки должны быть малыми, т. е. содержать более высокие степени
Za, и можно решить задачу в нерелятивистском приближении,
как было впервые сделано Бете [84].
Согласно второму порядку старой теории возмущений сдвиг
энергии, обусловленный тем, что электрон в состоянии п испу-
испустит и вновь поглотит фотон, равен
feraln
[ {\1к\){\1^\)
где суммирование производится по поперечным поляризациям
фотона и по всем электронным состояниям. Выберем теперь
4шп, удовлетворяющим условию
(ZaJ m < kmln -С (Za) m
(например, положим kmln « (ZaK'2m) и воспользуемся диполь-
ным приближением, которое может показаться до некоторой
степени сомнительным. Электронные состояния являются нере-
нерелятивистскими, поэтому а, можно заменить на v = p/m. Тогда
можно провести интегрирование по к, которое дает
„ |п 1?»-д» + *|1|(,1|р|и)р]. (8.86)
| J>m cn I
Теперь для этой части вычислений необходимо произвести пере-
перенормировку массы. Поскольку электромагнитная масса элек-
электрона Ьт уже содержится в его экспериментальной массе т, в
гамильтониане появится массовый контрчлен вида
_ _
2(т-Ьт) 2т
Он приводит к сдвигу энергии
который имеет ту же структуру, что и первый член в (8.86).
Поэтому последний включается в перенормировку массы. Поль-
Пользуясь тем, что 6min > Еп — Ет, получаем нерелятивистскую
часть лэмбовского сдвига в виде
(8.87)

182 ПОПРАВКИ ВЫСШИХ ПОРЯДКОВ К МАТРИЦЕ РАССЕЯНИЯ (ГЛ. 8
Последнее равенство служит определением величины Ё, кото-
которая по порядку величины ожидается ~ (ZaJtn. Теперь сумми-
суммирование по состояниям проводится с помощью следующего ком-
коммутационного соотношения:
(Ет - ?„) (п | р И2 = |(п | [[р, Н], р] | п).
т
Оно дает
In -^fs- (n |W | n> = ^f- In -^fs. | ^ (o) p. (8.88)
? 3m2 E
Объединяя найденное выражение с (8.84), получаем сдвиг энер-
энергии s-состояний водородоподобного атома с точностью порядка
a(ZaL:
Зпп3 \ 2Е 24 5j V '
Величина Ё была найдена Бете и др. [85] и в соответствии с на-
нашими ожиданиями оказалась равной 8,9 а?т для водорода. Для
получения полного лэмбовского сдвига с точностью порядка
a(ZaL к (8.89) следует еще добавить вклад аномального маг-
магнитного момента из (8.83).
Неудивительно, если читатель окажется неудовлетворенным
проведенным рассмотрением, в особенности использованием ди-
польного приближения, и тем, как мы обошлись с kmin. Любо-
Любознательному читателю мы рекомендуем ознакомиться с недав-
недавней работой Эриксена и Р1енни [86], в которой фотоны не разде-
разделяются на мягкие и жесткие.
В этой главе было показано, как расширить на одну степень
по а сверх низшего порядка правила написания элементов S-
матрицы. Мы встретились с трудностями, связанными с появле-
появлением расходящихся выражений, и преодолели эти трудности,
показав, что имеется хорошо определенный способ отделения
расходящихся выражений и включения их в константы, которые
перенормируют заряд и массу электрона, а также волновые
функции, описывающие распространение электрона и фотона.
Имеются ясные физические основания для проведения перенор-
перенормировок.
К параметру массы в уравнении Дирака должна быть добав-
добавлена электромагнитная масса, поскольку она уже содержится
в массе, измеряемой на опыте. Необходимо также перенормиро-
перенормировать заряд, чтобы учесть эффект статической поляризации ва-
вакуума. Наконец, требуется перенормировать волновую функцию
аналогично тому, как это делается в обычной нерелятивистской
теории возмущений (см. (8.47) и (8.48)). Тем самым учитывает-
учитывается поправка на амплитуду наблюдения электрона в сопрово-
сопровождении флуктуации, вызванных взаимодействием.

ЗАДАЧИ 183
Перенормировка является довольно тонкой операцией, так
как величины Zb Z2, Z3 и 8т, к несчастью, расходятся. Однако,
как мы видим, величины физических эффектов оказываются в
итоге конечными и независящими от обрезания. Более того, они
согласуются с опытом, как, например, в случае лэмбовского
сдвига и аномального магнитного момента электрона [41, 81].
В этом месте естественно спросить, какие новые проблемы
возникнут при переходе к еще более высоким порядкам по а.
Оказывается, что никаких, за исключением необходимости про-
проводить дополнительную вычислительную работу. Мы уже ввели
все необходимые перенормировки. Изложенные в этой главе
идеи и методы достаточны для того, чтобы, вычисляя S-матрицу
в любом (конечном) порядке по а, получать единственные, ко-
конечные и независящие от обрезания амплитуды любых физиче-
физических процессов (см. [50]).
ЗАДАЧИ
1. Проверьте унитарность амплитуды электрон-протонного рассеяния
вплоть до порядка е*. Для этого найдите абсорбтивную часть G.51), которая
отвечает промежуточным электрону и протону на массовой поверхности, и
покажите с помощью (8.33), что она равна соответствующему произведению
амплитуд второго порядка. Покажите также, что диаграммы на рис. 7.6 и 7.7
не приводят ни к каким другим абсорбтивным частям.
2. Проверьте унитарность амплитуды рассеяния до порядка е3, связав
мнимую часть поправки к вершине (8.60) с соответствующим произведением
амплитуды электрон-позитронного рассеяния второго порядка и вершины еу .
3. Покажите, что собственная масса, вычисленная из (8.35) с парамет-
параметром обрезания Л таким, что Л<т, линейно растет с ростом Л и отвечает
классической собственной энергии заряда, распределенного с радиусом
а ~ 1/Л.
4. Закончите вычисление лэмбовского сдвига в порядке a(ZaL, добавив
к (8.89) член из (8.83), отвечающий аномальному магнитному моменту. Про-
Проведите вычисления для s- и /^-состояний.
5. Постройте амплитуду рассеяния фотона на фотоне порядка е4 и по-
покажите, что она удовлетворяет калибровочной инвариантности и конечна.
6. Докажите теорему Фарри [88], согласно которой диаграмма в виде
замкнутой петли с нечетным числом исходящих фотонных линий равна нулю.
Из этой теоремы следует, что рассеяние света во внешнем поле (дельбрюков-
ское рассеяние) в наинизшем порядке квадратично по напряженности поля.
7. Путем явного вычисления убедитесь, что во втором порядке Zi = Z-2-
Проведите обрезание фотонного пропагатора, чтобы сохранить калибровочную
инвариантность.
8. Докажите (8.59).
9. Проверьте (8,76) и (8.78). .
10. Найдите радиационные поправки порядка а1п(92/'и2) и a\n(EjkmiD)
к рассеянию электрона в кулоновском поле при больших энергиях и передан-
переданных импульсах,

ГЛАВА 9
УРАВНЕНИЕ КЛЕЙНА —ГОРДОНА
§ 41. Введение
Можно использовать метод функции распространения и раз-
развить соответствующую технику вычислений для процессов с уча-
участием частиц со спином 0. Мы попытаемся описать такие ча-
частицы скалярной волновой функцией (р(х), имеющей всего одну
компоненту. Тем самым мы приходим к уравнению Клейна —
Гордона для свободной частицы
= 0. (9.1)
В гл. 1 это уравнение было отвергнуто, так как оказалось
невозможным определить сохраняющуюся положительно-опре-
положительно-определенную вероятность. Однако в результате дальнейшего рас-
рассмотрения первоначальные мотивы, заставившие нас отказаться
от (9.1), исчезли. Поэтому мы вновь возвращаемся к этому ура-
уравнению, приняв фейнмановскую интерпретацию состояний с от-
отрицательной энергией, движущихся назад во времени. Спин ча-
частицы несуществен для такой интерпретации, и мы убедимся в
том, что она справедлива для частиц с нулевым спином, так же
как и для электронов.
Аналогично тому, что было для электронов, мы придем к
следующей картине: наряду, например, с я+-мезоном, который
описывается решением уравнения Клейна — Гордона с положи-
положительной энергией, появляется также п~-мезон, интерпретируе-
интерпретируемый как п+-мезон с отрицательной энергией, движущийся назад
во времени.
Теперь отвлечемся на некоторое время и задумаемся над
тем, к каким частицам в природе можно применять уравнение
Клейна — Гордона. Стабильные элементарные частицы с нуле-
нулевым спином неизвестны, однако п-мезоны и /(-мезоны являются
почти стабильными кандидатами. Экспериментально обнару-
обнаружено [89, 15], что они одновременно рождаются и уничтожаются
в большом количестве, например, в следующих реакциях (р —¦
протон, п — нейтрон, Л° — нейтральная лямбда-частица, л+ —

§ 4Ц ВВЕДЕНИЕ
положительно заряженный п-мезон и т. д.):
(9.2)
Поэтому волновое уравнение для этих мезонов с нулевым спи-
спином должно учитывать возможные процессы рождения и анниги-
аннигиляции. Нельзя проследить за мировыми линиями таких частиц
во время процесса рассеяния, как это было возможно для элек-
электронов, взаимодействующих с фотонами. В частности, нельзя
проследить за мировыми ли-
линиями заряженных я- и /(-ме-
/(-мезонов даже в случае взаимо-
взаимодействия с фотонами, так как
имеется вклад диаграмм типа
изображенной на рис. 9.1. —*¦*-¦
Возможность рождения и
уничтожения одиночных бес-
бесспиновых частиц, подтверждае-
подтверждаемая на опыте, приводит к тому, Рис. 9.1. Вклад в электромагнитную
что теория взаимодействия та- структуру я-мезона.
ких частиц должна быть мно-
многочастичной. Лучше всего здесь подходит формализм кванто-
квантовой теории поля, но опять, как и для взаимодействия электро-
электронов и фотонов, мы сможем понять многие явления и провести
большое количество расчетов с помощью метода функции рас-
распространения, расширенного на случай мезонов, связанных с
источником, которому отвечал бы добавочный член в правой
части (9.1).
Если включить слабые взаимодействия, то мезоны с нулевым
спином уничтожаются [89, 15] также в реакциях, например, сле-
следующего типа (ц — мю-мезон, v — нейтрино):
Я+ —> Ц + -f- V,
д —> я -\- я -f- я , (У-ч)
-> Я0 + Ц+ + V.
Вследствие того, что взаимодействие, отвечающее за подобные
слабые распады (9.3), мало, заряженные я- и /(-мезоны имеют
очень большое время жизни, т ~ 10~8 сек, которое значительно
превосходит естественную единицу времени Ь/тс2 <. 10~23 сек,
образованную из величин й, с и масс я- или /(-мезона. Поэтому
в первом порядке теории возмущений по степеням константы
слабого взаимодействия можно пренебречь распадами (9.3) и
конечным временем жизни т ~ 10~8 сек при рассмотрении

186 УРАВНЕНИЕ КЛЕЙНА-ГОРДОНА [ГЛ.9
амплитуд процессов сильного взаимодействия типа (9.2). В этом
приближении я- и /(-мезоны считаются стабильными частицами
и описываются начальными и конечными свободными волно-
волновыми функциями.
Нейтральные я0- и /С°-мезоны, которые мы также хотим
включить в рассмотрение, имеют меньшее время жизни и рас-
распадаются в основном по следующим каналам [89, 15]:
Jt°->Y + Y> tjt«~ 106 сек,
К°->л+ + п~, т^-КГ10 сек.
Однако по сравнению с характерным временем 10~23 сек эти про-
процессы протекают все же очень медленно, и отвечающее за них
взаимодействие достаточно рассматривать лишь в наинизшем
порядке. Поэтому я0 и К0 также будут рассматриваться как ста-
стабильные в процессах сильного взаимодействия типа (9.2).
Кроме взаимодействий типа (9.2) и (9.3), в которых участ-
участвуют частицы со спином 0, заряженные я- и /С-мезоны взаимо-
взаимодействуют с фотонами и внешним электромагнитным полем.
Для того чтобы подчеркнуть сначала сходство с электродина-
электродинамикой дираковского электрона, мы в этой главе ограничимся
рассмотрением электродинамики частиц со спином 0. Метод
функции распространения для этих частиц будет развит на ос-
основе тех же физических принципов, что и в теории электронов.
С целью рассмотрения поведения мезонов во внешних полях при
низкой энергии, например связанных состояний я-мезоатомов,
мы осуществим нерелятивистский переход в уравнении Клей-
Клейна — Гордона и дадим его нерелятивистскую интерпретацию.
Более общая проблема слабых и сильных взаимодействий рас-
рассматривается в следующей главе.
§ 42. Пропагатор для уравнения Клейна — Гордона
Решения уравнения Клейна — Гордона удовлетворяют ура-
уравнению непрерывности, которое, согласно A.12), имеет вид
По теореме о дивергенции интеграл
Q=\d*x /о (х) = / \ (Рх ф'йСф, (9.4)
где введено полезное сокращенное обозначение
V7. С дь \ { да
сохраняется для решений уравнения (9.1).

S 42) ПРОПАГАТОР ДЛЯ УРАВНЕНИЯ КЛЕЙНА - ГОРДОНА 187
Решения уравнения Клейна — Гордона в виде плоских волн
с положительными и отрицательными частотами образуют а со-
совокупности полный набор. Нормированные в ящике объемом V
они имеют вид
где (Op = po > 0 и р2 = т2 в соответствии с условием Эйнштей-
Эйнштейна. Решения, нормированные в непрерывном спектре, записы-
записываются следующим образом:
i (9.5)
УBяK 2сор
о-частотнь
ювиям ор
d3x /<±>* (*) / dof& {x) = ± б3 (р -
для положительно- и отрицательно-частотных решений соответ-
соответственно. Они удовлетворяют условиям ортонормированности:
(9.6)
Обратим внимание, что для суперпозиции положительно-частот-
положительно-частотных решений, т. е. для
\ (9.7а)
величина Q положительна,
Q = / J d*x Ф<+>* (х)Х&+) W = + $ ^3РI a+ (P) Р. (9-76)
а для решений с отрицательной частотой, т. е. для
?-Чх)=\(Рра1(р)р-Цх), (9.8а)
эта величина отрицательна,
Q = i\ d3x ср<->* (х)^Ф(-> (х) = -\ d3p! а- (р) |2. (9.86)
Именно в этом пункте заключается трудность для вероятност-
вероятностной интерпретации решений уравнения Клейна — Гордона, так
как для произвольной суперпозиции решений в виде плоских
волн величина Q принимает как положительные, тэк и отрица-
отрицательные значения.
Займемся построением феинмановского пропагатора для ура-
уравнения Клейна — Гордона. Для этого найдем решения урав-
уравнения
(? *- + т2) АР {х' -x) = -V (xf - x), (9.9)
которое описывает распространение вперед во времени положи-
положительно частотных и назад во времени отрицательно-частотных

188 УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА [ГЛ.9
частей волн. Действуя по аналогии с теорией Дирака (см.
F.40) — F.46)), перейдем путем фурье-преобразования к им-
импульсному представлению, в котором AF имеет вид
• _ х)=
Благодаря малой мнимой добавке к массе пропагатор (9.10)
удовлетворяет требуемому граничному условию, которое со-
состоит в том, что только положительные частоты распростра-
распространяются вперед во времени, а отрицательные — назад. Как было
показано в гл. 6, контур интегрирования в (9.10) однозначно
задается этим условием.
Проверим, что контур интегрирования в (9.10) выбран пра-
правильно. Для этого проведем интегрирование по dp0, используя
теорему Коши. Получим
BjtK2a)p
- / J d3p f{,-> (хг) Ц-Г (х) 9 (t - t'). (9.11)
Возьмем волну общего вида, содержащую как положительные,
так и отрицательные частоты,
ф (х) == ф(+) (х) + ф(-) (х). (9.12)
Тогда из (9.6) и (9.11) прямым вычислением находим, что
кр(х'—х) обеспечивает распространение вперед во времени
только волн с положительными частотами
- IB (f - t) ф<+> (х', f) = J (Px AF (x' - х) i аГф(+) (х, () (9.13)
и назад во времени волн с отрицательными частотами
- /9 (/ - t') Ф<~> (х', f) = -\ d3x AF (х' - х) и?р<-> (х, 0- (9-14)
Формулы (9.13) и (9.14) аналогичны F.49) и F.50) для урав-
уравнения Дирака.
§ 43. Введение электромагнитных потенциалов
Взаимодействие мезона со спином 0 с электромагнитным по-
полем вводится, как и для уравнения Дирака, с помощью мини-
минимальной замены
рц-^ р'1 - e/f(x). (9.15)

5 43] ВВЕДЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ПОТЕНЦИАЛОВ ]?9
Сначала будем считать А»(х) приложенным внешним потен-
внешним потенциалом. Вводя (9.15) в уравнение (9.1), получаем
0. (9.16)
Для уравнения (9.16) по-прежнему имеется сохраняющийся по-
поток, который по аналогии с A.12) равен
- Ф (х) [(/ -^ + еА» (х)) ф* (х)]. (9.17)
Соответствующий сохраняющийся заряд имеет вид
Q=\d*x ф* (х) [iX- 2еЛ° (*)] ? (х). (9.18)
Амплитуда рассеяния на этом потенциале плоской волны,
описывающей падающий заряженный мезон, дается решением
уравнения (9.16). Принимая фейнмановское граничное условие,
согласно которому вперед во времени распространяются рас-
рассеянные волны только с положительными частотами, а назад —
с отрицательными, мы интегрируем (9.16) с помощью фейнма-
новского пропагатора (9.10):
(D, + /л2) ф (х, /) = - ie (^г Л* + A» -JL") ф + е'А^ф, (9.19)
где
V (у) = ie (^L А» (у) + А»(у)^- еЫ» (у) А» (у).
Уравнение (9.19) аналогично уравнению F.53) для дираковских
частиц, и решения обоих уравнений имеют близкий физический
смысл. Мы требуем, чтобы в результате рассеяния в будущее
распространялись только волны с положительными частотами,
отвечающие частицам с положительной энергией. Выполнение
этого требования обеспечивается интегрированием с фейнманов-
ским пропагатором в (9.19). Если воспользоваться (9.11), инте-
интегрирование дает
= Ф (х, t)-i\ cPp fW (х) 5 d*y 9 (/ - у0) /<+)* (у) V (у) ф (у) -
- i \ d3p /<-> (х) 5 d*y 9 (г/о - /) fУ* (У) V (у) ф (у). (9.20)
Это выражение содержит также волны с отрицательными часто-
частотами, которые распространяются назад, в прошлое. Однако с

190
УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА
[ГЛ. 9
точки зрения экспериментатора, наблюдающего за показаниями
приборов, поглощение в прошлом частицы с отрицательной энер-
энергией и зарядом е равносильно испусканию частицы с положи-
положительной энергией и зарядом —е. Таким образом, мы приходим
к фундаментальному предсказанию, допускающему экспери-
экспериментальную проверку, которое состоит в том, что для каждой
частицы в природе существует противоположно заряженная ан-
античастица.
Частица может не нести заряда и в этом случае она может
оказаться тождественной своей античастице, Такая частица су-
существует в природе — это я0, нейтральный п-мезон со спином 0.
Хотя п° не участвует в задаваемом (9.15) электромагнитном
взаимодействии, пропагатор свободных я°-мезонов может быть
построен в полной аналогии с изложенным в § 42. Поскольку
для я0 ток и заряд (9.4) равны нулю, то в отсутствие взаимо-
взаимодействий п° будет описываться действительным решением ф =
= ф* свободного уравнения Клейна — Гордона. Тогда фейнма-
новский пропагатор (9.11) будет, как и для заряженных мезо-
мезонов, соответствовать распространению положительно-частотной
части ф вперед во времени, а отрицательно-частотной — назад.
§ 44. Амплитуды рассеяния
Направляя мировые линии в разные стороны, т. е. вперед и
назад во времени, как показано на рис. 9.2, мы тем самым вклю-
включаем в рассмотрение, помимо амплитуд собственно рассеяния,
t \
X
(а)
Рис 9.2. Диаграммы для рассеяния частицы и античастицы, рождения и анни-
аннигиляции пары.
еще и амплитуды рождения и аннигиляции пар частица-антича-
частица-античастица в полной аналогии с изложенным ранее для электронов.
Вычисление амплитуды рассеяния или перехода производит-
производится путем последовательной итерации уравнения (9.19). Количе-
Количество итераций определяется требуемой точностью получения ф.
Свободное решение ф в (9.19) представляет собой нормирован-
нормированную свободную волну в отсутствие рассеяния, Амплитуда пере-

§ 44] АМПЛИТУДЫ РАССЕЯНИЯ 191
хода в состояние, в котором частица обладает заданным им-
импульсом р'+, получается путем проектирования рассеянной в ре-
результате взаимодействия волны на нормированную свободную
волну с импульсом р'+. Вероятность перехода дается тогда ква-
квадратом модуля этой амплитуды.
В обычном рассеянии мезонов (рис. 9,2, а) мы имеем после
рассеяния при t-*¦ оо волны с положительными частотами и ам-
амплитуда рассеяния находится путем выделения из рассеянной
волны (9.20) положительно-частотной проекции:
S - =\im[d3x /(t)s/Хф (*) =
= б3 (р; - р+) - i J *У ff* (У) V (у) ф (у); (9.21)
здесь Ф(у) дается уравнением (9.19), в котором свободная вол-
волна с положительной частотой f<+) (у) отвечает падающему ме-
мезону. Вероятность перехода равна 5 ' 2.
Для процесса рождения пары (рис. 9,2, г) мы вновь, как и
в (9.21), выделяем волны с положительными частотами, однако
на этот раз ф(у) представляет собой рассеянную волну, возник-
возникшую из падающей волны с отрицательной частотой f(~>(#) в
(9.19). В соответствии с (9.14) волна с отрицательной частотой
является «падающей» при уо~* +°°, поскольку посредством про-
пагатора АР(х — у) она распространяется только назад во вре-
времени. В полной аналогии с основными правилами, выведенными
в гл. 6 для случая позитронов, мы сопоставим распространению
назад решения с отрицательной частотой и квантовыми числами
р_ испускание антимезона, например я~-мезона, с положитель-
положительной энергией и 4-импульсом р~
Для нахождения амплитуды аннигиляции пары, изображен-
изображенной на рис. 9.2, в, мы выделяем при t —» —оо отрицательно-ча-
отрицательно-частотную часть рассеянной волны (9.20):
5Р_, Р+ = - Hm \ (Рх /<,->*(х)idU(У) =
(9.22)
здесь Ф(у) дается уравнением (9.19), в котором налетающий
я+-мезон описывается волной /(р+)(у) с положительной частотой
и -импульсом р+. Как обычно, налетающему я~-мезону с поло-
положительной энергией и 4-импульсом р- соответствует волна с от-
отрицательной частотой /•,"'*(«/), распространяющаяся от взаимо-
взаимодействия V (у) назад в прошлое.

Jg2 УРАВНЕНИЕ КЛЕЙНА — ГОРДОНА [ГЛ. 9
Наконец, рассеяние я~-мезона (или антимезона), изобра-
изображенное на рис. 9,2,6, дается формулой (9.22), где по-прежнему
Ф(у) определяется уравнением (9.19). Однако «падающая» от-
отрицательно-частотная волна п+-мезона описывается теперь функ-
функцией /(~)(#), которая соответствует конечному яг-мезону, ис-
испускаемому после рассеяния с положительной энергией и 4-им-
пульсом р'_, т. е.
5р_ р-_ = 63 (Р_ _ р'_) - / J d*y /<,->* (у) V (у) ф (у). (9.23)
Сравнение с методом функции распространения для пози-
позитронов, изложенным в гл. 6, показывает, что полученные сейчас
правила написания элементов 5-матрицы по своему физиче-
физическому смыслу совпадают с рассмотренными в гл. 6.
Практические правила вычисления вероятностей переходов
под действием электромагнитного взаимодействия могут быть
получены путем рассмотрения нескольких простых примеров,
как было сделано в гл. 7 для электронов.
§ 45. Процессы рассеяния низшего порядка
В качестве первого примера рассмотрим кулоновское рассея-
рассеяние я+-мезона в низшем порядке по е. В этом приближении член
e2AlxAil в (9.19) может быть отброшен.
Амплитуда перехода для диаграммы на рис. 9.3 находится из
(9.21), где надо положить ф{у)ж fp+)(y). При q s= pf — р,#0
\ член с б-функцией равен нулю и мы полу-
У# чаем
V f'Pi
/ ipt + p^^y)
f* = "(* + *>» 4"(?), (9.24)
где
Рис. 9.3. Кулоновское ^ С
рассеяние я+-мезона. /Iй ((?) s= \ d^y e4V A^ (у).
Форма тока в (9.24) напоминает независящую от спина часть в
разложении Гордона для тока электрона. Подставляя в (9.24)
выражение для A»{q) в случае статического кулоновского по-
потенциала
Л - со.) g^, (9.25)

§ 4S1 ПРОЦЕССЫ РАССЕЯНИЯ НИЗШЕГО ПОРЯДКА 193
мы получаем сечение путем обычной процедуры возведения в
квадрат, суммирования по конечным состояниям и деления на
падающий поток. По аналогии с G.10) находим
BяK ., Г Ze2(o>f
da = —- d'pf 2я6 (cuf - а,) у
Iv| ^ V f ';
= (9 26)
da 4p2p2 sin* F/2) • ^9-ZD'
Полученное выражение отличается от соответствующей фор-
формулы G.22) для электронов отсутствием множителя
[1 — р2 sin2 @/2)], который связан со спином.
Подобный результат получается и для кулоновского рассея-
рассеяния я~-мезонов. Из формулы (9.23), в которой /(-)*(г/) описы-
описывает лг-мезон с импульсом р- до рассеяния и ф(у) «/'г*(г/) от-
р_
вечает конечному я~, испускаемому после рассеяния (как пока-
показано на рис. 9.4), мы находим ч
(p_p) (q) \p
S ' = + — , ц (9.27) \
"-"- BяK^2«)_-2аI \
где q = р'_ — р_ по-прежнему обозна- f
чает переданный импульс. Формулы / %е
(9.24) и (9.27) отличаются только зна- 7
ком, что связано с разными знаками за- Jip_
ряда, я+ и я", и приводят к одинаковому /
сечению (9.26). /
Урок, извлеченный нами из проведен- рис_ д4- Кулоновское
ного вычисления, состоит в том, что я-ме- рассеяние эх--мезона.
зонной вершине ставится в соответствие
фактор ^(Рц + р^) вместо еуй Для электрона. Волновая функ-
функция нормируется множителем 1/д/2со, который заменяет
л/т/Е для электрона, и, разумеется, спиноры в данном случае
отсутствуют.
Правила для члена <А4цЛй во взаимодействии V (9.19) мы
получим из рассмотрения комптоновского рассеяния заряжен-
заряженного мезона. «Внешний потенциал» в данном случае склады-
складывается из поглощенных и испущенных фотонов, описываемых с
использованием «нормировки в непрерывном спектре» в виде
суммы двух членов (см. G.53)):
1, Х)еа'х
(9>28)
где / и % отвечают импульсу и поляризации.

194 УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА [ГЛ. 9
Поскольку комптоновская амплитуда в низшем порядке про-
пропорциональна е2, члены в V, линейные по е, необходимо проите-
рировать один раз. Тогда 5-матрица, имеющая порядок е2 и от-
отвечающая диаграммам на рис. 9.5, будет равна
Sfl = (- ief \ d*y d*z fpr (у) i [^- А» (у) + Лц (у) JL] X
X /Д, {у - г) i [-?- Л, (z) + Av (z) ¦?-] /<+) (z) +
d*y /<+)• (у) Лй {у) Л" (у) f(p+) (у). (9.29)
Подставляя сюда Лц из (9.28) и сохраняя только перекрестные
члены между выражением
УBяK 2k '
которое описывает поглощение фотона, характеризуемого (k,X),
и выражением
которое отвечает испусканию фотона с (k',Xf), после интегри-
интегрирования по пространственным координатам находим
Su = , (~'еJ =г BяL б4 {р + k - р' - k') X
(р
_ fe/J _ m2 e' • Bр - Л') - 2/е • в']. (9.30)
Полезно убедиться в правильности (9.30) путем проверки
инвариантности этой амплитуды относительно калибровочного
преобразования. Такой проверке мы уже подвергали в гл. 7 ам-
амплитуды для электронов. Легко установить, что Sfi обладает ин-
инвариантностью как по отношению к калибровочному преобразо-
преобразованию
e^-^ + Xft", (9.31)
примененному к начальному фотону, так и по отношению к пре-
преобразованию
'< + *% B)
над конечным фотоном.

46]
ПРОЦЕССЫ ВЫСШЕГО ПОРЯДКА
195
В выражении (9.30) удобно выбрать калибровку
е • р = г' ¦ р =
которая соответствует поперечной поляризации фотонов в ла-
лабораторной системе, т. е. в системе, где начальный мезон по-
покоится и имеет 4-импульс р — (т,0). Тогда в (9.30) оказывает-
оказывается отличным от нуля только вклад от члена Л^Л^, так как e-k =
= e'-k' = 0. Далее, по хорошо знакомой нам схеме переходим
К л'
к',Л'
р р+к р' р р-/с р' р
Рис. 9.5. Комптоновское рассеяние я-мезона.
от амплитуды к дифференциальному сечению. Для этого возво-
возводим (9.30) в квадрат, устраняем одну степень BяL84(/? + k —
— р' — k'), умножаем на фазовый объем конечных частиц
d?pf dsk'
и на BяK — величину, обратную начальному потоку в лабора-
лабораторной системе, а также на BяK—величину, обратную плотно-
плотности частиц в мишени. В итоге имеем
а2 (е • в'J
'lab = "да*" [ 1 + (k/m) A - cos 6)]2 '
Отсюда в пределе малой энергии фотона k —> 0 получаем клас-
классический томсоновский предел. Суммируя по поляризациям ко-
конечного фотона е' и усредняя для неполяризованного света по
начальным поляризациям, получаем
а2A +cos20)
О—.2 Г 1
lab
da\ __
dQ, ),.ъ —
2т2 [1 + (k/m) A - cosG)]2
(9.33)
§ 46. Процессы высшего порядка
Мы можем продолжить аналогию с методом функции распро-
распространения для электрона и вывести из разобранных примеров
правила вычисления диаграмм высшего порядка. Основные от-
отличия от правил для электрона состоят в следующем:
1. В вершине рассеяния мезона из состояния р^ в состояние
Рд (см. рис. 9.6) с любым направлением линий вперед и назад
во времени следует произвести замену
— ieyv- -* — ie (p> + pi1'). (9,34)

196 УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА [ГЛ. О
2. Добавочный член А^А** во взаимодействии (9.19) вносит
вклад')
2ie2gilV. (9.35)
Примером является амплитуда (9.30). Множитель i появляется
благодаря тому, что параметром разложения для этого члена
служит е2. Поэтому в порядке еп в результате я-кратной ите-
итерации (9.19) возникает множитель (—i)n, когда мы вычисляем
вклад от (9.34) в этом порядке. Если член АцА^ входит в вычис-
вычисления т раз, появляется множитель (—i)n~m(—l)m —
= (—i)n-2m(i)m; следовательно, в (9.35) возникает i. Необхо-
Необходимо постоянно помнить, что параметром разложения является
е, а не порядок взаимодействия.
Рис. 9.6. Диаграмма для Рис. 9.7. Диаграмма для
вершины, отвечающей взаимодействия вида
взаимодействию вида е^'
е<Р* (р' + Ph Ф^11.
Появление множителя 2 в (9.35) связано с. тем, что всегда
есть два способа сопоставить двум множителям в А^А^ кванты,
которые уничтожаются, рождаются или рассеиваются в вершине
(см. рис. 9.7). К амплитуде взаимодействия, которая соответ-
соответствует сумме всех диаграмм, вносящих вклад в данном порядке
по е, можно применить критерий калибровочной инвариантно-
инвариантности. Мы уже пользовались этим критерием для проверки
(9.30). Таким образом, мы имеем полезный и очень простой спо-
способ проверки правильности вычисления относительных вкладов
от членов р-Л + Л-р и Л-Л в (9.19).
3. Пропагатор внутренней линии, которой соответствует им-
импульс р, мы заменяем согласно
/ _ liP + m) i
p-r-m + ie ~ P2-m* + ie p2 - m2 + ie
т. е. делаем замену р + m -*¦ 1.
') Имеется исключение из этого правила — двум испускаемым из одной
точки фотонам, образующим замкнутую петлю, соответствует множитель 1/2
(см. задачу 9.11).

§ 46] ПРОЦЕССЫ ВЫСШЕГО ПОРЯДКА 197
4. Для внешних линий мы заменяем электронные спиноры
следующим образом:
(9.37)
Vf
Все остальные множители i и 2я в точности такие же, как
для электронов. Остается лишь вопрос об относительном знаке
минус. В случае электронов мы, руководствуясь принципом Пау-
Паули, производили антисимметризацию относительно перестановки
двух тождественных частиц. С другой стороны, эксперимент сви-
свидетельствует о том, что п-мезоны являются бозонами, т. е.
по ним имеется симметрия согласно статистике Бозе — Эйн-
Эйнштейна. В частности, в реакции
К+ -> п+ + я+ + я"
два я+-мезона испускаются в относительном s-состоянии. Кроме
того, есть серьезные теоретические основания, впервые указан-
указанные Паули, для связи между спином и статистикой. Эта связь
такова, что частицы с полуцелым спином подчиняются прин-
принципу запрета (являются фермионами), а по частицам с целым
спином имеется симметрия (они являются бозонами).
Вопрос о связи спина со статистикой рассматривается в кван-
квантовой теории поля [90]. Пока мы просто примем, что частицы со
спином 0 являются бозонами и подчиняются условию симмет-
симметрии. Это означает, что между диаграммами, отличающимися пе-
перестановкой бозонов, должен быть относительный знак плюс
вместо минуса для случая фермионов.
Теперь не будет множителей (—1) для замкнутых петель
или между диаграммами рассеяния и аннигиляции. Мы вводили
их в диаграммы для электронов, как, например, в амплитуды
(8.2) и (8.5), соответствующие диаграммам на рис. 8.1,6 и
8.1, д, исходя из принципа Паули в теории дырок. Для бозонов
нет заполненного моря с отрицательной энергией и относитель-
относительные знаки следует получать путем иных рассуждений.
В кулоновском рассеянии одинаковых бозонов между двумя
диаграммами, изображенными на рис. 9.8, имеется знак плюс.
Амплитуда рассеяния бозона на антибозоне получается отсюда
заменой знака энергии для двух линий; например, с помощью
подстановки
?2+->-/>2 (9-38)
мы получаем амплитуды для двух диаграмм, изображенных на
рис. 9.9.
Относительный знак двух амплитуд, соответствующих диа-
диаграммам на рис. 9.9, остается положительным, если замена

УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА
[ГЛ. 9
/
V
v
\
V
/
/
/
V
/ \ /
Рис. 9.8. Кулоновское рассеяние я+-мезона на я+-мезоне.
V\/V\/V\j(
/ \
U
\
Рис. 9.9. Кулоновское рассеяние зх+-мезона на я~-мезоне.
\
/
4ч У
\ / \
(а) (ф (в)
Рис. 9.J0. Вклады четвертого порядка в кулоновское рассеяние я+ — ц-

§ 47] НЕРЕЛЯТИВЙСТСКИИ ПРЕДЕЛЬНЫЙ ПЕРЕХОД 199
(9.38) является единственным изменением при переходе от диа-
диаграмм рассеяния (рис. 9.8) к диаграммам аннигиляции
(рис. 9.9). Формула (9.38) есть пример правила подстановки
(кросс-симметрии), с которым мы уже встречались для элек-
электронов (см., например, G.85)). Теперь мы распространили его
на амплитуды для бозонов.
Это правило приводит к положительному относительному
знаку всех трех амплитуд, изображенных на рис. 9.10. Ниже вер-
вершины у диаграммы 9.10, а и 9.10, в одинаковы, поэтому их отно-
относительный знак положителен. Поскольку за счет введения на
диаграмме 9.10, а дополнительного по сравнению с диаграммой
9.10,s взаимодействия между линиями и и v не возникает знака
минус, мы приходим к выводу, что замкнутая петля на диа-
диаграмме 9.10,6 не приводит к появлению множителя (—1).
Электромагнитное взаимодействие бозонов со спином 0, на-
например л- и /(-мезонов, в более высоких порядках, а также пе-
перенормировки можно рассмотреть в полной аналогии с преды-
предыдущей главой. Однако мы не будем вдаваться в детальное рас-
рассмотрение этих явлений, так как для сравнения с эксперимен-
экспериментальными данными необходимо учесть значительно более силь-
сильное взаимодействие п- и /С-мезонов друг с другом и с ядрами.
Обсуждению этого неэлектромагнитного взаимодействия посвя-
посвящена следующая глава.
§ 47. Нерелятивистский предельный переход
в уравнении Клейна — Гордона
Существуют физические явления, для изучения которых весь-
весьма желательно иметь приближенное описание я-мезонов в рам-
рамках обычной одночастичной квантовой механики с вероятност-
вероятностной интерпретацией. Такой подход можно применять, например,
к взаимодействию заряженных я-мезонов с атомными электри-
электрическими и магнитными полями в веществе, а также к пионным
атомам. Для анализа таких явлений мы попробуем сделать пе-
переход к нерелятивистскому уравнению Шредингера.
В самом начале гл. 1 мы отказались от уравнения второго по-
порядка Клейна — Гордона вследствие невозможности построить
точную одночастичную квантовую теорию с вероятностной ин-
интерпретацией. Мы отдали предпочтение уравнению Дирака, ко-
которое содержит первую производную по времени, как и нереля-
нерелятивистское уравнение Шредингера. Однако затем мы убедились
в том, что одночастичная картина для уравнения Дирака спра-
справедлива лишь для очень ограниченного круга явлений, таких,
например, как слабые медленно меняющиеся поля, когда имеет-.
ся широкая щель ~2тс2 между спектрами положительной и от-
отрицательной энергии. Именно такую физическую ситуацию мы

200 УРАВНЕНИЕ КЛЕЙНА - ГОРДОНА [ГЛ, 9
сейчас рассмотрим, когда будем строить приближенную одно-
частичную теорию на основании уравнения Клейна — Гордона.
В качестве первого шага приведения уравнения Клейна —
Гордона к форме уравнения Шредингера, т. е. к виду, содержа-
содержащему только первые производные по времени, перейдем от (9.1)
к паре уравнений первого порядка [91].
Введем определение
и перепишем (9.1) в виде
i^4f = (V2-m2)cp. (9.40)
Удобно ввести две линейные комбинации:
которые имеют простые нерелятивистские пределы. Для свобод-
свободной частицы с положительной энергией покоя имеем
ф~е-<^=-±-ф (9.42)
и в этом пределе
Q = (p~e-lmt, x = 0. (9.43)
Для частицы с отрицательной энергией, или античастицы, реше-
решение в том же пределе имеет вид
9 = 0 и % = (р~е+ш. (9.44)
Таким образом, 6 играет роль, аналогичную большим компо-
компонентам, а % —малым компонентам дираковского спинора.
В терминах 9 и % уравнение Клейна — Гордона записывается
так:
Введем более компактное двухкомпонентное обозначение
Ф = (х6). (9.46)
Тогда получим уравнение
г^- = #оФ, (9.47)
где гамильтониан свободной частицы имеет вид

§ 47] НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛЬНЫЙ ПЕРЕХОД 201
Хотя уравнение (9.47) имеет шредингеровскую форму, оно, как
и уравнение (9.1), не приводит к положительно-определенной со-
сохраняющейся вероятности, так как Но не является эрмитовым
оператором. Неэрмитова матрица ( _. _, J в члене, отвечаю-
отвечающем кинетической энергии, связывает вместе «большие» и «ма-
«малые» компоненты.
Пренебрегая V2 в низшем порядке для медленно движу-
движущейся частицы, мы приходим к уравнению Шредингера и к ре-
решениям (9.43) и (9.44) для положительной и отрицательной
частот соответственно. Заимствуя из гл. 4 технику Фолди —
Ваутхайзена для теории Дирака, мы можем последовательно
включить поправки, возникающие за счет члена, отвечающего
кинетической энергии. В данном случае матрица р = ( _. )
является неэрмитовым аналогом матрицы а, а ц=( „ _. J —
аналогом р, где аир — матрицы, осуществляющие преобразо-
ние уравнения Дирака. Рассуждая так же, как при выводе
D.1), положим
Ф' = в'яФ, (9.49)
где
S = T,f>8(p) = (J J)e(p). (9.50)
Отсюда находим, что при
нечетные операторы р исчезают из гамильтониана (здесь
р^ — V J . Преобразование, задаваемое формулами (9.49) —
(9.51), является неунитарным, и с его помощью неэрмитов га-
гамильтониан (9.48) приводится к следующему виду:
Н'о = eiSHoe~iS = Ti л/т2 + р2. (9.52)
В такой форме решения с положительной и отрицательной энер-
энергией полностью разделяются, а соотношение между энергией и
импульсом оказывается точно таким же, как для свободных
электронов. Единственное отличие (9.52) от D.1) состоит в том,
что в (9.52) нет удвоения числа решений за счет спиновой сте-
степени свободы. Поскольку гамильтониан Н'й эрмитов, в этом
представлении можно дать вероятностную интерпретацию ре-
решениям Ф'. Для решений с положительной частотой
( I ) a<+> (х) (9.53)
имеем
л/т2 + р2 а<+> (х) = со а<+> (х). (9.54)

202 УРАВНЕНИЕ КЛЕЙНА —ГОРДОНА [ГЛ.9
При этом плотность вероятности дается выражением
Р (х) = | а<+> (х) р, (9.55)
а энергия равна
J '<+>* (Х) H'Q (х) Ф'(+> (х) d?x. (9.56)
Для решений с отрицательными частотами запишем
ф'<-> (*) = e'V ( J ) а<-) (х). (9.57)
Собственные значения энергии находятся из уравнения, анало-
аналогичного (9.54):
Ут2 + р2а<->(х) = сора<->(х), (9.58)
а для вероятности имеем выражение типа (9.55):
Р (х) = | а<-> (х) |2. (9.59)
Однако теперь благодаря присутствию ц в (9.52) среднее от га-
гамильтониана равно собственному значению энергии, взятому со
знаком минус:
Мр = - J Ф'(->* (х) Н'о (х) Ф'1"* (х) d3x. (9.60)
Мы отождествим Ф'<~'*(х) с волновой функцией античастицы,
так как из (9.52) для свободной частицы имеем Н'О = Н'О* и со-
согласно методу функции распространения (см. 9.11), (9.10) и
(9.5)) вперед во времени распространяется подвергнутое комп-
комплексному сопряжению решение с отрицательной энергией.
Если имеется внешнее электромагнитное поле, то уравнение
Клейна — Гордона уже не удается привести к диагональному
виду, т. е. разбить на отдельные уравнения для положительных
и отрицательных частот. Однако, действуя так же, как при пере-
переходе от D.2) к D.4), можно добиться приближенной диагона-
лизации для случая слабых, медленно меняющихся полей. Вве-
Введем, как обычно, взаимодействие с полем в уравнение (9.1) пу-
путем минимальной замены
Рц ->¦ Рй - е\-
Тогда уравнение Клейна — Гордона, записанное в двухкомпо-
нентной форме (9.48), примет вид
I 1 \ я2 . / 1 0
J+U
где л = р — еА. Определение ф здесь такое же, как в (9.46) и
(9.41), с заменой (9.39) на
.dt
> = [~

§ 17| НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛЬНЫЙ ПЕРЕХОД 203
(Ф~А°). Если в D.2) мы отождествим
р-1-с; -!)¦
то придем к D.4) с заменой C на ц. В частном случае статиче-
статического внешнего поля получим приближенное уравнение Шредин-
гера, содержащее члены до порядка 1/т4:
с гамильтонианом
(9.62)
Первый член представляет собой разложение л] т2 + я2 и опи-
описывает релятивистский эффект увеличения массы; такой же член
был в теории Дирака. Последнее слагаемое в (9.62)—это дар-
дарвиновский член; он служит поправкой к классическому электро-
электростатическому взаимодействию точечного заряда eqp(x) подобно
поправке на «дрожание» в дираковской теории. Однако, в от-
отличие от D.5) и D.7), здесь он впервые появляется в порядке
1/т4.
До тех пор, пока мы ограничиваемся физическими задачами,
для которых процедура Фолди — Ваутхайзена является сходя-
сходящейся, и несколько первых членов ряда D.4) или (9.62) дают
результаты, близкие к точным, мы можем рассматривать вза-
взаимодействия мезонов в рамках нерелятивистской квантовой ме-
механики. С точностью до удержанных в Н' членов решения с по-
положительной и отрицательной частотой в этом представлении
разделяются и гамильтониан оказывается эрмитовым, поэтому
возможна традиционная вероятностная интерпретация, основан-
основанная на приведенных в гл. 1 постулатах.
Воспользовавшись (9.62) и записывая в этом представлении
решения с положительной частотой по аналогии с (9.53):
ф;<+> (Х) = e-'V (J) ф(+) (х)> (9>63)
получаем

204 УРАВНЕНИЕ КЛЕЙНА — ГОРДОНА [ГЛ. 9
Плотность вероятности равна
Р (х) = | Ф;(+) (х) |2 = | ^+) (х) Г, (9.65)
а собственное значение энергии Еп совпадает, как и в (9.56),
со средним значением гамильтониана:
Еп = \ Ч+)* « Н' (х, е) г|)<+> (х) Л, (9.66)
где Н' (х, е) — оператор, стоящий в левой части (9.64):
(9.67)
Решения с отрицательной частотой запишем в виде (9.57):
o;(->W = e+'V(J)^-)(x). (9.68)
Тогда из (9.62) найдем
Я" (х, - е) *«,-> (х) = ?„*<,-> (х). (9.69)
Мы вновь сопоставляем античастице комплексно-сопряженное
от решения с отрицательной энергией, так как ¦ф^"'* (х) удовле-
удовлетворяет уравнению
что отличается от (9.64) только знаком при е. Плотность ве-
вероятности равна
Р (х) = | Ф<->' (х) Р = | ^ (х) |2. (9.70)
Среднее значение гамильтониана вновь, как и в (9.60), равно
взятому со знаком минус собственному значению энергии:
еп = -
п
Поскольку решения с положительной и отрицательной частотой
отличаются только знаком заряда в (9.64) и (9.69), появляется
привлекательная возможность переопределить в рассматривае-
рассматриваемом представлении Фолди — Ваутхайзена вероятности и сред-
средние значения энергии путем введения диагональной матрицы
/ 1 0 Л
г\ = I 0 , I уже встречавшейся нам ранее:
^M. (9-72)
Еп = J Ф; (х) ч\Н'Ф'п (х) йЧ. (9.73)

§ 47] НЕРЕЛЯТИВИСТСКИЙ ПРЕДЕЛЬНЫЙ ПЕРЕХОД 205
Такое переопределение не сказывается на (9.65) и (9.66) для
решений с положительной частотой, но меняет знаки в (9.70) и
(9.71) для решений с отрицательной частотой. Собственные зна-
значения энергии теперь совпадают со средними значениями Н, ко-
которые по аналогии с обычной квантовой механикой стали поло-
положительными как для решений с положительной, так и с отри-
отрицательной частотой. Однако теперь Q(x)^0 для решений
с положительной частотой и Q (х) ^ 0 для решений с отрица-
отрицательной частотой и интерпретируется как плотность заряда для
частиц и античастиц соответственно.
Мы можем и далее развивать представление Фолди — Ваут-
хайзена, которое с точностью до удержанных в Н' членов и при
условии сходимости ряда по \\т совпадает с формализмом
обычной квантовой механики. Например, из (9.62) можно найти
уровни энергии и вероятности переходов для я-мезоатома с уче-
учетом релятивистской зависимости массы и дарвиновских попра-
поправок. Кроме того, связь с классикой и соотношения Эренфеста по-
получаются из
± (?) (9.74)
Интерпретация в терминах одночастичной плотности вероят-
вероятности применима только тогда, когда путем преобразования
Фолди — Ваутхайзена удается разделить решения с положи-
положительными и отрицательными частотами. Ею нельзя пользоваться
в задачах с сильными и быстро меняющимися полями, где необ-
необходимо учитывать появление я+я~-пар. В предположении, что
определения (9.72) и (9.73) справедливы и в общем случае, мы
можем вернуться к исходному представлению и исследовать
структуру выражений для заряда и энергии. Для этого выпол-
выполним следующее преобразование:
ф = е-«ф'. (9.75)
Здесь необходимо соблюдать осторожность, так как преобра-
преобразование, связывающее оба представления, не является унитар-
унитарным. Из (9.50) и (9.51) следует, что для свободной частицы
S = -S+. (9.76)
Учитывая, что r\S = — S\\, находим для энергии
<ор = J ф'р* (х) цЩФ'р (х) d3 х = J Ф*р (х) e-iS\H'0eiSOp (x) йН =
= J ФР (х) r\e-isH'oeis®p Md3x = $ Ф; (х)цН<>Фр (х) d3x. (9.77)

206 УРАВНЕНИЕ КЛЕЙНА — ГОРДОНА [ГЛ. 9
Таким образом, выражение для энергии не меняет своего вида.
Аналогично, используя (9.46) и (9.41), получаем для заряда
Q (x) сРх = ^ ф'р М ЧФ'р to d3x = J Ф; (х) цФР (х) d3x =
= J [6* (х) 6 (х) - %* (х) % (х)] д?х = -± \ ср* (х)Т0 Ф (*) d3x, (9.78)
что после умножения на 2т совпадает с полученным ранее вы-
выражением (9.4) для сохраняющегося заряда.
Близкие результаты получаются с учетом взаимодействия.
В этом случае преобразование Фолди — Ваутхайзена имеет, как
и в гл. 4, вид
ф' _ . . . etS"ei
где каждая из матриц S(/) удовлетворяет условиям
Поэтому плотность заряда, определенная, как в (9.78), с матри-
матрицей 11, вновь принимает простой вид в исходном представлении
и совпадает с выражением (9.17) для плотности заряда. Анало-
Аналогично для уровней энергии п+- и лг-мезонов в статическом
внешнем поле имеем
Е = J Ф'* (х)г\Н' (х) Ф' {х) dh = J Ф*(х)цН (х) Ф (х) d3x (9.79)
Полученные простые соотношения между средними значе-
значениями в двух представлениях наводят на мысль о введении мат-
матрицы т) = ( л —1 ) в °бЩее определение среднего значения:
<О')= \ Q)'*(xLO'{x)Q)'(x)d3x= J Ф*{х)чО{х)Ф{х)Л3х = (О); (9.80)
здесь О'(х) = eis0(x)e-is.
Без матрицы т) мы не получили бы такой простой связи ме-
между выражениями в двух представлениях. Введение матрицы т)
в определение (9.80) соответствует умножению на (—1) средних
значений, наблюдаемых для системы в состоянии с отрицатель-
отрицательной частотой. Это связано с требованием, чтобы решения с от-
отрицательной частотой распространялись назад во времени и
процессы испускания и поглощения менялись местами. При
этом физические наблюдаемые оказываются связанными со взя-
взятыми со знаком минус параметрами решений с отрицательной
энергией.
Для позитронов распространение назад во времени отрица-
отрицательных частот обеспечивается теорией дырок; для бозонов нет
теории дырок и мы должны либо довольствоваться тем, что дает

ЗАДАЧИ 207
метод функции распространения, либо обратиться к формализму
квантовой теории поля.
В заключение подчеркнем, что мы дали вероятностную ин-
интерпретацию решениям тех физических задач, относящихся
к бозонам, для которых последовательность преобразований
Фолди — Ваутхайзена сходится. В частности, для свободных ча-
частиц мы построили точное преобразование, разделяющее реше-
решения, соответствующие положительным и отрицательным часто-
частотам, или частицам и античастицам. Поэтому мы поступали
правильно, когда в (9.21), (9.22) и (9.24) рассматривали S-мат-
рицу как амплитуду вероятности.
Заряд, которым бозон отличается от антибозона, не обяза-
обязательно должен быть электрическим, а может иметь совсем дру-
другую природу. Существуют, например, мезоны К0 и К0, которые
электрически нейтральны, но являются античастицами по отно-
отношению друг к другу, различаясь знаком заряда, называемого
«странностью» [50]. Кроме того, бозон может вообще не нести
никакого заряда и в этом случае он совпадает со своей антича-
античастицей, как я°-мезон. В этом случае волновая функция является
действительной и Q(i) s 0.
ЗАДАЧИ
1. Вычислите в первом борновском приближении в лабораторной системе
дифференциальное сечение кулоновского рассеяния л+-мезона на К~-мезоне.
2. Вычислите в системе центра инерции дифференциальное сечение рас-
рассеяния л+-мезона на я+-мезоне и сравните с формулой G.84) для рассеяния
электрона на электроне.
3. Вычислите дифференциальные сечения тормозного излучения л+-ме-
зопа в кулоновском поле и рождения пары я+я~ и сравните с формулами
Бете — Гайтлера.
4. Найдите полное сечение рождения пары п+п~ в ультрарелятивист-
ультрарелятивистском пределе Е Э> tnc2 и сравните с аналогичным результатом для электрон-
позитронной пары.
5. Вычислите вклад пар я+я~ в поляризацию вакуума и дайте интер-
интерпретацию знаку полученного ответа.
6. Найдите электромагнитную собственную энергию я+-мезона и срав-
сравните с аналогичной величиной для электрона.
7. Проверьте, что для заряженных л-мезонов, как и для электронов,
перенормировочные константы для волновой функции и вершины во втором
порядке равны друг другу, т. е. Z, = Z2, А^ (р, р) = — di (p)ldpv'.
8. Найдите уровни энергии я~-мезона в кулоновском поле.
9. Установите классическое соответствие для уравнения Шредингера для
я-мезона с помощью выводимых из (9.74) соотношений Эренфеста.
10. Постройте фейнмановский пропагатор для векторных мезонов, удо-
удовлетворяющих свободному волновому уравнению
11. Приведите аргументы в пользу правила 4 из приложения Б, «Электро-
«Электродинамика бозонов со спином 0». Покажите, что с точностью до порядка е4
это правило приводит к унитарной амплитуде упругого ц+ — я~-рассеяния.

ГЛАВА 10
НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
§ 48. Введение
В этой главе мы применим метод функции распространения,
развитый для электромагнитного взаимодействия частиц со спи-
спином 0 и '/г, к другим типам взаимодействия элементарных ча-
частиц. Эти взаимодействия делятся на три различных класса.
Во-первых, имеется гравитационное взаимодействие, которое в
обычных лабораторных условиях характеризуется чрезвычайно
малой безразмерной константой, равной (MlM2G/hc) «* Ю~40, и
которым мы будем пренебрегать. Ко второму классу относятся
слабые взаимодействия, приводящие к превращениям одних ча-
частиц в другие, например р-расиад и распады п~-, К~- и ц-мезо-
нов (см. § 50). Слабые взаимодействия в области малых и сред-
средних энергий (<Cl Гэв) могут быть охарактеризованы безразмер-
безразмерной константой, имеющей величину от 10~5 до 10~6. Наконец,
существуют сильные взаимодействия с константой ^,1. Силь-
Сильное взаимодействие ответственно за силы, которые удерживают
нуклоны в ядре и за рождение частиц я, К, Л, 2 и S в реак-
реакциях типа (9.2).
Теория слабых и сильных взаимодействий не развита до того
уровня, чтобы вызванные ими эффекты могли быть рассчитаны
из общего принципа, такого, как, например, принцип эквива-
эквивалентности и требование ковариантности в теории тяготения или
принцип «минимального электромагнитного взаимодействия» (на
основе которого электромагнитное взаимодействие вводится пу-
путем замены [92] р^->рп — еА^). Не имея подобной фундамен-
фундаментальной исходной идеи, мы для выбора возможного вида
взаимодействия вынуждены обратиться непосредственно к экс-
экспериментальным данным, а также к принципам симметрии и
в первую очередь к лоренцевой инвариантности.
«Что представляют собой вершины?» — это центральный
вопрос, возникающий при рассмотрении слабых и сильных вза-
взаимодействий, и к нему мы сейчас переходим. Мы будем действо-
действовать в рамках метода функции распространения и ограничимся

5 49]
СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
209
вычислениями в низшем порядке по параметрам взаимодей-
взаимодействия. Это очень серьезное ограничение, если мы претендуем на
детальное описание экспериментальных данных. Для сильных
взаимодействий параметр разложения превышает единицу; в
теории слабых взаимодействий в ее современном несовершенном
виде диаграммы высших порядков зависят от параметра обре-
обрезания в интегралах, отвечающих замкнутым петлям, причем эта
зависимость такова, что расходимости не удается перенести в
перенормировочные константы, как это было сделано в гл. 8 для
электродинамики.
§ 49. Сильные взаимодействия
В 1935 г. Юкава [93] установил аналогию между сильными,
короткодействующими ядерными силами и электромагнитными
силами между частицами. Если кулоновское взаимодействие об-
обусловлено обменом виртуальным квантом, или фотоном, то, мо-
может быть, ядерные силы тоже вызваны обменом виртуальной
частицей, которая должна иметь целый спин. Для частицы со
спином 0 и массой ц мы можем вос-
воспользоваться пропагатором Клей-
Клейна— Гордона (9.36). Тогда ампли-
амплитуда рассеяния первого порядка, от-
отвечающая диаграмме на рис. 10.1,
примет вид
9
A0.1)
q2 — р,2 + ге '
?оУ—
Рис. ЮЛ. Нуклоп-нуклонное
взаимодействие за счет об-
обмена одним я°-мезоном.
В формуле A0.1) мы опустили все
факторы, связанные с вершинами,
в которых частица, изображенная
пунктирной линией, поглощается
или испускается нуклонами, изо-
изображенными сплошными линиями с начальными и конечными
импульсами р\, р2 и p'v p'2 соответственно. Инвариантный пере-
переданный импульс q2 н= (р, — pjJ = (р'2 — р2у пространственнопо-
добен (q2 < 0). В нерелятивистском пределе, когда кинетиче-
кинетические энергии отдачи нуклонов малы по сравнению с их энер-
энергиями покоя, в A0.1) можно положить q2 «—|q|2 и записать
ЯК'
I2 +
A0.2)
Переходя путем фурье-преобразования к координатному про-
пространству, находим, что Щ отвечает борновской амплитуде для

210 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
рассеяния на потенциале Юкавы
Радиус действия ядерных сил составляет ~10~13 см, т. е. при-
примерно одну треть классического радиуса электрона, поэтому ча-
частица, которой обмениваются нуклоны, должна иметь массу
Главным кандидатом на эту роль является я-мезон (пион) с
массой ~ 140 Мэв, открытый в 1947 г.; сейчас известны три типа
[94, 89, 15] я-мезонов, я+, я~ и я0, с примерно одинаковой мас-
массой. Считается, что эти я-мезоны с зарядами +е, —е и 0 соот-
соответственно вносят основной вклад в ядерные силы на больших
расстояниях, хотя более тяжелые частицы играют важную роль
при столкновениях с малым прицельным параметром и боль-
большим q2.
Экспериментально было установлено, что я-мезоны имеют
спин 0 и отрицательную «внутреннюю четность». Спин заряжен-
заряженного я-мезона можно установить, применяя принцип детального
равновесия к реакции
я+ + d ¦«->¦ р + р.
Вероятности протекания этого процесса в том и другом напра-
направлениях определяются статистическими весами; отсюда нахо-
находится спин я-мезона. «Внутренняя четность» определяется из
наблюдения захвата я~-мезона, находящегося на /С-оболочке в
атоме дейтерия, с образованием двух нейтронов:
я~ -+¦ d->n + п.
Из принципа запрета следует, что единственным возможным со-
состоянием двух нейтронов с / = 1 является ZP\-состояние, чет-
четность которого равна —1. Если к рассматриваемому процессу
сильного взаимодействия применим закон сохранения четности,
то я~-мезон тоже должен иметь отрицательную четность. При
этом мы, как обычно, предполагаем, что протон и нейтрон
имеют одинаковую внутреннюю четность. Это значит, что при
пространственном отражении B.33) их волновые функции пре-
преобразуются с одинаковой фазой ф=0, т. е. г|/(х', t) = -f уоф(х, t)
при х' = —x. Поскольку я~ захватывается со сферически-сим-
сферически-симметричной S-орбиты, то четность его волновой функции, равную
— 1, относят к «внутренней четности» я". Спин, равный 0, и от-
отрицательная внутренняя четность являются свойствами, общими
для я+- и лг-мезонов, которые, как указывалось в гл. 9, являют-
являются античастицами друг для друга. Спин я0 тоже равен 0, а его

§49] СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ 211
четность равна —1. Это следует из наблюдения распада на два
фотона
в совокупности с определением корреляции плоскостей поляри-
поляризации [95] «пар Далица»
Получив информацию о квантовых числах я-мезонов, мы
продолжим теперь рассмотрение ядерных сил, придерживаясь
аналогии с электродинамикой. Начнем с исследования изобра-
изображенного на рис. 10.1 процесса рассеяния протона на протоне за
счет обмена одним я°-мезоном. Будем считать, что протон 1 рас-
рассеивается в «я-мезонном поле», создаваемом протоном 2; такой
подход уже использовался нами (см. G.31)), когда мы интер-
интерпретировали рассеяние электрона на протоне как рассеяние в
электромагнитном поле Ар.(х), создаваемом протоном.
Попытаемся описать этот процесс с помощью уравнения Ди-
Дирака, подобного уравнению F.52), т. е.
(tV - Мр) Цр (х) = g0V^p (х) Фо (х), A0.3)
где константа go аналогична заряду е, а матрицу Дирака Г нам
предстоит определить. Для мезонного поля ср0 можно предло-
предложить уравнение типа G.27) и G.33), в котором знак гH = ±1
заранее не определен:
(? + ц§) Фо (х) = - go% (x) Г% (х) щ. A0.4)
Экспериментально установлено [96, 97], что ядерные силы с хо-
хорошей точностью сохраняют четность, следовательно, на урав-
уравнения A0.3) и A0.4) налагается требование сохранения четно-
четности, как и лоренцевой инвариантности. Тогда необходимо вы-
выбрать Г = ty5 для того, чтобы правая часть A0.4) была псевдо-
псевдоскаляром, как и левая часть.
Нетрудно убедиться в том, что уравнение A0.3) инвариантно
относительно преобразования зарядового сопряжения, поэтому
можно воспользоваться развитой в гл. 5 теорией дырок и уста-
установить соответствие между решениями с отрицательной энер-
энергией и волновыми функциями антипротонов. Волновая функция
антипротона определяется соотношением вида E.5):
и удовлетворяет тому же уравнению Дирака A0.3) при условии,
что мезоны п° и зарядово-сопряженный к нему совпадают, т. е,
(Фо)с = + Фо-

212 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Выбранная форма взаимодействия является, по всей вероят-
вероятности, неправильной или по крайней мере неполной. Уравнения
A0.3) и A0.4) выписаны только из соображений простоты и по
аналогии с электродинамикой. Никак не обосновано, например,
исключение взаимодействия, содержащего производные полей,
хотя в предыдущей главе при рассмотрении взаимодействия за-
заряженных я-мезонов с электромагнитным полем это взаимодей-
взаимодействие учитывалось. Таким образом, уравнения A0.3) и A0.4)
следует рассматривать как грубую, простую модель, ибо фан-
фантазия природы безусловно богаче той, что заложена в уравне-
уравнениях A0.3) и A0.4). Достоинство этой модели состоит в том,
что она позволяет установить общие свойства ядерного взаимо-
взаимодействия, которые сохраняются и при более общем рассмо-
рассмотрении.
Используя предложенную вершину я0 — р-взаимодействия,
мы можем теперь вычислить амплитуду, соответствующую диа-
диаграмме на рис. 10.1. Из A0.4) найдем в первом порядке поле
я°-мезонов, созданное током перехода частицы 2. Ток имеет вид
а искомое поле равно
Фо (х) = - ig0 J dV /Д, (х - х') [^ (*') /Y5+p2 (*')] По- (Ю-5)
Согласно A0.3) оно вызывает следующее изменение волновой
функции протона 1:
А^Р1 М = J <?х" SF (х - х") [go/Y5*Pl (*") Фо (*")]. (Ю.6)
По формулам F.53) и F.56) находим амплитуду рассеяния
Stt = (- igof J <*'*' d*x" [гЦ (*") /у5^ (*")] X
X *лЖ'-*Оло[^;(*0/у5ФР2 (*')]• (Ю.7)
Сравнивая A0.7) с аналогичными формулами G.32) и G.33),
мы заключаем, что изменения в правилах графической техники
состоят в замене вершины еу^ на igo\5 и пропагатора фотона
igllvDF(x — х') на пропагатор я°-мезона -\-ihF(x — х')т)о.
К A0.7) мы должны добавить обменный член, возникающий
благодаря тождественности двух протонов (ему отвечает диа-
диаграмма на рис. 10.2). Соответствующая амплитуда равна
= - (_ igof J dV d V pp< (x") /Y5^P] (*")] X
(Ю.8)

§ 49] СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ 213
Она отличается от A0.7) перестановкой волновых функций ко^
нечных протонов ¦ф ' (х) •*-> ¦ф ' (х) и знаком минус, который,
как и в G.82), обеспечивает антисимметрию начальных и конеч-
конечных протонных волновых функций относительно перестановки
протонов.
Рассеяние нейтрона на нейтроне описывается аналогичным
образом. Мы должны записать волновое уравнение для нейтро-
нейтрона, которое включает взаимодей-
взаимодействие с п°-мезоном. Кроме того, в \ п'
A0.4) добавляется нейтронный ^ г
источник. Мы можем опираться
на экспериментально установлен-
установленный факт равенства сил р — р и
я — л с точностью до поправок,
обусловленных электромагнит-
электромагнитным взаимодействием, например
кулоновским взаимодействием /р7
протонов [97, 98]. Поэтому есте-
естественно предположить, что ней- Рис. 10.2. Паулневская диаграмма
троны взаимодействуют с л°-ме- для двух протонов,
зонами так же, как протоны, если
не считать возможного различия в знаке, е0 = ±1. Таким об-
образом, волновая функция нейтрона удовлетворяет следующему
уравнению:
(«V - Ма) г|э„ (х) = - gotoiy^n (х) % (*), A0.9)
а уравнение A0.4) заменяется на
( ? + Но) Фо М = — &о [% (х) i\5i>P (х) — е(уф„ (х) iy5tyn (x)] rj0. A0.10)
Небольшую разность масс нейтрона и протона, Мп — Мр да
да 0,002 Мр, относят за счет электромагнитных эффектов, свя-
связанных с зарядом протона, и ею обычно пренебрегают, так же
как и всеми электромагнитными взаимодействиями. Амплитуда
рассеяния п — я, получаемая из A0.9) и A0.10), совпадает
с амплитудой рассеяния р — р, так как е^ = ± 1.
Когда мы переходим к рассмотрению рассеяния р — я, тре-
требуется учесть взаимодействие с заряженными я+- и я~-мезо-
нами. В низшем порядке в амплитуде учитывается только одно-
мезонный обмен, которому соответствуют, кроме диаграмм без
обмена зарядом (рис. 10.3, а), добавочные диаграммы с обме-
обменом зарядом (рис. 10.3,6).
При написании волнового уравнения для я+-мезонов мы
вновь будем руководствоваться экспериментально установлен-
установленным равенством (с точностью до электромагнитных поправок)

214
НЁЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
[ГЛ. 10
взаимодействий п — р и р — р в состояниях, разрешенных для
системы р — р.
Уравнение для п+-мезонов запишем по аналогии с уравне-
уравнением A0.10) для л;0-мезонов:
(П + |Л2+) Ф+ (х) = - g+1]+*n (x) iy^p (x). A0.11)
Связь входящих сюда величин т)+ = ± 1 и g+ с соответствую-
соответствующими величинами ц0 и go будет установлена ниже. Правая часть
Рис. 10.3. Диаграммы без обмена зарядом и с обменом зарядом для п — р-
рассеяния.
A0.11) приводит к появлению вершин перехода протона в ней-
нейтрон с испусканием я+-мезона (рис. 10.4).
Возникший я+-мезон может распространяться вперед и на-
назад во времени. Если он распространяется назад, то, согласно
(а)
Рис. 10.4. Вершины пере-
перехода р->п.
Рис. 10.5. Вершины пере-
перехода п -*¦ р.
изложенному в предыдущей главе, его отождествляют с п~-ме-
зоном, который движется вперед во времени и поглощается в
вершине, как показано на рис. 10.4, б.
Произведя комплексное сопряжение над A0.11), получим
уравнение для зарядово-сопряженнои частицы, т. е. я~-мезона,
( ?
Ф_ (*) = -
% (x). A0.12)

S «] СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ 215
Правая часть A0.12) соответствует вершинам, изображенным
на рис. 10.5.
Теперь мы должны добавить в волновые уравнения для ней-
нейтрона и протона члены, соответствующие переходам, изобра-
изображенным на рис. 10.4 и 10.5. Сравнивая A0.11) и A0.12)
с A0.3), A0.9) и A0.10), мы приходим к следующим волновым
уравнениям для протонов и нейтронов:
(ZV - Мр) г|)р (х) = goiys% (х) % (х) + g*+iys% (x) Ф+ (х),
^ A0.1 о)
(iV - Мп) Kfn {х) = - goBoiy^n(x)cpo (х) + ?+е+гу5% М Ф_ (х);
здесь знаковый множитель e.f = ±1 подлежит определению.
Чтобы установить ограничения на входящие в волновые ура-
уравнения константы, рассмотрим рассеяние п — р и выпишем ам-
амплитуды, отвечающие двум изображенным на рис. 10.3 диа-
диаграммам низшего порядка. Считая, что падающий нейтрон {р{)
рассеивается в мезонном поле, создаваемом протоном (р2), по-
получим по известным нам правилам
SU = (- ЗД (- ео) Л о \ dV <?x" Ry (x') iy5% (У)] X
X ibp (x' - x") [^ {x") /Y5% (
X
X ibp (x' - x") [ЧЦ (x") ly^ (*")]. A0.14)
Если бы вместо этого мы считали, что падающий протон рассеи-
рассеивается в поле, создаваемом нейтроном, то получили бы ампли-
амплитуду, отличающуюся от A0.14) заменой
Поэтому положим
е+ = 1, A0.15)
так как ответ не должен зависеть от нашей точки зрения.
Относительную величину констант g+ и g0 можно опреде-
определить, исходя из наблюдаемого равенства взаимодействий п — р
и р — р в состояниях, разрешенных для системы р — р принци-
принципом запрета. Сравним рассеяние р — р и р — п в антисимме-
антисимметричных относительно перестановки двух частиц состояниях.
Для этого представим себе на время, что нейтрон тождествен
протону, но по-прежнему взаимодействует как с нейтральными,
так и с заряженными мезонами. Тогда в амплитуду рассеяния
нейтрона необходимо добавить обменные диаграммы со знаком
минус, чтобы обеспечить требуемую антисимметрию состояния.

216 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Совокупность диаграмм, приводившихся ранее на рис. 10.3
и добавленных к ним обменных диаграмм, изображена на
рис. 10.6; там же указаны необходимые обозначения. Диаграм-
Диаграмма (в) является обменной по отношению к (а), а диаграмма
(г) —по отношению к (б). Сумма этих четырех диаграмм дает
(г)
Рис. 10.6. Сумма диаграмм однопионного обмена для р — п-рассеяния с учетом
паулиевских обменных и зарядово-обменных вкладов.
следующую S-матрицу, построенную в предположении, что ней-
нейтрон и протон тождественны и подчиняются принципу запрета:
X J dV d'x" { р„; (*') «y64>Pi (x')] /А, (*' - х") [^ {х") /
^ (х'Ц iAF {x' - х") ppj (x") /
Сравнение A0.16) с суммой A0.7) и A0.8) показывает, что
из требования равенства взаимодействий л — р и р — р в анти-
антисимметричных состояниях, разрешенных для системы р — р, вы-
вытекает следующее условие на константы связи:
Это уравнение имеет два решения:
|g+|2 = 0, ео = —1 A0.18)
\g+\2 = 2gl, ео=+1, по= —т!+. A0.19)
Первое из них, A0.18), отвечает обмену только нейтральными
мезонами. Очевидно, что в этом случае взаимодействия п — р
и р — р в одинаковых состояниях равны. Поскольку я+- и я~-ме-
зоны существуют и вершины типа изображенных на рис. 10.4
и 10.5, т. е. такие, в которых рождаются одиночные зт+- и я~-ме-

§ 49] СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ
зоны, входят в наблюдаемые реакции, например
мы должны выбрать второе решение A0.19).
Согласно A0.19) константа связи заряженных мезонов в
вершине (р— п) в д/2 раз больше, чем константа связи
я°-мезона в вершине (р—р). В амплитуду рассеяния входит
только квадрат модуля |g+|2, поэтому можно для удобства
выбрать константу g+ действительно; тогда
?+ = л/2~?о- A0.20)
Условие A0.19) ц+ — —% удобно заменить дополнительным
правилом написания фейнмановских амплитуд. Положим
и введем следующее дополнительное правило построения ампли-
амплитуды для любой диаграммы: амплитуда умножается на (—1)
если диаграмма содержит обмен нечетным числом заряженных
мезонов между нуклонами. Можно показать, что это правило
эквивалентно антисимметризации не только относительно пере-
перестановки линий п — пир — р на диаграмме, но также и отно-
относительно перестановки линий п — р. Последнее утверждение сле-
следует из того, что любая диаграмма с обменом заряженным ме-
мезоном переходит в диаграмму с обменом нейтральным мезоном
при перестановке линий нейтрона и протона (относительный
знак минус возникает благодаря противоположным знакам ве-
величин тH и х\+, которые входят в гшонный пропагатор). В низшем
порядке это очевидно; достаточно сравнить диаграммы на
рис. 10.6, а и б.
Для получения общего правила антисимметризации необхо-
необходимо рассмотреть два случая. Первый из них — это обмен пио-
пионом между двумя различными нуклонными линиями; иллюстра-
иллюстрацией служит рис. 10.7, а. Этот случай аналогичен тому, который
мы уже рассмотрели в низшем порядке.
Другой случай — когда пион испускается и вновь погло-
поглощается одним и тем же нуклоном — немного сложнее. Рассмот-
Рассмотрим, например, диаграмму на рис. 10.7,6; один из способов упо-
упорядочения этой диаграммы во времени показан на рис. 10.7, в.
Чтобы связать эту диаграмму с той, знак которой нам изве-
известен (т. е. без линии, отвечающей зт+-мезону), мы переставим
со знаком минус нейтрон и протон / и // и получим диаграмму,
показанную на рис. 10.7, г. Диаграмма 10.7, г имеет тот же знак,
что и 10.7,5, которая получается из 10.7, е перестановкой линий
/ и //. Собирая знаки минус (их два), мы видим, что если я+
испускается и поглощается одной и той же нуклонной линией,

218
НЁЭЛЕКТРОМАГМИТНЫЕ ВЗАИМОДЕЙСТВИ
[ГЛ. 10
7Г
p'
(+)
nh \p
(ф (Ф
У////////////////////////, 'УУУ/УУУУ/////////УУУУУУ//УУУУУУУУУУУУУУ,
II
V777777777777777777777777} '///////'////////////////////////////////
Рис. 10.7. Правила антисимметризации для обменов в системе п — р.

§ 49] СИЛЬНЫЕ ВЗАИМОДЕЙСТВИЯ 219
можно положить т)+ = т)о и приписать диаграмме такой же знак,
как у диаграммы, получаемой заменой л+ на я0.
Необходимо подчеркнуть, что мы путем чисто формального
построения расширили правило антисимметризации, которое в
случае р — р-рассеяния следовало из принципа запрета. По
отношению к системе п — р, когда частицы различимы и могут
рассеиваться в симметричных 3Si, lP\, 3D2,i,o и т.д. состояниях,
это правило есть не более чем удобный способ следить за зна-
знаками в приближении «зарядовой независимости», т. е. равенства
взаимодействий р — р, п — п и п — р в одинаковых состояниях.
Причина введения этого формального и сложного на вид
обобщения принципа запрета станет ясной в следующем пара-
параграфе, где будет дано простое единое описание протона и нейт-
нейтрона как двух состояний одной частицы — нуклона. Согласно
такой картине мы считаем, что при перестановке конечных р и
п, как на рис. 10.3, а и 10.3,6, в амплитуде рассеяния р — п
появляется знак минус по аналогии со знаком минус, возникаю-
возникающим благодаря принципу запрета между амплитудами рассея-
рассеяния р — р, изображенными на рис. 10.1 и 10.2').
Теперь мы определили все параметры, за исключением тH;
ео = е+ = +1 и г)+ = г\о с дополнительным условием антисим-
антисимметризации диаграмм, получаемых перестановкой протонной и
нейтронной линий. Для получения т^о заметим, что за счет взаи-
взаимодействия в A0.13) протон не всегда является просто прото-
протоном, но иногда представляет собой нейтрон и зт+-мезон (см.
рис. 10.4 и 10.5); следовательно, носителем электрического за-
заряда является как протон, так и зт+-мезон. Таким образом, элек-
электромагнитные токи протона и зт+-мезона не сохраняются в
отдельности.
В этом можно убедиться, вычисляя токи (нормированные на
единичный заряд), из приведенных выше волновых уравнений:
1 т^ ft w =1 -щ; (VA)=?*+фАфпф+ - *+ФЛ>1ур-.
Однако, если мы положим в A0.11)
Л+ = +1, A0.23)
') Условие A0.21) вместе с правилом антисимметризации применимо ко
всем процессам, включая те, которые определяют собственную энергию.

220 НЕЭЛЕК.ТРОМЛГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
то закону сохранения будет удовлетворять сумма протонного и
я+-мезонного токов
^[tf(*) + tf+(*)]==0. A0.24)
Мы примем A0.23), чтобы исключить возможность существова-
существования необнаруженных локальных источников и стоков электриче-
электрического заряда. Тогда из A0.21) следует
т!0 = т1+ (- 1. A0.25)
§ 50. Формализм изотопического спина
Собирая вместе условия A0.15) и A0.19) — A0.21), а также
A0.25), полученные из требования равенства амплитуд рас-
рассеяния п — п, п — рир — р в одинаковых состояниях, мы можем
переписать волновые уравнения A0.10) — A0.13) в следующей
форме, содержащей только одну действительную неизвестную
константу связи:
(iv - мр) цр = goiy5 ОрФо „+),
(,-V - лу % = g0iy5 (- i|yp0 + л/2 г|ур_),
( П + jig) Фо = - g0 (%1у5Ър ~ VY5*n).
( ? + И2+) Ф+ = - ?0 V2" %i\5%, A0.27)
(? + Ц2+) Ф_ = ( П + И2+) ф
Сходство уравнений для протона и нейтрона наводит на
мысль описать их единой нуклонной волновой функцией
A0.28)
Нуклонная волновая функция представляет собой восьмиком-
понентный спинор, четыре верхних компоненты которого соот-
соответствуют протонному спинору, а четыре нижних — нейтронному.
Свободное уравнение Дирака имеет диагональный вид, протон-
протонные и нейтронные компоненты не смешиваются. В приближении
«зарядовой независимости», когда Мр « Мп да М, имеем сле-
следующее простое уравнение:
(tV — М) ? = 0.
Для описания входящего в A0.26) взаимодействия необходимо
ввести недиагональные матрицы, которые смешивают протонные

§ 50] ФОРМАЛИЗМ ИЗОТОПИЧЕСКОГО СПИНА 221
и нейтронные волновые функции. Смешивание удобно записать
с помощью трех матриц Паули:
Подразумевается, что каждый из элементов этих матриц дей-
действует на все четыре компоненты г|зр или г|)п в A0.28), например
*¦*-(?)•
Мы обозначили матрицы символом т, чтобы отличить их от
спиновых матриц Паули or. Теперь уравнения A0.26) можно
объединить и записать в виде
(/V — М) W = g0iy5 (тд^фо + V2~ т+^ф+ + V2" t-^tP-); A0.30)
здесь
являются операторами, «повышающими» и «понижающими»
заряд.
Уравнение A0.30) можно привести к более компактному
виду, если ввести «вектор» ф с тремя компонентами
Ф = (ФьФ2,Фз), (Ю.32)
где
ф,
-~ (ф+ + ф_), ф2^-^г(ф+-ф_)> ф3^ф,
Тогда вместо A0.30) имеем
(/V -М)Ч = g0iy5 (т • ф) W. A0.33)
Аналогичным образом, пренебрегая малой разностью масс
п±- и я°-мезонов, т. е. полагая цо « ц+ « ц, уравнения A0.27)
можно объединить в одно приближенное уравнение для я-ме-
зонов:
(П + Ц2) Ф = - go^iy5rW. A0.34)
Прогресс, достигнутый введением компактных «изоспиновых»
обозначений для пионов и нуклонов, является чисто формаль-
формальным. Никакого нового физического содержания при этом не
было заложено. Мы можем считать, что в воображаемом «изо-
«изотопическом пространстве» W образуется как спинор, а ф как

222 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
вектор. Тогда оба волновых уравнения A0.33) и A0.34) оказы-
оказываются ковариантными относительно вращений в изотопическом
пространстве. Ковариантность обеспечена тем, что во взаимо-
взаимодействии мы ограничились членами, которые дают одинаковые
силы между протонами и нейтронами и между заряженными и
нейтральными пионами. Обратное утверждение также спра-
справедливо: любая совокупность инвариантных относительно вра-
вращений в изотопическом пространстве волновых уравнений при-
приводит к равенству взаимодействий в системах п — п, п — р и
р — р в одинаковых состояниях [96, 97].
Именно с этой целью — построить простую схему, в которой
протон и нейтрон являются двумя компонентами нуклонной
волновой функции Ч*", — мы выводили правила для фейнманов-
ских амплитуд в предыдущем параграфе.
С математической точки зрения формализм изотопического
спина совпадает с формализмом трехмерного углового момента.
Точно так же, как закон сохранения углового момента следует
из ковариантности волнового уравнения относительно вращений
в обычном трехмерном пространстве, закон сохранения изотопи-
изотопического спина вытекает из ковариантности A0.33) и A0.34) от-
относительно вращений в изотопическом пространстве. Однако
закон сохранения изоспина является приближенным, так как
уравнения симметричны только в пренебрежении электромаг-
электромагнитным взаимодействием и разностями масс р и п и я* и л°.
В этом приближении состояния систем из мезонов и нуклонов
можно диагонализовать по квадрату полного изотопического
спина /2 и третьей проекции изоспина /3, которая связана с пол-
полным зарядом системы.
При поворотах в изотопическим пространстве нуклонная вол-
волновая функция A0.28) преобразуется как двухкомпонентный
спинор, поэтому нуклону приписывается изотопический спин
У2. Третья проекция изоспина выбирается равной +7г для про-
протона и —'А Для нейтрона. Волновая функция мезона A0.32)
преобразуется как вектор с третьей проекцией 0 для зт°-мезона.
Таким образом, пионам приписывается /= 1.
Мезон-нуклонное рассеяние можно рассматривать как задачу
с двумя каналами / = 3/2 и / = '/г по изоспину. Мезон и нуклон
связаны с этими каналами по известным правилам сложения
моментов. В рассеянии р — р и п — п в приближении зарядовой
независимости участвует только канал с /= 1. Для системы
р — п /3 = 0 и рассеяние может идти через оба канала с / = 0
и /= 1. Вскоре мы рассмотрим несколько примеров применения
изоспина в задачах о рассеянии.
Подводя итоги, выпишем правила диаграммной техники в
рассмотренной модели A0.33) и A0.34) с зарядово-независи-
мыми взаимодействиями (сравните с § 34):

§ 50] ФОРМАЛИЗМ ИЗОТОПИЧЕСКОГО СПИНА 223
1. Нарисовать все связные диаграммы.
2. Каждой диаграмме поставить в соответствие амплитуду
с фактором
в каждой вершине.
3. Каждой внутренней нуклонной линии, соединяющей точки
х и у, ставится в соответствие пропагатор iSF(x — у)\, где 1
есть матрица размерности 2 X 2 в пространстве нуклонных изо-
спиноров. Каждой внутренней мезонной линии ставится в соот-
соответствие пропагатор ikF{x — у)Ьа&, где бар — единичная матрица
размерности 3X3, связывающая друг с другом операторы та и
тр, которые входят в вершины, соединяемые мезонной линией.
4. Для каждой внешней линии ввести волнэвую функцию.
Для нуклонной линии полезны проекционные операторы
Уг 0 + тз) и УгA—тз) для протона и нейтрона соответственно
и волновые функции Хр — ( п ) и %« == ( i ) • Например, волно-
волновая функция падающего нейтрона с квантовыми числами (р, s)
имеет вид
Для мезонной линии волновая функция содержит изотопическую
часть фе, где фе представляет собой единичный вектор в трех-
трехмерном пространстве изотопического спина пионов. Согласно
A0.32) вектор фе, выраженный через мезонные состояния с за-
зарядом -f-> — и 0 имеет следующие компоненты:
Фе+ = -^(и,о),
Ф1 = -^гA,-г(о)) (Ю.36)
фое = @,0,1).
Таким образом, в вершине, в которой поглощается налетающий
зх+-мезон или испускается конечный я~-мезон, соответствующий
Налетающему я+-мезону с отрицательной энергией, распростра-
распространяющемуся назад во времени, появляется, как в A0.30), изото-
изотопический фактор т • ф^ sa — (х, + /т2) = л] 2 т+, Для испуска-
испускания конечного я+ (или поглощения начального я~) соответ*
ствующий фактор равен т • ф^ = д/2 т_.

224 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
5. Согласно условию, принятому в конце § 49, два члена,
которым соответствуют диаграммы, топологически отличаю-
отличающиеся только перестановкой двух нуклонных линий, имеют про-
противоположные знаки. Каждой замкнутой нуклонной петле соот-
соответствует множитель (—1). Кроме того, в амплитуду входит
множитель (—1)", где Я — число античастиц в начальном со-
состоянии (см. F.56)).
В рассмотренной модели мы слепо следовали электродина-
электродинамике. Общие свойства, такие как сохранение изотопического
спина в пион-нуклонных взаимодействиях, справедливы во всех
порядках по взаимодействию, если пренебрегать малыми разно-
разностями масс и электромагнитными эффектами. Однако разложе-
разложение взаимодействия в ряд теории возмущений по степеням кон-
константы взаимодействия go полезно далеко не всегда, так как
?о/4л « 14 и эта величина вовсе не мала, как ее электродинами-
электродинамический аналог а ~ 1/137. Разложение по степеням go приводит
к расходящемуся ряду теории возмущений вместо сходящегося.
§ 51. Сохраняющиеся токи
Вводя изотопические обозначения A0.28) и A0.32) в диффе-
дифференциальный закон сохранения тока A0.23), получим
0I ,10.37,
где векторные обозначения относятся к изотопическому про-
пространству. Сохраняющийся электрический заряд, получаемый
интегрированием временной компоненты с ц = 0 по всему про-
пространству, равен
^^+(Ц^) ] (Ю.38)
Закон сохранения, следующий непосредственно из A0.33), имеет
вид
ik'l=4г V в 4: (*л*,+^v»)=°- A0>39)
Его называют законом сохранения нуклонного заряда. Полный
нуклонный заряд дается выражением
N = J ?+? <РХ = J ОХ + Ц>>„) йъх A0.40)
и в рассматриваемой модели сохраняется, так как сохраняется
разность между полным числом нуклонов (протонов плюс нейт-
нейтронов) и полным числом антинуклонов. Это видно, в частности,
из диаграмм на рис. 10.4 и 10.5, поскольку при любом упорядо-
упорядочении во времени непрерывная нуклонная линия проходит через

§ 52] ПРИБЛИЖЕННЫЕ МЕТОДЫ, НУКЛОН-НУКЛОННОЕ РАССЕЯНИЕ 225
каждую вершину. Вводя A0.40) в A0.38), получаем
/з = \ dh [I W+VF + (ф X фK] A0.42)
где величина
представляет собой третью компоненту изотопического спина.
Исходя из инвариантности A0.33) и A0.34) относительно вра-
вращений в изотопическом пространстве, естественно предположить,
что должна сохраняться не только проекция /3, а все три проек-
проекции изоспина. Прямой проверкой можно убедиться, что это
действительно так. Сохраняющийся изотопический ток имеет
вид
\(Х^). (Ю.43)
Сохраняющийся полный изоспин дается следующим выражением:
A0.44)
Сохранение электрического и нуклонного зарядов и изотопи-
изотопического спина является общим свойством теории, основанной на
уравнениях A0.33) и A0.34). Законы сохранения Q и N — это
строгие законы природы1); напротив, изотопический спин /
сохраняется только в пренебрежении электроманитным и сла-
слабым взаимодействиями. Последние нарушают зарядовую неза-
независимость сильных взаимодействий, следствием которой яв-
является симметрия уравнений A0.33) и A0.34) и сохранение
A0.43) и A0.44). Строго сохраняющейся величиной согласно
A0.41) остается только третья проекция изоспина /3. Таким об-
образом, на примере рассмотрения законов сохранения мы убеди-
убедились в том, что формализм изоспина позволяет полнее понять
смысл уравнений.
§ 52. Приближенные методы; нуклон-нуклонное рассеяние
В качестве примеров, иллюстрирующих как применение фор-
формализма изоспина, так и некоторые общие свойства взаимодей-
взаимодействия пионов и нуклонов, мы кратко рассмотрим два вопроса:
вклад однопионного обмена в нуклон-нуклонное взаимодействие
и пион-нуклонное рассеяние. Теперь мы можем записать ком-
компактное выражение для рассмотренных ранее диаграмм нуклон-
нуклонного рассеяния, изображенных на рис. 10.1—10.3. Сле-
') Обобщением N с учетом странных частиц является барионное число б,
которое оаначает разность между числом барионов (N, A, 2, S и т. д.) и ан-
тибарионов (см. [50]).

226 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕПСТВИЯ [ГЛ. 1»
дуя полученным правилам и переходя, как обычно, к импульс-
импульсному представлению, получим следующее выражение для ам-
амплитуды рассеяния:
X | Ы'п (Pl) »"V" (Pi) X,] (р/_р'J_ц2 [#« (Ps) 'V«
) X,] / / \2 2Dtf " fa) /Y5t« (P2)X2]| • A0.45)
Сравнение A0.45) с соответствующим выражением G.82) для
амплитуды электрон-электронного рассеяния показывает, что
имеется соответствие
Вместо V2 фигурирует BjtN, так как мы перешли к нормировке
в непрерывном спектре для внешних линий. В случае рассеяния
р — р изотопические факторы равны
3Xp) = 1 A0.46)
и два члена в A0.45), подобно выражениям A0.7) и A0.8), от-
отвечают прямому и обменному рассеянию двух тождественных
фермионов; аналогичная ситуация имеется в рассеянии п — п.
Для рассеяния р — п изотопический фактор равен
(Хр %)' (Х^"ТХ„) = — 1, в первом члене
(х;ГтХр) • (Х^ТХ„) = + 2 в обменном члене.
Поэтому амплитуда отличается от амплитуды рассеяния р — р
и п — п. Если, однако, мы рассмотрим рассеяние в состояние
системы р — п, симметричное по изоспину с /= 1 и /3 = 0, ко-
которое имеет вид
^ 1)], (Ю.47)
то оба изотопических фактора в первом и во втором членах
A0.45) становятся равными,
Х+тХп) = ^ (- 1 + 2) = -—. A0.48)

§ 52] ПРИБЛИЖЕННЫЕ МЕТОДЫ, НУКЛОН-НУК.ЛОННОЕ РАССЕЯНИЕ 227
Таким образом, полученная амплитуда рассеяния р— п равна
умноженной на \/-\/2 амплитуде рассеяния р— р или п — пи
антисимметрична относительно перестановки пространственных
переменных частиц.
Для рассеяния в антисимметричное изотопическое состояние
с / = 0, /3 = 0, которое имеет вид
\)*»V)-Xn№XplX)\, (Ю.49)
изотопические факторы в A0 45) равны
1
для первого члена и + 3/V2 для второго члена. Следовательно,
амплитуда рассеяния симметрична относительно перестановки
пространственных переменных (координат и спина) протона и
нейтрона и антисимметрична относительно перестановки их изо-
изотопических переменных.
Эти примеры показывают, как обобщенный принцип запрета
действует в системе NN. Нуклоны взаимодействуют только в
состояниях, антисимметричных относительно совместной пере-
перестановки их пространственных и изотопических координат.
В приближении зарядовой независимости амплитуды рассеяния
р — р и п — п равны амплитуде рассеяния р — п в симметричном
изотопическом состоянии A0.47) и соответственно в антисим-
антисимметричном пространственном состоянии. Это равенство вытекает
из A0.45), A0.46) и A0.48), если принять во внимание, что пол-
полные сечения р — р и п — п получаются, как и G.81), интегриро-
интегрированием только по половине фазового пространства, иначе мы
учли бы протоны и нейтроны дважды; таким образом, множи-
множитель 1/2 сокращается с (\j^J2f из A0.48).
В нерелятивистском пределе спинорная часть матричного
элемента в A0.45) упрощается следующим образом:
й{р\, s[)y,u(Pl, Sl)^u+(s[)a'^~Pl) h(s,), (Ю.50)
где u(si) означает двухкомпонентный паулиевский спинор; ра-
равенство A0.50) легко проверяется, если в спинорах перейти к
нерелятивистскому пределу. В этом пределе пропагатор мезона
переходит в фурье-образ потенциала Юкавы:
3 < (p.-pib ±Г
и тогда A0.45) оказывается амплитудой рассеяния порядка

228 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
на потенциале вида
V{ri, г2) = -Дг A - Рех) (ti ¦ т2) (а • V,) (а2 • V,) g~* ^' , A0.51)
где
' ^1я~
а оператор Рех производит перестановку волновых функций
нейтрона и протона и приводит к появлению второго члена в
A0.45). В соответствии с принципом запрета два нуклона
должны находиться в антисимметричном относительно переста-
перестановки состоянии, иначе оператор A — Рех), действуя на состоя-
состояние, дает нуль. Для двух нуклонов в s-состоянии потенциал
является притягивающим на конечных расстояниях г = |г! —
•—г2| > 0, как видно из усреднения A0.51) по углам
= -?- A - Рех) у т, • т2 «г, • а2 [ц* ??L - 4яб3 (г)]
и из того наблюдения, что это состояние, будучи симметричным
по пространственным координатам, должно быть антисиммет-
антисимметричным относительно перестановки спинов либо изоспинов. По-
Поэтому в s-состоянии
j (т, • т2) («г, • a,))s = (± [(т, + т2J - 6] [(а, + а2J - 6])$ =
= i [Г (Г + 1) -1] [5(S + 1) - J-] = - 1. A0.52)
Таким образом,
V. (г) = - 2/2 [^- —^- в» (г)]. A0.53)
При учете нестатических поправок отталкивание в виде
б-функции «размазывается», т. е. заменяется на отталкиватель-
ный кор на малых расстояниях (a short-range repulsive core
interaction). Сам по себе потенциал A0.53) не описывает дейт-
дейтрон и данные по рассеянию при низких энергиях. Это неудиви-
неудивительно, так как нет серьезных оснований надеяться на досто-
достоверность приближения статического одномезонного обмена. Дей-
Действительно, поскольку константа связи велика, gg/4jt~14,
нельзя пренебрегать вкладами от диаграмм высших порядков,
которые описывают процессы с многими мезонами. Однако

$ 53] МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ 229
можно показать [99], что последние дают вклад в основном на
малых расстояниях г и спадают, как е~п>1Т, при цг > 1, где
п — число участвующих в обмене мезонов.
Поэтому весьма обнадеживает то, что, как показал анализ
высших парциальных волн в разложении нуклон-нуклонной
амплитуды, формулы A0.45) и A0.51) хорошо описывают
наблюдаемые сдвиги фаз, если положить gl/4n « 14 в соответ-
соответствии со значением этой величины, получаемым из анализа дан-
данных по мезон-нуклонному /7-волновому рассеянию.
§ 53. Мезон-нуклонное рассеяние
Диаграммы Фейнмана на рис. 10.8 описывают рассеяние
мезона на нуклоне в низшем порядке по g\IAn. Согласно нашим
М
(a) F)
Рис. 10.8. Мезон-нуклонное рассеяние в низшем порядке, отвечающее
формуле A0.54).
правилам амплитуда рассеяния дается выражением
о 1 / ^ /О \4х4/ I \ 5Ш
Sl1 ~ J2ny-' Л/ ? ? 2а 2м ^2Л> ° ^' + Pi ~ ^2 — Pi) ^Ц
где
х
Х«(Р„ s,)xr (Ю.54)
Обратите внимание на кросс-симметрию матричного элемента
A0.54); он инвариантен относительно замены
* <72- A0.55)
Аналогичным свойством обладает рассмотренная ранее ампли-
амплитуда G.67) комптоновского рассеяния. Симметрия A0.55) со-
сохраняется и во всех высших порядках [50]. Она очевидным обра-

230 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ 1ГЛ. 10
зом следует из фейнмановских диаграмм — достаточно заме-
заметить, что для любой диаграммы, которая отвечает поглощению
падающего пиона до испускания конечного, как, например, на
рис. 10.8, а, найдется другая диаграмма, как на рис. 10.8,6, ко-
которая отличается от первой лишь тем, что начальный пион
поглощается после испускания конечного. Мы ограничимся рас-
рассмотрением области низких энергий [100], сохраняя в WI члены
порядка \JM для рассеяния в s-волне и порядка 1/М2 для р-вол-
нового рассеяния. Переходя к квадратам в знаменателях фейн-
фейнмановских пропагаторов и используя соотношение
«(/>') *Y5 {p + q + M) iy5u (p) = п (/»') qu (p),
находим
а»=
liiu (р2) за) \{ ?!}1+*
00.56)
Проводя вычисления в системе центра инерции с указанной
выше точностью, приводим A0.56) к виду
- ж"+ (s*) Х2+ (т • Ф2е*т • Ф> • ч2° • ч. -
- т • ф*т • ф2е*о • 4l(r • q2) и (s,) хг A0.57)
Первый член отвечает взаимодействию, которое не зависит от
спина и изотопического спина. В нерелятивистском случае в
борновском приближении это взаимодействие описывается по-
потенциалом
v w= + Srб3 (г)=6/2Л1 [^б3 (г)] • A0-58)
По теории возмущений он приводит к огромной длине рассея-
рассеяния, равной DМ/2/ц) 1/ц « 2/|л « 2,8-10~13 еж, где мы вновь по-
положили /2 = 0,08. Однако, поскольку взаимодействие является
отталкивательным и имеет малый радиус (в нерелятивистском
приближении A0.58) нулевой радиус), то вызванные им эф-
эффекты малы. Сильный, короткодействующий, отталкивательный
потенциал типа изображенного на рис. 10.9 приводит к сдвигу
s-фазы порядка б ~ qa, где радиус потенциала а дает в данном
случае длину рассеяния на этом потенциале. Из поправок на
отдачу нуклона можно ожидать, что a ~ 1/M и, следовательно,
s-волновая длина мезон-нуклонного рассеяния мала в противо-
противоположность большой амплитуде, «~- l/ц, полученной из необо-

53]
МЕЗОН-НУКЛОННОЕ РАССЕЯНИЕ
231
\V(r)
снованного применения борновского приближения к A0.53).
Эксперимент показывает, что это действительно так [15, 89,
94, 100].
Второй член в A0.57) отвечает р-волновому рассеянию. Вы-
Выражение такого вида получается во втором порядке нереля-
нерелятивистской теории возмущений. Если рассматривать нуклон как
нерелятивистскую частицу со спином '/г, Для которой спектр
промежуточных состояний между поглощением начального ме-
мезона и испусканием конечного включает только состояния с по-
положительной энергией, то можно воспользоваться A0.50) и
привести вершину взаимодействия к виду go(a-V) (т-фе)/2М.
Множитель 1/со в A0.57) возникает в этом приближении от
энергетического знаменателя и имеет знак плюс для амплитуды,
изображенной на рис. 10.8, а, и знак минус для амплитуды на
рис. 10.8,6. Напротив, первый член в A0.57), отвечающий рас-
рассеянию в s-волне, возникает благодаря прямым и обратным
переходам нуклона в море с отрица-
отрицательной энергией в промежуточном со-
состоянии. В этом случае при малых им-
импульсах нуклона Пуф ~ —1 и энерге-
энергетический знаменатель дает множи-
множитель— 1/2Л1
Из соотношения неопределенности
AEAt ~ 1 можно ожидать, что для рас-
рассматриваемых диаграмм взаимодей-
взаимодействие в /^-состоянии имеет больший
масштаб во времени, ~ 1/со, чем в s-co-
стоянии, ~ 1/М. Поэтому представля-
представляется естественным, что низкоэнергети-
низкоэнергетическая амплитуда рассеяния в р-со-
стоянии имеет более сильную зависи-
зависимость от энергии, чем амплитуда для
s-состояния. Если в /^-состоянии дей-
действует сильный притягивающий «потен-
«потенциал», то может образоваться резо-
резонанс.
Как впервые указал Чью [101], ре-
решающим является вопрос о знаке по-
потенциала в /5-состоянии. Независимо
от того, что использованный нами при
написании A0.57) метод теории возмущений качественно не-
необоснован, этот знак играет в рассеянии огромную роль и может
служить важным количественным критерием при анализе ам-
амплитуды рассеяния в р-состоянии. Чтобы ответить на этот во-
вопрос, удобно выделить из амплитуд проекции, которые отвечают
различным каналам с фиксированными значениями полного уг-
Рис. 10.9. Отталкивание на
малых расстояниях для s-
волнового я — п-рассеяния.

232 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 1С
лового момента / и полного изоспина /, так как переходы между
каналами с разными / запрещены законом сохранения углового
момента, а между каналами с разными / — законом сохранения
изоспина A0.44) (в приближении зарядовой независимости).
§ 54. Проекционные операторы для изоспина
и углового момента
Мы знаем, что согласно векторной модели сложения угловых
моментов полный изотопический спин системы из одного ну-
нуклона (с / = 7г) и одного мезона (с /= 1) может равняться
либо / = '/г, либо / = 3/г- Проекционные операторы для этих
двух состояний, Ру и Рг/ будут матрицами размерности 3X3
в изотопическом пространстве мезонов, натянутом на базисные
векторы A0.36), и матрицами 2X2 в пространстве нуклонных
изоспиноров A0.35). Операторы Р1/з и Р,д должны обладать
основными свойствами проекционных операторов:
Р1 = РЪ> Р% = РЪ' A0-596)
где 1 означает единичную матрицу в шестимерном простран-
пространстве, построенном как прямое произведение мезонного и нуклон-
ного изотопических пространств.
Эти операторы нетрудно найти, если заметить, что диаграм-
диаграмма без пересечения мезонных линий, изображенная на
рис. 10.8, а, должна приводить к чистой амплитуде с / = '/г, так
как она содержит только одну промежуточную нуклонную ли-
линию с / = 72 и / сохраняется в каждой вершине. Поэтому изо-
изотопические матрицы в диаграмме без пересечения должны быть
пропорциональны Р%!\
<ф* | />,А | фf> = от • ф*'т - ф^. A0.60)
Коэффициент а можно найти, вычисляя аналогичный матричный
элемент оператора PJh и используя равенство A0.596):
<ф2е I р\ I ф.)=? <ф2 | р,,. i ф;> <ф;
Таким образом, а = '/3 и

§ 54J ОПЕРАТОРЫ ДЛЯ ИЗОСПИНА И УГЛОВОГО МОМЕНТА 233
Оператор Р3/г находится теперь непосредственно из A0.59а):
<ф; | рЧг | фг>=фГ • ф? - j (т • фГ) (т • фг). (Ю.62)
Полученные результаты переносятся и на угловые моменты,
так как мы вновь складываем S = 7г с L = 1 для мезона, нахо-
находящегося в /^-состоянии относительно нуклона. Орбитальными
волновыми функциями я-мезона являются теперь векторы qi и
q2 по аналогии с ф, и ф^ в изотопическом пространстве, и вме-
вместо A0.61) и A0.62) теперь можно записать
здесь ? = |q1|==|q2l-
Эти операторы нормированы согласно
w <q21 Q? I я»><Q» 1 Q/1 Qi> = **/ <4a 1 Q* I fli>. (Ю.64)
где суммирование по трем ортогональным направлениям, как
и в случае изотопических проекционных операторов, мы заме-
заменили на интегрирование по сфере \ dQn. Подобная несуществен-
несущественная разница в условиях нормировки между Рг и Q, обусловлена
тем, что наблюдаемые мезоны всегда ориентированы в изопро-
странстве вдоль одного из трех направлений A0.36), которые
отвечают зарядам ±1 и 0, в то время как направления их им-
импульсов образуют континуум, отвечающий различным углам рас-
рассеяния.
Комбинированные проекционные операторы для собственных
состояний изоспина и углового момента представляют собой
произведения операторов Р и Q. Они определены следующим
образом:
ар — <5з — р г\
•s l J 11 Г ¦/а4''/»'
op __ ер — р Г)
(Юбб)
где первый индекс оператора &ц представляет собов удвоенное
значение изоспина, а второй — удвоенное значение углового мо-
момента. Операторы ^й, а = 1, ..., 4, обладают свойствами

234 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. !0
A0.59) и нормированы согласно
3
? S * v. I фх> <ф:'чя I *„< - «„л- (Ю.66)
Вводя проекционные операторы в A0.57), получаем следую-
следующее выражение для амплитуды пион-нуклонного рассеяния во
втором порядке теории возмущений и в нерелятивистском при-
приближении:
W
A0.67)
Обратите внимание на то, что амплитуда A0.67) отрицательна
только для канала C.3); это соответствует наличию притяже-
притяжения лишь в канале с / = / = 3/г [Ю0, 102, 103]. Эксперименталь-
Экспериментальное наблюдение резонанса в этом состоянии и малые сдвиги
фаз при низкой энергии в трех других р-состояниях качественно
согласуются с тем, что дает «потенциал», который приводит к
амплитуде A0.67).
§ 55. Сечения рассеяния пионов на нуклоне
Сечение рассеяния получается из A0.67) и A0.54) возведе-
возведением в квадрат и умножением на обычные множители, связан-
связанные с фазовым объемом. Для фиксированных начального и ко-
конечного спиновых состояний имеем
, 130212 Г / М \ { dbqz\/ М ,оп\ 1 .,
X б4 (<7, + Px-q2- P2),
что в нерелятивистском пределе в системе центра масс пере-
переходит в
Для конкретного процесса da/dQ вычисляется путем подстановки
в 5М соответствующей изотопической волновой функции я-мезона
ф^, импульса q(. и отвечающих данному процессу нуклонных
изоспиноров %г- Сечение, усредненное по спинам, получается, как
обычно, суммированием по спинам нуклона. В качестве при-
примера рассмотрим п+ — р-рассеяние, в которое дает вклад только

§ 56] СЕЧЕНИЯ РАССЕЯНИЯ ПИОНОВ НА НУКЛОНЕ 235
канал с / = 3/2, так как /3 = 3/г- Пренебрегая вкладами всех
других состояний, кроме / = / = 3/2, получаем из A0.65)
Суммируя по конечным и усредняя по начальным спинам нукле-
на, находим с помощью A0.69)
spins
spins
q, -y о • q, a • q2) =
Ч^ + 3(Я2-Я1J]- (Ю.70)
Подставляя это выражение в A0.68), получаем вклад состояния
с / = / = 3/2 в дифференциальное сечение п+ — /^-рассеяния в
системе центра инерции
где, как и раньше, мы обозначили
(юл)
f(
Полученное выражение A0.71) вряд ли можно считать досто-
достоверным, так как оно основано на борновском приближении, ко-
которое, как уже было показано, совершенно неприменимо для
s-волнового рассеяния. Важное достоинство A0.71) состоит, од-
однако, в том, что оно предсказывает угловое распределение вида
(l-f-3cos20) в хорошем согласии с экспериментальными дан-
данными для мезонов с энергией в районе от 150 до 200 Мэв. Кроме
того, установлено, что в этой области энергий отношения сечений
близки к значениям, вычисленным с учетом одного состояния
с I = J = 8/2:
а(п+ — р —ул+ — р): а(п~ — р—>п° — п)'.
:а(я~ —р->я- —р)=»9:2- 1. A0.72)
В предположении, что в данной области энергий основной
вклад в рассеяние вносит канал с / = / = 3/2, мы попытаемся
расширить применимость формулы A0./1) с помощью следую-
следующих двух общих соображений [100, 102, 103]. Во-первых, заме-

236
НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
(ГЛ. 10
тим, чго, за исключением области энергий вблизи порога,
A0.71) дает неправильную зависимость от энергии, так как
о —» оо при о—юо. Однако из условия унитарности следует огра-
ограничение сверху на величину полного сечения. В рамках метода
функции распространения трудно обсуждать вопрос об унитар-
унитарности S-матрицы [50], поэтому мы воспользуемся некоторыми
общими результатами нерелятивистской теории рассеяния, а
именно:
1. Для данного канала амплитуда рассеяния имеет вид
^ е" sin в =
q
тг-Лт
<7(ctg6 — i)
A0.73)
где q означает импульс каждой из частиц в системе центра
инерции, а б — сдвиг фазы в данном канале. Фаза б действи-
действительна, если отсутствуют неупругие каналы с теми же кванто-
квантовыми числами
2. Вклад канала с орбитальным моментом / и полным момен-
моментом / = / ± '/г в полное сечение ограничен сверху значением
tot
4яB7+П
2
3. При низких энергиях хорошее приближение дает разло-
разложение по эффективному радиусу:
qzi+\ ctg6 = a + ftco + cco2+ ... A0.75)
Второе замечание состоит в том, что, как говорилось в § 53,
благодаря малому энергетическому знаменателю, ~а>, и срав-
сравнительно большой продолжительности, ~ 1/со, /J-волнового взаи-
взаимодействия можно ожидать сильной энергетической зависимо-
зависимости фазового сдвига для /5-волны. Поэтому естественно думать,
что в A0.75) для канала C.3) поправки высших порядков
к борновскому приближению приведут к коэффициенту с, ко-
которым нельзя пренебречь и за счет которого усиливается при-
притяжение, даваемое борновским приближением.
Используя A0.73) и A0.74), перепишем A0.71) в виде
где
В этом порядке мы можем также записать
cos2 6), A0.76)
(Ю.77)
A0.78)

55]
СЕЧЕНИЯ РАССЕЯНИЯ ПИОНОВ НА НУКЛОНЕ
237
Сравнивая с A0.75), мы видим, что для воспроизведения ха-
характера поведения борновского члена в пределе со->0 необхо-
необходимо положить а = 0 и b = -f- (Зц2/4/2). Для определения сле-
следующего коэффициента с в разложении A0.75) и получения
формулы, включающей поправку на эффективный радиус к
длине рассеяния, мы должны выйти за пределы нашего низко-
низкоэнергетического борновского приближения.
Как мы уже отмечали, согласно A0.67) можно ожидать, что
для канала C.3) коэффициент с отрицателен, гак как в этом
канале в противоположность другим имеется притяжение.
Полагая в качестве низ-
низкоэнергетического при-
приближения
Я3 ctg 633 =
4Р
¦('-?)•
A0.79)
Яу
7
/V
N
(Ф
мы получим хорошее опи-
описание эксперименталь-
экспериментальных данных по п+—р-рас-
сеянию при /2 = 0,08, что
соответствует ё2/4я « 14
и юг ft 2,2ji.
Формула A0.79) была
впервые получена Чью и
Лоу [102] из мезонной тео-
теории с неподвижным ну-
клонным источником
(со/М -> 0) и без помощи
разложения по степеням
константы взаимодейст-
взаимодействия, которым мы пользо-
пользовались в A0.54).
Сингулярность ампли-
амплитуды рассеяния A0.77) в
точке со = 0 в «нефизической области», граница которой рас-
расположена при со = (и,, возникает благодаря обращению в нуль
энергетического знаменателя борновской амплитуды A0.54).
Таким образом, фейнмановские пропагаторы в A0.56) имеют
простые полюсы при энергиях мезонов в лабораторной системе
coi = —\х2/2М и 0J = +ц2/2М; coi и ©2-> 0 в нерелятивистском
пределе ц/М -> 0.
Все диаграммы высших порядков с одной нуклонной ли-
линией, соединяющей мезонные вершины, как на рис. 10.10, также
Рис. 10.10. Радиационные поправки
с одной нуклонной линией в промежутке.

238 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
приводят к членам с полюсами при со = 0, и эти члены вносят
вклад в вычеты в формулах A0.78) и A0.79) в этом полюсе.
Все другие диаграммы, изображенные, например, на
рис. 10.11, дают выражения, конечные при со = 0 для внешней
мезонной линии, и поэтому вносят вклад во второй член в
A0.79), который отвечает приближению эффективного ра-
радиуса1). Строя зависимость (q3 ctg дзз)/(о от щ и экстраполируя
в точку ш = 0, мы выделяем вклад амплитуд, изображенных на
рис. 10.10, который характеризует интенсивность такого про-
процесса, когда физический нуклон с Р2 = М2 испускает или погло-
я #_-
т.
г. ^
Ш
N ^Ч
(а) F)
Рис. 10.11. Вклады высших порядков.
щает мезон с мнимым импульсом \q\ —i\i и остается физиче-
физическим нуклоном с
(Р -f qf = М2.
Амплитуда этого процесса является, согласно Чью и Лоу, кон-
константой связи мезон-нуклон, численное значение которой, полу-
полученное из экстраполяции, равно /2 = 0,08 [104].
§ 56. Электромагнитная структура мезонов и нуклонов
Как мы уже отмечали, сильные взаимодействия оказывают
влияние на электромагнитные свойства мезонов и нуклонов.
Действительно, уже давно было известно, что протон обладает
аномально большим магнитным моментом, равным 2,79 цБ (где
jj,B = efi/2Mpc—ядерный магнетон Бора), вместо значения, рав-
равного 1,0 цБ, предсказываемого теорией Дирака для частицы с
зарядом е (здесь мы пренебрегаем радиационными поправками,
рассмотренными в гл. 7 и 8). Аналогично, нейтрон имеет маг-
магнитный момент, равный —1,91 цв, в то время как свободное
уравнение Дирака приводит к нулевому магнитному моменту
для нейтральной частицы.
Можно допустить существование аномальных магнитных мо-
моментов, если отказаться от принципа минимальности электро-
') Это утверждение, которое кажется правдоподобным для данных фейн-
мановских диаграмм, строго доказывается в следующем томе [50].

§ 56] ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА МЕЗОНОВ И НУКЛОНОВ 239
магнитного взаимодействия [92]. Вместо того чтобы вводить
электромагнитное взаимодействие в уравнение Дирака с помо-
помощью замены
(?^ A0.80)
мы можем добавить также дипольный член
где кр= 1,79, к„ = — 1,91.
Более продотворным является подход без попытки введения
новых параметров, как в A0.81), с сохранением минимальной
формы взаимодействия A0.80). В таком подходе считается, что
все отключения от A0.80), включая аномальные магнитные мо-
моменты к, обусловлены сильными взаимодействиями [105—108].
Подобным образом в гл. 8 было показано, что лэмбовское сме-
смещение атомных уровней и аномальный магнитный момент
электрона в пределах точности современных экспериментов мо-
могут быть объяснены взаимодействием электрона с фотонами.
Не вдаваясь в детальные вычисления и опираясь только на
принципы инвариантности, мы можем установить общий вид
изменений, вносимых в A0.80) сильными взаимодействиями.
/*¦
/ Протон
\ р Протон
V
{а) (Ф
Рис. 10.12. Электромагнитная вершина заряженного пиона и радиационная
поправка.
В данном случае требование лоренцевой инвариантности и со-
сохранение электромагнитного тока налагают существенные огра-
ограничения на электромагнитную вершину частицы. Рассмотрим
сначала я+-мезон и диаграмму на рис. 10.12,6, которая служит
«радиационной поправкой» к вершине на рис. 10.12, а.
Согласно нашим правилам изменение в электромагнитном
токе перехода на рис. 10.12, а, обусловленное диаграммой на

240 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ (ГЛ. 19
рис. 10.12,5, имеет вид
«(р„ + К) -е (р. + р»У+ (- '*<> V2J х
= е(р№ + <) + />/,Р). (Ю.82)
Значение интеграла 1^{р',р) не представляет большого инте-
интереса, так как он является всего лишь одним из членов ряда по
§2, который вполне может оказаться расходящимся. Важно,
однако, как эта добавка к электромагнитному току я+-мезона
ведет себя при лоренцевых преобразованиях, поскольку закон
преобразования является общим для всех порядков. Из A0.82)
ясно, что вычисление следа и интегрирование по импульсу при-
приводит к величине 1^,(р',р), преобразующейся как 4-вектор. Сле-
Следовательно, можно записать
УР'. P) = Pji(P2' P'2> (Р-РУ) + Р»Ш, Р'\ (Р~рУ)> (Ю.83)
где форм-факторы /i и f2 являются скалярными функциями трех
независимых скаляров р2, р' и (р — р'J, входящих в интеграл.
Если ограничиться рассмотрением рассеяния реального мезона
на потенциале, форм-факторы становятся функциями только
квадрата переданного 4-импульса q2 = {p' — pJ, так как р2 =
Дальнейшее ограничение на A0.83) следует из сохранения
тока: для q-n фурье-компоненты тока реального физического
мезона имеем
«Р/ц (Р', Р) = (/ - РТ /ц (/, Р) = 0. A0.84)
Для A0.83) при р2 = р/2 = ц2 получаем отсюда fi(q2) = /2(<72);
этот результат можно получить непосредственно из A0.82) тем
же способом и с той же неопределенностью, как в гл. 8 при рас-
рассмотрении поляризации вакуума.
Мы получили общий вид электромагнитного тока перехода
реального я+-мезона для рассеяния с переданным импульсом
qv-. Ток ^(р^ + Рд), отвечающий точечному взаимодействию, за-
заменяется на
< + /'^я(Л A0-85)
где функция FJl(q2), которую называют форм-фактором заря-
заряженного я-мезона, зависит только от инвариантного передан-
переданного импульса. Форм-фактор нормирован на единицу при нуле-
нулевом переданном импульсе, /гл@)= 1, причем здесь предпола-
предполагается, что перенормировка уже проведена, как в гл. 8, и заряд

! 56]
ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА МЕЗОНОВ И НУКЛОНОВ
241
е положен равным наблюдаемому физическому заряду я+-ме-
зона.
Изучение Fn(q2) требует применения более мощных методов,
чем теория возмущений [50]. Однако даже A0.85) налагает
сильное ограничение на форму дифференциального сечения рас-
рассеяния я+-мезона электромагнитным полем. Например, в низ-
низшем порядке по а отношение сечений при разных энергиях и
углах рассеяния, но при одинаковом q2 не зависит от Fn(q2) и
равно отношению, найденному в гл. 9 в пренебрежении силь-
сильными взаимодействиями.
Подобный результат получается также для электромагнит-
электромагнитного тока нуклона (и странных гиперонов). Благодаря спиновой
степени свободы нуклон может обладать двумя скалярными
форм-факторами. Появление второго форм-фактора отвечает
дополнительной возможности наличия магнитного момента у ча-
частицы со спином '/г.
'Протон
Протон
(а)
Протон
(Ф
Протон
Pr
Hpamofr
Рис. 10.13. Протонная электромагнитная вершина и радиационные поправки.
Для протона, например, диаграммы, которые надо учитывать
до порядка g°, изображены на рис. 10.13. Они вносят следую-
следующее изменение в протонный ток перехода:
п (//) еу^и (р) -> п (//) еу^и (р) +
X
^п{р')еТ»{р', р)и(р). A0.86)

242 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Снова, как и в случае тока я+-мезона, мы находим, что про-
протонный ток является 4-вектором. После интегрирования по им-
импульсам остаются 4-векторы р р'^ и у , которые могут быть
заключены в обкладки из протонных спиноров. Все остальные
матрицы у должны быть вида р, р' или ys- Однако матрицы ys
можно исключить, поскольку число п — N вершин четно и, сле-
следовательно, матрицы уб можно объединить попарно и использо-
использовать свойство y| = 1 • Кроме того, все факторы р' и р, в которые
входят матрицы у, можно переставить направо и налево к со-
соответствующим спинорам п(р') и и(р) и затем положить рав-
равными М (вспомните пример использования этого приема при
вычислении электромагнитной вершины электрона в гл. 8).
Таким образом, мы приходим к выводу, что A0.86) имеет
следующий общий вид:
п(р')еТ»(р',р)и(р) =
= ей (/) [дГ, (q2) + р;Г2 (?2) + уйГ3 И] " 0>). <10-87)
где Tt(q2), 1= 1, 2, 3, — скалярные функции q2. Те же рассуж-
рассуждения приводят к совпадающему с A0.87) представлению для
нейтронного тока.
Из сохранения тока вытекает соотношение между тремя
форм-факторами Yi{q2). По аналогии с A0.84) имеем
Отсюда получаем Fi (q2) = Г2(^2) и нуклонный ток принимает
следующий наиболее общий вид:
п (//) еГ» {р\ р) и (р) = ей (pf) [(Р(г + pi) Г, (q2) + Y(ir3 W\ « О»)-
При рассмотрении электромагнитной структуры нуклонов обыч-
обычно исключают вектор (Рц + уО, вводя
ct^v (P/V - Pv) =
с помощью представления Гордона для тока. Поскольку спиноры
п(р') и и(р) удовлетворяют свободному уравнению Дирака, мы
можем, используя непосредственно C.26), получить следую-
следующую эквивалентную форму записи:
= ей (р') [Y|lF, (q2) + ^§f kF2 (q2)] и (р). A0.88)
С таким выражением мы уже встречались при изучении радиа-
радиационных поправок к электронной вершине (см. (8.61)). Если
величина к положена равной аномальной части магнитного мо-

§ 56] ЭЛЕКТРОМАГНИТНАЯ СТРУКТУРА МЕЗОНОВ И НУКЛОНОВ 243
мента в единицах ядерного магнетона (кр = 1 ,79 и к„ = —1,91)
и е означает физический заряд протона, то ^@) = 1 и F\ @) — 1
для протона и Fi @) = 0 для нейтрона1).
Пользуясь формализмом изоспина, мы можем объединить
протонный и нейтронный токи в изоскалярную и изовекторную
части
е%+п(р') { Y(i [Fjs> (q2) + т3/*» (?2)] +
« (p) x -
%+ [If (p', P) + V'^ (/>'. P)] X, (Ю.89)
где
)
^s> = | (kp^p) + Kn^n)), ^' @) = - 0,06,
Ff = ^ (kp^p) - Knf ^n>), ^0) @) = + 1,85.
Для протона х+тзх = 1 и A0.89) переходит в протонный ток;
для нейтрона х+хз% = —1 и A0.89) дает ток нейтрона.
Из общего вида тока перехода A0.88) и A0.89) вновь вы-
вытекают существенные ограничения на форму дифференциаль-
дифференциального сечения рассеяния протона и нейтрона электромагнитным
полем. В борновском приближении по а = 1/137, но в любом
порядке по константе сильного взаимодействия получаем для
дифференциального сечения рассеяния электрона на физическом
протоне и нейтроне вместо G.46) следующее выражение:
dQ, ~~ 4E2[\ + B?/М) sin2 F/2)] sin4 F/2)
UU-Уи)
где 6 — угол рассеяния в лабораторной системе. Форм-факторы
F\ и F2 в отдельности находятся из сравнения результатов изме-
измерений при разных углах рассеяния и энергиях, но фиксирован-
фиксированном q2. Если результаты более чем трех измерений при данном
') Широко используются также форм-факторы
которые имерзт более наглядную геометрическую интерпретацию,

244 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
q2 отложить в виде зависимости величины
4 6 "\ Е>2 A I 2Е ¦ 2 6 "
от cos2 @/2) при фиксированном q2, то должна получиться пря-
прямая линия. Любые отклонения от нее означают ошибку в расче-
расчетах, связанных с электродинамикой явления; эти отклонения
нельзя отнести за счет незнания сильных взаимодействий или
погрешности в вычислении форм-факторов. Дело может, напри-
например, оказаться в неоправданности низшего приближения по а
либо в более глубоких причинах.
§ 57. Слабые взаимодействия
Слабые взаимодействия [109, 15, 17], наиболее известным
примером которых является р-распад, можно разделить на леп-
тонные и нелептонные. В лептонных взаимодействиях участвуют
ц-мезоны (ц~), электроны (е~) и два типа нейтрино (v, v')-
К лептонным относятся следующие процессы (вместе с соот-
соответствующими реакциями для античастиц ц+, е+, v, v'):
р-распад п
распад мюона \х~
распад пиона я~
ц-захват ц~
-*¦ Р
А
+ Р
-f e~ -f v,
- + V + v,
ц- -f v',
е" -f- v,
->п -f v'
A0.91а)
A0.916)
A0.91в)
A0.91г)
и, кроме того, большое число лептонных распадов с изменением
странности, благодаря которым странные частицы переходят
в нуклоны, лептоны и, возможно, пионы; например,
Примерами нелептонных распадов, в которых всегда уча-
участвуют странные частицы, являются
Л->р + я~, К+ -> я+ + п+ + п~.
Мы рассмотрим лептонные взаимодействия без участия
странных частиц; в настоящее время нет ясной картины слабых
взаимодействий с участием странных частиц, и мы не будем ка-
касаться этого вопроса. Проблема, с которой мы сталкиваемся при
рассмотрении реакций A0.91а,б, в), состоит в получении на
основе имеющихся экспериментальных данных структуры вер-
вершин взаимодействия в диаграммах, описывающих эти процессу.

58]
БЕТА-РАСПАД
245
Два основных принципа, на которые мы опирались при рас-
рассмотрении сильных взаимодействий, теряют здесь силу: чет-
четность и изоспин не сохраняются в слабых взаимодействиях.
§ 58. Бета-распад
Фундаментальный процесс A0.91а) ответствен за р-распад
в ядрах. Рассмотрим распад свободного нейтрона. Элемент
S-матрицы, который отвечает распаду (см. рис. 10.14), дол-
должен быть линеен по волновым функциям, описывающим на-
начальный нейтрон и конечные частицы, т. е.
XF . tr, гЛ (\ fl Q5M
ctRv6 VI > • • • » Л4/• \lu.^7л^
Как обычно, эрмитово-сопряженные волно-
волновые функции ip+ отвечают испускаемым час-
частицам (р,е~) или налетающим античасти-
античастицам (которые описываются решениями с
отрицательной энергией), распространяю- Рис. 10.14. р-распад.
щимся назад во времени, а г|) отвечают
налетающим частицам («) или испускаемым античастицам (v).
Поэтому, помимо р-распада, в A0.92) включены также все взаи-
взаимодействия типа
v -f n-> p -f e~.
В энергетически разрешенных ядерных переходах наблюдается
обратный р-распад, или испускание позитрона
р —>• п -\- е+ + v.
Этому процессу должен соответствовать матричный элемент,
аналогичный A0.92):
..., х4). A0.93)
Функции F и F в A0.92) и A0.93) должны определяться из
эксперимента. Исходя из общих принципов теории, мы сделаем
здесь единственное допущение, а именно
i? /v r у г \== р' (у у у и (in ад\
*2> 3> 4/ Bafiv \ 2» 1» 4' 3/' \iv.vtf

246 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Это равенство обеспечивает выполнение принципа детального >
равновесия для слабых взаимодействий и означает, что без
учета множителей, связанных с фазовым объемом, реакции
протекают с равной вероятностью справа налево и слева на-
направо1). То, что должен выполняться принцип детального рав-
равновесия A0.94), следует из малости отвечающего за р-распад
взаимодействия и унитарности S-матрицы. В отсутствие взаи-
взаимодействия 5-матрица сводится к единичной матрице Ьц. Запи-
Запишем S-матрицу в виде
Тогда условие унитарности (8.31) примет вид
Для р-распада правая часть имеет второй порядок по константе
слабого взаимодействия, а левая часть представляет собой раз-
разность двух величин первого порядка. В первом приближении
членами второго порядка можно пренебречь. Это приводит к ра-
равенству A0.94), если учесть, что при f ф i
Sfi = - iTfi.
Нейтрино является безмассовой нейтральной дираковской
частицей, и когда мы говорим, что в C-распаде нейтральным
партнером электрона является антинейтрино, мы тем самым
удовлетворяем твердо установленному на опыте закону сохра-
сохранения лептонного заряда. Для реакции A0.91а) это просто
вопрос определения; однако для я- и ц-распада сохранение леп-
лептонного заряда имеет четкий смысл. Наблюдаемые C-спектры
указывают также на то, что спин нейтрино равен У2- Позднее
обнаружение распада n~-*-e~-\-v подтвердило этот вывод. На-
Наконец, необходимо отметить, что отсутствие массы у нейтрино
приводит к отличию в условии нормировки волновой функции
нейтрино по сравнению с другими фермионами. Для решения
в виде плоской волны с квантовыми числами (k, s) запишем
*{V){X)= 42e1w U(V>(*' s)e~ik'X; A0-95)
здесь
u
и поэтому
') В терминах теории поля это отвечает эрмитовости гамильтониана в
теории возмущений.

§ 58] БЕТА-РАСПАД 247
Проекционными операторами для нейтрино являются
2
ЛИ' (k, s) = ? иа {k, s) пй (k, s) = k,
s = \
AW(k, s)=i»,(A, s)€6{k, s) = -k.
s = l
Удобно проводить нормировку, рассматривая нейтрино на-
наравне с электроном как частицу с конечной массой, и норми-
нормировать волновую функцию согласно изложенному в гл. 3, а за-
затем перейти к пределу /nv->0. Результат совпадает с A0.95).
После тридцати лет исследований функция F в A0.95) была
в конце концов полностью определена при низких энергиях, т. е.
для сравнительно больших относительных расстояний х,— Xj в
координатном пространстве. Простейшая гипотеза относительно
функции F состоит в том, что она обращается в нуль при боль-
больших относительных пространственно-временных расстояниях
Хг — Xj. Действительно, если размер области, где F отлична от
нуля, мал по сравнению с характерной длиной Ь/Е^с ~ 10~12 см,
отвечающей энергии р-распада Е$ ~ 1 ч- 10 Мэв, то в первом
приближении можно считать взаимодействие F точечным, т. е.
p4) (*I - Х2) 6М> (X, - Х3) б<4> (X, - Хд, A0.96)
где $~a|3Yfi — постоянная матрица, связывающая спиноры друг с
другом. Это приближение чрезвычайно хорошо согласуется со
всеми имеющимися сейчас экспериментальными данными. Пере-
Переходя с помощью фурье-преобразования от A0.96) к импульс-
импульсному представлению, получаем
2, k3, k4) =
, X2, X3, X4) =
k2 + k3 + k4) ^a3Y6. A0.97)
Таким образом, взаимодействие представляет собой постоянную
матрицу, умноженную на обычную б-функцию, выражающую
сохранение энергии-импульса в вершине взаимодействия. Этот
результат следует сопоставить с тем, который был нами получен
для нуклон-нуклонного рассеяния, обусловленного обменом
я-мезонами. Тогда мы имели
F~^-tJ- A0.98)
что отвечает потенциалу с радиусом ~ Ъ/цс. Если бы массу
я-мезона можно было сделать большой, то при малых д2

248 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
картина стала бы аналогичной C-распаду, т. е. мы получили бы
приближенно точечное взаимодействие четырех фермионов.
Если, наоборот, энергии частиц, участвующих в слабом взаи-
взаимодействии, например в обратном C-распаде
v + р—>п + е+,
возрастают, то можно ожидать, что взаимодействие станет нело-
нелокальным; возможно, что между системами р — п и е — v про-
происходит обмен тяжелым бозоном W+, как
показано на рис. 10.15, либо нелокаль-
нелокальность имеет более сложную природу [110].
Мы продолжим рассмотрение C-распа-
>хххххх^ да в рамках приближений A0.96) и
A0.97). В области низких энергий можно
пренебречь отдачей нуклона с точностью
до поправок ~q/M (где q — импульс от-
Рис 10 15 Возможный Дачи протона), а волновые функции ней-
обмен тяжелым 1Р*-бо- тРона и протона в A0.92) и A0.93) заме-
зоном при р-распаде. нить на постоянные спиноры. После воз-
возведения в квадрат и суммирования по
спинам для неполяризованных нейтронов и конечных частиц
получаем
VT
А, В
A0.90)
где pi и Е\ — 4-импульс и энергия частицы, i = (e, v, p, п). Вели-
Величины ТА и Тв означают матрицы, структура которых опре-
определяется структурой матрицы ^"a8Ye- В системе покоя нейтрона
эти матрицы постоянны, так как они зависят только от пере-
переменных нуклона. Поэтому после взятия следа в A0.99), который
должен иметь следующий общий вид:
где Л, В и С являются константами, Pe^pejEe и п^ = р^/?^, мы
находим для вероятности перехода в заданное конечное со-
состояние
VT
(ре + р„ + рр-рп). (ЮЛ 00)
Теперь для нахождения спектра электронов необходимо ум-
умножить это выражение на фазовый объем d3ped3p^dpp конеч-
конечного состояния и проинтегрировать по импульсам протона

$ 58) БЕТА-РАСПАД 24S
и нейтрино:
~ peEe{Mn - Mp-Eef(±+B) dEe. A0.101)
Таким образом, зависимость величины
dE ш 1ц _fFF (Ю.102)
от энергии Ее должна даваться выражением А/Ее + В. Было
обнаружено — не только в распаде свободного нейтрона, но и в
широком классе так называемых «разрешенных» ядерных пере-
переходов,— что спектр электронов удовлетворяет этому закону1)
и, более того, А = 0, т. е. величина A0.102) не зависит от
энергии.
Принято изображать спектр электронов на графике Кюри,
который представляет собой график зависимости величины
реЕе dEe
от энергии Ее. Изображаемая величина пропорциональна
(Мп — Мр — Ее), поэтому на графике Кюри ей соответствует
прямая линия. Отсутствие в A0.100) члена, пропорционального
А/Ее, объясняется конкретным видом взаимодействия, ответ-
ответственного за р-распад; к этому вопросу мы еще вернемся. Член
А/Ее принадлежит к так называемым «интерференционным чле-
членам Фирца». Последние явно отсутствуют во всех р-снектрах,
включая спектры запрещенных р-переходов, матричные элемен-
элементы которых пропорциональны скоростям нуклонов. Занятно, что
спектр электронов A0.101) при Л = 0 просто пропорционален
фазовому объему (E^peEedEe} и имеет статистическую форму,
как если бы вместо A0.100) матричный элемент был констан-
константой Sft ~ BяL б4 (ре + ру + рр — рп).
Обратимся теперь к структуре матрицы @~аау6 в A0.97). За-
Зафиксировав на время индексы у и б в A0.92), мы можем пред-
представить зависимость от индексов а и р в самом общем виде
с помощью 16 независимых комбинаций матриц у, введенных
в гл. 2:
>T(Vx)ae +
') Необходимо учитывать кулоновские поправки [111].

250 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Согласно B.38) матрицы 1, \5, ух, у5ух и аи в обкладках из
дираковских спиноров ty(x) и ^(х) образуют скаляр (S), псев-
псевдоскаляр (Р), вектор (V) и тензор второго ранга (Г) соответ-
соответственно. Тогда из A0.92) и A0.96) ясно, что для ковариантно-
ковариантности амплитуды относительно собственных преобразований
Лоренца необходимо, чтобы F<s> и Яр) были линейными комби-
комбинациями матриц 1 и ye. F{V)X и F(A)% — линейными комбинациями
матриц yt> YTYs> a FtT)U — линейной комбинацией аКх и аКху5.
В результате 5-матрица принимает вид
o(e-)
где
ая =
и
(
р, а, :
1
/ "
2Е
(Рр
г2 =
1ртег
VEpE
=(l,
= (l»
Пп
пЕе
п(Р,
Y5,
Ys>
Bл
Y.
Y",
A0.103)
Элемент 5-матрицы для обратного р-распада имеет такой же
вид с точностью до замены констант Ct и а{ на комплексно-со-
комплексно-сопряженные1) в соответствии с A0.94) и замены спинорных ин-
индексов согласно
Если мы вновь пренебрежем зависимостью нуклонных спиноров
от импульсов, тем самым ограничиваясь «разрешенными» пере-
переходами, выражение A0.103), записанное с помощью двухком-
понентных спиноров Паули, примет вид
Ж « («+«„) {С9пе (Pe) [I -f asYs] v, (p,) +
(ре) [1
«, (Ре) [1 + «Л] YbY», (P,)}. (Ю. 104)
') Точнее говоря,
at -> + а* для / = Л, V
а; -> — а) для / = 5, Р, Т.

§ 58] БЕТА-РАСПАД 251
Члены, содержащие константы Cs и Cv, вызывают разрешенные
переходы (S, V) «типа Ферми» с |Д5| = 0, а два других члена
(А, Т) ответственны за переходы «типа Гамова — Теллера» с
|А5|=1 для нуклонного состояния. Переходы типа Ферми
можно отличить от переходов типа Гамова — Теллера в ядерном
р-распаде, где уголовой момент начального и конечного состоя-
состояний фиксирован; в распад свободного нейтрона дают вклад те
и другие переходы.
Все члены в A0.104), пропорциональные «,-\5, нарушают со-
сохранение четности, и до 1956 г., когда появилась работа Ли и
Янга, их исключали, чтобы не нарушать инвариантность S-мат-
рицы относительно пространственной инверсии. Эксперименталь-
Экспериментальное обнаружение несохранения четности в слабых распадах, по-
последовавшее вслед за работой Ли и Янга [112], привело затем
к полному определению всех коэффициентов оц и С,- в ряде клю-
ключевых экспериментов [15, 17, 109].
Константы <Хг в членах, нарушающих сохранение четности,
определяются путем измерения продольной поляризации элект-
электрона. Один из методов нахождения этой поляризации состоит
в измерении право-левой асимметрии при рассеянии р-распад-
ного электрона на атоме. Мы определим поляризацию, как и в
G.95), согласно
где NR есть число «правовинтовых» электронов, т. е. электро-
электронов с положительной спиральностью, @)-n = +l, a NL есть
число «левовинтовых» электронов с @)-п — —1. Как для пе-
переходов типа Ферми, так и для переходов типа Гамова — Тел-
Теллера, и в ядрах, и в распаде свободного нейтрона поляризация
электрона в пренебрежении отдачей нуклона и после интегри-
интегрирования по углам нейтрино с хорошей точностью дается вы-
выражением
P = -i§^ = -|Pe|. A0.105)
В пределе ре-*1 испускаются только электроны с отрицатель-
отрицательной спиральностью. В том же пределе спиновый проекционный
оператор переходит, как и в G.107), в A—Ys)/2 и, таким обра-
образом, волновая функция левополяризованного электрона имеет
вид
lp фле-==ф1+^> A0.106)
Поэтому все константы «4 в A0.104) равны +1, ибо только в
этом случае осуществляется правильный переход к релятивист-
релятивистскому пределу. Поляризация при произвольном ре находится

262 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
введением C.19) и G.94) в A0.99), вычислением следов и инте-
интеграла по угловым переменным нейтрино. Теперь выражение
A0.104) упрощается и принимает вид
Ж = №.) К (Ре) 0 + Y.) (Cs + Cvy0) v9 (р,) +
f + CilY)o,(pv), A0.107)
где относительные величины постоянных Cs, Cv, Ст и Сд еще
подлежат определению.
Возведение Ш в квадрат и суммирование по спинам является
чисто вычислительной операцией, которую рекомендуется проде-
проделать в качестве упражнения. Для неполяризованных нуклонов
не возникает интерференции между переходами типа Ферми
(S, V) и типа Гамова — Теллера (А, Т). Более того, отсутствуют
интерференционные члены между S и V, а также между Л и Г,
так как эти варианты приводят к разным поляризациям нейт-
нейтрино. Действительно, переставив факторы (l + ys) направо, мы
увидим, что S- и Г-переходы приводят к испусканию антинейт-
антинейтрино с отрицательной спиральностью:
цлев („\_ "г V5 „лев
Uv {Pv) 2 v
v {Pv) 2 v \PvJ-
С другой стороны, при переходах типа V и А испускаются толь-
только антинейтрино с положительной спиральностью. Если нет
интерференции между S и V или Л и Г, то отсутствуют также
интерференционные члены Фирца, т. е. равен нулю коэффи-
коэффициент А в A0.100) и A0.101). В этот коэффициент дают вклад
члены типа
Если Га содержит четное число матриц у, то в Гв их должно
быть нечетное число, и наоборот; поэтому в член Фирца дают
вклад только интерференционные члены, которые, как мы ви-
видели, обращаются в нуль. Если бы нейтрино испускались с по-
поляризацией, меньшей, чем 100%, отсутствие членов Фирца озна-
означало бы, что взаимодействие содержит либо только члены типа
S или V, либо только типа А или Т. Однако в A0.107) входят
все четыре члена, и поэтому для получения дополнительной
информации о Cs, Cv, Сд и Ст необходимо указать экспери-
эксперименты по измерению коэффициента С в A0.100), т. е. по изме-
измерению угловой корреляции между электроном и антинейтрино.
Рассмотрим, например, чистый переход типа Ферми, содер-
содержащий только вклады S и V. Суммирование по спиновым пере-
переменным электрона и антинейтрино дает угловое распределение

§ 58] БЕТА-РАСПАД 2ЕЗ
испускаемого антинейтрино относительно электрона:
^(e)~Sp(^ + m)(l+Y6)(Cs + Y0Cv)^(C*+Y0Q(l-Y5) =
= 8?й?,[|С5|2A-ресозе) + |СИ2A +pecos6)], A0.108)
где 0 — угол между антинейтрино и электроном. Такое же рас-
распределение получается для обратного р-распада. Эксперимен-
Экспериментальное угловое распределение, найденное для почти чистого
перехода типа Ферми в Аг35 путем измерения направления вы-
вылета позитрона относительно ядра отдачи, приближенно имеет
вид A -f- pe cos 9), что указывает на векторный характер пере-
перехода. Аналогичное вычисление для переходов типа Гамова —
Теллера дает
^гтF)~?е?,[|Сл|2A __>. jocose)+ 4| Cr|2(l + у p. cose)].
A0.109)
Измерения для чистого перехода этого типа в Ne23 вместе с
другими данными по смешанным переходам указывает, что
|Сг/Сл|<С1. Тогда в пределе Ст/СА — 0 выражение A0.107)
упрощается и принимает вид суммы двух членов
а» «КХ) К (p.) Cyv° 0 - v5) о, (р,) +
V5H(P,). (ЮЛЮ)
Эта амплитуда отвечает испусканию антинейтрино с положи-
положительной спиральностью. Теперь осталось определить только амп-
амплитуды Cv и СА и их относительную фазу. Величины Cv и СА
находятся из измерений вероятности распада нейтрона и чистого
перехода типа Ферми в О14. Фаза определяется из измерения
углового распределения электрона относительно направления
спина нейтрона при р-распаде поляризованных нейтронов; это
распределение чувствительно к смеси V — А. Окончательный ре-
результат такой'):
^/2"CV = A,005 ± 0,003) • 10~5 -\ э G2),
мр
СА = (+ 1,250 ± 0,009) Cv si + аСу3). A0.111)
') Множитель I/V2 фигурирует по историческим причинам. Экспери-
Экспериментально определяется только относительная фаза Cv и СА- Принято вы-
выбирать константу Cv действительной и положительной.
2) Численное значение G взято из [113]. (Прим. перев.)
3) См. [114]. Большинство числовых данных, приводимых далее в этой
главе, взяты из данного источника. (Прим. перев.)

254
НЁЭЛЕКТРОМАГНИТНЫЁ ВЗАИМОДЕЙСТВИЯ
[ГЛ. 10
Вводя обозначения A0.111) в A0.110) и возвращаясь к реляти-
релятивистской форме записи, получаем следующую инвариантную
амплитуду р-распада:
- у,)*,
Естественно было бы рассматривать ЗЯ как амплитуду в пер-
первом порядке по взаимодействию и учесть эффекты высших по-
порядков, например такие, которым отвечают диаграммы на
рис. 10.16. Однако мы не знаем, как вычислять эти амплитуды
fp п р
(a) 0j
Рис. 10.16. Некоторые диаграммы высшего порядка для Р-распада.
в предположении A0.96) о локальности взаимодействия. Замк-
Замкнутые петли на таких диаграммах приводят к расходящимся
выражениям, которые нельзя отделить и заключить в перенор-
перенормировочные константы, как было сделано в гл. 8. Трудность
возникает из-за отсутствия бозонных пропагаторов между
нуклонными и лептонными вершинами, которые обеспечивают
сходимость при больших импульсах. Хотя мы имеем дело со
слабыми взаимодействиями, обладающими очень малой кон-
константой A0.111), вопрос о вкладе высших порядков не является
чисто академическим, так как сечения, полученные из A0.112)
для процессов рассеяния типа
растут как квадрат энергии [115] и имеют порядок величины
Когда энергия возрастает до Ец. м ~ 300 Мр ~ 300 Гэв, слабые
взаимодействия возрастают до масштабов сильных и эффекты
нелокальности и вклады высших порядков начинают играть ре-
решающую роль.

§ 59] ТЕОРИЯ ДВУХКОМПОНЕНТНОГО НЕЙТРИНО 255
§ 59. Теория двухкомпонентного нейтрино
Мы уже отмечали, что при р-распаде испускаются только
антинейтрино с положительной спиральностью. Соответственно
при обратном р-распаде испускаются нейтрино с отрицательной
спиральностью, в чем нетрудно убедиться, если учесть, что
амплитуда обратного р-распада получается из A0.112) по пра-
правилу A0.94). Поскольку нейтрино с положительной спирально-
спиральностью и антинейтрино с отрицательной спиральностью отсут-
отсутствуют как в р-распаде, так и во всех других слабых взаимо-
взаимодействиях, они представляют собой лишнюю степень свободы
в уравнении Дирака для безмассовой частицы и мы можем по-
попытаться от нее избавиться.
Уравнение Дирака для безмассовой частицы
i-^v = _/o-Vi|jv A0.114)
не содержит матрицы р, а соотношениям антикоммутации
A.16) для трех матриц щ, «2> «з
{a,,ak} = 26tk, a?=l A0.115)
удовлетворяют матрицы Паули размерности 2X2. Таким об-
образом,
а = 0. A0.116)
Напомним, что именно необходимость построить четвертую ан-
тикоммутирующую матрицу р привела к введению матриц раз-
размерности 4X4 в гл. 1.
Решение A0.114) и A0.116) в виде плоской волны с положи-
положительной энергией имеет вид
где Е = |р|, а спинор u(p,s) удовлетворяет уравнению
Еи(р, s) = a-pu{p, s). A0.118)
Решением уравнения A0.118) в обычном представлении матриц
Паули с осью г, направленной вдоль р, является
и(р, +) = (J). A0.119)
Оно описывает нейтрино с положительной спиральностью:
Чтобы получить нейтрино с отрицательной спиральностью, ко-
которое наблюдается в природе, мы должны выбрать решение

256 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
уравнения A0.115), в котором
а = -а, A0.120)
вместо A0.116). В этом случае A0.118) заменяется на
Еи{р,-) = -о-ри{р,-) A0.121)
и мы имеем решение, отвечающее нейтрино с отрицательной
спиральностью,
и(р, -) = (?)• (Ю.122)
Для того чтобы лучше понять связь этих двухкомпонентных
решений с уже хорошо нам знакомыми четырехкомпонентными
электронными спинорами, мы вернемся к уравнению Дирака
для частицы с массой т и выберем следующее представление
матриц аир:
/сг. 0 \ / 0 —1\
а,- = @( _ffJ. e=(-i о)- A
которое отличается от A.17) унитарным преобразованием
Тогда, вводя обозначение
,,,_(" (+)
мы можем записать уравнение Дирака A.13) в виде
(Ю.124)
В A0.124) верхние и нижние компоненты г)з перемешиваются
только массовыми членами, поэтому в пределе т -»- 0 возни-
возникают два несвязанных уравнения, соответствующие A0.114).
В одном из них а = а, как в A0.116), а в другом а = —а, как
в A0.120). В представлении A0.123)
Нетрудно убедиться, что решение
при т-»-0 отвечает нейтрино с положительной спиральностью,
так как

§ 59] ТЕОРИЯ ДВУХКОМПОНЕНТНОГО НЕЙТРИНО 257
Аналогично для
имеем
следовательно, решение г)з(—) отвечает нейтрино с отрицатель-
отрицательной спиральностью.
На возможность описания безмассовой дираковской частицы
двухкомпонентным уравнением впервые указал Вейль [116] в
1929 г., однако эта идея не была серьезно воспринята, так как
при переходе к двум компонентам исчезает матрица р и те-
теряется симметрия относительно Р-преобразования, задаваемого
согласно B.32) оператором Р = e'^fj.
После открытия несохранения четности в 1956 г. уравнение
Вейля было воскрешено в работах Ландау, Ли и Янга и Салама
[117, 118]. Они обратили внимание на то, что зарядовая чет-
четность С, которой соответствует оператор E.5), E.6), также не
сохраняется, однако имеет место инвариантность относительно
совокупности обеих операций СР, которую называют комбини-
комбинированной инверсией.
Согласно E.5) операция зарядового сопряжения состоит в
замене г)з(х, t) на г|)с(х, t) = Срф* (х, t), где матрица С удовле-
удовлетворяет E.4) и E.6). В новом представлении этим условиям
удовлетворяет матрица
В случае ДЕухкомпонентного нейтрино присутствие матрицы {5
в операторе зарядового сопряжения означает, что это преобра-
преобразование уже не является операцией симметрии, однако комби-
комбинированное преобразование СР есть операция симметрии. Дей-
Действительно, если г)з(х) представляет собой решение A0.114),
то решением оказывается и функция
ЪСР{х, 0 = Сф'(-х, fl = =F/<x2i|>*(-x, t), A0.125)
поскольку
jf + ia- V,) ЦСР (х, I) = + ia2 (/ ± - ia* ¦ Vx) ^ (- х, t) =
= Т ia2 [(- i jf-ia- V*') * (x\ /)]* = 0,
где x' = — x.
Волновая функция антинейтрино получается по аналогии с
E.7) и E.8) для электронов. Возьмем решение с отрицательной
энергией, проделаем над ним комплексное сопряжение и умно-
умножим на ia2. Например, решение с отрицательной энергией

258 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
уравнения A0.114) с а = —а для нейтрино с отрицательной
спиральностью имеет вид (Е = +|р|)
где
— Ev{—p,—) = — o-pv(- р, —),
v(-p, -) = (J). A0.126)
Согласно A0.125) волновая функция антинейтрино есть
Она, очевидно, также является решением уравнения Вейля с от-
отрицательной спиральностью. Таким образом, функция A0.127)
действительно отвечает частице с отрицательной спирально-
спиральностью, но в системе координат х' = —х, полученной простран-
пространственным отражением. Можно привести такую аналогию:
правша кажется в зеркале левшой. Точно так же антинейтрино,
обладающие отрицательной спиральностью в штрихованной си-
системе, имеют в нештрихованной системе положительную спи-
спиральность.
§ 60. Распад ц-мезона
В распаде ц-мезона (мюона)
ц- ->¦ е~ + 'v' + v
участвуют четыре фермиона, включая пару (е~, v). Такое сход-
сходство с р-распадом нейтрона позволяет предположить, что мат-
матричный элемент имеет такую же, как для C-распада, форму. По
аналогии с амплитудой обратного C-распада амплитуда про-
процесса
ц,+ —>• е+ •+¦ v -f- v'
находится из принципа детального равновесия. Вновь, как в
A0.112), мы объединяем волновые функции пары (е~, v), счи-
считая, что имеется связь вида
ue(p)yu(l-\5)Vv(k) A0.128)
(кинематические обозначения указаны на рис. 10.17).
Такая связь означает, что образующиеся при распаде ц~
антинейтрино имеют положительную спиральность, а электроны
полностью поляризованы против направления своего движения

60]
РАСПАД ц-МЕЗОНА
259
(позитроны от распада \i+ полнос1ью поляризованы по направ-
направлению движения). Поляризация нейтрино экспериментально не
исследовалась, но опыты показали, что, как и предсказывает
A0.128), электроны полностью поляризованы против направ-
направления своего движения [119, 120].
Элемент 5-матрицы для ц-распада принимает вид
. A0.129)
Параметр Л, определяющий поляризацию v', и константа
связи О должны быть найдены из наблюдаемого спектра элект-
электронов и вероятности распада.
Вероятность распада уг для случая неполяризованных ча-
частиц получается из A0.129) путем_ умножения \Sfi\2 на фазовый
объем конечных частиц d3p d3k d3k, введения проекционных опе-
операторов для суммирования по спинам, деления на 2, что соот-
соответствует усреднению по спинам \х~, деления на VT = BяLб4@)
с целью получить вероятность перехода, нормированную на еди-
единичный объем, и, наконец, деления
на плотность ц~, равную 1/BяK. В ре-
результате для вероятности перехода
имеем
d3k d3k v
2?\ 2Е- ^
к k
~2BлM 2Ер ) 2Е
XV{P-P-k-k)
spins
где
spins
X Sp [(/) + me) Ytl A -
A - Ys)]-
A0.130)
Рис. 10.17. ц-распад.
Из A0.130) следует, что в выражении для полной проинте-
проинтегрированной вероятности распада все, что стоит справа от
BЕР)~\ лоренц-инвариантно. Таким образом, величина, обрат-
обратная вероятности распада, пропорциональна энергии ЕР в соот-
соответствии с требованием теории относительности. В системе по-
покоя мюона эта величина есть его время жизни.

260 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Вычисляя следы, получаем
? | ЭХ |2 = 32G2 A + 1112) (к • рР ¦ k + к • кр ¦ Р) +
spins л
+ G2 (I + Г) Sp (b^YvY5) Sp (/>Y|lfYvYe). (Ю-131)
Произведение двух последних следов есть скаляр, антисиммет-
антисимметричный по k и Р, по k и р и линейный по всем четырем импуль-
импульсам. Можно записать его в виде
Sp (?y"PyvY5) Sp (pY^YvYs) = a(k-kp-P-k-pP-k). A0.132)
Для определения постоянной а зададим на время векторы
k, k, p, P в удобной для вычисления форме, но с условием, что-
чтобы выражение A0.132) не обращалось в нуль. Например, при
*и = ?ц = A,0, 0,0) и РA = р11 = @, 1,0, 0) выражение A0.132)
принимает вид
— а =
При суммировании по индексам ц и v дают вклад только две
комбинации: ц, — 2, v = 3 и ц = 3, v = 2. Таким образом,
— а = 2Sp (Y0Y2Y1Y3Y5) Sp (Y1Y2Y0Y3Y5) = + 32.
Тогда для A0.131) имеем
2) |ЗК|2 = 32О2[|1— 112 /г • fep • Р + И +Я|2^-р^-Р]. A0.133)
spins
Далее проинтегрируем по импульсам ненаблюдаемых нейтри-
нейтрино в A0.130). Поскольку |5W|2 линеен по k и Б, мы должны вы-
вычислить интеграл
\t§:kak*6\Q-k-k), A0.134)
где Q = Р — р. Этот интеграл преобразуется как лоренцев тен-
тензор второго ранга, и его удобнее всего вычислить в системе
центра масс двух нейтрино, где Q является чистым времени-
подобным вектором. В данной системе после несложных вы-
вычислений находим
J(O)=24-QoLg ^ ё g J"
Поскольку A0.134) является тензором второго ранга, мы можем
в любой лоренцевой системе записать ответ в виде
^ A0.135)

61] РАСПАД Я-МЕЗОНА 261
Объединяя A0.130), A0.133) и A0.135), получим
*=? pd%dQp {\1-м2ър-рн+т1-2р-р)+
%
+ | 1 + X р [- 4 (р • Р? + Зр ¦ Р (ml + ml) - 2/n*mf]}.
Интегрируя по углам вылета электрона и пренебрегая его мас-
массой покоя, т. е. полагая meIEv-*-0, имеем следующее распреде-
распределение по энергии электрона в системе покоя уг:
A0.136)
Наблюдаемое распределение с хорошей точностью согла-
согласуется со значением Л = +1, т. е. нейтрино, фигурирующее в
A0.129) в паре с \х~, также имеет отрицательную спираль-
ность1). Полагая 1=1 в A0.136) и интегрируя по всем энер-
энергиям электрона 0 < Ер ^ '/г^ц, получаем полную вероятность
распада ц-мезона
1 G2ml
Значение константы G, найденное из измеренного времени
жизни, равного
^ = B,197134 + 0,000077) • 10~6 сек,
с точностью до 2% совпадает со значением векторной константы
связи G = л/2 Cv для ядерного р-распада A0.111) (см. [122,
123]).
Мы получили очень сильное указание на универсальность
слабого взаимодействия между фермионами. Равенство констант
есть дополнительный аргумент в пользу правильности приня-
принятого нами описания взаимодействия. Теперь мы обратимся к
другим процессам, в которых участвуют лептонные пары (е~, v)
или {\и~, v'), и проверим, относится ли связь между лептонами
в этих процессах к (V — Л)-типу A0.128).
§ 61. Распад я-мезона
При построении элемента S-матрицы для распада я-мезона
A0.91) мы можем снова принять за исходный пункт (V — А)-
связь A0.128), которая прекрасно описывает р-распад и распад
') Энергетическая зависимость A0.136) при X = + 1 отвечает параметру
Мишеля р = 3/4 (см. "

262 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
мюона. В пользу этого предположения свидетельствуют два
экспериментальных наблюдения. Во-первых, обнаружено, что [i~
в распаде п~ —> уг + v' продольно-поляризован в направлении
своего движения. Тогда антинейтрино также должно быть поля-
поляризовано в направлении своего движения, т. е. иметь положи-
положительную спиральность, так как спин лг равен нулю. В системе
покоя я~-мезона частицы \i~ и v' испускаются с равными и про-
противоположно направленными импульсами и должны быть оди-
одинаково продольно-поляризованы (либо обе по направлению
своего движения, либо обе против), поскольку только в этом
случае суммарная проекция их углового момента на направле-
направление движения будет равна нулю. Вывод о том, что антиней-
антинейтрино имеет положительную спиральность, согласуется с
A0.128).
Второе экспериментальное наблюдение, свидетельствующее
в пользу A0.128), — это очень малое отношение вероятностей
распада
Я( п~>е + '*Л = 1,26- 10~4. A0.138)
Сильное подавление испускания электрона предсказывается
A0.128) благодаря фактору A—у$), который приводит к пол-
полностью поляризованным нейтрино с отрицательной спирально-
стью и антинейтрино с положительной. Переставляя этот фактор
налево, получаем п(р){\ +Ys). что в пределе vJc—*\ соответ-
соответствует испусканию электронов, продольно-поляризованных
только против направления движения (и позитронов, поляризо-
поляризованных по направлению движения).
Запрещенный: -* Q ^ Q *— $?= + 0
е~(отрицателдтя ^ ^Г ^ v(положительная
елиралшат-) ~ спираль/меть)
Разрешенный: -е Р
( ^_. v(положительная
cnupamHocmt) ¦* спиральносли)
Рис. 10.18. Сохранение спина в распаде я-мезона, приводящее к тому, что
как е~, так и v имеют положительную спиральность.
Однако, как мы уже отмечали и как показано на рис. 10.18,
в распаде п~ антинейтрино с положительной спиральностью со-
сопровождается электроном, продольно-поляризованным по на-
направлению своего движения. Поэтому получаемая из A0.128)
вероятность распада содержит фактор подавления, равный

§61)
РАСПАД я-МЕЗОНА
263
где [I — масса пиона. Он соответствует вероятности испускания
электрона, поляризованного по направлению движения. Более
тяжелый ц-мезон, испускаемый с энергией
является нерелятивистским; его спиновый проекционный опера-
оператор существенно отличается от A ±Ys), и заметного подавления
не возникает.
Итак, мы примем A0.128) в качестве лептонного члена в
матричном элементе для распада пиона и будем искать 4-вектор
или аксиальный вектор, на который должен быть умножен леп-
тонный член, чтобы получить инвариантную амплитуду пере-
перехода.
Поскольку спин я-мезона равен нулю, этот вектор должен
быть построен из двух независимых 4-векторов, характеризую-
характеризующих распад, 4-импульса я-мезона Рр, и 4-импульса нейтрино Аг^,
изображенных на рис. 10.19. Однако k^ не
дает вклада, так как kv^(k) = Q. Тем са-
самым структура матричного элемента для
распада я-мезона определяется однозначно;
он равен
?'= —^X
X [й (p) Y» A - Y5) «v (?)] Bя)« б4 (P - p - Й).
A0.139)
Постоянная G есть константа р-распада
A0.111), а коэффициент а, характеризую- рИс. 10.19. Распад
щий полную вероятность распада, может я-мезона.
быть разным для распада на ц~ и ег.
Повторяя выкладки, близкие к A0.130) — A0.137) (но более
простые), находим для вероятности распада
J BяK /J\
т„ ~~ BяN \2ц J
G21
<10140>
где т — масса испускаемого электрона или мюона.

264 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
Если постоянная а одна и та же для электронного и мюон-
ного каналов распада, то из A0.140) получаем следующее
отношение вероятностей:
(и2 —
lJ
я->-е + v \ / т„ V (и2 — mlJ ,
г^Ы—) -Г5—f^-= 1,з• ю-4,
что находится в хорошем согласии с экспериментально наблю-
наблюдаемым значением A0.138). Это говорит в пользу связи
A0.128), которая является универсальной для всех лептонных
распадов. Если бы не было строгого правила отбора, налагае-
налагаемого (V — Л)-связью, согласно которому нейтрино имеют
отрицательную спиральность, а антинейтрино — положитель-
положительную, отношение вероятностей не было бы таким чрезвычайно
малым, а было бы близко к значению, даваемому фазовым
объемом
По экспериментально измеренному времени жизни я-мезона,
равному т = B,6030 + 0,0023) • 10~8 сек, находим коэффициент
в A0.140):
|а|«0,92 ц. A0.141)
Предположение об универсальности связи A0.128) для всех
лептонных распадов позволяет определить поляризацию ^-ме-
^-мезона в распаде пиона. Зная ее, можно однозначно предсказать
параметр асимметрии в распаде ц-мезона, который характери-
характеризует корреляцию между направлением вылета электрона и на-
направлением спина ц-мезона в последовательном распаде
я- -* ц~ + v'
U е~ + v + v'.
Для определения асимметрии вычислим сначала поляриза-
поляризацию ц-мезона, испускаемого в заданный элемент телесного
угла, а затем найдем спектр электронов от распада этих
ц-мезонов.
Чтобы найти поляризацию ц-мезона в распаде пиона, вер-
вернемся к A0.139) и вычислим вероятность распада на мюон
с заданной поляризацией s. Введем, как в G.89) и G.90), спи-
спиновый проекционный оператор (l+Y5s)/2 и воспользуемся

§ 61] РАСПАД я-МЕЗОНА
265
техникой вычисления следов. Тогда вместо A0.140) получим
4я2 2?р 2 J 2?g 2?„
где Р и р представляют собой 4-импульсы пиона и мюона со-
соответственно. Вероятность распада максимальна для ц~ с поло-
положительной спиральностью, т. е. согласно G.94) при
Вероятность обращается в нуль, если р,-мезон имеет отрица-
отрицательную спиральность, sL = —sR.
Для получения вероятности распада ц-мезона, обладающего
заданной поляризацией s, мы возвращаемся к A0.129) и повто-
повторяем вычисления, подставляя Я, = +1 н пренебрегая массой
покоя электрона, т.е. полагая те/Ер^>-0. Спиновый проекцион-
проекционный оператор A +Y5^)/2 вновь позволяет свести суммирование
по спинам к вычислению следов:
electron
spin
X Sp [pYpA - Ys) *Yv0 - Ys)] = 64G2& • pk ¦ (P - mMs\
Интегрирование по переменным ненаблюдаемого нейтрино про-
производится, как в A0.135), и дает
^ _ G2 pdEpdQp
X {- Ц ^ [
В системе покоя ц--мезона имеем
— - 01
тр. /J
48я4 ">^р "~р "uu LV mM У ' Ер
Согласно A0.142) ц--мезон от распада пиона имеет положи-
положительную спиральность. Поэтому из G.94) следует
= — se • п = — cos 8.

266 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
где 8 — угол между направлением спина ц-мезона и направле-
направлением вылета электрона. Отсюда получае;и
т\Е% dEp d (cos 6) [з - 4 ^-] A - a cos 9),
где
а =
представляет собой параметр асимметрии, значение которого
совпадает с измеряемым на опыте [15—17, 109].
§ 62. Два типа нейтрино
Все рассмотренные нами лептонные взаимодействия характе-
характеризовались одним и тем же типом (V — Л)-связи A0.128) в
матричном элементе для лептонов. Это значит, что в слабых
взаимодействиях \i~ и е~ переходят в нейтрино с отрицательной
спиральностью. Природа, проявив скупость в том, что для устра-
устранения лишней степени свободы нейтрино позволила четности не
сохраняться, оказалась необъяснимо щедра, допустив существо-
существование двух типов нейтрино, v и v', очень похожих и в то же
время совсем разных. Нейтрино v, связанное в вершине с элект-
электронной линией, имеет отрицательную спиральность и нулевую
(либо очень малую) массу, так же как нейтрино v', связанное
с (.i. Тем не менее они различны ').
Первое указание на то, что имеются два типа нейтрино, было
получено из сравнения не слишком надежной теоретической
оценки вероятности радиационного распада по каналу
с ее экспериментальным значением, которое дается отношением
R (ц- -> е~ + у) о 0 .„-8
R (ц- -> е~ + v + v') <~Z'^' Ш ¦
Рассматриваемый процесс может идти в первом порядке
теории возмущений по слабому взаимодействию, только если
последнее обусловлено обменом промежуточным заряженным
векторным мезоном. Приняв эту гипотезу, можно произвести
расчет вероятности, рассмотрев диаграммы, изображенные на
рис. 10.20.
Хотя возникающие интегралы расходятся и результаты ра-
расчета нельзя поэтому принимать буквально, трудно получить
для приведенного выше отношения значение меньше, чем
') В лучшем случае они могут оказаться двумя разными парами компо-
компонент четырехкомпонентного нейтринного спинора.

§ 63] ГИПОТЕЗА О СОХРАНЯЮЩЕМСЯ ВЕКТОРНОМ ТОКЕ 267
К)-4—10~5. Однако эти диаграммы, так же как и все другие, об-
обращаются в нуль [124], если нейтрино v', соответствующее ц~,
отличается от нейтрино v, отвечающего е~.
Более надежный опыт для решения вопроса о существова-
существовании двух типов нейтрино был предложен Понтекорво и Швар-
Шварцем [115]. Идея состоит в том, чтобы с помощью пучка v' от ра-
распада пионов вызвать реакции типа
v' + 9!->^ + ^ или е.
Рождение ц в этой реакции было экспериментально обнаруже-
обнаружено, в то время как ни одного события с испусканием е не было
Wl?)
>xxxxxx«
Рис. 10.20. Распад ц -> е + у, который возможен, если нейтрино v и v'
тождественны.
найдено. Это говорит о существовании двух типов нейтрино.
Тем самым к вопросу «Чем, кроме массы покоя, отличаются
ц и е и зачем природе понадобились два заряженных лептона?»,
ответ на который никому не известен, теперь можно добавить
еще один вопрос: «Зачем нужны два типа нейтрино?».
§ 63. Гипотеза о сохраняющемся векторном токе
Распады л- и ц-мезонов, так же как ядерный р-распад, ука-
указывают, что лептонные пары (е, v) и (ц, v') связаны в матрич-
матричных элементах распада одной и той же связью типа (V—А).
Более того, из сравнения A0.112) и A0.129) с а=1,25, К =
= 1,00 и G « G можно сделать вывод о большом сходстве ме-
между нуклонной и лептоннои связями.
Естественно было бы ожидать, что облако сильно взаимо-
взаимодействующих я-мезонов, которым, в отличие от лептонов, ок-
окружены физические нуклоны, изменит векторную и аксиально-
векторную константы связи, введенные для «голых» нуклонов
в отсутствие сильного взаимодействия. Поэтому поразительным
представляется тот факт, что векторные константы для р-рас-
пада и р,-распада совпадают с точностью до 2%. Даже коп-
станта а = 1,25, которая дает отношение аксиальных частей

268 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
взаимодействия для нуклонов и лептонов, оказывается доста-
достаточно близкой к единице, чтобы, основываясь на этой близости,
строить интересные предположения.
Исследование электромагнитных взаимодействий электро-
электронов в гл. 8 и протонов в § 56 дает важный ключ к пониманию
равенства векторного тока взаимодействия нуклонов и лептонов.
Равенства (8.50) и (8.57) показывают, что вершинная функция
электрона за счет радиационных поправок перенормируется
фактором Z~l. Согласно (8.46) и (8.57) дополнительный фак-
фактор Z2 появляется также в элементах S-матрицы благодаря пе-
перенормировке волновой функции электрона. В низшем порядке
по а было установлено, что Z\ = Z2 (см. (8.54)) и, следова-
следовательно, эти эффекты взаимно компенсируются; было также ука-
указано, что равенство Z\ = Z2 справедливо во всех порядках и
является следствием тождества Уорда (8.51) [50].
Такое же положение имеется в электромагнитном взаимо-
взаимодействии протонов. Мезонные поправки, которым соответствует
рис. 10.13 и формула A0.86), перенормируют электромагнитную
вершину протона фактором (бесконечным в теории возмуще-
возмущений), аналогичным Z,, причем он вновь компенсируется обус-
обусловленной мезонами перенормировкой протонных волновых
функций. Это утверждение можно проверить с точностью до
второго порядка по мезон-нуклонному взаимодействию, показав,
что равенство (8.51) справедливо с учетом мезон-нуклонного
взаимодействия.
Из равенства перенормировочных постоянных следует очень
важный вывод: физические, наблюдаемые заряды электрона и
протона равны друг другу, если равны их «голые», неперенорми-
рованные заряды, так как изменение фотонного пропагатора за
счет поляризации вакуума одинаково сказывается на электроне
и протоне. Это свойство уже подразумевалось ранее при рас-
рассмотрении электромагнитной структуры протона, когда величина
.FiP)@) была положена равной 1 в A0.8).
Форма матричного элемента р-распада для векторной части
взаимодействия
-^Utn = -^fY^, A0.143)
где
имеет большое сходство с электромагнитной вершиной протона.
Это сходство становится еще более очевидным благодаря тому,
что мезонные поправки не влияют на коэффициент при у^ для
нулевого переданного импульса. Основное отличие состоит в
том, что при р-переходе заряд меняется на единицу. Герштейн

§ 63] ГИПОТЕЗА О СОХРАНЯЮЩЕМСЯ ВЕКТОРНОМ ТОКЕ 269
и Зельдович [125] и позже Фейнман и Гелл-Манн [122] предпо-
предположили, что векторный «ток» в р-распаде может быть получен
из электромагнитного тока путем изотопического поворота. По-
Последний можно производить благодаря зарядовой независимости
сильных взаимодействий.
Вспоминая, что согласно A0.89) электромагнитный ток ну-
нуклонов может быть записан в виде суммы изоскаляра и изовек-
тора, правило Фейнмана — Гелл-Манна можно сформулировать
следующим образом: векторный ток р-распада получается из
изовекторнои части электромагнитного тока /^ заменой
;з _^ /+ _
Л
V2"
;/2\
Это правило известно как гипотеза о сохраняющемся векторном
токе. В отсутствие радиационных поправок он в точности соот-
соответствует взаимодействию A0.143). С учетом радиационных
поправок векторная часть матричного элемента для р-распада
получается непосредственно из A0.89):
/+ = 2 -^(pOt+jyWfo2) + ^^Ч<72)] ТО- (Ю.144)
Поскольку из электрон-протонного рассеяния известно, что в
области —q2 <С \x2 форм-факторы приблизительно постоянны,
они могут быть заменены своими значениями в точке q2 = 0.
Тогда формула A0.144) принимает вид
О Г 3,70/(T,,v <7
(/)h+
A0Л45)
Мы видим, что по своему построению этот ток сохраняется, т. е.
Помимо того, что константа при /^ в A0.145) не перенор-
перенормируется, другим экспериментально проверяемым следствием
гипотезы о сохранении векторного тока является наличие в этой
формуле второго члена, названного «слабым магнетизмом» [126].
К сожалению, он имеет тот же порядок величины, что и по-
поправки первого порядка на отдачу нуклона при р-распаде, и
поэтому его трудно наблюдать на опыте. Однако слабый магне-
магнетизм был тем не менее обнаружен в блестящем эксперименте
[127] по изучению р-переходов ядер В12 и N12 в основное состоя-
состояние ядра С12.
Согласно гипотезе о сохранении векторного тока можно по-
получить правила диаграммной техники для слабых взаимодей-
взаимодействий из фейнмановских правил для электродинамики. Во-пер-

270
НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
[ГЛ. 10
вых, имеется полное соответствие между диаграммами для
р-распада и электромагнитных взаимодействий. Например,
электромагнитная структура описывается диаграммами на
рис. 10.21 вместо диаграмм на рис. 10.13.
В диаграммах на рис. 10.21, а и 10.21, в вместо еA+тз)/2
фигурирует фактор (с/д/2)т+. Диаграмма на рис. 10.21,6 соот-
соответствует «слабому пионному току», который вновь получается
(О)
\я°
(в)
Рис. 10.21. Векторная часть вершины слабого взаимодействия согласно гипо-
гипотезе о сохранении векторного тока.
из пионного электромагнитного тока вращением в изотопиче-
изотопическом пространстве. Пионную электромагнитную вершину можно
найти, взяв ток в A0.37) в качестве матричного элемента пере-
перехода; тогда вершина имеет в импульсном представлении сле-
следующий вид:
? = - ie (фе' X феK {К + Р J. 00.146)
где фе и фе , р яр' представляют собой изотопические волно-
волновые функции и импульсы начального и конечного мезонов.
Очевидное различие на коэффициент 2 между A0.146) и
A0.37) обусловлено тем, что в A0.37) имеются два способа со-
сопоставления волновых функций ф{х) начальным и конечным
частицам. Для получения вершины р-распада мы вновь заменим
третью компоненту на «повышающую» компоненту и е — на
О/д/2; в результате получим следующее выражение для пион-
ной вершины на рис. 10.21, б:
' X Фе), + i (Фе' X феJ][Х + PJ- 00-147)
Наличие во взаимодействии такого члена приводит к дру-
другому экспериментально наблюдаемому следствию, а именно

§ 64] ЧАСТИЧНО СОХРАНЯЮЩИЙСЯ АКСИАЛЬНЫЙ ТОК 271
существованию распада [15, 17, 109, 122, 125]
я+-*я° + е- + v. A0.148)
Матричный элемент с учетом сильных взаимодействий снова
связан с пионным электромагнитным током A0.85) посредством
изотопического поворота. Поэтому единственное изменение, вно-
вносимое в A0.147) мезонными радиационными поправками, со-
состоит в появлении пионного форм-фактора Fn(q2), который при
малых <72, участвующих в реакции A0.148), может быть положен
равным 1. Тогда можно вычислить вероятность рассматривае-
рассматриваемого распада, исходя из вершины A0.147). Расчет дает следую-
следующее значение для отношения этой вероятности к вероятности
доминирующего распада1):
R (я- -> ц,- + v) v
Таким образом, гипотезу о сохранении векторного тока мож-
можно кратко сформулировать следующим образом. Лептонный ток
¦ФеУнО — Y5)^v взаимодействует с «повышающей» компонентой
сохраняющегося изотопического тока A0.43), который по ана-
аналогии с электродинамикой рассматривают как ток перехода.
Экспериментально проверяемые следствия возникают благодаря
тому, что эта «повышающая» компонента определяется из тре-
третьей компоненты согласно зарядовой независимости сильных
взаимодействий; третья компонента может быть измерена в
электромагнитных взаимодействиях.
§ 64. Частично сохраняющийся аксиальный ток
Мезонное облако, окружающее нуклоны, влияет также на
аксиально-векторную, или типа Гамова—-Теллера, часть р-рас-
падного взаимодействия. Мы можем предположить, что именно
с этим мезонным облаком связано происхождение числа
а =1,25, характеризующего отношение аксиально-векторной
константы к векторной. Величина а близка к единице, а если
проделать перенормировку константы за счет связанных с ме-
мезонным облаком виртуальных эффектов по теории возмущений,
то получится логарифмически расходящееся выражение. Можно
поэтому сделать предположение, что для аксиально-векторного
р-распадного взаимодействия имеется приближенный закон со-
сохранения [128].
Поскольку в настоящее время отсутствует прогресс в объ-
объяснении величины а на основе этой не вполне отчетливой идеи,
или исходя из любых иных предположений, мы не будем более
') См. *Л. Б. Окунь, ссылка [109]. (Прим. перев.)

272
НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ
[ГЛ. 10
обсуждать величину а. Однако, как мы сейчас увидим, идея
о том, что в амплитуде слабого распада лептоны связаны с
«частично» сохраняющимся аксиально-векторным нуклонным
током, принесла некоторый успех в объяснении наблюдаемого
времени жизни я—мезонов.
Простейшая радиационная поправка к аксиально-векторному
току — это поправка, обусловленная одним я-мезоном; она изо-
изображена на рис. 10.22. Соответствующий член в инвариантной
амплитуде |3-распада имеет вид
аи1я = ^ (- ig л/2) [п
X
X «) [п(ре) Г(\ - Ye) о (*)], A0.150)
где Са/д/2 есть константа связи в амплитуде распада я*
A0.139), a g является константой сильного л — Af-взаимодей-
ствия. Добавочный множитель д/2 возникает из изотопической
матрицы для испускания заряженного пиона. Кинематические
обозначения введены на рис. 10.22. Возникает также ряд допол-
дополнительных вкладов первого порядка по слабому взаимодей-
взаимодействию от диаграмм типа изображенных
на рис. 10.23. Все вклады от диаграмм
на рис. 10.23 можно записать в виде
РА /~к
где
К (РР> Рп) =
= -?= п (Рр) [
Рис. 10.22. Вклад одно-
пионного обмена в акси-
аксиальную часть слабого
взаимодействия.
(<72)
= Рр+ рп.
По своей структуре это выражение похо-
похоже на электромагнитный ток A0.87) с той
разницей, что для получения аксиального
вектора сюда добавлена матрица у5. Если мы примем, что, по-
подобно диаграммам на рис. 10.23, все остальные вклады в f~l
преобразуются как «повышающая» компонента изотопического
вектора, то A0.151) можно упростить, показав, что
#-.,072) = 0. A0.152)
Это равенство следует из инвариантности сильного взаимодей-
взаимодействия относительно зарядового сопряжения и изотопической ин-

§ 64|
ЧАСТИЧНО СОХРАНЯЮЩИЙСЯ АКСИАЛЬНЫЙ ТОК
273
вариантности. Чтобы его доказать, повернем сначала f^ в изо-
изотопическом пространстве, заменив т+. в слабых вершинах
диаграмм на рис. 10.23, а на тз, а также в вершине испускания
я~-мезона, связанного с лептонами на рис. 10.23,6. Благодаря
п\
(а)
F)
Рис. 10.23. Аксиальные вклады в р-распад.
зарядовой независимости сильных взаимодействий f^ перехо-
переходит при этом в третью компоненту изотопического вектора; в
частности, для протона
= -щ п (р') [Y,Y5^. (q2) + «7,Y5^2 (q2) + Ptf
где
(q2)] и (р), A0.153)
Согласно зарядовой инвариантности сильного взаимодействия
дополнительные вклады в A0.151) от диаграмм на рис. 10.23
должны привести к току
f\kp', Р), который при заме-
замене протона на антипротон
преобразуется в точности
так же, как ток «голого»
протона:
?). A0.154)
Рис. 10.24. Слабая вершина для анти-
антипротона.
Рассеянию антипротона
из состояния с импульсом р
в состояние с импульсом р'
отвечает диаграмма на
рис. 10.24. В соответствии с результатами гл. 6 можно счи-
считать, что на ней изображен протон с отрицательной энергией,
движущийся назад во времени, который рассеивается из состоя-
состояния (—р') в состояние (—р). Его аксиально-векторный ток

274 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
имеет вид
о (р) YuYe» (рО = - "' (р) С~\уъСпт (рО е1* =
5«(p)ei*, A0.155)
где мы использовали соотношение E.8) (по поводу фазового
множителя см. рассуждения перед E.8)). Теперь мы должны
сохранить в токе A0.153) лишь члены, обладающие теми же
трансформационными свойствами, что и «голый» ток, поскольку
flc(~P, -P') = -71(P', Р)е'Ф- (Ю.156)
Отсюда нетрудно получить равенсгво A0.152).
Все вклады диаграмм типа изображенной на рис. 10.23,6 в
аксиально-векторную часть амплитуды могут быть записаны
как произведение выражения вида A0.150) на скалярную функ-
функцию q2. Все поправки к пион-нуклонной вершине приведут к
следующей форме взаимодействия:
где q == рп — рр, а 9Г (q2) является инвариантной функцией q2.
Это следует из того, что число вершин, в которые входят мат-
матрицы у5, всегда нечетно и все факторы рр и рп можно переста-
переставить направо и налево, где они, действуя на свободные дираков-
ские спиноры, дадут М. Таким образом, диаграммы типа пока-
показанной на рис. 10.23,6, на которых единственный мезон из
окружающего нуклон облака непосредственно связан с лепто-
нами, дают вклад только в $~г(<72) в A0.151). Выделяя из
&~2{q2) этот вклад, запишем
T2tf) = ?-2tf)-a8ff/]. (Ю.157)
Постоянная а связана с наблюдаемым временем жизни я—ме-
я—мезонов посредством A0.140), а форм-фактор ?Г(<72) в точке
q2 = \x2 может быть выражен через пион-нуклонную константу
связи g, как было показано в § 55. Полагая в A0.157) кон-
константу g равной наблюдаемой константе (я — N) -связи ?2/4я «
« 14, нормируем &'(q2) на 1 в точке q2 = ц2:
5г(м-2)=1. A0.158)
Относительно 3~2 ничего не известно. Однако, поскольку 2Г2
является коэффициентом при величине (?nYs, которая пред-
представляет собой поправку порядка (q/M) на отдачу нуклона, ЗГч
не наблюдается в р-распаде. Из предыдущего мы знаем, что
#¦,@) = —a = -1,25. A0.159)

§ 64] ЧАСТИЧНО СОХРАНЯЮЩИЙСЯ АКСИАЛЬНЫЙ ТОК 275
Воспользовавшись этими предварительными замечаниями,
мы можем теперь рассмотреть вопрос о частично сохраняю-
сохраняющемся аксиально-векторном токе. Если бы аксиально-векторный
ток строго сохранялся, условие
в применении к A0.151) привело бы к соотношению
или
Поскольку &~\@) Ф 0, это означало бы, что 5Гъ имеет полюс
при <72 = 0, что соответствует обмену безмассовой псевдоскаляр-
псевдоскалярной частицей. Представляется соблазнительным отождествить
этот полюс с я-мезонным в A0.157) и связать нарушение точ-
точного сохранения тока с существованием массы у я-мезона.
Таким образом, используя A0.151) и A0.157), мы приходим
к видоизмененной гипотезе:
= Нт п (Рр) y5 [- ^^
A0.160)
Делая дополнительное предположение, что в пределе ц2—»0 ин-
инвариантные форм-факторы мало отличаются от своих физиче-
физических значений, получаем из A0.160)
— 2/И5~, @) = + 2Ма = + 2М A,25) « agл/2. A0.161)
Отсюда следует численное предсказание
а|« 0,90ц,
которое с хорошей точностью согласуется со значением, получае-
получаемым из наблюдаемого времени жизни я^мезонов с помощью
A0.141). Подобное соотношение между вероятностью распада
я-мезона, постоянной Ферми G и константой взаимодействия
пион-нуклон было впервые получено Гольдбергером и Трейма-
ном [129] путем приближенных вычислений в дисперсионной
теории. Впоследствии Намбу, а также Бернстейн и др. [128] по-
получили его как следствие частичного сохранения аксиально-век-
аксиально-векторного тока.

276 НЕЭЛЕКТРОМАГНИТНЫЕ ВЗАИМОДЕЙСТВИЯ [ГЛ. 10
ЗАДАЧИ
1. Исследуйте инвариантность уравнений A0.3) и A0.4) относительно
операций зарядового сопряжения и обращения времени.
2. По какому закону должны при зарядовом сопряжении преобразовы-
преобразовываться функции ф+ и ф-, чтобы уравнения A0.12) и A0.13) оставались ин-
инвариантны?
3. Рассмотрев диаграммы шестого порядка, проверьте согласованность
условия выбора знака A0.21).
4. В приближении зарядовой независимости полезным преобразованием
симметрии является G-преобразование. Оператор G-преобразования опреде-
определяется следующим образом:
Установите, как преобразуются функции ф и f под действием этого опе-
оператора.
5. Проверьте, что в нерелятивистском приближении в порядке g% потен-
потенциал A0.51) приводит к амплитуде рассеяния A0.45).
6. Покажите, что потенциал A0.58) в порядке g$ приводит к S-волновой
части амплитуды я — Л^-рассеяния A0.57).
7. Используя свойства цикличности следа, покажите, что выражение
A0.82) преобразуется как лоренцев 4-вектор; обобщите это утверждение для
любого порядка. Интеграл \ d*k в A0.82) следует регуляризовать и расхо-
расходящуюся часть выделить в перенормировочную постоянную; эта операция не
влияет на трансформационные свойства.
8. Докажите, что электромагнитные форм-факторы в A0.85) и A0.89)
для задач рассеяния должны быть действительны при q2 < 0, если ток пере-
перехода эрмитов. Должен ли ток быть эрмитовым?
9. Рассмотрите возможные электромагитные форм-факторы л°- и /\°-ме-
зонов.
10. Покажите, что формула Розенблюта A0.90) дает наиболее общую
зависимость от угла рассеяния при фиксированной передаче импульса для
любой релятивистски-ковариантной структуры протона и электрона в при-
приближении однофотонного обмена между электроном и протоном.
11. Покажите, что выражение второго порядка A0.82) для форм-фактора
Fn(q2) может быть переписано в виде следующего спектрального представ-
представления:
и вычислите спектральную функцию р \q' ).
12. Докажите, что для протона и я+-мезона Zi = 22 с точностью до
членов порядка е2 и g2; получите отсюда равенство их перенормированных
зарядов при условии равенства «голых» зарядоя.
13. Рассчитайте фоторождение л-мезонов в низшем порядке по е и g-
Проверьте калибровочную инвариантность.
14. Вычислите электромагнитную собственную энергию нейтрона и про-
протона во втором порядке, используя A0.89) и аппроксимируя форм-факторы
их статическими значениями, т.е. полагая F{q2) -*¦ F@). Возникающие при
этом интегралы необходимо регуляризовать. Можно ли таким способом полу-
получить положительную разность масс нейтрона и протона? (См. [130].)
15. Постройте S-матрицу процесса л°->-2у, удовлетворяющую условиям
калибровочной и релятивистской инвариантности, и найдите вероятность рас-

ЗАДАЧИ 277
пада. Вычислите относительную вероятность рождения пары Далица:
л"-*¦ \ + е+ -\-е~. Наконец, рассмотрите распад на две пары Далица и пока-
покажите, что по корреляции плоскостей этих пар можно определить четность
л°-мезона (см. [131]).
16. Проверьте, что формула A0.105) дает правильное значение поляриза-
поляризации электрона, равное —| ре I, если матричный элемент Р-распада описывается
формулой A0.107).
17. Проверьте в низшем порядке по G2 формулу A0.113) для энергетич-
ной зависимости сечения реакции v + р ->- п + е+. Вычислите это сечение, ис-
используя пропагатор промежуточного ^-бозона и общий вид форм-факторов
в вершинах.
18. Проверьте, что для уравнения Вейля A0.114) имеется операция обра-
обращения времени.
19. Вычислите спектр электронов в [х-распаде с учетом всех пяти типов
связи S, Т, Р, V и А и сравните с формулой A0.136).
20. Если ц-распад происходит через №-мезон с конечной массой, как
изображено на рис. 10.15 для случая E-распада, спектр A0.135) меняется.
Найдите это изменение и свяжите его с изменением параметра Мишеля
(см. [551).
21. Определите вероятность реакции A0.148) и проверьте значение отно-
отношения A0.149).
22. Вычислите парциальные вероятности распадов
23. Вычислите парциальную вероятность образования пары Далица
в распаде
2° н» А0 + у,
Обсудите возможность определения относительной четности 2° и Л° в этом
распаде (см. [132]).
24. Какова общая структура амплитуды слабого распада
Найдите параметр асимметрии для случая поляризованных Л°.
25. Вычислите параметр асимметрии и поляризацию электрона в fS-pac-
паде поляризованных нейтронов.

ПРИЛОЖЕНИЕ А
ОБОЗНАЧЕНИЯ
Координаты и импульсы
Совокупность пространственно-временных координат (t, х, у, г) ^ (/, х)
образует 4-вектор со следующими контравариантными компонентами (с и h
положены равными 1):
„ц. _ (г0 1 2 з\ /, \
X =:;;= \Л , Л i Л , Л / = ^/, Л, (/, ^^.
Ковариантные компоненты получаются изменением знака пространственных
координат:
Х\1 === 1-^0» -*Ь л2, Хз) = I,?» — Л, — y, — Z) — §\LV% '
где
«Н
Принято условие суммирования, согласно которому по дважды повторяю-
повторяющимся индексам подразумевается суммирование (если не оговорено обрат-
обратное). Если два одинаковых индекса (по которым должно быть произведено
суммирование) оказались либо оба внизу, либо оба наверху, то в вычисле-
вычислениях была, по-видимому, допущена ошибка. Квадрат «длины» 4-радиус-век-
тора равен
„2 „ ГМ /2 2
X — ХпХ — I — л .
Аналогично определяется 4-импульс
р* — (Е, Рх, ру, рг).
Скалярное произведение двух 4-импульсов дается выражением
0
1
0
0
0
0
-1
0
0
0
0
— 1
Подобным же образом определяется произведение
х ¦ р = / • Е — х • р
Для 4-векторов р приняты нежирные обозначения, а для трехмерных векто-
векторов р — жирные.
Оператор импульса имеет в координатном представлении вид
1
i )

ПРИЛОЖЕНИЕ А 279
и преобразуется как контравариантный 4-вектор:
"¦¦•—
В этих единицах комптоновская длина волны частицы равна 1//п
(« 3,86-10-" см для электрона), а ее энергия покоя есть т (ж 0,511 Мэв
для электрона).
4-потенциал электромагнитного поля определен согласно
Тензор электромагнитного поля определяется следующим образом:
Напряженности электрического и магнитного полей в нековариантных обозна-
обозначениях имеют вид
Е = (F01, F02, Я3).
B = (F23, F31, Я2).
Матрицы Дирака и спиноры
Дираковский спинор для частицы с импульсом р и поляризацией s обо-
обозначается посредством иа (р, s), а для античастицы — посредством va (p, s).
В обоих случаях энергия po^sEp = + VР2 + tn2 положительна. Также в обо-
обоих случаях вектор s^ который в системе покоя имеет вид
5^= @, S<°>), S@)-S@)=l,
описывает направление спина частицы в системе покоя.
Матрицы у, входящие в уравнение Дирака, удовлетворяют условию анти-
антикоммутации
и связаны с матрицами а и Р посредством равенств
У = Pa, Yo = Р-
Обычно используется представление
О -\ )' w >-ч-\-о ОГ
где
\\ a2_f0 -i\ /1 О Л
ОГ \i OJ' ~\О -1 )
представляют собой матрицы Паули размерности 2X2, а 1 = (а i) есть
единичная матрица той же размерности. Часто встречаются следующие ком-
комбинации:
4^, yv],
В этом представлении компоненты a^v равны
0 a

280 ПРИЛОЖЕНИЕ А
где i, /, k = 1, 2, 3 в циклическом порядке и
01 . I
Для широко употребляемого «скалярного произведения» матрицы у с обыч-
обычным 4-вектором используются обозначения ')
Спиноры и и и удовлетворяет уравнению Дирака
(р — т) и (р, s) = 0,
. 05 + т) v (p, s) = 0.
Их явное выражение дается формулой C.7), однако для большинства при-
приложений достаточно знать проекционные операторы. Введем дираковски-со-
пряженные спиноры
п =k+y°,
v = v+y",
которые удовлетворяют уравнениям
й (р, s) (р - т) = 0,
v (р, s) (p + m)= 0.
Проекционные операторы имеют вид
Имеются следующие условия нормировки:
U(P,8)U(P,S) = 1,
б (р, s) v(p, s) = - 1 {А-г>
и условие полноты
2] [иа (p,s) пв (р, s) — иа (р, s) tip (p. s)] = бар.
s
При вычислении следов необходимо строить величины, эрмитово-сопря-
женные по отношению к данным матричным элементам. Для таких величин
имеем
[п (р', s') Г и (р, в)]+ = п (р, s) Г (р', s'),
где
г °r+v0.
¦ у 1 Y
См. примечание на стр. 26. (Прим. перев.)

ПРИЛОЖЕНИЕ А 281
Например.
Суммирование выражений (АЛ) по спинам дает проекционные операторы
для состояний с данной энергией:
ар /_j Э V 2т )afi'
(А.З)
[Л- (р)]ар- ~ ? »„ (р, S) бэ (р, S) =
ав
Полезным тождеством является разложение Гордона для тока
а о,-, /ц (р) = а (Р
Теоремы о следах и соотношения для матриц у
йЬ — a- b — ialivallbv.
След нечетного числа матриц у равен нулю:
Sp 1 = 4,
Spd6 =4a-b,
Sp 01B2C3^4 = 4 [ai • a2 • a3 ¦ a4 — ci\ ¦ a3 • a^ • 04 + a.\ • a4
Sp Y5a6 = 0,
Sp Ystfbci = 4/
- - 2d,
= 4a • 6,
Другие соотношения приведены в § 25.

ПРИЛОЖЕНИЕ Б
ПРАВИЛА ФЕЙНМАНА
Сечения процессов даются выражениями, которые можно разделить на
две части: во-первых, это квадрат абсолютной величины амплитуды ЗЯ, кото-
которая должна быть лоренцевым скаляром и в которой заключена информация
о физике процесса, и, во-вторых, фазовый объем и кинематические факторы.
Дифференциальное сечение da процесса с участием только бесспиновых ча-
частиц и фотонов записывается следующим образом:
b
где, как обычно, ш^ = V I Р р + т2, a vi и vj представляют собой скорости
начальных коллинеарных частиц. Затем это выражение интегрируется по всем
нерегистрируемым импульсам ?i . . . kn конечных частиц. Статистический фак-
фактор 5 для реакции с т тождественными частицами в конечном состоянии
равен
=ТТ
11
Для дираковских частиц *) фактор 1/2сор следует заменить на tn/Ep и вновь
учесть статистический фактор S; остальные факторы те же.
Дифференциальная вероятность распада частицы с массой М в ее системе
покоя равна
/ = 1
где все величины определены, как и прежде. Если в конечном состоянии
имеются фермионы, то вновь 1/2ш* -*¦ ni/Et; если начальная частица является
фермионом, фактор 1/2.W отсутствует.
') Если нормировать дираковские спиноры на 1т вместо 1, как в фор-
формуле (А.2), выражение (Б.1) можно применять и для фермионов. В этом
случае проекционные операторы для состояний с определенной энергией
имеют вид (т±р) вместо (А. 3).

ПРИЛОЖЕНИЕ Б 283
При необходимости производится суммирование по конечным поляриза-
поляризациям и усреднение по начальным.
Для нахождения инвариантной амплитуды SW необходимо изобразить все
фейнмановские диаграммы, отвечающие рассматриваемому процессу, за иск-
исключением диаграмм в виде изолированных вакуумных петель и собственно-
энергетических поправок к внешним линиям. Амплитуда SW(G'), соответствую-
соответствующая диаграмме G, строится путем сопоставления каждому элементу диаг-
диаграммы определенного фактора в амплитуде. Факторами, не зависящими от
конкретных деталей взаимодействия, являются:
1. Каждому бозону со спином 0, входящему в диаграмму, соответствует
фактор У Z. Фактор у Z находится путем вычисления точного мезонного
пропагатора Af (р) в пределе р2 -> р.2; А^ (р) -> Z Д/,- (р) при р2 ->¦ Ц2.
2. Каждой внешней фермионной линии, входящей в диаграмму, соответ-
соответствует уZ2 и (р, s) либо у Z2 v (p, s) в зависимости от того, отвечает эта
линия начальному или конечному состоянию; аналогично каждой фермион-
фермионной линии, выходящей из диаграммы, соответствует VZ2 п (р, s) лиСо
yZ2 v (p, s). Величина Z-i определяется путем предельного перехода
Пш S'F (р) = Z2SF (p).
3. Каждой внешней фотонной линии сопоставляется фактор е^ У Z3, где
при q2 -> О
+ калибровочно-инвариантные члены.
В вычислениях, проводимых в низшем порядке по теории возмущений,
эти величины Z можно положить равными единице. В высших порядках они
вместе с вершинными поправками перенормируют заряды, заменяя «голые»
заряды физическими.
4. Каждой внутренней фотонной линии с импульсом р соответствует
фактор
F^p p — m + ie, p2 — in2 + ie '
5. Каждой внутренней линии мезона со спином 0 и импульсом q отве-
отвечает величина
6. Каждой внутренней фотонной линии с импульсом q сопоставляется
величина
В теории с сохраняющимися токами калибровочно-инвариантными членами
типа q^qvt q^riy и т. д. можно пренебречь.
Для взаимодействия мезонов с нуклонами каждой внутренней мезонной
линии соответствует дополнительный изотопический фактор 6jj, а внешним
линиям соответствуют следующие факторы:
7. х и х+ сопоставляются начальным и конечным нуклонным спинорам,
ЗС = ( п ) отвечает протону и х = ( ) — нейтрону (аналогичные факторы
появляются для /(-мезонов и Н-гиперонов).

28}
ПРИЛОЖЕНИЕ Б
8. я-мезонам в начальном и конечном состояниях отвечают изотопические
функции фе и фе* соответственно, причем
Ф^± = А= A, ± i, 0) ф^0 = @, 0, 1)
(аналогичные факторы вводятся для 2-гиперонов).
9. Каждому внутреннему импульсу /, который не фиксирован законами
сохранения в вершинах, соответствует
С йч
J Bя)« •
10. Каждой замкнутой фермионной петле отвечает множитель (— 1).
11. Диаграммы, которые отличаются друг от друга только перестановкой
двух внешних тождественных фермионов, имеют противоположный относи-
относительный знак. При этом подразумевается не только перестановка двух тожде-
тождественных частиц в конечном состоянии, но и, например, перестановка началь-
начальной частицы и конечной античастицы.
Взаимодействие определяет тип и структуру вершин. Ниже приведены
правила для основных типов взаимодействия.
Спинорная электродинамика
Имеются два типа вершин, изображенных на рис. Б. 1, которые отвечают
следующей плотности гамильтониана, записанной в виде нормального произ-
произведения:
/ / о \i
Для данного типа взаимодействия справедливы следующие правила:
1. Каждой вершине сопоставляется фактор —<еУд-
2. Каждому массовому контрчлену отвечает величина ibm.
Рис. Б.1.
3. Заряд перенормируется следующим образом:
где точной вершине соответствует гд (р'< р)
= Z2 согласно тождеству Уорда.
ПРИ Р'
i = т и Zi =

ПРИЛОЖЕНИЕ Б 285
Электродинамика бозонов со спином О
Имеются три типа вершин, изображенных на рис. Б. 2, которые отвечают
следующей плотности лагранжиана:
( ~* * \
&, = - 1е0 : <р+ у-д^ -j^-j y.A^ + el'-A2:: <p+<p : + бц2 : Ф+<р :.
Для этих вершин справедливы правила:
1. Вершине взаимодействия с фотоном отвечает фактор — ie0 (р -\- р')ц-
2. Вершине с двумя фотонными линиями отвечает + 2/e
Рис. Б.2.
Рис. Б.З.
3. Каждому массовому контрчлену отвечает фактор (бц2.
4. Каждой замкнутой петле, содержащей только две фотонные линии, как
показано на рис. Б. 3, отвечает множитель '/г.
5. Перенормировка заряда производится, как в спинорной электродина-
электродинамике.
Мезон-нуклонное рассеяние
В зарядово-независимой теории гамильтониан содержит четыре члена
Хг = - Zt = : lg J?y5T ¦ фУ : - Ьт : W : - '/г бр.2 : ф • ф : + 'А бЯ, : (ф • фJ :,
которые изображены на рис. Б. 4 и Б.5.
Точки на рис. Б. 5 означают, что только значение / = 0 передается от
мезонной пары ij к паре rs (см. ниже правило 2). Правило для массовых
контрчленов то же, что и раньше, а другие правила гаковы:

286 ПРИЛОЖЕНИЕ Б
1. Каждой мезон-нуклонной вершине отвечает фактор goYa^a. который
дает константу взаимодействия заряженных мезонов с протонами, равную
V2go и ± go для взаимодействия нейтральных мезонов с протонами и ней-
нейтронами соответственно.
Рис. Б.4.
\
\
\
\
\ .••<" >
Рис. Б.5. Рис. Б.6.
2. Каждой вершине с четырьмя мезонами, изображенной на рис. Б. 5, со-
соответствует фактор — 2J6X6ij6r«.
3. Каждой замкнутой петле, содержащей две мезонные линии, как на
рис. Б. 6, отвечает множитель '/г-
Электродинамика бозонов со спином 1
Пропагатор векторного бозона имеет вид [— gy,v + k^ky/m2] (k2 — те2)"
вместо — gjiv/^2 для безмассового фотона, а внешняя линия содержит
вектор поляризации 8ц, как в случае фотона.
В электродинамике векторных бозонов имеются четыре типа вершин, изо-
изображенных на рис. Б. 7, которым соответствует следующая плотность лагран-
лагранжиана:
«О: [X Д VV<PV -

ПРИЛОЖЕНИЕ Б 287
Ниже по порядку приводятся факторы, соответствующие каждой из этих
вершин:
1. Фактор - ieo(p' + р)^а& + ieog&ya + ieop6ga&,
2. Фактор +/eg[2eilveaB-eiiaeBv-eilBeav].
3. Фактор /6p,2gag для каждого массового контрчлена.
4. Множитель 1/2 для каждой замкнутой петли, содержащий только две
фотонные линии.
ее р /
Рис. Б.7.
5. Вывод этих правил из канонической теории, а также рассмотрение
аномального магнитного момента и процедуры регуляризации можно найти
в работе [133].
Во всех приведенных выше примерах матрицы расположены в «естествен-
«естественном порядке». Для замкнутых петель это означает взятие следа. Изотопиче-
Изотопические индексы замыкаются с соответствующими индексами на другом конце
бозонной линии. При суммировании по поляризации фотонов
У, 8д (k, X) 8v {k, Я,)=ф — gjjV
к
и векторных мезонов
бц (к, X) ev (k, Л)=ф — guv + \ .

ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА
1. Рассеяние мюона на электроне (к § 27). В § 27 рассмотрена задача
о рассеянии электрона на бесструктурной дираковской частице (тяжелом элек-
электроне). Как там отмечалось, такое рассмотрение неприменимо к протону,
поскольку оно не учитывает его структуру и его аномальный магнитный мо-
момент, связанные с сильными взаимодействиями. Но эта задача буквально
соответствует задаче о рассеянии мюона на электроне, так как мюон в смыс-
смысле его электромагнитных свойств действительно отличается от электрона
только массой и не подвержен сильным взаимодействиям. Таким образом,
формулы § 27 остаются справедливыми, т. е. описывающими рассеяние мюона
на электроне, если в них заменить ер на е, а под М подразумевать массу
мюона.
Дифференциальное сечение рассеяния определяется формулой G.42), а
квадрат матричного элемента для случая неполяризуемых частиц — формулой
G.43). В системе центра инерции выражение для дифференциального сечения
имеет следующий вид:
= 551*2 Г(еЯ + р2J + (е? + р2 CQS2 dJ _ 2 (m2 + М2) р2 ^2 *1
(e + ?)Vsin*-5
где р — импульс в системе центра инерции, е = Vр2 + гп2, Е = у р2 + М2 —
энергия электрона и мюона, Ф — угол рассеяния, do — элемент телесного угла
(все в системе центра инерции).
2. Превращение электронной пары в мюонную пару (к § 32). При столк-
столкновении электрона и позитрона, кроме упругого рассеяния, может произойти
их аннигиляция с превращением в мюонную пару (положительно и отрица-
отрицательно заряженные мюоны). Этот процесс описывается второй диаграммой
(рис. 7.12,6), а амплитуда — формулой G.86), в которой надо опустить первый
член в квадратных скобках, заменить т2 на тМ и считать pt и <?, соответ-
соответственно импульсами ц.~- и |х+-частиц (р\ и q\ — по-прежнему импульсы элек-
электрона и позитрона). Из законов сохранения следует, что превращение воз-
возможно при Е > М, где Е — энергия электрона (позитрона) в системе центра
инерции.
Полное сечение превращения равно
4я а2 Л , М2 \ /, М
3 4?2 ^ ^ 2?2 У V 4Е'

ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА 289
Заметим, что эта формула неприменима непосредственно вблизи порога
процесса, где образующиеся мюоны нельзя считать свободными.
3. Неупругое рассеяние электрона на протоне (к § 56). В § 56 рассма-
рассматривалась задача об упругом рассеянии электрона на реальном протоне. Для
этого было модифицировано выражение для тока G.34), отвечающее «дира-
ковскому» протону. Эта модификация сводилась к замене / на (P/\J\Pi) —
матричный элемент точного оператора тока протона, учитывающего сильные
взаимодействия (но первого порядка по электромагнитным взаимодействиям).
Как было показано в § 56, этот матричный элемент может быть представлен
феноменологически в виде
й (Pf) Г> (Pt),
где Гц — вершинная функция протона, выражающаяся согласно A0.88) через
два инвариантных форм-фактора Fu F2, являющихся функциями от квадрата
переданного импульса q2. Таким образом, амплитуда рассеяния может быть
определена на основании простой диаграммы Фейнмана (рис. 7.3) с заменой
в протонной вершине Y^ на Г1*.
Аналогично можно рассмотреть задачу о неупругом рассеянии электрона
на протоне, т. е. процесс, в котором электрон теряет импульс q, а протон пре-
превращается в некоторую совокупность адронов. Для этого надо использовать
диаграмму рис. 7.3 или формулу G.31), заменив протонный ток Р1 на матрич-
матричный элемент тока
<« \P\Pi)
где \Pi) —начальное состояние протона с импульсом Я,, а \п) —конечное
адронное состояние.
Элемент матрицы рассеяния S/,-, отвечающий этому процессу, будет со-
содержать амплитуду
где, как и в § 27, рг и рг ¦— импульсы электрона до и после рассеяния, а
u(pl) 'и u(pt)—соответствующие дираковские амплитуды (мы опустили для
краткости спиновые индексы), q = pt — Pf.
Дифференциальное сечение рассеяния с образованием адронного состоя-
состояния п, вычисленное по обычным правилам, имеет следующий вид:
(в этой формуле и далее мы пренебрегаем массой электрона).
Просуммировав это выражение по спиновым состояниям электрона в ко-
конечном состоянии, усреднив по спиновым состояниям электрона в начальном
состоянии и просуммировав по всем конечным адронным состояниям и, мы
получим сечение рассеяния электрона на протоне при данном угле рассеяния
и данной потере энергии (инклюзивное сечение).
В качестве независимых переменных удобно выбрать инварианты

290 ДОПОЛНЕНИЯ РЕДАКТОРА ПЕРЕВОДА
Мы получим
где
>(Pn-Pt-4){Pi\!VL\n)(n\i]i\Pl).
n
Тензорная структура W^v определяется только двумя векторами, Pi и q.
Из этих векторов и метрического тензора g^v можно построить всего пять
независимых тензоров. Требования инвариантности относительно обращения
времени и сохранение тока накладывают три условия. Поэтому tt7^ опреде-
определяется двумя инвариантными функциями от двух переменных: <?2 и v. Мы
можем записать W^v в следующем виде:
4" " IIP
Выражение для сечения мы запишем в системе покоя протона, в которой
q2 = 4ei82 sin2 -^ , v = Mq0, Pipi = Me,
где Ei, 62 — соответственно начальная и конечная энергии электрона, а О —
угол рассеяния электрона,
da = de2 daM0TT ( W2 + ft7! tg2 -^ j.
Здесь dcrM0TT — сечение рассеяния релятивистского электрона в кулоновском
поле:
, a2 cos2*/2
аамотт = rfo2 —— . .
4е, sin2 0/2
Таким образом, неупругое рассеяние определяется двумя структурными
функциями двух инвариантов, Wi и W%. Если при больших энергиях адронная
структура такова, что не зависит от дополнительных размерных параметров
(типа масс), то Wi и №г могут зависеть только от безразмерных отношений
q2/v (автомодельность или масштабная инвариантность). Тогда Wi, W2 долж-
должны иметь вид
Заметим, что общее выражение для W^v может быть представлено в виде
U^v = J dH el"x (Pt | [/„ (x). /v (y)} | Pt),
где [/ц (х), /v (г/)) — коммутатор операторов тока в двух мировых точках.

ЛИТЕРАТУРА')
1. С. Швебер, Введение в релятивистскую квантовую теорию поля, ИЛ,
1963.
2. У. М. Jauch, F. Rohrlich, The Theory of Photons and Electrons, Cambridge,
Mass., Addison-Wesley Publishing Company, Inc., 1955.
3. H. H. Боголюбов, Д. В. [Цирков, Введение в теорию квантованных по-
полей, «Наука», 1976.
4. А. И. Ахиезер, В Б., Берестецкий, Квантовая электродинамика, «Наука»
1969.
5. X. Умэдзава, Квантовая теория поля, ИЛ, 1958.
6. /. Hamilton, Theory of Elementary Particles, London, Oxford University
Press, 1959.
7. F. Mandl, Introduction to Quantum Field Theory, New York, Interscience
Publishers, Inc., 1960.
8. P. Roman, Theory of Elementary Particles, Amsterdam, North Holland
Publishing Company, 1960.
9. Г. Вентцель, Введение в квантовую теорию волновых полей, Гостехиз-
дат, 1947.
10 /. Schwinger, Quantum Electrodynamics, New York, Dover Publications,
Inc., 1958.
11. P. Фейнман, Квантовая электродинамика, «Мир», 1964.
12. L. Klein (ed.), Dispersion Relations and the abstract Approach to Field
Theory, New York, Gordon and Breach, Science Publishers, Inc., 1961.
G. R. Sceaton (ed.), Dispersion Relations; Scotish Universities Summer
School, New York, Interscience Publishers, Inc., 1961.
13. G. F. Chew, S-Matrix Theory of Strong Interactions, New York, W. A. Ben-
Benjamin, Inc., 1962.
14*. В. Б. Берестецкий, E. М. Лифшиц, Л. П. Питаевский, Релятивистская
квантовая теория, ч. 1, «Наука», 1968.
15*. Е. М. Лифшиц, Л. П. Питаевский, Релятивистская квантовая теория,
ч. 2, «Наука», 1971.
16*. Р. Фейнман, Взаимодействие фотонов с адронами, «Мир», 1975.
17*. Дж. Бернстейн, Элементарные частицы и их токи, «Мир», 1970.
18*. С. Трейман, Р. Джекив, Д. Гросс, Лекции по алгебре токов, Атомиздат,
1977.
19*. Дж. Чью, Аналитическая теория S-матрицы, «Мир», 1968.
20*. В. Н. Грибов, Квантовая электродинамика (Материалы 9-й Зимней
школы ЛИЯФ, ч. 1), Ленинград, 1974.
21. В. Паули, Общие принципы волновой механики, Гостехиздат, 1947.
22. Л. Шифф, Квантовая механика, ИЛ, 1957.
') Литература, помеченная звездочкой, добавлена при переводе. Работы,
изданные на русском языке, цитируются по последним изданиям.{Прим. перев)

292 ЛИТЕРАТУРА
23. П. А. М. Дирак, Принципы квантовой механики, Физматгиз, 1960.
24*. Л. Д. Ландау, Е. М. Лифшиц, Квантовая механика, «Наука», 1974.
В. А. Фок, Начала квантовой механики, «Наука», 1976.
25. Е. Schrodinger, Ann. Phys. 81, 109 A926).
W. Gordon, Z. Physik 40, 117 A926).
O. Klein, Z. Physik 41, 407 A927).
* V. A. Fock, Z. Physik 38, 242 A926); 39, 226 A926).
26. P. A. M. Dirac, Proc. Roy. Soc. (London) A117, 610 A928); АП8, 351
A928).
27. H. E. Moses, Phys. Rev. 113, 1670 A959).
28. В. Паули, Теория относительности, Гостехиздат, 1947. «Принцип отно-
относительности». Сборник работ классиков релятивизма, ОНТИ, 1935.
* Л. Д. Ландау, Е. М. Лифшиц, Теория поля, «Наука», 1973.
29. R. H. Good, Jr., Rev. Mod. Phys. 27, 187 A955), в особенности Sec. Ill,
p. 190.
30. M. J. Lighthill, Introduction to Fourier Analysis and Generalized Func-
Functions, Cambridge, University Press, London, 1958.
* И. М. Гельфанд, Г. Е. Шилов, Обобщенные функции и действия над
ними, изд. 2-е, Физматгиз, 1959.
31. W. Gordon, Z. Physik 50, 630 A928).
32. Е. Schrodinger, Sitzber. Akad. Wiss. Physik-Math. 24, 418 A930).
33. T. D. Newton, and E. P. Wigner, Rev. Mod. Phys. 21, 400 A949)
(русский перевод см. в книге: Е. Вигнер, Этюды о симметрии, «Мир»,
- 1971, стр. 277—293).
34. О. Klein, Z. Physik 53, 157 A929).
35. L. L. Foldy, and S. A. Wouthuysen, Phys. Rev. 78, 29 A950).
36. С G. Darwin, Proc. Roy. Soc. (London) A118, 654 A928).
W. Gordon, Z. Physik 48, 11 A928).
37. Г. Бете, Э. Солпитер, Квантовая механика атомов с одним и двумя
электронами, Физматгиз, 1960.
38. М. Е. Rose, Relativistic Electron Theory, John Wiley and Sons, Inc., New
York, 1961.
39. W. E. Lamb, Jr., and R. С Retherford, Phys. Rev. 72, 241 A957).
40. W. E. Lamb, Jr., Repts. Progr. Phys. 14, 19 A951).
41. R. P. Feynman, Proc. 1961 Solvay Conf., Interscience, New York, 1962.
*S. J. Brodsky, S. D. Drell, Ann. Rev. Nucl. Science 20, 147 A970).
* B. E. Lautrop, A. Peterman, E. de Rafael, Phys. Rev. 3C, 193 A972).
42. E. Fermi, 1. Physik 60, 320 A930).
43. T. A. Welton, Phys. Rev. 74, 1157 A948).
44. L. L. Foldy, Rev. Mod. Phys. 30, 471 A958).
45. L. D. Huff, Phys. Rev. 38, 501 A931).
M. H. Johnson, and B. A. Lippman, Phys. Rev. 77, 702 A950).
46. H. A. Tolhoek, and S. R. de Groot, Physica 17, 17 A951).
. К. М. Case, Phys. Rev. 106, 173L A957).
H. Mendlowilz, and К- М. Case, Phys. Rev. 97, 33 A955).
M. Carrassi, Nuovo Cimento 7, 524 A958).
V. Bargmann, L. Michel, and V. L. Telegdi, Phys. Rev. Letters 2, 435
A959).
W. H. Louisell, R. W. Pidd, and H. R. Crane, Phys. Rev. 94, 7 A954).
A. A. Schupp, R. W. Pidd, and H. R. Crane, Phys. Rev. 121, 1 A961).
G. Charpak, F. J. M. Farley, R. L. Garwin, T, Muller, J. С Sens, V. I. Te-
Telegdi, and A. Zichichi, Phys. Rev. Letters 6, 128 A961).
47. O. Feinberg, Phys. Rev. 112, 1637 A958).
E. E. Salpeter, Phys. Rev. 112, 1642 A958).
48/ P. A. M. Dirac, Proc. Roy. Soc. (London) A126, 360 A930).
49: J. R. Oppenheimer, Phys. Rev. 35, 939 A930).

ЛИТЕРАТУРА 293
50')./. D Bjorken, and S. D. Drell, Relativistic Quantum Fields, McGraw-Hill
Book Company, Inc., 1965.
51. E. P. Wigner, Gottinger Nachr. 31, 546 A932) (русский перевод в книге
[33], стр. 262—276).
52. Е. С. G. Stukelberg, Helv. Phys. Acta 14, 32L, 588 A941).
* Г. А. Зисман, ЖЭТФ 10, 1163 A940); 11, 631 A941).
53. R. P. Feynman, Phys. Rev. 76, 749 A949) (русский перевод в книге: «Но-
«Новейшее развитие квантовой электродинамики», ИЛ, 1954, стр. 138).
54. R. P. Feynman, Phys. Rev. 76, 769 A949) (русский перевод в книге [53],
стр. 161).
55. Т. D. Lee, and С. N. Yang, Phys. Rev. 105, 1671 A957).
56. F. Low, Brandeis Univ. Summer School, 1959.
57. N. F. Mott, Proc. Roy. Soc. (London) A124, 425 A929).
58. С Moller, Ann. Phys. 14, 531 A932).
59. W. Pauli in: A. Flugge (ed.), Handbuch der Physik, vol. V, part 1, Sprin-
ger-Verlag, Berlin, 1958.
60. R. H. Dalitz, Proc. Roy. Soc. (London) A206. 509 A951).
61. O. Klein, and Y. Nishina, Z. Physik 52, 853 A929).
*/. Tamm, Z. Physik 62, 545 A930).
62. P. A. M. Dirac, Proc. Cambridge Phil. Soc. 26, 361 A930).
63. H. J. Bhabha, Proc. Roy. Soc. (London) A154, 195 A935).
64. H. Мотт, Г. Месси, Теория атомных столкновений, «Мир», 1969.
L. Wolfenstein, Ann. Rev. Nucl. Science, 6, 43 A956) (русский перевод
см. УФН 62, 71 A957)).
Н. A. Telhoek, Rev. Mod. Phys. 28, 277 A956).
65. M. Jacob, and О. С. Wick, Ann. Phys. (N. Y.) 7, 404 A959).
66. S. M. Berman, частное сообщение.
67. В. Гайтлер, Квантовая теория излучения, ИЛ, 1956.
68. W. Pauli, and F. Villars, Rev. Mod. Phys. 21,434 A949) (перевод в сбор-
сборнике: «Сдвиг уровней атомных электронов», ИЛ, 1950, стр. 139).
69. /. Schwinger, Phys Rev. 74, 1439 A948) (русский перевод см. в книге,
цитированной в [53], стр. 12).
70. Е. A. Uehling, Phys. Rev. 48, 55 A935).
R. Berber, Phys. Rev. 48, 49 A935).
71. Л. Д. Ландау, А. А. Абрикосов, И. М. Халатников, ДАН СССР 95, 773
A954).
Л. Д. Ландау, в сборнике: «Нильс Бор и развитие физики», ИЛ, 1958.
72. М. Gell-Mann, and F. Low, Phys. Rev. 95, 1300 A954) (перевод см. в
сборнике: «Проблемы современной физики». № 3, ИЛ, 1955, стр. 195).
73. R. H. Dalitz, Proc. Roy. Soc. (London) A206, 521 A951).
74. R. Karplus, N. M. Kroll, Phys. Rev. 77, 536 A950).
75. Г. А. Лоренц, Теория электронов и ее применение к явлениям света и
теплового излучения, Гостехиздат, 1956.
76. V. Е. Weisskopf, Phys. Rev. 56, 72 A939).
77. С. W. Allen, Astrophysical Quantities, University of London Press, Ltd.,
London, 1955.
78. J. Schwinger, Phys. Rev. 73, 416 L A948).
79. H. M. Foley, and P. Kusch, Phys. Rev. 73, 412 L A948).
80. C. Sommerfeld, Phys. Rev. 107, 328 A957) and Ann. Phys. (N. Y.) 5, 20
A958).
A. Peterman, Helv. Phys. Acta 30, 407 A957).
81. D. T. Wilkinson, and H. R. Grane, Phys. Rev. 130, 852 A963).
*/. С Wesley, and A. Rich, Rev. Mod. Phys. 44, 250 A975).
') Русский перевод этой книги готовится к изданию в издательстве «Нау-
«Наука» в 1978 г. (Прим. перев.)

294 ЛИТЕРАТУРА
82. У. Schwinger, Phys. Rev. 75, 651; 76, 790A949) (русский перевод в книге
[53], стр.'40, 78)".
3. D. R. - ¦ ~ '
83. D. R. Yennie, S. С. Frautschi, and H. Suura, Ann, Phys. (N. Y.) 13, 379
A961).
84. H. A. Bethe, Phys. Rev. 72, 339 A947) (русский перевод в книге [68] стр. 82).
85. Н. A Bethe, L M. Brown, and У. R. Stehn, Phys. Rev. 77, 370 A950).
С. L. Schwartz, and У. I. Tiemann, Ann. Phys. (N. Y.) 6, 178 A958).
86. G. Ericksen, unpublished dissertation, University of Minesota, 1959.
87. S. D. Drell, Ann. Phys. (N. Y.) 4, 75 A958).
88. W. Furry, Phys. Rev. 51, 125 A937).
89. M. Gell-Mann, and A. H. Rosenfeld, Ann. Rev. Nucl. Science 7, 407 A957)
(русский перевод в сборнике: «Проблемы современной физики», № 4,
ИЛ, 1958, стр. 14).
У. D. Jackson, The Physics of Elementary Particles, Princeton University
Press, Princeton, N. Y., 1958.
W. S. С Williams (ed.), An Introduction to Elementary Particles, Acade-
Academic Press Inc., New York, 1961.
* Ш. Глэшоу, УФН 119, 715 A976).
90. W. Pauli, Phys. Rev. 58, 716 A940) (русский перевод см. в книге: В. Пау-
Паули, Релятивистская теория элементарных частиц, ИЛ, 1947).
W. Pauli, V. Weiskopf, and L. Rosenfeld, Niels Bohr and the Development
of Physics, McGraw-Hill Book Company Inc., New York, 1955 (русский
перевод см. в книге: «Нильс Бор и развитие физики», ИЛ, 1958).
91. Н. Feshbach, and F. M. Villars, Rev. Mod. Phys. 30, 24 A958).
N. Kemmer, Proc. Roy. Soc. (London) A173, 91 A939).
S. Sakata, and H. Taketani, Proc. Math.-Phys. Soc. Japan 22, 757 A940).
W. Heitler, Proc. Roy. Irish Acad. Soc. A49, 1 A943).
92. M. Gell-Mann, Nuovo Cimento Suppl. 2, 848 A956).
93. H. Yukawa, Proc. Phys.-Math. Soc, Japan 17, 48 A935).
94. Г. Бете, Ф. Гофман, Мезоны и поля, т. II, ИЛ, 1958.
95. R. Piano, A. Prodell, N. Satnios, M. Schwartz, У. Steinberger, Phys. Rev.
Letters 3, 525 A959).
96. G. С Wick, Ann. Rev. Nucl. Science 8, 1 A958) (русский перевод см.
УФН 68, 201 A959)).
97*. Р. Блин-Стойл, Фундаментальные взаимодействия и атомное ядро,
«Мир», 1976.
98. D. Wong, and H. P. Noyes, Phys. Rev. 126, 1866 A962).
G. Breit, Rev. Mod. Phys. 34, 766 A962).
H. P. Noyes, Phys. Rev. 130, 2025 A963).
M. M. Levy, Phys. Rev. 88, 725 A952).
99. M. J. Moravcsik, and H. P. Noyes, Ann. Rev. Nucl. Science 11, 95 A961).
* K. Erkelenz, Phys. Reports 13, 191 A974).
100 Э. Хенли, В. Тирринг, Элементарная квантовая теория поля, ИЛ, 1963.
101. G. F. Chew, Phys. Rev. 95, 285 A954).
102. G. F. Chew, and F. E. Low, Phys. Rev. 101, 1570, 1579 A956).
103. G. С Wick, Rev. Mod. Phys. 27, 339 A955).
104. S. D. Drell, Rev. Mod. Phys. 33, 458 A961).
105. С. Д. Дрелл, Ф. Захариазен, Электромагнитная структура нуклонов ИЛ,
1962.
106. R. Hofstadter, Nuclear and Nucleon Structure, W A. Benjamin, Inc.,- 1963.
107. L. Hand, D. G. Miller, and R. Wilson, Rev. Mod. Phys. 35, 335 A963).
108. S. D. Drell, Intern. School Phys. «Enrico Fermi». Course XXVI. Varenna,
1962, Academic Press, 1964.
109. E. I. Konopinski, Ann. Rev. Nucl. Science 9, 99 A959).
L. B. Okun, XI Intern. Conf. on High Energy Phys., CERN, Geneva
A962).

ЛИТЕРАТУРА 295
S. Л1. Berman, Lectures on Weak Interactions, CERN Seminar A961)
(CERN 60—20).
C. Fronsdal (ed.), Weak Interactions and Topics in Dispersion Physics,
W. A. Benjamin, Inc., New York, 1963.
G. Danby, J. M. Gaillard, K- Guilianos, L. M. Lederman, N. Mistry,
M. Schwartz, J. Steinberger, Phys. Rev. Letters 9, 36 A962).
* Л. Б. Окунь, Слабое взаимодействие элементарных часгиц, Физматгиз
1963.
ПО. Т. D. Lee, and С. N. Yang, Phys. Rev. 119, 1410 A960).
111. E. J. Konopinski, and L. M. Langer, Ann. Rev. Nucl. Science 2, 261 A953).
112. T. D. Lee, and С N. Yang, Phys. Rev. 104, 254 A956) (русский перевод
см. в сборнике: «Новые свойства симметрии элементарных частиц» ИЛ
1957).
113*. В. Г. Ерозилимский, УФН 116, 145 A975).
114*. Particle Data Group., Rev. Mod. Phys. 48, No. 2, Part II A976).
115. 6. Понтекорво, ЖЭТФ 37, 1751 A959).
M. Schwartz, Phys. Rev. Letters 4, 306 A960).
T. D. Lee, С N. Yang, Phys. Rev. Letters, 4, 307 A960).
116. H. Weyl, Z. Physik, 56, 330 A929).
117. L. Landau, Nucl. Phys. 3, 127 A957).
Л. Д. Ландау, ЖЭТФ 32, 405 A957); 32, 407 A957).
118. Т. D. Lee, С. N. Yang, Phys. Rev. 105, 1671 A957).
A. Salam, Nuovo Cimento 5, 299 A957) (русский перевод см. в сбор-
сборнике: «Новые свойства симметрии элементарных частиц», ИЛ, 1957).
119. Р. С. Macq, К- М. Growe, and R. P. Haddock, Phys. Rev. 112,2061 A958).
120. O. Feinberg, and L. M. Ledirman, Ann. Rev. Nucl. Science 13, 431 A963).
121. L. Michel, Proc. Roy. Soc. (London) A63, 514 A950).
122. R. P. Feynman, and M. Gell-Mann, Phys. Rev. 109, 193 A958) (русский
перевод см. в сборнике. «Проблемы современной физики», № 4, ИЛ,
1958).
123. S. M. Berman, and A. Sirlin, Ann. Phys. (N. Y.) 20, 20 A962).
* K. Kleinknecht in: Proceedings of the XVII Int. Conf. on High Energy
Physics, London, 1974.
124. G. Feinberg, Phys. Rev. 110, 1482 A958).
125. С. С. Герштейн, Я- Б. Зельдович, ЖЭТФ 29, 698 A955).
126. М. Gell-Mann, Phys. Rev. Ill, 362 A958).
127. Y. К. Lee, L. W. Mo, and С 5. Wu, Phys. Rev. Lett. 10, 253 A963).
128. Y. Nambu, Phys. Rev. Letters 4, 380 A960).
J. Bernstein, S. Fubini, M. Gell-Mann, W. Thirring, Nuovo Cimento 17, 757
A960).
129. M. L. Goldberger, and S. B. Treiman, Phys. Rev. 110, 1178 A958).
130. R. P. Feynman, and G. Speisman, Phys. Rev. 94, 500 A954).
K- Huang, Phys. Rev. 101, 1173 A956).
131. N. M. Kroll, and W. Wada, Phys. Rev. 98, 1355 A955).
132. G. Feinberg, Phys. Rev. 109, 1019 A958).
G. Feldman, and T. Fulton, Nucl. Phys. 8, 106 A958).
133. T. D. Lee, and С N. Yang, Phys. Rev. 128, 885 A962).

Дж. Д. Бьёркен, С. Д. Дрелл
РЕЛЯТИВИСТСКАЯ КВАНТОВАЯ ТЕОРИЯ
ТОМ 1
Релятивиотская квантовая механика