Автор: Бронштейн И.Н. Семендяев К.А.
Теги: математика высшая математика математический анализ
Год: 1986
Текст
И.Н.БРОНШТЕЙН
К.А.СЕМЕНДЯЕВ
СПРАВОЧНИК
по
МАТЕМАТИКЕ
ДЛЯ ИНЖЕНЕРОВ И УЧАЩИХСЯ ВТУЗОВ
ИЗДАНИЕ ТРИНАДЦАТОЕ, ИСПРАВЛЕННОЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1986
SmmeebyUo
ББК 22.11
Б68
УДК 51
Авторы из ГДР, принимавшие участие в подготовке справочника:
P. BECKMANN, M. BELGER, H. BENKER, M. DEWEB,
Н. ERFURTH, H. GENTEMANN, S. GOTTWALD, P. GUTHNER,
G. GROSCHE, H. HILBIG, R. HOFMANN, H. KASTNER,
W. PURKERT, J. von SCHEIDT, TH. VETTERMANN,
V. WUNSCH, E. ZEIDLER
Бронштейн И. Н., Семендяев К. А. Справочник по математике
для инженеров и учащихся втузов.—13-е изд., исправленное. — М.: Наука,
Гл. ред. физ.-мат. лит., 1986.— 544 с.
Предыдущее, 12-е издание A980 г.) вышло с коренной переработкой,
произведенной большим коллективом авторов из ГДР, под редакцией
Г. Гроше и В. Циглера. В настоящее издание внесены многочисленные
исправления.
Для студентов, инженеров, научных работников, преподавателей.
Илья Николаевич Бронштейн
Константин Адольфович Семендяев
СПРАВОЧНИК ПО МАТЕМАТИКЕ
для инженеров и учащихся втузов
Редактор А И. Штерн
Художественный редактор Т. Н Кольченко
Технические редакторы В Н. Кондакова, С. Я. Шклнр
Корректоры Т С Вайсберг, Л С Сомова
И Б 12490
Сдано в набор 27.08.85. Подписано к печати 27.05.86 Формат
70 х 100/16. Бумага книжно-журнальная для офсетной печати.
Гарнитура тайме. Печать офсетная. Усл. п л. 44,2 Уел кр -отт 88.4.
Уч.-изд. л 72,22. Тираж 250000 экз. Заказ 60. Цена 4 р. 10 к.
Ордена Трудового Красного Знамени издательство «Наука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ордена Октябрьской Революции, ордена Трудового Красного
Знамени Ленинградское производственно-техническое объединение
«Печатный Двор» имени А М Горького Союзполиграфпрома при
Государственном комитете СССР по делам издательств, полиграфии
и книжной торговли
197136, Ленинград, П-136, Чкаловский пр., 15.
1702000000 - 106
053@2)-86
4
© Издательство «Teubner»,
ГДР, 1979
© Издательство «Наука»,
Главная редакция
физико-математической
литературы, 1980,
с изменениями, 1986
СОДЕРЖАНИЕ
От редакции 10
1. ТАБЛИЦЫ И ГРАФИКИ
1.1. ТАБЛИЦЫ
1.1.1 Таблицы элементарных функций 11
1. Некоторые часто встречающиеся постоянные A1) 2. Квадраты, кубы, корни A2). 3. Степени целых
чисел от 1 до 100 B9). 4. Обратные величины C1). 5. Факториалы и обратные им величины C2).
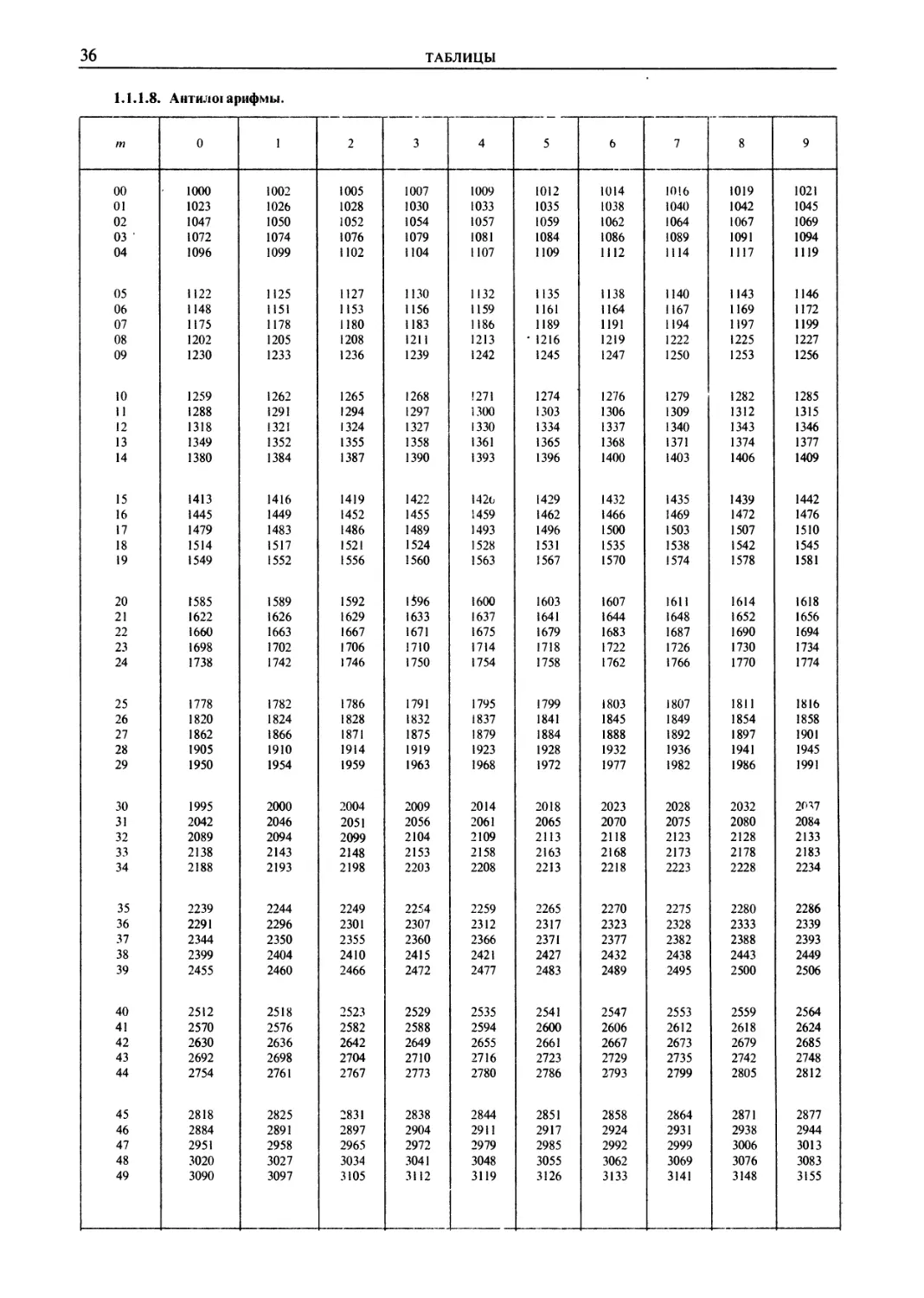
6 Некоторые степени чисел 2, 3 и 5 C3). 7. Десятичные логарифмы C3). 8. Антилогарифмы C6) 9.
Натуральные значения тригонометрических функций C8) 10. Показательные, гиперболические и тригонометрические
функции (для х от 0 до 1,6) D6). 11. Показательные функции (для х от 1,6 до 10,0) D9). 12.
Натуральные логарифмы E1). 13. Длина окружности E3). 14. Площадь круга E5). 15. Элементы сегмента круга
E7). 16. Перевод градусной меры в радианную F1). 17. Пропорциональные части F1). 18. Таблица для
квадратичного интерполирования F3)
1 1.2. Таблицы специальных функций 64
1. Гамма-функция F4). 2 Бесселевы (цилиндрические) функции F5). 3. Полиномы Лежандра (шаровые
функции) F7). 4. Эллиптические интегралы F7). 5 Распределение Пуассона F9). 6 Нормальное распределение
G1). 7. Х2-распределение G4). 8. /-распределение Стьюдента G6). 9. z-распределение G7). 10. F-распределение
(распределение v2) G8). 11. Критические числа для испытания Уилкоксона (84). 12. Х-распределение
Колмогорова—Смирнова (85).
1.1.3. Интегралы и суммы рядов 86
1 Таблица сумм некоторых числовых рядов (86). 2. Таблица разложения элементарных функций в степенные
ряды (87). 3 Таблица неопределенных интегралов (91). 4 Таблица некоторых определенных
интегралов (ПО).
1.2. ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1.2.1 Алгебраические функции ИЗ
1 Целые рациональные функции A13). 2. Дробно-рациональные функции A14). 3. Иррациональные
функции A16).
1.2.2. Трансцендентные функции 117
1. Тригонометрические и обратные тригонометрические функции A17). 2. Показательные и логарифмические
функции A19) 3. Гиперболические функции A21).
1.3. ВАЖНЕЙШИЕ КРИВЫЕ
1.3.1. Алгебраические кривые 123
1 Кривые 3-го порядка A23). 2. Кривые 4-го порядка A24).
1 3.2. Циклоиды 125
1.3.3. Спирали 128
1.3.4. Цепная линия и трактриса 129
2. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА
2.1. ЭЛЕМЕНТАРНЫЕ ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
2.1.1. Общие сведения 130
1. Представление чисел в позиционной системе счисления A30). 2. Погрешности и правила округления
чисел A31)
1*
СОДЕРЖАНИЕ
2 1 2 Элемешарная теория погрешностей 131
1 Абсолютные и относительные погрешности A31) 2. Приближенные границы погрешности функции A32)
3 Приближенные формулы A32)
2 1.3. Элементарные приближенные графические методы. 1. Нахождение нулей функции /(х) A32). 2 Графическое
дифференцирование A33) 3 Графическое интегрирование A33)
2.2. КОМБИНАТОРИКА
2 2 1 Основные комбинаторные функции 134
1 Факториал и гамма-функция A34) 2 Биномиальные коэффициенты A34). 3 Полиномиальный
коэффициент A35)
2 2 2. Формулы бинома и полинома 135
1 Формула бинома Ньютона A35) 2 Формула полинома A35)
2 2.3 Постановка задач комбинаторики 135
2 24 Подстановки 136
1. Подстановки A36). 2. Группа подстановок к элементов A36). 3. Подстановки с неподвижной точкой
A36). 4 Подстановки с заданным числом циклов A37) 5 Перестановки с повторениями A37)
2 2 5. Размещения 137
1 Размещения A37) 2 Размещения с повторениями A37).
2 2 6 Сочетания 138
1 Сочетания A38). 2 Сочетания с повторениями A38).
2.3. КОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СУММЫ,
ПРОИЗВЕДЕНИЯ, СРЕДНИЕ ЗНАЧЕНИЯ
2 3 1 Обозначение сумм и произведений 138
2 3.2 Конечные последовательности 138
1 Арифметическая прогрессия A39) ^2 Геометрическая прогрессия A39)
2 3 3 Некоторые конечные суммы 139
2 3 4 Средние значения 139
2.4. АЛГЕБРА
2 4 1. Общие понятия 140
1 Алгебраические выражения A40) 2 Значения алгебраических выражений A40) 3 Многочлены A41)
4 Иррациональные выражения A41). 5 Неравенства A42) 6. Элементы теории групп A43)
2 4.2 Алгебраические уравнения 143
1 Уравнения A43) 2 Эквивалентные преобразования A44) 3 Алгебраические уравнения A45) 4. Общие
теоремы A48). 5 Система алгебраических уравнений A50)
24 3 Трансцендентные уравнения 150
2.4 4 Линейная алгебра 151
1. Векторные пространства A51) 2. Матрицы и определители A56). 3. Сиаемы линейных уравнений A61)
4 Линейные преобразования A64). 5 Собственные значения и собственные векторы A66)
2.5. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
2 5 1. Алгебраические функции 169
1 Целые рациональные функции A69) 2 Дробно-рациональные функции A70) 3 Иррациональные
алгебраические функции A74)
2 52 Трансцендентные функции 174
1. Тригонометрические функции и обратные к ним A74). 2 Показательная и логарифмическая функции
A79). 3 Гиперболические функции и обратные к ним A80).
2.6. ГЕОМЕТРИЯ
2 6 1. Планимефия 183
26 2 Стереометрия 185
1 Прямые и плоскости в пространстве A85) 2 Двугранные, многогранные и телесные углы A86) 3
Многогранники A86) 4 Тела, образованные перемещением линий A88)
СОДЕРЖАНИЕ
2.6.3. Прямолинейная тригонометрия 189
1. Решение треугольников A90) 2. Применение в элементарной геодезии A91)
2 6 4. Сферическая тригонометрия 192
1. Геометрия на сфере A92). 2. Сферический треугольник A92) 3 Решение сферических треугольников
A92).
2.6.5. Системы координат 194
1. Системы координат на плоскости A95). 2 Координатные системы в пространстве A97)
2.6.6. Аналитическая геометрия 199
1. Аналитическая геометрия на плоскости A99) 2 Аналитическая геометрия в просфанствс B04)
3. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
3.1. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ .
ФУНКЦИЙ ОДНОГО И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3.1.1. Действительные числа 210
1. Система аксиом действительных чисел B10) 2. Натуральные, целые и рациональные чиспа B11) 3 Абеолкн-
ная величина числа B12). 4. Элементарные неравенства B12)
3.1.2. Точечные множества в R" 212
3.1 3. Последовательности 214
1. Числовые последовательности B14) 2 Последовательности точек B15)
3.1.4. Функции действительного переменного 216
1. Функция одного действительного переменного B16) 2 Функции нескольких дейспепельных переменных
B23).
3.1 5. Дифференцирование функций одного действительного переменного 225
1. Определение и геометрическая интерпретация первой производной Примеры B25) 2 Прошводные
высших порядков B26). 3. Свойства дифференцируемых функций B27) 4 Монотонность и выпукюоь
функций B28). 5. Экстремумы и точки перегиба B29) 6 Элементарное исследование ^функции
B30).
3.1.6. Дифференцирование функций многих переменных . N 2М
1. Частные производные, геометрическая интерпретация B30) 2. Полный дифференциал, проишодиая по
направлению, градиент B31) 3. Теоремы о дифференцируемых функциях многих переменных B32)
4. Дифференцируемое отображение пространства Rn в Rm, функциональные определи i ел и. неявные
функции; теоремы о существовании решения B33) 5 Замена переменных в дифференциальных выражениях
B35). 6. Экстремумы функций многих переменных B36)
3.1 7. Интегральное исчисление функций одного переменною 238
1. Определенные интегралы B38) 2 Свойства определенных интефалов B39) 3 Неопределенные
интегралы B39). 4. Свойства неопределенных интегралов B41) 5 Интегрирование рациональных функций B42)
6. Интегрирование других классов функций B44) 7 Несобственные ин тралы B47) 8 Геомефичеекие и
физические приложения определенных интегралов .B51)
3.1.8. Криволинейные интегралы 253
1. Криволинейные интегралы 1-го рода (интегралы но длине кривой) B53) 2 Сущее 1вование и
вычисление криволинейных интегралов 1-го рода B53) 3 Криволинейные иитралы 2-ю рода (ишегралы
по проекции и интегралы общего вида) B54) 4. Свойства и вычисление криволинейных интефалов 2-ю
рода B54). 5. Независимость криволинейных интегралов oi пути интегрирования B56) 6. Геомефичеекие
и физические приложения криволинейных инте1 ралов B57)
3.1.9. Интегралы, зависящие от параметра , 257
1. Определение интеграла, зависящего от параметра B57) 2 Свойства интегралов, зависящих oi
параметра B57). 3. Несобственные интегралы, зависящие от параметра B58) 4 Примеры интралов,
зависящих от параметра B60)
3.1.10. Двойные интегралы 2ъ0
1. Определение двойного интеграла и элементарные свойства B60) 2 Вычисление двойных интефалов
B61). 3. Замена переменных в двойных интегралах B62) 4 Геометрические и физические приложения
двойных интегралов B63)
3.1.11. Тройные интегралы 263
1. Определение тройного интеграла и простейшие свойства B63) 2 Вычисление г ройных hhici ралов
B64). 3. Замена переменных в тройных интегралах B65). 4 Геометрические и физические приложения
тройных интегралов B65).
СОДЕРЖАНИЕ
3.1.12. Поверхностные интегралы 266
1. Площадь гладкой поверхности B66). 2. Поверхностные интегралы 1-го и 2-го рода B66). 3. Геометрические
и физические приложения поверхностного интеграла B69).
3.1.13. Интегральные формулы 270
1. Формула Остроградского-Гаусса. Формула Грина B70). 2 Формулы Грина B70). 3 Формула
Стокса B70). 4. Несобственные криволинейные,- двойные, поверхностные и тройные интегралы B70)
5. Многомерные интегралы, зависящие от параметра B72).
3.1.14. Бесконечные ряды 273
1. Основные понятия B73). 2. Признаки сходимости или расходимости рядов с неотрицательными членами
B74). 3. Ряды с произвольными членами. Абсолютная сходимость B76). 4 Функциональные
последовательности. Функциональные ряды B77). 5. Степенные ряды B79). 6. Аналитические функции. Ряд Тейлора.
Разложение элементарных функций в степенной ряд B82).
3.1.15. Бесконечные произведения 285
3.2. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
3.2.1. Вариационное исчисление 287
1. Постановка задачи, примеры и основные понятия B87). 2. Теория Эйлера — Лагранжа B88). 3.
Теория Гамильтона — Якоби B94). 4. Обратная задача вариационного исчисления B95). 5. Численные методы
B95).
3.2.2. Оптимальное управление 298
1. Основные понятия B98) 2. Принцип максимума Понтрягина B98). 3. Дискретные системы C03) 4.
Численные методы C04).
3.3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
3.3.1. Обыкновенные дифференциальные уравнения 305
1 Общие понятия. Теоремы существования и единственности C05) 2. Дифференциальные уравнения 1-го
порядка C06). 3. Линейные дифференциальные уравнения и линейные системы C13). 4. Общие
нелинейные дифференциальные уравнения C25). 5. Устойчивость C25) 6. Операторный метод решения
обыкновенных дифференциальных уравнений C26) 7. Краевые задачи и задачи о собственных значениях C27).
3.3.2. Дифференциальные уравнения в частных производных 331
1. Основные понятия и специальные методы решения C31) 2. Уравнения в частных производных 1-го
порядка C33). 3. Уравнения в частных производных 2-го порядка C39).
3.4. КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
3.4.1. Общие замечания 357
3.4 2. Комплексные числа. Сфера Римана. Области 357
1. Определение комплексных чисел Поле комплексных чисел C57). 2. Сопряженные комплексные числа
Модуль комплексного числа C58). 3. Геометрическая интерпретация C58). 4. Тригонометрическая и
показательная формы комплексных чисел C58). 5 Степени, корни C59). 6. Сфера Римана. Кривые Жордана.
Области C59).
3 4.3. Функции комплексного переменного 360
3.4.4. Важнейшие элементарные функции 361
1. Рациональные функции C61) 2 Показательная и логарифмическая функции C61) 3
Тригонометрические и гиперболические функции C64).
3.4.5. Аналитические функции 365
i. Производная C65) 2 Условия дифференцируемости Коши —Римана C65) 3 Аналитические функции
C65).
3.4.6. Криволинейные интегралы в комплексной области 366
1. Интеграл функции комплексного переменного C66). 2. Независимость от пути интегрирования C66).
3. Неопределенные интегралы C66) 4 Основная формула интегрального исчисления C66). 5.
Интегральные формулы Коши C66)
3.4.7. Разложение аналитических функций в ряд 367
1. Последовательности и ряды C67). 2 Функциональные ряды. Степенные ряды C68). 3. Ряд Тейлора
C69). 4 Ряд Лорана C69). 5. Классификация особых точек C69). 6. Поведение аналитических функций на
бесконечности C70).
3.4.8. Вычеты и их применение 370
1. Вычеты C70). 2. Теорема вычетов C70). 3. Применение к вычислению определенных интегралов C71).
СОДЕРЖАНИЕ
3 49 Аналитическое продолжение 371
1 Принцип аналитического продолжения C71). 2 Принцип симметрии (Шварца) C71)
3 4.10 Обратные функции Римановы поверхности 372
1 Однолистные функции, обратные функции C72) 2. Риманова поверхность функции z = |/w C72). 3. Рима-
нова поверхность функции z — Ln w C73).
3 4 11 Конформные отображения 373
1 Понятие конформного отображения C73) 2. Некоторые простые конформные отображения C74).
4. ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ
4.1. МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
4 1 1 Основные понятия математической логики 376
1 Алгебра логики (алгебра высказываний, логика высказываний) C76) 2 Предикаты C79)
4 1 2. Основные понятия теории множеств 380
1. Множества, элементы C80). 2 Подмножества C80)
4 1 3 Операции над множествами 381
1 Объединение и пересечение множеств C81). 2. Разность, симметрическая разность, дополнение
множеств C81) 3 Диаграммы Эйлера-Венна C81) 4. Декартово произведение множеств C82) 5. Обобщенные
объединение и пересечение C82)
4.1.4 Отношения и отображения 382
1. Отношения C82) 2 Отношение эквивалентности C83) 3 Отношение порядка C83). 4. Отображения C84).
5. Последовательности и семейства множеств C85) 6 Операции и алгебры C85).
4.1 5 Мощность множеств 386
1. Равномощность C86). 2 Счетные и несчетные множества C86)
4.2. ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
4 2 1 Векторная алгебра 386
1 Основные понятия C86). 2. Умножение на скаляр и сложение C86). 3. Умножение векторов C88).
4 Геометрические приложения векторной алгебры C89).
4 2 2. Векторный анализ 390
1 Векторные функции скалярного аргумента C90) 2. Поля (скалярные и векторные) C91). 3. Градиент
скалярного поля C93). 4. Криволинейный интеграл и потенциал в векторном поле C94). 5 Поверхностные
интегралы в векторных полях C95). 6. Дивергенция векторного поля C97). 7. Ротор векторного поля C98).
8. Оператор Лапласа и градиент векторного поля C99). 9. Вычисление сложных выражений (оператор
Гамильтона) C99). 10. Интегральные формулы D00) 11 Определение векторного поля по его источникам
и вихрям D01) 12. Диады (тензоры II ранга) D02)
4.3. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
4 3.1 Плоские кривые 405
1 Способы задания плоских кривых. Уравнение плоской кривой D05). 2 Локальные элементы плоской
кривой D06) 3 Точки специального типа D07). 4 Асимптоты D09) 5 Эволюта и эвольвента
D10). 6 Огибающая семейства кривых D10).
4 3 2 Пространственные кривые 410
1 Способы задания кривых в пространстве D10). 2 Локальные элементы кривой в пространстве D10)
3 Основная теорема теории кривых D11).
4.3.3. Поверхности 412
1. Способы задания поверхностей D12) 2 Касательная плоскость и нормаль к поверхности D12).
3. Метрические свойства поверхностей D13). 4 Свойства кривизны поверхности D14). 5. Основная теорема
теории поверхностей D16). 6 Геодезические линии на поверхности D17).
4.4. РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4 4.1. Ряды Фурье 418
1 Общие понятия D18). 2. Таблица некоторых разложений в ряд Фурье D19) 3 Численный гармонический
анализ D23).
4 4 2. Интегралы Фурье 425
1 Общие понятия D25). 2 Таблицы трансформант Фурье D26).
СОДЕРЖАНИЕ
4.4 3 Преобразование Лапласа 437
1 Общие понятия D37) 2 Применение преобразования Лапласа к решению обыкновенных
дифференциальных уравнений с начальными условиями D38) 3 Таблица обратного преобразования Лапласа
дробно-рациональных функций D38)
5. ТЕОРИЯ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
5.1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
5 1 1 Случайные события и их верояхносчи 441
1 Случайные события D41) 2 Аксиомы 1еории вероятностей D42). 3 Классическое определение вероя!-
ности события D43) 4 Условные вероятности D43) 5. Полная вероятность Формула Байеса D43)
5 1 2 Случайные величины 444
1 Дискретные случайные величины D44) 2 Непрерывные случайные величины D45)
5 1 3 Моменты распределения 446
1 Дискретный случай D46) 2 Непрерывный случай D47)
5 1 4 Случайные век юры (многомерные случайные величины) 448
1 Дискретные случайные векторы D48) 2 Непрерывные случайные векторы D49) 3 Граничные
распределения D49) 4 Моменты многомерной случайной величины D49) 5. Условные распределения D50)
6 Независимоеib случайных величин D50) 7 Регрессионная зависимость D50) 8 Функции oi случайных
величин D51)
5 1 5 Характеристические функции 451
1 Свойства характеристических функций D52). 2 Формула обращения и теорема единственности
D52) 3 Предельная теорема д 1Я характеристических функций D52) 4 Производящие функции D53)
5 Характеристические функции мноюмерных случайных величин D53).
5 1 6 Предельные теоремы 453
1 Закон больших чисел D53) 2 Предельная 1еорема Муавра —Лапласа D54) 3 Центральная предельная
теорема D54)
5.2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
5 2 1 Выборки 455
1 Гистограмма и эмпирическая функция распределения D55). 2 Функция выборок D56) 3 Некоюрые
важные распределения D57)
5 2 2 Оценка параметров .• 457
1 Свойства точечных оценок D57) 2 Методы получения оценок D58). 3 Доверительные оценки D59)
5 2 3 Проверка гипотез (тесты) 460
1 Постановка задачи D60) 2 Общая теория D60) 3 г-критерий D61) 4 /-критерий D61) 5 Критерий
Уилкоксона D61). 6 Х—критерий D62) 7. Случай дополнительных параметров D63) 8 Критерий согласия
Колмогорова —Смирнова D63)
5 2 4 Корреляция и регрессия 464
1 Оценка корреляционных и pei рессионных характеристик по выборкам D64) 2 Проверка innoiejbi р = 0
в сиучае нормально распределенной 1енеральной совокупности D64) 3 Общая задача рефессии D65)
6. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
6.1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
,6 11 Постановка задачи линейного npoiраммирования и симплекс-метод 466
1 Общая постановка тдачи, i еомс! рическая интерпретация и решение за щч с шумя переменными D66)
2 Канонический вид ЗЛП, изображение вершины в симплекс-таблице D68) 3 Симплекс-метод при
заданной начальной таблице D69) 4 Получение начальной вершины D71). 5 Вырожденный случай и его
рассмотрение при помощи симплекс-метода D73) 6 Двойственность в линейном программировании D73).
7 Модифицированные методы, дополнительное изменение задачи D75)
6.2. ТРАНСПОРТНАЯ ЗАДАЧА
6 2 1 Линейная транспортная задача 477
62 2 Опускание начального решения * 478
62 3 Транспоржый метод 479
СОДЕРЖАНИЕ
6.3. ТИПИЧНЫЕ ПРИМЕНЕНИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
6.3.1 Использование производственных мощностей . . . . к 481
6.3.2. Задача о смесях 481
6.3.3. Распределение, составление плана, сопоставление 482
6.3.4. Раскрой, планирование смен, покрытие 482
6.4. ПАРАМЕТРИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6.4 1 Постановка задачи 483
6 4.2. Метод решения для случая однопараметрической целевой функции 483
6.5. ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6 5 1. Постановка задачи, геометрическая интерпретация 486
6.5.2. Метод сечения Гомори 487
1. Чисто целочисленные задачи линейного программирования D87). 2. Смешанно-целочисленные задачи
линейного программирования D88).
6.5.3 Метод разветвления 488
6.5 4. Сравнение методов ' 489
7. ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ И ИХ ПРИМЕНЕНИЯ
7.1. ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
7.1.1. Погрешности и их учет 490
7.1.2. Вычислительные методы 491
1. Решение линейных систем уравнений D91). 2. Линейные задачи о собственных значениях D95).
3. Нелинейные уравнения D96) 4. Системы нелинейных уравнений D98) 5 Аппроксимация D99) 6
Интерполяция E02) 7 Приближенное вычисление интегралов E06) 8 Приближенное дифференцирование E10).
9 Дифференциальные уравнения E10).
7 1.3 Реализация численной модели в электронных вычислительных машинах 516
I. Критерии для выбора метода E16). 2. Методы управления E16). 3. Вычисление функций E17).
7.1 4 Номография и логарифмическая линейка 518
1 Соотношения между двумя переменными - функциональные шкалы E18) 2. Логарифмическая (счег-
ная) линейка E19). 3. Номограммы точек на прямых и сетчатые номограммы E19).
7.1 5 Обработка эмпирического числового материала 520
1. Метод наименьших квадратов E21). 2. Другие способы выравнивания E22).
7.2. ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
7.2.1. Электронные вычислительные машины (ЭВМ) 523
1. Вводные замечания E23) 2. Представление информации и память ЭВМ E23) 3 Каналы обмена
E24). 4 Программа E24). 5. Программирование E24). 6. Управление ЭВМ E26). 7. Математическое
(программное) обеспечение E26). 8. Выполнение работ на ЭВМ E26)
7.2.2 Аналоговые вычислительные машины 527
1. Принцип устройства аналоговой вычислительной техники E27). 2 Вычислительные элементы аналоговой
вычислительной машины E27). 3. Принцип программирования при решении систем обыкновенных
дифференциальных уравнений E29). 4 Качественное программирование E30)
Список литературы 532
Предметный указатель 534
ОТ РЕДАКЦИИ
Справочник И. Н. Бронштейна и К. А. Семендяева по математике для инженеров и студентов втузов
прочно завоевал популярность не только в нашей стране, но и за рубежом. Одиннадцатое издание
вышло в свет в 1967 г. Дальнейшее издание справочника было приостановлено, так как он уже не
отвечал современным требованиям.
Переработка справочника была осуществлена по инициативе издательства «Teubner» с согласия
авторов большим коллективом специалистов в ГДР (где до этого справочник выдержал 16 изданий).
Было принято обоюдное решение выпустить этот переработанный вариант совместным изданием:
в ГДР - издательством «Teubner» - на немецком языке;
в СССР — Главной редакцией физико-математической литературы издательства «Наука» — на
русском языке.
В результате переработки справочник не только обогатился новыми сведениями по тем разделам
математики, которые были представлены ранее, но и был дополнен новыми разделами: «Вариационное
исчисление и оптимальное управление» (гл. 3.2), «Математическая логика и теория множеств» (гл. 4.1),
«Вычислительная математика» (гл. 7.1), и основными сведениями по вычислительной технике (гл. 7.2).
При этом был сохранен общий методический стиль справочника, позволяющий и получить фактическую
справку по отысканию формул или табличных данных, и ознакомиться с основными понятиями (или
восстановить их в памяти); для лучшего усвоения понятий приводится большое количество примеров.
В связи со столь основательным пересмотром справочника в ГДР весь текст был заново переведен с
немецкого языка.
При подготовке русского издания была произведена некоторая переработка, с тем чтобы по
возможности учесть требования программ отечественных вузов. Эта переработка в основном связана
с изменением обозначений и терминологии, которые у нас и в ГДР не всегда совпадают. Некоторые
разделы для русского издания были переписаны заново — это первые разделы из глав, посвященных
алгебре (гл. 2.4), математической логике и теории множеств (гл. 4.1). Менее значительной переделке
подверглись разделы, посвященные комплексным переменным (гл. 3.4), вариационному исчислению и
оптимальному управлению (гл. 3.2), вычислительной математике (гл. 7.1).
В таком виде справочник вышел в 1980 и в 1981 г.
В настоящем, 13-м (или 2-м переработанном) издании в справочник внесены многочисленные
исправления.
Редакция благодарит всех читателей, приславших свои замечания и исправления. С сожалением
отмечаем, что таких писем было немного. Основные исправления были внесены по результатам
рецензирования и дополнительного редактирования предыдущего издания.
Мы'повторяем свою просьбу к читателям присылать замечания в адрес редакции: 117071, Москва,
Ленинский проспект, 15, Физматлит, Редакция математических справочников.
1. ТАБЛИЦЫ И ГРАФИКИ
1.1. ТАБЛИЦЫ
1.1.1. ТАБЛИЦЫ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1.1.1.1. Некоторые часто встречающиеся постоянные.
Величина
я
2л
Зя
4л
я.2
я-3
я:4
я.6
я:180(=Г)
я-10800 (= Г)
я:648000 (=Г)
я2
У'п
/2я
]/^~2
е
е2
V"e
(/е
Л2
ек
е2п
п
g**)
fa
п
3,141593
6,283185
9,424778
12,566371
1,570796
1,047198
0,785398
0,523599
0,017453
0,000291
0,000005
9,869604
1,772454
2,506628
1,253314
1,464592
1,611992
2,718282
7,389056
1,648721
1,395612
4,810477
23,140693
535,491656
0,577216
0,434294
9,81
96,2361
3,13209
4,42945
*) С—постоянная Эйлера.
**) g — ускорение свободного падения
lgH
0,49715
0,79818
0,97427
1,09921
0,19612
0,02003
1,89509
1,71900
2,24188
4,46373
6,68557
0,99430
0,24857
0,39909
0,09806
0,16572
0,20736
0,43429
0,86859
0,21715
0,14476
0,68219
1,36438
2,72875
1,76134
1,63778
0,99167
1,98334
0,49583
0,64635
м/с2); здесь дане
Величина
1 я
1 2л
1.3л
1:4л
2:я
3-я
4 я
6л
180°:я
1О8ОО':л
648000":л
1-я2
/Гл
/ТТгл"
)/—*
f/ЗАп:
1:е
1:е2
\/пе
У'Т:е
г*2
е-п
1пя
1 Л/= In 10
1:*
1:2*
n]/~g
n\/~2g
п
0,318310
0,159155
0,106103
0,079577
0,636620
0,954930
1,273240
1,909859
57 ,295780
3437', 7468
206264",81
0,101321
0,564190
0,398942
0,797885
0,682784
0,620350
0,367879
0,135335
0,606531
0,716532
0,207880
0,043214
0,001867
1,144730
2,302585
0,10194
0,050968
9,83976
13,91552
) округленное значение g на уровне моря
lgn
1,50285
1,20182
1,02573
2,90079
1,80388
1,97997
0,10491
0,28100
1,75812
3,53627
5,31443
1,00570
1,75143
1,60091
1,90194
1,83428
1,79264
1,56571
1,13141
1,78285
1,85524
1,31781
2,63562
3,27125
0,05870
0,36222
1,00833
2,70730
0,99298
1,14350
на широте 45—50°.
12
ТАБЛИЦЫ
Интерполяция. Большинство помещенных ниже
таблиц даег значения функций с четырьмя
значащими цифрами для трехзначных аргументов.
Когда аргумент задан с большей точностью и,
следовательно, искомое значение функции не может
быть найдено непосредственно в таблицах,
необходимо прибегать к интерполяции. Наиболее
простой является линейная интерполяция, при
которой допускают, что приращение функции
пропорционально приращению аргумента. Если
заданное значение х лежит между приведенными в
таблице значениями х0 и хх = х0 + К которым
соответствуют значения функции v0 = f(xo) и
>'i = f(xi) = >'о + Ai то принимают
Интерполяционная поправка А легко
вычисляется с помощью таблицы
пропорциональных частей 1.1.1.17.
Примеры. 1) Найти 1,67542. В таблицах находим:
1,672= 2,789 и 1,682= 2,822; тогда Л = 33*). Из таблицы
пропорциональных частей получаем: 0,5-33 = 16,5; 0,04-33 =
= 1,3; -——Д = 16,5 + 1,3 * 18; 1,67542 = 2,807.
h
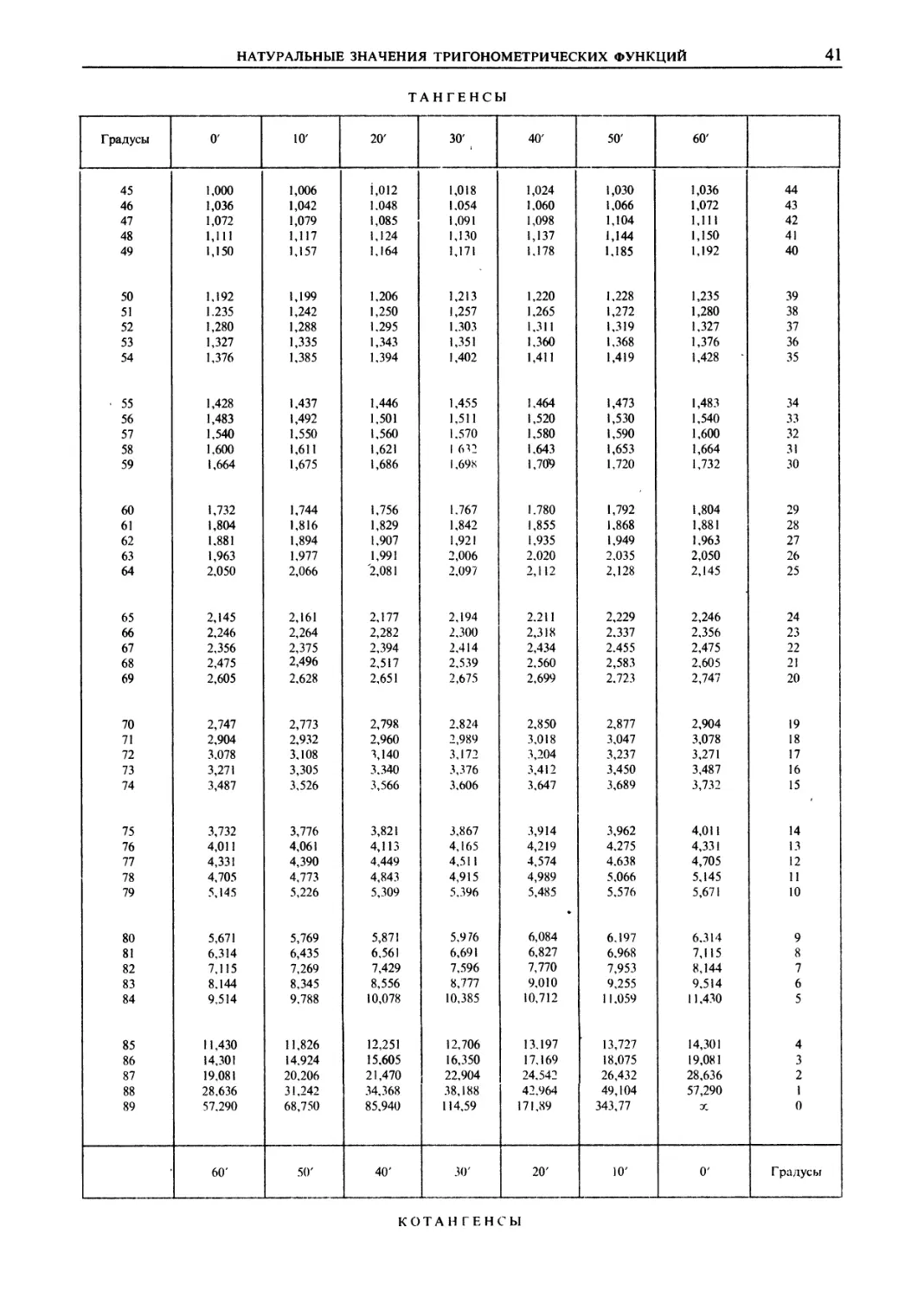
2) Найти tg79°24\ В таблицах находим: tg79°20' =
= 5,309 и tg79°30' = 5,396; тогда Л = 87; 0,4-87% 35;
tg79°24' = 5,344.
Погрешность линейной интерполяции не
превышает единицы последней значащей цифры,
если только две соседние разности Ао и Аг **)
различаются не больше чем на 4 единицы
(последнего знака). Если это условие не выполнено,
необходимо пользоваться более сложными
интерполяционными формулами. В большинстве
случаев достаточной является квадратичная
интерполяция по Бесселю:
к =
х — х0
h ;
/с A — Ас)
ki находится из габл. 1.1.1.18.
Пример. Требуется найти tg85°33'. По таблице
находим (И = 10'): к = 0,3, кх = 0,052; поправка равна 0,3-491 -
- 0,052 - 75 % 143; tg 85°33' = 12,849.
1.1.1.2. Квадраты, кубы, корни.
Объяснения к таблице. Таблица
позволяет находить квадраты, кубы, квадратные и
кубические корни с четырьмя значащими цифрами.
Для аргументов п, заключенных между 1 и 10,
величины и2, л3 находятся непосредственно из
таблицы, если значение аргумента дано с тремя
значащими цифрами. Например, 1,792 = 3,204. Если
же значение аргумента задано более чем тремя
значащими цифрами, необходимо прибегнуть к
интерполяции. Для этой таблицы погрешность
линейной интерполяции нигде не превышает
единицы последнего знака.
Для нахождения и2, и3 при п > 10 и п < 1
принимают во внимание, что при увеличении п в 10к
раз п2 увеличивается в 102* раз, и3 — в 103к
раз, т. е. перенос запятых у п на к разрядов
вправо вызывает перенос запятых у п2 на 2/с
разрядов вправо. При этом по мере надобности
к взятому из таблиц числу приписываются нули
справа' или слева. Например, 0Д792 = 0,03204;
1793 = 5735000*).
Корни квадратные для и, заключенных
между 1 и 100, могут быть найдены непосредственно
из таблицы (с применением линейной
интерполяции), а для любых п — по следующим
правилам.
1) Подкоренное число разбивают в обе стороны
от запятой на грани, содержащие по две цифры.
2) В зависимости от того, содержит ли первая
слева, не состоящая из нулей грань одну или
две значащие цифры, значение корня находят
в таблице соответственно в графе ]/п или J/10n.
3) В найденном значении корня запятую ставят,
исходя из того, что каждая грань подкоренного
числа, стоящая до запятой, дает для корня одну
цифру до запятой, а для чисел, меньших 1, каждая
состоящая из нулей грань после запятой дает для
корня один нуль после запятой.
Прим еры. 1) ]/гу9 = 4,889; 2) /23WO0 = 488,9; 3)
l/0,00'02'39 = 0,01546; 4) |/0,00'3 = 0,05477. (В последнем
примере под знаком корня на конце нужно мысленно добавить
один нуль, т. е. дополнить последнюю грань, и корень
следует искать в графе |/10и.)
Корни кубические для п, заключенных
между 1 и 1000, могут быть найдены
непосредственно из таблицы (с применением линейной
интерполяции), а для любых и - по следующим
правилам.
1) Подкоренное число разбивают в обе стороны
от запятой на грани, содержащие по три цифры.
2) В зависимости от того, содержит ли первая
слева, не состоящая из нулей грань одну, две
или три значащие цифры, значение корня находят
в таблице соответственно в графе ]/п, J/lOn или
j/lOOn. 3) В найденном значении корня запятую
ставят по тому же правилу, что и для квадратных
корней.
Примеры. 1) few - 2,880»»); 2) ]/39'000 = 62,06;
3) |^О,0ОО'О02'39 = 0,01337; 4) ^О.ООО'З - 0,06694; 5) |/^03 -
= 0,3107. (В последних двух примерах под знаком корня на
конце нужно мысленно добавить соответственно два нуля
и один нуль, т. е. дополнить соответствующую грань.)
*) Разность А и поправку обычно выражают в едини-
*) Лучше записать 1793 = 5,735- 106, избегая употребле-
цах разряда последней значащей цифры, не выписывая ния нулей для замены неизвестных цифр (точно: 1793 =
нулей и запятой впереди =5735 339)
**) Здесь подразумеваются обозначения- Xi = х0 + К **) Нуль на конце нужно сохранить, так как здесь он яв-
х2 = л0 + 2/?, х , -— х0 — /», ук = f{xk) (к — — 1, 0, 1, 2), Ао = ляется значащей цифрой и характеризует точность полу-
= Vi - Vo, At - r2 v'i, A_j — v0 — v-i ченного значения корня.
КВАДРАТЫ, КУБЫ, КОРНИ
13
I
Квадраты, к
п
1,00
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
,30
,31
,32
,33
,34
,35
,36
,37
,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
'бы, квадратные и кубические корни
Л2
1,000
,020
,040
,061
,082
,102
,124
,145
,166
,188
,210
,232
,254
,277
,300
,322
,346
,369
,392
1,416
1,440
1,464
,488
,513
,538
,562
,588
,613
,638
,664
1,690
,716
1,742
,769
,796
1,822
1,850
1,877
1,904
1,932
1,960
1,988
2,016
2,045
2,074
2,102
2,132
2,161
2,190
2,220
2,250
2,280
2,310
2,341
2,372
2,402
л*
1,000
1,030
1,061
1,093
1,125
,158
1,191
,225
,260
,295
,331
,368
,405
,443
,482
,521
1,561
1,602
,643
,685
,728
1,772
,816
,861
1,907
1,953
2,000
2,048
2,097
2,147
2,197
2,248
2,300
2,353
2,406
2,460
2,515
2,571
2,628
2,686
2,744
2,803
2,863
2,924
2,986
3 049
3,112
3,177
3,242
3,308
3,375
3,443
3,512
3,582
3,652
3,724
1,000
1,005
1,010
1,015
1,020
1,025
1,030
1,034
1,039
1,044
1,049
1,054
1,058
1,063
1,068
1,072
1,077
1,082
1,086
1,091
1,095
,100
,105
,109
,114
,118
,122
,127
,131
,136
,140
,145
,149
,153
,158
,162
,166
,170
,175
,179
,183
,187
,192
,196
,200
,204
,208
,212
,217
,221
,225
,229
,233
,237
,241
1,245
|/Юл
3,162
3,178
3,194
3,209
3,225
3,240
3,256
3,271
3,286
3,302
3,317
3,332
3,347
3,362
3,376
3,391
3,406
3,421
3,435
3,450
3,464
3,479
3,493
3,507
3,521
3,536
3,550
3,564
3,578
3,592
3,606
3,619
3,633
3,647
3,661
3,674
3,688
3,701
3,715
3,728
3,742
3,755
3,768
3,782
3,795
3,808
3,821
3,834
3,847
3,860
3,873
3,886
3,899
3,912
3,924
3,937
(/п
1,000
1,003
1,007
1,010
1,013
,016
,020
,023
,026
,029
,032
,035
,038
,042
,045
,048
,051
,054
,057
1,060
1,063
1,066
1,069
1,071
1,074
1,077
1,080
1,083
1,086
1,089
,091
,094
,097
,100
,102
,105
,108
,111
,113
,116
,119
,121
,124
,127
,129
,132
1,134
1,137
1,140
,142
.145
,147
1,150
1,152
1,155
1,157
f/10w
2,154
2,162
2,169
2,176
2,183
2,190
2,197
2,204
2,210
2,217
2,224
2,231
2,237
2,244
2,251
2,257
2,264
2,270
2,277
2,283
2,289
2,296
2,302
2,308
2,315
2,321
2,327
2,333
2,339
2,345
2,351
2,357
2,363
2,369
2,375^
2,381
2,387
2,393
2,399
2,404
2,410
2,416
2,422
2,427
2,433
2,438
2,444
2,450
2,455
2,461
2,466
2,472
2,477
2,483
2,488
2,493
4,642
4,657
4,672
4,688
4,703
4,718
4,733
4,747
4,762
4,777
4,791
4,806
4,820
4,835
. 4,849
4,863
4,877
4,891
4,905
4,919
4,932
4,946
4,960
4,973
4,987
5,000
5,013
5,027
5,040
5,053
5,066
5,079
5,092
5,104
5,117
5,130
5,143
5,155
5,168
5,180
5,192
5,205
5,217
5,229
5,241
5,254
5,266
5,278
5,290
5,301
5,313
5,325
5,337
5,348
5,360
5,372
14
ТАБЛИЦЫ
Продолжение
п
1,55
1,56
1,57
1,58
1,59
1,60
1,61
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
,70
,71
,72
,73
,74
,75
,76
,77
,78
,79
,80
,81
,82
,83
,84
,85
,86
,87
1,88
1,89
1,90
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
2,00
2,01
2,02
2,03
2,04
2,05
2,06
2,07
2,08
2,09
2,10
л2
2,402
2,434
2,465
2,496
2,528
2,560
2,592
" 2,624
2,657
2,690
2,722
2,756
2,789
2,822
2,856
2,890
2,924
2,958
2,993
3,028
3,062
3,098
3,133
3,168
3,204
3,240
3,276
3,312
3,349
3,386
3,422
3,460
3,497
3,534
3,572
3,610
3,648
3,686
3,725
3,764
3.802
3,842
3,881
3,920
3,960 . .
4,000
4,040
4,080
4,121
4,162
4,202
4,244
4,285
4,326
4,368
4,410
3,724
3,796
3,870
3,944
4,020
4,096
4,173
4,252
4,331
4,411
4,492
4,574
4,657
4,742
4,827
4,913
5,000
5,088
5,178
5,268
5,359
5,452
5,545
5,640
5,735
5,832
5,930
6,029
6,128
6,230
' 6,332
6,435
6,539
6,645
6,751
6,859
6,968
7,078
7,189
7,301
7,415
7,530
7,645
7,762
7,881
8,000
8,121
8,242
8,365
8,490
8,615
8,742
8,870
8,999
9,129
9,261
1,245
1,249
1,253
1,257
1,261
1,265
1,269
1,273
1,277
1,281
1,285
1,288
1,292
1,296
1,300
1,304
1,308
1,311
1,315
1,319
1,323
1,327
1,330
1,334
1,338
1,342
1,345
1,349
1,353
1,356
1,360
1,364
1,367
1,371
1,375
1,378
1,382
1,386
1,389
1,393
1,396
1,400
1,404
1,407
1,411
1,414
1,418
1,421
1,425
1,428
1,432
1,435
1,439
J,442
1,446
1,449
\'Ш
3,937
3,950
3,962
3,975
3,987
4,000
4,012
4,025
4,037
4,050
4,062
4,074
4,087
4,099
4,111
4,123
4,135
4,147
4,159
4,171
4,183
4,195
4,207
4,219
4,231
4,243
4,254
4,266
4,278
4,290
4,301
4,313
4,324
4,336
4,347
4,359
4,370
4,382
4,393
4,405
4,416
4,427
4,438
4,450
4,461
4,472
4,483
4,494
4,506
4,517
4,528
4,539
4,550
4,561
4,572
4,583
1,157
1,160
1,162
1,165
1,167
1,170
1,172
1,174
1,177
1,179
1,182
1,184
1,186
1,189
1,191
1,193
1,196
1,198
1,200
1,203
1,205
1,207
1,210
1,212
1,214
1,216
1,219
1,221
1,223
1,225
1,228
1,230
1,232
1,234
1,236
1,239
1,241
1,243
1,245
1,247
1,249
1,251
1,254
1,256
1,258
1,260
1,262
1,264
1,266
1,268
1,270
1,272
1,274
1,277
1,279
1,281
fV I o/i
2,493
2,499
2,504
2,509
2,515
2,520,
2,525
2,530
2,535
2,541
2,546
2,551
2,556
2,561
2,566
2,571
2,576
2,581
2,586
2,591
2,596
2,601
2,606
2,611
2,616
2,621
2,626
2,630
2,635
2,640
2,645
2,650
2,654
2,659
2,664
2,668
2,673
2,678
2,682
2,687
2,692
2,696
2,701
2,705
2,710
2,714
2,719
2,723
2,728
2,732
2,737
2,741
2,746
2,750
2,755
2,759
р 100/1
5,372
5,383
5,395
5,406
5,418
5,429
5,440
5,451
5,463
5,474
5,485
5,496
5,507
5,518
5,529
5,540
5,550
5,561
5,572
5,583
5,593
5,604
5,615
5,625
5,636
5,646
5,657
5,667
5,677
5,688
5,698
5,708
5,718
5,729
5,739
5,749
5,759
5,769
5,779
5,789
5,799
5,809
5,819
5,828
5,838
5,848
5,858
5,867
5,877
5,887
5,896
5,906
5,915
5,925
5,934
5,944
КВАДРАТЫ, КУБЫ, КОРНИ
15
Продолжение
п
2,10 '
2,11
2,12
2,13
2,14
2,15
2,16
2,17
2,18
2,19
2,20
2,21
2,22
2,23
2,24
2,25
2,26
2,27
2,28
2,29
2,30
2,31
2,32
2,33
2,34
2,35
2,36
2,37
2,38
2,39
2,40
2,41
2,42
2,43
2,44
2,45
2,46
2,47
2,48
2,49
2,50
2,51
2,52
2,53
2,54
2,55
2,56
2,57
2,58
2,59
2,60
2,61
2,62
2,63
2,64
2,65
4,410
4,452
4,494
4,537
4,580
4,622
4,666
4,709
4,752
4,796
4,840
4,884
4,928
4,973
5,018
5,062
5,108-
5,153
5,198
5,244
5,290
5,336
5,382
5,429
5,476
5,522
5,570
5,617
5,664
5,712
5,760
5,808
5,856
5,905
5,954
6,002
6,052
6,101
6,150
6,200
6,250
6,300
6,350
6,401
6,452
6,502
6,554
6,605
6,656
6,708
6,760
6,812
6,864
6,917
6,970
7,022
и*
9,261
9,394
9,528
9,664
9,800
9,938
10,08
10,22
10,36
10,50
10,65
10,79
10,94
11,09
11,24
11,39
11,54
11,70
11,85
12,01
12,17
12,33
12,49
12,65
12,81
12,98
13,14
13,31
13,48
13,65
13,82
14,00
14,17
14,35
14,53
14,71
14,89
15,07
15,25
15,44
15,62
15,81
16,00
16,19
16,39
16,58
16,78
16,97
17,17
17,37
17,58
17,78
17,98
18,19
18,40
18,61
\~п
,449
,453
,456
,459
,463
,466
,470
,473
,476
,480
,483
,487
,490
,493
,497
,500
,503
,507
,510
,513
,517
,520
,523
,526
,530
,533
,536
,539
,543
,546
,549
,552
,556
,559
,562
,565
,568
,572
,575
,578
,581
,584
,587
,591
,594
,597
,600
,603
,606
,609
,612
,616
,619
,622
1,625
1,628
|/10и
4,583
4,593
4,604
4,615
4,626
4,637
4,648
4,658
4,669
4,680
4,690
4,701
4,712
4,722
4,733
4,743
4,754
4,764
4,775
4,785
4,796
4,806
4,817
4,827
4,837
4,848
4,858
4,868
4,879
4,889
4,899
4,909
4,919
4,930
4,940
4,950
4,960
4,970
4,980
4,990
5,000
5,010
5,020
5,030
5,040
5,050
5,060
5,070
5,079
5,089
5,099
5,109
5,119
5,128
5,138
5,148
1,281
,283
,285
,287
,289
,291
,293
,295
,297
,299
,301
,303
,305
,306
,308
,310
,312
,314
,316
,318
,320
,322
,324
,326
,328
,330
,331
,333
,335
,337
,339
,341
,343
,344
,346
,348
,350
,352
,354
,355
,357
,359
,361
,363
,364
1,366
1,368
1,370
1,372
1,373 -
1,375
1,377
1,379
1,380
1,382
1,384
2,759
2f763
2,768
2,772
2,776
2,781
2,785
2,789
2,794
2,798
2,802
2,806
-2,811
2,815
2,819
2,823
2,827
2,831
2,836
2,840
2,844
2,848
2,852
2,856
2,860
2,864
2,868
2,872
2,876
2,880
2,884
2,888
2,892
2,896
2,900
2,904
2,908
2,912
2,916
2,920
2,924
2,928
2,932
2,936
2,940
2,943
2,947
2,951
2,955
2,959
2,962
2,966
2,970
2,974
2,978
2,981
f/ 100л
5,944
5,953
5,963
5,972
5,981
5,991
6,000
6,009
6,018
6,028
6,037
6,046
6,055
6.064
6,073
6,082
6,091
6,100
6,109
6,118
6,127
6,136
6,145
6,153
6,162
6,171
6,180
6,188
6,197
6,206
6,214
6,223
6,232
6,240
6,249
6,257
6,266
6,274
6,283
6,291
6,300
6,308
6,316
6,325
6,333
6,341
6,350
6,358
6,366
6,374
6,383
6,391
6,399
6,407
6,415
6,423
16
ТАБЛИЦЫ
Продолжение
п
2,65
2,66
2,67
2,68
2,69
2,70
2,71
2,72
2,73
2,74
2,75
2,76
2,77
2,78
2,79
2,80
2,81
2,82
2,83
2,84
2,85
2,86
2,87
2,88
2,89
2,90
2,91
2,92
2,93
2,94
2,95
2,96
2,97
2,98
2,99
3,00
3,01
3,02
3,03
3,04
3,05
3,06
3,07
3,08
3,09
3,10
3,11
3,12
3,13
3,14
3,15
3,16
3,17
3,18
3,19
3,20
«2
7,022
7,076
7,129
7,182
7,236
7,290
7,344
7,398
7,453
7,508
7,562
7,618
7,673
7,728
7,784
7,840
7,896
7,952
8,009
8,066
8,122
8,180
8,237
8,294
8,352
8,410
8,468
8,526
8,585
8,644
8,702
8,762
8,821
8,880
8,940
9,000
9,060
9,120
9,181
9,242
9,302
9,364
9,425
9,486
9,548
9,610
9,672
9,734
9,797
9,860
9,922
9,986
10,05
10,11
10,18
10,24
л*
18,61
18,82
19,03
19,25
19,47
19,68
19,90
20,12
20,35
20,57
20,80
21,02
21,25
21,48
21,72
21,95
22,19
22,43
22,67
22,91
23,15
23,39
23,64
23,89
24,14
24,39
24,64
24.90
'25,15
25,41
25,67
25,93
26,20
26,46
26,73
27,00
27,27
27,54
27,82
28,09
28,37
28,65
28,93
29,22
29,50
29,79
30,08
30,37
30,66
30,96
31,26
31,55
31,86
32,16
32,46
32,77
1,628
1,631
1,634
1,637
1,640
1,643
1,646
1,649
1,652
1,655
1,658
1,661
1,664
1,667
1,670
1,673
1,676
1,679
1,682
1,685
1,688
,691
1,694
1,697
1,700
1,703
1,706
1,709
1,712
1,715
,718
,720
,723
,726
,729
,732
,735
,738
,741
1,744
,746
,749
,752
,755
,758
1,761
,764
,766
,769
,772
,775
,778
,780
,783
,786
1,789
\/\0п
5,148
5,158
5,167
5,177
5,187
5,196
5,206
5,215
5,225
5,235
5,244
5,254
5,263
5,273
5,282
5,292
5,301
5,310
5,320
5,329
5,339
5,348
5,357
5,367
5,376
5,385
5,394
5,404
5,413
5,422
5,431
5,441
5,450
5,459
5,468
5,477
5,486
5,495
5,505
5,514
5,523
5,532
5,541
5,550
5,559
5,568
5,577
5,586
5,595
5,604
5,612
5,621
5,630
5,639
5,648
5,657
Г»
1,384
,386
1,387
,389
,391
,392
,394
,396
,398
,399
1,401
1,403
1,404
1,406
1,408
1,409
1,411
1,413
1,414
1,416
1,418
1,419
1,421
1,423
1,424
1,426
1,428
1,429
1,431
1,433
1,434
1,436
1,437
1,439
1,441
1,442
1,444
1,445
1,447
1,449
1,450
1,452
1,453
1,455
1,457
1,458
1,460
1,461
1,463
1,464
1,466
1,467
1,469
1,471
1,472
1,474
1^1 Он
2,981
2,985
2,989
2,993
2,996
3,000
3,004
3,007
3,011
3,015
3,018
3,022
3,026
3,029
3,033
3,037
3,040
3,044
3,047
3,051
3,055
3,058
3,062
3,065
3,069
3,072
3,076
3,079
3,083
3,086
3,090
3,093
3,097
3,100
3,104
3,107
3,111
3,114
3,118
3,121
3,124
3,128
3,131
3,135
3,138
3,141
3,145
3,148
3,151
' 3,155
3,158
3,162
3,165
3,168
3,171
3,175
{Лоои
6,423
6,431
6,439
6,447
6,455
6,463
6,471
6,479
6,487
6,495
6,503
6,511
6,519
6,527
6,534
6,542
6,550
6,558
6,565
6,573
6,581
6,589
6,596
6,604
6,611
6,619
6,627
6,634
6,642
6,649
6,657
6,664
6,672
6,679
6,687
6,694
6,702
6,709
6,717
6,724
6,731
6,739
6,746
6,753
6,761
6,768
6,775
6,782
6,790
6,797
6,804
6,811
6,818
6,826
6,833
6,840
КВАДРАТЫ, КУБЫ, КОРНИ
17
Продолжение
п
3,20
3,21
3,22
3,23
3,24
3,25
3,26
3,27
3,28
3,29
3,30
3,31
3,32
3,33
3,34
3,35
3,36
3,37
3,38
3,39
3,40
3,41
3,42
3,43
3,44
3,45
3,46
3,47
3,48
3,49
3,50
3,51
3,52
3,53
3,54
3,55
3,56
3,57
3,58
3,59
3,60
3,61
3,62
3,63
3,64
3,65
3,66
3,67
3,68
3,69
3,70
3,71
3,72
3,73
3,74
3,75
10,24
10,30
10,37
10,43
10,50
10,56
10,63
10,69
10,76
10,82
10,89
10,96
11,02
11,09
11,16
11,22
11,29
11,36
11,42
11,49
11,56
11,63
11,70
11,76
11,83
11,90
11,97
12,04
12,11
12,18
12,25
12,32
12,39
12,46
12,53
12,60
12,67
12,74
12,82
12,89
12,96
13,03
13,10
13,18
13,25
13,32
13,40
13,47
13,54
13,62
13,69
13,76
13,84
13,91
13,99
14,06
32,77
33,08
33,39
33,70
34,01
34,33
34,65
34,97
35,29
35,61
35,94
36,26
36,59
36,93
37,26
37,60
37,93
38,27
38,61
38,96
39,30
39,65
40,00
40,35
40,71
41.06
41,42
41,78
42,14
42,51
42,88
43,24
43,61
43,99
44,36
44,74
45,12
45,50
45,88
46,27
46,66
47,05
47,44
47,83
48,23
48,63
49,03
49,43
49,84 '
50,24
50,65
51,06
51,48
51,90
52,31
52,73
1,789
1,792
1,794
1,797
1,800
1,803
1,806
1,808
,811
,814
,817
1,819
1,822
,825
1,828
1,830
1,833
1,836
1,838
1,841
1,844
1,847
1,849
1,852
1,855
1,857
1,860
1,863
1,865
1,868
1,871
1,873
1,876
1,879
1,881
1,884
1,887
1,889
1,892
1,895
1,897
1,900
1,903
1,905
1,908
1,910
1,913
1,916
1,918
1,921
1,924
1,926
1,929
1,931
1,934
1,936
\/\0п
5,657
5,666
5,675
5,683
5,692
5,701
5,710
5,718
5,727
5,736
5,745
5,753
5,762
5,771
5,779
5,788
5,797
5,805
5,814
5,822
5,831
5,840
5,848
5,857
5,865
5,874
5,882
5,891
5,899
5,908
5,916
5,925
5,933
5,941
5,950
5,958
5,967
5,975
5,983
5,992
6,000
6,008
6,017
6,025
6,033
6,042
6,050
6,058
6,066
6,075
6,083
6,091
6,099
6,107
6,116
6,124
1,474
1,475
1,477
1,478
1,480
1,481
1,483
1,484
1,486
1,487
1,489
1,490
1,492
1,493
1,495
1,496
1,498
1,499
1,501
1,502
1,504
1,505
1,507
1,508
1,510
1,511
1,512
1,514
1,515
1,517
1,518
1,520
1,521
1,523
1,524
1,525
1,527
1,528
1,530
1,531
1,533
1,534
1,535
1,537
1,538
1,540
1,541
1,542
1,544
1,545
1,547
1,548
1,549
1,551
1,552
1,554
(УТой
3,175
3,178
3,181
3,185
3,188
3,191
3,195
3,198
3,201
3,204
3,208
3,211
3,214
3,217
3,220
3,224
3,227
3,230
3,233
3,236
3,240
3,243
3,246
3,249
3,252
3,255
3,259
3,262
3,265
3,268
3,271
3,274
3,277
3,280
3,283
3,287
3,290
3,293
' 3,296
3,299
3,302
3,305
3,308
3,311
3,314
3,317
3,320
3,323
3,326
3,329
3,332
3,335
3,338
3,341
3,344
3,347
J^lOOw
6,840
6,847
6,854
6,861
6,868
6,875
6,882
6,889
6,896
6,903
6,910
6,917
6,924
6,931
6,938
6,945
6,952
6,959
6,966
6,973
6,980
6,986
6,993
7,000
7,007*
7,014
7,020
7,027
7,034
7,041
7,047
7,054
7,061
7,067
7,074
7,081
7,087
7,094
7,101
7,107
7,114
7,120
7,127
7,133
7,140
7,147
7,153
7,160
7,166
7,173
7,179
7,186
7,192
7,198
7,205
7,211
18
ТАБЛИЦЫ
Продолжение
п
3,75
3,76
3,77
3,78
3,79
3,80
3,81
3,82
3,83
3,84
3,85
3,86
3,87
3,88
3,89
3,90
3,91
3,92
3,93
3,94
3,95
3,96
3,97
3,98
3,99
4,00
4,01
4,02
4,03
4,04
4,05
4,06
4,07
4,08
4,09
4,10
4,11
4,12
4,13
4,14
4,15
4,16
4,17
4,18
4,19
4,20
4,21
4,22
4,23
4,24
4,25
4,26
4,27
4,28
4,29
4,30
14,06
14,14
14,21
14,29
14,36
14,44
14,52
14,59
14,67
14,75
14,82
14,90
14?8
15,05
15,13
15,21
15,29
15,37
15,44
15,52
15,60
15,68
15,76
15,84
15,92
16,00
16,08
16,16
16,24
16,32
16,40
16,48
16,56
16,65
16,73
16,81
16,89
16,97
17,06
17,14
17,22
17,31
17,39
17,47
17,56
17,64
17,72
17,81
17,89
17,98
18,06
18,15
18,23
18,32
18,40
18,49
52,73
53,16
53,58
54J01
54,44
54,87
5531
55,74
56,18
56,62
57,07
57,51
57,96
58,41
58,86
59,32
59,78
60,24
60,70
61,16
61,63
62,10
62,57
63,04
63,52
64,00
64,48
64,96
65,45
65,94
66,43
66,92
67,42
67,92
68,42
68,92
69,43
69,93
70,44
70,96
71,47
71,99
72,51
73,03
73,56
7409
74,62
75,15
75,69
76,23
16,11
77,31
77,85
78,40
78,95
79,51
1,936
1,939
1,942
1,944
1,947
1,949
1,952
1,954
1,957
1,960
1,962
1,965
1,967
1,970
1,972
1,975
1,977
1280
1,982
1,985
1,987
1,990
1,992
1,995
1,997
2,000
2,002
2,005
2,007
2,010
2,012
2,015
2,017
2,020
2,022
2,025
2,027
2,030
2,032
2,035
2,037
2,040
2,042
2,045
2,047
2,049
2,052
2,054
2,057
2,059
2,062
2,064
2,066
2,069
2,071
2,074
/10Й
6,124
6,132
6,140
6,148
6,156
6,164
6,173
6,181
6,189
6,197
6,205
6,213
6,221
6,229
6,237
6,245
6,253
6,261
6,269
6,277
6,285
6,293
6,301
6,309
6,317
6,325
6,332
6,340
6,348
6,356
6,364
6,372
6,380
6,387
6,395
6,403
6,411
6,419
6,427
6,434
6,442
6,450
6,458
6,465
6,473
6,481
6,488
6,496
6,504
6,512
6,519
6,527
6,535
6,542
6,550
6,557
Г*
1,554
1,555
1,556
1,558
1,559
1,560
1,562
1,563
1,565
1,566
1,567
1,569
1,570
1,571
1,573
1,574
1,575
1,577
1,578
1,579
1,581
1,582
1,583
1,585
1,586
1,587
1,589
1,590
1,591
1,593
1,594
1,595
1,597
1,598
1,599
1,601
1,602
1,603
1,604
1,606
1,607
1,608
1,610
1,611
1,612
1,613
1,615
1,616
1,617
1,619
1,620
1,621
1,622
1,624
1,625
1,626
Р Ю/7
3,347
3,350
3,353
3,356
3,359
3,362
3,365
3,368
3,371
3,374
3,377
3,380
3,382
3,385
3,388
3,391
3,394
3,397
3,400
3,403
3,406
3,409
3,411
3,414
3,417
3,420
3,423
3,426
3,428
3,431
3,434
3,437
3,440
3,443
3,445
3,448
3,451
3,454
3,457
3,459
3,462
3,465
3,468
3,471
3,473
3,476
3,479
3,482
3,484
3,487
3,490
3,493
3,495
3,498
3,501
3,503
7,211
7,218
7,224
7,230
7,237
7,243
7,250
7,256
7,262
7,268
7,275
7,281
7,287
7,294
7,300
7,306
7,312
7,319
7,325
7,331
7,337
7,343
7,350
7,356
7,362
7,368
7,374
7,380
7,386
7,393
7,399
7,405
7,411
7,417
7,423
7,429
7,435
7,441
7,447
7,453
7,459
7,465
7,471
7,477
7,483
7,489
7,495
7,501
7,507
7,513
7,518
7,524
7,530
7,536
7,542
7,548
КВАДРАТЫ, КУБЫ, КОРНИ
19
Продолжение
п
4,30
4,31
4,32
4,33
4,34
4,35
4,36
4,37
4,38
4,39
4,40
4,41
4,42
4,43
4,44
4,45
4,46
4,47
4,48
4,49
4,50
4,51
4,52
4,53
4,54
4,55
4,56
4,57
4,58
4,59
4,60
4,61
4,62
4,63
4,64
4,65
4,66
4,67
4,68
4,69
4,70
4,71
4,72
4,73
4,74
4,75
4,76
4,77
4,78
4,79
4,80
4,81
4,82
4,83
4,84
4,85
л2
18,49
18,58
18,66
18,75
18,84
18,92
19,01
19,10
19,18
19,27
19,36
19,45
19,54
19,62
19,71
19,80
19,89
19,98
20,07
20,16
20,25
20,34
20,43
20,52
20,61
20,70
20,79
20,88
20,98
21,07
21,16
21,25
21,34
21,44
21,53
21,62
21,72
21,81
21,90
22,00
22,09
22,18
22,28
22,37
22,47
22,56
22,66
22,75
22,85
22,94
23,04
23,14
23,23
23,33
23,43
23,52
79,51
80,06
80,62
81,18
81,75
82,31
82,88
83,45
84,03
84,60
85,18
85,77
86,35
86,94 '
87,53
88,12
88,72
89,31
89,92
90,52
91,12
91,73
92,35
92,96
93,58
94,20
94,82
95,44
96,07
96,70
97,34
97,97
98,61
99,25
99,90
100,5
101,2
101,8
102,5
103,2
103,8
104,5
105,2
105,8
106,5
107,2
107,9
108,5
109,2
109,9
110,6
111,3
112,0
112,7
113,4
114,1
fn
2,074
2,076
2,078
2,081
2,083
2,086
2,088
2,090
2,093
2,095
2,098
2,100
2,102
2,105
2,107
2,110
2,112
2,114
2,117
2,119
2,121
2,124
2,126
2,128
2,131
2,133
2,135
2,138
2,140
2,142
2,145
2,147
2,149
2,152
2,154
2,156
2,159
2,161
2,163
2,166
2,168
2,170
2,173
2,175
2,177
2,179
2,182
2,184
2,186
2,189
2,191
2,193
2,195
2,198
2,200
2,202
j/lO/i
6,557
6,565
6,573
6,580
6,588
6,595
6,603
6,611
6,618
6,626
6,633
6,641
6,648
6,656
6,663
6,671
6,678
6,686
6,693
6,701
6,708
6,716
6,723
6,731
6,738
6,745
6,753
6,760
6,768
6,775
6,782
6,790
6,797
6,804
6,812
6,819
6,826
6,834
6,841
6,848
6,856
6,863
6,870
6,877
6,885
6,892
6,899
6,907
6,914
6,921
6,928
6,935
6,943
6,950
6,957
6,964
fn
1,626
1,627
1,629
1,630
1,631
1,632
1,634
1,635
1,636
1,637
1,639
1,640
1,641
1,642
1,644
1,645
1,646
1,647
1,649
1,650
1,651
1,652 .
1,653
1,655
1,656
1,657
1.658
1,659
1,661
1,662
1,663
1,664
1,666
1,667
1,668
1,669
1,670
1,671
1,673
1,674
1,675
1,676
1,677
1,679
1,680
1,681
1,682
1,683
1,685
1,686
1,687
1,688
1,689
1,690
1,692
1,693
3,503
3,506
3,509
3,512
3,514
3,517
3,520
3,522
3,525
3,528
3,530
3,533
3,536
3,538
3,541
3,544
3,546
3,549
3,552
3,554
3,557
3,560
3,562
3,565
3,567
3,570
3,573
3,575
3,578
3,580
3,583
3,586
3,588
3,591
3,593
3,596
3,599
3,601
3,604
3,606
3,609
3,611
3,614
3,616
3,619
3,622
3,624
3,627
3,629
3,632
3,634
3,637
3,639
3,642
3,644
3,647
{hoon
7,548
7,554
7,560
7,565
7,571
7,577
7,583
7,589
7,594
7,600
7,606
7,612
7,617
7,623
7,629
7,635
7,640
7,646
7,652
7,657
7,663
7,669
7,674
7,680
7,686
7,691
7,697
7,703
7,708
7,714
7,719
7,725
7,731
7,736
7,742
7,747
7.753
7,758
7,764
7.769
7,775
7,780
7,786
7,791
7,797
7,802
7,808
7,813
7,819
7,824
7,830
7,835
7,841
7,846
7,851
7,857
20
ТАБЛИЦЫ
Продолжение
п
4,85
4,86
4,87
4,88
4,89
4,90
4,91
4,92
4,93
4,94
4,95
4,96
4,97
4,98
4,99
5,00
5,01
5,02
5,03
5,04
5,05
5,06
5,07
5,08
5,09
5,10
5,11
5,12
5,13
5,14
5,15
5,16
5,17
5,18
5,19
5,20
5,21
5,22
5,23
5,24
5,25
5,26
5,27
5,28
5,29
5,30
5,31
5,32
5,33
5,34
5,35
5,36
5,37
5,38
5,39
5,40
23,52
23,62
23,72
23,81
23,91
24,01
24,11
24,21
24,30
24,40
24,50
24,60
24,70
24,80
24,90
25,00
25,10
25,20
25,30
25,40
25,50
25,60
25,70
25,81
25,91
26,01
26,11
26,21
26,32
26,42
26,52
26,63
26,73
26,83
26,94
27,04
27,14
27,25
27,35
27,46
27,56
27,67
27,77
27,88
27,98
28,09
28,20
28,30
28,41
28,52
28,62
28,73
28,84
28,94
29,05
29,16
114,1
114,8
115,5
116,2
116,9
117,6
118,4
119,1
119,8
120,6
121,3
122,0
122,8
123,5
124,3
125,0
125,8
126,5
127,3
128,0
128,8
129,6
130,3
131,1
131,9
132,7
133,4
134,2
135,0
135,8
136,6
137,4
138,2
139,0
139,8
140,6
141,4
142,2
143,1
143,9
144,7
145,5
146,4
147,2
148,0
148,9
149,7
150,6
151,4
152,3
153,1
154,0
154,9
155,7
156,6
157,5
fn
2,202
2,205
2,207
2,209
2,211
2,214
2,216
2,218
2,220
2,223
2,225
2,227
2,229
2,232
2,234
2,236
2,238
2,241
2,243
2,245
2,247
2,249
2,252
2,254
2,256
2,258
2,261
2,263
2,265
2,267
2,269
2,272
2,274
2,276
2,278
2,280
2,283
2,285
2,287
2,289
2,291
2,293
2,296
2,298
2,300
2,302
2,304
2,307
2,309
2,31.1
2,313
2,315
2,317
2,319
2,322
2,324
l/Юи
6,964
6,971
6,979
6,986
6,993
7,000
7,007
7,014
7,021
7,029
7,036
7,043
7,050
7,057
7,064
7,071
7,078
7,085
7,092
7,099
7,106
7,113
7,120
7,127
7,134
7,141
7,148
7,155
7,162
7,169
7,176
7,183
7,190
7,197
7,204
7,211
7,218
7,225
7,232
7,239
7,246
7,253
7,259
7,266
7,273
7,280
7,287
7,294
7,301
7,308
7,314
7,321
7,328
7,335
7,342
7,348
fn
1,693
1,694
1,695
1,696
1,697
1,698
1,700
1,701
,702
,703
,704
,705
,707
,708
1,709
1,710
,711
1,712
1,713
1,715
1,716
1,717
1,718
1,719
1,720
1,721
1,722
1,724
1,725
1,726
1,727
1,728
1,729
1,730
1,731
1,732
1,734
1,735
1,736
1,737
1,738
1,739
1,740
1,741
1,742
1,744
1,745
1,746
1,747
1,748
1,749
1,750
1,751
1,752
1,753
1,754
3,647
3,649
3,652
3,654
3,657
3,659
3,662
3,664
3,667
3,669
3,672
3,674
3,677
3,679
3,682
3,684
3,686
3,689
3,691
3,694
3,696
3,699
3,701
3,704
3,706
3,708
3,711
3,713
3,716
3,718
3,721
3,723
3,725
3,728
3,730
3,733
3,735
3,737
3,740
3,742
3,744
3,747
3,749
3,752
3,754
3,756
3,759
3,761
3,763
3,766
3,768
3,770
3,773
3,775
3,777
3,780
jhoo/i
7,857
7,862
7,868
7,873
7,878
7,884
7,889
7,894
7,900
7,905
7,910
7,916
7,921
7,926
7,932
7,937
7,942
7,948
7,953
7,958
7,963
7,969
7,974
7,979
7,984
7,990
7,995
8,000
8,005
8,010
8,016
8,021
8,026
8,031
8,036
8,041
8,047
8,052
8,057
8,062
8,067
8,072
8,077
8,082
8,088
8,093
8,098
8,103
8,108
8,113
8,118
8,123
8,128
8,133
8,138
8,143
КВАДРАТЫ, КУБЫ, КОРНИ
21
Продолжение
п
5,40
5,41
5,42
5,43
5,44
5,45
5,46
5,47
5,48
5,49
5,50
5,51
5,52
5,53
5,54
5,55
5,56
5,57
5,58
5,59
5,60
5,61
5,62
5,63
5,64
5,65
5,66
5,67
5,68
5,69
5,70
5,71
5,72
5,73
5,74
5,75
5,76
5,77
5,78
5,79
5,80
5,81
5,82
5,83
5,84
5,85
5,86
5,87
5,88
5,89
5,90
5,91
5,92
5,93
5,94
5,95
л2
29,16
29,27
29,38
29,48
29,59
29,70
29,81
29,92
30,03
30,14
30,25
30,36
30,47
30,58
30,69
30,80
30,91
31,02
31,14
31,25
31,36
31,47
31,58
31,70
31,81
31,92
32,04
32,15
32,26
32,38
32,49
32,60
32,72
32,83
32,95
33,06
33,18
33,29
33,41
33,52
33,64
33,76
33,87
33,99
34,11
34,22
34,34
34,46
34,57
34,69
34,81
34,93
35,05
35,16
35,28
35,40
и?
157,5
158,3
159,2
160,1
161,0
161,9
162,8
163,7
164,6
165,5
166,4
167,3
168,2
169,1
170,0
171,0
171,9
172,8
173,7
174,7
175,6
176,6
177,5
178,5
179,4
180,4
181,3
182,3
183,3
184,2
185,2
186,2
187,1
188,1
189,1
190,1
191,1
192,1
193,1
194,1
195,1
196,1
197,1
198,2
199.2
200,2
201,2
202,3
203,3
204,3
205,4
206,4
207,5
208,5
209,6
210,6
2,324
2,326
2,328
2,330
2,332
2,335
2,337
2,339
2,341
2,343
2,345
2,347
2,349
2,352
2,354
2,356
2,358
2,360
2,362
2,364
2,366
2,369
2,371
2,373
2,375
2,377
2,379
2,381
2,383
2,385
2,387
2,390
2,392
2,394
2,396
2,398
2,400
2,402
2,404
2,406
2,408
2,410
2,412
2,415
2,417
2,419
2,421
2,423
2,425
2,427
2,429
2,431
2,433
2,435
2,437
2,439
/Той
7,348
7,355
7,362
7,369
7,376
7,382
7,389
7,396
7,403
7,409
7,416
7,423
7,430
7,436
7,443
7,450
7,457
7,463
7,470
7,477
7,483
7,490
7,497
7,503
7,510
7,517
7,523
7,530
7,537
7,543
7,550
7,556
7,563
7,570
7,576
7,583
7,589
7,596
7,603
7,609
7,616
7,622
7,629
7,635
7,642
7,649
7,655
7,662
7,668
7,675
7,681
7,688
7,694
7,701
7,707
7,714
fn
1,754
,755
1,757
,758
,759
,760
,761
,762
1,763
1,764
1,765
1,766
1,767
,768
,769
,771
,772
1,773
1,774
1,775
1,776
1,777
1,778
1,779
1,780
1,781
1,782
1,783
,784
1,785
1,786
1,787
,788
1,789
1,790
1,792
1,793
1,794
1,795
1,796
1,797
1,798
1,799
1,800
1,801
1,802
,803
,804
,805
1,806
1,807
1,808
1,809
1,810
1,811
1,812
jXlO/i
3,780
3,782
3,784
3,787
3,789
3,791
3,794
3,796
3,798
3,801
3,803
3,805
3,808
3,810
3,812
3,814
3,817
3,819
3,821
3,824
3,826
3,828
3,830
3,833
3,835
3,837
3,839
3,842
3,844
3,846
3,849
3,851
3,853
3,855
3,857
3,860
3,862
3,864
3,866
3,869
3,871
3,873
3,875
3,878
3,880
3,882
3,884
3,886
3,889
3,891
3,893
3,895
3,897
3,900
3,90*2
3,904
j/ЛоОл
8,143
8,148
8,153
8,158
8,163
8,168
8,173
8,178
8,183
8,188
8,193
8,198
8,203
8,208
8,213
8,218
8,223
8,228
8,233
8,238
8,243
8,247
8,252
8,257
8,262
8,267
8,272
8,277
8,282
8,286
8,291
8,296
8,301
8,306
8,311
8,316
8,320
8,325
8,330
8,335
8,340
8,344
8,349
8,354
8,359
8,363
8,368
8,373
8,378
8,382
8,387
8,392
8,397
8,401
8,406
8,411
22
ТАБЛИЦЫ
Продолжение
п
5,95
5,96
5,97
5,98
5,99
6,00
6,01
6,02
6,03
6,04
6,05
6,06
6,07
6,08
6,09
6,10
6,11
6,12
6,13
6,14
6,15
6,16
6,17
6,18
6,19
6,20
6,21
6,22
6,23
6,24
6,25
6,26
6,27
6,28
6,29
6,30
6,31
6,32
6,33
6,34
6,35
6,36
6,37
6,38
6,39
6,40
6,41
6,42
6,43
6,44
6,45
6,46
6,47
6,48
6,49
6,50
35,40
35,52
35,64
35,76
35,88
36,00
36,12
36,24
36,36
36,48
36,60
36,72
36,84
36,97
37,09
37,21
37,33
37,45
37,58
3'7,70
37,82
37,95
38,07
38,19
38,32
38,44
38,56
38,69
38,81
38,94
39,06
39,19
39,31
39,44
39,56
39,69
39,82
39,94
40,07
40,20
40,32
40,45
40,58
40,70
40,83
40,96
41,09
41,22
41,34
41,47
41,60
41,73
41,86
41,99
42,12
42,25
210,6
211,7
212,8
213,8
214,9
216,0
217,1
218,2
219,3
220,3
221,4
222,5
223,6
224,8
225,9
227,0
228,1
229,2
230,3
231,5
232,6
233,7
234,9
236,0
237,2
238,3
239,5
240,6
241,8
243,0
244,1
245,3
246,5
247,7
248,9
250,0
251,2
252,4
253,6
254,8
256,0
257,3
258,5
259,7
260,9
262,1
263,4
264,6
265,8
267,1
268,3
269,6
270,8
272,1
273,4
274,6
Уп
2,439
2,441
2,443
2,445
2,447
2,449
2,452
2,454
2,456
2,458
2,460
2,462
2,464
2,466
2,468
2,470
2,472
2,474
2,476
2,478
2,480
2,482
2,484
2,486
2,488
2,490
2,492
2,494
2,496
2,498
2,500
2,502
2.504
2,506
2,508
2,510
2,512
2,514
2,516
2,518
2,520
2,522
2,524
2,526
2,528
2,530
2,532
2,534
2,536
2,538
2,540
2,542
2,544
2,546
2,548
2,550
[/Юл
7,714
7,720
7,727
7,733
7,740
7,746
7,752
7,759
7,765
7,772
7,778
7,785
7,791
7,797
7,804
7,810
7,817
7,823
7,829
7,836
7,842
7,849
7,855
7,861
7,868
7,874
7,880
7,887
7,893
7,899
7,906
7,912
7,918
7,925
7,931
7,937
7,944
7,950
7,956
7,962
7,969
7,975
\ 7,981
7,987
7,994
8,000
8,006
8,012
8,019
8,025
8,031
8,037
8,044
8,050
8,056 •
8,062
1,812
1,813
1,814
1,815
1,816
1,817
1,818
1,819
1,820
1,821
1,822
1,823
1,824
1,825
1,826
1,827
1,828
1,829
1,830
1,831
1,832
1,833
1,834
1,835
1,836
1,837
1,838
1,839
1,840
1,841
1,842
1,843
1,844
1,845
1,846
1,847
1,848
1,849
1,850
1,851"
1,852
1,853
1,854
1,855
1,856
1,857
1,858
1,859
1,860
1,860
1,861
1,862
1,863
1,864
1,865
1,866
f/\0n
3,904
3,906
3,908
3,911
3,913
3,915
3,917
3,919
3,921
3,924
3,926
3,928'
3,930
3,932
3,934
3,936
3,939
3,941
3,943
3,945
3,947
3,949
3,951
3,954
3,956
3,958
3,960
3,962
3,964
3,966
3,969
3,971
3,973
3,975
3,977
3,979
3,981
3,983
3,985
3,987
3,990
3,992
3,994
3,996
3,998
4,-000
4,002
4,004
4,006
4,008
4,010
4,012
4,015
4,017
4,019
4,021
f/lOOn
8,411
8,416
8,420
8,425
8,430
8,434
8,439
8,444
8,448
8,453
8,458
8,462
8,467
8,472
8,476
8,481
8,486
8,490
8,495
8,499
8,504
8,509
8,513
8,518
8,522
8,527
8,532
8,536
8,541
8,545
8,550
8,554
8,559
8,564
8,568
8,573
8,577
8,582
8,586
8,591
8,595
8,600
8,604
8,609
8,613
8,618
8,622
8,627
8,631
8,636
8,640
8,645
8,649
8,653
8,658
8,662
КВАДРАТЫ, КУБЫ, КОРНИ
23
Продолжение
п
6,50
6,51
6,52
6,53
6,54
6,55
6,56
6,57
6,58
6,59
6,60
6,61
6,62
6,63
6,64
6,65
6,66
6,67
6,68
6,69
6,70
6,71
6,72
6,73
6,74
6,75
6,76
6,77
6,78
6,79
6,80
6,81
6,82
6,83
6,84
6,85
6,86
6,87
6,88
6,89
6,90
6,91
6,92
6,93
6,94
6,95
6,96
6,97
6,98
6,99
7,00
7,01
7,02
7,03
7,04
7,05
42,25
42,38
42,51
42,64
42,77
42,90
43,03
43,16
43,30
43,43
43,56
43,69
43,82
43,96
44,09
44,22
44,36
44,49
44,62
44,76
44,89
45,02
45,16
45,29
45,43
45,56
45,70
45,83
45,97
46,10
46,24
46,38
46,51
46,65
46,79
46,92
47,06
47,20
47,33
47,47
47,61
47,75
47,89
48,02
48,16
48,30
48,44
48,58
48,72
48,86
49,00
49,14
49,28
49,42
49,56
49,70
274,6
275,9
277,2
278,4
279,7
281,0
282,3
283,6
284,9
286,2
287,5
288,8
290,1
291,4
292,8
294,1
295,4
296,7
298,1
299,4
300,8
302,1
303,5
304,8
306,2
307,5
308,9
310,3
311,7
313,0
314,4
315,8
317,2
318,6
320,0
321,4
322,8
324,2
325,7
327,1
328,5
329,9
331,4
332,8
334,3
335,7
337,2
338,6
340,1
341,5
343,0
344,5
345,9
347,4
348,9
350,4
\Г«
2,550
2,551
2,553
2,555
2,557
2,559
2,561
2,563
2,565
2,567
2,569
2,571
2,573
2,575
2,577
2,579
2,581
2,583
2,585
2,587
2,588
2,590
2,592
2,594
2,596
2,598
2,600
2,602
2,604
2,606
2,608
2,610
2,612
2,613
2,615
2,617
2,619
2,621
2,623
2,625
2,627
2,629
2,631
2,632
2,634
2,636
2,638
2,640
2,642
2,644
2,646
2,648
2,650
2,651
2,653
2,655
|/Шй
8,062
8,068
8,075
8,081
8,087
8,093
8,099
8,106
8,112
8,118
8,124
8,130
8,136
8,142
8,149
8,155
8,161
8,167
8,173
8,179
8,185
8,191
8,198
8,204
8,210
8,216
8,222
8,228
8,234
8,240
8,246
8,252
8,258
8,264
8,270
8,276
8,283
8,289
8,295
8,301
8,307
8,313
8,319
8,325
8,331
8,337
8,343
8,349
8,355
8,361
8,367
8,373
8,379
8,385
8,390
8,396
1,866
1,867
1,868
1,869
1,870
1,871
1,872
1,873
1,874
1,875
1,876
1,877
1,878
1,879
1,880
1,881
1,881
1,882
1,883
1,884
1,885
1,886
1,887
1,888
1,889
1,890
1,891
1,892
1,893
1,894
1,895
1,895
1,896
1,897
1,898
1,899
1,900
1,901
1,902
1,903
1,904
1,905
1,906
1,907
1,907
1,908
1,909
1,910
1,911
1,912
1,913
1,914
1,915
1,916
1,917
1,917
4,021
4,023
4,025
4,027
4,029
4,031
4,033
4,035
4,037
4,039
4,041
4,043
4,045
4,047
4,049
4,051
4,053
4,055
4,058
4,060
4,062
4,064
4,066
4,068
4,070
4,072
4,074
4,076
4,078
4,080
4,082
4,084
4,086
4,088
4,090
4,092
4,094
4,096
4,098
4,100
4,102
4,104
4,106
4,108
4,109
4,111
4,113
4,115
4,117
4,119
4,121
4,123
4,125
4,127
4,129
4,131
]^100/i
8.662
8,667
8,671
8,676
8,680
8,685
8,689
8,693
8,698
8,702
8,707
8,711
8,715
8,720
8,724
8,729
8,733
8,737
8,742
8,746
8,750
8,755
8,759
8,763
8,768
8,772
8,776
8,781
8,785
8,789
8,794
8,798
8,802
8,807
8,811
8,815
8,819
8,824
8,828
8,832
8,837
8,841
8,845
8,849
8,854
8,858
8,862
8,866
8,871
8,875
8,879
8,883
8,887
8,892
8,896
8,900
24
ТАБЛИЦЫ
Продолжение
п
7,05
7,06
7,07
7,08
7,09
7,10
7,11
7,12
7,13
7,14
7,15
7,16
7,17
7,18
7,19
7,20
7,21
7,22
7,23
7,24
7,25
7,26
7,27
7,28
7,29
7,30
7,31
7,32
7,33
7,34
7,35
7,36
7,37
7,38
7,39
7,40
7,41
7,42
7,43
7,44
7,45
7,46
7,47
7,48
7,49
7,50
7,51
7,52
7,53
7,54
7,55
7,56
7,57
7,58
7,59
7,60
49,70
49,84
49,98
50,13
50,27
50,41
50,55
50,69
50,84
50,98
51,12
51,27
51,41
51,55
51,70
51,84
51,98
52,13
52,27
52,42
52,56
52,71
52,85
53,00
53,14
53,29
53,44
53,58
53,73
53,88
54,02
54,17
54,32
54,46
54,61
54,76
54,91
55,06
55,20
55,35
55,50
55,65
55,80
55,95
56,10
56,25
56,40
56,55
56,70
56,85
57,00
57,15
57,30
57,46
57,61
57,76
350,4
351,9
353,4
354,9
356,4
357,9
359,4
360,9
362,5
364,0
365,5
367,1
368,6
370,1
371,7
373,2
374,8
376,4
377,9
379,5
381,1
382,7
384,2
385,8
387,4
389,0
390,6
392,2
393,8
395,4
397,1
398,7
400,3
401,9
403,6
405,2
406,9
408,5
410,2
411,8
413,5
415,2
416,8
418,5
420,2
421,9
423,6
425,3
427,0
428,7
430,4
432,1
433,8
435,5
437,2
439,0
2,655
2,657
2,659
2,661
2,663
2,665
2,666
2,668
2,670
2,672
2,674
2,676
2,678
2,680
2,681
2,683
2,685
2,687
2,689
2,691
2,693
2,694
2,696
2,698
2,700
2,702
2,704
2,706
2,707
2,709
2,711
2,713
2,715
2,717
2,718
2,720
2,722
2,724
2,726
2,728
. 2,729
2,731
2,733
2,735
2,737
2,739
2,740
2,742
2,744
2,746
2,748
2,750
2,751
2,753
2,755
2,757
/Юл
8,396
8,402
8,408
8,414
8,420
8,426
8,432
8,438
8,444
8,450
8,456
8,462
8,468
8,473
8,479
8,485
8,491
8,497
8,503
8,509
8,515
8,521
8,526
8,532
8,538
8,544
8,550
8,556
8,562
8,567
8,573
8,579
8,585
8,591
8,597
8,602
8,608
8,614
8,620
8,626
8,631
8,637
8,643
8,649
8,654
8,660
8,666
8,672
8,678
8,683
8,689
8,695
8,701
8,706
8,712
8,718
Г»
1,917
1,918
1,919
1,920
1,921
1,922
1,923
1,924
1,925
1,926
1,926
1,927
1,928
1,929
1,930
1,931
1,932
1,933
1,934
1,935
1,935
1,936
1,937
1,938
1,939
1,940
1,941
1,942
1,943
1,943
1,944
1,945
1,946
1,947
1,948
1,949
1,950
1,950
1,951
1,952
1,953
1,954
1,955
1,956
1,957
1,957
1,958
1,959
1,960
1,961
1,962
1,963
1,964
1,964
1,965
1,966
j/Ufo
4,131
4,133
4,135
4,137
4,139
4,141
4,143
4,145
4,147
4,149
4,151
4,152
4,154
4,156
4,158
4,160
4,162
4,164
4,166
4,168
4,170
4,172
4,174
4,176
4,177
4,179
4,181
4,183
4,185
4,187
4,189
4,191
4,193
4,195
4,196
4,198
4,200
4,202
4,204
4,206
4,208
4,210
4,212
4,213
4,215
4,217
4,219
4,221
4,223
4,225
4,227
4,228
4,230
4,232
4,234
4,236
f/\00n
8,900
8,904
8,909
8,913
8,917
8,921
8,925
8,929
8,934
8,938
8,942
8,946
8,950
8,955
8,959
8,963
8,967
8,971
8,975
8,979
8,984
8,988
8,992
8,996
9,000
9,004
9,008
9,012
9,016
9,021
9,025
9,029
9,033
9,037
9,041
9,045
9,049
9,053
9,057
9,061
9,065
9,069
9,073
9,078
9,082
9,086
9,090
9,094
9,098
9,102
9,106
9,110
9,114
9,118
9,122
9,126
КВАДРАТЫ, КУБЫ, КОРНИ
25
Продолжение
п
7,60
7,61
7,62
7,63
7,64
7,65
7,66
7,67
7,68
7,69
7,70
7,71
7,72
7,73
7,74
7,75
7,76
7,77
7,78
7,79
7,80
7,81
7,82
7,83
7,84
7,85
7,86
7,87
7,88
7,89
7,90
7,91
7,92
7,93
7,94
7,95
7,96
7,97
7,98
7,99
8,00
8,01
8,02
8,03
8,04
8,05
8,06
8,07
8,08
8,09
8,10
8,11
8,12
8,13
8,14
8,15
57,76
57,91
58,06
58,22
58,37
58,52
58,68
58,83
58,98
59,14
59,29
59,44
59,60
59,75
59,91
60,06
60,22
60,37
60,53
60,68
60,84
61,00
61,15
61,31
61,47
61,62
61,78
61,94
62,09
62,25
62,41
62,57
62,73
62,88
63,04
63,20
63,36
63,52
63,68
63,84
64,00
64,16
64,32
64,48
64,64
64,80
64,96
65,12
65,29
65,45
65,61
65,77
65,93
66,10
66,26
66,42
л-1
439,0
440,7
442,5
444,2
445,9
447,7
449,5
451,2
453,0
454,8
456,5
458,3
460,1
461,9
463,7
465,5
467,3
469,1
470,9
472,7
474^6
476,4
478,2
480,0
481,9
483,7
485,6
487,4
489,3
491,2
493,0
494,9
496,8
498,7
500,6
502,5
504,4
506,3
508,2
510,1
512,0
513,9
515,8
517,8
519,7
521,7
523,6
525,6
527,5
529,5
531,4
533,4
535,4
537,4
539,4
541,3
V»
2,757
2,759
2,760
2,762
2,764
2,766
2,768
2,769
2,771
2,773
2,775
2,777
2,778
2,780
2,782
2,784
2,786
2,787
2,789
2,791
2,793
2,795
2,796
2,798
2,800
2,802
2,804
2,805
2,807
2,809
2,811
2,812
2,814
2,816
2,818
2,820
2,821
2,823
2,825
2,827
2,828
2,830
2,832
2,834
2,835
2,837
2,839
2,841
2,843
2,844
2,846
2,848
2,850
2,851
2,853
2,855
\/\0п
8,718
8,724
8,729
8,735
8,741
8,746
8,752
8,758
8,764
8,769
8,775
8,781
8,786
8,792
8,798
8,803
8,809
8,815
8,820
8,826
8,832
8,837
8,843
8,849
8,854
8,860
8,866
8,871
8,877
8,883
8,888
8,894
8,899
8,905
8,911
8,916
8,922
8,927
8,933
8,939
8,944
8,950
8,955
8,961
8,967
8,972
8,978
8,983
8,989
8,994
9,000
9,009
9,011
9,017
9,022
9,028
1,966
1,967
1,968
1,969
1,970
1,970
1,971
1,972
1,973
1,974
1,975
1,976
1,976
1,977
1,978
1,979
1,980
1,981
1,981
1,982
1,983
1,984
1,985
1,986
t,987
1,987
1,988
1,989
1,990
1,991
1,992
1,992
1,993
1,994
1,995
1,996
1,997
1,997
1,998
1,999
2,000
2,001
2,002
2,002
2,003
2,004
2,005
2,006
2,007
2,007
2,008
2,009
2,010
2,011
2,012
2,012
J^10«
4,236
4,238
4,240
4,241
4,243
4,245
4,247
4,249
4,251
4,252
4,254
4,256
4,258
4,260
4,262
4,264
4,265
4,267
4,269
4,271
4,273
4,274
4,276
4,278
4,280
4,282
4,284
4,285
4,287
4,289
4,291
4,293
4,294
4,296
4,298
4,300
4,302
4,303
4,305
4,307
4,309
4,311
4,312
4,314
4,316
4,318
4,320
4,321
4,323
4,325
4,327
4,329
4,330
4,332
4,334
4,336
1^100/7
9,126
9,130
9,134
9,138
9,142
9,146
9,150
9,154
9,158
9,162
9,166
9,170
9,174
9,178
9,182
9,185
9,189
9,193
9,197
9,201
9,205
9,209
9,213
9,217
9,221
9,225
9,229
9,233
9,237
9,240
9,244
9,248
9,252
9,256
9,260
9,264
9,268
9,272
9,275
9,279
9,283
9,287
9,291
9,295
9,299
9,302
9,306
9,310
9,314
9,318
9,322
9,326
9,329
9,333
9,337
9,341
26
ТАБЛИЦЫ
Продолжение
п
8,15
8,16
8,17
8,18
8,19
8,20
8,21
8,22
8,23
8,24
8,25
8,26
8,27
8,28
8,29
8,30
8,31
8,32
8,33
8,34
8,35
8,36
8,37
8.38
8,39
8,40
8,41
8,42
8,43
8,44
8,45
8,46
8,47
8,48
8,49
8,50
8,51
8,52
8,53
8,54
8,55
8,56
8,57
8,58
8,59
8,60
8,61
8,62
8,63
8,64
8,65
8,66
8,67
8,68
8,69
8,70
66,42
66,59
66,75
66,91
67,08
67,24
67,40
67,57
67,73
67,90
68,06
68,23
68,39
68,56
68,72
68,89
69,06
69,22
69,39
69,56
69,72
69,89
70,06
70,22
70,39
70,56
70,73
70,90
71,06
71,23
71,40
71,57
71,74
71,91
72,08
72,25
72,42
72,59
72,76
72,93
73,10
73,27
73,44
73,62
73,79
73,96
74,13
74,30
74,48
74,65
74,82
75,00
75,17
75,34
75,52
75,69
и*
541,3
543,3
545,3
547,3
549,4
551,4
553,4
555,4
557,4
559,5
561,5
563,6
565,6
567,7
569,7
571,8
573,9
575,9
578,0
580,1
582,2
584,3
586,4
588,5
590,6
592,7
594,8
596,9
599,1
601,2
603,4
605,5
607,6
609,8
612,0
614,1
616,3
618,5
620,7
622,8
625,0
627,2
629,4
631,6
633,8
636,1
638,3
640,5
642,7
645,-0
647,2
649,5
651,7
654,0
656,2
658,5
V»
2,855
2,857
2,858
2,860
2,862
2,864
2,865
2,867
2,869
2,871
2,872
2,874
2,876
2,877
2,879
2,881
2,883
2,884
2,886
2,888
2,890
2,891
2,893
2,895
2,897
2,898
2,900
2,902
2,903
2,905
2,907
2,909
2,910
2,912
2,914
2,915
2,917
2,919
2,921
2,922
2,924
2,926
2,927
2,929
2.931
2,933
2,934
2,936
2,938
2,939
2,941
2,943
2,944
2,946
2,948
2,950
|/lO/i
9,028
9,033
9,039
9,044
9,050
9,055
9,061
9,066
9,072
9,077
9,083
9,088
9,094
9,099
9,105
9,110
9,116
9,121
9,127
9,132
9,138
9,143
9,149
9,154
9,160
9,165
9,171
9,176
9,182
9,187
9,192
9,198
9,203
9,209
9,214
9,220
9,225
9,230
9,236
9,241
9,247
9,252
9,257
9,263
9,268
9,274
9,279
9,284
9,290
9,295
9,301
9,306
9,311
9,317
9,322
9,327
2,012
2,013
2,014
2,015
2,016
2,017
2,017
2,018
2,019
2,020
2,021
2,021
2,022
2,023
2,024
2,025
2,026
2,026
2,027
2,028
2,029
2,030
2,030
2,031
2,032
2,033
2,034
2,034
2,035
2,036
2,037
2,038
2,038
2,039
2,040
2,041
2,042
2,042
2,043
2,044
2,045
2,046
2,046
2,047
2,048
2,049
2,050
2,050
2,051
2,052
2,053
2,054
2,054
2,055
2,056
2,057
4,336
4,337
4,339
4,341
4,343
4,344
4,346
4,348
4,350
4,352
4,353
4,355
4,357
4,359
4,360
4,362
4,364
4,366
4,367
4,369
4,371
4,373
4,374
4,376
4,378
4,380
4,381
4,383
4,385
4,386
4,388
4,390
4,392
4,393
4,395
4,397
4,399
4,400
4,402
4,404
4,405
4,407
4,409
4,411
4,412
4,414
4,416
4,417
4,419
4,421
4,423
4,424
4,426
4,428
4,429
4,431
[V100/1
9,341
9,345
9,348
9,352
9,356
9,360
9,364
9,368
9,371
9,375
9,379
9,383
9,386
9,390
9,394
9,398
.9,402
9,405
9,409
9,413
9,417
9,420
9,424
9,428
9,432
9,435
9,439
9,443
9,447
9,450
9,454
9,458
9,462
9,465
9,469
9,473
9,476
9,480
9,484
9,488
9,491
9,495
9,499
9,502
9,506
9,510
9,513
9,517
9,521
9,524
9,528
9,532
9,535
9,539
9,543
9,546
КВАДРАТЫ, КУБЫ, КОРНИ
27
Продолжение
п
8,70
8,71
8,72
8,73
8,74
8,75
8,76
8,77
8,78
8,79
8,80
8,81
8,82
8,83
8,84
8,85
8,86
8,87
8,88
8,89
8,90
8,91
8,92
8,93
8,94
8,95
8,96
8,97
8,98
8,99
9,00
9,01
9,02
9,03
9,04
9,05
9,06
9,07
9,08
9,09
9,10
9,11
9,12
9,13
9,14
9,15
9,16
9,17
9,18
9,19
9,20
9,21
9,22
9,23
9,24
9,25
75,69
75,86
76,04
76,21
76,39
76,56
76,74
76,91
77,09
77,26
77,44
77,62
77,79
77,97
78,15
78,32
78,50
78,68
78,85
79,03
79,21
79,39
79,57
79,74
79,92
80,10
80,28
80,46
80,64
80,82
81,00
81,18
81,36
81,54
81,72
81,90
82,08
82,26
82,45
82,63
82,81
82,99
83,17
83,36
83,54
83,72
83,91
84,09
84,27
84,46
84,64
84,82
85,01
85,19
85,38
85,56
658,5
660,8
663,1
665,3
667,6
669,9
672,2
674,5
676,8
679,2
681,5
683,8
686,1
688,5
690,8
693,2
695,5
697,9
700,2
702,6
705,0
707,3
709,7
712,1
714,5
716,9
719,3
721,7
724,2
726,6
729,0
731,4
733,9
736,3
738,8
741,2
743,7
746,1
748,6
751,1
753,6
756,1
758,6
761,0
763,6
766,1
768,6
771,1
773,6
776,2
778,7
781,2
783,8
786,3
788,9
791,5
|/«
2,950
2,951
2,953
2,955
2,956
2,958
2,960
2,961
2,963
2,965
2,966
2,968
2,970
2,972
2,973
2,975
2,977
2,978
2,980
2,982
2,983
2,985
2,987
2,988
2,990
2,992
2,993
2,995
2,997
2,998
3,000
3,002
3,003
3,005
3,007
3,008
3,010
3,012
3,013
3,015
3,017
3,018
3,020
3,022
3,023
3,025
3,027
3,028
3,030
3,032
3,033
3,035
3,036
3,038
3,040
3,041
j/lOn
9,327
9,333
9,338
9,343
9,349
9,354
9,359
9,365
9,370
9,375
9,381
. 9,386
9,391
9,397
9,402
9,407
9,413
9,418
9,423
9,429
9,434
9,439
9,445
9,450
9,455
9,460
9,466
9,471
9,476
9,482
9,487
9,492
9,497
9,503
9,508
9,513
9,518
9,524
9,529
9,534
9,539
9,545
9,550
9,555
9,560
9,566
9,571
9,576
9,581
9,586
9,592
9,597
9,602
9,607
9,612
9,618
2,057
2,057
2,058
2,059
2,060
2,061
2,061
2,062
2,063
2,064
2,065
2,065
2,066
2,067
2,068
2,068
2,069
2,070
2,071
2,072
2,072
2,073
2,074
2,075
2,075
2,076
2,077
2,078
2,079
2,079
2,080
2,081
2,082
2,082
2,083
2,084
2,085
2,085
2,086
2,087
2,088
2,089
2,089
2,090
2,091
2,092
2,092
2,093
2,094
2,095
2,095
2,096
2,097
2,098
2,098
2,099
4,431
4,433
4,434
4,436
4,438
4,440
4,441
4,443
4,445
4,446
4,448
4,450
4,451
4,453
4,455
4,456
4,458
4,460
4,461
4,463
4,465
4,466
4,468
4,470
4,471
4,473
4,475
4,476
4,478
4,480
4,481
4,483
4,485
4,486
4,488
4,490
4,491
4,493
4,495
4,496
4,498
4,500
4,501
4,503
4,505
4,506
4,508
4,509
4,511
4,513
4,514
4,516
4,518
4,519
4,521
4,523
\/100п
9,546
9,550
9,554
9,557
9,561
9,565
9,568
9,572
9,576
9,579
9,583
9,586
9,590
9,594
9,597
9,601
9,605
9,608
9,612
9,615
9,619
9,623
9,626
9,630
9,633
9,637
9,641
9,644
9,648
9,651
9,655
9,658
9,662
9,666
9,669
9,673
9,676
9,680
9,683
9,687
9,691
9,694
9,698
9,701
9,705
9,708
9,712
9,715
9,719
9,722
9,726
9,729
9,733
9,736
9,740
9,743
28
ТАБЛИЦЫ
Продолжение
п
9,25
9,26
9,27
9,28
9,29
9,30
9,31
9,32
9,33
9,34
9,35
9,36
9,37
9,38
9,39
9,40
9,41
9,42
9,43
9,44
9,45
9,46
9,47
9,48
9,49
9,50
9,51
9,52
9,53
9,54
9,55
9,56
9,57 '
9,58
9,59
9,60
9,61
9,62
9,63
9,64
9,65
9,66
9,67
9,68
9,69
9,70
9,71
9,72
9,73
9,74
9,75
9,76
9,77
9,78
9,79
9,80
«2
85,56
85,75
85,93
86,12
86,30
86,49
86,68
86,86
87,05
87,24
87,42
87,61
87,80
87,98
88,17
88,36
88,55
88,74
88,92
89,11
89,30
89,49
89,68
89,87
90,06
90,25
90,44
90,63
90,82
91,01
91,20
91,39
91,58
91,78
91,97
92,16
92,35
92,54
92,74
92,93
93,12
93,32
93,51
93,70
93,90
94,09
94,28
94,48
94,67
94,87
95,06
95,26
95,45
95,65
95,84
96,04
791,5
794,0
796,6
799,2
801,8
804,4
807,0
809,6
812,2
814,8
817,4
820,0
822,7
825,3
827,9
830,6
833,2
835,9
838,6
841,2
843,9
846,6
849,3
852,0
854,7
857,4
860,1
862,8
865,5
868,3
871,0
873,7
876,5
879,2
882,0
884,7
887,5
890,3
893,1
895,8
898,6
901,4
904,2
907,0
909,9
912,7
915,5
918,3
921,2
924,0
926,9
929,7
932,6
935,4
938,3
941,2
3,041
3,043
3,045
3,046
3,048
3,050
3,051
3,053
3,055
3,056
3,058
3,059
3,061
3,063
3,064
3,066
3,068
3,069
3,071
3,072
3,074
3,076
3,077
3,079
3,081
3,082
3,084
3,085
3,087
3,089
3,090
3,092
3,094
3,095
3,097
3,098
3,100
3,102
3,103
3,105
3,106
3,108
3,110
3,111
3,113
3,114
3,116
3,118
3,119
3,121
3,122
3,124
3,126
3,127
3,129
3,130
l/lOn
9,618
9,623
9,628
9,633
9,638
9,644
9,649
9,654
9,659
9,664
9,670
9,675
9,680
9,685
9,690
9,695
9,701
9,706
9,711
9,716
9,721
9,726
9,731
9,737
9,742
9,747
9,752
9,757
9,762
9,767
9,772
9,778
9,783
9,788
9,793
9,798
9,803
9,808
9,813
9,818
9,823
9,829
9,834
9,839
9,844
9,849
9,854
9,859
9,864
9,869
9,874
9,879
9,884
9,889
9,894
9,899
2,099
2,100
2,101
2,101
2,102
2,103
2,104
2,104
2,105
2,106
2,107 •
2,107
2,108
2,109
2,110
2,110
2,111
2,112
2,113
2,113
2,114
2,115
2,116
2,116
2,117
2,118
2,119
2,119
2,120
2,121
2,122
2,122
2,123
2,124
2,125
2,125
2,126
2,127
2,128
2,128
2,129
2,130
2,130
2,131
2,132
2,133
2,133
2,134
2,135
2,136
2,136
2,137
2,138
2,139
2,139
2,140
4,523
4,524
4,526
4,527
4,529
4,531
4,532
4,534
4,536
4,537
4,539
4,540
4,542
4,544
4,545
4,547
4,548
4,550
4,552
4,553
4,555
4,556
4,558
4,560
4,561
4,563
4,565
4,566
4,568
4,569
4,571
4,572
4,574
4,576
4,577
4,579
4,580
4,582
4,584
4,585
4,587
4,588
4,590
4,592 '
4,593
4,595
4,596
4,598
4,599
4,601
4,603
4,604
4,606
4,607
4,609
4,610
j^lOOn
9,743
9,747
9,750
9,754
9,758
9,761
9,764
9,768
9,771
9,775
9,778
9,782
9,785
9,789
9,792
.9,796
9,799
9,803
9,806
9,810
9,813
9,817
9,820
9,824
9,827
9,830
9,834
9,837
9,841
9,844
9,848
9,851
9,855
9,858
9,861
9,865
9,868
9,872
9,875
9,879
9,882
9,885
9,889
9,892
9,896
9,899
9,902
9,906
9,909
9,913
9,916
9,919
9,923
9,926
9,930
9,933
СТЕПЕНИ ЦЕЛЫХ ЧИСЕЛ ОТ 1 ДО 100
29
Продолжение
п
9,80
9,81
9,82
9,83
9,84
9,85
9,86
9,87
9,88
9,89
9,90
9,91
9,92
9,93
9,94
9,95
9,96
9,97
9,98
9,99
10,00
96,04
96,24
96,43
96,63
96,83
97,02
97,22
97,42
97,61
97,81
98,01
98,21
98,41
98,60
98,80
99,00
99,20
99,40
99,60
99,80
100,00
«з
941,2
944,1
947,0
949,9
952,8
955,7
958,6
961,5
964,4
967,4
970,3
973,2
976,2
979,1
982,1
985,1
988,0
991,0
994,0
997,0
1000,0
]/п
3,130
3,132
3,134
3,135
3,137
3,138
3,140
3,142
3,143
3,145
3,146
3,148
3,150
3,151
3,153
3,154
3,156
3,158
3,159
3,161
3,162
j/Юл
9,899
9,905
9,910
9,915
9,920
9,925
9,930
9,935
9,940
9,945
9,950
9,955
9,960
9,965
9,970
9,975
9,980
9,985
9,990
9,995
10,000
2,140
2,141
2,141
2,142
2,143
2,144
2,144
2,145
2,146
2,147
2,147
2,148
2,149
2,149
2,150
2,151
2,152
2,152
2,153
2,154
2,154
3,
yiOn
4,610
4,612
4,614
4,615
4,617
4,618
4,620
4,621
4,623
4,625
4,626
4,628
4,629
4,631
4,632
4,634
4,635
4,637
4,638
4,640
4,642
9,933
9,936
9,940
9,943
9,946
9,950
9,953
9,956
9,960
9,963
9,967
9,970
9,973
9,977
9,980
9,983
9,987
9,990
9,993
9,997
10,000
1.1.1.3. Степени целых чисел от
п
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
1
4
9
16
25
36
49
64
81
100
121
144
169
196
225
256
289
324
361
400
441
484
529
576
625
676
729
784
841
900
961
1024
1089
1156
1 до 100.
/|3
1
8
27
64
125
216
343
512
729
1000
1331
1728
2197
2744
3375
4096
4913
5832
6859
8000
9261
10648
12167
13 824
15625
17576
19683
21952
24389
27000
29791
32768
35937
39 304
1
16
81
256
625
1296
2401
4096
6 561
10000
14641
20736
28 561
38416
50625
65 536
83521
104976
130321
160000
194481
234256
279841
331 776
390625
456976
531441
614656
707281
810000
923521
1048 576
1185921
1336336
1
32
243
1024
3125
7776
16807
32768
59049
100000
161051
248832
371 293
537824
750 375
1 048 576
1419857
1889 568
2476099
3200000
4084101
5153632
6436343
7962624
9765625
11881376
14348907
17210368
20511149
24300000
28629151
33 554432
39135393
45435424
30
ТАБЛИЦЫ
Продолжение
п
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
и2
1225
1296
1369
1444
1521
1600
1681
1764
1849
1936
2 025
2116
2209
2 304
2401
2 500
2 601
2 704
2 809
2916
3025
3136
3 249
3 364
3481
3 600
3 721
ЗМ4
; чич
4 0%
4 225
4 356
4489
4624
4761
4900
5041
5184
5 329
5476
5625
5 776
5929
6084
6241
6400
6 561
6724
6889
7056
7 225
7 396
7 569
7 744
7921
8100
8281
8464
8649
8 836
9025
9216
9409
9604
9 801
10000
л*
42875
46656
50653
54872
59319
64000
68 921
74088
79 507
85 184
91 125
97 336
103 823
110 592
117649
125000
132651
140608
148 877
157464
166375
175616
185193
195112
205 379
216000
226981
238 328
250047
262 144
274625
287496
300763
314432
328 509
343000
357911
373248
389017
405224
421875
438 976
456 533
474 552
493 039
512000
531441
551368
571787
592 704
614125
636056
658 503
681472
704969
729000
753 571
778 688
804 357
830 584
857 375
884736
912673
941 192
970299
1000000
1500625
1679616
1874161
2085136
2313441
2 560000
2 825 761
3 111 696
3418801
3 748096
4100625
4477456
4879681
5 308416
5 764801
6250000
6765201
7311616
7 890481
8 503056
9150625
9834496
10 556001
11316496
12117361
12960000
13 845 841
14776 336
15 752961
16777216
17 850625
18974736
20151 121
21381376
22 667121
24010000
, 25411681
26873 856
28 398241
29986 576
31640625
33 362176
35153041
37015056
38950081
40960000
43046721
45212176
47458 321
49 787136
52200625
54700816
57289 761
59969 536
62742241
65 610000
68 574961
71639296
74805201
78074896
81450625
84934656
88 529281
92236816
96059601
100000000
52 521875
60466176
69 343957
79235168
90224199
102400000
115 856201
130691232
147008443
164916224
184528125
205 962976
229 345007
254803968
282475249
312 500000
345025251
380204032
418195493
459165024
503284375
550731776
601692057
656 356768
714924299
777 600000
844 596301
916132832
992436543
1073 741824
1 160290625
1252 332 576
1 350 125 107
1453 933 568
1564031349
1680700000
1804229 351
1934917632
2073071593
2219006624
2 373046875
2 535 525 376
2 706784157
2887174368
3077056 399
3 276800000
3486784401
3 707 398432
3939040643
4182 119424
4437053125
4704270176
4984209207
5277319168
5 584059449
5904900000
6240 321451
6590815232
6956883693
7 339040224
7 737 809 375
8153 726976
8 587 340257
9039207968
9 509900499
10000000000
ОБРАТНЫЕ ВЕЛИЧИНЫ
31
1.1.1.4.
п
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
Обратные
0
10000
9091
8333
7692
7143
6667
6250
5882
5556
5263
5000
4762
4545
4348
4167
4000
3846
3704
3571
3448
3333
3226
3125
3030
2941
2857
2778
2703
2632
2564
2500
2439
2381
2326
2273
2222
2174
2128
2083
2041
2000
1961
1923
1887
1852
1818
1786
1754
1724
1695
1667
1639
1613
1587
1562
1538
1515
1493
1471
1449
величины.
1
9901
9009
8264
7634
7092
6623
6211
5848
5525
5236
4975
4739
4525
4329
4149
3984
3831
3690
3559
3436
3322
3215
3115
3021
2933
2849
2770
2695
2625
2558
2494
2433
2375
2320
2268
2217
2169
2123
2079
2037
1996
1957
1919
1883
1848
1815
1783
1751
1721
1692
1664
1637
1610
1585
1560
1536
1513
1490
1468
1447
2
9804
8929
8197
7576
7042
6579
6173
5814
5495
5208
4950
4717
4505
4310
4132
3968
3817
3676
3546
3425
3311
3205
3106
3012
2924
2841
2762
2688
2618
2551
2488
2427
2370
2315
2262
2212
2165
2119
2075
2033
1992
1953
1916
1880
1845
1812
1779
1748
1718
1689
1661
1634
1608
1582
1558
1534
1511
1488
1466
1445
3
9709
8850
8130
7519
6993
6536
6135
5780
5464
5181
4926
4695
4484
4292
4115
3953
3802
3663
3534
3413
3300
3195
3096
3003
2915
2833
2755
2681
2611
2545
2481
2421
2364
2309
2257
2208
2160
2114
2070
2028
1988
1949
1912
1876
1842
1808
1776
1745
1715
1686
1658
1631
1605
1580
1555
1531
1508
1486
1464
1443
4
9615
8772
8065
7463
6944
6494
6098
5747
5435
5155
4902
4673
4464
4274
4098
3937
3788
3650
3521
3401
3289
3185
3086
2994
2907
2825
2747
2674
2604
2538
2475
2415
2358
2304
2252
2203
2155
2110
2066
2024
1984
1946
1908
1873
1838
1805
1773
1742
1712
1684
1656
1629
1603
1577
1553
1529
1506
1484
1462
1441
5
9524
8696
8000
7407
6897
6452
6061
5714
5405
5128
4878
4651
4444
4255
4082
3922
3774
3636
3509
3390
3279
3175
3077
2985
2899
2817
2740
2667
2597
2532
2469
2410
2353
2299
2247
2198
2151
2105
2062
2020
1980
1942
1905
1869
1835
1802
1770
1739
1709
1681
1653
1626
1600
1575
1550
1527
1504
1481
1460
1439
6
9434
8621
7937
7353
6849
6410
6024
5682
5376
5102
4854
4630
4425
4237
4065
3906
3759
3623
3497
3378
3268
3165
3067
2976
2890
2809
2732
2660
2591
2525
2463
2404
2347
2294
2242
2193
2146
2101
2058
2016
1976
1938
1901
1866
1832
1799
1767
1736
1706
1678
1650
1623
1597
1572
1548
1524
1502
1479
1458
1437
7
9346
8547
7874
7299
6803
6369
5988
5650
5348
5076
4831
4608
4405
4219
4049
3891
3745
3610
3484
3367
3257
3155
3058
2967
2882
2801
2725
2653
2584
2519
2457
2398
2342
2288
2237
2188
2141
2096
2053
2012
1972
1934
1898
1862
1828
1795
1764
1733
1704
1675
1647
1621
1595
1570
1546
1522
1499
1477
1456
1435
8
9259
8475
7812
7246
6757
6329
5952
5618
5319
5051
4808
4587
4386
4202
4032
3876
3731
3597
3472
3356
3247
3145
3049
2959
2874
2793
2717
2646
2577
2513
2451
2392
2336
2283
2232
2183
2137
2092
2049
2008
1969
1931
1894
1859
1825
1792
1761
1730
1701
1672
1645
1618
1592
1567
1543
1520
1497
1475
1453
1433
9
9174
8403
7752
7194
6711
6289
5917
5587
5291
5025
4785
4566
4367
4184
4016
3861
3717
3584
3460
3344
3236
3135
3040
2950
2865
2786
2710
2639
2571
2506
2445
2387
2331
2278
2227
2179
2132
2088
2045
2004
1965
1927
1890
1855
1821
1789
1757
1727
1698
1669
1642
1616
1590
1565
1541
1517
1495
1473
1451
1431
32
ТАБЛИЦЫ
Продолжение
п
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
0
1429
1408
1389
1370
1351
1333
1316
1299
1282
1266
1250
1235
1220
1205
1190
1176
1163
1149
1136
1124
1111
1099
1087
1075
1064
1053
1042
1031
1020
1010
1
1427
1406
1387
1368
1350
1332
1314
1297
1280
1264
1248
1233
1218
1203
1189
1175
1161
1148
1135
1122
1110
1098
1086
1074
1063
1052
1041
1030
1019
1009
2
1425
1404
1385
1366
1348
1330
1312
1295
1279
1263
1247
1232
1217
1202
1188
1174
1160
1147
1134
1121
1109
1096
1085
1073
1062
1050
1040
1029
1018
1008
3
1422
1403
1383
1364
1346
1328
1311
1294
1277
1261
1245
1230
1215
1200
1186
1172
1159
1145
1133
1120
1107
1095
1083
1072
1060
1049
1038
1028
1017
1007
4
1420
1401
1381
1362
1344
1326
1309
1292
1276
1259
1244
1229
1214
1199
1185
1171
1157
1144
1131
1119
1106
1094
1082
1071
1059
1048
1037
1027
1016
1006
5
1418
1399
1379
1361
1342
1325
1307
1290
1274
1258
1242
1227
1212
1198
1183
1170
1156
1143
ИЗО
1117
1105
1093
1081
1070
1058
1047
1036
1026
1015
1005
6
1416
1397
1377
1359
1340
1323
1305
1289
1272
1256
1241
1225
1211
1196
1182
1168
1155
1142
1129
1116
1104
1092
1080
1068
1057
1046
1035
1025
1014
1004
7
1414
1395
1376
1357
1339
1321
1304
1287
1271
1255
1239
1224
1209
1195
1181
1167
1153
1140
1127
1115
1103
1091
1079
1067
1056
1045
1034
1024
1013
1003
8
1412
1393
1374
1355
1337
1319
1302
1285
1269
1253
1238
1222
1208
1193
1179
1166
1152
1139
1126
1114
1101
1089
1078
1066
1055
1044
1033
1022
1012
1002
9
1410
1391
1372
1353
1335
1318
1300
1284
1267
1252
1236
1221
1206
1192
1178
1164
1151
1138
1125
1112
1100
1088
1076
1065
1054
1043
1032
1021
1011
1001
Объяснения к таблице обратных
величин. В таблице 1.1.1.4 даны с четырьмя
знаками значения величин 10000: и для
трехзначных аргументов, заключенных между 1 и 10.
Каждое число в таблице помещено в строке,
соответствующей первым двум значащим цифрам
аргумента (указанным в столбце и), и в столбце,
соответствующем третьей цифре аргумента.
Например, 10000: 2,26 = 4425. Если аргумент дан с
четырьмя знаками, то необходимо прибегнуть
к линейной интерполяции. Следует обратить
внимание на то, что здесь интерполяционные
поправки не прибавляются, а вычитаются.
Помещенные в таблице числа можно
рассматривать как десятичные знаки, следующие за
запятой в дроби 1: п; например, 1: 2,26 = 0,4425.
Для нахождения 1: п при и > 10 и п < 1
принимают во внимание, что при умножении п на 10*
величина 1:и умножается на 10~\ т.е. перенос
запятой у п на. к разрядов вправо вызывает
перенос запятой у 1: п на к разрядов влево и наоборот.
Например, 1: 22,6 = 0,04425 и 1:0,0226 = 44,25.
1.1.1.5. Факториалы и обратные им величины.
Факториалы.
п
х
2
3
4
5
6
7
8
9
10
п\
1
2
6
24
120
720
5040
40320
362880
3628800
п
11
12
13
14
15
16
17
18
19
20
п\
39916800
479001600
6227020800
87178291200
1307674368000
20922789888000
355687428096000
6402373705728000
121645100408832000
2432902008176640000
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
33
Величины, о б р а 1 н ы е факториалам*)
п
1
2
3
4
5
6
7
8
9
10
*) Для
0,0<»24802.
1 п\
1,000000
0,500000
0,166667
0,041667
0,0283333
0,0213889
0,0319841
0,0*24802
0,0527557
0,0627557
п
11
12
13
14
15
16
17
18
19
20
\:п\ применена сокращенная запись нулей
1 :я'
0,0725052
0,0820877
0,0916059
0,0^11471
0,01276472
0,01347795
0,01428115
0,0»515619
0,01782206
0,01841103
после запятой. Так, для 1
п
21
22
23
24
25
26
27
28
29
30
:8! вместо 0,000024802
0,01919573
0,02188968
0,02238682
0,02316117
0,02564470
0,02624796
0,02891837
0,02932799
0,03011310
0,03237700
написано
1.1.1.6. Некоторые степени чисел 2, 3 и 5.
/7
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2"
2
4
8
16
32
64
128
256
512
1024
2048
4096
8 192
16 384
32768
65 536
131072
262 144
524288
1 048 576
3я
3
9
27
81
243
729
2187
6 561
19683
59049
177147
531441
1 594 323
4782969
14348907
43046721
129 140163
387420489
1 162261467
3486 784401
5"
5
25
125
625
3125
15625
78125
390625
1 953125
9765625
48 828125
244140625
1220703 125
6103 515625
30517578125
152 587 890625
762939453125
3 814697 265625 ,
19073486 328125
95 367431640625
1.1.1.7. Десятичные логарифмы.
Объяснения к таблицам
логарифмов и антилогарифмов. Таблица 1.1.1.7
служит для нахождения десятичных логарифмов
чисел. Сначала для данною числа находится
характеристика ei о логарифма, а затем мантисса
из таблицы. Для трехзначных чисел мантисса
находится на пересечении строки, в начале которой
(графа N) стоят две первые цифры данного числа,
и столбца, соответствующего третьей цифре
нашего числа. Если заданное число имеет больше
трех значащих цифр, необходимо применить
линейную интерполяцию. При этом
интерполяционная поправка находится только на четвертую
значащую цифру числа; поправку на пятую цифру
имеет смысл делать только тогда, когда первая
значащая цифра данного числа равна 1 или 2.
Пример lg 254,3 = 2,4053 (к 4048 нужно прибавить
0,3 17 = 5,1)
Для нахождения числа по его десятичному
логарифму служит таблица 1.1.1.8 (таблица анти-
2 И Н. Ьронилейн, К А Семендяев
логарифмов)*). Аргументом в этой таблице является
мантисса заданного логарифма. На пересечении
строки, которая определяется первыми двумя
цифрами мантиссы (графа т), и столбца,
соответствующего третьей цифре мантиссы, в таблице
антилогарифмов находится цифровой состав искомого
числа. На четвертую цифру мантиссы должна быть
внесена интерполяционная поправка.
Характеристика логарифма позволяет поставить в
полученном результате запятую.
Примеры. lgx= 1,2763; х = 18,89 (к найденному в
таблице значению 1888 прибавляется 0,3 • 4 = 1,2; в
полученном результате отделяются запятой два знака, так как
характеристика равна единице). Если \gx = 2,2763, то х = 0,01889.
Эти результаты могут быть записаны также следующим
образом: Ю1-2763 = 18,89; 10-7237 = 0,01889 (так как
2,2763=-1,7237).
*) Число у, десятичный логарифм которого равен х,
называют антилогарифмом х Со1ласно определению
логарифма, эта функция совпадает с показательной функцией
у = 10х
34
ТАБЛИЦЫ
Десятичные логарифмы
N
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
0
0000
0414
0792
1139
1461
1761
2041
2304
2553
2788
ЗОЮ
3222
3424
3617
3802
3979
4150
4314
4472
4624
4771
4914
5051
5185
5315
5441
5563
5682
5798
5911
6021
6128
6232
6335
6435
6532
6628
6721
6812
6902
6990
7076
7160
7243
7324
1
0043
0453
0828
1173
1492
1790
2068
2330
2577
2810
3032
3243
3444
3636
3820
3997
4166
4330
4487
4639
4786
4928
5065
5198
5328
5453
5575
5694
5809
5922
6031
6138
6243
6345
6444
6542
6637
6730
6821
6911
6998
7084
7168
7251
7332
2
0086
0492
0864
1206
1523
1818
2095
2355
2601
2833
3054
3263
3464
3655
3838
4014
4183
4346
4502
4654
4800
4942
5079
5211
5340
5465
5587
5705
5821
5933
6042
6149
6253
6355
6454
6551
6646
6739
6830
6920
7007
7093
7177
7259
7340
3
0128
0531
0899
1239
1553
1847
2122
2380
2625
2856
3075
3284
3483
3674
3856
4031
4200
4362
4518
4669
4814
4955
5092
5224
5353
5478
5599
5717
5832
5944
6053
6160
6263
6365
6464
6561
6656
6749
6839
6928
7016
7101
7185
7267
7348
4
0170
0569
0934
1271
1584
1875
2148
2405
2648
2878
3096
3304
3502
3692
3874
4048
4216
4378
4533
4683
4829
4969
5105
5237
5366
5490
5611
5729
5843
5955
6064
6170
6274
6375
6474
6571
6665
6758
6848
6937
7024
7110
7193
7275
7356
5
0212
0607
0969
1303
1614
1903
2175
2430
2672
2900
3118
3324
3522
3711
3892
4065
4232
4393
4548
4698
4843
4983
5119
5250
5378
5502
5623
5740
5855
5966
6075
6180
6284
6385
6484
6580
6675
6767
6857
6946
7033
7118
7202
7284
7364
6
0253
0645
1004
1335
1644
1931
2201
2455
2695
2923
3139
3345
3541
3729
3909
4082
4249
4409
4564
4713
4857
4997
5112
5263
5391
5514
5635
5752
5866
5977
6085
6191
6294
6395
6493
6590
6684
6776
6866
6955
" 7042
7126
7210
7292
7372
7
0294
0682
1038
1367
1673
1959
2227
2480
2718
2945
3160
3365
3560
3747
3927
4099
4265
4425
4579
4728
4871
5011
5145
5276
5403
5527
5647
5763
5877
5988
6096
6201
6304
6405
6503
6599
6693
6785
6875
6964
7050
7135
7218
7300
7380
8
0334
0719
1072
1399
1703
1987
2253
2504
2742
2967
3181
3385
3579
3766
3945
4116
4281
4440
4594
4742
4886
5024
5159
5289
5416
5539
5658
5775
5888
5999
6107
6212
6314
6415
6513
6609
6702
6794
6884
6972
7059
7143
7226
7308
7388
9
0374
0755
1106
1430
1732
2014
2279
2529
2765
2989
3201
3404
3598
3784
3962
4133
4298
4456
4609
4757
4900
5038
5172
5302
5428
5551
5670
5786
5899
6010
6117
6222
6325
6425
6522
6618
6712
6803
6893
6981
7067
7152
7235
7316
7396
ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ
35
Продолжение
N
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
' 77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
0
7404
7482
7559
7634
7709
7782
7853
7924
7993
8062
8129
8195
8261
8325
8388
8451
8513
8573
8633
8692
8751
8808
8865
8921
8976
9031
9085
9138
9191
9243
9294
9345
9395
9445
9494
9542
9590
9638
9685
9731
9777
9823
9868
9912
9956
1
7412
7490
7566
7642
7716 '
7789
7860
7931
8000
8069
8136
8202
8267
8331
8395
8457
8519
8579
8639
8698
8756
8814
8871
8927
8982
9036
9090
9143
9196
9248
9299
9350
9400
9450
9499
9547
9595
9643
9689
9736
9782
9827
9872
9917
9961
2
7419
7497
7574
7649
7723
7796
7868
7938
8007
8075
8142
8209
8274
8338
8401
8463
8525
8585
8645
8704
8762
8820
8876
8932
8987
9042
9096
9149
9201
9253
9304
9355
9405
9455
9504
9552
9600
9647
9694
9741
9786
9832
9877
9921
9965
3
7427
7505
7582
7657
7731
7803
7875
7945
8014
8082
8149
8215
8280
8344
8407
8470
8531
8591
8651
8710
8768
8825
8882
8938
8993
9047
9101
9154
9206
9258
9309
9360
9410
9460
9509
9557
9605
9652
9699
9745
9791
9836
9881
9926
9969
4
7435
7513
7589
7664
7738
7810
7882
7952
8021
8089
8156
8222
8287
8351
8414
8476
8537
8597
8657
8716
8774
8831
8887
8943
8998
9053
9106
9159
9212
9263
9315
9365
9415
9465
9513
9562
9609
9657
9703
9750
9795
9841
9886
9930
9974
5
7443
7520
7597
7672
7745
7818
7889
7959
8028
8096
8162
8228
8293
8357
8420
8482
8543
8603
8663
8722
8779
8837
8893
8949
9004
9058
9112
9165
9217
9269
9320
9370
9420
9469
9518
9566
9614
9661
9708
9754
9800
9845
9890
9934
9978
6
7451
7528
7604
7679
7752
7825
7896
7966
8035
8102
8169
8235
8299
8363
8426
8488
8549
8609
8669
8727
8785
8842
8899
8954
9009
9063
9117
9170
9222
9274
9325
9375
9425
9474
9523
9571
9619
9666
9713
9759
9805
9850
9894
9939
9983
7
7459
7536
7612
7686
7760
7832
7903
7973
8041
8109
8176
8241
8306
8370
8432
8494
8555
8615
8675
8733
8791
8848
8904
8960
9015
9069
9122
9175
9227
9279
9330
9380
9430
9479
9523
9576
9624
9671
9717
9763
9809
9854
9899
9943
9987
8
7466
7543
7619
7694
7767
7839
7910
7980
8048
8116
8182
8248
8312
8376
8439
8500
8561
8621
8681
8739
8797
8854
8910
8965
9020
9074
9128
9180
9232
9284
9335
9385
9435
9484
9533
9581
9628
9675
9722
9768
9814
9859
9903
9948
9991
9
7474
7551
7627
7701
7774
7846
7917
- 7987
8055
8122
8189
8254
8319
8382
8445
8506
8567
8627
8686
8745
8802
8859
8915
8971
9025
9079
9133
9186
9238
9289
9340
9390
9440
9489
9538
9586
9633
9680
9727
9773
9818
9863
9908
9952
9996
36
ТАБЛИЦЫ
1.1.1.8.
т
00
01
02
03 '
04
05
06
07
08
09
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
Антило! арифмы.
0
1000
1023
1047
1072
1096
1122
1148
1175
1202
1230
1259
1288
1318
1349
1380
1413
1445
1479
1514
1549
1585
1622
1660
1698
1738
1778
1820
1862
1905
1950
1995
2042
2089
2138
2188
2239
2291
2344
2399
2455
2512
2570
2630
2692
2754
2818
2884
2951
3020
3090
1
1002
1026
1050
1074
1099
1125
1151
1178
1205
1233
1262
1291
1321
1352
1384
1416
1449
1483
1517
1552
1589
1626
1663
1702
1742
1782
1824
1866
1910
1954
2000
2046
2094
2143
2193
2244
2296
2350
2404
2460
2518
2576
2636
2698
2761
2825
2891
2958
3027
3097
2
1005
1028
1052
1076
1102
1127
1153
1180
1208
1236
1265
1294
1324
1355
1387
1419
1452
1486
1521
1556
1592
1629
1667
1706
1746
1786
1828
1871
1914
1959
2004
2051
2099
2148
2198
2249
2301
2355
2410
2466
2523
2582
2642
2704
2767
2831
2897
2965
3034
3105
3
1007
1030
1054
1079
1104
ИЗО
1156
1183
1211
1239
1268
1297
1327
1358
1390
1422
1455
1489
1524
1560
1596
1633
1671
1710
1750
1791
1832
1875
1919
1963
2009
2056
2104
2153
2203
2254
2307
2360
2415
2472
2529
2588
2649
2710
2773
2838
2904
2972
3041
3112
4
1009
1033
1057
1081
1107
1132
1159
1186
1213
1242
1271
1300
1330
1361
1393
142(;
1459
1493
1528
1563
1600
1637
1675
1714
1754
1795
1837
1879
1923
1968
2014
2061
2109
2158
2208
2259
2312
2366
2421
2477
2535
2594
2655
2716
2780
2844
2911
2979
3048
3119
5
1012
1035
1059
1084
1109
1135
1161
1189
• 1216
1245
1274
1303
1334
1365
1396
1429
1462
1496
1531
1567
1603
1641
1679
1718
1758
1799
1841
1884
1928
1972
2018
2065
2113
2163
2213
2265
2317
2371
2427
2483
2541
2600
2661
2723
2786
2851
2917
2985
3055
3126
6
1014
1038
1062
1086
1112
1138
1164
1191
1219
1247
1276
1306
1337
1368
1400
1432
1466
1500
1535
1570
1607
1644
1683
1722
1762
1803
1845
1888
1932
1977
2023
2070
2118
2168
2218
2270
2323
2377
2432
2489
2547
2606
2667
2729
2793
2858
2924
2992
3062
3133
7
1016
1040
1064
1089
1114
1140
1167
1194
1222
1250
1279
1309
1340
1371
1403
1435
1469
1503
1538
1574
1611
1648
1687
1726
1766
1807
1849
1892
1936
1982
2028
2075
2123
2173
2223
2275
2328
2382
2438
2495
2553
2612
2673
2735
2799
2864
2931
2999
3069
3141
8
1019
1042
1067
1091
1117
1143
1169
1197
1225
1253
1282
1312
1343
1374
1406
1439
1472
1507
1542
1578
1614
1652
1690
1730
1770
1811
1854
1897
1941
1986
2032
2080
2128
2178
2228
2280
2333
2388
2443
2500
2559
2618
2679
2742
2805
2871
2938
3006
3076
3148
9
1021
1045
1069
1094
1119
1146
1172
1199
1227
1256
1285
1315
1346
1377
1409
1442
1476
1510
1545
1581
1618
1656
1694
1734
1774
1816
1858
1901
1945
1991
20Я7
2084
2133
2183
2234
2286
2339
2393
2449
2506
2564
2624
2685
2748
2812
2877
2944
3013
3083
3155
АНТИЛОГАРИФМЫ
37
Продолжение
т
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
0
3162
3236
3311
3388
3467
3548
3631
3715
3802
3890
3981
4074
4169
4266
4365
4467
4571
4677
4786
4898
5012
5129
5248
5370
5495
5623
5754
5888
6026
6166
6310
6457
6607
6761
6918
7079
7244
7413
7586
7762
7943
8128
8318
8511
8710
8913
9120
9333
9550
9772
1
3170
3243
3319
3396
3475
3556
3639
3724
3811
3899
3990
4083
4178
4276
4375
4477
4581
4688
4797
4909
5023
5140
5260
5383
5508
5636
5768
5902
6039
6180
6324
6471
6622
6776
6934
7096
7261
7430
7603
7780
7962
8147
8337
8531
8730
8933
9141
9354
9572
9795
2
3177
3251
3327
3404
3483
3565
3648
3733
3819
3908
3999
4093
4188
4285
4385
4487
4592
4699
4808
4920
5035
5152
5272
5395
5521
5649
5781
5916
6053
6194
6339
6486
6637
6792
6950
7112
7278
7447
7621
7798
7980
8166
8356
8551
8750
8954
9162
9376
9594
9817
3
3184
3258
3334
3412
3491
3573
3656
3741
3828
3917
4009
4102
4198
4295
4395
4498
4603
4710
4819
4932
5047
5164
5284
5408
5534
5662
5794
5929
6067
6209
6353
6501
6653
6808
6966
7129
7295
7464
7638
7816
7998
8185
8375
8570
8770
8974
9183
9397
9616
9840
4
3192
3266
3342
3420
3499
3581
3664
3750
3837
3926
4018
4111
4207
4305
4406
4508
4613
4721
4831
4943
5058
5176
5297
5420
5546
5675
5808
5943
6081
6223
6368
6516
6668
6823
6982
7145
7311
7482
7656
7834
8017
8204
8395
8590 '
8790
8995
9204
9419
9638
9863
5
3199
3273
3350
3428
3508
3589
3673
3758
3846
3936
4027
' 4121
4217
4315
4416
4519
4624
4732
4842
4955
5070
5188
5309
5433
5559
5689
5821
5957
6095
6237
6383
6531
6683
6839
6998
7161
7328
7499
7674
7852
8035
8222
8414
8610
8810
9016
9226
9441
9661
9886
6
3206
3281
3357
3436
3516
3597
3681
3767
3855
3945
4036
4130
4227
4325
4426
4529
4634
4742
4853
4966
5082
5200
5321
5445
5572
5702
5834
5970
6109
6252
6397
6546
6699
6855
7015
7178
7345
7516
7691
7870
8054
8241
8433
8630
8831
9036
9247
9462
9683
9908
7
3214
3289
3365
3443
3524
3606
3690
3776
3864
3954
4046
4140
4236
4335
4436
4539
4645
4753
4864
4977
5093
5212
5333
5458
5585
5715
5848
5984
6124
6266
6412
6561
6714
6871
7031
7194
7362
7534
7709
7889
8072
8260
8453
8650
8851
9057
9268
9484
9705
9931
8
3221
3296
3373
3451
3532
3614
3698
3784
3873
3963
4055
4150
4246
4345
4446
4550
4656
4764
4875
4989
5105
5224
5346
5470
5598
5728
5861
5998
6138
6281
6427
6577
6730
6887
7047
7211
7379
7551
7727
7907
8091
8279
8472
8670
8872
9078
9290
9506
9727
9954
9
3228
3304
3381
3459
3540
3622
3707
3793
3882
3972
4064
4159
4256
4355
4457
4560
4667
4775
4887
5000
5117
5236
5358
5483
5610
5741
5875
6012
6152
6295
6442
6592
6745
6902
7063
7228
7396
7568
7745
7925
8110
8299
8492
8690
8892
9099
9311
9528
9750
9977
38
ТАБЛИЦЫ
1.1.1.9. Натуральные значения тригонометрических функций.
Угловой радиус разделен на шесть частей: шаг 10'.)
СИНУСЫ
Градусы
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0'
0,0000
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2519
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,500Q
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
60'
10'
0,0029
0,0204
0,0378
0,0552
0,0727
0,0901
0,1074
0,1248
0,1421
0,1593
0,1765
0,1937
0,2108
0,2278
0,2447
0,2616
0,2784
0,2952
0,3118
0,3283
0,3448
0,3611
0,3773
0,3934
0,4094
0,4253
0,4410
0,4566
0,4720
0,4874
0,5025
0,5175
0,5324
0,5471
0,5616
0,5760
0,5901
0,6041
0,6180
0,6316
0,6450
0,6583
0,6713
0,6841
0,6967
0,7092
50'
20'
0,0058
0,0223
0,0407
0,0581
0,0756
0,0929
0,1103
0,1276
0,1449
0,1622
0,1794
0,1965
0,2136
0,2306
0,2476
0,2644
0,2812
0,2979
0,3145
0,3311
0,3475
0,3638
0,3800
0,3961
0,4120
0,4279
0,4436
0,4592
0,4746
0,4899
0,5050
0,5200
0,5348
0,5495
0,5640
0,5783
0,5925
0,6065
0,6202
0,6338
0,6472
0,6604
0,6734
0,6862
0,6988
0,7112
40'
30'
0,0087
0,0262
0,0436
0,0610
0,0785
0,0958
0,1132
0,1305
0,1478
0,1650
0,1822
0,1994
0,2164
0,2334
0,2504
0,2672
0,2840
0,3007
0,3173
0,3338
0,3502
0,3665
0,3827
0,3987
0,4147
0,4305
0,4462
0,4617
0,4772
0,4924
0,5075
0,5225
0,5373
0,5519
0,5664
0,5807
0,5948
0,6088
0,6225
0,6361
0,6494
0,6626
0,6756
0,6884
0,7009
0,7133
30'
40'
0,0116
0,0291
0,0465
0,0640
0,0814
0,0987
0,1161
0,1334
0,1507
0,1679
0,1851
0,2022
0,2193
0,2363
0,2532
0,2700
0,2868
0,3035
0,3201
0,3365
0,3529
0,3692
0,3854
0,4014
0,4173
0,4331
0,4488
0,4643
0,4797
0,4950
0,5100
0,5250
0,5398
0,5544
0,5688
0,5831
0,5972
0,6111
0,6248
0,6383
0,6517
0,6648
0,6777
0,6905
0,7030
0,7153
20'
50'
0,0145
0,0320
0,0494
0,0669
0,0843
0,1016
0,1190
0,1363
0,1536
0,1708
0,1880
0,2051
0,2221
0,2391
0,2560
0,2728
0,2896
0,3062
0,3228
0,3393
0,3557
0,3719
0,3881
0,4041
0,4200
0,4358
0,4514
0,4669
0,4823
0,4975
0,5125
0,5275
0,5422
0,5568
0,5712
0,5854
0,5995
0,6134
0,6271
0,6406
0,6539
0,6670
0,6799
0,6926
0,7050
0,7173
10'
60'
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
0,7193
0'
89
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
Градусы
КОСИНУСЫ
НАТУРАЛЬНЫЕ ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
39
СИНУСЫ
Градусы
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
0'
0,7071
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
60'
10'
0,7092
0,7214
0,7333
0,7451
0,7566
0,7679
0,7790
0,7898
0,8004
0,8107
0,8208
0,8307
0,8403
0,8496
0,8587
0,8675
0,8760
0,8843
0,8923
0,9001
0,9075
0,9147
0,9216
0,9283
0,9346
0,9407
0,9465
0,9520
0,9572
0,9621
0,966,7
0,9710
0,9750
0,9787
0,9822
0,9853
0,9881
0,9907
0,9929
0,9948
0,9964
0,9978
0,9988
0,9995
0,9999
50'
20'
0,7112
0,7234
0,7353
0,7470
0,7585
0,7698
0,7808
0,7916
0,8021
0,8124
0,8225
0,8323
0,8418
0,8511
0,8601
0,8689
0,8774
0,8857
0,8936
0,9013
0,9088
0,9159
0,9228
0,9293
0,9356
0,9417
0,9474
0,9528
0,9580
0,9628
0,9674
0,9717
0,9757
0,9793
0,9827
0,9858
0,9886
0,9911
0,9932
0,9951
0,9967
0,9980
0,9989
0,9996
0,9999
40'
30'
0,7133
0,7254
0,7373
0,7490
0,7604
0,7716
0,7826
0,7934
0,8039
0,8141
0,8241
0,8339
0,8434
0,8526
0,8616
0,8704
0,8788
0,8870
0,8936
0,9026
0,9100
0,9171
0,9239
0,9304
0,9367
0,9426
0,9483
0,9537
0,9588
0,9636
0,9681
0,9724
0,9763
0,9799
0,9833
0,9863
0,9890
0,9914
0,9936
0,9954
0,9969
0,9981
0,9990
0,9997
1,0000
30'
40'
0,7153
0,7274
0,7392
0,7509
0,7623
0,7735
0,7844
0,7951
0,8056
0,8158
0,8258
0,8355
0,8450
0,8542
0,8631
0,8718
0,8802
0,8884
0,8962
0,9038
0,9112
0,9182
0,9250
0,9315
0,9377
0,9436
0,9492
0,9546
0,9596
0,9644
0,9689
0,9730
0,9769
0,9805
0,9838
0,9868
0,9894
0,9918
0,9939
0,9957
0,9971
0,9983
0,9992
0,9997
1,0000
20'
50'
0,7173
0,7294
0,7412
0,7528
0,7642
0,7753
0,7862
0,7969
0,8073
0,8175
0,8274
0,8371
0,8465
0,8557
0,8646
0,8732
0,8816
0,8897
0,8975
0,9051
0,9124
0,9194
0,9261
0,9325
0,9387
0,9446
0,9502
0,9555
0,9605
0,9652
0,9696
0,9737
0,9775
0,9811
0,9843
0,9872
0,9899
0,9922
0,9942
0,9959
0,9974
0,9985
0,9993
0,9998
1,0000
10'
60'
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
1,0000
0'
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Градусы
КОСИНУСЫ
40
ТАБЛИЦЫ
ТАНГЕНСЫ
Градусы
0
1
2
3
4
5
6
7
8
9
10
И
12
J3
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0'
0,0000
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
60'
10'
0,0029
0,0204
0,0378
0,0553
0,0729
0,0904
0,1080
0,1257
0,1435
0,1614
0,1793
0,1974
0,2156
0,2339
0,2524
0,2711
0,2899
0,3089
0,3281
0,3476
0,3673
0,3872
0,4074
0,4279
0,4487
0,4699
0,4913
0,5132
0,5354
0,5581
0,5812
0,6048
0,6289
0,6536
0,6787
0,7046
0,7310
0,7581
0,7860
0,8146
0,8441
0,8744
0,9057
0,9380
0,9713
1,0058
50'
20'
0,0058
0,0233
0,0407
0,0582
0,0758
0,0934
0,1110
0,1287
0,1465
0,1644
0,1823
0,2004
0,2186
0,2370
0,2555
0,2742
0,2931
0,3121
0,3314
0,3508
0,3706
0,3906
0,4108
0,4314
0,4522
0,4734
0,4950
0,5169
0,5392
0,5619
0,5851
0,6088
0,6330
0,6577
0,6830
0,7089
0,7355
0,7627
0,7907
0,8195
0,8491
0,8796
0,9110
0,9435
0,9770
1,0117
40'
30'
0,0087
0,0262
0,0437
0,0612
0,0787
0,0963
0,1139
0,1317
0,1495
0,1673
0,1853
0,2035
0,2217
0,2401
0,2586
0,2773
0,2962
0,3153
0,3346
0,3541
0,3739
0,3939
0,4142
0,4348
0,4557
0,4770
0,4986
0,5206
0,5430
0,5658 '
0,5890
0,6128
0,6371
0,6619
0,6873
0,7133
0,7400
0,7673
0,7954
0,8243
0,8541
0,8847
0,9163
0,9490
0,9827
1,0176
30'
40'
0,0116
0,0291
0,0466
0,0641
0,0816
0,0992
0,1169
0,1346
0,1524
0,1703
0,1883
0,2065
0,2247
0,2432
0,2617
0,2805
0,2994
0,3185
0,3378
0,3574
0,3772
0,3973
0,4176
0,4383
0,4592
0,4806
0,5022
0,5243
0,5467
0,5696
0,5930
0,6168
0,6412
0,6661
0,6916
0,7177
0,7445
0,7720
0,8002
0,8292
0,8591
0,8899
0,9217
0,9545
0,9884
1,0235
20'
50'
0,0145
0,0320
0,0495
0,0670
0,0846
0,1022
0,1198
0,1376
0,1554
0,1733
0,1914
0,2095
0,2278
0,2462
0,2648
0,2836
0,3026
0,3217
0,3411
0,3607
0,3805
0,4006
0,4210
0,4417
0,4628
0,4841
0,5059
0,5280
0,5505
0,5735
0,5969
0,6208
0,6453
0,6703
0,6959
0,7221
0,7490
0,7766
0,8050
0,8342
0,8642
0,8952
0,9271
0,9601
0,9942
1,0295
10'
60'
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
1,0355
0'
89
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
Градусы
КОТАНГЕНСЫ
НАТУРАЛЬНЫЕ ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
41
ТАНГЕНСЫ
Градусы
45
46
47
48
49
50
51
52
53
54
¦ 55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
0'
,000
,036
,072
,111
,150
,192
.235
,280
,327
,376
1,428
1,483
1,540
1,600
1,664
1,732
1,804
1,881
1,963
2,050
2,145
2,246
2,356
2,475
2,605
2,747
2,904
3,078
3,271
3,487
3,732
4,011
4,331
4,705
5,145
5,671
6,314
7,115
8,144
9,514
11,430
14,301
19,081
28,636
57.290
60'
10'
1,006
1,042
1,079
,117
,157
,199
,242
,288
,335
,385
1,437
1,492
1,550
1,611
1,675
1,744
1,816
1,894
1,977
2,066
2,161
2,264
2,375
2,496
2,628
2,773
2,932
3,108
3,305
3,526
3,776
4,061
4,390
4,773
5,226
5,769
6,435
7,269
8,345
9,788
11,826
14,924
20,206
31,242
68,750
50'
20'
1,012
1.048
1,085
1,124
1,164
1,206
,250
.295
,343
,394
,446
,501
,560
1,621
1,686
1,756
1,829
1,907
1,991
2,081
2,177
2,282
2,394
2,517
2,651
2,798
2,960
3,140
3,340
3,566
3,821
4,113
4,449
4,843
5,309
5,871
6,561
7,429
8,556
10,078
12,251
15,605
21,470
34,368
85,940
40'
30'
,018
.054
,091
,130
,171
,213
,257
,303
,351
,402
1,455
1,511
1.570
1 6^2
1,69<S
1.767
1,842
1,921
2,006
2,097
2,194
2,300
2,414
2,539
2,675
2,824
2,989
3,172
3,376
3,606
3,867
4,165
4,511
4,915
5,396
5,976
6,691
7,596
8,777
10,385
12,706
16,350
22,904
38,188
114,59
30'
40'
1,024
1,060
1,098
1,137
1,178
1,220
1,265
1,311
1,360
1,411
1,464
1,520
1,580
1,643
1,709
1.780
1,855
1,935
2,020
2,112
2.211
2,318
2,434
2,560
2,699
2,850
3,018
3,204
3,412
3,647
3,914
4,219
4,574
4,989
5,485
6,084
6,827
7,770
9,010
10,712
13,197
17,169
24,542
42,964
171,89
20'
50'
1,030
1,066
1,104
1,144
1,185
1,228
1,272
1,319
1,368
1,419
1,473
1,530
1,590
1,653
1,720
1,792
1,868
1,949
2,035
2,128
2,229
2.337
2.455
2,583
2,723
2,877
3,047
3,237
3,450
3,689
3,962
4,275
4.638
5,066
5,576
6.197
6,968
7,953
9,255
11,059
13,727
18,075
26,432
49,104
343,77
10'
60'
1,036
1,072
1,111
1,150
1,192
1,235
1,280
1,327
1,376
1,428 -
1,483
1,540
1,600
1,664
1,732
1,804
1,881
1,963
2,050
2,145
2,246
2,356
2,475
2,605
2,747
2,904
3,078
3,271
3,487
3,732
4,011
4,331
4,705
5,145
5,671
6.314
7,115
8,144
9,514
11,430
14,301
19,081
28,636
57,290
X
0'
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Градусы
КОТАНГЕНСЫ
42
ТАБЛИЦЫ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ (ШАГ 0,1 °)
СИНУСЫ
Градусы
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0
0,0000
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
1
Градусы
0,1
0,0017
0,0192
0,0366
0,0541
0,0715
0,0889
0,1063
0,1236
0,1409
0,1582
0,1754
0,1925
0,2096
0,2267
0,2436
0,2605
0,2773
0,2940
0,3107
0,3272
0,3437
0,3600
0,3762
0,3923
0,4083
0,4242
0,4399
0,4555
0,4710
0,4863
0,5015
0,5165
0,5314
0,5461
0,5606
0,5750
0,5892
0,6032
0,6170
0,6307
0,6441
0,6574
0,6704
0,6833
0,6959
0,7083
0,9
0,2
0,0035
0,0209
0,0384
0,0558
0,0732
0,0906
0,1080
0,1253
0,1426
0,1599
0,1771
0,1942
0,2113
0,2284
0,2453
0,2622
0,2790
0,2957
0,3123
0,3289
0,3453
0,3616
0,3778
0,3939
0,4099
0,4258
0,4415
0,4571
0,4726
0,4879
0,5030
0,5180
0,5329
0,5476
0,5621
0,5764
0,5906
0,6046
0,6184
0,6320
0,6455
0,6587
0,6717
0,6845
0,6972
0,7096
0,8
0,3
0,0052
0,0227
0,0401
0,0576
0,0750
0,0924
0,1097
0,1271
0,1444
0,1616
0,1788
0,1959
0,2130
0,2300
0,2470
0,2639
0,2807
0,2974
0,3140
0,3305
0,3469
0,3633
0,3795
0,3955
0,4115
0,4274
0,4431
0,4586
0,4741
0,4894
0,5045
0,5195
0,5344
0,5490
0,5635
0,5779
0,5920
0,6060
0,6198
0,6334
0,6468
0,6600
0,6730
0,6858
0,6984
0,7108
0,7
0,4
0,0070
0,0244
0,0419
0,0593
0,0767
0,0941
0,1115
0,1288
0,1461
0,1633
0,1805
0,1977
0,2147
0,2317
0,2487
0,2656
0,2823
0,2990
0,3156
0,3322
0,3486
0,3649
0,3811
0,3971
0,4131
0,4289
0,4446
0,4602
0,4756
0,4909
0,5060
0,5210
0,5358
0,5505
0,5650
0,5793
0,5934
0,6074
0,6211
0,6247
0,6481
0,6613
0,6743
0,6871
0,6997
0,7120
0,6
0,5
0,0087
0,0262
0,0436
0,0610
0,0785
0,0958
0,1132
0,1305
0,1478
0,1650
0,1822
0,1994
0,2164
0,2334
0,2504
0,2672
0,2840
0,3007
0,3173
0,3338
0,3502
0,3665
0,3827
0,3987
0,4147
0,4305
0,4462
0,4617
0,4772
0,4924
0,5075
0,5225
0,5373
0,5519
0,5664
0,5807
0,5948
0,6088
0,6225
0,6361
0,6494
0,6626
0,6756»
0,6884
0,7009
0,7133
0,5
0,6
0,0105
0,0279
0,0454
0,0628
0,0802
0,0976
0,1149
0,1323
0,1495
0,1668
0,1840
0,2011
0,2181
0,2351
0,2521
0,2689
0,2857
0,3024
0,3190
0,3355
0,3518
0,3681
0,3843
0,4003
0,4163
0,4321
0,4478
0,4633
0,4787
0,4939
0,5090
0,5240
0,5388
0,5534
0,5678
0,5821
0,5962
0,6101
0,6239
0,6374
0,6508
0,6639
0,6769
0,6896
0,7022
0,7145
0,4
0,7
0,0122
0,0297
0,0471
0,0645
0,0819
0,0993
0,1167
0,1340
0,1513
0,1685
0,1957
0,2028
0,2198
0,2368
0,2538
0,2706
0,2874
0,3040
0,3206
0,3371
0,3535
0,3697
0,3859
0,4019
0,4179
0,4337
0,4493
0,4648
0,4802
0,4955
0,5105
0,5255
0,5402
0,5548
0,5693
0,5835
0,5976
0,6115
0,6252
0,6388
0,6521
0,6652
0,6782
0,6909
0,7034
0,7157
0,3
0,8
0,0140
0,0314
0,0488
0,0663
0,0837
0,1011
0,1184
0,1357
0,1530
0,1702
0,1874
0,2045
0,2215
0,2385
0,2554
0,2723
0,2890
0,3057
0,3223
0,3387
0,3551
0,3714
0,3875
0,4035
0,4195
0,4352
0,4509
0,4664
0,4818
0,4970
0,5120
0,5270
0,5417
0,5563
0,5707
0,5850
0,5990
0,6129
0,6266
0,6401
0,6534
0,6665
0,6794
0,6921
0,7046
0,7169
0,2
0,9
0,0157
0,0332
0,0506
0,0680
0,0854
0,1028
0,1201
0,1374
0,1547
0,1719
0,1891
0,2062
0,2233
0,2402
0,2571
0,2740
0,2907
0,3074
0,3239
0,3404
0,3567
0,3730
0,3891
0,4051
0,4210
0,4368
0,4524
0,4679
0,4833
0,4985
0,5135
0,5284
0,5432
0,5577
0,5721
0,5864
0,6004
0,6143
0,6280
0,6414
0,6547
0,6678
0,6807
0,6934
0,7059
0,7181
, 0,1
1
0,0175
0,0349
0,0523
0,0698
0,0872
0,1045
0,1219
0,1392
0,1564
0,1736
0,1908
0,2079
0,2250
0,2419
0,2588
0,2756
0,2924
0,3090
0,3256
0,3420
0,3584
0,3746
0,3907
0,4067
0,4226
0,4384
0,4540
0,4695
0,4848
0,5000
0,5150
0,5299
0,5446
0,5592
0,5736
0,5878
0,6018
0,6157
0,6293
0,6428
0,6561
0,6691
0,6820
0,6947
0,7071
0,7193
0
Градусы
89
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
Градусы
КОСИНУСЫ
НАТУРАЛЬНЫЕ ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
43
СИНУСЫ
Градусы
45
46
47
48
49
50
51
52
53
.54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
0
0,7071
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
' 0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
1
0,1
0,7083
0,7206
0,7325
0,7443
0,7559
0,7672
0,7782
0,7891
0,7997
0,8100
0,8202
0,8300
0,8396
0,8490
0,8581
0,8669
0,8755
0,8838
0,8918
0,8996
0,9070
0,9143
0,9212
0,9278
0,9342
0,9403
0,9461
0,9516
0,9568
0,9617
0,9664
0,9707
0,9748
0,9785
0,9820
0,9851
0,9880
0,9905
0,9928
0,9947
0,9963
0,9977
0,9987
0,9995
0,9999
0,9
0,2
0,7096
0,7218
0,7337
0,7455
0,7570
0,7683
0,7793
0,7902
0,8007
0,8111
0,8211
0,8310
0,8406
0,8499
0,8590
0,8678
0,8763
0,8846
0,8926
0,9003
0,9078
0,9150
0,9219
0,9285
0,9348
0,9409
0,9466
0,9521
0,9573
0,9622
Х),9668
0,9711
0,9751
0,9789
0,9823
0,9854
0,9882
0,9907
0,9930
0,9949
0,9965
0,9978
0,9988
0,9995
0,9999
0,8
0,3
0,7108
0,7230
0,7349
0,7466
0,7581
0,7694
0,7804
0,7912
0,8018
0,8121
0,8221
0,8320
0,8415
0,8508
0,8599
0,8686
0,8771
0,8854
0,8934
0,9011
0,9085
0,9157
0,9225
0,9291
0,9354
0,9415
0,9472
0,9527
0,9578
0,9627
0,9673
0,9715
0,9755
0,9792
0,9826
0,9857
0,9885
0,9910
0,9932
0,9951
0,9966
0,9979
0,9989
0,9996
0,9999
0,7
0,4
0,7120
0,7242
0,7361
0,7478
0,7593
0,7705
0,7815
0,7923
0,8028
0,8131
0,8231
0,8329
0,8425
0,8517
0,8607
0,8695
0,8780
0,8862
0,8942
0,9018
0,9092
0,9164
0,9232
0,9298
0,9361
0,9421
0,9478
0,9532
0,9583
0,9632
0,9677
0,9720
0,9759
0,9796
0,9829
0,9860
0,9888
0,9912
0,9934
0,9952
0,9968
0,9980
0,9990
0,9996
0,9999
0,6
Градусы
0,5
0,7133
0,7254
0,7373
0,7490
0,7604
0,7716
0,7826
0,7934
0,8039
0,8141
0,8241
0,8339
0,8434
0,8526
0,8616
0,8704
0,8788
0,8870
0,8949
0,9026
0,9100
0,9171
0,9239
0,9304
0,9367
0,9426
0,9483
0,9537
0,9588
0,9636
0,9681
0,9724
0,9763
0,9799
0,9833
0,9863
0,9890
0,9914
0,9936
0,9954
0,9969
0,9981
0,9990
0,9997
1,0000
0,5
0,6
0,7145
0,7266
0,7385
0,7501
0,7615
0,7727
0,7837
0,7944
0,8049
0,8151
0,8251
0,8348
0,8443
0,8536
0,8625
0,8712
0,8796
0,8878
0,8957
0,9033
0,9107
0,9178
0,9245
0,9311
0,9373
0,9432
0,9489
0,9542
0,9593
0,9641
0,9686
0,9728
0,9767
0,9803
0,9836
0,9866
0,9893
0,9917
0,9938
0,9956
0,9971
0,9982
0,9991
0,9997
1,0000
0,4
0,7
0,7157
0,7278
0,7396
0,7513
0,7627
0,7738
0,7848
0,7955
0,8059
0,8161
0,8261
0,8358
0,8453
0,8545
0,8634
0,8721
0,8805
0,8886
0,8965
0,9041
0,9114
0,9184
0,9252
0,9317
0,9379
0,9438
0,9494
0,9548
0,9598
0,9646
0,9690
0,9732
0,9770
0,9806
0,9839
0,9869
0,9895
0,9919
0,9940
0,9957
0,9972
0,9983
0,9992
0,9997
1,0000
0,3
0,8
0,7169
0,7290
0,7408
0,7524
0,7638
0,7749
0,7859
0,7965
0,8070
0,8171
0,8271
0,8368
0,8462
0,8554
0,8643
0,8729
0,8813
0,8894
0,8972
0,9048
0,9121
0,9191
0,9259
0,9323
0,9385
0,9444
0,9500
0,9553
0,9603
0,9650
0,9694
0,9736
0,9774
0,9810
0,9842_
0,9871
0,9888
0,9921
0,9942
0,9959
0,9973
0,9984
0,9993
0,9998
1,0000
0,2
0,9
0,7181
0,7302
0,7420
0,7536
0,7649
0,7760
0,7869
0,7976
0,8080
0,8181
0,8281
0,8377
0,8471
0,8563
0,8652
0,8738
0,8821
0,8902
0,8980
0,9056
0,9128
0,9198
0,9265
0,9330
0,9391
0,9449
0,9505
0,9558
0,9608
0,9655
0,9699
0,9740
0,9778
0,9813
0,9845
0,9874
0,9900
0,9923
0,9943
0,9960
0,9974
0,9985
0,9993
0,9998
1,0000
0,1
1
0,7193
0,7314
0,7431
0,7547
0,7660
0,7771
0,7880
0,7986
0,8090
0,8192
0,8290
0,8387
0,8480
0,8572
0,8660
0,8746
0,8829
0,8910
0,8988
0,9063
0,9135
0,9205
0,9272
0,9336
0,9397
0,9455
0,9511
0,9563
0,9613
0,9659
0,9703
0,9744
0,9781
0,9816
0,9848
0,9877
0,9903
0,9925
0,9945
0,9962
0,9976
0,9986
0,9994
0,9998
1,0000
0
Градусы
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Градусы
КОСИНУСЫ
44
ТАБЛИЦЫ
ТАНГЕНСЫ
Градусы
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
0
0,0000
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
1
0,1
0,0017
0,0192
0,0367
0,0542
0,0717
0,0892
0,1069
0,1246
0,1423
0,1602
0,1781
0,1962
0,2144
0,2327
0,2512
0,2698
0,2886
0,3076
0,3269
0,3463
0,3659
0,3859
0,4061
0,4265
0,4473
0,4684
0,4899
0,5117
0,5340
0,5566
0,5797
0,6032
0,6273
0,6519
0,6771
0,7028
0,7292
0,7563
0,7841
0,8127
0,8421
0,8724
0,9036
0,9358
0,9691
1,0035
0,9
0,2
0,0035
0,0209
0,0384
0,0559
0,0734
0,0910
0,1086
0,1263
0,1441
0,1620
0,1799
0,1980
0,2162
0,2345
0,2530
0,2717
0,2905
0,3096
0,3288
0,3482
0,3679
0,3879
0,4081
0,4286
0,4494
0,4706
0,4921
0,5139
0,5362
0,5589
0,5820
0,6056
0,6297
0,6544
0,6796
0,7054
0,7319
0,7590
0,7869
0,8156
0,8451
0,8754
0,9067
0,9391
0,9725
1,0070
0,8
0,3
0,0052
0,0227
0,0402
0,0577
0,0752
0,0928
0,1104
0,1281
0,1459
0,1638
0,1817
0,1998
0,2180
0,2364
0,2549
0,2736
0,2924
0,3115
0,3307
0,3502
0,3699
0,3899
0,4101
0,4307
0,4515
0,4727
0,4942
0,5161
0,5384
0,5612
0,5844
0,6080
0,6322
0,6569
0,6822
0,7080
0,7346
0,7618
0,7898
0,8185
0,8481
0,8785
0,9099
0,9424
0,9759
1,0105
0,7
0,4
0,0070
0,0244
0,0419
0,0594
0,0769
0,0945
0,1122
0,1299
0,1477
0,1655
0,1835
0,2016
0,2199
0,2382
0,2568
0,2754
0,2943
0,3134
0,3327
0,3522
0,3719
0,3919
0,4122
0,4327
0,4536
0,4748
0,4964
0,5184
0,5407
0,5635
0,5867
0,6104
0,6346
0,6594
0,6847
0,7107
0,7373
0,7646
0,7926
0,8214
0,8511
0,8816
0,9131
0,9457
0,9793
1,0141
0,6
Градусы
0,5
0,0087
0,0262
0,0437
0,0612
0,0787
0,0963
0,1139
0,1317
0,1495
0,1673
0,1853
0,2035
0,2217
0,2401
0,2586
0,2773
0,2962
0,3153
0,3346
0,3541
0,3739
0,3939
0,4142
0,4348
0,4557
0,4770
0,4986
0,5206
0,5430
0,5658
0,5890
0,6128
0,6371
0,6619
0,6873
0,7133
0,7400
0,7673
0,7954
0,8243
0,8541
0,8847
0,9163
0,9490
0,9827
1,0176
0,5
0,6
0,0105
0,0279
0,0454
0,0629
0,0805
0,0981
0,1157
0,1334
0,1512
0,1691
0,1871
0,2053
0,2235
0,2419
0,2605
0,2792
0,2981
0,3172
0,3365
0,3561
0,3759
0,3959
0,4163
0,4369
0,4578
0,4791
0,5008
0,5228
0,5452
0,5681
0,5914
0,6152
0,6395
0,6644
0,6899
0,7159
0,7427
0,7701
0,7983
0,8273
0,8571
0,8878
0,9195
0,9523
0,9861
1,0212
0,4
0,7
0,0122
0,0297
0,0472
0,0647
0,0822
0,0998
0,1175
0,1352
0,1530
0,1709
0,1890
0,2071
0,2254
0,2438
0,2623
0,2811
0,3000
0,3191
0,3385
0,3581
0,3779
0,3979
0,4183
0,4390
0,4599
0,4813
0,5029
0,5250
0,5475
0,5704
0,5938
0,6176
0,6420
0,6669
0,6924
0,7186
0,7454
0,7729
0,8012
0,8302
0,8601
0,8910
0,9228
0,9556
0,9896
1,0247
0,3
0,8
0,0140
0,0344
0,0489
0,0664
0,0840
0,1016
0,1192
0,1370
0,1548
0,1727
0,1908
0,2089
0,2272
0,2456
0,2642
0,2830
0,3010
0,3211
0,3404
0,3600
0,3799
0,4000
0,4204
0,4411
0,4621
0,4834
0,5051
0,5272
0,5498
0,5727
0,5961
0,6200
0,6445
0,6694
0,6950
0,7212
0,7481
0,7757
0,8040
0,8332
0,8632
0,8941
0,9260
0,9590
0,9930
1,0283
0,2
0,9
0,0157
0,0332
0,0507
0,0682
0,0857
0,1033
0,1210
0,1388
0,1566
0,1745
0,1926
0,2107
0,2290
0,2475
0,2661
0,2849
0,3038
0,3230
0,3424
0,3620
0,3819
0,4020
0,4224
0,4431
0,4642
0,4856
0,5073
0,5295
0,5520
0,5750
0,5985
0,6224
0,6469
0,6720
0,6976
0,7239
0,7508
0,7785
0,8069
0,8361
0,8662
0,8972
0,9293
0,9623
0,9965
1,0319
0,1
1
0,0175
0,0349
0,0524
0,0699
0,0875
0,1051
0,1228
0,1405
0,1584
0,1763
0,1944
0,2126
0,2309
0,2493
0,2679
0,2867
0,3057
0,3249
0,3443
0,3640
0,3839
0,4040
0,4245
0,4452
0,4663
0,4877
0,5095
0,5317
0,5543
0,5774
0,6009
0,6249
0,6494
0,6745
0,7002
0,7265
0,7536
0,7813
0,8098
0,8391
0,8693
0,9004
0,9325
0,9657
1,0000
1,0355
. 0
Градусы
89
88
87
86
85
84
83
82
81
80
79
78
77
76
75
74
73
72
71
70
69
68
67
66
65
64
63
62
61
60
59
58
57
56
55
54
53
52
51
50
49
48
47
46
45
44
Градусы
КОТАНГЕНСЫ
НАТУРАЛЬНЫЕ ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
45
ТАНГЕНСЫ
Градусы
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
Градусы
0
1,0000
,0355
,0724
,1106
,1504
,1918
,2349
,2799
,3270
,3764
1,4281
1,4826
1,5399
1,6003
1 6643
1,7321
1,8040
1,8807
1,9626
2,0503
2,1445
2,2460
2,3555
2,4751
2,6051
2,7475
2,9042
3,0777
3,2709
" 3,4874
3,7321
4,0108
4,3315
4,7046
3,1446
5,6713
6,3138
7,1154
8,1443
9,5144
11,4301
14,3007
19,0811
28,6363
57,2900
1
0,1
1,0035
1,0392
1,0761
1,1145
1,1544
1,1960
1,2393
1,2846
1,3319
1,3814
1,4335
1,4882
1,5458
1,6066
1,6709
1,7391
1,8115
1,8887
1,9711
2,0594
2,1543
2,2566
2,3673
2,4876
2,6187
2,7625
2,9208
3,0961
3,2914
3,5105
3,7583
4,0408
4,3662
4,7453
5,1929
5,7297
6,3859
7,2066
8,2636
9,6768
11,6645
14,6685
19,7403
30,1446
63,6567
0,9
0,2
1,0070
1,0428
1,0799
1,1184
1,1585
1,2002
1,2437
1,2892
1,3367
1,3865
1,4388
1,4938
1,5517
1,6128
1,6725
1,7461
1,8190
1,8967
1,9797
2,0686
2,1642
2,2673
2,3798
2,5002
2,6325
2,7776
2,9375
3,1146
3,3122
3,5329
3,7848
4,0713
4,4015
4,7867
5,2422
5,7894
6,4596
7,3002
8,3863
9,8448
11,9087
15,0557
20,4465
31,8205
71,6151
0,8
0,3
1,0105
1,0464
1,0637
1,1224
1,1626
1,2045
1,2483
1,2938
1,3416
1,3916
1,4442
1,4994
1,5577
1,6191
1,6842
1,7532
1,8265
1,9047
1,9883
2,0778
2,1742
2,2781
2,3906
2,5129
2,6464
2,7927
2,9544
3,1334
3,3332
3,5576
3,8118
4,1022
4,4373
4,8288
5,2924
5,8502
6,5350
7,3962
8,5126
10,0187
12,1632
15,4638
21,2049
33,6935
81,8470
0,7
0,4
1,0141
1,0501
1,0875
1,1263
1,1667
1,2088
1,2527
1,2985
1,3465
1,3968
1,4496
1,5051
1,5637
1,6255
1,6909
1,7603
1,8341
1,9128
1,9970
2,0872
2,1842
2,2889
2,4023
2,5257
2,6605
2,8083
2,9714
3,1524
3,3544
3,5816
3,8391
4,1335
4,4737
4,8716
5,3435
5,9124
6,6122
7,4947
8,6427
10.1988
12,4288
15,8945
22,0217
35,8006
95,4895
0,6
0,5
1,0176
1,0538
1,0913
1,1303
1,1708
1,2131
1,2572
1,3032
1,3514
1,4019
1,4550
1,5108
1,5697
1,6319
1.6977
¦1,7675
1,8418
1,9210
2,0057
2,0965
2,1943
2,2998
2,4142
2,5386
2,6746
2,8239
2,9887
3,1716
3.3759
3,6059
3,8667
4,1653
4,5107
4,9152
5,3955
5,9758
6,6912
7,5958
8,7769
10,3854
12,7062
16,3499
22,9038
38,1885
114,5887
0,5
Градусы
0,6
1,0212
1,0575
1,0951
1,1343
1,1750
1,2174
1,2617
1,3079
1,3564
1,4071
1,4605
1,5166
1,5757
1,6383
1,7045
1,7747
1,8495
1,9292
2,0145
2,1060
2,2045
2,3109
2,4262
2,5517
2,6889
2,8397
3,0061
3,1910
3,3977
3,6305
3,8947
4,1976
4,5483
4,9594
5,4486
6,0405
6,7720
7,6996
8,9152
10,5789
12,9962
16,8319
23,8593
40,9174
143,2371
0,4
0,7
1,0247
1,0612
1,0990
1,1383
1,1792
1,2218
1,2662
1,3127
1,3613
1,4124
1,4659
1,5224
1,5818
1,6447
1,7113
1,7820
1,8572
1,9375
2,0233
2,1155
2,2148
2,3220
2,4383
2,5649
2,7034
2,8556
3,0237
3,2106
3,4197
3,6554
3,9232
4,2303
4,5864
5,0045
5,5026
6,1066
6,8548
7,8062
9,0579
10,7797
13,2996
17,3432
24,8978
44,0661
190,9842
0,3
0,8
1,0283
1,0649
,1028
,1423
,1833
,2261
,2708
,3175
1,3663
1,4176
1,4715
1,5282
1,5880
1,6512
1,7182
1,7893
1,8650
1,9458
2,0323
2,1251
2,2251
2,3332
2,4504
2,5782
2,7179
2,8716
3,0415
3,2305
3,4420
3,6806
3.9520
4,2635
4,6252
5,0504
5,5578
6,1742
6,9395
7,9158
9,2052
10,9882
13,6174
17,8863
26,0307
47,7395
296,4777
0,2
0,9
1,0319
1,0686
1,1067
1,1463
1,1875
1,2305
1,2753
1,3222
1,3713
1,4229
1,4770
1,5340
1,5941
1,6577
1,7251
1,7966
1,8728
1,9542
2,0413
2,1348
2,2355
2,3445
2,4627
2,5916
2,7326
2,8878
3,0595
3,2506
3,4646
3,7062
3,9812
4,2972
4,6646
5,0970
5,6140
6,2432
7,0264
8,0285
9,3572
11,2048
13,9507
18,4645
27,2715
52,0807
572,9572
0,1
1
1,0355
1,0724
,1106
,1504
,1918
,2349
,2799
,3270
,3764
1,4281
1,4826
1,5399
1,6003
1,6643
1,7321
1,8040
1,8807
1,9626
2,0503
2,1445
2,2460
2,3559
2,4751
2,6051
2,7475
2,9042
3,0777
3,2709
3,4874
3,7321
4,0108
4,3315
4,7046
5,1446
5,6713
6,3138
7,1154
8,1443
9,5144
11,4301
14,3007
19,0811
28,6363
57,2900
QO
0
44
43'
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Градусы
КОТАНГЕНСЫ
46
ТАБЛИЦЫ
1.1.1.10. Показательные, гиперболические
X
0,00
01
02
03
04
0,05
06
07
08
09
0,10
11
12
13
14
0,15
16
17
18
19
0,20
21
22
23
24
0,25
26
27
28
29
0,30
31
32
33
34
0,35
36
37
38
39
0,40
41
42
43
44
0,45
46
47
48
49
0,50
51
52
53
54
0,55
ех
1,0000
1,0101
1,0202
1,0305
1,0408
1,0513
1,0618
1,0725
1,0833
1,0942
,1052
,1163
,1275
,1388
,1503
,1618
,1735
,1853
,1972
,2092
,2214
,2337
1,2461
1,2586
1,2712
1,2840
1,2969
1,3100
1,3231
1,3364
1,3499
1,3634
1,3771
1,3910
1,4049
1,4191
1,4333
1,4477
1,4623
1,4770
1,4918
,5068
,5220
1,5373
1,5527
,5683
1,5841
1,6000
1,6161
1,6323
1,6487
1,6653
1,6820
1,6989
1,7160
1,7333
е~Х
1,0000
0,9900
0,9802
0,9704
0,9608
0,9512
0,9418
0,9324
0,9231
0,9139
0,9048
0,8958
0,8869
0,8781
0,8694
0,8607
0,8521
0,8437
0,8353
0,8270
0,8187
0,8106
0.8025
0,7945
0,7866
0,7788
0,7711
0,7634
0,7558
0,7483
0,7408
0,7334
0,7261
0,7189
0,7118
0,7047
0,6977
0,6907
0,6839
0,6771
0,6703
0,6637
0,6570
0,6505
0,6440
0,6376
0,6313
0,6250
0,6188
0,6126
0,6065
0,6005
0,5945
0,5886
0,5827
0,5769
shx
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
0,0600
0,0701
0,0801
0,0901
0,1002
0,1102
0,1203
0,1304
0,1405
0,1506
0,1607
0,1708
0,1810
0,1911
0,2013
0,2115
0,2218
0,2320
0,2423
0,2526
0,2629
0,2733
0,2837
0,2941
0,3045
0,3150
0,3255
0,3360
0,3466
0,3572
0,3678
0,3785
0,3892
0,4000
0,4108
0,4216
0,4325
0,4434
0,4543
0,4653
0,4764
0,4875
0,4986
0,5098
0,5211
0,5324
0,5438
0,5552
0,5666
0,5782
и тригонометрические функции (для х от 0 до 1,6).
chx
,0000
,0001
,0002
,0005
,0008
,0013
,0018
,0025
,0032
,0041
,0050
,0061
,0072
,0085
,0098
,0113
1,0128
1,0145
1,0162
1,0181
1,0201
1,0221
1,0243
1,0266
1,0289
1,0314
1,0340
1,0367
1,0395
1,0423
1,0453
,0484
1,0516
1,0549
1,0584
1,0619
1,0655
1,0692
1,0731
1,0770
1,0811
1,0852
1,0895
1,0939
1,0984
1,1030
1,1077
1,1125
1,1174
1,1225
1,1276
1,1329
1,1383
1,1438
1,1494
1,1551
thx
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
0,0599
0,0699
0,0798
0,0898
0,0997
0,1096
0,1194
0,1293
0,1391
0,1489
0,1586
0,1684
0,1781
0,1877
0,1974
0,2070
0,2165
0,2260
0,2355
0,2449
0,2543
0,2636
0,2729
0,2821
0,2913
0,3004
0,3095
0,3185
0,3275
0,3364
0,3452
0,3540
0,3627
' 0,3714
0,3799
0,3885
0,3969
0,4053
0,4136
0,4219
0,4301
0,4382
0,4462
0,4542
0,4621
0,4699
0,4777
0,4854
0,4930
0,5005
sinjc
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
0,0600
0,0699
0,0799
0,0899
0,0998
0,1098
0,1197
0,1296
0,1395
0,1494
0,1593
0,1692
0,1790
0,1889
0,1987
0,2085
0,2182
0,2280
0,2377
0,2474
0,2571
0,2667
0,2764
0,2860
0,2955
0,3051
0,3146
0,3240
0,3335
0,3429
0,3523
0,3616
0,3709
0,3802
0,3894
0,3986
0,4078
0,4169
0,4259
0,4350
0,4439
0,4529
0,4618
0,4706
0,4794
0,4882
0,4969
0,5055
0,5141
0,5227
COSJC
1,0000
1,0000
0,9998
0,9996
0,9992
0,9988
0,9982
0,9976
0,9968
0,9960
0,9950
0,9940
0,9928
0,9916
0,9902
0,9888
0,9872
0,9856
0,9838
0,9820
0,9801
0,9780
0,9759
0,9737
0,9713
0,9689
0,9664
0,9638
0,9611
0,9582
0,9553
0,9523
0,9492
0,9460
0,9428
0,9394
0,9359
0,9323
0,9287
0,9249
0,9211
0,9171
0,9131
0,9090
0,9048
0,9004
0,8961
0,8916
0,8870
0,8823
0,8776
0,8727
0,8678
0,8628
0,8577
0,8525
tgx
0,0000
0,0100
0,0200
0,0300
0,0400
0,0500
0,0601
0,0701
0,0802
0,0902
0,1003
0,1104
0,1206
0,1307
0,1409
0,1511
0,1614
0,1717
0,1820
0,1923
0,2027
0,2131
0,2236
0,2341
0,2447
0,2553
0,2660
0,2768
0,2876
0,2984
0,3093
0,3203
0,3314
0,3425
0,3537
0,3650
0,3764
0,3879
0,3994
0,4111
0,4228
0,4346
0,4466
0,4586
0,4708
0,4831
0,4954
0,5080
0,5206
0,5334
0,5463
0,5594
0,5726
0*5859
0,5994
0,6131
ПОКАЗАТЕЛЬНЫЕ, ГИПЕРБОЛИЧЕСКИЕ И ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
47
Продолжение
X
0,55
56
57
58
59
0,60
61
62
63
64
0,65
66
67
68
69
0,70
71
72
73
74
0,75
76
77
78
79
0,80
81
82
83
84
0,85
86
87
88
89
0,90
91
92
93
94
0,95
96
97
98
99
1,00
01
02
03
04
1,05
06
07
08
09
1,10
ех
1,7333
,7507
,7683
',7860
,8040
,8221
,8404
,8589
1,8776
1,8965
1,9155
1,9348
1,9542
1,9739
1,9937
2,0138
2,0340
2,0544
2,0751
2,0959
2,1170
2,1383
2,1598
2,1815
2,2034
2,2255
2,2479
2,2705
2,2933
2,3164
2,3396
2,3632
2,3869
2,4109
2,4351
2,4596
2,4843
2,5093
2,5345
2,5600
2,5857
2,6117
2,6379
2,6645
2,6912
2,7183
ZJ456
2,7732
2,8011
2,8292
2,8577
2,8864
2,9154
2,9447
2,9743
3,0042
е~х
0,5769
0,5712
0,5655
0,5599
0,5543
0,5488
0,5434
0,5379
0,5326
0,5273
0,5220
0,5169
0,5117
0,5066
0,5016
0,4966
0,4916
0,4868
0,4819
0,4771
0,4724
0,4677
0,4630
0,4584
0,4539
0,4493
0,4449
0,4404 -
0,4360
0,4317
0,4274
0,4232
0,4190
0,4148
0,4107
0,4066
0,4025
0,3985
0,3946
0,3906
0,3867
0,3829
0,3791
0,3753
0,3716
0,3679
0,3642
0,3606
0,3570 >
0,3535
0,3499
0,3465
0,3430
0,3396
0,3362
0,3329
shx
0,5782
0,5897
0,6014
0,6131
0,6248
0,6367
0,6485
0,6605
0,6725
0,6846
0,6967
0,7090
0,7213
0,7336
0,7461
0,7586
0,7712
0,7838
0,7966
0,8094
0,8223
0,8353
0,8484
0,8615
0,8748
0,8881
0,9015
0,9150
0,9286
0,9423
0,9561
0,9700
0,9840
0,9981
1,0122
1,0265
1,0409
1,0554
1,0700
1,0847
1,0995
1,1144
1,1294
1,1446
1,1598
1,1752
1,1907
1,2063
1,2220
1,2379
1,2539
1,2700
1,2862
1,3025
1,3190
1,3356
chx
1,1551
1,1609
1,1669
1,1730
1,1792
1,1855
1,1919
1,1984
1,2051
1,2119
1,2188
1,2258
1,2330
1,2402
1,2476
1,2552
1,2628
1,2706
1,2785
1,2865
1,2947
1,3030
1,3114
1,3199
1,3286
1,3374
1,3464
1,3555
1,3647
1,3740
1,3835
1,3932
1,4029
1,4128
1,4229
1,4331
1,4434
1,4539
1,4645
1,4753
1,4862
1,4973
1,5085
1,5199
1,5314
1,5431
1,5549
1,5669
1,5790
1,5913
1,6038
1,6164
1,6292
1,6421
1,6552
1,6685
thx
0,5005
0,5080
0,5154
0,5227
0,5299
0,5370
0,5441
0,5511
0,5581
0,5649
0,5717
0,5784
0,5850
0,5915
0,5980
0,6044
0,6107
0,6169
0,6231
0,6291
0,6351
0,6411
0,6469
0,6527
0,6584
0,6640
0,6696
0,6751
0,6805
0,6858
0,6911
0,6963
0,7014
0,7064
0,7114
0,7163
0,7211
0,7259
0,7306
0,7352
0,7398
0,7443
0,7487
0,7531
0,7574
0,7616
0,7658
0,7699
0,7739
0,7779
0,7818
0,7857
0,7895
0,7932
0,7969
0,8005
sinx
0,5227
0,5312
0,5396
0,5480
0,5564
0,5646
0,5729
0,5810
0,5891
0,5972
0,6052
0,6131
0,6210
0,6288
0,6365
0,6442
0,6518
0,6594
0,6669
0,6743
0,6816
0,6889
0,6961
0,7033
0,7104
0,7174
0,7243
0,7311
0,7379
0,7446
0,7513
0,7578
0,7643
0,7707
0,7771
0,7833
0,7895
0,7956
0,8016
0,8076
0,8134
0,8192
0,8249
0,8305
0,8360
0,8415
0,8468
0,8521
0,8573
0,8624
0,8674
0,8724
0,8772
0,8820
0,8866
0,8912
COS*
0,8525
0,8473
0,8419
0,8365
0,8309
0,8253
0,8196
0,8139
0,8080
0,8021
0,7961
0,7900
0,7838
0,7776
0,7712
0,7648
0,7584
0,7518
0,7452
0,7385
0,7317
0,7248
0,7179
0,7109
0,7038
0,6967
0,6895
0,6822
0,6749
0,6675
0,6600
0,6524
0,6448
0,6372
0,6294
0,6216
0,6137
0,6058
0,5978
0,5898
0,5817
0,5735
0,5653
0,5570
0,5487
0,5403
0,5319
0,5234
0,5148
0,5062
0,4976
0,4889
0,4801
0,4713
0,4625
0,4536
tgx
0,6131
0,6269
0,6410 ,
0,6552
0,6696
0,6841
0,6989
0,7139
0,7291
0,7445
0,7602
0,7761
0,7923
0,8087
0,8253
0,8423
0,8595
0,8771
0,8949
0,9131
0,9316
0,3505
0,9697
0,9893
1,0092
1,0296
1,0505
1,0717
1,0934
1,1156
1,1383
1,1616
1,1853
1,2097
1,2346
1,2602
1,2864
1,3133
1,3409
1,3692
1,3984
1,4284
1,4592
1,4910
1,5237
1,5574
1,5922
1,6281
1,6652
1,7036
1,7433
1,7844
1,8270
1,8712
1,9171
1,9648
48
ТАБЛИЦЫ
Продолжение
X
1,10
11
12
13
14
1,15
16
17
18
19
1,20
21
22
23
24
1,25
26
27
28
29
1,30
31
32
33
34
1,35
36
37
38
39
1,40
41
42
43
44
1,45
46
47
48
49
1,50
51
52
53
54
1,55
56
57
58
59
1,60
ех
3,0042
3,0344
3,0649
3,0957
3,1268
3,1582
3,1899
3,2220
3,2544
3,2871
3,3201
3,3535
3,3872
3,4212
3,4556
3,4903
3,5254
3,5609
3,5966
3,6328
3,6693
3,7062
3,7434
3,7810
3,8190
3,8574
3,8962
3,9354
3,9749
4,0149
4,0552
4,0960
4,1371
4,1787
4,2207
4,2631
4,3060
4,3492
4,3929
4,4371
4,4817
4,5267
4,5722
4,6182
4,6646
4,7115
4,7588
4,8066
4,8550
4,9037
4,9530
е~х
0,3329
0,3296
0,3263
0,3230
0,3198
0,3166
0,3135
0,3104
0,3073
0,3042
0,3012
0,2982
0,2952
0,2923
0,2894
0,2865
0,2837
0,2808
0,2780
0,2753
0,2725
0,2698
0,2671
0,2645
0,2618
0,2592
0,2567
0,2541
0,2516
0,2491
0,2466
0,2441
0,2417
0,2393
0,2369
0,2346
0,2322
0,2299
0,2276
0,2254
0,2231
0,2209
0,2187
0,2165
0,2144
0,2122
0,2101
0,2080
0,2060
0,2039
0,2019
shx
1,3356
1,3524
1,3693
1,3863
1,4035
1,4208
1,4382
1,4558
1,4735
1,4914
1,5095
1,5276
1,5460
1,5645
1,5831
1,6019
1,6209
1,6400
1,6593
1,6788
1,6984
1,7182
1,7381
1,7583
1,7786
1,7991
1,8198
1,8406
1,8617
1,8829
1,9043
1,9259
1,9477
1,9697
1,9919
2,0143
2,0369
2,0597
2,0827
2,1059
2,1293
2,1529
2,1768
2,2008
2,2251
2,2496
2,2743
2,2993
2,3245
2,3499
2,3756
chx
1,6685
1,6820
1,6956
1,7093
1,7233
1,7374
1,7517
1,7662
1,7808
1,7957
1,8107
1,8258
1,8412
1,8568
1,8725
1,8884
1,9045
1,9208
1,9373
1,9540
1,9709
1,9880
2,0053
2,0228
2,0404
2,0583
2,0764
2,0947
2,1132
2,1320
2,1509
2,1700
2,1894
2,2090
2,2288
2,2488
2,2691
2,2896
2,3103
2,3312
2,3524
2,3738
2,3955
, 2,4174
2,4395
2,4619
2,4845
2,5073
2,5305
2,5538
2,5775
thx
0,8005
0,8041
0,8076
0,8110
0,8144
0,8178
0,8210
0,8243
0,8275
0,8306
0,8337
0,8367
0,8397
0,8426
0,8455
0,8483
0,8511
0,8538
0,8565
0,8591
0,8617
0,8643
0,8668
0,8692
0,8717
0,8741
0,8764
0,8787
0,8810
0,8832
0,8854
0,8875
0.8896
0,8917
0,8937
0,8957
0,8977
0,8996
0,9015
0,9033
0,9051
0,9069
0,9087
0,9104
0,9121
0,9138
0,9154
0,9170
0,9186
0,9201
0,9217
sin*
0,8912
0,8957
0,9001
0,9044
0,9086
0,9128
0,9168
0,9208
0,9246
0,9284
0,9320
0,9356
0,9391
0,9425
0,9458
0,9490
0,9521
0,9551
0,9580
0,9608
0,9636
0,9662
0,9687
0,9711
0,9735
0,9757
0,9779
0,9799
0,9819
0,9837
0,9854
0,9871
0,9887
0,9901
0,9915
0,9927
0,9939
0,9949
0,9959
0,9967
0,9975
0,9982
0,9987
0,9992
0,9995
0,9998
0,9999
1,0000
1,0000
0,9998
0,9996
COS X
0,4536
0,4447
0.4357
0,4267
0,4176
0,4085
0,3993
0,3902
0,3809
0,3717
0,3624
0,3530
0,3436
0,3342
0,3248
0.3153
0,3058
0,2963
0,2867
0,2771
0,2675
0,2579
0,2482
0,2385
0,2288
0,2190
0,2092 f
0,1994 '
0,1896
0,1798
0,1700
0,1601
0,1502
0,1403
0,1304
0,1205
0,1106
0,1006
0,0907
0,0807
0,0707
0,0608
0,0508
0,0408
0,0308
0,0208
0,0108
+ 0,0008
-0,0092
-0,0192
-0,0292
tgx
1,9648
2,0143
2,0660
2,1198
2,1759
2,2345
2,2958
2,3600
2,4273
2,4979
2,5722
2,6503
2,7328
2.8198
2,9119
3,0096
3,1133
3,2236
3,3413
3,4672
3,6021
3,7471
3,9033
4,0723
4,2556
4,4552
4,6734
4,9131
5,1774
5,4707
5,7979
6,1654
6,5811
7,0555
7;6018
8,2381
8,9886
9,8874
10,983
12,350
14,101
16,428
19,670
24,498
32,461
48,078
92,620
1255,8
-108,65
-52,067
-34,233
ПОКАЗАТЕЛЬНЫЕ ФУНКЦИИ (ДЛЯ х ОТ 1,6 до 10,0)
49
Кратные значеныч я и к/2 dili вычис /спич тригоио метрических ф\акции при х > 1,6
п
1
2
3
4
5
// я/2
1.57080
3,14159
4,71239
6.28319
7,85398
// я
3.14159
6,28319
9.42478
12.56637
15,70796
6
7
8
9
10
п я/2
9.42478
10,99557
12,56637
14.13717
15,70796
п- я
18,84956
21,99115
25,13274
28,27433
31,41593
Примеры. 1) sin7,5 = sinEя/2-0,35398) = cos0,35398 = 0,9380 (линейная интерполяция). 2) sin29=.sin(9я+0,72567)=
-sin0,72567= -0,6637 (линейная интерполяция).
1.1.1.11. Показательные функции (для л от 1,6 до 10,0)*).
л
1.60
1.61
1,62
1.63
1.64
1,65
1,66
1.67
1.68
1.69
1,70
1,71
1,72
1.73
1,74
1,75
1,76
1.77
1,78
1.79
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,90
1.91
1,92
1,93
1,94
ех
4.9530
5,0028
5,0531
5.1039
5,1552
5,2070
5,2593
5.3122
5,3656
5,4195
5,4739
5,5290
5,5845
5,6407
5.6973
5,7546
5,8124
5,8709
5.9299
5,9895
6,0496
6,1104
6,1719
6,2339
6,2965
6,3598
6,4237
6,4883
6,5535
6,6194
6,6859
6,7531
6.8210
6,8895
6.9588
*' Для вычисления
ех - е~х
sn х = — - , сп х =
е~х
0,2019
0.1999
0,1979
0,1959
0,1940
0,1920
0,1901
0,1882
0,1864
0,1845
0,1827
0,1809
0.1791
0,1773
0,1755
0.1738
0.1720
0,1703
0,1686
0.1670
0,1653
0,1637
0.1620
0,1604
0,1588
0,1572
0.1557
0.1541
0,1526
0,1511
0,1496
0,1481
0,1466
0,1451
0,1437
X
1,95
1,96
1,97
1,98
1,99
2,00
2,01
2,02
2,03
2,04
2.05
2.06
2,07
2,08
2,09
2,10
2.11
2,12
2,13
2,14
2.15
2.16
2,17
2.18
2,19
2.20
2,21
2,22
2,23
2,24
2.25
2,26
2,27
2,28
2,29
i иперболических функций
е*~-Х- thx =
shx 1 -
ch x 1 +
X
е
7.0287
7,0993
7.1707
7,2427
7,3155
7,3891
7,4633
7,5383
7,6141
7,6906
7,7679
7,8460
7,9248
8,0045
8.0849
8.1662
8.2482
8.3311
8,4149
8,4994
8.5849
8,6711
8,7583
8,8463
8,9352
9,0250
9,1157
9,2073
9,2999
9,3933
9,4877
9,5831
9,6794
9,7767
9,8749
при х > 1,6
е~х
0.1423
0,1409
0.1395
0,1381
0,1367
0,1353
0.1340
0.1327
0.1313
0.1300
0.1287
0,1275
0.1262
0.1249
0.1237
0.1225
0,1212
0,1200
0,1188
0,1177
0,1165
0.1153
0.1142
0.1130
0.1119
0,1108
0.1097
0.1086
0,1075
0,1065
0,1054
0,1044
0,1033
0.1023
0,1013
X
2,30
2,31
2.32
2,33
2,34
2.35
2,36
2.37
2.38
2,39
2.40
2,41
2,42
2.43
2,44
2,45 •
2,46
2,47
2,48
2,49
2,50
2,51
2,52
2,53
2,54
2,55
2,56
2,57
2,58
2,59
2,60
2,61
2,62
2.63
2,64
ех
9,9742
10,074
10,176
10,278
10,381
10,486
10,591
10,697
10,805
10,913
11,023
11,134
11,246
11,359
11,473
11,588
11,705
11,822
11,941
12,061
12,182
12,305
12,429
12,554
12,680
12,807
12,936
13,066
13,197
13,330
13,464
13,599
13,736
13,874
14,013
е~х
0,10026
0,09926
0,09827
0,09730
0,09633
0,09537
0,09442
0,09348
0,09255
0,09163
0,09072
0,08982
0,08892
0,08804
0,08716
0,08629
0,08543
0,08458
0,08374
0,08291
0,08208
0,08127
0,08046
0,07966
0,07887
0,07808
0,07730
0,07654
0,07577
0,07502
0,07427
0,07353
0,07280
0,07208
0,07136
можно пользоваться следующими формулами:
50
ТАБЛИЦЫ
Продолжение
2,65
2,66
2,67
2,68
2,69
2,70
2,71
2,72
2,73
2,74
2,75
2,76
2,77
2,78
2,79
2,80
2,81
2,82
2,83
2,84
2,85
2,86
2,87
2,88
2,89
2,90
2,91
2,92
2,93
2,94
2,95
2,96
2,97
2,98
2,99
3,00
3,01
3,02
3,03
3,04
3,05
3.06
3,07
3,08
3,09
3,10
3,11
3,12
3,13
3,14
3,15
3,16
3,17
3,18
3,19
3,20
3,21
3,22
3,23
3,24
ех
14,154
14,296
14,440
14,585
14,732
14,880
15,029
15,180
15,333
15,487
15,643
15,800
15,959
16,119
16,281
16,445
16,610
16,777
16,945
17,116
17,288
17.462
17,637
17,814
17,993
18,174
18,357
18,541
18,728
18,916
19,106
19,298
19,492
19,688
19,886
20,086
20,287
20,491
20,697
20,905
21,115
21,328
21,542
21,758
' 21,977
22,198
22,421
22,646
22,874
23,104
23,336
23,571
23,807
24,047
24,288
24,533
24,779
25,028
25,280
25,534
е~х
0,07065
0,06995
0,06925
0,06856
0,06788
0,06721
0,06654
0,06588
0,06522
0,06457
0,06393
0,06329
0,06266
0,06204
0,06142
0,06081
0,06020
0,05961
0,05901
0,05843
0,05784
0,05727
0,05670
0,05613
0,05558
0,05502
0,05448
0,05393
0,05340
0,05287
0,05234
0,05182
0,05130
0,05079
0,05029
0,04979
0,04929
0,04880
0,04832
0,04783
0,04736
0,04689
0,04642
0,04596
0,04550
0,04505
0,04460
0,04416
0,04372
0,04328
0,04285
0,04243
0,04200
0,04159
0,04117
0,04076
0,04036
0,03996
0,03956
0,03916
X
3,25
3,26
3,27
3,28
3,29
3,30
3,31
3,32
3,33
3,34
3,35
3,36
3,37
3,38
3,39
3,40
3,41
3,42
3,43
3,44
3,45
3,46
3,47
3,48
3,49
3,50
3,51
3,52
3,53
3,54
3,55
3,56
3,57
3,58
3,59
3,60
3,61
3,62
3,63
3,64
3,65
3,66
3,67
3,68
3,69
3,70
3,71
3,72
3,73
3,74
3,75
3,76
3,77
3,78
3,79
3,80
3,81
3,82
3,83
3,84
ех
25,790
26,050
26,311
26,576
26,843
27,113
27,385
27,660
27,938
28,219
28,503
28,789
29,079
29,371
29,666
29,964
30,265
30,569
30,877
31,187
31,500
31,817
32,137
32,460
32,786
33,115
33,448
33,784
34,124
34,467
34,813
35,163
35,517
35,874
36.234
36,598
36,966
37,338
37,713
38,092
38,475
38,861
39,252
39,646
40,045
40,447
40,854
41,264
41,679
42,098
42,521
42,948
43,380
43,816
44,256
44,701
45,150
45,604
46.063
46,525
0,03877
0,03839
0,03801
0,03763
0,03725
0,03688
0,03652
0,03615
0,03579
0,03544
0,03508
0,03474
0,03439
0,03405
0,03371
0,03337
0,03304
0,03271
0,03239
0,03206
0,03175
0,03143
0,03112
0,03081
0,03050
0,03020
0,02990
0,02960
0,02930
0,02901
0,02872
0,02844
0,02816
0,02788
0,02760
0,02732
0,02705
0,02678
0,02652
0,02625
0,02599
0,02573
0,02548
0,02522
0,02497
0,02472
0,02448
0,02423
0,02399
0,02375
0,02352
0,02328
0,02305
0,02282
0,02260
0,02237
0,02215
0,02193
0,02171
0,02149
л:
3,85
3,86
3,87
3,88
3,89
3,90
3,91
3,92
3,93
3,94
3,95
3,96
3,97
3,98
3,99
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
ех
46,993
47,465
47,942
48,424
48,911
409,402
49,899
50,400
50,907
51,419
51,935
52,457
52,985
53,517
54,055
54,598
60,340
66,686
73,700
81,451
90,017
99,484
109,95
121,51
134,29
148,41
164,02
181,27
200,34
221,41
244,69
270,43
298,87
330,30
365,04
403,43
445,86
492,75
544,57
601,85
665,14
735,10
812,41
897,85
992,27
1096,6
1212,0
1339,4
1480,3
1636,0
1808,0
1998,2
2208,3
2440,6
2697,3
2981,0
3294,5
3641,0
4023,9
4447,1
е"х
0,02128
0,02107
0,02086
0,02065
0,02045
0,02024
0,02004
0,01984
0,01964
0,01945
0,01925
0,01906
0,01887
0,01869
0,01850
0,01832
0,01657
0,01500
0,01357
0,01228
0,01111
0,01005
0,00910
0,00823
0,00745
0,00674
0,00610
0,00552
0,00499
0,00452
0,00409
0,00370
0,00335
0,00303
0,00274
0,002479
0,002243
0,002029
0,001836
0,001662
0,001503
0,001360
0,001231
0,001114
0,001008
0,000912
0,000825
0,000747
0,000676
0,000611
0,000553
0,000500
0,000453
0,000410
0,000371
0,000335
0,000304
0,000275
0,000249
0,000225
НАТУРАЛЬНЫЕ ЛОГАРИФМЫ
51
.Y
8,5
8,6
8,7
8,8
8,9
X
е
4914,8
5431,7
6002,9
6634,2
7332,6
— х
е
0,000203
0,000184
0,000167
0,000151
0,000136
х
9,0
9,1
9,2
9,3
9,4
.Y
е
8103,1
8955,3
9897,1
10938
12088
е
0,000123
0,000112
0,000101
0,000091
0,000083
X
9,5
9,6
9,7
9,8
9,9
10,0
X
е
13360
14765
16318
18034
19930
22026
Продолжение
— X
е
0,000075
0,000068
0,000061
0,000055
0,000050
0,000045
1.1.1.12. Натуральные логарифмы.
N
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
0
0,0000
0,0953
0,1823
0,2624
0,3365
0,4055
0,4700
0,5306
0,5878
0,6419
0,6931
0,7419
0,7885
0,8329
0,8755
0,9163
0,9555
0,9933
1,0296
1,0647
1,0986
1,1314
1,1632
1,1939
1,2238
1,2528
1,2809
1,3083
1,3350
1,3610
1,3863
1,4110
1,4351
1,4586
1,4816
1,5041
1,5261
1,5476
1,5686
1,5892
1
0,0100
0,1044
0,1906
0,2700
0,3436
0,4121
0,4762
0,5365
0,5933
0,6471
0,6981
0,7467
0,7930
0,8372
0,8796
0,9203
0,9594
0,9969
1,0332
1,0682
1,1019
1,1346
1,1663
1,1969
1,2267
1,2556
1,2837
1,3110
1,3376
1,3635
1,3888
1,4134
1,4375
1,4609
1,4839
,5063
,5282
,5497
,5707
,5913
2
0,0198
0,1133
0,1989
' 0,2776
0,3507
0,4187
0,4824
0,5423
0,5988
0,6523
0,7031
0,7514
0,7975
0,8416
0,8838
0,9243
0,9632
1,0006
1,0367
1,0716
1,1053
1,1378
1,1694
1,2000
1,2296
1,2585
1,2865
1,3137
1,3403
1,3661
1,3913
1,4159
1,4398
1,4633
1,4861
1,5085
1,5304
1,5518
1,5728
1,5933
3
0,0296
0,1222
0,2070
0,2852
0,3577
0,4253
0,4886
0,5481
(Г,6043
0,6575
0,7080
0,7561
0,8020
0,8459
0,8879
0,9282
0,9670
1,0043
1,0403
1,0750
1,1086
1,1410
1,1725
,2030
1,2326
1,2613
,2892
1,3164
,3429
1,3686
1,3938
1,4183
1,4422 г
1,4656
,4884-
1,5107
1,5326
1,5539
1,5748
1,5953
4
0,0392
0,1310
0,2151
0,2927
, 0,3646
0,4318
0,4947
0,5539
0,6098
0,6627
0,7129
0,7608
0,8065
0,8502
0,8920
0,9322
0,9708
1,0080
1,0438
1,0784
1,1119
1,1442
1,1756
1,2060
1,2355
1,2641
1,2920
1,3191
1,3455
1,3712
1,3962
1,4207
1,4446
1,4679
1,4907
1,5129
1,5347
1,5560
1,5769
1,5974
5
0,0488
0,1398
0,2231
0,3001
0,3716
0,4383
0,5008
0,5596
0,6152
0,6678
0,7178
0,7655
0,8109
0,8544
0,8961
0,9361
0,9746
1,0116
1,0473
1,0818
1,1151
1,1474
1,1787
1,2090
1,2384
1,2669
1,2947
1,3218
1,3481
1,3737
1,3987
1,4231
1,4469
1,4702
1,4929
1,5151
1,5369
1,5581
1,5790
1,5994
6
0,0583
0,1484
0,2311
0,3075
0,3784
0,4447
0,5068
0,5653
0,6206
0,6729
0,7227
0,7701
0,8154
0,8587
0,9002
0,9400
0,9783
1,0152
1,0508
1,0852
1,1184
1,1506
1,1817
1,2119
1,2413
1,2669
1,2975
1,3244
1,3507
1,3762
1,4012
1,4255
1,4493
1,4725
1,4951
1,5173
1,5390
1,5602
1,5810
1,6014
7
0,0677
0,1570
0,2390
0,3148
0,3853
0,4511
0,5128
0,5710
0,6259
0,6780
0,7275
0,7747
0,8198
0,8629
0,9042
0,9439
0,9821
1,0188
1,0543
1,0886
,1217
1,1537
1,1848
1,2149
1,2442
,2726
,3002
1,3271
1,3533
1,3788
1,4036
1,4279
1,4516
1,4748
1,4974
. 1,5195
1,5412
1,5623
1,5831
1,6034
8
0,0770
0,1655
0,2469
0,3221
0,3920
0,4574
0,5188
0,5766
0,6313
0,6831
0,7324
0,7793
0,8242
0,8671
0,9083
0,9478
0,9858
1,0225
1,0578
1,0919
1,1249
1,1569-
1,1878
1,2179
1,2470
1,2754
1,3029
1,3297
1,3558
1,3813
1,4061
1,4303
1,4540
1,4770
1,4996
1,5217
1,5433
1,5644
1,5851
1,6054
9
0,0862
0,1740
0,2546
0,3293
0,3988
0,4637
0,5247
0,5822
0,6366
0,6881
0,7372
0,7839
0,8286
0,8713
0,9123
0,9517
0,9895
1,0260
1,0613
1,0953
1,1282
1,1600
1,1909
1,2208
1,2499
1,2782
1,3056
1,3324
1,3584
1,3838
1,4085
1,4327
1,4563
1,4793
1,5019
1,5239
1,5454
1,5665
1,5872
1,6074
52
ТАБЛИЦЫ
Продолжение
N
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
0
1,6094
1,6292
1,6487
1,6677
1,6864
1,7047
1,7228
1,7405
1,7579
1,7750
1,7918
1,8083
1,8245
1,8405
1,8563
1,8718
1,8871
1,9021
1,9169
1,9315
1,9459
1,9601
1,9741
1,9879
2,0015
2,0149
2,0281
2,0412
2,0541
2,0669
2,0794
2,0919
2,1041
2,1163
2,1282
2,1401
2,1518
2,1633
2,1748
2,1861
2,1972
2,2083
2,2192
2,2300
2,2407
2,2513
2,2618
2,2721
2,2824
2,2925
1
1,6114
1,6312
1,6506
1,6696
1,6882
1,7066
1,7246
1,7422
1,7596
1,7766
1,7934
1,8099
1,8262
1,8421
1,8579
1,8733
1,8886
1,9036
1,9184
1,9330
1,9473
1,9615
1,9755
1,9892
2,0028
2,0162
2,0295
2,0425
2,0554
2,0681
2,0807
2,0931
2,1054
2,1175
2,1294
2,1412
2,1529
2,1645
2,1759
2,1872
2,1983
2,2094
2,2203
2,2311
2,2418
2,2523
2,2628
2,2732
2,2834
2,2935
2
1,6134
1,6332
1,6525
1,6715
1,6901
1,7084
1,7263
1,7440
1,7613
1,7783
1,7951
1,8116
1,8278
1,8437
1,8594
1,8749
1,8901
1,9051
1,9199
1,9344
1,9488
1,9629
1,9769
1,9906
2,0042
2,0176
2,0308
2,0438
2,0567
2,0694
•2,0819
2,0943
2,1066
2,1187
2,1306
2,1424
2,1541
2,1656
2,1770
2,1883
2,1994
2,2105
2,2214
2,2322
2,2428
2,2534
2,2638
2,2742
2,2844
2,2946
3
1,6154
1,6351
1,6544
1,6734
1,6919
1,7102
1,7281
1,7457
1,7630
1,7800
1,7967
1,8132
1,8294
1,8453
1,8610
1,8764
1,8916
1,9066
1,9213
1,9359
1,9502
1,9643
1,9782
1,9920
2,0055
2,0189
2,0321
2,0451
2,0580
2,0707
2,0832
2,0956
2,1078
2,1199
2,1318
2,1436
2,1552
2,1668
2,1782
2,1894
2,2006
2,2116
2,2225
2,2332
2,2439 '
2,2544
2,2649
2,2752
2,2854
2,2956
4
1,6174
1,6371
1,6563
1,6752
1,6938
1,7120
1,7299
1,7475
1,7647
1,7817
1,7984
1,8148
1,8310
1,8469
1,8625
1,8779
1,8931
1,9081
1,9228
1,9373
1,9516
1,9657
1,9796
1,9933
2,0069
2,0202
2,0334
2,0464
2,0592
2,0719
2,0844
2,0968
2,1090
2,1211
2,1330
2,1448
2,1564
2,1679
2,1793
2,1905
2,2017
2,2127
2,2335
2,2343
2,2450
2,2555
2,2659
2,2762
2,2865
2,2966
5
,6194
,6390
,6582
,6771
,6956
,7138
,7317
,7492
,7664
,7834
1,8001
1,8165
1,8326
1,8485
1,8641
1,8785
1,8946
1,9095
1,9242
1,9387
1,9530
1,9671
1,9810
1,9947
2,0082
2,0215
2,0347
2,0477
2,0605
2,0732
2,0857
2,0980
2,1102
2,1223
2,1342
2,1459
2,1576
2,1691
2,1804
2,1917
2,2028
2,2138
2,2246
2,2354
2,2460
2,2565
2,2670
2,2773
2,2875
2,2976
6
1,6214
1,6409
1,6601
1,6790
1,6974
1,7156
1,7334
1,7509
1,7681
1,7851
1,8017
1,8181
1,8342
1,8500
1,8656
1,8810
1,8961
1,9110
1,9257
1,9402
1,9544
1,9685
1,9824
1,9961
2,0096
2,0229
2,0360
2,0490
2,0618
2,0744
2,0869
2,0992
2,1114
2,1235
2,1353
2,1471
2,1587
2,1702
2,1815
2,1928
2,2039
2,2148
2,2257
2,2364
2,2471
2,2576
2,2680
2,2783
2,2885
2,2986
7
1,6233
1,6429
1,6620
1,6808
1,6993
1,7174
1,7352
1,7527
1,7699
1,7867
1,8034
1,8197
1,8358
1,8516
1,8672
1,8825
1,8976
1,9125
1,9272
1,9416
1,9559
1,9699
1,9838
1,9974
2,0109
2,0242
2,0373
2,0503
2,0631
2,0757
2,0882
2,1005
2,1126
2,1247
2,1365
2,1483
2,1599
2,1713
2,1827
2,1939
2,2050
2,2159
2,2268
2,2375
2,2481
2,2586
2,2690
2,2793
2,2895
2,2996
8
1,6253
1,6448
1,6639
1,6827
1,7011
1,7192
1,7370
1,7544
1,7716
1,7884
1,8050
1,8213
1,8374
1,8532
1,8687
1,8840
1,8991
1,9140
1,9286
1,9430
1,9573
1,9713
1,9851
1,9988
2,0122
2,0255
2,0386
2,0516
2,0643
2,0769
2,0894
2,1017
2,1138
2,1258
2,1377
2,1494
2,1610
2,1725
2,1838
2,1950
2,2061
2,2170
2,2279
2,2386
2,2492
2,2597
2,2701
2,2803
2,2905
2,3006
9
1,6273
1,6467
1,6658
1,6845
1,7029
,7210
,7387
,7561
1,7733
1,7901
1,8066
1,8229
1,8390
1,8547
1,8703
1,8856
1,9006
1,9155
1,9301
1,9445
1,9587
1,9727
1,9865
2,0001
2,0136
2,0268
2,0399
2,0528
2,0656
2,0782
2,0906
2,1029
2,1150
2,1270
2,1389
2,1506
2,1622
2,1736
2,1849
2,1961
2,2072
2,2181
2,2289
2,2396
2,2502
2,2607
2,2711
2,2814
2,2915
2,3016
ДЛИНА ОКРУЖНОСТИ
53
т
1
2
3
4
5
lnlOw
2,3026
4,6052
6,9078
9,2103
11,5129
.13. Длина окружности.
Объяснения к таблице 1.1.1.12
натуральных логарифмов. В отличие от таблиц
десятичных логарифмов здесь даны как мантиссы,
так и характеристики. Логарифмы чисел,
заключенных между 1 и 10, находятся непосредственно
в таблице, причем на третий и четвертый
десятичные знаки должна быть внесена
интерполяционная поправка. Для чисел, больших десяти или
меньших единицы, натуральные логарифмы
находятся с помощью помещенных в конце таблицы
значений логарифмов степеней 10.
d
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
0
3,142
3,456
3,770
4,084
4,398
4,712
5,027
5,341
5,655
5,969
6,283
6,597
6,912
7,226
7,540
7,854
8,168
8,482
8,796
9,111
9,425
9,739
10,05
10,37
10,68
11,00
11,31
11,62
11,94
12,25
12,57
12,88
13,19
13,51
13,82
14,14
14,45
14,77
15,08
15,39
15,7|
1
3,173
/3,487
3,801
4,115
4,430
4,744
1 5,058
5,372
5,686
6,000
6,315
6,629
6,943
7,257
7,571
7,885
8,200
8,514
8,828
9,142
9,456
9,770
10,08
10,40
10,71
11,03
11,34
11,66
11,97
12,28
12,60
12,91
13,23
13,54
13,85
14,17
14,48
14,80
15,11
15,43
15,74
2
3,204
3,519
3,833
4,147
4,461
4,775
5,089
5,404
5,718
6,032
6,346
6,660
6,974
7,288
7,603
7,918"
8,231
8,545
8,859
9,173
9,488
9,802
10,12
10,43
10,74
11,06
11,37
11,69
12,00
12,32
12,63
12.94
13,26
13,57
13,89
14,20
14,51
14,83
15,14
15,46
15,77
3
3,236
3,550
3,864
4,178
4,492
4,807
5,121
5,453
5,749
6,063
6,377
6,692
7,006
7,320
7,634
7,948
8,262
8,577
8,891
9,205
9,519
9,833
10,15
10,46
10,78
11,09
11,40
11,72
12,03
12,35
12,66
12,97
13,29
13,60
13,92
14,23
14,55
14,86
15,17
15,49
15.80
4
3,267
, 3,581
3,896
4,210
4,524
4,838
5,152
5,466
5,781
6,095
6,409
6,723
7,037
7,351
7,665
7,980
8,294
8,608
8,922
9,236
9,550
9,865
10,18
10,49
10,81
11,12
11,44
11,75
12,06
12,38
12,69
13,01
13,32
13,63
13,95
14,26
14,58
14,89
1.5,21
15,52
15,83
5
3,299
3,613
3,927
4,241
4,555
4,869
5,184
5,498
5,812
6,126
6,440
6,754
7,069
7,383
7,697
8,011
8,325
8,639
8,954
9,268
9,582
9,896
10,21
10,52
10,84
11,15
11,47
11,78
12,10
12,41
12,72
13,04
13,35
13,67
13,98
14,29
14,61
14,92
15,24
15,55
15,87
6
3,330
3,644
3,958
4,273
4,587
4,901
5,215
5,529
5,843
6,158
6,472
6,786
7,100
7,414
7,728
8,042
8,357
8,671
8,985
9,299
9,613
9,927
10,24
10,56
10,87
11,18
11,50
11,81
12,13
12,44
12,75
13,07
13,38
13,70
14,01
14,33
14,64
14,95
15,27
15,58
15,90
7
3,362
3,676
3,990
4,304
4,618
4,932
5,246
5,561
5,875
6,189
6,503
6,817
7,131
7,446
7,760
8,074
8,388
8,702
9,016
9,331
9,645
9,959
10,27
10,59
10,90
11,22
11,53
11,84
12,16
12,47
12,79
13,10
13,41
13,73
14,04
14,36
14,67
14,99
15,30
15,61
15,93
8
3,393
3,707
4,021
4,335
4,650
4,964
5,278
5,592
5,906
6,220
6,535
6,849
7,163
7,477
7,791
8,105
8,419
8,734
9,048
9,362
9,676
9,990
10,30
10,62
10,93
11,25
11,56
11,88
12,15
12,50
12,82
13,13
13,45
13,76
14,07
14,39
14,70-
15,02
15,33
15,65
15,96
9
3,424
3,738
4,053
4,367
4,681
4,995
5,309
5,623
5,938
6,252
6,566
6,880
7,194
7,508
7,823
8,137
8,451
8,765
9,079
9,393
9,708
10,02
10,34
10,65
10,96
11,28
11,59
11,91
12,22
12,53
12,85
13,16
13,48
13,79
14,11
14,42
14,73
15,05
15,36
15,68
15,99
54
ТАБЛИЦЫ
Продо. жжение
d
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
-&,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
0
15,71
16,02
16,34
16,65
16,96
17,28
17,59
17,91
18,22
18,54
18,85
19,16
19,48
19,79
20,11
20,42
20,73
21,05
21,36
21,68 .
21,99
22,31
22,62
22,93
23,25
23,56
23,88
24,19
24,50
24,82
25,13
25,45
25,76
26,08
26,39
26,70
27,02
27,33
27,65
27,96
28,27
28,59
28,90
29,22
29,53
29,85
30,16
30,47
30,79
31,10
31,42
1
15,74
16,05
16,37
16,68
17,00
17,31
17,62
17,94
18,25
18,57
18,88
19,20
19,51
19,82
20,14
20,45
20,77
21,08
21,39
21,71
22,02
22,34
22,65
22,97
23,28
23,59
23,91
24,22
24,54
24,85
25,16 |
25,48
25,79
26,11
26,42
26,73
27,05
27,36
27,68
27,99
28,31
28,62
28,93
29,25
29,56
29,88
30,19
30,50
30,82
31,13
2
15,77
16,08
16,40
16,71
17,03
17,34
17,66
17,97
18,28
18,60
18,91
19,23
19,54
19,85
20,17
20,48
20,80
21,11
21,43
21,74
22,05
22,37
22,68
23,00
23,31
23,62
23,94
24,25
24,57 .
24,88
25,20
25,51
25,82
26,14
26,45
26,77
27,08
27,39
27,71
28,02
28,34
28,65
28,97
29,28
29,59
29,91
30,22
30,54
30,85
31,16
3
15,80
16,12
16,43
16,74
17,06
17,37
17,69
18,00
18,32
18,63
18,94
19,26
19,57
19,89
20,20
20,51
20,83
21,14
21,46
21,77
22,09
22,40
22,71
23,03
23,34
23,66
23,97
24,28
24,60
24,91
25,23
25,54
25,86
26,17
26,48
26,80
27,11
27,43
27,74
28,05
28,37
28,68
29,00
29,31
29,63
29,94
30,25
30,57
30,88
31,20
4
15,83
16,15
16,46
16,78
17,09
17,40
17,72
18,03
18,35
18,66
18,98
19,29
19,60
19,92
20,23
20,55
20,86
21,17
21,49
21,80
22,12
22,43
22,75
23,06
23,37
23,69
24,00
24,32
24,63
24,94
25,26
25,57
25,89
26,20
26,52
26,83
27,14
27,46
27,77
28,09
. 28,40
28,71
29,tK
29,34
29,66
29,97
30,28
30,60
30,91
31,21
5
15,87
16,18
16,49
16,81
17,12
17,44
17,75
18,06
18,38
18,69
19,01
19,32
19,63
19,95
20,26
20,58
20,89
21,21
21,52
21,83
22,15
22,46
22,78
23,09
23,40
23,72
24,03
24,35
24,66
24,98
25,29
25,60
25,92
26,23
26,55
26,86
27,17
27,49
27,80
28,12
28,43
28,75
29,06
29,37
29,69
30,00
30,32
30,63
, 30,94
31,26
6
15,90
16,21
16,52
16,84
17,15
17,47
17,78
18,10
18,41
18,72
19,04
19,35
19,67
19,98
20,29
20,61
20,92
21,2.
21,55
21,87
22,18
22,49
22,81
23,12
23,44
23,75
24,06
24,38
24,69
25,01
25,32
25,64
25,95
26,26
26,58
26,89
27,21
27,52
27,83 '
28,15
28,46
28,78
29,09
29,41
29,72
30,03
30,35
30,66
30,98
31,29
7
15,93
16,24
16,56
16,87
17,18
17,50
17,81
18,13
18,44
18,76
19,07
19,38
19,70
20,01
20,33
20,64
20,95
21,27
21,58
21,90
22,21
22,53
22,84
23,15
23,47
23,78
24,10
24,41
24,72
25,04
25,35
25,67
25,98
26,30
26,61
26,92
27,24
27,55
27,87
28,18
28,49
28,81
29,12
29,44
29,75
30,07
30,38
30,69
31,01
31,32
8
15,96
16,27
16,59
16,90
17,22
17,53
17,84
18,16
18,47
18,79
19,10
19,42
19,73
20,04
20,36
20,67
20,99
21,30
21,61
21,93
22,24
22,56
22,87
23,19
23,50
23,81
24,13
24,44
24,76
25,07
25,38
25,70
26,01
26,33
26,64 .
26,95
27,27
27,58
27,90
28,21
28,53
28,84
29,15
29,47
29,78
30,10
30,41
30,72
31,04
31,35
9
15,99
16,30
16,62
16,93
17,25
17,56
17,88
18,19
18,50
18,82
19,13
19,45
19,76
20,07
20,39
20,70
21,02
21,33
21,65
21,96
22,27
22,59
22,90
23,22
23,53
23,84
24,16
24,47
24,79
25,10
25,42
25,73
26,04
26,36
26,67
26,99
27,30
27,61
27,93
28,24
28,56
28,87
29,19
29,50
29,81
30,13
30,44
30,76
31,07
31,38
ПЛОЩАДЬ КРУГА
55
1.1.1.14. Площадь круга.
d
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8 .
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
5,0
5,1
5,2
5,3
5,4
5,5
0
0,7854
0,9503
1,131
1,327
1,539
1,767
2,011
2,270
2,545
2,835
3,142
3,464
3,801
4,155
4,524
4,909
5,309
5,726
6,158
6,605
7,069
7,548
8,042
8,553
9,079
9,621
10,18
10,75
11,34
11,95
12,57
13,20
13,85
14,52
15,21
15,90
16,62
17,35
18,10*
18,86
19,63
20,43
21.24
22,06
22,90
23,76
1
0,8012
0,9677
1,150
1,348
1,561
1,791
2,036
2,297
2,573
2,865
3,173
3,497
3,836
4,191
4,562
4,948
5,350
5,768
6,202
6,651
7,116
7,596
8,093
8,605
9,133
9,676
10,24
10,81
11,40
12,01
12,63
13,27
13,92
14,59
15,27
15,98
16,69
17,42
18,17
18,93
19,71
20,51
21,32
22,15
22,99
23,84
2
0,8171
0,9852
1,169
1,368
1,584
1,815
2,061
2,324
2,602
2,895
3,205
3,530
3,871
4,227
4,600
4,988
5,391
5,811
6,246
6,697
7,163
7,645
8,143
8,657
9,186
9,731
10,29
10,87
11,46
12,07
12,69
13,33
13,99
14,66
15,34
16,05
16,76
17,50
18,25
19,01
19,79
20,59
21,40
22,23
23,07
23,93
3
0,8332
1,003
1,188
1,389
1,606
1,839
2,087
2,351
2,630
2,926
3,237
3,563
3,906
4,264
4,638
5,027
5,433
5,853
6,290
6,743
7,211
7,694
8,194
8,709
9,240
9,787
10,35
10,93
11,52
12,13
12,76
13,40
14,05
14,73
15,41
16,12
16,84
17,57
18,32
19,09
19,87
20,67
21,48
22,31
23,16
24,02
4
0,8495
1,021
1.208
1,410
1,629
1,863
2,112
2,378
2,659
2,956
3,269
3,597
3,941
4,301
4,676
5,067
5,474
5,896
6,335
6,789
7,258
7,744
8,245
8,762
9,294
9,842
10,41
10,99
11,58
12,19
12,82
13,46
14,12-
14,79
15,48
16,19
16,91
17,65
18,40
19,17
19,95
20,75
21,57
22,40
23,24
24,11
5
0,8659
1,039
1.227
1,431
1,651
1,887
2,138
2,405
2,688
2,986
3,301
3,631
3,976
4,337
4,714
5,107
5,515
5,940
6,379
6,835
7,306
7,793
8,296
8,814
9,348
9,898
10,46
11,04
11,64
12,25
12,88
13,53
14,19
14,86
15,55
16,26
16,98
17,72
18,47
19,24
20,03
20,83
21,65
22,48
23,33
24,19
6
0,8825
1,057
1,247
1,453
1,674
1,911
2,164
2,433
2,717
3,017
3,333
3,664
4,011
4,374
4,753
5,147
5,557
5,983
6,424
6,881
7,354
7,843
8,347
8,867
9,402
9,954
10,52
11,10
11,70
12,32
12,95
13,59
14,25
14,93
15,62
16,33
17,06
17,80
18,55
19,32
20,11
20,91
21,73
22,56
23,41
24,28
7
0,8992
1,075
1,267
1,474
1,697
1,936
2,190
2,461
2,746
3,048
3,365
3,698
4,047
4,412
4,792
5,187
5,599
6,026
6,469
6,928
7,402
7,892
8,398
8,920
9,457
10,01
10,58
11,16
11,76
12,38
13,01
13,66
14,32
15,00
15,69
16,40
17,13
17,87
18,63
19,40
20,19
20,99
21,81
22,65
23,50
24,37
8
0,9161
1,094
1,287
1,496
1,720
1,961
2,217
2,488
2,776
3,079
3,398
3,733
4,083
4,449
4,831
5,228
5,641
6,070
6,514
6,975
7,451
7,942
8,450
8,973
9,511
10,07
10,64
11,22
11,82
12,44
13,07
13,72
14,39
15,07
15,76
16,47
17,20
17,95
18,70
19,48
20,27
21,07
21,90
22,73
23,59
24,45
9
0,9331
1,112
1,307
1,517
1,744
1,986
2,243
2,516
2,806
3,110
3,431
3,767
4,119
4,486
4,870
5,269
5,683
6,114
6,560
7,022
7,499
7,992
8,501
9,026
9,566
10,12
10,69
11,28
11,88
12,50
13,14 ¦
13,79
14,45
15,14
15,83
16,55
17,28
18,02
18,78
19,56
20,35
21,16
21,98
22,82
23,67
24,54
56
ТАБЛИЦЫ
Продолжение
d
5,5
5,6
5,7
5,8
5,9
6,0
6,1 -
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6 "
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
0
23,76
24,63
25,52
26,42
27,34 '
28,27
29,22
30,19
31,17
32,17
33,18
34,21
35,26
36,32
37,39
38,48
39,59
40,72
41,85
43,01
44,18
45,36
46,57
47,78
49,02
50,27
51,53
52,81
54,11
55,42
56,75
58,09
59,45
60,82
62,21
63,62
65,04
66,48
67,93
69,40
70,88
72,38
73,90
75,43
76,98
78,54
1
23,84
24,72
25,61
26,51
27,43
28,37
29,32
30,29
31,27
32,27
33,29
34,32
35,36
36,42
37,50
38,59
39,70
40,83
41,97
43,12
44,30
45,48
46,69
47,91
49,14
50,39
51,66
52,94
54,24
55,55
56,88
58,22
59,58
60,96
62,35
63,76
65,18
66,62
68,08
69,55
71,03
72,53
74,05
75,58
77,13
2
23,93
24,81
25,70
26,60
27,53
28,46
29,42
30,39
31,37
32,37
33,39
34,42
35,47
36,53
37,61
38,70
39,82
40,94
42,08
43,24
44,41
45,60
46,81
48,03
49,27
50,52
51,78
53,07
54,37
55,68
57,01
58,36
59,72
61,10
62,49
63,90
65,33
66,77
68,22
69,69
71,18
72,68-
74,20
75,74
77;29
3
24,02
24,89
25,79
26,69
27,62
28,56
29,51
30,48
31,47
32,47
33,49
34,52
35,57
36,64
37,72
38,82
39,93
41,06
42,20
43,36
44,53
45,72
46,93
48,15
49,39
50,64
51,91
53,20
54,50
55,81
57,15
58,49
59,86
61,24
62,63
64,04
65,47
66,91
68,37
69,84
71,33
72,84
74,36
75,89
77,44
4
24,11
24,98
25,88
26,79
27,71
28,65
29,61
30,58
31,57
32,57
33,59
34,63
35,68
36,75
37,83
38,93
40,04
41,17
42,31
43,47
44,65
45,84
47,05
48,27
49,51
50,77
52,04
53,33
54,63
55,95
57,28
58,63
59,99
61,38
62,77
64,18
65,61
67,06
68,51
69,99
71,48
72,99
74,51
76,05
77,60
5
24,19
25,07
25,97
26,88
27,81
28,75
29,71
30,68
31,67
32,67
33,70
34,73
35,78
36,85
37,94
39,04
40,15
41,28
42,43
43,59
44,77
45,96
47,17
48,40
49,64
50,90
52,17
53,46
54,76
56,08
57,41
58,77
60,13
61,51
62,91
64,33
65,76
67,20
68,66
70,14
71,63
73,14
74,66
76,20
77,76
6
24,28
25,16
26,06
26,97
27,90
28,84
29,80
30,78
31,77
32,78
33,80
34,84
35,89
36,96
38,05
39,15
40,26
41,40
42,54
43,71
44,89
46,08
47,29
48,52
49,76
51,02
52,30
53,59
54,89
56,21
57,55
58,90
60,27
61,65
63,05
64,47
65,90
67,35
68,81
70,29
71,78
73,29
74,82
76,36
77,91
7
24,37
25,25
26,15
27,06
27,99
28,94
29,90
30,88
31,87
32,88
33,90
34,94
36,00
37,07
38,16
39,26
40,38
41,51
42,66
43,83
45,01
46,20 '
47,42
48,65
49,89
51,15
52,42
53,72
55,02
56,35
57,68
59,04
60,41
61,79
63,19
64,61
66,04
67,49
68,96
70,44
71,93
73,44
74,97
76,51
78,07
8
24,45
25,34
26,24
27,15
28,09
29,03
30,00
30,97
31,97
32,98
34,00
35,05
36,10
37,18
38,26
39,37
40,49
41,62
42,78
43,94
45,13
46,32
47,54
48,77
50,01
51,28
52,55
53,85
55,15
56,48
57,82
59,17
60,55
61,93
63,33
64,75
66,19
67,64
69,10
70,58
72,08
73,59
75,12
76,67
78,23
9
24,54
25,43
26,33
27,25
28,18
29,13
30,09
31,07
32,07
33,08
34,11
35,15
36,21
37,28
38,37
39,48
40,60
41,74
42,89
44,06
45,25
46,45
47,66
48,99
50,14
51,40
52,68
53,98
55,29-
56,61
57,95
59,31
60,68
62,07
63,48
64,90
66,33
67,78
69,25
70,73
72,23
73,75
75,28
76,82
78,38
ЭЛЕМЕНТЫ СЕГМЕНТА КРУГА
57
1.1.1.15. Элементы сегмента круга.
1.1.1.15.1. Длина дуги и площадь сегмента для хорды, равной единице.
Подъем
(отношение стрелки
к хорде) И/а
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,10
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,20
0,21
0,22
0,23
0,24
0,25
Длина
дуги /
,0003
,0011
,0024
1,0043
,0067
1,0096
1,0130
1,0170
1,0215
1,0265
1,0320
,0380
1,0445
1,0515
1,0590
1,0669
1,0754
1,0843
1,0936
1,1035
1,1137
1,1244
1,1356
1,1471
1,1591
Площадь
сегмента
0,0067
0,0133
0,0200
0,0267
0,0334
0,0401
0,0468
0,0536
0,0604
0,0672
0,0740
0,0809
0,0878
0,0948
0,1018
0,1088
0,1159
0,1231
0,1303
0,1375
0,1448
0,1522
0,1596
0,1671
0,1747
Подъем
(отношение стрелки
к хорде) h/a
0,26
0,27
0,28
0,29
0,30
0,31
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
Длина
дуги /
1,1715
1,1843
1,1975
1,2110
1,2250
1,2393
1,2539
1,2689
1,2843
1,3000
1,3160
1,3323
1,3490
1,3660
1,3832
1,4008
1,4186
1,4367
1,4551
1,4738
1,4927
1,5118
1,5313
1,5509
1,5708
Площадь
сегмента
0,1824
0,1901
0,1979
0,2058
0,2137
0,2218
0,2299
0,2381
0,2464
0,2548
0,2633
0,2719
0,2806
0,2893
0,2982
0,3072
0,3162
0,3254
0,3347
0,3441
0,3536
0,3632
0,3729
0,3828
0,3927
1.1.1.15.2. Длина дуги, стрелка, длина хорды и площадь сегмента
для радиуса, равного единице.
Центр.
угол а°
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Длина
дуги /
0,0175
0,0349
0,0524
0,0698
0,0873
0,1047
0,1222
0,1396
0,1571
0,1745
0,1920
0,2094
0,2269
0,2443
0,2618
0,2793
0,2967
0,3142
0,3316
0,3491
0,3665
0,3840
0,4014
Стрелка h
0,0000
0,0002
0,0003
0,0006
0,0010
0,0014
0,0019
0,0024
0,0031
0,0038
0,0046
0,0055
0,0064
0,0075
0,0086
0,0097
0,0110
0,0123
0,0137
0,0152
0,0167
0,0184
0,0201
/
~h
458,37
229,19
152,80
114,60
91,69
76,41
65,50
57,32
50,96
45,87
41v70
38,23
35,30
32,78
30,60
28,69
27,01
25,52
24,18
22,98
21,89
20,90
20,00
Длина
хорды а
0,0175
0,0349
0,0524
0,0698
0,0872
0,1047
0,1221
0,1395
0,1569
0,1743
0,1917
0,2091
0,2264
0,2437
0,2611
0,2783
0,2956
0,3129
0,3301
0,3473
0,3645
0,3816
0,3987
а
~h
458,36
229,18
152,78
114,58
91,66
76,38
65,46
57,27
50,90
45,81
41,64
38,16
35,22
32,70
30,51
28,60
26,91
25,41
24,07
22,96
21,77
20,77
19,86
Площадь
сегмента
0,00000
0,00000
0,00001
0,00003
0,00006
0,00010
0,00015
0,00023
0,00032
0,00044
0,00059
0,00076
0,00097
0,00121
0,00149
0,00181
0,00217
0,00257
0,00302
0,00352
0,00408
0,00468
0,00535
58
ТАБЛИЦЫ
Продолжение
Центр.
угол а°
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
Длина
дуги /
0,4014
0,4189
0,4363
0,4538
0,4712
0,4887
0,5061
0,5236
0,5411
0,5585
0,5760
0,5934
0,6109
0,6283
0,6458
0,6632
0,6807
0,6981
0,7156
0,7330
0,7505
0,7679
0,7854
0,8029
0,8203
0,8378
0,8552
0,8727
0,8901
0,9076
0,9250
0,9425
0,9599
0,9774
0,9948
1,0123
1,0297
1,0472
1,0647
1,0821
1,0996
1,1170
1,1345
1,1519
1,1694
1,1868
1,2043
1,2217
1,2392
1,2566
1,2741
1,2915
1,3090
1,3265
1,3439
1,3614
1,3788
Стрелка h
0,0201
0,0219
0,0237
0,0256
0,0276
0,0297
0,0319
0,0341
0,0364
0,0387
0,0412
0,0437
0,0463
0,0489
0,0517
0,0545
0,0574
0,0603
0,0633
0,0664
0,0696
0,0728
0,0761
0,0795
0,0829
0,0865
0,0900
0,0937
0,0974
0,1012
0,1051
0,1090
0,1130
0,1171
0,1212
0,1254
0,1296
0,1340
0,1384
0,1428
0,1474
0,1520
0,1566
0,1613
0,1661
0,1710
0,1759
0,1808
0,1859
0,1910
0,1961
0,2014
0,2066
0,2120
0,2174
0,2229
0,2284
/
И
20,00
19,17
18,41
17,71
17,06
16,45
15,89
15,37
14,88
14,42
13,99
13,58
13,20
12,84
12,50
12,17
11,87
11,58
11,30
11,04
10,79
10,55
10,32
10,10
9,89
9,69
9,50
9,31
9,14
8,97
8,80
8,65
8,50
8,35
8,21
8,07
7,94
7,82
7,69
7,58
7,46
7,35
7,24
7,14
7,04
6,94
6,85
6,76
6,67
6,58
6,50
6,41
6,33
6,26
6,18
6,11
6,04
Длина
хорды а
0,3987
0,4158
0,4329
0,4499
0,4669
0,4838
0,5008
0,5176
0,5345
0,5513
0,5680
0,5847
0,6014
0,6180
0,6346
0,6511
0,6676
0,6840
0,7004
0,7167
0,7330
0,7492
0,7654
0,7815
0,7975
0,8135
0,8294
0,8452
0,8610
0,8767
0,8924
0,9080
0,9235
0,9389
0,9543
0,9696
0,9848
1,0000
1,0151
1,0301
1,0450
1,0598
1,0746
1,0893
1,1039
1,1184
1,1328
1,1472
1,1614
1,1756
1,1896
1,2036
1,2175
1,2313
1,2450
1,2586
1,2722
а
~h
19,86
19,03
18,26
17,55
16,90
16,29
15,72
15,19
14,70
14,23
13,79
13,38
12,99
12,63
12,28
11,95
11,64
11,34
11,06
10,79
10,53
10,29
10,05
9,83
9,62
9,41
9,21
9,02
8,84
8,66
8,49
8,33
8,17
8,02
7,88
7,73
7,60
7,46
7,34
7,21
7,09
6,97
6,86
6,75
6,65
6,54
6,44
6,34
6,25
6,16
6,07
5,98
5,89
5,81
5,73
5,65
5,57
Площадь
сегмента
0,00535
0,00607
0,00686
0,00771
0,00862
0,00961
0,01067
0,01180
0,01301
0,01429
0,01566
0,01711
0,01864
0,02027
0,02198
0,02378
0,02568
0,02767
0,02976
0,03195
0,03425
0,03664
0,03915
0,04176
0,04448
0,04731
0,05025
0,05331
0,05649
0,05978
0,06319
0,6673
0,07039
0,07417
0,07808
0,08212
0,08629
0,09d59
0,09502
0,09958
0,10428
0,10911
0,11408
0,11919
0,12443
0,12982
0,13535
0,14102
0,14683
0,15279
0,15889
0,16514
0,17154
0,17808
0,18477
0,19160
t19859
ЭЛЕМЕНТЫ СЕГМЕНТА КРУГА
59
Продолжение
Центр.
угол ос°
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
ПО
111
112 •
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
Длина
ДУГИ /
1,3963
1,4137 .
1,4312
1,4486
1,4661
1,4835
1,5010
1,5184
1,5359
1,5533
1,5708
1,5882
1,6057
1,6232
1,6406
1,6581
1,6755
1,6930
1,7104
1,7279
1,7453
1,7668
1,7802
1,7977
1,8151
1,8326
1,8500
1,8675
1,8850
1,9024
1,9199
1,9373
1,9548
1,9722
1,9897
2,0071
2,0246
2,0420
2,0595
2,0769
2,0944
2,1118
2,1293
2,1468
2,1642
2,1817
2,1991
2,2166
2,2340
2,2515
2,2689
2,2864
2,3038
2,3213
2,3387
2,3562
2,3736
2,3911
Стрелка h
0,2340
0,2396
0,2453
0,2510
0,2569
0,2627
0,2686
0,2746
0,2807
0,2867
0,2929
0,2991
0,3053
0,3116
0,3180
0,3244
0,3309
0,3374
0,3439
0,3506
0,3572
0,3639
0,3707
0,3775
0,3843
0,3912
0,3982
0,4052
0,4122
0,4193
0,4264
0,4336
0,4408
0,4481
0,4554
0,4627
0,4701
0,4775
0,4850
0,4925
0,5000
0,5076
0,5152
0,5228
0,5305
0,5383
0,5460
0,5538
0,5616
0,5695
0,5774
0,5853
0,5933 ~
0,6013
0,6093
0,6173
0,6254
0,6335
/
~h
5,97
5,90
5,83
5,77
5,71
5,65
5,59
5,53
5,47
5,42
5,36
5,31
5,26
5,21
5,16
5,11
5,06
5,02
4,97
4,93
4,89
4,84
4,80
4,76
4,72
4,68
4,65
4,61
4,57
4,54
4,50
4,47
4,43
4,40
4,37
4,34
4,31
4,28
4,25
4,22
4,19
4,16
4,13
4,11
4,08
4,05
4,03
4,00
3,98
3,95
3,93
3,91
3,88
3.86
3,84
3,82
3,80
3,77
Длина
хорды а
,2856
,2989
1,3121
1,3252
1,3383
1,3512
1,3640
1,3767
1,3893
1,4018
1,4142
1,4265
1,4387
1,4507
1,4627
1,4746
1,4863
1,4979
1,5094
1,5208
1,5321
1,5432
1,5543
1,5652
1,5760
1,5867
1,5973
1,6077
1,6180
1,6282
1,6383
1,6483
1,6581
1,6678
1,6773
1,6868
1,6961
1,7053
1,7143
1,7233
1,7321
1,7407
1,7492
1,7576
1,7659
1,7740
1,7820
1,7899
1,7976
1,8052
1,8126
1,8199
1,8271
1,8341
1,8410
1,8478
1,8544
1,8608
а
__ J
5,49
5,42
5,35
5,28
5,21
5,14
5,08
5,01
4,95
4,89
4,83
4,77
4,71
4,66
4,60
4,55
4,49
4,44
4,39
4,34
4,29
4,24
4,19
4,15
4,10
4,06
4,01
3,97
3,93
3,88
3,84
3,80
3,76
3,72
3,68
3,65
3,61
3,57
3,53
3,50
3,46
3,43
3,40
3,36
3,33
3,30
3,26
3,23
3,20
3,17
3,14
3,11
3,08
3,05
3,02
2,99
2,97
2,94
Площадь
сегмента
0,20573
0,21301
0,22045
0,22804
0,23578
0,24367
0,25171
0,25990
0,26825
0,27675
0,28540
0,29420
0,30316
0,31226
0,32152
0,33093
0,34050
0,35021
0,36008
0,37009
0,38026
0,39058
0,40104
0,41166
0,42242
0,43333
0,44439
0,45560
0,46695
0,47845
0,49008
0,50187
0,51379
0,52586
0,53806
0,55041
0,56289
0,57551
0,58827
0,60116
0,61418
0,62734
0,64063
0,65404
0,66759
0,68125
0,69505
0,70897
0,72301
0,73716
0,75144
0,76584
0,78034
0,79497
0,80970
0,82454
0,83949
0,85455
60
ТАБЛИЦЫ
Продо 1жение
Центр.
угол а
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
Длина
дуги /
2,3911
2,4086
2,4260
2,4435
2,4609
2,4784
2,4958
2,5133
2,5307
2,5482
2,5656
2,5831
2,6005
2,6180
2,6354
2,6529
2,6704
2,6878
2,7053
2,7227
2,7402
2,7576
2,7751
2,7925
2,8100
2,8274
2,8449
2,8623
2,8798
2,8972
2,9147
2,9322
2,9496
2,9671
2,9845
3,0020
3,0194
3,0369
3,0543
3,0718
3,0892
3,1067
3,1241
3,1416
Стрелка h
0,6335
0,6416
0,6498
0,6580
0,6662
0,6744
0,6827
0,6910
0,6993
0,7076
0,7160
0,7244
0,7328
0,7412
0,7496
0,7581
0,7666
0,7750
0,7836
0,7921
0,8006
0,8092
0,8178
0,8264
0,8350
0,8436
0,8522
0,8608
0,8695
0,8781
0,8868
0,8955
0,9042
0,9128
0,9215
0,9302
0,9390
0,9477
0,9564
0,9651
0,9738
0,9825
0,9913
1,0000
/
h
3,77
3,75
3,73
3,71
3,69
3,67
3,66
3,64
3,62
3,60
3,58
3,57
3,55
3,53
3,52
3,50
3,48
3,47
3,45
3,44
3,42
3,41
3,39
3,38
3,37
3,35
3,34
3,33
3,31
3,30
3,29
3,27
3,26
3,25
3,24
3,23
3,22
3,20
3,19
3,18
3,17
3,16
3,15
3.14
Длина
хорды а
,8608
,8672
,8733
,8794
,8853
,8910
,8966
1,9021
1.9074
1,9126
1,9176
1,9225
1,9273
1,9319
1,9363
1,9406
1,9447
1,9487
1,9526
1,9563
1.9598
1,9633
1,9665
1,9696
1,9726
1,9754
1,9780
1,9805
1,9829
1,9851
1,9871
1,9890
1,9908
1,9924
1,993.8
1,9951
1,9963
1,9973
1,9981
1,9988
1,9993
1,9997
1,9999
2,0000
а
h
2,94
2,91
2,88
2,86
2,83
2,80
2,78
2,75
2,73
2,70
2,68
2,65
2,63
2,61
2,58
2,56
2.54
2,51
2,49
2,47
2,45
2,43
2,40
2,38
2,36
2,34
2,32
2,30
2,28
2.26
2,24
2,22
2,20
2,18
2,16
2,14
2,13
2,11
2г09
2,07
2,05
2,04
2,02
2,00
Площадь
сег мента
0,85455
0,86971
0,88497
0,90034
0,91580
0,93135
0,94700
0,96274
0,97858
0,99449
1,01050
1,02658
1,04275
1,05900
1,07532
1,09171
,10818
,12472
,14132
,15799
.17472
,19151
,20835
,22525
,24221
,25921
,27626
,29335
,31049
,32766
,34487
,36212
,37940
,39671
,41404
,43140
,44878
,46617
,48359
,50101
,51845
,53589
,55334
1,57080
Объяснения к таблицам 1.1.1.13,
1.1.1.14 и 1.1.1.15.
Таблицы 1.1.1.13 и 1.1.1.14 дают значения
длины окружности и площади круга диаметра d,
лежащего между d = 1,00 и d = 10,0, с четырьмя
значащими цифрами. Если диаметр круга лежит вне
этих границ, то площадь или длина окружности
определяется для диаметра \0kd или 10"kd.
Найденное число затем умножается в случае длины
окружности соответственно на 10* или 10"*, а в
случае площади круга — на 102к или 10к. Если
число значащих цифр у d больше трех, необходимо
прибегнуть к интерполяции.
Примеры. 1) Для d = 69,3 длина окружности равна
217,7, а площадь круга 3772. 2) Для d = 0,693 длина
окружности равна 2,177, а площадь круга 0,3772.
В таблицах 1.1.1.15 даны элементы сегмента
круга (рис. 1.1). Таблица 1.1.1.15.1 относится к
сегментам кругов любых
радиусов с длиной хорды, равной
единице. Если при
заданном подъеме (отношении
стрелки к хорде) длина
хорды равна а, то приведенное
в таблице значение длины
дуги должно быть умножено
на а, а площадь сегмента -
на а2.
Таблица 1.1.1.15.2 содержит данные,
относящиеся к любым сегментам одной и той же
окружности радиуса, равного единице. Если длина
радиуса равна г, то табличные значения /, h и а
Рйс 1 1
ПРОПОРЦИОНАЛЬНЫЕ ЧАСТИ
61
должны быть умножены на г, а площадь сегмента -
на г2. Если задаются длина дуги / (или хорда а)
и стрелка h, то радиус сегмента г равен
отношению / (или а) к табличному значению длины дуги
(или хорды), соответствующему данному значению
l/h (или a/h).
Пример. Если длина хорды кругового сегмента а =
= 40 см, а стрелка А = 6 см, то для нахождения длины дуги
/ вычисляем величину А/а = 0,15 и умножаем
соответствующее табличное значение / (таблица 1.1.1.15.1) на 40:
/ = 40 • 1,0590 = 42,36 см. Радиус сегмента г и центральный
угол а определяются с помощью таблицы 1.1.1.15.2. Для
a/h = 6,67 табличное значение для а равно 1,1010 и а = 66,8°
(линейная интерполяция). Отсюда следует, что г = 40:1,1010 =
= 36,33 см. Теперь можно определить длину дуги / с
помощью таблицы 1.1.1.15.2: / = 36,33 • 1,1661 = 42,36 см.
Примеры использования
1) 52° 37 23"
50° = 0,872665
2° = 0,034907
30' = 0,008727
7' = 0,002036
20" = 0,000097
3" = 0,000015
0,918447
52° 37' 23" = 0,91845 рад
таблицы 1.1.1.16.
2) 5,645 рад
5,235988 = 300°
0,409012
0,401426
0,007586
0,005818 =
0,001768
0,001745 =
23°
20'
6'
Радиан — это плоский
соответствующая длина
(обозначение: рад). Дуга,
радиусу, имеет градусную
0,000023 = 5"
5,645 рад = 323° 26' 5"
угол, для которого
дуги равна радиусу
длина которой равна
меру 57°17'44,8".
1.1.1.16. Перевод
Уюл
1°
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Дуга
0,017453
0,034907
0,052360
0,069813
0,087266
0,104720
0,122173
0,139626
0,157080
0,174533
0,191986
0,209440
0,226893
0,244346
0,261799
0,279253
0,296706
0,314159
0,331613
0,349066
градусной
Угол
21°
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
меры в раднанную. (Длина дуги
Дуга
0,366519
0,383972
0,401426
0,418879
0,436332
0,453786
0,471239
0,488692
0,506145
0,523599
0,541052
0,558505
0,575959
0,593412
0,610865
0,628319
0,645772
0,663225
0,680678
0,698132
Угол
45°
50
55
60
65
70
75
80
85
90
100
120
150
180
200
250
270
300
360
400
Дуга
0,785398
0,872665
0,959931
1,047198
,134464
,221730
,308997
,396263
,483530
,570796
,745329
2,094395
2,617994
3,141593
3,490659
4,363323
4,712389
5,235988
6,283185
6,981317
окружности радиуса
Угол
1
:
з
4
5
6
7
8
9
10
20
30
40
50
Дуга
0,000291
0,000582
0,000873
0,001164
0,001454
0,001745
0,002036
0,002327
0,002618
0,002909
0,005818
0,008727
0,011636
0,014544
1)
Угол
1"
2
3
4
5
6
7
8
9
10
20
30
40
50
Дуга
0,000039
0,000044
0,000048
0,000097
0,000145
0,000194
0,000242
0,000005
0,000010
0,000015
0,000019
0,000024
0,000029
0,000034
1
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
.1.1.17. Пропорциональные части.
11
1,1
2,2
3,3
4,4
5,5
6,6
7,7
8,8
9,9
21
2,1
4,2
6,3
8,4
10,5 •
12,6
14,7
16,8
18,9
12
1,2
2,4
3,6
4,8
6,0
7,2
8,4
9,6
10,8
22
2,2
4,4
6,6
8,8
11,0
13,2
15,4
17,6
19,8
13
1,3
2,6
3,9
5,2
6,5
7,8
9,1
10,4
11,7
23
2,3
4,6
6,9
9,2
11,5
13,8
16,1
18,4
20,7
14
1,4
2,8
4,2
5,6
7,0
8,4
9,8
11,2
12,6
24
2,4
4,8
7,2
9,6
12,0
14,4
16,8
19,2
21,6
15
1,5
3,0
4,5
6,0
7,5
9,0
10,5
12,0
13,5
25
2,5
5,0
7,5
10,0
12,5
15,0
17,5
20,0
22,5
16
1,6
3,2
4,8
6,4
8,0
9,6
11,2
12,8
14,4
26
2,6
5,2
7,8
10,4
13,0
15,6
18,2
20,8
23,4
17
1,7
3,4
5,1
6,8
8,5
10,2
11,9
13,6
15,3
27
2,7
5,4
8,1
10,8
13,5
16,2
18,9
21,6
24,3
18
1,8
3,6
5,4
7,2
9,0
10,8
12,6
14,4
16,2
28
2,8
5,6
8,4
11,2
14,0
16,8
19,6
22,4
25,2
19
1,9
3,8
5,7
7,6
9,5
11,4
13,3
15,2
17,1
29
2,9
5,8
8,7
11,6
14,5
17,4
20,3
23,2
26,1
20
2,0
4,0
6,0
8,0
10,0
12,0
14,0
16,0
18,0
30
3,0
6,0
9,0
12,0
15,0
18,0
21,0
24,0
27,0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
62
ТАБЛИЦЫ
Продолжение
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
31
3,1
6,2
9,3
12,4
15,5
18,6
21,7
24,8
27,9
41
4,1
8,2
12,3
16,4
20,5
24,6
28,7
32,8
36,9
51
5,1
10,2
15,3
20,4
25,5
30,6
35,7
40,8
45,9
61
6,1
12,2
18,3
24,4
30,5
36,6
42,7
48,8
54,9
32
3,2
6,4
9,6
12,8
16,0
19,2
22,4
25,6
28,8
42
4,2
8,4
12,6
16,8
21,0
-25,2
29,4
33,6
37,8
52
5,2
10,4
15,6
20,8
26,0
31,2
36,4
41,6
46,8
62
6,2
12,4
18,6
24,8
31,0
37,2
43,4
49,6
55,8
33
3,3
6,6
9,9
13,2
16,5
19,8
23,1
26,4
29,7
43
4,3
8,6
12,9
17,2
21,5
25,8
30,1
34,4
38,7
53
5,3
10,6
15,9
21,2
26,5
31,8
37,1
42,4
47,7
63
6,3
12,6
18,9
25,2
31,5
37,8
44,1
50,4
56,7
34
3,4
6,8
10,2
13,6
17,0
20,4
23,8
27,2
30,6
44
4,4
8,8
13,2
17,6
22,0
26,4
30,8
35,2
39,6
54
5,4
10,8
16,2
21,6
27,0
32,4
37,8
43,2
48,6
64
6,4
12,8
' 19,2
25,6
32,0
38,4
44,8
51,2
57,6
35
3,5
7,0
10,5
14,0
17,5
21,0
24,5
28,0
31,5
45
4,5
9,0
13,5
18,0
22,5
27,0
31,5
36,0
40,5
55
5,5
11,0
16,5
22,0
27,5
33,0
38,5
44,0
49,5
65
6,5
13,0
19,5
26,0
32,5
39,0
45,5
52,0
58,5
36
3,6
7,2
10,8
14,4
18,0
21,6
25,2
28,8
32,4
46
4,6
9,2
13,8
18,4
23,0
27,6
32,2
36,8
41,4
56
5,6
11,2
16,8
22,4
28,0
33,6
39,2
44,8
50,4
66
6,6
13,2
19,8
26,4
33,0
39,6
46,2
52,8
59,4
37
3,7
7,4
11,1
14,8
18,5
22,2
25,9
29,6
33,3
47
4,7
9,4
14,1
18,8
23,5
28,2
32,9
37,6
42,3
57
5,7
11,4
17,1
22,8
28,5
34,2
39,9
45,6
51,3
67
6,7
13,4
20,1
26,8
33,5
40,2
46,9
53,6
60,3
38
3,8
7,6
11,4
15,2
19,0
22,&
26,6
30,4
34,2
48
4,8
9,6
14,4
19,2
24,0
28,8
33,6
38,4
43,2
58
5,8
11,6
17,4
23,2
29,0
34,8
40,6
46,4
52,2
68
6,8
13,6
20,4
27,2
34,0
40,8
47,6
54,4
61,2
39
3,9
7,8
11,7
15,6
19,5
23,4'
27,3
31,2
35,1
49
4,9
9,8
14,7
19,6
24,5
29,4
34,3
39,2
44,1
59
5,9
11,8
17,7
23,6
29,5
35,4
41,3
47,2
53,1
69
6,9
13,8
20,7
27,6
34,5
41,4
48,3
55,2
62,1
40
4,0
8,0
12,0
16,0
20,0
24,0
28,0
32,0
36,0
50
5,0
10,0
15,0
20,0
25,0
30,0
35,0
40,0
45,0
60
6,0
12,0
18,0
24,0
30,0
36,0
42,0
48,0
54,0
70
7,0
14,0
21,0
28,0
35,0
42,0
49,0
56,0
63,0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
ТАБЛИЦА ДЛЯ КВАДРАТИЧНОГО ИНТЕРПОЛИРОВАНИЯ
63
Продолжение
1
2
3
.4
5
6
7
8
9
,
2
3
4
5
6
7
8
9
71
7,1
14,2
21,3
28,4
35,5
42,6
49,7
56,8
63,9
81
8,1
16,2
24,3
32,4
40,5
48,6
56,7
64,8
72,9
72
7,2
14,4
21,6
28,8
36,0
43,2
50,4
57,6
64,8
82
8,2
16,4
24,6
32,8
41,0
49,2
57,4
65,6
73,8
73
7,3
14,6
21,9
29,2
36,5
43,8
51,1
58,4
65,7
83
8,3
16,6
24,9
33,2
41,5
49,8
58,1
66,4
74,7
74
7,4
14,8
22,2
29,6
37,0
44,4
51,8
59,2
66,6
84
8,4
16,8
25,2
33,6
42,0
50,4
58,8
67,2
75,6
75
7,5
15,0
22,5
30,0
37,5
45,0
52,5
60,0
67,5
85
8,5
17,0
25,5
34,0
42,5
51,0
59,5
68,0
76,5
76
7,6
15,2
22,8
30,4
38,0
45,6
53,2
60,8
68,4
86
8,6
17,2
25,8
34,4
43,0
51,6
60,2
68,8
77,4
77
7,7
15,4
23,1
30,8
38,5
46,2
53,9
61,6
69,3
87
8,7
17,4
16,1
34,8
43,5
52,2
60,9
69,6
78,3
78
7,8
15,6
23,4
31,2
39,0
46,8
54,6
62,4
70,2
88
8,8
17,6
26,4
35,2
44,0
52,8
61,6
70,4
79,2
79
7,9
15,8
23,7
31,6
39,5
47,4
55,3
63,2
71,1
89
8,9
17,8
26,7
35,6
44,5
53,4
62,3
71,2
80,1
80
8,0
• 16,0
- 24,0
32,0
40,0
48,0
56,0
64,0
72,0
90
9,0
18,0
27,0
36,0
45,0
54,0
63,0
72,0
81,0
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1.1
к
0,000
0,002
0,006
0,010
0,014
0,018
0,022
0,026
0,030
0,035
0,039
0,043
0,048
0,052
0,057
0,061
0,066
.1.18. Таблица для
*i
0,000
0,001
0,002
0,003
0,004
0,005
0,006
0,007
0,008
0,009
0,10
0,011
0,012
0,013
0,014
0,015
к
1,000
0,998
0,994
0,990
0,986
0,982
0,978
0,974
0,970
0,965
0,961
0,957
0,952
0,948
0,943
0,939
0,934
квадратичного интерполирования.
к
0,066
0,071
0,075
0,080
0,085
0,090
0,095
0,100
0,105
0,110
0,115
0,120
0,125
0,131
0,136
0,142
0,147
*1
0,016
0,017
0,018
0,019
0,020
0,021
0,022
0,023
0,024
0,025
0,026
0,027
0,028
0,029
0,030
0,031
к
0,934
0,929
0,925
0,920
0,915
0,910
0,905
0,900
0,895
0,890
0,885
0,880
0,875
0,869
0,864
0,858
0,853
к
0,147
0,153
0,159
0,165
0,171
0,177
0,183
0,190
0,196
0,203
0,210
0,217
0,224
0,231
0,239
0,247
0,225
*1
0,032
0,033
0,034
0,035
0,036
0,037
0,038
0,039
0,040
0,041
0,042
0,043
0,044
0,045
0,046
0,047
к
0,853
0,847
0,841
0,835
0,829
0,823
0,817
0,810
0,804
0,797
0,790
0,783
0,776
0,769
0,761
0,753
0,745
к
0,255
0,263
0,271
0,280
0,290
0,300
0,310
0,321
0,332
0,345
0,358
0,373
0,390
0,410
0,436
0,500
*1
0,048
0,049
0,050
0,051
0,052
0,053
0,054
0,055
0,056
_А057
0,058
0,059
0,060
0,061
0,062
к
0,745
0,737
0,729
0,720
0,710
0,700
0,690
0,679
0,668
0,655
0,642
0,627
0,610
0,590
0,564
0,500
64
ТАБЛИЦЫ
Всем значениям к, заключенным между
смежными числами столбца к (как правого, так и
левого), соответствует одно и то же значение ки
помещенное между этими смежными значениями
к. «Критическим» (табличным) значениям к
соответствует вышележащее /с,.
Примеры. 1) Для к =0,8 находим /cj =0,040 (так же
как и для всех других к, заключенных между 0,797 и 0,804
или между 0,196 и 0,203).
2) Для к = 0,3 (или для к = 0,7) кх = 0,052.
1.1.2. ТАБЛИЦЫ СПЕЦИАЛЬНЫХ ФУНКЦИЙ
1.1.2.1. Гамма-функция.
X
1
1,00
01
02
03
04
1,05
06
07
08
09
1,10
11
12
13
14
1,15 '
16
17
18
19
1,20
21
22
23
24
1,25
Г(\)
1,00000
0,99433
0,98884
0,98355
0,97844
0,97350
0,96874
0,96415
0,95973
0,95546
0,95135
0,94740
0,94359
0,93993
0,93642
0,93304
0,92980
0,92670
0,92373
0,92089
0,91817
0,91558
0,91311
0,91075
0,90852
0,90640
л*
1,25
26
27
28
29
1,30
31
32
33
34
1,35
36
37
38
39
1,40
41
42
43
44
1,45
46
47
48
49
1,50
Г(у)
0,90640
0,90440
0,90250
0,90072
0,89904
0.89747
0,89600
0,89464
0,89338
0,89222
0,89115
0,89018
0,88931
0,88854
0,88785
0,88726
0,88676
0,88636
0,88604
0,88581
0,88566
0,88560
0,88563
0,88575
0,88595
0,88623
Y
1,50
51
52
53
54
1,55
56
57
58
59
1,60
61
62
63
64
1,65
66
67
68
69
1,70
71
72
73
74
1,75
Г(л-)
0,88623
0,88659
0,88704
0,88757
0,88818
0,88887
0,88964
0,89049
0.89142
0,89243
0,89352
0,89468
0,89592
0,89724
0,89864
0,90012
0,90167
0,90330
0,90500
0,90678
0,90864
0,91057
0,91258
0,91467
0,91683
0,91906
V
1,75
76
77
78
79
1,80
81
82
83
84
1,85
86
87
88
89
1,90
91
92
93
94
1,95
96
97
98
99
2,00
Г(л-)
0,91906
0,92137
0,92376
0,92623
0,92877
0,93138
0,93408
0,93685
0,93969
0,94261
0,94561
0,94869
0,95184
0,95507
0.95838
0,96177
0,96523
0,96877
0,97240
0,97610
0,97988
0,98374
0,98768
0,99171
0,99581
1,00000
Значения гамма-функции для х < 1 (х Ф 0, — 1,
— 2, ...) и для х > 2> могут быть вычислены при
помощи формул
Г (х) = — ~, Г (х) = (х
Примеры. 1) Г@,7) = ГA,7)/0,7 = 0,90864/0,7 = 1,2981.
2) ГC,5) - 2,5 • ГB,5) = 2,5 • 1,5 • ГA,5) = 2,5-1,5-0,88623 =
= 3,32336.
БЕССЕЛЕВЫ ФУНКЦИИ
65
1.1.2.2.
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
Бесселевы (цилиндрические) функции.
Jo(x)
+ 1,0000
0,9975
0,9900
0,9776
0,9604
+ 0,9385
0,9120
0,8812
0,8463
0,8075
+ 0,7652
0,7196
0,6711
0,6201
0,5669
+ 0,5118
0,4554
0,3980
0,3400
0,2818
+ 0,2239
0,1666
0,1104
0,0555 '
0,0025
-0,0484
0,0968
0,1424
0,1850
0,2243
--0,2601
0,2921
0,3202
0,3443
0,3643
-0,3801
0,3918
0,3992
0,4026
0,4018
-0,3971
0,3887
0,3766
0,3610
0,3423
-0,3205
0,2961
0.2693
0,2404
0,2097
Jx(x)
+ 0,0000
0,0499
0,0995
0,1483
0,1960
+ 0,2423
0,2867
0,3290
0,3688
0,4059
+ 0,4401
0,4709
0,4983
0,5220
0,5419
+ 0,5579
0,5699
0,5778
0,5815
0,5812
+ 0,5767
0,5683
0,5560
0,5399
0,5202
+ 0,4971
0,4708
0,4416
0,4097
0,3754
+ 0,3391
0,3009
0,2613
0,2207
0,1792
+ 0,1374
0,0955
0,0538
+ 0,0128
-0,0272
-0,0660
0,1033
0,1386
0,1719
0,2028
-0,2311
0,2566
0,2791
0,2985
0,3147
Y0(x)
— х
-1,5342
1,0811
0,8073
0,6060
-0,4445
0,3085
0,1907
-0,0868
+ 0,0056
+ 0,0883
0,1622
0,2281
0,2865
0,3379
+ 0,3824
0,4204
0,4520
0,4774
0,4968
+ 0,5104
0,5183
0,5208
0,5181
0,5104
+ 0,4981
0,4813
0,4605
0,4359
0,4079
+ 0,3769
0,3431
0,3070
0,2691
0,2296
+ 0,1890
0,1477
0,1061
0,0645
+ 0,0234
-0,0169
0,0561
0,0938
0,1296
0,1633
-0,1947
0,2235
0,2494
0,2723
0,2921
Yx(x)
— ос
-6,4590
3,3238
2,2931
1,7809
-1,4715
1,2604
1,1032
0,9781
0,8731
-0,7812
0,6981
0,6211
0,5485
0,4791
-0,4123
0,3476
0,2847
0,2237
0,1644
-0,1070
-0,0517
+ 0,0015
0,0523
0,1005
+ 0,1459
0,1884
0,2276
0,2635
0,2959
+ 0,3247
0,3496
0,3707
0,3879
0,4010
+ 0,4102
0,4154
0,4167
0,4141
0,4078
+ 0,3979
0,3846
0,3680
0,3484
0,3260
+ 0,3010
0,2737
0,2445
0,2136
0,1812
/о (х)
1,000
1,003
1,010
1,023
1,040
1,063
1,092
1,126
1,167
1,213
1,266
1,326
1,394
1,469
1,553
1,647
1,750
1,864
1,990
2,128
2,280
2,446
2,629
2,830
3,049,
3,290
3,553
3,842
4,157
4,503
4,881
5,294
5,747
6,243
6,785
7,378
8,028
8,739
9,517
10,37
11,30
12,32
13,44
14,67
16,01
17,48
19,09
20,86
22,79
24,91
0,0000
0,0501
0,1005
0,1517
0,2040
0,2579
0,3137
0,3719
0,4329
0,4971
0,5652
0,6375
0,7147
0,7973
0,8861
0,9817
1,085
1,196
1,317
1,448
1,591
1,745
1,914
2,098
2,298
2,517
2,755
3,016
3,301
3,613
3,953
4,326
4,734
5,181
5,670
6,206
6,793
7,436
8,140
8,913
9,759
10,69
11,71
12,82
14,05
15,39
16;86
18,48
20,25
22,20
К0(х)
X
2,4271
1,7527
1,3725
1,1145
0,9244
0,7775
0,6605
0,5653
0,4867
0,4210
0,3656
0,3185
0,2782
0,2437
0,2138
0,1880
0,1655
0,1459
0,1288
0,1139
0,1008
0,08927
0,07914
0,07022
0,06235
0,05540
0,04926
0,04382
0,03901
0,03474
0,03095
0,02759
0,02461
0,02196
0,01960
0,01750
0,01563
0,01397
0,01248
0,01116
0,009980
0,008927
0,007988
0,007149
0,006400
0,005730
0,005132
0,004597
0,0041119
К,(х)
X
9,8538
4,7760
3,0560
2,1844
1,6564
1,3028
1,0503
0,8618
0,7165
0,6019
0,5098
0,4346
0,3725
0,3208
0,2774
0,2406
0,2094
0,1826
0,1597
0,1399
0,1227
0,1079
0,09498
0,08372
0,07389
0,06528
0,05774
0,05111
0,04529
0,04016
0,03563
0,03164
0,02812
0,02500
0,02224
0,01979
0,01763
0,01571
0,01400
0,01248
0,01114
0,009938
0,008872
0,007923
0,007078
0,006325
0,005654
0,005055
0,004521
3 И Н Бронштейн, К А Семендяе
66
ТАБЛИЦЫ
Продолжение
X
5,0
5,1
5,2
5,3
5,4
5,5
5,6
5,7
5,8
5,9
6,0
6,1
6,2
6,3
6,4
6,5
6,6
6,7
6,8
6,9
7,0
7,1
7,2
7,3
7,4
7,5
7,6
7,7
7,8
7,9
8,0
8,1
8,2
8,3
8,4
8,5
8,6
8,7
8,8
8,9
9,0
9,1
9,2
9,3
9,4
9,5
9,6
9,7
9,8
9,9
10,0
J0(x)
-0,1776
0,1443
0,1103
0,0758
0,0412
-0,0068
+ 0,0270
0,0599
0,0917
0,1220
+ 0,1506
0,1773
0,2017
0,2238
0,2433
+ 0,2601
0,2740
0,2851
0,2931
0,2981
+ 0,3001
0,2991
0,2951
0,2882
0,2786
+ 0,2663
0,2516
0,2346
0,2154
0,1944
+ 0,1717
0,1475
0,1222
0,0960
0,0692
+ 0,0419
+ 0,0146
-0,0125
0,0392
0,0653
-0,0903
0,1142
0,1367
0,1577
0,1768
-0,1939
0,2090
0,2218
0,2323
0,2403
-0,2459
Jx(x)
-0,3276
0,3371
0,3432
0,3460
0,3453
-0,3414
0,3343
0,3241
0,3110
0,2951
-0,2767
0,2559
0,2329
0,2081
0,1816
-0,1538
0,1250
0,0953
0,0652
0,0349
-0,0047
+ 0,0252
0,0543
0,0826
0,1096
+ 0,1352
0,1592
0,1813
0,2014
0,2192
+ 0,2346
0,2476
0,2580
0,2657
0,2708
+ 0,2731
0,2728
0,2697
0,2641
0,2559
+ 0,2453
0,2324
0,2174
0,2004
0,1816
+ 0,1613
0,1395
0,1166
0,0928
0,0684
+ 0,0435
4х)
-0,3085
0,3216
0,3313
0,3374
0,3402
-0,3395
0,3354
0,3282
0,3177
0,3044
-0,2882
0,2694
0,2483
0,2251
0,1999
-0,1732
0,1452
0,1162
0,0864
0,0563
-0,0259
+ 0,0042
0,0339
0,0628
0,0907
+ 0,1173
0,1424
0,1658
0,1872
0,2065
+ 0,2235
0,2381
0,2501
0,2595
0,2662
+ 0,2702
0,2715
0,2700
0,2659
0,2592
+ 0,2499
0,2383
0,2245
0,2086
0,1907
+ 0,1712
0,1502
0,1279
0,1045
0,0804
+ 0,0557
Yx(x)
+ 0,1479
0,1137
0,0792
0,0445
+ 0,0101
-0,0238
0,0568
0,0887
0,1192
0,1481
-0,1750
0,1998
0,2223
0,2422
0,2596
-0,2741
0,2857
0,2945
0,3002
0,3029
-0,3027
0,2995
0,2934
0,2846
0,2731
-0,2591
0,2428
0,2243
0,2039
0,1817
-0,1581
0,1331
0,1072
0,0806
0,0535
-0,0262
+ 0,0011
0,0280
0,0544
0,0799
+ 0,1043
0,1275
0.1491
0,1691
0,1871
+ 0,2032
0,2171
0,2287
0,2379
0,2447
+ 0,2490
Щх)
27,24
29,79
32,58
35,65
39,01
42,69
46,74
51,17
56,04
61,38
67,23
73.66
80,72
88,46
96,96
106,3
116,5
127,8
140,1
153,7
168,6
185,0
202,9
222,7
244,3
268,2
294,3
323,1
354,7
389,4
427,6
469,5
515,6
566,3
621,9
683,2
750,5
824,4
905,8
995,2
1094
1202
1321
1451
1595
1753
1927
2119
2329
2561
2816
Ix(x)
24,34
26,68
29,25
32,08
35,18
38,59
42,33
46,44
50,95
55,90
61,34
67,32
73,89
81,10
89,03
97,74
107,3
117,8
129,4
142,1
156,0
171,4
188,3
206,8
227,2
249,6
274,2
301,3
331,1
363,9
399,9
439,5
483,0
531,0
583,7
641,6
705,4
775,5
852,7
937,5
1031
1134
1247
1371
1508
1658
1824
2006
2207
2428
2671
К0(х)
0,00
3691
3308
2966
2659
2385
2139
1918
1721
1544
1386
1244
1117
1003
09001
08083
07259
06520
05857
05262
04728
04248
03817
03431
03084
02772
02492
02240
02014
01811
01629
01465
01317
01185
01066
009588
008626
007761
006983
006283
(Ю5654
005088
004579
004121
003710
003339
003006
002706
002436
002193
001975
001778
Кг(х)
0,00
4045
3619
3239
2900
2597
2326
2083
1866
1673
1499
1344
1205
1081
09691
08693
07799
06998
06280
05636
05059
04542
04078
03662
03288
02953
02653
02383
02141
01924
01729
01554
01396
01255
01128
01014
009120
008200
007374
006631
005964
005364
004825
004340
003904
003512
003160
002843
002559
002302
002072
001865
ЭЛЛИПТИЧЕСКИЕ ИНТЕГРАЛЫ
67
1.1.2.3. Полиномы Лежандра
V =/>,(*)
0,0
0,05
0,10
0,15
0,20
0,25
0,30
0,35
0,40
0,45
0,50
0,55
0,60
0,65
0,70
0,75
0,80
0,85
0,90
0,95
1,00
-0,5000
-0,4962
-0,4850
-0,4662
-0,4400
-0,4062
-0,3650
-0,3162
-0,2600
-0,1962
-0,1250
-0,0462
+ 0,0400
0,1338
0,2350
0,3438
0,4600
0,5838
0,7150
0,8538
1,0000
(шаровые функции).
0,0000
-0,0747
-0,1475
-0,2166
-0,2800
-0,3359
-0,3825
-0,4178
-0,4400
-0,4472
-0,4375
-0,4091
-0,3600
-0,2884
-0,1925
-0,0703
+ 0,0800
0,2603
0,4725
0,7184
1,0000
Р4(х)
0,3750
0,3657
0,3379
0,2928
0,2320
0,1577
+ 0,0729
-0,0187
-0,1130
-0,2050
-0,2891
-0,3590
-0,4080
-0,4284
-0,4121
-0,3501
-0,2330
-0,0506
+ 0,2079
0,5541
1,0000
Р?х)
0,0000
0,0927
0,1788
0,2523
0,3075
0,3397
0,3454
0,3225
0,2706
0,1917
+ 0,0898
-0,0282
-0,1526
-0,2705
-0,3652
-0.4164
-0,3995
-0,2857
-0,0411
+ 0,3727
1,0000
рь(х)
-0,3125
-0,2962
-0,2488
-0,1746
-0,0806
+ 0,0243
0,1292
0,2225
0,2926
0,3290
0,3232
0,2708
0.1721
+ 0.0347
-0,1253
-0,2808
-0,3918
-0,4030
-0,2412
+ 0,1875
1,0000
Р7(х)
0,0000
-0,1069
-0,1995
-0,2649
-0,2935
-0,2799
-0,2241
-0,1318
-0,0146
+ 0,1106
0,2231
0,3007
0,3226
0,2737
+ 0,1502
-0,0342
-0,2397
-0,3913
-0,3678
+ 0,0112
1,0000
Р0(х)=1,
р5 (х) = 4-F3х5 - 70х3 + 15х),
о
Р6(х) = — B31х6 - 315х4 + 105х2 - 5),
16
р7 (
D29x7 - 693х5 + 315х3 - 35х).
1.1.2.4. Эллиптические интегралы.
1.1.2.4.1. Эллиптические интегралы 1-го рода: F(k, <р), к =¦ sina.
ф
0°
10
20
30
40
50
60
70
80
90
0°
0,0000
0,1745
0,3491
0,5236
0,6981
0,8727
1,0472
1,2217
1,3963
1,5708
10°
0,0000
0,1746
0,3493
0,5243
0,6997
0,8756
1,0519
1,2286
1,4056
1,5828
20°
0,0000
0,1746
0,3499
0,5263
0,7043
0,8842
1,0660
1,2495
1,4344
1,6200
30°
0,0000
0,1748
0,3508
0,5294
0,7116
0,8982
1,0896
1,2853
1,4846
1,6858
40°
0,0000
0,1749
0,3520
0,5334
0,7213
0,9173
1,1226
1,3372
1,5597
1,7868
50°
0,0000
0,1751
0,3533
0,5379
0,7323
0,9401
1,1643
1,4068
1,6660
1,9356
60°
0,0000
0,1752
0,3545
0,5422
0,7436
0,9647
1,2126
1,4944
1,8125
2,1565
70°
0,0000
0,1753
0,3555
0.5459
0,7535
0,9876
1,2619
1,5959
2,0119
2,5046
80°
0,0000
0,1754
0,3561
0,5484
0,7604
1,0044
1,3014
1,6918
2,2653
3,1534
90°
0,0000
0,1754
0,3564
0,5493
0,7629
1,0107
1,3170
1,7354
2,4362
ос
3*
68
ТАБЛИЦЫ
1.1.2.4.2. Эллиптические интегралы
Ф
0°
10
20
30
40
50
60
70
80
90
0°
0,0000
0,1745
0,3491
0,5236
0,6981
0,8727
1,0472
1,2217
1,3963
1,5708
10°
0,0000
0,1745
0,3489
0,5229
0,6966
0,8698
1,0426
1,2149
1,3870
1,5589
20°
0,0000
0,1744
0,3483
0,5209
0,6921
0,8614
1,0290
1.1949
1,3597
1,5238
30°
0,0000
0,1743
0,3473
0.5179
0,6851
0,8483
1,0076
1,1632
1,3161
1,4675
2-го рода: Е(к,
0
40°
0,0000
0,1742
0,3462
0,5141
0,6763
0,8317
0,9801
1,1221
1,2590
1,3931
i
50°
0,0000
0,1740
0,3450
0,5100
0,6667
0,8134
0,9493
1,0750
1,1926
1,3055
ф), к = sina.
60°
0,0000
0,1739
0,3438
0,5061
0,6575
0,7954
0,9184
1,0266
1,1225
1,2111
70°
0,0000
0,1738
0,3429
0,5029
0,6497
0,7801
0,8914
0,9830
1,0565
1,1184
80°
0,0000
0,1737
0,3422
0,5007
0,6446
0,7697
0,8728
0,9514
1,0054
1,0401
90°
0,0000
0,1736
0,3420
0,5000
0,6428
0,7660
0,8660
0,9397
0,9848
1,0000
1.1.2.4.3.
a°
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Полные
К
,5708
,5709
,5713
,5719
,5727
,5738
,5751
,5767
,5785
,5805
,5828
,5854
,5882
,5913
,5946
,5981
,6020
,6061
1,6105
1,6151
1,6200
1,6252
1,6307
1,6365
1,6426
1,6490
1,6557
1,6627
1.6701
1,6777
1,6858
эллиптические инте!рал!
?
1,5708
1,5707
1,5703
1,5697
1,5689
1,5678
1,5665
1,5649
1,5632
1,5611
1,5589
1,5564
1,5537
1,5507
1,5476
1,5442
1.5405
1,5367
1,5326
1,5283
1,5238
1,5191
1,5141
1,5090
1,5037
1,498!
1,4924
1,4864
1,4803
1,4740
1,4675
ос°
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
К
1,6858
,6941
,7028
,7119
,7214
,7312
,7415
,7522
,7633
,7748
,7868
,7992
,8122
,8256
,8396
,8541
1,8691
1,8848
1,9011
1,9180
1,9356
1,9539
1,9729
1,9927
2,0133
2,0347
2,0571
2,0804
2,1047
2,1300
2,1565
,i: к
' = sina
Е
1,4675
1,4608
1,4539
1,4469
1.4397
1,4323
,4248
,4171
,4092
,4013
,3931
,3849
,3765
,3680
,3594
,3506
,3418
,3329
,3238
,3147
,3055
,2963
1,2870
1,2776
1,2681
1,2587
1,2492
1,2397
1,2301
1,2206
1,2111
a°
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
К
2,1565
2,1842
2,2132
2,2435
2,2754
2,3088
2,3439
2,3809
2,4198
2,4610
2,5046
2,5507
2,5998
2,6521
2.7081
2,7681
2,8327
2,9026
2,9786
3,0617
3,1534
3,2553
3,3699
3,5004
3,6519
3,8317
4,0528
4.3387
4,7427
5,4349
ОО
Е
1,2111
,2015
,1920
,1826
,1732
,1638
,1545
,1453
,1362
,1272
1,1184
1,1096
1,1011
1,0927
1,0844
1,0764
1,0686
1,0611
1,0538
1,0468
1,0401
1,0338
1,0278
1,0223
1,0172
1,0127
1,0086
1,0053
1,0026
1,0008
1,0000
я/2 1
Л. f__*!!„ Г
РАСПРЕДЕЛЕНИЕ ПУАССОНА
69
1.1
г
0
1
2
3
4
5
6
7
8
г
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2.5. Распределение Пуассона.
X
0,1
0,904837
0,090484
0,004524
0,000151
0,000004
-
-
-
-
0,2
0,818731
0,163746
0,016375
0,001092
0,000055
0,000002
-
-
-
0,3
0,740818
0,222245
0,033337
0,003334
0,000250
0,000015
0,000001
-
-
0,4
0,670320
0,268128
0,053626
0,007150
0,000715
0,000057
0,000004
-
-
0,5
0,606531
0,303265
0,075816
0,012636
0,001580
0,000158
0,000013
0,000001
-
0,6
0,548812
0,329287
0,098786
0,019757
0,002964
0,000356
0,000036
0,000003
-
0,7
0,496585
0,347610
0,121663
0,028388
0,004968
0,000696
0,000081
0,000008
0,000001
0,8
0,449329
0,359463
0,143785
0,038343
0,007669
0,001227
0,000164
0,000019
0,000002
}.
0,9
0,406570
0,365913
0,164661
0,049398
0,011115
0,002001
0,000300
0,000039
0,000004
-
-
-
-
-
-
-
-
—
1,0
0,367879
0,367879
0,183940
0,061313
0,015328
0,003066
0,000511
0,000073
0,000009
0,000001
-
-
-
-
-
-
-
—
1,5
0,223130
0,334695
0,251021
0,125510
0,047067
0,014120
0,003530
0,000756
0,000142
0,000024
0,000004
-
-
-
-
-
-
-
2,0
0,135335
0,270671
0,270671
0,180447
0,090224
0,036089
0,012030
0,003437
0,000859
0,000191
0,000038
0,000007
0,000001
-
-
-
-
—
2,5
0,082085
0,205212
0,256516
0,213763
0,133602
0,066801
0,027834
0,009941
0,003106
0,000863
0,000216
0,000049
0,000010
0,000002
-
-
-
—
3,0
0,049787
0,149361
0,224042
0,224042
0,168031
0,100819
0,050409
0,021604
0,008102
0,002701
0,000810
0,000221
0,000055
0,000013
0,000003
0,000001
-
—
3,5
0,030197
0,105691
0,184959
0,215785
0,188812
0,132169
0,077098
0,038549
0,016865
0,006559
0,002296
0,000730
0,000213
0,000057
0,000014
0,000003
0,000001
—
4,0
0,018316
0,073263
0,146525
0,195367
0,195367
0,156293
0,104196
0,059540
0,029770
0,013231
0,005292
0,001925
0,000642
0,000197
0,000056
0,000015
0,000004
0,000001
70
ТАБЛИЦЫ
Продолжение
г
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
4,5
0,011109
0,049990
0,112479
0,168718
0,189808
0,170827
0,128120
0,082363
0,046329
0,023165
0,010424
0,004264
0,001599
0,000554
0,000178
0,000053
0,000015
0,000004
0,000001
-
-
-
-
-
-
-
-
-
-
5,0
0,006738
0,033690
0,084224
0,140374
0,175467
0,175467
0,146223
0,104445
0,065278
0,036266
0,018133
0,008242
0,003434
0,001321
0,000472
0,000157
0,000049
0,000014
0,000004
0,000001
-
-
-
-
-
-
-
-
-
6,0
0,002479
0,014873
0,044618
0,089235
0,133853
0,160623
0,160623
0,137677
0,103258
0,068838
0,041303
0,022529
0,011264
0,005199
0,002228
0,000891
0,000334
0,000118
0,000039
0,000012
• 0,000004
0,000001
-
-
-
-
-
-
-
7,0
0,000912
0,006383
0,022341
0,052129
0,091226
0,127717
0,149003
0,149003
0,130377
0,101405
0,070983
0,045171
0,026350
0,014188
0,007094
0,003311
0,001448
0,000596
0,000232
0,000085
0,000030
0,000010
0,000003
0,000001
-
-
-
-
-
8,0
0,000335
0,002684
0,010735
0,028626
0,057252
0,091604
0,122138
0,139587
0,139587
0,124077
0,099262
0,072190
0,048127
0,029616
0,016924
0,009026
0,004513
0,002124
0,000944
0,000397
0,000159
0,000061
0,000022
0,000008
0,000003
0,000001
-
-
-
9,0
0,000123
0,001111
0,004998
0,014994
0,033737
0,060727
0,091090
0,117116
0,131756
0,131756
0,118580
0,097020
0,072765
0,050376
0,032384
0,019431
0,010930
0,005786
0,002893
0,001370
0,000617
0,000264
0,000108
0,000042
0,000016
0,000006
0,000002
0,000001
-
10,0
0,000045
0,000454
0,002270
0,007867
0,018917
0,037833
0,063055
0,090079
0,112599
0,125110
0,125110
0,113736
0,094780
0,072908
0,052077
0,034718
0,021699
0,012764
0,007091
0,003732
0,001866
0,000889
0,000404
0,000176
0,000073
0,000029
0,000011
0,000004
0,000001
0,000001
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
71
1.1.2.6. Нормальное распределение.
1.1.2.6.1. Плотность распределения вероятности ф(х) =
= —п— е х /z нормированного
нормального распределения.
центрированного
О х
Рис. 1.2
V
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
U
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
4,6
4,7
4,8
4,9
0
3989
3970-4
3910~~4
3814 4
3683
3521 4
3332 ~\
3123 4
2897
2661 ~ 4
2420 ~\
2179
1942
1714
I497
1295 4
1109~4
9405";
7895 ~5
6562 ~5
5399 ~5
4398"^
3547 ~5
2833"^
2239
1753"^
1358"^
1042" 5
7915~6
5953
4432"^
3267"^
2384"°
1723 °
1232
8727"^
6119"^
4248"^
2919~^1
1987
1338~8
8926 \
5894"*
3854 ~ я
2494 -\
1598 \
1014"°
6370 I
3961"^
2439 v
1
3989
3965
3902
3802
3668
3503
3312
3101
2874
2637
2396
2155
1919
1691
1476
1276
1092
9246
7754
6438
5292
4307
3470
2768
2186
1709
1323
1014
7697
5782
4301
3167
2309
1667
1191
8426
5902
4093
2810
1910
1286
8567
5652
3691
2387
1528
9684 ~У
6077
3775
2322
2
3989
3961
3894
3790
3653
3485
3292
3079
2850
2613
2371
2131
1895
1669
1456
1257
1074
9089
7614
6316
5186
4217
3394
2705
2134
1667
1289
9871 ~6
7483
5616
4173
3070
2236
1612
1151
8135
5693
3944
2705
1837
1235
8222
5418
3535
2284
1461
9248
5797
3598
2211
3
^ 3988
3956
3885
3778
3637
3467
3271
3056
2827
2589
2347
2107
1872
1647
1435
1238
1057
8933
7477
6195
5082
4128
3319
2643
2083
1625
1256
9606
7274
5454
4049
2975
2165
1560
1112
7853
5490
3800
2604
1766
1186
7890
5194
3386
2185
1396
8830
5530
3428
2105
4
3986
3951
3876
3765
3621
3448
3251
3034
2803
2565
2323
2083
1849
1626
1415
1219
1040
8780
7341
6077
4980
4041
3246
2582
2033
1585
1223
9347
7071
5296
3928
2884
2096
1508
1075
7581
5294
3661
2506
1698
1140
7570
4979
3242
2090
1334
8430
5274
3267
2003
5
3984
3945
3867
3752
3605
3429
3230
ЗОН
2780
2541
2299
2059
1826
1604
1394
1200
1023
8628
7206
5960
4879
3955
3174
2522
1984
1545
1191
9094
6873
5143
3810
2794
2029
1459
1038
7317
5105
3526
2411
1633
1094
7263
4772
3104
1999
1275
8047
5030
3112
1907
6
3982
3939
3857
3739
3589
3410
3209
2989
2756
2516
2275
2035
1804
1582
1374
1182
1006
8478
7074
5844
4780
3871
3103
2463
1936
1506
1160
8846
6679
4993
3695
2707
1961
1411
1003
7061
4921
3396
2320
1569
1051
6967
4573
2972
1912
1218
7681
4796
2965
1814
7
3980
3932
3847
3725
3572
3391
3187
2966
2732
2492
2251
2012
1781
1561
1354
1163
9893 ~5
8329
6943
5730
4682
3788
3034
2406
1888
1468
ИЗО
8605
6491
4847
3584
2623
1901
1364
9689 ~7
6814
4744
3271
2232
1508
1009
6683
4382
2845
1829
1164
7331
4573
2824
1727
8
3977
3925
3836
3712
3555
3372
3166
2943
2709
2468
2227
1989
1758
1539
1334
1145
9728
8183
6814
5618
4586
3706
2965
2349
1842
1431
1100
8370
6307
4705
3475
2541
1840
1319
9358
6575
4573
3149
2147
1449
9687 "8
6410
4199
2723
1749
1112
6996
4360
2690
1643
9
3973
3918
3825
3697
3538
3352
3141
2920
2685
2444
2203
1965
1736
1518
1315
1127
9566
8038
6687
5508
4491
3626
2898
2294
1797
1394
1071
8140
6127
4567
3370
2461
1780
1275
9037
6343
4408
3032
2065
1393
9299
6147
4023
2606
1672
1062
6676
4156
2561
1563
Замечание. Например, 3989 означает 3989- 10~4.
72
ТАБЛИЦЫ
1.1.2.6.2. Фу н к ция распределения Фо (х) — <р (t) dt = -== le { ^dt нормированного
J ]/2n J
и центрированного нормального распределения.
О х
Рис 1 3
*
о,с
о,
о,:
о,:
0,4
0,f
\
0,6
0,'
0,i
0,9
1,0
1,
i,:
i,:
)
1,4
1,5
1,6
1,-
1
1,8
1,9
2,0
2,
2,2"
*)
2,3
0
0,0 000
398
793
0,1 179
554
915
0,2 257
580
881
0,3 159
413
643
849
0,4 032
192
332
452
554
641
713
772
821
860
966
892
759
Начиная с
892
означает
1
040
438
832
217
591
950
291
611
910
186
437
655
869
049
207
345
463
564
649
719
778
826
864
474
895
559
2
080
478
871
255
628
985
324
642
939
212
461
686
888
066
222
357
474
573
656
726
783
830
867
906
898
296
3
120
517
910
293
664
0,2 019
357
673
967
238
485
708
907
082
236
370
484
582
664
732
788
834
871
263
900
969
4
160
557
948
331
700
054
389
708
995
264
508
729
925
099
251
382
495
591
671
738
793
838
874
545
903
581
згою места, значение Ф0(х) приведено
ФоB,30) =
0,4892759.
5
199
596
987
368
736
088
422
734
0,3 023
289
531
749
944
115
265
394
505
599
678
744
798
842
877
755
906
133
6
239
636
0,1026
406
772
123
454
764
051
315
554
770
962
131
279
406
515
608
686
750
803
846
880
894
908
625
7
279
675
064
443
808
157
486
794
078
340
577
790
980
147
292
418
525
616
693
756
808
850
883
962
911
060
8
319
714
103
480
844
190
517
823
106
365
599
810
997
162
306
429
535
625
699
761
812
854
886
962
913
437
9
359
753
141
517
879
224
549
852
133
389
621
830
0,4 015
177
319
441
545
633
706
767
817
857
889
893
915
758
с семью знаками после запятой. Например, запись
НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
73
Продолжение
.Y
2,4
2,5
2,6
2,7
2,8
2,9
3,0
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4,0
4,1
4,2
4,3
4,4
4,5
5,0
0
0,4918
025
937
903
953
388
965
330
974
449
981
342
986
501
990
324
993
129
995
166
996
631
997
674
998
409
998
922
999
276
999
519
999
683
999
793
999
867
999
915
999
946
999
966
999
997
1
920
237
939
634
954
729
966
358
975
229
981
929
986
938
990
646
993
363
995
335
996
752
997
759
998
469
998
964
999
305
999
539
999
696
999
802
999
872
999
918
999
948
999
968
2
922
397
941
323
956
035
967
359
975
988
982
498
987
361
990
957
993
590
995
499
996
869
997
842
998
527
999
004
999
333
999
557
999
709
999
811
999
878
999
922
999
951
999
969
3
924
506
942
969
957
308
968
333
976
726
983
052
987
111
991
260
993
810
995
658
996
982
997
922
998
583
999
043
999
359
999
575
999
721
999
819
999
883
999
925
999
953
999
971
4
926
564
944
574
958
547
969
280
977
443
983
589
988
171
991
553
994
024
995
811
997
091
997
999
998
637
999
080
999
385
999
593
999
733
999
826
999
888
999
929
999
955
999
972
5
928
572
946
139
959
754
970
202
978
140
984
111
988
558
991
836
994
230
995
• 959
997
197
998
074
998
689
999
116
999
409
999
609
999
744
999
834
999
893
999
932
999
957
999
973
6
930
531
947
664
960
930
971
099
978
818
984
618
988
933
992
112
994
429
996
103
997
299
998
146
998
739
999
150
999
433
999
625
999
755
999
841 ¦
999
898
999
935
999
959
999
974
7
932
443
949
151
962
074
971
972
979
476
985
110
989
297
992
378
994
523
996
242
997
398
998
215
998
787
999
184
999
456
999
641
999
765
999
848
999
902
999
938
999
961
999
976
8
934
309
950
600
963
189
972
821
980
116
985
588
989
650
992
636
994
810
996
376
997
493
998
282
998
834
999
216
999
478
-999
655
999
775
999
854
999
907
999
941
999
963
999
977
9
936
128
952
012
964
274
973
646
980
738
СУ» ОС
989
992
992
886
994
991
996
505
997
585
998
347
998
879
999
247
999
499
999
670
999
784
999
861
999
911
999
943
999
964
999
978
74
ТАБЛИЦЫ
1.1.2.7. х2~РаспРеДеление*
В таблице приведены значения (в процентах) квантилей х2 (т) в зависимости от числа степеней
свободы т и вероятности а.
Рис 1.4
т
1
2
3
4
5
6
7
8
9
10
И
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
0,99
0,00016
0,020
0,115
0,30
0,55
0,87
1,24
1,65
2.09
2,56
3,1
3.6
4,1
4,7
5,2
5,8
6,4
7,0
7.6
8,3
8,9
9,5
10,2
10,9
11,5
12,2
12,9
13,6
14,3
15,0
0.98
0,0006
0,040
0,185
0,43
0.75
1,13
1.56
2,03
2,53
3,06
3,6
4,2
4,8
5,4
6,0
6,6
7,3
7,9
8,6
9,2
9.9
10,6
11,3
12,0
12,7
13,4
14,1
14,8
15,6
16,3
0,95
0,0039
0,103
0,352
0,71
1,14
1,63
2,17
2,73
3,32
3,94
4,6
5,2
5.9
6,6
7,3
8,0
«.7
9,4
10,1
10,9
11,6
12,3
13,1
13,8
14,6
15,4
16,2
16,9
17,7
18,5
0,90
0,0! 6
0,211
0,584
1,06
1,61
2,20
2,83
3,49
4,17
4,86
5,6
6,3
7,0
7,8
8,5
9,3
10,1
10,9
11,7
12,4
13,2
14,0
14,8
15,7
16,5
17,3
18,1
18,9
19,8
20,6
0,80
0,064
0,446
1,005
1,65
2,34
3,07
3,82
4,59
5,38
6,18
7,0
7,8
8,6
9,5
10,3
11,2
12,0
12,9
13,7
14,6
15,4
16,3
17,2
18,1
18,9
19,8
20,7
21,6
22,5
23,4
0,70
0,148
0,713
1,424
2,19
3,00
3,83
4,67
5,53
6,39
7,27
8,1
9,0
9,9
10,8
11,7
12,6
13,5
14,4
15,4
16,3
17,2
18,1
19,0
19,9
20,9
21,8
22,7
23,6
24,6
25,5
0,50
0,455
1,386
2,366
3,36
4,35
5,35
6,35
7,34
8,34
9,34
10,3
11,3
12,3
13,3
14,3
15,3
16,3
17,3
18,3
19,3
20,3
21,3
22,3
23,3
24,3
25,3
26,3
27,3
28,3
29,3
0,30
1,07
2,41
3,67
4,9
6,1
7,2
8,4
9,5
10,7
11,8
12,9
14,0
15,1
16,2
17,3
18,4
19,5
20,6
21,7
22,8
23,9
24,9
26.0
27,1
28,2
29,2
30,3
31,4
32,5
33,5
Х^-РАСПРЕДЕЛЕНИЕ
75
Продолжение
а
0,20
1,64
3,22
4,64
6,0
7,3
8,6
9,8
11,0
12,2
13,4
14,6
15,8
17,0
18,2
19,3
20,5
21,6
22,8
23,9
25,0
26,2
27,3
28,4
29,6
30,7
31,8
32,9
34,0
35,1
36,3
0,10
2,7
4,6
6,3
7,8
9,2
10,6
12,0
13,4
14,7
16,0
17,3
18,5
19,8
21,1
22,3
23,5
24,8
26,0
27,2
28,4
29,6
30,8
32,0
33,2
34,4
35,6
36,7
37,9
39,1
40,3
0,05
3,8
6,0
7,8
9,5
11,1
12,6
14,1
15,5
16,9
18,3
19,7
21,0
22,4
2,3,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37,7
38,9
40,1
41,3
42,6
43,8
0,02
5,4
7,8
9,8
11,7
13,4
15,0
16,6
18,2
19,7
21,2
22,6
24,1
25,5
26,9
28,3
29,6
31,0
32,3
33,7
35,0
36,3
37,7
39,0
40,3
41,6
42,9
44,1
45,4
46,7
48,0
0,01
6,6
9,2
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
0,005
7,9
10,6
12,8
14,9
16,8
18,5
20,3
22,0
23,6
25,2
26,8
28,3
29,8
31,3
32,8
34,3
35,7
37,2
38,6
40,0
41,4
42,8
44,2
45,6
46,9
48,3
49,6
51,0
52,3
53,7
0,002
9,5
12,4
14,8
16,9
18,9
20,7
22,6
24,3
26,1
27,7
29,4
30,9
32,5
34,0
35,6
37,1
38,6
30,1
41,6
43,0
44,5
45,9
47,3
48,7
50,1
51,6
52,9
54,4
55,7
57,1
0,001
10,8
13,8
16,3
18,5
20,5
22,5
24,3
26,1
27,9
29,6
31,3
32,9
34,5
36,1
37,7
39,3
40,8
42,3
43,8
45,3
46,8
48,3
49,7
51,2
52,6
54,1
55,5
56,9
58,3
59,7
т
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
76
ТАБЛИЦЫ
1.1.2.8. ^-распределение Стьюдента.
В таблице приведены значения (в процентах) квантилей
свободы т и вероятности а.
am в зависимости от числа степеней
Рис. 1.5
т
1
2
3
4
5
6
7
8
9
10
12
14
16
18
20
22
24
26
28
30
ос
а
0,10
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1.812
1,782
1.761
1,746
1,734
1,725
1,717
1,711
1,706
1,701
1,697
1,645
0,05
12,706
4,303
3,182
2,776
2,571
2,447
2,365
2.306
2,262
2,228
2,179
2,145
2,120
2,101
2,086
2,074
2,064
2,056
2,048
2,042
1,960
0,025
25,452
6,205
4,177
3,495
3,163
2,969
2,841
2,752
2,685
2,634
2,560
2.510
2,473
2.445
2,423
2,405
2,391
2,379
2,369
2,360
2,241
0,020
31,821
6,965
4,541
3,747
3,365
3,143
2,998
2,896
2,821
2,764
2,681
2,624
2,583
2,552
2,528
2.508
2,492
2,479
2,467
2,457
2,326
0,010
63,657
9,925
5,841
4,604
4,032
3,707
3,499
3,355
3,250
3,169
3,055
2,977
2.921
2,878
2,845
2,819
2,797
2,779
2,763
2,750
2,576
0,005
127,3
14,089
7,453
5,597
4,773
4,317
4,029
3,833
3,690
3,581
3,428
3,326
3,252
3,193
3,153
3,119
3,092
3,067
3,047
3,030
2,807
0,003
212,2
18,216
8,891
6,435
5,376
4,800
4,442
4,199
4,024
3,892
3,706
3,583
3,494
3,428
3,376
3,335
3,302
3,274
3,250
3,230
2,968
0,002
318,3
22,327
10,214
7,173
5,893
5,208
4,785
4,501
4,297
4,144
3,930
3,787
3,686
3,610
3,552
3,505
3,467
3,435
3,408
3,386
3,090
0,001
636,6
31,598
12,941
8,610
6,859
5,959
5,405
5,041
4,781
4,587
4,318
4,140
4,015
3,922
3,849
3,792
3,745
3,707
3,674
3,646
3,291
z-РАСПРЕДЕЛЕНИЕ
77
1.
п
\
2
3.
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
ос
1.2.9. z-распределение
(см. 5.2.1
.3).
г
1
4,1535
2,2950
1,7649
1,5270
1,3943
1,3103
1,2526
1,2106
1,1786
1,1535
1,1333
1,1166
1,1027
1,0909
1,0807
1,0719
1,0641
1,0572
1,0511
1,0457
1,0408
1,0363
1,0322
1,0285
1,0251
1,0220
1,0191
1,0164
1,0139
1,0116
0,9949
0,9784
0,9622
0,9462
2
4,2585
2,2976
1,7140
1,4452
1,2929
1,1955
1,1281
1,0787
1,0411
1,0114
0,9874
0,9677
0,9511
0,9370
0,9249
0,9144
0,9051
0,8970
0,8897
0,8831
0,8772
0,8719
0,8670
0,8626
0,8585
0,8548
0,8513
0,8481
0,8451
0,8423
0,8223
0,8025
0,7829
0,7636
3
4,2974
2,2984
1,6915
1,4075
1,2449
1,1401
1,0672
1,0135
0,9724
0,9399
0,9136
0,8919
0,8737
0,8581
0,8448
0,8331
0,8229
0,8138
0,8057
0,7985
0,7920
0,7860
0,7806
0,7757
0,7712
0,7670
0,7631
0,7595
0,7562
0,7531
0,7307
0,7086
0,6867
0,6651
4
4,3175
2,2988
1,6786
1,3856
1,2164
1,1068
1,0300
0.9734
0,9299
0,8954
0,8674
0,8443
0,8248
0,8082
0,7939
0,7814
0,7705
0,7607
0,7521
0,7443
0,7372
0,7309
0,7251
0,7197
0,7148
0,7103
0,7062
0,7023
0,6987
0,6954
0,6712
0,6472
0,6234
0,5999
5
4,3297
2,2991
1,6703
1,3711
1,1974
1,0843
1,0048
0,9459
0,9006
0,8646
0,8354
0,8111
0,7907
0,7732
0,7582
0,7450
0,7335
0,7232
0,7140
0,7058
0,6984
0,6916
0,6855
0,6799
0,6747
0,6699
0,6655
0,6614
0,6576
0,6540
0,6283
0,6028
0,5774
0,5522
6
4,3379
2,2992
1,6645
1,3609
1,1838
1,0680
0,9864
0,9259
0,8791
0,8419
0,8116
0,7864
0,7652
0,7471
0,7314
0,7177
0,7057
0,6950
0,6854
0,6768
0,6690
0,6620
0,6555
0,6496
0,6442
0,6392
0,6346
0,6303
0,6263
0,6226
0,5956
0,5687
0,5419
0,5152
8
4,3482
2,2994
1,6569
1,3473
1,1656
1,0460
0,9614
0,8983
0,8494
0,8104
0,7785
0,7520
0,7295
0,7103
0,6937
0,6791
0,6663
0,6549
0,6447
0,6355
0,6272
0,6196
0,6127
0,6064
0.6006
0,5952
0,5902
0,5856
0,5813
0,5773
0,5481
0,5189
0,4897
0,4604
12
4,3585
2,2997
1,6489
1,3327
1,1457
1,0218
0,9335
0,8673
0,8157
0.7744
0,7405
0,7122
0,6882
0,6675
0,6496
0,6339
0,6199
0,6075
0,5964
0,5864
0,5773
0,5691
0,5615
0,5545
0,5481
0,5422
0,5367
0,5316
0,5269
0,5224
0,4901
0,4574
0,4243
0,3908
24
4,3689
2,2999
1,6404
1,3170
1,1239
0,9948
0,9020
0,8319
0,7769
0,7324
0,6958
0,6649
0,6386
0,6159
0,5961
0,5786
0,5630
0,5491
0,5366
0,5253
0.5150
0,5056
0,4969
0,4890
0,4816
0,4748
0,4685
0,4626
0,4570
0,4519
0,4138
0,3746
0,3339
0,2913
00
4,3794
2,3001
1,6314
1,3000
1,0997
0,9643
0,8658
0,7904
0,7305
0,6816
0,6408
0,6061
0,5761
0,5500
0,5269
0,5064
0,4879
0,4712
0,4560
0,4421
0.4294
0,4176
0,4068
0,3967
0,3872
0,3784
0,3701
0,3624
0,3550
0,3481
0,2952
0,2352
0,1612
0,0000
78
ТАБЛИЦЫ
1.1.2.10. F-распределение (распределение у2)*).
Рис 1.6
т2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
1
161
4052
18,51
98,50
10,13
34,12
7,71
21,20
6,61
16,26
5,99
13,74
5,59
12,25
5,32
11,26
5,12
10,56
4,96
10,04
4,84
9,65
4,75
9,33
4,67
9,07
4,60
8,86
4,54
8,68
4,49
8,53
4,45
8,40
2
200
4999
19,00
99,00
9,55
30,82
6,94
18,00
5,79
13,27
5,14
10,92
4,74
9,55
4,46
8,65
4,26
8,02
4,10
7,56
3,98
7,21
3,89
6,93
3,81
6,70
3,74
6,51
3,68
6,36
3,63
6,23
3,59
6,11
3
216
5403
19,16
99,17
9,28
29,46
6,59
16,69
5,41
12,06
4,76
9,78
4,35
8,45
4,07
7,59
3,86
6,99
3,71
6,55
3,59
6,22
3,49
5,95
3,41
5,74
3.34
5,56
3,29
5,42
3,24
5,29
3,20
5,18
*) В таблице даны значения
шрифт) в зависимости от числа
т2- число степеней свободы для
4
225
5625
19,25
99,25
9,12
28,71
6,39
15,98
5,19
11,39
4,53
9,15
4,12
7,85
3,84
7,01
3,63
6,42
3,48
5,99
3,36
5,67
3,26
5,41
3,18
5,21
3,11
5,04
3,06
4,89
3,01
4,77
2,96
4,67
квантиле*
степеней
меньшей
5
230
5764
19,30
993
9,01
28,24
6,26
15,52
5,05
10,97
4,39
8,75
3,97
7,46
3,69
6,63
3,48
6,06
3,33
5,64
3,20
5,32
3,11
5,06
3,03
4,86
2,96
4,70
2,90
4,56
2,85
4,44
2,81
4,34
6
234
5859
19,33
99,33
8,94
27,91
6,16
15,21
4,95
10,67
4,28
8,47
3,87
7,19
3,58
6,37
3,37
5,80
3,22
5,39
3,09
5,07
3,00
4,82
2,92
4,62
2,85
4,46
2,79
4,32
2,74
4,20
2,70
4,10
7
237
5928
19,35
99,36
8,89
27,67
6,09
14,98
4,88
10,46
4,21
8,26
3,79
7,00
3,50
6,18
3,29
5,61
3,14
5,20
3,01
4,89
2,91
4,64
2,83
4,44
2,76
4,28
2,71
4,14
2,66
4,03
2,61
3,93
8
239
5981
19,37
99,37
8,85
27,49
6,04
14,80
4,82
10,29
4,15
8,10
3,73
6,84
3,44
6,03
3,23
5,47
3,07
5,06
2,95
4,74
2,85
4,50
2,77
4,30
2,70
4,14
2,64
4,00
2,59
3,89
2,55
3,79
9
241
6022
19,38
99,39
8,81
27,34
6,00
14,66
4,77
10,16
4,10
7,98
3,68
6,72
3,39
5,91
3,18
5,35
3,02
4,94
2,90
4,68
2,80
4,39
2,71
4,19
2,65
4,03
2,59
3,89
2,54
3,78
2,49
3,68
10
242
6056
19,39
99,40
8,79
27,23
5,96
14,55
4,74
10,05
4,06
7,87
3,64
6,62
3,35
5,81
3,14
5,26
2,98
4,85
2,85
4,54
2,75
4,30
2,67
4,10
2,60
3,94
2,54
3,80
2,49
3,69
2,45
3,59
11
243
6082
19,40
99,41
8,76
27,13
5,94
14,45
4,70
9,96
4,03
7,79
3,60
6,54
3,31
5,73
3,10
5,18
2,94
4,77
2,82
4,46
2,72
4,22
2,63
4,02
2,57
3,86
2,51
3,78
2,46
3,62
2,41
3,52
12
244
6106
19,41
99,42
8,74
27,05
5,91
14,37
4,68
9,89
4,00
7,72
3,57
6,47
3,28
5,67
3,07
5,11
2,91
4,71
2,79
4,40
2,69
4,16
2,60
3,96
2,53
3,80
2,48
3,67
2,42
3,55
2,38
3,46
i i'| (тх, т2) для а = 0,05 (светлый шрифт) и для а = 0,01 (полужирный
свободы тх и т2 (w1 —число степеней свободы для большей дисперсии,
дисперсии).
F-РАСПРЕДЕЛЕНИЕ
79
Продолжение
14
245
6143
19,42
99,43
8,71
26,92
5,87
14,25
4,64
9,77
3,96
7,60
3,53
6,36
3,24
5,56
3,03
5,00
2,86
4,60
2,74
4,29
2,64
4,05
2,55
3,86
2,48
3,70
2,42
3,56
2,37
3,45
2,33
3,35
16
246
6169
19,43
99,44
8,69
26,83
5,84
14,15
4,60
9,68
3,92
7,52
3,49
6,27
3,20
5,48
2,99
4,92
2,83
4,52
2,70
4,21
2,60
3,97
2,51
3,78
2,44
3,62
2,38
3,49
2,33
3,37
2,29
3,27
20
248
6209
19,44
99,45
8,66
26,69
5,80
14,02
4,56
9,55
3,87
7,39
3,44
6,16
3,15
5,36
2,93
4,81
2,77
4,41
2,65
4,10
2,54
3,86
2,46
3,66
2,39
3,51
2,33
3,37
2,28
3,26
2,23
3,16
24
249
6235
19,45
99,46
8,64
26,60
5,77
13,93
4,53
9,47
3,84
7,31
3,41
6,07
3,12
5,28
2,90
4,73
2,74
4,33
2,61
4,02
2,51
3,78
2,42
3,59
2,35
3,43
2,29
3,29
2,24
3,18
2,19
3,08
30
250
6261
19,46
99,47
8,62
26,50
5,75
13,84
4,50
9,38
3,81
7,23
3,38
5,99
3,08
5,20
2,86
4,65
2,70
4,25
2,57
3,94
2,47
3,70
2,38
3,51
2,31
3,35
2,25
3,21
2,19
3,10
2,15
3,00
40
251
6287
19,47
99,47
8,59
26,41
5,72
13,74
4,46
9,29
3,77
7,14
3,34
5,91
3,05
5,12
2,83
4,57
2,66
4,17
2,53
3,86
2,43
3,62
2,34
3,43
2,27
3,27
2,20
3,13
2,15
3,02
2,10
2,92
50
252
6302
19,48
99,48
8,58
26,35
5,70
13,69
4,44
9,24
3,75
7,09
3,32
5,86
3,02
5,07
2,80
4,52
2,64
4,12
2,51
3,81
2,40
3,57
2,31
3,38
2,24
3,22
2,18
3,08
2,12
2,97
2,08
2,87
75
253
6323
19,48
99,48
8,57
26,27
5,68
13,61
4,42
9,17
3,72
7,02
3,29
5,78
3,00
5,00
2,77
4,45
2,61
4,05
2,47
3,74
2,36
3,49
2,28
3,30
2,21
3,14
2,15
3,00
2,09
2,86
2,04
2,79
100
253
6334
19,49
99,49
8,55
26,23
5,66
13,57
4,41
9,13
3,71
6,99
3,27
5,75
2,97
4,96
2,76
4,42
2,59
4,01
2,46
3,71
2,35
3,47
2,26
3,27
2,19
3,11
2,12
2,98
2,07
2,86
2,02
2,76
200
254
6352
19,49
99,49
8,54
26,18
5,65
13,52
4,39
9,08
3,69
6,93
3,25
5,70
2,95
4,91
2,73
4,36
2,56
3,96
2,43
3,66
2,32
3,41
2,23
3,22
2,16
3,06
2,10
2,92
2,04
2,81
1,99
2,71
500
254
6361
19,50
99,50
8,53
26,14
5,64
13,48
4,37
9,04
3,68
6,90
3,24
5,67
2,94
4,88
2,72
4,33
2,55
3,93
2,42
3,62
2,31
3,38
2,22
3,19
2,14
3,03
2,08
2,89
2,02
2,78
1,97
2,68
ос
254
6366
19,50
99,50
8,53
26,12
5,63
13,46
4,36
9,02
3,67
6,88
3,23
5,65
2,93
2,71
4,31
2,54
3,91
2,40
3,60
2,30
3,36
2,21
3,17
2,13
3,00
2,07
2,87
2,01
2,75
1,96
2,65
'
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
80
ТАБЛИЦЫ
w2
18
19
20
21
22
23
24
25
26
27
28
29
30
32
34
36
38
40
42
44
46
1
4,41
8,29
4,38
8,18
4,35
8,10
4,32
8,02
4,30
7,95
4,28
7,88
4,26
7,82
4,24
7,77
4,23
7,72
4,21
7,68
4,20
7,64
4,18
7,60
4,17
7,56
4,15
7,50
4,13
7,44
4,11
7,40
4,10
7,35
4,08
7,31
4,07
7,28
4,06
7,25
4,05
7,22
2
3,55
6,01
3,52
5,93
3,49
5,85
3,47
5,78
3,44
5,72
3,42
5,66
3,40
5,61
3,39
5,57
4,37
5,53
3,35
5,49
3,34
5,45
3,33
5,42
3,32
5,39
3,29
5,34
3,28
5,29
3,26
5,25
3,24
5,21
3,23
5,18
3,22
5,15
3,21
5,12
3,20
5,10
3
3,16
5,09
3,13
5,01
3,10
4,94
3,07
4,87
3,05
4,82
3,03
4,76
3,01
4,72
2,99
4,68
2,98
4,64
2,96
4,60
2,95
4,57
2,93
4,54
2,92
4,51
2,90
4,46
2,88
4,42
2,87
4,38
2,85
4,34
2,84
4,31
2,83
4,29
2,82
4,26
2,81
4,24
4
2,93
4,58
2,90
4,50
2,87
4,43
2,84
4,37
2,82
4,81
2,80
4,26
2,78
4,22
2,76
4,18
2,74
4,14
2,73
4,11
2,71
4,07
2,70
4,04
2,69
4,02
2,67
3,97
2,65
3,93
2,63
3,89
2,62
3,86
2,61
3,83
2,59
3,80
2,58
3,78
2,57
3,76
5
2,77
4,05
2,74
4,17
2,71
4,10
2,68
4,04
2,66
3,99
2,64
3,94
2,62
3,90
2,60
3,86
2,59
3,82
2,57
3,78
2,56
3,76
2,55
3,73
2,53
3,70
2,51
3,65
2,49
3,61
2,48
3,57
2,46
3,54
2,45
3,51
2,44
3,49
2,43
3,47
2,42
3,44
6
2,66
4,01
2,63
3,94
2,60
3,87
2,57
3,81
2,55
3,76
2,53
3,71
2,51
3,67
2,49
3,63
2,47
3,59
2,46
3,56
2,45
3,53
2,43
3,50
2,42
3,47
2,40
3,43
2,38
33
2,36
3,35
2,35
3,32
2,34
3,29
2,32
3,27
2,31
3,24
2,30
3,22
7
2,58
3,84
2,54
3,77
2,51
3,70
2,49
3,64
2,46
3,59
2,44
3,54
2,42
3,50
2,40
3,46
2,39
3,42
2,37
3,39
2,36
3,36
2,35
3,33
2,33
3,30
2,31
3,25
2,29
3,22
2,28
3,18
2,26
3,15
2,25
3,12
2,24
3,10
2,23
3,08
2,22
3,06
8
2,51
3,71
2,48
3,63
2,45
3,56
2,42
3,51
2,40
3,45
2,37
3,41
2,36
3,36
2,34
3,32
2,32
3,29
2,31
3,26
2,29
3,23
2,28
3,20
2,27
3,17
2,24
3,13
2,23
3,09
2,21
3,05
2,19
3,02
2,18
2,99
2,17
2,97
2,16
2,95
2,15
2,93
9
2,46
3,60
2,42
3,52
2,39
3,46
2,37
3,40
2,34
3,35
2,32
3,30
2,30
3,26
2,28
3,22
2,27
3,18
2,25
3,15
2,24
3,12
2,22
3,09
2,21
3,07
2,19
3,02
2,17
2,98
2,15
2,95
2,14
2,91
2,12
2,89
2,11
2,86
2,10
2,84
2,09
2,82
10
2,41
3,51
2,38
3,43
2,35
3,37
2,32
3,31
2,30
3,26
2,27
3,21
2,25
3,17
2 24
3,13
2,22
3,09
2,20
3,06
2,19
3,03
2,18
3,00
2,16
2,98
2,14
2,93
2,12 /
2,89
2,11
2,86
2,09
2,82
2,08
2,80
2,06
2,78
2,05
2,75
2,04
2,73
11
2,37
3,43
2,34
3,36
2,31
3,29
2,28
3,24
2,26
3,18
2,24
3,14
2,22
3,09
2,20
3,06
2,18
3,02
2,16
2,99
2,15
2,96
2,14
2,93
2,13
2,90
2,10
2,86
2,08
2,82
2,07
2,79
2,05
2,75
2,04
2,73
2,03
2,70
2,01
2,68
2,00
2,66
12
2,34
3,37
2,31
3,30
2,28
3,23
2,25
3,17
2,23
3,12
2,20
3,07
2,18
3,03
2,16
2,99
2,15
2,96
2,13
2,83
2,12
2,90
2,10
2,87
2,09
2,84
2,07
2,80
2,05
2,76
2,03
2,72
2,02
2,69
2,00
2,66
1,99
2,64
1,98
2,62
1,97
2,60
F-РАСПРЕДЕЛЕНИЕ
81
Продолжение
14
2,29
3,27
2,26
3,19
2,22
3,13
2,20
3,07
2,17
3,02
2,15
2,97
2,13
2,93
2,11
2,89
2,10
2,86
2,08
232
2,06
2,80
2,05
2,77
2,04
2,74
2,01
2,70
1,99
2,66
1,98
2,62
1,96
2,59
1,95
2,56
1,93
2,54
1,92
2,52
1,91
2,50
16
2,25
3,19
2,21
3,12
2,18
3,05
2,16
2,99
2,13
2,94
2,11
2,89
2,09
2,85
2,07
2,81
2,05
2,78
2,04
2,75
2,02
2,71
2,01
2,69
1,99
2,66
1,97
2,62
1,95
2,58
1,93
2,54
1,92
2,51
1,90
2,48
1,89
2,46
1,88
2,44
1,87
2,42
20
2,19
3,08
2,15
3,00
2,12
2,94
2,10
2,88
2,07
2^3
2,05
2,78
2,03
2,74
2,01
2,70
1,99
2,66
1,97
2,63
1,96
2,60
1,94
2,57
1,93
2,55
1,91
2,50
1,89
2,46
1,87
2,43
1,85
2,40
1,84
2,37
1,83
2,34
1,81
2,32
1,80
2,30
24
2,15
3,00
2,11
2,92
2,08
2,86
2,05
2,80
2,03
2,75
2,00
2,70
1,98
2,66
1,96
2,62
1,95
2,58
1,93
2,55
1,91
2,52
1,90
2,49
1,89
2,47
1,86
2,42
1,84
2,38
1,82
2,35
1,81
2,32
1,79
2,29
1,78
2,26
1,77
2,24
1,76
2,22
30
2,11
2,92
2,07
2,84
2,04
2,78
2,01
2,72
1,98
2,67
1,96
2,62
1,94
2,58
1,92
2,54
1,90
2,50
1,88
2,47
1,87
2,44
1,85
2,41
1,84
2,38
1,82
2,34
1,80
2,30
1,78
2,26
1,76
2,23
1,74
2,20
1,73
2,18
1,72
2,15
1,71
2,13
40
2,06
2,84
2,03
2,76
1,99
2,69
1,96
2,64
1,94
2,58
1,91
2,54
1,89
2,49
1,87
2,45
1,85
2,42
1,84
2,38
1,82
2,35
1,80
2,33
1,79
2,30
1,77
2,25
1,75
2,21
1,73
2,17
1,71
2,14
1,69
2,11
1,68
2,09
1,67
2,06
1,65
2,04
п\
50
2,04
2,78
2,00
2,71
1,97
2,64
1,94
2,58
1,91
2,53
1,88
2,48
1,86
2,44
1,84
2,40
1,82
2,36
1,81
2,33
1,79
2,30
1,77
2,27
1,76
2,25
1,74
2,20
1,71
2,16
1,69
2,12
1,68
2,09
1,66
2,06
1,65
2,03
1,63
2,01
1,62
1,99
75
2,00
2,71
1,96
2,63
1,92
2,56
1,89
2,51
1,87
2,46
1,84
2,41
1,82
2,36
1,80
2,32
1,78
2,28
1,76
2,25
1,75
2,22
1,73
2,19
1,72
2,16
1,69
2,12
1,67
2,08
1,65
2,04
1,63
2,00
1,61
1,97
1,60
1,94
1,58
1,92
1,57
1,90
100
1,98
2,68
1,94
2,60
1,91
2,54
1,88
2,48
1,85
2,42
1,82
2,37
1,80
2,33
1,78
2,29
1,76
2,25
1,74
2,22
1,73
2,19
1,71
2,16
1,70
2,13
1,67
2,08
1,65
2,04
1,62
2,00
1,61
1,97
1,59
1,94
1,57
1,91
1,56
1,89
1,55
1,86
200
1,95
2,62
1,91
2,55
1,88
2,48
1,84
2,42
1,81
2,36
1,79
2,32
1,77
2,27
1,75
2,23
1,73
2,19
1,71.
2,16
1,69
2,13
1,67
2,10
1,66
2,07
1,63
2,02
1,61
1,98
1,59
1,94
1,57
1,90
1,55
1,87
1,53
1,85
1,52
1,82
1,51
1,80
500
1,93
2,59
1,90
2,51
1,86
2,44
1,82
2,38
1,80
2,33
1,77
2,28
1,75
2,24
1,73
2,19
1,70
2,16
1,68
2,12
1,67
2,09
1,65
2,06
1,64
2,03
1,61
1,98
1,59
1,94
1,56
1,90
1,54
1,86
1,53
1,83
1,51
1,80
1,49
1,78
1,48
1,75
00
1,92
2,57
1,88
2,49
1,84
2,42
1,81
236
1,78
2,31
1,76
2,26
1,73
2,21
1,71
2,17
1,69
2,13
1,67
2,10
1,65
2,06
1,64
2,03
1,62
2,01
1,59
1,96
1,57
1,91
1,55
1,87
1,53
1,84
1,51
1,80
1,49
1,78
1,48
1,75
1,46
1,73
т2
18
19
20
21
22
23
24
25
26
27
28
29
30
32
34
36
38
40
42
44
46
48
СП
J\)
ее
Dj
60
65
70
sn
oil
100
125
150
200
400
1000
00
1
4,04
7,20
4,03
7,17
4,02
7,12
4,00
7,08
3,99
7,04
3,98
7,01
3,96
6,96
3,94
6,90
3,92
6,84
3,90
6,81
3,89
6,76
3,86
6,70
3,85
6,66
3,84
6,63
2
3,19
5,08
3,18
5,06
3,16
5,01
3,15
4,98
3,14
4,95
3,13
4,92
3,11
4,88
3,09
4,82
3,07
4,78
3,06
4,75
3,04
4,71
3,02
4,66
3,00
4,63
3,00
4,61
3
2,80
4,22
2,79
4,20
2,78
4,16
2,76
4,13
2,75
4,10
2,74
4,08
2,72
4,04
2,70
3,98
2,68
3,94
2,66
3,92
2,65
3,88
2,62
3,83
2,61
3,80
2,60
3,78
4
2,57
3,74
2,56
3,72
2,54
3,68
2,53
3,65
2,51
3,62
2,50
3,60
2,49
3,56
2,46
3,51
2,44
3,47
2,43
3,45
2,42
3,41
2,39
3,36
2,38
3,34
2,37
3,32
5
2,41
3,43
2,40
3,41
2,38
3,37
2,37
3,34
2,36
3,31
2,35
3,29
2,33
3,26
2,31
3,21
2,29
3,17
2,27
3,14
2,26
3,11
2,23
3,06
2,22
3,04
2,21
3,02
6
2,30
3,20
2,29
3,19
2,27
3,15
2,25
3,12
2,24
3,09
2,23
3,07
2,21
3,04
2,19
2,99
2,17
2,95
2,16
2,92
2,14
239
2,12
235
2,11
2,82
2,10
2,80
7
2,21
3,04
2,20
3,02
.2,18
2,98
2,17
2,95
2,15
2,93
2,14
2,91
2,13
2,87
2,10
2,82
2,08
2,79
2,07
2,76
2,06
2,73
2,03
2,69
2,02
2,66
2,01
2,64
8
2,14
2,91
2,13
2,89
2,11
2,85
2,10
2,82
2,08
2,80
2,07
2,78
2,06
2,74
2,03
2,69
2,01
2,66
2,00
2,63
1,98
2,60
1,96
2,55
1,95
2,53
1,94
2,51
9
2,08
2,80
2,07
2,79
2,06
2,75
2,04
2,72
2,03
2,69
2,02
2,67
2,00
2,64
1,97
2,59
1,96
2,55
1,94
2,53
1,93
2,50
1,90
2,46
1,89
2,43
1,88
2,41
10
2,03
2,72
2,03
2,70
2,01
2,66
1,99
2,63
1,98
2,61
1,97
2,59
1,95
2,55
1,93
2,50
1,91
2,47
1,89
2,44
1,88
2,41
1,85
2,37
1,84
2,34
1,83
2,32
11
1,99
2,64
1,99
2,63
1,97
2,59
1,95
2,56
1,94
2,53
1,93
2,51
1,91
2,48
1,89
2,43
1,87
2,40
1,85
2,37
1,84
2,34
1,81
2,29
1,80
2,27
1,79
2,25
12
1,96
2,58
1,95
2,56
1,93
2,53
1,92
2,50
1,90
2,47
1,89
2,45
1,88
2,42
1,85
2,37
1,83
2,33
1,82
2,31
1,80
2,27
1,78
2,23
1,76
2,20
1,75
2,18
F-РАСПРЕДЕЛЕНИЕ
83
Продолжение
14
1,90
2,48
1,89
2,46
1,88
2,43
1,86
23
1,85
2,37
1,84
2,35
1,82
2,31
1,79
2,26
1,77
2,23
1,76
2,20
1,74
2,17
1,72
2,12
1,70
2,09
1,69
2,08
16
1,86
2,40
1,85
2,38
1,83
2,34
1,82
2,31
1,80
2,29
1,79
2,27
t
1,77
2,23
1,75
2,19
1,72
2,15
1,71
2,12
1,69
2,09
1,67
2,04
1,65
2,02
1,64
2,00
20
1,79
2,28
1,78
2,26
1,76
2,23
1,75
2,20
1,73
2,18
1,72
2,15
1,70
2,12
1,68
2,06
1,65
2,03
1,64
2,00
1,62
1,97
1,60
1,92
1,58
1,89
1,57
1,88
24
1,75
2,20
1,74
2,18
1,72
2,15
1,70
2,12
1,69
2,09
1,67
2,07
1,65
2,03
1,63
1,98
1,60
1,94
1,59
1,91
1,57
1,88
1,54
1,84
1,53
1,81
1,52
1,79
30
1,70
2,12
1,69
2,10
1,67
2,06
1,65
2,03
1,63
2,00
1,62
1,98
1,60
1,94
1,57
1,89
1,55
1,85
1,53
1,83
1,52
1,79
1,49
1,74
1,47
1,71
1,46
1,70
40
1,64
2,08
1,63
2,00
1,61
1,96
1,58
1,94
1,58
1,90
1,57
1,88
1,54
1,85
1,52
1,79
1,49
1,75
1,48
1,72
1,46
1,69
1,42
1,64
1,41
1,61
1,39
1,59
50
1,61
1,97
1,60
1,95
1,58
1,91
1,56
1,88
1,54
1,85
1,53
1,83
1,51
1,79
1,48
1,73
1,45
1,69
1,44
1,66
1,41
1,63
1,38
1,57
1,36
1,54
1,35
1,52
75
1,56
1,88
1,55
1,86
1,52
1,82
1,50
1,79
1,49
1,76
1,47
1,74
1,45
1,70
1,42
1,64
1,39
1,59
1,37
1,56
1,35
1,53
1,32
1,47
1,30
1,44
1,28
1,41
100
1,54
1,84
1,52
1,82
1,50
1,78
1,48
1,75
1,46
1,72
1,45
1,70
1,43
1,66
1,39
1,60
1,36
1,55
1,34
1,52
1,32
1,48
1,28
1,42
1,26
1,38
1,24
1,36
200
1,49
1,78
1,48
1,76
1,46
1,71
1,44
1,68
1,42
1,65
1,40
1,62
1,38
1,58
1,34
1,52
1,31
1,47
1,29
1,43
1,26
1,39
1,22
1,32
1,19
1,28
1,17
1,25
500
1,47
1,73
1,46
1,71
1,43
1,67
1,41
1,63
1,39
1,60
1,37
1,57
1,35
1,53
1,31
1,47
1,27
1,41
1,25
1,38
1,22
1,33
1,16
1,24
1,13
1,19
1,11
1,15
00
1,45
1,70
1,44
1,68
1,41
1,64
1,39
1,60
1,37
1,56
1,35
1,53
1,32
1,49
1,28
1,43
1,25
1,37
1,22
1,33
1,19
1,28
1,13
1,19
1,08
1,11
1,00
1,00
m2
48
50
55
60
65
70
80
100
125
150
200
400
1000
00
84
ТАБЛИЦЫ
1.1.2.11. Критические числа для испытания Уилкоксона (см. 5.2.3.5).
а = 0,05
15
14
13
12
11
10
9
8
7
6
5
4
3
2
п\
4
_
-
8,0
9,0
47,5
46,0
43,5
41,0
38,5
36,0
33,5
31,0
28,5
26,0
23,5
20,0
17,5
14,0
5
_
7,5
9,0
10,5
48,0
45,0
43,0
40,0
38,0
35,0
33,0
30,0
27,0
24,0
21,0
18,0
15,0
6
_
8,0
10,0
12,0
13,0
47,5
45,0
42,5
40,0
37,5
34,0
31,5
29,0
25,5
23,0
19,5
15,0
7
_
9,5
11,0
12,5
15,0
16,5
47,0
44,0
42,0
39,0
36,0
33,0
30,0
27,0
24,0
20,0
16,0
8
8,0
10,0
12,0
14,0
16,0
18,0
19,0
46,5
43,0
40,5
38,0
34,5
32,0
28,5
25,0
21,5
17,0
9
9,0
11,5
13,0
15,5
17,0
19,5
21,0
22,5
45,0
42,0
39,0
36,0
33,0
30,0
26,0
22,0
18,0
10
10,0
12,0
15,0
17,0
19,0
21,0
23,0
25,0
27,0
44,5
41,0
37,5
34,0
30,5
27,0
23,5
18,0
11
10,0
13,5
16,0
18,5
20,0
22,5
25,0
26,5
29,0
30,5
42,0
39,0
36,0
32,0
28,0
24,0
19,0
12
11,0
14,0
17,0
19,0
22,0
24,0
26,0
28,0
30,0
33,0
35,0
40,5
37,0
33,5
29,0
25,5
20,0
13
12,0
15,5
18,0
20,5
23,0
25,5
28,0
30,5
32,0
34,5
37,0
38,5
38,0
35,0
30,0
26,0
21,0
14
13,0
16,0
19,0
22,0
25,0
27,0
29,0
32,0
34,0
37,0
39,0
41,0
43,0
39,0
35,5
32,0
27,5
22,0
15
16
,8
19
20
21
22
23
24
п\
2
3
4
5
6
7
8
9
10
11
12
13
14 .
а = 0,01
15
14
13
12
11
10
9
8
7
6
5
4
3
2
п2
4
_
-
-
61,5
59,0
55,5
53,0
49,5
46,0
42,5
40,0
36,5
33,0
29,5
25,0
20,5
~
15
5
_
-
12,5
62,0
58,0
55,0
52,0
49,0
45,0
42,0
38,0
35,0
31,0
27,0
22,0
—
16
6
_
12,0
14,0
16,0
61,5
58,0
54,5
51,0
47,5
44,0
40,5
36,0
32,5
28,0
23,5
—
17
7
_
14,0
15,5
18,0
20,5
61,0
57,0
53,0
50,0
46,0
42,0
38,0
34,0
30,0
25,0
~
18
8
_
15,0
18,0
20,0
22,0
25,0
59,5
56,0
52,5
48,0
44,5
40,0
35,5
31,0
25,5
19,0
19
9
13,5
17,0
19,5
22,0
24,5
27,0
29,5
5в\о
54,0
50,0
46,0
42,0
37,0
32,0
27,0
20,0
п2
20
10
15,0
18,0
21,0
24,0
26,0
29,0
32,0
34,0
56,5
52,0
48,5
44,0
38,5
34,0
28,5
21,0
21
11
16,5
20,0
22,5
26,0
28,5
31,0
33,5
36,0
39,5
54,0
50,0
45,0
41,0
35,0
29,0
22,0
22
12
17,0
21,0
24,0
27,0
30,0
33,0
36,0
39,0
42,0
44,0
51,5
47,0
42,5
37,0
30,5
23,0
23
13
18,5
22,0
25,5
29,0
32,5
35,0
38,5
41,0
44,5
47,0
50,5
49,0
44,0
38,0
32,0
24,0
24
14
20,0
24,0
28,0
31,0
34,0
38,0
41,0
44,0
47,0
50,0
53,0
56,0
51,0
45,5
40,0
32,5
25,С
25
п\
3
4
5
6
7
8
9
10
11
12
13
14
^-РАСПРЕДЕЛЕНИЕ
1.1.2.12. /-распределение Колмогорова — Смирнова (см. 5.2.3.8).
к
0,32
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,40
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,50
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,60
0,61
0,62
0,63
0,64
0,65
Q(K)
0,0000
0,0001
0,0002
0,0003
0,0005
0,0008
0,0013
0,0019
0,0028
0,0040
0,0055
0,0074
0,0097
0,0126
0,0160
0,0200
0,0247
0,0300
0,0361
0,0428
0,0503
0,0585
0,0675
0,0772
0,0876
0,0987
0,1104
0,1228
0,1357
0,1492
0,1632
0,1778
0,1927
0,2080
Я.
0,66
0,67
0,68
0,69
0,70
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,80
0,81
0,82
0,83
0,84
.0,85
0,86
0,87
0,88
0,89
0,90
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,99
0,2236
0,2396
0,2558
0,2722
0,2888
0,3055
0,3223
0,3391
0,3560
0,3728
0,3896
0,4064
0,4230
0,4395
0,4559
0,4720
0,4880
0,5038
0,5194
0,5347
0,5497
0,5645
0,5791
0,5933
0,6073
0,6209
0,6343
0,6473
0,6601
0,6725
0,6846
0,6964
0,7079
0,7191
1,00
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,10
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,20
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,30
1,31
1,32
1,33
0,7300
0,7406
0,7508
0,7608
0,7704
0,7798
0,7889
0,7976
0,8061
0,8143
0,8223
0,8299
0,8374
0,8445
0,8514
0,8580
0,8644
0,8706
0,8765
0,8823
0,8877
0,8930
0,8981
0,9030
0,9076
0,9121
0,9164
0,9206
0,9245
0,9283
0,9319
0,9354
0,9387
0,9418
X
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,50
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
1,60
1,61
1,62
1,63
1,64
1,65
1,66
1,67
0,9449
0,9478
0,9505
0,9531
0,9556
0,9580
0,9603
0,9625
0,9646
0,9665
0,9684
0,9702
0,9718
0,9734
0,9750
0,9764
0,9778
0,9791
0,9803
0,9815
0,9826
0,9836
0,9846
0,9855
0,9864
0,9873
0,9880
0,9888
0,9895
0,9902
0,9908
0,9914
0,9919
0,9924
X
1,68
1,69
1,70
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,80
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,90
1,91
1,92
1,93
1,94
1,95
1,96
1,97
1,98
1,99
Q(K)
0,9929
0,9934
0,9938
0,9942
0,9946
0,9950
0,9953
0,9956
0,9959
0,9962
0,9965
0,9967
0,9969
0,9971
0,9973
0,9975
0,9977
0,9979
0,9980
0,9981
0,9983
0,9984
0,9985
0,9986
0,9987
0,9988
0,9989
0,9990
0,9991
0,9991
0,9992
0,9993
X
2,00
2,01
2,02
2,03
2,04
2,05
2,06
2,07
2,08
2,09
2,10
2,11
2,12
2,13
2,14
2,15
2,16
2,17
2,18
2,19
2,20
2,21
2,22
2,23
2,24
2,25
2,26
2,27
2,28
2,29
2,30
2,31
0,9993
0,9994
0,9994
0,9995
0,9995
0,9996
0,9996
0,9996
0,9996
0,9997
0,9997
0,9997
0,9997
0,9998
0,9998
0,9998
0,9998
0,9998
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
0,9999
1,0000
86 ТАБЛИЦЫ
1.1.3. ИНТЕГРАЛЫ И СУММЫ РЯДОВ
1.1.3.1. Таблица сумм некоторых числовых рядов.
3)
5)
7) 7 >+1) " ry+2T + Fi + '""L
8)
9)V ! = JL.
Zj("~ 1)(и+ 1) 1-3
1 }
11-13 +'"'~ 2
oo
Zl _J 1 _J_
п(и+ 1)(и + 2) ~ 1-2-3 + 2-3-4 +'" ~ 4'
12) > , ' , -^-Г**^*...-. '
1-2.../ 2-3. ..(/+1) ¦'" (/-l)-(/-l)!'
11 n2
1 1
17)
Lj n* 24 34 72°
„=1 n=l
Числа Бернулли Вк
19)
1 1 1 я2кB2к-1)
20)
oo
у, „_! i j_ j L
V 1 _ 1 11 _ к2кB2к- 1)
21) ^Bп-1Jк =1 + ^+ ^Г+ +*+•-- 2.BЛ), «*•
ТАБЛИЦА РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
87
Таблица первых чисел Бернулли
к
вк
1
1
6
2
1
30
3
1
42
4
1
30
5
5
66
6
691
2730
7
7
6
8
3617
510
9
43867
798
10
174611
330
11
854513
138
22)
Числа Эйлера Ек
Z 1 1_ _1 1_ 7t2fc+1
( ' Bn-lJfc + 1 32fc+1 + 52fc + 1 ~ 72fc+1 + "*~ 22k + 2-{2k)\ к'
Таблица первых чисел Эйлера
к
1
1
2
5
3
61
4
1385
5
50 521
6
2702765
7
199 360981
1.1.3.2. Таблица разложения элементарных функций в степенные ряды.
Функция и область
сходимости
Разложение в ряд
(а±хГ
(| х | ^ а при т > 0)
\х\^а и а + х^0
при 0 > m > — 1,
| х | < а при т < — 1
(т > 0) *)
(|х|<1)
A±х)^
(|х|<1)
A±хI/3
(М<1)
dlxI'2
(Ы<1)
A±хK/2
(|х|<1)
A±хM'2
(Их)'
(|х| < 1 при т^ 1;
I х К 1 и 1 ± х ф 0
при 0 < т < 1)
A±хГ1/4
(| х | ^ 1 и 1 ± х Ф 0)
(| х | < 1 и 1 ± х Ф 0)
A + х)-1'2
(I х | < 1 и 1 ± х Ф 0)
Биномиальный ряд
преобразованием к виду сГ ( 1 ± —) сводится к нижеследующим рядам.
Биномиальные ряды с положительным показателем
1•3 2 1-3-7
TIT* ± ~4~-
1-2
12
1-2-5
_ ЬЗ-7- 11
4-8-12-16
Ь 2 • 5 - 8 4
3-6-9-12 Х ±-
4
» 1 ' 1 ' 3 • 5 х4 +
" 2-4-6-8 *'"
Ь 2 Х+ 2-4 + 2-4-6 + 2-4-6-8 Х +>>
,5.53 ,5-3-1 , 5-3-11 А
1J- 2 ^ ' 2-4 л "" 2-4-6 л 2-4-6.8 л +
Биномиальные ряды с отрицательным показателем
15
i - Ь5'9 з 1-5-9-13 4 _
+ 4-8-12 Х 4-8-12-16 Х +"
¦ __!_ 1-4 2_1-4-7 з 1-4-7-10 4_
+ ТХ+Т^6"Х + 3-6-9 Х + 3-6-9-12Х + "
- J_ l '3 2 _ 1-35 з 1-3-5-7 4_
+ 2Х+ 2-4Х + 2-4-6Х 2-4-6-8Х +>"
*) При m натуральном разложение содержит m + 1 членов.
ТАБЛИЦЫ
Продолжение
Функция
и
облас гь
сходимости
A
A
A
A
A
A
A
±
х I
±
х|
±
х|
±
A х |
A
A
A
A
A
A
±
х|
±
х|
±
х)
<
х)
<
х)
<
х)
<
х)
<
х)
<
х)
<
-1
1)
-3/2
1)
-2
1)
-5/2
1)
-3
1)
-4
1)
-5
1)
Разложение в ряд
sin х
(I х | < оо)
sin (x + а)
(| X | < 00)
COS X
(I х | < оо)
cos (x + а)
(I х | < оо)
tgx
(I х | < л/2)
Ctg X
(О < | х | < к)
sec х
([ х | < я/2)
cosec х
(О < | х | < п)
е*
(I х | < оо)
1-2 3'5 2-3-5-7 з 3-5-7-9 4_
+ 2Х+ 2-4Х + 2-4-6 Х + 2-4-6-8Х + '' '
1 + 2х + Зх2 + 4х3 + 5х4 + ...
- А 5-7 2 _ 5jJN9_ з 5-7-9- 11 4 _
+ 2Х+ 2-4Х + 2-4-6Х + -4-6-8 Х + ''
1 + j^2~B • Зх + 3 • 4х2 + 4 - 5х3 + 5 - 6х4 + ...)
1 + —-yyB • 3 • 4х + 3 • 4 • 5х2 + 4 • 5 • 6х3 + 5 • 6 • 7х4 + .. )
1 + — 2 *3 4 B • 3 * 4 • 5х + 3 • 4 • 5 ' 6х2 + 4 ' 5 ' 6 ' ?х3 + 5 • 6 - 7 • 8х4 + ...)
Тригонометрические функции
I
(-1Г
Bи- 1)!
Ex" sin (я + ля/2)
* i—L.= sin a
л!
2! 3!
х2 х4 хб
1 -L и U
1Т+ 1Г "бТ
У х" cos {a + t
La "!
2! 3!
Bи)!
с+ 3 х + 15 х + —х + 2835~Х +-"
^ =J _/^ x^ 2xl_ x^_ \
2и)! х \3 45 945 + 4725 )
Показательные функции
Zx" х
х х2 х3
ТАБЛИЦА РАЗЛОЖЕНИЯ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ
89
Продолжение
Функция и область
сходимости
д. = ^ .п а
(|х|<оо)
X
е* - 1
In х
(х>0)
In х
@ < х < 2)
In х
(х > 1/2)
In A + х)
(-1 <х< 1)
In A - х)
(-1<х<1)
In О Artk v
1 -X
(|х|>1)
In | sin х |
In cos x
(|х|<я/2)
In | tg x |
@<|х|<я/2)
arcsin x
arccos x
V (* In af _
n = O
x V
f (x-1J
n = 0
V ! +i <*-
Lj n
я=1
n=l
Z. » " V
n= 1
00
n = 0
2 /
n = 0
V 22n
Y 22n-l{22n
n=l
In I v 1 I \
1П | X | + 7
Y 1-3-5.
X ' Ij 2-4-6
я=1
я y l-
2^/2
n=l
Разложение в ряд
x In a (x In aJ (x
1! 2! '
+ i By. x BiX>
' Bn)\ 2 2 ] 2!
In аK
3!
В х4 В хб
4! ' 6!
Логарифмические функции
Гх-l (x-
- 1Jя+1 ^L х+ 1 ' 3(х +
О" , п (х-1J
(х-1) 2 1
- 1 (х - IJ (х - IK
х 2х2 Зх3
= х .—+ — — + ...
X2 X3 X4 X5
+ 2 + 3 + -J-+ -J-+
( X3 X5 X7
->(* ] J
"+1 *\х ' Зх3 ' 5х5
"^„х2" х2 х
Bи)! П|Х| 6 18
2и)! 2 12
B—-DB
пBпу.
IK + 5(x+lM +
х - IK (х - IL
3 4
¦¦¦)
¦)
h lx^+-)
4 хб
0 2835 ' *"
хб 17х8
45 2520 •¦
j 7
3 +90
Обратные тригонометрические
..B«-1)х2и + 1 х3
.. Bп) Bи + 1) 2-3
3-5.. B/1- l)x2n + 1 я
•4-6...Bи)Bи+1) 2
1-Зх5 ЬЗ
2-4-5 2-4
/ х3 1
\Х ' 2-3 ' 2 •
¦¦]•
62
2835 Х ' ¦-
функции
-5х7
-6-7 ' •••
Зх5 1 • 3 • 5х7 | \
4-5 ' 2-4-6-7 " )
90
ТАБЛИЦЫ
Продолжение
Функция и область
сходимости
arctg х
(|х|<1)
arctg х
arcctg x
sh x
(| х | < оо)
chx
(|х|<оо)
th x
A х | < я/2)
cth x
@ <| х | < я)
sch x
(|х|<я/2)
csch x
@ < | х | < я)
Arsh x
Archx**)
Arth x
Arcth x
V( 1Г *2п+1 х
Zj 2m+ 1
п = О
+ к V in+i
~ 2 [_j ' Bп
п = О
..о
V^ V2n-1 V3
\ х х I
Aj Bм-1)! ~ ' 3!
Y х2" х2 д
/_j {2n)\ ~ 2' <¦
n = O
V (-l)n + 122nB2n- 1)
Zj B«)!
1 7 Я 1
x ' L Bn)! "
1 i ^ ("ir Ex2" 1
n=l
1 Y 2(-iyiB2"'1 -
x ' /j Bn)!
n = l
/ j 2 4-6...
n=l
Г „ y,.3.s
/ j ^tt " 1 3
n = 0
Zj Bm + l)x2n+1 x '
n = O
*) Первый член берется со знаком + при
**) Функция двузначная (см. 1.2.2.3)
Разложение в
X3 X5 X7
3 5 7 +'"
1 +я 1 + 1
1 я / x3 x5 x7
Гиперболические
x5 x7
4 x6
1 x x3 2x5
C x ' 3 45 ' 945
_ _LX2 + 5 x4 _ 61 x6 + 1
1) D 2.-1 1 x , 7x3
BnX x . 6 ' 360
ряд
1_+ 1
+ ...J
х7 1 х9
х7
472Т+---
385 х8
31х5
15 120
Обратные гиперболические функции
•Bл-1) 2n+1 1
2пBп+\) Х Х 2 • 3 Х
-B.-1) Д 1 Г
-2П'2П X2"J ^1ПМ
5 х7
._iy_+^y.+ _iT_+...
х > 1 и со знаком — при х <
з 1-3 5 1-3-5 7
1 2-4-5 Х 2-4 6 7 Х ' •
1 1-3 1-3-5
2 • 2х2 2 • 4 • 4х4 2 • 4 • 6 • 6х6
-1.
¦¦¦¦]
_ ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 91_
1.1.3.3. Таблица неопределенных интегралов. ной функции входит выражение, содержащее
Общие у казан и я. 1. Постоянная интегриро- 1п/(х), его следует понимать как 1п|/(х)|; знак
вания опущена всюду, за исключением случаев, абсолютной величины везде для простоты опущен.
когда интеграл может быть представлен в различ- 3. В тех случаях, когда первообразная функция
ных формах с различными произвольными по- представлена в виде степенного ряда, ее нельзя
стоянными. выразить через конечное число элементарных функ-
2. Во всех формулах, где в состав первообраз- ций.
1.1.3.3.1. Интегралы от рациональных функций.
Интегралы, содержащие ах + Ъ.
Обозначение: X = ах + Ь.
1) \Xndx = 1 Хи+1 (пф -1; при п= -1 см. № 2). 2) -?- = — In X.
J a(n+ 1) . J X а
Г J +2 Ъ
3) \xXndx = -J7 ^у\Х 17—
J а2 (п + 2) а2 (п -
4) j x"Xm dx = -^tj- UX - Ь)т Xя dX
3) \^П^ = -г7--^Х^2 - -^---Х^ {пФ -X, -2;прип=-1, -2 см. №№ 5 и 6).
(применяется при т < п или при т целом и и дробном, в этих случаях (X — Ь)т раскрывается по формуле
бинома Ньютона (см. 2.2.2.1); пф —1, —2, ..., — т).
a a2 J
xdx Ъ
~ХГ=~а1~Т +
8) J "x^= ^(W-2)x-2 + (п-1)х«-;(w # ^2)-
9I^=Я^2-2ьх+ь21п410I
Х2'Х ^;Х-2ЫпХ-^).
12)
13)
Г х2</х 1 Г -1 26 Ь2 1
J -X"-= ^U-3)X«-3+ (,-2) Х-2" (,-l)X-J (" # J' 2' 3)-
X + 2Х2/
17) j?^_= -L[(w_-^_4 + (п з3^и_з- ^я_2+ ^.^ (w# !, 2, з, 4).
18) f^=_lln^.
20)
24)
26)
27)
28)
Г dx Г 1 2 1 J_ Х"|
J х2Хъ ~ a[2b2X2 +VTJt~aVx~~~br~ П~х~\
Г rfx 1 Г 2, X 2аХ X2 1
J х3Х Ьъ |_ х х 2x2J
Г ^х 1 Г 21 X а3х X2 ЗаХ1
Г dx 1 Г А" 4а3х а*х2 X2 4aXl
J ?3^- - И6" ln T+ "IT" ^+ 2^~ —1
92 ТАБЛИЦЫ
если знаменатель члена под знаком ? обращается в нуль, то такой член заменяется следующим:
Обозначение: А = bf - ад.
31) "Х+ dx = ~+ тг1п(/х + в\ 32)
ln{fx + g). 32) fj?r-WЧт
f f J (ax + b)(fx + g) A ax + b
х dx 1Ь а
33) - = — — In (ах 4- Ь) - — 1п(/х + а) (А # 0).
34) \(ах^х + д) = ~{ ^ + fin ?±|) (A * 0).
35) Г- ^-^-= » _L^n?±iL (а#Ь).
J (а 4- х) (о 4- х) (а — о) [о 4- х) (а — о) b 4- х
f x2dx 62 а2 Ь2-2ао
36) 7 Г77 о-= /^ ^ Г + 77 оп (Я + х) + Т. Т1~1п ° + х) (« ^ Ч-
J (а + х) (о 4- хJ F - а) (о 4- х) F - аJ (Ь - аJ
37) ^- г2-= ~ 2 ( + ) 4- _ з In а-~~- (а ф Ъ)'
,9Л Г xdx 1 / а Ъ \ а + Ъ а + х
38) J (а + хJ(Ь + хJ = (а^ЬJ"!, аТГ+ bTx~J + {a~=W ЬТ~ ( ^
39)
Г х2^х _ -1 / a2 b2 \ lab а + х
J (a + хJ(Ь + хJ ~ (а - ЬJ [а + х + Ь + х) + (а - ЬK П Ь + х (а * '*
Интегралы, содержащие ах2 + Ьх + с.
Обозначения: X = ах2 + Ьх + с, А = 4ас — о2.
г 2 2ах + Ь , А лч
I -^=-arctg -т=— (для А > 0),
40) J^J 1/Д ^
2 2ах + Ь 1 2ах + Ь1/
LArth ^± Lln1^ (для А < 0).
Г rfx 2ах + Ь 2а- Г dx v ллч
J х^= ~1пГ+ xj -Y (см- № 40)-
f dx 2ях + Ь / 1 За \ 6а2 Г dx
«>
Г х2 dx (b2 - lac) x + be 2c С dx
48) J IT- ¦ TEx + Tj X <CM- № 40)-
Cx2dx -x с Cdx (и-2N f xdx
49) j ^= Bл-3)а^-'+ B733Oj ^ - (krJ
fxmdx_ x"-1 (m-l)c fxw~2dx (n-m)b Гхт'^х
} J Хп ~ Bп-т- \)аХп~1 + Bл - m - 1)а J Jf" Bп - т - \)а J X"
{тф2п- 1; при т = 2м - 1 см. № 51).
Гх2п~Чх _ 1 С x2"-3dx с С x2n~3dx Ъ [x2n~2dx
J Xя a J X a J X a J X
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
93
52)
53)
55)
№40)-
f4-rx*!T-T-\ir (cM-
J хХ 2с X 2с J X
f dx _ 1 Ь Cdx I С dx
J xX" 2c(n - I)*" 2c] X" с ) хХ"-1'
J
1 Bи + m - 3)а С dx (n + m-2)b С dx
:xm-lX"-1 (m-l)c J xm'2Xn ~ (m-l)c J x^*" (W > j'
xmX" (m- l)cxm"
f ^x _ 1 Г f\ (/х + ^J~| 2gfQ - bf С dx
' J (/x + d* = 2(cf2-gbf + g2a)lJln X J + 2\cf2 - gbf + g2a) J X (CM' 9 '"
Интегралы, содержащие а2 ± x2.
Обозначения:
x
arctg —
a
. .x 1, a + x
Arth — = — In
a 2 a - x
x 1 x 4- a
Arcth — = —- In для знака — при I x I > a.
a 2 x — a
для знака +,
для знака — при \х\< а,
В случае двойного знака в формуле верхний знак относится к X = а2 -I- х2, а нижний — к X = а2 — х2.
5r±z- -v- <"''0)-
69)
72)
74)
76)
78)
80)
82)
x3dx
2X 4X2'
dx
1 1 x>
2A 2a4X T 2e6 X'
J x2A- " Л + a3 • ' J x2AT2 " a*x + 2a*X + 2a> K
f dx _ _LX ^x ^L_x JLy ™ f
J x2X3 a6x + 4a4X2 + 8«6X + 8a7 J j
Г <*x _ ! - ! i- x lnx onfA_
JxA 2a x zaA a A JxA
1
2a6v2
1
!a2x:
+
<
1
п6Х
1
2a4
+ д
lnx2
1
a*X:
Интегралы, содержащие аъ ± х3.
Обозначение: X = a3 ± x3; в случае двойного знака в формуле верхний знак относится к X = а3 + х3,
3 3
а нижний - к
4 dx
a° - x°.
1 . (a±xJ
85)
86)
Cdx 1
j 1Г= ± б?-
f х rfx I a2 x ax + х2 1
j IT" бТ1п (а±^ ± ^Т
1
2хха
___ | _ (CM. № 83).
2х х а
xdx
ldx 1
— = ±ylnX.
94
ТАБЛИЦЫ
2dx
: 89)
90) | ^-= ^ JL± ± I ^ (см. № 83). 91) I -^ = ^з-ln ^-.
dx 1 1 . x3 л Г dx 1 1 Cxdx
92)
94)
95)
1 x3 f
з^]п1Г 93) J
1 f
(cm. № 85).
96) ^3^2-= -
Интегралы, ее
Tn- v <CM- №83»-
Интегралы, содержащие a4 + x4.
[ dx 1 х2 + ах)/2 + а2 1
1/2
99)
f x2rfx 1 x2 + ax)/2 + a2 1
Jfl4x4 4a |/2 x2 - ax ]fl + a2 2a j/2
arctg
j/2
—y
Интегралы, содержащие а4 — х4.
f dx 1 , а + х 1 х Г х dx 1 а2 + х:
101) -г т= —т-1п + —r-arctg—. 102 —. г = -^-ln —2
J а4 - х4 4а3 а - х 2а3 а J а4 - х4 4а3 а1 - х
ЮЗ) f -P^r = tUii "^ - -Larctg -. 104) Г -^^ = - 1 In (а4 - х4).
J а4 - х4 4а а - х 2а а J а* - х 4
Некоторые случаи разложения дроби на элементарные.
105)
106)
где А =
107)
где А =
108)
1
1
Y_J
(а + bx) (f + gx) fb-ag\a + bx f + ах /
1 ABC
-+ —+
(х + а)(х + b)(x + с) х + а х + fc х + с'
1
Л В С D
-+ т-+ +
1
x + а х + Ъ х + с х + d'
1
(Ь - а)(с - a)(d - а)' (а - Ъ)(с - b)(d - Ъ)
1 1/6 а
и т. д.
fb-ag \a
f + ах2 /
1.1.3.3.2. Интегралы от иррациональных функций.
Интегралы, содержащие ух и а2 ± Ь2х.
Обозначения :
Y =
arctg -
а
для знака +,
1 а + Ь]/х
— In j=r для знака —.
В случае двойного знака в формуле верхний знак относится к X = а2 + b2x, a нижний -«¦ к
f 2 1/? 2а2/^ _ 2а3 v
= а2 — Ь2х.
111)
)/х^х
_ _
Ь2Х ~ аЬъ
+ ^У- но) J
У 112)
"?^х 2)/? За2)Д За
"х2""" ±"ьуЗГ+ ь4х VY'
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
95
113)
115)
ДГ|/х" ab '
dx
—-Y. 114)
Г dx _ 2 2b
J xTx^'a^Tx^^
116I ]^W=~^n^+~^^+~^
Другие интегралы, содержащие ух.
f |/x dx 1 х + a l/
117) -Л 5-= 7=-ln 7= т^ ~7=-arctg —= .
'Ja4 + x2 2a)/2 x-al/2x4_a2 a]/2 a2 - x
Г dx 1 b^J
f l/^dx 1 e + l/x 1 /x Г dx 1
119) -^ r=T-ln -r arct% —' 120) 7-= г-5-li
J a4 - x2 2a a - j/x « « J (a4 - x2) ]/x 2a3
a]flx
V
l/x
Интегралы, содержащие ]/ах + b.
Обозначение: X = ax + b.
121) |/Xdx= —)/I3.
J 3a
123) |x2l
126)
124)
2Ca2x2-4abx + 8b2)
15?
127)
128)
129)
130)
131)
133)
135)
138)
139)
142)
143)
J X]/X
J X2/X = ~ ~b^~ 2b) x]/x
I
I
ДЛЯ Ь < 0.
а С dx
X X
dx
(см. № 127).
:=- (см. № 127).
(cm. № 127).
_ Bn-3)af dx
¦1"BH-2)bJx-il/F Ш)
xl/x
(см. № 127).
137)
(см. № 127).
J x(/x3 bj/jf |
Jx2l/X3 bxj/x Ь2]/Х 2b2 ) x]/x
.27).
ГЛГ"/2^х 2ХИ/2
J -7— "V-
х(п~2I2
С dx 2 If
J 35^" (W-2)b^-2v2+Tj
dx
96
ТАБЛИЦЫ
145)
' dx _
x2Xnl2 " bxX(n
1 па Г dx
7^2I2 ^"J xXn/2 •
Интегралы, содержащие у ах + b и |//х + g.
Обозначения: X = ax + b, Y = fx + g, A = bf - ag.
146)
147)
149)
150)
151)
152)
153)
154)
dx
arctg
У-5
для af < О,
для
dx
Y]/X
2a/
arctg
i__ (тас № 146). 148)
для Д/ < 0,
Г dx
2J/X
i ln f]/x - |/a/
k /a? n 77?T7a/
l/xy
CyXdx 2VX А С dx
для А/ > 0.
(cm № 146).
(cm. № 146).
и. № 149).
j 77
155, J^y-Ac
' +
(см. М .53).
Г
Интегралы, содержащие у.а2—х2.
Обозначение: X = а2 — х2.
157) \]/~Xdx = — ( x l/T + a2 arcsin — \ 158) \x]/rXdx=
J 2 V aJ J 3 ^_ -_
159) x2l/x^x= -—[/X3+ —xl/x +a2 arcsin— . 160) x3 l/x dx = V—-- - a2 ——..
J 4K 8\ a/__J 5 3
161) I Jl - = |/x-aln fl + ^-. 162)
- - arcsin —.
163)
[]fxdx ]fx 1 fl + l/x 1Л„ Г rfx .x _ fxrfx /-
-—r—= - -—iz--\ In . 164) -7=^= arcsin—. 165) -T=^= —VX.
J x3 2x2 ^ 2a x } ]fx a ' J \/X V
166) |
x2 dx x
~7F= ~T
а2 . x t^t
—-arcsin—. 167)
2 a ' J
a
V 2
—7=--= a2
\fx 3
168) f-iL-^- —In a+vX . 169)
J xl/x ax J
л J x
a +
l]fx
2a2 x2
171)
fl/F^-Uxl/x1* ^/X+ ^
-^-Y 172)
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
97
173)
xj/x1 ^xj/x3 a4xj/x
a6 х
i
6 24
174) \х*]ГТих=Ц- '
]/~Xldx l/x3 ,_ a + l/x
= + a2/X-a3ln - .
176)
-Vх 3a2 . x
агсяп—.
2 2a
fx 3a a- "~
178)
x Г xdx 1
- 179) J
180) f^-rAr-"«in4-. 181)
182)
184)
/X1
* dx 1
Г
J xTj
183)
Интегралы, содержащие ух2 + a2.
Обозначение: X =x2 + a2.
185) /X rfx = у ( x /X + a2 Arsh —j + С = у [x /x + a2 ln(x + /x)] + d.
186)
187) fx2
188) |x3
190)
191)
193)
195)
197)
\x]/~Xdx = — l
+ a2 Arsh—) + С = x/^1 ~ -^-[x/x+a2ln(x-H
йу4 о
x x
+Arsh —
x a
[VXdx _
J x2 -~
C]fxdx = _ /X^_ j.
J X ZX Zfl
+ln(x
192)
194)
С - f ^ - ^.
C,
f <** _ K^ 19g) f dx _ _^X_+ _l_in a + /X
J x2l/x a2x' J x3l/x 2a2x2 2a3 x
200)
201)
202)
jx
a x
——Arsh 1- С =
16
Arsh
24 16 16 a
a4xl/x a
h
4 И Н. Бронштейн, К. А. Семендяев
98
ТАБЛИЦЫ
204)
][X ) x]fx3 a2/* a3
212>
f
dx
dx
3 3 а + 1
2a2x2l/* 2а4]/* 2а5 х
Интегралы, содержащие ух2 — a2.
Обозначение: X = x2 — a2.
C]/Xdx ][X x ][X r-
K 2 -= - +Arch — + C= - + \n(x+yX)+Cl.
214)
215)
216) |х31/Л:Лх
218)
219)
221)
223)
225)
227)
213) j/X rfx = у ^x /X - a2 Arch ^ + С = у [x /^ - a2 In (x + j/x)] + Cx.
[x2 fxdx = ^/^ + -^fx V* ~ al Arch -) + С = ?-\fx* + -^-[x/x -a2\n(x + /*)]
J 4 o\ a/4 о
x3 yXdx «J-—+ —^ . 217) N^ =J/\Y-
aarccos—.
~ arccosA
f
= Arch| + С =ln(x
Jx!l/jf a2x
a2/x. 224)
226)
2a2x2 2a3
^-Arch ^-) + С
228)
+
230)
Г
\x3
232)
cldx
Зх
231)
Ъа2
\
Зх
За2
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
99
233)
235)
r\Z~X*dx ]fTb
J — 1^
* За о
— тага:05т 234)
1 .1 а
7= =-arccos —.
a2\fx a2 x
7=^ -—?=-— —-г-arccos—.
2a2x2]/J 2aA]/X 2as x
Интегралы, содержащие у ax2 + bx + с. ^а
Обозначения: X = ax2 + bx + с, A = Aac —b2, k= ——.
A
241)
242)
\w"
1
j~AnB]/a~X +2ax + b) + С для a > 0,
1 9/jv 4- h
для a > 0, A > 0,
для a > 0, A = 0,
для a < 0, A < 0.
I/A
lnBax + ft)
1 . 2ax + b
arcsin
Г dx =2t
J x"j7F
744^ Г dx _ 2Bax + b) 2fc(n-l) Г
] J л:Bи+1)/2 "Bп-1)АХBи-1)/2 + 2n - 1 J
f ^_ Bax + b)/x l Г
за|/х
dx
^r+2/cJ.
245)
246)
247)
248)
249)
251)
253)
255)
256)
257)
4*
fe 241).
J7F- « a"J
4a(n+ 1)
J
(см. № 241). 250)
{
Bb2-4ac)x-
aAj/T
dx
(см. * 241).
(см. № 241).
(см. № 246).
\xXyXdx= —j — XyXdx
Г yBn + 3)/2 l /•
xXi2n + l)l2 dx = — ХBи+1)/2 dx (см. №
J B« + 3)a 2a J
fx2 /X^x = (x - pi ^+ ^Iz^i Г
J \ 6a/ 4a 16a2 J
248).
(см. № 245).
100
ТАБЛИЦЫ
( 1 , 1]fcX 2c \
_ln — + — +ь) + С
]/c \ * x J
258)
dx
1 bx + 2c
7--Arsh ?=-—+ С i
]/ ]/X
1 bx + 2c
1 bx + 2c
arcsin —,
/
259)
260)
261)
С dx _ ]fx b Г dx_
J x2 l/x ~ ex 2c J x /X
для с > О,
для с > О, ,Д > О,
для с > О, Д = О,
для с < О, Д < О.
(см. № 258).
(см. № 241, 258).
(см. № 241, 258).
(см. № 248, 260).
f YBn+l)/2 yBn+l)/2 h Г Л уBи-1)/2
262) dx = Д- + 4- Х<2и>/2 dx + с dx
J x 2n + 1 2 J J *
Интегралы, содержащие другие иррациональные выражения.
dx
265)
f , f - ^-/ax2 + Ьх. 264) f
J x]/ax2 + bx bx v J
Г
J ]
x — a
, = arcsin .
)/lax -x2 a
]/lax-
266) Г]/lax - x2 dx = ——
, / =¦ . x — a
— — у lax — xz + a arcsin .
; - x^ 4- -z-arcsin
f
J (ax2 +
b)]/fx
xl/ag -bf
r arctg ——= {ag - bj > 0),
2]/b]/bf-ag
In
" V < 0).
x2 + g -
(и+1)а
269)
к
(n-\)a
/ax 4- b
x l/x" + a2
27.)
!-,
]/xn - a
2 а
= —arccos -—-
267)
268)
270)
272) .
J у a3 - x
Рекуррентные формулы для интеграла от дифференциального бинома.
273) хм (ахп + b)p dx = ! xm + 1 (ax* 4- Ь)р + npb хт (ах11 + b)"'1 dx
J т + ир+lL J J
= -—; — — xm+1 (axn + b)p+1 + (m 4- n + np + 1) xm (дхи 4- h)p+1 dx
bn (p 4- 1) |_ J J
= l |xw + 1 (ax" 4- b)p+1 - a (m + n 4- ир 4- 1) j xm + n (ax* 4- b)p dx
= — xm-n+l ^axn _|_ ^)P+1_ (m _ и + 1)^ ХП'~"(ДХИ + b)pdx .
a(m4-«p4-l)j_ J J
1.1.3.3.3. Интегралы от тригонометрических функций.
Интегралы, содержащие синус.
sin
274) | sin axdx = cos ax. 275)
sin2 a.
ix dx = -— x sin 2ax.
2 4a
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 101
276) sin3 ax dx ^ ~ - cos ax + —cos3 ax. 277) sin4 ax dx = — х — -—sin lax + ^— sin 4ax.
8 4а 32а
Jsin" ах cos ах п — 1 Г
sin" ах dx = — ь sin" ax dx (п > 0 — целое).
па п J
Г sin ах х cos ах Г . 2х / х2 2 \
279) х sin ах dx = = : 280) х2 sin ах dx = —=- sin ах - =- с
J a2 a J а2 \ а аъ)
Г э • , П*2 6 V [х3 6х\
х sin ах dx = —= j- sin ах — —г cos ах.
J \ a2 aAJ \а a3 J
х" sin ах dx = — -—cos ах + -- х"~l cos ах dx (п > 0).
J a a J
281)
282)
283)
284)
285) I "'~"~-dx =
Г sin ax , sin ax Г cos ax dx
- -dx = + a ¦— (cm. № 322).
J x2 x J x
Г sin ax 1 sin ax a f cos ax ,
dx- -j-+ -T-dx (cm. № 324).
J xn n - 1 x" n - 1 J x"
286) = \cosGcaxdx = —In tg =—In (cosec ах — ctg ах).
J sin ax J а 2 а
f dx 1 „ ч Г dx cos ах 1 , ах
287) -у--= ctg ах. 288) — = - ^—^^ + -—In tg -—-.
J sinz ах a J sinJ ax 2a sinz ax 2a 2
f dx I cos ax n — 2 С dx
289) - = -. -^-—-, + -r—-7 {n > 1).
J sin ax a(n — 1) sin ' ax n — 1 J sin ax
f xdx 1
----- - 2
J sin ax аг
f xdx 1 / (a
290) ----- - 2~[ax+ W
J sin ax аг \ 3-3!
1 / (axK 7 (axM 31 (axO 127 (ax)
[ax+ W+ + +
291)
292)
Г x ^/x х 1
-.- з = - — ctg ax H r In sin ax.
J sm2 ax a a2
С х dx х cos ax 1 и — 2 Г х dx
I = — — |- (п > 2).
J sin" ах (п — 1) a sin" ах (п — \)(п — 2) a2 sin" ах п — 1 J sin"" 2 ax
С dx 1 / п ах \ С dx 1 / к ах \
Ш) j гжг= -тЧ" т) Ш)) ггж-аГ-т1Чт+ т-}
295) Г **е_. = _ ?tg(« _ ef\+ 4-|„cosf^--
J 1 + sin ax a \ 4 2 / a2 \ 4
f x dx x I n ax\ 2 , . / я aj
296) r- - = ctg I -- - - — -+ — In sin — - -
J 1 — sin ax a \4 2 ] a \ 4 2
, sin ax dx 1 / n ax
297) =±x+._tg—+ —
1 1 ± sin ax a \4 2
298)
dx 1 / n _ ax \ 1 ax
sin ax(Y± sinVx) = ~a '8\T + ~2~) + ~a 'ё "Г
f _.._*___-_
J A + sin axJ
, v.v 1 / n ax \ 1 % f n ax
W I Г, -~..-.Ж = - 2aM-4 - T - ^ ( 4" " T
fsin t tit
назы
*) OiipciejiemibiH иигс!рал называется интегральным синусом.
x3 x5
+
*) В„ чисча Ьсриулпи
102 ТАБЛИЦЫ
300) J A-ш«г гг
„<4 f sin axdx 1 /я ах\ 1 3/я ах
Г sin ахdx 1
j (l-sina*J = " 27
Jl+sm2ax 2j/2a
„л/чч Г sin ахdx
302) j
dx 1
5 = — tg ax.
cos ax a
305) f sin ax sin bx dx = ^ ^X - S1" ^ + *j[ * (I a I ^ 1 fe <> ПРИ l«l = lfcl CM- № 275)-
)x
2(a-b) 2(a + b)~
306)
307)
f_*L
J b + с sin
arctg ; — (Ь2>сг),
1\/ьг-с2 УЬ1 - с2
1 -In
l/c2-ft2 btg^
Г *inaXdX -?L-!L f *^_ (см. № 306).
J Ь + с sin ах с с J b + с sin ах
308) f -, .^ . . = -i-ln tg H. _ ^ f *E ,CM. № 306).
J sin ах (Ь + с sin ax) ab 2 b J b + с sin ax
f ^x - с cos ax Ь Г dx
J (b + с sin axJ ~ a(b2 - c2) (b + с sin ax) b2 - c2 } b + с sin ax
Г sinaxdx _ b cos ax с Г dx
J (Ь + с sin axJ ~ a (c2 - b2) (b + с sin ax) c2 - b2 J b + csin ax
Г dx 1 l/b2 + c2 tg ax
311) -= ^Ц = arctg I —J? (b > 0).
J b2 + c2 sin2 ax b]/b2 2 b
Ц = arctg I —
sin2 ax ab]/b2 + c2 b
dx 1 ]/b2 - c2 tg ax
b
l/c2 - b2 tg ax + b
In V; (c2 >b\b> 0).
2ab]/c2-b2 J/c2-b2tgax-b
Интегралы, содержащие косинус.
313) | cos ax dx = ~ sin ax. 314) | cos2 ax dx = — x + ——sin 2 ax.
cos axdx = — sin ax. 314) cos2 с
J a J
315) cos3 axdx = — sin ax sin3 ax. 316) cos4 axdx = — x H sin 2 ax + ——- sin 4 ax.
J a 3a J 8 4a 32a
-,„-,4 f « , cos" ax sin ax n-1 f _,
317) cos"axdx= 1 cos" 2axdx.
J па п J
.... f , cos ax x sin ax f , 2x /x2 2 \ .
318) xcosaxdx= 5 h . 319) \x2 cos ax dx = —=- cos ax -b I r- sin ax.
J a2 a J a2 \ a a3 /
„m f 3 j {I*2 6\ /x3 6x\ .
320) x5 cos ax dx = —= j- cos ax + r sin ax.
J V e « / V « « /
321) x"cosaxdx= X SmaX -— x" sinaxdx.
J a a J
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
103
~~„ч i cos ax dx cos ax f sin ax dx
323) = = a (cm. № 283).
1 x2 x I x
(* Ф 1) (см. № 285).
324) J x15 = " (w-l)x"-1 " ^rj Xя
325) —-—= sec ax dx = — In tg ( ^-+ ~ ) = — In (sec ax + tg ax).
J cosax J a \ 2 4 / a v
„~,ч С dx 1 лл„ч С dx sin ax 1 , /я ax \
326) —= =—tgax. 327) = = = + —lntgl—+ — .
J cos2 ax a * 'J cos3 ax 2acos2ax 2a B\4 2)
dx 1 sin ax и - 2 f dx .
328) —- = —; —n 1 г ъ (n > ¦
J cos"ax a(n - 1) cos" x ax n — 1 J cos"~2ax
[ xdx = 1 Г
J cosax a2 [ 2
¦
4-2! 6-4!
¦ в1(ах)8 I 1385'ю'10 , .
86! 108!
8-6!
10-8!
Bn + 2)Bn)!
,
.,л. С xdx х 1
330) —5 =—tg ax + -=-ln cos ax.
J cos2 ax a a2
331)
332)
xdx x sin ax 1
cos" ax (n — 1) a cos""i ax (n — 1) (n — 2) a2 cos" ax
dx
1 ax
cos ax a 2 '
J;
I
f <*x 1 ax „,„ f
Jrr^x-=Ttgi- 333)Ji3
334) f —?*E -tg ^+ 4-lncos " 335) f ^
J 1 + cos ax a 2 a2 2 J 1 -
__„ f cosaxdx 1 ax _л_ч Г cosaxdx
336) =x tg—-. 337) =-
J 1 + cos ax a 2 J 1 - cos ax
«.„Лч f dx 1 , /и ax \ 1 ax
338) г- r- = — In tg — + -^r- tg ^r-.
J cos ax A + cosax) a \4 2/ a 2
лллч Г ^х 1 . /it ax\ 1 ax
J cos ax A-cosax) a \4 2/ a 2
n-2 С xdx
г s-2 in > 2).
n- 1 J cos" ax
cdx x ax 2
= ctg -r- + -г
cosax a 2 a2
1 ax
a ° 2 '
ax
dx
ax 1
344)
346)
347)
1 ax 1 з ax f rfx . 1 ax 1 3
=2a-tg^-+6a-tg T- 341)J d-cosa^'-^^T-^8
1 ax 1 , ax Г cosaxrfx 1
^'8— frT'g T- 343)J (l-cosax)^27C
. 345) f, dX2 = f ,
' J 1 - cos2 ax J si
ax 2]/la
1 + cos2 ax
f__*L
J b + с cc
Ь + с cos ax
|; при
см. № 314).
-arctg
> c2),
¦) Определенный интеграл-
(х>0) называется интегральным косинусом и обозначается Ci(x):
где С — постоянная Эйлера.
**) Е„ - числа Эйлера.
104 таблицы
f cos ax dx x b С dx
348) = - (см. № 347.
J Ь + с cos ах с с J b + с cos ax
349) f * г- -1-lntgf ^+ f) -^ Гт—^ (см. № 347).
J cos ax (b + с cos ax) ab \ 2 4 J b ] b + с cos ах
350) f '* = """" -* f *E (см. № 347).
J (b + с cos ахJ а (с2 - Ь2) (Ь + с cos ax) c2 - b2 J b +- с cos ax
Г cos axdx b sin ax с С
351) r=-= ——= =7— —— -y 5-
J (b + ccosaxJ a(b2 - с2)(Ь + с cos ax) b2 - c2 J b +
(cm № 347).
ax
353)
— с" cos ax
arctg
ab ]/b2 - с2
1 b tg ax - ]/c2 - b2
In — \ (c2 >b2, b> 0).
^ 2ab ]/c2 -b2 b tg ax + ]/c2 - b2
Интегралы, содержащие синус и косинус.
354) sin ax cos ax dx = —- sin2 ax. 355) sin2 ax cos2 ax dx = — .
J 2а J о 32а
356) sin" ax cos ax dx = —-. — sin" +1 ax (n Ф — 1).
Г 1
357) sin ax cos" axdx = -. — cos"+1 ax (и # — 1).
Г sin"~1axcosw + 1ax n — 1 Г . , .
358) sin"axcosMaxdx= - a(n + m) + ^~+~m~\ «*cosm axdx
(понижение степени л
sin"+1axcosm~ * ax m — 1 Г . „ M _,
= -. г 1 sin ax cos ax ax
a (n 4- m) n + m J
(понижение степени т
359) [-. =-lntgax. 360) f-r-j-^ = - [in tg(^ + ^-) - -Д-
J sin ax cos ax a J snraxcosax a |_ \4 2 ] sin a.
361) Jsi
4
363) Г —3 = — fin tg ax + -—\ \ 364) I . 2 dX ~2 = - -2- ctg 2ax.
J sin ax cos3 ax a \ 2 cos2 ax J J sin2 ax cos2 ax a
„^ Г dx 1 Г sin ax 1 3, fn ax\~]
365) L<*-2 = = — г : +—lntg — + •
J sin axcosJax a [_ 2 cos ax sin ax 2 \4 2 /J
„,,. f dx 1 / 1 cos ax 3, ax \
366) ^-* i = — ^—-^ + — In tg -— .
J sinJaxcoszax a \ cos ax zsm'ax 2 2 )
367) I ~ ^4 = —t ,/ n-i + I d-^i (" ^ l) (CM- № 361' 363)-
J sin ax cos ax a (w — 1) cos ax J sin ax cos ax
Г . я dX = -. *. w_1 + I — n_2dX (л Ф 1) (cm. № 360, 362).
J sin ax cos ax a(n — l)sin ax J sin ax cos ax
Г dx _ 1 1 n + m-2 С dx
J sin" ax cos ax a(n-l) shV^axcos1" ax n-\ J sin" ax cosm ax
эниже]
J sir?
368)
369)
(понижение степени и; и? > 0 и и > 1),
1 1 n + m-2f dx
a(m-l) sin"axcosWI~1ax m-1 J sin"axcosm~2ax
(понижение степени ш; я > 0 и w > 1)
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
105
sin ax dx
1 1
= — sec ах-
a cos ax a
sin ax dx
- г + с = тг" tg2ax + d.
2а cos2 ax 2а
1 „__ С sin2 ах dx 1 . 1 /тс ах \
——-~х—-. 373) = sin ах + — In tg — + — .
а (и - 1) cos" l ax J cos ах а а \ 4 2 )
1 Г sin ax 1 /n ax\l
"a"L2cos2ax ~TlntgVT+ ~Y)\
1 С dx
" 1 ax n — \ J cos" 2
a(n-l)cos"
(см № 325, 326, 328).
378)
cos" ax
379) [*^-dx-.
J cos ах
1 /sin2 ax \ f sin3 axdx 1 / 1 \
— — + in cos ax . 377) = = — cos ax + .
a \ 2 J J cos2 ax a \ cos ax J
1 Г 1 1 1
7L(n-l)cos'-ra7 " (n - 3) cos"" 3 ax J (" * *' " # 3)'
sin"~1ax f sin" ax dx
+ (n # 1}>
a(n — 1) J cos ax
380) I -
1
Г sin"
^-dx
ax
\?П tF IK
sinn+lax n-m + 2 Г sin"ax
- — _ , - I _ _ u
a(m — ljcos 'ax m—\ J cosm z ax
sin" ax n-1 Г sin" ax dx
a(n — m) cosm ~1 ax n — m J cosm ax
l axdx
a(m — l)cos'
x n — 1 Г sin" l a
^a~x ~ ^~ГJ ^os-2
381)
382)
cos axdx
Г cos
J si
siir ах
cos ах dx
Г cos
__
J si
1 1
—. _ cosec ах.
a sin ах а
1 , ctg21
—
2a sin2 ax
f c
386)
J
ax dx
387)
cos3 axdx
\( ax\ С cos2 a
— cosax + lntg-— . 385) —r~i
a\ 2 ) J sin3
С
J
. \
sin ax .
J
383)
axdx
ax
f cos a
—:
J sin"
1
1
г
n — 1 \ a sin
1 /cos2 ax . \
— — + In sin ax
a \ 2 J
384) fcos2flX^
J sin ax
Г cos2 a
J "lin7
!
f cos" ax cos"~! ax Г cos" ax dx
390) — dx = — -- + : (л Ф 1).
J sin ax a(n - 1) J sin ax
* cos" + 1ax n — m + 2 С cos" ax d.
a(w — ljsin ax m— 1 J sinm~2a.
cos""г ax n — 1 С cos"
a (n — m) sinm ~l ax n — m J si
a(« - l)sin" ! ax '
2a~Vsin2ax "" *° 2
1 / cos ax , ax\
Ilntg—-.
2 /
f cos3 axdx 1/. 1 \
388) —r-5 = sin ax + .
J sin2 ax a \ sin ax /
391)
cos" ax dx
ax dx
" 2 axdx
{m Ф n),
Г
J ^nTx
) ~ ~
092)
393) J^f—^-T
-ЗПДЧ I
J cosax(l ± cosax) a
sin ax dx
cos
a(m — l)sin'
1
\n l ax n-1 f cos" 2 ax dx
-—^п — —r—r-2 (m Ф 1).
)sm ax m— 1 J sinm ax
1 ax
2aA + cos ax) + 2a"lntg ~T
1
J
2a A ± sin ax) 2a
395)
n_ ax\
4 + 2 /
J si
cos ax dx _ 1 1 ± sin ax
sin ax A ± sin ax) a sin ax
cos axA ±sinaxj = 2a(I ± sin ax)
Г
} J
397) Г ^1аЛ.^ = _
J sin ax A ± cos ax)
1
1 / я ах \
± 2a~ " tg \T + T"/
1 1 ax
2а(Г±Гсо8 flxf ± 2я tg ~2~'
106 ТАБЛИЦЫ
398) f^-ELfi
J sin ax ±
± cos ax 2 2a
axdx x
= +
sin ax ± cos ax 2
x 1 , , .
= — + —— In (sin ax ± cos ax).
С cos axdx x 1 , .
399) = -f — + -—In (sin ax ± cos ax).
J sin L —° — ° °"
400) f_—? ',„,,(« ±JL\ 40!) f- *L- ±Jlnfl±tg^\
J sin ax ± cos ax a 1/2 \ 2 8 / J 1 + cos ax ± sin ax a \ 2 /
„ f dx 1 , ax + 0 . с с
402) — = Intg , где sin0= tg0 = —.
J 6 sin ax + с cos ax a]/b2 + c2 2 \/b2 + c2 b
*~^ f sin axdx 1 , ,, „ ,ллч Г cos axdx 1 ,
403) = ln(b + с cos ax). 404) = —ln(b + с sin ax).
J о + с cos ax ac J b + с sin ax ac
405)
d(x^)
С dx С \ V
— = , где sin 0
J Ь + с cos ax + /sin ax J b +/c2 +/2sin(ax + 0)
(см.-№ 306).
dx 1 (с \ С dx I ctgax + b
l2 2 2 - 2 = ~Г~ arctg —tgax . 407) —= 5 , . , = In .
о cos ax + с sin ax aoc уь ) J b cos ax — с sin ax 2aoc ctgax — b
408) sin ax cos bxdx= ^ t M ^—^-^ (a2 / Ь2; при a = b см. № 354).
406)
Интегралы, содержащие тангенс.
409) Г tg ax dx = - — In cos ax. 410) | tg2 ax dx =
J a J
411) tg3 axdx = — tg2ax + — lncosax. 412) tg"axdx=— —-tg" ax - tg" axdx.
J 2a a J a(n - 1) J
A ,4f J ax3 a3x5 2a5x7 17aV 22иB2и - OB.a2""^2"*1
413) jxtgaxdx =— +_г+-5Г+-1_-+...+ ____ +...•).
414) |^XA=ax + ^L+ ^L+ilg- + .,.+ ^^^ff' ' +...*)¦
416) I ,„ ^7. t = ± у + 2a"ln(sin ax ± cos ^ 41?) I /ЛГТ~ = ^ + ^rln(sin ax ± cos ax).
Интегралы, содержащие котангенс.
418) ctg ax dx = — In sin ax. 419) ctg2 axdx= -
J a J
420) fctf «Ac = - ^^- '"SinaX. 421) fctg"ax^ = - C'f"aX- f ctg-axdx (« # 1).
J 2a a J a(n - 1) J
22nBna2n~lx2n+i
—-...- g>| + ^ ...*).
Г ctg axdx _ 1 ax (axK 2 (axM 22nBn(axJ"-1
}J x " ax 3 135 4725 '" Bn - l)Bn)! "' ''
424) f?^i
1.1.3.3.4. Интегралы от других трансцендентных функций.
Интегралы от гиперболических функций.
426) sh ax dx = — ch ax. 427) ch ax dx = — sh ax.
J a } a
428) sh2 axdx = —— shaxchax - —-x. 429) ch2axdx = —shaxchaxH x.
J 2a 2 J 2a 2
f?^dx=--i—ctg-ax («#-1). 425) f —^f— = f^L (cM. № 417)
J sin2 ax a(n+l) J 1 ± ctgax J tgax ± 1
*) В„ — числа Бернулли.
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 107
—sh" l ax ch ax sh" 2 ax dx (n > 0),
430) |sh"<«<<x=< a" j " 1+2 Г
sh"+1 axchax sh"+2 axdx (n < 0; n Ф -1).
a{n + 1) n + 1 J
{1 л — 1 Г
—sh ax ch"" * ax + ch" ax dx (n > 0),
an n J
1 n + 2 f
shaxch"+1ax + ch"+2 axdx (n < 0; л # -1).
Ф + 1) и + 1 J
432) |-^-=— lnth^. 433)
J shax a ^
434) xshaxdx = —xchax 2-snax- 435) xchaxdx = —xshax ~i
' J a a2 J a a2
436) th ax dx = — In ch ax. 437) cth ax dx = — In sh ax. 438) th2 ax dx = x -
a
439) cth2axdx = x . 440) sh ax sh fex dx = —= ^(a sh fex ch ax - fe ch fex sh ax) (a2 ф b2).
J o, J a — о
441) ch ax ch fex dx = —~ -^(a sh ax ch fex - fe sh fex ch ax) (a2 Ф fe2).
J a - fe
442) ch ax sh fex dx = —^—-^-(a sh fex sh ax - fe ch fex ch ax) (a2 Ф fe2).
443) I sh ax sin ax dx = ——(ch ax sin ax — sh ax cos ax).
1 2a
444) I ch ax cos ax dx = —(sh ax cos ax + ch ax sin ax).
445) I sh ax cos ax dx = —(ch ax cos ax + sh ax sin ax).
1 2a
446) I ch ax sin ax dx = —— (sh ax sin ax — ch ax cos ax).
.j.
Интегралы от показательных функций.
447) \eaxdx = —eax. 448)
[xeaxdx = ^-(ax - 1). 449) f
JV
453) l^^-i-ln-
456>Jfe?^
yj (ac>0),
1
2a]/-bc
In \ (fee < 0).
*) Определенный интеграл —dt называется интегральной показательной функцией и обозначается Ei(x). При х>0
интеграл расходится в точке t = 0; в этом случае под Ei(x) понимается главное значение несобственного
интеграла (см. 3.1.7.7):
j ?*-с + ь.|х 1 +
где С - постоянная Эйлера.
108 ТАБЛИЦЫ
Г „«* е~ Г^пХ*-?Ш-± \™- (см. » 45,).
J A + ахJ сг{\ + ах) J а я J х
Г еах С е"х
459) ?вдс sin bx dx = —2 тт{я s^n Ьх — Ъ cos hx). 460) ?»"* cos frx dx — -j y(° cos ^x + ^ s'n
461) eax sin" x dx = — -^—х-^-(л sin x - и cos x) + —?- f ?ядс sin" x dx (см. № 447, 459).
J a2 + n2 a2 4- и J
462) ea* cos" x dx = C°S—^-{a cos x + и sin x) + , ~ , eax cos" x dx (см. № 447, 460).
J a2 + n2 a2 + n2 J
f хея* гах
463) xeflX sin fex^x = —> rr(« sin bx — b cos /?x) r ;-т^-Г(«2 — ^2)sin frx — 2аЬ cos hx].
J a2 + b2 {a2 + b2J
464) xeax cos /?x ^x = 2 2 (a cos bx + b sin bx) - —у—-^rj- [(a2 - /?2) cos />x -f 2«b sin bx].
Интегралы от логарифмических функций.
465) Jlnx^x = xlnx-x. 466) J(lnxJ^/x = x(lnxJ -2xlnx + 2x.
467) J (In xK dx = x (In xK - 3x (In xJ + 6x In x - 6x.
468) J (In x)" dx = x (In x)" - n j (In x)"-l dx (n Ф - 1).
470)
471,
472)
m+1 Г lnx 1 ~|
\_m 4- 1 (m 4- IJ J
xm (In x)" dx = ' - - xm (In xf~ l dx (m Ф - 1, л ф - 1) (см. № 470).
J m+1 m 4- 1 J
f(lnx)n (lnx)" + 1 Г lnx lnx 1
dx = —. 474) —zrdx = - j-- -= г аи Ф 1 .
J x л 4- 1 J xm {m-\)xm x (m - VJ xm x
С xm dx С е~у
476) = dy, где j; = - (m + l)ln x (см. № 451).
J lnx J )i
f ^ ... -' p-4
J х'(\пхУ х'-Чп-ЩпхУ1-1 n-\ J
(л#1).
IX) Xr {П — 1ДШЛ|" П — 1 J Xr ^111 X)"
8)J X 18 900 ---„Bn+l)! •¦ }'
483) I In cos x dx = -
484)
6 60 315 иBи + 1)!
7x5 22"B2"~1 —
+ + ^
9 450 л Bл +
485) | sin In x dx = —(sin In x - cos In x). 486) cos In x dx = —-(sin In x + cos In x).
Г-4-назы,
Jlnr
*) Определенный интеграл называется интегральным логарифмом и обозначается li х При v> 1 интеграл расходится
J 'n'
в точке /=1; в этом случае °под интегралом понимается главное значение несобственною интефала Интегральный
логарифм связан с интегральной показательной функцией1 li.v = Ei (In x).
**) В„ — числа Бернулли.
ТАБЛИЦА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВШ9
Г In A + х) х2 х3 к"
487) J ~——dx = х - J2 + зг- ••• + (- I)" ^ + •••
Интегралы от обратных тригонометрических функций.
С х х / Г х (х2 а2 \ хх
488) arcsin — dx - х arcsin — + ]/а2 - х2. 489) хarcsin — dx - I — — 1 arcsin— + -r
J a a J я \ 2 4 / a 4V
490) x2 arcsin — dx = —arcsin—- + — (x2 + 2a2)]/a2 - x2.
J a 3 a 9
Г
J
arcsin— dx 3 5
Г a x 1 x3 1 • 3 x5 1 • 3 • 5 x
} J + + ^
x a
arcsin — dx
«arcsin — dx /~2 j
492) = arcsin In — 493) arccos — dx = x arccos ]/a2 — x2.
J x x a a x J a a r
I X ( \ CL \ XX /
494) x arccos —dx = I — I arccos у a2 — x2.
J a \ 2 Л / a 4 ?
r „3 „ <
x2arccos — dx — — arccos (x2 + 2a2)]/a2 — x2.
J a 3 a 9 y
Г-
I"
495)
J
x
, arccos — dx ,
. а _л _^ 1 x3 1-3 x5 1-3-5 x7
496) | _ __ 2 ,nx_ ^ _ _.___ _______ ______
,7^ 1 x 1 a + ^x2
497) =- arccos 1 In .
1 x2 x a a x
I x x a I x \ x cix
498) arctg — dx - xarctg -1п(я2 + х2). 499) xarctg — dx = -^(x2 + a2)arctg .
Ja a 2 J a 2 a 2
x x3 x ax2 fl3
500) I x2 arctg — dx = — arctg —- + —In (a2 + x2).
1 a 3 a 6 6
501)
1-
Г x xn + 1 x а С xn + ldx
xn arctg — dx - ——-arctg — -——T (n # - 1).
J a n + \ a n + 1 J a + xz
X
arctg—п
__.___.
X
arctg—dx Л iii
С a 1 x 1 a2 + x2
503) 2 = - - arctg —-In j—.
x ь a 2a
x
—dx
« aicig —мл С А
504) ± = - ——rarctg- + —^— * 2х (и # 1).
J х" (п - \)х" ' я и - 1 J хя *(я2 + х2)
505) arcctg — dx — xarcctg 1 In (я2 -f x2). 506) xarcctg — dx = —(x2 + я2) arcctg 1 .
Jfl я 2 Jfl2 я2
Г . x x3 x ях2 я3 , -j ~
х2 arcctg — dx = —-arcctg 1- In (я2 + x2).
J я З я 6 6
f x x"+' x а С xn+ldx
Xя arcctg— dx -arcctg— + — T (n Ф - 1 .
J я n+1 я n+ljfl2+x2
507)
508)
x
arcctg- dx
с 2 я ' 32я3 52я5 ¦ 72я
KdX 1 х 1 я2+х2
510) I — т arcctg — + --In у—.
1 "г х а 2а х
110 ТАБЛИЦЫ
. arcctg — dx
511) '
Интегралы от обратных гиперболических функций.
512) | Arsh — dx = xArsh — - l/x2 + a2. 513) | Arch — dx = x Arch— - ]/x2 - a2.
} a a J я а
514) Arth — dx = xArth — + — ln(</2 - x2). 515) Arcth — dx = x Arcth— + — ln(x2 - a2).
J a a 2 J a a 2
1.1.Э.4. Таблица некоторых определенных интегралов*).
1.1.3.4.1. Интегралы от показательных функций (в сочетании с алгебраическими,
тригонометрическими и логарифмическими).
+ 00
1) Г xne~ax
J
dx = Г(П^1} **) (а > 0, п > - 1).
В частности, при натуральном п этот интеграл равен n\/a"+l.
' п + 1 \
(а > 0, п > -1).
2) J XV"-2 dx = --^^у
\-3...Bki)]/n
В частности, при п целом и четном (п = 2/с) этот интеграл равен ~^пТ\—t+i/2—» а ПРИ и Целом
А:!
и нечетном (и = 2/с -I- 1) он равен k'+l .
3) ^"e2jc2 rfx = V_!L_ (fl > 0). 4) f x2^--2 rfx = j4- (fl > 0).
J 2л J 4aJ
2a
f x2^--2 rfx
J
6) +f 4^ = ^-. 7) f 4*L - =1.
J ex - \ 6 J г* + 1 12
8)
10)
П)
0
+ оо
J
0
т
0
I
0
e-exsinx
X
е~х lnxd
е~х ln2xi
+00
= arcctg a = arctg— (a > 0). 9) ?~x In x dx = - С « -0,5772 ***).
— rY
1.1.3.4.2. Интегралы от тригонометрических функций (в сочетании с
алгебраическими).
*) Более полные таблицы определенных интегралов см • Г р а д ш т е й н И. С.? Рыжик И. М. Таблицы интегралов,
сумм, рядов и произведений.—М : Наука, 1971; Прудников А. П, Брычков Ю. А., Маричев О. И. Интегралы
и ряды - М . Наука, 1981.
**) Г — гамма-функция
***) с — постоянная Эйлера
****) B(.v, у) = -~т-— Г~ бе1а-функция, или эйлеров интеграл 1-го рода, Г (л) — гамма-функция, или эйлеров интеграл
2-го рода
ТАБЛИЦА НЕКОТОРЫХ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 111
Эта формула справедлива для любых аир (последнее равенство - при аир натуральных);
к/2 п/2 л/2
сет применяться для |/sin x dx, j/sin x dx, ? и т. п.
ооо |/cosx
Г Л, 0>о,
f sin ах ) 2' ' Г sinpx , [Г(р/2)]
13) т"'*" 1 к л 14) ~r-^=2 -щ-*
-у, ж 0, о
если р — рациональное число с нечетными числителем и знаменателем.
. _ч Г sin ax nas l С cos ax dx
15) —dx = ——, 0 < s < 2. 16) =оо (а # 0, а - произвольное число).
о
+ 00
Г
О
П
- —, а < 0.
Г COSflX
J
0
f sinx ^
— cos bx л
X
+ 00
С cosx
ln-
1
(а,
h
Ь>0).
20)
I
0
sin x cos ax
X
dx= -
19)
j x a j x
о о
0,
V* if*
71 .... COS ЯХ 7С
--"' '•¦""'I 23) I 7-rZ2dx=-2>
0
24) j!!^Ldx = I-|fl|. 25)
0 - oo - oo
я/2 к/2
cosxt
/l - k2 sin2 x" /c
о о •
nil
26) J 7ПГте7= 5Г1П TIT |/C|<L 2?) b, „¦, =T-arcsm/c, |/c| < 1.
28) J, ,"",;-, =^(K-E)*)
l/l - /c2 sin2 x
я/2
29)
о
nil
С
1.1.3.4.3. Интегралы от логарифмических функций (в сочетании с
алгебраическими и тригонометрическими).
• Г In In— dx= -(
31) | lnln— dx = -C » - 0,5772**). 32) | ——-dx = -— (сводится к № 6).
о
*) Е и К — полные эллиптические интегралы: Е = Е(/с, л/2), К = F(k, п/2)
**) С — постоянная Эйлера.
112
ТАБЛИЦЫ
33)
: = Г(а+ 1)*) (-1 <а < oo).
46)
я/2 я/2 я
In sin x dx = In cos x dx = In 2. 40) x In sin x dx =
oo о
я/2 +oo
sin xln sin xdx = In 2 — 1. 42) —
0 о
+ 00
f 5!
0
я
1 In (a
0
fin (a2-
о
n/2
J'
39)
43)
44)
45)
7i2ln2
2 "
\nxdx= -—(C + lna)*) (o>0).
x 2
¦-b2
2abcosx
-{
2n\na
(Ь ^ a > 0).
1.1.3.4.4. Интегралы от алгебраических функций.
48) f a(l fdx 2 Г2g+1 A Yd Г(" +
f xa(l - xfdx = 2 Гx2g+1 A - xYdx = Г(" + П^(Р ^ 1} = B(oc + 1, p + 1) (a > - 1, P> -1)**).
J J Г (a + p + 2)
(сводится к № 10).
49)
+ 00
J A + x)xe ~ sT
50)
52)
A—
dx
аГ
1±±
53)
f rfx
—
J 1 + 2x <fos a +
x2 2 sin a
л\ сич С dx a l Л
a<— . 54) =_._._ о <?i<—
2 / J 1 + 2x cos a + x2 sin cj \ 2
*) С — постоянная Эйлера.
**) B(x, у) = —^— \~ бета-функция, Г(х) — гамма-функция.
ЦЕЛЫЕ РАЦИОНАЛЬНЫЕ ФУНКЦИИ
113
1.2. ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Действительная функция от действительного
переменного х — это однозначное отображение /
подмножества действительных чисел во множество
действительных чисел: у =/(х). Множество точек
с координатами (х, /(х)) называется графиком
функции. Графики функций — это в общем случае
кривые, которые пересекаются с каждой прямой,
параллельной оси у, не более чем в одной точке
(см. также 2.4).
1.2.1. АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
1.2.1.1. Целые рациональные функции.
Постоянные функции. Функция у = О
отображает каждое действительное число х в число
нуль. Считается, что она не является никакой
(конечной) степенью аргумента. Ее график — ось
х. Функция у = а (а ф 0) есть функция нулевой
степени от аргумента. Графиком такой функции
является прямая, параллельная оси х и
пересекающая ось у в точке @, а).
Линейные функции: у = ах + b (а ф 0).
Графиком такой функции является прямая,
проходящая через точки А( — Ь/а, 0) и В@, Ь)
(рис. 1.7, а). При Ь = 0 точки А и В совпадают
У
а)а<0 б)а>0
Рис 1.7
и прямая проходит через начало координат
(рис. 1.7,6).
Функция имеет один нуль:
х0 = - Ь/а.
Если а > 0, то функция монотонно возрастает;
если а < 0, то она монотонно убывает. Если Ъ = 0
и а > 0, то говорят, что у прямо пропорционально
х, а а называют коэффициентом
пропорциональности.
Квадратичные функции: у = ах2 + Ьх + с
(а Ф 0). График — парабола с осью симметрии,
б)а<0
Рис 1 8
параллельной оси у, и вершиной С(-Ь/Bа),
Dас - Ь2)/Dа)) (рис. 1.8). Функция имеет не больше
двух нулей. График пересекает ось у в точке
В @, с). В случае А = 4ас — Ь2 < 0 он пересекает
ось х в точках Ах ((-b - /^Д)/Bа), 0)и А2((-Ь +
+ ]/ — Д)/Bа), 0). При А = 0 кривая касается оси
х в точке {-Ь/{2а), 0) (касание 2-го порядка);
при А > 0 точек пересечения с осью х нет. Если
а > 0, то функция в точке х^ = - Ь/Bа) (абсцисса
вершины) имеет минимум, а при а < 0 —
максимум (см. 3.2.1).
Функции третьей степени:
у = ах3 + Ьх2 + сх + й(аф 0).
График этой функции может иметь различный
вид. У него имеется по крайней мере одна (а
может быть, и две, и три) точка пересечения с
осью х и ровно одна точка перегиба. У функции
либо нет экстремумов, либо их два (в последнем
случае один максимум и один минимум). Для
более точного описания кривой нужны значение
коэффициента а, значение А = Ъас — Ъ2 и значение
дискриминанта функции
D = Ъ2с2 - 4асг - 4ЬЧ - 21 a2d2 + 18 abed.
Если а > 0, то у -* — оо при х -* — оо и
У^> +ОО При Х-> +00.
Если а < 0, то у -+ + оо при х -*• — оо и
у^—оо при х-* +оо.
При А > 0 функция не имеет экстремумов,
имеется точка перегиба Е (рис. 1.9, а).
Ж ^* О
а)Л>0,а<0 5)А=0,а>0
Рис. 1.9
б)Л<0,а>0
При А = 0 функция не имеет экстремумов,
имеется точка перегиба Е. Касательная в точке
перегиба Е параллельна оси х (рис. 1.9,6).
При А < 0, а > 0 у функции имеется один
максимум в точке xmax = ( — b — ]/ — А)/(За) и один
минимум в точке xmln = ( — b + j/-A)/Ca); имеется
точка перегиба Е (рис. 1.9, в).
При D > 0 кривая пересекает ось х в трех
точках: Аи А2, А3.
При D = 0 у кривой две или одна точка
пересечения с осью х, причем ровно в одной
точке пересечения имеет место касание. При этом
точка касания в первом случае считается второго,
а во втором случае — третьего порядка.
При D < 0 имеется одна (простая) точка
пересечения с осью х.
Точка перегиба Е имеет координаты
Ь 2Ь3 - 9abc \
+ d ] и является центром сим-
За' 27а2 J
метрии кривой. Касательная в точке Е имеет
наклон tg ф = А/(За). Если А = 0, то график этой
функции называется кубической параболой
(рис. 1.9,6).
114
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Целые рациональные функции л-й
степени:
у = апх" + ап- i
+ а0, ап ф О,
и > 0 - целое. Графики этих функций - кривые без
особых точек и без асимптот, имеющие не более
п точек пересечения с осью х, не более п — 1
экстремумов и не более и - 2 точек перегиба,
Рис. 1.10
чае а > 0 получаются растяжением ординат в а раз,
а в случае а < 0 — растяжением в \а\ раз и
последующим зеркальным отображением
относительно оси х.
1.2.1.2. Дробно-рациональные функции.
Обратная пропорциональность:^
= а/х, а фО. График такой функции -
равносторонняя гипербола с действительной полуосью
J/21 а | (расстояние от вершины до центра), с
центром в начале координат и с асимптотами —
осями координат. Функция имеет один полюс
1-го порядка (см. 2.5.1.2.2) в точке х = 0.
Экстремумов нет. При а > 0 функция в интервалах
( — оо, 0) и @, +оо) монотонно убывает, график
лежит внутри первого и третьего квадрантов,
вершины гиперболы — в точках А (уа, у а) и
В(—]/а, — ]/а). Говорят, что у обратно
пропорционально х (рис. 1.12). При а < 0 функция в тех
причем в случае нескольких экстремумов
максимумы и минимумы чередуются (рис. 1.10). При
п ^ 1 графики — кривые n-го порядка (см. 1.3).
и-нечетное. Существует по меньшей мере
одно пересечение с осью х и при п ^ 3 по
меньшей мере одна точка перегиба. Число
экстремумов при п ^ 3 всегда четно, а число точек
перегиба нечетно. Если ап > 0, то при х -> - оо
имеем у-* — оо, а при х->+оо имеем _у->+оо.
Если ап < 0, то, наоборот, при х -* — оо имеем
у-* +оо, а при х-> +оо имеем у-> — оо.
п — четное. При п ^ 2 существует по меньшей
мере один экстремум функции. Число экстремумов
при п ^ 2 всегда нечетно, а число точек перегиба
четно. Если ап > 0, то при х-* —оо или х -> + оо
всегда )>->+оо. Если ап < 0, то при тех же
условиях у-* — оо.
Степенные функции:)/ = хи, и^2- целое.
Все графики этих функций проходят через точку
A, 1) и касаются оси х в точке @, 0). Их иногда
называют параболами п-го порядка. Тогда @, 0)
считается точкой и-кратного касания кривой с
осью х (ср. n-кратный нуль, см. 2.3.2). Если п
четно, то функция имеет в точке х = 0 минимум
и график симметричен относительно оси у
(рис. 1.11, а). Если п нечетно, то точка @,0)-
точка перегиба с горизонтальной касательной и
1
\
\
\\
\\
\
\
-/
У
к.
0
7 1 '
6 if *V
5 \ 1
4 I I
з II
2 1/
1 }А
1 X
У
т
1
1
/|
4
3
2
1
0
-1
-2
-3
-4
^ь
|/
/
Г
1 X
AV
~-~— х
Рис. 1 12
же интервалах монотонно возрастает, график лежит
внутри второго и четвертого квадрантов,
вершины гиперболы - в точках /1'(-|/М, \/\~а~\) и
#'(l/l«|. - l/M) (Рис- 1-12, штриховые кривые).
Дробно-линейные функции: у =?
агх + b2'
D =
Ф 0, a2 Ф 0.
Графики
функций — также равносторонние гиперболы с
действительными полуосями j/2 | D | /1 а2 |, с центрами
С( — Ь2/а2, а^/аз) и с асимптотами, параллельными
осям координат и проходящими через С. Функции
имеют один полюс 1-го порядка в точке
У
0
\
с
X
Рис 111
кривая симметрична относительно начала
координат (рис. 1.11,6). Графики функций у = ах" в слу-
Рис. 1.13
хр=—Ь2/а2. Экстремумов нет. Если D < 0, то
функции в интервалах (- оо, - Ь2/а2) и (- Ь2/а2, + оо)
монотонно убывают, вершины гипербол находятся
ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ
115
У\р\\
I «2 I /
2°. Функция у =
а Ф 0. График
01 ( У\Р\\
| а2 | ' а2 \ а2 | /
leal/
Если ?> > О, то функции в данных интервалах
монотонно возрастают, а вершины гипербол
находятся в точках
а2
а2
Некоторые нелинейные дробно-
рациональные функции.
1°. Функция у = а -\ 1—2*' ^ ^ 0» с # 0.
График такой функции (рис. 1.14) также
распадается (подобно графикам дробно-линейных
^1
|а2|' а2 \ а2 \
б)с<0,Ь>0
г)С<О,Ъ<0
Рис. 1.14
функций) на две ветви, так как функция имеет
полюс 2-го порядка в точке хр = 0. Ось у и
прямая, уравнение которой имеет вид х — а = О, -
асимптоты этой кривой.
Одна из двух ветвей кривой пересекает
асимптоту у — а = О в точке А (— с/Ь, а), в то время как
другая ветвь при Ъ < О монотонно возрастает, а
при Ъ > О монотонно убывает. Функции имеют один
экстремум в точке х — —2с/Ь с соответствующим
значением функции у = а — Ь2/Dс) (точка В на
рис. 1.14). Точка перегиба С имеет координаты
(-Зс/Ь, а - 2Ь2/{9с)). При Л = 4ас - Ь2 < 0 кривая
дважды пересекает ось х: в точках
При Л = 0 кривая касается оси х в точке
{-Ь/Bа), 0). Если Л > 0, то точек пересечения с
осью х нет.
ах2 + Ьх + с
этой функции симметричен относительно
вертикальной прямой, уравнение которой имеет вид
х = - Ь/Bа), а ось х является для нее
асимптотой (рис. 1.15). Вид кривой существенно
определяется значением дискриминанта Л = Лас — Ъ2.
а)А>0
Рис. 1.15
1
Так как график функции у = - 2
— ах2 — Ьх — с
ляется зеркальным отображением относительно
оси х графика данной функции, то достаточно
ограничиться случаем а > 0. Функция не имеет
нулей.
а) А > 0. Для каждого значения х функция
положительна и непрерывна; в точке хтах =
= —Ь/Bа) она имеет максимум, равный 4а/А.
В промежутке ( —оо, хтах] она монотонно
возрастает, а в промежутке [хтах, +оо) монотонно
убывает. График имеет точки перегиба
в(х j/L зл с(х
DI лтах ~~ г- » a I» I л«пах
V 2а\Гъ Л/ V
2a]/b
с наклонами касательных в этих точках
tg ф! = а2 C/ДK/2 и tg ф2 = - а2 C/ЛK/2
соответственно (рис. 1.15, а).
б) Д = 0. В точке хр = —Ь/Bа) функция имеет
полюс 2-го порядка, а для всех остальных значений
х функция положительна и непрерывна. В
интервале (-оо, хр) она монотонно возрастает, а в
интервале (хр, +оо) монотонно убывает
(рис. 1.15,6).
в) Д < 0. Функция имеет в точке хтах = - Ь/Bа)
максимум, равный 4а/Д, а в точках хр _
= Хтах + У^А/Bа) и хР2 = хтах - ]/^~Д/Bа) -
полюсы 1-го порядка. В промежутке ( — оо, хР2) она
положительна и монотонно возрастает, в
промежутке (Хр2, хтах] отрицательна и монотонно
возрастает, в промежутке [xmax, xpi) отрицательна
и монотонно убывает, в промежутке (хр , +оо)
положительна и монотонно убывает. Для всякого
значения х, за исключением х = хр и х = хр ,
функция непрерывна (рис. 1.15, в).
3°. Функция у — —5 \ > ас ?* 0. На
ах2 + Ьх + с
тех же основаниях, что и в предыдущем
примере, можно ограничиться случаем а > 0. График
этой функции пересекает ось х в начале координат
и имеет асимптотой ось х (рис. 1.16). Обозначим
Д = Аас - Ь2.
116
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
у\ в
а)А>0
фД=0,Ь>0 52)A=0,b<0
ос и/5 разных знаков
u2m-~-u, в^)А<0,
хи/3 отрицательны ее и/3 положительны
Рис. I 16
а) А > 0. Для каждого значения х функция
непрерывна и имеет в точках xmin = ус/а и
*тах = у с/а минимум и максимум со значениями
( — Ъ — 2)/ас)/А и ( — b + 2\/ас)/А соответственно.
В промежутке ( — сю, xmin] она монотонно
убывает, в промежутке [xmin, xmax] монотонно
возрастает, в промежутке [хтах, +оо) монотонно
убывает. Существуют три точки перегиба
(рис. 1.16,а): корни уравнения а2хъ — Захс — be = 0.
б) А = 0. Из того, что ас ф 0 и а > 0,
следует, что b ф 0, с > 0. Для каждого значения х
имеем ах2 + Ьх + с = а\х + Ь/Bа)J. В точке
хр = — Ь/Bа) функция имеет полюс 2-го порядка,
а при всех остальных значениях х она непрерывна.
График имеет одну точку перегиба х = Ь/а.
1) b > 0. В точке xmax = b/Ba) функция имеет
максимум со значением функции 1/B6). В
промежутке (-оо, хр) она монотонно убывает, в
промежутке (хр, хтах] монотонно возрастает, а в
промежутке [хтах, +оо) монотонно убывает
(рис. 1.16,6i). 2) b<0. В точке xmin = Ь/Bа)
функция имеет минимум со значением 1/BЬ).
В промежутке (-оо, xmin] она монотонно убывает,
а в промежутке [xmin, xp) монотонно возрастает,
в промежутке (хр, +оо) монотонно убывает
(рис. 1.16, б2).
в) А < 0. Многочлен в знаменателе имеет два
различных действительных корня в точках
а = (-Ь - /^А)/Bа) и C = (-Ь + |/^Д)Д2а), и так
как ар = с/а Ф О, то а, C ф 0. Функция имеет в
точках xpi = а и Хр2 = р полюсы 1-го порядка.
1) а < 0, р > 0. В интервалах ( — оо, а), (а, Р),
(Р, +оо) функция монотонно убывает и не имеет
экстремумов (рис. 1.16,»!). 2) а < 0, Р < 0. Функция
имеет в точке xmin = — у с/а минимум, а в точке
¦*max = У~с/а максимум. В промежутках (-оо, ос),
(а> xmin], [xmax, + оо) она монотонно убывает, в
промежутках [xmin, p), (p, xmax] монотонно
возрастает (рис. 1.16,в2). 3) а > 0, Р > 0. Функция
имеет в точке xmin = — ус/а минимум, а в точке
^max = ]/с~/а максимум; в промежутках (-оо, xmin],
[xmax, p), (p, +оо) она монотонно убывает, в
промежутках [xmin, а), (а, xmax] монотонно возрастает
(рис. 1.16, в3). Единственная точка перегиба —
корень уравнения а2х3 — Захс — be = 0.
Рис. 1 17
4°. Степенные функции у =
= ах~", а ф 0, п — целое
положительное число. У этих
функций нет экстремумов, в точке
Хр = 0 они имеют полюс
порядка п, их графики при четном
п симметричны относительно
оси у, а при нечетном п
центрально симметричны относи-
тельно начала координат.
Координатные оси — асимптоты
кривых. При а > 0 и п четном
функции в интервале @, + оо)
монотонно убывают, а в
интервале (—,оо, 0) монотонно
возрастают; при а > 0 и п нечетном
функции в обоих интервалах
монотонно убывают. При а < 0
графики функций получаются
вертикальным отражением относительно оси х
графиков у = \а\х~". Если а = 1, то графики
проходят через точку А(\, 1). На рис. 1.17
показаны графики функций у — х~2 и >' = х~3.
1.2.1.3. Иррациональные функции.
Квадратный корень из линейного
двучлена: у = ± ]/ах + Ь, а Ф 0.
Рассмотрим случай, когда перед радикалом
взят знак +. Если а > 0, то везде в области
определения —Ь/а ^ х < + оо у
функция неотрицательна и --^
монотонно возрастает. Если
а < 0, то везде в области
определения — оо < х < —Ь/а
функция неотрицательна и
монотонно убывает.
Функция равна нулю при х =
= —Ь/а, ее график
представляет собой часть параболы с вершиной { — Ь/а, 0)
и параметром р = а/2, лежащую над осью х
(рис. 1.18). Если перед радикалом взят знак —,
то график получается зеркальным отражением
относительно оси х графика у = + у ах + Ь.
Оси парабол совпадают с осью х. Ср. 2.6.6.1.2.
Квадратный корень из
квадратного трехчлена: у= + ]/ах2 + Ьх + с, а ф 0.
1) а < 0, А = 4ас — Ь2 > 0. В этом случае
выражение не определяет никакой действительной
функции с непустой областью определения.
2) а < 0, А < 0. Область определения - отрезок
[а, р], где а = (-Ь + /^А)/Bа) и р = (-Ь-
- ]/ - А)/Bа). Функция имеет в точке Ь/Bа)
максимум, равный у'А/Dа) (перед корнем знак +), и
а)а<0,Л<0 б)а>0,А>0 в)а>0,А<0
Рис 1 19
ТРИГОНОМЕТРИЧЕСКИЕ И ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
117
минимум, равный - |/а/Dя) (перед корнем знак
-); на концах области определения она равна нулю.
График функции представляет собой часть эллипса
с центром {-Ь/{2а), 0) и вершинами в точках
А, В, С, D, лежащую в верхней полуплоскости
(рис. 1.19,а) (перед корнем знак + ) и в нижней
полуплоскости (рис. 1.19,6) (перед корнем знак -).
3) а > 0, А > 0. Функция определена при любом
значении х, не имеет нулей, но при х = -Ь/{2а)
имеет минимум, равный |/А/Dа)^перед корнем
знак +), и максимум, равный - |/Д/Dа) (перед
корнем знак -). График состоит из ветвей
гиперболы с центром (-Ь/Bа), 0) и осью х в
качестве мнимой оси (рис. 1.19,6); при этом
верхняя ветвь соответствует знаку + перед корнем,
а нижняя — знаку — .
4) а > 0, А < 0. Область определения этой
функции распадается на промежутки ( —оо, а],
[Р, +оо), где а = (-Ь-/^А)/Bа), $ = (-Ь +
+ ]/^Д)/Bа). Функция обладает двумя нулями в
граничных точках области определения.
График состоит из двух ветвей гиперболы
с центром (-Ь/Bа), 0) и осью х в качестве
действительной оси (рис. 1.19, в); при этом части
гипербол, лежащие в верхней полуплоскости,
соответствуют знаку + перед корнем, а лежащие в
нижней полуплоскости — знаку — .
Степенная функция: у = хк, к = т/п, т,
п — взаимно простые целые числа, п^ ±1.
1) к > 0. Функция имеет один нуль при х0 = 0,
и график проходит через точку A, 1). Если и
четное, то область определения — промежуток
[0, +оо). Если п нечетное, то она определена
в)
Рис. 1 20
при любом значении х. Если п нечетное, a m
четное, то ось у - ось симметрии графика; если
пит нечетные, то график центрально
симметричен относительно начала координат. Если
п> т, то ось у — касательная к кривой в точке
@, 0); если т > п, то касательная в точке @, 0) -
ось х (рис. 1.20).
2) к < 0. При хр = 0 функция имеет полюс /с-го
порядка — точку разрыва (точка разветвления с
неограниченно возрастающим модулем значения
функции). При п четном она определена в
интервале @, +оо), а при п нечетном - для любого
У
1
0
^\
/
х-Ф
-— —
X
У
1
0
1
V
Л
/
Рис.
X
5)
1.21
У
1
0
\y=*'2/J
^^
1 X
б)
значения х ф 0. Экстремумов нет. Графики этих
функций проходят через точку A, 1) и имеют
асимптотами оси координат. Они обладают теми
же свойствами симметрии, что и кривые,
описанные в 1) (рис. 1.21).
1.2.2. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
1.2.2.1. Тригонометрические и обратные
тригонометрические функции.
Общая синусоидальная
зависимость: у = Л sin (сох + (ро), А > 0, со > 0.
1) При /4 = 1, со = 1ифо=0 имеем
обыкновенный синус: y = sinx. Это периодическая функция
с периодом Т = 2п (см. 2.5.2.1). Ее график -
синусоида (рис. 1.22, а) пересекающая ось х в
точках В„ с координатами (ия, 0) (п — любое целое
число), которые одновременно являются точками
перегиба кривой. Касательные в этих точках
образуют с положительным направлением оси х
угол либо я/4, либо -я/4. Максимумы
функции лежат в точках хтаХя = я/2 + 2пя, минимумы -
в точках xmjn = —я/2 + 2пя. Значения функции
у удовлетворяют неравенству -1 < у ^ 1.
2) График общей синусоиды с амплитудой Л,
круговой частотой со и фазой ф0 представлен
на рис. 1.22,6 (незатухающее гармоническое
колебание; о затухающем гармоническом колебании
Рис. 1.22
см. 1.2.2.2). Его получают из синусоиды аффинным
преобразованием: растяжением в А раз в
направлении оси у, растяжением в 1/со раз в
направлении оси х и последующим параллельным
переносом по оси х на -фо/со. Функция имеет
период Т = 2я/со и нули в точках (пп — фо)/со.
Максимумы расположены в точках (я/2 — ф0 +
+ 2ия)/со, минимумы — в точках (— я/2 — ф0 +
+ 2ия)/со. Все значения функции удовлетворяют
неравенству - А < у ^ А.
Косинус: у = cosx. Так как cosx = sin(x +
+ я/2) для любого х, то функция cos х представ-
118
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
ляет собой частный случай общей
синусоидальной зависимости: А = со = 1, ф0 = я/2. Поэтому
ее график - сдвинутая по оси х на -я/2
синусоида (рис. 1.23). Нули — в точках я/2 + «я,
Рис. 1.23
максимумы — в точках 2ля, минимумы — в точках
Bл + 1) я. Период Т = 2я.
Тангенс: y = tgx. Область определения этой
функции представляет собой бесконечное число
открытых интервалов ( — я/2 + ля, я/2 + ля), где
л - любое целое число. В каждом из этих
интервалов функция монотонно возрастает и имеет нуль
в точке хОи — ля. Функция периодична с периодом
Т = я. В точках (я/2) + ля функция имеет полюс
Рис. 1.24
1-го порядка. Точки пересечения ее графика с
осью х - это одновременно и точки перегиба.
Касательные в этих точках составляют с
положительным направлением оси х угол я/4
(рис. 1.24).
Котангенс: y = ctgx. Область определения
этой функции представляет собой бесконечное
число открытых интервалов (пп, (п + 1)я), где п —
любое целое число. В каждом из этих
интервалов функция монотонно убывает и имеет один
нуль в точках хОи = (я/2) + пп. Функция
периодическая с периодом Т = я. В точках пп она
имеет полюс 1-го порядка. Точки пересечения
Рис. 1 25
ее графика с осью х — это одновременно и точки
перегиба. Угол, образуемый в этих точках
касательными к кривой с положительным
направлением оси х, равен —я/4 (рис. 1.25). В
области определения справедливо равенство
ctg х = — tg ((я/2) + х).
Секанс: j/ = secx. Эта функция определена в
открытых интервалах (- (я/2) + ля, (я/2) + ля)
соотношением sec х = 1/cos x и имеет в точках
хРп ~ (%№ "*" пп полюсы 1~го порядка. Функция
периодична с периодом Т = 2я (рис. 1.26). При
любом х из области определения справедливо
Рис. 1 26
Рис. 1 27
неравенство | sec х | ^ 1, минимумы функции
находятся в точках 2ля, максимумы — в точках
Bл + 1)я.
Косеканс: у = cosecx. Функция определяется
в открытых интервалах (ля, (л + 1)я) равенством
cosec х = 1/sin x; она периодична с периодом
Т = 2я и имеет в точках хрп = ля полюсы 1-го
порядка (рис. 1.27). Так как при любом х из
области определения справедливо равенство
cosec х = sec (x — я/2), то график совпадает со
сдвинутым на я/2 по оси х графиком функции
у = sec х. Функция имеет минимумы в точках
яDл + 1)/2 и максимумы в точках яDл + 3)/2.
Арксинус: y = arcsinx. Эта функция
является обратной к функции у = sin x на отрезке
— я/2 < х ^ я/2 (рис. 1.28). Таким образом, ее
область определения — 1 < х ^ 1, а область
значений - я/2 ^ у ^ я/2. Функция монотонно
возрастает и имеет нуль при х0 = 0. Ее график —
часть синусоиды, зеркально отраженной
относительно прямой х — у = 0 (биссектрисы первого и
Рис. 1.28
1.29
третьего квадрантов). График имеет в начале
координат точку перегиба; касательная в этой
точке составляет с осью х угол ср = я/4 (см.
также примечание в конце 1.2.2.1).
ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ ФУНКЦИИ
119
Арккосинус: >; = arccos х. Эта функция
является обратной к функции у = cos х на отрезке
О ^ х ^ я. Таким образом, ее область
определения — 1 ^ х < 1, а область значений 0 < у ^ я
(рис. 1.29). Функция монотонно убывает. Ее график -
часть косинусоиды, зеркально отраженной
относительно прямой л: — у — 0. График имеет в точке
@, я/2) точку перегиба; касательная в этой точке
составляет с осью х угол ф = Зя/4 (см. также
примечание в конце 1.2.2.1).
Арктангенс: у = arctg х. Эта функция
является обратной к функции у = tg x на интервале
— я/2 < х < я/2. Следовательно, ее область
определения — оо<х< +оо, а область значений
-я/2 < у < я/2 (рис. 1.30). Функция монотонно
Рис. 1.30
возрастает и имеет нуль при х0 = 0. Ее график
получают зеркальным отражением
соответствующей ветви графика функции у = tg x относительно
прямой х — у = 0. В начале координат функция
имеет точку перегиба; утл, образуемый
касательной в этой точке с осью х, равен ф = я/4.
Прямые у + я/2 = 0 и у - я/2 = 0 - асимптоты
при х-*— оо и х -> + х соответственно (см. также
примечание в конце 1.2.2.1).
Арккотангенс: у = arcctgx. Эта функция
является обратной к функции у = ctg x на
интервале 0 < х < я. Следовательно, ее область
определения — оо < х < 4- оо, а область значений
О < у < я (рис. 1.31). Функция монотонно убывает
У
s It
—*=^
к
0 Ч" х
Рис. 1.31
и не имеет нулей. Ее график получают
зеркальным отражением соответствующей ветви
графика функции у = ctg x относительно прямой
х - у = 0. - Этот график имеет точку перегиба
(О, я/2); угол, образуемый касательной в этой точке
и осью х, равен ф = Зл/4. Прямые у = 0 и
у — я = 0 — асимптоты при х -> + оо и х -> — оо
соответственно (см. также нижеследующее
примечание).
Примечание Если х - фиксированное действительное
число, — 1 ^ х ^ 1, то множество всех действительных чисел
у, для которых x = siny, обозначают Arcsinx;
следовательно, Arcsin х = {у | х = sin у} В каждом таком множестве
Arcsin х существует единственное действительное у0 =
= arcsin х, которое называется главным значением
Arcsinx. Отсюда следует: у ? Arcsinx тогда и только тогда,
когда имеется целое число и, при котором у =
= (— 1)"arcsinх + пп. Соответственно получают: у е Arccos x
тогда и только тогда, когда существует такое л е Z (Z —
множество целых чисел), что у = + arccos x + 2пп.
Далее, у е Arctg х при х е (— оо, + оо) тогда и только тогда,
когда существует такое neZ, что у = arctg x + пп;
у е Arcctg х тогда и только тогда, когда существует такое
и е Z, что у = arcctg x + пп
Графики многозначных функций Arcsin x, Arccos x,
Arctg х, Arcctg х изображены соответственно на рис. 1.28 —
1.31 штриховыми линиями.
1.2.2.2. Показательные и логарифмические
функции.
Показательные функции: у = еЪх =
= ехр {Ьх}, Ъ ф 0 (их называют также
экспоненциальными). Функция (рис. 1.32) определена при
всех значениях х, не имеет ни нулей, ни
экстремумов. Ее значения всегда положительны.
Обозначив а = еь, имеем еЬх = ах для всех значений х,
а > 0, а ф 1. При Ъ > 0 (т. е. а > 1) функция
монотонно возрастает, при Ъ < 0 (т. е. О < а < 1)
она монотонно убывает. Важные частные случаи:
у = ех — ехр х,
График проходит через точку @, 1) и имеет ось х
в качестве асимптоты при х -*¦ — оо.
Логарифмические функции: у = logflx,
а > 0, а ф 1. Они являются обратными функциями
Рис. 1 33
для показательных функций. Область значений:
- оо < у < +оо. Обозначая Ъ = In а, имеем в области
120
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
определения loga x = (l/fr)lnx, Ъ ф 0. При а > 1
(т. е. Ъ > 0) функция монотонно возрастает, при
0 < а < 1 (т. е. b < 0) она монотонно убывает
(рис. 1.33). Важный частный случай: а = е (т. е.
Ъ = 1), у = In х. График проходит через точку
A,0) и имеет асимптотой ось у. При каждом
отличном от нуля значении Ъ функции у — еЪх и
у = {\/Ь)\пх взаимно обратны; их графики
совмещаются друг с другом при зеркальном
отражении относительно прямой х — у = 0.
Функции у = Ье'{ах) = Ьехр{- (ахJ}, а Ф 0,
Ъ > 0. Функция (рис. 1.34) определена при всех
значениях х, ее область значений: 0 < у ^ Ъ.
д=/
В промежутке — оо < х ^ 0 она монотонно
возрастает, а в промежутке 0 ^ х < + оо монотонно
убывает и имеет при х = 0 максимум утах = Ъ.
График симметричен относительно оси у и
имеет две точки перегиба: ВA/(ау2), bye) и
С( — 1/(ау2), bye). Касательные в этих точках
имеют угловые коэффициенты tgcpj = — aby2/e и
tg Ф2 = ab \/2/е. Важный частный случай: Ь =
= 1/(а |/2тс), а = а |/2 (это гауссова кривая — кривая
нормального закона распределения ошибок,
ср. 1.1.2.6.1).
Функции у = аеь* + cedx, abed ф 0. Функции
(рис. 1.35) определены при всех значениях х.
Их рассматривают как сумму функций ух = аеЪх
и у2 — сеЛх (о частных случаях 6=1, d = — 1 и
а = с = 1/2 или а = — с = 1/2 см. 1.2.2.3). Можно
выделить четыре типа, для каждого из которых
существует четыре случая. Для каждого типа
рассматривается один случай. Графики функций в
остальных случаях получают из графика
рассмотренного случая путем зеркального отображения
относительно оси х, оси у или обеих осей.
а) ас > 0, bd>0. На рис. 1.35, а изображен
случай а > 0, с > 0 и b > 0, d > 0. Функция
монотонно возрастает; Экстремумов и нулей нет.
График не имеет точек перегиба, ось х —
асимптота.
б) ас > 0, bd<0. На рис. 1.35,6 изображен
случай а > 0, с > 0, b > 0, d < 0. Функция имеет
минимум в точке xmin, не имеет нулей. В
промежутке ( — оо, xmjn] она монотонно убывает, а в
промежутке [xmin, +oo) монотонно возрастает.
График не имеет точек перегиба и асимптот.
в) ас < 0, bd > 0. На рис. 1.35, в изображен
случай а > 0, с < 0, b > 0, г/ > 0. Функция имеет
один максимум в точке хтах, нуль при
In (-с/я)
In (с/я)
Х° = ~~ь /—' пРомежУтке ( — оо, хпах] она
монотонно возрастает, а в промежутке [хтах, + оо)
монотонно убывает. График имеет одну точку
перегиба, ось х — асимптота.
г) ас <O,hd< 0. На рис. 1 35, г изображен случай
а < 0, с > 0 и b < 0, d > 0. Функция не имеет
экстремумов, монотонно возрастает и имеет один
нуль в х0. У графика одна точка перегиба.
Асимптот нет.
Экстремальные значения (типы б) и в)) в точке С
достшаются при х = (\/(d — b))- In( — ab/(cd)), d ф b.
Нули (типы в) и г)): х0 = (i/(d - b))-\n{-a/c),
d ф b. Точка пересечения с осью у: А@, а + с),
абсцисса точки перегиба D (типы в) и г)):
х = (\/(d - b))-\n{-ab2/(cd2)), d ф b.
Функции у = aebx f сх = яехр {Ьх + сх2}, ас Ф
ф 0. Графики этих функций симметричны
относительно прямой 2сх + b = 0. У функций нет нулей,
но есть один экстремум в точке Л (— Ь/Bс),
аехр{-Ь2/Dс)}).
Различают два типа графиков функций,
которые изображены для случая а > 0 на рис. 1.36
а)С>0
б)с<0
Рис 1 36
(при я < 0 нужно зеркально отобразить кривые
относительно оси х).
а) с > 0, а > 0. Экстремум — минимум; функция
в промежутке ( — оо, xmin] монотонно убывает, а в
промежутке [xmin, + оо) монотонно возрастает.
Точек перегиба и асимптот нет (рис. 1.36, а).
б) с < 0, а > 0. Экстремум — максимум;
функция в промежутке ( — оо, хтах] монотонно
возрастает, а в промежутке [хтах, +оо) монотонно
убывает. Ось х — асимптота (рис. 1.36,6) Точки
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ
121
перегиба имеют координаты
-Ь-]/2с
Функции>> = яхьесх = ахь ехр (сх), abe # 0. Если
в качестве b взягь любое отличное от нуля
действительное число, то функции при b > 0
определены в промежутке 0 ^ х < + оо, а при
b < 0 — в промежутке 0 < х < + оо. Здесь снова
достаточно рассмотреть случай а > 0 (при а < 0
графики получаются зеркальным отображением
относительно оси х).
а) с > 0, Ь> 1 (рис. 1.37, а). График касается
оси х в точке @, 0). Функция монотонно
возрастает.
б) с > 0, Ь = \ (рис. 1.37,6). График проходит
через точку @, 0) и касается в этой точке
прямой х — у — 0. Функция монотонно возрастает.
О х О
a)c>O,b>f
У
1с 0
х 0] х
в)с>0,0<Ь<1
х 01
г)с>0,Ь<0
е)с<О,Ь=1
^ х 0\
ж)с<0,0<Ь<1 з)с<0,Ь<0
Рис 1 37
в) с > 0, 0 < b < 1 (рис. 1.37, в). График касается
оси у в точке @, 0) и имеет точку перегиба С
с абсциссой (|/Ь — Ь)/с. Функция монотонно
возрастает и не имеет экстремумов.
г) с > 0, b < 0 (рис. 1.37, г). Ось у — асимптота.
Функция имеет минимум в точке х = —Ь/с и
монотонно убывает в промежутке @, —Ь/с], а в
промежутке [ — Ь/с, +оо) монотонно возрастает.
д) с < 0, Ь>\ (рис. 1.37, д). График касается
оси х в точке @, 0) и имеет две точки перегиба
С и D с абсциссами хс = (b + ]/~b)f{ -с) и
*Z) = (b - yb)/{ — c). Ось х - асимптота. Функция
имеет максимум при х = -Ь/с. В промежутке
[0, -Ь/с] монотонно возрастает, а в промежутке
[ — Ь/с, +оо) монотонно убывает.
е) с < 0, Ь=1 (рис. 1.37, е). График проходит
через точку @, 0) и касается в этой точке
прямой ах — у = 0. Существует только одна точка
перегиба С с абсциссой Х(- = — 2/с, аналогичная
рассмотренной в д), и единственный максимум
при х = — 1/с.
ж) с < 0, 0 < b < 1 (рис. 1.37, ж). График
касается оси у в точке @, 0). Существует только
одна точка перегиба С с абсциссой хс =
= (Ь + уЬ)К — с) и единственный максимум при
х = - 1/с.
з) с < 0, Ь < 0 (рис. 1.37, з). Оси координат —
асимптоты. Функция монотонно убывает в
интервале @, + оо).
Функции у = Ае~ах sin (сох + (р), А > 0, а > 0,
со > 0. Графики этих функций (рис. 1.38)
представляют собой при х ^ 0 затухающие
гармонические колебания, если интерпретировать х как
Рис. 1 38
время, а у как отклонение (при а = 0 -
незатухающие гармонические колебания, см. 1.2.2.1).
Кривая располагается в области, ограниченной
графиками функций у = Ае~ах и у=—Ае~ах
(изображены штриховыми линиями), имеющими ось
х в качестве асимптоты.
Координаты точек касания Ак рассматриваемой
кривой с графиками функций у = Ае~ах и
у = — Ае~ах равны
хк = , ук = (— 1) Ае ,
со
к — целое. Точки пересечения с осями координат:
В (О, A sin ф), Ск ((кп — ф)/со, 0); точки экстремума
(абсциссы точек Dk): (кп — ф +
+ arctg(co/a))/co; абсциссы
точек перегиба Ек: (кп - ф +
+ 2arctg(co/a))/co;
логарифмический декремент: 8 =
= In \Ук/Ук + 1 I = ап/(й.
1.2.2.3. Гиперболические
функции.
Гиперболический си- ¦
ех - е~х
ну с: у = sh х = .
Функция нечетная,
монотонно возрастающая. Ее график
(рис. 1.39) центрально
симметричен относительно начала ко- Рис 1 39
ординат Точка @, 0) является
точкой перегиба кривой. Угол наклона ф
касательной в'точке @, 0) равен я/4.
У
0
7
/
/
3
2 1
Ж
1 2*х
-1
-2
-з
-4
122
ГРАФИКИ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
Гиперболический косинус: у = ch x =
ех + е~х
. Эта функция в промежутке (— оо, 0]
монотонно убывает, а в
промежутке [0, + оо)
монотонно возрастает, имеет при
х0 = 0 минимум со
значением функции, равным единице.
Ее график (рис. 1.40)
симметричен относительно оси
у и является цепной
линией (см. 1.3.4). В
окрестности точки /4@, 1) он
хорошо аппроксимируется
графиком функции у = \ + х2/2
Рис !-40 (парабола на рис. 1.40
изображена штриховой линией,
касание 3-го порядка).
Гиперболический тангенс: у = th x =
— —. Функция монотонно возрастает, все
-2 -/ 0
ее значения лежат
между -1 и 1. График
(рис. 1.41) центрально
2 3 X симметРичен
относительно начала координат.
Точка @, 0) является
точкой перегиба кривой.
Угол наклона (р
касательной в точке @, 0) равен
и у + 1 = 0 - асимптоты
при х-* + ао и х -> — оо соответственно.
Гиперболический котангенс: у —
ех + е~х
= cth х = 1—. В интервалах (— оо, 0) и @, + оо)
ех - е х
функция монотонно убывает; в точке хр = 0 она
имеет полюс первого порядка. Нулей нет.
График функции (рис. 1.42) центрально
симметричен относительно точки @, 0). Прямые у - 1 = 0,
я/4. Прямые у — 1=0
Рис. 1.42
у + 1 = 0 — асимптоты при х-» + оо и х-* — оо
соответственно; прямая х = 0 — вертикальная
асимптота.
Ареасинус: y = Arshx = ln(x + J/x2 + 1). Эта
функция является обратной функцией для
> = sh х на интервале (—оо, +оо) и поэтому
монотонно возрастает. График (рис. 1.43)
получают зеркальным отражением графика у = sh x
относительно прямой х — у = 0. Точка @, 0) —
центр симметрии кривой и одновременно точка
перегиба. Угол наклона (р касательной в точке
@, 0) равен я/4.
Ареакосинус: у = Arch х = ln(x ± |/х2 — 1).
Эта функция двузначная. Она является обратной
2
функцией для у = ch х в промежутке [0, + оо)
и в промежутке ( — оо, 0]. Ее область
определения 1 ^ х < + оо. В области определения
верхняя ветвь монотонно возрастает, а нижняя
монотонно убывает. Ее график (рис. 1.44)
касается в точке ,4A, 0) прямой, параллельной оси у,
7 X
Рис 1.44
и является графиком у = ch x, зеркально
отраженным относительно прямой х — у = 0.
1 , * +х
Ареатангенс: у = Arth х = — In .
Эта
функция является обратной функцией для y = thx
на интервале ( —оо, +оо). Ее область
определения — 1 < х < 1, область значений — оо < у < + оо.
Функция нечетная, монотонно возрастающая.
График функции (рис. 1.45) центрально симметричен
-4 -3 -2 -/ 0
1 X
-1
1 2 3
-2
-3
-4
Рис. 1.46
относительно точки @, 0), причем эта точка —
одновременно и точка перегиба. Касательная в этой
точке имеет угол наклона ф = я/4, прямые
х—1=0 и х+1=0 — асимптоты. График
функции получается зеркальным отражением графика
у = th х относительно прямой х — у = 0.
КРИВЫЕ 3-ю ПОРЯДКА
123
1 х+1
Ареакотангенс: y = Arcthx = -In
Эта
2 х-1"
функция является обратной функцией для у =
= cth х в обоих интервалах монотонности
( — оо, 0) и @, + оо). Следовательно, ее область
определения распадается на интервалы (-оо, -1)
и A, +оо), в которых она монотонно убывает.
Ее график (рис. 1.46) центрально симметричен
относительно точки @, 0); он получается путем
зеркального отражения относительно прямой
х — у = 0 графика у = cth x и имеет асимптоты
у = 0, х + 1 = 0, х - 1 = 0.
1.3. ВАЖНЕЙШИЕ КРИВЫЕ
Если F(x, у) = 0 - уравнение, имеющее решения
и не являющееся тождеством (см. 2.4.1.2), и если
Q - {(а, Ь) | F (а, Ь) = 0} - множество всех
упорядоченных пар действительных чисел а и Ь, для
которых F (а, Ь) = 0, то множество L =
= {М(а, b)\{a, b)eQ} всех точек М плоскости,
имеющих в какой-либо системе координат S
координаты а и Ь, называют плоской кривой,
определенной в S уравнением F(x, у) = 0. Если
F(x, у) представляет собой, в частности,
выражение у — /(х) и система координат декартова, то
кривая L является графиком функции у = /(х)
(см. 1.2). Таким образом, уравнение кривой зависит
не только от вида кривой, но и от системы
координат.
Кривая L называется алгебраической кривой
порядка п, если имеются декартова система
координат и многочлен F(x, у) переменных х,
у степени п такой, что F (х, у) = 0 является
уравнением кривой L в этой системе
координат.
В полярной системе координат (см. 2.6.5), как
правило, ограничиваются уравнениями вида
р = /(ф). Тогда р=/(ф) рассматривается как
уравнение кривой L в полярных координатах.
Если х = x(t) и у = y(t) — две функции,
определенные в одном и том же промежутке /, и
S - декартова система координат, то обе эти
функции называются параметрическим
представлением кривой
L={M(x(t),y(t))\teI].
1.3.1. АЛГЕБРАИЧЕСКИЕ КРИВЫЕ
Об алгебраических кривых 1-го и 2-го
порядков см. 2.6.6.1.
1.3.1.1. Кривые 3-го порядка.
Полукубическая парабола (рис. 1.47).
Уравнение кривой: агхъ - у2 = 0, л > 0.
Параметрическое представление: х = t2,
на К кривой в точке с абсциссой
х: К = 6а/( ]/х D + 9а2хK/2).
Длина / дуги кривой от начала
координат до точки М с
абсциссой х:/ = (D + 9а2хK/2 - 8)/B7а2).
Локон Аньези (рис. 1.48).
Уравнение кривой: {х2-\-а2)у-
— а3 = 0, а > 0. Асимптота:
у = 0. Радиус кривизны в
вершине у4@, а): Яд = а/2.
Точки перегиба: В(а/уЗ, За/4),
С(-а/]/з, За/4). Угловые
коэффициенты касательных в точках
перегиба: tg ср2 = - 3 )/з/8, tg q>i = 3 |/з/8.
Площадь между кривой и асимптотой: S = па2.
Декартов лист (рис. 1.49). Уравнение
кривой: х3 -\- у3 — Ъаху = 0, а > 0. Параметрическое
представление: х = 3at/(l + t3), у = 3at2/(l + t3),
— oo<t<—l и — l<t<+oo. Если обозначить
через M(t) точку кривой, соответствующую
значению параметра t, а через (p(f) угол между
МО и положительным направлением оси х, то будет
справедливо равенство tg ф @ = t. Начало координат
О — узловая точка кривой. При — 1 < t < + оо
кривая проходит из
второго квадранта через
точку @, 0) (Г = О) и А
в точку @, 0) (t -+ + оо);
при - оо < t < - 1
кривая, начинаясь в точке
У\
-as
-а
Рис. 1.49
Рис. 1.50
Рис. 1.47
(О, 0), располагается в четвертом квадранте. Оси
координат - касательные к кривой в точке @, 0).
Радиус кривизны в точке @, 0) обеих ветвей
кривых: Ro = За/2. Уравнение асимптоты: х + у + а = 0.
Вершина: А (За/2, За/2). Площадь петли: Sx = 3a2/2;
площадь между кривой и асимптотой: S2 = 3a2/2.
Циссоида (рис. 1.50). Уравнение кривой:
х3 + (х — а) у2 = 0, а > 0. Параметрическое
представление: х = a?2/(l + t2),y = at3/(l + t2), - оо < t <
< + оо; t = tg <p (t), где ср (t) - угол между лучом
ОМ и положительным направлением оси х
(М (t) - текущая точка кривой). Уравнение в
полярных координатах: рм = a sin2 (p/cos (p.
Геометрическое определение: точка М находится на кривой,
если она лежит на луче, выходящем из начала
124
ВАЖНЕЙШИЕ КРИВЫЕ
координат, и | МО | = | PQ |, где Р - вторая точка
пересечения луча с окружностью радиуса а/2 и
центром (а/2, 0), a Q — точка пересечения луча с
прямой х — а = 0. Точка @, 0) - точка возврата
кривой. Асимптота: х - а = 0; площадь между
кривой и асимптотой: 5 = Зпа2/4.
Строфоида (рис. 1.51). Уравнение кривой:
(х + а) а2 + {х - а) у2 = 0, а > 0. Параметрическое
представление: х = a(t2 — l)/(t2 + 1), у = at(t2 —
- l)/(t2 + 1), -оо <t < +ао; t = tg <p(t), где ф(?) -
угол между прямой МО и положительным
X
Рис. 1.51
направлением оси х (М = M(t) - текущая точка
кривой). Уравнение в полярных координатах:
р = — a cos 2<p/cos ф. Геометрическое определение:
точка М лежит на кривой, если она лежит на
луче, выходящем из А (-а, 0), и \PM\-\PO\,
где Р — точка пересечения луча с осью у, О —
начало координат (на рис. 1.51 \РМХ\=\РО\ =
= | РМ2 I). Начало координат - узловая точка
кривой, прямые х + у = 0 и х — у = 0 - касательные
к кривой в О. Асимптота: х — а = 0. Вершина:
А( — а, 0). Площадь петли: Si = 2а2 — па2/2;
площадь между кривой и асимптотой: S2 = 2а2 +
+ па2/2.
1.3.1.2. Кривые 4-го порядка.
Конхоида Никомеда (рис. 1.52).
Уравнение кривой: (х - аJ{х2 + у2) — 12х2 =0, а > 0,
Рис. 1.52
/ > 0. Параметрическое представление: х = а + /cost,
у = a tg t + I sin f, —n/2<t<n/2- правая ветвь,
n/2 < t < Зп/2 — левая ветвь. Уравнения в
полярных координатах: р = (a/cos ф) + / — правая ветвь,
р = {a/cos ф) — / — левая ветвь. Геометрическое
определение конхоиды Никомеда: конхоида*) прямой
х — а = 0 относительно О. Асимптота: х — а — 0
(для обеих ветвей). Вершины: А(а + 1, 0)—
правая ветвь, D(a — l, 0) — левая. Точки перегиба
правой ветви: В и С; их абсцисса —
наибольший корень уравнения х3 - Ъа2х + 2а(а2 - I2) = 0.
Для левой ветви следует различать три случая:
а) 1<а (рис. 1.52,а). Точка О — изолированная
точка кривой (О в этом случае в
параметрическом представлении не содержится). Левая ветвь
имеет две точки перегиба, абсцисса которых —
второй по величине корень выписанного выше
уравнения, б) 1>а (рис. 1.52,6). О — узловая
точка кривой, касательные в О имеют угловые
коэффициенты |/г — а2/а или — |//2 — а2/а, радиус
кривизны в О: Ro = l\/l2 - а2/Bа). в) I = a
(рис. 1.52, в). Точка О совпадает с вершиной D
и является точкой возврата.
Улитка Паскаля (рис. 1.53). Уравнение
кривой: (х2 4- у2 - ахJ - I2 (х2 + у2) = 0, а > 0, / > 0.
Рис 1 53
В параметрической форме (при а < I точка О не
включается): х = a cos21 + I cos t, у = a cos t sin t +
+ Isint, 0 < ? < 2л. Уравнение в полярных
координатах (при а<1 без точки О): р = асо8ф + /.
Геометрическое определение (без О как
изолированной точки): конхоида окружности с радиусом
а/2 и центром (а/2, 0) относительно О. Вершины
А (а + /, 0), В (а — I, 0). Экстремумов четыре, если
а > /, и два, если а ^ /:
С, D, E, Flcost ¦¦
/ ± ]
8а2
Dа)
/ 2а2 + /2\
Точки перегиба G, HI cos t = ——-— I
существуют, если а < I <2а. Если / < 2а, то существуют
две точки: /(-/2/Dа), \]/4а2 - 12/Dа)) и К(-12/Dа),
— IУ4а2 — /2/Dа)), обладающие общей касательной.
При а < I точка О — изолированная точка кривой,
при а > I точка О — угловая точка с двумя
касательными (угловой коэффициент касательных
*) Конхоидой данной кривой называется кривая,
получающаяся при увеличении или уменьшении радиуса-вектора
каждой точки данной кривой на постоянный отрезок /
Если уравнение кривой в полярных координатах имеет вид
р = /(ф)> то уравнением ее конхоиды будет р = / (ф) ±/.
Конхоида Никомела — конхоида прямой линии
циклоиды
125
у а2 — 12/1 и — у а2 — 12/1) и радиусом кривизны
|/а2 - /2/2, при а = I точка О — точка возврата
(см. кардиоиду).
Кардиоида (рис. 1.54). Уравнение кривой:
(х2 + у2)(х2 + у2 -2ах) - а2у2 = О, а > 0. В
параметрической форме: х = a cos t A + cos t), у =
= a sin t A + cos f), 0 < t < 2л. Уравнение в полярных
координатах: р = а(\ + cos ф). Геометрическое
определение: частный случай улитки Паскаля (см. выше)
или частный случай эпициклоиды (см. 1.3.2).
Вершина: АBа, 0); точка возврата — точка О.
Координаты экстремумов С и D: хс = xD = За/4,
УС = ~Уй = V^XO Ч>С = ~Ф?> = яДрс = Pd = За/2.
Площадь: S = Ъка2/2 (шестикратная площадь круга
с диаметром а). Длина кривой: s = 8а.
Овалы Кассини (рис. 1.55). Уравнение
кривой: (х2 + у2J - 2с2(х2 - у2) - (а4 - с4) = 0,
с > 0, а > 0.
В полярных координатах: p2=c2cos2cp±
± ус4 cos2 2ф + (а4 — с4). Геометрическое
определение: точка М плоскости лежит на кривой,
а)а ^ с|/2(рис. 1.55, а). Вершины: Л (j/fl?~+ с2, 0),
С(- )/а2 + с2, 0), Я@, j/a2^"?), D@, - /а2-с2).
Если а = с |/2, то кривизна в точках В и D
равна нулю (кривая имеет с касательными в В
и D касание 3-го порядка).
6)с<а<су2 (рис. 1.55,6). Имеются четыре
точки перегиба: Р, L, М, N. Их координаты:
хР = -xL = хм = -хдг = {/(т - л)/2, уР = yL =
= -УМ = ~ УЫ = l/(m + л)/2, где m = j/(a4 - с4)/3,
и = (д* _ с4)/C<2). Точки ? и G, а также К и I
имеют при су 2 > а общие касательные. Их
координаты: х? = -xG= - хк = х/ = ]/4с4 - а4/Bс),
УЕ = УС = - УК = ~У1 = «7Bс).
в) а = с Лемниската (см. ниже).
г)_а^< г (рис. 1.55, в). Пересечения с осью х:
А(\/аГ+72, 0), C(-l/V+c2, 0), Р()/с2-а2, 0),
Q(- \/с2 - а2, 0). Координаты точек Е, G, I, К:
хЕ = Xj = -xG = -хк = /4с4 - а4/Bс),
2/B)
= ~У1
G
-УК =«2/Bс).
уЕ = yG =
Лемниската (рис. 1.56). Уравнение кривой:
(х2 + у2J - 2а2 (х2 - у2) = 0, а > 0. В полярных
Рис 1 56
координатах: p = a]/2cos29. Геометрическое
определение: точка М плоскости лежит на
кривой, если произведение ее расстояний до
фиксированных точек Fi(a, 0) и F2(-a, 0) постоянно:
| F,M | • | F2M | = (| F,F2 |/2J. (Частный случай овала
Кассини.) Начало координат — узловая точка с
касательными у = + х, она же - точка перегиба.
Пересечение кривой с осью х: /4(а|/2, 0),
С(-ау2, 0); координаты точек Е, G, I, К:
хЕ = х7 = -xG = -хк = а|/з/2,
УЕ = Ув = ~У1 = -УК = я/2.
Радиус кривизны: г = 2а2/Cр); площадь каждой
петли: S = а2.
1.3.2. ЦИКЛОИДЫ
Циклоидой называется кривая, описываемая
точкой, отстоящей на фиксированное расстояние
от центра круга, катящегося без скольжения по
данной кривой - направляющей циклоиды.
Обыкновенная циклоида (рис. 1.57).
Направляющая кривая - прямая линия.
Уравнение в декартовых координатах: acos((x +
если произведение ее расстояний до фиксирован- + ]/у Bа - у))/а) = а - у, а > 0. В параметрической
ных точек Fx и F2 постоянно: | MF1 || MF2 \ = а2; форме: x = a(t - sin t), у = аA -cost), -oo<t<
при этом Ft и F2 имеют координаты Fx (с, 0), < +оо, а - радиус катящейся окружности,
F2(-c, 0). Форма кривой зависит от отношения t = z_ MCXB называется углом качения. Точки
Ф' возврата: OkBkna, 0). Вершины: Ak(Bk - \)па, 2а).
а<с
Рис. 1.55
126
ВАЖНЕЙШИЕ КРИВЫЕ
Длина дуги ОМ: s = 8я sin(t/4), M(t)~ текущая
точка; длина дуги одной ветви OAxOi'. s = 8а.
Площадь между дугой OA^Oi и осью х:
S = Зпа2. Радиус кривизны: R(t) = 4asin(t/4). Радиус
У
Рис. 1 57
кривизны в вершинах: RA — 4а. Эволюта циклоиды
(см. 4.3.1.5) — такая же циклоида (на рис. 1.57
изображена штриховой линией).
Укороченная и удлиненная
циклоиды (тро-хоиды) (рис. 1.58). Уравнения в
параметрической форме: х = a(t - X.sin t), у =
= а(\ — A,cost), a — радиус окружности; t = z. MCXP
(угол качения); Ха = С^М (при X > 1 (рис. 1.58, а) -
удлиненная циклоида, при X < 1 (рис. 1.58, б) —
укороченная циклоида). Вершины Ак(Bк — 1)тсд,
Рис. 1.58
A + X) а) - максимум с радиусом кривизны
RA = аA + ХJ/Х и ВкBкпа, A - Х)а) - минимум
с радиусом кривизны Rr = аA - ХJ/Х. Длина дуги
2я
BkBk + l: a J |/l + X2 — 2Xcostdt. Площадь, заштри-
о
хованная на рис. 1.58: S = па2 B + X2). Радиус
кривизны: R(t) = . Узловые
X(cost-X)
точки Dk удлиненной циклоиды: Bкпа, а(\ —
- ]Д2 — to)), где t0 — наименьший
положительный корень уравнения t — X sin t — 0. Укороченная
циклоида имеет точки перегиба:
Е2к (а(- arccos X + 2кп - X]/\ - X2), аA - X2)),
E2k+l(a(arccosX + 2кп - Х]/\-Х\ а{\ - X2)).
Эпициклоиды (рис. 1.59). Направляющая
кривая - окружность радиуса Ь; окружность радиуса
а катится без скольжения вне ее. Уравнения
в параметрической форме:
х = (а + b) cos ф - a cos ((а + Ь) ф/а),
у = (а + b) sin ф - a sin ((a + b) ф (а),
— оо < ф < +оо, ф = z. COAi.
Вид кривых зависит от отношения т = Ь/а.
а) т — целое положительное число. Кривая
состоит из т равных друг другу дуг,
«обходящих» направляющую окружность (рис. 1.59, а).
Достаточно рассмотреть изменения ф от нуля до
2л, так как кривая далее переходит сама в себя.
При т = 1 получается кардиоида (см. 1.3.1.2).
Точки возврата Ак при 1 < к < т получаются при
значениях параметра ф^ = 2(к - \)п/т; вершины
Вк — при фВл = B/с — \)п/т.
б) т = p/q, p и q — положительные, целые,
взаимно простые числа. Кривая состоит из р
равных друг другу пересекающихся дуг (рис. 1.59,6).
Кривая замкнута. Промежуток изменения
параметра: 0 ^ ф < 2qn.
в) Если т иррациональное, то кривая состоит
из бесконечного числа равных друг другу дуг.
Кривая не замкнута. Длина дуги между двумя
точками возврата: 8(a + b)/m. Площадь между
дугой и направляющей окружностью: 5 =
= па2{2а + ЪЬ)/Ь. Радиус кривизны:
4а (а + b)sin(*Kp/Ba))
2а+ b '
4а (а + Ь)
в вершинах Вк:
Bа + Ъ)
циклоиды
127
Гипоциклоиды (рис. 1.60). Направляющая
кривая - окружность радиуса Ь; окружность
радиуса а катится без скольжения внутри нее.
Уравнения в параметрической форме:
х = (Ь — a)coscp + acos{(b — а)ц>/а),
у = (Ь - a) sin ф - a sin ((b - а) ф/а),
b > а, — оо < ф < оо.
Так как b > а, то всегда т = Ь/а> 1. При т = 2
гипоциклоида вырождается в диаметр
направляющей окружности. (О числе равных друг другу
дуг кривых и параметрических интервалов см.
эпициклоиды. Там же см. и значения
параметров точек возврата и вершин.) Длина дуги
одной ветви (между двумя точками возврата):
8(Ь — а)/т. Площадь между одной ветвью и на-
a) m=3
правляющей окружностью: S = па2{ЗЬ - 2a)/b.
Радиус кривизны:
и вершинах Вк:
Ь-2а
Ла(Ь-а)
Ь-2а '
При т — 3 гипоциклоида с тремя ветвями
(рис. 1.60,а); длина кривой: s = 16a; площадь,
ограниченная кривой: 2па2. В частном случае
т = 4 получается астроида (рис. 1.60,6).
Уравнения в параметрической форме: х = Ьсо83ф,
у = Ь8ш3ф, 0 ^ ф < 2тс; в декартовых координатах:
Х2/3 + ^2/3 = fo2/3} ШИ (х2 + у2 _ Ь2K + 21Х2у2Ь2 = О
(алгебраическая кривая 6-го порядка). Длина кривой
равна s = ЬЬ = 24а; площадь, ограниченная
кривой: S = 3nb2/S = 6ка2.
Удлиненная и укороченная эпи- и
гипоциклоиды (рис. 1.61 и 1.62). Уравнения
в параметрической форме удлиненных и
укороченных эпициклоид:
(а + Ь) ф
х = (а + b) cos ф - Ха cos
у = (a + b) sin ф - Ха sin
а
{а + Ь)ф
а > 0, b > 0,
СМ, - оо < ф < + оо
(для удлиненной эпициклоиды X, > 1, рис. 1.61, а;
для укороченной X < 1, рис. 1.61,6).
Рис. 1.61
Параметрические уравнения удлиненной и
укороченной гипоциклоид:
х = (Ь — a) cos ф + Ха cos
' = (b — a)sinq> — Xasin
a
> - а)ф
a
Ь > а > 0, Ха = СМ, — оо < ф < + оо
(для удлиненной гипоциклоиды X > 1, рис. 1.61, а;
для укороченной X < 1, рис. 1.62,6). Частные
случаи:
а) гипоциклоида b — 2а\ х = аA+ Х,)созф,
у = а(\ — A,) sin фД т* 1,0^ф< 2я. Кривая — эллипс
с полуосями аA+Х) и \а{\-Х)\ (см. 2.6.6.1);
128
ВАЖНЕЙШИЕ КРИВЫЕ
б) эпициклоида Ь — а:
х = aBcos<p - Xcos2<p), у = aBsincp -
О ^ ф < 2п,
есть улитка Паскаля (см. 1.3.1.2; следует, однако,
/ У
/ /
[/
ч.
\ X
\ N
/
/
f
0
ч
\д
V
п *\
7 ' \
J / \
у \
< \
у
Рис. 1.62
обратить внимание на другое положение кривой
относительно координатной системы).
1.3.3. СПИРАЛИ
Архимедовы спирали (рис. 1.63). Кривая
представляет собой путь, описываемый некоторой
точкой, движущейся с постоянной скоростью v
Рис. 1.63
по лучу, вращающемуся около полюса О с
постоянной угловой скоростью со. Уравнение в полярных
координатах: р = аф, а = v/(o > 0, - оо < ф < оо.
Первая ветвь: 0 ^ ср < + ос; вторая: — аз < ф ^ О
(на рис. 1.63 изображена штриховой линией).
Каждый луч ОК пересекает кривую в точках
Аь А2,...,Лп,..., находящихся друг от друга на
расстоянии А(А( + j = 2па. Длина дуги ОМ:
s = а(ф]/ф2 + 1 + Arsh ф)/2; для больших ф имеем
lim s/ф2 = а/2. Площадь сектора МХОМ2\
ф -+ +OD
а2(фг — ф?)/6. Радиус кривизны: К(ф) = а(ф3 +
+ 1K/2/(ф2 + 2).
Гиперболические спирали (рис. 1.64).
Уравнения в параметрическом виде: х = (acost)/t,
у = (asint)/t, -oo <t < 0 и 0<f<+oo. Кривые
состоят из двух ветвей, расположенных
симметрично относительно оси у. Первая ветвь:
— оо < г < 0 (на рис. 1.64 штриховая линия);
вторая ветвь: 0<t < +oo. В полярных координатах
уравнение первой ветви: р = а/| ф - л |, - оо <ф<л;
второй ветви: р = а/ф, 0 < ф < +оо. Для обеих
ветвей прямая у — а = 0 — асимптота (ф -» — л
и ф -¦ 0), а точка О — асимптотическая точка
(ф-> — оо и ф -+ +оо). Площадь заштрихованного
сектора М^ОМ^. S = а2A/ф2 - lApi)/2. Существует
lim S = а2/Bф2). Радиус кривизны (вторая ветвь):
Ф
Ф2
Логарифмические спирали (рис. 1.65).
Уравнение в полярных координатах: р = ае*ф,
а>0, — оо < ф < +оо. Кривая пересекает все лучи,
Рис. 1 65
выходящие из точки О, под одним и тем же
углом а. При этом k = ctg а. При а = л/2,
т. е. при к — 0, кривая вырождается в окружность.
Полюс О — асимптотическая точка кривой. Длина
дуги MiM2: s = (р2 - pi)|/l + k2/k; длина дуги
ОМ от начала до точки М с полярным радиусом р:
s0 = pj/l + к2/к. Радиус кривизны: R(p) =
= j/l +k2p.
Развертка (эвольвента) окружности
(рис. 1.66; ср. также 4.3.1.5). Если А - некоторая
ЦЕПНАЯ ЛИНИЯ И ТРАКТРИСА
129
определенная точка на окружности радиуса а с
центром в О, а М — произвольная точка
эвольвенты, то длина дуги АВ равна длине отрезка
MB. Уравнения в параметрической форме:
х = acoscp + аф sin (р, у = а sin ср — acpcoscp,
-оо<ф<+оо, (р = г! МО А.
Кривая состоит из двух ветвей, симметрично
расположенных относительно оси х (при
-оо<ф^0 и 0<ф<+оо), с общей течкой в
У
Точка О — центр симметрии кривой. Имеются
две асимптотические точки:
Рис. 1.66
точке возврата А {а, 0). Длина дуги AM:
s = аф2/2. Радиус кривизны: Я(ф) = а | ф |. Все
центры кривизны лежат на окружности радиуса
а с центром в О.
Клотоида (рис. 1.67). Кривая проходит через
точку О, причем величина, обратная радиусу
Рис. 1.67
кривизны (сама кривизна), в каждой точке М
кривой пропорциональна длине дуги кривой
s = ОМ, т. е. \/R = sa2 (множитель
пропорциональности 1/а2). Уравнения в параметрической
форме*):
х = а ]/тс f cos ——du, у = а ]/я f sin — -~-du,
о 2 о 2
- оо < t < +oo, t = s/(a\/n), s = 6ti, a > 0.
*) Эти интегралы не выражаются через элементарные
функции.
5 И. Н. Бронштейн, К. А. Семендяев
А(а]/п/2,
B{-a]/n/2, -a
1.3.4. ЦЕПНАЯ ЛИНИЯ И ТРАКТРИСА
Цепная линия (рис. 1.68). Форму цепной
линии принимает гибкая тяжелая нерастяжимая
нить, подвешенная в двух точках.
Уравнение в декартовых координатах:
у = ach(x/a), a > 0. Кривая подобна графику
функции y = chx (см. 1.2.2.3) (преобразование подобия:
х = ах, у — ау). Вблизи вершины А @, а) кривую
а
У
А
0
м/
кр
X
Рис. 1.68
можно приблизить параболой у = а + х2/Bа)
(на рис. 1.68 штриховая линия). Длина дуги AM:
s (х) = a sh (x/a). Величина площади
криволинейной трапеции О AMP: S (х) = as (x) = a2 sh (x/a),
где М (х) - текущая точка кривой с абсциссой х.
Радиус кривизны: R = у2/а = ach2(x/a).
Трактриса. Пусть М — произвольная точка
кривой, Р — точка пересечения касательной в М
с осью х; тогда \PM\-a, или, иными словами:
если к одному концу нерастяжимой нити длины
а прикреплена точка М, а другой конец нити
движется по оси х, то М описывает трактрису
(линию влечения, рис. 1.69). Уравнение правой
ветви в декартовых координатах:
х = aln((a + ]/а2 - у2)/у) - j/a7^/ =
= a Arch (а/у) - ]/а2 - у2, а > 0, 0 < у ^ а.
Уравнение левой ветви получается заменой х
на —х. Оба уравнения возведением обеих частей
в квадрат можно привести к одному. Точка
А @, а) — точка возврата, ось х - асимптота, ось у -
ось симметрии. Длина дуги AM: s(y) = а\п{а/у);
при этом lim | s(у) - х(у)}| = аA - In2) % 0,3069 a.
Радиус кривизны: R (у) = а]/а2 - у2/у; соответ-
ствующая кривая центров кривизны (эволюта,
см. 4.3.1.5) — цепная линия (на рис. 1.69
штриховая линия) с уравнением у = a ch (x/a).
2. ЭЛЕМЕНТАРНАЯ МАТЕМАТИКА
2.1. ЭЛЕМЕНТАРНЫЕ ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
2.1.1. ОБЩИЕ СВЕДЕНИЯ
2.1.1.1. Представление чисел в позиционной
системе счисления. Для представления чисел
применяют цифры или, точнее говоря, цифровые ряды
или (цифровые) слова, которые образуются путем
упорядочения конечного числа знаков из
конечного множества основных знаков (алфавита
системы счисления).
Представление натуральных чисел.
Различают два типа систем счисления:
непозиционные (примером которых может служить
римская система счисления) и позиционные. В
позиционной системе счисления выбирают некоторое
натуральное число р, большее единицы, и
используют его в качестве базисного числа (р-ичная
система счисления); для р, равного единице,
позиционной системы счисления не существует.
Вводят р основных знаков, называемых цифрами.
Эти знаки используют для образования
цифровых последовательностей, которые служат для
представления натуральных чисел. (Будем
обозначать цифры так: а0, аи...,ар-1.) Каждой
цифровой последовательности, образованной только из
одной цифры, однозначно сопоставим одно из
р — 1 первых натуральных чисел или нуль. Тогда
всякое натуральное число а имеет точно одно
представление в р-ичной системе счисления:
а = bsps + bs- ^* + ... + bop°,
где s обозначает однозначно определенное
натуральное число, bo,...,bs- цифры, причем bs -
цифра, отличная от цифры, соответствующей
нулю. Ряд знаков bsbs-i...b0 является цифровым
представлением числа а. Число нуль
представляется последовательностью, состоящей из одной
цифры, соответствующей нулю. В позиционной
системе представляемое число образуется
аддитивно, причем каждая цифра bj имеет числовое
значение (число, которое соответствует цифре bj)
и позиционное значение (вес) pJ, если bj стоит
на j-м месте, считая справа (счет начинают с нуля,
а не с единицы!). Аддитивный вклад этой цифры
в значение числа равен bjpJ.
Десятичная система: р -10, цифры 0, 1, 2, 3, 4, 5,
6, 7, 8, 9. Например,
3-105 + 2-10* + 0-103 + 0-102 + 9-101 + 1 • 10° - 320091.
Двоичная система (бинарная, или диодная, система):
р ш 2, цифры 0, L*). Например,
*) Чаще используются цифры 0 и 1.
Записанная в двоичной системе счисления
последовательность L0L00LL обозначает число, значение которого в
десятичной системе есть 83; действительно, 64 + 16 + 2 +
+ 1-83.
Чтобы иметь возможность представлять в
позиционной системе также и некоторые
рациональные числа, позиционные значения цифр в записи
числа распространяют на степени р с
отрицательными показателями. Для выделения
позиционного значения (веса) р° необходим
дополнительный знак (знак дробности), в качестве которого
обычно берется запятая (иногда точка). Этот знак
размещается в цифровой последовательности
непосредственно справа от цифры с позиционным
значением р°. В соответствии с этим цифровая
последовательность bsfrs-i b0, b-lb-1...b-r
обозначает число, заданное р-ичным
представлением
+ Ь_2р + ... + b-rp~r.
Цифра b-r может иметь числовое значение
нуль.
Примеры. Десятичная система: 23,040 - 2 • 101 +
+ 3-10° + 0-10-* + 4- 10" а + 0- ИГ3,
Двоичная система: L0, 0LL • L «.21 + 0• 2° + 0• 2"х +
+ L-2'2 + L.2~3. Запись числа L0, 0LL в десятичной
системе есть 2,375; действительно, 2 + 0,25 + 0,125 » 2375.
Каждое число, представимое в позиционной
системе счисления последовательностью цифр
конечной длины, является рациональным числом.
Наоборот, в каждой позиционной системе можно
представить точно только некоторое
подмножество рациональных чисел (зависящее от выбора р).
Например, рациональное число 1/3 не может быть
представлено в десятичной системе счисления в
виде конечной последовательности цифр; 1/25 в
десятичной системе записывается как 0,04, а в
двоичной системе счисления 1/25 конечной
последовательностью цифр представлено быть не может.
Если а/b — рациональное число (а и b — взаимно
простые натуральные числа), то а/b может быть
точно представлено в позиционной системе с
базисом р тогда и только тогда, когда каждый
простой множитель в разложении числа b
является простым множителем в разложении р.
Таким образом, в десятичной системе пред-
ставимы только такие рациональные числа а/Ь
(a, b — взаимно простые), у которых b содержит
лишь простые множители 2 и 5.
АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ПОГРЕШНОСТИ
131
2.1.1.2. Погрешности и правила округления чисел.
Как было замечено в 2.1.1.1, не каждое
рациональное и тем более не каждое
действительное число можно представить в позиционной
системе в виде конечной цифровой
последовательности. Поэтому приходится применять
приближенные значения представляемого числа,
содержащие ограниченное число цифр. К этому
прибегают и тогда, когда точное число содержит
конечное, но слишком большое число цифр.
Простейшим способом получения
приближенного значения числа является отбрасывание цифр
в его точном изображении (обрыв), начиная с
некоторог о разряда. При этом погрешность
приближения, т. е. разность z - а, где z — точное число,
а — его приближение, всегда положительна и не
превосходит единицы разряда последней
сохраняемой цифры.
Примеры приближенных значений чисел,
полученных отбрасыванием разрядов:
1.570 - приближенное значение для я/2 (* 1,570796...);
1,414 — приближенное значение для |/2 (* 1,414213...);
0,210-приближенное значение для 27/128 (% 0,210875).
Отбрасывание разрядов является простейшим
способом округления чисел. Применяются и другие
способы округления, из которых наиболее
употребителен следующий-
1) Если за последней сохраняемой цифрой
следует цифра 0, 1, 2, 3 или 4, то никаких
изменений в приближенное значение числа,
представленного последовательностью
предшествующих ей цифр, не вносится (округление с
недостатком).
2) Если за последней сохраняемой цифрой
следует 9, 8, 7, 6 или 5, то к ней
прибавляется единица. Если последняя сохраняемая
цифра 9, то она заменяется на 0 и на единицу
повышается цифровое значение предшествующей ей
цифры. Если эта цифра также 9, то действуют
таким же образом до тех пор, пока не
встретится цифра, отличная от 9 (округление с
избытком).
Иногда применяется дополнительное правило:
3) Если за последней сохраняемой цифрой
следует лишь цифра 5 или цифра 5, за которой все
остальные цифры нули, и если последняя
сохраняемая цифра имеет четное значение,
осуществляется окружение с недостатком; в противном
случае — округление с избытком.
Примеры приближенных значений чисел, полученных
таким округлением:
1.571 - приближенное значение для я/2;
1,414 - приближенное значение для ]/2;
0,211 - приближенное значение для 27/128;
10,000 - приближенное значение для 9,9995;
9,998 - приближенное-значение для 9,9985.
В то время как при отбрасывании разрядов
приближенное значение а числа z никогда не
превосходит z, при округлении приближенное
значение может быть больше или меньше числа z.
Если аг — приближенное значение z, полученное
при окружении с недостатком или избытком с г
десятичными разрядами после запятой, то
погрешность округления равна | аг — z | < 0,5 • 10~г.
Приближенные значения, полученные при
округлении, не обязательно должны иметь только
значащие цифры (ср. 10,000 и 9,9995). Цифры в
записи приближенного значения а числа z
называются верными цифрами, если | а — z | не
превосходит половины позиционного значения
последней цифры числа а. Запись приближенного
значения, полученная путем отбрасывания и округления,
состоит только из верных цифр.
Эти правила обеспечивают погрешность, не
превосходящую по абсолютной величине половины
единицы разряда последней сохраненной цифры.
Все цифры округленного числа в таком случае
оказываются верными, хотя фактически они могут
и не совпадать с соответствующими цифрами
в записи точного числа (см. примеры).
Приближенное число обычно характеризуют
количеством сохраненных разрядов после запятой
или количеством значащих цифр. К значащим
цифрам относятся все цифры, кроме нулей слева.
Так, например, числа 253; 70,2; 0,00375 имеют
по три значащие цифры. При записи
приближенных чисел все значащие цифры должны быть
верными, если погрешность числа не указывается
каким-либо другим способом.
При округлении чисел, больших 10, не следует
писать нули, не являющиеся верными цифрами,
а нужно выделять множитель вида 10й. Так,
например, число 139796,7, округленное до трех
значащих цифр, следует записывать в виде
1,40-105 или 14,0-104.
2.1.2. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ
ПОГРЕШНОСТЕЙ
2.1.2.1. Абсолютные и относительные
погрешности. Приближенные значения чисел
появляются не только в результате обрыва и
округления. Каждое измеряемое значение некоторой
величины в общем случае также есть
приближенное значение этой величины (ср. 7.1.1). Если а
обозначает приближенное значение числа z, то
а — z называется истинной погрешностью а, а
(а — z)/z — истинной относительной погрешностью
а. Но так как в большинстве случаев z
неизвестно, то неизвестны как истинная, так и
истинная относительная погрешности. Напротив,
часто можно указать граничную величину
истинной погрешности, т. е. положительное число Да,
для которого выполняется неравенство | а — z | ^
< Да, или а — Аа < z < а + Да; Да называется
пределом (границей) погрешности, или предельной
абсолютной погрешностью, или сокращенно
абсолютной погрешностью а; да = Да/а — предельной
относительной погрешностью или сокращенно
относительной погрешностью а. Относительная
погрешность а часто указывается в процентах.
Примеры. 1) Если а, - приближенное значение
числа z, полученное путем обрыва (ср. 2.1.1.2), причем
пг содержит г знаков после запятой, то в качестве
абсолютной погрешности может быть выбрано Лаг« 10~р.
Если а, получено округлением, то абсолютная
погрешность равна Даг-0,5 10~г.
2) Число 3,14 есть приближенное значение числа п.
Так как 3,14159 также является приближенным
значением тс с пятью цифрами после запятой, то 0,0016
может быть выбрано в качестве абсолютной погрешности.
Тогда относительная погрешность равна O'f^^6 * 0,00051,
или 0,051 %.
132
ЭЛЕМЕНТАРНЫЕ ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ
sinx з
sin x 5
COSX з
cosx я
tgx*
tgx*
\/a~2~+
ex*\
ln(l +
Формула
S X
S X - X3/6
tl
й 1 - x2/2
X
x + x3/3
x % a + x/2a
+ x % I/a - x/2a3
x) * I/a - x/a2
4-х
x)*x
0,1%
± 0,077
± 0,580
±0,045
± 0,386
± 0,054
± 0,293
-0,085^2-,0,093^
-0,05 \a2 -r 0,052a2
± 0,031a
± 0,045
± 0,002
Относительная погрешность не превышает
1%
Интервал — d < х < d обозначается ±d;
интервал а < х < b обозначается о-гЬ
±0,245
±1,005
±0,141
± 0,662
±0,172
±0,519
- 0,247д2 + 0,328а2
-0,157fl2~0,166a2
± 0,099а
-0,134^-0,148
± 0,020
10%
± 0,786
± 1,632
± 0,451
±1,036
±0,517
± 0,895
-0,607a2-rl,545a2
-0,448а2ч-0,530о2
± 0,301а
- 0,375 ч- 0,502
-0,176ч-0,230
2.1.2.2. Приближенные границы погрешности
функции. Пусть /(хь..., хк) - функция переменных
хь...,хк. Часто требуется знать предельную
абсолютную погрешность А/:
и~11
при условии, что для значений переменных
xi,..., Xfc известны предельные абсолютные
погрешности Ащ. Если/(хь ..., хк) имеет непрерывные
частные производные f'X( по переменным х(,
i — 1, ..., к, то обычно полагают (ср. 3.1.6.3)
Примеры. 1) f(xlt х2) = Xi -f x2:
А (а, + аг) = ^ax + Да2 (/^ = 1, /^ = 1);
2)У(хь x2) = Xl-x2:
Д(а, +а2) = Да1 + Да2 (Д, = 1, ГХг = -1);
3) /"(.х) = с • х {с - постоянная):
4)/(xlf
-я) = Afl-|f| (/i-0;
Д (ai • a2) « Д«1 • | a2 I + Да2
А (о
\а2.
¦flat
j*Ai
-1/х
Дс»1
ll'TalT
, f -
ь 'х2 ~
* \а2\
+ Да2.
-.xi/x
AM
\an\
Д (sin a) « Да • | cos a |
Да ,
1«1 '
cos x).
{1/2) ^ ^ Ai-
l«lA'2 I ~ l«l I I «2 I '
Если функция /(х) задана таблицей, то А/
находят посредством линейной интерполяции из
таблицы в том случае, если Аа меньше, чем
величина шага х в таблице вблизи а. Чаще всего
А/ можно найти прямо из таблицы.
Пример. Для а = 1,30 и Да = 0,01 найдем Г(л) из
табл. 1.1.2.1- ГA,30) = 0,89747 Вследствие равенств
ГA,29) = 0,89904 и Г A,31 ) = 0,89600 можно положить
Д (Г A,30)) = 0,002 и за приближенное значение Г A,30)
принять число 0,897.
2.1.2.3. Приближенные формулы. Во многих
случаях сложные функции можно приблизить
более простыми. Для этого часто используют
первые члены разложения в ряд Тейлора
(ср. 3.1.14.6). В таблице на этой странице
указаны некоторые приближенные формулы и
относительные погрешности в соответствующих
интервалах.
2.1.3. ЭЛЕМЕНТАРНЫЕ
ПРИБЛИЖЕННЫЕ
ГРАФИЧЕСКИЕ МЕТОДЫ
2.1.3.1. Нахождение нулей функции /(х). Для
определения приближенного значения нуля
функции/(х) может применяться график этой функции
(ср. 1.2). Иногда, как показывает следующий
пример, целесообразно представить функцию в виде
суммы двух слагаемых.
Пример. Найти приближенное значение нуля функции
/(х) = sin х — х + 3. Так как sin х — х + 3 = 0 в случае,
ГРАФИЧЕСКОЕ ИНТЕГРИРОВАНИЕ
133
когда sin х = х — 3, то абсциссы точек пересечения графиков
функций g(x) = sinx и й(х) = х-3 как раз и есть нули
f(x). Функция sinx затабулирована (ср. 1.1.1.10), ее график
легко построить. График функции h (х) = х — 3 — прямая,
которую также легко построить (ср. 1.2.1.1).
Полученные приближенные значения могут быть
улучшены посредством правила ложного
положения и методом Ньютона (ср. 7.1.2.3).
2.1.3.2. Графическое дифференцирование. Если
имеется график функции /(*), то точки графика
функции f'(x) могут быть получены следующим
способом.
1) На оси х в области задания функции
f(x) выбираем последовательность точек
хи х2,...,х„.
2) На отрицательной части оси х вне области
задания функции /(х) выбираем точку Р — полюс
построения. Длина b отрезка РО называется
полюсным расстоянием.
3) В точках кривой/(х) с абсциссами х, строим
нормали к кривой. Для этого пригодно
прямоугольное карманное зеркало (лучше всего
металлическое), которое вертикально Ставят на плоскость
чертежа. Если кривая без излома переходит в свое
зеркальное отражение, то ребро зеркала покажет
направление нормали.
4) На каждую из полученных нормалей опускаем
перпендикуляры из Р, которые пересекают ось у
в точках Qt. Эти перпендикуляры проходят
параллельно касательным в точках (xf, /(х<)).
5) Точка пересечения прямой, проходящей через
Qi параллельно оси х, с прямой х = х^ является
точкой графика/'(х) (рис. 2.1).
Рис. 2.1
Масштаб/' (х) зависит от используемых
масштабов тх по оси х и ту по оси у и от
полюсного расстояния Ь. Если ^ и т] - длины
отрезков между точками с координатами
@, 0) и (х, 0) и соответственно между @, 0)
и @, у), то х = тх?, и у = туг\. Тогда, обозначив
ординаты точек построенной кривой через г\\ для
наклонов прямых, построенных параллельно
касательным, получим
2.1.3.3. Графическое интегрирование. Если
имеется график функции /(х), то график функции
х
F(x)= J f(t)dt можно приближенно заменить ло-
*о
маной следующим способом.
1) Разделим отрезок / = [х0, х]
промежуточными точками разбиения на частичные отрезки
1к. При этом следует обратить внимание на то,
чтобы относительные экстремумы функции /(х)
не лежали внутри частичных отрезков.
2) Для каждого частичного отрезка часть
плоскости между осью х и/ кривой /(х) заменим
(приблизительно) равновеликим прямоугольником,
проведя параллель к оси х так, чтобы
отброшенная часть площади была примерно равной
добавленной (заштрихованы на рис. 2.2). Пусть
b
тх dy
ту dx '
таким образом,
Рис. 2.2
xfc есть абсцисса точки пересечения, определенная
однозначно (вследствие 1) прямой, параллельной
оси х, с графиком /(х) на частичном отрезке
1к; тогда точка пересечения этой же прямой с осью
у имеет координаты @, /(хк)).
3) Выберем на отрицательной полуоси х и вне
области задания функции /(х) точку Р - полюс
построения. Пусть b обозначает длину отрезка
РО (полярное расстояние).
4) Проведем через точку Qo = (х0, 0) параллель
к прямой, проходящей через точки Р и @, /(xj).
Пусть эта параллель пересекает прямую х = хх
в точке Qi. Через Qx проведем параллель к
прямой, проходящей через точки Р и @, /(х2)).
Пусть эта параллель пересекает прямую х = х2
в точке Q2 и т.д. Ломаная QoQi-Qn есть
приближенный график функции F(x).
Пусть снова (как и в случае .графического
дифференцирования) х = тх?, у = тух) и Нк -
длины отрезков между точками (хк, 0) и Qk. Тогда
для Y = F{x) выполняется соотношение Y = myH.
Если по методу графического дифференцирования
с тем же полюсом Р в точках с абсциссами
xfc (к > 0) построить точки кривой производной
функции F(x), то получим точки (xfc,/(хк)).
Отсюда для масштабов следует, что
ту = mY/(mxb),
YYly = УПхТПуЬ.
134
КОМБИНАТОРИКА
2.2. КОМБИНАТОРИКА
2.2.1. ОСНОВНЫЕ
КОМБИНАТОРНЫЕ ФУНКЦИИ
2.2.1.1. Факториал и гамма-функция. Функция
/(и), для которой
при всех целых неотрицательных л, называется
п-факториалом и обозначается л!. Для любого
натурального л имеем л! = 1 • 2 •... • л.
Примеры. 1!-1;2!«1-2-2;6!-1-2-3-4.5-6-720.
Значения функций л! и 1/л! см. в
табл. 1.1.1.5.
Для приближенного вычисления л! в случае
очень больших чисел л пользуются формулой
Стирлинга
или
1п(л!) « ( л + у)ш" - и + у1пBя).
Определение гамма-функции Г(х) ло Эйлеру.
Для всех действительных чисел х > О
(ср. 3.1.9.4)
Определение гамма-функций Г(х) ло Гауссу.
Для всех действительных чисел х, кроме
{О, -1, -2, -3,...},
л!лх
Г(х)= lim —— .
При х > 0 оба определения дают одинаковую
функцию.
Основные свойства гамма-функции (см.
также 3.1.9.4).
ГA)= 1, Г(х+ 1) = хГ(х),
Г(х)ГA-х)=-Д—,
Г(х)Г(-х)= : .
xsinrcx
Некоторые специальные значения
гамма-функции: Г(-1/2)= —2]/те, ГA/2) = |/я.
Таблицу значений функции см. в 1.1.2.1. График
функции см. на рис. 2.3.
Полюсы Г(х): хр = 0, -1, -2, -3,...
Вследствие первых двух свойств для всех
натуральных чисел л имеем Г(л + 1) = л!. Поэтому
гамма-функция может рассматриваться как
обобщение факториала. Для приближенного вычисления
значения функции Г(х) при больших
положительных значениях х может быть использована
формула Стирлинга: Г(х + 1) « (х/е)х]/2пх.
по
-5ГЛ-3 -2-1 О i 2 3 4 х дляГ(х)
-2
-3
-4
-5
Рис. 2.3
2.2.1.2. Биномиальные коэффициенты. Для всех
целых неотрицательных чисел л, к функция
d (или (?)):
. для 0 ^ к ^ л,
С*=< к\(п-к)\ для 0 =
U
называется биномиальным коэффициентом.
Читается: С из л по к (или л над к).
Значения биномиальных коэффициентов могут
быть последовательно определены из так
называемого треугольника Паскаля:
&
1
1 1
1 2 1
13 3 1
14 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
7 21 35 35 21 7 1
Каждый коэффициент образуется путем
сложения двух стоящих над ним (справа и слева).
Крайние значения известны для любого л:
С? = Сп„ = 1. В строке с номером л слева направо
стоят значения С?, Сп\ С%,...,Спп-
Область определения биномиальных
коэффициентов можно расширить: именно, для всех
действительных а и для всех целых /с ^ 0 функция
1 при к = 0,
B.2)
также называется биномиальным
коэффициентом.
Для целых а ^ 0 оба определения
совпадают.
ПОСТАНОВКА ЗАДАЧ КОМБИНАТОРИКИ
135
Примеры.
3!E-3)! ~J
(-А- -2(-2-1)(-2-2)
I 3J 3!
-4,
Свойства биномиальных коэффициентов. Для
целых и ^ 0, fc ^ 0 справедливо свойство
симметрии:
С; = С;"*, или
©-(.-.)¦
B.3)
Для действительных а, Ъ
теоремы сложения:
имеют место
ситнгь-
B.4)
Если а = Ь = п, где и - целое неотрицательное,
то из B.3) и B.4) следует (ср. также 2.2.2.1),
что
2.2.1.3. Полиномиальный коэффициент.
Определенная для всех натуральных п и всех наборов
неотрицательных целых чисел [/сь /с2,...,fcr], для
которых t k, = it, функция C.(*i.*a,...,U или
п\
называется полиномиальным коэффициентом.
Примечание. Биномиальный коэффициент С* есть
частный случай полиномиального коэффициента Cn(fcb k2),
где kt = к, к2 = п — к.
= 60
Примеры. С6B, 1,3)
С12B, 3, 3, 4) -
277200.
2.2.2. ФОРМУЛЫ БИНОМА
И ПОЛИНОМА
2.2.2.1. Формула бинома Ньютона. Для всех
действительных чисел а, Ъ и для всех
натуральных чисел п
Ъ)п= ? Скпап~кЬк =
к = 0
= С°па"Ь° + С1па"
Примечание. Биномиальные коэффициенты
формулы B.6) составляют в треугольнике Паскаля строку с
номером и.
Если заменить Ъ на -Ь, то из формулы
B.6) следует
...+. Сппа%п. B.6)
П ример. (а - fcL - а* - 4а3Ь + 6а2Ьг - АаЬъ + Ь4.
Из B.6) получаем
? С; = 2я при а = Ь = 1, B.7)
л = о
f (-l)kCi| = 0 при а = 1, Ъ = -1. B.8)
fc = 0
Вычитанием или сложением B.7) и B.8) получим
равенства
при этом в первом случае т - наибольшее
нечетное число, а во втором — наибольшее четное число,
не превосходящее п.
2.2.2.2. Формула полинома. Для любых отличных
от нуля действительных чисел аь а2,...,аг и
любого натурального п
(ai + а2 + ... 4- аг)" =
2j Cn\Kit к2, ...,fcr)fljia22...д?г.
fei + /с2 + ... + /с, = и
B.9)
При этом суммирование распространяется на все
наборы неотрицательных целых чисел (ки к2,...,кг),
для которых ? /с,- = п.
i= 1
При а^ = а2 = ... = аг = 1
Пример, {а + b + сK = С3C, 0, 0)а3 + С3B, 1,
+ С3B, 0, 1)а2с + С3{1, 2, 0)аЬ2 + С3{1, 1, 1)аЬс +
+ С3A, 0, 2)ас2 + С3@, 3, 0)Ь3 + С3@, 2, 1)Ь2с +
+ С3@, 1, 2Nс2 + С3@, 0, 3)с3
+ ЪаЬг + баЬс + Зас2 + Ь3 + ЗЬ2с + ЗЬс2 + с3.
2.2.3. ПОСТАНОВКА ЗАДАЧ
КОМБИНАТОРИКИ
Во многих математических исследованиях
встречаются комбинаторные задачи, своеобразие
которых целесообразно показать на примерах.
1. Сколькими способами можно расставить на
полке 10 различных книг? (Ср. 2.2.4.1.)
2. Как велико число различных отображений,
переводящих множество из п элементов в себя?
(Ср. 2.2.4.1.)
3. Сколько различных шестизначных чисел
можно составить из цифр 1, 1, 1, 5, 5, 9?
(Ср. 2.2.4.5.)
136
КОМБИНАТОРИКА
4. В турнире принимают участие восемь команд.
Сколько различных предсказаний относительно
распределения трех первых мест (по результатам
соревнований) можно сделать? (Ср. 2.2.5.1.)
5. Сколько различных трехбуквенных слов
можно составить из 32 букв алфавита, не обращая
внимания на то, имеют ли смысл составленные
из букв слова или нет? (Ср. 2.2.5.2.)
6. Сколькими способами можно из множества
к (различных) элементов выбрать г элементов?
(Ср. 2.2.6.1.)
7. Как велико число различных результатов
бросаний двух не отличимых друг от друга
кубиков? (Ср. 2.2.6.2.)
Приведенные примеры показывают, что в
задачах комбинаторики интересуются вообще числом
различных выборок определенных объектов, причем
в зависимости от вида дополнительных
требований следует различать, какие выборки считаются
одинаковыми и какие различными.
2.2.4. ПОДСТАНОВКИ
2.2.4.1. Подстановки. Каждая
последовательность к различных предметов с учетом порядка
называется перестановкой этих предметов. Если
пронумеровать места этих предметов слева
направо: 1, 2,...,/с, то можно сформулировать
следующее определение:
взаимно однозначное отображение р*
конечного упорядоченного множества М = {sb s2,...,sk] из
к элементов на себя называется подстановкой
элементов множества М.
Перестановки из к элементов множества М
отличаются друг от друга только порядком
входящих в них элементов.
Число Рк = Р{рк) всех перестановок рк из к
различных элементов равно
Рк = к\. B.10)
Примеры. Для примеров 1 и 2 п. 2.2.3 из
B.10) следует: имеется 101 = 3628 800 различных способов
расстановки на полке 10 книг и и! взаимно однозначных
отображений, переводящих множество из п элементов в себя.
2.2.4.2. Группа подстановок к элементов. Если
выбрать М = {1, 2,...,к}, то каждую подстановку
рк этих элементов можно записать как матрицу
из двух строк:
где
/1
2 3....
S2 S3 ...
B.11)
pk(i)
для всех ie{l,...,fc}.
Это делает возможным определение произведения
р\ • р\ двух подстановок к элементов как
последовательного проведения обоих преобразований:
Для этого записывают обе подстановки в виде
матриц и переставляют столбцы второго
множителя так, чтобы первая строка второго множителя
совпадала со второй строкой первого множителя.
Матрица произведения состоит из первой строки
первого множителя и преобразованной второй
строки второго множителя:
/1 2 3 ... к \ /sj s2 s3 •
\Si S2 S3 ...
Пример 1
-С
1 2 3.
Справедливы следующие утверждения.
1) Для каждых двух подстановок р* и р\
элементов множества {1, 2,...,fc} произведение
р\ • р\ есть однозначно определенная
подстановка рк.
2) Произведение есть ассоциативная (но
не коммутативная) бинарная операция:
3) Для подстановки рк = ( "' I
{тождественная подстановка) при всех р* имеет
место равенство pk-pk - pk-pk = pk.
4) Для каждой подстановки рк = ( "' ) су-
Vi «2 ... V
ществует обратная подстановка (fr)" =
(«1 «2 • • • sfc\ w
1, для - которой выполняется
соотношение (р*)~1 -рк = р* • (рк)"х = р?.
Вследствие 1)-4) и B.10) все подстановки р*
элементов множества {1, 2,...,/с} образуют
(см. 2.4.1.6) группу порядка к\.
Эта группа называется симметрической
группой Sk.
Пример 2. Элементы симметрической группы S3.
'»-(з")'*-(*"}'1"Aз"^
Если в матрице подстановки р*
элементов множества {1, 2,..., к} встречаются два столбца
для которых s4 < $j, a tt>tj
(или s( > sj, a tt < tj), то такая пара столбцов
называется инверсией подстановки рк.
Подстановка называется четной или нечетной
в зависимости от того, четно или нечетно число
встречающихся в ней инверсий.
Пример 3. Если Z(p?)-число инверсий, то для
подстановок примера 2:
Z(pe3)
i, Z(p|) = 3,
Отображение группы Sk во множество
{ —1, 1}, определенное следующим образом:
Х(рк) = 1,еслирк — четная подстановка, и х(Л — — 1»
если рк — нечетная подстановка, называется
характеристикой подстановки группы Sk. Вследствие
равенства х(р\'Л) = X(Pi)'X(P2) это отображение
гомоморфно.
Множество всех четных подстановок
множества {1,...,/с} образует подгруппу группы Sk
порядка /с!/2. Эта подгруппа называется
знакопеременной группой.
2.2.4.3. Подстановки с неподвижной точкой.
Если рк - подстановка множества М = {1, ..,к}, то
РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ
137
каждый элемент i е М, для которого рк (i) = /,
называется неподвижной точкой подстановки рк.
Пример. Для подстановок примера 2 п. 2.2.4.2
справедливо следующее: р] имеет неподвижную точку 3,
р\ — точку 1, р\ — точку 2, р] имеет неподвижные точки
1, 2 и 3; pi и р\ таковых не имеют.
Число F(pk) всех подстановок множества
{1, ..., /с}, имеющих по крайней мере одну
неподвижную точку, равно
B.12)
где С{ — биномиальные коэффициенты. Число
G(p^) всех подстановок множества {1,...,&},
имеющих в точности одну неподвижную точку, равно
B.13)
Пример. Пять человек занимают места 'за столом,,
не обращая внимания на разложенные на столе именные
карточки. В общей сложности они могут разместиться
5! = 120 способами. В
F(p5) = С\А\ - С|-3! + С\2\ - d 1! + С2-0! = 76
случаях по крайней мере один человек и в
случаях в точности один человек займет отведенное ему
место.
2.2.4.4. Подстановки с заданным числом
циклов. Если матрицу подстановки рк перестановкой
столбцов можно привести к виду
/Sj S2 S3 ...Sr_! SrSr+l ...Sk\
\S2 S3S4...S, Si fr+1 ... ft/
то рк задает взаимно однозначное отображение
S|-*S|+1, i = 1, 2,...,г - 1, sr-*su множества
{sb s2,...,sr} на себя, которое называется циклом
длины г и обозначается Zr-(su s2»•••,$»•). В
соответствии с этим каждой неподвижной точке
соответствует цикл длины 1.
Каждую подстановку рк можно однозначно (с
точностью до порядка сомножителей) представить
в виде произведения циклов, не имеющих общих
элементов.
Примеры.
Л
1 2 3 4 5 б\
23 1 546Г
A, 2, 3)D, 5) F).
Для .числа Р{к, s) подстановок р*, которые могут
быть представлены в виде произведения s циклов,
имеют место рекуррентные формулы
P(fe,fe)*l, ?(*, 1)-(*-1)! при Л > 1, B.14)
P(/c,s) = P(/c- 1,5- 1) + (/с-1)-Р(/с- 1, s)
при к > s > 2.
Пример Имейся РC, 3) = 1 подстановка группы S3
(ср. пример 2 и 2 2.4.2) с тремя циклами: pl\
РC, 1) = 2 подстановки с одним циклом: р\ и р|;
РC, 2) = РB, 1) + 2РB, 2)= 1 +21 = 3 подстановки с двумя
циклами: р\, р\ и pi
2.2.4.5. Перестановки с повторениями. Если
рассматривать упорядоченные ^-наборы из множества
М, которые состоят не только из различных
элементов множества М, то получим
перестановки с повторениями.
Пусть А/ = {sb..., sp} - непустое множество из р
элементов и iu i2, ..., ip — натуральные числа та-
р
кие, что ? ij = к. Каждый упорядоченный набор к
чисел pkix i i, содержащий элемент Sj ровно ij
раз A<7<р), называется перестановкой
множества М с повторением.
Примечание. При f, = i2 ~ ... = jp = 1 получим
перестановки множества из р элементов.
Число CtO'i» hi-'-Jp) различных перестановок
множества М с повторениями равно*)
где
Пример. Имеется СбC, 2, 1) =
B15)
= 60 различных
шестизначных чисел, содержащих трижды цифру 1, дважды
цифру 5 и один раз цифру 9 (ср. пример 3 п. 2.2.3).
2.2.5. РАЗМЕЩЕНИЯ
2.2.5.1. Размещения. Любой упорядоченный
набор г различных элементов множества М,
состоящего из к элементов, называется размещением
а) из к элементов по г.
Примечание. Каждое размещение акг есть взаимно
однозначное отображение упорядоченного множества
{1, 2,...,г} во множество М. Из определения следует, что
г < к. При г-к получаем подстановки множества М.
Число А^- А (ак) различных размещений есть
/с!
(к-г)\
¦¦к{к-
1). B.16)
Примеры. 1) Имеется А\ различных взаимно
однозначных отображений множества {1, 2} во множество
{аи а2, а3, а4}, т. е. А\ = 12.
2) Имеется А\ — 336 различных способов распределения
трех первых мест при восьми командах, участвующих в
соревновании (ср. пример 4 п. 2.2.3).
2.2.5.2. Размещения с повторениями. Любой
упорядоченный набор г элементов множества М,
содержащего к элементов, называется размещением
с повторениями ак из к элементов по г.
Примечание. Каждое размещение с повторениями
# есть однозначное отображение упорядоченного множества
{1, 2,...,г} в М. При этом возможно, что г > к.
Число Л(а{) различных размещений с
повторениями есть
А(ак) = кг. B.17)
Пример. Число различных трехбуквенных слов,
которые можно составить из 32 букв алфавита, есть
(ср. пример 5 п. 2.2.3).
•) Ср. 2.2.1.3.
138
КОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СУММЫ, ПРОИЗВЕДЕНИЯ, СРЕДНИЕ ЗНАЧЕНИЯ
2.2.6. СОЧЕТАНИЯ
2.2.6.1. Сочетания. Любое подмножество из г
элементов множества, содержащего к элементов,
называется сочетанием скг из к элементов по г.
Примечание. Если объединить все размещения
а* из к элементов по г, состоящие из одних и тех
же элементов (не учитывая расположения), в классы
эквивалентности, то каждому классу будет соответствовать
ровно одно сочетание dL и наоборот. ,
Примеры. I) Пары [Sl, s2}, {su s3}, {si,4
{*2, S3}, {si, «¦}, {sit s4) исчерпывают все сочетания из
четырех элементов по два.
2) Имеется одно сочетание из к элементов по О
(т.е. не содержащее ни одного элемента) - это пустое
множество.
Число Сгк = С(ск)
равно
С'к =
всех различных сочетаний
к\
г\{к-г)\ '
B.18)
Пример. В числовом лото надо выбрать 5 чисел из
90. Для этого существует С|О-43949268 способов (ср.
пример б п. 2.2.3).
2.2.6.2. Сочетания с повторениями. Объединим
все размещения а, с повторением из к
элементов по г, состоящие из одинакового количества
одних и тех же элементов (без учета
расположения), в классы эквивалентности. Каждый класс
эквивалентности называется сочетанием с
повторением скг из к элементов по г.
Примечание. Два размещения ак и а'к или йк и
а'к принадлежат одному сочетанию ск или ск
соответственно только тогда, когда существует перестановка рТ
множества {1, 2, ..., г) такая, что для всех ie{\, 2, . , г]
имеет место равенство
или я* @
#V@)-
Ср. примечания в 2.2.5.1, 2.2.5 2 и 2 2.6.1.
Число /* = С(скг) различных сочетаний с
повторением из к элементов по г равно
^-i (fc + r-1)!
fk
B.19)
'-1 K+r~l r\(k-l)\
Пример. При наличии двух неразличимых кубиков
можно получить f\ = Cf = 21 различный результат бросаний
(ср. пример 7 п. 2.2.3).
2.3. КОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ, СУММЫ,
ПРОИЗВЕДЕНИЯ, СРЕДНИЕ ЗНАЧЕНИЯ
2.3.1. ОБОЗНАЧЕНИЕ СУММ
И ПРОИЗВЕДЕНИЙ
Если яь а2,... ,ап — (конечная)
последовательность действительных чисел (ср. 2.3.2), то можно
составить конечную последовательность сумм и
произведений.
Для конечных сумм и произведений чисел
приняты обозначения:
п л
? ах = ах + а2 + ... + ап, Па,- = а± -а2-...-а„.
i=l «=i
B.20)
Входящая в выражения B.20) переменная z
называется индексом суммирования (индексом
умножения), а целые числа 1 и п — пределами
суммирования (пределами умножения). Значение суммы
(произведения) не зависит от обозначения индекса
суммирования (индекса умножения) — это так
называемая немая переменная:
п п п
i=l j=l k=l
Иногда бывает необходимо перейти к новому
индексу суммирования с одновременным
изменением пределов суммирования. Так, например,
полагая в первой сумме i = k + г, где г — целое число,
а к — новый индекс, получим, что новые пределы
по индексу к равны соответственно 1 - г и п - г
и
2.3.2. КОНЕЧНЫЕ
ПОСЛЕДОВАТЕЛЬНОСТИ
Конечная (действительная) числовая
последовательность есть однозначное отображение
множества Ап = {1, 2,...,п}, п ^ 1, во множество
действительных чисел. При этом образ натурального
числа ieAn обозначается а, и называется
членом последовательности. Последовательность
обозначается посредством [д,]".
Последовательность может быть задана прямым перечислением ее
членов или каким-нибудь алгебраическим
выражением.
Примеры. 1) Последовательность, заданная прямым
перечислением членов:
[a,]f = 4, -1,3/5,4,4.
2) Последовательность, заданная алгебраическим
выражением:
[3/-/2]?
2, 0, -4, -10, -18.
Если задана последовательность [aj" =
= йь й2,...,й„, п>1, то из нее можно образовать
другую последовательность:
= a2 - a,, a3 - a2, ..., а„ - an_,;
B.21)
она называется последовательностью первых
разностей последовательности [«,]". Если п > 2, то
из последовательности первых разностей можно
снова образовать последовательность первых
разностей, которую называют последовательностью
вторых разностей исходной последовательности.
Если продолжать так дальше, то процесс
оборвется на последовательности (и - 1)-х разностей, так
как она состоит только из одного члена.
Если [rfj 1 — последовательность первых
разностей последовательности [«J", то
а2 - аи dx + d2 = a3 - аи ..., ? dx = а„ -
B.22)
СРЕДНИЕ ЗНАЧЕНИЯ
139
Если cii = О, то ап равно сумме п — 1 членов
последовательности первых разностей.
конечная последовательность [aj" называется
постоянной, если существует такое действительное
а, что а, = а для всех ie{l,...,n}. В
соответствии с этим конечная последовательность длины
п = 1 постоянна.
2.3.2.1. Арифметическая прогрессия. Конечная
последовательность называется арифметической
прогрессией Л-го порядка, если последовательность
ее первых разностей постоянна (а{ — a,_i = d —
разность арифметической прогрессии).
Последовательность называется арифметической прогрессией
т-го порядка, если последовательность т-х
разностей постоянна, а (т - 1)-х не постоянна.
Если [а;]" — арифметическая прогрессия 1-го
порядка и d — ее разность, то
а сумма членов равна
sn = в\ + а2 + ... + а„ =
= ? а,- = л (а! + а„)/2 = п^ + (и - 1)ш//2.
» = 1
Если [а;]" — арифметическая прогрессия
порядка т, то существует многочлен
такой, что для всех /е{1, ..., п) выполняется
равенство а, = Рт (/).
При т = 1 для последовательности [а,]" с
постоянной разностью d этот многочлен имеет
вид
д. = di + («i — d).
Пример. Последовательность [**]" ¦¦ 1, 2а, •••, n3
есть арифметическая прогрессия 2-го порядка, Pa(Q«i2.
Последовательность первых разностей имеет вид ДОГ1,
где <*, ¦« 0 + IJ - <а - 2i + 1. Последовательность вторых
разностей записывается в виде ДОГ2» где rf,-2A+1)+
+ 1-B*+1)-2.
Если рассматривать [г1]? как последовательность первых
разностей последовательности ДОГ1, то ДОГ1 есть
арифметическая прогрессия 3-го порядка. Тогда существует
многочлен третьей степени по i такой, что при всех i
выполняется равенством - с3/3 + сг\г + cxi + c0. Если выбрать
ах - О, то первые четыре члена последовательности
ДОГ1 будут равны 0, 1, 5, 14. Из системы уравнений
i*c3 + i3c2 + icx + с0 - а, при / - 1, 2, 3, 4 (или из одной
из интерполяционных формул (ср. 7.1.16.1)) для неизвестных
коэффициентов сг, са, си с0 получаем
с3 ш 1/3, с2 - -1A ci - 1/6, с0 - О
и, далее,
ш у р т 2»* + Зя» + я т Bя + 1)(я + 1)я
2.3.2.2. Геометрическая прогрессия. Каждая
последовательность [а,]", у которой частное от деления
двух соседних членов постоянно: а, + 1/я«=Я для
всех ie{l,...,w — 1}, называется геометрической
прогрессией. Число q называется знаменателем
геометрической прогрессии.
Общий вид членов геометрической прогрессии:
сумма всех членов геометрической прогрессии
{q Ф 1) равна
q"-l
2.3.3. НЕКОТОРЫЕ КОНЕЧНЫЕ СУММЫ
2) Р + (Р + 1) + (р + 2) + ... + (р + и)
3) 1
4) 2
5) 1:
7) 1:
8) V
9) V
+ 3 + 5-
+ 4 + 6 -
1 . л2 _|_ '
> + з2 + :
v + 24 +:
f ... + Bп-1) =
f ... + 2и = п (п +
2 2 И(
и2
52 + ... + Bп- 1)
53 + ... + Bл-1)
54 + ... + «4 =
п(и + l)B/i
«2;
1);
п +
(п +
4
2 _ '
3 = i
+ 1)
\)Bп
6
'
«Dи2
3
п2Bп
(Зп2 -
2
+ 1)
-1)
2-i);
h 3« — 1)
30
2.3.4. СРЕДНИЕ ЗНАЧЕНИЯ *)
Если заданы п (не обязательно различных)
действительных чисел аь а2,...,Дт то число
(а! + а2 + .
называется средним арифметическим чисел а?,..., л„,
a mn = / — (а2 + а\ + ... + а2) — средним
квадратичным чисел аь ..., а„. Если а и b —
неотрицательные действительные числа, то
тс = ^а~ь
называется средним геометрическим чисел а и b
или средним пропорциональным чисел а и Ь.
Из равенства m2G = ab следует, что а: mG =
= mG:b.
Для среднего арифметического тд{а, Ъ) и
среднего геометрического mG(a, b) неотрицательных
чисел а и b справедливы следующие утверждения:
1) mG(a, Ь)^тд{а, Ь);
2) а, тд (а, b), b - арифметическая прогрессия
1-го порядка; a, mG{a, b), b - геометрическая
прогрессия. Если а и b - длины отрезков, то
отрезки длин тд{а, Ь) и mG(a, b) можно
построить циркулем и линейкой (рис. 2.4 и
2.5).
*) О средних значениях см. также 3.1 14.
140
АЛГЕБРА
Золотое сечение. Если а > 0, то разложение
этого числа на два положительных слагаемых
х и а — х называется золотым сечением числа а,
Рис. 2.4 Рис 2.5
если х является средним геометрическим чисел
а и а — х. Из равенства х = \/а(а — х) следует:
х='—(]/5- 1)а« 0,618а.
Если считать а длиной отрезка, то отрезок
длиной х определяется построением, приведенным
на рис. 2.6.
Из равенства х2 = а (а — х) = а2 — ах следует, что
а2 = х2 + ах = х(х + а), в соответствии с чем а
Рис. 2.6
есть среднее геометрическое чисел х и х + а.
Таким образом, если х делит число а в золотом
сечении, то а в свою очередь делит в золотом
сечении число х + а.
2.4. АЛГЕБРА
2.4.1. ОБЩИЕ ПОНЯТИЯ
2.4.1.1. Алгебраические выражения. В
современной математике алгеброй называют науку о
системах объектов («величин»), над которыми
определены операции, аналогичные сложению и
умножению действительных чисел. Различные объекты
могут иметь различные имена, а для
обозначения операций над ними применяются различные
знаки. Существенной частью алгебры является
грамматика алгебраических выражений,
определяющая правила построения выражений из имен
объектов, знаков операций и вспомогательных
знаков (так называемых разделителей). Мы
ограничимся употреблением простейшей системы
обозначений, при которой величины обозначаются
отдельными буквами, быть может, с подстрочными
индексами (например, х, у3, «152)*). Будем
считать также определенными основные действия:
сложение (-(-), вычитание (-), умножение (• или х) ¦ *)
и деление (: или /). Умножение и деление
считаются действиями более старшими, чем
действия сложения и вычитания. В выражениях,
содержащих несколько знаков действий,
выполняются сначала все более старшие действия, а
затем младшие. Действия одинакового
старшинства выполняются по порядку, слева направо.
Для изменения порядка действий могут
применяться скобки. Правильные выражения должны
содержать одинаковое количество открывающих и
закрывающих скобок, которые всегда могут быть
объединены в систему вложенных пар. Первыми
должны выполняться действия внутри самых
внутренних скобок (не содержащих скобок внутри
себя), затем внутри скобок следующего уровня
и т. д. Для удобства иногда употребляются
скобки разного вида, как-то: ().[]>{}•
однако они должны встречаться парами и не нару-
*) В алгоритмических языках (см. 7.2.1),
допускающих только линейную запись (в одну строку),
используются имена из нескольких букв и цифр,
начинающиеся всегда с буквы, например: уЗ, abc, beta\.
**) Если употребляются только однобуквенные имена,
знак умножения может быть опущен, например, вместо
Ъ-аЬ можно писать ЗаЬ.
шать систему вложенности; например, выражение
(а • {Ь + с) - d] неправильное. Если допускается
нелинейная запись, то изменение порядка действий
при делении может быть показано записью
«в два этажа» - с горизонтальной чертой в
качестве знака деления (а также косой чертой), т. е. записи
^±АИ (а + Ь)/(с + d) - j)
(a + b):(c + d)fu
с + а
равноценны.
Возведение в целую степень определяется как
повторное умножение и обозначается знаком t или
подстрочной записью показателя степени:
а-а- ...а обозначается а ] п или а". Возведение в
л раз
степень рассматривается как действие более
старшее, чем умножение и деление. Например, а | т/п
совпадает с (а | ю)/п, а не с а | (т/п)*).
2.4.1.2. Значения алгебраических выражений.
Если не ограничиваться свойствами
алгебраических выражений самих по себе как абстрактных
выражений, то возникают вопросы, связанные с
интерпретацией этих выражений на некоторой
конкретной системе допустимых объектов, которые
могут замещать алгебраические величины. Мы
ограничимся рассмотрением алгебраических
выражений над какими-либо системами чисел,
допускающими упомянутые выше действия (см. 3.1.1
и 3.4.2). Поскольку при этом алгебраические
выражения могут быть вычисляемы, если входящим
в них величинам придавать числовые значения,
их иногда называют арифметическими
выражениями.
Следует заметить, что основными действиями^
являются сложение и умножение.
Если рассматривать только натуральные (целые
положительные) числа, то вычитание - действие,
обратное сложению, - не всегда окажется
выполнимым и потребует введения нуля и отрицательных
целых чисел; деление (на число, отличное от нуля) -
действие, обратное умножению, — окажется
выполнимым, если мы введем в рассмотрение рацио-
*) Возведение в нецелую степень определено ниже
(см. 2.4.1.4).
ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
141
нальные числа. Существуют разнообразные системы
чисел, допускающих вычисление произвольных
рациональных (т. е. использующих только четыре
арифметических действия) выражений, например
числа вида а + ЪуЗ, где а и Ь - рациональные.
При рассмотрении алгебраических выражений
во многих случаях выделяют некоторые
основные величины (переменные), отличая их от других,
называемых коэффициентами или параметрами.
При этом возможно считать допустимыми для
основных величин и для параметров различные
системы чисел. Так, например, рассматривая
алгебраические уравнения (см. 2.4.2) с целыми или
действительными коэффициентами, можно искать
корни среди целых, действительных или
комплексных чисел.
Алгебраические выражения можно
преобразовывать, заменяя одно выражение другим. Такие
преобразования называются допустимыми
(тождественными), если после преобразования
выражение будет сохранять свое значение при
подстановке любых чисел допустимых систем. При
преобразованиях используются основные свойства
арифметических действий (здесь и далее в этом
пункте знак равенства употребляется в смысле
тождественности):
коммутативность (перестановочность):
а + b - Ъ + а, а-Ь — Ъ-а\
ассоциативность (сочетательность):
а + (Ь + с) = (а + Ь) + с, а-(Ь-с) = (а-Ь)-с\
дистрибутивность (распределительность):
а • (Ь + с) = а - b + a • с.
Из этих свойств вытекают формулы действий
над степенями:
хт • х" = хт+", (х • у)т = хт • у, (хт)п = хт ¦",
хт/х" — хт~п, (х/у)т = хт/ут.
Некоторые формулы преобразований:
(х ± уJ = х2 + 2ху + у\
(х + у + ... + t + иJ = х2 + у2 + ... + t2 + и2 +
-I- 2ху + ... + 2х* + 2хм + ... + 2уи + ... + 2tu,
(х ± уK = х3 ± Ъх2у + Зху2 ± у3,
(х±у)п (см. 2.2.2.1),
(х + у)(х - у) = х2 - у2,
хп -у" = (х- y){xn~l +xn~2y + x"-V +
ражение можно представить
(суммы одночленов):
А1Х1 + Аг-Хг Л- ..
виде многочлена
АЯ-ХЯ
где Ai — коэффициенты выражения, не содержащие
переменных, a Xt — произведения степеней
переменных. Многочлен обычно располагают в порядке
убывания или возрастания степеней какой-нибудь
переменной либо суммы степеней всех
переменных. Одночлены, в которых выражения Xt
тождественны, т. е. содержат одинаковые переменные
в одних и тех же степенях, называются
подобными и обычно приводятся — объединяются в один,
коэффициент в котором равен сумме
коэффициентов приводимых одночленов. Сумма
степеней всех переменных в одночлене называется
степенью этого одночлена. Наибольшая из
степеней одночленов называется степенью многочлена.
Сумма, разность и произведение многочленов
также являются многочленами. Степень суммы или
разности не превосходит наибольшей из степеней
слагаемых, степень произведения равна сумме
- степеней сомножителей.
Деление многочленов (с остатком). Если Р(х)
и Q (х) — многочлены по х степеней пит
соответственно, п ^ т, то всегда существуют однозначно
определенные многочлены Г(х) степени п - т и R (х)
степени, меньшей чем w, такие, что тождественно
р (х) = Q (х) • Г(х) + R (х). Для нахождения частного
Т(х) и остатка R(x) выполняют деление Р(х)
на Q(x).
3r4
Зх4
Прим
Юах3
-бах3
-4ах3
-4ох3
ер.
+ 22а2х2
+ 9а2х2
+ 13а2х2
+ 8а2х2 -
5а2х2 -
5а2х2 -
24а3х
- 24а3х
- 12а3х
12а3х +
10а3х +
+ Юа4
10а4
15а4
х2 - 2ах + За2
Зх2 - 4ах + 5а2
- 2а3х - 5а4
Таким образом, Зх4 - Юах3 + 22а2х2 - 24а3х + 10а4 =
= (х2 - 2ах + За^НЗх2 - 4ах + 5а2) + (-2а3х - 5а4).
Если Я(х) = 0 (нулевой многочлен), то
многочлен Q(x) называется делителем многочлена
Р(х). Для нахождения общего наибольшего
делителя двух многочленов Р(х) и Q(x)
применяется алгоритм Евклида. Выполняется цепочка
делений до получения остатка, равного нулю:
2у + X2
Rm-i(x) = Rm-i(x). Tm(x) + Rm(x\
-...-ху2к~1 +у2к).
2.4.1.3. Многочлены. Если в алгебраическом
выражении основные величины (переменные)
участвуют только в действиях сложения, вычитания
и умножения, включая возведение в целую степень,
то такие выражения называются целыми
рациональными (см. 2.5.1). Используя свойства
арифметических действий, любое целое рациональное
выПредшествующий ему остаток Rm(x) является
общим наибольшим делителем. Если он не
содержит х, то многочлены Р(х) и Q(x)
называются взаимно простыми.
2.4.1.4. Иррациональные выражения.
Обобщение понятия о степени.
Извлечение корня определяется как действие,
обратное возведению в степень. Корнем m-й степени
142
АЛГЕБРА
из х (обозначается ух) называется величина у, т-я
степень которой равна х: (J/x) = х. При т четном
ух существует (среди действительных чисел) только
при х ^ 0, причем допустимы два значения
корня - положительное и отрицательное. Для
определенности знак корня в этом случае будем
всегда брать положительным, так что
ухт = | х |. При т нечетном существует
единственное значение ух, знак которого совпадает со
знаком х.
Из определения следует, что
при условии, что соответствующие корни
существуют.
Выражения, содержащие знак корня (радикал),
называются иррациональными.
Примеры преобразований иррациональных выраже-
ний
1) 1/хД27) - /2ху/D/) - /2x^/B1 у |) (при у # 0, ху ^ 0);
2) )/х1(Ауг>) - \/2xy*z/(%y3z>)
(при у Ф 0, г * 0);
+ У) (при х3 + у * 0);
¦ |/(х + и)/2 + |/(х - и)/2,
где и = |/х2 - у (при у ^ 0, х2 - у > 0).
Понятие возведения в степень может быть
обобщено на нулевой, отрицательные и дробные
показатели при помощи формул (для допустимых
значений х)
Примеры. Неравенство х2 + 1 > 0 - тождественное;
х2 + у2 + 5 < 0 - невыполнимое; 2х + 4 > 0 - выполнимое
(оно справедливо при х > - 2).
Некоторые универсальные
неравенства.
1) |а + Ь|^|я| + |Ь|, | fli + a2 + ... + а„ | ^
2) \a\ + \b\^\a-b\^\\a\-\b\\.
3) I (ai + а2 + ... + а„)/п | ^
^ 1/(^1 + а2 + ... + а2)/п (равенство имеет место
только при а1 = а2 = ... = ап).
4) Неравенство Коши — Буняковского:
{афх + a2b2 + ... + а„Ь„J ^
K(al + а\ + ... + а2)(Ы + Ь§ + ... + Ь2)
(равенство имеет место тогда и только тогда,
когда aak = fibk для всех к=\,...,п и некоторых
а, р, |а| + |Р|>0).
5) Неравенство Минковского (при р^ 1):
(I fli + bj |p + | а2 + Ь2 \р + ... + | ап + Ьп \рI1р ^
Выполнимые неравенства.
„ fll + й2 + _,. йп
при а,-^ 0 (i = 1, 2,..., п)
Среднее геометрическое положительных чисел
меньше их среднего арифметического или равно
ему (см. 2.3.1). Равенство имеет место, только
если ах = а2 = ... = а„.
2) Неравенство Чебышева. При 0 < ai ^ а2 <
^ ... < ап и 0 < Ь\ ^ Ь2 ^ ... ^ Ь„
... + ап bi + b2 + ... + Ь„
a2b2 + ... + anbn
Приведенные в 2.4.1.2 формулы для действий со
степенями остаются в силе.
Пример. (|/?+ {/? + $Ф
ty?) = (х1'2 + х2/3 + х3/4 + х7'12)(х1/2 - х1/3 + х1/4 + х5/12)
2_х7/б _х
хз/4 _xi3/i2 _
2.4.1.5. Неравенства. Два алгебраических
выражения, соединенные одним из знаков <, ^, >,
^, ф, образуют неравенство. Неравенство
называется тождественным или универсальным, если
оно выполняется (в арифметическом смысле) для
любых действительных значений входящих в'
неравенство величин. Неравенство называется
выполнимым, если существует непустое множество
значений входящих в неравенство величин, при
подстановке которых неравенство оказывается
справедливым, и невыполнимым, если таких значений не
существует.
При
b2 + ... + bn
... + anbn
3) Обобщенные неравенства Чебышева. При
...<а„ и 0 < Ь\ ^ Ь2 ^ ... ^ bn, k
натуральном
к
к
При 0 «
y»«;-+<|jt±ii±i;
УРАВНЕНИЯ
143
Неравенства называются эквивалентными, если
они выполнимы для одних и тех же
значений входящих в них величин или если они
невыполнимы.
Основные свойства неравенств
(эквивалентные преобразования).
1) Если А\ < А2, то А2 > А\.
2) Если А\ ^ А2 и А2 ^ Ль то А\ = А2.
3) Если /4i < А2 и А2 ^ Аз, то Ai < Л3.
4) Если А\ < А2 и Лг ^ Лз или А\ ^ А2 и
Л2 < Аъ, то ^1 < Л3.
5) Если А\ ^ /42Иу43 ^ Л4,то ^i + Л3 ^ А2 + А*.
6) Если Л! < Л2 и Л3 > 0, „ то Л1Л3 ^ А2АЪ.
7) Если /4i ^ Л2 и Л3 < 0, то Л1Л3 ^ А2АЪ.
8) Если 0 < А\_ ^ А2 или /li ^ А2 < О, то
lMi > I/A2.
Решить неравенство, содержащее неизвестную
величину, - значит определить множество значений
неизвестного, при которых неравенство
выполнимо,— множество решений неравенства. Для
отыскания решения используются эквивалентные
преобразования.
Примеры решения неравенств.
1) 5х + 3 < 8х + 1. Используя свойство 5), прибавим
к обеим частям неравенства -8х-3; получим -3x^-2.
Используя свойства б) и 7), получим решение
х > 2/3.
2) Неравенство первой степени ах + Ь > О*). При а > О
имеем х>-Ь/а, при д<0 имеем х<-Ь/в, а при а-О
неравенство тождественно для Ь>0 и невыполнимо для
Ь<0.
3) х2 < а. При а < 0 неравенство невыполнимо, при
а «О получаем х-0, при а>0 решением является
множество значений, определяемое двойным неравенством
4)х3>о./При а<0 неравенство тождественно, при
л>0 решением является множество значений х,
определяемое следующими условиями: или х>|/а, или
х<-]/2.
5) Неравенство второй степени ах2 + Ьх + с > 0 (а * 0)
может быть преобразовано к виду я((х + р/2J + ?>) >0,
где р = Ь/а, D«Dос-Ь2)/Dа2). При D>0 неравенство
тождественно при а > 0 и невыполнимо при а < 0. При
D < 0, используя свойства неравенств и примеры 3) и 4),
получим, обозначив х% - -р/2 - j/^Б, х2 = -р/2 + /^7),
что х < xi или х > х2 при а > 0, Xi < х < ха при а < 0.
2.4.1.6. Элементы теории групп. Алгебраическая
система G, в которой определена одна операция,
ставящая в соответствие двум любым элементам
системы какой-либо третий элемент этой системы,
называется группой, если эта операция
(обозначаемая * ) обладает следующими свойствами:
1) (а * Ь) * с = а * (Ь * с) для всех a, b, ceG -
ассоциативность;
2) существует «нейтральный» элемент е такой,
что е * а = а * е = а для всех aeG;
3) для каждого aeG существует обратный
элемент х такой, что а*х = х*а = е.
Если, кроме того, для любых элементов а
и Ъ выполнено соотношение а * Ъ — Ъ * а, то
группа называется коммутативной, или абелевой.
*) Знак неравенства < можно перевести в ^
умножением неравенства на —1. Если вместо ^ стоит >, то
при решении возможность равенства должна быть
отброшена
В качестве знака операции обычно
употребляют знак + (аддитивная группа) или •
(мультипликативная группа). Для аддитивной группы
нейтральный элемент называется нулем, а обратный
к а элемент обозначается —а. Для
мультипликативной группы нейтральный элемент называется
единицей, а обратный элемент обозначается а~1.
Коммутативная аддитивная группа называется
кольцом, если в ней определена, кроме операции
сложения, вторая операция - умножение,
обладающая дистрибутивностью: a-(b + c) = a-b + ac и
{a + b)-c = a-c + b-c для любых элементов a, b и с.
Примером кольца может служить Z —
множество всех целых чисел.
Если операция умножения в кольце обладает
свойством ассоциативности a-(be) = {a-b)-c или
коммутативности ab — Ь-а, то кольцо называется
соответственно ассоциативным или
коммутативным.
Если в ассоциативном и коммутативном
кольце существует единичный элемент е, т. е.
а • е = е • а = а для любого а, и для каждого
элемента а, отличного от нуля, существует
обратный элемент а~1 (т.е. кольцо, из которого
исключен нуль, образует мультипликативную
группу), то кольцо называется полем. Примерами
полей могут служить множество всех
рациональных чисел, множество всех действительных чисел
и множество всех комплексных чисел.
Отображение алгебраической системы G в
другую систему G' называется гомоморфизмом, если
каждому элементу aeG соответствует
определенный элемент а' е G', причем если с = а * Ь, то
с' = а' *'Ь' (# - операция, определенная в G, #' -
операция, определенная в G'). Если такое
отображение взаимно однозначно, оно называется изо-
мдрфизмом.
2.4.2. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
2.4.2.1. Уравнения. Пусть G обозначает
множество чисел, так называемую основную область,
и а, Ь, с,..., х, у, z — переменные. Это знаки,
вместо которых могут стоять элементы основной
области или ее подмножества, так называемой
основной области переменных, или области
изменения. Из чисел и переменных могут быть
построены алгебраические выражения (см. 2.4.1),
например: 8, -3/5, Bх - \)/а {а Ф 0), ]/а1 - 1.
Определение выражения можно распространить на
неалгебраические выражения, к которым относятся,
например, ар (|3 действительное), ех, \ogay, sinx,
arccos z.
Под областью определения X выражения с п
переменными хь х2,..., хи и соответствующими
областями изменения Хи Х2,...,Хп понимают
множество всех последовательностей (?i, Ъ,2,-..,?„),
fyeXt (i = 1, 2,...,л), для которых данное
выражение переходит в число из области G, если
переменные х,- заменить на ^.
Если G — множество всех действительных чисел, то
выражение Bх + 1)/5 имеет, например, в качестве области
определения всю область изменения х, в то время как
область определения выражения 5/Bх + 1) содержит все числа
области изменения х, за исключением -1/2.
144
АЛГЕБРА
Два выражения 7^ (хь х2, .., х„), Т2(хи х2,..., хп)
от переменных xi, х2,..., хп называются
эквивалентными по отношению к области определения X,
если соотношение 7\ (?ь ?2, •••, U = ^2(^1, ?2, •••
..., ?„) выполняется для всех последовательностей
(^ь \ъ ••-, U^X (ср. 2.4.1.5). Переход от
выражения 7\ к эквивалентному выражению Т2
называется эквивалентным преобразованием выражений.
Это понятие зависит от областей определения
выражений; так, у а2 = а для неотрицательных
действительных чисел есть эквивалентное
преобразование, но не является таковым для
множества всех действительных чисел.
Пример. Выражения Зх/2 + 5х/2 и 4х эквивалентны
по отношению к множеству всех действительных чисел,
в то время как а + b + 1 и а + (Ь2 — \)/{Ь — 1) не
эквивалентны по отношению к этому множеству, так как
выражение а + (Ь2 — l)/(b — 1) не определено при Ь — 1.
Если два выражения Ть Т2, содержащие
переменные, связать знаком равенства: Ti = T2, то
получается уравнение; 7\ и Т2 называются
соответственно левой и правой частями уравнения.
Если выражения Ti и Т2 не содержат
переменных, то имеется высказывание о равенстве,
которое либо истинно, либо ложно. Уравнение
представляет собой высказывание, которое
переходит в истинное или ложное только после замены
переменных их значениями.
Решение. Множество решений. Пусть
Т\ (хь х2,. ..,х„) = Т2(хь х2,...,х„) есть уравнение
с п переменными, и пусть X — соответствующая
область определения. Тогда каждая
последовательность чисел (?i, ?2»•••»?«)» элементы ?* которой,
будучи подставленными вместо соответствующих
переменных х,- в уравнение, переводят его в
истинное высказывание, называется решением или
корнем этого уравнения. Решить уравнение —
значит найти все его решения, т. е. найти его
множество решений.
Пример. C, 2) есть решение уравнения Зхх — 2х2 = 5
(хь х2 действительны), множество решений есть
{(E + 2f)/3, t); t - произвольное действительное число}.
Уравнение называется разрешимым или
неразрешимым в зависимости от того, имеет оно решение
или нет. Если все последовательности чисел
(?ь ^2,...,^„)еХ являются решениями уравнения,
то оно называется тождеством относительно X.
Так, уравнение х2 = 2 для рациональных х
неразрешимо, а для действительных х разрешимо.
Уравнение |/? = а есть тождество по отношению
к множеству всех неотрицательных
действительных чисел.
Уравнения с параметрами. Иногда в уравнении
с п переменными часть переменных можно
рассматривать в качестве так называемых неизвестных
т переменных @ < т < п), а остальные — в
качестве параметров. Тогда решения уравнения
могут зависеть от параметров.
Пример. Если в уравнении 5х - 2у = z + 1 все
переменные считаются неизвестными уравнения, то это есть
уравнение относительно переменных х, у и z и, например,
тройка A, 0, 4) есть решение этого уравнения. Если же z
рассматривать как параметр, то получается уравнение
относительно х и у, решением которого является, например,
(z + 3, 2z + 7)
Эквивалентные уравнения: Два уравнения с п
переменными хь х2,.. ,х„, принадлежащими одной
и той же области изменения, называются
эквивалентными над этой областью изменения,
если их множества решений совпадают. Например,
уравнения х2 = 4 и х3 = 8 эквивалентны над
множеством натуральных чисел, но не эквивалентны
над множеством целых чисел, так как в последнем
случае множества решений суть { — 2, 2} и {2}
соответственно.
Уравнения, тождественные по отношению к
одинаковым областям изменения, всегда
эквивалентны (это справедливо и для двух неразрешимых
уравнений); если два уравнения эквивалентны
третьему, то они эквивалентны друг другу
{транзитивность эквивалентности) (ср. 2.4.1.5).
2.4.2.2. Эквивалентные преобразования.
Эквивалентное преобразование — это преобразование,
которое переводит уравнение в эквивалентное.
Преобразование, переводящее уравнение Gi в
уравнение G2, эквивалентно тогда и только тогда,
когда для множеств решений L\ и L2 уравнений
Gi и G2 выполняется равенство L\ = L2. Если,
напротив, L\ ф L2, то преобразование называется
неэквивалентным.
Примеры (областью изменения в дальнейшем всегда
будет множество действительных чисел).
1) Преобразование уравнения d: 3x-4 = 8 + 5x в
уравнение G2: 2x=-12 является эквивалентным, так как
2) Если уравнение
12 + 4х 2х - 1
переписывают в
х + 3 5-х
виде A2 + 4х)E - х) = Bх - 1)(х + 3), то производят
неэквивалентное преобразование, так как Lx = {7/2} с {7/2, -3} = L2;
в этом случае Lt a L2. Если в качестве области изменения
брать, например, множество положительных действительных
чисел, то указанное преобразование является эквивалентным,
так как в этом случае Lt = L2 = {7/2}.
3) Еще один пример неэквивалентного преобразования
подобного типа дает переход от|/х + 7 = 2х-1 кх + 7 =
= Bх - IJ, так как U = Щ с {2, -3/4} = L2.
4) При неэквивалентных преобразованиях решения могут
и теряться, т е. Lt r> L2. Например, если перейти от
уравнения d: х3 - 4х2 = 5х к уравнению G2: х2 - 4х - 5 = 0,
то получим Li = {-1, 0, 5} => L2 = { - 1, 5}.
Теоремы об эквивалентных преобразованиях
уравнений (ср. 2.4.1.5).
1. Уравнение Ti = T2 эквивалентно уравнению
Т\ = Т'2, если Ti эквивалентно Т\ и Т2
эквивалентно Т'2.
2. Уравнение Т\ = Т2 эквивалентно уравнению
Т2 = 7Y
3. Уравнение Ту = Т2 эквивалентно уравнениям
Ti + Тъ = Т2 + Т3 и Тх - Тъ = Т2 - Т3, если 7 3
есть выражение, определенное во всей области
определения уравнения Тх = Т2.
4. Уравнение 1\ = Т2 эквивалентно уравнениям
TiT3 = Т2ТЪ и Ti: Гз = Т2: 73, если Тъ
определено и отлично от нуля во всей области
определения уравнения Ti — Т2.
Чтобы решить уравнение, т е. чтобы
определить множество его решений, в общем случае
посредством эквивалентных преобразований
составляют цепочку уравнений, первое есть заданное
уравнение, а последнее — уравнение такой простой
структуры, что его решение можно найти
непосредственно. По построению каждые два соседних
уравнения цепочки эквивалентны друг другу; вслед-
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
145
ствие транзитивности эквивалентности все
уравнения цепочки эквивалентны друг другу; в частности,
исходное уравнение эквивалентно последнему
уравнению. Следовательно, найдя множество решений
последнего уравнения, мы находим также множество
решений исходного уравнения.
Примеры. 1)-^-
F v x
2-х х + 2
(х —
действительное);
2) 5(х + 2)B - х) + 2х(х + 2) = ЗхB - х);
3) -5х2 + 20 + 2х2 + 4х = 6х - Зх2;
4) 20 = 2х; 5)х = 10.
Проделанные преобразования эквивалентны для всех
х Ф -2, 0, 2. Следовательно, искомое множество решений
имеет вид L\ = L5 = {10}.
2.4.2.3. Алгебраические уравнения.
Общее понятие. Каноническая
форма. Любое уравнение Р(хи...,х„) = 0, где
P(xi,...,xn) есть многочлен (отличный от нулевого)
относительно Хь...,хи, называется алгебраическим
уравнением относительно переменных xi,...,xn.
Коэффициенты многочлена могут при этом быть
как постоянными, так и параметрами (т. е.
переменными, отличными от хь...,хп) или функциями
таких параметров.
В соответствии со сказанным, например, Зх2 — х + 5=0,
пх - 1 = 0 - алгебраические уравнения относительно х, а
х2 + 2у2 - ху - 3 = 0 - алгебраическое уравнение
относительно х l/i у. Уравнение у3 — у sin х — 2 sin2 х — 7 = 0 не
является алгебраическим относительно х и у, но если х
рассматривается как параметр, то и это уравнение будет
алгебраическим относительно у.
Неалгебраическими уравнениями являются, например,
/4х - 7 + 5 = 1 - 2х3,
г - 8х + 15 х-3'
sin х - е* + 5 = 0.
Среди неалгебраических уравнений те уравнения,
в которые переменные, рассматриваемые как
неизвестные, входят под знаками трансцендентных
функций (см. 2.5.2), называются
трансцендентными уравнениями (см. 2.4.3).
Иногда неалгебраические уравнения можно
преобразовать в алгебраические (не обязательно
эквивалентные исходным).
Примеры. Уравнение —
эквивалентно
алгебраическому уравнению 2х2 + Зх — 20 = 0.
Уравнение -j-
х-5
1
никакому алгебраиче-
х2 - 8х + 15 х-3
скому уравнению не эквивалентно; оно выполнено для
всех х, кроме х = 3 и х = 5.
Уравнение 7 — х = ух — 1 можно преобразовать в
алгебраическое уравнение х2 - 15х + 50 = 0, но это уравнение
не эквивалентно исходному. Алгебраическое уравнение
имеет множество решений {5, 10}, в то время как исходное
уравнение выполняется только при х = 5.
Всякое алгебраическое уравнение относительно х
можно записать в виде
Аохп
0;
Ао ф 0, п > 1;
Аг называются коэффициентами уравнения, п — его
степенью.
Если все коэффициенты А( являются
параметрами, то уравнение называется общим
алгебраическим уравнением относительно х степени п.
Если алгебраическое уравнение разделить на
Ао Ф 0, то, обозначая А(/Ао = д,- (/=1, 2,..., и),
получим каноническую форму алгебраического
уравнения и-й степени относительно х:
а2хп~
... -h an-i
а„ = 0.
Корни алгебраических уравнений до четвертой
степени включительно выражаются через
коэффициенты при помощи конечного числа
алгебраических операций. В этом случае каждое решение
выражается в радикалах, т. е. представляет собой
выражение, содержащее только знаки
арифметических операций и извлечения корней; показатели
этих корней — целые числа р ^ 2, а подкоренные
выражения суть рациональные функции
коэффициентов или сами содержат радикалы.
Алгоритмы решения
алгебраических уравнений с одним неизвестным.
Линейные уравнения (уравнения 1-й степени).
Каждое линейное уравнение есть алгебраическое
уравнение 1-й степени, т. е. неизвестное
встречается только в 1-й степени. Существуют также
уравнения, эквивалентные линейному.
Например, уравнение (х — 1)(х + 3) = (х -. ХЦ\ 2) над
множеством R действительных чисел эквивалентно линей-
5 ~>
ному уравнению 4х-13 = 0. Уравнение - *- , - - *"— =
= — над множеством R\{1, 3, 5} эквипален , щ-
нейному уравнению х - 13 = 0. Иррациональное
уравнение ух + 2=1 над множеством всех действительных чисел
эквивалентно уравнению х + 1 = 0.
Линейное уравнение с одним неизвестным х
и областью изменения R имеет вид ах + b = 0,
а ф 0, ах - линейный член, Ъ — свободный член.
Это уравнение имеет одно решение: х = — Ь/а.
При изменении множества, над которым
определяется решение, изменяется и разрешимость уравнения.
Так, уравнение 2х + 5 = 0 неразрешимо над
множеством натуральных чисел.
Квадратные уравнения (уравнения 2-й степени).
Каждое алгебраическое уравнение 2-й степени
называется квадратным уравнением. Квадратное
уравнение относительно х с областью изменения
R (или множеством комплексных чисел С)
имеет вид
ах2 + Ьх + с = 0, а ф 0,
где ах2 - квадратный, Ьх - линейный и с -
свободный члены. После деления на а получаем
каноническую форму: х2 + рх + q ш 0, где р = Ь/а,
q = с/а — действительные параметры.
Число действительных решений квадратного
уравнения х2 + рх + q = 0 зависит от знака
дискриминанта D — q — (р/2J:
если D < 0, то имеется два решения (два
действительных корня);
если D = 0, то имеется одно решение (два
действительных совпадающих корня);
если D > 0, то нет действительных решений
(два комплексных корня).
Если в качестве области изменения неизвес1-
ного взять множество комплексных чисел, то
квадратное уравнение всегда имеет два решения:
действительные — в случае D ^ 0 и комплексно
сопряженные - в случае D > 0.
146
АЛГЕБРА
Вследствие того, что Лас — b2 = 4a2D, в качестве
дискриминанта можно использовать выражение
А = 4ас — Ь2, знак которого определяет вид решения
квадратного уравнения ах2 4- Ьх + с = 0.
Решение квадратного уравнения.
1-й способ. Применение формулы.
а) Для уравнения вида ах2 + Ьх + с¦ = 0 имеем
а{х - а)(х - р) (или х2 4- рх + q =
уравнение ах2 + Ьх + с = 0 (или
-b + ]/b2 -Лас
Xi. 2 = V-Z •
2a
б) Для уравнения вида х2 4- рх 4- q = 0 имеем
х1>2 = -р/2±]/(р/2J - q = -р/2±\Ш.
Эти формулы справедливы всегда, если в
качестве области изменения неизвестного выбрано
множество комплексных чисел. Если область
изменения есть множество действительных чисел, то
надо потребовать еще, чтобы выполнялось
неравенство D < О (или А < 0).
2-й способ. Разложение на линейные
множители. В случае, если удается разложить
квадратный трехчлен на линейные множители:
ах2 + Ьх + с =
= (х-а)(х-
х2 4- рх 4- q = 0) имеет множество решений L =
Кубические уравнения (уравнения 3-й степени).
Уравнение 3-й степени, или кубическое уравнение,
имеет вид
ах3 4- Ьх2 4- сх 4- d = 0, а ф 0,
где а, Ь, с, d - действительные, при этом ах3 -
кубический, Ьх2 — квадратный, сх — линейный и d —
свободный члены. После деления на а уравнение
принимает канонический вид:
х3 4- гх2 4- sx 4- t = 0, (*)
где г = b/a, s = с/а, t = d/a.
Делая в уравнении (#) замену неизвестного
у = х 4- (г/3) (х = у — (г/3)), получаем так называемое
приведенное уравнение:
3s - г2
где р =
2г3
3
Число действительных решений кубического
уравнения зависит от знака дискриминанта
D = (р/3K 4- {q/2J (эта величина получается
умножением на (-1/108) дискриминанта, введенного в
1.2.1.1):
Решение кубического уравнения.
1-й способ. Разложение левой части на
линейные множители. Если удается найти
разложение ах3 + Ьх2 4- сх 4- d — а(х — а)(х — р)(х — у),
то уравнение ах3 4- Ьх2 4- сх 4- d = 0 имеет
множество решений {а, C, у}. Достаточно найти
разложение вида ах3 4- Ьх2 f сх 4- d = а(х — а)(х2 +
4- рх 4- а) (выделение линейного множителя); тогда
одно решение есть х2 = а, а два других
находятся путем решения квадратного уравнения
х2 4- рх 4- ст = 0. Очевидно, выделение линейного
множителя всегда возможно, если известно одно
решение уравнения или это решение можно
подобрать (см. 2.4.2.4).
2-й способ. Применение формулы Кардано
Формула Кардано для кубического уравнения
х3 4- гх2 4- sx 4-1 = 0 относится к его приведенному
виду у3 4- ру 4- q = 0. В этом случае
= и 4- v,
У 2 = ~
Уз = -
и 4-
2
и 4-
V
V
¦ +
и
и
—
2
-
V
V
i]/3 = etu 4- e2v,
j'j/з = 62w 4- ад
v = ]/-q/2-]/Dt
D = (p/3K + (q/2J, 81>2=(-1 :
Посредством замены xk = yk — (r/3) (k — 1, 2, 3)
из yk получим решения xk данного кубического
уравнения.
В случае D < 0 кубическое уравнение имеет
три действительных решения. Если применять
приведенные выше формулы, то корни будут
выражаться через комплексные величины. Избежать
этого можно следующим образом (см. также 3-й
способ). Положим р = j/ — р3/27, cos ф = — q/{2p).
Тогда решениями приведенного уравнения у3 +
+ РУ + Я = 0 будут
У! = 2|!/рсо8(ф/3),
у2 = 2 ]/р cos (ф/3 + 2л/3),
Уз = 2 |/р cos (ф/3 4- 4л/3),
от которых заменой хк = ук — (г/3) снова можно
перейти к решениям заданного кубического
уравнения х3 4- гх2 4- sx 4- t = 0.
D<0
D = 0
x действительное
Одно действительное решение
Три действительных решения
Одно действительное решение и одно
действительное двукратное решение или одно
действительное трехкратное решение (последнее в случае
Р = Я = 0)
х комплексное
Одно действительное и два комплексно
сопряженных решения
Три действительных решения
Одно действительное решение и одно
действительное двукратное решение или одно
действительное трехкратное решение (последнее в
случае р — q = 0)
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
147
Пример. Кубическое уравнение х3 - 6х2 4 21х - 52=0
заменой х»у + 2 преобразуем к приведенному виду
у3 4 9у - 26 - 0 (здесь р = 9, q = -26, D = 27 4 169 = 196).
Применение формулы Кардано дает ух = 2, у2 =
«-14 2<]/3, уз » -1 - 2i]/3; следовательно, xt = 4,
Решение уравнения 4-й степени.
1-й способ. Разложение на линейные
множители. Если удается произвести разложение
многочлена ах* + Ьх3 4- сх2 + dx + е = а(х — а) х
х (х — C)(х — у)(* — 5), то уравнение
3-й способ. Применение вспомогательных
величин, которые могут быть вычислены при
помощи таблиц. В приведенном уравнении
У3 + РУ + Q. — 0 положим Я = (sign q)]/\ p |/3.
Вспомогательная величина (р и при ее помощи
корни уи у2, Уз определяются в зависимости от
знаков р и D = (р/3K 4- (q/2J из таблицы:
ах4 +
+ сх2 4-
= 0
имеет множество решений {а, C, у, 8}.
Достаточно найти разложение левой части уравнения
4-й степени в произведение двух квадратных
трехчленов: тогда решение уравнения 4-й
степени сводится к решению двух квадратных
уравнений.
У\
Уг
Уъ
2/?з
Ф
- 2/?cos —
-2Rcos(-- +
/ф
-2/?cosl —4
т)
/><0
Z>>0
-2*ch
R ch -
f
4 i|/3 Л sh -*?-
-2Ksh|
Л sh ^- 4 /
/7>0
/~ Ф
Пример. y3-9y + 4-0, p- -9, « = 4, 2)= -23 <0,
- j/i - 1,7321, cos ф - -V - 0,3849, ф » 67°22'.
yi * -2|/Зсо8 22°2Г - -3,4641 0,9242 - -3,201,
у г - -2j/3 cos 142e27 = (-3,4641)-(-0,7929) = 2,747,
• уз - -2|/3cos262°27 * (-3,4641).(-0,1314) = 0,455.
Приближенное решение уравнения см. 7.1.2.3.
Уравнение 4-й степени имеет вид
ах4 4- Ьх3 4- сх2 4- dx 4- е = 0, а ^ 0,
где а, Ь, c,d,e- действительные; посредством
замены у = х 4- Ь/Dа) данное уравнение переводим в
приведенное уравнение
у* + ру2 + qy + г = 0,
где р, q и г — рациональные функции
коэффициентов a, h, с, d, e.
Вид решения этого уравнения зависит от вида
решения его кубической резольвенты
гъ 4- 2pz2 4- (р2 - 4r)z - q2 = 0.
Если область изменения неизвестного есть
множество С комплексных чисел, то имеет место
следующее:
2-й способ. Если zb
бической резольвенты, то
Уг = {]fil 4- ]fz~2 4-
z2, z3 — корни
кусуть решения приведенного уравнения у* + ру2 +
4- qy 4- г = 0 (при этом знаки перед радикалами
j/^i"» l/^г"» l/^7 выбирают так, чтобы выполнялось
равенство |/z7]/z7l/^" = —q). Далее посредством
замены х = у - Ь/Dа) находят решения исходного
уравнения 4-й степени.
Пример. Уравнение х4 — 25х2 4 60х — 36 = 0 имеет
кубическую резольвенту г3 - 50z2 4 769z - 3600 = 0 с
решениями Zi-9, z2 = 16, z3 = 25; для того чтобы
yzlyzlyzl = -60, знаки перед всеми корнями надо взять,
например, отрицательными, т.е. |/zi = — 3, |/гг = — 4,
|/z3 = -5. Отсюда получим корни исходного уравнения:
xi — 1» Х2 — 2, х3 = 3, х4 = —6.
3-й способ. Если в уравнении
ах4 4- Ьхъ + сх2 4- dx 4- е — 0
Кубическая резольвента
Все корни действительны и положительны *)
Все корни действительны, из них один положительный
и два отрицательных*)
Один действительный корень и два комплексно
сопряженных корня
*) Согласно теореме Виета, произведение корней zu z2,
Уравнение 4-й степени
Четыре действительных корня
Две пары комплексно сопряженных корней
Два действительных корня и два комплексно
сопряженных корня
г3, равное q2, должно быгь всегда положительным {q ф 0)
148
АЛГЕБРА
замены x*
выполняется равенство b = d = 0, то мы имеем так
называемое биквадратное уравнение ях4 + сх2 + е = 0.
Посредством замены переменного х2 = t это
уравнение переводится в квадратное уравнение
at2 4- ct 4- е = 0. Из решений tu t2 этого уравнения,
полагая х2 = t, получают корни исходного
уравнения 4-й степени.
Если коэффициенты уравнения х4 4- гх3 4- sx2 +
4- tx 4- и — 0 удовлетворяют соотношению г3 4- 8t =
= 4rs, то уравнение 4-й степени может быть
решено при помощи квадратного уравнения:
х4 4- гх3 4- 5Х2 4- Гх + и
х (х2 + ~ J 4- и = 0. После
заданное уравнение 4-й степени переходит в урав-
2 ( г2\
нение г 4- I s ——-If + м = 0, решая которое,
получаем затем решения исходного уравнения.
Приближенное решение уравнения см. 7.1.2.3.
Уравнения высших степеней. Уравнения 5-й и
более высоких степеней в общем случае
принципиально неразрешимы в радикалах. Чаще всего
их решают приближенными методами (см. 7.1.2.3).
Если можно подобрать решение хь то выделением
линейного множителя (х - хх) решение заданного
уравнения сводится к решению уравнения
меньшей степени.
Частные виды уравнений высших степеней,
т решений хь х2,...,хт двучленного уравнения
хт = а (т > 1 целое, а положительное) получают
при помощи формулы Муавра (см. 3.4.2.5) в виде
xk+l
«г-/ 2А
= ]/ a ( cos —
2кп . 2кп\
4- i sin ),
т
к = 0, 1, ..., т - 1.
Уравнение х2т + ахт + b = 0 заменой
переменного хт = у переводится в квадратное уравнение
у2 4- ay 4- b = 0. Если оно имеет решения уи у2, то
при помощи двучленных уравнений хт = ух или
хт = у2 находят корни исходного уравнения.
2.4.2.4. Общие теоремы. Если хг - корень
уравнения
Р„(х) = хи + аххп~х + а2хп~2 + ... + а„-хх + а„ = 0,
го многочлен Р„(х), стоящий в левой части
уравнения, делится на (х — Xi) без остатка и
получаемое частное есть многочлен Ри_! (х) степени
и- 1:
Рп(х) = (х-х1)Р„_1(х).
В общем случае остаток от деления Р„(х)
на (х - xi) равен Pn(xi):
Pn(x) = (x-x1)Pn_1(x)-f Р„(*1).
Если Р„(х) делится без остатка на (х - xt)fc, но
уже не делится на (х — х1)к+1, то Xi называется
к-кратным корнем уравнения Р„(х) = 0 (корнем
кратности к). В этом случае Xi есть общий
корень полинома Р„(х) и его производных
вплоть до (к — 1)-го порядка.
Основная теорема алгебры. Каждое
алгебраическое уравнение п-й степени
хи + а{хп~ 1 + ... + аи_ !* + а„ = 0,
коэффициенты которого at (i = 1,...,л)—
действительные или комплексные числа, имеет ровно п
корней, действительных или комплексных, если
/с-кратный корень считать за к корней.
Если корни многочлена Р„(х) равны хь х2,...,хг
и кратности их равны соответственно <хь ос2,...,аг
(? «I = п), то многочлен представим в виде
произведения:
Рп(х) = х" 4- fli
4-... 4- an_ix 4- ап =
= (х - X!)ai (х - х2)а2... (х - хг)\
и соответствующее уравнение имеет вид
(х - xi)ai (х - х2)а2... (х - хг)"г = 0.
Решение уравнения Р„ (х) = 0 можно упростить
путем перехода к уравнению, имеющему те же
самые корни, что и Р„ (х) = 0, но уже однократные
(простые). Так как кратные корни многочлена
Ри(х) являются также корнями производной
Р^(х), то определяют наибольший общий делитель
Т{х) многочленов Р„(х) и Р'п(х). Тогда уравнение
Q(x) = 0, где Q(x) = Ри(х)/Г(х), имеет те же самые
корни, что и Р„ (х) = 0, но каждый из них имеет
кратность 1.
Уравнение с действительными коэффициентами.
Если уравнение х"Ч- flix"~1 + ... 4- я„- iX 4- ап = 0
с действительными коэффициентами имеет
комплексный корень хх = a 4- ip (p ф 0), то оно имеет
также корень хх = a - ф и притом той же
кратности, что xt. Поэтому число строго комплексных
корней уравнения с действительными
коэффициентами всегда четно. Следовательно, уравнение
нечетной степени с действительными коэффициентами
имеет по крайней мере один действительный
корень.
В разложении на множители левой части
уравнения Ри(х) = 0 с действительными
коэффициентами наряду с множителем (х — xY)p, где
ху — комплексный корень, имеется также и
множитель (х - ху)р. Объединив каждую такую пару
множителей, получим разложение левой части
на действительные множители:
= (x-x1)ai(x-x2)a2...
...(х - х*)а*(х2 4- pix 4- <
и- I «, + 2
+ Чх)\
Здесь xi, x2,...,xk — действительные корни
уравнения, а / пар комплексно сопряженных
решений — корни квадратных множителей х2 4- р,х + </,
(i = 1, 2,...,/). Отсюда следует, что (р{/2J - qt < 0.
Так как каждый из квадратных множителей
х2 4- ргх 4- qt положителен при любых
действительных значениях х, то справедливо следующее
утверждение: если уравнение аохп 4- flix" +
4- ... 4- an-ix 4- а„ = 0 не имеет действительных
корней, то при любых х левая часть имеет
знак коэффициента а0. Из этого следует
утверждение: если в уравнении четной степени ап/ао<0,
то уравнение имеет по меньшей мере два
действительных корня разного знака.
Теорема Виета. Для уравнения
х" + а^хп~1 4- ... + an-ix 4- а„ = 0
ОБЩИЕ ТЕОРЕМЫ
149
имеет место следующая зависимость между
корнями уравнения (с учетом кратности) и его
коэффициентами а{ {i = 1, 2,...,и):
Х2
Х„ =
- аъ,
Таким образом, если уравнение имеет
целочисленные коэффициенты и целочисленное решение,,
то это решение является делителем свободного
члена.
Теорема Виета для квадратного и
кубического уравнений.
х2 + рх + q = 0: х3 + rx2 + sx + t = 0:
+ х2 = -р,
+ х2 + х3 = -г,
Х2Х3 = S,
Теорема Штурма. При помощи теоремы Штурма
можно определить число действительных корней
уравнения с действительными коэффициентами.
Прежде чем сформулировать теорему Штурма,
опишем используемый здесь алгоритм. Отделим
кратные корни заданного уравнения Р(х) = 0, т. е.
перейдем к уравнению Q (х) = 0, которое имеет те
же корни, что и данное, но кратности 1.
(Напомним, что Q(x) = Р(х)/Т(х), где Г(х) —
наибольший общий делитель Р(х) и Р'(х).) Затем составим
последовательность Q(x), Q'(x), Qi(x),...,Qm(x)
следующим образом (алгоритм Евклида):
R2(x)Q1(x)-Q2(x),
Qm . 2 (x) - Rm (x) Qm _! (x) - Qm (x),
(деление с остатком); Qt - остатки от деления,
взятые с противоположным знаком (см. 2.4.1.3).
Так как в последовательности Q(x\ Q'{x\
Qi(x\...,Qm(x) степени многочленов монотонно
уменьшаются, то процесс деления оборвется после
конечного числа шагов. Как известно, посредством
такого деления с остатком отыскивается
наибольший общий делитель исходных многочленов
Q{x) и Q'(x). Но так как по предположению
Q(x) имеет только простые корни, то наибольший
общий делитель Qm(x) многочленов Q(x) и Q'{x)
есть постоянная.
Положив в многочленах х = ? (? —
действительное число), получим последовательность
действительных чисел (Ш Q'&\ fi 1 (?),...,Q«(S). Если
в этой последовательности два соседних числа
имеют различные знаки, то говорят о перемене
знака. Пусть w(?) означает число перемен знака,
причем если некоторые из чисел &(?) — нули,
то при подсчете числа перемен знаков их
пропускают.
Теорема Штурма утверждает: если а и b (а < Ь)
не являются корнями Q(x), то разность w(a)-
— w(b) равна числу действительных корней Q(x)
в промежутке [а, Ь].
Чтобы найти число всех действительных
корней уравнения, нужно найти промежуток,
содержащий все корни, и применить к нему теорему
Штурма. Для этого служит
Правило Ньютона.- Пусть
Р(х) = аохп + ^х" -I-... + аи_!Х + ап = 0,
а0 > 0,
— уравнение n-й |,степени. Число g такое, что
Р(х) > 0, F(х) > 0,..., Р{п~1)(х) > 0 для всех х > д,
есть верхняя граница действительных корней
уравнения Р(х) = 0. Число h есть нижняя граница
действительных корней этого уравнения, если ( — h)
есть верхняя граница действительных корней
уравнения Р( — х) = 0.
1 них корней урапч
Пример. Найти число действи
ния х4 - 5х2 + 8х - 8 = 0. Имеем
Р(х) = х4 - 5х2 + 8х - 8, Р'(х) = 4х - 10х + 8,
Р" (х) = 12х2 - 10, F" (х) =-- 24х
Заметим, что Р"'(х)>0 для всех х>^ сети <; " 0 Дале<*
Р"(х)>0 и Р*(х)>0 для д^\% но i"(i <Л) Так к-и
Р(х)>0 при х > 2, то д = 2 есть верхняя iраним !>ч>
действительных корней этого уравнения Если irr мер.
применить к Р(—х) = х4 — 5х2 — 8х — 8, го в к-ачечве г<ор>
ней границы получим 3, т.е. /i = -3 есть нижняя ¦рани--
всех действительных корней1 заданного уравнения
Следовательно, все действительные корни данного уравнения лежат
в промежутке [ — 3, 2]; определим их число при помочи
теоремы Штурма. Прежде, всего заметим, что Р(\) не
имеет кратных корней. Вычислим многочлены
Р(х) = Q(x) = х4 - 5х2 + 8л - 8.
Р/(х) = 0'(х) = 4х3- Юх + 8
g1(x) = 5x2 - 12x+ 16.
Q2(x)= -3.x+ 284,
Так как в дальнейшем важен только -»чак тг ,>
многочленов, то для упрощения вычисления мно
Q{ делимое или делитель можно умножать ни сое я< » "К
положительный множитель. При х= — 3 полу»аг^ < ^ -^
довательность 4, -70, 97, 293, -1; при
последовательность 4, 20, 12, 278, 1 Таким >•
w( — 3) = 3, wB) = 1, и уравнение имеет и-(--З) ^
действительных корня. Если вычислить еще, на при >
w@) = 2, то мы найдем, что один корень нахоио'
интервале (-3, 0), другой - в интервале @, 2)
Правило знаков Декарта. Число положительных
корней (подсчитанное с учетом их кратности)
уравнения
0
Р(х) = аохп
ап
не больше числа перемен знака в последова-
150
АЛГЕБРА
тельности я0, аи...,ап коэффициентов Р(х) и может
отличаться от него лишь на четное число. Если
уравнение имеет только действительные корни, то
число его положительных корней равно числу
перемен знака в ряду коэффициентов.
Пример. Коэффициенты уравнения х* + 2х3 - х2 +
+ 5х-1=0 имеют знаки + + - + -, т. е. знак
изменяется трижды. Согласно правилу Декарта, это
уравнение имеет или три, или один положительный корень.
Так как при замене х на -х корни уравнения меняют
знаки, а при замене х на х + h их величины
изменяются на h, то при помощи правила Декарта можно
оценить число отрицательных корней, а также число
корней, больших И. В нашем примере заменой х на
-х получим, что х* - 2х3 - х2 - 5х - 1 = 0, т. е. уравнение
имеет один отрицательный корень. Замена х на х + 1 дает
уравнение х4 + 6х3 + 11х2 + 13х + 6 = 0, т. е. все
положительные корни нашего уравнения (число которых один или
три) меньше 1.
В частности, каждое уравнение четной степени,
первый и последний коэффициенты которого
имеют различные знаки, имеет по меньшей мере
один положительный и один отрицательный корни.
Каждое уравнение нечетной степени имеет по
меньшей мере один действительный корень того
же знака, что и {-ап/а0); число его
действительных корней другого знака — четное число
(или нуль).
Правило Декарта позволяет также оценить
число действительных корней уравнения Р{х) = 0
в промежутке [а, Ь]. Для этого надо применить
правило знаков приведенным выше способом к
уравнению Р (у) = 0, где у = (а - х)/{х - Ь).
2.4.2.5. Система алгебраических уравнений. Если
заданы т уравнений с п неизвестными и
требуется найти последовательности из п чисел,
которые одновременно удовлетворяют каждому из
т уравнений, то мы имеем систему уравнений.
Если все т уравнений линейны, то говорят о
системе линейных уравнений; такие системы могут
решаться методами линейной алгебры (см. 2.4.4.3).
Проиллюстрируем на примерах методы решения
для некоторых часто встречающихся типов
нелинейных систем уравнений.
Примеры. 1) Даны уравнение 1-й степени и
уравнение 2-й степени, каждое с двумя неизвестными:
х2 + у2 + Зх - 2у = 4,
х + 2у ш 5.
Линейное уравнение решается относительно одного из
двух неизвестных (х = 5 — 2у) и полученное выражение
подставляется в квадратное уравнение. Получаем квадратное
уравнение относительно одного неизвестного
у2 —у Л = 0, которое решается, как обычно: у\ = 2,
у2 = 18/5. Получаем множество решений заданной системы
уравнений: L= {A, 2); (-11/5, 18/5)}.
2) Даны два уравнения 2-й степени с двумя
неизвестными:
решений исходной системы уравнений:
L={A, 2);(-1, -2); B, 1); (-2, -1)}.
3) Даны два уравнения 2-й степени с двумя
неизвестными:
х2 + у2 + Зх - 2у - 17,
ха + у2 + х - у - 12.
Вычитанием уравнений получим, что 2х - у - 5. Если
от заданной системы уравнений перейти к эквивалентной,
содержащей любое из исходных уравнений и полученное
линейное уравнение, то будем иметь случай, рассмотренный
в примере 1). Для исходной системы уравнений получаем
множество решений {C, 1); F/5, 13/3)}.
4) На плоскости хОу требуется найти уравнение
окружности, проходящей через три точки, например B6, А),
(9, 21), A7, 17); получаем три уравнения 2-й степени с тремя
неизвестными:
Так как у - 2/х, то из первого уравнения получаем
биквадратное уравнение х* - 5х2 + 4 = 0, которое
посредством замены х2 = г переводим в квадратное уравнение
относительно t. Из множества решений квадратного
уравнения tt = 1, t2 = 4 находим корни биквадратного
уравнения, а затем (вспомнив, что у - 2/х) и множество
где с, d - неизвестные координаты центра, г - неизвестный
радиус. Взяв любые два из этих уравнений и вычитая
одно из другого, получим линейное уравнение с двумя
неизвестными. Вычитание второго уравнения из первого
дает -с + <* + 5«0, вычитание третьего из первого дает
-9с + Ш + 57 = 0. Полученная система имеет решение с - 2,
d ш - 3. Подставив эти значения в одно из исходных
уравнений, получим г = 25.
2.4.3. ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
Общее понятие. Примеры. Уравнение, в
котором неизвестное входит в аргумент
трансцендентных функций, называется трансцендентным
уравнением (см. 2.4.2.3). К трансцендентным
уравнениям принадлежат показательные уравнения,
логарифмические уравнения и тригонометрические
уравнения. В общем случае трансцендентные
уравнения могут быть решены только при помощи
приближенных методов. В некоторых особых
случаях трансцендентные уравнения можно все же
свести к алгебраическим уравнениям.
Показательные уравнения
(приводимые к алгебраическим).
1. Неизвестное находится только в показателях
степеней выражений, над которыми не
производится операций сложения и вычитания. Тогда
логарифмирование общего уравнения (с
произвольным основанием) приводит к цели.
Пример. 3*«=4*-2-2х; xlog3 «(х - 2)log4 + xlog2,
откуда
х« 21og4 m log 16
log 4 - log 3 + log 2 log (8/3) •
2. Неизвестное х входит только в показатели
степени выражений, основания которых являются
целыми степенями одного и того же числа к.
Тогда заменой неизвестного у = к* можно
получить уравнение, алгебраическое
относительно у.
Пример. 2*-l = Sx-2-4'-2. Основания выражений,
содержащих х, суть целые степени 2; заменой неизвестного
у = 2* переводим исходное уравнение в уравнение
у3 - 4у* - 32у =* 0 с решениями уг - 8, у3 - -4, уэ - 0.
Отсюда получаем, что Xi = 3; других действительных
корней не существует.
ВЕКТОРНЫЕ ПРОСТРАНСТВА
151
Трансцендентные уравнения, содержащие
неизвестное только в аргументе гиперболических
функций, можно привести к уравнениям
рассмотренного вида, если гиперболические функции выразить
через показательные.
Пример. 3 ch х = sh х + 9,
- + з,
2 2
е* + 2е~х — 9 = 0. Заменой переменного у = е* получим
уравнение у2 - 9у + 2 = 0, алгебраическое относительно у, с
решениями yit2 = 9±j 73 , откуда следует, что хх = 1пу1а&
* 2,1716 и х2 = In y2 « -1,4784.
Логарифмические уравнения
(приводимые к алгебраическим).
1. Пусть неизвестное х входит только в
аргумент логарифма или уравнение содержит
логарифмы от одного и того же выражения А(х\
где А (х) - многочлен. Тогда замена переменного
вида у = logj, А (х) приводит к алгебраическому
относительно у уравнению. Из решений этого
уравнения получаем решения исходного уравнения
при помощи таблицы логарифмов.
Пример. 4-lgf-yxj = 3 l/lgfyx\ Полагая у =
= l/lgI — х I, получаем 4 — у2 — Ъу с множеством решений
{1, -4}. Из i=mgfi-x) следует у* = 10, т.е.гх = 4;
решение у2 = —4 для исходного уравнения — постороннее.
2. Пусть неизвестное х входит только в аргумент
логарифмов одного и того же основания а,
и все уравнение есть линейная комбинация
выражений вида m,logaP,(x) (m,-- рациональные числа,
Pi — многочлены относительно х). Тогда уравнение
можно привести к виду loga Q (х) = А, где Q (х) -
многочлен, или, потенцируя, к алгебраическому
уравнению Q (х) — аА = 0.
Пример.
21og5Cx- l)-log5A2x + l) = 0,
f
Проверка показывает, что L = {2} есть множество решений
исходного уравнения.
3. Пусть неизвестное х входит только в
аргумент логарифма, и уравнение содержит только
логарифмы с одним и тем же аргументом, но с
различными основаниями. Тогда в некоторых
случаях уравнение можно решить после приведения
логарифмов к одному основанию и
использования свойств логарифмов.
Пример. Iog2(x- 1) +log3(х- l) + log4(x- 1) =
log* 2
lOg4(x - 1) =
Iog34,
= 3 + log34, Iog4(x - I)(log24 + Iog34 + 1) = 3
Iog4(x-1)= 1, x = 5.
Тригонометрические уравнения
(приводимые к алгебраическим). Пусть
неизвестное х или пх 4- а (и — целое) входит только в
аргументы тригонометрических функций. Тогда,
применяя тригонометрические формулы, приводим
уравнение к виду, содержащему лишь одну
тригонометрическую функцию аргумента х. Эту
функцию полагаем равной у и решаем
алгебраическое относительно у уравнение. Решив его,
определяем (в общем случае при помощи таблиц)
неизвестное х. При этом, ввиду периодичности
тригонометрических функций, следует принимать
во внимание многозначность решения. При
переходе от данного уравнения к уравнению,
содержащему только одну тригонометрическую
функцию относительно х, иногда бывают
необходимы неэквивалентные преобразования
(например, возведение в квадраг при наличии
радикалов). Поэтому необходимо сделать
проверку, чтобы исключить появившиеся
посторонние решения.
П ример. 4sinx = 4cos2x — l;4sinx = 4(l— sin2x) — 1;
после замены переменной у = sin х получим 4у2 + Ау - 3 = 0
с решениями уг = 1/2, у2 = - 3/2. Решение у2 не дает
действительных решений заданного уравнения (|sinx|^l);
ух дает х = я/6 + 2кп и х = 5я/6 + 2кп (к = 0, ± 1, ±2,
±3,...).
2.4.4. ЛИНЕЙНАЯ АЛГЕБРА
2.4.4.1. Векторные пространства.
2.4.4.1.1. Понятие векторного
пространства. Непустое множество V, для
элементов которого определено сложение ( + ) и
умножение (•) на действительные числа, называется
действительным векторным пространством V = [F,
+ , •] или линейным пространством*), а элементы
V называются векторами, если выполнены
следующие аксиомы:
1) Для любых двух элементов а, ЬеУ
существует один элемент а + be V — сумма а и b
(внутренний закон композиции).
2) Ассоциативность. Для любых а, b, ceV
справедливо равенство а + (Ь 4- с) = (а + Ь) + с.
3) Коммутативность. Для любых а, ЬеУ
справедливо равенство а + b = b + а.
4) Для любых а, b е V существует х е V
такой, что а + х = Ь.
5) Для любого аеКи любого действительного
числа а имеется элемент а- ае V — произведение
элемента а на число а (внешний закон
композиции)**).
6) Ассоииативностъ. Для любого aeV н любых
действительных чисел a, p справедливо равенство
(оф)а = а(|3а).
7) Для любого аеК справедливо равенство
1а = а.
8) Дистрибутивность. Для любых а, be К и
любых действительных чисел а, C справедливы
равенства а (а + Ь) = аа + ab и (а + C) а = аа 4- (За.
Замечание. При определении умножения вместо поля
действительных чисел можно положить в основу другие
поля К. Тогда говорят о векторном пространстве над
полем К; в частности, о «действительном векторном
пространстве» или о «комплексном векторном
пространстве», если К есть соответственно поле действительных
или поле комплексных чисел.
Примеры. 1) Векторное пространство упорядоченных
пар (х, у) действительных чисел х, у с законами
композиции
(х, у) + (х', У) = (х + х',. У + /),
<х(х, у) = (ax, ay).
*) Векторными пространствами иногда называются
только линейные пространства, имеющие конечный базис
(см. 2.4.4.1.4).
**) Элемент а а обычно обозначается аа
152
АЛГЕБРА
2) Векторное пространство конечных
последовательностей (хь х2,...,х„) действительных чисел с законами
композиции
а(*ь х2,....,х,,) = (ахь ах2,...,ах,,).
3) Векторное пространство многочленов ? а^х' с за-
конами композиции
f о,х' + f ft,* = f (о, + Ь{)х1 + ? а{х> (п > т),
i
4) Векторное пространство функций, непрерывных на
замкнутом отрезке, с законами композиции [/ + д] (х) =
= /(х) + 0(х), [ое/](х) = ot/(x).
5) Векторное пространство геометрических векторов на
плоскости, причем сложение и умножение на действительное
число определены обычным образом (см. 4.2.1).
Правила действий с элементами векторных
пространств. Из аксиом 1) —8) следует, что
действия с элементами векторного пространства
производятся, в сущности, так же, как и с числами;
по отношению к сложению и умножению на
действительные числа справедливы, грубо говоря,
«обычные» правила, в частности:
1) Существует, и притом только один,
нейтральный по отношению к сложению элемент 0 такой, что
а + 0 = а для любых а е К; 0 называется
нулевым вектором.
2) Для каждого вектора ае V существует
единственный обратный по отношению к сложению
элемент (-а)еКтакой, что а + (-а) = О; вектор
( — а) называется противоположным вектору а.
3) Уравнение а + х = Ь, где a, b е V, разрешимо
единственным образом; решение хе V называется
разностью векторов b и а, пишут: х = b — а.
В частности, 0 — а = — а.
4) Законы ассоциативности и коммутативности
сложения, так же как и дистрибутивные законы,
методом полной индукции можно обобщить на
любое конечное число слагаемых.
5) Для векторов a, b е V и действительных
чисел а, C выполняются соотношения:
a) a + (-b) = a-b; б) -(-а) = а;
в) - (а + Ь) = -а - Ь; г) - (а - Ь) = -а + Ь;
д) Оа = 0; е) аО = О,
ж) (-а)а = а(-а), (-1)а= -а;
з) а (а - Ь) = аа - ab, (а - р) a - аа - (За.
2.4.4.1.2. Векторные подпространства.
Пусть К-векшрное пространство и
[/-непустое подмножество в V. Если V по отношению
к тем же операциям сложения и умножения само
является векторным пространством, то U
называется векторным подпространством (пространства)
V. Чтобы проверить, является ли V векторным
подпространством V, не требуется доказывать
истинность всех аксиом, так как имеет место
критерий: U@ Ф U Я V) есть векторное
подпространство V тогда и только тогда, когда для
любых a, bet/ и любого действительного а
справедливы включения а + be (/ и аае I/
(замкнутость U по отношению к операциям + и •).
Примеры. 1) Всякое векторное пространство имеет
два тривиальных векторных подпространства, а именно:
само себя и то, которое содержит нулевой вектор в
качестве единственного элемента.
2) В векторном пространстве конечных
последовательностей действительных чисел (х,, х2, ..., х„)
подмножество, содержащее все такие последовательности, что
ci*i + С2*2 + ... + с„хп = О (с{ — фиксированные
действительные числа), образует векторное подпространство по
отношению к операциям сложения и умножения,
определенным для последовательностей.
3) В векторном пространстве многочленов
подмножество всех многочленов степени, меньшей л, образует
векторное подпространство по отношению к операциям
сложения и умножения, определенным для многочленов.
4) Пусть S — непустое множество векторного
пространства. Всякое выражение вида Х^ + А.2а2 + ... +
+ Х,аг, где Xi, Х,2, ..., К — произвольные действительные и
аь а2, ..., areS. называется линейной комбинацией
элементов S. Множество всех линейных комбинаций векторов
из S образует векторное подпространство.
5) Если U\ и U2 — векторные подпространства
одного и того же векторного пространства V, то их
пересечение Ui f\ U2 также есть векторное подпространство
пространства V. То же самое справедливо и для пересечения
большего числа подпространств.
6) Пусть S - произвольное множество векторов
векторного пространства V. Можно рассмотреть
пересечение всех векторных подпространств пространства И
содержащих S. Это снова есть векторное подпространство, а
именно наименьшее векторное подпространство, содержащее
S. Его называют линейной оболочкой множества S и
пишут: &(S) = f){Ua: (/„-векторное подпространство V
Если S = 0, то S? (S) есть векторное подпространство
из V, содержащее только нулевой вектор.
Если S^0, то Se (S) наряду с S содержит в качестве
векторного пространства всякую линейную комбинацию
векторов из S Так как множество всех линейных
комбинаций S само образует векторное подпространство из V,
содержащее S, a JS? (S) есть наименьшее векторное
подпространство, обладающее этим свойством, то J??(S) состоит
как раз из всех линейных комбинаций векторов из S:
R; a^eS; г — натуральное число>
Из Si^S2 следует &y{S) с J^(S2). Если U есть
векторное подпространство из V, то &(U) = U, и наоборот.
Если векторное подпространство U пространства Иможно
представить как линейную оболочку множества S векторов
из V, то S называется системой, порождающей U.
7) В то время как для двух векторных подпространств
Ui и U2 пространства V их пересечение вновь является
векторным подпространством, для их объединения это в
общем случае не так. Наименьшее векторное
подпространство из К содержащее U1\JU2, т.е. Se{Ul{JU2),
называют суммой Ui + U2 (или композицией) Ul и U2. Оно
состоит из всех векторов х = Х!+х2, где XieLfb x2el/2-
2.4.4.1.3. Линейная зависимость.
Непустое конечное множество S - {аь ..., а*}
элементов векторного пространства V называется
линейно зависимым, если существуют
действительные числа Хи ..., \к, не все равные нулю и такие,
что
Х&х + ... + Х&ь = 0.
Если это соотношение имеет место только при
Хг as... = Xk = 0, то множество S называется
линейно независимым. Вектор хеК называется
линейно зависимым от S, когда он является линейной
комбинацией векторов из S, т.е. если xeif(S).
В случае, если x?i?(S), вектор х называется
линейно независимым от S.
ВЕКТОРНЫЕ ПРОСТРАНСТВА
153
Примеры. 1) Вектор х = C, -7, 0) векторного
пространства упорядоченных троек действительных чисел
линейно зависит от множества
S = {A, -1, 0); @, 1, 1); C, 0, 5); B, -1, 3)},
так как, например, х = 2A, -1, 0) - 3C, 0, 5) + 5B, -1, 3),
S()
2) Вектор х = C, — 7, 0) не является линейно зависимым
от множества S = {@, 1, 1); @, —2, 5)}, так как каждая
линейная комбинация векторов из S дает, очевидно, вектор,
первая координата которого равна нулю, т. е. вектор х
линейно независим от S.
3) Нулевой вектор линейно зависит от каждого
множества S, так как 0e&(S) для любого S.
Множество S векторов из К называется линейно
зависимым, если существует по крайней мере один
вектор xeS, который линейно зависит от 5\{х}.
Если любой вектор xeS линейно не зависит от
5\{х}, то S называется линейно независимым.
Примечание. В случае, когда S — непустое
конечное множество, это определение эквивалентно определению,
данному в начале пункта.
Из этого следует, в частности, что пустое
множество 5 = 0 линейно независимо. Множество
S в {0}, содержащее только нулевой вектор 0,
линейно зависимо, так как
Из определения следует: каждое множество S,
содержащее линейно зависимое подмножество 5',
само линейно зависимо. Действительно, если S'
линейно зависимо, то по крайней мере для одного
х е S' справедливо х б & (S' \ {х}) и вследствие
^f(S'\{x})cif(s\{x}) также и xeX{S\{x}).
Справедливо утверждение: каждое
подмножество S' линейно независимого множества S
само является линейно независимым. Если S' = 0,
то 5' линейно независимо, а в случае S' Ф 0
утверждение следует из предыдущего утверждения.
В частности, любое конечное подмножество S'
линейно независимого множества S само линейно
независимо. И наоборот, из линейной
независимости всех конечных подмножеств 5' множества
S следует линейная независимость 5.
Примеры. 1) В векторном пространстве
упорядоченных пар действительных чисел множество {C, 0); (-1, 2);
G, 1)} является линейно зависимым, так как справедливо
равенство 5 C, 0) + (-1, 2) - 2 G, 1) = @, 0).
2) В векторном пространстве многочленов множество
S = {х3", п — натуральное} линейно независимо ввиду того,
что каждое конечное подмножество {x^vi, xrv*, ..., x^v»}
элементов из S линейно независимо, так как из
предположения XjX3vi + X2x3v2 + ... + XAx3v* = 0 (для любого х)
следует, что все коэффициенты X, (i = 1,2, ..., к) равны нулю.
3) В векторном пространстве многочленов множество
{х3 + 2х2; 2х3 + 2х2 - 6х + 4; -х2 + Зх; х2 - 1}
является линейно зависимым множеством векторов, так
как, например,
2 (х3 + 2х2) - Bх3 + 2х2 - 6х + 4) -
-2(-х2 + Зх)-4(х2- 1) = 0.
4) В векторном пространстве комплексных чисел над
полем действительных чисел множество {1, /} является
линейно независимым множеством, так как соотношение
Xi • 1 + Х2 • / = 0 выполняется с действительными X! и Х2
только при Xt = Х2 = 0. В векторном пространстве
комплексных чисел над полем комплексных чисел множество
{1, /} линейно зависимо. Xt• 1 + Х2 i = 0 при Xi = i, X2 = — 1.
Другие свойства линейной
зависимости.
1. Если 5 линейно независимо, a S(J{x}
линейно зависимо, то х есть линейная комбинация
векторов из S.
2. Если S линейно независимо, х линейно
независимо от S, то S (J {х} также линейно независимо.
3. Если 5 линейно независимо, аь ..., лкеБ, то
из соотношения
следует, что Xi = ць ..., Хк = \iki т. е. к линейно
независимому S всегда можно применить «принцип
приравнивания коэффициентов».
Если S линейно зависимо, то это уже не так;
например, для ai = C, 0), а2 = (-1, 2), а3 = G, 1)
имеем
7*l -3a2-a3 = 2a! - 4а2 +а3.
2.4.4.1.4. Базис. Размерность. Если В —
система векторов, порождающая векторное
пространство F, то каждый вектор xeV можно
представить в виде линейной комбинации векторов
из В. Если, кроме того, система В линейно
независима, то представление х в виде линейной
комбинации векторов из В определено однозначно.
Такая линейно независимая порождающая
система В называется базисом пространства V.
Итак, если К=[К + ,-] есть векторное
пространство, то каждое подмножество В я V такое,
что 1) & (В) — V и 2) В линейно независимо,
называется базисом пространства К
Примеры. 1) В векторном пространстве R" всех
упорядоченных ^-последовательностей действительных
чисел множество В = {ех = A, 0, 0, ..., 0); е2 = @, 1, 0, ..., 0);...
• ••; еи = @, 0, 0, ..., 1)} есть базис; он называется
каноническим базисом пространства R".
2) В векторном пространстве всех многочленов множество
В = {1, х, х2, ...} есть базис, так как В линейно
независимо и каждый многочлен р(х) можно записать в виде
линейной комбинации элементов из В:
р(*) =
***.
3) В векторном пространстве всех решений уравнения
Зх + 4у - z = 0, например, множество В = {A, 0, 3); @, 1, 4)}
является базисом, так как В линейно независимо и каждое
решение уравнения можно представить в виде х = (х, у, z) =
= Х.1 A, 0, 3) + Х2@, 1, 4) (см. 2.4.4.3).
4) Векторное пространство, состоящее только из
нулевого вектора 0, имеет В = 0 в качестве (единственного)
базиса вследствие того, что JSf @) = {0}, и линейной
независимости 0.
Справедливы следующие утверждения о
существовании базиса и его свойствах.
1. Каждое векторное пространство имеет (по
меньшей мере один) базис. Каждая
порождающая система векторного пространства содержит
базис. Из этого, в частности, следует: если V'—
векторное пространство, порождаемое конечной
системой, т. е. имеет место равенство V = & E),
где S - конечное множество, то V имеет конечный
базис.
2. Каждый базис В векторного пространства
V есть минимальная порождающая система V,
т. е. (a) Se (В) = V; (б) для всех В таких, что В с В,
справедливо соотношение & (В1) # V. Наоборот,
154
АЛГЕБРА
каждое подмножество В с \\ удовлетворяющее
условиям (а) и (б), является базисом V.
3. Каждый базис В векторного пространства V
есть максимальное линейно независимое
подмножество пространства V в следующем смысле:
(а) множество В линейно независимо; (б) для
всех В' таких, что множество В' => В, В' линейно
зависимо. Наоборот, каждое подмножество
В с V, удовлетворяющее условиям (а) и (б),
является базисом V.
4. Пусть В - базис векторного пространства
К и пусть S — линейно независимое подмножество,
содержащее т векторов из V. Тогда в В всегда можно
найти такое подмножество В*, также состоящее
из т векторов, что множество (B\B*)[j S, в
котором векторы из В* заменены на векторы из S,
снова будет базисом V. Другими словами, это
означает, что некоторое подмножество из т
векторов базиса можно заменить на заданное
линейно независимое подмножество, состоящее
из т векторов, без потери при этом свойства базиса.
Таким образом, всегда можно построить базис,
содержащий заданную линейно независимую
систему векторов.
При помощи утверждений 2-4 можно
построить базисы векторного пространства V,
порождаемого конечной системой. Для этого или
«сокращают» порождающую систему V последова-
1ельным отбрасыванием векторов, которые
являются линейной комбинацией остальных
векторов, до тех пор, пока «сокращенная»
порождающая система не станет линейно независимой, или
добавляют к линейно независимому множеству
V" вектор хт + ь который не является линейной
комбинацией векторов из 7™, затем к Tm+l =
— Tm{J {xm+il добавляют вектор xm+2, не
являющийся линейной комбинацией векторов 7™+1,
и т. д. до тех пор, пока «расширенное» линейно
независимое множество V (« ^ т) не станет
порождающей системой V. Предположение, что «К
порождается конечной системой», обеспечивает
обрыв обоих процессов после конечного числа
шагов. Векторное пространство, порождаемое
конечной системой, называется конечномерным.
В частности, все базисы конечномерного
векторного пространства состоят из одинакового
количества векторов; число базисных векторов,
одинаковое для всех базисов векторного
пространства, называется его размерностью и
обозначается dim V. Векторное пространство,
содержащее только нулевой вектор, имеет
размерность нуль. Если векторное пространство не
порождается конечной системой, то оно называется
бесконечномерным.
Примеры. 1) Векторное пространство R"
упорядоченных л-последовательностей действительных чисел имеет
размерность п (dim R" = и), так как канонический базис, а
следовательно, и любой базис R" содержат п векторов.
2) Векторное пространство перемещений на плоскости
двумерно, так как каждые два непараллельных вектора
образуют базис этого векторного пространства.
3) Векторное Пространство многочленов бесконечномерно.
Если векторное пространство V имеет
размерность « ^ 1, то каждый базис Fecib линейно
'независимое множество из п векторов. И наоборот,
каждое линейно независимое множество,
содержащее п векторов из К есть базис V. Это
дает удобный для практических исследований
критерий базиса, если известна размерность
векторного пространства.
Соотношение dim V= и ^ 1 выполняется тогда
и только тогда, когда в V существует по крайней
мере одно линейно независимое множество,
состоящее из « векторов, в то время как все множества,
содержащие п + 1 векторов, линейно зависимы.
Пусть V— конечномерное векторное
пространство, a U, Ui и U2 — векторные подпространства
V. Тогда справедливы следующие утверждения:
1) dim U < dim V и dim U = dim V только тогда,
когда U = V;
2) из Ui Я U2 и dim V\ = dim U2 следует
Ul = U2;
3) dim {U1 П U2) + dim {Ul + U2) = dim V^ +
4- dim U2-
Координаты. Пусть V— «-мерное
пространство (п ^ 1) и В = {аь а2, ..., а„} - базис К
Вследствие 1-го свойства базиса {?? (В) — V)
каждый вектор xeVможно представить как линейную
комбинацию векторов из В: х = х^ -I- х2а2 +
+ ... + хяа„, и вследствие линейной независимости
В это представление х единственно (с точностью
до порядка слагаемых). Если базисные векторы в В
каким-нибудь образом упорядочить, то каждому
вектору х можно взаимно однозначно поставить
в соответствие упорядоченную и-последователь-
ность (хь х2, ..., х„) действительных чисел — его
координаты.
Пусть V — n-мерное векторное пространство
(п ^ 1) и В = {аь а2, ..., а„} — базис V, базисные
векторы которого а, стоят в фиксированном
порядке *). Если х е V, то однозначно определенные
коэффициенты в представлении х
х,а, в виде
линейной комбинации векторов В называют
координатами х по отношению к В и пишут: х =
= (хь х2, ..., х„)в.
Вместо векторов V можно производить
вычисления с сопоставленными им по отношению к В
упорядоченными n-последовательностями
координат в соответствии со следующими утверждениями.
Упорядоченная n-последовательность координат,
поставленная в соответствие сумме х + у векторов
х и у по отношению к В, получается как сумма
упорядоченных n-последовательностей
координат, сопоставленных по отношению к В
векторам х и у. Упорядоченная «-последовательность
координат вектора ах по отношению к В равна
упорядоченной «-последовательности координат
вектора х по отношению к В, умноженной на а.
Вследствие этого взаимно однозначное
соответствие между «-мерным векторным
пространством V и векторным пространством
упорядоченных «-последовательностей действительных чисел
является изоморфизмом. Справедливо следующее
утверждение: каждое «-мерное векторное
пространство изоморфно векторному пространству
упорядоченных «-последовательностей действительных
чисел.
Преобразование координат. При
переходе от одного базиса В = {al5 a2, ..., а„}
*) Всюду в дальнейшем будем понимать базис именно
ВЕКТОРНЫЕ ПРОСТРАНСТВА
155
аГ
а!
а*
= АТ
ai
а2
, то
х„
= А
"*?
х*_
векторного пространства Vk другому базису В* =
= {а^, af, ..., а*}, конечно, изменяются
координаты вектора хе V. Пусть х = (хь х2, ..., xn)g =
= (xf, xf, ..., x*)g*. Если (базисные векторы af
базиса В* связаны с базисными векторами а,
базиса В уравнениями а* = ? akiak (i = 1, 2, ..., п),
то для координат х, и xf одного и того же вектора
х имеет место следующее соотношение: хк =
= I aikxf (к = 1, 2, ..., п).
Матричный способ записи:
Если
где А есть матрица из элементов aik, а Л — матрица,
транспонированная по отношению к А. Говорят,
что координаты х преобразуются контраградиент-
но по отношению к базисным векторам.
Пример. Пусть R3 есть векторное пространство
упорядоченных троек действительных чисел, В - {еь е2, еэ} -
канонический базис R3 и В* - {«! -A, 1, 1), а2 -A, 1, 0),
а3 - A,0,0)} - другой базис R3. Тогда вектор х - C, -1, 2)в
имеет по отношению к В* координаты х«B, -3, 4Jg*,
так как at - et + е2 + еэ, а2 - et + е2, а3 * еь т. е. хх - xf +
+ *J + *f» X2 ш *f + jcJ, х3 e xf, откуда следует: xf = хэ =
«2, х| ¦ х2 - х3 - -3, х| - X! - х2 « 4.
2.4.4.1.5. Евклидовы векторные
пространства. Чтобы иметь возможность ввести
в векторном пространстве понятия «длина вектора»
и «угол между двумя векторами», его следует
снабдить дополнительной структурой — метрикой.
Это делается при помощи скалярного
произведения.
Пусть V= [V, +, •] — действительное векторное
пространство. Функция (р: Кх K-+R, которая
каждым двум векторам х и у из К ставит в
соответствие действительное число, называется скалярным
произведением в V, если она обладает следующими
свойствами:
1) дистрибутивностью: ф (хх + х2, у) = Ф (хь у) +
+ ф(х2, У);
2) коммутативностью: ф(х, у) = ф(у, х);
3) однородностью: ф(ах, у) = аф(х, у) (а-
действительное);
4) положительной определенностью: ф (х, х) > 0
для всех х Ф 0.
Действительное векторное пространство V=
= [К +, •, ф] с таким скалярным произведением ф
называется евклидовым векторным
пространством. Вместо ф (х, у) часто пишут (х, у) или х • у.
Примеры. 1) В векторном пространстве V2
упорядоченных пар чисел (х, у) скалярное произведение зададим,
например, так:
((*ь М (** Уг)) - 9*,х2 - 6х^2 - Ьуххг + 5уху2.
Выполнение свойств 1) - 3) проверяют вычислением, а
свойство 4) справедливо вследствие того, что
((хь Уг), (хь у2)) = 9х? - ^х^, + 5у\ = (Зхх - 2yxf + у\ > 0
для всех (хь ух) Ф @, 0).
2) В векторном пространстве R" упорядоченных
«-последовательностей действительных чисел скалярное
произведение определим так:
((ХЬ Х2, . .. , Хн), (уг, у2, ..., у„)) = Xrft + Х2у2 + ..'. + Х„у„.
3) В векторном пространстве всех непрерывных на
[-я, я] функций скалярное произведение определим
соотношением (f,g) = — J f(t) д (t) dt.
Модуль вектора. Пусть V — евклидово
векторное пространство. Под модулем (нормой,
длиной) || х || вектора хе К понимают
неотрицательное действительное число || х || = |/(х, х). Вектор
с модулем, равным 1, называется единичным
вектором; для каждого вектора а Ф 0 вектор
а/1| а || единичный.
Из свойств скалярного произведения вытекают
следующие свойства модуля: для всех х, yeV и
всех действительных чисел а
1) || х || ^ 0, || х || = 0 тогда и только тогда,
когда х = 0;
2) || ах || =|а|||х||г
3) II х + у || ^ || х || + || у || (неравенство
треугольника).
Если заменить в последней формуле х на х — у,
а затем у на у — х, то получим, что | || х || —
~ II У II I ^ II х — у ||. Знак равенства возможен
только тогда, когда у = 0 или х = осу, а ^ 0.
Имеет место неравенство Коши — Буняковско-
го: | (х, у) | < || х || || у ||. Знак равенства возможен
тогда и только тогда, когда множество {х, у}
линейно зависимо.
На основании неравенства Коши — Буняков-
ского величину угла между векторами х Ф 0 и
у Ф 0 можно определить как действительное
число ф, которое удовлетворяет двум условиям:
(х, У)
х II II у ||
и 0 ^ ф < п.
Ортогональность. Два вектора х, у
евклидова векторного пространства V называются
ортогональными, если (х, у) = 0. В частности,
нулевой вектор 0 ортогонален каждому вектору из
V. m-последовательность {хь х2, ..., хт} векторов
х, евклидова векторного пространства называется
ортогональной системой, если она не содержит
нулевого вектора и векторы х, попарно
ортогональны, т. е. х, # 0 и (х„ Xj) — 0 для любых i и j
(i Ф j); она называется ортонормированной
системой, если, кроме того, все векторы х, являются
единичными, т. е. если
0 при i Ф j,
1 при i = j.
Ортонормированная система, которая
одновременно является базисом векторного пространства,
называется ортонормированным базисом.
Свойства ортогональной системы.
1. Каждая ортогональная система линейно
независима.
2. Если координаты двух векторов х, у заданы
относительно ортонормированного базиса В:
х = (хь х2, ..., хп)в, у = (уг, у2, ..., уп)в, то их
скалярное произведение равно (х, у) = ххух +
+ x2j>2 + ... + хпу„.
156
АЛГЕБРА
3. Каждое евклидово векторное пространство
конечной размерности имеет ортонормированный
базис.
Такой ортонормнрованный базис можно
получить методом ортогонализацш (Грама —
Шмидта) из любого базиса евклидова векторного
пространства конечной размерности V путем
«последовательной ортогонализации». Если {аь а2, ...
..., аи} — базис К то из него получают
ортогональную систему {Ьь Ь2, • • •, Ь„}, где
(/с = 2, 3, .... п).
>,•> b,)
Тогда
bi
bH
-
ортонормированный базис К
П р и м е p. {(-1, 2, 3,0); @, 1, 2, 1); B, -1,-1, 1)} - базис
векторного подпространства U векторного пространства
упорядоченных четверок действительных чисел. Скалярное
произведение определено соотношением ((хь х2, х3, х4), (уи у2,
Уь У*)) — *\У\ + *гУ2 + *зУз + х^у*. Тогда методом орто-
юнализации получим ортогональную систему {bb b2, b3}:
Ь,=(-1, 2, 3, 0),
Ь2=@, 1, 2, 1)-у(-1, 2, 3, 0) = уD, -1, 2, 7),
Ь3 = B, -1, -1, l) + -i(-l, 2, 3, 0)-уD, -1, 2, 7) =
= ^G,2,1,-4).
Если перейти, наконец, от Ь; к соответствующим
единичным векторам, то получим искомый ортонормированный
базис векторного подпространства U в следующем виде:
I -!--(-1, 2, 3, 0); -L-D, -1, 2, 7); -4гG,
(у 14 у 10 у 10
\ 2, 1, -4I.
Ортогональные векторные
подпространства. Два векторных подпространства С/ь
U2 евклидова векторного пространства V
называются взаимно ортогональными (обозначается:
V11. U2), когда для любого хе 1/х и любого у е U2
справедливо равенство (х, у) = 0. Если U —
векторное подпространство пространства V, то
множество U = {х | хе V и (х, и) = 0 для всех ие U}
называется ортогональным дополнением U в V.
Ортогональное дополнение С/1 с
определенными в К операциями вновь является векторным
подпространством U1 = [С/1, +, •], при этом
выполняется соотношение U f] U1- = {0}. Если,
кроме того, V— пространство конечной
размерности, то (С/1I = U и U + U1 = V, откуда следует,
что dim U1 = dim V- dim U. Так как U + U1 = V,
то каждый вектор хеК можно представить в
виде х = u + v, где ue U, a v e VL; учитывая, что
U p| U-L = {0}, разложение вектора х в сумму такого
вида единственно. Вектор и называется
ортогональной проекцией вектора х на U, a v —
ортогональной составляющей вектора х, перпендикулярной
U. Для всех а е U справедливо соотношение || v || =
= || х — и || < || х — а ||, т. е. перпендикуляр v
имеет известное свойство «кратчайшего
расстояния».
2.4.4.1.6. Гильбертово пространство.
Многое из сказанного в 2.4.4.L5 о евклидовом
векторном пространстве остается справедливым и
в том случае, если это пространство
бесконечномерно, хотя некоторые утверждения, в которых
упоминается размерность и,.нуждаются в уточнении.
Наиболее важным обобщением понятия евклидова
пространства является гильбертово пространство Н,
определяемое следующими свойствами:
1) Н — бесконечномерное векторное
пространство.
2) Для векторов х, уеН определено скалярное
произведение (х, у), для которого справедливы
свойства 1) — 4) скалярного произведения
евклидова пространства. Величина || х || = (х, хI/2
называется нормой элемента хеЯ.
3) Для любой последовательности векторов
х„еЯ(и = 1,2,...), для которой lim || хп — хт || =
и, т -* оо
= 0, существует вектор х е Н такой, что lim || x —
И -> 00
— х„ || =0 (свойство полноты).
Бесконечная последовательность векторов в Я
называется линейно независимой, если любое
конечное подмножество этой последовательности
линейно независимо.
При помощи процесса ортогонализации для
любой линейно независимой последовательности
можно построить ортонормированную систему,
эквивалентную исходной последовательности в том
смысле, что линейные оболочки подмножеств их
первых п элементов совпадают для любого п.
Если уи у2, ... — ортонормированная система,
то ряд
сходится тогда и только тогда,
когда ]Г а? < оо. При этом
=1
(теорема Пифагора в гильбертовом
пространстве).
В любом бесконечномерном подпространстве
Hi с Я (в том числе и в самом Я) существует
ортонормированный базис В(уи у2, ...), т. е. такой
ортонормированный набор векторов, что для
произвольного элемента xeHi справедливо
разложение х = ? (х, yi)yh где ряд сходится по норме.
yteB
Хорошо известным примером гильбертова пространства
/2, элементами которого являются последовательности
действительных чисел (хи х2, ..., хт ...), для которых ряд
? | х, |2 сходится. Скалярное произведение элементов {xj и
« = 1
{у{} определяется как (х, >>) = JT х,у,. Ортонормированным
базисом в /2 может служить последовательность векторов
в! =A,0,0,. ..),<?2 = @, 1,0,...),... ,е„ = @, ..., 0, 1, 0, ...),...
2.4.4.2. Матрицы и определители.
2.4.4.2.1. Понятие матрицы. Если тп
выражений расставлены в прямоугольной таблице
из т строк и п столбцов:
"яп а12 ... aL
«21 «22 ••• «2
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
157
то говорят о матрице размера т х л, или
сокращенно об т х л-матрице; выражения aik называются
элементами матрицы. Положение элемента в
таблице характеризуется двойным индексом; первый
индекс означает номер строки, второй - номер
столбца, на пересечении которых стоит элемент
(нумерация строк производится сверху вниз, а
столбцов - слева направо). Элементами матрицы,
как правило, являются числа, но иногда и другие
математические объекты, например, векторы,
многочлены, дифференциалы и даже матрицы.
Матрица обозначается следующими способами:
«и •
«mi ¦¦¦ атн/
«mi ... ««п
а также || aik || или (а1к).
Матрица размера л х п называется
квадратной матрицей порядка п. Квадратная матрица || aik \\
порядка л называется:
верхней треугольной матрицей, если aik = О
для всех i > к;
нижней треугольной матрицей, если aik = О
для всех i <к;
диагональной матрицей, если aik — О для всех
единичной матрицей, если
ГО при i Ф к,
при i = к.
«/* = oi
ГО
ik = <
(.1
Элементы аи, т. е. элементы, стоящие в таблице
на диагонали квадрата, проходящей из левого
верхнего угла в правый нижний, — на главной диагонали
матрицы, - называются главными диагональными
элементами или просто диагональными
элементами; элементы aitn-i+1 0 = 1, ..., л), т.е.
элементы, стоящие на диагонали, которая проходит
из правого верхнего угла в левый нижний
(побочная диагональ матрицы), иногда называются
побочными диагональными элементами. В случае
т х «-матриц элементы пц (i = 1, ..., min (m, n))
также называют главными диагональными
элементами или просто диагональными элементами.
Сумма главных диагональных элементов
называется следом (Spur, Trace) матрицы и
обозначается SpA или Тг А.
Матрица размером 1 х л, состоящая из одной
строки, называется матрицей-строкой; аналогично
говорят о матрице-столбце, если речь идет о
матрице размера т х 1; т х л-матрица, все элементы
которой равны нулю, называется нулевой т х л-
матрицей и обозначается О. Каждая таблица вида
%кг %кг
%кх %кг
%К
1 < i'i < i*2 < • • • < ir < w; 1 < кх < к2 < ... < ks < п,
которая получается из т х «-матрицы || aik ||
вычеркиванием части строк и столбцов, называется
подматрицей матрицы || aik \\. По определению
матрица || aik \\ сама должна быть причислена к
своим подматрицам. Если элементы строк матрицы
А — II aik II расставлены в столбцы (при этом
одновременно элементы столбцов расставляются
в строки), то полученная матрица называется
транспонированной к Л и обозначается АТ = || aj ||,
если ajk = aki.
2.4.4.2 J. Определитель квадратной
матрицы. Каждой квадратной матрице А ~
= || aik || порядка п с действительными или
комплексными элементами можно однозначно
поставить в соответствие действительное или
комплексное число D, которое называется определителем
матрицы А:
D = det A = det
а12 ... ah
«21 «22
«11 «12 ••• «1и
«21 «22 ••• «2я
«п2
«ия
¦Z(-DZin)aua2i2...anin
причем сумма должна быть распространена на все
подстановки тг набора чисел 1, 2, ..., «. Таким
образом^ из элементов матрицы А сначала
составляют все возможные произведения
из п сомножителей каждое, содержащие по одному
элементу из каждой строки и по одному из каждого
столбца. Знак (-l)z(n) определяется числом
Z (я) — числом инверсий подстановки
Mi h ... U
(см. 2.2.4). Полученные и! слагаемых и
составляют в сумме det A.
Определитель обозначается также Л и | aik |.
Если D =* | aik | — определитель порядка п, то
минором Mik элемента aik называют
определитель порядка п - 1, получающийся из D
«вычеркиванием» 1-й строки и к-ro столбца. Под
алгебраическим дополнением Aik элемента aik понимают
минор Mtk, домноженный на (-l)i+*:
«11 «12-"«l,fc-l «1,*+1 -.«In
«21 «22"«2.k-l «2,fc+l "«2и
= (-!)<¦»
Примеры.
2)
«22 «23
«31 «32 «33
" «13«22«31 — «11«23«32 — «12«21«33
«и1 «и2 •.•«*,*-! «пД+1 •
'И «12
= «П«22 - «12«21-
«11«22«33 + «12«23«31 + «13«21«32 ~
158
АЛГЕБРА
С в о и с i в а определителей. Если рас-
смагривать строки определи 1еля D порядка и
как векторы zb z2, . , zn, го свойства определителя
D(zu z2, ..., zn) с вектор-строками zx удобно
сформулировать так:
1) Перестановка строк может изменять лишь
знак определителя D.
D(zu . , z,-, .. , zk, . . , zn) =
- -D(zb . ., zk, .., z,, . ., zj;
в общем случае
D(zb z2, .. , ги) = (--l)ZGt)D(znA), zKB)> , zn(n)),
1де я — подс1ановка чисел 1,2, ., п. a Z (к) — число
ее инверсий.
2) Общий для всех элементов строки множитель
можно выносить за знак определителя:
D (zb z2, .. , azk, ..., zn) = olD (zb z2, ..., zk, ..., zn).
3) При сложении двух определителей,
различающихся только одной строкой, соответствующие
элементы этой строки складываются:
D(zb z2, ..., zk, ..., zn) + D(zu z2, ..., zk, ..., zn) =
= D(z,, z2, .. , zfc + zfc, . ., гД
4) Прибавление кратного А.-Й строки к i-й строке
не изменяет значения определителя D(i#/c):
D(zb z2, ..., zh ..., zk, ..., zw) =
= Z)(zb z2, ..., z.-fotZfc, ..., zk, ..., zB).
5) D(zb z2, ..., zn) = 0 тогда и только тогда,
когда {zj, z2, .., zn} есть линейно зависимое
множество векторов. В частности, D — 0, если одна
строка D состоит из нулей или если две строки D
равны или пропорциональны друг другу.
6) Определитель не изменит своего значения,
если поменять в нем местами строки и столбцы,
г. е. транспонировать определитель Поэтому все
свойства, сформулированные для строк, верны
и для столбцов
Теорема разложения. Если D — | aik | —
определитель /1-го порядка, то
D = Z aikAik - Z akiAkh I < k ^ л,
т. е. сумма произведений всех элементов какой-
либо строки (или столбца) на соответствующие
им алгебраические дополнения равна значению
определителя. Сумма произведений всех элементов
какой-либо строки (или столбца) на ал1ебраические
дополнения соответствующих элементов другой
строки (или другого столбца) равна нулю:
X akiAti = X aikAu = 0, k # /.
i = 1 j = 1
Суммируя сказанное, получаем
(D, если k = I,
диагональных элемешов».
°kiAli = Z °ikAU =
0, если k Ф I
Вычисление определителей. Значение
определи геля 2-го порядка вычислявкя по
мнемоническому правилу «произведение главных
диагональных элементов минус произведение побочных
Для нахождения значения определителя 3-ю
порядка также можно указать мнемоническое
правило, так называемое правило Саррюса: приписать
к определителю справа два первых столбца,
не меняя их порядка, и составив сумму
произведений элементов главной диагонали и
элементов, параллельных ей, из которой затем вычесть
сумму произведений элементов побочной
диагонали и элементов, параллельных ей.
€Ц 1 СНг & з
0>2\ &Ч2 Ф&
Определители более высоких порядков тоже
можно вычислять по определению, однако это
требует больших усилий. Чаще поступают
следующим образом: определитель л-ro порядка
сводят к определителям (п — 1)-го порядка,
последнее — к определителям (п — 2)-го порядка и т. д.
до тех пор, пока не получат определители 3-го
или 2-го порядка. В основе этого принципа
«постепенного понижения порядка» лежит теорема
разложения: определитель л-го порядка D
записывается в виде суммы определителей порядка
л — 1 («раскладывается по элементам i-й строки
или /с-го столбца»); к каждому из этих
определителей порядка л — 1 вновь может быть применена
теорема разложения. Если все элементы i-й строки
определителя Д кроме одного, равны нулю, то
сумма, полученная после применения теоремы
разложения, содержит не более одного отличного от
нуля слагаемого. Таким образом, вычисления
существенно упростятся, если перед разложением
определителя по элементам /-й строки как
можно большее их число будег превращено в нули
Это становится возможным благодаря
применению свойств определителей (особенно свойства 4)).
Пример.
2 9 9 4
2 -3 12 8
4 8 3-5
12 6 4
2 4 9 4
2 -7 12 8
4 0 3-5
10 6 4
(свойство 4))
2
4
1
4
1
2
8
-5
4
-7
2
4
1
3
1
2
4
-5
4
+ 0
= 0-21
(теорема
2
4
1
3 4
1 С
2 4
разложения)
= J-21
1
4
1
1
1
2
0
-5
4
(свойство 5)) (свойство 4))
Г 1 -51 4 -51]
-2W - = -21 {D+10)-A6 + 5)} -+147
(.2 4| 1 4IJ
(теорема разложения)
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ
159
Вычисление определителя оказывается еще более
удобным, если, применяя свойства 1)- 5), его можно
преобразовать4 так, чтобы все элементы, стоящие
слева и ниже главной диагонали а1Ь Д22>--->яПл>
были равны нулю. Как легко понять на
основании теоремы разложения, значение определителя
получается тогда просто как произведение членов,
стоящих на главной диагонали.
2.4.4.2.3. Ранг матрицы. Квадратная
матрица называется невырожденной (неособенной) или
вырожденной (особенной) в зависимости от того,
отличен ее определитель от нуля или равен нулю.
Матрица А Ф О (см. О в 2.4.4.2.1) имеет
ранг rang (A) = р, если А имеет по меньшей мере
одну невырожденную (неособенную) подматрицу
порядка р, а все квадратные подматрицы А
более высоких порядков вырождены (особенные).
Если дополнительно положить rang(O) = 0, то
каждой матрице будет сопоставлено одно
неотрицательное целое число - ранг матрицы.
Пример.
rang
Г 1 -2 -3 <Л
2 3 8 7_:
L-. I i-ij
так как подматрица 2-го порядка L 3 невырождена, а
вое подматрицы 3-го порядка вырождены.
Теоремы о ранге. Если рассматривать
строки (или столбцы) матрицы А как векторы
гъ z2, ..., гт (или $ь s2, ..., sj, то теоремы о ранге
матрицы А с вектор-строками z, удобно
формулировать так:
1. Если rang A = р, то существует линейно
независимое множество из р вектор-строк матрицы А,
в то время как все множества из а вектор-
строк (а > р) матрицы А линейно зависимы. Иначе
говоря, ранг матрицы А равен максимальному
числу линейно независимых вектор-строк
матрицы А.
2. Ранг матрицы А не изменяется при
следующих преобразованиях:
а) при перемене местами двух строк;
б) при умножении одной строки на число
с^О;
в) при сложении любого кратного одной строки
с другой строкой;
г) при транспонировании А.
Так как rang A = rang (A ), то теоремы,
указанные выше для строк, справедливы и для
столбцов.
Вычисление ранга. Нахождение ранга
матрицы А = || aik \\ Ф О сводится к тому, чтобы
при помощи теоремы 2 матрицу А перевести в
трапециевидную матрицу А' того же ранга:
А'=
О 022-¦• flip «2.P+1 •••«2и
то о ...о о ...о
р столбцов п—рстолбцов
р строк
т — р строк
в которой: а) все элементы, стоящие ниже главной
диагонали, равны нулю; б) либо все элементы
последних т — р строк обращаются в нуль, либо
т = р; в) все элементы главной диагонали а'ц,
^22» •••> flpp ОТЛИЧНЫ ОТ НуЛЯ.
Если применить определение ранга к матрице
А', то получим непосредственно, что rang (Л') = р
(т. е. ранг матрицы А' равен числу главных
диагональных элементов, отличных от нуля), и
тогда rang (Л) = rang (Л') = р.
Чтобы преобразовать матрицу А ф О в
трапециевидную матрицу А' равного ранга, поступают
следующим образом:
1) Так как не все элементы А равны нулю,
то перестановкой строк и столбцов можно
добиться того, чтобы первый диагональный
элемент был отличен от нуля (а\ i ф 0).
2) Сложением первой строки, умноженной на
соответствующий множитель, с другими строками
всегда можно добиться, чтобы все элементы
первого столбца, стоящие ниже а'ц, были равны нулю.
3) Теперь или уже получена желаемая форма
матрицы, или в строках со 2-й по т-ю имеется
по крайней мере один ненулевой элемент, который
при помощи перестановки строк и столбцов может
быть поставлен на второе место в главной
диагонали. Тогда снова выполняем операции этапа
2) применительно ко 2-й строке и получаем, что
все элементы 2-го столбца, стоящие ниже 2-го
главного диагонального элемента, равны нулю
и т. д., пока через конечное число шагов не
получим трапециевидную матрицу.
Этот, метод называется алгоритмом Гаусса.
Пример.
rang
Г 1-2-3 о"|
2 3 8 7 =
L-i I i-ij
[1 -2 -3 0~1 П -2 -Зо1
О 7 14 7 I = rang I О 1 2 1 1 =
О -1 -2 -1J [_0 0 00 J
= rang
Для матриц с большими по величине
элементами можно использовать теорему 26), чтобы
получить матрицу равного ранга с элементами,
меньшими по величине.
2.4.4.2.4. Элементарная алгебра
матриц. Равенство матриц. Две матрицы
А = II я*-* II размера г х s и В = || bik || размера
р х а называют равными, если они имеют
одинаковый размер и все элементы, стоящие на одних
и тех же местах, равны между собой, т. е. если
г = р, s = о и aik = hik при всех i и к. Тогда
пишут А = В.
Сумма матриц одинакового разме-
р а. Сумма А + В двух матриц одинакового
размера А = || aik || и В = || bik || есть матрица
С = II cik || того же размера с элементами
Cik = ciik + bik при всех i и к. Таким образом,
сложение матриц одинакового размера происходит
поэлементно.
Умножение матрицы на
действительное число. Произведение матрицы
А = || aik || на действительное (комплексное) число X
есть матрица ХА = \\ Xaik \\, т. е. умножение матрицы
160
АЛГЕБРА
на действительное (комплексное) число происходит
поэлементно.
Свойства сложения и умножения
на числа.
1. Сложение матриц одинакового размера
ассоциативно, коммутативно и обратимо.
Уравнение А + X = В с матрицами одинакового
размера А = || aik || и В = || bik || имеет в качестве
единственного решения X = В — А = || bik — aik || —
разность матриц В и А.
2. Среди матриц одинаковою размера имеется
одна нейтралййая по отношению к сложению
матрица — ну.Щвая матрица» О, все элементы
которой равны нулю.
3. Для каждой матрицы А = || aik || существует
(и притом единственная) матрица, обратная по
отношению к сложению, так называемая
противоположная для А матрица — А = || —aik\\. В
соответствии с определением разности получаем
О-А = -А. Далее, имеем В-\-{-А) = В-А и
~(-А) = А.
4. Умножение матрицы А на действительные
(комплексные) числа X, \i подчиняется правилам:
(k\i)A = Цц/4), \-А = А. Далее, О А = О, X 0 = 0
и (-l)-A = -A.
5. Сложение и умножение на числа связаны
дистрибутивными законами; для матриц А и В
одинакового размера и произвольных
действительных (комплексных) чисел X, ц
(X + \i)A = ХА + \хА, Х{А + В) = ХА + ХВ.
Свойства 1 — 5, взятые вместе, показывают, что
множество всех матриц одинакового размера
образует действительное (комплексное) векторное
пространство (см. 2.4.4.1).
Умножение сцепленных матриц.
Матрицы А — || aik \\ размера т х п и В = \\ bik \\
размера г х s называются сцепленными, если
п = г, т.е. число столбцов первой матрицы равно
числу строк второй матрицы. При этом матрицы
В и А могут оказаться не сцепленными,
если s ф т.
Произведение АВ двух сцепленных матриц А
и В есть матрица С = (cik) размера т х s, где
Q* = Z aijbjk> T- е- элемент, стоящий в i-й строке
и /с-м столбце матрицы произведения, получается
в виде скалярного произведения /-й вектор-строки
матрицы А на /с-м вектор-столбец матрицы В.
-3
1 4 2 I
_-3 6-5J bs ?J
Свойства умножения матриц.
1. Умножение сцепленных матриц
ассоциативно.
2. Умножение матриц, вообще говоря,
некоммутативно. Так, в приведенном примере
произведение В А не определено, так как матрицы В и А
не сцеплены. Если даже существуют оба
произведения АВ и В А, то они могут отличаться
друг от друга.
3. Существуют делители нуля, т. е. А Ф О,
В Ф О, произведение А В которых есть нулевая
2
-1
16
8
2
3
8
0
2
-5
24
16
I ГО 0 01
"LoooJ-
j
матрица; например,
Г5 2-2
L9 2 -3
Следовательно, из того, что АВ = О, А Ф О,
нельзя сделать заключение, что В — О, и аналогично
из АВ — АС, А ф О, в общем случае не следует,
что В = С.
4. Существует одна мафица, нейтральная по
отношению к умножению, —квадратная единичная
матрица п-го порядка Еп. Тогда для любой
матрицы А размера т х п
АЕ„ = ЕтА = А.
5. Сложение и умножение матриц связаны
дистрибутивными законами: еспи А и В имеют
одинаковый размер и сцеплены с С, то
(А + В) С = АС + ВС; если С сцеплена с матрицами
А и В одинакового размера, то С(А + В) =
= С А + СВ
На множестве квадратных матриц порядка п
всегда выполнимы как сложение, так и
умножение, так как каждые две п х «-матрицы имеют
одинаковый размер и сцеплены. По отношению к
сложению и умножению это множество образует
кольцо матриц.
6. Для квадратных матриц А и В равных
размеров det{AB) — det A det В
1. Если А и В — сцепленные матрицы, то для
транспонированных матриц (ср. 2.4.4.2.1) выполнено
равенство (АВI = ВГАТ.
Нахождение обратной матрицы.
Если задаться вопросом о существовании
матрицы А, обратной для квадратной матрицы. А
порядка п по отношению к умножению, т. е. такой,
что АА~х — Еп, то вследствие свойства 6
невырожденность матрицы А является необходимым
условием существования обратной матрицы, так как
в случае вырожденности А было бы dQt(AA~x) =
= det A ¦ det A " i = 0 ф 1 = det ?„.
Если А — матрица п-ю порядка, то ее
невырожденность есть необходимое и достаточное условие
существования матрицы А~х такой, что АА"Х = Еп
При этих условиях матрица А "\ обратная для А,
определена однозначно. Кроме того, А~1А = Еп.
Далее, для п х м-матриц 4 и В справедливы
формулы
(АВI =В'А\ (А~1У1 =А.
Вычисление обратной матрицы.
1-й способ Метод неопределенных
коэффициентов в применении к АХ — Еп приводит к п
линейным системам п уравнений с п неизвестными
каждая (см. 2.4.4.3.3). Решение каждой из этих
п систем уравнений дает столбец искомой матрицы
X = А *.
2-й способ.
~ det A
где Aik — алгебраическое дополнение элемсша alk
матрицы А То, что эта матрица удовлетворяет
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
161
уравнению АХ = Е„, легко установить, вычисляя
матрицу АА~1 при помощи теоремы разложения.
Пример.
[32 Л1 Г -2 -5 Л
Решение матричных уравнений.
Матричное уравнение с неизвестной матрицей X,
которое приводится к виду АХ = В или ХА = В,
может быть решено методом неопределенных
коэффициентов. Использование этого метода
приводит к решению систем линейных уравнений
для столбцов или строк искомой матрицы X
(см. 2.4.4.3). Для уравнения АХ = В возможны
следующие основные случаи.
1. Уравнение не имеет решения: матрица А
имеет размер т х и, матрица В имеет размер
г х s и тф г, а также т = г, но rang (A) <
2. Уравнение имеет бесконечное множество
решений: матрица А имеет размер т х и, матрица В
имеет размер т х s и rang (A) = rang (А | В) < п *).
3. Уравнение имеет единственное решение:
матрица А имеет размер т х и, матрица В
имеет размер т х s и rang (A) = rang (Л | В) = и;
в частности, если А и В — квадратные матрицы
n-го порядка и А - невырожденная матрица;
в этом случае уравнение ЛХ = В имеет
единственное решение X = А~1В.
2.4.4.2.5. Специальные классы матриц.
Квадратная матрица А называется:
симметрической, если АТ = А;
кососимметрической, если А = — А;
ортогональной, если Л не вырождена и АТ = А~1.
Пусть А - квадратная матрица с комплексными
элементами; А — матрица, комплексно
сопряженная к А, т. е. получаемая из матрицы А
заменой ее элементов на комплексно сопряженные.
Матрица А называется:
эрмитовой, если АТ = А;
косоэрмитовой, если А = —А;
унитарной, если А не вырождена и АТ ' = А~1.
матрица,
Г2131
«мер. 10 5
I 3 5-4J
[¦"
L-3 5 Oj
симметрическая
кососимметрическая матрица,
| - ортогональная матрица.
матриц специальных
[cos <p sin <р~|
-sincpcoscpj
Свойства
классов.
1. Для каждой матрицы А матрицы ААТ и
АТА являются симметрическими.
2. Любую квадратную матрицу А можно
разложить в сумму симметрической и кососиммет-
рической матриц:
А = у(
АТ) + у (Л - Ат).
3. Если матрицы А и В ортогональны, то
ортогональны также матрицы АВ и А~К
4. Квадратная матрица А ортогональна тогда и
только тогда, когда вектор-строки (или вектор-
столбцы) матрицы А образуют ортонормирован-
ную систему.
5. Для ортогональной матрицы dot A = +1.
6. Любая ортогональная матрица 2-го порядка
имеет вид
[cos ф sin ф ~|
— е sin ф б cos cpj'
где е = ± 1 и ф е [0,2л) — некоторый угол.
2.4.4.3. Системы линейных уравнений.
2.4.4.3.1. Понятие системы линейных
уравнений. Система m линейных уравнений с
п неизвестными хь х2,...,хп (см. 2.4.2.3)
... + а2пх„ = Ъ2,
называется системой линейных уравнений или,
точнее, m х п-системой линейных уравнений', а,* —
коэффициенты, Ь, — свободные члены системы. Если
все hi = 0, то мы имеем однородную систему
линейных уравнений, в противном случае говорят
о неоднородной системе линейных уравнений.
n-последовательность чисел (с i, с2,..., сп) называется
решением т х n-системы линейных уравнений, если
ее элементы, подставленные в заданном порядке
вместо неизвестных, удовлетворяют каждому из т
уравнений и принадлежат заданной области
изменения. (Если нет специальных оговорок, то
область изменения всех неизвестных — множество
действительных чисел.) Совокупность всех
решений системы называется множеством решений.
Две системы линейных уравнений называются
эквивалентными, если они имеют одинаковые
множества решений.
2.4.4.3.2. Решения системы линейных
уравнений. Однородные системы линейных
уравнений всегда разрешимы, так как и-последо-
вательность @, 0,...,0) удовлетворяет всем
уравнениям системы. Решение @, 0,...,0) называют
тривиальным решением. Вопрос о решениях
однородной системы линейных уравнений
сводится к вопросу о том, существуют ли, кроме
тривиального, другие, нетривиальные решения
или нет.
Например, однородная 2 х 3-система линейных
уравнений
2xj + х2 - х3 = 0, х2 + х3 = О
имеет множество решений L - {k(l, - 1, 1)}; X. -
произвольное действительное число; иначе говоря, хг = Хи
Хг = — К х3 — X при любом действительном X является
решением системы. Напротив, однородная 2 х 2-система
уравнений
2хх + х2 = 0, xt - х2 = О
имеет только тривиальное решение: L = {@, 0)}.
Среди неоднородных систем линейных уравнений
существуют неразрешимые системы; например,
*) Матрица (А | В) получается путем правостороннего
присоединения матрицы В к матрице А.
xi + 2х2
х, + 2х2 = 2.
6 И. Н Бронштейн, К. А. Семендяев
162
АЛГЕБРА
Система линейных уравнений
5х! + х2 = 2,
Xi - 2х2 = 7
имеет единственное решение Х{ = 1,х2 = — 3,mraL = {A, —3)}.
Напротив, система уравнений
2хх +х2-х3= -5,
разрешима неоднозначно; при любом действительном X
значения хх = — 2 + X, х2 = — X, х3 = 1 + X дают решение
системы:
шений и получить затем решения системы в виде
линейных комбинаций этих п — р линейно
независимых решений.
2. Множество решений Lm x «-системы
линейных уравнений Ах = Ь состоит из всех
упорядоченных n-последовательностей вида х0 + х*, причем
х0 —"некоторое частное решение данной системы,
а х* пробегает значения всех решений
соответствующей однородной системы Ах = 0:
L={(-2, 0,
Теория систем линейных уравнений может быть
наглядно и просто описана при чомощи матриц:
«11 «12 ••• «1я
«21 «22 ---«гг.
_ «ml «m2 ••• «mn J
x2
Систему линейных уравнений
«11*1 + «12*2 + ... +
+ «22*2 + • • • +
{х0 4- х*, где х0 - постоянный вектор такой,
что Ах0 = Ь, а Ах* = <
«ml*l + «т2*2 + . . . + «тлХи = Ьт
можно записать в виде Ах = Ъ.
Характер множества .решений этой системы
зависит теперь только от rang (Л) (ранга матрицы
коэффициентов А системы) и от rang {А | Ъ)
(ранга так называемой расширенной матрицы
коэффициентов (А \ Ь)).
о.}
(Для иллюстрации этой теоремы следует
рассмотреть первый и последний из приведенных
выше примеров.)
2.4.4.3.3. Способы решения линейных
уравнений.
Алгоритм Гаусса. Нахождение множества
решений системы линейных уравнений основывается
на том, что от заданной системы при помощи
эквивалентных преобразований переходят к системе,
которая решается «проще», чем исходная система,
и эквивалентна заданной. Эквивалентными
преобразованиями системы линейных уравнений
являются :
1) перемена местами двух уравнений в системе;
2) умножение какого-либо уравнения системы на
действительное число с Ф 0;
3) прибавление к одному уравнению другого
уравнения, умноженного на произвольное число.
Эти эквивалентные преобразования системы
линейных уравнений Ах = Ъ вызывают в матрице
коэффициентов Лив расширенной матрице
коэффициентов (А \ В) только преобразования,
сохраняющие ранг, а именно приводят к
перестановке строк, умножению строки на число,
отличное от нуля, и прибавлению к одной строке
другой, умноженной на произвольное число.
Справедливо также обратное: если преобразовать
Ранг
1. rang (A\ Ь) Ф rang (A)
2. rang (А | b) = rang (А) = р
а) р = л
б) р < п
Ах = Ъ (т уравнений,
п неизвестных)
система неразрешима
система разрешима
решение единственно
решение не единственно
Частный случай Ь = 0,
(однородная система Ах=0)
этот случай не может иметь места при
Ь = 0, т. е. однородная система
разрешима всегда
система имеет только тривиальное
решение
система имеет нетривиальные решения
Структуру множества решений описывает
следующая теорема.
1. Множество решений L однородной т х п-
системы линейных уравнений Ах = 0 есть
векторное подпространство векторного пространства
упорядоченных ^-последовательностей
действительных чисел, т. е. любая линейная комбинация
решений системы вновь есть решение системы.
Если rang (A) = р, то
dim L = п — р.
В случае р < п можно выбрать п — р
неизвестных, построить п — р линейно независимых ре-
матрицы А и (Л j Ь) в матрицы А' и (А' \ Ь')
соответственно равных рангов, применяя к строкам
допустимые преобразования строк (см. 2.4.4.2.3),
сохраняющие ранг, то системы
Ах = Ъ и А'х = Ъ'
будут эквивалентными. Алгоритм Гаусса состоит
в том, чтобы получить матрицы А' и (А' \ Ь')
трапециевидной формы.
В случае, если исходная система Ах = Ь
разрешима (пусть rang (A) - rang (A \ b) = р),
вследствие трапециевидности матриц А' и {А' \ Ь')
эквивалентная система А'х = Ь' может быть записана
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
163
в виде
а'цхг + а\2х2 + ... + я'1рхр =
= Ь\ - a'i,p+
а'ггХг + ... + а2рхр = Ь'2 — а'2, р+ i
i - ... - а\пхп,
- ... - а2пхи,
р = Ь'р - ар>р
-...- арихи.
Эту систему называют треугольной системой.
Так как rang A = rang (A | Ь) = р, то множество
решений есть (и - р)-мерное многообразие;
следовательно, п — р неизвестных хр+1,...,х„ можно
выбрать произвольно: хр+1 = А,ь хр + 2 = А,2, ...,х„ =
= ХИ-Р; остальные неизвестные хь х2,...,хр
получаются из треугольной системы последовательно
как функции параметров X,:
Если для получения трапециевидных матриц
А' или {А'\Ь') требуется еще перестановка
столбцов, то этого достигают перенумерацией
неизвестных в системе уравнений Ах = Ь.
Примеры. 1) Xj — 4х2 + 2х3 =—1,
2xj - Зх2 - х3 - 5х4 = -7,
3xi - 7х2 + хэ-5х4=-8.
Здесь
rang
П -4 2 0 -1~|
2-3-1-5-7 =
[j -7 1 -5 -8J
= rang
1-4 2 0-1
0 5-5-5 -5
0 5 -5 -5 -5 _
1 -4 2 0 -1 ~|
0 1-1-1-1
_ о о о о о J
Из этого заключаем:
а) rang (Л) = rang (A \ b), т. е. система разрешима;
б) решение неоднозначно: 4 — 2 = 2 неизвестных могут
быть выбраны произвольно;
в) треугольная система имеет вид
xi - 4х2 = -1 -2х3, х2 * -1 + х3 + х4.
Если положить х3 = Я.1, х4 = Х2, то получим
х2 = -1 + Xi + Х2, xi = -5 + 2X.i + 4Х2» т. е. множество
решений L={(-5, -1, 0, 0) + М2, 1, 1, 0) + Х2D, 1, 0, 1); Я*
/=1,2- произвольные действительные числа}. Тогда
соответствующая однородная система Ах = 0 имеет, очевидно,
множество решений L={XlB, 1, 1, 0) + Х2D, 1, 0, 1); Х(-
произвольные действительные числа}.
2) 2х, + Зх2 - х3 = 2,
7хх + 4х2 + 2х3 » 8,
3xj - 2х2 + 4х2 = 5.
Тогда
rang
-12 3 2
2 7 4 8
4 3-25
= rang
(Здесь произведена перестановка трех первых столбцов.)
Отсюда заключаем: rang (A) = 2, rang (A | b) = ^следовательно,
система неразрешима: L = 0.
3) *i - х2 + х3 = 12,
2xj + Зх2 — х3 = 13,
Зх2 + 4х3 = 5,
— Зхх + х2 + 4х3 = —20.
Здесь
rang =
* 1 -1 1 12 Г1 -1 1 12 Т
2 3 -1 13 I I 0 5 -3 -11 I
I = rang I I =
034 5 1034 5|
_-3 1 4 -2<J Lo -2 7 16 J
1
0
0
0
-1
-2
0
0
1
7
29
0
12-1
16
58
0
= rang
1
0
0
0
-1
-2
0
0
1
7
1
0
12 -
16
2
0
= rang
Отсюда заключаем:
а) rang (Л) = rang (/4 | Ь).= 3, т. е. система уравнений
разрешима;
б) решение единственно;
в) треугольная система имеет вид
хх - х2 + х3 = 12,
- 2х2 + 7х3 - 16,
откуда найдем L = {(9, -1, 2)}. Соответствующая
однородная система Ах — 0 имеет только тривиальное решение.
Правило Крамера. Если мы имеем частный
случай и х л-системы линейных уравнений Ах = Ь
такой, что rang (A) =? rang {А | Ь) = и, то вследствие
невырожденности А единственное решение х можно
представить в виде х = А~гЬ. Воспользовавшись
формулами для обратной матрицы из 2.4.4.2.4,
получим
in A2l ... А„Г
*12 ^22 .-. Лп2
х2
1
ь2
^Ain A2n ... А,
где Aik — алгебраическое дополнение элемента aik
матрицы А. Тогда /-я координата х, находится
по формуле
1 '2 + ... + 4А.) =
Ли
«21
... Ьх .
... ь2 .
... ьп .
..аи
¦ апп
1 ... I ... И
где о*феделитель Dh стоящий в числителе,
получается из D = det А заменой i-го столбца на
столбец Ь. Следовательно, для и х и-системы
линейных уравнений Ах = Ъ такой, что D = det А Ф 0,
получим единственное решение х = (хь х2,...,хя) ,
где х,- = Dt/D (i = 1, 2,...,п).
Пример. 2х! + х2 + 3х3 = 9,
хх-2х2-1- хэ= -2,
Зх! + 2х2 + 2х3 = 7.
Здесь
2 1 3
1 -2 1
3 2 2
13,
9 1 3
-2 -2 1
7 2 2
= -13,
6*
164
АЛГЕБРА
2 9 3
1 -2 1
7 2
= 26,
2 1 9
1 -2 -2
3 2 7
с линейной оболочкой У? (фМ) образа множества М:
() (
= 39,
26_.
13"
13
2.4.4.4. Линейные преобразования.
2.4.4.4.1. Основные понятия.
2.4.4.4.1.1. Понятие линейного
преобразования. Пусть V и V - действительные
векторные пространства. Однозначное отображение
Ф пространства V в пространство V называется
линейным преобразованием V в V\ если
выполняются условия:
1) ф(х + у) = ф(х) + <р(у) для любых х, yeV;
2) ф (X, • х) = X • ф (х) для любого х е V и всех
действительных А..
(При этом операции в V могут быть
определены иначе, чем в V, хотя из соображений
простоты они обозначаются теми же знаками
« + » и «•».)
Если V=V, то ф: V-+V называют также
линейным оператором в V или линейным
преобразованием пространства V.
Если х' = фх, то х' называется образом
(изображением) х при отображении ф, х -
прообразом (или оригиналом) х' при преобразовании
Ф, а множество {хе V\ фх = х'} называется полным
прообразом (или полным оригиналом) элемента х'
при преобразовании ф. Если М есть
подмножество из К, то фМ = {х'еК'|х'= ф(х), хеМ}
называют множеством образов элементов из М
(образом множества М) мри преобразовании ф.
Если М' - подмножество \м V, то М = {хе F| фхе
еМ'} называе1ся полным прообразом множества
М' при преобразовании ф.
Примеры. 1) Преобразование q>i: R3 -> R2 такое, что
ф1 (хь х2, хз) = (xi, х2), линейно.
2) Преобразование ф2 пространства R" в векторное
пространство многочленов не выше (п — 1)-й степени такое,
что Ф2(хь х2 х„) = xt + x2t + x3t2 + ... + xHt*~l, линейно.
-3) Преобразование ф3 векторного пространства С00
бесконечно дифференцируемых функций в себя такое, что
Фз/ = /' для всех /еС°°, линейно: ф3 есть линейный
оператор в С00.
4) Преобразование ф4: V-*V такое, что ф4х = О' для
любого xeV (С есть нулевой вектор из К'), линейно;
его называют нулевым преобразованием.
5) Преобразование ф5: R3 -*¦ R2 такое, что ф5 (хь х2, х3) =
= (хь 1), не является линейным, так как
= (х, + у„ 2) Ф (х, + уи 1) - Ф5 [(хь х2, х3) + (уь у2, уз)]-
2.4.4.4.1.2. Свойства линейных
преобразований. Для каждого линейного
преобразования ф: V-+V имеем:
1. Образ нулевого вектора 0 пространства V
всегда является нулевым вектором 0' в V:
фО = О'.
2. Линейная комбинация элементов из К всегда
преобразуется в линейную комбинацию
соответствующих элементов из V с теми же
коэффициентами. Поэтому для каждого подмножества
М ^V образ линейной оболочки S? (M) совпадает
Если, в частности, В является базисом V, то
фК= ф^(В) = ^?(фВ). Отсюда следует, что
линейное преобразование ф: V-+ V однозначно
определено уже множеством образов фВ базиса В.
3. Если S — линейно зависимое множество
векторов из V, то (pS — также линейно зависимое
множество векторов пространства V. С другой
стороны, линейно независимые множества
посредством преобразования ф могут перейти в линейно
зависимые множества. Поэтому образ базиса В
пространства Vb общем случае — лишь
порождающая система пространства фК.
4. Если U - векторное подпространство из V,
то фС/ есть векторное подпространство из V.
Если V конечномерно, то размерность dim фК
пространства образов ф V называют рангом
линейного преобразования ф: гаг^ф = сНтфК.
5. Если U' - векторное подпространство
пространства фИи U - полный прообраз U' по
отношению к ф, то U является векторным
подпространством в К
Свойства 3 — 5 означают, что линейное
преобразование сохраняет свойство линейной
зависимости, а свойство быть подпространством
сохраняется как у образов, так и у прообразов.
В частности, вследствие свойства 5 множество
К9 всех тех векторов из V, образом которых при
преобразовании ф является нулевой вектор из V,
образует векторное подпространство пространства
V, называемое ядром Kv линейного
преобразования ф: Кегф = К^ где К9 = {хе V: фх = О'}.
Если Ку конечномерно, то его размерность
называют дефектом линейного преобразования ф:
Defekt ф = dim Kv. Если ф: V -> V и V —
конечномерное векторное пространство, то
rang ф + Defekt ф = dim V.
Примеры. Для примеров 1)-4) линейных
преобразований имеем (см. 2.4.4.4.1.1):
Кф1 = {@, 0, х3); х3 - любое действительное число);
Defekt Ф1 = 1; rang фх = 2.
*ф2 = {@. 0. •••¦ 0)}; Defekt ф2 = 0; гап8ф2 - п.
*Фз = U'-f = с01*1}' Dekkt Фз - 1; rang ф3 не определен
(так как С00 бесконечномерно).
Кф4 = V; если V конечномерно, то Defekt ф4 - dim V;
rang ф4 = 0.
Ядро линейного преобразования позволяет
ввести разбиение пространства V на классы
элементов, имеющих одинаковые образы: два
элемента из V принадлежат ^-одному и тому же
классу, т. е. имеют один и тот же образ при
преобразовании ф, тогда и только тогда, когда их
разность принадлежит ядру ф.
2.4.4.4.1.3. Взаимно однозначные
линейные преобразования. Линейное
преобразование ф: V-*V называется взаимно
однозначным,, если из фх = ц>у следует х = у. Взаимно
однозначный линейный оператор из К в К
называется также невырожденным оператором в
пространстве V; остальные операторы называются
вырожденными операторами.
В соответствии с этим из приведенных примеров
линейных преобразований взаимно однозначным является
лишь ф2; ф, таковым, например, не является, так как
Ф. A, 1, 1)-ф1 A, 1, 5), хотя A, 1, 1),*A, 1, 5).
ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ
165
Для любого линейного преобразования (р:
V-* V следующие высказывания попарно
эквивалентны :
1) ф взаимно однозначно;
2) для каждого линейно независимого
множества S пространства V множество ф5 есть
линейно независимое множество пространства У\
3) К, = {0}.
Из 2), в частности, следует, что образ базиса
V при взаимно однозначном преобразовании ф
является базисом фК Для конечномерного
векторного пространства V и взаимно однозначного
преобразования ф имеем сйтфК=сИтК
2.4.4.4.2. Представление линейных
преобразований с помощью матриц.
Пусть V и V — конечномерные векторные
пространства, dim V = п, dim V = т, В — {аь а2, ...
..., ап] - базис К, В' = {Ьь Ь2, ..., Ъп) - базис V.
Всякое линейное преобразование ф: V-+V
образами <раь фя2, • -, фяп векторов базиса В
определено однозначно, так как каждый вектор
xeV есть линейная комбинация векторов В и
вследствие этого его образ фх есть
соответствующая линейная комбинация векторов базиса фВ.
Если записать образы уа^, ц>а2, ..., <рап векторов
В в координатах базиса В', то ф будет
определяться однозначно посредством т • п координат
векторов фя, (/ = 1, 2, ..., п) относительно В',
которые можно расставить в т х «-матрице А так,
чтобы к-й столбец матрицы А состоял из
координат вектора ц>ак относительно В'. И наоборот,
каждой т х и-матрице А по отношению к
фиксированной паре базисов (В, В') можно единственным
образом сопоставить линейное преобразование ф:
К-> V, если рассматривать столбцы А как
координаты образов векторов В относительно В'.
Итак, между множествами линейных
преобразований ф: V-*V\ где dim V = п, dim V = т,
и множеством т х «-матриц существует взаимно
однозначное соответствие при фиксированных
базисах В пространства К и В' пространства V. Если
В = {аи а2, ..., а„} и <рак = (а1к, а2Ь ..., атк)в„
то ф можно записать в виде матрицы:
А =
(Так как А зависит еще и от выбранной пары
базисов (В, В'\ то точнее было бы написать
А(В, ву)
Пример. Пусть линейное преобразование <р: R4 -¦ R3
задано образами векторов базиса В пространства R4:
ФA, -2, 0, 3) = (-9, 7, 1), <р@, 0, 1, -1) = C, -3, 3),
<рA, 0, 3, 0) = D, 0, -2), фA, -1, 1, 0) = @, 1, -1).
(Координаты относятся к каноническому базису пространства
R4 и соответственно к каноническому базису пространства
R3.) Тогда, найдя ф-образы векторов еь е2, е3, еА
канонического базиса пространства R4 и записав их координаты
относительно канонического базиса пространства R3
(ср. 2.4.4.1.4), получим матрицу А, описывающую
преобразование ф по отношению к паре канонических базисов. Для
этого выразим е( в виде линейных комбинаций векторов
заданного базиса В и найдем уе( в виде соответствующих
линейных комбинаций заданных векторов фВ. Записав
координаты векторов (ре, относительно канонического базиса,
окончательно получим
А =
3 -2
«11
_ «ml
«12 ..-
«22 .-.
«m2 •••
«In
«2n
«mn
Если перейти от пары базисов (В, В') к новой
паре базисов (В, В'), то описывающая ф матрица
А,в в>, перейдет в матрицу
А ГГ- 1 Л С
Л(В, В') - 1 Л(В, В') '
причем столбцы матрицы S (соответственно Т)
будут состоять из координат векторов В
относительно В (соответственно В' относительно В').
Матрицы одинакового размера, которые получаются
одна из другой право- и левосторонним умножением на
невырожденные матрицы, называются эквивалентными.
Эквивалентность матриц есть отношение эквивалентности,
которое разбивает множество матриц одинакового размера
на классы эквивалентных матриц. Число этих классов
равно min (/и, п) + 1, где т х п — размер рассматриваемых
матриц.
Вследствие этого две матрицы, описывающие одно и то
же линейное преобразование относительно различных пар
базисов, эквивалентны. Обратно, эквивалентные матрицы
относительно соответствующих пар базисов задают одно
и то же линейное преобразование.
Линейному преобразованию ср: V-*¦ V соответствует
единственный класс эквивалентных матриц
Если V — V, т. е. если ф — линейный оператор
в V, то для двух матриц Ав и А^ описывающих
линейный оператор ф относительно различных
базисов В, В, вследствие В = В' и В = В'
выполняется равенство
Квадратные» матрицы Ах и А2, для которых
А2 = S~1AlS, где S — невырожденная матрица,
называются подобными. Подобие матриц есть также
отношение эквивалентности.
Аналогично сформулированному выше можно
утверждать: линейному оператору (р в пространстве V
соответствует единственный класс подобных матриц.
Свойства всех матриц одного и того же класса
эквивалентности или одного и того же класса
подобия тесно связаны со свойствами линейных
преобразований, описываемых этими матрицами.
Укажем некоторые из них:
1. Если ф: V-+ V — линейное преобразование
и А<в „,ч — матрица, описывающая ф относительно
пары'базисов (В, В'), то для образа фх элемента
х е V справедливо соотношение
где х# — вектор-столбец, составленный из
координат вектора х относительно В, (фх)^, — вектор-
столбец, составленный из координат вектора фх
относительно В'.
По этой формуле наряду с образом можно
определить также полные прообразы, что сводится
к отысканию решения системы линейных
уравнений (см. 2.4.4.3).
2. Все матрицы класса эквивалентности,
соответствующего линейному преобразованию ф:
V-+V (К# К'), имеют одинаковый ранг, и
rang (A) = rang ф для всех А из класса
эквивалентности, соответствующего ф.
166
АЛГЕБРА
3. Все матрицы класса подобия,
соответствующего линейному оператору ф в пространстве V,
имеют одинаковый ранг, одинаковый
определитель, одинаковый след, одинаковый
характеристический многочлен и одинаковые собственные
значения (см. 2.4.4.5).
В частности, линейный оператор невырожден
тогда и только тогда, когда матрицы
определяемого им класса подобия невырождены.
2.4.4.4.3. Операции над линейными
преобразованиями. Если ср: V-*V\ <p':
V-* V, \|/: V -*¦ V" суть линейные преобразования,
то определим
сумму ф + ф': V-*V как (ф + ф') х = фх + ф'х
для любого xeV;
произведение ф на число а, т. е. аф: V-+ V
(а - действительное), как (аф) х = а (фх) для
любого х е V;
произведение \|/ф: V-+ V" как (ij/ф) х = \|/ (фх) для
любого х е V (последовательное выполнение, или
композиция, линейных преобразований).
Преобразования ф + ф', аф и \|/ф также
являются линейными преобразованиями.
Если К, V, V" - конечномерные векторные
пространства с базисами В, В\ В" и линейные
преобразования ф, ф', \|/ заданы соответственно
матрицами Ар.ву А\в,ву С(В',В")> то:
линейное преобразование ф + ф' относительно
(В, В') задается матрицей А + А';
линейное преобразование аф относительно (В, В')
задается матрицей olA;
линейное преобразование \|/ф относительно
(В, В") задается матрицей С А.
Так как операциям над линейными
преобразованиями соответствуют аналогичные операции над
задающими их матрицами, то множество
линейных преобразований пространства V в V имеет
такую же структуру, как и множество матриц,
задающих эти преобразования. Отсюда следует:
1. Множество линейных преобразований V в V
с определенными на нем действиями сложения
и умножения на действительные числа образует
векторное пространство.
2. Множество линейных операторов
пространства V с определенными в нем действиями
сложения и умножения образует кольцо.
2.4.4.4.4. Обратный оператор. Для
невырожденных операторов ф: V -* V можно поставить
вопрос об операторе ф, обратном к ф, т.е.
таком, что фф = ф-1ф = ?, где е —
тождественный оператор, т. е. такой, что ex = x для любого
х е V. Если ф V = V, то существует обратный к ф
оператор ф, определяемый следующим образом:
(р~1х = у тогда и только тогда, когда фу = х.
Вследствие невырожденности ф оператор ф
определен однозначно, и можно показать, что
Ф вновь является линейным оператором в
пространстве V.
Предположение <pF= V необходимо для того, чтобы
каждый элемент из V можно было рассматривать как
образ при преобразовании <р некоторого элемента из V.
В случае конечномерного векторного пространства V это
предположение всегда выполнено.
Если ф, \|/ - невырожденные операторы в V
такие, что фК=\|/К= F, то
взаимно обратны;
3) если V конечномерно и преобразование ф
относительно базиса В задается матрицей А, то
преобразование ф относительно того же базиса
задается матрицей А~1;
4) если V конечномерно, то множество
невырожденных операторов пространства V по отношению
к умножению образует группу.
2.4.4.5. Собственные значения и собственные
векторы.
2.4.4.5.1. Собственные значения и
собственные векторы матриц. Пусть
А - п х «-матрица. Любой вектор xeV, x Ф О,
для которого Ах = Хх, где X — некоторое число,
называется собственным вектором А, а X —
принадлежащим или соответствующим ему
собственным значением матрицы А.
Уравнение Ах = Хх эквивалентно уравнению
(А — ХЕ) х — 0. Это однородная система линейных
уравнений, нетривиальные решения которой
являются искомыми собственными векторами. Она
имеет нетривиальные решения только тогда, когда
rang (А - ХЕ) < п, т. е. если det (А - ХЕ) = 0.
Многочлен det {A - ХЕ) называется
характеристическим многочленом матрицы А, а уравнение
det (А — ХЕ) = 0 — характеристическим уравнением
матрицы А; его решения являются собственными
значениями матрицы А. Если X,- - собственные
значения А, то нетривиальные решения
однородной системы линейных уравнений (А — XtE) x = 0
суть собственные векторы Л, принадлежащие
собственному значению Х(. Множество решений этой
системы уравнений называют собственным
подпространством матрицы А, принадлежащим
собственному значению Xt; каждый вектор х # 0
собственного подпространства является
собственным вектором матрицы А (само собой разумеется,
в собственном подпространстве определены
линейные операции « + » и «•»).
Примеры. 1) Собственные значения матрицы А =
= I _4 « найдем из характеристического уравнения
det (А - ХЕ) =
3-Х -2
= X2 - 4Я. - 5 = 0, Xi - 5, Х2 =
-4 1-Х
= -1. Собственное подпространство А, принадлежащее
Хг ш 5, есть множество решений системы уравнений
¦м-
т. е. L, = {ц (-1, 1); ц - действительное число}.
Аналогично найдем собственное подпространство,
принадлежащее Х2 = -1: L2 = {й A, 2); ц - действительное
число}.
2) Матрица А
-и1,:
имеет характеристическое
уравнение X2 - ЛХ + 5 ш 0 и, следовательно, собственные
значения Xi ш 2 + i, Хг = 2 - \. Действительных собственных
векторов нет. Над комплексным полем собственному значению Хх
принадлежат собственные векторы jci = цA, i — 1), а
собственному значению Хг - собственные векторы х2 = ц(-1, i + 1);
здесь ц - произвольное комплексное число, не равное нулю.
3) Матрица А =
имеет собственные значения
\х = Х2 = 2; отсюда получаем собственное
подпространство Lx- L2 = {ц A, 1); ц - произвольное действительное
число).
СОБСТВЕННЫЕ ЗНАЧЕНИЯ И СОБСТВЕННЫЕ ВЕКТОРЫ
167
2.4.4.5.2. Теоремы о собственных
значениях и собственных векторах.
1. Подобные матрицы имеют одинаковые
характеристические многочлены и, следовательно,
одинаковые собственные значения.
2. Если Хь Х2, ..., Х„- собственные значения
матрицы А, то
ли в каждом классе эквивалентности матрица
диагонального вида? Оказывается, существует:
если rang ф = г, то всегда можно построить такую
пару базисов, что матрица, задающая ср, имеет
вид
1 0 0 ... О ... О
О 1 0 ... О ... О
Это можно использовать как необходимый
критерий правильности вычисления собственных
значений. Далее, из того, что det A = [~[ Xh следует,
что матрица А невырождена только тогда, когда
нуль не является собственным значением А.
3. Если Хи Х2, • • •» К- (попарно) различные
собственные значения матрицы А и хь х2, ..., хг —
соответствующие им собственные векторы (Х(
принадлежит х(), то {хь х2, ..., хг} есть линейно
независимое множество векторов.
4. Если матрица А имеет собственное значение
X, то для любых чисел с0, си ..., ск матрица
к
В = ? сгАх (здесь А1 = А и А0 = Е) имеет соб-
1 = 0
к
ственное значение ? с {к1. Отсюда, в частности,
i = 0
следует: если А имеет собственное значение X, то
Ат (т — натуральное число) имеет собственное
значение Хт. Для невырожденной матрицы А это
высказывание справедливо и при целых
отрицательных числах т, если положить Ат = А~к =
= (А~1)к (где к= -т есть натуральное число).
5. Каждая матрица А удовлетворяет
собственному характеристическому уравнению, т. е. если
Y, с{Х1 — характеристический многочлен Л, то
? CiA1 = 0 {теорема Гамильтона — Кэли).
1 = 0
Для определенных классов матриц
справедливы частные предложения:
1. Все собственные значения симметрической
матрицы действительны.
2. Собственные пространства, принадлежащие
различным собственным значениям
симметрической матрицы, взаимно ортогональны.
3. Все собственные значения ортогональной
матрицы по модулю равны единице.
4. Собственным значением ортогональной
матрицы наряду с X является также А,.
2.4.4.5.3. Применение теории с о б-
ственных значений.
2.4.4.5.3.1. Задача о нормальной
форме для линейных операторов. Пусть (р:
V-*V (V Ф V) — линейное преобразование
конечномерных векторных пространств и А - матрица,
описывающая ср относительно пары базисов (В, В')
(см. 2.4.4.4.2). Вопрос состоит в том, можно ли
надлежащим выбором пары базисов найти
матрицу, описывающую ф и имеющую особенно простой,
а именно диагональный (отличными от нуля
могут быть только элементы главной диагонали),
вид. Так как линейному преобразованию <р
сопоставлен единственный класс эквивалентных
матриц, то вопрос можно поставить так: существует
О 0 0 ... 1 ... О
О 0 0 ... О ... О
О 0 0 ... О ... О
(здесь г элементов главной диагонали равны
единице, остальные равны нулю).
Если поставить тот же самый вопрос по
отношению к линейным операторам в пространстве
V, то ответ получить гораздо труднее, так как
в этом случае можно «варьировать» уже не два
базиса (в V и V'\ а только один (в V). В этом
случае справедливо следующее утверждение.
Линейный оператор (р: V -* V относительно базиса
{аь а2, ..., ап} описывается диагональной
матрицей тогда и только тогда, когда базисные векторы
обладают свойством фа,- = Xtah где Х{ — некоторые
действительные числа. Эти числа Х( и являются
элементами диагональной матрицы.
Всякий вектор х ф 0, для которого фх = А,х,
где X — некоторый скаляр, называется
собственным вектором линейного оператора ф, а X —
собственным значением оператора ф,
принадлежащим этому собственному вектору.
Следовательно, линейный оператор ф
относительно базиса В описывается диагональной
матрицей тогда и только тогда, когда базисными
векторами являются собственные векторы, и вся
постановка задачи сводится к вопросу о
существовании базиса из собственных векторов оператора
ф. Для того чтобы существовал базис из
собственных векторов, т. е. для того, чтобы линейный
оператор ф имел п линейно независимых
собственных векторов, необходимо и достаточно,
чтобы все собственные значения оператора ф
были действительными и для каждого
собственного значения X кратности р выполнялись
равенства
rang (ф - Xz) = rang {А — ХЕ) - п — р,
где А — какая-либо матрица, задающая ф. Это
означает, что собственное подпространство,
принадлежащее собственному значению кратности р,
должно иметь размерность р (чтобы для р
совпадающих собственных значений получить р
линейно независимых собственных векторов).
Поставленная проблема не всегда разрешима,
так как не обязательно все собственные значения
линейного оператора должны быть
действительными и может случиться, что для кратных
собственных значений нельзя получить требуемого числа
линейно независимых собственных векторов.
Однако симметрический оператор в евклидовом
векторном пространстве всегда может быть описан
диагональной матрицей относительно
подходящего ортонормированного базиса, так как всегда
можно получить ортонормированный базис,
состоящий из собственных векторов
симметрического оператора. (Линейный оператор ф в евклидо-
168
АЛГЕБРА
вом векторном пространстве V называется
симметрическим, если (фх, у) = (х, <ру) для всех х, уе V.)
Вычисление собственных значений и
собственных векторов линейного оператора ср производится
путем определения собственных значений и
собственных векторов какой-либо матрицы
оператора (р.
2.4.4.5.3.2. Приведение матрицы к
диагональному виду. Задача состоит в том,
чтобы для п х n-матрицы А подобрать такую
матрицу С, чтобы матрица А' = С~1АС имела
диагональный вид. Эта задача тесно связана с
задачей онормальной форме линейных операторов.
Если относительно базиса В линейный оператор
Ф в пространстве V описывается матрицей А&
то ищем базис В\ по отношению к которому
описывающая ф матрица Aq> имеет диагональный
вид. Так как матрицы Ag и Ав> должны быть
подобны, то эта задача сводится к отысканию
такой матрицы С, чтобы матрица А# = С~1А^С
имела диагональный вид. Если задача разрешима,
то В' должен состоять из собственных векторов
оператора ф, т. е. столбцами искомой матрицы С
должны быть координаты собственных векторов,
образующих базис В'.
Задача всегда разрешима, если матрица А
симметрическая, так как тогда все собственные
значения действительны и размерность
собственного подпространства, принадлежащего
собственному значению А,, совпадает с кратностью X.
Вследствие ортогональности собственных
подпространств, принадлежащих различным
собственным значениям, для симметрических матриц
А всегда можно найти такую ортогональную
матрицу С, что С~1АС = СТАС имеет
диагональный вид.
Пример. Для того чтобы привести к диагональному
виду матрицу
Например, Ф = х\ + 4х2 — 6xtx2 является квадратичной
формой, так как
Г2-1 2-1
¦ -1 2-2 ,
L 2 -2 5J
найдем сначала ее собственные значения: Xi = 7, Х2 = Х3 = 1;
отсюда получаются собственные пространства:
^i = {ц A. - 1, 2); ц — действительное},
^2 = {Hi A. 1, 0) + ц2 (-2, 0, 1); ць ц2 - действительные}.
Далее получаем ортонормированную систему
собственных векторов:
Г|/б 1/2 1/5 )
1 -A, -1, 2); *—{\t 1, 0); ^j-(-l, I, 1».
Таким образом, посредством С = —
матрица А преобразуется в А' -
2.4.4.5.3.3. Преобразование
квадратичных форм к главным осям. Под
квадратичной формой относительно переменных
хь х2, ..., х„ понимают выражение вида х^кх,
где х = (хь х2, ..., х„) и А = || aik || —
симметрическая матрица, aik - действительные числа.
Матрица А называется матрицей квадратичной формы.
Постановка задачи такова: найти такую
ортогональную матрицу С, чтобы после введения
новых переменных уи у2, ..., у„ при помощи
уравнения х = Су данная квадратичная форма
содержала только слагаемые с квадратами текущих
координат: хтАх _ r>Xiyl + Х2у\ + ... + Хпу1.
Такой вид квадратичной формы называют канони-.
ческим.
После замены переменных х = Су форма х Ах
переходит в форму у (С АС) у, которая должна
содержать только слагаемые с квадратами
переменных. Таким образом, задача равнозначна
следующей: найти ортогональную матрицу С такую,
чтобы матрица С АС имела диагональный вид.
Это всегда возможно для симметрической матрицы
А, если в качестве столбцов искомой матрицы С
выбрать ортонормированную систему собственных
векторов матрицы формы А. Тогда посредством
замены х = Су квадратичная форма приводится
к виду Х1у1 + Х2у\ + ... + Хпу1, где Xt —
собственные значения матрицы А с учетом кратности.
Собственные векторы матрицы А, стоящие в
столбцах С, называются главными осями
квадратичной формы, а процесс преобразования
квадратичной формы в ее каноническую форму
называется приведением к главным осям или
приведением к каноническому виду.
Каноническая форма определяется однозначно
с точностью до нумерации переменных yt.
Пример. Для того чтобы квадратичную форму
Ьх\ + 5x1 + 7х§ - 4xtx2 + 4x2x3 привести к каноническому
виду, вычислим собственные значения и соответствующие
собственные подпространства матрицы
Г 6-221
-2 5 0 . По
L 2 0 7J
лучим Я.,=3, Х2 = 6, Х3 = 9; L, = {nB, 2, -1)}, L2-
= {ц(-1, 2, 2)}, L3 = {nB, -I, 2)}. Так как собственные
значения попарно различны, то соответствующие им
векторы попарно ортогональны, и, чтобы получить
ортонормированную матрицу, их нужно только пронормировать.
• Г 2 -1 21
Заменой х = — \ 2 2 -1 \у заданная форма приводит-
L-1 2 2J
ся к каноническому виду Ъу\ + Ьу\ + 9у\.
Если все собственные значения симметрической
матрицы А положительны (все отрицательны, все
неотрицательны, все неположительны), то для всех
х#0 квадратичная форма х Ах положительна
(соответственно отрицательна, неотрицательна,
неположительна) *).
Пример. Для действительных чисел хь х2, х3 таких,
что (xi, x2, хэ)^@, 0, 0), справедливо неравенство
Зх? + 10х| - 3x1 + 4х2х3 > 4x1 - 2х? - 10х§ -I- 4ххх2, так как
в этом случае 5х\ + 6х2 + 1х\ - 4xjX2 + 4х2х3 > 0, ибо
матрица полученной квадратичной формы имеет только
положительные собственные значения: X, = 3, "Кг - 6, Х3 = 9.
Критерий положительной определенности квадратичной
формы (критерий Сильвестра) приведен в 3.1.6.6.
*) Квадратичная форма в первом и втором случаях
называется определенной (положительно определенной или
отрицательно определенной) и в двух других случаях —
положительно или отрицательно полуопределенной.
ЦЕЛЫЕ РАЦИОНАЛЬНЫЕ ФУНКЦИИ
169
2.5. ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
К элементарным функциям относятся
рациональные функции, степенные функции,
тригонометрические функции и обратные к ним,
показательные и логарифмические функции,
гиперболические функции и обратные к ним, а также
функции, представимые в виде суммы, разности,
произведения, отношения или суперпозиции
перечисленных функций («функции, заданные
формулами», т. е. представимые в виде аналитического
выражения, причем областью определения
элементарной функции является множество всех чисел,
для которых ее аналитическое выражение имеет
смысл).
К неэлементарным функциям относятся, например:
j 1 для рациональных х
1 0 для иррациональных х
(функция Дирихле): f функция у = [х] (целая часть от х),
т. е. у равно наибольшему целому числу, не превосходя-
щему х: функция
_ Г sin х
' = Лтоо1 + *2'
функция
-dx (интегральный синус): функция у = Г (х) =
= J е~Чх l dt (гамма-функция).
2.5.1. АЛГЕБРАИЧЕСКИЕ ФУНКЦИИ
2.5.1.1. Целые рациональные функции.
2.5.1.1.1. Определение целой
рациональной функции. Функция / называется
целой рациональной функцией (или многочленом),
если она может быть представлена в виде
y=f(x)=
B.23)
для любого х (из области определения *)); числа
а0, аи ..., ап действительны (или комплексны);
а0 ф 0; п е N (или и = 0). Правая часть называется
многочленом (относительно переменного х), числа
а{ — коэффициентами многочлена, число п —
степенью целой рациональной функции (или степенью
многочлена). Представление B.23) единственно,
т. е. функции
f(x) = ? ап-кх\ д(х) = ? Ь„-*х*
*=0 *=0
равны тогда и только тогда, когда т = п и ак = Ьк
для к = 0, 1, 2, ..., п. Выражение B.23) называется
канонической формой представления целой
рациональной функции. Многочлен степени 1 называется
линейным.
Примеры. 1) /i (х) = с — постоянная функция,
степень /i равна 0.
2) h (x) ш х, степень /2 равна 1.
3) /з (х) - Gх + 1) (Зх + 5), степень /3 равна 2.
4) /4 (х) = |/7з х2 - 2 ]/1 х3 + cos 4 ' х, степень /4
равна 3. 5
*) Если для функции /, заданной аналитическим
выражением, область определения не задана явно, то под этим
всегда следует понимать множество всех действительных
чисел х0, для которых аналитическое выражение у = f (x)
дает действительное число / (х0).
Графики целых рациональных функций для
некоторых частных случаев приведены в 1.2.1.1.
2.5.1.1.2. Разложение на линейные
множители. Многочлен ? an-kxk, п ^ 1, назы-
*=о
вается приводимым, если он может быть
представлен в виде произведения многочленов низших
степеней; в противном случае он называется
неприводимым.
Многочлены нулевой степени (константы) не
являются ни приводимыми, ни неприводимыми;
многочлены первой степени всегда неприводимы.
Возможность разложения на множители
многочленов степени, большей единицы, зависит от
выбора области определения коэффициентов,
которая, в общем, не обязательно совпадает с
множеством действительных чисел.
Пример. Многочлен х4 — 7 неприводим, если
считать, что коэффициенты многочленов должны быть
рациональными числами. Если же в качестве области определения
коэффициентов взять множество действительных чисел, то
х4 - 7 = (х2 + |/7) (х2 - ]/l). Если же допустить
существование комплексных коэффициентов, то данный многочлен
может быть разложен на линейные множители:
Х4 _ 7 = (х - (рТ){х + ifyl)(x + fi)(x - ф%
Основная теорема алгебры. Любая целая
рациональная функция л-й степени с
коэффициентами из множества комплексных чисел может быть
разложена на п + 1 сомножителей, один из которых
имеет нулевую степень, а п множителей линейны
с единичными коэффициентами при переменном:
? an-kxk = ао(х - ах) (х - а2)... (х - а„).
Здесь а4 — комплексные числа. Если а0, аи ..., а„ —
действительные числа, то для каждого линейного
множителя (х — afc) с комплексным afc в
разложении содержится линейный множитель (х - ал), где
afc — число, комплексно сопряженное к afc.
Если область определения коэффициентов
сужена до множества действительных чисел, то
любая целая рациональная функция и-й степени
может быть разложена на множители первой и
второй степени:
X an-kxk = ао(х - ai)(x - a2)...
*=о
.. (х - а,) (х2 + рхх + qi)... (х2 + р,х + qt), B.24)
где 2/ + r = n, a aOi <хь ..., ar, ръ ..., ph qu ..., qt -
действительные числа.
2.5.1.1.3. Корни целых рациональных
функций. Число X; называется корнем (нулем)
целой рациональной функции / с
действительными коэффициентами, если
f(*j) = t
= 0.
Если X! является корнем целой рациональной
функции/степени п, то существует целая
рациональная функция fi степени п — 1 такая, что для
каждого х, принадлежащего множеству D области
определения /г имеет место равенство /(х) =
= (х - xx)fi (x). Если, помимо этого, корнями /
являются числа х2, х3, . • •, хг, то существует
170
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
целая рациональная функция /г степени п - г (г < и)
такая, что для всех xeD имеет место равенство
f(x) = (x-Xl)...(x-xr)fr(x).
Число Xj называется корнем кратности kj
(или корнем kj-го порядка), если существует целая
рациональная функция /^. такая, что
/(Х) = (Х-ХЩ(Х) ИА.(Х;)#О.
Учитывая кратность корней, целую
рациональную функцию / степени п можно представить
в виде
/(х) = (х - х^ (х - x2f> ...(х- xs)k* g (х), B.25)
s
где ? kj = r, g (x) - целая рациональная функция
степени п — г. Из выражения B.25) следует: целая
рациональная функция степени п имеет не более и
различных корней; если число корней равно п,
то она может быть представлена в виде
произведения и линейных множителей и одного множителя
нулевой степени. Число корней (с учетом их
кратности) является четным или нечетным в
зависимости от того, является ли степень функции /
четной или нечетной; если степень целой
рациональной функции с действительными
коэффициентами нечетна, то функция имеет по крайней мере
один действительный корень.
Примеры. 1) /(х) = х* - х3 - 5х2 - х - 6 имеет корни
Xj = — 2 и х2=3. Других действительных корней нет.
Поэтому для этой функции существует представление
/(х) = (х + 2)(х-3)(х2 + 1).
2) /(х) - х8 - х7 - Их6 + Их5 + ЗОх4 - 58х3 - 12х2 +
+ 88х — 48 имеет корень xt = 1 кратности 2, корень х2 — 3
(однократный) и корень х3 = -2 кратности 3. Отсюда
получаем разложение
f(x) = (х - IJ (х - 3) (х + 2K (х2 - 2х + 2).
Корни и графики функций. Каждому корню
функции / однозначно соответствует точка пересечения
(или точка касания, если порядок корня равен
четному числу) графика функции с осью абсцисс.
В точке, соответствующей однократному корню,
график имеет наклон, отличный от нуля; в точке,
соответствующей многократному корню, наклон
равен нулю, т. е. касательная к графику в
точках, соответствующих многократным корням,
совпадает с осью абсцисс.
Вычисление корней. Вычисление корней целых
рациональных функций сводится к решению
л
алгебраических уравнений ? яи_кхк = 0 (см. 2.4.2.3).
fc = 0
2.5.1.1.4. Поведение целых
рациональных функций на бесконечности.
Поведение целой рациональной функции / степени п
на бесконечности зависит:
1) от знака коэффициента а0 при хл;
2) от четности или нечетности п.
X
X
п
аО
lim fix)
-> +00
lim fix)
-> -00
Четное
>0
00
00
-
-
<0
00
CO
Нечетное
ao>O
-f GO
— 00
-
<0
00
00
Из того, что целые рациональные функции
непрерывны во всей своей области определения,
следует, что любая целая рациональная функция
четной степени всегда ограничена либо сверху, либо
снизу, а целая рациональная функция нечетной
степени не ограничена ни сверху, ни снизу.
2.5.1.1.5. Частные случаи. Линейные
функции - это целые рациональные функции первой
степени: /(х) = аох + аи а0 Ф 0. Они монотонно
возрастают при а0 > О и монотонно убывают при
а0 < 0. Графиками линейных функций являются
прямые, которые пересекают координатные оси в
точках Ai-ai/ao, 0) и В@, ах) (см. 1.2.1.1).
Квадратичные функции — это целые
рациональные функции второй степени: /(х) = аох2 + ахх +
+ а2, а0 Ф 0. Преобразуя, получим
Графиком квадратичной функции является пара-
( ах а\\
бола с вершиной С - -—, а2 - -—, которая
\ 2а0 4а0)
своими ветвями направлена в сторону
положительных (я0 > 0) или отрицательных (а0 < 0)
ординат (см. 1.2.1.1).
Степенные функции (с положительным
показателем степени) — это целые рациональные функции
fix) = х" (n e N). Графики этих функций
симметричны относительно оси ординат при четном и и
центрально симметричны относительно начала
координат при нечетном п; они называются
параболами п-го порядка (см. 1.2.1.1).
2.5.1.2. Дробно-рациональные функции.
2.5.1.2.1. Определение
дробно-рациональной функции. Функция / называется
рациональной функцией, если она представима в
виде отношения двух целых рациональных
функций Р (х) и Q (х), т. е. в виде
где ao Ф 0, bo Ф 0, n, m e N (или m, n = 0). При m = 0
это целая рациональная функция. При т > О
функция / называется дробно-рациональной
функцией.
Примечание. Выражение B.26) называется
канонической формой представления дробно-рациональной
функции f если функции Р(х) и Q(x) не имеют общих корней.
Если Р(х) и б(х) имеют общие корни хь ..., хк, то
/(*) =
Р(х)
где целые рациональные функции Pi(x) и Qi (х) не имеют
общих корней. Следовательно, их отношение f\ (x) =
= Piix)/Qxix) является канонической формой представ-
_Р(х)
ления функции /i. Выражение /(х) =
описывает функ^
цию/, значения которой совпадают со значениями/! во всей
области определения/i, исключая точки Xjij = 1, 2, ..., к), в
которых функция / не определена. Расширяя область опреде-
ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ
171
ления функции /, получим функцию /2 такую, что
{f{x), если х Ф xj,
lim Дх), если х = х} и предел конечен
х-*х;
0=1,2,..., Ас).
Функция /2 совпадает с функцией fx.
Примеры.
1) /i M = -р— (канонический вид).
-J/5
2) /г (х) = -j——(канонический вид).
2(х-3)
Дробно-рациональная функция /(х) = Р (x)/Q (х)
называется правильной дробно-рациональной
функцией, еели степень многочлена Q(x) больше, чем
степень многочлена Р(х) (примеры 2) и 3)), и
неправильной в противном случае (пример 1)).
Последнюю, разделив числитель на знаменатель
(см. 2.4.1.3), можно разложить на сумму, состоящую
из целой рациональной функции и правильной
дробно-рациональной функции.
Зх2 - 4х + 3 , 2
Пример, /(х) = = Зх -
2.5.1.2.2. Нули и полюсы
дробно-рациональных функций. Действительное
число Xj называется нулем или корнем рациональной
функции/(х) = P(x)/Q(x), представленной в
канонической форме, если Р (xj) = 0, a Q (xj) Ф 0. Если при
этом X; является корнем кратности г многочлена
Р(х), то Xj называется корнем кратности г
функции /(х). Таким образом, нахождение корней
рациональных функций сводится к нахождению
корней целых рациональных функций.
Действительное число х( называется полюсом
дробно-рациональной функции /(х) = Р (x)/Q (x),
представленной в канонической форме, если
Q (xf) = 0, а Р (х{) Ф 0. Если при этом х,- является
корнем кратности г многочлена Q(x), то х,
называется полюсом порядка г.
х2 - 1
Пример. Правильная функция Дх) = хз + Х2 _ 8х _ 12
имеет два однократных корня х, = 1 и х2 = -1, полюсы
х3 = 3 (полюс 1-го порядка) и х4=-2 (полюс 2-го
порядка).
В окрестности полюса х, значение функции
растет неограниченно, т.е. lim |/(x)|=+oo;
х-> х,
прямая х = х, является асимптотой графика этой
функции.
О поведении дробно-рациональной функции
в окрестности полюса х, можно сделать вывод по
знакам значений /(х, + е) и /(х, - е), где е -
достаточно малое положительное число.
Пример. х{ = 4 является полюсом функции /(х) =
х — 1
—5—т—; при малом е > О
х2 - 4х
4 + е- 1
= 3-fe
" D + еJ -4D + б) 4е + е2
4-e-l 3-е
! D-?J_4D-е) -4е + е3
2.5.1.2.3. Поведение
дробно-рациональных функций на бесконечности.
Если дробно-рациональная функция / задана в
виде
j = O
где а0 Ф 0 и Ьо Ф 0, то для всех х Ф О
1 я*-*
/м =
>о ,
х"м (х)
xmv (х)'
где lim u(x) = a0 и lim v(x) = b0. Таким
х-»±оо х-+±оо
образом, получаем:
а) При т = п
хпи(х) м(х)_
хт v (х) v (х)'
следовательно,
lim fix)- lim Л?> *
x -* ± oo x -> ± oo V (x) bo
т. е. прямая у = ao/bo является асимптотой
графика функции /.
б) При п < т
х»и(х) = и(х)
xmv(x) xm~nv(xY
следовательно,
lim /(x)= lim -4^-^ = 0,
х -*- ± oo х -> ± оо Xт п v (х)
т. е. асимптотой является ось абсцисс.
в) При п > т
хпи(х) _ х"-ти(х)
xmv(x)~~~v(x) ¦
Поведение функции на бесконечности зависит от
знака дроби ао/Ьо и от того, четно или нечетно
число п — т. Для всех трех случаев, обозначив
ао/Ъо — с, получаем следующую таблицу:
lim f(x)
Х-> +00
lim f(x)
Х-* -00
т = n
с
с
n < m
0
0
n > m
п — т
четно
+ 00
+ оо
— 00
— 00
п — т
нечетно
с>0
+ оо
— 00
с<0
— 00
+ оо
<0.
2.5.1.2.4. Степенные
дробно-рациональные функции. Простейшими дробно-
рациональными функциями являются степенные
функции с целым отрицательным показателем
172
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
f(x) =
n= -1, -2, -3,...
Если п нечетно, то (- х)и = - (х"), т. е. эти
функции являются нечетными; графики их
представляют собой кривые типа гиперболы, центрально
симметричные относительно начала координат.
Асимптотами этих графиков являются
координатные оси. В точке х = 0 эти функции не определены.
Степенные функции с четным (отрицательным)
показателем степени являются четными функциями,
т. е. (- х)п = хп. Их графики симметричны
относительно оси ординат. Асимптотами этих графиков
являются ось абсцисс и ось ординат
(положительное направление). В точке х = 0 эти функции не
определены.
Если в выражении B.26) т = 1, и < 1, то
получается дробно-линейная функция
( \ =
a°x + ai
где b0 Ф О и аф0 — aob1 Ф 0. Функция / имеет
корень xt = —а1/а0 (если а0 Ф 0) и полюс х2 = —bi/b0.
При х -+ ± оо значения функции стремятся к
ао/Ьо. Графиком функции/является равносторонняя
гипербола, ветви которой расположены
симметрично относительно точки М ( , — I. (Графики
V ^о Ьо)
дробно-рациональных функций см. в 1.2.1.2.)
2.5.1.2.5. Разложение
дробно-рациональных функций на элементарные
дроби. Для интегрирования рациональных
функций в общем случае необходимо разложить
их на сумму простейших рациональных дробей.
Если
/м =
Р(х)
ем
<с = 0
j=0
где Р (х) и Q (х) не имеют общих корней, п < т
и Ьо = 1, то /(х) единственным образом
представляется в виде
г, ч АП . ^12 . . Alkl
(х -
(х-хО2 (х-хЛ
^22
+ (х-х2) + (х-х2J +-"+(х-
(х-х,)
х,J
J "
(x-xsf*
(х2 + Plx + qx) (x2 + ptx + qiJ
(x2 + p2x + q2)
•-(X2-
f B22 + C22x ( + B2i2 + С
(x2+p2x + 42J '" (x2+p2x-
CrlX
(x2
(x2 + prx + ^r)
5п„ + Crl x
где kb lj, r, s — натуральные числа; Лд, B^fc, CJk,
qj, Pj — действительные числа; х{ - корни функции
Q (x); кроме того, Ц- - qj < 0 (/ = 1, 2, ..., г).
Слагаемые в выражении B.27) называются
элементарными (простейшими) дробями.
Частные случаи.
1) Если уравнение Q (х) = 0 имеет только
однократные действительные корни, например хь
х2, ..., хот, то B.27) имеет вид
№¦¦
Q(x)
A2 Am
¦ + — + ... + ¦
х — х2
х-хт
2) Если уравнение Q (х) = 0 имеет
действительные, но не обязательно однократные корни,
например Xj — корень кратности kj, то B.27) имеет
вид
ем
Ых-
3) Если уравнение Q (x) = 0 имеет также и
комплексные, но только однократные корни, то B.27)
имеет вид
к I
Bj + Cjx
Q(x)
+ 4}
Методы разложения на
элементарные дроби. Сначала функция приводится к
каноническому виду (см. B.26)); в случае
неправильной дробно-рациональной функции выделяется
целая рациональная часть и значение
коэффициента при члене с наибольшим показателем
степени в многочлене, находящемся в знаменателе
оставшейся правильной дробно-рациональной
функции, приводится к 1. Далее, для разложения
на элементарные дроби требуется, чтобы было
известно множество решений уравнения Q (х) = О,
т. е. представление Q (х) в виде произведения
(см. B.24)). Для определения коэффициентов при
разложении на элементарные дроби существуют
различные методы; поясним некоторые из них на
примерах.
Метод неопределенных коэффициентов.
Пример
Запишем
2х2 - 4х + 2
(х - IJ х - i (х - IJ '
Умножая обе части на (х — IJ, получим х = А^х + (Аг — At).
Приравнивая коэффициенты при одинаковых степенях х,
получим Аг = \ и /42 — /4i = 0; следовательно,
1
sx-l
1
Пример 2.
B.27) /(х).
Р(х)
Q(x)
2х4 + 2х2 - 5х
!х4 + 2х2-5х + 1
х(х2 + х+ IJ
ДРОБНО-РАЦИОНАЛЬНЫЕ ФУНКЦИИ
173
Запишем
В2 + С2х
Jy*> x x2 + x+l т(х* + х+!Г
Умножим обе части на х(х2 + х + IJ:
2х4 + 2х2 - 5х + 1 *
*i4i(x2 + х+ IJ +(Bt + Ctx)(x2 + х+ 1)х + (В2 + С2х)х.
Умножив B.28) на (х — 2K, получим
Зх4 - 9х3 + 4х2 - 34х + 1
G+1р "
= Al3 + {x-2)[Al2+{x-2)Al
левой и правой частях, получим
/1, + С, «2, 2/1,+Й!+ С, =0,
ЗЛ.+В, + С, + С2 = 2, 2/t,+B,+B2=-5, И, «1.
Отсюда i4i - С! = С2 =» 1, Bi — -3 и В2 = -4. Таким
образом.
одинаковых степенях а в Устремив х в обеих частях к 2, получим А13 = -3. Умножив
B.28) на (х + ЗJ и устремив затем х к -3, получим А22 = -5.
Простое преобразование выражения B.28) дает в результате
3 5 Зх - 1
/(*)
(х-2K т (х + 3J (х-2)(х + 3)
-4 + х
с2 + х+ Г
Метод подстановки численных значений.
Пример 3.
Р(х) х2 + х-1 _ х2 + х-1
_dii_4- .
х _ 2 г (х - 2J х + 3'
B.29)
Аналогичным образом (т. е. умножая B.29) на (х — 2J или
на (х + 3) и устремляя х к 2 или к -3) получаем Ах2 = 0,
А21 = 2. Преобразуя B.29) в равенство ^_2^у^ -
/W
3 - х2 - 2х
х + 3 х-2
приходим к разложению
-, получим, что /4И = 1. Таким образом,
Запишем /(х) = ——+ —~ + _3 . Полагая
последовательно для х значения 1, -2 и 3, получим систему
- — = At +-у/12 - А3, —8^= —г'41 ~ /*2 —4^у4э»
"+1м
/М-
х - 2 (х - 2K х + 3 (х + ЗJ"
Примечание 1. Для случая, рассмотренного в
примере 1, т. е. для разложения /(х) вида
Решение этой системы: Ах = 1/2,
Таким образом, получаем разложение
-1/3, А3 = 5/6.
<2 (х) х — хх х — х2 х — хт
по вышеописанному методу предельных значений имеем
,Р(х)
А(
lim {x-
X -+ X
(/= 1, 2, ..., т).
/w 2x"" 3(х+1)х6(х-2)-
Метод предельных значений.
Пример 4.
, Зх4 - 9х3 + 4х2 - 34х + 1
С другой стороны,
х5 - 15х3 + 10х2 + 60х - 72
lim -вМ._ to CMCW =g.
X -^ Xj X - XJ X-+Xj X~ XJ
и, значит, разложение на элементарные дроби
окончательно может быть записано так:
Зх4 - 9х3 + 4х2 - 34х
'" (х-2K (х + 3J
/(*) =
Запишем
ew
= V P(*j)
; х-2 (х-2J (х-2K х + 3 (х + 3)
Таблица к п. 2.5.1.3.
тг. B.28)
Примечание 2. Для случая, рассмотренного в
примере 4, неопределенные коэффициенты можно искать по
Степенная функция
Иррациональная функция
Область значений/
Точки перегиба
Поведение функции на интервалах
монотонности
п = 2т — 1; meN
g(x) = xn
r-y-x для -оо<х<0
/(ХН y
1/х для 0 < х < + оо
— 00 < у < +00
м0 (о. о)
монотонно возрастает
л = 2m; meN
?(*) = *"
/W = l7x
0<х< +оо
0 <^ < +оо
нет
монотонно
возрастает
0<х < +оо
— оо < у < 0
нет
монотонно
убывает
174
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
формулам
А" = 2Т х1™2 С(Х " 2K/(Х)]"' Л22 = х Ит_ з [(Х + 3J/(Х)]'
2.5.1.3. Иррациональные алгебраические
функции. Простые иррациональные алгебраические
функции, называемые также степенными функциями
с дробными показателями степени вида 1/л, где п —
натуральное число, являются обратными к
степенным функциям с натуральными показателями
степени. В случае четного показателя степени
существуют две обратные функции; для
нечетного показателя - одна обратная функция.
Графики иррациональных функций см. в
1.2.1.3; свойства приведены в таблице на стр. 173.
2.5.2. ТРАНСЦЕНДЕНТНЫЕ ФУНКЦИИ
Неалгебраические функции называются
трансцендентными (см. 2.5.1). К наиболее важным
трансцендентным функциям относятся
тригонометрические функции, показательные функции,
гиперболические функции, а также функции,
обратные к ним.
2.5.2.1. Тригонометрические функции и
обратные к ним.
2.5.2.1.1. . Определение
тригонометрических функций. Пусть круг радиуса г с
центром в начале (прямоугольной декартовой)
системы координат
V\ пересекает
положительную ось абсцисс
в точке S (рис. 2.7).
Движущаяся по
окружности точка Р с
координатами ?, г\
определяет угол SOP,
величину которого (в
радианах или в
градусах — см. 2.6.3)
обозначим через х. При
этом х положительно,
если точка Р, начиная
движение из точки S, пробегает окружность в
направлении против часовой стрелки
(положительном направлении). Тригонометрические
круговые функции (функции угла) определяются
следующими равенствами:
синус: f(x) = sin х = —;
косинус: f(x) = cos x = —;
РИС. 2.7
тангенс: f(x)
tg x = —;
котангенс: fix) = ctgx = —;
Л
секанс: f(x) — secx = —;
косеканс: f{x)= cosec x = —.
Область определения тригонометрических
функций состоит из множества действительных чисел х,
за исключением значений, обращающих в нуль
знаменатель.
Примечания. 1) Косинус (лат. «complement
sinus» — дополнительный к синусу) является синусом
дополнительного угла, и, наоборот, синус является
косинусом дополнительного угла; соответственно также тангенс и
котангенс или секанс и косеканс находятся друг с другом
в отношении функция — кофункция, т. е. имеют место
равенства (х - в радианах)
. /я \ . /я \
cos х = sin I —— х I, sin x = cos I — — x I,
ctgx = tgfy-xj, tgx=ctg(y-x\
/я \ /я \
cosec x = sec I —— x I, sec x = cosec I —— x I.
2) Благодаря простым соотношениям sec x = 1/cos x и
cosec x = 1/sin x функции секанс и косеканс используются
на практике сравнительно редко (в основном в астрономии).
В связи с этим подробные сведения о свойствах этих
функций здесь приводиться не будут.
3) Если в определении круговых функций специально
выбрать г = 1, то значения тригонометрических функций
могут быть определены (при 0 ^ х < я/2) как длины
следующих отрезков (см. рис. 2.7): sinx соответствует PL; cosx
соответствует OL; tgx соответствует P'S; ctgx
соответствует S'P".
Периодичность
тригонометрических функций. Так как положения движущейся
по окружности точки, соответствующие двум
углам, величины которых отличаются на число,
кратное 2я, совпадают, то значения всех
тригонометрических функций периодически
повторяются, т. е. имеют место равенства sin х = sin (х + 2кп),
cos х = cos (x + 2кп), а для тангенса и котангенса
даже tg х = tg (x + кп) и ctg x = ctg (x 4- кп), при
этом к = 0, ±1, ±2, ...
Соотношения в прямоугольном
треугольнике. Для значений аргумента х между
О и я/2, рассматриваемого в качестве угла
прямоугольного треугольника, имеем следующие
соотношения для тригонометрических функций:
aba
sin х = —, cos х = —, tg х = —,
с с b
be с
ctg x = —, sec x = —, cosec x = —,
ah a
где (рис. 2.8) a — длина противолежащего катета,
b — длина прилежащего
катета, с — длина
гипотенузы.
Графики
тригонометрических функций см. в
1.2.2.1, таблицы значений
функций - в 1.1.1.10.
Вспомогательные
методы для нахождения
значений, которые не
могут быть непосредственно определены из
таблиц.
2.5.2.1.2. Свойства тригонометрических
функций.
1) Значения тригонометрических функций для
аргументов, значения которых лежат между
я/2 и 2я, сводятся к значениям функций от аргу-
Рис. 2.8
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ОБРАТНЫЕ К НИМ
175
Область определения
Область значений
Нули
Полюсы
Длина периода
Экстремумы в точках
Точки перегиба
\
Четность функции
/(х) = sin х
— оо < х < +00
-1 </(*)< +1
х = кп >
нет
2л
л
х = у + кп
х = кп
нечетная
/(х) = cosx
— оо < х < +оо
-1 </(*)< + 1
х = у + кп
нет
2л
х = кп
X = — + &Я
четная
/(*) = tgx
— 00 < X < +00
х Ф у + кп
— оо < /(х) < + оо
х = кп
л
х = у + кп
л
нет
х = кп
нечетная
fix) = ctgx
- 00 < X < + 00
— оо </(х) < + оо
л
х- + кп
х — кп
л
нет
л
X = у + /СЛ
нечетная
ментов, лежащих между 0 и тс/2, при помощи
следующих формул приведения:
sin ( —- + х 1 = cos х,
sin (я ± х) = + sinx,
sin I — л ± х 1 = - cos х,
cos I — + х J = — sin x, cos (я ± x) = — cos x,
cos I — - n ± x I = ± sin x,
tg fy + *)*= -ctgx,
± 1, ±2,...
4) Значение любой тригонометрической
функции для значений аргумента между я/4 и я/2 может
быть сведено к значению дополнительной
функции для дополнительного угла. Это используется
в таблицах тригонометрических функций.
5) При выполнении различных действий с
тригонометрическими функциями полезно знать
значения функций для некоторых углов и знаки
значений функций в четырех тсвадрантах:
= ±tgx,
tgfytt + XJ *= + CtgX,
ctg (я ± х) = ± ctg х,
tgX.
2) Значение тригонометрической функции / от
отрицательного аргумента может быть выражено
через значение соответствующей функции от
положительного аргумента при помощи соотношений
/(-х)=/(х) для косинуса и /(-х)=-/(х) для
синуса, тангенса и котангенса.
3) Для определения значений
тригонометрических функций при значении аргумента | х | ^ 2я
нужно учитывать периодичность
тригонометрических функций (см. 2.5.2.1.1).
Радианы
Градусы
sinx
cosx
tgx
ctgx
0
0°
0
1
0
л
~6
30°
У
2
1
l/з
/з
Л
т
45°
ft
2
2
1
1
л
т
60°
ф.
2
1
2
/з
1
W
л
т
90°
1
0
0
Квадрант
I
II
III
IV
Аргумент
0<JC<T
/с
у < X < Л
Л<Х<уЛ
у л < х < 2л
sinx
+
+
-
-
cosx
+
-
-
+
tgx
+
-
+
-
ctgx
+
-
+
-
176
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
2.5.2.1.3. Соотношения между триго- Приравнивая действительные и мнимые части, по-
нометрическими функциями. лучаем
Связь между функциями с одинаковым значе- п п1 п_2 -г ,
j,4 COS ПХ — COS X — С-и COS X Sin X ~r
нием аргумента*).
+ C4cos"xsin4x - Cjcos"xsin6x -I-...,
. , , sin x
sin2x + cos x =1, tgx=^-, tgxctgx=l, sin nx = Cwicos«- ix sin x_
sec2 x — tg2 x =1, ctg x = , sin x • cosec x = 1,
smx
cosec2 x — ctg2 x = 1, cos x • sec x = 1.
Теоремы сложения для суммы и разности
аргументов *).
sin (х ± у) — sin х cos у ± cos x sin у,
cos (х ± у) = cos х cos у + sin x sin у,
tg X + tg j/
ctg(x±y) =
ctg x ctg у + 1
ctg у ± ctg x
sin (x + у + z) = sin x cos у cos z + cos x sin у cos z +
+ cos x cos у sin z — sin x sin у sin z,
cos (x + у + z) = cos x cos у cos z — sin x sin у cos z —
— sin x cos у sin z — cos x sin у sin z.
Теоремы сложения для кратных аргументов.
2tgx
sin 2x = 2sin x cos x = г—,
1 + tg2 x
л 2 2 1 - tg2 X
cos 2x = cos x — sin x = r—,
1 + tg2 x
sin 3x = 3 sin x — 4 sin3 x,
cos 3x = 4 cos3 x — 3 cos x,
sin 4x = 8 cos3 x sin x — 4 cos x sin x,
cos 4x = 8cos4 x — 8 cos2 x + 1,
2tgx 2
tg2x =
ctg 2x =
tg 4x =
ctg 4x =
1 - tg2 x ctg x - tg x'
ctg2 x - 1 _ ctg x - tg x
2ctgx 2
» . . •» /-»+
. ctg 3x =
1 - 3 tg2 x
4tgx-4tg3x
1 - 6 tg2 x + tg4 x'
ctg4 x - 6 ctg2 x + 1
4 ctg3 x - 4 ctg x
3ctg2x-l
Для больших значений n выражения для sin nx
и cos их получают, пользуясь формулой Муавра
для комплексных чисел (см. 3.4 2):
cos nx + i sin nx = (cos x + i sin x)" =
= Z ikCjcosn~'cxsinkx.
*) Следует заметить, что правые части приводимых
формул могут быть неэквивалентны левым частям при
некоторых значениях аргумента.
- C3cos"~3xsin3x -I- C;Jcos"~5xsin5x - ...
Для функций половинного аргумента имеют
место следующие соотношения (знак + или —
выбирается в соответствии с тем, в какой четверти
(квадранте) находится угол - аргумент х/2):
tgy -±
X
ctgy =
1 - COS X
1 - cos х sin x
1 + COS X 1 + COS X
1 — cos x
sin x
- cosx
sin x 1 + cos x
. — cos x 1 — cos x
sinx
Теоремы сложения для суммы и разности
функций.
х + у х - у
sin х + sin у =2 sin —-—cos
2 '
x + у . x — у
sin x - sin у =2 cos —-—sin —-—,
x + у x - у
COS X + COS у = 2 COS COS ,
- . X + у . X - у
COS X - COS у = - 2 Sin — Sin —,
cos x ± sin x = 1
tg x ± tg у =
sin (x ± y)
ctg x ± ctg у = ±
tg x + ctg у
cos x cos у
sin (x ± y)
sin x sin у
cos(x-y)
cos x sin у
cos (x + y)
ctgx-tgj; = —v
sin x cos у
Произведения тригонометрических функций.
sin (x + у) sin (x - у) = cos2 у - cos2 x,
cos (х + у) cos (х — у) = cos2 у — sin2 х,
sin x sin у = — [cos (x - у) - cos (x + у)],
cos х cos у = —- [cos (х - у) + cos (х + у)~\,
sin х cos у = — [sin (x - у) + sin (x + у)],
cos х sin у = — [sin (x + у) - sin (x - у)],
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И ОБРАТНЫЕ К НИМ
177
sin х sin у sin z = — [sin (x + у - z) +
+ sib(y + z - x) + sin(z + x - 3;) - sin(x + у 4- z)],
sin x cos у cos z = — [sin (x 4- у - z) —
— sin (y + z — x) + sin (z + x — y) 4- sin (x 4- у + z)],
1 г
sin x sin >; cos z = — [ - cos (x 4- у - z) 4-
+ cos C/ + z — x) + cos (z + x — y) — cos (x 4- у 4- z)],
cos x cos у cos z = — [cos (x + у — z) +
+ cos (y 4- z - x) 4- cos (z 4- x - y) 4- cos (x 4- у 4- z)],
tg x + tg у tg x - tg у
tgxtgy
ctg x ctg у
tgxctgy =
ctg x 4- ctg у ctg x - ctg у
ctg x 4- ctg у ctg x — ctg у
tg x 4- tg у tg x - tg у
tg x + ctg у tg x - ctg у
ctg x 4- tg у ctg x - tg у
Соотношения между квадратами
тригонометрических функций с одинаковым значением
аргумента.
характер, что в математической форме записывается
в виде функции /(х) = A sin (сох 4- <р) (где А, со, <р —
действительные числа и А Ф О, со ф 0). Если сравнить
график функции /(х) = A sin (сох + ф) = A sin со (х 4-
4- ф/со) с графиком функции у = sin x, то видно,
что параметр А вызывает сжатие (| А \ < 1) или
растяжение (| А \ > 1) графика вдоль оси ординат;
если А < 0, то график будет к тому же зеркально
отражен относительно оси абсцисс; параметр со
изменяет (наименьший) период колебаний, период
становится равным 2я/|со|; слагаемое ф вызывает
смещение графика функции вдоль оси абсцисс на
| ф/со [ единиц (см. 1.2.2.1 и рис. 1.22).
Пример. График функции /(х) = - 2 sin B.x + я/4) по
сравнению с графиком функции 0(x) = sinx зеркально
отражен и сжат в два раза относительно оси абсцисс,
растянут в два раза вдоль оси ординат и сдвинут на я/8 в
отрицательном направлении оси абсцисс. Наименьший
период функции / равен я.
Физическая интерпретация
функции /(х) = A sin (сох 4- ф). Если выбрать в качестве
независимого переменного время t, то получим
f(t) — A sin (cor 4- ф). Здесь ф — это смещение по
фазе, или «начальная фаза», Т = 2л/со — «период
колебаний», v = \/Т= co/Bti) — «частота
колебаний», со = 2к/Т = 2п\ — круговая, или циклическая,
частота (число колебаний за 2л секунд) и А —
sin2x
COS2JC
tg2x
Ctg2*
sin2*
1 — sin2x
sin2*
1 - sin2 x
1 — sin2*
sin2x
cos2*
1 - cos2 *
1 — cos2 *
cos2*
cos2*
1 — cos2 *
tg2*
1 4- tg2 *
1
1 + tg2 *
tg2*
ctg2*
1
1 4- ctg2 *
1 4- ctg2 *
1
ctg2*
sec2*
sec2 x - 1
sec2x
1
sec2*
sec2 * — 1
1
sec2* — 1
соsec2 *
1
cosec2 *
cosec2 * — 1
cosec2 *
1
cosec2 * — 1
cosec2 * — 1
Степени тригонометрических функций.
sin2x = —A - cos2x),
cos2x = —A 4- cos2x),
sin3 x = —C sin x - sin 3x),
cos3 x = — C cos x 4- cos 3x),
sin4 x = — (cos 4x - 4 cos 2x 4- 3),
8
cos4 x = — (cos 4x 4- 4 cos 2x 4- 3).
Для вычисления sin"x и cos"x при больших
натуральных показателях степени п можно испольЗо-
вать* формулы для sin их и cos их (см. выше).
2.5.2.1.4. Синусоидальная функция
общего вида /(х) = A sin (сох + ф). Многие
процессы в природе и технике имеют колебательный
«амплитуда колебаний». Если А зависит от
времени по закону А = A (t) = e~Rt, где R > 0, то
амплитуда постепенно уменьшается (затухающее
колебание; см. 1.2.2.2). Если колебания
накладываются друг на друга, то результат определяется
как сумма синусоидальных величин; если
колебания имеют одинаковую частоту, то их сумма
имеет ту же частоту:
? Ak sin (ш 4- Фд) = A sin (cot 4- ф).
*= 1
При п = 2 имеют место следующие соотношения:
tg<P
А = у А\ 4- АI 4- 2AiA2 cos (ф2 —
Ах вшф, 4- А2 sin ф2
! 4- А2
Функцию/(?) = A sin (cof 4- ф) можно также
представить в виде f(t) = a sin oat 4- b cos cof, причем
A = \/a2 4- b2, a/A — cos ф, b/A = sin со.
2.5.2.1.5. Определение обратных
тригонометрических функций. Функции,
обратные к тригонометрическим функциям, назы-
178
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
ваются обратными круговыми или обратными три- 2.5.2.1.7. Соотношения между обрат-
гонометрическими функциями.
Пусть к — целое число.
Функции,
обратные
к функциям
рассматриваемым
на каждом из
промежутков
называются
и обозначаются <
у — cos х
у = ctg х /
2к - 1 2к 4- 1
ными тригонометрическими
функциями.
arcsin х = - arcsin (- х) =
arccos x = я - arccos (- х)
я . х
¦- —— arcsin x = arcctg ,
[кп, (* + 1)я]
2* - 1 2к+1
(Ля, (fe 4- 1) я)
арксинусом *),
арккосинусом,
арктангенсом.
arctg x = - arctg (- х) =
у = Arcsin х,
у = Arccos х,
у = Arctg х,
у — Arcctg х.
я х
= arcctg x = arcsin ,
2 /ТТх1
arcctg x = я — arcctg (— x) =
я x
= arctg x = arccos :
2 yi+x2
Суммы и разности обратных
тригонометрических функций.
arcsin х + arcsin у =
Наиболее часто применяются обратные
тригонометрические функции, которые получаются, arcsin x — arcsin у =
= arcsin (x |/l - у2 + у ]/\ - х2)
при ху ^ 0 или х2 + у2 ^ 1;
= я - arcsin (х у\ - у2 + у \/\ - х2)
при х > 0, у > 0 и х2 + у2 > 1;
= —п - arcsin (x |/l - у2 + у ]/\ - х2)
при х < 0, у < 0 и х2 + у2 > 1;
если положить в вышеприведенных интервалах = arcsin(xl/l — у2 — yl/l — х2)
к = 0 (так называемые главные значения; они
обозначаются соответственно arcsin x, arccos x, arctg х, при ху ^ 0 или х + у < 1;
arcctg x).
Примеры, arcsin 0 = 0, arccos A/2) = я/3, arctg I = я/4,
arcctg |/з = я/6.
2.5.2.1.6. Свойства обратных
тригонометрических функций.
= я - arcsin (x |/l - у2 - у ]/l - х2)
при х > 0, у < 0 и х2 + у2 > 1;
= -я - arcsin (x]/l - у2 - у |/l - х2)
при х < 0, >> > 0 и х2 4- у2 > 1;
Область определения
Область значений
Монотонность
Точки перегиба
>> = arcsin х
- 1 <х< + 1
монотонно
возрастает
@,0)
-
у = arccos х
— 1 < jc < 4- 1
0 <у < я
монотонно
убывает
@, я/2)
-
у = arctg jc
— с» < jc < +оо
монотонно
возрастает
@, 0)
я я
-у, т
>> = arcctg х
- 00 < X < + 00
0 <>> < я
монотонно
убывает
@, я/2)
Графики обратных тригонометрических функций arccos x + arccos у =
см. в 1.2.2.1. Таблицы значений обратных три-
гонометрических функций см. в 1.1.1.9 и 1.1.1.10. = arccos (ху - \/1 - х* ]/\ - у2) при х 4- у > 0;
*) Arcus - дуга; запись у = Arcsin х означает, что у есть = 2я — arccos (ху — j/l — х2 |/l — _у2)
величина такого угла в радианах, синус которого равен х
(лат.: arcus cuius sinus x est). при х 4- у < 0;
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ
179
arccos х — arccos у =
= - arccos (ху + |/l - х2 ]/\ - у2) при х $* у;
= arccos (xy + J/l — x2 ]/l — у2) при х < у;
х + у
arctg х + arctg у = arctg
\-ху
при ху < 1;
X +¦ V
= п + arctg при х > 0, ху > 1;
= -я + arctg
1-ху
х + у
1 —
при х < 0, ху > 1;
arctg х — arctg у = arctg
х-у
1 + ху
при ху > — 1;
= п + arctg
1 + ху
при х > 0, ху < — 1;
х — у
= - п + arctg при х < 0, ху < - 1.
1 + ху
логарифмическая
2.5.2.2. Показательная
функции.
2.5.2.2.1. Определение показательной
и логарифмической функций. Функция /
называется показательной, если для каждого
значения х, принадлежащего области определения,
имеет место равенство
у=Ях) = а',
где а > О — действительное число, а ф 1.
Областью определения функции /(х) = ах
является множество действительных чисел; так как
ах > О для всех х, то множеством значений функции
является множество положительных
действительных чисел. При а > 1 функция является строго
возрастающей, при 0 < а < 1 - строго
убывающей.
Так как ах*ах2 = ах^ + **, то каждая
показательная функция / удовлетворяет теореме сложения
f(x\)f(x2) =/(*i + *2)- Функция, обратная к
показательной функции у = ах, называется
логарифмической функцией и обозначается у = logex.
Существование логарифмической функции
обеспечивается строгой монотонностью
показательной функции на всей ее области
определения. Логарифмическая функция определена только
для положительных значений аргумента.
2.5.2.2.2. Частные случаи
показательных и логарифмических функций. Если
умножить значения функции на действительное
положительное число /с, т. е. перейти к функции
д(х) = ках, то в силу равенства ках = ax+logak это
означает сдвиг графика функции / на \ogak единиц
в положительном направлении вдоль оси абсцисс.
Если в выражении /(х) = ах в качестве а взять
число е = lim ( 1 Н ) , трансцендентное число
п ~* оо \ п )
е = 2,718 281828459045..., то получим
показательную функцию /(х) = ех, играющую важную роль в
естественных науках. Значения функции е* с любой
точностью можно вычислить при помощи
степенного ряда (см. 3.1.14.6):
Применения функции/(х) = е*. Процессы
(органического) роста: д (f) = до^г{во — начальная величина, с —
постоянная роста).
Процессы распада: m(t) = moe~"(mo - начальная
величина, X — постоянная распада).
Затухающие колебания: /"(() = e~ktsin (cor + <р) (см.
2.5.2.1.4). 2
Теория ошибок: /(*) = е х (кривая Гаусса - функция
ошибок).
Функция, обратная к у = е*, обозначается у = In x.
Так как loge (kx) = \ogak + logflx, то график
функции д (х) = loge (kx), где к > 0, получается из графика
функции /(хI = logax сдвигом последнего на \ogak
единиц в положительном направлении оси ординат.
2.5.2.2.3. Свойства показательной
и логарифмической функций.
Область
определения
Область
значений
Монотонность
Нули
Точки пересечения
с осью ординат
lim fix)
Х-> +00
lim fix)
х-^ -ос
Область
определения
Область
значений
Монотонность
Нули
Точки пересечения
с осью ординат
lim fix)
х-> +оо
lim fix)
х -> — ос
У = а\
а> 1
-00 <Х < +00
0 < у < +оо
монотонно
возрастающая
нет
у=\
+ 00
0
У=\о%аХ,
а> 1
0 <х < +оо
-оо < у < +оо
монотонно
возрастающая
х=1
нет
+ 00
не имеет
смысла
0<а< 1
— оо < х < +оо
0 < у < +оо
монотонно
убывающая
нет
у=\
0
+ 0О
y=logax,
0<а<1
0 < х < +оо
-оо < у < +оо
монотонно
убывающая
х= 1
нет
— 00
не имеет
смысла
180
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
Графики показательных и логарифмических
функций см. в 1.2.2.2. Таблицы значений
показательной и логарифмической функций см. в 1.1.1.10 —
1.1.1.12.
2.5.2.3. Гиперболические функции и обратные
к ним.
2.5.2.3.1. Определение
гиперболических функций.
Синус гиперболический
ех - е~х
у = sh х =
Тангенс гиперболический
ех - е~х
у = th х =
* е* + е~х
Секанс гиперболический
2
у = sch х ¦¦
ех + е х
Косинус гиперболический
ех + е~х
у = ch х =
Котангенс гиперболический
ех + е~х
Косеканс гиперболический
2
Графики гиперболических функций см. в 1.2.2.3.
Таблицы значений гиперболических функций
см. в 1.1.1.10.
2.5.2.3.3. Соотношения между
гиперболическими функциями. Приведенные
ниже равенства аналогичны соотношениям между
тригонометрическими функциями.
Замечение. Равенства, в которых гиперболические
функции / встречаются в форме f\x) или f(ax), могут быть
получены по аналогии с выводом соотношений для
соответствующих тригонометрических функций, если формально
заменить sin х на / sh х и cos х на ch х, где /2 = -1 (см.
также 3.4.1).
Примеры. cosaх + sin2дс« 1 преобразуется в ch2x +
+ i2 sh2 х ш ch2 x - sh2 х ш l; sin 2x « 2 sin x cos x
преобразуется в i sh 2x « 2i sh x ch х, или sh 2x « 2 sh x ch x.
Основные соотношения:
shx
thx =
cthx =
schx =
cschx :
chx'
chx
shx'
thx
shx'
cthx
chx '
у = csch :
ex -
ch2 x - sh2 x = 1,
sch2 x + th2 x = 1,
cth2 x - csch2 x = 1,
th x cth x = 1.
2.5.2.3.2. Свойства гиперболических функций.
Область определения
Область значений
Нули
Асимптоты
lim f(x)
х-> ±оо
Монотонность
Экстремумы
Точки перегиба
Четность функции
у = shx
— оо < х < +00
У
— 00 < у < +00
х = 0
нет
± 00
монотонно
возрастает
нет
х = 0
нечетная
у = chx
- оо < х < + оо
1 <у < + оо
нет
нет
+ оо
на (- оо, 0)
монотонно
убывает,
на @, + оо)
монотонно
возрастает
минимум х = 0
нет
четная
у = thx
— оо < х < +оо
- 1 <у < + 1
х = 0
у** ± 1
± 1
монотонно
возрастает
нет
х = 0
нечетная
у = cth х
- оо < х < + оо
ХФО
— оо <у < — 1
+ 1 < у < + оо
нет
х = 0
у= ± 1
± 1
на (- оо, 0)
монотонно
убывает,
на @, + оо)
монотонно
убывает
нет
нет
нечетная
ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ И ОБРАТНЫЕ К НИМ
181
Соотношения между квадратами гиперболических функций с одинаковым значением аргумента
Sh2x+l
slAr+1
-
Ch2x-1
Ch2x
Ch2x
Ch2x-1
th2x
l-th2x
1
l-th2x
1
cth2x
1
cth2 x - 1
Cth2X
cth2x-l
1
cth2x
1 —sch2x
sch2x
1
sch2x
1
l-sch2x
csch2x
1
csch2x
1 +csch2x
csch2x
1
1 +csch2x
csch2x+l
Теоремы сложения для суммы и разности
аргументов.
sh (х ± у) = sh х ch у ± ch x sh у,
ch (х ± у) = ch х ch у ± ch x sh у,
thx + thy
th(x±y) =
cth(x±>>) =
1 ± th x th у'
1 ± cth x cth у
cth x ± cth j/
Теоремы сложения для двойного и половинного
аргументов.
sh 2х = 2 sh х ch x,
ch 2x = sh2 x 4- ch2 x,
2 thx
th2x =
cth 2x =
1 + th2 x'
1 + cth2 x
2 cth x '
sh — = )/(chx - l)/2 при x ^ 0,
sh — = - ]/(ch x - l)/2 при x < 0,
ch — = |/(ch x + l)/2,
x sh x ch x — 1
2 ch x + 1 sh x
sh x ch x + 1
, x
cth —
2
2 ch x - 1 sh x
Сумма и разность гиперболических функций.
2 '
ch x + ch у = 2 ch * У ch *
chx-ch3; =
2 '
-У
2 '
th x ± th у
sh(x±y)
ch x ch у '
Формула Муавра.
(ch x + sh х)и = ch nx ± sh nx.
2.5.2.3.4. Определение обратных
гиперболических функций. Функции,
обратные к гиперболическим, называются также ареа-
функциями. Они определяются следующим
образом :
ареасинус
у = Arsh х, если х = sh у;
ареакосинус *)
у = Arch х, если х = ch у;
ареатангенс
у = Arth х, если х = tg у;
ареакотангенс
у = Arcth х, если х = cth у.
Явное выражение обратных гиперболических
функций через логарифмические функции. Если
приведенные в 2.5.2.3.1 функциональные уравнения
разрешить относительно х и затем формально
поменять переменные местами, то получим
у = Arsh х = In (х + |/х2 + 1),
у = Arch x = In (x — j/x2 — 1)
(для x^l и — оо < у < 0),
у = Arch х = In (х + \/х2 — 1)
(для
= Arth х = In / = — In
]/ 1 - х 2 1 - >
(при | х | < 1),
А .. ,/x+l 1х+1
у = Arcth х = In / = — In
У }/ х- 1 2 х- 1
(при | х | > 1).
*) Следует учесть, что у = ch x не во всей области
определения - монотонная функция Следовательно,
обратную функцию получают отдельно для каждого из двух
промежутков монотонности
182
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
2.5.2.3.5. Свойства обратных
Область определения
Область значений
Нули
Асимптоты
Поведение на
бесконечности
Точки перегиба
Четность функции
у = Arsh х
-00 <Х < +00
— оо < у < +00
х=0
нет
lim Arsh x ~ ± оо
Х-* ±00
х=0
нечетная
гиперболических функций.
у = Arch х
1 <Х < +00
0<у < +оо
или
-оо <j> <0
х=1
нет
lim Arch x = + оо
Х-» +00
для Arch х = In (x + j/x2 - 1);
lim Arch x = — оо
x-> +oo
для Archx = ln(x-l/x2- 1)
нет
ни четная,
ни нечетная
у — Arth х
-1<х< +1
— оо < у < +оо
х=0
х=±1
х=0
нечетная
у = Arcth х
-00 <Х < -1
+ 1 < X < +00
-оо < у < +оо
нет
у=0
х=±1
lim Arcth x = 0
х-* ±оо
нет
нечетная
Графики ареафункций получаются из графи- зеркальным отражением относительно прямой
ков соответствующих гиперболических функций у = х (см. 1.2.2.3).
2.5.2.3.6. Соотношения между обратными гиперболическими функциями.
Arshx
Archx
Arthx
Arcth x
Arshx
±Arshj/x2- 1
Arsh X
]/хг-Х
Arsh *
|/x2-l
Archx
±Arch/x2+l
+ Arch l
j/l-x2
+Arch
/x2-l
Arthx
Arth
j/x2+l
+ArthK
Arth-
Arcth x
Arcth v~
X
+ Arcth —
Arcth-
X
Во втором столбце таблицы принято, что
Arch x = In (x 4- |/х2 - 1),
и для х > 0 берется знак +, а для х < 0 берется
знак —.
Arsh х ± Arsh у = Arsh (х ]/\+у2 ± у j/l-f-x2),
Arch x ± Arch >> = Arsh (ху ± ]/{х2 - 1) (у2 - 1)),
х±у
Arth х ± Arth у = Arth
1 ± ху '
1 + XV
Arcth х ± Arcth у = Arcth — ~
:: ± У
ПЛАНИМЕТРИЯ
183
2.6. ГЕОМЕТРИЯ
2.6.1. ПЛАНИМЕТРИЯ
Треугольник. Сумма двух сторон в
треугольнике (рис. 2.9) больше третьей стороны: b + о а.
Сумма углов в треугольнике равна 180°: а +
+ р + у = 180°.
Треугольник определен, если задан
какой-нибудь из следующих наборов его элементов: 1) три
Рис. 2.9
Рис. 2.10
стороны; 2) две стороны и угол между ними;
3) сторона и два прилежащих к ней угла. Если
заданы две стороны и угол, противолежащий
одной из сторон, то при помощи этих элементов
можно построить либо два, либо один, либо ни
одного треугольника (рис. 2.10); подробнее см.
2.6.3.1.2.
Медианой называется отрезок прямой,
соединяющий вершину треугольника с серединой
противолежащей ей стороны. Медианы треугольника
пересекаются в одной точке — центре тяжести
треугольника (рис. 2.11) - и делятся этой точкой в
отношении 2: 1 (считая от вершины). Длина медианы,
проведенной к стороне а, равна
]/2 (Ь2 + с2) - а2
(см. также 2.6.3.1.2).
Биссектрисой треугольника называется
лежащий в треугольнике отрезок прямой, которая
а
Рис. 2.11
Рис. 2.12
делит его внутренний угол пополам. Биссектрисы
треугольника пересекаются в одной точке,
являющейся центром вписанной окружности (рис. 2.12);
о радиусе вписанной окружности г см. 2.6.3.1.2.
Длина биссектрисы угла а вычисляется по формуле
(см. также 2.6.3.1.2)
У be [(Ь + сJ - а2]
/а= bT~c '
Центр описанной окружности
находится в точке пересечения
перпендикуляров, восставленных
к сторонам треугольника в их
серединах (рис. 2.13); о радиусе
описанной окружности R см.
2.6.3.1.2.
Высотой треугольника называется отрезок
перпендикуляра, опущенного из вершины
треугольника на противоположную сторону. Высоты
треугольника пересекаются в одной точке, называемой
Рис. 2 13
его ортоцентром; о длинах высот ha, hb, he*)
см. 2.6.3.1.2.
Высота, медиана и биссектриса, опущенные на
одну и ту же сторону, совпадают, если две другие
стороны треугольника равны (равнобедренный
треугольник). Совпадения двух из этих отрезков
достаточно для того, чтобы треугольник был
равнобедренным.
Для равностороннего треугольника {а = Ь = с)
центры вписанной и описанной окружностей, центр
тяжести и ортоцентр совпадают.
Средней линией называется отрезок прямой,
соединяющий середины двух сторон
треугольника; она параллельна третьей стороне и равна
половине ее длины.
Площадь треугольника:
S = bhb/2 = (ab sin y)/2 = гр =
= abc/DR) = ]/р{р-а){р-Ъ){р-с\
где р = (а + b + c)/2.
Прямоугольный треугольник (рис. 2.14): с -
гипотенуза, а и b — катеты. Имеют место
равенства: а2 + Ь2 = с2 (теорема
Пифагора), h2 = тп, a2 = тс, Ь2 = пс.
Площадь: S = ab/2 = (a2 tg P)/2 =
= (с2 sin 2P)/4.
Тригонометрические
формулы, относящиеся к треугольнику,
см. в 2.6.3.1.1.
Треугольники (а также
многоугольники с одинаковым
числом сторон) подобны, если у них
соответственные углы равны и сходственные стороны
пропорциональны. Для подобия треугольников
достаточно выполнения одного из следующих условий:
1) три стороны одного треугольника
пропорциональны трем сторонам другого; 2) два угла
одного треугольника равны двум углам другого;
3) две стороны одного треугольника
пропорциональны двум сторонам другого треугольника, а
углы, заключенные между ними, равны.
Площади подобных фигур пропорциональны
квадратам соответствующих линейных элементов
(сторон, высот, диагоналей и т. п.).
Параллелограмм (рис. 2.15). Основные свойства:
1) противоположные стороны равны; 2)
противоположные стороны
параллельны; 3) диагонали в
точке пересечения делятся
пополам; 4) противоположные
углы равны. Наличие у
четырехугольника одного из
двух последних свойств или
равенства и параллельности
одной пары противоположных сторон вызывает
как следствия все остальные свойства.
Диагонали и стороны связаны соотношением
d\ + d\ = 2 [а2 + b2). Площадь: S = ah.
Прямоугольник и квадрат. Параллелограмм
является прямоугольником (рис. 2.16), если: 1) все
углы прямые или 2) диагонали равны (одно из
этих свойств есть следствие другого). Площадь:
а
Рис. 2.15
*) hb означает высоту, опущенную на строку b
треугольника.
184
ГЕОМЕТРИЯ
Прямоугольник есть квадрат (рис. 2.17), если
а = Ь. Имеют место формулы d — а |/2 « 1,414а;
а = ]/2 d/2 « 0,707d. Площадь: 5 = а2 = Л2/2.
санный четырехугольник, рис. 2.21, а). Около
четырехугольника можно описать окружность тогда
и только тогда, когда а + у = |3 + 6=180о
(вписанный четырехугольник, рис. 2.21, б). Для вписанного
а
Рис. 2.18
Рол*б. Параллелограмм является ромбом
(рис. 2.18), если у него: 1) все стороны равны, или
2) диагонали взаимно перпендикулярны, или 3)
диагонали делят углы параллелограмма пополам
(одно из этих свойств влечет как следствия два
остальных). Площадь: S = ah = a2 sin a = dld2/2.
Трапеция — четырехугольник, у которого две
стороны параллельны, а две другие не
параллельны (рис. 2.19), а и Ь — основания трапеции,
И - высота, т — средняя линия (отрезок прямой,
соединяющий середины непараллельных сторон):
т = (а + Ь)/2. Площадь: S = (а + b) h/2 = mh. Если
?
/77
а
Рис. 2.19
Рис. 2.20
d = с, то говорят о равнобочной трапеции. В этом
случае
S = [а - с cos у) с sin у = (Ь + с cos у) с sin у.
Четырехугольник (рис. 2.20). Сумма углов
всякого выпуклого четырехугольника равна 360°;
а2 + Ь2 + с2 + d2 =d\ + d\ + 4m2, где т - отрезок,
соединяющий середины диагоналей. Площадь:
S = (d1d2 sin a)/2.
В четырехугольник можно вписать окружность
тогда и только тогда, когда а + с = b + d (onu-
четырехугольника ас + Ы = dxd2. Площадь
вписанного четырехугольника:
где
S = ]/{р - а){р - Ъ){р - с){р - d),
d)/2.
Многоугольник (рис. 2.22). Если число сторон
равно п, то сумма внутренних углов равна
Рис. 2.22
Рис. 2.23
180° (п — 2). Сумма внешних углов равна 360°.
Площадь определяют, разбивая многоугольник на
треугольники. ,
Если у многоугольника все стороны и углы
равны между собой, то говорят о правильном
многоугольнике (рис. 2.23). Для правильных
многоугольников с п сторонами имеют место
следующие соотношения: центральный угол а = 360%,
внешний угол |3 = 360°/п, внутренний угол у =
= 180° - р. Если R — радиус описанной окруж-
Элементы правильных многоугольников.
Обозначения: п — число сторон, S — площадь, а — сторона, R — радиус описанной окружности,
г — радиус вписанной окружности
3
4
5
6
7
8
9
10
12
15
16
20
24
32
48
64
а*
0,4330
1,0000
1,7205
2,5981
3,6339
4,8284
6,1818
7,6942
11,196
17,642
20,109
31,569
45,575
81,225
183,08
325,69
S
1,2990
2,0000
2,3776
2,5981
2,7364
2,8284
2,8925
2,9389
3,0000
3,0505
3,0615
3,0902
3,1058
3,1214
3,1326
3,1366
S
5,1962
4,0000
3,6327
3,4641
3,3710
3,3137
3,2757
3,2492
3,2154
3,1883
3,1826
3,1677
3,1597
3,1517
3,1461
3,1441
_R
а
0,5774
0,7071
0,8507
1,0000
1,1524
1,3066
1,4619
1,6180
1,9319
2,4049
2,5629
3,1962
3,8306
5,1012
7,6449
10,190
г
2,0000
1,4142
1,2361
1,1547
1,1099
1,0824
1,0642
1,0515
1,0353
1,0223
1,0196
1,0125
1,0086
1,0048
1,0021
1,0012
а
R
1,7321
1,4142
1,1756
1,0000
0,8678
0,7654
0,6840
0,6180
0,5176
0,4158
0,3902
0,3129
0,2611
0,1960
0,1308
0,0981
а
г
3,4641
2,0000
1,4531
1,1547
0,9631
0,8284
0,7279
0,6498
0,5359
0,4251
0,3978
0,3168
0,2633
0,1970
0,1311
0,0983
г
R
0,5000
0,7071
0,8090
0,8660
0,9010
0,9239
0,9397
0,9511
0,9659
0,9781
0,9808
0,9877
0,9914
0,9952
0,9979
0,9988
г
а
0,2887
0,5000
0,6882
0,8660
1,0383
1,2071
1,3737
1,5388
1,8660
2,3523
2,5137
3,1569
3,7979
5,0766
7,6285
10,178
ПРЯМЫЕ И ПЛОСКОСТИ В ПРОСТРАНСТВЕ
185
ности, а г - радиус вписанной окружности, то
сторона а = 2 ]/r2 - г2 = 2R sin (a/2) = 2r tg (а/2).
Площадь: S = nar/2 = nr2 tg (а/2) = nR2 (sin а)/2 =
= /ш2 ctg (а/2)/4.
Данные об отдельных правильных
многоугольниках см. в таблице их элементов на стр. 184.
Окружность. Радиус г, диаметр d.
Углы, связанные с окружностью *): вписанный
угол а = В&/2 (рис. 2.24), угол между хордой и
касательной Р = At/2 (рис. 2.24), угол между
хордами у = (ИЗ + Й))/2 (рис. 2.25), между секущими
Рис. 2.25
Рис. 2.26
а = (DE — ВС)/2 (рис. 2.26), между секущей и
касательной р = (fE - Тв)/2 (рис. 2.26), между
касательными а = (ВЕС - ВЁС)/2 (рис. 2.27).
Пересекающиеся хорды (рис. 2.25):
АС • AD = АВ • АЕ = г2 - т2.
Секущие (рис. 2.26):
АВ • АЕ = АС • AD = AT2 = т2 - г2.
Длина окружности С и площадь круга S:
n = C/d* 3,141592653589793...,
С = 2кг « 6,283г,
С = 2 ]/n~S « 3,545 |/S,
S = nr2 » 3,142r2,
5 = m*2/4 « 0,785d2,
r = C/Btc) « 0,159C,
^ = 2j/5/i% 1,128 j/5;
см. также таблицы 1.1.1.13 и 1.1.1.14.
Сегмент и сектор (рис. 2.28). г — радиус, / —
длина дуги, а - хорда, а - центральный угол (в
*) В этих равенствах фигурирует не длина дуги, а ее
угловая мера, совпадающая с мерой соответствующего
центрального угла
градусах), h — стрела сегмента:
а = 2 ]/2hr - h2 = 2r sin (a/2),
h = r - ]/r2 - {a2/A) = r A - cos (a/2)) = {a/2) tg (a/4),
/ = 2тшх/360«0,01745га.
Приближенно:
2) l*\/a2 + (\6h2/3).
Площадь сектора: S = яг2а/360 « 0,00873r2a.
Площадь сегмента:
Si = г2 [(тса/180) - sin a]/2 = [lr-a(r- Л)]/2.
Приближенно: Si» h Fа + 8Ь)/15. Таблицы для 5Ь
/, h и а см. в 1.1.1.15.
Круговое кольцо (рис. 2.29). D = 2R — внешний
диаметр, d = 2г — внутренний диаметр, р = (R +
+ г)/2 - средний радиус, Ъ-R — r- ширина
кольца.
Площадь кольца: S = n(R2 -r2) = n(D2 -d2)/4 =
= 2яр8.
Площадь части кольца (заштрихована на
рис. 2.29) с центральным углом ф (в градусах)
равна
2.6.2. СТЕРЕОМЕТРИЯ
2.6.2.1. Прямые и плоскости в пространстве.
Две прямые (несовпадающие), лежащие в одной
плоскости, либо имеют одну общую точку, либо
не имеют ни одной. В последнем случае они
Рис. 2 30
параллельны. Если через две прямые нельзя
провести плоскость, они называются
скрещивающимися.
Угол между скрещивающимися прямыми
определяется как угол между параллельными им
прямыми, проходящими через одну точку (рис. 2.30).
Расстояние между скрещивающимися прямыми
186
ГЕОМЕТРИЯ
Рис. 2.31
равно длине отрезка прямой, пересекающей обе
заданные прямые и перпендикулярной к ним.
Две плоскости (несовпадающие) или
пересекаются по одной прямой, или не имеют общих
точек. В последнем случае они параллельны.
Совпадающие плоскости также считаются
параллельными. Если две плоскости перпендикулярны
одной и той же прямой или если на каждой из
них имеются по две пересекающиеся прямые,
соответственно параллельные между собой, то эти
плоскости параллельны.
Прямая и плоскость. Прямая может лежать
целиком в данной плоскости, иметь с ней одну
общую точку или не
иметь ни одной. В
последнем случае прямая
параллельна плоскости.
Угол между прямой и
плоскостью измеряется
углом между прямой и ее
проекцией на плоскость
(рис. 2.31). Если прямая перпендикулярна двум
пересекающимся прямым на плоскости, то она
перпендикулярна любой прямой на плоскости
(перпендикулярна плоскости).
2.6.2.2. Двугранные, многогранные и телесные
углы. Двугранный угол — фигура, образованная
двумя полуплоскостями, выходящими из одной
прямой. Двугранный угол измеряется своим
линейным углом ЛВС (рис. 2.32), т. е. углом между
перпендикулярами к ребру DE двугранного угла,
восставленными в обеих плоскостях (гранях) из
одной точки.
Многогранный угол OABCDE (рис. 2.33)
образуется несколькими плоскостями (гранями),
имеющими общую точку (вершину) и пересекающимися
последовательно по прямым О А, ОВ, ..., ОЕ
(ребрам). Два ребра, принадлежащие одной грани,
образуют плоский угол многогранного угла, а две
соседние грани — двугранный угол. Многогранные
углы равны (конгруэнтны), если они при
наложении совпадают; для этого должны быть равны
соответствующие элементы (плоские и
двугранные углы) многогранных углов. Если
соответственно равные элементы многогранного угла располо-
Рис. 2.32
Рис. 2.33
Рис. 2.34
жены в обратном порядке, многогранные углы
при наложении не совпадают; в этом случае их
называют симметричными, т. е. они могут быть
приведены в положение, изображенное на
рис. 2.34.
Выпуклый многогранный угол лежит целиком
по одну сторону от каждой его грани. Сумма
плоских углов z. ЛОВ + z. ВОС + ... + z. EOA
(рис. 2.33) любого выпуклого многогранного угла
меньше 360° (или 2я).
Трехгранные углы равны, если они имеют:
1) по равному двугранному углу, заключенному
между двумя соответственно равными и одинаково
расположенными плоскими углами, или 2) по
равному плоскому углу, заключенному между
двумя соответственно равными и одинаково
расположенными двугранными углами,
или 3) по три соответственно
равных и одинаково расположенных
плоских угла, или 4) по три
соответственно равных и одинаково
расположенных двугранных угла.
Телесный угол — часть
пространства, ограниченная прямыми,
проведенными из одной точки
(вершины) ко всем точкам какой-либо
замкнутой кривой (рис. 2.35). Он
характеризует угол зрения, под
которым из вершины видна данная кривая. Мерой
телесного угла является площадь, вырезаемая
телесным углом на сфере единичного радиуса с
центром в вершине. Например, для конуса с углом
при вершине 120° телесный угол равен я (см.
формулы в 2.6.2.4).
2.6.2.3. Многогранники. Обозначения: К-объем,
S — полная поверхность, М — боковая поверхность,
h — высота, F — площадь основания.
Многогранник — тело, ограниченное
плоскостями.
Призма (рис. 2.36). Основания — равные
многоугольники; боковые грани — параллелограммы.
Рис. 2.35
Рис. 2.36
Рис. 2.37
Призма называется прямой, если ее ребра
перпендикулярны плоскости основания. Призма
называется правильной, если она прямая и ее
основания — правильные многоугольники.
Имеют место соотношения: М = pi, где / -
ребро, р — периметр сечения призмы плоскостью,
перпендикулярной ребру; S = М + 2F; V = Fh.
Для треугольной призмы, усеченной не
параллельно основанию, V = (а + b + с) Q/3 (рис. 2.37),
где а, Ъ, с — длины параллельных ребер, Q —
площадь перпендикулярного сечения.
Для и-гранной призмы, усеченной не
параллельно основанию, V = IQ, где / - длина отрезка
прямой ВС, соединяющего центры тяжести
оснований, Q — площадь сечения, перпендикулярного
этой прямой.
Параллелепипед (рис. 2.38) — призма, у которой
основания — параллелограммы. В параллелепипеде
МНОГОГРАННИКИ
187
все четыре диагонали пересекаются в одной точке
и делятся в ней пополам. Параллелепипед
называется прямоугольным, если он прямой (прямая
Усеченная пирамида (плоскость сечения
параллельна основанию, рис. 2.43). Если F - площадь
нижнего основания, / — площадь верхнего
основания, h — высота (расстояние между основаниями),
а и А — две соответственные стороны оснований,
то
V = h [F + / + \/Ff~\/3 =± hF [I + (а/А) + (а/ЛJ]/3.
Для правильной усеченной пирамиды М — (Р +
+ р) Ь/2, где Р и р^- периметры соответственно
О
Рис: 2.38
а
Рис. 2.39
призма) и его основания - прямоугольники. В
прямоугольном параллелепипеде (рис. 2.39) все
диагонали равны. Если a, by с — ребра прямоугольного
параллелепипеда, ad- его диагональ, то d2 =
= а2 + b2 +c2, V= abc, S = 2{ab + bc + са).
Куб - прямоугольный параллелепипед с
равными ребрами: а = Ъ = с, d2 = За2, V = а3, S = 6а2.
Пирамида (рис. 2.40). Основанием является
какой-либо многоугольник, боковые грани -
треугольники, сходящиеся в одной вершине.
Пирамида называется п-угольной, если в ее основании
лежит и-угольник; V — Fh/3.
Рис. 2.43
нижнего и верхнего оснований, Ъ - высота
боковой грани (апофема).
Обелиск. Нижнее и верхнее основания
являются прямоугольниками, расположенными в
параллельных плоскостях; противоположные боковые
грани одинаково наклонены к основанию, но не
пересекаются в одной точке (рис. 2.44). Если
Рис. 2.40
Рис. 2.41
Если пирамида пересечена плоскостью (рис. 2.41),
параллельной основанию, то
SAt
SO1
AXA BtB CiC
площадь ABCDEF
площадь AxBiCxDiEiI
¦f—У.
\soj'
где SO — высота пирамиды, т. е. отрезок
перпендикуляра, опущенного из вершины на основание.
Пирамида называется правильной, если в ее
основании лежит правильный многоугольник, а
высота проходит через его центр. Для правильной
пирамиды М = pb/2 (где р — периметр основания,
a b - высота боковой грани (апофема)).
Треугольная пирамида (рис. 2.42). Если О А = а,
ОВ = Ь, ОС = с, ВС = р, CA=q и АВ = г, то
а, b и аь &! — стороны оснований, h — высота, то
V = h [Bа + ах) Ь + Baj + a) 6J/6 =
= h [ab + (а + aj (Ь + Ь0 + аф^/6.
Клин. Основание - прямоугольник, боковые
грани — равнобедренные треугольники и
равнобочные трапеции (рис. 2.45);
V = Bа + ах) bh/6.
Правильные многогранники. Все грани — равные
правильные многоугольники, и все многогранные
У2 =
1
288"
0
r2
Я2
a2
1
r2
0
P2
b2
1
42
P2
0
c2
1
a2
b2
c2
0
1
1
1
1
1
0
Рис. 2.46
188
ГЕОМЕТРИЯ
Элементы правильных многогранников (а — длина ребра).
Название
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
Число граней и их форма
4 треугольника
6 квадратов
8 треугольников
12 пятиугольников
20 треугольников
Число
ребер
6
12
12
30
30
вершин
4
8
6
20
12
Полная
поверхность
1,7321л2
6л2
3,4641л2
20,6457л2
8,6603л2
Объем
0,1179лЗ
лЗ
0,4714лЗ
7,6631лЗ
2,1817лЗ
углы равны. Существует всего пять правильных
многогранников (рис. 2.46), данные о которых
представлены в таблице элементов правильных
многогранников.
Теорема Эйлера. Если е — число вершин
выпуклого многогранника, / — число граней и к —
число ребер, то е — к + / = 2.
Примеры см. в таблице правильных
многогранников.
2.6.2.4. Тела, образованные перемещением
линий. Обозначения: К-объем, S - полная
поверхность, М — боковая поверхность, h — высота,
F — площадь основания.
Цилиндрическая поверхность (рис. 2.47)
образуется прямой линией (образующей),
перемещающейся параллельно заданному направлению вдоль
некоторой кривой (направляющей).
Рис 2 47
Рис. 2 48
Цилиндр (рис. 2.48) — тело, ограниченное
цилиндрической поверхностью с замкнутой
направляющей и двумя параллельными плоскостями,
являющимися основаниями цилиндра. Для любого
Рис 2 49
Рис 2 50
цилиндра (р — периметр основания, рг —
периметр сечения, перпендикулярного образующей, Q —
площадь этого сечения, / — длина образующей)
имеем М = ph = pj, V — Fh = Ql.
Круговой прямой цилиндр имеет в основании
круг, и его образующие перпендикулярны
плоскости основания (рис. 2.49). Пусть R — радиус
основания; тогда М = 2nRh, S = 2nR (R + h), V = nR2h.
Усеченный круговой цилиндр (рис. 2.50).
-nR2
^ +h2
Отрезок цилиндра — «копыто» (обозначения см.
на рис. 2.51; а = <р/2 - в радианах).
V=h\a (ЗД2 - а2) + 3R2 (Ь - R) а]/(ЗЬ) =
= hR3 [sin а - (sin3 а)/3 - а cos а]/Ь,
М = 2Rh [F - R) а 4- а\/Ь
(формулы остаются в силе при b > R, (р > п).
Цилиндрическая труба (рис. 2.52). R и г -
внешний и внутренний радиусы, 5 = R - г, р = (R +
+ г)/2 (средний радиус);
V = nh (R2 - г2) = nhd BR - 5) =
= кпд Bг + 8) = 2nhbp.
Коническая поверхность (рис. 2.53) образуется
прямой линией (образующей), перемещающейся
Рис. 2.51
Рис. 2.52
Рис 2.54
вдоль кривой линии (направляющей) и имеющей
неподвижную точку (вершину).
Конус (рис. 2.54) — тело, ограниченное
конической поверхностью с замкнутой направляющей
ПРЯМОЛИНЕЙНАЯ ТРИГОНОМЕТРИЯ
189
и плоскостью, образующей основание. Для любого
конуса V = hF/3.
Круговой прямой конус (рис. 2.55) имеет в
основании круг, и его высота проходит через центр
Рис. 2.55
Рис. 2.56
круга (/ - длина образующей, R - радиус
основания).
М = nRl = kR ]/r2 + h2, S = nR(R + /),
V = nR2h/3.
Усеченный прямой конус (рис. 2.56).
/ = ]/h2 + (R- rJ, М = nl(R + г),
V = Kh (R2 + г2 + Rr)/3, H = h + hr/(R - r).
Конические сечения см. в 2.6.6.1.
Сфера - поверхность шара (рис. 2.57).
(Обозначения: R - радиус сферы, D = 2R — диаметр
сферы.) Любое сечение сферы
плоскостью есть круг. Под
большим кругом — кругом
радиуса R — понимают
сечение сферы плоскостью,
проходящей через ее центр.
Через всякие две точки
сферы (не являющиеся
противоположными концами
диаметра) всегда можно провести
только один большой круг.
Меньшая дуга этого
большого круга является кратчайшим расстоянием на
сфере между данными точками. О геометрии на
сфере см. 2.6.4.1. Поверхность сферы и объем
шара:
Рис. 2.57
S = 4nR2
s
V = 4nR3/3
V =
R
R
* 12,57Я2,
= \/36nV2z
% 4Д89Я3,
= (|/sVic)/6 я
5
= nD2 я 3,142D2,
» 4,836 j/F2,
F = пйъ/6 я 0,5236i
s 0,09403 t/51,
= (|/5/я)/2* 0,2821 j/S,
= jV/D*)
Шаровой сектор (рис.
s-
- 2a-
nR Bh + a),
»
Рис. 2.58
* 0,6204 ^F.
2.58).
V = 2тсЯ2й/3.
?E
Рис. 2.59
Шаровой сегмент (рис. 2.59).
а2 = h BR -h\ M = 2nRh = n(a2 + h2),
S = n BRh + a2) = к {h2 + 2a2\
V = nh Ca2 + /i2)/6 = nh2 CR - h)/3.
Рис. 2.60
Рис. 2.61
Шаровой слой (рис. 2.60).
R2 = а2 + [(а2 - Ъ2 - /i2)/B/i)]2, M = 2nRh,
S = n {2Rh + а2 + b2),
V=nh (За2 + ЗЬ2 + h2)/6.
Если Vi — объем усеченного конуса, вписанного
в шаровой слой (рис. 2.61), и / — его образующая,
то V-V1 =nhl2/6.
Тор (рис. 2.62) — поверхность, образованная
вращением окружности вокруг оси, лежащей в
Рис. 2.62
Рис 2.63
плоскости этой окружности и не пересекающей ее.
S = 4n2Rr « 39,48Яг, S = n2Dd « 9,870Ш,
V= 2n2Rr2 я 19,74Яг2, V= n2Dd2/4 « 2,467Ш2.
Бочка (рис. 2.63). Для круговой бочки
(образующая — дуга окружности) приближенно
V» 0,262й BD2 + d\ или V» О,О873й BD + dJ.
Для параболической бочки
V=nh (8D2 + 4Dd + 3d2)/60 я
я 0,05236/j (8D2 + 4Dd + З^2).
2.6.3. ПРЯМОЛИНЕЙНАЯ
ТРИГОНОМЕТРИЯ
Радианное измерение углов. Наряду
с обычным в практике градусным измерением
углов, при котором полный угол равен 360°,
прямой угол 90°, каждый градус делится на
60 минут A° = 60'), минута - на 60 секунд (Г = 60"),
используют безразмерное радианное измерение
углов, прежде всего в теоретических вопросах,
190
ГЕОМЕТРИЯ
особенно для тригонометрических функций (см.
2.5.2.1). При этом величина центрального угла а
в произвольном круге определяется как отношение
длины дуги /, на которую этот угол опирается,
к радиусу R:< a = 1/R. В круге радиуса 1
(единичном круге) радианная мера угла равна длине дуги,
которую вырезают стороны этого угла. За единицу
измерения принимается радиан — центральный
угол для дуги, длина которой равна радиусу.
Радианная мера полного угла равна In,
прямого угла я/2. Если ос - мера угла в градусах, а
а — мера того же угла в радианах, то переход от
одной меры к другой производится по формулам
а=Ж«' "Т* (Z30)
Таблицы для перевода градусов в радианы см.
в 1.1.1.16.
2.6.3.1. Решение треугольников.
2.6.3.1.1. Решение прямоугольного
треугольника. Обозначения: а, Ь — катеты,
с — гипотенуза, а, р - углы, противолежащие
соответственно сторонам а и Ь.
Основные соотношения:
sin а = cos р = а/с, cos а = sin C = b/c, B.31)
tg а = ctg p = a/b, ctg а = tg p = Ъ/а. B.32)
2.6.3.1.2. Решение косоугольного
треугольника. Обозначения: а, Ь, с — стороны,
а, Р, у - противолежащие им углы, р = (а + b +
+ с)/1 - полупериметр, R - радиус описанной
окружности.
Основные соотношения:
а + р + у = 180°.
Теорема синусов.
a b с
1R.
B.33)
sin а sin р sin у
Теорема косинусов.
с2 =а2 + Ъ2 -labcosy. B.34)
Дополнительные соотношения:
Теорема тангенсов.
a-b tg((a-p)/2) tg((a-p)/2)
а + b tg ((a + Р)/2) ctg (y/2)
Теорема половинного угла.
PiP-с)
B.35)
B.36)
B.37)
cos — =
Формулы Мольвейде.
а + Ь _ cos ((a - р)/2)
с ~ sin (у/2) "
a-b sin ((a - P)/2)
cos (y/2)
cos ((a - p)/2)
cos ((a + P)/2) '
sin ((« - P)/2)
sin ((a +
B.39)
B.40)
Формула косинусов (теорема о проекциях).
с = a cos p + b cos a. B.41)
Формула тангенсов.
с sin a с sin C
tgy =
b — с cos a a — с cos
B.42)
Остальные соотношения получаются из формул
B.34)-B.42) соответствующей циклической
перестановкой сторон а, Ь, с и соответственно углов
Основные случаи решения
треугольников.
I. Даны сторона и два прилежащих угла,
например с, а, р. Тогда третий угол также
известен: у = 180° - a - р. Стороны определяются по
формуле B.33):
sin a sin P
sin у
sin у
II. Даны две стороны и угол между ними,
например а, Ь, у.
1) Решение при помощи формулы B.34):
Ь2 + с2 - а2
с = у а2 + b2 — lab cos у, cos a =
2bc
Р = 180° - а - у.
2) Решение при помощи формулы B.35):
а — В а — b у
ig~l~-~a~Tb °tgT'
a-P a+p
зная —-— и —-—, можно вычислить аир,
sin у
III. Даны две стороны и угол,
противолежащий одной из них, например a, b, a (a — против a).
. п b
sin p = — sin a;
a
решение существует только тогда, когда b sin a ^
Различные случаи.
1) а > Ь; угол противолежит большей стороне;
тогда a > Р, Р < 90° и треугольник определяется
однозначно.
2) а = Ь\ тогда a = р и равнобедренный
треугольник определяется однозначно.
3) а < Ь\ угол противолежит меньшей стороне:
За) b sin a < а; имеются два решения Pj и р2,
Pi + р2 = 180°;
36) b sin a = а; одно решение р = 90°;
Зв) b sin a > а; нет решений.
Далее, у = 180° - a - р, с = а
si
IV. Даны три стороны: а, Ь, с.
Из B.34): cos a =
Ь2
Ibc
Вычисление других величин в
треугольнике (см. также B.6.1)).
ПРИМЕНЕНИЕ В ЭЛЕМЕНТАРНОЙ ГЕОДЕЗИИ
191
Радиус описанной окружности R (см. также
теорему синусов B.33)).
4 cos (a/2) cos (P/2) cos (y/2) '
Радиус вписанной окружности г.
\/(р-а)(р-Ь)(р-с)/р;
а Р у
r = ptgtg^tg^;
ару
г = 4R sin — sin — sin —;
r = (p-c) tg-±-.
Высота hc на сторону с.
hc = a sin P = b sin a.
Медиана тс на сторону с.
mc = — ]/a2 + Ь2 + lab cos у.
Биссектриса 1У угла у.
, 2accos(P/2)
2fcc cos (a/2)
Площадь S.
а + с
1
S = — ab sin y;
S = 2R2 sin a sin p sin y;
. sin a sin P , sin a sin I
2 sin у
Формула Герона.
2 sin (a -Ь р) "
B.43)
B.44)
B.45)
B.46) - =
B.47)
B.48)
B.49)
B.50)
B.51)
B.52)
B.53)
S = rp = ]/p{p - a)(p - b)(p - c). B.54)
2.6.3.2. Применение в элементарной геодезии.
Определение недоступного расстояния.
В точках А, В могут быть измерены углы а, р,
у и 5 между направлениями к точкам Р и Q
и заданной прямой АВ (рис. 2.64). Пусть известно
а
Рис. 2.64
Применяя дважды теорему синусов B.33),
получим половину разности искомых углов. Выпишем
формулы:
АР/а = sin y/sin A80° - a - р - у) =
= sin y/sin (a + p + у),
BQ/a = sin a/sin (a + у 4- 5),
b/AP = sin p/sin \|/, b/BQ = sin 5/sin <p.
Из этих соотношений прежде всего получаем
b sin p sin у sin б sin a
a sin \|/ sin (a + p + y) sin ф sin (a + у + 5) '
B.56)
откуда
sin ф
sin 5 sin a sin (a + P + y)
B.57)
sin v|/ sin P sin у sin (a + у 4- 5)
где т| - вспомогательный угол. Применяя
операции сложения и вычитания, имеем
sin ф — sin \|/ ctg ц — 1
2 cos ((ф +
sin ф + sin \|/ ctg л + 1 '
ctg 45° ctg л - 1
2 sin ((ф +
ctg л + ctg 45° '
B.58)
: tg ((Ф + *)/2) ctg D5° + л) =
= tg((a + y)/2)ctgD5<^).
Отсюда можно определить е2 = (ф - \|0/2, и
тогда
ф:
+ e2,
- 82.
B.59)
Подставляя в B.56), получим искомое расстояние.
Обратная задача. Пусть положение трех
точек А, В, С определено_относительно друг друга
при помощи отрезков АС = а и ВС = Ь, а также
углом /L АС В = у. Пусть в точке Р измерены
углы: z. СРА = а и z. СРВ = р. В общем случае
расстояние а = АВ (или b - PQ) и требуется найти
PQ (или АВ).
Для решения необходимо определить углы ф
и \|/. Так как р является углом при вершине как
в треугольнике ABS, так и в треугольнике PQS,
имеем
B.55)
можно найти положение точки Р относительно
точек Л, В, С, т. е. однозначно определить
отрезки х, у, z (рис. 2.65). Для этого только
необходимо, чтобы точка Р не лежала на окружности,
описанной вокруг треугольника ABC. Имеем
Ф + \|/ = 360° - (а + р + у) = 2еь
B.60)
sin ф = — sin a,
а
sin v|/ = — sin p,
b
192
ГЕОМЕТРИЯ
откуда
sin ф Ъ sin а
sin \|/ a sin р
= ctg л,
B.61)
где г| — вспомогательный угол. Опять получаем
выражение B.58) и определяем ф и \|/ из
выражений B.59). Подставляя эти значения в B.60),
найдем z, а при помощи теоремы синусов B.33)
получим затем х и у.
2.6.4. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
2.6.4.1. Геометрия на сфере.
Большой круг. Если пересечь шар
плоскостью, проходящей через его центр, то в сечении
шара получим большой круг, радиус которого
равен радиусу шара. Если точки А и В не
являются противоположными концами диаметра, то
через них можно провести только один большой
круг; длина меньшей его дуги является
наикратчайшим расстоянием на сфере между этими
точками (геодезическая линия). Большие круги играют
на сфере роль, аналогичную роли прямых на
плоскости.
Двумя различными точками А и В, лежащими
на сфере, определяется пучок плоскостей. Каждая
плоскость пучка пересекает шар по некоторому
кругу. Если А и В не являются
противоположными концами диаметра, то плоскость пучка,
проходящая через центр шара, определяет
наибольший круг пучка — большой круг. Остальные круги
называются малыми кругами; плоскость,
перпендикулярная плоскости, содержащей большой круг,
пересекает шар по наименьшему кругу.
Измерение дуг и углов на сфере.
Измерение расстояний на сфере проводится вдоль
дуг большого круга. Длина дуги большого круга
между точками А и В равна
Яа,
B.62)
где R — радиус шара, а — соответствующий
центральный угол (измеряемый в радианах). Если
ограничиться случаем единичной сферы (радиус R = 1),
то любую дугу большого круга можно
охарактеризовать соответствующим центральным углом
в радианах. Угол пересечения дуг двух больших
кругов измеряется линейным углом между
касательными к большим кругам в точке пересечения,
или, что одно и то же, двугранным углом,
образованным плоскостями больших кругов.
Сферический двуугольник. При
пересечении двух больших кругов на поверхности
шара образуются четыре сферических
двуугольника. Площадь сферического двуугольника с
углом а:
i = 2Д2а.
B.63)
2.6.4.2. Сферический треугольник. Три
пересекающихся больших круга образуют на сфере
сферический треугольник. Три точки А, В и С,
из которых никакие две не являются
противоположными концами диаметра, определяют три
больших круга, которые пересекаются в точках
А, В, С и диаметрально противоположных к ним
точках А', В', С и делят поверхность шара на
восемь сферических треугольников (рис. 2.66). При
этом стороны (дуги больших кругов) и
соответственно углы некоторых из этих треугольников
меньше я (R = 1); такие сферические треугольники
называются треугольниками Эйлера. Здесь
рассматриваются только треугольники Эйлера.
Рис. 2.66
Примечание. Треугольник ABC, не являющийся
треугольником Эйлера, с углом у = z. AB > п, отличается
от полусферы, которая определяется большим кругом,
проведенным через точки А и В, только на треугольник
Эйлера ВАС с углом ^ В А = 2я - у.
Для треугольника Эйлера (со сторонами а, Ь, с
и противолежащими им углами а, Р, у) имеют
место следующие утверждения.
1) Неравенство треугольника. Сумма двух
сторон больше третьей, разность двух сторон меньше
третьей:
а + Ь>с, \а-Ь\<с. B.64)
2) Сумма двух углов меньше, чем третий угол,
увеличенный на я:
а + Р < у -f я. B.65)
3) Наибольшая сторона противолежит
наибольшему углу:
а < Ь, если а < Р;
а = Ь, если а = р.
4) Сумма углов заключена между я и Зя,
сумма сторон - между 0 и 2nR (R - радиус сферы):
я<а + р + 7<3я, o<a + b + c < 2nR. B.66)
Таким образом, сумма углов сферического
треугольника всегда больше 180°. Разность
<х + Р + у-я = б B.67)
называется сферическим избытком или
сферическим эксцессом. Через эту величину определяется
площадь сферического треугольника:
S = R2e. B.68)
2.6.4.3. Решение сферических треугольников.
В этом пункте мы ограничимся случаем
единичной сферы (радиус R = 1).
2.6.4.3.1. Основные соотношения.
Теорема синусов.
sin Ь
sin у
B.69)
Теорема косинусов сторон.
cos с = cos a cos b + sin a sin b cos у. B.70)
РЕШЕНИЕ СФЕРИЧЕСКИХ ТРЕУГОЛЬНИКОВ
193
Теорема косинусов углов.
cos у = —cos a cos р + sin а sin р cos с. B.71)
Теорема половинного угла.
у 1 / sin (р - a) sin (р - Ь)
tg — = / : ,
2 ]/ sin p sin (p — с)
sin (р — a) sin (р — Ь)
sin a sin b
у 1 / sin p sin (p - с)
2 |/ sin л sin Ъ
где 2р = а + b + с.
Теорема половинной стороны.
«gy =
cos — =
где 2Р = а + р + у-л:.
Аналогии Непера.
-sin Psin(P - у)
sin(P
sin
sin(P
- a) sin (P -
P sin (P - y)
sin a sin P
- a) sin (P -
P)'
P)
sin a sin p
с a- |
tg — cos ——
a + b a + |
—-—cos ——
с a - В а -b a + P
,gySin-_=tg--sin —-,
у а -b a + P a + b
ctg у cos —— = tg -—— cos -——,
у . a-b a-З.я+Ь
ctg — sin
2 b 2 2 •
Формулы Деламбра (Гаусса).
у a + b с a — (
sin — sin = sin — cos
.у a + b
sin — cos
с a + p
= cos — cos — ,
B.72)
B.73)
B.74)
B.75)
B.76)
B.77)
B.78)
B.79)
у a — b с a — p
cos — sin — = sin — sin , B.80)
у а — b c.a + p
cos — cos = cos — sin —-—. B.81)
(Из соотношений B.70) —B.81) соответствующей
циклической перестановкой сторон а, Ь, с и углов
а, р, у получаются остальные соотношения.)
Основные случаи решения
треугольников.
1а) Даны три стороны.
Из B.72)
a 1 / sin (p — b) s
2 |/ sin p sin
- b) sin (p - c)
p sin (p - a)
Из B.70)
cos a — cos b cos с
cos a = —
sin b sin с
7 И Н Бронштейн, К А Семендяев
16) Даны три угла. В противоположность
плоскому треугольнику сферический треугольник
в принципе однозначно определяется тремя
углами. При этом должны быть выполнены
неравенства B.65) и B.66). Решение аналогично случаю 1а)
по формуле B.73) или B.71).
Па) Даны две стороны и угол между ними,
например а, Ь, у.
1) Решение по формуле B.70):
cos с = cos a cos b + sin a sin b cos у,
cos a - cos b cos c
sin b sin с
cos b — cos a cos с
sin a sin с
однозначно определяет с, a, p.
2) Решение по формулам B.76) и B.77):
однозначно находим (а + р)/2 и (а — р)/2, а тем самым
аир. Формула B.69) дает
sin a
sin <:• = sin у ;
sin a
с должно быть выбрано большим (меньшим),
чем Ь, если у больше (меньше), чем р.
Нб) Даны сторона и два прилежащих угла,
например с, а, р.
1) Решение при помощи формулы B.71).
2) Решение при помощи формул B.74) и B.75)
(аналогично Па)).
Ша) Даны две стороны и угол, противолежащий
одной из этих сторон, например a, b, a.
• о sin Ь .
sin p = -г-—sin a;
sin a
решение существует только тогда, когда sin b sin a^
^ sin a.
Различные случаи.
1) sin a > sin b; следовательно, sin a > sin p;
таким образом, a > p, если а > b, и наоборот;
p определено однозначно.
2) sin a = sin b; следовательно, sin a = sin P;
как и в случае 1), р определено однозначно.
3) sin a < sin b\ следовательно, sin a < sin p.
За) sin b sin a < sin а; имеются два решения pt
и P2; Pi +Р2 = я;
36) sin b sin a = sin а; одно решение Р = я/2;
Зв) sin b sin a > sin а; решений нет.
Далее, разрешив формулы B.74) или B.75)
(B.76) или B.77)) относительно tg (г/2) (ctg (у/2)),
получим с и у.
Шб) Даны два угла и сторона, противолежащая
одному из них, например а, а, р.
Решение аналогично Ша): sin b = sin я;
sin a
затем используются аналогии Непера B.74) - B.77).
Вычисление других величин,
связанных со сферическим
треугольником. _
Радиус описанного круга R.
ctg R . I/ _ зт(Р-а)мп(Р-РM1п(Р-7). Bg2)
sin P
ctg R — ctg — sin (a — Р),
где 2Р = а + р + у - п.
B.83)
194
ГЕОМЕТРИЯ
Радиус вписанного круга г.
> — a) sin (p — b) sin (p — с)
sin p
; B.84)
tg r = tg у sin (р - а), B.85)
где 2р = а + b + с.
Сферический избыток е {формула Уильера).
p р-я p - b p - с
у g 2 tg ~Y~ig ~T~
B.86)
где 2Р = e.
Связь между сферической
тригонометрией и прямолинейной
тригонометрией.
Справедлива теорема Лежандра: площадь
сферического треугольника с малыми сторонами
(поэтому и с малым сферическим избытком)
почти равна площади плоского треугольника с
теми же сторонами; каждый угол плоского
треугольника примерно на одну треть сферического
избытка меньше, чем соответствующий угол
сферического треугольника.
Теорема синусов, теорема косинусов и теорема
о половинном угле в сферической тригонометрии
для малых сторон (или, что то же самое, для
большого радиуса шара R) переходят в
соответствующие теоремы прямолинейной (плоской)
тригонометрии.
2.6.4.3.2. Решение прямоугольных
треугольников. Обозначения: a, b — катеты,
с — гипотенуза, а и р — углы, противолежащие
соответственно сторонам а и Ь.
С
Рис. 2 67
Основные соотношения:
sin a = cos (90° - а) = sin a sin с, B.87)
sin b = cos (90° - b) = sin p sin c, B.88)
cos с = sin (90° - a) sin (90° - b) = cos a cos b, B.89)
cos а = sin (90° - a) sin p = cos a sin p, B.90)
cos P = sin (90° - b) sin а = cos b sin a, B.91)
sin a = cos (90° - a) = ctg (90° - b) ctg p =
sin b :
tg b ctg p,
B.92)
= cos (90° - b) = ctg (90° - a) ctg a = tg a ctg a,
B.93)
cos с = ctg a ctg p, B.94)
cos a = ctg (90° - b) ctg с = tg b ctg c, B.95)
cos P = ctg (90° - a) ctg с = tg a ctg с B.96)
Эти основные соотношения могут быть
получены из правила Непера, если расположить пять
элементов прямоугольного треугольника
(пропустить прямой угол) по кругу в том порядке, как
они находятся в треугольнике, и заменить при
этом катеты а и b их дополнениями до 90°
(рис. 2.67), то косинус каждого элемента будет
равен произведению синусов двух не прилегающих
к нему элементов, а также произведению
тангенсов двух прилегающих к нему элементов.
Формулы B.87) и B.88) можно получить из
B.69); B.89) - из B.70); B.90) и B.91) - из B.71).
2.6.5. СИСТЕМЫ КООРДИНАТ
Системой координат Z п-мериого аффинного
пространства Ап (см. 2.6.6) называется множество,
состоящее из некоторой точки О аффинного
пространства (начала координат) и п линейно
независимых векторов ль ..., х„, которые
принадлежат векторному пространству Уп аффинного
(см. 2.6.6) пространства Ап (ль ..., х„ образуют
в У„ базис): I = {О; хь ..., х„]. Каждая точка Р
аффинного пространства А„ единственным образом
может быть представлена линейной комбинацией
п векторов, выходящих из точки О:
Р = 0
Хнх„).
Числа Хг, ..., Х„, записанные в виде
упорядоченной последовательности, называются
координатами точки Р относительно системы координат L.
В комплексной записи: Р — Pz — (ku ..., Х,„I. Если
базис хь ..., х„ ортонормирован, то ? называется
прямоугольной декартовой системой координат.
Если Zi = (О; х„ ..., .х„} и I2 = {Q; >'ь ..., у„] -
две системы координат аффинного пространства
Ап, а Р — точка этого пространства с
координатами относительно 1( и 12 соответственно:
то имеют место следующие формулы перехода:
Строками матрицы А являются координаты
векторов у,, ..., >'„ в базисе хь ..., xh. Строками
матрицы В являются координаты векторов хь ...
..., х„ в базисе >-ь ..., у„ (см. 2.4.4.1.4 и 2.4.4.1.5).
В однородных системах координат (называемых
также пропорциональными системами координат),
к которым относится, например, барицентрическая
система координат, отдельная координата не
имеет непосредственного значения для
определения положения точки. Положение точки
определяется отношением координат друг к другу.
Барицентрическая система координат ? в
n-мерном аффинном пространстве А„ определяется
заданием п + 1 точек Рь Р2, ..., Р„ + ь не лежащих
в одной гиперплоскости, принадлежащей А„.
Барицентрическими координатами точки Р являются
такие (положительные или отрицательные) веса mh
которые, будучи приписаны точкам Р, (/= 1, ...
..., п + 1), образуют систему, центр тяжести
которой есть точка Р: Pi = (wb ..., mn+1)z. Если
умножить барицентрические координаты точки
(веса) на одно и то же число, то положение
определяемой ими точки не изменится.
СИСТЕМЫ КООРДИНАТ НА ПЛОСКОСТИ
195
Пусть даны барицентрическая система
координат Е, состоящая из точек Рь ..., Р„+ь и
система координат Zt аффинного пространства
А„: Ех = {О; хь ..., хп]. Пусть координаты точек
Рь ..., Рл + 1 в системе Zt суть Piz = (х,ь . •., x,n)i
(i = l, ..., п + 1). Преобразование координат
точки Р = (хь ..., xnki = {ти ..., mn + l)z
осуществляется по формулам
V т y
хк = —~, М = ? т, (/с = 1, ..., п). B.97)
М
Суммирование производится по /от 1 до п + 1.
Если mf неизвестны, а хк известны, то B.97)
представляет собой однородную систему из п уравнений
с п + 1 неизвестными ти т2, ..., т„+1. Одно из
ненулевых т, может быть выбрано произвольным
образом.
Системой координат I на плоскости или в
пространстве называют в общем случае систему, состоящую из
точек, прямых, лучей, векторов, кривых или других
элементов плоскости или пространства, по отношению к которой
можно охарактеризовать положение тела на плоскости или
в пространстве А именно, положение каждой точки Р
плоскости или пространства относительно такой системы
однозначно определяется некоторым набором чисел. Эти
числа, записанные в виде упорядоченной
«-последовательности, называются координатами точки Р относительно
системы координат ?. Р = Pz = (х, у, .., z)^
2.6.5.1. Системы координат на плоскости.
2.6.5.1.1. Прямолинейные системы
координат на плоскости.
Прямолинейная система координат на плоскости состоит из
фиксированной на плоскости точки О {начало
координат) и двух пересекающихся в этой точке
прямых #! и д2 {координатных осей): L = {О; дъ д2].
На каждой из этих прямых лучам, выходящим из
точки О, приписывается положительное и
отрицательное направление; кроме того, на каждой
при проектировании прямыми, параллельными
осям координат, на координатные оси (см. рис. 2.68),
взятые со знаком плюс или минус в зависимости
от того, лежит ли проекция точки Р на
положительной (положительный знак координаты) или на
отрицательной (отрицательный знак координаты)
части координатной оси, Эти координаты
совпадают с координатами в двумерном аффинном
пространстве, если базисные векторы системы
координат имеют единичную длину.
Ковариантными координатами точки Р
являются длины ортогональных проекций отрезка ОР
на координатные оси. Ковариантные координаты
в аналитической геометрии не употребляются.
Ниже мы будем рассматривать только контра-
вариантные координаты.
Угол со между положительными частями обеих
осей называется координатным углом. При со = 90°
система координат называется прямоугольной (или
декартовой) системой координат*); в противном
случае система координат называется косоугольной.
В декартовой системе координат ковариантные
и контравариантные координаты совпадают.
Обычно в прямолинейной системе координат на
плоскости первую ось называют осью х или осью
абсцисс, а вторую — осью у или осью ординат.
Оси делят плоскость на четыре части — квадранты
(см. рис. 2.68). Положение точки Р с абсциссой а
и ординатой Ъ относительно системы координат
Е сокращенно записывается в виде Р = Р1 = {a, b)z.
Если другие координатные системы одновременно
с рассматриваемой не употребляются, то индекс Z
может быть опущен.
2.6.5.1.2. Криволинейные системы
координат на плоскости. Криволинейные
системы координат на плоскости являются
обобщением прямолинейных. Криволинейная система
координат на плоскости представляет собой два
97 98 9S
Рис 2.68
Рис 2.69
прямой выбирается масштаб для измерения длин
(рис. 2.68). Без ограничения общности масштабы
измерения длины обеих прямых можно считать
одинаковыми (в противном случае масштаб одной
оси умножением на некоторое постоянное число
можно привести к масштабу другой оси).
Контравариантными координатами (или
параллельными координатами) точки Р являются
длины проекций отрезка ОР, кбторые получаются
*) Эта система координат совпадает с декартовой
системой координат, определенной в начале 2.6.5, для случая
п - 2. В литературе часто применяется также для общих
косоугольных координат понятие «декартовы координаты».
Тогда при со = 90° {wx = vv2 = w3 = 0) появляется понятие"
«прямоугольные декартовы координаты». В последующем
под декартовыми координатами всегда следует понимать
координаты прямоугольной системы координат, оси
которых имеют одинаковые единицы масштаба.
196
ГЕОМЕТРИЯ
однопараметрических семейства кривых (семейства
координатных линий). Через каждую точку Р
плоскости при этом проходит только одна кривая
каждого семейства. Две кривые, принадлежащие
разным семействам, имеют ровно одну общую
точку. Оба значения параметров, при которых
кривые из двух семейств кривых проходят через
одну и ту же точку Р, называются криволинейными
координатами точки Р. На рис. 2.69 изображена
такая координатная система с семействами кривых
/s и gt (s, t — параметры).
Часто применяющейся криволинейной системой
координат является полярная система координат.
Она состоит из заданной фиксированной точки О
плоскости (полюса), концентрических окружностей
с центром в точке О и лучей с началом в точке
О, один из которых называется полярной осью
(рис. 2.70). Параметрами обоих семейств кривых
(полярными координатами) являются радиус р для
<p=f5C
=/80°
>
?(
к
>
га
Щ:
f-90°
V-270°
Рис 2 70
семейства концентрических окружностей
(полярный радиус, или расстояние. до полюса) и угол (р
между полярной осью и лучом для семейства
лучей (полярный угол). Полярный угол считается
положительным при отсчете от полярной оси
против часовой стрелки и отрицательным при
отсчете в обратном направлении. Точка Р в
полярных координатах изображается так: Р = (р, (р).
2.6.5.1.3. Преобразование координат
на плоскости. Параллельный
перенос системы координат. Если
прямолинейная система координат ? = {O',gx, д2]
преобразована переносом на вектор OQ в систему
координат 2У = {Q; д\, д2] с началом в точке
Q = (я, Ь)^ и координатными осями д\ и д'2,
параллельными осям дх и д2, то имеют место
следующие формулы преобразования: х' = х — а,
у' = у - Ь. При эгом Р = (х, y)z = (*', /)?' (рис. 2.71).
Поворот системы координат.
Координатная система ? с координатным углом со
при повороте на угол ер переходит в
координатную систему Е'; формулы преобразования имеют
вид
sin (со + ф) sin ф
х = х Н — у,
sin со sin со
sin ф sin (со — ф)
у' = : л; Н г V.
sin со sin со
При этом Р = (х, }>)х = (*', У')г (рис. 2.72).
Рис 2 72
Если со = 90° (поворот декартовой системы
координат на угол ф), то получаем
х' = х cos ф + >' sin ф, / = — х sin ф + у cos ф.
Пусть ? - прямолинейная система координат
с координатным углом со, ?i — прямолинейная
система координат с координатным углом юь
Е2 — полярная система координат, полярная ось
которой ?2 совпадает с осью х в ?. Пусть,
далее, начала координат систем ? и Hi совпадают
с полюсом системы Е2 (этого всегда можно
добиться параллельным переносом систем
координат Е и EJ.
Тогда, если точка Р, имеющая в этих трех
системах координаты Р = (х, у)% — (хь yt)^ —
= (р, ф)х2, задана только относительно одной
системы координат, то ее координаты в других
системах могут быть найдены по формулам
sin (со — a) sin (со — р)
X = ; Xi + : У\,
sin со sin со
sin а
sin
Уи
sin со sin со
sin p sin (со — |
sin (p - а)
р sin (со — ф)
sin (со — а)
" "sin (Р"^]^'
р sin ф
р = j/x2 + у2 + 2ху cos со, ф = arctg
у sin со
у cos со + х
Рис 2 71
где а — угол между положительными
направлениями оси х в Z и оси А"! в Z^ p — угол между
положительными направлениями оси х в Е и оси у
КООРДИНАТНЫЕ СИСТЕМЫ В ПРОСТРАНСТВЕ
197
в Lj (со'! = р — а; а, |3 считаются положительными
при отсчете от полярной оси против часовой
стрелки).
2.6.5.2. Координатные системы в пространстве.
2.6.5.2.1. Прямолинейные системы
координат в пространстве.
Прямолинейная система координат Е в пространстве
состоит из заданной фиксированной точки О
пространства {начала координат) и трех прямых
9и 9 г, 0з> не лежащих в одной плоскости и
пересекающихся в точке О,— координатных, осей (осей
х, у, z, или соответственно оси абсцисс, оси
ординат и оси аппликат): ? = {О; ди д2, Уз}- Три
плоскости, содержащие пары координатных осей,
называются координатными плоскостями
(плоскостями ху, xz и yz). На каждой из трех осей лучам,
выходящим из точки О, приписываются
положительное и отрицательное направления и на каждой
прямой выбирается масштаб длины (рис. 2.73).
Рис 2 73
Без ограничения общности можно считать, что
масштабы длин всех трех осей равны (этого всегда
можно добиться умножением масштаба каждой
оси.на соответствующее число). Пусть косинусы
между положительными направлениями осей х, у
и z (координатных углов) равны соответственно
cos z. (у, z) = vvb cos /L (z, x) = w2 и cos zi (x, y) =
= vv3. При Wj = w2 = w3 = 0 система координат
называется
прямоугольной (или декартовой)
системой координат; в
противном случае система
координат называется
косоугольной *). В
зависимости от взаимного
расположения
положительных направлений осей
возможны правая и левая
координатные системы
(рис. 2.74). Ковариантны-
ми координатами точки Р являются расстояния от
точки до трех координатных плоскостей, взятые
с соответствующими знаками.
Контравариантными координатами
(параллельными координатами) точки Р являются длины
отрезков прямых, которые проектируют точку Р
поочередно на каждую из трех координатных
плоскостей параллельно координатной оси, не
лежащей в этой плоскости (см. рис. 2.73), взятые
с соответствующими знаками. В декартовой
системе координат ковариантные и контравариантные
координаты совпадают. Координата точки
положительна, если точка лежит по ту же сторону от
координатной плоскости, проходящей через две
координатные оси, куда указывает положительное
направление третьей координатной оси. В
противном случае координата точки отрицательна.
Пространство разбивается гремя
координатными плоскостями на восемь октантов, знак
каждой отдельной координаты в которых
определяется в соответствии с таблицей:
Октант
X
У
z
I
+
+
+
II
-
+
+
III
-
-
+
IV
+
-
+
V
+
+
-
VI
-
+
-
VII
-
-
VIII
+
-
-
*) См сноску в 265 1.1.
Точка Р с абсциссой а, ординатой b и
аппликатой с относительно системы координат S
записывается так: Р = Рх = (а, Ъ, с^. Если
одновременно другие системы координат не используются,
то индекс S можно опускать.
2.6.5.2.2. Криволинейные системы
координат в пространстве. Криволинейные
системы координат в пространстве являются
обобщением прямолинейных. Они состоят из трех
однопараметрических семейств поверхностей.
Через каждую точку Р пространства проходит
только одна поверхность каждою семейства. Значения
параметров для этих трех поверхностей и
являются криволинейными координатами точки Р.
Часто применяющимися криволинейными
системами координат являются сферическая система
координат и цилиндрическая система координат.
Сферическая система координат состоит из
заданной фиксированной точки О (полюса)
пространства, из ориентированной прямой д,
проходящей через точку О, из полуплоскостей,
ограниченных этой прямой (одна из них называется
полуплоскостью нулевого меридиана), из конических
поверхностей с вершинами в точке О и с прямой
g в качестве оси и из сфер с центром в точке О.
Параметром семейства сфер является радиус
сферы р (полярное расстояние), параметром
семейства полуплоскостей — угол ф, который полу-
плоскость образует с полуплоскостью нулевого
меридиана (географическая долгота). Параметром
семейства конических поверхностей является их
угол раствора 0. Угол 0 измеряется между
положительным направлением прямой g и образующей
боковой поверхности конуса (географическая
широта). Положительные направления отсчета
показаны на рис. 2.75. В сферических координатах
точка Р изображается в виде Р = (р, ср, 0).
Цилиндрическая система координат состоит из
заданной фиксированной точки О (начала
координат), ориентированной прямой д, проходящей
через эту точку, из плоскостей, перпендикулярных
прямой д, из полуплоскостей, которые ограничены
198
ГЕОМЕТРИЯ
прямой д (одна из них называется плоскостью
нулевого меридиана), и из цилиндров, осью которых
является прямая д. Параметром семейства
перпендикулярных д плоскостей является расстояние z
от точки О до плоскости: z положительно
Рис. 2 75
Рис. 2 76
(отрицательно), если плоскость пересекает
положительную (отрицательную) часть прямой д.
Параметром пучка полуплоскостей является угол (р,
который полуплоскость образует с полуплоскостью
нулевого меридиана. Положительное направление
отсчета показано на рис. 2.76. Параметром
семейства цилиндров является радиус цилиндра р.
В цилиндрической системе координат точка Р
изображается в виде Р = (ф, р, z).
2.6.5.2.3. Преобразование координат
в пространстве.
Параллельный перенос. Система
координат Е = {О; 0i, д2, дъ) переносом на вектор
OQ преобразуется в систему координат Е' =
= {Q; 0ь 9ъ 9'ъ) с
началом координат в точке
Q — (а, Ь, с)? и координат-
ми осями 0'ь д'2 и д'ъ,
2 параллельными осям ди
~*п'а2 и Яъ-, при помощи
^ следующих формул
(рис. 2.77): х' = х - а,
у' = у — Ъ, z' = z — с. При
этом Р = (х, у, z)L =
Рис. 2.77
Поворот
системы координат.
Поворот декартовой
системы координат Е = {О; ди д2, д3} вокруг
проходящей через начало координат оси д с
направляющими косинусами
cos z_ @Ь д) = a, cos z. @2, д) = р, cos z. (g3, g) = y
на угол 9 переводит ее в систему координат
Е' = {О; 0i, 02, 0'з} (рис. 2.78) при помощи
следующих формул перехода:
х' = х (cos 9 + а2 A - cos 9)) + у (у sin 9 +
+ ар A - cos 9)) + z (-p sin 9 + ау A - cos 9)),
y' = x(-ysin9 + раA -cos 9)) +
-I- у (cos 9 + р2 A - cos 9)) + z (a sin 9 + py A - cos 9)),
z' = x (P sin 9 + ya A - cos 9)) + у (-a sin 9 +
+ yP A - cos 9)) + z (cos 9 + y2 A - cos 9)).
Здесь P = (x, y, z)z = (x\ y', z')i<-
Если известны направляющие косинусы углов
между осями декартовых систем ЕиГс общим
началом, то имеют* место формулы:
х' = /хх + т^у + nlz, у' = 12х + т2у + n2z,
z' = /Зх + тъу + n3z,
где /,-, mh nt {i = 1, 2, 3) — направляющие косинусы.
В векторной форме:
х' = хА,
где
х' = (х\ у', z'), х = (х, >', А
Матрица перехода
А =
/i h hi
ttl\ Wl2 WI3 I
является ортогональной (см. 2.4.4.2.5).
Если заданы две системы координат Е и Е'
с совпадающими началами координат и известны
косинусы углов между положительными
направлениями осей системы Е (оси х, у, z) и системы
Рис 2 78
E (оси x', y', z'), а также косинусы wb w2, vv3
координатных углов системы Е (см. 2.6.5.2.1), то,
зная положение точки Р в системе ?', можно
вычислить положение той же точки в системе Е
по нижеследующим формулам.
Пусть Р = (х, у, zjj; = (x\ у', z')z-; тогда
A - W2) X - (и'3 - wtw,) У - (н>2 - waw,) Z
х- g2 - - - ,
A - w|) У - (wt - w2H'3) Z - (w3 - wt w2) X
- (w2 -
- (wt - vv2w3) У
52
где 52 = 1 + 2w1w2M'3 - w2 - w2 - w3,
X = x' cos z. (x', x) + y' cos z. (/, x) + z' cos z. (z\ x),
У = x' cos z. (x\ y) + у' cos z. (/, y) + z' cos z. (z', y),
Z = x' cos ^ (x', z) + y' cos z, (y', z) + z' cos z. (z', z).
Пусть декартова (Е), цилиндрическая (Ej) и
сферическая (Е2) системы координат согласованы
начала координат систем I., I<i и Е2 совпадают,
главные прямые д систем Е] и Е2 совпадают
с осью z системы Е, ограниченные прямой д
полуплоскости нулевого меридиана систем Ъх и Е2
содержат положительную часть оси х системы Е.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
199
Тогда координаты точки Р относительно трех
систем Е, Z] и ?2, связаны друг с другом
следующими формулами.
Если Р = (х, у, zfc =(р, ф, z\x =(р, ф, 0)l2, то
n х = р cos ф = р sin 0 cos ф,
у = р sin ф = р sin 9 sin ф,
SteJ Z — Z = p COS 0,
р =
• + zz, ф = arctg —,
0 = arctg
j/x2 + у
— = arccos -
\/x2 + y2 + z2
2.6.6. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Аффинное /7-мерное пространство Ап над
векторным пространством У„ есть множество Ап,
каждой паре элементов которого Рь Р2 поставлен
в соответствие вектор из К„, обозначаемый далее
PiP2, причем 1) для любых Р{ е А„, хеУп
существует один и только один элемент Р2 е Ап, для
которого Pj>~2 = х; 2) f\P2 + Р2РЪ = Р^3 для всех
Р\, Рг, Ръ^Ап- Элементы Ап называются его
точками; вектор Р\Р2 называется вектором
переноса из точки Рх в точку Р2.
Подмножество La Ап называется плоскостью
в А„, если вместе с точками Ро, Рь ..., Р„ оно
содержит также любую такую точку Р, что Р0Р
есть линейная комбинация векторов Р0Рь ...
..., РоР„- Размерность подпространства Vn,
порожденного векторами Р0Р, Ро, Р е L, называется
размерностью плоскости L. Гиперплоскостью
называется плоскость размерности (п — 1).
Аналитическая геометрия на плоскости и в
пространстве относительно системы координат
двумерного или трехмерного аффинного
пространства или относительно прямолинейной
параллельной системы координат отличается весьма
незначительно. Как наиболее часто применяемой в
дальнейшем прямолинейной параллельной системе
координат будет отдаваться предпочтение.
2.6.6.1. Аналитическая геометрия на плоскости *).
Расстояние d между двумя точками в
параллельных или полярных координатах Pi = (хь yik =
= (Рь <Pik2 и Р2=(х2, y2h1=(p2, 4>2к2
вычисляется по следующим формулам:
d = l/pf + pi- 2pip2 cos (ф2 - фО =
= l/(*2-XiJ+0>2 -У\J + 2 (x2 - xj) {y2 -yj cos ю.
В декартовых координатах d =
= l/(x2 - XlJ + (y2 - y,J.
В последующем (если нет специальной
оговорки) всегда имеются в виду декартовы
координаты. >
Координаты середины отрезка PiP2:
*1 + Х2 У1+ У2
*) Векторное изображение (представление в векторной
записи) дается только в 2.6.6.2. Оно совпадает с
представлением (векторным изображением) в векторной записи
для плоскости, если опускаются последняя компонента
векторов и последняя строка и последний столбец матриц
Координаты точки Р, которая делит отрезок
—> т d(Pu P)
Р\Р2 в отношении —=
ИХХ
п
nyi
п
+
+
+
d(P
тх2
т
ту2
'» Р2
X, ¦
1
Уг -
)
4-;
+
t-)
_ ^.
^2
п + т
1+А, "
При X < 0 точка Р лежит вне отрезка PiP2.
Координаты центра тяжести системы из п
материальных точек Р, = (хь у) с массами m,- (i =
= 1, 2, ..., и):
У =
i щ
Ориентированная площадь S многоугольника
с вершинами в точках Рь ..., Р„:
S = у [(*i - х2) {yi + Уг) +
+ (*2 ~ *з) (Уг + Уз) + • • • + (хя ~ *i) (Уп + Ух)].
Ориентированная площадь треугольника с
вершинами в точках Рь Р2, Р3:
У2
Уз
При вычислении по этим формулам площадь
получается положительной, если обход вершин в
порядке нумерации происходит против часовой
стрелки, и отрицательной в противном случае.
Если S — О, то Рь Р2, Р3 лежат на одной прямой
(необходимое и достаточное условие).
2.6.6.1.1. Прямая. Каждая прямая на
плоскости в параллельных координатах представима
в виде Ах + By + С = 0, а в полярных координатах -
в виде р cos (ф — а) = р, где р — расстояние от
полюса до прямой, а — угол между полярной
осью и нормалью к прямой.
Если А = О {В = 0), то прямая параллельна оси
х (оси у). Если С = 0, то прямая проходит
через начало координат.
Если В Ф 0, то равенство Ах + By + С = 0 можно
записать в виде у = кх + Ъ. Прямая пересекает
ось у в точке Р = @, Ь).
В декартовой системе координат к — угловой
коэффициент прямой: /c = tgoc (a - угол между
осью х и прямой).
Прямая может быть задана точкой Рх = (хь ух)
и угловым коэффициентом к или двумя точками
Pi = (xi, yi) и Р2 = (х2, у2).
Уравнение прямой, проходящей' через данную
точку в заданном направлении: у — У\ = к(х — хг).
Уравнение прямой, проходящей через две задан-
у у. % %.
ные точки: = . Имеет место ра-
венство к ¦
У2 -У\
У2 ~ У1
Х2 -
Х2 - Xi
Уравнение прямой в отрезках: 1 = 1.
а Ъ
Прямая пересекает ось х в точке А = (а, 0) и
ось у в точке В — @, Ь).
200
ГЕОМЕТРИЯ
Нормальное уравнение прямой: х cos ос +
+ у sin а — р = 0, где р — расстояние от прямой до
начала координат, а а- угол между нормалью
к прямой и осью х.
Нормальное уравнение прямой можно получить
из уравнения Ах + By + С = 0, умножив его на
нормирующий множитель ц = +\/]/А2 + В2. Знак
ц должен быть противоположен знаку С. Косинусы
углов, образуемых прямой с осями координат,
называются направляющими косинусами. Если
z. (ось х, прямая) =у и z. (ось у, прямая) = 8, то
cos 5 = cos (90° - у) = sin у, cos2 у + cos2 8=1.
Расстояние d от точки Рх = (\ь >'i) до прямой,
задаваемой уравнением х cos а + у sin а — р = 0,
равно модулю числа d = хх cos а + ух sin а — р
(подстановка координат точки в нормированное
уравнение прямой). По этой формуле d
положительно, если точка Рг и начало координат
лежат по разные стороны от прямой. В
противном случае d отрицательно.
Координаты (х0, у0) точки пересечения двух
прямых, задаваемых уравнениями
Ах х + В^ + С г =0, А2х + В2у + С2 = 0,
вычисляются по формулам
х0 =
Если
В2
At В,
А2 В2
= 0,
С, А,
У° а~вх '•
А2 В2
прямые параллельны
(ki = к2, или А1/А2 = Вх/В2). Угол ф пересечения
двух прямых (отсчитываемый против часовой
стрелки) находится из любого из соотношений
tg<p=AlB2-A2Bl
COS ф =
При к{ — прямые перпендикулярны.
к2
Прямая Аъх + В3у + С3 = 0 проходит через
точку пересечения этих прямых, если
1 В, (
А2 В2 С2 =0.
Л, Въ Съ
2.6.6.1.2. Кривые 2-го порядка. Кривой
2-го порядка на плоскости называется множество
точек, координаты которых удовлетворяют
уравнению
ах2 +- 2Ьху + су2 + 2dx + 2«?у + / = 0, B 98)
где я2 + Ь2 + г2 Ф 0.
В матричной форме:
гАгТ
2угт
Я = (
= 0,
После приведения уравнения кривой к
каноническому виду (см. 2.6.6.2) кривые могут быть
классифицированы следующим образом (условие Х{ > 0
всегда может быть достигнуто заменой переменных
или умножением обеих частей уравнения на — 1).
1-й случай. Центральные кривые (существует
центр симметрии). Общее уравнение кривей в
каноническом виде: А^х2 4- Х2у2 + # = 0, где Х{ > 0.
Классификация происходит согласно следующей
таблице:
>0
>0
>0
<0
<0
с/
<0
>0
0
0
Вид кривой
эллипс (рис 2 79)
в действительных числах уравнение не
имеет решения (мнимый эллипс)
одна точка @, 0) (пара мнимых
пересекающихся прямых или вырожденный
эллипс)
гипербола (рис. 2 88)
пара пересекающихся прямых
2-й случай. Параболические кривые (центра
симметрии нет). Общее уравнение кривой в
каноническом виде (с А.! > 0): \{х2 + 2hy + k = 0.
Классификация происходит согласно следующей
таблице:
h
0
0
0
к
любое
<0
0
>0
Вид кривой
парабола (рис 2 96)
пара прямых, параллельных оси v
двойная прямая (ось v)
пара мнимых параллельных прямых
г = (х,
Кривые 2-го порядка на плоскости часто
называются коническими сечениями, так как они
могут быть получены в сечении плоскостью
прямого кругового конуса. Если секущая плоскость
не проходит через вершину конуса, то сечение
будет гиперболой, параболой или эллипсом
соответственно в зависимости от того, параллельна ли
секущая плоскость двум или одной образующей
конуса или не параллельна ни одной. Если
секущая плоскость проходит через вершину конуса,
то получаются распадающиеся конические сечения.
Параллельные прямые получаются, если конус
вырождается в цилиндр (вершина конуса уходит
в бесконечность).
Кривые 2-го порядка могут быть также
определены при помощи фокального свойства: кривая
2-го порядка есть геометрическое место точек,
для которых отношение расстояний до заданной
точки F (фокуса) и до заданной прямой
(директрисы) есть величина постоянная, равная е
(эксцентриситету). При е < 1 получается эллипс,
при е = 1 — парабола, при е > 1 — гипербола.
Кривая 2-го порядка однозначно определяется заданием
пяти точек общего положения через заданные пять точек
проходит одна и юлько одна кривая 2-го порядка Если
хо1я бы три тчки лежа! на одной прямой, го получас 1ся
распадающееся коническое сечение
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
201
Полярное уравнение. В полярных
координатах кривые 2-го порядка имеют уравнение
1 + e cos ф
(р — параметр, е — эксцентриситет данной кривой,
полюс находится в фокусе, полярная ось
направлена от фокуса к ближайшей вершине). Для
гиперболы этим уравнением
определяется только одна
ветвь.
Последующие
рассмотрения относятся к
~^г кривым 2-го порядка в
каноническом виде.
Эллипсом называется
множество
(геометрическое место) всех точек
М = (х, у), для которых
сумма расстояний до
двух заданных
фиксированных точек Fj = ( + с, 0) и F2 = ( — с, 0) (фокусов)
постоянна (равна 2а) (рис. 2.79). Расстояния гх =
= | FXM | и г2 = | F2M | вычисляются по формулам
гх = а — ех,
г 2 = а + ex.
Элементами эллипса являются: большая ось
АВ = 2а; малая ось CD = 2b; вершины Ау В, С и D;
фокусы F1=( + c, 0) и F2=(-c, 0), где
с = |/я2 — Ь2; эксцентриситет е = с/а (е < 1);
фокальный параметр р = Ь2/а (половина хорды,
проведенной через фокус параллельно малой оси).
Каноническое уравнение эллипса (координатные
оси совпадают с осями эллипса) имеет вид
Параметрическое задание имеет вид
х = a cos t, у = b sin f, 0 ^ t ^ 2n.
В полярных координатах (связанных с фокусом)
имеем
Р =
1 + е cos ф
е < 1.
Директрисы — прямые, параллельные малой оси
и находящиеся на расстоянии d = а/е от нее
d-
Рис 2 80
(рис. 2.80). Для любой точки эллипса М = (х, у)
справедливо соотношение r1/dl = r2fd2 = e.
Диаметры — хорды, проходящие через центр
эллипса; они делятся в центре пополам
(рис. 2.81). Геометрическим местом середин хорд,
параллельных одному из диаметров эллипса, снова
является диаметр, который называется
сопряженным заданному. Если к и к' — угловые
коэффициенты двух
сопряженных диаметров,
то кк' = ~Ь2/а2.
Далее, если длины двух
сопряженных
диаметров равны 2аi и 2ЬЬ
а а и р - острые углы
между диаметрами и
большой осью (к =
= -tgoc, к' = tgP), то
\ sin (ос + C) == ab,
Рис281
(теорема Аполлония).
Касательная к эллипсу в точке М ¦¦
имеет уравнение
хх0 уу0
(*о, Уо)
Нормаль и касательная к эллипсу в точке М
являются биссектрисами соответственно
внутреннего и внешнего углов, образованных радиусами-
векторами, проведенными из фокусов эллипса в
эту точку (рис. 2.82). Прямая Ах + By + С = 0
касается эллипса тогда и только тогда, когда
А2а2 + В2Ь2 - С2 = 0.
У.
Т 1
\ °
—\
_>
%.
Н{х,-ф
Рис 2 82
Радиус кривизны R
(см. рис. 2.82):
Рис. 2 83
в точке М = (х0,
ab
где и - угол между нормалью и радиусом-
вектором, проведенным из фокуса в точку М
ее пересечения с эллипсом.
Для вершин А и В (см. рис. 2.79)
R = Ь2/а = р; для вершин С и D R = а2/Ь.
Площадь: S = nab. Площадь сектора: ВОМ =
= —arccos— (рис. 2.83). Площадь сегмента:
MBN — ab arccos ху.
а
Длина эллипса:
U-4-6
где Е(е) = Е(е, я/2) - полный эллиптический интег-
202
ГЕОМЕТРИЯ
рал 2-го рода. Если положить = X,
а + Ъ
Приближенные формулы:
п(а + Ь)
64 - ЗХ4
64 - 1вХ2'
Окружность — частный случай эллипса (а = Ь\
так что ее свойства вытекают из свойств
эллипса. Оба фокуса совпадают с центром
окружности (с = 0).
б)
Рис. 2 84
Уравнение окружности с центром в начале
координат и радиусом R (рис. 2.84,а): х2 + у2 = R2.
Уравнение окружности с
центром в точке С =
М(х,у) = (х0, у 0) и радиусом R
(рис. 2.84, б);
в параметрической форме
(рис. 2.85):
х = х0 + R cos r,
у = у0 + R sin f,
Рис. 2.85
где г — угол, образованный подвижным радиусом
с положительным направлением оси Ох, 0 ^ t ^ 2тг.
Уравнение B.98) описывает окружность тогда и
только тогда, когда Ъ = 0, а = с # 0 и e2 + d2-
— af > 0. Канонический вид уравнения (рис. 2.84)
в этом случае: х2 + у2 = R2.
М
Рис 2 86
Рис. 2.87
Уравнение окружности в полярных координатах
имеет вид (рис. 2.86)
р2 - 2pp0cos((p - (ро) + ро = Я2;
здесь (ро, (ро) — полярные координаты центра
окружности. Если центр лежит на полярной оси
и окружность проходит через полюс (рис. 2.87), то
уравнение принимает вид р = 2R cos ф.
Гиперболой называется множество точек, для ко-
горых абсолютная величина разности расстояний
до двух заданных фиксированных точек Ft = ( + с, 0)
и F2 = (— с, 0) (фокусов) постоянна (равна 2а < 2с).
Точки, для которых гх — г2 — 2а (гг = \ MFX I,
г2 = | MF2 |), принадлежат одной ветви гиперболы
(на рис. 2.88 - левой); точки, для которых
г2 - rt = 2а, принадлежат другой (правой) ветви.
Рис. 2.88
Расстояния /*! и г2 вычисляют по формулам
rj = + (ех - а), г2 = ± (ех + а). Верхний знак
соответствует правой ветви, нижний — левой.
Элементы гиперболы: действительная ось
АВ — 2а.; вершины Л, В; центр О; фокусы
Fb F2, лежащие на действительной оси по обе
стороны от центра на расстоянии с(> а) от него;
мнимая ось CD = 2b(b = ус1 — а2); фокальный
параметр р = Ь2/а (половина хорды, проведенной
через фокус перпендикулярно действительной оси)
и е = с/а > 1 — эксцентриситет (см. рис. 2.88).
Каноническое уравнение гиперболы (оси
координат совпадают с осями гиперболы) имеет вид
Уравнение в параметрической форме: х = a cht,
у = bsht, —oo<t<+ao.
Уравнение в полярных координатах:
Р
Р =
е> 1.
1 4- е cos ф
Директрисы — прямые, перпендикулярные
действительной оси и пересекающие ее на
расстоянии d = а/е от центра (рис. 2.89). Для любой точки
М (х, у) гиперболы — = — = е.
d d
Рис. 2 89
Касательная к гиперболе в точке М(х0, Уо)
ххо УУо Л ,,
имеет уравнение —г — = 1. Касательная и
а о
нормаль к гиперболе являются биссектрисами
соответственно внутреннего и внешнего углов,
образованных радиусами-векторами, проведенными
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
203
из фокусов в точку касания (рис. 2.90). Прямая
Ах + By + С =0 касается iиперболы тогда и
только тогда, когда А
Рис 2 90
Асимптоты гиперболы (рис. 2.91) — прямые, к
которым ветви гиперболы неограниченно
приближаются при удалении в бесконечность. Угловые
коэффициенты асимптот: к = ± tg5 = ±b/a. Урав-
Ь
нения обеих асимптот: v= ±—х.
а
Отрезок касательной Т7\ между асимптотами
делится точкой касания пополам: ТМ = МТХ.
Площадь треугольника ТОТ1 между касательной
Рис 2 91
Рис. 2 92
и обеими асимптотами равна ab (для любой
точки гиперболы М). Если через точку М
провести две прямые MF и MG, параллельные
асимптотам, то площадь параллелограмма OFMG
равна —
'+Ь2
Сопряженные гиперболы (рис. 2.92)
b2
(вторая изображена на рис. 2.92 штриховой
линией) имеют общие
асимптоты. Действительная
ось каждой из них равна
мнимой оси другой, и
наоборот.
Диаметры — хорды
данной и сопряженной ей
гипербол, проходящие
через их общий центр; они
делятся в центре пополам.
Два диаметра с угловыми
коэффициентами к и к'
называются сопряженными, если Ь2/а2 = кк'.
Каждый из обоих диаметров делит хорды данной или
сопряженной ей гиперболы, параллельные другому
диаметру, на две равные части *) (рис. 2.93). Если
Рис 2 93
*) Из двух сопряженных диаметров только один
(для которого \k\<h/a) пересекает данную гиперболу.
Получающаяся при згом хорда - диаметр в узком смысле
слова - делится в центре пополам.
длины сопряженных диаметров равны 2ах и 26ь
а а и р - острые углы, образованные этими
диаметрами с действительной осью (а > р), то
a\-b\ = a2 -b2, ab = a1b1sin(a- P).
Радиус кривизны R в точке М = (х0, >>о)
(см. рис. 2.90):
о , Уо
cos' и
где и — угол между нормалью и радиусом-
вектором, проведенным из фокуса в точку касания.
В вершинах А и В (см. рис. 2.88) R = р — Ь2/а.
Рис 2.94
Площадь сегмента гиперболы (рис. 2.94):
AMN = ху - аЫп ( — + — J = xv - ab Arch —.
\а b/ a
„ л _ ab ab 2\OS\
Площадь 0AMG = 1 In (отрезок
4 2 с
MG параллелен асимптоте).
Равнобочная гипербола имеет равные оси: а = Ь.
Ее уравнение: х2 - у2 = а2. Асимптоты
равнобочных гипербол перпендикулярны друг другу. Если
выбрать асимптоты в качестве осей координат
(рис. 2.95), то уравнение равнобочной гиперболы
будет иметь вид ху = а212.
Рис. 2 95
Рис. 2.96
Парабола - это множество точек М = (х, у),
равноудаленных от фиксированной точки {фокуса)
F = (р/2, 0) и от данной прямой {директрисы)
(рис. 2.96): | MF | = | Ж | = х + —.
Элементы параболы: ось х — ось параболы,
вершина О, фокус F = {р/2, 0), директриса (прямая,
перпендикулярная оси х; уравнение: х = -р/2)
и фокальный параметр р (расстояние от фокуса
до директрисы, или половина хорды, проходящей
через фокус перпендикулярно оси х).
Эксцентриситет параболы е равен единице.
204
ГЕОМЕТРИЯ
Каноническое уравнение параболы у2 = 2рх (см.
рис. 2.96); в полярных координатах: р =
р
= ; с осью, параллельной оси у:
1 + COS ф
у = ах2 + hx + с. Фокальный параметр параболы,
задаваемый последним уравнением: р = 1/B | а |).
При а > 0 парабола обращена вершиной вниз
(рис. 2.97), при а < 0 — вершиной вверх; координаты
вершины: х0 = -Ь/{2а), у0 = Dас - Ь2)/{4а).
/°
Рис 2.97
Рис. 2 с
Под диаметром параболы понимают прямую,
параллельную оси параболы. Диаметр делит
пополам хорды, параллельные касательной,
проведенной в конце диаметра (рис. 2.98). Если
угловой коэффициент этих хорд равен к, то
уравнение диаметра имеет вид у = р/к.
Уравнение касательной (рис. 2.99) к параболе в
точке М = (х0, у0)'- УУо = Р(х + х0). Касательная и
нормаль к параболе являются биссектрисами углов
между фокальным радиусом-вектором точки
параболы и диаметром, проходящим через эту же
точку. Отрезок касательной к параболе между
точками касания и пересечения с осью параболы
(осью х) делится пополам касательной,
проведенной через вершину параболы (осью у):
TS = SM, TF = FM, ТО = ОР = х0.
Прямая у — кх + Ъ касается параболы тогда и
только тогда, когда р = 2Ък.
yt
s
" 0
G
\F
1
p
V
Рис 2 99 Рис. 2 100
Радиус кривизны параболы в точке М = (xl5 yj):
R= (P + ^iK/2 P _
i/^ COS3 М р2 '
где п = | MiV | - длина нормали MN (рис. 2.99).
В вершине О радиус кривизны R = р.
Площадь сегмента параболы M0N равна двум
третям площади параллелограмма PQNM
(рис. 2.100). Площадь OMR =— ху.
Длина дуги параболы от вершины О до
М = (х, у):
ОМ =
¦V-
Приближенно при малых значениях —
2.6.6.2. Аналитическая геометрия в пространстве.
Расстояние между двумя точками Р^ — (хь уъ zj,
Рг = (Х2> Уг-, zi) B параллельной системе координат
равно
d = l(x2 - xtJ + (у2 - у,J + (z2 - zO2 +
+ 2(у2 - yi){z2 - ^i)^i + 2(z2 - zt)(x2 - Xi)w2 +
+ 2(х2-х1)(.у2->;1)и>з]1/2,
где wb w2, w3 — косинусы координатных углов
(см. 2.6.5.2.1). В декартовых координатах
d = l/(x2 - xjJ + (у2 - уО2 + (z2 - zxf.
Координаты середины отрезка Р\Р2:
х = -*-—-, У = -^у-2-, z = -i---^-.
Координаты точки Р, которая делит отрезок
—> т P~J>
PiP2 в отношении —= > = X:
¦ шх2
Хх2
п + т
У\ + тУг
п + т
Z{ + mz2
п + т
1+ X
1
Если X < 0, го точка Р лежит вне отрезка
РуР2. Координаты центра тяжести Р (х, уь z)
системы п материальных точек Рг = (хь yh z{)
(i = 1,.,.,/i) с массами mf:
-л z —
? w«
Ориентированный объем треугольной пирамиды
с вершинами в точках Рь Р2, Р3 и Р4:
V = —
6
х2 У2
Хз Уъ
х4 у4
22
23
Z4
1
1
1
1
1
- Уг Zi - z2
Объем положителен, если ориентация тройки
векторов PiP2, P1P3, Р\Ра совпадает с ориента-
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
205
цией системы координат. Если V = 0, то четыре
точки лежат в одной плоскости (необходимое и
достаточное условие).
В дальнейшем мы будем рассматривать только
декартовы системы координат.
2.6.6.2.1. Прямая. Каждая прямая в
пространстве может быть задана системой линейных
уравнений относительно координат (пересечение
двух плоскостей, рис. 2.101):
Ахх + Вху + Cxz + Dx = 0,
B.99)
А2х + В2у + C2z + D2 = 0.
Или в векторной форме:
rNj + D, = 0, rN2 + D2 = 0,
где г = (х, у, z), N, = {Ah Bt, С,) (i = 1, 2).
формуле
Рис 2 101
Рис. 2.102
Прямая может быть задана точкой Рх = (хь уи
zx) и параллельным ей вектором (направляющим
вектором) R = (/, т, п) (рис. 2.102). Тогда уравнение
прямой в координатной форме имеет вид*)
У -У\
/
B.100)
в векторной форме.
(г - гх) х R = 0 или г = Г! + RX,
где r = (x, v, z), Г! = (хь уи zx)\
в параметрическом виде:
х = хх + /X., у = >»! + mX., z =
nX.
При этом между B.99) и B.100) существует
следующая связь:
вх
в2
сх
с2
, т —
с2
^2
' "~
А
А
1 #i
2 В2
Прямая однозначно определяется двумя
точками Pj =(хь уи zx) и Р2 = (х2, )ъ. Z2)- Уравнение
прямой:
в координатной форме (см. сноску):
у2 -
B.101)
в векторной форме.
(г - rt) х (г2 - rj = 0 или г = Г! + Х(г2 - ri),
где г2 — rt есть направляющий вектор R прямой:
R = (/, т, п) = (х2 - хь у2 - уь z2 - zx).
Расстояние d от точки Р3 = (-^з» Уз» 2з) ^о
прямой, заданной в виде B.100), вычисляется по
*) В случае, если знаменатель какой-либо из дробей
равен 0, то равен 0 и соответствующий числитель
/2 + т2 + п2
Кратчайшее расстояние d между двумя
прямыми, заданными уравнениями
/i
х — х2
"Т2"~
.V - Ух
^ ~ У2
т2
z — :
пх
z - z2
п2
может быть вычислено по формуле
- х2 У\- у2 zx - z2
h mi «i
l2 m2 n2
d= —~
t
/2
т2
2
тх
т2
пх
п2
2
+
«1
п2
B.102)
Две прямые пересекаются тогда и только
тогда, когда стоящий в числителе формулы
B.102) определитель обращается в нуль (d = 0).
Если уравнения обеих
прямых объединить в
систему и решить ее
относительно х, у, z, то
будут получены
координаты точки пересечения.
Угол пересечения двух
прямых равен углу меж-''
ду направляющими
векторами Rj и R2 этих
прямых;
JR1R2
Рис 2 103
2.6.6.2.2. Плоскость. Каждую плоскость в
пространстве можно задать линейным уравнением
относительно координат (рис. 2.103):
Ах + By + Cz + D = 0. B.103)
В векторной форме-
rN + D = 0, N = (А, В, С), г = (х, у, z).
Перпендикулярный плоскости вектор N
называется нормалью к плоскости. Если | N | =
= у А2 + В2 + С2 = 1, то уравнение плоскости
может быть записано в виде
х cos а + у cos Р + z cos у — р = 0, р^0
(нормальное уравнение плоскости).
Умножением на нормирующий множитель
+ — (знак которого противоположен
\/а2 + в2 + с2
знаку D) уравнение B.103) может быть приведено
к нормальному;
А
±
]/а2 + в2 + с2'
в
\fA2+B2
С
cos у = ± —-====
}/А2 + В2
206
ГЕОМЕТРИЯ
суть направляющие косинусы нормали; р —
расстояние от начала координат до плоскости.
Если в уравнении B.103) D — 0, то плоскость
проходит через начало координат. При А = 0
(В = 0, С = 0) плоскость параллельна оси х
(оси у, оси z), при А = В = 0 (Л = С = 0,
В = С = 0) плоскость параллельна плоскости ху
(плоскости xz, плоскости yz).
Уравнение плоскости в отрезках:
а о с
Эта плоскость пересекает оси координат в точках
Pi = (а, 0, 0), Р2 = @, Ь, 0)и?3 = @, 0, с).
Плоскость однозначно определяется:
(I) тремя своими точками Рх = (хь yly zj,
Р2 = (*2> У г, z2) и Р3 = (*з> Уз, z3), не лежащими
на одной прямой;
(II) двумя своими точками Рх и Р2 и
параллельным плоскости направлением, задаваемым
вектором R =(/, т, п), не параллельным РХР2\
(III) точкой Pi и двумя параллельными
плоскости направлениями, задаваемыми двумя
линейно независимыми векторами Rx = (/ь ть иД
r2 = (/2, т2, «г);
(IV) точкой и ненулевым вектором N = (Л, В, С),
коллинеарным вектору нормали к плоскости.
Тогда уравнения плоскости получаются
следующим образом:
Случай (I):
х -хх у -
*2 ~ *i Уг-
-*\ Уз - У\
= 0;
в векторной форме: (г - rj (r2 - гг) (г3 — гх) = 0
(смешанное произведение векторов),
гь Г2» гз — радиусы-векторы трех точек Рь Р2,
Ръ, а г = (х; у; z).
Случай (II):
х — хг у — y\ z — zx
*2 - *i Уг - У1 Z2~ zt
I m n
= 0;
в векторной форме: (г - гх) (г2 - r2) R = 0.
Случай (III): х — хх у — у\ z —
h mi «i = 0;
/2 т2 п2
в векторной форме: (г - г{) RiR2 = 0.
Случай (IV): А (х - хх) + В(у - yj +
в векторной форме: (г — rj N = 0.
Множеством решений системы, состоящей из
уравнений нескольких плоскостей, является точка
или линия пересечения этих плоскостей (прямая).
Если система уравнений не имеет решений, то
плоскости не имеют общих точек,.
Угол пересечения ср двух плоскостей равен
углу между векторами нормалей Nb N2 к
соответствующим плоскостям:
Угол пересечения \|/ между плоскостью и прямой
\J/ = 90° - х (X - Уг«л между вектором нормали N
к плоскости и направляющим вектором R прямой):
|NR|
sin \(/ = —-
cos х
2.6.6.2.3. Поверхности 2-го порядка.
Поверхностями 1-го порядка в пространстве
называются такие множества точек, координаты которых
удовлетворяют уравнению вида
ацх2 + а22у2 + a33z2 + 2al2xy + 2al3xz + 2a23yz +
+ 2a14x + 2^24^ + 2a34z + a44 = 0; B.104)
в матричной форме:
гЛгТ+2агГ+а44 =0,
г = (х, yt z), А :
«И Я12 «13
а21 а22 а2Ъ
L a3l a32 д33_1
а = (д14, а24, «34) (А Ф О).
Приведение к каноническому виду.
При параллельном переносе системы координат
на вектор г*, координаты которого
удовлетворяют уравнению Аг* = — а, в уравнении
поверхности 2-го порядка исчезают линейные члены.
Уравнение принимает вид
Ьцх' + Ь22/ + b33z' + 2bl2x'y' + 2b13x'z' +
+ 2b23y'z + Ь44 = 0, B.105)
где х', /, z' - координаты относительно новой
системы координат ?'.
В матричной форме: г'Вг'? + Ь44 = 0, г'=
= (х', /, z'), В = || />^ ||. (Начало новой системы
координат Р является центром симметрии
поверхности 2-го порядка, т. е. если г' = (х', у', z') —
точка поверхности, то — г' = (— х', — /, — z') —
также точка поверхности 2-го порядка.) Матрицы А
и В - симметрические (аи = ayi и Ьи = Ьп), ггб^
этому их собственные значения действительны,
а собственные векторы ортогональны.
При последующем преобразовании
(преобразование к главным осям) к системе координат
Ъ" с началом координат, остающимся в точке Р,
и осями координат, совпадающими по направлению
с собственными векторами, уравнение
поверхности 2-го порядка приобретает вид
Хх (х"J + ^2 (у"J + Х3 (z"J + с44 = 0, B.106)
где Хг, Х2, Х3 — собственные значения матрицы В.
В матричной форме:
г"Ст"Т+ с44 = 0, т"т= (х", у", z"),
= о х2 о ,
Lo о ^3J
где х", у" и z" — координаты точки на
поверхности 2-го порядка относительно ?". Если
собственное значение имеет кратность к, то к линейно
независимых собственных векторов следует орю-
гонализировать при помощи метода Грама-
Шмидта (см. 2.4.4.1.5).
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
207
Если еь е2, е3 — ортонормированные
собственные векторы, принадлежащие В, то уравнение
B.106) получается из уравнения B.105), если
положить г' = t'D . Здесь D — матрица, столбцы
которой составлены из координат ортонормиро-
ванных собственных векторов матрицы В {D
ортогональна). Уравнение B.106) называется
каноническим уравнением поверхности 2-го порядка. Оси
координат являются осями симметрии
поверхности.
Если система уравнений Ат* = — а не имеет
решений (не существует центра симметрии), то
по крайней мере одно из собственных значений
равно нулю. Приведение к каноническому виду
производится аналогично случаю ненулевых
собственных значений. Необходимо следить лишь за
тем, чтобы в случае двукратного собственного
значения, равного нулю, собственный вектор был
выбран так, чтобы он был ортогонален вектору а
(свободному члену): агг = 0. Этим обеспечивается
исчезновение двух линейных членов в уравнении
B.104). После преобразования к главным осям
уравнение поверхности 2-го порядка приобретает
вид
Х1х'2 + Х2у'2 + mz' = 0 B.107)
(при эгом возможно равенство Х2 = 0); У, /,
z' — координаты относительно системы Е'.
В дальнейшем предполагается, что
поверхности 2-го порядка приведены к каноническому
виду (формулы B.106) и B.107)). Тогда возможна
следующая классификация (условие ^ > 0 всегда
может быть выполнено путем замены переменных
или умножением уравнения на — 1).
Поверхности 2-го порядка с
центром симметрии.
х2 у2 z2
Эллипсоид (рис. 2.104): -у + р~ + ^-= 1, где
a, b и с - полуоси.
Рис 2.104
Рис. 2.105
Если а = Ь> с, то имеем сплющенный
эллипсоид вращения, получающийся при вращении
х2 z2
эллипса —г- + —Z- — 1, лежащего в плоскости Oxz,
а2 с2
Канонический
>0
>0
>0
>0
>0
>0
>0
>0
'¦ >0
<0
<0
0
0
0
вид: Ххх2 + Х2у 4
>0
>0
>0
<0
<0
<0
0
0
0
0
0
0
0
0
X3z2 + d = 0.
d
<0
>0
0
<0
>0
0
>0
<0
0
*о
0
<0
>0
0
Поверхность
эллипсоид
мнимый эллипсоид
вырожденный эллипсоид - мнимый конус с
действительной вершиной
однополостный гиперболоид
двуполостный гиперболоид
эллиптический конус (ось конуса — ось г)
цилиндр с мнимыми образующими
эллиптический цилиндр
пара мнимых пересекающихся плоскостей
гиперболический цилиндр
пара пересекающихся плоскостей, параллельных оси z
пара параллельных плоскостей, перпендикулярных оси х
пара мнимых параллельных плоскостей
координатная плоскость (плоскость Oyz)
Канонический вид: Х{х2 + Х2у2 + mz = 0.
м
>о
>о
>о
>о
<о
0
m
<0
<0
*о
Поверхность
эллиптический параболоид
гиперболический параболоид («седло»)
параболический цилиндр
Некоторые свойства поверхностей 2-го порядка
(заданы в каноническом виде).
вокруг его малой оси (рис. 2.105). При
а = Ъ < с имеем вытянутый эллипсоид вращения,
208
ГЕОМЕТРИЯ
который получается
при вращении
лежащего в плоскости Oxz
х2 z2
эллипса —г- Н—г- = 1
а2 с2
вокруг его большой
оси (рис. 2.106). При
а = Ь = с имеем сфе-
У ру х2 + у2 + z2 = а2.
Сечение
эллипсоида любой плоскостью
есть эллипс (в частном
случае - круг). Объем
эллипсоида равен
4
— nabc, объем сферы
равен — па3.
Однополостный гиперболоид (рис. 2.107):
a2 b2 V~ '
а и Ъ — действительные полуоси, с — мнимая
полуось. (О прямолинейных образующих см. в конце
раздела.)
Рис. 2 106
Рис. 2.107
Рис 2 108
Двуполостный гиперболоид (рис. 2.108):
х2 у2 z2
с — действительная полуось, а и b — мнимые
полуоси.
Для обоих гиперболоидов сечения,
параллельные оси z, — гиперболы (для однополостного
гиперболоида может быть пара пересекающихся
прямых); сечения, параллельные плоскости Оху,—
эллипсы.
Если а = Ь, то гиперболоид может быть
получен вращением гиперболы с полуосями а и с
вокруг оси z: мнимой — в случае
однополостного и действительной — в случае двуполостного
гиперболоида.
Конус (рис. 2.109)
2 * L2 ~Т~ — W
а2 Ь2 с2
имеет вершину в начале координат; за его
направляющую кривую может быть взят эллипс
с полуосями а и Ь, плоскость которого
перпендикулярна оси z и находится на расстоянии
с от начала координат. Этот конус является
асимптотическим для обоих гиперболоидов
Рис 2 109
Рис. 2 ПО
х2 у2 z2
—г-Н = =- = ± 1, т.е. каждая из его обра-
а2 Ь2 с2
зующих при удалении в бесконечность
неограниченно приближается к обоим гиперболоидам
(рис. 2.110). Если а = Ь, то имеем прямой
круговой конус.
Поверхности 2-го порядка, не
имеющие центра симметрии.
Эллиптический параболоид (рис. 2.111): z —
X" V
= ~т+ тт- Сечения,
а ЬА
параллельные оси z, —
параболы; сечения, параллельные плоскости Оху,—
эллипсы. Если а = Ь, то имеем параболоид
вращения, получаемый при вращении параболы
z = х2/а2, лежащей в плоскости Oxz, вокруг ее оси.
Объем части
параболоида,
отсекаемой плоскостью,
перпендикулярной его
оси, на высоте h,
равен — nabh, т. е.
равен половине
объема эллиптического
цилиндра с такими
же основанием и
высотой.
Гиперболический
параболоид (рис.
2.112):
Сечения,
параллельные плоскости Oyz,—
конгруэнтные
(одинаковые) параболы;
сечения, параллельные
плоскости Oxz, —
также конгруэнтные
параболы; сечения, па-
Рис. 2 111
Рис. 2 112
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
209
раллельные плоскости Оху,— гиперболы (а также
пары пересекающихся прямых).
Общие свойства. Прямолинейной
образующей поверхности называется прямая линия,
Рис. 2.113
Рис. 2.114
целиком лежащая на данной поверхности;
например, прямолинейные образующие конической
или цилиндрической поверхности.
Однополостный гиперболоид (рис. 2.113)
х2 у2 z2 Л
—-z--\—т. =- = 1 имеет два семейства прямо-
а2 Ьг с2
Ь2
линейных образующих:
X 2 / у\ X Z
а с \ bj\ac
а
с
b '
и и v - произвольные величины.
Гиперболический параболоид (рис. 2.114)
х2 у2
z = —; =" также имеет два семейства
а2 Ь2
зующих:
a b \a
a b \ a b
здесь и и v — также
произвольные величины. Через
каждую точку поверхности
в обоих случаях проходят
две прямые: по одной
образующей из каждого
семейства (на рис. 2.113 и 2.114 __
показано лишь по одному
семейству прямых).
Цилиндры. Форма
цилиндра определяется его направ-^
ляющей. Мы будем считать
ее расположенной в
плоскости Оху, а образующие —
параллельными оси z. Тогда
имеются три цилиндра 2-го
порядка:
эллиптический цилиндр (рис. 2.115)
при a = b = R получаем прямой круговой цилиндр
х2 + у2 = R2;
Рис. 2.115
-
ЗГ
——-.
--.
z
и
у
1
1
1
1
1
1
?.1-1
1
1
1
^——
—.
—
z
У
Рис 2.116
Рис. 2.117
гиперболический цилиндр (рис. 2.116)
х2 )>*
~J~ b2 " '
параболический цилиндр (рис. 2.117)
у2 = 2рх.
3. ОСНОВЫ МАТЕМАТИЧЕСКОГО АНАЛИЗА
3.1. ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
ФУНКЦИЙ ОДНОГО И НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
3.1.1. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Числа, с которыми обычно приходится иметь
дело — натуральные, целые (положительные и
отрицательные), рациональные и иррациональные, —
составляют множество действительных чисел.
3.1.1.1. Система аксиом действительных чисел.
Множество R действительных чисел может быть
охарактеризовано следующими шестнадцатью
аксиомами.
Аксиомы сложения.
1. Для любых чисел a, beR определено
единственное число a + beR, называемое суммой
чисел а и Ь.
2. Для любых a, beR имеет место
соотношение а + b = b + а*) (коммутативность).
3. Для любых a, b, ceR имеет место
соотношение а + (Ь + с) = (а + Ь) + с
(ассоциативность).
4. Существует число OeR такое, что а + 0 = а
для всех aeR. Число 0 носит название нуль.
5. Для любого числа aeR существует -число
beR такое, что a -Ь b = 0.
Аксиомы умножения.
6. Для любых чисел a, beR определено
единственное число а beR, называемое произведением
чисел а и Ь.
7. Для любых a, beR имеет место
соотношение ab = b-а (коммутативность).
8. Для любых a, b, ceR имеет место
соотношение а • (Ь • с) = (а • Ь) ¦ с (ассоциативность).
9. Существует число 1 е R такое, что 1 • а = а
для всех aeR. Число 1 носит название
единица.
10. Для любого aeR, а Ф 0, существует beR
такое, что а-Ь = 1.
11. Для любых a, b, ceR имеем а-(Ь + с) =
= а-Ь + а-с (дистрибутивность).
Таким образом, множество R образует
относительно сложения коммутативную группу, а
множество R без «уля образует коммутативную
группу относительно умножения.
Следствия из аксиом сложения и
умножения. 1) Для двух действительных чисел
а и b имеется ровно одно действительное число
х такое, что а + х = Ь. Число х называется
разностью чисел b и а и обозначается b — а.
При этом говорят, что b — уменьшаемое, а —
вычитаемое и а вычитается из Ь. В случае
О — а пишут —а. Таким образом, число b из
аксиомы 5 однозначно определено.
2) Для любого aeR имеем: а = — ( — а), —0 = 0.
3) Для любых а, Ь, с, deR имеем: b — а — d — с
эквивалентно тому, что а + d — b + с;
(b + d)-(a + c) = (b-a) + (d- с);
(b + с) - (а + d) = (b - а) - (d - с).
4) Из а • b = 0 следует, что либо а = 0, либо
/> = 0.
5) Для действительных чисел а и Ь, где а ф 0,
существует единственное действительное число х
такое, что а-х = Ь. Число х называется частным
(дробью) от деления b на а и обозначается
b
— или Ь/а. При этом b называется делимым
а
(числителем), а а — делителем (знаменателем).
6) Для любого aeR\{0} имеем —— = а.
7) Для любых а, Ь, с, deR\{0} равенство
b d . ,
— = — эквивалентно тому, что а • d = b - с; кроме
а с
того,
b d_
а с
Ь/а
"dfc"
_ bd
а-с'
Ь-с
*) Тождественность двух действительных чисел
выражается при помощи знака равенства. Если а и h - различные
действительные числа, то пишут а Ф Ъ.
8) Для любых a, beR и любого ceR\{0}
выполняется соотношение
a b a + b
с с с
9) Для любого aeR справедливо равенство
-a = (-l)-a.
10) Для любых a, beR выполняется равенство
-(ab) = (-a)-b.
11) (-1).(-1)=1.
Множество R действительных чисел обладает
вследствие указанных свойств алгебраической
структурой поля (коммутативного тела).
Кроме того, в R вводится отношение порядка
(«больше», «меньше», «равно»), удовлетворяющее
следующим аксиомам.
НАТУРАЛЬНЫЕ, ЦЕЛЫЕ И РАЦИОНАЛЬНЫЕ ЧИСЛА
211
Аксиомы порядка.
12. Для двух чисел a, beR имеет место одно
(и только одно) из трех соотношений: а < Ь, а = Ь,
а> Ь.
13. Для любых a, b, ceR таких, что а<Ь
и Ь < с, справедливо соотношение а < с
{транзитивность).
14. Для любых a, b, ceR таких, что а < Ь,
справедливо соотношение а + с <Ь + с.
15. Для любых a, b, ceR таких, что а < Ъ и
с > О, справедливо соотношение а-с < Ь-с.
Если а < Ь, то говорят, что а меньше Ъ
(или Ъ больше а); в этом случае пишут также
Ъ > а. Если или а < Ь, или а = Ь, то пишут
а ^ Ь. Действительные числа, удовлетворяющие
неравенству а > О, называются положительными;
действительные числа, удовлетворяющие
неравенству а < О, называются отрицательными.
Следствия из аксиом порядка.
1) Если а < Ь, то_^а> —Ъ. 2) Если а<Ъ и
с < d, то а + с < b + d. 3) Если а < b и с < d,
причем b > О и с > О, то а-с < b-d. 4) 1 > 0.
5) Если я > 0, то \/а > 0.
16. Принцип непрерывности Дедекинда. Пусть
множество R действительных чисел разделено на
два класса Кг и К2 так, что: а) классы К^
и Х2 не пусты; б) каждое действительное число
относится только к одному классу; в) из
условий аеК{ и Ь<а следует, что ЪеК^.
Тогда существует единственное действительное
число 5 такое, что все действительные числа,
удовлетворяющие неравенству а' < s, принадлежат
классу Ки а все действительные числа,
удовлетворяющие неравенству а" > s, принадлежат классу
К2. Число s называется сечением множества
действительных чисел.
Множество R действительных чисел
полностью определяется указанными аксиомами 1 — 16.
Геометрическое изображение
действительных чисел. Если на прямой g
заданием точки О и единичного вектора введена
система координат, то каждая точка М прямой g
однозначно определяется своей координатой х.
Таким образом, каждой точке М прямой g
соответствует одно действительное число х, и обратно:
каждому действительному числу х соответствует
одна точка М прямой д. Прямая д называется
числовой прямой. Таким образом, точки прямой д
и соответствующие им действительные числа могут
употребляться равнозначно. При этом говорят:
точка а лежит левее b (или b лежит правее а)
в случае, если а < Ь. В частности,
отрицательные числа лежат левее нулевой точки О, а
положительные числа — правее точки О.
3.1.1.2. Натуральные, целые и рациональные
числа. К понятию натуральных чисел приходят
в процессе счета. Натуральные числа получаются
путем последовательного прибавления 1, начиная с 1.
Множество натуральных чисел NcR обладает
следующими свойствами:
1. leN.
2. Из п е N следует п + 1 е N.
3. Если и е N, то п — 1 е N тогда и только
тогда, когда п ф 1.
4. Если М — подмножество N со свойствами:
а) 1еМ; б) из пеМ следует п+\еМ, то
Свойство 4 выражает тот факт, что таким путем
последовательного прибавления получаются все
натуральные числа. Это свойство называется
аксиомой индукции. Оно позволяет проводить
доказательства по индукции.
Принцип доказательства по методу полной
(математической) индукции. Пусть А (п) —
зависящее от neN утверждение. Если доказано, что:
а) А(\) выполняется; б) при условии, что А(п)
справедливо для некоторого и, верно также А{п+\)
(шаг индукции), то А (п) справедливо для всех
П ри мер. Доказать правильность утверждения А(п):
для всех ие!\. Очевидно, что /1A) верно. Пусть А (и)
верно для некоторого числа не1\; тогда
V к= — п(п+ 1) + (п+ 1) = —(м+ 1)(п + 2).
k=i 2 1
Следовательно, верно также А{п+\). Тогда, согласно
аксиоме индукции, утверждение А (л) верно для всех neN.
Из принципа непрерывности Дедекинда вытекает
Аксиома Архимеда. Для каждого
действительного числа а существует натуральное число п
такое, что а < п.
Сумма и произведение натуральных чисел
суть натуральные числа. Однако если п ^ т, то
п — m$N. Следующее определение приводит к
такому расширению области натуральных чисел, в
котором операция вычитания выполнима
неограниченно: действительное число g называется целым
числом, если существуют такие натуральные числа
п и т, что g — п — т.
Сумма, разность и произведение целых чисел —
всегда целые числа. Множество целых чисел Z
образует коммутативное кольцо. Частное от деления
целых чисел не всегда есть целое число.
Действительное число а называется
рациональным, если существуют такие целые числа дх и д2
(&2 Ф 0), что a = gjg2. В противном случае а
называется иррациональным.
Числа 0J и д2 не определены однозначно
числом а: числитель и знаменатель дроби могут
быть домножены на одно и то же целое число
9\. 9iP
р (р # 0): — = . Множество рациональных
92 9гР
чисел обозначается Q.
Каждое действительное число может быть
записано в виде десятичной дроби. При этом
рациональным числам и только им соответствуют
периодические десятичные дроби. Однако, например,
разложение в десятичную дробь действительного
числа у 2, т. е. такого однозначно определенного
положительного действительного числа, квадрат
которого равен 2, не является периодическим.
Таким образом, J/2 — иррациональное число.
Множество рациональных чисел бесконечно и счетно,
а множество иррациональных чисел несчетно
(см. 3.1.2). Множества Q и R\Q всюду плотны
в R, т. е. в каждом интервале {х | а < х < Ь} суще-
*) Индукция может начинаться не с 1, а с любого
числа Ho^N (n0 ^ 1). В этом случае А(п) верно для
всех п е N, п ^ п0
212
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
ствуют как рациональные, так и иррациональные
числа.
3.1.1.3. Абсолютная величина числа. Число
| а |, fleR, удовлетворяющее соотношению
м
{а при а ^ О,
— а при а < О,
называется абсолютной величиной числа а (таким
образом, | а | = ]/?).
Для любых a, beR
1) \а\>0, |-fl| = |a|, a<|fl|;
2) если | л | = 0, то это эквивалентно тому, что
3)
\а\.\Ь\,
(неравенство
треуголь4) |а + Ь|^|а|
ника);
5) 1М-|Ь||<|а-Н
3.1.1.4. Элементарные неравенства. Для
действительных чисел Я|, Ь, (i=l,...,и) имеют место:
обобщенное неравенство треугольника
неравенство Коши — Буняковского
Если aeR, а>-1 и /ieN, то A + а)" ^ 1 + ия
(неравенство Бернулли).
Если aeR, O^a^l и weN, то A + а)" ^
Если neN и п ^ 6, то (w/З)" < и! < (я/2)".
Пусть a 1,...,а„ — действительные числа. Тогда
Ап — (ах + а2 4-... 4- а„)/л называется средним
арифметическим,
Gn = \/а^а2.--cin, аг ф 0, — средним
геометрическим.
м„=т
-, а,- т^ 0, — средним
+ l/a2 + ...
гармоническим чисел flb...,fln.
Если «, > 0 (/ = 1,...,и), то
3.1.2. ТОЧЕЧНЫЕ МНОЖЕСТВА В R"
Множество М называется конечным, если
либо оно пусто, либо найдется натуральное п
такое, что М может быть взаимно однозначно
отображено на подмножество Nn a N: Nn =
= {х | xeN, х ^ п} (т. е. может быть занумеровано
не более чем п числами). В противном
случае М называется бесконечным. Бесконечное
множество М называется счетным, если существует
взаимно однозначное отображение множества М на
N. Конечное или бесконечное счетное множество
М называется не более чем счетным. В
противном случае М называется несчетным множеством.
Примеры. 1) N и Q — бесконечные счетные множества.
2) Множества R и R\Q несчетны.
Множество точек из R" называется точечным
множеством. При п = 1, т. е. для случая числовой
прямой R, точечные множества называются также
числовыми множествами.
Примеры. 1) Множество М — {(хи x2)|xi+X2<l}
является точечным множеством из R2 (внутренность
единичной окружности) *).
2) М = {(х,, х2, х3) 11 х, | < 1/2, i=l, 2, 3} - точечное
множество из R3 (куб с ребром, равным 1).
3) М = {х|0^х<1}- числовое множество.
Числовое множество М называется
ограниченным сверху, если существует CeR такое, что
х<С для всех хеМ. Число С называется
верхней границей множества М. При этом говорят,
что число С ограничивает М сверху; М называется
ограниченным снизу, если существует число
CeR такое, что С < х для всех хеМ. При
этом говорят, что С ограничивает М снизу
(С — нижняя граница М). Множество М
называется ограниченным, если оно ограничено и сверху,
и снизу.
Число G называется верхней гранью (точной
верхней границей), числового множества М, если
G есть верхняя граница и для любого
действительного 8 > 0 существует такое х' е М, что
G - 8 < х'.
Число g называется нижней гранью (точной
нижней границей) числового множества М, если g
есть нижняя граница и для любого
действительного 8 > 0 существует такое х' е М, что
х' < g + 8.
Верхняя и нижняя грани числового множества
М обозначаются соответственно
G = sup М = sup х,
хеМ
¦ inf М = inf х.
хеМ
Таким образом, для ограниченного сверху
(снизу) множества М число supM (infM) является
наименьшим (наибольшим) числом,
ограничивающим М сверху (соответственно снизу). Если
sup Me M (infMе М), то это число называется
максимальным (минимальным) элементом
множества М и обозначается
max М = max х (соответственно min М = min x).
хеМ хеМ
Всякое непустое ограниченное сверху (снизу)
числовое множество имеет, и притом только
одну, верхнюю (нижнюю) грань.
Примеры. 1) Множество M = {x|xeQ, 0<х<1}
является ограниченным. Всякое чиедо С ^ 1 ограничивает М
сверху. Далее, supM=l, infM = min M = 0. Множество М
не имеет максимального элемента.
2) Множество N ограничено снизу, но не ограничено
сверху.
3) Для множества М = {х|х = 1 4- -^-^—, ие1Ч} имеем
п
supM = maxM = 3, infM = 2. Множество М не имеет
минимального элемента.
Пусть a, beR, a < b. Тогда множество («, Ь) =
= {х | xeR, а < х < b} называют интервалом,
множество [a, 6] = {x|xeR, a ^ x ^ b) - отрезком
(сегментом), а множества [a, b) = {x|xeR,
а ^ х < Ь] и (а, Ь] = {х | xeR, а < х ^ /;} —
полуинтервалами; для интервалов, полуинтервалов и
отрезков часто используется общий термин
промежуток, а и b - концы промежутка, число
b — а — длина промежутка. Рассматриваются также
*) В последующем для геометрической наглядности
всегда будет рассматриваться декартова система
координат.
ТОЧЕЧНЫЕ МНОЖЕСТВА В Rn
213
неограниченные интервалы:
(а, +оо) = {x|xeR, a < х},
[а, + оо) = {х | х е R, а ^ х},
(-со, а) = {х | хеR, х < а},
(- оо, я] = {х | х е R, х ^ а}.
Пусть Р(хь...,х„) и Q(yb...,>'„) - две точки
пространства R"-; тогда число
у i=i
называется расстоянием между точками Р и Q.
В случае и = 1 получаем d(P, Q) = | хх — у^ |.
Пусть е > 0, и пусть Р — точка пространства
R". Тогда множество
называется е-окрестностью точки Ро. е-окрест-
ность точки Ро состоит, таким образом, из всех
внутренних точек л-мерного шара радиуса е
с центром в точке Ро- Иными словами, е-
окрестность Ро есть множество точек
пространства R", расстояние которых до точки Ро меньше е.
В случае п = 1 Е-окрестность точки Р(х) есть
интервал (х — б, х + е). Множество U(P0)^Rn
называется окрестностью Ро, если оно содержит
какую-нибудь е-окрестность Ро.
Множество McR" называется ограниченным,
если оно может быть заключено в «-мерный
шар конечного радиуса. Диаметром множества
называется верхняя грань расстояний между его
точками.
Точка QeRn называется предельной точкой
множества М с R", если в каждой ?-окрестности
точки Q найдется отличная от нее точка из М.
Точка множества М, не являющаяся предельной
для М, называется изолированной.
Если Q — предельная точка множества М, то
в каждой е-окрестности точки Q лежит
бесконечно много точек из М. Предельная точка
множества М может не принадлежать этому
множеству.
Примеры. 1) Конечное множество не имеет
предельных точек.
2) Множество М = {х | х = 1 + (и + l)/n, neN} имеет
предельную точку х = 2.
3) Каждое рациональное число является предельной
точкой множества иррациональных чисел.
4) Каждое действительное число является предельной
точкой множества рациональных чисел.
5) Каждая точка пространства R" — предельная точка
этого пространства.
Теорема Больцано — Вейерштрасса. Любое
бесконечное ограниченное множество в R" имеет по
крайней мере одну предельную точку.
Пусть М — множество из R". Множество точек
R", не принадлежащих М, называется
дополнением М.
Пусть М' — множество всех предельных точек
множества М. М' — называется производным
множеством множества М. Множество М = М \J M'
называется замыканием М.
Справедливы следующие включения: (MJ с М',
М. Кроме того, М = М.
Множество McR" называется замкнутым, если
оно содержит все свои предельные точки, т. е.
М' с М. Множество McR" называется открытым,
если для каждой точки РеМ существует е-
окрестность Ut (P), такая, что Ue (P) с М. Пустое
множество замкнуто и открыто одновременно.
, а) Множество McR" замкнуто тогда и только
тогда, когда его дополнение открыто.
б) Пересечение произвольного числа замкнутых
множеств есть замкнутое множество.
в) Объединение конечного числа замкнутых
множеств есть замкнутое множество.
г) Пересечение конечного числа открытых
множеств есть открытое множество.
д) Объединение произвольного числа открытых
множеств есть открытое множество.
Примеры. 1) Любое конечное множество точек
замкнуто.
2) Для любого точечного множества его производное
множество и его замыкание замкнуты.
3) Множество Q не открыто и не замкнуто в R.
4) Пространство R" является как открытым, так и
замкнутым множеством.
5) Множество М = {1/л | «eN} с R не открыто и не
замкнуто в R.
6) Любая е-окрестность точки PeR" - открытое
множество.
7) Промежуток [я, Ь] с R является замкнутым
множеством.
Точка Р множества MgR" называется
внутренней точкой множества М, если существует
е-окрестность Uz (P) такая, что U? (P) я М. Точка
PeR" называется внешней точкой для множества
М, если она является внутренней точкой его
дополнения. Точка Р называется граничной
точкой множества М, если в любой е-окрестности
точки Р есть как точки множества М, так и его
дополнения. Множество всех граничных точек
множества М называется границей М.
Примеры. 1) Все точки множества М = @, 1) <= R
внутренние.
2) Каждое иррациональное число есть граничная точка
множества Q.
3) Множество Мх = {(хь х2)|х? + х\ > 1} является
множеством всех внешних точек множества Мг = {(хь х2) | х\ +
+ х|<1}. Единичная окружность является границей М,
иМ2.
Множество М с R" называется линейно связным,
если любые две его точки можно соединить
непрерывной кривой (образом отрезка при
непрерывном отображении), все точки которой
принадлежат этому множеству. Множество М
называется связным, если не существует таких
открытых Gj и G2, что McG,|J G2, Gx f] G2 = 0,
a Mf]G{ и Mf]G2 одновременно непусты.
Линейно связное множество связно.
Если McR" — открытое связное множество, то
любые две точки из М можно соединить
ломаной, полностью расположенной в М. В
частности, открытое связное множество линейно связно.
Пример. Кольцо М = {(хь х2) 10 < а < х\ + х\ < Ь) с
с R2 является связным множеством.
Открытое связное точечное множество
называется областью. Ограниченная область G
называется односвязной областью, если ее граница —
связное множество. В противном случае G
называется многосвязной областью. Объединение
214
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
области G и ее границы называется замкнутой
областью.
Если область G односвязна, то любая
замкнутая кривая без самопересечений, лежащая в G,
может быть стянута в точку путем
непрерывной деформации внутри области G.
Неограниченная
у замкнутая
у////////омасгпь
Рис 3.1
Неограниченная
ддусШная
область
Трвхпбязная
odnncrnh
Рис 3.2
Примеры. 1) Множество М - {(хь х2) \ х\ + х\ < 1}
односвязно.
2) Кольцо М = {(хи х2) 10 < а < х\ + х\ < Ь} является
двусвязнбй областью.
3) Множество М = 1(хь х2) | (х, - IJ + х\ < -у 1 (J
Множество McR" называется выпуклым, если
вместе с любыми двумя точками Р, Qe M ему
принадлежат все точки соединяющего их отрезка.
Пример. Прямоугольник М = {(хь х2) 11 x, |< a, \ х2 К
< Ь} с R2 — выпуклое множество.
Если каждой точке РеМ поставить в
соответствие некоторую окрестность U(P), то
совокупность этих окрестностей образует покрытие
множества М. При этом разным точкам может
быть сопоставлено одно и то же множество,
являющееся их общей окрестностью. Поэтому
покрытие множества может состоять и из
конечного набора окрестностей.
Лемма Гейне — Бореля о конечном покрытии/
Если McR" — замкнутое ограниченное множество,
то из любого покрытия множества М открытыми
множествами можно выбрать конечное покрытие.
3.1.3. ПОСЛЕДОВАТЕЛЬНОСТИ
3.1.3.1. Числовые последовательности.
3.1.3.1.1. Ограниченность,
сходимость. Примеры. Однозначное отображение
множества натуральных чисел во множество
действительных чисел R называется числовой
последовательностью или, короче,
последовательностью ф(л) = а„; пишут: <р = {«„}.
Последовательность {а„} называется ограниченной, если
существует такое число К е R, что | а„ \ ^ К для
всех neN.
Число а называется пределом
последовательности {а„}, если для любого е > 0 йайдется
такое натуральное N *), что для всех я ^ N
выполняется неравенство \ап — а \ < е. Если
последовательность {ап) имеет предел а**), то говорят,
ч го последовательность {а„} сходится к пределу а.
При этом пишут: lim an = а или а„-+а. Если
п -> оо
последовательность сходится к «, то вне любой
е-окрестности а лежит лишь конечное число членов
этой последовательности. Последовательность, не
.. имеющая предела, называется расходящейся.
Примеры. 1) Последовательность {1/и} сходится к
нулю: если задать произвольное е > 0 и выбрать
N > 1/е, что всегда возможно в силу принципа Архимеда,
то для всех п ^ N имеет место соотношение 11/л - 01 =
= 1/л < 1/N < е.
2) Последовательность {л} является неограниченной и
расходящейся.
3) Последовательность {(-1)"} является ограниченной и
расходящейся.
4) Последовательность {(л + О/и} сходится, и
lim (л + 1)/л = 1.
Л-* 00
5) Последовательности {(-1)"/"} и {^"}, \q\ < 1,
сходятся к 0.
6) Последовательность «i =2, а„ = —( а„
(л > 2) сходится и имеет пределом J/2.
-х +
1
7) Для а > 0 имеем lim
л -¦ оо
|/д
Последовательность {а„} называется
возрастающей (неубывающей), если. а„+1^ап для всех
neN. Последовательность {а„} называется строго
-z-> не является связным.
*) Вообще говоря, зависящее от с
**) Последовательность может иметь только один
предел.
ПОСЛЕДОВАТЕЛЬНОСТИ ТОЧЕК
215
возрастающей, если ап+1>ап для всех neN.
Последовательность {ап} называется убывающей
(невозрастающей), если ап+1^ап для всех neN.
Последовательность {ап} называется строго
убывающей, если а„+1 < а„ для всех weN. Возрастающая
и убывающая последовательности называются
монотонными последовательностями.
3.1.3.1.2. Теоремы о числовых
последовательностях. Для числовых
последовательностей справедливы следующие теоремы.
1. Любдя сходящаяся последовательность
ограничена.
2. Монотонная последовательность сходится
тогда и только тогда, когда она ограничена.
Если возрастающая (убывающая)
последовательность сходится, то ее предел совпадает с
верхней (нижней) гранью множества ее значений.
3. Критерий сходимости Коши.
Последовательность {а,,} сходится тогда и только тогда,
когда для любого е > 0 существует такое *)
NeN, что для всех п ^ N и т^ N имеет место
неравенство \ап — ат\ < е.
4. Пусть последовательности {ап} и {Ь„} таковы,
что lim ап = a, lim bn = b. Тогда lim {а„Ь„) =
п-* оо п-* оо л-* со
= ah и для любых a, |3eR выполняются
соотношения
lim (ая„ + рЬ„) = ая + рЬ.
п -» оо
Если, кроме того, b Ф О, то, начиная с
некоторого номера, все Ь„ ф О и lim (an/bn) = a/b.
П -> 00
5. Если {а„} сходится к а, то {|а„|} сходится
к \а\.
6. Пусть lim а„ = а > 0. Тогда, начиная с не-
п —» да
л /— * /~
которого номера, все ап > О и lim |/л„ = ]/я.
и -+ оо
7. Из lim а„ = а следует, что lim O^ + ... +
и -¦ со л —» оо
+ ап)/п = а.
8. Если последовательность {«„} ограничена, а
последовательность {Ьп} сходится к нулю, то
последовательность {а„Ьп} также сходится к нулю.
9. Если для членов последовательности {ап}
имеет место двойное неравенство А < а„ ^ В и
существует lim а„ = а, то А < а ^ В.
п -* ос
10. Если все члены последовательности {ап}
попарно различны, то lim а„ = а существует тог-
п —» оо
да и только тогда, когда множество значений
{flw|neN} ограничено и а является его
единственной предельной точкой.
11. Если ап ^ Ь„ ^ с„ и lim а„ = lim с„ = а, то
п —*¦ оо и —> оо
последовательность {/?„} сходится и lim bn - a.
п -*¦ оо
Пусть {а„} — заданная последовательность, и
пусть {пк} — строго возрастающая
последовательность (/ceN, nkeN). Последовательность {а )
называется подпоследовательностью последовательности
Если последовательность {«„} имеет
определенный конечный предел а или ее предел
равен оо *), то такой же предел имеет и любая
подпоследовательность {ап }.
Если последовательность {а„} не имеет определенного
предела (конечного или бесконечного), то это не означает,
что и подпоследовательность {ап } не имеет предела
(конечного или бесконечного). Если подпоследовательность
{а„ } имеет предел (конечный или бесконечный), то его
называют частичным пределом для последовательности \а„).
Из любой ограниченной последовательности {а„\ всегда
можно извлечь такую подпоследовательность {ап^, которая
сходилась бы к конечному пределу (теорема Больцано —
Вейерштрасса). Если последовательность {а„} не ограничена,
то из нее всегда можно выделить подпоследовательность,
имеющую частичный предел (например, бесконечный).
Итак, для любой последовательности {ап} независимо от
того, ограничена она или нет, существуют частичные
пределы (конечные или равные ±оо). Наибольший и
наименьший из этих частичных пределов всегда существуют
и обозначаются соответственно
liman (верхний предел последовательности {а„}),
lima, (нижний предел последовательности {а„}).
Равенство этих пределов есть условие, необходимое и
достаточное для существования предела (конечного или
бесконечного) последовательности {а„}
Примеры. 1) Последовательность {A + 1/п)"} строго
возрастает, ограничена и вследствие этого сходится. Ее
предел обозначается буквой е. Число е = 2,71828... играет
важную роль в качес1ве основания натуральных
логарифмов.
2) Последовательность {1/и2} строго убывает,
ограничена и, следовательно, сходится. Ее предел
inf{l/«2 | /ieN} =0.
3) Для чисел яь...,яг; Ьх bseR таких, что аг Ф О,
К Ф О,
С 0 при г < s,
«о/^о при г = s,
+00 при г > s и ао/Ьо > О,
- оо при г > s и ао/Ьо < 0.
4) Последовательность {«„}: а„ = (-1)" + — ограничена
п
и расходится. Ее подпоследовательность < 1 + хт-> сходится
2/с
к + 1, а подпоследовательность < -
— 1, При этом Тип а„ = +1,
п -*¦ оо
тельность
lim
п -* оо
2/с+ 1 }
сходится к нулю;
сходится к
— 1. Последова-
следовательно,
— > также сходится к нулю.
3.1.3.2. Последовательности точек. Однозначное
отображение ф множества N в пространство R"
называется последовательностью точек из R":
<p(fc) = Pk{x\, ..., x*)eR"**);
пишут: ф = {Рк}.
Последовательность точек {Рк} называется
ограниченной, если множество ее значений
{Pk|/ceN} с R" ограничено. Точка Р0(х°и ..., xj)
*) Вообще говоря, зависящее от е
*) То есть для любого Е > 0 существует такое
/VeN, что |а„|>? для всех п > N. Аналогично
определяются пределы + оо и — оо
**) Далее координаты точек опускаются ради простоты
записи.
216
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
называется пределом последовательности {Рк},
если lim d (Рк, Ро) = 0, т. е. если расстояния от
/с-> эо
точек Рк до Ро образуют сходящуюся к нулю
числовую последовательность. Если
последовательность {Рк} имеет пределом Ро, то говорят,
что она сходится к пределу Ро. При этом пишут:
Hm Pk = P0*).
k-+ oo
Последовательность, не имеющая предела,
называется расходящейся.
Если последовательность сходится к Ро, то
вне любой е-окрестности точки Ро лежит лишь
конечное число членов данной
последовательности.
Последовательность точек {Рк(х\, ..., xj)}
сходится к Ро (х?, ..., xj) тогда и только тогда,
когда сходятся последовательности
соответствующих координат, т. е. когда lim xj = х? для s = 1,
к^> оо
2, ..., п.
Примеры. 1) Последовательность точек {Рк} из
R2:(x*, хк2) = {(к + l)/k, l/к) ограничена и сходится к точке
РоA, 0), так как lim
1, lim -r
k-*<x> k
2) Последовательность {Рк} точек из R2: (x*, Xj) =
= A//с2, к3 - 1) не ограничена и расходится, поскольку
lim {к3 - 1)= +оо.
it-юо
Так как сходимость последовательностей точек
из R" может быть сведена к сходимости числовых
последовательностей, то большинство теорем о
числовых последовательностях переносится на
последовательности точек. В частности:
1. Всякая сходящаяся последовательность точек
ограничена.
2. Критерий сходимости Коши:
последовательность точек {Рк} сходится тогда и только
тогда, когда для любого е > 0 найдется такое N е N,
что для любых к, I ^ N справедливо неравенство
d(Pk, Р,) <е**).
3.1.4. ФУНКЦИИ ДЕЙСТВИТЕЛЬНОГО
ПЕРЕМЕННОГО
3.1.4.1. Функции одного действительного
переменного.
3.1.4.1.1. Определение, графическое
изображение, ограниченность. Пусть А
и В — множества в R. Однозначное отображение
/ множества А в В называется действительной
функцией одного действительного переменного***)
(см. также 4.1.4.5). Множество А называется
областью определения функции / и обозначается
D(j). Элемент yeW(f), который ставится в
соответствие элементу xeD(f), обозначается f(x) и
называется значением функции f в точке х.
Множество {/(х) | xeD(f)} cz В называется
множеством значений / и обозначдется W(f).
Функция /полностью определена, если известна
область ее определения и для каждого значения
*) Последовательность точек в R" может иметь не
более одного предела
**) Это — так называемое свойство полноты
пространства R".
***) Пока речь идет о действительных функциях
действительного переменного, мы будем их кратко называть
функциями
xeD(f) известно значение функции /(х), т.е.
известно правило, по которому находится это
значение. Правило установления соответствия
х -*f(x) часто может быть выражено в форме
аналитической зависимости.
Следует различать обозначения / и f(x).
Символом / обозначают функцию, в то время как
/(х) есть Значение функции / в точке xeD(f).
Однако простоты ради используют выражение
«функция /(х)», понимая под этим функцию,
определенную посредством отображения х ->/(х)
при xeD(f).
Графическое изображение
функции. Пусть х и у — координаты точки Р в
декартовой системе координат. Множество {Р(х, f(x))\xe
eD(/)} cR2 называется графиком функции/. При
этом координата х называется абсциссой или
аргументом, координата у = f(x) — ординатой
или значением функции, а уравнение у =/(х) —
функциональной зависимостью.
Важным вспомогательным средством при
построении графика функции или при выяснении ее
характерных свойств является построение таблицы
значений функции, в
которой для известных значений
аргумента указаны
соответствующие значения
функции. Графики и таблицы для
важнейших элементарных
функций приведены в 1.1.1.2
и 2.5.
Функция/не обязательно
должна быть задана явно —
уравнением у =/(х). Она
может быть определена также неявно - уравнением
F (х, у) = 0, (х, yjeMc R2, параметрически (х = х (г),
у = y(t), fe?cR) и т. д.
Примеры. 1) Функция y=/(x) = |x|, D(f) = R,
имеет область значений W(f) = {у \ у ^ 0} (рис. 3.3)
2) Всякая последовательность действительных чисел
{«„} является функцией с областью определения N и
областью значений
Рис 3 3
3) Функция f:
nx + 2 Г I при x Ф 0,
f(x) — lim = \
n _> да nx + 1 B при x = 0,
имеет область значений И^(/) = {1, 2}
4) Уравнение ух — sin x = 0 определяет функцию
Сумма, разность, произведение и частное
функций / и д определяются следующим образом:
) =f(x)g(x),
=D(f)f]D(gl
д
Если f — взаимно однозначная функция, то
обратное к / отображение g также однозначно, т. е.
тоже является функцией (см. 4.1.4.4).
Обратное отображение д, соответствующее
взаимно однозначному отображению /, такому,
ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
217
что D (/) я R, W(f) Я R, называется обратной
функцией по отношению к функции /
Очевидно, что D(g)=W(f), W(g) = D(f),
/[</(х)] = х при xeD(g), g [/(%)] = х при xeD(/),
а функциональная зависимость у = /(х)
эквивалентна функциональной зависимости х = д (у).
Для того чтобы из функции у =f(x) получить
обратную функцию д, необходимо разрешить
уравнение у = f(x) относительно х и (в том случае, если
в дальнейшем независимое переменное будет
обозначаться посредством х) поменять переменные
х и у местами. При этом графиком обратной
функции д является график функции /, зеркально
отраженный относительно прямой у — х.
Примеры. 1) Функция / (.х) = х2, D{f)=W(f) =
= {х|х^0}, имеет обратную функцию д{х) = ]/х. На всей
области D(f) = R функция y2 не имеет обратной.
2) Функцией, обратной к показательной функции
/(х) = ех, D(f) = R, является логарифмическая функция д(х) =
= lnx, D(g) = {х|х>0}.
3) Функция f(x) = s\nx имеет в D(f) = [-n/2, л/2]
обратную функцию д (х) = arcsin x, D(g)=[-\, 1]. На всем
множестве R функция sin x не имеет обратной.
Если / и д — функции одного переменного, то
функция F, определенная соотношением у =
= F(x) = g [/(х)] на области определения D(F) =
= {xeD(J)\ f(x)eD(g)}, называется сложной
функцией или суперпозицией (а также композицией)
функций / и д и обозначается gof. Следует иметь в
виду, что здесь операция проводится справа
налево.
Пример. Если f(x) = ax + b, D(f)=R и д(х) = ]/х,
D(д) = {х | х ^ 0}, то до f(x) = g[f (x)] = \/ах + Ь. Область
определения есть D(g° f) = {х \ ах + b ^ 0}.
Функция / называется ограниченной на
множестве Е cz D (/), если существует такое число А,
что |/(х) | ^ А для всех хеЕ. Функция / называется
ограниченной сверху (снизу) на Е, если множество
значений / при хеЕ ограничено сверху (снизу).
Верхняя (нижняя) грань множества М значений
функции / на Е называется верхней (нижней)
гранью функции J и обозначается sup f(x) (inf /(*)).
хе? хеЕ
Если число supf(\nff) на Е принадлежит
соответствующему множеству значений М, то оно
называется наибольшим (наименьшим) значением
/ на Е и обозначается max/(x)(min/(x)). При
хе? хеЕ
этом говорят, что функция /достигает на Е своего
максимального (минимального) значения.
Примеры 1) Функции /, (х) = sin x, f2 (x) — cos x
ограничены на R, так как для всех xeR имеем |sinx|^l,
|cosx |^1. При этом
sup sin x = sup cos x = max sin x = max cos x = 1.
xeR' xeR xeR xeR
2) Функция /(у) = х2 ограничена на R снизу, но не
ограничена сверху. Однако f ограничена на любом ограниченном
подмножестве ? с R. ,,
Функция /(х) = ?«„-/¦*', ао Ф 0, называется
1 = 0
целой рациональной функцией или многочленом
п-й степени. Многочлен нулевой степени
называется константой. Функция называется
(дробной) рациональной функцией, если она является
частным от деления двух многочленов. Рациональная
функция называется правильной, если степень
многочлена в числителе меньше степени
многочлена в знаменателе.
Графиком функции, равной константе, является
прямая, параллельная оси абсцисс; графиком
многочлена первой степени — прямая,
пересекающая ось абсцисс под некоторым (не нулевым и
не прямым) углом; графиком многочлена второй
степени — парабола.
X2 + X - 1
х3- 1
является правильной рациональной функцией.
Пример. Функция /(х) =
ЗЛА 1.2. Предел функции одного
переменного. Пусть функция / определена в
некоторой окрестности точки х0, за исключением,
быть может, самой точки х0. Говорят, что функция
/ имеет в точке х0 предел, равный А, и
обозначают: lim f(x) = А, если для любого е > 0
х->х0
найдется такое 5 > 0 *), что для всех х,
удовлетворяющих неравенству 0 < | х — х0 | < 8,
выполняется соотношение |/(х) — А\ <е.
Другими словами, f имеет в точке х0 предел,
равный А, если для каждой е-окрестности точки А
существует такая 5-окрестность точки х0, что все
точки 5-окрестности, за исключением, быть
может, точки х0, отображаются функцией/в е-окрест-
ность точки А.
Пусть функция / определена в некоторой
окрестности точки х0, за исключением, быть может,
самой точки х0. Функция/имеет в точке х0 предел А
тогда и только тогда, когда для любой числовой
последовательности {х„], такой, что xneD(f),
х„ # х0 и lim х„ = х0, выполняется равенство
И -> 00
lim f(xn) = A.
п —* оо
Примеры. 1) Функция f(x) = х имеет в любой точке х0
предел, равный х0, так как для любой последовательности
{х„}, такой, что lim х„ = хо, имеем
п -* оо
lim f(xn) = lim х„ = х0.
и -+ оо и -¦ оо
2) Функция f(x) -
( 1 при х ^ О,
( 0 при х < О
не имеет предела в 0. Если, например, взять
последовательности х„ = 1/и и хж = — 1/т, то получим
lim х„ = lim xm = 0, lim f{xH)=\, lim /(хж) = 0.
и—*оо т —> оо п -* оо т —> оо
3) Функция f(x) = 1/х не имеет предела в 0. Иначе
должна была бы сходиться к конечному пределу
последовательность {/A/и)} = {л} (meN).
Критерий Коши. Пусть функция / определена
в окрестности х0, за исключением, быть может,
самой точки х0. Функция / имеет предел в точке х0
тогда и только тогда, когда для любого е > О
существует такое 5 > 0, что для всех хь х2,
удовлетворяющих условию 0<|х1— хо|<5, 0<
< | х2 — х0 | < 8, имеет место неравенство | f(xx) —
-J(x2)\ <?•
Иногда важно знать поведение функции справа
(соответственно слева) от точки х0, так что
целесообразно ввести следующее определение.
*) 5, вообще говоря, зависи г от с
218
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Функция / имеет в точке х0 предел справа (еле- Основные теоремы о пределах
ва), равный А и обозначаемый / (х + 0) (/(х - 0)), функций.
Если для одного из пяти случаев: х -* х0,
х -> х0 ± 0, х -* ± оо существуют \imfl(x) = Al,
lim/2(x) = A 2, то
a) lim (cji (x) + c2f2 (x)) = с^ + с2А2;
= lim f(x) =
х -> х0 + О
(f(x0 - 0) = lim f(x) = A),
x -»• x0 - 0
если для любого е > 0 найдется такое 8 > О, что
для всех х из интервала (х0, х0 + 5) ((х0 - 5, х0))
имеет место неравенство | f(x) — А \ < е.
Пример. Для функции / =
1 при х ^ О,
О при х < О
б) \imfl(x)f2{x) = AlA2;
в) lim Д (х)//2 (х) = AJA2, если Л2 # 0.
Пример lim х sin х = lim x lim sin x = 0.
x ^ 0 x -> 0 x -> 0
/(+0)= lim Дх)=1,
х- +0
3.1.4.1.3. Вычисление пределов. Для
вычисления пределов функций пользуются
указанными выше определениями и теоремами, а также
следующими приемами.
I. Определение предела посредством преобра-
Функция / имеет в точке х0 предел тогда и зования функциональной зависимости к удобному
/(-0)= lim /
х- -0
= 0.
только тогда, когда в точке х0 существуют
пределы этой функции как справа, так и слева, и
они равны.
Определение предела может быть обобщено
на случай, когда х неограниченно возрастает
(соответственно убывает), в предположении, что
область определения функции не ограничена.
Это позволяет выяснить характер поведения
функции «в бесконечности».
Пусть область определения функции не ограни-
виду.
Примеры 1) lim '- = lim (x" + х"~2 +
х -* 1 х ~ ! х -> 1
.. + X + 1) = И
j/l + X - 1 1 1
2) lim - = lim —zA =-'
x -> 0 x x -»0 |/1 + x + 1 2
II. Правило Лопиталя. Если при х -* х0 (соот-
чена сверху (снизу); тогда / обладает при х -> + оо ветственно х -> ± со) в функции F (х) возникают
(х_> _ оо) презлом, равным Л, если для любого неопределенности вида - или -, то для вычисле-
е > 0 существует такое х ь что для всех х > х! (х < х г) ~
имеет место неравенство | /(х) — А \ < е.
Обозначение:
lim /(х) = А ( lim f(x) = A).
х-+ 4- оо х-+ — оо'
Пример. lim — = 0. Если взять xt = — (е > 0),
х-> +оо х е
то для всех х
будем иметь
О оо
ния iim F(x) (соответственно lim F(x)) мож-
X -+ Хо X -¦ ± ОС
но зачастую* успешно применять следующие
правила.
На) Пусть функции / и д определены и
дифференцируемы в некоторой окрестности U (х0) точки
х0, за исключением, быть может, самой точки х0.
Пусть, далее, lim /'(х) = lim д (х) = 0 и д' (х) ф О
X -> Х0 X -¦ Х0
Наконец, можно определить также понятие при хе t/(xo)\ {х0}. Если при этом
«бесконечно большая функция», т. е. функция, зна- /'(*)
чения которой неограниченно возрастают (по аб- .^ „ TTTyT = ^'
солютной величине) при приближении аргумента к
какой-либо точке, в окрестности которой функция то
определена. Обзор возможных определений
предела дан в табл. 3.1.
Таблица 3.1
1 1
X ^ Xj
.in, Щ-
А.
Предел функции / в точке
.V = XQ
«Обращение функции / в
бесконечность» в точке v = х()
Обозначение
lim / (х) = А
х -* х0
lim = + оо
х -»¦ х0
lim f(x) — оо
х-*х0
lim f(x) = оо
х -*х0
Определение
Для каждого е > 0 существует 5 (е) > 0 такое, что для всех х,
удовлетворяющих условию 0<|х — хо|<5, имеет место
неравенство \f(x) - А\<г
Для любого М существует 6 (М) > 0 такое, что для всех х,
удовлетворяющих условию 0 < | х — х0 | < 8, имеет место
неравенство f(x) > М
Для любого М существует 5 (М) > 0 такое, что для всех х,
удовлетворяющих условию 0<|х — хо|< 5, имеет место
неравенство fix) < М
Для любого М существует 5(Л/)>0 такое, что для всех х,
удовлетворяющих условию 0<|х —х()|<8, имеет место
неравенство |/(х)|> М
ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
219
- Продолжение
Обозначение
Определение
Предел функции / при х -*
-* + ее, соответственно
х -» — оо
lim f(x) = А
х -*¦ +оо
Для любого 8 > 0 существует хо (е) такое, что для всех v ^ х0 имеет
место неравенство \f(\) - А\< е
lim f(x) = A
X -* — 00
Для любого е>0 существует ло(е) такое, что для всех y< v()
имеет место неравенство | f (х) — А | < е
«Обращение функции / в бес-
конечность» при х-* +оо,
соответственно х-»—оо
lim /(x) = +оо
X -» +00
Для любого М существует х0 (М) такое, что для всех х ^ х0
имеет место неравенство / (х) > М
lim f(x) = +оо
х -> — оо
Для любого М существует х{)(М) такое, что для всех v < л()
имеет место неравенство /(v)> M
lim f(x) = — оо
х -> +оо
Для любого М существует \'0(Л/) такое, что для всех
х> \() имеет место неравенство /(х)< М
lim f(x) = — оо
X -* +00
Для любого М существует л() (Л/) такое, что для всех
х < v() имеет место неравенство f(x) < М
lim / (х) = оо
х-* +00
Для любого М существует х()(М) такое, что для всех
х ^ х0 имеет место неравенство | f(x)\ > М
lim /(x) = оо
х-* — оо
Для любого М существует х()(М) такое, что для всех
х ^ х0 имеет место неравенство | / (х) | > М
Пределы справа и слева
lim f{x) = A
х - х0 + О
Для любого е > 0 существует 5(е)>0 такое, что для всех х,
удовлетворяющих условию 0 < y — v() < б. имеет место неравенство
| / (х) - А | < 8
lim f(x) = A
х -> х0 - О
Для любого е > 0 существует 8 (е) > 0 такое, что для всех х.
удовлетворяющих условию 0 < х0 — х < 5, имеет место неравенство
I / (-V) ~ Л \ < 8
«Обращение функции / в
бесконечность» справа и
слева в точке
lim f
х -* х0 + О
Для любого М существует 6(М)>0 такое, что для всех х,
удовлетворяющих условию 0 < л - х0 < 5, имеет место неравенство
f(x) > Л/
lim f(x) = +оо
х; -> х0 - О
Для любого М существует 8 (М) > 0 такое, что для всех х,
удовлетворяющих условию 0 < х0 - v < б, имеет место неравенство
f(x)>M
lim J (x) = -оо
х -> х0 + О
Для любого М существует 8 (М) > 0 такое, что для всех х,
удовлетворяющих условию 0 < х — х0 < 8, имеет место неравенство
/(х)< М
lim f(x) = -оо
с - хо - О
Для любого М существует 8 (М) > 0 такое, что для всех v,
удовлетворяющих условию 0 < х0 — v < б, имеет место неравенство
lim f(x) = оо
х -> х0 + О
Для любого М существует б (М) > 0 такое, что для всех х,
удовлетворяющих условию 0 < х — х0 < б, имеет место неравенство
\Г(х)\> М
lim /(x) = оо
х -¦ х0 - О
Для любого М существует б (Л/) > 0 такое, что для всех л\
удовлетворяющих условию 0< v() — v < 5, имеет место неравенство
|/(х)|> Л/
Соответствующее утверждение имеет место и = lim g (x) = 0, а также д' (х) ф 0 при х > а.
в том случае, когда lim J(x)= lim д(х)=оо, а х-» + оо
J
также при х - х. ± О." " *° " "* *"
Нб) Пусть функции / и д дифференцируемы
при х > а {а > 0) и, кроме того, lim f(x) =
+
Тогда,если
Л, то
lim '—/—r = Л.
-> + оо д \х)
220
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Аналогичное утверждение справедливо при
lim д(х) = оо, а также при х -> — со.
х -> + ос
Прим &р-Ы. 1) Пусть /(х) * sin х, д (х) = х, х0 = 0. Из
cosx , „ . .. sinx
hm —-—= 1, согласно На), следует, что lim = 1.
х->0 ' х-*0 х
2) lim
COS X — 1
4) lim (xlnx)= lim ' _, = lim r
x-*+0 x -» + 0 x x-* +0 ~x
= lim (-x) = 0.
x-> +0
5) lim x I arctg x —— I = lim
x -» + оо \ 2/ x-* + <
arctg x —
= lim
x-> + oo
A+x2)
(-1)
(-1)
+ lim x
X-+ + 00
6) lim ((я - 2x) tg x) = lim
x -* n/2 х-* я/2 ct8 x
= lim ((-2)(-sin2x)) = 2.
х — я/2
III. Если/непрерывна в точке x0 и lim g (x) = x0,
x -*¦ a
то (см. 3.1.4.1.4) lim/@(x))=/(xo).
x-* a
Примеры. 1) lim A + xI/JC = lim eln{l+x)lx =
x — 0 x -> 0
lim In A 4- x)/x
2) lim Xх = lim exlnx = e° = 1.
x — +0 x-» +0
IV. Использование разложения функции в ряд
Тейлора.
х —sinx
Пример, lim з
х-0 х
lim
х-0
1
т
3.1.4.1.4. Непрерывные функции
одного переменного. Функция / называется
непрерывной в точке xoeD(f), если для любого
е > 0 существует такое 5 > 0, что для всех х,
принадлежащих D (/) и таких, что | х — х0 \ < 5, имеет
место неравенство | f(x) — f(x0) \ < е.
Примеры. 1) Функция f(x) — C непрерывна в точке
х0 е R. Если взять произвольное е > 0, то для любого
положительного 5 и всех х, таких, что | х - х0 | < 6, имеем
|/(х)-/(хо)|-|С-С|-0<ь '
2) Функция /(х) = х непрерывна в точке х0 е R. Если
положить 5 = 6, причем е > 0 - произвольное число, то
для всех х, таких, что | х — х0 | < 5, имеем | f(x) — f{x0) | =
= | х - х01 < 5 = е.
Между непрерывностью функции / в точке х0
и существованием предела / в х0 имеется
следующая связь:
функция /, определенная в некоторой
окрестности х0, непрерывна в точке х0 тогда и только
тогда, когда существует предел функции f в точке
х0, равный /(х0), т.е. ко1да lim f(x) =/(x0).
v -> х0
Функция f непрерывна в точке xoeD(f) тогда
и только тогда, когда для любой числовой
последовательности {х„\, такой, что xneD(f) и lim хп —
п-> оо
= х0, имеет место равенство lim /(*„) = f(x0).
п -* ос
Примеры. 1) Функция
_ Г 1 при х ^ 0,
1 0 при х < О
I npi
не является непрерывной в точке х0 = 0.
2) Функция Дх) = 1/х не является непрерывной в точке
3) Функция
fix)
{xsin
о
= 0.
A/х) при х/0,
при х = О
на мно-
каждой
непрерывна в точке х0 =
Функция / называется непрерывной
жестве ?с/)(/), если j непрерывна
точке хоеЕ.
Если / не является непрерывной в точке х0
(разрывна или имеет разрыв в точке х0), то х0
называется точкой разрыва функции /.
Грубо говоря, непрерывность функции f
означает, что в результате небольшого изменения
значения аргумента значение функции также
изменяется мало. Если D(/) — промежуток и график
функции/на Е с D(f) является куском «сплошной»,
непрерывной кривой, то / непрерывна на Е.
Основные свойства непрерывных
функций.
Сумма, разность и произведение непрерывных
функций также являются непрерывными
функциями.
Если / непрерывна и не равна нулю в точке х0,
то 1// также является непрерывной в точке х0.
Многочлен непрерывен во всех точках
множества R.
Дробно-рациональная функция непрерывна
во всех точках, в которых ее знаменатель отличен
от нуля.
х4 — 2х2 + 3
Пример. Функция f(x) = 3—j непрерывна на
множестве R\ {1}.
Пусть функция / непрерывна и положительна
(отрицательна) в точке х0. Тогда существует
такая окрестность U (х0) точки х0, что для всех
хе U (xo)P) D(f) имеет место неравенство /(х) > О
(/(х) < 0).
Любая функция, представимая в виде суммы
степенного ряда, непрерывна в точках, лежащих
внутри интервала сходимости этого ряда.
Если функция /непрерывна в точке х0, а функция
д — в точке/"(х0), то сложная функция ^о/непрерывна
в точке х0.
Пример. Из непрерывности функций f(x) = sin x и
д (х) = е* в R следует непрерывность сложной функции
Аналогично понятию одностороннего предела
вводится понятие непрерывности справа и слева.
Функция f называется непрерывной справа (слева)
в точке xoeD(/), если для любого е > 0 сущест-
ФУНКЦИИ ОДНОГО ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
221
вует такое 6 > 0, что для всех xeD(f),
удовлетворяющих условию 0 ^ х — х0 < 5 @ < х0 — х < 5),
имеет место неравенство |/(х) — /(х0) | < е.
Функция/непрерывна в х0 тогда и только тогда,
когда она непрерывна в х0 как справа, так и слева.
Пример. Функция
/(*) =
1 при х ^ О,
О при х < О
О справа, но не является непре-
и порядок
непрерывна в точке х0 =
рывной слева.
3.1.4.1.5. Точки разрыва
величины функций.
1. Устранимый разрыв. Пусть функция /
определена в окрестности точки х0 и не является
непрерывной в этой точке. Функция / имеет в точке х0
устранимый разрыв, если существует lim /(x) = А.
х->х0
При этом функция
f/(x) при xgD(/)\{x0},
[ А при х = х0
/¦(*)¦
непрерывна в точке х0.
Пример. Функция
/(*) =
1 при х Ф О,
2 при х = О
имеет устранимый разрыв в точке х0. Функция f*(x)=l,
D(f*) = R, непрерывна в точке х0 = 0.
2. Конечный разрыв {скачок функции). Пусть
для функции / существуют lim f(x) = A,
х -> х0 - 0
lim f(x) = В, причем А ф В. Тогда говорят,
v -> .ко + 0
что функция / имеет в точке разрыва х0 скачок,
равный по величине \ В — А\.
Пример. Функция
М-
{1 при .
0 при
при х < О
имеет в точке 0 скачок, равный 1.
3. Бесконечный разрыв. Если для функции /
имеет место соотношение lim | /(х) | = оо, то
х-»х0
точку х0 называют точкой бесконечного разрыва
функции [.
Пример. Функция [(х) = 1/х имеет бесконечный
разрыв в точке х0 = О
Точки устранимого и конечного разрывов
называются также точками разрыва 1-го ~рода.
Точками разрыва 2-го рода являются точки
бесконечного разрыва и те точки, в которых не
существует конечного предела либо справа, либо слева.
График функции с
точками разрыва 1-го и 2-го рода
показан на рис. 3.4. Точки А,
D, F, G — точки разрыва 1-го
рода {A, F, G — конечного
разрыва, D - устранимого);
В, С, Е- 2-го рода {В,
Е — бесконечного разрыва).
Пример.
Дробно-рациональная функция имеет не более чем
конечное число точек бесконечно-
Функция f называется кусочно непрерывной на
отрезке / = [а, Ь] a R, если / непрерывна во всех
точках xel, за исключением конечного числа
точек разрыва 1-го рода.
4. Порядок величины функций. Следующие
определения дают возможность сравнивать две
функции.
Если для функции [, определенной в
окрестности точки х0, имеет место равенство
lim
х -* v0
/w
I x - x0 Is
где с>0 и seR\{0}, то точка хо называется
нулем функции [порядка s в случае s > 0 и точкой
бесконечного разрыва функции [порядка ( — s)
(полюсом порядка s) в случае s < 0.
Если lim |xs/"(x)| = с, где о 0, seR\{0}, то
х -> ос
говорят, что функция/(х) является бесконечно малой
порядка s при х -> оо, если s > 0 (соответственно
бесконечно большой порядка ( — s) при х -> эс, если
s <<))•).
Не для всякой функции, удовлетворяющей
условию lim |/(x)| = oo, можно указать порядок
.X -> ОС
«обращения в бесконечность». Например,
показательная функция растет при х -+ + оо быстрее,
чем любая степень Xs.
Примеры. +) Для функции sin х точка 0 является ну-
sinx
лем порядка 1, так как lim —
х->0 J
2) Функция f(x) = x" является бесконечно большой
порядка п при х-юо, так как lim |x""x"|= 1.
Х-* 00
Для сравнения порядка величины двух
функций / и g употребляются символы о и О
(читается: «о малое» и «О большое»). Если для двух
функций / и g существует такая функция И, бесконечно
малая при х -»х0 (соответственно при х-> ± ос),
что f=gh (в частности, если lim (f/g) = 0), то
пишут:
f(x) = o(g(x)).
Читается: «/(х) есть о малое от д(х) при х -> х0»
(соответственно «при х -> ± оо»).
Пример, sin к = о (ух) при х -> 0.
Если для двух функций / и д существует такое
MgR, что —т—г <М при х->х0 (соответственно
9(х)
при х -> ± оо), то пишут:
f(x) = O(g(x)).
Читается: «/(х) есть О большое от д(х) при х -+ х0»
(соответственно «при х-> + оо»).
Пример. Так как lim
= 1, то sinx = О(х)
при х-*0.
3.1.4.1.6. Теоремы о функциях,
непрерывных на отрезках. Всякая функция,
непрерывная на отрезке / = [а, Ь~\ **), ограничена на /.
Рис
го разрыва.
*) При х -> + оо определение аналогично.
**) В концевых точках а и b функция / должна быть
односторонне непрерывна
222
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Пример. Функция /(х) = —г-——, х > 1, /"(!)= — ке,
D(f) — [I, a] (а > 1), непрерывна на D(f) и. следовательно,
ограничена.
Теорема Вейерштрасса. Для каждой функции,
непрерывной на / = [а, Ь], существуют т =
= min/(x), М = max/(x).
хе/ хе/
Пример. Функция f из предыдущего примера
достигает на [1, л] своих верхней и нижней граней
Теорема Коши о прохождении через нуль. Если/
непрерывна на [а, Ь] и /(а) > 0, f(b) < О, то
существует точка х е [а, Ь], в которой / обращается в нуль
(аналогичное утверждение имеет место в случае
Да) < О, ДЪ) > 0).
Пример. Функция f(x) = -"— - In x непрерывна на
[1, f] Из Д1) > 0, f(e) < 0 следует существование точки
\'ое[1, <•], в которой / обращается в нуль
Теорема о промежуточном значении. Пусть /
непрерывна на [а, Ь\ и пусть т = min/(x) < max/(x) =
хе/ хе/
= М и а е (ш, М). Тогда существует точка х0 б
е(«, Ь), в которой /(х0) = а. Таким образом,
W(f) = [m, M].
Функция / называется убывающей
(возрастающей) на [я, Ь] я D(f), если для любых хь х2е
е[я, Ь] таких, что xt < x2, имеет место неравенство
f(xi) ^Дхг) (Дх\) ^Дхг))- Функция / называется
строго убывающей (строго возрастающей) на [а, Ь\
если для любых хь х2е[а, Ь] таких, что xi < х2,
имеет место неравенство/(xt) >/(x2) (/(*i) </(x2)).
Если / является убывающей или
возрастающей, то она называется монотонной функцией.
Показательная функция f(x) = ex строго возрастает на
каждом замкнутом отрезке [а, />], так как для \i < х2
имеем е*2 ~ Xl > 1, откуда следует eXl < eXl
Свойства монотонных функций.
1. Возрастающая (убывающая) на [а, Ь] функция
/ непрерывна на [а, Ь~\ тогда и только тогда, когда
она принимает каждое значение из промежутка
[/D ЛВД ([/(Ь), Да)]).
2. Если / монотонна на [«, Ь~\, то она может
иметь на [а, Ь] не более чем счетное множество
точек разрыва, и каждая ее точка разрыва — 1-го
рода.
3. Пусть / непрерывна и строго возрастает
(убывает) на [а, Ь]. Тогда на множестве [/(а),
ЛЧ] ([/(Н Лfl)]) определена непрерывная строго
возрастающая (убывающая) функция д, обратная
для/
Пример. Функция /(х) = е* непрерывна и строго
возрастает на любом [а, Ь], W(f) — {у \ у > 0}
Обратная для нее функция д(х) = \пх, D(g) =
= {х|х>0}, также непрерывна и строго возрастает в D(g)
Функция / называется равномерно непрерывной
на М с D (/)? если для любого е > 0 найдется
такое 5 > 0*), что для любых хь х2еМ таких, что
I *i — Х2 I < S» выполняется неравенство |/(xj —
Пример. Функция f(x) = 1/х непрерывна при хе@,
1). но не является равномерно непрерывной в интервале
@, 1)
Если /"равномерно непрерывна на М,
то/непрерывна на М. Если множество М ограничено и
замкнуто, то верно и обратное: всякая
непрерывная на [а, Ь~\ функция равномерно непрерывна на
[«, Ч.
3.1.4.1.7. С п еци ал ь н ые виды функций.
1. Периодические функции Функция /
называется периодической, если найдется такое 7 ф 0, что из
xeD(f) следует х + ТеD(/), x-TeD(f) и f(x + Т) = /(х).
Наименьшее положительное Т; удовлетворяющее
указанным условиям, называется периодом функции /.
Пример Функции sin x и cos x - периодические с
периодом 2л.
2 Функции ограниченной вариации. Пусть
Z — разбиение отрезка [а, Ь~\ с точками разбиения а =
= х0 < х, <...<; х„_ , < х„ = h Если / — такая функция, что
[а, Ь] с: ?>(/), то число V(f, Z) = ? |/"(xt)-/"(*»-1)| назы-
k= 1
вается eapuaifuevi функции f относительно разбиения Z Если
существует конечная верхняя грань V(f, [a, /?]) = supK(/, Z)
по всем разбиениям отрезка [а, /?], то она называется
полной вариацией функции f на отрезке [а, Ь]. При этом f
называется функцией ограниченной вариации*).
Свойства функций ограниченной
вариации
1) Всякая монотонная на [а, Ь~] функция является функцией
ограниченной вариации.
2) Всякая дифференцируемая на [а, Ь~\ функция,
производная которой ограничена на [а, Ь], является функцией
ограниченной вариации.
3) Функция, определенная на [а, Ь], является функцией
ограниченной вариации тогда и только тогда, когда она
представима в виде разности двух возрастающих функций.
4) Всякая функция ограниченной вариации интегрируема
по Риману (см. 3.1 7.1).
Примеры. 1) Если / возрастает на [«, />], ю
V(U [fl, b-]) = f(b)-f(a).
2) Функция
Г х cos (л/2х) при \ > 0,
~ \ 0 при х = 0
не является функцией ограниченной вариации на отрезке [0, 1]
При разбиении 0 < - — < < . < — < --- < I получа-
2п 2п — \ 3 2
ем V(f, Z) = ]Г —, откуда вследствие расходимости ряда
*=i K
3. Абсолютно непрерывные функции.
Функция /называется абсолютно непрерывной на отрезке [//, Ь] с
a D (/), если для любого е > 0 существует такое 6 > 0, что
для любой конечной системы содержащихся в [а, /?]
непересекающихся отрезков Ik = [xk-l. xk] таких, что ? (хк —
— хк_ ,) < 6, выполнено неравенство
Всякая абсолютно непрерывная на [«, Ь] функция
является равномерно непрерывной функцией и функцией
ограниченной вариации.
4. Полунепрерывные функции Функция /,
определенная в некоторой окрестности точки х0, называется
полунепрерывной снизу (сверху) в х0, если для любой после-
*) Число 5 не зависит от выбора хь х2
*) Функции ограниченной вариации могут быть как
непрерывными, так и разрывными С другой стороны,
существуют непрерывные функции неограниченной
вариации (см. пример 2).
ФУНКЦИИ НЕСКОЛЬКИХ ДЕЙСТВИТЕЛЬНЫХ ПЕРЕМЕННЫХ
223
довательности {х„} такой, что lim х„
п -> оо
ИЩ f{xH)>f(xo)
n -> оо
/(*»)</(*<>))•
Функция / называется полунепрерывной в точке х0, если
f полунепрерывна в точке х0 сверху или снизу.
Пример. Функция Дирихле
|1 при xeM = Qp|[0, 1],
(О при хе[0, 1]\Л/
является полунепрерывной сверху при хоеМ и
полунепрерывной снизу при х0 е [0, 1] \ Л/. При этом/разрывна в каждой
точке своей области определения.
5. Функции, удовлетворяющие условию
Липшица. Если для функции /, для которой [д, Ь] с: D (/),
существует гакая постоянная L, что для любых хь х2е[д, Ь]
выполняется неравенсгво |/(xt) — /(х2) | < L\ xt — x2 |, то
говорят, что функция f на отрезке [д, Ь] удовлетворяет
условию Липшица с постоянной Липшица, равной L
1) Каждая функция, удовлетворяющая на [а, Ь] условию
Липшица, является абсолютно непрерывной функцией.
2) Всякая дифференцируемая на [а, Ь] функция,
производная которой ограничена на [д, Ь], удовлетворяет
условию Липшица.
Пример. Функция /(х) = ух не удовлетворяет
условию Липшица на @, 1], так как множество {1/|/х|хе@, 1)}
не является ограниченным.
3.1.4.2. Функции нескольких действительных
переменных.
3.1.4.2.1. Определение, графическое
изображение, ограниченность.
Определение функции одного действительного переменного
(см. 3.1.4.1.1) будет теперь обобщено на функции п
действительных переменных. Область определения
такой функции — подмножество в R". Точку,
которой в декартовой системе координат
соответствует последовательность (хь ..., х„), обозначают
Р(хь ..., х„) или, кратко, Р(х^).
Пусть /IcR^BcR. Однозначное отображение
/ множества А в множество В называется
(действительной) функцией п действительных
переменных (см. также 4.1.4.5). Множество А называется
областью определения f и обозначается D(f). Образ
yeW(f) элемента (хь ..., х„> = (х() = Р(х.)еD(/)
обозначается/(хь ..., х„), или/(х,), или/(Р). Число
/(xi, ..., х„) называется значением функции в точке
(хь ..., х„). Множество )/(Р) | PeD(f)} <= В
называется множеством значений f и обозначается
W(f).
Каждой точке (хь ..., х„)еD(/) <= R"
соответствует только одна точка у = /(хь ..., xJeR.
Уравнение y=f(xu ..., х„), как и в 3.1.4.1,
называется функциональной зависимостью. Функция /
не обязательно должна быть задана явно —
уравнением у =/(хь ..., х„), но может быть, например,
задана неявно — уравнением вида F (хь ..., хп; у) —
= 0.
Пример. Правилом сопоставления (х,, х2) -»/(х1, х2) =
=*х2 + х2, (хь x2)eR2, определяется функция с областью
определения D(f) = fjl2 и множеством значений W(f) =
= {у lye К, у>0}. Уравнением функции / является
уравнение у = х2 + х\.
Графическое изображение функции
двух переменных. Для функций двух
переменных хь х2, как и для функций одного переменного,
возможно геометрическое представление (в
декартовых координатах хь х2, у пространства R3).
Множество точек
{Р(хи *2,/(хь х2))\(хи x2)eD(/)}cR3
называется графиком функции / Таким образом,
для построения графика функции/значение функции
f(xu xi) откладывается на прямой, проходящей
через точку (хь x2)eD(f), в направлении оси у.
Для большинства рассматриваемых на практике
функций точки Р образуют поверхность в
пространстве R3, которая и является графиком функции
/. Вспомогательным средством при построении
графика или выявлении основных свойств функции
является построение таблицы значений, в которой
для конкретных точек области определения указаны
соответствующие значения функции. Для функции
более чем двух переменных аналогичная
наглядная геометрическая интерпретация, вообще говоря,
уже невозможна.
Линии уровня, поверхности уровня.
Если с е W(f), то точечное множество
{(хь ..., хп)|/(хь ..., xn) = c}CR"
называется поверхностью уровня функции /. Таким
образом, на поверхности уровня функция / имеет
постоянное значение. В
случае п = 2 это точечное
множество называется линией
уровня.. Линия уровня — это
спроектированная на
плоскость Xi0x2 кривая
пересечения графика функции / с
плоскостью, параллельной
плоскости Xi0x2.
Примеры. 1) Линии уровня
функции y=f(xu x2) = x? + xi
/)(/)=R2, суть окружности с Рис. 3.5
центром в точке @, 0). Если
пересечь график f плоскостью,
содержащей ось у, то полученная кривая пересечения будет
параболой. Таким образом, график функции / представляет собой
параболоид вращения (рис. 3.5).
2) Линии уровня /(хь х2) = х^г, ?>(/) = R2, суть
гиперболы (или пара пересекающихся прямых — при с = 0).
График функции/-гиперболический параболоид.
3) График функции Дхь х2) = X! + х2, D (/) = R2,-
плоскость, содержащая точку @, 0). Линии уровня/- прямые.
Функция /, где D (/) е R", называется
ограниченной сверху (снизу) на Е с D (/), если множество
{/(хь ..., х„)|(хь ..., хп)еЕ] ограничено сверху
(снизу) в R. Функция / называется ограниченной на
Е, если / ограничена на Е как сверху, так и
снизу.
Пусть функция / ограничена на Е a D(f) a R"
сверху (снизу). Верхняя (нижняя) грань множества
М = {/(х,) | (Xi)eE) значений функции/на Е обозна-
' чается sup f(xt) (inf f(xt)).
(xt)eE (xt)eE
Если sup/ (inf/) на множестве Е принадлежит
множеству М, то ее называют наибольшим
(наименьшим) значением функции f на Е и обозначают через
max f(xt)
(xt)eE
( min f(xt)).
(x,)eE
Примеры. 1) Функция f(xl4 x2) = x\ + x|, D(f) = R2
ограничена на D(f) снизу, но не является ограниченной
сверху.
2) Функция /(хь х2) = х, + х2, D (/) = R2, ограничена на
2
224
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Функция/такая, что D (/) a R", называется
однородной степени к, если для любого
действительного числа X > О и любого (хь ..., xn)eD (f) точка
(А,хь ..., Ъс„) лежит в D (/) и имеет место равенство
f(Xxu ..., Ъси) = ^/(*ь .... хн).
Теорема Эйлера. Если однородная функция / с
показателем однородности, равным к,
дифференцируема, то имеет место соотношение
- = /с/(хь...,хй).
dxt
Примеры. 1) Квадратичная форма f(xt, ..., х„)
/>(/) = R2,- однородная степени 2.
{(*»
2) Функция /(хь ..., хя)=
i >0, t
1, ..., и},-однородная степени -1/2.
3.1.4.2.2. Пределы, функций многих
переменных. Определения предела из 3.1.4.1.2
теперь обобщаются следующим образом. Пусть
функция / определена в некоторой окрестности
точки Ро (xf) eD(f) a R", за исключением, быть
может, точки Ро. Функция / имеет в Ро предел,
равный А и обозначаемый lim /(Р) = А, если для
Р-*Р0
каждого е > О существует такое 5 > 0, что для
всех точек Р(х,), удовлетворяющих условию
О < d(P, Ро) < 5, имеет место неравенство \f(P) —
- А | < е.
Пусть функция / определена в некоторой
окрестности точки Ро, за исключением, быть может,
самой точки Ро. Функция / имеет в точке Ро
предел, равный А, тогда и только тогда, когда
для любой последовательности точек {Рт} такой,
что Рт G D (/), Рт Ф Ро и lim Рт = Ро, имеет место
т -* оо
равенство lim f(Pm) = A.
I т —* оо
Пусть область определения функции / не
ограничена в R". Функция / имеет при Р -> оо предел,
равный А и обозначаемый lim f(P) = А, если
Р->00
для любого е > 0 существует число Ъ > 0 такое,
что для всех PeD(f), удовлетворяющих условию
d(P, 0) > b, имеет место неравенство \f(P) - А\ <е.
Теоремы о пределах из 3.1.4.1.2 легко
обобщаются на функции многих переменных.
Примеры. 1) Для всех Р0(х?, xf)eR2 справедливо
соотношение
(x,H(x?)
2) Функция
(Х2-Х?J
О
при (х„ х2) Ф @, 0),
при (xi, х2) = @, 0)
не имеет предела в точке @, 0): если, например, рассмотреть
последовательность {\/к, 1//с2}, то получим lim {1/&, \/к2} =
к-*сс
= @, 0), a lim /A/Лс, 1/к2) = + оо.
к-* оо
3.1.4.2.3. Непрерывные функции
многих переменных. Функция / называется
непрерывной в точке PoeD (/) с R", если для
каждого б > 0 существует такое 5 > 0, что для
всех PeD(f), удовлетворяющих условию d(P,
Ро) < 8, имеет место неравенство
Таким образом, если f непрерывна в точке Ро,
то для любой е-окрестности /(Ро) существует
такая 8-окрестность U6 (Ро) точки Ро, что для
всех Pet/s(P0) значения функции f(P) лежат в
е-окрестности f(P0).
Пример. Функция /(хь ..., х„) = ? хк, D(/) = R",
непрерывна во всех точках Р(х?, ..., x°)eD(/). Если
указать произвольное е > 0 и положить 8 = e/j/и, то для
всех Р(хь ..., х„), удовлетворяющих условию d(P, P0)<b,
на основании неравенства Коши - Буняковского получим, что
I Ixk-x?|<
I (** " 4)
Функция / определенная в окрестности Ро,
непрерывна в Ро тогда и только тогда, когда /
имеет в Ро предел, равный значению функции в
этой точке, т.е. когда lim f(P) — f(P0).
Функция / определенная в окрестности точки
Ро, непрерывна в Ро тогда и только тогда, когда
для всех последовательностей точек {Р,}, для
которых PiED(f) и hm Р, = Ро, выполняется равен-
/ ~> ОО
ство \imf(Pt)=f{P0).
/-»• 00
Пример. Функция
при (хь х2) Ф @, 0),
О при (хь х2) = (О, О),
имеет разрыв в точке @, 0), так как последовательность
{1/к, 1/к} имеет предел lim {1/к, 1/к} - @, 0), a lim f{\/k,
к-юо к->со
1/к} = 1/2 #/@, 0).
Из непрерывности функции / следует, что
математические операции lim и / можно
переставлять: если найти вначале значения функции /(Р«),
а затем предел lim /(Pj), то получим значение
/-+ ОО
функции в точке предела lim Р, = Ро.
1-> 00
Определения и теоремы для непрерывных
функций одного переменного (см. 3.1.4.1.4)
можно перенести на функции многих переменных.
Функция / называется непрерывной на
множестве Е cz R", если она непрерывна во всех
точках множества Е.
Функция / называется равномерно непрерывной
на множестве Е, если для любого е > 0
существует 5 > 0 такое, что для любых Рь Р2еЕ,
удовлетворяющих условию d(Pu P2) < 5, выполнено
неравенство |/(Pi) -f(P2) I < е-
Пусть заданы п функций фь ..., (р„, таких, что
и
D ((ft) с: R\ P| D (ф,) = D ф 0 (i, j = \, ..., n), и
ОПРЕДЕЛЕНИЕ И ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПЕРВОЙ ПРОИЗВОДНОЙ
225
функция/, такая, что [<pi{ti, ..., tk), ..., Ф„(?ь ...
..., tk))eD(f)cz R" для всех (tu ..., tk)eD.
Отображение F, которое каждому набору к чисел
(tx, ..., tk)eD ставит в соответствие число
F{tu •••, '*)=/[<Pi('b ••-, tk), ..., фи(гь ..., tk)],
называется сложной функцией.
Пример. Пусть ф, (f)~cosf, ф2(f) = sinr, ?>(ф,)«
»Р(ф2)-[0, 2я) и f(xu x3)«xi + xi, 0(/)«RA Тогда
F(t)-j (cos t, sin 0 * cos21 + sin2 f - 1, D{F)~ [О, 2я). F (t)
является сложной функцией.
Свойства непрерывных функций.
1) Сумма, разность и произведение
непрерывных функций являются непрерывными
функциями. Частное непрерывных функций -
непрерывная функция в точках, в которых знаменатель
отличен от нуля.
2) Если / непрерывна в точке Ро и /(Ро) > 0
(/(Ро) < 0), то существует окрестность U (Ро)
точки Ро такая, что для всех Ре U(P0)f] D(f)
выполнено неравенство /(Р) > 0 (/ (Р) < 0).
3) Если / непрерывна на ограниченном
замкнутом множестве Е, то / ограничена на Е.
4) Всякая непрерывная на ограниченном
замкнутом множестве Е функция равномерно
непрерывна на Е.
5) Всякая непрерывная на ограниченном
замкнутом множестве Е функция достигает на нем своих
наибольшего и наименьшего значений.
6) Теорема о промежуточном значении. Если /
непрерывна в области*) Е и f(P]) = a, f(P2) = b
для Рь Р2е?, причем а < Ь, то для каждого
уе(а, Ь) найдется точка РеЕ, в которой /(Р) = у.
7) Если / непрерывна на D (/) cR" и функции
фь ..., ф„ непрерывны на /)(ф,) cR"(i = l, ..., п),
то сложная функция F, составленная из / и
фь ..., ф„, непрерывна на D(F).
3.1.5. ДИФФЕРЕНЦИРОВАНИЕ
ФУНКЦИЙ ОДНОГО
ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО
3.1.5.1. Определение и геометрическая
интерпретация первой производной. Примеры. Если / —
функция одного переменного и хое(а, Ь), то
функция ф, определенная равенством
-/_» /М-/(*о)
называется разностным отношением функции /
в точке х0**).
Геометрическая интерпретация.
Пусть на графике функции / в координатной
системе х, у заданы фиксированная точка Р0(х0, Уо) и
подвижная точка Р(х, у), и пусть секущая,
проведенная через эти точки, образует угол р с
положительным направлением оси х. Тогда
t Ay = у'-уо
Ах х — х0
f(x)-f(x0)
х — х0
Разностное отношение функции / в точке х0 равно,
таким образом, угловому коэффициенту секущей,
проведенной через точки Р и Ро (рис. 3.6).
*) Напомним, что область связна.
**) Следует обратить внимание на то, что х0 —
фиксированная точка.
Функция / называется дифференцируемой в
точке хое(а, Ь), если существует предел
разностного отношения функции / в точке х0:
/М-/Ы
lim ф (х) = lim
х -> х0 х -> х0
х - х0
Этот предел называется производной функции / в
точке х0.
ах ах ах х = х0
Геометрическая интерпретация.
Если на графике функции подвижная точка Р(х, у)
стремится к точке Ро (х0, у0) (см. рис. 3.6), то, вообще
говоря, изменяется также угловой коэффициент
секущей. Если существует производная функции /
в точке х0, то прямую, проходящую через точку
^о (*о, У о) и такую, что tg (а) = /' (х0), где а - угол
наклона этой прямой, называют касательной к
графику функции/в точке Ро (х0, yQ). Таким образом,
уравнение касательной есть у — /(х0) =/'(хо)(х —
-х0).
Функция / называется дифференцируемой справа
(слева) в точке х0, если существует предел справа
(слева) lim ф(х) ( lim ф(х)) разностного
х->хо + 0 х-*хо — 0
отношения ф в точке х0. Этот предел
называется производной справа {слева) функции f в точке
х0 и обозначается /'+ (х0), /' (х0 + 0) (/'_ (*о), /' (*о -
-0)).
Если существует /' (х0), то функция /
дифференцируема справа и слева в точке х0 и /'+ (х0) =
= /'_ (х0) = /' (х0). Обратно, если существуют
односторонние производные /'+ (х0), /'_ (х0) и /'+ (х0) =
= /'_(х0), то существует также f'(x0) =/'+ (х0) =
= /'-Ы.
Функция / называется дифференцируемой на
множестве Е, если она дифференцируема во всех
точках хоеЕ*). Функция / называется
дифференцируемой, если она дифференцируема на D(f).
Если / дифференцируема, то функция /',
определенная соответствием х->/'(х), называется
производной функции f.
Примеры. 1) Функция /(х) = х дифференцируема в
каждой точке .xoeR, и
М= Ит
f(x)-f(x0)
lim
¦ х0
*) Функция f, дифференцируемая на Е = [а, Ь], должна
быть дифференцируема в точках а и h односторонне
8 И. Н Бронштейн, К А. Семендяев
226
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Таблица 3 2
Функция
С (const)
X
xn
1
X
1
}х
l7x
shx
ах
lnx
logex
lgx
sin x
cosx
tgx
ctgx
secx
Производная
0
1
их"
1
x2
n
xn+1
1
¦if*
1
ch x
a*ln x
1
1 1
— loga e = —
x xln a
1 j 0,4343
x ~ x
cosx
— sinx
5— = sec2 x
cos x
1 ,
r-5— = —cosec x
sin x
sinx
— = tg x sec x
cos^x
Функция
cosec x
arcsin x
arccos x
arctg x
arcctg x
arcsec x
arccosec x
ch x
thx
.cthx
Arshx
Archx
Arth x
Arcth x
Производная
cosx
—^—= — ctgxcrsecx
sin x
1
1
|/ 1 — x2
1
1 '
x j/x2 - 1
1
sh x
1
ch2 x
1
1
l/F+~x2
l
1
Г-Х2"
2) Для функции f(x)~C (С - постоянная) имеем
ГЫ-о.
3) Показательная функция f(x) = е* дифференцируема,
и fix)-f'{x) Для всех -xeR-
4) Для всех xeR имеем (sinх)'= cosx, (cosx)'= -sinx.
5) Любой степенной ряд дифференцируем во всех
точках, лежащих внутри интервала сходимости.
6) / (х) = ]/х не является дифференцируемой в точке
х0 = 0, так как не существует конечного предела
не дифференцируема в точке х0 = 0, так как не существует
предела lim sin(l/x).
х-*-0
8) f(x) = | х | является дифференцируемой справа и
слева в точке х0 = 0. Но так как /'+@) = +1, /1@)= -1,
то / не дифференцируема в точке хо = 0.
Графики функций из примеров 6) - 8) показаны
соответственно на рис. 3.7, а — в. Они не обладают
касательными в точке @, 0)*).
9) Пусть /"дифференцируема и / (х) > 0 для всех xeD(f).
Г
Производная функции In f, т. е. (In /)' = --, называется
логарифмической производной функции /.
10) Для вычисления производной функции /(х) = х\
D(f)= {x | х > 0}, следует найти вначале
логарифмическую производную (In f(x))' - j = In x + 1. Отсюда
получается f'(x) = x*(ln x + 1).
Производные важнейших элементарных
функций приведены в табл. 3.2.
3.1.5.2. Производные высших порядков. Пусть
производная /' функции / дифференцируема в
точке xoeD(f). Тогда (f'(x))'\x = Xo называется
второй производной функции / в точке х0.
Обозначение:
. „„, VL.
Г Ы - /(
7) Функция
хо) = -jjprf(*o) = (d2fldx2) (x
fix)-
Г xsin(
I о
in(l/x) при х / 0,
при х = 0
*) По определению каса гельная к графику функции не
может быть вертикальной.
СВОЙСТВА ДИФФЕРЕНЦИРУЕМЫХ ФУНКЦИЙ
227
Действуя подобным образом, определяют п-ю
производную, или производную п-го порядка, функции
/ в точке х0:
/(п) (*о) = (/(и} W)' I х = Хо = ?гЯ*о).
Производные /C), /D), /E), f{6\ ... обозначаются
также/,/™,/v,/VI, ...
Если существует /(п)(х0), то функция /
называется п раз дифференцируемой в точке х0. Имеет
место следующее равенство:
Функция / называется п раз непрерывно
дифференцируемой на множестве Е, если она п раз
дифференцируема в точке хеЕ и /(и) непрерывна
на Е.
Пример, п-я производная многочлена и-й степени есть
постоянная.
Дальнейшие примеры производных высших
порядков элементарных функций приведены в
табл. 3.3.
Таблица 3.3
Функция
Xю
lnx
log^x
/х
sinx
COSX.
sinA:x
cosfcx
shx
chx
n-я производная
m(m - \){m - 2)...{m -n+ l)xm~"
(при целочисленном т и п > m
л-я производная равна 0)
( пя-1 (Я--1)! 1
( } lna xn
knekx
(\na)nax
(kin afakx
sinU-^-)
cosvx+^-;
kncos(kx+^-\
shx при четном n, chx при
нечетном n
ch x при четном л, sh x при
нечетном n
3.1.5.3. Свойства дифференцируемых функций.
1. Функция, дифференцируемая в точке х0,
непрерывна в этой точке.
2. Пусть функции/! и/2 дифференцируемы в точке
х0. Тогда функция Ci/t + c2/2, где сь c2eR, также
дифференцируема в точке х0 и
(ci/i + c2/2)' | Хо = cj\ (х0) + с2/'2 (х0).
Произведение fxf2 также дифференцируемо в
точке х0, и имеет место следующее правило диффе-
(ЛЛП,
8*
»(хо)/2 (^о) + /i (^о)/2 (^о)-
В случае, если /2{х0)^0, частное fjf2
дифференцируемо в точке х0, и имеет место следующее
правило дифференцирования дроби:
/'1Ы/2Ы-/1Ы/2М
(/2ЫJ
Примеры. 1) Функция
руема в точке xoeR, и
е» sin x дифференци-
f (х0) = f xo (sin х0 + cos x0).
2) Функция /"(x) = tg.v дифференцируема в точках
xeR\{x|x = B/c+ l)ic/2, k = О, ±1, ±2, ...},
ГЫ-
cos2 х0 + sin2 х0
I + tg2x0 = —2—•
cos2 x0
3. Пусть функции / и ф дифференцируемы
соответственно в х0 и t0, и пусть х0 = <р (t0).
Тогда сложная функция /((p(f)) дифференцируема
в точке to и обладает производной
(/ (ф))' If = г0 = /' [Ф Ml - Ф' ih)-
Примеры. 1) Функция f(x) — e"nx дифференцируема
в точках xoeR, и
(л-0)
sin ло cos л0.
2) Показательная функция общего вида f(x) = ах
{а > 0) дифференцируема в точке xoeR, и так как а* = ех1па,
то
4. Пусть функция / дифференцируема и строго
монотонна на (а, Ь). Пусть также в точке хое(а, Ь)
производная /' (х0) не равна нулю. Тогда обратная
функция д(у) дифференцируема в точке у0 =/(х0),
и ее производная есть
(д(у))'\
'У = Уо '
ГЫ'
Примеры. 1) Показательная функция f(x) = e*
удовлетворяет условиям теоремы 4. Следовательно.
g (у) = In у дифференцируема в точке у0 = ех°. Ее производная
есть
2) Для xgR имеем (arctgx)' = Т.
5. Если функции /i и /2 и раз дифференцируемы
в точке х0, то функция /j/2 также п раз
дифференцируема в точке х0, и имеет место формула
Лейбница:
если считать, что/|0) (х0) =/, (х0) (/ = 1, 2).
Для функций, дифференцируемых в интервале,
имеют место следующие теоремы.
Теорема Ролля. Пусть функция / непрерывна на
[а, Ь] и дифференцируема в (а, Ь). Если/(а) =/(Ь),
то найдется по крайней мере одна точка хое(а, Ь),
в которой /' (х0) = 0.
Таким образом, при выполнении
предположений этой теоремы график функции / имеет в точке
х0 касательную, параллельную оси х. Из теоремы
228
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Ролл я следует, в частности, что между двумя
нулями многочлена находится по крайней мере один
нуль производной этого многочлена.
Теорема Лагранжа (о конечном приращении).
Если функция / непрерывна на [а, /?] и
дифференцируема в (а, Ь\ то найдется по крайней мере одна
точка хое(а, Ь), в которой
При х0 = 0 этот ряд называется также рядом
Маклорена. Следовательно, если lim Rn(x) = 0
п -> оо
при хе(х0 — а, х0 + а), то функция/(х) может быть
аппроксимирована в (х0 — а, х0 + а) многочленом
и-й степени / ^—(х — xo)v (см. также 3.1.14.6).
/ , v!
J\x«>- ь-а ¦
Положив Ъ — а = к и 0 = (х0 — а)/к, получим
k)=f(a)+f'(a + Qk)k, причем 9е@, 1).
Геометрическая интерпретация.
Если для функции/выполняются условия теоремы
Лагранжа, то к графику функции / можно
провести по меньшей мере одну касательную,
параллельную секущей, проведенной через точки {а,
f(a)), (b, f(b)). Теорема Лагранжа является
обобщением теоремы Ролля.
Если / дифференцируема на {а, Ь) и f (х) = О
для всех хе(а, Ь), то / (х) = С = const.
Теорема Коши. Пусть функции fug непрерывны
на [а, Ь~\, дифференцируемы в (а, Ь), и пусть
д'(х) ф О для всех хе(а, Ь). Тогда существует по
крайней мере одна точка хое(а, Ь), в которой
9' (xq) g (b) - g (a)'
Пусть функция / дифференцируема п + 1 раз в
(х0 — а, х0 + а) (а > 0). Тогда для всех хе(х0 —
— а, х0 + а) имеет место формула Тейлора:
/м =
-(х-ХоГ + Я„М =
(л+1)!
~(х -xo)v + rn+l(x),
6е@, 1).
Величина Rn(x) называется остаточным
членом {в форме Лагранжа) формулы Тейлора.
В частном случае, когда х0 = 0, получается
формула Маклорена:
В случае п = 0 формула Тейлора сводится к
теореме Лагранжа. Если f бесконечно
дифференцируема в (х0 — а, х0 + а) (i.e. имеет в (х0 — а,
х0 + а) производные всех порядков) и для всех
хе(х0 — а, х0 + а) имеет место равенство
lim Rn(x) = 0, то функцию / можно представить
П-* 00
в виде суммы ряда Тейлора:
Пример. Показательная функция /(х) « е* бесконечно
дифференцируема в R. Из соотношения /"" ¦ / для всех
weN получается формула Маклорена:
Zv! (й+1I
Для каждого xeR имеем lim —-х" + 1-0, и,
("+ 1)'
00
> —
следовательно, ё*« > —г. В частности, отсюда следует:
3.1.5.4. Монотонность и выпуклость функций.
Функция /, дифференцируемая на (а, Ь), возрастает
(убывает) на (а, Ь) тогда и только тогда, когда
/'(х)^0 (/'(х)^0) для всех хе(а, Ь). Если при
этом не существует интервала (а, р) с (а, Ь) такого,
что f'(x) = O для всех хе(а, р), то j строго
возрастает (убывает).
Таким образом, угол наклона касательной к
графику дифференцируемой возрастающей
(убывающей) функции является неотрицательным
(неположительным).
Если для дифференцируемой функции /: а)
/(х0) ^ 0, б) для каждого х ^ х0 выполняется
условие /' (х) ^ 0, то /(х) ^0 при х ^ х0.
Примеры. 1) Для функции f(x)«е* при любом
xeR имеем /'(х) *=/(х) > 0. Следовательно, / строго
возрастает на R.
2) Функция /(x) = x-sinx строго возрастает на / =
= @, 2тс), так как для хе/ имеем /'(х) = 1 — cosx > 0.
Поскольку /@) ш 0, то / (х) ш х - sin х > 0 при хе/, а отсюда
и при всех х > 0.
3) Функция /(х) = е~* + х- 1 строго возрастает на
[0, +оо), так как f (х) =* -е~х + 1>0 при х > 0. Отсюда,
так как /(х) «= 0, следует, что /(х) > 0, т. е. е~х > 1 - х при
х>0.
Дифференцируемая на (а, Ь) функция/называется
выпуклой вниз (соответственно строго выпуклой
вниз) на {а, Ь), если f(x2)^f(xl)+f'(xl)(x2-x1)
(соответственно
f(x2)>f(xl)+f'{xl)(x2-xl))
для любых хь х2е(а, Ь) таких, что X! Ф х2.
Дифференцируемая на {а, Ь) функция /
называется выпуклой вверх (соответственно строго
выпуклой вверх*)), если /(х2) </(*i) +f'{xi)(x2 - Xi)
(соответственно f(x2) < f (xx) +f(x1)(x2 - хг)) для
любых хь х2е(а, Ь) таких, что хх ф х2.
для всех хе(х0 — а, х0 + а).
*) Часто в литературе используют вместо «выпуклый
вниз» термин «вогнутый», а вместо «выпуклый вверх»
просто «выпуклый», такая терминология имеется и в
некоторых разделах этого справочника.
ЭКСТРЕМУМЫ И ТОЧКИ ПЕРЕГИБА
229
Геометрическая интерпретация
выпуклости функции. Из неравенств,
указанных в определении выпуклости, следует, что
график функции /, выпуклой вниз, нигде не лежит
под касательной к нему. Если /строго выпукла вниз,
то график /, за исключением точки касания, всегда
лежит над любой касательной к нему.
Соответствующие утверждения имеют место и для случая
выпуклости вверх.
Пример. Функция/(х) = х2 строго выпукла вниз в
D{f) = R, так как для любых х,, x2eR таких, что xt Ф х2,
выполнено неравенство х\ > х? + 2хх (х2 - ху) = 2х!Х2 - х?.
Критерии выпуклости функции.
1. Дифференцируемая на (а, Ь) функция/выпукла
вниз (вверх) на {а, Ь) тогда и только тогда, когда
/' возрастает (убывает) на (а, Ъ). Функция / строго
выпукла вниз (вверх) на (а, Ь) тогда и только тогда,
когда /' строго возрастает (убывает) на (а, Ь).
2. Дважды дифференцируемая в (а, Ь) функция
/выпукла вниз (вверх) на (а, Ь) тогда и только тогда,
когда для всех хе(а, Ъ) имеет место неравенство
Примеры. 1) Показательная функция f(x) = ex
строго выпукла вниз на R, так как для любого xeR
имеем: /' (х) = ё* > 0 - строго возрастающая в R функция.
2) Функция/(х) = cos х строго выпукла вверх в интервале
(-я/2, я/2), так как для всех хб(-я/2, я/2) имеем /"(х) =
« - cos х < 0.
3.1.5.5. Экстремумы и тонки перегиба. Пусть
функция / определена на (а, Ь), и пусть х0 е (а, Ь).
Значение /(*,) называется локальным минимумом
{максимумом) функции / на {а, Ь), если существует
окрестность U (х0) точки х0 такая, что U (х0) а (а, Ь),
и для всех xeU(xo)\{xo} выполнено неравенство
Максимум или минимум функции / называется
{локальным) экстремумом функции / на (а, Ь).
Экстремумы функции/на (а, Ь) являются, таким
образом, наибольшими или наименьшими
значениями функции относительно некоторой
окрестности. Они отличаются, вообще говоря, от
наименьшего т = min /(х) и наибольшего М =
хе(а, Ь)
= max /(x) значений функции на всей области
хе(а, Ь)
определения. Если, однако, / выпукла вниз (вверх)
на {а, Ь) и имеет минимум (максимум) в {а, Ь), то он
совпадает с т(М). Наибольшее (наименьшее)
значение функции / дифференцируемой на [а, Ь],
достигается либо в одной из точек локального
максимума (минимума), либо на одном из концов
отрезка [а, Ь]. Таким образом, если множество
локальных максимумов (минимумов) конечно и
если известны все локальные максимумы
(минимумы) функции / на [а, Ь] и значения функции
в точках а и Ь, то перебором можно определить
max /(х) ( min /(х)).
хе[а, Ь\ хе[а, Ь]
Пример. /@I=0 является локальным минимумом
функции/(х) = х2 на [-1, +1], который совпадает с
наименьшим значением /на [—1, +1].
Необходимое условие существования
экстремума. Если/(х0) является экстремумом
дифференцируемой функции / то /' (х0) = 0. Касательная к
графику функции / проходящая через точку
(*о» /(хб))> параллельна оси х.
Пример. Так как /@) = 0 является минимумом
функции /(х) = х2, то /' @) = 0.
Достаточные условия существования
экстремума.
1. Если/дважды дифференцируема в точке х0 и
/'(хо) = 0, а /"Ы>0 (/"(хо)<0), то функция /
имеет в точке х0 локальный минимум (максимум).
2. Пусть / к раз дифференцируема в точке х0.
Далее, пусть /(v)(x0) = 0 при v = 1, ..., к — 1 и
f{k) (хо) Ф 0- Если к четное, то / имеет в точке х0
при f(k) (х0) > 0 минимум и при /(к) (х0) < 0
максимум. Если к нечетно, то экстремума нет.
Примеры. 1) Функция /(х) = х4 имеет локальный
минимум в точке х0 = 0, который совпадает с абсолютным
минимальным значением / в R, так как / в R четыре раза
непрерывно дифференцируема и
/'@) =/"@) =/'"@) = 0, /<4>@) = 4! > 0.
2) Для функции /(х) = х3 в точке х0 = 0 выполняется
необходимое условие экстремума /'@) = 0. Однако /@) = 0
не является точкой экстремума функции /.
3) Функция /(х) = х3 + х2 — х — 1 имеет минимум в
точке х0 = 1/3 и максимум в точке х2 = -1. Однако,
поскольку lim /(х) = - оо, lim /(х) = + оо, у функ-
х -* — оо х-» + оо
ции / в R нет наибольшего и наименьшего значений.
4) Пусть среди прямоугольников с одинаковым
периметром необходимо найти максимальный по площади.
Если а, Ь — длины сторон прямоугольника, то его площадь
равна S = fl'ft. Из условия Р = 2{а + b) = const > 0 следует,
что Ъ - Р/2 - а и S {а) = а (Р/2 - а). Решение задачи сводится,
таким образом, к нахождению максимального значения
функции S, где D(S) = [0, Р/2]. Уравнение S'(a)=-2fl +
+ Р/2 = 0 имеет единственное решение а0 = Р/4. Так как
S"(a0) = — 2 < 0, то S имеет в точке а0 = Р/4 локальный
максимум, который вследствие того, что S @) = S (Р/2) = 0,
совпадает с максимальным значением S. Искомый
прямоугольник есть квадрат со стороной а = Р/4.
5) Пусть заданы п значений измеримой величины
я,, ..., а„. Число х (среднее значение) должно быть
определено так, чтобы сумма квадратов отклонений величин
ак от х принимала минимальное- значение, т. е. надо
определить минимум функции
/W-I К-*J> *>(/) = R-
Уравнение /'(х) = — 2 ? (ак — х) = 0 имеет
единственна 1
ное решение х0 = — ? ак. Из того, что /" (х0) = 2п > 0,
п * = i
следует, что / имеет в точке х0 локальный минимум,
который совпадает с минимальным значением / в R.
Искомое среднее значение равно среднему арифметическому
значений измеряемой величины.
Предположения о дифференцируемости функции
/ в необходимых (соответственно достаточных)
условиях экстремума могут не выполняться, но тем
не менее функция / может иметь экстремумы.
Например, функция /(х) = | х | не дифференцируема
в точке х0 = 0, однако имеет в ней минимум. В
подобных случаях нужно пытаться найти значения
экстремумов непосредственно на основе
определения. При этом важным вспомогательным средством
являются соображения о монотонности вблизи
исследуемых точек. Функция /(х) = | х |, например,
является строго убывающей при х < 0 и строго
возрастающей при х > 0. Следовательно, /@) = 0
является ее минимумом.
Пусть функция/дифференцируема в некоторой
окрестности точки х0. Функция / имеет в точке
230
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
х0 точку перегиба тогда и только тогда, когда
функция/' имеет в точке х0 локальный экстремум.
Геометрическая интерпретация.
Если/имеет в точке х0 точку перегиба, то график
функции / в точке (х0, f(x0)) «перегибается» через
касательную к нему в этой точке, т. е. в некоторой
окрестности точки х0 кривая при х < х0 и гфи
х > х0 лежит по разные стороны от касательной.
Необходимое условие существования точки
перегиба. Если функция / дважды дифференцируемая
в некоторой окрестности точки х0, имеет в х0
точку перегиба, то /" (х0) = 0.
Достаточное условие существования точки
перегиба. Если / в некоторой окрестности точки
х0 к раз дифференцируема, причем к нечетно,
к > 3, и/(у)(х0) = 0 при v = 2, 3,... ,к - 1, а/(к)(х0) Ф
ф 0, то функция / имеет в х0 точку перегиба.
Примеры. 1) Функция /(х) = х3 имеет в точке х0 = 0
точку перегиба, так как /" @) = 0, /'" @) « 6 Ф 0.
2) /(x) = sinx имеет в хо=0 точку перегиба;
/"@) = - sinO = 0, /'"@) = - cosO - - 1 Ф 0.
3.1.5.6. Элементарное исследование функции.
При помощи дифференциального исчисления во
многих случаях можно получить представление о
поведении графика функции, не заполняя подробных
таблиц значений функции, которые в большинстве
своем неудовлетворительно отражают важнейшие
качественные свойства функции, такие, как точки
разрыва, локальные экстремумы или нули функции.
Такое исследование функции включает в себя
приведенные ниже этапы, которые могут быть
проведены на основе методов, описанных в 3.1.4.1,
3.1.5.4 и 3.1.5.5.
1. Определение нулей функции /(решение
уравнения/(х) = 0), четности (нечетности) и периодичности.
2. Определение интервалов непрерывности и
дифференцируемости.
3. Классификация точек разрыва функции /
и исследование ее поведения «на бесконечности».
4. Определение локальных экстремумов и точек
перегиба.
5. Определение интервалов монотонности и
выпуклости.
6. Вычисление соответствующих значений
функции.
7. Выполнение эскиза графика функции.
Пример. Будем исследовать график функции
— при х > 2,
Х2+1
X2 - 1
— 4х
4) Единственное решение уравнения /' (х) = -г~г—~7\г~
= 0
/(*)•
при х < 2.
1) Функция / не имеет нулей.
2) / непрерывна на R\{1, -1}. Так как /'_ B) = -8/9,
/'+ B) = 0, то / не дифференцируема в точке Xi = 2.
Следовательно, функция / дифференцируема на R\{2, 1, —1}
(см. 3.1.5.3).
3) При х < 2 /(х) = (х-1J(х+1) + 1. Точки х2 = 1 и
х3 = — 1 являются, таким образом, точками разрыва 2-го
рода. Далее,
lim f(x)
l0
lim f(x) = + oo,
l0
lim /(x) = lim f(x) = — oo,
l0 l0
lim f{x) = 5/3, lim f(x) = 1.
-» + 00 X-* — 00
есть x0 = 0. При x < 2 и х ф ± 1 получим, что /" (x) =
= ~г—тгу-. Из того, что /"@)= -4<0, следует, что /
(X 1)
имеет в 0 локальный максимум. Функция / не достигает в
области определения наибольшего и наименьшего значений.
Так как у уравнения /"(х) = 0 нет действительных
решений, то / не имеет точек перегиба.
5) При хе(-оо, -1) и хе(- 1, 0) /'(х) > 0.
Следовательно, / строго возрастает в этих интервалах. При хе@, 1) и
хеA, 2) f'(x) < 0, откуда следует, что/строго убывает в этих
интервалах.
/ 2
Рис. 3.8
При хе(—1, +\)f"(x)<0 и, следовательно, / строго
выпукла вверх в (-1, +1) При хе(-оо, -1) и хеA, 2)
/"(х)>0. Следовательно, / строго выпукла вниз в этих
интервалах (рис. 3.8).
3.1.6. ДИФФЕРЕНЦИРОВАНИЕ
ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
3.1.6.1. Частные производные, геометрическая
интерпретация. Пусть функция / определена в
некоторой окрестности точки Ро (х?,..., xj) e R". Функция
/называется дифференцируемой по хк, если
существует предел разностного отношения
lim (/(.х?, ..., х?_ь хк, х?+ь ..., х„0)-
х*->х?
— J\XU ..., Xk-i, Xk, Xk+iy ..., Xn))/(Xk — Xk),
этот предел называется частной производной
функции f (по хк) в точке Ро и обозначается
df(xl x*l о 0
dxk Jхк\ и , п)
Частная производная функции / по хк в точке
Ро (х?, ..., xj) равна, таким образом, обыкновенной
производной функции действительного
переменного хк, которая получается из /, если переменные
х, для i Ф к положить равными xf.
Функция / называется дифференцируемой по
каждому из переменных в EcD(f), если для /
на Е существуют частные производные по каждому
из переменных хь ..., хи. Функция / называется
непрерывно дифференцируемой в точке PoeD(f),
если/дифференцируема по каждому из переменных
в некоторой окрестности точки Ро и все частные
производные df/dxk (k = 1, ..., п) непрерывны в Ро.
Пример. Функция /(х,, х2) = r*i sinх2
дифференцируема по каждому из переменных в R2, и
f'xx (х?, х!0 = ех° sin xl f'x2 (х?, х°2) . ех° cos x°2;
более то о, / является непрерывно дифференцируемой в R2.
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ, ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ, ГРАДИЕНТ
231
При п > 1 из дифференцируемости/в точке Ро по
каждому из переменных не следует, вообще говоря,
непрерывность / в точке Ро. Функция / из
примера 2) в 3.1.4.2.2 разрывна в точке @, 0), несмотря
на то, что / дифференцируема в @, 0) по Xj и х2:
Л,(о, о) = /;2(о, о) = о.
Геометрическая интерпретация
частной производной. Пусть /- функция
двух переменных, дифференцируемая по каждому
из переменных в точке Ро(хо, Уо)- Рассмотрим
плоскость П, проходящую через точку Р0(х0, у0)
параллельно плоскости xOz, т. е. плоскость у = у0.
По определению f'x(x0, y0) есть число, равное
tg ф, где ф - угол между касательной к кривой
пересечения плоскости П и графика (см. 4.1.4.4)
функции / и плоскостью хОу (рис. 3.9).
Рис. 3.9
Соответственно f'y(x0, Уо) представляет собой
тангенс угла наклона касательной к кривой
пересечения плоскости х = х0 с графиком функции /
и плоскость хОу.
Производные высших порядков. Пусть функция /
на открытом множестве Е a D (/) с: R"
дифференцируема по хк. Тогда f'Xk является функцией с
областью определения D itf'Xk) = Е. Функция /
называется в точке РоЕЕ дважды дифференцируемой
(по хь х,), если функция /^ в точке Ро
дифференцируема по х,. Для второй производной / по хк и х,
используется обозначение —z—\ или Гхкхг (Ро)-
Посредством полной индукции определяют
частную производную r-го порядка:
д / У1/ \ I = d'f(p0) =
Ч\ dxir-, • • • dxh ) I ро = дх/г• • • 6xh x'i '"Х'Г о)'
Пример. Для функции / = rx' sin x2 имеем
f"Xx
При определенных предположениях можно
менять порядок вычисления частных производных
функции. Пусть / непрерывна в некоторой
окрестности U (Ро) точки Ро g R". Если существуют частные
производные/'^,/'^, f"xx в U (Ро) и они непрерывны
в точке Ро, то существует частная производная
/x,xfc B ро и f'XlXk(Po) = /Wo)-
3.1.6.2. Полный дифференциал, производная по
направлению, градиент. Пусть область
определения D(f) функции / содержит окрестность точки
P0(xi> •••» *?), п ^ 1. Функция / называется
дифференцируемой в точке Ро, если для любых
Р(хи ..., х„) из этой окрестности
f(P) - /(Ро) = t f'Xk
- X°k) + р (Р, Р0) *! (Р),
где р (Р, Ро) = |/kE (xk - хк0J и ^lim Rt (P) = 0.
Линейная часть
df(P)= if'Xk(Po)(xk-x°k)
приращения f(P) —/(Ро) называется полным
дифференциалом функции / в точке Ро.
График функции / определяемой равенством
называется касательной плоскостью к графику
функции / в точке Ро.
Если / дифференцируема в точке Ро, то /
непрерывна в Ро и дифференцируема по каждому
из переменных хь ..., х„. Однако, если функция
непрерывна и дифференцируема по каждому из
переменных хь ..., хя в точке Ро, она не обязательно
дифференцируема в этой точке. Если же/непрерывно
дифференцируема в точке Ро, то /
дифференцируема в точке Ро.
Пример. Функция
0 при (х,, х2) - @, 0)
непрерывна в R2. При (хь х2) Ф @, 0)
/' @,0)= lim Ц*-
1 0
/х2@, 0) = 0.
Следовательно, / дифференцируема в R2 по xt и по х2. Из
того, что • lim f'x A/w, l/n) = 1/2 Ф f'x @, 0), следует, что
п-* оо l
f'x не является непрерывной в @, 0). Функция/не
дифференцируема в Ро@, 0), так как в противном случае (если
положить, в частности, что х, = х2 -* 0) должно было бы иметь
место разложение /(хь х2)-/@, 0) = —-х, = |/2xi/?, (P),
где lim Ri (P) - 0, что невозможно, ибо Ri(P) = l/2/4.
Р-*Ро
Геометрическая интерпретация
полного дифференциала функции
двух переменных. Пусть Ро(х0, Уо) — точка
из области определения функции z =/(x, у).
Если положить dx = х — х0, dy = у — у0, dz = z — z0,
то в случае дифферениируемости функции / в Ро
232
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
получается формула разложения
/(Р) - /(Ро) = df(P) + р (Р, Ро) R, (Р),
где lim R1(P) = 0.
Если отложить вертикально из Р (х0 + dx,
Уо + dy) (соответственно Ро (х0, у0)) значение
функции /(Р) (соответственно /(Ро)), то получим
соответствующие точки поверхности графика
функции /. Если же в
точке Р взять приближенное
значение/"(Ро) + df(P), то
получим точку плоскости,
касательной к графику
функции в гочке Ро, ле-
_ жащую над точкой Р.
У Полный дифференциал
df(P) является
приращением значения функции,
если поверхност ь графика
/ заменена касательной
плоскостью к нему,
проведенной в точке Ро (рис. 3.10). Это приближение
тем точнее, чем меньше р(Р0, Р)-
Производная по направлению. Пусть /определена
в некоторой окрестности точки Ро (х?, ..., x°)eR",
и пусть m — единичный вектор в R" (|ш| = 1) с
координатами w,=cosa, (i = 1, ..., n), r^e a,-
углы между вектором m и положительными
направлениями осей координат. Предел
1 ¦"" " " х„Ч/шл)-/Й ..., х°п)]
(если он существует) называется производной
функции f в точке Ро по направлению m и
обозначается д/(Р0)/дт.
Производная функции / по направлению m
равна, следовательно, обыкновенной
производной такой функции одного переменно1О, которая
получена из / путем сужения области ее
определения до отрезка прямой, проходяще! о через точку
Ро в направлении вектора т.
Пример. Пусть /(хь х2) « х? + х|, Ро=(°> 0). и «
= {1/|/2, \/\/2}. Тогда
dm
lim |
4^' 4=0 "'(О, 0I= lim г = 0.
1/2 1/2/ J t-+0
Если/дифференцируема в точке Ро, то существует
производная по направлению функции f в Ро
относительно произвольного единичного вектора m и
г'Хк {Ро) cos <хк.
dm
Если/дифференцируема по каждой из координат
в точке Ро, то вектор {/^ (Ро),/^(Ро), ..., /^(Ро)}
называется градиентом функции f в точке Ро и
обозначается символом grad/(P0).
Если / дифференцируема в гочке Ро, го
где справа стоит скалярное произведение. Если m —
вектор в касательной плоскости к поверхности
уровня /(хь ..., хп) = const, то
M^- = grad/(P0).m=0.
В общем случае
= | grad/(P0) | cos(grad/(P0), m).
Свойств-а градиента.
1. Градиент функции / перпендикулярен
поверхности уровня /.
2. Направление градиента есть направление
наиболее быстрого роста функции / (т. е.
направление наибольшей производной по направлению).
Примеры. 1) Пусть /(хь х2, х3) = 1/г, где
г ш ]/х\ +xl + xl, D(f) ш R3\ {0, 0, 0} (ньютонов потенциал
центрально симметричного силового поля). Тогда
grad/(P)= 3~{xi' X2» хз}- Поверхностями уровня при
этом являются сферы с центром в точке начала
координат @, 0, 0). Производная функции / в точке
Р(х,, х2, х3) по направлению m равна
dm
2) Для функции / из примера 2) в 3.1.4.2.2 в точке
Ро@, 0) существует производная по любому направлению,
несмотря на то что / разрывна в точке Ро.
3.1.6.3. Теоремы о дифференцируемых
функциях многих переменных.
Дифференцирование сложной
функции. Пусть функция / дифференцируема в точке
Р0(х?,...,х?), и пусть фь...,ф„ — функции одного
переменного, дифференцируемые в точке toe(a, b)
и такие, что х? = ф,(Г0) (»'= 1» 2,..., и). Тогда
сложная функция, составленная из/ и фь...,ф„ (см.
3.1.4.2.3), дифференцируема в точке t0, и ее
производная равна
dt
?,.-, хи°)фИ*о).
Пример. Пусть функция /(хь х2) непрерывно
дифференцируема в R2. Далее, пусть х, = q>i(f) = rcosf,
х2 = ф2@ — г sin t, где г = const. Сложная функция F{t) =
= /(г cos r, r sin f) имеет производную
F't @ = г [ -f'x {(г cos t, r sin t) sin t + f'x% (r cos t, г sin t) cos r].
Дифференцирование неявных
функций. Если функция F(x, у) непрерывно
дифференцируема в области Е с R2 и существует
функция у =/(х), определенная в (а, Ь) и такая, что
для всех хе(а, Ь) уравнение F(x,f(x)) = 0
выполняется, и если, кроме того, F'y(x, f{x)) # 0, то
/дифференцируема в (а, Ь) и для каждого хе(а, Ь)
справедливо равенство (ср. 3.1.6.4)
= о,
Примеры. 1) Уравнением
F(x, у) ш х3 + / ш 0, х < 0, yeR,
неявно определяется функция у = /(х) = 31п(-х).
Для нахождения f'{x) не обязательно разрешать
уравнение Р(х, у)-0 относительно у: достаточно продифферен-
ДИФФЕРЕНЦИРУЕМОЕ ОТОБРАЖЕНИЕ ПРОСТРАНСТВА R* в Rw
233
цировать F(x, /(х)) = О относительно х и получить
Зх2 + ey-f'{x) = О, откуда f'(x) » -3/х.
2) Пусть F(x, у) - х - sin у, -1<х<+1, .уе(-я/2,
+ я/2). Решением уравнения F(x, )>) = О относительно у
является у =/(х) = arcsin x. При помощи неявного
дифференцирования получаем 1 — cosy/'(x) = 0; следовательно,
/'М-
1
3.1.6.4. Дифференцируемое отображение
пространства R" в R"; функциональные определители;
неявные функции; теоремы о существовании решения.
Пусть в некоторой области GcR" определены
функции /i,...,/m. Если записать сокращенно:
х = (х,,...,х„),
Формула Тейлора функции двух переменных.
Пусть функция j на множестве
Е = {(х, y)eR2 | (х - х0J +(у- у0J < 5, 5 > 0}
г + 1 раз дифференцируема. Тогда для всех
(х, у)еЕ справедлива формула
f(x, у) -
(*, У).
При этом
д
,-xo)-- +
дк
дхк(
+
/
ь°
(у-
dkf
!
и + 1)! '
- Уо) —
0V
dkf
дх°ду1
Г')
dkf
д
0 дх
д
дх°
V
х0 + 9(V- \0), З'о + 9C'- \о)
где 0е(О, 1). Величина Rn(x, у) называется
остаточным членом (в форме Лагранжа) формулы
Тейлора для функции f.
Если при (х, у)еЕ имеет место равенство
lim Rn(x, у) = 0, то можно использовать формулу
п -> оо
Тейлора для того, чтобы в некоторой
окрестности точки (х0, >'о) приблизить функцию /
многочленом п-й степени. Формула Тейлора легко может
быть обобщена на функции более чем двух
переменных.
Если /дифференцируема в области Е с R2 и для
всех (х, у)еЕ выполнены соотношения /*(х, у) =
= f'y(x, у) = 0, то /" постоянна.
Пример. Если разложить функцию f(x,y) =
= sin x sin у в точке (х0, Уо) =» @, 0) вплоть до остаточного
члена R3(x, y\ то получим
sin х sin у ш ху + Ri{x, у).
+ (Зх2>> + y*)s\n 9xcos9y],
где 0 < в < 1. Из | cos 6х | < 1, | sin вх | < 1 в силу неравенства
треугольника следует, что
Таким образом, при небольших значениях | х | 4-1 у \
функция /(х, >¦) близка к функции /i(x, у) = ху, графиком
которой является гиперболический параболоид.
то отображением х -> f (x) определяется функция f
с областью определения D(f) = G и множеством
значений W{f) ст. Rm. Функция f называется
непрерывной, соответственно дифференцируемой, по
каждой из координат в G, если все функции
/,•(/ = 1,...,л) непрерывны, соответственно
дифференцируемы, по каждой из координат хь...,х„
в области G. Аналогично определяется непрерывная
дифференцируемость отображения f.
Пусть функция f определена в области G a R"
и дифференцируема в точке P0(x(},...,x°)eG. по
каждой из координат. Матрица размера п х т
дА
дхк
р
А
дхх '"
_ дх„'" дх„ J
называется функциональной матрицей функции f
в точке Ро. В случае т = п определитель этой
матрицы
...Л)=
)
dx
называется функциональным определителем или
якобианом функции f в точке Ро.
Пример. Якобиан функции fi(xt, х2) = х\ - х|,
/iUi, x2) = 2xtx2 равен
Шъ1Д. =4((х?J+(х$J).
с(х,, х2) 0
Свойства дифференцируемых
отображений.
1. Если область GcR" посредством непрерывно
дифференцируемой на G функции f
отображается на множество C'cR" и если для всех
PeG якобиан -—-1--'-"-'—— отличен от нуля, то
г;(х,,...,хи)
G' также является областью.
2 Пусть f является на G с R" непрерывно
дифференцируемой функцией. Пусть также в точке
#0.
д(хи...,х„)
Тогда существует окрестность U(Ро) точки Ро,
которая отображается функцией f на некоторую
окрестность V точки f(P0) взаимно однозначно.
При этом в V существует непрерывно
дифференцируемая обратная функция g*).
Таким образом, система уравнений
*) В этой теореме утверждается только локальная
обратимость Функция f не обязательно взаимно однозначна
на всей области G.
234
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
разрешима относительно переменных хь...,х„ в
некоторой окрестности точки, в которой якобиан
отличен от нуля, т. е. существуют непрерывно
дифференцируемые функции д\,..,дп такие, что
Пример. Системой уравнений
3'1 = Уi(p, <p) = pcos<p, у2 = f2(p, <p) = psin(p
определено отображение области G - {(р, ф)| р > 0, ере
е[0, 2я)}с=К2 на R2\{0, 0}. Функции /,, f2 непрерывно
дифференцируемы в G, и
d If и Г г) _
^(Р, Ф)
COSlp
рсовф
= Р-
Поскольку р > 0, ю указанная выше система уравнений
разрешима в некоторой окрестности произвольной точки
области G относительно р и фе[0, 2л). Получаем
' arctgO>2/.vt) при ух > О, у2 > О,
я + arctg(y2/yx) при >-, < О,
2я + arctgO'2/yi) при vi > 0, у2 < О,
я/2 при ух = 0, у2>0,
Зя/2 при ух -0, у2 <0. _
Легко видеть, что эти формулы решения справедливы
г(Уи У2)--
для всех точек из G. Заданное посредством формул
У<=//(р» Ф)(' = 1. 2) отображение G на R2\{@, 0)} взаимно
однозначно.
Теорема об умножении якобианов. Пусть
функции /ь...,/„, заданные уравнениями у( =
= /,(хь...,хп) (/=1,...,и), и функции ди...,дп,
заданные уравнениями х,; = gt (zb..., zn) (i = 1,..., л),
дифференцируемы по каждой из координат. Тогда
функции Fu...,Fn, определенные уравнениями
где 1 = 1,...,и, дифференцируемы по каждой из
координат и соответствующий якобиан равен
d(Fu...,Fn) d(fu...,/„) d(gu...,gn)
d(zu...,zn) г(хь...,хй) d(zu...,zn)'
Функции /i,.,/m называются зависимыми в
G cz R", если в DcR" существует функция, не
равная тождественно нулю ни в одной подобласти
области D и удовлетворяющая в каждой точке
(xb...,xJeG соотношению
Следующая теорема дает критерий того, что
данная система непрерывно дифференцируемых
функций является зависимой.
Пусть функции/ь...,/т непрерывно
дифференцируемы в ограниченной области G с R". Тогда:
1. При т>п функции /ь...,/ш всегда
зависимы.
2. При т = п функции /ь...,/п
зависимы в G тогда и только тогда, когда якобиан
——-—'-—- тождественно равен нулю в G.
3. При т<п функции/ь...,/те зависимы в G,
Примеры. 1) Функции Л (х,, х2) = <"*» + X2Ji(Xi, x2) ~
_ еХ\ - х2 независиМы в каждой ограниченной области
в R2, поскольку d(fi<fi\ = -2e2xi*O.
d(xu x2)
2) Функции /i(x,, х2) = sin(xt - х2% f2(xu x2) «
= cos(.x, - хг) являются зависимыми в R2, так как
sin2 (х, - х2) + cos2 (xj - х2) - 1 = 0.
Для всех (xi, x2)eR2 имеет место
если ранг матрицы
схк
меньше т.
равенство
^0
д(хи х2)
Неявные функции. Пусть в некоторой
области G плоскости хОу задана функция F,
и пусть линия уровня функции F, определенная
соотношением F(x, у) = 0, является графиком
некоторой функции /, заданной уравнением у — /(х).
В этом случае для всех xgD(/) выполняется
равенство F (х, / (х)) = 0, и говорят, что функция /
задана неявно уравнением F(x, у) — 0 или что
уравнение F (х, у) = 0 является однозначно
разрешимым относительно у. Может оказаться, что
уравнение F(x, у) = 0 однозначно разрешимо не в
общем виде, т. е. не для всех (х, у) е М =
= {(х, у) | F(x, у) = 0}, а лишь локально, т. е. в
некоторой окрестности некоторой точки из М.
Пример. Линия уровня, заданная в плоскости хОу
уравнением F(x, у) ш х2 + у2 - 1 = 0, представляет собой
окружность единичного радиуса, которая не может быть
графиком функции _у = /(х). Уравнение F(x, у) = 0, вообще
говоря, однозначно неразрешимо. Однако верхняя по-
ловина окружности есть график функции у - fx (x) =
= |/1 — х2. Следовательно, уравнение F(x, у) — 0 является
однозначно разрешимым относительно у при у ^ 0. Точно
так же уравнение F(x, y)*=0 однозначно разрешимо
относительно у при у < 0. При этом неявно заданная таким
образом функция есть у = /2(х) = — j/l — х2. Ее график —
нижняя половина окружности.
Пусть функция F и ее частная производная
F'y непрерывны в области G с R2. Пусть также
F(x0, Уо) = 0, (х0, >>0)eG, F;(x0, уо) Ф 0. Тогда
существует единственная непрерывная функция /,
задаваемая уравнением у = /(х), которая определена
в некоторой окрестности U(x0) в точке х0,
удовлетворяет соотношению / (х0) = у0) и в
некоторой окрестности К(х0, Уо) точки (х0, у о) условия
F(x, у) = 0, (х, }>)еК(хо, у0) и у = /(х), xeU(xo\
равносильны. В частности, для каждого xe(J{x0)
выполняется равенство F(x, /(x)) = 0.
Если функция F к раз непрерывно
дифференцируема, то / также к раз непрерывно
дифференцируема (см. 3.1.6.3). (Соответствующее
утверждение верно, естественно, и для решения
уравнения F (х, у) — 0 относительно х.)
Если grad F (Ро) Ф 0, то через точку Ро проходит
только одна линия уровня функции F.
Пример. Уравнение F(x, у) = хеу - уе* + х = 0
однозначно разрешимо относительно у в некоторой
окрестности точки @, 0), так как F является непрерывно
дифференцируемой в R2 и F'y{0, 0) = -1 ф 0. Однако
(явное) решение у — f(x) этого уравнения не определяется
элементарной функцией. Тем не менее можно, согласно
3.1.6.3, вычислить производную f в точке х0 = 0:
f'((\\ — Гх\У1 У} _ Т
/@)-~ f;(o, о)'
Обобщенная теорема о разрешимости неявных
функций. Пусть в некоторой области G cr R"+m
заданы т функций Fu...,Fm от п + т перемен-
ЗАМЕНА ПЕРЕМЕННЫХ В ДИФФЕРЕНЦИАЛЬНЫХ ВЫРАЖЕНИЯХ
235
ных хь...,.х„; yi,...,ym
уравнений:
посредством следующих
Достаточные условия однозначной
разрешимости системы уравнений F,(xb...,xn; yi,...,ym) = 0
(i = l,...,/w) относительно .Уь...,.ут даются
следующей теоремой
Пусть функции Ft в ш которой окрестности U
точки P0(x?,...,jcJ; у?, ...,y°)eG непрерывны и
непрерывно дифференцируемы относительно
yi ,ут. Пусть, далее,
#0.
Тогда существует такая окрестность V точки
^о = ^о (хЬ • • •. х°н) и, кроме того, существует такая
(однозначно определенная окрестностью V) система
определенных и непрерывных в V функций
/i,...,/m, что
и для каждой точки (хь...,хл)е V выполняется
равенство
Если все функции F, /с раз непрерывно
дифференцируемы, то все fi также к раз
непрерывно дифференцируемы.
Если уравнения F,(xb...,xn; yi,...,ym) = 0
однозначно разрешимы относительно yi,...,ym, то
говорят, что этой системой уравнений неявно
определяется функция f = (/i,...,/m) с областью
определения ?>(f) = V a R" и множеством значений
W(f) с Rm.
Для вычислений производной dfk/dxr (к =
= 1,...,т; 1 < г < и) прибегают к обобщенному
правилу дифференцирования сложных функций в
окрестности точки Ро:
0 =
dFj_
dxr
Определитель, образованный из коэффициентов
этой системы линейных уравнений относительно т
неизвестных dfk/dxr (к = \,...,т), есть якобиан
d(Fu...,Fm)
который, согласно условию теоремы, не равен
нулю в окрестности точки Ро. В этой
окрестности система линейных уравнений однозначно
разрешима относительно dfk/dxr (к = 1,...,т).
3.1.6.5. Замена переменных в дифференциальных
выражениях.
I. Если / есть функция одного переменного,
заданная уравнением y = f(x), то при замене
переменного х = ср(г) зачастую необходимо выра-
dnf
зить производные — — (п = 1, 2, 3,...) через произ-
а х
водные функций / ° ф и ф от t. Для первых
трех производных по правилу дифференцирования
сложной функции получаются следующие формулы
(/ и /°Ф сокращенно обозначены через у)*):
dy I dy
dx ~ ф'@ dt '
- Зф'(г)ф"(<> ^-+ [3(Ф"(ОJ - Ф'(
Если заменить зависимое переменное у на и
посредством формулы у = ф (м), то
dy ,t\du d2y
d
ги
dx v"; dx ' dx2 Y v ' dx2
d3y f d3u n du d2u
dx3 dx3 dx dx2
Ф
+ ч
\dxj '
При замене х и у на t и и посредством
уравнений х = ф(г, м), у = vj/(t, и) справедливы
формулы
di|/ dv|/ du
dy dt du dt
dx dip dip du
dt du dt
*y i(dy\ d
dx2 dx \ dx J dx
dt du
dip dip
_ dt du
1 d
dip dip du dt
dt du dt
_
du
dt
du
dt
Ht
~dT
Пример. Декартовы координаты х,
полярными координатами р, ф посредством
х = р cos ф, у = р sin ф.
В этом частном случае получают
4у _ р' sin ф + р cos ф
dx p' cos ф — р sin ф'
d2y р2
+ 2p' - pp"
-
+ -i—r~
du dt
dip du
du dt —
у связаны <
формул
dx (p' cos ф — р sin фK'
где р' = dp/dy, р" - d2p/d<p2.
П. Если функция / двух переменных задана
уравнением со =/(х, у), то при замене переменных
х = ф(м, v), у = \J/(m, v)
частные производные dco/dx, du>/dy и частные
производные d(o/du, dw/dv связаны друг с другом
соотношениями
dco
"du~
d(d d\\/
dy dv '
*) В последующих формулах все функции
предполагаются достаточное число раз дифференцируемыми
236
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
откуда следует, что
да) дсо
-— + В —-,
ди dv
— = С — h и ——,
ду ди dv
где А, В, С и D суть функции от и и v.
Вторые частные производные вычисляются по тем же
формулам, но применяемым не к со, а к частным
производным дю/дх и ды/ду, например:
д2(о д
~^'Jx~
дх
д (
5\
дА
- н ь
ди dv du du
В —I =
dB day
+ B—-—+ —-—+ -—
+
dB dco\
dudv
д2ы дА да
I | J
dv2 dv ди dv dv У
Точно так же вычисляются производные высших
порядков.
Пример. Выразить оператор Лапласа
л,.. _ д2со ^ ?2<»>
в полярных координатах х = р cos
дю дсо , da
у = р sin ф. Имеем
dx™*+TySmlp-
^_= _
откуда следует:
да
дх
да
~ду~~
да (
дх*
COS (f
вШф
да
э sin ф + -г—р cos ф,
dy
da sinp
dp p
da cos ф
dp p
da
c>'
da
dy
дх2
4~
dp
( , da^ _ sin ф da\ _
\ dp p dq>)
p с?ф\ dp p d<p)
Аналогично вычисляют
d2a
A,, d2a , 1 d2a . 1 da
dp p dtp p dp
Для функций более чем двух переменных
можно получить аналогичные формулы замены
переменных.
3.1.6.6. Экстремумы функций многих
переменных. Пусть функция / определена в некоторой
области G ci R" и Ро - точка в G. Значение
функции в этой точке /(Ро) называется (локальным)
минимумом, соответственно (локальным)
максимумом функции / в G, если существует
окрестность U (Ро) с G точки Ро такая, что для всех
точек PeU{Р0)\{Р0} имеет место неравенство
/(Р)>/(Р0), соответственно /(Р) </(Р0).
Максимум или минимум функции / называется также
(локальным) экстремумом функции / в G.
Значение локального экстремума функции / в
точке Ро является наименьшим или наибольшим
значением функции в некоторой окрестности
точки Ро, однако оно не совпадает, вообще
говоря, с наименьшим или наибольшим значением
функции в области G.
Пример. Функция/(хь х2) = х? + х\ имеет минимум
в точке @, 0), равный f@, 0) — 0, который совпадает с
наименьшим значением / в R2.
Необходимое условие
существования экстремума. Если/(Р0) — экстремум
функции /, дифференцируемой по каждой из
координат в некоторой окрестности U(P0) точки Ро,
то выполняются равенства f'x.(Po) = 0 (i = l,...,n).
Примеры. 1) Для функции J (хи х2) = х2 + х\ имеют
место равенства f'Xi @, 0) - /^ @, 0) = 0.
2) Функция f(xi, х2) = XjX2, D(f) — R2, не имеет в точке
@, 0) экстремума, несмотря на то что равенства
/^@, 0) = /^@, 0) = 0 выполняются.
Достаточные условия
существования экстремума. Пусть функция / дважды
непрерывно дифференцируема в G с О(/) с R" и в
точке PoeG выполняются равенства /'х.(Ро) = 0
(i=l,...,n). Если, кроме того, положительно
(отрицательно) определена квадратичная форма*)
Q(zu...,zn)=
то функция /имеет минимум (максимум) в точке Ро,
а если форма Q(zu ..., zn) неопределенная, то
функция / не имеет экстремума в точке Ро.
Если Q(zI,...,zn) не является ни неопределенной, ни
определенной, то требуется дополнительное исследование,
чтобы решить, является ли/(Ро) экстремумом.
Частный случай п = 2. Квадратичная форма
Q{zu z2) положительно или отрицательно
определена тогда и только тогда, когда
Гх,Х1Ро) Гх,Х1Ро) >0
ГХ2Х1(го)ГХгХ1(Ро)
Форма Q(zi, z2) положительно (отрицательно)
определена, если, кроме того, выполнено
неравенство fXiXi (Ро) > 0 (fXiXi (Ро) < 0). При D(P0) < 0
квадратичная форма Q(zu z2) - неопределенная.
В случае D(Po) = 0 необходимо дополнительное
исследование.
Пример. Для вычисления значения экстремума функции
1
D(P0) =
f(xu *г) - ух» " 4Xi*2 + 9х* + Зх> "
прежде всего находятся решения системы
/Х2(х,, х2) = -4
18х2 - 14 - 0.
Единственное решение этой линейной системы уравнений
есть (х?, х5) = A, 1). Из того, что fXlXl{UD-L
/W1' D-18, rXlX2lU D--4, следует, что D(l, 1) =
= 2>0; в точке A, 1) функция f имеет экстремум и
поскольку fxX {U 1)=1>0, это минимум: /A, 1)=-5.
*) Квадратичная форма Q(zt,...,zn) = ^ (tijZiZj назы-
вается положительно (отрицательно) определенной, если для
всех (zb ..,zn)eR"\{0,. .,0} имеет место неравенство
Q(z{,...,zn) > 0 (Q(zu...,zn) <0). Если Q(zb...,zn) принимает
как положительные, так и отрицательные значения, то
Q(zu ,zn) называется неопределенной (см также 2.4.4.5.3.3).
Форма Q{zu...,zn) является положительно (отрицательно)
определенной тогда и только тогда, когда все
собственные значения матрицы (а1}) являются положительными
(отрицательными) (см. 2.4 4.5), или (критерий Сильвестра)
тогда и только тогда, когда все главные миноры
det(a,-j-)f, j=l (k = 1, .. , п) положительны (имеют знак (—1)*)
ЭКСТРЕМУМЫ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
237
Нахождение условных
экстремумов. В многочисленных задачах на
экстремальные значения (нахождение экстремума
некоторой функции) из естественных наук, техники и
экономики множество точек, на котором ищут
экстремум, подчинено определенным условиям,
которые зачастую заданы в форме
дополнительных уравнений.
Пример. Необходимо определить значение экстремума
функции /(х,, х2) - *i + х2 при дополнительном условии
х,х2 »4.
Общая задача на поиск условного экстремума
может быть сформулирована следующим образом:
найти все экстремумы и наибольшее и
наименьшее значения функции /(хь.. ,хп), определенной в
области GcR", для точек Р(хи...,х„),
удовлетворяющих дополнительным условиям
Ф,(.хь...,х„) = 0 (/ = 1,...,ш),
где ф ь..., фш — действительные функции,
определенные в G.
Необходимые условия
существования условного экстремума. Пусть
функции /, фь...,ф„ непрерывно дифференцируемы в G
и ранг функциональной матрицы (d<pt/dxk) равен т.
Положим
L = f + ? ^Ф*
который совпадает с наибольшим значением F при
выполнении указанных выше условий.
Два примера задач па жстрему.мы
I Метод наименьших квадратов Пусть в плоскости
хОу заданы N + 1 точек (v,-, m,) (/ = 0, 1, . ,N), где х, # y^
при \ ф ) Нужно найти функцию у= f(x, a0, ,а„. х),
зависящую oi v и or п параметров а0, «,, Л„-\ {п < /V), график
которой как можно лучше приближается к указанным точкам
(рис 3 11) Согласно методу наименьших квадратов, эти
параметры выбираются 1ак, чтобы величина
N
(функция L называется функцией Лагранжа с
множителями A,i,...,A,m, где Xi,...,Xm —
произвольные действительные числа). Если / в точке
Р0(х?,...,xJ)eG при дополнительных условиях
имеет экстремум, то справедливы соотношения:
a) L'Xj(P0) = f'Xi(P0) +
была наименьшей Ее пи для величины Q воспользоваться
1еорией экстремумов, ю при соответствующих
предположениях о дифференцируемости / получаются необходимые
условия для определения параметров «0, «i, ¦,«„-{
PQ/C(ij = O (/ = (), 1, ,/?-!) Эти уравнения называются
норма 1ьпыми уравнепичми
Если, в частности, выбрать в качестве / многочлен
относительно х / (\, «„, ,а„- \) = X tt*-v*' то с учетом того,
* = 0
что в этом случае
2 X I a^-m
б) L'K(P0) = щ(Р0) = 0 (k= l,...,m).
Таким образом, необходимыми условиями
существования условного экстремума функции / в
точке Р при дополнительных условиях ц>к = 0
(к = 1,...,ш) являются следующие п + т уравнений:
в качестве системы нормальных уравнений получим
следующие п линейных уравнений (ср 2.4 4 3)
/ 1 OXi
к= 1
{Р) = 0
с n + ffl неизвестными х,,...,х„, А.ь...Дте.
Пример. Среди всех прямоугольников с постоянным
периметром надо найти наибольший по площади. Пусть
х, у-длины сторон прямоугольника, тогда F(x, у) - ху -
его площадь. Дополнительное условие: ф(х, у)- х + у - м/2 ¦ 0.
Система
Ц(х, У) - F'x(x, у) + Хф;(х, у) ш у + \ ш О,
l;k у) - Fy(x, у) + хФ;(х, у). х + х «о,
U(х, у) - ф(х, у) - х + >• - м/2 - 0
имеет единственное решение х0 - у0 » -Хо » м/4. Легко
заметить, что F в точке (х0, Го) имеет локальный максимум,
для краткости здесь использованы символы Гаусса
N
[W] = ?m,,v? (к = 0, ,/j- 1)
2 Опреде wiiue оппшма \ьного местоположении Для N
заданных местоположений, изображенных на рис 3 12
iочками P,(y,, »,) (i =¦ 1. ,/V), необходимо определить такое
местоположение (такую точку <Ро(*о, У о))-, сумма расстояний
от которою до всех остальных наименьшая Следователыто,
д тя Fo должен достшаться минимум футткции
N
"(v0. V0) = X «v* ~ л'оJ +(Vk~ \oJI12
238
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Необходимые условия даются системой двух нелиней- (рис. 3.13). Число
N
V
_ 2
'Li «** ~ xoJ + (Ук - УоJI'2 '
N
у _ 2 V Ув-Ук
^Z.((^-^oJ + (yk-VoJI/2-
*= l
Решение этой нелинейной системы уравнений является,
вообще говоря, сложной задачей.
называется интегральной суммой относительно
разбиения Z.
Функция /(х) называется интегрируемой на
отрезке [a, b] в смысле Римана, если существует
а=хп
хл...х^
Рис. 3 12
Если выбрать в качестве нулевого приближения
N N
го при помощи интерационных формул получим
N
\
i= 1
N
i= 1
JV
V
У - x,)>
[к) _ x\2
) — xi)
xt
+ (/ok)
j
y,
1
- yd2I12
= 0, 1,...).
((xW - xtJ + (y*g - yd2I»
3.1.7. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ФУНКЦИЙ ОДНОГО ПЕРЕМЕННОГО
3.1.7.1. Определенные интегралы. Пусть функция
/(х) определена и ограничена на отрезке
[a, b\ a <b. Произведем разбиение Z отрезка
[а, Ь] на «элементарные отрезки» введением точек
х, (/ = 0, 1,...,л):
а = х0 < Xi < х2 < ... < х„-1 < хп = Ъ.
Обозначим через A(Z) длину наибольшего
элементарного отрезка разбиения Z, т. е. A(Z) =
= max (xt — Xi-i). В каждом элементарном от-
1 ^ i ^
резке выберем произвольное число ^, (х,_ i
х,-)
Рис. 3.13
число / со следующим свойством: для любого
е > 0 найдется такое 8 (е) > 0, что при любом
разбиении Z, для которого A(Z)<5, выполняется
неравенство | a (Z) — I \ <г независимо от выбора
?4. Число / называется определенным интегралом
функции /(х) на отрезке [а, Ь].
Обозначение:
l=]f{x)dx;
х называется переменным интегрирования, а и b -
соответственно нижним и верхним пределами
интегрирования.
Этому определению равносильно следующее:
/(х) интегрируема на [а, Ь], если для всякой
последовательности Zn разбиений, для которых
lim A (ZJ = 0, последовательность a (ZJ соответ-
П-* 00
ствующих интегральных сумм независимо от
выбора внутренних точек ?к всегда сходится (она
сходится в таком случае к одному и тому же
предельному значению, которое и есть
интеграл).
Если интегрируемость /(х) уже известна, то
достаточно найти предел последовательности
а (ZJ для какой-нибудь последовательности
разбиений Zn, удовлетворяющей условию lim A(Zn) =
П-+ 00
= 0.
Верхние и нижние суммы Дарбу. Пусть М,-
и w, — соответственно верхняя и нижняя грани
/(х) в элементарном интервале [х,_ь х,] для
разбиения Z отрезка [а, Ь]. Числа S{Z) =
п п
= X М,(х,- - х,-!) и s(Z) = X "»i(x, - Xi-i) назы-
i = 1 i = 1
ваются соответственно верхней и нижней суммами
разбиения Z.
Критерий интегрируемости Римана. Функция
/(х), определенная и ограниченная на [а, Ь],
интегрируема на [а, Ь] тогда и только тогда, когда
для любого е > 0 существует число 5 (е) > 0 такое,
что для любого разбиения Z, где A (Z) < 8,
выполняется неравенство S{Z) - s (Z) < е.
Классы функций, для которых интеграл Римана
всегда существует:
а) функции, непрерывные на [а, Ь~\;
б) функции, ограниченные на [а, Ь] и имеющие
конечное число разрывов;
в) ограниченные и монотонные на [а, Ь]
функции.
СВОЙСТВА ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
239
Геометрическая
интерпретация
определенного инте-
Рис 3 14
В /f77^kn fH Ределенного инте-
.2? отрезке [а, Ь], то J /(х) dx
представляет собой
площадь области,
ограниченной осью х, графиком
f(x) и прямыми х = а и х — b (рис. 3.14).
Если /(х)^0 на [а, Ь], то площадь соответ-
ь
ствующей фигуры равна —\f(x)dx.
3.1.7.2. Свойства определенных интегралов.
1. ]f(x)dx = 0.
2. Перестановка пределов интегрирования: если
ь
существует J/(x) dx при а < Ь, то существует
]f(x)dx= -]f(x)dx.
b a
3. Если существуют интегралы j/(x)dx и
b Ъ
\f{x)dx, то существует также \f(x)dx и для
любого взаимного расположения точек я, Ь, с
]f(x)dx=]f(x)dx+lf(x)dx.
ь
4. Если существует jf(x)dx, то для любой
постоянной а
5. Если существуют интегралы \f(x)dx и
x, то существует также
J [/ (а) + д(х)] dx = j/(x) dx +jg(x) dx.
6. Если всюду на [с/, Ь] выполнено неравенство
х)^д(х) и существуют j f(x)dx и §g(x)dx, то
b b
$ f(x)dx ^$g(x)dx.
В частности, если m ^ / (х) ^ М, то
т (Ь — а) ^ f / (x) dx ^ М (Ь — а).
ь
7. Если существует J/(x)dx, то существует
ь а
также J|/(x)|dx, и
8. Первая теорема о среднем значении. Если
/(х) интегрируема на [а, Ь] и m^f(x)^M, то
существует число ц, w < |i ^ M, такое, что
В частности, если /(х) непрерывна на [а, Ь],
то существует число ?, а <? < 6,
такое, что
Геометрическая
интерпретация; между а и b существует ~q
такое ?, что площадь фигуры
ABCD равна площади прямо- Рис. 3.15
угольника AB'CD (рис. 3.15).
9. Обобщенная первая теорема о среднем
значении. Если / (х) и g (x) интегрируемы на [а, Ь],
*и ^ / (х) ^ М и либо всегда g (x) ^ 0, либо всегда
g (х) ^0, то / (х) g (x) интегрируема на [я, />] и
существует число ц, m ^ ц ^ М, такое, что
ь ь
В частности, если/(х) непрерывна, то
существует такое число ?, а < ^ < Ь, что
f/W^(x)rfx=/(^)ffir(x)rfx.
а а
10. Вторая теорема о среднем значении. Если
/(х) монотонна и ограничена, а # (х) интегрируема,
то на [а, Ь~\ существует такая точка ?, что
]f{x)g (x) dx=f{a)\g (x) rfx + / (Ь) J ^ (x) dx.
а а ^
11. Если функция/(х) интегрируема на отрезке
[а, Ь], то функция
F(x)=J/(t)^
а
на отрезке [а, Ь] непрерывна, а если /(х)
непрерывна на [а, Ь], то функция F (х) имеет на [а, Ь]
производную, причем F' (х) = / (х).
12. Интегрирование посредством разложения
в ряд. Если функции/„ (х) (п = 1, 2, 3, ...)
интегрируемы на [а, Ь], а бесконечный ряд ]Г /„ (х)
сходится равномерно (см. 3.1.14.4) на [а, Ь], то
сумма ряда / (х) также интегрируема на [а, Ь] и
ь * /ь \
ff(x)dx= ? (ifAx)dx).
а и= 1 \а /
О вычислении определенных интегралов и
дальнейших свойствах см. 3.1.7.4 и 3.1.7.7.
3.1.7.3. Неопределенные интегралы.
Первообразная функция. Функция F(x), дифференцируемая
240
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
в некотором интервале {а, Ь), называется
первообразной функцией для функции f(x) в этом
интервале, если для каждого хе(а, Ь) справедливо
равенство F'{x) = /(х).
Примеры. /(x) = cosx, F(x) «* sinx, хе(~ оо, оо);
Дх) - 1 г F(x) ш arcsin х, хе(-1, 1); /(х) - -k F(x) -
l/l - х* *
-ln|xf (x#0).
Если F,(x) и F2(x)-flBe первообразные
функции для f(x) на одном и том же отрезке, то
проинтегрирован:
'
они различаются на адди-
тивную постоянную: F2 (x) =
= Fx (х) + С, т. е. графики
всех первообразных функций
образуются из одного из них
сдвигом по оси у (рис. 3.16).
х Пример. Функции Fx (x) »
¦» - arccos х и F2 (х) ¦» arcein x
Рис 3 16 имеют для хе(-1, 1) одинако»
вую производную l//l - х2 и,
следовательно, являются первообразными функциями для
1/j/l - х2, поэтому
arcsin х - - arccos x + С;
так как arcsin 0-0, агссовО«я/2, то С«я/2 и,
следовательно,
arcsin х + arccos x » я/2.
Неопределенным интегралом функции f(x) на
некотором интервале называют множество всех
первообразных функций функции/ (х) на этом
интервале; обозначение:
if(x)dx.
Если F(x) какая-нибудь первообразная функция
для /(х), то
где С — произвольная постоянная.
Поэтому примеры, приведенные в начале пункта, можно
записать так:
Jcosx</x »»einx + C;
dX ' ¦ - (хе(-\, 1));
(х Ф 0).
Вычисление неопределенных интегралов при
помощи соответствующих правил интегрирования
стараются свести именно к табличным интегралам.
Зачастую, однако, неопределенный интеграл от
некоторой элементарной функции невозможно
выразить через элементарные функции (представить в
замкнутой форме). Эго происходит уже при
интегрировании таких простых функций, как
f~x , sin .y/.y, cos.v/x, I/In .x.
Для того чтобы проинтегрировать подобную
функцию, можно произвести разложение
подынтегральной функции в ряд и использовать свойство
12 и 3.1.7.2
Пример. е~*1'' т | _xz + x4/2!-x6/3! + ...
Этот степенной ряд сходится равномерно на всяком
ограниченном интервале, поэтому может быть почленно
5-2! 7-3!
Тем самым находится представление интеграла в виде
хорошо сходящегося степенного ряда.
Интеграл может быть приближенно вычислен
разными способами (см. 7.1.2.7).
Не представимые в замкнутой форме (т. е. не
являющиеся элементарными функциями), но важные
для практики интегралы затабулированы, например:
dx
In х
(интегральный логарифм),
С d(n (эллиптический интег-
, = F(k, ф) рал \.го рода (см.
Jo 1/1-Л2 sin2 ф 1.1.2.4)).
Таблица основных интегралов.
Постоянная интегрирования опущена; указания об
интервале определения сделаны только тогда, ког:
да речь идет не об интервале (-оо, оо).
Степенные функции
х
хп dx = ——- (и Ф - 1; х ф 0, если п < 0)
* dx ¦-
0С+ 1
(а Ф — 1 — действительное, х > 0)
| —= ln|x| (x#0)
I х
Показательные функции
= ex
= ~~- (аФ
1пя
Тригонометрические функции
J sin х dx = — cosx
j cos x dx = sin x
Jtgx</x= - In | cos x | (х?Ч2/с+ 1) —
f ctg x dx = In | sin x | (x ф kn)
*7- = tgx
-ctgx (x ф kn)
cos x
' dx
Гиперболические функции
J sh x dx = ch x
j" ch x dx = sh v
j th x dx = In ch x
\cthxdx = ln|shx| (v#0)
j
ch2x
dx
sh2x
J sh2x
= thx
= - cth x
СВОЙСТВА НЕОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
241
Дробно-рациональные функции (а ф 0)
— = —arctg —
х2 а а
dx
1 х
— Arth — (| х | < a),
a a
-In
a + x
3. Если F(w) — первообразная функция для/(w)
в интервале /, то для произвольных постоянных
а, Ъ {аф 0)
jf {ax + b)dx = —F(ax + b) + С,
причем х лежит в интервале, для которого
и = ах + bel.
dx
— Arcth — (\x\>a).
а а
При
мер. I
-т
—In
2а
х + а
(аФО)
4. Если /(х) имеет в некотором интервале
непрерывную производную и /{х)ф 0, то
j
Иррациональные функции {а ф 0)
]/а2 - х
= arcsin — (| х | < а)
а
Пример
, f У х ff * </х - у In A + sin2 x) + С.
Arsh (x/a),
ln(x +j/я5^
Arch (x/a),
х2)
In I x + j/x2 - a21 (| x | > fl)
J /x2 - „2
Выражение определенного
интеграла через неопределенный (основная
теорема дифференциального и интегрального исчислений,
теорема Ньютона — Лейбница). Если для функции
/(х), интегрируемой по Риману на отрезке [а, Ь],
существует непрерывная функция F(x) на [я, ?>],
являющаяся первообразной функцией для /(х) на
[л, Ь] (в частности, если /(х) непрерывна на
[л, Ь]\ то определенный интеграл \f{x)dx можно
а
вычислить по формуле
]f{x)dx = F{b)-F{a)\
для записи правой части используются символы:
,. _ . JJ или F(x)|J.
Пример. 1) \ сое х </х - [sin x]j
sin Ь — sin a\
— ¦" [In х]* ш In Ь - In а ш
n —, если я > 0, b > 0.
Геометрическая интерпретация
первообразной функции. Если S(х) —
площадь криволинейной трапеции, ограниченной
неотрицательной функцией /(х), прямыми,
проходящими через {а, 0) и (х, 0) и параллельными оси
у, и осью х (рис. 3.17), то
S(x) = F(x)-F(a),
где F{x) — любая первообразная функция для/(х)
на отрезке [«, Ь].
3.1.7.4. Свойства неопределенных интегралов.
1. Аддитивность неопределенного интеграла:
J(/(x) + g{x))dx = \f{x)dx + \g{x)dx.
2. Постоянный множитель ос можно выносить
за знак интеграла:
5. Интегрирование по частям. Если м(х) и v{x)
имеют в некотором интервале / непрерывные
производные, то
j и (х) v' (х) dx = и (х) f (х) — J и' (х) у (х) dx.
Примеры. I) Jxsinxdx = x(-cogx)-Jl'(-cosx)</x=s
= -xcosx + sinx + С.
2) In х dx ¦» I In x • I • </x ¦« x In x — I — xdx =
¦ xlnx-x + C (определено в любом интервале, где х > 0).
Интегрирование по частям определенных
интегралов. Если функции и и v имеют на
[а, Ь] непрерывные производные, то
ь ь
J и (х) у' (х) dx = [и (х) и (х)]* - J и' (х) у (х) dx.
6. Интегрирование подстановкой (заменой
переменного). Если функция f(z) непрерывна на
[а, р], функция z = g(x) имеет на [я, Ь]
непрерывную производную и а ^ д{х) ^ р, то
причем после интегрирования в правой части
следует сделать подстановку z = g(x).
Пример, sin3 х cos x dx = \z* dz**—z
Зачастую этой формулой пользуются справа
налево; для того чтобы определить §f(z)dz,
вводят функцию z = g(x) и вычисляют
$f{9(x))g'{x)dx; после этого при помощи обратной
функции х = h (z) нужно вернуться к исходному
переменному х (обратная функция х = h{z)
существует, если д' (х) ф 0 на [а, Ь~\).
Примеры.
I) — —;
подстановка z * tg x,
хе(-я/2, л/2); значит, г* » flf'(x)« 1/cos2 z ?t 0 и х • arctg z.
Тогда
Г dz
J (i/jt^K
« cos x rfx » sin x + С »
Г+С.
242
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
2) Jl/«2 — z2dz: делаем замену r = «cosx, хе@, я),
гак что у'(х) = — rtsin.v ф О и .v = arccos (г/и); тогда
j ]/а2 - z2dz = \ ]/а2 - a2 cos2 x(-a sin х) dx = - a2 J sin2 .v </х.
Далее, так как sin2 х = — A - cos 2х\ то
J sin2 x dx = у I x - -у sin 2x J
+ С = -~(x - sinxcosx) + C,
но sin x = ]/\ - cos2 x = — У a2 - z2, и после введения
обратной функции получим, что
JJ/V - z2 (/г = - у arccos-y + ^ J/V - z* -I- С.
Правило подстановки (замена переменного) для
определенных интегралов. Если функция/(х)
непрерывна на [а, Р], а функция g строго монотонна,
имеет на [а, Ь] непрерывную производную и
g(a) = oi. g{b) = $, то справедливы следующие
равенства (z = g(x); обратная функция х = h(z)):
= \ f(z)dz,
в (а)
Р Мр)
J/(z)dz= J
а Л (а)
В отличие от правила подстановки для
неопределенных интегралов, согласно которому
необходимо вернуться к исходному переменному,
здесь при подстановке нужно сразу изменить
пределы интегрирования.
Пример, f У а2 - z2dz\ подстановка r = «cosx (л ^
-«
5» х > 0 для - а < z ^ «) дает
J У а2 - z2 dz - -«2 J sin2 x dx = + 4"«2 JA ~ cos 2x) </x =
Можно прежде вычислить неопределенный интеграл (см.
приведенный выше пример);
J ]/а*~^? dz = - ~arccos - + — {/а2 - г2 Г = ~ а2п.
3.1.7.5. Интегрирование рациональных функций.
Дробно-рациональная функция R (х) — отношение
двух многочленов Q{x) и Р(х), не имеющих
общих множителей:
Q(x) Ьохт + Ь1хт-1 +... + Ьт
P(x)
aox"
Рациональные функции всегда интегрируются в
элементарных функциях. Их интегралы являются
линейной комбинацией следующих функций:
рациональных функций, логарифма линейных двучленов,
логарифма квадратичных трехчленов, арктангенса
линейных двучленов.
Если степень Q(x) больше или равна степени
Р(х), то прежде всего делением Q{x) на Р(х)
выделяют целую часть. Тогда получают сумму,
состоящую из многочлена и правильной
рациональной функции R(x) = j (x) + —-——, причем степень
Р(х)
Qj (х) меньше степени Р(х) и многочлены Qi{x)
и Р(х) не имеют общих множителей.
Пример. - v —
F F .\2 +1
Многочлен/(х) можно сразу же
проинтегрировать: если
\f{x)dx =
т — п + 1
—хт'
+ ... + cm_nx + С.
Если деление выполнено, то производится
разложение дробно-рациональной функции
на
г (х)
Р(х)
простейшие
дроби,
раскладывается на сумму дробей, которые
затем легко проинтегрировать. Это разложение
на простейшие дроби тесно связано с разложением
знаменателя Р(х) на множители. Делением
числителя Qi{x) и знаменателя Р(х) на а0 можно
всегда достичь того, чтобы коэффициент при
старшем члене многочлена Р(х) был равен 1. По
основной теореме алгебры (см. 2.5.1.1.2) имеем
Р(х) = (х - fll)*i ...(х - ar)k'(x2 + Plx + 4,)'1...
где av (v = 1,..., г) — действительные нули кратности
kv многочлена Р(х), в то время как
квадратные трехчлены не имеют действительных нулей,
т. е. pj — 4дм < 0, ц = 1,..., s. Получение такого
представления в виде сомножителей и является,
собственно, главной проблемой при интегрировании
конкретной дробно-рациональной функции. Далее,
каждому из сомножителей Р(х) соответствует
некоторое число простейших дробей B.5.1.2.5), а
именно каждому сомножителю вида (х - af
соответствует сумма простейших дробей
АЛ А
х — а (х — аJ '" (х — а)к
и каждому сомножителю вида (х2 + рх + qI
соответствует сумма простейших дробей вида
Bjx + d , В2х + С2 , t B^ + C,
х2 + рх + q (х2 + рх + qJ
... -+¦
(х2 + рх + цI
Постоянные Aj, Bj, C} рассматриваются сначала
как неизвестные.
Пример. Я(х)= -o-xVlp_ j •
Разложение знаменателя дает
Р(х) = х6 + х4 - х2 - 1 = (х - 1)(х -I- 1)(х2 + IJ.
Таким образом,
в
Сх + D ^ Ex + F
Для определения коэффициентов А, В, С, О, Ь", F
левую и правую части умножаем на знаменатель Р(х) и
отбрасываем ею.
В вышеприведенном примере после умножения на
знаменатель (х - 1)(х + 1)(к2 + IJ имеем
х + 2 = А(х + 1)(х2 + IJ + В(х - 1)(х2 + IJ +
-I- (Сх + D)(x -
|)(*2
(?х + F)(x -
1).
Приравнивание коэффициентов при одинаковых степенях
х в многочленах, стоящих слева и справа (от \5 до х°),
ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
243
дает систему уравнений
V3
Y4
X
X2
X1
x°
0
0
0
0
1
2
- A + В + С,
= A-B + D,
-2A + 2B + E,
m 2A - 2B + F,
-И+В-С-
=A-B-D-
E,
F,
откуда Л-j, B--J, С--|. D--J. Я - ~i
F» -1.
Таким образом, имеет место разложение
х 4- 2
3
2х + 4 4х + 8 1
x2 + l (x2 + lJJ
Интегрирование простейших (элементарных)
дробей. После того, как разложение на
простейшие дроби осуществлено, достаточно
проинтегрировать полученные дроби. Дроби, знаменатель
которых имеет а своим действительным корнем,
интегрируются по формулам
Adx
1
J (х - а)*
Интеграл от дроби
v- 1 (х-аУ1
Bx + C
rnpnp2-4q ¦
(x2 + px + qy
< О, т. е. когда знаменатель имеет комплексно-
сопряженные корни, преобразованием числителя
при v > 1 приводится к виду
dx =
(х2 + рх
В Г Bx + p)dx
рВ
2
dx
2(v-
(c
V
dx
При v = 1 после аналогичного преобразования
получим
Г Вх + С ,
+ рх + q
Вычисление интегралов вида
dx
dx
/v =
х2 + рх + q)v
производится по рекуррентной формуле
2Bv-3)
1
2х
-/v-l,
(v - 1)D* - p2)
которая позволяет свести вычисление интеграла
/v после v — 1 шагов к вычислению интеграла
f
¦ + px + q
Значение последнего интеграла равно
2 2х + р
h = arctg + С.
]/4<7 — р2 j/4g — р2
Таким образом, интегрирование простейшей дроби
_ JL Г x2+22dx - -1- V f ,*** а.
и по рекуррентной формуле
Дальнейшие примеры. 1.
как степень многочлена в числителе равна степени многочлена
в знаменателе, то, прежде чем приступить к разложению
на простейшие дроби, нужно произвести выделение целой
части. Имеем
Далее,
В
(хд -\у х - 1 (х - 1)* х + 1 (х + 1)а '
Умножение на общий знаменатель дает
2х2 - 1 - А(х + 1J(х - 1) 4- В(х + 1)а +
+ С(х- 1J(х + 1) + D(x- IJ.
Значения некоторых коэффициентов (здесь В и D) часто можно
получить быстрее, чем методом приравнивания
коэффициентов, — подстановкой нулей знаменателя. Если подставить в
уравнение х » 1, то получим, что 2 — 1 «¦ 4В, т, е. В — 1/4.
Если подставить х =» -1, то получается 2 - 1 «40;
следовательно, D ш 1/4, Приравнивая коэффициенты при.х3 и х°,
получаем уравнения 0«*/1 + С и -\=*-A
следовательно, А « 3/4, С « - 3/4.
Итак, получаем
1 1
3,
+ с*
2х3 - Зх
+ 4ln
2(х2- 1) " 4
х+ 1
+ С.
; у знаменателя нет вещественных нулей;
разложение на квадратичные множители дает х* + 1 «=
» (х2 - |/2х + 1)(х2 + |/2 + 1), а разложение на простейшие
дроби -
1 т BjX + Сх + В3х + Сг
)/2
х+\
-|/2х+1
Приравниванием коэффициен i ов находим
2>
1 .,
2/Г
'*4+l 2l/2 ix2 + ]/2x+\ 21/2 J x2 -^ I
244
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Применяясоответст») к'чциеформулы для интегрирования
простейших дробей -»??-t_i—f получаем, чго
X + рх + if
lfx + l/i
Т" J 1 А ^Х " —/I
2|/2 х +|/2х+ 1 2J/2
ifl ~
^ +
ш—L-in(x2 + /2x + l) + -~rarctg(|/2x+ l) + Clt
4|/2 2^/2
2|/2 J x2-l/2x+l *" 2]/2 L2 " Х
- i) + C2
кратное чисел и, т,..., дает в итоге интеграл от
рациональной функции.
4. Теорема Чебышева. Интеграл Jxm(a + bxn)p dx
(a, b — произвольные постоянные, т, n, p —
рациональные числа) — Интеграл от
дифференциального бинома - может быть выражен в элементарных
функциях только тогда, когда одно из чисел р,
т + 1 т + 1
, 1- р является целым.
п п
а) р — целое; подстановка t — j/x, где г —
наименьшее общее кратное знаменателей чисел т и
п, приводит к интегралу от рациональной функции.
^ т + 1 „ г / —
б) целое; подстановкой t = ya + bx", где
и
г — знаменатель дроби р, получаем интеграл от
рациональной функции.
ч т + 1
в) 1- р — целое; при помощи подстановки
следовательно, в итоге получаем
f ~^~ ш -JL-
J x + l 4j/2
-, где г — знаменатель дроби р, полу-
чаем интеграл от рациональной функции.
-7=r-arctg(l/2x - 1) + С (С т С\ + Cj). Пример. I т= </* ш Ь
Таблицы интегралов рациональных функций
см. в 1.1.3.3.
3.1.7.6. Интегрирование других классов функций.
В дальнейшем R(u, v, w,...) означает
рациональную функцию от аргументов и, v, w,...
Приводимые ниже интегралы подходящей
подстановкой могут быть сведены к интегралам от
рациональных функций.
3.1.7.6.1. Интегрирование
иррациональных функций.
1. |Я(х, у ах + b)dx; в результате замены
переменного t = ]/ах + Ь, т. е. х = —(tn — b),
dx = — tn~l dt, получаем
Г" .. f (f-b \n ,
R (x, У ax + b)dx = \ Rl , t ]— tn~l dt,
J J V a J a
т. е. интеграл от рациональной функции.
Пр„МеР. J l/^+JL^x-2jf?±f/t, где
*-/хП.
(ad-Ьсф 0); подстанов-
итак, т ш - 1/2, и « 1/4, /) « 1/3, (т + t )//i » 2 - целое.
, x-(r3-l)*, </x» I2r2(f3-lK</r,
±^{М» . 7) + с . i.A +
7 7
5. |Я(х, )/дх2 + 2Ьх + c)dx (а ф 0).
Эти интегралы можно свести к интегралам от
рациональных функций, от тригонометрических или
гиперболических функций (они рассматриваются
в 3.1.7.6.2). Преобразуем выражение
ах2 + 2Ьх + с = —(ах + ЬJ Н
а а
и рассмотрим три возможных случая:
а) ас — Ь2 > 0; тогда интересен лишь случай
а > 0, так как при а < 0 всегда ах2 + 2Ьх + с < 0.
Заменой переменного t = —
+ 2bx + с = —
получаем,
что
ЧТО
ас - Ь2
+ 1), откуда следует,
а - ctn'
dx = n (ad —
/ах2 + 2Ьх + с) dx =
/ас - Ь2
7 ^2"'
нальной функции.
^2"' приводит к интегралу от
рациоГ ]/ac-b2 b I ac-
J \ a a ]/ a
а
Л2"
\\dt-
J
з. [я(х,1/^^±1,1/^^±А,..Ъх;
J V pcx + d ^сх + <Г /
вка f = / -
\)dt.
cx + d
, где г-наименьшее общее
Дальнейшая подстановка, а именно t = sh и
(можно применять и подстановку t = tgn), при-
водит к интегралу от рациональной функции от
ИНТЕГРИРОВАНИЕ ДРУГИХ КЛАССОВ ФУНКЦИЙ
245
функций shw и спм:
f Rt (t, ]/t2 + 1) dt = f Rt (sh u, ch м) ch м du.
б) ас — b2 = 0; тогда в подынтегральном
выражении содержится полный квадрат, и, извлекая
квадратный корень, получаем интеграл от
рациональной функции.
]/ах2 + 2Ьх + с, а затем приравнивают
коэффициенты при одинаковых степенях х у многочленов
слева и справа.
Пример. /
в) ас - Ь2 < 0; подстановкой t =
лучаем, что ]/ах2 + 2Ьх + с =
ах + b
2-1
]/х2 - 2х
Применяя описанный способ, получаем, что
/ = (ах2 + bx + c)l/x2-2x + A [ dx .
J l/x2 - 2х
при
b2 -ас
Дифференцируя обе части, имеем
Зх3 - 8х2 + 4х
а > О и \/ах2 + 2Ьх + с= V у 1 -1* при
а <0.
В результате приходим к интегралу вида
J Ri (t, ]/t2 - \)dt, если а > О, и J Rx (t, ]/\-t2)dt,
если a < 0. В первом случае используют
подстановку г = ch и (или t = sec и), во втором случае
t = cos м (или t = sin u); получают соответственно
]/х2 - 2х
=B«x + b) l/x2 - 2x + (r?x2 + bx+c)
x- 1
Пример. I — dx : «c - b2 = -1 < 0
J l/x2 - 2x
(случай в)).
Делаем замену переменного г = х-1; следовательно,
х = г + 1, dx » df. Тогда (при г = ch м)
|/x2 - 2х
= ln(r
sh "
г~^~\) + С = ln(x - 1 + |/x2 - 2x) + С
Одной из трех подстановок Эйлера интегралы
рассматриваемого вида можно также сразу свести
к интегралам от рациональных функций:
а) если а > 0, то делают замену
б) если с > 0, то делают замену
, /—1—^ f xf + l/c,
]/ах2 + 2Ьх + с = < v
I xt-yc;
в) если ах2 + 2Ьх + с имеет два разных
действительных корня а и р, то делают замену
]/ах2 + 2Ьх + с = t (х - а).
6. Интегралы специального вида
f PJx)dx
, где Рп (х) - многочлен n-й сте-
J l/ax2 + 2*,л т- .
пени, можно свести к более простому интегралу
Г dx
t . Полагают
J ]/ax2 + 2bx + c
J l/ax2 + 2bx + с
= Pn.l(x)\/ax2 + 2bx + c + A \
Jl
dx
, (*)
)/ax2 + 2bx + c
где Pn-i (x) — многочлен степени п — 1,
коэффициенты которого еще не определены. Для нахождения
коэффициентов этого многочлена и числа А
дифференцируют левую и правую части равенства (*),
полученный результат умножают на
|/х2-2х ]/х2-2х
откуда после умножения на |/х2 — 2х и приравнивания
коэффициентов при соответствующих степенях х следует:
о=1, Ъ = -3/2, с* = -1/2, А = -1/2. Таким образом,
J I/
l/x2 - 2х
2 - 2х) + С
(см. предыдущий пример).
7. Эллиптические интегралы. Интегралы вида
j R (х, ]/ахъ + Ьх2 + сх + е) dx,
j/?(x, |/ах4 + Ьх3 + сх2 + ех + /) dx,
как правило, не выражаются через элементарные
функции; тогда они называются эллиптическими
интегралами. В результате ряда преобразований
можно каждый такой интеграл свести к
элементарным функциям и к эллиптическим интегралам
первого, второго или третьего рода:
Г dt
. -t2){\ -k2t2)
dt
Г (l-k2t2)dt
J ]/tt-t2)a-k2t2)'
+ht2)]/{\ -t2){\ -k2t2)
)(l-k2t2)
@<k< 1).
Если сделать подстановку
то получим соответственно
sin v|/ @ < v|/ < тс/2),
- к2 sin2 ф
- fc2 sin2
J A + /isin2v|/)l/l-/t2sin2\J/
Эллиптические интегралы первого, второго и
третьего рода в лежандровой форме.
Соответствующие определенные интегралы обозначаются
по Лежандру F(/c, (p), E(k, ф), П(Л, к, ф):
l/l - к2 sin2 ф
246
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
г—===П(Л, /с,
'A
Эти функции, кроме переменного (р, содержат
еще параметр к или параметры h и к; они зата-
булированы (см. 1.1.2.4).
3.1.7.6.2. Интегрирование
трансцендентных функций.
1. J Я (sin х, cosx)dx. Делаем замену
переменного, полагая t = tg (x/2) (— п < х < п), а
следовательно, х = 2arctgf, dx = л dt. Тогда
1 + t2
cos х = 2 cos2 —- - 1 = г
2 1 +t2
- 1
1 -t2
It
+ t2
откуда
R (sin x, cos x) dx = I ЯI —-^y,
т. е. в итоге получаем интеграл от рациональной
функции.
При
Г 1 + sin х , I I +t2 2
мер. dx - I 5~- rdt =
F J 1 - cos x I 1 -t2 I + f2
•/ 1 +t2
= 21n|rj-y-ln(l
TT71
ln si f " ctg f
В частных случаях можно применять и более
простые подстановки: если функция R(sinx, cosx)
нечетна относительно sinx, т. е. Я (-sinx, cosx) =
= -R(sinx, cosx), то подстановка t = cosx
приводит к интегралу от рациональной функции;
если Я (sinx, cosx) нечетна относительно cosx,
т.е. Я (sinx, — cosx)= —Я (sinx, cosx), то
подстановка t = sin x дает интеграл от рациональной
функции; если, наконец, Я (-sinx, -cosx) =
= Я (sin x, cos х), то подстановкой t = tg x получают
интеграл от рациональной функции.
Примеры. 1) —Др-rfx. При помощи подстановки
cos х, dt = — sin x dx получают
f-™fi-dx = - frf4= -V+ С = --V- + С.
J cos3x J Г 2r 2cos^x
2) "^ г—X ,2 ¦ i • Здесь подстановка r = tgx
J <rcos2x + b2sm2x e
tg2xcos2x
Г dx_ Г (\+t2) dt
J ^cos2 x~Vb2 sin2 x " J (a2 + b2t2) A + t2) ~
- f-T%-2 "\arctgf-f) + C = \arctgf^tg x)
Ja2 + b2r ah \a J ab \a J
3) Jsin"xdx. Если п = 2т,+ 1, то полагаем f = cosx;
f sin2m+1xrfx = J(l -cos2x)msinxdx = - J(l - t2)mdt =
:-cosx + C:^p
2m + 1
¦+С.
В частности,
J sin3 xdx = — cos x + ?°-5-— 4- C.
Если и = 2m, то по формуле Муавра получаем
sin2mx = L j, | cos2mx- C2mcos2(m- l)x + ...
(-l)myC7m
Следовательно,
J sin2m х dx =
... + {-\)т-хСтг-х sin2x + (-l)mC3wx 1 + С
4)Jcos"xrfx. Если л = 2m + 1, то полагаем f = sinx;
Jcos2m+1x</x = J(l -sin2xrcosxrfx = J(l -t2)mdt =
--».- -n, з ¦ •• . v v -m 2m+{
Если п = 2m, то по формуле Муавра получаем
cos2m x = 2*_ , cos 2mx + C\m cos 2 (m — 1) x 4-...
... 4- C\m ' cos 2x + -^- С
Следовательно,
(cos2mxdx = ^ii^ — sin2mx+ —--rC2msin2(m - l)x + ...
J 22m [ m m - 1 2m v ;
• ... + П?" * sin 2x -f C1mx + C.
В частности,
Jcos4x</x= -^-(-ysin4x4-4sin2x4-6xj + C.
5) jsin",xcosmxdx. Если п (или m) нечетно, то
подстановка f = cosx (или t = sinx) приводит к интегралу от
рациональной функции. Например,
J sin2 xcos3 xdx = Jsin2 x(l - sin2 x)cosxdx = \t2(\-t2)dt,
t = sin x.
Если оба показателя степени четны (или нечетны), то
подстановка t = tg x приводит к интегралу от рациональной
функции. Если, в частности, пит положительные, то
можно использовать преобразования
sin х cos x = ^Y-, sin2 x =
Например.
J sin2 x cos4 x dx = {(sin x cos xJ cos2 x dx
-J- | sin2 2x(l + cos 2x) dx = -^ sin2 2xcos 2x dx +
~— | A - cos 4x) dx = -I- sin3 2x 4- --- x - -— sin 4x -
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
247
7) |ctg" x dx = -
-' x - j
ctg"-2 x dx.
2. JR(emx, enx,...,epx)dx (m, n,...,p —
рациональные числа). В результате подстановки t = 6х
получают интегралы вида — R (tm, f,..., tp) dx. Если
г - наименьшее общее кратное знаменателей дробей
т, п,...,р, то подстановкой и = yt получают
интеграл от рациональной функции.
3. J/?(shx, chx)dx. Эти интегралы можно
вычислить, заменив гиперболические функции на
показательные.
Случаи Jsh"xdx, \chnxdx, J sh" x chm x dx
рассматриваются аналогично соответствующим
интегралам от тригонометрических функций.
) - j
arctg x R' (x) dx = arctg x R(x)
J arcsin x R' (x) dx —
= arcsin x R (x) - t
R(x)dx,
-R(x)dx.
Пример, jln
TJ2jJ"J 25J2x + 5 5 J B* + 5JJ ~
Приме, J^
- - 2 arctg e* + С.
Интегралы вида
4. J Р (x) eax dx, 5. J Р (x) sin (ax + 0) dx,
6.
7.
8.
где Р (х) - многочлен от х, можно вычислить,
применив один или более раз формулу
интегрирования по частям.
Примеры. 1) Посредством однократного
интегрирования по частям
Таблица интегралов трансцендентных функций
находится в 1.1.3.3.
3.1.7.7. Несобственные интегралы. При введении
определенного интеграла предполагалось, что
функция /(х) ограничена, а интервал
интегрирования конечен. Несобственные интегралы
являются обобщением определенных интегралов на случай
неограниченных функций и бесконечных
пределов интегрирования.
Интегралы с неограниченными
подынтегральными функциями. Пусть функция /(х)
ограничена и интегрируема на каждом отрезке
а ^ х < Ь - 8, где 0 < е < Ь - а, но lim /(х) = оо.
х-+Ь
-а-
P'(x)eaxdx
получают интеграл от функции с многочленом, степень
которого на единицу ниже, так что в результате и
интегрирований по частям можно вычислить исходный
интеграл.
2) В случае интеграла Jea*sin(<xx + $)dx однократное
интегрирование по частям приводит к соотношению
Если существует предел
/= lim ff(x)dxy
?-> +0 a
(*)
a J
^-U«cos (ax + p) + — Г^ cos (ax + f})rfx;
a a J
интегрируя по частям второе слагаемое:
eax sin (ax + p) dx =* - — eax cos (ax + p) +
¦-^У*** sin (ax н
lxsin(ax + P)</x,
и объединяя интегралы, появляющиеся справа и слева,
получаем, что
то он называется сходящимся несобственным
интегралом от /(х) на [а, Ь] и его, как и ранее,
ъ
обозначают J f(x)dx, т. е.
[f{x)dx= lim f /(x)rfx.
a ?-> +0 a
Если же предел (¦) не существует, то
ь
§f(x)dx называется расходящимся несобственным
а
интегралом.
Если же /(х) ограничена и интегрируема при
а < х < Ь, то несобственный интеграл сходится и
совпадает с определенным интегралом в прежнем
смысле.
sin (ax
L«,« + с.
а' + а'
Интегралы вида
9. Jlnx?'(x)</x, 10. J arctg xЯ'(*)<**,
11. j arcsin x Я'(х)й(х,
где Л' (х) — производная некоторой рациональной
функции R(x), можно интегрированием по частям
свести к уже рассмотренным случаям:
|1пхД'(х)<*х = 1пхЯ(х)- \^^-dx,
г=г при 0 < х ^ 1 - е, где
Примеры. 1) /(х) =
0 < е < 1, ограничена и непрерывна; следовательно,
интегрируема. Предельное значение
/ = lim —--—= lim [arcsin(l-e)-arcsinO] *
е-* +0 J |/i _ x2 e-+ 4-0
= arcsin 1 = я/2
существует; гаким образом, -~~г~- = -—.
У»-*1 2
248
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
2) /(х) * —-— при 0 < х < 1 - ?, где 0 < е < 1,
ограничена и непрерывна, но
j/(x)dx сходится, то по определению полагают
с ъ с ъ
1-е
|im Г -J*_
в-+0 J *-J
lim [-ln(l-
е-* +0
« lim (-Ine) = +00;
?-> +0
следовательно,
[-toll-*
расходится.
Аналогично определяется несобственный
интеграл для функций, которые на каждом отрезке
а + s ^ х ^ Ь, где 0 < е < Ъ — а, ограничены и
интегрируемы, но lim /(х) = оо:
]f{x)dx= lim J f(x)dx.
a Z-* +0a + e
Примср./(х)= ——; пусть сначала 0 < а < 1:
1 1
|dx/jc"« lim f^-- lim -1-A_е>-•)»-!_;
таким образом, интеграл сходится.
При а ^ 1 ^~- расходится, так как при а > 1
lim .
lim
и при а'
i
lim — ш Mm In— =+оо.
?-> +0J х б-» +0 Е
Пусть/(х) не ограничена в окрестности обоих
концов отрезка [а, У]. И пусть с - любая
внутренняя точка отрезка [а, У]: а < с < Ь.
Если каждый из интегралов j/(x)dx и
\f{x)dx сходится, то по определению
Пример, fix) - - * а т -1, Ь - 1:
/1-х2
1 0 1
Г to ш Г </х Г rfx ш *_ ji.
~т~ "" I ,, "г j 2 2
или, подробнее,
Ь С-?! Ь
J/(x)rfx= lim J /(x)rfx+ lim f /(x)^x.
a ?x-^+0 a e2-*+°c + ?2
Оба предела нужно вычислять по отдельности.
Если в этом смысле несобственный интеграл
расходится, но существует предел
lim Г J/(x)dx+ }/(х)</Д
?- +0L а с+е J
то его называют главным значением
несобственного интеграла в смысле Коши. Он обозначается
тем же символом
Ь
либо v. p.
x, что и сам интеграл,
dx
Пример. Главное значение интеграла J —— равно
'_*?_+ f -AEJLtofW);
„ш
е- +
ъ
тогда как несобственный интеграл —~ (а < с < Ь) не
существует.
Интегралы с бесконечными пределами. Пусть
функция /(х) определена при х ^ а и
интегрируема на каждом отрезке а ^ х ^ Ь. Если
существует предел
ь
1= lim ff(x)dx,
Ь -*¦ +00 а
то он называется сходящимся несобственным
интегралом от /(х) на интервале [а, +оо) и
обозначается через j f(x)dx; таким образом,
J f{x)dx= lim {/(x)dx.
а Ь -> +OO a
Если же предел / не существует, то интеграл
\ f{x)dx называется расходящимся несобственным
интегралом.
Примеры.
1) J
lim \e~*xdx
Ь-* ооо
Если, наконец, /(х) не ограничена в
окрестности некоторой внутренней точки с отрезка
с
[а, Ь~\ и каждый из интегралов J/(x)dx,
= — lim (I - е~Л) =» —, если a > 0, и интеграл сходится;
a b-* +00 a
если же a < 0, то интеграл расходится.
Л?* ш f*. lta JL_( 1 _,).
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ 249
если а>1; если же 0 < а < 1, то несобственный интеграл которых она не ограничена. Тогда интервал
расходится как при а = 1: [а, +оо) разбивают на соответствующие частичные
+* * , интервалы и на каждом из этих частичных
^-« lim — ш Hm In b = + оо, интервалов вычисляют несобственные интегралы.
J x b-> +coJ х Ь-++со Если они сходятся, то интеграл на [а, +оо)
определяется как сумма интегралов на этих
так и при 0 < а < 1: частичных интервалах.
+ оо ь Критерии сходимости. Они формулируются для
J "x5""^ J'+ooJ ^"Sfc J'+oo 1-a^ e~^"+GOi интегралов вида J f{x)dx; для других типов
справедливы аналогичные утверждения*).
. % 14 \ j *• Если Функция /(х) и д(х) неотрицательны
Аналогично определяется Jj(x)dx= и для х > х0 > а справедливо неравенство
+ оо
л f(x)^g(x), то из сходимости f g(x)dx следует
= lim \f{x)dx. a
Ь-> — 00 b +oo
a +oo сходимость j f (x) dx, а из расходимости
Если оба интеграла \ f(x)dx и $ f(x)dx +oo a +оо
00 а J f(x)dx — расходимость J g(x)dx.
сходятся, то определению полагают а °
2. Если функции f(x) и #(х) неотрицательны
+ 00 а +оо
а f/ \
J f(x)dx= $f{x)dx+ J f(x)dx. и существует lim J— = К (O^K^+oo), то
-00 x-+oo^W
Пример. 7 *.- f/(x)rfx+ 7/(х)Ас- ДЛЯ ^ < + °° из сходимости J ^(x)dx следует
J ' + Х J J +оо
сходимость J f(x)dx, а при К > 0 из рас-
0 с а
ш lim г-rX2-+ lim I i .* i " ходимости f g(x)dx следует расходимость
fc-^-OoJ1"-* С -» + 00 J * "•" X a
Ь О +oo
J f(x)dx, т. е. при 0 < /С < оо оба интеграла
- lim (-arctgfc)+ lim arctgс - —- + -у «я.
или одновременно сходятся, или одновременно
расходятся.
а Г^шное значение. Если несобственные интегралы „ случае интеграла ^ fl < ь> от неограниченной
-l/<X)dX " ! /<ХМХ Расходятся- а пРадел в окрестности х = Ь функции нужно рассмотреть
/ (Х)
? у, ч j предел lim ——-.
hm j f(x)dx существует, то он называется х_>ь_о0(х)
Ь-++сс-ь В качестве функций сравнения в случае
главным значением несобственного интеграла. Его +0°
+ оо J f(x)dx особенно удобно использовать функции
обозначают v. p. j f(x)dx. « b
д(х) = —^Г> а в случае интеграла \f(x)dx от
Пример. Так как функция fix) = х 2~ нечетна, то
1 + х неограниченной в окрестности точки х = Ъ функ-
—^-j-rfx = 0; отсюда получаем ции — д(х) = — —.
J 1 "г X уи — X)
-ь
Ь Ъ Ъ Ь +оо
Г Y^^-dx - f -^j- + f y^j- - f y-^i-. Примеры. 1) f {1**д dx. Подынтегральная функ-
крестност
+<»
Г 1"х
ция в окрестности точки х»0 не ограничена. По опре-
Таким образом, главное значение несобственного интег- делению
рала равно
Г f Inx
J 1b2
первое слагаемое — сходящийся интеграл, так как при
Г ,, 0 < а < 1 имеем lim х" д «0; второе слагаемое
Сам же несобственный интеграл ] г^х расходится. х-»+0 1+х
] г
*) Во многих случаях бывает достаточно уметь от-
Пусть функция f(x) на интервале \а, +оо) ветить на вопрос, сходится ли данный несобственный
обладает конечным числом точек, в окрестности интеграл или расходится
250
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
сходится, так как при 1 < а < 2 имеем
, In
Х-+00 1 +
lim x-^-- lim -^--^
ч I — — • И
J xl/l + х2
Ит
. . 1
спользуя д (х) — —*-, получаем
х
1; таким образом, дан-
lim /(х) = об и несобственный интеграл
х-*Ь-0
ь
\f{x)dx сходится, . то он равен площади за-
штрихованной на рис. 3.18
неограниченной области.
Щ
х- +оо 9W ^^оо х^1 +
ный интеграл сходится, так как сходится интеграл
[dx
1
3) —===== (к2 < 1). Рассмотрим функцию
J l/(l-x2)(l-/c2x2)
Ь X О
Рис. 3.18
Рис. 3.19
сравнения 9 (x) - • Тогда lim
l/l -x x-*l -
1
_ jaK как интеграл
*
сходится, то
1/2A-/c2)
сходится и данный интеграл.
Абсолютная сходимость несобственного интег-
+ 00
рала. Интеграл J f(x)dx называется абсолютно
а
сходящимся, если сходится интеграл J |/(x)|dx
(аналогичные определения имеют место для
других видов несобственных интегралов). Если
+ 00
J f(x)dx сходится абсолютно, то он сходится.
а
Пример. sm* dx - абсолютно сходящийся интег-
рал, так как, положив #(х)- 1/х3/2, получим
lim
х-* +оо
lim
= 0.
Связь между несобственными интегралами и
+ оо
бесконечными рядами. Интеграл J f(x)dx тогда
а
и только тогда является сходящимся, когда для
каждой числовой последовательности {х„} (х0 = а,
хн ^ а) такой, что lim х„ = + оо, ряд
п-* +оо . /
оо Хи+1
Z J f(x)dx сходится и имеет всегда одну и ту
и = 0 х
же сумму. Эта сумма и является значением
несобственного интеграла.
Многочисленные критерии сходимости для
бесконечных рядов могут, таким образом,
использоваться для исследования сходимости
несобственных интегралов, и, наоборот, интегральный
критерий (см. 3.1 14.2) сводит исследование сходимости
рядов к определению сходимости несобственных
интегралов.
Геометрический смысл
несобственных интегралов. Если функция /(х) на
отрезке а < х ^ Ъ непрерывна, / (х) ^ О,
Если f(x) непрерывна при х ^ 0, /(х)^0 и
несобственный интеграл J f{x)dx сходится, то
а
он равен площади заштрихованной на рис. 3.19
неограниченной области.
Действия с несобственными
интегралами. Свойства определенных интегралов
для несобственных интегралов переносятся на ин-
+ оо
тегралы вида J f(x)dx и другие несобственные
а
интегралы следующим образом:
+ 00 +оо
1. Если сходятся J f{x)dx и J g(x)dx, то
а а
сходятся также J Af(x)dx для любой постоян-
а
+ 00
ной Л и | (/(х) + g(x))dx, причем
а
7 Af(x)dx = A+[ f(x)dx,
а а
J (/ (х) + g(x)) dx= (f (x) dx + fg (x) dx.
2. Если F(x) — первообразная для/(х) в
интервале [а, +оо) и существует lim F(x), то
Х-» +00
где [F(x)]fl+0° = lim F{x)-F(a). В случае не-
Х-» +00
собственного интеграла от неограниченной
функции /(х) справедлива формула
если первообразная функция F (х) непрерывна
(точнее, допускает доопределение по непрерывности) в
точках, в окрестности которых функция /(х) не
ограничена.
Примеры. 1) Первообразная функция для
Дх) = j- есть
F(x) = -±_-ln -^--+ -^-arctg(/2x + 1) +
4|/2 х2_|/2х4 I 2/2
ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
251
(см. 3.1.7.5), и lim F(x)= —~, F@) = 0.
х-+00 2|/2
Таким образом,
f dx я
J {+х* 21/2'
2) Первообразная для /(х) = х~1/3 есть F(x) = -^х2/3;
она непрерывна при х = 0; следовательно, I -=— =
3) Первообразной для /(х) = 2 является F(x) =
= ln|x2 - 11; она имеет разрывы при х = ± 1. Применение
2
Г 2х
формулы к интаралу -j—— привело бы к неправиль-
-2
ному результату 0, тогда как этот интеграл —
расходящийся.
3. Интегрирование по частям. Если функции
и (х) и v (х) имеют на интервале [а, + оо)
непрерывные производные, существует lim u(x)v(x) и
X -» +00
+ оо +оо
j и' (х) v (x) dx сходится, то J и (х) v' (x) dx также
сходится и справедлива формула
J и (х) v' (х) dx = [и (х) v (х)]в+ « - J и' (х) v (x) dx.
а а
Примеры. 1) м(х) = х", v(x) *=e~x; lim xV*=0,
Х-* 00
J x"~xe~xdx сходится; отсюда следует, что
о
J x"e-xdx = n f y*-xe-*dx.
о о
В результате повторных интегрирований по частям
находим
Примеры. 1) Выше было доказано, что интеграл
+ f In: ,
j 2 "z сходится; разложим его на два слагаемых:
о
Г \nzdz ш Cjnz dz+ Г \nz_dz
J 1 + z2 J 1 + z2 J 1 + z2
0 0 1
Подставим z = 1/х во второе слагаемое разложения; тогда
+ оо О 1
[ }n\dz = [^rdx = - f ^т-dx;
J 1 +z2 J 1 + x2 J 1 + x2
отсюда следует, что
+ oo 1 1
f -Г5^ = f r^rdz - f J^rdx = 0.
J 1 + z2 J 1 + z2 J 1 + xx
, . , ,. In sin x
2)/= 1 In sin zdz сходится, так как lim =
о х->+0 V^
0 при 0 < a < 1. Если подставить z = 2х, то получим
/
/ = 2 J In sin 2x dx = 2 J In B sin x cos x) dx =
о о
я/4 я/4
= -|-1п2 + 2 J lnsinxrfx + 2 Jlncosxdx.
2 о о
В результате подстановки х = я/2 - м получаем
я/4 я/2
2 J In cos х </х = 2 Jin sin м du,
О
/
Jlnsinxdx + 2 flnsinx</x = -?-ln2 + 21;
О я/4 2
таким образом,
/= -(я/2) In 2.
2) w(x) « 1/х, v(x) - -cosx; тогда
Г m2Ldx -Г- ^1 + °° -
так как оба слагаемых в правой части имеют смысл.
В частности, отсюда следует существование -—— dx (так
как подынтегральное выражение при х = 0 остается
ограниченным).
4. Правило подстановки. Если функция f(z)
при z ^ а непрерывна, функция z = g (x) на [а, Ъ)
имеет непрерывную производную д' (х) ф 0 и # (а) = а,
lim ^(x) = +00, то
х-+Ь
\ f(z)dzJ\f{g{x))-g'{x)dx-
при этом интеграл, стоящий справа, может быть
как собственным, так и несобственным, и из
сходимости одного из интегралов следует
сходимость другого.
3.1.7.8. Геометрические и физические приложения
определенных интегралов.
Длина кривой. Если плоская кривая L
задана параметрически: х = (р(О, у = \|/(г)
(*о < * < h\ причем ф(г) и \|/(f) - непрерывно
дифференцируемые функции, то она имеет длину /,
вычисляемую по следующей формуле:
'=
Если кривая L — график непрерывно
дифференцируемой функции у = /(х) (х0 < х ^ хД то длина
этой кривой вычисляется по формуле
/
Если кривая L задана в полярных
координатах р = р (ф) (ф0 < Ф < Ф1), то ее длина может
быть вычислена по формуле
Ф1
Фо
252
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Для кривой в пространстве, заданной
параметрически: х = ф(г), у = \|/(f), z = х@ (*о < * < ti),
где ф (Г), v|/ (t), % @ - непрерывно
дифференцируемые функции, длина вычисляется по формуле
/ =
'2@ А.
Площадь. Если /(х) является
неотрицательной непрерывной на отрезке а < х < Ь функцией,
то площадь F криволинейной трапеции ABCD
(см. рис. 3.14) вычисляется по формуле
S=]f{x)dx.
Площадь S сектора ОАВ, ограниченного
кривой АВ, заданной в полярных координатах:
Р=0(ф) (фо ^ Ф < Ф1), и радиусами О А и ОВ
(рис. 3.20), определяется интегралом
Фо
Фо
О вычислении площадей см. также 3 1.8.6
или 3.1.10.4.
в
Рис. 3.20
Рис. 3.21
. Объем тела вращения. Пусть функция
/(х) неотрицательна и непрерывна на отрезке
а ^ х < Ь; объем V тела, получающегося в
результате вращения криволинейной трапеции аАВЬ
(рис. 3.21) вокруг оси х, определяется формулой
Объем V тела, заключенного между двумя
плоскостями х = а и х = Ь, в случае, если
площадь сечения, проведенного перпендикулярно оси.
О
Рис 3.22
х, есть известная функция х: 5 =/(х) (а ^ х s
(рис. 3.22), вычисляется по формуле
V=]f{x)dx.
Ь)
О вычислении объемов см. также 3.1.10.4 и
3.1.11.4.
Площадь поверхности тела
вращения. Площадь S поверхности тела вращения,
возникающего в результате вращения вокруг оси х,
кривой, заданной на отрезке а ^ х < Ъ
неотрицательной непрерывно дифференцируемой функцией
/(х), вычисляется по формуле
S =
Если вращающаяся кривая задана параметрически:
х = Ф (t), y = y\f(t) (to^t^ t^ vl/(t) ^ 0, то
S = 2n J vj/ (t
^'2(t) dt.
Центр тяжести. Координаты (?,, т\) центра
тяжести материальной кривой с линейной
плотностью 5(х), заданной в явном виде: у = /(х)
(а ^ х ^ Ь), выражаются следующим образом:
ь
ъ
Ц= ^|б(х)/(хI/1
где М - полная масса: М = J6(x)j/l+ [/'(*)]2tffx.
При постоянной плотности 5 (х) второе равенство
может быть приведено к виду
2тс/Л = 2n)f{x) l/l + t/Чх)]2 dx
(/ — длина кривой). Это — первая теорема
Гульдена площадь S поверхности тела вращения,
образующеюся в результате вращения некоторой
плоской кривой вокруг оси, не пересекающей
этой кривой, равна произведению длины кривой
на длину окружности, описываемой при этом
вращении ценiром тяжести кривой: S = 2пг\1.
Пример. При вращении окружности радиуса г вокруг
не пересекающей ее оси образуется тор (рис. 3.23). Если
масса распределена по окружности равномерно, го центр
тяжести лежит в центре окружности. Пусть d - расстояние
от центра до оси (d > г); тогда центр тяжести
описывает окружность длиной 2nd; отсюда по первой теореме
Гульдена получается площадь поверхности тора:
Координаты (?, г)) центра тяжести
криволинейной трапеции (рис. 3.24) с равномерно
распределенной массой (поверхностная плотность 6 = 1) и
СУЩЕСТВОВАНИЕ И ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ 1-го РОДА
253
y=f2(x)
площадью S вычисляются следующим образом:
ь ь
cf(x)dx, г) = -—
Из второго равенства следует вторая теорема
Гульдена: объем V тела, описываемого плоской
фигурой при вращении
ее вокруг оси, лежащей
в плоскости этой
фигуры и не пересекающей
ее, равен произведению
площади S этой фигуры
на длину окружности,
_». описываемой при враще-
% нии центром тяжести этой
Рис. 3.25 Фигуры: F=S-2^.
Пример. Объем тора
(см. рис. 3.23). Площадь
вращающегося круга равна яг2; таким образом, объем тора
равен V«nr2-2nd-2n2r2d.
О вычислении центров тяжести плоских фигур
и тел см. также 3.1.10.4 и 3.1.11.4.
Момент инерции. Момент инерции 1у
относительно оси у кривой у = /(х) (а ^ х < Ъ)
с линейной плотностью 8(х) вычисляется по
формуле
О
и концом в точке В и и = /(х, у) —
ограниченная функция, заданная в некоторой области,
содержащей кривую L. На L выбираются
произвольные точки А = Ао, Аи...,Ат-и Ап = В; тем
самым криволинейный отрезок АВ разбивается на
элементарные отрезки (разбиение Z) (рис. 3.26).
Рис. 3.26
Пусть длина отрезка кривой между At-X и
At (i = 1,...,«) равна As,-. Пусть, далее,
Mifeh Л/) — произвольная точка на элементарном
отрезке Л,_ь А{. Сумма
, r\t)As,
Момент инерции 1У относительно оси у
криволинейной трапеции (рис. 3.25) с постоянной
поверхностной плотностью 5 равен
ь
Iy = b\x2{f2{x)-fx{x))dx.
О вычислении моментов инерции см. также
3.1.10.4 и 3.1.11.4.
3.1.8. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
Криволинейный интеграл является обобщением
введенного в 3.1.7.1 определенного интеграла, при
котором функция интегрировалась вдоль отрезка
[а, 6] действительной оси; в случае
криволинейного интеграла функция интегрируется вдоль
кривой.
Отрезок плоской кривой, заданной
параметрически :
х = <р(г), у = v|/ (г) (ti О^г2),
называется гладким, если производные функций
Ф @ и v|/ (r) непрерывны и всегда ф' (t) +
+ vj/' (t) > 0. Точка со значением параметра tl
называется начальной точкой, а точка со
значением параметра t2 — конечной точкой отрезка
кривой. Кривая называется кусочно гладкой, если ее
можно разбить на конечное число гладких
отрезков кривой.
Аналогичное определение имеет место для
пространственных кривых, заданных
параметрически: х = ф(г), У = vj/(f), z = %{t) (ti^t^ t2).
3.1.8.1. Криволинейные интегралы 1-го рода
(интегралы по длине кривой). Пусть L — отрезок
кусочно гладкой кривой с началом в точке А
называется интегральной суммой относительно
разбиения Z. Обозначим через A(Z) максимальное
из чисел Ast:
A (Z) = max As,-.
1 i
Как и при определении обычного
определенного интеграла, число J называется
криволинейным интегралом 1-го рода, если оно обладает
следующим свойством: для любого е > 0
существует такое число 5 (е) > 0, что для любого
разбиения, удовлетворяющего условию A(Z) < 5, и
независимо от выбора точек М, выполняется
неравенство | S (Z) — / | < е.
Обозначения:
/= J/(x, y)ds, 1= J /(x, y)ds.
(L) (AB)
Аналогично определяется криволинейный
интеграл J f(x, y, z)ds 1-го рода от функции
(Q
и = /(х, у, z) трех переменных по отрезку L
пространственной кривой.
Криволинейный интеграл 1-го рода не зависит
от направления движения по кривой L, т. е. если
L проходится в противоположном направлении,
так что В — начало, а А — конец, то
j /(x, y)ds= f /(x, y)ds.
(BA) (AB)
3.1.8.2. Существование и вычисление
криволинейных интегралов 1-го рода. Если отрезок кривой
L представлен параметрически: x = x(s), у = y{s)
@ ^ s ^ /), причем / обозначает длину дуги участка
кривой L от начальной точки до точки,
отвечающей значению параметра s, то криволинейный
254
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
интеграл сводится к определенному интегралу:
fix,
y{s))ds,
(L)
и, таким образом, из существования одного
интеграла следует существование другого; из этой
формулы введением новых переменных
интегрирования можно получить и другие представления:
а) Если L— отрезок кусочно-гладкой кривой,
заданной параметрически: х = ф(?), y = y\t(t)
(ti^t^ t2), то
t2
f f{x, у)ds = J/(Ф(г), фit))l/^W+Vit)dt. (•)
(L) r,
Формально при вычислении криволинейного
интеграла нужно, таким образом, представить
функцию параметрически и по правилу
подстановки для определенных интегралов заменить
переменное s на t. Тогда в силу формулы
—- = |/ф' @ + y\f' it) непосредственно получаем
формулу (*).
Аналогично для кривой в пространстве имеем
(Ц
fix, у, z)ds
б) Если плоская кривая задана в явном виде:
= yix) ia^x^b), то
J /(x, y)ds=Sfix,
Щ
y'2ix)dx.
Пример. Пусть L — полуокружность радиуса г,
описанная вокруг начала координат, параметрическое
представление которой: х — г cos г, у = г sin t @ < t < я). Тогда
J yds - Jrsinf rdt = 2r2.
(L) °
3.1.8.3. Криволинейные интегралы 2-го рода
(интегралы по проекции и интегралы общего вида).
Пусть L — отрезок гладкой кривой с началом в
точке А и концом в точке В, и—fix, у)—
функция, заданная в области, содержащей L,
0 х0 х, х2
х = (xt> Уд, Mt = ($ь г|,). Тогда сумма
S(Z) = f/fe г\д Ахь Ах, = х, - х(_ь
Рис. 3.27
называется интегральной суммой, соответствующей
разбиению Z. (В отличие от интегральной суммы
при криволинейном интеграле 1-го рода здесь
/(?;> Л«) умножается не на длину As, элементарного
отрезка, а на величину Ах, его проекции на ось
х.) Обозначим через A(Z) наибольшее из
расстояний от /!,_! до А( A < i! < п).
Число / называется криволинейным интегралом
2-го рода, если для любого 8 > 0 существует
такое число 5 (е) > 0, что для каждого разбиения
Z, удовлетворяющего условию A (Z) < 6, и для
любого выбора промежуточных точек М, выполняется
неравенство | S(Z) - / | < е.
Обозначения:
/= I fix, y)dx, /= J fix,y)dx.
(Ц (АВ)
Криволинейный интеграл по кусочно гладкой
кривой определяется как сумма интегралов по
гладким отрезкам кривой, из которых
составляется данная кривая. Если начальная и конечная
точки совпадают, то получается криволинейный
интеграл по замкнутой кривой, который
обозначается следующим образом:
$/(х, y)dx.
Аналогично можно определить для плоской
кривой число
J /(x, y)dy,
(L)
а для пространственной кривой — числа
J /(х, у, 2) dx, J fix, у, z) dy, J fix, y, z) dz.
Щ Щ (L)
Если на одной плоской кривой определены две
функции Р(х, у) и Qix, у), то под
J Pix,y)dx + Qix, y)dy
понимают сумму обоих интегралов J P(x, y)dx и
1 Q(x, y)dy, т.е.
Ш
f P(x, y)dx + Qix, y)dy =
(L)
= J P(x, y)dx+ f Qix, y)dy.
(L) (L)
Аналогичным образом для пространственной
кривой понимается интеграл
J P(x, у, z)dx + Qix, у, z)dy + Я(х, у, z)dz
и ограниченная на L. Выберем на L
произвольные точки А = Ао, Аи...,А„-и Ап — Ъ. При этом
получается разбиение Z кривой L на
элементарные отрезки (рис. 3.27).
Пусть М, — произвольная точка, лежащая на L
между Л,_! и А{ ii =!,...,«), и пусть
от трех функций Р(х, у, z), Qix, у, z) и Д(х, у, z)
трех переменных.
3.1.8.4. Свойства и вычисление криволинейных
интегралов 2-го рода. Обычный определенный
интеграл есть частный случай криволинейного
интеграла, когда в качестве кривой L выбирают
СВОЙСТВА И ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ 2-го РОДА
255
отрезок оси х. Оба интеграла имеют аналогичные прерывна и у(х), то
свойства: ь
\af{x,y)dx = a\ f(х, у)dx (a = const), I /<*' ^dx = Sf<*• У(*»dx-
Щ (L) (L)
J (fix, У)+д(х, y))dx = J /(х, у)Лс + Ых,>-)</х. Примеры. I) / = ^xydx + (у - x)dy, , де L - огрезок
^ ' * ' ' ' параболы у = х2 с началом в точке @, 0) и концом
Если кривая L состоит из двух кривых L, в точке A, 1). Параметрическое задание кривой L: х = г,
1 >• = г2 @^ г ^ 1). Следовательно,
И 1^2, ТО
/ = J [f3 + (f2 - rJf] dt = JCr3 - 2t2)dt = -^-.
2) / = f xvdx + vzdy + zx dz, где L - один виюк винто-
(L) '
«ой линии х = a cos t, у = a sin t, z = bt @ ^ г < 2я);
/ s J (- </3 sin21 cost + a2 bt sin t cost + ab2t cos t)dt = —~a2b.
f /(x, y)dx= J /(x, j;)</jc+ f f(x, y)dx.
Ш (L,) (L2)
Если направление интегрирования по L меняют,
принимая В за начальную точку, а А — за
конечную, то
J /(х, .уМх=- J /(х, Я</х.
(В/1) • (А В)
Аналогичные формулы верны для криволиней- Связь криволинейных интегралов
ного интеграла по пространственной кривой. 1-го и 2-го рода. Если L — гладкая кривая
Криволинейный интеграл зависит от начальной на плоскости или гладкая кривая в простран-
и конечной точек и в общем случае также от стве, касательная к которой имеет с координат-
пути L, соединяющего обе точки. Он не зависит ными осями углы а, C или а, |3, у, то
от пути тогда и только тогда, когда обращается
в нуль на каждой замкнутой кривой (см. также 1 р(*> y)dx + Q(x, y)dy = J (P cos a + Qcosp)ds
3.1.8.5). (V iL)
Вычисление. Если L — гладкий отрезок
кривой, заданной параметрически: х = q>(f), y = vj/(f)
('i <t^t2), и функция f{x, у) непрерывна на L, I ?{*> У* z)dx + Q(x, у, z)dy + Я(х, у, z)dz =
то существуют криволинейные интегралы (L)
fix, y)dx и j f(x, y)dy и справедлив следую-
Щ (L)
щий переход к определенным интегралам:
(Ц
fix, y)dx= J/4<P(r),
fix, y)dy= f
Аналогично для кривой в пространстве,
заданной параметрически: х = (р@, у = v|/(f), z = x(t)
(?! ^ f ^ г2)» получаем, что
J/(x, у, z)dx=\
j /(x, y, z)dy= Sfivit),^it),xit)Wit)dt,
J jix, y, z)dz= !fiq>it),^it),iit))x'it)dt.
Щ r,
Формально нужно, таким образом, как и при
замене переменного в определенных интегралах,
заменить переменные интегрирования х, у и z
на переменное t, используя параметрическое
представление L. Это непосредственно приводит к
указанным формулам для вычисления
криволинейных интегралов.
Если кривая L задана уравнением у = у(х)
(а ^ х ^ Ь) и наряду с непрерывностью /(х, у) не-
= J (Р cos а + Q cos p + R cos y) ds.
Если в случае плоской кривой ввести угол
(хГп) между положительным направлением
нормали (получаемым из направления касательной
поворотом на я/2 против часовой стрелки) и
осью х, то, учитывая, что (х,^п) = а + я/2,
получим
J P dx + Q dy = f [F sin (x» - Q cos (x»] ds.
Пример. Пусть L — кривая, не проходящая через
ачало координат, и Р = y/r2, Q = — х/r2 (г = |/х2 + у2). Тог-
J ra-rf* r2^ J ^2sin(x,n)+ r
Щ
Преобразуем этот криволинейный интеграл 1-го рода.
Обозначим через (хГг) угол, который составляет радиус-
вектор г с осью х (рис. 3.28); тогда
x/r = cos (хГг), у/г = sin (хГг).
Обозначим через (г,лп) угол между радиусом-вектором и
Hi
0
/
—L
X
Рис 3.28
256
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
нормалью к L; тогда (г/Ъ) - (хГп) - (хрг). Таким образом, или
(?) (L)
Этот так называемый интеграл Гаусса геометрически
представляет угол, под которым кривая L видна из начала
координат. Если кусочно гладкая кривая L является простой
замкнутой кривой (т. е. образом окружности при
непрерывном взаимно однозначном отображении), то значение
интеграла Гаусса равно 2я, если L окружает начало координат
и пробегается против часовой стрелки, и равно 0, если
начало координат лежит вне L.
3.1.8.5. Независимость криволинейных интегралов
от пути интегрирования. Значение криволинейного
интеграла, взятого вдоль пути L, соединяющего
данную начальную точку А с конечной точкой В,
вообще говоря, зависит от пути L.
Условия независимости
криволинейного интеграла от пути.
Двумерный случай. Если функции Р(х, у)
и Q(x, у) вместе со своими частными
производными дР/ду и dQ/dx непрерывны в области G,
то криволинейный интеграл j P dx + Q dy не
(L)
зависит от выбора кривой L, целиком лежащей
в G и соединяющей А и В, если в G существует
однозначная функция U (х, у), производные которой
удовлетворяют условию
dU/dx =
dU/dy
т.е. если Pdx + Qdy является полным
дифференциалом функции U. Криволинейный интеграл может
быть тогда вычислен по следующей формуле:
J Pdx + Qdy = U(В)- U(А).
Если область G односвязна, то необходимым
и достаточным признаком существования функции
U (х, у) является выполнение условия
интегрируемости
дР_
77
?
дх
для всех точек области G.
Вычисление функции U(x, у). Если
(*о> Уо) - фиксированная точка, а (х, у) -
переменная точка односвязной области G и если
выполнено условие
интегрируемости, то
криволинейный интеграл
J Pdx + Qdy, взятый по
произвольной кривой L,
соединяющей эти точки
и лежащей в области G,
является искомой
функцией U(x, у). В случае,
когда кривая,
соединяющая точки (х0, Уо) и
(х, у) в G, состоит из двух отрезков,
параллельных координатным осям (рис. 3.29), имеем
17(х, у) = j P& yo)dZ3 + J Q(x, r\)dr\ + С,
*о Уо
Рис. 3 29
V(x, у) = J Q(x0, Л)«*Л + SP& У№ + С.
Уо х0
Примеры. 1) Р(х, у)ш
Пусть G является односвязной областью, не содержащей
начало координат. Тогда в С функции Р, Q, дР/ду,
dQ/dx непрерывны и
ду дх
Криволинейный интеграл J Pdx + Qdy, следовательно,
(L)
не зависит от выбора пути в G, и при (х0, у о) ** @, 1),
у > 0 получаем, что
¦ + с.
В области, содержащей начало координат,
криволинейный интеграл не зависящим от пути не является. В
противном случае он должен был бы обращаться в нуль
при интегрировании по окружности радиуса г с центром
в начале координат; однако в этом случае
2я
j Pdx + Qdy= f (sin21 -I- cos2 t)dt =2n*0.
(L)
2) Функцию U (x, у) можно найти также следующим
образом: пусть Р(х, у) = х + у, Q(x, у) — х — у; тогда
равенство дР/ду - dQ/dx всегда выполнено. Искомая функция
U (х, у) должна удовлетворять условию dU/dx = Р = х + у.
Интегрированием по х получаем U =—х2 + ху + ц>{у) с
постоянной интегрирования ф(у), зависящей от у.
Из условия dV/dy = Q следует теперь, что х + у'(у) =
— х — у, откуда у'{у)=—у, следовательно, фО')™
= —^у2 + С. Таким образом,
V(x, y) = -jx2 + xy-±y2 + C.
Трехмерный случай. Пусть G — некоторая
односвязная пространственная область, т. е.
область, которая наряду с каждой замкнутой
кривой содержит также некоторую поверхность,
границей которой является эта кривая (в этом
смысле область между двумя концентрическими
сферами является односвязной поверхностью, а тор
(см. рис. 3.23) - нет). Пусть функции Р(х, у, z),
Q (х, у, z) и R (х, у, z) вместе с частными производ-
дР дР dQ dQ dR dR
ными —, —, , —, , непрерывны в
ду dz dz дх дх ду
G. Если А и В — две точки в G, то
криволинейный интеграл
J Pdx + Qdy + Rdz
(Ц
не зависит от выбора кривой L, соединяющей
эти точки, тогда и только тогда, когда существует
функция U(x, у, z), для которой
dU
dU
3U
т. е. когда подынтегральное выражение
криволинейного интеграла является полным дифференциалом
некоторой функции U{x, у, z).
СВОЙСТВА ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА
257
Необходимым и достаточным условием
существования функции V(х, у, z) является
выполнение условий интегрируемости
dz ду' дх dz' ду дх
в предположении, что функции Р, Q, R вместе
с частными производными непрерывны в G.
Функция Щх, у, z) может быть вычислена
при помощи криволинейного интеграла, взятого по
любой кривой L, соединяющей точку (х0, у0, z0)
с точкой (х, у, z) и лежащей в G. Если отрезки,
параллельные координатным осям (рис. 3.30), лежат
в G, то получим
формулу
U(x, у, z) =
а координаты центра тяжести равны
4- ]r(x, у,
Рис 3 30
или пять других
формул, аналогичных
этой, которые получатся, если выбрать другие пять
путей интегрирования, частичные отрезки которых
параллельны координатным осям.
П р и м е р. Р = х2 - yz, Q = у2 — xz, R = z2 — ху. Условия
интегрируемости выполнены во всем пространстве; для
(х0, Уо, г0) = @, 0, 0) получаем
U (х, у, z) = Ь2 d% + ] л2 dt] + ) (С2 - ху) d^ + С ш
0 0 0
= у х3 + — у3 + — z3 - xyz + С.
3.1.8.6. Геометрические и физические
приложения криволинейных интегралов.
1. Ориентированная площадь S области,
ограниченной плоской замкнутой кривой L:
S = ~ Ф х dy - у dx.
При этом S получается положительной или
отрицательной в зависимости от того, где
находится область G при обходе по границе L — слева
или справа.
Пример. Площадь области, ограниченной эллипсом
х2 у2
—у- + -JJ- — 1; параметрическое задание эллипса: х = a cos t,
у = Ъ sin t @ < t < 2я). Тогда
2я
= — l
S = — lab (cos2 t + sin2 t) dt = abn.
2. Масса и центр тяжести кривой L. Если
масса гладкой кривой L распределена с линейной
плотностью 5 (х, у, z), то полная масса кривой
вычисляется по формуле
М
J 6 (х, у, z) ds,
(L) (L) (L)
Пример. Вычислим массу и координаты центра
тяжести циклоиды х = г (t — sin О» У — г A - cos t) @ < / < 2я)
с равномерно распределенной массой E = 1):
2я
(L) О
% - — Г х <fc * ^-г2 Г(? — sin Г) |/2 j/l-c
2я
3. Работа силы вдоль кривой L. Если Рех -f
+ бе2 + ^е3 — сила, которая вдоль кривой L
меняется по величине и направлению ({еь е2, е3} —
ортонормированный базис), то при движении
материальной точки единичной массы под влиянием
этой силы совершается работа
А = \Р dx + Qdy + Rdz.
(L)
Работа тогда и только тогда не зависит от
пути L, соединяющего две точки, когда
подынтегральное выражение является полным
дифференциалом некоторой функции U (х, у, z) (так
называемого потенциала силового поля). В этом случае
работа вычисляется как разность потенциалов
в данных точках.
Пример. Если компоненты силы равны Р = х/г3,
Q - У/г*> ^ = Фг, где г « Ух2 + у2 + г2, то существует
потенциал, а именно U(x, у, z)*= - 1/г, и сила совершает вдоль
некоторой кривой L, соединяющей точки (х* у* z0) и
(*ь У и z\) и не проходящей через @, 0, О), работу
Л - U (хх, ylt г,) - U (х0, у* z0).
3.1.9. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ
ОТ ПАРАМЕТРА
3.1.9.1. Определение интеграла, зависящего от
параметра. Если функция / (х, у) определена при
а<х<Ь, с ^ у ^ d и при каждом фиксированном
у интегрируема по х, то равенство
F(y)=
x, y)dx
определяет на отрезке [с, dt] некоторую функцию
F переменного у, называемого в этом случае
параметром.
С ydx
I — г
что легко прове-
Пример, arcsin v
рить подстановкой z = ху.
3.1.9.2. Свойства интегралов, зависящих от
параметра. Если функция /(х, у) непрерывна при а ^
^ х ^ Ь, с ^ у ^d, то функция F (у) также
непрерывна при с 4: у ^ d. В частности, F (у) можно
9 И Н. Бронштейн, К А Семендяев
258
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
интегрировать. При этом
(повторный интеграл); порядок интегрирования
может быть изменен:
I df{x'y) dx)dy=i (j/(x'y) dy)dx'
Скобки могут быть опущены, если
договориться, что внешнему знаку интеграла ставится в
соответствие внешний дифференциал. Если частная
производная df/dy непрерывна, то функцию F (у)
можно дифференцировать по у и
F' (у) =
Интегрирование и дифференцирование по
параметру интегралов, зависящих от параметра, часто
используют для вычисления определенных
интегралов.
Примеры. 1) Функция /(х, у) = ху и производная
df/ду = ху In х при 0 ^ х < 1, у > 0 непрерывны. Из того, что
F(y)
= Гх^х = Г—Т L_
следует равенство
Дифференцируя равенство I xy dx =
о
тельно п раз, получим
l
1ХУAП
x)Hdx--
(-1)"/»!
2) Функция / (х, у) = ху при 0 < х < 1, а < у < Ь (а > 0)
непрерывна; поэтому порядок интегрирования может быть
изменен:
и 1»
J J x' dx dy~ \\xy dy dx.
Из того, что
x»-x«
lnx '
следует формула
Г **-** d _ ln b + 1
J ln x X~ a + Г
Переменные пределы
интегрирования. Если ф (у) и \|/ (у) непрерывны и
дифференцируемы при с ^ у < d и если / (х, >>) имеет
непрерывную частную производную по у в области,
содержащей точки (х, у) с <р (у) < л; ^ \|/ (у), с <
Рис. 3.31
< У < d (рис. 3.31), то зависящий от параметра
интеграл
¦ (У)
F (у) = J / (х, у) dx
при c^y^d можно дифференцировать, и его
производная имеет вид
ду
- /(ф Ы, у) ф' (у).
С (у — х)"
Пример. F{y)= ——j f(x)dx; f(x) непрерывна;
а = const; тогда
Г (у)
f -хУ1
-J (И-1)Г
Посредством последующих дифференцирований найдем
Fin+l){y)=f(y)-
3.1.^.3. Несобственные интегралы, зависящие от
параметра. Часто рассматриваются несобственные
интегралы, зависящие от параметра, например
J J/A - xJ A - y2x2)
¦f oo
J x>-le-'dx (y>0).
При этом первый интеграл берется от функции,
неограниченной при х = ±1, а второй — на
бесконечном интервале. Оба типа интегралов имеют
сходные свойства, поэтому ограничимся
рассмотрением только одного из них.
Равномерная сходимость. Пусть ин-
+ 00
теграл J / (х, у) dx сходится при каждом у из
а
некоторого интервала /. Этот интеграл называется
равномерно сходящимся на /, если для каждого
е > 0 существует точка х (е), не зависящая от
у el и такая, что для любого Ъ > х (е)
выполняется неравенство
J f{x,y)dx
b
+ (XI
Пример. Интеграл J ye~yx dx при у ^ 0 сходится и
о
представляет, таким образом, некоторую функцию F {у),
дится, так как при Ь > х (е) ««^ , , o-yxAvA^_ . _Ldy = ln^_
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА 259
причем F @) = 0; при у > 0 имеет место сходимость, так как Пример. +f e~yx dx при у > о 0 равномерно схо-
* _ Ьу О
\ уе ху dx = J е~г dz = 1 - е Ьу. +00 j
0 ° дится, и F (у) = j" e"** dx = —, откуда следует, что
На каждом отрезке 0 < с < у ^ d интеграл равномерно схо-
' имеем I Г _ „ ,
JJ
f ye~xydx= J e~z dz = e~b'<e~bc<e. c ° c
ь Ьу С другой стороны, после изменения порядка интегри-
„ рования имеем
Достаточные признаки
равномерной сходимости. ? Г г e-«_e-««*
1. Если существует функция ср (х) такая, что J у y*dydx= J ~ dx:>
при х ^ х0 > а и при всех у е / о с о
I / (х, у) | ^ Ф (х), следовательно,
+ оо Г е-"-е-'* d
и если интеграл J <p (x) dx сходится, то J ^ dx = ln—.
а о
+ 00
J / (х, у) dx равномерно сходится на /. В случае неравномерной сходимости изменение порядка
а интегрирования, как показывает следующий пример, может
+ «> оказаться невозможным: пусть а > О, Ь > 0 и
Пример. J e~xy sin x dx; при х > 0, у ^ у0 > 0 имеем +»
о Г _^ _Ья е-«у_е-ьу
|е~"8Н1х|<е~*'о = ф(х) и f e~xyodx сходится; следова- J У
о 1
тельно, } e'^sinxdx равномерно сходится при у>уо>0. отск>Да
° С С е~ау-е-Ьу
+ r°° \F (у) dy = dy;
2. Интеграл j f(x)g (х, у) dx равномерно схо- J J У
0 °
дится на /, если J/(x)dx сходится, а функция так как, с другой стороны, J (шГ"* - Ье~Ьху) dy =
а е-ах_е-Ъх °
д (х, у) на / равномерно ограничена и монотонна = ~ » то ПРИ а * b
по х. . +в +(В .
Пример. Интеграл
дится, так как несобственный интеграл
+ Г Sinx f f (ае--*> - Ье-Ьху) dx dy - \ [{ае-^-Ъе~Ьху) dy Ax =
I е у dx равномерно схо- j J J J
J x oi io
0 1 ao
Г sin x - f — dy + — dx =
J -т-dxявля- J У J x
ется сходящимся (см. 3.1.7.7), а функция д(х,у) = е~ху при ^^ b
равномерно ограничена (е~ху 4: 1) и монотонна по х. = dx = In — Ф 0.
Если функция/(х, у) при х ^ а, уе/ непрерыв-
+ оо Если, кроме того, при у е / существует и непре-
на и J / (х, у) dx равномерно сходится, то функ- рывна функция f'y (х, у) при х ^ а и интеграл
00
+ оо J f'y (х, у) dx равномерно сходится на J, то
функция F (у) = J /(х, >>) dx непрерывна на /, т. е. для а
а ция F (у) дифференцируема на / и имеет произ-
любого уое1 водную
Km 7 / (*, У) dx = 7 / (*. У о) dx. F' (у) = +f /; (х, у) dx.
У^Уо а а
При этих условиях F (у) можно интегрировать, +J sin x
и при с, del имеем Пример. F {у) = I e~xy —~dx, y>0.
о
J ff(x,y)dxdy= Slf{x,y)dydx. +f sinx . +» x, . .
Jc 3 a / Интегралы e"*" dx, J g"x' sin x dx равномер-
J x 0
0
Интегрирование и дифференцирование несоб- но сходятся при у>уо>0. Отсюда вытекает, что для
ственных интегралов, зависящих от параметра, любого у > 0 выполняется равенство
часто используются при вычислении несобствен- р, _ _ V0 .ху . .
ных интегралов. 0
9*
260
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Интеграл можно вычислить:
f -» • j fcosx + ysinx _-Л+а> 1
- e *y sin x dx = -—=Ц e xy = - 5-,
0
так что F {у) = -1/A + у2). Отсюда F (у) = С - arctg у. Так
как lim F (у) • 0, то С = я/2 и
у-* +оо
Г ,„ sin х , я
I е ~7~ = Т " arctg y;
в частности, при
+ 00
f S'" Х А _ Л
3.1.9.4. Примеры интегралов, зависящих от
параметра.
1. Бета-функция (эйлеров интеграл 1-го рода):
Этот интеграл есть функция от параметров х и у;
он сходится при х > О, у > 0 и расходится, если
либо х < О, либо у ^ 0.
Свойства бета-функции.
1) В (х, у) = В (у, х).
2) В (х, у) = -гтт—ГВ (*. ^ " *)•
х + у - 1
3) В (х, л) =
= U 2, ...
4) В (х, у) =
(и-1)!
х(х+ 1)(х + 2)...(х +л- 1)
при
+ 00
5) В (х, 1 - х) =
(О < х < 1).
sin хп
2. Гамма-функция (эйлеров интеграл 2-го рода):
Г(х)= J
dt.
Этот несобственный, зависящий от параметра х
интеграл сходится при х > 0, а при х ^ 0
расходится. Подстановками и — е~' и и = \nt получаем
соответственно
5) Связь с бета-функцией:
6) Закон дополнения:
Г (х) Г A - х) = -г^— @ < х < 1).
SinXTC
7) Закон удвоения Лежандра:
/ 1 )/
Теорема умножения:
8) Формула Раабе: J In Г (и) du = x (In x -
- 1) + In j/2ic.
9) Формула Гаусса:
г(*) , ^ Г i-f-1 ,
о
, С = lim ( )
п —> оо \ / ^ ^
(С — постоянная Эйлера
С = 0,577 215 664 901 532...).
10) Формула Коши:
In n I,
Г(х)
ы, Г(х)= J
Свойства гамма-функции.
1) При х > 0 гамма-функция непрерывна и
имеет непрерывные производные любого порядка:
Г(я)(х) = J e~tfc~l(\ntYdt.
о
2) Представление Гаусса (в виде произведения):
(л-1)!
Г'(х)
Г(х)
Некоторые интегралы, связанные с гамма-
функцией, содержатся в 1.1.3.4.
3.1.10. ДВОЙНЫЕ ИНТЕГРАЛЫ
3.1.10.1. Определение двойного интеграла и
элементарные свойства. Пусть S — ограниченная
область *) плоскости х, у с кусочно гладкой
границей, и пусть функция/(х, у) определена и
ограничена на S. Посредством
сетки кусочно гладких
кривых (рис. 3.32)
область S разбивают на
конечное число
элементарных областей Si(i = 1,
2, ..., л) с площадями
AS,- (разбиение Z); пусть
A (Z) — наибольший из
диаметров элементарных
областей 5,
получающихся при разбиении Z.
В каждой из
элементарных областей выбирается
произвольная точка Mt — (xh yt). Число a (Z, {М,}) =
Рис. 3.32
Г W ~ и ^ "X х (х + 1) (х + 2)... (х + л - 1) (Х > 0)' = I / (хь л) Аи ставится в соответствие каждому
3) Функциональное равенство: Г (х + 1) = хГ (х).
4) Г(л+ 1) = л! (л = 0, 1, 2, ...).
*) В 3.1.10-3.1.13 термин «область» всегда означает
«замкнутая область».
ВЫЧИСЛЕНИЕ ДВОЙНЫХ ИНТЕГРАЛОВ
261
разбиению Z и выбору ючек М^5, и называется
интегральной суммой, соответствующей разбиению
Z и выбору точек М,е5,.
Функция / (х, у) называется интегрируемой по
области S (в смысле Римана), если существует
число / со следующим свойством: для каждого
е > 0 найдется 5 (е) > 0 такое, что для каждого
разбиения Z области S, для которого A (Z) < е,
и независимо от того, какие точки М, выбираются
в элементарных областях, выполняется неравенство
| a (Z, {М^) — I j < е. Число / называется двойным
интегралом (Римана) от / (х, у) по области S
и обозначается следующим образом:
(S)
I = tff(x,y)dxdy.
(S)
Эквивалентным этому определению является
следующее: /(х, у) интегрируема по S, если для
каждой последовательности Zn разбиений с
lim A (Zn) = 0 последовательность соответствую-
п—»оо
щих интегральных сумм a (Zn, {M\H)}) всегда
сходится независимо от выбора промежуточных
точек {М|и)} (в этом случае все последовательности
интегральных сумм сходятся к одному и тому же
значению, которое и есть двойной интеграл).
Интегрируемые функции.
а) Каждая непрерывная на S функция является
интегрируемой по S.
б) Каждая ограниченная на S функция, которая
непрерывна на S, за исключением точек, лежащих
на конечном числе !ладких кривых, интегрируема
по S; значения функции на таких кривых можно
произвольно изменять (если только измененная
функция остается ограниченной), не меняя значения
интеграла.
Свойства двойных интегралов. Если
функции интегрируемы по области, то имеют
место следующие свойства.
1) Аддитивность относительно
подынтегральных выражений:
Я [Я*, У) + в(х9 y)]dxdy =
(S)
= ff / (х, у) dx dy + \\g (x, у) dx dy.
(S) (S)
2) Аддитивность относительно областей: если
Su S2 — две области без общих внутренних точек,
то
Я f(x,y)dxdy =
= JJ/(x, y)dxdy+ JJ/(x, y)dxdy.
(Si) (S2)
3) Постоянный множитель можно выносить за
знак интеграла:
Я Af (х, у) dxdy = A j'jY (х, у) dx dy.
(S) (S)
4) Если для каждой точки (х, y)eS
выполняется неравенство / (х, у) < g (x, у), то
5) Если /(х, у) интегрируема по 5, то функция
| / (х, у) | также интегрируема по 5 и
| tff{x,y)dxdy\^ \\\f{x,y)\dxdy.
(S) (S)
6) Если m является нижней, а М — верхней
границей для /(х, у) на S, и если AS - площадь
области S, то
т AS ^ Я/ (*> У) dxdy^M AS.
(S)
7) Теорема о среднем значении. Если / (х, у)
непрерывна в (связной) области S, то
существует по меньшей мере одна точка (?,, r\)eS
такая, что
SSf(xty)dxdy=f&r\)AS.
8) Если {Sn} — последовательность областей с
площадями ASn и диаметрами ри и если каждая
область содержи i точку М и lim р„ = 0 (в этом
п~* оо
случае говорят, что последовательность Sn
стягивается в точку М), то для непрерывной функции
/(х, у) существует предел
(дифференцирование по области).
3.1.10.2. Вычисление двойных интегралов.
а) Если
S = {(х; у) | а ^ х ^ Ъ, у, (х) ^ у ^ у2 (х)},
где уь у2 — непрерывные функции на [а, Ь~\
(рис. 3.33), то
Ъ/Уг(*) \
Я/ (х, у) dx dy — J ( j / (x, у) dy I dx,
(S) «4iW '
т. е. двойной интеграл может быть вычислен в
результате двух последовательно проведенных
простых интегрирований. Скобки можно опустить,
g(x,y)dxdy.
(S)
(S)
Рис 3.34
если условиться, что второму знаку
интеграла соответствует первое переменное
интегрирования.
б) Аналогичная формула имеет место для
S = «x, У)|х1(у)^х^х2C;), с*
(рис. 3.34):
(S)
J(x,y)dx)dy.
с \ v, (v)
262
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Пример. Пусть S — область, заключенная между
кривыми у = |/х и у = х2 (рис. 3.35); тогда а = О, b = \,
yt (х) - х2, у2 (х) = \/х; отсюда
(S)
S J f{x,y)dydx;
О х2
если, в частности, / (х, у) = ху, то
||/(х, y)dxdy= j j
(S) 0 х2
Область S может быть описана также в форме б), где с — О,
d = 1, х, (у) = у2, x2 (у) = }/>>. Тогда
E)
О у2
/(х,
в) Если область 5 можно разбить на конечное
число областей, заданных, как в случаях а) или б)
(ПП
Рис. 3.35
Рис. 3.36
(рис. 3.36), то для вычисления интеграла по S
используется свойство 2) из 3.1.10.1.
3.1.10.3. Замена переменных в двойных
интегралах. Пусть функции х = х (и, v) и у = у (u, v)
взаимно однозначно отображают открытую
область G, содержащую область G плоскости м, v
с кусочно гладкой границей, на открытую
область Р, содержащую область S плоскости ху,
и пусть S — образ G, причем в О функции х (м, v),
у (м, v) и их первые частные производные
непрерывны, а якобиан отличен от нуля:
J =
д (х, у)
д («, v)
дх дх_
~дп dv
ду ду
ди dv
#0.
Если функция /(*, у) непрерывна на S, то
справедлива следующая формула:
Я/ (х, у) dx dy= Я / (* («> »)> У ("> "Я I JI du dv-
(S) (G)
Выражение \J\dudv называется элементом
площади в криволинейных координатах и, v.
Формула преобразования остается верной и тогда,
когда сделанные предположения нарушены вдоль
конечного числа кусочно гладких кривых, при
условии, что функция / (х, у) и якобиан остаются
там ограниченными.
Специальные криволинейные
координаты.
1. Полярные координаты. Пусть S — область,
полученная взаимно однозначным отображением
области G плоскости р, ф, определяемым
функциями х = р cos ф, у = р sin ф. Тогда | J \ -
г (х, у)
р и
д(р, ф)
Я/ (*» у) dx dy = Я/ (р cos ф» р sin ф) р dP ^ф-
(S) (G)
П р им е р. / (х, у) = ху, и область S — четверть круга:
х2 + у2 < R2, х > 0, у ^ 0; функции х = р cos ф, у = р sin ф
также задают область S, являющуюся взаимно однозначным
(за исключением отрезка р — 0) образом области
G = {(р; ф) 10 < р < R, (
Тогда
\\ху dx dy = р2 sin ф cos ф р dp d<p =
(S)
(G)
R я/2
С С Г Г cos2<d~1*/2
= 1 I р3 sin ф cos ф dip dp = J p3 4\о dp =
0 0 0
2. Обобщенные полярные координаты. В случае,
когда область интегрирования S ограничена эл-
х2 v2
липсом —j + —j- = 1, удобны обобщенные
полярные координаты
имеем
х = ар cos ф, у = bp sin ф; тогда
д (х, у)
д (р, ф)
1 2я
Я/ (х, у) dS = J J / {ар cos ф, bp sin ф) abp dq> dp.
(S) 0 0
3. Если область S ограничена астроидой с
параметрическим представлением x = acos3f,
>> = a sin3 Г @ < t < 2я) (рис. 3.37), то вводят
криволинейные координаты х = и cos3 у, у = и sin3 у. Для
фиксированного v получаются прямые,
проходящие через начало координат; и = const дает
семейство астроид, J = Зи sin2 v cos2 v.
ОПРЕДЕЛЕНИЕ ТРОЙНОГО ИНТЕГРАЛА И ПРОСТЕЙШИЕ СВОЙСТВА
263
3.1.10.4. Геометрические и физические
приложения двойных интегралов.
Истолкование двойного интеграла как объема.
Если / (х, у) ^ 0 на S, то двойной интеграл
(S)
интерпретируется как объем цилиндрического тела,
основанием которого служит область 5 плоскости
х, у и которое сверху ограничено поверхностью
z = f (х, у) (рис. 3.38). Если, в частности, / (х, у) =
= 1, то получают объем цилиндра с плоскостью
Рис. 3.38
Рис. 3.39
z = 1 в качестве верхнего основания. Объем этого
цилиндра численно равен площади AS области 5:
AS = JJ dx dy.
(S)
Примеры. 1) Найти объем цилиндрического тела, в
основании которого находится круг х2 + у2 < ay, z — 0 и
которое сверху ограничено частью поверхности сферы
х2 + у2 + г2 = а2 (рис. 3.39). На основании симметрии можно
записать, что
У = 2 JJ ]/а2 - х2 - у2 dx dy,
(S)
где S - полукруг х2 + у2 ^ ay, x > 0. В полярных координатах
х = р cos ф, у — р sin ф область S описывается неравенствами
0 < р < a sin ф, 0 < ф < я/2, поэтому
я/2 a sin ф
V = 2 J J ]/а2 - р2 р dp dtp.
0 0
Подставим во внутренний интеграл t = j/a2 - р2; имеем
я/2 a cos ф 2 я/2
V= -2 J J t2 dtdy = - T a3 J (cos3 <p - 1) </<p.
0 a J 0
Используя преобразование cos3 <p = — cos q> + — cos 3<p,
получаем окончательно
i-(f-4>
2) Найти площадь области, ограниченной астроидой
х = а cos3 U У = a sin3 t @ < t < 2я) (см. рис. 3.37). В
результате введения криволинейных координат х = и cos3 v, у =
= u sin3 v (см. 3.1.10.3) получаем
AS = 11 dx dy =
(S)
а 2я a 2я
= 1 Зы sin2 r cos2 v dv du — 3 \ и du I — sin2 2u rfv =
0 0
0 0
2я
Центр тяжести и масса. Координаты ? и г)
центра тяжести области 5 с массой, распределенной
с плотностью 8 (х, у), определяются по формулам
Л=-Т7 b(x,y)ydS,
(S) (S)
где M — масса области S: M = JJ 5 (jc, j) dS.
(S)
Момент инерции. Момент инерции 1Х плоской
области S с массой, распределенной с плотностью
5 (х, у), относительно оси х есть
(S)
момент инерции 1У относительно оси у:
(S)
полярный момент инерции относительно начала
координат:
(S)
3.1.11. ТРОЙНЫЕ ИНТЕГРАЛЫ
3.1.11.1. Определение тройного интеграла и
простейшие свойства. Пусть задана ограниченная
пространственная область *) V, граница которой
является кусочно гладкой поверхностью (см.
3.1.12). Пусть функция / (х, у, z) определена и
ограничена в области V. Посредством выбора сети
кусочно гладких поверхностей строится некоторое
разбиение Z области V на конечное число
элементарных областей К, (i = 1, 2, ..., л) с объемами А К,.
Пусть A (Z) — наибольший диаметр
элементарных областей Vh и пусть М, (х„ yh z.) -
произвольная точка в каждой элементарной области К,.
Число су (Z, {М,}) = ? /(х„ yh z{) AVt называется
интегральной суммой, соответствующей разбиению
Z и выбору точек М, е Vr
Функция / (х, у, z) называется интегрируемой
по области V, если существует число / со
следующим свойством: для каждого е > 0 существует
число 5 (е) > 0 такое, что для каждого разбиения
Z, удовлетворяющего условию A (Z) < 5,
независимо от выбора точек М, выполняется
неравенство |cr(Z, {Mt}) — 11 < e. Число / называется
тройным интегралом функции/ (х, у, z) по области
V и обозначается следующим образом:
(V)
(У)
Этому определению интегрируемости
эквивалентно следующее: функция/(х, у, z) интегрируема
по V, если для каждой последовательности Zn
разбиений области К, для которой lim A (ZJ =
И -> 00
= 0, последовательность a (Zn, {M\n)})
интегральных сумм всегда сходится независимо от выбора
точек Л/, (в этом случае все последовательности
*) См. сноску к 3.1 10.
264
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
интегральных сумм сходятся к одному и тому же
значению, которое и есть значение интеграла).
Интегрируемые функции.
а) Каждая непрерывная на V функция является
интегрируемой по V.
б) Каждая ограниченная на V функция, кото-
рая непрерывна на V, за исключением точек,
лежащих на конечном числе гладких поверхностей,
является интегрируемой по V. Если функция в
точках таких поверхностей произвольно изменяется
(однако так, что измененная функция остается
ограниченной), то значение интеграла не изменится.
Свойства тройных интегралов.
Тройные интегралы имеют свойства, соответствующие
рассмотренным в 3.1.10.1 для двойных интегралов.
3.1.11.2. Вычисление тройных интегралов.
1. Пусть V является цилиндрическим телом,
проекция которого на плоскость х, у есть область
S и которое ограничено снизу поверхностью z =
— z\ (х, у), а сверху — поверхностью z = z2 (x, у),
Рис. 3.40
где zu z2 — непрерывные функции в S (рис. 3.40);
тогда
Щ f (х, у, z) dx dy dz = I] Г f У /(x, у, z) dz) dx dy.
\ 2, (x, y) '
(V)
(S) \ 2
Интегрированием по z тройной интеграл сводится
к двойному интегралу по области S.
Если область S плоскости х, у определена при
этом неравенствами а < х <; Ь, у у (х) ^ у < у2 (х),
где уь у2 — непрерывные функции на \а, Ь], то
Ь Уг (х) z2 (х, у)
= J j j / (х, у, z) dz dy dx.
a y, (x) z, (x, y)
Пример. Пусть К-тело, ограниченное эллипсоидом
х2 v2 z2
—5~+ ^Ч- -^2~e 1; тогда S состоит из точек (х, у),
удовлетворяющих неравенству х2/а2 + у2/Ь2 < 1; таким образом,
имеем
ДО/(х, у, z)dxdydz =
(У)
ffj / (х, у, z) dx dy dz =
(У)
1 / х2 у2
A i/e2_x2 с у ~~с?~1>1~
e
= f
_fl _^_Ja%
f (x, у, z)dz dy dx.
xi -i/ ~г
2. Пусть V лежит между плоскостями х = а
и х = ь, а каждая плоскость х = const, где а^
V
Рис. 3.41
^ х ^ Ь, пересекает область V по плоской области
Sx (рис. 3.41); тогда
Ь
Щ f (x, у, z) dxdy dz = l( Ц f (x, у, z) dy dz) dx.
(V) a (Sx)
Пример. Пусть И-тело, ограниченное конической
поверхностью R2x2 = h2 (у2 + z2) (рис. 3.42); этот конус лежит
между плоскостями
^{Rx/hJ. Тогда
Рис. 3.42
0 и х - Л, и Sx- круг у2 + z2
Ш* Л
например,
f (х, у, z)
то интеграл по плоской области Sx можно вычислить
введением полярных координат у = р cos <p, z = р sin <p:
l W
Делаем подстановку и = ]/р2 +
х l/l -h (К/ЛJ
/(x, y, z)dz</x</y,
¦ff
E)
а так как 5 полностью описывается неравенствами
du = ^j-(l-
Поэтому значение искомого тройного интеграла равно
h
{l(x)dx= *Lh2(l-h).
ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ТРОЙНЫХ ИНТЕГРАЛОВ
265
3.1.11.3. Замена переменных в тройных
интегралах. Пусть посредством функций х = х (и, v, w),
у = у (и, v, w), z = z (м, у, w) производится взаимно
однозначное отображение открытого множества,
содержащего область G пространства м, и, w,
ограниченную кусочио гладкими поверхностями,
на открытое множество, содержащее область V
пространства х, у, z, и V есть образ G при этом
отображении. Если эти три функции х, у, z
вместе со своими первыми частными
производными непрерывны в G и
J =
д (х, у, z)
д (и, v, w)
дх
~ди~
ду
ди
dz
ди
дх
~dv
ду
dv
dz
~dv~
дх
dw
ду
dw
dz
#0,
то для каждой непрерывной функции /(х, у, z)
справедлива формула
(У)
= JJJ / (х (м, у, w), у (w, v, w), z (м, v, w))\J\ du dv dw.
(G)
Выражение \J\dudvdw называется элементом
объема в криволинейных координатах и, v, w.
Эта формула преобразования остается верной
также и тогда, когда на конечном числе кусочно
гладких поверхностей указанные условия нарушены
(если, однако, функция / (х, у, z) и якобиан
остаются ограниченными).
Специальные криволинейные
координаты.
1. Сферические координаты. Пусть область V
получена из области G взаимно однозначным
отображением х = р sin 9 cos ф, у = р sin 9 sin ф,
z = p cos 9; при этом J = p2 sin 9. Тогда
ДО/ (х, у, z) dx dy dz = ДО/(Р sin 9 cos q>,
(У) (G)
p sin 9 sin ф, р cos 9) p2 sin 9 dp dф d9.
Элемент объема в сферических
координатах есть, таким образом,
р2 sin 9 dp dф d9.
Пример. Пусть V- область
в пространстве, ограниченная
сферой х2 + у2 + z2 = 2az и двумя
коническими поверхностями х2 +
+ у2 = z2 tg2 а, х2 + у2 = z2 tg2 p*
<у) (рис. 3.43). В
сферических координатах р, ф,
6 область V определяется
неравенствами 0 < р < 2а cos в,
Отсюда
Рис 3.43
0 < ф < 2я,
р 2а cos в 2я
Jff/(x' >. z)dxdydz = f J f /(р sin в cos ф,
(И) а 0 0
р sin в sin ф, р cos 0) р2 sin 6 dip dp dQ.
2. Обобщенные сферические координаты: х =
= ар sin 9 cos ф, у = Ьр sin 9 sin ф, z = cp cos 9.
Тогда J = abcp2 sin 9.
3. Цилиндрические координаты: х = р cos ф,
у = р sin ф, z = z. Тогда J = р.
3.1.11.4. Геометрические и физические
приложения тройных интегралов.
1. Объем пространственной области: в случае
частного вида подынтегральной функции /(х, у,
z) = 1 тройной интеграл по V представляет собой
объем AV области V:
ДО idxdydz = AV.
(У)
Пример. Если И-тело, описанное в примере в
3.1.11.3, то его объем равен
Р 2а cos в 2л
dxdydz=[ Г Г р2 sin 6 <*<р dp <*в =
(V) а О О
р\2а cos в р
Г 2np2sine</p</e=^y- [%a
cos3 в sin в dQ ш
а О
16я , Г cos*в Т8 4я з, 4 ¦
~3~ 4~ = "у (
2. Масса тела К Если пространственная
область V заполнена массой с плотностью 5 (х, у, z),
то полная масса V равна
М = jjj 5 (х, у, z) dx dy dz.
(V)
3. Центр тяжести. Если ?, г|, ? являются
координатами центра тяжести пространственной
области, заполненной массой с плотностью
6 (х, у, z), то
У, zt
у, z) dx dy dz.
(У)
1Я
(И)
(У)
4. Момент инерции. Моменты инерции
пространственной области V, заполненной массой с
плотностью 5 (х, у, z), относительно осей х, у и z
равны соответственно
(У)
W(z
(У)
(У)
Пример. Найти момент инерции относительно оси z
тела V, ограниченного круговым цилиндром х2 + у2 = а2,
0 < z < А, которое равномерно заполнено массой с
плотностью 5=1. Введем цилиндрические координаты;
266
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
h2na
/, = ПТ(х2 + у2) dV - J Г Гр2р </р */ф <
(К) 0 0 0*
0 0
Л2я h
(К)
где Л К = яа2Л - объем тела V.
5. Гравитационное притяжение. Сила
гравитационного притяжения F, с которой
пространственный объем V, заполненный массой с плотностью
5 (х, у, z), по закону Ньютона действует на
материальную точку Р = (?, т|, 0 с массой 1, имеет
компоненты
}- л
JJJ
(V)
где г = |/(x - У2 + (
ционная постоянная.
- лJ + (z ~ О2, Y -
гравита3.1.12. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
Кусок поверхности S, заданный в
параметрической форме: х — х (и, v), у = у (и, v), z = z (и, v),
где точка (м, v) пробегает некоторую область *)
G плоскости и, v, называется гладким, если раз^
личные пары значений (u, v) дают разные точки
S, частные производные функций х (и, v), у (и, v),
z (и, v) непрерывны и
rang
"dx dy dz
du du du
дх ду dz
dv dv dv
Если поверхность S состоит из конечного
числа гладких кусков поверхности, то S
называется кусочно гладкой.
Гладкая поверхность S называется
двусторонней, если в каждой точке поверхности можно
выбрать нормаль так,
что при обходе каждой
замкнутой кривой,
лежащей на S, мы,
непрерывно изменяя нормаль при
движении по кривой,
возвращаемся в исходную
точку кривой с тем же
направлением нормали.
Стороны двусторонней
поверхности могут быть, таким образом,
охарактеризованы направлением соответствующих нор-
Рис. 3.44
малей. Не двусторонней, т. е. односторонней
поверхностью, является, например, лист Мёбиуса
(рис. 3.44).
Всюду в дальнейшем под поверхностью
понимается двусторонняя поверхность.
3.1.12.1. Площадь гладкой поверхности. Пусть
поверхность S задана параметрически: х = х(м, у),
у = у (и, v)t z — z (и, у), где точка (u, v) пробегает
некоторую область Г плоскости и, v. Тогда
площадь AS поверхности определяется поверхностным
интегралом
AS = JJ ]/EG-F2 du dv,
(П
где Е
(dxV (dy\2 (dz\2 F_dx'dx
\du~) +\du~) +\du~)' du dv +
dy dy dz dz /я^\2 /я,Д2 /я,\2
du dv du dv'
подынтегральное выражение dS = ]/EG - F2 du dv
называется элементом поверхности.
Если S задана явно уравнением z = <p (х, у),
причем (х, у) пробегает область S' (проекцию
области S на плоскость хОу), то
AS = JJ j/l + р2 + q2 dx dy,
(S1)
где p = dz/dx, q = dz/dy.
Примеры. 1) Найти площадь поверхности части
сферы х2 + у2 + z2 = а2, высекаемой цилиндром х2 + у2 = ау
(см. рис. 3.39).
Параметрическое представление сферической
поверхности:
х = a sin 9 cos <р, у = a sin 0 sin ф,
a cos 8;
таким образом, и = 9, v = ср; находим Е = a2, F — 0, G —
= a2 sin2 0; следовательно, У EG - F2 = «2 sin 9.
Уравнение границы области интегрирования
получается подстановкой параметрического представления в
уравнение окружности: sin 9 = sin <p. Отсюда получим, что
четверть искомой поверхности, лежащая в первом октанте,
характеризуется следующими значениями параметров: 0<
< Ф < я/2, 9 < ф, 0 < 9 < я/2. Следовательно,
я/2ф
AS = 4 J J a2 sin 9 dQ dip = 4a2
0 0
я/2
J A - cos ф) d<p =
0
- 4а2 (я/2 - 1).
2) Кусок поверхности z = xy, лежащий над кругом
х2 + у2 < К2, имеет площадь
Преобразуя этот интеграл при помощи полярных
координат х = р cos ф, у = р sin ф, получим
2я R
AS = j j р ]/\ + р2 dp d<p = ^- ((I + Л2K/2 - 1).
0 0
2-го
*) См. сноску к п. 3.1.10.
3.1.12.2. Поверхностные интегралы 1-го и
рода.
Определение поверхностного
интеграла 1-го рода. Пусть некоторая функция
/(х, у, z) определена и ограничена на гладкой
поверхности S. Пусть Z обозначает некоторое
разбиение поверхности S на конечное число
элементарных поверхностей S, (i = 1, 2, ..., п) с площа-
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 1-го и 2-го РОДА
267
Рис. 3.45
дями ASt, A (Z) — наибольший из диаметров
элементарных поверхностей St и М, = (xf, yh z{) —
произвольная точка на соответствующей
элементарной поверхности
Pi (рис. 3.45). Число
ь Уь zt)ASt
называется
интегральной суммой,
соответствующей разбиению
Z и выбору точек
{м,}. ¦
Если существует число / со следующим
свойством : для каждого е > 0 найдется такое 6 (е) > О,
что для каждого разбиения Z, удовлетворяющего
условию A (Z) < 5, и независимо от выбора точек
М, выполняется неравенство | cr (Z, {MJ) — / | < е,
то / называется поверхностным интегралом
1-го рода от /(х, у, z) по поверхности S.
Обозначение: / = Jf/(х, у, z) dS.
(S)
Для случая / (х, у, z) = 1 число / равно
площади AS поверхности S.
Вычисление поверхностного
интеграла 1-го рода (сведение к двойному
интегралу). Если поверхность задана
параметрически: х = x(u,v), у = у (и, v), z — z (и, v), причем и
и v пробегают область Г плоскости и, v, то
(S)
= JJ /(х (м, v), у {и, v), z (и, v)) ]fEG~- F2 du dv.
(П
Если поверхность задана явно уравнением
z = ф (х, у), причем (х, у) пробегает область' S', то
tff(x,y,z)dS =
(S)
= Я /(*> У- Ф (*> У)) V1 + Р2 + Я2 dx dy.
(SI
Для случая, если S представлена уравнениями
вида х = \|/ (у, z) или у = % (*» z)> верны
аналогичные формулы.
Примеры. 1) Пусть поверхность S является сферой
радиуса г с параметрическим представлением х = r sin G cos <p,
у = г sin 9 sin ф, z = r cos в; тогда Г есть прямоугольник
Я/(х, у, 2)</S =
E)
= JJ / (г sin 0 cos ф, г sin 9 sin ф, г cos 0) г2 sin 9 dQ Лр =
(П
2яя
= r2 f f / (г sin 9 cos ф, г sin 9 sin ф, г cos 0) sin 9 dQ dq>.
0 0
2) Пусть S - цилиндрическая поверхность х2 + у2 = я2,
0<z</t; ее параметрическое представление: х = a cos ф,
у = вмпф, z = z; тогда /EG - F2 = а, Г является
прямоугольником 0 Л
Я / (х' ^» z) ^ — Я / (а cos Ф» а s'n Ф» z) <* d<P dz =
(S) (Г)
hln
= а J f / (a cos ф, a sin ф, z) d<p dz.
0 0
Определение поверхностного
интеграла 2-го рода. Ориентация
двусторонней незамкнутой поверхности: выбирается
определенная сторона поверхности S; обход замкнутой
кривой на S считается согласованным с выбранной
стороной, если образуется правый винт, т. е. из
конца вектора нормали обход кажется
происходящим против часовой стрелки.
Пусть в точках поверхности 5, однозначно
проектирующейся на плоскость х, у и заданной
явно гладким уравнением z — ср (х, у), определена
ограниченная функция / (х, у, z). Пусть Z —
разбиение поверхности S на конечное число
элементарных поверхностей S, (i = 1, 2, ..., и), A (Z) -
наибольший диаметр элементарных поверхностей,
М{ — (х„ yh z,) — произвольная точка, выбранная
на элементарной поверхности 5,. Пусть выбрана
определенная сторона поверхности, т. е.
поверхность 5 ориентирована. Тогда установленное
направление обхода границы каждой
элементарной поверхности 5, определяет направление
обхода в плоскости х, у границы проекции S,'.
Площадь AS'i этой проекции берется со знаком
плюс, если граница проекции S't проходится в
положительном направлении; в противном случае -
со знаком минус (рис. 3.46). Число
cj(Z,
ь уь
называется интегральной суммой,
соответствующей разбиению Z и выбору точек {М,}. В
противоположность образованию интегральных сумм
ц
/
AS[>0
поверхностных интегралов 1-го рода, здесь / (М,)
умножается не на площадь ASt элементарной
поверхности 5„ а на ориентированную площадь
AS[ проекции Sj поверхности S,- на плоскость х, у.
Если существует число / со следующим
свойством : для каждого г > 0 найдется такое 8 (е) > О,
что для каждого разбиения Z, удовлетворяющего
условию A (Z) < 5, независимо от выбора точек М\
выполняется неравенство | a (Z, {М,}) — / | < е, то
268
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
/ называют поверхностным интегралом 1-го рода
от/ (х, у, z) dx dy по ориентированной поверхности
S. Обозначение:
I=Slf(x,y,z)dxdy.
(S)
Если S проектируется на плоскость х, у
неоднозначно, но ее можно разбить на конечное число
поверхностей, для каждой из которых такая
однозначная проекция существует, то поверхностный
интеграл по 5 определяется как сумма интегралов
по отдельным поверхностям.
Если S имеет однозначную проекцию на
плоскость у, z или х, z, то аналогично можно
определить два других поверхностных интеграла 2-го
рода:
JJ /(х, у, z)dydz, ft f (х, у, z) dz dx,
(S) (S)
где в соответствующих интегральных суммах
стоят площади проекций 5, на плоскости у, z и х, z.
Наконец, для трех функций Р (х, у, z), Q (х, у, z),
R (х, у, z), определенных на S, эти интегралы
можно сложить и определить более общий
поверхностный интеграл 2-го рода.
JJ P dy dz + Q dz dx + R dx dy =
(S)
= ffPdydz + tf
E) (S)
Jj Rdxdy.
E)
Вычисление поверхностного
интеграла 2-го рода (сведение к двойному
интегралу).
1. Пусть поверхность 5 имеет явное
представление: z = ф (х, у), причем (х, у) изменяются в
области 5', а ф непрерывна в 5'. Тогда
поверхностный интеграл по той стороне S, для которой
угол между нормалью и осью z является острым,
вычисляется по следующей формуле:
Я / (*. у. z)dx
(S)
Я
(S')
*» ^ ф (*. у)) dx
Если выбрана другая сторона поверхности, то
Я / (х, у, z) dxdy= - Я / (х, У, Ф (х, у)) dx dy.
(S) (S')
Аналогично получаем, что
Я / (х, yt z) dy dz = Я /(¦(* 4 У, z)dydz,
(S) (Sf)
где поверхность S задана уравнением х = \J/ (у, z),
S' — проекция 5 на плоскость у, z, а поверхностный
интеграл берется по той стороне, нормаль к
которой образует с осью х острый угол. Точно
так же
Я/(х, у, z)dzdx= JJ/(x, X(z, *)> z)dzdx,
(S) (S')
где поверхность S задана уравнением у = % (*•> *),
S' — проекция S на плоскость х, z, а
поверхностный интеграл берется по той стороне, нормаль
к которой составляет с осью у острый угол.
2. Если поверхность S задана в
параметрической форме: х = х (м, v), у = у (и, v), z = z (и, v), то
Я/(х, у, z)dxdy =
(S)
= ± Я / (х ("» у)' У ("¦ ")' z ("» v^ С du dv>
(П
Sif(x,ytz)dydz =
(S)
= ± Я / (* ("» y)' У («* y)' z ("* y)) ^ du dv>
Я / (x, у, z) dz rfx =
(S)
= ± Я / (x ("'y)' >¦ ("»y)'z ("¦y))
(П
д (и, v)'
д(и, v)'
с = ~{
д (
д (м, v)
положительный знак перед интегралом справа
выбирается тогда, когда ориентация области Г
плоскости и, v соответствует ориентации
поверхности (г. е. обход контура на Г и его образа на
поверхности одновременно согласованы с верхней
стороной Г и выбранной стороной поверхности).
Для суммы трех интегралов получаем
Я Р dy dz + Q dz dx + R dx dy =
(S)
= ± Я (pA + QB + RC')du dv-
(П
Связь между поверхностными
интегралами 1-го и 2-го рода. Если а, р,
у — углы нормали к выбранной стороне
поверхности с осями х, у и z, то
Я Р dy dz + Q dz dx + R dx dy =
(S)
= fj (P cos a + Q cos p + R cos y) dS,
(S)
т. е. стоящий слева поверхностный интеграл
2-го рода преобразуется в стоящий справа
поверхностный интеграл 1-го рода.
Для двух различных незамкнутых поверхностей
S, и S2 с одной и той же границей С (стороны
которых согласованы с
заданным обходом контура С)
поверхностный интеграл
Я Р dy dz 4- Q dz dx -t- R dx dy
(S)
имеет в общем случае
разные значения (рис. 3.47), т. е.
в общем случае он не
обращается в нуль на замкнутой
поверхности (аналогично за- Рис 3.47
висимости от пути
криволинейного интеграла). Если функции Р, Q, R,
дР/дх, dQ/ду, dR/dz непрерывны в
«пространственно односвязной» области V (т. е. в области,
которая наряду с каждой замкнутой поверхностью
содержит также и область, ограниченную этой
поверхностью), то поверхностный интеграл по
ГЕОМЕТРИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ПОВЕРХНОСТНОГО ИНТЕГРАЛА
269
всякой замкну!ой поверхности S и V обращается
в нуль тогда и ю.1ько то[да, когда
+
дх ду
dz
следует, что
Пример. Пусть (х, у, z) — некоторая точка поверхности
S, а fe л, Q - точка вне S, и
Функции Р =
- и их произ-
водные ^, ^, -^- непрерывны при (х, у, г) # & т\, Q, и
5Р 5Q ЗЛ л
имеет место равенство -г— + -^=- + -=— = 0; таким образом,
дх ду dz
для этих функций интеграл JJ Pdydz + Qdzdx + R dx dy
(S)
равен нулю по каждой замкнутой поверхности,
ограничивающей тело, не содержащее точки (?, т|, Q.
Переход к поверхностному интегралу 1-го рода:
Если (rpn) - угол между радиусом-вектором г точки (х, у, г)
поверхности и нормалью к 5 в точке (х, у, г), то
ЛК= \\zdxdy= JГх(в, <p)C<ffl</q>
E) (Г)
= J j с cos Q ab sin Q cos QdQdy-
О О
я 1 4я
= abc-2n J cos2 0 sin 6 </6 = 2abcn J u2du=* — abc.
О -1 3
Центр тяжести и сила притяжения.
Если поверхность S покрыта массой с поверхностной
плотностью 5 (х, у, z), то пдлная масса поверхности
S равна
Я
у, z)dS;
координаты (?, r|, Q центра тяжести равны
Ь = -^ jjx 5 (х, у, z) dS, Ц = ~ J|y8 (х, у, z) dS,
Ct= — \\zB(x9y,z)dS;
= cos (дС ') cos а + cos (у7т) cos р* + cos (гГг) cos у = cos (гГп),
так что для поверхностного интеграла получаем, что
Геометрически этот интеграл представляет собой
телесный угол, под которым из точки D, ц, Q видна
поверхность S. Если поверхность S замкнута, то его значение
равно 4л, если точка (^, г), Q лежит внутри области,
ограниченной S, и 0, если (?,, л, 0 лежит снаружи.
3.1.12.3. Геометрические и физические
приложения поверхностного интеграла.
Объем тела. Объем АV тела V,
ограниченного кусочно гладкой поверхностью S, можно
различными способами вычислить как
поверхностный интеграл 2-го рода:
AV = ff z dx dy, или AV = Jf x dy dz,
(S) (S)
AV
— \\xdydz + ydzdx + zdxdy,
причем интегралы следует брать по внешней
стороне поверхности S.
г
Пример. Пусть пространственная область V ограничена
эллипсоидом х2/а2 + у^/Ь2 + z2fc2 - 1. Параметрическое
представление этой поверхности есть
х = a sin 0 cos ф, у = b sin 0 sin ф, z — c cos в,
где 0 ^ 0 < л, 0 ^ ф ^ 2я (область Г плоскости ф, 0). Отсюда,
компоненты силы притяжения F этого
распределения массы, действующей на материальную точку
Мо = (х0, у0, z0) единичной массы, равны
-bdS,
1
(S)
где у — гравитационная постоянная.
Пример. Пусть поверхность конуса (см. рис. 3.42)
Й2х2 — h2 (у2 4- z2) покрыта массой с плотностью 8=1. Из
условия симметрии т| = ? = 0; так как поверхность 5 задана
уравнением
причем у иг пробегают внутренность круга у2 + z2 = Л2,
получаем
dydz.
После введения в плоскости у, z полярных координат
у =в р cos ф, z = p sin ф получаем, что
2л Л
2я
3
О О
а так как М = яЛ |//i2 + R2, то $ = у Л.
270
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
3.1.13. ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ
3.1.13.1. Формула Остроградского — Гаусса.
Формула Грина. Пусть пространственная область*)
V ограничена кусочно гладкой поверхностью S
и Р(х, у, z), g(x, у, z), Я(х, у, z) - функции,
непрерывные в открытом множестве, содержащем V\J 5,
вместе с производными дР/дх, dQ/ду, dR/dz; тогда
справедлива следующая формула (формула
Остроградского — Гаусса):
' дР dQ с
дх ду (
= IJ Р dy dz + Q dz dx + R dy dx,
(S)
причем поверхностный интеграл 2-го рода, стоящий
справа, следует брать по внешней стороне
поверхности S, ограничивающей область V.
Формула Грина для плоской области:
Pdx + Qdy.
j
(Ц
ж
E)
Эта формула преобразует двойной интеграл по
области S в криволинейный
интеграл по границе L
области S, причем
криволинейный интеграл берется по
контуру L, пробегаемому в по-
ложительном направлении
(рис. 3.48). Эта формула спра-
ведлива, если контур L является
кусочно гладким, а функции
Р(х, y)f Q(x, у), дР/ду, dQ/dx непрерывны в
открытом множестве, содержащем S\jL.
Пример. По формуле Остроградского - Гаусса для
р = х3, б = у3, R = z3 получаем, что
О
Рис. 3.48
Я x3dydz + y3dzdx + z3dxdy
(S)
ДОС
(У)
2 + У1 + z2)dv-
Если, в частности, S является сферой х2 + у2 + z2 = I?2,
то тройной интеграл после введения сферических
координат равен
R к 2л
12я
ооо
3.1.13.2. Формулы Грина. Пусть в открытом
множестве G, содержащем пространственную
область V, ограниченную кусочно гладкой
поверхностью S, заданы функции Р(х, у, z), Q(x, yt z),
непрерывные в области G вместе со своими
вторыми частными производными. Тогда справедлива
первая формула Грина (или подготовительная):
ГГ дО
PAQdV= P —dS -
'(у) (S)
MdP_dQ_.dP_tQ_.tL
дх дх ду ду dz
(У)
dz
где AQ =
d2Q d2Q d2Q
-, а через дР/дп и dQ/dn
дх2 т ду2 т dz2
обозначены производные функций Р и Q
соответственно в направлении внешней нормали к S.
При тех же предположениях справедлива
вторая формула Грина:
(У)
(S)
Дня случая плоской области эти формулы имеют
вид
Я
(S)
PAQdS =
(Ц
где 5 — область плоскости х, у; L — ее граница,
обходимая в положительном направлении (см.
дР дО
рис. 3.48); —— и — производные в направле-
дп дп
д2Р д2Р
нии внешней нормали к кривой L; АР = -z-j- + -~r-
3.1.13.3. Формула Стокса. Пусть система
координат является правой, пусть кусочно гладкая
двусторонняя незамкнутая поверхность 5,
ограниченная кусочно гладким контуром L, расположена
внутри пространственной области V, и пусть
функции Р(х, у, z), Q(x, у, z), R(x, у, z) вместе со
своими первыми частными производными
непрерывны в V. Тогда справедлива следующая
формула (формула Стокса):
z\
*) См. сноску к 3.1.10.
(S)
причем путь интегрирования L проходится так,
чтобы направление обхода вместе с
нормалью к выбранной сто- z
роне поверхности S
образовывало правый винт (рис. 3.49).
3.1.13.4. Несобственные
криволинейные, двойные,
поверхностные и тройные интегралы. В
случае многомерных интегралов
несобственные интегралы
можно определить так же, как в
одномерном случае. Эти определения аналогичны
для криволинейных, двойных, поверхностных и
тройных интегралов, и поэтому достаточно их
привести, например, для двойных интегралов.
Двойные интегралы от
неограниченных функций. Пусть функция f(x, у) не
ограничена в окрестности некоторой точки Мо
ограниченной области S и интегрируема по всякой
Рис. 3.49
НЕСОБСТВЕННЫЕ КРИВОЛИНЕЙНЫЕ, ДВОЙНЫЕ, ПОВЕРХНОСТНЫЕ И ТРОЙНЫЕ ИНТЕГРАЛЫ 271
области 5\G(М0), где 17 (Мо) - произвольная
окрестность точки Мо. Тогда, если для любой
последовательности окрестностей UH точки Мо,
диаметры которых стремятся к 0, существует предел
lim Я Я*> y)dxdy = It
ограничена, однако
где S\ UH обозначает область, полученную
исключением точек окрестности Un из S, то / называется
сходящимся несобственным двойным интегралом
от функции /(х, у) по 5; обозначение:
'-ЯЯ*. y)dxdy.
(S)
Если предел существует не для всякой
последовательности Um то интеграл JJ/(x, y)dxdy назы-
(S)
вается расходящимся.
Если в 5 всегда f(x, у) ^ 0, то при выборе
окрестностей Un можно ограничиться кругами.
Данное определение можно распространить на
тот случай, когда /(х, у) не ограничена в
окрестностях большего числа точек или в окрестностях
гладких кривых.
Пример. Пусть S - круг х2 + у2
2 2/2
= (х2 + у
р
2)~а/2;
и f(x, у)
(
; если а > 0, то/(х, у) не ограничена в
окрестности начала координат. Так как /(х, у) ^ 0, то можно
ограничиться кругами. Пусть UH - круги с радиусами
р„, lim р„ = 0. Если в области S\ Un введены полярные
л —> оо
координаты, то
12я
(Т dxdy
л-юо JJ (х + У У л->оо
о J
(S\
р„ О
Р
= lim 2я
п-+ао
1
«1 ! = 2я
J'P. 2-а
при 0 < а < 2,
в то же время при а > 2 предел не существует; следовательно,
при 0 < а < 2 несобственный интеграл сходится и
S'
dx dy
2я
при 0 < а < 2;
при а ^ 2 несобственный интеграл расходится.
Аналогично доказывается, что несобственный тройной
ССС dxdydi
интеграл --^ j 2wT по шаРУ vc центром ъ начале
(У)
координат сходится, если 0 < а < 3, и расходится, если а ^ 3.
Признак сходимости. Если f,g —
неотрицательные функции в области S, интегрируемые в
дополнениях окрестностей точки Мо, и если в некоторой
окрестности точки Мо функция /(х, у)/д(х, у)
остается ограниченной и интеграл }jg(x, у)dxdy
(S)
является сходящимся, то Jj/(x, у)dxdy также
(S)
сходится.
В качестве функции сравнения можно
использовать функцию
д(х, у) = ((х-хоJ+(у-уо)У°'2,
где Мо = (х0, Уо).
Пример. Область S есть круг х2 + у2 < 1, функция
/(х, у) »= In ух2 + у2 в окрестности точки Мо = @, 0) не
lim l/x2 + у2 In l/x2 + у2 = 0.
(х,>0-@,0)
Таким образом, функция/(х, у)/д (х, у), где д (х) = (х2 + у2)' ш,
остается ограниченной; отсюда следует сходимость
интеграла
Двойные интегралы по
бесконечной области. Пусть S — неограниченная область,
имеющая границей кусочно гладкую кривую, а
/(х, у) — некоторая заданная в S функция, которая
интегрируема по каждой конечной подобласти
области S. Если для любой последовательности
SH ограниченных подобластей таких, что каждая
ограниченная подобласть области S содержится во
всех 5„ при п > «о, существует предел
lim Jj/(x, y)dxdy = I,
n-+cO(Sn)
то этот предел / называют сходящимся
несобственным двойным интегралом от функции
/(х, у) по 5; обозначение:
i = а Ах, у) dxdy.
(S)
Если предел существует не для всякой
последовательности Sn, то интеграл JJ/(x, у)dxdy назы-
(S)
вается расходящимся.
Если /(х, у) ^ 0 всюду в неограниченной
области S, то члены последовательности SH можно
выбрать следующим образом: Sn = S f] Km где К„ —
круги с центром в начале координат, радиусы
которых ри удовлетворяют условию lim1 р„ = оо.
Примеры. 1) Пусть S является областью х ^ 0, у > О,
и пусть /(х, у) = е~ (*2 + З'2). Так как /(х, у) ^ 0 в S, то в
качестве 5„ можно взять последовательность четвертей
кругов с радиусами р„, lim р„ = оо. Тогда после перехода
п-* оо
к полярным координатам имеем
Р„я/2
О О
поэтому
lim —-^U -e~P-2) = ^-,
и, следовательно,
2) Пусть S — первый квадрант, х ^ 0, у > 0; /(х, у) =
= sin (х2 + у2). Если SB — последовательность четвертей
кругов с радиусами pm lim р„ = оо, то
S
sin{x2+у2)dxdy
п-> оо
Т?-
= I sin
11
^-(l-cos(p2));
272
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
так как у полученной числовой последовательности предела
не существует, то несобственный интеграл Jf sin (х2 + у2) dx dy
(S)
является расходящимся.
Наконец, можно определить несобственный
двойной интеграл для случая, когда и область
интегрирования, и функция f(x, у) (в окрестности
некоторых точек) не ограничены.
Замена переменных в
несобственных интегралах. Формулы преобразования
для двойных интегралов (см. 3.1.10.3) и тройных
интегралов (см. 3.1.11.3) остаются в силе (в
аналогичных предположениях) также для несобственных
интегралов, если хотя бы один из двух
интегралов в этих формулах сходится.
Пример. В интеграле
i - *W- у*/ь2
где область S ограничена эллипсом
dxdy
; 1, подын-
тегральная функция в окрестности эллипса не ограничена.
Введением обобщенных полярных координат х = ар cos <p,
y — bpsin<p интеграл преобразуется к следующему виду:
следовательно,
Я
(S)
dxdy
]/i-x2/a2-y2/b2
3.1.13.5. Многомерные интегралы, зависящие от
параметра. Пусть S - ограниченная область
плоскости х, у; I — интервал ?-оси, а функция
/(х, у, ?) для каждого ?е/ интегрируема на S.
Тогда для ? е / двойной интеграл определяет
функцию
x, у, Qdxdy.
(S)
Интеграл, зависящий от параметра ?,, имеет
следующие свойства:
1) если функция/(х, у, ?) непрерывна, то функция
F(?) также непрерывна на /;
2) если, кроме того, /(х, у, ?) обладает
непрерывной частной производной по ?,, то F (?)
дифференцируема на / и
г Ю-|| M^i
- dx dy.
Аналогичные свойства имеют криволинейные,
поверхностные и тройные интегралы, зависящие
от параметра.
Пример.
Пусть функция р (х, у, г) непрерывна в К Если точка (?, r\, Q
не лежит в V% то функция -^ — —v-^ непрерывна в V;
0% Г Г
следовательно, F(?, т), Q дифференцируема по ^ и имеет
производную
Так как подынтегральное выражение также обладает
непрерывной частной производной, то под знаком интеграла
можно продифференцировать еще раз; получим
Аналогично вычисляются частные производные по ц и
Сложением получаем, что
а;2
= 0.
Для несобственных криволинейных, двойных,
поверхностных и тройных интегралов, зависящих
от параметров, как и в одномерном случае (см.
3.1.9.3), непрерывность подынтегрального
выражения уже не является достаточным условием для
того, чтобы обеспечить непрерывность интеграла
по параметру; дополнительно необходима
равномерная сходимость этих интегралов.
Равномерная сходимость несобственного
двойного интеграла. Пусть Р = (х, у) и М = (?, г|) —
точки ограниченной области S, a f(P, M) —
некоторая заданная в S функция, которая в
окрестности Р = М не ограничена. Интеграл
JJ/(P, M)dSP=
r\)dxdy
является несобственным интегралом, зависящим
от параметров. Он называется равномерно
сходящимся в точке MoeS, если для любого е>0
найдется такое 5 (е) > 0, что для всех точек М,
удаленных от Мо на расстояние, не превышающее
5, и для всех окрестностей U точки Мо, диаметры
которых не превышают 5, выполняется неравенство
, M)dSP\<e.
Если интеграл JJ/(P, M)dSP сходится равно-
(S)
мерно в точке Мо, то функция
P, M)dSP
непрерывна в точке Мо.
Пример. Пусть V - некоторая ограниченная область в
пространстве х, у, г; р(х, у, z) - ограниченная на К функция:
| р(х, у, z) | < С - const. Если Р = (х, у, z) и М - {\, л, Q -
точки из V, то
гМР - )/(x-
есть несобственный тройной интеграл, зависящий от точки М.
Покажем, что он сходится в каждой точке Мое V
равномерно, так что функция
(У)
ОСНОВНЫЕ ПОНЯТИЯ
273
непрерывна в И Для произвольной окрестности U точки
Мо и шара Vh радиуса б с центром в Мо, содержащего U
(рис. 3.50), вследствие
ограниченности р(х, у, z) имеем
dVP
гмр'
Если теперь МеК6, то
шаР ^26 с центром в М и
радиусом 25 содержит шар Vs
с центром в Мо. Тогда
Рис. 3.50
(Ч) (Им)
После введения сферических координат с полюсом в
точке М получим
0 0 0
Таким образом,
Р(Р)
ГМР
dVP
для всех Me V6, где 6 < 6(е) =
< 8я52С < е
—, и любой окрестности
U точки Мо, диаметр которой меньше 8 (б). Это доказывает
равномерную сходимость рассматриваемого интеграла.
3.1.14. БЕСКОНЕЧНЫЕ РЯДЫ
3.1.14.1. Основные понятия. Если {ап} —
числовая последовательноть, то последовательность
Si
+ а2>
называют последовательностью частичных сумм
(бесконечного) ряда, который обозначают
ах + аг + ... + ап + ... или
а„;
ап называют общим членом ряда.
Если последовательность частичных сумм
имеет (конечный) предел S, т. е. lim Sn = S, то ro-
И-» 00
ворят, что ряд
? ая = а1+а2 + а3 + ... C.1)
сходится и имеет сумму S, и пишут ? а„ = S.
и=1
Если последовательность частичных сумм не имеет
(конечного) предела, то бесконечный ряд C.1)
называется расходящимся. Тем самым
сходимость ряда сводится к сходимости
последовательности его частичных сумм.
Примеры. 1) Ряд ]Г aqn -a + aq + aq2 + ... (беско-
я = 0
нечная геометрическая прогрессия) сходится при | q \ < 1, и
Чтобы это показать, рассматривают последовательность
Zl -qH+l
aqk => а и вычисляют пре-
1 -q
дел последовательности SH:
lim Sn =
2) Ряд
1... расходится, так как
последовательность частичных сумм SH = n неограниченно возрастает.
3) Ряд ? (— 1)" = — 1 + 1 — 1 + ... является расходя-
и=1
щимся, так как последовательность частичных сумм Sn
принимает значения 0 и -1 для четных и нечетных п
соответственно.
Критерий Кош и. Числовой ряд сходится
тогда и только тогда, когда для любого е > 0
найдется такое натуральное JV, что для всех n ^ N
и любого натурального к выполняется неравенство
= \ап+1 + ... + ан+к\
Отсюда сразу получается необходимый признак
сходимости ряда: последовательность членов
сходящегося ряда должна стремиться к нулю:
lim а„'— 0.
п —* оо
Это условие не является достаточным, как
показывает пример ряда ) ln| I H—): имеем
Zln( 1 + — ):
(¦4)-»
lim In
п —* оо
однако ряд расходится (частичные суммы
SH = У 1п( 1 + —) = VAпA + 5) - Ins) = ln(l + п)
S=l 1=1
неограниченно возрастают).
Пример. Ряд У -г—г т- расходится, так как
lim а„ = lim
Если отбросить первые п членов ряда, то
получится ряд
оо
ап+1 + ал+2 + ... = X as,
s = n+l
который называется n-м остатком ряда и
обозначается через Rn.
274
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Основные свойства сходящихся при г > к + 1 сходится, а при г < к + 1 расходится. Напри-
рядов. мер, для ряда
1) Отбрасывание или изменение конечного числа ^ 2и3/2 + 4
членов ряда не влияет на сходимость (или расхо-
димость) ряда.
2) Если все члены сходящегося ряда умножить
на множитель с, то его сходимость не нарушится неравенство
(сумма ряда умножится на с). 2и3/2 + 4 _ л3/2B + 4л~3/2) 3
,, . ? * , Л3 + 1 ~ Л3A+Л) ^"и372"
3) Два сходящихся ряда ? а„ и ? а« с сум-
н = 1 я = 1 справедливо для всех л, удовлетворяющих условию 4л 3/2 ^ 1;
мами S и S' можно почленно складывать или вычи- следовательно, для л > N - П^б] ¦). Так как ряд
тать. Ряд ? (ап ± а'п) сходится и имеет сумму ) -Т[Т сходится, то сходится также данный ряд. Ряд
n=i Ljn
S ± S'. "J
± J
4) Если ряд сходится, то его члены можно V ^ + * расходится, так как 2п™ + f > -.
уппировать в порядке их следования. Полученный Z^ п + 1 л + l л
группировать в порядке их следования. Полученный
ряд сходится, и его сумма равна сумме исходного
ряда.
3.1.14.2. Признаки сходимости или расходимости
рядов с неотрицательными членами. n=1
I. Ряд с неотрицательными членами сходится веНство ttV^— справедливо для достаточно боль-
V 1
2) Ряд > 7.——- при р > 0 расходится, так как нера-
/ Л1плг
тогда и только тогда, когда последовательность
частичных сумм ограничена сверху.
Примеры. 1) Гармонический ряд у — расходится.
п~1
(In л)" " л
Так как
tB = tx + у (t, - f,-1
л - 1 _ л + 2
—J— -—2~»
— сходится, так как -— < -у при л ^ N = 2.
п п п
III. Признак Даламбера. (А) Если су-
последовательности чисел qn — "** •> построенной
оо
из членов ряда ? аю ая > 0, для всех л ^ N вы-
л= 1
ЯЯ+1
полняется неравенство
- ^ q < 1 (q — фиксиро-
следовательность г„ и Sn не ограничены.
ванное число, не зависящее от и), то ряд ? д„ схо-
я=1
2) Ряд V JL-при а < 1 расходится, а при а > 1 сходится. дится» еа1И ™я всех и > N имеет мест0 неравенство
Утверждение для а < 1 следует из примера 1) (а = 1) и
признака сравнения рядов с положительными членами.
II. Признак сравнения рядов с
положительными членами. Пусть даны два
оо оо
ряда с неотрицательными членами ? ап и ]Г Ь„.
я=1 п=1
Если существует натуральное число N такое, что
неравенство а„ ^ Ьп выполнено для всех п ^ N, то
оо
из сходимости ряда ? Ь„ следует сходимость ряда
аю а из расходимости ряда 2j a» ~ расходи-
1 и=1
мость ряда ? Ья.
и=1
то ряд Л а„ расходится.
я=1
ан+1
(Б) Если последовательность , построенная
из членов ряда ? а„, а„ > 0, имеет некоторый пре-
дел р, lim
я+1
Я-+0О «к
= р, то при р < 1 ряд ? а„
сходится, а при р > 1 расходится (если lim
= оо, то ряд 5] а„ также расходится) (предель-
и=1
ньш признак Даламбера).
Примеры. 1) Ряд ? ая, где
*) Квадратные скобки обозначают целую часть числа,
заключенного в них, т. е. наибольшее целое число, не
превосходящее данного, т. е. [л + х] = л при 0 < х < 1. В частности,
ПРИЗНАКИ СХОДИМОСТИ ИЛИ РАСХОДИМОСТИ РЯДОВ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ 275
При р = 1 предельный признак Даламбера не дится при р < 1 и расходится при р > 1; ряд расхо-
дает ответа на вопрос, сходится данный ряд или дится и при р = оо.
,. и При р = 1 предельный признак Коши не дает
расходится. Для ряда ? - имеем Ът^ —^ = ответа на вопрос 0 сходимости. д^ обоих рядов
= 1, и даряд расходится, а, с другой стороны, для V ^_ и V± имеем Ит ^ . lf но первый из
Z1 „2 / J И / 1 П и -> 00
— также имеем Km rj-= 1, но и=1 и=1
п n-юо (л j них сходится> а второй расходится.
этот ряд сходится. «
Примеры. 1) Ряд У -т—rj- сходится, так как
Замечание. Если а„ > О и ан+1/ан = 1 + А./и + &¦•> гДе «^2
ряд J] | а„ | сходится, то при X < 1 ряд j ая сходится, а при
* " s 1 - расходится. В частности, если lim |/^ = jjm _JL= о < 1.
И* + С,»!
л-»оо 1пл
а„ rt + drf-1 +... + dk „_ V/*Y
2) Ряд > I — I сходится при всех х ^ О, так как
(к - натуральное число), то ряд ? а„ сходится при di —
и=1
- Ci > 1. Напротив при </х - сх < 1 ряд расходится (признак V0* ~ ~ и lim Кл» " 0 < 1.
Гаусса). nJ* °°
Примеры. 1) Рад ^-сходящийся, так как 3) Рад }хЧг) *" СХОДИТСЯ *"" ВСВХ * УДОШ1СГВ°-
ряющих условию 0 < х < 1/е, так как lim уощ = ех < 1
lim , Ит ?±i. l<i. и-оо
и_юо и-*оо2и 2 (см. 3.1.3.1); для всех х > 1/е рад расходится.
00
2) Для ряда Vn!^Y(x>0) имеем V- Интегральный признак (Коши,
.= ! Маклорен). Пусть данный ряд имеет вид ? ан =
я=1
л °°
-^±i = , " x|Vt и lim x = —. = L /(")' пРичем/(л) есть значение в точке х — п
При х < е рад сходится, а при х > е расходится; при х = е некоторой функции /(х), определенной при
предельный признак Даламбера (Б) не дает ответа. Однако X ^ п0. Если f(x) МОНОТОННО убывает И в области
из (А) видно, что отношения 5;±J-=—I—(, = е) всегда определения справедливо неравенство /(*)>«,
о» A + 1/пУ "
больше 1, так как A + 1/л) < е\ таким образом, при х = е ряд то РЯД L ап СХОДИТСЯ тогда И ТОЛЬКО тогда,
расходится. и=1
V1 * «-+1 и когда сходится несобственный интеграл f f(x)dx
3) Ряд ) — расходящийся, так как -^?-= г и «
?j,n ^ ая п + 1 "о
У1.3...B„-1) 1 (см. 3.1.7.7).
d, — Cj = 1. Напротив, рад ) — ^ сходится,
/ j 2*4... Bп) и
00 |
Примеры. 1) Ряд ? — расходится, так как функция
f(x) = 1/х при х ^ 1 положительна и монотонно убывает и,
/>
IV. Признак Коши. (А) Если существует кроме того, | — = lim Г—= lim ln(D) = oo.
натуральное число N такое, что для числовой * х D-><x> J x D-*co
последовательности {]/а„}, построенной из членов •
* . 2) Ряд / —;—jt-j.—».+ (а > 0) сходится, так как
ряда 2^ аю ап > 0. Для всех п ^ N справедливо не- ^ и in и (in (in л))
равенство \^п ^ q < 1 (q - фиксированное число, ф я /{х) ш t „ри х > 3 положительна,
00 X Ш X (Ш (In X)j
не зависящее от п), то ряд % ап сходится. Если для монотонно убывает и, кроме того,
бесконечного множества чисел п ^ N имеет место +00
неравенство уап ^ 1, то ряд ? а„ расходится. /(х)</х =
и=1 •*
оо 3
(Б) Пусть lim уап = р, где X fl« ~ Ряд с не- . / 1 1
и~*°° и=1 оо "d^ooV <t{\n(\nD)T + a(ln(ln3»°
отрицательными членами. Тогда ряд ? ан схо-
и=1 т.е. несобственный интеграл сходится.
276
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
3.1.14.3. Ряды с произвольными членами. Абсо- при помощи формулы Эйлера получаем
лютная сходимость. Ряд называется
знакочередующимся, если его члены являются (поочередно) ¦ sin(n + — jx-sin — х
положительными и отрицательными. Такой ряд Vcoskx « —-^ 2/ —
можно записать в виде
2«ь
2 sin — х
= сх - с2 + съ - с4 + ... + (-l)" сп + ..., C.2)
где с„ > О для любого и (если первый член ряда
отрицателен, то исследуют - ? ( —1)"~х ся).
У sin/be ¦¦
Поэтому
C.2)
Признак Лейбница. Если для членов ряда
cos Hex
1
sin
х
У
и оба исходных ряда при х Ф 2тк <т « 0, ± 1, ±2, ...)
сходятся по признаку Дирихле.
Абсолютная и условная сходи-
оо
мость. Ряд Y, ап называется абсолютно сходя-
п= 1
оо
щимся, если ряд ? \ап\ из абсолютных величин
п=1
членов исходного ряда сходится. Ряд ? а„
Hashing
вается условно сходящимся, если он сходится, но
00
не абсолютно, т. е. ряд ? | а„ | расходится.
00
Если ряд Y ап сходится абсолютно, то он схо-
и= 1
дится в обычном смысле, т. е. из сходимости ряда
н. I. 2 (см. 3.1.14.5). Имеем | In 2 - ? (- ЦТ4t»\ «1Д" + » ? , ^, бедует сходимость ряда ? а..
Другие признаки сходимости. " '^^ ^^ ^ того ^^ исследовать
Признак Абеля. Если ряд ? Ь, сходит- сходимость знакопеременного ряда ? а„, прежде
ся, а последовательность {а„} (п = 1, 2, ...) моно-
сп > сп+! (п = /с, к + 1,...) и lim си = О,
п-> оо
то ряд сходится.
Остаток у знакочередующихся рядов можно
00
легко оценить. Если ряд ? (—l)"^ сходится и
имеет сумму S, то остаток Rn = S - ? (- l)s x cs
s= 1
имеет знак (—1)" и |Яи|^си+1.
Пример. Ряд У (— 1)" — сходится, так как св =
= — > = С.+1 и lim — =0. Сумма этого ряда рав-
П П + 1 п —? т п i
тонна и ограничена, то ряд
а„Ьп схо-
дится.
Признак Дирихле. Если частичные суммы
ряда ? Ъп ограничены, | Sn \ < М, а. последователь-
ность {ап} монотонна и lim ап = 0, то ряд ? а„Ь„
п -*¦ оо и= 1
сходится.
всего строят ряд Y I °«I и исследуют его при по-
и= 1
мощи признаков, описанных в 3.1.14.1. Если ряд
Y I Ди I сходится, то сходится также и ряд
Y ап (но если ряд абсолютно расходится, то о его
и= 1
сходимости ничего сказать нельзя).
Примеры. 1) Ряд У (-\f~l — сходится условно,
Примеры. 1) Если числа ал > 0 образуют
сходящуюся к нулю монотонную последовательность, а
оо
Ьн = (-1)""\ то ряд X (- XT'l ая сходится. Таким образом,
признак Лейбница является частным случаем признака
Дирихле. я-1 «-1
00 00
2) Ряды ? q,sinnx и ? a.cosnx сходятся для всех шимся.
2) Ряд ^--(.-Э)-при,>1 схо.
не является сходя-
хФ2тъ (т = 0, ±1, ±2, ...), если последовательность {ап}
монотонно стремится к нулю. Из равенства
как члены ряда
2 sin (яр)
дится абсолютно, так
удовлетворяют неравенству
ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ. ФУНКЦИОНАЛЬНЫЕ РЯДЫ
277
sin(r»P)
¦ 1, 2, ... Следовательно, ряд Сумма ряда Y^ равна е" (см. 3.1.14.6, пример 2));
Lj
- сходится абсолютно при а > 1 и любом действи-
тельном р.
Свойства абсолютно сходящихся
рядов.
I. В абсолютно сходящемся ряде
последовательность членов может быть изменена любым
образом, при этом характер сходимости ряда и
величина его суммы не изменятся. Сходящиеся
ряды, суммы которых не зависят от
последовательности членов, называют иногда безусловно
сходящимися.
Если ряд сходится условно, а а — любое
заданное число, то члены ряда можно так
переупорядочить, что преобразованный ряд будет сходиться и
число а будет его суммой {теорема Римана).
II. Под произведением двух бесконечных рядов
а„ и
понимают ряд, образованный из
всевозможных произведений а„Ьк (и, к = 1, 2, ...).
Эти произведения а„Ьк можно упорядочить,
вообще говоря, многими способами и получить
тем самым различные ряды. Следующая теорема
дает условие того, чтобы все эти ряды сходились
и имели одну и ту же сумму.
Теорема Коши. Если ряды ? а„ и X К схо"
и=1 л= 1
дятся абсолютно и имеют суммы А и В
соответственно, то все их произведения также сходятся
абсолютно и имеют сумму А'В. В этом случае
справедлива формула
\я=1 /\я=1 / n=i\«=i
(формула умножения Коши).
Формула умножения Коши имеет место и
оо оо
тогда, когда один из двух рядов ? ап или ]Г Ъп
и=1 и=1
сходится абсолютно, а другой ряд просто сходится.
Ряд-произведение в этом случае просто сходится,
но, быть может, не абсолютно.
Пример. Ряд / —г*) сходится абсолютно для всех х
I см. признак К
оши для ряда
При помощи фор-
мулы умножения Коши вычисляется произведение
1L^)\Z^
^v
полученный результат можно записать следующим
образом: е*еу = ех+у (теорема сложения для показательных
функиий).
3.1.14.4. Функциональные последовательности.
Функциональные ряды. Отображение множества
натуральных чисел N во множество действительных
функций одного переменного х, определенных на
промежутке /, называется функциональной
последовательностью и обозначается
{/„ (х)} или Д (х), /2 (х), /з (х), ...; C.3)
функции /„ (х) называются членами
последовательности. Каждое значение хе/, для которого
последовательность C.3) имеет некоторый (конечный)
предел, принадлежит области сходимости этой
последовательности. Таким образом,
последовательность определяет в области своей сходимости
некоторую функцию
/(х)= lim /и(х),
л-> оо
которая называется предельной функцией (или
пределом) последовательности. В дальнейшем
предполагаем, не ограничивая общности, что область
сходимости совпадает с областью определения /.
Для того чтобы охарактеризовать предельную
функцию, используют понятие равномерной
сходимости. Функциональная последовательность
сходится к предельной функции /(х) равномерно
в /, если для любого е > 0 найдется такое N (е), не
зависящее от х, что для всех п > N (е) и для всех
хе/ выполняется неравенство
Обозначение: /„ (х) Zt/(x).
Если существует такое е > 0? что для каждого
числа N имеется по меньшей мере одно п > N и
х0 е / такие, что | /и (х0) — /(х0) | > е, то говорят, что
последовательность сходится неравномерно.
Примеры. 1) Функциональная последовательность
{/я(х)}=< -——2~г\ сходится для любого хе/ = [0, 1] к
функции f(x) = 0. Эта сходимость является равномерной
в /, так как для любого е > 0 можно найти такое N (е),
например [1/Bе)] + 1 (где [1/Bе)] означает наибольшее
целое число, которое меньше или равно 1/Bе)), что для всех
и > N = N(е) и всех xel выполняется неравенство
2) Функциональная последовательность
сходится при любом xel = [0, 1] к функции f(x) = 0. Для
любого фиксированного дс > 0 достаточно выбрать
— + 1 таким, чтобы выполнялось неравенство
/я (х) < — <е- Однако эта сходимость в / не является
пх
равномерной. Если выбрать ? < 1/2, то, каково бы ни было
N, можно указать такие п> N и xel (например, п = N 4- 1,
х = 1/(N + 1)), что/„(х) > е (при данном выборе п и х имеем
*) По определению 0! = 1.
278 ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
Критерий Коши равномерной схо- Действительно, 1 - cos ^-= 2 sin2-^ < ^-, так как
димостифункциональнойпоследова- п п п
тельности. Последовательность C.3) сходится к I sin х | < | х |^ Но \х | < С, где С - max (| а |, | Ь |). Тогда
предельной функции равномерно в / тогда и только 0 < 1 - cos — < 2 ( —J .
тогда, -когда для каждого е > 0 существует не за- «,"
висящее от х число N (б) такое, что при п ^ N и для V 2С2
любого m ^ 1 Ряд 2,~?~ сходится и является маж°Рантой да«ного
1/и+«М-/пМ1<е
функционального ряда.
для всех xeD одновременно.
Функциональные ряды. Бесконечный Признак Абеля равномерной схо-
ряд (см. 3.1.14.1), построенный из функциональной д и м о с т и. Ряд ? ап (х) Ьн (х) s ах (х) Ъх (х) + ...
последовательности «=i
v г / ч ••• + <U*)M*) + ... сходится для всех хе/ равно-
мерно, если ряд ? Ь„(х) сходится в J равномерно
называется функциональным рядом. Понятия и равномерНо ограниченная последовательность
«область сходимости», «предельная функция» и {пп{х)} для каждого хе1 является монотонной,
«равномерная сходимость» переносятся на функцио- Признак Дирихле равномерной
нальную последовательность частичных сумм »
с / \ V- г i \ п - о/ \ сходимости. Ряд У аи(х)Ь„(х) = а1(х)Ь1(х) + ...
$п(х) = 2- Л М- Разность между суммой 5(х) „=i
s=l
. „ ... + а„ (х) Ь„ (х) + ... сходится для всех х е / равно-
сходящегося функционального ряда и одной из его я
частичных сумм 5„ (х) называют остатком и обозна- мерно, если частичные суммы Sjj(x) = J] Ь„(х)
чают я=1
д (х) _ 5 (х) — S (х) = равномерно ограничены (| Sj (х) | ^ М, М — const),
" а последовательность {а„(х)} монотонно и равно-
Z°° /-/\_/- /\_i_/- /\i мерно стремится к нулю.
7s l-V = Jn+l \x) ~T Jn + 2\x) + •••
Признак Вейерштрасса равномер- Пример. Ряд ^^^-х" сходится на отрезке
ной сходимости рядов. Ряд У /п(х) схо-
и= 1 [0, 1/2] равномерно, так как ряд ? х" на отрезке [0, 1/2]
дится на промежутке / равномерно, если существует сходится равномерно (см „ризнак вейерШТрасса; мажоран-
сходящийся числовой ряд ^ ап с положительны- тойэ например, является ? A/2)"), а последовательность
ми членами такой, что для всех п ^ N и всех х е / f (и + 1)") f/ l Y0
выполняется неравенство {а"(х)} = j ~^J = {{1 + И) ) монотонно возрастает и
ограничена (граница, например, е).
00 Свойства равномерно сходящихся
Ряд ? ап называется мажорантой функцио- рядов.
n=1 I. Пусть функции/„(х) (п = 1, 2, ...) определены
? - . v на отрезке / = [а, ЬЛ и непрерывны в некоторой
нального ряда 2^ /и(х)- «
и=1 точке х = х0 этого отрезка. Если ряд ? /и(х) схо-
Примеры. 1) Функциональные ряды ^^„sinnx и дится на / равномерно, то сум^а/(х) ряда также
непрерывна в точке х = х0. Тогда
? а„ cos nx сходятся в каждой конечной области равномерно, оо оо
я~1 1*т S/»(х)= 2] ^т /вD
• Х-+Х0и=1 я=1 Х-^Х0
если ряд J] а» абсолютно сходится. Так как |а„smлх|<
II. Пусть функции/и(х) (п — 1, 2,...) непрерывны
то ряд X 1«-1 может быть вы" „я лт„^^ / =, Гп hi „ „„m. ряд f /и(:
я=1
бран в качестве мажоранты.
ся на / равномерно и имеет сумму fix). При этих
2) Функциональный ряд ,
' * F условиях ряд можно почленно интегрировать (т. е.
^ / х \ поменять местами знак бесконечной суммы и знак
2 f 1 - cos — J интегрирования):
J/Wdx=lt fH(x)dx = f J/«Wrfx.
в каждом интервале (a, Ь) является равномерно сходящимся. a an=i n=i a
СТЕПЕННЫЕ РЯДЫ
279
Замечания. 1) Для почленного
интегрирования ряда достаточно, чтобы функции/„ (х) (л = 1,
2, ...) были интегрируемы на [a, ft] (не
обязательно непрерывны).
оо
2) Равномерная сходимость ряда ? /я(х) не
является необходимой для перестановочности
знака интегрирования со знаком бесконечной
суммы или для непрерывности суммы ряда.
III. Пусть функции /„ (х) (л = 1, 2,...) на отрезке
/ = [a, ft] имеют непрерывные производные /я (x).
Если на этом отрезке ряд ? /„ (х) сходится, а ряд,
я=1
оо
составленный из производных ? /и(х), сходится,
и=1
и притом равномерно, то сумма /(х) ряда
Yj fn(x) имеет на / непрерывную производную,
и= 1
причем
Замечания. 1) Если ряд ? /„(х) сходится
я=1
оо
хотя бы в одной точке /, а ? f'n(x) сходится на /
равномерно, то ряд ? /„ (х) на / сходится равно
и=1
мерно.
2) Свойства рядов I —III нетрудно перенести на
функциональные последовательности. Например,
свойству I соответствует следующее: пусть функции
/и (л) (л = 1, 2, ...) заданы на отрезке / = [а, ft] и
непрерывны в некоторой точке х = х0 этого отрезка.
Если функциональная последовательность
сходится на / равномерно, то предельная функция
/(х) этой последовательности непрерывна в точке
х = х0 и
lim lim /и(х)= lira lim /и(л)= lim /(x).
п-юо х->х0 х-*хоп-юо х-+х0
Примеры. 1) Пос. 1едователыюсть fn (х) — -—. 2
сходится на [0, 1] равномерно. Предельная функция /(х) = О
непрерывна. Далее, по свойству II
1
+ И2) |\_
л 2 = 0</х = 0.
2) В ряде
U
- функции /„ (х) = -
- непрерывно
дифференцируемы на произвольном отрезке [о, 6]. Ряд
в силу неравенства —3— < ~т~ сходится на
[а, 6] равномерно, так же как и ряд > cos их, состоящий
из производных/^ (х), так как
cosnx
_ ,. . V1 sin их .
Следовательно, сумма f(x) ряда > —3— непрерывно диф-
•«1
ференцируема на [а, Ь] и
Пусть F — множество функций, определенных
на отрезке / = [a, ft]. Множество F называется
равномерно ограниченным, если существует число
М такое, что |/(х) | < М для всех хе/ и для всех
функций f(x)eF (так что М не должно зависеть
от конкретной /е F). Множество F называется рав-
ностеЛенно непрерывным, если для любого е > О
существует 8>0 такое, что для всех хъ х2е/,
удовлетворяющих условию | хх — х2 \ < 5, и для
всех/eF выполняется неравенство \f{xx) —f(x2) \ <
< ? (так что 6 зависит только от е: Ь =Ь(е),
и не зависит от / и от хь х2е/).
Теорема Арцела-Асколи. Пусть на
/ = [a, ft] задано бесконечное множество функций F.
Если F равномерно органичено и равностепенно
непрерывно, то из него можно выбрать равномерно
сходящуюся последовательность.
3.1.14.5. Степенные ряды. Степенной ряд есть
функциональный ряд с общим членом
(ан — действительные числа):
- УоТ = ao + ai(y- Уо) +
+ <*г (У ~ УоJ + • • • + а„(у - уо)п + ...
Действительное число у0 называется центром
степенного ряда. Заменой переменного х = у — у0
этот степенной ряд преобразуется в степенной ряд
оо
? аих" = а0 + агх + а2х2 + ... + а„х" + ...
с нулевым центром. В дальнейшем ограничимся
исследованием рядов именно такого вида.
Существуют степенные ряды, которые
а) сходятся при всех х (всюду сходящиеся сте-
оо
V х"
пенные ряды); например, ряд / —- сходится для
любого х по признаку Даламбера:
J?
O<1;
ii-oo \x\n{n+ 1) и^оо л+
б) сходятся только при х = 0, например ? л!х",
так как
lim -
„-¦оо ni |X|
при х # 0 (признак Даламбера);
lim (| х | | л + 11) = оо > 1
И-> 00
280
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
в) для некоторых х # 0 сходятся, для других х
оо I х|п+ 1
расходятся, например ? х", так как lim -—— =
и = 0 П-+ 00 1*1
= lim |х| = |х|. Таким образом, этот ряд при
п-> оо
| х | < 1 сходится, а при | х \ ^ 1 расходится.
Свойства степенных рядов.
I. Если степенной ряд ? а„хп сходится при
п = 0
х = хь то он абсолютно сходится для всех х,
удовлетворяющих неравенству | х \ < | хх |, а если
степенной ряд расходится при х = х2, то он
расходится и для всех х, удовлетворяющих
неравенству | X | > | Х2 |.
П. Если степенной ряд ? анхп при некоторых
п = 0
х#0 сходится, а при остальных х расходится, то
существует, и только одно, положительное число г
такое, что степенной ряд при | х | < г сходится,
и даже абсолютно, а при \х\> г расходится. При
х = г и х = —г ряд может как сходиться, так
и расходиться. Число г называется радиусом
сходимости степенного ряда. Если г > 0, то
промежуток ( — г, г) называется интервалом сходимости
степенного ряда.
Для вычисления радиуса сходимости служит
теорема Коши — Адамара: радиус сходимости г
ряда ? а„хп равен обратной величине верхнего
и = 0
предела последовательности {]/|а„|}:
1
(при этом г = оо, если Пгп |/| а„ | =0, и г = О,
п л -* оо
если lim |/| а„ | = оо).
п -* оо
Верхний предел г числовой последовательности
{?>„} (ср. 3.1.3.1.2) есть верхняя граница множества
«точек сгущения» последовательности, т. е. для
любого е > 0 существует только конечное число
индексов п таких, что Ь„ > г + е, но для
бесконечного числа п справедливо неравенство Ъп > г — е.
Если для любого действительного числа С имеется
бесконечное множество индексов п таких, что
Ь„ > С, то говорят, что верхний предел равен 4- оо;
если, напротив, для любого действительного числа
С имеется только конечное число индексов и таких,
что Ь„ > С, то говорят, что верхний предел равен
-оо. Верхний предел существует всегда. Если
существует lim |/| ап |, то
п -* оо
Йт
—> оо
]/\a~nl
Радиус сходимости г степенного ряда ? апх"
п= 1
может быть вычислен также при помощи
признака Даламбера: если существует предел
Цт
q, то г = — (г = оо при q = 0 и г = О
Примеры. 1) Ряд ? пх* имеет радиус сходимости
я»0
г = 1, так как
1 J1
г b1
lim |7л lim ]/n
п-+ оо и-* оо
оо «
2) Ряд У — имеет радиус сходимости г = оо, так как
•so я!
lim
3) Ряд ? пх* расходится в граничных точках х = 1 и
х = — 1 интервала сходимости.
4) Ряд ? — имеет радиус сходимости г « 1, так как
lim ]/— = 1;
1-» 00 К И
; он сходится в граничной точке х=-1
(признак Лейбница) и расходится в граничной точке х = 1
(гармонический ряд) интервала сходимости.
5) Ряд ? ~ имеет радиус сходимости г = 1, так как
1 И
при q = оо).
абсолютно и в граничных точках х = ± 1 интервала
сходимости (о ряде У -г см. 3.1.14.2).
III. В каждой внутренней точке интервала
сходимости степенной ряд сходится абсолютно. Во
всяком замкнутом промежутке, который целиком
лежит в интервале сходимости, степенной ряд
сходится равномерно. Если степенной ряд сходится
при х = г (не обязательно абсолютно), то
степенной ряд на [0, г] сходится равномерно. (Если
степенной ряд расходится при х = г, то на
интервале [0, г) степенной ряд не может сходиться
равномерно.)
00 00
IV. Степенные ряды Хаяхл и ^С!+каи+кхи
и=0 п=0
{к =0, 1, 2, ...) имеют один и тот же радиус
сходимости (в частности, интервалы сходимости
со оо
степенных рядов ? а„хп и ? папхп~1 (к = 1) сов-
и=0 я=0
падают); однако в граничных точках интервала
сходимости эти ряды могут иметь различное
поведение.
V. Теорема единственности
разложения в степенной ряд. Если два ряда
Л апх" и J] Ьпхп сходятся в одном и том же
и=0 я=0
интервале \х\ <г и во всех его точках (или хотя
бы в бесконечном подмножестве точек, имеющих
нуль в качестве предельной точки) имеют
одинаковые суммы, то эти ряды совпадают, т. е. а„ = Ьп
для и = 0, 1, 2, ...
Данная теорема обосновывает метод сравнения
коэффициентов.
Примеры. 1) Пусть ..— *,. , . ^
уиу \иу 1 • 2... .п
для всех действительных а и всех натуральных п. Ряды
СТЕПЕННЫЕ РЯДЫ
281
»=о ««о
A + ху - > I )x" и A + xf - > ( )x"при |x| < 1 сходят- в) Степенной ряд У апхп внутри его интервала
Lj\n/ Lj\nJ n = o
ся абсолютно (см. 3.1.14.6, пример 2)); следовательно, сходимости можно почленно дифференцировать:
Это утверждение верно также и для концов
интервала сходимости, если ряд ? ш^х" схо-
дится в этих точках. Степенной ряд внутри интер-
вала СХОдимости можно дифференцировать любое
цисло раз ^ свойство IV):
Примеры. 1) Справедлива формула ln(t+x) =
= J] (-l)""—х" (см. 3.1.14.6, пример 3)), г = 1. При х ¦= 1 ряд
также сходится (см. признак Лейбница). Следовательно,
A + х)"+ь = \ (a + bjxm.
получается
Тем самым получается теорема сложения биномиальных
коэффициентов:
V
для любых действительных чисел а, Ь и всякого натураль-
2) Пусть /(х) = У апх* и ряд имеет ненулевой радиус
сходимости. Если /(х) - четная (или нечетная) функция,
то ряд ? a,x" содержит только четные (или нечетные)
VI. Если Yj ап (х — хо)п — степенной ряд с ра-
и = 0
диусом сходимости г > 0, то его сумму /(х) можно
разложить также в степенной ряд с центром в
любой точке X! из интервала сходимости:
где
(При этом все эти ряды, суммы которых равны
Ьп, сходятся (см. свойство IV), а для радиуса
сходимости гх нового ряда справедливо неравен-
ство г, > г - | хх - х0 |.)
VII. а) Сумма f{x) степенного ряда ? а»х"
п = 0
для всех значений х из интервала сходимости (-г, г)
есть непрерывная функция. Если степенной ряд схо-
дится при х = г, то сумма/(х) при этом значении
х также непрерывна (слева):
In 2
«
V(
2) Справедливо равенство
(СМ. 3.1.14.6, пример 3)), г = 1. Ряд при х = 1 (а также при
х = -1) сходится, так как
а Bи+1J п2 + п + 025
и Ь| — at = 2,5 — 1 = 1,5 > 1 (см. замечание к признаку Да-
ламбера). Согласно теореме Абеля о предельном значении,
имеем
-j = arcsin 1:
24.. .Bп) 2я+1
1 j 1.3 1 1.3.5 1
= 1 +У'Т+ 2^4'У "*~ 2-4-6 "У
} —Щ~
3) сУмма сходящегося ряда } *—Щ~ (см- пРизнак
Лейбница) может быть вычисленПледующим образом:
З1~^З1 ""
Hm f{x)
Х-*Г -0
ay.
Если степенной ряд сходится при х = —г, то сумма
f{x) при х = -г непрерывна справа (теорема
Абеля о предельном значении).
б) Степенной ряд У апхп всегда можно по-
„ = о
членно интегрировать на отрезке [0, х^, где
- lim fY(-l)V"</f= lim
4) Ряд функции Бесселя
если хх - один из концов интервала сходимости
и ряд сходится в хь то формула остается спра- удовлетворяет дифференциальному уравнению хи" + и' +
ведливой. + хм = 0. Этот ряд сходится при всех х, и выполняются
282
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
равенства
сходятся, то
и, согласно теореме о единственности разложения
функции в степенной ряд, выполняются
соотношения
1 = аосо,
0
атс„-т
при п ^ 1;
Если сложить эти ряды, то в качестве коэффициентов
при х2"'1 (и — 1, 2, ...) получаем
отсюда можно последовательно найти сп. Точно так
же можно представить отношение двух функций
g/f, являющихся суммами степенных рядов, как
сумму степенного ряда ? с„хп в некоторой ок-
и = 0
что и доказывает утверждение рестности нуля, если а0 =/@) Ф 0. Коэффициенты
Другие примеры к этим утверждениям даны в 3.1.14.6. с» вычисляются из соотношения
VIII. Действия со степенными ряда-
м и. а) Если /(х) = ? а„х" и д (х) = ? Ь„хп, то для
п=0 л=0
любого х, являющегося внутренней точкой
интервалов сходимости обоих рядов (см. свойство III),
можно построить сходящиеся ряды
if I
„=0\ т=0
б) Пусть д (х) - сумма степенного ряда с
ненулевым радиусом сходимости г: д (х) = ? Ьих",
и = 0
а /(м) - бумма степенного ряда с ненулевым ра-
00
диусом сходимости г': f(u) = ? а„ми. Тогда F (х) =
и = 0
=f(g(x)) снова есть сумма некоторого степенного
ряда: F(x) = ? с„х" — по крайней мере для тех х,
и = 0
для которых ряд I | Ьпхп | сходится и имеет сум-
и = 0
му, меньшую чем г'. Коэффициенты сп вычисляются
00
при помощи рядов: с„ = ? ambmn, которые абсо-
т = 0
лютно сходятся при условии, что | Ьо | < г', где
оо
(в (*))* = I Ььх". Другими словами, чтобы полу-
я = 0
чить степенной ряд для F(x), можно подставить
оо оо
м = I ^ix" B степенной ряд J] а„ми и привести
и=0 л=0
подобные члены.
в) Если функция /(х) в окрестности нулевой
оо
точки есть сумма степенного ряда I апх* и /@) =
и = 0
= а0 Ф 0, то функция 1//(х) в окрестности нулевой
точки также есть сумма некоторого степенного
оо
ряда У сих"; так как для малых х оба ряда
т. е. из системы Ь„ = ^ атсп„т для и = 0, 1, 2, ...
т = 0
Примеры приведены в 3.1.14.6.
3.1.14.6. Аналитические функции. Ряд Тейлора.
Разложение элементарных функций в степенной ряд.
Функция/(х) называется аналитической в точке х0,
если для всех х, удовлетворяющих условию
| х — х0 | < г, функция /(х) есть сумма некоторого
степенного ряда:
/(х)= ? ап(х-х0)п.
Каждая аналитическая в точке х0 функция ана-
литична также в некоторой окрестности х0 (см.
3.1.14.5, свойство VI). Сумма, разность и
произведение аналитических функций — снова
аналитические функции. Если функция /(х) - аналитическая
в х0 и Дх0) Ф 0, то функция 1//(х) - также
аналитическая в х0. Функция f(g (x)) аналитична в х0,
если д(х) аналитична в х0 и f(u) аналитична
в точке м0 =д(х0) (ср. 3.1.14.5, свойство VIII). Если
/(х) аналитична в х0, то в некоторой окрестности
х0 она дифференцируема любое число раз и
Си+лаи+*(х-х0)и.
Тогда
C.4)
(ряд Тейлора).
АНАЛИТИЧЕСКИЕ ФУНКЦИИ. РЯД ТЕЙЛОРА
283
Если функция /(х) в некоторой окрестности
точки х0 дифференцируема любое число раз, а
остаточный член в формуле Тейлора (см. 3.15.3)
стремится к нулю при п -> оо, то степенной ряд C.4)
имеет отличный от нуля радиус сходимости, а
функция /(х) аналитична в х0.
Эти соображения можно перенести на степенные
ряды с большим числом переменных. Функция
/(х, у), которую можно записать как сумму
степенного ряда от двух переменных:
п (X ~ Х0)т (у -
т, п — 0
с областью сходимости, содержащей точки (х, у)
с х Ф х0 и у Ф у0, называется аналитической в точке
(*(ъ УоУ Точка относится к области сходимости,
если степенной ряд в этой точке сходится. Для
степенных рядов нескольких переменных имеют
место теоремы, аналогичные сформулированным
в 3.1.14.5 для одного переменного.
Функция, аналитическая в точке (х0, у0),
дифференцируема по всем переменным любое число
раз, и
1 а"+и/(х0, у0)
птп mini dxndf '
Таким образом, разложение функции /(х, у), если
оно возможно, должно иметь вид
/(*, у) -
оо
I
0, у0)
mini дхтдуп
(х-х0Г{у-у0Г
{ряд Тейлора).
Примеры. 1) Функция /(х) = 1/A - х) является
аналитической в каждой точке х0, удовлетворяющей условию
|хо|<1. Разложение в степенной ряд для этой функции
в точке х0 получают следующим образом:
имеет радиус сходимости г = 1. Почленным
дифференцированием получаем для /(х) дифференциальное уравнение
A + x)f = а/, а в качестве решения — функцию/(х) = A + х)я,
так как /@) = 1. Таким образом,
A + х)- =
x"sl+flx+
11 = 0
fl(q-l)(q-2) .
1.2...и
. ,
для |х| < 1.
3) Функцию /(х) = a resin х при х = 0 можно разложить
в степенной ряд (ряд Тейлора). Если найти производную
/' М = 7j—2U/2» то ЭТУ Функцию при | х | < 1 можно раз-
ложить в следующий ряд:
/'(х)
(см. пример 2)). При | х | < 1 ряд можно почленно
проинтегрировать:
\f{t)dt = arcsinx =
Поэтому
arcsin x = x + —'— + ¦
3 x5
1-3-5 x7 l-3...Bn- 1) x2"+1
2-4-6 ' 7 "•"••• + 2-4...2л *2n+l
для |x|< 1. Справедливость формулы при х = ± 1 следует
из теоремы Абеля о предельном значении и из примера 2)
к свойству VII в 3.1.14.5.
Аналогичным способом получаются, например,
следующие ряды:
/<*)-
1
1
1-х 1-х0 1-(х-хо)/A-хо)
ДЛЯ |Х|<1,
(так как
при | q | < 1; см. 3.1.14.1, пример 1)). Ml + х) =
Ряд сходится при | х - х01 < 11 - х01 = г.
00
W
2) Ряд Е(х)= > =7- имеет радиус сходимости г = оо.
/ 1 п\
и-0
Почленно дифференцируя, получаем, что
X2
2
X4
4
для -1 <х< 1.
4) Для функции /(х) = sin x
О
«-1 »=0 к\
Функция ?(х) удовлетворяет дифференциальному уравнению
?(*) ш У{*)- Отсюда следует, что Е{х) = Се* и С = 1 в силу поэтому
?@) = 1. Таким образом,
при *
- при J
2п+
(л =0, 1,...),
(п = 0, 1,...);
есть функция, аналитическая всюду.
Ряд
/М-
Так как для и-го остатка ряда
_ х"-" { (-1)("+1)/2 sin Эх, п
Rn " (п+1)! | (_ If2 cos Эх, и
нечетное,
четное,
284
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
справедлива оценка | Я„ | < f—'¦¦¦¦¦ , a Mm RH — 0 при х е
(л+1)! п-»оо
е [а, Ь], то sin х представляется этим рядом для всех х.
Таким же способом можно показать, что (для | х | < оо)
коэффициентов Т„ следующие уравнения:
Zffl
Bт + 1)!Bл-2т)!
где л = 0, 1, 2, ... Отсюда легко вычисляются То = 1, 7*1 = 2,
Т2 = 16, Г3=272, Г4 = 7936, ...;
5) При помощи почленного интегрирования рядов
получаются разложения в степенные ряды некоторых интегралов,
которые в конечном виде через элементарные функции не
выражаются. Из равномерно сходящегося на любом
конечном промежутке ряда
7) Функцию
можно разложить в степенной ряд
в окрестности точки х = 0, предварительно доопределив ее
при х = 0 предельным значением 1. Положим
получается интеграл (для | х | < оо)
IX-T7T + --
x2"+1
Bл -
Так как (для | х | < оо)
Bл + 1)!
то отсюда следует формула
f *Ш±л, - Vr iv x2"+1
J t /_} 1} Bл+1)!Bл+1)
6) Функция F (х) = tg (x), как отношение аналитических
в точке х = 0 функций д(х) = sin x, /(x) ?= cos x, /@) = 1,
также аналитическая в точке х = 0. Можно найти разложение
этой функции в ряд; так как функция tgx нечетная, то
разложение содержит только нечетные степени х (см. 3.1.14.5,
свойство V):
Из соотношения tg x cos х = sin x и рядов для cos x
и sinx получаем
Вычислим коэффициенты рж используя теорему о
единственности разложения функции в степенной ряд:
Сравнивая коэффициенты при одинаковых степенях х,
получим :
коэффициент при х:
коэффициент при х":
--Al.O
4 (л — m)! m! л!
m = O
при л>2.
Можно в общем виде показать, что коэффициенты р\, -
рациональные числа;
Ро-1. Э1--1Д
Р24+1=О (Л = 1, 2,...),
где Вк - числа Бернулли (см. 1.1.3.1):
В, = 1/6, В2 - 1/30, В3 = 1/42, В4 = 1/30,
В5 = 5/66, В6 = 691/2730, J57 = 7/6, B8 = 3617/510,
В9 = 43 867/798, В,о = 174 611/330, Вп = 854 513/138.
У (У (-1Г- ь
Lj\U Bт+1)!Bл-2|я)!
— О 0
Некоторые авторы называют числами Бернулли
коэффициенты р„.
Пользуясь этим разложением, можно найти разложение
cthx. Действительно,
Заменив в этой формуле х на 2х, получим (для | х | < я)
Используя теорему о единственности разложения
функции в степенной ряд, получим для определения неизвестных
БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
285
Числа Бернулли используют также в следующих
разложениях:
8) Пусть f(x) — аналитическая в точке х = 0 функция:
/(х) * а + Ьх + сх2 + дх3 + <?х4 +/х5 + ...;
тогда/2 (х) - также аналитическая функция; при аФО
аналитическими будут функции
а при а > 0 - функции
Запишем первые члены разложения в степенной ряд в
окрестности точки х = 0 этих аналитических функций:
/2(х) = а2 + 2аЬх + (Ь2 + 2ас)х2 +2(ad + Ьс)х3 +
+ (с2 + lae + 2bd) х4 + 2 (а/+ be + cd) x5 + ...,
BЫ,с2 е ЪЬ2с
а2 а а3
~x
Ы с2 , ЪЬ2с 5Ь*
4а2" Sa2~+'l6^~~
1 1 Гд tx
(x) fa L 2а
]/f(x)
9) Обратная функция х = а (у) для аналитической функции
У =/(*) = ах + Ьх2 + сх3 + dx* + ex5. +fxb + ... (а ф 0) -
также аналитическая в точке у = 0и имеет разложение в ряд
д (у) = А у + By2 + Су3 + Dy* + Еу5 + Fy6 + ...,
BЬ2 - ас),
Ь
А ш -L, В = - -?-. с
D ш -LEafcc - а2</ - 5Ь3),
? - ^-Fa2bd + За2с2 + 1464 - а3* - 21а*>2с),
F — -ут-Gа3Ье + 7а3с</ + %Aab3c -
- a*f- 2%a2b2d - 2%a2bc2 - <
3.1.15. БЕСКОНЕЧНЫЕ
ПРОИЗВЕДЕНИЯ
Если {м„} - последовательность (числовая или
функциональная), то последовательность {Р„}, где
i = Uu Р2 = UXU2, • • ., Р„ =
Uk = UjM2 • . . Un, СО-
стоит из частичных произведений бесконечного
произведения, которое символически записывается
в виде
Если существует такое q, 0 < q < 1, что для
любого п выполнено неравенство 0 < м„ < q, то
lim Р„ = 0, т. е. предельное значение этого беско-
п —> оо
нечного произведения есть нуль, хотя ни один из
сомножителей ип не равен нулю. Но так как
естественно выделить бесконечные произведения,
равные нулю только тогда, когда хотя бы один
сомножитель равен нулю, то сходимость для
бесконечных произведений определяется иначе, чем
сходимость бесконечных рядов.
00
VI. Бесконечное произведение f] A + ап) рас-
сходящимся, если существует такое т, что для всех
п > т выполняется неравенство ы„ ф 0, и
последовательность частичных произведений PJJ1 = \\ ик
к = т+1
при п -*¦ оо сходится к отличному от нуля числу Um:
lim P™ = Um. Не зависящее от т действительное
п-> оо
число U = и{и2...итит называется значением
бесконечного произведения. Если предел lim PJJ1 равен
п -* оо
О, или оо, или —оо, то говорят, что бесконечное
произведение расходится к 0, или к оо, или к — оо.
Если предел Р™ при п -> оо не существует, то
бесконечное произведение называется неопределенно
расходящимся.
Из этого определения следует: сходящееся
бесконечное произведение тогда и только тогда
равно 0, когда один из сомножителей равен 0.
Примеры. 1) Бесконечное произведение
2
сходится и имеет значение 1/2, так как ин Ф 0 для всех п и
ао
I 111 ^ )
откуда
ПИ)
я = 2
зля всех п и
«-0-1H-i)-(i-i
2) Произведение I |( 1 —--) расходится к 0 (стремится
к 0), так как и„ Ф 0 для всех п и
откуда следует, что lim Рхя = 0.
п-+ оо
286
ДИФФЕРЕНЦИАЛЬНОЕ И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЯ
рт/ \ V. Если существуют как положительные, так и
3) Произведение I |( 1 + —J расходится к + оо (стре- отрицательные а„, то для сходимости бесконечного
}ш1 произведения достаточно, чтобы вместе с рядом
мится к + ооХ так как ы. Ф О для всех пи ^
. 2-3.4...(п+1)=л + 1[
ап сходился и ряд
а1-
VI. Бесконечное произведение \\ О + й«) Рас-
откуда следует, что Km Р„=+оо. и=1
и~*°° ходится к 0 тогда и только тогда, когда для
Основные теоремы для бесконеч- достаточно большого т справедливо соотношение
ных произведений.
00
I. Если сходится бесконечное произведение f] и„,
л=1
то сходится также и каждое остаточное произведение
оо
пп = П ит — мя+1"и+2 • • • Если бесконечное про-
(ср. II) lirh
П-* 00 к =
1 + ак) = — оо. Важные частные
случаи: существует номер т такой, что для всех
к^т ак < 0, а ряд ]Г а„ расходится или же ряд
и=1
? а„ сходится, а ряд ? а* расходится.
VIL Для произведений ? A + ап) с ап любого
изведение J~[ и„ имеет сходящееся остаточное про-
л=1
изведение я„, то сходится также и само бесконечное
оо
произведение Ц и„. Это означает, что добавка или знака справедливо следующее утверждение: беско-
отбрасывание "конечного числа членов не влияет нечное произведение Д d + «¦) сходится тогда и
на сходимость бесконечного произведения. только тогда корда ^ любого действительного
И. Если бесконечное произведение Ц ин сходит- числа е > 0 существует такое N (е), что для всех
и=1 n^N(e) и любого натурального р выполнено
неравенство
ся, то
lim nn = 1
п-* оо
lim и„ = 1.
П-* 00
Для всех w, начиная с некоторого, все
сомножители и„ сходящегося бесконечного произведения
больше нуля. На основании I и II, таким образом,
п <
т = п+ 1
Бесконечное произведение Ц A + а«) называет-
и=1
можно без ограничения общности считать все ип ся абсолютно сходящимся, если сходится произ-
оо
ведение |~[ A + | а„ |).
л= 1
VIII. Если П A + I ап I) сходится, то произведе-
ос
ние YI (^ + ап) сходится, т. е. из абсолютной схо-
и= 1
димости следует обычная сходимость бесконечного
произведения.
IX. Произведение \\ О + ап) сходится абсолют-
л=1
оо
но тогда и только тогда, когда ряд ? а„ схо-
положительными.
III. Для сходимости бесконечного произведения
00
YI и„ с положительными сомножителями и„ необ-
и=1
ходимо и достаточно, чтобы сходился ряд
оо
linn..
Если это условие выполнено и L— сумма этого
ряда, то
П — ГТ я= х
„У-j и* дится абсолютно (см. 3.1.14.3).
X. Порядок сомножителей у абсолютно сходя-
Часто бывает целесообразно записать произве- щегося произведения может быть изменен
произвольным образом, при этом не изменится ни
v характер сходимости, ни значение бесконечного
дение в виде
П
произведения.
Тогда, согласно II, условие lim(an) = 0 явля-
п —> оо
ется необходимым условием сходимости
произвеао я_ j
Примеры. 1) Произведение f] A + х2 ) абсолютно
сходится при | х | < 1 к величине
-. Абсолютная схо-
IV. Если для всех п^т справедливо^неравен- дамость данного произведения следует из абсолютной сходи-
ство а„ > 0 (или ан < 0), то произведение f] A + ап) мости ряда ? х2" 1 при |х| < 1 (см. IX). Значение произ-
сходится тогда и только тогда, когда сходится ряд ¦«*»» вычисляется следующим образом:
х4)...A +х2" )= 1 -х2",
ПОСТАНОВКА ЗАДАЧИ, ПРИМЕРЫ' И ОСНОВНЫЕ ПОНЯТИЯ
287
поэтому Р„ = 1-f2-. Следовательно, lim Pn = —1— для произведения. Далее,
2) Бесконечное произведение
Г(х)=^
+х/п
абсолютно сходится для всех хФ -к (к = О, 1, 2, ...).
Рассмотрим
:(х —
2/Г
л У х(х+1)(х-
Отсюда следует формула для гамма-функции
Lnxjn~= lim (-х-ТТТ7г)-х;
откуда, согласно IX, следует абсолютная сходимость следовательно, Г(х + 1) = х Г(х).
3.2. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Вариационное исчисление — математическая
дисциплина, посвященная отысканию экстремальных
(наибольших или наименьших) значений
функционалов. Под функционалом (линейным) понимается
числовая функция, определенная на некоторых
классах функций. Функционал ставит в
соответствие каждой функции из такого класса некоторое
число. Примером функционала является интеграл
ъ
J (х) = J х (t) dt, где х (t) — непрерывная функция,
а
определенная на отрезке [а, Ы]. Вариационное
исчисление является естественным развитием той
главы математического анализа, которая посвящена
задаче отыскания экстремумов функций.
Возникновение и развитие вариационного исчисления тесно
связано с задачами механики, физики и т. д.
В XX веке возник целый ряд новых направлений
вариационного исчисления, связанных с
интенсивным развитием техники, смежных вопросов
математики и особенно вычислительной техники. Одним
из основных направлений развития вариационного
исчисления во второй половине XX века является
рассмотрение неклассических задач вариационного
исчисления. Это направление получило название
оптимального управления. В основе решения задач
оптимального управления лежит общий
математический прием, который носит название «принцип
максимума Л. С. Понтрягина». Следует заметить,
что все основные необходимые условия
классического вариационного исчисления с обыкновенными
производными следуют из принципа максимума
Понтрягина.
3.2.1. ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ
3.2.1.1. Постановка задачи, примеры и основные
понятия.
Пример 1. Существенный импульс развитию
вариационною исчисления дала следующая, поставленная в 1696 г.
Иоганном Бернулли проблема, которая обычно называется
задачей о брахистохроне.
Между точками Ро и Р,, расположенными на различной
высоте, нужно провести соединяющую их кривую таким
образом, чтобы время падения тела, движущегося без трения
вдоль кривой из />о в Р, под действием силы тяжести,
было минимальным.
Для решения этой задачи построим декартову систему
координат с началом координат в точке Ро и с
вертикальной осью у, идущей в направлении лежащей ниже точки Р,.
Для случая, когда тело находится в момент начала падения
в состоянии покоя в точке Ро, из закона сохранения
энергии следует, что
тду = mv2/2,
откуда для скорости v имеем -р = v « \/2cjy, и тем самым
время падения t (с учетом, что ds = ]/\ + y'2dx) выражается
интегралом
Требуется найти функцию у(х), график которой соединяет
обе точки Ро@, 0) и Р, (хь yt), т. е. у@) =0 и y{xl) = yu и
которая минимизирует указанный интеграл.
Пример 2. Найти кратчайшую кривую между двумя
точками Р0(х0, у0) и Р, (х,, уг) в плоскости х, у, т. е. найти
функцию у{х), при которой
Р,
ds= J j/l+/2</x
принимает наименьшее значение; при этом функция у(х)
должна удовлетворять условиям ,у(хо) = .Уо' y{xi) = yx.
В обоих примерах отыскиваются функции у(х\
которые минимизируют функционал вида
'(У) «*!/(*, У, y')dx;
х0
при этом задаются граничные условия
Это — так называемая простейшая задача
вариационного исчисления.
Из всех классов функций, на которых ищется
экстремум, здесь будут рассматриваться только
класс непрерывных и класс непрерывно
дифференцируемых функций на отрезке [а, 6], которые мы
будем обозначать Со и С2 соответственно. Следует
отметить, что весьма существенно, в каком классе
ищется экстремум, так как он может существовать
в одном классе и не существовать в другом.
288
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Аналогом расстояния между двумя функциями
в каждом из рассматриваемых классов является
норма разности этих функций; понятие
нормы в этих классах определяется следующим
образом:
в Со 1М1с0= тах \У(*)\>
а^х^Ь
в С! IIУ lie = max \y(x)\+ max |/(х)|.
а<х< b a^x^b
В качестве е-окрестности Ut(y1) функции у1
понимают множество
U*(У1) = {у |yeCh \\y-y1 ||С| < е}, i = 0, 1.
Если для функции у0 из области определения
D(J) существует окрестность Ut(y°) такая, что
J(y°)>J(y)
VyeUt(y°)f)D(J\
то J {у0) называется (локальным) минимумом или
максимумом. Элементы из Ut(y°)f)D{J)
называются также функциями сравнения.
Понятие экстремума функционала нуждается
в уточнении. Говоря о максимуме или минимуме
(точнее, об относительном максимуме или
минимуме), мы имели в виду наибольшее или
наименьшее значение функционала только по отношению
к значениям функционала на близких кривых.
Однако близость кривых может быть понимаема
различно, как это видно из определения нормы.
Поэтому в определении максимума или минимума
надо указывать, какая близость имеется в виду
(в смысле класса Со или класса С\). Если
функционал J [у (х)] достигает на кривой у = у0 максимума
или минимума по отношению ко всем кривым, для
которых модуль разности у (х) — у0 (х) мал, т. е.
по отношению к кривым, близким к у = у0 (х)
в смысле нормы пространства Со, то максимум
или минимум называется сильным. Если же
функционал J \_у (х)] достигает на кривой у = у0 (х)
максимума или минимума лишь по отношению
к кривым у = у (х), близким к у = у0 (х) в смысле
нормы класса Сь т. е. по отношению к кривым,
близким к у = у0 (х) не только по ординатам, но
и по направлениям касательных, то максимум
или минимум называется слабым.
Аналогично тому, как это делают в случае
функций, число J (y°) называют наименьшим
(абсолютным минимумом) или наибольшим
(абсолютный максимум) значением, если
J(y°)<J(y) или J(y°)>J(y) VyeD(J).
Из определения нормы в пространствах Со и Сг
видно, что сильный экстремум является
одновременно и слабым, но не наоборот.
Основным элементом исследования в
вариационном исчислении являются понятия первой
и второй вариации функционала.
Положим F(e) = J (y° + eh) и рассмотрим
первую и вторую производные функции F(e) по
параметру е при е = 0.
Величины F @) и F" @) называют первой и второй
вариацией функционала J (у) и обозначают
соответственно 6J(y°, h) и 62J(/, h).
Условия bJ (y°, h) = 0 и 52J (y°, )
52J (y°, h) ^ 0 могут быть использованы при
формулировке необходимых условий экстремума
функционала J(y).
3.2.1.2. Теория Эйлера - Лагранжа. Задачей Ла-
гранжа в вариационном исчислении называют
описанную в 3.2.1.1 задачу нахождения экстремума
для функционала
ЛУ)= !/(*, У, y')dx.
C.5)
При этом требуется, чтобы искомые функции
у (х) i удовлетворяли граничным условиям
Если нет специальной оговорки, то
считаем, что у(х) имеет непрерывную
производную у'(х).
Необходимые условия экстремума.
Дифференциальное уравнение
Эйлера—Лагранжа. Если функция у0 (х) доставляет
функционалу J(y) слабый (локальный) экстремум,
то она должна являться решением
дифференциального уравнения Эйлера — Лагранжа:
Г, - ~Гу = о, (з.б)
или в другой форме:
/;-/;¦>-/;¦,/-/';,¦/' = о
(/ предполагается дважды непрерывно
дифференцируемой). Так как сильный (локальный)
экстремум есть одновременно и слабый (локальный)
экстремум, то дифференциальное уравнение
Эйлера - Лагранжа представляет собой также и
необходимое условие для сильного (локального)
экстремума.
Уравнение Эйлера - Лагранжа есть
дифференциальное уравнение 2-го порядка. Решения этого
уравнения называют экстремалями. Появляющиеся
здесь две постоянные интегрирования
определяются при помощи граничных условий
так что должна быть решена задача с граничными
условиями.
Пусть у0 (х) есть решение задачи C.5), т. е.
пусть существует экстремум. Для кривых
сравнения вида
yt(x)=y°(x) + Bh(x),
(е — малый параметр) имеем
J(yE)=-F(e) =
= J Дх, у0 (х) + eh (х), у01 (х) + eh' (x)) dx.
Таким образом, функционал F (е) есть функция
только параметра е. В силу предположения о том,
что у0 (х) есть решение, должно выполняться
соотношение
5J = F@) = 0. C.7)
ТЕОРИЯ ЭЙЛЕРА-ЛАГРАНЖА
289
Вычислим F(e):
F(?)= \^dx= \{f'yHx)+f'yh'(x))dx =
*1
- ?(/;)н
Из F @) = 0 в силу основной леммы
вариационного исчисления*) вытекает уравнение
Эйлера — Лагранжа.
Из краткого описания доказательства видно,
что предположение о существовании решения у°
данной вариационной задачи существенно. В то
время как в теории задач на экстремум для
непрерывных функций (заданных на замкнутом
множестве) теорема Вейерштрасса обеспечивает
существование решения задачи, в вариационном
исчислении существует трудность, заключающаяся
в том, что задачи, которые формулируются
корректно, в некоторых случаях не имеют решения.
Это означает, что существование решения данной
задачи в вариационном исчислении нуждается в
особых доказательствах.
До сих пор требовалось, чтобы функции у(х)
были обязательно непрерывно дифференцируемы.
Это требование можно ослабить. Так, например,
вариационная задача с подынтегральной функцией
f(x, у, у') имеет смысл уже тогда, когда требуется
только кусочная непрерывность первой
производной у{х). Остается теперь ответить на вопрос,
обладает ли эта функция сама по себе
производными более высокого порядка и удовлетворяет
ли уравнению Эйлера — Лагранжа.
Лемма Дюбуа — Реймона.
Пусть/дважды непрерывно дифференцируема по своим
аргументам. Если функция у непрерывно
дифференцируема и в точке у первая вариация функционала
J равна нулю, то для каждой точки х,
удовлетворяющей условию Лежандра f'y у (х, у, у') Ф 0,
существует окрестность, в которой функция у дважды
непрерывно дифференцируема и удовлетворяет
уравнению Эйлера — Лагранжа.
Пример 3. Найти экстремум функционала J (у) =
= J (У2 + У2 + 2Уе*)dx ПРИ У (°) ¦ °» У @ - е- Уравнение
о
Эйлера — Лагранжа имеет вид
0 или у" - у = е*.
~-
хе*
хе
Гаким образом, у(х) ш С\е~х + С2е* + -у. Используя
граничные условия, получаем
Х
2*
i
*) Если д(х) непрерывна и J h(x)g(x)dx - 0 для любой
х0
такой непрерывной функции, имеющей непрерывную
производную, что h(x0) = h(xl) = 0, то д(х) = 0 на [х0, xj.
10 И Н. Бронштейн, К. А. Семендяев
Специальные случаи задачи C.5).
а) Если / = /(х, у'), т.е. f'y = 0, то уравнение
Эйлера — Лагранжа имеет вид —- (f'y) = 0, так что
f'y = const есть первый интеграл этого уравнения.
Пример 4. Найти экстремум функционала
J {у) — $ (х2 + y'2)dx, у(— 1) » — 1, у{\) «a 1.
Из условия f'y- — const получаем, что у' ¦» Сь и,
следовательно, у(х) = Ctx + C2. Применяя граничные условия,
получим у (х) = х.
б) Если fsf{yty\ то /; = 0 и dfjdx =
Из уравнения Эйлера — Лагранжа следует, что
d
и, таким образом, -r-(f - у'f'y) = 0.
Следовательно, /— у f'y = const есть первый интеграл.
Пример 5. Задача о брахистохроне. Найти
экстремум функционала (см. пример 1)
J(y)'
Из того, что /— у'f'y- — const = Сi, следует соотношение
-у'— у °Ct. и тем самым y(l+/2jm
|/jr j/(l + /2).у
Используя замену / (х) = ctg (у (x)/2), получим, что у «¦
= 2К, sin2 (у/2) = К, A - cos у), / = 2/C,y'cos(y/2)sin(y/2) «
= ctg (у/2), т. е. dx/Kx - dv-2 sin2 (у/2), откуда вытекают
параметрические уравнения экстремалей:
х — К, (у - sin у) + К2, у = Кх A - cos у).
Полученные уравнения являются параметрическими
уравнениями циклоиды. Константы определяются из граничных
условий.
в) Если/=/(х, у) + а{х)у', то уравнение
Эйлера - Лагранжа упрощается и принимает вид
f'y = а! (х) (тривиальный случай).
г) Если /=/(У), то f'y = const, и тем самым
/ (х) = const = Сь т. е. экстремали являются
прямыми вида у(х) = Сгх + С2.
Следует учитывать, что экстремали не всегда
реализуют (локальный) минимум или максимум
функционала, так как уравнение Эйлера —
Лагранжа представляет собой только необходимое условие
экстремума.
Приводимые далее необходимые условия
экстремальности позволяют в определенных случаях
исключить те экстремали, которые не дают
экстремума функционалу.
Условие Лежандра. Используя вторую
вариацию 52J = F" @), получают необходимое
условие экстремума Лежандра: чтобы функция у(х)
доставляла слабый (локальный) минимум
(максимум) функционалу J (у), необходимо, чтобы для
хе[х0, Xi] имело место неравенство
fW (*> у (*)> у' (*)) > ° (fW (*. у (*)> у' (*)) < °)-
C.8)
290
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Пример 6. Найти минимум функционала
J(y)~ [(у12-13]/\+у'2)dx, .НО) «О, у(\)ш\.
о
Так как подынтегральная функция зависит только от у', то
экстремалями являются прямые. С учетом граничных условий
получаем j>(x)=»x. Условие Лежандра имеет вид /Jy =
» 2 - 13A + у2)'312 ^ 0. Для экстремали у(х) » х это
неравенство не выполняется, так что слабого локального
минимума не существует.
Условие Якоби. Пусть для функции у(х),
хе[х0, хх), выполнено строгое условие Лежандра,
т. е. f'y.y. (x, у, у') > 0. Если при этом функционал
J (у) имеет при у(х) слабый минимум, то для
точки xs, сопряженной с х0, должно выполняться
неравенство xs ^ хх. Сопряженная точка xs
определяется следующим образом. Пусть и (х) есть
решение дифференциального уравнения Якоби
±{Гу.у.и')-и(/;у--?-г;^ = о, „<*о) = о. C.9)
За xs принимают наименьший из корней функции
и (х), лежащих справа от х0. Если же и (х) справа
от х0 не обращается в нуль, то полагаем xs = cp
Пример 7. Найти минимум функционала
*i
J (У) - [(У2 + 2у/ - 16у2) dx, у @) - у0, Ух (*i) - Ух.
о
Уравнение Эйлера - Лагранжа у" + \Ьу — 0 имеет решение
у (х) = С, sin 4x + С2 cos Ax. Условие Лежандра выполнено
в строгой форме:
ft Ах* У(х), /(х))«2>0.
Уравнение Якоби C.9) имеет вид
и" + 16м « 0, м @) « 0,
так что его решение есть и (х)« Сх sin 4x. Поэтому для
сопряженной точки получаем значение х, » я/4, т. е. условие
Якоби выполнено в случае, если хх < тс/4.
Наряду с необходимыми условиями для слабого
локального экстремума существуют также
необходимые условия для сильного локального
экстремума. Как отмечалось, необходимые условия для
слабого экстремума представляют собой также
и необходимые условия для сильного экстремума,
но не наоборот.
Условие Вейерштрасса. Для
существования сильного минимума функционала J (у)
необходимо, чтобы для Е-функции Вейерштрасса
Е(х,у,у',1) =
= /(*, У, 0 -fix, У, У) - (/ - у') Г? (х, у, у') C.10)
во всех точках экстремалей у(х) для любого
числа / выполнялось неравенство
Е(х, у, у', /)^0. C.11)
Пример 8. Найти минимум функционала
J(y)-\y3dx, y@)»0, уA)-1.
Решение уравнения Эйлера - Лагранжа дает экстремаль
у(х)**х.
Условие Лежандра выполнено:
Г'уу - 6/ - 6 > 0.
Решение дифференциального уравнения Якоби
6м" = 0, м@)»0,
имеет вид и(х) «сх, так что для сопряженной точки имеем
х, — оо, т. е. это необходимое условие выполняется и на
экстремалях.
Для ?-функции Вейерштрасса получаем
Е(х, у, у, 0 = /3 - 1 - 3(/ - 1) « /(/2 - 3) + 2.
Очевидно, что эта функция не для всех значений /
неотрицательна, так что функционал может обладать при >'(х) = х
самое большее слабым локальным минимумом.
Угловые условия Вейерштрасса-
Эрдмана. Может оказаться, что
рассматриваемый функционал J (у) в классе непрерывно
дифференцируемых функций не обладает экстремумом.
Пример 9. Найти минимум функционала
Так как подынтегральная функция от х не зависит, то (см.
специальный случай б) задачи C.5))
у2 A - у'J + 2Уу2 A - у') - const - С,
есть первый интеграл уравнения Эйлера - Лагранжа. Отсюда
следует, что
у2 « 1 \- ил*
Поэтому экстремали имеют вид
Ja-(* + Ca)a-C..
Использование граничных условий приводит к кривой
(х - 3/4J - у2 - 9/16.
Конечные точки лежат, однако, на различных ветвях этой
гиперболы, так что непрерывно дифференцируемой
экстремали, которая связывает обе точки, нет. Так как
подынтегральная функция неотрицательна, то значение функционала
не может быть меньше нуля. Очевидно, что его нулевая
граница достигается для функции
0 для 0<х< 1,
которая хотя и непрерывна на отрезке [0, 2], но в точке
х * 1 не имеет производной.
Рассмотрим класс кусочно непрерывно
дифференцируемых функций. Точку (х, .у(х)) кусочно
непрерывно дифференцируемой функции у (х)
называют точкой перелома, если в точке х
производная слева Pi = У- (х) и производная справа р2 =
= у'+ (х) функции у существуют и не равны друг
ДРУ1У-
Информацию о том, существуют ли экстремали
с точками перелома, дают следующие условия
Вейерштрасса — Эрдмана.
Если (х, у) является точкой перелома
экстремали, то оба уравнения
Гу(х, У, Pi) =/;•(*» -У' Р2), C-12)
и-у'Гу)у = Р1=и-?Г,>)у = Р2 C.13)
должны иметь общее решение, для которого рх фрг.
Пример 10. Для задачи из примера 9 условия
Вейерштрасса - Эрдмана C.12), C.13) для точки перелома дают
-2у2A-Рг)«-2у2A-Р2),
У2 A " PiJ + 2y2Pl (I - Pl) ш у2 A - р2J + Ifpt A - Р2\
т. е. точки перелома могут появиться только при у » 0.
ТЕОРИЯ ЭЙЛЕРА-ЛАГРАНЖА
291
Естественные граничные условия;
условия трансверсальности. Наряду со
случаем задания граничных условий у(х0) и у{хг)
могут встречаться также случаи, когда: 1)
существует только одно (например, у(х0)) граничное
условие или граничных условий вообще нет;
2) граничное условие задается тем, что в точке х±
(неизвестной) верно равенство у {хх) = <р (хД т. е.
точка (хь у{хх)) должна лежать на заданной кривой
У = ф (*)•
Равенство нулю первой вариации функционала
J (у) дает, наряду с уравнением Эйлера — Лагранжа,
следующие условия для недостающих граничных
значений:
а) Если заранее известно только значение
функции у(х0) в граничной точке х0, то граничное
условие в точке xt определяется из уравнения
Гу(хиУ(х1),у'(хл)) =
C.14)
Аналогичное соотношение получается, если в
точке х0 не задано наперед значение функции.
Соотношение C.14) называется естественным
граничным условием.
б) Пусть в точке х0 граничное условие задано
в виде у(хо) = Уо, а в точке xt (переменной)
требуется, чтобы ^(xj) = (р(хД где у = (р(х) —
заданная кривая. В этом случае получается условие
трансверсальности
- У (*1)
М, У'(*i)) = 0, C.15)
с помощью которого определяется значение
функции y(xt).
Соотношение, аналогичное C.15), получается,
если на заданной кривой должна лежать точка
(*<ъ У(х0))-
Пример 11. Найти экстремум функционала
.НО)-1/2.
Уравнение Эйлера - Лагранжа принимает вид / - 1, так что
экстремалями являются функции у(х) - х2/2 + СХХ + С2.
Из у@) - 1/2 следует. Са - 1/2. Константа Ct получается
из C.14):
- 1 + С, + 0,5 + С, + 0,5 + 1 « 2Ci + 3 - 0,
т. е. Сх ш -3/2. Таким образом, экстремаль имеет вид
у(х)-(х'-Зх+1)/2.
Пример 12. Требуется определить кратчайшее
расстояние между точкой (х0, у0) и кривой y-f(x). Эта задача
сводится к задаче отыскания минимума функционала
Принцип Гамильтона. Вариационное
исчисление играет основополагающую роль в
составлении уравнений механики и теоретической физики.
Большинство этих уравнений может быть получено
на основе вариационного принципа при помощи
понятия энергии. Так, например, принцип
Гамильтона в механике системы точек состоит в
следующем.
Для системы такого рода переход из одного
состояния в другое за заданный отрезок времени
[f0, гх] происходит так, чтобы первая вариация
функционала
j = j(T- U)dt= jL<fr
'о 'о
равнялась нулю: движение системы осуществляется
функциями, которые среди всех допустимых
движений делают упомянутый выше интеграл
постоянным, т. е. уравнение движения системы совпадает
с уравнением Эйлера — Лагранжа для
функционала J. При этом Г означает кинетическую и U —
потенциальную энергию системы, a L— Т— U —
функция Лагранжа. Интерес здесь фокусируется
в первую очередь на обращении первой вариации
функционала J в нуль, а не на вопросе об
экстремуме. Задачи такого рода также называют
вариационными задачами.
Пример 13. Пусть материальная точка движется под
влиянием силы тяжести (свободное падение). При этом для
кинетической и потенциальной энергии имеют место
формулы
Г-тУ2/2 и[/»-тду
(т - масса, у (г) - высота точки ко времени г). Интеграл для
функции Лагранжа имеет следующий вид:
h U
'(У) - J (Г- U)dt - т J (У2/2 + gy)dt.
Согласно принципу Гамильтона уравнение движения
системы есть уравнение Эйлера - Лагранжа для функционала
ЛУ):
тд - mdy/dt - 0, т. е. у" - у;
таким образом,
y(t)-Ci + C2t + gt2/2.
Это - известное уравнение движения для свободного падения.
Известный из механики принцип Гамильтона
можно переносить и на другие физические
процессы, так что вариационные принципы
представляют собой общий метод составления уравнений
в математической физике.
Другие задачи. Наряду с задачами для
функционалов вида
J(y)=
x, У, y')dx
причем Xj неизвестно. Экстремали этого функционала -
прямые вида
у(х)ша{х-хо) + уо,
так как подынтегральная функция зависит только от у'.
Точка xt определяется из условия трансверсальности
l/l + У2 Ы + (Г Ы - / (хО) у' (x,)/|/l + у'2 (х,) - 0,
которое приводит к известному соотношению
ортогональности
10*
существуют также и другие постановки задач.
В дальнейшем в качестве условий экстремума
указываются только уравнения Эйлера — Лагранжа,
хотя существуют и другие необходимые условия,
аналогичные приведенным выше.
Задачи с высшими производными.
Для задачи нахождения экстремума функционала
*i
J(y)= !f(x, у, У, /', ..., /n))dx
292
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
с граничными условиями
У(хо) = Уо, УЫ = Уо,
!)(*о) = 3*"Ч
уравнение Эйлера — Лагранжа имеет вид
Л-?/>+?/> + •••+(-Г ?/>-<*
Пример 14. Найти экстремум функционала J Cv) *
Уравнение Эйлера - Лагранжа принимает вид
f> ~ ~k
*" -2у~4/+2у4>
/*) _ 2/ + у = 0;
оно имеет решение в виде
у(х) - ех(С1 + С2х) + c"x(C3 + С4х).
Использование граничных условий приводит к получению
искомой экстремали.
Задачи для нескольких функций. Для
задачи нахождения экстремума функционала
*i
1{Уи .-., Уп)= J7(*, Уи •-., У*, У\, ..-, y'n)dx
х0
с граничными условиями yt (х0) = yi0, y{ (xj =
= Уц {i = 1, ..., и) уравнения Эйлера — Лагранжа
имеют вид
fy,-?fy, = ° С-1 »)•
Задачи в параметрическом пред*
ставлении. Требование, чтобы искомая кривая
была задана явно: у = у(х), может существенно
сузить задачу. Общее рассмотрение достигается
при параметрическом задании кривой:
x = x{t), y = y{t).
Функционал
J= Sfix, У, y')dx
принимает при этом следующий вид:
J= \f(*(t\ y{t\ y(t)/x(t))x(t)dt,
to
где х и у — производные х и у по t;
подынтегральная функция не содержит явно независимое
переменное t и является однородной функцией
первой степени относительно х и у.
В общем случае рассматривают функционал
вида
*> У, х, У) dt,
to
причем подынтегральная функция является
положительно однородной функцией первой степени
относительно к и у, т. е.
f(x, у, ах, ау) = а/(х, у, х, у) для а > 0.
При этом предположении значение функционала
зависит только от вида кривой
и не зависит от специально выбранного
параметрического представления. Уравнения Эйлера —
Лагранжа имеют вид
Однако они не являются независимыми друг от
друга, так как на основании теоремы Эйлера
(для однородных функций) выполняется
соотношение
так что достаточно решить только одно из этих
уравнений.
Следует заметить, что получаемые решения
могут допускать представление в явной или
неявной форме, а не только в параметрической
форме.
Пример 15. Найти экстремум функционала
j-fliiirfr, x@)-.y@)«0, хA)шУA)ш\.
о х
Уравнения Эйлера - Лагранжа имеют вид
dt
Так как для отыскания экстремали достаточно решить только
одно уравнение, то используем более простое первое
уравнение:
^— )=»0, т.е. '-X-JL. ш у зу* „ (уу^ т const,
X2 ) X3
и, таким образом, y2f2 - CjX + C2. Используя граничные
условия, получаем у2 « х.
Задачи с дополнительными
условиями в виде уравнений. При нахождении
экстремума функционала
J= lf{x9 Уи -.., ут У\, ..-, y'n)dx
х0
с граничными условиями
и дополнительными условиями
а) gj(x, ylt ..., уп)=0 (/=1, ..., m; m < п),
или
Х1
б) J gfj(x, У1, -., У„, у'и —» ^)^х = 0
х0
(/ = 1, ..., w; m < п)
(изопериметрическая задача), или
в) gj(x, yl9 ..., ую у\, ..., у;) = 0
(/ = 1, ..., m; m < п),
уравнения Эйлера — Лагранжа принимают вид
причем так называемая функция Лагранжа L для
дополнительных условий а), б), в) имеет следующий
вид:
а) Цх, у, у', X)=f(x, у, ?)+ ? Xj(x)gj(x, у)
= x(t),
= y{t)
ТЕОРИЯ ЭЙЛЕРА-ЛАГРАНЖА
293
б) Цх, у, У, X) =/(х, у, у') + X Ijgjix, у, у');
7=1
в) Цх, у, у', X) = /(х, у, У)
При этом экстремали у,(х) и постоянные Х,;-
или функции А,,(х) (множители Лагранжа)
должны быть определены так, чтобы выполнялись
дополнительные условия и уравнения Эйлера
(ср. 3.1.6.6).
Формулы для функции Лагранжа показывают,
что здесь речь идет об обобщении известного
метода множителей Лагранжа при поиске
условного экстремума.
Достаточные условия экстремума.
В то время как для действительных функций
одного переменного условие /" (х0) > 0 (/" (х0) < 0)
является достаточным для того, чтобы в точке х0
функция /(х) имела минимум (максимум),
аналогичных условий для второй вариации 52J (т. е.
62J > 0 или b2J < 0) не хватает, чтобы получить
достаточные условия экстремума для
вариационной задачи. Для этого привлекают дополнительные
соображения, основанные на рассмотрении полей
экстремалей. В дальнейшем будет рассматриваться
достаточное условие для слабого и сильного
экстремумов только для задачи Лагранжа нахождения
экстремума функционала
3) знак функции ?(х, у, р, у') не изменяется во
всех точках (х, у), которые лежат достаточно
близко от экстремали у(х), и для всех значений у,
лежащих вблизи р(х, у(х)). Функция у доставляет
функционалу минимум при Е ^ 0 и максимум
при Е ^ 0.
б) Функция у(х) доставляет функционалу J (у)
сильный (локальный) экстремум, если
1) выполнены пп. 1) и 2) условий а);
2) функция ?(х, у, р, У) не изменяет свой знак
для всех точек (х, у), лежащих в достаточной
близости от у(х), и для любых значений у' (Е ^ 0 —
минимум, Е < 0 — максимум).
Пример 16. Найти экстремум функционала
¦I'1
dx,
Для этой задачи, решенной в примере 8, экстремаль у = х
удовлетворяет условиям Лагранжа и Якоби и может быть
включена в поле экстремалей у = Сх; ?-функция имеет вид
Е (х, у, р, у') - У3 - р3 - Зр2 (У - р) ш (у' - рJ (у + 2р).
Из выражения для ^-функции видно, что первый
сомножитель всегда неотрицателен, а второй положителен для
значений У, которые расположены около 1, т. е. у — х реализует
слабый (локальный) минимум функционала. Условие сильного
экстремума не выполнено, так как при у' < - 2 ^-функция
отрицательна.
Пример 17. Найти экстремум функционала
J(у) =
*, У,
у(х0) = у0, у(хх) = yv
Будем говорить, что экстремаль у = у(х) можно
расположить в поле экстремалей, если существует
семейство экстремалей у = у (х, С) (С - параметр)
такое, что
— оно покрывает определенную область G
плоскости х, у так, что через каждую точку G
проходит ровно одна экстремаль семейства;
- для данного С = Со получаем исходную
экстремаль у = у (х), причем экстремаль у = у (х)
лежит не на границе области G.
Поле экстремалей называется центральным,
если все кривые поля исходят из точки (х0, yo)eG
(центр семейства экстремалей). Наклон проходящих
через точку (х, у) экстремалей поля называется
градиентом поля в точке (х, у) и обозначается
Р(х, У); Р(х, У) как функция от (х, у) называется
градиентной функцией.
Достаточным условием для включения
экстремали в поле экстремалей (с центром (х0, у0))
является условие Якоби xs > хх.
При применении ?-функции Вейерштрасса,
определяемой соотношением
у, р, У) =
=/(*, У* У) -
У> Р)-(У' ~ P)fy'(*> У* Р)
(где р = р (х, у) — градиентная функция),
получаются следующие достаточные условия экстремума:
а) Функция у{х) доставляет функционалу J(y)
слабый (локальный) экстремум, если
1) у(х) является экстремалью, т. е.
удовлетворяет уравнению Эйлера - Лагранжа и граничным
условиям у(х0) = у0, у(хг) = ух\
2) у(х) может быть включена в поле
экстремалей;
Экстремали этой задачи имеют вид
у = х2 + Схх + С2.
Применение граничных условий дает у — х2 — х.
Условия Лежандра и Якоби выполнены. Экстремаль у = х2 - х
может быть включена в поле у = .х2 + Сх
Из соотношения Е (х, у, р, У) =¦ (У - рJ/2 видно, что
Е ^ 0 для всех у', так что экстремаль у = х2 — х реализует
сильный (локальный) минимум.
Задачи для функций многих
переменных.
Пример 18. Найти экстремум функционала
J(u) = Jf/(x, У. ", «4 u'Jdx dy, C.16)
G
м(х, у) = мо(х, у) для (х, y)eDG. C.17)
Здесь отыскивается функция и(х, у), которая определена
в области G плоскости х, у и принимает заданные значения
ио(х» У) на границе DG области С Кроме того, требуется,
чтобы w(x, у) имела непрерывные частные производные
и'х(х, у) и и'у{х, у).
Большинство из указанных выше условий экстремума
для функций одного переменного непосредственно
обобщается и на этот случай.
Так, например, в качестве необходимого условия слабого
(локального) экстремума функционала C.16) получаю г
следующее уравнение Эйлера — Лагранжа: если и дважды
непрерывно дифференцируема, то
л-?*-?*-»
C.18)
Это есть дифференциальное уравнение в частных
производных 2-го порядка. Так как значения функции и на границе
dG заданы, то краевая задача может быть решена.
Требование, чтобы функция и имела непрерывные
производные и'х и и'у, позволяет ослабить следующая
294
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Теорема Хаара. Равенство нулю первой
вариации J (у) из C.16) при непрерывной функции и
и кусочно непрерывных производных и'х и и'у
эквивалентно равенству
где S — любая односвязная часть множества G
(ограниченная кусочно гладкими кривыми), a L
представляет собой ее границу (при обходе в
положительном направлении).
Интегральное соотношение в теореме Хаара
играет ту же роль, которую ранее играло
уравнение Эйлера — Лагранжа.
Пример 19. Для функционала J (и) = JJ (и'х2 + и'}) dx dy
G
уравнение Эйлера - Лагранжа имеет вид
и'хх + и"уу = 0 {уравнение Лапласа).
Задачи Майера и Больца. Наряду с
задачей Лагранжа на практике встречаются также
задачи на нахождение экстремума функционала
J(y)
C.19)
J (У) = Fi (Уо (*i)) + J F2 (x, y0, .., У„ Уо, • •., y'n)dx
C.20)
с условиями
/,•(*, Уо, ..-, У» Уо, ..-, Уп) = 0
(i = 0, 1, ..., т; т < и),
yj(xo) = yjo (j = 0, I, ..., п), C.21)
yj(xi)=yji (/' = 0, 1, ... и).
Задачи такого вида называются задачей Майера
(C.19), C.21)) или задачей Больца (C.20), C.21)). Так
как задача Майера есть частный случай задачи
Больца (F2 = 0), то рассматривается только
последняя. Функционал F, 0>00ч)) из C.20) может быть
приведен посредством замены
у'п+! (х) = F\yo (у0 (х)) у'о (х), уп+1 (х0) = F, {у00),
к виду х
j F\yo (у0 (х)) у'о (х) dx + Fx {уооУ
Xq
Так как Fx {yOo) есть известная постоянная, которая
не оказывает влияния на поиск экстремума, то
задача Больца эквивалентна следующей задаче
Лагранжа нахождения экстремума функционала:
J(y) =
Xi
= И^оЫ/о + М*, Уо, .... Ую У'о, .... y'n))dx,
MX, У0, -.., Уп, УО, ¦•; Уп)=0
(/ =0, 1, ..., т; т < п),
У/(*о) =У]о (/ = 0, 1, ..., и),
УЛ^1) = >'Л 0 = 0, 1, .... п).
3.2.1.3. Теория Гамильтона — Якоби. Между
уравнениями Эйлера - Лагранжа и уравнениями
в частных производных 1-го порядка существует
важная связь, которая была открыта Гамильтоном
и развита Якоби.
В дальнейшем будем рассматривать только
функционалы вида
xi
J(y)= J fix, у, у') dx, у (х0) = Уо, У (xi) = Ух-
Предположим, что существует экстремальное
значение функционала. Пусть, например, J есть
минимальное значение функционала J (у), т. е.
J = J(y)= //(x, .v°, y°')dx.
х0
Пусть искомая функция у0 (х) соединяет точки
Ро(хо, Уо) и Pi(xb yi), т. е.
Величину J называют характеристической
функцией Гамильтона. Если считать, что функция у0 (х)
уже определена, то значение J будет зависеть только
от пределов интегрирования, т. е.
J = J(x0, >'о; хь yj.
Предположим, что точка Ро зафиксирована, а точка
Рх может перемещаться, т. е. Рх — Рх (х, у). Тогда
J = J (х, у),
т. е. J есть функция только координат. Можно
показать, что функция J (х, у) удовлетворяет
следующим формулам Гамильтона:
J'x=f(x, У, Р(х, у)) -р(х9 y)f'y(x, у, р(х, у)% C.22)
J',=fs(x, у, р(х, у)), C.23)
где р (х, у) = у0' - градиент.
Формулы C.22), C.23) играют в вариационном
исчислении фундаментальную роль. При помощи
этих формул можно вывести ряд условий
экстремума; в частности, уравнение Эйлера — Лагранжа
получается, если предположить, что J является
дважды непрерывно дифференцируемой функцией
по х и у. Исключая р (х, у) из формул Гамильтона,
получают уравнение Гамильтона — Якоби:
J'x + H (х, у, J'y) = 0, C.24)
где
Я(Х, у, J'y) = (pf'y (X, у, р) -/(X, у, р))р = V'(X, yt fy)
(Н — функция Гамильтона, или гамильтониан); р =
= у' (х, у, J'y) находим из уравнения C.23) (в
предположении, что f'y'y'\y' = p ф 0).
Уравнение Гамильтона — Якоби является
уравнением в частных производных 1-го порядка для
определения экстремума J(x, у) функционала J.
Общее решение C.24) может содержать наряду
с постоянными также и функции, которые можно
выбирать произвольно. Пусть
J = J(x, у, а)
есть однопараметрическое свойство решений, в
котором параметр а является существенным, т. е.
выступает не только как аддитивный член. Тогда
основная теорема теории
Гамильтона—Якоби позволяет утверждать следующее:
dJ(x, у, а)
функция, определенная из уравнения = b
да
ЧИСЛЕННЫЕ МЕТОДЫ
295
(b - произвольная постоянная), является общим
решением уравнения Эйлера - Лагранжа для
функционала J(y) в неявной форме.
Во многих случаях поиск решения уравнения
Гамильтона - Якоби оказывается более простым,
чем уравнения Эйлера - Лагранжа.
Пример 20. Найти экстремум функционала
х»
У(хо)~Уо,
Пример 21. Пусть дано уравнение
+ q(x)u=f(x)
Запишем формулы Гамильтона применительно к данному
случаю:
]/(х
+ р2) -р2]/х2 + //j/l + р2
Решение уравнения Гамильтона — Якоби
находим в виде
J (х, у) »(х2 sin a - 2xy cos a - у2 sin a)/2.
Из уравнения dJ/да « b/2 получаем общее решение уравнения
Эйлера — Лагранжа
х2 cos a + 2xy sin a — у2 cos a ¦ Ъ.
3.2.1.4. Обратная задача вариационного
исчисления. Необходимое условие того, что функция у(х)
доставляет экстремум функционалу J (у), приводит
к уравнению Эйлера - Лагранжа. Обратной
задачей вариационного исчисления называют задачу
построения по заданному уравнению в частных или
обыкновенных производных функционала J (у), для
которого это уравнение представляет собой
уравнение Эйлера - Лагранжа. Этот метод играет
важную роль при численном решении
дифференциальных уравнений с граничными условиями.
В общем случае, однако, построить функционал
J {у) по заданному дифференциальному уравнению
довольно сложно.
Частный случай. Рассмотрим уравнение
(в частных или обыкновенных производных) вида
Au=f,
где А — линейный дифференциальный оператор,
а/-известная функция. Пусть, далее, оператор А
симметричен, т. е. (Аи, v) = (и, Av), и положителен,
т. е. (Аи, и) ^ 0 (равно 0 только при и = 0).
Выражение (м, v) означает скалярное произведение
функций и и v. Если уравнение Аи =/ имеет решение,
то оно доставляет минимум функционалу
J(u)=(Au, u)-2(u,f).
Обратно, если существует элемент, который
реализует минимум функционала J (и), то этот элемент
является решением уравнения Аи =/
Выводы этой теоремы могут быть применены
для построения функционала по заданному
уравнению в частных или обыкновенных производных,
причем так, чтобы уравнение Эйлера — Лагранжа
для этого функционала совпадало с заданным
уравнением. Главная трудность состоит в
доказательстве того, что оператор А является
симметричным и положительным.
d ( du\
dx \ dxJ
с граничными условиями м (а) = и (Ь) = 0. При
предположениях, что функции р(х), р'(х), q(x) и /(а) являются
непрерывными и для каждого хе[а, Ь] выполняются неравенства
p(x)>Po>0, q(x)^O, оператор А является симметричным
и положительным:
» ь
(Аи, v) ш - (v(x) j;(p(x) J^jdx + jq(x)u(x)v(x)dx -
(p (x) u' (x) v' (x) + q(x)u (x) v (x)) dx = (u, Av)
(для v (a) = v {b) = 0), т. е. А симметричен. Если подставить
в это выражение v = и, то получим, что
ъ ь
(Аи, и) > р0 j(uf dx > j^-^ ju2 dx > 0,
т. е. оператор А положителен. Таким образом,
вышеупомянутое уравнение Аи =/ является уравнением Эйлера —
Лагранжа для функционала
Пример 22. Пусть дано уравнение Пуассона
Аи = — Дм з — и'хх — и'уу =/(х, у)
с граничными условиями
м(х, у) = 0 для всех (х, y)edG,
где 3G — граница области G, в которой ищется решение.
Тогда
а) (Аи, v) - (Av, и) -
- f (-(uv'y-vuy)dx
dG
если v(x, у) ш 0 при (х, y)edG, и
б) (Аи, и) ш - JJ и (ихх + и';у) dx dy -
G
ш - f (-uu'ydx + uu'xdy) + JJ(ii*
dG G
Из (Аи, и) « 0 следует и'\ + и'2 = 0, т. е. и (х, у) » 0, так
как и (х, у) = const и и (х, у) = 0 на dG.
Таким образом, оператор А является симметричным
и положительным, и для функционала J(u) получается
выражение
J (и) - Jf (и'2 + и'2 - 2/м) dx dy.
G
3.2.1.5. Численные методы. Во многих
практических случаях уравнение Эйлера - Лагранжа
нельзя решить точно и приходится использовать
приближенные методы. Для того чтобы решить
уравнение Эйлера - Лагранжа, можно привлекать
численные методы решения дифференциальных
уравнений (прежде всего метод сеток). Так как при этом
приходится решать краевые задачи, то часто
появляются трудности. Поэтому для численного
решения вариационных задач применяются прямые
методы. В этом случае вместо построения решения
296
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
дифференциальных уравнений пытаются построить
минимизирующую последовательность.
Если функционал J (у) ограничен на своей
области определения D (J) снизу, т. е.
inf J (у) — т > — оо,
yeD(J)
то каждую последовательность {/} из D(J), для
которой имеет место равенство
lim J {/} = m,
п-* оо
называют минимизирующей последовательностью.
Сама последовательность {уп} при этом не
обязательно должна сходиться. Кроме того, не всегда
имеются минимальные элементы у0 е D (J) (т. е.
j (у0) = щ). Зачастую относительно {/} можно
только сказать, что
= 1, 2, ...)
(метод релаксации).
В то время как при помощи уравнений
Эйлера — Лагранжа определяют локальный экстремум,
прямые методы позволяют находить абсолютный
экстремум. Правда, необходимы дополнительные
соображения относительно того, насколько
решения, найденные прямым методом, удовлетворяют
уравнению Эйлера — Лагранжа.
Метод Эйлера рассмотрим на примере
решения задачи нахождения экстремума функционала
решается методами дифференциального исчисления:
J (У) =
У, У') dx, у (а) = у„ у (Ь) = уъ.
Если отрезок [а, Ь] разбить на п равных
отрезков точками
а + i
. Ь-а
(i = 0, ..., п),
то на основе метода прямоугольников функционал
J (у) можно приблизить выражением
п 1
= h Z f(a + ih, y{, (y, + i - yt)/h)
i = 0
(h = (b — a)/n, y{ « y(a + ih)). Тем самым получаем
приближенную задачу на нахождение экстремума
для функции п — 1 переменных уъ ..., yn-i- . .
Пример 23. Найти экстремум функционала
J(y) - К/2 + У2 + 2xy)dx, y@) ш у(\) ш 0.
о
Отрезок [0, 1] разбивается на пять равных частей, и
Уз - У@,6), уА ш у@,8),, у5 ш уA) - О,
У @) * у'о = (у, - 0)/@,2), / @,2)« у\ =(у2- У1)/@Л
У' @,4)) * у'г - О'з - У2)/(О,2), у' @,6) * у'3 - (у, - у3)Ц0Л
у' @,8)« yt = @ - У4)/(О,2).
Приближенная задача на нахождение экстремума
функционала
^5 (У) -Я*. Уъ У» У*) - 0,2 ^ ^^±1Г-™J + У?
В следующей таблице сравниваются величины у,,
полученные на основе данного приближения, с точными
значениями у @,2 0 (округленными до четвертого знака):
/
1
2
3
4
У!
-0,0286
-0,0503
-0,0580
-0,0442
У @,2 0
-0,0287
-0,0505
-0,0583
-0,0444
Метод Ритца. При помощи этого метода,
как и при использовании метода Эйлера,
вариационная задача сводится к задаче отыскания
экстремума функций.
Основная идея заключается в следующем. Пусть
"ь М2» мз> • • • есть полная система функций в области
определения D (J) функционала J (у), т. е. каждая
функция у из D (J) может быть приближена с любой
степенью точности линейной комбинацией
функций щ:
причем число п зависит от требуемой точности.
Если эту линейную комбинацию подставить
в функционал J (у), то он окажется функцией
только параметров а,:
= /(«ь ..., ап).
Необходимым условием того, чтобы эта
функция принимала экстремальное значение
относительно параметров аи а2, ..., ап, является система
соотношений
Из этой системы нелинейных уравнений
определяются параметры а,-. Функции м, называют также
координатными функциями. Они подбираются
обычно таким образом, чтобы функция
уп = Ё ад
удовлетворяла граничным условиям задачи.
Пример 24. Решение задачи из примера 23 методом
Ритца.
Допустим, что используются координатные функции
и, (х) = х2 - х, м2(х) - х3 - х2 ия(х) ш х"+! - х".
Пусть п равно 2, т. е.
у2 (х) = fll (х2 - х) + а2 (х3 - х2), у2 @) = у2 A) - 0.
ЧИСЛЕННЫЕ МЕТОДЫ
297
Тогда
J (Уг (*)) - | ((а, <2х - 1) + а2 (Зх2 - 2х)J +
+ (а, (х2 -х) + а2 (х3 - х2)J + 2х (а, (х2 - х) +
+ a2(x3-x2)))dx=f(au а2).
Из условий f'ai ш 0 и /д = 0 вытекает, что
и, следовательно, ах - 69/473, а2 - 77/473, у2 (х) * G7х3 -
- 8х2 - 69х)/473.
Сравнение с точным решением у{х)» ~т~А^ - е~х)-х
дано в таблице.
/
/
1
2
3
4
л (а го
-0,0285
-0,0506
-0,0585
-0,0442
У @,2/)
-0,0287
-0,0505
-0,0583
-0,0444
Пример 25. Как следует из примера 22, уравнение
Лапласа
»« + v;, - о
есть уравнение Эйлера - Лагранжа для функционала
Пусть область G ограничена прямыми х = 0, у = 0,
х •+• у а» 1 и на ее границе dG задана функция v (х, у) =»х2 + у2.
Возьмем координатные функции вида
М*. У)~х2 + у2, ы, (х, у) ш хуA - х - у),
и2(х, у) = х2у{1 -х-у),...
и положим п ш 3, т. е.
Vi(x, у) ш х2 + у2 + aixy(l - х - у) + а2х2у(\ - х - у) +
+ а3з?уA -х-у).
Функция и0 (х, у) прибавляется для того, чтобы v3 (x, у)
удовлетворяла граничным условиям. Таким образом,
Из соотношений /^ = 0, f'U2 = 0, увз = 0 получим а\ =
« 3,0401, о2 » а3 = -0,0562, и, следовательно,
v3 (х, у) - х2 + у2 + ху A - х - у) C,0401 - 0,0562 (х + х2)).
Метод градиентного спуска. Так же как и для
задачи нелинейной оптимизации, для численного
решения вариационных задач можно применять
метод градиентного спуска.
Пример 26. Пусть требуется минимизировать
функционал
J(y)~
x, у, y')dx,
причем на функции у(х) не накладывается никаких
граничных условий.
Градиент функционала J (у) определяется в
гильбертовом пространстве (см. 2.4.4.1.6) следующим
образом. Если дифференциал Гато
v J(y + th)-J(y)
lim
0 t
(для таких h, что у + th e. D (J) в некоторой
окрестности точки t = 0) существует и равен (J' (у), И),
то У (у) называют градиентом функционала J (у).
Под скалярным произведением (и, v) при этом
понимают интеграл
j и (х) v (x) dx.
х0
В 3.2.1.2 было получено выражение
откуда для градиента получаем
Если у(х) является экстремалью, т. e./J, - —fy. = 0,
то J' (у) = 0. Используем этот градиент для
приближенного решения указанной выше задачи.
Исходя из известного начального приближения
у1 (х), построим последующие приближения по
формуле
Величину шага Р„ можно определить, например,
из условия
J (уп - (V (Л) = min J (yn - рJ' (/))•
!3^о
Заметим, что J (уп — |3J' (уп)) — функция только
параметра р; Для последовательности {у"} имеет
место цепочка неравенств
Пример 27. Рассмотрим решение задачи из примеров
23 и 24 на нахождение минимума функционала
(без задания граничных условий). Вычислим градиент
Пусть начальное приближение есть у1 (х) = 0. Это
означает, что J' (у1) = 2х и J (у1) = 0, откуда для первой
итерации следует:
J (У2) - 41 (Р2 + Р2х2 - Эх2) dx = 4
-p - -Ы *
т. е. р\ - 1/8, у2 (х) = -х/4, Лу2) = -1/12.
Аналогично делают следующие шаги. Процесс
останавливают, когда J' (/) = 0 или, например, когда разница двух
следующих друг за другом значений функционала становится
достаточно малой (например, ./(/) - J(/+1) < e).
Легко найти точное решение этой задачи.
Из уравнения Эйлера - Лагранжа у" - у — х ¦» 0 следует,
что у(х) = Схе* + Сге~х — х\ произвольные постоянные Сх
и С2 можно определить из (естественных) граничных условий
У@) = С,-С2-1»0,
УA) = С1^-С2е-1-1=0,
298
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
3.2.2. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
3.2.2.1. Основные понятия.
Пример 28. Рассмотрим прямолинейное движение
материальной точки. Состояние движущегося объекта можно
охарактеризовать функцией xt (t) и скоростью х2 (t). На
движение можно влиять выбором ускорения u(t). Уравнения
движения при этом имеют вид
х, ш х2, хг ш и.
Существенно, что состояние объекта,
описываемое указанным законом (системой обыкновенных
дифференциальных уравнений), изменяется под
внешним воздействием (управлением). Функции
*! (г), ..., xn(t), описывающие состояние объекта,
называют фазовыми координатами объекта. Вектор
х (t) с координатами х2 (t), ..., х„ (г) называют
фазовым вектором, «-мерное пространство точек х —
фазовым пространством. Состояние объекта
зависит от величин управления и^ (t), ..., ur(t), которые
объединяются в вектор управления u(t); г-мерное
пространство точек и называется пространством
управления.
Если х° = х (Го) есть начальное состояние
объекта, то состояние x(t) должно однозначно
определяться заданием х° и u(t)(t ^ t0).
Соответствующую кривую в пространстве состояний, исходящую
из точки х°, называют траекторией.
Пусть закон изменения состояния описывается
системой обыкновенных дифференциальных
уравнений {динамической системой):
*i =/i (*ь • •., *„, "ь • • •, «г, t),
*п =fn(Xl, ..-, Хп, UU ..., Ur, t),
или, в векторном виде,
х=/(х, и, t), te[t0, t^.
Если функции /,(х, и, t) и dfi/dxj (* = 1, ..., п)
непрерывно дифференцируемы по всем аргументам,
то говорят о непрерывной динамической системе.
Динамическая система
и г
/« = Z aU (О xj + Z bik @ м*>
j=l *=1
т. е.
/ = Ах + Ви,
где А есть п х n-матрица с элементами aiJt а. В —
п х r-матрица с элементами bik, называется
линейной.
Две динамические системы
х =/(х, и, t), z = g(z, и, t)
называются эквивалентными, если существует
невырожденная матрица Р размера п х п с
постоянными элементами такая, что
Z(t) = Px(t).
Тогда z = Px = Pf(p-izi щ t).
В общем случае вектор управления не может
выбираться произвольно, так как в силу реальных
технических условий на него накладываются
определенные ограничения. Пусть U есть подмножество
в пространстве управления, определенное,
например, посредством неравенств \щ\ ^ а,, или ||u|| ^ а,
или h (и) ^ 0, и пусть и (t) принимает значения
только из U; тогда U называется областью
управления (зачастую область U является замкнутой или
даже замкнутой, ограниченной и выпуклой).
Очень часто на u(t) накладываются
дополнительные требования гладкости. Если, например,
управляющие устройства работают безынерционно,
то это значит, что управление должно быть
кусочно непрерывным.
Управление называется допустимым на отрезке
[t0, rj, если
1) u(t) принимает значения только из U;
2) и it) кусочно непрерывна.
Состояние х1 называется достижимым из
состояния х° = х (t0), если существуют допустимое
управление и такое tx ^ t0, что для
соответствующей траектории х (tx) = x1. Множество всех
состояний, достижимых из х°, называют множеством
достижимости, относящимся к начальному
состоянию х° = х (t0) и области управления U. Если
при этом задано и Гь то говорят о множестве
достижимости, относящемся к х°, U и tt.
Если множество U выпукло, то для линейной
системы множество достижимости, относящееся
к фиксированному tu является также выпуклым
(множество достижимости в общем смысле при
этом не обязательно выпуклое).
Всюду в дальнейшем будем считать, что область
управления совпадает со всем пространством
управления. Если состояние х1 = 0 является
достижимым из состояния х° = х (t0), то говорят, что х° —
управляемое состояние в момент времени t0. Если
каждое состояние х° является управляемым в
момент времени t0, то систему для времени t0
называют управляемой; если каждое состояние х°
является управляемым для каждого t0, то систему
называют полностью управляемой (т. е. каждую
точку пространства состояний при любом
начальном моменте времени можно перевести в начало
координат).
Система управляема тогда и только тогда,
когда любая эквивалентная ей система является
управляемой. Однако это утверждение трудно
использовать для практического анализа.
Для линейной системы, у которой элементы
матриц А и В являются постоянными (автономная
линейная система), справедливо следующее
утверждение.
Пусть G есть матрица размера п х пг:
G = (B, AB, А2В, ..., А"-1 В);
линейная автономная система
х = Ах + Ви
является полностью управляемой тогда и только
тогда, когда выполняется равенство
rang G — п.
3.2.2.2. Принцип максимума Понтрягина. При
одинаковых начальных состояниях данной
динамической системы, но при разных допустимых
управлениях получают, вообще говоря, различные
функции состояний и, следовательно, различные
процессы (и (t), х (t)). Поэтому имеет смысл говорить
о таком процессе, который оптимален в некотором
смысле. Тогда говорят об оптимальном процессе:
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
299
соответствующее управление называют
оптимальным управлением, соответствующее состояние —
оптимальным и соответствующую кривую —
оптимальной траекторией.
Основная задача. Пусть задана
динамическая система
х =/(х, м, t)
с начальным условием х (t0) = x° и областью
упраьления U. Ищется такое допустимое
управление и соответствующая траектория, что для
фиксированного конечного момента времени t,
выражение
где с, — заданные постоянные, является
минимальным. (Очевидно, что речь идет о минимизации
линейной комбинации координат конечного
состояния.)
Введем присоединенную вектор-функцию р(г)
с координатами />, (г), ..., pn{t), удовлетворяющими
соотношению
Pi = ~ Z ^—Pj, Pi (ti) = -Ci (i = 1, ..., л).
Вводя обозначения с — (с,, ..., с„) , р ={р,, • • •
.... Рп)Т,
df/dx =
дх, дх.
дх,
дх„ дх„ дх„
получаем векторное представление:
i>=-Jx-p, p(h)=-c
Под функцией Гамильтона понимают
выражение
почти всех fe[r0, ^i] выполняется условие
тахЯ(р(?), x{t), к, t) = H(p(t), x(t), u(t), t).
ueU
Если нужно максимизировать J, то указанное
относительно Н условие максимума заменяется
соответствующим условием минимума или
граничное условие записывается в виде p(t,) = +с.
Существенное преимущество принципа
максимума по сравнению с классическими теоремами
вариационного исчисления состоит в том, что он
применим для любого (в частности, замкнутого)
множества U. Расширение класса возможных
областей управления U по сравнению с
классическим случаем открытых множеств весьма
существенно для приложений теории.
Если нужно минимизировать дважды
дифференцируемую по всем аргументам функцию
J = F[x(ti)l
то в принципе максимума Понтрягина начальные
условия для присоединенной системы следует
заменить на
Если нужно минимизировать функционал
J = J /о [х, м, t) dt,
to
где функция /0 удовлетворяет таким же условиям,
что и fh то функция Гамильтона определяется
формулой
Н = -/о + t pjh
i= 1
а присоединенная система имеет вид
и J о г-ч J j
Pi == " — / Pi э Pi \tI/ == 0 [I == 1, . . ., w).
Пример 29.
Найдем оптимальное управление, при котором функционал
Таким образом, динамическая и присоединенная
системы могут быть представлены в форме
канонических уравнений:
дН t ч
где
дН
градиенты Н по р и х.
дН
—— и —
др дх
Принцип максимума Понтрягина. Для того
чтобы процесс (u(t), x(t)) решал заданную
основную задачу (т. е. являлся оптимальным процессом
в смысле постановки задачи), необходимо
существование присоединенной функции р (г),
являющейся решением присоединенной системы с
соответствующим граничным условием и такой, что для
оказывается минимальным. Имеем
Я* . - (и + и2) + х2рх + ирг ш ХгРх -(\-рг)и- и2,
Pi=0, Pl A) = 0, р2 = -Рь Рг @ = 0,
т. е.
Pi (П - Рг it) » 0.
Следовательно,Я*= -u-м2» *"(м + т) +Т'
мум Я* доставляет и = -1/2.
Условие для конечной точки.
Условие трансверсальности. Условия в задачах
часто задаются в конечной точке x(t,). Так, в
дополнение к основной задаче на оптимальной
траектории часто должны выполняться условия
вида
300
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
причем предполагается, что функции Fk дважды
I I
\ OXi J
дифференцируемы по всем xt и якобиан I
\
имеет максимальный ранг т. Тогда условия Fk = 0
(к = 1, ..., т) определяют в пространстве состояний
некоторое гладкое многообразие.
Требуется найти такое оптимальное управление,
которое переводит точку х° = х (t0) в произвольно
выбранную точку этого многообразия. Если вектор
p{t{) перпендикулярен конечному многообразию,
т. е. если
0 = 1, ..., п)
Имеем 11 = 1, Fx (x) = х, - 1, F2 (х) = х2 - 1,
у
Ро у м
Pi A) = —>
т. е.
pl(t)=-Xl и р2@ = Х,г-Х1~Х2.
Тем самым максимум функции Гамильтона дает
оптимальное управление (очевидно, что р0 < 0 и можно принять
Po=-D
м@ = Хгг - Xj -X2.
Неизвестные параметры Хг и Х2 должны быть
определены так, чтобы система переводилась в конечную точку
при некоторых значениях параметров Ха (р0 < 0 —
постоянная), то говорят о выполнении условий
трансверсальности.
Конечные условия для р (t J в принципе
максимума Понтрягина должны быть заменены на эти
условия трансверсальности.
Если критерий оптимальности задан в
интегральной форме:
t\
f/0(x, и, t)dt,
to
то гамильтониан определяется формулой
H*=Pofo+ Ёй/ь
i=l
а присоединенная система имеет вид
а/о
Pi = -Р
Pi(ti)=-
2j Pj
1 »
дх{
1, • • -, л),
где р0 ^ 0 - постоянная. В том случае, когда
условия для конечной точки не заданы, можно сразу
записать, что р0 = — 1.
Важнейшие соотношения, устанавливаемые в
принципе максимума Понтрягина, приведены в
табл. 3.4.
Если / представляет собой подмножество
{1, 2, ..., и}, а конечные условия таковы, что
xt(ti) = x} для iel
(некоторые конечные координаты заданы), то
условие трансверсальности принимает специальный
вид:
f заданы для iel,
PiVi) =|p0Q для i$l.
Пример 30. Дано
Xj = Х2,
*i @) = х2 @) = 0, х, A) = х2 A) = 1.
х2 = и,
Надо найти оптимальное управление, при котором
минимизируется интеграл
Интегрируя уравнения состояния, получим, что
*i @ = -|U,f3 - 4" (*1 + ^2) t\ х2 (t) = -1 X,t2 - (Xi + Я.2) t.
о z z
Из условий Xj A) = х2 A) = 1 следуют линейные
уравнения для определения параметров >ч и Х2:
- -i- (X,
-1-Х, - (X, + Х2) -
так что оптимальное управление имеет вид
и (г) = - 6/ + 4.
Если на управление и накладываются
ограничения в форме неравенств (например, \и (t) \ < 1), то,
как легко видеть, найти оптимальное управление
становится значительно труднее.
Аналогично получают условие
трансверсальности для начальной точки в случае, если x(t0)
не задана, а только требуется, чтобы х (t0) являлась
точкой гладкого многообразия, описываемого
следующей системой:
Gp[x(fo)]=0 (P = l, .... 0-
Тогда для присоединенной векторной функции
должно выполняться условие
Pi(h)=-
(i = 1, • •., п).
Задачи со свободным конечным
временем. Во многих задачах конечное время tv
не задано, и тогда говорят о задачах со
свободным конечным временем.
В зависимости от задачи (основная задача,
другие виды критериев оптимальности, условия
в конечной точке) принцип максимума может быть
дополнен условием
max H(х{t)t м, p{t), t) = } ? ~р,Л
или (в случае, если критерий задается в
интегральной форме)
1 " df-
max Я* (х @, u, p(t), t) = J X -^р,Л.
ueU t{i = o ot
Если имеется автономная'система, т. е. функции
fi(x(t), u(t)) зависят от t неявно, то из того, что
dfi/dt = 0, сразу вытекает, что
max H(x{t), и, p(t)) = O
ueU
ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА
301
Е «
II
=1X1 v
с 3
•I 1
=1X11
IИ
i *
III
302
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
max Н* (х (г), и, р (t)) = 0.
ueU
Если нужно минимизировать tx — f0, то говорят
о так называемой временной оптимизационной
задаче (оптимизации по времени). В этом случае
критерий оптимальности можно также записать
в виде
Тогда
ifodt
Н* = Ро + Z Pifi = Ро + Н.
Дополнительное условие принимает вид
1 п df-
max H(x{t), и, p(t),t)= J ? -^-P,^-p0.
ue U ^1=1 ct
Пример 31. Дано
*! - JCi, Xa - U, 0 < U < 1.
Надо найти такое допустимое управление, чтобы точка
х{ @) - 1, х2 @) - -1 переводилась в точку хх (ti) - х2 (t2) - 0
за кратчайшее время *,. Следовательно,
Управление
A,
0,
Рг - -Pi-
если р2 > О,
если р2 < О,
очевидным образом максимизирует Н. При интегрировании
присоединенной системы получаем
Pi -*>ь Pi- -b
с неизвестными постоянными интегрирования Ьи Ь2.
Очевидно, рг не более одного раза претерпевает смену знака, т. е.
оно может не более одного раза дать переключение
управления с и-1 на и « 0 или с и - 0 на' и « 1.
При и ш 1 интегрированием системы состояний получаем
семейство траекторий
xi -yf2 + s2t + si, xa-t + ва
(*!, «2 - постоянные интегрирования). Исключая г, получим
семейство парабол
Соответственно для и - 0 имеем семейство прямых
х, - /у + ги х2 ш г2
(/*!, г2 - постоянные интегрирования). Очевидно, что никакая
прямая этого семейства не может пройти через конечную
точку, которую нужно достигнуть, так как тогда должно
было бы выполняться условие гх ¦ гг ш 0. Для семейства
парабол из условия х, - х2 - 0 сразу получается, что
*1 - -у si » 0, т. е. парабола х, - ~-х| проходит через
конечную точку. Так как х2 возрастает монотонно по г, то
попадание в конечную точку происходит, но на ветви
параболы
Так как эта парабола не содержит начальной точки, то
сначала необходимо управлять с и ¦ 0, пока не будет
достигнута нужная парабола, а затем сделать переключение
на и ш 1.
Время переключения t2 и полное время tt могут быть
легко вычислены.
Исходящая из начальной точки траектория получается при
ишО:
х» - -t + 1, ха ¦ -1.
Для t2 имеем хх»\х\ч или 1-г2--^, или t2 —1/2.
Достигнутое состояние есть
xt-l/2, x2--l.
Дальнейшее управление с и * 1 дает траекторию
Из условия xj (f,) - xa(f,)-0 следует, что г, — 3/2.
Для присоединенной функции p2t таким браэом, должны
выполняться следующие соотношения:
{< 0 при t < 1/2,
-0 при tm 1/2,
> 0 при t > 1/2,
т. е. b\ » 2b2t b\ < 0.
Дополнительное условие принципа максимума Понтряги-
на также выполнено.
Системы с распределенными
параметрами. В отличие от задач управления,
которые описываются обыкновенными
дифференциальными уравнениями, задачи, которые
описываются уравнениями в частных производных,
называют системами с распреде.и'нными
параметрами.
Для этих задач можно сформулировать
принцип максимума Понтрягина аналогично
рассмотренному выше.
Так, например, для задачи нахождения минимума
функционала
•/(«)= ? ciQifa Ь)
i = 1
при не U с
Qixy = fiix, У, Q, Q'x, Q'y, и) (i = 1, 2,...,я),
<2, (.х, 0) = ^ (х), Qi @, у) = cfi (у), ^ @) = en @),
где и — (ии •••, иг) — кусочно непрерывный вектор
управления, Q = (Qi, ..., Qn) — вектор состояния,
принцип максимума Понтрягина имеет следующую
форму:
для того чтобы процесс (м(х, у), Q(x, у))
решал данную задачу, необходимо существование
присоединенных функций N,-(x, у), являющихся
решением присоединенной системы
Nixy = H'Q. - (д/дх) H'Qix - (с/ду) H'Qiy,
Nix = - Щ
Q,r
Nt(a, b)= -с-
(/=1, 2, ..., n),
так что почти для всех (х, )>)е[0, а] х [0, /?]
выполняется условие максимума
тахЯ(х, v, N(x, у), Q(x, у), Q'x(x, У), Q'yi^ У)и) =
ueU
= Я(х, у, N(x, у), Q{x, у), Q'x{x, у), Q'y{x, у), м(х, у)),
Н= ?/V,(x,.v)/,(x, у, Q, ^, Q'y, и).
ДИСКРЕТНЫЕ СИСТЕМЫ
303
Пример 32. Найти минимум функционала
J(u)~\\(x-\)Qdxdy
00
при |и |< 1 с
Q'xy - - 2Q'X - Q'y -2Q + щ Q (x, 0) - Q @, у) - 0.
x у
Вводя функцию Q0(x, у) = JJ(*- \)Qdxd\\ получим основ-
00
ную задачу нахождения минимума функционала Q0(U 1)
при условии, чю \и\^ 1 и
Со,л - (v - I)Q. Qo(v, 0) - Qo@, у) ш О,
<?."» = -Шх - Q'y -2Q + ys Q(x, 0) - Q@, у) - 0.
Максимизация функции Гамильтона
Н - N0(x -\)Q + N(-2Q'X - Q'y - 2Q + n)
дает оптимальное управление
и (х, у) ш sign /V (x, у).
Решение присоединенной системы
No.*) « 0, Nxy » -2N + 2/V; + /V; + N0(x - I),
имеет вид /V0(y, v) = — 1, N(.y, f) « — [е*~{ — x)(l— e2ty "K
так что оптимальное управление выражается функцией
и(х, у) * sign ' {ех~' - х)A - еи>" ") = sign(fv~' - v).
Для систем, которые описываются
дифференциальными уравнениями в частных производных
другого вида, существуют аналогичные принципы
максимума.
Связь между теорией
оптимального управления и вариационным
исчислением. Теория оптимальных процессов
разрабатывалась для решения задач с замкнутой
областью определения. На основе этой теории
можно решать также и вариационные задачи.
Пример 33. Пусть задана задача Лагранжа (см.
3.2.1.2) нахождения жстремума функционала
J(x) ш f / (х, Y, /)<//, • x(f0) - .y°, x(tx) ш x1.
Учитывая, что х*и и
Эйлера
получим уравнение
3.2.2.3. Дискретные системы. Если область
определения функции состояния x(t) является
множеством конечного числа значений rb t2,...,t^ и
изменение состояния происходит согласно закону
*('*) = /(*('*-Д и(М **) (к = 1,...,N),
то говорят о дискретной системе. При этом
u(tk) является г-мерным вектором управления в
момент времени tk с областью управления Uk.
Вводя обозначения: uk — u(tk), xk = x(tk),
представим систему в виде
хк = f(xk~\ uk, tk) = jk(xk~\ ик).
Если положить tk = к, то систему можно
наглядно описать при помощи JV-ступенчатого процесса
(рис. 3.51). При этом хк есть выходное
состояние ступени к, хк'1 - соответствующее входное
-о г— 1_, к-1\ "\Тк у^-'Г" I ты
^—I Стипннь1\-*- • • • -ЛСщпень ку~- • •'• —\СтцпеньМ\-*-
П__1 J 1__ J L/ . J
Рис 3.51
состояние, а ик — управление, действующее на этой
ступени. Выходное состояние получается в
зависимости от входного состояния и
соответствующего управления.
Особое значение имеет следующая
оптимизационная задача. Дана система
хк = fk(xk-^ „*) (д- = l,...,jV),
где fk no меньшей мере один раз
дифференцируема по всем переменным, ukeUk (замкнутое),
начальное значение х° задано; найти такое
допустимое управление ик, чтобы сумма
? с{хР была минимальна (xf^ - координаты
;= 1
выходного состояния х ). Если нужно
минимизировать F[x ], то для каждой ступени вводят
величину состояния х?+1:
При помощи замены х(/) ¦»//(/) получают счедующую
задачу ошимального управления: найти экстремум
функционала
'i
J(U) ш f /(у, », t)lll, X » //, Х(/о) » .V°, .Y(/,) ш X1.
'о
Гамильтониан и присоединенная система имеют вид
Н* т ри - /(х, //, /),
Так как управление »(/) принимает значения из
открытой области, ю
щ ш р _ /;/(.Y, „, „ . о,
откуда может быть определен максимум или минимум
гамильтониана. Из этого равенства следует, что
Цель оптимизации — минимизировать х„+\.
Для таких систем могут быть сформулированы
некоторые типичные постановки задач,
подобно тому как это делалось для непрерывных
систем.
Гамильтониан ступени к (к = 1,...,N):
Присоединенный вектор рк и присоединенная
система ступени к:
„у-. ™' ?pb^L, „n__Ci
304
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ И ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Принцип максимума. Если ик оптимально в
смысле поставленной задачи, то необходимо
существование N присоединенных, отличных от нуля
векторов рк, представляющих собой решения
присоединенной системы и таких, что
дНк{р\ хк~\ ик)
—? = 0 в случае, если и лежит
внутри Uk, и Нк(рк, х*, ик) максимально в
случае, если ик лежит на границе Uk.
В отличие от так называемого сильного
принципа максимума для непрерывных процессов,
эту форму называют слабым принципом максимума.
3.2.2.4. Численные методы. Принцип максимума
(необходимое условие оптимальности) дает полную
систему для определения неизвестных величин.
Однако в нем не содержится никаких
алгоритмов для вычисления этих величин.
Как и при рассмотрении численных методов
вариационного исчисления, различают так
называемые прямые и косвенные численные методы.
Принцип максимума Понтрягина приводит к так
называемой задаче с граничными значениями в
двух точках для определения функции состояния
и присоединенной функции, причем дополнительно
должна быть решена задача максимизации.
Пример 34. Найти минимум функционала
J(«)*»y Ьсг@Л при условии, что | и | ^ 1 и х « х + к,
о
х @) « 0. Максимизация гамильтониана
достигается за сче1 оптимального управления
м@ «sign/> (г),
так что для определения x(t) и p(t) получают задачу с
граничными значениями в двух точках:
х «.v + signp, x@)«0,
Численные методы для приближенного решения
этой задачи и для требуемой приближенной
максимизации гамильтониана называют
косвенными методами. Эти методы определяют
величины, которые удовлетворяют необходимым
условиям оптимальности (принцип максимума).
Так же как в вариационном исчислении, для
приближенного решения задач оптимального
управления зачастую применяются так называемые
прямые методы. Они создают монотонно
убывающую последовательность значений
функционала, или минимизирующую последовательность
(определение см. в 3.2.1.5).
Значительную роль среди прямых методов
играют так называемые градиентные методы.
Градиент J'(u), определенный в 3.2.1.5, для
функционала
?!
./(«)= J/o(x, и, t)dt
Таким образом, для приближенного решения
задач оптимального управления теперь можно
применять известные градиентные методы
нелинейной оптимизации. Рассмотрим кратко три из них.
а) Метод градиента для задач без
ограничений. На управление и не
накладывается никаких ограничений. Исходя из
начального управления и1 (t), дальнейшие управления
вычисляют согласно правилу
м' + 1=и'-М'И (i=l, 2, ...).
б) Метод градиента для задач с
ограничениями:
61) Условный метод градиента.
Пусть u'(t) — начальное приближение. Дальнейшие
управления вычисляются согласно правилу
i/ получаются при этом как решения
линейной «вспомогательной задачи» нахождения мини-
tx
мума функционала fy'fa^vdt при veU.
'о
62) Проекционный метод градиента.
Пусть и1 (t) — начальное приближение. Дальнейшие
управления вычисляются согласно правилу
Рц означает при этом оператор
проектирования на множество U, т. е. нужно решить
«вспомогательную задачу»
min || w-u\
при
max \w(t) - u(t)\.
[ ]
Трудности всех трех методов заключаются в
выборе величины шага р\. Шаг должен быть
определен так, чтобы для соответствующих
значений функционала выполнялось неравенство
0 = 1, 2,...).
В методах 61) и 62) проблема выбора шага
дополняется еще решением вспомогательной
задачи.
Пример 35. Найти минимум функционала
с v = х + и, х @> = 0.
Для градиента получаем следующую формулу:
J'(u) « ~p{t) с р * -р + v, р{\) * 0.
Если никаких ограничений на управление и нет, ю из
метода а) следует, что
и'м « и1 + РХ /V * - /V + л', />' A) = 0.
ал=х* + м', х'@)«0.
При часто встречающемся ограничении |м@Ю при
помощи методов 61) и 62) получают
и' »{l -p,V + p\sign/>'
с x=f(x, и, t), x(t0) — х°, имеет вид
J'(u) = -H*'
с р = — Н'х, p{ti) = 0 и Н* = pf — /0.
( sign(u' + р,/)'), если | м' + р>' | > 1,
причем p'{t) и x'(f) вычисляются так же, как и на основе
метода а).
ОБЩИЕ ПОНЯТИЯ. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И ЕДИНСТВЕННОСТИ
305
3.3. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
C.25)
и я,
C.26)
Дифференциальное уравнение — уравнение,
содержащее неизвестную функцию одного или
нескольких переменных, независимые переменные и
производные неизвестной функции по
независимым переменным.
Примеры дифференциальных уравнений:
2 ~^г~ 4- 3 ^- + 4у = \, у(х) — неизвестная функция,
(I ) ~ *У* л + sin.y * °» УМ - неизвестная функция,
ах J ах
——— — ху2 -~ ~, г(х, у) — неизвестная функция.
дхду дх ду
C.27)
Решить дифференциальное уравнение - это
значит найти все неизвестные функции,
обращающие уравнение в тождество. В общем случае
неизвестные функции определяются
дифференциальным уравнением неоднозначно (если решение
вообще существует), поэтому на искомые
функции часто накладывают дополнительные условия.
3.3.1. ОБЫКНОВЕННЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
3.3.1.1. Общие понятия. Теоремы существования
и единственности. Обыкновенным
дифференциальным уравнением порядка г называется уравнение
(относительно неизвестной функции у одного
независимого переменного х) вида
Fix, y(x), /(*),...,
= 0,
C.28)
где г — порядок наивысшей производной,
входящей в уравнение. (Например, уравнение C.25)
имеет порядок 2, а C.26) — порядок 1.) Если
уравнение линейно по у, /,...,Уг), то оно
называется линейным (C.25) линейно, C.26) - нет).
Под дифференциальным уравнением в явной форме
понимают дифференциальное уравнение,
разрешенное относительно старшей производной:
У> (х) = / (х, у (х), у' (х),..., fх > (х)).
Уравнение вида C.28) называют
дифференциальным уравнением в неявной форме. Под
интегрированием уравнения C.28) понимают
нахождение функции у{х), которая удовлетворяет
этому уравнению. При этом функция у(х)
называется решением дифференциального уравнения.
Общее решение обыкновенного дифференциального
уравнения порядка г имеет вид
у = у(х; СЬ...,СГ),
где Сь..., Сг — произвольные постоянные. При
любом наборе конкретных постоянных получаются
частные решения.
Задача Коши (задача с начальными
условиями) есть задача о нахождении частного решения,
которое удовлетворяет г начальным условиям
У(х0) = Уо, ?{х0) = /о,..-.Уг~п(хо) = Уо"~1]-
Если известно общее решение, то для
решения задачи Коши постоянные С* находят из
уравнений
у(х0;
Г а"'1 1
—Гу(х; СЬ...,СГ)
L -ix
Краевая задача есть задача отыскания частного
решения, которое удовлетворяет г краевым
условиям на концах отрезка а ^ х < Ь, т. е. при
х = а и х = Ь. Дифференциальное уравнение может
обладать также особыми решениями, т. е.
решениями, которые нельзя получить из общего решения
путем подстановки конкретных значений для
постоянных С{ (ср. 3.3.1.2.2).
Графическое изображение частного решения
называют интегральной кривой. Общее решение
дифференциального уравнения r-го порядка
определяет r-параметрическое семейство интегральных
кривых. Обратно, каждое r-параметрическое
семейство
>> = >>(х; СЬ...,СГ)
определяет (при некоторых дополнительных
условиях) дифференциальное уравнение r-го порядка,
которое получается путем исключения постоянных
Съ...,Сг из уравнений
уо (х) = уо (х; сь...,Cr) (i = 0, 1,...,г)*).
Таким образом, дифференциальное уравнение
описывает семейство кривых.
Пример 1. Семейство всех окружностей на
плоскости (х - CiJ + (у - С2J - С\ содержит три параметра.
Трехкратное дифференцирование приводит к уравнениям
(х - С,) + (у - С2)у' = 0, 1 + (>- - С2)у" + (у'J = 0,
{У - Сг)у'н + Зу'(у"J =0. Исключая С2 из двух последних
уравнений, получаем
/'A +(/J)-ЗЯЯ3=0.
Система обыкновенных дифференциальных
уравнений для неизвестных функций у^ (х),...,)>„(х)
имеет вид
у и Уь
,Уп, У'и У
=0
1,2,..., т).
Решением системы обыкновенных
дифференциальных уравнений называется любая
упорядоченная совокупность функций yt (х),..., уи (х),
обращающих каждое уравнение в тождество.
Порядком системы называется число
г = ? г„ где г, — порядок /-го уравнения. Общее
i= 1
решение системы у{ = yi(x) (i = l,...,m) зависит
от г произвольных постоянных.
Каждое уравнение n-го порядка в явной форме
Уп)(х) = /(х, у'(х),...,у{п-1)(х))
306
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
путем введения новых неизвестных функций ух = у,
У г — у\ Уъ — /', •••»>'« = у(и~1} можно» преобразовать
в систему п дифференциальных уравнений
У\=У2, У2=Уз,'--,Уп-1=Уп, Уп=/{х,У1,...,Уп)-
Для систем вида
У1=Л(х, Уи -.., Уп) 0=1, 2,...,п) C.29)
справедлива следующая теорема существования и
единственности для задачи Коши.
Теорема Коши. Пусть выполнены
следующие условия:
1) функции/,-(х, уь...,у„) непрерывны и
ограничены (|/, | < Л) в замкнутой области
Itt-tfl^b, i = l, 2,...,*};
2) в замкнутой области G по переменным
Уь ..., уп выполняется условие Липшица с
константой Липшица L, т.е. для всех (х, уь ..., у„)
и (х, У1,...,у„) из G выполняется неравенство
-yk\
0 = 1, 2,...,«).
Тогда система C.29) с начальными условиями
Уг (х°) = У? имеет, и притом единственное, решение
для | х - х° | ^ а, где а = min (а, Ь/А).
Замечание. Условие Липшица выполняется
всегда, когда /, обладают ограниченными в
области G частными производными по ук, т. е. когда
Я fi(x, УI, ..., уп)
дУ
(i, к= 1, ..., и).
Если в теореме Коши опустить
предположение о том, что выполнено условие Липшица,
то в результате получим лишь теорему
существования решений при условии yt (х°) = у\0) (i = 1,
2, ..., п) (теорема Пеано).
Примеры дифференциальных уравнений,
которые не удовлетворяют условиям теоремы Коши,
рассматриваются в 3.3.1.2.2.
Зависимость решения задачи Коши
от начальных данных. Если функции
/,(х, Уь...,у„) 0 = 1, 2,...,и) в некоторой
окрестности U{x°, у?,..., у?) точки (х°, у?,...,у?)
удовлетворяют условиям теоремы Коши, то они
удовлетворяют этим условиям и в некоторой
окрестности 1/(?, Ль---»1!») каждой точки (?, Ль-^Ля),
достаточно близкой к точке (х°, уJ,..., у?).
Для каждой точки х, принадлежащей достаточно
малой окрестности точки ?, всегда существует
решение yl(x),...,yH(x) системы C.29),
удовлетворяющее условиям х = ?, yi(Z>) = 41,...,yn(fy = r]n.
В то же время эти функции, рассматриваемые
как функции от начальных значений %, т|ь...,т]п,
непрерывны в некоторой окрестности точки
(х°, у°,...,у°п).
Если функции /,, кроме переменных, зависят
еще и от параметров Pi,...,pm и если они
непрерывны по всем аргументам, то функции
У\у-уУш удовлетворяющие задаче Коши, суть
непрерывные функции параметров ри...,рт.
Общее решение системы C.29) содержит п
произвольных постоянных: у, =у,(х, СЬ...,С„), где
/ = 1, 2,...,п. Функция и(х, Уи----,Уп) называется
первым интегралом системы C.29), если и
постоянна вдоль кривых решения системы (постоянная
зависит от выбранного частного решения); п
первых интегралов получают путем решения
уравнений yt,= yt(x, Cb...,Q) относительно Ск.
Каждый первый интеграл удовлетворяет
дифференциальному уравнению
ди ди
ди
• •. + /„(*, Уь-.-,H-5-- = о,
и, обратно, каждое решение и этого
дифференциального уравнения дает первый интеграл системы
C.29). Тогда п первых интегралов системы C.29),
для которых соответствующие функции ик
(к = 1, 2,...,и) линейно независимы, образуют
общий интеграл системы C.29).
3.3.1.2. Дифференциальные уравнения 1-го
порядка.
3.3.1.2.1. Уравнения 1-го порядка в
явной форме. Частные виды уравнений.
Дифференциальное уравнение 1-го порядка в
явной форме имеет вид
/=/(*, у).
Если через точку М(х, у) проходит график
решения у = у(х) уравнения у'=/(х, у), то наклон
а касательной к графику в точке М(х, у)
определяется непосредственно из уравнения (так как
tg а = у'(х) = /(х, у)). Таким образом,
дифференциальное уравнение в каждой точке
рассматриваемой области задает направление касательной
к кривой решения. Совокупность этих направлений
образует поле направлений (рис. 3.52). Точка
/ I \ \\ \ \ \
Д7=/
Рис. 3 52
вместе с заданным в ней направлением называется
линейным элементом поля направлений. Точку
М(х, у) называют носителем линейного элемента.
Итак, интегрирование дифференциального
уравнения 1-го порядка / = /(х, у) геометрически
сводится к соединению элементов поля направлений
в интегральные кривые, касательные к которым
в каждой точке имеют направление, совпадающее
с полем направлений в данной точке.
Часто приходится иметь дело с полем
направлений, в котором встречаются вертикальные
направления, соответствующие полюсу функции /(х, у).
В этом случае у считают независимым
переменным и рассматривают уравнение
dx
1
dy fix, у)'
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
307
В области, в которой выполняются условия
теоремы Коши для уравнения в явной форме,
через каждую точку проходит единственная
интегральная кривая.
Пример 1. В области Gj (см. рис. 3.52) выполнены
условия теоремы Коши для уравнения т— " *» но не для
М.
в области С2 - наоборот.
Совокупность всех интегральных кривых
зависит от одного параметра. Уравнение
соответствующего однопараметрического семейства
кривых — общий интеграл дифференциального
уравнения 1-го порядка — содержит одну произвольную
постоянную. Чтобы из общего интеграла
/ (х, у, С) = 0 получить частный интеграл у = у (х)
(или х = х {у)), удовлетворяющий условию у0 = у (х0)
(или х0 = х(уо)), нужно найти постоянную С
из уравнения / (х0, у0, С) = 0.
Частные виды обыкновенных
дифференциальных уравнений 1-го порядка.
Дифференциальное уравнение с разделяющимися
переменными:
у
д{у)'
Общий интеграл имеет вид
Пример 2. /-— ~4у +ty, Путем вычисления
интегралов а _ Г т ^* <** полУчаем общий
интеграл
Пример 3. /--^--2. Из
общий интеграл у + In | у — 11 ¦ - 2х + С.
получаем
Однородное уравнение:
У =
х, У)
х, уУ
где Р и Q — однородные функции степени г, т. е.
Р {кх, ку) = кгР (х, у), Q (кх, ку) = k'Q (x, у).
Путем введения новой неизвестной функции
и = у/х такое уравнение приводится к уравнению
с разделяющимися переменными.
Пример 4. / ш 21—'* Здесь Р »Зу - 7х и
Q ш Ау - Зх - однородные функции степени 1. Полагая
. Оно
у»их, приведем уравнение к виду г1-1 ТРИ,
имеет общий интеграл х1 (Аи1 - 6и + 7) ~ С (см. пример 2).
Общий интеграл исходного уравнения имеет вид
V - 6уХ + 1Х% т С.
Уравнения вида
ах + by + с
Если аВ — ЬА ф 0, то заменой t = х — х0, и = у — у0,
где х0 и у0 — единственное решение системы
ах + by. + с = 0, Ах + By + С = 0, такое уравнение
сводится к однородному. Если аВ - ЬА = 0, то
полагают и = ах + Ьу, ? = х; в этом случае
уравнение сводится к уравнению с разделяющимися
переменными.
Пример 5. у'ш
. Здесь flB-fe/t--19*0
и замена и » у — -т^-, t"X-~ приводит к уравнению
Общий интеграл этого
уравнения
Пример б. / - -
-. Здесь аВ-ЬАш 0. Тогда
Аи2 - 6ш -(- 7г2 - С, был найден в примере 4. Таким
образом, Ау2 -г 10у - бху + 7х2 + 4х - С есть общий интеграл
исходного уравнения.
х-у
замена и - -х-Ьу приводит к уравнению ~-—2 с
общим интегралом и + In | -и + 11 - -2х + С (см. пример 3).
Общее решение исходного уравнения есть у + 1п|х->+1|-
- - х + С.
Уравнения в полных дифференциалах:
Р(х, y)dx + Q(x, y)dy = O,
C.30)
где дР/ду = dQ/dx.
Если в некоторой односвязной области функции
Р и Q непрерывны вместе со своими частными
производными 1-го порядка, то условие
дР 8Q
—— = —— необходимо и достаточно для того,
ду дх
чтобы существовала функция F(x, у) такая, что
dF(x, у) = Р(х, у) dx + Q(x, у) dy
dF 8F
—--=Р(х, у) и —-=Q(x, у).
дх ду
В этом случае F(x, у) = С есть общий интеграл
уравнения в полных дифференциалах. Функцию
F(x, у) можно найти по формуле (ср. 3.1.8.5)
|Q(x0,
Уо
F(x, y)= JPft, y
Хо
(х0 и у0 произвольны).
Пример7.(х-y)dx + (у -х)</^-0.ЗдесьдР/дут-1
и dQ/dx - -1 в любой односвязной области, не
содержащей точек оси абсцисс. Тогда
F(x, у) - J D - y)d% + J (л - ХоМл -
Получаем общий интеграл хЛу - 2у2х - 2 - Су - 0.
Если левая часть уравнения C.30) не является
полным дифференциалом (т.е. ~—Ф ~-г\ т0
\ су oxJ
иногда можно найти такую функцию ц(х, у)
(интегрирующий множитель), что
дифференциальное уравнение цР dx + \lQ dy = 0 будет
уравнением в полных дифференциалах. Интегрирующий
множитель ц (х, у) удовлетворяет
дифференциальному уравнению в частных производных
дх
308
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Любое частное решение этого уравнения
является интегрирующим множителем.
Часто уравнение в частных производных для
нахождения интегрирующего множителя ц можно
упростить, если считать ц функцией только х
(или у, или ху, или х/у). При этом
руководствуются следующими правилами:
1 дР дО
а) Если — —
Q \ ду ёх
-- f{x), то
б) Если — (
в)Если
= f{y), 10 \i(x, у) = \
dQ
дх
irr-^ ) = /(**)•
то jx(x, у) = ц(ху).
г) Если
1
¦ Рх V ду дх
то ц(х, y) = \i[—).
\ X J
Пример 8. (xya-,y4)dx+ A-xya)dy-0. Здесь
Считая, что ц - \и{уЬ получим У' jf^"- 1&) " "j?
или =И_ш - ^. Частное решение: ц««,у".
После умножения на ц получаем уравнение (х - у)с/х +
+ 0>~а -x)rf>> -0, которое является уравнением в полных
дифференциалах. Его общий интеграл имеет вид х2у - 2у2х —
- 2 - Су - 0 (см. пример 7).
Линейное дифференциальное уравнение:
C.31)
Это неоднородное относительно учу'
уравнение имеет интегрирующий множитель ц(х) =
= е* (х' ; общее решение получают по формуле
Q(x)\i{x)dx
Если заменить в ней неопределенный интеграл
на определенный интеграл с пределами
интегрирования х0 и х. то получим, что у(х0) = С.
Линейному неоднородному уравнению C.31)
ставится в соответствие линейное однородное
уравнение / + Р (х) у = 0 (однородное по
отношению к у и / — не путать с ранее
рассмотренным однородным по х и >>)•
Общее решение линейного дифференциального
уравнения наряду с изложенным выше методом
можно найти и иначе: у — и + у, где и — общее
решение линейного однородного уравнения и у-
какое-либо частное решение линейного
неоднородного уравнения.
Методом вариации постоянной, используя общее
решение линейного однородного уравнения, можно
найти частное решение линейного неоднородного
уравнения. Общее решение однородного уравнения
имеет вид и = Сле~* "(х>"х (см. дифференциальное
уравнение с разделяющимися переменными).
Предположим теперь, что Сх зависит от х, и выберем
d = С\(х) так, чтобы функция у = С^{х)е~^ ^х'
удовлетворяла уравнению C.31); получим частное
решение неоднородного уравнения:
Пример 9. у' + - г-"~-У " гг-—гг-
* х(х-1г х*(х-1)
хг
а) ц(х) ш - , и общее решение имеет вид
б) Найдем частное решение, проходящее через точку
х0 «2, >!о - 1/4. Имеем
и соответствующее частное решение равно
t4(x-l)f , 1 \ «ft Л 1
^Г\ 4j(r-rjr 4У х^'
У(х) -
Пример 10. Rl{t) + Ld-^&mE есть
дифференциальное уравнение для силы тока /(О в цепи, состоящей
из источника тока с напряжением ? - ?0 (постоянное
напряжение) или ?-?osinci)( (переменное напряжение),
сопротивления R и индуктивности L. Обозначая R/L»a
и Eo/L шЬ (a, b - постоянные), получим общее решение:
/(()-<
/(f) - Се"- -f Ь/а при ? - ?0,
при Е - ?0 sin со/.
Общее решение Се" линейного однородного уравнения
соответствует затухающему процессу, а второе слагаемое
в формуле для /(г) есть частное решение исходного
неоднородного уравнения, оно дает постоянную составляющую
силы тока. Для случая ?-?osinco( сила тока сдвинута по
фазе относительно напряжения на угол а.
Уравнение Бернулли
сводится к линейному дифференциальному
уравнению введением нового переменного z = yl~n:
z' + (l -n)P(x)z = (l -n)Q(x).
Пример 11. xa(x - 1)У -уа - x(x- 2) у «О, и-2.
Вводя новое переменное г - у" \ получим линейное
уравнение г! + -ij*—)--г . —y.-i Оно имеет общее
решение z - х ~д ¦-( ——. ^ ^ J (CMi пример 9); общее решение
X \Х~I /
исходного уравнения: у ¦
1 + С(х - 1)'
Уравнение Риккаши:
В общем случае это дифференциальное
уравнение неразрешимо в квадратурах. Если же
известно одно частное решение уь то введением
нового переменного z по формуле у = yt + 1/z
уравнение Риккати может быть сведено к линейному
дифференциальному уравнению
z' + {2Pyx +Q)z= -P.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
309
Если у 2 — другое частное решение, то
zv= \/(у2 — yi) есть частное решение линейного
уравнения для переменного z; это позволяет
упростить интегрирование уравнения. Если же
известны три частных решения уи у2, у3, то
общий интеграл уравнения Риккати имеет вид
У - У г . Уъ ~Уг
-С.
У - У1 Уз - У1
Заменой;; = -z'/P(x)zуравнение Риккати можно
привести к линейному дифференциальному
уравнению 2-го порядка (ср. 3.3.1.3.4)
Pz" - (Р' 4- PQ)z' + RP2z = 0.
z . P' + PQ
Заменой У = ~р~пл + b\xh где ° = 2Р*~*
уравнение Риккати можно привести к
канонической форме z' = z2 4- R (х), где R (х) = Р (— Ь' 4-
4- РЪ2 4- Qb 4- R).
Частный случай уравнения Риккати:
у' 4- ау2 = Ьхт, а # 0.
Оно разрешимо для m = 0 (уравнение с раз-
4/с
деляющимися переменными) и для т = —
1 — 2М,
(*=±1, ±2,...):
если к > О, то заменой >' = -=—I , х =
х2у ах
= х1/(т + 3) получаем, что —г + ау2=Ьхт, где
- ь , ь= а
Ш4-3' " " т + 3'
т 4- 1 _ 4(fe - 1)
W4-3 ~ 1 — 2(/с — 1) '
если к < О, то заменой у = ——л
х(Ьху + т 4- 1)'
_?-i/(m+n получаем, что —- 4- ау2 = Ьх™, где
-, ь=-
т + 1
Зт 4- 4
т + 1 '
+ 1)
(fc + 1)'
Указанные замены следует проводить, пока
получаемое т не оказывается равным нулю.
Пример 12. у' = у2 -Bх + \)у + (х2 + х + 1). Здесь
у, (х) = х есть частное решение Замена >' = х + 1/z
приводит к уравнению г' — z = — I с общим решением
2 — ?ух -f 1. Уравнение Риккати имеет общее решение
у = х + - х —. Замена ^ = z + Л, где 6 = х + 1/2,
приводит данное уравнение к канонической форме z = z2 — 1/4
Замена у = —z'/z приводит данное уравнение к уравнению
2-го порядка z" + Bх + I)z' + (.v2+x+ l)z = О
Пример 13. у' - Зу2 =X-Sl\m= -8/5, к = -2, в= -3,
Ь = 1. Замена у= --——-—, х = х5/3 приводит к
уравнению >•' -I- -| у2 = -5х~4/3, где т = - |, к = -1, й = -| ,
3.3.1.2.2. Дифференциальное
уравнение 1-го порядка, не разрешенное
относительно/.
1) Уравнение F(x, у, /) = 0 разрешимо
относительно у'. Пусть в данной точке (х0, у0)
уравнение F(x0, у0, р) = 0, где р = у', имеет
действительные корни Рь...,р„, функция F(x, у, р)
и ее первые частные производные непрерывны
по всем переменным в каждой точке х = х0,
У - У о, Р = Pi и —— ф 0. Тогда уравнение F(x, у, р) = О
др
распадается на п дифференциальных уравнений
вида /=/,(х, у), где/,(х0, у0) = д. Через точку
(х0, Уо) проходят точно п интегральных кривых.
Пример 14 Найти интегральную кривую уравнения
>''2 = |4у|, проходящую через точку @, 1). Здесь
F(x, у, р) = р2 — | 4у | Функции F, f--,(—, '-— непрерывны
при х = 0, >> = 1, р{ = 2 и рг = -2, и dF(O, 1, 2)/<5р = 4^0,
4^tO. Таким образом,
уравнение
<1ВД_-Ь _л?)
-Цр — '
р2 — | 4>' | = 0 распадается на два уравнения: у' — 21/| у \ и
/ = — 2|/|у| Через точку @, 1) проходят обе интегральные
кривые- у = (х 4- IJ и v = (х - IJ.
2) Уравнение F(x, у, у') = 0 разрешимо
относительно у. Известна тройка чисел (х0, у0, Ро). Для
которой F(x0, уо, Ро) =0 и уравнение F(x, д;, р) = О
разрешимо в окрестности (х0, ^о» Ро) относительно
у: y=G(x, р), т.е. у0 = G(x0, р0) и F{x, G(x, р), р) = 0.
Если рассматривать только такие решения
у = у(х), которые в окрестности точки х0 имеют
отличную от нуля непрерывную производную, и
если еще предположить, что G(x, p) имеет в
окрестности точки (х0, р0) непрерывные частные
производные по х и р и G'p(х0, Ро) = ° ^л
дР
то получим уравнение
dp _ р - G'x(x, p)
~dx~~ G;(x, p) '
разрешенное относительно производной. Решение
этого уравнения имеет вид р = р(х) или х = х(р);
после подстановки в уравнение у = G (х, р) получаем
решение исходного уравнения в виде у = у(х) или
У = у{р)> х — х{р) как параметрическое
представление.
Пример 15 еу -г 2ху' — у = 0 Выберем ючку
(•^о? Ро) произвольно, возьмем, например, @, 1); тогда
.Уо =еРо + 2хоро и (х0, >'о, Ро) = Ф, е, !)• Уравнение
принимает вид у = G (х, р), где G (х, р) — ер + 2хр и
С„@, 1) = е Ф 0 Таким образом, ~ = — или
</х ер + 2х
(fp + 2x)dp + pdx = 0 Решение это1 о уравнения
(интегрирующий множитель (д = /?) при условии />@) = 1 ccib
х= —2 C'P' a решение исходною уравнения в
параметрической форме имеет вид у — B — р) — е'\ х —
Р
1
= A — р) —2^р. Эти уравнения суть парамефическос
представление интегральной кривой уравнения е +2ху'— v = 0
в окрестности р = I (при условии х0 - 0, >'о — е, у'@) = 1)
Ь = — 5, а новая замена у = _- —--.-- , х = х3 — к урав-
х(-5ху-1/3)
нению у' - 15J'2 = 5 с разделяющимися неременными
3) Уравнение F(x, у, у1) = 0 разрешимо
относительно х. Пусть известна точка (х0, у о, Ро)»
в которой F(x0, Уо, Ро) = 0, и пусть в окрестности
310
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
этой точки уравнение F(x, у, р) — О можно
разрешить относительно х: х = Н(у, р). Ограничимся
решениями вида у = у(х), где р = у'(х) разрешимо
в окрестности (х0, Ро) относительно х: х = х(р).
Дифференцируя соотношение х = Н (у, р) по р,
получим уравнение
dp
рЩ - 1
\dp p dp]
с решением у = у{р) или Р = р(у)- Решение
исходной задачи получается в виде х = х(р) и
у = у(р) (р - параметр) или х = х{у).
Пример 16. х = уу' + (у'J. При этом F(x, у, р) =
= х-ур-р2 и Н(у, р) = ур + р2. Точка (х0, у0) может
быть задана произвольно с единственным условием:
-т(УоJ + *о >0; тогда существует по крайней мере одно
значение р0 такое, что х0 - уоро - pi — 0. Рассмотрим,
например, точку х0 = 0, у0 — 0, р0 = 0. Вспомогательное
линейное дифференциальное уравнение -~- + у
dp
dp
имеет решение у(р) - -р+
при у@)=0.
Р 1 ]/\-р2
Интегральная кривая уравнения х = уу' + (у'J*
проходящая через точку х0 = 0, у0 - 0 (/ @) = 0), имеет (в
окрестности р = 0) параметрическую форму
4) Уравнение Лагранжа
всегда интегрируется в квадратурах указанным
выше способом. Если а(р) + Ь(р)р = 0, то имеем
уравнение Клеро
У = У'* + /(/)•
Общее решение этого уравнения имеет вид
Линейный элемент (х0, Уо, Ро) уравнения
F(x, у, р) = 0, т. е. F(x0, у0, р0) = 0, называется
регулярным, если в окрестности точки (х0, у0)
существует единственная непрерывная функция
p = f(x, у) такая, что Ро=/(хо,Уо) и
F(x, у, f{x, у)) = 0. В этом случае
дифференциальное уравнение y'=f(x, у) в окрестности точки
х0 имеет единственную интегральную кривую,
проходящую через (х0, Уо) и такую, что
у'(хо)=ро. В противном случае линейный
элемент называется особым. Совокупность точек
(х, у) - носителей особых линейных элементов -
называется дискриминантной кривой уравнения.
Интегральная кривая, состоящая из особых
линейных элементов, называется особой, а ее уравнение
называется особым интегралом. Если функция
F(x, у, р) в окрестности линейного элемента
(*о> У& Ро) непрерывна и имеет непрерывные
частные производные F'x, F'y и F'p, то линейный
элемент регулярен только тогда, когда F'p(x0,
Уо, Ро) Ф 0. Если же F'p (х0, уо, Ро) = 0, то
линейный элемент будет особым.
Как правило, особый интеграл не получается
из общего ни при каком значении
произвольной постоянной. Для нахождения особого интеграла
дифференциального уравнения F(x, у, р) = 0, где
р = у', к этому уравнению присоединяют
уравнение F'p{x, у, р) = 0 и исключают р. Если
полученное соотношение является интегралом
исходного уравнения, то это особый интеграл. Если
известно уравнение семейства интегральных кривых,
т. е. общий интеграл данного уравнения, то для
нахождения огибающих кривых этого семейства,
дающих особые решения, могут быть применены
методы дифференциальной геометрии.
Пример 17. Р2((х - уJ - 1) - 2р + ((х - уJ - 1) - 0.
Общий интеграл находим, разрешая уравнение
относительно у и применяя описанный выше метод:
l/l +P2
Таким образом, (х - СJ + (у - Q2 = 1.
Дополнительное уравнение для нахождения особых
решений есть р{(х - у)* - 1) - 1 = 0. Исключение р приводит
к уравнению (х - уJ((х - уJ - 2) = 0, т. е. у «= х,
у = х -I- \/2, у*=х- У2. В данном случае у * х не
является решением исходного уравнения и, следовательно,
не дает особого решения. Два других выражения,
у = х + ]/2 и у=»х- /2, являются особыми решениями.
Эти особые решения можно получить также из общего
Рис. 3.53
решения как огибающие, исключая С из уравнений
(х - СJ + (у - СJ - 1 = 0, ^~ ((х - СJ + (у - СJ - 1) - О
(рис. 3.53).
Особые точки дифференциального уравнения.
Пусть
/= ^~=/(*, У), C-32)
где Р и Q — многочлены по х и у без общего
множителя: производная df/dy обращается в
бесконечность только в тех точках (х0, у0), в которых
Q(xo,yo) = 0. В этих точках как правая часть
уравнения —- = — (если Р(х0, у0) Ф 0), так
dy P(x, у)
и ее производная по х непрерывны. По теореме
существования и единственности через такую точку
проходит единственная интегральная кривая
х =д{у). Если Р(х0, }>о) = Q{x0, Уо) = 0 (при данных
предположениях это может быть только в
изолированных точках), то (х0, у0) называется
особой точкой дифференциального уравнения
C.32). Особых решений для такого уравнения не
существует.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 1-го ПОРЯДКА
311
Дифференциальное уравнение
dy ах + by
dx ex + ду
{ад -ЪсФЪ)
C.33)
(а, Ь, с, д — постоянные) имеет особую
изолированную точку @, 0). Через каждую другую точку,
достаточно близкую к @, 0), проходит
единственная интегральная кривая. Рассмотрим корни zx и
z2 характеристического уравнения
с — z a
a b-z
= z2 -(
+ (bc- ад) = 0
и приведем уравнение C.33) при zx Ф z2
посредством замены переменных х = Ах + By, y = Cx + Dy,
где постоянные А, В, С, D (А2 + В2 > 0, C2 + D2 >0)
можно найти из систем
= 0, ((c
= 0, \ g
\ gA+(b-z2)B
к дифференциальному уравнению
С + aD =
-zx)D-
а при z0
x = ax +
b-c
dx z2x '
== z2 посредством
~У> У — У — к уравнению
dx
zoy
ZqX
Эти (аффинные) преобразования не изменяют
характера особой точки. Решение уравнения C.34)
имеет вид у = C\x\Zl^2, а решение уравнения
C.35) - вид у = —х In | х | + Сх.
Z0
Случай 1. Корни Zi и z2 — действительные
и одного знака. Особая точка называется узлом.
Без ограничения общности можно считать, что
Zx ^ Z2> 0. ИЗ УСЛОВИЯ (при Zj > Z2)
dy_
dx
= ±
= 0
следует, что все кривые в особой точке
касаются друг друга, т. е. имеют в особой точке общую
касательную. Если zi = z2,
то из особой точки в
любом направлении
выходит единственная
интегральная кривая.
Наряду с этими
семействами кривых имеется
еще одна проходящая
через особую точку
интегральная кривая: jc = 0.
Пример 18.
dy -6x + 4y
~dx" -х + у '
Корнями характеристического
уравнения гг — Ъг + 2 « 0 яв-
Рис. 3.54 ляются z\ »2 и zj*l.
Замена х • -Зх + у, уш -2х +
dy 2y
+ у приводит к уравнению — — ——, интегральные кри-
dx х
вые которого задаются уравнениями у = Сх2 (рис. 3.54).
Пример 1».
-. Корни
характеристического уравнения г2 - 2г + 1 - 0 равны между собой:
z, х= гг ш 1. Замена х — 2х - 2у, у = у приводит к уравнению
_2.
х + у ^
Рис. 3.55
интегральные кривые которого задаются
уравнениями у - xln | х | + Сх (рис. 3.55).
Пример 20. -^» А Это уравнение уже имеет кано-
C.34) ническую форму. Корни характеристического уравнения
C.35)
Рис. 3.56
г2 - 2г + 1 ¦ 0 равны между собой: гх - гх - 1.
Уравнения интегральных кривых имеют вид у « Сх (рис. 3.56).
Случай 2. Корни z± u_ z2 —
действительные и разных знаков. Особая ^ючка называется
седлом. При zl/z2 = — к < 0 получаем общее
решение вида у = С | х \~к. Через особую точку проходят
только две интегральные кривые: Зс = 0 и у — 0.
Рис. 3 57
Пример 21. 4Х-т —-У-. Корни характеристического
уравнения г2 - 1 * 0 равны zx - 1 и гг « -1. Уравнения
интегральных кривых имеют вид ху = С (рис. 3.57).
312
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Случай 3. Корни zx и z2 — комплексно
сопряженные (но не чисто мнимые). Особая точка
называется фокусом. При замене переменных
х = Ах + By, у = Сх + Dy
коэффициенты А и В можно определить так, чтобы
они были комплексно сопряжены по отношению
к коэффициентам С и D. Так как х, у в общем
случае для действительных х и у будут
комплексными, то вводят новые переменные 5с, у,
полагая
Зс = 5с + iy и ~у = 5с — (у.
Характер особой точки При такой замене вновь
не меняется. Общее решение уравнения C.33) в
координатах 5с, у имеет вид
где
Eс2 + у2I'2 = Се-Ш**<Л8(у/х\
zi = р + iq, z2 = p - iq,
или в полярных координатах
5с = р cos ф, у = р sin ф: р = Се~ {р1ч) ф.
Это — семейство логарифмических спиралей в
плоскости х, у с асимптотической особой точкой.
Все кривые входят в особую точку, но не имеют
там определенной производной и совершают
бесконечное множество оборотов вокруг точки
(О, 0).
Рис. 3 58
dy 5х — Ау
Пример 22. ~- -=* г Y~- Характеристическое
уравнение имеет корни гх — — 1 + i, z2 e — 1 — U и замена
х = — C - i) х - у, у ш — C + 0 х - у приводит к уравнению
dy (\ + i)y - - -
-р- = т.—гр-: Наконец, замена х » х + iy, y**x-iy
приводит к уравнению
df =
d% f -У
решение которого имеет вид (рис. 3.58)
Случай 4. Корни z1 и z2 — чисто мнимые
сопряженные. Особая точка называется центром.
Переменные 5с, у (выбранные, как в случае 3) дают
интегральные кривые
^2 + У = С,
т. е. семейство замкнутых кривых, которые
окружают особую точку.
dy х
Пример 23. -г~= • Корни характеристического
уравнения 22+1=0 равны zx =» / и z2 = —/. Уравнения
интегральных кривых имеют вид х2 + у2 » Г (рис. 3.59).
Рис 3 59
dy
dy
Пусть в дифференциальном уравнении —— =
= . ' г- функции Р (х, у) и <2 (х, у) имеют
непрерывные частные производные, и пусть
,Р(х,у) = а(х- хо) + Ь(у- Уо)
Q(x, у) = с(х-хо) + д(у- уо)
где ад - be Ф 0 и
j (x, у\
i (x, у),
{Т
x. У)
ТьЦх-ХоГ+Ь-уоГУ»
lim
<2i (x, у)
Оказывается, что (за одним исключением) вид
особой точки (х0, Уо) данного дифференциального
уравнения будет тот же, что и у особой точки
уравнения первого приближения
dy _ а(х - хо) + b(y - уо)
dx с(х - хо) + д(у - Уо)'
Примечание 1. Если особая точка уравнения
первого приближения — центр, то особая точка
основного уравнения является центром или
фокусом.
Примечание 2. Если ад — be = 0, то для
определения вида особой точки требуется
рассмотрение членов высшего порядка.
3.3.1.2.3. Приближенные методы
решения уравнений 1-го порядка. Здесь
коротко упомянуты некоторые методы; ниже (см.
7.1.2.9) они будут рассмотрены подробно.
Метод последовательных
приближений (П и к а р). В предположениях теоремы
существования и единственности задача Коши
y'=f(x, у), у(хо) = а эквивалентна уравнению
у(х) = а+ lf(t,y(t))dt.
х0
Функции у„, вычисленные последовательно по
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
313
формуле
уя(х) = а
, yo(t)
равномерно сходятся в заданном промежутке к
искомому решению у(х).
Пример 24. у * х2 + у2, у @) = 1. Легко вычислить
= 1 -1+ f(f2 + l)</f=l+x + —
J 3 '
2х^
2х5
_
_.
Интегрирование при помощи рядов.
В предположении, что правая часть
дифференциального уравнения /=/(х, у) аналитична по х и у,
т. е. что она может быть разложена в степенной
ряд по х и у, решение задачи Коши
существует в виде
У(х)= I ак(х-х0)к, ак=уЫ(х0)/к1
к = 0
Замечания. 1) Коэффициенты ак можно
вычислить при помощи дифференциального уравнения
последовательным дифференцированием и
подставить в ряд; 2) часто составляют ряд с
неопределенными коэффициентами и затем вычисляют ак
из рекуррентной системы, которая получается,
если подставить ряд в дифференциальное
уравнение и приравнять коэффициенты при одинаковых
степенях (х — х0). Этот метод применим также к
дифференциальным уравнениям высшего порядка
и к системам.
Пример 25. У ш хг + у2, у@) » 1. Функция /(х, у) -
шх2 + у2 аналитична по х и у. Вычисления /к)@) про-
изволим, последовательно дифференцируя исходное
уравнение:
У@) -
/@) «
У"@) =
Получаем
у(х) ш 1 + х + yj-x2 + yj-x3 + -^-x* + ...
Графическое интегрирование. Этот
метод базируется на понятии поля направлений
(ср. 3.3.1.2.1). Интегральная кривая изображается
ломаной, выходящей из заданной начальной точки.
Она состоит из коротких отрезков, направление
каждого из которых совпадает с направлением
поля в начальной точке отрезка, являющейся
Рис. 3 60
при этом конечной точкой предыдущего отрезка
(рис. 3.60).
3.3.1.3. Линейные дифференциальные уравнения
и линейные системы.
3.3.1.3.1. Общая теория линейных
дифференциальных уравнений. Линейным
дифференциальным уравнением п-го порядка
называется уравнение вида
У(п) + Pi (х)У") + ... + рп-1 (х) / + рп (х) у' = Дх).
C.36)
Такие дифференциальные уравнения имеют
большое значение в приложениях; при этом функцию
/(х) часто называют возмущающей функцией.
Если/(х) = 0, то линейное дифференциальное
уравнение называется однородным; если /(х) ф 0, его
называют неоднородным. Коэффициенты pv(x)
предполагаются непрерывными в
рассматриваемом интервале (а, Ь).
Однородное уравнение. Если функции yv (x)
(v = 1, 2, ..., к) - решения однородного уравнения
в интервале (а, Ь), то и их линейная комбинация
(Cv — произвольные постоянные) является
решением линейного однородного дифференциального
уравнения.
Функции yv(x) (v = 1, 2, ..., к) называются
линейно зависимыми на интервале (а, Ь), если
существует к чисел С\, таких, что для любого
хе(а, Ь) справедливо равенство
к
1и
= i
v | > 0.
Если же это равенство возможно только при
условии, что d=... = Cfc = 0, то функции
У\(х), ..., ук(х) называются линейно независимыми.
Решения у1} у2, ..., у» однородного уравнения
линейно зависимы на (а, Ь), если определитель
Вронского {вронскиан)
W(x) = W(yi(x), ..., уп(х)) =
Уг
У'г
• •• Уп
... У'п
314
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
равен нулю в точке хое(а, Ь). Из равенства W(x0) ¦¦
= 0 в силу формулы Лиувилля
= W(xo)exp
(- ]Pl
^ Хо
(t)dt
жим, что коэффициенты Cv зависят от х.
Производные функций Су(х) найдем из системы уравнений
C\yi +
+ ... + Спуп = О,
следует, что W(x) = 0 на (а, Ь). Указанные п
решений однородного уравнения на {а, Ь) линейно
независимы, если определитель Вронского в точке
хое(а, Ь) не равен нулю^ткуда следует, что этот
определитель нигде не равен нулю на {а, Ь).
Каждое однородное дифференциальное
уравнение /7-го порядка всегда имеет фундаментальную
систему решений, т. е. п линейно независимых
решений. Если решения уь •••> Уп образуют
фундаментальную систему решений, то у(х) =
= Схух (х) + С2у2 (х) + ... + СпУп (х) есть общее
решение линейного однородного
дифференциального уравнения.
Если известно частное решение yt (x)
однородного дифференциального уравнения и-го порядка
на интервале (а, Ь) {ух (х) ф 0), то можно понизить
порядок дифференциального уравнения (сохраняя
его линейность) заменой переменных у = ух J и (х) dx.
Если их (х), ..., ип-! (х) — фундаментальная
система преобразованного уравнения, то функции
У\ М, Уг (х) = yl(x)\u1 (x) dx, ..., у„(х) =
= yn-l(x)Sun-l(x)dx
образуют фундаментальную систему решений
исходного уравнения.
Пример 26. х2A -х)/ + 2хB-х)/ + 2A +х).у = О.
В канонической форме это уравнение имеет вид
х(\-х)]
Чтобы обеспечить 'непрерывность коэффициентов,
выберем в качестве интервала (а, Ь) один из интервалов
(-оо, 0), @, 1), A, +оо). Частное решение этого уравнения
имеет вид yl(x) = x~2. Данное однородное
дифференциальное уравнение приводится посредством замены у =
= x~2f u(x)dx к уравнению и' + -j и =*0, решение
которого есть м(х)«(х-1J. Таким образом, у,(х)вх,
у2 (х) = х f (х — IJ dx «(х - 1K/Cх2) образуют
фундаментальную систему решений исходного уравнения. Так как
(х - IJ
W(x) = * ^— и, следовательно,
с\уГ2) + с2УГ2) +... + спУГ2) = о,
(смотря по тому, в каком интервале проводится
рассмотрение), то полученные решения линейно независимы. Общее
решение имеет вид
Неоднородное уравнение. Общее решение у
линейного неоднородного уравнения равно сумме
общего решения соответствующего однородного
уравнения z и частного решения у неоднородного
уравнения: у = z + у. Для вычисления у применяют
один из следующих методов.
Метод вариации постоянных.
Запишем искомое решение в виде общего решения
соответствующего однородного
дифференциального уравнения у = Сху^ + ... + Спуп и
предполоРешая эту линейную систему, получаем C'v, a
затем квадратурами получаем и Cv(x). В результате
частное решение линейного неоднородного
уравнения записывается в виде
При этом Wv(x) - определители, которые
получаются из определителя Вронского W(x) для функций
Ух (х), ..., у„(х), если элементы v-ro столбца
заменить на 0, 0, ..., 0,f(x). Полученное таким образом
частное решение у(х) уравнения C.36)
удовлетворяет условиям
Метод Кош и. В общем решении линейного
однородного дифференциального уравнения
выберем коэффициенты Cv так, чтобы при х = а
выполнялись условия у (а) = 0, / (а) = 0, ..., у(п~2) (а) = О,
yin~i)(a) =f(a), где а — произвольный параметр.
Если у(х, а) есть полученное таким образом реше-
х
ние однородного уравнения, то у(х) = J y(x, a)da-
х0
частное решение уравнения C.36), для которого
1
Пример27.х2A -х)/ + 2хB-х)/ + 2A +х)у = х2.
В канонической форме это уравнение имеет вид
„ 2B-х) , 2A +х) 1
У + х(\-х)У + х2A-х)У 1-х'
Для непрерывности коэффициентов ограничимся одним
из интервалов (-оо, 0), @, 1), A, оо). Общее решение
соответствующего однородного дифференциального уравнения есть
(х - IK
и W(x)«
(см. пример 26). Далее, W, (х) - (* а1J и W2 (х) - 2Х
эх х [х — i
Следовательно, для интервала @, 1) или (-оо, 0)
х , (х-1)(Зх-2)
ш~9+ 6х
откуда
(х - IK
Зх
1п|х-1| +
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
315
3.3.1.3.2. Линейные уравнения с
постоянными коэффициентами. Уравнение
п-го порядка с постоянными коэффициентами
имеет вид
аоу(п) (х) + fll/"-l) (х) + ... + а„_ ! у' (х) + апу(х) =
= /(х) (во#0).
Однородное уравнение. Однородному
дифференциальному уравнению аоу(п) + ... + а„у = О ставится
в соответствие характеристический многочлен*)
Рп (г) = aor" + а^""! + ... + а„. Этот многочлен
можно представить в виде
Рп (г) = «о (г - г^г... (г - ф (г - (Pl + iqi))h ...
где ? /cs + 2 ? /s = п. При этом rs — различные
5=1 5=1
действительные корни кратности ks, а ps + iqs,
Ps — itls — различные пары комплексно
сопряженных корней кратности ls (коэффициенты
характеристического многочлена действительны).
Отдельным сомножителям Р„(г) поставим в соответствие
следующие функции: (г - rs)s - функцию ys(x) =
= (Ы + b2sx + ... + bkssxks~ >) <А\а(г - (ps + iqM))l.(r -
- (Ps - iqs))ls - функцию
*x cos qsx
(dlg
sin qsx.
Количество всех коэффициентов — произвольных
постоянных bks, cks и dks - в точности равно п. Общее
решение однородного дифференциального
уравнения может быть записано в виде
У =
+ У2(х) + ... + ykv{x) +
П р и м е р 28. У5) - 2/4) + 8/ - 12/ + 8у - О,
Ps (г) «г5 - 2г4 + 8г2 - \2г + 8 -
-(г + 2)(г-A+ОJ(г-A-0)а.
Сомножителю (г + 2) соответствует функция ух (х) =
= bie~2x, а сомножителю (г — A + i)J(r — A — i)J
соответствует функция
«1 (х) = (с} + с\х) е* cos х + (d\ + d\x) ё* sin x.
Общее решение имеет вид
y(x) = ble-2x + ex[(c\ + c?x)cosx + (d\ +<f2x)sinx].
Неоднородное уравнение. Общее решение
линейного неоднородного уравнения с постоянными
коэффициентами можно представить в виде у =
= z + у, где z — общее решение однородного
уравнения, а частное решение у неоднородного
уравнения можно найти вариацией постоянных или
методом Коши. Еще один способ решения таких
уравнений — это операторный метод (см. 3.3.1.6).
Наиболее просто находится частное решение
линейного неоднородного уравнения с
постоянными коэффициентами, если правая часть
{возмущающая функция) имеет специальный вид.
Некоторые примеры. Пусть Qk (х) —
многочлен степени к. Если правая часть
уравнения имеет вид/(х) = Q^fx)^*, то частное решение
ищется в виде у = Rk (x) етх, где Rk (x) - многочлен
степени к с неопределенными коэффициентами, при
условии, что т не является корнем
характеристического многочлена Р„; частное решение ищется в
виде ^ = x4Rk (х) етх в случае, если т есть д-кратный
корень характеристического многочлена. Если
правая часть имеет вид f(x) = Qk(x)emx sinoax или
Qk (x) emx cos сох, то частное решение ищется в
виде у = етх (Rk (x) cos cox + Sk (x) sin сох), если т + /со
не является корнем характеристического
многочлена; частное решение ищется в виде у =
= xqemx (Rk (x) cos cox + Sk (x) sin сох), если т ± /со
является g-кратным корнем характеристического
многочлена. В обоих случаях Rk(x) и Sk(x) —
многочлены степени к с неопределенными
коэффициентами.
Если правая часть представляет собой
линейную комбинацию вышеуказанных функций, то
частное решение уравнения равно сумме решений,
соответствующих каждому члену линейной
комбинации.
Например, при /(х) = аетх, где Рп(т)ф0,
аетх
частное решение имеет вид у = ———; если т
является g-кратным корнем характеристического
многочлена, то частное решение имеет вид
Пример 29. /" - 3/ + у - Зу = бе3*.
Характеристический многочлен Р3 (г) = г3 - Зг2 + г - 3 = (г - 3)(г + /)(/¦ •«-
- i) имеет простой корень г = 3. Тогда у - — хеЪх и у =
*) Этот многочлен можно получить, подставив
выражение у = егх в дифференциальное уравнение.
= Tq-^3x + CV3* + С2 sin x + C3 cos х.
Пример 30. У + 4У + 4у = х2 + e*-sinx.
Характеристический многочлен имеет вид Р2 {г) = г2 4- 4г + 4 = (г - 2J.
Частное решение ищется в виде у = (Ах2 + Вх + С) +
+ De* + (? cos х + Fsinx). Подставим его в
дифференциальное уравнение
2А + De* - Ecosx-Fsinx + SAx + 4B + 4D** -
- 4? sin x + AF cos x + AAx2 + 4?x + 4C + 4Dex +
+ 4? cos x + AF sin x = x2 + e* - sin v.
Приравнивая коэффициенты, получаем систему
АА - 1, 8/4 + АВ * 0, 2А+ АВ + АС = 0,
9D - 1, 3? + AF - 0, - 4? + 3F = - 1.
Решая эту систему, находим вид частного решения
а общее решение исходного уравнения имеет вид
у = у + Схе2х + С2хе2х.
Дифференциальное уравнение Эйлера
может быть сведено к линейному
дифференциальному уравнению с постоянными коэффициентами
подстановкой сх + d = е*.
316
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Пример 31.
IK/"-(*+ 0/-З
Это уравнение при подстановке (х+1) = ?' переходит в
уравнение
1)\ Л и у вилл я
d2y dy
dy it
j - J ? Pkk (t) dt].
det (уи (х)) = det (уи (х0)) exp j - J ? Pkk (t) dt
1. Если yi(x) (i = 1, 2, ..., m) — набор m вектор-
решений линейной однородной системы, то их
(рассмотренное в примере 29) Следовательно, y(t)-
6 т
= 7оГ*31' + <V3' + C2 sin t + С, cos f, а общее решение дан- линейная комбинация у(х) = ? С.у, (х) есть век-
ного уравнения имеет вид '~'
у(х) = -(х + IK In | х + 1 | + С, (х + 1)J + С2 sin (In | х +
+ 1 |) + C3cos(ln|x + 1
тор-решение (С, - произвольные постоянные).
2. Если т > п, то т вектор-решений линейной
однородной системы всегда линейно зависимы на
(а, Ь).
3. Каждая линейная однородная система
3.3.1.3.3. Линейные системы диф- всегда имеет фундаментальную систему вектор-
ференциальных уравнений. Рассмотрим решений, т.е. п линейно независимых
вектор-решений. Если у! (х), ..., у„ (х) образуют фундамен-
линейную неоднородную нормальную систему
У\ (*) + Pi 1 (*) Ух (х) + р12(х) hW + ...
-'. + Pm(x)
У'г(х) + P2i (х)ух (х) + ргг(х)у2(х) + ...
¦-+Р2п(х)у
У'п (х) + рв1 (х) У1 (х) + рп2 (х) у2(х) + ...
тальную систему, то у (х) = ? С;у,- (х) (С,- — произ-
j=i
вольные постоянные) есть общее вектор-решение
системы.
4. Если m(x) = (w!(x), ..., и„(х))Т есть вектор-
решение линейной однородной системы и Mj (х) Ф 0
на (а, Ь), то число неизвестных функций в данной
системе можно уменьшить. Для этого нужно
решить систему уравнений
которая может быть записана также и в
векторной форме:
y'(x) + P(x)y(x)=f(x),
Р(х)
РнХ (Х) .-. Рпп (Х) J
Решением данной системы будет набор п функций
у (х) = ()>! (х), ..., у„ (х))г, называемый вектор-
решением. Если /| (х) = 0 (i = 1, ..., и), то система
называется однородной. Такие линейные системы
решаются при помощи приемов, аналогичных тем,
которые применялись для решения линейного
дифференциального уравнения n-го порядка.
Однородные системы. Данные т вектор-решений
yt(x) = (ytx(x), ..., yin(x))T(i= 1, 2, ..., m)
называются линейно зависимыми на интервале (а, Ь),
если существует т чисел С, таких, что
I Ctyt =0, ? | С, | >0.
;=i ;=1
Если же это равенство возможно лишь при
условии Сх = ... = Ст — 0, то т вектор-решений
называются линейно независимыми; п
вектор-решений однородной системы У((х) = (уц(х), ..., yin(x))T
(/ = 1, 2, ..., и) линейно независимы только тогда,
когда существует точка хое(а, Ь) такая, что
det уи (х0) Ф 0. Тогда det уи (х) ф 0 для всех
хе(а, Ъ). Это следует из обобщенной формулы
4М
состоящую из п — 1 однородных линейных
дифференциальных уравнений.
Пусть \ = (zq2, ..., zqn)T(q = 2, 3,..., n) -
фундаментальная система решений этой системы. Тогда
векторы yq (x) = vq (x) и he) + zq (x) {q = 2, 3, ..., и),
где zq = @, 2,2, ..., zqn)\
vq(x)= -
(q = 2, 3, ..., n),
вместе с вектором м(х) составляют
фундаментальную систему исходной однородной системы.
Пример 32.
2х2 + 1
Будем искать решение в виде у{ (х)
avx\ y2 (х) =
= ? Mv, где yi @) = 00= 1, У г @) = Ьо = 0. Подставим yi и у2
v-0
в систему, в которой первое уравнение предварительно
умножено на х2(х2+1), а второе - на х(х2+1). Тогда,
приравнивая коэффициенты при одинаковых степенях х,
получим: as — 0 для v = 1, 2,. . ; bv — 0 для v = 0, 2, 3, ...;/>, = 1.
Таким обра юм, м(*) = A, х)^ есть частное вектор-решение,
2х
причем м, (х) = 1 ф 0. Составим уравнение z'2 -г— г2 = 0
и найдем его решение z2 — (х2 ¦+ 1); тогда z2 = @, х2 + 1)^. Вы-
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
317
-J,
(x) dx т , В результате по-
числим v2(x)
лучим
УЛх) - - тО' *)Г+ <0' * + 1)Г- (~ Т' *г)Т
+ {Ах - Аг) + {Вх - Ах)х + (В2 - А2) - 0,
(В, - В2) + (ЗЯ, - ААХ) х + (ЗЯ2 - 4^а) - 0,
Фундаментальной системой решений будет
ух (х) ш и (х) - A. xtf л (х) - ( - А дс2O
откуда имеем: в, - 2АХ - 0, Ах - 2А2 + В2 - 0,2В, - ААХ - 0,
Вх + 2В2 - 4А2 ш 0. Следовательно, Ах » у В, и А2 -
ш~2^г + ~7**1' ^сли положить ВхшСх и В2»С2, то
получим общее вектор-решение
5. Для линейных однородных систем с
постоянными действительными коэффициентами (т. е.
— р^ = atj = const) фундаментальную систему
находят следующим образом (ср. 2.4.4.5). Сначала Таким образом, два линейно независимых вектор-решения
определяют корни характеристического много- данной системы имеют вид
члена / / v I \ \Т
Pll + Г р12 ... Pin
Рг\ Ргг Л- г ... р2п
Р»\
Рп2
Рпп
= 0.
Если гх - простой корень характеристического
уравнения Р(г) = 0, то, подставив решение ух (х) =
— ег\х(Аи А2, ..., Ап)Т(А( = const) в систему,
определим А{; они будут зависеть от одной
произвольной постоянной. Значит, и частное вектор-решение
будет содержать одну произвольную постоянную.
Если rt есть р-кратный действительный корень
уравнения Р (г) = 0,то, подставив у^ (х) = ег^х(А1 (х),
А2(х), ..., Ап(х))т (Л, (х) - многочлен степени
р - 1 с неопределенными коэффициентами) в
однородную систему, найдем коэффициенты всех
многочленов. Они будут выражены через р
произвольных параметров. Следовательно, получим
частное решение с р произвольными
постоянными.
Если гх - простой комплексный корень
уравнения Р(г) = 0, то корнем является также
комплексно сопряженное число г{. Решение ух (х) строится
только для одного из этих двух корней, так же как в
случае простого действительного корня (только
теперь А{ — комплексные постоянные). Тогда Re^j)
и \т(ух) являются действительными
вектор-решениями, соответствующими данной паре
комплексно сопряженных корней характеристического
уравнения.
Если гх является р-кратным комплексным
корнем уравнения Р(г) = 0, то поступаем, как и в
случае действительного р-кратного корня, а затем в
качестве вектор-решений, соответствующих
корням гх и ?и берем Re^j) и \т(ух).
Неопределенные постоянные (коэффициенты многочленов At)
берутся комплексными, как в случае простого
комплексного корня.
Пример 33. у\ - ух + уг - 0, у'г - 4у, + Ъуг - 0.
Характеристический многочлен имеет вил
Р{г).
-1+г +1
-4 +3+г
г, ~ -1 есть двукратный корень. Поэтому решение ищем в
виде у(х) ш е'х{Ахх + Аг% Вхх + В2)Т.
Подставив эти значения У\ и у2 в рассматриваемую
систему, после почленного умножения на е* получим,
Общий вид системы линейных однородных
дифференциальных уравнений 1-го порядка с
постоянными коэффициентами есть
W +
(х) = 0
1,2,..., п).
Если det (aik) не обращается в нуль, то систему
можно привести к рассмотренному выше
нормальному виду. Однако решение можно получить и
непосредственно из данной системы тем же
методом, что и в случае нормальной системы. Случай
det (aik) = 0 мы не рассматриваем.
Неоднородные системы. Общее вектор-
решение у неоднородной системы равно сумме
частного вектор-решения ~у неоднородной системы и
общего вектор-решения соответствующей
однородной системы.
Чтобы найти у, можно применить метод
вариации постоянных. Для этого произвольные
постоянные С, в общем вектор-решении
однородной системы заменяем неизвестными функциями
С,(х):
Я*)= t Ct(x)yt(x),
и затем подставляем полученное выражение в
неоднородную систему.
Для производных новых неизвестных функций
С\(х) получаем неоднородную систему линейных
алгебраических уравнений. Решая ее, находим
(после интегрирований) функции Су (х), ..., Сп(х).
Подставив эти функции вместо постоянных в
решение однородной системы, получим искомое
частное вектор-решение неоднородной системы.
Например,
C.36а)
есть частное вектор-решение неоднородной системы
при условии, что у (х0) = 0. При этом yi (х) =
= (уц (х), ..., yin(х))Т (/ = 1, 2, ..., л) - линейно
независимые вектор-решения однородной системы,
а Д (х) — определители, которые получаются из
det (yik (x)) заменой i-й строки на строку,
составленную из свободных членов/! (х),... ,/„(х)
неоднородной системы.
318
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Пример 34. у, - ух + у2 - х, у'2 - 4у\ + Ъуг » 2.
Подставляя в систему у(х) т С1(х)е'х1 у + -j, х) +С2(х)е~* х
х (—, 1J (см. пример 33), получим, что
(т+т)
Сх (х)+т
Отсюда С", (х) - 4е* (х - 1), С2 (х) - 4е* ( - х
интегрирования получаем
xCi (х)+с'2 {х)е*-
После
-i
(Зх - 7, 4х - \0)Т.
Общее решение имеет вид
- (Зх - 7, 4х - 10)г+ Схе-*(~ + -~, xY + С2е
Пример 35.
' 1 1 1
У1+ х(х2 + \)У1~ х2(х2 + \)У2Ш^'
Известно общее решение соответствующей однородной
темы (с
при этом
Известно общее решение соответствующей однородной
системы (см. пример 32): z(x)-C,(l, x)T+C2(—~, х2У\
D,-
detW.
1/х 1
-1/Х X2
1
-1/х
Х2 +
X
X
X2
1
-X2
2 т
+1.
1
1/х
X
1
¦ 0.
Находим теперь у, используя приведенную выше формулу
C.36а):
Р(х) - У1 (х) Г-~ rfx - In | х | A. х)т.
Общее решение имеет вид
Для случая, когда в правых частях уравнений
стоят функции специального вида Qk (x) emx (Qk (x) —
многочлен степени к), можно применить метод
неопределенных коэффициентов, который был
описан при рассмотрении линейного
дифференциального уравнения n-го порядка с постоянными
коэффициентами.
Замечание. Вышеуказанные методы можно
перенести и на системы линейных
дифференциальных уравнений более высокого порядка.
3.3.1.3.4. Линейные
дифференциальные уравнения 2-го порядка. Рассмотрим
уравнение
а(х)у" + Ь(х)у' + с(х)у = F(x).
Предположим, что существует интервал /, на
котором функции а(х), Ь(х), с(х) непрерывны и а(х) Ф 0.
Тогда дифференциальное уравнение можно
разделить на а(х) и к полученному уравнению
У" + р(х)у' + q(x)y=f(x),
нить общие положения из 3.3.1.3.1.
В частности, общее решение соответствующего
однородного уравнения (/(*) = 0) может быть
записано в виде
У = Сху, (х) + С2у2 (х),
где у1 (х) и уг (х) — линейно независимые частные
решения однородного уравнения, Сх и С2 - про-
1 извольные постоянные.
Если известно частное решение у^ (х)
однородного уравнения у^ (х) ф 0 на /, то заменой
переменных у = ух J у (х) dx порядок исходного уравнения
можно понизить; для у получим уравнение
Тогда
и уг (х) = Аух (х)
х/. ехр I - J p (s) ds I
J у? (О
dt
{А Ф 0 — произвольная постоянная) — два линейно
независимых решения однородного уравнения
f+p{x)? + q(x)y = 0.
Общее решение неоднородного уравнения имеет
вид
У = z + у,
где z — общее решение соответствующего
однородного уравнения, а у — частное решение
неоднородного уравнения.
Частное решение у может быть найдено методом
вариации постоянных по следующей формуле:
У(х) =
\f(x)y2(x)eir(x)<lxdx.
Предположим теперь, что существует точка х0,
в которой а (х), Ъ (х), с (х), F (х) - аналитические
функции, т. е. их можно разложить в сходящиеся
ряды по степеням л; - х0. Будем считать, что
а(хо)ф0.
Точки, в которых выполняются эти условия,
называются регулярными точками
дифференциального уравнения. Тогда решения этого уравнения
тоже могут быть разложены в ряды по степеням
(х — х0), сходящиеся в той же области, что и ряды
для коэффициентов. Эти решения можно найти
методом неопределенных коэффициентов. Для
этого искомое решение записывается в виде ряда
У(х)
а*(х ~ хоУ и подставляется в дифферен-
циальное уравнение. После приравнивания
коэффициентов при одинаковых- степенях х — х0
получаем формулы для отыскания av (v = 0, 1, ...).
Пример 36. у" + ху ш 0. Для х0 - 0 все сделанные
предположения выполнены. Предполагаемое решение >'(х)-
ш ? ОуХу подставляем в дифференциальное уравнение и
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
319
получаем
Из C.37) найдем два значения гх и г2 и с учетом
формул C.38) получим два решения:
следовательно,
для v= 1,2,...
По этим рекуррентным формулам все коэффициенты
выражаются через а0, сх: «2=0, а3--уу«0, «4=
Ы*)= f я<2>(*-*оГ'*.
v = 0
Построение общего решения исходного уравнения
зависит от связи между гх и г2.
Случай 1. гА - г2 - нецелое число. Тогда
У\ (х) и у2 (х) линейно независимы, и общее решение
Дифференциального уравнения имеет вид
-tV«i. «5=0, ..., и решение записывается в виде У(х) = Z ^(х - xo)v + ri + ? о[2)(х - xo)v+r2-
C хб \
1- —+ -.,.) +
3-4 + 3-4.6.7
Предположим теперь, что дифференциальное
уравнение при Г(х) = 0 можно записать в виде
(х - х0J у" + (х - хо) р (х) y' + q{x)y = O,
причем р(х) и q(x) аналитичны в точке х = х0.
Такая точка х0 называется регулярной особой точ-
коп (или слабо особой точкой). Можно показать,
что существует по меньшей мере одно
решение вида
у(х)= ? av(x-x0)v+r,
где число г не обязательно целое, причем ряд
сходится при | х - х0 | < R (если ряды,
соответствующие функциям р(х) и q(x), сходятся при
| х - х0 | < R). Подставляя ряды для функций у(х),
р (х) = ? pv (х - xo)v и q (х) = Ya 4v (x - xo)v
v=0 v=0
в исходное уравнение, получим
? av(r + v)(r + v - 1)(х - xo)r+v +
/ + I Pv (x - xoy ? av (r + v) (x - xor+v +
v = 0 v = 0
+ ? q,(x - xoy f Ov(x - xo)r+v = 0.
В предположении, что а0 Ф 0, вычислим
коэффициент при (х - хо)г в данном соотношении. Имеем
_ j\ r _|_ _ _q
C 37)
Это уравнение называется определяющим уравне-
нием для г. Коэффициент при (х — xo)r+v, v = 1, 2,...,
равен
flv [(г + v) (г + v — 1) -f Po (r + v) + </о] +
+ I CM' + v - s) + gj flv-. = 0. C.38)
Случай! Г! = г2. Тогда yi(x) = Cy2 (х)и можно
показать, что общее решение записывается в виде
П (х) + Уг (x), где >4 (х) = У1 (х),
v^4 / да
— хо)Г1 / 1——
+ (х — хо)Г
or
\
I
(х — xo)v.
С л у чай 3. г2 = гх - и, где «-натуральное
число. В этом случае общее решение имеет вид
у (х) = у 1(х\ + у2 (х\
У1 (х) = У1W. а
где
_
y2 (x) = gnyi (x) In (х - хо) + (х - хо)Г2 ? К (х- хо)\
v = 0
где д„ - коэффициент при хи в выражении
и +
х
_ J rlp(t)dt
+ *о))
Коэффициенты bv определяются из
дифференциального уравнения.
Замечание. В некоторых задачах требуется
найти решения уравнения у" + р (х) / + q (х) у = 0
для больших х, т. е. решения в виде бесконечных
рядов по переменному 1/х. Пусть р(х) и q(x) ана-
литичны при х = оо, т. е. их можно разложить в
сходящиеся ряды по переменному 1/х. Замена
переменного х = 1/z приводит к уравнению
dz2
2
Точка х = оо называется регулярной точкой
исходного дифференциального уравнения, если
z — 0 является регулярной точкой преобразованного
уравнения. Для этого необходимо и достаточно,
чтобы
р(х) = — + О(х), g(x) = 0(x~4)
при х-*оо. Решения имеют вид
320
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Точка х = оо называется регулярной особой где J-n(x) определяется рядом, получающимся
точкой, если z — 0 является регулярной особой точ- из ряда для Jn(x) заменой п на -п; при целом п
кой преобразованного дифференциального урав- справедлива формула
нения. Для этого необходимо и достаточно, чтобы , u*i t \
Общее решение уравнения Бесселя при целом п
имеет вид
при х-> оо. Соответствующее определяющее урав- у(х) = С^„(х) + C2Yn(x).
нение имеет вид г2 + A - р0) г + q0 = 0, и в случае,
если rl-r2 не целое число, решения представ- Функция Yn (x) (обозначается также Nn (x)) называет-
ляются рядами ся функцией Бесселя (функцией Неймана, функцией
в ю Вебера, цилиндрической функцией) 2-го рода п-го
yi(x)= У avx~ri~v, у2(х)= У avx~r2~v порядка; для нецелых чисел п она определяется
v = 0 V ' v = 0 V формулой
у / V4 Jn M COS (nn)-J.n(x)
rn \X) = :—; .
Дифференциальное уравнение Бесселя
am ynnj
x2y" + xy' + (x2 - п2) у = 0.
Для целого п функция Yn(x) определяется равен-
Точка х = 0 - регулярная особая точка, и оп- ством
ределяющее уравнение имеет вид г2 — п2 = 0. г , ч . ч т , ,
Jn(x)cos(mn) - J-m(x)
Отсюда следует, что гх = п и г2 = -п. Если подста- Yn(x) = lim
вить у(х) = ? avx"+v в уравнение, то после
приsinfmn)
равнивания коэффициентов при одинаковых
степенях х получим, что Bп — 1) ах = 0, vBn + v) av +
+ Оу_2 =0 при v = 2, 3,..., п. Из этих рекуррентных
формул следует, что
2
2Y
х >
для /с = 1, 2, ... и произвольного а0 ф 0. Решение,
1
полученное при а0 = 2пГ(п + п > определяет где m - близкое к и нецелое число, С - постоян-
функцию Бесселя (цилиндрическую функцию) 1-го
рода п-го порядка:
x (Ф (г +
Графики функций Jo (x), Jx (x), 32 (х) и J3 (x)
изображены на рис. 3.61.
ная Эйлера (С = 0,5772...) и
к
ф(к)= \ —, Ф@) = 0.
s= 1
Графики функций Уо (х) и Yt (x) изображены на
рис. 3.62.
В случае целого п часто удобно рассматривать
в качестве линейно независимых решений две
Рис. 3.61
Общее решение уравнения Бесселя в случае,
когда п не целое, имеет вид
Рис. 3.62
функции Н{п1] = Jn(x) + iYn(x) и Н{„2) = Jn(x) - iYn(x)
и записывать общее решение в виде
*) Относительно гамма-функции см. 2.2.1.1, 3.1.9.4
Функции Н[1) и Н{2) называются функциями
Бесселя 3-го рода п-го порядка (или функциями
Ганке л я).
В некоторых приложениях рассматривают
модифицированные функции Бесселя 1-го рода п-го
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
321
порядка чисто мнимого аргумента
Zl /x\2v+"
(п произвольное) и модифицированные функции
-3 -2 -у~
/ -I
/ '2
I -3
Важнейшие формулы для функции Бесселя
1-го рода п-го порядка:
C.39)
C.40)
C.41)
In
dJn
d
d
1x
jn (x) = Jn
(x)
X X
— (x"J (x1
dx "
•\x ИЛМ)
0 I 2 3 x
-4 -
Рис. 3.63
Частный случай: J'0(x)= — Jj(x);
2-1—1 1
^ (x) = -/14 ^/ TV f(! - J
J,5
a^
Частный случай:
j (х)- 2 Г СО8И А
JOW"-J A_ ,2I,2*-
О
Для целого п имеют место соотношения
x-Vn(x) = (-ir^^-JjoW (л =1,2,...),
-k~-x
Рис. 3.64
Бесселя 2-го рода п-го порядка (или функции Мак-
дональда)
—
j2n (х) = — cos (x sin t) cos Bnt) dt,
Jin+1W = — sin (^sin 0sin (Bn + U *) &u
Кп (х)
= (- 1Г 1/„ W (in (j) + CJ
Функции Бесселя при п = 0, 1, 2, ... можно
получить разложением известных функций в ряды
Лорана:
exp[x(t-r1)/2]=J0(x)+ ? (t« + (-t)-»)Jn(x),
или в ряды Фурье:
cos(xsinf) = J0(x) + 2
(n целое). Тогда функции
y(x) = ClIn(x) + C2I-n(x) для нецелого п,
y(x) = CJn(x) + С2К„(х) для целого л
дают общее решение уравнения и = 1
х2/' + х/ - (х2 + п2) у = 0.
00
Графики функций /0, /i и Ко, Кх показаны на sin(xsirit) = 2 ]T J2n-\(x)s\n(Bn - \)t).
рис. 3.63 и 3.64. « = 1
11 И. Н. Бронштейн, К А. Семендяев
322
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Сферические функции Бесселя
(и +
(и + 1/2
можно выразить через элементарные функции:
1/2)(х)
Jm (х) = (--У (fm (х) sin x-gm (x) cos x),
^-) (gm(x)smx +
кх /
+ /m(x)cosx)
(здесь т — и 4- 1/2; п = О, 1, 2, ...), где
т
1
2
3
2
5
2
7
2
9
2
11
2
1
1
V
.х" '
Л. _ А
ЛЧ Л'
105 45 .
Л4 .V2
945 420 15
0
1
з
А
х2
[05 _ Ю
•Vя х
945 105 j
Дальнейшие выражения можно получить из
рекуррешмых формул.
Для >,,(y), Н1„1){х) и Н(п2)(х) имеют место
соотношения, анало! ичные соотношениям C.39),
C.40) и C41) для Jn(x).
Важнейшие формулы для модифицированных
функций Бесселя 1-го рода п-го порядка:
2пКп(х) = х (Кп + 1 (х) - Кп-{ (х)),
2 Li
2-U
Частный случай:
K'o(x)= -
Для больших значений х справедливы следующие
асимптотические формулы:
где О A/х) - бесконечно малая величина порядка
1/х, т. е. хОA/х) остается ограниченной при х -юо.
Любая функция, которая является решением
дифференциального уравнения Бесселя, называется
цилиндрической функцией Zn(x) порядка п. Для
ZH=Jn, Zn = J-n справедливы формулы
Zw+1(x) = ~Zw(x)-Zn_1(x) =
Гипергеометрическое дифференциальное
уравнение имеет вид
хA - х)у" + (с - A + а + Ь)х)у' - аЬу = 0,
где а, Ь, с — постоянные. Регулярные особые
точки:
х = 0, тогда гх = 0 и г2 = 1 - с;
х = оо, тогда Г] = а и г2 = Ь;
х = 1, тогда гг =0 и г2 = с — а — Ь.
В окрестности регулярных особых точек общие
решения имеют следующий вид:
1) В окрестности точки х = 0
y(x) = C1F(a, b; с; х) +
+ C2x1~cF(a^c+ 1; b-c+ 1; 2 -с; х),
если 1 — с не нуль и не целое отрицательное число;
y(x) = ClF(a, b; с; х) +
¦C2f\ F(a, b; с;
X) In X + Yj arx'
¦]¦
если с = 1 (числа аг определяются из
рекуррентных формул).
2) В окрестности точки х = 1
у(х) = CxF(a, b; a + b - с + 1; 1 - х) +
С2A -x)c-fl-*F(c-b, с-а; с-а-Ь+ 1; 1 - х).
3) В окрестности х = оо
^(х) = С!Х-^(а, а-с + 1; а - b + 1; 1/х) +
-I- C2x"bFF, Ь-с+1; Ь-с+1; 1/х),
где F(a, Ь; с; х) = ?((а
к 0
! (c)k))xfc (числа
определяются равенствами (аH = 1 и (а)к =
= а (а + 1) (а + 2)... (а + к - 1) при /с > 0). Этот ряд
абсолютно сходится при | х | < 1, если с не нуль и
не целое отрицательное число; расходится при
| х | > 1, если а и b не являются целыми и
отрицательными, и при | х | = 1 ряд абсолютно сходится,
если с > а + Ь. При х = 1 ряд расходится, если
а и b не являются целыми и отрицательными,
если с < а + Ь, при х = — 1 ряд сходится условно,
если a + b-l<c^a + b, и расходится при
с ^ - 1 + а + Ь.
ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ И ЛИНЕЙНЫЕ СИСТЕМЫ
323
Некоторые важные соотношения для
гипергеометрической функции F(a, b; с; х) (| х \ < 1):
F(a, b; с; x) = F(b, а; с; х),
F(a, Ь; с; х) =
aF(a + \;с + 1;х) = cF(a;c;x) + (а - с) F(a;c + 1;х),
F(a; с, x) = exF(c — a; с; —х), F(c; с; х) = ех.
Функции F(a, Ь; с; х) и F(a; с; х) — частные
случаи обобщенной гипергеометрической функции
pFq(au аъ ..., ар\ с\, ..., cq; x) =
(о а> 0),
F(a,b;c; х) = — F (а + 1, b + 1; с + 1; х),
(с - а - i)F(a, b; с; х) + aF(a + 1, Ь; с; х) -
-(с- l)F(a,b;c- 1;х) = 0,
с [с - 1 +A + а + b - 2c)x]F(a, b; с; х) -
-с(с- 1)A -x)F(a,b;c- 1; х) +
+ (а - с)(Ь - c)xF(a, b; с + 1; х) = О,
F(a, />; с; х) = A - x)c-fl-"F(c - а, с - Ь; с; х),
30
¦ъ
где сь с2, ..., cq ф 0, —1, —2, ... Поэтому можно
записать
F(a, b; с; х) = 2FX (a, b; с, х),
F(«; с; х) = ^(я; с; х).
Существуют также обобщенные
гипергеометрические функции нескольких переменных; например,
для двух переменных:
F(.,b;c;l)= 3^G^)
(с - а - b > 0, с - а > 0. с - b > 0).
При некоторых значениях параметров
гипергеометрическая функция выражается через
элементарные функции, например:
F(a, л; а; х) = A - х)~" (а - произвольное),
\2* 2' 2' )
,2' 2' 2' / х
Вырожденное гипергеометрическое
дифференциальное уравнение:
ху" + (с — х) у' — ау = О,
или уравнение Куммера. Регулярная особая точка
есть х = 0, причем rt = О и г2 = 1 — с. В
окрестности х = 0 общее решение имеет вид
у(х) = C{F(a; с; х) + С2х1~с F(a - с + 1; 2-е; х)
для с ф 0, —1, —2, — 3, ... Функция F(a; с; х)
называется функцией Куммера или вырожденной
гипергеометрической функцией. Она разлагается в
степенной ряд
F(a,b,b;c;X,y) = ? ~
Дифференциальное уравнение Лежандра для
целых п ^ 0:
A -х2)/' -2х/ + и(и+ 1)у = 0.
Регулярные особые точки суть х = — 1 с
показателями гх = г2 = Оих = 1 с показателями г, = г2 — 0.
Введением нового переменного х = 1 — 2t уравнение
Лежандра приводится к гипергеометрическому:
10 - 0 ~f
= о,
где a = п + 1, Ь = -п и с = 1. Таким образом,
частное решение есть многочлен
/ 1 х\
Pn(x) = Fln+ 1, -л; 1; —у—К
так как ( —и)и = 0 для т > п. Многочлен Рп(х)
называется многочленом Лежандра степени п.
Многочлен Рп (х) — единственное линейно независимое
сходящийся при всех х.
Некоторые важные соотношения
для функции Куммера:
для с > а > 0,
1,0
= ^~F(a + n; с + п; х),
11*
решение уравнения Лежандра, ограниченное в
точках х= 1 и х= -1. На рис. 3.65 изображены
324
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
графики первых восьми многочленов Лежандра: мая функция при — 1 < х < 1, то разложение
РзМ = -2-Eх3-Зх),
Р4 <х\ _ __ И5х4 — ЗОх2 + 3)
8
р5 (х) = -^-F3х5 - 70х3 + 15х),
16
1
р7 (Х) = D29х7 - 693х5 + 315х3 - 35х).
16
Важнейшие соотношения для мно-
гочленов Лежандра.
есть многочлен л-й степени с коэффициентом - п 2
при старшей степени. Многочлен Ри(х) имеет ровно
л простых действительных корней в интервале
-1 <х< 1.
Для многочленов Лежандра справедливы
следующие формулы:
х±(х2 - 1I/2 cos Г)" dt
f dt
](:хТ(?"~1)Т7Гсо77рт (знак любой),
(л + 1) Р„+1 (х) = Bл + 1) хР„ (х) - лР„_! (х),
х2 _ ,) А_ {Рп (х)) = „ {хРп {х) _ Ри_ 1
где ск
= ( —-—) f(x) Pk (x) dx, сходится абсо-
лютно и равномерно на интервале (-1, 1).
Функции, связанные с многочленами Лежандра
Рп(х) соотношениями
(и = 0,1,2,...; т = 0, 1,..., л),
называются присоединенными функциями
Лежандра. Функции Р|Г(х) удовлетворяют уравнению
Справедливы равенства
при п' п ^ т ^ '
\(Рт(х)J dx = "*" '
и (и
f
J
1 -x2
(и —т)! 2п+ 1
при л = 0, 1,...; ю= 1,2,..., л,
2m (л-ал)!
при л = 0, 1,...; т = 1, 2,..., л.
Система присоединенных (для каждого т ^ 0)
функций Лежандра Р™(х) (л = т, т + 1, ...) полна в
Ы-1, 1).
Примеры присоединенных функций Лежандра
{Pi (х) = Р„(х), Р?(х) = 0 для т > л):
(х) = 3 A - х2) = -i(I - cos 29),
1, если л = m,
0, если пФ т.
Многочлены Лежандра можно получить разло-
жением функции A - 2xz + z2)~1/2 в ряд по степе-
ням z:
pi (x) =
= _ ± Eх2 - 1) A - х2I/2 = - — (sin 6 + 5 sin3 0),
2 о
, 15
Pl{x) = 15x(l -x2)= — cos0(cos0- cos30),
Если /(х)-дважды непрерывно дифференцируе-
= - -г C sin 0 - sin 30),
4
УСТОЙЧИВОСТЬ
325
где х = cos 9. Вообще
Рп„(х) = {-1)п \ Ъ • 5 ...Bп - 1)A -х2)л/2 =
= (-1)"-1-3-...-Bи- 1) sin" в
для п — О, 1, 2, ...
3.3.1.4. Общие нелинейные дифференциальные
уравнения. Общее уравнение имеет вид
f(x, у, /,...,/¦>) = 0.
Вопрос о существовании и единственности
решения задачи Коши решается сведением
рассматриваемого уравнения к системе дифференциальных
уравнений и применением к ней теоремы
существования и единственности п. 3.3.1.1.
Частный случай: уравнение у(п)(х) = /(х).
Общее решение находят путем
последовательного интегрирования:
у(х) = С1 + С2(х - х0) + ... + Сп(х - Хо)" +
при помощи формулы Коши последнее слагаемое
можно записать в следующем виде:
X Xi Х„_!
X
f(t)(x-ty-4t.
дает особое решение исходного урав-
Клеро z =
нения
Пусть левая часть уравнения/(у, /, ..., у{п)) = 0
не зависит явно от х. Подстановкой у' = р (у),
где у рассматривается как новое независимое
переменное, можно свести такое уравнение к
дифференциальному уравнению п — 1-го порядка, так
dky
dp
как —-j- выражается только через р, —,..., тт^Т*
В частности,
dy_
dx
dx2
= PdA
P dy*
d3y 2 d2p ( dp\2
dx3 dy2 \dyj '"'
П р и м e p 39. y2 (y - \)y" - (/K - у (у - 2){y'J
образованное уравнение имеет вид
0.
ПреРазделив на р (при этом р = 0, т. е. у - С, является
решением), получим дифференциальное уравнение Бернулли
(см. пример 11), решение которого имеет вид
У2 , V2
-, т. е. у' *
- 1)"
После интегрирования приходим к общему интегралу
исходного уравнения
В этих выражениях х0 не является дополнительной
постоянной: если в х0 заданы у(х0), у'(х0), ...
..., ^""^(хо), то
Пример 37. Решить уравнение у'"-1пх при условиях
УA)-3'о. УA)шУо. У{1)шУо>
Частное решение дается формулой
4 (х-0а1п*А-
•Уо
И у + \* ч «о + — х3 In х -
2! 6
36 2 418'
и общее решение имеет вид
у(х) ш i-x3 In х - -ii-x3 + С, + С2х + С3х2.
Пусть левая часть уравнения/(х, /к\ ук+1>, ...
..., /я)) « 0 не зависит явно от .у и его производных
до Ас — 1-го порядка включительно. Заменой yik) = z
это уравнение приводят к уравнению п — /с-го
порядка.
Пример 38. f - ху'" + (y"f » 0. Замена y"«z(x)
приводит к уравнению Клеро г -* хг' + (z'K «= 0. Его общее
решение есть z-CiX-C3. Отсюда следует, что у(х) =
х3 х2
« Ct -j— С? -г- + С2х + С3. Особое решение уравнения
о 2
Уравнение f (х, у, /, ..., у(п)) = 0, в котором / -
однородная функция относительно у, у',...,у(п\
допускает понижение порядка введением новой
неизвестной функции z = у'/у.
Пример 40. х2уу" = {у- ху'J. При замене z = (In у)' =
= у'/у получается линейное уравнение xV + 2x2 - 1, решение
которого имеет вид г = —j-+—. Общее решение
исходного уравнения получим, учитывая, что (In у)' = г. Тогда
В уравнении /(х, у, у',...,у{п)) = 0, левая часть
которого является полной производной, можно
понизить порядок.
Пример 41. у" ~ ху' - у = 0. Так как -^ (у' - xv) =
= у" - ху' - у = 0, то у' - ху = Сь откуда
Пример 42. уу" = 2 (УJ. Умножение обоих частей
уравнения на (у/) приводит к уравнению {\пу')'=(\пу2)',
откуда In/==1пу2 + 1пСь или / = Сху2. Общим решением
исходного уравнения будет у =s - (С,х + С2)~1.
3.3.1.5. Устойчивость. Пусть ——=/,•(*, хь...,х„)
at
(j = 1, 2,...,и) — система обыкновенных
дифференциальных уравнений. Пусть функции/, (/ = 1,2,..., п)
имеют непрерывные частные производные 1-го
порядка. Обозначим через х, = х, (t; t°, х?,..., xj)
(i = l,...,/i) решение данной системы с
начальными значениями х? при t = г°, т. е. х? = х,
326
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
(f°; t°, x?,...,.vj). Каждое частное решение системы
может бьп ь истолковано как координата дивжущей-
ся ма1ериальной точки (в и-мерном пространстве),
зависящая от времени t.
Движение точки с координатами х, =
= x,(r; f°, х?,...,xj) называется устойчивым в
смысле Ляпунова, если для каждого е > 0 можно
наЙ1и такое 5 > 0, что для всех | х? — х? | < 8
(i = 1,..., л) в промежутке t° ^ t < oo справедливо
неравенство
\х(Ц; t°, x?,...,x?)-x,(f; t°, х?,...,х?) | < е
(i = 1,...,и).
Каждое движение, которое не является
устойчивым, называется неустойчивым. Решение
х,=х,(г; г°, х?,. ..,х°) называется невозмущенным,
a x,=x,(f; t°, x?,...,xj) — возмущенным
движением Геометрически устойчивость означает, что
в каждый момент времени t ^ t° точка
траектории возмущенного движения лежит в достаточно
малой окрестности соответствующей точки
невозмущенного движения.
Посредством замены xt = xf + х, (г), где xf {t) =
= \i(t; t°, x°u ..., x°n) (/=1, 2, ..., n), введем
новые координаты хь ..., х„. Невозмущен-
иое движение в новых координатах описывается
уравнениями Зс{ (г) = 0 (/ = 1,..., п). Пусть эта замена
произведена и требуется исследовать
устойчивость тривиального решения x,(f) = 0 (/=1,...,и)
в смысле Ляпунова, т. е. требуется исследовать,
находится ли точка, соответствующая
возмущенному движению, в е-окрестности нуля при
t° ^ f < oo. В дальнейшем преобразованную
систему будем записывать без черточек над х,. Тогда
для правых частей системы справедливо равенство
/,(г; 0,...,0) = 0. Система ~~ = /,(/= 1,..., п)
может быть представлена в виде
atjxj + ф,- (г; хь ..., х„) (i = 1, ..., п),
причем ciij = -— (Г; 0,..., 0) = const (/, j = 1,..., и),
( Xj
i e. cijj не зависит от г. Система
dxi "
— = I atjxj (i = 1,...,л)
ai , = 1
называется системой, линеаризованной по отноше-
dx, "
нию к ---= 2, я.-Л + ф,-.
"' i=i
Достаточное условие устойчивости
тривиальною решения дает следующая теорема. Пусть
1) все корни характеристического уравнения
dxt A
линеаризованной системы —— = 2, аахь т- е- КОР"
dt
dx
решение системы —— = /, (i = 1, 2,..., п) устой-
dt
чиво. Кроме того, справедливо следующееутвержде-
ние: если хотя бы один корень
характеристического уравнения det(a0 - гЬи) = 0 имеет
положительную действительную часть и ф,-
удовлетворяют условию 2), то тривиальное решение системы
dx{
= ) i неустойчиво.
at
Важно определить, имеет ли
характеристическое уравнение корни с отрицательными
действительными частями. Для этого используется
следствие из критерия Рауса — Гурвица: все корни
уравнения
/(г) = апгп + а„_ хгп-1 + ... + ахг + а0 (а0 > 0)
имеют отрицательные действительные части тогда
и только тогда, когда положительны все
определители
= аи D2 =
ах а0
а3 а2
Dn =
а0
«2
О
О
... О
... О
н-2 «2«-3 «2и-4 •••
(где полагают ат = 0 при m > w).
3.3.1.6. Операторный метод решения
обыкновенных дифференциальных уравнений. Этот метод
состоит в том, что посредством интегрального
преобразования от дифференциального уравнения
переходят к вспомогательному алгебраическому
уравнению. Затем находят решения
преобразованного уравнения и из них при помощи
обратного преобразования получают решения заданного
дифференциального уравнения.
В качестве интегрального преобразования часто
используют преобразование Лапласа
+ 00
F(p) = L{f(t)}= f e-ptf(t)dt.
о
Сведения об условиях, при которых
изображение F(p) существует, о свойствах
преобразования Лапласа и таблицу изображений можно
найти в разделе об интегральных
преобразованиях (см. 4.4.3).
Применение операторного метода
к решению линейных
дифференциальных уравнений с постоянными
коэффициентами. Пусть требуется найти решение
задачи Коши
ни уравнения det (аи — гЬц) — 0, имеют
отрицательную действительную часть;
2) все функции ф, (Г; хь х,..., х„) удовлетворяют
условию |ф,(г; Хь-.^хЛ ^ М< Y, xf>1/2+a,
причем М — постоянная и а > 0. Тогда тривиальное
\ dtn dtn~ dt I
y@) = и,, У(О) = Уо,...,У"}(О) = y\>n-l),
КРАЕВЫЕ ЗАДАЧИ И ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
327
а, (/ = 0, 1,...,п) — постоянные. Преобразованием
Лапласа сведем данное уравнение, используя
обозначения L{y(t)} = Y(p) и L{f(t)}=F(p\ к
вспомогательному уравнению
Qn(n)Y(p) =
= <*о(Р*-1Уо + Р"'2Уо + •
относительно Yх(р) и Y2(р)', получим, что
t-Ca)pa
2(p+lJ
••• + «и-l^o + F(p),
или
где
или &,(/>) У(p) = Af(p) + F(p), где 6.(Р) =
= аор" + Uip"'1 + ... + а„. Решение полученного
уравнения имеет вид
Обратное преобразование, проведенное только
для вюрого слагаемого, дает решение
дифференциального уравнения с нулевыми начальными
значениями.
П р и м е р 43. >•'" - 3/ + у' - Зу = бе3'; у@) = 1, у'@) = 0,
>"@) = 1. В этом случае F(p) - LFe3') ~ -, и решение
р — 3
вспомогательною уравнения имеет вид
у, . _ р2¦_- Зр\ + 2 6
4 ' р3 ->2" + р- 3 (р - 3)(я3 ~ V + р - ЗГ
Для вычисления, обрат ною преобразования V(p)
раскладываем правую часть на простейшие дроби:
« (ПВг* + 15 __ _ 4 \
5 V Р2+ 1 (Л-ЗJ /)-3/
25
При помощи (аблицы преобразования Лапласа по этому
июбражению находим оригинал (см 4.4.3.3)
У it) ¦-
Применение операторного метода
к решению линейных систем с
постоянными коэффициентами. Дана
задача Кош и
I aiky'k(t) + X blky(t) = /,(f) (i = 1, 2,...,и),
У,@) = )>к> 0 = 1, 2,...fn)
при условии det(a(fc)#O. Применяя к этой системе
преобразование Лапласа, получим для
преобразованных функций Yj(p) = L(yi(t)) систему
Ё (№ + bik) Yk(p) = Ft(p) + X ад^о,
где F {(р) = Щ i{t)). Из эгой вспомогательной
системы находим Vk(/?), производим обратное
преобразование и получаем, таким образом,
решение задачи Кош и.
Пример 44. Найти общее решение системы
У'х ~ У\ + У2 = t, у'г - 4.V! + Зу2 = 2.
Положим у, @) = С,, у2@) = С2, решим вспомогательную
систему
(р-
)= z +C2
P2(p + 1):
у (п) С2р3 + B - С2 + ACJp2 - 2р + 4
2W= P2(P+D2
Проведя обратное преобразование, получим общее
решение
ух (t) = 3t - 7 + e~f (D + 2С, - C2)t + 7 + С,),
y2(r) = 4f - 10 + e~'((8 -2C2 + 4Cx)t +10+ C2.
3.3.1.7. Краевые задачи и задачи о
собственных значениях. Во многих случаях необходимо
решать не задачу Коши для дифференциальных
уравнений, а искать решение рассматриваемого
уравнения, которое в граничных точках отрезка,
заданного в области изменения независимых
переменных, удовлетворяет определенным условиям,—
решать так называемые краевые задачи.
Простейшие примеры.
а) Решить уравнение у" + у = 0' с краевыми
условиями у@) = у(п) = 0. Эта задача имеет одно
нетривиальное решение у(х) = sinx.
б) Решить уравнение у" + ау » 0 с краевыми условиями
у@) - у(п) = 0. Нетривиальное решение существует только
для неотрицательных а, являющихбя квадратами целых чисел.
в) Решить уравнение /' + у = 0 с краевыми условиями
у@)-уBп) и / @) = / Bл). Имеется два линейно
независимых решения: >>i(x) = sinx и y2(x) = cosx.
3.3.1.7.1. Краевые задачи. Функция
Грина. Требуется найти на отрезке а ^ х ^ Ъ
решение у(х) следующей краевой задачи:
L [u] = g (x),
где L[u] = fo(x)y" +/i(x)/ + f2(x)y
(/о не обращается в нуль; функции /0, Л» /г, У
непрерывны на а ^ х ^ Ь), с краевыми условиями
«iW =ЛЬ и2[у] =h2,
где
"i |>] = а\ у (а) + а\у'{а) + b\y{b) + bjy'(b),
и2 [у] = ^\yW) + о\у'{<*) + />2^(Ь) + Ь^уЧ^).
Пусть
rang(/l|B) = 2;
а^, bf и Л, — действительные числа.
Полагая у(х) = 0 и h{ = h2 = 0, получаем <к)//о-
родную краевую задачу, которая соответствует
данной неоднородной краевой _
задаче. Однородная
краевая задача всегда имеет
тривиальное решение
у (х) = 0. Если >! (х) и
у2 (х) - решения
однородной задачи, то С\у\(х) +
+ СгУг {*) — также
решение.
Определение
функции Грина
G (х, х)
сформулированной краевой задачи (рис. 3.66). Пусть G (х, х) —
функция, определенная в Q = {(х, х) | а ^ х ^ Ь,
а < х ^ Ь}, со следующими свойствами:
а
Рис 3 66
328
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
а) В каждом из обоих треугольников
D1 = {(х, х) | а ^ х ^ х < Ь) и D2 = {(х, х) \ а ^ х ^
^ х < Ь) функция G (х, х) дважды непрерывно
дифференцируема по х и удовлетворяет
однородному дифференциальному уравнению
/о/ + /i/ + fiy = 0.
б) Функция G (х, х) непрерывна в Q.
в) В интервале а < х < Ъ справедливо равенство
0, x) dG(x-0, х) 1
г) В интервале а <х <Ъ функция G (х, х), как
функция х, удовлетворяет однородным краевым
условиям их [G] = 0 и и2 [G] = 0.
Нахождение функции Грина. Если
yi{x) и у2(х) — два линейно независимых решения
однородного дифференциального уравнения
= 0, то положим
Поэтому функция Грина имеет вид
G(x, x) =
в D2,
в D,
и определим А^х), А2(х\ В^х) и В2(х) так,
чтобы удовлетворялись требования а) — г). Если
однородная краевая задача имеет только
тривиальное решение, то функция Грина существует и
определена однозначно.
Решение неоднородной краевой задачи L[zi] =
= д(х) при условии Ui [zj = m2[zx] = 0 получают
при помощи функции Грина
г1(х)=\б(х, x)g(x)dx.
а
Решение уравнения L[z2]=0 при условии
Mi [Z2] = Ль и2 [z2] = h2 получают, предполагая, что
zi{x) = C^y^ix) + С2у2(х), и определяя Сх и С2
из краевых условий. Решение и исходной задачи
равно Zj + z2. Таким образом, имеет место
следующее утверждение: если однородная краевая
задача имеет только тривиальное решение, то
неоднородная краевая задача разрешима однозначно.
Пример 45. Требуется решить краевую задачу
у" + к2у = х при условии у@)=1, уA) = 2 @ < к < тс).
Вычислим сначала функцию Грина G{x, x)
поставленной краевой задачи. Однородная краевая задача
у" + к2у ш 0, у{0) — у(\) = 0 имеет только тривиальное
решение; ух (х) = sin /сх, у2 (х) — cos kx — два линейно
независимых решения уравнения у" + кгу - 0. Определим функцию
Грина, положив
х)
{/Mxjsin
BxCxJsin
)s\nkx + A2(x)coskx для 0 ^ x < x ^ 1 (D2),
kx + B2{x)coskx для 0 < x < x < 1 {Dx).
Условие а) для функции Грина выполнено по
построению функции G(x, Зс). Условия б) и в) приведем
к уравнениям
Ах (х) - Bi (Зс) = - — cos /сх, А2 (х) - В2 (х) = — sin kx.
Из г) получаем, что
В2 (х) — — — sin kx и А2 (Зс) = 0,
х (х) =
sin kx cos к
к sin к
x)
sin kx cos к
к sin к
к sin к
1
к
к
jn^ я0 t
я0
G (x, x) =
()
/с sin fc
_sin/cxsin/c(l-x)
Л sin Л
Для решения задачи с однородными краевыми
условиями у" + к2у = х, .у(О) = 0, уA) - 0 находим
fc(x, x)xrfx= - f-S
J J
/с sin /с
_ I sin/cxsin/c(l - Зс) - .- х sin/cx
ksink к2 k2s\nk'
Для решения задачи у" + к2у = 0, у@)=1, у A) = 2
предполагаем, что z2(x) = Cjsin/cx + C2cos/cx, причем С\ и
С2 надо определить из условий z2@)=l и z2(l) = 2.
Получаем
г2 (х) = 2 ~ cos ^ sin/cx + coskx.
sink
Тогда решение поставленной краевой задачи имеет вид
y(x) = Zi(.x) + z2(x) =
= * + ГAzicpjl _ 1_1 sinЛх + cos кх.
/с L sin^ к sin Л J
Пусть в дальнейшем выполнены следующие
условия: функция/0 дважды непрерывно
дифференцируема, fi непрерывно дифференцируема и /2
непрерывна на рассматриваемом отрезке. Тогда
оператор L*, определенный формулой
называется дифференциальным оператором,
сопряженным к L. Для этого дифференциального
оператора имеет место следующая формула Грина,
справедливая для любых дважды непрерывно
дифференциальных функций у (х) и z(x):
] {zL[y] - yL* [z]} dx = [fozy' - y(zf0)' + f.zy] |J.
a
Если L [y] = L* [у], то L называется
самосопряженным оператором. Это имеет место тогда, когда
выполняется соотношение f'o = f x. Формула Грина
превращается в этом случае в
J {zL [у] - yL [z]} dx = [/о (z/ - ^)] |J.
sin kx cos к 1 . -
— -.—.—г -cos/ex.
к sin к к
Краевая задача называется самосопряженной,
если
а) L= L*;
б) для каждой системы значений
{у{а), ?{а), у(Ь\ у'(Ь); z(a), z'{a\ z{b), z'(b)},
для которой Ut[y]=0 и l/,[z]=0 (/==1,2),
выполняется условие
КРАЕВЫЕ ЗАДАЧИ И ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
329
Примеры функций Грина линейных краевых задач
Таблица 3.5
d2y
d2y
dx2 }
ft-
dx2
d(xdv\ n2y
dx \ dx ) x '
(n = 0, 1, 2, . .)
dx \ ' dx) 1 — x2
(/7 = 0, 1, 2, . )
(a, b)
@, 1)
(- 1, 1)
@, 1)
(-oo, oo)
@, 1)
(-1, 1)
@, 1)
@, 1)
(-1, 1)
Краевые условия
>@) = 0
>-(!) = 0
У @) "Ь у A) = 0
у' @) -f- у' A) = 0
'да
у ограничено в (-оо, оо)
>@) = 0
у{\) = 0
^(-l)-v(l) = 0
/(-1)-/A) = 0
>>(<>) = 0
у ограничено в окрестности
нуля
>'(!) = 0
у ограничено в окрестности
точек 1 и - 1
G(х, х) (а < х < х <Ь)
G(x, x)(a<x<x<b)
-A -х)х
— х
^-(хх + х - х - 1)
__L^x-x
2
sin Агл: sin Л: A — х)
к sin к
cosk(x - х + 1)
2к sin к
sh^xshA:(l - х)
~kshk
In х для п = 0,
(( \п \
" 2n\\f) "(vx)nj
для п = 1, 2,
1 (l+x \-x\">2
2п\\ - х 1 + х )
для п = 1, 2,
Условия L=L* и /0(a)detB-/o(b)det/4=0
необходимы и достаточны для того, чтобы
заданная краевая задача была самосопряженной. Второе
условие выполнено, если краевые условия имеют
следующий специальный вид (краевые условия
Штурма).
Функция Грина самосопряженной краевой задачи
симметрична, т. е. G(x, х) = G(x, x).
Пример 46. Краевая задача у" + кгу = х, у@) — 1,
уA) = 2 является самосопряженной. Во-первых, справедливо
соотношение L[y] — у" + кгу = L*[у], во-вторых,
det
и, таким образом, det В - det A = 0. Функция Грина,
вычисленная в примере 45, является симметричной:
-x)
к sin к
sin kx sin к A - х)
к sin /с
-для 0 < х < х < 1,
для 0 < х ^ х < 1.
3.3.1.7.2. Задача о собственных
значениях. Пусть краевая задача L[y] =0 при
условии и( [у] = 0 (/ = 1, 2) самосопряжена.
Задача. Требуется найти нетривиальные
решения (т.е. решения у(х)фО) однородной задачи о
собственных значениях для уравнения L[y] + A,}> =
== (/о/)' + JгУ + Ъ-У — 0 (к — комплексное число)
при условии, что Ut [у] =0 (/ = 1, 2).
Каждое такое решение у{х) называется
собственной функцией, соответствующей
собственному значению X.
Если X = 0 не является собственным значением,
т. е. при X = 0 имеется единственное решение
у(х) = 0, то существует функция Грина G(x, x),
и поставленную задачу можно свести к
интегральному уравнению с симметричным ядром
у(х)= -X3G(x, x)y(x)ax.
Свойства собственных значений
и собственных функций.
1. Собственные значения действительны, и для
каждого собственного значения существует
330
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
максимум две линейно независимые собственные
функции.
2. Для двух собственных функций yt (х) и у2{х),
соответствующих различным собственным
значениям, справедливо равенство
ь
j У1 {х) у2 (*) dx = 0 (ортогональность).
3. Собственные значения краевой задачи
образуют последовательность действительных чисел
Хо < Xi < Х2 < ... < Хп < ...,
стремящуюся к бесконечности.
Пусть собственным значениям Хи Х2, ^3,...
соответствуют собственные функции ух (х), у2(х),...
Пусть при этом Я,,- записано столько раз, сколько
ему соответствует линейно независимых
собственных функций. Методом ортогонализации можно
добиться того, чтобы
4. Каждую дважды непрерывно
дифференцируемую функцию z(x) при условии l/,-[z]=0
(i = l, 2) можно разложить в равномерно и
абсолютно сходящийся ряд по собственным функциям
задачи о собственных значениях:
Все собственные значения определенной задачи
о собственных значениях положительны (если
X = 0 не является собственным значением).
Собственным значениям А,ь Х2,...,Хк соответствуют
собственные функции ух, y2,...,yt (одному
собственному значению могут соответствовать две
собственные функции). Для собственного значения
Хк + 1 определенной задачи о собственных
значениях справедлива оценка
\zL[z]dx
\z2dx
a
для всех допустимых функций z, удовлетворяющих
ь
условиям J ytz dx = 0 для i = 1, 2, ..., /.
а
Собственные значения и собственные функции
задачи Штурма — Лиувилля
L [у] = - (/о/У - /, У = A4W * Е (*• Ь)'
где функции /о, /ь ^ дифференцируемы на
(a, b), a /0 и g положительны, при условии, что
z(x) =
где Cv=fz(x)yv(x)dx.
Для неоднородной задачи о собственных
значениях
U2M=y'(a)-y'(b) =
C.44)
L[y] +Xy = f, где {/,-1>] =0 0 = 1, 2), C.42)
справедлива следующая альтернативная теорема.
а) Если X не является собственным значением
соответствующей однородной задачи о
собственных значениях, то задача C.42) разрешима
однозначно.
б) Если X — собственное значение, то задача
C.42) разрешима тогда и только тогда, когда
для собственных функций у(х), соответствующих
ь
X, справедливо равенство J f (х) у (х) dx = 0. При
а
этом задача C.42) разрешима неоднозначно, так
как наряду с и (х) решением является также
и{х) + Су(х), где у(х) есть собственная функция,
соответствующая собственному значению X, С —
произвольная постоянная.
Функция z(x) называется допустимой, если
z (х) дважды непрерывно дифференцируема и
выполняется условие t/,[z]=O (/ = 1, 2). Краевая
задача называется определенной, если для каждой
допустимой функции z(x) справедливо неравенство
f z (x) L [z] (x) dx ^ 0.
Например, задача о краевых значениях
где f0 > 0 и / 2- < 0, является определенной, так как
| zL [z] dx = - jVo (z'J dx + J f2z2 dx ^ 0.
(условия периодичности), обладают следующими
свойствами помимо приведенных выше для общих
задач.
1. При краевых условиях C.43) каждому
собственному значению соответствует только одна
собственная функция. При краевых условиях C.44)
могут существовать две линейно независимые
собственные функции, принадлежащие одному
собственному значению (см. пример в) в начале
3.3.1.7).
2. При условиях g > 0, /0 > 0, f х ^ 0, а1а2.^ 0,
bxb2 ^ 0, (а1J + (а2J > 0 все собственные значения
положительны, исключая случай/^х)^ 0, а1 —Ь1 =0,
в котором X = 0 есть собственное значение с
собственной функцией у{х) = const.
3. Если заменить /о и j\ _ функциям_и /0,
Д такими, что /о^/о, /i^/i (/^/0,
А ^/Д то соответствующие собственные
значения возрастут, т. е. Хк ^ Хк (уменьшатся, т. е.
Хк ^ Х^. Неравенство g ^ g порождает
неравенство Хк ^ Хк, а неравенство g ^ g — неравенство
Хк ^ Хк.
4. Расширение интервала (а; Ь) ведет к
уменьшению собственных значений, соответствующих
краевым условиям у (а) = у [Ь) = 0 или краевым
условиям у'(а) = у'(Ь) = 0.
5. Каждое собственное значение, которое
соответствует краевым условиям
аху{а) + а2у'(а) = aly(h) + a2y'(b) = 0,
где а1/а2 ^ 0, есть неубывающая функция а1/а2.
ОСНОВНЫЕ ПОНЯТИЯ И СПЕЦИАЛЬНЫЕ МЕТОДЫ РЕШЕНИЯ
331
3.3.2. ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
В ЧАСТНЫХ ПРОИЗВОДНЫХ
3.3.2.1. Основные понятия и специальные методы
решения. Пусть дано соотношение
F{xu ..., х„, и, u'Xl, ..., и'Хп,
При этом F - функция указанных аргументов
xh и, и^ u^jXk, ... (j, /с = 1, 2, ..., п). Ищется
функция и (хь..., х„), удовлетворяющая этому
соотношению, т. е. такая, что F обращается в нуль
тождественно по хь..., хи, если вместо и подставить
функцию и (х 1,..., хи), а вместо м'х, и"х Xfc, • • • —
производные
, _ дц(хь...,х,,) „ _ д2и{хи...,хп)
ах.
dxjdxk
Такая функция м(хь хи) называется решением
или интегралом дифференциального уравнения в
частных производных. Нашей целью будет не
нахождение общего решения, а выделение
отдельных частных решений путем наложения
определенных дополнительных условий. При этом иногда
удается получить представление о совокупности
решений. Наивысший порядок входящей в
дифференциальное уравнение производной называется
порядком дифференциального уравнения. Если
функция F линейна по совокупности и, и'х_,
и"х х,..., то дифференциальное уравнение
называется линейным уравнением в частных производных.
Линейное уравнение в частных производных и-го
порядка в общем случае может быть записано
в виде
ди
дпи
¦1
д'и
= /(*,).
В аргументах для краткости написано Xj вместо
ди ди ди
Х1,...,хя, вместо ,..., и т.д. Уравне-
dxj dXi дхп
ние L[u] =f(xj) называется линейным
неоднородным, L [и] = 0 — линейным однородным
дифференциальным уравнением. Если их и и2 — решения
линейного однородного уравнения, то решением
является также С^ + С2и2, где С1 и С2 —
произвольные постоянные. Каждое решение и
(если оно существует) линейного неоднородного
уравнения можно представить как сумму частного
решения п этого уравнения и общего решения U
(т. е. решения, которое в общем случае зависит
от п произвольных функций) соответствующего
линейного однородного уравнения.
Если функция F линейна по высшим («-го
порядка) производным, т. е. коэффициенты при
высших производных зависят лишь от
производных и, u'x., u"XjXk,... ДО п - 1-го порядка, то
дифференциальное уравнение называется
квазилинейным; оно имеет вид
/ ди дпи \
F\ xj, м, —-,..., =
V dxJ д^..Мг'
Z( д"~1и \
Bit...iAxj, «, -., 1 х
h . V dxi»...djcjr/
Zdnu
im = n +
dx\'...dx]r
dn~lu \
...,— =0.
В уравнениях в частных производных
произвольные элементы общего решения, т. е. решения,
из которого получают все частные решения
(возможно, за исключением определенных «особых
решений;»), являются не константами, как в
случае обыкновенных дифференциальных уравнений, а
произвольными функциями. В общем случае число
произвольных функций будет равно порядку
дифференциального уравнения. В случае
дифференциальных уравнений с п независимыми
переменными произвольные функции будут, вообще говоря,
функциями п — 1 переменных.
Пример 47. Уравнение и"х х =/(х1э х2) —
линейное дифференциальное уравнение 2-го порядка с заданной
функцией f(xu x2). Общее решение имеет вид
х,х2
"(*ь х2)= J J f{U s)dtds + w(xl) + v(x2\
*,*2
где w(x,) и v(x2) - произвольные функции.
Пример 48. аи'Хх + ЬиХг =0 (a, b - постоянные).
Общее решение имеет вид
и » w (fexi - ах2),
где w (t) — произвольная дифференцируемая функция.
Пример 49. Уравнение C.27) - квазилинейное
уравнение в частных производных 2-го порядка по двум
независимым переменным.
Пример 50. Уравнение и"ххи"уу + и'х = /(х, у, z) не
является ни линейным, ни квазилинейным уравнением в
частных производных по трем независимым переменным.
Для каждого множества функций вида
м=/(*ь *2> w@(xb *2))), где / и у - заданные
функции от хь х2, w и хь х2 соответственно,
a w(t) — произвольная функция, может быть
найдено такое уравнение в частных производных,
что данное множество функций будет общим
решением этого уравнения. Для доказательства
продифференцируем w по х, и х2 и исключим W.
В получившемся дифференциальном уравнении
заменим w на функцию от хь х2 и и, разрешив
уравнение м = /(хь х2, w) относительно w.
Пример 51. Совокупность поверхностей вращения,
которые получаются при вращении плоских кривых вокруг
оси и, задается посредством формулы
и ш w (xf + х\).
Из соотношений u'Xl * 2xiw' (x? + х\) и иХг = 2x2w' {x\ + x\)
получаем соответствующее уравнение в частных
производных 1-го порядка: х2и'Хх - ххи'Хг * 0.
Система уравнений в частных производных
для функций мA), мB), ..., м(к)(.хь ..., х„) имеет
332
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
\...,и<к
OXj
OX
——,... =0,
OXi )
где / = 1, 2,...,h. Если имеется столько же
дифференциальных уравнений, сколько неизвестных
функций, т. е. к = h, то система называется
определенной системой; если h < к, то система
называется недоопределенной, и, наконец, при
h > к — переопределенной. Дифференциальное
уравнение 2-го порядка F(xb х2, м, u'Xl, u'X2, и'
) = 0 эквивалентно системе
и v ,
Л1Л2
F(x
b х2, м, р,
q'X2) = 0,
qX2
трех дифференциальных уравнений 1-го порядка для
трех неизвестных функций и, р и д(хь х2).
Система Л дифференциальных уравнений с h
неизвестными функциями иA\..., м(Л) (г, хь..., х„)
) C.45)
-Ft f,
(/ = 1, 2,...,/i) называется нормальной по
отношению к независимому переменному t, если правые
части F, не содержат производных функций
м(/) порядка выше /с, и производных по t порядка
выше А:, — 1.
Задача Коши для нормальных
систем уравнений. Требуется найти решение
wA), ...,w(n) системы C.45), которое при t = t0
удовлетворяет начальным условиям
)r''
(/, =0, 1,...Л - 1; i = 1, 2,...,Л).
Теорема Коши — Ковалевской. Если все функции
Ujf.iXj) в некоторой окрестности точки (х°) и
все функции F, из C.45) в некоторой
окрестности точки
.о ,,о,о .о, _eVVW)
можно разложить в степенные ряды, то
задача Коши имеет решение, которое в некоторой
окрестности точки (t°, x°) можно разложить в
степенной ряд. Это решение единственно в классе
функций, разложимых в степенной ряд. Отметим,
что по этой теореме имеем решение в малом,
т. е. в окрестности точки (t°, xj).
Пример 52. Система u'x = v'r v'x=-u'y нормальна по
отношению к х.
П р и м е р 53. Уравнение и", ш a2{uXiXi + ипХгх2)
нормально по отношению к t.
Специальные методы
интегрирования.
1. Разделение переменных. Во многих
случаях решения можно искать в виде
и = м (хь..., х„) = м1(х1)м2(х2,...,хи)
М = М1(Х1) + М2(Х2,...,ХИ),
если после подстановки предполагаемого решения
уравнение удается записать в виде
/ ди2 ди2 \
= F2\ х2,. .-,Х_ Мг, > >••• I-
2V Ъ w ^x2' 5х3' /
х2' xjXj' Тогда Ui и и2 должны удовлетворять уравнениям
/ du^ d2ui \
FAxu uu -—-, —4~,... =С,
V dxx dx\ )
г ( ди2 dU2 \ п
F2 х2,...,х„, и2, -—, -—,... =С,
V ах2 дх3 )
где С есть произвольная постоянная, которую
можно определить из дополнительных условий.
Таким образом, для их (xt) получим
обыкновенное дифференциальное уравнение, а второе
уравнение будет содержать на одно независимое
переменное меньше.
Пример 54. (м^J + (u'Xi)* ¦ 1. Предположим, что
и(хх, x2)»ul(xl) + U2(x2). Тогда из исходного уравнения
следует
Решая эти два обыкновенных дифференциальных
уравнения, получим для уравнения в частных
производных дву пар а метрическое семейство решений
м(хь х2) - <ixi + A - а2I/2х2 + b (a2 - С).
Пример 55. "xiXi"" мх2" ®* Предположим, что
w(xi, x2)-U|(xt)u2(x2). Тогда после разделения переменных
^""rfxT" ' м7 rfJCa " '
и решение имеет вид
;{;
Л + С2<хлахх)е~а *2,
а2 - С > 0,
Л2«С«О,
fl2 - - С > 0.
2. Метод суперпозиции. Этот метод
можно применять для линейных дифференциальных
уравнений. Он состоит в получении новых решений
из данного семейства решений посредством
суммирования или интегрирования.
Если м(хь ..., х„; к) — семейство решений,
зависящее от параметра к, то при определенных
предположениях о сходимости ряда или интеграла
функция
v{xu ..., хи)
хь ..., х„; к),
если к — дискретный параметр, или
ь
v (хь ..., х„) = J и (хь ..., х„; к) dk,
если к — непрерывный параметр, также является
решением заданного дифференциального
уравнения.
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 1-го ПОРЯДКА
333
Пример 56. их х — и'х = 0. В предыдущем примере
было показано, что
м(хь х2; а) = е
= е~а X2
cosax1
есть решение, зависящее от непрерывного параметра Тогда
x, da = {?)" Г*****
J е-"**
также является решением.
3.3.2.2. Уравнения в частных производных 1-го
порядка. С теоремой Коши — Ковалевской связано
предположение о разложимости в степенной ряд,
которое во многих случаях оказывается слишком
ограничительным. В дальнейшем будем
предполагать, что встречающиеся частные производные
существуют и непрерывны. Важнейшим результатом,
вытекающим из изложенного ниже, является
эквивалентность уравнения в частных производных
1-го порядка системе обыкновенных
дифференциальных уравнений.
Каждое решение и = м(хь х2) уравнения в
частных производных 1-го порядка (с двумя
независимыми переменными)
F{xux2, и, pltp2) = 0
может быть представлено как поверхность в
трехмерном пространстве. При этом касательная
плоскость в фиксированной точке (хь х2, и) поверхности
имеет уравнение
U -u=pl(Xl-
р2 (Х2 - х2);
Pi и Рг — решения уравнения F(xu хъ и, рх, p2) = 0,
если хь х2 и и фиксированы. Огибающая
семейства касательных плоскостей в точке (хь х2, и)
называется конусом Монжа в точке (хь х2, и).
Касательная плоскость поверхности решения в точке
(хь х2, и) должна касаться построенного в этой
точке конуса Монжа вдоль образующей.
Направления, которые определяются образующими конуса
Монжа, называются характеристическими
направлениями. Кривая в (хь х2, м)-пространстве, имеющая
в каждой точке характеристическое направление,
называется характеристикой (фокальной кривой);
она удовлетворяет условиям
ds
ds
du
C.46)
образуют на поверхности решения фокальные
кривые.
Квазилинейное уравнение в частных производных
1-го порядка:
u x2, и) Pi
ь х2, и)р2=а(хи х2, и).
Конус Монжа вырождается в этом случае
в ось Монжа, так что в каждой точке существует
только одно характеристическое направление.
Каждая поверхность и — и(хх, х2), образованная одно-
параметрическим семейством фокальных кривых,
есть поверхность решения уравнения в частных
производных, и обратно, каждая поверхность
решения образуется таким образом. Каждая
фокальная кривая, имеющая общую с поверхностью
решения точку, целиком лежит на этой
поверхности решения.
Общее уравнение в частных производных 1-го
порядка :
F(xbx2, и, рир2) = 0.
Предположим, что конус Монжа не вырожден.
Чтобы фокальная кривая целиком лежала на
поверхности решения, для рх (s) и р2 (s), кроме
условий C,46), должны выполняться соотношения
dPl/ds = -{pxFH
dp2/ds = - (p2F'u
C.47)
Система из пяти обыкновенных
дифференциальных уравнений C.46) и C.47) называется
характеристической системой дифференциальных
уравнений. Функция F является интегралом этой системы,
т. е. F = const вдоль интегральной кривой. Каждое
решение характеристической системы с F = 0
(нужно потребовать выполнения этого равенства
только для начального элемента) называется
характеристической полосой, и соответствующая
пространственная кривая xt (s), x2(s), u(s) —
характеристической кривой. Справедливо утверждение:
на каждой поверхности решения имеется одно-
параметрическое семейство характеристических
кривых и соответствующих характеристических
полос. Если характеристическая полоса имеет
общий элемент с поверхностью решения, т. е.
общие значения хь х2, и, рх, р2, то она целиком
принадлежит интегральной поверхности.
3.3.2.2.1. Задача с начальными
значениями. Приведенные в 3.3.2.2 результаты
легко переносятся на случай п независимых
переменных.
Квазилинейное уравнение в частных производных
1-го порядка с п независимыми переменными-
Последнее соотношение называется условием
полосы, которое выражает тот факт, что
функциями Xj (s), x2(s) и u(s), Pi(s), p2(s) определена
не только пространственная кривая, но
одновременно и касательная плоскость в каждой ее точке.
Система функций хь х2, и, ри р2,
удовлетворяющая системе C.46) и F = 0, называется фокальной
полосой. Каждая поверхность решения и (хь х2)
(интегральная поверхность) содержит
характеристические направления, так как поверхность
обязательно должна касаться конуса Монжа, и они
а,- (хь ..., х„, и) Pi = а (хь ..., х„, м)
Пусть задано п — 1-мерное многообразие
начальных значений G в (хь ..., х„,
^-пространстве:
JC,-=JC?(fb ..., *„_,), M = M°(fb..., Г„_,)
(|- 1, 2, .. , п),
334
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
причем
rang
дх°п ах?
дх°„ дх°п
C.48)
и многообразие не содержит двойных точек
проекции на (хь ..., хи)-пространство (т. е.
различным наборам значений (/, /„_,) соответствуют
различные наборы значений (хь ..., х„)). Искомым
будет решение и = m(xj х„) дифференциального
уравнения
а,/?, = я, которое содержит начальное
многообразие G, т. е. для решения должно
тождественно по tk выполняться равенство
и° = к(х?, ..., х°п).
Для этого решим систему
dXi du
—— = а{ (хь ..., х„, и), —- = а (хь .
ds ds
, хи, м)
" (/ = 1,2,..., и)
с начальными значениями х, |s=0 = *?, и |,=0 =
Решение будет зависеть от s и ti, ..., t«-i•
X, = X, (S, tu . . ., Г„_ t), U = U (S, tb • • ., fn- l) ,
(/ = 1, 2,..., n).
Если определитель
ax ... а„
D = _^
5(
(s, r,, ..., f.-i
дх,
дх„
дхп
fit. 1
dt. i
отличен от нуля на G, т. е. при 5 = 0, то, разрешая
в окрестности G уравнения х* = х, (s, tu •••, ?n-i)
(/ = 1, 2, ..., и) относительно s, ?ь ..., г„_ь получим
s = s(xb ..., х„), f* = tk{xu ..., х„)
(к = \,...,п- 1).
Подставляя эти функции в и = и (.s, гь ..., fw_i),
получим искомую интегральную поверхность и =
= w(xb ..., х„). Таким образом, в предположении
D |s=0 / 0 задача о начальных значениях разрешима
однозначно.
Случай 0^=0=0. Многообразие G
называется характеристическим для дифференциального
уравнения ? а,/?, = а, если существуют функции
/ = 1
Xk(tA, ..., tn-i) {k = 1, 2, ..., п — 1) такие, что в G
справедливы соотношения
Г~- (/=1,2,...,,),
(х?, ..., х°п,и°) =
dtk
Каждое характеристическое многообразие
получается из п — 2-параметрического семейства фокаль-
ных кривых, т. е. решений системы dx-Jds = F'p.,
du/ds = Y, PjF'p* i = 1, • •., n, и, обратно, каждое такое
семейство кривых образует характеристическое
многообразие. Если фокальная кривая имеет одну
общую точку с характеристическим многообразием,
то она целиком лежит в нем. Если D|s=0 = 0, то
для разрешимости задачи о начальных значениях
необходимо и достаточно, чтобы G было
характеристическим многообразием. В этом случае имеется
бесконечно много интегральных поверхностей и G
называется многообразием разветвления
интегральных поверхностей. Чтобы понять это, построим
нехарактеристическое начальное многообразие G',
которое пересекается с G и однозначно определяет
некоторую интегральную поверхность. Тогда G
лежит на образованной таким образом
интегральной поверхности.
Пример 57. upi+p2
Соответствующая система
обыкновенных дифференциальных уравнений
dx2 « du
——= 1, ~j-= 1 имеет решение
ds ds y
as
U0S + Xjo, X2 {S) » S + X20, U = S + U0.
а) Ищем интегральную поверхность, проходящую через G:
х? = t\ х°2 = и и° = I. Здесь
1 E, t) = ~S2 + tS + Г2, Х2 (S, t
и (s, t) = .s + t
есть решение системы обыкновенных дифференциальных
уравнений с начальными значениями G. Так как D|,-o =
= - t Ф 0, то и - х2 - единственная интегральная
поверхность. *
б) Для G: х?»^2, x°2 = t, uo»t имеем D|f.0 = 0,
но G - характеристическое многообразие при X-i = 1. Если
взять С: х? -/(О, х°2 ш г, м° - 0 (/' (t) * 0,/@) - 0), то G и С
пересекутся в @, 0, 0). Интегральная поверхность для С:
Xi я ум2 + f(x2 - и) содержит G. За счет выбора функции /
получаем бесконечно много интегральных поверхностей,
содержащих G.
в) Для G: х? - J-r2, х°2 - -*-f2, и0 « 1 имеем D |..о - О,
но G не является характеристическим многообразием, так
как необходимые для этого соотношения 1 »¦ \t, 1 ¦ Xt,
1 «А. 0 не выполняются ни для какого X. Для G не
существует интегральной поверхности. Если бы интегральная
поверхность существовала, то на G для определенных ри р2
выполнялись бы оба соотношения:
+ Рг - 1 \G
i + Рг -
— Pi'
- - Pi -tt
'0,
¦ - pxt - p2t m 0.
Но таких рх и р2 не существует.
Общее уравнение в частных производных 1-го
порядка с п независимыми переменными хь ..., х„:
F(xu ..., х„, и, ри .-., Рп) = 0 lpi= -
Пусть соответствующий этому уравнению конус
Монжа (огибающая семейства касательных
плоскостей к решениям) не вырожден. Пусть п — 1-мерное
начальное многообразие G C.48) в (хь ..., х„, м)-
пространстве заданием п функций
Pi=P?(ti,.-,tn-l) (i = l,2, ..., и)
дополняется до многообразия полос, причем
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 1-го ПОРЯДКА
335
условия полосы
ди°_
of^- (к = 1, ..., п- 1)
выполняются тождественно по tl,...,tH-l. Пусть
в дальнейшем соотношение между величинами
полос xf, u°, pf и
Г(х?,...,хио,М°,р?,...,рио) = 0
справедливо тождественно по tl9...9tH-i. Будем получим
искать решение и — м(хь ..., х„), содержащее
заданное многообразие полос; должны выполняться
равенства
(/ = 1,2, ..., и).
Рассмотрим для данного уравнения
характеристическую систему
ds "'«•
(i = l,2,..., и).
Если D # 0 вдоль Gb т. е. для 5 = 0 и в
окрестности Gb то получим
s = s(Xi, ..., vj, tk = ffc (хь ..., хи)
(к = 1, 2, ..., п- 1).
Подставив эти функции в формулы
Pi =
• м = м(хь .... х.)
в качестве единственного решения задачи с
начальными значениями с
ди
- = pi (хь ..., х„).
Случай D|s=o = 0. Здесь важную роль играет
понятие характеристического многообразия полос:
Gi называется характеристическим многообразием
полос, если имеется п — 1 функций Хк таких, что
соотношения
^5
На каждой интегральной поверхности уравнения
в частных производных F = 0 существует однопа-
раметрическое семейство характеристических
кривых и соответствующих характеристических полос.
Если характеристическая полоса имеет общий
с интегральной поверхностью и = м(хь ..., х„)
элемент, т. е. значения хь х2, ..., хт м, рь ..., р„
(п-иГх х\ ди^> •-'>*")
I U — U {Хи ..., Х„),
то полоса полностью принадлежит
соответствующей интегральной поверхности.
Найдем теперь решение характеристической
системы с начальными значениями
м |,=о = "° Сь • • -, *n-1), (i = 1, 2, .., n)
и получим
Xi = X,(S, tu ..., tn-i),
и =u(s, 11, ..., tn-0, (/ = 1, 2,..., n).
Справедливо соотношение
так как оно выполнено для s = 0 (см. выбор величин
полос). Важную роль играет величина
D =
Ь-.-Лп-l)
дхп
дхп
л
i=l к=О
- (F'x.
гР?
k л:
выполнены на Gx. Каждое характеристическое
многообразие полос получается из п — 2-параметриче-
ского семейства целиком лежащих в нем
характеристических полос, и каждая характеристическая
полоса, имеющая общий начальный элемент с
характеристическим многообразием полос, целиком
лежит в нем.
Если D\s=0=0, то для разрешимости задачи
с начальными значениями необходимо и
достаточно, чтобы Gi было характеристическим
многообразием полос. В этом случае существует
бесконечно много решений, получающихся таким
образом, что образуется многообразие G\, которое
имеет п — 2-мерное пересечение с Gx и для которого
¦и=и(хгх2)
Характеристическая
полоса
Рис 3.67
ИфО. Если решить теперь для G\ задачу с
начальными значениями, то G{ будет содержаться
в ее решении (рис. 3.67).
336
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Пример 58. F (хь х2, и, рь р2) = рхр2 - и.
Характеристическая система имеет вид
ds
dx2
ds
ds ~Pb ds ~Ръ
и характеристические полосы описываются равенствами
*i - Рго (е1 - 1) + х10,
х2 ^PioW- 1) + х20,
ы = иое2$, рх = р1Ое*, р2 = р2Ое*.
Ищем решение, проходящее через Gx:
х? =1, х§ = t, м° = f2,
Р? - t/2, p5 = 2t.
Для G, выполняются следующие условия:
а) rang f-^-. -^-J = rang @, 1) = 1 (условие C.48));
б) F | q = pip2 — и \q = t2 — t2 = 0 (соотношения между
величинами полос);
в) \ Р?-г—P2-^-=2t-2t = 0 (условие полосы).
ot ot ot
Решение характеристической системы с начальными
значениями из Gx имеет вид
x,(s, f) = 2f(e*- 1)+ 1,
при условии det(f'^.x)^0в рассматриваемой
области (хь ..., хи)-пространства называется полным
интегралом. Очень часто полные интегралы можно
получить разделением переменных (см. 3.3.2.1).
Если зависящее от параметра а семейство и =
= /(хь ..., х„; а) поверхностей решения
дифференциального уравнения имеет огибающую, то она
снова есть решение. Огибающая определяется тем,
что из условия f'a(хь ..., х„; а) = 0 находят а как
функцию хь ..., х„ и подставляют в м=/(хь ...
.... *„; а).
Из полного интеграла построением огибающей
можно получить общее решение. Предположим,
что щ = W,- (tь ..., г„_ j) (i = 1,2,..., и), причем w, -
произвольные функции от п — 1 переменных tk.
Из и — 1 уравнений
найдем tk как функции хь ..., х„. Подставив эти
функции tk (хь ..., х„) (к = 1,..., п — 1) в выражение
получим решение, зависящее от и произвольных
функций, т. е. общее решение.
Полный интеграл приводит к решению
характеристической системы дифференциальных
уравнений. Пусть м=/(хь ..., х„; аи ..., а„) — полный
интеграл уравнения в частных производных F = 0.
Из соотношений
Так как D|,*,o s
P\{s, 0 = y^.
О
= 2t / 0, то можно разрешить хх —
* - 1) + 1, x2 = у(с* - 1) + г относительно 5И(:
t=—Dx2-xx + 1),
. 4х2 + х, - 1
4х2 - Xi + Г
Подставив эти значения в и = t2e2*, получим решение
После подстановки в рх » — <> и р2 — tc* получим
т. е. выполняются равенства
ди ди
дхх х дх2 2'
3.3.2.2.2. Полные интегралы. Решение
уравнения в частных производных 1-го порядка
F(xb ..., х„, и, рь ..., р„) = 0,
зависящее от п параметров a, (i = 1, 2,..., п):
и =/(хь ..., х„; аи ..., ап),
где аь ..., а„, Ьь ..., Ь„ — произвольные параметры,
найдем
x, = x,(s, аи ..., ат Ъи ..., Ьп) (/=1, ..., п).
Эти функции, подставленные в правые части
соотношений
м=/(хь ..., х„; аи ..., а„),
df(xu ..., х„; аи ..., ап)
дх,
дают и (s, аи ..., а„, Ьь ..., Ьи) и р, (s, аь ..., ап, Ьь ...
..., Ь„). Кривые х,- = х,- (s), и — и (s), р, = р, (s) являются
характеристическими полосами.
Особое решение — это решение
дифференциального уравнения, которое получается в результате
исключения рь ..., р„ из п + 1 уравнений
F(xb ..., х„, и, рь ..., р„) =
F;,(*b •••» л» и, Ри ..., PJ =
i = 1,2,..., и).
Особое решение может быть получено также
из полного интеграла построением огибающей.
Исключив п параметров аи ..., ап из п 4- 1
уравнений
/(хь ..., х„; аи ..., а„) = и,
Д.(хь ..., хи; аь ..., а„) = 0,
получим особые решения.
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 1-го ПОРЯДКА
337
Примеры полных интегралов уравнений в частных производных.
Таблица 3.6
Дифференциальное
уравнение
F (Pu Pi) - 0
Пример:
Р? + Р§»1
Р\ =/(*!, Pi)
Р2=/(*2, Pi)
Пример:
Pi - х?р2 + х{е 2
Pi - / ("» Pi)
Пример:
и2 (pi + pi + 1) - 1
Fl (*ь Pi) - F2 (x2, p2) (=at)
ИЛИ
Pi -/l(Xi, «i)
Pi=fi(x2, a,)
Пример:
A (x.) p? + В (x2) pf - a (x,) + * (x2)
M = p,xi + p2x2+/(pt, p2)
Полный интеграл
и = atxx + fliX2 + a2 при F (ab a't) = 0
M=fl,X,+(l-fl?I/2X2+fl2
" ¦ f / (xi, <*i) rfxi + aix2 + a2
« - f / (*2, fll) rfX2 + fliX! + п2
1 , 1 , a,
w = у xf«i + у x\e + atx2 + a2
С du
при условии, что р-д (и, s) есть решение уравнения р - f (и, sp)
(*i - а2J + а?х| + 2Д1х2 (хх - а2) = A + а\) A - м2)
при условии, что
1 /1-й2 У/2
« = J /i (хь fli) dxt + J /2 (x2, ax) rfx2 + a2
f/a(x1) + aiy/2j Г/Ь(х2)-аЛ1/2^ ,
м = ахх, +a2x2 + f (au a2)
3.3.2.2.3. Контактные преобразова- соотношение
ни я. Канонические уравнения и кано- „
нические преобразования. В этом пункте du - YJpkdxk =
вновь рассматриваются уравнения в частных про- *=i
изводных 1-го порядка
F(xu ..., х„, м, ри ...,
C.49)
хт м,
pn)
(а V л \
I du — > рк ахк I,
V *-1 /
где
5м
р*=— (Л = 1,2,...,и).
^Х
Наряду с обычными точечными преобразованиями
Зс,- = Xj (X!,..., Х„) (/=1,2,..., П),
д(хи ..., Зс„)
такими, что — ф 0, можно рассматри-
д(хи ..., х„)
вать контактные преобразования. Преобразование
Зс,- = х,-(х1, ..., х„, и, рь ..., рп),
Pi =Pi(xlt ..., х„, и, Рь ..., р„) (/ = 1,2,..., и),
i/ rriwfx,, ..., Х„, U, Ри ¦•, Ри)»
для которого
d(Xi, ... , Зс„, п, pi, ... , р„)
г1(хь ..., хя, м, рь ..., р„)
называется контактным преобразованием, если
существует такая функция g ф 0, что выполнено
При этих преобразованиях полный дифферен-
п
циал du = J] Pfc ^xfc переходит в полный дифферен-
п
циал du = Л pfc dxfc. Необходимое и достаточное
условие того, чтобы функции
х,(хь ..., х„, м, рь ..., р.),
р,-(хь ..., хт м, plv..., ри),
й(хь ..., хи, и, рь ..., р„) (/ = 1,2, ..., и)
определяли контактное преобразование, для
которого справедливо тождество
du- Y, Pkdxk = g[du-Yu Pk
338
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
выражается уравнениями
[п, х,] = 0, [х„ Xj] = О,
{.Pi, Pjl = °> [Рь "] = 9Рь
[ph xj] = Ъцд (i = \, ..., n; j = 1, ..., л).
При этом для двух функций/, h(xu ..., х„, и,
Pi, ..., р„) квадратные скобки определяются
равенством
/. ч
- *;, (д.
Это контактное преобразование переводит
уравнение C.49) в новое уравнение
F(xu ..., хп, и, ри ..., р„) =
v = F(xb ..., хя, к, рь ..., р„) = 0
с решением м = п (хь ..., х„).
Возможно, что новое дифференциальное
уравнение F = 0 не содержит производных и,
следовательно, не является больше дифференциальным
уравнением в собственном смысле.
Пример 59. Преобразование Лежандра х, = ph pt - х„
и- - ]Г Х*Р* ~ и есть контактное преобразование:
/
«-f pkdx
В дифференциальном уравнении C.49) можно
ввести и = хп+1 как независимое переменное и
искать семейство решений хи + 1 =/(х1, ..., х„; С)
в неявной форме v{xu ..., хи, хп+1) = С. При этом
вместо Pi = u'x. в C.49) следует подставить -v'x./v'Xn + l
(i — 1, 2, ..., п). Таким образом, получим
дифференциальное уравнение, которое явно не зависит от v.
Пусть в дальнейшем полученное таким образом
уравнение нормально по отношению к
переменному, которое будет обозначено через t (ср. 3.3.2.1).
Тогда можно ограничиться исследованием
дифференциального уравнения Гамильтона — Якоби
р + Н(хъ ..., х„, г, ръ ..., рп) = 0
(р = u't, Pi = «у для функции и от п + 1
переменных хь ..., х„, t (переменное v снова обозначается
через и). Система характеристических
дифференциальных уравнений, соответствующих этому
уравнению Гамильтона — Якоби, имеет вид
dt
du_
~aT
dt
dH
d±
dt
-j-=--T-- C.5-1)
dt
Уравнения C.50) образуют определенную
систему из 2и обыкновенных дифференциальных
уравнений. Если из них найти xt(t) и p,(f), то u(t)
и p(t) получатсй из уравнений C.51) простым
интегрированием. Система обыкновенных
дифференциальных уравнений C.50), соответствующая
функции H(xi, ..., х„, t, Pi, ..., р„) от 2п + 1
переменных, называется канонической системой
дифференциальных уравнений или нормальной системой
дифференциальных уравнений. К системам такого вида
приводят многие задачи механики и
теоретической физики. Решение нормальной системы C.50)
часто находится проще при помощи
соответствующего уравнения Гамильтона — Якоби.
Теорема Якоби. Если известен полный
интеграл w=/(xb ..., .х„, t, #ь ..., а„) + а
дифференциального уравнения в частных производных
р + Я(хь ..., х„, t, pu ..., р„) = 0,
причем dei(f'x.a) ф 0, то уравнения
при 2и произвольных параметрах а, и Ьх дают 2и-
параметрическое семейство решений канонической
системы C.50).
П р и м е р 60. Задача двух тел. Движение двух
материальных точек, взаимно притягивающихся по закону Ньютона,
происходит постоянно в одной плоскости. Поэтому, приняв
положение одной из точек за начало координат, можно
записать уравнения движения в виде
fx_^dU_ d2y = dU_
dt2 dx' Ht2" ду'
где U ¦•
Эта система после введения функции Гамильтона
Н(х,у, р, q) = ±;{p2
x, у)
переходит в систему канонических дифференциальных
уравнений
dt dp' dt dq' dt = dx ' dt dy
dx dy ..
для величин х, у, р « -7-, q » ~г-. Интегрирование этих
at dt
уравнений эквивалентно задаче нахождения полного
интеграла уравнения в частных производных
В полярных координатах р, ф уравнение в частных
производных можно записать в виде
функция
РГЛ 2k2 a22\'2.
м«-а^-а2ф- Boi + — -^-J ds + a
Po
является полным интегралом. Его можно получить
разделением переменных -м(р, ф, t) - их (t) + и2 (р, Ф) с учетом того,
что для уравнения вида "р»/(р, и'щ) выражение w-j/(p,
a2)dp + a2q> + a есть полный интеграл. Из ы^ « -t0 и
"о2 ш - Фо получается общее решение
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
339
причем второе уравнение задает траекторию. Вычислив
последний интеграл и используя обозначения Р =
Л 2аха1\1г
\ Т*—) ' полУчим уравнени
к1' '
i - е2 sin (ф - ф0) '
т е при б < 1 - эллипс, при е = 1 - параболу и при е > 1 -
гиперболу.
Канонические преобразования.
Преобразование
X, = Х,-(х,, ..., Хп, /?,, ..., /?„),
, Хт Ли ¦•¦,Рп)
Pi = Ы
0 = 1,2, ..., п)
C.52)
называется каноническим преобразованием, если
канонические уравнения C.50) переходят в
канонические уравнения
1= -11L (/ = 1,2,..., л).
dt dxi
dxt _ дН
dt dpi '
Это условие должно выполняться для всех дважды
непрерывно дифференцируемых функций #(хь ...
..., х„, /»,, ..., /?„).
Преобразование C.52) является каноническим,
если существую i функция G(xb ..., х„, рь ..., рп)
такая, что справедливо соотношение
Z (Pk dxk - рк dxk) = dG
Z (** «*Л* - -x* «W = dG
Л= 1
(Рь xk должны быть выражены через х„ р, по
формулам C.52)). Функция Н (хи ... ,хп, рх, ... ,р„)
получается из Н при подстановке выражений х„ р{
через л„ ^ в соответствии с C.52). Это возможно,
гак как для каноническою преобразования всегда
справедливо равенство
Р ( X ,, . . . , Хю р,, . . -,Рп) _ j
Пример 61. и-1: x = |/xcos2/j, p = j/xsin2/?-
каноническое преобразование, так как для функции G =
= - (— sin Ар + 4/>) имеет место равенство
р dx — р dx
= I — -- sin 2р cos 2/) + р)
2р cos 2/) + р) rfx 4- 2х sin2 2/> rfp = dG.
Например, канонические уравнения
¦— = B |/х - 4х sin 2/j) cos 2/j,
--г- - sin2 2w =- sin 2p - 1
rff 2|/x
с функцией Я = x(l — sin2 2p) + \/xs\n2p переходят в
канонические уравнения
с Н = х2 + р
Усювия канонических преобразований,
записанные при помощи скобок Лагранжа.
Преобразование C.52) являе«ся каноническим тогда и только
тогда, когда тождественно выполняются
соотношения [xj, xk] = 0, [*,, pk] = bjk, [pj, p^ = 0 (j, к =
= 1,2,..., n). При этом скобки Лагранжа [ , ]
определены равенствами
—
дРк
ер
Условия канонических преобразований,
записанные при помощи скобок Пуассона. Преобразование
C.52) является каноническим тогда и только тогда,
когда выполняются соотношения
{xj, хк) = 0, (pj, рк) = 0, (хр рк) = bJk
(j, к = 1,2, ..., n).
Функции F, G(xb ..., хи, pu ••-, Ри) связаны с
преобразованными функциями F, G CcL,..., Зс„, рь ...
..., ри) соотношением (F, G) = (F, G). При этом
скобки Пуассона (,) определены формулой
дРк
eP
для произвольных непрерывно дифференцируемых
функций/и g (хь ..., х„, Pt,..., р„). Скобка Пуассона
имеет следующие свойства:
(/, 9) = " fa, Л (/' /) = 0, (/, const) = 0,
{тождество Якоби). Совокупность канонических
преобразований от 2л переменных образует группу.
3.3.2.3. Уравнения в частных производных 2-го
порядка.
3.3.2.3.1. Классификация.
Характеристики. Корректно поставленные зада-
ч и. Рассматривается линейное относительно
вторых производных уравнение в частных
производных 2-го порядка
au(xu ..., хя)
д2и
i.j=i
ди
+ F хь ...,х„, и,-—, .
дхх
ди
Jx~n
C.53)
с непрерывными коэффициентами aiy Произведем
невырожденное преобразование переменных
- / ч д(хь ..., х„)
х, =х;(хь ..., х„), --1 —Ц-фО
(i = l,2,...f я);
340
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
тогда коэффициенты а1} преобразуются в
рассматриваемой точке (х?, ..., xj) как коэффициенты
квадратичной формы ? ^ijPiPj B случае невырож-
«. J = 1
денного линейного преобразования р,- = ? A^q^
где
дх{
ЙуCс?,...,5с2)= X alk(xol,...,x°n)AilAjk.
l,k= I
Дифференциальному уравнению C.53)
сопоставляется квадратичная форма ? а1} (х?, ..., xj)ptpj
в точке (х?, ..., х?). Из линейной алгебры известно,
что эта форма линейным преобразованием pt =
= Yj bjiqj может быть приведена к каноническому
виду
^ и.
При этом числа г и m не зависят от вида
линейного преобразования. Согласно этому,
получаются следующие типы дифференциальных
уравнений в окрестности точки (х?,..., xj):
эллиптический тип: т = п, г = 0 или г = п;
гиперболический тип: т = п, 1 < г < я — 1;
нормальный гиперболический тип: т = п, г = \
или г = п — 1;
параболический тип: т < п;
нормальный параболический тип: т = п — 1,
г = 0 или г = т.
Эта классификация зависит от выбора точки
(х?, ..., xj). Например, уравнение Трикоми —уи'^х +
+ и"Уу = 0 является уравнением смешанного типа:
при у > 0 — эллиптическое, при у = 0 —
параболическое, при у < 0 — гиперболическое.
Если коэффициенты a(J постоянны и линейное
преобразование р,
^- приводит квадратич-
ную форму, соответствующую уравнению, к
каноническому виду, то преобразование независимых
переменных х, = ? Ьих} приводит дифференциаль-
;=i
ное уравнение также к каноническому виду:
Y д2п V1 д2п
i=l i=r+l
- / ди дп \
+ F хь ...,хи, м, --,..., -— =0.
\ Зх! 5xny
Пример 62. Уравнение колебаний (g > 0, р > 0)
г">2и
^ -ft2- = <iiv(P'gra(iM)-gM + F(f, хь ..., х„)
для м(г, хь . , х„) вследствие равенства div(p grad u) =
= / -—(р -—) является гиперболическим
дифференциальных, \ dxj
1 = 1
ным уравнением; при этом д, р и q определяются свойствами
колеблющейся среды, а функция F(t, xu ..., х„) выражает
интенсивность внешнего возмущения.
Частные случаи:
д2и , д2и ,, ,
-г-у- = а т—j- + f\t, х) — одномерное волновое уравнение
dt ох
описывает малые поперечные колебания струны;
dh
д2и J д2и д2и\ Г1 . ,
W~*\d?-+ ду2-) + Яи х' у)-*»"*
ное волновое
уравнение описывает колебания мембраны постоянной
плотности;
д2и г( д2и д2и д2и\ Г1
W = a{dxr+dyr+~d?r)+ HU X' У' Z) ~ трехмерное
волновое уравнение описывает распространение звука в
однородной среде и распространение электромагнитных волн
в однородной непроводящей среде. Этому уравнению
удовлетворяют также плотность и давление газа, потенциал
скорости, компоненты напряженности электрического и
магнитного полей и их потенциалы. Для краткости часто
пишут:
д2и
— а Дм,
где Дм =
д2и д2и
+ ... + zr^-y и называют По оператором Далам-
дх\ "• дх2„
бера и Д — оператором Лапласа.
Пример 63. Дифференциальное уравнение
распространения тепла и диффузии в среде (д > 0, р > 0)
ди
g — = div (p • grad м) - qu + F{t, x,,..., хя)
{уравнение диффузии) является параболическим. Если р, q -
постоянные величины, то получаем уравнение
теплопроводности
ди
= а2 Дм + /
П р и м е р 64. Для стационарных процессов, т. е. в случае,
когда
F(r, хь ..., xn) = F(x,, ..., х„),
u{t, х„ ..., хя) = м(х„ ..., х„),
уравнение колебаний
- div (p • grad м) + qu = F (хь ..., х„)
есть эллиптическое дифференциальное уравнение. Частными
случаями являются
Дм = — /(хь ..., хя) — уравнение Пуассона,
Ди = 0 — уравнение Лапласа.
Если искать решение волнового уравнения
д2и
dt2
— а2 Дм=/
при/ = /(хь ..., х„) eiwt в виде м (t, хь ..., хч) = м(х,, ..., х„)еш,
то для м получается уравнение Гельмголъца
Дм + к2п = - —/(хь х2, ..., хя)
— эллиптическое дифференциальное уравнение.
Характеристики (характерна иче-
ские поверхности). Пусть функция w(xb...
...,хи) {п ^ 2) имеет непрерывные частные
производные 1-го порядка, обладает тем свойством, что
на поверхности w = 0 выполнено соотношение
/ dw dw\
grad w = I -—, ..., — - I Ф 0, и удовлегворяет диф-
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
341
ференциальному уравнению 1-го порядка
i
|^=0. C.54)
Поверхность w(xb ..., х„) = 0 называется
характеристической поверхностью уравнения C.53),
а уравнение C.54) — характеристическим
уравнением для C.53). При п = 2 характеристические
поверхности превращаются в характеристические линии.
Пусть каждая поверхность семейства w(xb ...
..., хп) = с, а < с <Ь, является характеристической
поверхностью уравнения C.53). Так как grad w Ф О,
то это семейство заполняет область G: через
каждую точку области G проходит ровно одна
характеристическая поверхность. Если функция w дважды
непрерывно дифференцируема, то можно
произвести преобразование координат jq = w(xb ..., х„),
которое вследствие C.54) ведет к а^ = 0 в G.
П ример 65. Волновому уравнению и", — а2 ]? и"х~
соответствует характеристическое уравнение (w'tJ - а2 ? (Wx J.
* K//f \' Плоскости at + У xtb{ •
(где />ь ..., Ьпщ с - произволь-
л
ные числа такие, что ? bf «=
/-1
_^ » 1) образуют
характеристические поверхности. В дальней-
/ \ шем поверхность
* 2 "
Рис 3.68 г~\ ' Х *"
называется характеристическим конусом с вершиной в точке
(f°, х? xj). Часть характеристического конуса, для
которой a (t - t°) > ( ? (х, - хРJ J , обозначается Г + (f°,
/ " V/2
х? х?), а часть, для которой a{t -1°) < ? (х, - х?J ,
обозначается Г'(г°, х? х°) (рис. 3.68).
П р и м е р 66. Уравнение теплопроводности и', «¦ a2 j u"XjXj
имеет характеристическое уравнение ? (н-у2 -0 и
характеристические плоскости w ш t - с - 0.
я
Пример 67. Уравнение Лапласа ? м" «0 имеет ха-
я
рактеристическое уравнение J] (и>у2 « 0. Так как из
условия grad w — 0 следует, что w.» с, то уравнение Лапласа не
имеет действительных характеристических поверхностей.
Канонические формы уравнений с
двумя независимыми переменными.
Рассмотрим уравнение
. ди ди\
+ F х, у, и, —-, — = 0
1 дх ду)
C.55)
фициентами А, В, С, которые не обращаются в нуль
одновременно. Пусть А ф 0 в рассматриваемой
области (х, у)-плоскости (в противном случае С Ф 0;
в случае А — С = 0 преобразование х = х + у,
у = х - у приводит к дифференциальному
уравнению с А Ф 0). Если после замены переменных
х = х (х, у), у = у (х, у) коэффициенты А (х, у) и С (х, у)
обращаются в нуль, то для функций х(х, у) и
у(х, у) выполняются равенства
C.56)
= j(B ± (В2 - ACI'2) =j
D=B2 - АС.
Классификация дифференциальных
уравнений.
1. D > 0 — гиперболическое дифференциальное
уравнение. Семейство кривых w (x, у) = с такое, что
w'y Ф 0, изображает характеристики уравнения
C.53) только тогда, когда выражение w (x, у) = с
есть полный интеграл одного из двух обыкновен-
dy
ных дифференциальных уравнений —— = lt (x, у),
dy_
dx
*i У)- Оба полных интеграла hl (x, у) =
и п2 (х> у) = С2 этих дифференциальных уравнений
(таких, что h\y ф 0, h'2y Ф 0) определяют два
семейства характеристик уравнения C.55). Если эти два
семейства характеристик рассматривать как
координатные линии, то получим
x = hi (x, у), y = h2 (x, у),
д2п ( дп дп\ л
—--+ F х, у, п, —-, —г = 0,
5х5у \ дх ду J
так как fi (х, у) # 0. Замена переменных х = х + у,
у = х — у дает эквивалентную каноническую форму
д2п дЧ -(- - - дп дп
+F
с дважды непрерывно дифференцируемыми коэф-
Пример 68. Уравнение Три коми уи"хх + и"уу = 0. А = у,
В ш 0, С « 1; тогда D=-j;>0bC = {(х; у) | х2 + (у + 4J < 9}.
Имеем /,(х, ,у) = (->;I/2 и /2(х, у) = -(-у)/2, и общий
интеграл уравнения (/.уД/х = (-у)/2 есть Ci = jx + (-H3/2.
а общий интеграл уравнения dy/dx - ~(-у)/2 есть С2 =
»-у х — (—уK12. Преобразование х = ~х + ( — .vK/2, у =
¦в — х — (—уK12 приводит уравнение Трикоми в области G
к нормальному виду
2. D = 0 — параболическое дифференциальное
уравнение. В этом случае оба дифференциальных
уравнения C.56) совпадают, так как lt = /2 = В/Л.
Единственное семейство характеристик можно
определить из уравнения dy/dx = В/А при помощи
общего интеграла h (х, у) = с такого, что /ij, # 0.
Преобразованием координат х = h(x, у), у = х
дифференциальное уравнение C.55) приводится к
342
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
нормальному виду
д2п
ду2 +
Пример 69 v2uxx + 2хуиху + х2и'уу + хи'х + и = 0. А- у2,
В = ху, С = х2 и D = 0; roi да /t = х/у и у2 - х2 - с есть
общий интеграл дифференциального уравнения dy/dx — х/у.
Преобразование х = у2 — х2, у = х приводит к нормальной
форме этого дифференциального уравнения:
гиперболично) и начальным условиям
м@, хь ..., х„) = ио(хи ..., х„),
"dt ' "i^b--.,^
(где м0 и Ui — заданные функции). Задача Коши
может быть сформулирована более общим образом.
Пусть задана поверхность S: f = w(xb ..., х„)
такая, что
3. D < 0 — эллиптическое дифференциальное
уравнение. В этом случае lt (х, >') и 12 (х, у) -
комплексно сопряженные. Преобразование
^ (х, у) + h2 (х, у)
У =
h1(x,y)-h2{x,y)
2\ ' '
где hi (х, у) = Ci и h2 (x, у) = С2 суть комплексно
сопряженные общие решения обыкновенных диф-
dy dy
ференциальных уравнений — = /х (х, у) и — =
= h (*•> У% приводит дифференциальное уравнение
C.55) к нормальному виду:
дЧ_ д*п_ -/ дА. ^)\-о
дх2 ду2 \ ' дх' ду)
В этом случае действительных характеристик не
существует.
П р и м е р 70. Уравнение Трикоии уи"хх + и"уу = 0 в области
(/ \- + (у - 4J ^ 9. Из —- = i(y)~ l/2 или --- = ~i(y)~il2
с !едуег, что /», (х, у) = у3/2 - / — х или h2 (x, .
2 + / — х.
Преобразование х = )-3/2, у = -
виду уравнения Трикоми в G
х приводит к нормальному
Корректные постановки задач для
отдельных типов дифференциальных
уравнений 2-го порядка. Пусть исследуемое
дифференциальное уравнение в рассматриваемой
области G не меняет свой тип.
Гиперболические
дифференциальные уравнения. Пусть область G лежит в
(t, хь ..., хи)-пространстве Rn+1. Гиперболические
дифференциальные уравнения описывают
колебательные процессы. Для гиперболических
дифференциальных уравнений имеет смысл задача Коши:
найти в G при t > 0 дважды непрерывно
дифференцируемую функцию u(t, xu ..., х„),
удовлетворяющую уравнению
д2и V1 д2и Y д2и
I + l +
F[t,xl9...,xm«, — ..., ~^j C.57)
(на коэффициенты налагаются такие условия,
чтобы это дифференциальное уравнение было
dw dw
dw
т. е. S не является характеристикой, и функции и0,
Ui заданы на S. Ищется решение уравнения C.57)
в области t > w(xb ..., х„), удовлетворяющее в S
условиям
и
ди
—-
on
(д/дп — производная по нормали к S). При этих
условиях все производные искомой функции по
г, хь ..., х„ можно вычислить на поверхности S
из дифференциального уравнения и начальных
значений.
Эллиптические дифференциальные
уравнения. Пусть G — ограниченная область
в (хь ..., х„)-пространстве R". Эллиптические
дифференциальные уравнения описывают статические
состояния. Поэтому ищутся решения
дифференциальных уравнений, которые на границе dG
области G удовлетворяют условиям вида 1/и
ди \
+ g — = h. Функции f, g, h заданы и непре-
dnJdG
рывны на dG, причем / ^ 0, g ^ 0, / + g > 0. Такая
задача называется краевой задачей.
Различают:
краевые условия 1-го рода:
ди\
краевые условия 2-го рода: ——
дп 18G
краевые условия 3-го рода:
я;
1
—— +fu 1 = h.
дп ) \3G
Соответствующие краевые задачи называются
краевыми задачами 1-го, 2-го и 3-го рода. Для
уравнения Лапласа Ам = F(xb ..., хя) краевая задача 1-го
рода называется задачей Дирихле, а краевая задача
2-го рода — задачей Неймана.
Параболические
дифференциальные уравнения. Параболические уравнения
описывают процессы диффузии. Для этих
дифференциальных уравнений, например для уравнения
вида
ди
д2и
B>Д&>0 при 1У>0, $,eR),
ставятся задачи с начальным условием
и@, х,, ..., х„) = wo(xb ..., х„),
и0 — заданная функция на гиперплоскости t = О
в (г, хь ..., х„)-пространстве R"+1.
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
343
Для гиперболического уравнения C.57) имеет
смысл рассматривать также смешанную задачу.
Пусть G — ограниченная область в (хь ..., х„)-
пространстве и Zj - цилиндр над областью G, т. е.
ZT={(t, х„ ..., хи)|0<* <Т, (хь ..., xn)eG}.
Ищем функцию и(t, хи ..., х„) в ZT,
удовлетворяющую начальным условиям
м@, хь ..., х„) = ио(хи • •., хп), 1
ди , > на G (G - за-
--@, хь ..., х„) = и1(х1, ... хп) ) мыкание G)
и краевому условию
--
dn
fu
= h(t, хь ..., хп)
(Sf — боковая поверхность цилиндра Zj). При этом
на cG должно быть выполнено условие
совместности
Аналогичная смешанная задача может быть
поставлена и для параболических уравнений.
Рассматриваемые задачи должны
удовлетворять следующим физическим соображениям:
1) Решение должно существовать.
2) Решение должно быть однозначно определено.
3) Решение должно непрерывным образом
зависеть от данных задачи.
Задача, удовлетворяющая этим требованиям,
называется корректно поставленной задачей.
3.3.2.3.2. Общие методы построения
решений. Метод Фурье решения смешанной
задачи для гиперболических или параболических
дифференциальных уравнений так же, как и в
случае некоторых краевых задач для
эллиптических дифференциальных уравнений, состоит в
применении разделения переменных и принципа
суперпозиции (см. 3.3.2.1). Разыскиваются так
называемые формальные решения, т. е. решения в
виде бесконечных рядов, в которых каждый член
является решением дифференциального уравнения
и удовлетворяет краевым или начальным условиям.
При соответствующих предположениях о диф-
ференцируемости коэффициентов уравнения,
начальных и краевых условий можно добиться
сходимости рядов.
Однородное гиперболическое
дифференциальное уравнение. Ищем
решение u(t, хь ..., х„) задачи
д2и
L (Ф H)
с эллиптическим оператором
начальными условиями
= мо(х,, ..., х„), --
C.58)
ь -.., хп)
и краевыми условиями
/ ди\\
[hu+ g — =0 при t > 0.
V dnj\dG
При этом G — ограниченная область (хь ..., х„)-
пространства и 3G — граница G. В дальнейшем
предполагается, что собственные значения Хк
оператора L положительны, причем 0 < A.t < A.2 < ...,
а соответствующие собственные функции/к(хь ...
..., х„), определяемые равенством Lfk = Xkrfk и
dfk
такие, что hfk + g ——
дп
dG
= 0, действительны и в
пространстве L2(G) со скалярным произведением
образуют полную ортонормированную систему
(см. 3.3.2.3.4 и 3.3.2.3.5).
Формальное решение поставленной задачи:
u(t, хь ..., х„) =
= f (ak cos ]/xk t + bk sin ]/Xk t)fk (хь ..., хя), C.59)
* = i
причем коэффициенты aki bk выбраны так, что
оо
ио(хи ...,х„)= X ak/k(xb ...,х„),
оо
их (хь ..., х„) = X \/Хк bkfk (хь ..., хя),
C.60)
Формальное решение может быть записано также
в виде
u(t, хь ...,х„)= ? dksin(\/xkt + ek)fk(xu ..., хя),
Jk = 1
где dk = (ak + bk)xl2, sin ek = ak/dk, cos ek = bk/dk.
Здесь каждый член ряда определяет
гармоническое колебание с амплитудой dkfk и частотой ]/\к.
Неоднородное гиперболическое
дифференциальное уравнение. Пусть
вместо уравнения C.58) имеем неоднородное
дифференциальное уравнение
д2и
г — г= -
Кроме того, выполняются те же самые
условия и предположения, как и в случае однородного
гиперболического дифференциального уравнения.
Формальное решение имеет вид
4 (t, хь ..., хи) = / \ак cos ]/%к t + bk sin ]/%k t +
t
J^ \ck(s)sm\/Tk(t - s)dslfki
344
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
c»(t)= fF{t,xl,...,xn)fk(xlt...,xJdxl...dxn.
G C.61)
Заметим, что первые два слагаемых в фигурных
скобках дают решение однородного уравнения с
начальными значениями м0 и мь третье же слагаемое
дает решение неоднородного уравнения с и0 = их =
= 0. В частном случае
F(t, хь ..., х„) =
= О(хь ..., хп)/,(хь ..., xB)sin|/k|f
при м0 = и\ = 0 решение, этой задачи имеет вид
u(t, хь ..., х„) =
С /sinl/A^f r- \
Параболическое
дифференциальное уравнение. Рассмотрим уравнение
ди
г —-= -Lu + F(t, xlt ..., х„), (хь :.., xn)eG,
ot
при условии
при f > 0.
Пусть для L выполняются те же самые
предположения, что и в случае однородного
гиперболического дифференциального уравнения.
Формальное решение имеет вид
u(t, хь ..., хп) =
00 t
= I {a*-** + lck(s)e-W-*ds} fk{xu ..., xn).
*=1 0
При этом ак и ск задаются формулами C.60) и
C.61).
Эллиптическое дифференциальное
уравнение. Ищется решение и (t, хь ..., хи)
эллиптического уравнения
в области z, = {(f, х,, ..., х„)|(хь ..., xn)eG,
О < г < /} с
U \t = l tf 1 \Л 1 > • • • 5 Лиу,
/ш + cj -¦- ) =0, 0 < f < /.
Формальное решение этой краевой задачи имеет
вид
u(t, хь ..., х„)
sh]/Xk(l-t)
s)ck(s)ds>fk,
где ак и ск вычисляются по формулам C.60) и C.61),
a bk — по формуле
bk = ^ulfkrdxl...dxn;
G
Gk(t, t) - функция Грина краевой задачи -v"(t) +
+ Xkv (t) = 0 при условии v @) = v A) = 0 (см.
табл. 3.5 в 3.3.1.7.1).
Пример 71. Колебание закрепленной струны длины I.
Найти решение гиперболического дифференциального
уравнения
с начальными условиями и ||=,0 — мо(х), и', ||и0 = и, (х) и
краевыми условиями и\х^0 = и\х„,=0.
В этом примере G совпадает с интервалом 0 < х < /,
, d2v
L определяется формулой Lo = — а -г~г и соответствующая
задача о собственных значениях Lv = \v при v @) = v (/) = 0
, (пка\г
имеет положительные собственные значения Х4 = I —г- I с
У 2 я?х
-у sin —т— при к = 1, 2,...
Формальное решение задается рядом
пка
t H- bfc si
. пка \ . пкх
11П — — f >Sin —r—,
J
У2 f ... nkx .
— |M0(x)sin-j-rf
1/21
или рядом
/ ч Т/2 V, . пкх . (пка \
и (t, х) = У у ) dk sin — sin f — t + ek L
где rft = (a^ 4- blY11, sin ek = at/rfk, cos e» = bk/dk.
Если м0 дважды непрерывно дифференцируема, а ut
непрерывно дифференцируема, то ряд для и (г, х) равномерно
сходится. Если м0 четырежды непрерывно дифференцируема,
ja ux трижды непрерывно дифференцируема, то почленным
дифференцированием можно доказать, что u(t, x) есть
решение поставленной задачи.
Каждое гармоническое колебание образует стоячую волну
пка л Л fl . пкх
с собственной частотой —-— и амплитудой dk / -у-sin ——.
Точки нулевой амплитуды хОн = — / (я = 0,
называются >>зловылш точками, а точки .
, 2, ..., к)
2л+1
2к
~/ (п = 0,
1, ..., к— 1) — точками максимальной амплитуды или
пучностями. Гармоническое колебание с Я., = I —1 называется
основным тоном: прочие гармонические колебания с Х2,
Х.3, • • • — обертонами. Суммарное действие отдельных тонов
дает тембр звука струны.
Пример 72. Распространение тепла в конечном
стержне. Найти решение параболического уравнения
и', = агипхх
с начальным условием и\,=0 = ио(х) и краевыми условиями
и \х=0 = и \x=i — 0; G, L, Xk, fk имеют тот же смысл, что и в
примере 71; ск - 0, так как F(t, x) = 0. Формальное решение
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
u(t, х) = |/|
пкх
- Г , ч Ккх .
т uo(x)sm — pJx.
Пример 73. Продольные колебания стержня с одним
свободным и одним закрепленным концом, на который в
начальный момент времени действует постоянная сила р.
Найти решение гиперболического уравнения
с начальными условиями и |, = 0 = ио(х), и', |,«0 = Uj (x) и
краевыми условиями м^|х=о = 0 (свободный конец), u'x\x=l= pd.
x2pd
После введения новой неизвестной функции п = и —
поставленная задача переходит в задачу
п", = а ихх +
a2pd
с начальными условиями п || = 0 = ио(х) —
и однородными краевыми условиями
x2pd
~2Р '
G - интервал 0 < х < I. Задача о собственных значениях
dy
0 имеет
2^ ,
— а —V = ^У П]
dx2
" . //am У
неотрицательные собственные значения Хк = I —-— I и
1ующие собственные функции /k(x)= /—cos—-
ветств
Формальное решение задается рядом
х pd I/2 \^/_ пка , . пка \
и (г, х) = -^~ + \ — > I afc cos —f + Ь» sin -j-f С'
2/ у / / A I « /
пкх
s—;
при этом
2
Я, , . пкх .
мо(х, у) sin -~sin
in ——dxdy,
Задача о собственных значениях для
~«2 (i'« + Vyy) = Ху при условии t' \(-)q, = 0 - имеет
ные значения А
функции
\хк1 --у и соответствующие со(
Л.(х, У)= -—
Р уп | ЛЫ I
где x = pcos9, у = р sin ф (/с =0,1, . , /=1,2, )
цк, — положительные корни уравнения Jk(t)=()
функция Бесселя 1-го рода к -го порядка, см
Формальное решение поставленной задачи пши
в виде ряда
».,cos|^it| +
р 2п
/=| |мо(х, >¦)
о о
р 2к
%
(x) cos — — dx.
При вычислении членов ряда получаем ck(t) = O, к ^ 1.
Пример 74. Колебания закрепленной мембраны. Найти
эешение гиперболического уравнения
и'п = а2 {и"хх + и;,)
) начальными условиями u|t = 0 = "o(*> у), "tli = o = "i (x, у) и
сраевым условием м |^^ = 0 для прямоугольника Go =
= {(х, у) | 0 < х < р, 0 < у < q) или для круга G^ = {(х, ^) | х2 +
ьг<р2}.
Задачу о собственных значениях для прямо-
гольника: —a2(vxx + v'yy) = Xv при условии t; \fiGo = 0 —
•ешим, предполагая, чю у(х, у) = vx {x)v2(y), и получим в
(к2 12\
ачестве собственных значений Хк1 = n2a2i —^--\—2- I и в
ачестве ортонормированных собственных функций
. , 2 . пкх nly
fki(x, у) = -----=-sin --- sin - -
]/рч р q
{к, /=1, 2, ..)
огда решение поставпенной задачи для об наспи Gd им«>т
(см. 3.3 2.3.4)
Пример 75 Смешанная задача дги двумерно,*
нения теплопроводности. Найги решение парабол и
дифференциального уравнения
при условиях и|,.о ="о(х» А') и "IdG» ~ ° в о(";1ас111
= {(х, у)|0<х<р; 0 < у < q}. Собственные функ
собственные значения оператора Lv — —a2 (vxx + i'^)
дены в примере 74.
2 . я*х . я/v . , 2( к2
Формальное решение дается рядом
2 I Г . . . пкх nlv
j i,'0(v, v)sin sm
/nn J J ^' "
346
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Пример 76. Задача Дирихле для прямоугольника:
Gr = {(x, у)|О<х<р; 0<.у<4}.
Найти решение эллиптического дифференциального
уравнения
«« + и;, - о
при условии м@, у) = ио(у), и(р, y) = ul(y) и и(х, 0) =
= vo(x), м(х, q) = Vi{x).
Сначала решается задача с краевыми условиями
и{0, у) = м(р, у) = 0 и и{х, 0) = vo(x), u(x, q) = vx (x).
Решение задачи о собственных значениях: 1х = —
dx2
при условии v@) = v (р) — 0 — имеет вид fk (х) = /— sin
V Р Р
22
к2п2
и Хк
виде ряда
При этом формальное решение получается в
1/2 f . . . nkx . , Т/2 f . . . nkx ,
ak = Uj |t?o(x)sin — dx, bk= Uj h>i(x)sin dx.
о о
Аналогично решается задача с краевыми условиями
и @, у) = м0 (у), и (р, у) = Mi (у), и (х, 0) = и (х, q) = 0.
Сумма двух этих решений дает формальное решение
поставленной задачи.
Операторный метод. Так же как и для
обыкновенных дифференциальных уравнений, при
решении уравнений в частных производных можно
с успехом применять операторный метод, который
основан на переходе от искомой функции к ее
изображению (см. 3.3.1.6). Часто применяют
преобразование Лапласа:
При этом искомую функцию считают функцией
одного из независимых переменных и
рассматривают остальные переменные как параметры. Для
определения изображения искомой функции
получают, таким образом, дифференциальное уравнение
(вспомогательное уравнение), которое содержит
на одно независимое переменное меньше, чем
исходное уравнение. В частности, если исходное
уравнение имело два независимых переменных, то
в качестве вспомогательного уравнения получим
обыкновенное дифференциальное уравнение. Если
из полученного вспомогательного уравнения удается
найти изображение искомой функции, то сама она
или находится по таблице изображений, или
получается по формуле обращения (см. 4.4.3).
Пример 77. Одномерное уравнение теплопроводности
при постоянной температуре на концах стержня:
fl2"L — wj = 0 при х0 < х < хь t > 0,
с начальным условием t'lr=o==wo (м0 — постоянная) и
краевыми условиями и \x = Xq = А, и \xmXi = В (А, В - постоянные).
Вспомогательное уравнение для функции
п(р, х) = J e~ptu(t, x)dt
При и0 = 0 коэффициенты Ci(p) и с2 (р) в общем решении
вспомогательного уравнения п (р, х) = сх (р) ех \Pla +
+ c2(p)e~xVP'a вычисляются из преобразованных краевых
условий п(р, х0) = Л/р и п(р, Xi)- В/р. Если х0 = 0 и /1=0,
то получим
п(р,
psh—к—
а
и затем после обратного преобразования
u(t,.
X, 71 /J /С Xj
Пример 78. Пусть стержень длины / находится в
состоянии покоя и его конец х = 0 закреплен. 3 момент
времени t = 0 на свободный конец стержня действует
сила F. Найти решение гиперболического уравнения
и',', - а2ихх = 0для0<х</, г>0
с начальными условиями и|,,0 = 0, и',\,ш0 = 0 и краевыми
условиями м L - о = 0» "*!*-/ = F/E (Е - модуль упругости)
Вспомогательное уравнение имеет вид
d2u
Р -
—.f и с усло-
du
виями и \х*0 - 0 и — —
ах ,»i pt,
разованной задачи получим
В качестве решения преоб-
после обратного преобразования находим решение
поставленной задачи:
. Bл + 1)ях Bn + l)nat
, . Fx SFI V
3.3.2.3.3. Гиперболические
дифференциальные уравнения. Случай двух
независимых переменных. Каноническая
форма линейных гиперболических
дифференциальных уравнений с двумя независимыми переменными
имеет вид
x, У, U, U'x, и'у)
C.62)
с характеристиками х = const и у = const.
Предположим, что функция / непрерывна по всем
переменным и удовлетворяет условию Липшица
(например, условие Липшица выполняется, если / имеет
непрерывные частные производные по и, р и q):
|/(х, у, и, р, q)-f(x, у, м, р, q)\ ^
^M{\u-u\ + \p-p\ + \q-q\).
Тогда справедливы следующие теоремы
существования и единственности для соответствующих
корректно поставленных задач.
а) Задача с начальными значениями.
Существует однозначное решение уравнения C.62)
с начальными условиями и (х, ф (х)) = м0 (х) и
ди/дп(х, <р(х)) = Mi (х), где у = ф(х) — заданная кри-
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
347
вая С такая, что ф' (х) # 0, д/дп обозначает
производную по нормали к С и м0, Mi - произвольно
заданные непрерывные функции на кривой С такие,
что производная и'о существует и непрерывна.
Решение м(х0, у0) зависит только от начальных
значений на отрезке Со кривой С, отсеченном
характеристиками Р0В0 и ЛИо- Изменение
начальных данных вне Со не влияет на решение в точке
У
0
с
Q
х--
PL
~со,уо)
А, Ао
--а
п
-ц-Ь
х=а j
Рис 3 69
Ро. Отрезок Со называется областью зависимости
решения в точке Ро (рис. 3.69).
б) Задача с начальными значениями
на характеристиках. Пусть функция
п(х) непрерывно дифференцируема на
характеристике у = Ь, а функция g (у) — на х = а с условием
совместности h (а) — g (b). Тогда существует
единственное решение уравнения C.62), принимающее
заданные значения на характеристиках х = а или
у = Ь:
и (х, b) = h (x), и (а, у) = д (у).
Область зависимости решения в точке Pt
состоит из BiQlJ AXQ, т.е. изменение начальных
значений h, g вне #iB(J AtQ не влияет на решение
в точке Р1 (см. рис. 3.69).
в) Смешанная задача. Пусть и0(х) —
непрерывно дифференцируемая функция на С:
у = ф (х), а д (у) - на характеристике х = а, причем
выполнено условие совместности и0 (а) = д (ф (а)).
Тогда существует однозначное решение уравнения
C.62) в области вида B0QDB0 (см. рис. 3.69),
которое на С и на х = а принимает заданные значения
и (х, ф (х)) = и0 (х), и (а, у) = д (у).
Формулу решения в явном виде дйя задачи с
начальными значениями на кривой или на
характеристиках для дифференциального уравнения
d2u
= h(x, у),
ди
ди
^ + с{х' у)и>
получают методом Римана.
Предполагается, что функции a, b непрерывно
дифференцируемы и с, h - непрерывные функции.
Сопряженное к L дифференциальное выражение
определяемся формулой
d2v д д
Mv = ——— - — (av) - — (bv) + cv.
дхду дх ду
Если а — b = 0, то Lu = Ми и оператор L
называется самосопряженным. Функция G (х, у; х0, у0)
должна, кроме аргументов х, у, зависеть еще от
параметров х0, Уо и удовлетворять следующим
условиям:
1) G как функция х, у удовлетворяет
сопряженному дифференциальному уравнению MG — 0;
2) G;(x, у0; х0, у о) -b(x, yo)G(x, у0; х0, у0) =0
(для у = у0),
G'y(x0, у; х0, Уо) - а(х0, y)G(x0, у; х0, у0) = 0
(для х = х0);
3) G(x0, у0; х0) ^о) = 1-
Значения функции G на характеристиках х = х0
и у = у о определяются из условий 2) и 3). Тогда G
определяется однозначно из задачи с
начальными условиями на характеристиках для
уравнения Mv = 0. Такая функция G называется
функцией Римана, соответствующей дифференциальному
оператору L. Для функции Римана G(x, у; х0, >>0),
соответствующей L, и функции Римана Н(х, у; х0,
Уо), соответствующей М, справедлив так
называемый закон взаимности:
Н(х, у; х0, у о) = G(x0, у о', х, у),
т. е. функция Римана дифференциального
оператора L переходит в функцию Римана сопряженного
дифференциального оператора М, если поменять
местами параметры и аргументы. Если L —
самосопряженный оператор, то функция Римана
симметрична по отношению,к (х, у) и (х0, .Уо)- При
помощи функции Римана получают формулу
представления решения задачи с начальными
значениями для Lu = h(x, у) в точке Ро (х0, у0) (см.
рис. 3.69 и п. а)):
2и (Ро) = и (Ао) G (Ао; Ро) + и (Во) G (Во; Ро) -
- f l(u'xG - uG'x + 2buG) yn +
B0A0
+ (u'yG - uG'y + 2auG) xn) ds + 2 Jf hG dx dy,
I
если С представимо в виде х = х (s), у = у (s), где
5 — длина дуги и х' • у' Ф 0, а х„, у„ — компоненты
единичной нормали к С, внешней по отношению к
области Z = В0А0Р0В0. Правая часть этой формулы
может быть определена через начальные данные
u(x(s), y(s)) = uo(s), ^(x(s), y(s)) = u1(s),
ди
так как, зная и и —- вдоль С, мы знаем также
дп
и'х и и'у вдоль С.
Формула представления решения для задачи с
начальными значениями на характеристиках (см.
рис. 3.69 и п. .6)) имеет вид
u(Pl) = u(Q)G(Q; P,)- \G(u'y + au)x=ady-
Ух
- \G(u'x + bu)y-^bdx + ДО Gh dx dy,
a S
где S — прямоугольник P^B^QA^
Пример 79. Вычислим функцию Римана для уравнения
Ьи^и'ху —— и = 0. Оператор L является самосопряженным,
348
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
т. е. функция G симметрична. Если обратить внимание на
второе и третье условия для функции Римана, то можно
предположить, что G =g(z), где z = (х - хо)(у - у0), д @) = 1.
Обе характеристики в точке Ро(*о. Уо) удовлетворяют
уравнению z = 0. Функция g(z) является решением
уравнена da 1
ния 2 -т~г+ ~> ТУ~® ПРИ условии д@) = 1 или, если
сделать замену z = г2, решением модифицированного
уравнения Бесселя
dr
Отсюда 0-/о(|Л) и G(x, у; х0, >>0) - Ы/(* - хо)(у - у0))
есть искомая функция Римана (/0 (t) — модифицированная
функция Бесселя 1-го рода нулевого порядка (см. 3.3.1.3.4)).
Пример 80. Дифференциальное уравнение
распространения электрического тока по проводам (телеграфное
уравнение) имеет вид
аи',', + 2Ьи', + си = и'хх,
причем а > 0, b и с - постоянные. Для новой неизвестной
функции м, определяемой соотношением и ш йе~Ы1а,
получим уравнение
-«^ + Я»Й ' ' " ' Ь2~аС
у = — (mt - х) приводится к виду п?р - — й — 0. Из формулы
представления получается решение исходного уравнения,
которое удовлетворяет начальным условиям п|,_0 " "о(х).
п', \,s0 — ui (*)• Таким образом, подставив в формулу
представления функцию Римана G = /0 (|/(х - х0) (у - у0)) из
примера 79 и возвращаясь к исходным переменным, получим
w(x, t) = -у(и0(х - mt) + uo(x + mt)) +
]/m2t2 - (s - х2)
Частный случай: а = 1/р2, b - с = 0. Тогда т**р, п ш 0
и в силу того, что /0@) = 1, /,@):=0, получим решение
уравнения и',',— р2и"хх — 0 с начальными условиями и|(_0»
-i/0(x), «JI«-o-"iW в следующем виде (формула Далам-
бера):
О-т {"<>(*-/¦
Дифференциальное уравнение колеблющейся
струны, или одномерное волновое уравнение,
&и_ _ 2 д2и
= о
C.63)
имеет характеристики х ± at = const (рис. 3.70) и
преобразованием t = х — at, х = х + at может
быть приведено к каноническому виду Щ% = 0.
Уравнение C.63) имеет общее решение
u(t, x)=
at)+f2(x-at),
где /j и /2 — произвольные дважды непрерывно
дифференцируемые функции. Функция /2 (х - at)
описывает возмущение, которое исходит из точки
х0 в момент времени г = 0ик моменту времени t
приходит в точку х = х0 + at (рис. 3.71).
Отсюда следует, что эта функция описывает
волну, которая распространяется вправо со
скоростью а. Аналогично /i (x + at) описывает волну,
x-at=const
которое заменой независимых переменных х — — (mt + х), _ и /х\
Рис. 3.70
распространяющуюся влево со скоростью а.
Общее решение уравнения C.63) есть суперпозиция
этих двух волн.
Решение задачи с начальными значениями на
кривой С: t=Oc начальными условиями и @, х) =
ot
—ui\x) имеет вид
x + at
и (t, х) = 1 („0 (х - at) + и0 (х 4- at)) + ^ J Mi(SMS
(решение Даламбера, см. пример 80). Это решение
xo-at
xo*at
Рис. 3.71
показывает, что область зависимости АВ решения
и в точке Р отсекается обеими характеристиками,
проходящими через Р, на оси х (см. рис. 3.70).
Задача о закрепленной струне. Найти решение
уравнения C.63) с начальными условиями и @, х) =
= и0 (х), и',@, х) = мх (х), 0 < х ^ /, и краевыми
условиями и (Г, 0) = и (t, I) = 0. Пусть при этом и0
дважды и их один раз непрерывно
дифференцируемы и выполнены условия совместности и0 @) =
= м0 (/) = 0 и и^ @) = их (I) = 0. Если продолжить
начальные значения и0 и wt посредством формул
мо(-х) = -мо(х) и м1(-х) = м1(х) на отрезок
[ — /, /], а затем периодически на всю ось х, то
при дополнительных условиях u'q @) = u'q (I) = 0,
и\ @) = Mi (/) = 0 функция u0 на оси х дважды, а
функция и^ один раз непрерывно дифференцируемы,
и решение этой задачи дается решением Далам-
бера. Если исследовать эту задачу с точки зрения
колебаний, то удобно использовать метод Фурье
(см. пример 71).
Задача с данными на характеристиках. Пусть
на х — at = г задана функция h (t) и на х + at = s —
функция y(t) (см. рис. 3.70), и пусть они дважды
непрерывно дифференцируемы. Будем искать такое
решение уравнения C.63), чтобы u(r + at, t) = h(t)
и u(s - at, t) = g (t). При этом справедливо условие
совместности h\ 1 =
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
349
ответствующим образом функции fx и /2 в общем
решении уравнения C.63), получим решение этой
задачи:
u{t, х) =
2а
Задача с начальными значениями для
неоднородного одномерного волнового уравнения u't't — а2ихх =
= f(t, x) имеет решение
u{t, х) = —Ы* - ot) + ио(х + at)) +
— \\f(s,r)dsdr,
К
s < f, |r-
-s|}
(прингде К = {(s, г)
цип Дюамеля).
Случай более чем двух независимых переменных.
Решение задачи о начальных значениях для дву-
д2и ( 2
мерного волнового уравнения
Ot
- = а2(~
ь х2),
+ —г- при условиях и @, хь
дх\)
—(О, Xi, х2) = и1(х1, х2) дается формулой Пуассона
и(ихих2)=±-( ГГ .^Ы^Ы
Х2 +
±- dxx dx2 C.64)
(г2 = (Зс! — xtJ -f (x2 — x2J). При этом
предполагается, что и0 трижды и ut дважды непрерывно
дифференцируемы. Область К^ьХг) есть круг в (хь
х2)-плоскости с центром (хь х2) и радиусом at.
Пусть М,*1'*2'*3 [/] обозначает среднее
значение функции/(хь х2, х3) на сфере s,*1'*2'*3 радиуса
t с центром (хь х2, х3):
2п п
_L
Xl +1 cos ф Sin 9f
х2 + t sin ф sin 0, х3 + t cos 0) cos 0 dQ dcp.
Решение задачи о начальных значениях для
трехмерного волнового уравнения
д2и 2 / д2и д2и д2иs
dt2 \ дх2 дх2 д.
при условиях и@, хь х2, х3) = м0(хь х2, х3),
ди @, хь х2, х3)
= щ (хь х2, х3) (w0 трижды и их
dt ^
дважды непрерывно дифференцируемы) дается
формулой Кирхгофа
ь х2, х3)
Истолкование формул C.64) и C.65). Пусть
начальные возмущения и6 и их отличны от нуля
лишь в каждой области G вблизи начала координат.
Решение C.64) показывает, что вне области,
ограниченной огибающей Е таких окружностей S?i>JC2>,
что (хь x2)eG, имеет место состояние покоя;
напрдтив, решение внутри области, ограниченной
огибающей, в общем случае не равно нулю
Рис. 3.72
(рис. 3.72). Решение имеет только внешний
волновой фронт.
Формула C.65) показывает, что в общем
случае в области, ограниченной огибающей Et и
лежащей вне области, ограниченной Е2, решение
не равно нулю. В области, ограниченной Е2, и вне
области, ограниченной ?ь имеет место состояние
покоя (рис. 3.73). В этом случае решение имеет
четкий внешний и внутренний волновой фронт.
Поной
C.65)
Рис. 3 73
Неоднородное волновое уравнение u"t — а2Аи =
= f(t, xu ..., х„). Как и в случае неоднородных
обыкновенных дифференциальных уравнений,
общее решение складывается из частного решения
неоднородного уравнения и общего решения
однородного волнового уравнения. Для того
чтобы получить частное решение неоднородного
уравнения, пользуются принципом Дюамеля:
решают задачу с начальными значениями п„ — а2Аи =
= 0 при условии п @, хь . ,.,х„; s) = 0 и п',@, хь ... ,х„;
s)=f(s, хь ..., хи) для однородного волнового
уравнения с параметром s. Тогда функция
u(t, хь ..., хи) = |м(г —s, хь ..., х„; s)ds
о
представляет собой частное решение
неоднородного волнового уравнения с однородными
начальными условиями. Таким образом, общее решение
350
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
трехмерного волнового уравнения получается в
виде
и (г, хь х2, х3) =
u(t, p, 0, ф) = —cos(cof + /ср + с) (со = ко),
Р
u(t, р, 0, ф) =
'[^
: А | tA^cos (cof q: /ср) qp — sin (cor x /ср) | cjps 0
1 CCC \ а' ь 2' 3 7
i? JU -—»—i*.*.*»
где г2 = ? (х, - х,J. В случае двумерного волно-
i= 1
вого уравнения к решению однородного уравнения
нужно прибавить частное решение неоднородного
уравнения, например,
_ tt[ /ft *" x^didx.dx,
па J J J (а2 (I - О2 - fa - X,J - (*а - х2J) '
2па
где К - область (хь х2, ^-пространства,
определяемая неравенствами
(со = fcfl),
и (Г, р, ф) =
= Zm (fcp) [Л cos m<p + В sin тф] [AJ cos cor +
+ В1 sin cof] (m = 0, 1,... ; со = ка).
Здесь (р, ф, z) — цилиндрические координаты:
Xi = p cos ф, x2 = p sin ф, x3 = z; (p, 0, ф) -
сферические координаты: хх = p cos ф sin 0, x2 = p sin ф х
x sin 0, x3 = p cos 0 в R3; (p, ф) - полярные
координаты: Х!=рсо8ф, х2 = р81Пф в R2; Zm(x)-
цилиндрические функции (решение
дифференциального уравнения Бесселя) и Jj+1/2 - сферические
функции Бесселя (ср. 3.3.1.3.4), У; - шаровая
функция (см. 3.3.2.3.4), к — произвольная
постоянная.
3.3.2.3.4. Эллиптические
дифференциальные уравнения. Исследуется задача о
собственных значениях задачи Штурлга - Лиувиллн
Выражение
1м
п
= - > -—[р —-
IV-
Хь *2. Хз)
/(Г - -, Xl5 X2, X3)
xi dx2
(p ^—\ + qu =\u, (xi, ..., xJeG,
C.66)
с краевыми условиями
называется запаздывающим потенциалом, так как
функция / берется не в момент времени г, а в
более ранний момент времени.
При рассмотрении смешанной задачи в случае
волнового уравнения следует обратиться к 3.3.2.3.2.
Такие задачи часто можно решать методом Фурье.
Частные решения одномерного волнового
уравнения и'/, — а2и"хх = 0 имеют вид
и (г, х) = С cos (cof + Ct) cos (/ex + C2) (со = ка\
и (t, x) = Сi cos (cor + /ex) + C2 sin (cor + /ex) =
= С cos (cor + kx + c).
Частные решения двумерного и трехмерного
волнового уравнения u't't — а2 Аи = 0 имеют вид
и (г, хь ..., х„) = п (хь ..., х„) е±ш (со = ка),
где п есть решение уравнения Гельмгольца Ам +
+ к2п = 0 с произвольной постоянной к (ср. частное
решение уравнения Гельмгольца; см. 3.3.2.3.4).
Отсюда получаются следующие частные решения:
u(t, хь х2, х3) =
C.67)
(например, при р = 1 и q = 0 Lu = — Aw); при этом
G - ограниченная область с кусочно гладкой
границей 3G и д/дп обозначает производную по
нормали к dG. Пусть для (хь ..., xn)eG = G (J dG
справедливы следующие условия:
р(хь ..., хя)>0, q(xx, ..., х„)^0,
р непрерывно дифференцируема и q непрерывна
Пусть для (хь ..., xn)edG выполняются неравенства
/(хь ..., хи)^0, у(хи ..., xn)>0,f + y>0 и/, g
непрерывны. Ищем нетривиальные решения и
(т. е. ненулевые), которые дважды непрерывно
дифференцируемы в G и непрерывно дифференцируемы
в G.
Для L справедливы первая формула Грина
(к\ +к22+Ц=к2; со = ка\
u(t, р, ф, z)=
= Zm (р ]/к2 - К2) cos (cor + Kz + тф + с)
(т - 0, 1, ...; со = ка),
u(t, p, 0, ф) = — Jj+l/2{kp) У,@, ф)cos(ш + с)
(/ = 0,1,...; со = /еа),
...^ = jJP
G ,= i
— /w —dS + \\ quvcdxl...dxn
J dn JJ
ас с
Грина
Я(и1м — uLv) dxi... dxn = I p ( и — v -r— I <iS;
G dG
при этом предполагается, что и, v дважды непре-
J
ас
и вторая формула Грина
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-ю ПОРЯДКА
351
рывно дифференцируемы в G и один раз — в G;
dS есть элемент поверхности границы 8G.
Оператор L эрмитов (салгосопряженный), т. е.
выполняется равенство JJ uLv dxt... dxn = JJ vLu dx{...
G G
...dxn для всех u,veD, где функция и,
удовлетворяющая краевым условиям C.67), содержится
в множестве функций D, если она дважды
непрерывно дифференцируема в G, один раз — в G и
если \^(LuJdxl ...dxn < оо.
G
L — положительный оператор, i.e. (Lu, и) =
= \\uLudxx...dxn > 0 для всех ueD. Эго свойство
G
следует из неравенства
~—) dxi...dxn,
д) Каждая функция и е D может быть разложена
в равномерно и абсолютно сходящийся ряд по
собственным функциям оператора L:
оо
м(хь ..., х„) = ? скик(хи ..., х„),
ck =$$uukdxl... dxn. C.69)
G
е) Система собственных функций оператора L
плотна в L2 (G).
ж) Если ueD, то ряд C.69) можно почленно
продифференцировать по х,. Полученные при
этом ряды сходятся в L2 (G) к du/dxh т. е.
и»
'G ,Т7
G k=i
min
(л,, ..
p
xn)e<7
р(хи ..., х„), ueD.
Нетривиальное решение задачи о собственных
значениях задачи Штурма — Лиувилля C.66),
C.67) называется собственной функцией, а
соответствующее ей X — собственным значением.
Свойства собственных функций и
собственных значений поставленной задачи таковы:
а) Собственные значения оператора L
неотрицательны.
б) Собственные функции оператора L,
принадлежащие различным собственным значениям, взаимно
ортогональны, т. е. из Lu = Хи и Lu = Хп при X ф X
следует, что
Л ип dxx.. .dxn = 0.
G
в) X = 0 юлько тогда является собственным
значением оператора L, когда q = 0 и / = 0. При
этом X = 0 — простое собственное значение (т.е.
существует только одна собственная функция для
этого собственного значения) и и0 = const —
соответствующая ему собственная функция.
Для выявления дальнейших свойств заменим
краевые условия C 67) Будем считать, что
.дп \дС
0
2* 0). C.68)
г) Множество собственных значений оператора L
счетно и не имеет конечных точек накопления.
Для каждого собственною значения может
существовать только конечное число собственных
функций.
Таким образом, собственные значения можно
расположить в возрастающем порядке 0 ^ Хх <
^ Х2 < ... с Хк -+ оо при к -» оо; при эт ом Хк пишется
столько раз, сколько линейно независимых
собственных функций соответствует этому
собственному значению. Собственные функции
обозначаются как мь и2, ... и удовлетворяют условиям
1мк = Хкик (к = 1,2,...) и ukeD. Можно предпо-
тгать, что собственные функции ортонормиро-
(аны:
j j ukUi dxx dx2 ... dxn = bki.
з) Если подставить вместо р и q функции р и q
такие, что р ^ р, q ^ q, то это приведет к
возрастанию собственных значений, т. е. к Xk ^ Хк.
Аналогично для р ^ р и q ^ q получаем Хк ^ Хк.
и) Расширение области G влечет за собой
уменьшение собственных значений (при краевых
ди
условиях —— =0 или ыЬс = 0).
on BG
к) Каждое собственное значение Хк, которое
связано с краевыми условиями вида (fu +
= 0, где f/g ^ 0, есть неубывающая
3G
функция fig.
Замечание. Все результаты остаются в силе,
если задача Штурма - Лиувилля имеет вид
+ дм
Lu = Хри,
'— =0,
\dG
где функция р положительна и непрерывна в G.
Вместо элемента объема dxi...dxn в этом случае
вводят элемент объема р(хь ..., xjdx! ... dxn.
Для вычисления собственных значений и
собственных функций часто применяют метод Фурье,
который основан на разделении переменных (см.
3.3.2.1 и 3.3.2.3.2).
Пример 81. Пусть поставлена задача Шгурма-
Лиувилля
для области G = {(х, у)\х2 + у2 < R2} в (х, у)-прос1рансгве
В полярных координатах х = р cos cp, v = p sin ф, 0 ^ р < R
О < ф < 2л, дифференциальное уравнение имеет вид
дп
1_д2п
при условии, что u(R, ф) = 0, и при дополнительных условиях
на м(р, ф); п(р, ф)|р = о ограничена и п(р, ф) = м(р, ф + 2л),
полагая п(р, ф) = «;(ф) w(p), получим —v" = цг (при условии
v (ф) = I? (ф + 2л)) и р (pw')' + (р2Х. - ц) w = 0 (при условии
w@)#oo, w(/?) = 0). Из первой задачи о собственных
значениях для v легко вычислить цк = к2 и собственные функции
1
sin /сф,
/л
352
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Преобразование р ]/\ = р приводит дифференциальное
уравнение для w к дифференциальному уравнению для бесселевых
функций
учитывая условие vv(O) Ф оо, получим решение и>(р) =
= Л(|Др) (Л @ - функция Бесселя 1-го рода fc-ro порядка;
ср. 3.3.1.3.4). Здесь ЛAДя) = 0, т.е. \^XR = \ikJ, где цу
(/ = 1,2,...)- положительные корни функции Бесселя Jk (t).
В качестве собственных значений* и нормированных
собственных функций при ц* = к2 получаем
л Uy-S-
Таким образом, собственные значения и собственные
функции поставленной задачи о собственных значениях равны
Гармонические функции. Функция
и(хъ ..., х„), которая в области G пространства
R" дважды непрерывно дифференцируема и
удовлетворяет уравнению Лапласа Дм = 0,
называется гармонической функцией в G.
Некоторые виды гармонических
функций.
В декартовых координатах при п = 3:
д2и д2и д2и л
U (XU Х2, Х3) = ??*»*» + k2*2 + k*X*
(к( — произвольные комплексные числа такие, что
к\ + к\ + к2ч= 0),
м(хь х2, х3) = (at
b2x2)(a3
(a,-, bt (i = 1, 2, 3) — произвольные числа);
при п =2:
32м Л
5xf 5xi
м(хь х2) = е±/с(^+'Ы
«(^ь ^2) =(^i + Mi) («2 + h2x2)
(к, аи а2, bu b2 — произвольные числа).
В цилиндрических координатах
при п = 3:
хх = р cos ф, х2 = р sin ф, х3 = z,
1 д ( ди\ 1 д2и д2и
Разделение переменных и = их (ф) и2 (р) w3 (z)
приводит к трем уравнениям:
dip2
) = 0,
C.70)
C.71)
ная. Тогда
и (ф, р, z) = е - Kz Zm (Kp) (a cos тф + b sin тф),
м(ф, р, z) = e±Kz.
-J(acosm9 + bsinm9),
и (ф, р, z) = (А + Bz) (a + P In p) (а + Ьф)
(а, Ь, А, В, а, р - произвольные параметры), Zm(x) -
цилиндрические функции (решения
дифференциального уравнения Бесселя). Если потребовать, чтобы
гармоническая функция и была ограниченной при
р = 0, то вместо Zm (x) надо подставить функцию
Бесселя JOT(x) (ср. 3.3.1.3.4).
В сферических к о ор ди на та х при п = 3:
хх = р cos ф sin 0, х2 = р sin ф sin 0, х3 = р cos 0,
1
1
ди\
1 ^г +
1
д2и _
т р2 sin2 0 гф2" ~
Разделение переменных и = wt (ф) и2 (cos 0) иъ (р)
приводит к уравнениям
I1 , + ^2"i (ф) = 0. C-72)
, 2 cfo3(p)
^Р2
(s = cos0;m = O, ±1, ±2,..., ±7; ; = 0, 1, 2,...),
причем следует потребовать регулярности и2 для
0=0 и 0 = п. Тогда
и (р, 0, ф) =
= I Apj Н г—г- J P*/1 (cos 0) (a cos тф + b sin тф)
\ PJ /
с многочленами Лежандра PI'(s) (см. 3.3.1.3.4),
и(р, 0, ф) = ( V +-^г) УЦв, Ф) (/^ Ь2,...)
с шаровыми функциями
j
Yj @, ф) = ? PJ1 (cos 0) (am cos тц> + bm sin тф).
m = 0
При и = 2:
X! = р cos ф, х2 = р sin ф,
1 д ( ди\ 1 д2и л
и(р, ф)
1рм н——Uacosmip + Ь81птф),
^ (р, ф) = А + В In p
причем требование «i (ф) = «i (ф + 2л) учтено
условием, что т — целое; К — произвольная постоян- (А, В,а,Ь — произвольные параметры; т = 0,1,2,...).
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
353
Специальные решения уравнения
Гельмгольца Дм 4- к2и = 0.
В декартовых координатах хь х2, х3:
и (хьх2,х3) = ??'(*tx» + к2*г + к>х*) (к\ +к\ + к\ = к2),
и (хьх2,х3) = (а + Ьхх)АкгХг + *з*з) (к\ + к\ = к2),
и (хьх2,х3) = (а + Ьхх) (А + Вх2) е*кх\
В цилиндрических координатах:
xt = р cos ф, х2 = р sin ф, х3 = z.
Разделение переменных (в предположении, что
ы(р, ф, z) = «! (ф) м2 (р) м3 (z)) приводит к
дифференциальному уравнению C.70) для и1 (ф), к C.71)
для u3(z) и к уравнению
для и2(р), где т = 0, ±1, ±2, ... и К —
произвольная постоянная. Тогда
и (р, ф, z) = е±*г Zm (p ]/k*~+K*) (a cos шф +
+ b sin тф) (т = 0, 1, 2,...),
и (р, ф, z) = e±iXzZm (p ]/k2 - X2) (a cos тф +
4- b sin m<p) (К = АД
м (р, ф, z) = (A + Bz) Zo (kp) (a + Ь<р).
В сферических координатах:
Xj = р cos ф sin 6, х2 = р sin ф sin 0, х3 = р cos 0.
Разделение переменных (в предположении
и (р, ф, 0) = ых (ф) и2 (cos 0) ы3 (р)) приводит к
дифференциальному уравнению C.72) для и1 (ф), к
C.73) для и2 (s), где s = cos 0, и к уравнению
^из(р) | 2 ^3(р
dp2 p dp
для м3(р). Тогда
w(p, ф, 0) = —Jj+1/2(*p) У,@, ф),
1/Р
м(р, ф, 0) = —e±ikP,
Р
где У,@, ф) - шаровые функции и JJ+1/2 -
сферические функции Бесселя (ср. 3.3.1.3.4).
Шаровые функции. Под шаровой
функцией У| порядка / = 0, 1, ... понимают каждую
однородную гармоническую функцию степени /,
заданную на единичной сфере Sx с R". Шаровыми
функциями в R2 являются тригонометрические
функции
У, (ф) = я, cos /ф 4- b, sin /ф (/ = 0, 1, 2, ...),
а однородные гармонические многочлены имеют
вид
иi (хь х2) = р' (a, cos /ф + 6/ sin /ф) =
где z = х, + /х2.
Шаровые функции У,@, ф) в R3
удовлетворяют дифференциальному уравнению
V 50/ sin20
12 И Н Бронштейн, К А Семендяев
Функция У; является шаровой функцией 1-го
порядка тогда и только тогда, когда она
дифференцируема произвольное число раз и удовлетворяет
данному дифференциальному уравнению. Функции
Ф и Р (в предположении УЦ0, ф) = Р(со8 0)Ф(ф))
удовлетворяют следующим дифференциальным
уравнениям:
dip2
(т = 0,1,2,...), C.74)
s = COS 0,
C.75)
причем условие Ф (ф) = Ф (ф + 2я) учтено тем, что
т = 0, 1, 2, ... При т = 0 уравнение C.75) есть
дифференциальное уравнение для многочленов
Лежандра, а при т > 0 — дифференциальное
уравнение соответствующих функций Лежандра
(ср. 3.3.1.3.4). Функции
УГ@, ф) =
' Р? (cos 0) cos тф при т = 0, 1, 2,...,/,
. PJm|(cos0)sin|m^ при т = - 1, -2,...,-/
(/ = 0, 1, 2, ...) —шаровые функции в R3.
Шаровые функции /-го порядка (т = 0, ±1, ...
..., +/) линейно независимы, и каждая линейная
комбинация
e, ф)= I
d ф)
вновь является шаровой функцией.
Шаровые функции Y? образуют в пространстве
L2 (Si) ортогональную и полную систему функций.
Справедлива формула
0 0
>7(e, ф)Jsine</e^/ф =
= 2л:
Помимо указанных шаровых функций У, @, ф)
других шаровых функций 1-го порядка не существует.
Каждая функция feL2 (Si) может быть
разложена по шаровым функциям в ряд
/(в, Ф) =f Z аТ УГ(в, Ф) = ? У, (в, Ф),
/ = 0 т= -I 1 = 0
причем У,@, ф) вычисляются при помощи формулы
Лапласа:
0,<p)P,(cosa)sin0</0d(p;
a обозначает угол между направлением @, ф) и
направлением @, ф). Кроме того, справедлива
интегральная формула
\Y
= ——- У,@,
354
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Свойства гармонических функций.
а) Для гармонической функции м(хь ..., х„)
справедливо следующее представление при п ^ 3:
u(x)= -
1
дп
Л
dG
при и = 2:
dG
при этом х = (хь ..., хя), у = (уь ..., >>„), | х - у | -
евклидово расстояние между х и у: | х — у | = ((хх —
->'iJ + -.-+(xw-)>,,JI/2, a
2тгй/2
есгь площадь поверхности л-мерной единичной
сферы.
Каждая гармоническая функция аполитична,
т. е. в каждой точке G ее можно разложить в
сходящийся степенной ряд.
6t) Если функция и(х) гармонична в открытом
шаре К % с центром х = (хь ..., xj и радиусом R и
непрерывна в замкнутом шаре К^, to ее значение
в центре шара равно среднему значению по
поверхности шара Sr:
1
u(x-y)dSr
б2) Пусть для функции и(х),- непрерывной в G,
выполнено следующее условие. Предположим, что
для каждой точки xeG существует число го(х) > О
такое, что для всех г <г0 справедливо
соотношение
Тогда функция и(х) гармонична в G.
в) Если функция и (х) ф const гармонична в G
и непрерывна в G, то в области G она не может
принимать ни максимального, ни
минимального значения, т. е. справедливо неравенство
min u(x) < и (у) < max u(x), yeG.
xedG xedG
Принцип максимума: гармоническая в
области функция достигает максимального
значения на границе области.
Bt) Если и \дс = 0, то и (х) = 0 в G.
в2) Если функция и является гармонической в
области R" \ G, непрерывной в R"\ G и lim и (х) =
_ |х|->+оо
= 0, то
|w(.y)|< max|w(x)|, veR"\G.
xedG
Если, в частности, и \$q = 0, то и =. О в R"\ G.
в3) Если последовательность функций ии и2, ..._,
гармонических в области G и непрерывных в G,
сходится равномерно на границе 3G области G,
то последовательность равномерно сходится в G.
г) Если функция и(х) является гармонической
в G\{0} и удовлетворяет соотношению
при п ^ 3:
и(х)
lim
1*1-0 |х|"
при п — 2:
lim
u(x)
= 0,
= о,
то ее можно доопределить в точке х = 0 так, что
полученная функция будет гармонической в
области G.
д) Если последовательность функций мь м2, ...,
гармонических в области G, слабо сходится к
непрерывной функции и в G, т. е. lim J{ ukv dxx... dxn =
k -+0O G
= JJ uvdx1 ...dxn для всех бесконечно дифференци-
G
руемых в G функций v с компактным носителем в
G, то и — функция, гармоническая в G. ,
е) Если функция и является гармонической в R"
и удовлетворяет неравенству
| м (х) |
m, xeR",
с ^ О,
то и — (гармонический) многочлен степени, не
большей чем т.
ж) Посредством преобразования Кельвина
(отражение относительно сферы 5^ в R":
R2 R2
X,- = -р^Х, ИЛИ X,- = --2-Х,-
|х|2
Гх|2
(i = 1, 2, ..., «)) можно получить изображение
Кельвина функции м(х)
при п = 3:
_,_, R ( R2
при п = 2:
и (х) = и
Если и (х) — функция, гармоническая при
| х | > R, то п (х) - функция, гармоническая в
4\{}
з) Для функции и (х) ^ 0, гармонической в шаре
Kr и непрерывной в К% справедливо неравенство
Гарнака
- и @) при | х | < R.
(*-1*1
Краевые задачи для уравнений
Лапласа и Пуассона в R3.
Задача Дирихле для уравнения Лапласа Аи = 0:
найти функцию, гармоническую в G, которая
непрерывна в G и на границе dG области G
совпадает с заданной непрерывной функцией и0.
Задача Неймана для уравнения Лапласа Аи = 0:
найти функцию, гармоническую в G, которая
УРАВНЕНИЯ В ЧАСТНЫХ ПРОИЗВОДНЫХ 2-го ПОРЯДКА
355
непрерывна в G и на границе dG области G
имеет заданную непрерывную производную по
нормали Uj (здесь G - ограниченная область с
достаточно гладкой границей).
Аналогичные постановки задач получаются для
уравнения Пуассона Дм = -/. Если / непрерывно
дифференцируема в G и непрерывна в G, то
краевые задачи для уравнения Пуассона сводятся к
соответствующим краевым задачам для уравнения
Лапласа Av = О посредством замены и (х) = v (х) +
+ V(x), где для функции
выполняется равенство AV= —/
Задача Дирихле для Дм = 0 и для Ам =
-/разрешима однозначно. Задача Неймана для Ам = О
и Ам = —/разрешима однозначно с точностью до
аддитивной постоянной, если выполнено условие
J M1J5 + ffj/^ = 0.
dG G
Функция Грина задачи Дирихле.
Функция G(x, х) называется функцией Грина
оператора Ам в области G, если она обладает
следующими свойствами:
1. При всех xeG функция G(x, х) имеет вид
G(x, x) = --
1
- + д (х, х).
Функция д (х, х) гармонична в G и непрерывна в G
относительно х.
2. Если xeG, то G(x, x)|xe^ = 0.
Свойства функции Грина.
а) Функция G(x, х) - гармоническая в G\{x}
и непрерывная в G\{x} по переменному х.
б) Для х, xeG, х Ф х, выполнено неравенство
0 < G (x, x) <
1
| х — х |
в) Если dG - достаточно гладкая поверхность
(например, если параметрическое представление
dG непрерывно дифференцируемо без особых
« точек), то существует и
однозначно определена
функция Грина G(x, x);
G(x, x) = G(x, x).
Для построения
функции Грина в областях со
свойствами симметрии
часто применяют
принцип отражения.
П р и м е р 82. Найти
функцию Грина для шара Kr.
Пусть * - точка,
симметричная х относительно Sr. Тогда
Рис. 3 74
R2 .
х. Будем искать функцию Грина в виде
G(x, х) =
1
' 4я | х - х | 4тс | х - х |'
Коэффициент А подбирают так, чтобы G(x, x)lve5G =0- Из
подобия треугольников (Охх) и (хзёх), xeS^ (рис. 3.74),
следует,
12s
R \х-х\ _ R
что |ТГ" |*^*Т Ео1И выбрать А = ИГР то
условие G \хедс ~ ° будет выполнено. Искомая функция
Грина имеет вид
1 Л |Jcj
г | х - х | 4л 11 х |2х - R2x \'
С(х, х) =
Пример 83. Найти функцию Грина для
полупространства х3 > 0. Точка х = (х,, х2, — х3) симметрична
точке х = (хь х2, х3) относительно плоскости х3 = 0.
Для функции С(х, х)= 4яи'_-|~ йфГПГХ»»""
G(x» x)lxe^G=0 выполнено при А = 1. Тогда G(x, x) =
1 1
4я | х - х | 4я | х - х |
есгь искомая функция Грина.
Если решение м(х) задачи Дирихле для
уравнения Ам = —/дифференцируемо достаточное число
раз на границе dG области G, то оно представимо
формулой
, x)f(x)dx,
xeG.
Формула Пуассона
¦«-яг Я
Я
|Х|=К
для | х | < R дает решение задачи Дирихле для
шара Кц: Ам = 0, и \ Sr = мв, где функция м0
непрерывна на 5^.
Краевая задача -Ам = Хм +/(х), и \dG = 0, где
/ непрерывно дифференцируема в G и непрерывна
в G, эквивалентна интегральному уравнению
и(х) = Х JJJ G (х, х) и (х) dx + Ш G (х, х)/(х) d~x.
G G
Наименьшему собственному значению задачи
Ам + Хи = 0, м \qq = 0 принадлежит только одна
(с точностью до положительного множителя)
собственная функция м2 (х), для которой при xeG
выполняется неравенство мх (х) > 0.
Краевые задачи для уравнения
Лаплас а в R2. Действительная или мнимая часть
аналитической в комплексной плоскости функции
удовлетворяет уравнению Лапласа в R2.
Рассматриваются те же самые краевые задачи,
что и в R3. При этом задача Дирихле однозначно
разрешима для произвольной непрерывной
функции м0, заданной на dG. Задача Неймана
разрешается однозначно с точностью до аддитивной
постоянной, если выполнено условие
разрешимости J м0 dS = 0.
dG
Функция Грина задачи Дирихле Дм = 0, м \qq =
= м0 для области G есть функция G (z, z) со
следующими свойствами (пишут м(хь x2) = m(z), где
z = хх + ix2):
1) G (z, z) = -—In =— + g (z, z), причем
2я | z - z |
g (z, z) — функция, гармоническая в G и
непрерывная в G noz;
2) G(z, z)\zedG = 0.
Для функции Грина справедливо неравенство
0<G(z, i)< -^-
2n
ln^
2n \z-z\
-, zeG,
\
356
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
где d — диаметр области G. Кроме того,
справедливы все другие свойства, указанные для функции
Грина в R3.
Функция
G(z, 1)= - 2^-ln|w(z, 1I= - ^-Re(ln(w(z,l)))
является функцией Грина задачи Дирихле для
односвязной области G, где
w(z, z) =
w(z)-w(z)
1 — w(z)w (z)
(w обозначает функцию, комплексно сопряженную
по отношению к функции w = w (z),
отображающей G в единичный круг). Задача Дирихле для
круга | z | < R решается по формуле Пуассона
|z-z|2
¦*ЬН V.
а для односвязной области G с краевой функцией
«о — по формуле
u(z) =
Re
8G
— w (z) w (z)
3.3.2.3.5. Параболические
дифференциальные уравнения. Уравнение
теплопроводности
1 ди д2и д2и „^
— -г-в=тт++ гт (ЗЛ6)
х;
a2
дх;
есть простой пример параболического
дифференциального уравнения. Важнейшие свойства
проявляются уже в случае п = 1 и справедливы для
произвольного п.
Так называемая первая краевая задача
(смешанная задача) является типичной задачей для
параболических дифференциальных уравнений: найти
функцию и(t, х), которая в области G — {(f, x)\t0 <
< t <T, (p! (t) < x < ф2 (t)} удовлетворяет
уравнению
4* ft, C.77,
a2 dt дх2
непрерывна на G (J 0G и на Г = dG\ {(T, x) | (pi (T) <
< х < (р2 (Т)} (изображена на рис. 3.75 жирной
линией) принимает значения, определяемые
заданной непрерывной
^ функцией /.
Важно заметить,
что решение ищется
. ,,. для t > 0, если значе-
' 'г ния искомой функции
/x=<pf(t)
Рис 3.75
заданы при t = 0. В
общем случае при
t < 0 задача не имеет
решения. Уравнение
C.77) существенно из-
меняется, если t
заменить на —t. Это легко объяснимо из
физических соображений, так как уравнение C.77)
описывает необратимые процессы. При t < 0 задача
поставлена некорректно, если краевые условия
относятся к t = 0.
Имеет место принцип минимакса: каждое
решение u(t, x) уравнения C.77), определенное и
непрерывное на G (J 0G, принимает наибольшее и
наименьшее значения на Г, т. е. либо на нижней,
либо на боковых линиях, ограничивающих G.
Отметим два следствия.
1. Решение первой краевой задачи уравнения
теплопроводности однозначно определено в G.
2. Решение первой краевой задачи уравнения
теплопроводности непрерывным образом зависит
от заданной на Г функции f.
Наряду с поставленной краевой задачей часто
исследуют задачу с начальными значениями
(задачу Коши): найти функцию u(t, x), непрерывную и
ограниченную при t ^ 0, которая при t > 0
удовлетворяет уравнению C.77), а при t = 0 -
начальному условию u|f = o = "oM> гДе "оМ при всех х
определена, непрерывна и ограничена.
Решение этой задачи определено однозначно и
непрерывным образом зависит от функции мо(х).
Интеграл Пуассона
+ 00
и(и х)=__i г«j(i
дает решение задачи с начальными значениями.
Первая краевая задача для уравнения
теплопроводности C.76) также разрешима однозначно.
При этом краевую задачу следует формулировать
так: найти функцию u(t, хь ..., х„), непрерывную
в замкнутой области, которая внутри нее
удовлетворяет дифференциальному уравнению C.76), а
на t = 0 и боковых поверхностях совпадает с
заданной функцией / (рассматриваемая замкнутая
область ограничивается плоскостями t = 0 и t = Т, а
ее боковая поверхность может быть представлена
в виде объединения конечного числа гладких
поверхностей, вектор нормали которых нигде не
параллелен оси t).
Аналогичные результаты получим, если усло-
ди
вием =/на границе заменить на условие \- аи =/.
дп
Указанные выше результаты могут быть
перенесены на параболическое дифференциальное
уравнение общего вида
ди
/ j
д2и
ди
t, х„ ..., хи)-—+с(г, хь ..., хп)и
+ d(t, хь ..., х„),
если в каждой точке (/, хь ..., хи) рассматриваемой
области квадратичная форма
? au(t, хь ..., xjp^j
ОПРЕДЕЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
357
положительно определена и коэффициенты a,,-, bh
cud дифференцируемы достаточное число раз.
Частными решениями одномерного уравнения
теплопроводности являются
И(|, х) = е±**-№9
и (t, х) = А + Вх,
и(t, x) = ~-e-x2l^a2t) (t > 0)
(к, А, В — произвольные постоянные). Функция
есть частное решение «-мерного уравнения
теплопроводности, если uk(xl9 ..., .х„) есть решение
уравнения Гельмгольца Аи + к2и = 0 (см. 3.3.2.3.4).
Другими частными решениями уравнения C.76)
являются:
u(t,
uk(xi,
при п = J
u(t, хь х2, х
при п = 2
u(t, хи
1 2/D/2
1 2/2
t
A r2=.xf +
0, r2=x\ +
xl
3.4. КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО
ПЕРЕМЕННОГО
3.4.1. ОБЩИЕ ЗАМЕЧАНИЯ
Понятие комплексною числа представляет собой
расширение понятия действительных чисел. Многие правила
арифметики действительных чисел могут быть перенесены на
комплексные числа. Например, биномиальная теорема или
теория определителей оказываются справедливыми в
области комплексных чисел. Вообще на комплексную область
могут быть перенесены многие разделы действительного
анализа Так возник комплексный анализ, в основе которого
лежит теория аналитических функций
Исторически комплексные числа обязаны своим
возникновением главным образом попыткам найти решения
алгебраических уравнений
3.4.2. КОМПЛЕКСНЫЕ ЧИСЛА.
СФЕРА РИМАНА. ОБЛАСТИ
3.4.2.1. Определение комплексных чисел. Поле
комплексных чисел. Комплексным числом а
называют упорядоченную пару а = (ос, C)
действительных чисел со следующими свойствами:
1) Два комплексных числа «i = (аь рх) и а2 =
= («2» Р2) равны тогда и только тогда, когда
«! =ос2 и 0! = р2.
2) Сумма двух комплексных чисел а1 = (аь РО
и «2 = (<*2, Рг) определяется следующим образом:
(a,, h) + (а2, |32) = (
2).
3) Произведение двух комплексных чисел ах =
= (аь pj) и а2 = (а2, Рг) определяется следующим
образом:
(<хь Pi)-(a2, p2) =
= (ai<x2 - Pi
C.78)
4) Деление двух комплексных чисел ах = (аь рх)
и а2 = (а2, р2) определяется как действие,
обратное умножению:
fli («ь Pi) _ («1«2 + Р1Р2, «2P1 -«1Р2) =
«2 " («2, Р2) " " " " «2 + Р2
при a^ + pi # 0.
Действительные числа содержатся в множестве
комплексных чисел, а именно, все они являются
парами вида (а, 0); условимся в дальнейшем
писать (а, 0) = а.
Пары вида @, Р) называют (чисто) мнимыми
числами.
Пара i = @, 1) имеет специальное название —
мнимая единица. По правилу 3)
/2= -1.
Запись @, Р) для чисто мнимого числа
эквивалентна записи /р (так как @, 1) (р, 0) = @ • р-
- 1 • 0, 0 • 0 + 1 • Р) = @, Р)).
Каждое комплексное число а = (а, р) можно
записать в виде суммы действительного числа
a = (a, 0) и чисто мнимого числа ф = @, р):
а = (а, Р) = (а, 0) + @, р) = а + ф.
При этом а = Re а называется действительной
частью комплексного числа а, а р = Im a —
мнимой частью а.
Итак:
1*) Два комплексных числа равны друг другу
тогда и только тогда, когда равны их
действительные и мнимые части.
2*) я, + а2 = («! + /Рх) + (a2 + ip2) =
р2).
3*) Я! • а2 = (a, + /Pi) • (а2 + /р2)
4*) а1-= в*
а а
а2 а2 + /р2
+ Pi
lEi.j. • 2P
Пример 1.
(-l + 502C-4i)
1 + 3i
A - 10* -
10 + 7,-
5i
25) C-40A
-2A2 + 50C- 13i —
10
43 +
-30
12)
201/
, A0 + 701
1 5i-i
-7 + 10i
1 -5 =
358
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Таким образом, вычисления с комплексными
числами сводятся к выполнению действий над
действительными числами. Сложение и умножение
при этом коммутативны и ассоциативны. Кроме
того, для них имеет силу дистрибутивный закон:
а1 (а2 + аъ) = а^а2 + «1«з-
Комплексные числа образуют поле с нулевым
элементом 0 = @, 0) и единичным элементом 1 =
= A, 0).
3.4.2.2. Сопряженные комплексные числа.
Модуль комплексного числа. Под комплексным
числом, сопряженным к а = а + ф, понимают
комплексное число а, которое отличается от а только
знаком мнимой часги: а = а — ф. При этом имеют
место следующие соотношения:
а = а;
а — Ъ тогда и только тогда, когда а —
действительное число;_ _ _
а ± Ъ = а±Ъ, а- Ь = а- Ь, {а/Ь) = а/Ь, а • а = а2 +
+ Р2;
Re а = а = (а + а)/2 - действительная часть а;
Im а = Р = (а — а)/2/ — мнимая часть а.
Модуль | а | комплексного числа а есть
неотрицательное действительное число:
| = ]/а • а = |/а2 4-
Если а — действительное число, то модуль
совпадает с абсолютной величиной | а |. На модуль
комплексных чисел могут быть перенесены
различные неравенства для абсолютных величин. Так,
для любых комплексных чисел а, Ъ, ак, Ък верны
соотношения
I а • Ъ | = | а | • | Ъ |,
|я + 6|<|а| + |Ь| {неравенство треугольника),
* t\ak\2- t \bk\2
k=l k=l
{неравенство Kowu — Буняковского).
3.4.2.3. Геометрическая интерпретация.
Поставим в соответствие комплексному числу а = а +
+ ip на плоскости точку А, которая имеет
абсциссу х = ol и ординату у = р относительно
прямоугольной декартовой системы координат: А (а, Р)
(о_^ числе а также говорят как о точке). Если
О А = (а, р) — радиус-вектор точки А, то он также
может быть использован в качестве
геометрической интерпретации числа а (рис. 3.76). Таким
A(a,fl)
образом, множество точек плоскости, или
множество радиус-векторов соответствующих им,
взаимно однозначно соответствует множеству
комплексных чисел. Вся плоскость называется
комплексной плоскостью. Точки оси абсцисс —
действительной оси - соответствуют
действительным, а точки оси ординат — мнимой оси — чисто
мнимым комплексным числам. Комплексное число
а, сопряженное к л, изображается точкой А —
зеркальным образом точки А относительно
действительной оси (см. рис. 3J6).
Длина радиус-вектора О А комплексного числа
а = а + ф равна | а \ = |/а2 + р2 - модулю этого
числа, | а - Ь \ равен расстоянию между
соответствующими точками а и Ъ.
Геометрическое сложение: наглядная
интерпретация сложения (вычитания) двух,
комплексных чисел а = а + /р, Ъ = у + /5
осуществляется пщ помощи соответствующих
радиус-векторов О А = (а, Р), ОВ = {у, 8): сумме (разности)
-0
Л (а,-А)
Рис 3 76
Рис. 3.77
а ± Ь = (а ± у) + 1 (р ± 5) чисел а и Ъ соответствует
радиус-вектор О А ±ОВ = (а ± у, р ± 5) (см.
рис. 3.77 и 2.4.4.1).
3.4.2.4. Тригонометрическая и показательная
формы комплексных чисел. Аргументом
комплексного числа а = а + /р (Arg а) называют _угол <р0
(в радианах) между радиус-вектором О А = (а, р)
и положительным направлением действительной
оси (см. рис. 3.76), определяемый с точностью
до слагаемого, кратного 2л. Главное значение
аргумента: arg а = ср, -тс < (р0 < я; имеем: Arga =
= arg a + 2kn. Например, arg A + i) = тс/4.
Справедливы равенства: а = | а | cos ф0, Р =
= | а | sin ф0 (см. рис. 3.76).
Тригонометрическая форма комплексного
числа а:
а = | а | (cos (ф0 + 2kn) + i sin (ф0 + 2/стс))
(/с = 0, ±1, ±2, ...).
Тригонометрические и показательные функции
связаны формулой Эйлера cos <р + i sin <р = е19 (см.
3.4.5). Отсюда
а = | а | (cos ф + I sin ф) = | а \ ещ.
Таким образом, для каждого комплексного
числа возможны три представления:
алгебраическое, тригонометрическое и показательное.
П р и м е р 2. 1 + / |/з = 2 ( cos — + / sin —) = 2е'"/3, или
1 + i |/3 = 2 [cos (л/3 + 2kn) + i sin (я/3 + 2кп)] = 2е1 + 2кя)'
(если не ограничиваться одним главным значением arg a =
= Фо = л/3).
СТЕПЕНИ, КОРНИ
359
Модуль комплексных чисел вида е'ф равен 1.
Следовательно, в плоскости комплексных чисел
они располагаются на окружности радиуса 1.
Число 0 = 0+1-0 имеет неопределенный аргумент
и, следовательно, допускает представление 0 =
= 101 (cos ф + i sin ф) (ф любое).
Если а = | а | (cos ф + i sin ф), b = \b\ (cos \j/ +
+ / sin vj/), то
a • b = | a | | b | [cos (ф + \|/) + i sin (ф + \|/)] =
= \a\-\b\ei{*+*\ C.80)
татов (корней):
77Г~7 Г Фо + 2/стг . . Фо + 2кп 1
wk = v\a\\ cos 1- i sin ,
y [_ m m J
т. е. ]/~а определяет т различных чисел:
]fa = allm = {wk\k = 0, 1, ..., m - 1} =
= {w0, wl5 ..., wm_1}.
Для любого целого числа п имеет место
равенство wk+nm = wk, так что, кроме уже
указанных корней wk, никаких других, отличных от них,
\ = T^r[cos (ф - ф) + i sin (ф -
b \b\ \\
C.81)
Геометрическая интерпретация:
радиус-вектор произведения а • b получается
поворотом радиуса-вектора а на угол ф против часовой
I = IflUH*-*) т. / ф0
1 |?| ' быть не может. Решение w0 = |/|a|lcos
Дейстбитемьная ось
а/Ь
Рис. 3.78
стрелки и растяжением в \Ь\ раз. Аналогично
интерпретируется деление (рис. 3.78).
3.4.2.5. Степени, корни.
1) Натуральный показатель степени.
Возведение комплексного числа а в n-ю степень (п —
натуральное число) производится по формуле
Муавра
а" = [| а | (cos ф + i sin ф)]и =
= | а |" (cos иф + i sin иф) = | а \" е'Иф,
которую можно вывести из формулы умножения
C.80).
В частности, i° = 1, i1 = 1, i2 = -1, i3 = -1,
i4 = 1, /4и+* = ik (k — целое число).
Формула бинома, как и формула
геометрической прогрессии, верна.
2) Отрицательный целый показатель степени.
Полагаем ап = \/а~п (п < 0). Тогда для а", как
следует из формулы C.81), может быть
использована формула Муавра.
3) Дробный показатель степени. Показатель
степени имеет вид п = \/т, т - натуральное число.
Возведение а в степень 1/w называют также
извлечением корня т-й степени из а; каждое
комплексное число w такое, что wm = а, называют
корнем т-й степени из а:
Вычисление а1/т также осуществляется по
формуле Муавра, но теперь для п = 1/т. Однако,
в то время как все рассмотренные до сих пор
вычислительные операции имели однозначные
результаты, операция |/а дает т различных
резуль-h i sin —I уравнения wm = а называют главным
m J
значением у а.
Так как все wk имеют одинаковый модуль
|/| а |, то они в соответствии со значениями
аргументов (к = 0, 1, ..., т — 1) лежат в
т
вершинах правильного m-угольника с центром в
а
Рис. 3.79
начале координат. На рис. 3.79 изображено шесть
значений у а = {wk; к = 0, 1. ..., 5}.
Пример 3. Для уравнения w3 = 8/ имеем \/\ 8/1 =
= ^/8 = 2, Arg 8i = -у + 2/ся, следовательно,
+/sin № + **^: fc,q !, 2} -
-Ф + U -1/3 + U -2i}.
Эти три корня лежат в углах равностороннего треугольника
на расстоянии 2 от начала координат. Главное значение
равно |/3 + i.
Уравнение w2 = 1 имеет решение ]/—1 = {/, — *};
главное значение равно +<*.
3.4.2.6. Сфера Римана. Кривые Жордана.
Области. Комплексная плоскость с присоединенной
к ней бесконечно удаленной точкой называется
расширенной или замкнутой комплексной
плоскостью. Расширение комплексной плоскости одной-
единственной точкой описывается при помощи
числовой сферы Римана.
Пусть плоскость %, ц в декартовой системе
координат 5, Ц, С> рассматриваемая как
комплексная числовая плоскость, касается своим началом
@, 0) единичной сферы (сферы единичного
диаметра). Эта точка называется южным полюсом
360
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
5; диаметрально противоположная ей точка N —
северным полюсом. Если комплексное число а =
= а + if) задано на плоскости (?,, г|) точкой Р(а, р),
то точку пересечения Р' (?,, г), Q отрезка PN со
сферой можно рассматривать как новое
геометрическое представление числа а (рис. 3.80). Таким
Рис. 3.80
образом, каждому комплексному числу однозначно
соответствует одна точка единичной сферы,
которая в этом случае называется сферой Римана.
Если последовательность точек на плоскости
«удаляется» в бесконечность, то
последовательность изображений точек на сфере стремится
к северному полюсу N. Точка N соответствует
бесконечно удаленной точке числовой плоскости.
Построенное выше отображение плоскости на
сферу называется стереографической проекцией.
Стереографическая проекция сохраняет углы и
записывается посредством следующих формул:
1 + а2 + I
Непрерывной кривой называют множество
точек z = х + iy комплексной плоскости, если х =
= х (t), у = у (Г) при -oo^fj^^rz^+oo есть
параметрическое непрерывное представление
кривой на плоскости х, у. Например, комплексное
параметрическое представление эллипса с
полуосями a, b и с центром в начале координат
имеет вид
z = z(t) = a cos t + ib sin Г @ ^ t < 2%),
а представление окружности с центром в точке
z, = а + ip и радиусом г имеет вид
z = (а + г cos r) -I- i (Р + г sin 0 = 2!+ re"
@ ^ f < 2л).
Кривой Жордана называется непрерывная
кривая без кратных точек. Это означает, что
различным значениям параметра t (за исключением,
быть может, начального и конечного значения)
функцией z = z (t) ставятся в соответствие
различные точки z кривой. Если начальная и конечная
точки кривой совпадают, то кривая называется
замкнутой. Эллипс и окружность являются
примерами замкнутых жордановых кривых.
(Открытой) Ъ-окрестностъю точки а называют
множество всех точек z, для которых | z — а \ < 6,
5>0.
[Открытой) областью G замкнутой комплексной
плоскости называется связное открытое множество,
т. е. множество точек этой плоскости таких, что:
1) для любых точек a, beG существует
непрерывная кривая, соединяющая их и целиком лежащая
в G; 2) если ceG, то существует 6-окрестность
точки с, целиком лежащая в G (рис. 3.81).
Границей области G называется множество точек,
которые не принадлежат G, но в любой произвольно
Рис. 3.81
малой 5-окрестности которых всегда лежат точки
из G.
Область G конечной числовой плоскости
называют односвязной, если ее внутренние точки по
отношению к любой замкнутой кривой Жордана,
лежащей в G, принадлежат G; в противном
случае область многоевязна: кольцевая область двух-
связна, область G на рис. 3.81 трехевчзна.
Замкнутой областью называется объединение множества
точек области G и ее границы dG. Обозначение:
G = G (J dG.
3.4.3. ФУНКЦИИ
КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Если каждому значению переменного z = х +
+ iy из множества D расширенной числовой
плоскости по правилу / сопоставляется
определенное значение переменного w = и + iv из множества
W расширенной числовой плоскости, то f
называется комплексной (или комплекснозначпой)
функцией комплексного переменного z; D — область
определения, j (D) с W — область значений
функции f. Обозначение: w = / (z).
Связь с функциями действительного
переменного: так как w = и + iv = f (z) = / (х + iy), то
каждой числовой паре (х, у) такой, что x + iyeD,
в силу функциональной зависимости / ставится
в соответствие пара (м, v) такая, что и + iv e W,
т. е. и и v являются действительными функциями
действительных переменных х, у: и (х, у), v = v (x, у).
Функция w = f (z) может быть записана в виде
w = и (х, у) + iv (х, у) = Re f (z) + i Im / (z).
В различных вопросах теории и приложений
функций комплексного переменного существенное
значение имеет модуль функции
| w | = |/ (z) |
x~, y)Y 7~[v(x, y)f = Ф (х, у).
Поверхность | w | = (р (х, у), где | w \ — аппликата,
восставленная в точке z = х + iy, называется
рельефом функции (рис. 3.82) *). Так как модуль
*) Рельеф многих функций приведен в кнше Янке Е.,
Эмде Ф., Леш Ф. Специальные функции — М.. Наука,
1977.
РАЦИОНАЛЬНЫЕ ФУНКЦИИ
361
функции — величина неотрицательная, то ее рельеф
находится всегда над областью определения D
функции /, за исключением нулей функции.
\sin(x+iy)\
Нулем функции f называется такое значение z0
независимого переменного z, для которого
| f (z0) |=0, и, следовательно, / (z0) = 0.
Функция w = f (z) называется ограниченной в
области G ? D, если существует такое
положительное число М, что \f(z)\ < М для любой точки 2
в этой области.
Предел и непрерывность функции комплексного
переменного определяются аналогично
соответствующим понятиям для функций
действительного переменного.
Если представить / (z) в виде / (z) = / (х + iy) =
= и (л, у) + iv (х, у), то запись lim / (z) = а, где
#
20 = х0 4- iyo, а = а + i'P, эквивалентна следующей:
lim и (х, у) = а
(х, у)-*(х0, уо)
и lim v (х, у) = р.
(х, у)->(х0, -vo)
Это позволяет определить предел / (z) через
пределы действительной Re/(z) и мнимой Im/(z)
частей.
Пример 4.
(х + iyJ
+1 lim 2
(x, y)-@,0) l/x2-
Функция j (z) непрерывна в точке z0, если
функции и (х, у) и v (х, у) непрерывны в этой точке
как функции двух действительных переменных.
Функция f(z) называется непрерывной в области,
если она непрерывна в каждой точке этой
области. Как и для функций действительных
переменных, для рассматриваемых функций
справедливы теоремы о непрерывности суммы,
произведения, отношения непрерывных функций и сложной
функции от непрерывных функций. Согласно
этому, многочлен от z непрерывен во всей
z-плоскости, рациональная функция от z
непрерывна в ее области определения.
3.4.4. ВАЖНЕЙШИЕ
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
3.4.4.1. Рациональные функции. Целые
рациональные функции (многочлены w-й степени):
w = Pm(z)= ? cvzv
v = O
(cv — комплексные коэффициенты, ст ф 0).
Многочлен Рт (z) можно однозначно записать как
произведение:
jl (z - z/2.. .(z - zk)\
где
Рт (z) = cm (z - z
k
Л vp = w, a zb
zk — нули многочлена
P=i
с кратностями vb ..., vfc соответственно (основная
теорема алгебры).
Дробно-рациональные функции вводятся как
отношение двух многочленов w = — . Они
определены для всех z, для которых Рт ф 0. Деление
с остатком для неправильных
дробно-рациональных функций (т < п) осуществляют так же,
как и для функций действительного переменного.
Разложение на простейшие дроби правильных
дробно-рациональных функций (т > п) имеет вид
коэффициенты Арг находятся, как и в
действительном случае. Важной рациональной функцией яв-
az + Ъ
ляется дробно-линейная функция w =
(см.
0 + Ю = 0.
cz + d
3.4.11).
3.4.4.2. Показательная и логарифмическая
функции. Натуральная показательная функция —
показательная функция с основанием е:
z z2 z3 z"
определена во всей плоскости z. Имеет место
формула Эйлера
eiz = cos z + i sin z, C.82)
(где cos z и sin z определены в 3.4.4.3). Из нее
следует представление для ег:
zs = ex + iy = ex (cos у + i sin >^);
с другой стороны, для любых zx и z2 справедливы
362
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Некоторые элементарные функции
Функция /(z)
Модуль I/(z) I
Главное значение
аргумента*) arg(/(z))
/х2 + у2
у
arctg —
х2-у2
2ху
arctg
2ху
z — а
(а = а + ф)
(х-аJ
j/(x-aJ + (y-
arctg
y-f
(х2 + у2J
arctg
2ху
arctg (|/p2 +1 - p), P =,—;•
Lnz
arctg — + 2kn *)
arctg —
ех cos у
е* sin у
у + 2ия, п - целое
такое, что -жу +
+ 2пп < + п
sin х ch у
cos x sh у
j/sin2 x + sh2 у
arctg [ctg x • th y]
cos x ch у
—sin x sh у
|/cos2 x + sh2 у
arctg[-tgу thy]
shz
sh x cos у
ch x sin у
j/sh2 x + sin2 у
arctg [tg у • cth x]
chz
ch x cos у
sh x sin у
]/sh2 x + cos2 у
arctg [tg у • th x]
tgz
sin2x
cos 2x + ch 2y
sh2y
(-cos2
cos 2x + ch 2y
| cos 2x + ch 2y |
sh2y
arctg . '
6 sin2y
¦) К значению arctg— в случае u< Onv > 0(соответственноу < 0)следует прибавлять число +я (соответственно -я).
**) В„ — числа Бернулли.
ВАЖНЕЙШИЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ
363
Таблица 3.7
f(z) = и (x, у) + iv (x, у), z = x + i>, /c = 0,
Разложение в ряд функции f(z)
в окрестности z = 0 или z = 1
z
г2
-? «-<"+1>лм<м*о
f <-1Пи+1)A-1Л |г-1|<1
i Z ( Hz ~ ^"' 1 z — 1 1 < 1
b = 0 Vй /
У —— (z - 1)", | z - 1 | < 1,- разло-
л=1
жение Ln z для /с = 0
и = 0
!«-¦'¦"-
00
/ j Bn)!
R=l
Ul<|**)
±1, ±2,...
Нули z0 m: порядок нуля
z0 = 0, m = 1
z0 = 0, m = 2
z0 = oo, w — 1
z0 = оо, т = 2
z0 = 0, m = 1 — точка ветвления
порядка 2
z0 - 1, m - 1 для /с - 0
<r 94 0, | z | < со
z0 = kit, m = 1
z0 = ton, m = 1
z0 = kit, m = 1
Особенности z5 w: порядок
особенности
Полюс в z, = oo, m = 1
Полюс в Zj = со, т = 2
Полюс в гя = д, m = 1
Полюс в zs = 0, m = 2
Точка ветвления порядка 2:
г, = 0, т = 1;
точка ветвления порядка 2:
zs = 00, т = 1
zs = 0, 00 - точки ветвления
порядка т = оо
Z, = 00
— существенно особые точки
zs = оо — предельная точка
полюсов;
zs = / — + к) п - полюс, т = 1
364
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
формулы:
eZl + Z2 = eZleZl
(теорема сложения для показательной функции);
Re ez = ех cos у, Im ez = ех sin у, \ ez \ = ех,
arg ez = у + 2пк
{к определяется условием -я < у + 2я/с ^ я).
Функция ez является периодической с периодом
2я/. Область значений W функции ez охватывает
всю плоскость, кроме ее начала — точки О.
Множество Е = {z | — я < Im z < я} является
однолистной областью функции <г; его образ есть вся
плоскость, разрезанная вдоль отрицательной части
действительной оси.
Натуральный логарифм. Функция,
обратная функции w — ez в ее однолистной области
?, называется главной ветвью натурального
логарифма.
In z = In | z I + (poi,
^ n.
Другие ветви представляют собой обратные
к ег функции в полосах, которые получаются из
Е при помощи параллельного переноса на 2kni
{к= ±1, ±2, ...).
Обратное отображение натуральной
показательной функции во всей комплексной плоскости
обозначают Ln z: если z = \z\e rg z, то
Ln z = In | z | + i Arg (z) при z ф 0.
Таким образом, Ln z состоит из множества ветвей
функции:
Ln z = ln | z | + (p0/ + 1km, где к = 0, ± 1, ±2, ...
Пример 5. In (— 1) = ln | -1 \ + ni = ni,
Ln 1 - ln | 1 | + 2Ш = 2kni {k = 0, ± 1, ±2, ...),
In (-1) = ln | - i | - ni/2 = - Kill.
Для натурального логарифма справедливы все
формулы, которые имеют силу для
действительных чисел, если только в этих формулах
используются правильно выбранные ветви.
Общая показательная функция есть
многозначная функция, включающая в себя отдельные
ветви функции:
w = az = ez ln a.
Главную ветвь получают, когда берут главную
ветвь Ln a.
3.4.4.3. Тригонометрические и гиперболические
функции. Для любого z
sinz = z-iL+ ^-¦¦• = {r(e'i-e-z%
Для любого z справедливы соотношения
sin /z = i sh z, cos iz = ch z,
sh /z = i sin z, ch /z = cos z.
В частности, отсюда вытекают формулы для
действительного у:
sin yi = i sh j>, cos y/ = ch y,
sh j;/ = i sin y, ch yi = cos v.
Формулы, имеющие место для
тригонометрических и гиперболических функций действительного
переменного (ср. 2.5.2.1), справедливы и для
функций комплексного переменного. В частности,
вычисление sin z, cos z, sh z, ch z при z = x + iy
производится согласно теоремам сложения для
sin (a + Р), cos (а + Р) и т. д.
Пример 6. cos (x + iy) = cos v cos iy - sin x sin iy =
= cos x ch у — i sin x sh у; следовательно,
Re cos z — cos (Re z) ch (Im 2),
Im cos z = -sin (Re z) sh (Im z).
Функции tg z, ctg z, th z, cth z определяются
формулами
tgz =
thz =
cos z
shz
"chl'
ctgz =
cth z =
sin z
chz
~sT77'
Отображение w = sin z однозначно отображает
полосу Е = {z I —я/2 < Re z < я/2} плоскости z на
комплексную плоскость w, разрезанную вдоль
действительной оси от - оо до -1 и от 1 до + оо.
Отображение, обратное w = sin z в области Е,
дает главную ветвь Arcsin z, определенную на
комплексной числовой плоскости, разрезанной
указанным способом.
Аналогично получаются обратные функции
для других тригонометрических и гиперболических
функций.
Эти отображения можно выразить через Ln
при помощи следующих формул:
Arcsin z = - / Ln (i (z + |/z2 - 1)),
Arsh z = Ln (z +
Arccos z = - / Ln (z +
Arch z = Ln (z + j/z2 - 1),
1 i — z
Arctg z = Ln ,
2 i + z
1 т 1+2
Arth z = — Ln y—--,
1 _ z — i
Arcctg z = H Ln ,
2 z + i
cos z = 1 -_+_-.
z^
3!
z
Chz=l+ _
zJ
z4
4T"
Функции sin z, cos z имеют период 2л, а функции
sh z, ch 2 имею г период 2ni.
Arcth z = —- Ln
2
z - 1
Их главные значения выражаются теми же
формулами, только вместо Ln подставляют главную
ветвь логарифма In, например:
arcsin z = —i In (/ (z + j/z2 - 1)),
1 1 +z
arth z = — ln .
АНАЛИТИЧЕСКИЕ ФУНКЦИИ
365
В табл. 3.7 приведены выражения для
действительной и мнимой частей, модуля и
аргумента, а также некоторые другие сведения об
элементарных функциях комплексного переменного.
3.4.5. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
3.4.5.1. Производная. Функция vv=/(z),
определенная в окрестности точки z0, называется
дифференцируемой в точке z0, если существует предел
lim ^--~-
Az->0
Az
Этот предел называется производной функции
w =/(z) в точке z0. Обозначение: f (z0), (df/dz)(z0),
dfiz)
dz
. Если функция / (z) дифференцируема
в каждой точке z области G, то она называется
дифференцируемой в области G и ее производная
обозначается w', J'(z), — , dj/dz (геометриче-
dz
ский смысл производной см. в 3.4.11.1).
Если функции / (z) и g (z) дифференцируемы
в G, то функции
f(z)±g(z), f(z)-g(z), -~P~ (g (z) Ф 0)
также дифференцируемы в G. Правила
дифференцирования те же, что и для функций
действительного переменного (см. 3.1.5). Правило взятия
производной (цепное правило) для сложных функций
также остается неизменным.
Пример 7. Пусть w - C* + 4K, w ¦ w3, w = Ъг + 4;
dz dw dz
для всех z на z-плоскости.
3.4.5.2. Условия дифференцируемое™ Коши —
Римана. Функция / (z) = и (х, у) + iv (x, у),
определенная в области G. дифференцируема в точке
z e G, если и (х, у) и о (х, у) обладают в этой точке
непрерывными частными производными по х и по
у и удовлетворяют условиям дифференцируемости
Коши - Римана (более точно: Даламбера -
Эйлера)
du dv ди dv
дх ду' ду дх
Производную функции w по z можно вычислить
следующим образом:
dw
ди . dv dv ди
= — -I-1 — _ у — =
dz дх дх ду ду
ди
= 1х~1
ди
ду
dv dv
i_ ;
ду дх
Примере. Функция w - / (z) » | г |2 дифференцируема
только в точке z » 0: и » х2 + у1, v — 0, ы'х = 2х, и'у = 2>>,
1>'х = 0, v'y = 0. Частные производные непрерывны в точке
@, 0), и только там выполняются условия Коши - Римана.
Тогда
/' @) = и'х @, 0) + iv'x @, 0) = 0.
3.4.5.3. Аналитические функции. Однозначная
функция / (z) называется аналитической,
голоморфной или регулярной в точке z = z0 (соответственно
z = оо), если она дифференцируема в некоторой
окрестности z0 (соответственно если F(z)=/(l/z)
после доопределения в нуле по непрерывности
аналитична в точке z = 0; тогда определяют
/'(оо)= ~(z2F'(z))\z = 0).
Функция/(z) аналитична в z = z0
(соответственно z = оо) тогда и только тогда, когда ее можно
представить в некотором круге с центром в точке
z0 (соответственно оо) сходящимся степенным
рядом (соответственно рядом с
неположительными степенями z):
f(z)= f an(z-z0)n
и = 0
оо
(соответственно / (z) = ? bnz~n).
Функция называется аналитической в области
G, если она аналитична в каждой точке этой
области.
Следовательно, функция j (z) = | z |2 (см.
пример 8) нигде не аналитична (хотя
дифференцируема при z = 0); в то же время функция w =
= / (z) = z2 или w = / (z) = ez является
аналитической на всей плоскости z.
Точки, в которых / (z) является аналитической,
называются регулярными (правильными). Если / (z)
аналитична в G, за исключением некоторых точек,
то эти точки называют особыми. Точка z e G
называется изолированной особой точкой, если
вокруг нее можно описать круг, не содержащий
других особых точек. Элементарные функции (как
алгебраические, так и трансцендентные) являются
аналитическими на плоскости z, за исключением
некоторых изолированных особых точек.
Свойства аналитических функций.
1) Во всех правильных точках аналитические
функции имеют производные любого порядка.
2) Максимум значения модуля функции,
аналитической в замкнутой области G, достигается на
границе области (принцип максимума).
3) Если функция аналитична по всей плоскости
и ограничена в ней, то эта функция постоянна
(теорема Лиувилля).
4) Две аналитические в области G функции
тождественны в области G, если они совпадают
на какой-нибудь ее подобласти или хотя бы на
некотором бесконечном множестве, имеющем в G
предельную точку (теорема единственности
аналитических функций).
5) В области, где функция w = и + vi —
аналитическая, функции и и v необходимо являются
гармоническими функциями, т. е. удовлетворяют
уравнению Лапласа, что следует из условий
Коши — Римана. Зная гармоническую функцию и,
можно с точностью до аддитивной постоянной
определить сопряженную к ней гармоническую
функцию v:
:dy + ф (х),
где
v(x,y)= — с
J дх
(ди д Гди \
<р' х = -1 — + — — dv •
\ду дх J дх ')
Аналогично по v можно определить и.
366
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
3.4.6. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
В КОМПЛЕКСНОЙ ОБЛАСТИ
3.4.6.1. Интеграл функции комплексного
переменного. Контурным интегралом функции w = / (z)
по дуге С = АВ (путь интегрирования) в плоскости
z с начальной точкой интегрирования А (а) и
конечной точкой интегрирования В{Ь) называется
комплексное число
J/ (z) dz = lim ? / (Q (zv - zv_ J, C.83)
?- max | zv —zv_i |-*0 V= l
если этот предел существует и не^ зависит ни от
выбора точек разбиения а = z0, zb ..., zn_b zn — b
кривой С, ни от выбора промежуточных точек
^vez^zv a С (рис. 3.83).
Для существования комплексного контурного
интеграла необходима ограниченность и
достаточна непрерывность / (z) на гладкой кривой С.
B=Mn(zn)
'A=M0(z0)
Рис. 3 83
Если в определении C.83) разложить / (z) и z
на действительную и мнимую части, то очевидно,
что
J/ (z) dz = J [и (х, у) + iv (х, у)] d(x + iy) =
С С
= J и (х, у) dx - v (х, y)dy + i\v (x, у) dx + и (х, у) dy.
Тем самым свойства действительных
криволинейных интегралов переносятся на комплексные
контурные интегралы, как, например (см. 3.1.8):
1) \f(z)dz=- J f{z)dz, причем кривая в
АВ ВА
правом интеграле проходится от В к А.
2) if (z) dz= у (z) dz + J7 (z) dz, где D -
AB AD DB
промежуточная точка кривой С между А (а) и В (Ь).
3) Если оо е С, то в этом случае \f{z)dz
С
можно определить как несобственный интеграл.
4) Оценка интеграла: если на кривой С
функция / (z) ограничена и | / (z) | < М = const, то
где s — длина дуги АВ кривой С.
Вычисление интеграла, если путь
интегрирования определен гладким
параметрическим заданием z = z (t) (a ^ t ^ Р), причем z (а) = а
и z (р) = Ь, осуществляется по формуле
Р
\f{z)dz = \f{z{t))z'{t)dt =
3.4.6.2. Независимость от пути интегрирования.
Для того чтобы контурный интеграл от
непрерывной функции комплексной переменной,
определенной в некоторой односвязной области, не
зависел от пути, соединяющего две
фиксированные точки а и Ьу необходимо и достаточно,
чтобы функция была аналитической в этой
области, т. е. чтобы она была дифференцируема
в этой области. В этом случае пишут
\f{z)dz = ]f{z)dz.
с
Интегральная теорема Кош и. Если
f(z) аналитична в односвязной области G, то
интеграл J / (z) dz зависит только от выбора точек
С
а и Ъ кривой С, и не зависит от вида гладкой
кривой С, соединяющей а и Ъ внутри G.
Интеграл по замкнутой кривой обозначают
j f (z) dz и называют интегралом по замкнутому
С
контуру. Интегральная теорема Коши для такого
интеграла принимает вид: если / (z) аналитична
в односвязной области G, то для каждой
замкнутой в G кривой имеет место соотношение
§f(z)dz-.
С
0.
= J Re
z @) z' (?)] dt + i J Im [/ (z (t)) z' @] rfr.
3.4.6.3. Неопределенные интегралы. Если в
области G интеграл не зависит от пути
интегрирования и начальная точка ае G фиксирована, а
конечная точка пути интегрирования zeG
неременная, то
]f(z)dz = F(z),
причем F(z)=/(z); функция F (z) называется
первообразной аналитической функции / (z).
Первообразная функция зависит от выбора начальной
точки а. Две любые первообразные функции
отличаются друг от друга на аддитивную
постоянную. Совокупность всех первообразных
обозначают
(С — любая константа) и называют
неопределенным интегралом от / (z).
Неопределенные интегралы от элементарных
функций комплексного переменного вычисляются
по тем же формулам, что и интегралы от тех же
функций действительного переменного.
3.4.6.4. Основная формула интегрального
исчисления. Интеграл от функции /(z), аналитической
в G, равен приращению ее первообразной функции
при переходе из начальной в конечную точку
пути интегрирования:
ь
Sf(z)dz = F(b)-F(a).
3.4.6.5. Интегральные формулы Коши. Если
функция / (z) — аналитическая в некоторой
односвязной области, то ее значение в любой точке z
этой области, а также значения ее производных
любого порядка в этой точке выражаются через
значения этой функции на замкнутом контуре С,
окружающем эту точку, следующими интеграль-
ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
367
ными формулами Коши:
/м-
C.84)
/(О
где ? - переменная интегрирования; интегралы
вычисляются вдоль пути С, пробегаемого в
положительном направлении (против часовой стрелки).
Если же функция / (z) - аналитическая во всей
части расширенной плоскости, находящейся вне
замкнутого контура С, то значения / (z) и ее
производные в любой точке z этой области
выражаются при помощи тех же формул C.84),
однако интегралы при этом вычисляются вдоль
пути С, пробегаемого в отрицательном
направлении (по часовой стрелке).
Иногда, чтобы подчеркнуть направление
движения вдоль контура интегрирования С,
пользуются следующими обозначениями: т — против
часовой стрелки, у— по часовой стрелке.
Интегральные формулы Коши позволяют
находить значения
тегралов.
некоторых определенных
инПример 9. Положим / (г) = г (эта функция -
аналитическая функция во всей плоскости) и в качестве пути
интегрирования возьмем окружность С с центром в точке
z и радиусом г: ? = z + re1*. Тогда, согласно последней
формуле из C.84), имеем
¦+'" •¦"•- '"• </ф,
откуда, полагая г - О, получаем, что
2я
^ПГ" с Г f со. 9 + 1 (г «in »-*•) ^ _
О
2я 2я
I g со» «> cos ^r sjn ф_Мф) (/p + i fr сон * sin (rsin ф —
О О
Так как мнимая часть равна нулю, то
2я
f J 2яг"
^г со- ф cos (r sjn ф _ Пф) </ф = _-,
2я
J <^ •'" ф sin (r sin ф — лф) <1<р — 0.
0
3.4.7. РАЗЛОЖЕНИЕ
АНАЛИТИЧЕСКИХ ФУНКЦИЙ В РЯД
3.4.7.1. Последовательности и ряды. Последо-
00
вательности {«„} и ряды ]Г ап для комплексных
л=1
чисел а„ = а„ + /р„ (/ = 1, 2, 3, ...), а также понятие
их сходимости формально определяются так же,
как и соответствующие понятия для
действительных чисел (см. 3.1.3, 3.1.14).
Последовательность аг = ах + ipb а2 = сх2 +
+ iC2» • • • > ^и = а« + Фи» • • • называют сходящейся,
если сходится каждая из последовательностей
действительных чисел
¦2, ..-, а„,
•2, .... К
Тогда
lim а„ = lim (ая -
= lim а„ + i lim р„ = а +
п -> оо п -»сю
Пример 10.
lim
= lim
и-» оо
l/| л | cos — + /lim !/|л| sin —=!+/• 0 =
1,
если а ф 0 и ф0 есть arg а (рис. 3.84).
Поэтому запись lim an = а равнозначна тому,
п-* оо
что для любой зада!'ной е-окрестности точки а
(см. 3.4.2.6) существует
такое N (г), что все
члены последователь- ^
ности ап с номерами
и ^ N (e) попадают в
эту окрестность.
Последовательности {а„}, которые не
являются
сходящимися, называются
расходящимися.
Если комплексная
числовая
последовательность (как
последовательность точек
z-плоскости) такова,
что вне любого сколь угодно большого круга
этой плоскости находятся все точки этой
последовательности, за исключением конечного числа,
то говорят, что последовательность стремится к
бесконечности: lim а„ = оо.
п —> оо
Ряд
7 ;Дейсгви-
' тельная ось
Рис з.84
+ а2 + ... + ап + ... =
= to + /pi) + (а2
... + (а,
называется сходящимся, если сходится каждый из
рядов действительных чисел
ОС 1 + 0С2 + . . . + 0С„ + . . .
и
р1 + р2 + ... + р. + ...
368
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Тогда
Поэтому запись ? а„ = S равнозначна (в случае
п = 1
сходимости) тому, что последовательность
частичных сумм {Sn} = < ]Г av> является сходящейся.
Тогда
lim Sn =
П -> 00
Пример 11.
I2
Zi2-1 v1 (-ir
(рис. 3.85).
ряд сходится в некоторой точке z Ф а, то либо он
абсолютно сходится во всей комплексной плоскости
z, либо имеется такое число R > 0, что ряд
абсолютно сходится для всех z таких, что | z - а \ < R,
и расходится для | z — а \ > R. Круг | z — а \ < R
называется кругом сходимости ряда, а R —
радиусом сходимости. Радиус сходимости может
быть вычислен по формуле
R = 1/1, где / = Йт |7l~cJ-
п —* оо
На окружности | z — а | = R ряд может либо
сходиться, либо расходиться и обладает по меньшей
мере одной особой точкой, т. е. такой точкой zb
что не существует степенного ряда с центром в zx
и положительным радиусом сходимости, сумма
которого на общей части кругов сходимости
совпадала бы с суммой данного степенного ряда.
Если R = 0, то ряд сходится только в точке
z = 0; в случае R — Л- оо ряд всюду сходится.
Степенной ряд сходится всюду, когда
lim jTkJ = 0.
п -*¦ оо
Например, для [я!:" имеем R - 0; для ? — г = е"
я-0 я-0 П-
Пример 12. Ряд 1+а1+«2 + ...» ? «-« 1/A - а) имеем Я- + оо; для рядов f z" и ? — имеем R - 1.
сходится для всех а таких, что | д | < 1 (геометрическая
§0 прогрессия). Сумму ряда в
примере 11 можно очень
быстро вычислить при помощи
этой формулы для а - i/2.
Понятия
расходимости, а также абсолютной,
условной и безусловной
сходимости рядов с
комплексными членами
формулируются так же,
как и для
действительных рядов (см. 3.1.14);
аналогично
определяются и условия сходимости.
3.4.7.2. Функциональные ряды. Степенные ряды.
Для последовательности комплексных функций
/i B)>/2(z)> •••¦>fn(z)i ••• в пересечении их областей
определения D — f) Dt можно составить функцио-
i = 1
нальный ряд
Действительи
О
Рис 3 85
z) +
C.85)
Все точки zeD, для которых ряд сходится,
составляют область сходимости ряда, а предельная
функция F(z) называется суммой ряда:
Степенные ряды представляют собой
функциональные ряды вида
I cn(z-a)n;
п = 0
(сп — комплексные постоянные). Если степенной
Внутри круга сходимости степенной ряд
представляет собой аналитическую функцию. Ее
дифференцирование (интегрирование) по z
осуществляется путем почленного дифференцирования
(интегрирования) соответствующего степенного ряда.
Продифференцированный (проинтегрированный)
степенной ряд имеет тот же самый радиус
сходимости, что и первоначальный ряд. Это свойство
можно использовать для разложения аналитических
функций в степенные ряды.
Пример 13. Разложить функцию /(r)«arctgz в
степенной ряд в окрестности z*0.
Используем геометрическую прогрессию (см. пример 12)
Почленно интегрируя, получаем
23 z$ ZU+l
/(z)-arctg*-x--y+~-...+(-ir2^T+...
Теорема единственности. Два
степенных ряда ? cnzn и ? c'nz>l c равными радиусами
п=0 п=0
сходимости, отличными от нуля, совпадают
(т. е. сп = с'п), если они оба сходятся к одним
и тем же значениям для некоторой сходящейся
к внутренней точке круга сходимости бесконечной
последовательности попарно различных точек.
Сумму, разность и произведение сходящихся
степенных рядов можно тоже представить в виде
степенного ряда, который сходится внутри общего
круга сходимости исходных рядов. Если ряд
? cnzn имеет радиус сходимости R > 0 и с0 ф О,
существует такой степенной ряд ? anzn
п = 0
с ра-
РИД ЛОРАНА
369
диусом сходимости, отличным от нуля, что в не- виде степенного ряда Лорана
котором круге с центром в z = 0 «, ж
f(z) = X ak(z - af + X bk(z - a)~k, C.86)
v Л „* ?~i "
Преобразование степенных рядов.
Если аналитическая функция задана в виде
степенного ряда, сходящегося в круге Кц:
/¦м - ? V,
коэффициенты которого вычисляются по
следующим формулам:
то она может быть представлена в виде
ряда по степеням z — а в каждой точке а такой,
что | а | < R. Тогда /t (z) =
l " = X bn (z — a)n. Радиус схо-
димости
этого
степенного ряда не меньше
расстояния от а до границы круга
К: Ri ^ R - \а\. В случае
равенства точка касания Р
обоих кругов (рис. 3.86) яв-
Рис 3.86 ляется особой точкой для
/t (z). При Rx> R-\a\
область сходимости /i (z) выходит за пределы
области сходимости /(z); тогда говорят, что fx (z)
есть аналитическое продолжение /' (z) (см. 3.4.9.1).
3.4.7.3. Ряд Тейлора. Если f(z) - аналитическая
функция в круге К с центром в точке а (а Ф оо)
радиуса R > 0, то всегда существует степенной ряд
оо
X cn(z — а)п, сходящийся в круге Kt (| z — а | < Яь
где Л < Rj) к функции f(z). Коэффициенты ряда
являются комплексными числами, определяемыми
функ-
по формулам сп = —-—. Тем самым в
и!
ция / (z) представляется в виде ряда
Этот ряд называется рядом Тейлора функции f(z)
в окрестности Кх точки z = a.
Пример 14. Разложение In (I + z) в ряд в окрестности
точки г « 0. Имеем
(сходится при | z | < 1).
Если функцию можно разложить в степенной
ряд по степеням z — а, ю на основании теоремы
единственности для степенных рядов он должен
быть рядом Тейлора функции в окрестности
точки а.
3.4.7.4. Ряд Лорана. Если f(z) — функция,
аналитическая внутри некоторого кольца между двумя
концентрическими окружностями с центром а
(О < г ^ | z - а | ^ R, а Ф оо), то эта функция
единственным образом может быть представлена в
(С - произвольно выбранный замкнутый путь
интегрирования внутри кольцевой области, по
которому обходят точку а в положительном
направлении (против часовой стрелки)).
Первый ряд в формуле C.86) представляет собой
обычный степенной ряд, который называется
регулярной частью ряда Лорана, а второй ряд
называется главной частью ряда Лорана.
Формулу C.86) можно записать в следующем
виде:
f(z)=
ck{z-a)\
C.87)
где
3.4.7.5. Классификация особых точек. Понятия
правильной, особой и изолированной особой
точек даны в 3.4.5.3. Если функция f(z) —
аналитическая в окрестности точки а (но не обязательно
в самой а), то характер точки а определяется
разложением в ряд Лорана в окрестности этой
точки.
1) Если ряд Лорана не содержит членов с
отрицательными степенями (т. е. с„ = 0 при п < 0),
то ряд Лорана обращается в ряд Тейлора; при
этом или функция f(z) - аналитическая также и в
точке а (если f(a) = с0), или а является
устранимой особой точкой (lim f(z) = с0 Ф/(а)). В по-
z-*¦ а
следнем случае, полагая/(а) = с0, достигают того,
что функция становится аналитической в точке
z = а {особенность устранимая).
2) Если разложение в ряд Лорана содержит
только конечное число членов с отрицательными
степенями (все с„ = 0 при п < т < 0 и ст Ф 0), то
точка а называется полюсом т-го порядка функции
/(z). Обозначение f(a) = оо.
3) Если C.87) содержит бесконечное число
членов с отрицательными степенями, то а
называется существенно особой точкой функции f(z). .
Пример 15. /(z) = el/s имеет существенно особую
точку при z ш 0, так как разложение в ряд Лорана в
окресгности этой точки имеет вид
i
l
Пример 16. Функция f(z) = 1Дг - аK имеет полюс
3-го порядка в точке z ¦= а.
370
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Пример 17. Функция
/М-
имеет полюс 1-го порядка в точке z - 0.
Важнейшее свойство аналитических функций
выражает
Теорема Пикара (большая). Если/(z) -
однозначная аналитическая функция в окрестности
точки z — а, являющейся для нее существенно
особой точкой, то в каждой окрестности точки
z = а функция / (z) принимает любое
конечное значение, за исключением, быть может,
одного.
3.4.7.6. Поведение аналитических функций на
бесконечности. Определение функции,
аналитической на бесконечности (z = оо), дано в 3.4.5.3.
Исследование поведения функции f(z) в
окрестности точки z = оо в общем случае сводится
преобразованием z = l/? к изучению свойств в
окрестности точки ? = 0 комплексной плоскости
функции F(Q=f(l/Q. Таким образом, выводы
пп. 3.4.7.4, 3.4.7.5 могут быть перенесены на
случай z = оо.
Ряд Лорана функции /(z) в окрестности точки
z = оо формально имеет тот же вид, что и при
разложении в окрестности точки z = 0:
/«¦
¦ Е
к= - оо
C.88)
однако при этом точка z = oo: 1) существенно
особая, 2) регулярная или устранимая особая,
3) полюс порядка т — в зависимости от того,
сколько имеется членов с положительными
степенями z в разложении C.88): 1) бесконечно много,
2) совсем нет, 3) конечное число.
Например, многочлен m-й степени обладает
в точке z = оо полюсом m-го порядка.
3.4.8. ВЫЧЕТЫ И ИХ ПРИМЕНЕНИЕ
3.4.8.1. Вычеты. Если аналитическая функция
f(z) в точке z = а имеет изолированную особую
точку (см. 3.4.5.3), то коэффициент с-1 при степени
(z-a)~l в ряде Лорана функции/(z) называют
вычетом аналитической функции/(z) относительно
точки а. Обозначение: Res/(z) или Выч/fz). При
а а
аф оо
2т
а при а = оо
С
причем С - любая замкнутая гладкая кривая
Жордана, охватывающая точку z = а, которая
обходится против часовой стрелки в первом случае
(а Ф оо) и в противоположном направлении во
втором {а = оо).
Если / (z) имеет в точке z = а ф оо полюсы
m-го порядка, то разложение в ряд Лорана имеет
fiz\- C'm I C"OT+1 I ¦ с~1
J{Z)~ (zaf (zаГ'1 z-
I
(z-af (z-аГ'
+ f ck(z-a)k, C.89)
fc = 0
и вычет можно вычислить следующим образом:
с_ х = Res / (z) = —L— lim ^~ {(z - a)" f (z)}.
а . \т—l) - z—*a **z
C.90)
простые полюсы. Согласно C.90), имеем
В случае устранимой особенности вычет при
z Ф со всегда равен нулю. Для бесконечно
удаленной точки это уже не так; например, f(z) = 1/z
обладает в точке z = оо устранимой особенностью,
в то время как Res — = — 1.
z
3.4.8.2. Теорема вычетов. Если / (z) -
аналитическая функция в области G, за исключением
конечного числа точек аь а2,..., ак, и С - замкнутая
кусочно гладкая кривая, охватывающая особые
точки a,- (i = 1, ..., fc) и лежащая целиком в
области G, то
*
Для функции, аналитической всюду в
расширенной комплексной плоскости, кроме конечного
числа особых точек, сумма вычетов во всех особых
точках (включая точку z = оо) равна нулю.
Пусть/(z) - однозначная функция в области G,
включая границу С (кусочно гладкую замкнутую
кривую), и аналитическая, за исключением, быть
может, конечного числа полюсов внутри G. Если,
кроме того, /(г)Ф0 при zeC, a{ - нули кратности
af(i = 1, 2, ..., к), bt - полюсы порядка Pj(/=
= 1, 2, ..., т) внутри G, то для любой функции
g(z), аналитической внутри области G и на ее
границе G, справедлива следующая формула:
В частности, при д (z) = 1
к
(логарифмический вычет), где N = ? о^ —
количество нулей (с учетом кратности), а Р = ? pf — ко-
ПРИНЦИП АНАЛИТИЧЕСКОГО ПРОДОЛЖЕНИЯ
371
личество полюсов (с учетом порядка) функции
f(z) в области G, ограниченной контуром С.
3.4.8.3. Применение к вычислению
определенных интегралов. Теорема вычетов оказывается
особенно полезной для вычисления различных
несобственных
интегралов.
Если / (z) —
аналитическая функция во
всей верхней полупло-
Рис 3 87
скости Im z ^ 0, за
исключением
конечного числа особых
точек аи аъ ..., а„,
лежащих над действительной осью (рис. 3.87), и
если z = оо — по меньшей мере двукратная нулевая
точка f(z), то
J
Res/(z).
C.91)
(Граница С области G, т. е. области Im z ^ 0,
есть действительная ось.)
Пример 19. Вычислить интеграл 7Т~~2~
-ad
Функция /(г) = 5— аналитическая в области
Im г ^ О, исключая точку г = /, и обладает в точке г = оо
двойной нулевой точкой (г = оо - устранимая особая точка).
По формуле C.90) имеем
lim
Z-X
lim
1
2/
и, согласно C.91), получим, что
- 2я1 ir -
3.4.9. АНАЛИТИЧЕСКОЕ
ПРОДОЛЖЕНИЕ
3.4.9.1. Принцип аналитического продолжения.
Пусть/i (z),/2 (z) — функции, аналитические в Gb G2
соответственно, и пусть j\ (z) = f2(z) в Glf]G2 Ф 0
(рис. 3.88). Тогда говорят, что fi (z) аналитически
продолжается в
область G2 при
помощи /2 (z) и, наоборот,
/2 (z) аналитически
продолжается в
область Gx при помощи
/i D
Согласно теореме
единственности для
аналитических
функций (см. 3.4.5.3), любая из функций /х (z) и
/2 (z) определяется другой однозначно.
Следовательно, обе эти функции можно воспринимать
как элементы одной функции F{z\ которая
является аналитической в Gt (J G2.
Пример 20. Степенной ряд ? z" при | z \ < 1
определяет аналитическую функцию / (г) = т~г- в то вРемя
Рис. 3.88
как степенной ряд сходится только внутри единичного
круга, функция определена в замкнутой области
плоскости г и является аналитической, исключая точку
z = 1 — полюс 1-го порядка.
Тем самым представляет собой аналитическое
продолжение ? z" за единичный круг во всю комплексную
R-0
плоскость, за исключением точки 2=1.
Если аналитическое продолжение существует, то
оно может быть истолковано следующим образом.
Предположим, что аналитическая функция /
представлена в некоторой точке z0 в виде
степенного ряда с кругом сходимости \z — zo\ < г. Для
каждой точки z = zt внутри этого круга значения
f(zi), f'(zi), ... известны и определяют разложение
в ряд Тейлора в окрестности этой точки. Новый
степенной ряд сходится внутри круга | z — z\ \ < ги
который может иметь часть, лежащую вне первого
круга. Тем самым мы получаем аналитическое
продолжение функции /(z). Этот процесс может
быть продолжен; в результате образуется
«цепочка» пересекающихся кругов сходимости.
Объединение этих кругов дает область G, в
которой различные разложения в ряд определяют
аналитическую функцию F - аналитическое
продолжение функции /, причем разложения в
окрестности некоторых точек zeG рассматриваются
как разложения, определяющие значения функции
F(z) в этих точках z. Степенные ряды,
представляющие таким образом аналитическую функцию F
в своих кругах сходимости, называются
элементами функции F. Функция F определена однозначно,
если задан каждый ее элемент.
Метод сцепленных кругов используется обычно
вдоль какой-либо подходящей кривой, т. е. центры
кругов сходимости, начиная с начальной точки
кривой, располагают на выбранной кривой.
Теорема о монодромии. Пусть /0 —
аналитическая функция в области Go,
продолжающаяся (вдоль любой непрерывной кривой) в
область G (Go a G). Если G односвязна, то в ней
существует аналитическое продолжение F функции f0.
Если при помощи метода сцепленных кругов,
исходя из элемента fo(z) функции Fx (z) и
перемещаясь вдоль замкнутой непрерывной кривой,
возвращаются вновь в круг сходимости функции
/о (z) и полученное новое разложение/,, (z) определяет
в этой области значения, отличные от значений
/о (z) в тех же точках (это возможно лишь для неод-
носвязных областей), то /„(z) представляет собой
элемент другой функции F2 (z). В этом случае
Fx (z) и F2 (z) интерпретируются как различные
ветви некоторой функции F(x), определенной,
однозначной и аналитической на соответствующей
римановой поверхности (см. 3.4.10).
3.4.9.2. Принцип симметрии (Шварца).
1) Принцип непрерывности. Пусть две
односвязные области Gx и G2 не имеют общих
точек, но их границы имеют общую часть Г.
Если функции /х (z) и /2 (z), аналитические
соответственно в областях Gt и G2, непрерывны в
объединении Gj(Jr и F(jG2 соответственно и
совпадают во всех точках Г, т. е. /\ (z) = f2 (z) при
zgF, то функции/i (z) h/2(z) являются
аналитическими продолжениями друг друга.
372
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
2) Принцип симметрии. Пусть функция
w =/(z) аналитична в области G, граница которой
содержит дугу окружности или прямолинейный
отрезок Г, причем w непрерывна на Г; если
точки w = f(z) для zeT также располагаются
соответственно на некоторой дуге окружности или
прямолинейном отрезке Г*, то функция / (z) может
быть аналитически продолжена в область G*,
симметричную относительно Г; при этом значения
/(z) в точках, симметричных относительно Г,
будут симметричны относительно Г*.
Если функция f(z), аналитическая в области G,
имеет на гладкой дуге нулевые значения, то она
является тождественным нулем. Таким образом,
две функции, различные в некоторой области G,
не могут иметь совпадающие значения на какой-
либо гладкой дуге.
3.4.10. ОБРАТНЫЕ ФУНКЦИИ.
РИМАНОВЫ ПОВЕРХНОСТИ
Функции, обратные таким функциям, как ez,
sin z, которые многократно принимают одни и те же
значения при изменении z в области определения
D, служат примером многозначной зависимости
(vv = Ln z, vv = Arcsin z).
Взаимно однозначное соответствие между D и
областью значений функции W обеспечивается
при наложении на подобные функциональные
зависимости некоторых ограничений. Часто бывает
полезно представить многозначную функцию как
однозначную, определенную на римановой
поверхности. Такая поверхность состоит из некоторого
числа плоскостей z, или «листов»,
соответствующих ветвям функции /(z) и соединенных вдоль
особых кривых, называемых разрезами (см. ниже).
3.4.10.1. Однолистные функции, обратные
функции. Однолистной областью Е называют
область регулярности функции /(z), \ в которой
f(Zi) Ф/(г2) при zt Ф z2. Тогда f(z) называют
однолистной функцией в Е. При этом в Е
выполнено неравенство/'(z) Ф 0, f(z) имеет однозначную
обратную функцию z = g (vv), аналитическую в
области образов В однолистной области Е
плоскости vv, и
1
\.9 МУ = -77ТТ (weB> 2 = 9 И).
Производная W = nzn l функции w = zn равна
нулю при z = 0 и отлична от нуля при z # 0.
Следовательно, z" в окрестности точки z = 0 имеет
неоднозначную обратную функцию. Именно, если
радиус-вектор z = | z | е'ф (ср = arg z) заметает,
например, одну из углообразных областей Ек:
2пк п 2пк п ,
<Ф< + — {к = 0, 1, ..., и - 1)
п п п п
плоскости z, то соответствующий радиус-вектор
w = | z |" einv заметает всю плоскость w, за
исключением отрицательной части действительной оси
(ср. рис. 3.89, а с рис. 3.89, б). Углы <р = z. (zOx)
увеличиваются в п раз. Полному повороту радиуса-
вектора в плоскости z соответствуют п полных
поворотов в плоскости w.
Каждая из областей Ек (к = 0, 1, ..., п-Л)
для w = z" является однолистной областью и
отображается взаимно однозначно при помощи функции
vv = z" на плоскость п\ разрезанную вдоль
отрицательной части действительной оси; обозначим
эту плоскость Bk. Она покрывается п раз
значениями функции w = z", т. е. каждая Ек отображается
U
Рис. 3 89
на Вк точно один раз. Если представить себе
Вк (к = 0, 1, ..., и — 1) как п экземпляров так
называемых «листов», расположенных один над друг им,
то функция w = z" теперь может быть однозначно
обращена на каждом листе Вк, т. е. для каждой
ветви z = j/w имеем
2 = дк (w) = zk (w) = j7hv~| е^ No + 2kn)/n
(fc = 0, 1, ..., n- 1);
главное значение \|/0 = arg vv. Главное значение ]/vv
называют главной ветвью z0 (w). Областями
определений (соответственно областями значений)
ветвей z = zk (vv) являются Вк (соответственно Ек).
3.4.10.2. Риманова поверхность функции z = J/vv.
Как объединяются п ветвей zk(w) в одну функцию,
как они связаны? Если независимое переменное w
функции J/vv в плоскости w обходит точку w = 0
по некоторой замкнутой кривой в направлении
против часовой стрелки, начиная с argw= —я,
то при каждом обходе этой точки главное значение
\|/0 пробегает значения от —я до +я; в силу того
что -я < arg vv = \|/0 < + я и Arg vv = \J/0 + 2/ся,
показатель к при каждом переходе через
отрицательную часть действительной оси возрастает
на 1. Так как zk (vv) = |/| vv | е'Мо + 2/сл)/^ то такои
переход w через отрицательную часть
действительной оси означает переход от ветви zk(w) к
ветви zk+l(w). Итак, на этой оси п ветвей связаны
циклическим переходом (zozlz2.. .zn- tzn = z0).
Это дает возможность представить функцию
yw в плоскости w как бы состоящей из п листов
Вк (ср. 3.4.10.1), расположенных друг над другом
и разрезанных вдоль отрицательной части
действительной оси (подобно тому как рассматривалась
плоскость z). Для того чтобы объединить
отдельные листы Вк как области определения
соответствующих ветвей zk(w) в одну связную область
определения функции yw, соединим их друг с
другом согласно циклическому переходу ветвей zk(w)
вдоль лежащих друг над другом разрезов:
граница разреза, относящаяся к верхней полуплоскости
(Im (vv) ^ 0) листа Вк (обозначается знаком плюс),
«склеивается» с границей разреза, относящейся к
нижней полуплоскости (Im (vv) < 0) (обозначается
знаком минус) лежащего над ним листа Вк+1.
Последняя граница «плюс» ( + ) листа Вп-Х соеди-
ПОНЯТИЕ КОНФОРМНОГО ОТОБРАЖЕНИЯ
373
няется с границей разреза «минус» (-) листа Во.
Построенная таким образом и-листная поверхность
называется римановой поверхностью функции
z = jTw (рис. 3.90).
Каждый лист Вк взаимно однозначно
соответствует однолистной области Ек, и совокупность
РиманоВа
ность для
-и
Рис. 3 90
значений yw однозначно отображается на
соответствующую риманову поверхность.
Точки w = 0 и w = оо называются точками
ветвления п — 1-го порядка функции |/vv, так как
при n-разовом обходе в одном и том же
направлении вокруг этих точек мы снова возвращаемся
к первоначальной ветви (рис. 3.90).
3.4.10.3. Риманова поверхность функции z = Ln w.
Рассмотрение функций w = ez, z = Ln w проведем
по аналогии с функциями w = z", z = yw. В
качестве однолистных областей функция w = ez
обладает бесконечным множеством полос 2кп +
+ oc<Imz<2(/c+lOt + a (a- любая
действительная постоянная, к = 0, ±1, ±2, ...), которые
расположены параллельно действительной оси и
имеют ширину 2к. Каждая из них может быть
однозначно обращена, в силу чего появляется
бесконечно много ветвей функции z = zk = ln | w | +
+ i (\J/0 + 2kn) (главное значение vj/o = argw,
k = 0, +1, ±2, ...), которые в качестве области
определения имеют при а = — я плоскость w,
разрезанную вдоль отрицательной части
действительной оси. В связи с этим риманова поверхность
для функции Ln w имеет строение, аналогичное
строению римановой поверхности функции |/vv,
но с бесконечным числом листов.
При любом количестве обходов в одном
направлении вокруг точки w = 0 (w = оо) невозможно
вернуться к первоначальной ветви. Точки w = 0
и w = оо являются поэтому точками ветвления
бесконечного порядка, или так называемыми
логарифмическими точками ветвления.
Пусть для функции w =/(z) в некоторой
окрестности точки w = /(д) существует обратная функция
z*=g(w). Тогда, если [#(w)]' имеет в точке f(a)
нуль кратности т или полюс порядка т + 2, то
z = а Ф оо является точкой ветвления порядка т
функции / (z).
Пример 21. Для функции Жуковского w = — (z + — j
вышеуказанным методом находим в плоскости w точки
ветвления и>1-2 = ±1 1-го порядка. Функция w = \/z имеет
в точке z=0 точку ветвления и — 1-го порядка.
3.4.11. КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
3.4.11.1. Понятие конформного отображения.
Отображение w = f(z) = и (х, у) + iv (x, у) с областью
определения D и областью значений W конформно
в точке zeD, т. е. отображение w =/(z) сохраняет
углы между кривыми, проходящими через точку z
области D, как по величине, так и по ориентации
(рис. 3.91), если в этой области функция/fz)
аналитическая и /'(z)#0. Таким образом, бесконечно
У
и
х О
а)Пл.г б)Пл.ш
Рис 3 91
малый треугольник в окрестности точки z
отображается в подобный треугольник в плоскости w,
т. е. каждая сторона растягивается (или сжимается)
в отношении |/'(z)|:l и поворачивается на угол
arg(/'(z)) (рис. 3.92). В частности, каждое
конформное отображение преобразует два семейства взаимно
U
Ш.
or
Ж а
5)Плш
Рис 3.92
перпендикулярных координатных линий х = const
и у = const плоскости z в два семейства взаимно
ортогональных кривых на плоскости w. Обратно,
двум семействам координатных линий и = const
и v = const плоскости w соответствуют два
семейства взаимно ортогональных кривых на
плоскости z. Таким образом, при помощи
аналитических функций можно получить множество
прямоугольных криволинейных систем координат (т. е.
таких систем, в которых координатные линии
различных семейств пересекаются под прямым
углом). Рис. 3.93 показывает конформное
отображение w = z2, причем линии х = const и у = const
переводятся во взаимно ортогональные софокус-
ные параболы. В точке z = 0 конформность
нарушается. Первый координатный квадрант переходит
в верхнюю полуплоскость (контуры отображения
отмечены штриховкой).
Описанные выше отображения называют также
конформными отображениями 1-го рода, в то время
как отображения, которые оставляют
неизменной величину, но не ориентацию углов между
двумя кривыми (отображения с переворотом
углов), называются конформными отображениями
1-го рода (например, w = z). Отображение w =
= /(z) называется конформным в точке z = оо,
если w =/(l/z) = F(z) конформно в окрестности
точки z = 0.
374
КОМПЛЕКСНЫЕ ЧИСЛА. ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Задача построения отображения, которое ставит
в соответствие односвязной области Gi односвяз-
ную область G2, решается на основе теоремы
Римана об отображении. Для каждой
(открытой) односвязной области G в плоскости z,
кроме всей плоскости z, существует конформное
отображение w = / (z), которое устанавливает
взаимно однозначное соответствие между всеми
точками области G и внутренними точками
единичного круга | w | < 1; при этом аналитическая
функция / определена единственным образом,
если задан образ точки z0 области G и угол
поворота любой кривой, проходящей через эту точку,
т. е. / (z0) = w0 и arg/' (z0) = а, где w0 и а -
заданные величины.
Например, функция w = г взаимно однозначно
отображает верхнюю полуплоскость Imz > 0 на единичный
круг | w | < 1, причем точка z = / переходит в точку w = 0.
Однозначное конформное отображение верхней
полуплоскости Im z ^ 0 на и-угольник (и ^ 3)
определяется так называемым интегралом Кри-
стоффеля — Шварца
где внутренние углы «-угольника, равные а,я
@ < а,- < 2; i = 1, 2, ..., п), должны удовлетворять
дополнительному условию
п — 2; а{ явля-
ются точками действительной оси, которые
соответствуют вершинам л-уголышка; Ct Ф 0 и С2
являются комплексными числами, выбором которых
можно получить все многоугольники с п углами,
подобные данному многоугольнику. Если одна
из вершин, например ап, отображается в точку
w = оо, то интеграл приводится к виду
w = С\ ){t -
С2,
где С\ и С2 -постоянные параметры, а а\, а'ъ ...
..., a'n-i - некоторые точки действительной оси.
Хорошо изучены многие функции,
отображающие различные области на единичный круг или
верхнюю полуплоскость. Поэтому, когда ищут
нужное отображение области G^ на область G2,
то достаточно найти аналитические функции fx (z)
и f2(z), которые однозначно отображают Gi и G2
на единичный круг. Тогда функция д2 (z\ обратная
к f2(z), отображает единичный круг однозначно
на G2, так что функция, составленная из/! (z) и д2 (z),
дает искомое отображение Gt на G2.
Конформные отображения находят
применение в электротехнике, гидро- и аэродинамике и
других областях приложения математики.
3.4.11.2. Некоторые простые конформные
отображения. На рисунках даются графики сеток на
плоскости (изотермические сетки), которые
преобразуются в декартову прямоугольную сетку на
плоскости w. Штриховкой на рисунках отмечены
контуры тех областей плоскости z, которые
отображаются на верхнюю полуплоскость w, а черным
отмечена область, переходящая в квадрат с
вершинами @, 0) @, 1) A, 0) A, 1).
а) Линейная функция w = az + b (a = | а \ eitf Ф 0)
определяет конформное преобразование
расширенной плоскости z (рис. 3.94). Преобразование может
Рис. 3.94
быть разложено на три: t = ei<pz - поворот плоскости
на угол ф; s — rt — подобное растяжение в г = | а \
раз; w = s + b — параллельный перенос на Ь. В
результате фигуры в плоскости z преобразуются
в себе подобные,
дополнительно поворачиваясь
и сдвигаясь. Точки zx =
= и z2 = оо пере-
1 — а
ходят сами в себя.
б) Инверсия
1
w = —
z
(рис. 3.95). Точка z =
= \z\ef9 переходит в точ-
1 -но
ку w = -—-е |ф, т. е. осу-
I z I Рис. 3.95
ществляется инверсия
относительно единичного круга и зеркальное
отображение относительно действительной оси.
Внутренность единичного круга | z | ^ 1
переводится во внешнюю часть круга | w | ^ 1, и, наоборот,
НЕКОТОРЫЕ ПРОСТЫЕ КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
375
внешняя часть круга | z | < 1 — во внутреннюю
часть круга | w | < 1. Сама окружность | z | = 1
переходит в окружность | w | = 1. Точки z = 1
и z = -1 остаются на месте. Конформность
нарушается в точке z ~ 0.
Это отображение имеет особое значение, так
как оно дает возможность исследовать поведение
функций на бесконечности (см. 3.4.7.6).
в) Дробно-линейная функция w = -(ad —
cz + а
- be ф 0, с Ф 0) однозначно и конформно
отображает замкнутую плоскость z на плоскость w
(рис. 3.96). Верно и обратное: каждая
аналитическая функция, которая отображает взаимно
Рис. 3.96
однозначно и конформно замкнутую плоскость на
себя, является дробно-линейной.
Это преобразование можно разложить на три:
t = cz + d - линейная функция, s = инвер-
ad
s - линейная функция. В
a be —
сия и w = 1
с с
результате дробно-линейная функция переводит
окружность в окружность (если считать прямые
частным случаем окружности). Неподвижные точки
этого отображения удовлетворяют уравнению
az + b
cz + d
г) Квадратичная функция w = z2 отображает
плоскость z на двойную плоскость w.
Изотермическая сетка плоскости z состоит из двух семейств
гипербол: и = х2 - у2 и v = 2ху (рис. 3.97).
Конформность нарушается при z = 0, точки 0 и 1
остаются на месте.
д) Две ветви функции w = ]/z — квадратного
корня — отображают всю плоскость z: 1) на
верхнюю полуплоскость w; 2) на нижнюю
полуплоскость \ w. Изотермическая сетка плоскости z
Рис. 3.97
состоит из двух семейств софокусных парабол с
фокусом в начале координат и с осями,
направленными по положительному и отрицательному
направлениям действительной оси (рис. 3.98).
Рис. 3.98
Рис 3.99
Конформность нарушается при z = 0, точки z = 0
и z = 1 остаются на месте.
е) Логарифм бесконечно многозначен. Для
главной ветви функции w = Ln z(u = In | z | и
v = ф0 + 2kn) вся плоскость z переходит в полосу
— я < у ^ +п плоскости w. Изотермическая сетка
состоит из окружностей In | z | = const и лучей
Ф = const (рис. 3.99), т. е. является полярной
сеткой.
4. ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ
4.1. МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
4.1.1. ОСНОВНЫЕ ПОНЯТИЯ
МАТЕМАТИЧЕСКОЙ ЛОГИКИ
4.1.1.1. Алгебра логики (алгебра высказываний,
логика высказываний). Под высказыванием
понимается имеющее смысл языковое выражение,
относительно которого можно утверждать, что оно
либо истинно, либо ложно. Таким образом,
каждому высказыванию можно приписать
истинностное значение И (истина) или Л (ложь). Вместо
этих символов часто употребляются числа 1 и О
соответственно.
Пример 1. «5 есть простое число», «3 есть
делитель 7», «3 + 5 = 9». Здесь первое высказывание имеет
истинностное значение И, а два других - истинностные значения Л.
Уравнение «2 + х = 4» не является высказыванием. Однако
всякий раз, придавая переменной х определенные числовые
значения, будем получать высказывание.
Используя-частицу «не», а также союзы «и»,
«или», «если..., то...», «тогда и только тогда, когда»
и т. п., можно из одних высказываний строить
другие, новые высказывания. Истинностные
значения новых высказываний определяются при этом
только истинностными значениями входящих в них
высказываний. Построение из данных высказываний
(или из данного высказывания) нового
высказывания называется логической операцией. Знаки
логических операций называются логическими связками
(или просто связками). Логические связки могут
быть одноместные (унарные), двухместные
(бинарные), трехместные (тернарные) и т. д. В алгебре
логики логические операции чаще всего
описываются при помощи таблиц истинности. Для
одноместной операции «отрицание» (или «инверсия»),
отвечающей связке «не», таблица истинности
выглядит так (табл. 4.1):
Таблица 4.1
А
0
1
не А
1
0
Отрицание высказывания А (т. е. не А)
обозначается ~]А, или А, или ~Л и часто читается:
«отрицание А» или «не А».
В табл. 4.2 приведены основные двухместные
логические операции (и логические связки). В
первом столбце дается, как правило, наиболее
употребительное обозначение логической операции, во
втором — некоторые другие широко
распространенные обозначения той же операции, в третьем —
линейно упорядоченный набор истинностных
значений, отвечающий этой операции (линейное
упорядочение выполнено так: если Ах * А2 - результат
применения логической связки ¦ к высказываниям
Ах и А2, то первый элемент набора есть
истинностное значение выражения 0*0, второй
элемент — истинностное значение для 0*1, третий —
для 1*0 и четвертый - для 1*1). В четвертом
столбце таблицы помещены различные названия
рассматриваемой операции (и связки), в последнем
указано, как обычно читается выражение вида
А{*А2, где А% и А2 - высказывания, а * -
(условное) обозначение рассматриваемой связки.
Переменная, значениями которой являются
высказывания, называется пропозициональной
переменной.
Основными символами алгебры высказываний
являются:
а) пропозициональные переменные ри р2, Рз* •••;
б) одноместная связка ~~1 и двухместные связки
л, v, -», *->;
в) скобки ( ).
Пропозициональные переменные могут
обозначаться и другими буквами, например а, Ь, с, ...
Понятие формулы алгебры высказываний, или
пропозициональной формулы, вводится по
индукции:
1) выражение, состоящее только из
пропозициональной переменной, является
пропозициональной формулой;
2) если Нг и Н2 - пропозициональные
формулы, то каждое из выражений ~~| Яь (Hi л Н2),
{Нх v H2),(Hi -> Я2)и(Я! <-+Н2) -
пропозициональная формула;
3) последовательность основных символов
только тогда является пропозициональной
формулой, когда она построена в соответствии с 1)
и 2).
Пример 2. Выражения
Hi ш ((р, -+ р2) л ~| р3),
Иг s ((р, л ~| Рз) v "I (рх л р2))
являются пропозициональными формулами.
Пропозициональная формула, начинающаяся со
знака ~, называется отрицанием.
Пропозициональные формулы (Hx л Н2), (Ях v Н2), (Нг --> Н2) и
АЛГЕБРА ЛОГИКИ
377
Таблица 4.2
Обозначение
логической
операции
Ах лА2
Ах v А2
А —¦ А
л\ Л2
А1 © А2
Л\ ~ А2
АХ\А2
АХ1А2
Другие
обозначения
логической операции
АХ&А2
Ах А2
АХА2
min(/4j, Л,)
Ах +А2
max(/4j, A2)
Ах 2 А,
Ах =>А~2
А{ + А2
Ах v А2
Ах АА2
Ах = А2
А *-* А
л\ол\
А1 ° А2
Ах v А2
Набор истинностных
значений,
отвечающий данной
логической операции
0001
0111
1101
ОНО
1001
1110
1000
Название логической операции
и связки
конъюнкция, логическое
умножение, логическое «и»
дизъюнкция, логическое
сложение, логическое «или»
импликация, логическое
следование
сумма по модулю 2,
разделительная дизъюнкция,
разделительное «или»
эквиваленция, эквивалентность,
равнозначность, тождественность
штрих Шеффера,
антиконъюнкция
стрелка Пирса, антидизъюнкция,
функция Вебба, функция Даггера
Как читается выражение,
приведенное в первом
столбце
Ах и А2
Ах или А2
если Ах, то А,, Ах
имплицирует А2, Ах влечет А2
Ах плюс А2; либо Alt либо
А2
Ах тогда и только тогда, когда
А2\ Ах эквивалентно А2
неверно, что А{ и А2, /4, штрих
Шеффера А2
ни Ах, ни А2: Ах стрелка
Пирса /4,
(Нх ~ Я2) называются соответственно конъюнкцией,
дизъюнкцией, импликацией и эквиваленцией.
Как и в арифметических выражениях,
устанавливаются определенные правила сокращения записей
пропозициональных формул:
а) вместо ~1 Я пишут Я;
б) вместо #! л Н2 пишут НХН2;
в) считается, что приоритет применения связок
возрастает в следующем порядке:
<->, -¦, v, л, ~~|;
г) внешние скобки опускаются.
Пример 3.
((Pi -»Рг) а Pt) ш (pj -> р2) рз,
((Pi л ~) Рз) v П (Pi л р2)) т рхрз v р~[р~2~.
Сокращенная запись многократной
конъюнкции и дизъюнкции. Пусть Ни
Н2, Нъ, ... — пропозициональные формулы. Тогда
Hi = Ни
„+1 / п \
л Я, = ( л Hi л Нп+! I,
\
Hi v Я„+1 j.
1 и+1
v Я, = ЯЬ y^Ht
Пример 4.
(_л Н, = (((Я, л Н2) л Н3) л НА) = Н,Н2НгНА,
^ Н, = (((Я, v Я2) v Я3) v Я4) s Я, v H2 v Я3 v Я4.
В алгебре логики широко используются
алгебраический и функциональный языки. При
алгебраическом подходе логические операции
интерпретируются как алгебраические, действующие на
множестве из двух элементов, например на множестве
{0, 1}. При функциональном подходе каждой из
основных логических операций сопоставляется
определенная двузначная функция.
Функция/(хь х2, ..., хп), у которой ар1ументы
пробегают множество {0, 1} и которая на любом
наборе значений аргументов принимает значение
из того же множества {0, 1}, называется функцией
алгебры югики или булевой функцией. Булеву
функцию/(л'ь х2, ..., х„) можно задавать таблицей
(табл. 4.3). Здесь наборы значений аргументов
Таблица 4.3
v,.v2 xn_\xn
00 00
00. 01
00 . 10
00 1 1
11 10
1 1 ... 1 1
/(л-рЛ-.,, . ,xn..hxn)
/@,0, ,0,0)
/@,0,.. ,0,1)
/@,0, . .1,0)
/@,0, ,1,1)
AM, -,1,0)
/A,1,. ,1,1)
расположены в порядке возрастания их номеров:
сначала идет набор, представляющий собой
двоичное разложение числа 0 (этот набор имеет номер 0);
затем идет набор, являющийся двоичным
разложением числа 1 (набор, номер которого есть 1);
за ним следует набор, соответствующий числу 2,
и т. д. Последний набор в табл. 4.3 состоит из п
единиц и является двоичным разложением числа
378
МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
2" - 1. Имея в виду такое стандартное
расположение наборов, булеву функцию/(хь х2, ..., х„) иногда
задают набором OLoOLi...a н_ , в котором а,
представляет собой значение функции/(хь х2, ..., хи) на
наборе с номером i (i = О, 1, ..., 2я - 1).
Среди булевых функций особо выделяются так
называемые элементарные булевы функции,
которые тесно связаны с основными логическими
операциями (и связками) — отрицанием, конъюнкцией
и др.
Двухместными элементарными булевыми
функциями являются конъюнкция, дизъюнкция,
импликация, сумма по модулю 2, эквиваленция, штрих
Шеффера и стрелка Пирса. Каждая из
перечисленных функций обозначается и определяется так же,
как логическая операция с соответствующим
названием, приведенная в табл. 4.2. Отличие состоит
только в том, что символы Ai и А2,
рассматриваемые в табл. 4.2, следует толковать теперь как
булевы переменные (т. е. переменные, принимающие
значения из множества {0, 1}).
Имеются две одноместные булевы функции,
зависящие от переменного х: тождественная
функция ф 1 (х) и отрицание х - функция ф2 (х) (табл. 4.4).
Таблица 4.4
X
0
1
ф|(*)
0
1
Ф2(х)
1
0
Тождественная функция <pt (x) обычно обозначается
через х, а отрицание х — через ~~| х или х (ср.
с логической операцией «отрицание»). Обе
одноместные булевы функции считаются
элементарными.
Имеются две нуль-местные элементарные
булевы функции: это константы 0 и 1.
Каждой пропозициональной формуле можно
сопоставить по определенному правилу булеву
функцию :
1) пропозициональному переменному р,
сопоставляется тождественная булева функция х, (i =
= 1, 2, ...);
2) пусть пропозициональным формулам Н^ и Я2
уже сопоставлены булевы функции ф^ и ф#2
соответственно; тогда пропозициональной
формуле ~| Hi сопоставляется булева функция ф# ,
пропозициональной формуле Н{ л Я2 (соответственно
Нх v Я2, Нх -> #2 и Hl<-*R2) сопоставляется
булева функция ф^1 • ф#2 (соответственно ф^ v ф#2,
Булева функция фд, сопоставляемая по
описанному правилу пропозициональной формуле Я,
называется функцией истинности формулы Я.
Пусть ц>н, — функция истинности формулы Я,
0 = 1, 2); пусть {хь х2, ..., хи} - множество тех
переменных, которые встречаются хотя бы в одной
из функций фя и ф# . Пропозициональные
формулы Нх и Я2 называются эквивалентными (или
равносильными), если на всяком наборе (аь а2, ...
..., а„) значений переменных хь х2, ..., хп значения
функций фЙ1 и фЯг совпадают. Тот факт, что
пропозициональные формулы Н^ и Я2
эквивалентны, обозначается так: Нх = Н2 (или Hi = Я2).
Приводимые ниже основные эквивалентности
часто оказываются полезными при оперировании
с пропозициональными формулами и булевыми
функциями.
Основные эквивалентности:
Н = Н (правило снятия двойного отрицания);
Я л Я — Я (идемпотентность конъюнкции);
Н v Н = Н (идемпотентность дизъюнкции);
Hi*H2 = Н2 * Hi (коммутативность связки *,
где символ ¦ является общим обозначением для
связок л, v, <->);
(Hi *Н2)*Я3 = Нх* (Н2*Я3) (ассоциативность
связки *, где * - общее обозначение для связок
л, v, <->);
Hi л (Я2 v Я3) = (Hi л Я2) v (Hi л Я3)
(дистрибутивность конъюнкции относительно
дизъюнкции);
Hi v (Я2 л Я3) = (Hi v Я2) л (Hi v Я3)
(дистрибутивность дизъюнкции относительно
конъюнкции);
Hi л Я2 =Нг vH2 и Я! v Я2 =77! л"Я2
(правила де Моргана);
Hi v (Hi л Я2) = Hi и Hi л (Hi v Я2) = Hi
(правила поглощения);
Hi v (Hi л H2) = Hi ~~
v Я2 и Hi л (Hi v Я2) =
= Hi л Я2;
H2
* Н2 ==
НН =_Л (закон противоречия);
И v Я = И (закон исключенного третьего);
НИ = Н;
Я v И = И;
НЛ = Л;
Я v Л = Я.
Замечание. Употребляемая в нескольких
приведенных эквивалентностях буква И
(соответственно буква Л) обозначает такую
пропозициональную формулу, функция истинности которой
равна тождественно 1 (соответственно 0).
Пропозициональная формула л ptk
(соответственно л^р^), где ст*е{0, 1}, Р% = Р^ Р\-Р*к>
ik^iju J2, ••-, )п) Для всех к = 1, 2, ..., г и р,т Ф plfc
при т Ф к, называется элементарной конъюнкцией
(соответственно элементарной дизъюнкцией) над
множеством пропозициональных переменных {
pJ2
. Число г (число букв в формуле)
2 j
называется рангом элементарной конъюнкции
(соответственно элементарной дизъюнкции). Две
элементарные конъюнкции (соответственно
дизъюнкции) считаются различными, если хотя бы в одной
из них найдется выражение р/, не входящее
в другую.
Пример 5. Конъюнкции ргръ, р2, р*, />2» Рь РгРъ
являются попарно различными элементарными
конъюнкциями над множествами пропозициональных переменных
{Рг> Рз, Р*. Рб}. {Ри Рг> Рз» Ра}, {Рг> Рз» Ра} и т. д.
Пропозициональная формула у Hi
(соответственно л Hj), в которой Яь Я2, ..., Hs -
попарно различные элементарные конъюнкции
(соответственно дизъюнкции) над множеством пе-
ПРЕДИКАТЫ
379
ременных {р, , р, , ..., p{j и, кроме того, ранг
каждой конъюнкции Н} (соответственно
дизъюнкции Hj) равен п, называется совершенной
дизъюнктивной (соответственно конъюнктивной)
нормальной формой над множеством {р,- , р,2, ..., р, }.
Две совершенные дизъюнктивные (соответственно
конъюнктивные) нормальные формы считаются
одинаковыми, если совпадают множества
элементарных конъюнкций (соответственно дизъюнкций),
входящих в эти формы.
Справедлива теорема. Любая
пропозициональная формула Н fa , pi2, ..., р,я), в которую
входят только пропозициональные переменные
Pt^ Pi2, • • • > Р|и» принадлежащие множеству {р^, pJ2,...
..., pjj, либо эквивалентна Л (соответственно И),
либо эквивалентна в точности одной совершенной
дизъюнктивной (соответственно конъюнктивной)
нормальной форме над множеством переменных
{/V Pj2, •.-, PjJ-
П р и м е р 6. Пропозициональная формула Н = р2-* Рг v
v р2Рз эквивалентна совершенной дизъюнктивной
нормальной форме р2Рг v p2Pi, а также совершенной
конъюнктивной нормальной форме (р2 v р3) (р2 v р3). Над множеством
переменных {р2, р3, р5} формула Н эквивалентна
совершенной дизъюнктивной нормальной форме
РгРъРь v РгРъРь v р2РгРъ v p2p3Ps
и совершенной конъюнктивной нормальной форме
0>2 V Рз V Р5)(р2 V Рз V Р5)(Р2 V р3 V р5)(р2 V р3 V р5).
Если в определении элементарной конъюнкции
(дизъюнкции) заменить пропозициональные
формулы р°* на булевы функции х°*, то получится
определение элементарной конъюнкции (дизъюнкции)
в классе булевых функций. Аналогичным образом
можно получить для булевых функций определения
совершенных дизъюнктивной и конъюнктивной
нормальных форм.
Пусть/(хь х2, ..., х„) -булева функция,
отличная от тождественного 0. Тогда ее можно
представить в совершенной дизъюнктивной нормальной
форме, которая имеет вид
(i,
, ..., ст„)
1 2
Х2 ...
Здесь дизъюнкция берется по всем таким наборам
о = (аь ст2, •••, <*п) значений переменных хь х2, ...
..., х„, на которых функция/(хь х2, ..., хп) равна 1.
Если булева функция g{xlt x2, ..., х„) не равна
тождественно 1, то ее можно представить в
совершенной конъюнктивной нормальной форме,
применив, например, следующий метод: сначала
строится совершенная дизъюнктивная нормальная
форма для функции #(хь х2, ..., х„), а затем
отрицание полученной дизъюнктивной формы
преобразуется с использованием правил де Моргана.
Пример 7. Импликация xt-*x2 равна 1 на наборах
@, 0), @, 1) и A, 1). Поэтому совершенная дизъюнктивная
нормальная форма для нее имеет вид х?х2 v x?x2 v x}x2 г
s xlx2 v xtx2 v xjx2. Совершенная дизъюнктивная
нормальная форма для отрицания импликации такова: ххх2. Значит,
Xi-»x2=Xj-*x2= x,x2=X! vx2 — совершенная
конъюнктивная нормальная форма функции xt -*¦ х2.
4.1.1.2. Предикаты. Применяемые в математике
высказывания обычно представляют собой
описание свойств каких-либо математических объектов
или описание отношений (взаимосвязей),
существующих между этими объектами. Для анализа
закономерностей, присущих таким высказываниям,
средств алгебры высказываний уже недостаточно.
Возникает необходимость ввести понятие «выска-
зывательной функции», или предиката.
Множество рассматриваемых объектов J будем
называть предметной областью (или множеством
индивидов), а элементы, принадлежащие множеству
/, — индивидами.
Пример 8. Т- множество всех действительных чисел
и всех однозначных, всюду определенных действительных
функций действительного переменного.
Знаки (символы) и последовательности знаков,
которыми обозначают индивиды, называются
индивидными (или предметными) константами.
Замечание. Очень часто индивидные
константы отождествляются с теми индивидами,
которые ими обозначаются.
П ример 9. «Числовые» константы: 3; п; - |/2;
«функциональные» константы: In, sin, tg.
Индивидная (или предметная) переменная
представляет собой знак, обозначающий произвольный
индивид из некоторого непустого подмножества
множества индивидов; это подмножество
называется областью изменения данной переменной.
Пусть аи а2, ..., а„ — индивиды из предметной
области /. Рассмотрим какое-либо высказывание
06 этих индивидах и обозначим его через Р (аь а2,...
..., а„). Если и = 1, то Р{ах) выражает свойство
индивида ах. Если n ^ 2, то данное высказывание
описывает некоторое отношение между
индивидами дь а2, ..., а„ (порядок следования индивидов
существен!). Возьмем предметные переменные хь
*2> •••> *и (с областями изменения /ь /2, ..., 1„
соответственно; здесь Ik - подмножество
множества /, к = 1, 2, ..., п). Выражение Р(хь х2, ..., хи)
представляет собой логическую функцию, или
предикат; при каждом замещении предметных
переменных хь х2, ..., х„ индивидами (из
соответствующих множеств Ik) оно становится
высказыванием. Символ Р был использован здесь для
обозначения конкретного, индивидуального
предиката, т. е. в данном случае символ Р является
предикатной константой (постоянным
предикатным символом). Переменный предикатный символ
представляет собой знак (или последовательность
знаков), обозначающий произвольную
предикатную константу из некоторого (подходящего)
множества предикатных констант. Если Р —
переменный предикатный символ, то Р(х1} х2, ..., х„)
называется переменным предикатом (или просто
предикатом). Предикат, зависящий в точности от п
различных предметных переменных, называется
п-местным (или п-арным). Высказывание можно
толковать как нуль-местный предикат, т. е. как
предикат, не зависящий от предметных
переменных. В случае бинарных предикатов вместо записи
Р(хи х2) часто применяют запись хАРх2.
Пример 10. «х есть четное число» — одноместный
(унарный) предикат; «х есть делитель у» - двуместный
(бинарный) предикат. Оба предиката — индивидуальные.
Пусть Р (хь х2, ..., х„) - предикат, a yi -
индивидная константа, или предметная переменная,
7 = 1, 2, ..., п; тогда выражение Р (уь у2, •.., у„)
называется элементарной формулой.
380
МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
Пример 11. Рассмотрим бинарные индивидуальные
предикаты х, > х2, х, | х2 и Х| = х2. Символы >, | и =
означают, как обычно, «больше», «есть делитель» и «равно».
Выражения х, > 3, 7| 5 и х3 = х10 являются элементарными
формулами.
С элементарными формулами можно
оперировать так же, как с пропозициональными
переменными: к ним применимы все операции алгебры
высказываний. При помощи логических связок из
элементарных формул строятся новые, предикатные
формулы. Сами элементарные формулы тоже
считаются предикатными.
Пример 12. ПG|5лх>3) и И C | 9) v И (х = у) -
предикатные формулы. Их можно «прочитать» следующим
образом: первую - «неверно, что 7 - делитель 5 и х больше
3», вторую — «3 не делит 9 или х не равно у».
Использование только элементарных формул
и операций алгебры высказываний не дает
возможности преодолеть трудности, возникающие,
например, при попытке сформулировать на формальном
логико-математическом языке следующую
теорему: «уравнение х + 3 = 8 имеет целочисленное
решение». В связи с этим в рассмотрение вводятся
кванторы. Чаще всего ограничиваются только
квантором общности (обозначение: V; читается:
«для всех...») и квантором существования
(обозначение: 3; читается: «существует...»).
Расширим понятие предикатной формулы.
Будем считать, что предикатные формулы строятся
из элементарных формул при помощи логических
связок и кванторов всеобщности и существования.
Применение кванторов для построения формул
осуществляется по следующей схеме.
Пусть Н - предикатная формула их-
предметная переменная, которая может и не входить
в формулу Н. Тогда выражения (VxH) и (ЗхЯ)
считаются предикатными формулами (в этом
случае говорят, что Н есть область действия
соответствующего квантора — Vx или Зх).
Приписывание спереди к предикатной формуле
какого-либо квантора называется операцией
навешивания квантора (или связывания кваппюром).
Конкретное вхождение переменной х в
формулу Н называется связанным, если оно либо
непосредственно следует за каким-нибудь квантором,
либо содержится в области действия некоторого
квантора Vx или Зх. Если вхождение переменной
в формулу не является связанным, то оно
называется свободным. Переменная, входящая в
формулу Я, называется связанной (свободной), если в Н
имеется связанное (свободное) вхождение этой
переменной. Таким образом, переменная может
быть одновременно и свободной, и связанной
(в данной формуле).
Пример 13. Пусть Z - множество целых чисел. В
предикатной формуле (Vx(xeZ-+ 21 2х)) л (х > 5) переменная х
является и связанной (три ее вхождения в первый член
конъюнкции — связанные), и свободной (вхождение х в
формулу х > 5 - свободное). Областью действия квантора Vx
является формула xeZ-> 2 |2х. В формуле 3x(xeZ л х + 3 =
= 8), представляющей собой истинное высказывание, все три
вхождения переменной х — связанные.
Предметные переменные, входящие в
предикатные формулы, можно переименовывать в
соответствии со следующими правилами.
Связанное переименование. Пусть х — связанная
переменная в формуле Н. Произвольное вхождение
переменной х, непосредственно следующее за
каким-либо квантором, и все вхождения х,
принадлежащие области действия рассматриваемого
квантора, можно одновременно заменить на любую
переменную у, не входящую в формулу Н.
Свободное переименование. Пусть х — свободная
переменная в формуле Н. Все свободные
вхождения этой переменной в формуле Н можно
одновременно заменить на любую переменную у, не
входящую в формулу Н.
Посредством связанного переименования
любую исходную предикатную формулу можно
преобразовать к такой предикатной формуле, которая
не содержит ни одной предметной переменной,
являющейся одновременно и связанной, и
свободной.
Пример 14. Формулу Зх (х > 1 -» Vx (х > у л Зх (х 110)))
можно преобразовать к следующим формулам:
Зх, (х, > 1 -> Vx, (х, > >• л Зх2 (х2 | 10))),
Зх, (х, > 1 -¦ Vx2 (х2 > у л Зх2 (х21 10))), .
Зх, (х, > 1 -> Vx2 (х2 > у л Зх3 (х3 | 10))).
Ограниченные кванторы. Часто при
оперировании с кванторами удобно бывает
рассматривать только элементы некоторого заданного
непустого множества М, т. е. использовать
конструкции вида: «для всех хеМ...» и «существует
хеМ...» (символически их можно записать так:
«Vxe M...» и «ЗхеМ...»). Эти ограниченные кванторы
следует интерпретировать только как сокращение
при записи формул, содержащих обычные средства
выражения:
VxeM (H (х)) - сокращение для формулы Vx(хе
еМ->Я(х)),
ЗхбМ(Я(х)) — сокращение для формулы Эх(хе
еМ л Н(х)).
4.1.2. ОСНОВНЫЕ ПОНЯТИЯ
ТЕОРИИ МНОЖЕСТВ
4.1.2.1. Множества, элементы. Под множеством
понимают объединение в единое целое
определенных вполне различаемых предметов (объектов),
которые при этом называются элементами
образуемого ими множества. Если а — элемент
множества М, то это обозначают так: аеМ (читают:
«а принадлежит М» или «а - элемент М»), Для
обозначения того, что а не является элементом
множества М, применяют запись: афМ (или аёМ).
Два множества А и В равны (обозначение: А = В),
если они содержат одни и те же элементы, т. е.
А=В~Ух (хеА<->хеВ).
Множество можно описать, указав свойство,
присущее только элементам этого множества.
Множество всех объектов, обладающих свойством
Н(х), обозначают через {х|Я(х)} или {х: Н(х)}.
Если в качестве свойства в Н (х) выбрать какое-
нибудь свойство, которым не обладает ни один
объект, например свойство х Ф х, то ни для какого
объекта а не может выполняться соотношение
ае{х\ Н(х)}, и, следовательно, Уа(а$ {х \ Н(х)}).
Множество, не содержащее элементов, называется
пустым, и его обозначают символом 0.
4.1.2.2. Подмножества. Если все элементы
множества А являются также элементами множества
В, то говорят, что А содержится (или включается)
ДИАГРАММЫ ЭЙЛЕРА - ВЕННА
381
в В или что В содержит (или включает) А,
и обозначают это так: А сг в (или В з А). Если
А с в, то множество Л называется иодлшожеопвсш
множества В; если к тому же А Ф В, то Л
называют собственным подмножеством множества В
и применяют запись А а В. Отношения ^ и с
между множествами называются соответственно
включением и собственным включением. Довольно
часто, когда нет необходимости различать эти
два вида включений, применяют только
обозначение с Запись Аф В (соответственно АфВ) означает,
что множество А не является подмножеством
(соответственно собственным подмножеством)
множества В.
Для множеств А, В и С справедливы следующие
соотношения:
А я А, Аф А,
АяВлВяС^АяС, А Я В л В а С-+ А а С.
Между включением и равенством множеств
существует связь, отраженная в следующем
соотношении :
А=В<->АяВлВяА.
Из этого выражения вытекает часто используемый
метод доказательства равенства двух множеств:
чтобы доказать равенство множеств А и В,
достаточно обосновать оба включения А я В и В я А.
4.1.3. ОПЕРАЦИИ
НАД МНОЖЕСТВАМИ
4.1.3.1. Объединение и пересечение множеств.
Объединение A\jB множеств А и В представляет
собой множество, состоящее из элементов,
принадлежащих хотя бы одному из множеств А и В.
Пересечение А (~) В множеств А и В есть множество,
которое состоит из элементов, принадлежащих
каждому из множеств А и В. Множества А и В,
имеющие пустое пересечение, т. е. A О В = 0,
называются непересекающимися (или дизъюнктными).
Для множеств А, В и С справедливы
следующие соотношения:
A(jA = Af)A=A, A{JB = B{JA,
Af]B = Bf]A, (A\JB)\JC = A\J(B{JQ,
(A\jB)f](A[jC),
A{J(Af)B) = A,
A[J0 = A,
A[JB,
A ^
А я С л В я С -+ A(J В я С,
АяВ л A^C-*A^Bf)C.
4.1.3.2. Разность, симметрическая разность,
дополнение множеств. Разность А\В множеств А и В
(порядок множеств существен!) есть множество,
состоящее из таких элементов множества А,
которые не принадлежат множеству В. Симметрическая
разность ААВ множеств А и В представляет
собой множество, состоящее из элементов,
принадлежащих в точности одному из множеств А
и В, т. е. А А В = (А\В) (J (В\А).
Если /}??, то дополнение С^А множества А
относительно Е определяется так:
СЕА = Е\А.
Для множеств А, В и С справедливы следующие
соотношения:
А\В Я А,
А\А = 0, А\(А\В) = А О В,
AAB=(A{jB)\(Af]B),
(A\JB)\C = (A\C){J(B\C),
(А0В)\С = (А\СH(В\С),
A\(B\C) = (A\B) U (А О С), (А\В)\С = A\(B \J C),
Если А и В — подмножества множества ?, то
A[jCEA = E, AOCEA=0,
СЕ0 = ?, СЕСЕА = Л,
СЕ(А О В) = СЕА U СЕВ, А Я В~СЕВ Я СЕА.
4.1.3.3. Диаграммы Эйлера - Венна. Для
пояснения некоторых свойств операций над множествами
и различных соотношений между множествами
можно использовать диаграммы Эйлера — Венна,
на которых множества, подлежащие рассмотрению,
изображаются в виде совокупностей точек на
плоскости (рис. 4.1—4.7). Рис. 4.1 иллюстрирует
Рис. 4.1
' Рис. 4.2
Рис 4.3
Рис. 4.4
Рис. 4 5
Рис 4.6
Рис 4 7
382
МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
соотношение В я А, на рис. 4.2-4.6
заштрихованные области изображают соответственно
объединение A(jB, пересечение A Q В, разность А\В,
симметрическую разность А Л В и дополнение CgA.
Заштрихованная на рис. 4.7 область соответствует
множеству A f] (В (J С). Этот рисунок может
служить иллюстрацией к обоснованию равенства
Af](B[JC)=(Af]B)[J(Af]C).
4.1.3.4. Декартово произведение множеств.
Упорядоченной парой (а, Ь) двух элементов а, Ь
называется множество {{а}, {а, Ь}}. Для любых
элементов а, Ь, с, d справедливо соотношение
(а, Ь) = (с, d) <-> а = с л 6 = d.
Если а = 6, то (а, а) {{а}, {а}}. В случае, когда
элементы а и Ъ разные, (а, Ъ) ф {Ь, а).
Упорядоченный набор п элементов (аь ..., ап) определяется
по индукции:
при п = 2 (аь ..., а„) есть (аь а2);
при и > 2 (аь ..., аи_ ь аи) есть ((аь ..., а„_ х), а„).
Справедливо соотношение
(аь ..., ап) = (Ьь ..., &„)<-> ах = Ьх л ... л ап = Ъп.
Декартово произведение А х В двух множеств А
и В есть множество всех упорядоченных пар (а, Ь),
где аеЛ и be В, т. е.
Л х? = {(а, Ъ)\аеА л ЬеЯ}.
Для множеств А, В, С, Z) выполняются
следующие соотношения:
(A(jB)xC = (A xC)[j(BxC),
(A()B)xC = (AxC)\J{BxC)9
A x(B[JC) = (A xB)[J(A xC),
A x(Bf]C) = (A xB)f](A xC),
(A xB)U(CxD)cz(A{JC)x(BUD),
(A x B)f](C x D) = (A(\C) x (Bf]D),
A xB = 04-+A=0vB = 0,
АяСаВяп->А x В Я С х D.
Декартово произведение множеств
некоммутативно.
Декартово произведение Лх х ... х Ап п
множеств (сокращенно записывается в виде х А) есть
множество
{(аи ..., an)\a1eAi л ... л апеАп}.
Л
Если Ах — ... = А„ = А, то вместо х А{
употребляют запись Ап и получающееся декартово
произведение называют п-й декартовой степенью
множества А.
4.1.3.5. Обобщенные объединение и пересечение.
Пусть К — некоторое множество, которое назовем
множеством индексов, и пусть для всякого /сеК
Ак есть подмножество множества А. Тогда
множество {Ак\кеК} называется семейством
подмножеств множества А. Объединение семейства
подмножеств {Ak\keK} есть множество {x\3k(ke
еК а хеАк)}; его обозначают так: (J Ак (или
кеК
(J Ak). Пересечение семейства подмножеств вводят
К
только для непустых семейств. Если К Ф 0, то
пересечение семейства подмножеств {Ак \ к е К} есть
множество {х | \/к (к е К -> х е Ак)}; такое пересечение
обозначается через (~) Ак (или Q Ак). Если семей-
кеК К
ство подмножеств обозначают одной буквой,
например М, то объединение (пересечение) всех
подмножеств этого семейства записывают в виде |J M
(соответственно f] M).
Для семейств подмножеств М, N, которые при
рассмотрении пересечения предполагаются
непустыми, справедливы следующие соотношения:
М с N -+ IJ М Я ((J N) л (fl N) Я р| М.
Выпишем еще несколько соотношений,
используя первоначальные обозначения для объединения
и пересечения семейств подмножеств. Пусть
{Ak\keK}, {Bj|jeJ} — семейства подмножеств и
С — множество. Тогда справедливы равенства:
cf) U л* = U
keK keK
keK keK
U^niM= U
keK jeJ (k,j)eKxJ
ri4kUn*j- П (
keK jeJ (k,j)eKxJ
эти равенства останутся верными, если всюду в них
заменить знаки f] и (J на х. Далее, справедливы
соотношения:
с\ U 4k- П (c\4k), c\ n лк= и (с\лк),
keK keK keK keK
U Ak\c =
keK keK
П Ак\с = П
keK keK
в частности, так как Акя А для всех к е К, то
CA([j
Q( Г)
= U
4.1.4. ОТНОШЕНИЯ И ОТОБРАЖЕНИЯ
4.1.4.1. Отношения, п-местным (п-мерным)
отношением R на непустом множестве А называется
подмножество множества Ап, т. е. R я Ап. Если R
есть n-местное отношение на А и (аи ..., а„)е R,
то говорят, что отношение Я выполняется для
элементов аь ..., а„, и пишут: Ra^.M^ если же
(аи ..., а„)^К, то говорят, что отношение R не
выполняется для элементов аи ..., а„. В случае
двухместного (бинарного) отношения R вместо
Raxa2 употребляют запись axRa2.
Для каждого непустого множества А легко
указать два тривиальных «-местных отношения:
а) полное, или универсальное, отношение v,
которое выполняется для любых п элементов
множества А;
б) пустое, или нулевое, отношение л, которое
не выполняется ни для каких п элементов
множества А.
Очевидно, что v = Ап и v = 0.
Если R есть «-местное отношение на А и В —
непустое подмножество множества А, то ограниче-
ОТНОШЕНИЕ ПОРЯДКА
383
ние R на В (обозначается R \ В) есть множество
R f] Вп и, следовательно, является n-местным
отношением на В.
Для отношений естественным образом можно
ввести все те операции, которые были определены
для множеств. Например, если R и S - п-местные
отношения на А, то объединение R (J S и
пересечение Rf]S этих отношений также являются
«-местными отношениями (иногда объединение
отношений называют суммой, а пересечение — абсолютным
произведением). Если R есть «-местное отношение
на А, то его дополнение, рассматриваемое на
множестве А", часто называют отрицанием
отношения R и обозначают через R.
Для бинарных отношений, играющих
важную роль в математике, введен целый ряд
специальных понятий. Остановимся на некоторых
из них. *
Произведением R • S (относительным
произведением) двух бинарных отношений R и S, заданных
на множестве А, называется множество {(х, у) \ 3z(ze
еА) л (x,z)eR л (z,y)eS}.
Обратным (инверсным, дуальным) отношением
к отношению R, заданному на множестве А,
называется отношение R'1, определяемое следующим
образом:
R-1 = {(x,y)\(y,x)eR}.
Если R, S и Т- бинарные отношения на А, то
выполняются следующие равенства:
(RS)- Т= R(S- Т), (R U S)- Г= (R- T) (J (S- Т),
(R[JS)-l=R-l[JS-\
Пусть R — бинарное отношение на А. Тогда
множество {х\3у((х, y)eR)} называется прообразом
отношения R, а множество {у\3х((х, y)eR)} —
образом отношения R.
Ниже дается перечень важных свойств бинарных
отношений (здесь всюду R - бинарное отношение
на множестве А).
Свойст во
Рефлексивность
Антирефлексивность
(или иррефлексивность)
Транзитивность
Си мметричность
Антисимметричность
Асимметричность
Линейность
Связность
Равенство третьему
Трихотомия
Характеризующее условие
Ma(aRa)
Ma "I (aRa)
VflVftVc (aRb a bRc
Ma\lb(aRb^bRa)
4dib(aRbA bRa^
4dib(aRb-> ~]bRa
4a4b(aRb v bRa)
VaVb(aRbv bRa v
VeVfeVc (aRc a bRc
Vd1b(aRb v bRa v
-+aRc)
a = b)
a = b)
-+aRb)
a = b) a
л ~| ((aRb a bRa) v (aRb л
л а — b) v (bRa л
4.1.4.2. Отношение эквивалентности. Бинарное
отношение называется отношением
эквивалентности, если оно рефлексивно, симметрично и
транзитивно. Если R — отношение эквивалентности,
то вместо aRb пишут а~ц b (читается: а
эквивалентно Ь относительно R). Если на А задано
отношение эквивалентности R, то элементы множества А
можно разбить на попарно не пересекающиеся
классы эквивалентных друг другу относительно R
элементов. Эти классы называются классами
эквивалентности, а произвольный элемент класса
называется его представителем. Если а — какой-
либо представитель некоторого класса
эквивалентности, то этот класс обозначают [а]д. Множество
всех классов эквивалентности множества А
относительно R называется фактор-множеством
множества А относительно R и обозначается A/R.
Пересечение отношений эквивалентности,
заданных на множестве А, также является отношением
эквивалентности на А.
4.1.4.Э. Отношение порядка. Бинарное
отношение называется отношением нестрогого (строгого)
квазипорядка, если оно рефлексивно (соответственно
антирефлексивно) и транзитивно. Вместо термина
квазипорядок часто используют другие термины:
предпорядок, квазиупорядоченность, предупорядоче-
ние. Квазипорядок R на множестве А называется
направленным (или право направленным), если для
любых двух элементов a, be А найдется элемент
се А, удовлетворяющий условию aRc л bRc;
квазипорядок R на А называется обратно
направленным (или левонаправленным), если для всяких двух
элементов a, be А существует элемент се А, для
которого справедлива конъюнкция cRa л cRb.
Каждый нестрогий квазипорядок R на
множестве А индуцирует отношение эквивалентности
5 на А:
aSb*-+aRb л bRa
(здесь a, be А).
Нестрогий (строгий) квазипорядок называется
нестрогим (соответственно строгим) частичным
порядком, если он является антисимметричным
(соответственно асимметричным) отношением.
Вместо термина частичный порядок используют
также термины полуупорядоченность, частичная
упорядоченность, частичное упорядочение (а
иногда просто порядок, упорядочение).
Если R - нестрогий квазипорядок на А и S -
отношение эквивалентности на А,
индуцированное этим квазипорядком, то бинарное отношение
R* на фактор-множестве A/S, определяемое
соотношением
является нестрогим частичным порядком на A/S.
Если R — нестрогий (строгий) частичный
порядок, то вместо aRb пишут а < д b или а ^ b
(соответственно a<R b или а < Ь) и говорят: «Ь
больше (соответственно строго больше) а» или «а
меньше (соответственно строго меньше) Ь». Если
R - нестрогий частичный порядок на А, то
соотношение
a<b<->a^Rb а афЬ D.1)
(a, be А) задает на А строгий частичный порядок.
С другой стороны, если R — строгий частичный
порядок на А, то формула \
a^b<-+a <Rb v a — b D.2)
(a, be А) определяет на А нестрогий частичный
порядок.
Частичный порядок на конечном множестве
иногда удобно бывает изображать в виде специаль-
384
МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
ных диаграмм, которые называются
диаграммами Хассе. Если R — частичный порядок на А, то
построение диаграммы Хассе для отношения R
осуществляется следующим образом: элементы
множества А изображаются точками плоскости, и затем
две произвольные различные точки an b
соединяются отрезком прямой или дугой, если aRb и
~1 Эх (х Ф а л х ф b л aRx л xRb). Для того чтобы
различать случаи aRb и bRa друг от друга, при
выполнении соотношения aRb на отрезке прямой
или дуге, соединяющей точки а и Ь, рисуют
стрелку, направленную от а к b (или просто
изображают точку b выше точки а или справа от нее).
Пример 15. Пусть А = {ль а2, а3, а4, а5} и R =
* {(fl,, rti),(fl2, «2), («3, «а). («4, <U), (Я5. Ы («1. Ы (<»Ь «з), («1, «Д
(я,. я5)< («2, «5)» («з» «s)}- Тогда R - нестрогий частичный
порядок на А. Диаграмма
Хассе для R изображена
на рис. 4.8 («большие»
элементы нарисованы
справа от «меньших»).
Если на множестве
А задан частичный
порядок R, то оно
называется частично
упорядоченным.
Элемент аеА называется
непосредственно предшествующим элементу be A
(и элемент b называется непосредственно
следующим за элементом а), если aRb л ~\3х(х ф а л х Ф
Ф b л aRx л xRb). Два элемента а и b множества
А, частично упорядоченного отношением R,
называются сравнимыми, если aRb v bRa; в
противном случае они называются несравнимыми.
Пусть множество А частично упорядочено
отношением R. Элемент аеА называется
минимальным {максимальным) элементом множества А,
если в А не существует элемента х, отличного от а
и удовлетворяющего условию xRa (соответственно
aRx).
Пусть В - подмножество множества А,
частично упорядоченного отношением R. Верхней гранью
или мажорантой (соответственно нижней гранью
или минорантой) подмножества В в множестве А
называется всякий элемент хеА,
удовлетворяющий условию Чу (уе В -+(yRx v у = х))
(соответственно Vy (yeВ -> (xRy v у = х))). Если у множества В
существует хотя бы одна мажоранта (миноранта)
в А, то В называется ограниченным сверху (снизу)
в А. Если само множество А обладает мажорантой
(минорантой), то она единственна и называется
наибольшим (наименьшим) элементом множества А.
Наименьшая верхняя грань подмножества В, если
она существует, называется точной верхней
гранью подмножества В и обозначается sup В
(читается: супремум В). Аналогично наибольшая
нижняя грань подмножества В, если она существует,
называется точной нижней гранью подмножества
В и обозначается inf В (читается: инфимум В).
Элемент частично упорядоченного множества,
не имеющий непосредственно предшествующих
элементов, называется предельным.
Множество А, частично упорядоченное
отношением R, называется линейно (совершенно, просто)
упорядоченным (или цепью), если в нем сравнимы два
любых различных элемента. Отношение R
называется тогда линейным (совершенным) порядком.
Линейно упорядоченное множество А
называется вполне упорядоченным, если каждое
непустое его подмножество имеет минимальный
элемент. Упорядочение множества А называется при
этом полным.
Частичный порядок R на множестве А
называется индуктивным или правойндуктивным
(соответственно левоиндуктивным), если относительно R
всякая цепь множества А обладает точной верхней
(соответственно нижней) гранью.
Пример 16. 1) Всякое отношение эквивалентности
является нестрогим квазипорядком. 2) Пусть М -
семейство подмножеств (некоторого множества) и Я с
-отношение включения на М, т. е.
«с = {(Аи А2)\АхеМ л А2еМ л Ах с А2}.
Отношение К с является нестрогим частичным порядком.
3) Собственное включение Rc на семействе подмножеств
М есть строгий частичный порядок. 4) Обычное отношение
^ является линейным (нестрогим) порядком в множестве Z
целых чисел и полным упорядочением в множестве N
натуральных чисел.
Слабый принцип максимальности Цорна. Если
R — индуктивное упорядочение на множестве А,
то в А существует максимальный относительно R
элемент.
Сильный принцип максимальности Цорна. Если
R — частичный порядок на множестве А и любая
вполне упорядоченная (относительно R) цепь в А
имеет верхнюю грань, то в А существует
максимальный (относительно R) элемент.
Оба эти принципа эквивалентны друг другу, а
также следующим двум принципам.
Принципы максимальных, цепей (Хаусдорф —
Биркгоф).
1) В каждом частично упорядоченном множестве
существует цепь, максимальная относительно гео-
ретико-множественного включения с.
2) Всякая цепь частично упорядоченного
множества содержится в некоторой максимальной
(относительно включения ?) цепи этого множества.
4.1.4.4. Отображения. Отображением множества
А во множество В (функцией на А со значениями
в В) называется правило, по которому каждому
элементу множества А Сопоставляется один или
несколько элементов множества В. Для обозначения
отображения ф множества А в множество В
используют запись (р: А -* В. Если хеА, то множество
всех элементов из В, сопоставляемых при
отображении ф элементу х, обозначается через ф(х) и
называется образом элемента х. Образом
подмножества Ai множества А при отображении ф
(обозначение: (p(Ai)) называется объединение
образов всех элементов х из А±. Образ всего
множества А, т.е. ф(Л), называется областью
значений отображения ф. Если уеВ, то его полным
прообразом при отображении ф (обозначение:
Ф^)) называется множество всех элементов
из А, которым при отображении ф сопоставляется
элемент у. Всякий элемент из Ф^) называется
прообразом элемента у при отображении ф. Если
при отображении ф: А -> В каждому элементу из А
сопоставляется в точности один элемент из В, то
отображение (функция) ф называется однозначным.
Отображение, не являющееся однозначным,
называется многозначным. Если ф: А -> В —
однозначное отображение, то отображение ф: В -> А,
ОПЕРАЦИИ И АЛГЕБРА
385
сопоставляющее каждому элементу уеВ его
прообраз ф (у), называется обратным (для отображе-^
ния ф). Отображение ф является, вообще говоря,
частичным, т. е. не для всякого элемента из В
его образ при ф есть непустое множество. Кроме
того, отображение ф может быть и
многозначным.
Отображение ф: А-+В можно толковать как
отношение между множествами А и В, т. е.
отождествлять его с некоторым подмножеством М
декартова произведения А х В, называемым
графиком отображения ф и определяемым
следующим образом:
М = {(х, у)\хеА а уеВ а ф(х) = у}.
Однозначное отображение ф: А-+В
называется:
сюръективным (сюръекцией), если ф(Л) = В
(отображение «на»);
инъективным (инъекцией), если образы различных
элементов различны (отображение «в»).
биективным (биекцией, взаимно однозначным),
если оно сюръективно и инъективно.
Пусть ф!: А^В и ф2: В-* С — два
однозначных отображения. Тогда (однозначное)
отображение ф: А -*¦ С, сопоставляющее произвольному
элементу хеА элемент ф2(ф1(х))еС, называется
суперпозицией (произведением, композицией)
отображений ф, и ф2 и обозначается ф2оф1.
Через id^ обозначается тождественное
отображение множества А на него же, т. е. такое
(однозначное) отображение, которое каждому элементу
из А сопоставляет этот же элемент.
Однозначное отображение ср: А-+В является
биекцией тогда и только тогда, когда существует
(однозначное)отображение\|/: В ->
А,удовлетворяющее условиям \|/ о ф = id^ и ф ° \|/ = idg.
Однозначное отображение ф: А^В является
инъекцией тогда и только тогда, когда существует
(однозначное) отображение \J/: ф (А) -*¦ А,
удовлетворяющее условию \j/ о ф = id^.
Однозначное отображение ф: А^В является
сюръекцией тогда и только тогда, когда существует
(однозначное) отображение vj/: В -*¦ А,
удовлетворяющее условию ф о \J/ = idB.
4.1.4.5. Последовательности и семейства
множеств. Конечные и бесконечные
последовательности можно толковать как функции (отображения):
конечная последовательность, состоящая из т
элементов, — последовательность аи а2, ..., ат —
есть функция ф: {1, 2, ..., т) -* {аи а2, • ••> ят}
такая, что ф(/) = «,- (/=1, 2, ..., т); бесконечная
последовательность яь а2, ..., ат, ... есть функция
ф: N-*{flb a2, ..., ат, ...} такая, что ф(/) = а,- при
всяком /eN (здесь N — множество натуральных
чисел).
Семейство множеств можно ввести с помощью
понятия функции. Пусть J - множество индексов.
Тогда функция ф: J -* М, значениями которой
являются множества, есть семейство множеств.
Если ф — семейство множеств и для каждого
jeJ имеем ф(/) = Л7, то это семейство множеств
обозначают часто так: (Aj)jej.
Пусть (Aj)jej — семейство множеств. Функция
Ф: J -> (J Aj такая, что V/ (/ б J -*¦ ф (/') € Aj), назы-
J
вается функцией выбора для семейства (Aj)jej.
13 И. Н. Бронштейн, К. А. Семендяев
Множество всех функций выбора для семейства
множеств (Aj)jej есть декартово произведение
семейства (Aj)jej:
X Aj = {ф | ф - функция выбора для (Aj);ej}.
Ясно, что если Aj = 0 при некотором jeJ, то
X Aj = 0. Обращением этого высказывания яв-
jeJ
ляется следующий
Принцип выбора. Для каждого непустого
семейства непустых множеств существует функция
выбора.
Этот принцип эквивалентен принципу
максимальности Цорна.
4.1.4.6. Операции и алгебры, п-местная (п-арная)
операция со на множестве М (при п ^ 1) есть
однозначная функция из М" в М; при этом, вообще
говоря, не предполагается, что функция со
определена для всякого элемента множества М".
Если операция со не всюду определена на Мп, то
она называется п-местной частичной операцией.
Под нуль-местной операцией на М понимают
выделение элемента из М. Если аи ..., а„ —
элементы из М, то результат применения операции со
к этим элементам, т.е. со(аь ..., ап), часто
записывают в следующем виде: <йах...ап', при п = 2
применяют также запись al(oa2-
П р и м с р 17.1) Сложение действительных чисел есть
двухместная операция в множестве R действительных чисел.
2) Деление действительных чисел - двухместная частичная
операция в R. 3) Выделение какого-либо элемента из R
(например, 1) есть нуль-местная операция в R.
Универсальной алгеброй (или, короче, алгеброй)
называется пара <М; Q>, где М — некоторое
непустое множество элементов и О, - некоторое
непустое множество операций, определенных на
множестве М. Множество М называется носителем
или основным множеством алгебры. Если
некоторые из операций, входящих в множество Q,
являются частичными, то алгебра называется
частичной. Очень часто вместо «алгебра <М; Q>»
говорят просто «алгебра М».
Полугруппой называется алгебра <М; ~Г> с
одной бинарной операцией J, удовлетворяющей
ассоциативному закону: каковы бы ни были
элементы а, Ь, с из М,
Операция "|", удовлетворяющая ассоциативному
закону, называется ассоциативной. Группой
называется полугруппа, удовлетворяющая следующим
условиям:
а) в М есть такой элемент е (левая единица),
что для каждого элемента аеМ выполняется
равенство е~[а = а;
б) для каждого элемента аеМ существует
такой элемент Ь (называемый" левым обратным
для а), что bj a = е.
Группа <М; Х> называется абелевой, если
операция Т коммутативна, т. е. для любых а и b из
М выполняется равенство ajb = bja.
Кольцом называется алгебра <М; Т, -L> с двумя
бинарными операциями f и _1_, удовлетворяющими
следующим условиям:
а) относительно операции J множество М
образует абелеву группу;
386
МНОЖЕСТВА, ОТНОШЕНИЯ, ОТОБРАЖЕНИЯ
б) справедливы дистрибутивные законы:
для любых элементов а, Ь, с из М.
Операцию J часто называют сложением, а ± —
умножением. Нулевым элементом (нулем) кольца
называется такой элемент а, что ajb = bubja = b
для всякого ЬеМ. Нулевой элемент в кольце
единствен.
Кольцо называется ассоциативным, если
операция _1_ ассоциативна. Если операция 1
коммутативна, то кольцо называется коммутативным.
Если в кольце все отличные от нуля элементы
образуют группу относительно операции JL, то
кольцо называется телом. Если операция 1 к
тому же коммутативна, то тело называется полем.
4.1.5. МОЩНОСТЬ МНОЖЕСТВ
4.1.5.1. Равномощность. Два множества А и В
называются равномощными (обозначение: А ~ В),
если существует биекция ср: А-* В. Отношение
равномощности, рассматриваемое на любой
заданной совокупности множеств, рефлексивно,
симметрично и транзитивно, т. е. является
отношением эквивалентности.
Множество А называется конечным, если
существует такое натуральное число п, что
/l~{/c|/ceNv/c< и}, где N — множество
натуральных чисел; при этом говорят, что множество
А имеет и элементов.
Множество, не являющееся конечным,
называется бесконечным.
Каждое непустое подмножество конечного
множества конечно. Множество всех подмножеств
конечного множества конечно.
Каждое множество, содержащее бесконечное
подмножество, бесконечно. Множество всех
подмножеств бесконечного множества бесконечно.
Множество N натуральных чисел бесконечно;
следовательно, бесконечны множества Z (множество целых чисел),
Q (множество рациональных чисел), R (множество
действительных чисел), С (множество комплексных чисел).
Каждое бесконечное множество имеет
собственное подмножество, которому оно равномощно,
и наоборот, если множество равномощно
своему собственному подмножеству, то оно
бесконечно.
Никакое множество не является равномощным
множеству всех своих подмножеств.
4.1.5.2. Счетные и несчетные множества.
Множество А называется не более чем счетным, если оно
конечно или равномощно множеству N.
Множество А называется счетным, если А ~ N. Иногда
счетные множества называют счетно
бесконечными.
Бесконечное множество, не являющееся
счетным, называют несчетным.
Каждое несчетное множество бесконечно; каждое
бесконечное множество содержит счетное
подмножество. Каждое бесконечное подмножество
счетного множества счетно. Объединение и непустое
пересечение счетной совокупности счетных
множеств - счетные множества.
Множества Z и Q - счетные.
Множества R и С - несчетные.
4.2. ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
4.2.1. ВЕКТОРНАЯ АЛГЕБРА
4.2.1.1. Основные понятия. Величины, значения
которых могут быть выражены действительными
числами, называются скалярами (например, масса,
заряд, температура, работа и т. п.). Величины же,
значения которых определяются как числовым
значением, так и направлением в пространстве,
называются векторами (например, скорость, ускорение,
сила, напряженность электрического и магнитного
полей и т. д.).
Геометрический вектор — это направленный
отрезок в пространстве (обозначается: Р\Р2\ а, Ь,
с, ... ; а, Ь, с, ... ; здесь Рх - начальная точка, Р2 -
конечная точка, рис. 4.9). Длина вектора а
называется его модулем и обозначается | а |. Единичные
векторы — это векторы, длина которых равна
единице. Единичный вектор, имеющий то же
направление, что и вектор а, обозначают ао- Нулевой
л
вектор 0 - это вектор, начало и конец которого
совпадают; его модуль равен нулю, направление
неопределенное. Два вектора считаются равными,
если равны их модули и совпадают их
направления (см. рис. 4.9). Векторы, которые получаются
из данного вектора а путем параллельного
переноса (все такие векторы равны а), называют
свободными векторами, порождаемыми вектором а.
Векторы, которые получаются из а путем
параллельного переноса вдоль а (и лежат на одной
прямой), называются скользящими векторами,
порождаемыми вектором а (рис. 4.10). Если вектор
нельзя переносить по физическим причинам
(постоянная точка приложения), то говорят о
связанном векторе.
4.2.1.2. Умножение на скаляр и сложение. Если
а - действительное число и a - вектор, то
произведение а • а также есть вектор с длиной | а 11 а |
и направлением, совпадающим с направлением
вектора а при а > 0, и с направлением,
противоположным направлению вектора а при а < 0. В
частности, —а имеет длину, равную а, но
противоположное направление (рис. 4.11). Векторы а0 и а
Рис. 4 9
Рис 4.10
Рис. 4.11
Рис. 4.12
УМНОЖЕНИЕ НА СКАЛЯР И СЛОЖЕНИЕ
387
коллинеарны, причем а = | а | а0. При а = 0 считается,
что 0 • а = 0.
Сумма а + b двух векторов a, b определяется
следующим образом: а и b складываются при
помощи параллельного переноса, как показано
на рис. 4.12; вектор а + b есть вектор, который имеет
начало, совпадающее с началом а, и конец,
совпадающий с концом b (правило треугольника). Вообще
сумма а + b + ... + е нескольких векторов а, Ь, ...
..., е определяется как вектор f, который замыкает
ломаную, составленную из а, Ь, ..., е (рис. 4.13).
-ь
Разность а - b векторов a, b рассматривается
как сумма векторов а и — b (рис. 4.14).
Правила действий с векторами.
а + b = b 4- а, а 4- (Ь 4- с) = (а 4- Ь) 4- с,
а (Ра) = (аР) а, (а 4- Р) a = аа 4- ра,
а (а 4- Ь) = аа 4- ab, | аа | = | а | • | a |,
Под линейной комбинацией векторов a, b, ..., d
с действительными коэффициентами а, р, ..., 8
понимают вектор, имеющий вид
е = аа 4- Pb 4-... 4- 8d. D.3)
Два вектора a, b называются коллинеарными, если
имеются такие действительные числа а, Р, что
аа 4- pb = 0, причем а, р не равны одновременно
нулю (геометрический смысл: прямые,
проходящие в направлениях а и Ь, параллельны). Три
вектора а, Ь, с называются компланарными, если
существуют такие действительные числа а, р, у, что
аа 4- pb 4- ус = 0 и а, р, у не являются
одновременно нулями (геометрический смысл: a, b, с
параллельны одной плоскости). Если a, b не кол-
линеарны или а, Ь, с не компланарны, то их
называют линейно независимыми на плоскости или в
пространстве. Два ненулевых вектора a, b
ортогональны (обозначение: a_Lb), если они взаимно
перпендикулярны. Такие векторы всегда линейно
независимы. Три попарно ортогональных
ненулевых вектора а, Ь, с также образуют тройку линейно
независимых векторов.
Координаты вектора. Если заданы три
линейно независимых вектора еь е2, е3, то
каждый вектор а можно однозначно представить в
виде (рис. 4.15)
а = а1е1 + а2е2 4- а3е3. D.4)
Величины а1*) называются аффинными (или
контравариантными) координатами а относительно
*ьС2,е3. Это кратко записывается так: а = (а1, а2, а3).
Равные векторы, т. е. векторы, совпадающие при
параллельном переносе, обладают одинаковыми
*) Поставленные вверху индексы не надо путать с
показателем степени
13*
аффинными координатами. Если а = {a1, a2, a3), b =
= (b1, b2, b3), то справедливы следующие
соотношения:
аа = (ад1, аа2, аа3),
a + b = (а1 + b\ a2 + Ь2, а3 + Ь3).
Векторы еь е2, е3 на рис. 4.15 образуют
правую систему координат, потому что они имеют
такую же ориентацию, как соответственно большой,
Рис. 4.15
указательный и средний пальцы правой руки; в
противном случае говорят о левой системе
координат.
Если, в частности, в качестве еь е2, е3
выбирают правую систему из трех единичных
векторов i, j, k, попарно перпендикулярных друг
другу (рис. 4.16), то
a = axi + ayj + azk; D.5)
ах, ау, az называются прямоугольными
декартовыми координатами вектора а.
Если заданы два линейно независимых
вектора еь е2, лежащие в одной плоскости, то каждый
вектор а, лежащий в
этой плоскости, можно
Рис. 4.16
Рис. 4.17
M(x,y,z)
однозначно представить в виде а = alei 4- a2e2
(рис. 4.17).
Координаты точки. Поясним теперь
связь между координатами вектора и
координатами точки. Если
перенести, как на рис. 4.18, в
постоянную точку О (начало
координат) три единичных
вектора ф 1, j, k, попарно
перпендикулярных друг другу,
то получится прямоугольная
декартова система
координат. Каждой точке М од-
нозначносрответствует
вектор г = ОМ, который
называется радиус-векторов точки М. Декартовы
координаты вектора ОМ, отнесенные к i, j, k,
называются декартовыми координатами точки М.
Определенные таким образом координаты
соответствуют декартовым координатам, введенным в 2.6.5.
Рис. 4.18
388
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Выбирая вместо i, j, к три любых линейно
независимых вектора еье2,е3, получим косоугольную
систему координат. Аффинные координаты вектора
ОМ называются координатами точки М.
4.2.1.3. Умножение векторов. Скалярное
произведение векторов а, Ь, обозначаемое ab, (a, b), (a, b),
а • b или (а • Ь) есть число ab = | а | • | b | cos ф, где
Ф — угол между векторами а и Ь.
Под векторным произведением векторов а, Ь,
обозначаемым а х Ь, [а • b], [a, b], [ab] или [а х Ь],
понимают вектор с, имеющий длину | с | = | а х b | =
= | а 11 b | sin ф
(площадь
параллелограмма, построенного на
а и b как на сторонах)
и направленный
перпендикулярно к а и Ь,
причем так, что
векторы а, Ь, с = а х b
образуют правую
тройку векторов (рис. 4.19).
Свойства произведений.
1) ab = ba (коммутативность), но а х b =
= — (b х а) (антикоммутативность);
2) (аа) b = a (ab) и (аа) х b = а (а х Ь)
(ассоциативность) при умножении на действительное
число;
3) а (Ь + с) = ab + ас и а х (Ь + с) = а х b + a x с
(дистрибутивность);
4) ab = 0, если а и b взаимно перпендикулярны;
а х b = 0, если а и b коллинеарны;
5) аа = а2 = |а|2, а х а =0; D.6)
6) в общем случае a(bc)#(ab)c;
7) линейные комбинации векторов можно
перемножать, как скалярные многочлены, однако для
векторного произведения важна
последовательность сомножителей.
Пример 1. Ca
«6я2-яЬ-2Ь2, но (За-2Ь)хBа + Ь)«6(яхя)-4(Ьх
xi) + 3(ixb)-2(bxb)»4(axb)+3(ixb)-7(ixb).
Двойное векторное произведение а х (b x с) -
вектор, компланарный векторам b и с, вычисляемый
по формуле
а х (Ь х с) = b (ас) - с (ab). D.7)
В общем случае а х (Ь х с) # (а х b) x с.
Смешанное произведение (axb)c есть скаляр,
абсолютная величина которого равна объему
параллелепипеда, построенного на векторах
а, Ь, с как на ребрах. Смешанное произведение
положительно, если а, Ь, с образуют правую систему;
в противном случае оно отрицательно. Вместо
(а х Ь) с пишут также (abc) или abc. Перестановка
двух сомножителей в смешанном произведении
abc меняет знак: abc = — acb = — bac = — cba;
циклическая перестановка не меняет знака: abc =
= bca = cab. Три вектора тогда и только тогда
линейно независимы, когда abc Ф 0. Кроме того,
имеют место формулы
(а х Ь) (с х d) = (ас) (bd) - (be) (ad)
(тождество Лагранжа), D.8)
(abc)(efg) =
ae af ag
be bf bg
ce cf eg
Выражение'произведений в
прямоугольных декартовых координатах.
Если векторы а, Ь, с заданы в прямоугольных
декартовых координатах:
а = ах\ + ау) + azk, b = bx\ + by\ + bzk,
с = cx\ + cy) + czk,
то произведения вычисляются следующим образом.
Скалярное произведение:
ab = axbx + ayby + а А- D.10)
Векторное произведение:
а х b = (aybz - azby)i + (a2bx - axbz)\ +
+ (axby - aybx) k =
j
bx by bs
Смешанное произведение:
abc =
ax
bx
cx
ay
by
Cy
az
К
cz
D.9)
Выражение произведений в
аффинных координатах. Если известны аффинные
координаты двух векторов a, b относительно
линейно независимых векторов еь е2, е3, т. е.
а = а1е1 + а2е2 + а3е3, b = Ь1е^ + Ь2е2 + Ь3е3,
то для скалярного произведения
ab = alblele1 + a2b2e2e2 + a3b3e3e3 +
+ (alb2 + a2bl)^t2 + (a2b3 + a3b2)e2e3 +
+ (a3bl + a1b3)e3el,
для векторного произведения
a x b = (a2b3 - a3b2) e2 x e3 + (a3*1 - a1^3) e3 x ei +
+ (alb2-a2bl)e1 x e2.
Следует заметить, что ei x ej = e2 x e2 =
= e3 x e3 = 0. Чтобы упростить эти формулы,
вводят так называемые метрические коэффициенты
9и = e&j 0\ J = U 2, 3), gtj = дф
и взаимные векторы е1, е2, е3 по отношению к
векторам еь е2, е3:
е^К-^е.хе,), е2 = К (е3 х еД
e3=K~1(ei xe2),
где V = eie2e3. Если а, Ь разложить по взаимным
векторам, то получим
а = а^1 + а2е2 + я3е3, b = b^1 + b2e2 + b3e3.
Коэффициенты разложения ah bt называются
ковариантными координатами векторов а, Ь в
противоположность контравариантным
координатам а\ Ь1. Оба типа координат можно вычислить
следующим образом:
контравариантные координаты
а = a^i + a2e2 + я3е3, а1 = ае1, а2 = ае2, а3 = ае3;
ковариантные координаты
а = flje1 + «2е2 + a3e3, ai = аеь а2 = ае2, а3 = ае3.
Таким образом, получаем:
ГЕОМЕТРИЧЕСКИЕ ПРИЛОЖЕНИЯ ВЕКТОРНОЙ АЛГЕБРЫ
389
для скалярного произведения
ab = а^1 + a2b2 + аъЬ3 = albt + a2b2
D.11)
для векторного произведения
a xb=(e1e2e3)-1[(a2b3-fl3b2)e1 +
+ (a3bJ - alb3) e2 + (a1*J - a2bl) e3] =
Пусть 0 — начало координат и г = ОМ —
радиус-вектор точки М (см. рис. 4.18).
В декартовых координатах
г = xi + у\ + zk.
Ниже приводятся формулы в векторной записи и в
записи в декартовых координатах.
a1 «2 a3
b1 b2 b3
для смешанного произведения
(abc) =
a1 a* aJ
b1 b2 b3
В случае прямоугольных декартовых
координат, т. е. когда et = i, e2 = j, e3 = к, имеем е1 = i,
е2 = j, е3 = к (взаимная система векторов и
исходная совпадают). Следовательно, ковариантные
координаты идентичны контравариантным, т. е.
а1 = аи а2 = а2, а3 = аъ, и метрические
коэффициенты имеют простой вид gi3 = 5,,-, где 8у — так
называемый символ Кронекера:
{1 для i = У,
(/,;= 1,2,3). D.12)
О для / ф j
Рис 4.20
Рис. 4.21
Уравнение прямой, проходящей через точку
о(*о> У о, z0) параллельно а (рис. 4.20):
Г = Го + tu, — ОО < t < + 00,
х = х0 + tax, у = у0 + tay, z = z0 + taz.
Уравнение прямой, проходящей через две точки
о(*о> Уо, 20) и М1(х1, уи г^Дрис. 4.20):
г = r0 + t (
X = Х0 + t
- г0), - оо < t < +оо,
- J>o), z = zo + t(zl -z0).
. ,„„„4 /Л .Лч тт Уравнение плоскости, проходящей через точку
Формула D.11) переходит тогда в D.10). Для трех м( } и перпендикулярной вектору „
единичных векторов еь е2, е3 (правой системы), / л.7\\-
попарно перпендикулярных, верны следующие
таблицы произведений (например, е^г = 0, в! х е2 =
= е3):
el
е^
е,
1
0
0
е-.
0
1
0
«я
0
0
1
X
е,
е2
ei
0
е2
е^
0
-«1
ез
~е2
е1
0
Скалярное произведение
Векторное произведение
(рис. 4.21):
(r-ro)n = 0,
(х - х0) пх + (у -
- z0) nz = 0.
D.13)
4.2.1.4. Геометрические приложения векторной
алгебры. Векторная алгебра позволяет по-новому
представить формулы аналитической геометрии
(см. табл.)
Уравнение плоскости, проходящей через три
точки М0(х0, у0, z0), Mi(xb yu zt) и М2(х2, уъ z2):
г = г0 + f 1 (гх - г0) + t2 (г2 - г0), - оо < tut2 < +оо,
X = Х0 + t! (ХХ - Х0) +Ч2 (Х2 - Х0),
У = УО + t! (^! - ^о) + t2 (y2 - Уо),
Z = Zo + ti (Zj - Z0) + t2 (Z2 - Z0).
Если использовать D.13), то надо положить
п = (ri - г0) х (г2 - г0).
Название
Длина вектора а
Площадь параллелограмма, построенного
на векторах а и b как на сторонах
Объем параллелепипеда, построенного на
знака)
Угол между векторами а и b
Векторная формула
1 а | = /а7
5 = | а х b |
и-
ab
COS ф — j——-
Координатная формула в прямоугольных
декартовых координатах
|а| =
-
V =
cos
= ]/а2х + а\ + а\
\1\ ау <**
ах ау az
bx by b:
cx cy c.
2
+
a. ax
b: bx
ax ay
bx by
2
&xbx + aJby/ + Q.b,
j/a2 + a2 + a2 уЬ1 + b2 + b2
390
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Расстояние между точками М0(х0, Уо» ^о) и
- г0 | =
- х0J + (У1 - у0J
- z0J.
Если рассматривать только точки М плоскости
х, у, то радиус-вектор имеет вид г = xi + у\ и
получаются следующие
уравнения плоской геометрии.
Уравнение прямой, прохо-
дящей через точку Мо (х0, у0)
перпендикулярно п = пх\ + пу\
(рис. 4.22):
0
Mi (
(г-го)п=0,
Рис. 4.22 (х _ Хо) Пх + (у - у0) Пу = 0.
Расстояние между точками М0(х0, у0) и
Рис. 4.23
I Г! - Г0 | = ]/(Х! - X0J + (У1 - УоJ.
4.2.2. ВЕКТОРНЫЙ АНАЛИЗ
Векторный анализ используется при
исследовании векторных функций методами
дифференциального и интегрального исчисления. Он находит
широкое применение в дифференциальной
геометрии и физике.
4.2.2.1. Векторные функции скалярного
аргумента. Если каждому значению скалярного
аргумента t поставить в соответствие вектор x(t), то
x(t) называется векторной функцией {вектор-
функцией) скалярного
аргумента t. Если начало
вектора г (t)
(радиус-вектора) поместить в
постоянную точку О, то конец
радиус-вектора x(t) опишет
пространственную
кривую, которую называют
годографом векторной
функции (рис. 4.23).
Если t означает время, то x(t) описывает
траекторию движения материальной точки. Если
r(t) разложить по базисным векторам i, j, k
прямоугольной декартовой системы координат, то
причем компоненты x(t), y(t), z(t) являются
функциями от t. Параметрическое представление
пространственной кривой (годографа) или
траектории движения имеет вид
x = x(r), y = y(t), z = z(t).
Предел и непрерывность. Если
а(и) = flf ^t + а2п)е2 + а^з (е1е2Сз - базис) -
последовательность векторов, то вектор а = ахех + а2е2 +
+ а2е3 называется предельным вектором этой
последовательности (обозначается lim a(n) = а),
и -¦ оо
если д,- = lim a\n){i = 1, 2, 3).
Л -> 00
Вектор а = a^i + а2е2 + «зез называется
пределом векторной функции г (г) = rx (t)tx + r2(t)e2 +
+ r3(t)e3 при г —> Го (обозначается lim г (г)) если
lim r,(r) = д, (i = 1, 2, 3). В частности, г (г) назы-
t-*t0
вается непрерывной в точке fo> если lim r(t) = r(to)t
t-+t0
что эквивалентно непрерывности компонент rt(t)
в точке t0.
Дифференцирование векторной
функции. Если существует предел
—— = lim -
dt M-* 0
At)-r(t)
At
lim —,
Af-*O At
dx
то —- называется производной от г (г) в точке t
dt
(рис. 4.24). В другой записи:
г'(г) или г (г). В декартовой
системе координат:
Вектор x'(t) имеет
направление касательной к
годографу в точке t и направлен в Рис 424
сторону, отвечающую
возрастанию параметра t. Длина
x'(t) зависит от выбора параметра t. Если t есть
\dx\
длина дуги, то —J = i.
Если t означает время, а г (t) - траекторию
движения материальной точки, то г' (t) - вектор
скорости, | г' (t) | - величина скорости.
Правила дифференцирования.
dt'
— (Г! -»-Г2)= —-Н
dip
~df]
dxx
dt
dx
—
dt
(Ф (t) — скалярная
функция от г),
Г2 + Г1
dx2
dt'
dx2
—— (множители
dx
нельзя менять местами),
Если г (г) — единичный вектор, то годограф
лежит на единичной сфере и касательная всегда
dx Л
перпендикулярна радиус-вектору, т. е. г —- = 0.
dt
Производные высших порядков.
Рассматривая г'(г) при переменном t как векторную
функцию, производную от г'(г) обозначают через
d2x
—у, или x"(t), или x'(t). В декартовых координатах:
Если x(t) описывает движение материальной
точки, то г" (t) — вектор ускорения, \ х" (t) J —
величина ускорения. Аналогично определяются третья,
четвертая, л-я производные.
Разложение по формуле Тейлора имеет вид
lim \x{t) — а | = 0. Это равнозначно тому, что
Г-Wo
ПОЛЯ (СКАЛЯРНЫЕ И ВЕКТОРНЫЕ)
391
Это не что иное, как векторная сумма разложений
по формуле Тейлора для функций x(t + h), y(t + /?),
z(t + h)
Остаточный член имеет вид
z{n+1)(t + 63/i)k],
n+1 (n+l)\ L у" ' V1
причем 0 < 9,- < 1.
Дифференциал функции r(t) определяется
формулой
л-л.
dl
Векторные функции скалярного аргумента
находят приложение в теории кривых и в механике
точки.
4.2.2.2. Поля (скалярные и векторные). Если
каждой точке пространства М ставится в
соответствие скалярная величина U, то возникает
скалярное поле U (М) (например, поле температуры,
плотности в неоднородной среде, электрического
направления, потенциал силового поля). Если М
имеет декартовы координаты (х, у, z), то пишут
также U — U (х, у, z) или U = U (г) с векторным
аргументом (радиус-вектором г = ОМ = xi + у\ + zk).
Некоторые скалярные поля, а) Плоское
поле
U = U(x,y)*)
(U не зависит от z).
б) Центральное поле {сферическое поле)
U = U(]/x2 + у2 + z2)
(U зависит только от расстояния точки от начала
координат).
в) Осевое поле (цилиндрическое поле)
U
2 +у2)
(U зависит только от расстояния от точки до оси z).
Свойства скалярных полей можно наглядно
изучить при помощи поверхностей уровня. Это
поверхности в пространстве, на которых U обладает
постоянным значением. Они описываются
уравнением U(x, у, z) = const. В центральном поле все
поверхности сфер с центром в начале координат
являются поверхностями уровня. В осевом (ци-
линдрическом) поле все
поверхности круговых
цилиндров с общей осью образуют
поверхности уровня. В
плоском скалярном поле
линиями уровня называют кривые,
на которых U остается
постоянным. Они описываются
Рис 4 25 уравнениями U (х, .у) = const.
На рисунках принято
наносить только линии уровня, которые соответствуют
определенным значениям U, следующим друг за
15
*) Иногда плоским полем называют поле,
определенное для точек пространства и обладающее тем свойством,
что для всех точек любой прямой, параллельной некоторому
постоянному направлению, функция U имеет одно и то же
значение. Такое поле правильнее называть плоскопара i-
лелъиым; его изучение сводится к изучению поля в плоскости,
перпендикулярной этому направлению
другом через равные интервалы (например, U = 10,
15, 20, 25, 30; рис. 4.25). Чем ближе друг к другу
начерчены линии уровня, тем быстрее растет U.
Вспомним о горизонталях на географических
картах.
В отдельных случаях линии уровня могут
вырождаться в точки, а поверхности уровня - в точки
и линии.
Пример 2. На рис 4.26 соответственно: а) V = ху\
б) U ш у/х2; в) U - р2; г) U - 1/р, р = ]/х2 + у2.
234 W
Рис 4.26
Векторные поля. Если каждой точке М
пространства ставится в соответствие вектор V, то
говорят о векторном поле V (М) (например, поле
скоростей частиц движущейся жидкости, силовое
поле Солнца, поле электрической напряженности,
поле магнитной напряженности; рис. 4.27).
Рис. 4.27
Как и при скалярных полях, в декартовых
координатах записывают: V = V(x, у, z) или
V = V (г) (г - радиус-вектор). Векторное поле
можно записать в декартовых координатах в следующем
виде: V(x, у, z) = Kx(x, у, z)\ + Vy(x, у, z)\ +
+ V, (х, у, z)k. Компоненты Vx, Vy, Vs образуют
три скалярных поля и однозначно определяют
V (г) - векторную функцию векторного аргумента.
Некоторые векторные поля, а)
Плоское векторное поле
V = V(x, у), К=0
392
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
(V не зависит от z; векторы V (х, у) лежат в (х, у)-
плоскости или в плоскости, параллельной этой
плоскости, рис. 4.28).
Рис 4.28
б) Сферическое векторное поле
V = Ф (р) г, р = |/х2 + у2 + z2, г = xi + у\ + zk,
(если ввести в рассмотрение сферу радиуса р с
центром в начале координат, то V(r) в каждой
точке сферы имеет одну и ту же длину и
параллелен нормали к сфере в этой точке; рис. 4.29).
Рис. 4 29
Рис. 4.30
в) Цилиндрическое векторное поле
V = Ф(р)г*, р = j/x2 + у2, г* = xi + у]
(если ввести в рассмотрение круговой цилиндр с
осью z и радиусом р, то в каждой точке
поверхности цилиндра вектор V имеет одну и ту же длину
и параллелен нормали к поверхности цилиндра в
этой точке; рис. 4.30).
Важным частным случаем центрального поля
является силовое поле Солнца
(у - гравитационная постоянная, шз - масса Земли,
тс — масса Солнца).
Для наглядного представления векторных полей
используют линии тока. Это кривые, в каждой
точке которых вектор поля V (М) есть касательный
вектор (рис. 4.27).
Через каждую точку М поля проходит одна
линия тока. За исключением точек, в которых
поле \(М) не определено либо V(M) = 0, линии
тока никогда не пересекаются. В сферическом
векторном поле все прямые, проходящие через
начало координат, являются линиями тока; в
цилиндрическом векторном поле все прямые,
которые пересекают ось z перпендикулярно,
являются линиями тока. В декартовых координатах
дифференциальное уравнение линий тока имеет
где t — параметр линий тока.
Для плоского поля третье равенство отпадает.
Если линии тока записать в виде у = у (х), то
dy = Уу(х, у)
dx Vx(x, уУ
Цилиндрические координаты. Для
решения многих задач часто рекомендуется
использование цилиндрических координат р, ср, z
B.6.5.2), которые связаны с прямоугольными
декартовыми координатами следующим образом:
х = р cos ф, у = р sin ф, z = z.
Координатные линии:
Ф = const, z = const, p — переменное (прямые,
проходящие через ось z, параллельны (х,
^-плоскости);
z = const, p = const, ф — переменное
(окружности с центром на оси z и параллельные (х, у)-
плоскости);
р = const, ф = const, z — переменное (прямые,
параллельные оси z).
Каждой точке М ставятся в соответствие
три единичных вектора ер, еф, ег = к, которые
являются векторами,
касательными к координатным
линиям, и указывают
направление возрастания
соответствующей координаты как
параметра. Эти единичные
векторы ер, еф, ez = k
изменяются при переходе от
точки к точке в
противоположность базисным
векторам i, j, k прямоугольной
декартовой системы
координат. Но они в любой точке
М перпендикулярны друг
другу и образуют правую
систему (рис. 4.31).
Если разложить вектор V (М) по единичным
векторам ер, еф, ег, проведенным в точке М, то
получим
V (М) = Vp (М) ер + Vv (М) еф + К (М) ег,
где Vp, Vv, К называются цилиндрическими
координатами V(М) в точке М в противоположность
декартовым координатам Vx, Vy, К, которые
используются в разложении
V(M) = VX(M)\+ Vy(M)l + Vz(M)k.
а) Выражение декартовых координат через
цилиндрические координаты:
Ух — К cos ф - Vv sin ф,
Vy = Vp sin ф + Кф cos ф, К = К.
б) Выражение цилиндрических координат через
декартовы координаты:
УР = Ух cos ф + Vy sin ф,
Кф = - Vx sin ф + Vy cos ф, К = К.
Рис. 4 31
ГРАДИЕНТ СКАЛЯРНОГО ПОЛЯ
393
Цилиндрическое векторное поле имеет в
цилиндрических координатах вид
У = Ф(р)ер.
В случае плоского поля V(x, у) надо в
приведенных выше формулах положить К = 0. В
частности (рис. 4.32),
V = Kp(p, ср)ер+Кф(р, Ф)еф.
Сферические координаты. Иногда
полезно использовать сферические координаты
Рис. 4.32
Рис. 4.33
0, ф, р (см. 2.6.5.2), которые связаны с
декартовыми координатами формулами:
х = р cos ф sin 0, у = р sin ф sin 0, z = p cos 0.
Координатные линии:
Ф = const, p = const, 0 — переменное
(меридианы);
р = const, 0 = const, ф — переменное
(параллели — широты);
0 = const, ф = const, p — переменное (прямые,
проходящие через начало координат).
Как и в случае цилиндрических координат,
каждой точке М ставятся в соответствие
единичные векторы ев, еф, ер, которые являются
векторами, касательными к координатным линиям и
идущими в направлении возрастающих
значений параметра (рис. 4.33). Если V (М) разложить по
единичным векторам е9, еф, ер, то получим
V (М) = Кв (М) ев + Кф (М) еф + Vp (M) ер;
Vq, Кр> Vp — сферические координаты V(M).
а) Выражение декартовых координат через
сферические координаты:
Vx = Vp sin 0>cos ф - VV sin ф 4- V% cos ф cos 0,
Vy = Vp sin 0 sin ф + Кф cos ф + VQ sin ф cos 0,
V. = Vp cos 0 - Ve sin 0.
б) Выражение сферических координат через
декартовы координаты:
Vq — Vx cos 0 cos ф + Vy cos 0 sin ф — К, sin 0,
Vv= - Vx sin ф + Vy cos ф,
Vp = Vx sin 0 cos ф + Кф sin 0 sin ф + V, cos 0.
Единичные векторы ее, еф, ер перпендикулярны
друг другу и образуют правую тройку векторов.
Сферическое векторное поле задается уравнением
У = Ф(р)ер.
4.2.2.3. Градиент скалярного поля.
Производная по направлению и градиент. Пусть
п — единичный вектор и U (г) — скалярное поле.
Проведем через конец вектора г прямую в
направлении п (рис. 4.34). Все точки прямой имеют радиус-
векторы вида г Ч- гп, МП
где t — действительное
число. Если
рассматривать U (г) только на этой
прямой, то получаем
функцию f(t) = U (г + гп). О
Производная/' @) называ- Рис 4 34
ется тогда производной
U (г) в точке г в
направлении п, короче, производной по направлению:
an
Таким образом, из определения производной как
предела следует
ди(г)
-- lim
Af-0
U (г + Afn) - U (г)
= /'@).
Запишем векторы г, п в декартовых координатах:
г = xi + у] + zk, n = nxi + nj 4- nzk.
Тогда для дифференцируемого поля U
dU(r) BU(t) dU{r) dU(r)
дп
дх
ду
dz
Градиентом поля U (г) называется вектор
(обозначение: grad U), определяемый в каждой
точке поля соотношением
dU dU . 3U ш
grad U = —-i + -—j + ^-k;
дх ду dz
dU(r)
дп
= n grad U.
dU
n
Часто вектор grad U обозначают также —— или
or
VI/. Полный дифференциал функции U (г) с
использованием обозначения grad U можно записать
следующим образом:
dU = d-^-dx 4- 3-^-dy 4- Щ-dz = (grad U)dr.
дх ду dz
Интерпретация градиента.
Рассмотрим в качестве примера U (г) температурное поле
Цг). Поверхности уровня
являются поверхностями
постоянной температуры; пусть
п — единичный вектор,
который построен
перпендикулярно поверхности уровня в
точке М в направлении
возрастающих значений Т
(вектор нормали) (рис. 4.35).
Тогда градиент grad T в
точке М имеет направление
нормали п, и его длина равна производной в
дТ(т)
направлении нормали
дп
М
О
Рис. 4.35
-. Тем самым
определение grad T не зависит от вида координатной
системы (инвариантное определение). Чем быстрее
растет Т, тем больше | grad T\. В точках, в которых
Т имеет максимум или минимум, grad T = 0.
Градиент можно определить инвариантно при
помощи пространственной производной
скалярного поля (см. 4.2.2.5). Градиенты играют важную
роль в теории потенциалов (см. 4.2.2.4).
394
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Координатное представление:
еи еи еи
grad U = — i + ~] + —к
дх ду dz
(декартовы координаты),
. „ dU I dU dU
grad G = -r— ep + -—еф 4- -r-e,
dp p p dq> ф dz
(цилиндрические координаты),
l ai/ ai/
:—— -r—еф + ——eD
p sin 9 д<р ф , dp p
. r, i at/
grad G = —ee H
p dG "
(сферические координаты).
Свойства градиента. Если с -
постоянная, то
grad с - 0, grad cU = с grad U,
grad^ 4- U2) = grad l/j 4- grad U2,
grad(UlU2)= t/igrad (/2 + t/2gradl/b
grad ФA/)=^-gradC/,
grad (V!V2) = (Vi grad) V2 + (V2 grad) Vt +
4- V, x rot V2 4- V2 x rot Vb
grad (сг) = с (с — постоянный вектор).
Выражения rot V и (V grad) V объясняются в
4.2.2.7 и 4.2.2.8. Если U зависит только от г = | г |,
то grad U (г) = V(г)— (сферическое поле); в
частности, grad г = — (поле единичных векторов).
Согласно формуле Тейлора, в первом
приближении имеем
U (г + а) = U (г) + a (grad U (г)) 4-...
4.2.2.4. Криволинейный интеграл и потенциал в
векторном поле. Пусть заданы векторное поле
V (г) и кривая АВ (А — начальная точка, В -
конечная точка). Криволинейный интеграл J V dr есть
АВ
скаляр, получаемый следующим образом (рис., 4.36):
Рис. 4.36
1) Разбиваем АВ точками А = Ао, Аи Аъ ...
..., Л„_1, Ап = В на п отрезков, приближенно
изображаемых векторами г,-г,_1=Аг1; это
разбиение обозначаем через Zn.
2) Векторы Дг,- образуют ломаную, которая
аппроксимирует кривую АВ. Наибольшую из длин
кривых Ak-iAk, к = 1, ..., и, назовем мелкостью
разбиения A(Zn).
3) На границе или внутри каждой элементарной
дуги Af-iAi выбирается произвольная точка М„
имеющая радиус-вектор г„ и составляется сумма
Sz =
V(f,)Ar,.
4) Если имеется такое число /, что для любого
заданного е > 0 существует такое 5(е) > 0, что
| SZn - 11 < б
для всевозможных сумм Sz с A(Zn) < 5(e), то
говорят, что криволинейный интеграл существует и
равен / = f Vrfr. Криволинейный интеграл можно,
АВ
таким образом, аппроксимировать как угодно точно
при помощи сумм Sz, если только разбиение
кривой достаточно мелко. Если рассТЯЬтреть
некоторую последовательность разбиений Zb Z2, Z3,... с
lim A(Z,,) = 0 и если криволинейный интеграл
/; -> оо
существует, то
/ = lim Sz = lim ? V (г,) Дг,.
п -* оо J" п -» оо ; = 1
Если выбрать декартову систему координат
dr = dx\ 4- dy\ + dzk,
V (x, y, z) = Vx\ + Vy\ + Kzk,
то можно записать также /\
f V dr = f Vx dx + Vydy 4- Vzdz.
Рис 4-37
AB
AB
Если кривая АВ имеет параметрическое задание
х = x(t), у = y(t), z - z(f), причем параметр t
пробегает значения t^ < t ^ tg (t^, tg соответствуют
А, В), то криволинейный интеграл можно свести к
определенному интегралу
Xdr =
Тв
\dt.
Криволинейный интеграл существует, в частности,
если производные х'(t), /(г), z'(t) непрерывны
(непрерывны касательные к кривой) и непрерывны
функции Vx(x(t),y(t),z(t)), Vy(x(t),y(t),z(t)), K(x(f),
y(f), z(t)) (непрерывность векторного поля V(r)
вдоль кривой АВ).
Свойства (рис. 4.37):
| \(v)dx= f \(r)dr+ J
ABC AB ВС
AB BA
I(Vi(rLV2(r))(/r= | V!(r)rfr+ J
/IB /IB /IB
J cV(r)rfr = c j V(r)dr{c = const).
AB AB
ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ В ВЕКТОРНЫХ ПОЛЯХ
395
Криволинейный интеграл по замкнутой кривой
обозначается символом § V dr.
Механический смысл. Если V (г) — силовое поле,
то Р = J V <йг означает работу, которую совершает
АВ
сила V при переносе материальной точки из А в В
вдоль кривой АВ.
Независимость от пути интегрирования. Если
рассматривают две различные кривые Сь С2,
которые соединяют точки А и В (рис. 4.38), то
соответствующие криволинейные интегралы в общем
векторное поле обладает
потенциалом:
Рис. 4.38
случае будут иметь различные значения.
Векторное поле V(r) называется консервативным
(потенциальным) в области G, если криволинейные
интегралы в G зависят только от начальной точки А
и конечной точки В (это эквивалентно тому, что
криволинейные интегралы вдоль замкнутых
кривых в области G всегда равны нулю). Если, в
частности, V (г) - силовое поле, то это означает,
что совершенная работа не зависит от пути, а
зависит только от положения начальной и
конечной точек кривой. Если компоненты VXi Vy, К имеют
непрерывные частные производные 1-го порядка
в односвязной области G, то V(r) тогда и только
тогда консервативно в G, когда
rot V = О,
или, в координатной записи,
dV*__ dVy_ d_Vl__dV1_ дК _ дУх
ду дх dz ду' дх dz
Эти условия называются условиями
интегрируемости.
Потенциал. Если для векторного поля V(r)
существует функция U (г) такая, что V = grad U, т. е.
в декартовых координатах
х " дх ' у " ду ' z " dz '
то U (г) называется потенциалом векторного поля
К (г)*). В этом случае У dr = (grad U)dr - dU;
следовательно,
АВ
J
АВ
U(B)- U(A).
Если А = А (г0), В = В (г0), то это можно
записать и так:
l/(r)-l/(ro)=JV*.
Го
Если поле V(r) имеет потенциал, то оно
консервативно. И наоборот, каждое консервативное
Го
При этом А (г0) —
постоянная точка и интеграл
можно вычислять вдоль любой рис 4 39
кривой, которая связывает А
с В (г). Значение U (г0) можно произвольно задавать.
В декартовых координатах часто выбирают
ломаную, звенья которой параллельны
координатным осям (рис. 4.39). Тогда
X
U (х, у, z)= U (х0, у0, z0) + J Vx (х, )>о, z0) dx +
+ f K,(x, у, zo)dy+ \V2(x,y,z)dz.
Уо Zo
Потенциал U (г) в области G определен всегда с
точностью до аддитивной постоянной.
Пример 3. а) Поле притяжения Земли:
V = -0k, U = -gz.
б) Силовое поле Солнца, находящегося в точке г = 0:
v_ Y"»C г v
г1 г'
в) Напряженность поля электрического заряда Q,
находящегося в г=0:
4кеог'
Здесь у - гравитационная постоянная, д - ускорение силы
тяжести, n\Q — масса Солнца, /из — масса Земли, ео —
диэлектрическая постоянная. В электрическом поле U
означает напряжение.
4.2.2.5. Поверхностные интегралы в векторных
полях. Пусть задана плоская площадка X,
ограниченная замкнутой ориентированной кривой С
(рис. 4.40). Вектор нормали п является единичным
¦) В физике потенциалом <р(г) в точке г называют
иногда величину, противоположную по знаку.
Рис. 4 40
вектором, который направлен перпендикулярно к
2 и выбран так, что из конца вектора п обход
контура С кажется происходящим против часовой
стрелки. Сторона площадки, обращенная к вектору
п, называется положительной стороной. Каждой
ориентированной плоской площадке Е можно
поставить в соответствие вектор S, имеющий
направление п и модуль, равный ее площади 5.
Выберем декартову систему координат и обозначим
через ?ху, 1У, и Ъ2Х проекции Е на плоскость х, у,
плоскость у, z и плоскость z, х соответственно.
Пусть площади этих проекций равны Sxy, Syz и
396
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Ssx. Тогда
S = Sn = Syzi + Szx] + Sxyk.
Если дана изогнутая площадка (рис. 4.41), то ее
можно ориентировать, выделяя одну сторону как
положительную. Под вектором нормали в точке М
понимается единичный вектор, который
перпендикулярен к Е в точке М и конец которого расположен
с положительной стороны Е. Граница области Е
ориентируется таким образом, что обход границы
из конца вектора нормали выглядит обходом
против часовой стрелки.
/45,
Рис. 4.41
Рис. 4.42
Поверхностные интегралы. Три
различных вида поверхностных интегралов в
векторном анализе образуются следующим образом:
1) Поверхность Е, на которой выбрана
положительная сторона, разбивается на п
элементарных площадок Ef (рис. 4.42) с площадями AS,-. Это
разбиение обозначается Zn. Под мелкостью
разбиения A(Zn) понимается наибольшее из чисел
du •••> dn, где dt — диаметр площади Е,-, т. е.
верхняя грань расстояний между точками площадки Е,.
2) Внутри или на границе каждой элементарной
площадки выбирается точка Mt и в этой точке
проводятся нормальный к поверхности вектор п
(соответствующий выбранной стороне) и вектор
AS, = AStn (направление которого п, а модуль ASf).
3) При заданной функции U (М) или заданном
векторном поле V(M) составляем следующие
интегральные суммы:
;= ? C/(M,.)AS,-,
i=l
= t V (Щ AS,,
= I V(M,)xAS...
Тогда мы определяем:
а) поток скалярного поля:
!<!> = ff C/rfS= lim У U (Mi) AS,;
i A(Zn)-0,= i
б) скалярный поток векторного поля:
Hm f У (М() ASt;
A(Zn)->0i=i
в) векторный поток векторного поля:
1C) = f f у x dS = lim f V (M^ x AS,.
A(Z)Ofi
Например, поток скалярного поля определяется
следующим образом: для любого заданного
е > 0 существует 8 (е) > 0 такое, что
для всех возможных интегральных сумм S<?\
которые удовлетворяют неравенству A (Zn) < 5 (е)
(аналогично для /B), 1C)). Следовательно, интегралы
можно с требуемой точностью аппроксимировать
суммами, если только разбиение поверхности
достаточно мелко. В частности, для
последовательности разбиений Zb Z2, Z3, ... такой, что
lim A (Zn) = О, всегда
п -*¦ оо
lim
п-> оо
lim X
П -* 00 i=l
если только интеграл существует (аналогично для
1B\ 1<3)).
Интегралы по замкнутой поверхности
обозначаются символами § U dS, g V dS, § V х dS.
При этом подразумевается, что векторы нормали
п должны быть направлены наружу.
Декартовы координаты. Если
поверхность задана в виде z — z(x, у) (рис. 4.43), то
поверхностные интегралы можно вычислить, полагая
дх
ду
Этот вектор имеет направление вектора нормали п
в точке М (х, у, z(x, у)). Его модуль приблизительно
Рис. 4.43
равен величине площади элементарной площадки,
проекция которой на плоскость х, у соответствует
прямоугольнику, который строится на М0(х; у),
у), М2(х; y + dy) [\dS\=dS =
-Я-
- V,(x, у, z(x, у))
Ukldxdy:
J
дх
', dx dy
--Vx^)k dxdy.
ДИВЕРГЕНЦИЯ ВЕКТОРНОГО ПОЛЯ
397
Двойные интегралы при этом должны браться
по всей проекции Иху поверхности Е на плоскость
х, у; переменная z заменяется в
подынтегральных выражениях на z (х, у). В частности, поверхност-
dz(x, у)
ные интегралы существуют, если z(x, у),
dz(x, у)
— —
ду
непрерывны (непрерывно меняется вектор
нормали, или, как говорят в этом случае,
непрерывно меняется касательная плоскость) и функции
U(x, у, z(x, у)), Vx(x, у, z(x, у)), Vy(x, у, z(x, у)),
Vz(x, у, z(x, у)) непрерывны (непрерывность U (М),
V(M) на поверхности).
Параметрическое представление общего вида.
Если поверхность X имеет параметрическое
представление
х = х (и, v), у = у (и, v), z = z (и, у),
то поверхностные интегралы можно вычислить,
учитывая, что
ди dv
и беря получающиеся двойные интегралы по
области плоскости и, v, в которой изменяются
параметры и, v. При этом
дг дх . ду dz
ди ди' ди ди
dv dv
Отсюда следует:
dv
dv
du
?l dz дх\-
dv dv du J
(dx dy dx dy\ 1
\ du dv dv du) J
r ( dz dx dx dz \
y\du dv dv du J
du dv dv
Аналогичная формула получается для в)
вычислением V х dS. В подынтегральных выражениях
интеграла а) следует положить U = U (х (и, v),
у (и, v), z (и, v)) (аналогично для Vx, Vy, Vs в б) и в)).
Производная по объему. Под
производной по объему скалярного поля U (М) или
векторного поля V (М) в точке М понимают величины
трех типов, которые получают следующим образом.
1) Точка М окружается замкнутой поверхностью L,
которая охватывает область с объемом V. 2)
Вычисляется интеграл по поверхности I
(§ U dS, §V dS или §V x dS).
z z z
3) Определяется предел отношения этого интеграла
к объему V, когда X стягивается в точку М, так
что V стремится к нулю. В частности,
§UdS
grad U = lim
К-оо V
(см. 4.2.2.3). Производные по объему векторного
поля приводят к понятиям дивергенции (см. 4.2.2.6)
и ротора (см. 4.2.2.7).
4.2.2.6. Дивергенция векторного поля.
Дивергенцией divV векторного поля V(M) называют
следующую производную по объему поля в точке М:
Рис 4.44
divV(M)= lim .
v-*0 У
Если М изменяется, то div V образует скалярное
поле. В другой записи: —— или VV.
дг
§ V dS есть скалярный поток
Z
векторного поля через
замкнутую поверхность ?,
которая окружает точку М и охва- У_
тывает область G с объемом
К(рис. 4.44). Векторы нормали
п направлены наружу.
Для того чтобы пояснить
эти понятия, рассмотрим
текущую жидкость. В этом
случае каждой точке из области потока в момент
времени t ставятся в соответствие плотность
р(М, t) и вектор скорости v(M, t). Скалярный
поток векторного поля и = pv (плотность потока)
равен тогда
Am
pv dS = lim .
Ar-0 At
При этом величина Am равна массе, которая
протекает через ? за отрезок времени от t до t 4- At;
Am положительна, если из области, ограниченной
?, вытекает больше массы, чем втекает (источники
находятся в области G). Это течение массы
вызывается изменением плотности жидкости, текущей
в G. Понятие дивергенции позволяет описать
поведение этой плотности в отдельной точке. В нашем
примере
div р (М, 0 v (M, t) = -
др(М, г)
Ft "
Это уравнение описывает закон сохранения массы и
называется уравнением непрерывности.
Вообще div V есть мера источников поля
V (М). Если в области G div V = 0, то векторное
поле V(M) в этой области называется свободным
от источников. Если, например, в вакууме имеются
электрические заряды с плотностью заряда р, то
напряженность электрического поля Е,
создаваемого этими зарядами, удовлетворяет уравнению
б0 div Е (М) = р (М)
(е0 — диэлектрическая постоянная); div Е = 0 в
области G означает, следовательно, что в G нет
никаких зарядов (заряды являются
источниками Е).
398
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
Формулы для вычисления дивергенции:
.. ж, dVx dVy dK
divV= —- + —-^ + —-
ox dy dz
(в декартовых координатах),
p dp p дф dz
(в цилиндрических координатах),
р
p sin 0 дф
— (в сферических координатах).
р sin 0
Правила вычисления дивергенции:
div с = 0, div cV = с div V,
div(Vi +V2) = divV1+divV,
div (l/V) = U div V + V grad (/
(в частности, div re = — I,
r J
div(Vi x V2) = V2rotV1 -
При этом с = const, с = const. В центральном поле
div Ф (г).г = ЗФ' (г) + гФ' (г), div г = 3.
Правила вычисления см. также в 4.2.2.9.
4.2.2.7.. Ротор векторного поля. Ротором (вихрем)
rotV векторного поля V(M) называют
производную по объему V поля V в точке М:
rotV(M) = lim- .
V-+0 v
Если М изменяется, то rotV образует векторное
д
поле. Другая запись: -xV или V х V (или иног-
дт
да curl V).
Понятие ротора rotV можно ввести наглядно
при помощи понятия циркуляции векторного поля
Г = |V dt вдоль замкнутой кривой С. В консерва-
С
тивном векторном поле (см. 4.2.2.4) всегда Г = 0.
Если С — замкнутая линия тока (рис. 4.45), то
Г Ф 0. Следовательно, в консервативном векторном
поле не могут появляться замкнутые линии тока.
Рис. 4.45
Рис. 4.46
Циркуляция Г есть мера завихренности поля; rot V
позволяет локализовать эти вихри следующим
образом (рис. 4.46): 1) в точке М задается единичный
вектор нормали п; 2) через М проводят
небольшую площадку L площади S, для которой п является
нормалью, контур С ограничивает эту площадку
и обходит п против часовой стрелки; 3) вычисляют
предел отношения циркуляции Г к 5, когда диаметр
d(L) площадки Z стремится к нулю (С и I стя-
гиваются в точку М):
n rot V :
lim
j \dr
С
Этот предел n rot V есть проекция rot V (M) на
направление п. В частности, если V — поле скоростей
вида
V(r) = ro(n хг)
(вращение всех точек пространства с постоянной
угловой скоростью со вокруг оси
с направлением единичного
вектора п (рис. 4.47)), то
rot V (г) = 2соп,
т. е. rot V имеет в каждой точке
направление оси вращения, а
длина вектора rot V равна
удвоенной угловой скорости. В
произвольном поле скоростей
равенство rot V (М) = 0 означает, что в точке М нет
(локального) вращательного движения. Если
вообще rot V = 0 в области G, то векторное поле
в G называется безвихревым. Вихревыми линиями
называются линии тока векторного поля rot V.
Координатное представление:
ду
Рис- 4-47
rotV =
dx
рф dz
4—
i j k
d d d
dx dy dz
V V V
(декартовы координаты),
dVz
dz
-)••¦
p Эф /
p dp
(цилиндрические координаты),
<7ф р
д(рК)
i dv
[
p sin 0 \ dQ
(сферические координаты).
Правила вычисления ротора:
rot с = 0, rot c\ = с rot V,
rot(Vi Н-У2) = го1У! +rotV2,
rot (U\) = U rot V + (grad U) x V,
rot (V! x V2) = (V2 grad) Vt - (V2 grad) V2 +
При этом с = const, с = const. Вывод этих
формул см. в 4.2.2.9. (Определение (Vgrad)V см.
в 4.2.2.8.)
ОПЕРАТОР ЛАПЛАСА И ГРАДИЕНТ ВЕКТОРНОГО ПОЛЯ
399
4.2.2.8. Оператор Лапласа и градиент векторного
поля. Пусть U (М) — скалярное поле; тогда оператор
Лапласа &U определяется следующим образом:
Координатное представление имеет вид:
Агг д2и d2U d2U
AU = —=- + -т-=- + -г-т- (декартовы координаты),
дх2 ду2 дг
1 д
dU
I d2U d2U
(цилиндрические координаты),
д2U
d2U 2_ dU_
~ dp2 p dp p2sin20 дц>2
1 д2и 1
еи
(сферические координаты).
Дифференциальное уравнение AU — О называется
дифференциальным уравнением Лапласа и играет
большую роль во многих задачах
математической физики.
Оператор Лапласа векторного
поля. Пусть V (М) — векторное поле; тогда AV
определяют как
АV (М) » grad div V (М) - rot rot V (М). D.14)
В декартовых координатах:
dz2
d2vz
дх2 + ду2
ду2
dz2
В других системах координат AV имеет очень
сложное выражение. В этом случае следует
пользоваться формулой D.14) и соответствующими
выражениями для grad 17, div V, rot V (см. 4.2.2.3, 4.2.2.6,
4.2.2.7).
Градиент векторного поля. Пусть
V (М) — векторное поле и а — вектор. Определяют
/ ^xr v V(r + A*a)-V(r)
(a grad) V = Iim — ~ —.
дг-о At
Выражение (a grad) V называют градиентом
векторного поля V по вектору а. Если п - единичный
вектор, то выражение (n grad) V равно производной
по направлению —-—векторного поля (см. 4.2.2.3).
дп
В декартовых координатах:
(a grad) V = (a grad Vx) i + (a grad Vy)\ + (a grad Vz) k
(cp. 4.2.2.1). Вообще имеем формулу
2(agrad) V = rot(V x a) 4- grad(aV) 4 adiv V -
— V div a — a x rot V — V x rot a.
Разложение векторного поля в первом приближе-
нии записывается так:
V (г) = V (г0) + ((г - г0) grad) V (г0) + .. .
Под градиентом векторного поля понимают диаду
O = grad-V (см. 4.2.2.12).
4.2.2.9. Вычисление сложных выражений
(оператор Гамильтона). В декартовых координатах
можно при помощи формального оператора
дх
f
ду
который называют оператором Гамильтона или
набла-оператором, записать все приведенные выше
выражения значительно проще:
дх
ду
dz
rotV
= V х V,
dx dy
i j k
дх ду dz
V V V
vx yy vz
d2U d2U d2U
AV = (AVX) i + (Щ) j + (AVZ) k = (VV) V,
(agrad)V =
= (a grad Vx) i + (a grad Vy) j + (a grad Vz) k = (a V) V.
Свойства оператора Гамильтона.
Для того чтобы вычислить сложные выражения
вида gradfl/^), div(C7V), rot^ x V2) и т.д.,
можно использовать следующие формальные
правила:
1) Выражение записывается как формальное
произведение с V.
2) Если V стоит перед линейной комбинацией
(с^Х + c2Y), где X, Y - функции точки (скалярные
или векторные), то
V(cxX + c2Y) = сi VX + c2VY {ct = const).
3) Если V стоит перед произведением функций
точки X, Y (скалярных или векторных), то
оператор V применяется поочередно к каждой из этих
функций (над нею в этом случае ставят знак |) и
результаты складываются:
I 1
V(XY) = V(XY) + V(XY); D.15)
аналогично . , .
V (X YZ) = V (X YZ) + V (XYZ) + V (X YZ).
Постоянные величины или постоянные векторы
не снабжаются знаком |.
4) Выражения V (AT), V (X Y) и т. д.
преобразуются по правилам векторной алгебры таким образом,
чтобы за оператором V стояла только величина,
снабженная знаком |. При этом оператор V
рассматривается как вектор.
5) Наконец, формальное произведение с V
записывается снова как выражение векторного анализа,
400
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
например
tMVl/2)l
Vx(VxV2) = V,x rotV2
и т. д. При этом после вычисления знак [ не пишут.
Эти формальные правила учитывают, что, с
одной стороны, V — вектор, а с другой —
дифференциальный оператор. В D.15) неявно содержится
правило дифференцирования произведения. Знак |
указывает на сомножитель, который
дифференцируется.
Пример 4. Оператор V действует на линейную
комбинацию (с,» const):
1) snd(c,C/, + c2U2) - V(clUl + c2U2) -
- CiVUi + c2VU2 - c, grad (/, + c2 grad U2\
2) div(ctV, + c2\2) - W(cl\l ¦+ c2V2) -
¦ f|Wj + c2W2 m a div V, + c2 div V2;
3) rot(c,V, + caV2) - V x (c,V, + c2V2) *
«c,(Vx Vi) + c2(V x V2) - c, rot V, + c2rot V,.
Пример 5. Оператор V действует на произведение
двух функций:
U2 {
()
I I
UJ + Vx (VC/a) - U2 grad Vx + I/, grad l/a;
2) div (l/V)« V (l/V) - V (UV) + V (l/V) -
4 4
- V(Vl/) + (/(W)- Vgrad I/ -I-1/div V;
3)div(Vt x V2)-V(V, x Va)-V(V, x Va) + V(V, х V2)-
-Vj(Vx V») -V,(Vx Va) - V2 rot Vt - V» rot V2;
I I
4) grad (V,Va) - V(V,V2) - VCVjVa) + У(У,Уа) -
- (VaV)V, + V2 x (V x V.) + (V,V)V2 + V, x (V x V2) -
- (V2 grad) Vi + V2 x rot V, + (V, grad) V2 + Vi x rot Va.
При вычислении надо принимать во внимание
тождество Лагранжа b(ac)«(ab)c + a x (b x с).
Пример 6. Двукратное применение оператора:
1) div rot V т V(V x V)« 0 для любого векторного поля
V (формально вследствие а (а х и) ¦ 0);
2) rot grad U - V х (VI/) - 0 для любого скалярного
поля U (формально вследствие а х аи ж 0);
3) rot rot V - V х (V х V) - V(W) - (W)V -
- grad div V - AV.
Здесь снова использовано тождество Лагранжа. Иногда
вместо V используется символ -г~.
О вычислении интегралов см. 4.2.2.10.
4.2.2.10. Интегральные формулы.
Преобразование объемного интеграла в
поверхностный интеграл. Пусть G -
пространственная область, ограниченная замкнутой
поверхностью S; пусть вектор нормали п направлен наружу
(рис. 4.48). Тогда
dU(xt у, z)
dx dy dz =
t/cos(n, x)dS D.16)
Рис. 4.48
(аналогично для у, z). При этом cos (n, x) = in
(косинус угла между вектором нормали и осью х).
Формула D.16) верна при очень общих
предположениях: функция U должна быть непрерывна в
окрестности G (J S и иметь в окрестности G (J S
непрерывные ограниченные первые частные
производные; поверхность S должна иметь, за
исключением конечного числа угловых точек и ребер,
непрерывно меняющиеся (ср. 4.2.2.5) касательные
плоскости, при этом телесные углы в угловых
точках и внутренние углы в точках ребер должны
быть больше нуля. Из соотношения D.16)
получаются следующие формулы (dv=dxdydz):
а) Интегрирование по частям:
dx
= JfUlU2cos(n, x)dS
S
-ЛЬ
dU2
~дх~
dv
(аналогично для у и z).
б) Формула Гаусса - Остроградского:
H,cos(n, y)+ Kcos(n, z))dS;
в векторной записи:
в) Первая формула Грина (однократное
интегрирование по частям):
dy2
_ <П>( —— cos (п, х) + —— cos (п, у) +
Л V дх дУ
S
^-cos(n, z)jU2dS-
! dU2 dUi dU2 dUt dU2 . ,
+ -z =—+ ~z r— )dv;
x dx dy dy dz dz
G
в векторной записи:
G
= §U2 (grad Ux) dS - JJj grad V, grad U2 dv;
S G
в частном случае при U2 = 1 имеем
Г Г j At/1
G S
dU
l/1)rfSs |j ^-
величина
dU
дп = (grad U) n = — cos (n, x) +
dU . . dU . ,
+ ——cos(n, у) н—-—cos(n, z) называется производ-
ду dz
ной по нормали
ОПРЕДЕЛЕНИЕ ВЕКТОРНОГО ПОЛЯ ПО ИСТОЧНИКАМ И ВИХРЯМ
401
г) Вторая формула Грина (двукратное
интегрирование по частям):
Используя символ оператора Гамильтона, все
эти формулы можно записать операторно; для
D.16) имеем
/я-
cos (n, х) i + cos (n, у) j 4- cos (n, z) k),
D.17)
Пример 9. JJJ</i>rotVsJJJ'fo07* V) = $</Sx V.
G G S
Пример 10. JJf rfpAl/ з JJJdi;V(Vl/)«#</SVt/
G G S
$</Sgradl/.
S
Пример 11.
или, кратко,
G S
Пример 7. JJJdvgrad U s JJJrfr VV - § dS t/.
G G 5
Пример 8.
- # </S C/2 VUi & § dS (grad (/,) (/2 (первая формула
S S
Грина).
Пример 12. fnWff
G G
- UlAU1)dv «#</8A/2УС/, - ^1Vt/2) (вторая формула
S
Грина).
Преобразование двойного
интеграла в криволинейный. Пусть 5 -
ограниченная плоская область с граничной кривой
С, которая ориентирована так, что S лежит слева;
тогда наряду с формулой D.16) справедлива
формула
[ j
dxdy = Фи cos(n, x)ds D.18)
(аналогично для у). При этом cos (n, х) есть косинус
л угла между внешней нормалью
(Т),х) п и осью х (рис. 4.49); ds —
*\ дифференциал длины дуги.
Теорема верна при очень общих
^—»*^^ / предположениях: функция U
^ч/^ должна быть непрерывна в ок-
Рис 449 рестности 5(JC и иметь в ней
непрерывные ограниченные
первые частные производные; граничная кривая С
должна обладать непрерывно изменяющимися
касательными, за исключением конечного числа
точек излома, причем внутренние углы в точках
излома должны быть больше нуля. Из D.18)
следует формула Грина
\\{dt-d?)dxdy=ydx+Qdy Dл9)
5 С
(ср. 3.1.13).
Преобразование поверхностного
интеграла в криволинейный интеграл.
Пусть ? — площадка с кусочно гладкой границей L,
которая ориентирована, как на рис. 4.41. Пусть
U непрерывно дифференцируема в окрестности I.
Тогда
JKf
cos(n, у) —cos(i
ду
\ Г
1, z)\dS=<bUdx
D.20)
(аналогичные формулы получаются циклическими
перестановками х, у, z). При этом cos (n, у) = nj,
cos (n, z) = nk (косинус угла между вектором
нормали п и осью у, соответственно осью z).
Из D.20) следует, что jj rot V dS = § V dx {теорема
I L
Стокса). Используя символ оператора Гамильтона,
из D.20) формально получим
D.21)
JJ dS х V = § dr.
Z L
Пример 13. JJrotVdSs JJ</S(V x
S I
= J}(</S x V)V =
z
L
Пример 14. JJrfS x gradl/s JfrfS x VU = idrU
I 1 L
4.2.2.11. Определение векторного поля по его
источникам и вихрям. Пусть G —
пространственная область, которая вместе с любой замкнутой
кусочно гладкой кривой содержит некоторую
двустороннюю кусочно гладкую поверхность,
опирающуюся на этот контур. Гладкое векторное поле Е
тогда и только тогда является безвихревым в
области G, т. е. rot E = 0, когда в G существует функция
U такая, что Е = grad U {U — потенциал поля,
см. 4.2.2.4).
Поля без источников
(соленоида л ь н ы е). Пусть G — пространственная область,
которая вместе с любой замкнутой поверхностью
содержит и ограниченное ею тело. Гладкое
векторное поле Н тогда и только тогда является
соленоидалъным в области G, т. е. div H = 0, когда
в G существует векторное поле А такое, что
Н = rot А (А — векторный потенциал поля).
Источники и вихри. Надо найти векторное поле
V (г) в ограниченной области G с заданными
источниками р (г) и вихрями w (г), т. е. в области G
решить систему уравнений
div V = р (г), rot V = w (г).
Эта задача решается однозначно, если вдоль
границы заданы значения Vn (n — вектор нормали),
т. е. на границе dG области G
Vn = /(г);
при этом должны выполняться следующие
дополнительные условия:
div w = 0, JJJ p dv = § fdS.
G dG
402
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
В предположении, что.функции р, wx, wy, ws
обладают в G непрерывными и ограниченными
первыми частными производными, а граница dG
является достаточно гладкой, решение ищется
следующим образом:
1) Найти поле Уь для которого в области G
div Vi = p, rot \t = 0.
Условие Vx = grad U приводит к уравнению
AC/ = р с частным решением
при этом г = xi + yj + zk, г' * x'i -I- у'\ + zit,
j г - г' | - ]/(х - х'J + (у- у'I + (z - z'J. Если под
р понимают плотность массы, то С/(г)
представляет собой потенциал размещения этой массы,
a Vt* grad U — соответствующую силу. Если под
р понимают плотность зарядов, размещенных в
вакууме, то U/e0 (8o - диэлектрическая
постоянная) — электрический потенциал, создаваемый р, и
л U Vj
Е =* grad —s соответствующая напряжен-
е0 е0
ность электрического поля.
2) Найти поле У2, для которого в области G
div V2 » 0, rot V2 « w.
Условие V2 = rot А приводит к уравнению АА » w,
причем divA = 0. Частное решение:
А(Г):
l CCC*(T')dx'
4*JJJ |r-
D.22)
Если под w понимают вектор плотности тока
зарядов, то V2 = rot А является полем
напряженности магнитного поля. Равенство D.22) дает
требуемое решение в предположении, что w равно
нулю вне данной области G. Если это не имеет
места, то w нужно продолжить на область Gb
охватывающую G, так, чтобы: a) wn было
непрерывно на dG; б) wn = 0 на dGt; в) divw s= 0 в слое
Gj\G. Тогда в равенстве D.22) нужно
интегрировать по области Gt.
3) Найти поле V3, для которого в области G
divV3
rotV3
а на границе dG выполняется соотношение
V3n=/*(M)-/-V1ii-V2ii.
Замена V3 = grad T приводит ко второй краевой
задаче теории потенциалов:
ДЧГ = 0 в области G;
—— е й grad *F « /* на границе dG.
dn
Искомое поле V получается тогда как сумма
V - Vi + V2 + V3.
4.2.2.12. Диады (тензоры II ранга). Диады находят
применение, например, в теории упругости. Их
часто обозначают так же, как тензоры (тензор
деформаций, тензор напряжений).
Линейные векторные функции. Под
линейной векторной функцией ФУ понимают
отображение, которое каждому вектору V ставит
в соответствие некоторый вектор V = ФУ; при
Ф (сХ) - сФ V, Ф (V, + V2) * ФУД + ФУ2.
Если рассматривать вращение всего
пространства вокруг оси, которая имеет направление
единичного вектора п, на угол <р (рис. 4.50), то в первом
приближении (ф или |г| мало)
г' в г 4- фп х г + ...
При этом Фг = фп х г - линейная
векторная функция (бесконечно
малый поворот). Каждую линейную
векторную функцию можно
представить в виде
D.23)
с постоянными векторами аь Ь,. Если еь е2, е3 -
три линейно независимых вектора, то под
координатами линейной векторной функции ФУ
относительно этого базиса понимают числа
(U-1, 2, 3)
(е1, е2, е3 - взаимные для еь е2, е3 векторы;
ср. 4.2.1.3). С использованием координат ФУ
представляется в виде
ФУ «
D.24)
Для построения конкретных линейных векторных
функций имеется три возможности:
а) Инвариантное (независимое от
координатной системы) построение при помощи
геометрических или физических величин (например,
бесконечно малый поворот D.23), тензор деформаций,
тензор напряжений).
б) В фиксированной системе координат с
базисными векторами еь е2, е3 задаются числа о/ и ФУ
определяется формулой D.24); при переходе к
другой системе координат величины а} преобразуются,
как простой ковариантный или контравариантный
тензор 2-го порядка.
в) В каждой системе координат задаются числа
а/, которые преобразуются так же, как и в б),
и ФУ определяется по формуле D.24).
Диады. Для того чтобы удобнее было
вычислять линейные векторные функции, вводят
формально диадное произведение a b двух векторов
а и b с обоими дистрибутивными свойствами:
+ a2a2)-b = at (в! -b) + a2 (а-b),
а-Oib, + p2bi) - Pi d-bi) + P2 (ab2);
множители в произведении a b нельзя менять
местами. Далее формально определяются правила:
(a-b)c«a(bc)*), c(a-b)-(ca)b, D.25)
(ab)*=(b-a), D.26)
(ab) x с = a(b x с), ex (a-b) = (с х a)b, D.27)
(ab)(cd) = (bc)(ad). ^ D.28)
Под диадой понимают конечную сумму диадных
*) (be) - скалярное произведение (см. 4.2.1.3). Умножение
формального диадного произведения a b на вектор дает
некоторый вектор.
ДИАДЫ (ТЕНЗОРЫ II РАНГА)
403
произведений
ф=
Каждой диаде Ф можно приписать линейную
векторную функцию:
ФУ = ?a,(b,V)
(ср. D.25)). Две диады Ф, ? считаются равными
тогда и только тогда, когда ФУ = 4*V для любых
векторов V. Под УФ мы понимаем линейную
векторную функцию
УФ= ?(Va,)b,
Если посредством равенства
Ф*= I(arbf)*=
определить диаду Ф *, сопряженную с Ф, то можно
записать УФ = Ф*У. Всегда Ф** = Ф. Диаде
л п
с х Ф = ? с х (а,- • Ь^ = Yj (с х а«)' bi
»= 1 i=i
(ср. D.27)) ставится в соответствие линейная
векторная функция
(СхФ)У=
Если
— другая диада, то произведению
Ф?= t (arb,)(crd7)= t (b.c,)(aD)
«,7=1 i,j=l
(ср. D.28)) соответствует линейная векторная
функция
(ФЧ>)У = ?
Всегда (Ф?) V = Ф (VV).
Координатное представление диад.
Если векторы як, Ък, входящие в Ф = ? afcbfc,
к= 1
заданы в некоторой декартовой системе координат:
Ък=(Ьк)х\+(Ьк)у\-
то, согласно формальному перемножению и
объединению подобных членов, имеем
Ф = ахх\ i + аху\ - j + аХ2\ к + аух\ i + ауу] • j +
+ ayz\ • k + azxk • i + axyk • j + a22k • k. D.29)
Новые числа ахх, axy, ..., azz называются
декартовыми координатами диады Ф. Если в более общем
случае
з з
а<с = Yj ((lkYej, К = Y, (&fc)i e''
то после формальною перемножения и
объединения соответствующих членов получаем
з
Ф = ? ajej-e1.
Линейная векторная функция, соответствующая
этой диаде, имеет вид
ФУ= ? я/е,(е'У) = ? ( ? Vla
i,j=l j=l\i=l
Числа а{ называются координатами Ф
относительно базисных векторов еь е2, е3. Они совпадают
с координатами линейной векторной функции ФУ.
В частном случае декартовых координат (et =e! =i,
е2 = е2 = j, е3 = е3 = к) справедливы равенства а\ =
— ахх> а2 = аху> «3 = ахг и Т- Д- ПОД СЛвдоМ Ф ПОНИ-
мают число
Sp Ф = а\ + а\
= ахх +
которое не зависит от выбора декартовой системы
координат (инвариант).
Симметрические и
антисимметрические диады. Диада Ф называется
симметрической, если Ф = Ф*; Ф называется
антисимметрической, если Ф = — Ф*. В декартовых координатах
(см. D.29)) симметричность диады означает, что
аху = аух, axz = azx, ayz = azy; антисимметричность
диады означает, что ахх — ауу — а2: = 0, аху = — аух,
ах, = — azx, ayz — — azy. Каждую диаду Ф можно
представить в виде
Ф = Фг + Фи I
при этом Фс = —-(Ф + Ф*) — симметрическая диада
и Фа = — (Ф — ф*) — антисимметрическая диада.
Чтобы геометрически осмыслить симметрическую
диаду, поставим в соответствие каждой
симметрической диаде уравнение 2F = гФг = 1, или, в
декартовых координатах, уравнение
ахх*2 + ауУУ2 + azzz2 -1- 2ахуху + 2ax,xz + 2ayzyz = 1,
которое является уравнением поверхности 2-го
порядка (эллипсоид, гиперболоид, цилиндрическая
поверхность) с центром в точке (О, О, 0). Эта
поверхность называется тензорной поверхностью.
Ее уравнение принимает особенно простой вид
{нормальная форма симметрической диады):
если совместить оси системы координат с
главными осями тензорной поверхности. В декартовой
системе координат Ф имеет вид
Ф =
• k.
Линейная векторная функция, соответствующая
этой диаде, имеет вид
Фг = \хх\ + X,2yj + ^zk-
Если А,! > 0, Х2 > 0, Х,3 > 0 (тензорная
поверхность — эллипсоид), то вектор Фг получается из
г = х\ + у) + zk путем растяжения в направлении
трех координатных осей, или, что то же самое,
в направлении главных осей поверхности.
Собственные значения Я.,- определяются в результате реше-
404
ВЕКТОРНОЕ ИСЧИСЛЕНИЕ
ния уравнения третьей степени относительно X:
ахх - X аху a
аху
= 0.
ауу - X azy
axz azy а„ - X
Главные оси h, удовлетворяют уравнению ФЬ,- =
= >А
Чтобы дать геометрическое пояснение
антисимметрической диады, запишем произвольную
антисимметрическую диаду в декартовых координатах
в виде
Ф = 0i • i - az\ • j + пу\ • k + az\ • i + Oj j - ax\ k -
-ayk i + axk j + Ok k.
Соответствующая ей линейная векторная функция
имеет вид
Фг = а х г =
i j к
ax ay az
x у z
Если положить а = фп и считать, что ф мало,
то Фг будет представлять собой бесконечно малый
поворот.
Векторный градиент. В 4.2.2.8 был
рассмотрен градиент векторного поля (agrad)V.
Векторным градиентом Ф векторного поля V
называется диада, для которой при постоянном векторе а
справедливо соотношение
Фа = (a grad) V.
Пишут: Ф = gгad•V; в декартовых координатах
(V = Vxi + Vy\ + Vzk)
дх
дх
су
(M)
дх
этой диады за-
ду ду
Так как координаты
висят от точки М, то в каждой точке М находится
своя диада (поле диад). Для (a grad) V получается
(agrad)V=a(grad-V) =
dvy
evy
Диады Фс, Фа (ф = фс + фа), соответствующие
Ф = grad • V, имеют вид
дК\
-^-)k- D30)
dVZt
дх ду
дх
2\дх
dz
2\ду dz
дх
dz
2
I/ Г, \J Ту 1
IT" if к*
ду
dz
При помощи этих диад можно записать
разложение векторного поля в первом приближении в виде
V (г) = V (го) + ((г - го) grad) V (г0) =
= V (г0) + (г - г0) Фс + (г - г0) Фа; D.31)
Фс, Фа вычисляются в точке г0. Далее,
(г - г0) Фа = — rot V (г0) х (г - г0). D.32)
Механический смысл. Пусть при
деформации упругой среды точка М (г) перемещается
в г' = г + V (г) (V (г) - вектор сдвига). Если
исследовать V(r) в малой окрестности г, то соотношение
D.31) показывает, что деформация состоит из
переноса (V (г0)), растяжения ((г - г0) Фс) и бесконечно
малого поворота ((г - г0) Фа), причем ось поворота
имеет направление rot V (г0), а угол поворота —
величину — | rot V (г0) |. Величина Фс называется
тензором деформаций. Наряду с ним важную роль
играет тензор
напряжений Ч1. Пусть задана
упругая среда, находящаяся
под воздействием сил
напряжения. Для
поддержания равновесия
выделенного элемента с
объемом v (рис. 4.51) в
каждом малом элементе
нужно к каждому элементарному кусочку его границы
с нормалью п, направленной во внешнюю
сторону, приложить силу, имеющую величину
Рис. 4.51
AF =
T AS.
D.33)
Диада Ч? (тензор напряжений) симметрична и
зависит от поверхностной точки М. Поверхностные
силы, действующие на и, равны, таким образом,
F = § Ч* dS.
Диада Ч? (тензор напряжений) симметрична и
зависит от поверхностной точки М. Поверхностные
силы, действующие на v, равны, таким образом,
Дивергенция и ротор. Аналогично 4.2.2.6,
4.2.2.7 определяются для диад дивергенция и ротор:
Div Ф = lim
lim
§dS x Ф
D.34)
D.35)
Если Ф имеет в декартовых координатах
представление D.29), то
= (?а^ д^ да\
[ дх + ду + dz /
I UUxy UUyy (/O,j, 1 , / VUX~ VUy* < , .
+117 + ~di + ~дТу + \дх~^ ~di + ~dz~r
D.36)
СПОСОБЫ ЗАДАНИЯ ПЛОСКИХ КРИВЫХ
405
\ dv dz ) \ ду dz )
(см. 4.2.2.2), можно формально записать:
grad • V = V • V, D.40)
Div Ф = УФ, D.41)
Rot Ф = V х Ф. D.42)
Формулы D.17) и D.21) также справедливы для
диад.
Пример 15.
•к. D.37)
JJJ Div Ф dv = JJJ dv (УФ) = § dS Ф
G G 8G
D.43)
(теорема Гаусса — Остроградского).
Если Ф представить в виде Ф = at • i + а2 • j + а3 • к, Пример 16
то получим, что щ Rot ф dv = jjj Л(ухф)= § dS х Ф. D.44)
G G 3G
Пример 17.
Div Ф = (div a,) i + (div a2) j + (div a3) к, D.38)
Яо1Ф = (rotai)i + (rota2)j + (rot a 3) к. D.39)
Вычисление диад при помощи one- ? ?
ратора Гамильтона. Используя оператор V (теорема Стокса).
Ф)= JJ(</S x У)Ф= § dr<t> D.45)
Z С
4.3. ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
В дифференциальной геометрии кривые линии
(плоские и пространственные) и поверхности
изучаются методами дифференциального исчисления;
поэтому функции, входящие в уравнения,
предполагаются непрерывными и имеющими
непрерывные производные до того порядка, который
необходим по характеру исследуемого вопроса. Это
условие может нарушаться только для отдельных
особых точек кривой или поверхности (например,
для точек разрыва или излома кривой). При
изучении геометрических образов по их уравнениям
различают свойства, зависящие от выбора системы
координат (например, пересечение кривой или
поверхности с осями координат, наклон
касательной, точки максимума или минимума и т. п.),
и инвариантные свойства, не изменяющиеся при
преобразовании системы координат и
принадлежащие собственно кривой или поверхности
(например, точки перегиба, вершины кривой, кривизна,
кручение и т. п.). С другой стороны, различают
локальные свойства, относящиеся к весьма малым
частям кривой или поверхности (например,
кривизна, линейный элемент поверхности, угол между
кривыми в точке пересечения), и свойства кривой
или поверхности в целом (например, число вершин,
длина замкнутой кривой, площадь замкнутой
поверхности). Локальные свойства изучают обычно
при помощи формулы Тейлора.
4.3.1. ПЛОСКИЕ КРИВЫЕ
4.3.1.1. Способы задания плоских кривых.
Уравнение плоской кривой. Плоскую кривую
аналитически можно задать одним из следующих способов:
в декартовых координатах:
в явном виде:
у = у(х), хе<а, b); D.46)
в неявном виде:
F(x,y) = 0, {x,y)eG; D.47)
в параметрическом виде:
x = x(t), y = y(t\ te(ai, p>; D.48)
в полярных координатах:
р = р(ф), фб<а,
D.49)
где (а, Ь} — промежуток на числовой прямой, G —
область на плоскости.
Пример 1 (рис. 4.52). a) y = sinx; б) x-t2, у = г3;
в) р = дф, а > 0.
Рис. 4.52
Положительное направление кривой
соответствует возрастанию х (см. D.46)),- t (см. D.48)),
Ф (см. D.49)).
Переход от неявного вида к явному.
Если (х0, у0) — точка кривой, т. е. F (х0, у0) = 0,
и F'y (х0, Уо) Ф 0, то уравнение F (х, у) = 0 в
некоторой малой окрестности точки (х0, Уо) можно
однозначно разрешить относительно у: у = у{х). Кроме
того, справедливы формулы
У =
Fy(x,y(x))'
- (F'yJ ?"xx + 2F'xF'yF'xy - (F'xJ F"yy
406
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Если F'x (х0, >>о) Ф О, то можно разрешить
уравнение F(x, у) — 0 относительно х: х = х(у); тогда
в формулах D.50) следует поменять местами х и у.
Если же F'x (х0, у о) = F'y(x0, у0) = 0, то точка (х0, у0)
называется особой точкой (сингулярной точкой)
(см. 4.3.1.3).
Переход от параметрического вида
к явному. Обозначим производные от .x(r), y(t)
через х(t), у(t). Если х(f0) # 0, то уравнение х — x(t)
можно разрешить в некоторой малой окрестности
t0 относительно t (t - t (x)). Тогда получим
уравнение в явном виде: у =/(х) = y(t (x)). Справедливы
равенства
Если у (t0) Ф 0, то у = у @ можно разрешить
относительно г (t = f (у)) и получить х = д (у) = х (t (у));
в этом случае в формулах D.51) следует поменять
местами х и у. При x(t0) = y(t0) = 0 точка кривой,
соответствующая значению t — t0, называется
особой (сингулярной) точкой (см. 4.3.1.3).
4.3.1.2. Локальные элементы плоской кривой.
Касательная к кривой в точке М определяется
как предельное положение секущей, проходящей
через М и соседнюю точку N кривой, при условии,
что N стремится к М (рис. 4.53).
Рис. 4.53
Рис. 4.54
Нормаль - прямая, перпендикулярная
касательной в точке касания М. Направление на
касательной и нормали выбирается так, как показано на
рис. 4.54, т. е. положительное направление
касательной указывает в сторону положительного
направления кривой, а положительное направление
нормали получается при повороте положительного
направления касательной на 90° против часовой
стрелки. Вектор касательной t (вектор нормали л)
представляет собой единичный вектор,
совпадающий с положительным направлением касательной
(направлением нормали):
Пример 2. Кривая у = sin х; / = cos x. Уравнение
касательной в точке (\'о, Уо) имеет вид у — sin х0 = (х — х0) cos x0;
в частности, при х0 = у0 = 0* у = х.
Пример 3. Кривая F (х, у) = х2 + у2 — 25 — 0
(окружность радиуса 5); F'x — 2х, F'y = 2y. Уравнение касательной
в точке (х0, у0) имеет вид 2х0 (х - х0) + 2у0 {у - у0) = 0; так
как Хо + у о = 25, то хх0 + уу0 = 25; в- частности, при х0 = 3
и у0 — 4* Зх + 4v = 25.
Пример 4. Кривая х = t2, у = г3; х = 2г, у = Зг2.
Уравнение касательной в точке (х0, у0), где х0 = to, у0 = г3,, имеет
вид 3/§ (х - х0) - 2t0 (у - Уо) = 0. Таким образом, у =
= ^-х - ±-t30 при t0 Ф 0.
Для плоских кривых приняты следующие
обозначения (рис. 4.55).
Рис. 4.55
а) В декартовых координатах:
МТ= -?-
\y)/l+yf2\
У_
У
PN ш | уу' |
б) В полярных координатах:
(отрезок касательной),
(отрезок нормали),
(подкасательная),
(поднормаль).
MN' -
ОТ*
/р2 + р'2
Pi
Р'
(отрезок полярной
касательной),
(отрезок полярной
нормали),
(полярная подкасательная),
ON' =в | р' | (полярная поднормаль).
Угол ф между двумя кривыми у — У\(х) и у «
= У2 (*) в общей точке (х0, Уо) равен углу между
положительными направлениями касательных
(измеренному против часовой стрелки) и может быть
вычислен по формуле
tg(p =
Уг (*о) - У\ (*о)
x^(to)y2(to) - x2(to)yx(to)
'*1(*о)*а(го) + *1('о)л(«о)#
Таблица 4.5
Форма задания кривой
D.46)
D.47)
D.48)
Уравнение касательной в точке (х0, г0)
У - Уо = У'о(х ~ хо>
(FyH(y - у0) + (F'xH(x - х0) = 0
Уо *о П
Уравнение нормали в точке (х0, Vq)
- У'о(У ~ Уо> = х ~ хо
(F'x)o(y-yo)~(F',)o(x-xo)
хо (х - хо) + Уо(У~ Уо) - 0
Здесь уо = у'(х0), у о = y(h)> (F',)o = ^;(х0, у о) и т. д.
(см. D.50), D.51)).
Длина дуги кривой у = у(х) (x = x(f), y = y(t))
между точками Ml(xi,yl), М2(х2,У2) (рис. 4.56)
ТОЧКИ СПЕЦИАЛЬНОГО ТИПА
407
вычисляется по формуле
П р и м е р 5. 1) у = ch х, К = 1/ch2 x;
+ y'2(x)dx =
Рис 4 56 = J ]/x* (f) + .
/,
здесь х,- = x(ti), i = 1, 2.
Дифференциалом длины дуги называется
величина
ds = ]/dx2 + dy2 = j/l + у'2 (x) dx = ]/x2 (t) + y2 (r) </r.
Этот дифференциал в первом приближении равен
расстоянию между точками Mt и М2, когда эти
точки находятся на достаточно близком расстоянии
друг от друга. Для кривой р = р (ф) в полярных
координатах длина дуги равна
Ф2 Ф2
s = | ds = J ]/р2 + р'2 </<р,
Ф1 Ф1
а дифференциал длины дуги составляет
ds = |/р2 + р'2 dq>.
Если через а(М) обозначить угол между
положительным направлением оси х и положительным
направлением касательной в точке М (измеренный
против часовой стрелки), то кривизна К кривой
в точке М определяется как предел
N-+M \MN\
(где 5 = a (N) - а (М) - угол смежности, a | MiV | -
длина дуги кривой между точками М и N;
рис. 4.57). Для прямой имеем К = 0. Чем больше
| К |, тем сильнее изогнута кривая.
Рис 4 57
Рис. 4.58
Представление о знаке К дает рис. 4.58.
Таблица 4.6
Способ задания
кривой
D 46)
D 47)
D 48)
D 49)
Кривизна К в точке М
К- У"{Х
К ~ A 4- /2K/2
р2 + 2р'2 - рр"
Л — ~ Г~Т~7 ' ~лТгг>
Рис 4.59
Кругом кривизны в точке М кривой называется
предельное положение окружности, проходящей
через точку М и две другие близкие точки N и Р
(рис. 4 59), когда N и Р
стремятся к М. Радиус этой
окружности называется
радиусом кривизны R.
Справедливо равенство R = 1/| К \
(К — кривизна). Центр С
круга кривизны называется
центром кривизны.
4.3.1.3. Точки
специального типа. Точка М кривой
называется точкой перегиба,
если касательная в точке М пересекает кривую
(см. рис. 4.58, в), так что в точке перегиба К = 0,
и если К меняет знак в точке, то это — точка
перегиба. Чтобы найти точки, в которых К = 0,
необходимо, согласно табл. 4.7, решить следующие
уравнения:
у = у(х): К = /'(*) = 0,
F (х, у) = 0: К = F"XXF'2 - 2F'xF'yFxy + F"yFx2 = 0,
Fx2 + F'2 ф 0;
x = x (Г), у = у (t): К = ху - ух = 0,ч х2 + у2 Ф0;
р = р (ф): К = р2 + 2р'2 - рр" = 0, р2 + р'2 Ф 0.
Затем достаточно проверить, меняет ли К знак
при прохождении через найденную точку.
Таблица 4.7
Способ задания
кривой
D.46)
D47)
D.48)
D.49)
п -
Координаты %, х] центра
— х -
у"
х'(\ +у'2)
у"
F'x (F'x2 + F'2
F2yF'xx - 2F'xF'yF'xy +
fy (f;2 + f;
F;2F'xx - 2F'xF'yF"xy
У (x2 + у2)
ху — ух
х (х2 + j'2)
С кривизны
)
F'x2F"yy '
2)
+¦ Fl2F"yy
(р2 + р'2) (р cos Ф 4- р' sin ф)
(р2 + р'2) (р sin
Ф Р2 + 2р'2
ср — р' cos ф)
-рр"
. Тогда у -
Пример 6. у =
= 0 при х,,2 = ± 1Д/з. При переходе через каждую из точек
Xi<2 величина у" меняет знак; следовательно, существуют две
точки перегиба: ( ' |), (- ' }).
408
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Пример 7. F sx2 - у2 - a2 = 0 (гипербола); F'x = 2х,
F' = - 2у, F:r = 0,Г;=-Г„«2;К2 8>>2 - 8x2. Уравнения
x2 - у2 - a2 -0, x2 - у2 * 0 несовместны при а Ф 0; таким
образом, у гиперболы нет точек перегиба.
Пример 8. х = л( f —— sin f L >> =л( 1 —r-cosf I
{укороченная циклоида); х ¦= a I 1 —r- cos f L у »-у- sin f, x =
= -y sin f, у -в у cos f, X s ~- B cos f - 1); точки перегиба:
-a ±i. ±2,...).
Пример9.р =—y=~, I
= -=- - точка перегиба.
" ф 2?
в^
Точки кривой, в которых кривизна К имеет
экстремум (максимум или минимум), называются
Рис. 4.60
вершинами; например, эллипс (рис. 4.60) имеет
вершины в точках А, В, С, D.
Особые точки кривых в
параметрическом представлении. Если кривая задана
в виде х = х (г), у = у (г) и х {t0) = у (t0) = 0, то,
согласно 4.3.1.1, задание кривой в окрестности t0
в виде у — у (х) или х = х 0>) не всегда
осуществимо. Поведение кривой в окрестности t0 исследуют,
используя разложение по формуле Тейлора (х0 =
х = х0 + — х (t0) (t - t0J + — х (t0) (t - toK + ...,
Уо
+ ^7'y(to)(t - t0J + ±-'y (to) (t - hK + ...
2!
3!
5)
6) (xo.yo)
Рис. 4.61
Пример 10. x*xo + (r-roJ + .... y~yo + (t-hK+'-
(точка возврата, рис. 4.61, л).
Пример U. x«xo + (f- t0J + ..., y = }0 + (t- 'о)* -
- (f - 'оM + ••• (точкл возврата, рис. 4.61,6).
Пример 12. х » х0 + (г - /оJ + (f - fo)* + • • •» У - 3\> +
+ (t - t0J - (t - to)A + ... (кривая кончается в точке (х0, .Уо);
рис. 4.61, в). Для вычисления наклона касательной необходимо
найти предел
Urn
Для упрощения исследования часто рекомендуется
сделать замену переменных т = t — t0, ? = .х — х0, г\ = у — Уо
Особые точки кривых, заданных в
неявном виде. Если кривая задана в виде
F(x, y) = 0 и F(xo,yo) = F'x(xo,yo) = Ffy(x0,y0) = 0,
то согласно 4.3.1.1, в окрестности точки (х0, уо)
задание кривой в виде у = у(х) или х = х{у) может
оказаться невозможным. В этом случае
осуществляют разложение по формуле Тейлора в
окрестности (х0, .Уо)- Разложение до членов 2-го порядка
имеет вид
F = a(y- у0J + 2Ь(х - хо)(у - у0) +
4- с (х - х0J + ... = 0,
где а = Fyy (х0, у0), Ь = Fnxy (х0, у0), с = F*x (x0, уо\
А = ас- Ъ2.
Если не все коэффициенты а, Ь, с равны нулю,
то решение квадратного уравнения а(у — у0J +
+ 2Ь (х - х0) {у - Уо) + с (х - х0J = 0 дает
уравнения касательных к кривой в точке (х0, Уо)-
Случай 1. л#0. Уравнения касательных
имеют вид
= k± {x _ Хо).
у-уо = (-Ь± /T
Если А > 0, то у = уо, х = х0 - единственное
решение ((х0, Уо) — изолированная точка кривой;
рис. 4.62, а). Если А < 0, то через (х0, Уо) проходят
Рис. 4.62
две ветви кривой с наклонами касательных,
равными к+ {(х о, у о) — двойная точка; рис. 4.62,6).
Если А = 0, то соотношениями х — х0 =
= % cos у -и sin a, у - у0 = ? sin a + r\ cos a, tg a =
= — b/u вводится новая система координат (сдвиг
начала координат в точку (х0, Уо) и поворот на
угол а). Тогда получим
F= (а + с)л2 + ... = 0.
При рассмотрении этого уравнения нужно
принимать во внимание члены более высокого (выше
второго) порядка. Здесь могут встретиться:
изолированная точка (см. далее пример 14), точка
возврата (пример 15), точка самоприкосновения
(рис. 4.62,в, пример 16).
Случай 2. а = 0, с ф§ (сводится к случаю 1,
если поменять местами х и у).
Случай 3. а = 0, с = 0, Ъ Ф 0. Имеются две
ветви кривой с касательными у = у0, х = х0
(двойная точка). Преобразованием координат х - х0 =
= г| — ^, У — Уо — Ц + ?> получаем, что F =
= 2Ь (л2 - k2) + ... = 0 (случай 1).
Если все коэффициенты а, Ь, с равны нулю,
то следует рассмотреть члены 3-го или «-го по-
ТОЧКИ СПЕЦИАЛЬНОГО ТИПА
409
рядка разложения по формуле Тейлора. В этом
случае могут встретиться точки кратности п
(рис. 4.62, г).
П ри мер 13. F(x, у) т (х2 + у2J - 2(х2 - у2) = 0
(лемниската):
F'x - 4х(х2 + у2 - 1), F', ш 4у(х2 + у2 + 1).
Система F'x-F',** 0 имеет три решения: @, 0), A, 0),
(-1, 0), но только @, 0) удовлетворяет условию F - 0. Так
как аяГ„@,0)«4, Ь = 0, с *-4, Л - ас - Ь2 - -16 <0,
то @, 0)-двойная точка; уравнения касательных: у * ± х.
Пример 14. F (х, у) - у2 + х4 » 0; кривая состоит
только из изолированной точки @, 0). _
Пример 15. F (х, у) з у2 - х3 = 0, у=±\/х3; кривая
определена только при х^0; @, 0)-точка возврата с
горизонтальной касательной.
Пример 16. F(x,y)*y2 -х4*0, у = tx2; обе ветви
кривой касаются друг друга в @, 0) - точке
самоприкосновения.
Особые точки кривых, заданных
в полярных координатах. Пусть мы имеем
Р =/(ф)- Если Ит/(ф) = 0 при ф -> + оо или ф ->
-> — оо, то р = 0 — асимптотическая точка (вокруг
Рис. 4 63
Рис. 4.64
этой точки кривая закручивается бесконечное число
раз, неограниченно приближаясь к ней; рис. 4.63).
Пример 17. р « ае*, lim ае* « 0 (логарифмическая
<р-* —оо
спираль).
Кривая, заданная выражением у =/(х), имеет
при х = х0 точку разрыва (рис. 4.64, а), если
функция /(х) в этой точке испытывает скачок. В
точках разрыва первой производной кривая скачком
меняет свое направление (точка излома; рис. 4.64,6).
Пример 18. /(х) - 0 при х < 0, f(x) = 1 при х 5» 0
(х » 0 - точка разрыва).
Пример 19. /» | х I, /' « -1 при х <, Г = +1 при
> 0 (х » 0 — точка излома).
В общем же случае все точки, в которых кривая
ведет себя так же, как на рис. 4.61-4.64
(независимо от способа представления), называются
особыми точками кривой. Обратим внимание на то,
что в случае параметрического задания кривой
определение двойных точек очень затруднительно,
так как двойной точке соот-
ветствуют различные
значения параметра. В этом случае
удобно перейти к неявной
форме задания.
4.3.1.4. Асимптоты. Если
кривая какой-либо своей
частью неограниченно
удаляется от начала координат, то
эта часть (бесконечная ветвь
кривой) может иногда иметь
асимптоту — прямую, к
которой кривая неограниченно приближается или с
одной стороны (рис. 4.65, а), или пересекая ее
(рис. 4.65,6).
Параметрический вид. Если кривая
задана в параметрическом виде: х = x(t), у = y(t), то
для нахождения асимптот ищут значения t = tt
такие, что х (t) -+ оо или у (t) -> оо при t ->¦ t,• ± 0.
В случае, если
1) х (t) -*¦ оо, но у (t) -+ а Ф оо, прямая у = а
является горизонтальной асимптотой;
2) У @ -¦ оо, но х (г) ->• д # оо, прямая х = а
является вертикальной асимптотой;
3)j'@"~>°o» x(f)->oo, необходимо вычислить
^ = lim ^f, Ь = lim (j>(f) - fcx(f));
если оба предела существуют, то кривая имеет
асимптоту у = кх + Ъ.
Явный вид. Если кривая задана уравнением
вида у = у (х) и существует число я такое, что
у -*¦ оо при х -> я + 0 или при х -* а — 0, то прямая
х = а - вертикальная асимптота. Для определения
горизонтальных и наклонных асимптот у = кх + Ъ
при х -*¦ + оо вычисляются пределы
3>(*)
lim
-» + 00
lim (у (х) - кх),
если они существуют (аналогично для х -+ — оо).
Пример 20. х« " , у » п (tg t - г), т > 0, п > 0, t, =
cos t
п
"• ••-
lim
x(r)
O
lim y(f)= ± оо,
±O
*= lim — (sin r - г cos r) = —,
t-*txm *""
lim L(tgf-f)- — -^-U
= л lim
sin f - t cos r - I
.. cos / — cos t + г sin t nn
« и urn ; = —r—,
г-,, -миг 2
симптота: у =» их/m — nn/2.
Аналогично для t2 получаем асимптоту у = пх/т + ия/2
и т. д.
Алгебраическая кривая. Пусть кривая
задана в виде F (х, у) = 0, причем F(x, у) является
многочленом от х и у (т — наибольшая степень х).
1) Горизонтальная асимптота у = а. Положим
х = 1/?, и умножением на ?т Уничтожим ^ в
знаменателях. Если получающееся таким образом
уравнение G (?, у) = 0 имеет (неизолированное)
решение у = а, Ъ, = 0, то прямая у = а является
горизонтальной асимптотой.
2) Вертикальная асимптота х = а. Чтобы ее
получить, следует в случае 1) поменять местами
хну.
3) Наклонная асимптота у = kx + b. Подставим
у = кх + Ъ в F (х, у) = 0 и расположим члены
полученного таким образом многочлена по убывающим
степеням х:
F(x, /ex+ *>)=/! (/с, Ь)хи+/2(/с, Ь)х"-*+...
Если уравнения fx (к, Ь) = 0, /2 (/с, Ь) = 0 имеют
решение, то у = кх + 6 является наклонной
асимптотой.
Пример 21. F(x, у)гх2(у- 1) + 2х- 1 = 0, х = у,
¦^-(у - 1) + -|- - 1 - 0, (у - 1) + 2? - $2 = 0.
410
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Для
что у -* 1
> ± 0 и тем самым для х -» ± оо получаем,
ш 1 - горизонтальная асимптота.
Пример 22. F (х, у)
х2 (у - 1) + 2х- 1 = 0, у «у,
Для ? -¦ + 0 и тем самым для у -* + оо получаем,
что х -» — 0. Следовательно, х = 0 является (односторонней)
вертикальной асимптотой.
Пример 23. х3 + .V3 - Зяху = 0 (декартов лист),
F (х. Ах + ft) з A + к3)х3 + 3 (k2h - ки)х2 + ...; полагая 1 +
+ к3 = 0 и /с2/» — ка — 0, имеем систему с решением к = — 1,
/) = —я; уравнение асимптоты: у = - х - «.
4.3.1.5. Эволюта и эвольвента. Эволюта данной
кривой представляет собой кривую, состоящую
из центров кривизны данной кривой. Она же
является огибающей нормалей этой кривой.
Параметрический вид уравнений эволюты ?, = ?(х), г\ —
= ц (х) или ? = \ (Г), г| = г| (г) можно получить на
основании формул табл. 4.7, положив там у = у (х)
или х = x(t), у = y(t).
П р и м е р 24. Найдем эволюту параболы у = х3.
Согласно табл. 4.7
Если положить х = /,? = х, т| = г, то будем иметь
уравнение эволюты в параметрическом виде х = - At3 у =
, или, после исключения г, в виде у « — + 3
(рис. 4.66).
Эвольвента. Если кривая Г2 является
эволютой Гь то Г! называется эвольвентой
(инволютой) кривой Г2. Каждая нормаль МС
эвольвенты является касательной к эволюте. Длина дуги
CCi эволюты равна приращению радиуса
кривизны эвольвенты (рис. 4.66): ССХ — МХСХ - МС.
Рис. 4 67
На основании этих свойств эвольвенту Тх можно
считать «развертывающей» кривой Г2,
получающейся из Г2 разматыванием натянутой нити.
Данной эволюте соответствует семейство эвольвент,
каждая из которых определяется первоначальной
длиной натянутой нити (рис. 4.67).
Для нахождения эвольвенты на основании
формул из* табл. 4.7 получаем систему обыкновенных
дифференциальных уравнений.
4.3.1.6. Огибающая семейства кривых. Под
огибающей семейства кривых понимается кривая,
которая в каждой своей точке касается некоторой
кривой из заданного семейства. Обе прямые на
рис. 4.68 представляют собой огибающие семейства
окружностей. Если семейство кривых задано в виде
ИХ
Рис. 4 68
F (х, у, С) = 0, то уравнение огибающей получают,
исключая С из пары уравнений
F(x,>- С) = 0, |^(х, .у, С) - 0.
При этом необходимо, чтобы выполнялись
неравенства F"cc ф 0; F'xF"Cy - F'yF"Cx Ф 0.
Пример 25 (рис. 4.68). ? «(х - О2 + у1 - г2 = 0, г -
=в const (семейство окружностей); F^ s — 2 (х — С) = 0, FGC e
»+2*0. Исключая С из этих уравнений огибающей,
получим у2 — г2 а> 0, т. е. две параллельные прямые.
4.3.2. ПРОСТРАНСТВЕННЫЕ КРИВЫЕ
4.3.2.1. Способы задания кривых в пространстве.
Кривая в пространстве обычно задается в
параметрическом виде:
x = x(r), y = y(t), z = z{t\ D.52)
где аО<|3(— оо^ а, р^ + оо). Если обозначить
через г = xi + yj 4- zk радиус-вектор точки М (х, у, z),
то D.52) можно записать в векторной форме:
г(Г),
D.53)
Производные по t будут обозначаться точками;
например, x(t) представляет собой первую
производную от x(f) no t. Будем писать
Положительное направление на кривой в
пространстве соответствует увеличению значения
параметра i. Кривую в пространстве можно задать
и как линию пересечения двух поверхностей:
F (х, у, г) = 0, G (х, у, z) = 0.
4.3.2.2. Локальные элементы кривой в
пространстве. Длина дуги между двумя точками Мо и М
пространственной кривой, соответствующими
значениям параметра t0, t, равна
s = j ds,
D.54)
dt
= \dr\.
Если зафиксировать точку Мо, то в качестве
нового параметра кривой можно ввести s
(натуральный параметр); s положителен, если М следует
за Мо (в смысле задаваемого при помощи t
положительного направления). Тогда получим х = х (s),
у = у (s\ Z = Z (s), ИЛИ Г = Г (s).
Разложение в ряд Тейлора. В
окрестности точки Мь соответствующей длине дуги Si =
= М0Ми справедливо равенство
r(s)
ds
2! ds2
d3r(Sl)
3! ds3
D.55)
ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ КРИВЫХ
411
или в координатной записи (для x(s))
dx(Sl) I d2x(si)t
* v " 2! </s2
Если заменить s на г, то соответствующие
формулы будут справедливы для г (г).
Касательная. Единичный вектор t = —-—
as
совпадает с направлением касательной в точке М
и указывает в положительном направлении кривой.
Главная нормаль и кривизна.
Единичный вектор п, сонаправленный вектору ~тт~*
называется вектором главной нормали к кривой
в точке М. Справедливы равенства
Коэффициент К ^ 0 называется кривизной кривой
в точке М. Величина R — \/К называется радиусом
кривизны. В случае плоской кривой кривизне
приписывают еще знак + или - (см. 4.3.1.2). Если
кривизна во всех точках кривой равна нулю (К ш 0),
то мы имеем дело с прямой в пространстве.
Сопровождающий трехгранник.
Вектор касательной t всегда перпендикулярен вектору
главной нормали п. Если дополнить t и п
перпендикулярным к ним единичным вектором b = t x в
(вектор бинормали) до правой тройки единичных
векторов, то получим тройку векторов t, n, b,
которую называют сопровождающим
трехгранником в точке М пространственной кривой (рис. 4.69)
Бинормаль
Спрямляющая
плоскость
Соприкасающаяся
плоскость
Нормальная
плоскость
Насательная
Рис. 4.69
Согласно формуле D.55), кривая с точностью до
членов 2-го порядка малости лежит в плоскости,
натянутой на t и п (соприкасающаяся плоскость),
на D и b натянута нормальная плоскость, на t
и Ь - спрямляющая плоскость.
Кручение. Кручение пространственной
кривой г = г (s) в точке М (s) определяется формулой
Г - 1/т - R2 (dt (s)/ds, d2t (s)/ds2, d3t (s)/ds3) -
x' y' z'
x" y" z"
x'" y'" zm
(x + y + z)
(x' — первая производная
no s и т. д.). Если кручение
во всех точках кривой
равно нулю (Те 0), то мы
имеем дело с плоской
кривой. Если в некоторой
фиксированной точке Mi
кручение Т = 0, то,
согласно формуле D.55),
кривая в окрестности
точки Мх с точностью
до членов 3-го порядка
представляет собой
плоскую кривую. Знак Т
позволяет определить
направление закручивания
кривой; Г>0 означает,
что для наблюдателя,
стоящего на соприкасающейся плоскости,
натянутой на t, n, в направлении b кривая закручивается
вверх против часовой стрелки (правый винт;
рис. 4.69); Т < 0 соответствует левому винту.
Общий параметрический вид. Если
кривая задана в виде D.52), то
к*- 1 _ r2f2 - (rfJ
R2 ~ (г2K ~
(х2 + у2 + z2)(x2 + у2 + z2) - (кх + уу + zzJ
Рис. 4.70
T= — -J
(х2 + у2 + z2K
х у z
х у z
x'yz
1
(г2K
R2
D.56)
(х2 + у2 + z2K'
Пример 26. Вычислим кривизну и кручение
винтовой линии
х = a cos t, v — a sin t, z — bt, a > 0
(b > 0 — правая винтовая линия, рис 4 70, h < 0 — левая
винтовая линия). Заменим параметр t длиной дуги
' \\/х2 + у2 + z2 dt = t |/V + />2;
]/а2 + b2
таким образом, кривизна
\/а2
]/а2 + Ь2
постоянна. Согласно D 56), кручение
— a sin t a cost b
— a cos t — a sin t 0
/а2+Ь2\2 flsinr -acost 0
~ V a ) [(- a sin tJ + {a costJ + b2~Y ~
также постоянно.
4.3.2.3. Основная теорема теории кривых.
Формулы Серре — Френе. Для
производных от векторов t, it, b сопровождающего
трехгранника справедливы так называемые формулы Серре —
Френе:
ds
ds
ds
412
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Основная теорема теории кривых.
Если на отрезке 0 ^ s^ а заданы две непрерывные
функции К (s) ^ 0, T(s), то с точностью до
расположения в пространстве существует единственная
кривая L: г = г (s), 0 < s < а такая, что s
представляет собой длину дуги, а кривизна и кручение
кривой L равны соответственно K(s) и T(s).
Построение кривой L проводится так:
а) Система D.57) представляет собой систему
девяти обыкновенных дифференциальных
уравнений для компонент векторов t, n, b. Заданием
t @), п @), b @) (задание сопровождающего
трехгранника в точке s = 0) решение системы D.57)
t (s), n (s), b (s) определяется однозначно.
б) Если, далее, задан г@) (s = 0 — начальная
точка кривой), то r(s) получаем по формуле
г E) = г @) + f t (s) ds.
4.3.3. ПОВЕРХНОСТИ
4.Э.З.1. Способы задания поверхностей.
Уравнение поверхности. Поверхность в
трехмерном пространстве можно определить
следующим образом:
в явной форме:
z = z(x, у); (х, y)eG; D.58)
в неявной форме:
F(x, у, z) = 0; (х, у, z)eU; D.59)
в параметрической форме:
х = х (и, у), у = у (и, у), z = z (и, v); (и, v) e G; D.60)
в векторной форме:
г = г(м, v); (u, v)eG; D.61)
где G — плоская область, U — пространственная
область.
Здесь D.61) представляет собой совокупность
уравнений вида D.60), записанную в векторной
форме, причем г = xi + у\ + zk означает радиус-
вектор точки поверхности М(х, у, z):
г (и, v) = х (и, v) i + у (и, v) j + z (и, v) k.
Пример 27. Уравнение сферы радиуса R с центром
в точке О@, 0, 0) имеет вид
F(x, у, z) = x2 + y2 + z2 -R2= 0;
в параметрической форме @ < и < 2п, 0 < v < я):,
х = R cos и sin у, у — R sin и sin у, z — R cos v;
в векторной форме: г = (R cos и sin v)\ + (R sin и sin v)\ +
+ (R cos v) k.
Криволинейные координаты на
поверхности. Если в формулах D.60)
зафиксировать параметр
v (v = vk), то получим
уравнение кривой на
поверхности,
называемой координатной
линией v = vk (рис. 4.71).
Аналогично при
фиксированном и (и = м,)
получится координат-
ная линия и = щ. В
Рис 4 72
общем случае эти
координатные линии
покрывают сплошь всю
поверхность. Точке Мь
которая является точкой
пересечения координатных
линий и = ии v = Vi,
поставим в соответствие
криволинейные
координаты (ии vx).
Координатные линии ориентируют
в направлении
возрастающих значений параметров.
Параметры и, v на сфере (рис. 4.72) имеют
следующий смысл: и — долгота, v — полярный угол,
отсчитываемый от северного полюса. Линии
и = const (соответственно v = const) представляют
собой параллели (соответственно меридианы).
Тензорные поля на поверхности.
Положим м1 =u,u2=v. Если на поверхности заданы
две функции ^(м1, и2) (а = 1, 2), которые при
переходе от системы координат и* к системе координат и'*
на поверхности преобразуются по формулам
а'ь(и'\ и'2) = ~^ау(и\ и2), D.62)
то аЛ(иг, и2) называют один раз ковариантным
тензорным полем на поверхности. В D.62)
использовано (как и во всем разделе 4.3) соглашение о
суммировании: суммирование от 1 до 2
производится по одинаковым верхним и нижним греческим
индексам. Функции я^'"а^' ) (т-е- набор из
2/с + 2/ функций) образуют к раз ковариантное и I
раз контравариантное тензорное поле на
поверхности, если при переходе от системы ма к системе
ит они преобразуются по формулам
duyi диу2 дик ди1 dui 6ii § l 2
= 6V°~i ди"^''' ди1^ Уи^Г'"' dubi V-• -Ъ (" ' " )•
4.3.3.2. Касательная плоскость н нормаль к
поверхности. Сопровождающий
трехгранник. Пусть поверхность отнесена к
криволинейным координатам м, v. Тогда векторы, касательные
Нормаль
Рис 4.73
в точке М(и, v) к координатным линиям и и v
соответственно, определяются по формулам
Рас. 4.71
ov
dv
МЕТРИЧЕСКИЕ СВОЙСТВА ПОВЕРХНОСТЕЙ
413
Единичные векторы ei = -—-, е2 = -—-
I 1*1 I I Г2 I
опре- выполняется условие
= 0,
деляют (при условии, что они неколлинеарны)
касательную плоскость в точке М (рис. 4.73).
Касательная плоскость к поверхности в точке М
представляет собой плоскость, в которой лежат все
касательные к кривым на поверхности, проходящим
через точку М.
Единичный вектор нормали N в точке М есть
вектор, перпендикулярный к касательной плоскости
в точке М и направленный таким образом, что
еь е2, N образуют правую тройку векторов.
Справедливо равенство
Тройка векторов еь е2, N, зависящая от точки
поверхности, называется сопровождающим
трехгранником. Вектор
dS = (п (и, v) x r2 (и, v)) du dv
по направлению совпадает с N(du>0, dv > 0);
его длина | dS | = | rt x r2 I du dv приближенно
равна площади криволинейного параллелограмма,
натянутого на точки (м, t;), (и + du, v), (и, v + dv)
(рис. 4.74).
Уравнение касательной плоскости
и нормали к поверхности.
dF__dF dF
дх dy dz
точка Мо называется особой точкой (конической
точкой). Разложив функцию F(x, у, z) по формуле
Тейлора в окрестности точки (х0, у о* z0), получим,
что касательные ко всем проходящим через Мо
кривым не лежат в одной плоскости, а образуют
конус 2-го порядка, уравнение которого имеет вид
J &F
+ \-dJd-z
'•-zo) +
62F
(d2F\ 82F(x0, у0, z0)
где —-=- = \ и, sv, и/ и т д
\ дх2 Jo дх2
ные производные 2-го порядка обращаются в нуль,
то мы имеем конус 3-го или более высокого
порядка.
4.3.3.3. Метрические свойства поверхностей.
Первая квадратичная форма
поверхности. Пусть поверхность задана в векторной
форме: г = г(м, v). Если u = u(t)t v — v(t)y то
г = г (t) = г (и (t), v (t)) представляет собой кривую
на поверхности. Справедливо равенство
dr , du , dv
dt ~ " dt v dt'
Дифференциал длины дуги, согласно D.54), имеет
вид
ds2 = {drJ = Edu2 + IF dudv + G dv2, D.63)
Способ
задания
поверхности
Уравнение касательной плоскости в точке
Мо (*о, Уо, z0): а (х- х0) + b (у - у0) + с (z - zo) =
Параметрическое уравнение нормали
к поверхности в точке Мо (х0, у0, z0):
х — х0 = at, у — Уо = bt, z — z0 — ct
D 58)
D 59)
D 60)
D.61)
dz (x0, y0) dz (x0, y0)
p = с = — i
dx dy
dF (x0, y0, zQ) dF (x0, Уо, z0)
— p =
dx
dy\
du /0 \ du
{dvjo \dv
(r - r0) N (Mo) = 0
, b =
dy
(x0, уо, zq)
dz
(
dujo \du
dvjo \dv
диH \du
дЛ (ё
dvH \dv
г = г0 + fN (М0)
г — радиус-вектор «текущей» точки М (х, у, z) касательной плоскости (нормали к поверхности). Фиксированная точка
, ч / ^х \ dx (м0, v0)
Мо имеет криволинейные координаты (и0, у0); I —- I = и т.;
\oujo си
П ри мсp 28. Для сферы F mx2 + уг + z2 - R2 -0 урав- гДе
нение касательной плоскости в точке Мо(хо, у0, z0) имеет
вид х0 (х - х0) + Уо (у - Уо) + z0 (z — z0) » 0, или хох + уоу +
'R2.
Уравнение нормали к поверхности:
у * t
- оо < г < + оо.
Особые точки поверхности. Если в
точке М(х0, уо, z0) поверхности F (х, у, z) — О
dr dr
du dv
дх дх dy dy dz dz
du dv du dv du dv '
414
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Если поверхность задана в виде z = z(x, у), то
дх ду
Выражение в правой части формулы D.63)
называется первой квадратичной формой поверхности.
Если положить
и1 = и, и2 = v,
011 = ?, 012 = 021 = F, 022 = G,
то, используя соглашение о суммировании (см.
4.3.3.1), первую квадратичную форму можно
записать в виде
ds2 = gapdu*dut.
При переходе к другой криволинейной системе
координат и'а на поверхности получим ds2 =
du'V, причем справедливо равенство
ди&
ди'*
Таким образом, функции да$ представляют собой
координаты дважды ковариантного тензорного
поля (метрический тензор) (см. D.62)). Положим
0 = det0ap = ?G-F2, д11 = G/g, д21 = д12 = -F/g,
д22 = Е/д. Справедливо равенство #ар0Ру = 5". При
переходе от системы и* к системе м'а функции да*
(соответственно д) преобразуются по формулам
у ди1 ди& У
(дважды контравариантное тензорное поле)
(соответственно
(и1, и2) ди1 ди2 ди2 ди1 \
и'1, и'2) ~ ди'1 дп^~ диТГ^и1Т)'
где
д(и\ и2)
d(ufl
Чтобы криволинейным системам координат
на поверхности поставить в соответствие
ориентацию г) = ±1, выберем в качестве положительной
(г) = +1) некоторую фиксированную систему Uq,
а для произвольной системы и* определим г)
как знак функционального определителя: г) =
5 (м1, и2)
¦¦ sign
Тогда тензоры Леви-Чивита
(дискриминантные тензоры)
1/0
преобразуются так же, как #ар и 0ар соответственно.
П р и м е р 29. Для сферы г - R (cos u sin vi + sin и sin »j +
+ cos»k) имеем
F»0, G-Я2;
таким образом, ds2 - Л2 (sin2 vdu2 + dv2).
Первая квадратичная форма определяет все
метрические свойства поверхности.
Длина дуги. Длина дуги кривой г = г (и (г),
v (t)) на поверхности между точками, соответствую-
щими значениям параметра t0 и f, равна
t
Площадь поверхности. Кусок
поверхности, который образуется, когда параметры м, v
пробегают область D плоскости м, v, имеет площадь
JJ dS = ff ]/EG-F2 du dv.
D D
Угол между двумя кривыми на
поверхности. Если r = r(ul(t), vx (t)\ T = r(u2(t),
v2(t)) — две кривые на поверхности г = г(м, i>),
которые пересекаются в точке М, то угол
пересечения а (угол между положительными
направлениями касательных в точке М) вычисляется по
формуле
Еи\й2 + F(uiV2 + Viu2) + Gv1v2
cos a = .
yEuj + IFuybi + Gv\ yEu\ + 2Fu2v2 + Gb\
где ui (соответственно п2) — первые производные
от их (t) (соответственно и2 (t)) при значении
параметра, соответствующего точке М, и т. д.
Отображение одной поверхности в
другую. Пусть поверхности
= ri(u, v)
г2(м, v)
заданы в одной и той же области D плоскости
параметров и и v (возможно, после замены
параметров). Если точке Мх поверхности Sx с радиус-
вектором Ti (и, v) поставить в соответствие точку
М2 поверхности S2 с радиус-вектором г2 (и, v), то
мы получим взаимно однозначное отображение
одной поверхности на другую. Это отображение
называется: 1) сохраняющим длину, если при нем
длина произвольной кривой остается неизменной;
2) сохраняющим углы (конформным), если при нем
не изменяется угол между двумя произвольными
пересекающимися кривыми; 3) сохраняющим
площадь (эквиареальным), если при нем не
изменяется площадь произвольного куска поверхности.
Отображение
Сохраняющее длину
Сохраняющее угол
(конформное)
Сохраняющее площадь
(эквиареальное)
Необходимое и достаточное
условие, накладываемое на
первую квадратичную форму
?, = ХЕ2, F, = XF2, G, = XG2,
Х(и, v)>0
?,G, -F\ = E2G2 -F22
В таблице ?,-, Fh G, — коэффициенты первой
квадратичной формы поверхности St(i = 1, 2).
Данные соотношения должны выполняться в каждой
точке поверхности.
Каждое отображение, сохраняющее длину,
является конформным и сохраняющим площадь.
Каждое конформное и сохраняющее площадь
отображение сохраняет длину.
4.3.3.4. Свойства кривизны поверхности.
Выражение в правой части формулы
-</N dx = Ldu2 + 2Mdudv + N dv2
называется второй квадратичной формой поверх-
СВОЙСТВА КРИВИЗНЫ ПОВЕРХНОСТЕЙ
415
ности. Она определяет свойства кривизны
поверхности. Справедливы равенства
У EG - F2
i =
1 =
d2x
du2
dx
~дп
дх
dv
d2x
du dv
dx
~du~
dx
dv
d2x
dv2
dx
~du~
dx
~dv
n
]/EG-
d2y d2z
du2 du2
dy dz
du du
dy dz
dv dv
d2y
du dv (
dy
du
dy
dv
d2y
dv2
dy
du
dy
~dv~
\
^EG - F2
г*'
*
d2z
)u dv
dz
du
dz
dv
d2z
dv2
dz
du
dz
dv~
Если положить w1 as и, и2 = v и Ьц — U Ьц = Ь21 —
» М, b22-Nt то вторую квадратичную форму
можно записать в следующем виде:
При переходе от системы ма к системе и'*
справедливо равенство
где
ди1 диь
здесь б - знак функционального определителя:
B 2)
е = sign -—1—jf-. Следовательно, функции оая
д(и1, и2)
представляют собой координаты дважды кова-
риантного псевдотензора. Положим по
определению b = det bejJ = LN - М2; величина Ъ
преобразуется по тому же закону, что и g (см. 4.3.3.3).
Главные кривизны. Для фиксированной
точки поверхности М всегда можно выбрать
декартову систему координат х, у, z такую, что
начало координат лежит в А/, а плоскость х, у
совпадает с касательной плоскостью,
проходящей через М. В этой системе координат поверхность
(в некоторой окрестности точки М) можно
представить в виде z = z (х, у), причем
г@, о) = ^=^ = о.
дх ду
Соответствующий сопровождающий трехгранник
в точке Мо состоит из трех единичных векторов
вь е2, N = ег х е2, которые направлены по
координатным осям. Разложение по формуле Тейлора
в окрестности точки М имеет вид
1 d2z@, 0) 2 a2z@, 0)
2 s= - х "Ь XV ~f"
2 дх2 dxdy
1 d2z@, 0) 2
Поворотом декартовой системы координат вокруг
оси z можно добиться того, чтобы выполнялось
равенство
(М2+*2) +
Величины ки к2 называются главными
кривизнами; Ri = -—^ R2 = т главными радиусами кри-
ki k2
визны; К = kik2 — гауссовой кривизной; Н =
= -y(fci +k2) —средней кривизной в точке М.
Пример 30 Для сферы радиуса R
В выделенной системе координат, в которой
поверхность может быть представлена в виде
D.64), квадратичные формы в точке М имеют
особенно простой вид:
(drJ = dx2 + dy2,
-dNdr^kidx2 + k2dy2.
Для произвольной системы координат на
поверхности справедливы равенства
к - — - LN -М2
g~ EG-F2'
LG - 2FM + EN
2(EG-F2) '
Главные кривизны ки к2 — корни квадратного
уравнения
к2 - 2Нк + К = 0.
Существенное преимущество применения
тензорного исчисления в дифференциальной геометрии
состоит в том, что, зная величины в некоторой
удобной системе координат и зная их поведение
при преобразовании, можно тотчас же написать
выражение этих величин в произвольной системе
координат и*. Главные кривизны при изменении
ориентирования меняют только свой знак
(псевдоскаляры); следовательно, К при переходе к
произвольной системе и* не изменяется (скаляр). Чтобы
найти выражение для К в системе мв, необходимо
лишь построить скаляр, который в выделенной
системе координат совпадает с к^к2. Таким образом,
мы получаем скаляр b/д. Аналогично можно
построить псевдоскаляр для Я.
Классификация точек
поверхности (формула D.64)) позволяет определить вид
поверхности в окрестности точки Мо (в
выделенной системе координат). Благодаря этому в
окрестности Мо получаем следующую классификацию:
416
ДИФФЕРЕНЦИАЛЬНАЯ ГЕОМЕТРИЯ
Название точки
Эллиптическая точка
Круговая точка
Гиперболическая точка
Параболическая точка
К =
К =
к =
к =
а) к*
б) к
Аналитическое
кхк2 >0 (т. е LM
к1к2>0, кх = к2
кхк2 < 0 (т. е. Ш -
кхк2 = 0 (т. е. LM
+ к22*0
1 = *2 = 0
определение
- N2 > 0)
- N2 < 0)
- N2 = 0)
В окрестности точки Мо поверхность
с точностью до членов 3-го порядка
ведет себя как
эллипсоид
сфера
однополостный гиперболоид
цилиндр
плоскость
Поверхности, для которых Н = О, называются
минимальными. Поверхности, для которых К =
= const, называются поверхностями постоянной
кривизны. Простейшие
примеры: К > 0 —
сфера, К < 0 —
псевдосфера (поверхность
вращения трактрисы;
рис. 4.75).
Поверхность
называется линейчатой,
если она получается
при движении в
пространстве прямой
(например, конус,
цилиндр,
однополостный гиперболоид,
гиперболический
параболоид). Если
поверхность при этом
может быть развернута
на плоскость, то
говорят о
развертывающейся поверхности
Рис. 4.75 (например, конус,
цилиндр). Во всех
точках развертывающейся поверхности К = 0;
следовательно, LN — М2 =0.
Если пересечь поверхность плоскостью,
проходящей через нормаль к поверхности в точке М,
то образующаяся кривая называется нормальным
сечением в точке М. Всегда существуют два взаимно
перпендикулярных направления, в которых
кривизна соответствующих нормальных сечений в
точке М равна главным кривизнам kl и к2. Эти
направления соответствуют направлениям осей
выделенной системы координат и называются
направлениями главной кривизны, а
соответствующие сечения - главными нормальными сечениями
поверхности. Если секущая плоскость образует
с осью et угол а, то кривизна /сдг нормального
сечения в точке М равна
kN = ki cos2 a + k2 sin2 а
(формула Эйлера).
Пусть поверхность задана в векторной форме:
г = г (и, v). Кривизна нормального сечения в точке
М, имеющего направление Атм + \irv, равна
_ ЬаРХ.Чр _ LX2 + 2МХц + N\i2
~ g^X* " EX2 + 2FX\i + G\i2 '
где X1 =Х, X2 = р.. Направления главных кривизн
Хги + цг„ можно получить, определив X, ц из
уравнения
или, более подробно, из уравнения
X2 (FN - GM) + X\i (EN - GL) + ц2 (ЕМ - FL) = 0.
D.65)
В направлениях главных кривизн кривизна
нормального сечения kN принимает экстремальные
(максимальное и минимальное) значения, равные
главным кривизнам /сь к2.
Линии кривизны — кривые r — r(u(t), v(t)) на
поверхности, направления касательных к которым в
каждой точке совпадают с одним из направлений
главной кривизны. Их дифференциальные
уравнения можно получить из формулы D 65),
положив X = du/dt и ц = dv/dt. Если секущая плоскость,
проходящая через точку М, образует с нормалью
к поверхности в точке М угол у ф 0, то кривая,
являющаяся линией пересечения плоскости и
поверхности, называется наклонным сечением
поверхности. Кривизна к наклонного сечения в
точке М вычисляется по формуле
к = kN cos у
(теорема Менье).
Кривизна произвольной кривой
на поверхности. Пусть г = г (и (t), v (t)) —
произвольная кривая на поверхности. Кривизна
кривой в точке М равна кривизне наклонного сечения
поверхности в точке М, которое образуется при
пересечении поверхности с соприкасающейся
плоскостью кривой в точке М, натянутой на вектор
касательной и вектор главной нормали. Зная
главные кривизны в точке М, можно,
следовательно, вычислить кривизну всех кривых на
поверхности, проходящих через эту точку.
4.3.3.5. Основная теорема теории поверхностей.
Деривационные формулы Гаусса и
Вейнгартена. Изменение сопровождающего
трехгранника (см. 4.3.3.2) описывается так
называемыми формулами для производных:
д2' s |~= Пргв + bapN (Гаусс),
ди*ди*
-—= -gaybyara (Вейнгартен),
ди
где г,- = дг/ди1. Все индексы пробегают значения
от 1 до 2. По одинаковым верхним и нижним
индексам производится суммирование от 1 до 2.
Символы Кристоффеля Г«р вычисляются по
формуле
'*&_ dgps _ ддЛр\
<Р ди« диъ )'
Они не обладают свойствами тензоров. Формулы
для производных представляют собой систему
дифференциальных уравнений в частных производных
первого порядка для компонент векторов гь г2, N.
ОСНОВНАЯ ТЕОРЕМА ТЕОРИИ ПОВЕРХНОСТЕЙ
417
Условия интегрируемости. Из
равенств
я2г ?2n d2N
О Га
ди^ди*
получаются так называемые условия
интегрируемости:
ди2 аи1
[2^M+(r!i-r22)fe12-f Г?^22 = 0,
СГ>12 ^1J2 ,-.1 , , /т-1 г-2 \ и i г2 l л
---— —i Г22ЬП +A 12- Г22)Ь12 + Г 12Ь22 = О
D.66)
(формулы Майнарди — Кодацци),
Ь = bnb22 - Ь\2 = Rl2 i2 D.67)
(формула Гаусса). Здесь
**¦ а C, у • = р + * Р<т * ay — ~у7 ] «а ] Ру D.06)
есть тензор кривизны Римана.
Так как К = fr/g, то формула Гаусса
(основная теорема Гаусса) может быть записана
в виде К = R\2\iIq- Отсюда следует, что гауссову
кривизну можно выразить только через
коэффициенты Е, Г, G первой квадратичной формы и
первые и вторые производные от них.
Следовательно, кривизна К может быть определена
только из измерений на поверхности, без
рассмотрения окружающего пространства (свойство
внутренней геометрии поверхности). При
отображениях, сохраняющих длину, кривизна К в
соответствующих точках одинакова. Так как для сферы
(плоскости) К = \/R2 (К = 0), то сферу никогда
нельзя отобразить на плоскость, сохраняя длину.
Основная теорема. Если заданы функции
gu(u\ u2) = E(u, v),
gl2(u\ u2) = g21(u\ u2) = F(u, v),
g22(u\ u2) = G(u, v)
(дважды непрерывно дифференцируемые) и
blx (и1, и2) = L(u, v),
Ь12(и\ и2) = Ь21(и1, и2) = М(и, v),
Ь22(их, и2) = N (и, v)
(один раз непрерывно дифференцируемые), для
которых выполнены условия интегрируемости
D 66), D.67), и, кроме того, для любых
действительных чисел X, ц таких, что X2 + ц2 ф 0,
справедливо неравенство EX2 + 2FX\i + G\i2 > 0, то
существует поверхность г = г(м, v) (трижды
непрерывно дифференцируемая), коэффициенты первой и
второй квадратичных форм которой совпадают
с заданными функциями. Поверхность определена
однозначно с точностью до движения в
пространстве (сдвига и поворота).
Построение этой поверхности проводится
следующим образом:
1) На основании формул Гаусса и Вейнгартена
для производных однозначно находится
сопровождающий трехгранник гь г2, N, если он задан в
некоторой фиксированной точке М (и0, v0).
2) Так как = га,
ди*
то отсюда можно
вычислить г (и, v); r (и, v) определяется однозначно,
если поверхность проходит через точку М.
4.3.3.6. Геодезические линии на поверхности.
Геодезические линии. Кривая на
поверхности называется геодезической линией, если в
каждой точке главная нормаль к кривой и нормаль к
поверхности коллинеарны. Кратчайшая линия,
лежащая на поверхности и соединяющая две
точки поверхности, всегда является частью
геодезической линии. На плоскости геодезическими
линиями являются прямые. На сфере окружности
больших кругов (например, нулевой меридиан и
экватор) суть геодезические линии. Геодезические
линии на искривленной поверхности соответствуют
прямым на плоскости. Геодезическая линия г =
= г (s) = г (и (s), v (л)) (s — длина дуги)
удовлетворяет дифференциальному уравнению
d2u*
du*
~ds~
= 0 (а =1,2), D.69)
ds2 • PY ds ds
и, обратно, всякое решение этого
дифференциального уравнения представляет собой
геодезическую линию (о символах Кристоффеля Гру см. 4.3.3 5).
Если поверхность задана в явном виде, z = z(x, у),
то дифференциальное уравнение геодезической
линии у — у (х), z = z (х, у (х)) имеет вид
dz\2 ( dz\2\ fy__dz_ (?z_(d/
dy~) ) Jx2" dx dv2 \dxy
1 +
dx
()Z V^Z
vx dx dy
dz d2z
cy dy2
dx
dv cxdvJ dx
——Z
dv dx2
Геодезическая кривизна. Для кривой
на поверхности г = г (s) = г (и (s), v (s)) (s — длина
дуги) всегда существует разложение вида
= N ¦
ds
Если кривая представляет собой нормальное
сечение в точке М, то в этой точке kg — 0 и kN равна
кривизне нормального сечения; вообще kN в точке
М равна кривизне нормального сечения,
проходящего через М, с той же касательной, что и r(s);
kg называется геодезической кривизной. Кривая на
поверхности тогда и только тогда является
геодезической линией, когда kg = 0.
Пусть S — кусок поверхности, ограниченной
простой замкнутой кривой 8S с геодезической
кривизной kg и длиной дуги s; тогда
§ kg ds + JJ k dS = 2тг D.70)
dS S
(теорема Гаусса — Бонне); JJ k dS называется пол-
S
ной кривизной куска поверхности. Полная кривизна
замкнутой поверхности, которую можно взаимно
однозначно и взаимно непрерывно отбрани ь на
сферу (тор), всегда равна 4л (нулю)
14 И Н Бронштейн, К А Семендяев
418
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4.4. РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ
И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4.4.1. РЯДЫ ФУРЬЕ
4.4.1.1. Общие понятия. При решении многих
задач физики и математики необходимо
осуществить разложение периодической функции с
периодом 2тс в ряд по тригонометрическим
функциям:
~+ ) (ак cos kx + bk sin kx). D.71)
Ряд вида D.71) называется рядом Фурье, а
разложение функции в ряд Фурье составляет задачу
гармонического анализа. В приложениях зачастую
ограничиваются конечным числом членов и
получают при этом приближение функции
тригонометрическим многочленом. Если рассматривается
гильбертово пространство L2( —тс, я)*), то система
функций
, cos х, sin x, cos 2x,
\/2п ]/п уп 1/тс
—— sin 2х, —rcos3x, ——-sin3x, ...
уп уп уп
является полной ортонормированной системой.
Отсюда следует, что при приближении функции
/(x)eL2( — n, п) тригонометрическим многочле-
ном sn (х) =
_«• +V
(otk cos kx + pk sin kx) средне-
квадратичная погрешность б2 = J (/ (х) — sn (x)Jdx
— Я
минимальна тогда и только тогда, когда в качестве
otfc, pk выбраны так называемые коэффициенты
Фурье функции /(х), которые определяются
следующим образом:
= — /(х) cos kxdx (k = 0, 1, 2, ...),
— я
D.72)
-И
f{x) sin kxdx (k = 1, 2, ...).
Отсюда следует, что для каждой функции
/(x)gL2(-tc, тс) сумма
sn (х) = —- + у (ak cos kx + bk sin kx),
fc=i
где ак и bk вычислены по формулам D.72), cxo-
*) Гильбертово пространство, в котором всюду плотно
евклидово пространство непрерывных функций на отрезке
Я
[ — я, я] со скалярным произведением (/", g) = J f(x)g(x)dx
дится к / в смысле среднего квадратичного:
lim }(f(x)-sn(x)Jdx = 0.
п -*¦ оо _К
Во многих случаях представляет интерес
вопрос: когда ряд Фурье сходится в обычном
смысле, т. е. поточечно, и каким образом он
описывает функцию/(х)? На так поставленный вопрос
дает ответ теорема Дирихле. Пусть j (х)
удовлетворяет в ( — тс, я) так называемым условиям Дирихле:
а) интервал ( — тс, тс) можно разбить на конечное
число интервалов, в которых /(х) непрерывна и
монотонна; б) если х0 является точкой разрыва
функции /(х), то существуют /(х0 + 0) и /(х0 — 0).
Тогда ряд Фурье функции /(х) сходится и имеет
место равенство
lim
— + / (я*
cos kx + bk sin kx)
=
J
/(х), если / непрерывна в х,
/(х + 0)+/(х-0)
в противном случае.
Если представить функцию /(х) периодически
продолженной на всю ось с периодом 2тс, то
утверждение теоремы Дирихле будет справедливо
для всех х.
Если раскладываемая в ряд Фурье функция имеет
период 21, то рассматривают интервал ( —/, /). При
этом коэффициенты ряда Фурье вычисляются по
формулам
<-h = -г
1,2,
=1, 2, ...
D.73)
ряд Фурье функции /(х) имеет вид
00 ¦
ао W кпх , . кпх\
— ч- > I я* cos —j- + bksin —— J.
В этом случае все вышеприведенные утверждения
остаются в силе.
Ряд Фурье
s (х) = 1- ) (ак cos kx + bk sin kx)
может быть также записан в одной из следующих
форм:
s(x) = -^-+ \ Ak sin {kx + фД
2 / j
ТАБЛИЦА НЕКОТОРЫХ РАЗЛОЖЕНИЙ В РЯД ФУРЬЕ
419
где Ак - \' ак f bk~, tg фА =
ckeik\
ск= -„ f{x)e ikxtlx =
flo/2.
если А = 0,
(ak - ihk), если к > 0,
(a k +
если А: < 0.
С и м м e i p и я. Если / (л) в ( — я, тс) — четная
функция, 1 е / ( — v) = / (х), то коэффициен гы Фурье
находятся по формулам
ак= I / (х) cos к.х A.x, Ьк = 0 D.74)
При этом ряд Фурье функции /(л) имеет вид
ао \
----- + > akcoskx
D.75)
Если / (х) — нечетная функция, те / ( — х) =
— —/(л), то коэффициенты Фурье находят по
формулам
ак = 0, Ьк = r / (x) sin кх dx. D 76)
я J
о
При пом ряд Фурье функции / (.х) имеет вид
s (х) = ? hk sin kx.
D.77)
Разложение на интервале @, я).
Если функция /(х) задана на интервале @, я) и
удовлегворяе! условиям Дирихле, го ее можно
разложить как в ряд по косинусам вида D.75),
так и в ряд по синусам вида D 77); в первом
случае коэффициен 1Ы вычисляются по формулам D.74),
а во втором — по формулам D.76) Оба ряда в
интервале @, я) дают значение функции / (х) в
точках непрерывности функции / (х) и величину
/(v + 0)+y(x-0) . ,, v
в точках разрыва функции / (х).
СХнтако вне @, я) эти разложения описывают
разные функции. Ряд по косинусам дает такую
функцию, которая получается из/ (х) путем четного
продолжения на соседний интервал ( — я, 0) и
периодическою продолжения с периодом 2я вне
( — я, я) (рис 4 76, а) Ряд по синусам дает такую
функцию, которая получается из f(x) путем
нечетною продолжения на (—я, 0) и периодическою
продолжения с периодом 2к вне ( — я, я) (рис. 4 76, б).
-2л
-2п
У
^L
\2п х
6)
Рис 4 76
Если / (х) задана на интервале @, /), то формулы
D.74) (соответственно D.76)) записывают в
следующем виде.
соответственно
/
ак = 0, Ьк = -— / (х) sin —— а
Тогда ряд D.75) (соответственно D.77))
принимает вид
а0 V1 кпх
* (х) = "Г" + / °к cos ~~Г
I соответственно
() у)
Lj l J
k= 1
4.4.1.2. Таблица некоторых разложений в ряд
Фурье. Ниже приведены разложения в ряд Фурье
некоторых простейших функций, которые заданы в
определенных интервалах и продолжены
периодически вне их. Для некоторых разложений дано
графическое изображение формы кривой.
Разложения относятся к интервалу ( — я, я) или к @, я).
В общем случае разложения периодических
функций нередко могут быть получены путем
изменения масштаба как по оси х, так и по оси у
А
-4Т
V
-2Т
У
/
1
/ \/
0 2Т
А у
4Т
/
6Т
Пусть, например, дана функция у — х: + 1 при
0 < х < 2Т с периодом 2Г(рис. 4.77). Посредством
замены переменных
14*
420
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
(х - Т) п Отсюда при помощи указанной выше замены,
= получаем функцию 1 в табл. 4.8, т. е. принимая во внимание свойство линейности раз-
функцию Y=X, заданную на интервале ложения в ряд Фурье, получим искомое раз-
— п < X < тс, с периодом 2я. Согласно этой таблице, ложение:
получаем У(Т+1
( sin X sin 2x sin Зх
У-21— J~+~T
2Т
1 . 2жх 1 Зпх
sin+sin
Таблица 4.8
1 у = X При — 71 < X < 71,
А
-ч/о
А А А А
sin х sin 2x sin Зх
При значениях аргумента ±кп ряд дает, согласно теореме
Дирихле, значение функции, равное 0
s Зх cos 5x
_ / sin х sin 2x sin Зх
'-*-2(,—г-+—г—+—т
4. у.
— (тс 4-х) при — я
4 / . sin Зх sin i
У = — \
ч .
A\ УК . ,_
\ —а при — я < x < О,
5. v = <
( а при О < х < я, а ;
Л 2n3nin5it
4а ( . sin Зх sin 5x
f Ci при — я < x < 0,
6 V = <
[ с2 прч 0 < х < я;
I I
I i i
i i i
-3n-2rt-rt О
! + с'2 Сх — с2
2
sin Зх sin 5х
¦¦¦¦)
0 при -я<х<-я + а, -а<х<а, я-а<х<я,
7. у = ^ а при а < х < я - а,
— а при — я + а < х < — а, д>0, 0<а< я/2;
( cos а sin х 4- — cos За sin Зх + — cos 5а sin 5x 4-... I
-П/2
Ы \rt-a Зп/2 П ?
ЯП | 2rt5h/2
ТАБЛИЦА НЕКОТОРЫХ РАЗЛОЖЕНИЙ В РЯД ФУРЬЕ
421
Продолжение
8 у =
a (v: + я)
при - а ^ х < а,
при a < х ^ л — а,
при - л + а < y ^ -а,
при я — a < х < я,
- при - л < y ^ -я + а, а > О, 0<а< я/2,
1
sin а sin х + -у-sin За sin 3y + --j- sin 5а sin
В частоеiи, при а = я/3 получаем
У =
n y - ^-sin 5х + 2- sin 7х - --у -sin 11 х +
cos 2y cos 3y
У = -^ — 4 ( COS Y - -p- + з2
10 y:
- y2 при -я < x ^ 0.
Y2 1фИ 0 ^ Y < Я,
sin 2x sin 3x
-3n-2it-Tt
sin 3y sin 5y
-yj—+ - -5з ~
при in
11 у = x (я - y) при 0 ^ x ^ л
и четно продолжена на (-я, 0),
' cos 2y cos 4x cos 6y
12 у = x (я - y) при 0 ^ х ^ я
и нечетно продолжена на ( — л, 0),
8 / sin 3y sin 5y
13 у = ,4y2 + By + С при — я < x < л,
sin kx
14 у = | sin y | при — л ^ х ^ л,
4 / cos 2
cos 4y cos 6y
i i i
\ 3 + 3 5+ 57+
-п 0 n 2n 3n
15 у = cos y при 0 < x < я
и нечепю продолжена на (-я, 0),
4/2sin2x 4 sin 4x 6 sin 6y
-п у.0
0 при -я ^ \ ^0,
Sin Y
1 1
т + 2
при
Sill Y
U
9
я '
5; \ S
( COS
1 1
i; Л,
2y
3
cos 4y
f 3 5 ~Л
cos 6\
5" 7
Jn
422 РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Продолжение
17 у — cos мх при — л ^ д: ^ л, где м — произвольное не целое действительное число,
Зх
2м sin мл ( 1 cos х cos 2х cos 3.
л \ 2м2 и2 - 1 + ~п*^~4 м2-<
18 у = sin мх при — л < x < л, где м — произвольное не целое действительное число;
2 sin мл ( sin х 2 sin 2x 3 sin Зх
м2 -4 м2 -9 +
V
sin мл / sin х
\
19 v = х cos х при — л < х < л;
1 . 4 sin 2x 6 sin Зх 8 sin 4x
v = —г- sin х -
2 "" л ' 22 - 1 З2 - 1 ' 42 - 1
20 у = х sin х при — л < х ^ л;
1 _ / cos 2x cos Зх cos 4x
y = l-Tcos.v-2l +
21 у = ch мх при — л ^ х < л, м#0;
_ 2м sh мл ( 1 cos х cos 2x cos Зх
22. у = sh мх при — л < х < л;
2 sh мл ( sin х 2 sin 2x 3 sin Зх
23 у = еах при — л < х < л, а ф 0;
у = - sh «л I ~
z 1- / —5 гт~(A cos kx — k sin /ex) I
|_ 2a Lj a +k J
В последующих примерах имеют в виду не столько задачу о том, как разложить данную функцию в ряд
Фурье, сколько обратный вопрос: к каким функциям сходятся некоторые простые тригонометрические
ряды ?
24. Y5^=_lnBsin4o<*<2T, 25. Y *=?-- *-=-*-, 0 < х < 2*.
/_j к \ 2/ /_j к 2
к= 1 к = 1
V cos ^х Зх2 - бпх + 2я2
Zn^=—п—•
26.
к = 1
2Ъ Z"F—-Jln
= f Lf2sin4)d(+ У^; 0<х^2Л f t-= --^ =1,20205...\
J J V 2/ Zj* \Z-/(c3 25,79436... У
О О fcl \
fc=l 0 О fc=l "fc=l
V'sin kx x3 - Зях2 + 2я2х
k= 1
QO
J\J. / у — t) — 111 I Z CUt) ~~ I, — Tt ¦v. Л s 71.
/ j К у /
fe= 1
n2 - 3x2.
31. > (-l)k+1 —v— =—, -жх<я. 32.
fc2 12
fc= 1 k=1
ЧИСЛЕННЫЙ ГАРМОНИЧЕСКИЙ АНАЛИЗ 423
33. " Y( - 1 )к + 1 -~-2Х- = I In I 2 cos -I- ) dz, - п < х < тт.
V\ n , cos kx V^ . . , 1 Г , Г, (' t \
34 )(_i)k41 _ — — = )(-l)k+1 -r- - \dz In 2 cos — ЫГ, -тс<х<я.
/ & / к J I V 2 /
к - 1 fc -= 1 0 0
35 Y(-l)k+lS-^4-= "—1^-"' -n^x^n. 36. Y — Ц^т1 — = -yln(tgy\ 0<
Jk=l k = 0
37. ) ''-- = —, 0 < x < я. 38. ) —— -—-= — 0 ^ x ^ n.
/_j 2k+[ 4 A B^+ IJ 8
ZcosBfe+ l)x
-BГ+Ж-
40.
t=0 0 0 fc=0
YsinB/,- + l)x _ 7c2x-7T.x2 Y1 k cosB/c + l)x _ 7t л: ^r
/ f 2A' +П3~ 8 ' "^>-^- • / \ ) 2fe _j_ | 4' 2 2
к - 0 к = 0
4, t(
3 я/2-
V tcosBfc+l)x 1 Г
44 z("'^ ¦<2Г+,г=-2
2-лс
Г
J
V1 . sin Bk + l)x ях к п
46 2(
47 Y(-P*sin<2* + 1)v ' Г
B/c ¦+¦ l)x 1 Г Г / t\ J
4.4.1.3. Численный гармонический анализ. Если тему относительно скалярного произведения
в промежутке 0 -^ х < L функция j (х) известна
kL < v-п
только в дискретной системе точек хк = -~-(Л=0, ^ д) = — ) /Ы)-д(хк) D 78)
1, . ,N—1), то задача ее приближенного пред- к~Г^
ставления тригонометрическим многочленом ре-
шается следующим образом. ?еРга над в ~ знак комплексного сопряжения).
Система функций Отсюда следует, что тригонометрический многочлен
в,Ы = ехр!//«,}, к, I = 0, 1...., N - 1, "^ ^' , }
2KXk tvW- ^^w- 2,с'ехр{""ттDЛ9)
где ак = , образует орюнормированную сие- ,^q j^q
424
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
N - 1
" 2ni jjf}'
j = 0
принимает в точках хк значения f(xk), т. е. решает
задачу тригонометрической интерполяции. При
этом отрезок этого многочлена дает наилучшее
приближение к f(x) в смысле метрики D.78) по
сравнению с аналогичным тригонометрическим
многочленом, но с другими коэффициентами.
Так как
«p{2*tfi-}-«p{-2«l(N -/)!}.
то из формулы D.80) следует, что
cl = cN_l, (/=1, 2,...,и-1),
—-—
([х] - целая часть х: наибольшее
целое число, не превосходящее х); коэффициент
с'о (а при четном N также и с„) действителен.
Если обозначить ак = ск + c^_j(, bk = i (ck — сдг _ ^),
1 < к ^ п — 1, и а0 = 2с0, а при N четном аи = 2с„,
то формула D.79) примет вид
Последний член возникает только при N четном.
При этом для вычисления ах и Ьх служат формулы
N - 1
D.82)
/v- l
i = — у
/ = 0, 1,...,и, Ьо = Ь„ = 0.
Погрешность интерполяции f(x) — Tjy(x) в
точках, не являющихся узловыми, существенно зависит
от членов более высоких порядков в разложении
f(x) в бесконечный ряд Фурье.
Если N = pq, то для вычисления коэффициентов
с, можно применить формулы
р-1
= — / f(xm+Jq)exp\ -2ni—>,
Р L I Р)
/ f
D.83)
функций, заданных р значениями, совпадающими
с f{x) в точках xm+Jq (/= 0,...,р — 1). По ним
вычисляются окончательные значения с,. Разлагая р
на множители, можно рекуррентно применять
формулы D.83) для вычисления сгт. Такой
способ вычислений, позволяющий значительно
сократить их объем, называется быстрым
преобразованием Фурье. Особенно эффективным является
этот метод, когда N — 2s. В этом случае формулы
D.83) могут быть записаны в виде следующих
соотношений:
crjk х = у(cjk + ехр{-(/«,}cj,k+q),
J1 (;
D.84)
где g = 2r~\ p = 2s~r, ar = я/р.
Полагая сначала г = s и cq* = f(xk) и переходя
рекуррентно по формулам D.84) от г к г — 1,
получим в результате значения с°о, равные искомым
коэффициентам с,-.
Используемые при этом значения exp{-i/ar}
также вычисляются рекуррентно:
при j четном
ехр {-№} =ехр
j -/yar+1i,
при j нечетном
ехр{-(/аг} =
ехр<-
2 cos ar
где cos аг =
+cosar +
Величины сгт являются коэффициентами Фурье q
Вычисления по формулам D.84) требуют числа
действий порядка iVlog2 N вместо N2 по формулам
D.80).
Для действительных коэффициентов Фурье а,
и bj формулы D.84) можно преобразовать к
следующему виду:
</*1 = у№ + cos;ar• arJtk+q - sinja, • Ь5,*+в),
O^k^q- 1,
Zi E ;
D.85)
*1 = -j(brJk + smja.r'a'jtk+q -h cosja.r-brj<k+q),
1-U
arJtk+q + cosjoir-brlk+q),
P
Как и в формулах D.84), здесь g = 2r-1, p = 2s~r,
ar = п/р. Рекурсия начинается с г = s, аод = 2/(хл),
bo* = 0. При этом всегда ?>о* =: ^р/2, * = 0.
ОБЩИЕ ПОНЯТИЯ
425
Для синусов и косинусов справедливы формулы :
при j четном
cos jot, = cosyar+b
sin
при j нечетном
cos jctr =
2 cos ar
sinyar =
(sin —у—ar+1j + sin( -y—a,.+
2cos ar
Формулу для cos ar см. выше.
На практике кроме N = 2s часто встречается
также N = 3 • 2s. В этом случае можно
воспользоваться формулами D.83), полагая р = 2s, g = 3,
а для вычисления crm (m = 0, 1, 2) трижды применить
формулы D.84).
Так как формулы D.79) при х — Xj совершенно
аналогичны формулам D.80), то метод быстрого
преобразования Фурье с успехом применяется в
случаях, когда требуется вычислить значения
тригонометрического многочлена Т^(х) с известными
коэффициентами в точках х} = — @ ^ j ^ N — 1).
4.4.2. ИНТЕГРАЛЫ ФУРЬЕ
4.4.2.1. Общие понятия. Непериодическая
функция f(x) не может быть разложена в ряд
Фурье. Однако при определенных предположениях
из разложения в ряд Фурье на интервале (-/,/)
посредством предельного перехода при / -> + оо
получают разложение / в так называемый интеграл
Фурье. Пусть /(х) в любом конечном интервале
подчиняется условиям Дирихле (см. 4.4.1.1)
и является абсолютно интегрируемой, т. е.
+ оо
J |/(х) \dx < +оо. Тогда для всех х имеет место
формула
/(х)= J (a(y)cos(xy) + b(y)sin(xy))dy, D.86)
где
| /(и)со
i) cos (yu) du,
D-87)
Ь(у) = — f (и) sin (yu)du.
п J
Правая часть формулы D.86) называется
интегралом Фурье функции /(х), а вычисляемые,
согласно D.87), коэффициенты напоминают по
своему виду коэффициенты ряда Фурье. В точках
разрыва функции /(х) правая часть формулы
D.86) принимает значения, равные
В то время как разложение в ряд Фурье
дает представление периодической функции (с
периодом 21) в виде суммы гармонических
колебаний с частотами у„ = п— (п = 1, 2,...), интеграл
Фурье представляет функцию f{x) как бы в виде
суммы бесконечно большого числа колебаний с
непрерывно изменяющейся частотой у; говорят, что
интеграл Фурье дает разложение функции в
непрерывный спектр.
Важным достаточным условием сходимости
интеграла Фурье служит признак Жордана —
Дирихле. Если функция /(х) в каждом
конечном интервале имеет не более чем конечное
число точек разрыва, / является функцией
ограниченной вариации в каждом конечном интервале и
f |/(х)|<*х<оо, то
j (a (y) cos {xy) + b {y) sin (xy)) dy =
о
/(x) в точках непрерывности /,
— if(x + 0) + f{x - 0)) в точках разрыва.
При этом а (у), Ь(у) определяются согласно
D.87). Интеграл Фурье может быть также записан
следующим образом:
+ оо +00
Г (и) cos у (м — x)du,
D.88)
или (в комплексной форме) в виде
~ [dy [/{и)е»<ы
Внешний интеграл в D.88) понимается в смысле
главного значения. Формула D.88) может
восприниматься как суперпозиция следующих двух формул:
\/2п
fix)-
+ 00
2^ J
|/2jc
f(x)eiyxdx,
F(y)e-ixydy.
D.89)
D.90)
Функция F(y\ которая поставлена в
соответствие функции /(х) согласно D.89), называется
трансформантой Фурье или преобразованием Фурье
функции/(х), а сам переход от/к F называется
преобразованием Фурье. Если задана трансформанта
Фурье F(y), то посредством так называемого
обратного преобразования Фурье D.90) получают
снова/(х). Вообще говоря, F — комплексная
функция и для действительных /. Исходная функция
/(х) также может принимать комплексные
значения, обладая действительным аргументом х.
Трансформанта Фурье существует, если /(х)
удовлетворяет указанным выше условиям
справедливости формулы D.86). При этом интеграл в
426
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
D.89) понимается, вообще говоря, в смысле главного
значения. Преобразование Фурье в D.89) можно
составить из косинус-преобразования и
синус-преобразования Фурье. Косинус-преобразование Фурье
и обратное к нему определяются формулами
о
f(x)cos(xy)dx,
D.91)
(у) cos (xy)d у;
соответственно синус-преобразование и обратное к
нему — посредством
Fs(y)
f{x)sin{xy)dx,
D.92)
¦ПЬ-
(y)sin(xy)dy.
Многообразные применения преобразования
Фурье в теории вероятностей (теория
характеристических функций), при решении краевых задач и
сингулярных интегральных уравнений (метод
Винера — Хопфа), а также в электронике и других
технических областях обусловливаются главным
образом следующими теоремами.
Теорема- о свертке. Если функции j и д
имеют трансформанты Фурье, то трансформанга
Фурье свертки двух функций
((f*g)(x)=+[f(y)g(x-y)dy)
с точностью до ]/2п равна произведению
трансформант Фурье сомножителей:
=- I (
2п J
]/
— оо
Теорема непрерывности. Если
lim +j \fn(x)-f(x)\dx = O,
Для четной функции f(x) имеет место
равенство F(y) = Fc(y) (при у < О Fc(y) продолжается
четным образом); для нечетной f(x) имеет место
равенство F(у) = iFs(у) (при у < 0 Fs(y)
продолжается нечетным образом). В общем случае /(х)
разлагается на сумму четной и нечетной функций:
у (/(*)
/(-*)),
Отсюда следует, что
при этом Gc(y) есть косинус-трансформанта Фурье
функции д (х), a Hs (у) — синус-трансформанта
Фурье функции h(x). Следовательно, можно в
принципе ограничиваться косинус- и
синус-трансформантами Фурье.
Свойства трансформант Фурье.
1. Если f(x) абсолютно интегрируема в
интервале ( — оо, +оо), то функция
F(y)-
1/2* J
f(x)eixydx
непрерывна при — оо < у < + оо и стремится к
нулю при у -> + оо.
2. Если для некоторого натурального числа п
функции f{x) и x"f (x) абсолютно интегрируемы
в интервале ( — оо, +оо), то F(y) n раз
дифференцируема и все производные F' (у),..., Fin) (у)
стремятся к нулю при у -> + оо.
3. Если f(x) и первые и - 1 производных
стремятся к нулю при х -* + оо, а п-я производная
/(и)(х) в интервале (— оо, + оо) абсолютно
интегрируема, то lim y"F (у) = 0.
у -> ± оо
lim Fn(y) =
(Fn, F являются трансформантами Фурье функций
/„, соответственно /), причем Fn{y) равномерно
сходятся к непрерывной функции F(y) на числовой
прямой.
Теорема о дифференцировании. При
преобразовании Фурье операция
дифференцирования преобразуется в умножение на независимое
переменное; точнее говоря, если j (х) кусочно
дифференцируема, / (х) и f'(x) имеют
трансформанты Фурье, и если G{y) есть грансформанта
Фурье функции/'(х), то G(y)= —iyF{y), где F(y)
есть трансформанта Фурье функции /.
Преобразование Фурье bR" (общая
теория). Рассмотрим множество ?(R") так
называемых быстро убывающих функций на R":
в (R-)
(R-); sup | x*D°j (х) | < со};
xeR"
а = (аь...,ос„),
^ О,
х» = *?•... ?, D'/=~T---V. 1*1= !>•
dxix...dxnn ' = 1
При /(x)eS(R") трансформанта Фурье F(>')
(j = (>ь...,у„)) определяется посредством формулы
F(jO = —L=- f/(x)f1<x^^x,
где <х, у} = X х)Уг
Теоремы, аналогичные указанным для R1,
остаются справедливыми.
4.4.2.2. Таблицы трансформант Фурье.
Встречающиеся в таблицах сокращения пояснены в конце
раздела.
ТАБЛИЦЫ ТРАНСФОРМАНТ ФУРЬЕ
427
К осин ус-преобразование Фурье
J(x)
( 1, 0 < х < а,
\ 0, х > а
( х, 0 < х < 1,
< 2 - х, 1 < х < 2,
[ 0, х > 2
Г 0, 0 < х < а,
) —, х > а
К X
1
( —, 0 < х < а,
1 0, х>а
СО, 0 < х < а,
) , х > а
(а + хУ1 (а>0)
(а-хГ1 (а>0)
(а2 + х2)-'
(а2 X2)
Ъ Ь
Ь2 + (а-хJ Ь2 + {а + хJ
а + х а — х
Ъ2 + (а + хJ ' Ъ2 + (а - хJ
(а2 + х2)-1/2
Г (а2-х2Уи2, 0<х<а,
(О, х>а
х~\ 0<Re v< 1
е ах
F w = у 7 | -^(х) cos (хз>) ^
]/2 sin(ay)
-У^СЦау)
W
1С (ау)
V'y
1 - 1С (ay)
V'y
У— [-si (ay) sin (ay) - Ci (ay) cos (ay)]
|/|- |cos (ay) Ci (ay) + sin (ay) i^- + Si (ay) jl
]/n sin (ay)
|/2 ,
/2я c"to cos (ay)
\/2пе-ь>яп{ау)
|/| K» to)
1/yJ.M
|/Isin(^.)rA_v)/-.
1/I_JL__
|/ л a2 + у2
428
. РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Продолжение
е-Ьх_е-ах
X
е-ах
l/x
хпе~ах
x"-le-~
1
X
U x
2
g
f In x, 0 <
{ 0, x>
Inx
(x2-a2)
(х2-а2Г>
^ln(l+x
In
a + x
b-x
.-.nx
I
1 e*-
x< 1,
1
X
n —
a
n(toc)
/(x)
F (y) = /— / (x) cos (xy) dx
V n J
0
1 ln( + yl)
^'"V^ + J-V
fa + (a2+y') V'2
/-n!a" + 1 (a2 +y2)-(n+1) ) (-\)mC2nm+l (Ц
|/-| Г (v) (a2 + y2)"v/2 cos U arctg — j
]/2k
V2 2
~2~a e
g (cos У lay — sin l/2ay)
1/T Si(y)
l/y V ^ /
l/y — (sin (ay) Ci (ay) - cos (ay) si (ay))
l/y — {sin (ay) [Ci (ay) - In (ab)] - cos (ay) si (ay)}
j/S [(Ci (y)J + (si (y)J]
/ I-*- [cos (by) — cos (ay)~\ + cos (by) Si (by) +
' + cos (ay) Si (ay) — sin (ay) Ci (ay) —
"~ / 2 И a^ + "T 'n (fl2 + ^2) + У arctg ( —)
sin (by) Ci (by)\
ТАБЛИЦЫ ТРАНСФОРМАНТ ФУРЬЕ
429
Продолжение
/(*)
F (у) = /— / (х) cos (ху) dx
р ~ by р~ аУ\
Ь2-х2
|/2я
(cos (
- 2 |/2я si (
1 -
1 — cos (ay)
У
sin (ax)
x sin (ax)
— e~ab ch (by), у <a,
-I/- e~by sh(afe), y>a
sin (ax)
x (x2 + fe2)
y<a,
y>a
x sin (ax)
J_r__a_±JL
L2 + (a +
{a -yJ J
-arctg —
sin2 (ax)
2]/ln
sin (ax) sin (bx)
1 . (a + bJ- у2
—— In гт2 .т
sin2 (ax)
У > 2a
430
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Продолжение
/(*)
¦nl
f (x) cos (xy) dx
sin3 (ax)
- {(.v + За) In {у +-3а) + (у - За) In | у - За | -
- (у + а)\п(у + а) - (у - аIп\ у - а\
sin3 (ax)
— \/ — (За2 — у2), 0 < v < а,
y = a,
y>3a
1 - cos (ax)
1 - cos (ax)
— (a - у), у < а,
cos (ax)
n e~ab ch (by)
1/т-
У1
к e~hych (ab)
e bx cos (ax)
i • +.__L_ 1
- yJ fc2+(a + ).J"j
6x cos (ax)
+e2aby
^yctg(ax)
>-) (e2ab - 1)-
sin (ax2)
sin [a A - x2)]
|/2a
1 / я J
— cos I a + -r+ -j—
2a V 4 4й
sin (ax2)
sin (ax2)
ТАБЛИЦЫ ТРАНСФОРМАНТ ФУРЬЕ
431
Продолжение
fix)
е~ах sin (bx2)
cos (ax2)
cos [a A - x2)]
e-cos(fcx2)
1 . fa\
— sin —
x \xj
1 . fa\
sin 1 — 1
(jsH4)
1 (a\
—— cos -
j/x ^ /
Vj/x^ Vх/
—— sin (a j/x)
sin (a [/x)
X
—=¦ cos (a |/x)
j/x
^-cos (b \/x)
j/x
,-а^со8(а/х)
-a j/x
[cos (a j/x) - sin (a j/x)]
j/x
f(y)= /— /(x)cos(xy)^x
0
1 2 2 2-1
-Лг- [sin B l/^) + cos B ]/7y) - e~2 Vay]
2 ]/y
—X— [sin B^) + cos B ]/a~y) + e~2V<*y]
2 у а
—?-rr- [cos B ]/ay) - sin B j/ay) + e~2*ay~\
— [cos B у'ay) - sin B \/ay) + e Vayi
2 j/a
¦iHS*($)-'(S-e)]
432
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Сыну с-преобразование Фурье
Г 1, 0 < х < а,
@, х > а
Г х, 0 < х < 1,
< 2 - х, 1 < х < 2,
1 0, х > 2
1
X
| ~, 0<х<а,
(.О, х > а
С 0, 0 < х < а,
1 —, х > а
У. X
1
f ——, 0<х<а,
(О, х>а
С 0, 0 < х < а,
(я + х) {а >ф
(я-х) (а>0)
X
7Гхт
(а2-х2Г1
b b
b2 +~G/ ~'xlr ~ bT+(c7~+~\j~2
а + х а — х
Ь2 + (а + хJ Ъ2 + {а- хJ
F(y) = |/^- J fix) cos (xy)dx
0
1/2 1-cos (ay)
V к у
4J/|y-2sinysin2^
Щ
Щ Si (ay)
-Щ si (ay)
1
2S (ay)
1 - 2S (ay)
fy
2 ]/~y
U— [sin (ay) Ci (ay) - cos (ay) si (ay)]
l/-|- Г sin (ay) Ci (ay) - cos (ay) f-y + Si (ay) j
1/— — [sin (ay) Ci (ay) - cos (ay) Si (ay)]
|/2я t?"*1*' sin (ay)
]/2n e~by cos (ay)
ТАБЛИЦЫ ТРАНСФОРМАНТ ФУРЬЕ
433
Продолжение
fix)
X
а2 — х2
1
х (а2 - х2)
1
х (а2 + х2)
x~v, 0 < Re v < 2
е-ах
X
X
|/х е~ах
е-ах
х^Хе-ах
1
е 2 A-е~хГ1
2
хе ах
-1/2 я,*
x~il2e a"
F (у) = L/-^- / (x)-sin (xy) rfx
0
- U^j cos (ay)
] / я 1 - cos (ay)
|/ 2
1/я 1-е~ау
у 2 a2
|/я a2+y2
I 2 2^ )
' w = 0 \a J
/— Г (v) (a2 + vz) sin v arctg —
V n ' L aA
-4=- th (я.у)
|/2я
|/I JL,-,'^
. ./'I ^
- —- e * [cos ]/lay + sin j/2a>']
I/-- e * sin |/2av
434
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Продолжение
fix)
{
n x, 0 < x < 1,
X x > 1
lnx
X
In x
j/x
x(x2 -a2) ln(bx)
x(x2-a2y1ln(—\
eax In x
In
In
a + x
b-x
a + x
a — x
i ln(a + xJ
x2 \ a — x J
In
1
X
2 + x2 + x \
72+X2-xJ
X
U
2 + (b + xJ \
2 + (b — xJ /
n | 1 - a2x2
X2
sin (ax)
X
1/2 +f
^ 00 — If — I / (x) sin (xy) dx
0
1/7 a(y)-c-
V * у
-In у
1 /тс
— 1/ -у (С + In у)
1 Гтс ~|
l/y [cos (ay) (In (ab) - Ci (ay)) - sin (ay) si (ay)]
— /— [cos (ay) Ci (ay) + sin (ay) si (ay)]
1?*Ы—Ш-«-т'-"Ч
Viil
n ( —- J + cos (by) Ci (by) - cos (ay) Ci (ay) 4- sin (fey) Si (by) -
,t — sin (ay) Si (ay) + — [sin (by) + sin (ay)]}
]/ln
sin (ay)
[1 — cos (ay) — ay si (ay)]
-rj/4 . /jA
— 1/— [C + In (ay) - cos (ay) Ci (ay) - sin (ay) Si (ay)]
l/S [С + In (ay) - Ci (ay)]
-4=r-ln
у + а
y-a
ТАБЛИЦЫ ТРАНСФОРМАНТ ФУРЬЕ
435
Продолжение
f(x)
j/(x)sin
(ху) dx
sin (ax)
_
— a, у > а
sin (ях)
— sin y, 0 ^ у < 7t,
sin (ax)
- sh (by), 0 < у < а,
-sh (ab), у > а
e bx sin (ax)
]/2n
e~bx sin (ях)
e'bxl sin (ax)
fib
2b
sin2 (ax)
— |/2л, 0<у<2а,
> 2a
sin (ax) sin (bx)
' 0, 0 < у < a - b,
— |/2я, a - b < у < a + b,
0, у > a + b
sin (ax)
-4 ^~ [(J' + 2«)ln СУ + 2a) + (y - 2a) In | у - 2a | - 2y In y~\
sin2 (ax)
а-^У 0<v<2a,
у >2а
cos (ax)
0, 0 < у < а,
j- 1/2я, у = a,
436
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
Продолжение
x cos (ax)
sin (ax2)
sin (ax2)
X
cos (ax2)
cos (ax2)
X
f(x)
( 1/t e~by ch {abX
|/2LCUJ-SU
\h\c(y2\ s(y2
mLcU;+sU
a c-a2/By)
lyfy
+00
F(y)=\/— /(x)sin(xy)ax
0
0 < у < а,
у > а
)*-№M4)]
NT
Преобразование Фурье. В большинстве случаев оно может быть составлено указанным в 4.4.2.1
способом из косинус-преобразования Фурье и синус-преобразования Фурье.
/(х)
Г А, а < х < Ь,
\ 0, х<аих>Ь
Г х", 0 < х < Ь,
[О, х<0йх>6
(и=1, 2,-3, ...)
гтт-, Re v > 0
(а + ix)v
7—1-гт^, Re v > 0
(а - jx)v
F(y) = \/bz [f{x)eix4x
-^=-(,--^)
у]/2и
| ft,/"'*-* у>0,
1 0, у < 0
Га у > а
Обозначения, используемые в таблице:
С - постоянная Эйлера (С = 0,57721...);
+ 00
F(z) = J е~Ч2~1йг, Rez > 0 {гамма-функция);
где /v(z) — e iny>l2Jv{zein/2) (функции Бесселя мнимого
аргумента)',
1 Г cost ,
— —г-dt,
2п J lA
у
]/2п
. (интегралы Френеля)',
ОБЩИЕ ПОНЯТИЯ
437
Si(x) =
Г sin r
J t
Ci(x)= -
(интегральный синус);
cos t
Г cos 1
J ~
dt [интегральный косинус).
4.4.3. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4.4.3.1. Общие понятия. Преобразование Лапласа
является интегральным преобразованием, которое
тесно связано с преобразованием Фурье и
обладает аналогичными свойствами. Оно очень часто
используется в технических дисциплинах, в
особенности в электротехнике и технической кибернетике.
Комплекснозначная функция f(x) действительного
переменного t называется оригиналом, если она
определена при t ^ 0, интегрируема на @, + со) и
имеет экспоненциальный порядок:
\f(t)\^Kest, s = const. D.93)
Функцию
F{p)= J e-X
D.94)
где р — комплексный параметр, называют
изображением (иногда трансформангой) оригинала f(t)
и пишут F(p) = L [/(*)]. Интеграл D.94) абсолютно
сходится при Re p > s, где s — постоянная из
D.93). Следовательно, изображение F(p) существует
в полуплоскости Re p > s. Изображение F(p) в этой
полуплоскости является аналитической функцией от
р, которая стремится к нулю при Rep->+oo
и остается ограниченной в любой полуплоскости
Re p. ^ .s0, где s0 > s.
Следующие девять теорем являются основанием
для широкой применимости преобразования
Лапласа. Названия теорем соответствуют
операциям, которые выполняются над функциями-
оригиналами.
1. Теорема о сложении (линейность
преобразования)- L[alfl{t) + a2f 2{t)~\ =
2. Теорема о свертке:
-x)f2(z)dx =L[/!(r)]L[/2@], i.e. свертке во
множестве оригиналов соответствует обычное
произведение функций во множестве изображений.
3. Теорема об интегрировании:
L J / (т) Jx = —F(p), F(p) = L[/]. Следовательно,
Lo АР
интегрированию в области оригиналов
соответствует деление изображения на независимое
переменное.
4. Теорема о дифференцировании:
Qn~lfo — - — pfo{n2)—fo{nl\ где
/bk) = lim -—-г- Эта теорема является одним
f-»+0 dtk
из важнейших обоснований описанных в 4.4.3.-2
применений преобразования Лапласа к решению
обыкновенных дифференциальных уравнений с
начальными условиями.
5. Теорема о запаздывании: L\_f(t —
b)] b[()l
6. Теорема о подобии: При а > О имеет
место формула L\_f(at)] = —F( — 1.
7. Теорема о смещении: L[e~uf(t)\ =
8. Теорема об умножении: L\_t"f(t)~\ =
9. Теорема о делении: Если для —f(t)
выполнимо преобразование Лапласа, то имеет место
+ 00
формула L —f(t) = F(q)dq.
Пример. Справедлива формула L A) =
Р
Для того чтобы получить отсюда L[jn\ принимаем во
внимание, что -~\—) = (-1)" -~гг- Тогда по теореме об умно-
«F \Р/ Р
жении получаем, что L[f~\ — —^j- Отсюлл, согласно
теореме о смещении, имеем L[tTx'r"] = г"~Т\йм"
(р + К)
Этот пример показывает, что зачастую изображения
можно находить без сложного вычисления ninei рила
Лапласа, а лишь путем использования теорем 1-9.
Обратное преобразование Лапласа.
Оригинал при преобразовании Лапласа.
определяется по своему изображению однозначно. Имеет
место следующая теорема об обращении
преобразования Лапласа (комплексная формула
обращения).
Если F(p) — аналитическая функция в области
Re р ^ 5, lim F(p) = 0 равномерно относительно
|р|-»со
s + ioo
arg р и j | F(p) 11 dp | < + oo, то F(p) является
изображением для функции
s+ia
fit)
2ni J
eptF(p)dp.
Особую значимость для приложений имеет
обратное преобразование дробно-рациональных
функций относительно р. Такую функцию
достаточно разложить на элементарные дроби и,
воспользовавшись теоремой о сложении, ограничиться
обратным преобразованием элементарных дробей.
Функцию-оригинал для элементарной дроби можно
взять из таблиц, например из 4.4.3.3.
Пример 1. Найдем функцию-оригинал F[p)
1
I
1
1
Pip + «)'
. Оригинал находится по
Р (р + я) ар о(р + а]
теореме о сложении при помощи таблицы из 4.4 3 3
f(t) = ±-(\~e~at).
438
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
4.4.3.2. Применение преобразования Лапласа к
решению обыкновенных дифференциальных
уравнений с начальными условиями. Большое
преимущество при решении задачи Коши для
обыкновенных дифференциальных уравнений
посредством преобразования Лапласа состоит в том,
что искомое частное решение получают
непосредственно, а не подгоняют общее решение к
заданным начальным условиям.
Пусть задано линейное дифференциальное
уравнение n-го порядка с постоянными
коэффициентами (а0 Ф 0, п > 0) aoy{n)(t) + aiyin~l){t) + ...
... + an-iy'(t) + any{i) = f(t) и начальными
условиями у@) = уо, /@) = /о,...,У"-1)@) = з;о(и~1).
Применение преобразования Лапласа к
дифференциальному уравнению с учетом теоремы о
дифференцировании и начальных условий приводит
во множестве изображений к уравнению вида
+ Уо(аоРп~
) (аор
при этом Y(p) = L[y(f)] - изображение искомого
решения, F{p) = L[/(f)] - изображение правой
части исходного уравнения, a Q(p) = аорп + а^рп~1 + ...
... + ап — характеристический многочлен
дифференциального уравнения. Отсюда получается, что
^ ^Q(P) Q(p)
Если yl (О и >>2 @ являются оригиналами
функций 1/0(р) и P(p)/Q(p) (они могут быть получены
разложением на элементарные дроби), то для
искомого решения, согласно теореме о свертке,
получается формула
Решения Y1(p),...,Yn(p) этой системы должны
быть затем подвергнуты обратному
преобразованию для того, чтобы получить решения
yi{t\...,yn(t) исходной задачи Коши.
Пример 2. ?(t) + 2y(t)mf(t\ где/@-2[(* + 1)/ +
+ A + 2;)], >>@)-1. Преобразование Лапласа приводит к
уравнению рУ(р)-1 + 2У(р)« L[/@], откуда Y(p)~
г-+ —Цк Согласно таблице из 4.4.3.3 и теореме
р + 2 р + 2
о свертке, получаем, что
y(t) ш e-2t + 2 J«ra(|-T)[(T + \)e%2 + A + 2т)]</т.
о
Вычисление интеграла завершает поиск решения задачи:
y(t) ш / + 2г.
Пример 3. /*)(t) + 2y"'(t) + 2y"(t) + 2y'(t) + y(t)mQt
где у@)-/@)«0, /@)«-2, /'@)-4. Преобразование
Лапласа дает
(р4 + 2р3 + 2р2 + 2р + 1) Y(p) - -2р.
Характеристический многочлен имеет корень -1 кратности
два и простые корни ±i. Следовательно, Y(p)m
-2р
™ г* Разложение на элементарные дроби имеет
-2р
вид
Сравнивая коэффициенты, находим /4-0, 6-1, С - -1,
0-0, т.е. У(р)«
получается в итоге
~
-. По таблице из 4.4.3.3
,у@-*<?"'-sin*.
Пример 4. Решить задачу Коши для системы
Так как правые части системы имеют простой вид, то
она может быть легко преобразована:
рУ1(р)+Уа(Р)--1-г+
При этом F(p) вычислять не нужно.
Совершенно аналогично можно решать систему
дифференциальных уравнений с постоянными
коэффициентами. Если задана система уравнений
У\ @ + «1 \У\ (t) + ... + alnyn{t) = /i (t),
УМ + ап1У1 (t) + ... + annyn(t) = fn(t)
с начальными условиями yt @),...,yn@), то
преобразованием Лапласа она переводится в систему п
линейных алгебраических уравнений относительно п
искомых изображений Yг (р),..., Yn (p):
(р + flll) Y^p) + al2Y2(p) + ... + alnYn(p) =
= Fx (p) + yi @),
«2iУi (P) + (P + a22) Y2(p) + ... + a2nYn(p) =
Y i (p) + an2 Y2 (p) + ... + (p + ann) Yn (p) =
РУ1(Р)+У*(Р)--
Отсюда получаем
Yl(p)m7jL
а(Р) - ^1 (Р)
Раскладывая на простейшие дроби:
р2-р + 2 А Вр + С
(Р - t)(p3 + 1) р - 1 р* + \'
и приравнивая коэффициенты, получаем Л - 1, fi - 0, С - -1,
-Ц а * , . Из таблицы находим
т. е. Yx (р) ш —^ j-*—-. Из таблицы
р — 1 р + 1
>>! @ »• е1 - sint. Оригинал y3(t) непосредственно указан в
таблице: у2(Oncost.
4.4.3.3. Таблица обратного преобразования
Лапласа дробно-рациональных функций. Функции в таблице
расположены по возрастанию степени знаменателя.
Таблица является полной вплоть до степени
знаменателя, равной 3, а также содержит несколько
функций, знаменатели которых — многочлены
степени 4.
ТАБЛИЦЫ ОБРАТНОГО ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
439
М/Ю]
i
р
1
р + а
1
Р2
1
Р (Р + л)
1
(р + rt) (р + Ь)
Р
{р + rt) (p + Л)
1
(Р + «J
____Р
(р~ + иJ ~
1
Р _ _
1
р2 + а"
1
(р4-/>J"+~я2"
1
?'
1
р2 (р 4- rt)
1
р (р 4- rt) (p 4- Ь)
1
Р (Р 4- rtJ
1
(р 4- rt) (p + /))(/? + с)
Р
(р 4- rt) (p 4- h) (p 4- 0
Р2
(р 4- rt) (р 4- h) (р + с)
1
(р 4- rt) (р 4- ЬJ
Р
(р + rt) (p 4- ЛJ
я2
(р 4- rt) (р + ЬJ
1
(pTrtF
р
(Р + яK
N
Я»
1
e-at
t
— d-e )
(„-at <,-bt\
Ь — rt
a — b
te~at
e~M {I -at)
— sh {at)
ch (яг)
1
— stn (at)
a »
cos (at)
— е~ы sin(rtf)
e "' 1 cos (at) sin (at) J
i'2
1 , -at
a2
1
rtfc (rt — b)
a2
Пr h\ i'~at 1 In r\ r~bt 1 (h n\ r~ct~\
(a-b)(b-c)(c-a) l[C b) l ' (" ° C ' (& fl) C J
1 h(ft ")f-|fc(r ,):-,:(, b)r-l
(rt - b) (Ь - с) (с - rt)
Xn2 ir h\ c~at 1 h2 (a r\ r~bl 1 r2 ^/i л^ г~сЧ
(rt - ft) (ft - f) (c - rt)
1
(b-rtJ (t ' {b a)tl )
1
i nr~at 1 Г/j I ht (h n\ я~*П1
(ft - rtJ l ^ ' Lfl ' ЬГ F ^ ° h
\
(b - aJ
440
РЯДЫ ФУРЬЕ, ИНТЕГРАЛЫ ФУРЬЕ И ПРЕОБРАЗОВАНИЕ ЛАПЛАСА
L [/ (г)]
fit)
Рл
(Р + с,)'
р [(/> + bJ + а2]
(р + а) (р2 + h2)
(Р + и) [(р + hJ + с2]
р
(р + а) [{р + hJ НЬ с2]
Р2
(Р + а) [(р + ЬJ + с2]
/>3 (р + а)
1
Р2 iP + a) iP + b)
1
р2 (р + аJ
1
(р + аJ (р + Ь):
1__
(Р + оL
J
(р + о
ip2 +
ip2 +
Тр2~+
ip2 +
1
р
(?Т
Трг+
[(У+~
P2ip2
fL
а2
а2
с?
а2
а2
'с?
с?
Ь)
+
1
)ip2 + b2)
Р
) ip2 + b2)
р_2______
р*
) ip2 + b2)
Т
Т
1
'Та'У
а2)
(l-2at+ ~
-A -c
а2 + Ь2
l-ae'"' + a cos ibt) + b sin (ht)"]
a2 + b'
- (a2e '" - ab sin ibt) + h2 cos ibt))
I Г lf _hl / ч a-b _ht . . Л
- -3 2~ e - e C0S СГ + e Sln («¦')
(/) - aJ + с2 L <" J
> Г ,, hi ab-b2-c2 ы . . 1
ar-flp + f2 [-^-'" + «- cos (cf) , sm (cr)J
'г-—у- a
ib - ar + с |_
+ i(ct - bJ + c2 - a2) e~hl cos ict) -
II 1
jt + —
a a set
a+k 1 1 _<<f 1 .„,
~c7h*+ ~с^Ь~1 + a2 ib - a) * b2 (a - b) e
~2~t A + e'"') + -3~
1 2-1
2- — sin (at) - -r sin (/>0
- cr [ a b J
t
cos («0 - cos ibt)~\
— a sin («r) + b sin (/>r)]
b2 - a
1
1
b2 - a2
[-«2 cos iat) + Л2 cos ibt)]
1 Г1 . 1
—-у-\ — sin (at) — t cos (at)
2a2 la J
27'sin (at)
— B cos (at) — at sin («r))
е~ы Г 1 1
-yi- — sin («') - r cos («')
sin (at))
a J
5. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
5.1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
5.1.1. СЛУЧАЙНЫЕ СОБЫТИЯ
И ИХ ВЕРОЯТНОСТИ
5.1.1.1. Случайные события. Многие явления в
природе, технике, экономике и в других областях
носят случайный характер, т. е. невозможно точно
предсказать, как явление будет происходить.
Оказывается, однако, что течение и таких
явлений может быть описано количественно, если
только они наблюдались достаточное число раз
при неизменных условиях. Так, например, нельзя
при бросании монеты предсказать, выпадет «герб»
или «цифра». Однако если бросать монету очень
часто, то можно заметить, что отношение числа
бросаний с выпадением «цифры» к общему числу
бросаний мало отличается от 1/2 и тем менее
отклоняется от 1/2, чем больше совершено
бросаний.
Теория вероятностей дает математическую
модель для описания случайных явлений такого
рода в объективной действительности. Так как
многие реальные процессы подвержены случайным
воздействиям, то основы этой теории важно знать
специалистам, занимающимся естественными,
техническими, а также и общественными науками.
Случайный эксперимент, или опыт, есть процесс,
при котором возможны различные исходы, так что
заранее нельзя предсказать, каков будет
результат. Опыт характеризуется тем, что его в
принципе можно повторить сколько угодно раз. Особое
значение имеет множество возможных, взаимно
исключающих друг друга исходов опыта.
Возможные, исключающие друг друга исходы
опыта называются его элементарными событиями.
Множество элементарных событий обозначается
через Е.
Пример 1. Однократное бросание игральной кости.
Возможные исключающие друг друга исходы этого опыта -
выпадения одного из чисел 1, 2, 3, 4, 5, 6. Множество Е
состоит из шести элементарных событий еи е2, е3, е4, es, e6,
причем элементарное событие et означает: выпадает число /.
Пример 2. Одновременные бросания двух игральных
костей. Множество Е элементарных событий состоит здесь
из 36 элементов еи, ех2> ••»*'бб> причем элементарное
событие еи означает: на первой кости выпадает /, а на
второй j.
Примерз. Определение длительности службы
электрической лампы. Элементарные события можно отождествить
с множеством положительных чисел, дополненным
символом + 00.
Помимо элементарных событий, часто
интересны события более сложной природы, например
в случае игральных костей событие «выпадает
четное число» или в случае определения
длительности службы лампы событие «длительность
службы не менее 3000 часов».
Пусть осуществляется некоторый опыт, и пусть
Е - множество его элементарных событий. Каждое
подмножество А с Е называется событием.
Событие А происходит тогда и только тогда, когда
происходит одно из элементарных событий, из
которых состоит А.
Пример 4. В примере 1 подмножество А = {е2, е4, е6]
образует событие «выпадает четное число». Событие
«выпадает четное число» в случае двух игральных костей
происходит тогда и только тогда, когда происходит одно
из элементарных событий, содержащихся в подмножестве
А = {eij\i +j четно}. В примере 2 подмножество
Л = We» *64» ?55* *5б» ^65» ^бб} множества Е может быть
интерпретировано как событие «сумма выпавших очков не
менее 10».
В примере 3 А — C000, + оо] может быть
интерпретировано как событие «электрическая лампа служит больше
300с часов».
Подмножества Е, а следовательно, и само ?,
и пустое множество 0 интерпретируются, согласно
общему определению, как события. Так как Е
состоит из всех элементарных событий, а при
каждом опыте обязательно происходит одно из
элементарных событий, то, таким образом, Е
происходит всегда. Такое событие называется
достоверным событием', его мы будем обозначать
буквой U. Пустое множество 0 не содержит
элементарных событий и, следовательно, никогда не
происходит. Такое событие называют невозможным
событием; его мы будем обозначать буквой И
Пусть Аъ А2,...,А„ — события, т.е.
подмножества некоторого фиксированного множества Е
элементарных событий. Тогда объединение
A j (J A2 (J ... (J Ап снова есть событие, так как оно
является подмножеством Е. Объединение
Ai\J A2(J...(jAH происходит тогда и только
тогда, когда происходит хотя бы одно из
событий Аь А2,..., А„. Событие Ах (J A2 (J ... (J AH
называют суммой событий Аи А2,...,А„. Его часто
обозначают А\ + А2 + ... + А„.
Точно так же пересечение А1 f] А2 (*)... f] А„
событий Ai есть снова некоторое событие.
Пересечение Ах 0 А2 (~)... f] An происходит тогда и
только тогда, когда происходят одновременно все
At. Событие Aj f] A2 [)... f] An называется
произведением событий Аи А2,...,А„. Его часто
обозначают так: А1А2...Ап.
Пример 5. Пусть при определении длительности
жизни Ах есть событие «продолжительность жизни лежш
между 0 и tj», a A2 — событие «продолжительность жизни
442
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
лежит между tx и f2»; тогда Ai\J А^ есть событие
«продолжительность жизни лежит между 0 и t2».
Пример 6. Если при одновременном бросании двух
костей Ах есть событие «сумма очков не менее 11»,
а Аг - событие «выпадает одинаковое количество очков»,
то Aif]A2 есть событие «выпадают две шестерки».
Пример 7. Пусть в случае двух игральных костей
Ах есть событие «сумма выпавших очков не более 2»,
а А2 - событие «сумма выпавших очков не менее 5»;
тогда A if] А 3 есть невозможное событие: Ах(\Аг»У.
Два события Ах и А2 называются
несовместными, если A1f\A2 = V, т.е. если события Ах
и А2 не могут произойти одновременно.
Если А — некоторое событие, то дополнение
А = Е\А также является подмножеством Е, т.е.
некоторым событием. Событие А происходит тогда
и только тогда, когда не происходит А; А
называется событием, противоположным
(дополнительным) А. События А и А всегда
несовместны: A f) A = V.
Пример 8. Если при каком-нибудь измерении А
есть событие «измеренная величина не менее о», то Л есть
событие «измеренная величина менее о».
Для действий со случайными событиями (суммы,
произведения, дополнения) справедливы формулы
элементарной теории множеств:
. A[JB = B\JA, Af]B = Bf]A
(коммутативность),
(ассоциативность),
= (Af]C)[j(Bf]C),
(A f] B)[j С = (A [j С) f](B[jQ
(дистрибутивност ь),
A[jB = Af]B, A[)B = A\JB
(формулы де Моргана),
A[JA = U, Af)A = V.
Для того чтобы построить теорию
вероятностей, нужно событиям поставить в соответствие
вероятности, которые будут давать количественную
оценку возможности их осуществления. Если Е
несчетно (как, например, в опыте «определение
продолжительности службы электрической лампы»),
то не всем подмножествам Е разумно ставить
в соответствие вероятность. Нужно ограничиться
определенным классом событий. События этого
класса называются случайными событиями. Они
являются предметом теории вероятностей. Если Е
конечно, то этот класс совпадает с классом всех
событий. Оказывается, что класс случайных событий
всегда можно выбрать так, чтобы, во-первых,
не появилось никаких математических трудностей
при введении вероятностей и, во-вторых, чтобы все
интересующие нас на практике события находились
в выбранном классе, т. е. являлись случайными
событиями в математическом смысле. Поэтому
для естествоиспытателя и инженера важно знать,
что все интересующие его случайные события
являются также случайными в смысле
математической теории, так что изложенная ниже
аксиоматика теории вероятностей применима к ним.
5.1.1.2. Аксиомы теории вероятностей. Пусть опыт
повторяется п раз и при этом подсчитывается,
как часто происходит интересующее нас событие.
Допустим, что оно произошло т раз. Отношение
— = Wn(A) называется относительной частотой
п
(или кратко — частотой) случайного события А в п
опытах. При этом 0 ^ ^„(/4) ^ 1. Практика
показывает, что во многих случаях при увеличении п
частота приближается к некоторому постоянному
значению. В свое время понятие вероятности
случайного события пробовали определить как
предел частоты. Это привело, однако, к
теоретическим и математическим трудностям, которые не
удавалось преодолеть. В современной теории не
делается попыток дать определение понятию
вероятности; его считают основным понятием,
удовлетворяющим некоторым аксиомам.
Формулировка аксиом, принадлежащая А. Н.
Колмогорову, опирается на следующие свойства частоты,
которые можно рассматривать как опытные факты:
1. Для больших п частота ^„(Л) колеблется
все меньше около определенного значения.
2. Wn(U)=\.
3. Wn(A[J В) = Wn(A) + Wn{B), если Л и В
несовместны.
Аксиомы теории вероятностей.
1. Каждому случайному событию А поставлено
в соответствие число Р (А), 0 ^ Р (А) ^ 1, которое
называют вероятностью А.
2. Вероятность достоверного события равна 1:
P(U)=i.
3. Аксиома аддитивности. Если Аъ
А2, ..., А„, ... — попарно несовместные случайные
события, т. е. At f] Aj - V при i Ф j, то
E.1)
Для конечного числа попарно несовместных
событий Ль А2, ..., А„ аксиома аддитивности дает
соотношение
P(Ai U /42(J---U/1'«)=='P^i) + P(^2)+-
в частности,
откуда следует, что P(V) = 0, т. е. вероятность
невозможного события равна нулю. Из E.1) следует,
что Р(А (J А) = Р(А) + Р(А), так как А и А
несовместны. Учитывая, что A (J A = U, и аксиому 2,
получаем
Р(Л)= 1 -РИ). E.2)
Для произвольных (не обязательно попарно
несовместных) случайных событий Аг, А2, ..., Ап имеет
место неравенство
E.3)
Фактическое определение вероятности некоторого
случайного события чисто теоретически часто
невозможно. В этих случаях необходимо произвести
достаточное число испытаний и принять
относительную частоту рассматриваемого события в
качестве приближенного значения вероятности. Так,
например, нет ни математической, ни
биологической теории, которая позволяет вычислить априори
вероятность Р(А) случайного события «рождение
близнецов». Для определения Р(А) нужно
использовать статистику большого числа рождений и под-
УСЛОВНЫЕ ВЕРОЯТНОСТИ
443
считать, как часто происходило это событие. Тогда
соответствующую частоту можно приблизительно
принять за вероятность Р (А). Определение Р (А) по
частоте иногда называется «статистическим
определением» вероятности. Речь здесь, однако, идет не
об определении вероятности, а об ее оценке
(см. 5.2.2).
5.1.1.3. Классическое определение вероятности
события. Если опыт таков, что он подразделяется
только на конечное число элементарных событий,
которые к тому же являются равновероятными, то
говорят, что речь идет о классическом случае. Для
опытов этого типа теорию вероятностей
разрабатывал еще Лаплас. Примерами таких опытов
являются бросания монеты (два равновероятных
элементарных события) или бросания игральной кости
(шесть равновероятных элементарных событий).
В классическом случае из аксиом для вероятности
Р(А) события А получаем
Р(А)= —
число элементарных событий,
благоприятных для А
E.4)
число всех возможных элементарных
событий
При этом под «элементарными событиями,
благоприятными для А», понимают такие события,
осуществление которых ведет к осуществлению А;
иными словами, это события, из которых состоит А
(понимаемое как подмножество Е). Лаплас
использовал E.4) для определения вероятности. (Формула
E.4) непригодна, например, в случае фальшивой
игральной кости.)
П р и м е р 9. Пусть правильная игральная кость брошена
один раз, и пусть А есть событие «выпадает четное число».
Благоприятными для А являются элементарные события е2,
е4, е6. Всего имеется шесть возможных элементарных
событий. Следовательно, Р (А) = 3/6 « 1/2.
Пример 10. Пусть одновременно бросают две
игральные кости, при этом выигрыш выплачивается, если сумма
выпавших очков не менее 10. Как велика вероятность
выигрыша? Имеется 36 элементарных событий. Благоприятными
для А являются элементарные события е4в» еб*> ?35> е5б> ?(,$-,
ебб. При этом etJ означает: на первой кости выпадает i, на
второй j. Тогда Р (А) = 6/36 = 1/6.
В классическом случае часто используют формулы
комбинаторики, например, для того, чтобы вычислить число всех
возможных элементарных событий.
Пример 11. Игра в лото: угадать «к чисел из л»,
например спортлото 6 из 49. Какова вероятность получить
главный выигрыш, указав к чисел правильно? Имеется одно
благоприятное событие, при котором происходит выигрыш
главного приза игры. Число всех элементарных событий
равно числу возможных выборок к чисел из п чисел без
учета порядка и без повторов, т. е. равно С*. Таким
образом, вероятность главного выигрыша в спортлото равна
1 1
CU 13983816"
5.1.1.4. Условные вероятности. Вероятность
некоторого случайного события А, как правило,
изменяется, если уже известно, что произошло
некоторое другое случайное событие В.
Вероятность А при условии, что событие В с
вероятностью Р(В)Ф0 уже произошло, обозначается
Р (А/В) и называется условной вероятностью А при
условии В.
Пример 12. Пусть одновременно бросают две
игральные кости. Пусть А — событие «сумма очков не менее 10»,
В - событие «сумма очков четная». Если известно, что В
произошло, то для А имеется 18 возможных элементарных
событий (например, е1х возможно, а е12 нет); из них
благоприятными для А являются eA6t e6*, ess, е6ь-
Следовательно, Р(/4/В) = 4/18 = 2/9.
Пример 13. Пусть имеются две урны. В первой
находятся пять белых и пять черных шаров, во второй - один
белый и девять черных. Опыт состоит в том, что наугад
выбирается урна и наугад из нее вынимается шар. Пусть В
есть событие «вынутый шар белый» н А, - события «шар
вынимается из i-й урны» (i - 1, 2). Тогда Р{В/АУ) = 5/10 =
= 1/2,/>(В/Л2)= 1/10.
Условная вероятность удовлетворяет
следующим соотношениям (которые можно считать
определением):
Р(А(^В)
Р (Л/В) = -~^-А Р (В) Ф 0, E.5)
Р\В)
E.6)
Если их разрешить относительно Р(А^\В), то
получают правило умножения:
Р [А П В) = Р (В) Р (А/В) = Р(А)Р (В/А), E.7)
т. е. вероятность произведения двух случайных
событий равна произведению вероятности одного
события на условную вероятность другого при
условии, что первое событие произошло.
Два случайных события А и В называются
независимыми, если осуществление одного не
влияет на вероятность осуществления другого, т. е.
если
Р(А/В) = Р(А). E.8)
Тогда правило умножения имеет вид
Р(А()В) = Р(А)Р(В), E.9)
т. е. вероятность произведения двух независимых
событий равна произведению их вероятностей. Так
как формулы E.8) и E.9) эквивалентны, то для
определения понятия «независимость двух
случайных событий» часто используется соотношение
E.9).
Случайные события Ах, А2, ..., А„ называются
независимыми в совокупности, если для каждого т
и каждой m-комбинации /ь ..., im, где 1 < ^ < ... <
< im ^ п, выполняется соотношение
Случайные события Ах, А2, ..., А„ называются
попарно независимыми, если для произвольных /, j
(i Ф j) At и Aj независимы.
Из независимости в совокупности следует
попарная независимость, но не наоборот.
5.1.1.5. Полная вероятность. Формула Байеса.
Предположим, что достоверное событие Е можно
представить в виде суммы п попарно несовместных
событий, т. е. U = Ах (J A2 [j ... (J Ап, где At f] Aj =
= Кпри / Ф j. Тогда для любого случайного
события В выполнено соотношение
В = (Alf]B)[j(A2 C\B)\J... U (Anf)B).
Согласно аксиоме аддитивности, отсюда следует,
что Р (В) = ? Р (В Р) Л,). Если применить формулу
E.7), то получим
Р(В)= Y,P(Ai)P(B/Ai).
E.10)
444
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Эта формула называется формулой полной
вероятности.
Пример 14. Пусть даны три урны I типа: два белых
и шесть черных шаров; одна урна II типа: один белый и
восемь черных шаров. Пусть наудачу выбирается урна,
а оттуда - шар. Обозначим через В событие «вынутый шар, —
белый»; его вероятное!ь Р(В). Обозначим через Ах событие
«выбрана урна I типа», а через А2 — событие «выбрана урна
II типа». Тогда B = (Bf]Ai)\J(Bf]A1I так как Axf)A2 = V.
Следовательно,
Р(В) = Р(АХ)Р(В/АХ) + Р(А2)Р(В/Аг).
Но />(/!,) = 3/4, Р(Л2)
= 1/9. Окончательно:
: 1/4; Р(В/АХ) ш 2/8 = 1/4, Р(В/А2) -
F{U>- 4 4 + 4 9 " "*-
31
144'
Пусть предпосылки закона полной вероятности
выполнены. Тогда можно вычислить вероятность
события А( при условии, что событие В произошло.
Для этого служит формула Байеса, или формула
вероятности гипотез:
Р(Аг)Р{В/Ад
P{AJB)=-
E.11)
Пример 15. Проводится гот же эксперимент, что и
в примере 14. Пусть вынут белый шар. Какова вероятность
того, что он вынут из урны I типа?
Р{АХ)Р(В1АХ) + Р{А2)Р(В/А2)
_27_
ЗГ
4 9
5.1.2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Действительное переменное, которое в
зависимости от исхода опыта, т. е. в зависимости от
случая, принимает различные значения, называется
случайной величиной.
Пусть X — некоторая случайная величина.
Функцией распределения F (х) случайной величины X
называется функция
F(x) = Р{Х <х). E.12)
Значение функции распределения в точке х0, таким
образом, равно вероятности того, что случайная
величина принимает значение, меньшее х0. В
теории вероятностей случайная величина полностью
характеризуется своей функцией распределения,
т. е. может рассматриваться как заданная, если
задана ее функция распределения. При помощи
функции распределения можно указать вероятность
того, что случайная величина попадает в заданный
полуоткрытый промежуток:
= F(b)-F(a).
E.13)
Функция распределения F {х) произвольной
случайной величины обладает следующими свойствами:
1)
= 0.
lim F(x)=l, lim F (x) -
X —*¦ + 00 X —» — 00
2) F(x) монотонно не убывает, т. е. при
имеет место неравенство F(xl)^F(x2).
3) F(x) непрерывна слева.
5.1.2.1. Дискретные случайные величины.
Случайная величина X называется дискретной, если
она может принимать только конечное или счетное
множество значений. Таким образом, она
характеризуется значениями хь х2, ..., которые она может
принимать, и вероятностями рг = Р (X = х,), с
которыми она принимает эти значения и которые
должны удовлетворять условию ?р^=1.
Однозначное отображение множества х,- на множество р,-
рассматривается как функция вероятности
дискретной случайной величины. Для функции
распределения дискретной случайной величины имеем
F(x)= ? Pi-
EЛ4)
Суммирование производится по всем i, для
которых х,- < х. Таким образом, F (х) является
ступенчатой функцией со скачками высотой pt
в точках х, (рис. 5.1).
5.1.2.1.1. Индикатор события. Пусть А -
некоторое случайное событие, где Р (А) = р.
Случайная величина
"to,
если А происходит,
если А не происходит,
называется индикатором А (характеристической
случайной величиной). Возможными значениями
являются 0 и 1; соответствующие вероятности: р0 =
= Р(Х=0)=1-р, Pl=P(X=\) = p.
5.1.2.1.2. Биномиальное
распределение. Пусть некоторый опыт повторяется п раз
и отдельные опыты этой серии не зависят друг
от друга. Пусть в каждом опыте может произойти
или не произойти событие Л, а вероятность его
осуществления в отдельном опыте не зависит от
номера опыта и равна р. Пусть Х(п) — число
наступлений события А в такой серии из п опытов.
Очевидно, что возможные значения случайной
величины Х(п) суть числа О, 1, 2, ..., п. Вероятности
Р(п, к) = Р(Х{п) = к) вычисляются по
биномиальному закону:
=\-p
0,
п).
E.15)
Случайная величина называется биномиально
распределенной с параметрами пир, если
возможные значения О, 1, ..., п она принимает с
вероятностями Р(п,к), задаваемыми формулой E.15).
Параметры пир полностью определяют
биномиальное распределение. На рис. 5.2 показаны
«полигоны» биномиальных распределений для п =
= 20 и различных р. При этом соответствующие
НЕПРЕРЫВНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
445
р=0,9
Р (и, к) отложены по ординате и соединены
ломаной линией.
Начиная с Р (и, 0), вероятности Р (п, к) могут
быть легко вычислены по следующей рекуррентной
формуле:
Pin. к) <„-* + 1)р
Р(п,к-1)
kq
Пример 16. Вероятность рождения мальчика равна
0,515. Как велика вероятность того, что из десяти наугад
выбранных новорожденных будет шесть мальчиков?
Предположение независимости может считаться выполненным.
Следовательно, для искомой вероятности имеем Р(А) = РA0,6) =
= С?о @,515N @,485L % 0,2167.
Пример 17. В урне N шаров, из которых ровно М
белых. Из урны п раз вынимался шар и после регистрации
снова возвращался в урну. Какова вероятность события, что
белый шар был зарегистрирован к раз? Эта вероятность
Р(п, к) вычисляется при помощи биномиального закона
E.15):
E.17)
^J(l-^-) (fc-0.1 п).
Биномиальный закон описывает в самой общей
форме осуществление признака в выборке объемом
п с возвратом.
Пример 18. Пусть вероятность получения
бракованного изделия равна 0,01. Какова вероятность того, что среди
100 изделий окажется не более трех бракованных? Согласно
биномиальному закону и закону сложения, получаем, что
Р(Л) - С?оо@,01)°@,99I00 + С|оо@,01I @,99)" +
+ С?Оо@,01J@,99)98 + С?оо@,01K@,99)97 = 0,9816.
5.1.2.1.3. Гипергеометрическое
распределение. В урне находится N шаров, из
которых ровно М белых. Пусть один за другим
без возврата (или одновременно, что одно и то же)
вынимается п (< М) шаров. Тогда вероятность
того, что среди этих вынутых п шаров будет к
белых, равна
/-•к s-n — k
Pn,M(п> *) = М "~М (к = 0, 1, ..., п). E.18)
CN
Случайная величина называется распределенной
гипергеометрически, если возможные значения 0,
1, ..., п она принимает с вероятностями Рдг д/(л,к),
определяемыми формулой E.18). Числа N, М, п —
параметры распределения.
Гипергеометрическое распределение, таким
образом, описывает осуществление признака в
выборке без возврата. Если N очень велико по сравнению
с п, то не имеет существенного значения,
возвращаются шары обратно или нет, и формула E.18)
может быть приближенно заменена формулой E.17)
биномиального распределения.
5.1.2.1.4. Распределение Пуассона.
Случайная величина называется распределенной по
закону Пуассона, если она принимает счетное
множество возможных значений 0, 1, 2, ... с
вероятностями
|= —е-" (к = 0,1,...).
E.19)
Число X называется параметром распределения.
Распределение Пуассона может использоваться
в качестве хорошего приближения биномиального
распределения, если п велико, а р мало. Тогда
в качестве X нужно взять пр (см. 5.1.5).
Пример 19. Машина проехала 100000 км. Пусть X —
число проколов шины на этом расстоянии. Тогда X можно
считать случайной величиной, распределенной по закону
Пуассона (с подходящим X), т. е. вероятность трех проколов
шины равна ^г-е'^.
Пример 20. Рассмотрим пример
= 0,01. Таким образом, 1000,01 = 1,
I3
18. Имеем п = 100,
-L + JL= 0,9810,
1°
0! '
что дает хорошее совпадение с точным значением, однако
вычисляется гораздо быстрее.
Распределение Пуассона затабулировано для
различных X (таблица в 1.1.2.5).
5.1.2.2. Непрерывные случайные величины.
Случайная величина называется непрерывной, если ее
функцию распределения (интегральную функцию
распределения) можно представить в виде
F(x)= lf{t)dt.
E.20)
Неотрицательная интегрируемая функция f(x)
называется плотностью распределения. Так как
lim F(x) = 1, то должно выполняться условие
> + 00
E.21)
При заданной плотности вероятности в силу
E.13) и E.20) вероятность того, что случайная
Рис 5.3
величина попадает в заданный промежуток, равна
(рис. 5.3)
ь
Р(а^Х <b) = F(b)-F(a) = f/(x) dx. E.22)
а
Вероятность Р(Х = а), т. е. вероятность того, что
непрерывная случайная величина равна заданному
446
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
действительному числу, всегда равна 0. Отметим,
что из равенства Р {А) — 0 не следует, что А
является невозможным событием, хотя P(V) = 0.
Для любого р из интервала @, 1) наименьшее
число хр, для которого F (хр) = р, называется р —
квантилью непрерывной случайной величины х.
5.1.2.2.1. Равномерное распределение.
Случайная величина называется равномерно
распределенной на [а, Ь], если ее плотность вероятности
Ь-а
О а Ь х
Рис. 5.4
на [а, 6] постоянна, а вне [а, Ь] равна 0 (рис. 5.4).
Так как J fix)dx = 1, то
- оо
1
/(*) =
b-a'
5.1.2.2.2. Нормальное распределение
(распределение Гаусса). Случайная
величина называется распределенной нормально, если она
имеет плотность вероятности следующего вида:
f{x) =
E.23)
здесь а и а — параметры распределения.
Функция E.23) представляет собой колоколооб-
разную кривую. Параметр а - точка максимума,
через которую проходит ось симметрии, параметр
ст - расстояние от этой оси до точки перегиба.
Если ст мало, то кривая высокая и заостренная;
если ст велико, то она широкая и плоская. Рис. 5.5
-з
-г
/
-/
0,8
0
У
Рис. 5 5
показывает нормальное распределение при а — О
и различных ст.
Если случайная величина X имеет нормальное
распределение с параметрами а и ст, то говорят,
что X распределено нормально согласно закону
N(х; а, ст), и пишут: XeN(x; а, ст). Функция <р(х) =
= е~х /2 (а = 0, ст = 1) называется плотностью
нормированного и центрированного нормального
распределения. Плотность вероятности (р (х) и соот-
X
ветствующее распределение Ф (х) = J <р (г) dt зата-
- оо
булированы (см. таблицы в 1.1.2.6.1 и 1.1.2.6.2).
Функцию Ф часто называют гауссовым интегралом
ошибок (таблица в 1.1.2.6.2 дает Ф0(л:)= —р=.-х
\ ]/2я
х j е~'2/2 dt, Ф (х) = Фо (х) + — 1. Особое значение
о 2/
нормального распределения в теории и практике
основывается в значительной степени на
центральной предельной теореме (см. 5.1.6; там также даны
примеры нормального распределения случайной
величины).
5.1.2.2.3. Экспоненциальное
распределение. Случайная величина называется
экспоненциально распределенной, если она имеет
следующую плотность вероятности:
(Хе"Хх при х ^ О,
/00 = ]
10 при х < 0.
Число X называется параметром распределения.
О 1 2 3 X
Рис 5.6
П р и м е р 21. Длительность службы электролампы
можно рассматривать с хорошим приближением как
экспоненциально распределенную величину. На рис. 5.6 показана
плотность вероятности экспоненциального распределения
сХ-1.
5.1.3. МОМЕНТЫ РАСПРЕДЕЛЕНИЯ
5.1.3.1. Дискретный случай. Пусть X есть
дискретная случайная величина с возможными
значениями хь х2, ... и рк = Р(Х = хк).
Число v, = ? х1крк называется (в случае абсо-
к
лютной сходимости ряда) i-м начальным
моментом случайной величины X (или ее распределения)
0=1,2,...).
Число [1,- = ?(хк - Vifpk называется i-м цент-
к
ральным моментом X.
Особое значение имеют первый начальный
момент Vi и второй центральный момент ji2.
5.1.3.1.1. Математическое ожидание.
Первый начальный момент
называется математическим ожиданием X и
обозначается через MX. Математическое ожидание
определяет положение центра распределения в
следующем смысле: если считать рк массами,
помещенными в точках хк действительной оси, то MX —
координата центра тяжести этой системы.
Свойства математического
ожидания.
1) Математическое ожидание постоянной а
(которую можно считать дискретной случайной вели-
НЕПРЕРЫВНЫЙ СЛУЧАЙ
чиной с одним возможным значением а,
принимаемым ею с вероятностью 1) равно этой
постоянной:
Ма — а.
2) Математическое ожидание суммы равно
сумме математических ожиданий:
М (Xi + Х2) = МХХ + МХ2. E.24)
3) Математическое ожидание произведения
постоянной величины на случайную величину равно
произведению постоянной на математическое
ожидание случайной величины: М(аХ) = аМХ.
4) Математическое ожидание произведения двух
независимых случайных величин равно
произведению их математических ожиданий:
Х2) = (МХ1)-(МХ2). E.25)
П р и м е р 22. Биномиальное распределение с параметра-
ми и, р:
E26)
П р и м е р 23. Гипергеометрическое распределение с
параметрами N, М, л:
MX у
Пример 24. Распределение Пуассона с параметром X:
E.28)
Таким образом, параметр X здесь имеет значение
математического ожидания.
ет мало
1 ,
12
MX
а)
C бела/f о
¦ 1
0123456781
MX
S)
Рис 5 7
5.1.3.1.2. Дисперсия. Второй центральный
момент называется дисперсией случайной величины
X и обозначается через DX, т. е.
DX = X (хк - MXJ рк = М(Х - MXJ. E.29)
Для вычисления дисперсии часто полезна
следующая формула:
DX = MX2 - (MXJ. E.30)
Корень квадратный из дисперсии называется
разбросом, или стандартным отклонением, или
средним квадратичным отклонением и обозначается
через ох-
<5X = ]/DX. E.31)
Величина ст (или DX) есть мера рассеяния
распределения относительно математического
ожидания. На рис. 5.7 показано дискретное распределение
с малым (а) и большим (б) рассеянием.
Свойства дисперсии.
1) Дисперсия постоянной величины равна нулю:
2) Дисперсия произведения постоянной
величины на случайную величину равна произведению
квадрата постоянной величины на дисперсию
случайной величины:
D (аХ) = a2DX.
3) Дисперсия суммы постоянной а и случайной
величин равна дисперсии случайной величины:
D(a + X) = DX.
4) Дисперсия суммы двух независимых
случайных величин равна сумме дисперсий этих величин:
D(Xl
DX2.
Пример 25. Биномиальное распределение:
DX - j? (k - прJ C№<f-k - npq, E.32)
\ E.33)
Пример 26. Гипергеометрическое распределение:
Пример 27. Распределение Пуассона:
DX ш X, ах - jA. E.35)
5.1.3.2. Непрерывный случай. Пусть X -
непрерывная случайная величина с плотностью
вероятности f(x). Тогда величина
v(=7 xif(x)dx E.36)
называется (в случае абсолютной сходимости
интеграла) /-м начальным моментом случайной величи-
+ оо
ны X [i = 1, 2, ...). Величина ц, = J (x-vl)if{x)dx
называется i-м центральным моментом случайной
величины X.
5.1.3.2.1. Математическое ожидание.
Первый начальный момент
Vl =MX= J xf{x)dx
E.37)
называется математическим ожиданием случайной
величины X. Математическое ожидание MX дает
положение центра тяжести распределения массы,
которое задается «плотностью распределения
массы» f(x).
448
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Математическое ожидание в непрерывном
случае обладает теми же свойствами 1) — 4), которые
были отмечены для дискретного случая.
Пример 28. Равномерное распределение на [а, Ь]:
ь
J Ь-а 2
Пример 29. Нормальное распределение N(х; а, а):
+ 00
J угпа
— 00
Следовательно, параметр а имеет значение математического
ожидания.
Пример 30. Экспоненциальное распределение:
MX
о
5.1.3.2.2. Дисперсия. Второй центральный
момент
ц2 = DX = f (х - MXJf(x) dx E.38)
- ao
называется дисперсией случайной величины X.
Величина у DX = а называется разбросом, или
стандартным отклонением, или средним квадратичным
отклонением случайной величины X. Справедлива
формула
DX = М (X - MXJ = MX2 - {MXJ. E.39)
Дисперсия в непрерывном случае обладает теми
же свойствами 1) - 4), которые были отмечены для
дискретного случая.
Пример 31. Равномерное распределение на [а, Ь]:
Пример 32. Нормальное распределение N(х; я, а):
DX- f (х - аJ —±г-е- <* - e)M2a»)rfx » a*.
J ^a
Параметр а имеет здесь значение разброса ах-
Таким образом, нормальное распределение полностью
определено заданием математического ожидания и среднего
квадратичного отклонения.
Пример 33. Экспоненциальное распределение: DX -
- 1А2.
5.1.4. СЛУЧАЙНЫЕ ВЕКТОРЫ
(МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ)
Совокупность (Х1, Х2, ..., Хп) случайных
величин называется п-мерным случайным вектором.
Такой случайный вектор может быть
охарактеризован своей п-мерной функцией распределения:
F(xu ...,
P(Xl<xl, ..., Х„<х„). E.40)
Функцию F(хи х2, ..., х„) часто также называют
кратко распределением вектора (Хх, ..., Х„) или
совместным распределением величин Хи ..., Хп.
Если рассматривать величины Хи ..., Х„ как
координаты некоторой точки в л-мерном евклидовом
пространстве, то положение точки {Хи ..., Хп)
зависит от случая, а значение функции F(xb ..., хн)
есть вероятность того, что точка оказывается в
полуоткрытом параллелепипеде Хх < хъ ..., Хп<хп
с ребрами, параллельными осям. Вероятность того,
что точка окажется в параллелепипеде я, ^ Xt < Ь,
(/= 1, 2, ..., п), определяется формулой
Р(ах ^Хх <Ьи ..., an^Xn<bn) = F(bu ..., bn) -
E.41)
здесь piii2 ik = F(clt ..., cn) A ^ U < i2 < ... < ik ^ n),
где с,- = at , ct = at , ..., ct = a,-, а все остальные
c,-bj.
Для двумерного случайного вектора, в
частности, получаем
P(fl! ^Xl< bu a2^X2< b2) =
= F (Ьь Ь2) - F {Ьи а2) - F (аи Ь2) + F (аи а2).
Свойства п-м ерной функции
распределения.
1) lim F(xu ..., х„)= 1, lim F(xu...,xn) = 0.
Xj-* + 00 Xj-* — 00
7=1,...,л ;=1,...,м
2) F(xu ..., х„) монотонно не убывает по
каждому переменному.
3) F(xu ..., xj непрерывна слева по каждому
переменному.
4) Для произвольных я„ bh at < bt (i = 1, ..., и),
правая часть равенства E.41) неотрицательна.
5.1.4.1. Дискретные случайные векторы.
Случайный вектор (Хь ..., Х„) называется дискретным,
если все его компоненты являются дискретными
случайными величинами. Если х^] (к = 1, 2, ...) —
возможные значения j-й компоненты, то функция
вероятностей ptl.../n вектора (Хи ..., Х„)
определяется следующим образом:
Pix in = P{x,= xi;\ x2 = х%\ .., хп = х|;>).
Для функции распределения по аналогии с E.14)
справедливо соотношение
F(xu...,xn)= Z Pi, /• <5-42)
х% < Ч
к= 1, 2, ...,п
Суммирование производится по всем наборам ik,
для которых х\кк] < хк для всех / = 1, 2, ..., п.
П р и м е р 34. Полиномиальное распределение. Пусть в
некотором опыте всегда происходит одно из попарно
несовместимых событий Аи ..., Ак. Пусть р(-Р(А(). Так как
Ai\J...\jAkmUuAlf\AJmVnp№l+JtTO
l Пусть
опыт проводится п раз, причем отдельные опыты этой серии
являются независимыми. Обозначим через Х( число
реализаций А, (/-1 к) в п опытах. Тогда каждая из
случайных величин Xj может принимать только конечное
множество значений 0, 1 п. Таким образом, вектор (Хи ...
.,., Хк) является дискретным случайным вектором. Для его
функции вероятностей имеем
гР\-Р
t + /д + ... + /» « л. E.43)
Случайный вектор с функцией вероятностей E.43)
называется полиномиально распределенным.
ГРАНИЧНЫЕ РАСПРЕДЕЛЕНИЯ
449
5.1.4.2. Непрерывные случайные векторы.
Случайный вектор называется непрерывным, если его
функцию распределения можно представить в виде
F(xb...,xn) = J ... f /(*ь..., g*!...^;
— 00 —00
/(хь ..., х„) называется плотностью распределения
вектора (Хи ..., Х„) или совместной плотностью
величин Хи ..., Х„. Вероятность того, что
случайный вектор (Я*!, ..., Хп) окажется в области G
«-мерного пространства, можно записать
следующим образом:
.,xjdxl...dxn. E.44)
Поэтому плотность должна удовлетворять условию
7 ...+f/(x1,...,xll)rfx1...dx1,= l. E.45)
Пример 35. Равномерное распределение. Вектор (Хи ...
..., Х^ называется распределенным в области G равномерно,
если он имеет плотность, постоянную в G и равную 0 вне G.
В силу E.45) эта постоянная должна быть равна l/V(G), где
V(G) - объем области G.
Пример 36. Нормальное распределение. Вектор (Хи...
..., Х„) называется нормально распределенным, если он имеет
плотность вида
Се~ Q (*ь • • •»*¦).
! хя)
E.46)
Здесь Q — некоторая положительно определенная
квадратичная форма от х, - «,, ..., х„ - ан (at — постоянные),
постоянную С можно вычислить из условия E.45). В случае п = 2
Рис. 5.8
плотность нормального распределения может быть приведена
к следующему виду (определение ак, ок, р см. в 5.1.4.4;
рис. 5.8):
, E.47)
5.1.4.3. Граничные распределения. Пусть F(xb ...
..., х„) — функция распределения случайного
вектора (Хи ..., Хн). Тогда
P(Xh<xh, ..., Xik<xik) = F(cu ..., с„)
A < i! < i2 < ... < i* < и),
где cj = xf , ..., Cj = xf , а все остальные с, = + оо,
называется к-мерным граничным распределением
F(xb ..., х„). Оно является функцией распределения
fc-мерного случайного вектора (Х,^, ..., А^). В
частности, при к = 1 получаются распределения
отдельных компонент:
, +оо, ..., хь +оо, ..., +оо) =
В дискретном случае функцию вероятностей /с-мер-
ного граничного распределения получают
суммированием по индексам, номера которых отличны
от |ь ..., ik; в непрерывном случае плотность
граничного распределения получают
интегрированием по переменным, номера которых отличны от
*ь ..» ik-
Общее число /с-мерных граничных
распределений равно Cj.
П р и м е р 37. Пусть дана двумерная дискретная
случайная величина (Хи Х2) с функцией вероятностей pik =
= P(Xt =* x\l), Х2 = хк{г)). Тогда функции вероятностей
отдельных компонент получаются как граничные
распределения:
Р{ХХ = АХ)) = ^Лъ Р(Х2 = 42)) - ^ А*.
П р и м е р 38. Пусть задана трехмерная случайная
непрерывная величина с плотностью f(xu хг, хг). Тогда,
например, плотность вектора (Хь Х2) получают как двумерное
+ 00
граничное распределение: g (хь х2) = J J\xu x2, x3) dx3,
Плотность третьей компоненты получают также как граничное
+00+00
распределение: h(x3)= f f /(хь х2, x3)dxxdx2.
— оо — оо
5.1.4.4. Моменты многомерной случайной
величины. Особый интерес представляют первые и
вторые моменты. Если случайный вектор (Хь ..., Хп)
дискретен, то числа
называются первыми начальными моментами
(Хи ..., Х„). В непрерывном случае первые
начальные моменты определяются формулой
= J •••
E.49)
0=1,..., n);
v, являются математическими ожиданиями
отдельных компонент: v, = MX у
Вторые начальные моменты vy и вторые
центральные моменты \ijk определяются следующим
образом :
дискретный случай:
., v v(j)v(t)n /с сл\
Vjk = 2_, ХУ'Х\ Pi j , (D.DUj
j'l, . ., in
непрерывный случай:
vjt = j ... j xjxkf(xlt ...,xn)dXl...dxn, E.52)
+ 00 +00
= J ... J {Xj - Vj) (xk ~ vk)/(xb ..., х„) dxx... ^хи.
E.53)
Говорят, что соответствующие моменты
существуют, если интегралы в правых частях E.48) -
E.53) сходятся абсолютно. Имеем
\iJk = M l(Xj - MXj)(Xk - MX,)] =
= М (XjXk) - MXjMXk = vjk -
15 И Н Бронштейн, К. А. Семендяев
450
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Величины цп равны дисперсиям отдельных
компонент:
Ил = DXj = a].
Величина \ijk = vjk — VjVk называется ковариацией
(корреляционным моментом) случайных величин
Xj, Xk и обозначается через co\(Xj, Xk). Матрица
II К/* \\j k = i . ,п называется матрицей ковариации
(корреляции). Параметр
_ cov (Xj, Xk) E54)
J ]/DXjDXk
называется коэффициентом корреляции между Xj
и Xk. Он лежит между —1 и +1.
Две случайные величины X и У называются
некоррелирующими, если их коэффициент
корреляции (их ковариация) равен нулю.
П р и м е р 39. Параметры в формуле E.47) для плотности
двумерного нормального распределения имеют следующие
значения: ах = МХи а2 = МХ2, ах = ]/DX~u o2 = ]/ЪТъ a
р = C°v' b^-ii (коэффициент корреляции между Хх и Х2).
В случае n-мерного нормального распределения для
плотности E.46) имеем
~ у Е Ьц (xi - at) (xj - aj)
f(xu...,xH) = Ce ' ;
здесь параметры а{ и bi} имеют следующие значения: а{ =
= МАГ,, Ьи = Лу/Л, где Л = det (Д,Д (Ау) - матрица
алгебраических дополнений матрицы ковариации. Таким образом,
л-мерное нормальное распределение, так же как в
одномерном случае, полностью определено заданием первых и вторых
моментов.
5.1.4.5. Условные распределения. Пусть (X, Y) -
случайный вектор, a F (х, у) - его функция
распределения.
Функция
F(x/y)= lim
Р(Х
Y<y + h)
Y^y +
E.55)
называется условным распределением X при условии,
что У принимает значение у. Аналогично
определяется F(y/x).
В дискретном случае для условной функции
вероятностей имеем
Pik
Pik
E.56)
В непрерывном случае для условных плотностей
имеем
f(x/y)= т^~
*, У)
x, у)
-.E.57)
Sf(x,y)dx
В знаменателях формул E.56) и E.57) стоят
граничные распределения компонент, определяющих
условие.
5.1.4.6. Независимость случайных величин.
Случайные величины Хи ..., Х„ называются
независимыми (ср. E.9)), если
F(xu ..., xw) = F1(x1)...Fw(xn), E.58)
где Fj (jcj) — функция распределения i-й компоненты
Xi (одномерное граничное распределение). В то
время как в общем случае о совместном
распределении, если известны распределения отдельных
компонент, ничего сказать нельзя, в случае
независимости случайных величин функция F(xb ..., х„)
полностью определена через распределения
отдельных компонент.
Пример 40. Ведется стрельба по мишени.
Допустим, что вертикальное отклонение X и горизонтальное
отклонение У относительно центра имеют нормальное
распределение
XeN(x; 0, at), YeN(y; 0, a2).
Можно считать, что X и Y независимы. Тогда для
плотности вектора (X, У), обозначающего место попадания
пули, имеем
\/2п<у2
Следовательно, (X, Y) распределено нормально с
параметрами ai = а2 = 0, аь ст2, р = 0.
Примечание. Независимость в практических
случаях обосновывается не проверкой E.58), а рассуждениями
или статистическими тестами. Тогда равенство E.58) считается
следствием.
Для независимых случайных величин
справедливы некоторые очень важные и часто
используемые теоремы о математическом ожидании и
дисперсии. Если X и У независимы, то
M(XY) = MXMY.
E.59)
Отсюда и из определения ковариации тотчас
следует: из независимости X и У вытекает
некоррелированность X и У
В случае нормального распределения из
некоррелированности следует и независимость, что
становится очевидным, если в формулу E.47)
подставить р=0и применить функциональное равенство
для экспоненты.
Дисперсия суммы независимых случайных
величин равна сумме дисперсий, т.е. D(Xi + ...
... + Хп) = DXt + ... 4- DXm если Хи ..., Хп
независимы.
5.1.4.7. Регрессионная зависимость. Для многих
явлений в природе и технике типичны
стохастические (случайные) зависимости. Между двумя
случайными величинами имеется стохастическая
зависимость в общем случае тогда, когда
существуют некоторые случайные факторы, которые
влияют на обе случайные величины, и
некоторые факторы, действующие только на первую или
только на вторую случайную величину.
Следовательно, если
X=f(Zu ..., Zm, Xlt ..., Xj),
Y = g(Zu ..., Zm, Уь ..., УД
то X и У стохастически зависимы. В теории
регрессии особое значение имеет задача: предсказание
интересующей нас случайной величины У, если
другие случайные величины, от которых стохастически
зависит У, приняли конкретные значения.
ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
451
5.1.4.7.1. Линии регрессии. Кривые в
плоскости х, у, определяемые уравнениями
называются линиями регрессии У относительно X и
соответственно X относительно У При этом
M(Y/X - х) - математическое ожидание У при
условии, что X приняло значение х. В случае
непрерывных X и У имеем
yf(y/x)dy,
M(X/Y=y)= J xf(x/y)dx.
При этом f(x/y) или f(y/x) — условные плотности.
Линии регрессии имеют следующий смысл:
наилучшее предсказание У при условии, что X = х0 есть
у{х0). При этом «наилучшее» означает, что для
произвольной функции и(Х) справедливо
неравенство М(У- и(Х)J ^ М(У- у(Х)J. Это можно
выразить и так: функция регрессии у(х) есть
функция, минимизирующая среднюю
квадратичную ошибку величины предсказания Уна основании
значений X. Соответствующим образом можно
интерпретировать и х(у).
5.1.4.7.2. Прямые регрессии. Случайные
величины X и Y называются линейно
коррелированными, если линии регрессии являются прямыми.
Эти «прямые регрессии» задаются следующими
уравнениями:
регрессия Уотносительно X: у — цу +
E.60)
регрессия X относительно У: х = \ix + $х/у(у ~ Иу)»
E.61)
величины Ру/Х и Рлуу называются
(теоретическими) коэффициентами регрессии. Они
вычисляются следующим образом:
СУ у
-—
Р>
СТ v
При этом р есть коэффициент корреляции X и У:
и сх — yDX, <Ту=|//)У Входящие в формулы
E.60), E.61) параметры \ix и Цу — математические
ожидания X и У: ц# = MX, \iy=MY.
В том случае, когда Хи Уне являются
линейно коррелированными, по формулам E.60) и E.61),
используя E.62) и E.63), можно составить уравнения
двух прямых. Они также называются линиями
регрессии и в этом случае являются линейными
аппроксимациями истинных линий регрессии.
5.1.4.8. Функции от случайных величин. Пусть
дан непрерывный случайный вектор (X, У);/(х, у) —
его плотность. Требуется найти распределение
случайных величин X + У, X ¦ Y, —.
Сумма X + Y есть также непрерывная
случайная величина, и ее плотность равна
/(z)=+f/(*> z-x)dx.
Если X и У независимы, так что f(x, у) —
= fi(x)f2(y), то
f(z)=+ffl(x)f2(z-x)dx. E.64)
Следовательно, плотность суммы есть свертка
плотностей отдельных слагаемых.
Пример 41. Пусть вектор {X, Y) распределен
нормально, а функция f(x, у) задана формулой E.47). Тогда
для плотности X + Y получаем
1 (z-jcH+a,)J
f{z) = 1 е 2 ст? + 2^^г + а§.
Следовательно, величина Z — X + У снова нормально
распределена с параметрами )/а? + 2рахо2 + oj, at + a2.
В случае независимости имеет место и обратное: если
сумма двух независимых случайных величин нормально
распределена, то и отдельные слагаемые распределены
нормально.
Произведение. Пусть (X, У) - случайный
вектор и Z = X У. Тогда для плотности имеем
Отношение. Пусть (X, У) - случайный
вектор; отношение X/Y есть некоторая случайная
непрерывная функция с функцией плотности
f(z) = +f x/(zx, x)dx- } xf(zx, x)dx.
0 -oo
5.1.5. ХАРАКТЕРИСТИЧЕСКИЕ
ФУНКЦИИ
Под характеристической функцией v|/(f)
случайной величины X понимают математическое
ожидание случайной величины е \
y\,(t) = M(eitX), E.65)
где t — действительный параметр.
Если F (х) — функция распределения X, то
J eitxdF(x).
E.66)
В случае дискретного распределения с xfc =
= k, k = 0, 1, 2, ...
Ф @ = Z
E.67)
(ряд Фурье с коэффициентами рк). В случае
непрерывного распределения
^(t)=+feitxf(x)dx E.68)
(интеграл Фурье).
Пример 42. Пусть X подчиняется закону Пуассона
с параметром X. Тогда характеристической функцией будет
E.69)
15s*
452
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Пример 43. Пусть X равномерно распределена на
{-а, а). Тогда
°Ч- dx
sin (at)
at
Пример 44. XeN(x;
ческой функцией будет
а, о). Тогда характеристи-
iat - -
E.70)
5.1.5.1. Свойства характеристических функций.
1) Характеристическая функция равномерно
непрерывна на всей действительной оси.
2) Для любой характеристической функции \|/(г)
выполняются соотношения
\|/@) = 1, |\|/(г)|^1 (-оо<*< +оо).
3) Если Y=aX + b с постоянными а и Ь, то
\J/y(t) = tyx (at) eibt {^x ~ характеристическая
функция X).
Используя характеристические функции, можно
легко вычислить моменты.
Если случайная величина X обладает моментом
порядка и, то характеристическая функция X п раз
дифференцируема по t и при к ^ п
\l/(fc)@) = ifcMx* = rV E.71)
Пример 45. Пусть X нормально распределена с
параметрами а и а. Следует вычислить MX и DX.
Согласно E.7ОХ \|r (t) = e 2 . Тогда в силу E.71)
fvj = \|г' @) = ia и - v2 = \|Л@) = - а2 - а2. Следовательно,
МX = Vl = а и DX ш v2 - v? - о2 + л* - а2 - а2.
Для приложений имеет большое значение тот
факт, что характеристическая функция суммы
независимых случайных величин равна
произведению их характеристических функций.
Если случайные величины Х1 и Х2
непрерывны, то плотность суммы, согласно E.64), есть
свертка обеих плотностей. Это свойство, таким
образом, есть не что иное, как теорема о свертке
преобразования Фурье (см. 4.4.2).
Пример 46. Применения теоремы о свертке. Пусть
случайная величина X распределена биномиально с
параметрами пир. Требуется найти ее характеристическую
функцию. Как известно, X можно интерпретировать как
число осуществлений события А в п независимых
испытаниях, если вероятность осуществления А в каждом
испытании есть р. Поэтому X можно записать в виде суммы
{0,
1,
0, если А не осуществляется в у'-м опыте,
если А осуществляется в j-м опыте.
%. причем Ы|)
q + ре", где q = 1 -p; таким образом,
По условию X} - независимые случайные величины.
Следовательно, согласно теореме о свертке, имеем \j/jf (t) =»
E72)
5.1.5.2. Формула обращения и теорема
единственности. Пусть F (х) — функция распределения, а
\|/ (t) — характеристическая функция случайной
величины X. Если хи х2 - точки непрерывности
F(x), то
1 Г e-itx1_e-itx2
F (х2) - F (Xl) = — ton - ф (Г) Л.
*Я с -» + оо J «
E.73)
Если случайная величина X непрерывна, а /(х) -
плотность F(x), то формула E.73) упрощается:
+ 00
E.74)
Таким образом, плотность получается из
характеристической функции обратным
преобразованием Фурье.
Из формулы обращения следует, что функция
распределения случайной величины однозначно
определяется ее характеристической функцией.
Если, например, каким-либо образом для X
o2t2
iat z—
получена характеристическая функция е 2 ,
то, согласно теореме единственности и формуле
E.70), XeN(x; а, а).
Пример 47. Пусть две независимые случайные
величины нормально распределены: XeN(x; au at), YeN(y;
«2» 02Х Требуется найти распределение для X + Y. Так как
то, согласно теореме о свертке,
ia2t-
аг) t - -
оЬ2
Вследствие теоремы единственности единственное
распределение, имеющее эту функцию распределения, есть N (х + у;
«1 + «2» jA*i + of). Таким образом, случайная величина
X + Y снова распределена нормально с параметрами а =
= ах Л- а2 и а = ]/а\ + а\.
Пример 48. Пусть X и Y— независимые случайные
величины, подчиняющиеся закону Пуассона:
к\ к\
Требуется найти распределение суммы X + У. По формуле
E.69) находим ^х(t) = ebi («"" l\ i|ry= «**(«*~ 0.
Вследствие независимости и согласно теореме о свертке
В силу теоремы единственности единственным
распределением, имеющим E.75) в качестве характеристической
функции, является пуассоновское распределение с
параметром Xt + Я.2. Таким образом, сумма двух независимых
случайных величин, подчиняющихся закону Пуассона, снова
распределена по закону Пуассона с параметром А.} + Х2.
Примечание. Здесь также имеет место обратное: если
сумма двух независимых случайных величин распределена
по закону Пуассона, то и слагаемые распределены по
закону Пуассона.
5.1.53. Предельная теорема для
характеристических функций. Последовательность {^„М}
функций распределения называется сходящейся
в основном к функции распределения F(x), если во
всех точках непрерывности lim FK(x) = F(x).
и-> оо
В дискретном случае сходимость в основном
FN(x) к F(x) означает, что соответствующие
ЗАКОН БОЛЬШИХ ЧИСЕЛ
453
функции вероятностей сходятся: ркп) -*¦ рк для имеем
всех к.
В непрерывном случае из сходимости в основном
следует (если /„ (х) непрерывны), что
подпоследовательность fnk(x)-+f(x) для почти всех х.
Если последовательность {Fn(x)} функций
распределения сходится в основном к функции
распределения F(x), то последовательность
соответствующих характеристических функций {\|/„(г)}
сходится к v|/ (t) - характеристической функции
F (х). Эта сходимость равномерна в каждом
конечном интервале.
Большое значение имеет обратная теорема:
если последовательность характеристических
функций {\|/„(г)} сходится к непрерывной функции
\|/(г), то при некоторых условиях
последовательность их функций распределения {Fn(x)} сходится
в основном к некоторой функции распределения
F (х) и \J/(f) есть характеристическая функция F (х).
Примечание. Условие обратной теоремы
выполняется, в частности, если выполняется одно из двух
условий:
1) {*Ы0} сходится равномерно на каждом конечном
интервале к функции \|/(f).
2){\|/n(t)} сходится к характеристической функции \|/@-
Пример 49. Пусть Р(п, fc) = CjpfoT* (fc = 0,l п) -
последовательность биномиальных распределений с
параметрами п, рщ и lim npn - X. К какому распределению
я-*оо
сходится эта последовательность? Соответствующая
последовательность характеристических функций \\iH(t)= ^„ +
+ ^*РпГ> очевидно, сходится к функции \|/ (f) = er \e ~ *).
Следовательно, предельное распределение является пуассо-
новским распределением:
Хк _х
5.1.5.4. Производящие функции. В случае
дискретных случайных величин, которые могут принимать
только значения 0,1, 2,..., часто вместо
характеристических функций используют производящие
функции.
Пусть рк является функцией вероятностей
некоторой дискретной случайной величины X
указанного типа, a z - комплексный параметр. Тогда
называется производящей функцией
случайной величины X. Функция (р (z) —
аналитическая в круге | z | < 1. Ее предел при z -> eif дает
характеристическую функцию X.
Производящие функции имеют свойства,
аналогичные свойствам характеристических функций.
5.1.5.5. Характеристические функции
многомерных случайных величин. Под характеристической
функцией п-мерной случайной величины понимают
математическое ожидание величины exp I i ? tkX
¦>
E.76)
где tu ..., ?„-действительные параметры.
Пример 50. Характеристическая функция п-мерного
нормального распределения имеет вид
¦ С i О - exp (i I aktk - -i ? bjktjt\ \ E.77)
\ * l j.k / v
где (bjk) — матрица ковариации. В частности, для п = 2
¦ (*ь h) - exp ifati + a2t2) - у
E.78)
Если Хи ..., Хп -.независимые случайные величины, то
где \К - характеристические функции отдельных компонент
X*
Если Z = Xt + X2 + ... + XH и +(tu ..., t.) -
характеристическая функция вектора (Хи ¦-, XJ, то
5.1.6. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
5.1.6.1. Закон больших чисел.
Последовательность {Х„} случайных величин называется
сходящейся по вероятности к случайной величине X,
если для любого г > 0 выполняется равенство
lim Р(|АГИ-ЛГ|<6)= 1.
я -* со
Говорят, что последовательность случайных
величин Xlt X2t ... подчиняется слабому закону
больших чисел, если для любого е > 0 справедливо
равенство
lim Pi I-
п-оо VI Л
другими словами, если
< е = 1, E.79)
zn = — ) хк — ) мхк
п / j п / j
сходится к 0 «по вероятности».
Для вывода слабого закона больших чисел важно
неравенство Чебышева. Пусть X — случайная
величина, имеющая конечную дисперсию. Тогда для
любого б > 0 справедливо неравенство
DX
—Г-.
E.80)
Теорема Чебышева. Если Хи Х2, ...—
последовательность попарно независимых
случайных величин, дисперсии которых равномерно
ограничены, т. е. DXk < С для каждого /с, то эта
последовательность подчиняется слабому закону
больших чисел.
Прямым следствием отсюда является
теорема Бернулли. Пусть т — число осуществлений
события А в п независимых испытаниях, и пусть
в каждом таком испытании А имеет вероятность
р. Тогда частота — = Wn (А) стремится «по
вероятности» к р, т. е.
lim P(\WH(A)-p\<s)=l E.81)
п -*¦ оо
для любого е > 0.
Если Хи Х2, ... —последовательность попарно
независимых случайных величин с равными мате-
454
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
матическими ожиданиями МХХ = МХ2 = ... = а, а
DXk равномерно ограничены, то для любого е > О
справедливо равенство
lim Р\
E.82)
Соотношение E.82) является теоретической
основой правила среднего арифметического при
измерениях. Пусть нужно измерить неизвестную
величину а. Из-за случайных ошибок измерения
повторяются п раз, причем отдельные измерения
независимы друг от друга: /с-е измерение может
быть описано случайной величиной Хк. Если в
процессе измерения нет систематической ошибки, то
МХк = а. Тогда, согласно E.82), построением
среднего арифметического измеренных значений
при достаточно большом п с вероятностью, сколь
угодно близкой к 1, получается значение, сколь
угодно приближающееся к искомой величине а.
Последовательность {Хп} случайных величин
называется почты наверное сходящейся к случайной
величине X, если
lim Р ( (J (| Хк - X | ^ е)) = 0 для любого е > 0.
Л -> СО \fc > л /
Говорят, что последовательность случайных
величин Хи Хъ ... подчиняется усиленному
закону больших чисел, если
E.83)
для любого е > 0,
другими словами, если —
«почти наверное» сходится к 0.
Теорема Колмогорова. Если
последовательность {Х„} независимых друг от друга слу-
00
чайных событий удовлетворяет условию / —¦?- <
Lj n
и=1
< + оо, то она подчиняется усиленному закону
больших чисел.
О связи между усиленным и слабым законом
можно сказать следующее: если
последовательность {Х„} случайных величин подчиняется
усиленному закону, то она подчиняется и слабому, но не
наоборот.
5.1.6.2. Предельная теорема Муавра — Лапласа.
5.1.6.2.1. Локальная предельная
теорема. Если вероятность осуществления события
А в п независимых опытах постоянна и равна
р@<р<1), то вероятность Р(п, k) = Ckpkq"~k
того, что в этих опытах событие А происходит
ровно к раз, удовлетворяет соотношению
lim
Р(п, к)
¦¦ 1,
E.84)
Другими словами, биномиально
распределенная случайная величина асимптотически
распределена нормально с параметрами а = пр и а =
= \/npq.
Пример 51 Пусть вероятность появления в
производстве бракованной детали равна 0,005 Как велика
вероятность того, что среди 10000 деталей 40 окажутся
бракованными? Итак, следует определить Р(п, к) при
п = 10000, к = 40, р = 0,005. Согласно E 84),
Р(и, к)»
\/2п]/npq
\_(k-
2
-прJ
npq J ^
k — пр
\/npq = 7,05, ^-^r= -1,42
]/npq
Следовательно,
P(n, /с)*
7,05
1/2»
Из табл. 1.1.2.6.1 находим ф A,42) = 0,1456 Таким образом,
Р(п, /с) = -у——% 0,0206. При вычислении по точной
формуле получаем Р(п, к) к 0,0197
5.1.6.2.2. Интегральная предельная
теорема. Пусть X — биномиально
распределенная случайная величина с параметрами пир.
(Следовательно, X можно интерпретировать как число
осуществлений события А в п независимых
испытаниях с Р (А) = р в отдельном испытании.) Тогда
равномерно относительно аиЬ(-оо < а <Ь < +оо)
выполняется соотношение
lim Р
X -пр
]fnpq
= Ф0(Ь) - Ф0(а).
E.85)
Пример 52. Пусть имеется ситуация, описанная
примере 51 Ищется вероятность того, что в ящике
10000 деталей находится не более 70 бракованных
/ -50 Х-пр _ 20
^^
\ |/49,75 ]/npq j/49,75
|/2л
-7,09
= Ф0B,84)-Ф0(-7,09)
Так как Фо (- х) = - Фо (х), то Р (X < 70) = Фо B,84) + Фо G,09).
Из таблицы найдем ФОB,84) = 0,4977; ФОG,О9) уже нет в
таблице, так как оно отличается от 0,5 крайне мало. Таким
образом, Р (X < 70) « 0,9977.
5.1.6.3. Центральная предельная теорема. Пусть
{Хп} - последовательность независимых
случайных величин, и пусть
у (xt - мх)
E.86)
где х =(к -
ГИСТОГРАММА И ЭМПИРИЧЕСКАЯ ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ
455
Величины Zn называются нормированными и
центрированными суммами {DZn = 1, MZn = 0). Пусть
Ф„(х) являются функциями распределения Zn, a
Fk (х) - функциями распределения Хк. Обозначим
Bl = Yj DXb Bn > 0- Необходимым и достаточным
условием выполнения равенства
E.87)
является следующее условие (Линдеберга): для
любого е > 0
(X-MXkJdFk(x) = 0.
k=i \X -МХк\>гВп
E.88)
Примечание. Условие выполняется, в
частности, если все Хк имеют одинаковое
распределение, у которого первый и второй моменты
конечны.
Условие E.88) означает, что отдельные слагае-
Xt - МХ(
мые ; из которых, согласно формуле
В„
E.86), состоит Zn, равномерно малы. В этом случае
смысл центральной предельной теоремы состоит
в следующем. Если случайную величину можно
представить как сумму большого- числа не
зависящих друг от друга слагаемых, каждое из которых
вносит в сумму лишь незначительный вклад, то
эта сумма распределена приблизительно
нормально.
Пример 53 Пусть проводится измерение и X —
случайная ошибка измерения Если случайная величина X
появляется в результате аддитивного наложения большого
числа не зависящих друг от друга факторов, порождающих
ошибки, каждый из которых оказывает на ошибку малое
влияние, то величину X можно считать распределенной
нормально.
Пример 54 Пусть X - длина березового листка,
случайно выбранного из некоторого множества сорванных
листков. Тогда X есть случайная величина, получающаяся
наложением многих малых, не зависящих друг от друга
факторов Поэтому для X может быть принято нормальное
распределение
5.2. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
5.2.1. ВЫБОРКИ
Задачи математической статистики состоят в
том, чтобы на основании знания некоторых свойств
подмножества элементов, взятых из некоторого
множества, сделать какие-нибудь утверждения о
свойствах этого множества, называемого
генеральной совокупностью. В генеральной совокупности
нас обычно интересует некоторый признак, который
обусловлен случайностью и может иметь
качественный или количественный характер.
Пример 55. Автомат производит валы. Множество
всех валов, произведенных при определенных, остающихся
неизменными производственных условиях, образует
генеральную совокупность Если интересующим признаком
является, например, диаметр, то этот признак имеет
количественный характер
Пример 56. Поточная линия производит охотничьи
патроны. Множество всех патронов, произведенных при
некоторых остающихся неизменными условиях, составляет
генеральную совокупность Если нас интересует способность
патрона функционировать или отказывать, то это
качественный признак.
Интересующий нас параметр некоторой
генеральной совокупности может быть представлен
в математической модели некоторой случайной
величиной X. В количественном случае X есть
сам признак; для качественного же признака,
например типа «хороший — плохой», X можно
определить так:
0, если «хороший»,
1, если «плохой».
Под случайной выборкой объема п понимается
выбор п объектов из генеральной совокупности,
причем выбор отдельных объектов производится
независимо один от другого. Результатом
случайной выборки объема п является совокупность
(хь ..., хп) значений признака.
П р и м е р 57 Совокупность @, 0, 0, 1, 0, 0, 0, 0, 0, 0)
является выборкой объема 10 из партии патронов Таким
образом, здесь девять хороших и один плохой патрон
Тот факт, что можно сделать много выборок
объема п и получить различные совокупности
значений признака, ведет к следующему
абстрактному определению понятия выборки.
Пусть имеется генеральная совокупность, в
которой признак X имеет распределение F(x).
Тогда п-мерный случайный вектор (Xlt ..., Хп), в
котором величины X, независимы друг от друга
и все имеют распределение F (х), называется
математической выборкой объема п. Каждая
реализация (хь ..., х„) случайного вектора
{Хи ..., Х„) есть выборка.
В случае, если это не вызывает недоразумений,
прилагательное «математическая» опускается.
5.2.1.1. Гистограмма и эмпирическая функция
распределения. Пусть имеется выборка (хь ..., хп) —
так называемая таблица наблюденных значений —
из генеральной совокупности с признаком X.
Пусть распределение X неизвестно. Для того чтобы
получить первое представление об этом
распределении в случае количественного признака,
составляют так называемую гистограмму. Производят
разбиение действительной оси на конечное число
граничащих друг с другом промежутков Дь ..., Ак.
Затем подсчитывают число т, выборочных
значений, лежащих вА;A ^ j'^ /с). Эти числа называются
групповыми частотами. Над А; рисуют
прямоугольник высоты mjn (относительные частоты
попадания в интервалы). Возникающий таким образом
ступенчатый график называется гистограммой
выборки.
Пример 58. Из текущей продукции авт омата была
сделана выборка в 350 валиков, признаком X является
отклонение диаметра валика от номинального размера
Табл 5 1 даег соответствующее статистическое
распределение
456
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Таблица 5.1
Статистическое распределение отклонений от номинала
350 валиков из продукции автомата
i
1
2
3
4
5
6
7
8
9
10
11
12
Д/, мм
от -0,230 до -0,210
от -0,210 до -0,190
от -0,190 до -0,170
от -0,170 до -0,150
от -0,150 до -0,130 .
от -0,130 до -0,110
от -0,110 до -0,090
от -0,090 до -0,070
от -0,070 до -0,050
от -0,050 до -0,030
от -0,030 до -0,010
от -0,010 до +0,010
Всего
Щ
3
8
19
37
53
60
64
49
31
17
7
2
350
т//«
0,009
0,023
0,054
0,106
0,151
0,171
0,183
0,140
0,088
0,049
0,020
0,006
1,000
На рис. 5.9 показана соответствующая
гистограмма.
т?/п
0,200-
Ц/00
Рис. 5.9
Удобным способом получить представление
о распределении X, приемлемом и при
качественных признаках, является построение эмпирической
функции распределения. Для данного
действительного числа х подсчитывается число выборочных
значений, меньше х. Обозначим это число через
тп (х). Функция Fn (х) = — называется эмпири-
п
ческой функцией распределения выборки (хь ..., х„).
Она является ступенчатой функцией.
О /,0 2,0 3,0 4,0 X
Рис. 5.10
Пример 59. Пусть при откармливании 10 животных
зарегистрированы следующие прибавки в массе (в
килограммах): 2,0; 2,8; 2,3; 3,4; 2,9; 2,8; 3,0; 3,2; 3,0; 2,8. На рис. 5.10
изображена соответствующая эмпирическая функция
распределения.
Функция Fn(x) может рассматриваться как
приближение истинного распределения F(x)
генеральной совокупности. Примем обозначение
Dn= max \Fn(x)-F(x)\. E.89)
— oo < x < +oo
Для любых непрерывных функций распределения
выполняется соотношение
lim P
п -* оо
raeQ(X)= ? (-1)*e~lk2^2. Отсюда вытекает,
*=-оо,
что при п -+ оо почти наверное Dn сходятся к 0;
другими словами, при п -*¦ оо последовательность
Fn(x) эмпирических функций распределения почти
наверное равномерно сходится к функции
распределения F(x) признака X в генеральной совокупности.
5.2.1.2. Функции выборок. Пусть (Хи ..., Хп) -
математическая выборка. Случайная величина Zn =
= Z(Xi, ..., Хп) называется функцией выборки.
Пример 60. Пусть ДГ = —
Реализация х =
= — ) х, при конкретной выборке называется
эмпирическим средним выборки (хь ..., х„).
Пример 61. Sa= —Ц- )(Xt - Xf. Реализация s2 -
п- 1 ?j
t — 5сJ называется эмпирической дисперсией
выборки (хь ..., х,).
Вопрос о распределении функции выборки
является основной задачей математической
статистики.
В случае малой выборки (п относительно мало)
представляет интерес распределение функции
выборки Zn. В случае большой выборки (п велико)
достаточно знать асимптотическое распределение
Zm т. е. предельное распределение Zn при и ^ оо.
Не существует общего критерия, который
позволял бы решить, когда выборка может считаться
большой, а когда малой. В то время как
распределение одной функции выборки уже при п = 30
можно с очень хорошим приближением заменить
асимптотическим распределением, для другой
функции выборки подобное приближение и при
п — 100 все еще невозможно.
Пример 62. Пусть признак X распределен нормально
по N(x; а, а). Тогда X распределено нормально по
N(x; а, о/\/п).
Пример 63. Пусть DX < + оо. Тогда X
асимптотически распределено нормально по N(x; MX, yDX/n).
Пример 63 показывает, что для определения
асимптотического распределения нужны только
очень слабые предпосылки, которые практически
всегда выполнены. Для вычисления точного
распределения функции выборки, как показывает
пример 62, необходимо знать распределение
признака X генеральной совокупности.
СВОЙСТВА ТОЧЕЧНЫХ ОЦЕНОК
457
5.2.1.3. Некоторые важные распределения.
Х2-ра сп ре дел ен и е. Пусть Xt, ..., Хп —
независимые случайные величины, где XiEN(x; а, а)
для всех /. Совокупность (Хи ..., Х„) можно
понимать как выборку объема п из генеральной
совокупности, в которой признак X распределен по
N(x; а, а). Рассмотрим функцию выборки %2 =
1
Распределение этой величины
называется %2-распределением с п степенями
свободы. Табл. 5.2 содержит плотность распределения
для х2 и некоторые функции выборки, тесно
связанные с х2.
Распределение Т = X/Y с независимыми X и У,
где X нормально распределено с законом
N (х; 0, 1), a Y = xlyn (c n степенями свободы),
называется t-распределением или распределением
Спгьюденгпа с п степенями свободы. Оно имеет
плотность
Г((Л+
1 + —
E.90)
]/кпГ(п/2)
Х2-распределение и ^-распределение
табулированы; х2-распределение табулировано до п = 30.
Таблица 5.2
Некоторые распределения, связанные с %2
Величина
х2= jrl/*.-"J
х=|/> I (*,-«)>
Плотность распределения
при х ^ 0
x<n/2)-l?-x/2
2П/2Г (я/2)
Г(п/2)
2п/2Г(л/2)
Это объясняется тем, что
'* асимптотически
распределено с законом N (х; ]fln + 1, п), и это
приближение при п = 30 уже является достаточно
точным (табл. 1.1.2.7, 1.1.2.8). Пусть независимые
случайные величины ^,(/=1, ..., Wi) и Yj(j =
= 1, ..., «2) нормально распределены с законом
JV(x; 0, а). Введем отношение
F =
W
E.91)
i~~YJ
Причем обозначения rj = щ — 1, г2 = и2 — 1.
Распределение F называется F-распределением со
степенями свободы (гь г2) (табл. 1.1.2.10).
Распределение Z = In yF называется Z-pacnpe-
делением со степенями свободы (гь г2) (табл. 1.1.2.9).
5.2.2. ОЦЕНКА ПАРАМЕТРОВ
В цехе на поточной линии изготовляются
патроны для винтовок. Пусть вероятность того,
что произвольно выбранный патрон негоден,
равна р. Для того чтобы точно определить р, пришлось
бы расстрелять все патроны, что не представляет
собой разумного способа проверки. Для оценки
величины р делается выборка. Признак X является
качественным :
0, если патрон годный,
1, если патрон негодный.
Тогда MX = 0A — р) + 1 • р = р; таким образом,
речь идет о том, чтобы оценить MX при помощи
сделанной выборки. Рассмотрим функцию выборки
Х = -
которая имеет значение относительной частоты
негодных патронов в выборке объема п. Если
(хь ..., хп) - реализация выборки, то
является, согласно закону больших чисел,
приближенным значением неизвестного р. В общем случае
задача оценки неизвестного параметра у (который
как-либо связан с генеральной совокупностью,
например, у = MX) на основании выборки
означает следующее. Нужно задать функцию выборки,
реализация которой в некотором смысле могла бы
рассматриваться как приближение у. Такая функция
выборки называется точечной оценкой у.
5.2.2.1. Свойства точечных оценок. Оценка
Г(Х1у ..., Х„) параметра у называется
состоятельной, если Г (Хи ..., Х„) сходится по вероятности
к параметру у, т. е. если для любого 8 > 0
выполняется равенство
lim P(\T(XU
п -* оо
Хя) - У I
Пример 64. 1) X есть состоятельная оценка MX.
2) S2 есть состоятельная оценка для DX - а2.
Оценка называется несмещенной, если ее
математическое ожидание равно оцениваемому
параметру.
Пример 65. 1)
-i-\
X есть несмещенная оценка MX. 2) MS2 = ) M(Xt —
п — 1 /__,
- XJ - a2; S2 есть несмещенная оценка a2.
Оценка Г = Г (Хи..., Хп) параметра у называется
асимптотически несмещенной, если
lim MY = у.
п -»• оо
458
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Каждая несмещенная оценка является
асимптотически несмещенной, так как MY = у для любого
конечного п.
Пример 66. Иногда в качестве оценки о2
используется также
S*2 - - V(Xt - XJ, MS*2 = -^- а2.
Эта оценка не является несмещенной, однако она является
асимптотически несмещенной, так как lim MS*2 = a2.
Л-> 00
Оценка Fj параметра у называется более
эффективной, чем другая оценка Г2, если М (Г\ — уJ ^
^ М (Г2 - уJ. Если обе оценки несмещенные, то
это означает: DYX ^ DF2. При достаточно общих
условиях для дисперсий оценок одного и того же
параметра можно указать положительную нижнюю
границу.
Оценка, дисперсия которой в
действительности принимает это минимальное значение,
называется эффективной. Она является наилучшей
оценкой в том смысле, что лучше всего
использует информацию, имеющуюся в выборке.
Однако во многих случаях эффективные
оценки не существуют.
5.2.2.2. Методы получения оценок.
5.2.2.2.1. Метод моментов. Для
параметров, которые известным образом составляются
из моментов, оценку получают, заменяя моменты
через так называемые эмпирические моменты. В
качестве /с-го эмпирического начального момента
берут функцию выборки
В качестве эмпирического центрального момента
/с-го порядка берут функцию выборки
Пример 67. Математическое ожидание — первый
(начальный) момент. Следовательно, метод моментов в
качестве оценки для MX дает величину
Пример 68. Дисперсия есть второй (центральный)
момент. Метод моментов дает в качестве оценки для
DX - а2 величину
Пример 69. Для ковариации метод моментов дает
оценку
E.92)
Пример 70. Для коэффициента корреляции, согласно
методу моментов, получается оценка
E,93)
п
Ковариацию и коэффициент корреляции можно
рассматривать только тогда, когда в генеральной
совокупности появляются два интересующих нас
параметра: X и У. Выборка объема и состоит
тогда из последовательности пар ((хь ух\ (х2, Уг)»--
.-.,(** Уп)\
5.2.2.2.2. Метод наибольшего
правдоподобия. Пусть дана выборка (хь..., х„) объема
и из генеральной совокупности с непрерывно
распределенным признаком X. Пусть плотность
вероятности X содержит неизвестный параметр у,
который следует оценить по выборке, и имеет
вид /(х, у).
Функцией правдоподобия называют функцию
параметра у, определяемую соотношением
L(xu...,xn; у) = /(хь y)f{x2, y)...f(xmy).
E.94)
Рассмотрим случай дискретного X с
возможными значениями хи х2,... и вероятностями
Р(Х = xj) = Pj(y). Обозначим через хг наибольшее
из возможных значений, которые встречаются в
выборке, а через /ь /2,... ,/г — абсолютные
частоты, с которыми появляются значения хь...,хг
в выборке
В этом случае функцией правдоподобия
называют функцию параметра у, определяемую
соотношение
L(xi, ..., х„; у) = р{* (у)pi2 (у) ...pir(y). E.95)
Метод наибольшего правдоподобия состоит в
том, что в качестве оценки параметра у берется
значение, при котором функция правдоподобия
достигает своего максимума. Это значение у
является функцией Х1,...,х„:
у = Г(хь...,х„).
Соответствующая функция выборки Г (Хи..., Х„)
называется наиболее правдоподобной оценкой у.
Параметр у (и одновременно Y(Xly...,Xn))
находят, решая относительно у уравнение
?-а E.96)
ду
Часто вместо E.96) используют уравнение
1 dL д In L
- = о.
E.97)
Если плотность/(х, Уь-..,У/) или функция
вероятностей Р(Х = xk) = pk(yi,...,Yz) зависит от /
параметров, то наиболее правдоподобную оценку системы
параметров yi,...,y/ получают решением системы
уравнений
dyt
E.98)
ДОВЕРИТЕЛЬНЫЕ ОЦЕНКИ
459
d\nL
откуда
= 0
E.99)
а = — ) хк = х и а2 = — ) (х»
- лJ = s
Следо-
Наиболее правдоподобные оценки имеют
некоторые замечательные свойства. При достаточно
общих условиях они являются состоятельными и
асимптотически нормально распределенными
(однако не всегда несмещенными), и имеют среди всех
асимптотически нормально распределенных оценок
наибольшую эффективность. Справедливо
следующее положение: если вообще имеется
эффективная оценка, то она получается методом
наибольшего правдоподобия.
Пример 71 Следует оценить вероятность р
некоторого события А Пусть
У _ | 0, если А не происходит,
[ 1, если А происходит,
есть индикатор события А (см 5.1.2); Р(Х = 0) = Ро(р) =
= 1 - р, Р(Х = 1) = Pi (р) = р Пусть в п независимых
наблюдениях событие А происходит т раз, т. е fo = n — m,
/i = т Таким образом, согласно E 95), имеем L = рт{\ — р)п~т,
= о Отсюда следует, что p=
(частота А) Следовательно, wn(A) есть наиболее
правдоподобная оценка неизвестного р.
Пример 72 Пусть X распределено по закону
Пуассона с неизвестным параметром X Проведем выборку и
получим значения хь ,х„ (х, - целые числа). Пусть г —
наибольшее из наблюдавшихся в выборке чисел,/0,...,/г—
абсолютные частоты, с которыми числа 0, 1. 2,. .,г появ-
ляются в выборке,
формуле E 95), L
ТВ-)'
получаем
ii.
ok Lj \ К
-7-е \ Тогда, согласно
В соответствии с E 97)
откуда
вательно, (х, s* ) есть наиболее правдоподобная оценка
параметров (я, а2) Мы уже знаем, что s* не является
несмещенной оценкой, а только асимптотически несмещена
5.2.2.3. Доверительные оценки. Точечная оценка
дает оценочное значение соответствующего
параметра из данной выборки, но ничего не дает для
точности и достоверности оценки. Такие данные
поставляют доверительные оценки (границы).
Пусть (X1,..., Хп) есть некоторая математическая
выборка из генеральной совокупности с признаком
AT, распределение которой зависит от
параметра у. Пусть ае@, 1). Пусть Г(Хи...,Хп) и
Г(Хи...,Х„) - такие функции выборок, что при
произвольном значении параметра у выполняется
равенство
Р(Г(Хи...,Хп)<у<Г(Хи...,Хп))=\ -а.
E.100)
Тогда случайный интервал (Г, Г) называется
доверительной оценкой параметра у с мерой
надежности 1 — а.
Если имеется реализация (хь...,хя) выборки
(Xif...,Х„), т.е. если произведена выборка, то
реализация доверительной оценки дает интервал
(у, у) и в большом ряду выборок истинное значение
у лежит примерно в A — а)-100% случаев внутри
вычисленных доверительных границ. Равенство
E.100) можноинтерпретировать и так: случайный
интервал (Г, Г) «покрывает» истинный параметр с
вероятностью 1 — а.
5.2.2.3.1. Доверительная оценка
неизвестной вероятности по большим
выборкам. Частота Wn(/1) является точечной
оценкой р = Р{А); она асимптотически нормально
распределена с MWn{A) = p, DWn(A) = pq/n.
Если XeN(x; а, ст), то eN(x; 0, 1). За-
к = х Величина х есть, таким образом, дадим а. Величина za такая, что
наиболее правдоподобная оценка для X и вместе с тем
состоятельная, асимптотически нормально распределенная
оценка параметра X распределения Пуассона.
Пример 73 Пусть X распределено нормально с
неизвестными параметрами а и а. Их следует оценить,
исходя из выборки (хь ,х„) объема п Функция
правдоподобия
Р( -z.
\/2к
= 2ФоBа)=1-0С,
L(xb
, ст2)=
1
ехр -
Следовательно,
In L = - -|1
- V(
> (хк - аJ \.
_ аJ.
может быть найдена из уравнения
2O0(za)= 1 -а
E.101)
при помощи табл. 1.1.2.6.2.
Если эти рассуждения применить к Wn(A), то
по заданному а можно найти za так, чтобы
]/pq/n
Согласно E 99), получаем следующие уравнения для
определения а и а2>
dlnL 1 V, \ с
—— = -у ) (xk - a) = С
да ст / /
Wn(A)-p
< za
1 - а.
Из неравенства
Wn-p
< za следует, что
^-) - р( 2Wn + ^-
W2n < 0,
460
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
откуда можно вычислить оба значения p{Wn), p{Wn),
которые представляют доверительные оценки для р.
Если а выбрано достаточно малым, то случайный
интервал (p{Wn), p(Wn)) «покрывает» р с мерой
надежности, близкой к 1.
5.2.2.3.2. Доверительная оценка а при
неизвестном ст из нормально
распределенной с законом ЛГ(х; а,
^генеральной совокупности. Оценка основана на том
факте, что при высказанных предположениях вели-
Х-алГ
чина —-—J/л удовлетворяет t-распределению с
о
т = и - 1 степенями свободы. Следовательно, на
основании табл. 1.1.2.8 по заданному а можно
отыскать число *.,„_!, для которого справедливо
равенство
1 -а.
]fn ]fn
Таким образом, случайный интервал
S S \
X 7=-?а,„-ь X -\—-prt^n-y I есть доверитель-
ная оценка а с мерой надежности р = 1 — а.
5.2.2.3.3. Доверительная оценка а при
неизвестном а из генеральной
совокупности, нормально распределенной
с законом N (х; а, а). Отправной точкой
является тот факт, что при заданных предпосылках
(n-l)S2 2
величина ^ удовлетворяет х
-распределению с п — 1 степенями свободы. Из табл. 1.1.2.7
по заданному а и т = п — 1 степеням свободы
определяют два числа сх и с2 такие, что
Р(%2 < с,) = 1 - Р(х2 > сО = у, Р(Х2 > с2) = у,
С\ = хГ-я/2, с2 = Ха/2- Например, для a = 0,02 и
т = 19 получаем, что сх = Хо,99 = 7,6 и с2 = Xo.oi =
= 36,2. Числа сь с2 определены так, что
- < с2\ = 1 -
a,
c2
_ . /(«-OS2 (n-l)S2\
Таким образом, , есть до-
V С2 С, ) к f
верительная оценка ст2 с мерой надежности 1 — а.
5.2.2.3.4. Доверительные интервалы
асимптотически нормально
распределенных оценок. Если Г есть некоторая
асимптотически нормально распределенная
точечная оценка у, то za определяется формулой
E.101) и для этого za справедливо соотношение
Z*< ^г
откуда получается доверительная оценка у с мерой
значимости 1 — а. Пример- 73 был конкретным
использованием этого общего соображения.
5.2.3. ПРОВЕРКА ГИПОТЕЗ (ТЕСТЫ)
5.2.3.1. Постановка задачи. Пусть два
предприятия производят провод. Пусть X — прочность на
разрыв провода, изготовленного на предприятии А;
Y — прочность на разрыв провода, изготовленного
на предприятии В; X, Y можно считать
нормально распределенными и независимыми. Пусть
на основании многолетних наблюдений известны
&Х и СТУ- С каждого предприятия был взят и
проверен провод из 50 катушек. При этом
получились средние прочности на разрыв:
х = 120,8 кгс/мм2 (предприятие А) и
у — 128,2 кгс/мм2 (предприятие В). Следует
проверить, можно ли считать это расхождение
случайным или оно является значительным
(существенным). Мы выдвигаем гипотезу, что расхождение
случайно, т. е. истинные средние прочности на
разрыв совпадают. Следовательно, тогда гипотеза
#0 (нулевая гипотеза) может быть
сформулирована так: MX = MY. При этой гипотезе величина
X-Y
]/D{X-Y)
(X-Y)\Tn
распределена по закону N(x;,0, 1). Для заданного
or (a называется вероятностью погрешности или
уровнем значимости) из табл. 1.1.2.6.2 можно
определить величину 2а такую, что P(|Z|>za) =
= l-2O>o(za)=a.
Конкретная выборка дает для «величины теста»
Z значение z. Если | z | > гю то говорят, что z
лежит в критической области. Тогда при
однократном проведении опыта происходит событие,
вероятность которого меньше а. Согласно
опытному факту, описанному в 5.1.1.2, в этом случае
гипотеза MX — MY должна быть отвергнута.
Говорят, что наблюдавшееся расхождение
значительно. Если вычисленное z не лежит в
критической области, т. е. | z | < za, то можно лишь
утверждать, что предложенная гипотеза не
противоречит материалу наблюдений.
Пусть в рассмотренном вначале конкретном
примере &х = 8»0 кгс/мм2, ay = 9,4 кгс/мм2. Тогда
/D(X - Y) = W^- + (-^у- = 1,75 кгс/мм2. Если
взять в
a = 0,05,
качестве вероятности погрешности
то получим, что za = 1,96,
- ^~-= -4,23, \z\ > za = 1,96. Таким
образом, вычисленное z лежит в критической
области. Следовательно, гипотеза MX = MY должна
быть отвергнута, т. е. качественное различие
между продукциями предприятий А и В
существенно и его нельзя объяснить случайностью выборки.
5.2.3.2. Общая теория. На основании материала
выборки следует проверить гипотезу Но. Гипотеза
Но может быть, например, гипотезой о равенстве
определенных параметров распределения, о
равенстве законов распределения, о некоррелированности
двух случайных величин и т. д. Для проверки
КРИТЕРИЙ УИЛКОКСОНА
461
такой гипотезы необходима контрольная
величина Т, которой является соответствующим
образом выбранная и приспособленная к задаче
функция выборки. По заданному уровню
значимости а (чаще всего выбираются а равным
0,05, или 0,02, или 0,01) определяется область
В — так называемая критическая область,
удовлетворяющая условию
Р(ТеВ\Н0 верна) < а. E.102)
Область В можно найти практически, если
известно распределение (или по меньшей мере
асимптотическое распределение) контрольной
величины Т.
Метод проверки состоит в следующем.
Производится выборка, которая дает частное значение
t контрольной величины Т. Если teB, т.е. если
осуществляется событие, имеющее очень малую
вероятность а, то от гипотезы Но отказываются.
Если ?>не лежит в В, то можно заключить, что
данные наблюдения не противоречат принятой
гипотезе.
Ошибочное решение, когда гипотеза Но
отвергается, хотя она и верна, называют ошибкой
первого рода. Чем меньше а, тем меньше
вероятность того, что совершается ошибка первого рода.
Ошибочное решение, когда гипотеза Но не
отвергается, хотя она неправильна, называют
ошибкой второго рода. Если а задано, то, согласно
условию E.102), критическую область В можно
выбрать бесконечно многими способами. Ее
выбирают так, чтобы вероятность допустить ошибку
второго рода была по возможности наименьшей.
Критические области рассматриваемых в
дальнейшем тестов выбираются именно с этой точки
зрения.
5.2.3.3. Г-критерий. f-критерий служит для
сравнения двух средних значений из нормально
распределенных генеральных совокупностей в
предположении, что дисперсии &х и аУ равны, хотя
и неизвестны. Таким образом, проверяемая
гипотеза Яо утверждает, что MX = MY. Пусть
(Xi,...,Xni), (У1,..., УП2) — независимые случайные
выборки из обеих генеральных совокупностей;
они могут иметь совершенно разные объемы. В
качестве контрольной используют величину
X - Y
п1п2(п1+п2-2)
E.103)
При сделанных предпосылках (нормальная рас-
пределенность X и У и равенство дисперсий)
и в предположении, что гипотеза Но правильна,
Т удовлетворяет r-распределению Стьюдента с
к — пх + п2 — 2 степенями свободы. Поэтому
критическая область В критерия может быть
установлена следующим образом. Для уровня
значимости а из табл. 1.1.2.8 определяется rak, где
к — nY + п2 — 2.
Если вычисленная (согласно E.103)) реализация
t удовлетворяет неравенству \ t \ > ?а> к. то гипотезу
Но отвергают.
По отношению к предпосылке «нормальной
распределенности» r-критерий не очень
чувствителен. Его можно применять, если статистические
распределения обеих выборок не имеют нескольких
вершин и не слишком асимметричны. Предпосылка
ст^ = ау во многих случаях может быть
обоснована на содержательном уровне; гипотезу
°Х = СТУ можно проверить и по F-критерию
(см. ниже).
Пример 74. Нужно проверить влияние двух
различных кормовых смесей на увеличение веса свиней. Для
этого 10 свиней кормили только первой кормовой
смесью, а 10 других свиней - только второй (пг - п2 = 10).
Пусть X — увеличение массы при одной кормовой смеси,
a Y - при другой. Величины X и Y можно считать
нормально распределенными (центральная предельная
теорема). Так как дисперсия увеличения массы складывается из
свойств отдельных животных, а эти свойства действуют
независимо от питания, то можно принять ах = о у
Таким образом, выполнены предпосылки для
применения г-критерия. Получились следующие эмпирические'средние
значения: х — 112,1 кг, у = 100,2 кг. Эмпирические дисперсии
равны соответственно s^ = 211, s^ = 86. Согласно E.103),
получаем
112,1-100,2
|/9-211 +9-86
V
10-10A0+ 10-2)
10+10
• IX
Для а = 0,05 и к = 10 + 10 - 2 = 18 из табл. 1.1.28 находим
'о.05,is = 2,101. Так как 11 \ > t^, то гипотеза Но отвергается.
Следовательно, с вероятностью погрешности 0,05 можно
сказать, что один корм лучше другого.
5.2.3.4. F-критерий. Гипотезы о дисперсии имеют
в технике, большое значение, так как а2 есть
мера таких числовых характеристик, как точность
машин, погрешности измерительных приборов,
точность технологических процессов и т. п.
F-критерий служит для проверки гипотезы
&Х = аУ ПРИ условии, что X и У распределены
нормально. Из каждой генеральной совокупности
производятся выборки объема пх и п2. В качестве
контрольной величины используют отношение
эмпирических дисперсий F = S\/S\ или F —
— S\/S\ (смотря по обстоятельствам, большую
дисперсию выбирают в качестве числителя).
Величина F удовлетворяет F-pacnpeделению с (ть т2)
степенями свободы (тх = пх - 1, т2 = п2 - 1).
Критическая область выбирается следующим образом.
Для уровня значимости а при р = а/2 и
соответствующих степенях свободы ть т2 из
табл. 1.1.2.10 выбирают значение Fp.mi mi. Если /,
вычисленное по выборке, больше, чем это
критическое значение, то гипотеза должна быть
отклонена с вероятностью погрешности а (тех значений
а, которые указаны в таблице, достаточно для
практических целей).
Пример 75. Двумя измерительными приборами X
и У произведены соответственно 10 и 20 измерений.
Получились следующие эмпирические дисперсии: sfc = 12,2, s\r=
= 8,0. Тогда /=5^/5^=12,2/8,0=1,525. Из табл. 1.1.2.10
для уровня доверительности а = 0,10 находим /^05; 9,19 =
= 2,42. Так как вычисленное значение / меньше, чем
критическое значение, то различие между s^ и s^
незначительно, т. е. гипотеза, что оба измерительных прибора
одинаково точны, не противоречит данным наблюдений.
5.2.3.5. Критерий Уилкоксона служит для
проверки, относятся ли две выборки к одной и
той же генеральной совокупности; другими
словами, гипотеза Яо: F^(x) = Fy(x) проверяется
посредством одной выборки (xb...,xWi) из X и одной
выборки (yi,...,y,i2) из У. Относительно
распределений X и У никаких предположений не делается.
462
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Способы проверки, при которых не делается
предположений о распределении в генеральной
совокупности, называются способами, свободными от
параметров, в противоположность рассматривавшимся
до сих пор параметрическим критериям, в
которых предполагалась нормальная распределенность
X и Y. Значения хь...,хИ1 и уи...,уПг обеих
выборок упорядочиваются вместе по их величинам.
Пусть, например, для п^ = 4 и п2 = 5 получилась
следующая последовательность: Уъ^ъ^^У].У2^2У^Угх\-
В случае yj < x,- говорят, что пара значений
(хь у^ образует инверсию. В нашем примере х3 и
х4 образуют по одной инверсии (с у5), х2 образует
три инверсии (с у2, Уи ys), а хх образует пять
инверсий (со всеми yj). В качестве контрольной
величины принимается и — полное число инверсий.
Если гипотеза верна, то и не должно слишком
сильно отклоняться от своего математического
ожидания Ми ¦¦
От гипотезы отказывают-
ся, если
больше определенного
критического значения ил. Критическое значение иа
берут для заданного уровня значимости из
табл. 1.1.2.11. Для больших пх и п2, для которых иа
нельзя взять из табл. 1.1.2.11, справедлива формула
Уп1п2(п1 + п2 + 1)
12 '
причем za определяется, согласно E.101), из
табл. 1.1.2.6.2.
Пример 76. Из двух партий некоторой продукции
было взято по 12 деталей и для каждой из них измерен
определенный признак. Нужно проверить гипотезу о том, что
этот признак в обеих партиях имеет одинаковое
распределение, другими словами, что производственный процесс
от партии к партии изменяется несущественно.
Табл. 5.3 показывает результаты измерений.
Критерий согласия %2 служит для проверки
гипотезы Яо о том, что Fx(x) - Fo (х), где Fx (х) -
функция распределения X, a Fo (x) — заданное
(гипотетическое) распределение.
Рассмотрим сначала случай, когда F0(x)
полностью определено, т. е. не содержит неизвестных
параметров. Область значений случайной
величины X делится на конечное число
непересекающихся множеств (так называемых классов) ДЬ...,Д*.
При непрерывном X классы Д, являются
промежутками, при дискретном X - группами
возможных значений X. Пусть р, есть «теоретическая
вероятность» того, что X попадает в Д„ если
гипотеза Но верна. Если Д4 = [ah Ь,), то
pi = F0{bi)-F0{ai). E.104)
Теперь из X производится выборка (Хи...,Хн)
объема п. Пусть М, - число значений выборки
в Д,-. Тогда
? Pi =1, ? Mt = п.
Разбиение на классы довольно произвольно.
Необходимо, однако, чтобы для граничных классов
выполнялось неравенство пр, ^ 1, для остальных
классов npi ^ 5; этого всегда можно добиться за
счет укрупнения классов. Если разбиение на
классы удовлетворяет указанным требованиям, то
контрольная величина равна
^)-, E,05)
В предположении, что гипотеза Но верна, X
имеет асимптотическое х2-распределение cm = к — 1
степенями свободы. Так как %2 есть мера
отклонения истинного распределения от гипотетического, то
гипотеза отвергается, если значение, вычисленное
Таблица 5.3
Результаты измерений деталей, взятых из двух партий некоторой продукции
Партия
1(х)
и (у)
Номер детали
1
0,8
3,1
2
1,9
2,7
3
3,0
1,8
4
3,5
4,0
5
3,8
0,2
6
2,5
U
7
1,7
3,6
8
0,9
2,1
9
1,0
1,4
10
2,3
4,7
11
3,3
2,8
12
3,4
1,6
Упорядочивание по величине дает: 0,2 (у); 03 (х);
0,9(х); 1,0(х); 1,1 (у); 1,4 (у); 1,6 (у); 1,7 (х); 1,8 (у); 1,9(х);
2,1(у); 23(х); 2,5(х); 2,7(у); 2,8Ы; 3,0(х); 3,1 (у); 33(х);
3,4(х); 3,5(х); 3,6(у); 3,8(х); 4,0(у); 4,7(у).
Число инверсий есть м = 1 + 1 + 1 -
+9 + 9 + 9 + 10 = 69. Следовательно,
-721 = 3. Для а = 0,05 из табл. 1.1.2.11 получаем, что
ц, = 35,0. Таким образом, гипотезу Но: F^(x) = Fy(x) не
следует отвергать.
5.2.3.6. х2-критернй. При помощи
рассмотренных до сих пор критериев можно было
проверить, являются ли некоторые различия, имеющиеся
в материале наблюдений двух выборок,
существенными (значимыми) или случайными. Обратимся
теперь к критериям, при помощи которых
проверяют, удовлетворяет ли рассматриваемая
случайная величина X заданному закону распределения
F0(x). Они называются критериями согласия.
по конкретной выборке согласно E.105),
превышает определенное критическое значение. Это
критическое значение у? для заданного уровня
значимости а и т = к — 1 степеней свободы находят
из табл. 1.1.2.7. Если х2 ^ Х«. то гипотеза
отвергается. Для п > 30 значение у? находят уже не из
табл. 1.1.2.7, а вычисляют по формуле
где z2a, определяемое равенством 2O0(z2a) = 1—2а,
вычисляется из табл. 1.1.2.6.2.
Пример 77. От аппаратуры, применяемой при
проведении тиража лотереи, требуется, чтобы для 90
возможных значений имелось равномерное распределение. Для
проверки в аппарат было положено пять шаров и
проведено п = 100 проверочных выниманий по одному шару.
Распределение F0(x) определяется в соответствии с пред-
КРИТЕРИЙ СОГЛАСИЯ КОЛМОГОРОВА - СМИРНОВА
463
положением равномерного распределения пяти возможных
значений X (X — номер вынутого шара) следующей функции
вероятности: р( = 1/5 для i=l,...,5. Здесь классы — сами
возможные значения. Таблица 5.4 содержит результаты
вниманий т( и данные, нужные для вычисления х2-
Таблица 5.4
Результаты выниманий при 100 пробных тиражах
i
1
2
3
4
5
Сумма
Число /и,-
испытаний,
в которых
был вынут
шар /
18
19
21
26
16
100
npi
20
20
20
20
20
100
m/ - npi
-2
-1
6
-4
0
npi
0,20
0,05
0,05
1,80
0,80
2,90
Для а = 0,05 и т = 5 - 1 = 4 степеней свободы из
табл. 1.1.2.7 найдем х» — 9,5. Так как вычисленное х2 — 2,9
меньше, чем &?, то результаты тиража не дают повода
сомневаться в равномерном распределении.
5.2.3.7. Случай дополнительных параметров.
Чаще всего гипотетическое распределение Fo (х)
установлено неоднозначно, и гипотеза говорит лишь
о том, что F0(x) относится к определенному
множеству функций распределения F(x;,$b ...,0г),
которое зависит от г параметров. Например,
гипотеза могла бы гласить: «X имеет
нормальное распределение» (здесь есть два параметра
а и а), или «X имеет распределение по закону
Пуассона» (здесь имеется один параметр X). В этом
случае поступают следующим образом: по выборке
получают наиболее правдоподобные оценки
параметров Эь ...,§, и принимают F0(x) — F(x; $ь ...
..., ЭР), затем по формуле E.104) вычисляются ри а
по E.105) - величина %2. Если производится оценка
г параметров, то остается только т = к — г — 1
степеней свободы. В остальном критерий остается
прежним.
Пример 78. При помощи измерительного прибора
было проведено 200 измерений известных расстояний, и
случайная погрешность измерения записана в микрометрах.
Действительная ось была разделена на девять промежутков,
которые указаны в табл. 5.5.
Таблица 5.5
Статистическое распределение случайной
погрешности
измерения в 200 измерениях
Номер
промежутка
1
2
3
4
5
6
7
8
9
Интервал в мкм
меньше — 15
от -15 до -10
от —10 до —5
от -5 до 0
от 0 до 5
от 5 до 10
от 10 до 15
от 15 до 20
больше 20
Частота /и/
6
11,5
15,5
22
47,5
42
28
17
10,5
ваются поровну как одному, так и другому классу.
Проверяется гипотеза Но о том, что случайная погрешность
измерения X распределена нормально. Следовательно,
гипотетическое распределение имеет плотность
f{x; a, a) =
1
которая содержит два неизвестных параметра а и а. По
этой выборке, состоящей из 200 измерений, были вычислены
наиболее правдоподобные оценки для а и а. Они дают
х = 4,60 мкм и s* = 95,2 мкм2. Таким образом, функция
распределения F0(x), используемая для проверки, имеет
плотность
Отсюда по табл. 1.1.2.6.2 можно вычислить р,. Например,
= -1 _ ф0 B,00) = -j - 0,4772 = 0,0228,
р2 =Р(-15<Х <
= Фо(-1,49) - Фо(-2,00) = ФоB,00) - ФоA,49) =
= 0,4772-0,4319 = 0,0453.
Табл. 5.6 содержит р, (i=l,...,9) и все данные,
необходимые для вычисления х2-
Таблица 5.6
Таблица вычисления для X2-критерия
i
1
2
3
4
5
6
7
8
9
Сумма
Щ
6
11,5
15,5
22
47,5
42
28
17
10,5
200
Pi
0,0228
0,0453
0,0954
0,1557
0,1968
0,1928
0,1466
0,0864
0,0582
1,000
npi
4;56
9,06
19,08
31,14
39,36
38,56
29,32
17,28
11,64
200,00
npi
0,45
0,66
0,67
2,68
1,68
0,31
0,06
0,05
0,11
6,61
Дробные значения ш, появляются из-за того, что
значения, попадающие на границу классов, обычно приписы-
Таким образом, вычисление дает х2 = 6,61. Так как
производится оценка двух параметров, то мы имеем теперь
9-2-1=6 степеней свободы. Для а = 0,05 и m = 6 из
таблицы 1.1.2.7 получаем х* = 12,6. Так как вычисленное х2
меньше табличного, то гипотеза о нормальной распределен-
ности случайной погрешности измерения соответствующего
прибора не противоречит материалу наблюдений на уровне
значимости 0,05.
5.2.3.8. Критерий согласия Колмогорова -
Смирнова. Этот критерий использует непосредственно
эмпирическую функцию распределения X (см. 5.2.1).
В основе лежит функция выборки
Dn= sup \FH(x)-F0(x)\,
-00 < X < +00
причем Fn (x) - эмпирическая функция
распределения, a F0(x) — гипотетическое распределение. Имеет
464
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
место равенство
lim P
П -* 00
Vn
Контрольная величина ]/nDn асимптотически
имеет функцию распределения Q(X). Для уровня
значимости а из табл. 1.1.2.12 берут такое
значение Хо, при котором Q(k0) = 1 - а. Если ynDn >
>'Х0, то гипотезу Яо о том, что X
распределена по закону F0(x), отбрасывают. Критерий
Колмогорова — Смирнова в общем неприменим,
если в F0(x) входят оценки параметров, которые
были произведены по той же самой выборке,
по которой была вычислена Fn(x).
5.2.4. КОРРЕЛЯЦИЯ И РЕГРЕССИЯ
5.2.4.1. Оценка корреляционных и регрессионных
характеристик по выборкам. Для случайного
вектора (X, Y) выборка (объема п) дает п пар
значений признака (хь у^\ (х2, .УгХ•••»(*»»» Уп)- В этом
случае говорят о связанной выборке в
противоположность независимым выборкам, где
совершенно независимо друг от друга наблюдаются
«! значений х и п2 значений у. Для прямых
регрессии E.60), E.61) могут быть даны оценки;
точнее говоря, теоретические характеристики
регрессии E.62), E.63) можно оценить по выборке.
По функциям выборки из 5.2.2.2, в частности
E.92) и E.93), получаются следующие оценки: для
\ix' х = — ) х{; для цу: у = —
п l_j п
- уJ. Для ковариации получают в качестве
оценки так называемую эмпирическую ковариацию
п — 1 l_j
заменяя в
E.62), E.63) теоретические величины их оценками
(эмпирическими величинами), получают оценки для
теоретических корреляционных и регрессионных
характеристик. Например, эмпирический
коэффициент корреляции:
SXSY
E.106)
Аналогично получаются эмпирические
коэффициенты регрессии:
sY mXY
77=
sx mXy
EЛ07)
и эмпирические прямые регрессии:
у = у + bY/x(x - х), х = х + bX/Y(У ~ У)-
При приблизительно линейно коррелированных X и
Y при помощи этих прямых регрессии можно
сделать наилучшее предсказание для Y при данном
значении X или наилучшее предсказание для X
при заданном значении Y. Вопрос о том, имеется
ли приблизительно линейная корреляция между
X и У, только в редких случаях может быть
решен теоретически. Это удается, например, если
известно, что (X, Y) распределены нормально.
Тогда линии регрессии являются прямыми, т. е.
имеется точная линейная корреляция. В общем
случае рассуждение проводится следующим
образом. Каждое значение выборки (X,, у,)
представляет одну точку в плоскости х, у, так что
полная выборка дает совокупность точек в
плоскости х, у. На рис. 5.11 приведены три примера
х 0
б)
Рис. 5.11
X 0
таких совокупностей точек. На рис. 5.11, а график
у(х) (см. 5.1.4.7) является параболической кривой,
обращенной выпуклостью вверх; здесь
предположение о линейной корреляции было бы неверным.
На рис. 5.11,6 график у (х) — приблизительно
прямая. Таким образом, здесь можно приближенно
принять линейную корреляцию. В случае
рис. 5.11, в следует предполагать отсутствие
корреляции.
При предположении приблизительно линейной
корреляции г есть мера силы связи между X
и Y. Величина | г |, близкая к 1, означает очень
тесную связь, в то время как величина | г |,
близкая к 0, говорит об очень слабой связи
или об ее отсутствии.
5.2.4.2. Проверка гипотезы г = 0 в случае
нормально распределенной генеральной совокупности.
В исследованиях корреляции очень важным
является вопрос о том, действительно ли имеется
корреляция, отличная от нуля, или ее нет, т. е.
существенно ли отлично от нуля значение г.
Следовательно, нужно проверить гипотезу г = 0.
Для этого от конкретной оценки г, согласно
E.106), переходят к соответствующей функции
выборки R согласно с E.93). В предположении,
что X и Y распределены нормально, величина R
распределена асимптотически нормально по закону
N(x; r, ад), где
1-г2
Следовательно, критическая область может быть
определена так. Для а из табл. 1.1.2.6.2 по формуле
E.101) вычисляют za. Если для вычисленного по
выборке г справедливо неравенство | г | > zTsr, то
гипотеза г = 0 отклоняется. Этот критерий годится
только для больших выборок. Для малых выборок
можно построить критерий на основании того
ОБЩАЯ ЗАДАЧА РЕГРЕССИИ
465
факта, что при данных предпосылках величина
о
— ]/п - 2 удовлетворяет г-распределению
\/l-R2
Стьюдента с п — 2 степенями свободы.
5.2.4.3. Общая задача регрессии. Пусть
случайная величина Y зависит от к переменных
Xi,...,xk и распределена нормально с дисперсией
а, не зависящей от xj, и математическим
ожиданием
В этом случае говорят, что Xj определяют Y
только в среднем.
Пример 79. В технике часто встречаются случайные
величины следующего типа: y=a + Pif+p2f2 + ...+ Pkf* + Z(f),
где Z(t)eN(t; 0, a); t означает время.
Если положить х} = ti (/= l,...,fc), то очевидно, что
Y — случайная величина описанного выше типа.
Задача состоит в том, чтобы посредством серии из п
независимых наблюдений (у/, xu,...,xu) (i = 1, ...,л) оценить
неизвестные параметры a, Pi,...,P*, входящие в
соотношение E.108). Отдельные наблюдения удовлетворяют
соотношению E.108) не точно: появляется ошибка 5,, и
yt = a + Pixu + ... + р4хы + 5,. E.109)
Относительно 5, предполагается следующее: 1) все б,
независимы друг от друга; 2) bteN(t; 0, а) для всех L
Тогда для плотности вектора (8Ь ..., 5„) справедлива
формула
из которой, заменяя 5, согласно E.109), получаем
функцию правдоподобия для оценки ос, рь...,р\:
Уравнения наибольшего правдоподобия
E.112)
дают оценки a, fih которые точно совпадают со
значениями, вычисленными для неизвестных параметров а, {3,
по методу наименьших квадратов. Например, в одномерном
случае
yt = а + рх, + 6|, а = у - рх,
i xf-пЛ
=l /
Техника проведения вычислений
в 7.1.5.1.
6. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
6.1. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6.1.1. ПОСТАНОВКА ЗАДАЧИ
ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
И СИМПЛЕКС-МЕТОД
6.1.1.1. Общая постановка задачи,
геометрическая интерпретация и решение задач с двумя
переменными. Линейным программированием
называется раздел математики, в котором изучаются
методы нахождения минимума или максимума
линейной функции конечного числа переменных при
условии, что переменные удовлетворяют конечному
числу дополнительных условий (ограничений),
имеющих вид линейных уравнений или линейных
неравенств.
Таким образом, задача линейного
программирования (ЗЛП) в общем случае может быть
сформулирована следующим образом.
Найти такие значения действительных
переменных хь х2, .-., х„, для которых целевая функция
принимает минимальное значение на множестве
точек, координаты которых удовлетворяют
условиям
4- а12х2 + ... 4- auxn = bu
a12xx + a22x2 + ... 4- a2nxn = b2t
«mi^i + am2x2 + ... + атяхя = Ьж,
Здесь коэффициенты ay, bh pj {i = 1, 2, ..., m; j =
= 1, 2, ..., и) - действительные числа. Без
ограничения общности можно предполагать, что
В матричном виде задачу линейного
программирования можно сформулировать так:
где х=(хь ..., xn)TeRn, A — матрица (atj)
размера m х и,
Р = (ри Р2, ..., Рп)Т,
Ь = (ЬиЬ2у ...,
(последнее неравенство означает, что bx ^ 0, ...
..., bm ^ 0; аналогичный смысл имеет неравенство
х ^ 0). Индекс у целевой функции означает, что
ищется минимум этой функции. Если ищется
максимум целевой функции G (х) = р^хх + ... 4- рпхп,
то это равнозначно отысканию минимума функции
б(х)= -G(x) = (-Pl)xu ..., +(-Рп)хИ. Если в
дополнительных условиях имеется неравенство,
например anxt + ... + ainxn < bh то введением
вспомогательного переменного у можно перейти к
уравнению anxi + ... 4- ainxn + у = bt. Для нового
переменного также справедливо неравенство у ^ 0;
в целевую функцию оно входит с коэффициентом 0.
Если для переменного xj не задано условие xi > 0,
то могут быть введены, например, новые
переменные x'j и xj с дополнительными условиями x'j ^ 0
и хj > 0, причем Xj = x'j — х']. Поэтому в
дальнейшем мы будем рассматривать в основном только
задачи минимизации целевой функции Q(x) при
условиях, заданных линейными уравнениями с
неотрицательными свободными членами bh и в
предположении неотрицательности переменных.
Эти задачи мы и будем называть задачами
линейного программирования.
Точка х = (хь ..., х„)Т, удовлетворяющая всем
условиям, называется допустимой точкой.
Множество всех допустимых точек называется
допустимой областью. Если после отбрасывания
одного условия допустимая область не
изменяется, то это условие называется лишним.
В задачах с двумя переменными можно
отказаться от перехода от неравенств к уравнениям,
так как линейное неравенство aiXi + а2х2 < b
допускает непосредственную геометрическую
интерпретацию: все точки, удовлетворяющие этому
неравенству, лежат на прямой a^xi + а2х2 = b и в
одной из двух полуплоскостей, на которые эта
прямая делит плоскость. Если заштриховать
полуплоскость, не удовлетворяющую неравенству,
и проделать это для всех неравенств в
отдельности, то часть плоскости, оставшаяся в конце
концов незаштрихованной, и образует допустимую
область.
F.1)
Для того чтобы найти полуплоскость,
удовлетворяющую условию I, построим сначала прямую Xj + 2х2 = 12
Приме
II: xt
Ill: xt н
IV: xt
V:
6min (^) =
p 1.
<8,
h x2 ^ 3,
>0,
x2 ^ 0,
= xj + 2,5x2.
ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ
467
(@; 6) и A2; 0) - точки ее пересечения с осями), затем
возьмем произвольную точку, не лежащую на этой
прямой, и проверим, удовлетворяют ли ее координаты
неравенству I или нет. Если удовлетворяют, то вся
полуплоскость, в которой находится эта точка, является
допустимой (по отношению к этому условию). В противном
случае полуплоскость является недопустимой и на рисунках
заштриховывается. Таким же образом поступим с
условием II и снова исключим точки, не входящие в
допустимую область. Графическое изображение двух этих
неравенств дано на рис. 6.1. Затем переходим к условиям III, IV и
V. Все точки плоскости, не исключенные условиями I-V,
Рис. 6.1
образуют допустимую область. Вследствие
неотрицательности переменных она всегда лежит в первом квадранте
плоскости. На рис. 6.2 изображена допустимая область для
нашего примера.
Точки, в которых целевая функция принимает
значение 17, лежат на прямой х1+2,5х2 = 17 линии уровня
?=/7 Х2
Q = 17, принадлежащей числу 17 (на рис. 6.2 эта линия
обозначена точками). Все линии уровня, принадлежащие
каким-либо другим значениям, также являются прямыми,
параллельными прямой Q ш 17. Если сместить прямую
Q = 17 параллельно самой себе в одном направлении, то
значения, принадлежащие линиям уровня, уменьшатся;
при параллельном переносе в другом направлении они
увеличатся. В каждой точке допустимой области целевая
функция принимает значение, принадлежащее той линии
уровня, на которой лежит эта точка. Направление, в котором
следует осуществлять сдвиг, чтобы достичь меньших
значений целевой функции, можно найти построением
другой линии уровня, например линии Q = 15. Путем
параллельного переноса прямой Q = const в направлении меньших
значений целевой функции в допустимой области
достигают того, что эта прямая будет пересекать допустимую
область по части ее границы. (В общем случае
параллельная прямая может либо пересекать допустимую
область в одной точке, либо проходить по отрезку, лучу или
прямой.) В примере 1 это точка Р, лежащая на линии
уровня, принадлежащей числу 3 (см. рис. 6.2). Все другие
допустимые точки лежат на линиях уровня,
принадлежащих большим значениям. Все точки, лежащие на линиях
уровня с меньшими значениями, являются недопустимыми.
Таким образом, точка Р есть искомая оптимальная точка.
Заметим, что оптимальная точка является угловой
точкой допустимой области. Точка Р не есть
относительный минимум целевой функции, так как линейная
функция вообще не имеет относительных экстремумов, т. е. Р
не может быть найдена методами дифференциального
исчисления.
Все задачи линейного программирования с
двумя переменными можно решить при помощи
а=/
Одно из „
условии
излишне
графического метода, объясненного на этом
примере.
Множество всех оптимальных решений
задачи линейного программирования выпукло.
Для пояснения рассмотрим допустимую область
примера 1 (с целевой функцией QminM = *i + *2;
рис. 6.3). Минималь- %
ное значение прини- Q=6 ,
мается целевой
функцией не только в «=«7\,
обеих угловых точках
Pi и Р2, но и на всем
отрезу между ними.
Некоторые примеры
допустимых областей
даны на рис. 6.4.
Соответствующие ,
особенности могут
встретиться и в задачах
линейного
программирования с более чем
двумя переменными.
Допустимая
область для задач в R".
Обобщая двумерный
случай, допустимую
область в
пространстве R" можно
рассматривать как
пересечение конечного
числа полупространств.
Она образует так
называемое многогран-.
ное множество. Точг
ка называется
вершиной допустимой
области в R", если она
является допустимой
и представляет собой
точку пересечения п
линейно
независимых гиперплоскостей.
(Каждое линейное
уравнение задает
гиперплоскость.
Каждому линейному
неравенству
сопоставляется ограниченное
гиперплоскостью
полупространство;
гиперплоскость получают,
заменяя знак
неравенства знаком
равенства.) Вершина
называется вырожденной,
если она является
точкой пересечения
более чем п
гиперплоскостей. Вершину
х нельзя представить
в виде выпуклой
линейной комбинации двух других точек допусти-
1 2
мой области (равенство х = Хх + A — Х)х при всех
1 2
допустимых х ф х не выполняется ни для каких
X, удовлетворяющих условию 0 < X < 1). Всякая
Луч
Точка.
Пустое
множество
468
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
допустимая область имеет конечное число вершин.
Если допустимая область образована п
неравенствами xj>0(/=1, ..., и) и т уравнениями, то
она может иметь самое большее СЦ+т вершин.
Если допустимая область ограничена и не пуста,
то она является выпуклым многогранником, и задача
линейного программирования в этом случае
всегда разрешима, а оптимальное значение целевой
функции достигается по крайней мере в одной из
вершин многогранника. Если допустимая область
пуста, то задача линейного программирования
неразрешима. Если допустимая область не
ограничена (см. первый пример на рис. 6.4), то задача
линейного программирования может быть
разрешимой или неразрешимой. Если задача имеет
решение, то всегда имеется по меньшей мере одна
вершина, где достигается оптимальное значение
целевой функции.
Если допустимая область является
многогранником, то каждая допустимая точка х имеет по
меньшей мере одно представление вида
где ? Xt = 1, Xi^O при 1 = 1, ..., к, причем
1 к
х, ..., х — вершины многогранника.
Если многогранное- множество имеет по
меньшей мере одну вершину, то каждая точка множества
имеет по меньшей мере одно представление вида
к i к j
х = ? Xtx + ? \ijr,
где ? Xi = 1, Xi ^ 0 при i — 1, ..., k, \ij ^ 0 при
;
y = l, ..., h; x — вершины и г — направляющие
векторы неограниченных ребер многогранного
множества.
6.1.1.2. Канонический вид ЗЛП, изображение
вершины в симплекс-таблице. Основным алгоритмом
решения задач линейного программирования
является симплекс-метод (см. 6.1.3). Его можно
применять в том случае, когда задача
программирования задана в специальном, каноническом
виде. Позднее будет показано, как каждую задачу
линейного программирования с непустой
допустимой областью можно привести к такому виду
(см. 6.1.4).
В рассмотренной в 6.1.1.1 формулировке
уравнения ЗЛП
F.2)
атпх„ =
имеют канонический вид, если каждое i-e
уравнение содержит переменное х^. такое, что
коэффициент перед ним в этом уравнении равен 1,
а во всех других уравнениях равен 0. Если при этом
bi ^ 0,..., bm ^ 0, то говорят о допустимом
каноническом виде. Переменные х^ называются
базисными, остальные — свободными.
В следующем примере, относящемся к допустимому
каноническому виду, мы отметим базисные переменные
подчеркиванием:
3xi + хг_+ 2хз - 5,
xi - 4хз + х* « 1.
Здесь Xt « 2, А.2 «= 5, Хэ » 4. Если уравнения заданы в
канонической форме, то целевая функция легко может быть
выражена через свободные переменные. Если целевая
функция имеет вид
Q (х) * х» + 13х2 + 2х3 + 17х4 + 3xs,
то вычитанием из этого выражения первого уравнения,
умноженного на 13 (так как там выделено переменное х2,
а в целевой функции х2 имеет коэффициент 13), второго
уравнения, умноженного на 3, и, наконец, третьего уравнения,
умноженного на 17, получим целевую функцию Q{x) =
=-52*! + 35х3 + 109. Вместе с уравнениями
канонического вида и условиями знака она описывает ЗЛП в
каноническом виде:
3xi + Хг + 2х3 «= 5,
+ Зхз +
9,
F.3)
, х2>0, ..., х5>0,
-52х1 +35хэ + 1О9.
Значение величины Qmin при нулевых значениях
свободных переменных обозначим через Qo- Здесь Qo = 109.
6.1.1.2.1. Симплекс-таблица. ЗЛП
канонического вида может быть записана в таблице
следующего вида. Левый крайний столбец содержит
Симплекс-таблица
В общем случае
Для примера F.3)
2
5
4
1
3
1
1
-52
3
2
3
-4
35
5
9
1
-109
номера Xt базисных переменных, верхняя строчка -
номера Xm+j свободных переменных. В точке
пересечения строки, соответствующей значению
Xh и столбца, соответствующего Xm+j, стоит
коэффициент atxm+j при свободной переменной в урав-
СИМПЛЕКС-МЕТОД ПРИ ЗАДАННОЙ НАЧАЛЬНОЙ ТАБЛИЦЕ
469
нении /, в котором выделена базисная переменная
х^. Соответственно справа записаны постоянные
члены уравнений, внизу — коэффициенты целевой
функции от свободных переменных, а в правом
нижнем углу записано значение — QQ.
Каноническому виду ЗЛП или
соответствующей симплекс-таблице сопоставляется точка
Получим канонический вид уравнений
х^ - 4х3 + х4 =1,
= Ьь ХХ2 =
= bm
= ... = хк = 0.
Координаты этой точки удовлетворяют п линейно
независимым условиям ЗЛП: т уравнениям и п — т
неравенствам х, ^ 0 для свободных переменных.
Если, кроме того, Ь, ^ 0 (допустимый канонический
Х^ вид), то точка является
допустимой и,следовательно,
вершиной (см. 6.1.1).
В примере F.3) получается
точка Xi = 0, хг = 5, х3 = 0, х4 = 1,
х5 = 9. Если сравнить задачу F.3)
с задачей, содержащей только
два переменных:
Зх, + 2х3 ^ 5, -xt + Зх3 ^ 9,
xi - 4х3 < 1, X! ^ 0, х3 > О,
б= -52х, + 35х3+ 109,
Рис. 6 5
и представляемой графически на плоскости хи х3
(рис. 6.5), то, рассматривая х2, х5, х4 как
вспомогательные переменные, получим, что искомая вершина есть
начало координат.
6.1.1.2.2. Свойства вершин и
обращение базисов. Вершина, полученная при помощи
ЗЛП канонического вида, обладает следующими
свойствами: п — т ее координат имеют значение
О (свободные переменные); т координат имеют
значение ^0 (базисные переменные); вектор-
столбцы матрицы А, соответствующие базисным
переменным, линейно независимы, т. е. образуют
базис пространства Rm. Невырожденная матрица,
составленная из этих вектор-столбцов,
называется базисной матрицей.
Если число линейно независимых уравнений
среди условий ЗЛП в пространстве R" равно т,
то эти условия в совокупности необходимы и
достаточны для того, чтобы определяемая ими
точка была вершиной допустимой области (в том
числе и в случае, когда ЗЛП задана не в
каноническом виде).
Если вершина известна, то всегда можно найти
соответствующий канонический вид ЗЛП,
умножив матрицу коэффициентов и столбец «правых
частей» слева на матрицу, обратную базисной.
При таком преобразовании системы уравнений
допустимая область не изменяется.
В примере F.3) точка хх = 1, х2 = 2, х3 = 0, х4 = 0,
х5 = 10 по указанному выше критерию также является
вершиной, так как столбцы в F.3), соответствующие
базисным переменным хь х2, xs, образуют невырожденную
матрицу и, следовательно, линейно независимы:
базисная
матрица
[3 101 Г 3 1 (Л Г0 0 1-1
-.0.1 -,.. = ,0-3 .
1 о oJ L 1 о oJ Lo i iJ
Найдем канонический вид, соответствующий этой вершине:
[00 1ПГ 31 2005-1 Г 10-4 101П
10-3-10 3019 = 01 14 -30 2 L
0 1 1J L 10 4 1 0 1J LO 0 1 1 1 loJ
+ 14х3 - Зх4
- Х3
^ = Ю,
из которого сразу можно найти вершину. Чтобы получить
канонический вид ЗЛП, следует, кроме того, привести
целевую функцию к новым свободным переменным х3, \4
6.1.1.2.3. Базисные решения. Вершина,
обладающая указанными в 6.1.1.2.2 свойствами,
соответствует допустимому базисному решению.
Если вершина имеет т положительных координат
(т — число линейно независимых
уравнений-условий), то соответствующие переменные должны
быть выбраны в качестве базисных переменных, и
тогда вершине отвечает точно одно базисное
решение. Если вершина имеет меньше чем т
положительных координат (вырожденная вершина),
то ей, возможно, отвечают несколько базисных
решений.
Зная базисное решение, всегда можно
однозначно найти вершину.
6.1.1.3. Симплекс-метод при заданной
начальной таблице. Так как решение ЗЛП достигается
(по крайней мере) в вершине допустимой области,
то достаточно рассмотреть значения целевой
функции только в вершинах.
Данной допустимой симплекс-таблице
соответствует одно базисное решение, т. е. одна вершина.
Проверка выделяет ту вершину, которую следует
считать оптимальной. В других случаях способ
ведет или к заключению, что задача
неразрешима (т. е. минимальное значение целевой функции
в допустимой области равно — оо), или к новому
базисному решению, в котором значение целевой
функции не больше, чем в первом. В общем случае
после конечного числа шагов достигается вершина,
в которой целевая функция имеет оптимальное
значение. При наличии вырожденных вершин в
очень редких, исключительных случаях может
оказаться, что мы снова и снова будем проходить
один и тот же цикл базисных решений,
относящихся к одной и той же вырожденной вершине. Этот
особый случай будет рассмотрен в 6.1.5.
Допустимой симплекс-таблице соответствует точка
минимума, если все коэффициенты целевой функции
неотрицательны:
Тогда минимальное значение целевой функции
равно Qo *).
(Этот критерий становится понятным, если
вспомнить, что все переменные в целевой функции
Q = Рхт+1хХт+1 + ••• + РКХК + ^o МОГУТ
принимать только неотрицательные значения.) Если
все коэффициенты целевой функции положительны,
то вершина, соответствующая таблице, является
единственной оптимальной точкой.
Если критерий не выполнен, т. е. не все
коэффициенты целевой функции неотрицательны, то
следует перейти от одного допустимого базисного
*) Условие р^ < 0, ..., р^ < 0 есть критерий
максимальности; исходя из него, можно описать также дальнейшие
этапы метода максимизации целевой функции (заметим, что
умножением целевой функции на — 1 можно легко перейти
от максимизации к минимизации).
470
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
решения к соседнему допустимому, т. е. такому,
в котором множества базисных и свободных
переменных изменены на один элемент. В
невырожденном случае этому геометрически
соответствует переход от одной вершины к другой вдоль
ребра допустимой области (обе вершины
принадлежат одному ребру). Этот процесс называют
также симплекс-шагом или заменой базиса.
Опишем последовательно его этапы.
1) Выбор разрешающего столбца:
среди элементов последней строки таблицы
выбирается любой Pj* < 0, и соответствующий
столбец называется разрешающим. В качестве Pj*
рекомендуется выбирать минимальное Pj.
2) Выбор разрешающей строки: если
ау* < 0 для всех элементов разрешающего
столбца, то минимума не существует (целевая
функция в допустимой области не ограничена
снизу). Если это не так, то для всех
положительных ау* нужно вычислить отношения bt/ay*. Строка
i, для которой отношение минимально, называется
разрешающей строкой i*:
. b( bt*
mm = ;
ay* > 0 fly* fl/*/*
общий элемент а,*;* разрешающего столбца и
разрешающей строки называется разрешающим
элементом.
3) Замена базиса при помощи
разрешающего элемента a^j* — процесс,
производящий в таблице преобразования канонического
вида, при котором базисное переменное х,*
становится свободным и одновременно свободное
переменное Xj* становится базисным. Если w — какое-
либо значение в таблице, то через w будем
обозначать значение, стоящее в новой таблице на
том же самом месте:
а) i* = /*, i = i для всех i Ф i*,
)* = i*, J =j для всех j Ф]*.
б) at*j* = ; аи* = - аи*щ*;* для всех i Ф /*,
J ai*j* J J
Pj* = —pj*at*j*.
в) dt*j = ai*jat*j* для всех ]ф}*\ Ьг* = Va,*/. (*)
Отметим, что элементы правого столбца и
нижней строки пересчитываются по тому же
принципу, что и элементы в центральной части
таблицы. То же имеет место и в г) и д).
г) ai} = atj — at*jay* для всех i ф i* и j' Ф j*,
Pj = Pj — &i*jPj* Для всех j Ф j*.
При вычислениях вручную рекомендуется
проделать вычисления г) по столбцам для каждого
j ф j*. Заметим, что
(новый столбец) = (старый столбец) -
( = bf — b>i*aij* для всех i ф i*, (-Qo) =
b
/то, что уже \
I стоит в новом j
I столбце после Г
\выполнения в)/
/ разреша-
I ющий стол-
\бец
«То, что уже стоит в новом столбце после
выполнения в)» есть число at*jf постоянное при
пересчете каждого столбца.
Правый столбец таблицы преобразуется
аналогично нормальному разрешающему столбцу,
остается неизменным также правило
преобразования такого столбца, сформулированное в г).
Единое для столбца число, уже имеющееся после в),
здесь есть Ь,*.
i
i*
-. j
... ay
... у
... Pj
... j*
ay*
'" 1 a**J* 1 '•'
... Pj*
¦>
i
... j
... ay
Uj*j
... Pj
... j
... ay*
... apj*
... pj*
bi
bi
-Qo
Всегда должно получаться Ь, ^ 0 и (— Qo) ^
>(-Qo)- Может случиться, что р} < 0, хотя р} ^ 0.
Пример 2.
Xi — x3 +3x4
x2 + 3x4
+х3 — Зх4 +х5
F.4)
Gmin = 4Xt - 6X3 + 9Х4 = 66.
ЗЛП задана в канонической форме. Запишем
соответствующую симплекс-таблицу:
8
2
7
6
5
2
0
2
0
-2
4
3
-1
0
0
1
?
-6
4
3
3
0
0
-3
9
1
2
6
6
2
-66
ПОЛУЧЕНИЕ НАЧАЛЬНОЙ ВЕРШИНЫ
471
1) Выбор разрешающего столбца:
имеется только один отрицательный коэффициент
в целевой функции (— 6). Следовательно, j* = 3
(разрешающий столбец есть ( — 1, 0, 0, 1, 1) ).
Разрешающий столбец содержит положительные
элементы (а63 = 1, а53 = 1).
2) Выбор разрешающей строки:
найдем min F:1, 2: 1) = 2( = Ь5/а53). Следовательно,
/* = 5. Разрешающий элемент а53 = 1. Он обведен
рамкой.
3) Замена базиса:
а) В левом столбце новой таблицы на место 5
ставится 3. Наоборот, в верхней строке вместо 3
запишем 5. Остальные индексы остаются на своих
местах.
б) Место элемента а53 — 1 в новой таблице
занимает а53 = 1: «5 3 = 1 • 1 = 1-
в) В новой таблице место разрешающего столбца
(кроме разрешающего элемента) займет столбец:
— (то, что уже стоит в новом столбце после
выполнения б)) • (разрешающий столбец, кроме
разрешающего элемента),
т.е. а83 = -1-(-1)= 1, а2Ъ = -1-0 = 0, а1Ъ =
= -10 = 0, аьъ= -Ы = -1, р3= -1-(-6) = 6.
В новой таблице место разрешающей строки
(кроме разрешающего элемента) займет строка:
(то, что уже стоит в новой строке после
выполнения б)) • (разрешающая строка, кроме
разрешающего элемента),
д т.е. я51 = 1-(-2)= -2, Й54 = 1-(-3)= -3,
Ь5 = 1 • 2 = 2. Таким образом, мы получили
следующие элементы новой таблицы:
8
2
7
6
3
1
-2
5
1
0
0
-1
1
6
4
-3
2
г) В столбец, стоящий под 1 {j = 1), мы
должны внести в новой таблице следующие
элементы (кроме элемента —2, уже стоящего там
после в)):
«81
«21
«71
«61
Pi -
=
«81
«21
«71
«61
_ Pl -
+ (-«5l)
«83
«2 3
«73
«63
- P* -
а21 =0-(-2)-0 = 0,
а71=2-(-2)-0 = 2,
аб1=0-(-2).1=2,
Pl =4-(-2).(-6)= -8.
Пересчитав оставшиеся два столбца, получим
полную таблицу:
8
2
7
6
3
1
0
0
2
2
-2
-8
5
1
0
-1
1
6
4
rt
0
3
-3
-9
3
- 2
6
4
2
-54
2:3
4:3
Пока критерий минимальности не выполнен,
необходимы дальнейщие замены базисов. Они
приводят к следующим таблицам:
8
4
7
6
3
8
4
7
1
3
1
0
0
2
| 2|
-2
-8
6
0
0
-1
1/2
4
5
1
0
0
-1
1
6
5
1
0
1
-1/2
0
2
2
0
1/3
0
-1
1
3
2
0
[ 1/3 |
1
-1/2
0
-'
3
2/3
6 6 2
2 2 2
4
-48
3
2/3 2/3: 1/3
4 41
1
6
-40
8
2
7
1
3
6
0
0
-1
1/2
1
4
5
1
0
1
-1/2
0
2
4
0
3
-3
3/2
0
3
3
2
2
2
6
-38
В последней таблице все коэффициенты целевой функции
неотрицательны (даже положительны). Следовательно, в
точке *! =2, х2 = 2, х3 = 6, х4 = 0, х5 = 0, х6 = 0, х7 = 2,
х8 = 3 целевая функция принимает минимальное значение
Qo= - (- 38) = 38 (Переменным, индекс которых стоит в
верхней строке, в базисном решении приписывается значение
0; это свободные переменные. Каждое из переменных,
индекс которых стоит в левом столбце, приравнивается к
числу, записанному в правом столбце той же самой строки;
это базисные переменные)
6.1.1.4. Получение начальной вершины.
6.1.1.4.1. Метод искусственных
переменных. Для оптимизации целевой функции
посредством симплекс-метода должна быть задана
симплекс-таблица, соответствующая допустимому
базисному решению. Рассмотрим ЗЛП с п
переменными, не имеющую еще канонического вида
(ср. F.2)). Введением искусственного переменного
472
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
xn + i в каждое i-e уравнение (i = 1, ..., т) и другой
целевой функции G мы приходим к следующей
вспомогательной задаче, всегда имеющей решение:
alnxn
F.5)
Если исходная задача F.2) имеет допустимую точку,
то дополним ее, положив хи + 1=0, ..., хп+т = 0,
до допустимой точки х задачи F.5). Так как G (х) ^ 0
для всех допустимых точек F.5), то точка х такая,
что G (х) = 0, есть оптимальная точка
вспомогательной задачи. ^
Примечание. Если оптимальной точкой
вспомогательной задачи является такая точка Зс, что G (х) > 0, то
исходная задача F.2) не имеет допустимых точек и потому
неразрешима.
6.1.1.4.2. Решение вспомогательной
задачи. Уравнения вспомогательной задачи F.5)
имеют канонический вид. Все искусственные
переменные выбираются базисными, а все
остальные — свободными. Преобразование целевой
функции к небазисным переменным (ср. F.2)) дает
следующий результат:
.) хп +¦
F.6)
Следовательно,
« + 1
п + т
1
аи
- X ап
i=i
таблица
п
аи
-?*
i=i
К
-tbt
<=i
есть допустимая симплекс-таблица для F.5).
Поэтому оптимальное решение вспомогательной
задачи может быть найдено при помощи симплекс-
метода. Как только какое-либо искусственное
переменное станет небазисным, соответствующий ему
столбец может быть опущен.
6.1.1.4.3. Переход от оптимальной
таблицы вспомогательной задачи к
начальной таблице исходной задачи.
В оптимальной таблице вспомогательной задачи
вычеркиваются все столбцы, где соответствующими
свободными переменными являются
искусственные переменные.
Случай I. Оптимальное значение целевой
функции положительно (т. е. число, стоящее в
правом нижнем углу таблицы, отрицательно).
Тогда допустимая область исходной задачи пуста,
исходная задача неразрешима.
Случай II. Оптимальное значение целевой
функции равно G (х) = 0.
Случай На. Среди базисных переменных нет
искусственных. Тогда базисное решение,
представленное таблицей, есть допустимое базисное решение
исходной задачи. Остается только пересчитать
целевую функцию Q (х) исходной задачи в функцию
свободных переменных и внести в таблицу новую
строку целевой функции.
Случай Пб. Среди базисных переменных есть
по меньшей мере одно искусственное переменное.
Этот случай сводится к случаю На следующим
методом. Если все коэффициенты в строке,
соответствующей искусственному базисному
переменному, равны 0, то строка в таблице вычеркивается.
(Это может повторяться не более т- г раз, где
m — число строк, а г — ранг матрицы А.) В противном
случае какой-либо отличный от нуля коэффициент
в этой строке выбирается разрешающим,
производится замена базиса симплекс-методом и столбец,
принадлежащий искусственному свободному
переменному, вычеркивается.
Пример 3.
Зх, + 2х3 - х5»
х, - х2 + х3
х,>0, ..., х5>0, Q =
-12,
5 5,
• 6,
F.7)
х2 - х3 + Здс4 - х5.
Начальная таблица соответствующей вспомогательной
задачи (G(x) « х6 + х7 + хв):
6
7
8
Г71
1
1
-5
2
0
-1
0
1
3
2
1
1
—4
4
0
0
1
5
-1
0
0
1
12
5
6
-23
Решение вспомогательной задачи:
1
7
8
6
1/3
2
0
-1
0
1
3
2/3
1/3
1/3
-2/3
4
0
0
LU
-1
5
-1/3
1/3
1/3
-2/3
4
1
2
-3
1
7
4
2
0
-1
0
1
3 8
2/3 .
1/з :
1/3 1
-1/3
5
-1/3
pi/з]
1/3
-1/3
4
1
2
-1
1
5
4
2
-1
-3
1
0
3
1
1
0
0
7
5
3
1
0
ДВОЙСТВЕННОСТЬ В ЛИНЕЙНОМ ПРОГРАММИРОВАНИИ
473
Мы пришли к случаю На. Целевая функция задачи F.7),
пересчитанная в функцию переменных х2, х3, имеет вид
Q(x) = — Зх2 — 2х3 + 10, и таблица
!
5
4
2
-1
-3
1
_з
3
1
1
0
— 2
5
3
1
-10
есть допустимая начальная таблица для F.7).
6.1.1.5. Вырожденный случай и его
рассмотрение при помощи симплекс-метода. Как было
упомянуто в 6.1.1.3, применение симплекс-метода
может натолкнуться на трудности, если вершина,
соответствующая симплекс-таблице, вырождена и
имеет несколько базисных решений. В этом случае
при некотором i в таблице Ъг = 0. Тогда в
качестве разрешающей строки обычно следует
выбирать как раз строку, в которой Ь{ = 0; значение
целевой функции при замене базиса не изменяется.
Теоретически (в практических примерах
чрезвычайно редко!) может случиться, что после
нескольких замен базиса мы снова придем к такой же
таблице и, следовательно, никогда не достигнем
оптимального значения (это явление называется
зацикливанием). Если симплекс-метод снова и снова
приводит к вырожденным таблицам без изменения
при этом целевой функции, он дополняется таким
образом, чтобы препятствовать появлению таких
циклов. Метод дополнения геометрически может
быть истолкован как предварительное внесение
малых изменений в правые части условий,
посредством чего граничные гиперплоскости
допустимой области сдвигаются так, что вырожденных
вершин больше не существует.
6.1.1.5.1. Лексикографический
порядок векторов. Вектор х = (хь ..., Хк)Т
называется лексикографически меньшим, чем вектор
У — (Уь ---¦> У к) (обозначается х^у), если
существует такое j, что Xi = уи ---, x,-i = yj-u *j < yj.
Тогда пишут также у > х.
Пример 4. >>>-0 означает, что первая отличная от 0
компонента у положительна (последующие компоненты
могут быть произвольными).
6.1.1.5.2. Дополнение к симплекс-
таблице. Каждая правая часть bt дополняется
до вектора (bt, bn, ..., bim) при помощи т других
чисел так, чтобы векторы удовлетворяли условию
(fen, ..., bim)T>- 0 и были линейно независимы.
Это условие выполнено, например, если положить
Ьц =1 и bik = 0 при i Ф к. Далее, - Qo дополняется
до вектора { — Qo, — Qu • •-, —Qm)T произвольными
числами (например, нулями). Получаем таблицу
^¦w+1 • ^n
bi
-Qo
bu
-Q\
• b\m
-Qm
6.1.1.5.3. Дополнение к
симплекс-методу (см. 6.1.1.3).
2) Частные Ь./а^*, образованные для всех i
таких, что а«* > 0, объединяются в векторы-частные
/ bi bn bim\T
—, , ..., ; лексикографически мини-
гг аг аг)
мальныи среди них соответствует строке /*.
36) Ь(*к = Ь(*ка^* для всех к.
Зд) bik = bik — bpkciij* для всех i ф i* и всех к;
i-Qk) = (-Qk)- bt*kPj* для всех к.
Получаемые таким образом векторы всегда
будут удовлетворять условию (Ь„ Ьп, ..., bim) > 0;
линейная независимость этих векторов будет также
обеспечена. Выполнение соотношения ( — Qo,
-бь .... -Qm)TX-Qo, -бь .... -Qmf
гарантирует, что при дальнейших вычислениях мы никогда
не вернемся к однажды уже рассмотренной таблице.
Этот расширенный симплекс-метод может
применяться в общем случае.
Пример 5. Следующая таблица представляет собой
пример, в котором существует возможность после
нескольких замен базиса снова вернуться к той же самой таблице:
1
2
3
!
2
-1
4
-1
-1
-1
5
-1
-1/2
-3
6
3
1
8
0
0
2
Последовательно можно выбрать следующие пары
значений (i*. ;¦): A, 3), B, 4), C, 5), D, 6), E, 1), F, 2).
Полученная таким образом таблица будет тождественна исходной.
Если же снова выбрать j* - 3, но применить симплекс-метод
с лексикографическим расширением:
1
2
3
1
и
-1
4
-1
-1
-1
5
I
-1/2
6
3
1
8
0
0
2
1
0
0
0
1
0
то вектор @, 1, 0) , возникающий при i = 1, будет
лексикографически больше, чем вектор @, 0, 1/2) , соответствующий
i = 2; таким образом, следует выбрать /* = 2, после чего
возникает новая таблица:
1
3
2
-1/2
1/2
1/2
4
-1/2
-1/2
-3/2
5
-3/4
-1/4
-13/4
6
5/2
1/2
17/2
0
0
2
1
0
0
-1/2
1/2
1/2
Метод, примененный к этой таблице, ведет к выводу, что
задача неразрешима, так как целевая функция в допустимой
области не ограничена снизу.
6.1.1.6. Двойственность в линейном
программировании.
6.1.1.6.1. Теоремы двойственности.
Каждой ЗЛП можно сопоставить точно одну
двойственную ей ЗЛП; связь задается следующим
образом.
474
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Исходная ЗЛП
1 2 1
ЛцХ + А12х ^Ь,
1 11
А21х + А22х — Ь,
Двойственная ЗЛП
1 2 1
Г1 Т2 2
12 12
х ^ 0, х - произвольное, и ^ О, м - произвольное,
1Т1 22
пах(") =#" + &"•
1Т1 22
Qmin(x) = р1 х + р1 х;
При этом векторы переменных х и м и
соответственно векторы правых частей и
коэффициентов целевой функции разложены на два
вектора, а матрица коэффициентов состоит из
четырех подматриц.
В частности, в первой задаче по знаку
ограничено ровно столько переменных, сколько есть
неравенств среди условий во второй задаче.
Важные частные случаи:
уравнений, из которой можно найти
оптимальное решение первичной задачи.
Теневые цены. Если заданы две задачи,
соответствующие первому из вышеприведенных
«важных частных случаев», то для каждого i
оптимальное значение х,- называется теневой ценой
единицы ингредиента, ограниченного i-м неравенством
двойственной задачи. Ее величина показывает,
насколько увеличилось бы оптимальное значение G,
если бы граница р( этого переменного увеличилась
на единицу. Теневая цена совпадает с
коэффициентом целевой функции при i-м свободном
переменном в оптимальной канонической форме
двойственной задачи, так что ее можно определить
без рассмотрения первичной задачи.
6.1.1.6.2. Двойственный симплекс-
метод. Двойственный симплекс-метод копирует
вычисления в таблице заданной задачи, которые в
случае применения симплекс-метода следовало бы
выполнять в двойственной задаче.
ЗЛП
Ах^Ь, Х^О, 6min(x) = pTX
Ax^b, x - произвольное,
<2min(x) = p7x
Двойственная ЗЛП
АТи^р, и^О,
Gmax{u) = bTu
ATu = b, u>0,
-Gmin(u)=-bTu
Замечания
Если р>0, то при помощи вспомогательных переменных в
двойственной задаче можно сразу найти начальную таблицу
В то время как первичная задача задана без ограничений знака,
двойственная ей задача имеет вид ЗЛП
Теоремы двойственности. Если
рассмотреть задачу, двойственную к двойственной
задаче, то снова придем к исходной задаче.
Если в одцой задаче допустимая область
пуста, то в другой целевая функция неограничена
снизу (при минимизации) или сверху (при
максимизации).
Если разрешима одна задача, то разрешима и
другая; оптимальные значения целевых функций
при этом одинаковы. Если первичная задача имеет
допустимую точку х, а двойственная задача —
допустимую точку и, то обе задачи разрешимы и
G (и) ^ max G = min Q ^ Q (x).
Если для двух допустимых решений G (и) = Q (х),
то и и х — оптимальные решения.
Теорема о дополняющей
нежесткости. Если х и и допустимы в первичной,
соответственно двойственной задаче, то для
того, чтобы они были оптимальными решениями,
необходимо и достаточно выполнение
следующего условия:
I 1 2 1
и (АцХ + А12х — Ь) = О,
II 2 !
х (Аци + A2i и — р) — 0.
Это означает, что в точке, где достигается
оптимальное значение, никогда не может одновременно
быть так, чтобы i-я компонента вектора решения
была положительна, a i-e неравенство второй
задачи выполнялось строго.
Если известно оптимальное решение и
двойственной задачи, то, подставив его в приведенное
выше условие, получим линейное уравнение для х.
1 2 1
Вместе с А21х + А22х = Ъ они составляют систему
Симплекс-таблица, соответствующая
каноническому виду ЗЛП (ср. 6.1.1.2), называется
двойственно-допустимой, если рк ^ 0 для всех
коэффициентов целевой функции, т. е. для к = т +
+ 1, ..., п. Геометрически этой таблице
соответствует точка пересечения п граничных
гиперплоскостей допустимой области (которая,
однако, не обязательно является допустимой
точкой).
Двойственный симплекс-метод дает
последовательность двойственно-допустимых таблиц до
тех пор, пока не будет найдена допустимая
таблица. По критерию минимальности симплекс-
методом тем самым будет найдена оптимальная
точка. Геометрически это значит, что мы подходим
извне (через точки пересечения, которые не
являются допустимыми) к оптимальной вершине
допустимой области. Двойственно-допустимой
таблице соответствует точка минимума, если
все правые части неотрицательны: bt ^ 0,..., bm ^ 0.
Если этот критерий не выполнен, то переход
к новой таблице разбивается на следующие этапы.
1) Выбор разрешающей строки: среди
Ь{ < 0 в таблице выбирается произвольное число
Ь,*, а соответствующая строка называется
разрешающей; в качестве Ь,* рекомендуется выбирать
минимальное Ь(.
2) Выбор разрешающего столбца:
если at*j > 0 для всех элементов разрешающей
строки, то минимума не существует (допустимая
область пуста). Если это не так, то для всех
отрицательных а,*у составляется частное pj\ at*j |.
Столбец _/, в котором частное минимально, выбирается
в качестве разрешающего столбца f:
Pj pj*
mm J =——-.
at*j < 0 I at*j | \<n*j* |
МОДИФИЦИРОВАННЫЕ МЕТОДЫ, ДОПОЛНИТЕЛЬНОЕ ИЗМЕНЕНИЕ ЗАДАЧИ
475
3) Замену базиса производят, как и в случае
симплекс-метода (см. 6.1.1.3).
Двойственно-допустимая таблица называется
двойственно-вырожденной, если все pj = 0.
6.1.1.7. Модифицированные методы,
дополнительное изменение задачи.
6.1.1.7.1. Модифицированный
симплекс-метод. Предположим сначала, что ЗЛП
уже имеет канонический вид (в противном
случае см. 6.1.1.7.3) и переменные перенумерованы
так, что хп-т+и ..., х„ являются базисными:
Qmin
Xj ^ О ДЛЯ j = 1,...,И,
S!*! + ... + е„_мХ„_т + YO-
Эта ЗЛП представлена в следующей основной
таблице:
п — т+ 1
л
аи
ami
п-т
... ах п—т •
... ат>л —т
• • ел-т
Я-/И+1
X)-. '•-..
0
0
... и
а ... о
'••,.. 'о
о
'
В.
"То '
Введем следующие обозначения: р = (Рь...,рт)Т,
а; = (аи,...,ат^ для ; = 1,...,(л - т), а, = @,...
...,0, 1, 0,...,0) с 1 на (/ — и + т)-м месте для
7 = (п — т + 1),..., п.
Модифицированная
симплекс-таблица. Место симплекс-таблицы занимает
следующая модифицированная симплекс-таблица:
F.10)
первую расстановку чисел в которой получим,
подставив на места, обозначенные буквами,
соответствующие данные основной таблицы.
Для описания свойств модифицированной
симплекс-таблицы введем следующие обозначения:
I
1 ... п—т
PI -Pn-m
n — m+1
a\,n-m+\ -aln
ив, n—m ¦+¦1 **• mn
Pn-m+l -Pn
n
^m
-Qo
Левый столбец указывает индексы базисных
переменных.
Столбец Ъ содержит значения базисных
переменных в точке пересечения, представленной
таблицей (при Ь ^ 0 — вершина).
Величина Qo есть значение целевой функции
в этой точке пересечения.
Величины Pi,...,pn являются коэффициентами
целевой функции, выраженной через свободные
переменные.
Столбцы матрицы А являются столбцами
канонического вида, соответствующими
переменным хп-т+1,...,х„; при этом А — матрица,
обратная базисной.
Все эти свойства сохраняются при переходе
к новой, модифицированной симплекс-таблице по
приведенному ниже методу.
Допустимой модифицированной симплекс-
таблице соответствует точка минимума, если все
коэффициенты целевой функции неотрицательны:
Рх ^ 0,..., рп > 0. Тогда минимальное значение
целевой функции равно Qo.
Переход к новой таблице. В случае,
если этот критерий не выполнен,
модифицированный симплекс-метод ведет точно к таким же
переходам от вершины к вершине, как и симплекс-
метод, изменяется лишь способ преобразования.
Определяются только те значения симплекс-
таблицы, которые используются для нахождения
разрешающего элемента. Затем проводится замена
базиса только для тех значений, которые стоят
в модифицированной симплекс-таблице. Основой
метода является тот факт, что, зная матрицу,
обратную базисной, мы можем в случае
надобности полностью найти канонический вид
(см. 6.1.1.2).
1) Выбор разрешающего столбца:
среди pj < 0 в таблице выбирается произвольное
Pj* < 0; если j* ^ и - т + 1, то соответствующий
столбец канонического вида известен; в
противном случае мы находим его по формуле
(a1;*,...,amj*)^= Adj* и вносим в таблицу. В любом
случае столбец, соответствующий _/*, является
разрешающим.
2) Выбор разрешающей строки
производится, как и в случае симплекс-метода
(ср. 6.1.1.3).
3) Замена базиса при помощи
разрешающего элемента at*j* осуществляется
проще, чем в случае немодифицированного
симплекс-метода, так как индексы столбцов
фиксированы и соответствующая верхняя строка остается
неизменной. Обозначим через w элемент новой
таблицы, стоящий на месте элемента w. Тогда
а) Xt — Xt для всех i # i*; X,,* = j*;
б) ui*j = apj/apj* для всех j' = (п — m + 1),...,и;
о,* = bp/apj*;
в) dij = afj - dpjdij* для всех i Ф i* и всех
; = (п - т + 1), ..., и, а pj = pj - dpjpj* для всех
j = (n — т + 1), ..., п. (Ср. указание, данное в 3 г)
при описании симплекс-метода (см. 6.1.1.3).)
Если (л — m + 1) ^ j*, то это не означает
неприменимости д формул, приведенных в б) и в).
г) bt = bi- b,*a,y* для всех i Ф i*, -Qo = (-Qo) -
476
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Правая часть вычисляется таким же образом,
как столбцы в в).
д) р. = е,- + р <Xj для всех j = 1,...,п — т
(вектор р уже известен из результата в)).
После вычислений всегда должно получаться,
что hi ^ О и ( — Qo)X~Qo)- Может случиться,
что pj < О, хотя pj ^ 0. Коэффициенты целевой
функции при новых базисных переменных должны
быть равны 0; их можно положить равными 0
сразу.
Для вырожденного случая справедливо все, что
было изложено относительно симплекс-метода.
Преимущества
модифицированного симплекс-метода. В случае симплекс-
метода ошибки округления могут неограниченно
расти от таблицы к таблице, так как на каждом
шаге переход к следующей таблице определяют
данные таблицы, имеющие некоторую
погрешность. Напротив, в случае модифицированного
метода применяются е,-, а,-, определенные из
основной таблицы. К тому же после
определенного достаточно большого числа шагов мы можем
«обновить» все данные (устранить ошибки
округления), взяв из основной таблицы базисную
матрицу (образованную из а,, соответствующих
базисным переменным
в порядке их
следования в модифицированной таблице) и найдя
обратную ей. Так возникает обновленная матрица А,
при помощи которой можно вычислить
обновленные b = Лр, рТ=—еТА и -Qo = -eTb.
Остальные pj (j = 1, ..., m) вычисляются по формуле
Pj = Zj — pT0ij при помощи обновленного р и данных
основной таблицы. Таким образом, вся
модифицированная таблица может быть вычислена
непосредственно на основе данных основной таблицы,
если только заданы индексы базисных переменных.
Далее, модифицированный метод ведет к
уменьшению количества вычислений по сравнению с
симплекс-методом, если число переменных по
крайней мере в три раза.больше, чем число уравнений,
и многие коэффициенты равны нулю.
Пример 6. Мы снова используем пример 2, который
уже был решен при помощи симплекс-метода. В качестве
основной таблицы имеем:
8
2
7
6
5
1
2
0
2
0
-2
4
3
-1
0
0
1
1
-6
4
3
3
0
0
-3
9
8
,
0
0
0
0
0
2
0
1
0
0
0
0
7
0
0
1
0
0
0
6
0
0
0
1
0
0
5
0
0
0
0
1
0
1
2
6
6
2
-66
8
2
7
6
5
1
4
3
-6
4
9
8
1
0
0
0
0
0
2
0
1
0
0
0
0
7
0
0
1
0
0
0
6
0
0
0
1
0
0
5
0
0
0
0
1
0
1
2
6
6
, 2
-66
Отсюда получим первую модифицированную симплекс-
таблицу (найдем в соответствии с 1) j* = 3, вычислим
(ai3, ..., а5з)Т=Аа3 и внесем в таблицу (разумеется, при
практическом использовании - сразу в ту же самую таблицу).
В соответствии с 2) найдем /¦ = 5, так как ЬА: а43 =
= 6:1 =6, Ь5:а53 = 2:1 =2.
Следовательно, число 1, взятое в рамку, является
разрешающим элементом. В соответствии с 3) получим
вторую таблицу:
8
2
7
6
3
1
-8
5
0
4
-9
8
1
0
0
0
0
0
2
0
1
0
0
0
0
7
0
0
1
0
0
0
6
0
0
0
1
0
0
5
!
0
0
_1
1
6
3
2
6
4
2
-54
Она изображает ту же самую вершину, которая была
получена после первого симплекс-шага в 6.1.1.3. После
следующих трех модифицированных симплекс-шагов мы
получим модифицированную симплекс-таблицу вершины, для
которой выполняется критерий минимальности (так же
как после трех симплекс-шагов была найдена
оптимальная симплекс-таблица той же самой вершины).
6.1.1.7.2. Модифицированный
двойственный симплекс-метод. Данному
каноническому виду ЗЛП, как и в 6.1.1.7.1,
сопоставляется основная таблица и модифицированная
симплекс-таблица. Мы применяем те же
обозначения, что и в 6.1.1.7.1.
Если (еь...,е„_ JT^ 0, то (при любом знаке
Р,) может быть применен двойственный симплекс-
метод, так как задан двойственно-допустимый вид.
Его также можно перевести в
модифицированный вид (с теми же преимуществами, которые
указаны в 6.1.1.7.1).
Критерий минимальности для
модифицированного двойственного симплекс-метода такой же,
как и в случае двойственного симплекс-метода.
Если критерий минимальности не выполнен,
то переход к новой модифицированной симплекс-
таблице осуществляется следующим образом.
1) Выбор разрешающей строки:
среди Ь, < 0 в таблице выбирается произвольное
Ь,* < 0 (например, наименьшее Ь,); затем
вычисляются отсутствующие элементы этой
разрешающей строки i*:
ai*j = {ai*n_m+l,...,ai*n)aj для j = 1,...,я - m
и вносятся в таблицу.
2) Выбор разрешающего столбца:
j* определяется, как и в двойственном симплекс-
методе; если j* ^t n — m + 1, то соответствующий
столбец канонического вида уже известен. В
противном случае он вычисляется по формуле
первая таблица
8
2
7
6
5
1
4
3
-1
0
0
1
.
п
-6
4
9
8
1
0
0
0
0
0
2
0
1
0
0
0
0
7
0
0
1
0
0
0
6
0
0
0
1
0
0
5
0
0
0
0
1
0
1
2
6
6
2
-66
первая таблица с внесенными в нее разрешающим
столбцом
ЛИНЕЙНАЯ ТРАНСПОРТНАЯ ЗАДАЧА
477
(ау*,...,ат^)т= Aotj* и вносится в имеющуюся
таблицу.
3) Замена базиса при помощи
разрешающего элемента а,*.* делается, как и в
случае модифицированного симплекс-метода.
6.1.1.7.3. Получение начальной
вершины. Если данная ЗЛП еще не имеет
канонического вида, то он может быть получен путем
решения вспомогательной задачи F.5), как в
6.1.1.4.1. Модифицированный симплекс-метод может
быть применен также для решения этой
вспомогательной задачи; однако столбцы,
соответствующие вспомогательным переменным, здесь
вычеркивать нельзя. Если найдена оптимальная
модифицированная симплекс-таблица вспомогательной
задачи такая, что Qo = О, то в качестве «новой
целевой функции» вспомогательной задачи может
рассматриваться исходная целевая функция *). Затем
вычисления продолжаются при помощи
модифицированного симплекс-метода с тем
дополнительным условием, что столбцы, соответствующие
искусственным переменным, не используются в
качестве разрешающих столбцов (критерий
минимальности относится соответственно только к другим
столбцам).
Существует также метод нахождения первой
двойственно-допустимой модифицированной
таблицы. Но модифицированный двойственный метод
(так же как двойственный) чаще всего используется
тогда, когда такая таблица задана непосредственно.
6.2.1. ЛИНЕЙНАЯ ТРАНСПОРТНАЯ
ЗАДАЧА
6.2. ТРАНСПОРТНАЯ ЗАДАЧА
? Xij = bi для i = 1,..., т;
Линейные транспортные задачи составляют
особый класс задач линейного программирования.
Задача заключается в отыскании такого плана
перевозок продукции с т складов к п
потребителям, который требовал бы минимальных затрат.
Если потребитель j получает единицу продукции
(по прямой дороге) со склада i, то возникают
издержки Pij. Предполагается, что транспортные
расходы пропорциональны перевозимому
количеству продукции, т. е. перевозка к единиц продукции
вызывает расходы кри.
Далее, предполагается, что
у>= ?>> F.И)
где b( есть количество продукции, находящееся
на складе i, и о, — потребность потребителя j.
Замечание. Если ? bt >
.=1
о,-, то количест-
я
во продукции, равное ? bt - ]Г я,, остается на
складах. В этом случае мы введем «фиктивного»
потребителя п+1 с потребностью ? Ь,-- ? а} и
i=i j=i
положим транспортные расходы pitn + l равными 0
для всех i. Если ? bt < ]Г а/, то потребность не
«=1 j=i
может быть покрыта.
В этом случае начальные условия должны
быть изменены таким образом, чтобы потребность
в продукции могла быть обеспечена.
Обозначим через хи количество продукции,
поставляемое со склада i потребителю j. В
предположении F.11) нам нужно решить следующую
ЗЛП:
xtJ = а} для / = 1,...,л;
Xij^O для I = 1,...,/и и j = 1,...,п;
Kmin=i iPliXl,
Транспортную задачу мы можем
характеризовать транспортной таблицей и таблицей издержек:
Допустимый план перевозок будем представлять
в виде транспортной таблицы:
Сумма элементов строки i должна быть равна
bh а сумма элементов столбца j должна быть
равна о,, и все 3c,-j должны быть неотрицательны.
Пример 7.
20 5 10 10 5
F.12)
*) В случае Qo > 0 в оптимальной точке
вспомогательной задачи допустимая область исходной задачи
пуста; следовательно, сама задача неразрешима.
478
ТРАНСПОРТНАЯ ЗАДАЧА
Мы получаем следующую ЗЛП:
+ *12 + Х13 + *14 + *15
•+ Х24
= 15,
= 15,
- х33 + х34 + х35 = 20,
= 20,
= 5,
= Ю,
= 10,
¦¦ 5;
Х34
хи > 0 для i=l, 2, 3; j = 1, 2, 3, 4, 5;
ц+ 6х12 + Зх13 + 5х14 + 9х15 + 6х21 + 4х22 + 7х23 + Зх24 + 5х25 + 2x3j + 5х32 + Зх33 + х34 + 8х35.
Такие задачи целесообразно решать при помощи
особого варианта симплекс-метода - так
называемого транспортного метода (см. 6.2.3).
Все транспортные задачи имеют оптимальное
решение. Если все значения и, и bt в условии
транспортной задачи целочисленны, то
переменные xtJ во всех базисных решениях (а также и
в любом оптимальном базисном решении) имеют
целочисленные значения.
6.2.2. ОТЫСКАНИЕ НАЧАЛЬНОГО
РЕШЕНИЯ
В транспортной таблице [
а\ ... ап
выберем ячейку (/*, j*) и запишем в ней xt*j*
= min{bj*, uj*}*):
Ьх
hi*
'ьт
а\
... aj* ... ап
а) Если ft,-* ^ о.-*, то остальные ячейки строки
I* вычеркиваются (все содержимое склада i*
поставляется в у*) и Oj* заменяется на (в/* — ft/*), a
ft/* — на 0.
б) Если ft/* ^ а.-*, то остальные ячейки столбца
у* вычеркиваются (потребитель j* уже получил всю
продукцию) и ft,* заменяется на (ft/* — a.-*), a
а.-* — на 0.
*) В случае min{ft/*t fly*} = 0 в таблицу вносится 0.
Следует различать внесение 0 и невнесение какого-либо
числа вообще!
Полученная таблица содержит на одну строку
или на один столбец меньше, чем предыдущая.
В полученной таблице выбирают новую ячейку и
повторяют предыдущие рассуждения до тех пор,
пока в таблице не окажется ни одной свободной
ячейки.
В результате каждой ячейке исходной таблицы
можно сопоставить либо зачеркнутую ячейку,
либо ячейку, в которую внесено число Хц. Тем
самым найдено базисное решение: переменные,
соответствующие зачеркнутым ячейкам, являются
свободными переменными; остальные являются
базисными, и им мы сопоставим значения Зс,7.
В каждой строке и в каждом столбце будет
стоять по меньшей мере одно базисное
переменное (возможно, со значением 0, что соответствует
вырожденному случаю).
Для того чтобы найти наиболее экономичное
начальное базисное решение, обычно выбирают
ячейку (/*, _/*), которой соответствуют
минимальные транспортные издержки: min рц = ppj*.
Если же выбирают верхнюю левую ячейку, то
метод выбора называется правилом
северо-западного угла.
Разберем отыскание начального решения на примере 7.
I. Применение правила северо-западного угла: в верхнюю
левую ячейку записываем min {15, 20} = 15, а остаток строки
вычеркнем:
5 10 10 5
15
20
В левую верхнюю ячейку получившейся таблицы
записываем min{5, 15} = 5, а остаток столбца вычеркнем:
5 10 10 5
0 15
10 1ПН
20
ТРАНСПОРТНЫЙ МЕТОД
479
В конце концов получим таблицу
[Т]
10 I
ГГЛ
15
Г201
10 5
Ей соответствует базисное решение х15 = 15,
*2i = 5, х22 = 5, х23 = 5, х33 = 5, х34 = 10, х35 = 5
(базисные переменные); остальные переменные
являются свободными, и в базисном решении им
соответствует значение 0.
II. Найдем min ptJ = 1 = р34. В ячейку C, 4) за-
Uj
пишем min {20, 10} = 10 и остаток четвертого
столбца вычеркнем. Найдем minpy = 2 = p31. В ячейку
C, 1) запишем min {10, 20} = 10 и остаток третьей
строки вычеркнем. Найдем minptJ = 3 = р13. В
;/з
ячейку A, 3) запишем min {15, 10} = 10 и вычеркнем
остаток третьего столбца. Продолжая таким
образом дальше, получим таблицу
о |]QJ]
ШИВ
10 20
20
10
5
10
6.2.3. ТРАНСПОРТНЫЙ МЕТОД
Пусть имеется транспортная таблица,
соответствующая начальному решению, ху = хц для
базисных переменных, хи = 0 для свободных
переменных (ячейки, соответствующие свободным
переменным, остаются пустыми). Далее, нам требуется
таблица расходов с заданными ри. (Ниже мы
постоянно будем ссылаться на пример 7 из 6.2.1.)
Отыскание симплекс-множителей.
Заполним таблицу расходов, оставив ячейки,
соответствующие свободным переменным, пустыми.
В крайний правый столбец внесем значения
неизвестных мь...,мш, в нижнюю строку - значения
неизвестных vu...,vH (рис. 6.6). Эти т + п
неизвестных для всех (i, j), соответствующих базисным
переменным, должны удовлетворять линейной
системе уравнений щ + Vj = рц.
Для всех базисных решений эта система имеет
треугольный вид, ранг ее матрицы равен
п + т - 1. Следовательно, систему всегда можно
решить следующим способом.
Полагают vn = 0. Если значения к неизвестных
A < /с < л + m - 1) определены, то в системе всегда
Ри
Ри
Pml
•
Л,
Ру
Рщ
• : •
• : •
Рщ
Pin
Рта
uL . . . tij . . . un
Рис. 6.6
имеется уравнение, одно из неизвестных в котором
уже найдено, а другое еще нет.
Переменные щ и Vj называются симплекс-
множителями. Иногда они называются также
потенциалами, а транспортный метод — методом
потенциалов.
Пример 8.
5
6
4
7
3
1
8
v2
V5
v5 = 0 -> u3 = 8, так как м3 + и5 — p3s = 8, -» у* = —7, так как
и3 + vA = рз4 =1» -*¦ ^з = — 5, так как и3 + у3 = 3, -*¦ и2 =
= 12-и>2 = — 8-»»! = -6-nii = 11.
Симплекс-множители нужны для того, чтобы
найти свободную ячейку (i, /), которая при замене
базиса переходит в базисную (это соответствует
отысканию разрешающего столбца в симплекс-
методе).
Для определения симплекс-множителей мы
вносим на свободные места в таблице значения
Pij = Plj — Щ — Vj
(коэффициенты целевой функции, пересчитанные для
свободных переменных). Если все р'ц ^ 0, то
базисное решение оптимально (см. критерий
минимальности). В противном случае вы выбираем
произвольное р'ар < 0, чаще всего наименьшее. Индексом
оф помечено свободное переменное хар, которое
должно войти в базис. Соответствующую ячейку
транспортной таблицы мы отметим знаком +.
Пример 9
Ри-
5
6
2
6
4
5
3
7
3
5
3
1
9
5
8
5
6
4
7
3
1
8
11
12
-6 -8 -5 -7 0
Минимальный элемент — 7 -¦ (а,
5
6
0
3
4
5
-3
7
3
1
-2
1
_2
-7
8
= B, 5)
480
ТРАНСПОРТНАЯ ЗАДАЧА
Кроме ячейки (а, р) транспортной таблицы,
мы пометим знаками — и + другие занятые
числами ячейки таким образом, чтобы в каждой
строке и каждом столбце транспортной таблицы
число знаков + было равно числу знаков -.
Это всегда можно сделать единственным образом,
причем в каждой строке и каждом столбце
будет содержаться максимум по одному знаку +
и по одному знаку -.
Пример 10.
15
5
5
-_^
5
5
15
5
10
5
+
5
5~
>
10
+
5~
Знак + поставлен в ячейке B, 5). Соответственно в
последнем столбце должен быть поставлен знак -, это
можно сделать только в ячейке C, 5). Следовательно,
знак + должен быть поставлен в последней строке. В
ячейке с числом 10 этого сделать нельзя, так как тогда
в соответствующем столбце не было бы знака -, и т. д.
Затем мы определяем минимум М из всех
элементов, помеченных знаком -, и выбираем
ячейку (у, 6), где этот минимум достигается.
В нашем примере с М = 5 можно выбрать (у, 8) =
= B, 3); при этом (у, 5) определяет базисное переменное,
которое должно стать свободным, т. е. базисное
переменное, соответствующее индексу разрешающей строки симплекс-
метода.
Переход к новой транспортной таблице (замена
базиса) происходит следующим образом:
а) В ячейку (а, р) новой таблицы записывается
число М.
б) Ячейка (у, 8) остается пустой.
в) В других ячейках, помеченных знаками -
или +, число М вычитается из стоящего в
ячейке числа ( —) или складывается с ним ( + ).
Результат вносится в соответствующую ячейку
новой таблицы.
г) Непомеченные числа переносятся в новую
таблицу без изменений. Остальные ячейки новой
таблицы остаются пустыми.
Пример 11.
15
5
5
5"
5"
15
5
10
5
+
5"
10
>
10
5
0
Получается новая транспортная таблица, и
повторяется ход предыдущих рассуждений. После
конечного числа шагов критерий минимальности
будет выполнен (если не учитывать
теоретически возможного зацикливания в случае
вырождения).
Пример 12. Ниже воспроизведен ход решения примера
7 из 6.2.1.
15
15
20
20
15^
5
5
5
10
5
5+
10
10
5
+
5~
5
6
0
-6
3
4
5
-8
-3
7
3
-5
-2
1
-7
-2
-7
8
0
11
12
15
5"
+
5
10
10
5+
0"
15"
5
О4"
5
+
10"
10
5
5
6
-7
3
4
-2
4
7
3
8
5
1
5
5
8
-1
-1
5
6
2
3
4
5
-3
0
3
1
-2
1
5
5
7
5
5~
10 +
5
10
+
10"
5
5
6
2
3
4
5
3
3
3
1
-2
1
5
5
7
5
15
5
10
К =
5
5
150
5
5
2
2
1
4
3
3
5
3
1
3
1
3
5
5
-1
-3
-2
ЗАДАЧА О СМЕСЯХ
481
Первая транспортная таблица была получена в 6.2.1
при помощи правила северо-западного угла (составление
первой вспомогательной таблицы и второй транспортной
таблицы было описано выше). Затем поочередно находятся
новая вспомогательная и новая транспортная таблицы до
тех пор, пока (после четырех замен базисов) не будет
достигнут минимум.
Следует обратить внимание на предпоследнюю
транспортную таблицу, так как она совпадает с найденной при
помощи улучшенного метода отыскания начального решения
в 6.2.2; если начать с нее, то потребуется лишь одна
замена базиса.
В вырожденном случае, как и в симплекс-
методе, особый метод для предотвращения
зацикливания применяется только тогда, когда после
нескольких последовательных шагов М становится
равным 0.
Если дана вырожденная транспортная таблица
(ее можно узнать по имеющемуся 0), то, заменив
ат на ат + пг и все bj на bi + ?, где е > 0
подразумевается очень малым, исправим значения
Хц базисных переменных так, чтобы для новых
а, и bj получилось базисное решение. Это всегда
можно сделать единственным образом (как и при
отыскании симплекс-множителей).
15
5
5
10
10
5
0
15
15
20+е
20+е
5 + Е
10+е
10+е
5 + е
15+2е
5-е
5 + е
10+е
10+е
5-2е
Зе
Если полученный таким образом элемент хк1
окажется отрицательным, то в этой же. строке
должен найтись положительный (еще до изменения)
элемент хкг и в этом же столбце —
положительный элемент 5csl. Тогда ячейка (s, r) свободна,
отмечаем ее знаком + и проводим замену базиса.
Так можно избавиться от всех отрицательных
значений *).
Затем при помощи транспортного метода
расчеты продолжают дальше (вырождение уже никогда
больше не встретится). Устремляя б -¦ 0, приходим
к оптимальному решению исходной задачи.
6.3. ТИПИЧНЫЕ ПРИМЕНЕНИЯ ЛИНЕЙНОГО
ПРОГРАММИРОВАНИЯ
6.3.1. ИСПОЛЬЗОВАНИЕ
ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ
Пример 13. Требуется изготовить четыре вида изделий
А( в количествах от at до Ьг (i = 1, 2, 3, 4). Себестоимость
одного изделия составляет р{. Каждое изделие А( требует
ац минут рабочего времени на каждом из станков М}
(/ = 1, 2, 3), общее время использования которых должно
быть заключено в пределах от п} до mj минут. Надо
найти план производства с минимальной себестоимостью.
Переменное х, - число изделий вида Ah которое следует
произвести.
М о дел b.aijXi + a2Jx2 + a3Jx3 + <»4j*4 < ntjдляj = 1,2,3;
aijXi + a2Jx2 + a3Jx3 + a4Jx4 ^ ni для j * 1, 2, 3; Xj < bh
для /=i, 2, з, 4; &,<„(*) = p,x,+p2x2+ 5.3.2. ЗАДАЧА О СМЕСЯХ
Пример 14. Требуется изготовить сплав из трех
металлов М,, каждый с плотностью aiU содержанием углерода
а12 и содержанием фосфора а13, которые могут быть
использованы в количествах от а\ до Ь\ и стоят р{ рублей за
килограмм. Сплав должен иметь плотность в пределах от
Л! до ть содержание углерода от л2 до т2 и содержание
фосфора от л3 до гл3; сплав должен быть произведен в
количестве с килограммов и быть при этом как можно
более дешевым.
Переменное х, « (количество затраченного
металла М()/с.
Модель, как и в 6.3.1, где нужно положить
а, = а\1с, bi = b'i/с.
Другие примеры
м
Виды квалифицированных
кадров
Сельскохозяйственные
культуры
Виды скота
-,
Учреждения, готовящие
квалифицированные кадры
Рабочая силы, техника
Рабочая сила, скотные
дворы, корма
Вариант. Если р, - прибыль на единицу продукции,
то ищем maxQ(x).
Замечание. При больших количествах изделий
требованием целочисленности можно пренебречь; при
вычислениях в единицах серий или объемов эта трудность чаще
всего отпадает сама собой. Если действительно встретится
описанный выше случай, то в громоздких задачах
рекомендуется применять специальный симплекс-метод для «дву-
сторонне ограниченных задач». Однако чаще всего для
многих j имеем п} = 0 или т} = со (соответствующее
неравенство излишне), а для многих i имеем я, = 0 или Ь, = оо
(соответствующее неравенство тождественно условию знака
или излишне); тогда методы решения, изложенные в
6.1.1, имеют одинаковую эффективность.
*) Часто бывает достаточно везде заменить е на -е.
16 И. Н. Бронштейн, К. А. Семендяев
482
ТИПИЧНЫЕ ПРИМЕНЕНИЯ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Другие примеры.
Примеры.
Mi
Кормовые средства
Отопительный газ
Сорта свеклы
аи
Содержание питательных
веществ, содержание
вредных веществ
Калорийность, содержание
серы и пыли
Урожайность листьев,
урожайность клубней
6.3.3. РАСПРЕДЕЛЕНИЕ, СОСТАВЛЕНИЕ
ПЛАНА, СОПОСТАВЛЕНИЕ
Пример 15 Требуется изготовить т видов продукции
Pj в количествах я, Имеется п станков М{ с bt минутами
рабочего времени. Каждая единица продукции Pj может быть
изготовлена по выбору на любом станке; это требует
с^ минут и стоит ри рублей Надо найти наиболее
экономичное распределение продукции по станкам.
Переменное xtj — количество продукции Pjy
произведенной на станке М{
Модель
? xtJ — Qj для j = 1,..., т;
для t = 1,...,и;
хи ^ 0 для всех (i, j),
Модель является обобщением транспортной модели. Задача
может быть решена при помощи симплекс-метода.
Вариант Требуется минимизировать общее рабочее
время станков (и рабочее время обслуживающих их рабочих).
Модель аналогична приведенной выше, но с целевой
функцией Q= X I сцхц.
Другие
Сельскохозяйственные
культуры
Предприятия
Продукция
Поставки в
квартале j
примеры.
Мг
посевные
площади
источники
энергии
предприятия
продукция в
квартале /
х
1
затраты
1
P.V
доход от
урожая
степень
использования
прибыль
(производственные
затраты) +
+ (затраты
на хранение)
max
max
max
min
Замечание. В случае ci} = 1 можно применить
транспортный метод после того, как путем введения
фиктивного Рт+х мы получим XaJ = Z^- В случае
необходимости некоторые распределения могут быть исключены
(например, при составлении плана надо учитывать, что
продукцию, произведенную в третьем квартале, нельзя вывезти
во втором), для этого достаточно положить в
соответствующих ячейках ри = оо.
При п = m, dj = 1, bt = 1, си = 1, xue{0, 1} при всех i и ;
как частный случай получается задача о сопоставлении.
п
п
п
п
п
Pj
изделий
предприятий,
которые нужно
построить
поездов,
которые следует
составить
штатных единиц
видов
деятельности
п
п
п
п
п
Мг
предприятий
месторасположений
путей
работников
работников
Ри
производственные
затраты
затраты на
освоение
маневры
производительность
затраты
времени
min
min
min
max
min
Решение можно найти при помощи транспортного
метода (с модификацией, чтобы не допустить вырождения).
6.3.4. РАСКРОЙ,
ПЛАНИРОВАНИЕ СМЕН, ПОКРЫТИЕ
Пример 16. Для заготовок в виде стержней длины /
каждый имеются варианты раскроя Z, (/ = 1, 2, 3, 4, 5, 6).
Требуется получить а} частей Т} длины 1} 0=1. 2, 3, 4).
При каждом варианте раскроя получается к{] частей Tj.
(При этом кп1г + ки12 + ki3l3 + kuU < /• Это условие,
наложенное на коэффициенты, содержится в определении «вариант
раскроя» и не является условием оптимизации.) Требуемое
количество частей должно быть получено из минимального
количества стержней.
Переменное х, — число стержней, разрезанных
согласно варианту Z,.
Модель: к^х1 + кг)х2 + k3jx3 + k4Jx4+k5Jx5 + k6jx6 > a,
при ; = 1, 2, 3, 4; x, ^ 0 при i = 1, 2, 3, 4, 5, 6;
Qmm(x) = Xt + X2 + X3 + X4 + X5 + X6.
Замечание. Вводя вспомогательные переменные и
умножая уравнения на — 1, сразу придем к двойственно-
допустимому каноническому виду; таким образом,
целесообразно применить двойственный или модифицированный
двойственный симплекс-метод.
Другие примеры.
Сырье
Доски (из опилок и
стружки)
Ткань, свернутая в
/-метровый рулон, или лист
жести ширины /
Более мелкие доски
/^-метровые полотна ткани
или полосы жести ширины 1}
Планирование смен в библиотеках и продажу билетов
в кассах также можно моделировать подобным образом:
Z, — возможные в течение дня смены; Т/ — определенное
время дня; ки = 1, если Z, предусматривает работу во
время Tj, в противном случае кц — 0; aj — число
работников, требующихся в момент времени Гу; xt - количество
работников смены Z(. В частном случае aj=l, кие{0, 1}
возникают задачи о покрытии, которые, разумеется, надо
всегда решать методами целочисленного линейного
программирования.
Пример 17. Для строительства гидроэлектростанций
могут быть использованы шесть мест Zt (/=1,...,6).
Каждая ГЭС Zf могла бы обслужить (ktJ« 1) или не
обеспечить (kl} = 0) некоторые из четырех регионов. После
сооружения минимального количества электростанций каждый
ПОСТАНОВКА ЗАДАЧИ
483
четырех районов лолжен быть «покрьп» хотя бы один
ран
если в Z, построена ГЭС, и
Переменное \,
\, — 0 н противном случае
Модель 1акая же, как модель раскроя, но с
условием «1 - а2 = <>i - Чл = 1 и с дополнительным условием
«v, = 0 или х,- = 1» при 1=1. 2, 3. 4, 5, 6
В а р и а и г ы примера Пусть расходы на строительство
Z, равны Pi Ищется наиболее дешевое «покрытие» всех
местностей Целевая функция в лом случае' Qmin = p{xt +
<- р2х2 + PiXs 4- p4v4 + P5X5 + Р(,хь Можно потребовать также
л-крашое покрытие -* а,---п
Другие примеры.
Фазы регулирования
уличного движения
Кандидаты в экспедицию
Потоки движения, которым
надо дать дорогу
Требующиеся знания
(медицина, радио, иностранные
языки)
6.4. ПАРАМЕТРИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6.4.1. ПОСТАНОВКА ЗАДАЧИ
Если все коэффициенты условий и целевой
функции зависят от одного или нескольких
параметров, то говорят о параметрическом
программировании. Практически применимые методы
существуют для случая, когда от параметра
линейно зависят только коэффициенты целевой функции
(см. 6.4.2). Случай, когда от параметра линейно
зависят только правые части условий, может
быть сведен к первому путем рассмотрения
двойственной задачи (см. 6.1.1.6). Законченная
теория, которая, однако, ведет к очень
громоздким вычислениям, имеется также для случая, когда
коэффициенты целевой функции линейно зависят от
нескольких параметров (при помощи двойственной
задачи также рассматривают зависящие от
параметров' постоянные члены условий). Аналогичное
утверждение имеет место, если от параметров
линейно зависят как коэффициенты целевой
функции, так и постоянные члены условий.
Для случаев, когда от параметров зависят
коэффициенты при переменных в условиях, общих
методов еще не существует.
6.4.2. МЕТОД РЕШЕНИЯ ДЛЯ СЛУЧАЯ
ОДНОПАРАМЕТРИЧЕСКОЙ
ЦЕЛЕВОЙ ФУНКЦИИ
Пусть ПЗЛП (параметрическая ЗЛП)
tfnxi + ... + аих„ = Ьи
рассматривается при всех t, — 00 < f < -f 00.
(Другие типы задач линейного
программирования с однопараметрической целевой функцией
сводящиеся к этому типу, описаны в 6.4.1.)
Геометрическая интерпретация в
случае двух переменных (ср. 6.1.1.1). При
всех значениях t задачи
flnX! + al2x2 ^ bu
Qmin
*i + am2x2 ^ b
xt > 0, x2 ^ 0,
+<?lO*l +(P2
имеют одинаковую допустимую область. С
изменением t линии уровня постепенно «вращаются».
На рис. 6.7 изображено пять положений линий
уровня при этом «вращении». Из рисунка видно,
что при t — tOi t = ti, t = t2 оптимальной точкой
является одна и та же вершина. При t = t3
оптимальны две соседние вершины (и все ребро
между ними). При большем t = f4 оптимальна
только одна новая вершина.
Если вершина ПЗЛП является оптимальной
точкой при t = t0, то существует определенный
промежуток t ^ t0 ^ 1 такой, что для целевой
функции, зависящей от t, в этом промежутке
указанная вершина оптимальна, в то время как
при t, лежащем вне его, она оптимальной не
является. (При этом возможно t = — 00,1 = + 00, t = 1.)
Этот промежуток называется тогда областью
устойчивости вершины. Если Е1 и Е2 — две
вершины и t' лежит внутри обеих областей
устойчивости, то области устойчивости тождественны.
Нетождественные области устойчивости имеют
максимум одну общую точку.
Пусть ПЗЛП имеет оптимальное решение по
крайней мере для одного значения параметра.
Тогда в интервале — оо < t < +00 имеется
конечное число характеристических значений
t0 < t! < t2 < ... < tr таких, что,
а) при t < t0 не существует решения ПЗЛП
(этот интервал может быть пуст, t0 = —00);
б) сегмент tt < t ^ ti + 1 при каждом i = 0, 1,...,г— 1
является областью устойчивости по меньшей мере
одной вершины ПЗЛП, tt^t ^ tt может быть
областью устойчивости вершины при определенных
1 = 0, 1,...,г;
в) при t > tr не существует решения ПЗЛП (этот
интервал может быть пуст, tr = + 00).
16*
484
ПАРАМЕТРИЧЕСКОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Если рассматривать оптимальное значение
целевой функции для каждой ПЗЛП с фиксированным
t как функцию U то получим функцию
оптимальных значений боСО-
Функция оптимальных значений непрерывна,
вогнута и кусочно линейна на интервале значений
U для которых ЗЛП разрешима. Точками излома
являются характеристические значения
tl9 *2....Л-1.
Метод решения. Основная идея метода
состоит в решении ПЗЛП для фиксированных
значений t и последовательном изменении t от
одного характеристического значения tt к другому.
Рассмотрим ПЗЛП канонического вида, которую
можно получить, как описано в 6.1.4. Строка
симплекс-таблицы, отведенная под целевую
функцию (ср. 6.1.2), заменяется на две строки: одну
для pj, другую для qr Соответственно
-Qo — - Qop - Qoqt. При замене базиса обе строки
преобразуются в отдельности, как обычная строка
целевой функции:
'т'-т+\
Р}-
-т+\
Р1п
"Cop
(здесь буквами обозначены числа в
соответствующей таблице; вообще они не являются числами
из первоначально заданной ПЗЛП).
Если не известно ни одного значения г, для
которого ПЗЛП разрешима, можно поступить
следующим образом. Сначала найдем оптимальное
решение для произвольно большого t. Это означает,
что в качестве элементов «управляющей строки»
для выбора разрешающего столбца нам требуются
только qjy если они отличны от нуля, a pj
нужны только в том случае, если qi — 0. Таким
образом, мы будем выполнять шаги симплекс-
метода до тех пор, пока это возможно. В
результате придем к одному из двух случаев.
Случай I. Все qt в полученной таблице не
меньше 0, и там, где qj = 0, везде Pj > 0. Это
значит, что мы получили оптимальную таблицу,
соответствующую вершине с областью
устойчивости, простирающейся до tr = + оо.
Тогда дальше мы поступаем, как описано ниже
в разделе «Определение левой границы области
устойчивости».
Случай И. Случай I не имеет места, т. е.
при отрицательном элементе управляющей строки
все atJ соответствующего столбца в таблице не
превышают 0.
Рассмотрим тогда (независимо от р} и qj) все
столбцы, содержащие только неположительные
элементы aiy
Пусть соответствующее множество индексов
есть J. Определим t' как наибольшее t, для
которого Pj + qjt^O при всех jeJ. Если такого ? не
существует, то ПЗЛП не имеет оптимального
решения ни при каких t.
Используем pi + q/ в качестве новой
управляющей строки и применим симплекс-метод. Если
он ведет к оптимальной вершине, то t' = tr является
правой границей ее области устойчивости, и далее
мы поступаем, как описано в разделе
«Определение левой границы области устойчивости». Если
симплекс-метод не приводит к оптимальной
вершине, то это происходит потому, что по отношению
к новой управляющей строке вновь имеет место
случай И. Опять повторяя все рассуждения,
получаем t" и т. д. После конечного числа шагов
мы получим tr или установим неразрешимость
задачи.
Определение левой границы
области устойчивости. Пусть мы знаем
правую границу rv+1 области устойчивости и
оптимальную таблицу соответствующей вершины Е.
Выберем t* чуть меньше, чем tv + i (при tv+1 = оо
возьмем достаточно большое положительное число).
Имеются две возможности: 1) таблица еще
оптимальна при г*, и t* является внутренней точкой
области устойчивости вершины Е; положим в этом
случае Е = Е*; 2) таблица больше не является
оптимальной для f*, тогда fv + 1 есть левая граница
области устойчивости вершины Е. Вычислим
оптимальную таблицу, соответствующую f *, при помощи
симплекс-метода. Если оптимальной вершины не
существует, то fv+1 = t0 и ПЗЛП неразрешима при
значениях параметра, меньших tv+1. Если
оптимальная вершина существует, то мы обозначим ее
через Е*; точка t* — внутренняя точка ее области
устойчивости.
В оптимальной таблице, соответствующей
вершине ?, определим минимальное t> для
которого все pj + qjt не меньше 0 (это может быть
и - сю). Полученное значение есть (v.
Продолжая применять этот метод, мы получим
решение ПЗЛП для всех f, при которых оно
существует.
Примечание 1. Метод упрощается, если
известно значение параметра, для которого ПЗЛП
разрешима. Сначала при помощи симплекс-метода
определим соответствующую оптимальную
таблицу. После этого применим метод «определения
левой границы области устойчивости» ко всем
характеристическим значениям, лежащим слева от
этого значения, и аналогичный метод
«определения правой границы области устойчивости» ко
всем характеристическим значениям, лежащим
справа. В оптимальной таблице, соответствующей ?*,
в этом случае надо найти максимальное значение
t, для которого все pj + qjt ^ 0.
Примечание 2. Если задана верхняя граница
t^x* выше которой значения t нас не интересуют,
то применим симплекс-метод с целевой функцией,
соответствующей *„,„. Если получим оптимальное
значение, то используем tmax в качестве tv+l при
«определении левой границы области
устойчивости». Если же нет, то продолжаем вычисления,
как в случае П.
Примечание 3. Если задана нижняя
граница, ниже которой значения t нас не интересуют,
вычисления прекращают сразу как только
характеристические значения t или значения t', ;",...
в случае II будут меньше значения (mln.
СЛУЧАЙ ОДНОПАРАМЕТРИЧЕСКОЙ ЦЕЛЕВОЙ ФУНКЦИИ
485
Примечание 4. Вырождение вершин играет
такую же роль, как и при решении
непараметрической задачи линейного программирования; здесь
мы не будем специально на этом
останавливаться.
Пример 18.
хх - х5 + 2х6 = 3,
х2 + х3 + х6 = 2,
х, ^0 х6^0,
Qmin =(-3-3r)x3+(l -t)xs+(l + 3t)x6.
Мы сразу находим начальную вершину и составляем
соответствующую таблицу (см. ниже) и управляющую строку
для больших t Таблица не является оптимальной при
произвольно больших t, так как в столбце j = 3 (и, кроме
того, в столбце j = 5) стоит отрицательный управляющий
элемент. Мы выбираем столбец j — 3 в качестве
разрешающего столбца и вычисляем следующую таблицу (см. ниже).
Управляющий коэффициент, соответствующий j = 5, все еще
отрицателен. Но мы не можем выбрать столбец / = 5
в качестве разрешающего столбца: имеет место случай II.
Множество J есть {5}; определим наибольшее t такое, что
р5 + q5t в l — t ^ 0 -»t' — 1. Мы составляем управляющую
строку с t' = 1 и устанавливаем оптимальность таблицы.
Таким образом, tr = 1. Для значений t*, чуть меньших
чем 1, таблица остается оптимальной. Определим
наименьшее t, для которого все pj + qjt не меньше 0.
1 - t >0~>г ^ 1,
4 + Ы $s 0 -> t ^ - 2/3,
Запишем новую управляющую строку при г =-2/3. При
г*, чуть меньшем чем —2/3, таблица больше не является
оптимальной, так как управляющий коэффициент при j = 6
становится отрицательным.
Выбираем столбец у = 6 в качестве разрешающего
столбца и т. д. Четвертая таблица при г*, несколько меньшем
чем — 1, не является оптимальной; она соответствует
вершине, область устойчивости которой состоит только из
t = -1.
Результат. При 1 < г < оо оптимальной таблицы не
существует. При — 2/3 < г < 1 оптимальна вторая таблица,
Q0(t) = —6 — Ы. При — 1 ^ t ^ —2/3 оптимальна третья
таблица, Qo @ = - 2. При - х ^ t < — 1 оптимальна пятая
таблица, (МО = 3 + St.
4
1
2
/-¦ 00
3
0
0
?
-3
-3
<0
5
_ |
_ j
0
1
-1
<0
6
1
2
1
1
3
>0
1
3
2
0
0
4
1
3
/-> х
/= 1
/= -2/3
2
0
0
1
3
3
>0
6
1
5
-1
_ j
0
1
-1
<0
0
5/3
6
?
2
1
4
6
>0
10
0
1
3 -»
2
6
6
12
2
6
—> 1
3
/= -2/3
i = -1
2
0
0
?
3
3
1
0
5
-1
1
1
5
5
5/3
0
4
1
-2
-1
-4
-6
0
2
1
1
1
2
0
2
2
6
1
2
/ = — 1
3
0
0
1
-3
-3
0
5
-1
1
2
2
0
4
1
-2
-1
1
-3
2
1
1
1
-1
-3
2
6
1
5
t = -1
f -> — ос
3
1
-1
1
-5
с
0
>0
2
1
-1
1
-2
-2
0
>0
4
0
-1
-1
1
-1
2
>0
2
0
1
-3
-5
2
486
ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Пример 19 Постановка задачи видна из левой таблицы: t' = 1/4, a tr = t" = 0. Правая таблица оптимальна при
всех t < 0
1
2
t-* х
/= 1/4
з ;
1
1/10
-2
1
>0
-7/4 •.
4
-1
20
-80
<0
0
2
1/10
0
0
0
1
3
/= 1/4
/ = 0
t -*¦ — ас
2
-10
10
20
-10
70/4
20
>0
4
-10
-10
0
-70
-70/4
0
>0
1
1
2
-1
7/4
2
Пример 20 Постановка задачи видна из левой таблицы. Имеем случай tr = оо.
1
2
t-*¦ х
/= -1
3
0
1
1
1
>о •
0
4
1
1
' 2
1/2
>0
3/2
1
1
0
0
0
3
/= -1
/ —* — х
2
0
1
-1
-1
0
>0
4
1
1
1
-1/2
3/2
>0
1
1
-1
-1
0
6.5. ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
6.5.1. ПОСТАНОВКА ЗАДАЧИ,
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
Если к задаче линейного программирования
(см. 6.1.1) добавить еще условие, что все или
некоторые переменные могут принимать только
целочисленные значения, то получим задачу
целочисленного линейного программирования.
Чисто целочисленное программирование —
линейное программирование с требованием цело-
численности для всех переменных.
Смешанно-целочисленное программирование —
линейное программирование с требованием цело-
численности только для некоторых, а не для всех
переменных.
Если все переменные могут принимать только
значения 0 или 1, то говорят о булевом
программировании (чисто булевом). Если это справедливо
лишь для некоторых переменных, то говорят о
смешанно-булевом программировании.
Примеры применения целочисленного
линейного программирования содержатся в задачах об
использовании производственных мощностей (см.
6.3.1), если имеющиеся мощности не могут быть
использованы по частям, в задачах о смесях
(см. 6.3.2), если компоненты смесей могут
добавляться только определенными порциями; в
транспортных задачах (см. 6.2), в задачах о распределении
(см. 6.3.3), в задачах о раскрое и покрытии
(см. 6.3.4) и во многих других случаях.
Геометрическая интерпретация и
разрешимость задач с двумя переменными
вытекает из изложенного в 6.1.1, если принять во
внимание, что в случае чисто целочисленной задачи
допустимыми точками являются только точки
координатной сетки (точки с целочисленными
координатами) в допустимой области ЗЛП. В случае
смешанно-целочисленной задачи получаются
отрезки прямых в допустимой области ЗЛП.
Пример 21.
2.Y, + х2 ^ 4, 2л, + 3\-2 < 6,
л, > 0, v2 ^ 0, *,, х2 - целочисленные,
Qmin - --*i ~ *2-
Для решения целочисленных задач линейного
программирования разработаны разнообразные
методы:
а) метод сечения (см. 6.5.2);
б) метод разветвления (см. 6.5.3);
в) доказательство целочисленности всех
базисных решений соответствующей ЗЛП для частных
классов задач (например, транспортная задача в
6.2.1); в этом случае решение ЗЛП, независимо
от требования целочисленности, дает решение
целочисленной задачи линейного
программирования;
г) приближенные методы, которые дают
хорошие допустимые решения (но в общем случае
неоптимальные).
Ч1К К) ЦК'ЮЧИСП ННЫ1 ЗЧ1ЛЧИ „'ШШ ИНОГО II 14I РЛММИРОВАНИЯ
487
Замечание к г). Поиск (возможно,
длительный) допустимой точки координатной сетки,
ближайшей к решению ЗЛП, часто ведет к
практически пригодному решению. В некоторых приме-
Олтимум
1111 п 1111 fti 111 ifl 1111 ffi 1111 f\ 11111T1 1P5?
p - оптимальная точка для ЗЛП
рг- ближайшая кр точка сетки
р'- оптимальная точка сетки
Рис 6 8
pax, однако, он может дать точки, лежащие
как угодно далеко от оптимальной (рис. 6.8).
6.5.2. МЕТОД СЕЧЕНИЯ ГОМОРИ
6.5.2.1. Чисто целочисленные задачи линейного
программирования. Сначала решается ЗЛП,
соответствующая целочисленной задаче линейного
программирования. Если ее оптимум Р является
точкой координатной сетки, то Р — решение
целочисленной задачи. В противном случае к ЗЛП
добавляется еще одно условие («сечение»), такое,
что все допустимые точки координатной сетки
удовлетворяют ему, а точка Р — нет.
Геометрически это значит, что Р и
окрестность Р отсекаются от допустимой области ЗЛП.
Решается новая ЗЛП и т. д. Надлежащим методом
построения сечений можно достичь того, что после
конечного числа шагов возникнет ЗЛП,
оптимальная точка которой целочисленна и тем самым
является решением первоначальной целочисленной
задачи линейного программирования. Первый
метод такого рода был разработан Гомори в
1958 г., и на его основе с тех пор было
развито несколько методов. Постоянное добавление
условий ведет к тому, что задача решается
при помощи двойственного или
модифицированного двойственного симплекс-метода.
Указание к построению модели. Если
первоначально задача содержит дополнительные
условия в форме неравенств, то посредством
введения вспомогательного переменного перейдем
к ЗЛП с условиями-равенствами. Если постоянный
член и все коэффициенты неравенства целочисленны,
то на вспомогательное переменное также можно
наложить требование целочисленности. Неравенства
с рациональными коэффициентами перед введением
вспомогательного переменного следует умножить
на общий знаменатель рациональных
коэффициентов. Неравенства с иррациональными
коэффициентами приводят (если иррациональные числа не
приближены рациональными и не преобразованы
так, как указано выше) к
смешанно-целочисленным задачам программирования, так как в этом
случае для вспомогательных переменных нельзя
потребовать целочисленности.
Построение сечений. Пусть {w] -
дробная часть числа vv, 0 < {vv} < 1. Например,
{4,1} =0,1 вследствие того, что 4,1=4 + 0,1, но
{-4,1} = 0,9, так как -4,1 = -5 + 0,9.
Пусть задана оптимальная таблица из т строк,
соответствующая ЗЛП, на все п переменных которой
наложено еще дополнительное требование
целочисленности. Пусть строка, соответствующая в
симплекс-таблице базисному переменному х,-, есть
i | а^х... ад,и т | bi, причем bt нецелочисленное. Тогда
к таблице приписывается еще одна строка,
соответствующая условию п + 11 — {а,^}... — {«/х„_ж} I —
— {bi}, и хя+1 рассматривается как целочисленное
вспомогательное переменное такое, что хи + 1^0.
После этого применяется двойственный симплекс-
метод.
Указания к использованию метода.
Если в процессе вычислений получится
оптимальная таблица, в которой вспомогательное
переменное имеет положительное значение, то
соответствующая строка может быть вычеркнута. Таким
образом, мы воспрепятствуем чрезмерному
увеличению числа строк.
Выбор среди нескольких нецелочисленных bt в
таблице может быть произвольным; рекомендуется
выбирать Ь( с максимальной дробной частью
Если ясно, что оптимальное значение целевой
функции должно быть целым, то строка целевой
функции тоже может быть использована для
построения сечения.
Может случиться, что, хотя допустимая область
ЗЛП не пуста, она не содержит ни одной точки
координатной сетки. Этот случай распознают
так же, как и при использовании двойственного
симплекс-метода (не находится разрешающих
столбцов).
П р и м е р 22
2\, f \2 + у., = 4.
2\, t 3y: 4- л-4 -6,
\,, v,. v, \4 — нее о о п.ше 0 и целочислепны,
() . = - у, - Y-,
Сначала мы ре
не гочие-ieiiHocib) при
им ЗЛП (не обращая внимания на
помощи симплекс-метола
1
>
4
1 2
1
1 2
2
1 2
m
LJ
1 2
2 1
2
з
3/4
- I 2
! 4
4
-1 4
1 2
1 4
3'2
1
5 2
488
ЦЕЛОЧИСЛЕННОЕ ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
В оптимальном решении ЗЛП х, нецелочисленно.
Поэтому из соответствующей строки мы должны построить
сечение и решить новую ЗЛП при помощи двойственного
симплекс-метода:
1
2
5
3
3/4
-1/2
-3/4
1/4
4
-1/4
1/2
н
1/4
3/2
1
-1/2
5/2
1
2
4
3
1
-1
1
0
5
-1/3
2/3
-4/3
1/3
5/3
2/3
2/3"
7/3
Мы используем i — 4 для построения сечения (для
этого целесообразно сразу оставлять пустую строку в новой
таблице) и снова применим двойственный симплекс-метод:
1
2
4
6
3
I
1
0
0
5
-1/3
2/3
-4/3
В
1/3
5/3
2/3
2/3
-2/3
7/3
1
2
4
5
3
1
_1
1
0
0
6
-1/2
1
-2
-3/2
1/2
2
0
2
1
2
Оптимальная точка целочисленна; следовательно, набор
*! = 2, х2 = х3 = О, х4 = 2 является оптимальным
решением целочисленной задачи линейного
программирования (если бы вычисления были продолжены, то строка,
соответствующая х5, могла бы быть вычеркнута).
Если рассматривать х3, х4
как вспомогательные
переменные, то задачу графически
можно изобразить в плоскости
хь х2; сечения имеют вид
2х!+х2«*4 и 2х! + 3х2<6
(рис. 6.9).
6.5.2.2.
Смешанно-целочисленные задачи
линейного
программирования. Основная идея — та
же самая, что и в чисто
целочисленном случае;
нецелочисленные Ь, в
таблице, конечно, только
тогда дают повод для построения сечения, когда
на соответствующее базисное переменное наложено
требование целочисленности. Однако строятся
сечения по-другому:
п + 1 Iflfl.,5*., • • • aiXn_тЬХп т | -
— 1 для ал ^ О,
\N Прямые
сечений
Рис. 6.9
где 5>
Пример 23. Рассмотрим ЗЛП из 6.5.2.1 (пример 22),
но потребуем целочисленность только для v,. Вычисления
до получения оптимальной точки аналогичны примеру 22
Затем вводится сечение и применяется двойственный
симплекс-метод:
г 1
2
5
i
3
3/4
-1/2
1/4
4
-1/4
1/2
-1/4
1/4
3/2
1
-1/2
5/2
1
2
3
5
1
-2/3
-4/3
1/3
4
-1/2
2/3
1/3
1/6
1
4/3
2/3
7/3
{*>•}
Оптимальная точка имеет координаты х, = I, х2 = 4/3,
х3 = 2/3, х4 - 0.
В геометрической интерпретации примера 22 сечение
равнозначно дополнительному условию 4х, + Зх2 < 8.
6.5.3. МЕТОД РАЗВЕТВЛЕНИЯ
Предположение, что переменные могут
принимать только целочисленные значения (т. е. в
практических применениях чаще всего конечное
число значений), дает возможность решить задачу
проверочной подстановкой всех допустимых
значений в целевую функцию и сравнением
полученных значений. Удобной для использования
эта идея, однако, становится лишь тогда, когда
полный перебор может быть сокращен
дополнительными рассуждениями. Эти рассуждения
основаны на принципе разветвления комбинаторного
программирования. Для решения общей чисто- и
смешанно-целочисленной задач линейного
программирования возникает, таким образом, следующий
метод.
Для оценки целевой функции на некотором
множестве допустимых решений целочисленной
задачи служит оптимальное решение
соответствующей ЗЛП (так как, если к ЗЛП добавить
требования целочисленности, оптимальное значение не
может улучшиться). Множество допустимых
решений постепенно расщепляется по мере того, как
для оптимальной таблицы с нецелочисленными
Ь,- = [Ь,] + {&,} ([«] — целая, а {а} — дробная часть
числа а, 0 ^ {а} < 1) ставятся две задачи: I и II (см.
пример 24) с условиями xt ^ [Ь(] или х,- ^ [?,] +1.
Допустимые области обеих задач, взятые вместе,
содержат все допустимые решения целочисленной
задачи.
Рекомендуется сначала проводить разветвление
для тех /, при которых {Ь,} максимально
близко к 0,5.
Разветвление, конечно, следует проводить
только для таких i, для которых х, должно быть
целочисленным. Для того чтобы иметь
возможность по мере надобности просто добавлять новые
условия, используют двойственный симплекс-метод.
Пример 24. Задача Лцелочисл-
-2vt + 2v2 + x3 = 3,
2v, + 2v2 + \-4= 13, F 13)
СРАВНЕНИЕ МЕТОДОВ
489
все vb х2, *3, Х4 ^ 0. *ii хг — целые,
<?„,,„-2х,-3х2.
Двукратное применение симплекс-метода к А (пусть это
будет Лцелочисл без требования целочисленности) приводит
к оптимальной таблице
2
1
4
1/4
1/4
1/4
3
1/4
-1/4
5/4
4
5/2
7
х, имеет в этой таблице нецелочисленное значение.
Расщепление
/III Х^З-Х, -Х5 = 3
при помощи уравнения, полученного из последней строки
таблицы:
должно быть пересчитано к небазисным в данный момент
переменным х4, х3.
В общем случае в качестве формального
метода расщепления строки i задачи с п переменными
и т строками получим:
И
| -a
J -{bt}.
п.
В нашем примере получаются таблицы А I
и А II.
А\
I 2
I 1
\\Ъ
4
1/4
1/4
-1/4
1/4
3
1/4
-1/4
1/4
5/4
4
5/2
-1/2
7
All
II 2
| i
V
4
1/4
1/4
1/4
1/4
3
1/4
-1/4
-1/4
5/4
4
5/2 -
1/2
7
Теперь обе задачи решаются при помощи
двойственного симплекс-метода. Если в оптимальной
точке для jq и х2 не получаются целочисленные
значения, то задача разветвляется дальше (при
помощи наиболее удобного оптимального значения)
и т. д.
На рис. 6.10 показан ход решения примера 24;
там указаны оптимальные значения хь х2 и
целевой функции.
, х2 " 7/2, ff- -W2
АН
/
?r3,*2-7/2,0-S/2
Допустимая область
пуста
АПП
АПП
Допустимая область
пуста
Рис. 6.Ю
Решение А I I II дает оптимальное решение
целочисленной задачи линейного программирования Лцелочисл, Qo - - 5.
Допустимые точки задачи ^целочисл* содержащиеся в
А II, имеют значения целевой функции не менее -9/2,
т. е. больше, чем Qo-
Допустимые точки задачи >4целочисл< содержащиеся в
A I I I I, имеют значения целевой функции не менее —5,
т. е. среди них могли бы быть точки с оптимальным
значением Qo (это можно было бы исследовать путем
дальнейшего разветвления), но во всяком случае - не
допустимые точки задачи Лцелочисл с меньшим, чем Qo, значением
целевой функции.
6.5.4. СРАВНЕНИЕ МЕТОДОВ
В некоторых примерах больших вычислительных
затрат требуют методы сечения, в других -
методы разветвления. Оба пути решения интенсивно
разрабатываются, так что постоянно появляются
новые варианты, эффективность которых, в общем,
едва ли может быть оценена. При использовании
вычислительных устройств методы разветвления,
как правило, требуют большего объема памяти, но
численно они устойчивее. В обоих методах
трудность состоит в том, что надо решить,
рассматривать ли число bh несущее в себе погрешности
округления, как целое или нет.
7. ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
И ИХ ПРИМЕНЕНИЯ
7.1. ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Одна из важнейших задач вычислительной
математики — установление правил вычисления
(алгоритмов), при помощи которых исходные данные
(вход) при использовании ранее созданных
вспомогательных схем и устройств (таблиц, настольных
вычислительных машин, аналоговых
вычислительных машин, цифровых вычислительных машин
и т. д.) преобразуются в выходные данные
(выход):
Вход
Реализатор
алгоритма
Выход
Для создания таких правил на основе
теоретических положений должны быть проведены
особые, ориентированные на возможности
практической реализации рассуждения.
Пример ! Нужно вычислить наименьший корень
уравнения х2 — 20х + 1 = 0 Но теоретический результат
х = 10 - J/99 как основа для проведения вычисления
неудобен, если вычисление должно проводиться с постоянным
числом десятичных знаков (например, три). 10,0 — 09,9 = 00,1
Если же применить эквивалентное выражение 10-|/99 =
= A0 -+• |/99)~ \ то получится пригодный алгоритм, 1ак как
теперь A0,0 + 09,9)"' = 19.9 =0,05
Некоторые общие положения
1. Математические аналитические методы
решений зачастую оказываются непригодными для
использования в качестве вычислительных
алгоритмов.
2. Алгоритмы должны быть по возможности
изменяемыми в зависимости от набора исходных
данных; заметим, что границы изменения этих
данных не всегда известны.
3. Метод может применяться как алгоритм
только тогда, когда он полностью схематизирован.
Это означает, что в каждый момент должно быть
однозначно установлено, какой следующий шаг
должен быть сделан.
4. Алгоритм должен строиться преимущественно
рекурсивно. Рекурсивный алгоритм состоит из
относительно небольших составных частей, которые
неоднократно реализуются для различных наборов
значений.
5. Вычислительный алгоритм должен быть
конечным, т. е. приводить к результату за
конечное число шагов. Бесконечные математические
модели (последовательности, ряды и т. п.) должны,
согласно этому, приводиться всегда к конечному
представлению.
6. Вычислительный алгоритм может содержать
лишь такие операции, которые являются
выполнимыми на используемых вычислительных
устройствах (или согласуются с вычислительной машиной).
7.1.1. ПОГРЕШНОСТИ И ИХ УЧЕТ
Если величины представляются численно (т. е.
посредством конечной р-разрядной дроби), то они
реализуются лишь приблизительно, с некоторой
погрешностью. В соответствии с общепринятыми
в математике обозначениями теоретическое, или
точное, значение величины обозначают так же,
как и саму величину: х, у, z,...,a, b, с, d,.... Чертой
сверху мы будем помечать соответствующие
значения, содержащие погрешность, т. е. числа, с
которыми мы фактически проводим вычисления.
В соответствии с этим 8(х) = х — х обозначает
истинную погрешность; 8(х) и 8(х) — ее нижнюю,
соответственно верхнюю, границу, А (х) = тах(|8(х)|,
| Ь{х) |) — максимальную погрешность; р(х) =
= 8(х)/х - относительную истинную погрешность х.
Следовательно,
х = х - 8(х), 8(х) ^ 8(х) < 8(х), | х - х | ^ А(х).
Для проведения численного расчета нужно знать,
каковы исходные данные, с какой точностью
должны быть получены выходные данные, какова
возможная точность выполнения операций и какой
алгоритм должен быть применен в связи с этим.
Существует три источника погрешностей; 1)
погрешность входных данных, 2) погрешность метода
(обрыва), 3) погрешность округления (машинная
погрешность).
Исследование погрешности выхода является
очень сложной проблемой. Если мы
рассматриваем отдельный вычислительный шаг вида
х = д(аи а2,...,ан), в котором выходная величина
должна быть вычислена согласно правилу д по N
Исходным данным, то истинную погрешность
8(х) = х-х можно разложить на следующие три
составляющие:
8(х) = 8м(х) + 8вв(х) + 8с(х).
Погрешность метода (погрешность обрыва):
Она является мерой отклонения вычислительной
модели от точной и может появляться даже тогда,
когда исходные данные точны (например, целые
числа).
РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ УРАВНЕНИЙ
491
Погрешность, обусловленная вводом:
*>ввМ = 0(яь «2, ••-, а^)-д(аи а2, ..., as).
Эта погрешность является оценкой распространения
погрешности ввода при вычислении.
Дополнительная погрешность, случайная
погрешность :
Ъс{х) = х-д (аь аъ..., aN).
Она является мерой погрешностей,
присоединяющихся от машинной реализации действий.
Максимально точная оценка погрешности
метода есть составная часть каждого
вычислительного метода. Она совершенно не зависит от
того, как этот метод реализуется.
Погрешность, обусловленную входными
данными, можно заметить и оценить, если алгоритм
прост и удовлетворяет некоторым дополнительным
условиям. Для сложных задач простые и
непосредственные методы исследования распространения
погрешности перестают действовать. Нужно
принимать во внимание, что эта часть погрешности
не зависит от реализации вычислений.
Число разрядов арифметики, кодирование,
фиксированная или плавающая запятая, особые
операции, сделанные с двойной точностью, и
т. п. имеют непосредственное влияние на
распространение погрешности. До сих пор существенные
результаты имелись в трех направлениях:
— в статистических исследованиях накопления
погрешностей;
— в детерминированном анализе
распространения погрешности при общих методах по Уилкок-
сону;
— в арифметике интервалов.
В противоположность разрабатывавшимся до
последнего времени моделям в арифметике
интервалов точная модель х = g{at, а2,...,а^)
заменяется на алгоритм, который использует интервал
как величину входа и дает в качестве выхода
интервал x = g(ali а2,...,ан) с
а, = [Л, < л, < В,], х = [Хх < х < Х2].
Таким образом, надо принимать в расчет
непосредственно интервалы, так что надобность в
специальном исследовании погрешностей отпадает.
К настоящему времени уже имеется целый ряд
алгоритмов арифметики интервалов. Так как эта
арифметика должна охватывать все случаи, то
зачастую оказывается, что выходные интервалы
очень велики; в связи с этим арифметика точек
с более точным слежением за
погрешностями приводит все-таки к более точным
результатам.
Величина дополнительной погрешности зависит
в первую очередь от функционирования
вычислительной техники. Главные причины больших
случайных погрешностей:
— метод обрыва и округления, принятый в
машине;
— потеря значащих разрядов при вычитании.
Если два числа одного порядка величины,
содержащие погрешность, вычитаются, то разность,
смотря по обстоятельствам, может оказаться и
чисто случайным числом. Тогда, если это число
входит в дальнейшие расчеты, возникают большие
случайные относительные погрешности; например,
3,1415613-3,1415524 = 0,0000089; от восьми
значащих цифр остались только две;
- техническое состояние машины;
- потеря разрядов при превышении
допустимой разрядности представления чисел (например,
при делении на маленькие числа).
Вычислительный алгоритм состоит из целого
ряда отдельных операций, которые снова и снова
повторяются. При этом погрешности выхода
каждого шага оказываются входными погрешностями
следующей операции, а точный анализ
погрешностей становится далее все более трудным, и
часто ограничиваются только оценками.
Вычислительный метод называется
устойчивым, если для любого е > 0 существует такое
8 > 0, что максимальная погрешность вывода
меньше е при максимальной погрешности ввода,
меньшей 6.
7.1.2. ВЫЧИСЛИТЕЛЬНЫЕ МЕТОДЫ
7.1.2.1. Решение линейных систем уравнений.
Рассмотрим неоднородную систему линейных
уравнений
а2нхп = Ь2,
+ а22х2
оИ1*1 + 0*2*2 + ... + атхп = Ьп,
т. е. Ах«Ь, которая в предположении, что
det А Ф 0, имеет для любых правых частей
уравнений однозначно определенное решение
х = (хь х2,...,хя)^ Для отыскания этого вектор-
решения имеется два вида методов: вычисление
на основе метода исключения и вычисление на
основе методов последовательных приближений
(итераций).
7.1.2.1.1. Прямые методы (метод
исключения Гаусса).
1) Простой метод Гаусса. Известный
метод исключения (см. 2.4.4.3.3) после
преобразования в алгоритм состоит из двух циклических
процедур.
Преобразование матрицы А в
матрицу треугольного вида.
1. Пусть k = 1.
2. Следует проверить, отлично ли afcfc от
нуля.
3. Если да, то к-я строка становится рабочей
строкой. Если нет, то меняем к-ю строку на
/-ю (/ > к), в которой а1к Ф 0.
4. Для i\ — к + 1, к + 2,...,л вычисляем новые
матричные элементы, которые обозначим, подобно
прежним, по правилу:
для j — к,
Для j Ф к,
а'и = О
аналогично представим новые правые части
уравнений :
492
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
5. Увеличиваем к на единицу, если к ^ п — 2,
и начинаем снова с п. 2. В итоге получим
верхнюю треугольную матрицу
А' =
О а22 ... а'2п
0 0 ... а'пп
вектор-решен ия
Вычисление
(хь х2,..., х„)т:
1. х„ = Ь'п/а'пп.
2. Для i = п — 1, п - 2,..., 1
2) Метод Гаусса — Жордан а.
Модифицируем простой метод Гаусса, а именно в п. 4
позволим номеру строки i пробегать значения от
1 до к — 1 и от к + 1 до и. Это приведет к
тому, что все элементы /с-го столбца, за
исключением диагонального элемента, становятся
равными 0, и вместо верхней треугольной матрицы
мы получаем теперь в конечном результате
диагональную матрицу
г-«'и 0 _.
А' -
L 0
Тем самым расчет вектор-решения существенно
упрощается:
x = (b\/a'll,...,b'Ja'JT.
Тем не менее число операций в этом методе
больше, чем в простом методе Гаусса.
Решающее значение для точности вычисления
имеет деление на акк, необходимое при расчете
q{. Поэтому условие п. 2 метода Гаусса для
выбора диагонального элемента слишком слабо
с точки зрения точности, и часто применяют
следующую схему.
Перестановкой строк и столбцов (последние
должны быть «помечены» и восстановлены при
построении вектор-решения) добиваются того,
чтобы элемент, который имеет наибольшую по
модулю величину среди всех элементов, не
использовавшихся ранее в качестве диагональных
элементов, оказался диагональным.
Пример 2. Процесс полной диагонализации методом
Гаусса - Жордана (табл. 7.1).
Колонки s, и 5, даны для контроля:
Si = X a'ik + b\ + Si = 0.
fc = l
3) Связанный алгоритм (способ
Гаусса — Банашевича). Можно прийти к
очень наглядной и компактной вычислительной
схеме, если отдельные шаги гауссова метода
6 1
А
>-<
Ь
6
s
t
t I
Рис 7 1
исключения расположить так, чтобы работать
только с числами, которые в дальнейшем не
обрабатываются и могут быть просто «переписаны».
Таблица 7.1
¦
1
2
3
1
2
3
2
3
1
2
3
А
-1 3/2 1
2 1 0
-1 -1 7/4
0 2 1
2 1 0
0 -1/2 7/4
0 2 1
2 0 -1/2
0 0 2
0 2 0
2 0 0
0 0 2
2)
>,
9/2
-1
7/2
4
-1
3
4
-3
4
2
-2
4
ч
-6
-2
-13/4
-7
-2
-17/4
-7
3/2
-6
-4
0
-6
47
1/2
диагональ
1/2
диагональ
-1/2
1/4
-1/2
1/4
диагональ
Si
0
0
0
0
0
0
0
0
0
РЕШЕНИЕ ЛИНЕЙНЫХ СИСТЕМ УРАВНЕНИЙ
493
Таблица 7.2
а,
«п 2
«21 "б
«31 2
«41 4
2
-3
1
2
т. -1
К2 -1
х= 1
а2 1
«12 3
«22 -5
«32 -5
«42 6
3
4
_2
0
т2 1
-1
7
а3
«»з -1
«23 0
«33 6
«43 2
1
-3
1
4
т3 -5
-1
3
а4
«14 0
«24 2
«34 "б
«44 -3
0
2
-2
5
и -1
-1
-2
а -30
20
-45
-3
58
20
15
7
-10
Кз 0
-31 ^^"^
^<^ -31К,
-24
54
6
-67
-24
-18
-6
5
к4 о
Вычислительная схема (рис. 7.1, табл. 7.2):
*¦• = - I «о- - bh
<** = - Z «,-*, <* = - z л,.,
1 = 1 j = 1
I- 1
dik = «ik - Z cndib d\k = «l*,
Когда надо решать несколько уравнений с одной
и той же матрицей, но с различными правыми
частями, рекомендуется произвести
вычисление обратной матрицы; тогда вектор-решение
х = А'1Ь можно вычислить простым
перемножением матриц.
Для этого решают одновременно п систем
уравнений Aylk) = e(k) с правыми частями
U — si -
fl"
Численный пример:
Проверка
- Z
= -i-F- 2-3) = О,
)= -1.
"" ' лля всех
^з I тЛ - а = О, К4 X т*'* - I -s* = °
Все схемы позволяют решать параллельно
несколько систем уравнений с одинаковой
матрицей А и различными столбцами правых частей.
Для этого требуется лишь иметь нужное число
столбцов Ь.
4) Нахождение обратных матриц.Для
каждой невырожденной матрицы А существует
магрица А~\ для которой АА'1 = А~1А = Е
является единичной матрицей. Матрицу А~1 называют
матрицей, обратной к А (см. 2 4.4.2.4).
и составляют обратную матрицу из
вектор-решений у{к) (к = 1, 2,...,/7) как вектор-столбцов.
Пример 3. Найти матрицу, обратную А (способ
Гаусса - Жордана. См. табл. 7.3).
7.1.2.1.2. Метод итерации. Возможны
разнообразные способы приведения векторного
уравнения Ах — b = 0 к виду х = Мх + с путем
выполнения подходящих эквивалентных
преобразований. В этой форме решение х определяется
как неподвижная точка линейного
преобразования Тх = Мх + с, которую определяют методом
последовательных приближений. Векторная
последовательность {.v
образом:
х{т +1) = Мхш + с,
, определенная следующим
т = 0, 1,.
где х@) — постоянный заданный начальный вектор,
сходится к вектор-решению х, если матрица М
не вырождена и удовлетворяет неравенству
|| М|| =sup (||Mx||, ||x || ^ 1}
или любая другая норма в пространстве матриц.
При этом справедливы оценки
Цх""»-л-|| = т-Р--||хA)-х<°>||.
1 -р
494
ЗЛРМННТЫ ЧИСЛЕННЫХ MF ГОДОВ
Таблица 7.3
.
2
3
2
3
1
3
1
2
3
?
1
2
I
3
0
0
1
0
1
0
0
А
2
3
1
4
У
1
12
0
0
0
1
0
?
1
3
1
4
1
5
1
12
4
15
1
6
1
180
0
0
1
1
0
0
1
2
1
3
4
~6
9
-36
30
Е
0
1
0
1
0
-6
_ j
-36
192
-180
А-1
1
0
1
0
1
0
1
30
-180
180
Ч
диагональ
1
2
1
3
-
-
к = 1
-6
-
диагональ
_ j
А: = 2
-
-
-15
-
30
диагональ
Аг = 3
1) Метод Якоб и. Если А = L + D + R с равенства || L + R || < inf | аи |. Если в качестве
составляющими матрицами
"о
О
L =
а2х 0
а31 аЪ2 0
нормы выбрать суммарную норму строки
|| А || = max ? | ay |, то получим важный результат:
i
"«и
R =
«22
0 fl12 ...
0 0 Й23--
метод Якоби сходится в предположении, что
/V'
(условие доминирования диагонали).
2) Метод Гаусса - Зейделя:
М = MG= -{L+ D)~lR.
Формула итерации:
(L + D)x(m + i) = -Rxlm) + b, xi0) задано.
Таким образом,
? яух]" + 1> = Ь,- t flyxf>;
следовательно,
1 / " l"
x(m+l) _| у (m) , у (m+1) _ l
«ii \y = ,•+ i j = i
(i= 1, 2,...,w).
Метод сходится при || D (L + Я) || < 1; доста- Вычислительная схема и пример,
точным условием этого является выполнение не- Итерационный метод Гаусса — Зейделя (табл. 7.4).
0 "
aln
то в этом методе М = Mj = — D l (L + R) и
Таким образом,
ЛИНЕЙНЫЕ ЗАДАЧИ О СОБСТВЕННЫХ ЗНАЧЕНИЯХ
445
Таблица 7.4
п
0
1
2
3
4
5
6
Матрица А
24
-1
1
0
0
2,250
2,00683
1,99900
1,99999
2,00000
-2 2
21
2
1
0
-2,7976
-3,01097
-3,00008
-3,00001
-3,00000
2
28
-2
0
1,1195
1,00067
1,00009
1,00000
1,00000
Далее не требуется!
1
-1
-2
20
(и)
0
-1,9982
-1,99938
-1,99999
-2,00000
-2,00000
-Ь
-54
61
-28
45
Сходимость при || (L + D) lR \\ < 1.
Достаточными условиями этого являются, например:
а) А симметрична и положительно определена;
л
б) X I «у I < I «н I для всех I.
7.1.2.2. Линейные задачи о собственных
значениях. Принципиально имеется много
возможностей для вычисления собственных значений Xj
и принадлежащих им собственных векторов Xj
матрицы А, которые определены и связаны
посредством соотношения Axj = XjXj. Поэтому при выборе
принимают во внимание, вообще говоря, не только
вычислительную точку зрения, но и метод,
который будет учитывать поставленную цель и
особенности матрицы.
Мы ограничимся рассмотрением только
некоторых методов при дополнительном предположении
симметричности (т. е. А = А).
7.1.2.2.1. Прямые методы. Цель прямых
методов — одновременное определение всех
собственных значений, а также собственных векторов
по единому методу. Поэтому можно говорить о
численном преобразовании к главным осям, потому
что собственные векторы А являются вектор-
столбцами матрицы преобразований X, а
собственные значения Xj — диагональными элементами
диагональной матрицы D в преобразовании
ХТАХ = D (см. 2.4.4.5.3).
1) Решение характеристического
(векового) уравнения. Собственные значения Xj
являются корнями многочлена Рд (X) = det(A — ХЕ),
коэффициенты которого можно вычислить
различными способами по элементам матрицы. Для
численного нахождения решений уравнения
РА(Х) = 0 следует обратиться к 7.1.2.3.
Собственные векторы каждого собственного
значения получаются как вектор-решения системы
линейных уравнений Ах = XjX, и их находят при
помощи соответствующих методов (см. 7.1.2.1).
Однако надо отметить, что этот метод
нарушает принцип непосредственного приложения
(ср. 7.1.3.1) и все более и более оттесняется
другими.
2) Метод Якоб и. Рассмотрим матрицы
1 0 ... 0 ... 0 ... 0
0 1 ... 0 ... 0 ... 0
0 0 ... 10 ... 0 ... 0
0 0 ... cos ф ... sin ф ... 0 — р-я
0 0 ... 0 1 ... 0 ... 0
0 0
1 0... 0
0 0 ... — sin ф ... cos ф ... 0 — q-я
0 0 ... 0 ... 0 1... 0
0 0 ...
р-й столбец //-и столбец
получившие название матриц элементарных
вращений Якоби. Всегда можно определить угол ф
в интервале ( — л/4, я/4) так, что в
преобразованной матрице А' = 7pqA7pq элементы ci'pq = a'qp
обращаются в нуль.
В матрице А" = T^qA, очевидно, меняются
лишь р-я и q-я строки, при этом:
a"qj = apjsin ц> -f aqjcosy, a'/j = fly для i # p, q.
В матрице А' = A"Tpq изменены по сравнению с
А" только р-й и </-й столбцы:
flip = «Гр cos ф - a"q sin ф,
a'iq — fl«''psin ф + fl^cos ф, fly = a'ij для / # p, q.
Если объединить обе части, то для элементов
в точках пересечения р-х и g-х строк и столбцов
получим
а'рр = аррcos2 ф - 2аpq cos ф sin ф 4- aqqsin2 ф,
a'qq = cipp sin2 ф + 2a рц cos ф sin ф + aqq cos2 ф,
a'pq = fl^p=(flPP - flM)cos фвш ф + apq{cos2 ф - sin2 ф).
496
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Следовательно, элементы a'pq и a'qp становятся
нулями, если
ао„ — ааа п к
ctg2cp=—Ц- =-, где - —<ф <—.
2ам 4 4
Идея метода состоит в вычислении матрицы
преобразования X как произведения таких
специальных матриц, которые находятся методом
итерации.
Если к А' снова применить элементарное
вращение Якоби, то в нуль обращаются еще два
других элемента, а элементы, которые ранее были
равны нулю в А', не становятся отличными
от нуля.
Итак, метод Якоби включает следующие
действия (k-й шаг):
1. Выбор элемента a(k)q из матрицы А{к).
2. Вычисление A{k+l) = TjqAik)Tpq (к = 0, 1,...).
3. Обрыв при ? I а<и+1) I < ?, е > 0 задано.
В противном случае - переход к к + 1-шагу.
При обрыве матрица А{к) имеет диагональный
вид с точностью, определяемой е, диагональные
элементы являются приближениями собственных
значений, а столбцы матрицы произведения всех
примененных Тм являются приближениями
собственных векторов.
Сходимость метода очень существенно зависит
от последовательности элементов в процессе. Она
доказана для
а) классического метода Якоби: выбор в
качестве основного, ведущего элемента наибольшего по
абсолютной величине внедиагонального элемента,
б) циклического метода Якоби: выбор элемента,
согласно заранее определенной последовательности,
способом строки или столбца. Метод создан для
автоматического счета (на ЭВМ).
7.1.2.2.2. Методы итерации. Под ними
понимают все методы, задача которых -
целенаправленное вычисление отдельных собственных
значений или векторов.
1) Простая векторная итерация
(степенной метод, метод Мизеса) для
вычисления наибольшего по величине собственного
значения. Если матрица А обладает простым
превалирующим собственным значением Xi
(I A-i | > | Х2 | > | ^з I > • • • > I К I), то векторная
последовательность, определяемая соотношением
х(т +1) = Ахм = Ат+ 1Х(О)> х<о) задано,
асимптотически сходится к собственному вектору
ylt принадлежащему А.ь х{т) ~ Х™суи если
начальный вектор х@) обладает компонентой в
направлении собственного вектора ^i- Собственное
значение можно вычислить следующим образом:
или, лучше,
Xi = lim R (x(w)).
m -*¦ oo
Во второй формуле R (х) означает частные Релея:
R (х) = хТАх/хТх.
Собственный вектор можно вычислить по
асимптотической формуле только при наличии
нормировки. Собственный вектор в направлении ух
определяется как
Уп/\\ У1 II = Нт хр>/|| х(т) || (/ = 1, 2,...,и).
т -* оо
Без такой нормировки метод численно неустойчив.
Наименьшее по абсолютной величине
собственное значение можно найти, если принять во
внимание, что оно равно обратной величине
наибольшего собственного значения матрицы А~1
(обратная векторная итерация).
2) Дробная итерация. Этот метод должен
применяться тогда, когда нужно определить
отдельное собственное значение вместе с
соответствующим собственным вектором. Его
использование опирается на знание такого хорошего
приближения Хк искомого \к, что величина
| Хк — Хк | мала по сравнению с \Xj — Хк\, j ф к,
и на то, что собственные значения расположены
изолированно. _
Матрица В (Хк) — А — ХкЕ имеет собственное
значение \ik = Хк — Xh для собственного вектора хк
матрицы А. В самом деле, В (Хк) хк = Ахк - Хкхк =
= Хкхк - Хкхк = {Хк - Хк) хк. Но тогда \хк ! есть
доминантное собственное значение матрицы В~1(кк)
для достаточно произвольного начального вектора
х@). Поэтому, если х{т + 1) = ?-1х(т),илиВх(т+1)==х(м),
ТО
Ы~1= lim R(x{m)), Xk = Xk+ lim /TV)-
т -* оо т -» ос
Кроме того, последовательности х\т)/\\ х{т) ||
сходятся к компонентам нормированного
собственного вектора ук/\\ ук ||.
7.1.2.3. Нелинейные уравнения. Пусть функция
y = f{x) при а^х^Ь определена и непрерывна.
Пусть, далее, имеются два числа xt и х2 такие,
что а < Xt < х2 ^ Ь. Если /(xj) и /(х2) имеют
противоположные знаки, то между xt и х2
существует хотя бы один корень функции f(x).
1) Итерационные методы. Нелинейное
уравнение/(х) = 0 можно эквивалентным
преобразованием многими способами привести к виду
g(x) = h(x).
Пример 4.
v2 - In х - 2 = 0, f(.\) = v2 - In v - 2;
ex = xe2, g\x) = ex , Л(х) = x^2 и т. д.
Построение сходящейся числовой
последовательности {х(т)}* = о по правилу g{xim + i)) = h{x{m))
при заданном х|0) называется итерационным
методом вычисления корня х/у.
Вследствие предположенной непрерывности
предельное значение такой последовательности
является корнем, потому что из соотношений
lim x(m) = а и lim x{m+1) = a в силу непрерыв-
т -* оо т -* оо
ности g и h имеем g (я) = h (я), т. е. л = х/у.
Достаточные условия сходимости: д' (х) и
/2'(*) непрерывны в некоторой окрестности х/у,
х@) лежит в этой окрестности и в этой
окрестности \д'(х)\ > \h'(x)\.
НЕЛИНЕЙНЫЕ УРАВНЕНИЯ
497
Таблица 7.5
l-Vm+l-.Vm|
\Xm~XN\
0
1
2
3
4
0,15
0,138
0,1379373
0,1379349
0,1379348
,9775
,980956
,9809733
,9809740
,9809740
0,012
0,0000627
0,0000024
0,0000001
0,0120652
0,0000627
0,0000025
0,0000001
0,0000000
Дальше не заполняется, потому что процесс останавливается. Данные последней колонки на
практике неизвестны и приведены для того, чтобы показать, что разность двух последовательных
итераций вполне характеризует сходимость
Пример 5. х1 — In х — 2 = 0, In х = х2 — 2,
следовательно, 0(х) = 1пх, Л(х) = х2-2.
Из пересечения графиков этих функций находим
х@) = 0,15; д'(х) = 1/х, й'(х) = 2х, откуда 1/х > 2х для
0 < х < l/j/2 % 0,707.
Выбором функций д (х) и И (х) можно получить
ряд хорошо сходящихся методов.
Метод Ньютона:
откуда
Сходимость имеет место тогда, когда
—-j- < 1 В ОКреСТНОСТИ Хуу. ЕСЛИ Хдг
является простым корнем, то выполняются
соотношения /' (xN) Ф О и /?'(*jv)#O. Следовательно,
для начального значения х@) должно выполняться
неравенство
Итерационная формула имеет вид
Метод секущих (правило ложного
положения, метод хорд):
= I, 2, . . .),
Здесь х@) и хA) — два заданных числа таких, что
/(х@))/(хA))<0.
Простая итерация. Если д(х) = х, то
х(т+1) = Л(х(И|)); условие сходимости": \h'(x)\<\.
Если х(т) достаточно близко к хдг, то для
погрешности г(т) = х/у — х(т) справедливо
следующее соотношение:
г(т) * h'(xN)r*m-l) « (h'(xN))m(xN - х@)).
Пример 6. Нахождение значения квадратного корня.
хм = у'а, т. е. х# есть корень уравнения х2 - а = 0, а > 0;
1 / а\
записав уравнение в виде х = — I x H I, получим
-И-5-
- хы)-
Неравенство |й'(х)|<1 равносильно д/х2 < 3, отсюда
следует, что единственным условием на х@) является
(х@)J > а/3.
2) Вычисление корней
рациональных функций. Если
Р„(х) = а0 + ахх + а2х2 + ... + а„хп, а„ Ф 0,
и все а, действительные, то нелинейное уравнение
имеет точно п корней
xN ,
(см.
имеет точно п корней xN , xN , ..., xN (см.
2.4.2.4). Некоторые из них или все могут" быть
действительными, некоторые могут совпадать
(кратные корни). Число комплексных корней четно,
и наряду с комплексным корнем z существует
также сопряженный ему корень z. Согласно этому
многочлен нечетной степени имеет по крайней
мере один действительный корень.
Если некоторый корень xN известен, то Р„(х)
можно разделить без остатка на линейный
множитель (х — Xjiy); следовательно, для вычисления
других корней степень многочлена можно
уменьшить.
Вычисление значений функции и ее
производных осуществляется при помощи указанного
разложения на линейные множители по схеме Горнера
(см. 7.1.3.3).
Конечно, все изложенные в 1) методы с
соответствующими изменениями могут быть применены
и к многочленам. Но существует также большое
количество специальных методов, которые по
аналогии с методами решения задач на нахождение
собственных значений могут быть подразделены
на прямые и итерационные методы в зависимости
от того, вычисляются ли все или только отдельные
корни.
Метод Лобачевского — Греффе (как
пример прямого метода). Для простоты
предположим, что многочлен
Р? (х) = а\Р (х - х</>) (х - j
- х\Р)
имеет только действительные и простые корни
х\р (к = 1, 2, ..., п), |хр+\ | < |xF>| (i = 1, ..., п - 1).
Новый многочлен P(nJ+l)(x) находим по следующей
схеме (табл. 7.6).
498
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
P(J) JJ) JJ
+
4\
Таблица 7.6
Для корней этого нового многочлена
справедливо неравенство
(к = 2, 3,
и);
последнее означает, что корни изолированы друг
от друга. Кроме того, | х\Р | = | хЦ+1) |2.
Можно показать, что при сделанных
предположениях процесс нахождения многочлена P|j, '(х)
практически заканчивается после конечного числа
шагов, когда все двойные произведения в табл. 7.6
становятся равными нулю с точностью до
погрешности округления. Тогда | х\^\ | пренебрежимо мало
по сравнению с | х\М^ |, где М = 2\ к - число
итераций, и следовательно,
откуда находим х[м^; корни исходного
многочлена легко вычисляются путем извлечения корня.
Знаки корней можно определить при помощи
простых дополнительных соображений или
непосредственно проверкой.
Метод применим также как к многочленам с
кратными действительными, так и к многочленам
с комплексными корнями, однако последний
этап - нахождение корней, а также критерий
окончания процесса - несколько видоизменяется.
Следует заметить также, что при практическом
проведении вычислений по схеме табл. 7.6
необходимо все коэффициенты представлять в виде
а = Ьтс, где b = 2 или Ь = 10.
7.1.2.4. Системы нелинейных уравнений. Если
непрерывные функции jx (x), /2 (х), ...,/„ (х) от п
независимых переменных х = (хь х2, ..., хи)
заданы в общей области определения D с R" и имеется
вектор хдг е D, для которого fj (хдг) = 0 для всех ;,
то хдг называется вектор-решением системы
нелинейных уравнений /(х) = 0:
(/(*» = 1л(х),/2(х), ...,/лх)O:
Задача нахождения такого вектора-решения является
обобщением задач в 7.1.2.1 и 7.1.2.3.
1) Линеаризация. Нелинейное
представление /(х) заменяют подходящим линейным
отображением L(x) = Ах + b {A - матрица размера
п х п). Тогда при определенных условиях
решение xl системы L(x) = 0 оказывается
подходящим приближением к хдг.
Метод Ньютона - Канторовича(ли-
неаризация через разложение по формуле Тейлора).
Пусть х@) — начальное приближение х#, и пусть
fj(x) по меньшей мере один раз непрерывно
дифференцируемы в ?>; тогда
/W-/(*")
а (Л. А.-.А)
д(хи х2, ..., хя)
Отбрасывая остаточный член Д(х), получаем
где А — матрица Якоби
х2, ..., х„)
sX@)
Предположим, что А невырождена. Тогда система
у = /(х) однозначно разрешима в окрестности х@).
Согласно этому, метод описывается следующей
схемой:
1. Выбор приближения х@) значения х#.
2. Вычисление матрицы А (х°).
3. Решение zA) системы А (х@)) z + f (x@)) = 0
.A) = х@) + , "•
дает новое приближение х(
- zA), для
которого процесс повторяют до тех пор, пока изменение
z(i) не окажется в пределах погрешности.
Пример 7. Метод Ньютона — Канторовича для двух
нелинейных уравнений (табл. 7.7).
2) Метод итерации. Эквивалентное
преобразование /(х) = 0 к виду х = 0(х) дает
возможность определить х как неподвижную точку
отображения д(х) на D по итерационной формуле
х(м + 1) = 0(х(и)), х(О) задано.
Имеет место следующая теорема о сходимости
построенной таким образом последовательности
векторов {х(т)}0°° к решению x#.
Пусть R — прямоугольный параллелепипед в и-
мерном пространстве:
R = {xeR* | ak < xk < bk, 1 < k < n).
АППРОКСИМАЦИЯ
499
Таблица 7.7
j= ]
• 2
У = з
/, (x, y) = 2- x2 - y2
h (x, y) = 1 - x2 + y2
Q
1
-0,125
0
-0,0024
0,0011
2
2
2,5
2,5
2,45
2,45
Точно- x
= 2x, -hy =
~2y
2
-2
1,5
-1,5
1,4167
1,4167
Щ
%
0,25
-0,25
-0,025
-0,04167
-0,0003
-0,0012
yu-1)
Пуск
1
1
1,25
0,75
1,2247
0,7071
Пусть вектор-функция д (х) определена на R и
удовлетворяет следующему условию: существует
действительная постоянная L, 0 < L < 1, такая, что
\\д(х)~ g(z)\\ ^L||.x-z||
х, zeR
Тогда:
1) Уравнение х = д(х) обладает точно одним
решением хуу в R.
2) Определенная выше итерационная
последовательность сходится к xjv для любого начального
вектора x{0)eR.
3) Справедлива оценка
7.1.2.5. Аппроксимация. Большое число
специальных задач по аппроксимации можно понимать и
рассматривать как частный случай общей проблемы
аппроксимации.
Рассматривается векторное пространство V,
элементами которого являются функции / какого-
либо класса, определенные на одной и той же
области М, и в котором определена норма р(/),
обладающая теми же свойствами, что и норма в
евклидовом и гильбертовом пространствах (более
точно общая постановка задачи аппроксимации
рассматривается в функциональном анализе). Пусть
/ - элемент из V и G — подпространство V. Тогда
общая проблема аппроксимации AP(f. G, p(f))
состоит в следующем: найти функцию g(x)eG
такую, что
D(f, G, p(f))= inf {p(f -g)}=p(f-g).
Функция g(x) называется наилучшим приближением,
соответствующим AP(f, G, p(/)), число D(f, G, p) —
дефектом.
С практической точки зрения речь идет о замене
численно не выражаемой функции/через
вычисляемую функцию geG no возможности более точно,
т. е. так, чтобы для заданного действительного
числа б > 0 подходящим выбором G получить
дефект, меньший е.
При решении AP(f, G, р) должен быть найден
ответ на следующие вопросы:
а) Существует ли наилучшее приближение #?
б) Однозначно ли определено #?
в) Как можно вычислить gl
7.1.2.5.1. Проблема линейной
аппроксимации в гильбертовом
пространстве. Пусть V — гильбертово пространство
со скалярным произведением (/, д) и нормой р (/) =
= II j II = ]/{f, f\ и пусть, кроме того, Gn я V
есть и-мерное подпространство V. Задача AP(f,
Gn, || ||) имеет однозначно определенное решение
g такое, что (д — /, h) = 0 для всех heGn. Если {hi,
h2, ..., hn] — некоторый базис Gn, то д = ? 4n)hk,
причем
(/=1, 2, .... п),
\\f-в IIя = (/ - 9, f - д) = II / II2 - Z
»b /)•
Матрица системы линейных уравнений для
вычислений коэффициентов разложения скп)
называется матрицей Г рама базиса {hj}. Будем
обозначать ее An(h}). Эта матрица является
симметричной (эрмитовой для комплексною
гильбертова пространства) и положительно
определенной.
Частные случаи АР подчиняются этой теории.
1) Гармонический анализ,
разложение Фурье:
V=L2(-n, к),
= {sin be, cosfoc}2 = 0
(см. 4.4.1).
2) Метод наименьших квадратов
V — пространство интегрируемых функций,
определенных на [а, Ь\ с интегрируемым квадратом.
Скалярное произведение функций f(x), g(x) опре
ь
деляется как \f(x)g(x)dx. Такое пространство
а
иногда обозначается R2(a, Ъ); пусть Gn+l—
множество всех многочленов Рп с действительными
коэффициентами степени не больше п.
500
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Сформулируем задачу AP(f, Gn + i, || |[): для
заданной функции / найти многочлен Р„ (х) =
= а0 + diX + а2х2 + ... + а„хп такой, чтобы для всех
многочленов Рп из Gn + i выполнялось неравенство
] (f(x) - Рп (х))> dx < J {f(x) - Р„ (х))> dx.
а а
Набор hk = х* (к = 1, 2, ..., п + 1) степенных
функций выступает как естественный базис Gn+U a
коэффициенты ао> • » ^и минимального многочлена
определяются из системы уравнений
Рекуррентная формула: (и + 1) Ри +1 (х) = Bп +
+ 1)хРп(х) — пРп-х (х).
Корни: Рп(х) имеет на [-1, 1] ровно п раз-
личных действительных корней.
Дальнейшие соотношения ортогональности:
J
1
= 0, I, ..., п- 1),
Ptt(x)dx-.
1 = 0 а а
(к= 1, 2, ..., Л+ 1),
т. е. из системы уравнений
(/с = 1, 2, ..., л + 1).
Отметим, что эта система малоудобна для
вычислений и может решаться только с
посредственной точностью. Например, при а — 0 и Ь = 1
матрицей этой системы является матрица Гильберта
1/1 1/2
1/2 1/3
... 1/л
_ 1/w 1/(и + 1) ... 1/Bл- 1)_
норма которой с возрастанием п неограниченно
растет.
Система уравнений становится особенно
простой, если в качестве базиса {hu h2, ..., hn]
подпространств Gn + 1 выбирать ортогональные
многочлены. Для таких многочленов Q, (х)
справедливы равенства
ъ
$Qi(x)Qj(x)dx = O для 1Ф].
а
Если, кроме того,
\Q2(x)dx=\ (/ = 0, 1, ..., и),
а •
то говорят, что многочлены Qt (x) образуют орто-
нормированную систему.
Для отрезка [а, Ь] = [—1, 1] это общеизвестные
многочлены Лежандра
Лпул/ 2"(и!) dx" v /5
Ортогональность:
J Pn(x)Pm(x)dx = 0 для m # п,
Если наилучшее приближение Рп (х) на сегменте
[—1, 1] ищется в виде линейной комбинации
многочленов Лежандра
* = 0
то для отыскания коэффициентов 4П) система
уравнений существенно упрощается:
Ч1!'
D2(f,
1 n 1
= J p (x)л - Q][ J/w л w
Пример 8. Найти парабопу, которая наилучшим об-
разом аппроксимирует функцию у = sin t на отрезке [0, я]
в смысле квадратичного отклонения.
1 Преобразование отрезка
-- - 1, у- sin — (х + 1) L -l
2 Многочлены Лежандра
Р0(х)=1, Р,(х) = х, Р2(х
3 Коэффициенты разложения1
1
4. Аппроксимация.
Р2 @ =
10 .-'Д
АППРОКСИМАЦИЯ
3) Разложение по обобщенным
ортогональным многочленам:
V=R2([a, Ц; q (x)), Gn+1 = {/>„}•
В этом пространстве скалярное произведение
образовано с помощью неотрицательной
интегрируемой весовой функции q(x):
ъ
(и, v) = { и (х) v (x) q (x) dx.
Для специальных весовых функций и
нормированного отрезка [—1, 1] известны
соответствующие ортогональные многочлены. Например, для
1
1.
многочлены Чебышева
Т„ (х) = cos (n arccos х), — 1 ^ х =
Ортогональность:
{О для т ф и,
я/2 для т = п ф О,
я для т = п = 0.
Тт(х)Тп(х)
Рекуррентная формула:
Тп+1(х) = 2хТ„(х)-Тп.1(х)
Т0(х)= 1, Т!(х)
(и=1, 2, ...);
Корни: Т„ (хк) = 0 для xk = cos (Bк + 1) я/Bи))
(к = 0, 1, ..., п — 1), т.е. на [—1, 1] существует
точно п действительных корней.
Точки экстремума: |7^(х)|<1, — l^x^l;
Tn(Xl) = (-\I для х, = cos (/я/и) (/ = 0, ..., п), т.е.
на отрезке [—1, 1] точно п + 1 действительных
точек экстремума.
Разложение по многочленам Чебышева можно
практически реализовать также, исходя из
разложения Тейлора, сходящегося на [-1, 1], заменой
степеней х на многочлены Чебышева, учитывая,
что
7.1.2.5.2. Приближение Чебышева. Мы
рассматриваем пространство V= С [а, Ь] функций,
определенных и непрерывных на [а, Ь], и ставим
задачу аппроксимации AP(f, G, р) с нормой
где В — некоторое подмножество отрезка [а, Ь].
В качестве системы функций G обычно берут
множества многочленов Р„.
1) Равномерное приближение. Если В совпадает
со всем отрезком [а, Ь], то
p(f)= sup {|/(x)|}= max |/(x)|.
хе[«, b] xe[a, b]
Пусть Gn + 1 = Р„ - векторное пространство
многочленов степени не выше п с вещественными
коэффициентами. Тогда верны следующие
высказывания:
1. Существует единственный (минимизирующий)
многочлен
Pn(x)eGn+l с D(f, Gn+1, || ||с) =
= max \f(x)-Pn(x)\^ max \f(x)-Pn(x)\
xe(a, b) xe[a, b]
для всех PneGn + 1.
2. Теорема Чебышева об альтернансе. Всегда
существуют множество п + 2 точек а ^ х0 < х^ < ...
. ..<х„+1 ^Ь и однозначно определенный
многочлен Рп(х) такие, что
\f(xj)-Pn(xj)\=D(f, Gn+U
(xj) - Pn {xj)) + (f(xj+l) - Pn (x
1)) = 0
для j = 0, 1, ..., л. _
Очевидно, что Р„(х) = Р„(х). Множество точек
х0, хь ..., х„+1 называется чебышевским альтер-
нансом.
3. Теорема Вейерштрасса. Для каждой функции
/(х), непрерывной на [а, Ь], и любого действитель-
ного числа е>0 можно указать такой многочлен
Р(х), что
х2=^(Т0(х)+Т2(х)%
4. В каждом разложении по многочленам
Чебышева (см. 7.1.2.5.1) ]Г ajTj(x) частичная сумма
j = 0
Пример 9. е* = 1+х + 0,5х2 + 0,16667х3 + 0,04167х4 +
Разложение по многочленам Чебышева:
Р4(х) = 1,2656ГО + 1,1250^ + 0,270872 + 0,04177, + 0,005274.
На этом примере мы хотим пояснить важное свойство
разложения по чебышевским многочленам: если ищется
приближение 3-го порядка, то
Р3(х) = 1,265670 + 1,12507, + 0,270872 + 0,04177,
дает оптимальный результат такого приближения. Если же
положить в основу разложение Тейлора и просто опустить
члены, начиная с 4-го порядка, то получим погрешность, в
8 раз большую.
Sn(x)= t ajTj(x)
j=0
является минимизирующим многочленом для
Sn+i(x) относительно Gw + b т.е. из неравенства
max \Sn + l(x) - Рп(х)\
xe[a, Ь]
max \
хе[а, b]
(для всех Pn(x)eGn + 1) следует:
Для практического определения
минимизирующего многочлена Рп чаще всего используются
свойства 2 и 4.
Алгоритм Ремеза. Исходя из множества
М@) _ fv@nn+l п < Y@) ^ @) ^ х „(О) ^ l
— \ j i j = o» и ^ ло ^ XI <^ ... <^ xn+i ^ о, как
начального приближения чебышевского альтернан-
502
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
са, согласно свойству 2, определяют
соответствующий Р(п0) (х) и дефект.
Заменой отдельных или всех элементов
множества М@) добиваются уменьшения величины
дефекта, приходя тем самым к новому множеству
МA), с которым поступают аналогично, и т. д.
Процесс заканчивается, когда в пределах точности
вычислений уменьшение дефекта оказывается
невозможным.
Пример 10 у(.\-) = г\ /i = 1, заданы три точки.
М@) -1 0 1
\{.\f)) 0,368 1.000 2,718
-Ь D@) = 0,368,
„<«>.( 1) + hl0) + Dt0) = 2,718.
Решая эту систему уравнений, получаем
Р\0)(х) = 1,175 х + 1,272, ?>@) = 0,272,
шах \Рт{х) - е* | = 0,286 для хк = 0,2.
vk = - 1 + fc 0,1
Попому в М@) мы меняем \:B0) = 0 на 0,2*
М{1) -1 0,2 1
v(vf) 0,368 1.221 2,718
Решая соответствующую систему уравнений,
получим теперь
Р\и(х) = 1,175л: + 1,264, DA) = 0,278.
Максимум погрешности \Р\1)(х)-сх\ в окрестности
0,2 с величиной шага 0,01 равен 0,279 для х = 0,16.
МB)- -1 0,16 1
Но при данном числе точек это приводит к тому же
самому ^многочлену Тем самым мы должны
рассматривать P(|U(V) B пределах нашей точности как наилучшее
приближение первой степени функции ех
Метод телескопа (приближенная
равномерная аппроксимация). Если
/(х)еС(а, Ь) и ? ckFk (x) — функциональный ряд,
равномерно сходящийся к/(х), то в качестве
приближения наилучшей аппроксимации Р„(х)
выбирают
При этом
Sn(x)= ? chFh(x).
S.-P.
оказывается минимальной, если речь идет о
разложении / по многочленам Чебышева.
2) Дискретная аппроксимация
Чебышева. Если xi < х2 < ... < хуу являются N
опорными точками, то вводят дискретную норму
Чебышева
Рассмотрим задачу
AP(f, Gn + U
При N > п + 1 справедливы высказывания,
аналогичные высказываниям в случае непрерывной
аппроксимации Чебышева. Численно задача может
быть решена методами линейного
программирования (см. 6.1).
При п + 1 = N речь идет об интерполяционной
проблеме (см. 7.1.2.6), и соответствующий
минимизирующий многочлен называют тогда
интерполяционным многочленом. При и + 1 = N он
определяется однозначно, а при л > N — нет.
7.1.2.6. Интерполяция.
7.1.2.6.1. Интерполяционный
многочлен. Пусть на сегменте [а, Ь] заданы и + 1
опорных (узловых) точек а ^ х0 < хх < х2 < ... < хп ^ Ь.
Пусть, кроме того, заданы п + 1 действительных
чисел у} d = 0, 1, ..., п) (например, как значения
функции / (х) в узловых точках). Тогда имеем
следующую задачу интерполяции.
Найти многочлен /я(х) степени не больше п
такой, что In (xj) = yj для 0 <./ ^ и.
Интерполяцию применяют главным образом
тогда, когда относительно / известны только
дискретные значения функции у = /(х), и, чтобы
вычислить другие ее значения между узловыми
точками (интерполяция) или за отрезком узловых
точек (экстраполяция), ее приближают многочленом
/и(х), причем
f(xj) = IH(xj) (/ = 0, 1, ...,и).
Всегда существует только один
интерполяционный многочлен (который может быть представлен
в различной форме).
Форма Лагранжа:
А
М)Е
J=o
(х - хо)...(х - xj.l
)...(x - х„)
Нетрудно видеть, что Lj(xj) = 1, Lj(xk) = 0 при
к Ф у, и> следовательно, /„ (х^) = уу
Форма Ньютона:
М*)= Z CjNj(x),
7 = 0
N0(x)=U
Nj(x) = (X - ХО)(Х - Х!)...(Х - Xj-t)
0=1,2, ...,„),
Cj = [XqXj ... Xj~\ = [XjXj- i ... Xo],
где
[xJx;_1...x0] =
1
- X0
(LXJXJ- 1 • • • *l] ~ [Xj- ! ... X0]),
0 = 0, 1, ..., n).
г)
Gn+l=Pn.
Выражение [xoxi...xj называется разделенной
разностью.
Для определения многочлена в форме Ньютона
применяют разностную схему или схему спуска:
ИНТЕРПОЛЯЦИЯ
503
Коэффициенты Cj многочлена Ньютона рав- Многочлен Лагранжа-
ны числам в'верхнем спускающемся ряду (обведены _
рамкой). зЫ-
j
0
1
2
з
Xj
ч
x2
ы
В
Vi
У1
V'3
>'i - Уо
Xl - Xo
X2 -Xi
Уз - Vi
[xtx2] - [xoxi]
x2 - x0
[x2x3] - [x,x2]
X3 - Xi
[x3x4] - [x2x3]
x4 - x2
[XjXj+lXj+2Xj+3]
[X1X2X3] - [x0XiX2]
X3 -Xo
[X2X3X4] - [X1X2X3]
X4 - Xi
Пример II fi(i<o)K(kfiiue интерполяционного ино-
IfHli
{\\<. i ь \ 1 - 4., \2 = 6, X3 == 8. V4. » 10, у 1 = 1, v2 — 3,
¦-- к \>4 •- 20
Mnoi оч юл Иьююна
/з(ч)= I -т 1 (v 4)+ ' (v -4)(x -6) +
р (х -4)(\ -6)(х -8) =
^x ~ 6i(x_T 8H*_zi9L (x-4)(x-8)(x- 10)
" 'D 1" 6) D - 8) D - 10) + ' F - 4) F - 8) F - 10) +
+ 8 (*-4)(x-6)(x-10) (x-4)(x-6)(x-8)
(8-4)(8-6)(8- 10) " A0- 4)A0-6)A0- 8)
= - Jo (x - 6)(x - 8)(x - 10) + ~ (x - 4)(x - 8)(x - 10) -
48'
- у (х - 4)(х - 6)(х - 10) +~-(х - 4)(х - 6)(х - 8),
-- 24 Av' - 27 v2 -I 142 v -240)
/3(х) = -2jBx3 - 27х2 + 142х - 240).
j
0
1
л
3
4
6
10
У]
?
3
о
20
5
~2
6
3
8
7
T
1 4
6 8
1
12
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Если функция /(х), подлежащая интерполяции,
достаточное число раз дифференцируема, то можно
вывести формулу для погрешности интерполяции:
f(x) - /я(х) = -——— (х - хо)(х - Xi)...(x - хи),
(и + 1)'
где Ъ, — некоторое число, расположенное между а и Ъ
и зависящее от х.
Часто применяют равноотстоящие узловые
точки (узловые точки, расположенные на равном
расстоянии друг от друга):
х0 = а, хх = х0 + Л, х2 = х0 + 2й,..., х„ = х0 + nh = Ъ
(т. е. h = (b - а)/п). Как легко видеть, в этом случае
разделенные разности выражаются через простые
разности:
1
[хкхк + 1 ...xfc+m] = ———Ашук,
m\hm
где
А°Ук = Ук, А1Ук = Ук+1 - Ук, &тУк = А (Ат~ 1ук)
(т = 2, ..., к).
Разностная схема упрощается. Формула
Ньютона принимает вид
М*) = Уо + — А^о(^ - х0) 4-
Правила вычисления:
- хо)(х - xt)
+ -777 А"Уо (х - х0) (х -
п\п
• • • (х - хп_ у).
Если положить х = х0 + th, где t может быть
действительным числом между нулем и п, то
предыдущая формула примет вид
t^A2j> +
k\
Вычисление и использование разностей может
быть формализовано введением операторов.
Важнейшие операторы и формулы.
Тождественность: 1ук = ук.
Сдвиг: Еук = ук+1 = у {хк + /i), Epyk = ук+р =
= У (** + Р^)> р действительно.
Разность:
&Ук — Ук + i — Ук~ опережающая разность,
Vjfc = Ук~ Ук-i - запаздывающая разность,
= Ук+а/2) - Л-A/2) - центральная разность.
Среднее значение:
?-
Д)« =
д» = (?-/)«= j; ci(-irjEJ,
АЕ =
V? = ?V = А и др.
Приведенные формулы следует понимать так,
что результаты применения операторов правой и
левой части к функциональным значениям ук
или fk=f(xk) оказываются тождественными.
Операторы допускают широкие формальные
преобразования (возведение в степень, формула бинома
и т. д.).
Важнейшие формы интерполяционного
многочлена при равноотстоящих узлах приведены в
табл. 7.8.
7.1.2.6.2. Сплайн-интерполяция.
Интерполяция на больших отрезках, т. е. с
относительно большим количеством узловых точек, имеет
дополнительные трудности. С одной стороны, при
больших расстояниях между узловыми точками
точность очень мала, а с другой стороны,
интерполяционные многочлены высокого порядка на
концах отрезка значительно колеблются, что
существенно искажает поведение функции. Это становится
особенно важным при последующем
дифференцировании.
Отчасти при решении таких задач оказывает
помощь кусочная интерполяция более низкого
порядка: интерполяция осуществляется по
небольшому количеству узловых точек отрезка и затем
многочлены объединяют в общую
интерполяционную функцию. При этом в точках стыковки обычно
терпит разрыв уже первая производная.
Для получения интерполяционных формул с
гладкими производными все возрастающее
значение получает сплайн-интерполяция.
Пусть заданы п + 1 узловых точек. Функцию,
интерполирующую /(х) на [a, b~], будем искать
теперь не среди многочленов Р„(х), а среди так
называемых сплайн-функций Sk(x) степени к.
Пусть К„ — система узловых точек (узлов) а =
= х0 < хА < ... < х„ = Ь. Функция Sk(x)
называется сплайн-функцией степени k ^ 0 на Кт если
а) SjkWeC*-1^ Ч;
б) Sk (x) - многочлен степени не больше к при
[Ху_ь Xj.
Множество сплайн-функций на Кп обозначается
Л-и/2)) = у
()
Сплайн-функция Sk(x)eSk(Kn) называется
интерполирующей сплайн-функцией, если
Sk(xj) = yj = f(x) (/ = 0, 1, .... п).
В приложениях часто бывает достаточно
выбрать к = 3 и применить так называемую
кубическую сплайн-интерполяцию. Обозначим
1, 2;j = 0, 1, ..., и).
Таблица 7.8
Ньютон (равноотстоящие опорные точки), х = х0 + th,
f(x) = f0 + С}А/о + С2Д2/0 + .. + СТА"/о + с?+1Л"+1/("+1) ($);
х = х„ — sh,
/(х) =/„ - ClsVfn + C2V2/n -... + (-!)" C"sVnfn + (- l)n+1Cns+1/T+1/(n +
Гаусс, I: x = x + t/i,
f(x)=f, + C/5/I + 1/2 + C252/,- + C3+153/1 + 1/2 + C*+Ib*fi + . + C"t++lA hT + 1
Гаусс, II.
An = Bn = n/2, если n четно; Л„ = (n — l)/2 и В„ = (и 4- l)/2, если и нечетно.
Бессель. Ubkfi +1/2 = у Ek/i + &*/< + i)j. x = х, + гЛ, и = 2г + 1,
г — A/2)
Эверетт: (п = 2г + 1, s = 1 — t), x = х,- + th,
f(s) = sft + С3 + 152/,. + С55 + 254/< + •¦ + tji+l
Стирлинг- Ubkfi = -у (8*/<-1/2 + 5k/i+1/2) j, x = х,- + гЛ,
, / Г , \ ч / , t ± \
f (х) = /,¦ + С; I \ibfi + — 5 /,- I + С,+ j I fioJ/,- + — о /, I + . + остаточный член
(Эта формула получается как среднее арифметическое обеих формул Гаусса. Так же определяют остаточный член!)
Так как s(x) на каждом частичном сегменте Для однозначного их определения в зависимости
есть многочлен степени не выше третьей, то для от решаемой задачи добавляются еще два уравнения.
xe\_Xj~i, Xj] Нормальны й случай (N):
hJ hJ
и, следовательно,
(х_
Периодический случай (?) (т.е. /(х +
())))
s° =s s? = s
Здесь s}, cJU cj0 неизвестны для j = 1, 2, ..., п. Заданное сглаживание на грани-
Последние исключаются в силу требования цах (^):
sj ^
Система уравнений G.2) в названных случаях
видоизменяется следующим образом.
Случай (TV). Добавляются два уравнения:
Дифференцируя эту функцию и учитывая, что Sfl~1 6 +S" 3 h + ^"
s' (x) на всем отрезке и, в частности, в узлах должна
быть непрерывна, окончательно получаем систему Случай (Р). Первое уравнение заменяется на
уравнений
„2 "J , „2 "J + "¦/+* , „2 "J+l Sl , Ь S2 ~7~+ 5" Т~= г! L
5j-l ~7~ "*" SJ т rSj+i — J О О W2 «1
6 3 6
/•_! 2 n - 1) G 2)
и добавляется новое уравнение:
—
j+l j
относительно п+ 1 неизвестных sj, s2, ..., 52
S2 Ь_ S2 H_ S2
6 " 6 "
hn
506
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Случай (R). Первое и последнее уравнения
заменяются соответственно на
У1 ~У\
У\ ~УО
я-1 Ч- A + ц/2)К
~ Уп-1 Уп-1 - Уп-1
Таким образом, система содержит только п — 1
неизвестных: sf, ..., si-t.
Пример 12. Сплайн-интерполяция функции /(х) = sin x,
и = 4.
Речь идет о периодическом случае; мы используем
G.2) и случай (Р).
У
0
1
2
3
4
Xj
0
7t/2
7t
Зя/2
2я
yj
0
1
0
— 1
0
hj
я/2
я/2
я/2
я/2
у, _ у, - 1
1
-1
-1
1
G.2):
(Р): 5? я/3 + si я/12 + sj я/12 = - 4/я,
¦ si я/12 + sf я/3 + s| я/12 = 0,
. sj я/12 + si я/3 + si я/12 = 4/я,
(Р): s? я/12 + si я/12 + si я/3 = 0.
Матрица системы симметрична. Легко получить, что
5?=-12/я2, 5§ = 0, si = 12M s2 = sg = 0.
Из формул G.1) получается сплайн-функция
(- 4/я3) х3 + C/я) х, 0 < х < я/2,
D/я3) (х - яK - C/я) (х - я), я/2 < х < я,
D/я3) (х - яK - C/я) (х - я), я < х < Зя/2,
(- 4/я3) (х - 2яK + C/я) (х - 2яХ Зя/2 < х < 2я.
Важно, что наряду с до сих пор известными
свойствами интерполирующая сплайн-функция
имеет еще два экстремальных свойства:
1) Среди всех интерполирующих, дважды
непрерывно дифференцируемых на [а, Ь] функций
ф(х) только интерполирующая сплайн-функция
степени 3 доставляет функционалу J (<р) =
х„
= J (ф" (х)J dx минимум, т. е.
s(x) =
для всех функций ф (х) таких, что ф (х,) = у}.
2) Для всех S(x)eS^(Kn) и дважды непрерывно
дифференцируемых функций / таких, что f(xj) — у^
справедливо соотношение
1 (/ (х) - 5 (х)J dx < J (f(x) - S (x)J dx,
причем равенство возможно только для
интерполирующей сплайн-функции:
Свойство 1), по существу, означает, что кривизна
интерполирующей кривой является минимальной -
свойство, которое приближенно реализуется
упругой линейкой (английское «spline»), закрепленной
в узлах интерполяции. Такова механическая
интерпретация сплайн-интерполяции.
7.1.2.7. Приближенное вычисление интегралов.
Под этой задачей понимают (приближенное)
вычисление значения определенного интеграла
ь
J/(x)rfx при условии, что известны отдельные
а
значения подынтегральной функции и некоторые
ее общие свойства. Будем далее предполагать, что
/(х) — (кусочно) непрерывная функция.
Формулы среднего значения. По
теореме о среднем значении интегрального
исчисления (см. 3.1.7.2) имеем
ь
\f(x)dx = (Ъ - a
< Ь,
М,
где т - наименьшее, а М - наибольшее значения
функции /(х) на отрезке [а, Ь].
На этой теореме фазируется следующий
общий принцип. Пусть на [а, Ь] заданы п + 1 узловых
точек а = х0 < хх < ... < х„ = Ь, в которых известны
значения подынтегральной функции у* =/(**)
(к = 0, 1, ..., и). Если М (уо, у и ..., уп) есть какое-
нибудь из средних значений, образованное из
..,у„)^ max yk,
к=гО,...,п
уп), получаем
форто, полагая /(?) ^ М(у0, .
мулу среднего значения:
J/(x) dx = (Ь - а) М (у0, У и
•, Уп) + К [/]
- J. [/] + «»[/].
где К„ [/] - погрешность интегрирования.
Для практических целей целесообразно
наложить некоторые дополнительные требования:
а) Функция М (уо, • • •, уп) должна быть линейной:
zb ..., ау„ + pzn) =
и ..., >>„)+ $M(z0, zx, ..., zn).
Тогда
б) Для надлежаще выбранного семейства
функций {fck(x)}k=0 должны выполняться равенства
Rn [hk] = 0, к < п, т. е. для этих функций формула
среднего значения должна быть точной.
Оба требования могут быть одновременно
выполнены, если использовать взвешенное
среднее арифметическое:
М(у0
\i = 0 / i = 0
р(уь р,-> 0.
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
507
Таблица 7.9
п
1
2
3
4
5
6
7
2
6
8
90
288
840
17280
Названия: п =
л =
Рс
1
1
7
19
41
751
Pin
•
4
3
32
75
216
3577
Ргп
1
3
12
50
27
1323
Ргп
32
50
272
2989
1, формула трапеции,
1, формула парабол (Симпсона), х0 < ? <
1, формула Ньютона.
7
75
27
2989
х„,
Р5п
19
216
1323
Рбп
41
3577
Рт
751
Rt
~ 9о~/D) (У
- ?/»»
~ 945"^' '® ¦
~ 12096 * ®
1400 ^ ®
/"(8) /t\
518400у vs>'
Согласно этому определению, в формуле
остается еще свобода выбора, а именно: число опорных
точек, расположение опорных точек, выбор весов.
Погрешность интегрирования Rn [/] существенно
зависит от этого выбора.
Целое семейство формул среднего значения
возникает при интегрировании вместо f(x)
интерполяционного многочлена Лагранжа /и(х):
шается вследствие одновременного увеличения
погрешности метода, так что для больших
промежутков обычно выбирают п < 7. Чаще
интегрирование осуществляется по формулам невысокого
порядка для частичных отрезков. В качестве
примера приведем формулу Симпсона:
a +jh, 7 = 0, 1, ..., 2N, h=(b- a)/BN),
¦
f(x)dx =
~(Уо
2у2 + 4у3
При равноотстоящих узловых точках полу- 2) Формулы для и = 2/с и п = 2А; + 1 имеют
чаются формулы, называемые формулами Ньюто- погрешности одного порядка. Поэгому при заданг
на — Котеса (табл. 7.9): ном числе точек эти формулы часто бывает удобным
. комбинировать.
Пример 13 Вычисление In 2 =
I dx
()абл 7 10)
Z
Pin,
a = x0, b = xn.
Формулы Ньютона — Котеса характеризуются
Ъ — а . тем, что они точно интегрируют многочлен степени
п. Можно показать, что этим требованием веса pjn
определяются однозначно.
Вообще формулы интегрирования, для кото-
Замечания. 1) Выигрыш точности, достигав- рых Rn [xm] = 0 для 0 ^ т ^ п и Rn [хп + 2] # 0, на-
мый при повышении порядка, частично умень- зываются формулами порядка п.
508
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Таблица 7.10
I
0
1
2
3
4
5
6
7
8
9
10
xt
1,0
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
1,000000
0,909091
0,833333
0,769231
0,714286
0,666667
0,625000
0,588235
0,555556
0,526316
0,500000
Pi
4
1 1
4
1 1
4
1 1
4
1 1
4
h "
у Z РЫ
0,182321
0,336471
0,470002
0,587781
0,693138
Pi
-1
-4
1 -1
4
1 1
4
1 1
4
1
у Z РЫ
0,095311
0,405462
0,530624
0,641847
Pi
1
3
3
1
it h Z Ptyi
о
0,262363
Если узловые точки или, может быть, их число
не заданы с самого начала, то можно попытаться
определить веса и узловые точки таким образом,
чтобы получалась формула как можно большего
порядка. Это приводит к так называемой
квадратуре Гаусса.
Квадратура Гаусса. Если w(x) —
положительная весовая функция, то всегда можно
определить коэффициенты Ain и узловые точки х,„
(i = 1, 2, ..., п) так, чтобы
\f(x)w(x)dx =
= )Ainf(xitt) + -
ь
(х) dx,
пп (х) =(х- х1п) (х - х2п) ...(х- хпп),
а ^ х1п < х2п < ... < хпп ^Ь, а < ^ < Ь.
Формула имеет порядок, равный 2п — 1 :
а) Узловые точки xin являются корнями
многочлена степени п из семейства {Рт(х)}^°=0
многочленов, получаемых ортогонализацией семейства
{xk}fc*o относительно w(x) (см. 7.1.2.5.1):
ь
J Р( (х) Р- (х) w (x) dx = 0 при i Ф j.
б) Веса Ain вычисляются интегрированием
соответствующих многочленов Лагранжа:
Ain=\Lin(x)w(x)dx.
Особые случаи (не ограничивая общности,
полагаем а = -1, Ъ = 1).
Формула Гаусса — Лежандра (табл. 7.11):
w(x)=l, Рт(х) — многочлены Лежандра (см.
Таблица 7.11
п
1
2
3
4
5
6
i
1
1
2
1
2
3
1
2
3
4
1
2
3
4
5
2
3
4
5
6
*w
0
0,5773503
-0,5773503
0,7745967
0
-0,7745967
0,8611363
0,3399810
-0,3399810
-0,8611363
0,9061798
0,5384693
0
-0,5384693
-0,9061798
0,9324700
0,6612094
0,2386192
-0,2386192
-0,6612094
-0,9324700
2
1
1
0,5555556
0,8888889
0,5555556
0,3478548
0,6521452
0,6521452
0,3478548
0,2369269
0,4786287
0,5688889
0,4786287
0,2369269
0,1713245
0,3607616
0,4679139
0,4679139
0,3607616
0,1713245
ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
7.1.2.5.1, а также 3.3.1.3.4):
2A-х?)
22и+1(л!L
Пример 14. Квадратура Гаусса — Лежандра*
«12
J = f sin t dl, n = 2
--"-~~~ о
Преобразуем промежуток интегрирования к отрезку
]
1), dt =
У - ~
~ f мпГ-*-(х + 1I dx,
4K1 - Ш - °'32589' 4т(>+Ml
J = -*-@,32589 + 0,94541) + у-^Г
7t
= 0,99848 f -j -^-y sin t,
Я
0 < x < y
Фактическая ошибка составляет -0,00152 Эю хороший
результат для формулы с двумя узловыми точками, что
подчеркивает значение таких методов интегрирования.
Формула Гаусса - Чебышева: w(x) = l/|/l - х2,
Рт (х) - многочлен Чебышева 7^,(х) (см. 7.1.2.5.1),
Ain = п/п для всех i; xin = cos (B/ — 1)я/Bп)),
Г (яиМJ ^
Пример 15 J (x4/^l -x2)t/x.
Если аыбрать п = 3, то 2и — 1 = 5 и результат должен
быть точен:
Г3 (х) = 2хТ2 (х) - Г, (х) = 2х {2х2 - 1) - х = 4х3 - Зх,
l/3 0 |/з
Гх4
9 9
(известный точный результат!)
Квадратуру Гаусса целесообразно применять
тогда, когда функция аналитична или достаточно
плотно табулирована. В других случаях можно
взять не такие точные, но более простые формулы
Ньютона — Котеса.
Метод экстраполяции. Линейность
формул среднего значения делает возможным
получение улучшенных значений интеграла при
помощи линейных комбинаций.
Пусть f/(x) dx = Jl0 [/] + Д'о [/] - линейная
формула интегрирования порядка (п — 1), т. е.
Д'о [х*] = 0, 0 ^ к ^ п - 1, но Д'о [хл] Ф 0. Тогда
)f(x) dx = pJ'o [/] + q (Л2 [/] + J\l2 [/]) + R [/],
о
где p = -1/B" - 1) и q = 2"/B" - 1), является
формулой порядка n (т. e. R [хи] = 0). Идея
доказательства для многих методов экстраполяции так
важна, что ее имеет смысл привести. Пусть,
например, Rl0 [хл] = с/и + \ где с — постоянная, не
зависящая от длины/ промежутка
интегрирования. Тогда, очевидно, R [хи] = pcln + 1 + q2c(l/2)tt + 1 =
= d"+1 (p 4- q/2n). Но при указанном выборе р и q
выражение в скобках равно нулю.
При практическом использовании обычно не
пользуются формулами, а оперируют с числовыми
значениями по следующей схеме:
Too
\
I
l
/7-2
Ж
/7-3
Г
•
...
...
...
Простейший случай получаем при
формулы трапеций:
п = 1 из
Ti0 = -±y
b-a
Имеем
-)'
Ь-а
= 0, 1, ...).
и т. д. Справедлива формула
г 2 Titk-i — Ti-lk-1
=1, 2, ...),
согласно которой мы можем по мере надобности
вычислять значения Tik, к > 0, в
последовательности, указанной в схеме стрелками.
Можно показать, что и столбцы, и косые строки
сходятся к значению интеграла. Схему можно
легко программировать. Так как при этом методе
погрешности также нарастают с увеличением
порядка величины, то продвигаются самое большее
до к = 7, давая i возможность возрастать до
тех пор, пока «гнездо» равных чисел в схеме не
покажет, что в пределах точности вычислений
метод привел к получению результата.
510
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Пример 16.
2
Ce'dx
J *
«3,059116.
3,059116 /
А
^v
U
3,06
3.09 3,0591
3,059 3,05911
3,07 3,05911 ^"
3,0591 ^"
3,06 <Г^^З,О5Ж
3,05911 ^*~^
3,06 3,059117
3,059116
3,059
7.1.2.8. Приближенное дифференцирование.
Приближенное определение производных функций
должно всегда проводиться с особой
осторожностью, так как известно, что дифференцирование
в противоположность интегрированию
сопровождается «разбалтыванием».
Пример 17. Функция f(x) = e sin (х/е2), е > 0,
удовлетворяет неравенству | f(x) |< е, но - 1/е < /' (х) ^ 1/е
Если выбрать е очень маленьким, то у мало изменяющейся
Рис. 7.2
функции /(х) производная будет принимать очень большие
значения (рис. 7.2).
Численное дифференцирование. Мы
исходим из того, что функция/(х) задана конечной
последовательностью пар значений (х,, ft), и ищем
приближенные значения f\, /", /"', ... величин
/'(х,),/''(*<),/'''(*.), ..
Если значения функции в точках сетки xt
считаются точными в пределах точности вычисления,
то дифференцируют интерполяционные
формулы (см. 7.1.2.6.1). Для выведения соответствующих
формул часто пользуются формальным методом
операторов (см. 7.1.2.6.1).
df
Введем оператор Dft = ——
ах
Основная формул а:
Е,
К 62\1/2 5\
hD = In E = ln(/ + А) = 21п( ( / + —J + — 1.
Пример 18.
В качестве формулы численного
дифференцирования мы применяем конечную частичную
сумму этого разложения:
Если значения функции заданы как результаты
измерений и требуется исследование поведения
производных, то необходимо численное
сглаживание с последующим дифференцированием (см.
7.1.5).
Таблица 7.12
Некоторые
Уо =
/о =
У'о =
Уо =
Уо =
У'6 =
у"
у'6 =
У'6 =
у'6'=
У'о-
to-,
1
ft {~У~ *
1
1
1
1
1
1
1
iw(-'
1
1
важные формулы
Формула
' (№> У] = У' (/Л) )
Л)
2 + 16y_i —30^0+ 16_у 1 -
у{ +4^2 —Уз)
1 — 20уо + 6у i + 4>'2 — Уз
3,.2 + 228,.,-420,0 +
+ 2(%i + 15у2- 12><3 +
_!+ 10>'о— 12yt 4-6^2 —
дифференцирования
2у,)
Оценка
погрешности
1 ,, ,„
-6Ну°—'
+ {6h*yo5) + ...
+ y*Vo" + ..
+ -LA^) +...
7.1.2.9. Дифференциальные уравнения.
7.1.2.9.1. Задача решения
обыкновенных дифференциальных уравнений с
начальными условиями. Имеется большое
число частных случаев дифференциальных
уравнений, которые можно проинтегрировать в
конечном виде; однако большинство задач с
дифференциальными уравнениями может быть решено только
численно. Простейшим методом является метод
ломаной Эйлера, легко реализуемый графически.
Пример 19. /(x)*/(v, >(x)), y{a)=s __
Рис 7.3
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
511
Схема вычислений (рис. 7.3): х{ = а + ih (/ = 0, 1, ..., N), Для точного решения дифференциального
У(«) = /(а, s) = tg<p0, уравнения у'(х) = /(х, у(х)) в узлах xs справедлива
формула
У1=з + hy'(a) = s + hf(x0, у(*<,)), .
/i =/(хь yO = tg9l, J>(*;+i) = y(xj) + /i/(x,, >>(х;)) + т/'(р^2
У2 = У1 + A/, = у, + А/(хь У1),
y't=f(x{, tt)-tg«p,,
Л+i = Л + hf(xh yt) (i = 0, 1, ..., N - 1).
Пример 20. / = х//3, уA)=1. Точное решение:
y(x) = ((x2 + 2)/3K/2. Результаты по методу Эйлера (см.
табл. 7.13).
Таблица 7.13
Результаты вычислений по методу Эйлера
*|
1
2
3
4
5
Л = 0,10
1,00
2,72
6,71
14,08
25,96
h = 0,01
1,00
2,82
6,99
14,63
26,89
Точно
1,00
2,83
7,02
14,70
27,00
Общие понятия. Локальной погрешностью
обрыва называется погрешность, которую делают
при переходе от Xj к xj+u если заменяют
дифференциальное уравнение конечным выражением.
Конечное приближение по методу Эйлера имеет
1
вид yj+l = yj + hf(xj, yj), так что Ej = —h2y"(^j)
является локальной погрешностью обрыва.
Погрешностью обрыва называется погрешность у (xj) —
— у^ возникающая при сложении (аккумуляции)
локальных погрешностей обрыва при некотором
фиксированном j. (В смысле 7.1.1 она является
погрешностью метода 5м (х,).) Погрешностью
округления называется доля погрешности,
возникающая при фактическом проведении вычислений, а
также вызванная этими округлениями
нарастающая неустранимая погрешность.
Одношаговые методы. Если в формуле
ломаной Эйлера заменить f(xjt yj) на более общее
выражение f(xj, yj\ то возникает общая формула
одношагового метода:
yj+! = yj + hf(Xj, yj)t >'o = s (/ = 0, 1, ...).
Вместо дифференциального уравнения решается
нелинейное разностное уравнение.
Таблица 7.14
Формулы типа Рунге — Кутта
Порядок
ошибки
обрыва
Л3
А4
А5
Формула
/-у<*|+**)
/=!*1+т*3
? = ±(kl+2k2 + 2k3-kkj
Вспомогательные величины
ki =/(*» У&
k2=f(Xi + h, yt + hkj
кх - как указано выше
кх - как указано выше,
*з =/(*! +Л, yi + 2hk2-hkx)
кх — как указано выше,
*2 =/(*< +у, tt + y*lj,
ki - как указано выше,
iw(*+y.*+4*i).
*Э =/(*!+у. Л + уМ,
Название
Улучшенная ломаная
Формулы Хойне
Формула Рунге-Кутта
512
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Важнейшими одношаговыми методами
являются
Методы типа Рунге — Кутта. Здесь
/(*/» У]) строится как весовое среднее значений
функции /(х, у) в определенным образом
выбираемых точках (х, у) = (?fc, T|fc) так, что локальная
погрешность обрыва имеет порядок выше h.
Знание порядка локальной погрешности не имеет
практического значения для прямой оценки
фактической погрешности обрыва или округления.
Общие оценки погрешностей другого типа
являются большей частью также слишком грубыми.
Поэтому для оценки погрешностей, для
управления ходом вычислений или в данном случае для
управления величиной шага (под этим понимают
зачастую очень выгодное изменение величины
шага h в зависимости от достигнутой точности)
в настоящее время широко применяют принцип
Рунге. Пусть погрешность метода имеет
порядок к. Приближенное значение у(х), вычисленное
в точке х с величиной шага h, обозначим через
У(х, h). Тогда в точке х = х0 + 2nh имеем (по
определению порядка погрешности метода)
у(х) - У(х, h) к A2nhk + 1 =A(x- x0)Л\
у (х) - У(х, 2/i) » An Bh)k+1 =A(x- x0) 2kh\
т. е.
У(х, 2Л) - У(х, h) » А (х - хо)A - 2к) h\
и, следовательно,
У{х)-Г{х,
У(х, h) - У(х, 2h)
2*-1
Одношаговые методы используют для
вычисления последующего значения yj+l только
информацию из полуинтервала \_yjf yj+i) и поэтому всегда
применяются в том случае, если вычисляются
первые значения (начальная процедура) или если о
свойствах непрерывности решения известно мало.
Если кривые решения являются достаточно
гладкими и известны некоторые начальные
значения, то точность аппроксимации решения может
быть увеличена благодаря учету к > 1
предшествующих значений.
Многошаговые методы основываются
на замене дифференциального уравнения
/(*)-/(*, У MHO, y(a) = s
при постоянном
к-го порядка
? а^Уп+j
aik) Ф 0, (аф)
шаге h разностным уравнением
yn+j) =
(Ы>*>J * 0, n = 0, 1, 2, ...,
Тем самым погрешность при шаге h выражается
через приближенные значения при шагах h и 2й.
величины yo = s, yu ..., yk-x являются заданными
значениями (требуется начальная процедура!).
Каждый способ этого вида однозначно
определяется двумя многочленами:
pfc (г) = akk)zk + 4*>_! z*"! 4- ... + а%\
и поэтому говорят о (р, о)-методе (см. табл. 7.15).
Если степень многочлена crfc меньше степени
многочлена рк, то говорят о явном (или
открытом) методе, а если степени равны, то говорят о
неявном (закрытом) методе.
Важнейшие (р, <з)-методы
Таблица 7.15
а B)
Определение коэффициентов
Адаме {k —\t 2, ...) явный метод
A - t) In A - t)
частный случай к = 1: a (z) = 1; ломаная Эйлера
Адаме - Мултон (к = 1, 2, ...) неявный метод
частный случай к = 1: a (z) = — A + z) правило трапеции
In A - О
Нистрём (к = 2, 3, ...) явный метод
k-i / |V
I/ii-T
t B - О
A - о in A - О
частный случай к = 2: a (z) = 2z правило средней точки (центра)
Хенричи - Милн (к = 2, 3, ...) неявный метод
частный случай к = 2: о (z) = — (z2 + 4z + 1) метод Милна
In A - 0
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
513
Замечание. Формулы часто записываются
при помощи разностей. Пересчет легко
осуществляется по операторным формулам (ср. 7.1.2.6.1):
yn+j = &ую Е* = ? C'jA', A' = А (А-1).
1 = 0
При помощи явных формул (и + /с)-е значение
вычисляется непосредственно по к
предшествующим значениям уп+к-и у„+к-2, •-, Уп-
Неявные формулы содержат подлежащее
вычислению значение уп+к как в линейной, так и в
нелинейной частях формулы, т. е.
акк)Уп+к = F(yn+k, Уп+к-и •••, Уп\ h).
Часто уп+к находят при помощи итерационного
процесса:
уп+к = lim уЦ>+ь
j-+co
= 1,2,...,
>й задаются как начальные приближения.
Две формулы с одинаковым порядком ошибки
можно связать в так называемый метод
предсказания — уточнения, который действует по
следующей схеме: по явной формуле «предсказания»
вычисляется приближение и подставляется в правую
сторону неявной формулы «уточнения», которая
дает улучшенное значение.
Пример 21. Адаме (/с = 4):
У +
-59/(хи+*_2, yn+k_2) +
+ 37/(хя+к-з, уи+*-з)-9
Адаме — Мултон (к = 3):
+ (9/(* Л)+ 19/(^
*-1. Уп+k-i)-
Обе формулы имеют одинаковый порядок ошибки.
Сходимость. Приближенный метод называют
сходящимся порядка р > О, если для всех
lim -—
Уп-У(х„)
= Л < оо.
Одношаговый метод является сходящимся,
если выполнены следующие условия:
а) величина /(х, у, И) при х0 < х ^ хдг,
— оо < у < +oo,0^/i</io как функция трех
переменных^ является непрерывной;
б) /(х, у, 0) = /(х, з') ПРИ ^о < х < хдг,
— оо < у < + оо;
в) |/(х, у, /i)-/(x, z, fc)|<L|y-z|, L= const,
при хо < x ^ xjv, -oo<>;< +00, 0</i^/i0.
Из этих трех условий наиболее
существенными являются условия а) и б), так как в)
выполняется для рассмотренных методов большей
частью автоматически, когда дифференциальное
уравнение имеет однозначное решение.
(р, <з)-метод сходится на [а, Ь] равномерно
(lim max | у„ - у{хп) \ = 0)
/1->0х„е[а, У]
тогда и только тогда, когда
а) сходится используемая начальная процедура;
б) все корни многочлена р (z) лежат в замкнутом
единичном круге (| z | < 1), причем корни zk,
| zk | = 1, являются простыми корнями (корневое
условие);
в) выполнено условие аппроксимации р A) = 0 и
р'A) = аA).
7.1.2.9.2. К раев ые задачи для
обыкновенных дифференциальных
уравнений (см. 3.3.1.7). Мы ограничимся линейными
краевыми задачами вида
L|>]=r(x),
i 0
0 = 1, ...,' п),
Rt !>] = t (*аУ(]) W + ьиУи) № (i = 1, • • • > n),
j = 0
j i (x), r (x) — непрерывные на [а, Ь] функции,
Каждое решение можно представить в виде
линейной комбинации:
у{х) = уо(х)+ X diyi(x),
i= I
где функции у,(х) являются линейно
независимыми решениями однородного уравнения L[y] = О
(фундаментальная система), а у0 (х) — частное
решение неоднородного уравнения L[y] = r. Если
эти функции заданы, то коэффициенты dt
вычисляются из системы линейных уравнений
d.R,
= Ci - Rt [jo] (i = 1, 2,..., л);
на этом основывается часто употребляемый метод
сведения к задаче с начальными значениями.
Путем подходящего задания начальных значений
Atj из L|>J = O и yf(a) = Aij (i = 1, 2,..., п - 1;
j = 1, 2,..., п) определяют фундаментальную
систему. Если система краевых (граничных) условий
содержит по крайней мере одно отдельное гранич-
л- 1
ное условие Яг [у] = ? ацУ(Л(а) = сь то у0 также
легко может быть вычислено как решение задачи
с начальными значениями.
Пример 22. Сведение к задаче с начальными
значениями:
граничные условия: >>(-1) = уA) = 0, - 1 ^ х ^ 1.
Полагаем у (х) - ух (х) + осу2 (х), где у, удовлетворяет
первому граничному условию и неоднородному
дифференциальному уравнению:
Так как уA) = ^A) + ау2A) = 0, то a = -У1 A)/у2A).
Вторым важным классом методов являются
эвристические методы. Пусть М — множество
решений дифференциального уравнения на
постоянной основной области G функций, т. е.
M = {y(x)\yeG и L[y] = r},
и пусть N = {y(x)\yeG и Rt[y] = ci} есть
множество решений граничных уравнений; тогда
множество решений L краевой задачи есть
пересечение этих двух множеств: L = М f]N.
17 И Н Бронштейн, К А. Семендяев
514
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Пусть Мр а М — множество функций из М,
которое определяется р параметрами Сь С2, ..., Ср:
Мр={у|уеМ,
и аналогично
Np = {y\yeN,
Cu ..., С,)},
, Сь ..., Ср)};
для yeNp L[y]=r + e{x, Сь ..., Ср),
для уеМр Я, [у] = с, + б, (х, Сь ..., Ср).
Если теперь потребовать, чтобы в качестве
приближения для решения краевой задачи была бы
взята та функция, при которой
1) значение е(х, Сь ..., Ср) становится как можно
меньше, то речы идет о методе областей;
2) значение 5,(х, Сь ..., Ср) становится в
известном смысле минимальным на Мр, то говорят о
краевом методе.
Такие методы можно применять для решения
как обыкновенных дифференциальных уравнений,
так и дифференциальных уравнений с частными
производными. В случае обыкновенных
дифференциальных уравнений почти исключительно
применяется метод областей.
Особенно важным является линейный случай,
когда в качестве параметрического множества
Np берется множество всех линейных комбина-
р
ций вида Ф(х, Сь ..., Ср) = vv0 + ]Г Cjwj(x)- При
этом w0 удовлетворяет неоднородным граничным
условиям Ri [w0] = ch в то время как линейно
независимые wj (x) удовлетворяют однородным
уравнениям Rt [vv,] = 0.
Таблица 7.16
Важнейшие методы областей
Название
Метод
квадратичной ошибки:
непрерывный
дискретный
Метод Галёрки-
на (метод ортого-
нализации)
Метод частичных
областей
Метод коллокаций
Требование минимальности
б(х; Сь С2, ..., Ср)
ь
J е2 dx -у min
л
? е2 fa) -> min; хь ..., х„ е [о, Ь\
i= 1
п > р
ь
J evj (x) dx = 0
для ;= 1, 2, ..., р
[t>y(x)]f-линейно независимая
система непрерывных функций
ti <t2<...<tp+le[a, Ь],
'У е(х, Си ..., Cp)dx = 0
h
для i = 1, 2, ..., р
tx <t2< ... < tp 6 [а, Ь] (точки кол-
локации)
e(f,; Сь С2, ..., Ср) = 0
для i = 1, 2, ..., р
7.1.2.9.3. Разностные методы решения
краевой задачи для уравнения
Пуассона (на плоскости). Изложение теории и
практического применения разностных методов для
обыкновенных дифференциальных уравнений и
уравнений с частными производными в рамках
этого справочника невозможно. Поэтому задачи и
основные идеи рассматриваются на ряде
конкретных примеров.
Задача. Пусть О, есть область на плоскости
х, у с границей Г. Ищется функция и (х, у), которая
в П удовлетворяет уравнению Пуассона
Дм = и"хх Л- и"уу = g (x, у).
Важнейшие краевые задачи:
!) "(х. УI(х,у)еГ = ф(*» У)-1-я краевая
задача, задача Дирихле.
2)
ди (х, у)
= vj/ (x, у) — 2-я краевая
задача, задача Неймана.
3) аи(х, у) + b —^—- = х(х, у) для (х, у) на
Г - 3-я краевая задача.
Разностные методы. Рассматривается не
континуум точек плоскости х, у, а счетное
множество дискретных точек Pi} = (xh yj).
Примеры форм сеток см. на рис. 7.4.
Прямоугольная
координатная
сетка
(Х0
(хР
,у0)
h
yj'
из
Координатная сетка
V
Координатная сетка
') f из шестиугольников
7у
Рис. 7.4
(
{ .
/
/
<
)
X
\
\
1—
1
(
/
4
\
> 1
)
V
\
а)
6)
Рис. 7.5
Дискретизация задачи.
1) Область. Если область Q разместить на
сетке, то одни точки сетки попадут внутрь области,
а другие окажутся снаружи ее. Дискретная «область»
Q* состоит из точек сетки, лежащих внутри
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
515
области Q; точки сетки, ближайшие к границе и
лежащие либо внутри, либо снаружи (это зависит
от постановки задачи!), рассматривают как
точки дискретной границы Г*. В этом случае
дискретная область ft* = Q*(Jr* состоит только
из точек сетки (рис. 7.5, а). Вторая возможность
заключается в том, что добавляют точки
пересечения Г с прямыми сетки как нерегулярные
граничные точки (рис. 7.5, б).
2) Уравнение. Производные, встречающиеся в
рассматриваемом дифференциальном уравнении,
заменяются в каждой точке сетки Рц = (xh yjj на
соответствующие разностные отношения, причем
локальная погрешность обрыва может быть
оценена (см. 7.1.2.8). Так, например,
дх
1
Такие конечные выражения называют также
молекулами и пишут их в виде наглядных структурных
формул.
Пятиточечные молекулы для оператора Лапласа:
+ O(h'),
+ 0(h2)
(квадратная сетка).
3) Граничные условия. Если область П такова,
что для достаточно простой сетки при
соответственно выбранном расположении граница Г
состоит только из сеточных прямых, то краевые
значения задаются в граничных сеточных точках
и вводятся в соответствующие молекулы, если
они включают такие точки.
Пример 23. Прямоугольники в прямоугольной или
квадратной сетках.
Задача Дирихле. В зависимости от того,
содержит ли область Q* только регулярные или
также нерегулярные точки сетки (см. выше),
заданные граничные данные перерабатываются двумя
способами:
а) Определяются краевые значения в
регулярных граничных точках путем интерполяции из
заданных значений на границе Г. Тогда имеет
место представленный выше простой случай
(рис. 7.6, а).
б) Непосредственно включаются заданные
краевые значения в нерегулярных точках и
применяются асимметричные молекулы вблизи границы
(рис. 7.6, б).
Пример 24. Уравнение Пуассона в прямоугольнике:
Сетка: (х„ у,) = (*й, j/i),
п* = {(№; jh) | 0 < / < 4, 0 < j < 3} - регулярная граница.
Ди(х, y)**f(x, у), м|г = ф A-я краевая задача).
17*
Q
Г
\
\
h P
R
\
s
\
и(РЫ
u(S) =
г
a)
Асимметричная
молекула
_ Коэффициенты
находятся с помощью
ряда Тейлора
\
б)
Рис. 7.6
При применении первой из двух указанных молекул для А
имеем
C/i-u + 1/i+i.j + Vu-i + C/,.i+l - AUU = h2fu
как дискретный аналог уравнения Пуассона. (Через UtJ
здесь обозначено приближение для u(xt, у^ = иц.)
Если записать все уравнения, для которых «центральный
элемент» u(J является внутренней точкой (т. е. 1 < i ^ 3,
1 < j < 2), то получим
h2f2l,
12 + U3
h- 4t/n
22 - 4l/21
32- 4U3l = h2fiu
13 - 4Ul2 = h2fl2,
i1- 4U22 = h2f22,
i- 41/32 = h2f32.
Подчеркнутые значения являются заданными краевыми
значениями и могут быть перенесены в правую сторону.
Тогда в качестве дискретного аналога поставленной задачи
получается следующая система линейных уравнений:
-4
1
0
1
0
0
1
-4
1
0
1
0
0
1
-4
0
0
1
1
0
0
-4
1
0
0
1
0
1
-4
1
0
0
1
0
1
-4
Uu
u3l
ui2
u22
u32
- h2fn
h2f2i
h2fl2
h2f22
h2f32
-u0l
~u20
-uAi
-u02
-u23
-
u42
-u10 -
-u30
-ul3
-u33 .
Матрица этой системы демонстрирует все характерные
признаки матриц, которые возникают при применении
разностных методов:
- матрицы, как правило, большие;
-матрицы симметричны и имеют блочную структуру;
- матрицы являются разреженными, т. е. они содержат
много нулей.
516
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Для решения систем линейных уравнений с такими
матрицами применяют обычно итерационные методы,
хотя в последнее время разработан ряд прямых методов,
использующих блочную структуру. Численно эти методы
часто оказываются выгодными, однако их недостатком
является отсутствие универсальности.
Порядок, в котором пробегаются точки сетки при
проведении итераций, влияет на вид матрицы уравнений
и имеет тем самым решающее влияние на условия и
сходимость итерационного процесса.
7.1.3. РЕАЛИЗАЦИЯ ЧИСЛЕННОЙ
МОДЕЛИ В ЭЛЕКТРОННЫХ
ВЫЧИСЛИТЕЛЬНЫХ МАШИНАХ
Численный метод еще не является
программируемым алгоритмам, который состоит из
отдельных операций, протекающих в однозначной
последовательности, обладает определенным началом, а
также достижимым после конечного числа шагов
концом и, следовательно, в принципе может быть
реализован машиной.
7.1.3.1. Критерии для выбора метода. Для
решения поставленной задачи имеется, как правило,
целый ряд методов.
Выбор определенного метода численного
решения задачи и его окончательное преобразование в
программируемый алгоритм всегда представляют
попытку оптимизации, причем известные исходные
положения V( и добавочные требования F,
выступают как дополнительные условия, важнейшими
из которых являются следующие:
Исходная информация:
Vx — постановка задачи и общие
предположения о решении;
V2 — дополнительная информация об исходных
данных (например, числовая область, специальный
тип матрицы, вид числового материала и др.);
К3 - общая структура машины (например,
емкость памяти, время обращения, арифметическое
устройство, стандартные функции, язык
программирования и др.);
Уд. — представление чисел, арифметика,
округление, точность специальных операций;
и т. д.
Требования:
Fj — специальное требование к выходным
данным (выводу) (например, целочисленные решения,
требование точности, выдача промежуточных
результатов, графическое изображение и др.);
F2 — степень универсальности (должна ли
решаться единичная задача, или требуется
универсальное программное обеспечение относительно
допустимого набора входных данных);
F3 - минимизация стоимости (времени счета);
F4 — ограничения памяти.
Эти условия частично противоречат друг другу,
и поэтому при попытке их удовлетворения
стараются добиваться определенного оптимума. Для
этого используют эмпирические правила.
Основной принцип выбора метода состоит в
следующем принципе непосредственного
приложения: нужно выбирать по возможности метод,
который решает именно поставленную задачу, а
не ведет к решению побочно через некоторые
подзадачи. Классический пример: собственные
значения не вычисляются как корни
характеристического многочлена (см. 7.1.2.2).
«Математически элегантные» решения зачастую
являются непросматриваемыми относительно
распространения погрешностей и устойчивости и
неблагоприятными численно.
- Теоретическая сходимость при численной
реализации не является гарантией
вычислительной сходимости. С другой стороны, теоретически
расходящиеся методы могут быть численно
пригодны.
— Дополнительная информация о вводе,
промежуточных результатах или выводе должна быть
по возможности использована полностью, чтобы
способствовать уменьшению погрешностей
(например, симметрия, порядок величин, знаки,
нули и т. д.).
Важнейшими причинами чрезмерного
накопления погрешностей являются частое использование
разностей (что приводит к потере значащих цифр)
и деления на числа неизвестного порядка величины
(что ведет к переполнению разрядной сетки); этого
следует избегать искусной организацией программы.
7.1.3.2. Методы управления. Каждый
практически использующийся алгоритм не устанавливает
однозначно последовательность выполняемых
операций заранее для любого набора исходных данных.
Фактический ход процесса определяется
параметрами управления Х„, значения которых вычисляются
в ходе реализации. В качестве параметров
управления выступают и промежуточные результаты, и
некоторые специальные величины (например,
нормы векторов или матриц, порядки величин,
число шагов, адреса ячеек памяти, объем памяти
и т. п.). Результат анализа величин Х„ и управляет
процессом.
Таблица 7.17
Таблица важнейших контрольных вопросов при анализе Хп
Контрольные вопросы
Хп<а1 (а — заданное число)
Хп = а1
Хп< Ап? (Ап — вычисленная константа)
ХП<ХП_Х1
Вычислительное время > Т (Т задано)
Замечания
нуждается в априорной оценке для определения а. Если а = е при управлении
обрывом итераций, то е не может быть выбрано произвольно малым, иначе
ошибка округления может исказить обрыв или совсем ему помешать
осторожно! При образовании разности существует опасность потери точности
контроль применять только при целочисленных переменных!
Ап определяется апостериорно
применяется для проверки теоретической монотонности параметра
Обеспечивает аварийный останов при ненаступлении конца циклического
процесса (например, при отсутствии сходимости итерации)
ВЫЧИСЛЕНИЕ ФУНКЦИЙ
517
7.1.3.3. Вычисление функций. Арифметическое
устройство цифровой вычислительной машины,
как правило, в состоянии выполнить лишь четыре
основных арифметических действия и элементарные
логические операции, а в особых случаях также и
определенные специальные операции, как, например,
вычисление скалярного произведения или
квадратного корня. Значения элементарных функций,
максимум или минимум п чисел, сумма, целая
часть или знак числа и т. п. определяются при
помощи универсальных подпрограмм (стандартные
функции).
Главные методы вычисления
функций.
1) Многочлен — схема Горн ера.
Действительный многочлен
Р„ (х) = а0 + «I* + ... + а„хп
характеризуется в ЭВМ вектором (а0, аи ..., ап; п).
Полная схема Горнера содержит все операции,
выполняемые при вычислений значения многочлена
и его производных при заданном значении
аргумента х = х0:
а<0)
a[l) flilA а<Ц ... а\" '<#>
Общее правил о: a[j) = а% 1) +
j = 1, 2,..., п + 1; к = п, п - 1, ...J - 1
j = 1,2,..., и+ 1;
к = и, п - 1, ...,0.
Пример 25. х0 = — 1,
2
2
2
1
-2
-1
-2
-3
-2
0
1
1
3
4
5
-1 1
-1 2
-2[3|
-4
ы
Частные случаи.
а) Выделение линейного множителя:
Рп(х): (х - х0) ¦-= а{пихп~ 1 + а(п1\ хп~ 2 + ...
Пример 26.
Bх4 + х3 - х + 1): (х + 1) = 2х3 - х2 + х - 2 +
х+ Г
б) Значение функции в точке х = х0'.
рпЫ = 41}; 2(-1L + (-1K - (-1) + 1 = з.
в) Значения производных в точке х = x'q:
г) Разложение Тейлора в точке х
Рп(х) = а@1) + а\2)(х -
Пример 27.
2х4 + х3 - х +1 - 3 - 6(х + 1) + 9(х + IJ -
-7(х +
- хо)п.
2(х+ IL.
2) Разложение в ряд. Разложения в ряд
для представления констант или функций
являются общеизвестными (см. 3.1.14.2 и 3.1.14.5).
Вопрос о сходимости рядов с числовой точки зрения
имеет второстепенное значение. Разложение в ряд
является численно пригодным, если ошибка обрыва
при достаточно малом числе членов является
настолько малой, что численный результат в
машинном представлении оказывается точным
(при этом сам ряд может даже расходиться!).
Требуемая здесь универсальность представления
означает, что для всей области определения
представляемой функции значения функции должны
быть представлены с машинной точностью. Этого
достигают при помощи разложения в единичных
случаях.
К быстро сходящимся рядам относятся
разложения Тейлора для ех, sin x, cos x, sh x и др.
Рассмотрим, например, разложение для sinx:
sinx= f (-l)Jx2j + 1/Bj + l)L
j=0
В этом случае ряд знакопеременный, и поэтому
ошибка обрыва Rn(x) по величине не больше,
чем первое отброшенное слагаемое. Для того
чтобы вычислить у — sin х для всех х с требуемой
точностью, достаточно в силу периодичности и
монотонности функции на отрезке 0 < х ^ л/2
оценить ошибку обрыва только при х = л/2:
\R2J(n/2)\^(n/2Jj+l/Bj+ 1)!; если требуется
вычислить sin х с точностью до восьмого знака, то
нужно взять ; = 7, так как (л/2I5/15! < 8 • 10~10.
Внимание] Оценка ошибки, согласно теореме
о знакопеременных рядах, может оказаться
численно неправильной, так как ошибки округления
ведут себя не знакопеременно!
Ускорение сходимости (примеры).
1) Преобразование Эйлера. Используя
операторную формулу (см. 7.1.2.6.1)
518
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
получим
Уо - У1 + Уг ~ Уг + •••
Пример 29.
Рассмотрим в качестве примера один из способов
вычисления я. Из разложения arctgx = х - — х3 + ...
следует я/4 « arctg 1 ш 1 - 1/3 + 1/5 - 1/7 + ... Этот ряд
сходится очень медленно (для точности до четвертого знака
требуется теоретически около 10000 членов; практически
ошибки округления при этом уже испортят результат!).
При применении вышеупомянутого преобразования (после
отделения ведущих членов) нужный результат получают
значительно быстрей:
1 - 1/3 + 1/5 - ... - 1/19 - 0,76046.
1/21
1/23
1/25
1/27
1//29
Ук
0,04762
0,04348
0,04000
0,03704
0,03448
А?
-414
-348
-296
-256
66
52
40
» «г
-14
2
-12
1/21 - 1/23 + 1/25 - 1/27 + 1/29 «
« 0,02381 + 0,00104 + 0,00008 + 0,00001 - 0,02494,
я/4 - 0,76046 + 0,02494 - 0,7854.
специальных
2) Использование
свойств.
я „ 1 1
а) Теоремы сложения: — = 2 arctg h arctg — +
4 5 7
+ 2 arctg—.
о
б) Специальные преобразования: посредством
соотношения A 4- х)/A — х) = р2/(р2 — 1) из
формулы
1 +х
1,
— In
2 1-х
1
1
= х + —¦ хл + — хэ + ...
получаем, что
TLV-1 3Bp2-lK
Если р > 2 — простое число, то (р + 1) четно и
lnp является суммой логарифмов целых чисел,
меньших р, и быстро сходящегося ряда.
Пример
3) Метод выделения. Находим разложение
данного, медленно сходящегося ряда по схеме:
(медленно сходящийся} _
\ Ряд )~
_ (ряд с известной} (быстро сходящийся\
~ у суммой J у ряд )'
7.1.4. НОМОГРАФИЯ
И ЛОГАРИФМИЧЕСКАЯ ЛИНЕЙКА
Повсюду там, где физико-технические
параметры выступают в многообразных связях и
зависимостях и где из числовых значений
некоторых величин должны быть быстро определены
одна или несколько других величин без
предъявления слишком высоких требований к точности,
используются номографические вспомогательные
средства, к которым в первую очередь можно
отнести широко используемое вычислительное
устройство — счетную линейку.
7.1.4.1. Соотношения между двумя
переменными - функциональные шкалы. Пусть на отрезке
MN установлена начальная точка А, из которой
вдоль MN в определенном направлении
откладывается единичный отрезок АЕ = ех. Пусть
у = /(х) для а < х ^Ь является монотонной
функцией. Если из точки А откладывают
ориентированный отрезок тх = exf(x) с конечной точкой
Рх (индекс должен напоминать обозначение
независимого переменного), то получают взаимно
однозначное и определенное данной функцией
/(х) соответствие между числами х и точками Рх
носителя шкалы MN.
Если у точки Рх для подходящим образом
выбранной
аргументов
равноотстоящей последовательности
= xt = а + ih
помещают отметку аргумента xh то получают
Рис. 7.7
шкалу функции, или функциональную шкалу
(рис. 7.7).
По определению к А и Е соответственно
относят значения аргумента х„ и хе, для которых
/(х„) = 0 и f(xe) = 1. Можно разбить шкалу на
части, вдоль которых выбираются по мере
надобности различные значения шага аргумента.
Пример 30./(х)-ха, 0<х<6 (рис. 7.8).
01 2 3 4 5 6
Mil | | |
АЕ Ря
Рис 7.8
При применении функциональных шкал для
оси х кривые, являющиеся графиками данных
функций, спрямляются (рис. 7.9).
ЛОГАРИФМИЧЕСКАЯ (СЧЕТНАЯ) ЛИНЕЙКА
519
1 2 3 4 5 б X
У
№
14
12
10
8
6
2
0
1
2
Ц=Х2
3 х
Рис. 7.9
Логарифмическая (счетная) линейка (рис. 7.12).
Шкалы A, R, С размещены на движке и, таким
образом, подвижны относительно других шкал.
Установление соответствия между делениями
различных шкал становится возможным, даже когда
применяемые шкалы не лежат в непосредственной
близости, благодаря бегунку, расположенному
подвижно относительно всех шкал.
П р и м с р 32. Что можно вычислить с тремя заданными
шкалами установкой движка?
(D) - (С) - (В) Llgx + L\gy = у lgz,
7.1.4.2. Логарифмическая (счетная) линейка.
Если расположить три шкалы функций
относительно друг друга так, чтобы одна из них была
смещена относительно двух других, то сложение
ту
Рис. 7.10
отрезков будет реализовывать определенное
функциональное соотношение между тремя
переменными (рис. 7.10):
егк (z) = exf(x) + eyg (у),
h (z) = 5l/(x) + ^-
ez ez
h (z) = af(x) + bg (y).
Последнее соотношение называется ключевым
уравнением.
Каждое уравнение F (х, у, z) = 0, которое может
быть приведено к такому виду (а, Ъ —
действительные числа;/(х) и g(у) - функции от х,
соответственно у), реализуется на соответствующей
счетной линейке.
Пример 31. Счетная линейка для расчета полного
сопротивления двух параллельно расположенных
проводников (рис. 7.11).
2 1 1/2 t/3
t-
2 1
1/4 1/5 1-1+
—J ¦— Г*,
1/3 t/4 Rt
??."!•
?.
10
Рис. 7.11
100
В^-
to
~1оое=
bgx
10
100
r!°
e=L/2
&L
10
10
Li-
0,5
e=L Цх
Цх
e=L х
-Н
Рис. 7.12
(A)-(L)-(R) ylgx
lg j/x + .y= - lg
и т. д.
И без того большое многообразие возможностей
может быть еще значительно увеличено, если
учитывать многократные перемещения. Это
обстоятельство и простота употребления объясняют
большое распространение счетной линейки.
7.1.4.3. Номограммы точек на прямых и сетчатые
номограммы. Для представления функции z = /(x, у)
номографическим способом в плоскости без
вспомогательных технических средств имеются
две возможности.
1) Номограммы из выравненных
точек. Точкам трех несущих кривых ставят в
соответствие три переменные х, у и z.
Значения переменных х, у и z считаются
соответствующими, если отвечающие им точки на
носителях Рх, Ру и Р, расположены на прямой (рис. 7.13).
X
Рис. 7.13
a b
Рис. 7.14
Специальному расположению носителей всегда
отвечает соответствующая форма соотношения
F (х, у, z) - 0, представляемая номограммой. Это
соотношение называется ключевым уравнением.
Главные формы номограмм из выравненных
точек с прямолинейными носителями:
а) (т2 -тх):а
Ътг — Ътх = ату — ams, mz =
(ту — mz):b (рис. 7.14),
ату + Ътх
а + Ъ
520
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
ezh (z) =
a + b
еуд (у)
a + b
exf(x),
a + b-
a + b'
(Эта номограмма является, таким образом,
практически эквивалентой логарифмической
линейке.)
Т.
>s?
Рис. 7.15
б) ту: тх = (pes — mz): m, (рис. 7.15),
pez - h (z) ez ^ eyg (y) _p
ezh(z) exf(xY h(z) exf(Xy
— mxmy = — mxmz sin a + — mymz sin |
(рис. 7.16),
1 sin a sin j
(
mz
1
h(z)
my
с sin a
g(y)
mx
dsinfi
-
ч
ч
ч
ч
ч
4
4
1 II 1 1 rrJ
4
4
4
ч
Рис. 7.16
2) Сетчатые номограммы. Пусть на
плоскости в декартовой системе координат (и, v)
заданы три семейства кривых с параметрами
семейств х, у, z. Если кривые семейств,
соответствующие значениям х, у и z, пересекаются в одной
точке, то эти значения параметров в силу
соотношения F (х, у, z) = 0 рассматриваются как
соответствующие друг другу.
Здесь каждой форме — сетчатой номограмме —
соответствует определенное ключевое уравнение.
Примеры с двумя осепараллельными
семействами :
а) my:mz + mx: mzctga = 1 (рис. 7.17),
my + mx tg a = mz,
df(x)tgct.\
\ \
\
v
\\
\
\
N
\
k 2
\^
У
\
Рис. 7 17
(Таким образом, этот вид номограммы также
эквивалентен счетной линейке.)
У
Рис. 7.18
б) mz:mx = g(y) (рис. 7.18),
7.1.5. ОБРАБОТКА ЭМПИРИЧЕСКОГО
ЧИСЛОВОГО МАТЕРИАЛА
Пример 33. При постоянном напряжении 1 В в
зависимости от повышения сопротивления АЛ от Ro = 1 Ом
измеряется сила тока /:
АЛ
0 0,2 0,5 1,0 1,5 2,0 2,5 3,0 3,5
1 0,833 0,667 0,540 0,400 0,333 0,286 0,250 0,222
Какой вид имеет по возможности простая
функция / = / (ЛЯ), наилучшим образом описывающая
эгу зависимость?
Так как числа как измеренные значения всегда
содержат случайные погрешности, то нельзя
ожидать, что интерполирующая функция (см. 7.1.2.6.1)
решает задачу наилучшим образом! Более того,
желательно провести по измеренным точкам такую
кривую, чтобы некоторая заданная мера для
отклонений оказалась минимальной.
Последняя задача является основной задачей
выравнивания {сглаживания) результатов
измерений — вывода эмпирических формул.
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
521
Пусть задано множество F(at, а2, ..., ап)
функций/(х; ах, ..., а„) и множество пар
действительных чисел (хь yt)fLi, N > п. Ищется такая функция
/(х; аи ..., an)eF, для которой
для всех /е F. Здесь р является некоторой
известной мерой отклонений
и тем самым описывает принцип (критерий)
выравнивания.
Внимание! Мы занимаемся только решением
этой задачи. Обоснование применения того или
иного критерия выравнивания дается
статистикой (см. 5.2.2.2).
7.1.5.1. Метод наименьших квадратов. Этот
принцип выравнивания был разработан
Гауссом и применялся с большим успехом в
обыденных и астрономических измерениях. Критерий
выравнивания имеет вид
N
Если погрешности et подчиняются нормальному
распределению, то этот критерий может
рассматриваться как статистический (принцип
максимального правдоподобия; см. 5.2.2).
Для простоты будем считать, что параметры
at (i — 1, 2,..., п) входят в / линейно, т. е.
/(х; аи а2, ..., а„) =
= *i/i М + «ifг (х) + ... + ajn (x).
Тогда
=1
необходимым условием экстремума р являются
равенства
п N N
/c=l /=1 i
(J = I-.я).
При использовании способа Гаусса записи
суммирования
N
I /M = [/(*)]
i=l
эти нормальные уравнения принимают вид
I ** [Л (x)fj М] = [yfj (*Н (/ = 1, 2,..., п).
Частный случай fk(x) = х* (к = 1, 2,..., п)
приводит к сглаживающему многочлену, и
нормальные уравнения принимают вид
t а.1У+'-2:] = [ух'-1] о = 1,2,...,«).
fc=l
На практике используют минимальное,
насколько возможно, число параметров.
Для этого сначала визуально проверяют, лежат
ли точки измерения, например, вблизи функции —
константы, прямой у = ах + Ь, параболы и т. д.,
и в соответствии с этим используют то или иное
предположение.
7.1.5.1.1. Выравнивание
непосредственных наблюдений. Если известно, что при
измерении yh i = 1, ..., N, речь идет о значениях
теоретически постоянной величины; или из
графического изображения вытекает соответствующее
предположение, то значение этой константы
может быть приблизительно определено путем
выравнивания значений измерений. Эта
постоянная у называется средним значением измерений.
Согласно 7.1.5.1 получаем единственное
нормальное уравнение
N
N
Видно, что среднее арифметическое наблюдений
какой-либо величины выравнивает эту величину
согласно методу наименьших квадратов.
Если vt = у - у{ обозначает случайную
погрешность, то [vv~\ принимает минимальное значение для
у= тгЫ и Ы = о.
N
,1/ м
1~ |/ N-1
Величину т = |/ ^ Ji называют средней
грешностью отдельного yt; отношение ту = m/yN
называется средней погрешностью среднего и
применяется в записи результата измерений в
виде у = у ± ту.
7.1.5.1.2. Выравнивание прямыми у =
= а + Ьх. Необходимым и достаточным условием
того, чтобы точки измерения МДхь yt) лежали на
прямой, является пропорциональность первых
разностей х и у, т. е. Ад'./Ах,- = const.
Если это соотношение приближенно
выполняется, то прямую у = а + Ьх можно
рассматривать как кривую выравнивания.
Коэффициенты прямой удовлетворяют,
согласно 7.1.5.1, двум нормальным уравнениям:
aN + b[x-] = [yl
откуда
Ы [*2] -
х]-, ь=м1ху^-1у^х
(Правило Крамера, см. 2.4.4.3.3.)
Пример 34.
X
0,5
1,0
2,0
2,5
3,0
У
0,62
1,64
3,70 с
5,02
5,74
Ну
1,02
2,06
1,32
0,72
Ау/Ах
2,04
2,06
2М_
1,44
522
ЭЛЕМЕНТЫ ЧИСЛЕННЫХ МЕТОДОВ
Четвертое значение измерения явно выделяется из
рамок кажущейся линейной зависимости, что указывает
либо на закономерное дополнительное влияние, либо на
побочную ошибку измерения. Если с уверенностью можно
сказать, что имеет место последнее, то это значение
опускают, в противном случае оно должно учитываться.
Выравнивание при помощи прямой дает следующий
результат: а = -0,409, Ь - 2,053; следовательно, у *
= 2,053х - 0,409.
Линеаризация. Если данные измерения
приблизительно удовлетворяют уравнению вида
то может быть построена линейная связь путем
преобразования X = /(х), Y- д(у) и, следовательно,
может иметь место выравнивание (следует
сравнить также с процессом спрямления, см. 7.1.4.1).
Пример 35 (см. пример 33). Если точки измерения
нанести на график, то получают гиперболическую кривую,
и можно предположить, что верно соотношение у = 1Да + Ьх).
Положив Х = хи Y = 1/у, получим линеаризованную форму
7.1.5.1.3. Параболическое
выравнивание
у — ах2 + Ьх + с.
Характеристическая величина:
Const,
т. е. вторые разделенные разности должны быть
постоянными.
Нормальные уравнения:
cN + Ь [х] + а [х2] = [у],
с[х] + Ь[х2] + а[х3] =[ху1
с [х2] + Ъ [х3] + а [х4] = [х2у\
Пример 36. У-у-68.
X
-2
0
3
4
б
9
У
35
50
68
70
76
84
Y
-33
-18
0
2
8
16
ДУ
15
18
2
б
8
ДУ/Дх
7,5
6
2
3
8/3
Д (ДУ/Дх):
'(xi+2-xj)
-0,3
— 1
-0,3
-0,06
При таком поведении вторых разностей параболическое
выравнивание еще может быть обосновано. Система
имеет вид
6с + 20Ь+146а«-25,
20с + 146Ь + 1028а = 266,
146с + 1028Ь + 8210а » 1484.
Решение. У = -18,4 + 6,5х - 0,30х2,
у ш 49,6 + 6,5х - 0,30х2.
7.1.5.2. Другие способы вырав
1) Метод выбранных точек. Сначала
точки измерения изображаются графически и
визуально определяется подходящая
эмпирическая формула:
y=f(xt; au ..., an)eF(au ..., а„).
Для вычисления параметров проводится
гладкая кривая Г, которая «хорошо» подходит к
точкам Мj, причем так, чтобы проявлялись
качественные признаки графического представления
функции из F.
Тогда на Г выбирается п точек Nj (/' = 1, 2,..., и.)
и из системы уравнений
а2,
/ = 1, 2,..., п)
вычисляются параметры аи а2, ..., а„ функции
Хотя метод и нагляден, но он очень груб и никоим
образом не учитывает статистического
распределения погрешностей (т. е. не может быть
статистически обоснован).
2) При приближении по методу средних
точки измерения Mt (i = 1, ..., N) разбиваются
на и равных или почти равных групп
Для определения параметров требуют, чтобы
i j
EJ = Z eit = Z (/(X»V fli» a2, -.., an) ~ У1) = 0
для / = 1, 2, ..., и.
Пример 37 (ср. пример 36). Параболическое
выравнивание:
/(х, а, Ь, с) « ах2 + Ьх + с.
X
-2
0
3
4
6
9
У
35
50
68
70
76
84
Х2
4
0
9
16
36
81
е
4а - 2Ь + с - 35
с-50
9а + ЪЬ -1- с - 68
16а + АЬ + с - 70
36а + 6Ь + с - 76
81а + 9* + с-84
Щ
М2
Щ
м4
щ
Группы^ ^ 1 - {Ми
Система уравнений:
13а + Ь + с - 153,
16а + 4Ь + с - 70,
117а + 15Ь + 2с- 160.
М3}; Лгш{МА)-1 Мъ
Решение:
/- 50,1 + 6,0х - 0Д5х2
(см. 7.1.5.1.3).
Эмпирические формулы, конечно, еще не
являются законами, но их получение может быть
важной предварительной ступенью для открытия
теоретически обоснованных функциональных
соотношений между физическими величинами. Почти
классическим примером этого является открытие
закона излучения Планка на основе построения
трех эмпирических формул.
ВВОДНЫЕ ЗАМЕЧАНИЯ
523
7.2. ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
7.2.1. ЭЛЕКТРОННЫЕ
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ (ЭВМ)
7.2.1.1. Вводные замечания. Созданные за
несколько последних десятилетий электронные
вычислительные машины получили в настоящее
время широкое распространение и используются
в самых различных областях для обработки
информации. Сюда относятся: разнообразные
вычислительные работы, как научно-технического, так и
экономического характера;
информационно-поисковые работы, связанные с организацией хранения
больших объемов информации и поиска в них;
наконец, работы по автоматическому управлению,
позволяющие принимать управляющие решения
по постоянно поступающим потокам информации.
В данном разделе даются вкратце некоторые
общие сведения о работе ЭВМ и связанные с
этим понятия.
Всякая ЭВМ имеет в своем составе следующие
основные части (см. схему):
Основная
память
Центральный
процессор
Устройство
управления
1) устройства ввода и вывода (внешние
устройства), обеспечивающие связь ЭВМ с внешней
средой;
2) запоминающие устройства {накопители, или
память), позволяющие хранить исходную
информацию, промежуточные и окончательные
результаты;
3) процессоры, осуществляющие элементарные
операции переработки информации;
4) устройства управления, контролирующие
процесс обработки информации;
5) операционную систему — совокупность
программ, обеспечивающих взаимодействие
отдельных частей ЭВМ в процессе ее работы.
7.2.1.2. Представление информации и память
ЭВМ. Любая информация в ЭВМ представляется
в закодированном виде и изображается
совокупностью битов — элементов, могущих принимать
только одно из двух значений — 0 или 1. Наиболее
употребительные виды информации — символьная
и числовая. Символьная состоит из символов, набор
которых образует алфавит данной ЭВМ. Каждый
символ кодируется определенной комбинацией
фиксированного числа битов, образующих байт.
Наиболее употребительная длина байта — 8 или
6 битов.
Числа, вводимые в ЭВМ (или выводимые из
ЭВМ), обычно записываются в десятичной системе
счисления со знаком « + » или « —» и с
использованием точки для отделения целой части от
дробной. Кроме того, для расширения диапазона
допустимых чисел и удобства записи разрешается
добавление множителя вида 10-", где п —
натуральное число. Такой множитель записывается
определенным условным образом, чаще всего в
виде Е ± п. Так, например, 0,000045 можно
записать в виде 45Е — 6 или 4.5Е — 5. Записанные таким
образом числа могут быть закодированы, так же
как и другая символьная информация. Необходимые
для этого символы всегда входят в алфавит.
Однако внутри ЭВМ для выполнения операций,
а также большею частью и для хранения в памяти
числа записываются в двоичной системе счисления,
причем на каждое число отводится одинаковое
количество битов, образующих машинное слово*).
Употребительны две внутренние формы записи
числа — с фиксированной или плавающей точкой.
При фиксированной точке каждый бит в машинном
слове соответствует определенному двоичному
разряду, т. е. его значение @ или 1) умножается
на определенную степень числа 2. Чаще всего
применяется система записи, в которой старший
разряд соответствует (— 1)-й степени числа 2, т. е.
все изображаемые числа меньше 1, или такая, в
которой младший разряд соответствует 0-й
степени числа 2, т. е. все изображаемые числа — целые.
При плавающей точке числа представляются
в виде та?, где т — мантисса (число, записываемое
с фиксированной точкой), а — основание счисления
B, 10, 16**)), р — целое число со знаком — порядок
числа. В машинном слове содержатся, занимая
определенные биты, мантисса и порядок со своими
знаками.
Машинное слово содержит целое число байтов.
Вводимая в ЭВМ информация размещается в
памяти ЭВМ. Память состоит из элементов,
которые могут иметь два физических состояния и
способны поэтому запоминать значения битов @ или
1), изображающих информацию. Совокупность
элементов, предназначенных для хранения одного
машинного слова, образует одну ячейку памяти. Все
ячейки памяти перенумерованы последовательно;
номер ячейки называется ее адресом***).
При работе ЭВМ происходит постоянный
обмен информацией между различными
устройствами, постоянная засылка и выборка содержимого
*) В некоторых ЭВМ используется двоично-десятичная
система, когда число представляется в десятичной системе,
а каждая десятичная цифра - в двоичной, занимая по 4 бита
в машинном слове.
**) Изображение числа в двоичной системе можно
рассматривать как запись в шестнадцатеричной системе,
объединяя каждые 4 бита в одну шестнадцатеричную цифру,
и наоборот.
***) В некоторых ЭВМ перенумерованы подряд
{адресуемы) все байты. В этом случае адресом ячейки является адрес
ее первого байта.
524
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
той или иной ячейки памяти. Время,
затрачиваемое на одно обращение к памяти, и объем памяти
являются основными факторами, определяющими
производительность ЭВМ. Повышение
быстродействия памяти вызывает, как правило, удорожание
ЭВМ. При необходимости иметь большой объем
памяти и для уменьшения стоимости часто памяти
ЭВМ придают иерархическую структуру, при
которой она состоит из нескольких уровней,
обладающих разным быстродействием. В процессе
работы информация по мере надобности может
пересылаться с одного уровня на другой. При этом
различают внутреннюю и внешнюю память.
Устройство управления имеет непосредственный доступ
(по адресу) к любой ячейке только внутренней
памяти. Информация, хранящаяся во внешней
памяти, может быть использована только после ее
пересылки во внутреннюю память. Обмен между
внутренней и внешней памятью осуществляется
только для группы ячеек, расположенных подряд
и образующих блок. Таким образом, во внешней
памяти адресуемыми элементами являются блоки.
Наиболее употребительна внешняя память на
магнитном слое, нанесенном на ленты, диски или
цилиндры (барабаны).
7.2.1.3. Каналы обмена. Ввод информации в ЭВМ
и вывод результатов ее обработки осуществляются
при помощи внешних устройств.
Предназначенная для ввода информация дблж-
на быть предварительно записана в
закодированной форме на каком-либо носителе, доступном для
восприятия внешними устройствами ЭВМ. Такими
носителями могут бьп ь бумажные перфоленты или
перфокарты, магнитные ленты или диски. Для
обмена информацией между внешними
устройствами и ЭВМ, а также для обмена между
внутренней и внешней памятью служат каналы обмена.
В процессе обмена через канал может
осуществляться простейшая переработка информации,
например ее перекодирование. Обмен с внешними
устройствами и внешней памятью происходит
более медленно, чем работает процессор ЭВМ,
поэтому обычно такой обмен совмещают с
работой процессора следующим образом. При
возникновении потребности в обмене у решаемой
задачи работа процессора прерывается и
включается соответствующий канал. Процессор может
выполнять в это время работу для какой-либо
другой задачи. Необходимо только, чтобы задачи
использовали различные области памяти и эти
области были защищены, т. е. никакая задача не
могла бы испортить данные или программы,
находящиеся в области, отведенной для другой
задачи. По окончании обмена вновь возникает
прерывание, и процессор может вернуться к
первоначальной задаче. Такой режим работы
называется мультипрограммным.
7.2.1.4. Программа. Для выполнения любой
задачи обработки информации вычислительного,
логического или другого характера должен быть
задан алгоритм обработки. Описание такого
алгоритма, предназначенное для восприятия его
машиной, называется программой.
Работа центрального процессора ЭВМ состоит
из последовательного выполнения различных
элементарных операций. Для каждой операции
исходными данными являются один или два операнда.
Для хранения операндов, их адресов и другой
вспомогательной информации используются
регистры — простейшие запоминающие устройства
объемом в одно машинное слово. Устройство,
в котором получается результат элементарной
операции, называется сумматором.
Для решения задачи на ЭВМ алгоритм решения
должен быть в конечном счете разбит на
элементарные операции. Описание одной элементарной
операции называется командой. Команда должна
содержать сведения о том, откуда взять операнды,
какие выполнить действия, куда послать результат.
Набор элементарных операций и способ их
описания образуют систему команд. В настоящее
время наиболее распространенной системой
команд является одноадресная, при которой команда
состоит из адресной части и кода операции. Одним
из операндов является содержимое сумматора,
адресная часть позволяет найти второй операнд
и (или) указывает, куда направить результат. Код
операции характеризует выполняемую операцию и
способ использования адресной части.
Адресная часть команды может иметь
различную структуру. Часто приходится выполнять одни
и те же команды, в которых адреса операндов
(или результатов) могут быть переменными. В
таких случаях выделяют постоянную и переменную
составляющие адреса; последнюю размещают в
каком-либо вспомогательном регистре. В команде
указываются постоянная составляющая и адрес
(номер) вспомогательного регистра. Иногда
применяется косвенная адресация, когда адрес операнда
образуется в какой-либо ячейке памяти,
определяемой адресной частью команды.
Наряду с простыми командами зачастую
используются команды более сложной структуры,
позволяющие описывать укрупненные операции,
например операции обмена. Такие команды обычно
называют макрокомандами. По существу,
макрокоманды заменяют некоторые определенные
последовательности элементарных команд.
Совокупность команд, описывающая весь
процесс решения задачи, образует объектную
(машинную) программу. Программа сама является одним
из видов исходной информации задачи и
размещается в памяти ЭВМ. В одном машинном слове
обычно размещается одна-две команды,
макрокоманды могут занимать более одного слова.
7.2.1.5. Программирование. Написание
алгоритма задачи в виде объектной программы является
сложной и трудоемкой работой, которую обычно
поручают самой ЭВМ. Исходными данными для
этой задачи является содержательное описание
алгоритма, называемое исходной программой. Для
того чтобы такое описание могло быть понято
машиной, оно должно быть написано на каком-
либо алгоритмическом языке. Существует большое
число алгоритмических языков, наиболее
распространенным из которых являются фортран, алгол-60,
кобол, PL-1.
Текст исходной программы на алгоритмическом
языке состоит из отдельных предложений,
называемых операторами. Операторы делятся на
исполняемые, которые описывают какие-либо действия,
выполняемые над данными, и неисполняемые,
которые содержат некоторую необходимую
информацию о данных и о выполнении программы.
ПРОГРАММИРОВАНИЕ
525
Конструкции каждого языка должны
удовлетворять определенным формальным требованиям,
совокупность которых определяет синтаксис языка.
Смысловое содержание языковых форм
описывает семантика языка. Совокупность языковых
средств, допустимых на данной ЭВМ, образует ее
систему программирования. Каждый
алгоритмический язык должен позволять описывать
соответствующие алгоритмы точно, полно и так,
чтобы это описание понималось однозначно.
Процесс написания исходной программы
(программирование) обычно состоит из нескольких
этапов. На первом этапе t рассматривается общая
структура алгоритма, он разбивается на составные
части и составляется грубое, неформальное
описание последовательности этих частей. Основными
структурами, при помощи которых может быть
построен любой алгоритм, являются:
1) последовательное выполнение (рис. 7.19);
2) повторение (цикл) (рис. 7.20 и 7.21);
Рис. 7.19 Рис. 7.20
Рис. 7.21
3) альтернатива (условное выполнение) (рис. 7.22
и 7.23);
Рис. 7.22
Рис. 7.23
4) ветвление*) (рис. 7.24).
На рис. 7.19 — 7.24 ромбики означают проверку
какого-либо условия (два выхода — «выполняется»
или «нет»), прямоугольники - элемент алгоритма.
Эти структуры могут использоваться рекурсивно.
*) Ветвление можно описать как последовательность
альтернатив, однако использование структуры ветвления
может заметно упростить программу
Рис. 7.24
Следующим этапом является детализация
элемента, выделенного на предыдущем этапе, и
рассмотрение его внутренней структуры и т. д. При
этом используются те же основные структуры.
Конечное описание (исходная программа) состоит
уже из элементарных операторов языка, полностью
формализовано и должно быть синтаксически
правильным.
В процессе программирования разрабатываются
и структуры данных, как исходных, так и
промежуточных и окончательных. При этом может
оказаться необходимым учитывать особенности
используемой ЭВМ, в первую очередь объем и
структуру памяти. За этим исключением, исходная
программа в основном не зависит от типа ЭВМ,
на которой реализован данный алгоритмический
язык.
На начальных этапах выявляется
целесообразность разбиения программы на модули, т. е. на
отдельные части, которые могут
программироваться независимо. Модульное программирование
особенно эффективно, когда приходится иметь дело
с несколькими тематически близкими программами,
имеющими общие части. Запрограммированные
заранее модули могут затем включаться в
различные программы. Передача информации от одного
модуля к другому выполняется обычно через
внешнюю память, хотя в различных языках
имеются и другие способы такой передачи.
Некоторые части программ, повторяющие один
и тот же алгоритм, удобно выделять в
подпрограммы. Подпрограммы программируются
независимо от основной программы и хранятся в ЭВМ
отдельно от нее. При возникновении в основной
программе потребности в алгоритме, выполняемом
подпрограммой, происходит вызов подпрограммы
и ее выполнение, после чего вновь продолжается
работа основной программы. При вызове
необходимая информация из основной программы может
передаваться в подпрограмму в виде параметров,
от которых зависит подпрограмма.
Процесс получения объектной программы из
исходной является одним из видов работ,
выполняемых ЭВМ. Программы, выполняющие такие
работы, называются компиляторами шги
трансляторами и являются составной частью общего
математического обеспечения ЭВМ.
Фактически трансляторы переводят исходную
программу не сразу в объектную программу, а в
некоторую промежуточную форму, написанную или
526
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
на языке ассемблера, или в виде объекта загрузки.
Оба этих языка близки к машинному языку команд,
однако в них вместо истинных адресов фигурируют
относительные, или символические, адреса, а также
содержится некоторая управляющая информация.
Окончательная объектная программа получается
после работы специальных программ — ассемблера
и загрузчика, составляющих часть монитора.
7.2.1.6. Управление ЭВМ. Работа ЭВМ
происходит в основном полностью автоматически.
Функции человека-оператора сводятся к начальному
пуску ЭВМ, к смене переменных внешних
источников информации - пакетов перфокарт,
магнитных лент и дисков - и к реакции на запросы ЭВМ
(главным образом о подготовке тех или иных
устройств) через пульт управления.
Наиболее употребительными системами
организации работы ЭВМ являются пакетная
обработка и разделение времени *). При пакетной обработке
в ЭВМ загружается несколько задач (пакет),
которые и выполняются последовательно или
параллельно в зависимости от наличия ресурсов. При
операциях обмена возникают прерывания,
позволяющие на время прекращения решения одной
задачи включать в решение другую.
При разделении времени несколько
пользователей связаны с ЭВМ через устройства ввода-
вывода {терминалы), поочередно подключаемые
автоматически к ЭВМ. Вводя информацию
(данные и программу) через терминал, пользователь
имеет возможность давать машине задания и
реагировать на ее ответы, осуществляя так
называемый диалоговый режим. Время работы
программы в среднем мало по сравнению со временем
обмена и временем реакции, поэтому ЭВМ
успевает обслужить несколько пользователей.
Помимо взаимодействия с внешней средой и
организации выполнения работ устройство
управления обеспечивает работу центрального
процессора, расшифровывая коды операции и адреса
в очередной команде и выбирая эту команду
в зависимости от сигналов, получаемых от
процессора. Все эти функции осуществляются как
соответствующими аппаратными средствами, так
и специальными программами, входящими в так
называемую операционную систему, составляющую
неотъемлемую часть ЭВМ.
7.2.1.7. Математическое (программное)
обеспечение. Совокупность программ, используемых при
работе ЭВМ, составляет ее математическое
обеспечение. Его обычно разделяют на специальное
математическое обеспечение, складывающееся из
программ пользователей, предназначенных для
решения тех или иных конкретных задач, и общее
математическое, в которое входят операционная
система, библиотека подпрограмм общего
назначения и ряд других программ, обеспечивающих
функционирование ЭВМ.
Операционную систему обычно делят на
супервизор и монитор**). Главной функцией супервизора
является управление задачами, состоящее в
основном в распределении ресурсов ЭВМ (куда отно-
*) Работа ЭВМ, входящих в АСУ (автоматические
системы управления), здесь не рассматривается.
¦*) Эти термины не всегда одинаково используются.
сятся прежде всего память и время центрального
процессора) между задачами в процессе их
выполнения — динамически. Монитор осуществляет
управляющие функции в пределах одной задачи,
обеспечивая компиляцию частей программы,
написанных на разных языках, их загрузку и
связь, взаимодействие задачи с внешней
памятью и т. п.
Составляя задание для ЭВМ, пользователь,
кроме программы решения своей задачи, должен
давать ряд указаний операционной системе
относительно требуемых ресурсов, используемых языков
программирования и т. п. Такие указания пишутся
на языке управления заданиями.
Важной частью общего математического
обеспечения является система управления данными,
рассматриваемая обычно как часть операционной
системы. При работе ЭВМ во внутренней и
внешней памяти хранится большое число наборов
данных, относящихся к различным задачам. В их число
входят и программы, по которым задачи
решаются. На языках программирования и языке
управления заданиями эти наборы делятся на смысловые
единицы (записи, файлы), идентифицированные
своими именами. В памяти ЭВМ наборы данных
размещаются на физических единицах (блоках),
характеризуемых адресами. Система управления
данными должна обеспечивать размещение
возникающих записей и файлов в свободных блоках
памяти и возможность их выборки по мере
надобности.
7.2.1.8. Выполнение работ на ЭВМ. Для
выполнения каких-либо работ на ЭВМ необходимо
прежде всего ознакомиться с возможностями
используемой ЭВМ. Определив общую схему
выполнения задачи и выходных данных, можно
составлять программу на каком-либо алгоритмическом
языке с учетом особенностей реализации языка на
данной машине.
Далее необходимо программу отладить, т. е.
устранить возможные ошибки, для чего задачу
решают на каких-либо вспомогательных данных
(тестах), таких, чтобы правильность результатов
можно было легко проверить.
Процесс отладки обычно распадается на две
стадии. Первая — выявление технических и
синтаксических ошибок (типа опечаток), вторая —
методическая отладка, когда ищутся ошибки алгоритма,
а также возможности его улучшения. Необходимо
иметь в виду, что в больших программах весьма
трудно обеспечить устранение в процессе отладки
всех ошибок, в связи с чем следует проводить
отладку небольших частей программы отдельно,
постепенно связывая их между собой.
После завершения отладки окончательный текст
фиксируется путем записи его во внешней памяти.
Если предстоит решать большое число вариантов
с различными данными по неизменной программе,
то для того, чтобы избежать повторной
трансляции, записывается объектная программа.
Если решение задачи занимает много времени,
необходимо в программе предусмотреть опорные
точки, т. е. запись во внешнюю память
промежуточных результатов. Такая запись должна
позволять возобновить решение задачи с
момента последней записи в случае сбоя в
работе ЭВМ.
ВЫЧИСЛИТЕЛЬНЫЕ ЭЛЕМЕНТЫ АНАЛОГОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЫ
527
7.2.2. АНАЛОГОВЫЕ
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
7.2.2.1. Принцип устройства аналоговой
вычислительной техники. Принцип устройства аналоговой
вычислительной техники основывается на
реализации математических моделей техническими
средствами, причем математические объекты
представляются в качестве измеряемых физических величин,
а математические операции реализуются в виде
соответствующих физических законов.
Существуют механические, пневматические,
гидравлические и электронные аналоговые
вычислительные машины.
Проводятся опыты с оптическими аналоговыми
вычислительными машинами (АВМ). Мы
ограничимся здесь электронными АВМ. В табл. 7.18
перечислены характерные отличия АВМ от
цифровых вычислительных машин.
этому вычислительный элемент может иметь три
положения:
1) «сброс», pr = L (т. е. приложено рг)\ в этом
положении выход у вычислительного элемента
равен входу у0 на клемме начального значения
со знаком « —»;
2) «вычисление», pr = ps = 0; интегратор
производит интегрирование;
3) «прерывание», ps = L; интегратор запоминает
значение напряжения на выходе, т. е. оно остается
в этом положении постоянным независимо от того,
что подается на вход.
В случае pr — ps = L интегратор находится
в положении «сброс» (преимущественное
включение).
Обычно интеграторы управляются
централизованно, т. е. в вычислительной машине
управляющие напряжения рг и ps включаются для этих
интеграторов одновременно. Отсчет времени начи-
Таблица 7.18
Признаки
Представление информации
Действия над информацией
Точность
Возможность применения
Программирование
Числовая область
Выдача результатов
Цифровая
Последовательность цифр
алгоритмы
теоретически не ограничена
универсальна
алгоритмы решения и
обработки
очень велика
цифровая таблица (таблица
знаков, текст) или кривые
Аналоговая
Значения физических
величин
выбранные
соответствующим образом физические
законы
ограничена принципиально
специальные задачи
уравнения задачи
мала
кривые, отдельные
результаты измерений, таблицы
Электронная аналоговая
Электрические потенциалы
законы теории электричества
0,2 — 2% на вычислительный
элемент
системы обыкновенных
дифференциальных уравнений
дифференциальные уравнения
для зависимых переменных
- 1 ^ у < 1
начерченные кривые, кривые
на осциллограммах, отдельные
результаты измерений, таблицы
7.2.2.2. Вычислительные элементы аналоговой
вычислительной машины. АВМ построены по
блочному принципу и содержат операционные
усилители, которые чаще всего конструируются
как сменные вставные блоки. Подключение
операционных усилителей в поле программирования
осуществляется посредством штеккеров и шнуров.
б вычислительных машинах, к которым
предъявляются более высокие требования, поле
программирования является сменным. После соединения
с входными цепями и цепями обратной связи
вычислительные усилители (усилитель постоянного
напряжения:
Ua= -sUe,
Ue — входное напряжение, Ua — выходное
напряжение, s > 105) становятся вычислительными
элементами, которые выполняют определенные
операции.
Важнейший вычислительный элемент
интегратор содержит, кроме того, еще два выключателя
(реле), которые приводятся в действие двумя
управляющими напряжениями pr, ps. Благодаря
нается {t = 0) в момент перехода из положения
«сброс» в положение «вычисление» и
заканчивается (t = te) в момент перехода из положения
«вычисление» в положение «прерывание» или
«сброс».
Переключение положений может
осуществляться с пульта управления при помощи часов
или другого датчика времени, а также по
программе.
Различают два рода работы:
1. Однократное вычисление: «сброс» —
«вычисление» - «прерывание».
2. Повторяющееся вычисление: постоянная
смена положений «сброс» и «вычисление»,
начинающаяся по стартовому сигналу, происходит до
сигнала остановки.
Кроме интеграторов, управляемых
централизованно, в больших вычислительных машинах
имеются свободно управляемые интеграторы, в которых
управляющие напряжения рг и ps могут быть
запрограммированы по отдельности. Таблица 7.19
дает обзор вычислительных элементов аналоговой
вычислительной машины.
528
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
Таблица 7.19.
Название
Символ
Функция
Замечания
Потенциометр:
заземлен
открыт
у = ах
у = х2+а(х{-х2)
а — действительное число, 0<а<1.
Регулировка потенциометра зависит
от последующего сопротивления
нагрузки
Сумматор
Инвертор
У = -
а/ (чаще всего целочисленны,
например, я/е{1, 10}) — постоянные
входные сопротивления
Центрально
управляемый интегратор
Свободно
управляемый интегратор
/ = - Ь Y,
i=l
У@)=-Уо
у' = -х
у@)--у0
У = —Уо ~b I E
a/, b (чаще всего целочисленны,
например а/, Ье{1, 10}) —
постоянные входные сопротивления, у0
постоянно. Часто встречающийся
случай•
0 < ti < t2 < te
(LnPH,<,,,
[О при t^tt;
fO при t < t2,
[L при t ^ t2
Мультипликатор
(параболический
умножитель)
С правильным знаком всегда
умножаются функции, которые подаются
на входы, обозначенные « + »
Генератор
функции
EZ>
/— непрерывная действительная
функция, кусочно линейная или
постоянная (аппроксимация с помощью
ломаной)
Компаратор
(реле с разностным
усилителем)
ix >z2: y = Xi
z, <z2: y = x2
zy = z2: неустойчиво
xx и х-, могут быть также
управляющими напряжениями
Открытый
усилитель
5 > 105, применение для особых
целей
Постоянные
функции
У= -1
Постоянные функции представлены
в виде клемм на поле
программирования Следует различать
напряжение вычисления +1 и
управляющее напряжение L
ПРИНЦИП ПРОГРАММИРОВАНИЯ
529
7.2.2.3. Принцип программирования при решении
систем обыкновенных дифференциальных уравнений.
В аналоговой вычислительной машине кусочно
непрерывные действительные функции переменного t
на сегменте 0 ^ t < te могут представляться (и быть
получены) в виде потенциалов, зависящих от
времени. При этом функции являются решениями
системы обыкновенных дифференциальных
уравнений с начальными условиями (задача Коши).
Дифференциальные уравнения программируются,
а начальные значения задаются как постоянные
функции. Мы пренебрегаем в этом разделе
технически обусловленными ограничениями
(ограничение сегментом [—1, 1], ограничение показаний
потенциометров 0 ^ а < 1) и рассматриваем
качественное программирование (составление плана
согласования).
План согласования для
обыкновенного дифференциального уравнения
в явной форме (см. 3.3.1.1). Рассмотрим в
качестве примера у"' = f(y, у', у", t), у@) = аи у' @) =
= 02, у" @) = аъ, где аи а2, а3 — положительные
действительные числа.
Первый шаг. Составление цепочки из трех
интегралов (соответственно порядку
дифференциального уравнения) (рис. 7.25); следует обратить
внимание на перемену знака при интегрировании
и перемену знака у задаваемых начальных
значений.
Второй шаг. Получение функции z = t в
качестве решения задачи z' = 1, z@) = 0.
Третий шаг. Получение f(y, y\ у", t) при
помощи вычислительных элементов
вычислительной машины. Запись результата у = у (/).
Пример 38. у" = - (а2 у, у @) = 0, / @) = - to, to > a
План согласования - рис. 7.26. (Выходы на записывающее
устройство и t не указаны. См. также пример 40.)
Пример 39. у\ = - ty\ + у2> у2 = - ухуг + ауе~аг1,
У\ @) = Уг @) - 0, у'2 @) = - а3, уз @) = аА, а( > 0; найти
решение при 0 < t < ге.
План согласования — рис. 7.27. Вспомогательную
функцию г2=*е~аг* получим как решение задачи о начальных
значениях z2 = - a2z, z2 @) = 1. В случае многоканального
записывающего устройства ух и у2 могут записываться
одновременно; в противном случае вычисления проводятся
дважды и уу и у2 записываются одно за другим.
Запись/бающее
устройшбо
(ордината)
Запись/бающее
устройшбо
(абсцисса)
Рис. 7.25
Рис. 7.26
Запись/бающее
устройстбо
(ордината)
Записывающее 4
устройство '
(абсцисса)
Рис 7 27
530
ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
7.2.2.4. Качественное программирование. На
выходах операционного усилителя могут получаться
только такие функции, значения которых лежат
между —1 и 1. Кроме того, в большинстве
случаев требуется отобразить отрезок 0 ^ t < te
независимой переменной задачи на временной
промежуток 0 < Т1^ Теу реализуемый в вычислительной
машине (и соответствующих устройствах вывода).
Это делается при помощи однородных линейных
преобразований.
1) Нормировка функций. Так как все
рассматриваемые функции кусочно непрерывны на
сегменте, то они ограничены. Поэтому для каждой
функции x(t), представимой в вычислительной машине,
существует верхняя граница ее значений;
обозначим ее через х*:
W (fe[(Ue]-V|x(t)|^x*).
При этом — 1 ^ х (t)/x* ^1 их (t)/x* представима.
Выходы инверторов и мультипликаторов не
нуждаются в нормировке, так как их нормировка
вытекает из нормировки на входах. Если в
качестве пределов выбрать верхние границы, то
получим оптимальное преобразование, при котором
усилители (возможно, за исключением
мультипликаторов) полностью пронормированы.
2) Преобразование независимого переменного.
При помощи преобразования T=Xt отрезок
0 ^ t ^ te отображается на отрезок 0 ^ Т ^ Те, где
Те = Xte. При этом нормированные функции задачи
(нормированные переменные задачи) становятся
машинными переменными:
x(t) = x(T/X)/x*.
Так как интегрирование в вычислительной машине
может происходить только по переменному Т
(действительное текущее время), то для
интегрирования получается следующее преобразование:
а = А/с: т = 0-*а = 0,
х = t -
dx = r
х(стЛ) 1
При X > 1 ,X < 1 и X = 1 говорят соответственно
о растягивании отрезка времени, сжатии и
программировании в истинном времени. При помощи
этих преобразований из плана согласования
получается нормированный план согласования, или схема
вычислений. Рис. 7.28 изображает переход от плана
согласования к нормированному плану согласова-
y=-sin cut
Рис. 7 29
Записывающее
устройство
[ордината)
Рис. 7 30
КАЧЕСТВЕННОЕ ПРОГРАММИРОВАНИЕ
531
ния в случае сумматора и интегратора согласно
уравнениям:
план согласования:
У= ~ Уо-
*i + a2x2)dx;
нормированный план согласования:
((
V У* )\xl
_ у0 Г /a.xf х, а2х? х2\
"~ J-* J \Ху* х, + by* xfj •
Пример 40. Нормировка плана согласования примера
38. В этом простом примере решение получается сразу:
у ш - sin tof и У ш - cocos cof, т. е. у* = 1 и у* « со.
Начальные значения нормированных функций: у@) = 0, У@)//* =
- - 1.
Если принять во внимание, что не обязательно
обе постоянные интеграторов а и Ъ выбирать
равными 1, то в качестве плана согласования
получается рис. 7.29. Мы видим, что схема на рис. 7.26
применима только при 0 < со < 1 (из-за
потенциометра начальных значений), в то время как
нормированный план согласования без больших затрат
при 0 < (й/(каЬ) <1 и при соответствующем выборе
а, Ь и X делает доступным гораздо большую
область по со. На выходе инвертора получают
функцию sin cot, а на выходе первого интегратора —
функцию cos Ш (схема генератора синусоидальных
колебаний). Схема оптимальна, все усилители
полностью промодулированы.
Пример 41. Нормировка плана согласования примера 39.
Нетрудно найти t* = t, и zf — 1. Остальные пределы
оцениваются. Подставляя оценочные значения, проводят
проверку. Если усилитель перемодулирует, то предел для выхода
усилителя выбран слишком малым; если модуляция
недостаточна, то предел выбран слишком большим. На рис. 7.30
показан нормированный план согласования.
СПИСОК ЛИТЕРАТУРЫ
1.1. Общие руководства, справочники и таблицы
1 1 Математическая энциклопедия.—М.- Советская
энциклопедия, т 1-5, 1977-1985.
1.2. Выгодский М. Я. Справочник по элементарной
математике.-М.: Наука, 1986.
1.3. Цыпкин А. Г. Справочник по математике для
средней школы.-М.: Наука, 1983
1.4. Корн Г, Корн Т. Справочник по математике для
работников и инженеров.—М • Наука, 1984.
1.5. Таблицы Барлоу.— М.: Наука, 1975
1.6. Хохлов А И Математические таблицы—М.* Наука,
1980.
1 7 Двайт Г. Б Таблицы интегралов и другие
математические формулы.— М : Наука, 1983.
1.8 Градштейн И. С, Рыжик И. М. Таблицы интегралов,
сумм, рядов и произведений.-М.: Наука, 1971.
1.9. Справочник по специальным функциям. — М : Наука,
1979
1.10. Янке Е., Эмде Ф, Лёш Ф. Специальные функции.—
М : Наука, 1977
111. Бейтмен Г., Эрдейн А. Таблицы интегральных
преобразований в двух томах. СМБ.- М.: Наука, 1969, 1970.
1 12. Бейтмен Г., Эрдейи А Высшие трансцендентные
функции в трех томах СМБ - М.: Наука, 1969, 1973, 1974.
1.13. Большее Л. Н., Смирнов Н В. Таблицы математической
статистики — М : Наука, 1983.
1.14. Саве лов А. А Плоские кривые.—М • Физматгиз, 1960.
2.2. Комбинаторика
2 1 Рыбников К А Введение в комбинаторный анализ —
М.- Изд-во МГУ, 1972
2.2. Ежов И И., Скороход А. В., Ядренко М И. Элементы
комбинаторики.-М.. Наука, 1977.
2 3. Кофман А. Введение в прикладную комбинаторику.—
М.. Наука, 1975
2.4 Сачков В Н. Комбинаторные методы дискретной
математики — М.. Наука, 1977.
2.4. Алгебра
2.5. Курош А Г. Курс высшей алгебры.- М • Наука, 1983
2 6 Кострикин А И. Введение в алгебру.— М.: Наука, 1977.
2.7 Ван дер Варден Б Алгебра - М.: Наука, 1979.
2.8. Мальцев А. И. Основы линейной алгебры.— М • Наука,
1975
2.9. Воеводин В В Линейная алгебра.-М.: Наука, 1981.
2 10 Воеводин В В Вычислительные основы линейной
алгебры - М : Наука, 1977
2.11. Ильин В А, Позняк Э Г Линейная алгебра-М..
Наука, 1978
2.12. Гельфанд И. М Лекции по линейной алгебре.—М."
Наука, 1971.
2.6. Геометрия
2 13 Погорелое А. В. Элементарная геометрия.— М.: Наука,
1977.
2 14. Понтрягин Л С Знакомство с высшей математикой.
Метод координат — М. Наука, 1977
2 15 Ефимов Н. В Краткий курс аналитической
геометрии.- М Наука, 1975
2.16 Погорелое А. В. Аналитическая геометрия.— М • Наука,
1978
2.17. Александров П. С. Курс аналитической- геометрии и
линейной алгебры — М.: Наука, 1979.
2.18. Волынский Б А. Сферическая тригонометрия.—М..
Наука, 1977
3.1. Дифференциальное и интегральное исчисления
3.1. Понтрягин Л. С Знакомство с высшей математикой
Анализ бесконечно малых — М.: Наука, 1980.
3 2. Никольский С М Курс математического анализа в
двух томах - М.: Наука, 1975.
3 3. Кудрявцев Л. Д Математический анализ в двух
томах.—М.: Высшая школа, 1980.
3 4 Ильин В А , Позняк Э. Г Основы математического
анализа в двух томах -М.: Наука, 1971, 1980.
3.5 Будак Б М , Фомин С. В Кратные интегралы и ряды.-
М.: Наука, 1967
3.6. Воробьев Н Н Теория рядов.-М.: Наука, 1979.
3 7. Колмогоров А Н, Фомин С В. Элементы теории
функций и функционального анализа.— М.. Наука, 1981.
3.8 Треногий В А. Функциональный анализ.-М.: Наука,
1980.
3.2. Вариационное исчисление и оптимальное управление
3 9. Гельфанд И. М., Фомин С. В. Вариационное
исчисление - М : Физматгиз, 1962.
3 10 Понтрягин Л. С, Болтянский В. Г, Гамкрелидзе Р В.,
Мищенко Е. Ф. Математическая теория оптимальных
процессов.—М.: Наука, 1983.
3.11. Алексеев В. М., Тихомиров В. М., Фомин С. В.
Оптимальное управление. — М.: Наука, 1979
3.12 Федоренко Р. П. Приближенное решение задач
оптимального управления. СМБ.-М.- Наука, 1978
3.3.1. Обыкновенные дифференциальные уравнения
3 13. Понтрягин Л. С. Обыкновенные дифференциальные
уравнения.-М.: Наука, 1982.
3.14 Петровский И. Г. Лекции по теории обыкновенных
дифференциальных уравнений - М . Наука, 1970.
3.15. Степанов В. В. Курс дифференциальных уравнений.—
М.. Наука, 1966.
3.16. Карташев А. П, Рождественский Б. Л.
Обыкновенные дифференциальные уравнения и основы
вариационного исчисления.—М.: Наука, 1980.
3.17. Камке Э Справочник по обыкновенным
дифференциальным уравнениям. — М : Наука, 1976.
3.18 Тихонов Н. И., Васильева А. Б., Свешников А. Г.
Обыкновенные дифференциальные уравнения.— М.:
Наука, 1980.
3.3.2. Дифференциальные уравнения в частных производных
3 19. Петровский И. Г. Лекции об уравнениях с частными
производными.-М.: Физматгиз, 1961.
3.20 Тихонов А. Н., Самарский А. А. Уравнения
математической физики — М.: Наука, 1972.
3.21 Бицадзе А. В Уравнения математической физики.-
М • Наука, 1976.
3 22 Владимиров В. С Уравнения математической физики. -
М.- Наука, 1976
3.23 Годунов С. К Уравнения математической физики.-
М.: Наука, 1971
ЛИТЕРАТУРА
533
3 24 Muxaii юв В П Дифференциальные уравнения в частных
производных — М Наука, 1983
3 25 Камке Э Справочник по дифференциальным
уравнениям в частных производных первого порядка — М
Наука, 1966
3.4. Комплексные числа. Функции комплексного переменного
3 26 Лаврентьев М А , Шабат Б В Методы теории
функций комплексного переменного. — М • Наука,
1973.
3 27 Маркушевич А И Краткий курс теории
аналитических функций — М Наука, 1978
3 28 Тихонов А Н , Свешников А Г Теория функций
комплексного переменного — М • Наука, 1979
3.29 Бицадзе А В Основы теории аналитических функций.—
М Наука, 1969.
3 30 Привалов И И. Введение в теорию функций
комплексного переменного.— М.: Наука, 1984.
3 31. Шабат Б. В Введение в комплексный анализ Ч. I, II —
М.. Наука, 1985
3 32 Сидоров Ю В, Федорюк М В, Шабунин М И
Лекции по теории функций комплексного
переменного - М : Наука, 1982.
4.1. Множества, отношения, отображения
4 1. Александров П С Введение в теорию множеств и
общую топологию — М Наука, 1977
4 2 Новиков П С Элементы математической логики. —
М Наука, 1973.
4 3 Яблонский С. В. Введение в дискретную математику. —
М Наука, 1986
4 4 Менде чьсон Э Введение в математическую логику —
М. Наука, 1984
4 5 Ершов Ю Л., Палютин Е. А Математическая
логика - М.- Наука, 1979
4.2. Векюрное исчисление
4 6 Кочин И Е Векторное исчисление и начала
тензорного исчисления - М Изд-во АН СССР, 1961
4 7 Лаптев Г Ф Элементы векторного исчисления.—М."
Наука, 1975
4.3. Дифференциальная геометрия
4 8 Погорелое А В Дифференциальная геометрия — М :
Наука, 1974
4-9 Дубровин Б А., Новиков С. П, Фоменко А Т.
Современная геометрия — М.: Наука, 1979
4.4. Ряды Фурье, интегралы Фурье
и преобразование Лапласа
4.10 Романовский П. И Ряды Фурье. Теория поля
Аналитические и специальные функции. Преобразование
Лапласа - М : Наука, 1980
4 11 Диткин В. А., Прудников А. П. Интегральные
преобразования и операционное исчисление. СМБ.—М.:
Наука, 1974
4 12 Брычков Ю. А , Прудников А П. Интегральные
преобразования обобщенных функций — М : Наука,
1977
4.13 Владимиров В С Обобщенные функции в
математической физике — М • Наука, 1979.
4 14 Никифоров А. Ф., Уваров В. Б Специальные функции
математической физики — М : Наука, 1984.
4 15 Арсенин В. Я. Методы математической физики и
специальные функции — М.. Наука, 1984.
4 16 Крылов В. И., Скобля Н. С Методы приближенного
преобразования Фурье и обращения преобразования
Лапласа.-М.: Наука, 1974
5. Теория вероятностей
и математическая статистика
5.1 Кошогоров А. Н. Основные понятия теории
вероятностей.- М Наука, 1974.
5.2. Прохоров Ю. В., Розанов Ю. А. Теория вероятностей.
СМБ -М • Наука, 1973.
5 3 Гнеденко Б. В, Хинчин А. Я. Элементарное введение
в теорию вероятностей.—М.: Наука, 1976.
5 4 Боровков А А Курс теории вероятностей.—М.: Наука,
1976.
5.5. Пугачев В. С. Теория вероятностей и математическая
статистика.-М.: Наука, 1979.
5 6 Ивашев-Мусатов О. С. Теория вероятностей и
математическая статистика.—М.: Наука, 1979.
6.1. Линейное программирование
6 1. Еремин И. И., Астафьев Н. Н. Введение в теорию
линейного и выпуклого программирования.— М.: Наука,
1976.
6.2 Карманов В Г. Математическое программирование.—
М.: Наука, 1986.
6 3. Моисеев Н. Н., Иванилов Ю. П., Столярова Е. М.
Методы оптимизации.-М.: Наука, 1978.
6.4. Иванилов Ю. П, Лотов А. В. Математические модели
в экономике.— М.: Наука, 1979.
7.1. Элементы численных методов
7.1 Фаддеев Д. К., Фаддеева В. Н. Вычислительные
методы линейной алгебры.— М.: Физматгиз, 1963.
7 2. Васильев Ф. П. Численные методы решения
экстремальных задач.-М.: Наука, 1980.
7.3 Бахвалов Н. С Численные методы (анализ, алгебра,
обыкновенные дифференциальные уравнения).— М.:
Наука, 1975.
7 4. Марчук Г. И. Методы вычислительной математики.—
М.: Наука, 1980.
7.5. Дьяченко В. Ф. Основные понятия вычислительной
математики.— М.: Наука, 1977.
7.6. Крылов В. И., Бобков В. В., Монастырский П. И.
Вычислительные методы в двух томах.—М.: Наука,
1976, 1977.
7.7. Никольский С. М. Квадратурные формулы.— М.: Наука,
1979
7 8 Самарский А. А. Теория разностных схем.- М.: Наука,
1977.
7.9 Тихонов А. Н., Арсенин В. Я. Методы решения
некорректных задач.—М.: Наука, 1979.
7.10. Самарский А. А., Николаев Е. С. Методы решения
сеточных уравнений.—М.: Наука, 1978.
7.11. Годунов С. К., Рябенький В. С. Разностные схемы.—
М : Наука, 1977.
7.12. Хованский Г. С. Основы номографии.- М.: Наука, 1976.
7.13. Панов Д Ю. Счетная линейка.-М.: Наука, 1982.
7.2. Вычислительная техника
7.14. Королев Л. П. Структуры ЭВМ и их математическое
обеспечение.-М.: Наука, 1978.
7 15. Карцев М. А. Архитектуры цифровых вычислительных
машин — М.: Наука, 1978.
7.16. Урмаев А. С. Основы моделирования на АВМ.-М.:
Наука, 1978.
7.17. Ершов А. П. Введение в теоретическое
программирование.-М.: Наука, 1975.
7 18. Любимский Э. 3., Мартынюк В. В., Трифонов Н. П.
Программирование. — М.: Наука, 1980.
7.19. Криницкий Н. А., Миронов Г. А., Фролов Г. Д.
Программирование и алгоритмические языки.— СКБ.—
М.: Наука, 1979.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютная величина числа 212
— сходимость несобственного
интеграла 250
ряда 276
Абсцисса 195, 197, 216
Автономная система 298
Адрес 523
Адресная часть 524
Аксиома Архимеда 211
— Дедекинда 211
— индукции 211
— непрерывности 211
Аксиомы действительных чисел 210
— порядка 211
— сложения 210
— теории вероятностей 442
— умножения 210
Алгебра 140, 385
— высказываний 376
Алгебраическая кривая 123, 409
Алгебраические функции 169-174,
разложение в ряд 87
— —, графики 113
Алгебраическое дополнение 157
— уравнение 145
высших степеней 148
— — квадратное 145
— — кубическое 146
линейное 145
— — 4-й степени 147
Алгоритм 490, 516
— Гаусса 159, 162
— Гаусса — Банашевича 492
— Евклида 141, 149
— обработки 524
— Ремеза 501
Алгоритмический язык 524
Аналитическая функция 282, 283, 365
Аналитическое продолжение 369, 371
Аналогии Непера 193
Антикоммутативность 388
Антирефлексивность 383
Антисимметричность 383
Апофема 187
Аппликата 197
Аппроксимация 499
Аргумент комплексного числа 358
— функции 216
Ареакосинус 181, график 122
Ареакотангенс 181, график 123
Ареасинус 181, график 122
Ареатангенс 181, график 122
Ареафункции 181
Арифметика интервалов 491
Арифметическая прогрессия 139
Арккосинус 178, график 119
Арккотангенс 178, график 119
Арксинус 178, график 118
Арктангенс 178, график 119.
Асимметричность 383
Асимптота 409
— вертикальная 409
— гиперболы 203
— горизонтальная 409
— наклонная 409
Асимптотическая точка 409
Ассемблер 526
Ассоциативная операция 385
Ассоциативность (сочетательность) 141,
151, 210
Ассоциативный закон 385
Астроида 262, 263
Аффинное пространство 199
Базис 153
— канонический 153
— ортонормированный 155
Базисное решение 469
Байт 523
Барицентрические координаты 194
Бесконечно большая 221
— малая 221
Бесконечное произведение 285
— — абсолютно сходящееся 286
— - неопределенно расходящееся 285
— - расходящееся 285
— — сходящееся 285
— —, частичное произведение 285
Бета-функция 260
Биекция 385
Биквадратное уравнение 148
Бинарное отношение 382
Бином дифференциальный 244
— Ньютона 135
Биномиальный закон распределения
444
— коэффициент 134
— ряд 87, 88
Бинормаль 411
Биссектриса 183, 191
Бит 523
Большой круг 189, 192
Бочка (круговая, параболическая) 189
Булева функция 377
Булево программирование 486
Булевы переменные 378
Быстро сходящийся ряд 517
Быстрое преобразование Фурье 424
Вариационная задача Больца 294
— — изопериметрическая 292
Лагранжа 294
Майера 294
Вариационные задачи в
параметрическом представлении 292
— — для нескольких функций 291
— — с высшими производными 291
Вариационный принцип 291
Вариация функции 222
полная 222
— функционала A-я, 2-я) 288
Вектор 151, 386
— бинормали 411
— геометрический 386
— главной нормали 411
—, длина (модуль, норма) 155, 386
— единичный 155, 386
— касательной 411
-, координаты (компоненты) 154, 387
— нормали 411, 413
— нулевой 152, 386
— противоположный 152
— свободный 386
— связанный 386
— скользящий 386
— управления 298
Векторная функция (вектор-функция)
390
— — линейная 402
Векторное подпространство 152
— поле 391
безвихревое 398, 401
консервативное (потенциальное)
395
— — плоское 391
соленоидальное 401
Векторное поле сферическое 392
— — цилиндрическое 392
— произведение 388
двойное 388
— пространство 151
бесконечномерное 154
— — гильбертово 156
— — действительное 151
— — евклидово 155
комплексное 151
— — конечномерное 154
— — нульмерное 154
Векторно-скалярное произведение 388
Векторный градиент 404
Вектор-решение системы 316, 317, 498
Вектор-столбец 158
Вектор-строка 158
Вектор-функция 390
Векторы взаимные 388
— коллинеарные 387
— компланарные 387
—, линейная комбинация 387
— линейно зависимые, независимые 152,
153, 387
— ортогональные 155, 387
— равные 387
—, сложение, умножение на скаляр
151, 386, 387
Вероятность 442
— погрешности 460
— полная 444
— условная 443
Вершина конуса 188
— кривой 408
— кривой 2-го порядка 201, 202
— многогранника 186
— многогранного угла 186
— треугольника 183
Ветвь гиперболы 202
— функции 372
Вещественные числа (см.
Действительные числа)
Винтовая линия 255, 411
Включение 381, 384
— собственное 381
Внешние устройства 524
Внешняя точка множества 213
Внутренняя точка множества 213
Вогнутая функция 228
Возмущающая функция 313, 315
Возмущенное (невозмущенное)
движение 326
Возрастающая последовательность 214,
215
— функция 222
Волновое уравнение 340, 341
двумерное 340, 349
— — неоднородное 349
одномерное 340, 348, 349
— — трехмерное 348, 349
Вполне упорядоченное множество 384
Вронскиан 313
Вспомогательные переменные 466
Выборка без возврата 445
— большая, малая 456
— с возвратом 445
Выпуклая функция 228
Выпуклое множество 214
Выпуклый многогранный угол 186
Выравнивание прямыми 521
— результатов измерений 520
Высказывание 376
Высота пирамиды 187
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
535
Высота трапеции 184
- треугольника 183, 191
Вычет 370
- логарифмический 370
Вычисление квадратного корня 497
- корней рациональных функций 497
Вычислительные элементы АВМ 527
Вычитаемое 210
Гамильтониан 294, 301
— ступени к 303
Гамма-функция 134, 169, 260, 287, 436
Гармоническая функция 352, 365
Гармонические колебания 343
Гармонический анализ 418, 499
численный 423
— многочлен 353
— ряд 274
Гауссов интеграл ошибок 446
Гауссова кривизна 415
Генеральная совокупность 455
Геодезическая кривизна 417
— линия 417
на сфере 192
Геометрическая прогрессия 139
бесконечная 273
Гильбертово пространство 156, 499
Гипербола 200, 202
— равнобочная (равносторонняя) 114,
203
Гиперболическая спираль 128
Гиперболические функции 180, 364
Гиперболический косеканс 180, график
122
— косинус 180, график 122
— котангенс 180, график 122
— параболоид 208
— секанс 180, график 122
— синус 180, график 122
— тангенс 180, график 122
Гиперболическое уравнение 341, 342,
346
— —, задача с начальными
значениями (задача Коши) 346
— — однородное, неоднородное 343
Гиперболоид двуполостный 208
— однополостный 208
Гипергеометрическая функция 323
— — вырожденная 323
— — обобщенная 323
Гипергеометрическое распределение
445
— уравнение 322
— — вырожденное 322
Гиперплоскость 199
Гипотенуза 183
Гипоциклоида 127
Гистограмма 455
— выборки 455
Главная ветвь корня 372
— — логарифма 364
— диагональ матрицы 157
— нормаль 411
Главное значение аргумента 358
корня 359
логарифма 359, 364
— — несобственного интеграла 248, 249
— — обратной тригонометрической
функции 119, 178
— нормальное сечение 416
Главные кривизны 415
Главный радиус кривизны 415
Годограф 390
Голоморфная функция 365
Гомоморфизм 143
Гравитационное притяжение 266, 269
Градиент 232, 297, 304
— векторного поля 399
— поля экстремалей 293
— скалярного поля 393
— функционала 297, 304
Градиентная функция 293
Граница множества 212, 384
— — верхняя (нижняя) 212
— области 213, 360
Граничная точка множества 213
Граничные условия (см Краевые
условия)
Грань многогранника 187
— многогранного угла 186
— функции верхняя (нижняя) 217, 223
— числового множества верхняя
(нижняя) 212, 384
График отображения 385
— функции ИЗ, 216
двух переменных 223
Графическое дифференцирование 133
— интегрирование 133
— — дифференциальных уравнений 313
Группа 143, 385
— абелева 143, 385
— аддитивная 143
—, единица 143
-, - левая 385
— коммутативная 143
— мультипликативная 143
—, нейтральный элемент 143
—, нуль 143
—, обратный элемент 143
-, левый 385
— подстановок 136
— — знакопеременная 136
— — симметрическая 136
Групповые частоты 455
Двойной интеграл 261
— —, вычисление 261
— —, замена переменных 262
как объем 263
несобственный 271
— — по бесконечной области 271
— —, теорема о среднем значении 261
Двугранный угол 186
Двуполостный гиперболоид 208
Действительная ось 358
— часть комплексного числа 357
Действительные числа 210, 357
— —, геометрическое изображение 211
Декартов лист 123, 410
Декартова система координат 195, 197,
387
— степень множества 382
Декартово произведение 382
Декартовы координаты 195, 197, 387
Деление в крайнем и среднем
отношении 140
— многочленов (с остатком) 141
— отрезка в данном отношении 199,
204
Делимое 141, 210
Делитель 141, 210
— многочлена 141
— нуля 160
Деривационная формула Вейнгартена
416
Гаусса 416
Десятичная дробь 130, 211
Детерминант (определитель) 157
Дефект 499
— линейного преобразования 164
Диагональ 183
— матрицы главная, побочная 157
Диаграмма Хассе 384
Диаграммы Эйлера-Венна 381
Диада 402
Диадное произведение 402
Диады симметрические
(антисимметрические) 403
Диаметр кривой 2-го порядка 201, 203
— множества 213
— окружности 185
Диаметры сопряженные 201, 202
Дивергенция 397
Дизъюнкция 377, 378
Динамическая система 298
автономная 298
— — линейная 298
непрерывная 298
управляемая 298
Директриса кривой 2-го порядка 200,
201, 202
Дискретная аппроксимация Чебышева
502
— норма Чебышева 502
— система 303
Дискретный аналог задачи 515
Дискриминант квадратного уравнения
145
— кубического уравнения 113, 146
Дискриминантная кривая 310
Дискриминантный тензор 414
Дисперсия 447, 448
Дистрибутивность
(распределительность) 141, 151, 210
Дистрибутивный закон 210, 386
Дифференциал вектор-функции 391
— Гато 297
— длины дуги 407
— полный 231
— функции двух переменных 231
Дифференциальное уравнение 305
— — в частных производных 331
— — — — — гиперболического типа
340
— — — — — квазилинейное 331, 333
— — — — — линейное 331
однородное
(неоднородное) 331
— — — — — параболического типа
340
1-го порядка, 2-го
порядка 334, 339
— — — — — смешанного типа 340
— — — — — эллиптического типа 340
— — обыкновенное 305
Дифференциальный оператор 328
— — самосопряженный 328
— — сопряженный 328
Дифференцирование вектор-функции
390, 391
— дроби 227
— интеграла по параметру 258, 259
— Несобственных интегралов 259
— неявной функции 232, 234, 235
— по области 261
— произведения 227
— ряда (почленное) 278
— сложной функции 227, 232
Дифференцируемая функция 225, 231,
365
— — по х/( 230
— — справа (слева) 225
п раз 227
Длина вектора (модуль, норма) 155, 386
— дуги 406, 410, 414
— кривой 251
— окружности 185
— промежутка 212
Додекаэдр 188
Долгота 197
Дополнение множества 213, 381
Допустимая область 466, 467
— точка 466
— функция 330
Допустимое управление 298
Допустимый план перевозок 477
Достижимое состояние 298
Дробная часть числа 487
Дробно-линейная функция 172, 361,
374, графики 114
Дробно-рациональная функция 170,
217, 361, графики 115-116
Дробный показатель степени 174, 359
Дробь 210
Евклидово пространство 155
Единица 210
Естественное граничное условие 291
Зависимые функции 234
Загрузчик 526
Задача выравнивания 520
— двух тел 338
— Дирихле 342
, граничные условия 515
— — для прямоугольника 346
уравнений Лапласа и Пуассона
354, 355
— —, разностные методы 515
— Коши (задача с начальными
условиями) 305, 341
— —, теорема существования и
единственности 306
536
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Задача Лагранжа 288, 294
— линейного программирования 466
— — — двойственная 473
, канонический вид 468
— — — о планировании смен 482
— — — о покрытии 482
— — — о производственных
мощностях 481
— — — о раскрое 482
— — — о распределении 482
о смесях 481
— — — о сопоставлении 482
— — — параметрическая 483
— — — целочисленного 486
— на собственные значения (о
собственных значениях) 329, 495
— — — — для круга 345
— — — — — прямоугольника 345
— — — — однородная 329
— Неймана 342
для уравнений Лапласа и
Пуассона 354, 355
— о брахистохроне 287, 289
— о закрепленной струне 348
— с граничными значениями в двух
точках 304
— с данными на характеристиках 348
— с начальными значениями 347
— смешанная 342
— Штурма-Лиувилля 330, 350
Закон больших чисел 453
— — — слабый 453
— — — усиленный 454
— взаимности 347
— дополнения 260
— композиции 151
— Пуассона 445
— удвоения Лежандра 260
Замена базиса 470
— переменного 235, 262, 265, 272
Замкнутая кривая 360
Замкнутое множество 213
Замыкание 213
Запись 526
Знакопеременная группа 136
Знакочередующийся ряд 276
Знаменатель дроби 210
Значение функции 216, 223
— — наибольшее, наименьшее 217, 223
Значения признака 455
Золотое сечение 140
Изображение 164
Изолированная точка 408
— — множества 213
Изоморфизм 143
Изопериметрическая задача 292
Икосаэдр 188
Импликация 377, 378
Инверсия 374
— перестановки 136
Инволюта (см. Эвольвента кривой)
Индекс суммирования 138
— умножения 138
Индивидная переменная 379
Индивидные константы 379
Индивиды 379
Индикатор события 444
Индуктивный порядок 384
Индукция 211
Интеграл Гаусса 256
— двойной 261
—, зависящий от параметра 257, 272
— контурный 366
— кратный 261, 263
— криволинейный 253, 254
— Кристоффеля —Шварца 374
— неопределенный 240, 366
— несобственный 247, 248, 271
— определенный 238
— по замкнутому контуру 366
— поверхностный 267, 268
— Пуассона 356
— с бесконечными пределами 248
— с неограниченной подынтегральной
функцией 247
— табличный 240
— тройной 263
Интеграл Фурье 425
— Эйлера 260
— эллиптический 240
Интегралы от алгебраических функций
94, 100-112, 244
— — гиперболических функций 106 —
107, 247
— — дробно-рациональных функций
91-94, 242
— — иррациональных функций 94 —
100, 112, 244
логарифмических функций 108-
109, 111-112, 247
— — обратных гиперболических
функций ПО
— — — тригонометрических функций
109-110, 247
— — показательных функций 107 —
108, ПО, 247
— — рациональных функций 91—94,
242
— — степенных функций 240
— — тригонометрических «.функций
100-106, 110-111, 246 "'•
— Френеля 436
Интегральная кривая 305
особая 310
— поверхность 333, 334
— показательная функция 107
— сумма 238, 253, 254, 261, 267
— теорема Коши 366
Интегральные формулы 270, 400
Коши 367
Интегральный косинус 103. 437
— логарифм 108, 240
— признак сходимости 275
— синус 101, 169, 437
Интегратор 527
Интег рирование дробно-рациональных
функций 242
— иррациональных функций 244
— несобственных интегралов 259
— по частям 241, 251, 400
— подстановкой (замена переменного)
241, 242, 251
— разложением в ряд 239
— рациональных функций 242
— трансцендентных функций 246
— элементарных дробей 243
Интегрируемая функция 238, 261, 263
Интегрирующий множитель 307
Интервал 212
— неограниченный 212
Интерполяционная поправка 12
Интерполяционные форму пы 504
Интерполяционный многочлен 502
Бесселя 505
Гаусса 505
Лежандра 502
Ньютона 502, 505
Стирлинга 505
Эверетта 505
Интерполяция 12, 502
— квадратичная 12
— кусочная 504
— линейная 12
Инфимум 384
Инъекция 385
Иррациональное выражение 142
Иррациональные функции 174,
графики 116-117
— числа 211
Исследование функций 230
Истинностное значение 376
Исходная программа 524
Итерационные методы 496
— — для нелинейных уравнений 498
Итерация дробная 496
— простая 497
— — векторная 496
Каноническая система
дифференциальных уравнений 338
— форма уравнения 341
Канонические преобразования 339
— уравнения динамической системы
299
Канонический базис 153
Каноническое уравнение кривой 2-го
порядка 200
— — поверхности 2-го порядка 207
Кардиоида 125
Касательная к графику функции 225
— к кривой 2-го порядка 201, 202, 204
— к плоской кривой 406
— к пространственной кривой 411
— плоскость 413
— — к графику функции 232
Катет 183
Качественное программирование 529
Квадрант 195
Квадрат 184
Квадратичная форма 168, 236
— —, главные оси 168
— — каноническая 168
— — неопределенная 236
— — поверхности первая, вторая 414
— — положительно (отрицательно)
определенная 168, 236
-, критерий Сильвестра 236
— — полуопределенная 168
— —, приведение к главным осям 168
Квадратичная функция 170, 375,
график 113
Квадратная матрица 157
— — вырожденная (особенная) 159
невырожденная (неособенная) 159
Квадратное уравнение 145
Квадратура Гаусса 508
Квазилинейное уравнение 331, 333
Квазипорядок 383
Квантор 380
— общности 380
— ограниченный 380
— существования 380
Класс эквивалентности 383
Классификация дифференциальных
уравнений 339
— кривых 2-го порядка 200
Клин 187
Клотоида 129
Ключевое уравнение 519
Ковариантные координаты 195, 197,
388
Ковариация 450
Код операции 524
Колебание мембраны 345
— струны 344
Коллинеарные векторы 387
Кольцо 143, 385
— ассоциативное 143, 386
— коммутативное 143, 386
— круговое 185
— матриц 160
Команда 524
Комбинаторные задачи 135
Коммутативная операция 385
Коммутативность (перестановочность)
141, 151, 210
Коммутативный закон 385
Компилятор 525
Компланарные векторы 387
Комплексная плоскость 358
— функция 360
Комплексно сопряженная матрица 161
— сопряженные числа 358
Комплексные числа 357
— —, алгебраическое представление
358
— —, показательная форма 358
, тригонометрическая форма 358
Композиция линейных
преобразований 166
— отображений 385
— функций (суперпозиция) 217
Конечная числовая последовательность
138
Конечное множество 212, 386
Конечные суммы, формулы 139
Коническая поверхность 188
Конические сечения 189, 200
Константа 217
— предикатная 379
Константы 378
Контактное преобразование 469
Контравариантные координаты 195,
197
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
537
Кон граградиен гное преобразование
координат 154
Контурный интеграл 366
Конус 188, 208
— Монжа 333
— прямой круговой 189
— усеченный 189
Конформное отображение 372
— - первого, второго рода 372
Конхоида 124
— Никомеда 124
Конъюнкция 377, 378
Координатные линии 196, 412
— оси 195, 197
— плоскости 197
— углы 195, 197
— функции 296
Координаты барицентрические 194
— аффинные 378
— вектора 154, 387
— декартовы 195, 197, 387
— ковариантные, контравариантные
195, 197, 387, 388
— косоугольные 195, 197, 388
— криволинейные 195, 197, 412
— полярные 196, 262
— середины отрезка 199, 204
— сферические 197, 393
— точки 194, 197, 387
деления отрезка в данном
отношении 199, 204
— — пересечения двух прямых 200
— центра тяжести 199, 204
— цилиндрические 197, 392
Корень квадратный, кубический, л-й
степени 141
— многочлена 169
— уравнения 148
Корневое условие 513
Корректно поставленная задача 343
Корреляционный момент 450
Корреляция 450
Косвенная адресация 524
Косеканс 174, график 118
Косинус 174, график 117
Косинус-преобразование Фурье 426
Косинусы направляющие 200, 206
Косоугольная система координат 195,
197, 388
Котангенс 174, график 118
Коэффициент корреляции 450, 451, 464
— пропорциональности ИЗ
Коэффициенты регрессии 451
— Фурье 418
Краевая задача 306, 327, 342
— — однородная, неоднородная 327,
329
— — определенная 330
первая 356
— — самосопряженная 528
Краевой метод 514
Краевые задачи для уравнений
Лапласа и Пуассона 354
— условия 1-го, 2-го, 3-го рода 342
Штурма 329
Кратный интеграл 261, 263
Кривая алгебраическая 123, 409
— второго порядка 200
— — — параболическая 200
— — — центральная 200
— гладкая 253
— Жордана 360
— замкнутая 360
— интегральная 305
— кусочно гладкая 253
— нормального закона распределения
120
— плоская 123, 251, 405
— пространственная 252, 410
Кривизна кривой 407, 411
— на поверхности 416
— поверхности 415
Криволинейные координаты 195, 197,
412
Криволинейный интеграл 253
— — в векторном поле 394
Гаусса 256 .
— — 1-го рода, 2-го рода 253, 254
— — по замкнутой кривой 254
Критерий базиса 154
— выпуклости функции 229
— интегрируемоеiи по Риману 238
— Коши 217, 273, 278
— параметрический 461
— Рауса - Гурвица 326
— свободный от параметров 461
— Сильвестра 236
— согласия 462
— — Колмогорова —Смирнова 463
— сходимости Коши 215, 216
— - несобственных интегралов 249
— Уилкоксона 461
F-критерий 461
/-критерий 461
Х-критерий 462
Круг 185
— кривизны 407
— сходимости 368
Круговое кольцо 185
Круговые функции (см. Тригономе!-
рические функции)
Кручение кривой 411
Куб 187
Кубическая парабола 113
— резольвента 147
Кубическое уравнение 146
Кусочно гладкая кривая 353
— непрерывная функция 221
Левая система координат 197, 387
Лексикографический порядок 473
Лемма Гейне —Бореля 214
— Дюбуа - Реймона 289
Лемнискаш 125, 409
Линеаризация 498, 522
Линеаризованная система 326
Линейная зависимость (независимость)
векторов 152, 153
— ин1ерполяция 12
— комбинация векторов 152
— оболочка 152
— система дифференциальных
уравнений 316
— — — — однородная, неоднородная
316, 317
— функция 113, 170, 374
Линейно зависимое (независимое)
множество 152, 153
— зависимые функции 313
— независимые векторы 152, 153
— упорядоченное множество 384
Линейное дифференциальное
уравнение 305, 308, 313, 318, 331
— — — 2-го порядка 318
— — - я-го порядка 313
— — — однородное, неоднородное 313,
314, 315, 331
— — — с постоянными
коэффициентами 315
— подпросфанство 199
— преобразование 164
— — взаимно однозначное 164
— —, представление в виде матриц 165
— программирование 466
— пространство (см. Векторное
пространство)
— уравнение (алгебраическое) 145
Линейный оператор 164
— — вырожденный (невырожденный)
164
— — обрашый 166
— — симметрический 168
— — i ождественный 166
— элемент особый 310
— — поля направлений 306
— — регулярный 310
— — уравнения 310
Линейчатая поверхность 416
Линии вихревые 398
— кривизны 416
— регрессии 451
— тока 392
— уровня 223, 391
Лист Декарта 123, 410
— Мёбиуса 266
Логарифм 364, 373
— десятичный 33
Логарифм натуральный 364
Ло1 арифмическая линейка 519
— производная 226
— спираль 128, 409
— точка ветвления 373
— функция 179, 373, график 119
— —, разложение в ряд 89
Логарифмическое уравнение 151
Логическая операция 376
— функция (предикат) 379
Логические связки 376
Локон Аньези 123
Ломаная Эйлера 510, 512
Мажоранта 278
Макрокоманда 524
Максимальный (минимальный) элемент
множества 212, 384
Максимум функции 229, 236
— — локальный 229, 236
— функционала 288
— — абсолкпный 288
— — сильный 288
слабый 288
Масса 257, 263, 265
Математическая выборка объема п 455
Математическое обеспечение 526
— ожидание 446, 447
Матрица 157
— базисная 469
— верхняя (нижняя) треугольная 157
— вырожденная (особая) 159
— Гильберта 500
— Грама 499
— диагональная 157
— единичная 157, 160
— квадратичной формы 168
— квадратная 157
— ковариации (корреляции) 450
— комплексно сопряженная 161
— кососимметрическая 161
— косоэрмитова 161
— коэффициентов 162
— — расширенная 162
— невырожденная (неособая) 159
— нулевая 157, 160
— обратная 160, 493
— ортогональная 161
— противоположная 159
— размера т х п 157
— разреженная 515
-, ранг 159
— симметрическая 161
-, след 157
— транспонированная 157
— трапециевидная 159
— треугольная 157
— унитарная 161
—, элемент 157
— элементарных вращений Якоби 495
— эрмитова 161
— Якоби 498
Матрица-столбец 157
Матрица-строка 157
Матрицы подобные 165
— равные 159
—, сумма, разность, произведение на
число 159
— сцепленные, умножение 160
— эквивалентные 165
Матричное уравнение 161
Машинное слово 523
Медиана 183
Мера надежности 459
Меридианы 412
Метод Адамса 512, 513
— Адамса -Мултона 512, 513
— вариации постоянной 308, 314
— выбранных точек 522
— выделения 518
— Галеркина 514
— Гаусса —Жордана 492
— Гаусса - Зейделя 494
— градиента 304
— — проекционный 304
— — условный 304
— градиентного спуска 297
— исключения Гаусса 491
538
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Метод итерации 493, 496, 498
— квадратичной ошибки 514
— коллокаций 514
— Коши 314
— краевой 514
— Лобачевского-Греффе 497
— ломаной Эйлера 510
— математической индукции 211
— Мизеса 496
— Милна 512
— многошаговый 512
— моментов 458
— наибольшего правдоподобия 458
— наименьших квадратов 237, 499, 521
— неопределенных коэффициентов 173
— неявный (закрытый) 512
— Нистрёма 512
— Ньютона 497
— Ньютона — Канторовича 498
— областей 514
— одношаговый 511, 513
— ортогонализации 156, 514
— Пикара 312
— подстановки нулей знаменателя 243
— — численных значений 173
— последовательных приближений Пи-
кара 312
— потенциалов 479
— предельных значений 173
— предсказания — уточнения 513
— приравнивания коэффициентов 243
— проверки 461
— разветвления 488
— разделения переменных 332
— релаксации 296
— Римана 347
— Ритца 296
— Рунге-Кутта 511, 512
— сведения к задаче с начальными
значениями 513
— секущих 497
— сечения Гомори 487
— сравнения коэффициентов 282
— средних 522
— степенной 496
— суперпозиции 332
— сходящийся 513
— — порядка /? 513
— телескопа 502
— Фурье 343
— Хенричи - Милна 512
— хорд 497
— частичных областей 514
— Эйлера 296, 511
— эксiраполяции 509
— явный (открытый) 512
— Якоби 494, 496
Методы градиентные 304
— итерации 493, 496
— прямые (косвенные) 296, 304, 491, 495
— разностные 514
— эвристические 513
Метрические коэффициенты 388
Метрический тензор 414
Минимальная поверхность 416
Минимальный многочлен 500
Минимизирующая
последовательность 296, 304
Минимум функции 229, 236
локальный 229, 236
— функционала 288
— - абсолютный 288
— — сильный 288
слабый 288
Минор 157
Миноранта 384
Мнимая единица 357
— ось 358
— часть комплексного числа 357
Мнимое число 357
Многогранник 186
— правильный 187
Многогранное множество 467
Многогранный угол 186
, вершина, грани, ребра 186
выпуклый 186
— —, плоский угол 186
Многолистная поверхность 372
Многообразие разветвления 334
Многосвязная область 213, 360
Многоугольник 184
- правильный 184
Многочлен 141, 169, 217, 361
- интерполяционный 502
—, каноническая форма 169
-, корень (нуль) 169
-, - кратности к 170
—, коэффициенты 169
- Лежандра 323
- неприводимый 169
- приводимый 169
-, степень 141, 169
Многочлены взаимно простые 141 -
-, деление с остатком (алгоритм
Евклида) 141
- Лежандра 323, 500, 508
- ортогональные 500
- Чебышева 501
Множества дизъюнктные 381
- равномощные 386
Множество бесконечное 212, 386
- выпуклое 214
- достижимости 298
- замкнутое 213
- значений функции 216, 223
- индексов 382
- конечное 212, 386
- линейно связное 213
- не более чем счетное 212, 386
- несчетное 212, 386
- ограниченное 212, 384
- — сверху (снизу) 212, 384
- открытое 213
- производное 213
- пустое 380
- равномерно ограниченное 279
- равностепенно непрерывное 279
- связное 213
- счетное 212, 386
- точечное 212
- числовое 212
Множители Лагранжа 293
Множитель интегрирующий 307
- нормирующий 200, 205
Модуль 525
- вектора 155, 386
- действительного числа (см.
Абсолютная величина)
- комплексного числа 358
- функции 360
Молекула 515
- асимметричная 515
- пятиточечная для оператора
Лапласа 515
Момент инерции 253, 263, 265
- корреляционный 450
- начальный 446, 447, 449
- случайной величины 447
- — — многомерной 449
- центральный 446, 447, 449
- эмпирический 458
Монитор 526
Монотонная последова i ельность 215
- функция 222
Мощность множества 386
Мультипрограммный режим 524
Набла-оператор 399
Наблюденные значения 455
Наибольшее (наименьшее) значение
функции 217, 223
Наибольший (наименьший) элемент
множества 384
Наклон касательной (см. Угловой
коэффициент)
Наклонное сечение 416
Накопители 523
Направление закручивания 411
Направляющая конической
поверхности 188
— цилиндрической поверхности 188
Направляющие косинусы 198, 200, 206
Направляющий вектор 205 j
Натуральные числа 211
Натуральный логарифм 364
, главная ветвь 364, 373
— параметр 410
Начало координат 195, 197, 387
Невозрастающая (неубывающая)
последовательность 215
— (—) функция 222
Нелинейные уравнения
дифференциальные 325
Неоднородная краевая задача 327
— система дифференциальных
уравнений 316
Неоднородное дифференциальное
уравнение 308, 313, 343
Неопределенный интеграл 240, 366
Неподвижная точка 493
подстановки 136
Непрерывная кривая 360
— слева (справа) функция 220
— случайная величина 445
— функция 220, 224, 361
Непрерывно дифференцируемая
функция 230, 233
Непрерывный спектр 425
Неравенства 142, 212
— эквивалентные 143
Неравенство 142
— Бернулли 212
— выполнимое (невыполнимое) 142
, - Гарнака 354
— Коши — Буняковского 142, 155, 212,
358
— Минковского 142
—, решение 143
— тождественное 142
— треугольника 155, 192, 212, 358
— — обобщенное 212
— универсальное 142
— Чебышева 142, 453
обобщенное 142
Несобственный интеграл 247, 248
— — абсолютно сходящийся 250
— —, главное значение 248, 249
двойной 271
— — зависящий от параметра 258
— — , критерий сходимости 249
равномерно сходящийся 258
— — расходящийся 247, 248
сходящийся 247, 248
тройной 272
— —, функция сравнения 249
Неубывающая последовательность 215
— функция 222
Неявная функция 216, 223, 234, 235
Нижняя грань множества 212, 384
— — функции 217, 223
Номограмма из выравненных точек 519
Номограммы сетчатые 520
Норма вектора (модуль, длина) 155,
156, 386
— элемента в гильбертовом
пространстве 156, 499
Нормаль 406, 413
Нормальная плоскость 411
— система дифференциальных
уравнений 332
Нормальное распределение 446, 449
— сечение поверхности 416
— уравнение прямой 200
— — плоскости 205
Нормированное распределение 446
Нормировка функции 529
Нормирующий множитель 200, 205
Носитель линейного элемента 306
Нули многочлена 169
— рациональной функции 171
— функции 221, 361
Нуль 143, 210
Обелиск 187
Область 213, 360
— зависимости решения 347, 348
— замкнутая 214, 360
— многосвязная 213, 360
— односвязная 213, 360
— определения функции 216, 223, 360
— пространственно односвязная 268
— сходимости 277
— управления 298
О большое, о малое 221
Образ (изображение) 164
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
539
Образ отношения 383
— отображения 384
Образующая конуса 188
— прямолинейная 209
— цилиндра 188
Обратная задача вариационного
исчисления 295
— пропорциональность 114
— функция 217
Обратное преобразование Лапласа 437
Обратные гиперболические функции
(ареафункции) 122, 181
— — —, разложение в ряд 90
— тригонометрические функции 118,
119, 178
, разложение в ряд 89
Общий интеграл дифференциального
уравнения 307
Объединение множеств 381
Объект загрузки 526
Объектная программа 524
Объем тела 263, 265, 269
вращения 252
Обыкновенное дифференциальное
уравнение 305
— — — в неявной форме 305
в полных дифференциалах 307
— — — , интегрирование с помощью
рядов 313
— — — линейное 308, 313
— — — нелинейное 325
неоднородное 313
, общее решение 305
— — — однородное 307, 313
— — — первого порядка 306
— — — с разделяющимися
переменными 307
, частное решение 305
Овалы Кассини 125
Огибающая 310, 336
— семейства 410
Ограниченная последовательность 214
— функция 217, 361
— — сверху (снизу) 217, 223
Ограниченное множество 212, 384
Однолистная область 372
— функция 372
Однополостный гиперболоид 208, 209
Однородная краевая задача 327, 329
— система линейных уравнений 161
Однородное дифференциальное
уравнение 307, 313, 331
линейное 313
Односвязная область 213, 256, 360
Одношаговый метод 511, 513
Окрестность 213, 360
?-окрестность 213, 360
Округление числа 131
— — с избытком, с недостатком 131
Окружность 185, 202
— вписанная (описанная) 191
—, длина 185
-, уравнение 202
Октант 197
Октаэдр 188
Операнд 524
Оператор Гамильтона (набла) 399
— Даламбера 340
— Лапласа 340, 399
— линейный 164
— обратный 166
— положительный 351
— самосопряженный 328, 347, 351
— тождественный 166
— эллиптический 343
— эрмитов 351
Операторный метод решения
уравнений 326, 346
Операторы 524
Операционная система 523, 526
Операция «-местная (л-арная) 385
— навешивания квантора 380
— нульместная 385
— сложения, умножения 386
Опорные точки 526
Определенный интеграл 238
Определитель 157
— Вронского 313
—, вычисление 158
Определитель, разложение по
элементам строки (столбца) 158
Определяющее уравнение 319
Оптимальная траектория 299
Оптимальное состояние 299
— управление 299
Оптимальный процесс 298
Оптимизационная задача 302, 303
Ордината 195, 197, 216
Оригинал 164, 437
Ориентация поверхности 268, 414
Ориентированная площадь 199, 257
Ориентированный объем 204
Ортогональная проекция 156
— система 155
— составляющая 156
Ортогональное дополнение 156
Ортогональные векторы 155
— многочлены 500
— подпространства 156
Ортонормированная система 155, 500
— — полная 418
Ортонормированный базис 155, 156
Ортоцентр 183
Осевое поле (цилиндрическое) 391, 392
Основание трапеции 184
Основная теорема алгебры 148, 169, 361
Основные эквивалентности 378
Особая точка 310, 365, 369, 406, 408,
409
— — изолированная 365, 408
кривой 408
— — поверхности 413
, полюс порядка т 369, 370
регулярная 319, 365, 370
— — существенно 369, 370
— — устранимая 369, 370
Особое решение 336
Особые точки дифференциального
уравнения 310
— — — — регулярные 319, 320
Особый интеграл 310
Остаток 273, 278
Ось абсцисс 195, 197
— аппликат 197
— кривой 2-го порядка 201, 202, 203
— ординат 195, 197
Отклонение среднее квадратичное 447
— стандартное 447, 448
Открытое множество 213
Отладка программы 526
Относительная погрешность 131
Отношение бинарное 382
— квазипорядка (предпорядка) 383
— w-местное (л-арное) 382
— полное (универсальное) 382
— порядка 383
— пустое (нулевое) 382
— частичного порядка 383
— эквивалентности 383
Отображение 233, 384
— биективное 385
—, график 385
— дифференцируемое 233
— инъективное 385
— конформное 373
— многозначное 384
— непрерывное 233
—, образ (прообраз) 384
— обратное 385
— однозначное 384
— поверхностей 414
— сюръективное 385
— тождественное 385
— эквиареальное 414
Отрезок 212
— цилиндра 188
Отрицание 376
— высказывания (инверсия) 376
Отрицательное число 211
Оценка асимптотически несмещенная
457
— более эффективная 458
— доверительная 459
— наиболее правдоподобная 458
— несмещенная 457
— состоятельная 457
— точечная 457
— эффективная 458
Пакетная обрабожа 526
Память 523
— внешняя, внутренняя 524
Парабола 123, 170, 200, 203, график
113, 114
—, уравнение 203
Параболические кривые 200
Параболический цилиндр 209
Параболическое выравнивание 522
— уравнение 340, 342, 344, 345, 356
Параболоид вращения 208
— гиперболический 209
— эллиптический 209
Параллелепипед 186
— прямоугольный 187
Параллели 412
Параллелограмм 183
Параллельные плоскости 186
— прямая и плоскость 186
— прямые 186
Параллельный перенос системы
координат 196, 198
Параметр 141, 144, 257
— распределения 445
— фокальный 201, 203
Первообразная 240, 366
Первый интеграл системы 306
Переименование свободное (связанное)
380
Переменная свободная, связанная 379
Перенос, вектор переноса 196, 198
Пересечение множеств 381
Перестановка 136
— с повторением 137
Подстановка 136
— обратная 136
— тождественная 136
— четная, нечетная 136
Период функции 222
Периодическая функция 174, 222
Пи (число) 185
Пирамида 187 ,*«.
— правильная 187
— треугольная 187, 204
— усеченная 187
План согласования 529
— — нормированный 530
Плоский угол многогранного угла 186
Плоское поле 391
— — векторное 391
Плоскость 205
— и прямая 186, 206
Плотность распределения 445
— — вектора 449
нормального 446, 449
— совместная 449
Площадь кольца 185
— криволинейной трапеции 252
— круга 185
— многоугольника 184, 199
— параллелограмма 183
— поверхности 414
— — тела вращения 252
— прямоугольника 183
— сегмента 185
— сектора 185, 252
— треугольника 183, 191, 199
— четырехугольника 184
Поверхностный интеграл 267, 268
— — в векторном поле 396
— — 1-го рода, 2-го рода 267, 268
Поверхность 412
— второго порядка 206
— — —, классификация 206
, приведение к каноническому
виду 206
— гладкая 266
— двусторонняя 266
— коническая 188
— кусочно гладкая 266
— линейчатая 416
— минимальная 416
— многолистная (риманова) 372
— односторонняя 266
— ориентированная 395, 414
— постоянной кривизны 416
— развертывающаяся 416
— уровня 223, 391
— цилиндрическая 188
540
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Поворот системы координат 196, 198
Погрешность 490
— абсолютная 131
— второго рода 461
— дополнительная 491
— интерполяции 504
— истинная 131, 490
— — относительная 131, 490
— максимальная 490
— метода 490
— обрыва 490, 511
— — локальная 511
— обусловленная входом 490
— округления 131, 511
— первого, второго рода 461
— предельная 131
— приближения 131
— случайная 491
Подкасательная 406
Подматрица 157
Подмножество 381
— собственное 381
Поднормаль 406
Подобные матрицы 165
— треугольники (многоугольники) 183
Подпоследовательность 215
Подпрограмма 525
Подпространство 152
Подстановки Эйлера 245
Показательное уравнение 150
Показательные функции 179, 361,
364, графики 119
— —, разложение в ряд 88, 363
Покрытие 214
Поле 143, 386
— без источников 401
— векторное 391
— направлений 306
— скалярное 391
— экстремалей 293
— — центральное 293
Полином (см. Многочлен)
Полиномиальное распределение 448
Полиномиальный коэффициент 135
Полная вариация функции 222
— кривизна 417
— ортонормированная система 418
Полное упорядочение 384
Полнота 156, 216
Полный дифференциал 256
— интеграл 336
— прообраз 164, 384
Положительное число 211
Полугруппа 385
Полуинтервал 212
Полукубическая парабола 123
Полунепрерывная функция 222
Полуупорядоченность 383
Полюс 196
— дробно-рациональной функции 171
— северный, южный 359, 360
— функции 369, 370
Полюсное расстояние 133
Полярная ось 196
— система координат 196
Полярное расстояние 197
— уравнение кривой 2-го порядка 201
Полярные координаты, замена
переменных 262
Полярный угол 196
Поправка интерполяции 12
Порождающая система 152
Порядок 383
— величины функции 221
Последовательность 214, 215, 367
— возрастающая (убывающая) 214
— конечная 138
— монотонная 215
— невозрастающая (неубывающая) 214,
215
— неравномерно сходящаяся 277
— ограниченная 214, 215
— первых (вторых) разностей 138
— постоянная 139
— равномерно сходящаяся 277
— расходящаяся 214, 216, 367
— строго возрастающая
(убывающая) 214, 215
— сходящаяся 214, 216, 277, 367
Последовательность точек 215
— функциональная 277
— числовая 214
Постоянная Липшица 223
— Эйлера ПО, 260, 320, 436
Постоянные функции 113
Потенциал векторного поля 395
— запаздывающий 350
— силового поля 257
Потеря значащих разрядов при
вычитании 491
Поток векторный 396
— скалярного поля 396
— скалярный векторного поля 396
Почленное дифференцирование ряда
279, 281
— интегрирование ряда 278, 281
Правая система координат 197, 387
Правило знаков Декарта 149
— Крамера 163
— ложного положения 497
— Лопигаля 218
— Непера 194
— Ньютона 149
— подстановки 241, 242, 251
— Саррюса 158
— северо-западного угла 478
— средней точки 512
— трапеции 512
— треугольника 387
Правильная дробно-рациональная
функция 171
— точка функции 365
Правильные многогранники 187
Правый винт 267
Предел вектор-функции 390
— последовательности 214, 216, 277
— — векторов 390
верхний (нижний) 215, 280
— функции 217, 218, 219, 361
— — многих переменных 224
справа (слева) 218, 219
Пределы интегрирования 238
— суммирования 138
— умножения 138
Предельная теорема для
характеристической функции 452
— — интегральная 454
— — локальная 454
— — Муавра — Лапласа 454
— — центральная 454, 455
— точка множества 212
— функция 277
Предельный элемент множества 374
Предикат 379
— двухместный (бинарный) 379
— индивидуальный 379
— я-местный («-арный) 379
— одноместный (унарный) 379
— переменный 379
Предикатная константа 379
— формула 380
Предикатный символ 379
Предметная область 379
— переменная 379
Представление Гаусса 260
Преобразование Кельвина 354
— координат 154, 196, 198
— — когредиентное (контраградиент-
ное) 154
— Лапласа 326, 346, 437
— Лежандра 338
— Фурье 425
— Эйлера 517
Приближение 499
— наилучшее 499
— равномерное 501
— чебышевское 501
Приближенное дифференцирование 510
— значение числа 131
— — —, верные цифры 131
— интегрирование 506
Приближенные формулы для
элементарных функций 132
Приведенное уравнение 146
Призма 186
— правильная 186
— прямая 186
Признак Абеля 276, 278
Признак Вейерппрасса 278
— Гаусса 275
— Даламбера 274
— Дирихле 276, 278
— Жордана —Дирихле 425
— инте1ральный 275
— Коши 275
— Лейбница 276
— Маклорена 275
— сравнения рядов с положительными
членами 274
Принцип выбора 385
— выравнивания 521
— Гамильтона 291
— Дюамеля 349
— максимума 304, 365
— — для гармонических функций 354
Понфягина 287, 299, 302
слабый 304
— непрерывности 371
— — Дедекинда 211
— Рунге 512
— симметрии Шварца 372
— Цорна 384
Принципы максимальных цепей 384
Присоединенная вектор-функция 299
— сис1ема 302, 303
Присоединенные функции Лежандра
324
Присоединенный вектор 303
Программа 524
Программирование 524, 525
Программное обеспечение 526
Прогрессия арифметическая 139
— геометрическая 139
Произведение бесконечное 285
— матриц 160
— отображений 385
— подстановок 136
— рядов 277
— чисел 210
Производная 225, 365
— вторая 226
— высших порядков 227, 231
— логарифмическая 226
— по направлению 232, 393
— по нормали 406
— по объему 397
— порядка п 227
— слева, справа (левая, правая) 225
—, таблица 226
— частная 230
Производное множество 213
Производящая функция случайной
величины 453
Промежуток 212
Прообраз (оригинал) 164, 384
— отношения 383
— оюбражения 164, 384
полный 164, 384
Пропозициональная переменная 376
— формула 376
Пропозициональные формулы
эквивалентные (равносильные) 378
Пропорциональная швисимость
прямая, обратная 113, 114
Простейшая дробь 172
— задача вариационною исчисления
288
Пространственная кривая 410
Пространство векюрное 151
— гильберюво 156, 499
— евклидово 155
— управления 298
Процессор 523
Прямая 199
— в пространстве 205
Прямолинейная обра$ующая 209
Прямоугольная система координат
195, 197, 387
Прямоугольник 183
Прямоугольный параллелепипед 187
— треугольник 183
Прямые методы 295, 304, 491
Псевдосфера 416
Пу1ь интегрирования 366
PaGoia силы вдоль кривой 257
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
541
Равенство фегьему 383
Равнобедренный треугольник 183
Равнобочная гипербола
(равносторонняя) 114, 203
— трапеция 184
Равномерно непрерывная функция
222, 224
— ограниченное множество 279
— сходящаяся последовательность 277
— сходящийся интеграл 258, 272
ряд 278
Равномерное приближение 501
— распределение 446, 449
Равностепенно непрерывное
множество 279
Радиан 61, 190
Радикал 142
Радиус кривизны 407, 411
— - главный 415
— кривой 2-го порядка 201, 203, 204
— окружности 185, 202
— — вписанной (описанной) 191
— сходимости 280, 368
Радиус-вектор 196, 387
Разброс 448
Развертка окружности 128, 129
Развертывающаяся поверхность 416
Разделение времени 526
— переменных 332
Разделенная разность 502
Разложение в ряд Лорана 368
Тейлора 228, 283, 368
_ _ _ _ численно пригодное 517
Фурье 418, 419
— дроби на простые (на
элементарные) 94
— на множители 148
— — простейшие дроби 361
— по многочленам Чебышева 501
~ — ортогональным многочленам 501
— — собственным функциям 330, 351
— элементарных функций в ряд 87
Размер матрицы 157
Размерность пространства 154
Размещение 137
— с повторением 137
Разностная схема 502
Разностное отношение 225, 515
— уравнение 511
Разностные операторы 502
Разность арифметической прогрессии
139
— запаздывающая 504
— множеств 381
— — симмефическая 381
— опережающая 504
— первая, вторая 139
— центральная 504
— чисел 210
Разрез 372
Разрешающая строка 470
Разрешающий столбец 470
— элемент 470
Разрыв функции 220, 224
— — бесконечный 221
— — конечный (скачок) 221
— — 1-го, 2-го рода 221
— — устранимый 221
— —, точка разрыва 220
Разрывная функция 220
Ранг линейного преобразования 164
— матрицы 159
— —, вычисление 159
Распределение 444
— асимптотическое 454
у — биномиальное 444
— вектора 448
— Гаусса 446
— 1ипергеометрическое 445
— граничное 449
— нормальное 446, 449
— полиномиальное 448
— Пуассона 445
. - равномерное 446, 449
— случайной величины 444
' — Стьюдента (/-распределение) 457
— условное 450
— экспоненциальное 446
— F (F-распределение) 457
Распределение Z (Z-распределение) 457
~ X2 (X^распределение) 457
Распространение тепла 344
Расстояние между двумя точками 199,
204, 213, 390
— — прямыми 205
— от точки до прямой 200, 205
Расходящаяся последовательность 214,
216, 367
Расходящееся произведение 285
Расходящийся несобственный интеграл
247, 248
— ряд 273
Расхождение (см. Дивергенция)
Расширенная матрица коэффициентов
162
Рациональная функция 170, 217
— — правильная 217
— — целая 217
Рациональное число 211
Ребро многогранника 186
— многогранного угла 186
Регистр 524
Регулярная точка дифференциального
уравнения 318
— — — — особая (слабая особая точка)
319, 320
— — функции (правильная) 365
— функция 365
Резольвента кубическая 147
Рекуррентная формула 243
Рельеф функции 360
Рефлексивность 383
Решение треугольников 190
— — сферических 193
Риманова поверхность 372
Ромб 184
Ротор (вихрь) 398, 404
Ряд 273, 367
— абсолютно сходящийся 276
— безусловно сходящийся 277
— бесконечный 273
— биномиальный 87, 88
— быстро сходящийся 517
— гармонический 274
— знакочередующийся 276
-, критерий Коши 273
— Лорана 369
— —, главная часть 369
— —, регулярная часть 369
— Маклорена 228
—, необходимый признак сходимости
273
—, общий член 273
-, остаток 273, 278
— равномерно сходящийся 278
— расходящийся 273
— с комплексными членами 367
— с неотрицательными членами 274
— степенной 279, 368
-, сумма 273, 368
— сходящийся 273, 367
— Тейлора 228, 282, 283, 369
— условно сходящийся 276
— функциональный 278, 368
— Фурье 418
-, частичная сумма 273
— числовой 273
Самосопряженный оператор 328, 347,
351
Свертка плотностей 451
Связанный алгоритм 492
Связки 376
Связное множество 213
Связность 383
Сглаживающий многочлен 521
Сегмент (см. Отрезок) 212
— кривой 2-го порядка 201, 203, 204
— круга 185
— шаровой 189
Седло (особая точка) 312
Секанс 174, график 118
— гиперболический 180
Сектор круга 185
— шаровой 189
— эллипса 201
Секущая 185
Семейство подмножеств 382
Сетка 514
Сечение в множестве действительных
чисел 211
Сила притяжения 269
Символ 523
— Кронекера 389
Символы Гаусса 237
— Кристоффеля 416
— Х7, О (о малое, О большое) 221
Симметрическая группа 136
Симметричность 383
Симплекс-метод 469
— двойственный 474
— — модифицированный 475, 476
Симплекс-множитель 479
Симплекс-таблица 468
— двойственно-вырожденная" 475
— двойственно-допустимая 474
— модифицированная 475
Симплекс-шаг 470
Синтаксис языка 525
Синус 174, график 117
— гиперболический 180, 364
Синусоида 117
Синусоидальная функция 177
Синус-преобразование Фурье 426
Система динамическая 298
— дифференциальных уравнений 305,
331
— — — в частных производных 331
— — — — — — нормальная 332
— — — — — — определенная (недо-
определенная) 332
— — — — — — переопределенная (не-
доопределенная) 332
— — — обыкновенных 305
-, общее решение 305
— — — —, общий интеграл 306
— — — —, первый интеграл 306
— — — —, порядок 305
— каноническая 338
— команд 524
— — одноадресная 524
— координат 194, 195, 197, 387
барицентрическая 194
декартова 194, 195, 197, 387
косоугольная 195, 197, 388
— — криволинейная 195, 197
левая (правая) 197, 387
— — однородная 194
— — полярная 196
прямоугольная 195, 197, 387
— — сферическая 197
— - цилиндрическая 198
— линейных уравнений 161
— — — однородная, неоднородная 161
— — — треугольная 163
— программирования 525
— с распределенными параметрами 302
— счисления 130
— — двоичная 130
— — десятичная 130
— — позиционная (непозиционная) 130
— управления данными 526
— управляемая 298
— уравнений алгебраическая 150
Системы уравнений эквивалентные 161
Скаляр 386
Скалярное поле 391
— - осевое (цилиндрическое) 391
— — плоское 391
— — центральное (сферическое) 391
— произведение 155, 388
Скачок функции 221
Скобки Лагранжа 339
— Пуассона 339
Скрещивающиеся прямые 185
След матрицы 157
Сложная функция 225, 232
Слой шаровой 189
Случайная величина 444
— — дискретная 444
— — линейно коррелированная 451
— — непрерывная 445
— — характеристическая 444
— выборка объема 455
Случайные величины независимые 450
— — некоррелированные 450
542
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Случайные события 442
— — независимые 443
— — — в совокупности 443
— — — попарно 443
Случайный вектор 448
— — дискретный 448
— — непрерывный 449
Смешанная задача 343
— — для гиперболического
уравнения 343, 347
двумерного уравнения
теплопроводности 345
— производная 231
Смешанное произведение 388
Собственная функция 329, 351
Собственное значение 329, 351
— — матрицы 166
— — оператора 167, 351
— подпространство матрицы 166
Собственный вектор матрицы 166
— — оператора 167
Событие 441
— достоверное 441
— невозможное 441
— противоположное (дополнительное)
442
— элементарное 441
События независимые 443
— несовместные 442
— случайные 442
—, сумма, произведение 441
Совершенная дизъюнктивная
нормальная форма 379
— конъюнктивная нормальная форма
379
Совершенно упорядоченное множество
384
Совместная плотность 449
Совместное распределение 448
Соленоидальное поле 401
Соприкасающаяся плоскость 411
Сопровождающий трехгранник 411, 413
Сопряженные гиперболы 203
— диаметры 201, 202
— дифференциальные выражения 347
— комплексные числа 358
Состояние достижимое 298
— управляемое 298
Сочетание 138
— с повторением 138
Спираль Архимеда 128
— гиперболическая 128
— логарифмическая 128, 409
Сплайн-интерполяция 504
Сплайн-функция 504
Спрямляющая плоскость 411
Сравнимые (несравнимые) элементы
384
Среднее арифметическое 139, 212
— гармоническое 212
— i еометрическое 139, 212
— значение 506
— — измерений 521
— квадратическое отклонение 447, 448
— квадратичное 139
— пропорциональное 139
Средняя кривизна 415
— линия фапеции 184
— —'треугольника 183
— ошибка наблюдения 521
— — среднего 521
Стандартное отклонение 447, 448
Степенная функция 170, графики 114,
116, 117
Степенной метод 496
— ряд 279, 368
— — абсолютно сходящийся 280
всюду сходящийся 279, 368
— —, круг сходимости 368
— — равномерно сходящийся 280
— —, радиус сходимости 280, 368
, центр 279
Стереографическая проекция 360
Стохастическая зависимость 450
Стрелка Пирса 378
Строфоида 124
Сумма векторов 151, 387
— Дарбу (верхняя, нижняя) 238
— нормированная и центрированная 455
Сумма по модулю B) 378
— ряда 273
— чисел 210
Сумматор 524, 528
Супервизор 526
Суперпозиция отображений 385
— функций 217
Супремум 384
Существенно особая точка 369, 370
Сфера 189, 412
— Римана 360
Сферическая система координат 197
Сферические координаты 265, 393
— функции Бесселя 322
Сферический двуугольник 192
— избыток (эксцесс) 192, 194
— треугольник 192
Эйлера 192
Сферическое поле 392
Схема вычислений 530
— Горнера 517
— — полная 517
— спуска 502
Сходимость абсолютная 250, 276
— безусловная 277
— в основном 452
— по вероятности 453
— почти наверное 454
— равномерная 258, 272, 277
— ряда условная 276
— среднеквадратичная 418
Сходящаяся последовательность 214,
216
Сходящийся ряд 273, 367
Сцепленные матрицы 160
Сюръекция 385
Таблица значений функции 216, 223
— издержек 477
— интегралов 91 — 112
— истинности 376
— наблюденных значений 455
— обратного преобразования Лапласа
439-440
— производных 226
— разложений в ряд Фурье 420—423
— трансформант Фурье 427-436
Тангенс 174, график 118
— гиперболический 180
Тангенсоида 118
Тело 386
Теневая цена 474
Тензор деформаций 404
— дискриминантный 414
— кривизны Римана 417
— Леви-Чивита 414
— метрический 414
— напряжений 414
Тензорные поля на поверхности 412
Теорема Абеля 281
— альтернативная 330
— Аполлония 201
— Арцела — Асколи 279
— Бернулли 453
— Больцано — Вейерштрассд 213, 215
— Вейерштрасса 222, 501
— Виета 148, 149
— вычетов 370
— Гамильтона — Кэли 167
— Гаусса —Бонне 417
— — основная 417
— Гаусса —Остроградского 405
— Гульдена 1-я, 2-я 252, 253
— Дирихле 418
— единственности аналитических
функций 365
— — разложения в степенной ряд 282
— — степенных рядов 368
— Колмогорова 454
— косинусов 190, 192, 193
— Коши 222, 228, 277, 306
— Коши —Адамара 280
— — интегральная 366
— Коши - Ковалевской 332
— ЛагрЯнжа 228
— Лежандра 194
— Лиуви.ия 365
— Менье'416
Теорема Ньютона - Лейбница 241
— о дополняющей нежесткости 474
— — монодромии 371
— — неявных функциях 234, 235
промежуточном значении 222, 225
— — свертке 426, 437
— — среднем значении A-я, 2-я) 239
— — — — для двойных интегралов 261
— об умножении якобианов 234
— основная алгебры 148, 169, 361
— Пеано 306
— Пикара (большая) 369
— Пифагора 156
— половинного угла 190, 193
— половинной стороны 193
— разложения определителя 158
— Римана 277
об отображении 374
— Ролля 227
— синусов 190, 192
— Стокса 405
— тангенсов 190
— умножения для гамма-функций 260
— Хаара 294
— Чебышева 244, 453
— — об альтернансе 501
— Штурма 149
— Эйлера 188, 224
— Якоби 338
Теоремы двойственности в линейном
программировании 474
— о непрерывных функциях 221, 225
— о пределах функций 218
— о ранге 159
— о собственных значениях и
собственных векторах 167
— о числовых последовательностях 215
— предельные 453
— сложения 176, 181
Теория Гамильтона-Якоби 294
— Эйлера-Лагранжа 288
Терминал 524
Тест 524
Тетраэдр 188
Тождество Лагранжа 388
— Якоби 339
Тор 189, 252
Точка асимптотическая 409
— ветвления 373
— — логарифмическая 373
— возврата 408
— гиперболическая 416
— двойная 408
— излома 409
— изолированная 213, 408
— коническая 413
— кратности 409
— круговая 416
— перегиба 230, 407
— разрыва 220, 409
— — бесконечного 221
— — 1-го, 2-го рода 221
— самосоприкосновения 408
— эллиптическая 416
Точки общего положения 200
— сетки 515
Траектория 298, 390
Трактриса 123
Транзитивность 211, 383
Транслятор 525
Транспонированная матрица 157
Транспонированный определитель 158
Транспортная задача 477
— таблица 477
Транспортный метод 478, 479
Трансформанта Фурье 425
Трансцендентные уравнения 145, 150
— функции 117, 174
Трапеция 184
Треугольник 183
— Паскаля 134
— прямоугольный 183
— равнобедренный 183
— равносторонний 183
— сферический 192
— Эйлера 192
Тривиальное решение (системы
уравнений) 161
Тригонометрические уравнения 151
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
543
Тригонометрические функции 174
— —, разложение в ряд 88
Тригономефический многочлен 418,423
Трихотомия 383
Тройной интеграл 263
Трохоида 126
Угловой коэффициент прямой 199
Угловые условия Вейерштрасса —
Эрдмана 290
Угол двугранный 186
— между век юрами 155
— — кривыми 406, 414
— — плоскостью и прямой 186, 206
— — плоскостями 206
— - прямыми 200
— — скрещивающимися прямыми 185
— многогранный 186
—, радианное измерение 189
— смежности 407
— телесный 186
— трехгранный 186
Узел 311
Узлы 504
— равноотстоящие 504
Улитка Паскаля 124, 128
Уменьшаемое 210
Универсальная алгебра 385
Упорядоченная пара элементов 382
Упорядоченное множество 384
Упорядоченность 383
— линейная 384
— полная 384
— совершенная 384
— частичная 383
Упорядоченный набор 382
Управление 298
— допустимое 298
— оптимальное 299
Управляемая система 298
Уравнение 144
— алгебраическое 145
— Бернулли 308
— Бесселя 320
— биквадратное 148
— волновое 340, 348
— Гамильтона-Якоби 294, 338
— Гельмгольца 340, 350
— дифференциальное 305, 331
— диффузии 340
— касательной плоскости 413
— квадратное 145
— квазилинейное 331, 333
— Клеро 310
— колебаний 340
— кубическое 146
— Куммера 323
— Лагранжа 310
— Лапласа 294, 340, 352, 399
— Лежандра 323
— линейное 145, 305, 313, 331
— логарифмическое 151
— непрерывности 397
— нормали к поверхности 413
— первого приближения 312
— плоской кривой 123, 405
— плоскости 205, 389
— поверхности 412
— показательное 150
— прямой 199, 205, 389, 390
— Пуассона 295, 340
— -, дискретный аналог 514
— —, разностные методы 514
— распространения тепла 340, 344
— Риккати 308
— с параметрами 144
— телеграфное 348
— теплопроводности 340, 356
— трансцендентное 145, 150
— тригонометрическое 151
— Трикоми 340, 341, 342
— Эйлера 315
— Эйлера - Лагранжа 288, 292, 293
— Якоби 290
Уравнения высших степеней 148
— жви валентные 144
Уровень значимости 460
Усеченная пирамида 187
Усеченный конус 189
— цилиндр 188
Ускорение сходимости 517
Условие аппроксимации 513
— Вейерштрасса 290
— Вейерштрасса —Эрдмана 290
— Дирихле 418
— доминирования диагонали 494
— Лежандра 289, 290
— Липшица 223, 306
— трансверсальности 291, 300
— Якоби 290
Условия интегрируемости 256, 257,
417
— Коши —Римана
(Даламбера—Эйлера) 365
— периодичности 330
Условная сходимость 276
Условный экстремум 237
Устойчивое (неустойчивое) движение
326
Устойчивость в смысле Ляпунова 326
Устойчивый вычислительный'мегод 491
Устранимая особенность 369, 370
Устройства ввода и вывода 523
— управления 523
Фазовое пространство (пространство
состояний) 298
Фазовые координаты 298
Фазовый вектор 298
Файл 526
Факториал (и-факториал) 134
Фактор-множество 383
Фокальная кривая 333
— полоса 333
Фокальное свойство 200
Фокальный параметр кривой 2-го
порядка 201, 202, 204
Фокус 200, 201, 202, 312
—, особая точка 312
Форма Лагранжа 502
— Ньютона 502
Формула Байеса (формула вероятности
гипотез) 444
— Бесселя 505
— Вейнгартена 416
— Гаусса 260, 416, 505
— Гаусса —Лежандра 508
— Гаусса - Остроградского 270, 400,
405
— Гаусса — Чебышева 509
— Герона 191
— Грина 270, 328
первая, вторая 270, 350, 400, 401
— Кардано 146
— Кирхгофа 349
— косинусов 190
— Коши 260
— Лейбница 227
— Лиувилля 314
— — обобщенная 316
— Маклорена 228
— Муавра 176, 181, 359
— неявная 513
— Ньютона 505, 507
— Ньютона —Котеса 507
— Остроградского - Гаусса 270, 400,
405
— парабол 507
— полинома 135
— полной вероятности 444
— представления 347
— преобразования двойного интеграла
в криволинейный 401
— — объемного интеграла в
поверхностный 400
— — поверхностного интеграла в
криволинейный 401
— Пуассона 349, 355, 356
— Раабе 260
— Симпсона 507
— Оирлинга 134, 505
— Стокса 270
— тангенсов 190
— Тейпора 228, 233
— —, остаточный член (в форме
Лагранжа) 228, 233
Формула Тейлора функции ,ш>.\
переменных 233
— трапеций 507
— Уильера 194
— умножения Коши 277
— Эверегга 505
— Эйлера 358, 361, 416
Формулы Гамильтона 294
— Гаусса 416
— Даламбера (Гаусса) 193
— де Моргана 442
— конечных сумм 139
— Коши (интегральные) 367
— Майнарди — Кодацци 417
— Мольвейде 190
— порядка п 507
— приведения 175
— Серре — Френе 411
— среднего значения 506
— типа Рунге —Кутга 511
Фундаментальная система 314, 316, 513
Функции зависимые 234
— линейно зависимые (независимые) 313
Функционал 287
Функциональная зависимость 216, 223
— матрица 239
— последовательность 277
— шкала 518
Функциональный определитель
(якобиан) 233
— ряд 278, 368
Функция 216
— абсолютно непрерывная 222
— алгебры логики 377
— аналитическая 282, 365
— бесконечно большая'221
— - малая 221
— Бесселя 320, 436
— — модифицированная 321
— - 1-го, 2-го, 3-го рода 320
— — сферическая 322
— Вебера 320
— вероятности 414
— вогнутая 228
— возрастающая (убывающая) 222
— выбора 385
— выборки 456
— выпуклая 228
— - вверх (вниз) 228
— Гамильтона 294, 299, 338, 471
— Ганкеля 320
— гармоническая 352, 365
— гиперболическая 180, 181, 364
— гипергеометрическая 323
— голоморфная 365
— Грина 328, 355
— — задачи Дирихле 355
— двух переменных 223
, линии уровня 223
— — —, таблица значений 223
— действительная (вещественная) 113,
216, 223
— действительного переменного 113,
216, 223
— Дирихле 169
— дифференцируемая 225, 365
я раз 227
— дробно-рациональная 170, 217, 361
— Жуковского 373
— интегрируемая 238, 261, 263
— иррациональная 174
— истинности формулы 378
— комплексная (комплекснозначная)
360
— комплексного переменного 360
— Куммера 323
— кусочно непрерывная 221
— Лагранжа 237, 291, 292
— Лежандра присоединенная 324
— линейная 113, 170, 374
— логарифмическая 119, 179, 364
— Макдональда 321
— монотонная 222
— невозрастающая (неубывающая) 222
— Неймана 320
— непрерьюная 220, 224, 361
— — слева (справа) 220
— непрерывно дифференцируемая 230
— нескольких переменных 223
544
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Функция нескольких переменных
дифференцируемая 231
по^ 230
— — — непрерывная 224
ограниченная 223
— — — однородная 224
— — — равномерно непрерывная 224
сложная 225
— неявная 216, 223, 234, 235
— обратная 217
— ограниченная 217, 223
— ограниченной вариации 222
— оптимальных значений 484
— первообразная 240, 366
— периодическая 222
— показательная 119, 179, 361, 364
— полунепрерывная сверху (снизу)
222
— правдоподобия 458
— равномерно непрерывная 222, 224
— разрывная 220
— распределения 444, 448
— — интегральная 445
— — многомерная 448
— — эмпирическая 456
— рациональная 170, 217
— регулярная 365
— Римана 347
— сложная 217, 225
— сравнения 249, 271, 288
— степенная 170, 171
— строго возрастающая (убывающая)
222
— — выпуклая вверх (вниз) 228
— трансцендентная 174
— удовлетворяющая условию
Липшица 223, 306
— целая рациональная 169, 217, 361
— целевая 466
— цилиндрическая 320, 322
— четная (нечетная) 419
— шаровая 353
— ех 179
^-функция Вейерштрасса 290
Характеристика 333
— подстановки 136
Характеристики 340
Характеристическая кривая 333
— поверхность 341
— полоса 333
— система уравнений 333
— функция Гамильтона 294
— — случайной величины 451, 453
Характеристические линии 341
— направления 333
Характеристический конус 341
— многочлен матрицы 166
— — уравнения 315
Характеристическое многообразие 334
полос 335
— уравнение 311, 341
— — матрицы 166
Хорда 185
Целая рациональная функция
(многочлен) 169, 217, 361, график 113
— часть числа 169
Целевая функция 466
— — однопараметрическая'483
Целое рациональное выражение 141
Целочисленное линейное
программирование 486
Целые числа 211
Центр кривизны 407
— кривой 2-го порядка 200, 201, 202
-, особая точка 312
— симметрии кривой 2-го порядка 200
— тяжести 252, 257, 263, 265, 269
Центральное поле (сферическое) 391
Центральный процессор 524
Цепная линия 122, 129
Цепь 384
Цикл подстановки 137
Циклоида 125, 257
— удлиненная (укороченная) 126, 408
Цилиндр 188, 209
— гиперболический 209
— параболический 209
— прямой круговой 188, 209
— усеченный 188
— эллиптический 209
Цилиндрическая поверхность 188
— система координат 198
— труба 188
— функция 320, 322
— — порядка п 322
Цилиндрические координаты 265, 392
Цилиндрическое тело 264
Циркуляция векторного поля 398
Циссоида 123
Цифра 130
Частичная сумма ряда 273
— упорядоченность 383
Частичное произведение 285
Частичный предел 215
Частная производная 230
Частное 141, 210
Частные Релея 496
Часгота события 442
Чебышевский альтернанс 501
Четырехугольник 184
Числа Бернулли 86, 284
— Эйлера 87
Численно пригодное разложение в ряд
517
Численное дифференцирование 510
— преобразование к главным осям
495
— решение задачи 516
— — характеристического уравнения
495
Численные методы вычисления
функций 517
Числитель 210
Число действительное (вещественное)
210
— иррациональное 211
— комплексное 351
Число мнимое 351
— натуральное 211
— положительное (отрицательное) 2 И
— рациональное 130, 211
— целое 211
— е 11, 179, 215
— л 11, 185
Числовая последовательность 214
— прямая 211
Шар 189
Шаровая функция 353
Шаровой сегмент, сектор, слой 189
Широта 197
Штрих Шеффера 378
Эвольвента кривой (инволюта) 410
— окружности (развертка) 128
Эволюта кривой 410
Эйлеров интеграл 1-го, 2-го рода 260
Эквивалентные преобразования
уравнений 144
Эквиваленция 377, 378
Экспонента 179
Экспоненциальное распределение 446
Экстраполяция 502
Экстремаль 288
Экстремум функции 229, 236
— — локальный 229
— — условный 237
— функционала 288, 293
Эксцентриситет 200, 201, 202
Элементарная дизъюнкция 378
— конъюнкция 378
— формула 379
Элементарные (простейшие) дроби 172
— события 441
Эллипс 200, 201
Эллипсоид 207
— вращения вытянутый (сплющенный)
207
Эллиптическая точка 416
Эллигпический интеграл 67, 68, 245
— - в лежиндровой форме 245, 246
— — 1-х о, 2-1 о, 3-го рода 245
— — полный 108
— опера юр 343, 350
— параболоид 208
— цилиндр 209
Эллиптическое уравнение 340, 342, 35С
Эмпирическая дисперсия выборки 456
— ковариация 464
— функция распределения 456
Эмпирические прямые pei рессии 464
Эмпирический коэффициент корреляции
464
— — регрессии 464
Эмпирическое среднее выборки 456
Эпициклоида 126, 127
Ядро линейного преобразования 164
Язык управления заданиями 526
Якобиан 233