М. В. Козлов, А. В. Прохоров
ВВЕДЕНИЕ
В МАТЕМАТИЧЕСКУЮ
СТАТИСТИКУ
ИЗДАТЕЛЬСТВО
МОСКОВСКОГО
УНИВЕРСИТЕТА
1987

УДК 519
Козлов М. В., Прохоров А. В. Введение в математическую ствтнстику.—
М.: Изд-во МГУ, 1987. —264 с.
Книга предназначена для начального изучения математической статистики.
Основные понитни, задачи и методы математической статистики вводятся на
примере простых статистических моделей. Значительное внимание уделено, с од-
одной стороны, численным и графическим иллюстрациям, с другой — логическим
основам математической статистики.
Для студентов университетов, обучающихся по специальностям «Матема-
«Математика», «Прикладная математика», «Механика».
Библиогр. 26 иазв. Ил. 13.
Рецензенты:
академик А. И. Колмогоров,
д-р физ.-мат. наук Ю. Н. Тюрин
Печатается по постановлению
Редакцнонно-нздательского совета
Московского университета
Учебное издание
Михаил Васильевич Козлов,
Александр Владимирович Прохоров
ВВЕДЕНИЕ Б МАТЕМАТИЧЕСКУЮ СТАТИСТИКУ
Зав. редакцией С. И. Зеленский
Редакторы А. А. Локшич, Ф. И. Горобец
Технический редвктор Г. Д. Колоскова
Корректоры //. Л. Мушникова, 7. С. Ми.ичкова
ИБ № 2612
Сдвно в набор 05.06.86. Подписано к печати 05.02.87.
Л-62050 Форнат 60X90/16 Бумага тип. № 3
Гарннтурв литературная. Высокая печать
Усл. печ. л. 16,5 Уч.-изд. л. 17.04
Тираж 11000 экз. Звказ Ni 405
Цеиа 78 коп. Изд. № 4492
Ордена «Знак Почета» издательство Московского университета.
103009. Москва, ул. Герцена. 5/7.
Типография ордена «Знак Почета» изд-ва МГУ.
119899, Москвв, Ленинские горы
1702060000-076 1М_87 @ издательство Московского
077@2)—87 университета, 1987 г.

ОГЛАВЛЕНИЕ
Предисловве . . , , 6
Глава I. СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ: НАЧАЛЬ-
НАЧАЛЬНЫЕ ПОНЯТИЯ 8
§ I, Вероятность и частота 8
1. Введение. 2. Таблица случайных чисел. 3. Парадокс де Мере.
4. Общая вероятностная модель. 5. Закон больших чисел
§ 2. Эмпирическое распределение вероятностей • 15
1. Эмпирическое распределение дискретной случайной величины.
2. Эмпирическая функция распределении. 3. Статистика Колмогоро-
Колмогорова. 4. Выборочные среднее и дисперсии.
§ 3. Порядковые статистики и задачах оценивании 22
1. Порядковые статистики. 2. Оценивание содержимого урны.
3. Оценка параметра равномерного распределении. 4. Оценивание
параметра сдиига экспоненциального распределении. 5. Доверитель-
Доверительный интервал. 6. Выборочные квантили. 7. Равномерное распреде-
распределение. 8. Доверительные интервалы для квантилей. 9. Совместное
распределение пары порядковых статистик.
§ 4. Параметры сдвига и масштаба: графический анализ .... 31
1. Семейство сдвига-масштаба. 2. Вероятностная бумага. 3. При-
Примеры графического анализа.
§ 5. Экспоненциальное распределение и пуассоиовский процесс . . 36
1. Экспоненциальное распределение. 2. Пуассоновский процесс.
3. Условное распределение точек пуассоновского процесса. 4. При-
Пример.
§ 6. Оценивание параметров экспоненциального распределения ... 44
1. Оценивание параметра сдвига при известном параметре масшта-
масштаба. 2. Оценивание параметра масштаба при известном параметре
сдвига. 3. Точечные оценки ц и о. 4. Распределение интервалов
между порядковыми статистиками. 5. Дисперсии несмещенных оце-
оценок ц*. о*; интериальиое оценивание ц, о. 6. Оценивание по пер-
первым г порядковым статистикам.
§ 7. Свеленяя о иажнейших непрерывных распределениях в /?'... 51
1. Гамма-распределение. 2. Экспоненциальное распределение. 3. Нор-
Нормальное распределение. 4. Распределение ха с я степенями свобо-
свободы. 5. Бета-распределение. 6. Равномерное распределение. 7. Распре-
Распределение Фишера, или /^-распределение. 8. Распределение Стьюдента,
или /-распределение.
§ 8. Нормальное распределение: оценивание параметроп, сравнение
двух выборок 58
1. Доверительные оценки для ц и о2, когда один нз параметров
известен. 2. Несмещенная оценка дисперсии. 3. Доверительные ин-
интервалы для ц я о2, когда оба napu.veipa неизвестно;. 4. Сравнокп?
дисперсии в двух выборках. 5. Задача сравнения средних ц, и ц?.
6. Пример.
Глава II. ЛИНЕЙНАЯ СТАТИСТИЧЕСКАЯ МОДЕЛЬ ... 69
§ 9. Оценивание коэффициентов линейной модели 69
1. Введение. 2. Примеры линейных моделей. 3. Линейная статисти-
статистическая модель. 4. Несмещенные оценки с минимальной дисперсией:
3

матрица полного ранга. 5. Наилучшие оценки в случае матрицы
неполного ранга. 6. Пример: модель с матрицей' неполного ранга.
7. Наилучшие оценки как оценки наименьших квадратов
§ 10. Ковариации, канонвческаи форма линейной модели, обобщении 80
I. Матрицы из случайных элементов. 2. Матрица ковариации.
3. Ковариации наилучших оценок. 4. Пример оптимального выбора
матрицы модели. 5. Каноническая форма линейной модели. 6. Оце-
Оценивание дисперсии. 7. Обобщенней лннейнаи модель
§11. Поридковые линейные оценки дли параметров сдвига и масштаба 89>
1. Обобщенная, линейная модель для семейства сдвига-масштаба.
2. Наилучшие несмещенные оценки. Э. Симметричное распределение.
4. Пример: равномерное распределение иа интервале (ц, ц+а).
5. Пример: экспоненциальное распределение. 6. Пример: нормальное
распределение. 7. Цензурироваинаи выборка. 8. Упрощенные ли-
линейные оценки.
§ 12, Многомерное нормальное распределение . . , . . . . '01
1. Невырожденное нормальное распределение. 2. Случайные векто-
векторы с вырожденной матрицей ковариации. 3. Вырожденное нормаль-
нормальное распределение. 4. Распределение проекций стандартного нор-
нормального вектора.
§ 13. Доверительное оценивание и проверка гипотез в линейной модели
с нормальными наблюдениями . . ........ 109
1. Распределение вектора оценок. 2. Доверительнме области для
параметров и параметрических функций. 3. Проверка гипотез с по-
помощью доверительных эллипсоидов. 4. Пример: сравнение средних
в нескольких нормальных выборках.
Глава III. ДОСТАТОЧНЫЕ СТАТИСТИКИ 116
§ 14. Статистическая модель, подобные статистики , 116
1. Статистическая модель. 2. Подобные статистики.
§ 15. Достаточные статистики в двскретной модели 120-
I. Введение. 2. Примеры. 3. Достаточные статистики: определенве.
4. Критерий достаточности. 5. Достаточные и минимальные доста-
точвые разбиения.
§ 16, Достаточные статистики в непрерывной модели Ш
1. Примеры достаточных статистик. 2. Определение достаточной
статистики, теорема факторизации. 3. Экспоненциальные семейства,
минимальная достаточность.
§ 17. Достаточность и несмещенное оценивание ........ 152
1. Полные достаточные статистики. 2. Наилучшие несмещенные
оценки в дискретной модели. 3. Наилучшие несмещенные оценки в
непрерывной модели.
§ 18. Информации в статистике 168
I. Байесовский подход в статистике. 2. Информация по Шеннону.
3. Информации по Кульбаку. 4. Информация по Фишеру.
§ 19. Неравенство Фреше—Рас—Крамера , г 185
1. Скалярный параметр. 2. Векторный параметр. 3. Границы дис-
дисперсии при нарушении условий регулярности.
Глава IV. ПРАВДОПОДОБИЕ 198
§ 20. Метод максимума правдоподобия 198
1. Функцнк правдоподобик. 2. Оценки максимального правдоподо-
правдоподобии. 3. Метод Монте-Карло в модели сдвига-масштаба.
§ 21. Критерий отношении правдоподобий 211
1. Проверка статистических гипотез. 2. Лемма Неймана—Пирсона.
3. Примеры. Равномерно наиболее мощные критерии. 4. Близкие ги-
гипотезы, б, Сложные гипотезы,
4

§ 22. Последовательный критерий отношения правдоподобий . . . 226
1. Метод последовательного статистического анализа. 2. Последо-
Последовательный критерий отношения правдоподобий. 3. Среднее число
наблюдений в последовательном критерии.
Глава V. БОЛЬШИЕ ВЫБОРКИ 235
§ 23, Асимптотические свойства оценок 235
1. Состоятельность. 2. Состоятельность оценок максимального прав-
правдоподобии. 3. Асимптотическая нормальность. 4, Преобразонание
статистик. 5. Асимптотическая нормальность выборочных квантилей.
6. Асимптотическая нормальность оценок максимума правдоподобия.
7. Асимптотическая эффективность оценок максимума правдоподо-
правдоподобия. 8. Асимптотическая достаточность. 9. Векторный параметр,
10. Оценинание параметров сдвига и масштаба.
§ 24. Асимптотические свойстна критерия отношения правдоподобий . 256
1. Скалярный параметр. 2. Векторный параметр, 3. Полиномиальное
распределение.
Литература ................ 264

ПРЕДИСЛОВИЕ
По замыслу авторов книга должна служить учебным посо-
пособием для студентов-математиков, знакомых с элементами теории
вероятностей в объеме семестрового курса. Она написана на ос-
основе курсов, читавшихся авторами для студентов механико-мате-
механико-математического факультета Московского университета, специализи-
специализирующихся в области теории вероятностей и математической ста-
статистики.
Среди книг, рассчитанных на первоначальное изучение пред-
предмета, особое место занимают классические труды Г. Крамера
[20] и Б. Л. Ван дер Вардена [10]. Написанные более 30 лет
назад и воспитавшие поколения вероятностников, они пользуются
заслуженным авторитетом и сейчас. Элементы математической
статистики являются составной частью общих курсов по теории
вероятностей, среди которых следует назвать учебники Б. В. Гне-
денко [17], Ю. А. Розанова [18], Б. А. Севастьянова [19],
В. Н. Тутубалина [21]. Недавно изданное учебное пособие по ма-
математической статистике А. А. Боровкова [12] рассчитано на
студентов старших курсов и аспирантов. Отметим также учебник
для вузов Г. И. Ивченко, Ю. И. Медведева [22]. При работе над
книгой авторы использовали методические достижения отечест-
отечественной н зарубежной литературы по математической статистике,
а также опыт и традиции преподавания вероятностных дисцип-
дисциплин на механико-математическом факультете и факультете вы-
вычислительной математики н кибернетики Московского универси-
университета. Особо отметим работу Д. Кокса, Д. Хинкли [14], а также
уже упоминавшуюся книгу Б. Л. Ван дер Вардена, логическая
ясность, простота изложения и отчетливое представление при-
прикладной стороны предмета в которой служили нам образцом.
Книга начинается со знакомства с некоторыми основопола-
основополагающими понятиями математической статистики на примере про-
простейших статистических моделей (гл. I, II). Значительное внима-
внимание уделяется здесь числовым н графическим иллюстрациям, то-
тогда как логика предмета отнесена на второй план. Достаточно де-
детально изучается линейная статистическая модель. Эта модель,
во-первых, служит хорошим источником материала для педагоги-
педагогической практики, во-вторых, открывает подход к теоретическим и
прикладным аспектам регрессионного и дисперсионного анализа.
В настоящей книге линейная модель должна еще и подготовить

читателя к восприятию теоретических основ статистики, которым
уделяется серьезное внимание в последующих разделах.
Вопросам использования информации, содержащейся в стати-
статистических данных, для построения статистических выводов и
формализации самого понятия информации в статистике посвя-
посвящена гл. III, содержащая разделы: достаточность, несмещенное
оценивание, информация в статистике, нижние границы дисперсии
оценок. Гл. IV объединяет некоторые приемы построения стати-
статистических оценок и критериев, основанных иа понятии правдопо-
правдоподобия. Гл. V посвящена асимптотическим свойствам оценок мак-
максимального правдоподобия и критерия отношения правдопо-
правдоподобий.
Ограниченный объем книги не позволил включить некоторые
важные статистические процедуры и затронуть другие разделы
современной математической статистики. Вместо этого авторы
более детально, с большим количеством примеров и повышенным
вниманием к логической стороне вопроса разобрали такие фун-
фундаментальные понятия статистики, как статистическая модель,
достаточность, правдоподобие. Авторы надеются, что тщательная
проработка материала книги поможет читателю самостоятельно
разобрать темы, затронутые нами лишь частично, по другим ис-
источникам, среди которых мы выделим капитальный труд
М. Дж. Кеидалла, А. Стьюарта [24—26]. Библиографический
список в конце книги включает в основном издания иа русском
языке и ии в какой мере ие претендует иа полиоту.
Авторы пользуются возможностью выразить благодарность
своим учителям и коллегам — сотрудникам кафедры теории веро-
вероятностей и кафедры математической статистики и случайных про-
процессов механико-математического факультета МГУ. Авторы бла-
благодарны сотрудникам факультета Н. Н. Марчук, Т. В. Нистрато-
Нистратовой, Т. В. Козьмииой, О. Б. Фисунеико, а также студентам и
аспирантам кафедры математической статистики и случайных
процессов за помощь в оформлении рукописи. Рассматривая кни-
книгу как очередиой шаг в разработке методики преподавания ма-
математической статистики, авторы отдают себе ясный отчет в не-
несовершенстве своего труда и будут благодарны всем, кто выска-
выскажет свои замечания и предложения.
М. В. Козлов, А. В. Прохоров

ГЛАВА I
СТАТИСТИЧЕСКИЕ МОДЕЛИ И МЕТОДЫ:
НАЧАЛЬНЫЕ ПОНЯТИЯ
§ 1. ВЕРОЯТНОСТЬ И ЧАСТОТА
1. Введение.
Процесс познания окружающего мира включает наблюдение и
эксперимент. Результаты наблюдений во многих случаях можно
представить последовательностью действительных чисел
Для того чтобы из ряда наблюдений можно было извлечь по*
лезную информацию, необходимо иметь модель явления. Вероят-
Вероятностные модели оказываются чрезвычайно плодотворными при
анализе явлений, исходы хеЯ? которых обладают некоторой сте-
степенью неопределенности. Понятие неопределенности в теории ве-
вероятностей формализуется путем введения распределения веро-
вероятностей на множестве % всех возможных наблюдений х. В про-
простейшем случае, когда Я? —конечное или счетное множество, за-
задаются вероятности р(х) всех его элементов х, так что О^()^
<1 и
Любое подмножество Л=Я? называют в этом случае событием, а
его вероятность определяют формулой
Пример 1 (случайный выбор с возвращением). Представим
себе урну с N шарами, занумерованными числами от 0 до N — 1,
и рассмотрим опыт, который заключается в n-кратном извлечении
шара «наугад» с последующим его возвращением в урну. Все
возможные неходы опыта могут быть представлены множеством
из Nn последовательностей:
Я?={х=(х, х»):х,=0,.1 N—1; i=l п).
На 9В задается равномерное распределение вероятностей: р(х) =
8

¦=ЛМ» для всех хеЯ?, что отражает равную степень неопределен-
неопределенности каждого возможного нехода.
Пример 2 (случайный выбор без возвращения). Если из
урны с N шарами последовательно извлекаются «наугад» п ша-
шаров без возвращения, n<N, то возможные исходы описываются
множеством нз N(N— 1)... (N — n+l)=Nl/(N — n)\ последова-
последовательностей:
Я?={х= (хи х2,• • •,хп) :дс<=0, \,...N—\, ХгФх}
при
1ФГ, i,/=l л},
а распределение вероятностей на Я?_ снова равномерное: для лю-
любого х
Взаимоотношение явления и его вероятностной модели имеет
статистический характер, т. е. обнаруживается при повторных
наблюдениях за явлением. Частоты исходов в длинном ряду ис-
испытаний стабилизируются, их колебания с ростом числа испыта-
испытаний уменьшаются. Этот эмпирический факт, называемый зако-
законом устойчивости частот, наблюдается в самых различных ситуа-
ситуациях. Уже выходя за пределы реального опыта, полагают, что
при неограниченном повторении частоты стремятся к пределам,
которые и принимают за вероятности соответствующих исходов
или событий.
2. Таблица случайных чисел.
Обратимся к табл. 7.1, а книги Л. Н. Большее а н Н. В. Смир-
Смирнова [1], содержащей 12500 «случайных цифр», которые можно
представлять себе как реализацию опыта, описанного в приме-
примере 1 при N=10, л =12500. Проследим за изменчивостью частот
появления цифры «0» с ростом числа наблюдений. Для облегче-
облегчения анализа сгруппируем первые 100 цифр таблицы (считывае-
(считываемой по строкам) по 10 цифр, последующие 900 —по 100 цифр,
следующие 9000 — по 1000. Наблюдаемые числа и частоты нулей
по группам и суммарно собраны в табл. 1.
Нетрудно подметить, глядя на последний столбец таблицы 1,
что колебания частоты т/п с ростом п затухают.
3. Парадокс де Мере.
Рассмотрим задачу, которая, как утверждают, возникла за
игорным столом и была предложена в 1654 г. Паскалю. Игрок де
Мере полагал, что вероятность р\ получить хотя бы одну едини-
единицу при бросании четырех игральных костей (событие А) меньше
вероятности рг выпадения одновременно двух единиц хотя бы
раз при 24 бросаниях двух костей (событие В), и ставил в игре на
событие В.
SL

Таблица 1
Колебание частоты появления нуля в 10000 случайных цифр
Число ваблю-
девай в группе
10
10
10
10
10
10
10
10
10
10
100
100
100
100
100
100
100
100
100
1000
1000
1000
1000
1000
1000
1000
1000
1000
Чвсло нулей
в группе
2
1
0
2
0
2
0
2
3
2
14
9
13
8
16
14
6
9
8
97
106
99
91
97
91
100
117
89
Частота нулей
в группе
0,2
0,1
0,0
0,2
0.0
0,2
о.о
0,2
03
0,2
0,14
0,09
0,13
0,08
0,16
0,14
0,06
0,09
0,08
0,097
0,106
0,099
0,091
0,097
0,091
0,100
0,117
0,89
Накопленное
число наблю-
наблюдений, п
10
20
30
40
50
60
70
80
90
100
200
300
400
500
600
700
800
900
1000
2000
3000
4000
5000
6000
7000
8000
9000
10000
Накопленное
чнсло нулей, т
2
3
3
5
5
7
7
9
12
14
28
37
50
58
74
88
94
103
111
208
314
413
504
601
692
792
909
998
Накопленная час-
частота нулей, т/п
0,2
0,15
0,10
0,15
0,16
0,116
0,100
0,112
0,133
0,140
0,140
0,123
0,125
0,116
0,123
0,125
0,117
0,114
0,1110
0,1040
0,1046
0,1032
0,1008
0,1001
0,0988
0,0990
0,1010
0,0998
Однако эти вероятности легко вычисляются:
Р(А) =pi = l — E/6L=0,5177..., Р(В) =р2= 1 — C5/36J4=
=0,4914...
Поскольку де Мере не были доступны эти вычисления, то свои
заключения он мог бы основывать на опытных данных. Предста-
Представим себе, что опыт с бросанием четырех игральных костей и опыт
из 24 бросаний двух игральных костей повторяются п раз. Ре-
Результат t-ro испытания, t=l, 2, ..., п, опишем парой (xt, yi), по-
полагая Xi=\ A/1=1), если произошло событие А E), и полагая
# = 0 (t/i=0), если событие А (В) не произошло. Обозначим через
l=\
Естественный вопрос заключается в том, насколько основатель-
основательным является сравнение вероятностей р\ и рг по их частотам
10

ninin и n&jn. Ниже приводятся результаты
игры с помощью таблицы случайных цифр из [1].
моделирования
л
mW „in
mm п/п
25
0,68
0,52
50
0,54
0,50
100
0,53
0,48
250
0,488
0,508
Как видно, хотя Р\>р2, но при п=250 нам «не повезло» —
trfnln < т®/п. Остановив «игру» на этом п, мы могли бы сделать
ошибочное заключение, что pi<p2.
В теории описанному опыту соответствуют две независимые
последовательности испытаний Бернулли с вероятностями поло-
положительного исхода («успеха») в одном случае р\, в другом — р2.
Введем случайные величины (ел. в.) v, и v2, равные числу успе-
успехов в каждой из этих последовательностей.
Вероятность события {vi<v2} для больших п рассчитаем при-
приближенно, пользуясь теоремой Муавра—Лапласа. Сл. в.
vl = (vi—npi)/ynpiqi, q
l—pi, 1=1, 2,
A)
независимы и приближенно нормально распределены с нулевым
математическим ожиданием и единичной дисперсией. Неравенство
vi<v2 после подстановки в него A) запишем в виде
Так как разность независимых нормальных сл. в. распределена
нормально, то левая часть B) при больших п имеет распределе-
распределение, близкое к нормальному, с математическим ожиданием и дне-
персней, равными
i-o—Угш-о=о
M (VPtfi vl — УШг У») =
Таким образом, имеем приближенное равенство (обозначе-
1 + №
= 1.
ние
—ft)+Q.5
11

функция распределения стандартного нормального закона, а сла-
слагаемое 0,5 — поправка на дискретность. Используя таблицу нор-
нормального распределения, для различных п получаем
п
P(v»<vt)
25
0,42
50
0,39
100
0,35
250
0,18
1000
0,12
Итак, даже при я =1000 приблизительно 12 шансов из 100 за то,
что vi окажется меньше V2 и будет сделан неправильный вывод,
что рх<ръ
4. Общая вероятностная модель.
В современной теории вероятностей под вероятностной мо-
моделью понимают тройку объектов (Q, s4, ff>), называемую веро-
вероятностным пространством. Здесь Q — некоторое множество, эле-
элементы которого со называются элементарными событиями, st—
система подмножество множества Q, называемых событиями, & —
вероятностная функция, ставящая в соответствие каждому собы-
событию А число 9*(А), 0<^(Л)а^1, называемое его вероятностью.
В соответствии с аксиоматикой Колмогорова требуется, чтобы
система событий была замкнута относительно перехода к допол-
дополнению и конечному или счетному объединению:
, i=\, 2, ...
а также содержала все Q: Q&s? и притом &(Q) = l (легко ви-
видеть, что конечное или счетное пересечение событий также яв-
является событием); вероятностная мера & должна обладать свой-
свойством счетной аддитивности: если Aif[Aj=0 при 1ф\% то
где индекс i пробегает конечное или счетное множество.
Вероятностная модель явления ставит в соответствие резуль-
результатам наблюдений
Xl, X2,...,Xn C)
последовательность случайных величин (ел. в.)—функций на Q:
*i(<o), X2(<o) *„(©). D)
Полагают, что наблюдения C) являются значениями величин D)
при осуществлении ш. Несмотря на различие объектов C) и D),
в математической статистике принято называть и то и другое
12

выборкой. Статистическим закономерностям числовых данных ре-
реального эксперимента C) отвечают вероятностные утверждения
для случайных величин D).
5. Закон больших чисел.
Табл. 1 составлена по результатам испытаний, порождающих
последовательность «случайных» цифр. Здесь х<е{0, 1, 2,...,9},
Xi(<u) — независимые ел. в., принимающие значения 0, 1, 2,...,9
с равными вероятностями />=1/10. Обозначим через т» число
появлений цифры 0 в первых п испытаниях. Анализ последнего
столбца 1 привел нас к заключению, что частота нуля тп/п с
ростом п совершает затухающие колебания вблизи 1/10. Это —
выражение эмпирического закона устойчивости частот. Соответ-
Соответствующее математическое утверждение — закон больших чисел
C. Б. Ч) для ел. в. Х{. Введем индикаторную ел. в.
'{x,w»=o
I, если Xi (©) = 0,
), если Х<(©)^0,
i=i
Тогда 3.Б.Ч. в усиленной форме выражается соотношением
?* (limvJn=p) = 1.
Л-мо
Для практических целей полезно иметь оценки вероятностей
0>(\vjn-p\<6)
при конечных п. Это можно сделать, используя распределение
вероятностей величины vn:
&>(Vn=m) =Cnmpm(\ — р)п-"\ т=0, 1, 2,.... га, E)
где р=1/10. Для /t=10 расчет по формуле E) дает следующие
значения (см. табл. 5.1 биномиального распределения в [1]):
т
SF (vn < m)
0
0,3486
0,3486
0
0
1
,3874
,7360
2
0.1937
0,9297
3
0,574
0,9871
0
0
4
,0111
,9982
5
0,0014
0,9997
0
0
6
,0001
,9998
При п=100 иепосредственные вычисления по формуле E) не-
нецелесообразны. Хорошее приближение к биномиальному распре-
13

делению E) дает в этом случае распределение Пуассона:
^1m = 0) 1,2
от!
где Л=я/?=10. По табл. 5.3 пуассоновского распределения в [1]
находнм приближенные значения вероятностей
PI
1
0,3639
2
0,5711
3
0,7340
4
0,8490
5
0,9215
6
0,9620
7
0,9822
8
0,9914
При л =1000 для расчета E) надо воспользоваться нормаль-
нормальным приближением
х
( "пгпр <х\ ^ ф(х)= 1 С
\ -/npq ) /2я J
Выпишем для нескольких значений х приближенные значения ве-
вероятностей
из таблицы значений функцни нормального распределення:
X
Рх
1
0,6827
2
0,9545
2,6
0,9916
3
0,9973
Подведем итог приведенным расчетам в форме следующего
соотношения:
^4|vn/n — 0,1 |>6)sa;= 0,01, F)
где при л =10 следует брать 6=0,3; при л=100 —6=0,08; при
„=1000-6=0,025.
Статистический смысл неравенства F) выясняется при много-
многократном повторении опыта, порождающего п случайных цифр.
Допустим, результаты большого числа N таких опытов представ-
представлены последовательностями
х?, 4Л xf, /=1, 2 N,
G)
и пусть mf— число нулей в G). Обозначим через Mt число
тех последовательностей G), для которых выполнено неравенство
|т^/л-р|<6.
14

Тогда имеет место приближенное равенство
MJN?s\— о,
выражающее закон устойчивости частот в примеиении к событию
f 2. ЭМПИРИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЯ
1. Эмпирическое распределение дискретной случайной велн-
Предположим сначала, что X дискретна и принимает значения
а, Ь, с,... с. вероятностями
Р(в), р(Ь), р(с)
По ряду наблюдений
Xi, Х2,..,Хп A)
вычисляем частоты р(х)=тн(хIп исходов х=а, Ь, с,.... Набор
частот
{р(а), /)(&)....} B)
представляет собой дискретное распределение вероятностей:
его называют эмпирическим распределением (э. р.), отвечающим
наблюдениям A). Э.р. B) является оценкой теоретического рас-
распределения ел. в. X:
{р{а),р(Ь)....). C)
Пример 1. Пусть теоретическое распределение — биноми-
биномиальное:
p(/)=C»ipi(l—p)*-i, /=0, 1 ft. D)
Смоделируем выборку объема л-40 из распределения D) с па-
параметрами А=250, р=0,1, объединяя первые 10000 случайных
цифр из [1] в л=40 групп по 250 цифр и подсчитывая число Xi
нулоП в i-й группе, i—1, 2 40. Результаты представлены ниже:
32
30
25
30
26
26
21
2S
31
22
24
24
22
18
27
31
31
29
31
32
13
30
24
30
25
19
19
22
28
24
17
24
24
23
17
23
26
25
28
20
Эмпирическое и теоретическое распределения представлены в
табл. 2.
15

Таблица 2
Вероятности р (/) = С^р'A—/>)*->;
А — 250: р = 0,1 и их оценки р (/)
по выборке объема л = 40
/
<13
13
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
>32
0,0
0,025
0,05
0,025
0,05
0,025
0,025
0,075
0,05
0,15
0,1
0,075
0,025
0,05
0,025
0,1
0,1
0.05
0,0
рA)
0,0019
@,003)
0,020
0,028
0,038
0,048
0,059
0,068
0,076
0,081
0,083
0,081
0,076
0,068
0,059
0,048
0,038
0,028
Таблица 3
Эмпирическая и теоретическая функции
распределения 7*(х), F(x) для выборки
из биномиального распределения;
b{x)=\F(x)-F{x)\
X
13
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
0,025
0,075
0.1
0,15
0,175
0,2
0,275
0,325
0,475
0,575
0,65
0,675
0,725
0,75
0,85
0,95
1
0,01
0,05
0,07
0,10
0,15
0,21
0,27
0.34
0,42
0,5
0,58
0,66
0.73
0,79
0,85
0,89
0,92
Д (О
0,015
0,025
0,03
0,04
0.025
0,01
0,005
0,015
0,055
0.075
0,07
0,015
0,005
0,04
0,00
0,06
0,08
Теоретическое распределение рассчитано приближенно с
мощью локальной предельной теоремы Муавра—Лапласа:
по-
Ф(*) =
/2S'
E)
значение рA3) вычислено непосредственно по формуле D)
(в скобках указано приближенное значение по формуле E)).
Как видно из табл. 2, относительная погрешность оценки
в интервале 17</<32 достигает 150%. Очевидно, для хорошей
оценки распределения C) необходимо, чтобы доля наблюдений,
приходящихся на каждую из представляющих интерес вероятно-
вероятностей, была достаточно велика. Этого можно добиться группиров-
группировкой, оценивая вероятности не отдельных значений, а группы зна-
значений.
С теоретической* точки зрения намного более полезным яв-
является представление эмпирической информации в виде функции
распределения (ф. р.)
?
/«?*
16

В табл. 3 и на рис. 1 проводится
сравнение F(x) с F(x)=9t(X<.
<х), рассчитанной с помощью
интегральной теоремы Муавра —
Лапласа.
Абсолютная погрешность
Д(х) = \F(x)—F(x) | достигает
0,08 при 13<х<32, а относитель-
относительная погрешность [b(x)/F(x)]X
Х100% при 17<х<32 не превос-
превосходит 40%.
2. Эмпирическая функция рас-
распределения.
12 Я 16 18 20 22 24 26 28 30 3234
Рис. 1. Эмпирическая функция рас-
распределения выборки нз биномиаль-
биномиального распределения р(/)=С^р'A—
р)*-), *=250; р=0,1 н ее нор-
нормальное приближение
Распределение вероятностей
произвольной случайной величи-
величины X характеризуют функцией
распределения (ф.p.) F(x). При
фиксированном х F(x) определяется как вероятность события
{¦?<*}, и ее можно оценить частотой этого события в ряду на-
наблюдений A). Соответствующую частоту принято обозначать
Fn(x). Иногда желательно отметить в обозначениях зависимость
Fn(x) отх=(хих2,...,хп\:
/VI*) =рп(х; хи х*,...,хп) =Fn(x; х).
Используя индикаторы, получаем следующую формулу:
(/д=1| если утверждение А истинно, и /а=0- в противном
случае).
Функция Fn(x), так, как она определена, есть функция рас-
распределения дискретной ел.в., принимающей значения Х\, *2.•••
..., хп с вероятностью 1/л (если какие-то k из Xi совпадают меж-
между собой, то их общему значению приписывается вероятность
kin), и ее называют эмпирической функцией распределения
(э. ф. р.).
Перейдем к вероятностной модели повторных испытаний —
последов ательности
Х\, Лг.• • -,Xn F)
независимых ел.в. с одинаковой ф. p. F(x). В математической
статистике принято употреблять одни и те же термины для ха-
характеристик последовательности ел. в. F) и принятых ими в ре-
17

зультате опыта значений A). В частности,
х,<х}, Х-=(Х} Хп).
также называют э. ф. р. Подчеркнем, что Fn(x; X) при каждом
фиксированном х— случайная величина. Так как
NlFn(x; X)=-±r
то из неравенства Чебышева получаем следующую оценку для
отклонения Fn{x) от F(x):
?an\Fn(x; X)-F(x)\>t)^F(x)(l-F(x))t-*. G)
Лучшую оценку для вероятности в левой части соотношения G)
при больших л можно получить применением интегральной тео-
теоремы Муавра—Лапласа:
*(V7\Fa{x; X)-F(x)\>t)*52(\-ib[t/)fF(x)(l-F(x)))). (8)
Заметим, что правые части G) и (8) зависят от величины F(x),
которую мы как раз и пытаемся оценить по результатам наблю-
наблюдений. Заменяя F(x)(l— F(x)) ее наибольшим возможным зна-
значением 1/4, эту зависимость мы устраним, но ценой огрубления
оценки.
3. Статистика Колмогорова.
Рассмотрим следующую меру расхождения э. ф. р. и теорети-
теоретической ф. р.
называемую статистикой Колмогорова.
Лемма. Распределение вероятностей ел. в. DV(X) не зависит
от ф. p. F{x)=&>(XjS^.x), если только F{x)—непрерывна.
Доказательство. Мы покажем, что распределение ел. в.
?>„(Х) совпадает с распределением D,,{\), где Y= (У.,..., Y,,) —
вектор из независимых равномерно распределенных на [0, 1]
ел. в. Предположим вначале, что F(x) строго монотонная и
F~l(y)—обратная к ней функция. Случайные величины У< =
=/-"(А",) иезазкенмы, л их общая ф. р. при 0<г/<1 равна
18

т. е. Yi равномерно распределена на [0,1]. Для э. ф.р.
Rn(y,V), У=(Уи -.., Yn),
имеем при 0<у<1
/I
Отсюда получаем
sup \Fn(x; X)-F(a)|- sup \Fn(F-l(y); X)-
<F(x)<l 0<tf<l
p \
x:0<F(x)<l
-F{F-l(y))\ - sup \Rri(y; \)-y\. (9)
0<y<\
Остается заметить, что в точках ,v, где F(.v)=0 или F(a-) = 1, с
вероятностью 1 Fn(x; \)=F(x), а войду монотонности Fn a F по
х также и sup \Fn(x; X) — F(x)\ по множеству всех таких х ра-
равен 0. Таким образом, правая и левая части соотношения (9) с
вероятностью единица равны Dn(\) и Dn(\) соответственно.
Следовательно, распределение Dn(X) для ел.в. X, распределен-
распределенных по закону F(x), совпадает с распределением Dn(\[) для ел.в.
Y, распределенных равномерно на отрезке [0,1].
Если F(x) не обязательно строго монотонна, то положим при
0<у<1
F-*(y)=s\ip{x:F(x)=y}.
Заметив, что супремум достигается ввиду непрерывности F{x) и
что поэтому при 0<у<1
нетрудно обнаружить, что проведенные выше рассуждения для
случая строго монотонной F{x) сохраняются без изменения и
для общего случая. ¦
Практическое значение доказанной леммы заключается в том,
что можно выбрать распределение вероятностей F(x) из сообра-
соображений наибольшей простоты численного расчета вероятностей
9>(Dn>6)=a и табулировать набор значений (п, б, а). Напри-
Например, если взять F(x)=sR(x)=x, O^jf^l, то расчеты сводятся к
вычислению объема «-мерной области, высекаемой в единичном
кубе условием
sup |/?„(*; xv хг *„)— jf|>6.
<<l
Как бы трудоемки ни оказались вычисления, но, проделав их
однажды, мы обеспечиваем возможность в случае любой непре-
19

рывноГ| ф. p. F(x) указать а и 6 такие, что при данном п выпол-
выполнено соотношение
n(x; X)— .F(jc)|>6)=a.
A0)
Иначе говоря, полоса Fn(x; Х)±б, —оо<х< + оо, ширины 2в
с границами, строящимися по выборке, с вероятностью 1—а за-
заключает внутри себя неизвестную ф. p. F(x).
Таблицы для значений п= 1A) 100 (от 1 до 100 с шагом 1) и
а=0,01; 0,02; 0,05; 0,1; 0,2 приведены в [1].
Пример 1 (продолжение). Для биномиальной ел. в. X с
параметрами fe = 250, р = 0,1, п = 40 нормированную ел. в. Х* =
= (X— kp)/l/kp(\—р) можно в силу теоремы Муавра—Лапласа
с известной степенью приближения считать распределенной по
нормальному закону с параметрами 0 и 1. Учитывая сказанное,
можно полагать, что для X* соотношение A0) будет выполняться
с некоторой небольшой погрешностью. Выпишем из табл. 6.2 [1]
несколько пар значений а, б, для которых ^(ZLo>6) =а:
(П)
Из рис. 1 и табл. 3 с учетом равенства
sup|Fn{х; х*)-Ф(х)| = sup |Fn(х; х)-Ф((*-kp)lVkp(\-p))\,
Ж
A
б
0,2
0,16547
0,1
0,18913
0,05
0,21012
0,02
0,23194
0,01
0,25205
находим Dn=0,095. Полученное отклонение надо рассматривать
как умеренное, если взглянуть на A1), откуда вытекает, что от-
отклонение на большую величину 0,165 и то происходит в средней
в одном случае из пяти. Н
А. Н. Колмогоровым было найдено предельное распределение
статистики Dn при и->-оо:
< у) =
, У>0,
к(У)= f; (-
Ряд для К (у) быстро сходится, и три члена этого ряда уже мо-
гу 1 обеспечить достаточную степень точности. Таблицу функции
20

К(у) можно найти в [1] (табл. 6.1). Выпишем несколько зна-
значений а=1 — К(у):
A2)
Пример 1 (продолжение). Имеем Vn-Dn = V40-0,095 = 0,60.
Из первого столбца A2) получаем, что примерно в 84 случаях
из 100 следовало бы ожидать отклонен ;е 0,60 или более, т. е. мы
имеем дело с довольно «удачными» результатами наблюдений.
Полезно сравнить точные значения для а, представленные в
A1), со следующими приближенными, получающимися из A2):
у
а
0
0
,60
.84
0
0
,65
.8
0,
0,
77
6
0
0
.90
,4
1
0
.08
О
1
0
,23
.1
1
0
.36
,05
1
0
.52
,02
1
0
,63
.01
а
b = y!Vn
0.2
0.17077
0.1
0,19449
0,05
0,21505
0,02
0,24035
0,01
0,25774
Итак, уже при п = 40 приближение ф. p. Dn с помощью асимпто-
асимптотической формулы очень хорошее. Абсолютная ошибка в опреде-
определении б, такого, что !P(Dw>6)=*a, для а от 0,01 до 0,2 состав-
составляет около 0,005; относительная ошибка в худшем случае равна
примерно 2,2%.
4. Выборочные среднее и дисперсия.
Поскольку э. ф. p. Fn(x) оценивает теоретическую ф. p. F(x),
то можно ожидать, что для функционалов T(F) от F оценкой бу-
будет служить значение T(Fr,), вычисленное по э. ф. p. Fn. К. числу
важнейших функционалов относятся среднее и дисперсия:
Поскольку Fn(x; Х\, Хч хп) отвечает дискретному распре-
распределению с вероятностями 1/л в точках Хи то
n n
T2 {F,,{x; x)) - — V (Xi -II = — Vx?-
П м П mm
x2 =-. si
(-1
21

или, переходя к случайным величинам,
п
7\(Fn(;c; Х)) = Д-?х, = Х,
n n
T 1С I». V\\— ' V^/Y Y\J ^ V^ V2 YJ C2
П АЫ П «v
l-l i-1
Выборочные среднее X и дисперсия So2, как мы увидим в
дальнейшем, оказываются во многих случаях хорошими и, в не-
некоторых отношениях, оптимальными оценками теоретических
значений.
§ 3. ПОРЯДКОВЫЕ СТАТИСТИКИ В ЗАДАЧАХ ОЦЕНИВАНИЯ
1. Порядковые статистики.
Расположим наблюдения
Х\, Хз, •.., Хп A1
в порядке возрастания и перенумеруем их заново:
|. B)
Фактически хц), »=1, 2,...,я, — действительные функции пере-
переменных A):
i(i, X2 хп):
{min(*, Xi-lt xi+i хп), i=\,...,n);
Функцию от результатов наблюдений принято называть стати-
статистикой. Статистики х((о, k=l, 2,...,n, называются порядковыми,
последовательность B) часто называют вариационным рядом.
При переходе от наблюдений A) к случайным величинам
Xi, X2, ..., Хп C)
терминология сохраняется: X(k>, определенное тем же способом,
что и Л(ц,, называется k-й порядковой статистикой, а
-^A)^-^B)^ • • • ^-fyn) D)
— вариационным рядом. Отметим, что э. ф. р. зависит от наблю-
наблюдении через порядковые статистики:
Fn{x; Xi,...,Хп) =Fn(x; Хц),...,Х(П)).
22

Иногда бывает желательно подчеркнуть зависимость порядковых
статистик Xi() от п. В таком случае наряду с обозначениями D)
будем употреблять следующие:
i=l, 2,...,п.
E)
Порядковые статистики широко используются в статистиче-
статистических задачах. Рассмотрим некоторые примеры.
2. Оценивание содержимого урны.
Предположим, что урна содержит неизвестное число шаров N,
занумерованных числами от 1 до N. С целью определения N со-
совершается повторный выбор с волвр; щением объема п. Пусть
Х\, Х2,...,хп — номера извлеченных шаюв. Естественно в качест-
качестве оценки R предложить максимальное из наблюдений:
#=*<*>• F)
Шуточную интерпретацию этой задачи дает В. Феллер [2],
предлагая для оценки числа зарегистрированных в городе авто-
автомобилей встать на перекрестке и записывать номера проезжаю-
проезжающих автомобилей. Приведенные ниже результаты моделирования
этой задачи с помощью таблицы случайных чисел показывают,
что предлагаемая статистическая процедура приводит к хорошим
оценкам. Пусть N=10000, л =10; по табл. 7.1, о [1] получены сле-
следующие значения Х(П) для 10 независимых выборок л-;, .... .vn:
9590, 8947, 9533, 9901, 9511, 9885, 7990, 9776, 9055, 9352. G)
Сл. в. Yi = Xf-N~l g хорошей степенью приближения могут рас-
рассматриваться как равномерно распределенные на [0,1], так что
Для ряда значений у и п=10 имеем
у
0.79
0,1
0.74
0.05
0.63
0.01
Отсюда можно сделать заключение, что в среднем в одном
случае из 10 в качестве оценки N= 10 000 будет появляться зна-
значение .V^7900. Поэтому появление в G) значения 7990 не сле-
следует считать особенным.
Совершенно ясно, что оценка F) всегда дает заниженный ре-
результат: N^X. Вычисляя
23

найдем
Оценку ft можно поправить, устранив систематическое смещение.
Пренебрегая погрешностью, запишем
МA + 1/л)#=ЛЛ (8)
Исправленные значения G) выглядят так (с точностью до еди-
единицы):
10549, 9841, 10486, 10891, 10462, 10873, 8789, 10753, 9960, 10287.
Свойство оценки A + 1/л)#, выражаемое формулой (8), назы-
называется несмещенностью. Вообще говоря, несмещенность — полез-
полезное свойство оценки. Заметим, однако, что устранение смещения
в рассматриваемом случае приводит к увеличению в A + 1/пJ =
= 1,2! раз дисперсии оценки (\-\-l//i)K по сравнению с Л (и во
столько же раз увеличивается выборочная дисперсия ряда (9)
по сравнению с G)).
Возвращаясь к ситуации, когда /V неизвестно, но достаточно
велико, можно по результатам наблюдений av, i=l п, подо-
подобрать такое число М, что последовательность xJM могла бы с
достаточной степенью точности рассматриваться как выборка из
равномерного распределения из отрезка [0, в], где Q^N/M неиз-
неизвестно. В следующем примере эта задача рассматривается более
подробно.
3. Оценка параметра равномерного распределения.
Пусть A)—выборка из равномерного распределения на [0, 0]
с неизвестным 0, C)—соответствующие независимые равномер-
равномерно распределенные ел. в. Поскольку MA'j=e/2, то для оценки 6
можно предложить статистику
Оценка A0), очевидно, несмещенная: М7"(Х) = 0. Учитывая
DX 0/12, получаем
DT{X)=—DXl = ~-
Статистика Хм имеет следующие ф. р., среднее и дисперсию:
^=(n + 2);+i),0'. A1)
24

Сравнивая статистики (l + l/n)Xln) и 7"(Х), замечаем, что обе
они несмещенно оценивают 0, ио дисперсия первой из них, рав-
равная (л(п+2))-'02, в (л+2)/3 раза меньше дисперсии второй.
Для измерения качества оценки часто используют ту или иную
характеристику разброса ее распределения вероятностей, чаще
всего дисперсию. С этой точки зрения оценка Х(п) (или A + 1/л)Х
ХА',„.) существенно лучше, нежели 7"(Х). При больших п сравне-
сравнение Х(п) и Т(\) можно провести более детально. В соответствии
с центральной предельной теоремой при ?>0
?*(\Т{Х)— е|</е/]/Зп)я5 1 —2Ф(— t). A2)
В свою очередь из A1) мы получаем при
«г (о < е-х(п) < ю/п)=«г (х(п)
= 1 —A—*/л)п*5 1— е-'. A3)
Фиксируем U и <2 так, что
1_а= 1 —2Ф(—7t)= 1—е-'-.
Из A2) и A3) вытекает, что с вероятностью, приблизительно
равной 1 — а, выполняется каждое из следующих неравенств:
Т(\) (l+/1/Vn)-1<e<7'(X) (I-fi/уЗя)-1. A4)
Х(п)<в<^(«)A-^2/я)-1. A5)
Таким образом, при больших п ширина первого и второго интер-
интервалов, накрывающих неизвестное значение 0 с вероятностью
1 — а, равна соответственно
Из соотношений A2), A3) вытекает, что сл.в. 7"(X)/X(n) с высо-
высокой вероятностью принимает значение, близкое к 1. Поэтому ин-
интервал, основанный на статистике Т(\), шире интервала, постро-
построенного по Х(п), примерно в l/n-2ti/y3t2. Прн а=0,05 имеем U =
•=1,96, <2 = 2,99, и множитель при Уп равняется 0,76.
4. Оценивание параметра сдвига экспоненциального распре-
распределения.
Предположим, что сл.в. C) независимы и имеют одну и ту
же плотность f(x— 6), где
0, х<0.
Распределение с плотностью f(x) и ф. р. /г(х) = 1 — егх, х>0,
называется экспоненциальным. Оно часто употребляется в теории
надежности как распределение времени до выхода из строя (от-
25

каза) изделия. «Сдвинутое» экспоненциальное распределение
/(х-0), 0>О. интерпретируют как наличие «гарантийного* сро-
срока 0, в течение которого отказ произойти не может.
Порядковая статистика х<и служит естественной оценкой б,
ее распределение дается формулой
,.... Х„>х) = «г»'*-*», л->0,
откуда получаем
= \ — е~\ A6)
т. е. интервал Хц, -г—^—^—^- <0<ХA) с вероятностью 1-а
накрывает неизвестное значение 6.
Среднее значение распределения f(x — 0) равно 6+1, и пото-
потому для оценки 0 можно также предложить статистику 7"(Х) =
= Х— 1. Легко подсчитать, что
М7"(Х)-в,
С другой стороны, из A6) находим
Сравнивая дисперсии оценки 7"(Х) и оценки Х(|)— 1/п (с устра-
устраненным смещением), приходим к выводу, что если измерять ка-
качество оценок значениями их первых двух моментов, то оценка
Х(|)— 1/м предпочтительнее оценки 7"(Х). Используя центральную
предельную теорему, найдем, что распределение X—1 — 6 при
больших п приближенно нормально с нулевым средним и диспер-
дисперсией 1/и:
&(\]'п(Х— 1 — 8) КО - 1—2Ф(—0,
откуда интервал
.V-1 -//|'л<8<.Т-1+//У/Г
ширины порядка 1/f'n накрывает неизвестное 0 с вероятностью
примерно 1 — 2Ф(—О, В то время как аналогичный интервал
A6) имеет длину порядка 1/п.
5. Доверительный интервал.
Для оценивания неизвестного параметра 0 по результатам
наблюдений в разобранных примерах сначала предлагались
так называемые точечные оценки — статистики, значения которых
считались приближением к 0. Погрешность оценивания характе-
характеризовалась двумя первыми моментами оценки —средним и дис-
дисперсией. С другой стороны, рассматривалась интервальная
оценка
7"i(X, а)<0<7-2(Х, а),
26

такая, что вне зависимости от того, каково истинное значенье
параметра 6, оно заключено в данном интервале с вероятностью
1 —а. В этой случае говорят, что построен а-доверительный ин-
интервал для 6, или, иначе, доверительный интервал с коэффициен-
коэффициентом доверия 1 — а (если написанное выше неравенство выпол-
выполняется с вероятностью, приближенно равной 1 —а, то говорят о
приближенном а-доверительном интервале). Отметим, что в
предыдущем параграфе была построена а-доверительная полоса,
заключающая внутри себя неизвестную ф. p. F(x).
6. Выборочные квантили.
В приведенных выше примерах крайние порядковые стати-
статистики выступают в качестве оценок неизвестного параметра, ко-
который определяет «крайнюю» точку носителя распределения ве-
вероятностей выборки. Другое важное применение порядковых ста-
тистнк возникает в задачах оценивания функции, обратной к
теоретической ф. р. Назовем р-квантилью непрерывной ф. р.
F(x) решение xP=xP(F) уравнения
F{xP)-p, 0<р<1. A7)
Для р—1/2 хр называется медианой распределения, для р=1/4
и р=3/4 употребляется название квартиль. Если F строго моно-
монотонна, то xp"F-l(p) определяется соотношением A7) однознач-
однозначно, в прртивном случае для некоторых р уравнение A7) имеет в
качестве решения целый отрезок [х, х] значений хр. Так как при
этом F(x) — F(x)—p, то
<?(Х<=[х, x))-F(x)-F(x)=0.
С точки зрения теории вероятностей значения х из \х, х) вообще
можно не принимать во внимание. Таким образом, неоднознач-
неоднозначность решения уравнения A7) несущественна. Чтобы устранить
связанные с отмеченной неоднозначностью формальные неудоб-
неудобства, можно принять за хР при рф\/2 наименьший корень урав-
уравнения A7): хр**х. Для медианы хщ в случае неоднозначности ее
определения удобнее принять середину отрезка [х, х].
Если р=А/я, 1<?<л—1, то уравнение A7), записанное для
э. ф. р., имеет своим наименьшим решением Хц,,:
Fn (х,Л); *!,..., хп) =p=k/n,
и поэтому x(h) может рассматриваться как естественная оценка
квантили хР. В случае произвольного р выборочной кеантилью
обычно называют X[nrj+i, где [а] обозначает целую часть чис-
числа а.
Нетрудно найти ф. р. порядковой статистики (в предположе-
предположении независимости ел. в. C)):
27

<*) = <*• (Fn (x, X) ^ k/n) =
=Z own-
n
где было использовано, что ел. в. J] /{*,<*} есть число успе-
1
1—1
хов в п испытаниях Бернулли с вероятностью успеха F(x).
7. Равномерное распределение.
В случае независимой выборки из равномерного распределе-
распределения: F(x)=x, 0<х<1, из A8) получаем
5> (X,*) < х) = ? CU1 A -*)"-<. A9)
Дифференцируя A9) по х, имеем
л я—1
или
I. B0)
Таким образом, для ф. р. A9) имеет место следующее представ-
представление
Функция двух переменных
В (а, Ь)= J /—«A —О»-1*, а > 0, Ь > 0, B2)
о
носит название бета-функции Эйлера. Плотность распределения
B1)
[В(а, 6)]-|дсв-1A—хI*-1, 0<х<1, B3)
28

называется бета-плотностью (с параметрами а, Ь), а соответ-
соответствующая ф. р.
К (а, Ь) = [В (а, б)] J f°-' A - /)МЛ, 0 < .* < 1. B4)
называется неполной бета-функцией. Как вытекает из A9), B1),
lx(k, n-k + 1) = ? CU'A -х)"-'. B5)
Для вычисления /х(а, Ь) составлены таблицы (см. [1]). Из
A8) и B5) получаем, что ф. p. k-k порядковой статистики от не-
независимой выборки объема п с непрерывной ф. p. F(x) может
быть выражена через неполную бета-функцию:
?(Xlh&x)=lFlX)(k, n-k+\). B6)
8. Доверительные интервалы для квантилей.
Формула B6) приводит к важному статистическому приложе-
приложению—доверительный границам и интервалам для квантилей не-
непрерывной теоретической ф. р. Именно, подставляя в B6) р-кван-
тиль, получаем
^(*,*,<*р)-/р(*, n-k+\), B7)
т. е. X[h) является нижней а-доверительной границей для р-кван-
тилн хр с а=1 — Ip(k, n — k+\). Аналогично
9>(Х^Хр) = \-1рA, n-1+l), B8)
т. е. Х1П является верхней а-доверительной границей для кванти-
квантили Хр.
При k<l с вероятностью 1 Xltl)<Xw, поэтому
1 -?(xP<Xlh)) -
т. е. доверительный интервал
Х№)<хР<Х(/) B9)
имеет коэффициент доверия
1 —а = /р(Л, п — k+l)— 1P{1, n — 1+l). C0)
Наиболее часто используют доверительный интервал B9) для
медианы распределения xU2, так как для симметричных распре-
распределений медиана совпадает с математическим ожиданием (если
оно существует). Правда, как мы увидим, в случае нормальной
выборки, а также если выборка большая, интервальная оценка,
основанная на порядковых статистиках, проигрывает по сравне-
сравнению с другими методами интервального оценивания.
29

9. Coumclihoc распределение пары порядковых статистик.
Аналогично A8) можно найти совместную ф. р. двух порядко-
порядковых статистик Xih) и Xw, k<l. При х<у
r=ft s=/—г
(=1
х F(*)' (F(«/)- F (x))' A -
Если ф. р. F(x) имеет плотность /(*), то пара (Xlh)t Xin) имеет
совместную плотность, которую можно получить, дифференцируя
по х и у их совместную ф. р. Полезнее, однако, сделать предель-
предельный переход при б-»-0, б>0, в следующем выражении (предпола-
(предполагаем х<у):
C1)
Используя равновероятность всех п\ перестановок Х,,< Х,,< ...
< Х/а). запишем C1) в виде
Х,<...<Х„). C2)
Выражение C2) эквивалентно при 6-»-0 следующему:
< ... <Л'„). C3»
Действительно, если, скажем, в интервал (х, х + 6] попало зна-
значение еще одной ел. в., то вероятность в C2) оценивается сверху
величиной
(F(x+6)-F(x))*(F(y+6)-F(y))~f*(x)f(yN\ «WO,
в то время как вероятность в C3) имеет порядок б2 (при
/(*)/<//)^0)- Используя независимость ел.в. Xf, i=l,...,n, рав-
нозер'.':-!тиость (k—1)! перестановок из 'Хи ..., X/. .\ и (/ — k —
— 1>: лерестаиовок vz Хх.и... ,Х„, получаем для C3) выражение
6~-п! & [X, < ... < Х,_, < л) ^ (.v < X, < л- -г 6) я
х j* (х + л < х„л ,<...< xL_, ¦< у) а° (у < х, <у Л) х
У <Р !,, г 6 < X,,,<...< *,) - о-',;! .-_1_ f (a/--' (f (л- -F- 6)-
30

- F(*
— « — ')
l 6)y-i. C4)
Пределом выражения C4) является совместная плотность
пары порядковых статистик {Xw, Xm), k<l, в точке (х, у), х<у,
и этот предел равен
п\
F(.vf->/(A-)X
(k — \y.(l — к — 1)! (и — iy
X (F(y)-F{x))i-«-*f(y)(\-F(y)r-!. C5)
§ 4. ПАРАМЕТРЫ СДВИГА И МАСШТАБА: ГРАФИЧЕСКИЙ АНАЛИЗ
I. Семейство сдвига-масштаба.
Значительный теоретический и прикладной интерес представ-
представляет статистическая модель независимых наблюдений
Хи А'2)... ^» A)
с общей ф. р. вида F((x—ц)/а), где F(x)—известная непрерыв-
непрерывная ф. р., а параметры сдвига и и масштаба а>0, вообще гово-
говоря, неизвестны. Нормированные ел. в.
Yi={Xi-li)la, i=\, 2 л, B)
очевидно, также независимы и одинаково распределены, а их об-
общая ф.р. равна
^(У,О) =^((Х, - fi)/o<x) =^(Х,««+м) =F(x).
Семейство ф. p. F((x — ц)/а) может быть образовано из лю-
любой ф. p. F(x), однако в математической статистике и ее прило-
жениях употребляют сравнительно небольшой набор распреде-
распределений, которые благодаря особым теоретическим свойствам ча-
часто используются в реальных задачах. К числу таких распреде-
распределений относится прежде всего нормальное
Параметры ц н а семейства Ф((х — м)/а) имеют хорошо из-
известный вероятностный смысл:
MX,- =г. ц + afAYt = ц + о
J= f te~"'2 dt = ц,
— Л
ос
DX( - огМУ2 = о2 -4= [ /2<г-<'. -' Л - о2.
31

Отмешм i а к же семейство экспоненциальных распределений,
задающееся плотностью
г-*, х>0,
Здесь МУ, = 1, DY(=\ и ц ,
Приведем еще один интересный пример, когда семейство ф. р.,
не являющееся сдвиго-масштабным, становится таким после пре-
преобразования. Распределение с ф. р.
-(*/P)*], х>0, (ЗУ
возникает в теории экстремальных значений и часто (под назва-
названием распределение Вейбулла) употребляется в качестве распре-
распределения времени жизни изделия в задачах надежности. Пусть
ел. в. X имеет ф. p. G(x). Тогда ел. в. Z—\nX имеет ф. р.
= 1 — ехр [ — p-vev*] = i _exp [ _6хр (Y (x—In р*))].
Таким образом, если случайная выборка Xit i=l,...,n, взята из
семейства C) с параметрами р>0, у>0. то Zi = \nXu i=l,...
...,п, является случайной выборкой из семейства F((x— ц)/а),
где
F(x) = l — ехр [—expxj, D)
л параметры ц, а связаны с р, у формулами
Отметим, что ф. р. D) также возникает в теории экстремаль-
экстремальных значений.
2. Вероятностная бумага.
Во многих случаях теоретические соображения или предше-
предшествующий опыт позволяют высказать предположение о том, что
случайная выборка х\, хц,...,хп взята из распределения F((x —
— ц)/а) с известной непрерывной F(x), но неизвестными ц, а.
Используя статистический материал х\, хц,...,хп, желательно
проверить это предположение. Соответствующая задача относится
к области теории проверки статистических гипотез. Существуют
различные принципы и разработаны различные методы решения
подобных задач, однако предварительный графический анализ
данных остается полезным инструментом исследования, особенно
для небольшой выборки.
Эмпирическая ф. р. является естественным приближением тео-
теоретической ф. р., но, за исключением выборки из равномерного
распределения (когда теоретическая ф.р. — прямая линия), гра-
графическая подгонка ф. р. из семейства F((x—ц)/ст) к э. ф. р.
32

представляет, очевидно, определенные трудности. Преодолеть их
можно, сраспрямив» график /?((дс— ц)/а). С этой целью, предпо-
предполагая, что F(x) непрерывна и строго монотонна в точках х, в ко-
которых 0<F(x)<l, введем отображение полосы —оо<дс< + оо,
0<у<1 в плоскость по формуле
(х, у)-+(х, F-Чу)), E).
где F~l(y) — функция, обратная к F(x). Отображение E) по ус-
условиям, наложенным на F(x), взанмно-однозначно и взанмно-не-
прерывно в области своего определения. Прн этом отображении
(х, F(x))-+(x, F->(F(x))) = (x, x), F)
т. е. график y = F(x), 0<у<1, переходит в прямую линию у=х
(илн ее интервал, если существуют такие значения х, что F(x) = l
или F(x)=0). Далее,
(х,
т. е. график F({x — ц)/а), ф. р. из рассматриваемого семейства,
переходит в прямую линию
Опишем вытекающую отсюда методику. Пусть Fn(x) — э. ф. р.
случайной выборки из семейства F((x — ц)Дт). График y=Fn(x)
преобразуем в y = F~l(Fn{x)) и подберем наиболее тесно приле-
прилегающую к нему прямую линию
у-(*-?)/* G)
Прн этом а—котангенс угла наклона прямой G) к оси х —
будет служить оценкой параметра а. Оценкой ц будет абсцисса
точки пересечения прямой G) с осью х. Если график у =
= F~l(Fn(x)) систематически уклоняется от линейной зависимо-
зависимости, то есть все основания сомневаться в том, что наблюдаемые
данные взяты из распределения F((x—ц)/а).
При фактической реализации указанного приема нет необхо-
необходимости строить целиком график y=F-l(Fn(x)), а следует отме-
отметить только точки (X(f), F-^iln)), i—l,...n, отвечающие скачкам
Fn(x), и подгонять прямую к этим точкам. Ввиду неудобств, свя-
связанных с точкой (*(„), F-'(l)), обычно строят точки (jcA), F-'X
Х('7(я+1))), 1 = 1, ..., п. Более удачным является выбор точек в
виде uG), F-i((/_o,5)/n)), i=l, 2 п.
Для графической работы с семейством сдвига-масштаба
М(*--ц)/а) удобно изготовить так называемую вероятностную
бумагу, выбрав по оси ординат неравномерный масштаб и при-
приписав точке с декартовой координатой у новую координату у'=
~F(u). В новой системе координат ху' непосредственно наносятся
точки (*A), (j — 0,5)/гс). Оцифровка осн ординат для нормального
закона показана на рис. 2.
2 М. В. Козлов, А. В. Прохоров 33

3. Примеры графического анализа.
С помощью таблицы случайных чисел образована выборка
объема я=10 из нормального закона с ц=1, а=2:
—2,504; 0,342; —1,512; 1,636; 4,062; 1,698; —0,916; 0,882;
1,830; —1,168.
Рис. 2. Изготовление нормальной ве-
вероятностной бумаги
1,5
1
0,5
0
0,5
1
1,5
9
I i
-
-
-
У
/
•
I I
1 i 1 ! .
Х-
• ^г _
-
-
-
1 1 1 1
-з -г -1 о
12 3*5
X
Рис. 3. Точки (x,t... Ф-'(A—0.5.10))
и прилегающая прямая для нскус-
ственнип нормальном выоорки
По таблице функции, обратной к нормальной, из [1] находим
ф-1(-
i
i—O,.
10
L)
(-
6E)
-H,125
7D)
(—H,385
8C)
(-H,675
9B)
( )l,036
10.1)
(-) 1,645
Точки (*(«, Ф-1 ((i — 0,5)/10)), 1=1, 2,..., 10, отмечены на
графике (рис. 3), и подобрана на глаз прямая
у=(дс — ц)/а, илн х =
где ц = 0,44; а=1,87. Выборочные среднее и дисперсия равны
х^ -j^xi --0.435; s\ = ±?х*-? - 2,976; s0 = 1,725.
i-l
Как видно, графическое приближение дает оценки ц, а. близ-
близкие к выборочным. Щ
34

В следующей таблице приведены данные о ежегодном потреб-
потреблении в фунтах на душу населения мясных продуктов, включая
птицу и рыбу, в США с 1919 по 1941 г. (считывать по стро-
строкам) [3]:
171
568
146
.3
,0
,7
167
164
160
.0
.7
.2
164,
163.
15G.
5
0
8
169.
162.
156.
3
1
8
179,
160.
1G5.
4
2
4
179
161
174
,2
,2
,7
172.
165,
178,
6
8
7
170,
163,
5
5
(8)
Эти данные предлагается описать моделью
(9)
где / обозначает год, xt — потребление в этот год. Полином а+
+ bt-rrt2+dt3 призван отразить неслучайные изменения перемен-
переменной xt и называется трендом, коэффициенты а, Ь, с, d подлежат
7920 25 30 35
Рис. 4 Ежегодное потребление мяса
в США в 1919—1941 гг. н полино-
полиномиальное приближение
0,99
0,95
0,9
0,7
0,5
0,3
0,1
0,05
0,01
т—1—1—1—
_
-
-
j
S
7 л i i
1—1 1—г—;
х* -
-
i i i
/«5 150 155 160 165 ПО 175 180
Рис. о. Данные о потреблении мяса
в США в 1919—1941 гг., нанесенные
на нормальную вероятностную бу-
бумагу
подбору по наблюдениям (8); е( — случайные колебания в еже-
ежегодном потреблении, их полагают независимыми, одинаково нор-
нормально распределенными ел. в. с нулевым средним и неизвестной
дисперсией. Значения (8) и аппроксимирующий их полином изоб-
изображены на рис. 4.
Попробуем с помощью описанного выше графического приема
проанализировать данные (8) на предмет того, нельзя ли их рас-
рассматривать как выборку из нормального распределения, т. е.
считать, что коэффициенты Ь, с, d в (9) равны нулю, и полагать
колебания в ежегодном потреблении чисто случайными, не содер-
содержащими тренда. Графическое построение на рис. 5 показывает
удовлетворительное согласие с проведенной на глаз прямой
м= 166,5, а = 7,33. A0)
С другой стороны, приведенный в книге [3J статистический ана-
показывает, что данные (8) следует описывать моделью (9),
35

как это и представлено на рнс. 4. Противоречие в толковании
статистических данных (8) позволяет обратить внимание на сле-
следующий важный вывод.
Любой статистический прием направлен на проверку одних
сторон вероятностной модели и не улавливает отклонения в дру-
других направлениях. Поэтому при анализе данных надо ясно пред-
представлять себе, какие предположения о модели не ставятся под
сомнение, а что подлежит проверке по результатам наблюдений.
При графическом анализе (см. рнс. 4) предполагалось, что на-
наблюдения независимы и одинаково распределены, и проверялась
гипотеза о нормальности их общего распределения. Если исход-
исходные предположения нарушены, то и выводы, которые делаются в
отношении проверяемой гипотезы, несостоятельны.
Отметим, кстати, что э. ф. р. не меняется при перестановке на-
наблюдений xi, X2 хп\ иначе говоря, она является функцией по-
порядковых статистик дсA), дсB> Х(Пу В частности, наблюдения
t/i=x(j), ?=1,...,л, имеют ту же э. ф. р., что н дс(, »=1, 2,..., л, н
если не обратить на это внимание, то по результатам анализа
э.ф.р. можно для значений уи i=l,...,n, ошибочно принять тот
же вероятностный закон, что и для дс,-.
§ 5. ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ И ПУАССОНОВСКИЙ
ПРОЦЕСС
1. Экспоненциальное распределение.
Стандартное экспоненциальное распределение определяется
плотностью
е-", х>0,
О, д:<0,
и имеет ф. p. F(x) = 1 — е~х, х>0. Обычно в распределение A)
вводится масштабный параметр и рассматривается ф. p. F(xja)
или F(kx), k = a~l. Параметр а является средним значением рас-
распределения. Важность распределения A) в теории и приложе-
приложениях связана с его характеристическим свойством, называемым
«отсутствием памяти»: если ел. в. X имеет плотность A), то при
х, у>0
: + у\Х>х)=Р(Х>х+у, Х>х)/Р(Х>х) =
Допустим, что X описывает случайное время до наступления
некоторого события. Тогда знание того, что это событие не про-
произошло до момента х, никак не сказывается на его появлении
после момента х: остающееся время ожидания имеет то же самое
экспоненциальное распределение.
36

Отмеченное свойство распределения A) становится более про-
прозрачным, если обратиться к схеме Бернулли. Допустим, что в
моменты времени, кратные некоторому шагу /i>0, совершаются
испытания Бернулли с вероятностью успеха p = Xh. Пусть vi—
номер испытания, при котором произошел первый успех, иХ{А) =
= /ivx— случайное время до появления первого успеха. Так как
q=l—p,
TO
I, B)
где [а] означает целую часть а. Устремим теперь h к нулю. Оче-
Очевидно, правая часть B) будет иметь предел ег*-х, т. е. в рассмат-
рассматриваемом предельном процессе распределение времени ожидания
первого успеха сходится к экспоненциальному (с масштабным
параметром Аг1).
2. Пуассоновский процесс.
С экспоненциальным распределением тесно связан так назы-
называемый пуассоновский процесс. Обратимся к уже использовав-
шейся схеме испытаний Бернулли. Обозначим через V1 + V2+...
...+Vft номер k-то по порядку успеха, &=1, 2 Нетрудно ви-
видеть, что
^К = «х, v, = «„..., vm = пт) =
>«!. V, > Л Vm > Пт)= П Л
Для величин X^h)=hvi — временных интервалов между после-
последовательными успехами — получаем при х\, хц,...,хт>0
9>(X\*>xltXp>x Х»>>хт)-*П«"ХГ/. А-^°. C)
т. е. совместное предельное распределение ел.в. Xj4-i=l,...,m,
соответствует независимым экспоненциально распределенным
ел. в. с масштабным параметром А,. Допустим, что Х\, Х^,...—
последовательность независимых ел. в. с экспоненциальной плот-
плотностью Хе~1х, х>0. Из C) вытекает, таким образом, что при лю-
любых т, хи...,хтк А-э-0
S> (Х}*> < х, Х?) < хт) -»- ^ (Хх < х, Хт < хт). D)
Сходимость многомерных функций распределения D) влечет
за собой сходимость вероятностей любых событий, связанных с
этими величинами:
37

ГJ, A-M). E)
где Bm — борелевское множество ш-мерного пространства Rm.
В частности, для Вт вида
соотношение E) превращается в следующее
ут) +Р (S, < У! 5,„ < ут), А -*0. F)
где
S(*) = X|*)+...+X)*). S/^X^-...-i-Х,, / --=1.2
Отметим на числовой оси точки
S}*>, S<">, ...,S<"> G)
Говорят, чго последовательность случайных точек G) образует
случайный точечный процесс иа прямой. Аналогично получаем
точечный процесс
S., S2.....SJ (8)
Утверждение F) означает, что точечный процесс G) сходится по
распределению к точечному процессу (8), образованному сум-
суммами Sj = X\+ ... +Xj, /=1, 2,..., независимых экспоненциаль-
экспоненциальных ел. в. с параметром X. Процесс (8) называется пуассонов-
ским.
Обозначим через N^x^ и A^@,xj число точек на временном
интервале @, jej в процессах G) и (8), соответственно:
(9)
W(o,х] = fn <=> Sm •< х, Sn,4-i > x.
Событие {Л^}о1>х]=~т) происходит тогда и только тогда, когда в
последовательности из п= [x/h] испытаний Бернулли происходит
ровно т успехов, а его вероятность равна
Устремляя h к нулю, находим
& (#<*>„ - т) - С;," (Х/г)"' A —Щп-" = (п%'1]'П A —ЯЛ)" X
X A —Ц A —М ... A - JIL^-\ A — M)-m -* (b-)"'/m! • <?-'•*. A0)
Принимая во внимание F) и (9), получаем отсюда
&(N@.xi=m)~-!i??- е-'-". (И)
т.
38

Это хорошо известное распределение Пуассона с параметром
Пуассоаовскии процесс был определен как последовательность
(8) моментов появления сточек», или ссобытин», на осн х. Фор-
Формула (9) определяет случайный процесс W@,X], х>0, т. е. функ-
функцию, сопоставляющую каждому х>0 случайную величину Лг@.х>
Процесс W(o,xh х>0, тоже называется пуассоновскнм. В следую-
следующей лемме отражены важнейшие свойства процесса N{OlX]. Поло-
Положим при х<у
Лемма 1. Пусть xo = O<Xi<х2< ... <хк. Тогда ел. e.N(Xil .*,] .
( = 1,2 k, независимы и
Г(NlXi._vXi] =m)=
Доказательство. Как и при выводе A1), используем предель-
предельный переход от схемы Бернулли. Положим
— ДГ(А) _
Тогда
х
A3)
Устремляя h к нулю, получаем с учетом E), что правая часть
A3) стремится к
Smx+...+mk<xk, S,,ll+...-f,nft+i yxk) = Si(N(x. vx.) —mlt i^ 1, ... k).
A4)
С другой стороны, поскольку величины A'jJ1 x j , как числа ус-
успехов на непересекающихся отрезках испытаний Бернулли, неза-
независимы, то левая часть A3) равна
(-1
Переходя к пределу при Л-»-0, найдем, что левая часть A3) стре-
стремится к
1,
П(Х(Х/-АУ_1))ОТ' с-Х(*,-*,._,) A5)
т,!
Приравнивая A4) и A5), получаем требуемый результат.
39

3. Условное распределение точек пуассоновского процесса.
Следующие утверждения о пуассоновском процессе и о неза-
независимых экспоненциально распределенных ел. в. имеют важное
теоретическое и прикладное значение:»
Лемма 2. Пусть Xt, X2,... — независимые экспоненциально
распределенные с параметром А. ел. в., Sn = Xi+ ... +Хп, л =
= 1. 2. ..., Л'<о,*) — построенный по последовательности Sn nyac-
соновский процесс. Тогда
(I) плотность распределения ел. в. Sn равна
Le-ut .v>0,
0 x<0;
(II) условная совместная плотность ел. в. Si Sn при усло-
условии ел. в. Sn+i равна
fs,.. ,sn\sM(yi У„\Уп+\)=-?—, 0<у1<...<уп<уп+1,
и равна нулю для остальных значений переменных;
(III) совместная плотность ел. в. Z(I)=S//Sn+i, i—1, 2, .... п,
раёна
и равна нулю для остальных значений переменных;
(IV) при условии события Nl0,X]=n совместная плотность рас-
распределения ел. в. St, i—l, 2,...,n, (моментов появления точек в
пуассоновском процессе) равна
^ . . .<У„<Х,
и равна нулю при остальных значениях переменных.
Замечание. Если Uu U2,...,Un — независимые и равно-
равномерно распределенные на [0, 1] ел.в., U{i), t=l,.. .,n, — порядко-
порядковые статистики, то, очевидно, все п! перестановок t//,<f/f,< ... <
<1/,'л являются равновероятными событиями и поэтому
A6)
Выбирая Bt= (ut, щ + 6) при 0<«i<...<«„ и достаточно малом
б>0, получаем, что A6) будет равно п!бп, т. е. совместная плот-
плотность величин ?/«) равна
40

Следовательно, результаты (II) и (IV) означают, что услов-
условные плотности
fa sn\sn*i И fa ^"(О,*]
совпадают с плотностями порядковых статистик из равномерного
распределения на [0, Sn+\] и [0, *] соответственно. ¦
Доказательство. (I) Из формул (9) и A1) и того факта, что
из события 5„+1^х вытекает Sn<*, получаем
т. е.
^e-4 A7)
Последовательно используя A7) при л=1, 2,... и принимая во
внимание, что S\ = XU имеем для ф. р. ел. в. Sn:
A8)
Дифференцируя A8) по х и производя сокращения, находим
плотность распределения ел. в. 5„:
(II) Пусть 0<у1<у2<... <уп+\. Выберем 5>0 таким, что
У\+Ь>у2, Уг+&<Уз yn+b>yn+i. Тогда с учетом леммы 1
получим
F(yi<Sl < у, + S, yt<St <yt + 6 yn+x <Sn+i < yn+x + S) =
П e'^i+i-*!-** = (Лб^+^^е"^*». B0)
Поделив выражение B0) на 5n+1 и устремив 5 к нулю, получим
/s. sn+1 (i/i yn+i) = *.n+le-ky"+i, 0<yt<. ..<yn+l. B1)
Поскольку с вероятностью единица 0<5i<... <5n+i, то для
значений ух уп+и не входящих в B1), совместная плотность
равна нулю. Поделив плотность B1) на выражение для fsM (*л-м),
"виденное в (I), получаем требуемый результат.
(Ш) При 0<^1<х2<... <хп<1 и 5>0 таком, что
i+i, i = l,...,я — 1, имеем
41

V
B2)
где интегрирование ведется по (л+1)-мерному множеству
В» = {{уи ¦ ¦ -,Уп+\) ¦ Xi<yi/yn+i<Xi + 6, i=l л).
Подставляя B1) в B2), легко видеть, что интеграл B2) сводится
к повторному
J
= 5» j
о
- 5"n!. B3)
где мы использовали, что интеграл от плотности /s(l+1 (</)--
Xe~Xyynjn\ равен 1. Из B2) и B3) вытекает, что совместная плот-
плотность S,7S,,+i. /=1, ..., п, на множестве 0<.vi< ... <.v,,<l посто-
постоянна и равна л!. Очевидно, она равна нулю для остальных значе-
значений переменных.
(IV) Это утверждение доказывается аналогично (II).
Из утверждения (III) леммы 2 вытекает следующий критерий
проверки гипотезы об экспоиенциальиости случайной выборки.
Допустим, наблюдаются результаты п независимых испытаний
хи хч,...,хп и имеется предположение, что соответствующие ел.в.
Хи Xi,...,Xn независимы и имеют одну и ту же экспоненциаль-
экспоненциальную плотность Хе~кх, х>0 с неизвестным ?.. Если предположение
верно, то значения
n~L B4)
можно рассматривать, в соответствии с замечанием к лемме 2,
как порядковые статистики для независимой выборки из равно-
равномерного на [0, 1] распределения. Отсюда возникает возможность
применить различные способы проверки согласованности наблю-
наблюдений с заданной (известной) теоретической ф. р.
4. Пример.
Следующие данные представляют собой количество летных
часов между последовательными отказами установки для конди-
кондиционирования воздуха на самолете типа «Боинг-720» [4]:
42
23
246
71
261
21
И
37
12
14
7
20
11
120
5
16
14
12
90
62
120
1
47
11
16
225
52
71
14
95

Считая промежутки между отказами независимыми, проверим
предположение об экспоненциальном законе распределения этих
промежутков с помощью графического приема, описанного в
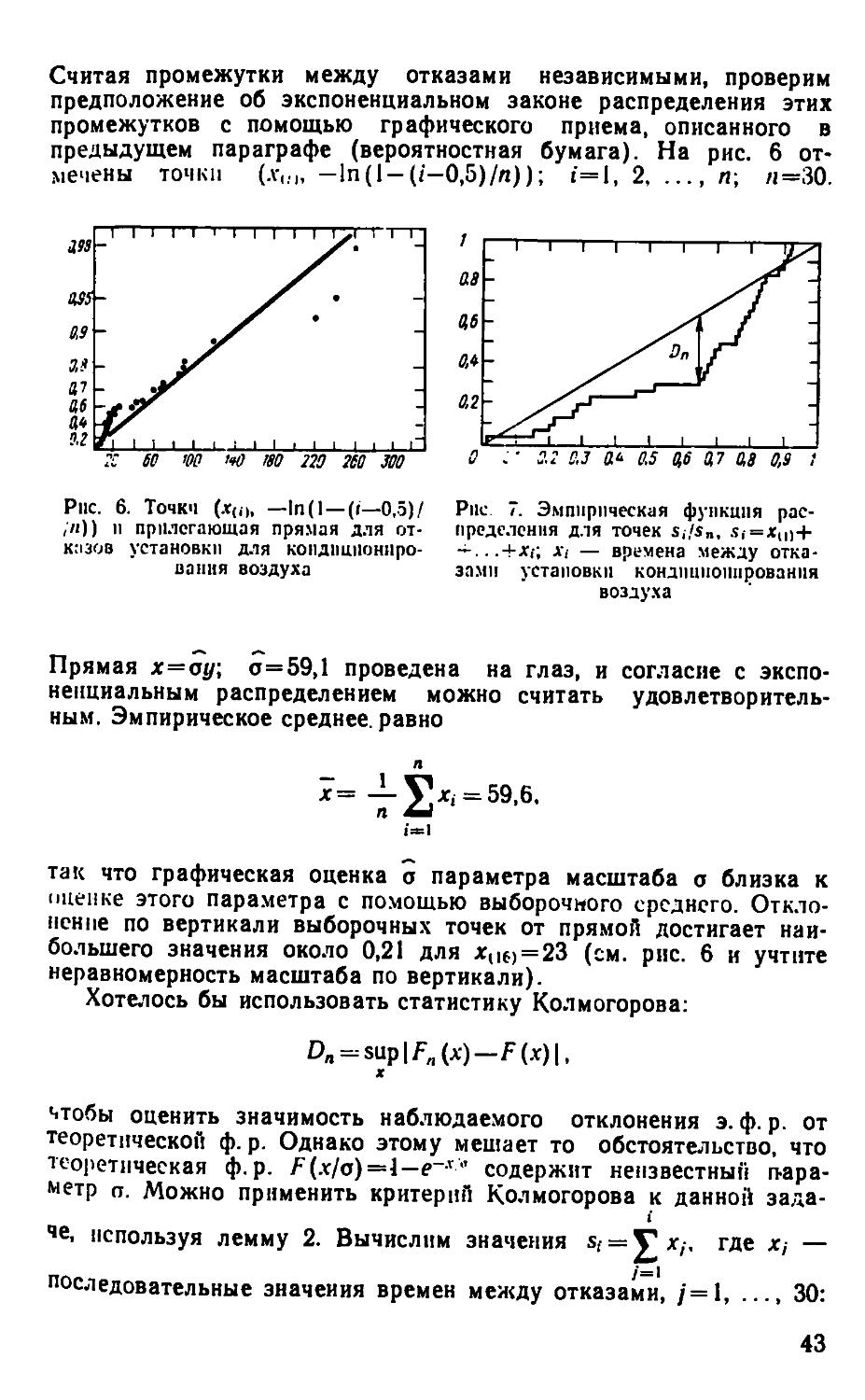
предыдущем параграфе (вероятностная бумага). На рис. 6 от-
отмечены точки (л-,.„ -ln(I-(/-0,5)/n)); i = l, 2, ..., п; /j=30.
as
zss
0,9
а*
ал
0,6
0,"
о,г
1 1 1 1
-
Ш\ ! 1 1
11111 'v:' ¦ ¦-
^т • —
i t I I i I i | | I \~
?C 60 '00 '*0 180 220 210
0.2 0,3 a* 0,5 0,6 0,7 0,8 0,9 1
Pnc. 6. Точкч (лГ(о, —InA —(i—0,5)/ Pile 7. Эмпирическая функция рас-
,«)) и прилегающая прямая для от- предслення для точек s,/Sn, s,=xu)+
кизов установки для кондпшюниро- — ...+хг. А"/ — времена между отка-
иапия воздуха зя.ми установки кондиционирования
воздуха
Прямая х=оу\ о=59,1 проведена на глаз, и согласие с экспо-
экспоненциальным распределением можно считать удовлетворитель-
удовлетворительным. Эмпирическое среднее, равно
x =
1=1
так что графическая оценка о параметра масштаба о близка к
iщенке этого параметра с помощью выборочного среднего. Откло-
Отклонение по вертикали выборочных точек от прямой достигает наи-
наибольшего значения около 0,21 для x,|f) = 23 (см. рис. 6 и учтите
неравномерность масштаба по вертикали).
Хотелось бы использовать статистику Колмогорова:
чтобы оценить значимость наблюдаемого отклонения э. ф. р. от
теоретической ф. р. Однако этому мешает то обстоятельство, что
теоретическая ф.p. F(x/o)=l—e~x° содержит неизвестный п-ара-
метр о. Можно применить критерий Колмогорова к данной зада-
задаче, используя лемму 2. Вычислим значения s, = Vx/. где х, —
последовательные значения времен между отказами, / = 1, .... 30:
43

23 284 371 378 478 512 574 621 846 917
1163 1184 1226 1246 1251 1263 1383 1394 1397 1411
1482 1493 1507 1518 1534 1624 1625 1641 1693 1788
После деления на S3o=1788 получаем следующий ряд значений
5» .. — с ./с_- I — 1 OQ*
¦*(!) ~~~- ^ 1/^30» * ~~~ * » * * * у А*7.
0.0128 0,1588 0,2074 0,2114 0,2785 0,2863 0,3210 0,3473
0,4731 0,5128 0,6504 0,6621 0,6856 0,6968 0,6996 0,7063
0,7734 0,7796 0,7813 0,7891 0,8288 0,8350 0,8428 0,8485
0,8579 0,9082 0,9088 0,9177 0,9468
Э.ф.р. для 2@, i=l, ..., 29, представлена ма рис. 7. Далее имеем
?>„ = 0,6504 — — = 0,2056, /29 Dn = 1,107,
3*(VnDn>\,\07)i9 I —/C(l, 107) =0,173,
т. е. примерно в 17 случаях из 100 могло бы наблюдаться такое
же или большее отклонение.
§ в. ОЦЕНИВАНИЕ ПАРАМЕТРОВ ЭКСПОНЕНЦИАЛЬНОГО
РАСПРЕДЕЛЕНИЯ
1. Оценивание параметра сдвига при известном параметре
масштаба.
Пусть Xi, i = l, ..., п, — независимые ел. в. с плотностью
(Г7((*—ц)/о), где
Пх) =
Распределение вероятностей ел.в. X, сосредоточено на (ц, +оо),
и, как мы уже видели в § 3, п. 4, оценить ц можно с помощью
статистики X(t). Распределение вероятностей Х(п легко находится
, .... Х„>х) =<?-«<*->/•¦, х>ц, A)
среднее н дисперсия равны
= o2/n2. B)
Считая параметр о известным, смещение оценки X(i} можно
исправить, рассматривая вместо нее Х(п—а/п. Если о неизвестно,
то можно попытаться заменить в формуле Х^—а/п неизвестное о
его оценкой по той же выборке.
2. Оценивание параметра масштаба при известном параметре
сдвига.
Рассмотрим задачу оценивания о, предполагая, что \i извест-
известно. Поскольку
МХ, = ц + о, C)
44

а качестве оценки о можно предложить
Оиенка Г(Х) — несмещенная, ее дисперсия равна о*/п. Так как
У,= (Х,-ц)/о, i-1. 2 п, D)
— ел.в. со стандартной экспоненциальной плотностью /(*), то
п
для плотности распределения ел.в. V Kj можем воспользовать-
ся формулой, выведенной в § 5:
Распределение с плотностью g {у/2)/2 играет важиую роль в ста-
гистнке и называется хн-квадрат распределением с 2п степенями
свободы; обозначение х22л. Отметим, что экспоненциальное распре-
распределение с плотностью 1/2е~х/2 является в то же время xVpacnpe-
делением. Подробнее о х2-распределенни будет идти речь в следу-
следующем параграфе.
Л
Из сказанного следует, что статистика 2 V Yt имеет х2гп-рас-
пределение, и поскольку
(-1
го, используя обозначения хр для р-квантили распределения х2гп,
получаем
Таким образом, а-доверительныи интервал для о можно записать
в форме
ха2<2пТ(Х)/о<х1-аП или 2/!Т(Х)/*,_в/2<о<2пГ(Х)/ха/2.
Указанный интервал является симметричным в том смысле, что
одинаково вероятно, окажется истинное значение о слева или
справа от этого интервала. Легко построить тем же способом и
несимметричный а-доверительныи интервал.
Функция распределения %гп табулирована (см. [1]), там же
указаны квантили хр распределения х2п для большого набора зиа-
ici-ин р н п—\ A) 100 (п от 1 до 100 с шагом 1).
Пример 1. Построим искусственную выборку объема л=20
- п>;;-,;1мстрами ц = 1, о = 2 с помощью таблицы случайных чисел
45

[1]. Если U — равномерно распределенная ел.в., то при 0<л<эс
?>(—In
т. е. ел. в. —In U имеет стандартное экспоненциальное распределе-
распределение. Выборку г,-, /=1, ..., п, из равномерного на [0, 1] распреде-
распределения получим группировкой по 4 цифры табл. 7.1, а [1]. Затем
строим выборку .Vi, /=1, .... п, по формуле л,=—21пг.+ 1:
7,442 2.90G 4,481 3,239 1,725 3,8-14 1,982
3,372 7.550 2,458 2,009 1,353 3,219 4.288
5,374 3,294 1,244 3,346 3,949 1,491
Вычисляем
1,244; х= 3,4283.
Если предположить, что значение параметра а = 2 известно, то
в качестве несмещенной оценки ]i получаем хп,—о/20= 1.244—
—0,1 = 1,144. Если предположить, что ц известно, то получаем не-
несмещенную оценку а: Т(х)=х—ц=2,4283. По табл. 2.2,а [1] на-
находим значения квантилей распределения /24с:
25 = 24,433; л-0,975 = 59,342
и вычисляем границы доверительного интервала с коэффициентом
доверия 0,95:
2пТ (х) /д-о.975-1.636; 2пГ (х) /л-0.о25=3,975.
3. Точечные оценки ц и о.
Когда оба параметра неизвестны, оценку о можно получить,
заменяя в D) ц на его оценку Х()):
а=Х—X(i).
Из A) и C) вытекает, что а — смещенная оценка:
поэтому несмещенной оценкой будет
п
--X(i))- E)
п — 1 п — l
Несмещенной оценкой параметра ц, очевидно, будет служить
ц* = ХA)-о*/я. F)
4. Распределение интервалов между порядковыми статисти-
статистиками.
Лемма 1. Пусть У,, i = l, ..., п, — независимые ел. в. со
стандартной экспоненциальной плотностью f(y) = e-y, y>0, a
}'(i)^KB)^.. .^К(п) — порядковые статистики. Тогда ел. в. 2,=
46

= (л—i+l) (У(,)— Yu-d), ' = 1. ¦••. «. У@)=0, независимы и имеют
ту хе плотность f(z).
Доказательство. Легко видеть, что события
Yit <Yit <...</,„.
где (i'i, B, ..., in) — перестановка из чисел A, 2, ..., п), равнове-
равновероятны. Поэтому, полагая Y<0)=Y0=0 и выбирая *,->0, »'=1, ..., и,
получаем
Kf_1)>x1-,i = l л) =
= «!<*» (К,- К, _, >Xi/(n-i + 1), i = 1 n) =
= и! \ e-U'dy, \ е-Ч'йу....
J J
= п! i e~vxdyx . . I ^ ¦"¦'«—• dyn—\ — e n
t'n lx «• !
CD X
J «) 2 1
Замечание. Лемму 1 можно рассматривать как одно из
следствий свойства отсутствия последействия экспоненциального
распределения. Представим себе, что У,, i = l, ..., п, — времена
жизни п приборов, поставленных одновременно на испытания. Тог-
Тогда У(П — время до отказа самого «плохого» прибора и, как сле-
следует из A), имеет плотность п е~"\ у>0. Момент Y{i) ввиду свой-
свойства отсутствия последействия экспоненциального распределения
можно рассматривать как начальный момент работы для остав-
оставшихся -«в живых» п—1 приборов. Следовательно, Yw—У,,) — вре-
время до отказа самого «плохого» из этих п—1 приборов имеет рас-
распределение с плотностью (л—1)е-{'1п1\ у>0, и т. д. Эти рассужде-
рассуждения можно сделать строгими, но приведенное выше доказатель-
доказательство короче.
Теорема 1. Пусть ел. в. Xj, i=l, ..., п, независимы и оди-
одинаково распределены с плотностью о~|е-(А'~>')/а, х>ц. Тогда ел. в.
nX(l), (n—i + l) (*(,¦,—Х(,-|>), 1 = 2, .... /г,
немшиимы, пА'(|, имеет плотность 0-1<;-(*-"»)/", х>пи, а
(«—/г I) (/Yf;,—Xi,_n), i — 2, ..., п, имеют ойинаковую плотность
о' '<?• ''•¦¦¦, х>0.
47

Доказательство. Из формулы D) имеем, что к ел. в.
У<о= (Я<п—ц)/о, i=l п,
применима лемма 1. Используя ее, получаем, что ел. в.
п(ХA)-ц)/о, fn-i+l)(X«>-X<i-,>)/o, « = 2 л, G)
независимы и одинаково распределены с плотностью е~х, х>0.
5. Дисперсии несмещенных оценок ц*, о*; интервальное оце-
оценивание ц, а.
Легко проверить, что
{—2 ¦=:>
-XA)=o-. (8)
Применяя теорему 1, находим дисперсии несмещенных оценок:
п
1=2
(~2
(9)
л* (л — 1)л,
Из G) вытекает, что ел.в. 2(л— 1)о*/о имеет распределение
%2(n-i) (см- п- ^)» а независящая от о* ел.в. 2л(Х0)—ц)/о имеет
Хг'-распределение (т. е. распределение с плотностью '/гв""*'2»
х>0). Отсюда вытекает следующая процедура построения дове-
доверительных интервалов для ц и о.
Пусть хр — р-квантиль распределения х^л-ц» т°гда а-дове-
рительныи интервал для о имеет вид
2 (л-1) о*/*.-а/2<о<2 (п-1) а*/ха/2. A0)
Для построения доверительного интервала для ц рассмотрим
ел. в.
,-Ц) = 2п(Х(|)-ц)/а (П)
2(п- 1)о* 2(л— 1)о*/о
Сл. в. A1) представлена как отношение двух независимых ел. в.,
имеющих хн-квадрат распределения, домноженная на л—1, она
имеет распределение Фишера F2.nn-\)(c\i. п. 7 § 7). Пусть хр —
48

р-квантиль этого распределения. Тогда получаем р-довернтельный
интервал для ц:
Х0)—ДС1-в/2а*/п<ц<ХA)—xt/3a*/n. A2)
Пример 1 (продолжение). Для экспоненциальной выборки
с ц= 1, о = 2 имеем
20
хA) = 1,244; ? (дс@- хA)) = 44,93;
1=2
20
о'--i-]g(xA-,-x(I)) = 2,364; ц-=дсA)--1-о-= 1,125.
1-2
С помощью таблиц квантилей Хзв находим по формуле A0) до-
доверительный интервал для о с а=0,05:
2-44,98/56,895<o<2-44,93/22,878, или 1,579<а<3,927.
Квантили хр распределения F2,38 для pi = 0,025 и р2 = 0,975 рассчи-
рассчитаны в примере § 7, п. 7:
xPt =0,025; хр, =4,071.
[учаем доверительный г
1,244—4,071 • 2,364 • 0,05<ц< 1,244—0,025 • 2,364 • 0,05,
Отсюда и из A2) получаем доверительный интервал для ц с р =
= 0,05:
или
6. Оценивание по первым г порядковым статистикам.
До сих пор рассматривались статистические процедуры, осно-
основанные на результатах *,, ( = 1, .... п, независимых одинаково
распределенных наблюдений. Фактически все статистические вы-
выводы зависели от наблюдений через порядковые статистики г,,,
/=1 п. В некоторых приложениях возникает задача оценива-
оценивания по некоторому подмножеству порядковых статистик. Напри-
Например, при испытании изделий на надежность может быть приме-
применен следующий план испытаний: выбирается определенное г^.п,
и испытания продолжаются до момента появления r-го по порядку
отказа. Результатами наблюдений в таком случае оказываются
значения первых г порядковых статистик *(,), i — l, .... г. Прове-
Проведенные выше построения для полной выборки легко переносятся н
на эту ситуацию.
Итак, пусть Хи), /=1, ..., г, г^п, — первые г порядковых ста-
статистик для случайной выборки X,, /=1, .... п, из экспоненциаль-
экспоненциального распределения с параметрами \i н о. Из теоремы 1 вытекает,
что ел. в.
@-X<i-i>), t = 2, .... г, A3)
49

независимы и имеют плотность — е-*0. Оценкой о, теоретичес-
теоретического среднего, служит выборочное среднее наблюдений Z,:
1=2
A4)
При г=п формула A4) совпадает с E). Отметим, что переход
от наблюдений Хщ, «=1 г, к Z(=(/t-i+l) {Хщ-Хо-п), «=
=2, .... г, приводит к некоторой потере информации, так как,
чтобы восстановить последовательность XU), i=l, .... г, из Z,,
1=2, .... г, необходимо еще знание Х,„. На самом деле, как мы
увидим в гл. III, вся нужная для оценки о информация содержит-
содержится в Z=(Z2, .... Zr).
Оценка 2, очевидно, несмещенная, ее дисперсия равна
<т2/(г-1). В качестве оценки ц естественно взять (ср. с F))
A5)
Эта оценка также несмещенная,нее дисперсия равна о2г/((г—1)х
Хн-). (ср. с (9)). Доверительные интервалы для ц и о строятся
н<| основании теоремы 1 и имеют тот же вид A0) при п=т и A2)
со следующими изменениями: вместо о*, определяемой формулой
E). берется 2, определяемое в A4); квантили хр и х'„ в A0) и
A2) берутся соответственно для распределений X-V-d и ^-'.-с—<••
Пример 1 {продолжение). Проведем по формулам A4), A5)
вычисление оценок, построенных по xUh i'=l, ..., г, для трех слу-
случаев г = 5. г=Ю. г= 15 и объединим результаты в таблицу вместе
со случаем полной выборки (г = 20):
О'
,i*
5
3,161
1,086
!0
2.914
1,009
2.
1,
15
728
108
2,
1.
20
364
125
1еоретнческне значении: ц— 1, а -2.
50

§ 7*. СВЕДЕНИЯ О ВАЖНЕЙШИХ НЕПРЕРЫВНЫХ
РАСПРЕДЕЛЕНИЯХ В Я1
1. Гамма-распределение.
Стандартная плотность задается формулой
/(*)=Ю, *<о.
где
ж.
5
— гамма-функция Эйлера, р — параметр, называемый парамет-
параметром формы. Обычно рассматривают гамма-распределение, содер-
содержащее еще и масштабный параметр л. Примем обозначение
С(>., р) для распределения с плотностью
ер-1е-?.дс) х > о. B)
Центральные моменты распределения ?7A, р) равны
-, r>-p. C)
[¦
о
Из формулы A) интегрированием по частям легко получить
Г(р+1)=рГ(р). D)
Отметим также известную нз анализа формулу ГA/2)=)'л. При-
Принимая во внимание D), из C) находим среднее и дисперсию
G(l )
^xf(x)dx = p,
E)
Iх р ~}х ~р'
Центральный момент [xr](x)dx порядка г>—р распределения
С(/., р) получается домножением выражения C) на л~г; среднее
» дисперсия равны соответственно р/К и р/К2.
Лемма 1. Пусть Xt — независимые ел. в. с распределением
С(/., р), i = l, 2 п. Тогда Х\ + ... + Х„ имеет распределение
*' К материалу этого параграфа можно обращаться по мерс необходимости.
51

Доказательство. Без ограничения общности положим Я = 1.
Достаточно рассмотреть случай и = 2. По форм у vie свертки ([2],
т. 2) плотность ел. в. Х\+Х2 равна при х>0
/*,-№(*)= J/jr.(O/*.(*-O*'
х
(
J
Сделав замену переменных s=xt, приведем выражение для
fxt+x, (x) к виду
Так как интеграл от плотности равен 1, то постоянный множитель
с равен 1/Г(р1+рг) (см. A)), что и доказывает лемму при п—-2.
Отметим попутно доказанную формулу
G)
Из леммы 1 вытекает, что распределение С(Х, р) при больших р
приближается нормальным с теми же средним и дисперсией. Дей-
Действительно, если р=п — натуральное число, то соответствующая
ел. в. распределена как сумма п независимых ел. в. с распределе-
распределением G(X, I) u применима центральная предельная теорема для
одинаково распределенных слагаемых. Если р не натуральное, то
к сумме добавляется еще одно слагаемое с распределением
G(K, р—\р\), где \р\ — целая часть р, которое асимптотически
пренебрежимо.
2. Экспоненциальное распределение.
Экспоненциальное распределение с плотностью У.е~Хх, х>0,
является частным случаем гамма-распределепия с параметром
формы, равным 1, и обозначается G(k, 1). Из леммы 1 вытекает,
что сумма п независимых С(а, ^-распределенных ел.в. имеет
распределение G(X, n). Этот результат был получен ранее другим
сг.о-обом (§ 5. лемма 2). Среднее и дисперсия экспоненциального
рги-и;/*>делс1ш>! О (к, \) равны л1 и ?.~2 соответственно.
52

3. Нормальное распределение.
Нормальное распределение в стандартной форме имеет плот-
плотность
ф(х)=се-*'/г, — оо<х< + оо,
где константа с=1/У2л находится из условия нормировки:
+ 00
1= J
— OB
00 1
о
Нормальное распределеиие с плотностью
обозначим через N(\i, о2). Плотность стандартного нормального
распределения, как правило, будет обозначаться <р(х), а соответ-
соответствующая ф. р. — Ф(х). Центральные моменты распределения
N@, 1) нечетного порядка, очевидно, равны нулю, а четного —
. ?„угА- L
/я J /я
о
Принимая во внимание формулы Г(р+1)=рГ(р) и
получаем рекуррентное соотношение
откуда для центрального момента порядка 26 получаем
BА—1)B*—3)-...-3-1. ¦ (9)
Пусть ел. в. X имеет распределение Л'(О, 1). Тогда в соответ-
соответствии со сказанным
МХ=0, DX=\.
Сл. в. aX+\i, о>0, имеет среднее ц, дисперсию о2, а ее плотность
равна о~'<р((х—ц)/°)« т- е- с11-в. оХ+ц имеет распределение
Л'(ц, о2). Таким образом, ц и о2 являются соответственно средним
и дисперсиеП распределения N(\i, о2). ¦
53

Лемма 2. Пусть X,- — независимые ел. в. с распределением
N(\n, о,2), 1 = 1, 2, ..., п. Тогда ел. в. Х{ + ... + Хп имеет распре-
распределение N(\ii + ... + \i,,, О|2 + о22+.. . + о,.2).
Доказательство проведем для п-2. Положим У,= (Х,—ц)/о,
и запишем
Легко видеть, что достаточно установить, что ел. в. У| + а}'г, а
— аг/ои имеет распределение #@, 1 + а2). По формуле свертки
Проведем преобразования показателя экспоненты в интеграле
A0):
•*' - (У - vJ/a2 = -V2 ( 1 -i- 4") - 2x0 -т а-
\ а- у а*
Подставляя A1) в A0), получаем, что
_±(J !__)-. _±_к1_
где
2ла
— м
очевидно, не зависит от у, т. е. является постоянной. Сравнивая
A2) с (8), получаем требуемое утверждение.
4. Распределение х2 с п степенями свободы.
Это распределение определим как распределение суммы п
квадратов независимых ел. в. с общим распределением Л'@, 1).
Пусть ел. в. А' имеет распределение Л'@, 1), тогда ф. р. А'2 равна
при х>0
Fx- (л)=з» (х2 < л)=гр (-V^< х<У7)~ф [Vx) -ф (- VI),
а ее плотность равна
54

Сравнивая полученное выражение для /х-(х) с формулой B),
заключаем, что квадрат стандартной нормальной ел. в. имеет рас-
распределение G A/2, 1/2). Отсюда и нз леммы 1 получаем, что
хи-квадрат распределение с п степенями свободы совпадает с
распределением G(l/2, п/2). Для хн-квадрат распределения при-
принято независимое обозначение х2«. Отметим, что экспоненциальное
распределение GA 2, 1) совпадает с у,22, а сумма п независимых
G A/2, 1)-распределенных ел. в. имеет распределение хгт> с чем
мы уже встречались в § 6.
Функция распределения %2п табулирована, при больших я
можно пользоваться нормальным приближением. Если ел. в. У
имеет распределение у*п, то (см. E))
МУ=п, DY=4п/2 =2л,
л ввиду центральной предельной теоремы
5. Бета-распределение.
Это распределение задается плотностью
О , х> 1, .v<0.
где
р>, 6) = Jx—'A— х)"-\
— бета-функция Эйлера, а>0, ft>0 — параметры. Функция рас-
распределения, которая называется также неполной бета-функцией,
обозначается /*(а, Ь). Учитывая формулу связи бета- и гамма-
функций (см. 7))
В(а, Ь)=Г(и)Г(ЬIГ(а-
Отметим очевидное тождество
/.t(o, й)==1-/(,-л,(й, а), (J5)
которое учитывается при составлении таблиц ф. р. и квантилей.
Обозначив через xP(Ix(a, b)) р-квантнль распределения /v(a, b),
имеем нз A5)
1 —1\-*ри<аМ) {Ь, а) - Р,
a)) = \-xp(I(a, b)). ¦ A6)
55

Между ел. в. с гамма- н бета- распределениями имеется интерес
ная связь, используемая в статистике и устанавливаемая в сле-
следующей лемме.
Лемма 3. Пусть ел. в. X и Y независимы и имеют распределе-
распределения G(>,, а) и О(Я, Ь) соответственно. Тогда ел. в. Z = X/(X+Y)
имеет ф. р. /г(а, Ь).
Доказательство. Рассмотрим отношение U=X/Y и, не ограни-
ограничивая общности, положим Х=1. Для ф. p. U получаем при ы>0
Дифференцируя, находим плотность
ОС <8
fu («) - f fy (У) fx (Щ ydy= ' f у^-Ч-У (иу)-1 e-"vy dy =
J Г (а) Г (fi) J
о о
• A7)
Г(а)ГF)
о
Так как
х A _2)-2 = 11?±^.гв-. A _2)«-«. A9)
v ' Г(а)ГF) ' v '
6. Равномерное распределение.
Равномерное распределение на (О, 1) является частным слу-
случаем бета-распределения с параметрами а=Ь = \; это распределе-
распределение подробно рассматривалось в § 2.
7. Распределение Фишера, или F-распределение.
Это распределение определяется как распределение ел. в.
у _ Х/т _ пХ
Y
Yin mY '
где X и Y независимы и имеют распределения %2т и %2п соответ-
соответственно. Для f-распределения принято обозначение Fm,n, парамет-
56

ры тип называются степенями свободы. Так как ySwm
ssG(l/2, A/2), то плотность ел.в. U=X/Y получается из формулы
A7) пр» а=пг/2, Ь=п/2, откуда получаем, что при v>0
fv @) ... Л f (Л. v) = Г((т + Я)/2) m«/2,,»/2ym/2-. („ +
п ¦ \ п ) Г (т/2) Г (я'2)
B1)
Из B1) и A7) легко получаем значения для центральных момен-
моментов /о.»i» распределения:
+ /)Г(я0 .)
о
Г(т)Г(л)
) Г
-0 .)
о
\т) Г(т)Г(л) '
Из A8), A9) имеем
откуда устанавливаем связь распределения Фишера с бета-рас-
бета-распределением
FV(v)=Fnu/m(v)=Imvnn+mv)(m/2, tl/2). Щ
Из формулы B0) имеем
Обозначив через Av(Fm,n) /)-квантнль распределения Fm,n, полу-
получаем из B2) следующее тождество:
(F«,m). B3)
которое учитывается при составлении таблиц квантилей /¦'-рас-
/¦'-распределения. Щ
В книге [1] приведены таблицы квантилей xp(Fm,n) для ряда
значении р и
ш=1AI0, 12, 15, 20, 24, 30, 40, 60, 120, ос,
п=1A), 30, 40, 60, 120, с».
Интерполяцию рекомендуется проводить по аргументам 1/т, 1/п,
57

для чего значения аргументов т>!0, я>30 сыбраиы из у\т>вик
постоянства шага по переменным 1//н, 1/я, что упрощает вычисле-
вычисления.
Пример. Найдем .\\.(Г-2.за) Для значении pi=0.025 и />:=0.975
По табл. 3.5 [1] находим
xPl (Fj.so) - 4,1821; д>, (F2iW) -¦ 4,0510,
х„, (F30.2) - 39,465; л>, (FA0.2) - 39,473.
Линейной интерполяцией по 1/п находим
ХР, (F2.3*) = ХГ, (F2.30) + (Л>, (fs.40) -XP, (f s.30» (-^" - -^" )"' X
-Ы4,1821-:-(—0,1311)(— 0,00833)"' (—0,007017)-
30 /
-4,071;
хР, (fas.a) - 39,465 + (—0,00833)"' (—0,007017) 0,008 = 39,4717;
xPl (Fs.3b) - (*л Сз».»)) = C9,4717)-' - 0,025.
8. Распределение Стьюдента, или t-распределеиие.
Это распределение определяется как распределение ел. в.
Ш B4)
где ел. в. А' и У независимы н имеют распределения Л"@, 1) и
Х2п соответственно; параметр п называют числом степеней свободы
/-распределения. Плотность ел. в. Т, очевидно, симметричная:
Замечая, что Т2 имеет /^.н-распределенне и что при t>0
ЫО-М-О--- Fr(t%
получаем из B1) при /» = 1, />0:
С ростом и распределение ел. в. Т приближается к W@, 1).
§ 8. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ: ОЦЕНИВАНИЕ
ПАРАМЕТРОВ, СРАВНЕНИЕ ДВУХ ВЫБОРОК
1. Доверительные оценки для ц и о2, когда один из параметров
известен.
Рассмотрим выборку Х-, (=1, ..., it, из нормального распреде-
распределения Xщ, о2) со средним ц и дисперсией о2. Точечными оценка-
оценками ц и о2 служат выборочные среднее и дисперсия
58

x-_-.±Vх„ So2=-LУ(X,-x)* = IVxl-x\
П ±mi II •*» ft **
1=1 1=1 1=1
Предположим вначале, что один из параметров (.i пли а2 извес-
гтен. В случае известного а величина
TM-Y—ц)/а A)
имеет нормальное распределение /V@, 1) (см. § 7, п. 3), и а-дове-
рптельный интервал для ц получаем из соотношения
&> (jfo/2 < К" (X —ц)/а < Х|_а.2) =- а,
или
ГХ-<кв/а/1^Г)=а.
где .v, — а-квантиль распределения Л'@, 1). Ввиду симметрии
.А/@, 1) имеем х„=—Х\-а, следовательно, a-доверительнын интер-
интервал можно представить в виде
X —a.V|_a/2/l/"/T<ц < X + oxi-a'-ilVn. Ш
Допустим, что |j, известно, а требуется оценить о2. Для точеч-
точечного оценивания а2 естественно вместо выборочной дисперсии
взять статистику
которая отличается от S\ заменой выборочного среднего на тео-
теоретическое. Для построения интервальной оценки образуем ве-
величину
п
' ~ Ъ-ИJ. B)
имеющую распределение %2п (см- § 7, п. 4). Отсюда получаем
а-довернтельнын интервал для о2 в виде
(X,— цJ,
i=i t=i
где л*,» — а-кваптнль распределения х2»-
2. Несмещенная оценка дисперсии.
В случае независимой выборки из произвольного распределе-
распределения выборочное среднее является несмещенной оценкой теоретичес-
теоретического среднего
59

Однако выборочная дисперсия имеет смещение
MS5-_ М (-L ? X?- -L- ? Х,Х,) = MXf-
1-1 (,/=1
L MX?- -?nli (MX,J = f 1 - —)
Поэтому обычно вместо S20 рассматривают несмещенную оценку
?_ S6=-L- V (X, -X)*.
1 ° ni^jv
3. Доверительные интервалы для ц и о2, когда оба параметра
неизвестны.
Допустим, что оба параметра \\. и о2 распределения Л'(|л, о2)
неизвестны. Для построения интервальных оценок вместо величин
A), B) образуем следующие:
п
Vri()C-n)lS, -l?(Xt-X)«. C)
?-1
Введем нормированные ел. в.
У,= (Х,-ц)/о,/-=1 п,
которые независимы и N@, 1)-распределены. Так как
то величины C) можно переписать в виде
Таким образом, распределения вероятностей величин C) не за-
зависят от неизвестных параметров ц и а2, и для построения дове-
доверительных интервалов остается лишь найти эти распределения.
Лемма 1. Пусть У,, » = 1, ..., л, независимы, N@, ^-распре-
^-распределены, С=[сц, i, /=1, .... п] — ортогональная пхп-матрица:
2г,,с,ч = 0 при \фк, у d--, 1. Положим
_ ijYj, iv=\ Я. E)
60

Тогда ел. в. Zit i = l, .... п, являются независимыми. Л/(О, 1)-рас-
1)-распределенными. При этом
Доказательство. Совместная плотность ел. в. У/, t=l п,
равна
(-1
Совместная ф. р. ел. в. Z,-, t= 1, .... л,
F_. .=<f>(Z,<21, i=l
ZB1? .... 2Л)
л
4Yi<2t' /=1 л)
равна ннтегралу от плотности G) по области
л
Произведем в этом интеграле замену перемениых по формулам
л
f( = 5]ty0/, i = \ п. (8)
Так как матрица С ортогональна, то из (8) вытекает
r-i /-I
[Ортогональное преобразование сохраняет длины векторов:
Л ЯП ЯП
Следовательно, подынтегральная функция G) в новых перемен-
переменных сохраняет прежний вид. Якобиан перехода от перемениых
У> к V; ввиду ортогональности матрицы [с,-/] равен 1, так что

что доказывает первое утверждение леммы 1. Равенстве F) вы-
вытекает из (8), (9). ¦
Выберем в условиях леммы 1 ортогональную лХл-матрицу
С=[сп] так, чтобы с„,= 1/Уп, /"=1, ..., п. Значения сц при хФп
нам не важны, лишь бы матрица С была ортогональной (напри-
(например, ;1егко проверить, что годятся с,-/ в форме
/< «)• Тогда
1 = 1 1=1 (=1
E (У.—Yf-^t Yf-nV-
t fc ?
1=1 1=1 1=1 1=1
Учитывая C), D) и определения %2„ и /,,_i (см. § 7), приходим
к следующему утверждению.
Лемма 2. Пусть X:, i=l, ...,«, независимы и N(\i, а2)-распре-
а2)-распределены. Тогда
--»»
1=1 1=1
независимы и распределены соответственно N@, 1) и %2п-\, а отно-
отношение
имеет распределение tn-\ Щ.
Из леммы 2 получаем а-доверительный интервал для о2:
< {n — D&lx*;., (X,-;_i), (Ю)
где .va(Xn-i)—«-квантиль Х^_граспределения, и и-доверительный
интервал для ц:
Х-х^а о (<„_,)S/1/n < ц < X —хв.,4 (/„_,) S/Vn, (И)
где x,(/n-i) — a-квантиль /л-грасмределення. Если в A0) или
A1) оставить лишь одно неравенство, то получим односторонние
н/2-доверительные границы, верхние или нижние.
4. Сравнение дисперсии в двух выборках.
Одко из важных прпложенп» пзложемноп выше теернн отно-
относится к так называемой задаче о двух выборках. Допустим, име-
имеются лве независимые нормальные выборки:
Хк1, Хи, .... Xk!k, ft-1. 2. A2)
62

Обозначим через \\к н о*:, /г-^1, 2, средние н fliicnepcim ел.п. A2)
Бо многих экспериментальных исследованиях возникает вопрос
о сравнении по результатам испытании A2) значении о:2 и оД
A1 и (.i2. Это сравнение естественно проводить, опираясь на соот-
соответствующие выборочные характеристики
"к "*-'
хк=—Ухк1, si=^'-V (xki-xk)*.
Отношение
выборочных дисперсий имеет распределение, зависящее лишь от
отношения X = oi2/o22, но не от Ц| и цг- Таким образом, если речь
идет о сравнении ог и оЛ а параметры (.и и цг не представляют
интереса н являются, как говорят, мешающими параметрами, то
переход к статистике V полностью устраняет влияние этих меша-
мешающих параметров. Величина K~lV имеет в силу леммы 2 распре-
распределение fn,-i,n,-i. откуда для отношения л, неизвестных днепер-
снй можно написать а-довернтельнын ннтервал
V/Xi-a/2 (/Ч-l.,,,-! )< А. < l//.Va/2 (/Ч-1.П.-1 )• (И)
Если здесь оставить лишь одно неравенство, то получается одно-
односторонний а/2-довернтельный ннтервал.
Особенно часто в приложениях возникает вопрос, верно ли,
что ог = о22, т. е. ?.= 1. Говорят в этом случае, что необходимо
проверить гипотезу #,-, = {л=1}. Намболее широкая альтернатива
к Нп — это противоположное допущение, что }.ф\, однако значи-
значительный интерес представляют и тьк называемые односторонние
альтернативы Х>1 или /.<1 (случай а<1 сводится к л>1 пере-
переменой местами af u о?). Например, может быть известно, что
точность некоторого усовершенствованного измерительного прибора
или некоторой методики но крайней мере не хуже прежней :i за-
лача состоит в том. чтобы по результатам наблюдении A2) при-
принять или отклонить гипотезу ?.= 1 против альтернативы /.>!. На-
Наличие доверительного интервала A4) наводит на мысль сформу-
сформулировать следующий критерий: подставим в A4) л=1, н если
результаты наблюдений
*я. хп хк„к, *=1, 2, A5)
приводят к верному неравенству
y/*l-a/2<l^t'/jf,/2. A6)
где
r,k — 1 ifaJ
63

n*
-Г>>*. ft-1, 2. A7)
го считать гипотезу A,= l против двусторонней альтернативы "кф\
верней; в противном случае гипотезу отвергнуть.
Как мы уже не раз отмечали, статистические выводы о вероят-
вероятностных моделях обладают принципиальной неопределенностью.
Так, указывая u-доверительный интервал A4) для >., следует
помнить, что утверждение A4) о границах, в которых лежит
неизвестное К, может оказаться верным при одной реализации
опыта A2) н неверным при другой. Увеличивая в A4) значение
а, мы тем самым уменьшаем допуск для неизвестного X, но за это
расплачиваемся уменьшением коэффициента доверия 1—а к ука-
указываемым границам, т. е. уменьшаем долю верных заключений
при многократном использовании данной процедуры. Это замеча-
замечание равным образом относится и к задаче проверки статистичес-
статистической гипотезы А,= 1. Если предположить, что на самом деле гипо-
гипотеза А=1 верна, то тем не менее остается вероятность а, что вы-
выборочная точка A5) попадает за пределы области A6) и тем
самым верная гипотеза будет отвергнута. Значение а называется
уровнем значимости критерия. Обычно критерий задают не обла-
областью A6). принятия гипотезы, а дополнительной областью, кото-
которую называют критической областью. Для рассматриваемого
критерия эта область получается объединением выборочных точек
A5), удовлетворяющих одному из неравенств:
V<Xa/2 ИЛИ И>Х|_в/2. A8)
Совокупность критических множеств A8), зависящая от пара-
параметра а, собственно и определяет данный критерий. Иначе кри-
критерий A8) можно задать с помощью статистики критерия v =
«=5г/5г2 и указания того, какие значения критерия приводят к
отвержению гипотезы. Введенный критерий называют f-крите*
рнем. Щ
о. Задача сравнения средних ц, и ц2.
В начале нашего века англичанин Госсет, работая на фирме,
занимавшейся пивоварением, столкнулся со следующей пробле-
проблемой. Было необходимо сравнить теоретические средние ц: в неко-
некотором числе k^2 малых выборок. Затруднения заключались в
малости выборок, ибо в противном случае можно было рассчиты-
рассчитывать на приближенное равенство sr^ai2 и полагать xu's, распре-
распределенными приближенно нормально со средними ц, и дисперсиями
1/л. — такая техника работы в те времена широко применялась.
Госсет нашел точное распределение xrfs,, что совершило, по обще-
ему лрмлианкю, переворот в статистике. Идея избавиться от ме-
шак'-ш;;:-: параметров б последующем привела Фишера к созданию
дисперсионного анализа, простейшим примером которого является
64

изложенная выше методика сравнения дисперсии с помощью
F-критерия.
Рассмотрим задачу сравнения \ц и ц2 в двух независимых
нормальных выборках в предположении, что дисперсии одинаковые:
а,2 = О22 = а2 Статистика Х\—Хъ в таком случае имеет нормальное
распределение со средним \ц—\i2 и дисперсией ai2lnl + o22ln2 =
= a2(l/«i +1/л2) (см. § 7. п. 3), зависящей от неизвестного а. Для
оценивания а2 можно было бы воспользоваться любой из статис-
статистик Sit2. k=\, 2. Ясно, однако, что более точной будет оценка, ис-
использующая всю выборку. Именно ввиду леммы 2 и свойств рас-
распределения х2 (§ 7, п. 4) величина
((л,—l)S,2+(n2— l)S22)/o2
имеет Х^+„,_2-распределение и, следовательно, статистика
S2=((nl-l)S,2+(«2-l)S22)/(n1 + n2-2) A9)
является несмещенной оценкой о2, построенной по полной выборке.
Вспоминая, что дисперсия х^-распределения равна 2л, получаем,
что DS2=(ni + n2— 1)-'о2, в то время как DS,2= (л,— 1)-'о2.
Таким образом, отношение
Т = IXi — Xd — tei — V*) /20)
имеет распределение ?,,+„,-2. Отсюда получаем а-доверительный
интервал для разности средних (ср. A1))
I (И1-И2) -(*! -^l) К
Обычным образом строятся односторонние доверительные грани-
границы. Статистика критерия Стьюдента*1 для проверки гипотезы
#о = {ц1 = Ц2} имеет вид
где s2=((ni— 1M|2+(л2— l)S22)/(ni+n2—2). Если альтернативой
к /Уо служит Ц1>Ц2» то в критическое множество зачисляются все
выборочные точки A5), для которых статистика / принимает зна-
значения, большие некоторого заданного:
{хп, х1г, .... дс1я1, хп xtnt: t > с). B1)
Выбор числа с определяет уровень значимости, или, как еще го-
говорят, размер критической области. Полагая с = дса(?„1+Я|-2).
получаем одностороннюю критическую область размера а. При
*' Условия контракта, по которому Госсст работал с фирмой по инвоваре-
H«io, не давали ему свободы публикации, и его знаменитая работа была опуб-
л"кои;!|;,ч под скромным псевдонимом Student.
3 М. В. Козлов, А. В. Прохоров 65

альтернативе ц\ф^ критическая область размера и получается
объединением двух областей t>C\ и /<Сг.
Дисперсионный, или ^-критерий, A8) и /-критерий, или крите-
критерий Стьюдепта, B1) относят к числу так называемых критериев
значимости (их еще иначе называют критериями согласия). Зада-
Задача проверки гипотезы ставится в форме поиска функции от резуль-
результатов наблюдений — статистики критерия, — которая служила бы
подходящей мерой согласия наблюденных значений со статистичес-
статистическом моделью. По идее в зависимости от задачи слишком большие
пли слишком маленькие, или и те и другие значения статистики
критерия должны рассматриваться как противоречащие нулевой
гипотезе Но- В предположении, что гипотеза #0 верна, этн значе-
значения могут быть наблюдены с вероятностью а — уровнем значи-
значимости нашего вывода. Итак, отвергая гипотезу Но, мы должны
считаться с возможностью, что на самом деле гипотеза верна н
тем самым сделан ошибочный вывод. Значение а является веро-
вероятностью этой ошибки. Разумеется, есть и другая возможность
ошибиться — принять гипотезу Но, когда на самом деле она не-
неверна. К этому вопросу мы вернемся в гл. IV.
6. Пример [5].
В следующей таблице приведены результаты двух опытов над
мухами. Мухн подвергались действию яда в течение 30 с в первом
опыте и 60 с — во втором. Измерялось время от момента сопри-
соприкосновения мухи с ядом до момента, называемого временем ре-
реакции, когда вызываемый ядом паралич распространится на-
настолько, что муха уже не может стоять и падает. Количество мух
Таблица 4
Времена реакции ykl-, k= 1,2, двух групп мух на действие яда,
Xki = In Унп Vki = Ф Ш — 0.5)/я*)« «1 = 15, nt = 16
3
5
5
7
9
9
10
12
20
24
24
34
43
46
58
140
РиХ100%
3,1
9,4
15,6
21,9
28,1
34,4
40,6
46.9
53.1
59,4
65,6
71.9
78.1
84,4
90,6
96,9
vu
— 1,866
—1,316
—0.911
—0,775
-0,579
—0,401
—0,237
—0,077
0.077
0,237
0,401
0,579
0,775
0,911
1,316
1,866
*и
0,477
0,699
0,699
0,845
0,954
0.954
<
.000
,079
,301
.380
,380
,532
,634
,663
,763
',146
2
5
5
7
8
9
14
18
24
26
26
34
37
42
90
/>*•:< 100%
3,3
10,0
16,7
23,3
30,0
36,7
43.3
50,0
56,7
63,3
70,0
76,7
83,3
90,0
96.7
°Ч
— 1,838
— 1,281
—0,966
—0.729
—0.524
—0,339
—0.168
0,000
0,168
0,339
0,524
0,729
0,966
1,281
1,838
(
(
(
(
(
(
),301
),699
),699
),845
D.903
5,954
1,146
1,255
1,380
1,415
1,415
1,532
,568
1,623
1,954
66

в первом опыте Л| = 16, а во втором «2=15. В табл. 4 приведены
значения yik, k=l, 2, »—1, 2, ..., л*, — времена реакции в минутах
в порядке возрастания (порядковые статистики), а также значе-
значения pki=(i—0,5)/л* и Vki = Q>-l(pki), k=\, 2, i = l,- 2, .... nk, с
целью проверки данных на нормальность. Точки (у и, vu) отмече-
отмечены на рис. 8. Как видно, зависимость v от у далека от линейной
щ
к
90
10
50
JO
10
5
9,2
_ i i i i i i
- ,
: • •*
"Г*
у
— ¦¦¦¦>¦
11 ' ;
* -
LU1
-
• -30c '-
i i i i i i i i "
20 40 60 80 №0 '70 W
2 34 6810 20 30406080WOWO 400 1OQD
Рис. 8. Времена реакции на действие Рис. 9. Логарифм времен реакции на
яда группы из 16 мух на нормальной действие яда двух групп из 15 и
бумаге
16 мух на нормальной бумаге
и похоже, что эти точки хорошо укладываются на логарифмичес-
логарифмическую кривую вида v = a+b\ny. Значения х*, = 1пуы, k=l, 2, i =
= 1, 2 ft*, также приведены в табл. А, а на рис. 9 нанесены
точки (**,, ф~1(ры)), i=l, 2 т,. Графический анализ показы-
показывает, что наблюденные значения логарифма времен реакций, ко-
которые мы по условиям эксперимента считаем независимыми и
одинаково распределенными в пределах каждой выборки, могут
рассматриваться как наблюдения над нормальными ел. в. Основы-
Основываясь на этих допущениях, применим изложенную выше теорию
для сравнения этих выборок с целью выяснения влияния разницы
в длительности воздействия ядом на время реакции. Выборочные
средние и дисперсии равны
i-1,219; х2= 1,179; <я2 = 0,2080;
0,1930.
Начнем с вопроса о значимости различия выборочных дисперсий.
Наблюденное значение статистики Лкрнтерия равно
"нав. = Щ = 1.08 S Хо.5 (Л5.Ы) = 1,0033,
т. е. гипотеза oi2 = O22 при любом а, чуть меньшем 0,5, должна
быть принята. Итак, согласие наблюденных значений с предполо-
предположением oi2=022 очень хорошее, н мы принимаем эту гипотезу.
Считая О|2 = О22, проверим с помощью /-критерия гипотезу о
равенстве средних. Имеем
«1-^2=0,040; s2= A5s,2+ 14s22) /29 = 0,2008;
s /1/16+1/15-0,02594.
67

Наблюденное значение статистики f-критерия равно
t = (xx— xt)/{s Vl/Hi+l/n.) = 0,040/^0,02594 =
= 0,040/0,161 = 0,25 я хо.6 (ttu) = 0,2557,
и, следовательно, гипотеза Ц1 = цг принимается иа уровне значи-
значимости а<0,4, что также свидетельствует о хорошем согласии дан-
данных с гипотезой.

ГЛАВА II
ЛИНЕЙНАЯ СТАТИСТИЧЕСКАЯ МОДЕЛЬ
§ 9. ОЦЕНИВАНИЕ КОЭФФИЦИЕНТОВ ЛИНЕЙНОЙ МОДЕЛИ
1. Введение.
Модели, которые рассматривались до сих пор, включали пред-
предположение о независимости и одинаковой распределеиностн наб-
наблюдений. Для построения оценок функционалов от теоретической
ф. р. или ее параметров, имеющих вероятностный смысл, мы обра-
обращались к э. ф. р. Если для оценивания одной и той же величины
оказывалось возможным предложить более одной статистики, то
предпочтение отдавалось той, распределение которой теснее скон-
сконцентрировано вокруг оцениваемой величины. Если оценка несме-
несмещенная, то мерой рассеивания служила ее дисперсия. Сравнение
несмещенных оценок по величине их дисперсий является одним
из наиболее часто используемых в математической статистике
критериев. В некоторых статистических моделях оказывается
возможным поставить и решить задачу нахождения наилучших
по данному критерию оценок — оценок, имеющих минимальную
дисперсию в классе всех несмещенных. В этом и следующем па-
параграфах рассматривается более простая задача отыскания на-
наилучших несмещенных оценок в классе линейных функций от
наблюдений или от их порядковых статистик.
2. Примеры линейных моделей.
Пример 1. Пусть
У=(Уи У2 Yn)
независимая выборка из N(\i, а2) с неизвестными ц и а. Пред-
Представим наблюдения в форме
ei, i=l, ..., п, A)
где е,- — независимые N@, 1)-распределенные ел. в. Вводя л-мер-
ные векторы-строки 1 = A, 1, .... 1), е=(е!, ...,е„), запишем A)
в векторной форме
? = ц-1 + ов. B)
Поставим задачу отыскания линейной несмещенной оценки пара-
69

метра ц с минимальной дисперсией. Пусть b=(fc , Ь„) — чис-
числовой вектор, такой, что статистика
a C)
несмещенно оценивает ц (знак транспонирования ' означает пере-
переход к вектору-столбцу):
Отсюда следует, что вектор b должен удовлетворять условию
Дисперсия оценки C) равна
D(bY') -&,Ч>У, + .. . + b
Таким образом, оценка C) будет наилучшей, если вектор b имеет
наименьшую возможную длину, а сумма его координат равна 1.
Хорошо известно, что таким вектором является Ъ = п~11, т. е. на-
наилучшая линейная несмещенная оценка ц совпадает с выбороч-
выборочным средним
A= — II =
я
D)
t=-i
Подчеркнем следующее важное обстоятельство: при решении
задачи отыскания наилучшей линейной несмещенной оценки были
использованы лишь свойства моментов ел. вектора е:
Ме,=0, /=1, ..., п,
= l, .... п] =/,
E)
где / — единичная матрица. Если выполнены соотношения E),
то рассуждения, приводящие к оценке D), сохраняют свою силу и
когда ел. в. е., i=l , л, имеют произвольное совместное рас-
распределение вероятностей.
Пример 2 [6]. В следующей таблице приведены результаты
л=15 измерений влажности некоторого материала, проведенных
для градуирования прибора. Значения х, — влажность в процен-
процентах, измеренная некоторым методом достаточно точно, так что
можно сказать, что ошибка отсутствует, «/, — показания прибора
ДЛЯ
У/
материала
6,0
39
6,3
58
6,5
49
с влажностью х
6,8
53
7,0
80
7,1
86
7,5
115
'•
7,5
124
7,6
104
7.8
131
8,0
147
8,2
160
8.4
156
8,4
172
8.9
180
Предположим, что прибор осуществляет линейную связь между
измеряемой велничиой х и показанием у, но что каждое измерение
подвержено случайной ошибке^ а ошибки от опыта к опыту не-
70

коррелированы и имеют одинаковые дисперсии о2. Тогда для опи-
описания рассматриваемого опыта можно предложить модель
или
Y = 8,l + 82x+ae,
где ел. вектор е подчиняется условию E), a, 8i и 02 — неизвест-
неизвестные параметры, х= (хи Хг х„). Пусть а=(аь а2) — произ-
произвольный числовой вектор. Будем искать линейную оценку
несмещенно оценивающую линейную комбинацию неизвестных
параметров
8 0 e'
В частных случаях а=A, 0) и а=@, 1) получим соответствую-
соответствующие оценки для 0| и 62. По условию несмещенности
л л
мы = ? ь,му,=? ь( @t+е,*,) =
i=i i=-i
л л
каковы бы ии были 0| и 02. В таком случае
.=.1 .-i
или
(ЬГ, bx')=b[l', х'] = (а„ о,). F)
Дисперсия оценки bY' равна
л л
DbY' = ? ifoYi = ? Ь?о« = а* || b ||J. G)
i=-i .=-1
Таким образом, среди всех векторов, удовлетворяющих F), надо
найти тот, который имеет наименьшую длину. Заметим, что если
Ь — любой вектор, удовлетворяющий F), то его проекция на
линейное подпространство V, порожденное векторами 1, х, оче-
иидно, также удовлетворяет F), а длина проекции ие превосхо-
превосходит длины вектора. Поэтому при поиске вектора наименьшей
длины, удовлетворяющего F), мы ничего не потеряем, если ог-
ограничимся лишь теми векторами Ь, которые лежат в подпростран-
подпространстве V:
Ь=с,1+с2х. (8)
71

Подставляя (8) в условие несмещенности F), получаем
С|1Г+с2хГ=а|,
(9)
Определитель системы (9) равен
л л
2
i=-l
i-l
1=1
и отличен от нуля, если только \ф\, и в этом случае существует
единственный вектор b в форме (8), дающий несмещенную оцен-
оценку, а следовательно, соответствующая оценка bY' имеет мини-
минимальную дисперсию.
Вычисляем матрицу, обратную к матрице системы (9):
X
— ух
п
так что решение системы (9) предегавимо в виде
{Си С2) = (аи а2)Н.
Находим оценки параметров 6i, 62 (см. (8)):
ei-bY'-fo, сг)[\', х']'Y' = (fll, at)H[V, x'] Y' = A, 0)H[V, x']'Y'.
? ', x',] Y'.
Проведя элементарные выкладки, найдем окончательные формулы
для 6,, §2:
x
1=1
л л л л л л
1=1 {-1 1-1 1=1 1 = 1 *=-1
л л
Yt+nt
8,=:
1=1
72

.—*J.г' (? (*-
(=1
1=1
)\Z*\' ') 2 ¦
(-1
Для числовых данных нашего примера получаем
х= 7,466; # = 100,266;
л
*t = 846,260; х2 = 55,741;
•"=¦1
/(/If
по
50
?П
i 111111
"i ft 1111
1 1 1 1
•
1 111
III
11111
, ll 11
I 1 1 1 1
у
• ¦I ii
¦ ii i
Illl
^:
, i ill*
х}—пхг = 10,154;
= 12898,8;
, = 550,11; 62-54,176; вх = ^—6^= —294,21.
8
Рис. 10. Гроднуровка прибора для
измерения влажности
Пары (Xitfi) и прямая (/ = 6| + 6гХ изображены на рис. 10.
3. Линейная статистическая модель.
Определим линейную статистическую модель, полагая, что
вектор наблюдений ?=(У'Ь У2, ..., У„) имеет следующую струк-
структуру:
Y^XQ'+ae', или ?=вГ+ае, A0)
где Х=[хц, 1 = 1, .... п; /=1, ..., г], г^п, — известная числовая
матрица, 8=(8ь ... , 9г) — вектор неизвестных коэффициентов,
е= (еь ег ея) — случайный вектор, такой, что
Ме, = 0, i=l п, [Ме.-е/, «, / = 1, .... п] =/,
A1)
«>0— неизвестный параметр, / — единичная матрица.
Из A0) получаем, что вектор математических ожиданий наб-
наблюдений равен
а матрица ковариаций
Ry = [cov (Kj, К/), i, / = 1 n] = /?0е = a2/.
Введем векторы
73

так что
Х=[х,', х2', ..., х/],
и A0) можно записать в виде
Y=8iX| + 82X2+... + 8rXr + ae. A2)
Свое название модель A2) получила за то, что неизвестный век-
вектор среднего
8 ... +8гхг
лежит в линейном подпространстве VczRn, порожденном вектора-
векторами х , хг. Модель A2) можно задать в непараметризованном
виде:
A3)
где V — заданное каким-либо способом линейное подпростран-
подпространство. Выбирая ту или иную систему векторов, порождающих V,
приходим к форме A2). Нередко бывает полезно от уже заданной
в форме A2) модели перейти к другой, выбирая иначе систему
порождающих векторов.
4. Несмещенные оценки с минимальной дисперсией: матрица
полного ранга.
Пусть
— несмещенная оценка для
где а = (а , аг) — пронзвольный числовой вектор. Это значит,
что математическое ожидание оценки
м(bY') = ?&<мк<=b(elX;-г... + efX;)=охьх; +...+ егьх;
тождественно по 8|, ... , Qr совпадает с ав", откуда получаем
Ьх,'=аи .... bx/=5r, илн ЪХ = а. A5)
Условие A5) является необходимым и достаточным, чтобы ста-
статистика bY' несмещенно оценивала аЭ'.
Дисперсия оценки bY' равна
D (bY') = jr b] D Yt = a*
Если b — произвольный вектор, подчиненный условию A5), то
вектор проекции npvb, очевидно, также удовлетворяет соотноше-
соотношениям A5), т. е. статистика
(np.b)Y'
74

несмещенно оценивает величину аЭ', и в то же время ее дисперсия
с учетом теоремы Пифагора удовлетворяет неравенству
D((npvb)Y')=a2||npvb|!2<a2||b||2 = D(bY').
Отсюда следует, что в поисках линейной несмещенной оценки
с минимальной дисперсией можно ограничиться векторами Ь, ле-
лежащими в подпространстве V:
Ь = С|Х, + ... + с,хг=сХ'. A6)
Подставляя A6) в A5), приходим к системе уравнений для оп-
определения с (ср. (8), (9)):
сХ'А^а. A7)
Допустим, матрица X имеет полный ранг г. Тогда матрица Х'Х
невырождена, A7) имеет единственное решение при любом век-
векторе а:
с=а(Х'Л')-',
и наилучшая линейная несмещенная оценка величины аЭ' равна
A'/y. A8)
Выбирая a=6, = F,i, б,2 6,я). где 6</=0 при 1ф) и 6,< = 1
(символ Кронекера), получим иесмещенную линейную оценку для
О, с минимальной дисперсией:
%=bi(X'X)-^X'\'. A9)
Организуя оценки Qt в вектор-строку 6= (8|, .... 8г) и замечая,
что [б/, .... бл'] =/, запишем вектор наилучших линейных несме-
несмещенных оценок:
Q'=(X'X)-XX'\'. B0)
Наилучшая несмещенная оценка A8) параметрической функции
аО' может быть записана в виде аЭ'. Таким образом, доказана
Теорема Г. (Гаусс, Марков). Если матрица X линейной мо-
модели имеет полный ранг, то наилучшие линейные несмещенные
оценки параметров 8,- даются формулой B0). Если а=(аь ...
¦.., а,) — произвольный числовой вектор, то линейная несмещен-
несмещенная оценка параметрической функции аб' с минимальной диспер-
дисперсией единственна и дается формулой аб'.
5. Наилучшие оценки в случае матрицы неполного ранга.
Случай матрицы X неполного ранга возникает в моделях дис-
дисперсионного анализа. Векторы Xi,...,xr в этом случае линейно
зазисимы, и разложение вектора среднего MY по векторам систе-
системы Х|...хг не единственно. Можно, однако, образовать такие ли-
линейные комбинации неизвестных коэффициентов Qt, которые по
75

вектору MY восстанавливаются однозначно. Поясним на примере.
Пусть r=3, xi, х2 лииейио независимы, x3=X! + x2. Тогда
Поскольку разложение вектора ц по подсистеме Х|, х2 единствен-
единственно, величины 8| + 8з и 82 + 8з по вектору т\ восстанавливаются од-
иозиачио. Именно такого рода линейные комбинации неизвестных
параметров и оцениваются в линейной модели с матрицей X не-
неполного ранга.
Параметрическая функция аЭ' называется допускающей оцен-
оценку (или оцениваемой), если ее значение восстанавливается по
вектору 11 = в|Х1 + ... + вгХг, т. е. она является линейной функцией
от координат вектора tj:
Отсюда следует, что выполняются соотношения A5), т.е. для
допускающих оценку параметрических функций аЭ' и только для
них существуют линейные несмещенные оценки. Как и при выво-
выводе теоремы 1, при поиске наилучшей несмещенной оценки можно
ограничиться такими линейными функциями bY', что вектор beV,
т.е. имеет место представление A6) и при этом выполнено усло-
условие несмещенности A5). Такой вектор b существует и притом
только одни. Действительно, если bi и Ь2 удовлетворяют A5), то
для их разности получаем
(b,-b2)x/=0, i=l г. B1)
Но вектора bi, b2 лииейио выражаются через систему Х|,...,хг,
поэтому условие ортогональности B1) приводит к выводу b| = b2.
Следовательно, взяв любое решение системы A7) и подстав-
подставляя его в A6), мы найдем вектор Ь, для которого bY' является
линейной несмещенной оценкой аЭ' с минимальной дисперсией.
Итак, получена следующая
Теорема 2 (Гаусс, Марков). Если матрица X линейной мо-
модели имеет неполный ранг, то линейные несмещенные оценки су-
существуют только Оля таких параметрических функций ав', что
вектор а является линейной комбинацией строк матрицы X; в
этом случае существует единственная несмещенная оценка b*Y'
с минимальной дисперсией. Вектор Ь* может быть получен проек-
проектированием на V вектора Ь, отвечающего произвольной несме-
несмещенной оценке, либо подстановкой любого решения системы A7)
в формулу A6).
6. Пример: модель с матрицей неполного ранга.
В табл. 5 приведены годозые урожаи пшеницы (в центнерах
на акр) на шести английских сельскохозяйственных станциях за
три года [6]. Естественно, что годовой урожай на данной станции
76

есть величина, зависящая от многих неподдающихся учету обс-
обстоятельств. Табличные данные позволяют заняться исследова-
исследованием вопроса о том, как зависел урожай от года и расположения
станции. Предположим, что реализация факторов, связанных с
условиями данного года i и данной местности /, при некоторых
средних характеристиках всех других случайных факторов при-
Таблица 5
Годовые урожаи пшеницы (в центнерах на акр)
на шести английских сельскохозяйственных станциях
Год
1
2
3
Kb станции
A933)
A934)
A935)
1
19
32
26
,0
,4
.2
2
22,2
32,2
34.7
3
35.
43,
40.
3
7
0
4
32,
35,
29,
8
7
6
S
25.
28.
20.
3
3
6
б
35
35
47
,8
,2
.2
водит к урожаю ц,,-;- — некоторому неизвестному числу, которое
желательно оценить, а что наблюдается уц = ц,,-/ + ое,;-, где состав-
составляющая aetj представляет собой вклад в урожай неучитываемых
в данной модели факторов. Переходя к случайным величинам, за-
запишем
1,...,р, /=
7, /?=3,
Предполагая, что ел.в. е,у некоррелированы, Ме,/ = 0, Ме2</=1,
приходим к линейной статистической модели. В данной модели, не
считая о, имеется /л? = 3-6=18 неизвестных параметров. Число
наблюдений также 18, и оценить ц,; можно, только положив
Ui,-= У,-,-. Упростим модель, считая вклад в урожай, связанный с
факторами года и местности аддитивным:
q.
где \х — некоторый «средний» по годам и участкам урожай,
а,, Р/ — добавки (со знаком) в урожай, определяемые годом н
местностью. Конечно, адекватность упрощенной модели (как,
впрочем, и исходной) подлежит проверке, но данного статистиче-
статистического материала для этой цели недостаточно, и мы оставим этот
вопрос в стороне. Образуя вектор Y:
Y=(Y,,...,Yp). У,-.(У« Y,,),i-l /?,

представим линейную модель в виде
чо
\Ур)
\q
+ oe',
или
где в=(ц, ai op, pi p,), X = [x,',x2 xp+(?+1] —
/39X (p+q+l)-матрица линейной модели ранга p+q-l, 1,—
= (I,...,l)i 0„=@ 0)—^-координатные векторы, /<,— единич-
единичная ?Х ^-матрица.
Матрица Л не имеет полного ранга, и параметры ц, at, P/ не
являются оцениваемыми: они не могут быть линейно выражены
через координаты вектора среднего:
T|=(n+ai+p , 1.1+ai+p,, ц+02+Pi, ... ,
ц.+а2+Р„, ...,ц+ар+Рь...,ц+ар+Р,).
Зато оценку допускают, например, разности a,—ai, »= 2,...,/?, а
вектор (a2—ai, аз—ai,. ...ар—ai), очевидно, вполне характери-
характеризует влияние фактора года на урожай, что, собственно, и интере-
интересует экспериментатора. Поскольку ос2—ai = a8', где а=@,1,
—1,0,.... 0), то наилучшая оценка для аб' имеет вид bY', где
b — вектор из линейной оболочки столбцов матрицы X, такой, что
а = ЪХ. Легко проверить, что этим условиям удовлетворяет вектор
7-'(—1,, 1„ 0,
и, следовательно,
Аналогично оцениваются остальные он—ai, i=3,...,p.
Для представленных в табл. 5 данных находим
(
«г» i^
1
28.4
2
34,6
3
33,0
Таким образом, аг—ai=6,2; аз—ai = 4,6.
78

7. Наилучшие оценки как оценки наименьших квадратов.
К изложению теории несмещенного линейного оценивания име-
имеется другой подход, основанный на следующем соображении
двойственности. Пусть bY' — произвольная несмещенная оценка
своего математического ожидания (см. A4)):
Тогда наилучшая оценка, как мы знаем, имеет вид npv-bY'. Обоз-
Обозначая через /?"Э V ортогональное дополнение V в Rn, имеем
(пр, Ь) Y' = (пр„ Ь) (пр, Y + np^ev, Y)' = npv b (nPv, Y)' =
= (npv,b + np/?nev,b)(npv,Y)'=b(npv,Y)'.
Таким образом, чтобы перейти от оценки bY' к соответствующей
наилучшей, надо найти вектор np^Y. Условия проектирования вы-
выражаются соотношением
(Y-npvY)X=0. B2)
Записывая разложение
npvY=e1x,+ ...+erxr=eX' B3)
и подставляя его в B2), получаем так называемую нормальную
систему уравнений относительно в:
QX'X = YX. B4)
Если матрица X полного ранга, то от уравнения B4) приходим
к ранее полученным формулам B0) для вектора наилучших оце-
оценок в. В общем случае любое решение (Г системы B4) опреде-
определяет по формулам B3) вектор np^Y и, следовательно, наилучшую
оценку b(npvY)' с математическим ожиданием ЬЯб'=а6'.
Полезно перенести этот подход на модель в форме A3):
Y
Положим
Тогда т) несмещенно оценивает г\ и является наилучшей оценкой
т) в том смысле, что для любого вектора b дисперсия статистики
Ьт)', несмещенно оценивающей br}', минимальна в классе линейных
несмещенных оценок. Так как
i, Л)) ЬЛЬ
(./=1
70, используя частичную упорядоченность матриц
79

если А—В — неотрицательно (положительно) определенная, за-
заключаем, что в классе линейных несмещенных оценок вектора t|
имеется оценка (и она единственна) с наименьшей матрицей ко-
вариаций. Щ
Вектор проекции B3), как известно, дает решение следующей
экстремальной задачи:
ijY— npvY||2^ min ||Y— F,Xj+ ... +6rxf)||2-=
e. ef
n т
= min У (Yi — У e.-.v.-.f. B5)
o, вг гЧ \ • i
Приравнивая к нулю производные от выражения под знаком min
в B5), легко получить отсюда нормальную систему уравнений
B4). Метод отыскания неизвестных 9/, /=1,...,г, из условия
B5) называется методом наименьших квадратов. Определенные
нами выше оценки 6/, /=1,...,/\ и ав' могут быть также названы
оценками метода наименьших квадратов, или м.н.к.-оценками.
В такой форме эти оценки были использованы независимо Ле-
жандром A806) и Гауссом A809), который впоследствии вывел
оптимальные свойства этих оценок.
§ 10. КОВАРИАЦИИ, КАНОНИЧЕСКАЯ ФОРМА ЛИНЕЙНОЙ
МОДЕЛИ, ОБОБЩЕНИЯ
1. Матрицы из случайных элементов.
Пусть
Z=[Za, i'=l,... ,tn, /=1,...,л]
— тХл-матрица из ел. в. Z,, (при т=\ получаем вектор-строку,
при л=1 — вектор-столбец; lxl-матрицу не будем отличать от
ее элемента). Математическим ожиданием Z назовем матрицу
MZ= [MZ,7, i=\ m, /= 1,..., л],
составленную из математических ожиданий ее компонент (в
предположении, что они существуют). Оператор математического
ожидания, очевидно, перестановочен с операцией транспонирова-
транспонирования:
(MZ)'=MZ',
математическое ожидание суммы матриц равно сумме математи-
математических ожиданий:
= MZ<1>+MZ<2>,
носятс
(MZ)B.
а постоянные матричные множители выносятся за знак матема-
математического ожидания:
80

Проверим последнее свойство:
М (AZ) = [ М ? atkZkl] = [? вйМг*,] = А [Шк1] = 4MZ.
2. Матрица ковариаций.
Пусть
U-(?/,,?/,,...,?/„)
— случайный вектор. Используя представление
-МС/,), /, /=1 n]=(U-MU)'(U-MU)
и приведенные выше правила вычисления математического ожида-
ожидания, получаем для матрицы ковариаций вектора U формулу
Rv = М ((U—MU)'(U—MU)) = MU4J—MITMU.
Отметим некоторые свойства матрицы ковариаций. Очевидно, что
если а — постоянный вектор, то
При умножении случайного вектора на постоянную матрицу мат-
матрица ковариаций преобразуется по формуле
= A'RVA. A)
Действительно,
RVA = М (AWA)— M (A'W) M (VA) = A' (MU'U) A—
— A' (MU'){№) A = A' (MU'V—
Взяв в A) в качестве А матрицу-столбец а', запишем для дис-
дисперсии ел. в. Uaf
DUa' = #ua' = a#ua'. B)
Так как дисперсия неотрицательна, то из B) вытекает, что/?и —
неотрицательно определенная матрица.
Как известно из линейной алгебры, симметричную неотрица-
неотрицательно определенную матрицу можно привести к диагональной
форме:
C'RVC = A C)
при помощи подходящей ортогональной пХп-матрицы
С:СС'=С'С=1.
При этом матрица Л имеет на главной диагонали неотрицатель-
неотрицательные числа X/, 1=1,...,п, а если матрица Rv положительно опре-
81

делена, то все Л,>0. Домножнм C) слева н справа на матрицу
С н С соответственно:
Ru = САС = (СЛ^КСЛ'/2)',
где Л1/2 — диагональная матрица с элементами я)/2 на главной
диагонали. Полагая СЛ1/2=В', имеем
Rv = B'B, D)
причем ранг матрицы В совпадает с рангом Ru. Представле-
Представление D) будет неоднократно использоваться в последующем.
3. Ковариации иаилучших оцеиок.
Воспользуемся формулой A), чтобы найтн матрицу коварна-
цнй вектора наилучших несмещенных оценок 6 в модели с матри-
матрицей X полного ранга. Учитывая, что Ry = Rm=o4, получим
e = YX{X'X)~1, /?g- = (X'X)-lX'/?Y^(X'X)-1 = 0«(X'X)-1. E)
Отметим, что если матрица
*=[х,' х/]
состоит из ортогональных векторов х„ i = l,...,r, то матрицы Х'Х
н (Х'Х)~1 днагональны н оценки в,, i=\,...,r, некоррелнрованы.
Случаи ортогональной матрицы X оказывается интересным и в
некоторых других отношениях. Во-первых, нахождение в; не тре-
требует обращения матрицы. Затем поскольку в, находится в ре-
результате проектирования вектора наблюдений на направление
X,, то в случае, когда в процессе анализа модели решаем отбро-
отбросить некоторые х:, полагая, что истинные значения коэффициен-
коэффициентов при них равны нулю, нет необходимости заново проводить
вычисления оцеиок оставшихся коэффициентов, так как при этой
процедуре они не изменяются.
4. Пример оптимального выбора матрицы модели.
Рассмотрим пример, когда экспериментатор не привязан же-
жестко к данной линейной модели, а имеет некоторую свободу в
проведении эксперимента и, следовательно, в выборе матрицы X.
Допустим, что требуется найтн веса 0,-, i= ],...,г, предметов
[7]. Если каждый из предметов взвешивается k раз, то наилуч-
наилучшей несмещенной оценкой слу:киг выборочное среднее. Дисперсия
каж.чиЛ из оценок равна o2'k, где а2 — дисперсия отдельного
нзвешчвання, ;i всего производится n—rk взвешивании. По друго-
другому методу при каждом взвешивании выбирают две группы пред-
метол и размещают па двух чашечках весов, а затем уравновешн-
82

Бают гирями. Эксперимент может быть описан линейной мо-
моделью:
YQ B i=l,...f n,
где хц=—1, +1 или 0 в зависимости от того, положен ли /-Й
предмет на левую, правую чашку весов или ие участвует в i-м
взвешивании; У, — величина уравновешивающих гирь со знаком,
указывающим, на какую из двух чашек добавлен разновес. Пред-
Предположим, что X имеет полный ранг, и найдем дисперсию оценки
6ь для чего разобьем матрицу Х'Х на блоки, выделив угловой
элемент:
M Ч
где b=(xrx2' Хрх/), F — квадратная (п— 1) X (п— 1)-матри-
ца, так что ввиду E)
D9,=a2det/7det;r;r. F)
Выразим определитель матрицы Х'Х через компоненты разбиеиия.
Составим линейную комбинацию последних г—1 столбцов гХг-
матрицы Х'Х с коэффициентами — компонентами вектора F~lb'.
В результате получаем матрицу-столбец:
L ь- J
Вычитаем ее из первого столбца Х'Х. Так как определитель
при таких преобразованиях не изменяется, то, разлагая преобра-
преобразованный определитель по первой строке, получим
detX'X = det[ Hxill2-b/:"lb' b
Подставляя полученное выражение в F), находим
D6, =- о* (||xi ||«—bF-»b') -».
Минимальное значение D6i приобретает, когда вектор Xi имеет
наибольшую возможную длину, а вектор Ь=0, так как квадратич-
квадратичная форма b^'b' положительна, если только Ь#0.
[Проверим, что матрица /•""' положительно определена. Квад-
Квадратичная форма
положительна, если только а=^0, так как X имеет полный ранг.
Для вектора вида а=@, а2 ат)
откуда следует, что матрица F — положительно определена.
83

Пусть С — ортогональная (я-1) X (л-1)-матрица (СС'=С'СФ
= /), такая, что
C'FC=A,
где Л — диагональная (п—1)Х(я—1)-матрица с положительны-
положительными элементами на главной диагонали. Домножая это соотношение
на С слева и на С справа, получим
Очевидно,
откуда получаем
bf-'b'= ЬСЛ-'С'Ь'-ЬСЛ-^Л-^СЬ'- ||ЬСЛ1/2||2,
что и требовалось.]
Те же рассуждения применимы и к дисперсии любой другой
оценки 6„ i = 2 г. Итак, чтобы дисперсия оценок коэффициен-
коэффициентов 0,-, /=1,...,г, была минимальна, надо, если это выполнимо,
организовать взвешивание так, чтобы, во-первых, вектора х< не
содержали нулевых компонент, т. е. при каждом взвешивании
участвовали все предметы, и, во-вторых, матрица Х'Х была диа-
гональиа, т. е. столбцы X ортогональны друг другу. Минималь-
Минимальное значение дисперсии одинаково для всех оценок и равно о2/п.
Если я = г?, то дисперсия взвешиваний о2/п в г раз меньше, чем
дисперсия o2/k при fe-кратном взвешивании отдельных предметов
и том же общем числе взвешиваний п.
Приведем пример ортогональной матрицы из элементов ±1:
А —
1111
1-1 1-1
1 1-1-1
1-1-1 1
При г = п = 4 эксперимент с Х = А приводит к дисперсии оценок
а:/4; при г —А, п = 8, взяв Х'=[А', А'], получим дисперсию о2/8,
в то время как при взвешивании по отдельности эти дисперсии
равны соответственно о2 и о2/2.
5. Каноническая форма линейной модели.
Рассмотрим линейную модель следующего частного вида:
(Л = ф| + а6,-, 1 = 1,....s; С/, = об„ i-s+l,...,n,
Мб*-О, U-1 я; /?в = /. G)
где II = (L'i,...,i7n) — вектор наблюдений, ф= (\|л,.. .,t|?s) — век-
гор tit-iuuecTiibix коэффициентов. Теория наилучшего несмещенно-
84

го оценивания для модели G) сильно упрощается по сравнению
с обшей моделью предыдущего параграфа. Чтобы статистика
1=1 1=1 i=i
несмещенно оценивала, скажем, г|3[, очевидно, необходимо и дос-
достаточно выполнение условия fe[ = l, b2 = ... = bs = 0. Чтобы ее дис-
п
.2
персия о2У $ была минимальна, надо положить еще bs+i = ...
... = bn = 0. Таким образом, наилучшие несмещенные оценки коэф-
коэффициентов г|), равны
Такие же рассуждения показывают, что наилучшей оценкой па-
параметрической функции a[\|?i + ... + as4|-s будет a[ipi+...+asi|3s. Из
вторсн группы соотношении G) сама собой напрашивается оцен-
оценка дисперсии
^5> (8)
которая, очевидно, является несмещенной.
Покажем, что линейную модель общего вида:
У = 8Х' + ое, Ме, = 0, /= 1 п, #е = /,
X = [xj, X2, ... , х;], 8 = F1( 62, .... 6Г), (9)
ортогональной заменой переменных можно привести к виду G),
который называют канонической формой модели (9), и получить
заново оценки § исходя из оценок ^>. Обозначим через s ранг мат-
матрицы X. Выберем ортоиормированный базис в пространстве V
размерности s, порожденном столбцами матрицы X, и дополним
его до ортонормироЕанного базиса всего пространства /?". Обоз-
Обозначим через С ортогональную матрицу перехода к новым коор-
координатам:
и = уС, и-(и,,...,и„), у =(«/i.•••.</<.)• (Ю)
Домножим обе части соотношения (9) на матрицу С, положим
U = YC, 6 = cC. Так как вектор среднего ц = вХ' лежит в простран-
пространстве V, то его новые координаты можно представить в виде
(^ ;tys, 0,...,0), а новые параметры t|?i,...,^s связаны со
старыми соотношением
лС=9Х'С=(ч1)...,Чч, 0.....0). A1)
85

Замечая, что (см. A))
= C'RtC = С 1С = /,
от модели (9) приходим к G).
Подставляя >|>; = ?/,-, i=l,...,s, вместо -ф; в A1), получим сле-
следующие соотношения для нахождения 6:
eX'C=(Ux ?/„ 0 0). A2)
Умножая обе части равенства A2) на С'Х, имеем
QXfX=(Ul Us, 0 0)С'Х =
A3)
= (?/, Us, 0 0)[С'х,' Сх',].
По условию выбора нового ортонормированного базиса новые ко-
координаты любого вектора у из V начиная с s+1-й нулевые:
уС=(и, us, 0 0).
Следовательно, все векторы х,С, i=l,...,r, имеют последние
п—s координат нулевые, и потому A3) не изменится, если век-
вектор (U\,...,US, 0,...,0) заменить на (Ui,...,Un):
л у/ у {Т1 11 \ {*** V Л^А^Л^' V ЛЛ V / 1 Л \
чЗЛ Л ^™ I С/ 1 • • • • i ^ 71 / ^ ^* ^^ • *^ *^ Л ^~ Ж Л * 1 1 « I
Матричное уравнение A4) совпадает с нормальной системой
уравнений B4) § 9.
6. Оценивание дисперсии.
Пользуясь канонической формой G) модели (9), выразим
оценку о2 из соотношения (8) через исходные величины У„ i =
= 1,...,я. Из ортогональности матрицы С вытекает
л л
а из A2) получаем, что
У U\ = ||вХ'С||2=5Х'СС'Хв' = §Х'Хв'.
1 = 1
Таким образом,
(У^ ) (|||| Ц112). A5)
n — s \Аи1 / п — а
86

Воспользовавшись равенствами
перепишем A5) в следующей форме:
||pReVY|p= _J_||Y-§X'||*
ТХ ~™ S ТХ ~~™ S
Отметим, что сценка о2 — несмещенная, (см. (8)).
7. Обобщенная линейная модель.
Обобщим линейную модель, допуская, что компоненты вектора
е коррелированы:
Y = eX' + oe, Me = 0, #e = Q = [<7<,, i, /=1 я]. A7)
но при этом будем предполагать, что матрица Q известна и поло-
положительно определена. Рассмотрим только случай, когда матрица
X полного ранга. Представим матрицу ковариацни вектора е в
виде (см. D))
Q'B'B, A8)
где В — невырожденная /iX/t-матрица. Умножая обе части A7)
на В*1, получаем
Вектор 6 = еВ"' имеет единичную ковариационную матрицу (см.
A)):
#6 = (В-1)' #eB-» --= (В')-1 (В'В) В-1 = /.
Полагая
U = \B-\ W = X'B-\
приходим к обычной линейной модели:
U = 8lP'-ro6, M6--0, Нъ -I, A9)
причем матрица W имеет полный ранг. Покажем, как получить
наилучшие несмещенные оценки в обобщенной модели (!7), поль-
пользуясь уже известными нам результатами для обычной линейной
м;>лелц A9). Пусть d*U' — оценка с минимальной дисперсией,
1есмещенио оценивающая аО'. Тогда
87

является линейной несмещенной оценкой аб' в модели A7), и мы
покажем, что она имеет минимальную дисперсию. Допустим, что
biY' — такая несмещенная оценка аб', что
(B-l)'Y = Dd*\}'. B0)
Поскольку
b,B'U = b1Y'
несмещенно оценивает аб', а ввиду B0)
Db1B'U = Db1Y'<Dd*U,
то оценка (biB')U имеет дисперсию, меньшую минимально воз-
возможной. Полученное противоречие доказывает, что наилучшая
несмещенная оценка ав' в модели A7) имеет вид
d*(B-')'Y', B1)
где d* находится из условия, что d*U' является наилучшей не-
несмещенной оценкой ав' в модели A9). Используя формулу E)
наилучших несмещенных оценок, получаем
8 = XiW {W'W)-1 = YB-1 (В-1)'* (Х'В-1
= 4Q-*X(X'Q-lX)-1- B2)
Матрица ковариаций оценок 6 равна (см. E))
#~ = a2 {WW)-1 - а2 (Х'В-1 (В-1)'*) = a2 (X'Q-lX)~l. B3)
Оценка дисперсии принимает вид (см. A6))
02 ! (U—QW) (U — QW')' =
п — s
=—— (Y—ex'jB-1 (в-1)' ( y—ех')' =
п — s
= —!— (Y — eX^Q-^Y — 6Х')'. ¦ B4)
п — s
Представляется полезным дать еще и независимое изложение
теории наилучшего несмещенного оценивания для обобщенной ли-
линейной модели A7). Используем при этом геометрический под-
подход. Итак, необходимо минимизировать дисперсию линейной
оценки bY' параметрической функции ав':
DbY' = b#Yb' = о2 bQb' B5)
при условии несмещенности
ЬХ = а. B6)
Определим в пространстве R" скалярное произведение по фор-
формуле
<х, y>=xQy' B7)
88

и перепишем условие B6) в виде
bQ (Q~lX)= a. B8)
Задача минимизации квадратичной формы B5) при линейных ог-
ограничениях B8) решается в полной аналогии со случаем обычной
линей ной модели: <2 = /. Пусть вектор b удовлетворяет B8), тог-
тогда вектор Ь*, получаемый проектированием b в смысле скалярно-
скалярного произведения B7) на подпространство, порожденное столбца-
столбцами матрицы Q~[X, также удовлетворяет B8) и в то же время
имеет минимальный квадрат длины:
<b*. b*> = b*Qb*'.
Следовательно, вектор Ь, приводящий к наилучшей несмещенной
оценке, лежит в линейном подпространстве, порожденном столб-
столбцами Q'lX (ср. A6) §9):
b = c{Q-iX)' = cX'{Q-i)f. B9)
Подставляя B9) в B8), находим с:
таким образом, наилучшая несмещенная оценка имеет вид
что совпадает с B2).
§ 11. ПОРЯДКОВЫЕ ЛИНЕЙНЫЕ ОЦЕНКИ ДЛЯ ПАРАМЕТРОВ
СДВИГА И МАСШТАБА
1. Обобщенная линейная модель для семейства сдвига-мас-
сдвига-масштаба.
Рассмотрим независимую выборку
Х\, Лг,... ,Хп A)
с общей ф. p. F((x—ц)/о); ф. p. F(u) стандартизованных ел. в.
С/(=(Х(_Ю/о, ,= 1 п, B)
считается известной, параметры ц и 0>О неизвестны. Порядко-
Порядковые статистики ел. в. A) и B) связаны формулой
?/(/>-(*@-|0/<». ''-I п, C)
и так как ф. p. F(u) ел. в. С/, известна, то в принципе любые
характеристики ?/<,> могут быть рассчитаны. Положим
o = a,-t cov(t/(o. U{j)) = qih i,j=l,...,n,
89

и, учитывая C), запишем
X(i) = |x + at/(,) = n + aai + a(t/(.)—он), i=l,...,n. D)
Полагая
ХA)=У,; t/(,)—a, = e,, /=1,...,я, E)
представим D) в виде обобщенной линейной модели:
У, = ц + оа, + аег, i=\,...,n, F)
или в векторной форме:
Y = (ц, a) I I + oe,
1 =• A, .... 1), a— (av .... a,,), Me —0, RB —
2. Наилучшие несмещенные оценки.
Оценки ц, а находятся по формулам B2) § 10:
!^[1\ а'])- (8)
Производя перемножение, преобразуем последний сомножитель в
(8) к 2х2-матрице и найдем обратную матрицу:
Г iQ-ir iQ-ia' 1-1 = j_ r«Q-ia' -aQ-Ц' 1
LQЧ' Qi'J Д [IQ^' 1Q4' J
LaQ-Ч' aQ-ia'
где
д= (IQ-Ч') (aQ-'o')—AQVJ. A0)
Матричный множитель при векторе Y в формуле (8) равен произ-
произведению /гХ2-матрицы
Q-'[l'. a'] = [Q-lV, Q-'o'] A1)
на 2х2-матрицу (9). Результатом их перемножения будет «Х2-
матрица, столбцы которой являются линейной комбинацией столб-
столбцов матрицы A1):
4" IQ-1' («О»') + О*' (- lQ^o'),
д
Q-Ч' (—aQ-Ч') + О»' (IQ-Ч')] =
!', Q-Ч— Га + а'1H-Ч'].
90

Таким образом,
(ц.а)=4-(*Га', -YIV), Г = 0-»A'а-а'1H^. A2)
Ковариационная матрица вектора оценок (ц, с) равна
(см. B3) § 10). ¦
Для дальнейшего полезно иметь в виду равенство
Взяв математические ожидания и дисперсии от обеих частей ра-
равенства, получаем
1ее'=лМ{/,, lQl'=nD?/,=n. A4)
3. Симметричное распределение.
Рассмотрим случай симметричного распределения выборки
A), и пусть \i=NiXi. Стандартизованные ел. в. Ut, i—\,...,n, в
этом случае имеют распределение, симметричное относительно
нуля, так что векторы фи..., Un) и (—11\ —Un) одинаково
распределены. Следовательно, одинаково распределены и векто-
векторы, составленные из их порядковых статистик, т. е. V-»((/(d, ...
.... ?/<„)) и (—Uщ),.... — {/(п). Введем матрицу
//=[6'n, 6'n-U • • • I fill» в»"~ Fii. • • • . 6«п).
где 6./ — символ Кронекера: б,,= 1; 6// = 0 при /#/, и запишем
UW)H—VH.
Таким образом, векторы V и —\Н одинаково распределены.
В частности, совпадают их математические ожидания и матрицы
коварнаций
=— MVH, /?v = /?-vh.
откуда получаем
a = MV=— aH, Q=RV = H'
Заметим, что Н'=Н=Н-1 и 1//=1, получаем отсюда
lQ-la'-lHQ-lHa'=lQ-lHa'—lQ-'a',
т. е.
lQ-ia'=0=aQ-ir. A5)
91

Подставляя A5) в A2) и A0), находим
, A6)
ц= 1/ЛУГа'
A7)
о = 1/ЛУГГ=: 4Q-4t'/(aQrltt).
Подставляя A5) и A6) в матрицу ковариаций A3), получаем,
что ц и о некоррелированы, а их дисперсии равны
)
A8):
Do=o2/(aQ-'a').
Наилучшая линейная несмещенная оцеика ц имеет дисперсию,
не превосходящую дисперсии выборочного среднего:
поскольку X представима как линейная функция порядковых ста-
статистик и является несмещенной оценкой ц. Покажем, что равен-
равенство
осуществляется лишь при условии
Ql'-l'. A9)
и при этом \а = Х. Для доказательства воспользуемся тем, что не-
неравенство Коши—Буняковского—Шварца
(aQa')(bQb')>(aQb'J. B0)
обращается в равенство, лишь когда векторы пропорциональны:
а=?.Ь или Ь = Яа.
Выбирая b = b:Q-' и подставляя з B0), получаем
где неравенство выполняется при
a = /.biQ-' или
Полагая здесь a = bi = l, получаем
92

Но (см. A4))
\Q\'=n,
так что
IQ-Ч'^я,
а равенство имеет место, лишь когда
Q\'=W.
При этом из равенства lQV=n вытекает, что А,= 1. Таким обра-
образом,
причем равенство имеет место лишь при условии A9). Наконец,
из A9) вытекает, что Q~4'=V, и из A7) находим, что при этом
4. Пример: равномерное распределение на интервале (ц, ц+с).
Используя формулу B1) § 3 для плотности распределения
k-й порядковой статистики, находим в случае равномерного на
(ц, ц+о) распределения ел. в. A):
1)!
ft!(n + 1—ft)! J n+l n+l
и аналогично
ц2_ k(k+l) I ft y_
(n+!)*(" +2)
Для вычисления
используем формулу C5) § 3 для совместной плотности пары
порядковых статистик и запишем
<
-1 x
X (у— х)'-*-'A — y)n-'dxdy. B2)
Сделав замену переменных х = гу, y—v и заметив, что якобиан
перехода к новым переменным paseFi v, преобразуем интеграл в
B2) к виду
93

I I
о о
= f 2* A — zy-k-xdz f i>'+> A — vf-'dv =.
о i
С учетом проведенной выкладки из B2) получаем при k<l
* (" (
(n+\)(n
откуда
»(/+»)kl k(n-l+l) .
)' ^ '
Сравнив B1) с B3), замечаем, что формула B3) годится и при
k = l.
Проверим, что матрица
P=(n+l)(n+2)[pkt, *,/=l «],
Р** = 2, /?k-i.*~?ft.*-i«—l. Pki = 0, \k—l\>l,
является обратной к Q. Положим QP== [a*/, k,j=l,...,n], тогда
п
а«= ("+1)(« + 2)
Доопределим элементы <7*,; при Л и / принимающих значения 0 и
я-fl с помощью формулы B3). Легко проверить, что при k<s.j
ак1= (я+ 1) (п + 2) (—^,/-1
Отсюда при Л</ находим
ak,=—l— (-k(n-j + 2) + 2k(n-j+l)-k(n-j))=0,
п+ 1
а при ?=/, воспользовавшись симметрией матрицы Q, получаем
а// = —— (—fl'/-!
я+ 1
=--J-r(-(/+ 1)(я—У+ 1)
п+ I
Таким образом, Q"' = P. ¦
Оценки ц и о могут быть получены применением формул A2)
Мы воспользуемся более простыми формулами A7), так-как рас-
распределение элементов выборки симметричное, но для этого надо
перейти к параметру ц* = ц+а/2, равному среднему значению рас-
94

пределения элементов выоорки. о нивой параметризации полу-
получаем выборку из равномерного распределения на интервале (ц*—
—а/2; ц* + а/2), и соответствующая модель имеет вид
где матрица ковариаций вектора е остается прежней, а(* = а,-—1/2.
Проводя вычисления по формулам A7), имеем
l, 0, ...,0, 1)',
Q-ia" = (n + 1) (л + 2) (-1/2, 0. .... 0. 1/2),
a'Q-1^' = (п + 1) (n + 2) (n- l)/2 (n + 1),
-= YQ-4 7A0-4') = 1/2 (K,+ Vn)= 1/2(XA) + XW), B4)
o= YQ-»1'/(o*Q-V) = (n + 1) (^-^/(n- 1) =
-l). B5)
Так как ц = ц*—o/2, то наилучшая несмещенная оценка равна
(см. теорему 1 § 9)
-;^-гХA)--^:тХ(г,). B6)
Оценки ц* и а некоррелированы, дисперсии оценок равны (см.
A8))
D|? = о2 ((я + 1) (n + 2))-1, Do = 2o*((n- 1) (n + 2))-1,
D|T * D? + D (o/2) = о2 Cn -1) B (n2 -1) (n + 2)). B7)
5. Пример: экспоненциальное распределение.
В случае экспоненциальной ф.р. 1—ехр(—(х—|i)/o), х>ц,
стандартизованные ел. в. {/,• имеют плотность е~х, х>0, и, в соот-
соответствии с леммой 1 § 6, ел. в.
Z, = (n-i+1) ({/(„-{/(,-„), -?/(«-0. i=l я, B8)
независимы и имеют ту же экспоненциальную плотность е~*,
х>0. Из B8) имеем
'd{n— i+ 1), k = \ n,
откуда
aft = Mt/W = ? (n- i + I), B9)
95

<7«=»cov (?/(*), ВД = ? ? cov(Z(,
mln(*. ()
x.(n—i+l)-^/!—/+1)-1» j («—i+1)-2. C0)
1=1
Проверим, что матрица
P=[pkt,k,l=\ n],
p*.4-i =/>*-..* (n—k+\J, pkk=(n—k+\J+{n—ky C1)
является обратной к Q. Доопределим элементы pki и ^*^ при k и
/, равных 0 или л + 1, с помощью формул C1) и C0) (считая там
сумму по пустому множеству индексов равной нулю). Нетрудно
видеть, что при этом для \-^k<j<n справедлива формула
п
= Як.1-\ Pi-ui -г qkiPu + gk,i+i Pj,i+\¦ C2)
Поскольку p/-i,/+/?//+P/,/+i = 0, а при k<j
к
Як.!-\ + 4ki = 4k.l+i = J (я— i + \)~г,
то из C2) получаем, что внедиагоиальные элементы матрицы
QP — нулевые. Диагональные элементы QP также находим по
формуле C2):
Х=| Х-1
Таким образом, Q~l = P.
Перейдем к вычислениям наилучших несмещенных оценок \х,
о по формулам A2), A0). Имеем
а при
2
J-1
так что
Q-4'=(«2,0 0)'. C3)
96

Далее.
n
? Pkiai = Pk.k-i а-ь-i + Pkkak + Pk,k+i aft+i, C4)
где a, при всех / определены формулой B9). Подставляя в C4)
значения входящих туда величин, получаем
4-1
* *+l
x у (и— t+l)-1—(я — kJ ? (n—i+ \)-1=(n—k+\) — (n—k) = \,
так что
Q-'a'=l'. C5)
Из C3) и C5) находим
п п
*-| *=|
п
Q-1l'aQ-1=(«2, 0 0)'l, Q^o'lQ-1»!'^1, 0 0),
?=-i-Y((n2, 0 0)'1а'-1'(п2, 0 0)о')-
1-1
а ! Y((n«, 0, ...,0IГ-1'(п«. О, ...,0)Г) =
П* (П — 1J
_п у *_
X—I
-l). C7)
Выражение A3) для ковариационной матрицы вектора оценок
(ц, с) принимает вид
аА (п(п-\)Г> -(«(«-I))-1 1
[-(n(n-l))-1 («-I) J'
Оценки ц и о совпадают с оценками \i* и о* § 6.
4 М. В. Козлов, А. В. Прохоров 97

6. iif/Hiviv j>: нормальное распределение.
Для моментов порядковых статистик стандартизованных ел. в.
?/(«., в случае нормального распределения нет простых формул.
Покажем, однако, что в этом случае выполняется условие A9):
Ql'-Г. C9)
и, следовательно, выборочное среднее является наилучшей по-
порядковой линейной несмещенной оценкой теоретического среднего
|i. Как доказано в § 8, ел. в.
п л
u—LVUi и S6-=—V(ut-ur
П mm /I лет
<-1 '-!
независимы. В следующем параграфе будет показано (см. при-
пример в п. 3 § 12), что на самом деле О не зависит от вектора
(t/i—0,...,Un—О), а не только от его длины. Воспользовав-
Воспользовавшись этим, заметим, что порядковые статистики набора ел. в.
Ux—U,...,Un—U имеют вид ?/A>—0,..., ?/(„,—0 и как функции
вектора (U\—0,...,U,,— О) ие зависят от О. В таком случае
О-М0 (?/<*,—О) = M0t/,*,-l/n,
откуда
л п
П Л м П ami
i = l 1 = 1
что и дает C9).
7. Цензурированная выборка.
В технике и особенно в бпомедицпискнх исследованиях типич-
типичной является ситуация, когда из ряда порядковых статистик
Х^)^Х,о)^...<Х(„) для измерения доступна лишь часть. Мы уже
встречались с примером подобного рода в § 6, где рассматрива-
рассматривалась задача одновременного испытания на надежность п изделий
до момента выхода некоторого заранее установленного числа и—г
из них, а статические выводы делались по значениям Хи)<
^Х,2,<:...<:Х(„.г). Другой пример возникает в случае, когда в ря-
ряду наблюдений А'ь А'2 А'„ наибольшие, наименьшие или и те
и другие значения являются ненадежными и » расчет прини-
принимают лишь значения
AV.+1) < *(г,-7-2| < • • • < -V(,i-r2). Г у, Гг > 0. D0)
Если наблюдению доступен лишь ряд D0), где хотя бы одно из
чисел ги гг нулевое, то говорят, что выборка цензурнроваиа
(II тип цензурирования). Теория наилучшего несмещенного оце-
оценивании через .пшенные функции от цензурнрованных наблюдс-
98

ний D0) переносится автоматически на этот случай: достаточно
(X^+i), ... , Х(п_г,)) принять за новый вектор Y. Более того,
именно в случае цензурированием выборки этот метод оказыва-
оказывается особенно полезным, так как для полной выборки хорошие
оценки во многих случаях строятся проще другими методам».
Практическое значение теории линейных порядковых оценок
зависит от знания средних и ковармацпн порядковых статистик.
Явные выражения для а и Q, а тем более для Q можно полу-
получить в исключительных случаях, поэтому важное значение приоб-
приобретает расчет таблиц для Mt/A) и cov(U0U U(il) и коэффициентов
flii, «?: наилучших оценок
D1)
для наиболее часто используемых распределений. Большой набор
таких таблиц содержится у Сархана и Гринберга [8].
Пример 1 [9]. Ниже приведены значения х®, хад= Iog10.vw.
i= 1, 2, ... , 7, дней смерти и их логарифмов первых 7 из л =
= 10 мышей после вакцинации культуры туберкулеза.
41
1,613
44
1,644
46
1,663
54
1,732
55
1,740
58
1,763
60
1,778
На рис. 11 нанесены точки \хци
Ф-1 ((i—0,5)/10)). i=l, 2 7, °'7
и проведена иа глаз прямая х= 0,5
= o*y + Vi*; ц* = 1,747; а* = 0,090. цЗ
Согласие с нормальным зако-
законом логарифмов времен жизни '
можно считать удовлетворитель- №
ным. Коэффициенты аи, а2,- на- 1,6 1,7 1Д
ходим из табл. 10.С.1 Сархана п и п л. %
Р fi F Рис. !!. Логарифм дней смерти пер-
1 риноерга. вых 7 из 10 мышей после вакцинации
культуры туберкулеза на нормальной
бумаге
i
"и
и...
0
—0
1
,0244
,3252
0
—0
2
,0630
,1758
0
—0
3
,08!8
,1С58
0
—0
4
,0962
,0502
0
—0
5
,1089
,0006
0
0
6
,1207
,0469
0,
0.
7
5045
6!07
99

Значения ц и о находятся по формулам D1):
ц= 1,746; а = 0,091
и, как видно, близки к значениям ц*, а*, полученным графиче-
графически.
8. Упрощенные линейные оценки.
Расчет матрицы ковариаций порядковых статистик t/(,-, пред-
представляет значительные трудности. Поэтому был предложен упро-
упрощенный метод, дающий хорошие результаты по крайней мере для
нормальной выборки. Положим в формулах A0), A2) Q = /.
В результате
1=\
Д=A 1')(оо')-A«Т =
Га'= Г а а'—а' 1 а' =у а? Г— У а(а'<
1=1
1=1
ГГ=ГаГ—
г оценки параметров цио принимают вид
{=1
1 = 1
{=1
1=1
D2)
n
где ct — {q.i—a)/^(af—aJ. Формулы D2) применимы и к цен-
зурированным наблюдениям D0), если под Y понимать вектор
соответствующих порядковых статистик (a = MY, n — размер-
размерность вектора Y).
Пример 1 {продолжение). По табл. 10.В.1 Сархаиа н Грин-
Гринберга находим значения се,-= М ?/(,•>, t=l,...,5, се6=—се5, оп=—си:
j
а/
1
1,538
2
1,001
3
0,656
4
0,375
5
0,122
100

Рассчитываем *ц, "а по формулам D2) с Ч=(Х{\), .... Xi7)):
ц= 1,748; а = 0,094.
Результаты мало отличаются от наилучших несмещенных оценок:
ц= 1,746; а = 0,091.
§ 12. МНОГОМЕРНОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
1. Невырожденное нормальное распределение.
Нормальная ел. в. U\ с плотностью распределения ф(*) =
= е-*ч2/уг2я называется стандартной. Сл. в. Xi = oU\ + n имеет
плотность а"'ф((х—ц)/а) общего нормального закона #(ц, а).
Связь между U\ и Х\ послужит нам отправной точкой для введе-
введения многомерного нормального распределения.
Определение 1. Стандартным нормальным случайным век-
вектором назовем вектор
V=(UuU2t. ..,Un)
из независимых стандартных нормальных компонент.
Вектор U имеет математическое ожидание 0, матрицу кова-
риаций /, его распределение обозначим N„@, /).
Определение 2. Пусть а = (аи а2,...,а„) — произвольный
числовой вектор, В=\Ьц, i,j=l,...,n] — невырожденная число-
числовая матрица. Распределение случайного вектора
X = UB + a, A);
где U — стандартный нормальный вектор, назовем невырожден-
невырожденным п-мерным нормальным распределением.
Лемма 1. Нормальный вектор X, определенный формулой
A), имеет математическое ожидание л, матрицу ковариаций Q =
-В'В и плотность распределения вероятностей
-a)Q-'(x-a)'). B)
Доказательство. Следующая формула
C)
преобразования плотности справедлива при любом распределении
вектора U. Действительно, взяв А = {х :xi<;al,...,Xn<an} и ис-
используя замену переменных x5-' = U, запишем
f f|det5|-'/u(x5-1)dx1...dxn=f f/u (и
= P (U e ЛВ-') = P (U5e A),
т. е. ф. р. РA15еЛ) вектора UB представлена как л-мерный ин-
101

тсграл по множеству А от правой части C), которая, следова-
следовательно, является плотностью распределения вектора 115.
Воспользуемся формулой C), заметив, что плотность рас-
распределения вектора U в A) равна
/и (и) - /„, (и,) ... fvn («„) = (/§?)- exp (-1 /2 ии). D)
В результате получаем, что плотность /ив(х) дается формулой
B) пои а = 0. Переход к случаю а^=0 не вызывает затруднений.
Следствие 1. Если матрица В ортогональна: В'В = 1,. то
вектор X, определенный формулой A) при а = 0, имеет распреде-
распределение ;VH @, /).
Следствие 2. Функция f(x), заданная формулой B) при
любых а и положительно определенной Q, является плотностью
некоторого нормального вектора X. Действительно, представив Q
в виде В'В, где 5 — невырожденная матрица (см. D) § 10), тре-
требуемый вектор X можно определить по формуле A) с данными
В и а. ¦
Таким образом, можно дать эквивалентное определение л-мер-
ного невырожденного нормального распределения как распреде-
распределения с плотностью B). При этом а является вектором среднего,
а положительно определенная матрица Q — матрицей ковариа-
цнн этого распределения. Примем для него обозначение Nn(&,
Q). Ш
Отметим частный случай двумерного невырожденного нор-
нормального распределения, плотность которого записывают обычно
в виде
_2р
i О,
его матрица ковариаций равна
Лемма 2. Если вектор X имеет плотность B) с положитель-
положительно определенной матрицей Q, то он представим в форме A).
Доказательство. Представив Q в виде В'В (см. D) § 10) и
положив
U=(X—а) В,
найдем по формуле C)
/и (и) = /(Х_,)В-. (и) = | det 5-' | -' /х-а (иВ) =
= |det5|(/2ll)-n|detQ|-l'2exp( —l/2u5Q-lBV) =
102

так что вектор U имеет распределение М„@, /), а X выражается
через него по формуле A). ¦
В следующей лемме, а также всюду, где это полезно, будем
отмечать нижним индексом размерность вектора и квадратной
матрицы.
Лемма 3. Если \„= (Х\,.. .,Х„) имеет распределение Wn@n,
Qn) с невырожденной матрицей Qn=\qu, i,j=l, ..., п] uYfc = (Xfl,
Х,-„ ... ,ХфЛ < i1<i2< .. .<ifc<«, &<я, то вектор Ук име-
имеет распределение Nk@k, Qk), где Qk получается вычеркиванием
из Q,, строк и столбцов с номерами, отличными от i'i,•••.'*• В ча-
частности, компоненты Xi, i=l,...,n, являются N(Q, qu)-распре-
qu)-распределенными ел. в.
Доказательство. Не ограничивая общности, положим Yfc =
= (*¦ Хк). Пусть
Xn=UnB, В=[Ь\ Ь'п\, bi={bu bnl), 7 = 1,--,«, E)
и Un—Nn(On, /„)-распределенный вектор. Приведем систему век-
векторов bi, ..., bfc к ортонормированной системе С|, ..., с„ таким
образом, что
Ьу=Ь/,с,+ ...+Л//с/, ХцФ0, /=1, ...,л. F)
Матрица C=[c'i с'„] является ортогональной, и потому век-
вектор
Zn = UnC G)
имеет распределение Nn@n, In). Из E), F) и G) получаем
х,=и„ь;=и„ (х/гсг +...
Uncj = XllZ1+...+K,iZl, /=1,2, ...,л. (8)
Ограничивая индекс ; в соотношениях (8) значениями от 1 до k,
получаем, что вектор \к={Хи...,Хк) получен невырожденным
линейным преобразованием из вектора (Zu...,Zk), имеющего
iVfc@*. / )-распределение, и, следовательно, Yft — нормальный
вектор. Его среднее и матрица ковариаций, очевидно, таковы, как
это утверждается в лемме.
Следствие. Пусть В = [Ьц, t=l,...,n, /=1 m]—nXm-
матрнца ранга m, m<n, Qm = B'B, Un—N@n, /^-распределенный
вектор. Тогда вектор
имеет m-мерное нормальное распределение Wm(am, Qm) с невы-
невырожденной матрицей ковариаций Qm. Действительно, достаточно
дополнить матрицу В до невырожденной яХя-матрицы и восполь-
воспользоваться леммой 3.
Л е м м а 4. Пусть вектор Х= (Хи .... Хп) имеет невырожден-
невырожденное нормальное распределение, Y = (Xjt, .... X[m), Z = (Xtm+lt ...
• , Xit),ede (j'i, /о. •••.'«) — некоторая перестановка из чисел
103

A, 2 п). Если со\г(Х;к, Xt^^O, k=l m; /=m-f 1, ..., n, то
векторы Y н Z независимы.
Доказательство. Вектор (Y, Z), полученный из нормального
вектора X перестановкой координат, очевидно, нормален. Матрица
коварнаций вектора (Y, Z) имеет по условию вид
\ Rv Om.n-m]
Y.Z=|
[On—m,m Rz J
где 0,-,у обозначает /Х/'-матрнцу, целиком состоящую из нулей.
В таком случае
(V'Z) ~ о R-1
{.On-m.m *Z J
и плотность вектора (Y, Z) распадается в произведение двух нор-
нормальных плотностей: Nm@m, RY) и JVn_,,,(On_m, Rz), что и до-
доказывает утверждение.
2. Случайные векторы с вырожденной матрицей ковариаций.
Пусть Х=(Я|, ..., Я») —случайный вектор с произвольным за-
законом распределения, а=Л1Х и Q = Rx существуют, причем мат-
матрица ковариаций Q имеет ранг m<n. Покажем, что в этом слу-
случае распределение вероятностного вектора X—а сосредоточено в
некотором m-мерном линейном подпространстве пространства Rm.
Запишем представление (см. D) § 10)
vQv'=vB'Bv'=(vB'J
где пХп-матрица В'=[Ъ\,...,b'n] имеет ранг т. Для любого
вектора v= (oi, ...,«„) квадратичная форма
vQv'= v5'5v'=(v5'J
обращается в нуль на (п—т) -мерном линейном подпространстве
V={v:vQv' = 0}={v:v5'=0}. (9)
Следовательно, для ueV
DvX' = vQv'=0
и с вероятностью 1
vX'-MvX'=va', т. е. v(X'—а')=0.
Полученное соотношение показывает, что вектор X'—а' с вероят-
вероятностью 1 лежит в m-мерном подпространстве L, являющемся ор-
ортогональным дополнением к V. Как видно из (9), подпростран-
подпространство L порождается столбцами матрицы В'.
Нетрудно понять, что распределение вектора X—а не будет
сосредоточено нн в каком собственном подпространстве L*czL.
Действительно, если допустить, что с вероятностью 1 X—aeL*,
104

то найдется ненулевой вектор UeL и ортогональный к L*, такой,
что с вероятностью 1
u(X'—a')=0, uX' = ua'
и, следовательно,
' = DuX'=0,
т. е. ueV, что приводит к противоречию, так как V и L ортого-
ортогональны.
Замечание. Подчеркнем, что подпространство L, где сосре-
сосредоточено распределение вероятностей вектора X, определяется
матрицей Q и не зависит от выбора матрицы В в представлении
Q = B'B.
3. Вырожденное нормальное распределение.
Расширим понятие многомерного нормального распределения,
допуская, что в определении A) матрица В — любая ненулевая
«Хш-матрица. Таким образом, распределение вектора
A0)
при любых т, п, ненулевой матрице В н \Jn=(Ul,... ,Un) — стан-
стандартном нормальном векторе называется m-мерным нормальным
распределением. Невырожденное т-мерное нормальное распреде-
распределение получается из A0), когда матрица В имеет ранг m (см.
следствие к лемме 3). Если матрица В имеет ранг ft<m, то мат-
матрица ковариаций Q = B'B вектора Хт имеет ранг к н, как доказа-
доказано в предыдущем разделе, распределение вероятностей вектора
Х.-п—лт сосредоточено в ft-мерном подпространстве LcRm, явля-
являющемся ортогональным дополнением к подпространству
V={v:vQv' = 0}. A1)
Покажем, что распределение вероятностей в подпространстве L
задается 6-мерной нормальной плотностью. Выберем в L ортонор-
мированный базнс в|, ..., е* и дополним его векторами eft+i, ...
• •.,em до ортонормированного базиса всего Rm. Пусть старые ко-
координаты (Xi,.. .,хт) =х пространства R'" связаны с новыми
(.'/!, • •. ,Ут) =у формулой
С
где С — ортогональная матрица. Для xeL имеем ///;+i = ... = i/m = 0.
Поэтому вектор
Y,,,= (Xm—й„,)С
имеет координаты Yk+[ = ...= Ym = Q. Умножая A0) на С, запишем
\m = VnBC.
Отбросив в матрице ВС последние т—к (нулевых) столбцов и
обозначив полученную nX^-матрицу через А, имеем
(YY) VA A2)
A2)
105

где nXfc-матрица А имеет ранг k. Итак, в базисе ei,...,em век-
вектор Х,„—а,„ имеет координаты (Yu...,Yk, 0,...,0), причем ввиду
A2) вектор (Yi,...,)'„) имеет ^-мерную нормальную плотность
Nk @к, С В'ВС) = Nk @*. C'QC). ¦
Проведенные рассуждения показывают, в частности, что рас-
распределение вероятностей вектора Хт—ат от матрицы В зависит
только через матрицу ковариацнй Q=B'B. Поэтому мы сохраним
за нормальными распределениями общего вида обозначение
Wm(a, Q). Аналогично тому, как это сделано в следствии 2 из
леммы 1, легко показать, используя формулу Dа) § 10, что для
любого вектора а и любой ненулевой неотрицательно определен-
определенной матрицы Q существует вектор X с распределением NI&,
Q). Ш
Отметим еше одну полезную связь нормального распределения
общего вида с невырожденным нормальным. Выберем среди
столбцов лХт-матрицы
Я=[Ь', Ъ'т]
ранга k в представлении A0) какие-либо k линейно независимых
столбцов bf , bik, так что остальные столбцы через них ли-
линейно выражаются
b/ =
Тогда n.Xfc-матрица [b*,, ... ,b*J имеет ранг k, поэтому вектор
№, Xg - UB [b^, .... bj + (о, aim)
имеет невырожденное 6-мерное нормальное распределение, а ос-
остальные компоненты вектора X линейно выражаются через
Х X
ь;, Ц]=
,-, —а,,, ... , Xik— atk)'. Ш
Лемма 5. Пусть Xm=(Xit...tXm) — нормально распределен-
распределенный вектор, заданный формулой A0),
Y = (X,,. .... Xik), Z = (X/,, ... , Xjt),
ide (i'i, .... i"a) и (/"i,...,/'/) — две непересекающиеся последова-
последовательности индексов. Если
cov(X(j, Х/г)-0, s=l,... ,k\ г=\ I,
то векторы Y и Z независимы.
Доказательство. Из определения A0) вытекает, что вектор,
составленный из части компонент Хт, также имеет нормальное
106

распределение. Поэтому, не ограничивая общности, предположим,
что
Y= (Х\,... ,Хк), %={Xk+i,...,Xm),
cov(Xit X,)=0, i = l,...,k; j = k+l m.
Распишем матрицу В в формуле A0) в виде
B=[b', b'm],
так что
X,-a, = Vnb', = b',V'n,
cov(A',, X/)=/M(b,U'nUnb'/)=bIb'/, i = l k; /-*+l,...,m.
Используя некоррелированность компонент векторов Y и Z, полу-
получаем отсюда, что системы векторов (b|,...,bfc) и (Ь*+| Ь„,)
взаимно ортогональны. Выберем в каждой нз этих систем макси-
максимальные линейно независимые подсистемы (b,t, .... bip) и (b/,, ...
.... blq). Объединенная система (Ь„ Ь^, Ь,„ .... biq),
очевидно, линейно независима. Поэтому вектор
(X,,, ... , Х1р, Xh Х/?) =Un [b,, bip, b/,, ... , b,e]
имеет невырожденное нормальное распределение. И, применяя
лемму 4, заключаем, что случайные векторы (Х,„ ... , X, ) и (X/,,...
... , Xj ) независимы. Для остальных компонент вектора Y из
разложения
Ь/ = *7,Ь/. + ... + Л/рЬ<р, j < k,
вытекает, что они линейно выражаются через Xtl, .... X,- :
Xi-ai = V,tb\ = XhXll+ .. .+KipXip.
Диалогично оставшиеся компоненты вектора Z линейно выража-
выражаются через X/,, ... , X/ . Таким образом, компоненты векторов
Y и Z являются функциями двух независимых между собой сис-
систем: (X,,, .... Xip и (X/,, .... Х/7), и потому Y и Z сами неза-
независимы.
Лемма 6. Пусть Хп + нормальный вектор, \к=\„А, где А —
nxk-матрица. Тогда вектор Y* является либо нормальным, либо
постоянным.
Доказательство. Используя представление A0), получаем
и если матрица ВА ненулевая, то Y* — нормальный вектор. Щ
Пример. Пусть Х| Хп независимые ел. в. с общим нор-
нормальным распределением М(ц, о). Образуем случайный вектор
У=(У|. Y2>...,Yn+l) = (X,—Х,...,Хп—Х,Х), где X — выборочное
среднее. По лемме 6 Y — нормальный вектор, и так как
cov(Yit У„+|) =cov(Xi—X, X) =0, i = 1,..., л,
107

то Yn+l=X не зависит от {Yu...,Yn) = {X1—X,...,Xl(—X). Ранее
я _
(см. § 8) было установлено лишь, что X не зависит otV (Xt—XJ.
4. Распределение проекций стандартного нормального вектора.
Пусть пространство R" разложено в прямую сумму ортого-
ортогональных подпространств V\, V2,...;U — стандартный нормальный
вектор. Нас будет интересовать распределение векторов проекций
пру, U, ( = 1,2, Выберем ортонормированиые базисы: е|,...,е*
в V\, eft+i, ..., ek+i в V2, ¦¦• и объединим их в базис еь ..., е„
всего пространства Rn.
Пусть С — ортогональная матрица перехода от старых коор-
координат х =(*!,...,*„) к новым у= (t/i,...,уп):
хС=у, х=уС. A3)
Полагая С=[с'и с'2,...,с'„], су= (си,... ,с„/), отметим, что
С\1,...,сп; — координаты вектора еу в исходной системе коорди-
координат. Вектор
Y = UC=U[c',,...,cV| A4)
ввиду ортогональности матрицы С является стандартным нор-
нормальным (см. следствие 1 леммы 1). Поскольку
A5)
то по лемме 6 вектор (при, U, npy,U...) является нормальным.
Чтобы найти координаты пру,. U, t = 1,2 в исходной сис-
системе координат, подставим в A5) вместо е; вектор из их коорди-
координат с, в старой системе, / = 1,2,...,п, и, принимая во внимание
A4), запишем
„, и)' =[с;+1,.... cft+,][c;+l
Взаимные ковариации векторов проекций
с*1 К c'k\ K+i <+J K+v • • • •
равны нулю из-за ортогональности системы векторов Cj,сг,....
Поэтому случайные вектора np^ll, i = l,2, ... , — взаимно неза-
независимы. Наконец отметим, что
Цпри, U||« - Y\ + ... + Y\,
108

и, значит, квадраты длин проекций имеют /^распределения с чис-
числами степеней свободы, равными размерностям подпространств,
на которые производятся проектирования. Щ
Для дальнейшего полезно отметить, что распределение ел. в.
HU-fail2, где а — произвольный числовой вектор, зависит от а
лишь через его длину ||а||. Действительно, выберем в R" новый
ортонормироваииый базис, приняв за ei = a/||a||. Пусть в новом
базисе вектор U имеет координаты (Zlt Z2, ...,Zn) =Z, причем
Z — стандартный нормальный вектор; вектор а имеет координаты
(||а||, 0,...,0). Таким образом,
?. A6)
{=2
Распределение ел. в. A6) называется нецентральным ^-распре-
^-распределением, с п степенями свободы и параметром иецеитральиости
6 = II а1Г-. ¦
Для последующих применений сделаем еще одно замечание.
Между распределениями вероятностей величии ||U||2 и ||U-fa||2
имеет место при ila||#0 неравенство
^(||U+a||2>u)>i?(||U||2>u), A7)
которое легко вывести из A6), учитывая следующее очевидное
неравенство:
2>0.
Про случайные величины, связанные знаком неравенства A7),
говорят, что одна из иих стохастически больше другой.
§ 13. ДОВЕРИТЕЛЬНОЕ ОЦЕНИВАНИЕ И ПРОВЕРКА ГИПОТЕЗ
В ЛИНЕЙНОЙ МОДЕЛИ С НОРМАЛЬНЫМИ НАБЛЮДЕНИЯМИ
1. Распределение вектора оценок.
Мы будем рассматривать линейную модель:
Y=(y, Yn), e=@i....,e,)f r<n, A)
e=(ei,...,en), X=[x'lt...,x'r], xy= (хи, ...,Xn/),
/=!,. ...r.
Обозначим через V пространство, порожденное столбцами матри-
матрицы X, в котором лежит неизвестный вектор среднего:
r = eX'. B)
109

Размерность V обозначим через d=dimV. Наилучшая линейная
несмещенная оценка вектора среднего равна
ti=e,x,+... +егхг=е^'=пр1/ y.
Оценка дисперсии равна (см. A6) § 10)
^ W. C)
Если векторы xi х„ линейно независимы, то 0,-, i=\,...,r, од-
однозначно определены и могут быть представлены формулой
В противном случае разложение B) однозначно определяет толь-
только такие параметрические функции aiQi + ... + arQr, которые явля-
являются линейными функциями от координат вектора г\:
ae=bti'=bxe', ь=(б, ь„),
т. е. параметрические функции с коэффициентами, подчиненными
условию
й = ЪХ. D)
Наилучшей для ав' является оценка bY', где beV и удовлетво-
удовлетворяет D).
В этом параграфе мы дополнительно предположим, что вектор
е является стандартным нормальным. В таком случае нормаль-
нормальными являются векторы оценок 6, г\ (при этом
Мб = 6, Я$ = оЦХ'Х)-\
а также любой набор наилучших оценок параметрических функ-
функций
ь,ч/....,ь*ч'.
где b,eV, i=l,...,k. Оценка дисперсии C) является независимой
от ij, 9 и от любой совокупности оценок параметрических функ-
функций (см. п. 4 § 12), а ее распределение с точностью до парамет-
параметра масштаба совпадает с х2-распределением:
nP«"Gi' Y = nP«"Gv Ч + np^Qv °8 ~
так что
имеет распределение х2 с числом степеней свободы п—dim V.
ПО

2. Доверительные области для параметров и параметрических
функций.
Обозначим через </,-> элементы матрицы (Х'Х)~1. Тогда 0, имеет
распределение Л'(в,-, o2qij), а ел. в.
F,- - е,)/(о Vqii)=((§*—$)/(° W))/(o/o)
имеет /-распределение с числом степеней свободы n—d, где d=
= dim V, что позволяет строить доверительные интервалы для
0, в виде
) + A'l-a/2 (<n-d) О ]/^Г , E)
где хпA,„) —а-квантиль распределения tm.
Обычно представляет интерес одновременное доверительное
оценивание ряда параметров или параметрических функций. Рас-
Рассчитать вероятность одновременного выполнения нескольких не-
неравенств типа E) хотя и возможно, но весьма затруднительно.
Иной способ одновременного доверительного оценивания коэффи-
коэффициентов 6 (или параметрических функций) заключается в постро-
построении доверительного эллипсоида. Рассмотрим этот метод в при-
применении к оценке всего набора 6= Fi,...,6r). Воспользуемся тем,
что
г\—щ=пру Y—i|=npi/(Y—r\)=anpve,
и, следовательно, величина
а-2Ип-ч112=а-2|| F-8) ХТ-а-8 (^-в) Х'Х (в-в)'
имеет распределение %2 с числом степеней свободы d = dimV и. не
зависит от оценки дисперсии а2. Поэтому ел. в.
d-'a-2|ln—i\\\2 = d-la-2(Q—Q)X'X(Q—8)' F)
имеет распределение Fd,n-d, так что с вероятностью 1—а выпол-
выполняется неравенство
d-Ia-2@-8)A''X(e-e)/<A-I-a(F(f,n.rf). G)
Допустим, что матрица X имеет полный ранг: d=r. Тогда область
переменных @i,...,0r), удовлетворяющая G), представляет собой
эллипсоид, являющийся a-доверительным множеством в простран-
пространстве параметров Rr: неизвестная точка @i,...,0r) накрывается
эллипсоидом G) с вероятностью 1—а. Заметим, что доверитель-
доверительный эллипсоид G) (при d=r) получается из следующего не зави-
зависящего от выборки эллипсоида:
растяжением с коэффициентом а и переносом на вектор 8.
111

Линейная модель A) фактически определена подпростран-
подпространством V, в котором лежит вектор среднего г\; а-доверительным
множеством для вектора г\ является cf-мерный шар (d=d\mV):
T«(^.n-d), tieV. (8)
Выбирая различные базисы в пространстве V, будем получать
для координат вектора г\ в этих базисах описанные выше а-дове-
рительные эллипсоиды; в частном случае, когда базис ортонорми-
рованный, эллипсоид превращается в шар.
Если Vs — подпространство V размерности 5, то аналогично
(8) можно записать a-доверительный эллипсоид для "Hi =ПР1*Л-
Полагая ть= np^sY, имеем
(9)
В развернутой форме (9) имеет вид
riel'. A0)
3. Проверка гипотез с помощью доверительных эллипсоидов.
Рассмотрим линейную модель
Y=ii+ae, Че1«, A1)
где неизвестный вектор среднего г\ лежит в заданном линейном
подпространстве Vй размерности d. До тех пор пока мы рабо-
работаем с данной моделью, предположение r\^Vd не подвергается
сомнению. Естественной гипотезой в линейной модели оказывает-
оказывается предположение о том, что щ лежит в некотором подпростран-
подпространстве размерности ?<d: V*=V'd. Назовем это предположение ги-
гипотезой Н. Иначе можно записать
Рассмотрим a-довернтелышй эллипсоид A0) для вектора tis =
= npl,sii, Vt=VJQVk, s--d—k. В соответствии с методологией, ко-
которую мы уже неоднократно применяли в гл. I, если а-довери-
а-доверительный эллипсоид содержит вектор 0, то гипотезу H:r\s=0 сле-
следует принять на уровне значимости а. Подставляя tis = 0 в A0),
получаем статистику критерия для проверки гипотезы Н в виде
F =-jztl|rwev*viiv( j^-llnp^ev'YH2); A2)
в предположении Н она имеет рр
Оптимальные свойства сформулированного f-критерня будут
рассмотрены в других главах. Пока мы приведем некоторые до-
дополнительные соображения в пользу этого критерия. Заметим
112

прежде всего, что знаменатель статистики F, с точностью до пос~
юянного множителя, равен
l|np^0v,rfY||2 = l|V-npvrfY||2=||Y-?lll2 A3)
и представляет собой меру отклонения вектора наблюдений Y от
оценки его вектора среднего х\. Если гипотеза Н верна, то за
оценку вектора среднего следует принять вектор проекции Y на
подпространство Vk: r\k = npvi<4, и тогда мера отклонения Y от
щ равна ||Y — х\к\\2. Но
Y = npv* Y + np/0V* Y -
и, следовательно,
IIY -n* II2 = II i4Ve Vk Y t np^e va Y ||2 =
= l|np^e;*Y||2 + ||np^ev</Y||*. A4)
Отношение A4) к A3) равно
1 + II пр/e,* Y ||«/|| np^evrf Y ||« = 1 + ^5j F. A5)
Если гипотеза Н верна, то
v!, Y ||2 = о21| пр/е„* е ||2, A6)
т. е. увеличение A4) по сравнению с A3) вызвано только слу-
случайными причинами. Если же гипотеза Н нарушена, то
Y ||2 = || npvdQvk (il -г ое)||2 =
Величина A7) стохастически больше A6) (см. п. 4 § 12), и, сле-
следовательно, большие значения статистики A5) могут рассматри-
рассматриваться как свидетельство против гипотезы Н. С точки зрения за-
задачи проверки гипотезы статистика A5) равнозначна статистике
/•'. Подводя итог, отметим, что распределение статистики F сво-
свободно от мешающего параметра а, критическая область с довери-
доверительным уровнем а имеет вид
F>xl-rL(Fd-k,n-r,)- A8)
/¦-критерии A8) называют также дисперсионным критерием, так
как статистика F представляет собой отношение двух независи-
независимых оценок дисперсий: в знаменателе — несмещенная оценка о2,
в числителе — независящая от знаменателя статистика, являю-
являющаяся несмещенной оценкой а2 в предположении гипотезы Н.
113

4. Пример: сравнение средних в нескольких нормальных вы-
выборках.
Пусть имеется г незавнсимых выборок:
Y(-(V|, Yin.), i=l г, я1+...Ч-п, = п.
причем наблюдения внутри выборки независимые и ЛГ(ц,, о2)-рас-
о2)-распределенные. Положив Y==(Yi, ..., Yr) и обозначив через If, О/
вектора размерности /, целиком состоящие из 1 н 0 соответствен-
соответственно, образуем линейную модель
"in. 0Я1 ... 0„,
0„', й,...0л,
<4 \ ... Ц
A9)
где е=(еь ..., е„) — стандартный нормальный вектор. Матрица
X линейной модели A9) — ортогональная, поэтому легко нахо-
находятся оценки
1=1 Г.
Оценка дисперсии имеет вид
и — г
п.-
/=1
(=1 /Ы
(-1
Рассмотрим гипотезу Я:ц1 = Ц2=-. . = цг. Подпространство V*, где
в соответствии с гипотезой Н лежит вектор среднего ц, в данном
случае одномерно: k=\ и порождается вектором 1„. Вычисляем
г
II i4Vev* Y ||*« || пр,„ Y ||« -|| npv.ft Y ||« =--? ntf -nY*.
Таким образом, статистика критерия равняется
Приведем численный пример, заимствованный из [7]. Пронзво-
ди.чнсь измерения окружностей головы л=142 черепов, принадле-
принадлежащих к /¦--•') сериям, при -гтом /?i = 83, n2 = 51, «з = 8. Результаты
измерении приведены ниже в виде суммарных характеристик:
114

11277;
откуда
^=135,87; ^= 138,22; ц3 = 137,75;
r ni
#/=19428; ^= 136,817.
Дальнейшие вычисления удобно провести по формулам
Е Е ^tf-E «-W-E Е (yi-7)-(Y «*?-^i.
i
которые приводят соответственно к значениям 238,59 и 4616,4 —
— 238,59» 4378;
/ (^) = 119.29/31-50 = 3,79.
Найдем р-квантиль ^2,139-распределения для pi =0,95 и рг = 0,
по табл. 3.5 [1]. Имеем по таблице
xPl (F2,i2o) = 3,0718; xPl {F2,*) = 2,9957;
Xp, (F 2.120) = 3,8046; a>, (F2,x) = 3,6889.
Значения xp(Fm,n) для п=139 вычислим линейной интерполяцией
по аргументу 1/л:
xPl (F2.139) = xPl (F2.120) + (xPl (F2.*) —xPx (F2,i2o))X
xf— —)( —)"'-3,0718— C,0718— 2,9957H,1367 =
V 139 120 ) \ 120 ) V '
= 3,0614;
.v>,(f2. ш) = 3,8046—C,8046—3,6889H,1367 = 3,7888.
Итак, наблюденный уровень значимости
^0,025,
что можно рассматривать как неудовлетворительное согласие с
гипотезой. Во всяком случае для уровня значимости о = 0,05
^(¦;.б.т = 3,79 значительно превосходит границу л'0,95 = 3,0614, и на
этом уровне гипотеза должна быть отвергнута.
115

ГЛАВА III
ДОСТАТОЧНЫЕ СТАТИСТИКИ
§ 14. СТАТИСТИЧЕСКАЯ МОДЕЛЬ, ПОДОБНЫЕ СТАТИСТИКИ
1. Статистическая модель.
В предыдущих главах были приведены примеры реальных ста-
статистических данных и предложены вероятностные модели для их
описания. Объектом исследования являлась последовательность
ел. в. Xi — Xi(io), t=l, 2, ..., определенных на основном вероятност-
вероятностном пространстве (й, «s#, {&}) (см. п. 4 § 1). Вектор наблюдений
Х„= (Хи Хг, ..., Хп) определяет вероятностную меру Р:
Р(В)=^(о>:Х„(а>)<=В), A)
заданную на системе &&п так называемых борелевских множеств
Rn: 3bH — наименьшая система подмножеств Rn, включающая
множества вида {xn = (jti, ..., х„) : ai<xi<bi, i—l, .... л}, а,«:
<bi — произвольные числа, и замкнутая относительно перехода
к дополнению и образования счетного объединения. Меру Р(В)
мы будем называть распределением вероятностей вектора Х„.
В последующем мы встретимся с моделями, в которых число на-
наблюдении п заранее не фиксировано и результатами наблюдений
могут оказаться числовые векторы x,,= (jci, ..., хп) разной раз-
размерности п. Имея в виду это обстоятельство, введем отдельное
обозначение й? = {х} для пространства выборок х, не накладывая
ограничении на структуру этого множества, хотя, как правило,
речь будет идти о S8 = Rn, х = х„=(дг|, ..., хп). В случае выбо-
выборочного множества S6 произвольной структуры будем считать,
что в 96 выделена система & так называемых измеримых мно-
множеств. Система 38 должна содержать 85 как свой элемент, долж-
должна быть замкнута относительно перехода к дополнению и образо-
образованию счетного объединения. Отображение Х(со) множества Q в
$Е, такое, что для любого В&
называется измеримым; в случае, когда фиксирована мера &
па (il, s4), функции) А'(о») называют случайным элементом на
C5, 3S). Пару из множества и системы измеримых подмножеств
называют измеримым пространством; таковы пары (Q, зФ),
C?, JS). Название связано с возможностью задать меру на систе-
110

ме измеримых подмножеств — это мера 0* в случае (й, si-) н
мера Р, определяемая формулой
Р(В)=^(со:Х(со)(=В), B)
в случае пространства (SB, 98).
Предметом изучения теории вероятностей является отдельное
вероятностное пространство (й, «s#, J1). Как мы могли убедиться
в предшествующих главах, в математической статистике вероят-
вероятностная модель, которая предлагается для описания опыта, опре-
определена не полностью. И как раз задача статистики — уточнить
эту модель по результатам испытании. Другими словами, модель
математической статистики определяет, я целым семейством веро-
вероятностных мер {&} на (й, зФ), н тем самым объектом изучения в
математической статистике оказываете! семейство вероятностных
пространств {(й, «s#, &)}, где & принадлежит некоторому задан-
заданному множеству {&>}. Формула B) порождает семейство вероят-
вероятностных мер {Р} на измеримом пространстве (96, 98). Тропку
(96, &, {Р}) называют статистической моделью. Прн фиксирован-
фиксированном Р вероятностное пространство (96, 9S, Р) назовем выбороч-
выборочным. Если семейство {Р} параметризовано н имеет вид {Рв:0е6},
где 0 — скалярный или векторный параметр, то модель
(96, 9S, {Рв:0ев}) называют параметрической.
Приведем некоторые примеры уже известных нам статистиче-
статистических моделей.
(I) 96 = Rn; 9S=9Sn — система борелевских множеств в R"; ме-
мера Р/г, где F — одномерная непрерывная ф. р., задается п-мерной
ф. р. вида
F(xt)-...-F(xn),
что соответствует независимой выборке с ф. р. отдельного наблю-
наблюдения F(x). Семейство {Р^} образуется из всех Pf с непрерывной
ф. p. F. К этой модели мы по существу обращались прн довери-
доверительном оценивании теоретической ф. р. через э. ф. р. с помощью
статистики Колмогорова (§ 2), а также при построении довери-
доверительных интервалов для квантилей (§ 3).
(II) Измеримое пространство (#?, !%) и мера Pf те же, что н
в (I), но F пробегает множество ф. р., отличающихся сдвигом и
масштабом от некоторой заданной ф. p. Fo(x). (Например, F0(x) —
— 1—е~х, х>0 илн F0(x)=<b(x).) Семейство {Р} в данном случае
параметризовано: каждое Рм,0 задается парой чисел (\х, а), —оо<
<ц<°°, о>0.
(III) 80, 35 — те же, что и выше, семейство {Р} состоит из мер
Р следующего вида. Пусть F(xu ..., х„) — соответствующая Р
л-мерная ф. p., Fi(xi), F,7(.v., Xj) — наборы одномерных и двумер-
двумерных ф. р.:
Ft (xt) = F( + оо -foo, ;<?, -г оо +oo),
, .... +oo, xit +oo +oo, xh +oo, ...,+oo).
117

Предполагается, что выполнены следующие соотношения:
ОБ 09 09 00
J XiXjdFuiXi, X/)= J XidFi(Xi) J X/dF/ix,), i< /.
— 00 —ОЭ
ОЭ
Xi dFt (Xi) = Ь,х1х + ... + brXir = л,-, J (*< —Л,J dFi (x() = a2,
i = 1, .... n,
где A-,i, ..., xir, i—l, ..., n, — некоторые заданные числа (одни к
те же для всех Р), 6i, .... 0Г, о2 — числовые параметры, свои для
каждого Р. Множество всех распределений Р с указанными огра-
ограничениями на первые два момента и составляет семейство {Р}.
Легко понять, что в данном случае речь идет о линейной стати-
статистической модели с некоррелированными наблюдениями, с равны-
равными дисперсиями и матрицей модели X=[xij, i=l, ..., п\ /=
= 1, ..., г]. Следует подчеркнуть, что каждому элементу Р сопо-
сопоставлен набор параметров Fi, ..., Qr, о2), однако это соответствие
не является взаимно-однозначным. Поэтому семейство {Р} не яв-
является параметризованным.
(IV) В условиях предыдущего примера предположим допол-
дополнительно, что Р — n-мериое нормальное распределение. В резуль-
результате получаем параметрическую модель (см. § 13), где Ре,* есть
Nn(QX\ аЧ), 6= F, Qr), —оо<6,<оо, i=l г, а>0.
Проведенное нами различие между вероятностной и статисти-
статистической моделями приводит к различию в понятиях и обозначе-
обозначениях, которое раньше не всегда явно отмечалось. Это относится,
в частности, к понятию статистики.
Определение 1. Статистикой назовем любую функцию
7"(х), задающую измеримое отображение пространства {96, 3S) в
(/?', 2&\), т. е. такую, что для любого В^&&\
Векторной статистикой назовем упорядоченный набор статистик:
Таким образом, понятие статистики оказывается не связанным
с семейством мер {Р}. Переход от статистики к случайной величи-
величине — функции от выборки — производится подстановкой в 7"(х)
вместо х случайного элемента X. К сожалению, уступая традиции,
не всегда удается отказаться от употребления термина статистика
по отношению к ел. в. 7"(Х).
Заметим, что обозначение Т(\) не отражает зависимости от
распределения & (или Р). Это не приводит к путанице, когда
речь идет о вероятностях &>(Т(Х)^В), но для математического
ожидания мы введем явное указание на распределение: МР или
Мп, если семейство параметрическое.
118

2. Подобные статистики.
Существуют статистики 7"(х), для которых распределение ве-
вероятностен 7(Х) одно и то же для всех Р из заданного семейства
{Р}. Такие статистики называются подобными (они подобны слу-
случайным величинам). Рассмотрим несколько примеров.
(I) Пусть /?"-"¦ — выборочное пространство, Pf — мера в
R" "'-, задаваемая непрерывной ф. р., имеющей вид
... -F(xn)-F(xa+i)- ...
{Pf} — семейство всех таких мер. Положим х<'>= (jti, .... хи),
xB)=(.v)i+I хп+т), х=(хО, х<2>) и введем э. ф. p. Fn(x; х<0),
Fm(x; хB>). При фиксированном х каж; тя из этих э. ф. р. является
статистикой. Образуем статистики Сми; нова:
= sup(Fn(x; x<'))_Fm(
X
sup\Fn(x; x»))-Fm(x;
X
Совершенно аналогично статистике Колмогорова (см. п. 3 § 2)
проверяется, что распределение каждой из статистик Т+, Т одно
и то же для всех Ре{Р/}, и, следовательно, обе эти статистики
подобные.
(II) Пусть {Р„:—оо<ц<оо} — семейство распределений в Rn
с параметром сдвига ц: Р„ задается ф. p. F0(x\—\i)-F0(X2—)>¦)•••¦
л
... F0(xn—)i). Статистика Т(х) = '?{ (Ъ—хJ— подобная.
(-1
(III) Для семейства {Р„:0<а< + оо} в /?", где Р„ задается ф. р.
Fo(xi/a)Fo(x2/a)-... •F0(xnla), подобной статистикой будет
л
+
(IV) В линейной статистической модели с нормальными на-
наблюдениями (см. п. 3 § 13) статистика
I ш/[^г
является подобной в предположении, что верна гипотеза Н: век-
гор среднего лежит в V*.
(V) В модели сдвнга-масштаба статистики
-*J и -
«-1 ° 1=1
будут подобными при выполнении гипотезы |« = мо для первой
статистики и а=ао — для второй.
Поскольку распределение подобной статистики одно и то же
Ui/i всех мер Р в пределах рассматриваемого семейства {Р}, ио-
119

добная статистика не помогает уточнить вопрос о том, какое
именно из распределений Р лучше всего соответствует наблюден-
наблюденным данным. Зато подобную статистику можно использовать для
проверки соответствия модели наблюденным значениям (хотя бы
в отношении таких отклонений от модели, которые улавливает
данная подобная статистика). Например, в задаче о сравнивании
двух независимых выборок гипотеза о том, что наблюдения в
обеих выборках х<') и хB' имеют общую ф. р., помещают нас в ус-
условия примера (I). Понятно, что умеренные значения статистик
7"+(х), 7"(х) будут говорить в пользу такого предположения.
Благодаря подобию, критерии с критическими областями вида
Т+(х)>с, Т+(х)<—с имеют при любом с определенный уровень
значимости, не зависящий от выбора меры Р в пределах семейст-
ва {Р}.
Задача проверки данных на согласие с моделью, как мы мог-
могли убедиться в предыдущих главах, близка к вопросу о построе-
построении доверительного интервала для параметра. Как видно из при-
примера (V), этот вопрос также можно решать, имея подходящую-
подобную статистику.
§ 15. ДОСТАТОЧНЫЕ СТАТИСТИКИ В ДИСКРЕТНОЙ МОДЕЛИ
1. Введение.
Почему, наблюдая выборочную точку х в статистической мо-
модели (#?, 38, {Р}), можно рассчитывать на уточнение наших све-
сведении об истинном распределении вероятностей Р? Конечно, пото-
потому, что точка х, полученная в результате эксперимента с распре-
распределением вероятностей Р, несет информацию о своем распределе-
распределении вероятностен. Если статистическая модель уже выбрана, то
интерес представляет лишь та информация в х, которая служит
задаче различения элементов Р из {Р}. По многим причинам ста-
статистические выводы приходится основывать на одной пли несколь-
нескольких статнстнках-функииях от х. Как выбрать эти статистики, что-
чтобы не потерять информации по интересующему нас вопросу? На-
Например, рассмотренные в предыдущем параграфе подобные стати-
статистики несу г информацию лишь о таких чертах распределения Р.
которые являются общими для всех элементов из семейства {Р}
и, следовательно, ничего не дают для решения задачи о различе-
различении элементов Р. Нас интересует такой, по возможности мини-
минимальный, набор статистик G*| (х), ..., Г*(х)) =Т(х), который со-
содержал бы всю имеющуюся в х различающую информацию об
элементах Р и ничего лишнего. Такая статистика Т(х) будет на-
называться достаточной статистикой для нашей модели.
2. Примеры.
(I) Пусть a? = {x,,= (.v, л„):а/ = 0 или 1, i=l, .... и},
Р„ (х„) = 8$« A -8)"-\ sn = Xl+...+xn,
где О<0<1. Это хорошо известная схема испытаний Бернулли.
120

Для оценки параметра 0 — неизвестной вероятности — использу-
используется статистика sn{Q = sn/n. Допустим, статистика sn приняла не-
некоторое значение s. Что мы получим нового, если узнаем, какая
именно из CV выборок, содержащих ровно s единиц, осуществи-
осуществилась в результате эксперимента? Если мы рассматриваем случай
s,, = s, то естественно перейти к модели с выборочным простран-
пространством S?j = {x,, :*! + .. .+xn = s) и семейством условных вероятност-
вероятностных мер, получаемых из Ре сужением на 96%. Эти меры:
как видно, не зависят от 6, а все семейство состоит из единствен-
единственного элемента — равномерного распределения на 26%. Итак, до-
дополнительная вероятностная информация, содержащаяся в х„, по-
помимо той, что х„еЯ?4-, никак не связана с параметром 6, и потому
статистику sn следует признать содержащей всю информацию о
параметре 6.
Соображения, лежащие в основе приведенных рассуждений,
можно пояснить с иной точки зрения. Реализуем испытания Бер-
Берну л л и с помощью извлечения шаров из урны (либо по таблице
случайных чисел) по следующей схеме. Возьмем рациональное 6,
0<0<1, и урну с N шарами я+1 цветов, причем доля шаров 1-го
цвета равна биномиальной вероятности р, = С„'0'A—0)n~', i=
= 0, 1, .... п (в качестве N можно взять наименьшее число, при
котором все NPl, i = 0, I, .... п, целые). Кроме того, возь-
возьмем еще л+1 ури, причем уриа с номером i, t = 0, I, ..., п, содер-
содержит Сп' (Сп°=1) шаров, занумерованных С„' наборами (х\, ...
¦ ¦-, хи), х/ = 0- или 1, /= 1, ..., п, содержащими ровно i единиц.
Организуем теперь двухступенчатый выбор. На первом этапе вы-
выбирается шар из урны с шарами л+1 цветов и отмечается цвет i
вытащенного шара. На втором этапе из уриы с номером i извле-
извлекается шар и номер извлеченного шара — последовательность
(х\, .... х„) — объявляется результатом полного эксперимента.
Элементарный вероятностный расчет показывает, что результат
опыта — (*i, ..., х„) — представляет собой реализацию испыта-
испытании Бернулли с вероятностью 6 выпадения 1. С другой стороны,
поскольку вторая ступень нашего сложного опыта связана с па-
параметром 6 лишь через' номер i — результат первого этапа, совер-
совершенно ясно, что к информации о 6, содержащейся в исходе i
первой ступени опыта, вторая ступень ничего нового добавить ие
может.
(II) Пусть Я?={х„-=(;с, xR):xi-0, 1, 2 t=l, 2, ...
.... »}, а мера Ре соответствует независимой выборке из пуассо-
мовского распределения с параметром 0>О:
7
121

Оценкой параметра G — теоретического среднего выборки — слу-
жит выборочное среднее x — sjn, «„ —д] xt. Рассмотрим услов-
ную модель в предположении s,, = s с выборочным пространством
8t?s = {x:xi + .. . + x,, = s) и условной мерой
Pe(xn|a?s) = Pe(xn)/pe(a?s), х„ея?*. B)
Знаменатель в B) представляет собой вероятность того, что сум-
сумма независимых пуассоновских ел. в., с параметром 6 каждая, при-
примет значение s. Легко проверить, что при сложении двух незави-
независимых ел. в., распределенных по Пуассону с параметрами >. и ц
соответственно, получаемая ел. в. X+Y также имеет распределе-
распределение Пуассона с параметром А,+ ц:
г»0
— е-* —*- tr* = - У —-
г! (u — v)l и! ?Jv\(u —
0 0
о)!
Таким образом,
Ре (#0 = Fe (J X, = s) = г-* (n8)'/s!, B')
и для условной меры получаем выражение
л
Ух,
Р„(х„|#$) = е-»*Ъ а'/\пх,1)(г-»»(лву/я!Г' =¦¦
„ C)
которое не зависит от G. Отметим, что C) представляет собой
частный случай так называемого полиномиального распределе-
распределения (при и = 2 — биномиального с вероятностью 1/2). Отсюда сле-
следует, что искусственную выборку объема я из пуассоповского
распределения с параметром G можно построить, моделируя сна-
сначала пуассоповскую ел. в. с параметром пЬ: если она приняла
значение s, то моделируется опыт по случайному размещению s
шаров по л ящикам. Результат последнего опыта записываем в
виде набора (х\, Хз, ..., х„), где лг, — число шаров, попавших в
ящик с номером i. Легко видеть, что этот результат имеет поли-
122

номиальную вероятность C), а опыт в целом приводит к исходу
(.V|, л, ... х„) с вероятностью A). Итак, с точки зрения инфор-
информации о параметре 8 интерес представляет лишь первым этап ука-
указанного двухступенчатого опыта, результат которого выражает
статистика s,,.
(Ill) Пусть ??={x,, = (a-,, .y2, .... .v-,,) :.v,=l, 2, ..., /V, i=l, 2,...
• ••, n), P;v(x,.) =N~n, XjigI1, т. е. речь идет о выборке с возвра-
возвращением нз урны с Л' занумерованными шарами. Параметр Лг при-
принимает натуральные значения. Проверим, что условное распреде-
распределение зиборкн Х„ при условии, что Х(Н)=т, не зависит от пара-
параметра V. Имеем
= т) = ^n (*(»> < т) —<**л- {Хм< от — 1) =
/=1 п)— <
>N (Х„ - х„ | Х(п) = т) = #».v (Х„ = х„IР (Х(п) = от) =
Рассуждения, аналогичные проведенным в предыдущих примерах,
показывают, что статистика *(„> содержит всю информацию о па-
параметре W, которая имеется в выборке.
3. Достаточные статистики: определение.
Пусть (Я?, SS, {Р}) — дискретная статистическая модель: мно-
множество $в конечно, или счетно, a SS — система всех подмножеств
8В. В этом случае любая числовая функция 7"(х) является, оче-
очевидно, измеримой относительно 9S, т. е. будет статистикой. Для
любого Р нз семейства {Р} и для данной (вообще говоря, вектор-
нон) статистики Т(х) определим семейство условных мер Р*, по-
положив для любого В3&
Р4 (В) = Р (В П <х: Т (х) = t})/P ([х: Т (х) = t}), D)
где Ре{Р}, а индекс t при данном Р пробегает множество всех
значений, для которых знаменатель в D) отличен от нуля.
Определение 1. Статистика Т(х) называется достаточной
для дискретной статистической модели (SB, 9S, {Р}), если при
каждом t условные вероятностные меры Р* не зависят от Ре
s{P}.
Замечание 1. Полезно иметь в виду, что при каждом t
имеется, вообще говоря, свое подмножество множества {Р} мер Р
таких, что знаменатель в формуле D) отличен от нуля, и именно
для этих Р условные меры Р* должны совпадать между собой.
Более наглядным является случай параметризованного семейства
{Р(ь в ев}. Здесь определение достаточности Т(х) удобно
123

сформулировать так: существует семейство мер Р*, зависящих
от индекса t, таких, что равенство
Ре (В П {х: Т (х) = t})/Pe ({х: Т (х) = t}) - Р* (В) Dа)
выполняется для всех пар (в, t), при которых левая часть в
Dа) определена.
Замечание 2. Пользуясь тем, что
вместо условных мер D) в выборочном подпространстве [S6, &)
можно ввести условные вероятности
t) D6)
и дать определение достаточной статистики Т(х) как статистики,
для которой условные вероятности D6) не зависят от & в преде-
пределах семейства {5*} (при данном t рассматриваются лишь те &,
для которых D6) определено).
Из определения достаточной статистики Т(х) вытекает, что, как
и в разобранных выше примерах, статистика Т(х) содержит всю
информацию выборки х, полезную для различения элементов Р
из {Р}. Понятие информации при этом не формализовано, однако
содержательный смысл сказанного хорошо ясен, если искусствен-
искусственно моделировать выборку Xм с распределением Р. Повторим это
рассуждение в общем случае. Сначала реализуем опыт, который
по элементу Ре{Р} моделирует (вообще говоря, векторную) ел. в.
ТА', для которой
P(T« = t) = P(T(X)=t). E)
Затем по значению t, которое приняла ел. в. ТЛ), и заданному се-
семейству мер Р* строим ел. в. Xм с множеством значений
{x:T(x)=t} и вероятностями
= 1)=р'(х). F)
Перемножая E) и F), находим с учетом D)
т. е. Xм имеет то же распределение, что и X, но при этом только
первый этап моделирования зависит от Ре{Р} и, следовательно,
несет различающую элементы Р из {Р} информацию. Результат Тм
первого этапа, очевидно, может быть представлен в виде T<V1 =
=Т(ХЛ|), где Т(х) — рассматриваемая достаточная статистика.
Итак, в искусственном эксперименте достаточная статистика Т(х)
является носителем всей полезной различающей элементы Р из
{Р} информации.
Определение 2. Достаточная статистика S(x) называется
минимальной, если она представима как (вектор-) функция от лю-
любой достаточной статистики.
124

Понятно, что интерес к достаточным статистикам связан с
возможностью сократить ненужную информацию, содержащуюся
в выборке, и тем самым облегчить возможность последующего
анализа. Поэтому если от достаточной статистики Т(х) можно пе-
перейти с сохранением свойства достаточности к статистике it(T(x)),
где функция ij>(t) принимает одинаковые значения при некоторых
*1=/^2, то статистику ^>(Т(х)) следует предпочесть Т(х). Из опре-
определения минимальной достаточной статистики следует, что даль-
дальнейшее сокращение данных без потери нужной информации невоз-
невозможно. Мы покажем, что статистики, рассмотренные в примерах
(I) — (III), являются минимальными достаточными. Проведем
подготовительные рассуждения.
Пусть 77х) — достаточная статистика для дискретной модели
($?, Л, {Рв}) и /|=/=/г — два ее значения. Перейдем к статисти-
статистике \fG"(x)), где if(/)ss/ при t\=f=tt и ${t2)=ti, т. е. статистика
\fG(x)) совпадает с 7"(х), если последняя принимает любое зна-
значение, кроме /г, а выборки, для которых 7"(х)=^, она объединяет
с теми, для которых 7"(x)=fi. Рассмотрим условия, при которых
такое сокращение данных сохраняет свойство достаточности. Что-
Чтобы это имело место, условная вероятность
= х. Г(Х) = /.)
-U G)
не должна зависеть от 6 (при тех 6, для которых выражение G)
имеет смысл). Преобразуем числитель в G) по формуле условной
вероятности:
1 = 1.2. (8;
Ввиду достаточности статистики 7"(х) условная вероятность в (8)
от параметра 6 ие зависит (см. Dа)). Положим для краткости
(?!>e(X = x|r(X) = f<) = /JI-(x), t = l, 2, и перепишем условную
вероятность G) в виде
q(() U
Рг(х) + (А(х)-Pl(х)) с?>9(Г(Х) = <1)Ч-сУ>9(Г(Х)^/,)- <9>
Выражение (9) ие зависит от 6 (для 6 таких, что знаменатель в
(9) отличен от нуля), если либо р\(х)вар2(х), т. е. условное рас-
распределение выборки при значениях i\ и h достаточной статистики
7"(х) одно и то же, либо множитель при р2(х)—pi(x) в (9) ие за-
зависит от 0. Это будет так, если отношение
с*»в (Т (X) = tt) Р9({х:Г(х) = М)
с*»в (Т (X) = h) = Рв ({х: Т (х) = <х}) A0)
не зависит от 6. Обратимся к примерам (I)—(III).
125

В ппимрпр (I) 77хЛ=*.+ ...+*„, pt(xn) = Cn" при Т{хп) =
i, так что Pi(xnI?bP2(Xn) для t&t2. Отношение A0) равно
1 -б)л-'«). о < е < 1,
и, очевидно, зависит от 9 при 1\ФН. Следовательно, если от ста-
статистики Т(хп) перейти к ^(^(х,,)), где tp(/)==f при t^h и ty{h) =
= /i, т. о. объединить значения t\ и t2 статистики 7"(х„), то свойст-
свойство достаточности нарушается, и потому статистика 7"(x,,)=;ci +
+.. .'-r.v,, минимальна.
В примере (II) ситуация аналогичная: р<(х„) определяется
формулой C) и р\(хп)фр2(х„). Отношение A0) выражений B')
при s = /2 и s = t\ равно
н, очевидно, зависит от 0 при
В примере (III) Г(хп)=х(п), p,(xn) = (m,n—(m,—1)») при
*(«! — "»,• н, следовательно, Р\(х„)фр2(хп). Положим для опреде-
определенности m,\<m2. Тогда отношение A0) равно (т2п—
— (m2—l)n)/(m,n—(mi—1)"), если Л^>т2, и принимает значение
нуль, если m.\<N<m2, т. е. отношение A0) зависит от параметра
N, следовательно, статистика *<„> минимальна.
4. Критерий достаточности.
Для наглядности рассмотрим параметрическую модель
(X, Л, {Рд, 8ев)). Пусть Т(х) — достаточная статистика; по-
положим
*(t; 6) = Pe({x:T(x) = t}).
Основное соотношение Dа) можно записать в виде
вх), t=T(x).
Введя функцию
А(х) = РТ(ж)(х).
получаем
в)А(х), хей7. A1)
Разложение распределения вероятностей Рв(х) в модели
C7, о8, {Р9:ве6}) на множители в форме A1), где один
множитель Л(х) не зависит от 0е6, а другой — зависит от х че-
через некоторую статистику Т(х), назовем факторизацией этого рас-
распределения. Факторизация Р0(х) иееднпственна. Например, взяв
проп:ви:ьную не обращающуюся в нуль функцию ф(х) и положив
, А'(х)
126

получим из A1)
Рв(*) =
Всегда возможна тривиальная факторизация
Рв(х)=Рв(х)-1.
Итак, если статистика Т(х) достаточна, то имеет место фактори-
факторизация A1).
Верно п обратное. Пусть имеется факторизация A1), где
Т(х) — некоторая статистика, g(t; 6) — функция t, /i(x) — функ-
функция, не зависящая от 0. Покажем, что статистика Т(х) является
в таком случае достаточной. Так как все меры Pfl обращаются
в нуль на множестве {х:Л(х)=0}, то исключим эти х из дальней-
дальнейшего рассмотрения. Из A1) получаем
); в)А(х) =
= *(t; в) у. А(х). A2)
x€B,T(x)=t
При В = Я? из A2) получаем
Pe({x:T(x) = t» = *(t; в) ? А(х). A3)
T(x)=t
Положим
Р'(В)= ? А(х)/ ? А(х).
x6B.T(x)=t T(x)=t
Для 6 таких, что PQ({x: T(x) = tj) >0, поделив A2) па A3),
получаем, что условная мера совпадает с Р'{В) и, следовательно,
статистика Т(х) — достаточная. Таким образом, получена
Теорема факторизации. Для того чтобы статистка
Т(х) была достаточной для дискретной модели (9В, J&, {Ро:0«=
ев}); необходимо и достаточно, чтобы имела место факториза-
факторизация A1).
При соответствующих изменениях в обозначениях этот же ре-
результат, очевидно, справедлив для пепараметрнческих моделей.
Отыскание достаточных статистик с помощью теоремы факто-
факторизации сводится к анализу распределении выборки. Достаточ-
Достаточность статистик в примерах (I) — (III) с помощью теоремь: факто-
факторизации устанавливается немедленно. Рассмотрим еще пример.
(IV) Пусть в схеме испытании Бернуллн число наблюдений
заранее не фиксировано: испытания продолжают до случайного
момента появления r-го успеха, где г — заданное число. Множе-
Множество SB состоит из всех последовательностей x:i=(xi, .... х„),
*.=0 или 1, i=l, .... п; я=1, 2 содержащих ровно г единиц,
127

причем .г„=1. Вероятностная мера Рв> О<0<1, определяется фор-
формулой
где Л'(х) — число координат вектора х. В силу теоремы фактори-
факторизации W(x) — достаточная статистика.
5. Достаточные и минимальные достаточные разбиения.
Статистики Ti(x) и Т2(х), связанные взаимно-однозначным
преобразованием т/(х) =\J>(T2(x)), назовем эквивалентными. Экви-
Эквивалентные статистики несут одну и ту же информацию о стати-
статистической модели. Если одна из них достаточная, то достаточной
будет и другая. Сокращение данных, которое дает каждая из этих
статистик, одно и то же: системы подмножеств
{x:T,(x)-t,} и {x:T2(x)«t2},
где ti и t2 пробегают соответственно множество значений стати-
статистик Ti и Т2, совпадают.
Определение 3. Разбиение множества SS на подмножест-
подмножества 951, где t пробегает некоторое множество индексов:
[)t t, 0
t
называется достаточным для дискретной модели (Я?, SB, {P}), ес-
если условные меры
не зависят от Ре{Р} (для тех Р при данном t, для которых
Р(Я?H)
))
Если имеется достаточное разбиение, то разными способами
можно определить числовую функцию, постоянную на элементах
разбиения и принимающую разные значения иа разных элемен-
элементах. Эта функция будет достаточной статистикой. Полезно иметь
в виду, что если элементы разбиения {"У*} множества SS целиком
содержатся в элементах достаточного разбиения {SSt} (т. е. для
любого а найдется t = ta, что УаЕ.^1а)> то разбиение {фа} также
является достаточным. Действительно, для хе<уа отношение
Р (Х)/Р (Уа) ¦-= (Р (Х)/Р (#,
не зависит от Ре{Р}, поскольку разбиение {SSt} — достаточное.
Определим минимальное достаточное разбиение как разбиение,
элементы которого являются объединением элементов любого до-
достаточного разбиения (или совпадают с таким элементом). Пока-
128

жем, как строится минимальное достаточное разбиение в дискрет-
дискретной модели. Для наглядности рассмотрим параметрический
случаи.
В п. 3 (видели, что если достаточная статистика Т(х) такова,
что отношение (см. A0))
не зависит от веб, то, сохраняя свойство достаточности, можно
объединить элементы разбиения, соответствующие значениям t\ и
it статистики Т. Это же соображение лежит в основе приема мн-
Ш1маль::ого сокращения данных, о котором идет речь ниже. Имен-
Именно введем отношение xRy па множестве $6, полагая, что х связа-
связано с у отношением R тогда и только тогда, когда для каждого 0е
ев, такого, что Р0(х), Р0(у)>0, отношение Рв(х)/Рв(у) не зави-
зависит от G. а для всех G, для которых одно из Pg(x), Рд(у) равно
нулю, также равно пулю и другое. Отношение х/?у, очевидно, ре-
рефлексивно: xRx имеет место для любого х; симметрично: если
х/?у, то и у/?х, и транзитнвно: xRy, yRz=>xRz. Таким образом,
xRy есть отношение эквивалентности, и, как известно, множество
Я? разбивается па непересекающиеся классы $Ви
X=\iXt, ЗДЯ.-С, 5ф(, A4)
t
где / пробегает некоторое множество индексов, причем каждый
класс 95i состоит из множества всех элементов, которые эквива-
эквивалентны друг другу по отношению R. [Проверим сделанное утвер-
утверждение. Пусть хей1 произвольно. Обозначим через Ух множе-
множество всех элементов у, таких, что xRy. Тогда xRx, и, следователь-
следовательно, ХеУх. ПуСТЬ ZG^ ПРОИЗВОЛЬНО; ДОПУСТИМ, ЧТО Ух[\УгФ
Ф2>, тогда существует элемент и из их пересечения. Поскольку
xRu и zRu, то по симметрии u/?z, а по транзитивности xRz. Пусть
\^Уг, тогда zR\, и так как xRz, то по транзитивности xRv,
т. е. ve^i или VxEif*- Аналогично получаем У%Е.Уг, т. е.
Ух = Ух- Итак, система подмножеств Ух, хеЗ?, такова, что
любые два из них либо не пересекаются, либо совпадают. Опреде-
Определим функцию / = /(х) так, что /(xi)=/(x2), если Ух, — Ух„ и
'(xi)=?/(x2), если Ух,фУх,. Полагая Set=<yt, t=t(x), x<=9S', по-
получаем, как нетрудно понять, требуемое утверждение.]
Докажем, что разбиение A4) достаточное. Определим функ-
функцию
ФС х, у)=Рв(у)/Рв(х), х, у<=%„ A5)
|де Gc=0 — любое такое, что Рв(х) >0; если такого 0 не сущест-
существует, то положим i|-(/, х, у) =оо. Проверим, что определение A5)
корректно. Если при всех 0ев Рв(х) = О, то все в порядке: функ-
функция ф однозначно определена и принимает значение оо. Пусть 0i
такоио, что Pgt(x)>0. Тогда по определению класса S6t также
5 М. В. Козлов. А. В. Прохоров 129

11 Pq (У) > 0, а для всех 8 таких, что Р0 (х) > 0, верно равен-
равенство
что и требовалось установить. Пусть 0еЭ — любое фиксирован-
фиксированное. Допустим, что P0(j?/)>O и Pfl(x)>0. По определению
класса 861 в этом случае Р0(у)>О для всех уе#?<. Суммируя
A5), получаем
/, х)= ? !>(*, х, у) = Рв(#,)/Рв(х).
у 6 ¦»/
откуда
Рассуждения, приводящие к A6), справедливы при всех ,
таких, что Ре (х) > 0. Если при некотором 0 Р0(х) —0, то по
определению класса 8В t также и PQ(&t) = 0. Следовательно,
A6) справедливо при всех 0, таких, что P0(j?<)>O, и разбие-
разбиение A4) — достаточное.
Для доказательства минимальности разбиения A4) возьмем
произвольное достаточное разбиение {Уа), и пусть V(x) — по-
порождающая разбиение {^aj достаточная статистика (V(x) — лю-
любая функция, принимающая различные значения на различных
элементах разбиения). По теореме факторизации
Pe(*) = *(V(x); в)Л(х).
Ограничимся далее подмножеством 8?' = {x:li(x)>0), которое со-
содержит носители всех мер Р0(х). Пусть х, уе^" таковы, что
V(x)=V(y)=v. Тогда
P0(x) = g(v; в)А(х). Pe(y) = *(v; в) Л (у).
Если g(\; 9)=0, то Р0(х) = Р0(у) = О. Если же g(\- в)>0, то
и, следовательно, х, у находятся в отношении R и принадлежат
одному элементу достаточного разбиения A4). Итак, элементы
разбиения {<уа} содержатся в элементах разбиения {#?/}, что и
требовалось доказать.
В примере (IV)
Pe(x)/P0(y)=(i-e)JV(x)-JV(y).
и это отношение не зависит от 0, О<0<1, только если N(x) =
=N(y). Следовательно, разбиение с элементами
130

является минимальным достаточным, a .V(x) — минимальная до-
достаточная статистика.
Отметим, что если S(x) — минимальная достаточная стати-
статистика, то, например, (S(x), S(x)) также будет минимальна, так
как, очевидно, порождает то же разбиение. Поэтому в теоретиче-
теоретическом плане остается вопрос о выборе такоП минимальной доста-
достаточной статистики, которая имела бы наименьшую размерность.
К построению минимального достаточного разбиения имеется
еще н другой подход. Рассмотрим сначала случай, когда семейст-
семейство {Р} состоит из конечного числа элементов Ро, Pi, ..., Р*. Вве-
Введем статистику
L(x)=(P0(x), Р,(х) Р*(х)).
Покажем, что статистика L(x) — достаточная. Пусть х и у при-
принадлежат одному элементу разбиения, задаваемого статистикой
L(x):
L(x)«L(y),
т. е.
Р.(х) = Р,(у), «-0, 1, ...,k.
Очевидно, в таком случае точки х и у находятся в отношении R
и. следовательно, принадлежат одному элементу минимального
достаточного разбиения, A4). Итак, элементы разбиения, за-
задаваемого статистикой L(x), содержатся в элементах достаточно-
достаточного разбиения. Как было отмечено в начале раздела, отсюда сле-
следует, что статистика L(x) — достаточная.
Теперь мы преобразуем статистику L(x) в минимально доста-
достаточную. Предположим вначале, что носитель распределения Ро(х)
содержит носители остальных Pi(x):
{x:P,(x)>0}<={jc:P0(x)>0}. A7)
Дальнейшие построения проведем на подмножестве SS'=
= {х: Po(x)>O}s#?. Покажем, что статистика
Т(х) = (Р,(х)/Р0(х) Р*(х)/Р„(х))
является минимальной достаточной. Пусть х, уе#?' принадлежат
одному элементу минимального достаточного разбиения A4).
В таком случае отношение Р,(х)/Р*(у) не зависит от i при всех i,
таких, что Р.-(х), Р,(у)>0, а для остальных i P,(x) = Р,(у) =0.
Отсюда следует, что либо
Р.(х)/Р.(у) = Ро(х)/Ро(у),
либо Р, (х) = Р,(у)=0. Во всех случаях получается, что
Р«(х)/Ро(х) = Р,(у)/Ро(у)
Для всех i=l, .... k, т. е. Т(х)=Т(у). Таким образом, элементы
разбиения, порождаемого статистикой Т(х), содержат в себе эле-
з* 131

менты минимального достаточного разбиения (суженного на SB')
а потому Т(х) — минимальная достаточная статистика.
Если условие A7) не выполнено, то, положив
(-0
легко обнаружить, что статистика Т(х) с заменой Ро(х) на Ро*(х)
оказывается минимальной достаточной.
В случае произвольного сгмейства {Pfl:8e0} рассуждения
сохраняются без изменений, если выполнено условие, аналогичное
A7). Достаточное разбиение порождается системой статистик, за-
зависящих от 6 как параметра:
Цх; в) = Ре(х), 9е в. A8)
Если множество в конечно, то A8) можно рассматривать как
векторную статистику. В общем случае, ради краткости, систему
A8) назовем функциональной статистикой. При каждом фиксиро-
фиксированном 0 = во «координата;- L(x; 9») является обычной скалярной
статистикой, совокупность всех таких координат Цх\ 9) состав-
составляет функциональную статистику A8).
Минимальное достаточное разбиение порождается функцио-
функциональной статистикой
7(х; 9)=L(x; 9)/L(x; в„), 9<=в,
где 9оев таково, что для всех 9ев
{х:Рв(х)>0}с{х:Рв.(х)>0}.
В примере (II) выборки из пуассоновского распределения
п
L(x; 9)/L(x; 90) =. е-«<о-о.> @/0о)га
Прологарифмировав, получаем
п
In (L (x; 6)/L (х; 60)) = -п F -в,) + J] ц In (L j. A9)
Поскольку взаимно-однозначное преобразование приводит к экви-
эквивалентной статистике, то A9) также является минимальной доста-
достаточной. Как видно из A9), любая «координата» функциональной
статистики A9) выражается через любую другую с 9#90. Поэто-
Поэтому «избыточную» функциональную статистику A9) можно заме-
п
нить одной скалярной, например статистикой д xit и, следова-
тельно, эта статистика минимальна.
132

§ 16. ДОСТАТОЧНЫЕ СТАТИСТИКИ В НЕПРЕРЫВНОЙ МОДЕЛИ
1. Примеры достаточных статистик.
Мы будем рассматривать здесь статистические модели
(#?, 3S, {Р}), где SS — область в Rn, S5=Se[\S5n, а мера Р задает-
ся некоторой «-мерной плотностью. Эта модель, которую мы на-
назовем непрерывной, и дискретная модель, изучавшаяся в преды-
предыдущем параграфе, охватывают все наиболее важные области при-
применения математическом статистики к выборкам фиксированного
объема. К сожалению, полное изложение теории достаточных ста-
статистик в непрерывной модели требует привлечения понятий и ут-
утверждений, выходящих за рамки данной книги, хотя в идейном
отношении нет разницы между дискретным и непрерывным слу-
случаем. Математически подготовленный читатель может ознакомить-
ознакомиться с логически полноценным изложением общей теории этого и
некоторых других параграфов данной главы по многочисленным
отечественным и переводным монографиям по математической
статистике, список которых можно найти в конце книги.
Определение достаточной статистики будет дано в следующем
разделе, а пока займемся примерами достаточных (и на самом
деле минимальных) статистик, обращаясь к неформальному поня-
понятию информации, различающей элементы Р из {Р}. Отметим, что,
как н в случае дискретной модели, статистики Т(х„) и S(xn), свя-
связанные измеримым взаимно-однозначным преобразованием Ч\ яв-
являются эквивалентными носителями вероятностной информации
и будут называться эквивалентными. Полезнее, однако, несколь-
несколько более слабая форма эквивалентности:
на некотором множестве Р-меры 1 при каждом
(I) Пусть мера Pf задается многомерной плотностью вида
f{x\)f(x2)...f(xn), где f(x) — произвольная одномерная плотность.
Таким образом, статистическая модель (Rn, SSn, {Pf}) соответст-
соответствует последовательности п независимых одинаково распределен-
распределенных испытаний с неизвестным законом распределения, обладаю-
обладающим плотностью. Это непараметрическая модель, так как индекс f
здесь функциональный.
Покажем, что вариационный ряд Tn=(*(i), *B), .... *(„>) со-
содержит всю информацию о плотности f. Для этого заметим, что
и поэтому плотность Т„(Х„) равна при х\<Х2<...<хп
n\f{Xl)...f{xn).
Нетрудно понять, что условное распределение Х„ при условии
133

— равномерное и сосредоточено в п\ точках {tlx Un), где
(':. ¦•., in) — произвольная перестановка из индексов A, .... л).
Мы не будем проводить формального доказательства этого фак-
факта, а вместо этого сразу обратимся к моделированию, как это де-
делалось в дискретном случае. На первом этапе образуем последо-
последовательность ел. в. Yn= (У'ь У2. ••¦. Уп) с плотностью
fyn (У«) = nI f (Ух) f (У2) --f (Уп), У1 < Уг < ¦ • ¦ < Уп
и ^vn (у„) = 0 при остальных значениях аргумента. Затем постро-
построим независимую от Y,, последовательность ел.в. (vi, vs, .... vn),
которая с равными вероятностями принимает л! значений
(<i, 'г, •••, in) — перестановок из чисел A, 2 я). Определим
результат составного эксперимента как последовательность ел. в.:
Xn-(Xi. *, Хп), Xt =yv., i = 1, 2 я.
Найдем плотности распределения случайного вектора Х„. Выбе-
Выберем произвольные попарно различные числа х\, х2, .... хп и б>0,
такое, что интервалы (*,, jc, + 6], i = 1 л, попарно не пересека-
пересекаются. По данным хп найдем такую перестановку (ku k2 kn)
индексов (l,2,...t/i), что
**,<**.< •¦•<•«*„•
Тогда, учитывая, что У1<У2<---<Уп с вероятностью 1, получаем
/ = 1 л) =
=/, /= 1 л) =
= j ... j n\f(y1)Hyt)...f(yn)dy1...dyn{n\)-1.
Производя сокращение на л!, получаем отсюда, что случайный
вектор Х„ имеет плотность f(x\)f(x2)...f(xn). Итак, вектор Х„
получен в два этапа: на первом — образован вектор Т„ =
= (X(D, .... Х1п)), на втором — с помощью случайного механиз-
механизма, не зависящего от неизвестной плотности }{х), получен уже
сам вектор Х„. Проведенная конструкция показывает, что Т„ со-
содержит всю информацию о плотности f(x).
(II) Пусть 8?=R+n={xnt=Rn:xi>0, i=l п}, 3S=i
0R+", а мера Рв, 0<9< + оо, задается плотностью.
f (х„; 9) =9~" при xne/?+n, jc,<9, i= 1 л
134

и /(х„; 0)=О для остальных х„. Таким образом, рассматривается
случайная выборка объема п из равномерного на @, 0) распреде-
распределения. Мы покажем, что вся информация о параметре 6, содер-
содержащаяся в выборке х„, заключена в статистике jc(n)=max(jci, ...
..., хп). Используя предыдущий пример, перейдем от выборки
х„ к ее вариационному ряду Т„=(*A), .*B), .... .*<„)), не потеряв
при этом информации о параметре 6. Плотность распределения
Т„(Х„) запишем в виде
и положим ее равной нулю при остальных значениях tn. Так как
то
Отсюда условная плотность Хщ -^(„-о при условии Х1п) равна
при 0</,<...<<n<9
1)()n^1. B)
Функция
представляет собой совместную плотность порядковых статистик
случайной выборки объема п—1 из равномерного на @, t) рас-
распределения (ср. A)). Соотношение B) устанавливает, что
/х, х(п_„ i х(Я) ('i tn-i\tn)^g(tlt ...,tn-i; tn)
для всех /, 0, таких, что /х(п) @ > 0- Это означает отсутствие
дополнительной информации о 6 в значениях Хм, ..., Х(т,_п, если
известна Xin).
(Ill) Пусть, как н в предыдущем примере, ЗС =/?+, <® =лХ ,
а мера РЦ|0, —оо<ц< + оо, а>0, задается я-мерной плотностью
/(х„; |4. а)= fla-V((^-ji)ya), / (х) = ег', х > 0.
Покажем, что двумерная статистика
1-2
содержит всю информацию о двумерном параметре (и, о). Перей-
Перейдем от Х„ к Tn(Xn) = (^(i), ..., Х1п)), сохранив всю информацию
135

о (ц, a), a затем взаимно-однозначным преобразованием перей-
перейдем к вектору
У,.= (У,, .... К„), У/-(Л-/+1) (*«.-*(М>). /=1 п.
Ввиду леммы 1 § 6 ел. в. У;, /=1 л, независимы и экспонен-
экспоненциально распределены: У] — с плотностью (т-'ехр(—(у\—пц)/а),
t/i>'/;i, а У/, />2, — с плотностью а ехр{-у,1о), у/>0, т. е.
плотность распределения вектора Y,, равна
п
fy'°(y,,) = а-"ехр i—о-11? и—iqi'u ,
7-i
//,>0, /=2 л, 0,>nji. C)
По лемме I § 7
/-2
/-2 /-2
имеет распределение G(a~', /г—1) с плотностью
Совместная плотность пары (У1гУ,+ ... +Yn) = lXt, У (Х(/)— Я<о))
(-2
равна
D)
ft-г
(п — 2)! о"
Сделаем взаимно-однозначный переход от вектора Yn к вектору
Zn по формулам
ZX = YU Z> = y2 + ...+ y/, / = 2 п.
Якобиан перехода от Yn к Zn равен 1, так что ввиду C) и D)
?г°(*п) = °~пехР(-<Г'1 (zi + Zn—"V))> 0 < z2 < ... < гп, гх > /ij
136

Отсюда получаем при Z\>n\i, zn>zn~\>...>Zt>0:
fz zn_11 z,. zn B г„_11 zv zn) =
= /S* {zn)lfttzn (г,, гп) = (я- 2)!/zT2.
Таким образом, условная плотность Zi Zn-\ при условии Z\%
Zn не зависит от параметров ц, а, и, следовательно, вся информа-
информация о параметрах содержится в статистике
или в эквивалентной ей статистике (.\\d, x). Отметим, что оценки
параметров ц, а, с которыми мы встречались в § 6 и 11, являют-
являются функциями статистик (л'п), х).
(IV) Пусть Se=Rn, Я=Яп, а мера Р^,„, -оо<м<+оо, а>0,
задается n-мерпой нормальной плотностью
л
Bла)-»ехр (--1- Y (x,-
От случайного вектора Х„ с плотностью Л^(ц-1, а2/), где 1 =
= A, .... 1), / — единичная яХя-матрица, с помощью ортогональ-
ортогональной матрицы С, у которой последний столбец имеет вид n~uiV,
перейдем к вектору Yn = XnC, имеющему распределение
Л'(ц1С, а2/). При этом (см. п. 3 § 8)
сл.в._У,, i=l, ..., п, независимы, У„ имеет распределение
••'»'(ИУя, а), а вектор а~х{У\, ..., Уп-\) — стандартный нормаль-
нормальный. Вектор Y,, получен из Х„ взаимно-однозначным преобразова-
преобразованием и, следовательно, как носитель информации полностью экви-
эквивалентен Х„. Поскольку плотность распределения вектора
(У >'п-.)
л—1
сферически симметрична, то нетрудно понять, что условное рас-
распределение точки (Yi Уп_|) иа сфере yi-t .. .-ryl-\=r- —
Равномерное. Нам важно лишь, что это распределение не зависит
137

от ц и о. Проверим это, переходя к полярным координатам г,
<Р), ..., ф„_2 по формулам
(ф)
@<ф2<:я), G)
I d (г, ф1
i/,,_2 = /" sin qii этфг... sin ф„_з cos ф„_г @«:фп_2<:л),
(/„_, = г sin <pi sin ф2... sin ф„_з sin ф„_2 @<О.
При этом, очевидно, у? + ... + «Д-i —/*, а индукцией по п легко
установить, что якобиан перехода равен
1 Уп-i) =rn-2?t
п2фп_4 81пфп_з. (8)
Введем ел. в. R, Ф\, ..., Фп-2, связанные с Y\, ..., K,,-i теми же
соотношениями G), что координаты г, q>i, ..., ф„_2 связаны с
Ух, ..., уп-\. Вероятность попадания точки (/?, Ф|, ..., Фп-з) в
борелевское множество В вычисляется как интеграл
I ... I ft?.... Yn , {У, Уп-ййуг... dya-i (9)
В'
по области В', являющейся образом В при отображении G). Со-
Совершая в интеграле (9) замену переменных G) и учитывая F) и
(8), приведем его к виду
Г
(/2яа)""*1 ехр( - --L- г^ г»-вуф1 ... йф„_^г, A0)
в
где g, определенное в (8), является функцией только ф] <рп-г-
Из A0) вытекает, что совместная плотность ел. в. R, Ф\, ..., Фп-2
равна
лф ф„_ (г, Ф,. • • • . Ф.-2) - (/и a)-n+1 ехр ( - -±г
(И)
(Отметим, что полярные координаты находятся во взаимно-одно-
взаимно-однозначном соответствии с декартовыми при условии
г sin ф1 •.. .-sin фп-зт^О, но так как R вшФ)-.. .-зтФп-зт^О с веро-
вероятностью 1 по любой мере Р„.п, то никаких осложнений не возни-
возникает.) Поскольку о-2/?2 — о~2 (Кн- ... -г V«-i) имеет распреде-
распределение Xn-i=-C(l/2, (п —1)/2), то R2 имеет распределение
0A/Bо2), (/г-1)/2) с плотностью (см. B), § 7)
138

откуда
Лл^^е 2°\ A2)
Интегрируя A1) по множеству {/">()} и учитывая, что интеграл
от плотности A2) равен 1, найдем плотность
/ф, ф„_2 (ф! Цп-2) = с„ sinn-39! sin"-\2 • ... • sin2 ф„_4 sin ф„_3,
A3)
где с„ — постоянная, которая не зависит от ц и а. Совместная
плотность (И) равна произведению плотностей A2) и A3). Та-
Таким образом, случайный вектор (У,:, R, Фи ..., Ф„-г) находится
во взаимно-однозначном соответствии с вектором Х„, за исключе-
исключением множества значений Рм.„-меры нуль. Его плотность равна
/у^л.ф, Фп_г (Уп, Л фх ф„_2) =
= /y° (Уп) /й'° (О /Ф, Ф„_2 (Фх. • • • . фп-2).
Отсюда условная плотность величин Ф*, .... Ф„-2 при условии
ел. в. У„, R равна их безусловной плотности A3) и не зависит от
(ц, а). Следовательно, двумерная статистика
содержит всю информацию о параметрах ц, а. Вместо A4) мож-
можно рассматривать эквивалентные статистики
или G, s*), s2=^ZT
(=1
связанные с A4) взаимно-однозначным преобразованием. Таким
образом, выборочные среднее х и дисперсия so2 образуют доста-
достаточную статистику.
2. Определение достаточной статистики, теорема факторизации.
Как мы уже отмечали, понятие достаточной статистики в не-
непрерывной модели вполне аналогично дискретному случаю. Одна-
Однако математические топкости, связанные с введением условных ве-
вероятностен, не позволяют нам дать определение достаточной ста-
статистики в его общей форме. Мы будем рассматривать только па-
параметрические модели и, если не оговорено противное, только
такие статистики Tr(xn) = Gi (х„), ..., 7г(х„)), которые можно до-
139

полнить статистикой У„-.(хп) = (Y\{xn) Y,,-,{xn)) такой, что
замена переменных
и = Тх(кп) tr=Tr(xn), yi~Yi(xn), ...,yn-r=Yn-r(xn)
A6)
взаимно-однозначна на множестве Ре-меры единица при любом
0е0, а плотности меры Ро в координатах х„ и (t,, y,,_r) связаны
на множестве Ре-меры единица соотношением
Yn.r(xn)(tr, yn-r)\J\, A7)
tr. Ух Уп-r)
где
t, ..., хп)
— якобиан перехода от координат (tr, yn-r) к (х„).
Иначе говоря, предположение A6), A7) означает, что, во-пер-
во-первых, существует плотность случайного вектора (Tr(Xn), Yn-r(Xn)),
и, во-вторых, при использовании этой плотности для вычисления
интеграла
I • • • J /Wv,сх„) (tr, Уп-r)Л, ... dt4yl ¦. ¦ dyn-r
в
можно воспользоваться заменой переменных A6) и свести этот
интеграл к следующему
В'
где В' является прообразом В при отображении A6).
Определение. Пусть статистика Тг(х„) такова, что выпол-
выполняются предположения A6), A7). Если условная плотность, опре-
определенная при U, 8, таких, что /тг(хп)(М >0. формулой
хв
ие зависит от 8е8, то статистика Тг(хп) называется достаточной
для данной модели.
Отметим, что
се ас
/yxn)(t,)= J ... { /t^v-WW^. y^r)dy1 ...dyn-r.
— 3D —M
Теорема факторизации. В предположении A6), A7)
статистика Тг(х„) является достаточной тогда и только тогда, ког-
когда Оля любого 0=9 на некотором множестве Рв-меры единица вы-
выполняется равенство
/х„(х„: 0)=g(T,(x,,); 6)й(хл), A9)
140

где g{\.\ fl) и Л(х„) — неотрицательные измеримые функции ар-
аргументов \г и х„ соответственно, h(x,,) не зависит от 8.
Доказательство. Пусть статистика Т,(х„) — достаточная. По-
Положим
л для каждой пары (tr, yn-r), для которой существует 8е9, что
frr{Xn){tr)>0, ПОЛОЖИМ
r|t,). B0)
Ввиду достаточности статистики Т,(х„) функция /ii(t,, у„_,) фор-
формулой B0) задается корректно (и является функцией только от
tr, Уп-r), а равенство B0) при каждом 6, tr, для которых правая
часть определена, выполняется на множестве Р«-меры единица.
Учитывая введенные обозначения, из A8) получаем равенство
t,. Уп-r), B1)
справедливое на множестве Р0-меры единица, откуда, используя
A7), получаем
/х„(хп> = ?(ТЛх„); ejA^T^x,), Уя^(хя))|У|. B2)
Поскольку якобиан |/| не зависит от 8, то, полагая A = Ai|/|, по-
получаем представление A9).
Обратно, пусть имеет место факторизация A9). Определим
функцию A| (t,, у,,-,,) условием
li(x,,)=h,{tr, у„-г), t, = T,(xn), yn-r=Yn_r(xn)
и перейдем в A9) к координатам (tr, у„_г). Все дальнейшие рас-
рассуждения проведем на подмножестве 95, на котором Л|>0, Л>0.
Воспользовавшись формулой преобразования A7), перепишем
A9) в виде
г„ Yn.r(xn, (t,. Уп-r)\J\ = g{t,; 9)h,(tn yn-r). B3)
Найдем отсюда плотность статистики ТГ(Х„):
тг(хя) (tr) = J •.. J /ух„>. у„.^хя) (tr. Уп
= g(t,J 0) J ... j А,а, yn-r)\J\-ldyi ... dyn-r. B4)
Г.СЛИ g(\,\ 8)>0, то, поделив B3) на B4), получаем, что условная
'лотиооть равна
141

= h, (tn уя_,) i JI -l / J ... If К (tr, zn-r) IJI
— * —to
и не зависит от 6, что и требовалось установить. Щ
Достаточность рассматривавшихся в примерах (II) — (IV) ста-
статистик с помощью теоремы факторизации устанавливается совсем
просто. Например, расписав плотность случайной выборки из нор-
нормального распределения N([x, а) в виде
B5>
л л
обнаруживаем, что пара (V х(, У]а;I является достаточной ста-
(=1 (=i
тнстнкой, что было непосредственно проверено выше (см. A5)).
К примеру (I) теорема факторизации в предложенной выше фор-
форме неприменима, так как условное распределение выборки при
условии достаточной статистики — вариационного ряда — являет-
является дискретным. Это один из редких в приложениях случаев, когда
не выполняются ограничивающие предположения A6), A7). Обра-
Обратимся к другим примерам.
(V) Рассмотрим линейную статистическую модель с нормаль-
нормальными наблюдениями в канонической форме (см. G) § 10):
Ui=^i + a6i, i=l г; (Л = од/, i = r+ 1 л, B6)
где ^=(\fi. •••. фг). о>0 ~ неизвестные параметры, Fi, 62, ...
• ••» бп) — стандартный нормальный вектор. Плотность распреде-
распределения U равна
и?) =
i
(=1 i=l 1=1
По теореме факторизации, статистики
л
7, (и) = и,-, i — 1, ... , г, So (и) =— Л tii
П шт
142

образуют г+ 1-мерную достаточную статистику. Эквивалентная
ей статистика
л
G\(и) Г, (и), 5?(и)), 5? (и) = —^— V и]
также является достаточной. Заметим, что оценки >j), = 7,(u), o2 =
= 5r(u) параметров ip, о линейной модели были введены в § 10.
Аналогично обстоит дело и для нормальной линейной модели
в общей форме A) § 13 с матрицей X полного ранга. Плотность
распределения наблюдений в этом случае равна
.-1
, в = @1, ... , 6Г), B7)
Х=[х1, ...,х'г], х/ = (л;1/, .... хы), /=1, .... г.
Введем статистики 7",- (у), /=1 г, как коэффициенты разложе-
разложения проекции вектора у на подпространство V, порожденное век-
векторами х,,/=1, ..., г
... + Тг(у)хг.
Так как вектор
то, применяя теорему Пифагора, найдем
l|y—eJC'|la = ll (У—»pvy+ п^-у—вХ')||« = ||у—пр„у||« + ||пруу—вХ'|Г
И ^ II II*- II
Подставляя B8) в B7) и применяя теорему факторизации,
получаем достаточную статистику в виде
,(У). ••• • Тг(у), |
Остается заметить, что известные нам оценки параметров в, о ли-
чепной модели имеют вид
8, = 7\(у), «=1 г, а2 = 5,2(у).
(\1) Рассмотрим ценз\рпруемую выборку (см. п. 7 § 11)
X(ri+i, < X(ri4.j, < ... < A'(r,_rt), rlt r2 > 0, B9)
143

считая наблюдения Хи .... Хп независимыми N(n, а)-распределен-
а)-распределенными, а Г\, т-2. — фиксированными числами. Найдем плотность
распределения вектора
Y = [Ylt .... V.v.) —(X(,,.ri), X(,1+2), .... Х(Я-г^), N—n—г, — г.,,
в точке у=(у ух), У\<У2<..<Ух. Проведем вначале не-
нестрогие рассуждения. Плотность вероятности того, что какие-то
N из ел. в. Х\, ..., Хп примут значения у\<уч<...<ух, равна
N
п{п—\) ... (n—N+\)
где ф(.г)—Л'@, 1)-плотность. Вероятность, что слева от у\ и
справа от у.м окажется ровно г\ и го соответственно каких-то из
л—W оставшихся наблюдений, равна
где Ф(дс) — ф.р. закона Л^@, 1). Используя независимость, пе-
перемножим полученные выражения н получим
МУ) = -7-7
C0>
[Проведем формальную выкладку. Возьмем б>0 настолько ма-
малым, что интервалы (yit t// + 6), i = 1, .... W, не пересекаются и
запишем
^м>0(К/ е («//, у, + б], ;= 1 ЛО =
+ ? #V.o (>'/ -Xft/, К/ €= (у/, Л + б], } + 1 АГ). C1)
где суммирование ведется по всем п(п—1)...(л—,V+1) упорядо-
упорядоченным наборам индексов (kit kb .... kN) без повторения из мно-
множества 1, 2, .... п. Учитывая, что все слагаемые суммы C1) рав-
равны между собой, перепишем C1) в виде
T^zW^11 (maX {Xi X/J
Yl=Xrt+h Y,t=(yh y, + 6], ; = 1 N.
Xw,<min(X; Xlrt)),
144

где суммирование ведется по всем СЙ_^ неупорядоченным на-
наборам индексов iv t2, .... tV, без повторения из множества
{1, ..., Г|, л—г2+1, .... п}, a/lt /2, ••• .'г,— остающиеся элемен-
элементы этого множества. Снова учитывая, что слагаемые суммы C2)
равны между собой, получим для C2) выражение
C,?_.v я! ^„.а (max (Хх Х„) < Х,1+|, Х,1+/ е (*// /// + б],
(л — Л)!
/ -1 N, Х„_. < min (*,,_.+ *„)). C3J
Запишем очевидную оценку сверху для C3):
—2Ц ^м.а (max (Х1( .... Хг.) < //, + б, X,t+/ e («//, у,
/= 1, ... , ЛГ, yN < min (Х„_,,+ , Хп)) =
Аналогично получаем оценку снизу:
,35,
Разделив выражения C4), C5) на bN и устремляя б к нулю, при-
придем к C0).]
Из формулы C0) и теоремы факторизации нетрудно вывести,
что достаточной является четырехмерная статистика (при г,>0,
Г2>0)
N X
Если цензурирование одностороннее: rt=0 или г2=0, то у\ или у,\
соответственно надо отбросить, и достаточная статистика оказы-
оказывается трехмерной.
3. Экспоненциальные семейства, минимальная достаточность.
Рассмотрим непрерывную параметрическую модель
(X, Я, {Рв, ве61), где 6^@, 0„), k^ 1, 0е/?",
а плотности /е(х) меР ^в заданы формулой
145

/e(x) -Л(х) ехр (? 8,7, (x) + b F, 6,)). C6)
Семейство Ро в этом случае назовем k-параметрическим распреде-
распределением экспоненциального типа (в естественной параметризации).
Ряд важных семейств распределений повторной выборки пос-
после подходящей параметризации сводится к C6). Например, если
отдельное наблюдение в последовательности л независимых испы-
испытании имеет распределение G(K; p), то совместная плотность рав-
равна при л;,, .... х„>0 (см. B) § 7)
= (*1( .... хп)-1 ехр (р J 1п*,- X ? х( + In (Л""/Г (р)")), C7)
так что, полагая ®Х=Р, %~ — ^, 7Х= V lnx,-, 72= V х{, при-
приходим к C6). Другой пример: независимая выборка из распреде-
распределения ;V(fi, о) имеет совместную плотность
,38,
экспоненциального типа C6), если положить 8i = — 1/о2, 82 =
= ц/о-. В
Более общая экспоненциальная модель вида
/в (х) - h (х) ехр | у at (8) 7, (х) + 6 (8),, C9)
где 6= (8i... .,lh), 8e0s/?', фактически может быть сведена к
C6), если цвести естественную параметризацию i|), = a,(8). Чтобы
убедиться в этом, достаточно заметить, что ^(8) на самом деле
является функцией от a,F), i=l,...,k, поскольку ехр(&(8)) вы-
выполняет в C9) роль нормирующего множителя.
Отметим, что повторная выборка нз распределения экспонен-
экспоненциального типа снова принадлежит к этому типу:
146

(xl!|, x'2' x«'"))=
X
Поэтому в примерах C7), C8) можно было рассматривать толь-
только случай л=1. В
Из теоремы факторизации при дополнительных ограничениях
A6), A7) вытекает, что векторная статистика Т(х) = G|(х),...,
. ..,Г*(х)) является достаточной в модели C6). Отметим, что ог-
ограничения A6), A7) являются излишними при более широком
понимании достаточности. Как н в дискретной модели, интерес
представляют достаточные статистики, сокращающие данные в
наибольшей степени. Достаточную статистику S(x) назовем ми-
минимальной достаточной статистикой, если она представима как
(вектор-) функция от любой достаточной статистики.
С достаточной статистикой Т(х) свяжем достаточное разбиение
множества 95:
i:T(x) = t|. D0)
С минимальной статистикой S(x) связано минимальное достаточ-
достаточное разбиение — такое, что элементы любого достаточного раз-
разбиения содержатся в элементах минимального:
{x:T(x)=t}s={x:S(x)=st}.
Как и в дискретной модели, минимальное достаточное разбиение,
правда при некоторых ограничениях, образуется из классов экви-
эквивалентности по отношению R:
х/?у«=*/е(х)/ЫУ) не зависит от в. D1)
Проверим это утверждение на экспоненциальной модели C9). За-
Заметим, во-первых, что плотности C9) обращаются в нуль на об-
общем множестве {х:Л(х)=0} н потому можно исключить из рас-
рассмотрения все такие х. Далее, отношение
/в We (У) ехр(? a,(e)G\(x)-7\(y))j
1
1=1
для данных х, у не зависит от в, если либо Т(х)=Т(у), либо
функции 1, о,-(в), вев, 1 = 1,...,*, линейно зависимы и коэффи-
коэффициенты с, = 7\(х)—7\(у) таковы, что
0«=0. D2)
Если прн некоторых с\,...,ск, Ci2 + ... + cft2>0, имеет место равен-
равенство D2), то модель можно редуцировать, взяв из системы 1,
Мб), < = 1,..,?, максимальную линейно независимую подсистему
147

и j.iMeiniB в C9) остальные функции а,@) на линейное представ-
представление через эту систему. Поэтому мы предположим, что 1, а,@),
i = l ,к, — линейно независимые. В таком случае разбиение на
классы эквивалентности по отношению к D1) совпадает с доста-
достаточным разбиением D0). Покажем, что это разбиение минималь-
минимально. Пусть достаточная статистика S(x) такова, что
). D3)
По теореме факторизации, если S(x)=S(y)=s, то
/e(>0=gi(s; 6)Mx), /e(y)=g1(s; в)А1(у)
и для всех 0е6, таких, что gi(s; 0)>O, отношение
не зависит от в, т. е. Т(х)=Т(у), что н требовалось устано-
установить. Щ
Подчеркнем, что в D3) рассматриваются лишь такие мини-
минимальные статистики S(x), которые удовлетворяют ограничениям
A6), A7), и тем самым утверждение о минимальности Т(х) до-
доказано лишь в этом классе статистик. В примерах C7), C8)
требования A6), A7) удовлетворяются, и достаточные статистики
я л [п л
\Y lnxt, Y^ xt) и !^Л|1 $J*''' являются минимальными соот-
/=| 1=1 *=1 /=|
ветсизенно для выборок из распределений G(K; p) и N(n, a).
В линейной статистической модели с нормальными наблюдения-
наблюдениями B7) статистики B9), служащие оценками коэффициентов 6 и
а2, также янляются минимальными достаточными.
Равномерное распределение на @; 6) (см. пример (II)), экспо-
экспоненциальное распределение с параметрами сдвига-масштаба (при-
(пример (ill)У не принадлежат к семейству экспоненциального типа.
Характерная особенность этих распределений заключается в том,
что множество, где плотность распределения отлична от нуля
(носитель распределения), зависит от параметра, в то время как
в C6) носитель у всех распределений один и тот же — {x:/i(x)>
>0}. Однако минимальность рассматриваемых в примерах (II),
(III) достаточных статистик доказывается теми же рассужде-
рассуждениями, что и для семейств экспоненциального типа. Такое же
заключение справедливо и для цензурированной выборки приме-
примера (IV). ¦
К построению минимального достаточного разбиения имеется
н другой подход. Оказывается, что, как и в дискретной модели,
достаточное разбиение порождается следующей системой статне-
гик:
L(r.\ в), /о(х). в ев,
148

зависящих от 8 как от параметра, а минимальное достаточное
разбиение порождается функциональной статистикой
L(x; 9)/L(x; во); вев, D4)
в предположении, что существует такое воев, что носители всех
мер Ре содержатся в носителе Pgo.
Если носители всех мер Ре совпадают, то в D4) удобнее
перейти к логарифмам.
InL(x; в)—InL(x; во)=?(х;в), 8<=в. D5)
Рассмотрим, к чему приводит этот подход в экспоненциальной мо-
модели C9). Подставляя /е(х) из C9) а D5), получаем
g(x; в)=?(о1(в)-^(в,)O'4(х) + F(в)-6(во)), веб. D6)
1Ж.1
Следовательно, разбиение X, порождаемое совокупностью стати-
статистик D5), совпадает в этом случае с разбиением, порожденным
векторной статистикой Т(х) = G*1 (х),..., Тк(х)), которая, как мы
уже проверяли, является минимальной достаточной. Таким обра-
образом, в экспоненциальной модели C9) удается сократить мини-
минимальную достаточную функциональную статистику D5) до Л-мер-
ной векторной Т(х). Полезно отметить, что если в экспоненциаль-
экспоненциальной модели C9) система функций 1, а,-F), i=\,...,k, веб взята
линейно независимой, то, как нетрудно понять, можно подобрать
значения 8(|)ев, i = l,...,k, так, что матрица [а,(в(/))—а,(во),
i,j=l,...,k] невырождена, и из соотношений D6) 7"((х), i=l k,
могут быть линейно выражены через функции 1, g(x; 8(/))i
/fft
Перейдем к произвольной непрерывной модели (Й7, Ш,
= 6}), у которой носители всех мер Ре совпадают. Рассмот-
Рассмотрим пространство 2? всевозможных конечных линейных комби-
комбинаций:
; в/).
еде 0:^@, с-, — произвольные постоянные /=1,...,/, I — любое
натуральное. S7 является линейным пространством, вообще гово-
говоря, бесконечномерным. В случае экспоненциальной модели, как
мы только что видели, & конечномерно: 1, 7\-(х), i = l,...,fe, по-
пождает 9?. Допустим, что в 2* имеется не более чем счетный
'У'Млс. i, ф,(х), ]'=1,...,? [к может быть и °о), так что любой
149

элемент ф(х)е21 представим в виде конечной линейной комби-
комбинации элементов базиса:
В частности, это верно и для каждой функции g(x; в), вев.
В таком случае, 6-мерная статистика
(<Pi(x), (р2(х),...,(р*(х)), Л<оо, D7)
эквивалентна функциональной статистике g(x; в), Оев, так как
g(x; 6)ei? при любом вев, и поэтому линейно выражается че-
через систему. Отсюда совпадение разбиений, порождаемых систе-
системой статистик g(x; 0), 6е0, и 6-мерной статистикой D7), и, сле-
следовательно, статистика D7) минимально достаточна.
Интересно заметить, что если размерность k статистики D7)
конечна, то, записывая при каждом веб разложение элемента
g(x, 8)е2' по базису 1, (pi(#).•• ->ф*(*). получаем
*
In /в (х) - In /0(> (х) = g (х; в) = ? щ (в) ср, (х) + Ь (в),
i
откуда
/в (х) =/во (х) ехр (? at (в)(р, (х) + Ь(в)|, D8)
т. е. статистическая модель является экспоненциальной. Таким
образом, семейство распределений с общим носителем является
экспоненциальным тогда и только тогда, когда пространство SB
конечномерно. ¦
Рассмотрим, что дает описанный подход в модели с независи-
независимой повторной выборкой, когда плотность fB (x), 6е9, отдельного
наблюдения сосредоточена иа одном и том же множестве. Пусть
g (х; 0) = 1п /в (х)- In /во (*), в е 0, D9)
и 2" — линейное пространство функций (р(дс), порожденное ли-
линейными комбинациями функций системы D9). Допустим, что
1, ffi(x), i=\,...,k (k может равняться и оо) — базис 2", так что
при любом 8е0
т(в)
g(x; в)= ус,(в)ф,(дг)+с,(в). E0>
Из предыдущего вытекает, что 6-мерная статистика
является минимальной достаточной. Подчеркнем, что здесь всюду
150

x — скалярная переменная. Перейдем теперь к повторной неза-
независимой выборке объема п. Очевидно,
п
g(xn; в) = ?g(*,; 6),9se,
а из E0) вытекает, что
п т(в)
g (х„; в) = у ( Y ct @) ф, (*,) + с0 (в), =
т(в) п
= 2 с, @) j; ф,- (деу) ¦¦;- яе^ (в>.
В таком случае ясно, что 6-мерная статистика
W>i (х„). ...,¦» (xj), ifc (х„) = V Ф| (*/), i = l к, E1)
является минимальной достаточной.
Если размерность k статистики E1) конечна, то при n>k она
дает сокращение данных по сравнению с тривиальной достаточ-
достаточной статистикой — вариационным рядом. Заметим, что при этом,
как вытекает из D8), распределения отдельного наблюдения и
всей выборки принадлежат экспоненциальному типу. Однако при
условии k<n остается открытым вопрос о сокращении размерно-
размерности статистики E1) с сохранением достаточности.
Прц дополнительном предположении, что все плотности /е(х),
веб, непрерывно дифференцируемы на некотором общем для
всех интервале Д, мы докажем следующее утверждение: любые
s, ss^min(?, n), компонент статистики E1) функционально неза-
независимы. При k^.h отсюда, очевидно, следует, что размерность
статистики E1) не может быть понижена с сохранением свойства
достаточности. Действительно, пусть некоторая статистика
(Xi(x,,),...,x*(x,,)), Kk, является достаточной; тогда ввиду мини-
минимальности статистики E1) все ее компоненты ф,-(х„), t=l ft,
должны функционально выражаться через %\(хп),... ,Х'(Х«)- Но
поскольку l<k, это приводит к функциональной зависимости
Ь (х„) чМхп).
При k>n из сформулированного утверждения вытекает, что
размерность достаточной статистики не может быть сделана мень-
меньше п. В самом деле, в этом случае статистики ^\{х„),... ,г|зл(хп)
функционально независимы, и потому якобиан d(Hf\,...,^n)l
/д(х\,...,Хп) отличен от нуля на множестве Д" = {х„:х,еД,
i—l...,n). Следовательно, найдется интервал АеД, что на под-
подмножестве Д^сгД"' зависимости г|", = i}\(х„), /—1,...,«, можно одно-
однозначно разрешить относительно х„. Учитывая, что
151

получаем, что соотношения if* ==4)«CJcti>»•• •.*(")) также однозначно
разрешимы относительно *(i>,...,*(„). Итак, в некоторой области
Д" переменных xi,...,xn (имеющей положительную меру при
каждом бев) статистика (.vA), .... .v(n>) эквивалентна статистике
(ti (*(!>> •••.*(«>) Ч'л(*и>...., л'(,())). Поэтому достаточное раз-
разбиение, которое порождает вариационный ряд в области Д", явля-
является минимально достаточным, т. е. (jc(i>,.. .,*<«>) — минимально
достаточная статистика по крайней мере в области Д".
Докажем теперь сформулированное выше утверждение о функ-
функциональной независимости статистик \|?i(xn) г|?4(х„). Предпо-
Предположим противное. Тогда якобиан
= det[c4v(xri)/<3.v/> i, /=1 s]=det[v'i(x,), i, /»1 s] E2)
тождественно равен нулю в Д" = {хп : х,-е Д, i = l,...,n}. Приведем
это к противоречию с линейной независимостью системы
1, <pi (х),... ,ф*(х). Будем действовать по индукции. При s= 1 по-
получаем (p',(xi)==0, cp, (*,)== const, и противоречие получено. Допус-
Допустим, что d(^u---,^s-i)ld(xu...,Xs-iL^0. Тогда, разложив опре-
определитель в E2) по последнему столбцу, получаем для xne.V
Ais(f'i(xs)+... + Ass(ffs(Xs)^O, E3)
где AjS=AiS{xi,... ,xs-\) — алгебраические дополнения соответ-
соответствующих элементов определителя E2). Так как по предположе-
предположению индукции
то найдутся такие значения х° a-j-i» что A°s— Ass(x°
*s_i) ~фО. В таком случае из E3) получаем АиЧ^х,) + ...-*-
+ Asi(fs(xs) — const, А^фО, что приводит к противоречию с линей-
линейной независимостью функций
§ 17. ДОСТАТОЧНОСТЬ И НЕСМЕЩЕННОЕ ОЦЕНИВАНИЕ
1. Полные достаточные статистики.
Рассмотрим статистическую модель (SB, 31, {&})¦ Мы уже
встречались с различными примерами числовых функ-
функций <f(P) неизвестного распределения вероятностей вы-
выборки Р, которые требуется оценить по результатам наблюде-
наблюдений. Так, в модели независимых повторных испытаний обычно
152

представляют интерес математическое ожидание и дисперсия от-
отдельны о наблюдения. Б параметрических моделях (Я?, 36, {Ре.
бев}) возникает задача оценивания различных числовых функ-
функций (fF) от неизвестного параметра в.
Различают оценки точечные, когда по выборке х вычисляется
значение / некоторой статистики 7"(х) и это значение t предлага-
предлагается н качестве приближения к неизвестному ф(8) (<f (P)), и оцен-
оценки umjpeci/ibHiye, когда по выборке х строится интервал G*1 (х),
7*2 (•">). любая точка t которого рассматривается как возможное
значение неизвестного «г(в) (ф(Р)).
Сделаем замечание о термш.'о.юп:;'. Занимаясь задачей точеч-
точечного оценивания, приходится рассматривать различные статистики
7"(х) как возможные оценки <р@) (ф(Р)). Принято в таком слу-
случае. в:-:е зависимости от того, насколько хорошо 7"(х) приближает
негззе.тную функцию, называть статистику 7"(х) оценкой.
Определение 1. Оценка Т(х) функции ф(в) (ф(Р)) назы-
называется несмещенной, если
МвГ(Х) = ф(в), вев (МрГ(Х)=ф(Р), Ре{?}),
где X — случайная выборка.
Несмещенные оценки не всегда существуют, но в случае, когда
они имеются, естественной мерой качества оценки служит ее дис-
дисперсия DeT(X), в ев (DpT(X), Pe{P}).
Будем рассматривать для определенности параметрический
случаи. Допустим, что S(x) — достаточная статистика в мо-
модели C0, Я, {Ре- в ев}). Так как, по нашим представлениям,
S(x) содержит всю информацию о 6, содержащуюся
в выборке х, то, решая задачу оценивания фF), по-внди-
мому, целесообразно рассматривать лишь статистики вида
g(S(x)) — функции достаточной статистики S(x). Представляет-
Представляется, что при этом сужении класса рассматриваемых оценок мы не
должны потерять в качестве: если 7"(х) — оценка с определен-
определенным значением какого-то критерия качества, то должна найтись
оценка вида g(S(x)) с таким же или лучшим, чем у 7"(х), значе-
значением этого критерия. Мы убедимся в справедливости этого ут-
утверждения при решении задачи несмещенного оценивания, когда
за критерий качества принята величина дисперсии оценки. А пока
заметим, что многие оценки, встречавшиеся нам в первых двух
главах, являются функциями минимальной достаточной статисти-
статистики (см. § 15, 16).
Переход от произвольных статистик Т(х) к функциям от дос-
достаточной g(S(x)) облегчает решение задачи оценивания, если ста-
статистика S(x) существенно сокращает данные, например, когда
размерность S(x) невелика и не зависит от размерности выбор-
выборки. В этом случае можно надеяться, что условие несмещенности
Me?(S(X))-=?(G). в ев, A)
рассматриваемое как уравнение относительно неизвестной функ-
153

дни g(s), можно решить, а в множестве его решений отыскать
оценку с минимальной дисперсией.
Рассмотрим пример.
(I) Пусть
Я? = Я\-{х„е/?п:х|>0; t=l п), Я-Я„ПЯп+,
семейство Ре, 8>0, задается «-мерной плотностью
/0(хп) = впехр (—8 2 х,), х„е= R«+,
так что случайная выборка Х„ = (Xi,...,Xn) состоит из независи-
независимых ел. в. с плотностью распределения 8е~вдг, дс>0, каждая. Дос-
п
таточная статистика: S(xn)=?.Vi. Запишем уравнение A)
для (р(8)=8:
j=eI е>о. B>
Так как S(X,,) имеет распределение G(8, n) с плотностью (см.
пп. 1, 2 § 7)
Ъ^** S>° C)
то уравнение B) принимает вид
(n), 6>0. D)
Если g(s) — решение D), то, изменив его произвольным обра-
образом на множестве меры Лебега нуль, мы снова получим решение
уравнения D). Оказывается, что с точностью до такого рода не-
неоднозначности уравнение D) имеет единственное решение, кото-
которое нетрудно найти. Действительно, заменив в C) п на п—1, за-
запишем
нлн
ос
I
— Г(п) s"-' е-** ds = 6-*+" Г (я), 6 > 0. E)
s Г(п — 1)
Сравнивая E) с D) и замечая, что Г(л) = (п—1I, находим ре-
решение уравнения D):
154

Таким образом, несмещенная оценка параметра 0,
функцией достаточной статистики, имеет вид
6 (х„)=(«-1 )/?*,•. F)
Стоит отметить, что G является средним значением отдельно-
отдельного наблюдения и известной оценкой G является выборочное
л
среднее х = V х^п, которое есть, кстати, функция достаточной
статистки. Однако попытка оценить G с помощью (я), как ВИД*
но, приводит к смещенной оценке.
Полагая h(s)=g(s)s"-\ г|з@)=0'я+1Г(п), перепишем уравне-
уравнение D) в виде
со
9>0- G)
Проверим, что уравнение G) имеет не более одного решения h(s)
(с точностью до его изменения на множестве меры нуль). Функ-
Функция г|з(О), определенная формулой G), называется преобразова-
преобразованием Лапласа функции h(s). Существуют различные способы об-
обращать преобразование Лапласа — находить h(s) по -ф@). Мы
используем вероятностный подход (см.: Феллер [2], т. 2). Диф-
Дифференцируя G) k раз по 0, находим
\ (8)
о
Домножим (8) на 0*/*' и просуммируем по k<Qx:
Мы покажем, что при Q-*- +оо
s ^. J
11, если s< х,
Mi e-es ^. JO, если s > х,
откуда будет следовать, что при
(И)
E(-i:
г. е. первообразная Н(х) функции h(x) однозначно восстанавли-
восстанавливается по преобразованию Лапласа i|)(Q). Как известно, функция
h(x) восстанавливается по Н(х) с точностью до ее значений на
множестве меры Лебега нуль. Остается проверить соотношение
155

A0) Левая часть A0) равна вероятности того, что пуассоповская
ел. в. X с параметром 0s приняла значение, не превосходящее
8а\ По неравенству Чебышева
откуда при л'<5
2>(X^0x)=3>(X-0s^Q(xS))<S/(Q(X-S)J-+O, 6-00.
а при л->5
?>(X < 0л) - 1 -9> (X > 8.v) = 1 — $> (X -Os > 0 (л--s))J..-
^ 1—05/@ (A"—S)a)-> 1. 0-н-ОО.
Единственность решения уравнения G) можно выразить в сле-
следующей форме: если /i(s) такова, что
(/i(s)e-:isds=-0, 0>0,
6
то h(s)==0 всюду, за исключением множества меры нуль.
Определение 2. Семейство распределений Qq, 8?б,
на измеримом прсстранстве (^Л оФ) называется полным, если для
любой измеримой функции Л (у) уравнение
--= 0, 0 ев, A2)
где Y — случайный элемент в (йу, «s#, Qe), имеет только нулевое
решение /г(у)=О с точностью до изменения /i(y) на множестве
Qe-меры нуль при любом Оев.
Будем говорить, что уравнение
имеет существенно единственное решение, если для любых двух
решений gi(y), g:(y) этого уравнения множество
имеет Qg-меру нуль при любом Оев.
Если семейство распределений Qq полно, то решение урав-
уравнения несмещенности
Me?(Y)=<P@), 6 ев,
существенно единственно. В самом деле, пусть g\(y), |Ыу) —
два таких решения. Тогда /i(y)=gi(y)—8z(y) является решением
уравнения A2), », следовательно, множество {у:Л(у) = О} имеет
Qg-меру нуль при каждом Оев. ¦
Как мы видели в примере (I), семейство распределений G(Q,
п) полно на (/?', 3&\). Семейство распределений Рв в том же при-
156

мере не является полным на (/?", 3&п), п>\, так как, скажем,
Мв(Х,-Х2)=0, в<=0.
Определение 3. Статистика Т(х) на («2?, ^, {Ре, 0 ев})
со значениями в измеримом пространстве (У, зФ) называется
полной, если семейство ее распределений вероятностей
QQ(A) = Pe(x:T{x)<=A), А<=Л,
является полным.
Если достаточная статистика Т(х) полна н уравнение A) раз-
разрешимо, то его решение существенно единственно. Мы увидим,
что соответствующая несмещенная оценка имеет минимально воз-
возможную дисперсию. Рассмотрим примеры полных достаточных
статистик.
(II) Статистика *,„> з модели повторных независимых испыта-
испытаний с равномерным на @, в), в>0, распределением полна (см.
пример (II) § 16): из уравнения
о
мол (х(п)) = j л (/) «/«-'e-'-rf/ - о, о > о,
о
сразу получаем, что первообразная функции Л(<)*""' равна нулю,
а следовательно, h{t)—O всюду, кроме множества меры Лебега
нуль.
п
(III) Рассмотрим статистику /яа"(|), у (.v(()—.r(u)i в выбор-
(=2
ке из экспоненциального распределения с плотностью
(Г'ехр(—а (х— ц)), х>ц, — оо<ц<оо, о>0
л
(см. пример (III) § 16). Так как Х = пХ0) и У= ? (Х„, — X<d)
i=2
независимы и имеют соответственно экспоненциальную и гамма
плотности:
ехр(—уст-'), у>0,
то уравнение A2) преобразуем следующим образом:
ОС ОС «3D
0=(" f h (x, у) /?.° (х) /у (у) dxdy = f fY (x) dx \h(x, у) /у (у) dy =
mi 0 пц О
QC 00
- (' /J.» (jc) h° (a) dx = a-1 exp (яца~') j exp (— xa~l) h° {x) dx. A3)
nix nix
157

Рассматривая A3) как уравнение относительно ц при фикси-
фиксированном а, легко видеть, что, за исключением множества меры
•Лебега нуль, ha(x) = 0, так что для почти всех х
со
I
A4)
Используя полноту семейства G(cr', п—1), получаем Н(х, у)=0
для |!очти всех у при всех х, для которых выполнено A4), что и
п
доказывает полноту статистики {nx{i), У\ (хA) — а-A))).
1=2
(IV) В модели повторной выборки из распределения Л'(ц, а2)
п " _
полной является статистика (У] А*«> У] (*i— х)г)- Проверим
сначала, что распределение N(\i, о02) иа (/?', 3&\), где — оо<ц<
< -foo, ao2>0 — фиксировано, является полным. Воспользуемся
для этого тем, что двустороннее преобразование Лапласа
ФF)= f e-exg(x)dx, — oo<6< + oo, A5)
—00
однозначно определяет функцию g{x) для почти всех х.
Уравнение A2) для семейства N(\i, o02) после элементарных
преобразований принимает вид
-г оо.
которое приводится к A5) заменой переменного y=xjoo2, так чт0
Л(х)=О почти всюду.
п п
Положим X = YX" У" = Е (*«—-^)*- Так как X и У незави-
симы и имеют соответственно распределения N(n\i, а2) и
G(l/Ba2), (n—1)/2), то уравнение A2) для пары статистик
П | П
_
V х,-, V(*i — jcJJ записывается в виде
i=i 1=1
О =- ? ] h (х, у) fy (х) /« (у) dxdy = j /^" (jf) dx j Л (x, у) /« (у) dy.
0 О
]
—зо 0
Фиксируем а; пользуясь полнотой семейства ^х"|0.(х), —оо<ц<оо,
находим, что для почти всех х
о
158

Теперь, используя полноту семейства СA/Bа2), (п—1)/2) (см.
пример (I)), получаем, что для почти всех у и почти всех х
Цх,у)-0. Ш
Имеет место следующая
Теорема 1. Пусть плотность fe(x) принадлежит k-парамет-
рическому экспоненциальному семейству:
/в (х) = h (х) ехр (j\ at (в) Г, (х) + Ь (в)). в е= 0.
1=1
Если множество значений функции а(в) = (а\(в),. ..,аь(в)),
вев, содержит k-мерный параллелипипед, то Т(х) = (Г,(х),...,
. ..,7"*(х)) — полная достаточная статистика.
Доказательство теоремы можно найти в [11, 12].
2. Наилучшие несмещенные оценки в дискретной модели.
Рассмотрим дискретную статистическую модель (<#,о8, {Ре,
в ев}), и пусть Т(*) — полная достаточная статистика. Допус-
Допустим, что существует несмещенная оценка S(x) параметрической
функции <рF):
MeS(X)=(p(e), вев. A6)
Будем искать функцию g(t) такую, что
A7)
Введем разбиение {«2?t} множества 9С', порождаемое достаточной
статистикой Т(х):
«2?,={x:T(x)-t}. A8)
Запишем уравнение A7) в виде
Ф(в), веб, A9)
где суммирование при каждом 8е6 ведется по тем t, для которых
P(^?) >0. Из A6) имеем, что для всех бев
Ф (в) = JS (х) Рв (х) = Y, рв (*0 Y S (Х) Рв (х)/Рв {Х >' B0)
с теми же ограничениями на область суммирования по t, что и в
A9). Сравнивая A9) и B0) и учитывая, что ввиду полноты
7*(дг) решение уравнения A9) существенно единственно, обнару-
обнаруживаем, что
g(t)= ? S(x)Pe(x)/PeW). B1)
159

где семейство условных мер
Р* (х) = Рв (х)/Рв (Л?(), х €= Л?,, B2)
не зависит от в ввиду достаточности статистики Т(х). (Напом-
(Напомним, что формула B2) при данном t определяет меру Р'ОО.
если существует хотя бы одно Оев, для которого Р* (<2м) > О
и л.-.ч псех таких в значение Р1 (х), хе^ь одно и то же; см.
§ 13.) Перепишем формулу B1), задающую функцию g(t), с уче-
учетом B2) в обозначениях, не содержащих в:
=-- ? 5(x)P«(x). B3)
Итак, получено следующее утверждение.
Лемма 1. Если Т(х) — полная достаточная статистика в ди-
скретне й модели (&, Ш, {Ре. в ев}) и существует статистика
S(x), несмещенно оценивающая параметрическую функцию <рF),
то статистика g(T(x)), где g{t) задается формулой B3), также
несмещенно оценивает <р(в). Статистика g(T(x)) существенно
единственна. Щ
Формула B3) определяет g(t) вне зависимости от того, явля-
является :ш достаточная статистика Т(х) полной или иет — оценка
?(Т(х)) остается все равно несмещенной:
Таким образом, справедлива
Лемма 2. Если Т(х) — достаточная статистика в дискретной
модели («27,(JQ,{Рв,0ев}) и существует несмещенная оценка
S(x) параметрической функции ф(в), то статистика g(T(x)), где
g(t) определена формулой B3), также несмещенно оценивает
Ф(в).
Лемма 3. В условиях леммы 2 имеет место соотношение
DflS (X) = DQg (T (X)) + Мв E (X) -g (Т (X)))*. B4)
Доказательство. Для дисперсии S(X) имеет место следующее
представление:
J ? (S(x)-4>(e))«Pe(x)/Pe(tft). B5)
t xe-^t
160

где Хх определено в A8). Преобразуем внутреннюю сумму в
B5), используя обозначение B2):
у
B6)
Ввиду B3) среднее слагаемое в B6) равно нулю. Подставляя
B6) в B5), получим
= У (S (х) -g (t))* Ре (*,) + Deff (T (X)),
откуда и вытекает равенство B4).
Из формулы B4) следует, что DgS(X) > Dgg(T (X)), причем
равенство выполняется, лишь когда S(X) и g(T(X)) совпадают с
Рд-вероятностью единица. Если достаточная статистика Т(х)
полна, то имеется существенно единственная функция g(t), такая,
что g(T(x)) несмещенно оценивает q>F). Формула B3) при этом
определяет существенно одну и ту же функцию g(t), вне зависи-
зависимости от того, какая там взята несмещенная оценка S(x). В та-
таком случае, используя лемму 2, получаем, что g(T(x)) имеет наи-
наименьшую возможную дисперсию в классе всех несмещенных оце-
оценок. Подведем итог всему сказанному.
Теорема 2*>. Если Т(х) — достаточная статистика в дис-
дискретной модели (8S, SS, {P(j, 8е0}) и S (х) — какая-либо не-
несмещенная оценка параметрической функции фF), то статистика
g(T(x)), где g(t) определена формулой B3), также несмещенно
оценивает фF) м
De?(T(X))<DeS(X),
причем равенство соблюдается лишь при условии совпадения
#(Т(Х)) и S(X) с Ре-вероятностью единица. Если к тому же
достаточная статистика Т(х) полна, то g(T(x)) — существенно
*' Теоремы 2 и 3 являются вариантами теоремы Блекуэла — Колмогорова —
Рао, а также включают утверждение теоремы Лемана—Шеффе о полных дос-
достаточных статистиках.
С';, М. В. Козлов. А. В. Прохоров 161

единственная статистика, являющаяся функцией Т(х), которая
несмещенно оценивает фF), и она имеет наименьшую возможную
дисперсию в классе всех несмещенных оценок. Функция g(t) мо-
может быть найдена как решение уравнения
либо получена из формулы B3), где S(x) — произвольная несме-
несмещенная оценка ср@).
Рассмотрим примеры.
(V) Пусть
# = {х„= (*!,...,*„) :*, = 0 или 1, /=1 п),
Статистика 7(хп) — полная достаточная. Действительно, прирав-
приравнивая математическое ожидание к нулю:
(-0
—)'(\— 6)n = 0, B7)
t-o
получаем, что многочлен от переменного дс=6/A—6), лс>0, тож-
тождественно равен нулю. Следовательно, его коэффициенты равны
нулю, т. е. А(/)=0, /=0, 1,...,л.
Возьмем статистику Si(xn)=jC|. Поскольку
то оценка St(xn) — несмещенная. Далее, при T(xn)=t имеем
по формуле B2)
р' (х„)=в' A _е)л-'/(С„е' A -в)"-*)={С'п)-1
Вычисляя по формуле B3), находим
*г (#)"'= (САГ1 2 \=(Ci)-lC'nz!1 = t/n.
x,+ ...+xn=t-l
Таким образом, наилучшая несмещенная оценка 6 есть
1=\
162

Возьмем статистику S2(xn) = (X2—Х\J/2. Имеем
т. е. статистика S2(x,,) несмещенно оценивает 0A—0) — дис-
дисперсию отдельного наблюдення. По формуле B3) находим
~-LB
-тг
откуда получаем наилучшую несмещенную оценку для вA—в):
Она не совпадает с результатом подстановки в формулу вA—6)
наилучшей несмещенной оценки 6=Jc, но она совпадает с несме-
несмещенной выборочной оценкой днсперсин s2:
(-1
где мы учли, что дс^ = дс<.
(VI) Пусть
# = {x»=(*i х„):Х(=1, 2, .... JV; 1 = 1, .... п},
xnejr, iV=l, 2, ....
Проверим, что достаточная статистика Т(хп) —Х(П) является пол-
полной. Имеем (см. пример (III) § 15)
'—{t — l)n), t=l, 2, .... N,
откуда уравнение A2) приобретает вид
N
t«—(t — l)n), N=\, 2
или
A @ «"-('-1)") = 0. N=l, 2
6V,* 163

и потому Л(/)=0 при f—1,2, Наилучшая несмещенная оценка
N равняется ё(х1П)), где g(t) находится нз условия
N
Yg(t)trn(t«-(t-\r) = N, N=l,2, .... B8)
(-1
Из B8) получаем
g(N)(N»— {N— 1)")=./Vn+1— (N— l)n+1,
нлн
Прн больших t g(tO& t(n+\)/n.
Если Т(х) — достаточная статистика для дискретной модели
(Л?, SS, {Ря, 0ев}), то для любой статистики S(x) можно рас-
рассмотреть статистику g(T(x)), определенную формулой B3):
*(t)= ? S(x)P'(x), a?, = {x:T(x) = t},
xgfl?,
B9)
Р'(х) = Рв(х)/РвОД, бее.
Статистика g(T(x)) принимает постоянное значение на элементах
разбиения {&\}, и это значение равно среднему значению статис-
статистики S(x) по условной мере Р* (х). В теории вероятностей так
определенную g(T(x)) называют условным математическим ожи-
ожиданием S(x) при условии Т(х), нлн, иначе, при условии разбие-
разбиения {<2м}, и обозначают
). C0)
Индекс в в обозначениях C0) имеет чнсто формальный смысл:
объект, определяемый формулой C0), от 8 не зависит. Однако
если статистика Т(х) не является достаточной, то условное мате-
математическое ожидание C0), вообще говоря, зависит от 0 и уже не
представляет такого интереса для математической статис-
статистики.
3. Наилучшие несмещенные оценки в непрерывной модели.
В случае непрерывной модели (/?", 3&п, {Ро. вев}) мы рас-
рассматриваем лишь такие достаточные статистики Тг(хп) =
= G",(х„) Тг(хп)), что отображение *; = 7\-(хп), i=\ г, мож-
можно дополнить некоторыми статистиками Yn-r(xn) = (Y\(xn),...,
•.., Уя-г(Хл)) до взаимно-однозначного преобразования всего про-
пространства R" (кроме, быть может, множества Р^-меры нуль), н
это преобразование регулярно, так что можно делать обычную
замену переменных в интегралах (см. § 16).
164

Рассматривая различные несмещенные оценки S(xn) парамет-
параметрическом функции ф(в), мы будем предполагать, что отображение
(t,, s) = (Т,(х„), S(xn)) также можно дополнить до регулярного
преобразования всего /?". Из определения достаточности Т,(хп)
вытекает, что условная плотность
/Sxn>iW(s|tr)=/(s|tr) C1)
не зависит от 0.
Теорема 3. Пусть Тг(х„) — достаточная статистика в непре-
непрерывной модели (Rn, Лп, {Р«. б ев}), S(xn) — несмещенная
оценка фF) и пара Тг(х„), о(х„) удовлетворяет сформулирован-
сформулированным выше условиям регулярности. Положим
00
= \sf(s\\r)ds, C2)
—со
где условная плотность f{s\t,) определена формулой C1). Тогда
статистика ?(Тг(х„)) несмещенно оценивает фF):
DQg(Tr(*,))<DB(S{Xn)), C3)
и равенство достигается лишь при условии совпадения ?(ТГ(ХП))
и S{X.) с ^^-вероятностью единица. Если к тому же статис-
статистика Т,(хп) полна, то ?(Тг(х„)) — существенно единственная
оценка ср(в), являющаяся функцией Тг(х„), и она имеет наимень-
наименьшую дисперсию в классе несмещенных оценок. Функция g(tr)
мсжег быть найдена по формуле C2) либо как существенно един-
единственное решение уравнения
СО IX
<Р (в) = Лу <Т' (Х«» s J • • • $ 8 С') ^W <U *i' ¦ ¦ dt" в s 9- C4)
—ао —оэ
Доказательство проводится аналогично дискретному случаю с
заменой сумм на интегралы. Имеем с учетом C1)
Meg(Tr(Xn))=-. J ... \fVxn){\r)dtl...dtr f s/(s|tr)ds =
—ао —оо —со
со 00
= J ... J s/?(Xf,).Tr(xn) (s, tr) dsd^ ...dtr =
^00
00
J" ...
00 00 QO
—00 ^00 —CO
6 M. В. Козлов, А. В. Прохоров 165

Для дисперсии оценки S(xn) получаем
ос
DeS (Х„) « J (s - Ф (в))"- &х„) (s) ds =
= J ••• J E-ф
—эв —да
qo a x
= f ... J /тг,х„,Л? ... dtr } (s-<p @))» /(s|tr) ds. C5)
— CO CO »
Преобразуем интеграл по s в C5) к виду
J I(s-ff(t,)J + 2(s-g(t,))(g(tr)-q>(8)) +
-f(tf(tr)-«P(e))*]/(s|tr)ds. C6)
Ввиду C2) интеграл от среднего слагаемого в C6) обращается
к нуль. Подставляя C6) в C5), получаем
De (S (Х„)) .= Deg (Тг (Х„)) + Ме (S (Х„) -g (Т, (Хя)))«, C7)
откуда следует неравенство C3). Наконец, если статистика
Тг(х„) — полная, то решение уравнения C4) существенно един-
единственно, так что при любой несмещенной оценке S(xn) формулы
C1), C2) определяют существенно одну и ту же функцию g(tr),
н тем самым дисперсия оценки ^(ТГ(Х„)) минимальная.
Замечание 1. Пусть Тг(х„) — достаточная статистика, а
У(х„) — такая статистика, что отображение (tr, y) — (Tr(xn)t
Y(xn)) можно дополнить до регулярного преобразования всего
/?". Пусть несмещенная оценка Л(У(х„)) не обязательно имеет
плотность, например принимает лишь дискретные значения. Прос-
Просматривая доказательство теоремы 3, легко убедиться в том, что
оно сохраняется при замене S(x,,) на Л(У(хл)), если положить
8 (^) =\НУ) /у(Х„>| тг(Х„) (У | tr) dy. C8)
Таким образом, теорема 3 справедлива и для всех статистик ука-
указанного вида Л(У(Х„)).
Замечание 2. Отметим, что, как и в дискретном случае,
статистика g(T,(xn)), определенная в C2) или C8), называется
условным математическим ожиданием соответственно S(xn) или
Л(У(х„)) при условии статистики Тг(х„). Обозначение:
Me(S(xn)|Tr(xn)) или луМПХпЖТЛх»))- ¦
Используя теорему 3, получаем, что в примере (I) оценка
F) — наилучшая. В примере (III) повторной выборки из рас-
166

пределения с плотностью оехр(ог1(^—ц)), *>Ц, наилучшие
линейные несмещенные оценки о и ц, полученные в § 11, являют-
являются наилучшими в классе всех несмещенных оценок. То же верно
для повторной выборки из распределения N(\i, о2): выборочные
среднее и дисперсия — наилучшие несмещенные оценки. Щ
Рассмотрим дополнительные примеры.
(VII) Нормальная линейная модель в общей форме:
fdy'a(y)-={Vbio)-nexp (—-L-Hy-eX'H*) C9)
с матрицей X полного ранга приводится с помощью невырожден-
невырожденного линейного преобразования переменного у и невырожденного
линейного преобразования вектора параметров 6 к канонической
форме (см. п. 5 § 10, пример (V) § 16):
Оценки наименьших квадратов Э,, /=1, ..., г, о2 образуют (г+1)-
мериую достаточную статистику в модели C9) (см. пример (V)
§ 16). Ее полнота вытекает из полноты соответствующих оценок
в преобразованной модели D0), которые имеют вид
л
ф,(и)=и{, i = l, .... г, о2(и)=^—г V и*. D1)
i—r-rl
Для г=1 полнота статистики D1) доказана в примере (IV); для
г>\ доказательство полностью аналогично случаю г=\. Таким
образом, найденные в § 9 линейные несмещенные оценки 0, о2
для нормальной модели C9) являются оценками с минимально
возможной дисперсией в классе всех несмещенных оценок, а не
только оценок, линейных по наблюдениям.
(VIII) Рассмотрим, как в примере (I), повторную выборку из
распределения с плотностью Эехр(—0.v), .v>0. Статистика S(xn) =
=пх как было показано, — полная достаточная. Параметрическая
функция
ф,F)=ехр(—е/),
где О0 — любое фиксированное число, допускает несмещенную
оценку. Действительно, положим
II, если .Vj>/,
'{*>*) ~~\0, если *,<*,
тогда
Л=&>(Х .>О=--Ф|@). —оо<0<оо.
167

Следовательно, наилучшая несмещенная оценка <р<F) может
быть получена в виде (см. замечания 1, 2 к теореме 3)
Me (/{X.XJ IS («-»• D2)
Как показано в лемме 2 § 5, условная плотность
/x.ls^CvJs) D3)
совпадает с плотностью U(d, где U\, U2,...,Un-\ независимы и
равномерно распределены на @, s). Но
D4)
((s—u)/s)»-«, 0<u<s,
так что плотность D3) равна
(n-l)s-n+1(s-*,)n~2. 0<x,<s. D5)
По формуле C8) получаем
= .С 7U><) /*.!«*„> (*! Is) dJfi =
о
(s-^Г2^. D6)
о
Если s<j/, то I{Xl>t) —О ПР" 0<JCi<s и, следовательно,
g(s)=0. При 0<t<s имеем '{«,><) =1 пРи *<*i<s и '{*,><} =
= 0 при 0<л-|</, так что интеграл D6) равняется в этом слу-
случае интегралу от плотности D5) по области /<X|<s, т. е. равен
вероятности D4) при u — t. Таким образом,
10 при s < t.
(i-JLY-1 при ,>/.
\ s /
Наилучшая несмещенная оценка ф<@) равна
0 при S(xn)<f,
[ — t/S (х,,))""' при S (xj > t.
Наилучшая несмещенная оценка неизвестной функции распреде-
распределения 1—ф<F) = 1—ехр(—6/) в точке t равна 1—g(S(xn)).
§ 18. ИНФОРМАЦИЯ В СТАТИСТИКЕ
1. Байесовский подход в статистике.
Неопределенность в исходе опыта при его описании статисти-
статистической моделью ($?, Л, {Ре, в ев}) складывается из двух
168

составляющих: неопределенности вероятностного характера, обус-
обусловленном случайностью механизма, реализующего х по распре-
распределению вероятностей Ре, н неопределенности, связанной с
незнанием истинного значения 80 параметра 8, в соответствии о
которым реализуется х. Байесовский метод в статистике рассмат-
рассматривает вторую неопределенность также с позиций теории вероят-
вероятностей.
Рассмотрим для примера задачу выборочного контроля произ-
производства, когда параметр 8 описывает некоторые свойства партии
изделий и может рассматриваться как случайный, меняющийся
от партии к партии. Опыт прошлых наблюдений может быть
обобщен а форме задания распределения вероятностей Q пара-
параметра 0. Обозначим через О соответствующую случайную вели-
величину. В результате мы имеем пару случайных элементов X и в.
Пусть /в(х), /в(в)— плотности распределений Ро и Q соот-
соответственно. Тогда пара (X, в) имеет плотность /в(х)/в(8). За-
Зависимость случайной выборки X от ел. в. в характеризуется ус-
условной плотностью
/x»WeWe00: A)
Можно представить себе, что вначале реализуется значение ел. в.
0 с плотностью /«(9)« затем в соответствии с условной плот-
плотностью A) образуется случайная выборка X. Значение 0, приня-
принятое ел. в. С, неизвестно, значение х случайной выборки X наблю-
наблюдается. По результатам наблюдения х надо сделать выводы о
значении 0.
Назовем байесовской статистической моделью структуру, сос-
состоящую из статистической модели ($?, ев, {Р„, веб}), изме-
измеримого пространства @, &~) и вероятностной меры Q на нем,
называемой априорным распределением.
Выбор априорного распределения является принципиальным
моментом в байесовском методе. Примеры, подобные приведенно-
приведенному выше, когда распределение Q устанавливается на основе час-
частотных соображений по результатам прошлых наблюдений за яв-
явлением, весьма немногочисленны. В теории разработаны различ-
различные подходы к этой проблеме. Суть проблемы заключается в том,
каким способом можно перейти от априорных сведений или пред-
представлений неформального характера к заданию вероятностного
распределения на @, &~). Мы не будем здесь останавливаться
на этом вопросе, отметим лишь, что, несмотря на различие мето-
методологий частотного н байесовского методов в статистике, в конеч-
конечном счете они приводят к сопоставимым статистическим проце-
процедурам.
Если априорное распределение Q каким-то образом выбрано,
то задачу оценки 0 можно отнести к области чистой теории ве-
вероятностей. Случайный элемент в измеримого пространства
@, Э~) с распределением Q полностью определен своим распре-
распределением вероятностей. Информация о 0, содержащаяся в слу-
169

чайной выборке X, полностью заключается в условной плотности
(рассматриваемой на множестве {х : f x (х)>0}):
/в|Х(в|х)-/хв(х, в)//х(х) =
-/е (х) /в (8)//х (х) = /Х|в (х19) /в (9)//х (х), B)
где мы предполагаем, что меры Ро я Q задаются плотностя-
плотностя/х(х) = J ... J/e(x)/e (e)det ... d9». C)
ми и
Условную плотность B) параметра 9 называют апостериорной.
Формула B) представляет собой непрерывный аналог так на-
называемом теоремы Байеса. Легко понять, как трансформируются
выражения B), C), если одна из величин X, в или обе дискрет-
дискретны. Чтобы не вводить лишних обозначений, примем соглашение,
что в случае дискретных X, в под плотностями /в(в). /q(x) и
т. д. будут пониматься соответствующие распределения вероятно-
вероятностей: Pe(x), Q(9) и т. д. В таком случае формула B) сохра-
сохраняет свой прежний вид, если X или в дискретны, в формуле C)
интегралы заменятся на суммы, если в дискретно. Щ
Апостериорная плотность B) служит источником всех даль-
дальнейших статистических выводов о 9. Скажем, в качестве точечной
оценки берут обычно среднее значение по этой плотности:
t = l, .... *, D)
где
We«lx) =1 -1/eix(8lx)dei • ••• de--«de.+« • • • d<>*
— апостериорная плотность компоненты 6i вектора e=Fi,...,
Рассмотрим примеры байесовских моделей.
(I) Пусть (Х\,...,Хп)=Хп испытания Бернулли с неизвестной
вероятностью 0<9<1, априорное распределение есть бэта-рас-
бэта-распределение с плотностью В(а, 6)-'вв-|A—9)*"', 0<9<1 (см. п.
5 § 7). Тогда апостериорная плотность B) пропорциональна
eS(x«> (I _e)n-s<xa> e" A —вN,
S (х„) =xv ч- ... + хп, Х[ ^0 или 1
и является бета-плотностью с параметрами a + S(xn), b + n—S(xn),
т. е. параметры априорного распределения (о, Ь) с учетом ре-
результатов испытания изменились на
(a + S(xn), b + n—S{xa\).
170

Априорное среднее параметра 9 равно (см. § 7)
1
UB(a, Ь)-1 6е A — в)*~|?Ю=В(в+1. Ь)/В(а, b)^a/(a~b),
о
а апостериорное — {a + S(xn))/(a + b + n). Если число наблюде-
наблюдений п велико, то байесовская оценка (a + S(xn))l(a + b + n), како-
каковы бы ни были а>0 и Ь>0, приближается S(xn)ln — частотой
положительного исхода в испытаниях Бернулли.
(II) Пусть Х\,..,Х„ — независимые ел. в. с экспоненциальной
плотностью С (О, I), априорное распределение параметра 9 —
G(}., p) с некоторыми заданными X, р. Тогда апостериорная плот-
плотность пропорциональна
Q"e-s^n)ebP~\e-M) 8 > 0, 5 (х„) = Х\ -<- ... + хп,
т. е. представляет собой плотность распределения G(\+S(xn),
р + п). Найдем байесовскую оценку для функции надежности
Априорное среднее от ехр(—90 равно
J г о»
о
J г о») \*- + t) J г о»)
о о
Априорное среднее от ехр(—0^) равно
)))-(»+i» E)
Если п велико, то байесовская оценка E) близка к наилучшей
несмещенной оценке (см. пример (VIII) § 17):
однако байесовская оценка дает нетривиальный результат при
всех t, в том числе и t>S(xn). Щ
Лемма 1. Пусть Т(х) — достаточная статистика для стати-
статистической модели {&, 28, {Рв, 9ев}). Тогда для любого апри-
априорного распределения Q на @, 3~) имеет место равенство (на
подмножестве X, имеющем Р„-меру единица при любом 9)
/в|Х(в|х)=/в|Т(Х)(9|0, t = T(x), F)
где участвующие в F) плотности в дискретном случае понимают-
понимаются как распределения вероятностей.
171

Доказательство проведем для непрерывной модели. По крите
рпю факторизации (см. § 16)
/e(x)=/{(x)=g(T(x); в)Л(х) G)
на подмножестве X, имеющем Р^-меру единица, 8е6, так что
апостериорная плотность пропорциональна (см. B))
*(Т(х); в)/в(9). (8)
Покажем, что плотность /в|т(х>(®I*)' ^^(х), также пропор-
пропорциональна правой части (8). По формуле B4) § 16
/?<х) @ =-?('; e)Mt),
откуда по формуле B), примененной к паре Т(Х), в, находим
/в1Т(Х) (в 11) пропорциональна
(t6)/(9). (9)
Сравнивая (8) и (9), получаем утверждение леммы. Щ
Из леммы 1 вытекает, что при байесовском подходе понятие
достаточности играет ту же роль, что и в классической статис-
статистике. Именно, как следует из формулы F), по достаточной ста-
статистике восстанавливается апостериорное распределение В при
условии выборки х, а это и все, что нужно знать при байесовском
методе.
2. Информация по Шеннону.
Достаточная статистика выступает носителем всей полезной
информации о неизвестном параметре 9 как при классическом,
так и байесовском подходе. Но само понятие информации оста-
остается пока предметом наших представлений, не имеющим точного
математического выражения. В байесовском подходе и выборка
н параметр являются случайными элементами, и потому к ним
применимо хорошо известное и оказавшееся чрезвычайно полез-
полезным понятие информации (и энтропии), введенное Шенноном.
Пусть, для начала, X и в — дискретные случайные элементы,
определенные на некотором общем вероятностном пространстве
(Q, S4-, 9*) и отображающие его в измеримые пространства (Я?,
38) и @, &~) соответственно;
До проведения каких бы то ни было наблюдений все наши све-
сведения о значении, которое может в результате опыта принять в,
заключены в распределении вероятностей QF), которое в стати-
тнстпкс называют априорным. Если стало известно значение х,
172

принятое случайной выборкой X, то вся полнота знаний о 9 поп-
лощается о условном распределении:
называемом в статистике апостериорным. Таким образом, допол-
дополнительные сведения, содержащиеся в результате опыта, изменили
неопределенность наших представлении о возможном значении 9:
до опыта она выражалась априорным распределением вероятно-
вероятностей, после опыта — апостериорным. Представляется естествен-
естественным определить какую-либо меру расхождения между этими рас-
распределениями к с ее помощью измерять информацию, получае-
получаемую в результате опыта.
Первое, что может прийти в голову, это рассмотреть разность
в качестве такой меры. Однако мы уже имели возможность убе-
убедиться в § 15, 16, что отношение вероятностей или логарифм это-
этого отношения (т. е. разность логарифмов вероятностей) оказа-
оказались полезными при изучении информативных свойств выборки.
Также и здесь оказывается полезной логарифмическая мера рас-
расхождеиня:
/в., (в; x)-iog(s»(e.=e|x=x)/<?»(e«e)). (io)
называемая информацией, содержащейся в событии Л-»{Х»»х} от-
относительно события 5«={в«=6}. Поскольку
то информация, содержащаяся в В относительно А, равна инфор-
информации, содержащейся в А относительно В, и потому меру A0)
называют взаимной информацией между А и В. (Конечно, все де-
делается в предположении &(А), 3°(В)>0.) Перепишем A0} в сим-
симметричной форме:
Подчеркнем, что равенство информации не означает равнознач-
равнозначности выводов, которые можно сделать об А из знания В и, на-
наоборот, о в из знания А. Пусть, скажем, А=В, тогда #(В|/1) = 1
н информация в А относительно В, равная
log A/Г (В)) = log (UP (в »в)) - /в (в), A1)
полностью определяет событие В. Та же информация A1) недос-
недостаточна для определения А по В, если только А и В не совпа-
совпадают с вероятностью единица. Очевидно, дело заключается в том,
что собственная неопределенность событий А и В, вообще гово-
говоря, различна. Примем выражение A1) за собственную меру не-
173

определенности события В, или, 'н»"*1, •»•• /¦оЛ/ч.яомиуш информа-
информацию, содержащуюся в событии В о самом себе. Ее можно ин-
интерпретировать как информацию, необходимую для полного раз-
разрешения неопределенности относительно события В. С учетом
сказанного величину
A2)
можно назвать условной собственной информацией, содержащейся
в событии {6=6} при условии события {Х=х}, и интерпретиро-
интерпретировать как информацию, необходимую для определения события
{6 = 9}, после того как стало известно, что Х=х. Поэтому раз-
разность
может рассматриваться как информация, содержащаяся в собы-
событии ,'Х = х} относительно события {6 = 9} и, как видно, совпадает
с взаимной информацией A0).
Формулы A0) — A3) определяют понятие информации для от-
отдельных событий {6 = 9}, {Х=х}, тогда как желательно опреде-
определить информацию о 6 в X, как случайных элементах. Это дости-
достигается усреднением введенных количеств информации по всем
значениям участвующих там случайных величин.
Энтропия 6 определяется как среднее значение собственной
информации и задается формулой
#(в) = ]Г5>(е = 9)/в(9)= — y5>(9 = 9)log5>(9 = 9). A4)
в в
Средняя условная энтропия 6 при условии X определяется равен-
равенством
6.x
x). A5)
е.х
Средняя взаимная энтропия между 6 и X получается усредне-
усреднением формулы A3) и равна
/@, Х)=ЯF)-ЯF|Х). A6)
Определенная формулой A6) информация по Шеннону обла-
обладает рядом свойств, которые было бы естественно потребовать от
люио.1 формализации понятия информации. Перечислим эти свой-
свойства.
!. Информация всегда неотрицательна: /(в, Х)^0.
2. Если статистика Т(х) подобная, то /(О, Т(Х))=0.
174

3. И::фср:-:г.:;::л, содержащаяся в статистике, не превосходит
информации, содержащейся во всей выборке:
/(в, Т(Х))</(в, X).
4. Если Т(х) — достаточная статистика для
е=е}), то /(в,Т(Х))=/(в,Х).
Проверим свойства 2 и 4. В случае подобной статистики Т(Х)
получаем
/9 (в, х) log *<Т(Х)~.»|в~9) = log _^IW=iL = 0,
е»,!(Х). 1 с ?j»(T(X) = x) 6 5»(Т(Х)==х)
гак что равна нулю и средняя взаимная информация /(9,
Г(Х)).
Пусть Т(Х) — достаточная статистика. Рассмотрим
e) 07)
6,х
По формуле полной вероятности
т). A8)
Используя достаточность Т(Х), запишем факторизацию A1) из
§ 15:
|(X; 9)Л(х). A9)
Логарифмический множитель в A7) после подстановки A8),
A9) приобретает вид
T)). t = T(X). B0)
X
Учитывая, что (см. A3) § 15)
л(х). B1)
x:T(x)=t
и домножая числитель и знаменатель дроби в B0) на второй мно-
множитель в B1), получаем для выражения B0) значение
), B2)
где t—T(x). Подставляя B2) на место логарифмического множи-
множителя в A7) и снова воспользовавшись формулой полной вероят-
вероятности, находим
175

jt:T(X)-t
Для непрерывных моделей и непрерывного априорного раслрг-
деления информационные характеристики вводятся путем замены
ь формулах A0) — A6) дискретных распределении вероятностей
кп соответствующие плотности, а сумм — на интегралы. Запи-
Запишем, для примера, выражения для взаимной и средней взаимной
информации между в и X:
/в|Х (в, х) - log (/ед (в, х)//в (в) /х (х)), B3)
/ (в, X) = \¦ ... i /вд@, х) Твд (в,х) </8, ... <%/*, ... dxK B4)
Аналогично дискретному случаю доказываются сформулированные
выше информационные свойства подобных н достаточных ста-
тнетнк.
Рассмотрим одни пример.
(III) Допустим вначале, что параметрическое множестве 9 =
= {8i, 6j, ...,6r} конечно и выборка также дискретна. Запишем
взаимную информацию:
/в д (в,, у.) - 1о- (Р @ = 0, | X =-- х),'Р @ - 0,)). B5)
Задачу различения, какое именно значение приняла ел.в. в, бу-
будем решать следующим образом: при данном наблюде::н1; х в
качестве предполагаемого значения неизвестного параметра вы-
выберем 0j такое, что выборка содержит о нем наибольшую инфор-
информацию:
'ед@/,х)^/вд(е,,х), i-l т. B6)
Иначе говоря, выбирается такое значение 0j, что отношение егс
апостериорной вероятности к априорной наибольшее:
^@=в,!х=х)/^@=в^)>^(в=е{|х=х)/^(в=е,), «=i г.
B7)
Перепишем B7) в виде
^(х=х|е=в/)/^(х=х)^<^(х=х|в-е1)/<У8(х-х), i=\ г,
или
х|0 = е,), i=l г. B8)
Из B8) видно, что предложенное правило различения на самом
деле не зависит от априорного распределения. Если вообще отка-
176

заться от байесовского метода и записать неравенство B8) для
классического подхода:
Pfl.(xM>P0.(x), i-l г, B9)
го правило выбора B9) неизвестного значения параметра выгля-
выглядит так: в качестве оценки выбираемся такое 6,, при котором ве-
вероятность наблюденной выборки х максимальна. Этот метод но-
носит название метода максимума правдоподобия, к о нем будет
идти речь в следующей главе.
Отметим, что в непрерывном случае также можно рассмо-
рассмотреть правило B6), заменив дискретное распределения на плот-
плотности. Аналогично B9) имеем оценку в*=0*(х) максимального
правдоподобия:
3. Информация по Кульбаку.
В байесовской модели информация по Шеннону служила ме-
мерой расхождения между апостериорным и априорным распреде-
распределениями параметра. При классическом подходе также играют
важную роль меры расхождения, но уже между распределениями
Pp. I) зб. Фактически любая форма статистического вывода о
неизвестном параметре 9 модели (Х,Ш. [?q. О <н О}) представ-
представляет собой некоторый способ различения мер «°д по наблюденно-
наблюденному значению выборки. Если Pe^Pft, для некоторых 0,^62, то
понятно, что различить по выборке значения 9| и 02 невозможно.
С другой стороны, если носители мер Р(>, » Pq., не пересекаются,
то задача различения 9| и 02 становится тривиальной. Эти край-
крайние случаи не интересны для теории, но наводят на мысль, что
возможности различения 0i и 02 зависят от того, насколько рас-
расходятся между собой распределения Р^ и Pq,.
Предположим для определенности, что статистическая модель
непрерывна и меры Pq задаются плотностями /о(х). Инфор-
Информацией по Кульбаку в точке х для различения в пользу 0i против
0: называется величина
/@1:02,x)=log(/fli(x)//fls(x)). C1)
Выражение C1) равно разности логарифмов плотностей /ot(x) и
/й> (х) и как мера расхождения представляется довольно есте-
естественной. Возвратимся на время к байесовскому подходу и рас-
рассмотрим взаимную информацию по Шеннону между х и 0,-:
'е.х А. х) = 1о§ (/о, (х)//х 00). '=1.2. C2)
177

Составляя разность выражений C2), получаем
'е,х (°i. х) -7в,Х (е2. *) = log (/Ol Шь (х)) = / @Х: 92, х). C3)
Итак, различающая информация в пользу /о, против /о, в точ-
точке х по Кульбаку равна разности информации Шеннона о 9| и
8г, содержащихся в х, вне зависимости от априорного распреде-
распределения (при условии, что априорные плотности или априорные ве-
вероятности в точках 9i и 92 положительны).
Определим среднюю различающую информацию в пользу /о,
против /ог относительно меры Pot как среднее значение C1) пс
этой мере:
/ @Х: 02) = I ... j /^@1: 02; х) fQl (x) dxx... dxn =
= f ... \ fQi (x) log (/6l (x)//Oj (x)) dx,... rf.vn, C4)
где мы предполагаем, что носитель меры Р^ содержится в носи-
носителе Рв.,:
и интегрирование в C4) распространяется на все х, для которых
/oltx)>O. Иногда удобно вместо /@i:02) писать /х (в|:92),
чтобы подчеркнуть, что речь идет о различающей информации пс
всей выборке. С другой стороны, если Т = Т(х)—некоторая ста-
статистика, то аналогично C4) определяется различающая информа-
информация по статистике:
/т @!: 02) - J • • • \ :/?1 (t) log (/?' (t)//?^ (t)) dt, d\ = dt, ... dtk. C5)
Рассмотрим пример.
(IV) Пусть fi (xi, X2) есть двумерная нормальная плотность
Л/2@, Q), где (см. пример п. 1 § 12)
, f)f{) где ц>(х) — плотность
1). Тогда
log (f, (X,, Хг)Цг (X,. Х2)) - 2-> log A -р*) -а-] 2-> A -р*)-' X] +
Р A -PV агЧ1 Х1Х2-а=2-' A -р*)-' Х|-2"
Взяв математическое ожидание М| по мере с плотностью
}\ (х\, Xi) от обеих частей равенства и учитывая, что
178

получаем
/0:2)^2- ' Iog(l —рг)—2-1 A —Р2)-1 + Р2A —Р2)-1 —
— 2-' A — р2)-'+ 2-'+ 2-н = 2-' log(l—р2).
Таким образом, /A:2) является функцией только коэффициента
корреляции р. Щ
Перечислим некоторые свойства информации C4).
1. Информация всегда неотрицательна: /(9i: 9г)^0, причем
равенство имеет место тогда и только тогда, когда множество
{х : /(>! W Ф /в., (х)} имеет Ро,-меру нуль, i= 1, 2.
2. Если Т(х) — некоторая статистика, то
/т(х,(в1:е2)</х(в1:е2)
с равенством тогда и только тогда, когда Т(Х)—достаточная
статистика.
3. Пусть Х=(Х<'), Х<2>) и Х<'\ Х<2> — независимы при каждом из
распределений Р^ и Pq2. Тогда
Коротко: для независимых наблюдений информация склады-
складывается.
Проверим последнее свойство, предполагая, что меры Ре,.
t=l, 2, определяются плотностями. Имеем
'х">.х<*> Wi: 8*) = П /в4 (u, v) log (/Oi (u, v)//ei (u, v)) dudv, C6)
где du = du\. ..diik, dv=dv\.. .dvn-h, а интегралы в C6) соот-
соответственно fc-мерный no u и (я — k)-мерный по v. Ввиду незави-
независимости
/в, (u, v) -/5,)>х,„ (". v) =l%} (")/J2) (v), i = 1, 2. C7)
Подставляя C7) в C6) и записывая
log -^- = log —f- + log —?l , C8)
'Muv> ^ $
разложим интеграл C6) в сумму интеграла
Л = J J /J1,, (") /&, (v) bg ($„ (u)//^,, (u)) dudv C9)
и интеграла /г, получаемого из /| заменой логарифмического
члена на второе слагаемое из C8). Заменяя интеграл C9) по-
повторным и интегрируя сначала по dv, найдем, что C9) равен
J /jfr, (и) log ($,, (и)//$„ (и)) Л. «/хС1) (8,: 82).
Аналогично У2~'х<2> ^i:®*)» чт0 и дает требуемый результат.
179

Проверим равенство информации
когда статистика Т = Т(х)—достаточная. В соответствии с пред-
предположениями § 16 найдется статистика Y = Y(x) такая, что пре-
преобразование (t, y) = (T(x), Y(x)) регулярно и с вероятностью
единица взаимно-однозначно, так что
- Я /т\ (t. У) log (/?;Y (t, у) 7Vfv 0. у)) dtdy> D°)
где d\=dt\. ..dir, dy=dyi.. .dyu-r и интегралы имеют соответ-
соответствующую размерность. Подставляя в D0) факторизацию B3)
§ 16, приведем D0) к виду
Л ё (t; в,) ht (t, у) | J | -1 log (g (t; Qt)/g (<; вг)) dtdy. D1)
Заменим интеграл D1) повторным и проинтегрируем сначала по
у. Учитывая формулу B4) § 16
получаем для D1) выражение
f /0| (t) la? (/?• (t) /«* (t)) «t - /т,х, (в,: 8S),
что и требовалось установить.
4. Информация по Фишеру.
Предположим вначале, что 0 — скалярный параметр, и рас-
рассмотрим информацию по Кульбаку:
=Шх; 6)log(/(x; 0)//(x; 0 + Д0))Лс, D2)
где dx = dx\.. .dx,,, а интеграл понимается как я-мерный. Будем
предполагать, что носитель у всех мер Р8, 0^9, общий, а от
плотностей /(х; й) потребуем выполнение свойств регулярности,
которые мы не будем перечислять, но которые обеспечивают обос-
обоснованность проводимых ниже выкладок. Разложим логарифмиче-
логарифмический член в D2) по формуле Тейлора:
D3)
где 0./ лежит между 6 и 0-гД0. Поскольку (мы считаем лога-
логарифм натуральным)
180

|=-^-l=O, D4)
то, подставляя D3) в D2), имеем
*l0g!<X;e;) A6'dx. D5)
6) !
он
Положим
6)^^dxMe ¦
Тогда D5) можно переписать в виде
/(e:e+Ae) = V2/(e)A92+o(Ae2). D6)
Дифференцируя, получаем
a* log /(х; О) _ 1 ау(х;б) i / а/(х-,б) \г ,4?.
ае» /(х-.е) ае* /»(х;е> V аэ / " v ;
Но (ср. D4))
м ' <>У(Х; 0) _ С ау(х;О) ,.._0
поэтому, взяв математическое ожидание от обеих частей равен-
равенства D7), где полагаем х = Х, имеем
Формула D8) определяет информацию по Фишеру в выборке X о
параметре 8 (мы полагаем прн этом, что в — интервал в R]). При
условиях регулярности, для которых оправданы приведенные
выше выкладки, информация по Фншеру определяет по формуле
D6) информацию по Кульбаку для бесконечно близких значений
параметра fl и 8 + Д8. Используя равенство (см. D4))
M0(<91og/(X; 0)/ав)=О, D9)
запишем для /(G) эквивалентную формулу
I(Q)=DB(d\ogf(\; 0)/д0). E0)
Работая с информацией по Фишеру, мы будем всегда предпола-
предполагать, что выполнено равенство D9), что обеспечивается требова-
требованием совпадения носителей мер Ро и возможностью дифференци-
дифференцирования под знаком интеграла D4).
181

Если статистическая модель дискретна, то формула E0) за-
заменяется на следующую:
прн этом требуется выполнение равенства, аналогичного D9).
Перейдем к векторному параметру 6= @i,.. . ,0л), предпола-
предполагая, что 0 — область в Rh. Информационной матрицей Фишера
назовем матрицу ковариаций /(8) случайного вектора
dlog/(X; 9)/dG*), E2)
где X имеет распределение Ре. При этом предполагается, что
вектор E2) имеет нулевое математическое ожидание:
M02radelog/(X;9)=.-0, 9 ев, E3)
и, таким образом,
*Ф)= Щ[(gradelog/(X; 9))'gradelog(X; 9)]. E4)
Аналогично определяется информационная матрица Фишера
для статистики Т(х):
/т<х) (в) =М [(grade log/тех) (т W; 8))'grade log/Тда (т (*)>вI E5)
где /t(X) (t; 9)— плотность распределения Т(Х) в предположе-
предположении, что выборка имеет распределение Ре- В частности,
/(9)=/х(в).
Если выборка илн статистика дискретны, то плотности в E3),
E4), E5) заменяются на распределения вероятностей.
Перечислим некоторые свойства информации по Фишеру.
1. Если Т(Х) —подобная статистика, то /т(х>(9)=0, б ев.
2. Для любой статистики Т(Х) имеет место неравенство**
/т(Х)(в)</х(в). веб.
3. Если Т(Х)—достаточная статистика, то
/т(Х)(9)-/х(9), 9 ев.
4. Пусть Х= (ХС>, Х<2>), ХA>, Х<2> — независимы при каждом
Ре, веб, и для них определена информация по Фишеру. Тогда
Проверим свойство 4. Ввиду независимости Х<'> и Х<2)
A). "B); в) =log/x(l) (х«); 9) + log/xB) (х<«; 9)
*> Напомним, что знак неравенства А^В между матрицами означает, что
разность В—А неотрицательно определена.
182

grad0log/xA)xB)(X<»,X<*>;e)-
= gradelog/xA) (X«'>; 9) + grade log/x<2) (X«>; 0). E6)
причем векторы в правой части E6) независимы, имеют нулевое
математическое ожидание и у них существует матрица ковариа-
ций. В таком случае математическое ожидание вектора в левой
части E6) равно нулю, а его матрица ковариаций равна сумме
матриц ковариаций векторов в правой части, что и требовалось
установить.
Свойство 1 очевидно. Свойства 2, 3 ради сокращения выкла-
выкладок докажем для скалярного параметра и в дискретном вари-
варианте. Положим
Qe(t)= ? Рв(х).
x:T(x)=t
Рассмотрим
м
/ aiogPe(X) aiogQe(T(X)) \«_
el ав « J "
Распишем математическое ожидание в правой части E7):
S
Ре(х) Qe(T(x)) P«W1 Qe(,)
x t x:T(x)=t
t x:T(x)=t t t
Таким образом, левая часть E7) равна
/х(в)-/тс»(в). E8)
а так как правая часть E7) всегда неотрицательна, то свойство 2
установлено.
Допустим, что Т(х)—достаточная статистика. По теореме
факторизации (см. п. 5 § 15) равенство
Ре(х)=?(Т(х); в)Л(х), E9)
выполняется при каждом 6 на некотором подмножестве 30 в,
имеющем Рв-меру единица. Изменим при каждом 0 меру Рв на
подмножестве 30QXa Ре-меры нуль так, чтобы равенство
E9) выполнялось при всех х^ЗО. Формально статистическая мо-
модель при этом изменилась, но с содержательной точки зрения
183

такое видоизменение несущественно. Суммируя E9), находим
Qe(t)=?(t;6) ? А(х). F0)
x:T(x)=t
Подставляя E9), F0) в левую часть E7), обращаем ее в нуль,
что с учетом E8) доказывает свойство 3.
Отметим, что свойства 1, 3 допускают обращение, если нало-
наложить некоторые ограничения, исключающие «патологические»
случаи. Предположим, для краткости, что 8 — скаляр, а в — не-
некоторый интервал, и потребуем, например, чтобы производная
<91ogfT!X)(t; 9)/<Э9 F1)
была непрерывна по 0. Допустим, что /т(Х)(б) = 0, б ев, т. е.
Вв (д log Мх) (Т (X); 6)/с>0) = 0, бе 0,
и, следовательно, (см. E3))
;6)/c>6-0, 6e=;e, F2)
на подмножестве Э~ъ<=-3~ переменного / Qe-вероятности единица,
где Qe — распределение статистики Т(Х). В таком случае для
подмножества 0'?0, состоящего из всех рациональных точек из
в, соотношение F2) выполнено на некотором подмножестве Т'<=,
<=&", Qe-мера которого равна единице для всех веб'. По не-
непрерывности F2) выполнено при всех веб на W:
4-logMx>(t;e)-0, tedT', Оев,
и, следовательно,
te=ST', ве=0, F3)
где f(t)—плотность, не зависящая от 0. Но из этого вытекает,
что при всех 8е0
3" .У"
т. е. Qe(^"') = l при всех ве0, что доказывает подобие статисти-
статистики Т(х).
Чтобы доказать обращение свойства 3, воспользуемся следую-
следующим утверждением.
Лемма 2 [13, с. 62]. Пусть (X, с®, {Ро. 9 s 0}) — непрерыв-
непрерывная или дискретная модель. Тогда существует счетное подмноже-
подмножество 6'Е0, что для любого подмножества Х'^Х, для которого
при всех 8е0' верно Рд (X') = 0, это равенство справедливо и
для всех 8е0.
Предположим, что в — интервал прямой, статистика Т(х) та-
такова, что разность информации E8) обращается в нуль. Потре-
Потребуем от модели, чтобы производные
184

jLlogPe(x), J-\ogQ0(T(x)), Og0,
oQ ad
были непрерывны по 8 (прн х, для которых они определены).
Пусть в' — подмножество, определенное в лемме 2, в"— подмно-
подмножество рациональных точек из 0. Поскольку левая часть E7), по
предположению, обращается в нуль, то при каждом 8ев
-l-logPe(x)--iLloBQ0(T(x))=<) F4)
на подмножестве og^St?, имеющем Рв-меру единица. В таком
случае найдется подмножество $в'<=<%, что равенство (С4) спра-
справедливо при всех 0e0'U6" и хеЯ?, и при этом для 0s6'U6"
верно
Ре(Я?') = 1. F5)
По непрерывности равенство F4) выполнено при всех 8е0,
ей?', а ввиду леммы 2 равенство F5) выполнено при всех 8
Итак, с Ре-вероятностью 1 при каждом 8ев
JLlogPe(x) ^-logQe(T(x))-=0, 0<=8,
од ад
откуда
PQ(T())ft(), 8<=е,
где k(x) не зависит от 8, т. е. статистика Т(х) —достаточная. ¦
Основание логарифмов в рассмотренных нами информацион-
информационных мерах не является существенным и определяет лишь единицу
измерения. Расчеты в статистике удобнее проводить с натураль-
натуральными логарифмами.
§ 19. НЕРАВЕНСТВО ФРЕШЕ-РАО-КРАА1ЕРА
1. Скалярный параметр.
Обратимся к задаче несмещенного оценивания параметриче-
:кои 1|)\нкцни ср(8) в модели (ЙГ, JS,)[Pq, 8ев}). Пусть Т(х) —
достаточная статистика. Как было установлено в § 17, если за
эффективность оценки принять величину ее дисперсии, то можно
ограничиться оценками вида S(x)=g(T(x)), не проиграв в эф-
эффективности. Если же оценка ищется в виде /i(V(x)), где стати-
статистика V(x) не является достаточной, то происходит проигрыш в
эффективности, если только /j(V(X)) не совпадает с g(T(X))
с Рg-вероятностыо единица, 8ев. Интересно, что проигрыш в
эффективности несмещенного оценивания может быть оценен не-
непосредственно через количество информации по Фишеру. Напом-
Напомним, что информация по Фишеру не теряется при переходе от
вь'боркп х к достаточной статистике Т(х) и, напротив, умень-
уменьшается при переходе к статистике V(x), не являющейся доста-
достаточной.
7 М. В. Козлов, А. В. Прохоров 185

В качестве основания логарифмов в определении 1\ @; при-
примем число е. Вкладом выборки называют величину
{/(х; Щ= — \п[(х; 0) или — 1пРе(х), A>
от от
соответственно для непрерывной или дискретной моделей. В слу-
случае повторных независимых наблюдений
?/(х„; 8) «??/(*,; 0),
где U(xi\ 9) называется вкладом наблюдения Xt и определяется
формулой, аналогичной A). Мы предполагаем выполненным ус-
условие D9) § 18:
Mf/(Xi; 9)=0, B)
так что из B) получаем
/х„ F) = DeU (Х„; 6) - ? D(IU (A',; 0) - л/*, @).
Ниже мы докажем, что при некоторых условиях регулярности
дисперсия несмещенной оценки 5(х)=?(Т(х)), где Т(х)—про-
Т(х)—произвольная статистика, удовлетворяет неравенству Фреше—Рао—
Крамера:
C)
Если статистика Т(дс)—достаточная, то /т(х> @) — ^х (Щ и нера-
неравенство C) приобретает вид
DbS(X)>4>'(u)s/'x@). D)
Если статистика Т(Х) не является достаточной, то (см. п. 4 § 18)
/та,@)</хF).
и нижняя граница C) дисперсии любой несмещенной оценки, яв-
являющейся функцией Т(Х), больше, чем нижняя граница несме-
несмещенной оценки — функции всей выборки X.
В случае повторных независимых наблюдений неравенство D)
имеет впд
E)
Стоит подчеркнуть, что правая часть E) имеет порядок 1/л, так
что стандартное отклонение имеет порядок 1/Ул. Если оценка
5(х) смещенная:
то она является несмещенной оценкой фF), и, следовательно, не-
неравенства D), E) сохраняются с заменой <рF) на tj;@).
186

Рассмотрим примеры.
(I) %= {х„= (*! хп): Xi = О или 1, ?== I. .... л},
Рв(хп)=6Г(х")A-6)п-Г(х"), Г(х„)= у xit 0<6< 1.
Наилучшая несмещенная оценка параметра б имеет дисперсию
DG-(Xn)M)=9(l-9)/n.
Вычислим информацию по Фишеру, пользуясь независимостью и
одинаковой распределенностью ел.в. Хи...,Х„:
Так как
(Al In6+ A дг±) ln(lO)) = .ve
= (л-1—в)/Ч0A—О)),
то
так что в данном случае неравенство E) обращается в равенство.
(II) Для выборки из экспоненциального распределения мера
Рв, 9>0, задается плотностью
= 6"ехР (~6 j
i—l
Наилучшая несмещенная оценка 0 равна (см. пример (I) § 17)
Вычислим дисперсию Г(Х„):
о
Г (п — 2) " "п~2
б
187
* „о
Г (n) J Г(п-2)

Г(л) л —2
ie« -e«= -^. F)
Подсчитаем информацию Фишера:
Неравенство E) принимает вид
n. G)
Таким образом, минимальная достижимая дисперсия F) несме-
несмещенной оценки параметра 6 больше, чем граница G) Фреше—
Рао—Крамера. При больших п расхождение между F) и G)
пренебрежимо мало.
Для параметрической функции <рF)=0~', совпадающей со
л
л
средним значением отдельного наблюдения, оценка х —¦У] xjn —
несмещенная и является функцией полной достаточной
п
статистики V *;. Ее дисперсия равна 1/(л9J, и, с учетом <р'(9) =
=—б2, получаем для нижней границы E) значение
т. е. для наилучшей несмещенной оценки .v неравенство E) обра-
обращается в равенство. И
Условия, в которых будет доказано неравенство Фреше—Рао—
Крамера D), включают в себя прежде всего требование D9)
§ 18, сформулированное при определении информации по Фи-
Фишеру:
М„?/(Х; 6)=0, б€Ев. (8)
Так как
j ... j/x(x; 6)^ ...Лс„=1, (9)
то в предположении, что операцию дифференцирования по 9 мож-
можно перенести под знак интеграла, из (9) получаем
J
J J ~k /х (Х; 0) dXl ¦ ¦ • dXn = °-
188

Сравним левую часть A0) с выражением
t/х {х' b)/fx (х: 6))/х (х: 6)dXx • ¦ ¦dXn=
J (it/х {х
= J ... Jf/ (x; 6) /х (х; 6) dq ... dxa = NiJJ (X; 6). A1)
Различие между интегралами A0) и A1) заключается в том,
что интегрирование в A1) фактически производится лишь по но-
носителю меры Рв:
^в-{х:/х(х; 6)>0}. A2)
Очевидно, если верно соотношение A0), то (8) выполнено тогда
и только тогда, когда
j^-/x(x;e)dx1...dxn=O. A3)
Соотношение A3) выполнено, если
-?-/х(х; 6)= 0 при хе#е#в. A4)
Для повторной независимой выборки равенство (9) приобре-
приобретает вид
а требование A3) сводится к следующему:
= О. A5)
Еще одно требование, необходимое для доказательства нера-
неравенства D), — это возможность перенести операцию дифференци-
дифференцирования под знак интеграла в следующем выражении:
= -^-| ... JS(x)/x(x;
... dxn. A6)
С учетом условия A4) соотношение A6) можно переписать в
виде (ср. A1))
<p'(e) = Me(S(X)?/(X; 9)). A7J
Теорема 1. Допустим, что плотность выборки f\ (x, 6) диф-
дифференцируема по 8ев, в — интервал прямой, операция диффе-
дифференцирования по 8 перестановочна с интегрированием по х в ин-
интегралах A0), A6) и выполнено условие A4). Если S — несме-
189

щепная оценка параметрической функции q>@) и существуют дис-
дисперсии
DeS(X), Ое?/(Х;в)=/х(в),
то имеет место неравенство D); в равенство оно обращается то-
тогда и только тогда, когда S(\) является линейной функцией
вклада выборки:
; 0) A8)
на подмножестве Р»-вероятности единица.
Доказательство. Из условия теоремы вытекают соотношения
(8) и A7). Используя (8), перепишем A7) в виде
<p'(e)=M(S(X)-<p@))?/(X; 0).
По неравенству Коши—Шварца—Буняковского
V'(eJ<DeS(X)Det/(X; в),
причем равенство имеет место лишь при выполнении условия A8),
что и требовалось доказать. ¦
Замечание 1. Для дискретной модели сохраняются все
предшествующие рассуждения с заменой плотностей на распре-
распределения вероятностей и интегралов на суммы.
Замечание 2. Если Т(Х) = (Г, (X),..., ГГ(Х)) —статисти-
—статистика и fr(V, 0) удовлетворяет условиям теоремы 1, то для несме-
несмещенных оценок — функций Т(Х)—справедливо неравенство C).
Следствие. Если неравенство D) обращается в равенство
при всех* 9ев, то из A8) находим
^ @)-1, A9)
ох)
/х (х, G) - h (x) exp {A (Q) S (х) + В (G)), B0)
и при этом
В/(в)/Л'(в)=-ф(в). B1)
Наоборот, если /х(х; 0) имеет вид B0), то верно A9), а следо-
следовательно, A8), т. е. неравенство Фреше—Рао—Крамера D) об-
обращается в равенство. Таким образом, обращение неравенства
D) в равенство имеет место только в случае экспоненциальной
модели B0) и только для оценок, имеющих вид aS(x)+p (a, P —
любые постоянные), или, другими словами, для параметрических
функций вида
(Yi Ь — любые постоянные).
2. Векторный параметр.
Теорема 2. Допустим, что плотность выборки /х(х; в),
в= (8i,..., 6ь)ев (в — область в Rk) дифференцируема по каж-
190

дому 0/, /=1; .... k, векторная статистика S(x) = (S\(x),..., Sr(x))
несмещенно оценивает вектор-функцию <р@) = (ф1(в),...,фг@))
и имеют место соотношения
<Э0/
i~JSfx)Mx;
i—\,...,k, dx = dx\ .. .dxn, а интегралы понимаются как п-мер-
ные. Предположим также, что
<3/х(х; 6)/dG,= 0, i = I k при х:/х(х; 6)=0.
существует матрица ковариаций
и информационная матрица Фишера /хF) положительно опре-
определена, то *>
/?5(х,(в)>Д(е)/х-1(в)Д(в)', B2)
где
=[-^7Ф/(в),/ = 1, ...,г;/ = 1 ft]
ы штрих обозначает операцию транспонирования. Равенство в
B2) илеег лесго гогйа и только тогда, когда
8(х) = фF) + и(х; в) Л (в) B3)
на подмножестве Р'^-вероятности единица; А(в)—kXr-матри-
ца полного ранга, зависящая лишь от в.
Доказательство. Аналогично тому, как это сделано в случае
скалярного параметра, легко показать, что
MeU(X; 6) = 0, U(x; e) = gradln/x(x; 0),
^WJLln/xfX; в).
гак что
/х(в)-/?и(х;в» -iWeU'(X; 0)U(X; в),
B4)
AF) = Me(S(X) — MflS(X))'U(X; в).
Найдем ковариационную матрицу вектора
W(X; 6)=S(X)— MflS(X)— U(X; 6)/x' @) А' (в).
* См. сноску на с. 182.
191

Проведя элементарные преобразования, получаем с учетом B4)
tfw=Me(S— MeS—U/-1A')'(S— MeS—и/-'Д') =
что и дает утверждение B2) теоремы 2. Равенство в B2) воз-
возможно, лишь когда /?w = [0], т. е. с Ре-вероятиостыо единица
S (X) —M(|S (X)—U (X; в) I-1 (в) Л' (в) = 0, B5)
откуда и следует B3). Щ
Следствие 1. Пусть неравенство B2) обращается в равен-
равенство, А (в) обратима, Д-Мв). /х'ф). ф(в) непрерывны по 9. То-
Тогда найдутся такие функции /Л(в),...,//ГF), В (в), К(х), что
/х (х; в) = exp j jr Ht (в) S, (х) 4- В @) f К (х) j. B6)
1-1
т. е. статистическая модель является экспоненциальной.
Действительно, из B3) получаем, что вектор градиента по в
grade 1п / (*: в) = S (х) А-1 @) -q: {в)А-1 @)
непрерывно зависит от 0 и, следовательно, функция 1п/(х; в) —
дифференцируемая функция неременных в= (в|,.... вп) в обла-
области в. В курсах математического анализа доказывается, что в
этом случае
в
In / (х; в)- In / (х; в„) - :|" (S (х) А~1 (в) -(р (в) А-1 (в)) dV,
где криволинейный интеграл берется вдоль любого гладкого
пути, лежащего в области в и соединяющего точки во и 0, d\ —
векторный элемент пути, штрих обозначает транспонирование.
Производя интегрнроваиие, получаем представление B6).
Следствие 2. Если Х„ — повторная независимая случайная
выборка, то
1п/ХA(хп; 9)= ?1п/х,(*Г. в),
U(xn; e)-gradeln/xn(xfI; в)«
= У grade In/Х/(ад в) - f U(v'; в)>
n
„ (в) = /?и(Х„; в) "-=
192

и неравенство B2) приобретает вид
Rsix) (в) > — А (в) /*,' (в) Л (в)'. B7)
я
Рассмотрим пример.
(III) Для повторной независимой выборки из распределения
N{\i, о2) положим 9i = |i, 62= о2. Тогда
п
Ых; 6)= [V^Ttr
Меры Рд имеют общий носитель — все пространство R", и вы-
выполняются требования диффереицируемости интегралов теоре-
теоремы 2. Находим
-^"М*,; в) = ^-(_1„/й—Lme.-JLfc-e,)')-
откуда для вектора U(xi, 6) и симметричной матрицы 11'(хь 0)Х
f/(i; в) получаем выражения
U (лу, в) = ((.v, - 6,) О^-1, (.vt -ОО^-вГ1),
u'(xV 0)u(.vi; в) J «ГЧ*|-*.)' W.-ej'-^-ejo^l
Таким образом
Г
|(в) = Л\и'(Х1, 9) U (Л,; в)«|
Г ОТ1 0
О 20F
где мы использовали следующие соотношения для стандартной
нормальной ел. в. У| — (Xi—6i)/в»-1'2 (см. п. 3 § 7): M>V=0,
МУ|4=3. Поскольку
= @lt 02), Л (в)
[о ij-
то неравенство B7) для любой несмещенной оценки S(x), удов-
удовлетворяющей требованиям теоремы 2, принимает вид
B8)
193

В частности,
D5,(X)>o2/n, D52(X)>2oVrt.
Наилучшие иесмещениые оцеики
я п
S, (хп.) - 7- — V xt. Si (х„) =-- -J—
1 = 1 №|
очевидно, удовлетворяют требованиям регулярности теоремы 2, а
их матрица ковариаций равна
rVn О I
О 2а4/(« — I)J
где мы использовали, что X и 2 = V (X, —XJ независимы,
i=i
aTlZ имеет распределение У.\-\, т. е. oT'Z распределена как
сумма п—1 квадратов независимых N@, 1) ел. в. Сравнивая
B8) и B9), мы видим, что по 02 иижияя граница ие достигается,
но при больших п разница пренебрежимо мала.
3. Границы дисперсии при нарушении условий регулярности
Как видно из неравенства Фреше—Рао—Крамера, в регуляр-
регулярном случае дисперсия несмещенных оценок в повторной выборке
имеет с ростом п порядок ие выше п~К Если дисперсия оцеики
Г(Х„) имеет порядок 1/л, то нз неравенства Чебышева вытекает,
что отклонение оцеики от ее математического ожидания имеет
порядок 1/)'я.
В то же время были примеры, в которых порядок убывания
дисперсии равнялся 1/л2. Так было для выборки из равиомерного
на @, 8) распределения и статистики Х(„), а также для распреде-
распределения с экспоненциальной плотностью а~' ехр ((*— ц)/°) и ста*
тистики X(i). В обоих случаях оценивается точка разрыва плотно-
плотности f{x; 9) распределения отдельного наблюдения, или, другими
словами, точка излома функции распределения. Можно показать,
что, вообще говоря, точка хв, в которой ф. p. F(x; в) ие имеет
производной, может быть оценена по результатам повторной вы-
выборки с точностью, превышающей 1/)'л; здесь мы ограничимся
примером.
(IV) Пусть одномерное распределение повторной выборки со-
сосредоточено на интервале @, а(9)), а ф. p. F(x; в) вблизи точки
х=а(В) ведет себя следующим образом:
1— F(a(Q) — б, 9)~с6°, 6->0, <х>0, с>0.
В таком случае пр» л->-оо
194

{—cta). C0)
Таким образом, отклонение Х1П) от а (9) имеет порядок rrUa, так
что при а<2 статистика х(п) является лучшей оценкой а(9), чем
это можно было бы ожидать в регулярном случае. ¦
Неравенство Фреше—Рао—Крамера можно модифицировать
так, что оно даст нижнюю границу для дисперсии оценок и при
нарушении условий регулярности. Запишем в случае скалярного
параметра 9 условие несмещенности оценки 5(х) в точках 9 и
9+А9:
JS(x)fx(x;9)dx = <p(9);
C1)
J5(x)/x (x; 9 + A9)dx = (p(9 + A9),
или
J(S(x)-q>(e))Mx; 6)dx=0;
C2)
I (S (x)- ф (9)) fx (x; G + Л6) dx= ф (в + Л6) -ф F),
где d\=dx\ dxn, а интегралы понимаются как я-мерные. Вы-
Вычитая выражения C2) одно из другого, получаем
|E(х)-ф(е))Ае/х(х; в)Л-Дф(в). C3)
где Д9/Х(х; 6)=/х(х; 6 + А9)-/х(х; в), АФ(9)=Ф(9 + А9)-
Допустим, что для данного Д9
{х: fx (х; 6 + Л6) > 0} С {х: fx (x; 6) > 0}. C4)
Тогда, ограничивая область интегрирования в C3) правым мно-
множеством C4), перепишем C3) в виде
ГE(х)-ФF)) YV*^? k(»; в)Л = А«р(в). C5)
Применяя к C5) неравенство Коши—Шварца—Буняковского,
получаем
f 1УХ(Х'У dx, C6)
где интеграл в C6) берется по носителю меры Рв. В случае по-
повторной выборки и при соблюдении условия C4) имеем
Де/Х(х; 6) Л Х/
195

и интеграл в правой части C6) можно записать в виде
Xi(xi; е+до)
: в) j
+L C7>
Учитывая независимость ел. в. Jf|,..., Хп, а также, что
получаем для C7) выражение
)
C8)
где также было использовано равенство, аналогичное C7), но
для я=1. Таким образом, для повторной независимой выборки
неравенство C6) приобретает вид
i^L)' )"-¦) ,39)
(V) Рассмотрим частный случай примера (IV), полагая, что
плотность одномерного распределения повторной выборки равна
f{x; 9)=a9-«(e — x)a~\ 0<x<0,
и равна нулю при остальных значениях х. Найдем асимптотику
при Д0-И) математического ожидания, входящего в правую часть
C9), полагая Д9 =—96, б>0, что обеспечивает выполнение одно-
одномерного варианта условия C4). Проводя элементарные преобра-
преобразования, получаем
г (Ае/(*;0))' dx Г (/(*; 8-86)-Hx; 0))' dx_
J / (*; 0) J / (х; 0)
о о
е ее
= Г Пх\ 0-06)' dx_2[f(x; 9-06)dx+(/(x; Q)dx. D0)
J }{x\ 0) J J
0 0 0
Два последних слагаемых в правой части D0) дают в сумме —1,
и выражение D0) приводится к виду
90-6)
— 1+ f (aF— 96)-aF— 66—х)в-|)Чх-16вF—;
о
196

-—1+ fa(l — б)-М1— х)«-*(\ + ЬхA— х)-1I-^. D1)
о
Мы покажем, что при 6-И) выражение D1) эквивалентно сба, где
с—некоторая постоянная. Имея в виду эту асимптотику, отбро-
отбросим .в интеграле D1) множитель (•—б) и, положив у=\—х,
запишем остающееся выражение в si: те
i «
1 — б)'-»— 1) dy = 6«a f {г + б)-«-' (A -=- zI"^— I) dz,
где сделана замена переменного 2=6./-' — б, что н доказывает
наше утверждение, причем
00
с = a j г-»-1 (A + гу~а — 1) dz.
Возьмем 6a= (bn)-1, где b — произвольная постоянная. Тогда из
C9) находим
-1)-'^ D2)
0аф' (GJ{Ьп)-2а ((с (Ьп)-1 + 1)"— 1 )~х —
»(ссЬ'1 — 1)->п-2". D3)
Значение Ь можно выбрать так, чтобы максимизировать множи-
множитель при л-2/а в D3). Если ба взять порядка n~{+t или п~'-*, е>0,
то легко обнаружить, что правая часть D2) будет иметь порядок
оA)п-2а, где оA)-»0, я-»-оо. Следовательно, граница D3) яв-
является наилучшей возможной (по порядку), которую может дать
неравенство C9). Заметим, что оценка параметра в с помощью
порядковой статистики х(П), предложенная в примере (IV), как
раз дает оптимальный порядок отклонения (см. C0)).

ГЛАВА IV
ПРАВДОПОДОБИЕ
§ 20. МЕТОД МАКСИМУМА ПРАВДОПОДОБИЯ
1. Функция правдоподобия.
Положим
L(х; в) = f(х; в) или PQ (х), х<=%, вев,
соответственно для непрерывной или дискретной статистической
модели (jC. Л. {Рв, в ев}). В § 15, 16, рассматривая 1(х, в)
при каждом фиксированном 6 как статистику, мы видели, что со-
совокупность статистик {L(x, 6), бев} порождает достаточное раз-
разбиение 30. Это означает, что любые два наблюдения хA) и х<2),
для которых
e)=Z,(x<*>; в), вев. A)
несут равнозначную информацию о неизвестном параметре 6.
Если какая-то сihtiici плоская процедура даег purt/wnuuc м^.ты
для хО, х'2', удовлетворяющих A), то следует признать, что при
этом используется информация, не имеющая отношения к задаче
различения распределений Pfl, 0e8. Хотя некоторые вопросы тео-
теории приобретают более естественную математическую форму, если
допустить и такие процедуры, тем ие менее основное теоретическое
и прикладное значение имеют процедуры, которые для любых х(|;
и х'2' с совпадающими функциями Z.(x'-''; в) и Z.(xB); 0), 0=в,
приводят к одним н тем же статистическим выводам. Функция
L(x; в). е«=в, A)'
у которой в рассматривается как основное переменное, ах — как
параметр, называется функцией правдоподобия. Значение функ-
функции L(\; 0) при данном наблюдении х называется правдоподо-
правдоподобием 0 (или меры Ре) при этом х. Значительное практическое и
теоретическое удобство достигается переходом к логарифмам.
Функцию
/(х; в)=1п/.(х, в), е<=в,
называют логарифмической функцией правдоподобия. В схеме по-
повторной независимой выборки
198

/(x; 0)- J] l(Xi; в), l(x,; в) -Ип/(х,; в), i= 1 n. B)
i=i
Итак, функция правдоподобия L(x; в), вев, содержит всю ин-
информацию о неизвестном параметре 6, заключенную в выборке х.
Но, как мы знаем, возможно дальнейшее сокращение данных,
если перейти к минимальному достаточному разбиению, при кото-
котором в один класс помещаются выборки х<", х<2), для которых от-
отношение
L(xC); 6)/L(x<2>; e)=Jfe(x<»; x<2>)
не зависит от бев (см. подробнее п. 6 § 15, п. 3 § 16). Принцип,
требующий от статистической процедуры одинакового заключения
для выборок с пропорциональными функциями правдоподобия,
называется принципом правдоподобия. Как видно, он совпадает с
принципом достаточности, в соответствии с которым по выбор-
выборкам х<!» и хB) с одним и тем же значением минимальной доста-
достаточной статистики должны производиться идентичные статистиче-
статистические выводы. Подробное обсуждение различных принципов ста-
статистического вывода и их интерпретация содержатся в книге
Кокса и Хинкли [14].
2. Оцеики максимального правдоподобия.
Задг.-.а точечного оценивания, решаемая с позиций принципа
достаточности, приводит к оценкам, являющимся функциями ми-
минимальное достаточной статистики. При этом, однако, остается
открытым вопрос, какую именно из функций достаточной стати-
статистики следует выбрать для оценивания заданной параметрической
функции <р<6). Подход, основанный на выборе несмещенной оиеи-
ки с минимальной дисперсией, был подробно рассмотрен в § 17.
Этот подход эффективен, однако, лишь когда имеется полная до-
достаточная статистика небольшой размерности, что практически
сводится к моделям экспоненциального типа. Требование несме-
несмещенности также ограничивает возможности применения метода;
к тому же, ничто не препятствует существованию оценки 5(Х) с
небольшим смещением и среднеквадратическим отклонением
меньшим, чем дисперсия наилучшей несмещенной оценки. Реали-
Реализацией принципа правдоподобия в задаче точечного оценивания
можно считать оценивание по методу максимального правдопо-
правдоподобия: оценка 6(х), максимизирующая функцию правдоподобия
L(x; 6(x))>L(x; в), вев,
или, что то же, логарифмическую функцию правдоподобия, назы-
называется оценкой максимального правдоподобия (о. м.п.) парамет-
параметра в. Если статистическая модель дискретна, то в(х) есть такое
199

значение параметра 9, при котором вероятность Рв (х) наблю-
наблюденной выборки х наибольшая; в непрерывной модели плотность
/(х, 0) наблюденного значения выборки х становится максималь-
максимальной при значении 0 = 6(х).
Допустим, что ф@) = (ф| (в),.. .,<Fi(8)) есть некоторая век-
векторная параметрическая функция. Что следует понимать под
оценкой максимального правдоподобия функции <рF)? Не огра-
ограничивая общности, будем предполагать, что- система <piF),...
...,rf,(fl) функционально независима и ее можно дополнить до
взаимно-однозначного преобразования всего параметрического
пространства. Пусть, для краткости, l—k и отображение <р = ф@)
уже взаимно-однозначно. Функция правдоподобия ?(х; <р) в но-
новой параметризации и L(x; 0) связаны формулой
Г(х;<р(в))=Мх;е).
Максимизация по <р функции ?(х; <р), очевидно, эквивалентна
максимизации L(x; 0) по 0, и точки максимума связаны соотно-
соотношением
Ф=Ф@(х)). C)
Естественно определить о. м. п. любой параметрической функции
фF) как результат подстановки 0=0(х„) в оцениваемую пара-
параметрическую функцию. Отметим, что в задаче наилучшего несме-
несмещенного оценивания оценка для ф(8) ищется независимо для
каждой <}(ti). В
Отметим, что если Т(х)—достаточная статистика, то по тео-
теореме факторизации
/.(х;0)=А(х)?(Т(х);в),
я задача построения о. м. п. сводится к поиску максимума по 0
функции ?(Т(х); 6). Если точка максимума по в функции "(t; 0)
единственная, то о. м.п. 0(х) определяемся однозначно и является
фуи;,шей достаточном статистики Т(х). В^ частности, при соблю-
rciu.ii указанного условия получаем, что 8(х) является функцией
минимальной достаточной статистики. В
В случае, когда функция правдоподобия дифференцируема,
Kftv.o:iueHiie о. м. п. сводится к решению системы
о/(х- Щ',дп •• = •:), /=J,...,*, 0=(Oi, .... 0А),
насыпаемой системой уравнений правдоподобия. Точка максимума
функции /(х, 6) находится среди решений этой системы (а также
значении функции правдоподобия на границе области 6). В
Многие и:-, оценок, с которыми мы до сих пор встречались, яв-
являются оценками максимума правдоподобия. Рассмотрим некото-
некоторые ;:pi;:iepu.
A) Для испытаний Бернулли с вероятностью положительного
исхода 0 получаем
200

L(xn, B) =
l(xn; n
Для нахождения максимума приравняем нулю производную по О
логарифмической функции правдоподобия:
о=di (х„; в)/ае=s (хп) е-1- (п -s.(x,;)> (i -в)-* =
Производная д/(х„; 0)/д0 меняет знак с минуса на плюс при пере-
л
ходе через точку 6(х„)= — S(xn)~—\]х( = х, и потому х яв-
ляется о. м. п.
(II) Для повторной выборки из нормального распределения
N(\i, а2), полагая Gi = и» 02 = о2. получаем
/(хл; в)=-г
дЦх„;
dl (xn; Q)/d% = -n/262 + (J te-xJ + n (x- QJ*) / Bв|).
i-l
Приравнивая производные к нулю, находим
Так как (исключая случай х,
}i <в-в
= х, t= 1, ..., п)
дв?
&Ч (*п, в)
е=е
(-1
о,
(хп; е)
в-в
е;
в=в
8 М. В. Козлов, А. В. Прохоров
201

то дискриминант
{дЧ1дЬ\){дЩдЬ\) — тцд^дЬ^) > О
и, следовательно, в точке 8i, 82 функция правдоподобия достигает
максимального значения.
(III) Для повторной выборки из равномерного распределения
на @, в)
— {
I
0 в противном случае.
Функция L(xn; 0) равна нулю при 8е@; x(n)], делает б точке
8=.?(л) скачок величины xw~n, а затем монотонно убывает. Фор-
Формально о. м. п. не существует, однако если переопределить плот-
плотность распределения в исходной модели, положив f(x; 0)=B~' при
0<х^6, то фактически, не изменив модели, получим о. м. п.
6(хп) =*•(„,.
(IV) Для повторной выборки из экспоненциального распреде-
распределения с плотностью
е7'ехр(—(х—е,)ег'), x^qv — «><ei< + oo. ea>o,
получаем
/(х„; в,, Q2)=-n\nQ,-fi
Очевидно, при любом 8г максимум /(х„; 0,, 02) по 0| достигается
при
0t — min .v, —X(i).
Isgisgn
Далее, из уравнения
о=--а/(хп; о„ е2)/ао2- -n/e2-i- у (х(-ьл)Ь72
находим
Напомним, что полной достаточной статистикой в рассматриваемой
л
модели является (x(i)( y1^— x{i))) (см. пример (III) § 17), и
потому несмещенные оценки (см. п. 3 § 6)
02 — г Oj
п — 1
нм^еют минимальную дисперсию. Как видно, отличие между
@ь 02) и @|*, 02*) незначительно при больших п. ¦
202

Рассмотрим повторную выборку из семейства экспоненциаль-
экспоненциального типа с плотностью
/ (х; в) = Л (х) ехр (? в,Т, (х) + 6 (в)), в = @, Qh).
.•=1
Логарифмическая функция правдоподобия выборки равна
I (х„: 0) = ? In А (л-,) + ? 0, ? Г, (л,) 4 пЬ @).
Дифференцируя по 0„ t = l, .... k, приходим к системе уравнении
0 « d/ (хЛ; в)/дв, = ? Г, (х,) + пдЬ (в)/дв,, * = 1 ft. D)
/-i
Условием однозначной разрешимости системы D) является невы-
невырожденность матрицы
в) , .
Чтобы решение системы D) было точкой максимума функции
правдоподобия, достаточно, как известно, положительной опреде-
определенности матрицы
\-дЧ{хп; в)/<ЭО,<ЭО/, I, /«1, .... ft]. F)
При условиях регулярности, которые здесь выполнены, имеют
место соотношения (ср. D6) — D8) § 18)
м дЧ (Х„; 6) м dl (Х„; 6) dl (Х„; 6) . ,, .
~Ме *>&, =Мв—& 55;—• '•/-1 •
Так как матрица F) не зависит от хл (см. E)), то отсюда следу-
следует, что F) есть матрица Фишера /х„(8) и потому неотрицатель-
неотрицательно определена. Итак, при условии невырожденности матрицы
[d2b(Q)/dQidQj, i, j=\, ..., k] о. м. п. находится как единственное
решение системы D). Отметим, что поскольку статистика
S (х„) - (S, (х„) Sk (x,J), St (хл) = — ? Г, (х/), G)
п
является достаточной, то статистика 6(хл), эквивалентная S(xn),
является достаточной.
Напомним, что неравенство Фреше—Рао—Крамера обращаег-
ся в равенство для оценки G). При этом из соотношения
,,; G)-=0
203

и из D) вытекает (см. также следствие 1 теоремы 2 § 19)
С другой стороны, подставляя в D) 6=6(х„), находим
так что
0,, ы i k.
Таким образом, о. м. п. gradefe(G) параметрической функции
gradgfeF) является несмещенной, а ее ковариационная матрица
принимает минимально возможное значение:
(nix (в)) = [-п&ЫдЬт,, I, j = 1, ... , п]~К
Из теоремы 2 § 19 (см. следствие) и проведенных выше рас-
рассуждений вытекает следующее утверждение: если соблюдаются
условия регулярности и существует несмещенная оценка, обраща-
обращающая неравенство Фреше—Рао—Крамера в равенство, то эта
оценка является о. м. п.
(V) Пусть (Xi, Yi), /=1, .... п — повторная выборка из дву-
двумерного нормального распределения ЛЦО, Q) (см. пример п. 1
§12):
/ о> а'р \
V а2р а2 /"
Вводя параметризацию
<р_ ! <р =, Е (8)
Y1 2a»(»-P2) о»A—р»)
приведем плотность распределения отдельного наблюдения к виду
f(x, 1/) = Bя)-1ехр(ф|7|(х, y)+<fiTi{x, у)+Ь{цц, <р2)),
где
Г,(*. У)=хг+у\ Та(х, у) = ху, 6(ф„ ф8) = 1/21пDф?—Ф|).
Запишем систему уравнений D):
L Vr Iy\ дЬ(<Рь ф!() — 4ф1
п
(9)
п
дЬ (ф|, ф2) фд
204

Разрешая систему (8), находим
Р—Фа/2ф|, а2 = -2ф,Dф,2-ср:2). A0)
Из (9) и A0) получаем о. м.п.:
В гл. V будет показано, что оценки максимума правдоподобия
обладают рядом оптимальных свойств для выборок большого
объема (п-*-оо). В случае умеренных и небольших п свойства
о. м. п. изучались лишь для частных моделей. Затруднение заклю-
заключается в том, что о. м. п. в общем случае не выписываются в яв-
явном виде и для их нахождения приходится применять численные
методы.
(VI) Рассмотрим цензурированную выборку нз распределения
(ц, а2), полагая, что наблюдению доступны порядковые статис-
статистики Х(ц, ..., *(л), N=n—г, г>0. Логарифмическая функция прав-
правдоподобия при X(i)^.. .^х,л') имеет вид (см. пример (VI) § !б)
/(х; ц, о) = с +г 1пA — Ф((хт— ц)/а))— Nina—
Здесь Ф(х) — ф.р. нормального закона N@, 1), ф(х)=Ф'(дс).
Положим
N N
и выпишем систему уравнений правдоподобия
а»
(П)
да
Введем функцию
ВМвЛЙ.»гЛ
и перепишем систему A1) в виде
A2)
A3)
205

Подставляя уравнение A2) в A3), получим
502+а2Я(|J = о2A + |Я(|)). A4)
С другой стороны, воспользовавшись уравнением A2), имеем
a|=X(,V)—ц=Х(Л'>—х+ (х—ц) =X(.V)—x+afl(s),
откуда
o=(x(.V)-x)/(s-B(|)). A5)
Подставляя A5) в A4), получим уравнение для нахождения |:
Уравнение A6) решается численно. Подставляя его решение f
в A5), найдем а, а подставляя | и а в A2), найдем ц. Получим
для ц, а более удобные для применения формулы. Переставляя
члены выражения A4), используя A5) и полагая
4E)=fl(S)/(flF)-&). A7)
получаем
Подставляя A5) в A2), находим
Таким образом, о. м. п. представляются формулами
И =*+Х(?)(*<">—х), a2-s02+A.(f)(x(A)-fJ, A8)
где 5 определяется из уравнения A6).
Чтобы иметь практическую возможность пользоваться оценка»
ми A8), достаточно рассчитать для разных h = r/n таблицу реше-
решений уравнения A6):
(!-fl(Л. lJ-lB(h, t))l(l-B(h, 6))-v A9)
для значений у, взятых с некоторым шагом. Подставляя решение
g = s(Л, у) в формулу A7), получим таблицу значений Я,=л(Л, у).
Такая таблица, рассчитанная Коэном, приведена в [9, с. 147—
148].
Проиллюстрируем изложенную методику на примере (I) § 11,
где л=10; г=3; N = 7; й = 0,3; х= 1,70471; so2 = O,OO3514;
*(л-)= 1,778. Тогда v=so2/(*w—хJ = 0,654. Из таблицы, приведен-
приведенной в [9, с. 148], интерполяцией по у находим Л,=0,512. Подстав-
Подставляя в A8), получаем
(Г= 1,742; а=0,079.
Всестороннее обсуждение этого примера содержится на с. 150—
151 книги [9].
206

3. Метод Монте-Карло в модели сдвига-масштаба.
Рассмотрим статистическую модель, задаваемую п-мерной
плотностью вида
f{x; щ о)-о-"/.(о-'(х-й-1)), 1 = A 1), B0)
где f(x)—f(x; 0, 1) — некоторая известная плотность, ц, о —
неизвестные параметры. Модель B0) охватывает важный для
приложений случай цензурироваииой выборки, когда наблюдению
доступны порядковые статистики
У
и плотность наблюдений равна (ср. пример (VI) § 16)
My; и. °Н
= -^т F M
где F(t/) — ф. р. плотности f(t/). Это так называемый II тип цен-
цензурирования; модель B0) включает и I тип цензурирования, когда
наблюдаются значения а-A), попавшие в заранее известный интер-
интервал (t,s) (см. [9, §6.3]).
Покажем, как, используя искусственное моделирование выбор-
выборки с плотностью /(х), можно строить доверительные оценки для
параметров ц и а. Мы будем исходить из о. м. п. ц(х), а(х), хотя
метод применим к любым оценкам \х, о, для которых распределе-
распределение ел. в.
)-ц), ег-'о(Х), B1)
где X имеет плотность распределения B0), ие зависит от пара-
параметров ц н а. Покажем, что совместное распределение ел. в. B1)
не зависит от параметров ц, а, когда ц(х), а(х) — о. м. п. Фикси-
Фиксируем значения цО| оо параметров ц, а, и пусть Х(С> — случайная
выборка с плотностью /(х; ц0, оо), Y = o<r' (X(°>—цо\) — стандарт-
стандартный случайный вектор с плотностью /(у; 0, 1)=/(У). Очевидно,
и, а) =
L(aoY+no 1; й. a)=a-"/(a-'(оо?+ц0 1-ц 1)) =
= а0-я(о/а0)-лД (а/ао)-1 (Y—(ц—й0)/о01)) -
(и_Мо)/0о, а/а0). B2)
Пусть й(Х@>) и а(Х@)) — о. м. п. Как видно из B2), точку макси-
максимума ц(Х<0>), а(Х<°>) левой части выражения B2) можно связать
207

с точкой максимума функции L(Y; ц', а'), которая равна ц,'=»
=?(Y), d' = a(Y). Именно
ao-|(M(X<°)-Mo))=M(Y), ao-'a(XC))=a(Y). B3)
Итак, совместное распределение ел.в. B1) совпадает с распреде-
распределением ел. в. n(Y),"a(Y), что и требовалось установить.
Для приближенного численного расчета совместного распреде-
распределения вероятностей
Н(и, о)=^(й(?)<ы, o(Y)<o)
с помощью метода статистических испытаний необходимо иметь,
во-первых, алгоритм вычисления функций ц(х), о(х):
?(х; ц(х), о(х))=тах/.(х; ц, а)
й.о
и, во-вторых, устройство, моделирующее последовательность неза-
независимых испытаний:
Y<'\ Y» Y<*>, B4)
с плотностью /Y(i)(y)=/(y; 0, 1), 1=1, ...,N. По B4) строим
последовательность N независимых испытаний пар ел. в.:
(M(Y»),a(YO)),i-l N, B5)
с ф. p. H(u, v), откуда рассчитываем э. ф. p. HN(u, v) и полагаем
Н(и, v)^HK(u, v).
В результате получаем, используя B3):
Рц.а(х:<г^а(х) <«) = Я1(к)вЯA(, + во),
Р^.„ (х: а (х)-1 (ц (х) -ц) < г) = Р^.„(х: (ц (х) - и) а-^ (х)-1 а < v) =»
где
G (и) = JJ Л (х, у) dx dy; Л (х, у) =d*// (x,
1
Таким образом, a-доверительные интервалы для а и ц имеют вид
a (x)/(x,_«/2 (//J)-1 < a < a (x)/(xa/2 (Я^)-1, B6)
ц (х)-a (x) x,_a/2 (G)< и < ц (х) - 9 (х) xa/2 (G), B7)
где xa(//|) и xa(G) обозначают a-квантили соответствующих рас-
распределений.
Отметим, что знание совместного распределения оценок ц, a
позволяет вычислять доверительные интервалы для любой пара-
параметрической функции ф(ц, а). В частности, предположим, что
208

речь идет о повторной (цензурнрованной) выборке с одномерной
ф. p. F(a~l{x— ц)), где F(x) — известная ф. р. Покажем, как
строится доверительный интервал для
где t — любое фиксированное. Ввиду монотонности функции F
достаточно построить а-довернтельную границу для <р/(ц, <•)=*
= crl(t— ц), так как
Для краткости рассмотрим только верхнюю а-доверптельную гра-
границу. Имеем, используя B3):
д'° v ' о а(х) а а(х) )
= Ро,| (х: о-1 (/— ц) а (х)-1 -ц (х)Ъ (х)-1 < s). B8)
Положим
Ро,, (х : то (х)-1 - ц (х) а (х)-1 < s) - Qx (s). B9)
По результатам моделирования B5) стронм э. ф. p. Q,..v(s), так
что Qx(s)^Q,,y(s).
С помощью ф. p. Qx(s) находятся доверительные границы для
<pf(|.i, a)=a~l{t—ц) при любом /. Отступая от принятых обозна-
обозначений, a-квантиль распределения Q» обозначим через х«(т):
Ро.| (х : та (х)-1— ? (х) Ъ (х) < х,_„(т)) - 1 — а. C0)
Из B9) вытекает, что функция Qt(s) убывает по т и, следователь-
следовательно, функция y = Xi-a(x) возрастает по т. Предположим для !<рат-
кости, что Qx(s) непрерывна и строго монотонна по т, так что
функция y=Xi-a(i) имеет обратную т=х~-а(у)- Из соотношений
B8) и C0) получаем
1 -а = Рд.. (х: а (х)-1 (Г-ц(х)) < л,_а (а (/-ц)))--=
= Р»,о(х: xT-la (а (х)-1 (t— ц (х))) < a-1 (t -и)).
Таким образом, a-доверительная нижняя граница для а~'(/—ц)
равна
а для ^(ог-1^—ц)) она равна
209

Проиллюстрируем эту методику на примере повторной выборки
из распределения Вейбулла с ф. р.:
Преобразованием У, = 1пЯ, выборка Хх Х„ из распределения
f».i(x) переводится в выборку Yu .... У„ из распределения
Р(а~1(у—\х)), ц —In Э, о=у~\ F(y) = l—exp(—expy)
(см. п. 1 § 4). Томан, Бэйн, Антл*' рассчитали таблицы для по-
построения доверительных интервалов для различных п и несколь-
нескольких вариантов цензурирования. Воспользуемся их примером для
числовых данных по испытанию
* до разрушения шарнкоподшип-
^ ников. Ниже приводятся резуль-
о- щу/^ - таты *<,•) испытаний в миллионах
-i\- jr \ оборотов л=23 шарикоподшип-
шарикоподшипников (взятых ими из работы
Либлейна, Целена):
-2
t,5
Рнс. 12.Точки (ya\.F~l((i—0,$)!23)),
F(y\ =1—ехр(—ехру) и прилегающая
к ним прямая; ущ — логарифм чис-
числа оборотов (в миллионах) до раз-
разрушения выборки из 23 шарикопод-
шарикоподшипников
17,88
48,48
68,64
105,12
41,52
54,12
84,12
128,04
28,92
51,84
68,64
105,84
42,12
55,56
93,12
173,40
33,00
51,96
68,88
127,92
45,00
67.80
98,64
На рис. 12 нанесены точки (*/<,,, F~l ((i—0,5)/23)), j/(,,=ln*<,•,,
i=l, .... 23, F(y) = l—exp(—ехр у) и проведена на глаз прямая
где ^=4,38; а = 0,43.
Согласие точек (у^, F~l(i—0,5)/23) с линейной зависимостью
можно считать удовлетворительным. Соответствующие оценки р
и у равны:
р=ехр(ц)=79,8; f=ir-*=2,3.
Систему уравнений правдоподобия после некоторых преобразо-
преобразований можно записать в виде
п/у—п У хУ\пх(/У х? +
л л
1/V
1=1
•) Technometrics, 1969, т. 11, с. 445—560; 1970, т. 12, с. 363—371. Авторы
ие использовал» оппс.'штто нз\!и nfiuiero подхода, а опирались на частные
свойства распределения Вейбулла.
210

Численное решение приводит к значениям
Y = 2,102; (f=81,99.
Выпишем несколько значений квантилей ха распределения ел. в.
v/v= @/0)""', рассчитанных Томаном и др. методом Монте-Карло»
>v a
П >ч
22
24
0
0
0
,02
.752
.759
0
0
0
.05
.798
,805
0
0
0
,10
.843
,848
0,
1,
1.
90
320
301
0.
1,
1,
95
418
392
0
1
1
,96
,583
,504
Линейной интерполяцией по п находим а-доверительные гра-
границы для y при а = 0,1:
1.50 = Y/Xi-e/2 < Y < ?/** 2 - 2.62.
Выпишем несколько значений квантилей ха распределения ел.в.
рассчитанных Томаном и
а
22
24
0.02
-0.509
—0,483
0,05
—0,404
—0.384
др.:
0
—0
—0
.10
,314
,299
0
0
0
.90
,302
,288
0
0
0
.95
,398
,379
0
0
0
,98
,519
,494
Линейной интерполяцией по п находим а-доверительные границы
для р при а=0,1:
68,04 =¦- р ехр (— *i_a/2/Y) < р < р ехр (—*а. 2/y) = 98,76.
§ 21. КРИТЕРИИ ОТНОШЕНИЯ ПРАВДОПОДОБИЙ
I. Проверка статистических гипотез.
В гл. I, II нам неоднократно встречалась форма статистическо-
статистического вывода, называемая проверкой гипотез. Напомним некоторые
примеры. При сравнении средних двух независимых нормальных
выборок из Л'(ць а2) и Л'((!2, о2) рассматривалась гипотеза Но:
И1 = Иг- В линейной статистической модели по выборке из
'Vn(rj, a2/), где вектор tj принадлежит некоторому линейному под-
подпространству '/, проверялась гипотеза //0:iieV", где V — неко-
некоторое заданное линейное подпространство V. Наконец, когда име-
имеется a-довернтельнын интервал для некоторой параметрической
функции ф = ф@) статистической модели (X, Si, {Pe, в ев}),
211

возникает возможность проверить гипотезу #о:ф = фо, где фо —
любое фиксированное значение параметрической функции. Во всех
этих примерах имеется статистика 7(х), называемая статистикой
критерия, такая, что область отвержения гипотезы принимает вид
иле
«7а = {х : 7(х)<с'а, либо Г(х) >с"а}.
Сама гипотеза Яо могла быть представлена в форме
Я0:Ре{Р}0={Р}, A)
где {Р} — семейство распределений вероятностей рассматриваемой
статистической модели, а {Р}о — некоторое его подмножество. Во
всех встречавшихся нам задачах оказывалось, что вероятность
=a, Pe{P}o, B)
не зависит от Р при условии справедливости гипотезы Яо, т. е. для
всех Ре{Р}0. Вообще говоря, для проверки, одной и той же гипо-
гипотезы Я(, можно использовать различные статистики критерия.
В приложениях бывает иногда ясно, какие возможные отклонения
от гипотезы Яо необходимо проверить и, следовательно, на какой
статистике критерия остановить свой выбор. Но даже и в этом
случае весьма интересно оценить свойства выбранного критерия
по сравнению с другими.
В общем случае нет необходимости непременно связывать
понятие критерия со статистикой. Статистическим критерием для
проверки гипотезы A) назовем любую систему подмножеств
{Н7а} множества ЗС, индексированную числами а из интервала
(О, 1). Если при этом выполнено соотношение B), то а называ-
называется размером критической области Wa. Потребуем дополнитель-
дополнительно, чтобы
Будем говорить, что данный критерий отвергает гипотезу Яо на
уровне значимости а, если результат наблюдений х принадлежит
критической области Wa. Степень согласия данных с гипотезой
удобно характеризовать значением
a(x)=inf{a:xe=We},
так что х отвергается на уровне значимости а(х)+е и принима-
принимается на уровне а(х)—е, каково бы ни было 0<е<а(х). Чаще,
однако, используют набор стандартных значений а: 0,1; 0,05; 0,01
и др., и степень согласия наблюдения х с гипотезой Яо -характери-
-характеризуют наименьшим а из этого набора, для которого xsfa. Для
одного и того же наблюдения х при одних уровнях значимости
критерий отвергает гипотезу Яо, а при других — принимает. По-
Поэтому следует подчеркнуть, что теория проверки гипотез не рас-
рассчитана на такое ее применение, когда по результатам наблюде-
212

ний гипотеза Но будет на самом деле принята или отвергнута.
Применение статистического критерия к результатам наблюдений
есть форма извлечения из выборки полезной информации, даль-
дальнейшее использование которой зависит от наблюдателя.
Если сравниваются два критерия {Wa} и {Wa'}, то естественно
сопоставить критические области одного и того же размера. При-
Применение любой из критических областей U7, и Waf в предположе-
предположении, что для каждой из них имеет место B), приводит к одной
и той же вероятности так называемо!"; ошибки первого рода —
отвергнуть гипотезу Но, если на самом деле она верна. Говорят,
что совершена ошибка второго рода, если гипотеза Но принята,
когда она неверна. Чтобы уточнить математическую постановку
вопроса, введем непересекающееся с {Р}о семейство распределений
{P}i={P} и назовем гипотезу Ht : Pe={P}i альтернативной к гипоте-
гипотезе На из A) (гипотезу Но назовем нулевой). Будем оценивать ка-
качество критерия {We} по проверке гипотезы Но против альтернати-
альтернативы Я) набором вероятностей
Р = Р(^а), Ре{Р},. C)
При фиксированном а вероятность р рассматривают как функцию
от Р и называют функцией мощности критерия. Значение 1—{J
при любом фиксированном Р, равно вероятности ошибки следу-
щего вида: гипотеза Но принята, хотя она неверна, а выборка на
самом деле извлечена из распределения Pi. Если
Р(^'а)<Р(^«), Ре{Р}. D)
и хотя бы при одном Р неравенство D) является строгим, то кри-
критическую область Wa размера а следует предпочесть области того
же размера W'a, поскольку критическая область Wu обеспечивает
меньшую вероятность ошибки второго рода. Неравенство D) за-
задает отношение (частичного) порядка в множестве критериев, и
тем самым можно поставить вопрос о существовании оптималь-
оптимального критерия, мощность которого превосходит мощности всех
других критериев.
Поскольку функция мощности C) зависит еще от параметра а,
то сравнение критериев D) было бы целесообразно проводить при
всех а. В теории это, однако, привело бы к излишним усложне-
усложнениям, и потому принято изучать и сравнивать критические облас-
области, а не критерии, тем более что в приложениях критерии зада-
задаются обычно статистиками и наличие неравенства D) при каком-
либо одном а влечет, как правило, такое же неравенство и при
других уровнях значимости.
В связи со сказанным в теории принято критическую область
размера а называть также критерием размера а или даже просто
критерием. Индикаторную функцию области Wa:
ф(х) = 1, если xsf., н ф(х)=0, если хШ Wa, E)
называют критической функцией критерия Wa- Из контекста всег-
213

да будет ясно, идет ли речь о критерии как системе вложенных
критических областей либо как об одной такой области.
Параметрические модели, как и в задаче оценивания, играют
первостепенную роль в теории проверки статистических гипотез.
Пусть
тогда гипотезы о распределениях становятся гипотезами о пара-
параметрах
н0: е<=е0, Hi: е«=е,,
а функция мощности р (Э) •= Рц (№„) рассматривается как функ-
функция переменного 6. Рассмотрим примеры.
(I) Для повторной выборки из экспоненциального распределе-
распределения с плотностью /(дс)=ехр(—(лс—G)), лс>6, а-доверительный ин-
интервал для параметра 6 из п. 4 § 3 имеет вид
Критерий Wa размера а для проверки гипотезы #о:8 = 6<> против
альтернативы Hi : 0=?M}o выбираем в виде
Wa = {Xn : 80>*<1), либо Q0<xw+n-1 In (I—a)}.
Отметим, что включение в Wa точек хп, для которых дс<о<6о, не
влияет на размер критерия, так как подмножество {х„: *'<o^8o}
имеет Рво-меру нуль. Функция мощности критерия Wa:
р (в) = Рв (х„: дгA) < в0, либо *<i) > 0o— n-1 In A —а)) =
= 0^ 9 (A(ij-^ uoj + o7 g (ЛA) ^ о0—п шA—а))
принимает значения
1_ае"<е-0о) При 6—в0 < О,
рF)= A_а)е"(в-в.) при 0<в—во<—п-1 1пA—а), F)
1 при в— 60>— л-1 1пA— а).
Функция мощности Р@) принимает минимальное значение в точке
6о:рFо) = 1—а и монотонно стремится к 1, если 6-»-±оо. Если
п-»-оо, то при любом 8=7^00 РF) =spi">(O)-^l.
Рассмотрим другую альтернативу H+t : 0>0о В этом случае
представляется естественным взять критерий исходя из нижней
доверительной границы для 0:
Wha = {Xn : Оо<*и)-Ь/г-' InA—а)}.
Легко видеть, что функция мощности этого критерия дается пос-
последними двумя строками в F), и, следовательно, мощность одно-
одностороннего критерия W*a в области 0>Оо такая же, как и двусто-
двустороннего Wa.
214

(II) Для повторной выборки из нормального распределения
, 1) при проверке гипотезы Я0:ц = ц0 против альтернативы
Н+х : ц.>ц0 будем исходить из нижней доверительной границы
для и (см. п. 1 § 8):
W+a = {xn: цо<*—Xi-jyn},
где ха — а-квантиль распределения N@, 1). Мощность критерия
W+e равна
р+ (И) = Р+ (ц; а) =
п
= ^*о ( лГ- / , Х( >к л(ц0—ц)
v у п *шл
7
\
i.
0
\
'(M
\
¦
1
am) //
;N—
'/
/
M
Рис. 13. Функции мощности односто-
одностороннего и двустороннего критериев
отношения правдоподобий выборки
из нормального распределения
и представляет собой по ц ф. р. закона Л^(цо+*!-а/Уп, л-')
(рис. 13). Отметим, что р+(м)<а при (.1<ц0 и стремится к 0 при
|i-*~оо, так что критерий W+a не годится против альтернативы
Я 1 :ц<ц0. Критическая область для проверки гипотезы Яо про-
против альтернативы Н~х строится по верхней а-доверительной грани-
границе для |д:
Функция мощности критерия W~a получается из р+(ц) симметрич-
симметричным отражением относительно точки ц0 (см. рис. 13):
р-(ц) =Р"(м; а) =Ф (yni-yi+iio-xl-afyn)).
Против двусторонней альтернативы Я, : ц=^ц0 критерий и функция
мощности, основанные на симметричном а-доверительном интер-
интервале имеют вид
вале, имеют вид
р (ц) = р (ц; а)=
а/2).
215

Нетрудно проверить, что
Р(ц; а)<р+(^; а) при ц>Мо,
Р(ц; а)<р~(^; а) при ц<цо,
так что двусторонний критерий \V% менее мощен, чем W?a или
W~a, если его применять против соответствующих односторонних
альтернатив (см. рис. 13). Зато критерии W+a, W~a, имея боль-
большую мощность при односторонних альтернативах, дают неудовлет-
неудовлетворительное решение против альтернативы Нх : цф\ю. Щ
Отметим, что в обоих примерах критические функции рассмат-
рассматриваемых критериев являются функциями минимальной достаточ-
достаточной статистики Т(х). В результате задача фактически сводится
к проверке гипотезы о параметре распределения статистики Т(х)
по результату единичного испытания. Например, критерии №, из
(II) можно преобразовать в критерий
^а = [t-1 < Ио-xjVn, либо t >и,, + xi-jyn)
для проверки гипотезы Я0:ц = Ио по результатам наблюдений t
в модели (/?', 36, N(\jl, п~1)) против альтернативы Ht : цфцо.
2. Лемма Неймана—Пирсона.
Рассмотрим статистическую модель вида C0', &, {Ро, PJ), где
семейство вероятностных мер состоит всего из двух элементов.
Допустим, что
Яо:Р = Ро, Я,:Р = Р1, (8)
т. е. при каждой из гипотез Но и Н\ распределение выборки пол-
полностью определено. Такие гипотезы называются простыми (в ра-
разобранных выше примерах (I), (II) нулевая гипотеза была прос-
простой, а альтернативная — не простой). Оказывается, что критерий
максимальной мощности в случае (8) всегда существует. Посколь-
Поскольку функция мощности любого критерия Wa в постановке (8) сво-
сводится к двум вероятностям:
то задача поиска оптимальной критической области ставится сле-
следующим образом: среди всех подмножеств №„?#, для которых
выполнено равенство
.'9)
найти подмножество W*a, такое, что при всех Wa^&
A0)
Поясним, как строится это множество, а затем проведем фор-
формальное доказательство. Рассмотрим вначале следующую простую
ситуацию: #? = {*], х2 Xn), Ро(*<)=ЛМ, * = 1, ..., N- Заметим
216

прежде всего, что условие (9) выполнимо лишь прн a = a*=
k=l, 2, .... N—1. Равенство
выполняется для любого подмножества Wak, состоящего ровно
из к точек. Так как
то ясно, что, упорядочив вероятности
и положив
Wak={iXfi ik). A1)
мы придем к свойству A0).
Рассмотрим другой частный случай: множество SB то же самое,
но предположим, что Ро(*<)=тЛ где б>0, т, — некоторые целые
числа, т. е. набор вероятностей Po(*i), * = 1. •••• N, состоит нз со-
соизмеримых чисел. Трансформируем эту модель, заменив каждый
элемент х^8В на т, элементов *(A), .... Xi(mi) и положив
= 1 mi. i~l Н), Ро(*,(/))-= б,
-Pi (*)/«/. /=1 mi. i = l. --.'V.
Ясно, что исходная статистическая модель получается из транс-
трансформированной объединением групп элементов и сложением соот-
соответствующих вероятностей. Оптимальное множество в новой моде-
модели получается аналогично A1) упорядочиванием пар (/, /). мри
котором
Pi (
Поскольку вероятности Ti (*<(/)) равны между собой прн всех j
и любом фиксиросанном i, то упорядочивание A2) можно провес-
провести с соблюдением следующего свойства: вероятности Pi(*,•(/)),.
/=1, 2 nil, расположены в A2) подряд. В таком случае вся-
всякое подмножество №в?Й?, включающее все пары **(/) из ряда
A2) вплоть до пары вида *,(т,) прн некотором /, с одной сторо-
стороны, является оптимальным в новой модели, а с другой стороны,
после объединения групп элементов, переводится в множество
№*?#?, являющееся оптимальным в исходной модели. Запишем
отрезок из ряда A2):
... A3)
217
Так как
Po(*.)=Po(*.(l))m,=6m(,

го
Pl {х. A)) =_Pii?iL ^IiM. a =_PiIM. a.
и, следовательно, с учетом A3) получаем, что порядок в §в, по-
порожденный соотношением A2), индуцирует в 8S следующий по-
порядок:
Pi (Jty/Po К) ^ Pi K)/Po (**,) > • • •. A4)
и потому образованное выше оптимальное множество Wa может
быть описано так:
где А/, определены в A4), а А таково, что соблюдается равенство
(9). Итак, оптимальное множество Wa включает точки х с наи-
наибольшим отношением правдоподобий Pi(*)/Po(*)-
Поясним, что для непрерывной моделн имеет место то же са-
самое. Полагая носитель плотности /0(х) конечным, разобьем его
на конечное число областей Л/, i=l, ..., N, с объемами
|Д/|=б//о(х/), A5)
где .V, — некоторые точхн нз Д;, i=l, ..., N, а б выбрано настоль-
настолько малым, что можно пренебречь погрешностью в равенствах
N. A6)
Из A5) и A6) имеем
A7)
Используя разобранную выше днскретную модель с равновероят-
равновероятными исходами по мере Ро, получаем, что оптимальное множество
Wa строится нз областей А, с наибольшим отношением правдопо-
правдоподобий /i(x,)//o(x,), х,еД,-.
Лемма 1 (Нейман а—П и р с о и а). Для статистической
модели (8В, Л, {Ро, PJ) и гипотез Но: Р = Р0, Я,: Р = Р, при лю-
любом k область
B7* = {x:L,(x)/Lo(x)>A!} A8)
(где Li(x) — правдоподобие меры Р,, » = 0, 1) имеет наибольшую
мощность среди всех областей W того же или меньшего размера:
(П() A9)
где
B0)
Доказательство проведем для непрерывной моделн. Пусть (см.
E)) ф(х), ф*(х) — критические функции W н W* соответственно.
Рассмотрим функцию
(Ф*(х)-<р(х))(Ых)-*Ых». B1)
218

При xelV* оба сомножителя в B1) неотрицательны: первый —
так как ф*(х) = 1, а второй — по определению A8). При x§F
первый сомножитель в B1) равен — ф(х) и, следовательно, непо-
неположителен, а ввиду A8) и второй сомножитель неположителен.
В таком случае, полагая dx=dx\ ... dxn и рассматривая интеграл
как л-мерный, получаем
О < J (Ф* (х) -ф (х)) (Л (х) -kf0 (х)) dx =
-*(J9'(x)/0(x)dx-J9(x)/0 (*)<&)
= Р1 (W) -Р, (W) -к (Р, (W) -Po
Отсюда ввиду B0) следует A9). Щ
Лемма 2. Если множество V={x:fi(x)—kfo(x)—O) имеег
меру Лебега нуль, то соотношение A8) определяет единственную
с точностью до множества меры Лебега нуль наиболее мощную
критическую область заданного размера.
Доказательство. Из равенства Pi (W*) ¦= Pi (W) вытекает
0 = J (Ф* (х) -ф (х)) (Д (х) -А/, (х)) dx =
= j (ф'(х)-ф(х))(Мх)-*/0(х))*.
Но при хей?Э V и таких, что fr(x)—*/о(х)>О, имеем ф*(х) = 1 и,
следовательно, ф*(х)—ф(х)^0, а при хей? G V и таких, что
fi(x)—kfo(x)<Q, имеем ф*(х)=0 и, следовательно, <р*(х)—
—ф(х)^0. Таким образом, при x^.$B OV подынтегральная функ-
функция
(ф*(х)-ф(х))(Мх)-*Мх))>0.
и, следовательно, на самом деле эта функция равна нулю для
почти всех хей? Э V по мере Лебега. Но /i (х)—^/0(х)^0 на
S8QV, и потому ф*(х)=ф(х) для почти всех хей?е V, а следо-
следовательно, и для почти всех хей?. ¦
Критерий W*, определенный в A8), называют критерием отно-
отношения правдоподобий. Напомним, что в рассматриваемой статис-
статистической модели статистика Li(x)/L0(x) порождает минимальное
достаточное разбиение (см. подробнее п. 6 § 15, п. 3 § 16), так чго
статистика критерия W* является фунцией минимальной доста-
достаточной статистики.
3. Примеры. Равномерно наиболее мощные критерии.
(III) В условиях примера (I), обозначая через I^x >ej индн
катор множества {х„ : *(i)>0}, получаем
219

Если 0!>8о, то для xn таких, что во<*(!)<в|, отношение правдо-
правдоподобий B2) равно нулю, а при x(d>0i оно постоянно и равно
(89,). Положим для любого №=Л'
W = {xn:jc(!)<=^}. B3)
Тогда наилучшая критическая область W*a размера а для гипоте-
гипотезы 6 = 6о против простой альтернативы в = в|>80 получается с по-
помощью B3) нз одномерной области Ф*а:
W'*=Wa\JWa, Ce@o, в,). W'aEtfi. + °°).
где 1Г'а = 0, если Peo(W«)>a. и в таком случае в качестве №"»
берется любое подмножество из (8i, +oo) такое, что Peo(W*) =<*;
если же Pe.(W^) < ct, то №"„= (8|, +оо), а в качестве \Х"% берет-
берется любое подмножество интервала (80, 8i), так чтобы РР,(Wa) +
+ Р«. (W'u) =а. В частности, критерий W+a из примера (I) удов-
удовлетворяет всем перечисленным требованиям и, следовательно, яв-
является наиболее мощным.
Для 8|<8о отношение правдоподобий B2) равно +оо при
х„: 8|<*(|)<8о и равно e"i(>'~M при X(i)>8o. Следовательно, опти-
оптимальная область получается с помощью B3) нз одномерной об-
области
где WaS.(%> +»)—любое такое, что Pe.(W«)=a. Обсудим полу-
полученные в этом примере результаты. Во-первых, наилучшую кри-
критическую область против альтернативы 8|>6о можно выбрать
в виде
1—а)},
а против альтернативы 8|<8о, принимая во внимание, что
Pe.(xn:.f(i)<61)-01— в виде
П7-а={х„:х(!)<80}и^+а. B4)
Таким образом, критическая область W+, — одна н та же против
альтернативы 8)>G0 при любом 8i. To же самое верно и для W~*.
Более того, область W~a годится как оптимальная и против любой
альтернативы 8;>60, так как левое подмножество в объединении
B4) имеет меру нуль по Рц, и Р01, 8|>8о. В результате область
220

B4) является наиболее мощной протнв любой простой альтерна-
альтернатнвы 9; ^00- ¦
Определение. Рассмотрим статистическую модель
(SO, <®. {Pfl, 6еЭ}). Критерий №*„ размера а для проверки ги-
гипотезы Яо:6 = 6о протнв альтернативы Н\ : 8е01=в называется
равномерно наиболее мощным, если для любого 8е9| н любой
другой области W^SJ размера, не превосходящего а, выполнено
неравенство
PQ(Wa)^PQ(Wa), веб,.! B5)
(IV) В условиях примера II имеем
и
L(xn; \kJ/L(xn; щ) =
При Ц1>цо отношение правдоподобии возрастает с ростом х, н
поэтому наилучшая критическая область для проверки гипотезы
ц = цо протнв простой альтернатнвы ц = Ц|>ц0 нмеет внд
{J B6)
Из условия
a =PMi
получаем уравнение для определения ?,:
-l/n(io + *e/n=x1_a(yV(O, 1)).
откуда
ka = \io + xl^x(N@, \)I\Ш. B7)
Таким образом, критическая область B6), B7) равномерно наи-
наиболее мощная против сложной альтернативы щ>цо- Аналогично
область _
W-a=[xn : х<(ю+ха (ЛГ @, 1))№
является равномерно наиболее мощной против сложной альтерна-
альтернативы (I <цо. Как видно, в данном случае не существует области,
равномерно наиболее мощной . против сложной альтернативы
221

MMo- Для проверки гипотезы т = цо против сложной альтерна-
альтернативы Ц|^цо в примере (II) была предложена область №,=
= W\/2[}W~a/2t которую можно рассматривать как некоторый
компромисс. Как следует из леммы 2, область W* строго менее
мощная, чем W+* и W~a, против соответствующих односторонних
альтернатив.
(V) Рассмотрим повторную выборку нз однопараметрического
семейства распределении экспоненциального типа:
fo(x)=h(x)exp(a(Q)T(x)+b(Q)).
Отношение правдоподобий:
я
L(xn; 8,)/L(xn; 8„) -ехр (@(80-0F0)) ? Т (х,) + n (Ь (Qt)-Ь (%)))
зависит от выборки через достаточную статистику, и при ~^1;
—аF0)>0 наиболее мощная критическая область для гипотезы
8 = во против простой альтернативы 6 = 6|>в0 имеет вид
Если функция a (8) монотонна по 6 на некотором подмножестве
6'=6, включающем точку 80, то область №+а является равномер-
равномерно наиболее мощной против сложной гипотезы 6>60, ВеЭ'. В слу-
случае, если разность aF)-aF0) меняет знак при прохождении точ-
точки 0о, равномерно наиболее мощная критическая область против
гипотезы 6|<8о будет иметь вид
{
и, следовательно, не существует равномерно наиболее мощного
критерия против двусторонней альтернативы бт^бо-
4. Близкие гипотезы.
Хотя в рассмотренных выше примерах были найдены равно-
равномерно наиболее мощные критерии при сложных альтернативах,
существования таких критериев в общем случае ожидать не при-
приходится. Имеются различные варианты других постановок опти-
оптимизационных задач в теории проверки статистических гипотез.
Здесь мы остановимся на критериях, которые будут в определен-
определенном смысле равномерно наиболее мощными по отношению к
«близким» гипотезам //"ч : 8=@0, 8о+6), 6->-0, либо Н'\ : 9е
е(Оо—6, во), 6-*-0.
Для повторной выборки наиболее мощный критерий для гипо-
гипотезы О = Оо против простой альтернативы 80+б, 6>0, запишем
в виде
222

7<6) =
i. в0)
= {хп:/(хл; 60 + 6)-/(х„; 90)>*(в)}.
Предполагая функцию правдоподобия дифференцируемой по 6,
имеем при 6-*-0
Цх„; 80 + в)—/(х„; 80) =—"^ " й + о (б) =
B9)
1-1
Если, к примеру, вторая производная го 6 логарифмической функ-
функции правдоподобия /(*,; 6) ограничена по х„ то остаточный член
в B9) мал равномерно по х„ и область W& при малых 6 будет
близка к области
W={xn:dl(xn;Q0)ldQ>k), C0)
где выбор k определяет размер критерия W. Будем называть
критерий W локально наиболее мощным по отношению к близким
альтернативам 0>6о.
Для повторной выборки из распределения N(\x, 1) имеем
=*|—Мо.
и критическая область C0) принимает вид
что совпадает с равномерно наиболее мощным критерием против
сложной односторонней альтернативы 0>0О. Щ
(VI) Рассмотрим повторную выборку из распределения Кош и
с параметром сдвига
Имеем
так что статистика локально наиболее мощного критерия имеет
вид
Чтобы воспользоваться критерием C0), необходимо умегь вы-
вычислять его размер. Это можно сделать приближенно, используя
центральную предельную теорему. В условиях регулярности, прн
223

которых была введена информация по Фишеру (см. подробнее
п. 1 § 19), имеем
Ме (dl (X,; 6)/d6) = 0, De (dl (Хц 6),дв) = /х, F),
и нормальное приближение дает
п
Ре. I х„: Y д1 (*Г. %)№ > Vnl% @o) *,_« (N @. 1))) 55 1 -а. C1)
)
(-1
Нормальное приближение C1) практически бывает достаточным
уже при умеренных п, хотя следует иметь в виду, что чем меньше
а, тем погрешность в C1) больше.
5. Сложные гипотезы.
Предположим, что и нулевая гипотеза, и альтернатива
Но: ВеЭо, Н\: вевь
— сложные, т. е. параметрические множества в0 и 6| состоят бо-
более чем из одного элемента. Одна нз возможностей строить крите-
критерии в этом случае основана иа статистике
Тл (х) = sup L (х; в)/ sup L (х; в). C2)
Оев! 6<=6„
Полагая, что оба супремума в C2) достигаются, можно сказать,
что по выборке х строятся оценки максимума правдоподобия
8о(х) ив,(х):
L (х; 0, (х)) = max L (х; в), i = 0, 1,
Оев,
и затем сравниваются правдоподобия выборки х при этих самых
«правдоподобных» значениях параметра 6 при гипотезах //» и Н\,
как это делается в задаче проверки простой гипотезы против
простой альтернативы. Критерий
называют, как и в случае простой гипотезы, критерием отношения
правдоподобий. Употребляется и другой вариант критерия отно-
отношения правдоподобий, основанный на статистике
Тг (х) --- sup L (х; в)/ sup L (х; в), в = Эо U вх. C3)
Оев вев0
Так как
supL(x; в) = max (sup L(x; в), sup L(x; в)),
Оев 0ев0 Оев,
то
7-2(x)=max(l, ^(x)),
224

так что критерий
WM {T()k) C4)
при k^\ совпадает с
(VII) Рассмотрим линейную модель в канонической форме
с. нормальными наблюдениями:
»
(-1
и»)).
где 4>=(i|>i. ..., i|v), u=(«i ип). Проверим линейную гипоте-
гипотезу Но : i|;2 = ... =^_Л =0 против альтернативы Нк: ifi - ... ¦>- ^;_Л>
>0 с помощью критерия C4). Имеем
г я
/(и;*, (Т)=—2-inB^—^B(«,-*)•+ ^ «?)• C5)
Безусловный максимум логарифмической функции правдоподобия
по Ч> достигается, очевидно, при tf,- = и,-, 1=1, ..., г. Дифференци-
Дифференцируя C5) по а2 при if< = $> " приравнивая производные нулю, на-
находим
откуда
Отметим, кстати, что о. м. п. $ совпадают с наилучшими линейны-
линейными несмещенными оценками из § 10, а оценка а2 отличается мно-
множителем.
Проводя аналогичные вычисления в предположении, что верна
гипотеза Но, т. е. полагая в C5) ф| = ...=фг-*=0, находим
?<=«<• i=r—k г, ог = -^- J
Таким образом,
i-r+l
(u;|.S-(i 2 «;-)-n/2exp(-n/2).
г—*+I
225

и статистика Т2 из C3) принимает вид
/
(—г+1 *—г—*+1
где F(u) — статистика F-критерия из § 13. Из C6) вытекает, что
72(и) и f(u) задают один и тот же критерий. Этот же вывод, оче-
очевидно, справедлив в любой параметризации линейной модели.
§ 22. ПОСЛЕДОВАТЕЛЬНЫЙ КРИТЕРИЙ ОТНОШЕНИЯ
ПРАВДОПОДОБИЙ
1. Метод последовательного статистического анализа.
Мы будем рассматривать схему повторного выбора и задачу
о проверке простой гипотезы Яо: Р = Ро против простои альтерна-
альтернативы Н\ : Р = Р|, но в отличие от предыдущего допустим, что число
наблюдении заранее не фиксировано, а может зависеть от резуль-
результатов уже проведенных испытании. Определим статистическую
модель, отвечающую такому опыту.
Пусть (/?", Я», Р(п)) — последовательность вероятностных мо-
моделей (п=\, 2, ...). Предположим, что последовательность мер
Р<">, п=1, 2, .... согласована в следующем смысле: для любого
В&
xn+i) t (xi х„)еВя), A)
что по существу означает, что мера Р<я+|> в ЗВп+и суженная на
38„, совпадает с Р<л\ т. е. последовательность (/?". SB", P). п =
= 1, 2, ..., описывает неограниченно продолжающийся вероятност-
вероятностный эксперимент. Пусть #? = {x=(jt|, х2. ...) :х,е/?<'>, t=l, 2 }—
множество всех бесконечных последовательностей действительных
чисел. Примем обозначение [х]„=(а-|, .... хп) для конечного от-
отрезка последовательности х и [В]п = {[х]л: хеВ}, B^SS. Введем
минимальную систему SB подмножеств 95, содержащую все мно-
множества вида В = {х: [х]леЯп}> где В„^<ЯП, п = \, 2, ..., замкнутую
относительно перехода к дополнению и образования счетного объ-
объединения. Известная теорема Колмогорова утверждает, что при
условии A) может быть определена единственным образом мера
Р на 38, такая, что для любого В38
Р(х: [х]„еВп) = Р<">(Вп) B)
(см. [15, 16]). Равенство B) означает, что Р-вероятность любого
события, связанного с результатом только первых п испытаний,
совпадает с вероятностью соответствующего события в модели
(/?", 38П, Р(п))- Определенная так вероятностная модель (Я?, Я, Р)
соответствует опыту, состоящему из бесконечной последователь-
последовательности, вообще говоря, зависимых испытаний.
226

В случае, когда на каждом (Rn, S8n) задано семейство зерс.тг-
ностных мер {Ре*1, б ев} и каждая последовательность р§\
«=1, 2 удовлетворяет условию согласованности A), на из-
измеримом пространстве {SB, SB) определено, в соответствии с тео-
теоремой Колмогорова, семейство вероятностных мер {Pg, в ев}.
Статистическая модель (#, Я,{Ро. в ев}) отвечает опыту с бес-
бесконечным числом испытаний и неизвестным вероятностным рас-
распределением, принадлежащим семейству {Рд,в ев}. При такой
постановке интерес представляют такие статистические процедуры,
которые основываются на конечных отрезках [х]„ результатов
наблюдений. Введем статистику Лг(х) с натуральными значениями,
которая будет служить «моментом прекращения» наблюдении, так
что статистические выводы будут функцией от [x]nw- He вся-
всякая статистака N(\) годится в качестве такого рода момента,
так как естественно, чтобы решение о прекращении испытаний
было основано лишь на результатах уже проведенных испытаний.
Статистику N(х) с натуральными значениями назовем момен-
моментом остановки, если
N(x)=n=>N(y)=n для любого у : [у]п=[х]„. C)
Можно сказать, что свойство C) статистики N(\) означает, что
решение о прекращении наблюдений не предвосхищает будущее.
Последовательный статистический анализ включает в себя любую
статистическую процедуру, зависящую от хеЯ? лишь через
[х]л'(хь где N(x) — некоторый момент остановки.
Рассмотрим наиболее важную для приложений модель повтор-
повторных независимых испытаний, так что
Pefx^eB"» *„еВ<»>)= ПРв(х:*,бВ(")
для любых п, flOe^Si, « = 1 п, и Pg(x: xt e fl<") не зависит
от i при любом fle^i, x=(xi, х2, ...). Ниже нам потребуются мо-
моменты остановки специального вида. Пусть h(x) — некоторая
Лгизмернмая функция и
Sn(x)=h{xl)+... + h{xn), х=(хи .... х„, ...), п=1, 2 D)
Введем момент N(\) первого достижения последовательностью
D) интервала (а, +оо):
W(x)=n-«=>.S,(x)ii"(a, +oo), « = 1 п—1,
Sn(x)e(a, +oo). E)
Очевидно, что соотношения D), E) задают момент остановки.
Покажем, что если
(ie = MeA(X1)>0. в ев,
227

то ел. в. Л7(X) конечна с Pg-вероятностью единица:
Рв(ЛГ(Х)<оо) = 1, в ев. F)
Воспользовавшись усиленным законом больших чисел, имеем
-l- G)
Из G) вытекает, что при Pg-почти всех х найдется номер
Пд = лд(х), начиная с которого Sn (x) > лцд/2, и, следовательно,
момент остановки ЛР(х), определенный в E), удовлетворяет тре-
требованию F). Если Ц0=-г-оо, то, как известно, n-'S,,(x)—»-+ ос
на множестве Pg-вероятности единица и момент N(x) также яв-
является конечным.
2. Последовательный критерий отношения правдоподобий.
Рассмотрим модель повторных (неограниченно продолжаю-
продолжающихся) независимых испытаний. Введем отношение правдоподо-
правдоподобий
/?„(х)=/.([х]„; е,)/М[х]„; во) (8)
для отрезка наблюдений длины п, \=(xit x2, ...), [х]л =
= (Х|, х2, ..., хп). Мы видели, что для любого фиксированного п
критерий, основанный на статистике (8), максимизирует мощность
при простых гипотезе и альтернативе — Яо:в = во, #1:в=в|.
В критическую область входят все выборки, для которых отно-
отношение (8) превосходит заданное число:
{[x)n:Rn(x)>A). (9)
Наглядный смысл неравенства (9) состоит в том, что правдоподо-
правдоподобие параметра 8| при выборке [х]„ в А раз больше правдоподо-
правдоподобия во, и потому неравенство (9) следует рассматривать как оп-
опровержение нулевой гипотезы. Число А выбирают для обеспечения
заданного уровня значимости:
а=Рво(х:/?„(х)>>1),
так что в зависимости от а граница А может оказаться и меньше
1. Это означает, что для некоторых точек х отношение (9) меньше
единицы, но мы интерпретируем их в пользу гипотезы //.. Такое
обстоятельство, конечно, является не очень приятным, но для него
есть оправдание. Нулевая и альтернативная гипотезы входят в
постановку задачи несимметрично: нулевая гипотеза проверяется,
альтернативная гипотеза рассматривается как направление воз-
возможного отклонения от Но. Поэтому и вероятности первого и вто-
второго рода не равнозначны для экспериментатора: вероятность
ошибки первого рода а устанавливается заранее, что гарантирует
ее определенный уровень, удовлетворяющий исследователя, а
228

вероятность ошибки второго рода минимизируется за счет выбора
критерия. Другое замечание в отношении критерия с фиксирован-
фиксированным объемом выборки состоит в том, что неравенство (9) могло
иметь место при меньших значениях п и, следовательно, проведе-
проведены «лишние» наблюдения.
Определим последовательный критерий отношения правдопо-
правдоподобий, выбрав два числа А>1>В>0 и задав момент Л'(х) оста-
остановки наблюдений следующим образом:
N(x)=n**>Ri(x)e=(B, А), « = 1 л—1; Яп(х)Ш (В, А). A0)
Иначе говоря, значения отношения правдоподобий из интервала
(В, А) относятся к области «неуверенности» в принятии решений.
Но как только /?„ вышло из этого интервала, решение принимает-
принимается: при /?а'(х) (х) ^ А гипоте.ча Нл отвергается, при /?л(х, ix) < В
гипотеза Но принимается. Критическая область имеет, таким обра-
образом, вид
Вообще говоря, остается возможность неограниченного продолже-
продолжения испытании для выборок х, для которых B<R,,(x)<A при всех
п. Покажем, что множество таких х при несовпадающих Р,„ Р|
имеет меру нуль по каждой из этих мер, т. е. /V(x) удовлетворяет
требованию конечности F).
Рассмотрим для определенности случай, когда распределение
вероятностен отдельного наблюдения задастся плотностью /,,(.*)
при Но и fi(x) при Н\. Положим a=logi4>0, b=logfl<0,
Л (х) = log (/х (*)//„ (л)). Sn (х) - log Rn (x) = ? Л (х,).
(-1
Мы покажем, что
—oo<s:Moft(*,)<(), о<м,й(^,х+оо, A2)
откуда будет следовать, что (см. конец п. 1)
Ро(х:ЛГ(х)<оо)=Р,(х:ЛГ(х)<оо) = 1. A3)
Для доказательства неравенств A2) применим неравенство Йен-
сена для выпуклых функций: если <р(х) такова, что для любого
0<а<1 и любых хФу щ(х) + A—а)ч(у)<у(ах+(\—а)у), то
M(p(Z)<(p(MZ), A4)
в предположении, что MZ конечно и ( )
[Докажем A4), предполагая дополнительно, что ср(х) имеет
непрерывную вторую производную ф"(х)<0. По формуле Тейлора
имеем
, У)(х-у))(х-у)\ A5)
229

где 0<9(дг, у)<\. Подставляя в A5) y = NlZ, x=Z, запишем
<p(Z) — <p(MZ) :=<p'(MZ) (Z—MZ) +g(Z), A6)
где g(x)<0 при всех x^MZ. Взяв математическое ожидание от
обеих частей равенства A6), получаем в случае конечного
ЩA) :Mq>(Z) — (p(MZ)=Mg(Z)<0," что и дает A4). Если
Mcp(Z; бесконечно, то, отбрасывая в A6) неположительное сла-
слагаемое g(Z), получаем, что M<p(Z)=—оо, и неравенство A4)
установлено].
Запишем неравенство A4) для (p(Z)=h(Xi)=logfi(Xi)lfo(Xi):
MJi (X,) - Г log -^4" Л> М dx < log f Ш. /0 (х) dx ~ 0. A7)
аналогично
MJi(Xl)~[log^f1(x)dx~-[log-№-f1(x)dx>0. A7a)
J Ы*) J n\x)
Если в A7) на множестве положительной Ро-меры fi(x)=0, то
MoA(^i)=—оо, и аналогично Mih(Xi)=+oo, если /о(*)=О иа мно-
множестве положительной Pi-меры, так что неравенства A2) установ-
установлены и тем самым доказано, что N(x) конечно. Щ
Последовательный критерий W задается двумя параметрами
А, В, Л>1>В>0; его размер а и мощность р в принципе могут
быть рассчитаны по формулам
а =Р0 (х: RNix) (х) > А), р = Pt (x: RNW (x) > А).
Такой расчет представляет в общем случае сложную задачу, ре-
решение которой в явном виде не находится. Однако возможен
простой приближенный расчет. Мы покажем, что, выбрав
Л'=р/а, Я'=A-р)/A_а), A8)
мы получим последовательный критерий
W'={x:RN-{x)(x)^A'},
значения а', р' которого связаны с а, р неравенствами
1-р). A9)
Обычно при использовании последовательного критерия задаются
вероятностями ошибок первого и второго рода порядка 0,1ч-0,01.
В тпком случае неравенства A9) показывают, что каждая из ве-
вероятностей а' и A—р') для критерия W может лишь незначитель-
незначительно превысить и и A—Р) соответственно, а их сумма не превосхо-
превосходит и+ A—Р).
Покажем сначала, что
1-р-ВA-а)«:0. B0)
230

По формуле полной вероятности имеем
л—1
-Р, (х: Rn (x) >A,N (х) =п) Л-') =
= I J..J tt»(*i) • • • '«W-^ /i(*i) • • • /ifcPi • • • <**,, B1)
l Ё
?п= {[х]„: h (х\) ... Л (*») > Л/о (.vj • • • /о (*¦«). ^ (х) - п).
Поскольку подынтегральная функция в B1) неположительна на
множестве Еп, то получаем отсюда первое нз неравенств B0). Ис-
Используя соотношения
1 - а=--Р0(х : /?Л'(Х) (х)<В). 1- p-PJx: Ял,,», (х)<В),
аналогично получаем второе из неравенств B0):
X dA'!... dx., < 0,
Gn ={[x]n: Л (x,) ... А (х„) < ?/0(At) ... /0 (*„), N (x) -n).
Неравенства B0) перепишем в виде
а). B2)
Значения вероятностей а', E' для критерия W подчиняются нера-
неравенствам того же вида:
Подставляя сюда, значения А', В' из A8), находим
'/а', A-Р)/A-а)>A-р')/A-а'), B3)
или
что приводит к первым двум неравенствам в A9). Далее, из B3)
имеем
Р/а-1<р7а'-1, A-а)/A-р)-1
или
а/(р-а)>а7(Р'-а'). A-Р)/(Р-а)>A-р')/(Р'-а'). B4)
Складывая неравенства B4), получаем
(z'). B5)
231

При р—а, р'—а'>0 перепишем B1)) т» я т.™
или
—1 + 1/(а+1-РК— 1 + 1/(а'+1—Р'),
откуда и получаем третье из неравенств A9).
3. Среднее число наблюдений в последовательном критерии.
Случайный момент времени ЛГ(Х) является моментом первого
выхода траектории случайного блуждания
из интервала (b, a), a = log<4, b = \ogB. Докажем следующее тож-
тождество Вальда:
), i=0, 1. B6)
Проверим сначала, что M,N(X) конечно. Заметим, что
Далее,
^ (JV (X) > 2л) =<?», (S, (X) е (М). у «1 2п)<
< <Pi (S, (X) е (&,'с), Sn+k(X)-Sn (X) s (&-с, а-Ь),
i,k = \ п). B8)
Так как ел. в.
Sn+*(X)— Sn(X)=A(Xn+l)+... + A(Xn+*), *-l, 2 п,
не зависят от 5,(Х), /= 1, ..., п, то из B8) получаем
(b-a, а-Ь), /-1, .... п)J. B9)
Но вероятность в правой части B9) меньше единицы при некото-
некотором п, поскольку, как было доказано выше, момент выхода N(X)
из любого интервала (a, b) конечен с вероятностью единица. Та-
Таким образом, при некотором п0
232

и, аналогично, при любом k
Учитывая монотонность членов ряда B7), заключаем, что этот
ряд сходится.
Введем ел. в.
"ft
[1, если b<Sk<a, A:=0, 1 j —1, 50=0,
в противном случае.
Легко видеть, что
N (X) = у Y,, S,v«x) = А (X,) + ... + A (XW(x,) = V А (X/) Y,. C0)
Из C0) получаем
1-х
а, используя независимость Л (А',) и У/, имеем
М, ? А(Х,) К, = Y № (*/) М,У, =М{А (X,) ? М,К,. C1)
Переходя в C1) к пределу при п-*-оо, приходим к B6). Щ
Перепишем тождество B6) в виде
t=0,1. C2)
Воспользуемся приближенными равенствами
Sjv<x) ^ а либо SW(x) 35 Ъ, C3)
пренебрегая тем, что в момент выхода из интервала (Ь, а) стати-
статистика Sn выходит, вообще говоря, не на границу интервала, а за
его пределы. Понятно, что для обеспечения малых вероятностей
а и 1—р границы а и Ь по модулю должны быть велики по
сравнению со средней длиной шага блуждания M,h(A^i), что и
служит основанием для приблнжений C3). В результате получаем
(SNlX) >а) + ЪР{ (Smx) < Ь),
или
— a), M1Sw,x)^cp + 6(l—P). C4)
Подставляя C4) в C2), получаем приближенные значения для
среднего числа наблюдений в последовательном критерии:
я (aa + Ь A -а))/М0А (Хк),
C5)
я (ар + Ь A -
9 М. В. Козлов. А. В. Прохоров 233

Рассмотрим пример. Пусть ft(x)=q>(x—\ч), t=l, 2, где <р(*)*
плотность закона Л'@, 1) и |ю<М>- Имеем
J =М0 In (Д (*,)//„ (X,)) = Мо (-1/2 (Х,-
+ 1/2 (Х^ц,)") - (Их-|1о)*/2, J
Границы последовательного критерия выбираются из условия
A8):
с = 1п(р/а), & = 1п(A-р
Подставляя их в C5), получаем
Сравним среднее значение объема выборки в последовательном
критерии с числом наблюдений па.в в критерии отношения прав-
правдоподобий с фиксированным объемом выборки и тем же размером
а и мощностью р. Из примера (II) § 21 выпишем уравнение для
определения п=паЛ:
(ц,-Мо-*1-а/1^)), C6)
где ха — а-квантнль закона N@, 1), Ф(дс)=ф. р. N@, 1). Из C6)
получаем
li — Но))* •
В результате
При a=l—p = 0,05 находим a = 2,94; &=—2,94, и правые части
соотношении C7) равны 0,4897, что указывает на экономию после-
последовательного критерия в числе наблюдений.
Последовательный критерий отношения правдоподобий мини-
минимизирует средний объем выборки по отношению к любому дру-
другому последовательному критерию с теми же или меньшими ве-
вероятностями ошибок первого и второго рода (см. [11, гл. 3.
разд. 12) и [7, с. 429]).

ГЛАВА V
БОЛЬШИЕ ВЫБОРКИ
§ 23. АСИМПТОТИЧЕСКИЕ СВОЙСТВА ОЦЕНОК
1. Состоятельность.
Различные методы оценивания, с которыми мы познакомились
в предшествующих главах, позволяют строить оценки Г(х„) при
любом объеме выборки п. Свойства оценок при возрастании п
систематически нами ие рассматривались. В данном параграфе
мы остановимся вкратце иа некоторых общих свойствах оценок,
проявляющихся в модели повторной независимой выборки при
л->-оо. Чтобы подчеркнуть зависимость статистики Г(хп) от п как
от параметра, будем употреблять ниже обозначение Г<п>(х„) вме-
вместо 7"(х„).
Пусть при каждом п статистика Г(п)(х„) определена на изме-
измеримом пространстве (/?", ?В„), п=\, 2 Поскольку речь идет
об одном неограниченно продолжающемся эксперименте, то есте-
естественно предполагать, что меры Р("> на (/?", яп), я=1, 2, ....
согласованы. В таком случае от последовательности
(/?", В„, {Р(п)}), я—1, 2, ..., можно перейти к единой статистиче-
статистической модели (80, Я, {Р}), где SB состоит из бесконечных последо-
последовательностей x=(*i, X2, ...) (см. подробнее п. 1 § 22), и рассмат-
рассматривать статистики 7"(п)([х]п), зависящие от х через конечный от-
отрезок [х]„=(*1 х„). Такой подход, чрезвычайно важный для
теории вероятностей, иа самом деле не играет столь большой ро-
роли в статистике (исключение составляет последовательный стати-
статистический анализ). Тем не менее мы будем исходить из единой
статистической модели (8Б, ?8, {Р}) ввиду ее лучшего соответствия
мыслимому эксперименту и большей математической ясности.
Подчеркнем, что все последующие рассуждения сохраняют
полностью свое значение, если полагать, что рассматривается по-
последовательность моделей (Rn, Bn, {Р(п)}), и соответственно заме-
заменить символ вероятности Р иа Р(п) (при подходящем п).
Ради упрощения выкладок мы будем употреблять обозначение
х„ для отрезка (xt, ..., хп) бесконечной последовательности х =
= (*i, *2, ...)еЯ?.
Определение 1. Допустим, что при каждом п=\, 2, ...
статистика 7"<п)(х„) рассматривается как оценка некоторого функ-
функционала ф(Р), Ре{Р). Скажем, что последовательность оценок
9* 235

7"<п>(х„) (или, короче, оценка 7"<п>(х„)) состоятельна, если для лю-
любого е>0 и любого Р{Р}
P(xn:|7"<»)(x,,)-9(P)|>e)-0, л—оо. A)
В параметрическом случае вместо A) имеем
Рв(хл:|ГС)(хп)-ф(в)|>е)-^О, л-оо, е<=в. B)
В случае векторной статистики Т(п)(х„) и вектор-функции ф(9)
(или ф(Р)) состоятельность означает, что соотношения B) (или
A)) выполнены покомпонентно.
Если при фиксированном Р выполнено A), то говорят, что по-
последовательность ел. в. 7"<П)(Х„) сходится по вероятности к <р(Р),
и пишут
7»(ХП)^Ф(Р). C)
р
Можно также сказать, что разность соответствующих величин
в C) сходится по вероятности к нулю:
7»(Х„)-ф(Р)->0.
р
Состоятельность — это минимальное требование, которое сле-
следует предъявлять к любой разумной оценке 7"<">(х„), и все оценки
для модели повторной выборки, с которыми мы встречались ранее,
являются состоятельными.. Напомним некоторые из примеров.
Э. ф.p. Fn(x; х„) — состоятельная оценка теоретической ф. р.
F{x) в любой точке х. Состоятельность выборочных моментов
(среднего, дисперсии и др.) легко вывести, опираясь на следую-
следующие два утверждения.
Теорема Хин чина (см. [2, т. 1, гл. X, § 2; т. 2, гл. VII,
§ 7]). Если Xt, i=l, 2, ..., — последовательность независимых
одинаково распределенных ел. в. и NiXt = ц конечно, то при лю-
бом е>0
Лемма 1. Если каждая из последовательностей ел. в. 7",(ХП),
/'=1, ..., k, сходится по вероятности к некоторой постоянной а/
« g(U, •¦-, tn) — непрерывная в точке (сь ..., ak) функция, то
g (Г<»> (Х„), .... 7W (Х„) -* g (а, ак). D)
к Р
Доказательство леммы 1 проведем для краткости при 6 = 1.
Ввиду непрерывности функции g(t) в точке а для любого е>0
найдется б>0, что
{t:\t-a\<6)c={t:\g(t)-g(a)\<zh
236

и, следовательно,
P{xn:|g(rc>(xn))-g(c)|>e}<P{xn:|T(«>(xn)-c|>6}.
Но последняя вероятность стремится ввиду A) к нулю при п-+
->оо. ¦
Выборочная квантиль Х[„Р], „, 0<р<1 (либо Х[Лр>н.л)> где
хк,пшкХ(к) — k-я порядковая статистика вектора наблюдений х„,
является состоятельной оценкой теоретической квантили хп в
предположении, что уравнение p = F(x) имеет единственное реше-
решение х=хР и в точке хР функция F непрерывна. Докажем вначале
это утверждение для повторной выборки из равномерного на @, 1)
распределения. Как следует из леммы 2 § 5, если Xlt ..., Xn^i —
независимые экспоненциальные G(X, 1), S*=A^i+... +.Х*, ft—
= 1, .... n+ 1, то ел.в.
Zft.n=Sft/Sn+i, ft=l, .... n, E)
распределены как порядковые статистики повторной выборки из
равномерного на @, 1) распределения. Применяя закон больших
чисел, имеем
Sn+i/(n + 1) -*- к, SmPil[np] -*- Я,, п -»-оо,
откуда, воспользовавшись леммой 1, получаем
[пр] in+i nt+1 р
Пусть теперь F{x)-непрерывная ф. р. общего вида. Полагая
F-l(z)=sup{x:F(x)—z), легко видеть, что Xi=F~l(Zi), i=l, ....
.... п+1, представляет собой повторную выборку из распределе-
распределения F(x), F-x(Zk,n)—Xk,n- Применяя лемму 1, получаем
G)
Если F(x) имеет точки разрыва, то, применяя ту же конструкцию,
но доопределив функцию F~l (z) по монотонности, получим утвер-
утверждение G) для любой квантили хр, являющейся точкой непрерыв-
непрерывности F(x).
2. Состоятельность оценок максимального правдоподобия.
Рассмотрим параметрическую модель повторной неограничен"
но продолжающейся выборки {X, Л,{Ре. вев}). Это озна-
означает, что мера Ре, суженная на (/?", Лп)'-
=(*i.х», ...): х„ = (хх *„) еВп), Вп е Я„,
порождает параметрическую модель (Л", Лп, {Р§\ вбв}) п-крат-
иой повторной независимой выборки. Будем, для определенности,
237

рассматривать непрерывную модель, так что мера Pg11 порож-
порождается п-мериой плотностью вида
Оценка максимума правдоподобия 6(п> (хп) определяется усло-
условием
вев
L<»> (х„; в) -/ (xi; в) ¦..../ (*„; в), в = (в, вл).
Если функция правдоподобия дифференцируема по 6, а максимум
достигается внутри области в, то ои может быть найден решением
уравнений правдоподобия
<Э/<">(х„; в)/<ЭО,=О, t=l k,
/(n)(xn; e)=logL(xn, 9) (8)
и последующим отбором среди решений системы (8) точки гло-
глобального максимума. На самом деле при условиях регулярности
типа тех, которые использовались в § 18, 19, локальный макси-
максимум единствен и совпадает с глобальным. Поэтому и для теории
и для приложений представляет интерес оценка, являющаяся кор-
корнем системы (8) и называемая оценкой уравнений максимума
правдоподобия. Мы сохраним за любым корнем системы (8) обо-
обозначение 3<п)(Хл).
Теорема 1. Пусть плотность f(x-, в) отдельного наблюдения
дифференцируема по вев, где в — некоторый интервал прямой,
Рв =^Рв при любых во^вь Введем при каждом я=1, 2, ... мно-
множество
В„={х„: существует решение системы <ЭИп)(х„; в)/59;=0, i—
= 1 *}.
Тогда, во-первых,
Рв(х:хпеВ„)-И, я-+-оо,
и, во-вторых, для х„еВ„ можно выбрать корень в<п)(Хп) уравне-
уравнений правдоподобия (8), который является состоятельной оцен-
оценкой 9.
Доказательство. Пусть в0, в^в и Рв,=?Ро.. В п. 2 § 22 бы-
было показано, что
- оо < Me. (log (/ (Хх; OJ// (Xi; в0))) < 0. (9)
Применяя закон больших чисел к последовательности
/м (Х„; 6J - /w (Х„; в0) = ? log (/ (Xt; OJ// (X,; в0)),
238

получаем
Рво (х : /<«> (х„; в,) - /<"> (х„; во)< 0) -*¦ 1, п -*¦ оо. A0)
Определим
В'п = {х„: /<«> (х„; 0О + 6)< /<"> (х„; %), /<«> (хл; во-6)</<") (х„; в0)}, б>0.
В соответствии с A0)
а для х„еВ'„, очевидно, функция /(х„; 0) имеет внутри отрезка
[0о—6, 0о+6] локальный максимум, что доказывает первое утвер-
утверждение теоремы. Для решения 0(л)(х„) уравнения
(х„; 0)/д0=О,
принадлежащего определенному выше интервалу @о—6, 0о+6),
запишем
Рво(х: дИ* (х„; 1<л) (х„))/а0 = 0,. 10(л) (хп)- 8о|< 6)-*• 1, п -»оо,
что ввиду произвольности б доказывает и второе утверждение
теоремы 1.
3. Асимптотическая нормальность.
Состоятельность последовательности оценок Г'п)(хп), я =
= 1, 2, .... является предельным свойством и формально никак
не связана с качеством этих оценок при конечных п. Чтобы со-
состоятельная оценка Ип)(х„) стала полезным инструментом стати-
статистики, необходимо, хотя бы приближенно, вычислять вероятности
Рв(х:|Г<»)(хл)-ф(в)|<6). A1)
Одно из важнейших направлений в теории вероятностей — пре-
предельные теоремы — позволяет дать оценку вероятностей (II) при
больших п. Центральная предельная теорема занимает, в соответ-
соответствии со своим названием, ведущее место в теории и приложениях.
Речь идет о сходимости функций распределения (соответствующим
образом центрированной и нормированной последовательности
ел. в.) к нормальному закону
#в((Г<«>(Хп)-ме))/о„(е)<о-*Ф@. «-*°°- A2)
Зачастую, но далеко не всегда в качестве ц„@) и о„F) в A2)
можно взять соответственно среднее и корень из дисперсии ел. в.
Т(п)(\п)- Хорошо известна предельная теорема A2) для случая,
когда
где ел. в. Yt, i = l, ..., п, — независимы, одинаково распределены
239

и имеют конечную дисперсию. Если исключить искусственные при-
меры, то, явно или неявно, сходимость в A2) связана с суммиро-
суммированием независимых или слабо зависимых ел. в.
Определение 2. Последовательность оценок 7"(п)(х„), л=
= 1, 2, .... называется асимптотически нормальной, если выполне-
выполнено соотношение A2); |x,i(G) называется при этом асимптотическим
средним, о2„@) — асимптотической дисперсией оценки 7<п)(х„).
(Коротко: 7"tn)(Xn) асимптотически нормальна N(\in(Q), o2nF)).)
Параметры ц„ и а„ определены в A2) неоднозначно. Нетруд-
Нетрудно проверить, что если \i'n и о'„ удовлетворяют условиям ц'„ =
= ц« + оA)о„, о'п=о„A+оA)), л-»-оо, где оA), л-»-оо, обозна-
обозначает последовательность, стремящуюся к нулю, то в A2) можно
заменить цп, а„ на ц.'п, о'п. Действительно, используя преобразо-
преобразование
*п) — Р„ _ о„
°'n o'n \ <*•
сведем вопрос к следующему общему утверждению.
Лемма 2. Пусть последовательности ел. в. У„, Un, Vn, л»
= 1, 2, ..., таковы, что при всех у, таких, что G(y) непрерывна:
P(Yn<y)-+G(y), л-оо,
где G(y) — некоторая ф.р.,
Ua-*-\, Vn-*-0, n-*-oo. A3)
Тогда
P(Un(Yn+Vn)<y)-+G(y), n-+oo, A4)
во всех точках непрерывности функции G (у).
Доказательство. Пусть е>0 произвольно. Имеем
&(У„ + Уп<У)<*(Уп<У + е. IVJ<e) +
Переходя здесь к верхнему пределу по л и используя A3), полу*
чаем
. A5)
Проводя преобразования
<у-*, \Vn\>*)>
<у-г)-?
аналогично A5) находим
A6)
240

Из A5) и A6) ввиду произвольности е и непрерывности G(y) в
точке у получаем
\im8>(Yn + Vn<y)=G(y). A7)
Л->00
Далее покажем, что
YnVn-*0. A8)
Действительно, при любом а
n\>e, \Уя\<а) + ёЦ\У„\>а)<
A9)
Переходя в A9) к верхнему пределу по л, получаем
Urn sup?»( | У„ Vn | >е) <G(—a) + 1—G(a—0). B0)
Устремляя в B0) а к оо, приходим к A8).
Для доказательства A4) можно сначала воспользоваться ре-
результатом A7), а затем применить к ел. в. Yn'=Yn+Vn, V'n =
= t/.,-l н
последовательно A8) и A7). И
Когда Т{п>(хп) рассматривается как оценка параметрической
функции ф(в), то хорошо, если свойство асимптотической нор-
нормальности A2) выполнено для ц„ (в) =ф(в). В этом случае стати-
статистику 7<п)(х„) называют асимптотически несмещенной. Нормирую-
Нормирующий множитель о„@) в A2) характеризует в этом случае раз-
разброс распределения статистики вокруг оцениваемой параметриче-
параметрической функции. В частности, можно написать
Рв (х„: Г<«> (х„) - *,_« (N @,1)).о„ (в) < Ф (в)<
< 7™ (х„) - ха (N @,1)) <т„ (в)) s a, B1)
где степень приближения растет с увеличением л, xa(N@, 1)) —
a-квантиль распределения N@, 1). В предыдущей главе мы виде-
видели, что при соблюдении определенных условий регулярности при^
ближение оценки 7(п)(х„) к ф@) имеет с ростом п порядок 1/Ул.
Поэтому множитель опF) в A2) в статистике обычно имеет вид
о„(в)=о(в)/Ул, о(в)>0. Запишем окончательно наиболее важный
для статистики вариант предельного соотношения A2):
(еГ1 Vn~ (Г(«) (Хл) - Ф (в))< 0 -* ф (/), л -«- оо. B2)
4. Преобразование статистик.
В случае, когда имеет место B2), очень полезным оказывается
следующий простой результат.
241

Лемма 3. Пусть Т^пЦХп), л=1, 2, ..., асимптотически нор-
нормальна N(Q, л-'о2(8)) и g(t) — дифференцируемая функция,
g'(Q)?=O. Тогда gG"<n>(Xn)), л=1, 2 асимптотически нор-
нормальна N(g(Q)), g'(QJo(Q)bn->).
Доказательство. По формуле Тейлора
t; в)), B3)
где а(/; 8)-*-0 при /-»-8. Подставим в B3) / = 7"<">(ХП):
(Х„)- 9) х
B4)
Так как, очевидно,
в, л-^оо,
то второй множитель в B4) сходится по вероятности к 1, и, при-
применяя к B4) лемму 2, получаем требуемый результат. ¦
Асимптотическую нормальность B2) можно использовать для
построения приближенных (при больших л) доверительных интер-
интервалов. Один путь состоит в том, чтобы заменить в B2) о (8) на
оF(х„)), где 6(х„) — некоторая оценка 0. Более интересен под-
подход, основанный на применении леммы 3. Именно допустим, что
функция g(Q) выбрана так, что
Я'(е)о(8)=с, B5)
где с — постоянная. В таком случае оценка g(TM(xn)) асимпто-
асимптотически нормальна JV(gF), c2n~l), и, следовательно, приближен-
приближенный а-доверительный интервал для ?F) имеет вид
g (Г" (х„)) - х,_«/2 (N @,1)) c/Vh~< g F) <
(Х„)) - *а,2 (# @,1)) C/Vn~). B6)
Так как функция g(Q) монотонна, то, разрешая неравенства B6)
относительно 0, получим а-доверительный интервал для парамет-
параметра 6. Для нахождения gF) необходимо решить дифференциаль-
дифференциальное уравнение B5). Приведем пример.
(I) В схеме испытаний Бернулли с неизвестной вероятностью
6, 0<9<1, из предельной теоремы Муавра — Лапласа
вытекает, что статистика
242

является асимптотически нормальной N(B, л~'8A—8)). Преобра-
Преобразование g(Q) находим из уравнения B5) для с= 1/2:
= arcsin У& .
Таким образом, статистика arcsin у Тп (х„) асимптотически нор-
нормальна W(arcsinV6, Dл)).
5. Асимптотическая нормальность выборочных квантилей.
Пользуясь представлением E) порядковой статистики Zft,n по-
повторной выборки из равномерного распределения на @,1), полу-
получаем
(^) B7)
где Sm = Xi + ... + Xm, m=\, .... n+l; Xh /=1 n+1 — неза-
независимые ел. в., распределенные экспоненциально G@, 1). Прово-
Проводя элементарные преобразования над B7), получаем
(l-p)Sfc-p(Sn+,-Sfe):= „ / {
— k
Допустим, что k^kn-*-oo, n-*-oo, так что kjn-*p, 0<p<\, напри-
например kn = [np]. Применяя к суммам
(Sk-k)lVJ, (Sn+l-Sk-(n-{- \-k))lVn+\-k B9
центральную предельную теорему для независимых одинаково
распределенных слагаемых, получаем, что каждая из величин B9)
имеет в пределе нормальное распределение N@, 1). Принимая во
внимание независимость ел. в. B9), используя лемму 2 и закон
больших чисел для Sn+i/(n+l), получаем, что B8) имеет пре-
предельное распределение Л'@, рA—р)). Таким образом, Zk,n асимп-
асимптотически нормальна N(p, p(l—p)n~x).
Пусть F(x) — непрерывная ф. р., обладающая плотностью Цх).
Тогда F'^Zk.n) распределена как k-я порядковая статистика по-
повторной выборки из распределения F(x) (см. конец п. 1). Вычис-
Вычисляя производную обратной функции F~l(z), находим
Допустим, что /(а„)>0, где хр — р-квантиль распределения F, и
применим лемму 3 с g(t)=F~x(t). В результате получаем следую-
следующее утверждение.
243

Теорема 2. Если ф. p. F(x) имеет положительную плотность
f(x) в окрестности квантили хр, 0<р<1, то выборочная квантиль
Х повторной выборки из F (а) асимптотически нормальна
(l/B'
p, p(p)/(p))
В порядке иллюстрации рассмотрим повторную выборку на
нормального распределения #(ц,о2). Среднее ц является медианой
распределения. Выборочная квантиль Х[П/2], „ асимптотически нор-
нормальна N{[i, яо2/2п). Выборочное среднее нормально М(ц, o2fn).
Отношение дисперсии выборочного среднего к асимптотической
дисперсии выборочной медианы равно 2/л=0,6366.
6. Асимптотическая нормальность оценок максимума правдо-
правдоподобия.
Рассмотрим повторную независимую выборку и предположим
для определенности, что модель непрерывна. Пусть 8(п)(х„) - со-
состоятельный корень уравнения правдоподобия
д/(п)(х„; 6)/ав = 0. (ЗС)
Положим при любых бев, 6>0
Точный смысл утверждения о состоятельности корня 1)(п)(х„) со-
состоит в том, что существует, возможно не всюду определенная,
статистика 8(п)(хп), я=1, 2, ..., для которой при любых вев и
6>0 имеет место предельное соотношение
(см. п. 2). Выражаясь не точно, можно представить себе, что при
каждом бев мера Ре в основном сосредоточена на подмноже-
подмножестве В(е% и в пределах этого подмножества уравнение правдо-
правдоподобия C0) имеет корень, лежащий в интервале (8—6, 8+6).
В таком случае при 6>0 достаточно малом возникает идея линеа-
линеаризовать уравнение C0) в окрестности любой точки 8 и найти
приближенное решение этого уравнения для хлеВвл1. Фиксируем
произвольное бо^в и запишем по формуле Тейлора линейное
приближение для левой части уравнения C0):
dim(*\ е) a("W, е„) + д*11п)(х„; е.)(е_6)+а(Хя. е)
+ (е6
39 дВ дВ*
Для х„ е BeJ'e отбросим остаточный член в C1) и найдем при-
приближенное решение 6<п)(хп; 90) уравнения C1):
¦д(п) /„ . л v ft _ dl (xn; 8e) / 3*1 (xn; 80)
е (х„, в0) -в0 — i ———
244

Покажем, что статистика 6<п)(х„; Во), рассматриваемая по мере
Ре,, при выполнении некоторых условий регулярности асимпто-
асимптотически нормальна. Эти условия следующие:
(Л) Плотность распределения f(x\; 6) отдельного наблюдения
дважды дифференцируема при Йев, в — интервал прямой.
(B) Операция дифференцирования по 6 перестановочна с ин-
интегрированием по х в интегралах
а с а* с
" \ f (х • 6)dx — I /(#,; 8)dxt',
ав J й92 J
(C) df(Xl; в)/ав = О при x: f(xt; 6)=0.
В этих предположениях (см. § 19, 20)
Mea/(X!; 8)/ав = 0,
/х, (8) =Me (dl (Хх; О)/дб)* = -Ме(дЧ (X,; 8)/ав2), C3)
где 1{х\\ 6)=ln/(xi; 6). Используя соотношения
п
ч(хг, в)/ае,
представим C2) в виде
2<) ео)-ео) =
где ел. в. X,-, i=l, ..., п, имеют распределение Ре,. Применяя
центральную предельную теорему для одинаково распределенных
слагаемых, получим с учетом C3), что первый сомножитель в пра-
правой части C4) имеет в пределе при п->оо распределение ЛГ(О, 1).
Ко второму сомножителю в C4) применим закон больших чисел
(см. теорему Хинчина, п. 1) и с учетом C3),получаем,что он схо-
сходится по вероятности к единице. Таким образом, статистика
6("'(х„; 6о) по мере Ре, асимптотически нормальна ЛГ(80, (IXt (80) х
хя)).
Итак, построена последовательность статистик 6<п)(х„; 8), п =
= 1, 2, ..., зависящая от параметра вев. При каждом фиксиро-
фиксированном 6 статистика 8<п)(х„; 8) асимптотически нормальна
#(8, (/*, (8)п)~') по мере Ре. Однако рассматриваемая по ме-
мере Ре'^ЬРе статистика б"(п)(х„; 8) уже не обладает хорошими
качествами как оценка 0'. Таким образом, никакая из совокупно-
245

сти статистик 9<n)(xn; 6), 8е6, не пригодна как оценка парамет-
параметра 6. Вспомним теперь, что при каждом веб статистика
8(п)(х„; 6) по построению «близка» в области Ве'.в к оценке урав-
уравнения максимума правдоподобия 8(п)(хп). Можно сказать, что ста-
статистика 8<п)(х„) приближает всю совокупность статистик
§<п)(х„; 6), 8еЭ, причем каждую отдельную статистику
8("'(хп; 8) — в области переменного х„, имеющую Рв-меру, близ-
близкую к единице. Точный смысл утверждения состоит в следующем:
при каждом фиксированном 8oS0 имеет место сходимость по ве-
вероятности
(в(п)(Хл)-ео)/(е(я)(хл; во)-
C5)
Мы докажем C5) при одном дополнительном условии регуляр-
регулярности:
(D) существует третья производная по 8 плотности {(х; 8),
\d4(Xi; 8)/ав3|<А(х,), МвЛ(Х,)<оо, ве=е,
где h(x\) — некоторая независящая от 8 функция.
Для доказательства соотношение C5) запишем для левой ча-
части уравнения правдоподобия C0) разложение по формуле Тейло-
Тейлора до квадратичного члена:
а/(п)(хя; ео)
ае
ае*
ае»
C6)
где 8i=8i(xn; 8) лежит между во и в. Решение 6(п)(хп) уравнения
C0) с учетом C6) и C2) представим в виде
- у
.; eo)-eo)(i + [±
Выше было установлено, что
л дЧ1п) (Хя; %
Далее, в силу условия (D)
-р-^-/х, (в0),
C7)
C8>
1=1
246

-J- J] Л (X.) -^-* const, «-+ oo. C9)
Из C7), C8), C9) и состоятельности оценки 8(х„) вытекает
C5). Принимая во внимание лемму 2, получаем следующий ре-
результат.
Теорема 3. Предположим, что информация по Фишеру
ht (б), 8ев, положительна и выполнены условия (Л), (В),
(С), (D). Тогда любая состоятельная оценка уравнений максиму-
максимума правдоподобия асимптотически нормальна N (8, (/х, (8) я)).
В условиях теоремы запишем по формуле Тейлора
от(п>(хп; е> = av(n)(xn; е„) + (в _e ач№(х„; ер D0)
ae» ae»
Подставляя в D0) состоятельный корень 6 = 6(n>(xn) уравнения
правдоподобия C0) и используя (/)), получаем
| 1 ау(л)(хп;е(л)(хп))
дб*
Поскольку
п
— У h (X.) -р-* const, 8(я>(Хл)—80-=-*0, л-*оо,
то, применяя к правой части D1) лемму 2, заключаем, что
я-1 <э*/(л> (х„; е(л) (Х„))/ав« -я ^/(л) (хп; ео)/ае» -^ о, я
Отсюда и из C8) выводим, что
/г1 <э*/(л> (х„; е(л> (хя))/ае* --* /х, F). D2)
Соотношение D2) показывает, что при достаточно больших я на
множестве Р0-вероятности, сколь угодно близкой к единице, спра-
справедливо неравенство
д2/<»>(х„; е<»>(хп))/ав2<0,
т. е. состоятельный корень 6(х„) уравнения правдоподобия на са-
самом деле является локальным максимумом функции /(п)(х„; 6).
Более того, если Щп) {хп), в2Л)(х„)— два состоятельных корня
уравнения правдоподобия, то либо функция /(|1)(хп; 6) постоянна
на отрезке с концами б1Я>(хп), Of* (х„), либо между ними найдет-
247

ся точка 6з(п)(хл)> являющаяся локальным минимумом функции
ftn)(xn; 6). В последнем случае, очевидно,
0. D3)
Так как корень уравнения правдоподобия взп>(хп) заключен меж-
между состоятельным» корнями 0{п) (хя) и Oj^^xJ, то он также яв-
является состоятельным, и из D2) и D3) вытекает, что
x.hi» о-
Но это противоречит предположению /*, F) > 0, 6 е 6. Итак,
получен следующий результат.
Теорема 4. Предположим, что выполнены условия теоре-
теоремы 3 и производная df{x; 6)/58 не обращается в нуль тождест-
тождественно ни на каком интервале значений вев. Тогда с Ре-вероят-
Ре-вероятностью, стремящейся к единице при n-*-oo, и любом ве© функция
правдоподобия имеет единственный внутренний локальный макси-
максимум 6<п)(х„), который представляет собой асимптотически нор-
нормальную N (в, (/.v, F) л)~') оценку параметра в.
Следствие 1. Если функция правдоподобия /(п)(х„; 6) до-
достигает максимума во внутренней точке, то теорема 4 применима
к оценке максимума правдоподобия.
Следствие 2. Пусть ф(8) — дифференцируемая параметри-
параметрическая функция и ф'F)#0. В условиях теоремы 3, воспользовав-
воспользовавшись леммой 3, выводим, что фF(п)(х„)) асимптотически нормаль-
нормальна #(ф(8), ф'(8J(/х, (8)п)~'). Если фF) — обратимая на в
функция, то, выбирая в качестве нового параметра ф = ф(8), по-
получаем для функции правдоподобия в новой параметризации
= /(П)(хп; 6),
Ф(в))/Ар)
и, следовательно, оценка ф(п)(х„) уравнения правдоподобия
дЬп)(х„; ф)/дф=0 совпадает с оценкой ф(8(п)(хп)), что дает неза-
независимый вывод асимптотической нормальности последней оценки.
В случае, когда 6(п)(хп) является оценкой максимума правдоподо-
правдоподобия, заключаем в условиях теоремы 4, что оценка максимума
правдоподобия ф(8G1)(хп)) асимптотически нормальна # (ф@), ф'
7. Асимптотическая эффективность оценок максимума правдо-
правдоподобия.
Для выборки конечного объема оценка параметрической
функции фF), дисперсия которой совпадает с нижней границей
неравенства Фреше — Рао — Крамера, называется эффективной.
248

В § 19 было установлено, что эффективные оценки существуют
только в экспоненциальных моделях н при этом только для па-
параметрических функций вида ф(9) =<хфо(9)+р, где фо(9) опреде-
определяется по модели однозначно, а, р — произвольные постоянные.
Роль дисперсии как меры разброса оценки вокруг среднего на
самом деле не очень велика, если оценка хотя бы приближенно
не является нормально распределенной с параметрами, равными
ее среднему и дисперсии. Действительно, информация о разбросе
распределения оценки, которую дает дисперсия, полностью описы-
описывается неравенством Чебышева, а это довольно грубое приближе-
приближение по сравнению с нормальным приближением, если последнее
имеет место.
Переходя к выборкам большого объема, из теорем 3, 4 и след-
следствия 2 мы имеем, что асимптотическая дисперсия оценки макси-
максимума правдоподобия (или оценки уравнений максимума правдо-
правдоподобия) параметра 6 и любой дифференцируемой параметриче-
параметрической функции ф(9), ф'(9)#0 эквивалентна нижней границе нера-
неравенства Фреше — Рао — Крамера при л->оо. По этой причине
такие оценки называют асимптотически эффективными. Хотя дис-
дисперсия оценок максимума правдоподобия 6<л)(х„) может и не су-
существовать или быть больше, чем (/х,(в)л)~', указанное об-
обстоятельство практически не играет никакой роли для асимпто-
асимптотической задачи оценивания: оценка 6(п)(х„) при больших п при-
приближенно нормальна со средним 0 и дисперсией (/х, Ф)п)~\ так
что именно асимптотическая дисперсия оценки 8(п)(хп) определяет
ее разброс (или концентрацию) вокруг оцениваемого парамет-
параметра в.
8. Асимптотическая достаточность.
В условиях регулярности (А) — (/)) запишем разложение лога-
логарифмической функции правдоподобия по формуле Тейлора:
; 8)=/W)(xn; QJ + dl %; е°> (8-80) +
+± «-W.«.) F _ 6оJ + ^ от»Чу Ц (е -уз, D4)
где |8,—8о|<|9—80|.
Подставляя в D4) 8о=9(п)(х„) — состоятельный корень урав-
уравнения правдоподобия д/<п)(х„; в(||).(хп))/дв»"О и проводя элемен-
элементарные преобразования, получаем
/(п)(х„; 8)=/<л)(хп; bw(xn))-
- y h. F) {Vn(Q -V» (xn))Y + r« (xn; 6), D5)
249

где
у. п
Так как при п-*-оо
(е_
-(в_1
1-1
«Iв —в(г0(Хп)| >0
то
D6)
Перепишем D5) в виде
/(*; 8) -...•/(*„; 6) =/ (Xl; е(п) (х„)) •...•/ (х„; 8(п) (х„)) х
хехр (—]-1х, (8) (/п (8-6"" (х„))J) ехр (г<"> (х„; 8)). D7)
Из соотношения D6) вытекает, что при любом б>0 Ре-мера мно-
множества
{хп:|ехр(г(»)(хп; 6))-1|<б} D8)
стремится к единице при п-+оо. Если рассмотреть меру Р9 лишь
на множестве D8), то из D7) получается, что плотность меры
Ре ^точностью до множителя, близкого к единице, факторизует-
ся и 6('"(Хп) — достаточная статистика этой факторизации. В свя-
связи с этим статистику §<"'(х„). называют асимптотически достаточ-
достаточной. Напомним, что достаточность статистики означает независи-
независимость условного распределения выборки при условии статистики.
Поясним, что в этом отношении можно сказать в случае асимпто-
асимптотической достаточности, записав дискретный вариант соотношения
D7):
Рв(хя)=*(хя)ехр(—1-/х, (8)(V^@-8(n)(xn))J) ехр (г<"> (х„, 8)).
где g(x,,) = Рп(х„) при 6=0(")(x>i)- Отсюда для условной вероят-
250

постн выборки х°п при условии 8<")(xll)=< получаем выражение
(ср. п. 5 § 15)
Ре(*п°) = g(xg)exp(f<n'(xg; 6))
Ре (х„ : в"" (х„) = /) ? g (xn) ехр (г(л> (х„; в)) '
где х°„ таково, что в(п)(х°„)=Л Так как верно D6), то для выбо-
выборок х°„, имеющих подавляющую Ре-вероятность, условная вероят-
вероятность D9) асимптотически не зависит от 0.
9. Векторный параметр.
Когда параметр 6=@ ,8*) — векторный, то интерес пред-
представляет совместное асимптотическое поведение оценок
(8(in) (х„) О*0 (х„)) = 8(п) (х„) уравнений правдоподобия
„; в)/ав, = О, i-l к. E0)
При условиях регулярности, аналогичных (А) — (D), векторная
оценка 0("'(х„) параметра 6 в повторной выборке является со-
состоятельной (т. е. каждая ее компонента состоятельна) и асимпто-
асимптотически нормальной: распределение случайного вектора
У/7(в<">(Хп)-8) E1)
рассматриваемого по мере Ре имеет пределом 6-мерное нормаль-
нормальное распределение Nk(e, I~xl(ty), где /х,(8)— информацион-
информационная матрица Фишера отдельного наблюдения. Таким образом,
асимптотическая матрица ковариаций (IXi(B)n)~l оценок 8(п)(х„)
совпадает с нижней границей неравенства Фреше — Рао — Кра-
Крамера, и потому векторную оценку 8(п>(х„) называют (совместно)
асимптотически эффективной.
Наметим доказательство асимптотической нормальности, кото-
которое повторяет рассуждения для скалярного параметра. Запишем
линеаризованную в точке 8°= (8° 0°*) систему уравнений
правдоподобия
б/ Лш
6,-6^ = 0, i-l k. E2)
Случайный вектор
(Х„, 8)-^ J
251

представляется в виде суммы независимых одинаково распреде-
распределенных векторов:
grade«"" (X,; 6); Мgrade / (X,; 8) =0,
Mfl ((gradg /(n) (Xi; 8))' (grade I(n) (X,; 8))) = /x, (8).
Кроме того,
??*• •••'-' *]--'<-
Обозначив решение системы E2) через
8(л)(хп; в«)=EГ (х„; в»), .... вГ(х„; в»)).
подставляя 8*">(Xn; 8°) в E2) и переходя к случайным векторам
Хп, после элементарных преобразований получаем
ft
ft
L
П
По центральной предельной теореме для сумм независимых оди-
одинаково распределенных векторов предельное распределение векто-
вектора правых частей системы E3) — нормальное Nk@, /X| (8°)).
Каждый элемент матрицы системы E3)
E4)
сходится по мере Pfl0 в силу закона больших чисел к своему ма-
математическому ожиданию — соответствующему элементу матри-
матрицы /л, (8°). Матрица /х, (8°) предполагается положительно
определенной, так что с Pflo- вероятностью, сколь угодно близ-
близкой к единице, при л-*-<х матрица E4) невырождена. Разрешая
систему E3), получаем
Vn( 8(л)(Хл; в»)-в») =
т*2^- '¦'-> *Г-
Вектор ^л(9<"'(х„; в0)—8°) представляется, таким образом, в виде
252

произведения асимптотически нормального случайного вектора на
случайную матрицу, сходящуюся по вероятности к постоянной
матрице /*,' F°). Обобщая лемму 2, легко вывести отсюда, что
вектор Ул(В(м)(Х„; 8°)—8°) асимптотически нормален по мере
Рвв с асимптотической матрицей ковариаций, равной (ср. A) §10)
(/*,' (8°))' /х, (8°) (/*,' (8°)) = /*/ (8°),
где использована симметрия матрицы Фишера. Остается провести
оценки остаточных членов разложения по формуле Тейлора, как
это делалось для скалярного параметра, и показать, что состоя-
состоятельный корень 6(л>(х„) системы уравнений правдоподобия E0)
по вероятности Р^е эквивалентен (Кп)(.сп; 8°):
(8)п) (Х„) -е?)/F/(п) (х„; е«)- ей —0-> 1. / = 1 *.
10. Оценивание параметров сдвига и масштаба.
Найдем выражение для информационной матрицы Фишера по-
повторной выборки из семейства сдвига-масштаба с плотностью
crlf((x— |x)/o), где f(x) известна. Положив g(x)=\nf(x), имеем
/<"> fa; |i, a) = -In a + g (fa— ц)/а),
= —а~1 —а~2 (хк—
дЧ<п>/д\1*= o~*g" ((д
= а~2 + 2сг3 fa— ц) g' (fa—
= ar-*gr' ((xt- |i)/e) + a-8 fa -\i) g" (fa—
Обозначив через Y\ = (X—ц)/о нормированную ел. в. и учитывая,
что
Х1; ц,
0 = МмлЙ<"> (X,; ц, o)/Aj =0-^^ A + a-1 (Xt-\i) g' ((Xt —ц)/о)).
получаем
Систему уравнений правдоподобия
? Г' ((** -Ц)/<») =0, ? A + О-1 (xf -ц) «Г' ((х, -ц)/в)) = О
253

в общем случае приходится решать численно. Оценки уравнений
правдоподобия ц(п)(х„), а(п)(Хл) асимптотически нормальны
w2((n, о), (/*,(ц. о)я)), где /x.Oi, а) определяется формулой
E5). Подчеркнем, что асимптотическая ковариационная матрица
оценок зависит только от параметра а.
Если плотность f(x) симметрична относительно нуля: /(*) =
-/(-*), то g(x)=g(-x), g'(-x) g'(x), g"(-x)=g"(x), от-
откуда
Мо.1У,4Г(У,)-0.
Следовательно, матрица /*, (ц, о), а также матрица /х,1 (ц. о)
диагопальны. Таким образом, матрица ковариаций двумерного
нормального вектора, предельного для случайного вектора
является диагональной, т. е. предельное нормальное распределе-
распределение соответствует независимым компонентам. В таком случае го-
говорят, что оценки ц(п>(Х„) н о("'(Х„) асимптотически независимы.
Если плотность f(x) несимметрична, то, изменяя начало отсче-
отсчета, можно обратить внедиагональные элементы матрицы /\, (8)
в нуль. Действительно, положим
iYi) E6)
и введем новую параметризацию, положив j(x) =f(x+a), g(x)=*
= \nj(x)=g(x+a), и рассмотрим повторную выборку х\, ..., хп
из распределения a~lJ((x—ц)/а). Обозначая через М,,,,, операцию
математического ожидания по мере с плотностью а~7((*—м)/°К
получаем
олК,? (К,) = VL^xYjT Wi) = Mo., ((^-а) ? (К, - а)) =
= Mo., (Kt- a) f[ (Кх) = M0AYlg" (К,) -aM0Ag" (KJ = О,
,) = M_.i? (У,) = Мо.1? (К, - о) = Mo,i/ (YJ,
,) = JVU.iV?? (^х) =Мол (Уг -вI? (Kt- a) =
где при последнем переходе использована формула E6). Таким
образом,
где а определяется в E6), так что оценки ц.(п)(х„), а(п)(х„) асим-
асимптотически независимы. Точку а называют центром расположения
распределения, задаваемого плотностью f(x). Асимптотическая не-
254

зависимость оценок ц(п)(хи), о(п)(х„) облегчает их использование,
в частности расчет асимптотических доверительных интервалов.
Отметим, что условие регулярности (D) (точнее, его векторный
аналог) оказывается слишком ограничительным для данной мо-
модели, если рассматривать область параметров —оо<|д< + оо,
ст>0. При о-*-0 плотность a~lf((x—\i)/a) стремится к бесконечно-
бесконечности в окрестности точки x — \i и прсзводные по \i, а от l(x\ \i, a) —
— \п(о~1}((х—ц)/о)) не будут равномерно по ц, а ограничены ни-
никакой функцией Л (а-). Но если ограьмчить область изменения па-
параметров неравенствами |p,|<ci, ст>-С:.>0, где с\, с2 — произволь-
произвольные постоянные, то бтмечеиных затруднений уже не возникает.
Так как с\ можно взять сколь угодно большим, а с2 — сколь угод-
угодно малым, то сужение параметрический области не существенно
с. точки зрения приложений. Рассмотрим примеры.
(II) Для повторной выборки из нормального распределения с
плотностью а~1у((х—ц)/сг) получаем
g (х) = In ф (х) = — In ] 1я — х*/2,
g' (х) = -х,
Оценки максимума правдоподобия равны \i = x, a =
= 1/ —V(*<— ~х)г (см пример (II) § 20), а их асимптотичес-
Г "Я
кая матрица ковариаций равна по формуле E5)
1
0
О. м. п. для ф(ст)=(Т2, равная ф(ст)=ст2, имеет асимптотическую
дисперсию (ф'(ст)J DJl,<ra=4d2(i2n-12-1 = 2(i4n-1. Асимптотическая и
точная матрицы ковариаций оценок ц, ст2 равны соответственно
(см. пример (II) § 19).
'аг/п 0 1 Г ог/п 0
0 2а*/п J И [ 0 2о*(п—
Отметим, что условия регулярности (А), (В), (С) в рассматри-
рассматриваемом случае выполняются, а для выполнения (D) надо ограни-
ограничить область изменения параметров до |(.i|<Ci, a>c2, где о, с* —
произвольные положительные постоянные.
(III) Для повторной выборки из гамма-распределения с изве-
известным параметром формы р и плотностью f(x. ц, а) =
= <г7((*—\хIа), где
-*, х>0,
255

условия дифференцируемости плотности f(x, ц, а) могут нару-
нарушаться в точке \i=x. Приняв р>3, обеспечим существование вто-
вторых производных (условие (А)) и возможность перемены поряд-
порядка дифференцирования по параметрам и интегрирования по .v (ус-
(условие (В)). Условие (С) также выполнено (см. § 19, соотношения
A5) и далее). Если допустить, что р>4, то при ограничении об-
области изменения параметров до |(.i|<ci<<x, a>-c2>0 выполняет-
выполняется также и условие (D).
Имеем (см. C), D) § 7)
g(x)= -1пГ (р) + (р-1) lnx-х, g' (х) = (р- 1)/х- 1,
g"{x)-.-(p-\)lx\
Мол/ (Ух) =Мо., (- (р- \)IY\) = - 1/(р-2),
Mo.iK,/ (Уг) = -1, МолЯ/ (К,) = -(р-1).
Асимптотическая матрица ковариаций о. м. п. равна
)-1
1 р \ 2« [-1 (р-2)
Если начало отсчета перенести в центр расположения распре-
распределения
^"(У1) =р-2,
т. е. оценивать ц'=ц + а вместо ц, то по формуле E7) находим
Как видно, асимптотическая дисперсия о. м. п. ц'(х„) в р/2 раз
меньше дисперсии ц(х„); нетрудно проверить, что она совпадав!
с асимптотической дисперсией о. м. п. ц'(х„) в модели с извест-
известным а.
§ 24. АСИМПТОТИЧЕСКИЕ СВОЙСТВА КРИТЕРИЯ ОТНОШЕНИЯ
ПРАВДОПОДОБИЙ
1. Скалярный параметр.
Рассмотрим для повторной выборки асимптотические свойства
критерия отношения правдоподобий, введенного в п. 5 § 21, пола-
полагая, что нулевая гипотеза — простая, альтернативная — слож-
сложная:
#0:8 = 80, Я^бев,, в={60}ив1,
а параметр 8 — скалярный. Статистику критерия возьмем в виде
(х„) = L<"> (х„; Ъ* (xJ)/LM (х„;
256

где ^(п)(х„) — оценка уравнения правдоподобия р^
модели (Я?, 3S, {Ре, 8е6}). Будем предполагать выполненными ус-
условия регулярности (А) — (D) п. 6 § 23, так что имеется единст-
единственный (с Ре-вероятностью, стремящейся к единице при п-*-оо)
состоятельный корень 8<п)(Хл) уравнения правдоподобия, являю-
являющийся асимптотически нормальным N(b, ('яДв)/*)-1). Исполь-
Используя формулу Тейлора, имеем
\(хп) = №(хп; ес»(хп))-/<'"(хп; 80) =
= <Э/<"> (х„; .%)№ (8<«>(х„)-80) + -1-дЧ™ (х„; 80)/<Э6* (в<"> (хя)-
д№(хп; QJ/dQ(№(xn)%), A,
«5!
(х„; во» (хп))/дв-д1М (хп; во)/<Эв=
n; eo)/d0* (9"> (х^ — 00) +^-W»(xn; 84)/а83 F"» (х„)-80)з,
B)
где |е«—6о|<:|8<п)(хп)—6о|, t= 1, 2. Используя в B) равенство
«5/<п> (Хп; ее» (х„))/ав = О
и подставляя выражение для производной дЛп>(х„; 80)/д8 из B)
в A), получаем
1п Г<«) (х„) = - 1/2^/С) (хп; ej/de* (в<«) (хп) -80)« + 2г„ (х„), C)
где для остатка 2гп(х„) имеем (ср. C7), C9) § 23)
л
МХ„I< — y.h(X№n4Xn)-%\{Vn@*n)-W2 — 0 D)
" Я
при п-»-оо. Используя закон больших чисел и асимптотическую
нормальность оценки 8<п)(х„), выводим, что статистика
- -J- ^.! (в„) WW (х„; \)l№nIXl (в,) (бе» (х„) - 6^ E)
по мере Ре, имеет предельное распределение х2 с одной степенью
свободы. Отсюда и из C), D) заключаем, что статистика
21п 7"(">(х„) в предположении гипотезы Но имеет Х12'РаспРеДе-
ление.
Знание, хотя и приближенное, распределения статистики кри-
критерия делает возможным его практическое использование при
больших п. В критическую область включают большие значения
статистики критерия:
{хп:21пГС)(хп)>.г,_а(Х?)} F)
где Xe(Xi2) — а-квантиль распределения xi2- Размер критерия F)
257

с ростом п стремится к а. Статистику критерия F) можно заме-
заменить при больших п статистикой E) и получить критерий в форме
{х„: - дЧЫ (v, QJ/dQ* (в<«> (х„)- 80)г > *,-« (XI)}. G)
В свою очередь, используя соотношения
-L да (Х„; 80)/<Э8* -» - /л, (8о) ,
п р
ре.
ре.
можно вместо G) предложить любую из следующих критических
областей:
(8)
{х„ : Л*, (8<"> (х„)) п @(«) (х„) -%)* > *i-«(X)?)}. (9)
Используя представление (см. C7), C2) § 23)
8>>(ХП)-00 = -<Э/<">(ХП; 8„)/де №> (Х„; в^/дб»)-» х
хA^гп(Х„, в0)),
где
г„(Х„; во)^О, п-^оо,
ре.
имеем
/л. (в0) п @"» (х„) -W - /л. (во) (у^д№ (хп; в,)/5в j' x
х (J-a*/(")(xn; 9J/dWy*(\ + rn(xn; %))*. A0)
Так как предпоследний множитель в правой части (Ю) стремится
по мере Ре„ к /А.'Чбо), то из (8) получаем еще один критерий:
(Щ
Практическое удобство критерия A1) состоит в том, что для его
применения не требуется вычислять о. м. п. 6f<n)(xn).
Проведенные рассуждения показывают, что критические обла-
области F) — (9), A1) в предположении, что справедлива гипотеза
#о, асимптотически эквивалентны: любые две из них отличаются
на множестве, Ре,-мера которого стремится к нулю при п-*-оо.
Покажем, что функции мощности этих критериев в любой точке
6|, такой, что Ре,=?Ро.> стремятся к единице при п-*-оо. Рассмот-
Рассмотрим, как ведет себя статистика критерия F) по мере Ро,. когда
п-*-оо. Имеем
258

21n7-c)(xn)-2(/c>(x(n); Ихп))-^»(х„; в,))-:-
+ 2(f<">(xn; в,) —/<">(хя; 80)). A2)
Как мы уже знаем, первое слагаемое в A2), в предположении, что
верна гипотеза 6 = 8i, имеет в пределе Х12-распределение. Отсюда
вытекает, в частности, что для любого е>0 и всех достаточно
больших л
Ре, (х„: № (х„; 6"" (х„))-/<"> (х„; 8J) > 0) > 1 -е. A3)
Далее,
л
('(п)(; 8)/""( 6))iJ]l(/( 8)//(х,; 80)),
и так как (см. § 22, соотношение A7а))
о = Мв|1п(/(Х1; ej/AX,; 80))>0,
то
n-i (/w (Х„; 8,) - /<"> (Х„; 80)) — а > 0, п -+ оо.
ре,
Следовательно, для любого е>0 и всех достаточно больших п
Ре, (х„: л-* (/<«) (хл; в,) -/<"> (х„; в0)) > а/2) > 1 -е. A4)
Из A3) и A4) получаем для достаточно больших п
Р(л) (9i) = Ре, (х„: 2 In Л") (х„) > х,_а (х?)) ^
^ Рв, (х„: 2 (/<") (х^бО -/<«) (х„; 90)) > па) - е > 1- 2е.
Итак, для любой простой альтернативы 6|, такой, что Ро, т^Ре..
функция мощности критерия F) стремится к единице при п-*-оо.
Такое свойство критерия называют состоятельностью. Состоятель-
Состоятельными являются и все остальные критерии G) — (9), A1). Действи-
Действительно, в случае критерия (8) запишем
Vn (во) (х„) -80) = Vn (В"» (хп)-8,) + VT (8,-8,,). A5)
Первое слагаемое в правой части A5) асимптотически нормально
N @, /х, Fj)) по мере Ре,. Поэтому для любого е>0 найдется
t,>0, такое, что, начиная с некоторого п, множество
(Ь"Цхп) -8,J</e} A6)
имеет Ро,-меру большую, чем 1—е. Если к тому же п удовлетво-
удовлетворяет неравенству
It (%) КЛ^-во! > (х,_а (X?»l/a + tT,
то из A5) следует, что
P(n) (9i) = Ре, (х„: /х, (в0) п (§»•) (х„) - в0)* > .г,_а (Х^)) > 1- е.
259

Состоятельность критерия (9) доказывается аналогично, если
учесть, что
/х,(е(л)(Хп)) — /x.(Oi), л-оо.
ре,
Так же нетрудно установить состоятельность критериев G), A1).
Сравнить состоятельные критерии можно, изучая порядок бли-
близости к единице их функций мощности при различных 8. Можно
сравнить их по поведению функции в точках 0=8П, таких, что
8„-»-6'о, п-*-оо. Заметим, что асимптотически эквивалентные крите-
критерии имеют, вообще говоря, не эквивалентные при я-»-оо ошибки
второго рода. Это легко обнаружить, сравнивая, например, ста-
статистики критериев (8) и (9): при одном и том же члене
л((Г(т|)(х„)—воJ стоит множитель /х,(О0) в (8) и множитель,
близкий к /х, (8) по мере Ре, в (9).
Стоит отметить, что статистика критерия A1) является квад-
квадратом статистики локально наиболее мощного против односторон-
односторонних альтернатив критерия из п. 4 § 21. Поскольку двусторонний
локально наиболее мощный критерий существует лишь в исклю-
исключительных случаях, то компромиссная область A1) может рас-
рассматриваться как «оптимальная» для двусторонних близких аль-
альтернатив.
2. Векторный параметр.
В случае векторного параметра 0=(8i 8/,), пользуясь раз-
разложением по формуле Тейлора и асимптотической нормальностью
Nk (в, (/х, (в) й)) оценок 0(л> (х„) и асимптотической нормально-
нормальностью Nk{0, /х,(в)л) вектора grade(/"(Х„; в), получаем, что стати-
статистики векторных вариантов критериев F) — (9), (И):
W? (х„) = п (§(«) (х„) -в») Ix, (в») (Sw (х„) - &>)',
х„) = п (в<«> (х„) -6°) /Xl (всо (х„)) (в<«>(х„) -в»)'
имеют по мере Ре» предельное х*- распределение. Все эти крите-
критерии также являются состоятельными и асимптотически эквива-
эквивалентными.
3. Полиномиальное распределение.
Рассмотрим повторную выборку из распределения с исходами
1,2 ши вероятностями исходов р\, р2, .... рт\ Р1+Р2+...+
+рт=\. За вектор неизвестных параметров примем р =
= (Рь Рг, •¦-, Рт-\). Найдем вначале о. м. п. параметра р. Ис-
260

пользуя индикаторное обозначение, запишем логарифмическую
функцию правдоподобия отдельного наблюдения:
т—\
/¦=1
где /л=1, если А верно, /» = 0, если Л неверно. Далее,
т—1
п) (х„; Р) - ?l (jr': p) = S ln p/ E 7(*/=/} ^
л
+ In A —pi— . . . —pm-l ) Y h*^™)'
n
Xn; P)/3p, = PT1 ? /{x .=/) - A - pt— • • • - Pm-\ )~X X
Уравнения правдоподобия запишем в виде
Складывая соотношения A7), имеем
Подставляя A8) в A7), получаем p/n) = vJ"Vn, i= I
... ,m—1, где через v/n)/n обозначена частота нехода /'; /=1,
..., т—1.
Также и о. м. п. параметрической функции рт является частота
VCTJ/m исхода т. Статистика Н^'"' имеет вид
Найдем матрицу Фишера отдельного наблюдения. Имеем
d*l(x1;p)/dp2l = -pT2Ilxi_l)-(\-pl-...-pm-i)-
d*l(Xl; p)/dp,dpk=-(l-pl-...-Pm_l)-4{xi_m}, 1
p)/drf=-PTl-Pm\
р p)/dPidPk = -P-\ j ф k.
261

" 1
1
_ 1
1
1
1
... 1"
... 1
... 1
+
pTl 0 ... о
О рТ1 ... О
_ _ _ о о
Вычислим статистику W™:
п (v(n»/n—р) Ixt (P) (v("Vn—Р)'
m—1
/я—1
(=.1
Поскольку первое слагаемое правой части A9) равно
т-1
Р- ! ? Wn)- «ft) i2 =
-1
т—1
1=1
/п-1
i=l
то получаем
«р»
A9)
B0)
Итак, статистика W^ имеет предельное распределение Xm_i
Критерий со статистикой A9) называется х2-кРитер"ем Пирсона.
Выпишем статистику Wf\ используя A9), B0):
п (v(">/n —р) Ixt (v<n>/n)(v(n>/n—р)' =
m-l
-1 (v[n)- np,J1 =
Критерий со статистикой
1=1
v[n)
также называют критерием % •
Пример [5]. При считывании шкалы, когда последняя циф-
цифра оценивается на глаз, часто наблюдается предпочтение одних
цифр другим. Следующие данные представляют частоты послед-
последних инфр при 200 считываниях шкалы:
262

v/
0
35
1
16
2
15
3
17
4
17
5
19
6
11
7
16
8
30
9
24
Если считать, что наблюдатель не имеет предпочтений, то мы
имеем дело с повторной выборкой объема л = 200 из полиномиаль-
полиномиального распределения с 10 равновероятными исходами: гипоте-
гипотеза Но. Рассчитаем значение статистики A9):
v, —20
(v/-20)S/20
15
11,25
—4
0,80
—5
1,25
—3
0,45
—3
0,45
—1
0,05
—9
4,05
—4
0,80
—10
5,00
4
0,80
Получаемое значение есть 24, 90. По табл. 2.1а [1] для распреде-
распределения х2 ПР" числе степеней свободы 9 находим с помощью ли-
линейной интерполяции, что вероятностью наблюдать такое же или
большее значение равна 0,0031. Это выходит за предел минималь-
минимального уровня значимости 0,005, принятого в статистических табли-
таблицах, и гипотезу #о следует отвергнуть.
Рассчитаем для тех же данных значение статистики Wf\
Имеем
(V/-20)*
225
16
25
81
16
100
16
G.43
1,00
1,66
0,53
0,53
0,05
7,36
1,0
3,33
1.0
Значение статистики равно 22,55, вероятность наблюдать такое
же или большее значение равна 0,0074.
Для статистики W1"* имеем
v,7np/
In (Vj/npj)
v,- In (\j'npj)
1
0
19
,75
,56
,59
0
—0
—3
,8
,22
,52
0
—0
—4
,75
,29
.35
0
—0
—2
,85
,16
.72
0
—0
—2
,85
,16
.72
0
—0
—0
,95
,05
,55
0
—0
—9
,55
.59
.44
0
—0
—3
,8
.22
,52
1
0
12
.5
,405
.15
1
0
4
,2
,182
.32
Значение статистики равно 18,39, вероятность наблюдать такое
же или большее значение равна 0,030.

ЛИТЕРАТУРА
1. Большей Л. Н., Смирнов Н. В. Таблицы математической статистики.
М.: Наука, 1983.
2. Ф е л л с р В. Введение в теорию вероятностей и ее приложения, т. 1, 2,
М.: Мир, 1984.
3. А ил ер сен Т. Статистический анализ временных рядов. М.: Мир, 1976.
4. К о к с Д., Льюис П. Статистический анализ последовательностей собы-
событий. М.: Мир, 1969.
5. Хальд А. Математическаи статистика с техническими приложениями, М,:
ИЛ, 1956.
6. Шеффе Г. Дисперсионный анализ. М.: Наука, 1980.
7. Р а о С. Р. Линейные статистические методы и их применение. М.: Наука,
1968.
8. С а р х а и А., Гринберг Б. Введение в теорию порядковых статистик,
М.: Статистика, 1970.
9. Д ей в ид Г. Порядковые статистики. М.: Наука, 1979.
10. В а и дер Варден Б. Л. Математическая статистика. М.: ИЛ, 1960.
11. Л ем а н Э. Проверка статистических гипотез. М.: Наука, 1979.
12. Боровков А. А. Математическая статистика. М. Наука, 1984.
13. За кс Ш. Теория статистических выводов. М.: Мир, 1975.
14. Кокс Д., Хинкли Д. Теоретическая статистика. М.: Мир, 1978.
15. К о л м огор о в А. Н. Основные понятия теории вероятностей, изд. 2. М;
Наука, 1974.
16. Ширяев А. Н. Вероятность. М.: Наука, 1980.
17. Г н е д е н к о Б. В. Курс теории вероятностей. М.: Наука, 1969.
18. Р о з а н о в Ю. А. Теория вероятностей, случайные процессы и математи-
математическая статистика. М.: Наука, 1985.
19. С е в а с т ь и и о в Б. А. Курс теории вероятностей и математической ста-
статистики. М.: Наука, 1982.
20. К р а м е р Г. Математические методы статистики. М.: Мир, 1975.
21. Т у т у б а л и н В. Н. Теория вероятностей. М.: Изд-во МГУ, 1972.
22. И вч ей к о Г. И., Медведев Ю. И. Математическая статистика. М.:
Высшая школа, 1984.
23. Барра Ж.-Р. Основные поиития математической статистики. М.: Мир,
1974.
24. К е н д а л л М. Дж., Стьюарт А. Теория распределений. М.: Наука,
1966.
25. К е н д а л л М. Дж., Стьюарт А. Статистические выводы и связи. М.:
Наука, 1973.
26. Кендалл М. Дж., Стьюарт А. Многомерный статистический анализ и
временные ряды. М.: Наука, 1976.