Автор: Вайнштейн И.И. Федотова И.М. Ширяева Т.А.
Теги: математика теория вероятностей высшая математика математическая статистика
Год: 2004
Похожие
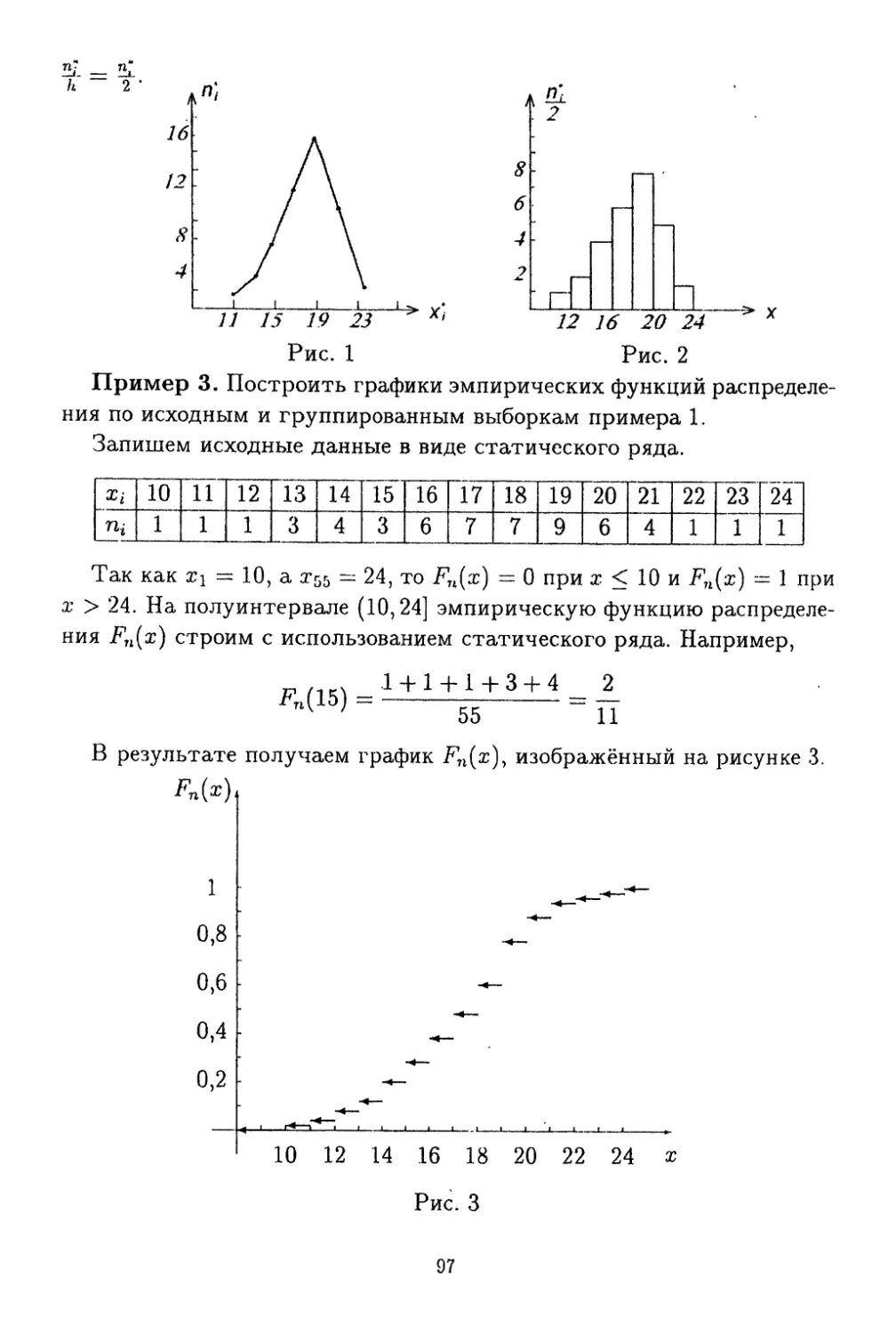
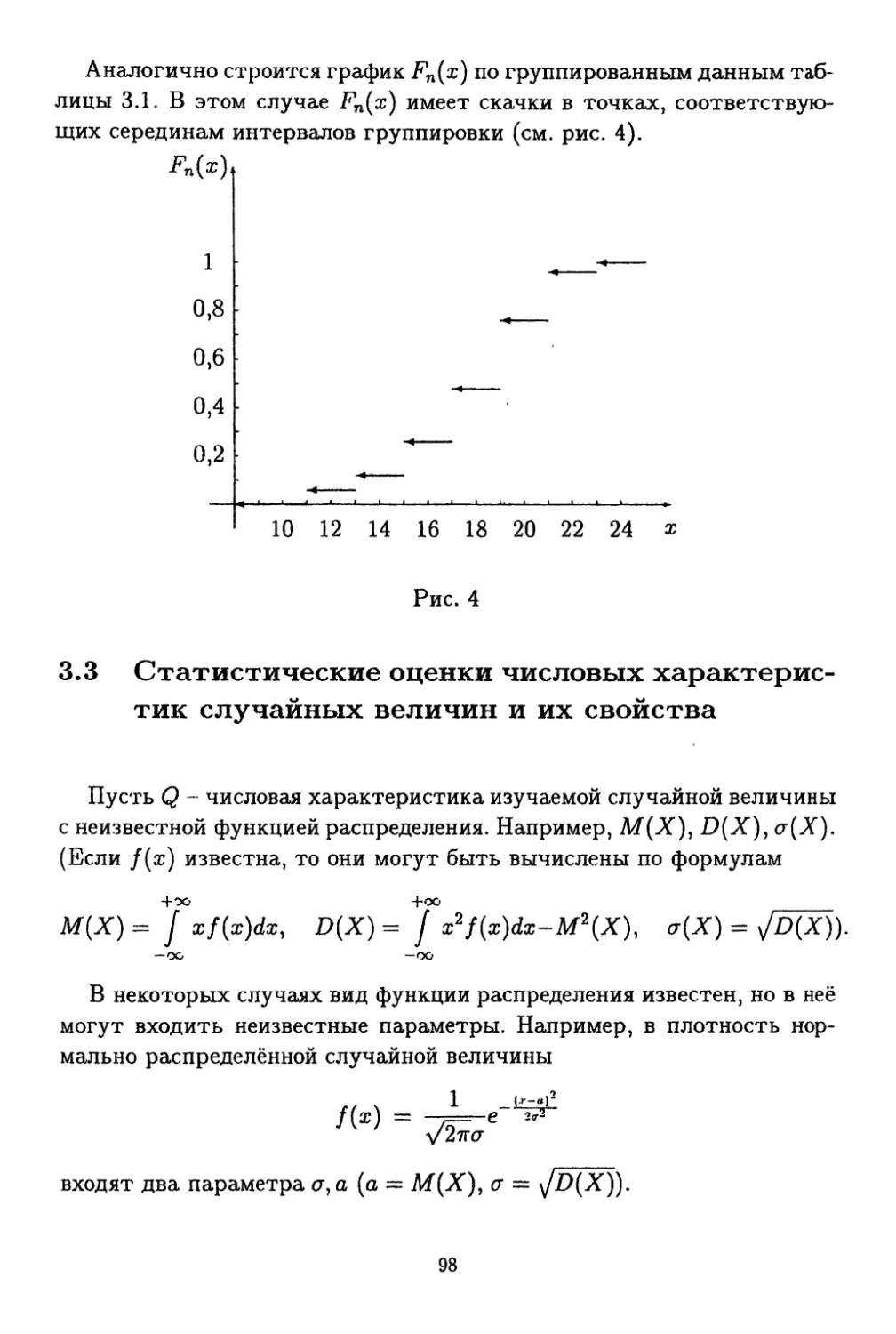
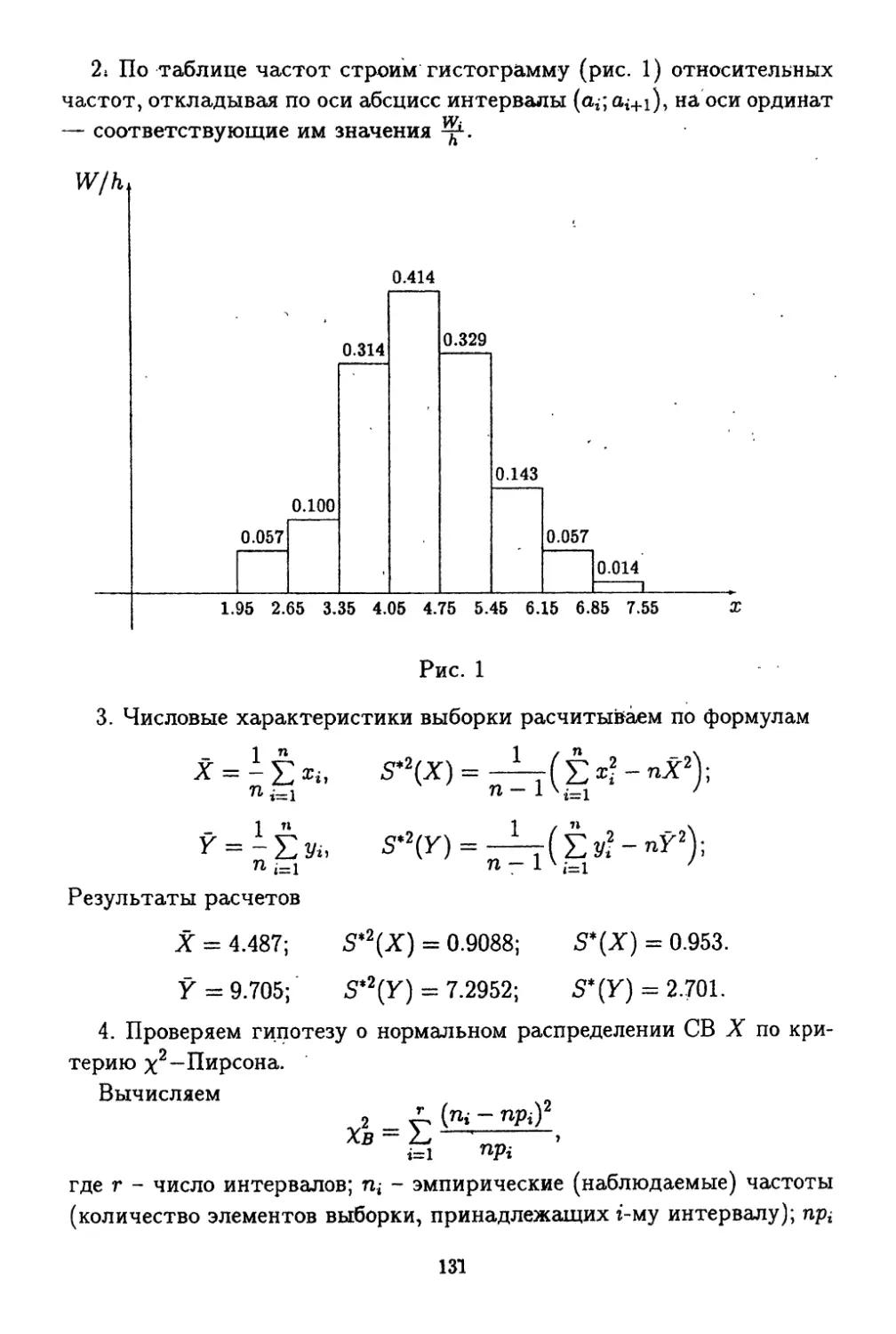
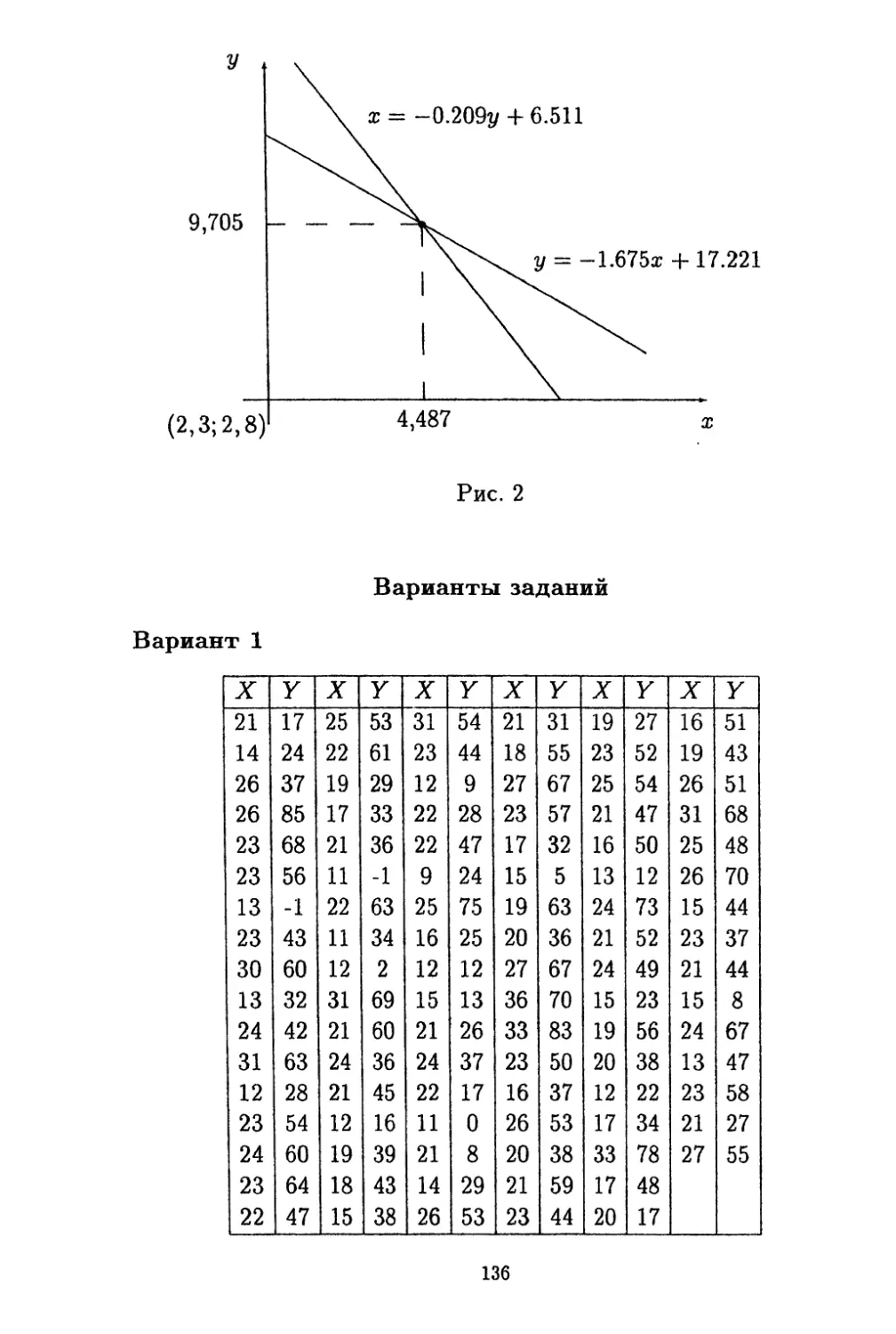
Текст
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ВЫСШАЯ МАТЕМАТИКА
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Красноярск 2004
УДК 51(07)
В93
Рецензенты:
А. М. Кытманов, докт. физ.-мат. наук, проф. КГУ;
И. О. Вогульский, докт. физ.-мат. наук, ведущий научный сотрудник
ИВМ СО РАН
В93 Высшая математика. Теория вероятностей и математическая статистика:
Учеб, пособие / И. И. Вайнштейн, И. М. Федотова, Т. А. Ширяева
Авторы:
И. И. Вайнштейн
И. М. Федотова
Т. А. Ширяева
Приведены теоретические сведения, методические указания по
решению задач по теории вероятностей и математической статистики
Студентам II и III курсов всех специальностей, обучающимся по
дистанционным технологиям
УДК 51(07)
@ Коллектив авторов, 2004
Печатается в авторской
редакции
Введение
Понятие вероятности восходит к древним временам, оно было из-
вестно уже античным философам. Мысль о том, что законы природы
проявляются через множество случайных событий, впервые возникла
у древнегреческих математиков. Она подробно изложена в поэме Лук-
реция Кара ”0 природе вещей”. Однако принято считать, что теория
вероятностей - сравнительно молодая ветвь математики. Ее развитие,
как самостоятельной науки, началось с переписки Паскаля и Ферма в
1656 году и было связано с решением задач, возникающих в азартных
играх. Эти задачи не укладывались в рамки существовавших тогда
математических моделей и стимулировали введение новых подходов и
идей.
В конце прошлого и начале этого века стали появляться более серь-
езные задачи естествознания (теория ошибок наблюдений, теория стрель-
бы, проблемы статистики), которые привели к дальнейшему развитию
теории вероятностей.
Основным объектом изучения теории вероятностей являются слу-
чайность или неопределенность, связанная с незнанием. Классический
пример -, выпадение герба при подбрасывании монеты. Но если рас-
сматривать случайные явления массового характера, то оказывается,
что и здесь действуют определенные закономерности. Поэтому корот-
ко можно сказать, что теория вероятностей изучает закономерности в
случайных явлениях.
3
Глава 1
Случайные события
1.1 Стохастические эксперименты. Пространство
элементарных событий
Исходными понятиями теории вероятностей являются понятия сто-
хаотического эксперимента и пространства элементарных событий. Сто-
хастическими называются эксперименты, результаты которых нельзя
предугадать заранее. Говоря об эксперименте в теории вероятностей,
мы не интересуемся его технической стороной, а только тем, какие
события в этом эксперименте могут наблюдаться, и что в результа-
те проведенного эксперимента действительно наблюдалось. Примеры
стохастических экспериментов: бросание монеты, бросание игральной
кости, проведение лотереи, азартные игры, стрельба по цели, поступ-
ление звонков на телефонную станцию.
Каждому стохастическому эксперименту можно поставить в соот-
ветствие некоторое множество Q, которое содержит полную информа-
цию о предполагаемых результатах при проведении этого экспериме-
та. Результаты эксперимента будем называть элементарными событи-
ями (или элементарными исходами). Элементарные события (исходы)
должны быть взаимоисключающими и равновозможными. Такое мно-
жество Q будем называть пространством элементарных событий.
Пример 1. Один раз бросают монету. Пространство элементарных
событий этого эксперимента имеет вид Q — {Г,Р}, где буква Г означа-
ет появление герба, буква Р - появление решки.
Пример 2. Бросают шестигранную игральную кость. Нас инте-
ресует число выпавших очков. Пространством элементарных событий
здесь будет множество Q = {1,2,3,4,5,6}
4
Пример 3. Вынимаем карты из колоды, содержащей 36 игральных
карт. Здесь 9 будет состоять из 36 элементарных событий, каждое из
которых есть одна фиксированная карта.
В приведенных примерах понятие равновозможйости элементарных
событий означает, что если взята монета, то она должна быть ’’пра-
вильной”, т.е. ее центр тяжести должен совпадать с центром симмет-
рии, то же относится и к игральной кости; а в колоде не должно быть
меченных карт.
В рассматриваемых примерах пространство элементарных исходов
О было конечным множеством. Но во многих задачах теории вероятнос-
тей приходится иметь дело с экспериментами, имеющими бесконечное
число исходов.
Примеры 4. Наудачу выбирают любое натуральное число. Данное
пространство элементарных исходов является бесконечным счетным
множеством.
Пример 5. Стрелок стреляет по круглой мишени, нас интересует
точка, в которую попала пуля. В качестве пространства элементарных
событий можно принять множество, состоящее из точек рассматрива-
емого круга и одной дополнительной точки О, обозначающей непопа-
дание стрелка в мишень. Данное пространство элементарных исходов
является бесконечным несчетным множеством.
Из приведенных выше примеров ясно, что можно рассматривать
различные типы пространств элементарных событий в зависимости
от того, какое число элементов они содержат:
1 тип: Q является конечным множеством.
2 тип: Q является бесконечным счётным множеством.
3 тип: Q является бесконечным несчётным множеством.
Задачи
Опишите пространства элементарных событий указанных ниже сто-
хастических экспериментов.
1. Симметричная монета подбрасывается 2 раза.
2. Одновременно бросают 3 монеты.
3. Наугад выбирается число из натурального ряда.
4. В урне а белых и /3 черных шаров. Из урны вынимается шар.
5. В квадрат [0,1] х [0,1] наудачу бросается точка.
6. Два человека условились встретиться в интервале времени [О, Т]
5
1.2 Случайные события
Определение. Подмножество пространства элементарных собы-
тий называется случайным событием.
Событие может состоять из одного или, нескольких элементарных;
исходов, а также может состоять из счетного или несчетного числа
элементарных исходов. События будем обозначать заглавными латин-
скими буквами А, В, С.
Пример 1. Монету бросают дважды, случайное событие А состоит
в том, что хотя бы один раз появится герб. Тогда Q = { ГГ, ГР, РГ,
РР }, А = { ГГ, ГР, РГ }
Пример 2. Случайным образом выбрано натуральное число. Пусть
А - событие, состоящее в том, что выбрано чётное число. Тогда Q =
{1,2,3,...},А = {2,4,...}.
Пример 3. Пусть есть проволока длиной 1 метр. Растягивают ее
за концы, в результате чего происходит разрыв в какой-то точке. Мно-
жество Q - это все точки на проволоке, которые математически можно
задать отрезком [0,1]. Пусть событие А состоит в том, что разрыв про-
изошел ближе к левому концу. Тогда А = [0, |).
Так как случайное событие есть подмножество множества Q, то для
них также можно ввести некоторые операции. Приведем таблицу, свя-
зывающую понятия теории вероятностей и теории множеств.
Обозна- чения Язык теории множеств Язык теории вероятностей
Q универсальное множество (для фиксированного эксперимента) пространство элементарных событий (элементарных исходов) достоверное событие
са элемент Q исход, элементарное событие
0 пустое множество невозможное событие
А некоторое подмножество Q случайное событие А
6
Продолжение таблицы.
Ас В А подмножество В из наступления события Д необходимо следует наступление В
AUB или А + В объединение множеств А и В - множеств точек, входящих или в А или в В объединение событий А и В - событие состоящее в том, что произошло А или В
АПВ или АВ пересечение множеств А и В - множеств точек, входящих и в А и в В пересечение событий А и В - г событие, состоящие в том, что одновременно произошли А и В
АВ = Ъ А и В иепересекающиеся множества событие А и В несовместны, то есть не могут наступить одновременно
А = П\А дополнение множества А, то есть множество точек, не входящих в А событие, состоящие в ненаступлении события А событие А-обратное событие к А, или противоположное событие
А\В разность множеств А и В событие, состоящее в том, что произойдёт событие А, но не произойдёт событие В
Пример 4. Бросаем игральную кость. Пусть событие А - выпало
четное число, событие В - выпало число кратное трем.
Тогда: ЛиВ = {2,4,6}U{3,6} — {2,3,4,6} - выпавшее число делится
или на 2, или на 3. А П В = {2,4,6} П {3,6} = {6} число делится и на
2 и наЗ. А — П \ А = {1,2,3,4,5,6} \ {2,4,6} = {1,3,5} - выпавшее
7
число нечетное.
, А \ В = {2,4} - число четное, но на 3 не делится.
Приведенные операции над событиями обладают следующими свой-
ствами: '
1. AUB = BUA.
2. АП В = Sri А.
3. AUA==Q.
4. АПП = А.
5. АП В С А.
6. A\At=0.
7. А = А.
8. (АиВ)ПС = АПСиВНС.
Эти свойства непосредственно следуют из определения операций над
событиями.
Задачи
1. Когда возможны равенства: АиВ = А,АПВ = А?
2. Из множества натуральных чисел N наугад взято одно число.
Событие А - число делится на 5, событие В - число оканчивается нулем.
Что означают события А, В, A U В, А П В, А \ В, А П В?
3. Совместны ли события А и A U В?
4. Доказать, что А П В = A U В.
5. Электрическая цепь между точками М и N приведена на схеме:
Событие Ai - выход из строя элемента а.;, где г = 1,2,3,4. Пусть
событие С - разрыв цепи. Записать С и С через А-к.
8
1.3 Классическое определение вероятности слу-
чайного события
В процессе развития теории вероятностей, как математической дис-
циплины, были сформулированы несколько определений вероятности
случайного события. Это было связано с тем, что, как указывалось
выше, существует 3 типа пространств элементарных событий. И для
каждого случая было дано свое определение.
Классическое определение вероятности случайного события предпо-
лагает, что пространство элементарных исходов Q является конечным
множеством.
Определение. Вероятностью Р(А) случайного события А назы-
вается отношение числа исходов, благоприятствующих событию А,
к числу всех возможных исходов стохастического эксперимента
Р(А) = ™
п
т - число благоприятных исходов (т.е. число элементов подмножес-
тва. А), п - число всех исходов (т.е. число элементов множества О/
Пример 1. В урне находятся I белых и к черных, и г синих шаров.
Наудачу вынимаем один шар. Найти вероятность того, что этот шар
будет белый.
Решение. Число всех возможных исходов данного эксперимента
равно п = 1+кА-г - количество всех шаров в урне. Число благоприятных
исходов равно т — I - количество белых шаров. Пусть событие А -
вынули белый шар. Тогда Р(А) =
Пример 2. Куб, все грани которого окрашены, распилен на тысячу
кубиков одинакового размера. Полученные кубики тщательно переме-
шаны. Найти вероятность того, что кубик, извлеченный наудачу, будет
иметь две окрашеные стороны.
Решение. Всего кубиков п — 1000. Куб имеет 12 ребер, на каждом
из которых по 8 кубиков с двумя окрашеными сторонами. Поэтому
Р(А) = * = 0.096.
Задачи
1. Случайно выбранная кость домино оказалась не дублем. Найти
вероятность того, что вторую так же взятую наудачу кость домино
можно приставить к первой.
9
2. Симметричную игральную кость бросают дважды. Пусть собы-
тие А состоит в том, что сумма выпавших очком равна 5. Найти Р(А).
3. Цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 написаны на карточках, кото-
рые тщательно перемешаны. Произвольным образом вынимаются три
карточки подряд и кладутся в ряд. Найти вероятность того, что чис-
ло, составленое из трех цифр, которые написаны на карточках, больше
587?
4. Из колоды в 36 карт вынимается одна карта. Найти вероятность
появления карты пиковой масти.
1.4 Элементы комбинаторики
Комбинаторным анализом (комбинаторикой) называется раздел ма-
тематики, рассматривающий законы о размещении объектов в соот-
ветствии со специальными правилами и нахождении числа способов,
которыми это может быть сделано. Методы комбинаторики играют
важную роль при вычислении классических вероятностей.
Изложим основные понятия комбинаторики.
Определение. Множество, состоящее из различных п элементов
будем называть п-множеством (все элементы множества различны
между собой)
Рассмотрим следующую задачу: из города А в город В ведут 2 доро-
ги, а из города В в город С ведут 3 дороги. Каким числом различных
путей можно совершить путешествие из города А в город С через город
В? Очевидно, что таких путей равно 2-3 = 6.
Приведенная задача хорошо иллюстрирует основной принцип комби-
наторики - правило умножения, которым мы часто пользуемся в жизни.
Сформулируем его в виде теоремы.
Теорема (основной принцип комбинаторики). Пусть имеется
щ-множество; п^-множествомножеств о. Число различных
комбинаций наборов элементов вида (а1,а2,.., ,ak), где а1 некоторый
7
элемент из щ-множества, а - некоторый элемент п^-множества,
..., ak - некоторый элемент п^- множеств а, равно щ • щ -... • пь-
Доказательство проведём методом математической индукции.
Пусть k = 2, то есть ni-множество и пг-множество. Рассмотрим раз-
личные пары (а1, а2), для этого составим прямоугольную таблицу так,
10
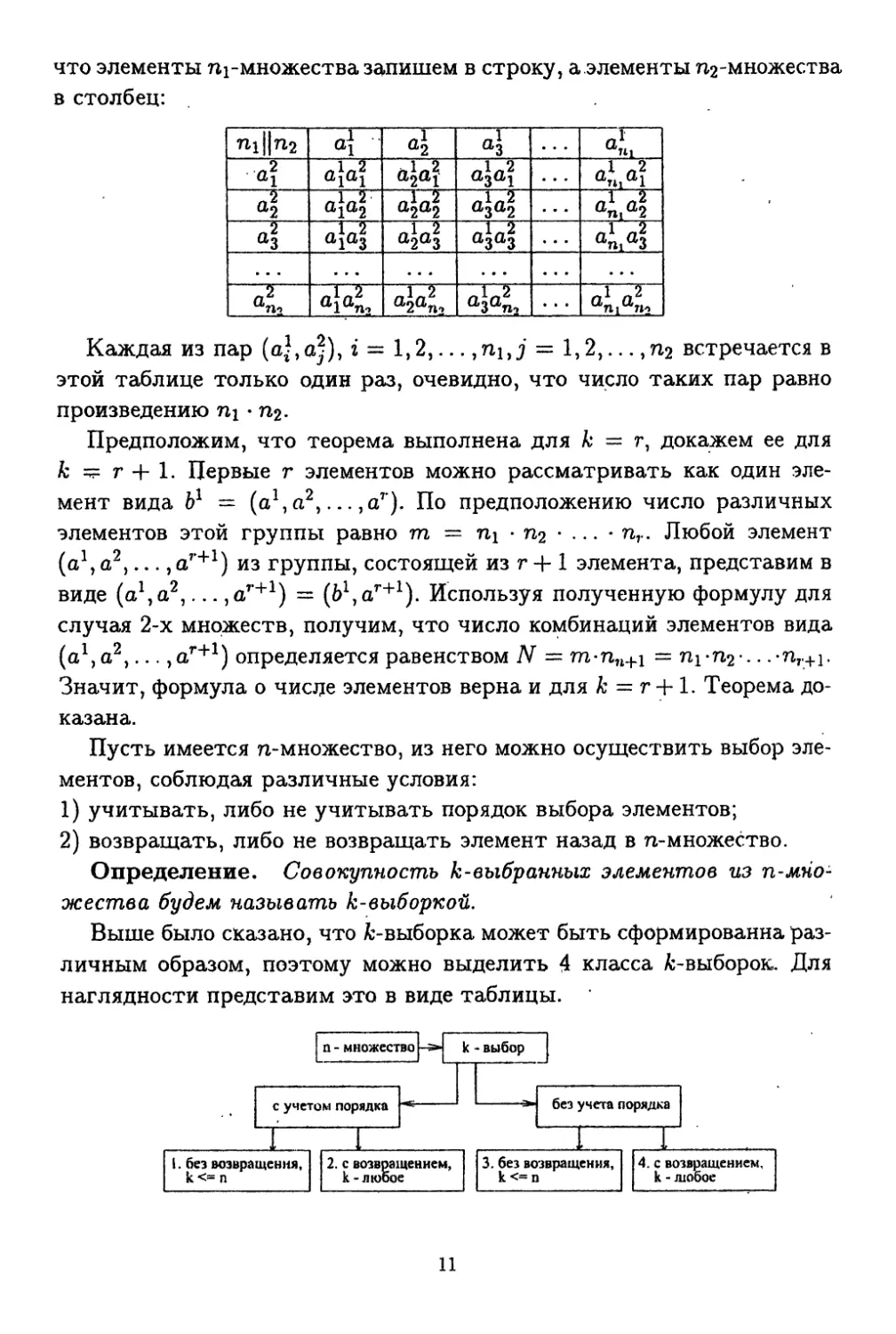
что элементы ni-множества запишем в строку, а элементы ^-множества
в столбец:
П1||п2 а] <4
а? а|а2 &2al 1 9 au,al
а2 a|a| a|a| . . . <4a2
аз Чаз a|a| a|a|
. . .
a2an. a3an.
Каждая из пар (a?, a2), i = 1,2,... ,nj, j = 1,2,... ,П2 встречается в
этой таблице только один раз, очевидно, что число таких пар равно
произведению щ 'Щ.
Предположим, что теорема выполнена для к = г, докажем ее для
к г + 1. Первые г элементов можно рассматривать как один эле-
мент вида Ь1 — (а1, а2,... ,аг). По предположению число различных
элементов этой группы равно т — щ • П2 • ... * пг. Любой элемент
(а1, а2,..., аг+1) из группы, состоящей из г Ч- 1 элемента, представим в
виде (а1,а2,... ,ar+1) = (b\ar+l). Используя полученную формулу для
случая 2-х множеств, получим, что число комбинаций элементов вида
(а1,а2,... ,аг+1) определяется равенством N — m-nn+i = щ-пу.. .-nr+i.
Значит, формула о чисде элементов верна и для к — г +1. Теорема до-
казана.
Пусть имеется n-множество, из него можно осуществить выбор эле-
ментов, соблюдая различные условия:
1) учитывать, либо не учитывать порядок выбора элементов;
2) возвращать, либо не возвращать элемент назад в п-множество.
Определение. Совокупность к-выбранных элементов из п-мно-
жества будем называть k-выборкой.
Выше было сказано, что fc-выборка может быть сформированна раз-
личным образом, поэтому можно выделить 4 класса fc-выборок. Для
наглядности представим это в виде таблицы.
11
Определение. К-выборку из п-множества с учетом порядка сле-
дования элементов без возвращения называют размещением из п эле-
ментом по к (очевидно, здесь к < п) и обозначают символом Акп.
Пример 1. Трехзначные номера машин без одинаковых цифр есть
выбор без возвращения с учетом порядка 3 элемента из 10, то есть
размещение из 10 по 3 - А|о.
Пример 2. Шестизначный телефонный номер из различных цифр
есть
Крайний случай, когда к — п, есть просто перестановка элементов
в п-множестве, за такой к-выборкой естественным образом закреплено
и название n-перестановка и обозначают ее символом Рп.
Пример 3. Расписание сдачи экзаменов по 5 предметам есть 5-
перестановка, т. е. Ргд.
Найдем число возможных различных размещений и перестановок
Рп. Будем обозначать это число тем же символом.
Теорема 1.
лЛ п!
п (п-ку.
Доказательство. Каждое размещение можно представить как ком-
бинацию (набор) из n-множества, (п — 1)-множества, (п — (п - 1))-
множества, так как выбор осуществляется без возвращения. По пра-
вилу умножения таких комбинаций n(n - 1)... (п — (к — 1)) — (пд:-д
(Напомним, что п! — 1 • 2 ... • п) Теорема доказана.
Следствие Рп = А™ — п! (т. к. по определению 0! = 1).
Примеры 4. В классе изучают десять предметов. В понедельник
6 уроков, причем все уроки различные. Сколькими способами можно
составить расписание на понедельник?
Решение. Расписание есть Тогда = 151200.
Определение. К-выборку из п-множества с учетом следования
экзаменов с возвращением называют размещением с возвращением
(или с повторением) из п элементов по к и обозначают символом В([
(очевидно, здесь к-любое, т.е. к <п или к > п).
Пример 5. Слово ’’мама” - есть размещение с возвращением из 33
элементов по 4 - Взз (т. к. в русском алфавите 33 буквы). Найдём число
размещений Вк.
Теорема 2. В7А; = пк.
12
Доказательство. Каждое размещение с возвращением можно пред-
ставить как комбинацию fc-элементов из п-множества, п-множества,...,
и-множества (всего п-множеств I’-штук). Применяя правило умноже-
ния получим, что
В-=пк
Теорема доказана.
Пример 6. Сколько ’’слов”, состоящих из четырех букв можно со-
ставить, используя а) русский алфавит, б) английский алфавит.
Решение. Каждое ’’слово” есть размещение с возвращением, поэ-
тому a) = ЗЗ4 = 1186121, б) = 264 = 456976.
Определение. К-выборку из п-множества без учета порядка сле-
дования элементов и без возвращения называют сочетанием из п эле-
ментов по к и обозначают символом (очевидно, здесь к <п).
Пример 7. Выбор студентом для изучения любых трех спецкурсов
из предложенных семи есть сочетание из 7 по 3 С?.
Найдем число различных сочетаний С*. .
Теорема 3.
Доказательство. Число сочетаний в k\ раз меньше чем число
размещений А*, т. к. если в каждом сочетании элементы переставить
между собой местами, то получим к1 размещений. Поэтому С„ = =
Теорема доказана.
Пример 8. В примере 7 студент может осуществить выбор спец-
курсов С? способов, т. е. С? = = 35.
Пример 9. Дано п точек, никакие 3 из которых не лежат на одной
прямой. Сколько прямых можно провести, соединяя точки попарно?
Решение. Каждая прямая - это выбор двух точек, из п, прдчем
в каком порядке выбраны точки не имеет значения. Поэтому число
z^2 n! (п-1)п
прямых, которые можно провести, равно 2 •
Определение, к-выборку из п-множества без учета порядка сле-
дования элементов и с возвращением называют сочетанием с возвра-
щением (с повторением) из п элементов по к и обозначают.символом
D^. (Очевидно, здесь к - любое, т. е. п < к или к < п).
Пример 10. Кость домино есть сочетание с возвращением (т. к.
есть ’’дубли”) из 7 элементов (0, 1, 2, 3, 4, 5, 6, 7) по 2 -Д?. Найдем
число различных сочетаний с возвращением.
Теорема 4. D* = C*+k_v
13
Доказательство. Сочетание с возвращением есть сочетание, .но
уже из (п + к — 1)-множества. Теорема доказана.
Прямей 11. В примере 10 рассматривалась кость домино теперь
понятно почему их 28 т.к. D* — Cy+2-i = ^8 ~ эдй “ ^2 “ 28-
Пример 12. Известно, что молекулы белка разлагаются на стан-
дартные аминокислоты. Аминокислота в свою очередь состоит из 3
нуклеотидов, возможно одинаковых. Нуклеотидов же всего 4: аденин,
тенин, гунин, цитании. Скодько стандартных аминокислот?
Решение. Каждая аминокислота есть выбор 3 нуклеидов без учетка
порядка с повторением из четырех, поэтому число всех аминокислот
равно Dl == = С| = gyji = 20
Приведем примеры, когда используются элементы комбинаторики
для нахождения вероятностей событий в случае конечного прстранст-
ва элементарных событий (классическое определение вероятности со-
бытия).
Пример 13. Колода из 36 карт перемешана. Найти вероятность
того, что все 4 туза расположены рядом.
Решение. Число возможных исходов п есть число возможных пе-
рестановок из 36 карт, т.е. п = P$q = 36!. Чтобы найти число бла-
гоприятных исходов представим, что сложили вместе тузы как одну
карту, тогда число таких перестановок будет Р32+1 = Рзз = 33!.. За-
тем учтем, что тузы тоже могут между собой быть перестановлены,
т.е. получим еще Р$ = 4! перестановок. Теперь воспользуемся прави-
лом умножения: всех благоприятных исходов будет т — Р33Р4 = 33!4!.
Тогда, если обозначим событие А - 4 туза расположенные рядом, то
р( 4'1 — та _ 33!4! _ 1
п ~ 36! — 1785’
Пример 14. В ящике имеется 15 тенисных мячей, из которых 9
новых й шесть старых. Для игры взяли 3 мяча. Найти вероятность
того, что все мячи новые.
Решение. Пусть событие А - взяли 3 новых тенисных мяча для
игры. ЭтЬ ёсть выбор без учета порядка и без возвращения. Поэтому
число всех возможных исходов п — С^ь. Благоприятными будут исхо-
ды, когда мячи берутся из 9 новых, т.е. число благоприятных исходов
равно т = Сд, Поэтому Р(А) = ™
Пример 15. В партии из к изделий г бракованых. Найти веро-
ятность того, что среди s выбранных наудачу для проверки изделий
ровно I окажутся бракованными.
14
Решение. Пусть событие А - взяли з издедий, среди которых I
бракованных- Число всех возможных способов взять з изделий из k
равно п = CJ. Благоприятными являются исходы, когда из общего
числа г бракованных изделий ровно I - это можно сделать С1Т способами,
а остальные s — I небракованные - количество способов выбора равно
поэтому число благоприятных исходов m = CltC[^r (использовали
с1 С'~1
правило умножения). Тогда Р(А) =
Задачи
1. В лоторее имеется 10 билетов: 5 выигрышных и 5 проигрышных.
Берется 2 билета. Какова вероятность проигрыша?
2. В урне А белых и В черных шаров. Из урны вынимают 2 шара.
Найти вероятность того, что оба шара будут белыми.
3. Нудачу взят телефонный номер состоящий из 5 цифр. Чему равна
вероятность того, что все цифры различные?
4. На полке стоят 15 книг, 5 из них в переплетах. Берут наудачу
3 книги. Какова вероятность того, что среди выбранных книг только
одна в переплете? . 1
5. При наборе телефонного номера абонент забыл две последние циф-
ры и набрал их наудачу, помня только что эти цифры нечетные. Какова
вероятность, что номер набран правильно?
6. Среди 100 фотографий есть фотография знаменитого артиста.
Взяли наудачу 10 фотографий. Какова вероятность того, что среди
них есть фотография артиста?
1.5 Статистическое определение вероятности слу-
чайного события
Классическое определение вероятности при переходе от простых при-
меров к рассмотрению сложных задач наталкивается на трудности
принципиального характера. Рассмотрим такой пример. Пусть име-
ется бесконечный натуральный ряд чисел. Наугад выбирается число,
найти вероятность, что оно четное. Из теории множеств известно, что
множество натуральных чисел и множество четных чисел находятся
во взаимно-однозначном соответствии, т.е. грубо говоря, сколько нату-
ральных чисел, столько и четных. Исходя из этого, если бы мы исполь-
зовали классическое определение вероятности события, то получили
15
бы, что искомая вероятность равна 1. Как видно из приведенного при-
мера, в случае бесконечных счетных пространств элементарных ихо-
дов, классическое определение вероятности события нельзя использо-
вать. Как поступить в приведенном примере? Если мы будем рассмат-
ривать только первые п членов натурального ряда, то тогда, используя
классические определения, вероятность того, что числд четное, будет
равна либо Рп(А) = 1/2, если п само четно, либо Рп(А) — если
п нечетно: п — 2к 4-1. Увеличивая п, получим, что Рп(А) все меньше
отличается от 0.5.
В общем случае, если проводятся длительные наблюдения над появ-
лением или непоявлением некоторого события А при большом числе по-
вторений испытаний, проходящих при неизменных условиях, то опыт
показывает, что число появлений или непоявлений события А подчиня-
ется устойчивым закономерностям. А именно, если через обозначим
число появлений события А при п независимых испытаниях, то ока-
зывается, что отношение при достаточно больших п сохраняет поч-
ти постоянную величину. Эту постоянную, являющейся объективной
числовой характеристикой явления, стественно назвать вероятностью
случайного события А. Поэтому Р. Мизес ввел следующее определение
вероятности события, которое называют статистическим
P(4) = lim —.
Имеется огромный опытный материал по проверке этого определения.
Приведем результаты экспериментов с бросанием монеты.
Экспериментатор : Бюффон
п - число бросаний р,п- число выпадений герба п
4040 2048 0,5080
Экспериментатор: К. Пирсон
п - число бросаний цп- число выпадений герба IhL п
12000 6019 0,5016
24000 12012 0,5005
16
1;6 Геометрическое определение вероятности слу-
чайного события
Если пространство элементарных событий О является бесконечным
несчетным множеством, то приведенные выше определения вероятнос-
ти случайного события использовать становится невозможно. Поэтому
определение вероятности было видоизменено, и появилось геометри-
ческое определение, где используется понятие меры множества.. Мера
множества - это его числовая характеристика. Если рассматривать
линейное множество, то его мера - это длина линии; если плоское мно-
жество, то, его мера - это площадь; если множество в пространстве, то
его мера -г это его объем.
Определение. Вероятностью случайного события А называется
отношение меры множества благоприятных исходов к мере множес-
тва всех исходов
mesA
mesft
Пример 1. Наудачу выбираются два числа из отрезка [0,1]. Найти
вероятность того, что их произведение меньше |
Решение. Пусть х, у - выбранные числа. Множество всех возмож-
ных исходов есть множество точек квадрата Q = [0,1] х [0,1]. Мно-
жество благоприятных исходов А = {(z,t/) 6 П : х • у < |} -это точки
квадрата которые лежат под кривой у —
\ 1 г 1 1
। \ г-. mesA — So — -4- / — dx = ~(1 4- In 2)
X. I 2 aX 2
--—1/2* 1/2
D . —
I ._____» mesCl = 1
o'1 ч 1. .
Р(Д) = -(1 + 1п2).
Пример 2. В любые моменты промежутка времени Т равновоз-
можны поступления в приемник 2-х сигналов. Приемник будет занят,
если разность между моментами поступления сигналов будет меньше
г. Найти вероятность того, что приемник будет занят.
Решение. Пусть х,у ~ моменты поступления сигналов в приемник.
Область возможных значений ж, у является квадрат Q = [0,Т] х [0)Г],
тпе$П = Т2. Приемник будет занят - событие А, если |я — у\ < г.
17
Данное множество лежит между прямыми х — у = г, и х — у = —г, или
у — х — г, ну = х±г.
Поэтому
mesA = SD = Т2 - 2 • 1(Т - г)2 = Т2 - (Т - г
&
Задачи
1. В круг радиуса R наудачу бросается точка. Найти вероятность
того, что точка попадет в круг радиуса г с тем же-центром..
2. На плоскость, разделенную паралельными прямыми, отстоящими
друг от друга на расстоянии 6 см, наудачу брошен круг радиусом 1
см. Найти вероятность того, что круг не пересечет ни одной.прямой.
3. На отрезке длины I наудачу выбраны две точки. Какова вероят-
ность того, что расстояние между ними меньше 0.3?..
4. Два парохода должны подойти к одному причалу. Время прихода
обоих пароходов независимо и равновозможно в течение данных суток.
Найти вероятность того, что одному из пароходов придется ожидать
освобождения причала, если время стоянки одного один час, другого
два часа.
5. На отрезке длиной L, наугад поставлены две точки. Найти ве-
роятность того, что из трех получившихся отрезков можно построить
треугольник.
6. Наудачу взяты два положительных числа х и у, каждое из ко-
торых не превышает 2. Найти вероятность того, что их призведение
меньше 1, а частное х/у не больше 2.
1.7 Аксиомы теории вероятностей
В современной математике принято аксиомами называть те пред-
положения, которые принимаются за. истину и в пределах данной тео-
рии не доказываются. Все остальные положения этой теории должны
выводиться чисто логическим путем из принятых аксиом. Формули-
ровка аксиом, т.е. тех фундаментальных положений, на базе которых
строится обширная теория, представляет собой не начальную стадию
развития математической науки, а является результатом длительного
18
накопленияг фактов и логического анализа полученных результатов с
целью выявления действительно основных первичных фактов. Именно
так складывались аксиомы геометрии, знакомство с которыми дается в
курсе элементарной математики, подобный же путь прошла теория ве-
роятностей. Впервые задача аксиоматического построения теории ве-
роятностей была поставлена и решена в 1917 г. С.Н/ Берштейном, ко-
торый исходил из качественного сравнения случайных событий. Но в
1939 году А.Н. Колмогоров предложил иной подход, который связывает
теорию вероятностей с теорией множеств и теорией функций. Именно
эта аксиоматика рассматривается ниже.
Пусть имеется множество -пространство элементарных событий
Q, А - некоторая система подмножеств множества П. А - называется
алгеброй, если
1. ПеЛ
2. Если А е А, В Е А, то A U В Е А, А П В Е А
3. Если А € А, то А Е А
Рассмотрим пространство Я и какую-нибудь выделенную систему
множеств А, образующую алгебру событий.
Определение. Вероятность на (Г2, А) есть числовая функция, опре-
деленная на множествах из А и обладающая следующими свойства-
ми:
I. Р(А) > 0 для любого А Е А
II. P(Q) = 1
III. Если А Г] В = 9, то Р(А U В) = Р(А) 4- Р(В).
Тройку (Q,A,P) называют вероятностным пространством.
Как видно, приведенное определение вероятности включает в себя
все изученные ранее определения, т.к. здесь Q может быть любого типа.
1.8 Свойства вероятности
Свойство 1. Вероятность невозможного события равна нулю
PW = о
Доказательство. Так как 0ПП = 0и0иП = П, то по аксиомам II
и Ш Р(П) = Р(0) 4- P(Q), т.к. P(Q) = 1, то Р(0) = 0.
19
Свойство 2. Вероятность противоположного события А равна
Р(А) = 1 - Р(А)
Доказательство. Так как Ли А .=? Q, А А А = 0,то по аксиоме III .
Р(А) + Р(А) = 1, тогда Р(А) — 1 —,Р(А).
Свойство 3. Если из наступления события А следует наступле-
ние события В (т.е. А в В), то Р(А) < Р(В).
Доказательство. Так как В ~ A U (А Г1 В), А А (А А В) = 0, то
по аксиоме III Р(В) = Р(А) + Р(А Г1 В), по аксиоме I Р(А А В) > О,
значит, Р(В) > Р(А).
Свойство 4. Для любого события А Р(А) < 1.
Доказательство. Так как любое событие А Е Q, то по свойству 3
Р(А) < P(Q) = 1
Свойство 5. Теорема сложения вероятностей случайных собы-
тий: Вероятность объединения двух событий равна сумме их веро-
ятностей без вероятности пересечения этих событий. Р(А U В) —
Р(А) +Р(В) — Р(АС\В).
Доказательство. Так как A U В — A U (В\(А А В)) и А А (В\(А А
В)) = 0, В = (В\(А А В)) + (А А В) и (В\(А А В)) А (А А В) = 0, то по
аксиоме III Р(А U В) = Р(А) 4- Р(В\(А А В)), Р(В) = Р(В\(А A Bj) +
Р(А А В), поэтому Р(А U В) = Р(А) + Р(В) - Р(А А В)
Свойство 6. Расширенная теорема сложения вероятностей собы-
тий
р( и Ак} = f Р(Ак) - Е Р(Ак п Л)+
к=1 к=1 к<1
+ s р(лпдп41)-- + (-1)"-1р(л1па2п-па„).
к<1<т
Доказательство проводится методом математической индукции.
Пример 1. На стеллаже библиотеки в случайном порядке расстав-
лены 15 учебников, причем 5 из них в переплете. Наудачу берется 3
учебника. Найти вероятность того, что хотя бы один из взятых учеб-
ников окажется в перелете.
Решение. Пусть событие А - хотя бы один учебник в перплете.
Тогда А - все 3 учебника без переплета. Р(А) ~ так как п = -
'-'15
20
все возможные исходы, т = Cf0 - благоприятные исходы (10 учебников
без переплета). Поэтому Р(А) = 1 - Р(А) = 1 - — 1 ~ Ц “ gi •
Пример 2. В ящике 12 белых, 7 черных, 11 синих шаров одинакого
радиуса. Наудачу вынимается шар. Найти вероятность, что шар не
белый.
Решение. Пусть событие А -вынули белый шар, В - черный, а С
- синий. Нужно найти Р(А), т.к. А — В U (7, то по теореме сложения
вероятностей Р(А) = Р(В) 4- Р(С) — Р(В П (7), но В П С — 0, значит,
Р(В П С) = 0, поэтому Р(Л) = Р(В) + Р(С) = ± + 11 = 15 = г так
как всего шаров 30.
Задачи
1. Среди одинаковых по внешнему виду 20 деталей находятся 4 бра-
кованы*. Наудачу берется 3 детали. Найти вероятность того, что среди
них хотя бы одна бракованная.
2. От коллектива бригады, которая состоит из 6-ти мужчин и 4-х
женщин, на профсоюзную конференцию выбирается 2 человека.Найти
вероятность того, что среди выбраных хотя бы одна женщина.
3. Производится стрельба по области D, состоящей из 3-х зон А1,А2,Аз.
Возможность попадания в Ai зону соответственно равны 0.5, 0.1, 0.17.
Найти вероятность попасть в область D.
4. На рынок поступила продукция 4-х обувных фабрик в соответ-
ствующих пропорциях 2:3:1:4. Фабрики, поставившие меньшее коли-
чество продукции, выпускают более качествнную продукцию. Найти
вероятность того, что случайный покупатель купит хорошую обувь.
1.9 Условная вероятность. Независимость событий
Рассмотрим вопрос о том, как определить вероятность какого-либо
события А при условии, что уже произошло другое событие В. Нач-
нем с примера. Пусть брошена игральная кость и результат неиз-
вестен, но известно, что выпало четное число. Мы хотим, зная эту
информацию, подсчитать вероятность того, что выпало число боль-
ше 3. Тогда речь идет об условной вероятности события А—{},В—
{}., {2}, {4}, {6}, .А{4}, {6}.,2j. Условную вероятность будем обозна-
чать символом Р(А/В). В приведенном примере Р(А/В} = С другой
стороны Р(В) = I = |; Р(А -В) = 1 = 1, тогда Р(А/В) = | = Ztfff =
21
2
з-
Пусть теперь Q - бесконечное несчетное множество. Определим услов-
ную вероятность Р(А/В), когда все исходы равновозможны. Так как
известно, что событие В произошло, то будем рассматривать толь-
ко те элементарные исходы, которые соответствуют событию В. Рас-
смотрим новое пространство элементарных событий = В. Выбе-
рем множество исходов из А, которое входит в В, обозначим его Ар
Ai = А А В. За условную вероятность Р(А/В) можно взять вероят-
ность события А при условии, что рассматриваются только, события
содержащиеся в В. Для нового пространства Qi эта вероятность равна
р/ А / Р\ — _ Р(АПВ)
Г(А/В) - - р(в) .
Поэтому условная вероятность определяется следующим образом:
Определение.Условной вероятностью события А при условии,
что произошло событие В с Р{В) > 0, называется число
Если это равенство записать иначе
Р(АПВ) = Р(А).Р(А/В),
то его называют теоремой умножения вероятностей событий.
Так как Р(А П В) = Р(В П А) = Р(В) • Р(А/В), то
Р(А) • Р(В/А) = Р(В) • Р(А/В).
Учитывая теорему умножения вероятностей, приведенная ранее те-
орема сложения Вероятностей может быть записана так: Р(А U В) =
Р(А) + Р(В) - Р(А) • Р(В/А) = Р(А) 4- Р(В) - Р(В) • Р(А/В).
Определение. События А и В называются независимыми, если
Р(А П В) = Р(А) • Р(В). Другими словами, события А и В незави-
симы, если условная вероятность события А равна безусловной'его
вероятности, т.е. Р(А) — Р(А/В), или Р(В) = Р(В/А\
Определение. События А\, Аг, Ап называются независимыми
в совокупности, если для любого набора индексов 1 < ki < к% < ... <
km < п выполняется равенство
. Р(АЬ1ПЛ2П-...ПЛЛт) = Р(Л1)-Р(А^)-...-Р(Акт)
22
Определение. События А\, Аъ, ..., Ап называются попарно неза-
висимыми, если P(AiC\Aj) = P(Ai)-P(Aj), для любых i,j> 1 < i < j <п.
Попарной независимости событий недостаточно для независимости
п событий в совокупности. Это показывает следующий пример.
Пример Бернштейна. На плоскость бросается тетраэдр, три гра-
ни которого окрашены соответственно в красный, синий и зеленый
цвета, а на четвертую нанесены все. три цвета. Событие А означает,
что при бросании тетраэдра на плоскость выпала грань, содержащая
красный цвет, событие В - грань, содержащая синий цвет, событие С
- грань, содержащая зеленый цвет. Так как каждый из трех цветов
содержится на 2-х гранях, то Р(А) = Р(В) = Р(С) = | Веро-
ятность пересечения любой пары введенных событий равна | |
так как искомая пара цветов есть только на одной грани. Это означает
попарную независимость всех трех событий. Но Р(Д А С А В) = | /
Р(Д) • Р(В) • Р(С) = то есть независимости в совокупности нет.
Пример 1. Пусть имеется электрическая цепь в виде:
Известно, что элементы А{ (г = 1,2,3) выходят из строя независимо
друг от друга с вероятностью pi. Найти вероятность того, что цепь
выйдет из строя.
Решение. Пусть событие Ai ={а»}, тогда Р(Д^) = р^ Событие А
- цепь вышла из строя,* тогда А = Дх U (Д2 А Д3), Используя теоремы
сложения и умножения вероятностей, а так же условия независимости
события Ai, получим, что
Р(Д) = Р(Дх) 4- Р(Д2 А Д3) - Р(Д1 А (Д2 А Д3)) =
Р(Дх) + Р(Д2) • Р(Д3) - Р(Дх) • Р(Д2) - Р(Дз) = Pi + Р2Рз - Р1Р2РЗ
Пример 2. Из урны, содержащей 3 белых и 2 черных шара, слу-
чайно без возвращения последовательно извлекаются шары. Найти ве-
роятность того, что чернь!й шар впервые появится при третьей испы-
тании.
23
Решение. Пусть событие А - при третьем испытании впервые по-
явился черный шар; событие Bi - при г-ом испытании появится черный
шар (г = 1,2,3). Выразим событие А через события А = В1ОВ2ПВз-
Поэтому по теореме умножения получим
Р(Л) = Р(В1ПВ2ПВ3) =
499 19 1
Р(Вг) • ЛВг/Вх) • Р(В3/(В1 П В2)) = -
Задачи
1. В двух урнах находятся шары, отличающиеся только цветом, при-
чем в первой урне 5 белых, 11 черных и 8 красных шаров, а во второй
соответственно 10, 8, 6. Из каждой урны наудачу извлекается по одно-
му шару. Какова вероятность того, что оба шара одного цвета.
2. Два спортсмена независимо друг от друга стреляют по одной ми-
шени. Вероятность попадания первого спортсмена 0.7, а второго 0.8.
Какова вероятность того, что мишень будет поражена.
3. Вероятность поломки первого станка в течение смены равна 0.2,
втрого 0.13, третьего 0.09. Чему равна вероятность того, что станки
потребуется налаживать в течение смены, если их поломка происходит
независимо.
4. В трех залах кинотеатра идут три различных фильма. Вероят-
ность того, что на определенный час в кассе 1-го зала есть билеты
равна 0.3; в кассе второго зала - 0.2; а в кассе 3-го зала - 0.4. Како-
ва вероятность того, что на данный час имеется возможность купить
билет хотя бы на один фильм.
5. Сколько надо бросить игральных костей, чтобы с вероятностью
меньше 0.3, можно было ожидать, что ни на одной из выпавших граней
не появится число 6.
6. Вероятность уничтожения цели при одном выстреле равна р. Най-
ти число выстрелов п, необходимых для поражения цели с вероятнос-
тью, большей или равной q.
7. Игрок А поочередно играет с игроками В и С по две партии. Ве-
роятность выигрыша первых партий для В и С равна 0.1 и 0.2 соот-
ветственно, вероятность выиграть во второй партии для В равна 0.3,
для С равна 0.4. Какова вероятность того, что а) первым выиграет В;
б) первым выиграет С.
8. Двое поочередно бросают монету, выигрывает тот, у которого
раньше появится орел. Какова вероятность выигрыша для каждого из
24
игроков.
9. Два стрелка поочередно стреляют по мишени до первого попада-
ния. Вероятность попадания для первого стрелка равна 0.2, для вто-
рого 0.3. Какова вероятность того, что первый стелок сделает больше
выстрелов, чем второй?
10. Какова вероятность Р(АПВ), если известна вероятность Р(А) =
а, Р(В) = Ь, и Р(А + В) = с.
1.10 Формула полной вероятности. Формула Бай-
еса
Пусть А - некоторое событие, которое может произойти с одним из
событий Hi, Яг» • ••> Нп, причем Я1, Яг, ..., Нп попарно несовместные
события, P(Hi) >0 и Е P(Hi) — 1-
г=1
Теорема (формула полной вероятности).
P(A) — ^P,P(Hi)-P(A/Hi).
1=1
п
Доказательство. Из приведенных условий следует, что А = U (Я2П
4=1
А). Далее, события АПЯ1, АП Яг, ..., АПЯП несовместны, поэтому ис-
пользуя теоремы сложения и умножения вероятностей, получаем, что
Р(А) = £ Р(Н< П А) = £ Р(Я2). Р(А/я2).
4=1 4=1
Теорема доказана.
Замечание. События Hi, Яг, ...,ЯП часто называют гипотезами.
Пример 1. Имеется три одинаковых урны, в первой урне 2 белых
и 1 черный шар, во второй, - 3 белых и 1 черный шар, в третьей - 2
белых и 2 черных шара. Наудачу берем урну и из нее вынимаем шар.
Найти вероятность того, что этот шар белый.
Решение. Рассмотрим три гипотезы Hi - взята первая урна; Яг
- взята вторая урна; Яз - взята третья урна. Событие А - появление
белого шара.
Так как гипотезы по условию задачи равновозможны, то P(Hi) =
Р(Яг) — Р(Яз) = |, условная вероятность события А при этих гипоте-
25
зах соответственно равна Р(А/Я1) — Р(А/Яз) = По
формуле полной вероятности находим, что Р(А) = + = Ц.
Пример 2. Некоторая деталь производится на двух заводах. Из-
вестно, что объем продукции первого завода в п раз превышает объем
продукции второго завода. Доля брака на первом заводе pi, а на вто-
ром р2- Найти вероятность того, что наугад взятая деталь окажется
бракованой.
Решение. Рассмотрим гипотезы: Hi - взята деталь 1-го завода; Н2
—, а условная вероятность Р(А /
п 4-1
1 /
—-г(Р1П + Р2)-
п 4-1
- взята деталь 2-го завода.
Тогда P(^) = Р(Я2) -
Я,) = ръ Р(Л/Я2" = р2.
Поэтому Р(А) = + ^-1
Можно решать и обратную задачу: опыт произведен, и в его резуль-
тате наблюдалось появление события А, как тогда надо оценить веро-
ятности гипотез HL, i — 1,2,... ,п, в связи с появлением этого события
А? Значит, надо найти условные вероятности P(Hi/A), i — 1,2,... ,n.
Из теоремы умножения вероятностей имеем, что
Р(А П Н^) - Р(А) • Р(Н£/Л) = Р(Н^) • Р(А/НО,
следует
Р(Я1М) = тт
Р(Л)
Выразим Р(А) с помощью формулы полной вероятности, тогда
Р(ЯМ) = i = 1 2 .
S Р(Я,) • Р(А/Я,)
Эта формула носит название формулы Байеса,
Пример 3. Два стрелка независимо один от другого стреляют на
одной линии, делая по одному выстрелу. Вероятность попадания в ми-
шень для первого стрелка 0.8; для второго — 0.4. После стрельбы в
мишене обнаружена одна пуля. Найти вероятность того, что эта пуля
принадлежит первому стрелку.
Решение. Пусть событие А — в мишень попала одна пуля. До опы-
та возможны следующуе гипотезы.
P(Hi) — ни первый, ни второй стрелок не попадает.
26
P{Hi) — оба стрелка попадают.
Р(Яз) — первый стрелок попадает, а второй нет.
Р(Я4) — второй стрелок попадает, а первый нет.
Вероятности этих гипотез:
Р(Я1) = 0.1 • 0.6 = 0.12; Р(Я2) = 0^8 • 0.6 = 0.48;
Р(Я3) = 0.8 • 0.4 = 0.32; Р(Я4) = 0.2 • 0.4 = 0.08;
Условные вероятности наблюдаемого события при этих гипотезах рав-
ны P(A/HJ = 0,Р(А/Я2) = 0,Р(А/Я3) = 1,Р(Л/Я4) = 1. После опы-
та, вероятности гипотез Я* будут равны:
PtA/HJ = 0,Р(А/Н2) = 0,Р(А/Н3) = O5TOI = 1>Р^/Н4) =
0.081 _
0.48 1+0.08 1 “ 7‘
Значит, вероятность тогб, что пуля принадлежит первому стрелку,
равна 5/7.
Задачи
1. В коробке есть 3 новых и 3 уже использованных теннисных мяча.
Для первой игры наудачу берут из коробки 2 мяча, а затем возвращают
их назад. Какова вероятность для второй игры из этой коробки наудачу
вынуть 2 новых мяча?
2. В урну, содержащую 4 шара, опущен белый шар, после чего из
нее наудачу извлечен один шар. Найти вероятность того, что извле-
ченный шар окажется белым, если равновозможны все предположения
о первоначальном составе шаров по цвету.
3. В пирамиде 5 винтовок, 3 из которых снабжены оптическим при-
целом. Вероятность того, что стрелок поразит мишень при выстреле
из винтовки с оптическим прицелом, равна 0.95, для вийтовки без оп-
тического прицела эта вероятность равна 0.7. Найти вероятность того,
что мишень будет поражена, если стрелок произвел один выстрел из
наугад взятой винтовки.
4. Вероятность поступления К вызовов на телефонную станцию за
промежуток времени t равна Р*(К). Считая число вызовов за любые два
соседних промежутка времени независимыми, определить вероятность
Р&.(К) поступления К вызовов за промежуток времени 2t.
5. Два станка производят одинаковые детали, которые поступают
на общий конвейер. Производительность первого станка вдвое боль-
ше производительности второго. Первый станок производит в среднем
60% деталей отличного качества, а второй - 84%. Наудачу взятая с кон-
вейера деталь оказалась отличного качества. Найти вероятность того,
что эта деталь произведена на первом станке.
27
6. Число грузовых автомашин, проезжающих по шоссе, на котором,
стоит бензоколонка, относится к числу легковых машин, проезжающих
по тому же шоссе как 3:2. Вероятность того, что будет заправляться
грузовая машина, равна 0.1; для легковой машины эта вероятность
равна 0.15. К бензоколонке подъехала машина для заправки. Найти
вероятность того, что это грузовая машина.
7. Батарея из 3-х орудий произвела залп, причем 2 снаряда попали
в цель. Найти вероятность того, что первое орудие дало попадание,
если вероятности попадания в цель первым, вторым и третьим орудием
соответственно равны 0.4 ; 0.3; 0.5.
1.11 Последовательные независимые испытания
(схема Бернулли)
Пусть проводится п последовательных независимых одинаковых сто-
хастических экспериментов (испытаний), в каждом из которых может
наступить или не наступить событие А. Под независимыми понимают-
ся такие эксперименты, в которых события, возникающие в результате
экспериментов, являются независимыми в совокупности. Так как испы-
тания одинаковы, то в любом из них событие А наступает с одинаковой
вероятностью, обозначим еер — Р(А). Вероятность противоположного
события А (ненаступления А) обозначим q = Р(Л) = 1 - р. Наступле-
ние события А обычно называют успехом, а ненаступление - неуспехом
(неудачей). Требуется найти вероятность Fn(rn) того, что событие А
в таких п опытах появится т раз.
Теорема. Pn(m) =
Доказательство. Рассмотрим событие В7П, состоящее в том, что
событие А появится в п опытах ровно т раз. Это событие может осу-
ществиться различными способами. Разложим событие В1п на объеди-
нение пересечений событий, состоящих в появлении или непоявлении
события А в отдельном опыте. Будем обозначать At- появление события
А в г-м опыте, Л< — непоявление события А в г-м опыте. Каждый ва-
риант события Вт должен состоять из т появлений события А и п — т
непоявлений, то есть Л, с различными индексами. Таким образом,
Вт = А1 • Аг •. •. Ат • Ат+1 •... • Лп 4- Ai • Лг • Аз •... • Лп_1 • Ап 4-...
28
... 4- Ai • A-2 *... * An_m • An_,n+1 An,
причем в каждое пересечение событие А должно входить т раз, а А
должно входить п — т раз. Число всех комбинаций такого рода равно
С'”1, то есть числу способов, какими можно,из п опытов выбрать т, в
которых произошло событие А. Вероятность каждой такой комбинации
по теореме умножения вероятностей равна pmqn~m. Так как комбина-
ции между собой несовместны, то по теореме сложения вероятностей,
вероятность события Вт равна
рп(тп) = р(я„) = От’”‘
с?
Теорема доказана.
Формула Рп{т) — C™pmqn~m называется формулой Бернулли.
Следствие. Пусть Рп(^1^2) — вероятность того, что событие
А произошло не менее и не более m2 раз в испытаниях. Тогда
Pn(mi;m2)= Е Ckpkqn~k
к~ЧП\
Доказательство.
JTto ~т1
Pn(mi; m2) = Р(ВП1 + Bmj+1 + ... + Bm,) = £ P(Bmi+k) =
i=0
m2
= L. Cnp q ,
k=m\
так как события ВШ1, Bmi+b • • •, &т2 независимы.
Пример 1. Игральная кость бросается 3 раза. Какова вероятность
того, что число ”5” выпало 2 раза.
Решение. Пусть событие А — выпадения числа ”5”, при одном
бросании кости, тогда Р(А) — 1/6. Здесь производится 3 независи-
мых испытания, нужно, чтобы ’’успех” осуществлялся 2 раза, поэтому
Пример 2. Система радиолокационных станций ведет наблюдение
за группой объектов, состоящей из 10 единиц. Каждый из объектов
может быть (независимо от других) потерян с вероятностью 0.1. Найти
вероятность того, что хотя бы один из объектов будет потерян.
Решение. Вероятность потери хотя бы одного объекта Рю(1;10)
можно было найти по формуле Рю(1; 10) — Рю(1) 4-Рю(2) 4-.. .4-Piu(10),
29
но проще воспользоваться вероятностью противоположного события -
ни один объект не потерян, тогда Рю(1; 10). = 1 — Рю(0) = 1 - 0.9 « 0.65.
Задачи
1. Вероятность попадания в цель при каждом выстреле из лука рав-
на j. Производится 6 выстрелов. Какова вероятность: а) ровно трех
попаданий, б) не менее двух попаданий. '
2. В семье 10 детей. Считая вероятности рождения мальчика и де-
вочки равными найти вероятность того, что в данной семье равное
количество мальчиков и девочек.
3. В помещении 4 лампы. Вероятность работы в течении года для
каждой лампы 0.8. Найти вероятность, что к концу года горят 3 лампы.
4. Два баскетболиста делают по 3 броска в корзину. Вероятность по-
падания мяча при каждом броске равна соответственно 0.6 и 0.7. Найти
вероятность того, что у обоих будет равное количество попаданий.
5. В 1693г. Джоном Смитом был поставлен следующий вопрос: оди-
наковы ли шансы на успех у трех человек, если первому надо получить
хотя бы одну шестерку при бросании игральной кости 6 раз, второму
- не менее 2-х шестерок при 12 бросаниях, а третьему — не менее 3-х
шестерок при 18 бросаниях.
1.12 Предельные теоремы для схемы Бернулли
Продолжим рассматривать последовательные независимые испыта-
ния. В предыдущем параграфе была получена формула Бернулли для
нахождения вероятностей Рп(^)- Но когда число испытаний п велико
применять эту формулу неудобно. Поэтому были доказаны предельные
теоремы для вероятностей Pn(m).
Пусть при больших п вероятность р уменьшается обратно прор-
ционально п, то есть это означает, что п • р ~ А, где А — некоторая
постоянная.
Теорема (Пуассона). Предположим, что призведение п -р яв-
ляется постоянной величиной, когда п неограниченно возрастает.
Обозначим А — п>р. т ~ ограничено. - Тогда для любого фиксирован-
ного А
А7П
lim Pn(m) = —-е“А.
30
Доказательство. По формуле Бернулли
г> „п—т
РДт) = Сп р q =
h!
(n — т)!
1
ml
п[п — 1)..
У- А)” (i-l) (1-1).
ml \ n j \ п/ \ п/ \ п / V п/
Так как для любого фиксированного ограниченного т имеет место
сходимость 1 - —> 1 при п —> оо, то Рп(т) « ~J-(1 - -)п
По второму замечательному пределу Jim. (1 - = е"А, Получаем,
что
i \ т ,
lim Рп(тп) — —7е~Х‘
n->0c- nk '
Теорема доказана.
Замечание. Теорема Пуассона применима, когда Р очень мало, а
п достаточно велико.
Пример 1. Радиоаппаратура состоит из 2000 элементов. Вероят-
ность отказа одного элемента в течении года равна 0.001. Найти веро-
ятность отказа: а) двух элементов за год, б) не менее двух элементов
за год.
Решение, а) Работа каждого элемента рассматривают как отдель-
ное испытание. Пусть событие Л — отказ элемента за год. По условию:
р = Р(Л) = 0.001, Л = пр — 2000-0.001 = 2. Тогда по формуле Пуассона
о
F2ooo(2) « 1 - 2,е-2 = 2е~г « 0.2707.
б) Здесь нужно найти ,Р2ооо (2; 2000) = 1 - Ргооо(О) - PaoooU) ~1-
2° 9 21 9 9
—е"2 - —е"2 = 1 - Зе"2 « 0.594.
Рассмотрим еще одну приближенную формулу для Pn(m), когда п
велико. Но при этом и число т тоже растет с ростом п, только неиз-
менной остается вероятность Р(Л) = р.
Теорема (локальная предельная — Муавра-Лапласа). Пусть
7П “ П ту
хп = и при п —> оо, m —> оо величины хп ограничены. Тогда
y/npq
1
y/npqPn(m) « -2==е »
V Z7T
31
Доказательство теоремы не приводим, его можно найти в [2].
Замечание. Для значений функции <р(х) = составлена
V 2тг
таблица. Функция <^(ж) является четной, то есть — <р(~х).
Пример 2. Найти вероятность того, что при 150 выстрелах мишень
будет поражена ровно 70 раз, если вероятность попадания при одном
выстреле равна 0.4.
Решение. Пусть событие А - попадание при одном выстреле, р =
Р(А) = 0.4, тогда q = 1 — р = 0.6. По теореме Муавра-Лапласа хп =
^~...50'0'4= « 1,67, и Р15о(7О) « ----—-....= v(1.67) « 0.0165,
>/150 0 4 0.6 k ’ >/150 • 0.4 • 0.6 V ’
t \ 1 л2
где <р\х) = —г=е 2 — значение этой функции сведены в таблицу 1
у2?г
(см. Приложение), поэтому, зная значение аргумента, находим значе-
ние <р(х).
Для вероятности Рп(т1;т2) того, что событие А наступило не менее
mi и не более m2 раз в п испытаниях, когда п велико тоже имеется
приближенная формула.
Теорема (интегральная предельная —Муавра-Лапласа). Пуст
т\ — пр mi — пр
ап = —, Ъп — —и при n -> oo,mi —> оо,Ш2 —> сю величины
y/npq y/npQ
ап и Ьп ограничены. Тогда
Рп(тх;т2) « -7= [ e~^dx
v2?ran
Доказательство теоремы не приводим, его можно найти в [2}.
1 а: .2
Замечание. Для значений функции Ф(х) == -7= / e~^dz составле-
V 2тг 0
на таблица 2 (см. Приложение). Функция Ф(т) является нечетной, то
есть —Ф(т) = Ф(—х). Тогда Pn(7ni;m2) = Ф(5П) ~ Ф(а?*)
Пример 3. Вероятность изделию некоторого производства оказать-
ся бракованным равна 0.005. Чему равна вероятность того, что из 10000
наудачу взятых изделий, бракованных оказывается не более 70.
Решение. По интегральной теореме Муавра-Лапласа чтобы найти
вероятность Pioooo(0; 70), нужно знать ап и 5П, Подсчитаем сначала их
значения:
32
О - 1ОООО • 0.002
а„ — у-- ==.« —7.09
710000 • 0.005 • 0.995
_ 70- 10000-0.002
Ъп — —2.84.
710000 • 0.005 • 0.995
Тогда Р1ООоо(О; 70) = Ф(2.84)-Ф(-7.09) = Ф(2.84) + Ф(7.09) « 0,9975.
Задачи.
1. Завод отправил в магазин 5000 лампочек. Вероятность того, что
лампочка разобьется равна 0,0002. Найти вероятность того, что в ма-
газин привезли не более трех разбитых лампочек.
2. Вероятность найти белый гриб среди прочих равна 1/5. Найти
вероятность того, что среди 300 грибов белых будет 75.
3. В партии из 1000 арбузов каждый арбуз оказывается неспелым с
вероятностью 1/4. Найти вероятность того, что спелых арбузов будет
больше 700.
4. Текст содержит 20000 букв. Каждая буква может быть непра-
вильно напечатана с вероятностью 0.0004. Какова вероятность, что в
тексте не менее 2-х опечаток.
5. Счетчик регистрирует попадающие в него частицы с вероятнос-
тью 0.9. Найти вероятность того, что он зарегистрировал не менее 95%
частиц, если в него попало 2000 частиц.
6. На прядильной фабрике работница обслуживает 800 веретен. Ве-
роятность обрыва пряжи в течении времени Т равно 0.005. Найти ве-
роятность того, что в течении времени Т будет не более 3-х обрывов
пряжи.
33
1.13 Последовательные зависимые испытания (це-
пи Маркова)
В схеме Бернулли изучаются последовательные независимые испы-
тания, но можно рассматривать зависимые испытания. Рассмотрим
самый простой вариант зависимых испытаний.
Пусть G есть некоторый эксперимент, который имеет конечное мно-
жество исходов {Е*!, , Еп}. Предположим, что мы неограниченно
повторяем эксперимент G, то есть производим последовательность исг
пытаний, в каждом из которых может осуществиться только одно из
событий Ei^ k = 1,2,... п.
Определение. Последовательность испытаний образует простую
цепь Маркова, если условная вероятность в г-м испытании (г = 1,2,...)
осуществиться событю Ek зависит только от того, каким было со-
бытие в (г — 1) испытании, и не зависит от событий произошедших
в более ранних' испытаниях. г
Исторически сложилось так, что при изложении цепей Маркова ис-
пользуют несколько иную терминологию; которую приведем ниже. Не-
которая физическая система G может находиться в одном из состояний
Ek) = 1,2,..., п. Она меняет своё состояние только в моменты времени
t\,t2).... Пусть Е]. означает, что система G пришла в состояние Ek в
момент времени tr, то есть на г-м испытании. Тогда для простой цепи
Маркова выполнено условие:
Лад;-1, ад.... Et.j = лад?1),
где lj — любые из {1,2,... ,n}, j = 1,2,... ,г — 1.
Далее ограничимся рассмотрением только однородных цепей Мар-
кова.
Определение. Однородной цепью Маркова называется цепь, в ко-
торой условная вероятность Р(Е£/Е^1) не зависит от номера ис-
пытания г, а зависит только от предыдущего и последующего со-
стояний, то есть Р(Е[/Е/’-1) = P(Ek/Ei) — pki— это вероятность
перехода из состояния Ei в состояние Ek за одно испытание, или,
как принято говорить, за один шаг.
Полная вероятностная картина возможных изменений, осуществля-
ющихся при переходе из одного состояния к непосредственно следую-
щему, задается матрицей
34
' Pll Р12 • • Pin
Р21 р22 • • • Р2п
Рп1 Рп2 • • • Рпп ;
Матрица Щ называется матрицей перехода за один шаг.
Пример 1. Пусть система G может находится в састояниях Е2,
Е$ переход из состояния в состояние происходит по схеме однородной
цепи Маркова с матрицей перехода Щ
1 1/2
Щ = 1/2
\ 1/3
1/6 1/3 \
О 1/2
1/3 1/3/
Если система находилась в состоянии Е\, то после изменения состо-
яния за один шаг она с вероятностью 1/2 остается в этом же состоянии,
с вероятностью 1/6 перейдет в состояние Е^у с вероятностью 1/3 пе-
рейдет в состояние Е%. Если система находилась в состоянии Т?2> то
остаться в этом состоянии она не может, а обязательно перейдет либо
в состояние Еь либо в состояние Е*з, причем этот переход осуществит-
ся с одинаковой вероятностью. Из состояния Е3 система может перейти
в любое из возможных состояний с одной и той же вероятностью 1/3.
Пример 2. Блуждания с отражением. Пусть частица, находящаяся
на прямой, блуждает по целым точкам между 0 и а. Если 0 < к < а, то
из точки к с вероятностью 1/2 частица переходит в к — 1 или к+1. Если
к равно 0 или а, то частица отражается, то есть переходит в точку 1
или в точку а — 1 соответственно с вероятностью 1. .
Запишем матрицу перехода Щ для данной системы G.
{ о
П1
1/2
О
1 о 0 ... О \
О 1/2 0 ... О
1/2 0 1/2 ... О
\ О 0 0 ... 1 0 /
Матрица П1 будет размерности (а + 1) х (а + 1).
Пример 3. Блуждания с поглащением. Если в примере (2) изме-
нить немного условия: попадая в точку 0 или а частица остается в них
с вероятностью 1.
Запишем матрицу перехода Щ для данной системы G.
35
Матрица П1 будет размерности (a-f-l)x(a-hl).
Рассмотрим каким условиям удовлетворяет матрица перехода Пр
1. Все элементы матрицы ры есть неотрицательные числа 0 < pki <
1 для всех fc,Z.
2. Так как из состояния Ek система обязательно переходит в лю-
бое другое возможное состояние, то сумма элементов каждой строки
матрицы П1 равна единице: Е ры = 1, k = 1,2, ...,п.
Пусть система G из состояния Ek в состояние Ei перешла за 2 шага,
найдем вероятность р&(2) такого перехода. Для этого воспользуемся
п
формулой полной вероятности: рм(2) = Е PkrPrh т.е. система из со-
! 7—1
стояния Ek перешла сначала за один шаг в любое другое возможное
состояние Ег, а затем уже из этого Ег состояния следующим шагом
перешла в состояние Ei. Каждое рн(2) есть элемент новой матрицы
перехода Щ за 2 шага, и как видим, тогда новая матрица Щ есть про-
изведение 2-х матриц: Щ = Пх *Пь
Если рассматривать вероятность рлДтп) - вероятности перехода из
состояния Ek в состояние Ei за т шагов, то аналогично по формуле
ПОЛНОЙ ВерОЯТНОСТИ МОЖНО ПОЛУЧИТЬ, ЧТО Pkl(jn) — Е PkrPvltp^ — 1).
Поэтому, применяя метод математической индукции, легко можно
показать, что матрица перехода П?п за т шагов есть m-тая степень
матрицы Пх, т.е. ПП1 = П™.
Пример 4. Матрица перехода за один шаг имеет вид: Пх =
Найти матрицу перехода за три шага.
Решение.
Пз = П|. Найдем сначала Щ
1/2 1/2
1/3 2/3
/1/2 1/2 \ / 1/2 1/2 \ / 5/12 7/12 \
112 ~ \ 1/3 2/3 J \ 1/3 2/3 / \ 7/18 11/18 J '
Теперь найдем Пз
36
/ 5/12 7/12 \ / 1/2 1/2 \ _
3 “ \ 7/18 11/18 / \ 1/3 2/3 )
_ / 29/72 43/72 \
~ \ 43/108 65/108 ) ’
Состояния, которые имеются, в цепи Маркова, могут быть между
собой, довольно различны по характеру. Поэтому вводится классифи-
кация состояний, которую очень коротко опишем ниже.
Определение. Состояние Ei называется несущественным, если
существует такое состояние Aj и такое число шагов т, чтор^(т) >
0, но Pji(k) — 0 для всех к. Все остальные состояния называются су-
щественными.
Несущественное состояние обладает тем свойством, что из него мож-
но с положительной вероятностью попасть в некоторое другое состоя-
ние, но из другого состояния вернуться в несущественное уже нельзя.
Так в примере 3 все состояния, кроме крайних Ец и Еа, несуществен-
ные, а состояния Е^ и Еа будут существенными.
В завершении этого параграфа приведем предельную теорему без
доказательства.
Теорема (Маркова).Если при некотором к > 0 все элементы
матрицы перехода Щ положительны, то существуют такие посто-
янные числа p.j(j — 1,2,...,п), что независимо от индекса i имеют
место равенства
lim Рц(т} = р7
(Другими словами, неважно из какого состояния вышла система, а
важно куда она идет, то есть важно направление ее движения ).
Задачи.
1. Вероятности перехода даются матрицей
П1 =
/ 1/2
1/2
U/2
1/3 1/6 \
1/3 1/6
1/3 1/6/
Чему равно число состояний? Найти вероятности перехода за два шага.
2. Пусть имеется маятник, у которого фиксируются только 2 положе-
ния: крайнее левое Е± и крайнее правое Записать матрицу перехода
для этой цепи Маркова. Есть ли здесь несущественные состояния?
37
3. Электрон может находиться на одной из 3-х орбит. Переход с
г—ой орбиты на j—ую переходит с вероятностью Найти матрицы
перехода за 1 и за 2 шага, постоянные с,.
4. Вероятности перехода даются матрицей
' 0 1/2 1/2 \
1/2 0 1/2 '
\ 1/2 1/2 О J
Есть ли здесь несущественные состояния? Применима ли предельная
теорема?
38
Глава 2
Случайные величины
2 .1 Случайные величины
В практической жизни часто приходится сталкиваться с различ-
ными величинами. Значения одних из встречающихся величин могут
быть известны (количество минут в часе, число членов парламента и
т.д.), значения же других величин можно найти из опыта, путем изме-
рения, пересчета (расстояния между двумя точками, число выпавших
гербов при бросании монеты 3 раза и т.д.). Величины, которые могут
принять в результате опыта любое из возможных значений, называют
случайными.
Можно привести много примеров таких величин: 1) число космичес-
ких частиц, попадающих на определенный участок земной поверхности
за сутки; 2) число вызовов, поступающих на телефонную станцию; 3)
размер уклонения точки падения снаряда от центра цели при стрель-
бе; 4) скорбеть молекулы газа. Несмотря на разнородность конкретного
содержания приведенных примеров, все они с точки зрения математи-
ки обладают общим свойством: каждая из этих величин под влиянием
случайных обстоятельств способна принимать различные значения, i
Определение. Случайной величиной £ называется функция, ото-
бражающая пространство элементарных исходов Q в множество дей-
ствительных чисел R; £ : Q -> R; £ — £(u;),a> Е П.
Пример 1. Монету бросают 2 раза. Нас интересует число выпаде-
ний герба. Здесь число выпадений герба — случайная величина. Ис-
ходное пространство элементарных событий Q имеет вид: Q = { рр,
рг, гр, гг }. Тогда определим случайную величину £ в виде схемы:
39
Q —> R
= pp —> o £(^i) — 0
U>2 — pr > 1 £(w2) — 1
CJ3 — rp —> 1 £(w3) = 1
cu4 = rr —> 2 £(cj4) = 2
Здесь £ принимает всего три значения: 0,1,2.
Пример 2. Пусть имеется круг радиуса L. В круг наугад бросает-
ся точка. Расстояние от центра круга до. выбранной случайной точки
- случайная величина Здесь исходное пространство элементарных
событий Q - все множество точек круга. Тогда определим случайную
величину £ в виде схемы: ,
То есть
£(с0)—центр круга) = О
точка окружности радиуса Z) = /,.0 < I < L
точка границы круга ) = L
В данном примере £ принимает значения из отрезка [О, L] 6 R-
Определение. Для любого исхода ы € Q значение £ — £(и>) назы-
вается реализацией случайной величины при данном исходе.
В зависимости от того, в множество какого типа - дискретное или
непрерывное, осуществляется отображение пространства Q, случай-
ные, величины можно разделить на 2 класса:
1. дискретные случайные величины;
2. непрерывные случайные величины.
В приведенных выше примерах задана дискретная случайная вели-
чина (пример 1), непрерывная случайная величина (пример 2).
40
2 .2 Дискретные случайные величины
Рассмотрим сначала дискретные случайные величины. Дискретная
случайная величина может принимать не более чем счетное число зна-
чений Ж1,Ж2, ....
Значение случайной величины £ наступает с некоторой вероятнос-
тью, обозначим ее pi — Р(£ — жг).
Соответствие, которое каждому значению х.ь дискретной случайной
величины £ сопоставляет его вероятность р.^ называется законом рас-
пределения случайной величины Закон распределения случайной ве-
личины £ удобно записывать в виде таблицы, которую называют рядом
распределения.
£ Х2 ХП
Р1 Р2 Рп
Если перечисленны все возможные значения случайной величины £,
то | Pi = Е Р(£ = Xi) = 1.
г=1 4=1
Пример 1. Случайная величина £ -число выпавших очков при од-
нократном бросании игральной кости. Построить ряд распределения
случайной величины
Решение.
Ряд распределения имеет вид:
е 1 2 3 4 5 6
Р 1/6 1/6 1/6 1/6 1/6 1/6
Так как случайная величина ( может принять одно из следующих
значений: 1,2,3,4,5,6; причем вероятность каждой реализации равна
1/6.
Пример 2. Пусть вероятность появления события А при каждом из
бесконечной последовательности испытаний равна р. Рассмотрим слу-
чайную величину £ - номер испытания, при котором произошло первый
раз события А. Найти ряд распределения случайной величины £.
Решение. Случайная величина £ может принимать любое целое
положительное значение 1,2,3,... .
Р(£ = 1) = - six? вероятность того, что событие А произойдет при
первом испытании, где р\ = р.
41
Р(^ — 2) = р2 - это вероятность того, что событие А не произойдет
при первом испытании, а произойдет при втором, тогда р% ~ (1 - р)р.
И т.д.
Р(£ ~ k) = Pk - это вероятность того, что событие А при первых
(fc — 1) испытаниях не произойдет, а произойдет только при А:—ом ис-
пытании, тогда р2 — (1 — р^к~^р. И т.д. .
Поэтому ряд распределения имеет вид:
е 1 2 к
р р (1 ~ Р)Р (1 -р^-'р
Задачи.
1. Устройство состоит из 3-х независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,1. Соста-
вить закон распределения числа отказавших элементов в одном опыте.
2. В урне 5 белых и 10 черных шаров. Вынули 2 шара. Построить ряд
распределения случайной величины £- числа вынутых белых шаров.
3. Производятся последовательные испытания 5 приборов на надеж-
ность. Каждый следующий прибор испытывается только в том случае,
если предыдущий оказался надёжным. Построить ряд распределения
числа испытанных приборов, если вероятность выдержать испытания
для каждого из них равна 0,5.
4. Вероятность попадания при каждом выстреле 0,8. Имеется 4 сна-
ряда. Стрельба ведется до первого попадания. Построить ряд распре-
деления израсходованных снарядов.
5. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны
3 детали. Составить закон распределения числа стандартных деталей
среди отобранных.
6. Дискретная случайная величина £ имеет закон распределения:
£ 0 7г/б 7г/2 5тг/6 7Г
р 1/10 3/10 1/10 2/10 3/10
Построить ряд распределения случайной величины р — sin(£).
7. Два баскетболиста поочередно забрасывают мяч в корзину до тех
пор, пока один из них не попадает. Построить ряд распределения слу-
чайного числа бросков, производимых каждым из баскетболистов, если
вероятность попадания для первого равна 0,4, а для второго 0,6.
42
2 .3 Функция распределения случайной величины
Для характеристики поведения дискретной случайной величины вы-
ше рассматривалась вероятность того, что £ принимает конкретные
значения. Но такой способ становится неприемлимым, если рассмат-
ривать непрерывную случайную величину, так как множество её зна-
чений бесконечно и сплошь заполняет некоторый отрезок или интервал
на числовой прямой. Поэтому можно рассматривать вероятости других
событий: таких, когда £ < ж, где х - некоторое действительное число.
Причем эти события можно определять для обоих классов случаев; как
дискретных, так и непрерывных.
Определение. Функцией распределения случайной величины £ на-
зывается функция F(x) = Р(£ < х), х € Я.
Функция распределения F(x) обладает рядом свойств.
Свойство 1. F(x) - неубывающая функция.
Доказательство. Пусть Xi < х^ тогда событие £ < Xi влечет за
собой событие £ < Х2> по свойству вероятности: Р(£ < xi) < Р(£ < #2),
т.е. F(xi) < Р(а?2), значит, функция Р(х)-неубывающая.
Свойство 2. Р(-оо) = 0, Р(+оо) = 1.
Доказательство. Так как событие (£ < —оо) = 0 (невозможное
событие); то Р(£ < —оо) = Р(—оо) = 0. Так как событие (£ < 4-оо) —
Q (достоверное событие), то Р(£ < оо) — F(oo) — 1.
Свойство 3. Функция F(z) непрерывна слева.
Доказательство. Пусть - произвольная монотонно возрас-
тающая последовательность, сходящаяся к точке ж, т.е. Jim.xn — х.
Обозначим через Ап событие (хп < £ < х). Тогда при i > j, At С Aj.
Поэтому Р(ЛП) = Р(хп < £ < я) = Р(а?) - F(zn), nlim.P(Al) =
Jim. (F(z) — F{xn)) = F(x) — Jim. F(xn) = F(x) — F(x — 0) = 0. Лемма
доказана.
Свойство 4. Для любых а <b выполнено равенство
Р(а < £ < b) ~ F(b) - F(a).
Доказательство. Рассмотрим событие: А = (£ < Ь), В = (£ < а),
С = (а < £ < 6). Тогда А = В + С\ причем В и С несовместны, по
теореме сложения вероятностей имеем, что Р(£ < Ь) = Р(£ < а)4-Р(а <
£ < Ь), значит, Р(а < £ < b) = F(&) — F(a). Лемма доказана.
43
Пусть интервал (а, 6) неограниченно уменьшают, т.е. b —> а. Тогда
вместо вероятности попадания в интервал будет получена вероятность
того, что является £ примет значение а.
Р(£ = а) = lim Р(а < £ < 6) = lim F(b) ~ F(a)
значение этого предела зависит от того, имеет ли функция F(a) в т.
х — а разрыв или нет. Если в т. а функция F(x) имеет разрав, то
Р(£ = а) равно значению скачка функции F(x) в т. а. Если F(x) в т. а
непрерывна, то Р(£ = а) = 0.
Следствие. Вероятность любого отдельно взятого значения непре-
рывной случайной величины равна нулю. Из того, что вероятность
события {£ = а} имеет вероятность равную нулю для непрерывных
случаев, не следует, что это событие не будет появляться, а следует
только, что при неограниченном повторении опыта это событие будет
появляться сколь угодно редко.
Пример 1. Дискретная случайная величина £ задана законом рас-
пределения.
£247
р 0,5 0,2 03
Найти функцию распределения F(rr) и начертить её график.
Решение. 1) Если х <2, то F(x) — 0, так как значений, меньших
числа 2, величина £ не принимает.
2 ) Если 2 < х < 4, то F(x)=0,5, так как £ может принять значение 2 с
вероятностью 0,5.
3 ) Если 4 < х < 7, то Р(ж)=0,7, так как £ может принять значение 2 с
вероятностью 0,5 и значение 4 с вероятностью 0,2, значит, одно из этих
значений, безразлично какое, £ может принять (по теореме сложения
вероятностей для несовместных событий) с вероятностью 0,54-0,2—0,7.
4 ) Если х > 7, то F(x) = 1, так как событие £ < 7 достоверно.
Поэтому искомал функция распределения имеет вид
0, х < 2,
0,5, 2 < х < 4,
0,7, 4 <х <7,
1, х>1.
График этой функции имеет вид.
44
Пример 2. Случайная величина £ имеет функцию распределения
F(x). Найти функцию распределения случайной величины tj — а£ + Ь,
где а 6 R, b 6 R, а > 0.
Решение. Обозначим функцию распределения случайной величины
т] через Fv(x). Тогда F^x) — Р(т} < х) — Р(а£+Ь < х) — Р(а£ < х-b) —
P(e<l(x-b)) = F(^)
Пример 3. Случайная величина £ задана функцией распределения
0,
F(x) = <
т < -1,
— 1 < X < д,
Найти вероятность того, что в результате испытания величина £ при-
мет значение из интервала (0,
Решение. Ptf е (0, |)) - F(|) - F(0) = (| • | + |) - (| - 0 + |) =
Задачи.
1. Дискретная случайная величина задана законом распределения
е 3 4 7 10
р 0,2 0,1 0,4 0,3
Найти функцию распределения и построить её график.
2. Случайная величина £ задана функцией распределения.
[ 0, х < 2,
F(z) = < 0,5(ж — 2), 2 < х < 4,
( 1, х > 4.
Найти вероятность того, что в результате испытания £ примет
значения:
45
а) меньшее 0,2.
б) меньшее 3.
в) не меньше 5.
г) ее(1,3).
3. Случайная величена £ имеет функцию распределения F(x). Найти
функцию распределения случайной величины т/ = а£,аЕ7?,1)а>0;
2) а <0.
4. Функция распределения случайной величины £ имеет вид:
0,
а 4- barcsin ж,
1,
х < — Ъ
-1 < х < 1,
X > 1.
Найти постоянные а и Ъ.
5. Опыт состоит из 3-х независимых бросаний монеты. Герб выпа-
дает с вероятностью 0,5. Для случайного числа появлений герба по-
строить график функции распределения.
2.4 Плотность распределения непрерывной случай-
ной величины
Пусть имеется непрерывная случайная величина £ с функцией рас-
пределения F(x). Пусть функция F(x) непрерывна и дифференцируе-
мая.
Определение.Плотностъю распределения случайной величины £
называется производная от функции распределения f(x) — F'(x).
Термин ”плотность распределения” используется неслучайно. Дей-
ствительно,
/(1) = ?(«) = lim + Д;> - f W = l,m
4 7 4 7 Дг->0 Дж Дг-и) Дж
так как рассматривается предел отношения вероятности попадения
случайной величины £ в интервал (ж,ж-|- Дж) к длине этого интервала,
причём длина интервала стремится к нулю. Поэтому /(ж) характери-
зует как бы плотность, с которой распределяются значения случайной
величины в данной точке.
Рассмотрим свойства плотности распределения.
46
Свойство 1. Плотность распределения есть неотрицательная функ-
ция: f(x) > 0.
Доказательство, /(а?) есть производная неубывающей функции
F(x)j значит /(ж) > 0.
ъ
Свойство 2. Р(а < £ < b) — J f(x)dx.
Доказательство. Так как первообразная функции /(ж) есть F(x),
ъ
то J f(x)dx = F(a) - F[b) = Р(а < С < Ъ\
Следствие 1. F(x) = j f(x)dx. (Так как F(x) — Р(£ < х) =
Р(—оо < £ < х) = / /(х)с/х).
4-ос
Следствие 2. f f(x)dx -- 1 (свойство нормировки).
Так как +f f(x)dx = F(-f-oo) — F(—оо) = 1—0=1.
Пример 1. Функция распределения непрерывной случайной вели-
чины £ задана выражением:
F(x) =
О,
ьх2
1,
х < О,
О < х < 1,
X > 1.
Найти: а;/(х);Р(£ £ (0,25;0,5)).
Решение. Так как функция распределения случайной величины £
непрерывна при х = 1, то ах2 — 1, значит, а = 1. Плотность распреде-
ления
Р(£ е (0,25; 0,5)) = F(0,5) - F(0,25) = 0,52 - 0,252 = 0,1875.
Задачи.
1. Функция распределения случайной величины £ имеет вид: F(x) =
а 4- barctgx, х £ (— оо, 4-оо). Найти: а, Ь, /(ж), 6 (-1,1)).
2. Плотность распределения случайной величины £ имеет вид:
s f jsinx, х £ (0, тг),
/й = ( 1, 3 £ (□,»).
Найти: F(x),P^ £ (0, |)).
47
3. Плотность распределения случайной величины £ имеет вид:
ft \ / х~ 2> х е (1,2),
/W=( О, ^(1,2).
Найти: F(z),P(£ е (1,2; 1,5)).
4. Функция распределения безотказной работы аппаратуры в тече-
ние времени t имеет вид: F(t) = 1-е”?,£ > 0,Т > О.Найти: /(z),P(£ Е
(0,2Т)).
2.5 Числовые характеристики случайных вели-
чин
В предыдущих параграфах были определены законы распределения
случайных величин. Каждый закон распределения представляет собой
некоторую функцию, и указание этой функции полностью описывает
случайную величину с вероятностной точки зрения. Но во многих во-
просах практики нет необходимости исчерпывающим образом описы-
вать случайную величину, достаточно бывает указать только отдель-
ные числовые параметры: например, какое-то среднее значение, око-
ло которого группируются возможные значения случайной величины;
какое-либо число, характеризующее степень разбросанности этих зна-
чений относительно среднего.
Рассмотрим числовые характеристики для дискретных и непрерыв-
ных случайных величин.
1. Дискретные случайные величины.
Определение. Математическим ожиданием дискретной случай-
п
ной величины ( называется число ME = £ xkPk- Если случайная ве-
1-1
личина £ имеет счетное число значений, то есть п = со, то тогда
математическое ожидание существует, если сходится ряд Е XkPk,
в противном случае, математическое ожидание не существует.
Математическое ожидание является вероятностным аналогом сред-
него арифметического. Если грубо оценить рл,то pk ~ Pk> где рь —
j^rrik-сколько раз встретилось значение когда проводилось N ис-
п Е Х-кТП*
пытаний. Поэтому МЕ> « Е —♦
48
Математическое ожидание обладает свойствами, которые следуют
из его определения.
Свойство 1. Математическое ожидание постоянной равно этой
постоянной.
Доказательство. Постоянную С можно рассматривать как дис-
кретную случайную величину, которая может принимать только одно
значение С с вероятностью 1, поэтому МС — С • 1 = С.
Свойство 2. Математическое ожидание суммы двух случайных
величин равно сумме их математических ожиданий. + — М£Ч-
Мр.
Доказательство. Пусть ai, ...,ап - возможные значения случайной
величины £, pi,... ,p7i ~ вероятности этих значений, ..., Ьт- возмож-
ные значения случайной величины ту, gi,..., qm - вероятности этих зна-
чений. Возможные значения £ + rj имеют вид + bi, 1 < k < n, 1 < I <
т. Обозначим р^-вероятность того, что £ примет значение ту - зна-
чениеЬг. Тогда М(£ + т?) = £ £(а* + 6()ры = Е <и( Е Ри)+Е( Е Ри),
&—1 Z—1 fc—1 I—1 k—1
но £ рк1 = рк, £ pki = qi, значит, М(£ + р) = М£ + Мр.
i=i i=i
Следствие. Математическое ожидание суммы конечного числа слу-
чайных величин равно сумме их математических ожиданий. M(£i-|-£2+
...4-£п)-М£1 + М£2 + ... + М£п.
Свойство 3. Математическое ожидание произведения двух неза-
висимых случайных величин равно произведению их математических
ожиданий M(£q) = М£Мр.
Доказательство. Воспользуемся обозначениями, которые были вве-
дены в доказательстве свойства 2. Тогда вероятность того, что £ту при-
мет значение akbk будет равна pkqi, то есть P(£q — акЬ^) = PkQi, так как
величины £ и ту независимы. Тогда по определению математического
ожидания М (£ту) = Е Е akbipkqi ~ Е &kPk Е Ьщ - M£Mtj.
k=l n=l
Следствие. Постоянный множитель можно выносить за знак мате-
матического ожидания М(С£) = СМ£.
2. Непрерывные случайные величины.
Пусть непрерывная случайная величина £ имеет плотность распре-
деления f(x\
Определение. Математическим ожиданием непрерывной случай-
ной величины £ называется число Mf, — f xf(x)dx. Говорят, что
-OQ
49
математическое ожидание случайной величины £ существует, если
несобственный интеграл сходится.
Математическое ожидание для непрерывных случайных величин
обладает теми же свойствами, что и математическое ожидание дис-
кретных случайных величин.
1. М(£ + у) = М^Му.
2. Если £ и ту независимы, то М(£ • ту) = М£ • Му.
3. М(С£) — СМ£, С— постоянная.
Предлагаем читателю доказать их самостоятельно.
Кроме математического ожидания, которое указывает некоторое сред-
нее значение случайной величины, можно рассматривать и средний
разброс случайной величины около своего математического ожидания.
Мерой этого разброса (рассеивания) служит дисперсия.
Определение. Дисперсией случайной величины £ называется ма-
тематическое ожидание квадрата отклонений случайной величины
от своего математического ожидания D£ = — М()2.
Поэтому для дискретных случайных величин D£ = Е (xi — Mfflpi,
i—l
4-ос
а для непрерывных случайных величин D£ = J (ж — M£)rf(x)dx. Ве-
личина а = называется среднеквадратическим отклонением.
Рассмотрим свойства дисперсии.
Свойство 1. Дисперсия постоянной равна 0.
Доказательство. DC — М(С - С)2 — 0.
Свойство 2. Если С - постоянная, то D(C£) = C2D£.
Доказательство. D(C£) = М(С£ - МС£)2 = M(C2tf - М£)2) -
C2D£.
Свойство 3. Дисперсия суммы двух независимых случайных вели-
чин равна сумме их дисперсий 4- ту) = D£ 4- Dy.
Доказательство. D(£+y) — М(£+у--М(£+у)2) — М((£-М£)+(?у—
Му))2 == D£ 4- £)7?4-2Л1((£ — М£)(у — Му)). Величины £,ту независимы,
поэтому независимы величины ( — М£ и у — Му, тогда М((£ — М^){у —
Му)) = М(£ - М£)М(у - Му) = 0.
Кроме характеристик положения случайной величины £ на прямой
используется ещё ряд других характеристик, каждая из которых опи-
сывает то или иное свойство распределения.
Определение. Начальным моментом k-ого порядка случайной ве-
личины £ называется математическое ожидание к-ой степени слу-
50
чайной велечины рк — M£k.
п ,
Очевидно, что для дискретных случайных величин щ ~ % х*-рИ
i—1
4-ос- ,
для непрерывных случайных величин рь — J х f(x)dx.
—оо
Определение. Центральным моментом k-ого порядка случайной
величины £ называется математическое ожидание k-ой степени слу-
чайной величины от своего математического ожидания.
Очевидно,что для дискретных случайных величин
Dk = ±- Mtfpi,
i=l
для непрерывных случайных величин
4-оо
Dk = f (х- M^)kf(x)dx.
—ОО
В частности, дисперсия - это центральный момент 2-го порядка. Для
нахождения дисперсии удобно пользоваться иногда формулой вида
= М^-(М^2. Действительно, DC, = М(£-М£У = М(?-2£М(+
(М£)2) = М? ~ М£) + (Ж)2 = М? - 2(М£)2 + (М^У = М? -
(Ж)2-
Пример 1. Дискретная случайная величина £ задана рядом распре-
деления
£ 2 5 8 19
р 0,2 0,3 0,4 0,1
Найти математическое ожидание и дисперсию случайной величины
С
Решение. = £ Xipi = 2 • 0,2 + 5 • 0,3 + 8 • 0,4 + 19 • 0,1 —7. Для
нахождения дисперсии используем формулу DC = МС~ — (МСУ
МС? = Е x2iPi = 22 - 0,2 + 52 - 0,3 + 82 - 0,4 + 192 - 0,1 = 70
DC = 70 - 72 = 70 - 49 = 21.
Пример 2. Плотность распределения непрерывной случайной вели-
чины С имеет вид:
, . f Зя2, х е [-1,0]
/W=[ О, г?[-1.0].
51
Найти математическое ожидание и дисперсию.
Решение.
f xf(x)dx— f xf(x)dx+ f xf(x) + *f xf(x)dx~ J'3x3dx =
-OG -OO -1 0 -1
3x4|0 „ 3
4 1-1 “4*
Дисперсия найдем по формуле D£ — М£2 — (М£)2.
М£2 = Тx2f(x) = ° Зж4<£г =
Поэтому Щ = 1- (-|)2 = i
Задачи.
1. Случайная величина £ задана рядом распределения
е 2 4 7 10 12
р 0,1 0,2 0,4 0,2 0,1
Найти математическое ожидание и дисперсию.
2. Два прибора испытывались на надежность. Вероятность отказа
первого прибора ОД, а второго 0,05. Найти математическое ожидание
и дисперсию случайного числа отказавших приборов.
3. Вероятность приема позывного сигнала одной радиостанции дру-
гой радиостанцией равна 0,2 при каждой посылке. Позывные подаются
каждые 5 секунд до тех пор, пока не будет получен ответный сигнал,
приннимаемый достоверно. Общее время прохождения позывного и от-
ветного сигналов равно 16 секунд . Найти среднее число подаваемых
позывных сигналов до установления двухсторонней связи.
4. Непрерывная случайная величина имеет равномерное распределе-
ние
хе(а’ь)
Д 0, х£(а,Ь).
Найти математическое ожидание и дисперсию.
5. Непрерывная случайная величина £ имеет показательное распре-
деление с параметром А > 0
о, х ( °’ х < 0
( 1 - е-Дт, х > 0.
Найти математическое ожидание и дисперсию.
6. Функция распределения случайной величины £ имеет вид (закон
арксинуса)
52
О, X < -1
| + - arcsine, -1 < x < 1
1, 1 < x.
Найти математическое ожидание и дисперсию.
2.6 Нормальное распределение (Гаусса)
Одним из наиболее часто встречающихся распределений является
нормальное распределение (Гаусса). Оно играет большую роль в те-
ории вероятностей, а связано это с тем, что нормальный закон рас-
пределения является предельным законом, к которому приближаются
другие законы распределения.
Определение. Непрерывная случайная величина £ имеет нормаль-
ное распределение, если ее плотность распределения имеет вид:
/(Ж) =
где а и а- некоторые постоянные, называемые параметрами распре-
деления.
Функция распределения F(x) принимает вид:
V^r До
Найдем основные числовые характеристики нормального распреде-
ления.
Математическое ожидание
М£ = I xf(x)dx — -^=- / хе
Сделаем замену переменной и = ~~ Тогда х — сги 4- a,dx = a du, а
пределы интегрирования остаются теми же, в чем нетрудно убедиться.
Получаем
, _ 1 г . ч . (У г , а г
М£ = —7= / (аи + а)е 2 du ~ —у= / ие 2 du-\—/ е 2 du.
53
Первый из интегралов в правой части полученного равенства, равен
нулю, как интеграл от нечетной функции в симметричных пределах, а
второй интеграл (так называемый интеграл Пуассона) равен т.е.
4-оо 2 __
У du — 5/2%
Тогда = х/2^ — а.
Значит, параметр а нормального распределения равен математичес-
кому ожиданию соответствующей случайной величины, т.е. — а.
Найдем дисперсию нормально распределенной случайной величины
Используем замену переменной и =
Тогда
1 4-оо , о ,
1 Г •> 9 _U /"О— —-7
DE — —/ а и/в 2 du = —=== и е 2 du.
у/^гст_^ y/^-L
Далее интегрируем по частям, полагая и = t,ue du = dv, откуда
dt — du,v — -е-^, поэтому
ГТ2 2
V
4-00 э
+ У e~^du).
-оо
Первое из слагаемых в скобках равно нулю, т.к. = 0, а
второе равно У2тг.
Значит, D£ = = <т2, Итак, дисперсия нормально распреде-
ленной случайной величины £ равна ст2, то есть — а2, ст есть среднее
квадратическое отклонение, так как а = \/D£ = у/v2 — о\ После вы-
числения математического ожидания и дисперсии становится ясным
вероятностный смысл параметров а и а нормального распределения.
График функции/(ж) = • ехр * (Рис. 1.)
54
Функция плотности нормального распределения f(x) с параметрами
а = 0, ст = 1 называется плотностью стандартного нормального рас-
пределения случайной величины, то есть для стандартной нормальной
случайной величины
г/ \ 1
/ W = ' ехР 2
V
Для вычисления вероятности попадания значения случайной величи-
ны, распределенной нормально, в заданный интервал (а,/3) обычно
пользуются специальной функцией
Эта функция называется функцией Лапласа или интегралом вероят-
ности. Ее значения даны в таблице 2 (см. Приложение) (табулирова-
ны). При использовании таблицы следует помнить, что функция Ф(х)-
нечетная функция, поэтому в таблице приведены ее значения только
для положительного аргумента.
Найдем вероятность попадания нормальной величины £ в интервал
(а,/3), используя стандартную нормальную величину. Для этого вве-
дем случайную величину т] = Тогда Mtj = 0, Dy = 1 (предлагается
читателю проверить самостоятельно). Неравенство а < £ < (3 равно-
сильно неравенству:
ст ст а
поэтому вероятности выполнения этих неравенств равны, то есть
55
Р(а < £ < /3) = Р(^^ < < ^г). Теперь можно записать
Р(а < £ < /3) = Р(-—- <т] < -) = -^= f ехр^- dx-
а а у 2тг _{х
1 -г2 1 0 _r2 1
--== / ехр“ dx = —7= / ехр~2~ dx Ч—7= / ехр~^“ dx —
—I exp 2 dx----------7= J exp 2 dx = —j= j exp 2 dx—
Zexp* d* = Ф(У >' Ф<“7^'
Итак, для нормально распределенной случайной величины с пара-
метрами а и а имеем, что
< £ < /3) = Ф(^) - Ф(^~^).
о а
В частности, можно посчитать вероятности
Р(|£-а|< а) = 0.6837;
Р(|£ — а| < 2сг) = 0.9545;
Р(|£- а| < За) = 0.9973;
Последнее из равенств называется правило ’’трех сигм”, оно пока-
зывает, что вероятность отклонения случайной величины £ от своего
математического ожидания а меньше, чем на Зег, близка к 1, то есть
такое отклонение является практически достоверным событием.
Пример 1.
Случайная величина £ распределена нормально с параметрами а =
8, а = 3. Найти вероятность того, что случайная величина в результате
опыта примет значение, заключенное в интервале (12.5,14).
Решение. Здесь а = 12.5,/3 = 14, поэтому р(12.5 < £ < 14) =
Ф(^) - Ф(^г-) = Ф(2) - Ф(1.5) = 0.4773 - 0.4332 = 0.0441. По
таблице 2 (см. Приложение) Ф(2) = 0.4773, Ф(1.5) = 0.4332.
Пример 2. Случайная погрешность измерения подчинена нормаль-
ному закону распределения с параметрами а = 0, о = 9. Проводятся три
независимых измерения. Найти вероятность того, что погрешность хо-
тя бы одного измерения не превосходит по абсолютной величине 3.
56
Решение. Найдем вероятность того, что погрешность измерения в
одном испытании не превышает 3.
3 — 3 3
Р(1С1 < 3) = Ф(г) - Ф(—) = 2Ф(-) = 0;2586
У У У
Вероятность того, что эта погрешность превышает 3 равна
р(|£| > 3) = 1 -р(|£| < 3) = 0.7414
Вероятность того, что во всех трех испытаниях погрешность измере-
ния превышает 3, по теореме умножения вероятностей равна произве-
дению вероятностей (р(|£| < З))3 = 0.4075, тогда искомая вероятность
равна 1 — (р(|£| < З))3 = 0.5925.
Задачи
1. Математическое ожидание нормальной случайной величины
а — 3, а среднее квадратическое отклонение а ~ 2. Написать функцию
плотности вероятности £.
2. Математическое ожидание и среднее квадратическое отклонение
нормально распределенной случайной величины £ соответственно рав-
ны 10 и 2. Найти вероятность того, что в результате испытания £
примет значение, заключенное в интервале (12,14).
3. Производится измерение диаметра вала без систематических оши-
бок. Случайные ошибки измерения £ подчинены нормальному закону
со средним квадратическим отклонением ст — 10. Найти вероятность
того,что измерение будет произведено с ошибкой, не превосходящей по
абсолютной величине 15мм.
4. Систематическая ошибка удержания высоты самолетом Н-20м, а
случайная ошибка характеризуется средним квадратическим отклоне-
нием, равным 50м. Для полета самолета отведен коридор высотой 100м.
Найти вероятность того, что самолет будет лететь ниже, внутри и вы-
ше коридора, если самолету задана высота, соответствующая середине
коридора.
5. Нормальная случайная величина £ есть ошибка измерения неко-
торого расстояния. При измерении допускается систематическая ошиб-
ка в сторону завышения на 1.2см., среднее квадратическое отклонение
ошибки измерения равно 0.8см. Найти вероятность того, что отклоне-
ние измеренного значения от истинного не превзойдет по абсолютной
величине 1.6см.
57
2.7 Некоторые вероятностные распределения
В теории вероятностей, кроме нормального распределения, исполь-
зуются еще ряд других распределений, некоторые из них приводятся
ниже.
I. Дискретные распределения
1. Вырожденное распределение - случайная величина £ сосредоточе-
на в точке а, то есть р(£ = а) = 1, его характеристики:М£ = a, D£ — 0.
2. Распределение Бернулли - случайная величина £ задана рядом
распределения Р(£ = к) = Ckpkqn~k, k = 0,1, ..,п, где q = 1 - p. Тогда
= np, — npq.
3. Геометрическое распределение - случайная величина £ задается
рядом распределения. Р(£ — к) = р(1 — p)k,k = 0,1,2,... Тогда М£ =
р ’ 4 р-
4. Распределение Пуассона - случайная величина £ задана рядом
распределения Р(£ — к) = ^е~х- Тогда М£ — A, _D£ — А.
II. Непрерывные распределения.
1. Равномерное распределение - случайная величина £ имеет функ-
цию плотности вероятности
°> г£М],
пх) ] * е ML
Тогда М( = 'ф, Df, =
2. Распределение Симпсона - случайная величина £ имеет функцию
плотности вероятности
f(T\ _ / 6^ “ • |а -h Ь - 2я|, х е [а, 6],
J{X>-\ о, a^ML
Тогда W - ^(а3 + Ь3 - 2(^)3),P£ = «
3. Показательное (экспоненциальное) распределение - случайная ве-
личина £ имеет функцию плотности вероятности
• / Ле-Ах', х > 0
= | о, ,<0'л>0-
Тогда = = j?-
58
4. Распределение Лапласа - случайная величина £ имеет функцию
плотности вероятности
/(ж) — х G [—оо,4-оо], А > 0.
Тогда
5. Распределение Вейбулла-Гнеденко - случайная величина £ имеет
функцию плотности вероятности
ч ( 2Аха-1е“Хх\ х > 0,
/W=1 0, х < 0
где а > 0, А > 0. Тогда М( = А^Ц j + 1), О$ = Л-}||Г(|) -^(Г( J))2],
где Г(ж) - гамма-функция.
6. Закон арксинуса - случайная величина £ имеет функцию плотнос-
ти вероятности
1
о,
Тогда М£ = 0, Df, = f.
7. Распределение Максвелла - случайная величина £ имеет функцию
плотности распределения
( ч [ ^£ж2е“/гг‘", х > 0,
fix} = < ’
k 7 1 0, ж<0.
Тогда = =
8. Гамма-распределение - случайная величина £ имеет функцию плот-
ности вероятности
^+*Г(«+1)Ж ’ х > и а > _1 Р > 0.
0, х < 0
Тогда М£ = (а + 1)/?, Щ = 02(а + 1), Г(а) = / x^e^dx.
9. Бета-распределение - случайная величина £ имеет функцию плот-
ности вероятности
г(1)-”г(б)жЛ z)6 \ же (0,1)
о, ж £(0,1).
59
Тогда - гамма-функция.
10. Распределение Рэлея - случайная величина £ имеет функцию
плотности вероятности
Тогда
11. Распределение Коши - случайная величина £ имеет функцию
плотности вероятности
= ----V’ А>0-
тг А2 4- (ж — ау
Тогда М£ = оо, £)£ = оо.
12. Логарифмически нормальное (логнормальное) распределение -
случайная величина £ имеет функцию плотности вероятности
Тогда М£ - е'^Щ = - 1).
13. Хи-квадрат распределение - случайная величина £ = Е где
гц - независимые нормально распределенные случайные величины с па-
раметрами 0,1. Тогда
f(x) - J 2"12Г(п/2}Х- 2> Х > °’
/( } I 0, X < 0.
И М£ = п, = 2п, Г(я) - гамма-функция, п - число степеней свободы.
14. Распределение Стъюдента- случайная величина £ — где ту-
нормально распределенная случайная величина с параметрами 0,1; рп -
независимая от ту величина с распределением Хи-квадрат с п степенями
свободы. Тогда плотность распределения
ж=о,^ = ^.
60
2.8 Закон больших чисел
Ранее уже отмечалось, что массовые случайные явления обладают
своими закономерностями. Свойство устойчивости в какой бы области
оно не проявлялось, коротко можно охарактеризовать так: конкретные
особенности каждого отдельного случайного явления почти не сказыва-
ются на среднем результате массы таких.явлений; случайные отклоне-
ния от среднего значения в каждом отдельном явлении в массе взаимно
погашаются, нивелируются, выравниваются. Именно эта устойчивость
средних и представляет собой физическое содержание ’’закона больших
чисел”, понимаемого в широком смысле слова: при очень большом чис-
ле случайных явлений средний их результат практически перестает
быть случайным и может быть предсказан с большой степенью опре-
деленности. В узком смысле слова ’’закон больших чисел” в теории
вероятностей понимается как ряд математических теорем, в каждой
из которых для тех или иных условий устанавливается факт прибли-
жения средних характеристик большого числа опытов к некоторым
определенным постоянным.
Рассмотрим сначала
Неравенство Чебышева.Лля любой случайной величины £, име-
ющей конечную дисперсию, при каждом е > 0 имеет место неравен-
ство:
Р(\£-М£\>£)<^.
Доказательство. Пусть /(ж) — функция плотности случайной ве-
личины £, то
Р(к - М(\ > е) = / f(x)dx.
Так как в области интегрирования > 1, то
У f(x)dx < ~ У (х - M£)2f(x)dx <
|£-М£|>е 6 |£-М£|>с
Неравенство доказано.
61
Следствие. Для любой случайной величины £ справедливо нера-
венство:
т-ж|>з/5^<
Доказательство. Пусть в неравенстве Чебышева е = тогда
Р(\£ - м(\ > Зд/Сё) < — 97 то есть Для любой случайной ве-
личины вероятность того, что отклонение случайной величины от ее
математического ожидания выйдет за пределы трех средних квадра-
тических отклонений, не может быть больше 1/9.
Теорема (Чебышева). Если Сь • • • — последовательное!™
попарно независимых случайных величин, имеющих конечные диспер-
сии, ограниченные одной и той же постоянной
D£i < С, D& < С,..., < С, то каково бы не было постояное
€ > О
П П Ь=1
Такая сходимость последовательности случайных величин называ-
ется сходимостью по вероятности.
Доказательство. Учитывая попарную независимость случайных
величин, получим, что
(1 п \ 1 п /1 п \ 1 п
Е = - Е M^,D - Еа- = -2 Е DU,
п k-1 / П k=l \п к-1 / k-1
так как < С, для всех fc, то D — п•
Используя неравенство Чебышева, имеем
Р{]^ t Е WI < е} > 1 -
n k=l п
fl п
Е2
Переходя к пределу при п —> оо, получим, что
1 71 J п
lim Р{\- Е & ~ “ Е W| < с} > 1.
Но так как вероятность не может быть больше единицы, то отсюда
и следует утверждение теоремы.
Следствие 1 (Теорема Бернулли). Пусть р — число наступ-
лений события А в п независимых испытаниях и р есть вероятность
62
наступления события А в каждом из испытаний. Тогда для любого
Е > О
lim Р(\— — р| < е) — 1
п-+оо 1
Доказательство. Введем случайные величины д* равные числу
появлений события А при к-м испытании, то есть д& есть либо 0, либо
1, имеем д = дх -Ь Д2 + •.. + дп, а так как Мр^ — р, Dpk ~ РЧ < то
теорема Бернулли — частный случай теоремы Чебышева.
Следствие 2 (Теорема Пуассона). Если в последовательности
независимых испытаний вероятность появления событиия А в к-м ис-
пытании равна то
п
.. £ Рк
lim Р(|С_Ы_I <е) = 1
Vln п 1 7
где д — число появлений события А в первых п испытаниях.
Доказательство. Рассмотрим случайные величины д& равные чис-
лу появления события А в к-м испытании. Тогда Мр^ = pk,Dpk =
РьЯк. < 4? и теорема Пуассона есть частный случай теоремы Чебыше-
ва.
В теореме Чебышева есть два жестких требования: 1) независимость
случайных величин; 2) конечность дисперсий случайных величин. При-
ведем без доказательства две теоремы, в которых эти условия заменены
на другие.
Теорема Маркова.Пусть имеется зависимые случайные величи-
ны £1>£г,Если
DELtk)
. -----> 0, п оо,
п1
то для любого е > О
Теорема Хинчина. Если случайные величины £i,... ,£п незави-
симы, одинаково распределены и имеют конечные математические
ожидания (а = то
п Ь=1
63
Пример 1. Используя неравенство Чебышева, оценить вероятность
того, что |£ - М£\ < 0.2, если D£ — 0.004.
Решение. Неравенство Чебышева Р(|£ — М£\ > е) < поэтому
Р(\£ ~ Ж1 < е) > 1 - тогда Р(|£ - М£\ < 0.2) > 1 - = 0.9.
Пример 2. Устройство состоит из 10-ти независимых работающих
элементов. Вероятность отказа каждого элемента за время Т равна
0.05. Оценить вероятность того, что абсолютноая величина разности
между числом отказавших элементов и средним числом отказов за вре-
мя Т окажется а) меньше 2-х; б) не меньше 2-х.
Решение, а) Обозначим через £ — число отказавших приборов за
время Т. Тогда £ — дискретная случайная величина с распределе-
нием Бернулли, поэтому = пр — 10 • 0.05 — 0.5; D£ = npq =
10 • 0.005 • 0.95 = 0.475. Как было сказано выше из неравенства Чебы-
шева следует, что Р(|£ — М£\ < е) > 1 - значит, Р(|£ — 0.5| < 2) >
1 - = 0.88.
б) По неравенству Чебышева получим, что Р(|£ — 0.5| > 2) < ~~ =
0.12
Пример 3. Последовательность независимых случайных величин
£1, ^2) • • • • • • , задана законом распределения
—па 0 па
2п2 х п2 2п2
Применима ли к заданной последовательности теорема Чебышева?
Решение. Для того, чтобы к последователности случайных вели-
чин была применима теорема Чебышева, нужно, чтобы выполнялись
два условия 1) случайные величины должны быть попарно независи-
мыми; 2) их дисперсии должны быть ограничены одной константой.
Первое условие обеспечено условием задачи. Проверим второе условие,
для этого сначала найдем М£п, а затем D£n.
Тогда
D^n = • (1 - ^2) + (™*)2 2^2 = °2
Итак, D£n = а2, значит, закон больших чисел для данной последо-
вательности случайных величин выполняется.
64
Задачи.
1. Дискретная случайная величина £ задана законом распределения
£ 0.3 0.6
р 0.2 0.8
Оценить Р(|£ — М£| < 0.2).
2. Дискретная случайная величина £ задана законом распределения
£ 0.1 0.4 0.6
р 0.2 0.3 0.5
Оценить Р(|£ - М£| > д/ОЛ).
3. В осветительную сеть параллельно включено 20 лампочек. Веро-
ятность того, что за время Т лампа будет включена, равна 0.8. Оце-
нить, что за время Т Р(|£ — М£| < 3 и Р(|£ — М£\ > 3.
4. Последовательность независимых случайных величин
£1, ^2, • • •, £п, • • • задана законом распределения
£п а
п+1 п
2п+1 2п+1
Применима ли к заданной последовательности теорема Чебышева?
5. Последовательность независимых случайных величин
£1, £2,..., £п,... задана законом распределения
3 0
£п
т
3
Верен ли закон больших чисел для данной последовательности слу-
чайных величин? (Использовать теорему Хинчина)
6. Последовательность независимых случайных величин
£1, £2,.. •, £п, • • • задана законом распределения
Верен ли закон больших чисел для заданной последовательности
случайных величин?
65
2.9 Характеристические функции
Определение. Характеристической функцией случайной величи-
ны £ называется комплекснозначная функция = Melt\ опреде-
ленная для всех действительных значений t.
Из определения следует, что для дискретной случайной величины с
рядом распределения
С • • • %к
Р Pl Р2 ... Pk
характеристическая функция будет определятся формулой
^(t) = f ea’*pk,
а для непрерывной случайной величины
^(t) - I el,xf(x)dx.
—oo
Рассмотрим свойства характеристических функций.
Свойство 1. = 1 для любой случайной величины £.
Доказательство. ^(0) —- MelQ^ = MeQ = М • 1 — 1
Свойство 2. |^(t)| < 1 для всех t £ R-
Доказательство.
|^(t)| — < М|ег<^| == Af|cos(t£) 4- i sin(t£)| =
= M^cos2(t£) + sin2(t£) = M • 1 = 1
Свойство 3. Для любых a,b € R <f>a£+b(t) — e^ip^at)
Доказательство, = = M(elta^ettb) = etbt(p^(at).
Свойство 4. Пусть случайные величины £i,<£2> • • • >£п независимы,
тогда ^+-+6. =
Доказательство. Учитывая независимость случайных величин, име-
ем, что = Д ^(0’
Свойство 5. Пусть случайная величина имеет абсолютный мо-
мент к-го порядка. Тогда <р^(0) = ikM^k, где </>^(0) — производная
к-го порядка функции
66
Доказательство. Используя формулу дифференцирования показа-
тельной функции, получим, что
—cpdt) = = м(^е^ = = ikMtfke*).
Если t — 0, то <ре(0) ~ ikM(£kelQ^) — ^М(^к • 1) = ikM£k. (Внесе-
ние дифференцирования под знак математического ожидания возмож-
но, так как математическое ожидание — это либо сумма, либо ин-
теграл) Значит, разложение в ряд характерестической функции, если
М\£< оо, имеет вид ^(t) = 1 + 4- o(|tn|).
Пример 1. Найдем характеристическую функцию для случайной
величины £ имеющей распределение Пуассона
P(£ = fc) = £e-A, * =0,1,2,....
^e(t) = S = е~А § = е-А g « - е“АеАе" =
(Здесь использовали разложение в ряд функции у = ех, ех — Е ^-)
Пример 2. Найдем характеристическую функцию нормального рас-
пределения случайной величины £. Случайная величина имеет функ-
1 (г-и)2
цию плотности вероятности , поэтому
[ eltxe-{-^r-dx — —JL_ f ettz~l dx
Сделаем замену переменной z = — ita. Тогда x = az 4- ita2 4-
a,dx = adz, поэтому
i oc-i+or 2
. [ e~^dz,
OO—2-f-Cr . 0.2^2
Известно, что J e~^dz = v2?r, значит, tp(t) = eia 2 .
—oc—i+a
Замечание. Для стандартной нормальной величины (параметры
0,1) характеристическая функция <p(t) = е~^
Если задана функция распределения случайной величины %, то ее
характеристическая функция находится однозначно. Но оказывается,
что по характеристической функции можно также однозначно задать
закон распределения случайной величины.
67
Теорема обращения. Справедливы следующие утверждения:
1. Для целочисленной случайной величины £
рк = Р(£ = к) = ] e~iuip(t)dt, к = 0, ±1, ±2,....
Z7T J
—7Г
2. Если характеристическая функция <p(t) случайной величины £
абсолютно интегрируема, то существует плотность распределения
/(ж), определяемая формулой
= -L у e-iix<p(f)dt
Теорема приводится без доказательства. Доказательство можно най-
ти в [1].
Пример 3. Найти закон распределения случайной величины £ с
характеристической функции </>(£) ~ cos t.
Решение. Характеристическая функция (p(t) = cos£ не является
абсолютно интегрируемой на всей прямой, поэтому предполагаем, что
£ — дискретная случайная величина.
Тогда характеристическая функция имеет вид
^(0 = 52 = 12 Pk^tXk + i 12 Pksmtxk.
t=i k=i k~i
Так как = cost, то ясно, что £ может принимать только 2 зна-
ченя: 1 и -1 с равными вероятностями, то есть
Рг = Ptf = -1) = 1/2, Р2 = Р(£ = 1) = 1/2.
Задачи.
1. Найти характеристическую функцию случайной величины, для
которой задана плотность вероятности
х \ 2х,х е [0,1]
= j 0,^ [0,1].
2. Найти характеристическую функцию случайной величины £, плот-
ность вероятности которой имеет вид:
/(х) =
68
3. Пусть <^(i) — характеристическая функция случайной величины
£. Найти характеристическую функцию случайной величины — £.
4. Пусть £ и г/ — независимые одинаково распределенные случайные
величины с характеристической функцией у?(£). Найти характеристи-
ческую функцию случайной величины £ — ту.
5. Найти закон распределения, которому соответствует характерис-
тическая функция (p(t) — 2/3-4-1/3 cos 3t.
2.10 Центральная предельная теорема
В рассмотренном выше законе больших чисел были указаны усло-
вия, когда суммы случайных величин сходятся по вероятности к неко-
торым предельным. Но ничего не было сказано про законы распределе-
ния предельных случайных величин. Предельные законы распределе-
ния являются предметом изучения центральной предельной теоремы,
которую иногда называют ”количественной формой закона больших
чисел”.
Сначала дадим определение сходимости, которой будем пользовать-
ся.
Определение. Последовательность случайных величин {£п} сла-
бо сходится к случайной величине если для любой непрерывной и
ограниченной функции выполняется условие при п -4 оо,
4-ос- 4-ос
У ip(x)dFn(x) -4 У* ^(x)dF(x),
—ос —ос
где Fn и F — функции распределения случайных величин Обо-
значается это Fn => F.
В дальнейшем нам понадобится:
Теорема непрерывности. Для сходимости Fn =4 F необходимо
и достаточно, чтобы 4>(t)npu каждом t, где и (p[t)
характеристические функции (п и
Доказательство теоремы не приводим, его можно найти в [1].
Пусть {Сп}^! — последовательность независимых, одинаково рас-
пределенных случайных величин. Пусть М(п = a, D£n = a2,Sn =
£ £^,Ф(т) - стандартный нормальный закон распределения (парамет-
ры 0,1).
69
Рассмотрим последовательность случайных величин (п ~
Теорема центральная предельная. Если 0 < о2 < оо, то при
п —> oO'F^x) => Ф(х),х Е (—оо,оо), ,Ф(я) — J e^^dt.
Доказательство. Без ограничнеия общности можно считать, что
а =? 0-, так как иначе можно было бы рассмотреть последовательность
= £п — а}^, при этом последовательность {£п} не изменится.
Учитывая теорему непрерывности достаточно доказать, что (р^п (0 —>
когда а = 0.
По свойству характеристической функции и так как & независимы
и одинаково распределены, имеем, что
. И—т— у4 C.L • t f t t
<p> = Me^" = Me = M П e‘^‘ = ^(-^=) = y,n(~V=)>
&\/П (Уу/П
где ^(0—характеристическая функция
Так как М(2 существует, то используем разложение в ряд функции
<р(0 (так как а — 0, то — М£2): <^(0 = ^(0)-f-t^,(0)-hy<p'r(0)-|-o(t2),
но 9?(0) — 1,^(0) = iM^i = 0,9?"(0) = i2M£2 — i2a2, поэтому <£>(0 ==
l-tV/2-bo(t2).
Найдем In £n(0
t t rr2 t t2
InC^) = In <pn(-^=) = nlny>(-^=) = nln(l - y(^)2+oi))
ay/п &y/n z ay/n a£n
Воспользуемся разложением в ряд функции 1п(1 — х) — -(ж + у +
£ + поэтому InC„(t) = п(-^ +о(Д)) -> co.
Итак, доказано, что при п —> оо ln(n(t) -» —у, тогда ^„(0 ->
е“"2", а это есть характеристическая функция стандартной нормальной
величины, значит, теорема доказана.
2.11 Системы двух случайных величин
В практических применениях теории вероятностей часто приходит-
ся сталкиваться с задачами, в которых результат опыта описывается
не одной случайной величиной, а двумя или.более случайными величи-
нами. Свойства системы нескольких случайных величин не исчерпыва-
ются свойствами отдельных величин, ее составляющих, помимо этого
70
она включает также взаимные связи (зависимости) между случайны-
ми величинами. Здесь мы рассмотрим только систему 2-х случайных
величин (£,??).
Определение. Функцией распределения системы 2-х случайных ве-
личин (£, у) называется вероятность совместного выполнения 2-х не-
равенств (£ < х,т} <у)
F(x,y) = Ptf<x,7} < у).
Функция распределения у) есть вероятность попадания случай-
ной точки (£, ту) в бесконечный квадрат с вершиной в точке (я, ?/), лежа-
щей левее и ниже ее. Функция распределения одной случайной величи-
ны £ - обозначим ее F^x) - представляет собой вероятность попадания
случайной точки в полуплоскость, ограниченную справа абциссой ж, а
функция распределения у - F^y) - вероятность попадания случайной
точки в полуплоскость, ограниченную сверху ординатой у.
Свойства функции распределения F(x, у) аналогичны свойствам функ-
ции распределения одной случайной величины.
1) Функция F(x, у) есть неубывающая функция обоих своих аргумен-
тов, то есть при Х2 > «1, F{x2,y) > F(x^y\ при У2 > Vi, F(x^y2) >
F(x,yi).
2) Повсюду на —оо функция распределения равна нулю F(xy —оо) =
F(-oo, у) — F(—оо, —оо) — 0.
3) При одном из аргументов, равном 4-оо, функция распределения
системы есть функция распределения случайной величины, соответ-
ствующей другому агрументу F(x,4-oo) = F^z), F(-f-oo,x) = Fr/(?/).
4) Если оба аргумента равны Ч-оо, функция распределения системы
равна 1. F(4-oo, Ч-оо) = 1.
5) Р(а < С < &, с < rj < d) = F(a, d) - F(a, с) - F(b, d) 4- F(a, d).
71
Введенная функция распределения существует для систем любых
случайных величин, как дискретных, так и непрерывных.
Систему дискретных случайных величин можно характеризовать
совокупностью вероятностей которые могут быть сведены в табли-
цу:
а?! ж2 хп
У1 Р11 Р12 Pin
У2 Р21 Р22 Р2п
Ут Рт1 Рт2 Ртп
Тогда одномерные законы: Р(£ — Xk) = Е Pkj — Pk, Р(у = yi) =
7=1
n
Е pit = pi.
Систему непрерывных случайных величин можно Характеризовать
плотностью распределения. Рассмотрим вероятность попадания (£,77)
в малый прямоугольник D со сторонами Да? и Ду.
P(^y)ED).
По пятому свойству функции распределения:
lim ——----------------
Дш—>0,Ду—>0 /хт./\у
m F(x + Да?,у + Ду) - F(x 4- Дж,у) - F(a?,y + Ду) 4- F(z,y)
Дг—>0.Ду—>0 ДжДу
Если функция F(a?,y) непрерывно дифференцируема, то
Кш Л1^1£2) = ^)=я„)
Дз:-*о, Дз/->о Да? Ду дхду
72
Функция f(x, у) называется плотностью распределения системы 2-х
случайных величин.
Тогда
х У
F(x,y) = / / f(x,y)dxdy.
ь d
Поэтому P(a < £ < 6, с < у < d} = f f f(x,y)dxdy.
Плотность распределения удовлетворяет следующим свойствам:
1) /(м) °-
2) / "7 f(x,y)dxdy = 1
—оо —ос
3) Одномерные плотности имеют вид:
/<(х) = Т f(x,y)dy; f^y) = *Ff(x,y)dx.
Пример 1.
Двумерная случайная величина (£,т?) распределена равномерно в об-
ласти Z), если
г/ ч ( (х>у) € D
где Sd - площадь области D.
Определение. Случайные величины £ и у называются независи-
мыми, если закон распределения каждой из них не зависит от того,
какое значение приняла другая величина. В противном случае £ и у
называются зависимыми.
Таким образом, дискретные случайные величины независимы, если
Р(£ = У = = Р(£ = • Р(Л = yj) = Pi 'Pj\ непрерывные
случайные величины независимы, если — fc • fir
Пример 2. Плотность распределения системы (£,??) имеет вид:
У) ir2(x2 + у2 + х2у2 4-1)
Определить, зависимы или нет £ и у.
Решение. Разлагая знаменатель на множители, имеем, что
/(Х)У) i 2V * 7l i
7г(1 + x2) 7Г(1 4-?/)
значит, £ и у- независимы.
73
Определение. Корреляционным моментом случайных величин £ и
rj называется
K(,v = М((£ - ме) • (г, - Ml}))
Для дискретных случайных величин
Kt.y = Е Efri - MCfah - Mr))ptj.
i—1 j=l
Для непрерывных случачайных величин
К(л = / / (* - w0(y - Mri)f(x,y)dxdy
— ОО —OG
Если случайные величины £ и Т}- независимы, то тогда = 0, но
существуют примеры, которые показывают, что хотя К^Г) = 0, случай-
ные величины £ и rj- зависимы.
Определение. Коэффицентом корреляции называется величина
г. =
у/Щу/Пг)
Свойства коэффицента корреляции
1) Для независимых случайных величин — 0.
2) |rU| < 1.
3) \r^\ = 1 тогда и только тогда, когда существуют такие числа
а / 0 и Ь, что rj = а£ 4- Ь.
Значит, коэффицент кореляции характеризует линейную зависимость
между случайными величинами.
Пример 3. Двумерное нормальное распределение имеет вид:
г (х~а1)2 , r(r-ai)(y-a2) _ (г/-а2)2
2(1 - r2)al (1 - г2)о\сг2 2(1 - r2)al
где ai = М£,а2 = Mrj.ai = - — r£sr
Если £ и Т] независимы, то двумерное нормальное распределение име-
ет вид:
74
fl , 1 г (я-ai)2 (y-a2)\
/(l-’> = 2^eXpf--------M---------Я~}'
Пример 4. Задана дискретная двумерная случайная величина (£,т/):
Ж 3 6
10 0,25 0,1
14 0,45 0,2
Найти коэффицент корреляции г^?/.
Решение. Найдем сначала и Мт/.
= £ *i(E Рц) = 3 • (0,25 + о, 45) + 6 • (0,1 + 0,2) =
i=i j=i
= 3-0,7+ 6-0,3 = 3,9.
Му = Е Рц) = Ю • (0,25 + 0,1) + 14 • (0,45 + 0,2) =
3=1 i=l
= 10-0,35 + 14-0,65 = 12,6.
Для вычисления дисперсии воспользуемся формулой D£ = Л1£2
(Ж)2-
Найдем М£2 и Му2.
Щ2 = 9-0.7 + 36-0,3 = 17,1.
Му2 = 100 • 0,35 + 196 • 0,65 = 162,4.
Поэтому
D£ = 17,1 - (3,9)2 = 17,1-15,21 = 1,89; = /Р£ = 1,7.
Dy = 162,4 - (12,6)2 = 162,4 - 158,76 = 3,64; ст,, = = 1,9.
Найдем корреляционный момент К^.
= Е Е - МЫу, - My)Pij = (3 - 3,9)(10 - 12,6) • 0,25+
+(6 - 3,9)(10 - 12,6) • 0,1 + (3 - 3,9)(14 - 12,6) • 0,45+
+(6-3,9)(14 - 12,6) • 0,2 - 0,06.
Тогда
75
Задачи.
1. Задана плотность распределения непрерывной случайной величи-
ны
,, . _ ( | sin х sin у, 0 < х <. тг,0 < у < тг
1[Х'У)~\ 0, (х,у) £ ([О,тг] х [О,тг]).
Найти коэффицент корреляции.
2. Задана дискретная двумерная случайная величина
»Д£ 2 5
0,4 0,15 0,35
0,8 0,05 0,45
Найти коэффицент корреляции т.
76
Типовой расчет
Теория вероятностей
Задача 1.
1) Из отрезка [0,3] наугад выбираем два числа. Найти вероятность
того, что их разность меньше 1.
2) На десяти одинаковых карточках написаны числа от 0 до 9. Найти
вероятность того, что наудачу образованное с помощью данных кар-
точек трёхзначное число делится на 2.
3) Из отрезка [0,3] наудачу выбираем два числа. Найти вероятность
того, что их сумма больше трёх.
4) На десяти одинаковых карточках написаны числа от 0 до 9. Найти
вероятность того, что наудачу образованное с помощью данных кар-
точек двузначное число делиться на 2.
5) Бросаем п игральных костей. Найти вероятность того, что на
всех костях выпало одинаковое число очков.
6) Бросаем четыре монеты. Найти вероятность того, что выпало
ровно два ’’герба”.
7) Бросаем три монеты. Найти вероятность того, что впало не боль-
ше двух ’’гербов”.
8) Найти вероятность того, что при случайном упорядочивании мно-
жества {1,2,..., 2п] каждое чётное число имеет чётный номер.
9) Из ящика, содержащего три билета с номерами 1, 2, 3 вынимают
по одному все билеты. Найти вероятность того, что хотя бы у одного
билета порядковый номер совпадёт с собственным.
10) Бросают две игральные кости. Найти вероятность того, что сум-
ма выпавших очоков делится на 6.
И) Какова вероятность того, что сумма двух наугад взятых по-
ложительных чисел, каждое из которых меньше либо равно 1, будет
меньше либо равна 1, а их произведение будет не больше 2/9.
12) Найти вероятность т^ого, что наудачу взятое трёхзначное число
77
окажется кратным 2, либо 5, либо и тому и другому одновременно.
13) Из 12 лотерейных билетов, среди которых 4 выигрышных, на-
удачу берут 6. Какова вероятность того, что хотя бы один из них вы-
игрышный.
14) В ящике 20 шаров с номерами 1,2,.. ., 20.. Наудачу выбирается
шесть шаров. Найти вероятность того, что среди них есть шары с
номерами 1 и 2.
15) Бросают 4 игральные кости. Найти вероятность того, что на
них выпадет по одинаковому числу очков.
16) Имеется пять отрезков, длины которых равны соответственно
1, 3, 5, 7, 9 единицам. Найти вероятность того, что с помощью .взятых
наудачу трёх отрезков из данных можно построить треугольник.
17) Из колоды карт (52 карты) наудачу извлекаются три карты.
Найти вероятность того, что это будут тройка, семёрка, туз (в ука-
занном порядке).
18) На полке в случайном порядке расставлено 40 книг, среди кото-
рых находится трёхтомник А. С. Пушкина. Найти вероятносто того,
что эти тома стоят в порядке возрастания номера слева направо, но не
обязательно рядом.
19) При наборе телефонного номера абонент забыл две последние
цифры и набрал их наугад, помня только, что эти цифры нечётны и
разные. Найти вероятность того, что номер набран правильно.
20) Из отрезка [а, Ь] наугад выбрали два числа. Найти вероятность
того, что их частное больше если а = 1,6 — 4.
21) Случайно выбран трёхзначный телефонный номёр. Чему равна
вероятность того, что все цифры различные.
22) Бросают две игральные кости. Какова вероятность того, что
сумма очков не меньше четырёх.
23) Найти вероятность того, что у случайно взятого четырёхзнач-
ного числа каждая следующая цифра меньше предыдущей.
24) На отрезке [а, Ь] наугад выбрали два числа. Найти вероятность
того, что их произведение меньше у, если а — 1, b = 5.
25) Если повернуть лист бумаги на 180й, то цифры 0, 1, 8 не изме-
нятся, цифры 6 и 9 переходят друг в друга, а остальные цифры теряют
смысл. Найти вероятность того, что случайно взятое трёхзначное чис-
ло не измениться при повороде листа бумаги на 180й.
26) На восьми одинаковых карточках написаны числа 2, 4, 6, 7, В,
11, 12, 13. Наугад беруться две карточки. Найти вероятность того, что
78
образованная из двух полученых чисел дробь сократима.
27) Из отрезка [а, Ь] наугад выбрали два числа. Найти вероятность
того, что их разность меньше либо равна |, если а = О, Ъ = 3.
28) Десять книг на одной полке расставляются наугад, Найти веро-
ятность того, что при этом три определённые книги окажутся постав-
ленными рядом.
29) Из отрезка [а, Ъ] наугад выбрали два у<исла. Найти вероятность
того, что их сумма больше, либо равна За, если а = 2, b = 5.
30) Нати вероятность того, что после случайного упорядочевания
элементов множества {1,2,... ,п} числа 1, 2, 3 стоят рядом в порядке
возрастания.
Задача 2. Игра между А и В ведётся на .следующих условиях: пер-
вых ход всегда делает А, он может выиграть с вероятностью pi, если
А не выигрывает, то ход делает В и может выиграть с вероятностью
gi. Если В не выигрывает, то А делает второй ход, который может
привести к его выигрышу с вероятностью р2- Если А вторым ходом
проигрывает, то победителем считается В. Найти вероятность выиг-
рыша для А и для В.
Pl Р2 41
1 0.4 0.5 0.8
2 0.5 0.4 0.7
3 0.3 0.5 0.9
4 0.9 0.7 0.9
5 0.2 0.5 0.8
6 0.8 0.9 0.6
7 0.7 0.6 0.5
8 0.1 0.3 0.7
9 0.3 0.3 0.1
10 0.8 0.5 0.3
11 0.5 0.7 0.6
12 0.2 0.5 0.7
13 0.7 0.8 0.9
14 0.6 0.5 0.2
15 0.3 0.4 0.8
Pl Р2 4i
16 0.1 0.3 0.9
17 0.4 0.3 0.6
18 0.7 0.1 0.9
19 0.2 0.5 0.7
20 0.3 0.5 0.6
21 0.9 0.8 А7_
22 0.4 0.6 0.8
23 0.2 0.3 0.8
24 0.3 0.5 0.1
25 0.9 0.7. 0.6
26 0.1 0.4 0.3
27 0,7 0.2 0.5
28 6.5 0.3 0.2
29 0.1 0.6 0.4
30 0.4 0.3 0.6
Задача 3.
а) На складе готовой продукции находится п изделий, среди которых
к высшего качества. Наудачу выбирают т изделий. Найти вероятность
79
того, что среди них I изделий высшего качества.
1. 71 — 7, k — 4, 772 = 2, 1 = 1.
2. п = 14, А: = 8, т = 4, 1 — 2.
3. п = 14, А: = 7, m = 5, Z = 3.
4. п — 7, 04 II ео II Е LeT II
5. п — 6, к = 4, 772 = 5, 1 = 1.
6. тг = 12, II o' II Е ОО II
7. тг = 12, 55м II 5 11 II ьо
8. 72 — 9, F—< II ОС? II S o' II
9. п — 9, к = 7, m = 5, 1 = 3.
10. 72 — 8, к = 4, m = 3, 1=1.
11. 72 — 8, 04 II ОО II s o' II
12. 72= 10, II СП 3 II уь. II со
13; 72= 10, к = 5, т = 3, 1 = 2.
14. 72 = 10, к = 4, 772 = 5, / = 2.
15. 72 = 10, ??- II си 3 II II ю
б) Из п аккамуляторов за год хранения к выходят из строя. Наудачу
выбирают т аккамуляторов. Определить вероятность того, что среди
них I исправленных.
16. 71 = 100, к = 9, 772 = 7, 1 — 4.
17. п = 100, к = 8, т = 6, 1 = 3.
18. 72 = 100, к = 7, т = 5, 1 = 3.
19. 72 = 100, к = 6, 772 = 4, 1 = 2.
20. 72 = 100, к = 5, 772 = 3, 1 = 1.
21. 72 = 80, к = 10, 772 = 7, 1 = 4.
22. 72 = 80, к = 9, об II о'' II Е
23. 72 = 80, к = 8, 772 = 5, 1 = 2.
24. 72 = 80, к = 7, 772 = 5, 1 — 3.
25. 72 = 80, к = 6, 772 = 4, 1 = 2.
26. 72 = 80, к = 5, т = 3, 1 = 2.
27. 72 = 80, к = 4, т = 3, 1 = 2.
28. 72 = 90, к = 10, 3 II ~сп II to
29. 71 = 90, к = 20, 772 = 6, 1 = 3.
30. 72 = 90, к = 10, 3 II wcn II to
Задача 4.
а) На складе находится щ изделий, изготовленных на заводе 1, П2
изделий - на заводе 2, п$ - на заводе 3. Вероятность того, что деталь,
изготовленная на заводе 1, высшего качества, равна pi. Для деталей
80
изготовленных на заводах 2и 3, эти вероятности равны Р2 п Найти.
вероятность того, что при проверке наудачу взятая деталь окажется
высшего качества. При проверке взятая деталь оказалась высшего ка-
чества. Какова вероятность того, что она была изготовлена на заводе
2?
1. щ = 10, п2 — 12, пз = 18, pi — 0,7, р2 — 0,8, р3 = 0,6.
2. П1 = 12, п2 = 24, п3 = 14, pi = 0,9, р2 = 0,7, р3 = 0,9.
3. П1 = 8, п2 — 18, п3 = 22, pi — 0,8, рг —0,9, р3 = 0,6.
4. rii = 20, п2 — 22, п3 = 12, pi = 0,5, р2 = 0,6, р3 = 0,8.
5. П1 = 24, п2 = 20, тг3 = 16, pi = 0,6, р2~0,8, р3 = 0,5.
6. П1 = 14, иг = 16, п3 — 20, pi = 0,8, р2 — 0,9, р3 = 0,7.
7. П1 = 15, п2 = 17, п3 — 19, pi = 0,6, р2 = 0,9, р3 = 0,9,.
8. rii — 20, п2 = 18, п3 — 12, pi = 0,9, Р2 = 0,7, р3 = 0,8.
9. щ = 16, п2 = 18, п3 — 10, pi =0,8, р2 = 0,7, р3 —0,6,
10. щ = 10, иг = 12, п3 = 20, pi = 0,7, р2 = 0,8, р3 — 0,9.
11. П1 = 20, п2 = 14, п3 = 18, pi = 0,9, р2 = 0,8, р3 = 0,8.
12. П1 = 18, п2 — 12, п3 = 16, pi = 0,8, р2 = 0,8, р3 = 0,7.
13. П1 = 12, П2 = 20, п3 = 18, pi=0,9, р2 = 0,6, р3 = 0,9.
14. П1=8, п2 = 10, 723 = 10, pi = 0,7, р2 = 0,8, р3=9,6.
15. 711 = 10, 712 = 8, п3 = 10, pi = 0,5, Р2 = 0)6, Рз = 0,7..
б) Две перфораторщицы набили на разных перфораторах по одина-
ковому комплекту перфокарт. Вероятность того, что первая перфора-
торщица допустила ошибку, равна pi, вторая - р2. Какова вероятность,
что при проверке наудачу взятая перфокарта оказалась с ошибкой?
Какова вероятность, что эта перфокарта была набита первой перфо-
ратощицей?
16. рг=0,05, р2 = 0,2. 17. рг = 0,25, р2 = 0,15.
18. pi = 0,15, р2 = 0,1. 19. Pi — 0,1, р2 = 0,5.
20. pi = 0,8, р2 = 0,1. 21. pi = 0,9, Р2 = 0,8.
22. pt = 0,9, рг = 0,7. 23. pi = 0,9, р2 = 0,6.
24. pi — 0,6, р2 = 0,9. 25. pi = 0,7, рг = 0,9.
26. pi = 0,8, Р2 = О,7. 27. рг =0,9, р2 = 0,8.
28. pi = 0,3, рг = О, 2. 29. pi =0,1, рг = 0,3.
30. pi = 0,6, рг = 0,4.
Задача 5.
а) Прибор состоит из п узлов. Вероятность безотказной работы в
течение гарантийного срока для каждого узла одинакова и равна р.
Выход из строя узлов независим друг от друга. Найти вероятность
81
того, что за указанный срок откажут два узла, не менее двух узлов.
1. 72 = 10, р = 0,8. 2. 72 = 6, р = 0,9.
3. 72 = 10, р = 0,6. 4. п = 5, р = 0,8.
5. 72 = 7, . р = 0,8; 6. . 72 = 7, р = 0,7.
7. 72 = 4, р = 0,9. 8. 72 = 5, р = 0,9.
9. 72 = 8, р = 0,8. 10. 72 = 8, р = 0,6.
11. 72 = 4, р = 0,7. 12. 72 = 6, £ = 0,6.
13. 72 = 4, р = 0,8. 14. п = 8, р = 0,7.
15. 72 = 8, р = 0,9.
б) Вычислительное устройство состоит из 1000 элементов, работаю-
щих независимо друг от друга. Вероятность отказа каждого элемента
за смену равна р. Найти вероятность того, что за смену откажут т
элементов.
16. т = 6, р = 0,024. 17. 7/2 = 2, р — 0,005.
18. 772 = 2, р = 0,002. 19. т = 3, р = 0,0025.
20. 772 = 6, р = 0,022. 21. 772 = 5, р = 0,0015.
22. 772 = 4, р = 0,002. 23. т = 4, р = 0,021.
в) Тираж книги 5000 экземпляров. Вероятность того, что в книге
имеется дифект брошюровки, равна р. Нати вероятность того, что ти-
раж содержит 772 неправильно сброшюрованных книг.
24. 772 = 6, р = 0,002. 25. 772 = 8, р = 0,0006.
26. т = 5, р = 0,0001. 27. 772 = 10, р = 0,001.
28. 772 = 7, р = 0,0001. 29. 772 = 9, р = 0,0003.
30. 772 = 10, р = 0,002.
Задача 6.
а) Бригада рабочих за смену изготовляет п деталей. Вероятность
того, что каждая изготовленная деталь высшего качества равна р. Ка-
кова вероятность того, что за смену изготовленно т деталей высшего
качества?
1. п = 725, р = 0,75. 772 = 525.
2. п = 750, р = 0,6. 772 = 625.
3. п = 625, р = 0,8. 772 = 570.
4. п = 150, р = 0,6. 772 = 75.
5. п = 400, р = 0,9. 772 = 165.
6. п = 225, р = 0,8. 772 = 165.
82
7. п - 192, р = 0,75. т — 150.
8. п - 245, р = 0,25. т — 70.
9. п — 625, р = 0,65. т = 370.
10. п — 600, р = 0,6. т — 375.
11. п — 300, р = 0,75. т — 240.
12. п = 400, р = 0,9. т — 372.
13. п — 400, р = 0,8. т — 330.
14. п — 800, р — 0,4. m — 600.
15. п = 800, р —0,5. т — 650.
б) При установившемся технологическом процессе завод выпускает
в среднем р% продукции первого сорта. Какова вероятности того, что
в партии из п изделий, прошедших через отдел технического контроля,
количество изделий первого сорта будет не менее mi и не более m2?
16. п = 725, р — 65. mi — 620, m2 “ 680.
17. п - 1000, р = 70. mi — 652, m2 — 760.
18. п — 625, р = 64. mi — 400, Tn% — 450.
19. п — 300, р — 45. mi — 75, m2 — 90.
20. п = 225, р-25. mi — 45, m2 — 60.
21. п = 400, р ~ 50. mi — 190, m2 — 215.
22. п — 625, р-36. mi — 225, m2 — 255.
23. п = 300, р- 75. mi — 215, m2 — 225.
24. п — 600, р — 40. mi — 210, m2 — 252.
25. п — 400, р — 90. mi — 345, m2 — 372.
26. п - 100, р = 80. mi — 72, m2 — 84.
27. п - 150, ч-Р — 60. mi — 78, m2 — 96.
28. п — 200, р — 65. mi — 0, m2 — 50.
29. п = 400, р- 55. mi — 100, m2 — 300.
30. п — 400, р — 60. mi — 50, m2 — 100.
Задача 7.
а) Вычислительное устройство состоит из п независимо работаю-
щих элементов. Вероятность выхода из строя каждого элемента оди-
накова и равна р. Составить закон распределения случайной величины
£ - числа отказавших элементов. Построить график функции распре-
деления F(a?). Найти М(£) и D(£).
83
1. п = 2, р = 0,4. 2. 71 = 3, р = 0, 12.
3. п = 4, р = 0,15. 4. 72 = 2, р = 0, 3.
5. п — 2, р = 0,25. 6. п = 3, р = 0,75.
7. п = 3, р —0,4. 8. тг = 4, р = 0,2.
9. 72—4, р — 0, 1. 10. 72 = 3, р = 0,15.
11. тг = 3, р = 0,2. 12. 72 = 2, р = 0,2.
13. 72 = 2, р = 0, 1. 14. 72 = 3, р = 0, 1.
15. п = 4, р = 0,5.
б) При обработке деталей на станке автомате вероятность выхода
размеров обрабатываемых деталей за границы ’’допуска’’ постоянна и
равна р. Для контроля качества отбирают п деталей. Построить гра-
фик функции, распределения F(x) случайной величины ( - числа не-
стандартных деталей. Найти D(£). Определить наивероятней-
шее число нестандартных изделий.
16. п = 5, р = 0,1. 17. тг = 5 р = 0,15.
18. п = 2, р = 0,2. 19. тг = 3 р = 0,25.
20. п = 4, р = 0,15. 21. п = 4 р = 0,1.
22. п = 3, р = 0,2. 23. тг = 4 р = 0,2.
24. п = 3, р=0,15. 25. тг = 3 р = 0,1.
26. тг = 2, р = 0,1. 27. тг = 2 р = 0,15.
28. тг = 4, р = 0,2. 29. п = 6 р = 0,1.
30. тг = 5, р = 0,2.
Задача 8.
Задана плотность распределения вероятностей /(ж). Определить ко-
эффициент а, функцию распределения F(x), М(£), D(£), вероятность
попадания случайной величины £ в интервал (а,/?). Построить графи-
ки функций /(ш) и F(x).
1. а = 0,/3 = 2. а = ~,0 = 3. а = 1,0-- 1 (а-х)2> я: €[-1,1], х 0[-1,1]. Зтг . . f asin2x, х Е [£, тт], = Т’^ = |0, ^[f.TT], - 9 / а^Х + Х ^’3]> “ J{X) “ S Л И ГЛ Qi
84
4.
a == 2,j0 = 3,/(х) = |
x £ [1Л],
x & [1) 4].
л /Э \ I acosz, хе -K, f,
“=o^=^./w=|0t 1(п4|].
6.
a = |>/3 = |,/(x) = |
ax2 + 1, x € [0,1],
0, xg [0,1].
7.
П /3 t( \ J "+~
a = 0,/3 =-,/(®) = I Q
® e [о, |],
^[o,|].
8.
a-2,/J=2,5,f(x) =
x e [2,3],
x 0 [2,3].
9.
a-2,/3 = 3,/(x)= “
x e [2,6],
x 0 [2,6].
10.
о = 2,Р = 2,5,/(1) = {“<1-2>'
IV) tb tt I/O) O]
11.
a = 4,f3 = 4,5,/(z) =
a(x — 4),
0,
x C [4,5],
x [4,5].
12.
n n \ I a cos ж,
« = 0,/? = -,/(x)^|0)
*e[o,f]>
* m il-
ls.
a = 2,/3 = 2,5,/(x) =
x e [2,3],
x (£ [2,3].
85
14.
а = °>0 = ~,/(х) = / ах2> *e[o,i],
2 I 0, a: £ [о, 1].
15.
16.
17.
18.
19.
20.
21.
22.
23.
a = 0,/3= ?f(x) = asinl> x£[0,%],
2 I °, x # [0, ^].
a = 0,/3 = 1 f(x) = / “ + 2, x e [0, |],
6’ I °> *£[o,j].
a = 0,/3 =, -,/(x) = / “sinr, x G [0, f],
4’ I °. xf£ [0,2].
a CL ( a । i
a = = W<a>
2 2 I 0, |x| >a.
ot-=2,/3 = 2,5>f(x) = [a^x~2l * 6 [2,3],
( °, x £ [2,3].
a = °^=~,f(x)=l ax’ x e [ОД],
2 ( 0, x g [0,1].
a = 0, p = 2, f(x) = ( a^3a: ~ x2)> [0,3],
I °> x& [0,3].
a = 0,/3 = 1,5, f(x\ = l a(x~ 1), x 6 [1, 2],
I 0, x £[1,2].
a = 0,13 = ~,f(x)=: I acosx> ®€[0,f],
4 I 0, x£ [0,2].
86
24.
а = о в - I f(x} _ / «sm3x, х G [0, |],
25. n а t< \ 1 asin2x, х 6 [0,5],
26. Л /Q i \ f % £ [0, 2], a = o,/3 = i,/M = |Oi
27. а — 1 2 fix} - / ax?’ ' l-2.2L
28. in 1 rf л 1 ax4> x e [-3,3],
29. <.=u = 3,/(I)=l;|,+4>’ “ 1 rZ31?’ 1 V, «Ьу_| 0,01.
30. a — о /3 — 1 ftx\ - J a^x + 3)> x e [~2> 2Ь
Задача 9.
Завод выпускает детали, стандартная длина которых а мм. Рас-
смотрим длину детали как случайную величину £, распределённую по
нормальному закону со средним квардатическим отклонением а и ма-
тематическим ожиданием а, определить: 1) вероятность того, что дли-
на наудачу выбранной детали будет больше а и меньше /3; 2) вероят-
ность отклонения длины детали от стандартного размера а более чем
6 мм.
1. а = 2.5, а = 1,а = 0,/3 = 2,5 = 3
2. а = 6, а = 3, а = 0, /3 = 5, S = 2
3. а = 2.5, а = 2, а 0.5,/3 = 1.5,5 = 2
4. а = 15, и = 2,а — 7,/3 = 9,5 — 3
87
5. а = 2, <т = 1, си = 0.5,/3 = 1,5 = 2
6. а = 18, ст = 3,а = 10,/3 = 24, <5 = 2
7. а = 36, ст = 6, а = 28,/3 = 42,5 = 3
8. а = 64, а = 8,а = 60,/3 = 70,5 = 5
9. а = 18, ст = 8, а = 12,/3 = 27,5 = 1.5
10. а = 26, <т = 6,а = 20,/3 = 30,5 = 2
11. а = 40, <7 = 4,а = 32,/3 = 42,5 = 4
12. а = 27, а = 3,си = 20, /3 = 25,5 = 2.5
13. а = 65, <7 = 8,а = 50,0 = 70,5 = 4
14. а = 28, <7 = 9,0! = 20,/3 = 32,5 = 3
15. а = 46, <7 = 9,а = 35,0 = 55,5 = 3
16. а = 55, а = 8, а = 40,/3 = 60,5 = 3.6
17. а = 12, о = 6,а = 4,0 = 15,5 = 1.2
18. а = 14, ст = 8,а = 6,0 = 17,5 = 2
19. а = 10, а = 4,а = 2,/3 = 15,5 = 1.5
20. а = 25, а = 6,а = 20,/3 = 27,5 = 1
21. а = 40, <7 = 6, а = 34,/3 = 43,5 = 1.5
22. а = 45, а = 5,а = 40,/3 = 48,5 = 3
23. а = 35, а = 4,а = 27,0 = 37,5 = 2
24. а = 10, а = 8,а = 8,/3 = 16,5 = 0.5
25. а = 30, <7 = 3,а = 24,/3 = 33,5 = 1.5
26. а = 48, а = 4, а = 45,0 = 56,5 = 3
27. а = 60, <7 = 6, а = 54,/3 = 70,5 = 2
28. а = 36, о = 8,0! = 30,0 = 40,5 = 2
29. а = 20, <7 = 3,0! = 17,0 = 26,5 = 1.5
30. а = 50, а = 5,а = 45,0 = 52,5 = 3
Задача 10.
Задана дискретная двумерная случайная величина 5 = (£, ту). Найти
коэффициент корреляции г.
’ЛС 0.2 0.6 0.9
2 0.1 0.3 0.12
4 0.07 0.28 0.13
2 4 5
1.0 0.25 0.17 0.13
1.5 0.16 0.08 0.21
1 2 5
0.3 0.22 0.1 0.17
0.6 0.06 0.27 0.18
3 5 6
2 0.18 0.12 0.33
6 0.2 0.08 0.09
88
»7\€ 2 3 5
5 0.1 0.15 0.25
7 0.25 0.1 0.15
vXf. 0.5 0.9 1.1
2 0.1 0.13 0.26
5 0.12 0.07 0.32
1 2 4
0.5 0.09 0.06 0.22
0.7 0.33 0.12 0.18
И)
0.2 0.4 0.7
2 0.1 0.15 0.25
5 0.25 0.1 0.15
13)
’ЛС 0.1 0.3 0.6
2 0.16 0.2 0.09
4 0.25 0.2 0.1
15)
’АС 0.5 0.9 1.1
2 0.18 0.12 0.35
6 0.22 0.06 0.09
17)
2 4 5
0.5 0.1 0.17 0.06
0.7 0.27 0.18 0.22
19)
’А£ 1 3 4
0.4 0.13 0.21 0.07
0.8 0.32 0.1 0.17
21)
Т)\£ 0.5 0.9 1.1
1 0.21 0.16 0.08
3 0.25 0.17 0.13
б) 6 9 10
0.1 0.15 0.1 0.25
0.3 0.1 0.25 0.15
8) 1 3 6
0.8 0.1 0.09 0.2
1.1 0.16 0.2 0.25
ю) 2 3 6
0.2 0.13 0.21 0.07
0.7 0.32 0.1 0.17
12) 1 3 5
0.2 0.13 0.21 0.07
0.9 0.32 0.1 0.17
14) 6 9 11
0.1 0.32 0.12 0.13
0.3 0.07 0.26 0.1
16) 3 5 6
1 0.1 0.15 0.25
2 0.25 0.1 0.15
18) ’/V; 2 3 6
2 0.06 0.27 0.18
5 0.22 0.1 0.17
20) 3 5 6
3 0.16 0.2 0.09
5 0.25 0.2 0.1
22) 1 3 5
0.2 0.18 0.12 0.35
0.9 0.2 0.06 0.09
89
»Л£ 6 9 11
23) 2 0.1 0.15 0.25
5 0.25 0.1 0.15
nV 0.2 0.4 0.7
25) 2 0.18 0.12 0.33
4 0.2 0.08 0.09
nV 2 3 6
27) 0.5 0.06 0.27 0.18
0.7 0.22 0.1 0.17
0.2 0.6 1.0
29) 3 0.13 0.21 0.07
5 0.32 0.1 0.17
0.1 0.3 0.6
24) 2 0.06 0.27 0.18
6 0.22 0.1 0.17
nV 3 5 6
26) 0.1 0.32 0.12 0.13
0.3 0.07 0.26 0.1
1 3 4
28) 2 0.21 0.16 0.08
5 0.25 0.17 0.13
nV 2 4 5
30) 0.4 0.1 0.15 0.25
0.8 0.25 0.1 0.15
90
Г лава 3
Математическая статистика
3.1 Задачи математической статистики
В теории вероятностей изучаются конкретные математические мо-
дели случайных явлений, событий. Если рассматривается некоторое
событие А, то задается способ вычисления вероятности события А -
Р(А), если изучается случайная величина X, то задается в какой-либо
форме ее закон (функция) распределения и затем, например, определя-
ются ее неслучайные характеристики- 'математическое ожидание, дис-
персия, среднее квадратическое отклонение. Или, зная функцию рас-
пределения двумерной случайной величины, делаем вывод о коррели-
рованное™ или некоррелированности ее компонент - вычисляя коэф-
фициент корреляции.
Задачи, которые рассматриваются в математической статистике,
являются в известной мере обратными к задачам теории вероятностей.
Так по известным реализациям изучаемых случайных событий (экспе-
риментальным статистическим данным) математическая статистика
разрабатывает методы подбора (построения) адекватной математичес-
кой модели случайного явления.
Выделим некоторые задачи.
1. Оценка неизвестной вероятности события, оценка числовых ха-
рактеристик случайных величин (M(X), D(X), а(Х)), оценка неиз-
вестной функции распределения, оценка параметров функции распре-
деления, вид которой известен, оценка зависимости одной случайной
величины от других случайных величин.
2. Проверка статистических гипотез. Например, гипотеза о виде не-
известного распределения.
91
Рассмотрим некоторые задачи, которые рассматривает математи-
ческая статистика на примере схемы Бернулли.
Пусть имеется п независимых испытаний и пусть в т из них про-
изошло событие А.
а) Проверка статистических гипотез.
Выдвигается гипотеза, что величина Р(А) (вероятность появления
события А в одном испытании) одна и та же, Р(Л) = ро, где ро ~ неко-
торое фиксированное значение. По относительной частоте — должны
установить справедлива гипотеза или нет.
б) Статистическая оценка неизвестных параметров.
Пусть требуется определить то число ро, которое можно принять за
вероятность Р(Л) в схеме Бернулли. В рассматриваем случае естест-
венно взять ро —
в) Доверительные интервалы.
Во многих случаях требуется указать интервал (а, 6), в котором с ве-
роятностью близкой к единице находится точное значение вероятности
Р(А). Такой интервал (а,Ь) называется доверительным интервалом.
3.2 Выборка. Эмпирическая функция распределе-
ния. Полигон. Гистограмма
Пусть X изучаемая случайная величина с функцией распределения
F(x).
Определение. Генеральной совокупностью случайной величины
называется множество всех ее возможных значений.
Предположим, что имеется возможность получать п ее значений,
например, экспериментально.
Определение. Выборкой объема п называется множество
^1? •••) ' (1)
п отдельных наблюдаемых значений случайной величины из ее гене-
ральной совокупности. Числа хп называются элементами (варианта-
ми) выборки. Числа пг} указывающие сколько раз число встреча-
ется в выборке - частотами.
Для того, чтобы по выборке можно было достаточно полно судить
(строить математическую модель) о случайной величине, она должна
92
хорошо представлять генеральную совокупность. Для этого каждый
элемент выборки должен быть отобран случайно, и все элементы долж-
ны иметь одинаковую вероятность попасть в выборку. Так, что экспе-
рименты должны быть независимы и не должны изменять изучаемую
случайную величину. Таким условиям будут удовлетворять выборки с
возвращением, когда обследуемые объекты в предыдущем эксперимен-
те возвращаются в изучаемую совокупность. Если объем генеральной
совокупности достаточно велик, а выборка составляет лишь незначи-
тельную ее часть, то различие между выборками с возвращением и
без возвращения стирается. В предельном случае, когда рассматрива-
ется бесконечная генеральная совокупность, а выборка имеет конечный
объем, это различие исчезает.
Итак, в результате п экспериментов получена выборка (1). Если
провести другую серию из п экспериментов, то, как правило, получит-
ся другая выборка
В связи с этим множество всех выборок объема п из рассматри-
ваемой генеральной совокупности можно рассматривать как значения
системы п случайных величин
Х1,Х2,...,Хп. (2)
Выборка (1) представляет собой одно из возможных значений п-
мерной случайной величины (2). И из наложенных требований на вы-
борки, можно считать, что случайные величины Xi независимы и рас-
пределены по тому же закону, что и рассматриваемая случайная ве-
личина X. (Имеет такую же функцию распределения, что и случайная
величина X).
В дальнейшем систему (2) будем обозначать ее конкретной реали-
зацией (1). Характеристики случайных величин, например, функция
распределения, математическое ожидание, дисперсия, полученные по
выборке, называются выборочными или эмпирическими, в отличие от
теоретических, для определения которых используется вся генераль-
ная совокупность.
Пусть X дискретная случайная величина. Оценим по выборке неиз-
вестные вероятности
Pi = Р(Х = Xi).
За оценку (приближенное значение) этих вероятностей принимают
93
относительные частоты
п
так как по закону больших чисел (теорема Бернулли) относительная
частота Wi по вероятности сходится к вероятности
nlim. P(|Wi — pi\ < е) — 1, для любого е > 0.
Определение. Последовательность (xi,ni), называется
статистическим рядом абсолютных (относительных) частот.
При большом объеме выборки строят группированные статисти-
ческие ряды. Для этого интервал, содержащий все элементы выборки
разбивают на к непересекающихся интервалов (ец,аг-+1), i = 0,
длины h. Например,
т Хпшх %min .
'=—~' („)
> З'ггшх 3'min ? j \
“ 1 + 3,322 lg п ( ’
В случае (3) берутся интервалы [a,, ai+1\
В случае (4), в качестве левого конца первого интервала берется
а0 — xmin — Затем ai — а$ 4- h, а 2 = ai 4- Л, и т. д. пока в последний
интервал попадет хгпах. Получаем интервалы (а.*,аг-+1]. Заметим, что в
формуле (4) вначале определяется длина интервалов, а затем устана-
вливается их число. Далее подсчитываются частоты п- - количество
элементов выборки, попавших в г-ый интервал. Обозначим через т*
середины полученных интервалов х* —
Определение. Последовательность пар называются груп-
пированным рядом частот, а (х*,^-) - группированным рядом отно-
сительных частот.
Для наглядности строят полигоны статистических или группиро-
ванных статистических частот - это ломаные с вершинами (т./,пг)
или (xi,n]\ А также полигоны относительных статистических или
группированных относительных частот - это ломаные с вершинами
(xi,ni/n) или (х*,п*/п).
Пусть X непрерывная случайная величина и (1) ее выборка.
Определение. Функция
(5)
94
где пх ~ число элементов выборки меньших х (пх = £ щ - сумма на-
Xi<x
копленных частот), п - объем выборки, называется эмпиритческой
функцией распределения.
Эмпирическая функция распределения обладает многими свойства-
ми функции распределения. Она равна нулю для х < xmin, и единице
для х > х1пах> и не убывает. Если в выборке все хп различны, то
эмпирическая функция распределения растет скачками величины £ в
каждой из точек х±, Ж2,..., хп. И в этом случае она совпадает с законом
распределения дискретной случайной величины, принимающей значе-
ния хп с вероятностями
Если теоретическая функция распределения F(x) определяет веро-
ятность события X < х, то Fn(x) определяет статистическую частоту
этого события в п экспериментах. В соответствии с законом больших
чисел (теорема Бернулли) при каждом фиксированном х эмпиричес-
кая функция распределения сходится по вероятности к теоретической
F(z).
nlim Р(| F(x) - Fn(x) | < е) = 1. (s > 0).
Замечание. Можно строить эмпирическую функцию распределе-
ния как по статистическим частотам, так и по группированным ста-
тистическим частотам для любых случайных величин.
Наглядной оценкой плотности вероятностей /(ж) (/(ж) — F'(x)) яв-
ляется гистограмма относительных частот. Пусть в соответствии с
(3) или (4) промежуток [ж„«п, ж?7Ша;] разбит на к интервалов (a^a^i)
длины Лип- число элементов выборки, попавших в г-й интервал
П1 + п2 + • • + nk ~ п-
Исходя из свойства функции плотности
P(ai < X < ai+1) « f(x)h (6)
при малых h, за оценку плотности /(ж) принимается
/п(®) = A- ai<x< ai+i, (7)
nh
здесь n^/^nh) - плотность относительных частот п*/п.
Определение. Гистограмма относительных частот состоит, из
прямоугольников с основаниями [a»,a4-+i] и высотами (7).
Площадь каждого прямоугольника равняется fn(x)h — и в со-
ответствии с (6), (7) оценивает вероятность попадания исследуемой
95
случайной величены в интервал (а^, а;+1) по выборке. Площадь же
всей фигуры, состоящей из прямоугольников, равна единице
& Ji* I А:
Е- - ~Еп.- = - = 1,
п п i-1 п
что соответствует свойству плотности вероятностей
4-оо
I ffxjdx = 1.
—ОО
Таким образом, сравнивая построенную гистограмму с графиками
известных плотностей, получают первую экспериментальную оценку
для неизвестной /(ж). Например, можно выдвинуть гипотезу о кон-
кретном законе распределения изучаемой случайной величины.
Пример 1. Представить выборку 55 наблюдений в виде таблицы
частот, используя 7 интервалов группировки. Выборка:
17 19 23 18 21 15 16 13 20 18 15 20 14 20 16 14 20 19 15
19 16 19 15 22 21 12 10 21 18 14 14 17 16 13 19 18 20 24
16 20 19 17 18 18 21 17 19 17 13 17 11 18 19 19 17
Размах выборки х1пах — хт{п = 24 — 10 = 14. Длина интервала
h — 14/7 — 2. Результаты группировки сведены в таблицу 3.1.
Т а б л и ц а 3.1
Номер интервала i Границы интервала Середина интервала я,’ Частота П* Накоп- ленная частота Относи- тельная частота Накоп. отн. частота Ё »'•;/»
1 10 12 11 2 2 0.0364 0.0364
2 12-14 13 4 6 0,0727 0,1091
3 14-16 15 8 14 0,1455 0,2546
4 16-18 17 12 26 0,2182 0,4728
5 18-20 19 16 42 0,2909 0,7637
6 20-22 21 10 52 0,1818 0.9455
7 22-24 23 3 55 0.0545 1.0000
Пример 2. Построить полигон группированных частот и гисто-
грамму относительных частот примера 1.
По результатам группировки (см. таблицу 3.1) строим полигон час-
тот (рис. 1) и гистограмму (рис. 2) - прямоугольники с высотами
96
Пример 3. Построить графики эмпирических функций распределе-
ния по исходным и группированным выборкам примера 1.
Запишем исходные данные в виде статического ряда.
Xi 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
n-i 1 1 1 3 4 3 6 7 7 9 6 4 1 1 1
Так как = 10, а Т55 — 24, то Fn(x) — 0 при х < 10 и Fn(x) — 1 при
х > 24. На полуинтервале (10,24] эмпирическую функцию распределе-
ния Fn(x) строим с использованием статического ряда. Например,
F"(15) =-----------------= и
55
В результате получаем график Fn(x), изображённый на рисунке 3.
F'n(x),
0,6
0,4
0,2
Рис. 3
97
Аналогично строится график Fn(x) по группированным данным таб-
лицы 3.1. В этом случае Fn(x) имеет скачки в точках, соответствую-
щих серединам интервалов группировки (см. рис. 4).
3.3 Статистические оценки числовых характерис-
тик случайных величин и их свойства
Пусть Q - числовая характеристика изучаемой случайной величины
с неизвестной функцией распределения. Например, М(X), <т(Х).
(Если /(ж) известна, то они могут быть вычислены по формулам
4-ос +ос
М(Х) = J xf(x)dx, D(X) = / x2f(x)dx—M2(X), а(Х) = Д>(Х)).
—ос -оо
В некоторых случаях вид функции распределения известен, но в неё
могут входить неизвестные параметры. Например, в плотность нор-
мально распределённой случайной величины
/(:С) ~ ^<7е 2"
входят два параметра а, а (а = М(X), ст = у/)(Х)).
98
Для получения приближённых значений (оценок) Q* числовых ха-
рактеристик случайных величин или параметров их функций распре-
деления Q (Q* « Q) используют выборочные значения (элементы вы-
борки).
Определение. Статистическая оценка Q* - это некоторая функ-
ция от результатов наблюдений (от выборочных значений), предна-
значенная для статистического оценивания неизвестных числовых
характеристик случайной величины и параметров ее функции рас-
пределения.
Имеем
Q* = T(XbX2,...,Xn),
где Q* - оценка величины Q. T(Xi, Х%,..., Хп) - функция от элементов
выборки, ее называют статистикой.
При фиксированной функции Т (статистике) оценка Q* зависит от
случайных выборочных значений, и связи с этим является случайной
величиной. Ее функцию распределения называют выборочным распре-
делением оценки. Оценка Q* зависит от выборочных значений и от
вида функции Т (статистики).
Ясно, что в качестве оценок следует брать такие статистки, значе-
ния которых для различных выборок были бы в определённом смысле
близки к истинным значениям оцениваемых параметров. Желатель-
но также, чтобы с увеличением объёма выборки надёжность оценки
возрастала.
Качество оценок характеризуется тремя основными свойствами.
1. Состоятельность оценки.
Определение. Оценка Q* = Т,(Х1,Л’2, ...,ХП) называется состоя-
тельной для Q, если она по вероятности сходится к Q при неогра-
ниченном увеличении величины п - объема выборки
Jim^PdQ* - Q\ < с) = 1, для любого е > 0.
2. Несмещённость оценки.
Определение. Оценка Q* = T(Xi, Х2, • • •, Хп) называется несмещн-
ной для величины Q, если
M(Q*) = Q,
т. е. математическое ожидание Q* равняется истинному значению
Q. В противном случае, смещённой.
99
При выполнении этого свойства, оценки не дают систематических
ошибок (в одну сторону) при изменении выборочных значений.
3. Эффективность оценки.
Пусть V среднеквадратическая ошибка оценки
V = M(Q* - Q)2.
Если оценка несмещённая, то
V = M(Q* - Q)2 = M(Q* - M(Qy? = D(Q*),
т. e. в этом случае ошибка оценки совпадает с её дисперсией. И яс-
но, что в этом случае оценка с наименьшей дисперсией являлась бы
наилучшей в смысле точности. И наилучшей была бы оценка с V = 0.
Но оказывается, для несмещённых оценок существует нижняя граница
для дисперсии ошибок, не равная нулю.
Определение. Несмещенная оценка Q* называется эффективной,
если она имеет наименьшую дисперсию среди других несмещенных оце-
нок.
Пусть QI = Ti(Xi,X2,-,Xi), Q2 ~ ?2(Xi,Х2,...,Хп) две различные
несмещённые оценки для Q. Если то оценка Qi более
эффективная, чем Q2.
Замечание. Значения рассмотренных оценок Q* зависят от выбор-
ки и являются случайными величинами (числами). В связи с этим их
называют точечными оценками.
3.4 Методы получения точечных оценок
3.4.1 Выборочные (эмпирические) числовые характеристи-
ки
Исходя из эмпирической функции распределения приходим к
1 п
X = - Z Xi - выборочное среднее, (8)
п i=i
1 п
S2 = - 52(Х.£ — X)2 - выборочная дисперсия, (9)
™ i=i
1 п ,
Pk = ~ ~ выборочный момент fc-ro порядка, (10)
п£=1
100
которые являются точечными .оценками соответственно для М(Х),
D(X), /ifc. (/ifc - теоретический начальный момент к-го порядка.)
Исследуем эти оценки. Учитывая, что Xt - независимые случайные
величины и имеют такую же функцию распределения, что и случайная
величина X (М(Х) = M(Xi) = а, D(X) = — °г2)> получаем
(In \ 1 / П \ 1 П
-£х; = -м =-ЕВД) =
2^ i=l / 21 \t=l / 22 1=1
=--£ а == — = а = М(Х). (11)
72 — j 72
Таким образом, выборочное среднее (8) является несмещённой оценкой
для математического ожидания.
Учитывая, что £>(Х») равномерно ограничены D(Xj,) = ст2, запишем
закон больших чисел (теорема Чебышева, стр. 62)
lim Р
In 1 71
-X Xi -±£М(хо
п i=l п i=1
< Е
= 1.
И в нашем случае
limP(|X-M(X)|<e) = l.
Значит, выборочная средняя X является и состоятельной оценкой для
математического ожидания.
Исследуем выборочную дисперсию S2. Вначале вычислим D(X).
(In \ 1 /п \ 1 п
-EXi EXi =-jSD(Xi) =
n 1=1 / 22 М=1 / 22 1=1
1 у 2 _ 21СТ2 _ °г2 _ Т>(Х)
П2 i=1 а п2 п п
(12)
Далее,
1 71 I П
s2 = - E(Xi - X)2 = - Е((Хг - а) - (X - а))2 =
п i=i п i=i
1 71 9 _ 7А 1 п
- EPG - а)2 - -(X - а) £(Х; - а) + i £(Х - а)2 =
г=1 27, =1 77, j— j
= 1 Е(Х< - а)2 - -(X - а)(Е Xi - па) + -п(Х - а)2 =
тг ,ix=1 п i=1 п
101
= - Е(*« - а)2 - ~(Х - а)п(Х - а) + (X - а)2 -
п j-1 п
= lf(X._o)2_(J?_a)2 (13)
п г=1
Теперь
M(S2) = М (- - а)2 - (X - а)2) -
\п<=1 7
= - £ М(Х{ - а)2 - М(Х - а)2 =
ni=i
= i Е M(Xi - M(Xi'))2 - М(Х - M(X))2 =
n»=l
1 71 1 n D(X}
= 1-nD[X',-^^Dm-^ = "^-D[Xy (14)
Здесь учли (11), (12). Получили, что
M(S2) = -—-7>(Х) / D(X),
n
и поэтому, выборочная дисперсия (9) является смещённой оценкой для
дисперсии.
Так как Jim. = 1, то из (14) получаем
lim M(S2) = lim —-D(X) = D(X),
и отсюда следует, что оценка (9) является асимптотически несмещён-
ной для дисперсии.
Возьмём вместо S2
s*2 = -^-7 E(Xi - X)2 = -^—S2 (15)
71> JL j Т2> JL
(5*2 - ’’исправленная” выборочная дисперсия).
Имеем
м<5’2) = ^M(s2) = =D(x)-
Так что оценка S*2 (15) является уже несмещённой дЛя D{X\ Можно
показать, что она является состоятельной для D(X\
102
Упражнение. Доказать, что
S2 = ~(±X2-nX2), S‘2 = -l-(EX?-nX2).
'L i—l П — 1 £—1
Замечание. На практике при больших п (п > 100) вместо S*2 ис-
пользуют S2.
Пример 4. Вычислить выборочную ’’исправленную” дисперсию для
выборки объема п — 10: 3, 7, 7, 0, 2, 1, 2, 3, 5, 4.
Предварительно находим
10 10 о - 34
£ Хг = 34, £ X* = 166, X = - 3,4.
*=1 г=1 Ю
Тогда
S*2 = “ 10 3>42) = 5’6-
3.4.2 Метод моментов
Пусть плотность вероятности /(х, Qi, ., Qk) изучаемой случай-
ной величины зависит от к параметров (неизвестных), Qb$2, • • •,Qk-
Метод моментов получения оценок Q^ - - • ,Qk состоит в следую-
щем:
приравниваются к первых теоретических Vj и эмпирических z7y (по
выборке) моментов, и из полученной системы к уравнений с к неиз-
вестными определяются оценки.
1 п +?° •
= / x’f(x,Ql,Q*2,...,X*k)dx (j = l,2,...,fc) (16)
П -ос
(XJ = z7?, i/j = M(Xj)). В (16) слева эмпирические, справа теоретичес-
кие моменты.
Замечание. В методе моментов можно приравнивать центральные
теоретические и эмпирические моменты
цк = М[(Х - М(Х))2], тк = 1 - X)2-
Ki=l
Пример 5. Найти методом моментов по выборке a?i, а?2,..., хп точеч-
ную оценку неизвестного параметра А показательного распределения,
плотность которого /(ж) = Ае~Хх (т > 0).
103
Решение. Приравниваем начальный теоретический момент перво-
го порядка (i/i равный М(X)) эмпирическому моменту первого порядка
равному X, получаем
М(Х) = X.
Приняв во внимание, что математическое ожидание показательного
распределения равно 1/А, имеем
1/Х = Х.
Отсюда
А = 1/Х.
Итак, искомая точечная оценка параметра А показательного распре-
деления равна величине, обратной выборочной средней
А* - 1/Х.
Пример 6. Найти методом моментов по выборке Ж1, ., хп точеч-
ные оценки неизвестных параметров а и а нормального распределения
f(x) = L=e-(«-«)2/(2<72)
Решение. Приравниваем начальный теоретический момент перво-
го порядка — М(Х) эмпирическому моменту первого порядка рав-
ному X, и также центральный теоретический момент второго порядка
/12 = D(X) центральному эмпирическому моменту второго порядка
m2 — S2
z/i -- X, /х2 — т2.
(М(Х) = X, D(X) = S2).
Приняв во внимание, что математическое ожидание нормального
о
распределения равно параметру а, дисперсия равна а имеем:
а = X, а2 = S2.
Отсюда получаем искомые точечные оценки параметров нормального
распределения:
а* = X, а* —
104
3.4.3 Метод максимального правдоподобия
Методом максимального правдоподобия получают такие оценки Q*,
при которых вероятность реализации рассматриваемых выборок (объ-
ёма п) максимальна.
Пусть X - дискретная случайная величина и её закон распределения
зависит от к неизвестных параметров Qi, Q2, ..., Qk.
Р(Х - Xi) = Pi(Qi,Q2,- •• ,<?!•), (Pi ф 0).
Тогда вероятность того, что случайные величины Х\, Х2, ...Хп, опре-
деляющие выборку, примут выборочные значения (1) равна
Z/(a?i, 3?2, • . . у ХПу QlyQ2z • • • ~ Р(Х} — Х\, Х2 = Х2у • • • у Хп — жп) —
- Р{Х. = xQP(X2 - х2)...Р(Хп = хп) - П Pi^Qi.Qi...., Qk\
i=i
Здесь учли предположение, что случайные величины Xi независимы
и имеют тот же закон распределения, что и случайная величина X, и
вероятность произведения независимых событий равна произведению
вероятностей этих событий.
Определение. Функция L называется функцией правдоподобия.
Она является законом распределения выборки и при фиксированных
выборочных значениях является функцией только неизвестных пара-
метров Qi у Q2y... yQk.
Как уже было сказано, за оценки берутся те значения параметров,
при которых функция правдоподобия (т. е. вероятность реализации вы-
борки) принимает максимальное (наибольшее) значение.
Таким образом, приходим к уравнениям для нахождения оценок (не-
обходимое условие экстремума)
^ = 0, 3 = 1,2,...Л . 117)
Конечно, необходимо проверить, что при найденных Q* из (17) функ-
ция правдоподобия будет принимать наибольшее значение.
На практике вместо функции L вводят логарифмическую функцию
правдоподобия In L
ь L - In П , Qk) - E InPl(Qlу Q2y..., Qk).
i-1 i=l
105
Точки экстремума функций L й In L совпадают, так как
dlnL _ 1 дБ
dQj LdQj
(18)
Пусть X - непрерывная случайная величина. И пусть её плотность
вероятности /(я, Qi, Q2> • • • 3 Qfc) зависит от неизвестных параметров
<21 > <2г, • • •, Qk-
Будем искать оценки неизвестных параметров из условия, что имен-
но при данной рассматриваемой выборке достигается максимальная ве-
роятность попадания выборок в n-мерный параллелепипед с центром
в (xi,T2,..., хп) и ребрами ДХ1, >АХп. Вероятность попада-
ния выборок в этот параллелепипед, с точностью до бесконечно малой
более высокого порядка, чем
У(ДХ1)2 + (ДХ2)2 + • • • + (ДХК)2,
равна
р = П Ж, Qi, , Qk) ьх, дх2... дхп =
г=1
= L(Ti,2?2, . . . Q11Q2, • • - , Qk)&XlkX2 • • • АХП,
где L - функция правдоподобия
ь = ПЖ,С1^2-..,ад.
Заметим, что вероятность Р и функция правдоподобия зависят только
от неизвестных параметров {xi зафиксированы). Тогда максимум ве-
роятности Р и функции правдоподобия достигается в одной и той же
точке.
На практике, так же как и в дискретном случае, переходят к лога-
рифмической функции правдоподобия In L.
Пример 7. Пусть X распределена по нормальному закону, парамет-
ры которого а — М(Х),& = неизвестны. Требуется по выборке
методом максимального правдоподобия получить оценки этих парамет-
ров.
Решение. Имеем
ffz.a.cr) — —2^
п
Ь(т1,т2,... ,жп,а,а) = П /(я», а, а) —
106
Л 1 1
II ------g 2<72 ~ .. g 1 = 1
i=i (jy/bv (ау/2л)п
In L = — —r f^Xi — a)2 — n In a -- nln л/2тг.
2cr2 £1
В соответствии с (18), получаем систему уравнений для нахождения
оценок
Отсюда
E(zi-X)2
2=1
Упражнение. Показать, что при этих значениях функция правдо-
подобия принимает наибольшее значение.
Как видно, оценки математического ожидания и дисперсии для нор-
мального распределения, полученные методом максимального правдо-
подобия, совпадают с выборочным средним и выборочной дисперсией, и
как было показано в п. 3, являются состоятельными оценками, причем
* *7
оценка а несмещенная, а оценка а - асимптотически несмещенная.
Можно еще показать, что оценка для а является эффективной, а не-
смещенная оценка для дисперсии
2=1
является асимптотически эффективной.
Пример 8. Найти методом максимального правдоподобия оценку
параметра А распределения Пуассона
. Xх'е
Рт(Х = Xi) = —j
где т - число произведенных испытаний; х^ - число появлений события
в г-ом (г ~ 1,2,... ,п) опыте (опыт состоит из т испытаний.) t
107
Решение. Составим функцию правдоподобия, учитывая, что Q — А:
L = p(ri; А)р(ж2; А)... р(хп; А) -
_А®1-е~л А®2-е-л Xх" • е~х _ Xi'е
11! Хъ\ Хп\ Х1\Х2]. ... хп1'
Рассмотрим логарифмическую функцию правдоподобия:
(п \
я* J In А — nA ~ 1п(ж1 . жп!).
£=1 /
Найдём первую производную от In L по А
dinL hXi
dX А “П'
Приравниваем первую производную к нулю
52 ^i/A - п = 0.
i-i
Отсюда,
А= 5></п = Х.
i=i
Найдём вторую производную от In L по А :
d2\nL п
------— < о
с!А2 А2 X
Следовательно, А = X -- точка максимума и, значит, в качестве оцен-
ки максимального правдоподобия параметра А распределение Пуассона
берем выборочную среднюю А* = X.
3.5 Интервальные оценки
3.5.1 Доверительный интервал и доверительная вероятность
Точечные оценки Q* являются случайными величинами и дают при-
ближенное значение оцениваемых параметров. В связи с этим, особое
значение имеет задача о нахождении по выборке интервалов, которые
108
с заданной вероятностью содержали бы (покрывали бы) истинное зна-
чение оцениваемых параметров. И тем самым можно было бы судить
о погрешности (точности) оценок.
Определение. Доверительным интервалом для параметра Q на-
зывается интервал
х2,хп),Q2(xlt хг,гп)),
содержащий (покрывающий) с заданной вероятностью (надежнос-
тью) 7 истинное значение параметра.
Доверительные интервалы строятся по выборке. Концы интервалов
зависят от элементов выборки и в связи с этим являются случайными
величинами.
Таким образом,
P(Qi < Q < <?2) = 7. (19)
Определение. Число у - называется доверительной вероятнос-
тью, а о = 1 — 7 уровнем значимости.
Выбор конкретного значения 7 зависит от рассматриваемой задачи,
так, чтобы вероятность а = 1 — 7 соответствовала практической не-
возможности маловероятного события. То есть, если Р(А) = 1 — 7, то
событие А считается практически невозможным. Заметим, что выбор
числа 7 в конкретной задаче определяется степенью тех опасностей, ко-
торые могут произойти, если все же произойдет событие Р(А) < 1 -7.
Как правило, за доверительную вероятность берут 7 > 0.95.
Будем строить доверительные интервалы для параметров, исполь-
зуя их точечные оценки.
3.5.2 Доверительный интервал для математического ожи-
дания нормально распределенной случайной величины
при известном среднеквадратическом отклонении а
Пусть случайная величина X распределена по нормальному закону
с неизвестным математическим ожиданием а и известным среднеквад-
ратическим отклонением ст, и имеется выборка (1). Тогда в системе
Xi, %2} • • •) %п, реализующей выборку из генеральной совокупности для
X, каждая компонента также распределена по нормальному закону с
М(Х() - a, a(Xi) = ст.
109
Возьмем за точечную оценку для а
1 п
а* =Х ==-УХ;,
n i=i
Выборочное среднее X является случайной величиной, и как сумма
нормально распределенных случайных величин с одинаковыми мате-
матическими ожиданиями и дисперсиями, также распределена по нор-
мальному закону, и в соответствии с (И), (12)
ад = а, <т(Х) = -^.
Vn
Доверительный интервал для а будем находить исходя из соотно-
шения
Р(\Х — а\ <£) = 7 (20)
(требуется найти величину 6.) Распишем левую часть соотношения
(20)
Р(|Х - а| < 3) = Р(а - 6 < X < а + 5) =
(а + 6 — а] (a — S — a\
-------- _ ф —
а I I °-)
у/п / \ ~^/п /
/-у/пЗА / у/п6\ (у/п6\
= Ф -— - Ф I --— = 2Ф I -— . (21)
\<т/ \ а / \ а /
Здесь воспользовались соотношением
Р(а < X < 0) = Ф(^) - Ф(^),
1 х ^2
Ф(х) = I e~^dt, Ф(—х) — —Ф(ж)
Ч/27ГI
для нормально распределенной случайной величины с математическим
ожиданием а и среднеквадратическим отклонением сг.
С учетом (21) потребуем выполнение (20)
ф (V55) = 7/2.
\ a J
По таблице 2 функции Лапласа Ф(ж) (см. Приложение) находим =
из условия
Ф(47) = I (22)
ПО
и далее
<5 = ^.
у/П
Таким образом, условие (20) выполнено. Перепишем его в виде
Р(|а - Х| < 6) = у.
Отсюда
р[х-^<а<Х+^} = 7) (23)
\ у/П у/П/ 4 7
И
\ у/П у/П)
- искомый доверительный интервал для величины а.
Пример 9. Случайная величина X имеет нормальное распределе-
ние с известным средним квадратическим отклонением а — 3. Найти
доверительные интервалы для оценки неизвестного математического
ожидания а по выборочным средним X, если объем выборки п - 36 и
задана надежность оценки 7 = 0,95.
Решение. Найдем t7. Из соотношения 2Ф(£) — 0,95 получим Ф(£) =
0,475. По таблице 2 (см. Приложение) находим t7 = 1,96.
Найдем 5 - точность оценки:
5 = i7a/v^ = (1,96 • 3)/\/36 = 0,98.
Запишем доверительный интервал (X — 0,98; X 4- 0,98). Например,
если X = 4,1, то доверительный интервал имеет следующие довери-
тельные границы:
X - 0,98 = 4,1 - 0,98 = 3,12; X + 0,98 = 4,1 + 0,98 = 5,08.
Таким образом, значения неизвестного параметра а, согласующиеся
с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08. Под-
черкнем, что было бы ошибочным написать Р(3,12 < а < 5,08) = 0,95.
Действительно, так как а—постоянная величина, то либо она заключе-
на в найденном интервале(тогда событие 3,12 < а < 5,08 достоверно
и его вероятность равна единице), либо в нем не заключена (в этом
случае событие 3,12 < а < 5,08 невозможно и его вероятность равна
нулю). Другими словами, доверительную вероятность не следует свя-
зываать с оцениванемым параметром; она связана лишь с границами
Ш
доверительного интервала,которые, как уже было у казано , изменяют-
ся от выборке к выборке.
Поясним смысл,который имеет заданная надежность. Надежность
7 = 0,95 указывает, что если произведено достаточно большое число
выборок, то 95% из них определяет такие доверительные интервалы,
в которых параметр действительно заключен; лишь в 5% случаях он
может выйти за границы доверительного интервала.
3.5.3 Доверительный интервал для математического ожи-
дания нормально распределенной случайной величины
при неизвестном среднеквдратическом отклонении
Пусть изучаемая случайная величина распределена по нормальному
закону, математическое ожидание а и а неизвестны.
Рассмотрим по выборке (1) случайную величину
Т =
S*/у/п'
(24)
где S'* - ” исправленное” выборочное среднее квадратическое отклоне-
ние )
1 п
S‘ = \—гП^-Х)2 (25)
(S* - точечная оценка для а).
Эта случайная величина имеет распределение, которое называется
распределением Стьюдента с k = п—1 степенями свободы. Плотность
распределения Стьюдента
S(t, n) = Вп 11 +
t2
п — 1
—оо < t < Н-оо,
В г(п/2)
п Г((п-1)/2)У^1)’
Г(р)= f x^e^dx
О
- гамма-функция Эйлера. Распределение Стьюдента не зависит от не-
известных параметров а и а (они не входят в формулу для плотности),
а зависит только от п -объема выборки.
112
Имеем
Р(|Т| < t7) = P(-t7 < Т < i7) = I S(t,n)dt = 2/ S(t,n)dt. (26)
-1Ц 0
Здесь учли, что S(t,n) четная функция по t. Далее, находим по таблице
3 (см. Приложение) распределения Стьюдента с к = п — 1 -- степенями
свободы величину i7 из условия
f S(t,n)dt = i/2, (27)
О
И расписывал соотношение (26) с учетом (24), (27), получаем искомый
доверительный интервал для величины а
\ уп у/П )
Пример 10. Количественный признак X генеральной совокупнос-
ти распределен нормально. По выборке объема п — 16 найдены вы-
борочная средняя X = 20,5 и ’’исправленное” среднее квадратическое
отклонение S'* = 0,8. Построить доверительный интервал для матема-
тического ожидания с надежностью 0,95.
Решение. Найдем £7, пользуясь таблицей 3 (см. Приложение), по
7 = 0,95 и п = 16 находим t7 = 2,13.
Найдем доверительные границы
X - t^S*/Vn = 20,2- 2,13 • 0,8/У16 = 19,774.
' X + t^S*/у/п = 20,2 + 2,13 • 0,8/У16 = 20,626.
Итак, с надежностью 0,95 по данной выборке неизвестный параметр
а заключен в доверительном интервале 19,774 < а < 20,626.
3.5.4 Доверительный интервал для среднеквадратического
отклонения нормально распределенной случайной ве-
личины
Пусть изучаемая случайная величина X распределена по нормально-
му закону. Ее среднее квадратическое отклонение неизвестно. Введем
случайную величину х ~ ”хи”
х = -у/п- 1, (28)
а
113
где S* - ” исправленное” среднее квадратическое отклонение (25). Ее
плотность распределения
хп-2е-ж3/2
= 2(п-2)/2Г((п-1)/2) ’
Распределение величины х не зависит от оцениваемого параметра а, а
зависит только от объема выборки.
Потребуем выполнения равенства
P(S* — <5 < ст < S* 4-5) = 7 (29)
(ищем 5).
Положим q = 8/S*. Запишем последовательно неравенства
S* - 6 < а < S* + 5,
S*(l - (5/S*) < сг < S*(l + 5/S*),
S*(l — g) < <т < S*(l 4-g), (30)
Пусть q < 1. Из неравенства (30) следует
1 1 1
S*(l + g) < а< S*(l-g)’
а/п — 1 S*\/n — 1 у/п — 1
1 + q (У 1 “ q
Отсюда, с учетом определения величины х (28), получаем
Уп --1 \/n — 1
— < х < п-------•
l + g 1-q
Вероятность выполнения этого неравенства и, следовательно, равно-
сильного ему неравенства (29) равна
Уп^Т/(1-д)
У /(ш,п)^ж=у.
Из этого уравнения можно по заданным п и 7 найти q.
На практике для отыскания q пользуются таблицей 4 (см. Прило-
жение). Определив по таблице q и вычислив по выборке S*, получаем,
в соответствии с (30), искомый доверительный интервал
S‘(l-g)<a <£♦(! +<?).
114
В случае q > 1, доверительный интервал имеет вид
О < а < S*(l + q).
Пример 11. Количественный признак X генеральной совокупности
распределен нормально. По выборке объема п = 25 найдено ’’исправ-
ленное” среднее квадратическое отклонение S* = 0,8. Найти довери-
тельный интервал, покрывающий генеральное среднее квадратическое
отклонение а с надежностью 0,95.
Решение. По таблице 4 (см. Приложение) по данным у = 0,95 и
п = 25 найдем q — 0,32.
Искомый доверительный интервал таков:
0,8(1 - 0,32) < а < 0,8(1+0,32),
или
0,544 < а < 1,056.
3.6 Проверка статистических гипотез
3.6.1 Статистические гипотезы
Пусть X - изучаемая случайная величина, и пусть ее закон распре-
деления неизвестен. Произведя выборку и построив гистограмму, мож-
но выдвинуть гипотезу о законе (функции) распределения изучаемой
случайной величины, сравнивая гистограмму с графиками известных
плотностей вероятностей.
Часто .гипотезу о законе распределения выдвигают из существа за-
дачи, определяющей изучаемую случайную величину. Так, например,
ошибка измерительных устройств, как правило, распределена по нор-
мальному закону.
Определение. Статистической гипотезой Н называется пред-
положение относительно параметров или вида функции (закона) рас-
пределения случайной величины X.
Статистическая гипотеза называется простой) если она одно-
значно определяет распределение случайной величины, или, если от-
носительно ее параметров она содержит только одно предположе-
ние. В противном случае она называется сложной.
115
Пример 12. Простой гипотезой является предположение о том, что
случайная величина X распределена по нормальному закону с мате-
матическим ожиданием а = 0 и среднеквадратическим отклонением
(7 = 1.
Пример 13. Если Л - параметр показательного распределения, то
гипотеза: А = 2 - простая, а гипотеза: А > 3 - сложная. Она состоит
из бесконечного множества простых гипотез Н: А = 5, где Ъ - любое
число, большее трех (стр. 58).
Определение. Проверяемая (выдвинутая) гипотеза называется
нулевой гипотезой и обозначается Ну.
Определение. Конкурирующей (альтернативной) называют ги-
потезу которая противоречит нулевой.
Выбор альтернативной гипотезы определяется из условий рассмат-
риваемой задачи.
Пример 14. Пусть проверяется гипотеза о равенстве параметра Q
некоторому заданному значению Qo, т. е- Ну: Q — Qy. В качестве аль-
тернативной гипотезы можно рассмотреть одну из следующих гипотез:
Hi : Q < Я2 : Q > QoJ #з • Q Qoi #4 : Q = Qi, где Qi заданное
значение, Qi Qy-
3.6.2 Статистические критерии для проверки гипотез. По-
строение критических областей
Для проверки нулевой гипотезы на основании выборочных данных
используют специально подобранную случайную величину К, точное
или приближенное распределение которой известно.
Определение. Величину К называют статистическим критери-
ем.
Статистика этого критерия (функция от выборочных значений)
называется статистикой Z критерия К.
Например, при проверке простой гипотезы Ну: Q — Qy в качестве
статистики критерия выбирают ту же статистику, что и для оценки
параметра Q, т.е. Q*.
Так же как и при построении доверительных интервалов выбирает-
ся уровень значимости си, такой, чтобы вероятность равная а соответ-
ствовала практической невозможности маловероятного события.
Пусть V - множество значений статистики Z и 14 С V - подмно-
116
жество, такое, что P(Z С Vk/Hy) — а, т. е., что условная вероятность
принадлежности значений критерия подмножеству Vk при условии ис-
тинности гипотезы Но равняется а.
Пусть zb - выборочное значение статистики Z, вычисленное по вы-
борке. Критерий проверки гипотезы формулируется следующим обра-
зом:
- гипотеза Ну отклоняется, если zB Е 14,
- гипотеза принимается, если zB 6 V \ 14.
Определение. Множество Vk называется критической областью.
Таким образом, множество V разбивается на два непересекающихся
подмножества: множество Vk ~ критическая область, множество V \ V/,
- область принятия гипотезы.
Положение критической области на множестве V зависит от форму-
лировки альтернативной гипотезы Яр
Например, если проверяется гипотеза Ну : Q — Qq, а альтернатив-
ная гипотеза Hi : Q > Qo (Q < Qo)> то критическая область разме-
щается на правом (левом) ’’хвосте” распределения статистики Z, т. е.
имеет вид неравенства Z > zi_a (Z < ztt), где zi_n и za - квантили
распределения Z при условии, что верна гипотеза Ну.
Определение. Квантилем ty порядка у распределения случайной
величины X является корень уравнения
Р(Х < Ц) = F(t,) = у.
В этом случае критерий называется односторонним, соответственно
правосторонним и левосторонним.
Если альтернативная гипотеза Hi : Q ф Qy, то критическая область
размещается на обоих ’’хвостах” распределения Z, т. е. определяется
двумя неравенствами Z < za/2 и Z > zi_aj2, и в этом случае критерий
называется двусторонним.
Нй: О=0(,
н,: е>еР
117
На рис. 5 показано расположение критической области Vk для раз-
личных альтернативных гипотез. Здесь - плотность распреде-
ления статистики Z критерия при условии принятия гипотезы (P(Z С
V\Vk) = \-a),
Таким образом, проверка статистической гипотезы может быть раз-
бита на следующие этапы:
1) сформулировать проверяемую (Но) и альтернативную (Hi) гипо-
тезы;
2) выбрать уровень значимости а;
3) выбрать статистику Z критерия для проверки гипотезы Но;
4) определить выборочное распределение статистики Z при условии,
что верна гипотеза Но;
5) в зависимости от выбранной альтернативной гипотезы опреде-
лить критическую область Vk одним из неравенств Z > 2i„q, Z < za
или совокупностью неравенств Z > ^i_a/2 и Z < zrt/2;
6) по выборке вычислить zb;
7) принять статистическое решение:
если zB е Vk, то гипотеза отклоняется как не согласующаяся с ре-
зультатами наблюдений;
если zB G V\Vfc, то принять гипотезу Но, т. е. считать, что гипотеза
Но не противоречит результатам наблюдений.
В результате проверки выдвинутой гипотезы могут быть допущены
ошибки двух типов
1) ошибка первого рода - отвергнута правильная гипотеза Но, когда
P(Z Е Vk/H0) = а;
2) ошибка второго рода - принята неправильная гипотеза (в дей-
ствительности верна альтернативная гипотеза), вероятность ошибки
второго рода /3 можно вычислять (для простой альтернативной гипо-
тезы Hi) по формуле
/з = p(z е v \ Vk/H,).
Пример 15. По паспортным данным автомобильного двигателя
расход топлива на 100 км пробега составляет 10 л. В результате изме-
нения конструкции двигателя ожидается, что .расход топлива умень-
шится. Для проверки проводятся испытания. 25 случайно отобран-
ных автомобилей с модернизированным двигателем, причем выбороч-
ное среднее расходов топлива составило X = 9,3л. Предположим, что
118
выборка расходов- топлива получена из нормально распределенной со-
вокупности со средним т и дисперсией а2 = 42. Используя критерий
значимости, проверить гипотезу, утверждающую, что изменение кон-
струкции двигателя не повлияло на расход топлива.
Проверяется гипотеза о среднем а нормально распределенной гене-
ральной совокупности. Проверку гипотезы проведем по этапам:
1. Проверяемая гипотеза Нц : а = 10, альтернативная гипотеза Hi :
2. Выберем уровень значимости се = 0,05.
3. В качестве статистики критерия используем оценку математи-
ческого ожидания - выборочное среднее X.
4. Так как выборка получена из нормально распределенной гене-
ральной совокупности, выборочное среднее также имеет нормальное
w сг2
распределение с дисперсией —
п
Яо, математическое ожидание
рованная статистика критерия
4 гт
= При условии, что верна гипотеза
этого распределения равно 10. Норми-
ТГ х-ю
U = имеет нормальное распре-
деление 7V(0,1), а — 0, а = 1.
5. Альтернативная гипотеза Hi : а < 10 предполагает уменьшение
расхода топлива, следовательно, нужно использовать односторонний
критерий. Критическая область определяется неравенством U < иа.
Учитывая, что
х
г^05 находим по таблице 2 (см. Приложение) из уравнения
Ф(ио.о&) = 0,05 — 0,5 —-0,45
или
Ф(-«0,05) = 0,45.
«о,<15 = -1,645.
6. Выборочное значение нормированной статистики критерия равно
9,3-Ю
u — -1 75.
yw
119
7. Статистическое решение: так как выборочное значение статисти-
ки критерия принадлежит критической области, гипотеза отклоня-
ется: следует считать, что изменение конструкции двигателя привело
к уменьшению расхода топлива.
Граница Хь критической области для исходной статистики X кри-
терия может быть получена из соотношения
^4/25
откуда получаем Х^ = 9,342, т.е. критическая область для статистики
Х< 9,342.
Пример 16.. В, условиях примера 12 предположим, что наряду с
гипотезой До : а — 10 л рассматривается альтернативная гипотеза
Н\ : а = 9 л. В качестве статистики критерия снова возьмем выбороч-
ное среднее X, Предположим, что критическая область задана следу-
ющим неравенством: X < 9,44 л. Найти вероятности ошибок первого
и второго рода для критерия с такой критической областью.
Решение. Найдем вероятность ошибки первого рода. Статистика
X критерия при условии, что верна гипотеза : а = 10 л имеет
нормальное распределение 7\Г(10, ^/4/25). По формуле
P(Z е П/Но) = а,
используя таблицу 2 (см. Приложение), находим
1 /9 44 - 10
а = Р[Х< 9,44/Но : а = 10] = - + Ф
- 1 + Ф(—1,4) = 1 - Ф(1,4) = 0,5 — 0,4192 « 0,08.
Это означает, что принятый критерий классифицирует ~ 8% авто-
мобилей, имеющих расход 10 л на 100 км пробега, как автомобили,
имеющие меньший расход топлива.
При условии, что верна гипотеза Hi : а = 9 л, статистика X имеет
нормальное распределение 7V(9, ^4/25). Вероятность ошибки второго
рода по формуле
P = P(Ze v\vk/H.)
равна
/ /9 44 - 9
(3 = Р[Х < 9,^/Hi : а - 9] - 1 - (о,5 + Ф
120
. : = 0,5 — Ф(1,1) = 0,5 — 0,3643 « 0,136;
Следовательно, в соответствии с принятым критерием 13,6% автомо-
билей, имеющих расход топлива 9 л на 100 км пробега, классифициру-
ются как автомобили, имеющие расход 10 л.
3.6.3 Проверка гипотез о виде функции распределения. Кри-
терий %2-Пирсона
Пусть проверяется гипотеза о виде функции распределения изучае-
мой случайной величины X. В этом случае за критерии проверки ги-
потезы берутся различные меры отклонения эмпирической функции
распределения Fn(x) от гипотетической F(x).
Например,
Z — max |Fn(x) — F(x)| - критерий Колмогорова
Z - У (Fn(x) - F(a:))25(a:)da:, <?(х) > 0,
У g(x)dx < оо - критерий Мизеса.
Подробно рассмотрим критерий х2~Пирсона.
Пусть X - непрерывная случайная величина. Разбиваем область ее
значений на г непересекающихся интервалов Дь Д2,..., Дг. тц - коли-
чество элементов выборки принадлежащих fc-му интервалу.
Pk = Р(Х е Afc), к = 1,2,...,г, 52 = п
ь=1
(для вычисления используется гипотетическая функция распределе-
ния). k ’
Если X - дискретная величина, то щ. - частоты, с которыми каждое
значение встречается в выборке, рь — Р(Х — ж^), которое вычисляется
по предполагаемому закону распределения случайной величины X. В
г
обоих случаях £ pk '== 1.
Если в функцию (закон) распределения входят I неизвестных па-
раметров, то их заменяют оценками, которые получаются, например,
методом максимального правдоподобия, после чего вычисляются р^.
121
За меру отклонения (за критерий) берется случайная величина
= (3D
к=1 пРк
Доказано, что при п —> оо независимо от закона распределения слу-
чайной, величины X, распределение величины х2 стремится к распреде-
лению х2 (” Хи-квадрат”) с (г — Z — 1)-степенями свобод^..На,практике
пользуются этим распределением для величины (31) (при фиксирован-
ном п) в случае прь > 10. Если в некоторых интервалах это условие не
выполняется, то их объединяют с соседними.
Далее по выборке вычисляется х| по формуле (31) и принимается
статистическое решение: гипотеза не противоречит выборке при за-
данном уровне значимости а, если Хв < если же Хв Х1-а> то
гипотеза отклоняется.
Здесь Х1-Л “ квантиль порядка 1 - а распределения х2 с (г - I - 1)
степенями свободы, который вычисляется по таблице б (см. Приложе-
ние).
Пример 17. Проверка гипотезы © распределении по закону Пуассо-
на. В первых двух столбцах таблицы 3.2 приведены данные об отказах
аппаратуры за 10000 часов работы. Общее число обследованных экзем-
пляров аппаратуры п = 757, при этом наблюдается
0 • 427 + 1 • 235 + 2 • 72 4- 3 • 21 + 4 • 1 + 5 • 1 = 451
отказ.
Проверить гипотезу о том, что число отказов имеет распределение
Пуассона:
д*
рк = Р[Х = к] = —е~Л, к = 0,1,..., при а = 0,05.
Оценка параметра А равна среднему числу отказов: А* = 451/757 «
0,6. По таблице 5 (см. Приложение) с А = 0,6 находим вероятности р^
и ожидаемое число случаев с к отказами (третий и четвертый столбцы
таблицы 3.2).
Для к — 4, 5 и 6 значения прк < 10, поэтому объединяем эти строки
со строкой для к = 3. В результате получим значения, приведённые в
таблице 3.3.
122
Т а б л и ц a 3.2
Число отказов к Количество случаев, в которых наблюда- лось к отказов, щ К Ожидаемое число случаев с к отказа- ми, npk
0 427 0,54881 416
1 235 0,32929 249
2 72 0,09879 75
3 21 0,01976 15
4 1 0,00296 2
5 1 0,00036 0
6 0 0,00004 0
Сумма 757 - -
Т а б л и ц а 3.3
к npk (nk - npk)2
0 427 416 0,291
1 235 249 0,787
2 72 75 0,120
> з 23 17 2,118
- - - 4 = 3,316
Так как по выборке оценивался один параметр А, то I — 1, число
степеней свободы равно 4—1 — 1=2. По таблице 6 (см. Приложение)
находим х995 = 5,99, так как < %9 95, то гипотеза о распределении
числа отказов по закону Пуассона принимается.
3.6.4 Выборочный коэффициент корреляции. Проверка гипо-
тезы о значимости коэффициента корреляции
Рассмотрим двумерную случайную величину (X, У) - систему из
двух случайных величин X и У.
Для выяснения их зависимости или независимости, коррелирован-
ности или некоррелированности вычисляют коэффициент корреляции
т
_ М((Х-М(Х))(У-М(У))) _ М(ХУ)-М(Х)М(У)
а(Х)а(У) ^ХИУ) ’ 1 >
123
Если случайные величины независимы, то их коэффициент корре-
ляции равен 0.
Если коэффициент корреляции не равен 0, то случайные величины
зависимы и называются коррелированными.
Если коэффициент корреляции равен 0, то случайные величины на-
зываются некоррелированными.
Коэффициент корреляции двух зависимых величин может быть не
равен нулю, а может и равен нулю.
Из некоррелированности еще нельзя заключить о независимости этих
величин. Можно построить пример, когда случайные величйны некор-
релированы, но зависимы.
Если же случайные величины X и Y распределены по нормальному
закону, то из некоррелированности вытекает их независимость.
Коэффициент корреляции удовлетворяет неравенству
-1 < г < +1
и если г = ±1, то Y и X связаны линейной функциональной зависи-
мостью.
Пусть в результате п независимых экспериментов получены п пар
значений случайных величин X, Y: (xb г/i), (я?2э, (хп,Уп)’
Исходя из определения коэффициента корреляции (32) и полученных
точечных оценок для математического ожидания и среднеквадратичес-
кого отклонения, приходим к выборочному коэффициенту корреляции
(Д ZiVij /п - XY
гв = S*(X)S’(y)
Так как выборка случайна, то выборочный коэффициент корреля-
ции является случайной величиной и может служить точечной оценкой
коэффициента корреляции случайных величин X и Y
Пусть выборочный коэффициент корреляции, найденный по выборке
не равен нулю. Ясно, что отсюда еще нельзя заключить, что коэффи-
циент корреляции генеральной совокупности также отличен от нуля.
В связи с этим проверяют гипотезу о равенстве нулю коэффициента
корреляции генеральной совокупности - значимости (существенности)
выборочного коэффициента корреляции.
Если выдвинутая гипотеза будет отвергнута, то выборочный коэф-
фициент корреляции значим, а величины X и Y коррелированье Если
124
гипотеза принята, то выборочный коэффициент корреляции незначим,
а величины X и Y некоррелированы.
Таким образом, имеем нулевую гипотезу Н$ : г — 0, при конкури-
рующей к ней гипотезы Hi : г 0.
Рассмотрим случай, когда двумерная слачайная величина (Х,У)
распределена по нормальному закону. В качестве критерия проверки
нулевой гипотезы берем случайную величину
Т = гвЛ/^2/л/Ь^. • (33)
Случайная величина Т при справедливости нулевой гипотезы имеет
распределение Стьюдента с к = п — 2 степенями свободы.
Так как конкурирующая гипотеза имеет вид г 0, критическая
область двусторонняя.
И теперь по выборке вычисляем в соответствии с (33) t&. Далее по
таблице 7 (см. Приложение) критических точек распределения Стью-
дента с п — 2 степенями свободы, при заданном уровне значимости а,
находим квантиль tfi.
Если |£в| < ~ нулевую гипотезу принимаем.
Если |tB| > - нулевую гипотезу отвергаем.
Пример 18. По выборке объема п = 122, извлеченной из нормаль-
ной двумерной совокупности, найден выборочный коэффициент корре-
ляции гв =• 0,4. При уровне значимости 0,05 проверить нулевую гипо-
тезу о равенстве нулю коэффициента корреляции при конкурирующей
гипотезе Hi : г ф 0.
Решение. Найдем выборочное значение критерия:
tB = Гв • л/^2/У1 - rl = 0,4- >/122 — 2/УГ^ 0,42 - 4,78
По условию, конкурирующая гипотеза имеет вид г 0, поэтому
критическая область - двусторонняя.
По уровню значимости а — 0,05 и числу степеней свободы к =
122—2 = 120 находим, по таблице 7 (см. Приложение) для двусторонней
критической области, критическую точку to,O5 = 1,98.
Поскольку tB > ta - нулевую гипотезу отвергаем. Другими словами,
выборочный коэффициент корреляции значимо отличается от нуля, т.
е. X и Y коррелированы.
125
3.6: 5 Линейная регрессия. Выборочное уравнение линейной
средней квадратической регрессии
Пусть (X, У) - двумерная случайная величина и случайные вели-
чины X и У зависимы. Важное прикладное значение имеет задача о
представлении одной из этих величин как функции от другой. Точное
представление У — #(.Х), как правило, невозможно, поэтому рассмат-
ривается приближенное представление У ~ д(Х).
Определение. Функция д называется наилучшим приближением
величины У в смысле метода наименьших квадратов, если M(Y —
g(X))2 принимает наименьшее возможное значение. И функция д(Х)
называется средней квадратической регрессией У на X.
Рассмотрим линейную среднеквадратическую регрессию, т. е. ли-
нейную функцию
д(Х) = аХ + Ь (34)
(параметры а и b подлежат определению), которая наилучшим образом
в смысле метода наименьших квадратрв среди всех линейных функций
аргумента X приближает величину У.
Рассмотрим функцию
F(a,b) = M((Y - аХ - Ь)2)
и найдем значения а и 6, при которых она принимает наименьшее зна-
чение.
Имеем
F(a,b) = М(((У - М(У)) - а(Х - М(Х)) + M(Y) -b- аМ(Х))2) =
= М((У - М(У ))2) + а2М((Х - М(Х))?) + М((М(У) - b - аМ(Х))2)-
-2аМ((У-М(У))(Х-М(Х)))+2М((У-М(У))(М(У)-5-аМ(Х)))-
-2aM((X - М(X)) • (М(У) - b - аМ(Х))) =
= M(Y - М(У))2 + а2М(Х - М(Х))2-
-2aM((Y - M(Y))(X - М(Х))) + (М(У) - b - аМ(Х))2. (35)
Здесь в выкладках учли, что М(Х — М(Х\) = О, М(С) = С, С = const.
Далее (35), с учетом (32), запишем в виде
F(a, b) = а2(У)+aV(X) - 2raa(X)a(Y) + (М(У) - Ь - аМ(Х}}2. (36)
126
Исследуем функцию F на экстремум. По необходимому условию эк-
стремума ,
ЭР
~ = 2аст2(Х) - 2га(Х)а(У) - 2(М(У) - Ь - аМ(Х)) • М(Х) = О,
9F
= -2(М(У) - Ъ - аМ(Х)) = 0.
Решая полученную систему относительно а и Ь, получаем
п = <YK
ст(Х)
Ь = М(У)-гМ(Х)^П.
Упражнение. Показать, что при этих значениях функция F(a, b)
принимает наименьшее значение. И оно равняется <т2(У)(1 - г2).
После подстановки найденных а и b в (34), получаем функцию сред-
ней квадратической регрессии Y на X
д(Х) = М(У) + г|^(Х-М(Х))
Определение. Прямая
y = M(Y) + r^(z- М(Х))
ст(А)
называется прямой среднеквадратической регрессии Y на X.
Определение. Величина
Д = а2(У)(1 - г2)
(37)
называется остаточной дисперсией Y на X.
Она определяет величину ошибки приближенного равенства.
Y ~ аХ 4- Ь. Если г — ±1, то ошибка равна нулю и тогда Y и X
связаны линейной функциональной зависимостью.
Аналогично получается прямая среднеквадратической регрессии X
на Y
x = M(X) + r^(y-M(Y)).
(38)
127
Теперь, заменяя в уравнениях (37), (38) сг(Х), а(У), М(Х), M(Y)
и г на их точечные оценки, получаем уравнения выборочных прямых
среднеквадратических регрессий Y на X и X на Y.
S*(X).
х = Х + - У).
128
Лабораторная работа
Математическая статистика
В вариантах заданий приведены результаты наблюдений случайных
величин (СВ) X, Y. Требуется:
1. представить выборку для СВ X в виде таблицы частот;
2. построить гистограмму относительно частот СВ X;
3. расчитать выборочные средние X, У, ’’исправленные” выборочные
дисперсии S*2(X), 5*2(У);
4. по критерию х2~Пирсона проверить гипотезу о нормальном рас-
пределении СВ X;
5. найти интервальные оценки математического ожидания М(Х) и
среднеквадратичного отклонения а(Х) в предположении, что СВ
X имеет нормальное распределение;
6. расчитать выборочный коэффициент корреляции гв;
7. проверить гипотезу о значимости выборочного коэффициента кор-
реляции гв;
8. найти выборочные уравнения линейной регрессии У на X и X на
У и построить их графики.
Примечание. В пп. 4, 5, 7 принять уровень значимости а = 0,05.
Пример.
Результаты наблюдений системы СВ X, У представленны в табл. 1.
129
Таблица 1
X Y X Y X Y X У X У X У X У
4,4 10,1 4,1 6,9 5,1 7,1 4,8 11,3 4,9 5,6 5,1 6,1 4,7 7,6
4,1 10,7 6,7 10.1 3,3 13,0 5,3 11,5 5,7 8,0 3.0 12,1 2.3 11.4
4,7 7,1 6,1 3,9 3,9 13,5 3,3 10,7 5,1 13,9 4,4 14,4 4,3
5,9 7,8 5,2 8,3 4,0 11,1 4,9 7,9 48: 6,2 3,6 £б i$,3
4,5 10,7 5,3 4,9 2,3 10,4 2,5 14,2 3,8 10,7 5,0 8,4 4,0 7,1
5,5 9,5 3,2 11,4 4,3 10,6 2,5 12,4 3,5 8,0 3,5 12,1 3,9 8,3
4,1 11,9 4,3 10,9 4,3 11,2 5,0 8,4 3,8 14,1 6.1 5,5 4,6 9,3
4,6 13,9 4,3 10,1 5,9 9,0 5,2 10,7 7,2 12,2 4,3 9;4 3,4 9.9
5,1 9,1 4,4 6.7 6,3 2,8 3,9 11,9 4.5 10,1 3,6 10.0 2.8 16.8
5,5 8,0 5,3 10,8 4,8 10,4 3.7 9,1 4.2 8,5 4,8 13,1 5,5 7.3
3,9 9,6 5,2 7,7 4,6 11,4 4,0 11,6 4,3 10,9 3,9 10,4 4,6 9,5
4,6 9,*7 6,2 5,7 3,3 12,8 3,9 13,3 4,1 11,9 3,9 12,6 4,7 12,3
6,5 5,5 4,9 9,1 4,9 9,8 7,2 3,3 5,8 4,5 4,7 11,0 4,9 6.3
5,7 3,9 4,9 9,3 4,0 11,7 3,7 10,6 3.8 9,8 4,2 10,9 4,3 12,0
5,0 13,1 3,4 7,0
1. Составляем таблицу частот. Длину интервала находим по фор-
муле:
Я'шах ^min
h =-----------.
1 + 3.3221g п
В нашем случае п = 100, a:min = 2.30, - 7.20. Следовательно,
7.20 - 2.30 .....
~ 1 + 3.3221g 100 ~ ’
Округляем полученное значение, полагая h = 0.70. В качестве левого
конца первого интервала берем точку
zmin “ = 2-30 - 0.35 = 1.95.
Составим таблицу частот (табл. 2).
Таблица 2
Интервалы (at;al+i) ^ = 7? Wjh
(1.95; 2.65] 4 0.04 0.057
(2.65; 3.35] 7 0.07 0.100
(3.35; 4.05] 22 0.22 0.314
(4.05; 4.75] 29 0J29 0.414
(4.75; 5.45] 23 0.23 0.329
(5.45; 6.15] 10 0.10 0.143
(6.15; 6.85] 4 0.04 0.057
(6.85; 7.55] 1 0.01 0.014
Е 100 1
130
2i По таблице частот строим гистограмму (рис. 1) относительных
Рис. 1
3. Числовые характеристики выборки расчитываем по формулам
Х = S*2(X) = -!— (Ё^-пХ2);
П i—1 П 1 ' 2=1 '
Y = - Ё у» S*2(Y) = Ё у! - п?2);
П i=i п — 1 4 ;-1 7
Результаты расчетов
Х = 4.487; S‘2(X) = 0.9088; £*(%) = 0.953.
У = 9.705; 5‘2(У) = 7.2952; 5*(У) = 2.701.
4. Проверяем гипотезу о нормальном распределении СВ X по кри-
терию х2—Пирсона.
Вычисляем
_ у (п< - w?o2
2=1 nPi
где г - число интервалов; п* - эмпирические (наблюдаемые) частоты
(количество элементов выборки, принадлежащих г-му интервалу); npi
131
- теоретические частоты, где pi = Р(а*-1 < X < сц) (вероятность
попадания СВ X на интервал (а^-^а»)).
Так как проверяется гипотеза о нормальном распределении СВ X,
то pi рассчитываются по формуле
п — Ф I —__ - ф 1
Рг \S^X}) \ S*(X)
где Ф(а?) - функция Лапласа.
Интервалы нужно выбирать так, чтобы в каждом интервале выпол-
нялось условие npi >10. Если для каких-то интервалов это условие не
выполнено, их следует объединить с соседними. Первый и последний
интервалы следует расширить до —оо и -f-оо, соответственно. Значения
функции Лапласа берутся из таблицы 2 (см. Приложение) (с учетом
Ф(-ж) = —Ф(я)).
Вычисляем вероятности pi :
,/2.65 — 4.487\
Pi = Р(-оо <х< 2.65) = ф(------——-------) - Ф(-оо) =
= Ф(-1.93) + 0.5 = -0.4732 + 0.5 = 0.0268;
.лм ,/3.35 — 4.487\ /2.65 — 4.487\
* = Р(2.65 < х < 3.35) = Ф( 0 953 ) - Ф( ) =
= Ф(—1.19) - Ф(-1.93) = -0.3830 + 0.4732 = 0.0902;
Аналогично,
рз = 0.2058;
р4 = 0.2875;
р5 = 0.2335;
р6 = 0.1161;
Р7 *= 0.0335;
./6.85 — 4.487\
р8 = Р(6.85 < х < +оо) = Ф(+оо) - Ф(-------------) =
= 0.5 - Ф(2.48) = 0.5 - 0.4934 = 0.0066;
Проверяем условие npi >10.
npi = 2.680 < 10;
пр2 = 9.020 < 10;
пр3 = 20.580 > 10;
132
пр4 — 28.750 > 10;
np5 = 23.350 > 10;
np6 = 11.610 > 10;
пр? = 3.350 < 10;
пр^ ~ 0.660 < 10;
Объединяем первый и второй интервалы в один - (—сю; 3,35], а также
шестой, седьмой и восьмой - (5,45;+оо).
Подсчитываем
Р(-оо < х < 3,35) = Р(-оо < х < 2,65) + Р(2,65 < х < 3,35) =
= 0,0268 + 0,0902 = 0,117.
Аналогично,
Р(5,45 < х < +оо) = 0,1562.
Составляем таблицу.
Таблица 3
Интервалы (^«, &i+l) Эмпир. частоты rii Вероятности Pi Теор. частоты npi (rij - npi)2 npi
(-00; 3.35] и 0.1170 11.70 0.0419
(3.35; 4.05] 22 0.2058 20.580 0.0980
(4.05; 4.75] 29 0.2875 28.750 0.0022
(4.75; 5.45] 23 0.2335 23.350 0.0052
(5.45; +оо) 15 0.1562 15.62 0.0246
S 100 1.0000 100.000 0.1719
Находим критическую точку = Хо,95- Число степеней свободы
равно г — Z — 1 (г - число интервалов, I - число неизвестных параметров
распределения.) В нашем случае число степеней свободы равно 5 - 2 -
1 = 2. По таблице 6 (см. Приложение) находим = 5.991.
Таким образом,
х| = 0.1719; = 5.991.
Так как Хв < Хь то гипотеза о нормальном распределении СВ А’ при-
нимается.
133
5. Находим интервальную оценку параметра а = М(Х) — мате-
матического ожидания СВ X. Доверительный интервал определяется
соотношением
где 6 = Число £7, где 7 = 1 — а = 0,95, находим по
таблице. В нашем случае t7 = 1,984. Тогда <5 = 1.984 ♦0.953/У100 =
0.189 и
X - 6 = 4.487 - 0.189 = 4.298;
X 4- 6 = 4.487 + 0.189 = 4.676;
Таким образом,
4.298 < а < 4.676 — искомый доверительный интервал.
Интервальная оценка параметра а = &(Х) находится по формуле
S*(X)(1 - q) < а(Х) < S*(X)(1 + q) при q < 1,
0 < о(Л') < S*(X)(1 4- q) при q > 1,
где q находится по таблице 4 (см. Приложение).
В нашем случае q = 0,143, S*(X) = 0.953. Получаем
0.953(1 - 0.143) < а < 0.953(1 4-0.143).
0.817 < а < 1.089 — искомый доверительный интервал.
Проведем корреляционный анализ случайных величин X и Y по вы-
борочным данным. 6. Найдем выборочный коэффициент корреляции
ГВ = £ ЪУ1 - ХуЪ(5‘(Х)5‘(У)).
\п i=l /
Результат расчета:
гв = | -1т Ё xiyi - 4.487 • 9.705) /(0.953 2.701) = -0.5910.
\100;=1 /
7. Проверяем значимость найденного коэффициента корреляции. Для
этого вычисляем ____
tB = - 2/У1 -
134
и сравниваем с tk = ta, найденным по таблице 7 критических точек
распределения Стьюдента (см. Приложение).
ta = 1,98.
В нашем случае
tB =
-0.591 - л/98
/1 - (-0.591 )2
= -7.253.
Так как |^в| > то выборочный коэффициент корреляции значимо
отличается от нуля, т. е. можно считать (с надежностью 7 = 1 — а —
1 — 0,05 = 0,95), что случайные величины X и Y коррелированы.
8. Найдем уравнение выборочной прямой среднеквдратической ре-
грессии Y на X'.
У = У + гв|^(*-Х).
В нашем случае
2 701
у = 9.705 - 0.591—-{х- 4.487)
и.Уэо
или
у = — 1.675а? 4-17.221.
Аналогично находим уравнение линии регрессии X на Y:
X = 4.487 - 0.591~ 9-705)
х = -0.209г/+ 6.511.
Построим графики полученных линий.
135
Варианты задании
Вариант 1
X Y X Y X Y X Y X Y X Y
21 14 26 26 23 23 13 23 30 13 24 31 12 23 24 23 22 17 24 37 85 68 56 -1 43 60 32 42 63 28 54 60 64 47 25 22 19 17 21 11 22 И 12 31 21 24 21 12 19 18 15 53 61 29 33 36 -1 63 34 2 69 60 36 45 16 39 43 38 31 23 12 22 22 9 25 16 12 15 21 24 22 11 21 14 26 54 44 9 28 47 24 75 25 12 13 26 37 17 0 8 29 53 21 18 27 23 17 15 19 20 27 36 33 23 16 26 20 21 23 31 55 67 57 32 5 63 36 67 70 83 50 37 53 38 59 44 19 23 25 21 16 13 24 21 24 15 19 20 12 17 33 17 20 27 52 54 47 50 12 73 52 49 23 56 38 22 34 78 48 17 16 19 26 31 25 26 15 23 21 15 24 13 23 21 27 51 43 51 68 48 70 44 37 44 8 67 47 58 27 55
136
Вариант 2
X У X У X У X У X У X У
28 18 21 23 31 18 12 25 25 15 25 14 22 18 22 4 15 28 23 41 35 39 13 -14 34 30 21 38 23 49 13 42 11 19 15 23 20 21 35 22 22 14 24 4 22 17 26 20 14 19 28 33 28 23 37 62 21 43 21 23 -1 34 37 43 12 15 16 51 21 17 25 23 32 17 17 16 27 19 24 31 23 26 20 19 18 36 17 27 25 48 26 25 27 32 19 38 40 52 43 20 29 21 20 19 30 18 30 22 21 15 32 29 14 18 23 22 16 16 23 19 29 50 25 51 23 54 20 38 59 15 16 31 23 26 13 23 16 34 15 23 21 26 19 25 12 18 21 27 9 23 28 27 22 19 57 20 30 32 41 20 43 29 28 30 35 10 37 46 52 25 20 8 20 32 22 27 17 24 26 21 24 26 16 22 21 32 17 16 67 26 49 32 44 41 47 48 51 14 18 23
Вариант 3
X У X У X У X У X У X У
45 18 30 34 21 30 16 26 27 25 23 21 26 13 33 20 22 14 22 12 18 13 13 21 12 27 22 16 14. 8 24 17 20 17 37 30 23 23 35 35 29 26 26 30 35 16 20 35 32 14 40 7 21 13 25 20 15 20 23 18 22 16 24 22 9 15 33 22 23 15 23 33 26 32 34 24 19 22 36 35 30 31 42 15 20 19 25 23 16 16 7 10 22 .18 20 15 10 18 18 12 27 17 30 41 22 26 25 38 15 32 22 29 39 25 40 6 31 23 29 12 15 14 13 17 12 26 18 14 17 9 16 10 32 17 23 9 9 41 10 26 20 29 32 25 14 25 26 30 15 13 10 37 23 33 15 27 15 13 15 13 21 24 15 12 18 21 27 28 8 19 32 27 28 26 30 27 20 35 14 29 35 24 36 31. 28 10 19 13 18 16 18 30 17 23 13 10 22 10 13 18
137
Вариант 4
X Y X Y X У X У X У X У
15 53 22 37 17 41 24 29 32 11 20 50
24 16 16 45 20 39 26 15 21 38 18 51
21 30 22 39 22 21 18 31 19 34 22 22
20 44 21 38 9 68 20 41 22 42 20 23
25 23 19 29 20 36 26 36 11 51 22 39
16 38 24 30 23 31 11 37 17 51 31 21
19 40 11 52 19 33 9 60 17 22 15 49
29 30 32 12 25 20 13 48 15 52 22 32
29 20 13 55 13 43 16 38 25 32 21 41
27 20 19 46 19 36 25 15 14 35 15 50
26 14 20 25 19 29 14 47 15 53 .22 23
13 38 22 26 4 63 20 27 15 42 22 35
20 27 19 47 33 24 23 20 22 33 25 36
17 42 10 47 28 23 15 33 20 34 13 48
21 36 31 21 22 .26 15 58 16 43 14 27
13 50 16 42 18 37 18 29 24 32
16 44 26 39 17 34 19 28 20 29
Вариант 5
X У X У X У X У X У X У
35 42 28 43 20 47 27 40 20 49 19 67
24 45 23 43 21 59 10 74 21 55 14 92
22 57 33 47 25 30 27 53 21 71 26 48
17 49 24 54 17 57 24 40 24 66 10 84
29 50 18 59 29 54 23 39 35 42 20 54
25 33 22 58 21 56 19 53 28 21 19 66
17 61 11 64 18 75 36 38 31 40 17 41
27 16 23 43 15 48 19 51 19 49 13 69
18 67 26 43 29 43 36 26 17 55 18 59
16 51 27 47 21 56 28 50 20 57 11 71
12 70 17 52 30 34 17 87 23 39 23 61
21 47 26 46 20 46 20 52 20 57 19 67
28 53 22 61 33 35 17 72 8 86 24 65
20 56 26 47 33 44 25 56 11 76 19 45
22 50 19 55 14 62 17 69 25 29 30 37
10 83 20 52 18 50 22 41 22 51
20 67 25 66 31 64 15 77 24 48
138
Вариант 6
X У X У X У X У X У X У
22 25 17 18 11 13 7 19 21 19 15 14 9 19 21 15 15 25 17 21 28 36 23 28 22 18 21 23 28 29 26 28 27 29 20 24 14 13 15 13 19 13 13 19 13 13 18 28 14 17 10 14 10 22 21 28 31 22 27 28 14 36 30 20 18 21 26 30 16 15 16 14 16 17 18 9 19 20 21 18 13 10 13 Д6 20 28 17 23 16 23 20 21 23 20 19 23 17 19 30 17 23 28 17 16 21 15 19 22 23 20 20 20 23 25 21 13 23 14 И 23 21 26 24 23 14 20 23 27 19 14 15 14 35 24 26 20 9 15 16 22 22 24 15 16 19 19 16 19 13 21 22 16 16 33 22 22 21 18 17 17 26 18 27 24 25 32 19 23 32 20 19 10 20 19 19 17 21 13 16 20 6 20 14 19 12 26 35 -17 25 26 26 29 25 34 18 28 17 24 19 32
Вариант 7
X У X У X У X У X У X У
.22 48 17 43 14 63 20 62 24 54 23 67
6 82 15 70 22 50 19 38 7 72 13 70
30 27 22 51 21 49 28 42 32 21 33 37
13 44 19 71 29 24 21 50 9 76 21 63
17 67 19 47 16 71 20 56 23 39 22 55
22 45 15 79 21 42 22 47 13 66 23 50
21 47 20 61 14 76 21 48 23 30 30 32
24 56 36 50 29 39 25 62 12 62 21 43
27 42 11 80 26 47 19 47 18 66 25 38
26 36 20 64 23 56 18 63 16 54 28 34
30 33 31 31 23 61 11 54 26 48 25 69
18 77 22 39 21 45 19 59 20 59 20 58
19 67 5 77 17 49 26 30 23 35 20 58
22 49 24 44 22 32 20 29 18 64 25 61
18 58 11 63 14 73 26 44 17 54 23 64
25 68 25 43 27 56 24 67 26 15
22 44 26 36 15 52 25 34 22 65
.139
Вариант 8
X У X У X У X У X У X У
12 18 23 14 20 19 14 8 17 17 18 21 15 7 22 8 16 26 29 35 15 39 33 12 2 29 13 20 33 22 20 43 15 10 11 19 22 9 15 13 17 15 10 20 11 20 12 17 12 17 6 22 42 31 5 23 23 14 17 5 38 18 22 13 32 15 26 7 6 20 23 13 26 11 13 13 14 16 18 23 14 17 15 19 15 11 33 38 26 47 15 26 15 24 19 27 42 19 34 26 45 30 18 18 13 20 15 19 23 18 14 14 16 18 20 14 11 13 16 33 10 12 32 20 27 44 20 21 23 12 24 13 28 23 36 13 16 12 25 24 21 20 15 12 16 16 19 21 9 15 10 13 16 23 18 51 34 28 34 15 16 35 30 29 30 19 22 15 19 19 17 20 16 16 23 20 21 12 18 8 13 14 20 13 15 22 20 19 34 37 28 29 14 14 12 22 10 33 22 27
Вариант 9
X У X У X У X У X У X У
15 14 И 14 11 10 12 9 15 10 12 21 16 12 12 11 12 28 36 36 34 56 56 25 37 34 32 46 27 14 48 39 40 51 16 14 16 16 8 13 13 18 18 9 17 15 11 15 14 12 11 40 48 30 35 50 36 37 36 28 34 30 39 42 38 22 39 48 17 10 16 13 19 14 6 13 15 10 11 12 11 13 15 15 12 31 41 33 39 46 30 58 42 34 46 46 46 42 23 42 38 49 13 13 14 12 14 13 12 13 19 16 13 14' 13 17 11 14 13 41 42 40 46 32 33 39 39 26 33 33 30 54 34 37 41 36 9 14 15 11 15 17 9 16 8 10 15 11 15 15 8 12 9 49 27 49 49 40 39 59 40 41 37 32 45 39 35 51 37 39 13 18 12 14 17 15 И 9 13 15 12 16 13 16 16 53 27 33 37 34 42 39 33 29 28 43 32 35 39 38
140
Вариант 10
X Y X Y X У X У X У X У
23 31 12 53 23 33 18 37 24 30 27 28
28 28 26 28 10 48 25 25 32 28 17 35
24 29 20 43 22 43 13 47 27 38 17 48
21 37 14 50 21 39 29 28 17 43 23 32
28 30 21 41 17 41 13 64 18 42 9 45
11 39 24 30 8 50 19 44 16 40 22 38
15 42 18 36 25 34 17 45 19 41 23 31
18 42 26 31 9 60 21 35 25 38 23 35
22 33 10 57 30 27 22 34 29 24 27 31
14 44 12 51 29 32 12 42 20 38 13 52
16 43 19 40 26 25 16 43 6 53 18 45
25 24 28' 36 25 31 14 41 21 38 24 39
20 39 20 48 32 20 27 31 15 50 15 47
12 39 28 23 24 36 20 44 16 49 20 44
21 36 11 53 21 31 33 25 23 35 20 45
17 47 24 33 27 29 30 21 22 41
31 24 20 40 19 35 16 48 19 36
Вариант 11
X У X У X У X У X У X У
45 18 30 34 21 30 16 26 27 25 23 21 26 13 33 20 22 33 14 15 24 7 16 9 11 27 19 11 8. 7 И. 22 12 12 37 30 23 23 35 35 29 26 26 30 35 16 20 35 32 14 40 17 24 9 21 28 24 23 22 17 25 24 14 14 18 21 19 35 23 15 23 33 26 32 34 24 19 22 36 35 30 31 42 15 20 14 11 18 22 15 12 17 19 10 15 26 18 22 23 27 14 10 30 41 22 26 25 38 15 32 22 29 39 25 40 6 31 23 29 16 29 9 12 15 24 13 23 8 19 22 14 25 6 21 18 11 9 41 10 26 20 29 32 25 14. 25 26 30 15 13 10 37 23 16 30 10 14 5 17 18 19 11 13 11 21 9 12 10 18 15 32 27 28 26 30 27 20 35 14 29 35 24 36 31 28 15 19 14 17 19 18 23 24 9 15 18 19 19 17 19
141
Вариант 12
X Y X Y X Y X Y X Y X У
19 36 12 44 21 23 18 24 23 17 16 37:
16 39 10 28 17 24 15 27 15 34 15 32
20 26 16 28 16 38: 17 40 15 47 19 33
26 19 16 28 18 31 17 20 15 43; 12 55
10 50 18 31 19 28 17 32 10 48 16 36
15 36 21 24 21 26 18 29 19 20 15.; 47
20 40 19 34 13 27 8 36 18 23 19, 45
8 42 19 29 12 43 12 .44 20 26 25 31
16 13 15 40 22 8 9 38 25 19 1Г 23
13 33 23 31 12 38 14. 41 19 37 24. 20
21 29 16 39 10 44 15 19 15 34 13 48
14 35 19 29 15 28 20 33 13 36 20 33
15 18 14 33 13 40 14 29 12 31 14 35
17 40 13 42 12 52 15 46 19 34 15 40
22 35 9 47 23 27 7 48 19 28 15 42
19 34 9 56 18 23 18 25 Г7 25
22 35 8 47 19 24 15 35 14 31
Вариант 13
X У X У X У X У X У X У
12,7 21 7,8 37 8,7 47 11,6 39 П,1 28 10,1 29
7,6 43 8,7 45 9,5 41 12,9 29 11,5 22 12,0 36
8,7 44 10,9 38 11,1 16 11,6 48 7,7 41 8,2 43
9,4 44 11,5 36 12,1 42 10,9 34 10,8 49 9,9 35
8,9 48 14,1 26 11,9 13 10,2 37 8,3 50 8,7 60
12,8 26 13,0 27 9,5 41 9,6 44 11,6 37 12,5 31
10,8 22 П,1 39 13,0 30 10,0 41 10,5 32 9,8 48
11,8 25 9,6 38 10,6 10$ 45 11,1 45 10,7 29 i2,l 21
9,5 32 8,4 53 36 12,1 12 9,4 55 6,2 73
10,6 35 9,8 26 9,3 57 10,4 31 10,0 27 8,1 47
6,6 41 11,6 33 9,4 32 П,7 44 10,0 51 11,0 25
9,6 50 10,0 48 6,4 59 10,1 34 12,2 39 10,3 42
10,1 37 12,2 32 9,2 33 10,3 33 13,6 31 14,5 30
10,7 38 8,6 37 11,4 42 10,3 32 10,9 39 13,6 28
9,0 53 11,0 30 5,5 75 10,0 37 7,8 ' 37 8,2 43
11,1 35 12,5 33 И,4 27 11,8 22 7,1 53
11,5 42 10,2 39 14,1 28 14,4 20 7,7 49
142
Вариант 14
X Y X Y X Y X Y X Y X Y
9 30 13 21 12 21 13 17 8 39 13 17
15 27 14 21 .8 33 13 23 11 35 11 21
10 23 14 23 11 38 12 27 13 22 7 38
10' 29 12 31 .11 31 15 16 9 27 12 26
12 27 12 17 12 32 10 26 И 24 11 18
14 26 8 38 12 25 12 26 12 28 13 27
7 33 13 27- 12 31 15 16 9 38 16 11
14 25 14 го 8 31 10 34 14 22 10 29
14 25 10 33 8 30 13 20 13 27 11 29
13 18 ;14 25 12 23 12 32 13 32 12 24
17 25 14 28 11 26 13 14 13 21 15 27
6 38 12 31 10 31 16' .17 13 20 11 27
13 26 15 13 14 '25 12 19 7 31 10. 32
10 29 13 16 10 31 16 16 9 32 11 30
10 31 15 13 12 22 10 27 13 25 12 25
13 20 14 18 12 25 12 24 12 23
13 27 9 25 13 22 13 20 14 21
Вариант 15
Х> Y X Y X Y X Y X Y X Y
12 42 39 13 38 35 34 39 31 23 41 8
37 23 43 17 19 40 12 39 35 26 40 31
45 7 25 18 36 16 37 28 32 28 28 30
39 35 24 40 30 30 23 39 40 27 38 10
38 20 41 21 35 24 33 25 27 33 49 23
29 25 49 24 30 34 12 33 34 15 24 38
14 36 40 •24 22 32 26 37 15 32 33 22
23 44 40 35 29 31 41 40 40 18 26 31
39 24 23 45 33 24 35 31 39 15 27 29
34 13' 26 42 28 39 47 30 27 31 47 25
12 34 34 37 38 19 22 35 41 35 16 27
28 29 17 33 49 24 48 34 21 35 57 31
41 48 36 35 40 32 35 27 48 24 25 44
38 32 38 24 45 27 15 34 27 22 24 42
24 44 36 .29 21 30 35 18 32 14 32 31
25 35 39 15 45 17 28 30 35 34
27 37- 56 19 32 41. 20 32 32 25
143
Вариант 20
X У X У X У X У X У X У
12,1 32 15,8 22 12,9 27 17,2 15 8,4 30 8,9 30
14,9 22 18,0 24 17,9 18 7,4 32 20,3 17 6,6 36
16,9 17 13,3 29 20,2 20 15,9 13 11,4 27 11,9 33
12,9 28 22,0 18 14,0 33 12,6 26; 14,1 19 17,0 11
15,1 24' 14,6 23 12,7 27 23,2 .8. 13,9 21 11,9 20
10,4 30 15,9 22 15,4 21 10,9 28 15,9 17 20,3 19
13,8 24 12,7 22 21,4 15 15,8 25 15,9 27 13,5 20
9,3 34 13,8 21 22,1 16 18,8 17 13,1 27 13,4 24
15,1 33 20,8 22 13,2 16 24,3 15 13,9 27 4,8 36
15,0 28 13,9 18 11,3 30 9,4 21 13,3 28 15,3 20
18,1 19 16,2 19 15,7 20 10,8 32 15,3 21 14,5 31
18,9 20 17,3 27 15,1 23 10,3 29 17,5 13 11,4 27
20,0 12 16,1 21 17,9 25 9,0 26 9,6 30 15,8 27
12,2 33 17,8 16: 15,4 26 П,7 28 16,2 11 13,6 24
17,7 13 13,9 24 14,3 31 10,3 30 14,2 19 18,3 21
15,4 14 16,8 20 17,1 18 18,2 10 18,7 21
16,0 15 15,6 15 11,0 27 18,9 23 10,7 21
Вариант 21
X У X У X ' У X У X У X У
12,2 24 14,1 12 П,1 27 9,9 34 12,3 35 12,9 22
13,1 27' 13,2 29 10,1 36 11,3 39 7,1 45 10,8 25
13,1 23 11,5 29 12,2 36 11,0 26 12,4 23 11,8 36
11,0 32 11,0 29 12,4 26 10,9 28 8,9; 35 12,3 31
12,2 36 11,6 28 11,2 24 10,1 28 11,2 31 11,6 32
8,9 38 11,6 25 10,8 34 14,2 17 11,9 19 11,7 20
10,4 38 14,7 24 13,4 18 10,5 28 12,2 34 10,5 27
9,3 37 7,9 42 12,7 31 12,9 22 7,1 48 10,2 31
8,1 39 11,5 32 11,9 21 9,8 27 11,2 29 8,0 38
10,8 27 10,7 41 9,1 40 11,0 16 9,6 32 9,0 41
7,9 47 10,8 43 12,8 27 10,2 36 9,6 41 9,5 29
9,8 31 9,3 32 11,3 35 14,2 32 12,0 34 И,1 35
12,1 31 12,6 20 10,7 32 10,8 35 10,3 25 8,7 30
8,9 31 11,8 34 8,4 42 П,4 31 12,1 22 12,7 33
13,3 15 8,5 30 И,1 34 7,4 36 11,2 34 12,3 23
10,6 31 7,1 39 9,3 37 11,0 31 11,7 30
9,9 39 9,4 34 8,7 42 6,4 37 11,5 25
146
Вариант 22
X Y X Y X Y X Y X Y . X У
60 35 45 67 39 49 63 55 46 39 40 40 59 51 43 60 61 37 71 63 25 57 37 50 55 33 58 62 48 41 43 66 25 25 55 47 39 45 47 57 47 50 40 45 52 30 36 40 53 52 37 50 50 36 83 26 19 69 54 65 34 47 43 63 80 45 49 55 50 68 53 54 34 60 74 53 61 48; 48 75 64 45. 44 71 65 41 44 41 42 50 40 40 28 43 41 49 36 45 41 62 20 34 44 78 44 56 43 50 57 28 59 47 56 ,31 25 42 74 34 57 51 38 41 46 57 55 36 60 45 73 51 72 67 54 47 46 24 .47 30 50 35 44 41 52 52 46 80 60 40 40 50 46 49 66 34 58- 58 59 61 40 59 33 65 20 60 60 54 52 36 49 44 34 39< 62 53 47. ,36 61 48 50 61 62 36 75 52 70 68 39 3.5 37 48' 57 43 59 24 49 59 68 18 39 32
Вариант 23
X У X У X. У X У X У X У
17 10 11 18: 21 17 6 9 13 15 8 15 11 15 13 12 10 34. 31 37 33 32 33 46 42 39 39 47 37 39 36 34 39 41 18 14 5 13 16 16. .9 19 11 5 12 13 15 19 9 12 12 32 38 33 36 38 37 37 28 39 48 37 38 34 31 ,38 40 42 9 15 13 14 13 14 .12 .15 13 13 7 16 17 14 17 20 18 41 35 40 37 ,39 37 39 38 37 38 43 36 32 37 34 30 34 , 3 11 11 14 12 15 14 11 11 8 8 14 16 10 18 8 17 47 30 39, 36 38 33 35 40 41 44 43 40 36 39 34 41 36 9 16 11 14 20 18 16 13 13 7 14 7 7 13 11 9 13 42 35 40 37 3.4 36 40 38 36 41 39 44 43 37 36 41 37 13 15 21 14 10 14 13 15 18 15 20 12 И 10 10 37 36 30 37 41 36 38 35 33 37 29 40 41. 41 42
147
Вариант 16
X Y X У X Y X У X У X У
36 20 18 20 41 20 29 18 41 16 40 20
37 24 35 20 39 18 41 12 40 9 37 17
50 12 42 11 42 20 34 23 38 19 22 21
24 22 42 22 45 15 20 23 36 14 43 14
31 15 24 27 .32 21 28 23 38 23 41 14
42 18 40 20 30 31 32 12 31 21 31 20
20 22 39 17 42 17 28 23 44 25 48 5
42 23 34 20 •40 15 38 25 .34 17 52 8
39 11 15 28 32 20 25 23 21; 28 33 26
33 20 46 16 35 18 31 25 28 27 37 23
29 33 21 20 37 17 29 20 12 27. 34 15
39 16 17 26 38 18 46 20 46' 20 43 17
33 19 28 28 28 24 31 17 33 21 23 25
24 24 36 23 34 16 37 19 32 21 41 24
25 30 40 17 38 15 26 22 42 12 36 27
50 12 33 24 35 13 39 ,10 31 23
29 19 29 20 39 •25 40 19 38 15
Вариант 17
X У X У X У X У X Y X У
21,1 76 16,7 75 18,9 72 14,7 99 18,9 41 20,9 61
9,5 85 25,8 114 15,0 48 25,5 62 23,6 60 32,2 60
24,9 87 25,7 80 22,5 65 16,1 79 15,6 99 20,5 76
21,9 70 18,2 77 15,2 63 16,8 67 21,4 64 19,9 90
14,3 44 27,7 66 18,3 69 15,6 53 15,0 60 25,5 73
10,2 51 23,8 59 13,2 80 8,8 53 15,8 81 19,5 66
14,8 48 22,4 83 19,4 66 23,0 81 23,1 78 16,5 74
16,5 67 20,2 49 20,2 65 29,1 73 24,7 50 19,7 56
24,6 31 20,9 88 25,1 45 13,4 64 10,1 69 13,6 68
18,3 76 17,9 99 18,9 57 23,0 72 12,1 82 .27,5 55
16,8 77 23,6 68 31,2 83 23,3 103 7,5 80 14,3 42
28,0 62 4,6 85 15,5 111 11,0 87 25,6 73 17,7 75
21,0 79 21,9 53 21,7 112 12,5 83 18,4 57 19,4 66
17,4 79 15,6 101 10,9 77 23,8 73 30,6 58 25,0 64
15,0 71 15,0 68 23,6 . 49 26,1 72 18,0 37 21,3 51
20,8 82 20,0 60 18,1 92 21,5 75 26,7 76
20,1 63 17,7 85 15,6 72 24,5 48 12,4 95
144
Вариант 18
X Y X Y X Y X Y X У X У
26 41 54 34 48 25 42 52 46 49 38 45 68 47 39 73 39 54 36 35 61 61 46 43 35 32 25 52 47 28 45 33 28 46 17 46 52 34 59 50 55 32 36 37 55 14 61 26 35 56 59 25 34 38 32 18 40 33 48 46 58 46 56 38 63 55 29 40 56 30 39 31 38 17 29 27 30 20 48 46 37 64 44 37 52 40 57 38 52 46 48 37 53 42 42 37 28 33 42 51 46 33 41 36 40 54 25 57 28 41 27 26 35 29 58 56 21 42 25 36 51 54 44 24 49 33 38 51 51 38 52 23 29 56 29 52 27 24 67 63 42 22 30 34 22 26 32 40 44 39 43 36 .40 51 47 41 37 51 .56 37 43 52 56 41 46 24 35 52 39 54 22 52 21 29 43 38 21 25 36 32 40 33 59 29 31 52 39 56 46 51 63 59 68 56 52 61 40 47 32 45
Вариант 19
X У X У X У X У X У X У
64 19 13 33 41 59 28 22 44 59 21 39 29 12 30 38 43 20 84 87 60 63 67 81 75 48 16 49 46 44 80 76 80 65 43 70 37 33 34 31 25 50 29 38 31 27 24 20 26 27 12 61 74 33 32 75 76 57 52 60 73 48 74 54 87 93 52 101 56 22 34 29 42 63 28 26 21 27 35 26 38 41 39 15 46 26 85 64 ,58 59 35 85 70 97 66 58 36 66 58 100 ,60 46 • 41 40 45 40 42 32 53 49 15 23 37 31 41 33 31 40 45 35 .55 59 72 39 44 40 40 95 67 51 53 51 82 42 75 56 39 49 55 21 38 26 33 37 33 36 52 35 37 42 38 28 24 51 39 29 68 51 57 75 73 57 62 25 46 48 75 58 91 •72 11 19 24 53 42 32. 30. 18 44 38 33 23 28 47 28 84 67 50 59 38 ,60 70 77 31 55 75 68 58 34 66
145
Вариант 24
X Y X Y X Y X Y X Y X Y
4,8 7,2 5,9 4,8 6,1 7,3 5,2 4,6 5,2 8,0 4,3 6,1
5,7 10,2 6,0 8,5 5,0 5,9 6,4 5,7 6,0 5,9 4,8 4,9
6,2 8,7 7,3 6,7 6,2 7,6 6,3 7,6 5,9 5,4 4,0 3,5
5,0 4,8 5,6 7,8 6,9 6,9 5,0 9,6 3,8 6,5 4,0 3,9
4,0 7,0 4,5 3,5 8,2 6,7 6,3 4,3 6,2 7,6' 4,7 6,7
4,4 6,4 6,6 6,7 4,0 5,9 6,0 4,8 5,6 6,8 5,6 9,2
6,1 7,5 5,9 6,0 4,6 4,3 2,7 4,0 6,2 8,3 4,6 7,6
7,2 8,0 7,4 6,5 4,4 7,3 4,5‘ 7,0 5,8 6,6 3,8 6,5
6,1 6,5 4,7 9,7 3,4 9,1 7,3 9,0 9,0 9,7 6,3 7,5
5,6 7,1 5,0 5,7 5,2 5,0 5,5 4,5 5,2 7,5 2,7 3,9
6,1 10,1 5,1 5,3 4,8 6,0 6,8 7,9 5,5 6,7 4,1 5,2
5,1 7,0 4,6 6,7 3,9 8,2 7,2 6,9 5,3 5,0 3,4 2,9
5,8 7,6 3,4 1,8 4,3 4,6 4,5 8,1 5,5 8,3 7,1 8,6
4,6 5,5 5,2 6,9 5,7 9,0 6,9 8,1 6,9 6,2 4,5 3,6
4,3 5,6 5,0 6,7 6,2 5,1 2,7 3,4 5,5 7,7 3,6 6,7
4,6 7,9 5,4 7,3 2,7 4,9 6,4 8,7 5,0 5,8
5,5 6,4 4,9 9,5 4,4 5,2 6,5 6,1 4,8 8,6
Вариант 25
X Y X Y X Y X Y X У X У
32 5,2 52 5,4 41 3,8 44 3,9 13 5,1 30 4,4
23 3,4 18 6,1 25 4,2 8 6,9 12 4,4 46 5,0
38 3,9 30 3,8 39 4,7 23 5,7 32 3,9' 31 5,6
42 2,7 32 4,9 33 3,6 27 6,3 38 4,7 35 3,8
25 6,2 18 5,1 35 3,2 39 3,5 22 6,6 22 4,2
40 4,8 33 3,5 31 4,3 25 5,6 35 4,9 22 5,2
21 4,7 42 4,3 23 6,0 20 6,6 38 4,7 14 6,3
34. 3,3 33 5,0 28 5,0 44 2,4 32 3,9 24 6,3
42 2,9 35 4,4 25 4,7 46 5,7 15 7,3 34 4,5
36 4,1 29 5,5 25 5,3 24 4,6 21 5,5 36 3,5
24 5,5 38 3,2 23 5,6 39 5,3 36 5,7 26 4,6
44 4,0 24 8,1 31 4,0 26 6,1 47 3,0 33 5,5
36 5,0 41 4,0 36 5,0 26 6,1 43 4,6 27 6,9
37 3,3 23 4,1 34 6,0 40 4,3 46 5,0 34 5,4
43 2,9 29 6,7 37 4,7 21 7,4 30 3,7 18 6,1
36 4,8 51 3,0 30 4,8 36 5,6 34 4,5
31 4,0 30 3,8 20 4,9 25 6,6 25 5,8
148
Вариант 26
X Y X Y X Y X Y X Y X Y
22 17 34 31 29 29 37 38 37 28 31 19
30 32 36 29 14 12 42 39 33 16 34 35
24 27 31 20 23 24 31 34 18 15 15 13
20 24 29 21 28 31 22 19 26 18 20 22
31 24 27 33 32 30 26 22 37 24 25 18
26 23 25 24 31 31 16 18 16 10 28 18
24 28 26 30 18 20 36 35 37 33 31 24
22 28 33 25 15 22 12 6 29 29 27 19
18 29 18 23 41 44 14 29 44 30 23 31
46 39 35 34 22 26 27 18 28 37 36 36
41 25 25 26 32 27 42 28 13 20 41 20
29 33 24 21 18 37 18 28 21 21 32 28
20 29 14 18 28 24 23 32 36 34 23 16
24 33 34 21 26 13 34 35 22 23 27 19
46 36 22 23 23 26 32 22 25 22 21 14
40 24 30 32 10 24 43 32 39 29
19 32 24 21 34 25 35 24 17 27
Вариант 27
X Y X У X У X У X У X У
6,8 5,4 5,0 4,5 4,6 3,2 3,5 5,0 6,3 2,9 2,4 5,1 4,8 2,8 4,6 3,6 8,6 8,7 4,7 5,4 5,7 7,0 3,9 5,0 7,5 5,6 3,9 4,1 2,9 5,7 3,0 6,0 5,4 8,8 6,5 7,1 8,3 5,3 5,7 3,1 3,9 1,5 6,0 6,9 6,2 4,8 4,2 2,2 6,2 6,9 4,6 4,9 3,8 6,5 4,3 4,6 4,8 3,0 4,1 6,5 6,9 5,3 5,7 2,8 4,3 7,7 5,8 4,2 6,7 7,9 4,2 3,9 4,6 4,0 6,2 4,0 3,8 6,2 3,7 3,9 5,8 9,6 4,4 5,3 5,3 5,8 7,1 5,2 3,6 5,1 3,7 5,9 3,9 5,2 5,5 3,7 5,4 7,4 7,2 6,7 6,3 2,9 5,1 4,5 4,9 4,2 5,1 5,3 5,8 2,5 6,2 6,3 6,8 5,8 3,7 2,8 3,9 5,1 4,4 6,2 3,1 2,4 4,7 4,8 6,3 8,7 2,3 5,4 6,9 4,0 4,1 4,0 4,7 4,6 5,7 6,6 5,6 4,9 7,0 4,8 6,1 7,4 7,5 6,6 6,4 6,4 7,6 8,3 6,8 3,8 7,7 4,2 5,8 5,0 3,3 6,8 5,1 4,6 5,3 4,8 4,7 6,4 7,6 7,9 5,9 7,3 6,2 6,2 4,9 3,2 2,4 4,5 4,8 7,3 7,1 7,9 4,6 5,1 6,3 6,1 4,9 6,3 3,9 7,0 2,9 3,9 4,4 5,7 7,8 6,0 6,1 4,0 5,8 6,7 7,2 4,8 6,7 4,6 7,0
149
Вариант 28
X Y X У X У X Y X У X У
2,7 3,0 4,4 5,2 3,3 3,2 5,8 4,0 3,2 2,4 4,4 3,6 4,3 5,6 4,4 4,7 1,7 4,2 2,5 4,3 6,1 5,8 5,5 7,1 4,5 3,1 4,9 5,5 3,6 5,7 6,0 5,5 4,8 2,5 6,1 2,8 3,3 4,8 3,4 4,1 1,9 4,4 3,0 4,1 2,3 3,8 4,8 4,3 2,9 4,5 4,0 7,1 4,2 3,2 5,5 4,7 5,4 3,5 5,6 3,5 5,9 3,9 2,9 5,5 5,7 3,8 5,9 5,0 3,1 3,5 3,4 4,8 4,2 3,8 3,7 4,8 1,2 5,5 5,0 3,2 3,6 4,2 4,6 5,0 3,0 3,2 6,0 5,6 4,1 5,9 4,4 3,9 7,4 2,4 5,4 5,5 4,9 4,8 6,0 5,1 7,0 4,4 3,4 3,2 5,6 4,1 4,0 5,8 4,1 3,1 5,0 4,4 3,9 4,3 3,8 6,2 6,2 3,7 3,3 5,2 4,6 6,1 4,9 4,5 6,1 6,6 4,5 5,2 6,2 5,3 6,2 5,3 6,3 7,7 4,7 2,8 4,3 4,7 4,4 4,5 2,1 2,8 3,6 3,9 4,9 4,5 2,1 3,5 3,7 3,1 4,1 5,3 4,3 5,2 6,4 5,8 4,2 4,4 3,7 6,2 5,4 4,1 5,5 5,0 5,0 5,0 7,3 4,4 6,0 6,8 5,2 4,4 4,1 1,6 3,9 2,9 5,3 5,6 4,4 3,3 4,0 2,2 4,7 4,1 3,4 5,4 5,1 4,6 3,0 4,7 5,5 6,7 8,0 7,1 ,5,8 5,4 2,6 5,7 5,5 4,5
Вариант 29
X У X У X У X У X У X У
18 72 17 68 14 91 16/ 86 19 55 13 103
16 75 20 57 11 101 15 77 15 96 16 94
17 86 13 89 20 69 22 54 27 26 22 85
15 59 18 86 22 54 20 67 9 103 17 76
16 78 18 66 15 86 8 93 10 87 12 91
16 74 7 104 9 103 20 75 14 80 10 83
14 86 17 97 17 89 20 92 8 89 11 103
14 98 16 95 15 75 25 39 18 69 15 93
16 68 13 66 18 86 12 78 17 78 16 86
10 104 12 90 17 81 13 111 15 98 17 98
17 86 16 56 10 127 16 84 16 83 14 98
14 80 17 103 10 99 15 83 16 86 12 113
12 88 9 119 15 82. 18 51 17 93 14 101
14 94 12 99 18 98 16 64 19 64 16 102
15 107 17 73 13 106 12 101 20 61 14 70
20 74 11 116 21 88 10 99 20 62
13 83 8 130 21 45 16 113 13 100
150
Вариант 30
X Y X Y X Y X Y X Y X Y
37 16 33 43 41 46 24 32 36 42 36 32 28 22 36 27 30 7,0 8,5 6,8 6,4 6,6 6,2 7,6 7,2 6,2 6,8 6,9 6,2 6,3 7,2 6,2 6,6 7,9 34 23 42 31 43 15 29 21 42 44 19 39 22 39 7 39 38 7,2 6,7 5,4 7,4 7,1 8,5 7,1 7,9 W 6,1 7,1 5,6 7,4 5,6 7,8 6,9 5,9 40 47 29 19 32 30 23 15 32 31 15 40 30 19 43 37 22 7,2 5,9 6,7 8,6 7,6 7,2 7,4 7,9 7,1 8,1 6,8 6,7 7,0 7,6 5,8 7,2 7,7 32 47 30 42 30 39 36 27 25 39 31 53 49 36 23 19 35 6,2 4,9 6,6 6,4 6,8 6,9 7,1 7,3 7,2 7,3 7,5 6,3 5,5 7,3 7,5 7,5 6,0 17 27 23 26 35 34 31 44 47 42 24 24 31 47 37 34 14 4,8 6,7 6,7 6,9 6,9 6,9 7,0 6,0 7,2 6,2 8,0 7,0 7,0 5,8 7,7 6,7 8,0 28 24 12 16 .52 40 29 29 16 24 23 34 .37 28 31 6,0 7,4 6,5 8,2 4,5 7,0 6,4 7,1 8,0 7,7 6,2 6,9 6,2 6,7 7,3
151
Приложение
Таблица 1. Таблица значений функции
/х 1
Пх) = ~Т5=е 2
\/ Z7T
X . 0 1 2 3 4 5 6 7 8 9
0,0 0,3989 3989 3989 3988 3986 3984 3982 3980 3977 3973
0,1 3970 3965 3961 3956 3951 3945 3939 3932 3925 3918
0,2 3910 3902 3894 3885 3876 3867 3857 3847 3836 3825
0,3 3814 3802 3790 3778 3765 3752 3739 3726 3712 3697
0,4 3683 3668 3652 3637 3621 3605 3589 3572 3555 3538
0,5 3521 3503 3485 3467 3448 3429 3410 3391 3372 3352
0,6 3332 3312 3292 3271 3251 3230 3209 3187 3166 3144
0,7 3123 3101 3079 3056 3034 ЗОН 2989 2966 2943 2920
0,8 2897 2874 2850 2827 2803 2780 2756 2732 2709 2685
0,9 2661 2637 2613 2589 2565 2541 2516 2492 2468 2444
1,0 2420 2396 2371 2347 2323 2299 2275 2251 2227 2203
1,1 2179 2155 2131 2107 2083 2059 2036 2012 1989 1965
1,2 1942 1919 1895 1872 1849 1826 1804 1781 1758 1736
1,3 1714 1691 1669 1647 1626 1604 1582 1561 1539 1518
1,4 1497 1476 1456 1435 1415 1394 1374 1354 1334 1315
1,5 1295 1276 1257 1238 1219 1200 1182 1163 1145 1127
1,6 1109 1092 1074 1057 1040 1023 1006 0989 0973 0957
1,7 0940 0925 0909 0893 0878 0863 0848 0833 0818 0804
1,8 0790 0775 0761 0748 0734 0721 0707 0694 0681 0669
1,9 0656 0644 0632 0620 0608 0596 0584 0573 0562 0551
2,0 0540 0529 0519 0508 0498 0488 0478 0468 0459 0449
2,1 0440 0431 0422 0413 0404 0396 0387 0379 0371 0363
2,2 0355 0347 0339 0332 0325 0317 0310 0303 0297 0290
2,3 0283 0277 0270 0264 0258 0252 0246 0241 0235 0229
1 2,4 0224 0219 0213 0208 0203 0198 0194 0169 0184 0180
152
Окончание табл. 1
X 0 1 2 3 4 5 6 7 8 9
2,5 0175 0171 0167 0163 0158 0154 0151 0147 0143' .0139
2,6 0136 0132 0129. 0126 01225 0119 0116 0113 оно 0107
2,7 0104 0101 0099 0096 Ь093 0091 0088 0086 0084 0081
2,8 0079 0077 0075 0073 0071 0069 0067 0065 0063 0061
2,9 0060 0058 0056 0055 0053 0051' 0050 0048 0047 0046
3,0 0044 0043 0042 0040 0039 0038, 0037 0036 0035 0034
3,1 0033 0032 0031 0030 0029 0028 0027 0026 0025 0025
3,2 0024 0023 0022 0022 0021 0020 0020 0019 0018 0018
3,3 0017 0017 0016 0016 0015 0015 0014 0014 0013 0013
3,4 0012 0012 0012 0011 ООН 0010 0010 0010 0009 0009
3,5 0009 0008 0008 0008 0008 0007 0007 0007 0007 0006
3,6 0006 0006 0006 0005 0005 0005 0005 0005 0005 0004
3,7 0004 0004 0004' 0004 0004 0004 оооз: 0003 0003 0003
3,8 0003 0003 0003 0003 0003 0002 0002 0002 0002 0002
3,9 0002 0002 0002 0002 0002 0002 0002 0002 0001 0001
Таблица 2. Таблица значений функции Лапласа
Ф(х) = j e~z2/2dz, Ф(—ж) = -Ф(х)
у2тг g
0 1 2 3 4 5 6 7 8 9
0.0 0.00000 00399 00798 01197 01595 01994 02392 02790 03188 03086
0,1 03983 04380 04776 05172 05567 05962 06356 06749 07142 07535
0,2 07926 08317 08706 09095 09483 09871 10257 10642 11026 11409
0,3 11791 12172 12552 12930 13307 13683 14058 14431 14803 15173
0,4 15542 15910 12276 16640 17003 17364 17724 18082 18439 18793
0,5 19146 19497 19847 20194 20540 20884 21226 21566 21904 22240
0,6 22575 22907 23237 23565 23891 24215 24537 24857 25175 25490
0,7 25804 26115 26424 26730 27035 27337 27637 27935 28230 28524
0,8 28814 29103 29389 29673 29955 30234 30511 30785 31057 31327
0,9 31594 31859 32121 32381 32639 32894 33147 33398 33646 33891
1,0 34134 34375 34614 34850 35083 35314 35543 35769 35993 36214
1,1 36433 36650 36864 37076 37286 37493 37698 37900 38100 38298
1,2 38493 38686 38877 39065 39251 39435 39617 39796 39973 40147
1.3 40320 40490 40658 40824 40988 41149 41300 41466 41621 41774
1,4 41924 42073 42220 42364 42507 42647 42786 42922 43056 43189
1,5 43319 43448 43574 43699 43822 43943 44062 44179 44295 44408
153
Окончание табл. 2
X 0 . 1 2 3 4 5 6 . 7 8 9
1,6 44520 44630 44738 44845 44950 45053 45154 45254 .45352 45449
1,7 45543 45637 45728 45818' 45907 45994 46080 46164 46246 46327
1,18. 46407 46486 46562 46638 46712 46784 46856 4бб2б 46995 47062
1,9 47128 47193 47257 47320 47381' 47441 47500 47558 47615. 47670
2,0 47725 47778 47831 47882 47932 47982 48030 48077 48124 48169
2,1 48214 48257 48300 48341, 48382 48422 48461 48500 48537 48574
2,2 48610 48645 48679 48713 48745 48778 48809 48840 48870 48899
2,3 48928 48956 48983’ 49010 49036 49061 49088 49111 49134 49158
2.4 49180 49202 49224 49245 49266 49286 49305 49324 49343 49361
2,5 49379 49396 49413 49430 49446 49461 49477 49492 49506 49520
2,6 49634 49547 49560 49573 49585 49598 49609 4Q621 49632 49643
2,7 49653 49664 49674 49683 49693 49702 49711 49720 49728 49736
2,8 49744 49752 49760 49767 49774 49781 49788 49795 49801 49807
2,9 49813 49Й19 49825 49831 49836 49841 49846 49851 .49856 49861
X 4(ж) . X Ф(й) X Ф(х) х '' * ф(»)
3.0 0,49865 3.1 049903 . 3,2 0.49931 3,3 0.49952 3.4 0.49966
3,5 0,49977 3,6 0,49984 . 3,7 0,49989 3,8 0,49993 3,9 0,49995
4,0 0,499968 4,5 0,49.9997 5,0 0,49999997
Та б л и ц а 3. Таблица значений t7J 7 = 0,95 (7 = 1-0?)
п п ty п п ^7
5 2,78 12 2,20 19 2,10 60 2,001
6 2,57 13 2,18 20 2,093 70 1,996
7 2,45 14 2,16 25 2,064 80 1,001
8 2,35 15 2,15 30 2,045 90 1,987
9 2,31 16 2,13 35 2,032 100 1,984
10 2,26 17 2,12 40 2,023 120 1,980
11 2,23 18 2,11 50 2,009 ОО 1,960
Таблица 4. Таблица значений д, 7 = 0,95 (7 = 1-0)
п Q п Q п 4 п 7 п Q
5 1,37 11. 0,59 17 0,42 35 0,26 80 0,161
6 1,09 12 0,55 18 0,40 40 0,24 90 0,151
7 0,92 13 0,52 19 0,39 45 0,22 100 0,143
. 8 0,80 14 0,48 20 0,37 50 0,21 150 0,115
9 0,71 15 0,46 25 0,32 60 0,188 200 0,099
10 0,65 16 0,44 30 0,28 70 0,174 250 0,089
154
Таблица 5. Распределение Пуассона
P(X = fc) = — е-\ Л = 0,6
к р к Р .
0 0,54881 4 0,00296
1 0,32929 5 0,00036
2 0,09879 6 0,00004
3 0,01976
Таблица 6. Критические точки распределения %2,
7 = 0,95 (а = 0,05)
к X2 к X2 к X2 к X2 к х2
1 3,841 7 14,067 13 22,362 19 30,144 25 37,652
2 5,991 8 15,507 14 23,685 20 31,410 26 38,885
3 7,815 9 16,919 15 24,996 21 32,671 27 40,113
4 9,488 10 18,307 16 26,296 22 33,924 28 41,337.
5 11,070 11 19,675 17 27,587 23 35,172 29 42,557
6 12,592 12 21,026 18 28,869 24 36,415 30 43,773
Таблица 7. Критические точки распределения Стьюдента
Уровень значимости а = 0,05 (двусторонняя критическая область)
k la к к к
1 12,7 10 2,23 19 2,09 28 2,05
2 4,30 И 2,20 20 2,09 29 2,05
3 3,18 12 2,18 21 о 2,08 30 2,04
4 2,78 13 2,16 22 2,07 40 2,02
5 2,57 14 2,14 23 2,07 60 2,00
6 2,45 15 2,13 24 2,06 100 1,98
7 2,36 16 2,12 25 2,06 120 1,98
8 2,31 17 2,11 26 2,06 ОО 1,96
9 2,26 18 2,10 27 2,05
155
Литература
1. Боровков А. А. Теория вероятностей. М.: Наука, 1976. 250 с.
2. Гнеденко Б. В. Курс теории вероятностей. М.: Наука, 1969. 340 с.
3. Ширяев А. А. Верятность. М.: Наука, 1980. 574 с.
4. Крамер Г. Математические методы статистики. М.: Мир, 1975.
648 с.
5. Гмурман В. Е. Теория вероятностей и матемтаическая статисти-
ка. М.: Высш, шк., 1998. 479 с.
6. Коваленко И. И., Филиппова В. А. Теория вероятностей и мате-
матическая статистика. М.: Высш, шк., 1982. 256 с.
7. Сборник задач по математике для втузов. Специальные курсы. /
Под редакцией А. В. Ефимова. М.: Наука, 1984. 606 с.
156
Содержание
Введение 3
1 Случайные события 4
1.1 Стохастические эксперименты. Пространство элемен-
тарных событий........................................ 4
1.2 Случайные события................................ 6
1.3 Классическое определение вероятности случайного со-
бытия ..................................\ ’......... 9
1.4 Элементы комбинаторики..............:........... 10
1.5 Статистическое определение вероятности случайного со-
бытия . ............................................. 15
1.6 Геометрическое определение вероятности случайного со-
бытия .............................................. 17
1.7 Аксиомы теории вероятностей..................... 18
1.8 Свойства вероятности .......................... 19
1.9 Условная вероятность. Независимость событий..... 21
1.10 Формула полной вероятности. Формула Байеса...... 25
1.11 Последовательные независимые испытания (схема Бер-
нулли) ............................................. 28
1.12 Предельные теоремы для схемы Бернулли........... 30
1.13 Последовательные зависимый испытания (цепи Маркова) 34
2 Случайные величины 39
2.1 Случайные величины............................. 39
2.2 Дискретные случайные величины................... 41
2.3 Функция распределения случайной величины........ 43
2.4 Плотность распределения непрерывной случайной вели-
чины .................................,.............. 46
2.5 Числовые характеристики случайных величин....... 48
2.6 Нормальное распределение (Гаусса)............... 53
157
2.7 Некоторые вероятностные распределения............ 58
2.8 Закон больших чисел.............................. 61
2.9 Характеристические функции....................... 66
2.10 Центральная предельная теорема.................. 69
2.11 Системы двух случайных величин................. 70
Типовой расчет 77
3 Математическая статистика 90
3.1 Задачи математической статистики................. 90
3.2 Выборка. Эмпирическая функция распределения/ Поли-
гон. Гистограмма ............1 . . . 91
3.3 Статистические оценки числовых характеристик случай-
ных величин и их свойства............................ 97
3.4 Методы получения точечных оценок ................ 99
3.4.1 Выборочные (эмпирические) числовые характерис-
тики ......................................... 99
3.4.2 Метод моментов .......................... 102
3.4.3 Метод максимального правдоподобия......... 104
3.5 Интервальные оценки . . ч . . . . ....'......... 107
3.5.1 Доверительный интервал и доверительная веро-
ятность ..................................... 107
3.5.2 Доверительный интервал для математического ожи-
дания нормально распределенной случайной ве-
личины при известном среднеквадратическом от-
клонении а................................... 108
3.5.3 Доверительный интервал для математического ожи-
дания нормально распределенной случайной вели-
чины при неизвестном среднеквдратическом от-
клонении ................................... 111
3.5.4 Доверительный интервал для среднеквадратичес-
кого отклонения нормально распределенной слу-
чайной величины................................... 112
3.6 Проверка статистических гипотез................... 114
3.6.1 Статистические гипотезы 114
3.6.2 Статистические критерии для проверки гипотез.
Построение критических областей . ................ 115
158
3.6.3 Проверка гипотез о виде функции распределения.
Критерий %2-Пирсона...................... 120
3.6.4 Выборочный коэффициент корреляции. Проверка
гипотезы о значимости коэффициента корреляции 122
3.6.5 Линейная регрессия. Выборочное уравнение ли-
нейной средней квадратической регрессии .... 125
Лабораторная работа 129
Приложение 152
Литература 156
159