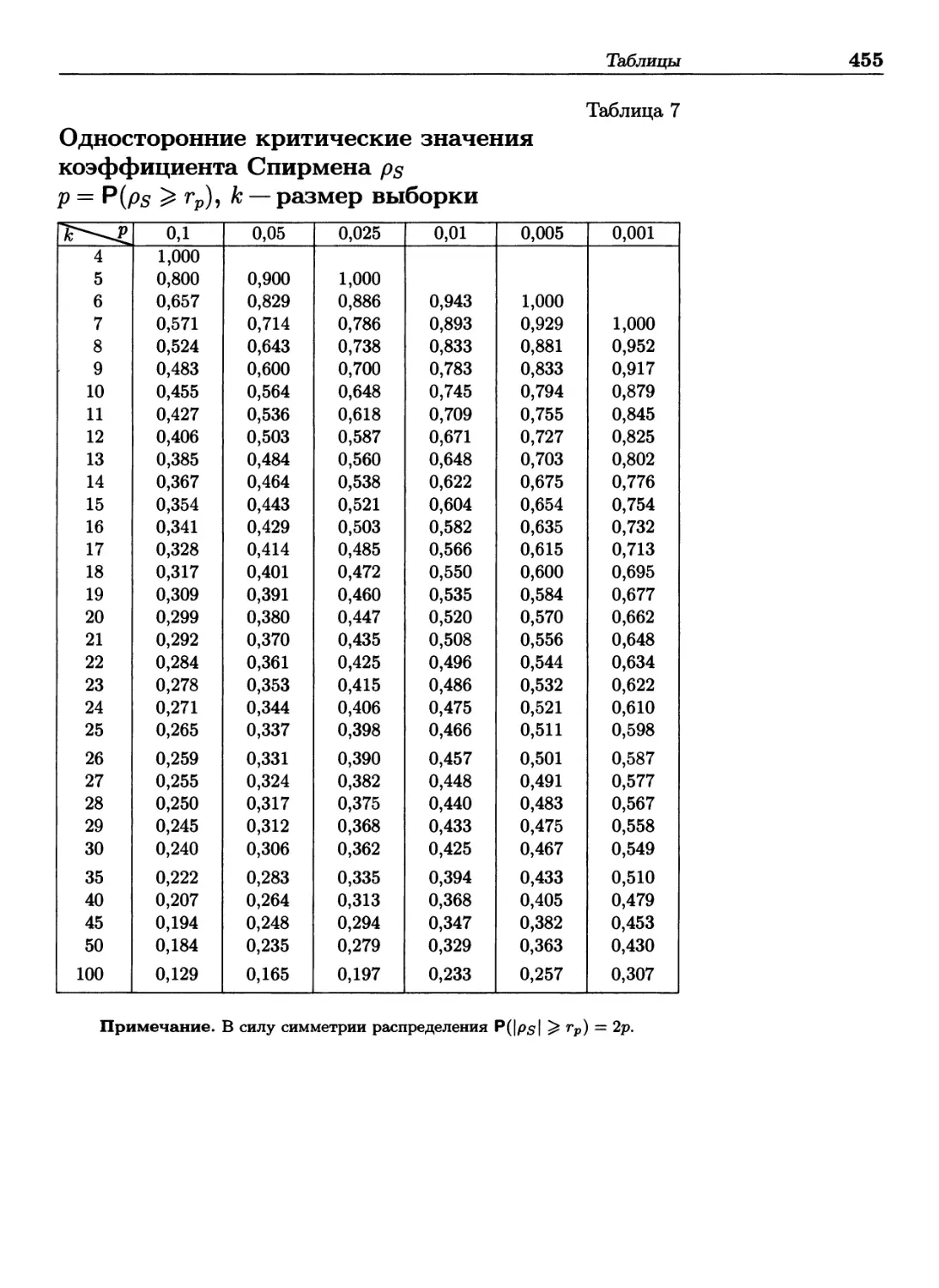
Автор: Лагутин М.Б.
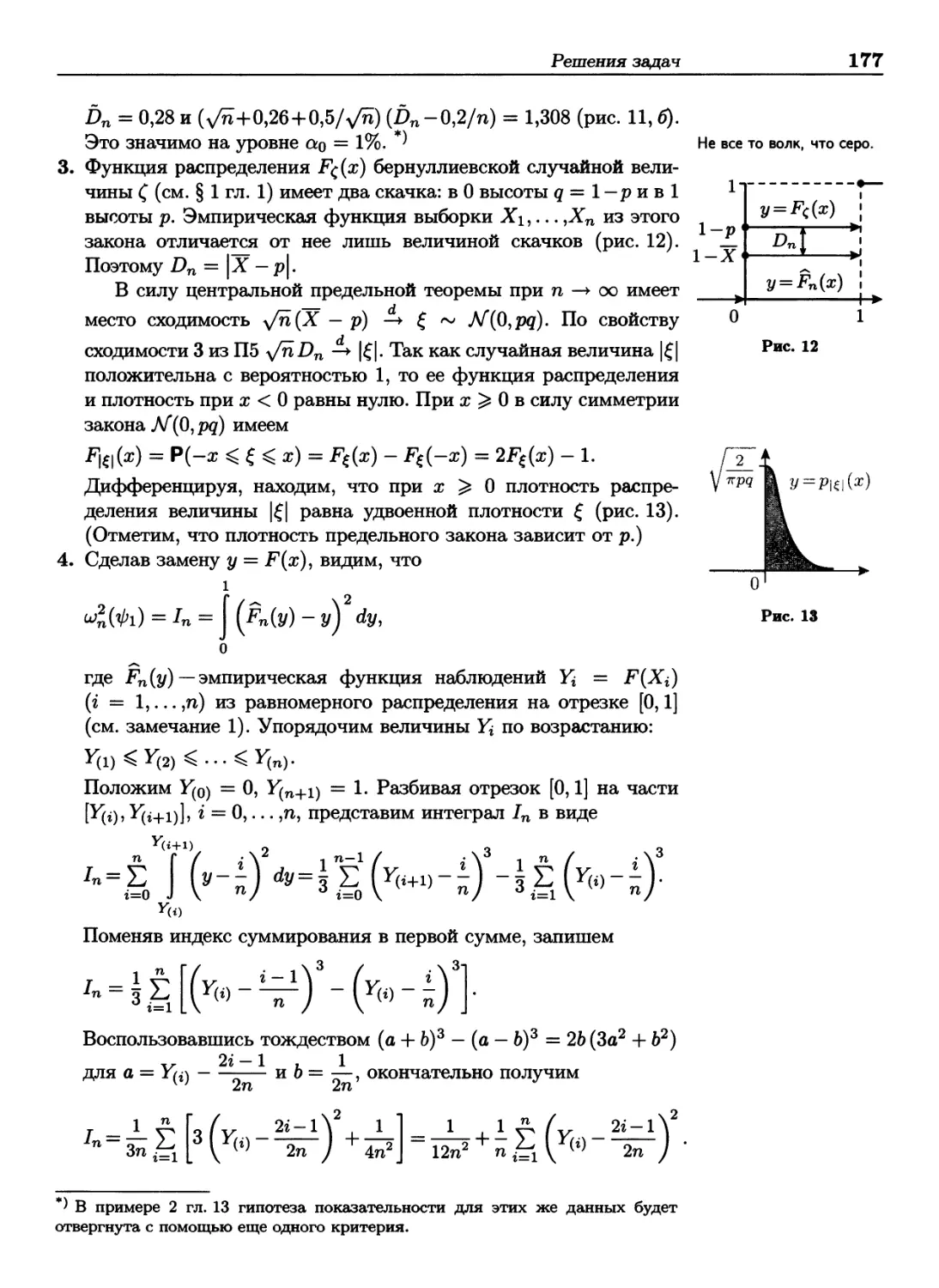
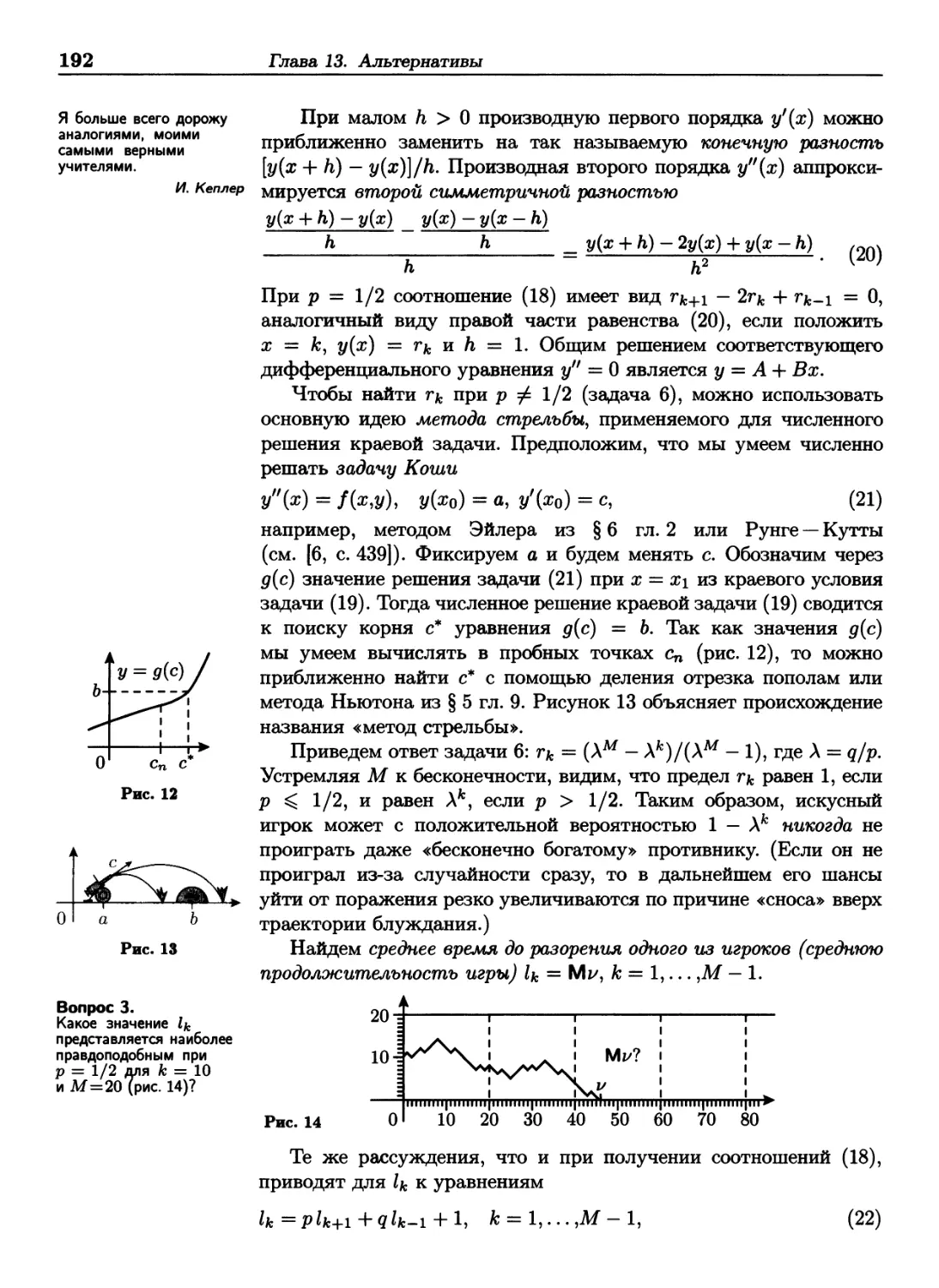
Теги: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 978-5-94774-996-0
Год: 2009
Текст
Μ. Б.Лагутин
НАГЛЯДНАЯ
МАТЕМАТИЧЕСКАЯ
СТАТИСТИКА
Учебное пособие
2-е издание, исправленное
Рекомендовано
Учебно-методическим объединением
по классическому университетскому образованию
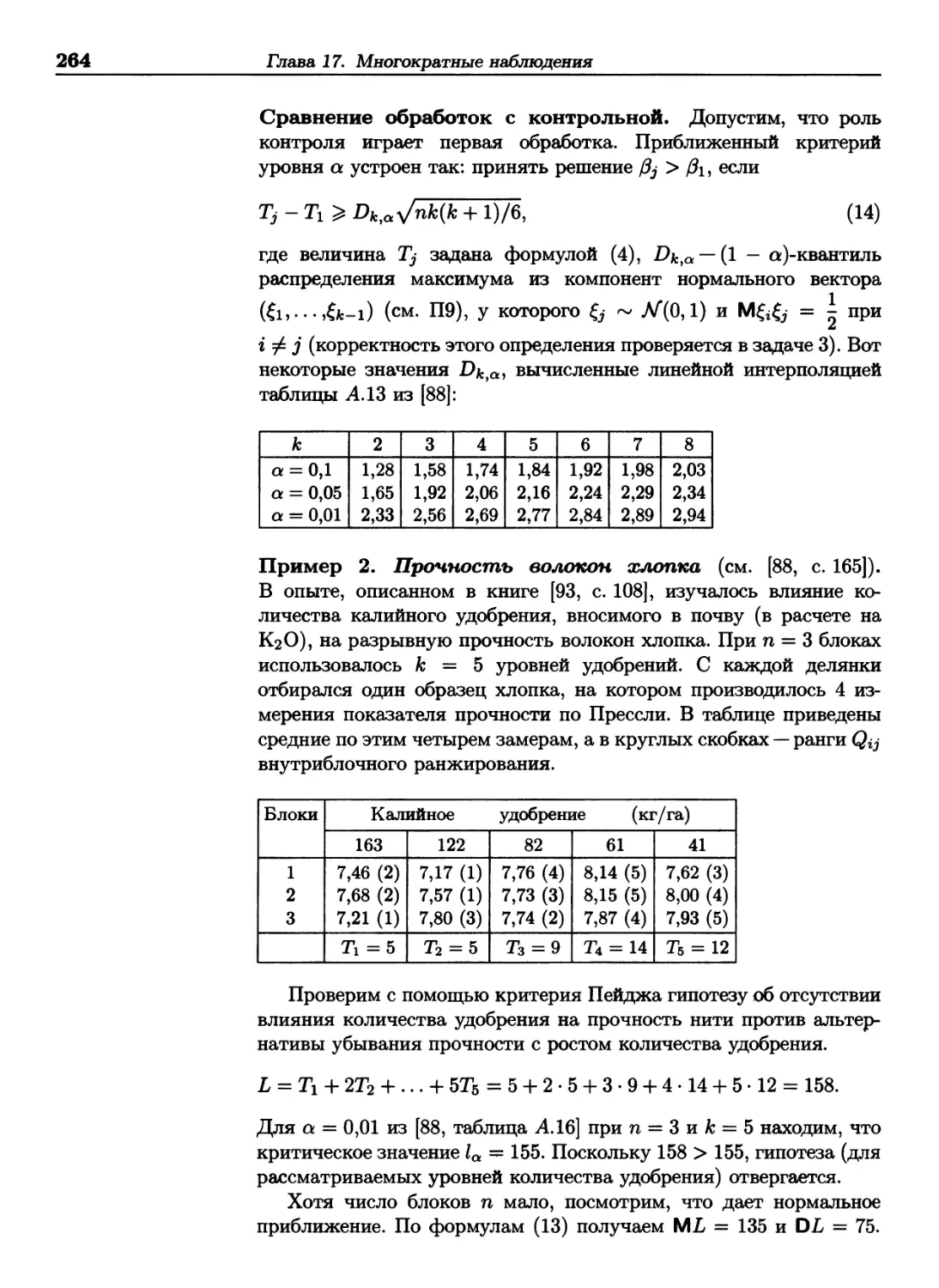
в качестве учебного пособия
для студентов высших учебных заведений,
обучающихся по направлениям «Математика»
и «Математика. Прикладная математика»
Москва
БИНОМ. Лаборатория знаний
2009
УДК 519.22
ББК 22.17
Л14
Рецензенты:
кандидат физ.-мат. наук Э. М. Кудлаев,
зав. каф. матем. статистики ф-та ВМиК МГУ
академик РАН Ю. В. Прохоров,
доктор физ.-мат. наук, проф. Ю. Н. Тюрин
Лагутин М. Б.
Л14 Наглядная математическая статистика : учебное пособие /
М. Б. Лагутин. — 2-е изд., испр. — М. : БИНОМ. Лаборатория
знаний, 2009. — 472 с. : ил.
ISBN 978-5-94774-996-0
Основы теории вероятностей и математической статистики
излагаются в форме примеров и задач с решениями. Книга также знакомит
читателя с прикладными статистическими методами. Для понимания
материала достаточно знания начал математического анализа.
Включено большое количество рисунков, контрольных вопросов и числовых
примеров.
Для студентов, изучающих математическую статистику,
исследователей и практиков (экономистов, социологов, биологов), применяющих
статистические методы.
УДК 519.22
ББК 22.17
Учебное издание
Лагутин Михаил Борисович
НАГЛЯДНАЯ МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Учебное пособие
Ведущий редактор М. Стригунова
Художник С. Инфантэ
Оригинал-макет подготовлен О. Лапко в пакете ВД^Х 2ε
с использованием кириллических шрифтов семейства LH
Подписано в печать 04.09.08. Формат 70 χ 100/16.
Усл. печ. л. 38,35. Тираж 2000 экз. Заказ 6743
Издательство «БИНОМ. Лаборатория знаний»
125167, Москва, проезд Аэропорта, д. 3
Телефон: (499) 157-5272, e-mail: binom@Lbz.ru, http://www.Lbz.ru
При участии ООО «ЭМПРЕЗА»
Отпечатано с готовых файлов заказчика в ОАО «ИПК
«Ульяновский Дом печати». 432980, г. Ульяновск, ул. Гончарова, 14
ISBN 978-5-94774-996-0 © Лагутин М. Б., 2009
© БИНОМ. Лаборатория знаний,
2009
ПРЕДИСЛОВИЕ
Перед Вами, уважаемый читатель, итог размышлений автора о
содержании начального курса математической статистики.
Настоящая книга —это, в первую очередь, множество занимательных
примеров и задач, собранных из различных источников. Задачи
предназначены для активного освоения понятий и развития у
читателя навыков квалифицированной статистической обработки
данных. Для их решения достаточно знания элементов
математического анализа и теории вероятностей (краткие сведения по теории
вероятностей и линейной алгебре даны в приложении).
Акцент делается на наглядном представлении материала и его
неформальном пояснении. Теоремы, как правило, приводятся без
доказательств (со ссылкой на источники, где их можно найти).
Наша цель —и осветить практически наиболее важные идеи
математической статистики, и познакомить читателя с прикладными
методами.
Первая часть книги (гл. 1-5) может служить введением в
теорию вероятностей. Особенностью этой части является подход
к освоению понятий теории вероятностей через решение ряда задач,
относящихся к области статистического моделирования (имитации
случайности на компьютере). Ее материал, в основном, доступен
школьникам старших классов и студентам 1-го курса.
Вторая и третья части (гл. 6-13) посвящены, соответственно,
оценкам параметров статистических моделей и проверке гипотез.
Они могут быть особенно полезны студентам при подготовке к
экзамену по математической статистике.
Четвертая и пятая части (гл. 14-21) предназначаются, в первую
очередь, лицам, желающим применить статистические методы для
анализа экспериментальных данных.
Наконец, шестая часть (гл. 22-26) включает в себя ряд более
специальных тем, обобщающих и дополняющих содержание
предыдущих глав.
Собранный в книге материал неоднократно использовался на
занятиях по математической статистике на
механико-математическом факультете МГУ им. М. В. Ломоносова.
Автор будет считать свой труд небесполезным, если, перелистав
книгу, читатель не потеряет к ней интереса, а захочет ознакомиться
Что за польза от книги без
картинок и разговоров?
Льюис Кэрролл,
«Приключения Алисы
в стране чудес»
4
Предисловие
Ей сна нет от французских
книг, а мне от русских
больно спится!
Фамусов в «Горе от ума»
А. С. Грибоедова
Никогда не теряй из виду,
что гораздо легче многих
не удовлетворить, чем
удовольствовать.
Козьма Прутков,
«Мысли и афоризмы»
с теорией и приложениями статистики как по этому, так и по
другим учебникам.
При работе над книгой образцом для автора была популярная
серия книг для школьников Я. И. Перельмана. Хотелось, по
возможности, использовать живую форму изложения и стиль,
характерный для этой серии.
Я благодарен моим коллегам по лаборатории Математической
статистики МГУ им. М. В. Ломоносова М. В. Козлову и Э. М. Куд-
лаеву за прочтение рукописи этой книги и полезные замечания.
М. Лагутин
К ЧИТАТЕЛЮ
В книге Д. Пойа «Математическое открытие» (см. [62] в списке
литературы) выделены три принципа обучения. Первым (и
важнейшим) из них является
Стимулирование
Надо заинтересовать учащегося, убедить в полезности изучения
предмета. Для успешности учебы необходимо четкое представление
о том, зачем нужна сообщаемая информация.
Приведем мнение по этому вопросу известного героя
детективного жанра (ведь восстановление по частностям общей картины
есть также и задача математической статистики).
«Мне представляется, что человеческий мозг похож на маленький
пустой чердак, который вы можете обставить, как хотите. Дурак
натащит туда всякой рухляди, какая попадется под руку, и полезные,
нужные вещи уже некуда будет всунуть, или в лучшем случае до
них среди всей этой завали и не докопаешься. А человек толковый
тщательно отбирает то, что он поместит в свой мозговой чердак. Он
возьмет лишь инструменты, которые понадобятся ему для работы, но
зато их будет множество, и все он разложит в образцовом порядке.
Напрасно люди думают, что у этой маленькой комнатки
эластичные стены и их можно растягивать сколько угодно. Уверяю вас,
придет время, когда, приобретая новое, вы будете забывать что-то
из прежнего. Поэтому страшно важно, чтобы ненужные сведения не
вытесняли собой нужных.»
А. Конан Дойл, «Этюд в багровых тонах»
Математическая статистика — один из наиболее часто
используемых в приложениях разделов математики. На результаты
практически любого научного эксперимента влияют неучтенные в модели
факторы, накладывается случайный шум. Методы математической
статистики, как правило, позволяют наиболее полно и надежно
извлекать полезную информацию из зашумленных данных. В книгу
включены многочисленные примеры применения статистических
методов для решения практических задач.
Чтобы побудить читателя глубже изучить теорию вероятностей,
на языке которой формулируются Статистические теоремы, многие
главы завершаются вероятностным^ парадоксом или
занимательным экспериментом.
Основа, подлинное
содержание всякого
познания доставляется
именно наглядной
концепцией мира, которая
может быть добыта лишь
нами самими и отнюдь
не может быть как-либо
преподана извне.
Артур Шопенгауэр,
«Афоризмы
житейской мудрости*
Студент — это не гусь,
которого надо
нафаршировать, а факел, который
нужно зажечь.
6
К читателю
То, что вы были
вынуждены открыть сами,
оставляет в вашем уме
дорожку, которой вы можете
снова воспользоваться,
когда в этом возникнет
необходимость.
Г. Лихтенберг,
«Aphorismen», Berlin,
1902-1906
При изложении
математического рассуждения
мастерство заключается
в умении дать
образованному читателю
возможность сразу, не
заботясь о деталях,
схватить основную идею;
последовательные дозы
должны быть такими,
чтобы их можно было
глотать «с ходу»; в случае
неудачи или если бы
читатель захотел что-либо
проверить, перед ним
должна стоять четко
ограниченная маленькая
задача (например,
проверить тождество;
две пропущенные
тривиальности могут
в совокупности
образовать непреодолимое
препятствие).
Дж. Литлвуд,
«Математическая смесь»
Всякое человеческое
познание начинается
с созерцаний, переходит
от них к понятиям
и заканчивается идеями.
И. Кант,
«Критика чистого
разума»
Следующим принципом обучения является
Активность
По-настоящему разобраться в некоторой теории можно лишь
самостоятельно решая задачи из данной области. Пассивного
чтения даже хорошего учебника, увы, недостаточно для подлинного
овладения предметом.
Каждая глава этой книги (за исключением дополнительных
глав 22-26) содержит задачи (с решениями). Они обычно
упорядочены по сложности, самые трудные отмечены звездочкой. Автор
надеется, что читатель попробует решить некоторые из
заинтересовавших его задач или, хотя бы, разберет решения, так как в них
содержится значительная часть материала. Кроме того, по ходу
изложения встречаются контрольные вопросы, ответы на которые
приведены в конце соответствующей главы.
Возможность активного усвоения материала во многом
определяется стилем его изложения.
Наконец, третий принцип -
фаз обучения
- это соблюдение последовательности
Исследование —► формализация —► усвоение
Важно начинать новую тему с содержательных примеров,
чтобы можно было «потрогать руками», прочувствовать ситуацию.
Можно попробовать придумать какой-нибудь способ решения
проблемы лишь на основе здравого смысла. Если он на самом деле
окажется бесполезным, то это лишь подтвердит важность теории,
позволяющей получить приемлемое решение.
Абстрактные определения становятся по-настоящему понятны
лишь тогда, когда они используются при решении конкретных
задач в различных моделях. В книге «Теория катастроф» В. И.
Арнольд пишет:
«Абстрактные определения возникают при попытках обобщить
«наивные» понятия, сохраняя их основные свойства. Теперь, когда
мы знаем, что эти попытки не приводят к реальному расширению
круга объектов (для многообразий это установил Уитни, для групп —
Кэли, для алгоритмов — Черч), не лучше ли в преподавании
вернуться к «наивным» определениям? (...) Пуанкаре подробно
обсуждает методические преимущества наивных определений окружности
и дроби в «Науке и методе»: невозможно усвоить правило сложения
дробей, не разрезая, хотя бы мысленно, яблоко или пирог.»
При написании этой книги автор старался следовать указанным
принципам обучения. Вероятно, какие-то методические приемы
окажутся полезными преподавателям статистики, хотя, безусловно
справедливо утверждал Козьма Прутков, что
У всякого портного свой взгляд на искусство!
Часть I
ВЕРОЯТНОСТЬ
И СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
Глава 1
ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
В основе математической статистики лежит теория вероятностей.
Аксиоматика теории вероятностей была разработана А. Н.
Колмогоровым (опубликована в 1933 г.). Читателю, возможно, известны
такие основные понятия этой теории, как независимость событий
или математическое ожидание случайной величины. Тем не
менее, будет полезно напомнить самое необходимое для дальнейшего
изложения (см. также приложение Ш*) и учебники [19], [39], [90]
в списке литературы).
§ 1. ФУНКЦИИ РАСПРЕДЕЛЕНИЯ И ПЛОТНОСТИ
Пример 1. Измерим время ξ от первого включения до
перегорания электрической лампочки.
Пример 2. Подбросим монетку. Если она упадет гербом вверх,
будем считать, что ξ = 1, иначе положим ξ = 0.
Обобщая эти примеры, представим, что проводится
эксперимент, результат которого (действительное число ξ) зависит от
случая. Как охарактеризовать случайную величину £, дать
вероятностный закон ее поведения?
Допустим, что возможно повторить эксперимент несколько раз.
Обозначим через £ι,...,£η полученные при этом значения. Тогда
для произвольной точки χ на прямой можно подсчитать νη —
количество значений, попавших левее χ (рис. 1).
Предположим, что существует некоторое число, к которому
будет приближаться частота vnjn при неограниченном увеличении п.
Естественно рассматривать это число как вероятность того, что
ξ не больше, чем х. Обозначим эту вероятность через Ρ (ξ ^ χ).
(Формальные определения понятий вероятности и случайной
величины приведены в Ш.)
Пример 3. На рис. 2 показан график частоты появлений
буквы «а» в стихотворении М. Ю. Лермонтова «Бородино». Размах
Вероятность — это
важнейшее понятие
в современной науке
особенно потому, что
никто совершенно не
представляет, что оно
означает.
Бертран Рассел, из
лекции, 1929 г.
Читал ли что-нибудь?
Хоть мелочь?
Репетилов
в «Горе от ума»
А. С. Грибоедова
Сперва аз да буки, а там
и науки.
Р: Probabilitas (лат.) —
вероятность.
*) П1 обозначает ссылку на раздел 1 приложения.
8
Глава 1. Характеристики случайных величин
Рис. 2
t ·
0,08
0,06
0,04
(
\ 500
1000
1500
» -ш—·—·
1 ►
2000 25^00 "
колебаний частоты быстро уменьшается, она стабилизируется ца
уровне чуть большем, чем 0,06. В таблице приведены вероятности,
с которыми встречаются в большом по объему тексте буквы
русского алфавита, включая «пробел» между словами (данные взяты
из [92, с. 238]). Отметим, что итоговая частота появлений буквы «а»
в стихотворении «Бородино», равная 162/2461 « 0,066, лишь
незначительно отличается от соответствующей вероятности 0,062.
0,175
Ρ
; о,040
я
0,018
X
0,009
о
0,090
в
0,038
ы
0,016
ж
0,007
е, ё
0,072
л
0,035
3
0,016
ю
0,006
а
0,062
к
0,028
ь, ъ
0,014
ш
0,006
и
0,062
м
0,026
б.
0,014
Ц
0,004
τ
0,053
д
0,025
г
0,013
щ
0,003
н
0,053
π
0,023
ч
0,012
э
0,003
0,045
У
0,021
й
0,010
Φ
0,002
Зафиксируем η и рассмотрим поведение частоты vnjn при
изменении «границы» χ (см. рис. 1). При сдвиге точки χ вправо,
количество значений £ι,... ,£п, оказавшихся левее #, будет
увеличиваться. Поэтому вероятность Р(£ ^ х) (как предел частоты) будет
неубывающей функцией от #, которая стремится к 1 при χ —► + оо
и стремится к 0 при χ —► — оо.
-If i—!-► Определение. Функция F^(x) = Ρ (ξ ^ χ) называется функцией
α " с распределения случайной величины £.
Рис. 3
Зная F^(x), можно найти вероятность попадания ξ в любой
промежуток (а,Ь] на прямой (рис. 3):
Р(а < £^ Ь) = Ρ(ξ О) - Ρ(ξ < а) = F*(b) - F€(a).
Если функция распределения F^(x) имеет разрыв в точке с, то
К°кП,£о доказать величина скачка Fe(c) - F€(c-) равна
формально, используя
свойство непрерывности ρ(ξ = β) = ρ{ξ ^ с) _ ρ{ξ < с)
§ 1. Функции распределения и плотности
9
Случайные величины мы будем задавать с помощью функций
распределения.
Определение. Случайная величина η равномерно распределена на
отрезке [0,1], если
{О при χ < О,
χ при 0 < χ < 1,
1 при χ ^ 1.
Такое распределение соответствует выбору точки наудачу из
отрезка [0,1], поскольку для любых 0 ^ а < Ь ^ 1 вероятность
попадания значения η в отрезок [а, Ь] равна его длине Ь — а (рис. 4).
Определение. Случайная величина г называется показательной
с параметром λ > 0, если
*«-{!..-
при χ ^ 0,
Хх при ж > 0.
График функции распределения FT(x) приведен на рис. 5.
Показательное распределение можно использовать для
описания времени эксперимента из примера 1.
Определение. Если существует такая функция Ρξ(χ) > 0, что для
произвольных а < Ь
ь
Ρ(α<ξ<6)= Lfc(a)<fc,
Рис. 5
Вопрос 2.
Чему равна Р(т > 3/λ)
точно и приближенно?
Ρ(α<Ξξ<:6)
υ=Ρξ(χ)
то говорят, что случайная величина ξ (или ее распределение
вероятностей) имеет плотность Ρξ(χ) (рис. 6).
Когда плотность существует, ее можно найти дифференцироваг
нием функции распределения:
/ \ d А? / \ ν Ft(x + Δχ) - Ft(x)
Таким образом, плотностью равномерной величины η является
функция /[о, ι] (здесь и далее Ια обозначает индикатор множества
А: 1а(х) = 1 при χ € А, 1а(х) = 0 при χ £ А), & плотностью
показательной величины г служит рТ(х) = λβ~λχ/[ο, +οο) (рис. 7).
Не у всякой случайной величины есть плотность. Например, ее
нет у дискретных (принимающих конечное или счетное ) число
значений) величин. Такова определяемая ниже бернуллиевская
случайная величина.
*) Множество называют счетным, если его элементы можно перенумеровать
натуральными числами.
У = Рг(х)
Рис.7
Я. Бернулли
(1654-1705), швейцарский
математик.
10
Глава 1. Характеристики случайных величин
1
\-р
y = Fc(x)
►!
О1 1 χ
Рис. 8
Вопрос 3.
Как выглядит график
функции распределения
дискретной случайной
величины ξ, принимающей
значения х\ < Х2 < ...
с соответствующими
вероятностями р± ,рг, · · ·?
Рис. 9
Определение. Случайная величина ζ имеет распределение
Берну лли с вероятностью «успеха» ρ (0 ^ ρ ^ 1), если она
принимает значения 0 и 1 с такими вероятностями: Ρ (ζ = 0) = 1 — ρ
иР« = 1)=р.
График функции распределения Fq(x) бернуллиевской
случайной величины ζ приведен на рис. 8. Распределение Бернулли при
ρ = 1/2 годится как вероятностная модель эксперимента из
примера 2. Значение ρ φ 1/2 отвечает случаю несимметричной монеты.
§2. МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
И ДИСПЕРСИЯ
Не всегда требуется полная информация о случайной величине £,
выражающаяся в ее функции распределения F^{x), Иногда
достаточно знать, где располагается область «типичных» значений £.
Одной из важных характеристик «центра» этой области является
математическое ожидание.
Проблема. На тонком стержне (числовой прямой) в точках с
координатами Хк находятся массы гпк (рис. 9). Где следует выбрать
точку а крепления стержня к вертикальной оси, чтобы
минимизировать момент инерции относительно нее 1а = Σ (xk — α)2ιη*?
Оказывается, точку крепления стержня надо поместить в центр
масс с = Σχ*>™>ΐΰ/Σπι*: (см· задачу 1). Вероятностными аналогами
центра масс с и момента инерции относительно него 1С служат
математическое ожидание и дисперсия.
Определение. Для дискретной случайной величины £,
принимающей значения #ι,#2ί··· с соответствующими вероятностями
РьР2) · · ·, математическим ожиданием называется число
М£ = 5>*Р*. (1)
к
Например, для бернуллиевской случайной величины ζ имеем
Μζ = 0·(1-ρ) + 1·ρ = ρ.
Определение. Когда у случайной величины ξ есть плотность
Ρζ(χ), ее математическое ожидание вычисляется по формуле
+оо
Μξ= χρξ(χ)άχ. (2)
Для показательной случайной величины г нетрудно подсчитать,
интегрируя по частям, что
Mr
= x\e~Xxdx = - у
e ydy = j
0 +
dy
1
λ
§2. Математическое ожидание и дисперсия
11
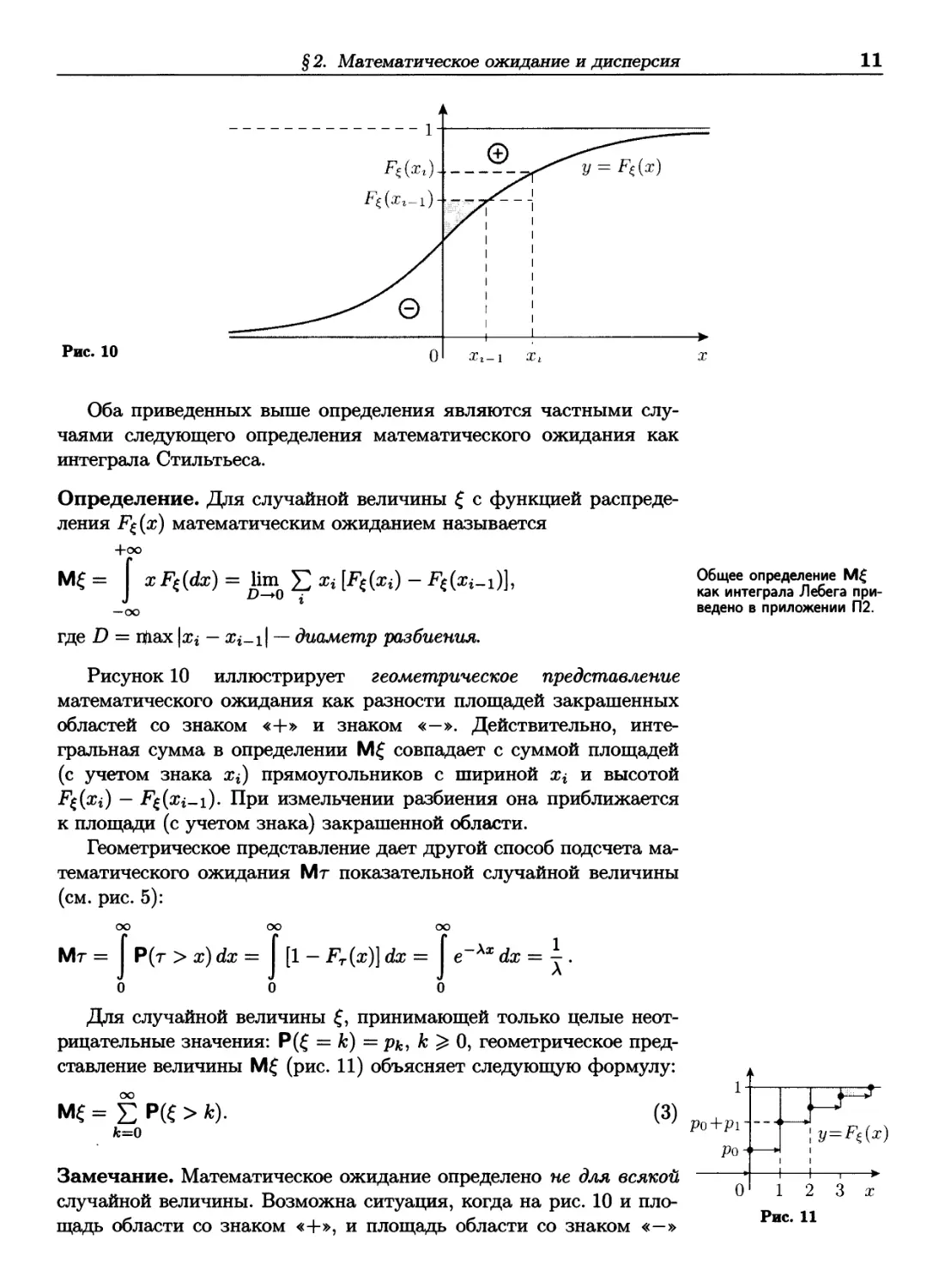
Рис. 10
Оба приведенных выше определения являются частными
случаями следующего определения математического ожидания как
интеграла Стильтьеса.
Определение. Для случайной величины ξ с функцией
распределения F^(x) математическим ожиданием называется
+оо
Щ = I xF^dx) = ton Σ Ъ №(хг) - F€(s<-i)],
—oo
где D = ifrax I X% %i—l
| — диаметр разбиения.
Рисунок 10 иллюстрирует геометрическое представление
математического ожидания как разности площадей закрашенных
областей со знаком «+» и знаком «—». Действительно,
интегральная сумма в определении Μξ совпадает с суммой площадей
(с учетом знака Xi) прямоугольников с шириной χ ι и высотой
Ρξ(χΐ) ~ Ρξ(χί-ι)· При измельчении разбиения она приближается
к площади (с учетом знака) закрашенной области.
Геометрическое представление дает другой способ подсчета
математического ожидания Mr показательной случайной величины
(см. рис. 5):
Mr
оо оо оо
= [ Р(т > х) dx = [ [1 - Fr(x)] dx = [ .
-x*dx = \.
Л
Общее определение Μξ
как интеграла Лебега
приведено в приложении П2.
Для случайной величины ξ, принимающей только целые
неотрицательные значения: Ρ (ξ = k) = р&, k ^ 0, геометрическое
представление величины Μξ (рис. 11) объясняет следующую формулу:
fc=0
(3)
Замечание. Математическое ожидание определено не для всякой
случайной величины. Возможна ситуация, когда на рис. 10 и
площадь области со знаком «+», и площадь области со знаком «—»
i
1 .
1
Po+Pi-
Ро-
0
^
1
1 »
]
» »
Ζ
у=Щх
! 3 χ
Рис. 11
12
Глава 1. Характеристики случайных величин
О. Коши (1798-1857),
французский математик.
равны оо. В этом случае возникает неопределенность вида оо — оо.
Например, для закона Коши с плотностью Ρξ(χ) = 1 /[π (1 + χ2)]
каждая из площадей есть
xpe(x)dx = - —^—~ dx = — т^—— 7г- b(l-fy) =оо.
J ^ξν; π J 1+χ2 2π J 1 + 2/ 2π ν У)\
0 0 0
Следовательно, Μξ не существует, несмотря на то, что 0 — nei
распределения (плотность Ρζ(χ) симметрична относительно 0).
ν=Ρξ(χ)
Рис. 12
Вопрос 4.
Как получить формулу (4)
с помощью свойств
математического ожидания из
приложения П2?
Вы давиче его мне
исчисляли свойства, но
многие забыли? — Да?
Чацкий в «Горе от ума»
А. С. Грибоедова
[В слове «давеча»
сохранена авторская
орфография.]
Обсудим теперь понятие дисперсии случайной величины.
Как правило, помимо Μ ξ бывает важно знать величину
типичного «разброса» значений ξ вокруг среднего. Мерой этого
«разброса» может служить стандартное отклонение y/Βξ (рис. 12), где
дисперсия Οξ определяется формулой
Οξ = Μ(ξ-ίΑξ)\
т. е. D£ — это среднее квадрата отклонения ξ от Μξ.
Для вычисления дисперсии полезно равенство
Οξ = Μξ2 - (Μξ)2.
(4)
Для примера вычислим дисперсию бернуллиевской случайной
величины ζ. Прежде всего, заметим, что ζ2 и ζ одинаково
распределены. Поэтому Μζ2 = Μζ = ρπΟζ = ρ — ρ2= ρ{\ — ρ).
§3. НЕЗАВИСИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН
Обычно вероятностную модель необходимо построить не для одного
эксперимента, а для серии опытов. В этом случае нередко можно
предполагать отсутствие взаимного влияния разных опытов друг
на друга, их независимость.
Определение. Случайные величины ξι,... ,ξη называются
независимыми, если для любых а* < Ь* (г = 1,... ,п)
η
Р(аг < & < fc, i = 1,... ,n) = JJ P(ai < & < bi).
В частности, если все а* = — оо, то для произвольных я ι,..., хп
Ρ (ξι < хи · · · An < Хп) = ΡξΛχι) * · · · * Ρξη(χη)- (5)
Независимые равномерно распределенные на отрезке [0,1]
случайные величины ryi,... ,ι/η можно считать координатами случайного
вектора, равномерно распределенного в n-мерном единичном кубе.
Действительно, равенство
P(a,i ^Vi^bi, i = 1,... ,η) = (bi - αϊ);... · (bn - αη),
§ 4. Поиск больных
13
Рис. 13
где 0 ^ di < bi ^ 1, означает, что вероятность попадания точки
(r/i,... ,77п) в произвольный параллелепипед с параллельными осям
координат ребрами и находящийся целиком внутри единичного
куба равна его объему (рис. 13 при η = 3). На самом деле,
параллелепипед можно заменить на любое множество А, для которого
определено понятие n-мерного объема.
Говорят, что бесконечная последовательность {&} образована
независимыми случайными величинами, если свойство
независимости выполняется для любого конечного набора из них.
Определение. Последовательность независимых бернуллиевских
случайных величин СьСг»··· с одинаковой вероятностью «успеха»
ρ называют испытаниями (или однородной схемой) Бернулли.*^
В заключение параграфа приведем интуитивно понятное
утверждение, которое часто применяется при доказательстве
статистических теорем.
Лемма о независимости. Пусть ξι,... ,£n+m — независимые
случайные величины; / и а — борелевские функции (см. приложе- Доказательство этой
' J * * ^J v ^ леммы можно найти,
ние П2) на Rn и Rm соответственно. Тогда случайные вели- например, в [48, с. 53].
чины 77i = /(ξι,... ,ξη) и 772 = #(£п+ь · · · £п+гп) независимы.
§4. ПОИСК БОЛЬНЫХ
Применим элементарную теорию вероятностей к решению одной
проблемы выявления больных (см. [82, с. 254]).
Во время второй мировой войны всех призывников в армию
США подвергали медицинскому обследованию. Реакция Вассер-
мана позволяет обнаруживать в крови больных сифилисом
определенные антитела. Р. Дорфманом была предложена простая
методика, на основе которой необходимое для выявления всех больных
число проверок удалось уменьшить в 5 раз!
Методика. Смешиваются пробы крови к человек и
анализируется полученная смесь (рис. 14). Если антител нет, то этой одной
проверки достаточно для к человек. В противном случае кровь
каждого человека из этой группы нужно исследовать отдельно,
и для к человек всего потребуется к + 1 раз провести анализ.
Вероятностная модель. Предположим, что вероятность
обнаружения антител ρ одна и та же для всех η обследуемых,
и результаты анализов для различных людей независимы, т. е.
моделью является последовательность из η испытаний Бернулли
с вероятностью «успеха» р.
Допустим для простоты, что η делится нацело на к. Тогда
надо проверить п/к групп обследуемых. Пусть X, — количество
ο#όόοο@ο#οοο#οο
Φ болен
О здоров
Рис. 14
\U
*) Если у каждой случайной величины ζΐ своя вероятность «успеха» pi, то схему
называют неоднородной.
14
Глава 1. Характеристики случайных величин
Вопрос 5.
Чем плох слишком
большой размер группы?
Вопрос 6.
Какая ошибка допущена
на рис. 15 в изображении
графика функции Н(х)
при малых р?
х.
\* + 1
Рис. 15
проверок, потребовавшихся в j-ft группе, j = 1,... ,η/Α;. Тогда
с вероятностью (1— р)к (все к человек здоровы),
с вероятностью 1 — (1— р)к (есть больные).
Обозначим общее число проверок Χι + ... + Xn/k через Ζ. Задача
заключается в том, как для заданного значения р*) определить
размер группы ко = &о(р), минимизирующий ΜΖ.
Согласно формуле (1) находим
МХ1 = 1-(1-р)к + (к + 1)-[1-(1-р)к]=к + 1-к(1-р)к.
Отсюда по свойствам математического ожидания (П2) имеем
MZ = MX1 + ... + MXn/k = l MXi=n[l + l/fc-(l-p)fc].
κ
Положим Н(х) = 1 + 1/х — (1 — р)х при χ > 0.
Для близких к нулю значений ρ минимум функции Η (χ)
достигается в точке #о, где хо — наименьший из корней уравнения
Н'(х) = 0, т. е. уравнения
1/я2 + (1-р)*1п(1-р)=0. (6)
Его нельзя разрешить явно относительно х. Поэтому, используя
формулу (1 — р)х « 1—рх при малых р, заменим Н(х) на функцию
Н(х) = 1 + 1/х — 1 + рх = 1/х + р#, имеющую точку минимума
^о = 1/л/р> причем Н(хо) = 2у/р. Для ρ = 0,01 получаем xq = 10
и Н(х0) = 1/5, т. е. MZ » п/5.**>
Не пропускайте их, они
еще не раз пригодятся
в дальнейшем!
Я занимался до сих пор
решением ряда задач,
ибо при изучении наук
примеры полезнее правил.
И. Ньютон,
«Всеобщая арифметика»
ЗАДАЧИ
1. Докажите, используя свойства математического ожидания (П2),
что функция /(а) = М(£ — а)2 при а = М£ имеет минимум,
равный D£.
2. Случайные величины ryi,...,ryn независимы и равномерно
распределены на отрезке [0,1]. Вычислите Μη и Dfj среднего
арифметического η = — (щ + ... + ηη).
3. Для случайных величин из задачи 2 найдите функцию
распределения FVin)(x), Мщп) и Dr7(n), где щп) = тах{г/1,... ,r/n}.
4. Обозначим через ι/ число «неудач» до появления первого
«успеха» в схеме Бернулли с параметром р. Вычислите Μ ν.
Указание. Примените формулу (3).
5. Рассмотрим следующую стратегию поиска больных. Все
обследуемые разбиваются на пары. Если объединенная проба крови
не содержит антител, то оба здоровы. В противном случае
исследуется кровь первого из них. Если этот человек здоров,
то другой должен быть болен, и в таком случае достаточно двух
*) Это значение можно оценить с помощью частоты выявления заболевания
в предыдущих обследованиях.
**) Асимптотика хо и #(#о) при ρ —► 0 исследуется в задаче 6.
Решения задач
15
тестов. Если же первый оказался больным, то кровь второго
также должна быть подвергнута анализу, и поэтому потребуется
три теста. Выясните, при каких значениях вероятности ρ
обнаружения заболевания у отдельного обследуемого данная стратегия
будет в среднем экономичнее индивидуальной проверки.
6? Пусть xq = хо(р) — наименьший из корней уравнения (6).
Докажите, что хо ~ 1/\/р и H(xq) ~ 2 у/р при ρ —► 0.*)
РЕШЕНИЯ ЗАДАЧ
1. С учетом свойств математического ожидания (см. приложе- Растолковать прошу,
ние П2) и формулы (4) находим, что функция
/(α) = Μ [ξ2 - 2αξ + а2] = Щ2 - 2аЩ + а2 = (а- Щ)2 + Οξ
есть квадратный трехчлен с минимумом в точке а = М£.
ι
2. Согласно формуле (2) Мщ = j xdx = 1/2. (Это можно понять
о
и без вычислений: плотность ρηι (χ) = 7[0, ι] симметрична
относительно прямой χ = 1/2.)
1
Далее, в силу следствия из П2 имеем Μη2 = J x2dx = 1/3.
о
Применяя формулу (4), получаем, что ϋηι = 1/3 — 1/4 = 1/12.
Наконец, согласно свойствам математического ожидания
и дисперсии из приложения П2 запишем:
Репетилов
в «Горе от ума»
А. С. Грибоедова
Μη = - (Mr/i + ... + Μηη) = Мщ = ^,
Οη = — (Dr/i + .
+ Опп) = ±*п = Ш
(во второй строке использована независимость случайных
величин Г/1,. .. ,77п).
Обратим внимание на то, что случайные величины щ и η
имеют одинаковое математическое ожидание, но дисперсия у η
в η раз меньше. Эти соотношения, очевидно, выполняются и для
произвольных независимых одинаково распределенных случай- QeMb отмерь а один —
ных величин ει,...,εη с конечной дисперсией. Такая модель отрежь,
используется для описания ошибок измерения.
3. Максимум из случайных величин r/i,..., ηη не превосходит χ
тогда и только тогда, когда все щ не больше, чем χ (рис. 16), ■
поэтому 0
FV(n)(x) = P (V(n) < я) = Ρ (ηι *ζ χ,... ,7fo ^ х).
г?2 ηη ηι r?(n)
• · · · J
χ 1
Рис. 16
*) Здесь f(p) ~ g(p) означает, что f(p)/g(p) —*■ 1.
16
Глава 1. Характеристики случайных величин
п-т — -■
В силу независимости случайных величин щ из формулы (5)
для χ £ [0,1] выводим, что
Fn<n)(x) = Ρ(*?1 < Х) ' ··· · P(Vn < Χ) = [P(l?l ^ *)]" =*П.
График соответствующей плотности
Ρη(η)(χ) = dFrjin)(x)/dx = пхп-11{ъЛ]
изображен на рис. 17 (для η > 2).
Применяя формулу (2), вычисляем
1 1
Мг/(п) = #п#п_1<&г = η \xndx = .
qqqqqpqqpq
οοοοο·οο·ο
12... *...
Рис. 18
Замечание. Интуитивно ясно, что длины отрезков, на которые
делят [0,1] взятые наудачу η точек, распределены одинаково
(см. задачу 7 из гл. 10). Поэтому самая правая из точек будет
находиться в среднем на расстоянии 1/(п + 1) от 1. [Однако,
наименьший из отрезков разбиения имеет длину порядка 1/п2
(задача 4 из гл. 4).]
ι
Наконец, Μη?, = J x2nxn~1dx = п/(п + 2), откуда в силу
соотношения (4) находим, что
Ощп) = п/(п + 2)- [п/(п + I)]2 = п/[(п + 1)2(п + 2)].
Замечание. Дисперсия Ощп^ с ростом п убывает намного
быстрее, чем дисперсия Dfj: порядок малости первой есть 1/п2,
второй — 1/п. Это связано с тем, что плотность ρηι (χ) = /[0? ц
имеет разрыв в точке х = 1.
Вероятность рк того, что до первого «успеха» в схеме Бернулли
будет ровно к «неудач», в силу независимости испытаний равна
qkp1 где q = 1 — ρ (рис. 18). Это так называемое геометрическое
распределение*^ Случайная величина ν дает пример дискретной
случайной величины, имеющей счетное множество значений:
Р(и = к) = рь к ^ 0. Суммируя геометрическую прогрессию,
находим Ρ(ι/> к) = Pk+i + Pfc+2 + · · · =qk+1p(l + q + ...) =qk+l.
Применяя формулу (3), получаем Μι/ = q + q2 + q3 + ... = q/p.
Пусть Yj — число проверок, потребовавшихся для j-й пары
обследуемых (J = 1,2,... ,n/2), q = 1 — р. Тогда
Yj = <
1 с вероятностью q2 (нет больных),
2 с вероятностью qp (первый здоров, второй болен),
3 с вероятностью (pq+p2)= p (в противном случае).
*) Вероятности pk образуют геометрическую прогрессию.
Решения задач
17
Согласно формуле (1), MYj = 1 · q2 + 2 · qp + 3 · ρ = 1 + Зр — ρ2.
Отсюда находим ожидаемое общее число проверок
ΜΖ=ΜΥ1 + ... + ΜΥη/2 = (η/2)ΜΥι=η(1 + 3ρ-ρ2)/2.
Следовательно, «парная» стратегия в среднем эффективней
индивидуальной проверки, когда 1+Зр—р2 < 2, т. е. при условии,
что ρ < (3 - \/Ь)/2 = 1 - κ « 0,382. Здесь κ = (у/Ь - 1)/2 «
« 0,618 обозначает «золотое сечение» — пропорцию,
почитавшуюся в древнегреческом искусстве и архитектуре, при которой
«меньшее» относится к «большему», как «большее» к «целому»:
(1-х) : к = к : 1 (рис. 19).
Любопытно, что при ρ ^ 1 — κ вообще не существует
стратегии проверки, которая экономичнее индивидуальной. Этот
красивый результат получил в 1960 г. П. Ангар (см. [82, с. 147]).
6. Положим ε = ε(ρ) = — ln(l — ρ). Разложение логарифма в ряд
при ρ —► 0 дает эквивалентность ε ~ р. Подставив ε в
уравнение (6), получим
1/х2 = εβ
(7)
у2е~у = ε.
(8)
Дифференцированием устанавливается, что левая часть
уравнения (8) на множестве {у ^ 0} имеет максимум Μ = 4е~2 в точке
У+=2.
Из рис. 20 очевидно, что при ε < Μ уравнение (8) имеет два
корня: у0 = Уо{е) —► 0 и у\ = у\{ё) —► оо при ε —► 0. Покажем,
что хо = yo/ε ~ l/y/ε. Для этого оценим xq снизу и сверху.
Из убывания функций 1/х2 и εβ~εχ при χ > 0 (рис.21)
вытекает, что в качестве оценки снизу можно взять величину х-,
определяемую равенством \/х2_ = ε, т. е. #_ = l/y/ε.
В качестве начальной оценки сверху возьмем #+ = 2/+/ε =
= 2/ε. Уточним ее методом итераций (см. рис. 21):
£e"£XL=x+=£e_2=1/^2|x=4=>< = e/Vi,
Так как е^1) = 1 + о(1), имеем х0 ~ 1/\/ε ~ VVP· Для
доказательства эквивалентности Н(х0) ~ 2 >/р остается
подставить найденную асимптотику в формулу, определяющую
функцию Н(х).
1-κ
Рис. 19
Покажем, что при достаточно малых ε это уравнение имеет два
корня: xq = #ο(ε) и х\ = χι(ε) — соответственно точка минимума
и точка локального максимума функции Н(х) (рис. 23).
Пусть у = εχ. Легко видеть, что (7) равносильно уравнению
У2е-у
> 2/о У+ = 2
Рис. 20
XQPC+X+
Рис. 21
18
Глава 1. Характеристики случайных величин
ОТВЕТЫ НА ВОПРОСЫ
Прошу мне дать ответ.
Софья
в «Горе от ума»
А. С. Грибоедова
У = Ft(x)
Pk
О Xk Xk+\
Рис. 22
У = Н(х)
Хо Χι
Рис. 23
Для меня давно уже
аксиома, что мелочи —
это самое важное.
А. Конан Дойл,
« Установление личности»
1. Возьмем Ак = (с — 1/fc, с], к = 1,2,... . Эти события вложены:
Ак D i4fc+i, причем с = Г\Ак- По свойству непрерывности (Ш)
ρ (ξ = с) = lim P(c - 1/fc < ξ ζ с) = F^c) - F^(c-). Отсюда
к—юо
заключаем, что если функция Fs(x) непрерывна, то вероятность
попадания ξ в любую фиксированную точку на прямой равна 0.
2. Р(т > З/λ) = 1 - Р(т < З/λ) = 1 - FT(3/A) = е"3 w 0,05. Те,
кто знаком с усиленным законом больших чисел (П6), могут
отсюда заметить, что только 5% приборов с показательным
временем работы до поломки служат более трех средних сроков
l/λ (согласно примеру к формуле (2)).
3. См. рис. 22.
4. Используем свойства 1 и 2 математического ожидания из П2:
Μ(ξ - МО2 = Μ[ξ2 -2ξΜξ-τ- (МО2] =
= Щ2 - 2 (МО2 + (МО2 = Щ2 - (МО2·
5. В группе очень большого размера к почти обязательно будут
присутствовать больные, и поэтому объединенная проверка
станет излишней.
6. На рис. 23 изображен правильный график Н(х) в случае
малого р. Действительно, Н(х) —► +оо при χ —► 0 и Н(х) —► 1
при χ —► +оо, причем в последнем случае функция 1/х убывает
медленнее, чем (1 — р)х, и поэтому график Н(х) приближается
к асимптоте у = 1 сверху.
Глава 2
ДАТЧИКИ СЛУЧАЙНЫХ ЧИСЕЛ
Пусть г/1,7/2,.. . — координаты точек, взятых наудачу из отрезка
[0,1], т.е. независимые и равномерно распределенные на
отрезке [0,1] случайные величины.
Проблема. Как построить числовую последовательность yi,y25 · · ·>
которую можно было бы рассматривать как реализацию случайных
величин г/1,7/2,...?
Элементы такой последовательности называются
псевдослучайными числами, а устройства (или алгоритмы) для их получения —
датчиками.
Бросая в воду камешки,
смотри на круги, ими
образуемые; иначе такое
бросание будет пустою
забавою.
Козьма Прутков
§ 1. ФИЗИЧЕСКИЕ ДАТЧИКИ
Простейшим физическим датчиком является, вероятно, рулетка
и подобные ей устройства. Рассмотрим вращающуюся с малым
трением вокруг оси стрелку, конец которой описывает окружность
единичной длины (рис. 1). Раскручивая повторно стрелку, будем
получать в качестве уьУ2> · · · координаты конца стрелки в местах
остановок.
Другой датчик основан на следующем утверждении из теории
вероятностей (см. [12, с. 242], [39, с. 49]).
Утверждение. Для того, чтобы случайная величина η была
равномерно распределена на [0,1] необходимо и достаточно, чтобы
оо
разряды Сг ее двоичной записи (т. е. η = Σ 2~г£) образовывали
г=1
схему Бернулли с вероятностью «успеха» ρ = 1/2 (см. § 3 гл. 1).
Таким образом, для получения одного псевдослучайного числа
с точностью до 2~п можно подбросить симметричную монетку п
раз и сложить 2~г для тех г (г = 1,... ,п), при которых выпадал
герб.
Вместо монетки можно использовать шум в электроприборах
(см. [58, с. 269]). Обозначим через Ti моменты времени, когда шум
переходит некоторый пороговый уровень С снизу вверх или сверху
0,25
Вопрос 1.
Как с помощью ζι>С2,· · ·
построить бесконечную
последовательность
независимых равномерно
распределенных на [0,1]
случайных величин
77ь?72,·--?
20
Глава 2. Датчики случайных чисел
Рис. 2
Вопрос 2.
Обратно, как из щ ,7/2, · · ·
получить схему Бернулли
СьСг,··· с заданной
вероятностью «успеха» р?
вниз (рис. 2). Положим & равной 0 или 1 в зависимости от того,
перейден ли порог во время первой или во время второй половины
цикла электронных часов, у которых длина цикла At намного
меньше, чем среднее время между переходами шума через
уровень С.
Этим и другим физическим датчикам свойственны следующие
общие недостатки:
1) для работы датчиков необходимо специальное оборудование,
которое обычно требует тщательной настройки;
2) опыт, использующий генерируемые физическим датчиком
числа, не воспроизводим в том смысле, что нельзя получить те же
самые yi,2/2, · · · при его повторном проведении;
3) физические датчики плохо совместимы с компьютерами, так
как время получения псевдослучайных чисел несоизмеримо велико
по сравнению со скоростью расчетов.
Для преодоления этих недостатков используют таблицы
случайных чисел и математические датчики.
Т1 обозначает табл. 1
в конце книги.
Рис. 3
§2. ТАБЛИЦЫ СЛУЧАЙНЫХ ЧИСЕЛ
Таблица случайных чисел представляет собой зафиксированные
результаты работы некоторого датчика. Обычно она имеет вид
последовательности псевдослучайных цифр, разбитых на группы
для удобства использования (см. Т1).
Каждый может составить собственную таблицу, вынимая из
шляпы бумажки с номерами от 0 до 9 или подбрасывая правильный
икосаэдр, у которого каждая из цифр нанесена на 2 из 20 граней
(рис. 3).
Как с помощью такой таблицы получать псевдослучайные
числа?
Сначала выберем наугад первое число; для чего можно, не глядя
в таблицу, загадать номера строки и столбца. Соответствующий
набор цифр принимается в качестве знаков после запятой в
десятичном представлении у\. Например, загадав в таблице Т1 строку 1
и столбец 2, получим у\ =0,09.
§ 3. Математические датчики
21
Далее, начиная с выбранного места, будем считывать таблицу
по столбцу (по строке или в любом другом порядке, который
не зависит от содержания таблицы) и получать уг> 2/з> · · · · Так,
считывая Т1 вниз по столбцу, генерируем
Vi = 0,09; у2 = 0,54; у3 = 0,42; у4 = 0,01; ...
Если требуются псевдослучайные числа с точностью не до двух,
а до четырех знаков после запятой, то нужно считывать также
и пары цифр, расположенные в соседнем столбце:
уг = 0,0973; у2 = 0,5420; у3 = 0,4226; у4 = 0,0190; ...
При всей своей простоте использование таблицы случайных
чисел может приводить к неверным заключениям (см. § 5), да
и сама таблица может оказаться недостаточно качественной.
В книге [72) в качестве случайных цифр предлагаются 20000
знаков после запятой в десятичном представлении числа π. Однако
среди первых 10000 цифра 0 встречается только 937 раз. Согласно
центральной предельной теореме (П6) для независимых
равновероятных цифр такое может наблюдаться не чаще, чем в двух случаях
из ста (см. также задачу 2 гл. 18).
Таблицы случайных чисел неудобны для использования в
компьютерных программах тем, что требуют для своего хранения
довольно много оперативной памяти. По этой причине для
генерации псевдослучайных чисел чаще применяют так называемые
математические датчики.
§3. МАТЕМАТИЧЕСКИЕ ДАТЧИКИ
Эти датчики обычно представляют собой рекуррентные
алгоритмы, генерирующие число уп по предыдущему числу yn-i-
Рассмотрим вначале простой, но довольно «плохой» датчик —
метод середины квадрата (Дж. фон Нейман, 1946). Зададим
произвольное четырехзначное*) число ко. Например, пусть ко = 8473.
Вычислим к$ = 71791729. Выделив средние 4 цифры, получим
к\ = 7917. Положим у\ = к\ · 10~4 = 0,7917. Затем вычислим
к\ = 62678889. Тогда к2 = 6788, у2 = 0,6788 и т. д. Ясно, что
1) выбор числа ко полностью определяет всю последовательность
2/1,2/2»···; 2) процесс зациклится не позднее, чем через 104
шагов (существует число, которое сразу воспроизводит самое себя:
37922 = 14379264); 3) можно так неудачно задать ко (например,
1000 или 0085), что уп = 0, начиная с некоторого п.
Более сложный и часто используемый на практике
мультипликативный датчик работает по следующей схеме. Задаются
стартовое число к0 (например, 1), множитель т и делитель d. Далее
*) Чтобы молено было использовать 8-разрядный калькулятор.
22
Глава 2. Датчики случайных чисел
Здесь запись «a mod 6»
обозначает остаток от
деления α на 6.
Рис. 4
последовательно вычисляются уь уг> · ■
А:п = (ш · A:n_i) mod d,
по формулам
J кп = {т-к,
\уп = kn/d.
(1)
Какие значения можно рекомендовать для чисел га и d? Выбор
простого числа с? = 231 — 1 = 2147483647 предпочтителен для
тех компьютеров, которые позволяют использовать 32 двоичных
разряда для представления целых чисел. Множитель га выбирают
так, чтобы последовательность fci, Afe,..., прежде чем зациклиться,
пробегала все возможные значения от 1 до d — 1. В результате
изучения статистических свойств датчика для различных
множителей Дж. Фишман и Л. Мур предложили использовать, в частности,
га = 630360016 или га = 764261123 (см. [58, с. 271]).
В программном обеспечении иногда встречаются быстро
работающие, но недостаточно качественные датчики. Так, датчик RAND
из библиотеки STDLIB Borland C++ зацикливается всего через 232
шага. В [31, с. 190] анализируется датчик RANDU (d = 231,га =
= 216 + 3 = 65 539), вошедший в SSP — библиотеку научных
программ для IBM-360. Оказывается, что все точки с координатами
(Узп-2)Узп-ъУзп) располагаются в точности на одной из 15
плоскостей вида 9узп-2 - бузп-i + Узп = &> где к = -5,... ,9, вместо того,
чтобы равномерно плотно заполнять единичный трехмерный куб
(рис. 4)*^.
В заключение, рассмотрим датчик (см. [58, с. 272]), который был
исследован Б. Уичманом и И. Хил лом в 1982 г. Чтобы получить уп,
запустим одновременно три мультипликативных датчика с
параметрами
rfi =30269,
d2 = 30307,
d3 = 30323,
rai = 171;
ra2 = 172;
ra3 = 170.
Каждый из них на n-м шаге генерирует у^, у^ и у'^ соответственно.
Положим уп = {у'п + у'п + Уп}·) гДе {'} обозначает дробную часть
действительного числа.
Этот датчик имеет период около 3 · 1013, что значительно
превосходит период датчика Фишмана и Мура 231 — 2
и на компьютере он работает в несколько раз быстрее.
2 · 109,
Природе разума свой- § 4. СЛУЧАЙНОСТЬ И СЛОЖНОСТЬ
ственно рассматривать
но^акНнеобходиУмыеНЫе' Проблема построения псевдослучайных чисел волновала в XX веке
б. Спиноза, «Этика», многие умы. Фон Мизес рассматривал бесконечные последователь-
часть 2, теорема XLIV НОСТИ, у КОТОрЫХ чаСТОТЫ СИМВОЛОВ СТабиЛИЗИруЮТСЯ ПО ПОДПО-
следовательностям. Какими подпоследовательностями при этом
*) Легко проверить, что 9кзп-2 — 6/сзп-1 + кзп = 0 mod 231
§ 4. Случайность и сложность
23
разумно ограничиваться — вопрос, который уточнял Черч.
Принципиально иной подход предложил А. Н. Колмогоров. Он провел
параллель между случайностью и алгоритмической сложностью:
случайным выглядит то, что очень сложно получить. Кстати, на
волновавший одно время общественность вопрос о возможности
получения кодированной информации из других миров А. Н.
Колмогоров отвечал, что если уровень развития иных космических
цивилизаций намного выше земного, то сообщения от них будут
восприниматься как случайный сигнал.
Приведем отрывок из [72, с. 177] о связи между случайностью
и сложностью.
«В связи с псевдослучайными числами возникает следующий
вопрос. В каком смысле их можно считать случайными, если они
получены с помощью детерминированных (неслучайных) алгоритмов?
В 1965-66 гг. Колмогоров и Мартин-Леф представили понятие
случайности в новом свете. Они определили, когда последовательность
из 0 и 1 можно считать случайной. Основная идея состоит в
следующем. Чем сложнее описать последовательность (т. е. чем длиннее
«самая короткая» программа, конструирующая эту
последовательность), тем более случайной ее можно считать. Длина «самой
короткой» программы, естественно, различна для разных компьютеров. По
этой причине выбирают стандартную машину, называемую машиной
Тьюринга. Мерой сложности последовательности является длина
наиболее короткой программы на машине Тьюринга, которая
генерирует эту последовательность. Сложность — мера иррегулярности.
Последовательности, длина которых равна N, называются
случайными, если их сложность близка к максимальной. (Можно показать,
что большинство последовательностей именно таковы.) Мартин-Леф
доказал, что эти последовательности можно считать случайными, так
как они удовлетворяют всем статистическим тестам на случайность.
Таким образом, сложность и случайность тесно взаимосвязаны. Если
программист собирается получать «настоящие» случайные числа,
то в силу результатов Колмогорова и Мартин-Лефа он сможет это
сделать только с помощью достаточно длинной программы. В то же
время на практике генераторы случайных чисел очень короткие. Как
совместить эти два факта?»
Что кажется подчас
лишь случаем слепым,
то рождено источником
глубоким.
Ф. Шиллер
На практике в отношении к математическим датчикам в
основном господствует «презумпция случайности»: алгоритм
используют, если не установлено, что он «плохой». Почти каждый датчик
выдает приемлемые по качеству псевдослучайные числа в
количестве нескольких десятков или сотен. Однако при моделировании
случайных процессов порой приходится генерировать многие
тысячи чисел. Непросто найти датчик, чтобы на таких длинных
последовательностях существующие методы проверки (см. § 2, гл. 12)
его не забраковали.
24
Глава 2. Датчики случайных чисел
§5. ЭКСПЕРИМЕНТ «НЕУДАЧИ»
В [82, с. 29] приведен пример задачи, при попытке решения
которой с помощью таблицы случайных чисел возникает интересный
парадокс.
ЗАДАЧА. Пусть Xq обозначает величину моей «неудачи»
(скажем, время ожидания в очереди, сумму штрафа или других
финансовых потерь). Предположим, что мои знакомые подвергли
себя опыту того же типа. Обозначим размеры их «неудач» через
Χι, Хг, · · · · Сколько (в среднем) знакомых придется мне опросить,
пока не встретится человек, размер неудачи которого не меньше,
чем у меня?
Формализуем задачу. Допустим, что Xq , Х\,... — независимые
величины с одной и той же непрерывной функцией распределения.
Введем случайную величину N = min{n ^ 1 : Хп ^ Хо}· Чему
равно математическое ожидание МЛГ?
Как будет показано ниже, ответ не зависит от того, какое
именно непрерывное распределение имеют случайные величины
Хп, поэтому будем считать, что они равномерно распределены на
отрезке [0,1].
Имея в виду усиленный закон больших чисел (П6), попытаемся
эмпирически оценить МЛГ средним арифметическим значений щ,
получаемых при моделировании ситуации с помощью таблицы Т1.
Сначала разыграем значение #0, выбирая наугад некоторое
число в таблице. Пусть, скажем, это будет третье число в первой
строке. Тогда xq = 0,73. Для моделирования #ι,#2,··· будем
считывать таблицу от выбранного числа вниз по столбцу. Получим
χι = 0,20, Х2 = 0,26, хз = 0,90. Этого достаточно, так как
0,90 ^ 0,73, поэтому πι = 3. Повторив опыт к раз, можно оценить
Вопрос 3. МЛГ с помощью η = (πι + ... + Пк)/к.
4βΜν°ΜΒΗο°^?Τ ра3 ^ теперь найдем ответ теоретически. Из непрерывности
распределения величины Хп следует, что P{Xq = Хп) — 0 при η ^ 1
(см. вопрос 1 гл. 1). Поэтому неравенство в определении случайной
величины N можно заменить на строгое. Далее,
Р(ЛГ > п) = Р(Х0 = тах{Х0Л,... Л»})· (1)
Если под знаком вероятности заменить Xq (слева от равенства) на
любую из Xi, г = 1,... ,п, то вероятность, очевидно, не изменится.
Поэтому вероятность того, что именно Xq окажется наибольшей
среди Xq^Xi, ... ,ХП, равна 1/(1+п) (и не зависит от распределения
при условии его непрерывности).
Поскольку случайная величина N принимает только целые
неотрицательные значения, то, согласно формуле (3) гл. 1,
получаем
MiV = !o;rhi = l + i + ! + i + ... = oo, (2)
так как гармонический ряд расходится (см. [46, с. 14]).
Чему равно п?
§5. Эксперимент «Неудачи»
25
Почему же попытка оценить МЛГ с помощью моделирования
приводит к результату, совершенно не похожему на теоретический
ответ? Этому можно дать несколько объяснений.
Прежде всего, используя псевдослучайные числа, округленные
до двух знаков после запятой, мы неявно непрерывную модель
заменяем дискретной: Р(Хп = г/100) = 0,01, г = 0,..., 99. Поэтому
Р(Х0 = Хп) Φ 0 при η ^ 1 и
юо ι
ΜΝ=Σ^, (3)
71=1 П
где, в отличие от формулы (2), суммирование членов
гармонического ряда идет до 100, а не до оо (см. задачу 4 ниже).
Воспользовавшись тем, что
оо
lim (У) lnra ) = 7 = - е~х Inxdx « 0,577,
m-°° \η=ι п ) J
о
где 7 обозначает постоянную Эйлера, получаем, что
MN « In 100 + 7 « 4,605 + 0,577 « 5,2.
Однако обычно моделирование дает еще меньшее значение. Это
происходит потому, что иногда экспериментатор, неудачно выбрав
Xq (например, 0,98), не желает долго ждать появления еще
большего псевдослучайного числа и выбирает другое xq — поменьше.
Тем самым он производит подгонку данных и, отбрасывая большие
значения гц, занижает результат.
Еще одной причиной несоответствия теории и моделирования
является малый размер выборки. Дело в том, что на результат
эксперимента сильно влияют редкие события — появления очень
близких к 1 значений xq, которые обычно не происходят при малом
числе испытаний.
Замечание. Используя в эксперименте псевдослучайные числа,
округленные до к знаков после запятой, получим MN « к In 10 + 7,
т. е. результат зависит от точности представления чисел χο,χι,... .
Эта ситуация напоминает тот факт, что длина береговой линии,
измеряемая по карте, зависит от ее масштаба (рис. 5). Таблица
случайных чисел аналогична так называемым фракталам —
геометрическим объектам, сколь угодно малые части которых подобны
целому.*^
Куда как чуден создан
свет!
Фамусов в «Горе от ума»
А. С. Грибоедова
Л. Эйлер (1707-1783),
швейцарский математик,
механик, физик и
астроном. В 1727-1741,
1766-1783 гг. работал
в России.
Рис. 5
Правильно в философии
рассматривать сходство
даже в вещах, далеко
отстоящих друг от друга.
Аристотель
*) См., например, А. Д. Морозов «Введение в теорию фракталов», Москва-
Ижевск: Институт компьютерных исследований, 2002.
26
Глава 2. Датчики случайных чисел
§6. ТЕОРЕМЫ СУЩЕСТВОВАНИЯ И КОМПЬЮТЕР
Рис. β
Верится с трудом...
Чацкий в «Горе от ума»
А. С. Грибоедова
Сегодня это
действительно слишком просто:
вы можете подойти к
компьютеру и практически
без знания того, что
вы делаете, создавать
разумное и бессмыслицу
с поистине изумительной
быстротой.
Дж. Бокс
Книга книгой, а своим
умом двигай.
Рис.7
Приведем пример из области численного решения
дифференциальных уравнений из [5, с. 85], показывающий, что нужно с
осторожностью относиться к компьютерным вычислениям.
Для приближенного решения задачи Коти
Гу'(я) = /(я,у),
I У(хо) = Уо
можно использовать метод Эйлера: Уг+ι = Уг + hf(xilyi)^ Xi+\ =
= Xi + ft, где ft > 0 —некоторый малый шаг (см. [6, с. 430]).
Рассмотрим пример. Пусть /(#,у) = —ж/у, у(—1) = 0,21.
График численного решения с шагом ft = 0,1 приведен на рис. 6.
На самом деле, правая часть уравнения —х/у имеет разрыв
при у = 0, поэтому теоретическое решение у = ^/1,0441 — х2
(переменные разделяются) не может быть продолжено в полуплоскость
у < 0. При yi « 0 касательная имеет большой наклон и метод
Эйлера «перепрыгивает» на другую интегральную кривую.
ЗАДАЧИ
1. Попробуйте придумать «свой» датчик случайных чисел (важно
не качество датчика, а оригинальность идеи).
2. Случайные величины 771,772,... — независимы и равномерно
распределены на [0,1]. Положим
К = {п ^ 2: 771 > 772 > · · · > Vn-i < Vn},
т. е. (К — 1) —длина «нисходящей серии».
а) Смоделируйте 20 значений случайной величины К с
помощью таблицы Т1 и оцените МК их средним арифметическим.
б) Найдите Μ К теоретически.
Указание. Вычислите вероятность Ρ (К > п) и примените
формулу (3) гл. 1.
3. Выполните то же самое для случайной величины L, где
L = min{n ^ 2: 771 + ... + Г7п > 1}
(рис. 7).
Указание. Для нахождения вероятностей P(L > η)
используйте формулу свертки (см. ПЗ).
4. Докажите формулу (3) с помощью свойств условного
математического ожидания (П7):
а) вычислите М(ЛГ | Х0 = #о) = Σ Р(^ > η \ Х0 = #ο)>
~ п=о
б) найдите ΜΝ по свойству 1 из П7.
Решения задач
27
5? Пусть случайная величина Μ равномерно распределена на
множестве {1,2,... ,п}: Р(М = га) = 1/п, га = 1,... ,п.
Случайная величина J равна остатку от деления η на, М. Найдите
lim P( J ^ М/2).
Рис. 8
Замечание. Ввиду рис. 8 кажется правдоподобным, что при
увеличении η распределение J будет приближаться к
равномерному на множестве {0,1,... ,М — 1}, и, следовательно, искомая Вопрос 4.
вероятность должна стремиться к 1/2. Однако на самом деле в ?ем заключэется
этот предел равен примерно 0,386.
РЕШЕНИЯ ЗАДАЧ
1. По-видимому, можно считать случайными последние четыре
цифры номеров телефонов из записной книжки.
2. Используя строки таблицы Т1, начиная с первой, получим
к\ = 3, &2 = 2,..., к\ + ... + &2о = 64» оценка для МАГ равна 3,2.
Ввиду симметрии любой порядок 771,..., г)п равновозможен.
Поэтому Р(К > п) = P(r/i > 772 > · · · > Ήη) = 1/п\. Отсюда
ОО ОО ι
по формуле (3) гл. 1 имеем ЬЛК = Σ Р(К > η) = Σ ~τ =
Λ ~. Λ п=0 п=0
= е « 2,718.
3. Так же, как и в предыдущей задаче, для моделирования
используем строки таблицы Т1. Получим 1\ = 4, /г = 3...,
/ι + ... + /го = 55, оценка для ML равна 2,75.
Пусть Sn = 771 + ...+ ηη. Тогда P(L>η) = Ρ(5η^ 1) = FSn(l).
Докажем по индукции с помощью формулы свертки (ПЗ), что
функция распределения Fsn(x) = хп/п\ при 0 ^ χ ^ 1.
(При произвольных χ функция распределения Fsn (x) задается
формулой (4) гл. 4.)
База. При η = 1 функция распределения Fsx (χ) = Fm (x) = #,
O^x^l.
Шаг. Так как Sn — Sn—i + ?7п> ГДО Sn—i и τ\η независимы, то
+оо χ
Если на клетке слона
прочтешь надпись
«буйвол», не верь глазам
своим.
Козьма Прутков
Подставив х = 1, находим P(L > η) = 1/п!. Следовательно,
случайные величины L и К из задачи 2 одинаково распределены,
ML = ЬЛК = е.
Иное (геометрическое) решение вытекает из того, что
подмножества точек n-мерного единичного куба, удовлетворяющие
неравенствам χχ + ... + хп ^ 1 и х\ ^ х^ ^ ... ^ #п,
представляют собой n-мерные симплексы*): первому из них,
*) Вершинами произвольного n-мерного симплекса служат (п + 1) точек из
пространства Мп, не лежащие ни в какой (п — 1)-мерной гиперплоскости.
28
Глава 2. Датчики случайных чисел
помимо начала координат (0,... ,0), принадлежат вершины куба
вида (0,... ,0,1,0,... ,0), а второму — вида (1,... ,1,0,... ,0) (рис. 9
для η = 3).
Линейное преобразование с верхнетреугольной матрицей
Ζ1 1
о ι
\о ... о υ
отображает первый симплекс на второй. Якобиан
преобразования (П9) равен 1, поэтому объемы не изменяются. При решении
задачи 2 было установлено, что второй симплекс имеет объем
1/п!.
4. Используем независимость и равномерную распределенность на
множестве {0; 0,01; ...; 0,99} случайных величин Х0> · · · > Хп-
P(N>n\X0 = x0) =
= Ppfi < а?о,..., Хп < хо\Хо = хо) ==
η
= Ρ(Χι < So, . . . , Хп < Χθ) = Π Р(Хг < Хо) = Хо-
г=1
Отсюда находим Μ(Ν\Χ0 = хо) = Σ χο = τ~Ζ—· Наконец,
n=o L х°
усредняя по жо, докажем формулу (3):
ΜΝ = Σ M(N\X0 = хо)Р(Хо = хо) =
хо
Л 0,99 Л 100 !
= J_ у L_ = Τ -
100/^п1-ж0 эт_1 η*
xq=0 n=l
5. Пусть /д/ = 2п/М — 2 [п/М], где [ · ] — целая часть числа. Так
как п = Μ [η/Μ] + J, то 0 ^ 1М = 2 J/M < 2. Отсюда
[/м] =
2гг1 _^ In] _ 12J] _ \ 1,
mJ LMJ~LMJ~\o,
если J^M/2,
если J < Μ/2.
В соответствии с формулой полной вероятности (П7) запишем
P(J > М/2) = - £ [/т] = - Σ Γί—1 - 2 ί-2-1 V
Ответы на вопросы
29
При η —► оо эта сумма стремится к интегралу
1 l/m
О l/(m+l)
=^Ife-^)=2(rbri+···)·
Из разложения ln(l -f χ) = χ — χ2/2 + #3/3 — ж4/4 +... получаем,
что искомый предел равен 2 In 2 — 1 « 0,386.
ОТВЕТЫ НА ВОПРОСЫ
1. Запишем СъС2>··· по диагоналям и по каждой ϊ-й строке
построим свою случайную величину щ:
VI <-&>С2>С4,С7, ···
V2 <~ Сз»Сб>С8> ···
VS <-Сб,С9, ···
2. Если щ ^ р, то положим & = 1, иначе ζ» = 0 (рис. 10).
3. Обычно получается результат около 2 или 3.
4. На рис. 8 изображен случай, когда Μ много меньше п. Однако, О
для всех Μ > 2п/3 (что происходит с вероятностью 1/3)
справедливо неравенство J < Μ/2 (рис. 11).
Μη 2Μ
Рис. 11
Глава 3
МЕТОД МОНТЕ-КАРЛО
— Думаю, вам не стоит
беспокоиться, — сказал
я.—До сих пор всегда
оказывалось, что в его
безумии есть метод.
— Лучше бы было сказать,
что есть безумие в его
методе, — пробормотал
инспектор.
А Конан Доил, «Записки
о Шерлоке Холмсе»
Замечательно, что
науке, начинавшейся
с рассмотрения азартных
игр, суждено было стать
важнейшим объектом
человеческого знания.
Лаплас, «Аналитическая
теория вероятностей»
П. Лаплас (1749-1827),
французский математик
У = φ(χ) ^Δ
ν/1
О .τ,
Рис. 1
Б. Тейлор (1685-1731),
английский математик.
В широком смысле методом Монте-Карло называется численный
метод решения математических задач при помощи
псевдослучайных чисел. Его название происходит от города Монте-Карло в
княжестве Монако, знаменитого своими игорными домами.
§ 1. ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ
Знакомство с методом начнем с рассмотрения задачи численного
интегрирования функции φ(χ), заданной на отрезке [0,1]. Как
ι
вычислить приближенно интеграл I = Ιφ{χ)άχΊ Пожалуй, про-
о
стейший способ — метод прямоугольников. Он состоит в замене I
г 1г / ^ г - 1/2
на интегральную сумму 1п = - 2^ φ\Χϊ), где %i = это
п i=i п
«узлы» равномерной сетки, т. е. середины интервалов разбиения
отрезка [0,1] на η равных частей (рис. 1).
При условии, что φ(χ) дважды непрерывно дифференцируема,
можно оценить погрешность метода прямоугольников δη = \Ι—Ιη\
так:
Доказательство. Положим а\ = х\ - —, Ь\ = Xi + —-. По
2п 2п
1 формуле Тейлора φ{χ) = φ(χί) + φ'(χί)(χ - ж<) + j </>"(£) (х ~ χί)2>
где χ е [α*, bi] и ξ = ξ(χ) е [α*, ЬЦ. Поскольку ^φ/(χί)(χ - χ^) dx = 0,
Ri = [φ(χ) - φ(χ%)] dx = 2 ψ"[ξ(χ)] (x ~ xi)2dx,
ai a,i
Остается применить неравенство
η
г=1
<Е1Д»1-
г=1
§2. «Правило трех сигм»
31
Таким образом, для гладких функций погрешность метода
прямоугольников имеет порядок малости 1/п2. Вопрос 1.
Метод Монте-Карло для вычисления интеграла / отличается „« ^выборе^
от метода прямоугольников тем, что в качестве «узлов» использу- «узлов» не середин,
о а правых концов отрезков
ются псевдослучайные числа yi,..., уп. разбиения?
Обоснование. Пусть случайные величины 171,772,.. . —
независимы и равномерно распределены на [0,1]. Положим & = φ(ηι). По
теореме о замене переменных из П2
оо оо 1
Щ\ = I <р(у) Рщ (У) dy = I <р(у) /[о, ι] dy = I ip(y) dy = Ι.
Согласно усиленному закону больших чисел (см. П6) имеем
■^ Μ£ι = J при η
-~* 1 1
ιη = - Σ 6 = - Σ φ(ν%)
00.
4=1
ηϊ=
i=l
Таким образом, если рассматривать псевдослучайные числа
yi,..., уп как реализацию щ,..., ηη, то с ростом η погрешность
приближения должна стремиться к нулю.
§2. «ПРАВИЛО ТРЕХ СИГМ»
Получим оценку для величины погрешности метода Монте-
Карло на основе центральной предельной теоремы (П6). Если
ι
О < D£i = J <р2(у) dy — I2 < 00, то при η —► оо
о
η
у/п{1п — 1) _ i=l d v
у/Щ1
y/nU&
где —* обозначает сходимость по распределению (см. П5), а
предельная случайная величина Ζ имеет функцию распределения
X
Ф(х) = Ρ(Ζζχ) = -^= [ е""2/2du
\/2π J
(рис. 2). Такая случайная величина называется стандартной нор-
мольной (обозначение: Ζ ~ΛΓ(0,1)).
В силу указанной сходимости/для любого χ ^ О при η —► оо
Р l·^^11 < *) - Р(-« < £ < *) = *(*) - *(-*)·
В силу симметрии имеем равенства
Ф(-х) = 1 - Ф(х) и Ф(а?) - Ф(-х) = 2 Ф(я?) - 1.
Для получения численных оценок рассмотрим подробнее
поведение функции Ф(х). К сожалению, ее нельзя выразить через
элементарные функции. Для приближенного вычисления Ф(х) можно
-3-2-10 1 2 3
Рис.2
32
Глава 3. Метод Монте-Карло
0«7о ^
Ч/<
95% А ■]
99,7%^
-3 -2-1 0 1
Рис
. 3
2 3
воспользоваться таблицей Т2. Рисунок 3 иллюстрирует некоторые
табличные значения.
Определение. Случайная величина X = μ + σΖ, где Ζ ~ ЛГ(0,1),
называется нормальной с параметрами μ и σ2 (обозначение:
Χ ~ Λ/Χμ,σ2)). При этом
Вопрос 2.
Как вы думаете, какие
три ошибки чаще всего
допускают студенты на
экзамене, пытаясь
написать формулу плотности
закона λί(μ,σ2)?
= 2
Рис. 4
(s-/i)2
2<г*
Какой вероятностный смысл имеют характеристики μ и σ2?
Нетрудно убедиться, что μ = MX, а σ2 = DX. Геометрический
смысл параметров μ и σ заключается в том, что прямая χ = μ
является осью симметрии плотности ρχ(χ)1 а μ ± σ — точками
перегиба ρχ(χ). Графики плотностей при μ = 0 и нескольких
значениях σ приведены на рис. 4.
Согласно определению случайной величины X и с учетом рис. 3
имеем
Ρ(μ - 3σ ^ Χ ^ μ + 3σ) = Ρ(|Ζ| < 3) » 0,997.
Другими словами, случайная величина Χ ~ Λ/^μ,σ2) принимает
значения из отрезка [μ — 3σ, μ + 3σ] с вероятностью 0,997, которую
зачастую не отличают от 1. Это утверждение известно на практике
как «правило трех сигм».
Возвращаясь к оценке погрешности метода Монте-Карло, заг
ключаем, что при достаточно больших η в соответствии с
«правилом трех сигм» выполняется неравенство
с вероятностью близкой к 1.
(2)
А
А/п,
^1 у
0 It Vj
Рис. 5
1
1
1 г>
1
§ 3. КРАТНЫЕ ИНТЕГРАЛЫ
Неразумно использовать метод Монте-Карло для вычисления
одномерных интегралов — для этого существуют квадратурные
формулы (см., например, [6, с. 375]), простейшая из которых —
рассмотренная выше формула метода прямоугольников. Дело в том, что
метод Монте-Карло имеет ряд существенных недостатков.
1) Оценка погрешности (2) имеет порядок малости 1/\/п в
отличие от порядка 1/п2 оценки (1). Это можно связать с тем,
что метод Монте-Карло нерационально использует информацию:
прямоугольники «случайной» интегральной суммы частично
перекрываются (рис. 5). (Вообще же, для математической статистики
это обычно, что оценка отстоит от оцениваемого параметра на
величину порядка 1/\/п, где п — число наблюдений.) Из-за мед-
§ 3. Кратные интегралы
33
ленной сходимости метод обычно применяют для решения тех
задач, где результат достаточно получить с небольшой точностью
(5-10%).
2) Для вычисления правой части формулы (2) надо знать,
1
чему равна D£i = ^2{y)dy — J2, или хотя бы уметь ее оцени-
о
вать.
3) В отличие от метода прямоугольников оценка погрешности
метода Монте-Карло справедлива лишь с некоторой
вероятностью.
Тем не менее, этот метод (или его модификации) часто
оказывается единственным численным методом, позволяющим решить
задачу. Особенно он бывает полезен для вычисления интегралов
большой кратности. Дело в том, что число «узлов» сетки возрастает
как nfc, где А: —кратность интеграла (так называемое «проклятие
размерности»). Так, чтобы найти интеграл по десятимерному кубу,
используя в качестве «узлов» только его вершины, надо 210 = 1024
раза вычислить значение интегрируемой функции. В практических
задачах эти вычисления могут оказаться довольно долгими,
например, когда для расчета значений требуется численное решение
систем нелинейных или дифференциальных уравнений.
Напротив, метод Монте-Карло не зависит от размерности:
чтобы найти приближенное значение интеграла
1 1
■ = J...J*xi,
,Xk)dx\.. .dxk
с точностью порядка 1/^/п достаточно случайно набросать η
точек в fc-мерный единичный куб (разбив псевдослучайные числа
на группы из к элементов) и вычислить среднее арифметическое
значений φ в этих точках. В частности, если функция — индикатор
некоторой области D, то с помощью метода Монте-Карло можно
приближенно определить объем этой области. Например, частота
случайных точек, попавших под дугу окружности на рис. 6 будет
служить приближением к π/4.
Отметим, что формула (2) оценки погрешности, полученная
для одномерного случая, сохраняется и для к > 1.
> х2 + у2 ζ 1
Рассмотрим модификацию метода Монте-Карло (см. [29, с. 124]),
которая называется расслоенной выборкой (выборкой по группам).
Каждую из сторон единичного fc-мерного куба разобьем на N равных
частей. При этом куб разбивается на η = Nk «кубиков» Δ< со
стороной Ι/iV. В каждом из Δ« (г = 1,... ,п) выбирается независимо
равномерно распределенная fc-мерная «точка» r/i = (ι^1 , *»* ^
и интеграл оценивается с помощью случайной суммы
..Л
Ιη = -Σ vim)·
(3)
34
Глава 3. Метод Монте-Карло
Рис. 7
Ж. Лагранж
(1736-1813), французский
математик.
Найдем порядок малости стандартного отклонения у ΌΙη при
увеличении п. Так как слагаемые в сумме из (3) независимы, то
01п
n i=l
(4)
Ввиду формулы (4) гл. 1 верно неравенство 0<р(г1{) ^ М<^2(7^).
Отсюда для ограниченной функции φ получаем оценку
foL ^ \fuil < м/у/й,
где Μ = max\<p(x)\. Это —обычный порядок точности. Однако
точность увеличивается, если колебания функции φ в пределах каждого
из Аг имеют порядок линейных размеров «кубиков». Это
выполняется, когда функция φ имеет ограниченные частные производные по
каждой из переменных χ у. \d<p/dxj\ ^ L, j = 1,... ,k (рис. 7).
Для получения оценки стандартного отклонения для таких
функций выберем внутри каждого Δ» произвольную
неслучайную точку yi (например, центр «кубика»), и, перемещаясь от yi
к tqi вдоль осей координат, по теореме Лагранжа о среднем
(см. [45, с. 277]) запишем
*Ш - V(l/i) = Σ «Г Uj) - yij)) , (5)
3 = 1 Ч 7
где α± —значения производных δφ/dxj в некоторых точках из Δ»
(зависящих от ту< и уг). Положим £У' = а\3' (η^ - j/j J.
Для произвольных случайных величин ξι,... ,£*, имеющих
конечный второй момент (П2) справедливо неравенство (задача 3)
к к
DEC* < Σ
щ.
(6)
Из него и формулы (5) следует, что
^офп) < Σ ν^ < Σ Jm (tf>)2.
3 = 1 3=1 V V '
Так как точки »|i и yi принадлежат Δ», то № \ ^ L/N — Ln~l^k.
Поэтому ϋφ(τιί) ^ L2k2n~2^k. Наконец, из равенства (4) выводим
оценку
JUL < Lkn-1'2-1'" = Cn"1'2"1".
Таким образом, порядок малости \ΏΪη меньше, чем порядок п~1^2
погрешности обычного метода Монте-Карло. Однако при к = 1
погрешность убывает со скоростью п-3/2, что медленнее скорости
сходимости п метода прямоугольников на гладких функциях.
Замечание. Для некоторого класса функций к переменных Холто-
ном и Соболем были построены (неслучайные) последовательности
«узлов», для которых погрешность имеет порядок lnfc η/η, что
на практике эквивалентно η
-1+ε
где ε > О сколь угодно мало.
Свойства, формулы и программы для их расчета содержатся в [74].
§ 4. Шар, вписанный в k-мерный куб
35
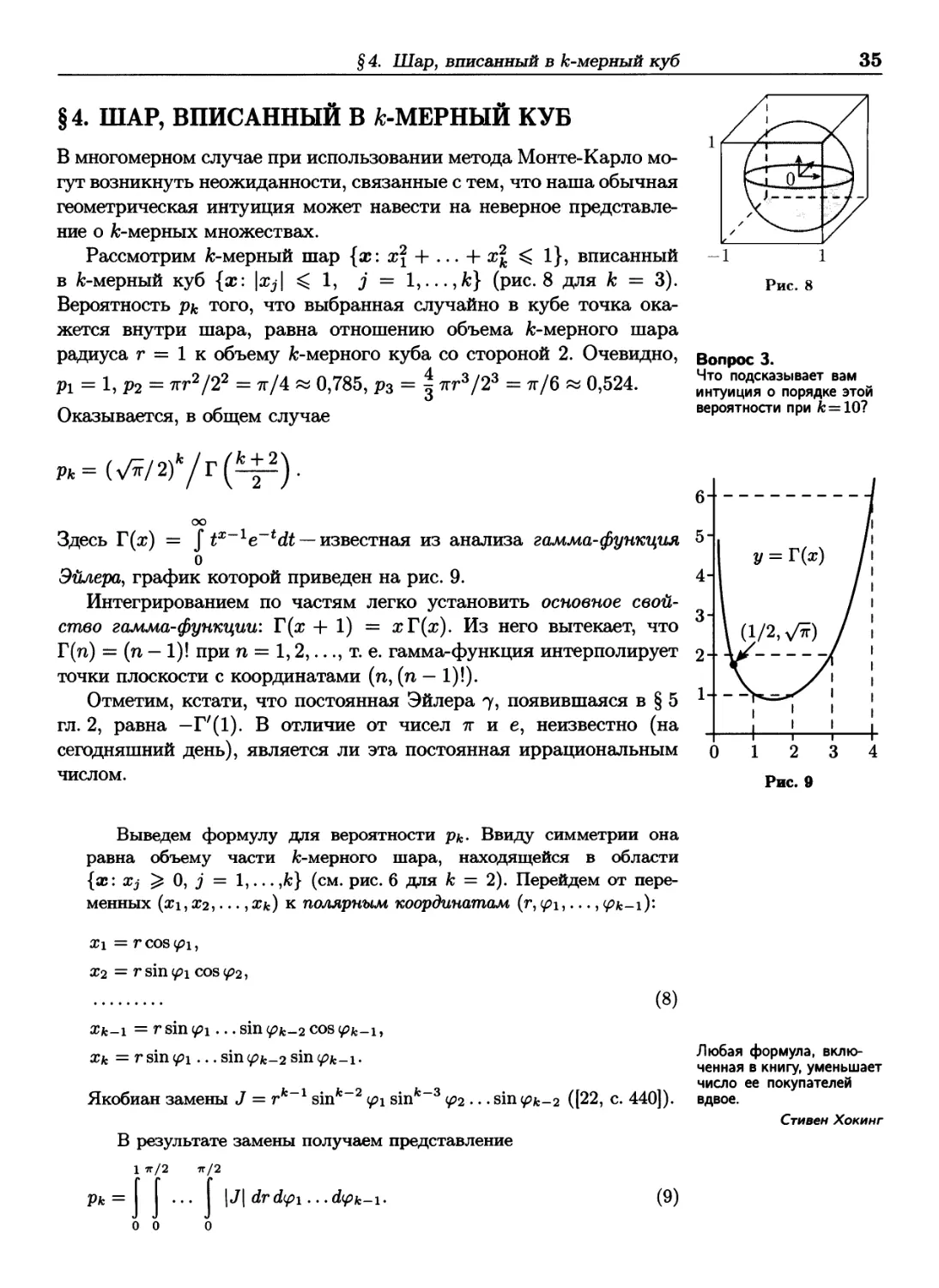
§4. ШАР, ВПИСАННЫЙ В А>МЕРНЫЙ КУБ
В многомерном случае при использовании метода Монте-Карло
могут возникнуть неожиданности, связанные с тем, что наша обычная
геометрическая интуиция может навести на неверное
представление о fc-мерных множествах.
Рассмотрим fc-мерный шар {х: х\ + ... + х\ ^ 1}, вписанный
в fc-мерный куб {х: \xj\ ^ 1, j = Ι,.,.,Α:} (рис.8 для к = 3).
Вероятность рк того, что выбранная случайно в кубе точка
окажется внутри шара, равна отношению объема fc-мерного шара
радиуса г = 1 к объему fc-мерного куба со стороной 2. Очевидно, вопрос 3
ft = hP2= «г*/*» = тг/4 « 0,785, р3 = | *г»/2» = π/6 « 0,524. Х^Гр^ой
Оказывается, в общем случае вероятности при к=10?
Рис. 8
Рк=Ш2)к/т{^).
Здесь Т(х) = J 1х~1е~ь<И — известная из анализа гамма-функция
о
Эйлера, график которой приведен на рис. 9.
Интегрированием по частям легко установить основное свой-
ство гамма-функции: Г(х + 1) = хГ(х). Из него вытекает, что
Г(п) = (п — 1)! при η = 1,2,..., т. е. гамма-функция интерполирует
точки плоскости с координатами (η, (η — 1)!).
Отметим, кстати, что постоянная Эйлера η, появившаяся в § 5
гл. 2, равна —Г'(1). В отличие от чисел π и е, неизвестно (на
сегодняшний день), является ли эта постоянная иррациональным
числом.
Выведем формулу для вероятности р&. Ввиду симметрии она
равна объему части fc-мерного шара, находящейся в области
{х: Xj ^ 0, j = 1,... ,k} (см. рис. 6 для к = 2). Перейдем от
переменных (χι, Х2, · · ·,Хк) к полярным координатам (г, φι,..., φΐε-ι)'-
хх = rcos<£i,
Х2 = rsin<£i cos<^2,
(8)
Xk-i = r sin φι... sin <pfc_2 cos φ^ι,
Xk = r sin φι... sinφ^-τ. sin φι<-\-
„fc-l oi„fc-2
Якобиан замены J = r sin 2 <^i sin φ2 ... sin <^fc_2 ([22, с 440]). вдвое.
Pfc
В результате замены получаем представление
1 π/2 π/2
= ... |J| άτάφι...άφ^-i.
(9)
Любая формула,
включенная в книгу, уменьшает
число ее покупателей
Стивен Хокинг
36
Глава 3. Метод Монте-Карло
Г. Вейль (1885-1955),
немецкий математик.
Доказательство этой
теоремы можно найти
в [29, с. 95]
Поскольку sirnpj ^ 0 при 0 ^ φ3 ^ π/2, знак модуля в
формуле (9) можно убрать, и кратный интеграл распадается в
произведение
1 тг/2
rk~ldr · lfc_2 ·... · /ι, где Im = sinm φάφ, τη = 1,..., к — 2.
о о
Первый сомножитель равен 1/к. Для вычисления 1Ш сделаем замену
у = sin2 ψ. Тогда Im = i}i/—1)/2(l - у)~1/2 dy = \в(^±1, j), где
1
B(rJs)=\yr-\l-yy-Uy=^p^;, r>0,*>0, (10)
J Г(г -f s)
о
— бета-функция Эйлера. Так как То = π/2 = ο ^ ( о' о )' το из фор-
мулы (10) следует, что r(j) = ^и 7m = (0F/2)r(^±±)/r(^).
При перемножении /т, т = 1,... ,fc — 2, гамма-функции перекрестно
сокращаются, что и приводит к указанному выше ответу, который
можно записать в явном виде:
_ ί (π/2)7 (2.4·6·...·ϋ5), если к = 2»,
Рк ~ \ (π/2)7 (3 · 5 · 7 ·... · к), если к = 2г + 1.
(И)
В частности, по первой из этих формул находим, что рго ~ 2,5 · 10 8.
Рассмотренный пример наглядно показывает, что может
потребоваться очень много псевдослучайных точек, чтобы получить
удовлетворительное приближение методом Монте-Карло для
интеграла от функции, принимающей большие значения на «тощих»
многомерных областях. При этом «тощими» могут оказаться
области, которые на первый взгляд таковыми не представляются.
§5. РАВНОМЕРНОСТЬ ПО ВЕЙЛЮ
Определение. Числовая последовательность χχ,Χ2, ···> где
Xi Ε [0,1], называется равномерной по Вейлю , если частота
попаданий точек χι на любой отрезок [а, Ь] С [0,1] стремится к его длине
b — а при η —► оо.
Согласно усиленному закону больших чисел (П6) реализация
r/i ,7/2, · · · последовательности независимых и равномерно
распределенных на отрезке [0,1] случайных величин обладает этим
свойством с вероятностью 1.
Существуют и неслучайные последовательности, равномерные
по Вейлю (см. задачу 5). Такой пример дает
Теорема 1. Пусть хп = {an}, где {·} обозначает дробную часть
числа, а — любое иррациональное число. Тогда последовательность
я ι, #2, · · · является равномерной по Вейлю.
§ 6. Парадокс первой цифры
37
Если последовательность #ι,#2, · · · равномерна по Вейлю, то для
произвольной интегрируемой по Риману на отрезке [0,1] функции
φ(χ) осуществляется сходимость (см. [45, с. 561])
1 п
п г=1
= Ι φ(χ)
ах при η —► оо.
(12)
Б. Риман (1826-1866),
немецкий математик.
При использовании равномерной по Вейлю последовательности
для вычисления кратных (в частности, двойных) интегралов
возможно такое (см. задачу 4), что при η —> оо
1 1
1 п
~ Σ ^(S2t-l»S2t) -+ С Φ
п i=l
у>(ж,у) d^dy.
о о
Определение. Числовая последовательность #ι,#2,..., гДе
#i Ε [0,1], называется вполне равномерной, если для
произвольного натурального числа к частота попаданий fc-мерных точек
(я(п-1)&+ь · · · ixnk) в любой находящийся внутри единичного
fc-мерного куба параллелепипед с параллельными координатным
осям ребрами стремится к его объему при η —> оо.
В начале тридцатых годов Д. Шамперноун доказал, что число
0,1234567891011121314151617181920212223...
(т. е. десятичные знаки являются последовательными натуральными
числами) обладает следующим свойством: частота, с которой любая
группа из к цифр встречается в его записи, стремится к 10_fc.
(Неизвестно, обладают ли этим свойством числа π и е.)
Отметим, что вполне равномерность — асимптотическое
понятие. Это означает, что конечный отрезок последовательности
можно как угодно «испортить», скажем, заменив все элементы
нулями, и тем самым сделать ее непригодной для вычислительных
целей.
Вопрос 4.
Будет ли (12) выполняться
оо
для φ(χ)= Σ'{χ=χί}.
i=l
при условии, что
последовательность
#ь#2,··· равномерна
по Вейлю, причем все Xi
различны?
§6. ПАРАДОКС ПЕРВОЙ ЦИФРЫ
Как вы думаете, с какой вероятностью число 2П начинается
с цифры 7? (Под вероятностью здесь понимается предел частоты
появления 7 при η —> оо, если он существует.) Если вы полагаете,
что эта вероятность равна 1/9, то ошибаетесь!
Действительно, 2П начинается с цифры т, 1 ^ т < 9, если
найдется такое Ζ, что т 101 < 2П < (ш + 1) · 10ζ. Логарифмируя,
получаем
log10 т + / < nlog10 2 < log10(m + 1) + /.
38
Глава 3. Метод Монте-Карло
Все три числа, участвующие в этом двойном неравенстве,
принадлежат отрезку [/, / + 1]. Поэтому, переходя к дробным частям, имеем
log10 m < {nlog10 2} < log10(m + 1).
Так как log10 2 — иррациональное число, то в силу теоремы 1
последовательность хп = {nlog10 2} является равномерной по Вейлю.
Отсюда искомая вероятность
Рт = logi0(m + 1) - bgio m
(13)
В частности, ρη = log10 8 — log10 7 « 0,058, что почти вдвое меньше,
чем 1/9 « 0,111.
Можно предложить пари (см. [72, с. 187]), что первая цифра
некоторого взятого наугад «большого числа» N окажется не
больше, чем 4. Вероятность выигрыша в нем для N = 2п — вовсе
не 4/9 « 0,444, а с учетом формулы (13) имеет значение
Pi + Р2 + Рз + Р4 = log10 5 - log10 1 « 0,699.
Любопытно, что подсчитанная по таблице 7.6 из [10] частота
выигрышей в этом пари для N = п\ (п = 1,... ,100) равна 0,68.
Как раз четыреста!...
Нет! триста...
ЗАДАЧИ
1. Сколько случайных точек надо бросить в единичный квадрат
(см. рис. 6), чтобы получить две верные цифры после запятой
Фыусоэ и Хлесгое* числ& π с BepoaTHOCTbIO (),997?
в «Горе от ума» "
А. с. Грибоедова 2. Используя разложение числа е в ряд, докажите, что хп =
= {en!} —► 0 при η —► оо.
3. С помощью неравенства Коши—Буняковского (П4) получите
неравенство (6).
4. Для датчика хп = {an}, где a > 0 — произвольное
иррациональное число, найдите предел частоты попаданий точек (#2г-ъ#2г)
в подмножество единичного квадрата
а) у < х,
б) х + у ^ 1 (рис. 10).
Указание. Для 0 < a < 1 выразите #η+ι через хп.
Б* Рассмотрим два числовых треугольника:
а) 1/2 б) 1/2
1/3 2/3 1/4 2/4 3/4
1/4 2/4 3/4 1/8 2/8 3/8 ... 7/8
Либо дождик, либо снег, БуДУт ли получаться равномерные по Вейлю последовательно-
либо будет, либо нет. сти, если считывать эти треугольники по строкам?
Решения задач
39
РЕШЕНИЯ ЗАДАЧ
1. Если «успехом» считать попадание точки под дугу окружности
х2 Л- у2 = 1 (см. рис. 6), то результаты бросаний образуют
схему Бернулли с вероятностью «успеха» ρ = π/4. Поскольку
дисперсия отдельного испытания в этой схеме равна р(1 — р), то
для частоты «успехов» 1п согласно формуле (2) имеем
\1п - тг/4| ^ Сп = 3ν/(π/4Κ1 πΖΐ) с вероятностью 0,997.
Оценка для погрешности вычисления самого π равна 4СП.
Приравнивая ее к требуемой точности 0,005, находим η « 970835.
Таким образом потребуется почти миллион точек!
2. Как известно из математического анализа,
1
e = 1 + h + h+·
где
1
(п+1)!
1
<
(п + 1)!
1
1 +
п!
+ ...=
1
(п + 2)!
1
п + 2 (п + 2)(п + 3)
+ ,
·)
(п+1)! ч
Поэтому {е п!}
1+2 + ?
·) = —
J (п +
η! εη <
п + 1
1)! '
0 при η
оо. Таким образом,
подпоследовательность равномерной по Вейлю
последовательности сама может и не обладать этим свойством.
3. Преобразуем квадрат левой части неравенства (6):
к /к к \2 / к \2
0Σ&=Μ(Σ6-ΜΣίί) =Μ(Σ3) =
= Μ Σ ί# = Σ Μ^, где $ =fc - Mfc.
Квадрат правой части неравенства (6) представляется в виде
Остается применить свойство (4) математического ожидания
из П2 и неравенство Коши—Буняковского (П4).
4. Прежде всего, можно считать, что 0 < a < 1, ибо иначе о/ = {а}
задает ту же самую последовательность хп.
Для таких а справедливо представление χη+ι = {хп + а}
(два возможных случая приведены на рис. 11). Таким образом,
#n+i = f(xn), где f(x) = {χ + α} (рис. 12). Поэтому все точки
(#2i-i,#2i) будут лежать на графике этой функции, вместо того,
чтобы равномерно плотно заполнять весь квадрат.
Доход не бывает без
хлопот.
40
Глава 3. Метод Монте-Карло
Вопрос 5.
Почему это верно?
у = {тпх}
1 ТПк-l П ТПк
Рис. 14
Далее, из равномерности по Вейлю последовательность
точек Xi вытекает, что ординаты х^% тоже обладают этим
свойством.
Так как х<ц ^ Х2%-\ тогда и только тогда, когда х<ц попадает
на отрезок [0, а], то частота в случае а) будет стремиться к а,
а не к 1/2 (площади треугольника), как должно быть для
«настоящего» датчика случайных чисел.
В случае б) из-за симметрии графика f(x) относительно
диагонали квадрата χ + у = 1 предел частоты равен 1/2.
Замечание. Мультипликативный датчик из § 3 гл. 2
Г кп = (га · A:n_i) mod d, ^ ^ f Уо = ko/d,
\уп = K/d
I 2/n+i = {m · уп}
также удовлетворяет соотношению уп+1 = /(Уп) с f(x) = {mx}
(рис. 13).
В [29] приведен ряд утверждений, из которых следует, что
при га —► оо этот датчик позволяет правильно вычислять
интегралы любой кратности.
В случае а) обозначим через га& = к{к + 1)/2 —общее число
элементов последовательности в к первых строках
треугольника. Пусть rrik-i < η < rrik (т. е. хп принадлежит к-ft строке).
Тогда хп = (п - m,k-i)/{k + 1) (рис. 14). Оценим сверху ι/η —
количество попаданий точек ж», г = 1,..., п, в промежуток (0, х]
при 0 < χ < 1 (здесь [ · ] — целая часть числа):
Аналогично оценим ι/η снизу:
j=i i=2 V l J
Отсюда -^ ^ ^ ^
6fc
-, где обе границы стремятся к χ при
ТПк U ТПк-\
к —► оо. Поэтому последовательность χι,Χ2,··· равномерна по
Вейлю.
В случае б) количество попаданий точек χι в промежуток
(0,1/2] для подпоследовательности вида
п'к = 2fc+1 — к — 2 (А: полных строк)
и для подпоследовательности вида
nl = 2к - к - 1 + 2*"1 (к - 1/2 строк)
одинаково и равно /& = 2fc — 1. При к —► оо получаем, что
Wnfc ~* 1/2) в то время как /fc/n'fc'
равномерности по Вейлю.
2/3,,что противоречит
Ответы на вопросы
41
Замечание. Рассмотрим частоту появлений произвольной
цифры на j-м месте после запятой в десятичном представлении
a) y/ri) б) log п. Оказывается, что в первом случае предел
1
к+
этой частоты равен —, что следует из равномерности по Вейлю ь ΪΤ '__
10'
последовательности хп = {у/п} (рис. 15). Во втором же случае
предела нет, а множество предельных точек представляет собой
некоторый отрезок внутри отрезка [0,1].
у = \[х
ОТВЕТЫ НА ВОПРОСЫ
1. По теореме Лагранжа φ(χ) = φ(χί)+φ'(ξ)(χ—Χί). Рассуждая так
же, как при выводе формулы (1), получаем оценку: δη ^ ~ ^/п,
где L = max |у/(ж)|. Таким образом, при использовании в ка-
честве «узлов» правых концов отрезков разбиения обычным
порядоком малости погрешности является 1/п. Причиной тому
служит отсутствие взаимной компенсации площадей со знаками
«+» и «-» на рис. 16, происходящей при выборе «узлов»
посередине.
2. В следующей формуле допущены все три ошибки:
1
(χ-β)2
/2πσ
Согласно формуле (11), вероятность рю ~ 2,5 · 10~3. Таким
образом, почти весь «объем» десятимерного куба сосредоточен
в его 1024 «углах». В результате в среднем только одна из 400
случайных точек попадает внутрь десятимерного шара.
Для интегрируемости по Риману на отрезке согласно критерию
Лебега необходимо и достаточно (см. [59, с. 34]), чтобы
функция была ограниченной, а множество ее точек разрыва имело
лебегову меру нуль (т. е. чтобы существовало покрытие этого
множества конечной или счетной системой интервалов, сумма
длин которых сколь угодно мала).
Равномерная по Вейлю последовательность обязана,
очевидно, быть всюду плотной в [0,1] (в любом интервале из [0,1]
должны присутствовать ее точки). Поэтому множеством точек
разрыва функции φ(χ) является весь отрезок [0,1].
Следовательно, эта функция не интегрируема по Риману. Однако φ(χ)
отличается от 0 только на счетном множестве точек #;, в силу
чего интеграл Лебега от нее существует и равен 0. В свою
очередь, левая часть формулы (12) при каждом η равна 1.
Подпоследовательность ординат х<ц генерируется датчиком {/Зг}
с иррациональным β = 2а.
Человек редко ошибается
дважды — обычно раза
три или больше.
Джон Перри Барлоу
А. Лебег (1875-1941),
французский математик
Глава 4
ПОКАЗАТЕЛЬНЫЕ И НОРМАЛЬНЫЕ ДАТЧИКИ
Нормальные герои всегда В этой главе мы расскажем, как с помощью псевдослучайных
идут в обход. чисел имитировать реализации случайных величин с заданным
И3 Ай^^бТ РаспРеДелением· Прежде всего, познакомимся со стандартным
способом моделирования — методом обратной функции. Затем
рассмотрим специальные датчики для показательного и нормального
законов.
§ 1. МЕТОД ОБРАТНОЙ ФУНКЦИИ
Допустим, что функция распределения F(x) непрерывна и строго
возрастает. Тогда на интервале (0,1) существует непрерывная и
монотонная обратная функция F~1(y) и справедливо
Утверждение 1. Если случайная величина η равномерно
распределена на отрезке [0,1], то случайная величина ξ = F-1^) имеет
функцию распределения F(x).
Доказательство. Так как 0 < F(x) < 1, то (см. рис. 1)
ОД = Ρ(ί < *) = P(F(f) ^ F(x)) = Ρ(η ζ F(x)) = F(x). Ш
Определение. Выборкой размера п из распределения F называ-
ется случайный вектор (£ι,...,£η)> компоненты которого незави-
\У— \х) симы и одинаково распределены с функцией распределения F(x).
Ввиду утверждения 1 для того, чтобы моделировать
реализацию #ι,... ,#п выборки (£ι,... ,£п) из распределения F, достаточно
Рис. 1 преобразовать псевдослучайные числа yi,... ,уп с помощью
обратной функции F~l.
Применим метод обратной функции для моделирования
выборки из показательного закона с функцией распределения F(x) =
= (1 — е~Хх) 1{х>0у. Найдем обратную функцию:
у = 1-е~Хх <=> х = --\п(1-у).
Поэтому формула для моделирования выглядит так:
Вопрос 1.
Нельзя ли предложить ~. _ _ i W1 — */Λ
похожую, но более х% ~ χ "Η1 Уг"
простую формулу,
дающую тот же результат? где у; (г = 1,... ,п) — псевдослучайные числа.
§ 2. Распределения экстремальных значений
43
Еще один пример применения метода обратной функции
содержится в задаче 1.
Замечание 1. Многие утверждения, выполняющиеся для
последовательности независимых и равномерно распределенных на [0,1]
случайных величин щ,г}2·,··· (например, усиленный закон
больших чисел или центральная предельная теорема из П6) остаются
верными и после преобразования, если «хвосты распределения»
1 — F(x) и F(—x) достаточно быстро убывают при χ —► -foo.
С другой стороны, в § 2 показано, что выборки из распределений
с «тяжелыми хвостами» ведут себя иначе.
§2. РАСПРЕДЕЛЕНИЯ ЭКСТРЕМАЛЬНЫХ
ЗНАЧЕНИЙ
Рассмотрим пример из [17, с. 18]. Пусть элементы выборки
(Χι,... ,ХП) имеют функцию распределения
Хвост сзади, спереди
какой-то чудный выем.
Чацкий в «Горе от ума»
А. С. Грибоедова
,-,/ ч J 1 - i ПРИ Х > е>
F(x) = { Inx
1 0 при χ < е.
(1)
Обозначим max{Xi,... ,ХП} через Х^ и вычислим приближенно
7 = Р(Х(п) > Ю7) ПРИ п = 4.*) С учетом независимости и
одинаковой распределенности случайных величин ΛΊ,... ,Хп запишем
Р(Х{п) < я) = Р(Хг ^ х,..., Хп < х) = [F(x)]n .
Поскольку In 10 « 2,3, а (1 — е)п « 1 — еп при малых ε, получаем
Л \ Л
1/4
-1_(1_7ЬПо) И1"(1_7^з)-Щ
(более точный подсчет η на калькуляторе дает значение 0,226).
Таким образом, примерно β каждом четвертом случае (!) значение
Х(4) будет превышать 107. Вопрос 2.
Оказывается, из-за того, что функция распределения F(x) Можно ш указать такую
' ' ^J —г г г π \/ последовательность
имеет «сверхтяжелый» правый «хвост» (рис. 2), распределение констант Ьп, чтобы
случайной величины Х^ чрезвычайно быстро с ростом п «ухо- Х(п)/Ьп—>0 прип-юо?
дат» на +оо, и никаким линейным преобразованием не удается
«вернуть» его в конечную область. Точнее: невозможно подобрать
такие «центрирующие» константы ап и «нормирующие» константы
Ьп > 0, чтобы последовательность (Х(п) — ап)/Ьп сходилась бы
по распределению (см. П5) к невырожденному закону**) (см. [17,
с. 82]).
*) Для выборки, скажем, из закона Л/"(0,1) ввиду правила «трех сигм» (см. § 2
гл. 3) такая вероятность ничтожно мала.
**) Распределение случайной величины ξ вырождено, если Ρ (ξ = const) = 1.
44
Глава 4. Показательные и нормальные датчики
Если такой закон для максимума выборки из некоторого
распределения существует, то он (с точностью до сдвига и масштаба)
обязательно принадлежит (см. [17, с. 66]) одному из трех типов
распределений экстремальных значений:
Тип I: F(x) = ехр{-е~х} , - оо < χ < оо;
О, χ ^ О,
ехр{-я"а}, х > 0;
exp {-(-s)Q}, s<0,
Тип II: F(x) = |
Тип III: F(x) = { **
Здесь типы II и III представляют собой однопараметрические
классы распределений с параметром a > 0.
В приведенной ниже теореме даются простые достаточные
условия «притяжения» (т. е. сходимости (Х(п) — ап)/Ьп для
некоторых ап и Ъп) к каждому из трех возможных типов.
Теорема 1. Допустим, что
1) lim ех[1 - F(x)] = β > 0, тогда Х(п) - 1η(/?η) Λ ξ, где
х—кх>
случайная величина ξ имеет функцию распределения типа I;
2) для некоторого а > 0 существует lim ха[1 — F(x)] = β > 0,
X—КХ>
тогда Χ(η)/(/3η)1/α —* г/, где случайная величина г/ имеет функцию
распределения типа И;
3) F(c) = 1, где с < оо, и для некоторого α > 0 существует
lim (с - z)-Q[l - F(x)] = β > О, тогда (/3n)1/Q(X(n) -с)Д(, где
ж—неслучайная величина ζ имеет функцию распределения типа III.
Доказательство. В первом случае
Ρ(Χ{η)-\η(βη)ζχ) =
= [F(z + ln(/?n))]n = [l-/? βχρ{-χ-\η(βη)} + ο(1/η)]η =
= [l-e~x/n + o(l/n)]n->ехр{-е~х} при га—>оо.
В остальных случаях доказательство аналогично. ■
Необходимые и достаточные условия «притяжения» были
получены Б. В. Гнеденко в 1943 г. (см. [17, с. 49]).
Возвращаясь к примеру функции распределения F(x), заданной
формулой (1), покажем, что неосуществимое с помощью линейного
преобразования, можно ъ этом случае осуществить с помощью
нелинейного. Положим Xi = ΙηΧ;. Очевидно, что функцией
распределения случайной величины Xi будет F(x) = (1 j I{x>iy.
§ 3. Показательный датчик без логарифмов
45
В силу теоремы 1 последовательность Х(п)/п сходится по
распределению к закону экстремальных значений И-го типа с a = 1.*)
Так как min{Xi,... ,ХП} = — тах{— ΛΊ,..., — Хп}, то
предельные распределения для минимума выборки получаются из законов
трех экстремальных типов с помощью преобразования
G(x) = l-F(-x).
Например, закону Ш-го типа соответствует функция
распределения 1 — ехр{—#α}, χ ^ 0. Это распределение известно в
теории прочности материалов под именем закона Вейбулла—Гнеденко
(«принцип слабейшего звена»). Его частным случаем при а = 1
является показательный закон с параметром λ = 1 (см. задачу 2).
§ 3. ПОКАЗАТЕЛЬНЫЙ ДАТЧИК
БЕЗ ЛОГАРИФМОВ
Выборку из показательного закона можно моделировать и без
вычисления логарифмов (см. [82, с. 59]). Для этого рассмотрим
таблицу из независимых равномерно распределенных на отрезке [0,1]
случайных величин
Vn, ϊ7ΐ2, ... Vij, ...
Ϊ721, ^22, ... V2j, ...
Ήα, ϊ)ϊι·> ... Vij, ...
Для г-й строки таблицы определим случайную величину Κι как
U ^ 2: Vn > Vi2 > ..· > Vi(j-i) < Vij}, т. е. (Ki - 1) —это длина
«нисходящей серии», начиная от начала г-й строки (см. задачу 2
гл. 2). С последовательностью независимых и одинаково
распределенных случайных величин К{ свяжем схему Бернулли, считая
«успехом» событие {Ki четно} и «неудачей» — {Ki нечетно}.
Утверждение 2. Обозначим через ν число «неудач» до первого
«успеха». Тогда Ρ(ι/ + ?7(ι/+ΐ)ΐ ^ ж) = 1 — е~х, χ > 0, т. е. сумма
числа «неудач» и первой величины в строке «успеха» показательно
распределена с параметром λ = 1.
Доказательство. Прежде всего, вычислим
Ρ(Κι > η, 77η < у) = Р(у >ηι\>ηΐ2>---> ηΐη)·
Последнее событие происходит тогда и только тогда, когда все η
точек попадают на отрезок [0, у] и оказываются упорядоченными
*) Переход от Χι κ Χχ сильно сжимает прямую с распределенной на ней
вероятностной массой, благодаря чему становится возможным получить предельный
закон дальнейшим линейным сжатием прямой.
46
Глава 4. Показательные и нормальные датчики
1
0
[ У = р{
/'''''
' ]
τ}(χ)
у = 1-е
[ X
Рис. 3
по убыванию. Каждому порядку точек соответствует одно из п!
равных по объему подмножеств n-мерного куба со стороной у
(см. задачу 3 гл. 2). Таким образом, Р(К\ > η,ηη ^ у) = уп/п\.
Отсюда имеем
Р(К1=п,щ1^у) = Р(К1>п-1,щ1^у)-Р(К1>п,щ1^у) =
Уп~1 Уп
(п-1)! п\
Суммируя по четным значениям п, находим
Р(ЛГ1четно,г?11<2/) = ^-| + ^-^ + ... = 1-е-«.
Если положить в этом равенстве у = 1, то получим, что вероятность
«успеха» ρ = Ρ (Κι четно) = 1 — е-1.
Вычислим совместное распределение случайных величин ν
= Ρ (Kj нечетно, j = 1,... ,г, Ki+i четно, η^+ιμ ^ у) =
= Ρ (Kj нечетно, j = 1,... ,г) Ρ (Ki+i четно, r7(i+i)i < у) =
-ι
= ql (l — e y), где g = 1 — ρ = e
Для завершения доказательства утверждения 2 потребуется
следующее утверждение (проверить которое предлагается в задаче 3).
Утверждение 3. Целая [ · ] и дробная {·} части показательной
случайной величины г с параметром λ = 1 независимы, причем
[г] распределена по геометрическому закону: Ρ ([г] = г) = дгр, где
ρ = 1—е-1, g = 1— ρ, а {г} имеет функцию распределения F{Ty(x) =
= - (1 - е-*) при 0 < χ < 1 (рис. 3).
Отсюда находим совместное распределение [т] и {г}:
Р(М = <, Μ < У) = Р(М = г) Р({т} < у) = ςτ* (l - е~У).
Оно совпадает с распределением ν и ?7(ι/+ΐ)ΐ· Следовательно,
ι/ + ?7(ι/+ΐ)ΐ и [г] + {г} = г распределены одинаково. ■
§4. БЫСТРЫЙ ПОКАЗАТЕЛЬНЫЙ ДАТЧИК*)
Вычисление In x на компьютере обычно основано на разложении
логарифма в ряд Тейлора, и для получения достаточной
точности надо выполнить около 20 арифметических действий (см. [6,
с. 362]). Из-за этого моделирование показательной выборки с
помощью метода обратной функции происходит довольно медленно.
*) Материал этого параграфа технически более сложен, но важен: леммы 1-3
будут неоднократно использоваться в дальнейшем.
§ 4. Быстрый показательный датчик
47
При расчете математических моделей (скажем, при определении
надежности системы, состоящей из элементов со «случайными»
временами работы и ремонта) показательный датчик обычно
является глубоко вложенной подпрограммой. Ввиду этого ускорение
его работы представляет значительный интерес. Оказывается, на
основе приводимой ниже теоремы 2 время моделирования можно
существенно уменьшить. Для ее доказательства потребуются
несколько новых понятий.
Определение. Случайная величина Τ имеет гамма-распределение χ.
с параметрами а > О и λ > 0 (обозначение: Τ ~ Γ(α,λ)), если ее
плотность (см. графики на рис. 4) задается формулой
„ /м\ Л <& — 1Л—λχ τ
Рт(:г) = —-х е /{ж>0},
где Г (а) — гамма-функция Эйлера (см. § 4 гл. 3).
Показательный закон является частным случаем
гамма-распределения при а = 1.
Момент к-го порядка МТк гамма-распределения равен
10<а<1
у=Рт(х)
Ла L*+«-VA*d* = r(Q + fc) = а(а +
Г(а) J \кГ(а)
l)...(g + fc-l)
Хк
(2)
Лемма 1. Если случайные величины Τι ~ Γ(αι,λ) и Τ<ι ~ Г(с*2,А)
независимы, то их сумма Τι + Τ<ι ~ Γ (αϊ + с*2, λ).
Доказательство. Без ограничения общности докажем эту лемму
при λ = 1. По формуле свертки (ПЗ) запишем плотность
х
о
Сделав замену t = ху, приведем выражение для рт1+т2(х) к ВИДУ
ι
Cat-^-V*. где C-j^L^jjr^a-y)··-1*.
О
Поскольку интеграл от плотности равен 1, без вычислений находим,
что константа С = 1/Γ(αι + аг).
Попутно была выведена формула (10) гл. 3, связывающая бета-
и гамма-функции:
ι
В(г18) = \уг-\1-Уу-Чу=ЩЩ, г>0,*>0. ■
а=11<а<2
,а>2
Вопрос 3.
Чему равна дисперсия
показательного закона?
48
Глава 4. Показательные и нормальные датчики
Вопрос 4.
Какую плотность имеет
вектор (ξ(ΐ),...,€(п)).
если компоненты
выборки распределены
с плотностью р(х)1
Рис. 6
Рис. 7
Определение. Набор ξ^ ^ £(2) < ... < £(п) упорядоченных по
возрастанию значений компонент выборки (£ι,...,£η) называется
вариационным рядом, а сами случайные величины ξ^) ~
порядковыми статистиками:
ξ{1) = min{fi,...,£n},
ξ{2) = max{min{fb... ,&_ь &+ь... ,fn}},
ξ{η) = max{£b...,£n}.
Лемма 2. Пусть случайные величины ryi,...,ryn независимы
и равномерно распределены на отрезке [0,1]. Тогда плотность
вектора (ί/(ΐ),...,^(η)) (см. П8) равна п! на множестве 5 =
= {х: 0 < χι < ... < хп < 1} и равна нулю вне этого множества.
Доказательство. Для произвольной точки (ж5,...,#^) из 5
построим «кубик» {х: х® ^ Х{ < #? + £, г = 1,... ,п} с ребрами
достаточно малой длины $, целиком лежащий в 5 (рис. 5 для η = 2).
Так как все перестановки η^ <η%2 < ... < r/in равновероятны, то
Ρ (я? < 4(0 <«? + ί, г = 1,...,п) =
= η! Ρ (ж? < ту< < ж? + ί, г = 1,... ,гг, 771 < ... < туп) = η! ίη.
Переход к пределу при δ —► 0 (см. П8) завершает доказательство.
■
Следствие. Рассмотрим так называемые равномерные спейсинги
Аг = »7(г) -»7(г-1), г = 1,... ,гг+1, щ0) = 0, 77(η+ΐ) = 1 (рис. 6). Вектор
(Δι,...,Δη) получается из (/7(1)? · · · )4(n)) c помощью линейного
преобразования с верхнетреугольной матрицей (см. ШО), на
диагонали которой стоят единицы. Якобиан преобразования равен 1.
По формуле преобразования из П8 плотность вектора (Δι,... ,Δη)
равна п\ в области {χ: χι +... + хп < 1, Xi > 0, г = 1,... ,п} и равна
нулю вне этой области.
Лемма 3. Пусть τ = (τι,... ,тп) — выборка из показательного
распределения с параметром λ, Si = τχ + ... + п (рис. 7). Тогда
вектор (Si/Sni... ,5η_ι/5η) распределен так же, как вектор
порядковых статистик (г7(1),... ,?7(η,—ι)) Для выборки размера η — 1
из равномерного распределения на [0,1].
Доказательство. То же самое линейное преобразование,
что и в следствии леммы 2, переводит случайный вектор
S = (5ι,...,5η) в вектор т. Используя независимость т^, по
формуле преобразования (П8) находим плотность S:
п
Ps(su^^sn) = l[\e-x^-Si-^=Xne-Xs\0 = so<s1<...<sn.
г=1
Положим Xi = Si/Sn, г = 1,... ,η - 1, Хп = Sn. Тогда Si = XiXn,
г = 1,... ,τι — 1. Нетрудно убедиться, что якобиан J этого преобра-
§4. Быстрый показательный датчик
49
зования равен #™ г. Отсюда плотность вектора X = (ΛΊ,... ,ХП)
рх(хи... ,хп) = И Ps(xix<n, · · · ,Χη-ιΧη,Χη) = \nXn~le~XXn (3)
на множестве {χ: 0 < х\ < ... < хп-\ < 1, #п > 0}.
Проинтегрировав по последней координате (см. П8), получим
оо
Ρ(χ1ι...,χη-θ(^ι»···^η-ι) = λη|χΓ1β-^ηώη = Γ(η) = (η-1^
о
на множестве {ж: 0 < #ι < ... < xn-i < 1}· И
Теперь все готово, чтобы сформулировать и доказать основной
результат этого параграфа.
Теорема 2. Пусть случайные величины ι/ι,...,ι/2η-ι независимы
и равномерно распределены на [0,1], £ι,... ,£η_ι —расставленные
в порядке возрастания величины rfo+i,... ,?72η-ι> £о = 0, ξη = 1.
Тогда вектор т; с компонентами τ[ = - у (& — &-ι) 1η(ι/ιΐ/2 · · · Ήη),
г = 1,... ,η, представляет собой выборку из показательного закона
с параметром λ.
Например, в случае η = 2 имеем
Τι = ~ д *7з hfaiTft), T2 = - - (1 - Г7з) 1η(τ7ι%)·
Экономия времени при моделировании возникает из-за того, что
для получения показательной выборки размера η требуется только
одно вычисление логарифма. Однако при этом приходится
генерировать 2п — 1 псевдослучайных чисел и упорядочивать по
возрастанию η -1 из них. Расчеты на компьютерах разных типов показали,
что практически оптимальным является вариант алгоритма при
η = 3 (см. [29, с. 27]). Такой датчик работает примерно вдвое
быстрее метода обратной функции.
Доказательство. Положим Х[ = &, г = 1,...,п - 1; Х'п =
1 п 1
= --rln(77i772...r7n) = Σ τ%·> гДе Тг = ~т 1пг7г· Согласно методу
г—1
обратной функции, случайные величины Т{ показательно
распределены с параметром λ, τ. е. τι ~ Γ(1,λ). При этом ri,... ,тп
независимы, будучи функциями от независимых величин щ (см. лемму
о независимости из § 3 гл. 1). Отсюда в силу леммы 1 выводим, что
х;~г(п,а),
т. е.
^(χ)=(^Ί)ίχη"ΐ6"λΧ^>0}·
Очевидно, случайный вектор (Х[,... ,^ή-ι) распределен так же,
как и вектор порядковых статистик (г7(1)> · · · ,г7(п,—ι)) дая выборки
50
Глава 4. Показательные и нормальные датчики
размера η — 1 из равномерного распределения на отрезке [0,1]. По
лемме 2 его плотностью является
Pixi^x^jfau · · · ,^η-ι) = (η - 1)!
в области {χ: 0 < χι < ... < χη-ι < 1}.
При этом (Х[1... ,Α^-ι) и Х'п независимы как функции от
независимых векторов (г7п+1,... ,r/2n-i) и (771,... ,r/n). Следовательно,
плотность вектора X' = (Х{,... ,Х^) имеет вид
Рх>(х\, · · · ,хп) = Р&'^х^Ы* · · · >χη-ι) Ρχ'η(χη) = ХпХп~1е~Ххп
в области {х: 0 < χι < ... < χη-ι < 1, #η > 0}, т. е. она совпадает
с задаваемой формулой (3) плотностью вектора X из леммы 3.
Осталось заметить, что X' преобразуется вт'с помощью того
же взаимно однозначного отображения, которое в лемме 3
перевоза один раз дерева не дит X в т: Т; = (Х{ - Χ;_ι)Χη, г = 1,... ,П - 1; тп = (1 - Xn-i)Xn
сруоишь. (убедитесь!). Поэтому векторы т'ит одинаково распределены. ■
§5. НОРМАЛЬНЫЕ СЛУЧАЙНЫЕ ЧИСЛА*)
Для моделирования реализации выборки из распределения Λ/^Ο,Ι)
с помощью метода обратной функции надо уметь вычислять
значения обратной функции Ф_1(у) к функции распределения Ф(х)
стандартного нормального закона. Приближенно это можно делать,
например, интерполируя достаточно подробную таблицу Ф~1(у)
или заменяя ее «близкой» функцией. Так, Хамакер (см. [58, с. 281])
предложил следующую аппроксимацию:
Ф~\у) « sign(y - 0,5)(1,238* (1 + 0,0262*)),
где
г = >/-1п(4у(1-у)),
sign(#) = <
—1, если χ < 0,
0, если χ = 0, — знак числа х.
1, если χ > 0.
Она обеспечивает две верные цифры после запятой для \Ф 1(у)\ ^
Другой метод приближенного моделирования основывается на
центральной предельной теореме (П6). Для независимых и
равномерно распределенных на [0,1] случайных величин 771,772...
согласно задаче 2 гл. 1 имеем Мт7г = 1/2, D77i = 1/12. Центральная
предельная теорема для суммы 5П = 771 + ... + 77п дает сходимость
(Sn - п/2) /у/гф2 ±*Ζ~ ΛΓ(0,1) при η — оо.
*) В табл. Т1 приведен фрагмент таблицы таких чисел из [10].
§ 5. Нормальные случайные числа
51
Взяв η = 12, получим случайную величину S\2 — 6, распределение
которой мало отличается от стандартного нормального закона
ЛГ(0,1).
Замечание 2. Обратим внимание на то, что, в отличие от Z, при
любом η случайная величина 5П ограничена. Используя формулу
свертки (ПЗ), можно доказать (см. [82, с. 42]), что функция
распределения суммы 5П имеет вид
Ήη(*0 = 3Σ(-ΐ)*σ*(*-*)ΐ,
п\ СГ{
fc=0
(4)
где /+ = тах{0, /}. На каждом из отрезков [г — 1, г], г = 1,... ,п, она
является многочленом степени η (Fsn (х) на [0,1] была вычислена
при решении задачи 3 гл. 2). На концах отрезков графики гладко
«состыкованы». На рис. 8 изображены соответствующие плотности
Psn(x) = (d/dx) FSn(x) для η = 1,2,3.
В заключение рассмотрим способ точного моделирования,
базирующийся на нелинейном преобразовании пары независимых и
равномерно распределенных на [0,1] случайных величин щ, щ в пару
независимых ЛГ(0,1) случайных величин Χ, Υ:
X = у/-2In771 cos(2π772), Υ = \/—2\пщ sin(2^2).
(5)
Доказательство. Для независимых ΛΓ(Ο,Ι) случайных
величин X и Υ плотностью вектора (Χ,Υ) служит
p{x,Y)(x,y) = -/=
*2
2 .
1
ч/2тг
*2 1 *2+ι/2
- е 2 = — ρ 2
2тг
Обозначим через R и Φ полярные координаты точки (Χ,Υ): Χ =
= RcosΦ1 Υ = RsmΦ. Используя формулу преобразования из П8
(якобиан замены равен г), находим плотность вектора (Д,Ф):
1 _ri
Р(Н,ф)(г,<р) = — е 2 г, г > 0, 0 < φ < 2тг.
Так как она распадается в произведение плотностей
_г2 ι
pR(r) = re 2 /{г>0} и рф(<р) = — /{0<ν?<2π})
то R и Φ независимы. Интегрируя плотности, вычисляем функцию
распределения Fr(t) = 1 — е~г /2 при г^Ои F<p(np) = φ/(2π) при
О < ν? ^ 2π.
Отсюда методом обратной функции получаем формулы для
моделирования случайных величин R и Ф: R = у^—2 In 771, Φ = 2π7/2,
которые только остается подставить в формулы замены
координат. ■
Задача 6 дает способ моделирования выборки из закона Коши
на основе датчика нормальных случайных чисел.
„=1 » = Ps»
^ η = 2
52
Глава 4. Показательные и нормальные датчики
§6. НАИЛУЧШИЙ ВЫБОР
Иногда приходится
полагаться на случай; ни
в чем нельзя быть вполне
уверенным в морском
сражении.
Г. Нельсон
Вопрос 5.
Почему при любом четном
η и m = n/2 вероятность
наилучшего выбора будет
не менее 1/4?
Сказка. В некотором царстве, некотором государстве жила-была
царевна. И приехали к ней свататься добры-молодцы, один другого
лучше. Заходили женихи в палаты царские по очереди да
кланялись царевне. Все бы хорошо, да вот беда — добры-молодцы уж
больно обидчивы! Коли сразу не давала своего согласия царевна,
садились на коня да и подавались восвояси. А ей-то о женихах
заранее ничего не ведомо, известно только, сколько всего их
пожаловало. Как тут царевне быть, как выбрать из них самого
достойного?
Вероятностная модель. Предполагая, что женихи
становятся в очередь в случайном порядке, будем считать, что
пространством элементарных событий (см. Ш) является множество всех
перестановок из η элементов: ω = (ii,...,in), где г& — различные
числа от 1 до п, а вероятностная мера — равномерная: ρ(ω) = 1/п!.
Удобно наглядно представлять перестановку в виде точек на
действительной прямой с координатами Χι,...,Χη, такими что Хк
находится правее Х^ если ik > Ц (см. [69, с. 15]). Точки появляются
одна за другой, и желательно остановиться на точке с наибольшей
координатой.
Обсуждение. Если царевна выберет первого «попавшегося»
жениха, то вероятность, что именно он окажется наилучшим, равна
всего лишь 1/п. Можно, пропустив га первых женихов (чтобы
осмотреться, какие вообще бывают женихи), затем остановиться
на том, кто понравится больше всех предыдущих, а если такого
не окажется —на последнем. Конечно, при этом не исключена
возможность упустить самого лучшего!
Оказывается, для произвольного η можно подобрать га£, при
котором эта вероятность будет больше, чем 1/е « 0,368.
Докажем это. Рассмотрим процесс появления точек Х{ на
прямой.*) Для следующей после первой точки имеются две
возможности—быть левее или правее (мы исключаем возможность
равноценных женихов). Вообще, после г-й точки имеется г +1
промежутков, куда может попасть следующая (г + 1)-я точка. Понятно,
что число всех возможных размещений равно 2 · 3 ·... · η = η!.
Предположим, что рассматриваемая стратегия приводит к
выбору к-й по счету точки (событие А*), к = га+1,... ,п. Такой выбор
означает, что все точки при г = га + 1,..., А: — 1 располагаются
левее крайней правой из первых пробных га точек, а к-я — правее
всех. На расположение первых га точек это не налагает никаких
ограничений, но для (га+1)-й точки имеется не га+1 промежутков,
а лишь га (она не может быть крайней правой), для (га+2)-й — лишь
*) Возьмите лист бумаги и карандаш и нарисуйте точки в соответствии с тем,
что написано ниже.
§ 6. Наилучший выбор
53
га+1 промежутков,..., для (к — 1)-й — лишь к —2 промежутков, для
к-й имеется единственная возможность — попасть правее всех
предшествующих, затем для (к + 1)-й имеется уже к + 1 промежутков
и т. д. Таким образом, при fc = m + l,...,n вероятность
_ 1-2·...-mm·...-(fc-2Hfc+l)·..
~ 1·2·3·...·η
P(^fc) 123·. ...η "(jfe-l)jfe·
Конечно, максимальная точка может попасть и в число
пропускаемых первых т. Обозначим это событие через Ат.
Пусть событие В означает остановку на максимуме. Рассмотрим
событие ВПАь, к = m+1,... ,η, состоящее в том, что остановка
произошла на А:-м шаге и привела к наилучшему выбору. Для случая,
когда fc-я по счету точка оказывается абсолютно максимальной,
для следующей (к + j)-Vl точки (j = 1,2,...,η — к) имеется не
к + j промежутков, куда она может попасть, а лишь к + j — 1 (она
не может попасть правее наибольшей). Это означает, что вместо
последних сомножителей (к + 1) ·... · η в формуле для Р(Ак) надо
взять к ·... · (п — 1), что влечет равенство Ρ (Β Π Ак) = т/[п(к — 1)].
Пользуясь формулой полной вероятности (П7) для разбиения
Ак, к = т,...,п, находим вероятность выбора «наилучшего
жениха» при заданном т:
Рт(в)= Σ Р(впАк) =
к=т+1
к=т К
Обозначим через т£ то значение т, при котором Рт(В) будет
наибольшей. В следующей таблице, взятой из [9, с. 38], для некоторых
значений η приведены соответствующие числа т£ и р^ = Рт* (В).
η
ГПп
Рп
2
0
0,5
3
1
0,5
4
1
0,458
5
2
0,433
7
2
0,414
10
3
0,399
20
7
0,384
50
18
0,374
100
37
0,371
1000
368
0,368
Можно доказать, что р^ убывает с ростом п. Из неравенства
η
т п^ 1 т Г dx _ т , т т п^ 1
И khm Ь^+ϊ ^^J^"~ ^ П^ ^ ^ к=тЬ
т
и того, что функция f(x) = —x\nx имеет максимум в точке
х* = е"1, вытекает, что р£ —► /(#*) = е-1 « 0,368.
Таким образом, предложенная стратегия является
оптимальной (в смысле максимума вероятности сделать наилучший выбор),
когда количество пропускаемых женихов приблизительно равно
целой части числа п/е.
В заключение отметим, что если ΑΊ,... ,ХП — выборка из
равномерного распределения на [0,1] (или, в силу метода обратной
функции,—из любого непрерывного распределения), благодаря тому,
54
Глава 4. Показательные и нормальные датчики
что Х{ ограничены сверху 1, существует стратегия, при которой
остановка на максимуме происходит с вероятностью не менее 0,58
(см. [9, с. 60]).
ЗАДАЧИ
Навык мастера ставит. 1. Пусть случайная величина Ζ имеет плотность Komu pz(x) =
= — ~-. Получите формулу для моделирования выборки из
7Г(1 +Х )
этого распределения методом обратной функции.
2. Выясните, к какому закону «притягивается»
а) максимум,
б) минимум выборки из показательного распределения с
функцией распределения F(x) = 1 — е~х при χ ^ 0.
Указание. Запишите функцию распределения минимума
и подберите ап и Ьп.
3. Докажите утверждение 3.
4* Пусть Δ(!) = πιίη{Δι,... ,Δη+ι}, где Δ& — k-ft спейсинг выборки
из равномерно распределенных на [0,1] случайных величин
(см. следствие в § 4). Установите на основе леммы 3 сходимость
распределения п2А^ при η —► оо к показательному закону
сА = 1.
Указание. Используйте свойства сходимости (П5) и закон
больших чисел (П6).
5? Для выборки τι,... ,тп из показательного распределения
а) убедитесь, что спейсинги Δ* = τ^) — T(i_i), г = 1,...,п,
независимы (здесь tq = 0);
б) найдите распределение минимального показательного спей-
синга.
6* Докажите, что если X и Υ — независимые ЛГ(0,1)-случайные
величины, то Ζ = Χ/Υ распределена по закону Коши.
Указание. Примените формулу преобразования плотности из
П8 при замене (Χ,Υ) -> (Χ/Υ,Υ).
РЕШЕНИЯ ЗАДАЧ
1. Прежде всего, вычислим функцию распределения случайной
величины Ζ:
χ
Fz(x) = - —^-2 =J + -arctg:z.
7Г J 1 + и * π
—оо
Отсюда получаем искомую формулу для моделирования
*г = tg[7T(j/< - 1/2)] = - Ctg(7H/i), (6)
где у ι — псевдослучайные числа.
Решения задач
55
2. а) Согласно теореме 1 для показательного закона с λ = 1 имеем:
Т(п) - Inn -+ f, где Ρ(ξ < χ) = exp {-e~x} (тип I).
б) Так как показательное распределение является частным
случаем закона Вейбулла—Гнеденко при α = 1, то предельный
закон для минимума выборки тщ также должен быть
показательным. Действительно, используя независимость и одинаковую
распределенность случайных величин т», г = 1,... ,п, запишем
η
Ρ(τ(ΐ) >αη + Ъпх) = Ц Р(т< > ап + Ьпя) = е-п<в»+ь-*>.
г=1
Взяв αη = 0 и Ьп = 1/п, видим, что случайная величина птщ
показательно распределена с λ = 1.
3. Для г = 0,1,..., 0^2/^1, д = 1—р = е-1 имеем:
При 2/ = 1 находим, что Р([т] = г) = дгр. Сложим вероятности
несовместных событий {[т] = г, {т} t^y}, г = 0,1,... ,η (Π7):
Р([т]< п, {т} < у) = ± (1-е"») £)«*? =
р »=0
= ^(1-е-»)Р([т]<п).
Устремляя здесь η —► оо, находим F{r}(2/) и, тем самым,
устанавливаем независимость случайных величин [г] и {г}.
4. Пусть (τι,... ,τη+ι) — показательная выборка с параметром λ =
= 1, £η+ι = τι + ... + τη+ι. Вектор равномерных спейсингов
(Δι,... ,Δη+ι) по лемме 3 распределен так же, как вектор
(Ti/Sn+i,... ,rn+i/Sn+i). Отсюда Δ(1) ~ Τ(ΐ)/5η+ι.
Согласно решению задачи 2, случайная величина тщ имеет
показательное распределение с параметром η +1. В силу закона
ρ
больших чисел (П6) Sn+i/(n + 1) —> Μτι = 1. Учитывая
непрерывность при χ > 0 функции φ(χ) = 1/х, из представления
„^ = |n/(„ + 1)f__|__(„ + 1)r(1)
по свойствам сходимости (П5) получаем в качестве предельного
закона показательное распределение с параметром λ = 1.
Доказанное утверждение также легко выводится из
следующего изящного результата Б. де Финетти (1964 г.): для
произвольных χι ^ 0,..., #η+ι ^ 0
Ρ (Δι > xu..., Δη+ι > χη+ι) = (1 - χι - ... - χη+ι)+,
где /+ = max{0, /}.*) Если положить h = χι =... = χη+ι, то
Ρ(Δ(1)>Λ) = [1-(η + 1)Λβ. (7)
*) Как его доказать, можно узнать из учебника [82, с. 57].
56
Глава 4. Показательные и нормальные датчики
Взяв h = χ/η2 для произвольного χ ^ О, видим, что правая
часть формулы (7) сходится к е~х при η —► оо.
5. а) Пусть для краткости λ = 1. С учетом ответа на вопрос 4
запишем плотность распределения вектора показательных
порядковых статистик:
η
^(г(1),...,г(п))(^Ь---^п) =п! Пе **> 0<^1 < ··· <^η·
г=1
Отсюда (аналогично следствию из § 4) по формуле
преобразования плотности (П8) для линейного отображения с якобианом 1,
находим плотность вектора спейсингов:
*>(*„....*.)(«ь · · · -u") = nl Пе-(и1+-+,ц) = nie_iUn+1_<
i=l i=l
в области {и: щ > О, г = 1,... ,п}. Таким образом, плотность
представляется в виде произведения плотностей. Поэтому
случайные величины Δ», г = 1,...,гг, независимы и показательно
распределены с параметрами η + 1 — г соответственно.
б) Используем этот результат для нахождения распределения
минимального спейсинга A(i) = min{Ai,. · · >Δη}·
η η
г=1 г=1
т. е. случайная величина Α(ΐ) распределена по показательному
закону с параметром п(п +1)/2. Ввиду свойств сходимости (П5)
отсюда следует, что предельным распределением для п2А^) при
η —► оо служит показательной закон с λ = 1/2.
6. Совместной плотностью независимых Л/"(0,1)-случайных
величин X и Υ является
, ν 1 _*£ 1 _Ζ Ι _*2+у2
Р(х,у,(зд) = ^е 27=е . =-е > .
Сделаем замену s = х/у, t = у. При этом якобиан
обратного преобразования равен t. Согласно формуле преобразования
плотности получаем
P(s,T)(*,t) = 1*1 P(x,Y)(*t,t) = \t\ — е" s 2 .
Интегрируя по ί, находим
2π J π(1+5 ) J π(1+5 )
-оо О
Другое доказательство вытекает из формул (5), периодичности
функции ctg и формулы (6) для моделирования Z:
X/Y = ctg(27TT72) ~ ctg (71772) ~ - ctg(^2).
Ответы на вопросы
57
ОТВЕТЫ НА ВОПРОСЫ
1. Если случайная величина η равномерно распределена на [0,1],
то 1 — η имеет, очевидно, такое же распределение. Поэтому для
моделирования можно использовать следующую формулу: Х{ =
= -jlnyi.
2. Возьмем Ъп = епСп, где 0 < сп —> оо при π —► оо. Для
любого χ > 0 при достаточно больших π выполняется условие
хепс" > е. Тогда Р(Х{п)/Ьп < я) = Р(Х{п) < хепс") =
= [1 - (псп + 1п#)_1]п —► 1 при η —► оо.
3. Для показательной случайной величины τ из формулы (2) при
α = 1 находим Мт = l/λ, Mr2 = 2/λ2, откуда
Dr = Mr2 - (Mr)2 = 2/λ2 - 1/λ2 = 1/λ2.
4. Вектор (£(ΐ),...,£(η)) получается из вектора равномерных
порядковых статистик (?7(ΐ),.. -,Щп)) с помощью преобразования
Xi = F_1(2/i), где F-1 (у)— обратная функция к функции
распределения элементов выборки. Очевидно, что якобианом об-
п
ратного преобразования служит J = J\ ρ{χι). Следовательно,
t=l
плотностью вектора порядковых статистик (£(i), · ·. ,£(п))
является функция
η
Р«(1),....*(п))(жь · · · ,яп) =п\ ]\р(хг) при χι <х2 <... <хп.
г=1
5. Обратим внимание на места в перестановке чисел η — 1 и п.
В том случае, когда число η — 1 попадает в первую половину
перестановки, а п — во вторую, рассматриваемая стратегия
приводит к наилучшему выбору. Из симметрии вероятность такого
расположения чисел η — 1 и η равна 1/4.
тация, моделирование.
Глава 5
ДИСКРЕТНЫЕ И НЕПРЕРЫВНЫЕ ДАТЧИКИ
§ 1. МОДЕЛИРОВАНИЕ ДИСКРЕТНЫХ ВЕЛИЧИН
Начнем с рассмотрения общего метода моделирования реализации
Simulation (англ.) —ими- #ι,...,#η выборки (£ι,...,£η) из произвольного дискретного
распределения. Положим pk = Ρ(£ι = с*;), к = 1,2,.... Разобьем
отрезок [0,1] на части длины рк и обозначим через гт сумму
т
Σ Рк (^о = 0). Если псевдослучайное число yi (см. гл. 2) попадает
к=1
в промежуток (τ^-ι,τ^·], то полагаем ж* = Cj (рис. 1).*)
Этот метод на самом деле является методом обратной функции
(см. § 1 гл. 4), если определить F~l(y) = inf {χ: F(x) ^ у} (рис. 2).
Для некоторых дискретных случайных величин можно
предложить специальные (более простые или более быстрые) датчики.
— -ц- ·? Так, для моделирования случайной величины ι/, имеющей геомет-
\)Pj у~ ^х' рическое распределение: pk = P(f = к) = (1 — р)кр, к = 0,1,...,
-*—^ достаточно подсчитать число «неудач» до первого «успеха» в схеме
Бернулли. Другой пример дает биномиальный закон.
1 +
ri-i + f
Xi = F-l(yi)
Определение. Случайная величина Zn имеет биномиальное рас-
Рис· 2 пределение с параметрами η и ρ (η = 1,2,...,0 ^ ρ ^ 1), если
Ъ{к,п,р) = Ρ(Ζη = к) = С*р*(1 -р)п~\ к = 0,1,...,η (рис.3).
(Здесь Ск = п\/[к\(п — к)\\ — число сочетаний из η по к).
{ ,η,ρ) Способ моделирования случайных величин с таким распределе-
~щ нием основан на следующем утверждении.
пР & п Утверждение 1. Пусть Ci?C2? · · · — схема Бернулли с вероятностью
Рис. 3 «успеха» р. Тогда число «успехов» в η испытаниях Ζη = ζι +... + ζη
имеет биномиальное распределение.
Доказательство. Докажем его по индукции, используя
непосредственно проверяемое тождество С^-1 + Ск = С^+1. В силу
леммы о независимости из § 3 гл. 1, случайные величины
*) В частности, для бернуллиевской случайной величины получаем способ
моделирования, предложенный в ответе на вопрос 2 гл. 2.
§ 1. Моделирование дискретных величин
59
Zn = Ci + · · · + ζη и Cn+i независимы. Поэтому
6(fc,n + Ι,ρ) =
= Ρ(Ζη = k) P(Cn+i = 0) + P(^n = k - 1) P(Cn+i = 1) =
= Σ cj-y-^i -p)n-fc+V(i -p)1_i =
i=0
= (^ + C*-1)pfe(l-p)"+1-fe. ■
На основе утверждения 1 с помощью свойств математического
ожидания и дисперсии из П2 получаем, что MZn = пр и DZn =
= пр(1-р).
Определение. Случайная величина N имеет распределение
Пуассона с параметром λ > 0, если для к = 0,1,...
р(к,Х) = Р(ЛГ = fc) = ^ e~\
Рисунок 4 дает представление о поведении ρ(λ;,λ) при λ > 1.
Легко вычислить математическое ожидание закона Пуассона:
оо оо \fc—1
Вопрос 1.
К какому предельному
закону сходится при п-юо
(Zn-np)/y/np(l-p)7
(Здесь вероятность
р€ (0,1) и не зависит
от п.)
С. Пуассон (1781-1840),
французский физик
μν=ς кР(к,\) = \ ς τπΰ
fc=l k=l V*- Ч1
= λ.
Замечание 1. Пуассоновское распределение получается
предельным переходом из биномиального при η —► оо, ρ —► 0, пр —► λ:
6(fc,n,p) = ^^^
_ Μ*
fc!
fe!
(1-рГ
(n-fc + l)pfc(1_p)n_fc =
[О":)--!'-^)»-')-
и математик.
Τ ^^Йи"^(^'А)
^
Е1 | |
0 λ к
Рис. 4
где (1— р)п —► е , а выражение в квадратных скобках стремится
к 1. Пуассоновское приближение биномиального распределения при
больших η и малых ρ иногда называют законом редких событий.
Для моделирования пуассоновской выборки понадобится
Утверждение 2. Пусть η,Τ2,... — независимые показательно
распределенные с параметром λ случайные величины. Положим 5П =
= τι + ... + τη, Ν — число значений 5η, η = 1,2,..., на отрезке
[0,1]. Тогда случайная величина N имеет распределение Пуассона
с параметром λ.
Доказательство. Согласно лемме 1 гл. 4 случайная величина
5η ~ Γ(η,λ), т.е. плотностьpsn(х) = Хпхп~1е~Хх/(п — 1)! при χ > 0.
Дифференцированием нетрудно проверить, что соответствующей
этой плотности функцией распределения является
FSn (x) = l- e~Xx "ff {\хУ/г\ при χ > 0. (1)
г=0
Вопрос 2.
Чему равна DAT?
а) Угадайте.
б) Вычислите.
60
Глава 5. Дискретные и непрерывные датчики
Sn 1 s
Рис. 5
Положим So = 0. Тогда с учетом положительности τη+ι находим
Р(ЛГ = п) = Р(5п<1,5п+1>1) = Р(5п^1)-Р(5п+1^1) = ^е-\
что и требовалось установить.
Докажем утверждение 2 другим способом. Для η ^ 1 запишем
равенство
Р(ЛГ = п) = Р(0 < 5η < 1,τη+ι > 1 - Sn).
Поскольку 5П и τη+ι независимы, их совместная плотность имеет
вид P(Sn,Tn+i)(*»t) = Psn(5)Prn+1(*)· Проинтегрируем ее по
множеству {0 ^ s ^ 1, t > 1 - s} (рис. 5):
1 оо 1
Р(ЛГ=п)=| | pSn(e)pTn+1(i)iftde=JpSn(e)P(rn+i>l-e)de=
0 1-s
J (n-1)!
.-1е-А..е-А(1-.)Л =
\ η
(n-1)
J'-1*-*
,-λ
Так как ζ Ρ(^ = η) = 1, то
η=0
P(jv = о) = ι - Σ ?(N = n) = e~A. ■
71=1
На основе утверждения 2 и метода обратной функции (см. § 1
гл. 4) получаем формулу для моделирования пуассоновских
случайных величин:
щ = min < к ^ 0: \\yij < е λ > ,
где yij — псевдослучайные числа (г = 1,2,...; j = 0,1,...).
§2. ПОРЯДКОВЫЕ СТАТИСТИКИ И СМЕСИ
Для выборки (ϊ7ι,...,ϊ7η) из равномерного распределения
на [0,1] найдем распределение к-й порядковой статистики щк)
(см. § 4 гл. 4).
Утверждение 3. FVk)(x) = £ Сгпх{(1 - х)п~\ 0 ^ х ^ 1.
г=к
77(i) Щк) У(г) У(п) Доказательство. «Успехом» будем называть попадание точки
0 х 1 ^ левее х (рис. 6). При этом случайные величины ζ* = I{Vi^.x}
Рис. 6
образуют схему Бернулли с ρ = ж, а число «успехов» имеет
биномиальное распределение. Другими словами, вероятность того,
что β точности г из η точек попадут левее (и, следовательно,
§ 2. Порядковые статистики и смеси
61
η — г точек правее) #, равна С^#г(1 — х)п~г. Но Р(г7(А:) ^ ж) —это
вероятность того, что по крайней мере к точек окажутся слева от
χ (г = /с,к + 1,... ,п). ■
Дифференцированием функции Fn{k) (x) вычисляем плотность:
рщк)(*) = Σ с*ахх*-\1 -х)п-<- Σ ση{η-ϊ)χ\ι-χ)»-*-1.
Так как последнее слагаемое во второй сумме равно нулю, запишем
Вопрос 3.
Какая функция
распределения у случайной
величины £(fc), если
компоненты выборки &
имеют непрерывную
функцию распределения F
>унк-
п-1
п—1—г
*!<*>(*) = Σ «^ ar-^l - *)п- - Σ ηΟ_! х»(1 - *)
Все слагаемые в первой сумме, кроме первого, сокращаются:
p4w(x)=nC*Z11xfc-1(l-x)n-*. (2)
Поскольку (п — 1)! = Г(п), из (2) и формулы (10) гл. 3 выводим при
0 < χ < 1, что
W*) = B(fc,n.fc + 1)* Μ1-*)
\П—fc
Определение. Случайная величина f/ имеет бета-распределение
с параметрами г > 0 и s > 0, если ее плотность задается формулой
Ри{х) = щ^ ЯГ_1(1 " z)S-1J{0<a:<l}·
Графики на рис. 7 дают представление о плотности ри(х) при
разных значениях г и s. В частности, при г = s = 1 бета-
распределение сводится к равномерному распределению на [0,1].
Другим частным случаем (при г = s = 1/2) является арксинус-
распределение с функцией распределения F(x) = - arcsin yfx на [0,1].
Оно возникает в качестве предельного закона для времени, в течение
которого находился в выигрыше первый из двух равных по силам
η
игроков: δη = Σ ^{5fc_i^o,5fc^o}, где Sk = Χι + ... + Xk, случайные
fc=l
величины Xi независимы, P(Xi = — 1) = Р{Х% = 1) = 1/2, г = 1,2,....
Тогда Ρ(δη/η ^ х) —► -F(x) при η —► оо (см. § 4 гл. 16).
Так как F(0,976) « 0,9 (рис. 8), то в среднем β каждом пятом
случае один из игроков будет лидировать на протяжении не менее
97,6% времени игры.
Легко подсчитать момент к-го порядка бета-распределения:
ι
шк = -^—, \xk+*-l(i - χ)'-1** = B{rJk:s).
B(r,s) J B(r,s)
(3)
62
Глава 5. Дискретные и непрерывные датчики
Рис. 9
Вопрос 4. _
Можно ли F(x)
представить в виде смеси
с положительными
весами других функций
распределения?
Вопрос 5.
Почему в этом примере
оо
fc=0
С. Η. Бернштейн
(1880-1966), российский
математик.
К. Вейерштрасс
(1815-1897), немецкий
математик.
Для того чтобы познакомиться с еще одним методом
моделирования (так называемым методом суперпозиции) потребуется ввести
понятие смеси распределений.
Определение. Пусть рк ^ 0, Y^Pk = 1, F^ (ж) —некоторые
к
функции распределения. Тогда функция распределения F(x) =
= J2pkFk(x) называется смесью распределений Fk(x) с весами рк-
Пример 1. Функция F{x), приведенная на рис. 9, представляет
собой смесь с весами 1/2 функций распределения F$(x) = I{x^i]
(т. е. ξ = 1с вероятностью 1) и Fv(x) случайной величины г/,
равномерно распределенной на отрезке [0,1].
Для моделирования случайной величины, функция
распределения которой является смесью, используется основанный на
формуле полной вероятности (П7)
Метод суперпозиции
1) Разыгрывается значение дискретной случайной величины,
принимающей значения к = 1,2,... с вероятностями рк (см. § 1).
Обозначим полученное в результате розыгрыша значение через ко.
2) Моделируется случайная величина с функцией
распределения Fk0 (x) некоторым способом (скажем, методом обратной
функции из § 1 гл. 4).
Пример 2. Пусть ξ распределена на [0,1] с плотностью р$(#),
оо
представимой в виде степенного ряда Σ акХк с а^ ) 0 ([29,
fc=o
оо
с. 20]). Положим рк = ак/(к + 1). Тогда р$(х) = £) Рк (к + 1)хк.
к=0
Но случайная величина Щк+i) = max{77i,... ,77fc+i}, где щ
независимы и равномерно распределены на [0,1], обладает плотностью
Рщк+1) (х) = (к +1) хк (см. задачу 3 гл. 1), т. е. Щк+i) имеет
бета-распределение с параметрами r = fc + lns = l, и для моделирования
ξ можно применить метод суперпозиции.
К сожалению, рассмотренный подход нельзя использовать, если
среди коэффициентов а& есть отрицательные. Однако для
непрерывных плотностей можно предложить способ приближенного
моделирования, основанный на аппроксимации их полиномами Берн-
\п—к
штейна
fn(x)=tf(^)ckxk(i-xY
Теорема Вейерштрасса. Если функция f(x) непрерывна на
отрезке [0,1], то fn(x) —► f(x) равномерно по χ при η —► оо.
Доказательство. Известно, что всякая непрерывная на отрезке
[0,1] функция ограничена: \f(x)\ ^ Μ < оо (см. [45, с. 193]). Кроме
§ 2. Порядковые статистики и смеси
63
того, она является равномерно непрерывной: для всякого ε > О
найдется δ > О такое, что \f{x) — f(y)\ ^ ε, коль скоро \х — у\ ^ δ
(см. [45, с. 446]).
Пусть Ζη — количество «успехов» в η испытаниях Бернулли
с вероятностью «успеха» х. Обозначим для краткости через рк
биномиальную вероятность 6(λ;,η,#) = Ρ(Ζη = А:), т. е.
Рк = С*хк(1-х)п-\ к = 0,1,..., п.
Отметим, что в силу теоремы о замене переменных (П2), полином
Бернштейна fn(x) равен M/(Zn/n).
Используя неравенство Чебышева (П4), получаем
.-х1>лг VIп I / η δ ηδ
ϊ*>*
Αηδ2
{fc:|±-x|>*}
Отсюда выводим равномерную по χ Ε [0,1] оценку погрешности
приближения:
\№-fn(x)\ = \£[f(x)-f(%)]Pk\
< Σ \f(x)-f(£)\pk+ Σ \f(x)-f(^)\pk<
{fc:|t-|<*} {*:|4-|>*}
Переход к пределу при ε-^Оип-^оо завершает доказательство.
Следствие. Непрерывную на отрезке [0,1] плотность f(x) можно
равномерно приблизить плотностями, в качестве которых годятся
нормированные полиномы Бернштейна
ι
fn(x) = fn(x)/dn, где dn = fn(x) dx.
В самом деле, из равномерной сходимости fn(x) к f(x) вытекает,
11 _
что dn = J* fn(x) dx —► J* /(ж) <£r = 1, т. е. /n(#) —► f(x) равномерно,
oo _ _
Для моделирования случайной величины ξη с плотностью /п(#)
методом суперпозиции представим нормированный полином fn(x)
в виде смеси:
Ш = Σ /Щт [(» + 1) С* **(1 - *)-fc], (4)
fc=0 "nV71 "г а;
где в квадратных скобках стоит (см. формулу (2)) плотность
(к + 1)-й порядковой статистики для выборки размера η + 1 из
64
Глава 5. Дискретные и непрерывные датчики
Дж. фон Нейман
(1903-1957),
американский математик.
равномерного распределения на [0,1]. Из формулы (4)
интегрированием получаем, что
При больших η равномерные порядковые статистики разбивают
отрезок [0,1] на примерно равные по длине части, так что
приближенное моделирование случайной величины ξ с плотностью f(x)
методом суперпозиции, основанное на формуле (4), по существу
является заменой ξ на дискретную случайную величину, принима-
k .(k\
ющую значения - с вероятностями, пропорциональными / - .
η \п/
§3. МЕТОД НЕЙМАНА (МЕТОД ИСКЛЮЧЕНИЯ)*)
Предположим , что случайная величина ξ распределена на отрезке
[а,Ь], причем ее плотность ограничена: max Ρξ(χ) = С < оо.
хе[а, Ь]
Случайные величины 171,772,... — независимы и равномерно
распределены на [0,1], Х{ = а + (Ь - α)η2ί-ι, У% = Сщ% (i = 1,2,...).
Таким образом, пары (Xi,Yi) независимы и равномерно
распределены в прямоугольнике [а, Ь] χ [0, С] (рис. 10). Обозначим через
ν помер первой точки с коордипатами (А"*,!*), попавшей под
график плотности Ρξ(χ), т. е. ν = min{z: Y\ ^ p^(Xi)}. Положим
оо
Xv — 2-jXrJ-{v=n\-
71=1
Утверждение 4. При выполнении приведенных выше условий
случайная величина Хи распределена так же, как £.
Доказательство. Пусть р — это вероятность попадания точки
(XiXi) под график плотности, q = 1 — р. Тогда вероятность
ρ = P(Yi ^ ρξ(Χι)) есть отношение площади под графиком
у = ρξ (χ) к площади прямоугольника:
]ρξ(χ)άχ
Р =
С{Ъ - а) С{Ъ - а) '
По формуле полной вероятности (см. П7) представим функцию
распределения Χν\
оо
FXv(x) = 9{Χν <ι)=ΣΡ(" = η,Χη ζ χ).
η=1
Принимая во внимание, что
{„ = η} = {Yi > pe(Xt),i = 1,... ,η - 1, Yn < ρξ(Χ„)},
) Материал этого параграфа не используется в дальнейшем.
§ 3. Метод Неймана (метод исключения)
65
и что события {Yi > ρξ(Χί),ι = 1,...,п-1} и {Υη ^ρξ(Χη)1Χη < χ}
независимы согласно лемме из § 3 гл. 1, получаем (см. рис. 10):
FX„(*) =
С»
= Σ P(Yi>Pt(Xi),i = l,...,n-l,Yn^pt(Xn),Xn^x) =
n=l
χ
= Σ qn-lP(Yn*iPdXn),Xn*ix)= Σ яп~1 α
η=1
οο
71=1
С(Ь-о)
Σ
fc
Pk
|Δ*|
Вопрос б.
Сколько в среднем точек
(Xi,Yi) потребуется
«вбросить» в
прямоугольник [a,b] χ [0,С]
для получения одного
значения ξ?
= Е«п_1[р*€(*)]=ад,
71=1
что и требовалось доказать. ■
В случае, когда площадь прямоугольника [a, b] х [0, С] значительно
превышает 1, время моделирования можно существенно
уменьшить, применяя модифицированный метод Неймана (расслоенную
выборку). Он состоит в разбиении [а, Ь] на отрезки Δ*, на каждом
из которых ρξ(χ) не намного отличается от Сk = max р$(х) (рис. 11).
хеАк
Тогда Ρξ(χ) представляется в виде смеси плотностей Д (ж):
Pt(x) = T,Pk Л (ж), где0<рь= p*(xdx, /fc(a?) = 5^ifi /Δ
fc J Pfc
Afc
Отсюда видим, что для моделирования случайной величины ξ надо:
1) разыграть номер отрезка разбиения А к с вероятностями рк\
результат розыгрыша обозначим через &о,
2) моделировать методом Неймана случайную величину с
плотностью Д0(х) ^ Ско/рко, бросая случайно точки в прямоугольник
Ак0 х [0, Ск0/рк0] до первого их попадания под график плотности
Д0 (х) или, что то же самое, в прямоугольник Ак0 χ [0, Ск0] до первого
попадания под график функции р^{х).
Из ответа на вопрос 6 и свойства 1 условного математического
ожидания (П7) следует, что среднее число бросаний будет равно
т.е. сумме площадей прямоугольников А к х [0,С&], которая при
измельчении разбиения стремится к 1, так как Ρζ(χ) — плотность.
Пример 3. Плотность показательной с параметром λ = 1
случайной величины г представляется в виде смеси (g = e_1,p = l — q):
оо оо
рТ(х) = е-х1[0,+оо)= Σ e"fce-(x-fc)/[fc,fc+1)= Σ (Якр) Р{т}(х~к)
к=0 к=0
(см. утверждение 3 гл. 4). Этот пример демонстрирует возможность
моделирования модифицированным методом Неймана случайной
величины, плотность которой имеет неограниченный носитель.*)
*) Носитель — множество, на котором плотность положительна.
66
Глава 5. Дискретные и непрерывные датчики
Замечание 2. Рассмотренный в § 3 гл. 4 способ
моделирования последовательности {т} без вычисления логарифмов,
является обобщением метода Неймана. Вместо бросания точек
в прямоугольник [α,6] χ [О, С] производится выбор случайных
точек r\i = (r7ii,?7i2> · · ·) из бесконечномерного единичного куба
/°° = [0,1] χ [0,1] х ... . Момент первого попадания под график
плотности Ρξ(χ), τ. е. в множество
{(х,у): a^x^b.O^y^ Ρξ(χ)},
заменяется на момент попадания в множество
Л = {у = (уьУ2, · · ·): У\ >Уч > · · · >Ук-1 <Ук,К четно} С/°°,
имеющее бесконечномерный объем ρ = 1 — е-1.
§4. ПРИМЕР ИЗ ТЕОРИИ ИГР
Представьте, что вам предложили принять участие в следующей
простой игре (см. [72, с. 54]). Одновременно со своим противником
вы называете одну из двух цифр— «1» либо «2» (поднимаете один
или два пальца). Если сумма названных цифр —четное число, то
вы выигрываете, а если нечетное, то проигрываете эту сумму.
Платежная матрица игры приведена на рис. 12. Стоит ли играть
на таких условиях?
Давайте разберем, к каким результатам приводят разные
стратегии в этой игре.
Прежде всего, заметим, что если бы вы сумели точно
предсказать следующую цифру противника, то смогли бы выиграть,
назвав такую же. Аналогичной возможностью играть в противофазе
обладает и противник. Поэтому обоим игрокам надо применять
случайные стратегии.
Однако, совершенно случайно (например, подбрасывая монету)
называть «1» или «2» игрокам также нет резона, так как в этом
случае их средний выигрыш равен +2 — 3 — 3 + 4 = 0 (говорят, что
игра имеет «нулевую сумму»).
Давайте сыграем! Ниже приведена последовательность из «1»
и «2», названных противником без учета вашего поведения.
Закройте эти цифры листком бумаги и, постепенно сдвигая его
вправо, попытайтесь угадывать следующую цифру. Запишите свои
выигрыши и проигрыши в соответствии в платежной матрицей,
изображенной на рис. 12, и подсчитайте итог.
21221211121121122112
Удалось победить? На самом деле эта игра выгодна для
противника: используя приведенную ниже стратегию, он сможет при
достаточно большом числе партий вас разорить!
Действительно, если вы называете «1» с вероятностью р\
и «2» с вероятностью 1 — pi, а противник —с вероятностями рг
Добрый пример лучше ста
слов.
(\
\ё
[*
4
+2
-3
Т|
-3
+4
/
Рис. 12
Вопрос 7.
Допустим, что противник
все же решил называть
«1» и «2» равновероятно,
невзирая на ваше
поведение. Как'вам
следует играть в таком
случае?
Задачи
67
и 1— р2> соответственно, то средний выигрыш за партию Ζ(ρι,ρ2) =
= +2ριρ2 - 3ρι(1 - Р2) - 3(1 - pi)p2 4- 4(1 - ρι)(1 - p2) = 12pip2 -
- 7pi - 7p2 + 4.
Поверхность 2 = Z(pi,p2) является гиперболическим
параболоидом («седлом»), в сечении которого плоскостью р% = 7/12
получается прямая, параллельная оси абсцисс: Ζ(ρι,7/12) = —1/12
(рис. 13). Таким образом, если противник называет «1» с
вероятностью 7/12 « 0,583 и «2» с вероятностью 5/12 « 0,417, то независимо
от значения pi вы будете в среднем проигрывать 1 за каждые 12
партий.
Приведенная выше последовательность из «1» и «2» была
получена с помощью последнего столбца таблицы случайных чисел Т1
в соответствии с оптимальной стратегией противника: если
очередное число в столбце меньше или равно 58, то записывалась «1»,
иначе— «2».
Однако, чтобы в серии независимых игр выиграть
определенную небольшую сумму 5 (скажем, S = 20) с вероятностью близкой
к 1, противнику потребуется вовсе не 125 (= 240) партий, а намного
больше (см. задачу 5).
Вопрос 8.
Допустим, что вам
известно значение до и то,
что противник не станет
его менять, как бы вы не
играли. Какой стратегии
следует придерживаться
в такой ситуации?
Рис. 13
Медленно, но верно.
IV, И
ЗАДАЧИ Счастье в том, чтобы без
^ помех упражнять свои
„ _ способности, каковы бы
1. Для равномерной порядковой статистики η^) сравните точку они ни были.
Максимума ПЛОТНОСТИ (так Называемую МОду распределения) Аристотель, «Политика»,
и Мщк).
2. Чему равно математическое ожидание случайной величины ξ
с функцией распределения F(x) из примера 1?
3. Пусть случайные величины X ~ Г(г,А) и Υ ~ Γ(θ,λ)
независимы. Проверьте, что тогда Χ/(Χ+Υ) имеет бета-распределение
с параметрами г и s.
Указание. Примените формулу преобразования плотности
случайного вектора из П8.
4. Выборка 77ι,... ,г/п взята из равномерного распределения
на [0,1]. Используйте леммы 1 и 3 гл. 4 для доказательства того,
что при п —► оо имеет место сходимость пщк) —* Τ ~ Г(А:,1), где
Щк) ~ &-я порядковая статистика.
Указание. Используйте свойства сходимости (П5) и закон
больших чисел (П6).
5. Допустим, что в примере из теории игр противник играет по
оптимальной стратегии (рг = 7/12), а вы равновероятно
называете «1» и «2» (pi = 1/2). Сколько примерно партий потребуется
противнику для выигрыша S = 20 с вероятностью 0,975?
Указание. Для оценки вероятности используйте центральную
предельную теорему (П6) и таблицу Т2.
68
Глава 5. Дискретные и непрерывные датчики
РЕШЕНИЯ ЗАДАЧ
1. Дифференцируя правую часть формулы (2), нетрудно
установить, что плотность случайной величины η^) имеет
максимум в точке гпк = (к — 1)/(п — 1). Ito формуле (3) находим
Мщь) — к/(п + 1) (выбранные наудачу η точек разбивают
отрезок [0,1] на η +1 интервалов в среднем одинаковой длины).
Плотность случайной величины щк) симметрична плотности
величины 77(п+1_*.) относительно прямой χ = 1/2. При к < (п+1)/2
мода Шк < МЩк)^ распределение «скошено» влево (правый
«хвост» тяжелее). При к > (п+ 1)/2 —наоборот.
2. Μξ = JxF(dx) = iJxF€(dr) + \lxF„{dx) = \ + \ = |.
3. Используем тот же прием, что и при решении задачи 6 гл. 4:
а) дополним случайную величину Х/(Х + Y) до двумерного
случайного вектора;
б) найдем его плотность по формуле преобразования (см. П8);
в) проинтегрируем плотность по последней координате.
Пусть и = х/(х + у), г/ = χ + у. Обратное преобразование
задается формулами ж = ш/, у = ν — гш, 0 < м < 1, ν > 0.
Отсюда dx/du = ν, dx/dv = г/, dy/du = —ν, dy/dv = 1 — u
n\J\=v.
Р(^)М = щт (uv)r-1(v-t«/)e-1e-,\ 0<ti<l,v>0.
oo
, ч «r-1(l-u)»-1 f r+s_i _„, ur-1(l-u)s_1
0
4. Пусть (τι,... ,rn+i) — показательная выборка с параметром λ =
= 1, Sk = η + ... + 7>. По лемме 1 гл. 4 Sk ~ Г(А;,1).
В силу леммы 3 гл. 4 Щк) ~ Sk/Sn+i- Согласно закону больших
ρ
чисел (П6) Sn+i/(n+l) —-» Μ η = 1. Из непрерывности функции
φ{χ) = 1/х при χ > 0 и представления
п -А. = п ( 1
П Sn+i n + 1 V5„+i/(n + l)
используя свойства сходимости (П5), получаем Г(А:,1) в качестве
предельного распределения для случайной величины пщк)-
5. Приведем решение, следуя [79, с. 107]. При pi = 1/2 и рг = 7/12
размер выигрыша в одной партии Χι имеет не зависящее от г
распределение: он принимает значения —3,2,4 с вероятностями
1/2,7/24,5/24 соответственно. При этом μ = ΜΧι = —1/12,
σ2 = DXi = ΜΛ?-(ΜΛΊ)2 « MX? = (9·12+4·7+16·5)/24 = 9.
Поскольку |μ| = 1/12 значительно меньше, чем σ « 3, в одной
партии преобладает случайный разброс, а не снос. Однако, при
продолжительной игре систематический отрицательный снос
W
Ответы на вопросы
69
Рис. 14
μ = —1/12 в соответствии с усиленным законом больших
чисел неминуемо (почти наверное) приводит к уходу траектории
блуждания на —оо (рис. 14).
Насколько быстро происходит этот уход?
Обозначим через 5П = Χι + ... + Хп размер выигрыша за
η партий. Тогда в силу центральной предельной теоремы (П6)
при достаточно больших η
P(Sn < -20) = Ρ (^^ к =™=ϋ») * Φ (-*> + "/") ,
где Ф(х) — функция распределения закона ΛΓ(Ο,Ι). Из таблицы
Т2 находим, что 0,975 « Ф(1,96) « Ф(2). Отсюда получаем
квадратное уравнение для определения требуемого числа партий:
п/12—6<^п—20 = 0. Оно имеет положительный корень щ « 5600.
Таким образом, пройдет немало времени, пока проигрышная
тенденция перевесит случайные колебания 5П.
На большом пути и малая
ноша тяжела.
Игра не стоит свеч.
Софья в «Горе от ума»
А. С. Грибоедова
ОТВЕТЫ НА ВОПРОСЫ
1. Для центрированных и нормированных сумм бернуллиев- Ответа не хочу, я знаю
ских случайных величин в силу центральной предельной тео- ваш ответ
ремы (П6) предельным законом является ЛГ(0,1).
2. Так как при η —► оо, ρ —► 0, пр —► λ биномиальное распределение
стремится к пуассоновскому, то можно предположить, что и
дисперсии сходятся: lim np(l — ρ) = λ. Однако, в общем случае
п—юо
из сходимости по распределению (П5) не следует сходимость
дисперсий, поэтому вычислим DN непосредственно:
ОО \fc-2
Μ [Ν(Ν - 1)] = Σ *(* - 1)ρ(*,λ) = λ2 Σ (k _ 2)! -
ΟΛΓ = Μ [Ν(Ν - 1)] + ΜΛΓ - (ΜΛΓ)2 = λ2 + λ - λ2 = λ.
-λ _ \2
= У,
3. Учитывая непрерывность F(x), воспользуемся методом
обратной функции (см. § 1 гл. 4):
*€<*,(*) = Р (*<*) < х) = Р (Ftiw) < F(x)) =
= р (Щк) < f(x)) = Σ с;ад<(1 - f(x))»-\
i=k
70
Глава 5. Дискретные и непрерывные датчики
Доказательство
законности суммирования
(тауберовой теоремы)
приведено, например,
в [33, с. 57].
Можно. Например, F{x) = ~ F(x) + ~ F(x). С другой стороны,
разложение на дискретную и непрерывную составляющие
единственно (см. [12, с. 53]).
оо
Степенной ряд Ρξ(χ) = Σ a,kXk сходится на [0,1]. Поэтому
fc=o
можно почленно интегрировать на (0,1). Будучи функцией
распределения,
ад = ς ^γ
fc=0 Л + l
JH-l
1 при χ —► 1.
Так как коэффициенты этого ряда неотрицательны, то его
можно суммировать при χ = 1.
6. Согласно задаче 4 гл. 1 в среднем потребуется Mi/+1 = q/p+1 =
= Ι/ρ = С (b — α) точек.
7. Всегда называя «2», вы будете выигрывать больше (+4), чем
проигрывать (—3).
8. Надо максимизировать Ζ(ρι,ρ2) = Ρι(12ρ2 — 7) — 7рг + 4 по
Pi € [0,1] при фиксированном значении рг- Очевидно, что для
Р2 < 7/12, максимум достигается при pi = 0, а для рг > 7/12 —
при pi = 1.
Часть II
ОЦЕНИВАНИЕ ПАРАМЕТРОВ
Эта часть книги рассчитана в основном на студентов, изучающих
математическую статистику. Поэтому к большинству утверждений
и теорем приведены доказательства, что может оказаться
полезным при подготовке к экзамену. Рассмотрено много примеров, на
которых проясняется смысл важнейших понятий статистики. Тем
читателям, кто интересуется в первую очередь методами обработки
прикладных данных, можно сразу после просмотра §§ 1-2 гл. 6
перейти к части III.
Глава 6
СРАВНЕНИЕ ОЦЕНОК
Если у тебя спрошено
будет: что полезнее,
солнце или месяц? —
ответствуй: месяц. Ибо
солнце светит днем,
когда и без того светло,
а месяц —ночью.
Но, с другой стороны:
солнце лучше тем, что
светит и греет, а месяц
только светит, и то лишь
в лунную ночь!
Козьма Прутков
Хг
0?
10 20 30 40
Рис. 1
Вопрос 1.
Может ли это значение
равняться
а) 28, 6) 100?
Анализируемые методами математической статистики данные
обычно рассматриваются как реализация выборки из некоторого
распределения, известного с точностью до параметра (или
нескольких параметров). При таком подходе для определения
распределения, наиболее подходящего для описания данных, достаточно уметь
оценивать значение параметра по реализации. В этой главе будет
рассказано, как сравнивать различные оценки по точности.
§ 1. СТАТИСТИЧЕСКАЯ МОДЕЛЬ
Эксперимент. Пусть 0 — некоторое неизвестное положительное
число. Ниже приведены (с точностью до 0,1) координаты χι десяти
точек, взятых наудачу из отрезка [0,0].
3,5 3,2 25,6 8,8 11,6 26,6 18,2 0,4 12,3 30,1
Они были получены по формуле Хг = 0у^, г = 1,...,10, где у ι —
псевдослучайные числа (см. гл. 2). Попробуйте угадать значение
параметра 0 с помощью рис. 1, на котором изображены эти точки.
С формальной точки зрения в данном эксперименте мы имеем
дело со следующей моделью: набор Х{ — это реализация
независимых и равномерно распределенных на отрезке [0,0] случайных
величин Xi с функцией распределения
ад = <
0, если χ ^ 0,
ж/0, если 0 < χ < 0,
1, если χ ^ 1
(рис. 2). Здесь 0 Ε θ = (0, +оо) — неизвестный параметр масштаба.
Статистическая модель. В общем случае задается
семейство функций распределения {Fo(x), 0 Ε θ}, где θ —множество
возможных значений параметра; данные #ι,...,#η
рассматриваются как реализация выборки ΛΊ,... ,Хп, элементы которой имеют
функцию распределения F$0 (x) при некотором неизвестном значе-
§ 2. Несмещенность и состоятельность
73
нии 0о € Θ. Задача состоит в том, чтобы оценить (восстановить) 0о
по выборке #ι,... ,#п, по возможности, наиболее точно.
Те, кто знаком с методом обратной функции из § 1 гл. 4, могут
представлять себе задачу так: кто-то задумал 0о, а затем получил
реализацию по формуле #; = ^1(у»), где у* — псевдослучайные
числа (рис. 3). Как «угадать» задуманное значение, основываясь
на наблюдениях #ι,... ,#п?
Будем оценивать 0о ПРИ помощи некоторых функций 0 от η
переменных я ι,... ,#п.*)
Для приведенных выше данных эксперимента в качестве оценок
неизвестного параметра масштаба можно использовать, скажем,
θι = #(п) = max{#i,... ,#п} и 02 = 2 (#ι+.. .+хп)/п. Интуитивно
понятно, что при увеличении η каждая из оценок будет приближаться
именно к тому значению 0, с которым моделировалась выборка. Но
какая из них точнее? Каким образом вообще можно сравнивать
оценки? Прежде чем дать ответы на эти вопросы, познакомимся
с важнейшими свойствами оценок — несмещенностью и
состоятельностью.
§2. НЕСМЕЩЕННОСТЬ И СОСТОЯТЕЛЬНОСТЬ
Определение. Оценка 0(#ι,... ,#п) параметра 0 называется
несмещенной, если М# 0(Χι,... ,Хп) = 0 для всех 0 Ε θ.
Замечание. Важно, чтобы условие несмещенности выполнялось
для всех 0 £ Θ. Тривиальный контрпример: оценка 0(#ι,... ,#п) =
= 1, идеальная при 0 = 1, при других значениях 0 имеет смещение
Ь(0) = М0-0 = 1-0.
Иногда представляет интерес получение оценки не для самого
параметра 0, а для некоторой заданной функции φ(θ).
Здесь индекс θ у М#
означает, что имеется
в виду математическое
ожидание случайной
величины θ(Χι,...,Χη),
где Xi распределены
с функцией
распределения Fq(x). В дальнейшем
этот индекс будет
опускаться, чтобы
формулы не выглядели
слишком громоздко.
Пример 1. Для выборочного КОНТРОЛЯ ИЗ Партии ГОТОВОЙ ПрОДуК- 6: bias (англ.) — смещение.
ции отобраны η приборов. Пусть Χι,... ,ХП — их времена работы до
поломки. Допустим, что Χι одинаково показательно распределены
с неизвестным параметром 0: F$(x) = 1 — е~вх, χ > 0. Требуется
оценить среднее время до поломки прибора
оо оо
φ(θ) = МХг = θ ί χε~θχάχ = i f
ye
■Uy=\
Вопрос 2.
Будут ли несмещенными
определенные выше
оценки 01 и 02?
(Посмотрите решения
задач 2 и 3 из гл. 1.)
По свойствам математического ожидания (П2) выборочное среднее
X будет несмещенной оценкой для функции φ(θ): MX = φ(θ).
*) Предполагается, что функции являются борелевскими (см. П2). В частности,
годятся любые непрерывные функции 0(χι,... ,хп)·
74
Глава 6. Сравнение оценок
Замечание, ^сли в примере 1 попытаться оценить сам параметр 0
при помощи 0 = 1/Х, то получим смещенную оценку. Это следует
из строгой выпуклости функции φ(χ) = 1/х при χ > О и
неравенства Иенсена (см. П4). Несмещенная оценка для 0 приведена
в задаче 6.
Следующий пример показывает, что не всякую функцию φ
в заданной статистической модели можно несмещенно оценить.
Пример 2. Пусть элементы выборки Xi имеют распределение Бер-
нулли с неизвестной вероятностью «успеха» 0 Ε θ = (0,1):
P(Xi = 1) = 0, Р(Х{ = 0) = 1 - 0.
В этой модели при η = 1 нельзя несмещенно оценить φ(θ) = 1/0.
Действительно, условие несмещенности имеет вид
φ(0) (1-θ) + £(1)0 = 1/0.
При 0 —► 0 линейная функция в левой части стремится к <р(0),
а гипербола в правой — к бесконечности.
Пример 3. Рассмотрим выборку из какого-либо распределения
с двумя параметрами μ и σ, где μ = Μ Χι и σ2 = DXi (скажем,
нормального закона Λί(μ, σ2) из § 2 гл. 3). По свойствам
математического ожидания (П2) выборочное среднее X несмещенно
оценивает параметр μ. В качестве оценки для неизвестной дисперсии
φ(σ) = σ2 можно взять выборочную дисперсию
S2 =1-±{Хг-х? =1-±х* -х2. (1)
п г=1 п г=1
Вопрос 3.
юмнстаоЭ не приводя* Однако, оценка 52 имеет смещение. Действительно, так как
вычислений, а опираясь случайные величины Xi независимы и одинаково распределены,
глЛКи тео^му^замене то» применяя свойства математического ожидания (П2) на основе
переменных (П2)? формулы (1), получаем:
\пг=1 п i,j=l / п г=1 п г=1
- Α Σ MXi MXj = MX2 - - MX2 - —i (MXi)2 = 5^1 DXi.
n2 ^ ^ η η η
Чтобы устранить смещение, достаточно домножить 52 на п/(п-1).
В нормальной модели Ν (μ, σ2) можно несмещенно оценить само
стандартное отклонение σ с помощью оценки σ = Cn^/nS2/(n — l)
§2, Несмещенность и состоятельность
75
- гамма-
(см. [15, с. 29]), где сп = ]^Г (^—^ /т (|) , Г(х) -
функция Эйлера, определенная ранее в § 4 гл. 3. Отметим, что
с ростом η коэффициент сп довольно быстро убывает к 1:
η
Сп
2
1,253
3
1,128
4
1,085
5
1,064
10
1,028
20
1,012
50
1,005
Само по себе свойство несмещенности не достаточно для того,
чтобы оценка хорошо приближала неизвестный параметр.
Например, первый элемент Χι выборки из закона Бернулли служит
несмещенной оценкой для θ: ΜΧι =0·(1 — θ) + 1 · θ = θ. Однако,
его возможные значения 0 и 1 даже не принадлежат θ = (0,1).
Необходимо, чтобы погрешность приближения стремилась к нулю
с увеличением размера выборки. Это свойство в математической
статистике называется состоятельностью.
Определение. Оценка 0(#ι,... ,#п) параметра θ называется
состоятельной, если для всех θ Ε θ последовательность
θη = Θ(Χ\,... ,Χη) —► θ при η —► οο.
ρ
Здесь —► обозначает сходимость по вероятности (см. П5):
для любого ε > 0 Р(|0П — 0\ > ε) —> 0 при η —► оо.
Состоятельность оценки (а точнее — последовательности оценок
{^п}) означает концентрацию вероятностной массы около
истинного значения параметра с ростом размера выборки η (рис. 4).
Как установить, будет ли данная оценка состоятельной? Обычно
оказывается полезным один из следующих трех способов.
1) Иногда удается доказать состоятельность, непосредственно
вычисляя функцию распределения оценки (задачи 1 и 2).
2) Другой способ проверки состоит в использовании закона
больших чисел (П6) и свойства сходимости 3 из П5. (Так, оценка
θ = 1/Х из примера 1 будет состоятельной ввиду непрерывности
функции φ(χ) = 1/х при χ > 0.)
3) Часто установить состоятельность помогает
Лемма. Если смещение Ъп(в) = Μθη—Θ и дисперсия Οθη стремятся
к нулю при η —► оо, то оценка θ состоятельна.
Доказательство. По неравенству Чебышева (П4)
p(ifln-fli>g)<M(*;2~g)2·
Но
М(0„ - Θ)2 = Μ(θη - Μθη + Μθη -Θ)2 = Μ [(θη - Μθη) + Ьп(в)}2 =
= Οθη + 2 Ьп(в) Μ(θη - Μθη) + ЬЦв) = Οθη + ЪЦв). ■
П2>П\
У=РвП1(х)
76
Глава 6. Сравнение оценок
Кто не рискует, тот не
пьет шампанского.
Если используется
функция штрафа
р(и) = |и|, то риск
называют абсолютным,
а если р(и) = и2 —
квадратичным.
§3. ФУНКЦИИ РИСКА
Проблема. Как измерить точность оценки?
Пусть p(u) ^ 0 обозначает функцию штрафа (потерь) в том
смысле, что мы платим штраф ρ(θ — θ) за отклонение оценки
θ(χι,... ,#п) от истинного значения параметра Θ. Обычно р(0) = О
и р(и) возрастает с ростом \и\.
Определение. Функцией риска оценки θ называется
Щ{в) = Щф{Хи...,Хп)-в),
т. е. средняя величина потерь при оценивании θ с помощью Θ.
_1_
An
RxiO)
1/2
Рис. 5
Рис. β
Рис. 7
Ri(9)
J К
о' θ
Рис. 8
Т. Байес (1702-1761),
английский математик.
Пример 4. Вычислим квадратичный риск частоты X для схемы
Бернулли из примера 2. В силу несмещенности X и свойств
дисперсии %(0) = М(Х - Θ)2 = ЩХ - MX)2 = DX =
= n~2D(Xi + .. .+Хп) = n_1DXi = θ(1-θ)/η (дисперсия случайной
величины Χι была найдена в § 2 гл. 1). График функции ϋχ(θ)
(верхняя часть параболы) для θ G (0,1) приведен на рис. 5.
Как же сравнивать оценки? Можно считать ту оценку лучшей,
у которой риск меньше. Но риск —это функция от Θ. Каким
образом выбрать «наименьшую» из двух функций, скажем, таких,
как на рис. 6? (Что больше, синус или косинус?)
Рассмотрим три подхода к этой проблеме.
1) Минимаксный (осторожный) подход заключается в
сравнении функций по их наибольшему значению на множестве θ
(см. рис. 7): выбирается та оценка, у которой при самом
неблагоприятном значении θ риск меньше. Таким образом, при этом
подходе выбор оценки диктуется желанием избежать крупного
штрафа, если θ окажется вблизи точки максимума функции риска.
Однако, возможна ситуация, когда минимаксный подход
противоречит здравому смыслу (рис. 8). В подобных случаях более
разумным представляется
2) Байесовский (интегральный) подход: сравниваются два
интеграла, Д = jRi(9)dQ и /2 = J#2(0)c?Q, где Q — некоторая
мера на множестве Θ. В частности, когда θ — скалярный параметр
и Q — равномерная мера на Θ, лучшей при таком подходе считается
оценка, у которой меньше площадь под графиком функции риска.
Байесовскими в математической статистике называются
методы, при которых априорная информация о параметре, если
таковая имеется, формализуется в виде некоторого распределения Q
(не обязательно вероятностного) на параметрическом множестве θ
(см. [38, с. 168]). При этом, если Q — вероятностная мера (см. Ш),
на сам параметр θ можно смотреть, как на случайную величину.
В некоторых ситуациях предположение о случайности параметра θ
§3. Функции риска
77
выглядит весьма естественно: «природа» как бы разыгрывает
значение θ в соответствии с распределением Q перед моделированием
очередной выборки.
На практике можно оценить функцию распределения меры Q по
частоте появления θ в ранее проведенных экспериментах. Иногда из
соображений равной возможности всех значений θ априори полагают,
что Q — это равномерная мера на множестве Θ.
3) Ограничение множества оценок: для некоторых
статистических моделей существуют оценки, обладающие равномерно мини-
мольным риском в заданном классе оценок (рис. 9).
Так, в нормальной модели из примера 3 оценки μ = X
и σ·
2 _
nS2/(n — 1) имеют равномерно минимальную
дисперсию среди всех несмещенных оценок с конечной дисперсией
(см. [50, с. 83]). То же самое справедливо (см. [50, с. 75]) для частоты
X как оценки неизвестной вероятности «успеха» в схеме Бернулли
и для несмещенной оценки 0з = maxiXi,... ,ХП} = 0ι
η η
параметра масштаба 0 в модели равномерного распределения на
отрезке [0,0] из § 1.
Для последней оценки согласно задаче 3 гл. 1 имеем
V η ) η2 (η + 1)2(η+
1
_(п±}У_ η θ2 =
(η + 1)2(η+2) η(η + 2)
Ρ.
(2)
Отметим, что за устранение смещения максимума θ\ пришлось
заплатить увеличением дисперсии в ( — J раз. Ввиду задачи 2
гл.1 дисперсия D02 = 4DX = 02/(Зп). Отсюда находим, что
отношение D03/D02 = 3/(п + 2) ^ 1 и стремится к 0 при η —► оо.
Сравним точность этих оценок для данных эксперимента. На
самом деле выборка была получена умножением на 0о = 35 десяти
псевдослучайных чисел из первой строки таблицы Т1. Легко
вычислить, что 02(#ъ· · · ,#п) = 28,1 и 0з(жь...,жп) = 33,1. Значит,
оценка 0з в данном случае точнее, а значение 02 оказалось даже
меньше, чем хю = max{#i,... ,#п} = 30,1.
В заключение, обсудим проблему выбора функции штрафа.
Во многих статистических моделях существуют несмещенные оценки
с равномерно минимальным риском для любой выпуклой (П4)
штрафной функции (см. [50, с. 79]).
С другой стороны, реальные (например, финансовые) потери
всегда ограничены. Но ни одна ограниченная на (—оо, +оо) функция
р(и) φ const не может быть выпуклой. К сожалению, для
ограниченных штрафных функций (скажем, для р(и) = const ·1{\ν\>δ})ι как
правило, не существует несмещенных оценок не только с равномерно,
но и с локально минимальным риском (см. [50, с. 81]).
К счастью, для выборок большого размера ситуация упрощается.
Для гладкой функции потерь ее разложение в ряд Тейлора в нуле
Рис. 9
78
Глава 6. Сравнение оценок
Взирая на солнце,
прищурь глаза свои, и ты
смело разглядишь в нем
пятна.
Козьма Прутков
дает
ρ(θ' - 0) = α + 6(0' -0) + с(0' - 0)2 + ε,
где остаток ε пренебрежимо мал при достаточно малом |0' — 0|.
Условия р(0) = 0 и р(и) ^ 0 влекут, соответственно, равенства α = О
и Ь = 0. Следовательно, р(0' — 0) = с(0; — 0)2 + ε. Таким образом,
для состоятельных оценок 0 минимизация риска Мр(0 — 0) при
больших п, по существу, равносильна минимизации квадратичного
риска М(0 — 0)2 (т. е. не зависит от конкретного вида функции р).
Однако, оценки, наилучшие при квадратичной функции потерь,
часто бывают слишком чувствительными к выделяющимся
значениям элементов выборки (так называемым «выбросам»). Эту
проблему мы рассмотрим подробнее в главе 8 при обсуждении
устойчивости оценок к «выбросам».
0,17 0,83
Рис. 10
Не всякой сказке верь.
§4. МИНИМАКСНАЯ ОЦЕНКА
В СХЕМЕ БЕРНУЛЛИ
Как было отмечено выше, выборочное среднее X в схеме Бер-
нулли — несмещенная оценка вероятности «успеха» 0, обладающая
равномерно минимальной дисперсией. Однако минимаксной (име-.
ющей наименьший максимум риска) для квадратичного штрафа
является (см. [50, с. 228]) оценка Ходжеса—Лемана
ё=х+тт^Ц-х)
(3)
Давайте проведем эксперимент по сравнению точности оценок X
И в.
1) Задумайте вероятность «успеха» во £ (0,1).
2) Смоделируйте выборку размера η = 9 из распределения
Бернулли с помощью таблицы Т1 (см. вопрос 2 гл. 2).
3) Вычислите значения оценок и определите, какая из них
оказалась ближе к во.
Например, пусть во = 0,17. По первой строке в таблице Т1
получаем реализацию выборки: 1, 1, 0, 0, 0, 0, 0, 1, 0 (если
число в таблице меньше 17, то пишем «1», иначе— «0»). Для таких
_ 1 3
Xi находим, что χ = ц « 0,333 и в = ^ = 0,375. Видим, что в данном
случае частота оказалась точнее. А как у вас?
Если проводить этот эксперимент многократно (каждый раз
загадывая новое значение 0о)> то примерно в половине случаев
оценка в будет ближе к 0о> ч^м х. Но согласно изложенной ниже
«теории» такое, казалось бы, должно происходить намного чаще!
Действительно, из рис. 10, на котором приведены графики
квадратичных рисков при η = 9 оценок X и в (см. задачу 4), следует,
что доля тех в, при которых Я§(в) < Λγ(0), равна примерно
0,83 — 0,17 = 0,66. Почему же на практике оценка в обычно
выигрывает лишь в 50% случаев?
Задачи
79
Объяснение. Дело в том, что, сравнивая X и 0, мы смотрим,
значение какой из них оказалось ближе к 0о, а не платим
квадратичный штраф за погрешность оценивания параметра 0о-
Другими словами, средний выигрыш в пари при ставке С на
оценку 0 равен_Ср((9) + (-С)[1 - р(0)] = 2С \ρ(θ) - 1/2], где ρ(θ) =
= Р(|0 - 0| < \Х - 0|). Игра выгодна, когда ρ(θ) > 1/2.
Функция ρ(θ) симметрична относительно 1/2. Нетрудно
вывести, что при ^ ^ 1/2
№
= 1-р(££<х<з)' где^ =
4(1 + ^п)
Ее можно вычислить, используя то, что случайная величина пХ
имеет биномиальное распределение (см. утверждение 1 гл. 5).
Предполагая равномерность выбора значения 0о из [0,1]
(байесовский подход), заметим, что при η = 9 площади над и под
уровнем 1/2 графика ρ(θ) на рис. 11 отличаются всего на 0,008.
Похожая ситуация возникает при оценке параметра сдвига μ
в нормальной модели Х% ~ ΛΓ(μ, σ2) с известным параметром
масштаба σ. Эта модель может использоваться для измерений, точность
которых заранее известна. В ней выборочное среднее X будет не
только несмещенной оценкой с равномерно минимальной дисперсией,
но и минимаксной оценкой для квадратичного риска. Тем не менее,
существует такая оценка Д, что Р(|Д — μ\ < \Х — μ\) > 1/2 при всех μ.
Эта оценка выглядит так:
μ = Χ- -1= sign(X) min{y/K\X\/c, Φ{-^\Χ\/σ)} ,
где Ф(х) —функция распределения закона ЛГ(0,1) (см. [15, с. 14]).
На хорошее всегда
найдется лучшее.
ЗАДАЧИ
1. Для случайных величин Х{ г = 1, ...,п, взятых^ наудачу из
отрезка [0,0], докажите состоятельность оценки θ ι = Χ(η) =
= max{Xb...,Xn}
а) непосредственно из определения,
б) применяя лемму из § 2.
2. ,Д[ля статистической модели из задачи 1 проверьте, что оценка
04 = (п + 1) Х(1), где Х(1) = min{Xb ... ,ХП},
а) не имеет смещения,
б) не является состоятельной.
3. Придумайте какую-нибудь несмещенную и состоятельную
оценку для параметра 0 в модели сдвига показательного
распределения (см. рис. 12)
Fb(x)
-{;
_ €-(χ-θ)
при χ > 0,
при χ ^ 0.
80
Глава 6. Сравнение оценок
4. Вычислите смещение, дисперсию и квадратичный риск
минимаксной оценки Ходжеса—Лемана в схеме Бернулли (см.
формулу (3)).
5. Для схемы Бернулли при η = 3 нарисуйте график абсолютного
риска X. Будет ли эта функция
а) непрерывной,
б) гладкой?
6. Для показательной выборки ΧΊ,... ,ХП из примера 1 положим
5П = Х\ + ... + Хп. Установите несмещенность оценок
а) 0 = (η — 1)/5п для параметра 0,
б) φ = (1 — t/Sn)n~ I{sn>t] Для функции надежности φ(θ) =
= Ρ(Χι > t) = е"**, где ί"> 0.
Указание. Примените лемму 1 гл. 4 и теорему о замене
переменных (П2).
7* Для модели из задачи 1 сравните дисперсии несмещенных
оценок 03 = ^— Х(П) и 05 = Χ(ΐ) + Х(п)·
Указание. Найдите функцию распределения F(x1y) и
плотность р(х,у) вектора (Х(!),Х(П)) и вычислите математическое
ожидание МХщХ(п) = J" J ху p(x,y)dxdy.
РЕШЕНИЯ ЗАДАЧ
1. а) Ввиду задачи 3 гл. 1 Fx(n)(x) = (χ/θ)η при 0 ^ χ ^ 0.
Поскольку Р(Х(П) ^ 0) = 1, Для любого ε из (0,0) имеем
Pflfli - 0| > ε) = Р(Х{п) ^ θ - ε) = (1 - ε/θ)η -> 0
при η —► οο.
б) Из той же задачи Μ0ι = —► 0 и D0i = -~- г -*0.
' ^ п + 1 (п + 1)2(птЬ2)
2. а) Очевидно, что случайные величины Х[ = 0 — Х^ г =
= 1,... ,п, также образуют выборку из равномерного
распределения на отрезке [0,0]. Поэтому случайная величина XL* =
= min{X{,... ,Χ^} = 0 - X(п) распределена так же, как
Χ(ΐ). Отсюда с учетом решения предыдущей задачи получаем
МХ{1) = 0 - МХ{п) = 0 - п0/(п + 1) = 0/(п + 1).
б) Используя независимость случайных величин Х^, находим,
что при η —+ оо
ρ(^>^+ε) = Πρ(^>^τ) =
V θ{η+\))
3. Рисунок 12 подсказывает взять Χ^ι) = πάα{Χ\,... ,Хп} в
качестве состоятельной оценки параметра сдвига. Поскольку
Решения задач
81
Ρ(Χ(ΐ) > 0) = 1, эта оценка имеет смещение. Вычислим его.
Для Δ = X(i) — 0 в силу независимости величин Х^ находим:
Ρ(Δ > χ) = Ρ(Χι > χ + 0) ·... · Ρ(Χη > χ + 0) = e"na\
Иными словами, случайная величина Δ имеет показательное
распределение с параметром п. С учетом ответа на вопрос 3
гл. 4 получаем ΜΔ = 1/п и ϋΔ = 1/п2. Следовательно,
0 = Х(!) — 1/п —несмещенная и состоятельная (в силу леммы
из § 2) оценка.
Другим решением задачи может служить несмещенная
оценка X — 1 (случайные величины Χι — Θ показательно
распределены с параметром 1). Ее состоятельность вытекает из закона
больших чисел (П6) и свойств сходимости (П5).
4. Минимаксную оценку 0 можно записать так:
0 = (1-εη)Χ + (1/2)εη, где еп = 1/(1 + у/п). (4)
Поскольку MX = 0 и DX = 0(1 — 0)/п, по свойствам из П2
смещение 6(0) = М0 - 0 = (1/2 - 0) εη, D0 = (1 - εη)2 DX =
= (1 — εη)20(1 - θ)/п. Таким образом, 0 —смещенная, однако
состоятельная (в силу леммы из § 2) оценка.
Квадратичный риск 0 легко найти по формуле, полученной
при доказательстве леммы: R§(0) = D0 + Ь2(0) = 1/[4(1 + \/п)2].
Замечание. Так как %<1/2) = 1/(4п), то Щ{в) < Д^(0)
в некоторой окрестности точки 1/2 при любом η (см. рис. 10).
Поэтому для достаточно близких к 1/2 значений параметра θ
оценка 0 предпочтительнее. Это и понятно: ввиду формулы (4)
она, являясь «взвешенным средним» X и 1/2, подправляет
оценку Х1 притягивая ее к 1/2.
5. Приведем решение для произвольного η (см. [15, с. 31]).
Абсолютный риск частоты X в схеме Бернулли есть
Дх(0) = Μ \Х - 0| = £ 11 - θ\ Сгпв\1 - θ)η~\
г=0 I П I
Пусть dj(0) = (0 - £)С£0*(1 - Θ)η~\ Так как MX = 0, то
, л = 1,2,. . . ,?Ί,
'fc-1 fc
Σ<^(0) = 0. С учетом этого для 0 G
г=0 L П nJ
абсолютный риск представляется в следующем виде:
%(0) = Е<к(в) - £χ(0) = 2ΣΜΘ) - Σ*(θ) = 2Σάί(θ).
г=0 г=к г=0 г=0 г=0
82
Глава 6. Сравнение оценок
Рис. 13
Аналогично выводу формулы (2) из § 2 гл. 5 устанавливается,
что правая часть равна 2C*Z{ 0fc(l —0)n_fc+1 (проверьте!). В
случае η = 3 имеем
%(*) = {
2(9(1 - (9)3 при О ОО/З,
402(1-0)2 при 1/3 < 0 ζ 2/3,
[2 03(1-0) при2/3^0^1.
График этой функции приведен на рис. 13. На отрезке 0,~
риск имеет локальный максимум при 0 = -т. Части графика на
\k-l к]
концах отрезков
(к = 1,2,3) не стыкуются гладко.
6. а) В силу леммы 1 гл. 4 случайная величина 5n ~ Г(п,0) с
плотностью psn(s) = 0nsn~le~98/Г(п) при s > 0. Далее, по
теореме о замене переменных из П2, определению и основному
свойству гамма-функции (см. § 4 гл. 3) имеем
о
б) Аналогично, сделав замену χ = 0(s — £), получим
оо оо
M^=|(l-*/*)n-1Ps(*)de=i^|(e-i)n-1e-fl'<fa=e-
et
7. Так как 0 — параметр масштаба для распределений оценок 0з
и 05, то достаточно найти отношение D05/D03 при 0 = 1.
Вычислим совместное распределение случайных величин Хщ
и X(n):
F(x,y)=P(X(1) ζχ,Х{п) ^у)=Р(Х{п) <у) -Р(Х(1)>я,Х(п) <у) =
(УП — (у—χ)η·> если 0<ж<у<1,
уп, если 0<я^у<1,
поскольку Ρ(Χ(ΐ) > а?,Х(п) < у) = Р(ж < Х< ^ у, г = 1,...,п),
а эта вероятность равна (у — #)п, если ж < у, и равна 0
в противном случае.
ПЛОТНОСТЬ р(х,у) = flgfy = П(П - 1)(у - ж)П"2/{0<а:<2/<1},
1 1
ЬЛХ(1)Х(п) = п(п — 1) J χ J y(y — x)n~2dy dx. С помощью замены
о χ
ζ = у — χ легко получить, что внутренний интеграл равен
(1 - х)п/ η + χ (1 - χ)71-1/ (η - 1).
Ответы на вопросы
83
Согласно определению бета-функции и формуле (10) гл. 3,
выражающей ее через гамма-функцию, находим:
МХ(1)Х(П) = (n-l) B(2,n + l) + nB(3,n) =
= [(η-1)Γ(2)Γ(η + 1)+ηΓ(3)Γ(η)]/Γ(η + 3).
Поскольку Г(п) = (п — 1)!, окончательно получаем, что
MX(1)X(n) = [(n-l)l!n!+n2!(n-l)!]/(n+2)! = l/(n+2).
С учетом свойств дисперсии (П2) и решений задач 1-2
D05 = DX(1) + DX(n) +2 (MX(1)X(n) - MX(1) MX{n)) =
w Vn + 2 n + 1 n+V V n/
^ ^ 2
Отсюда и из формулы (2) имеем 1 < D05/D03 = \—τη * 2
1 -+- 1/71
при η —► оо.
ОТВЕТЫ НА ВОПРОСЫ
1. а) Значение θ не может равняться 28, так как хю = 30,1.
б) Хотя значение 100 для θ теоретически возможно, но
интуитивно представляется крайне маловероятным (вероятность
получить наблюдаемое расположение точек при θ = 100 не
превосходит (тах^/0)п = 0,30110 « 6,1 · Ю-6).
2. Оценка θ ι всегда недооценивает θ и поэтому смещена.
Несмещенность оценки 02) очевидно, вытекает из симметрии
распределения величины Χι относительно 1/2 (откуда ΜΧι = 0/2)
и свойств математического ожидания (П2).
3. Для дискретной случайной величины £, принимающей значения
Хг (г = 1,... ,п) с одной и той же вероятностью 1/η, Μξ = χ.
В силу теоремы о замене переменных (П2)
Me=l-t*i ο*=±ς(*<-*)2·
n i=l n г=1
Таким образом, при любых χι проверяемое равенство — частный
случай формулы (4) гл. 1. Из пушки по воробьям.
Глава 7
АСИМПТОТИЧЕСКАЯ НОРМАЛЬНОСТЬ
Все верят в
универсальность нормального
распределения: физики
верят потому, что думают,
что математики доказали
его логическую
необходимость, а математики
верят, так как считают,
что физики проверили
это лабораторными
экспериментами.
А. Пуанкаре
Рис. 3
§ 1. РАСПРЕДЕЛЕНИЕ КОШИ
В [11, с. 178] приведено описание следующего эксперимента по
локализации источника излучения. В некоторой точке
трехмерного пространства с неизвестными координатами (а, Ь, с) находится
источник 7-излучения. Регистрируются координаты (#г»Уг)> г =
= 1,... ,п, точек пересечения траекторий 7-квантов с поверхностью
детекторной плоскости ζ = 0. Требуется оценить параметры а и b
по этим данным, предполагая, что направления траекторий
7-квантов случайны, т. е. равномерно распределены на сфере с центром
в точке (а,Ь,с) (рис. 1).
Какую оценку можно было бы предложить для (а, Ь)? Первое,
что приходит в голову,— это (Χ,Υ). Ясно, что точки пересечения
траекторий с плоскостью ζ = 0 располагаются гуще
непосредственно под источником излучения. В подобных случаях прибегают
к усреднению данных, чтобы, по возможности, устранить разброс
измерений (предполагается, что при этом происходит взаимная
компенсация отклонений в разные стороны).
Однако, в данном случае усреднение совершенно бесполезно.
Для объяснения, почему это так, рассмотрим одномерный
аналог эксперимента (двумерная модель разбирается в задаче 7): из
точки (0,1) выходит случайный луч (рис. 2), направление которого
равномерно распределено на нижней полуокружности с центром
(0,1). Случайная величина X — координата пересечения этого луча
с осью абсцисс. Какая плотность р(х) у этой величины?
Решение. Понятно, что плотность — четная функция.
Вычислим ее для χ ^ 0. Найдем сначала функцию распределения
F(x) = Р(Х ^ х) (см. рис. 2):
F(x) = Р{Х ^ 0) + Р(0 < X ^ х) = J + — = \ + - arctgx.
Δ 7Г ^ 7Г
Отсюда р(х) = F'(x) = 1/[π(1 + χ2)]. Это — плотность Коши. На
первый взгляд она похожа на плотность стандартного нормального
закона ЛГ(0,1) (рис. 3). Однако, они различаются по скорости
убывания к нулю при χ —► оо вероятностей Р(Х < —х) и Ρ(Ι ^ а;) (так
§1. Распределение Коши
85
называемых «хвостов распределения»). У закона Коши «хвосты»
намного «тяжелее». Ленивой лошади и хвост
Чем опасны «тяжелые хвосты»? Тем, что случайная величина втягость
с таким распределением с довольно существенной вероятностью
может принимать большие по абсолютной величине значения.
Поэтому в реализации выборки большого размера из такого закона
обязательно появятся одно или несколько наблюдений, которые
сильно отличаются от остальных (их называют «выбросами»).
В этом случае при оценивании «центра» распределения при
помощи выборочного среднего X произойдет резкое смещение оценки
в сторону наибольшего «выброса» (см. задачу 6). Куда один баран, туда
Из-за слишком «тяжелых хвостов» у закона Коши не суще- и все стадо
ствует даже математического ожидания (см. замечание в § 2 гл. 1).
Если бы оно существовало, то по усиленному закону больших чисел
(П6) среднее арифметическое сходилось бы к Μ Χι с вероятностью 1
при η —► оо. А что происходит с X для выборки из распределения
Коши? Чтобы выяснить это, используем характеристические
функции (П9):
оо
ψΧι (t) = MeitXl = (cos tx + г sin tx) p(x) dx =
—oo
oo
_ 1 f COStx
~ π J 1 + x2
tx ,
dx.
Этот интеграл, зависящий от параметра £, можно явно вычислить
с помощью теоремы о вычетах (см. [73, с. 239]). Ответ таков:
ΨχΑΐ) — e~l*L (Другой способ — применение к е-'*' обратного
преобразования Фурье из П9.) Отсюда, используя свойства 2 и 3
характеристических функций из П9 (при а = О, Ъ = 1/п), находим:
^x(t)=П^(*)=e-n|t|' <м«)=e_n|t/n|=e_|t|·
г=1
Таким образом, характеристическая функция среднего X
совпадает с характеристической функцией величины Χι. Так как
характеристическая функция однозначно определяет функцию
распределения (см. [90, с. 301]), то X также имеет распределение Коши
при любом п. Поэтому наблюдаемое значение X будет отклоняться
от 0 ничуть не меньше значений самих Х{.
Как же, все-таки, состоятельно оценить θ в модели сдвига
F(x — Θ), когда F — функция распределения закона Коши?
Подходящей оказывается, например, оценка, определяемая в следующем
параграфе.
86
Глава 7. Асимптотическая нормальность
§2. ВЫБОРОЧНАЯ МЕДИАНА
Рассмотрим ранее встречавшийся в § 4 гл. 4 вариационный ряд
X(i) < Х(2) < ... < Χ(η)ι состоящий из упорядоченных по
возрастанию элементов выборки (Χι,... ,ХП).
Определение. Выборочной медианой называется оценка
ч · " ' » МДЯ=/Х(*+1)' если η = 2*+ 1,
Х{1) Х{2) MEDX{n) |(X(fc) + X(fc+1))/2, еслип = 2А:
Рис. 4
(рис. 4 при η = 5).
Выборочная медиана MED служит оценкой для
теоретической медианы х\/2, которая определяется как решение уравнения
„/ ч у F(x) = 1/2, где F(x) — функция распределения элементов выборки.
^/ Для непрерывной функции F(x) решение всегда существует, но
| может быть не единственным (рис. 5).
~Щ ► Подобно математическому ожиданию (см. § 2 гл. 1), медиана
х ΧιJ2 является характеристикой, показывающей, где располагается
Рис. 5 «центр» распределения:
P(Xi ^ Xl/2) = Р(Хг > Xl/2) = \
(см. также задачу 4).
Пример 1. Модель радиоактивного распада ([68, с. 5]). Как
известно, радий (Да) с течением времени превращается в радон
(Rn). В момент распада атом радия излучает α-частицу — ядро
атома гелия (Яе), и происходит переход Ra —► Rn. Допустим,
что время г до распада отдельного атома Ra не зависит от
состояния других атомов и имеет показательное распределение:
pt = Р(т > t) = e~xt. Если имеется всего η атомов радия (в одном
грамме насчитывается приблизительно 1022 атомов), то среднее
число остающихся через время t атомов есть n(t) = npt = ne~xt.
Определяемая из равенства п(Т) = п/2 величина Τ (период
полураспада) не зависит от исходного количества Да: Τ = 1η2/λ (для
радия Τ « 1600 лет). На языке теории вероятностей Т —медиана
показательного распределения.
Какими свойствами обладает MED как оценка для #ι/2?
Теорема 1. Пусть элементы выборки имеют плотность р(#),
причем р(х\/2) > 0. Тогда при η —► оо
Эта сходимость вытекает (см. [50, с. 314]) из теоремы 2,
доказываемой в § 3.
Контрпример. Плотность р(х) на рис. 6 симметрична и равна 0
при |х| ^ а. При η —* оо MED для нечетных η будет принимать
§ 3. Выборочные квантили 87
бесконечное количество раз значения как из интервала (—оо, — а),
так и из интервала (а, + оо). Поэтому она не может сходиться ни
к какой из точек отрезка [—α,α].
При выполнении условий теоремы 1 выборочная медиана будет
состоятельной оценкой для #ι/2·
Более того, из теоремы 1 следует, что точность оценки MED при
больших η имеет порядок малости \j\fn. Действительно, умножая
(MED — X1/2) на у/п («коэффициент увеличения микроскопа»), мы
получаем нечто «практически ограниченное» (с вероятностью 0,997
по «правилу трех сигм» из § 2 гл. 3).
Задача 5 дает пример состоятельной оценки с иной
асимптотикой погрешности.
Возвращаясь к оценке параметра сдвига распределения Коши,
видим, что #!/2 = θ (это вытекает из симметрии плотности
случайной величины Х{ относительно 0), причем р(х\/2) — 1/я" > 0·
Следовательно, MED — состоятельная оценка для параметра сдвига.
Другие (более точные) оценки θ в этой модели будут приведены
в двух следующих главах.
Замечание. Для оценивания координат α и b в эксперименте
по локализации источника излучения можно было бы поставить
вторую детекторную плоскость, если излучение достаточно
сильное, чтобы пройти сквозь первую, или установить над плоскостью
непроницаемый экран с «окошком» и использовать
«сверхэффективность» (т. е. точность порядка 1/п) крайних членов усеченной
выборки (см. эксперимент по сравнению 2Х и Х(п) Для выборки из
равномерного распределения на [0, Θ] в § 1 гл. 6).
Тем не менее, рассмотренный пример поучителен тем, что такая
«естественная» оценка центра симметрии распределения и
«сгущения» наблюдаемых значений элементов выборки, как X,
оказывается несостоятельной, и поэтому требуются более сложные оценки.
§3. ВЫБОРОЧНЫЕ КВАНТИЛИ
Понятие теоретической медианы можно обобщить.
Определение. Пусть α Ε (0,1). Для непрерывной функции
распределения F теоретической a-квантилъю ха называется
решение уравнения F(x) = а (рис. 7).
Так же, как и в случае медианы (а = 1/2), это решение может
быть не единственным.
Оценить ха можно с помощью порядковой статистики Χ([αη]+ΐ)ι
где [ · ] обозначает целую часть числа. Эту оценку называют выбо-
Вопрос 1.
Почему MED
состоятельна? (См. свойства
сходимости из П5.)
1-
0
---yf
Xq,
У = F(x)
X
Рис. 7
88
Глава 7. Асимптотическая нормальность
рочной а-квантилъю. Ее состоятельность вытекает из следующей
теоремы.
Теорема 2. Пусть элементы выборки имеют плотность р(#),
причем р(ха) > 0 для заданного а € (О,1). Тогда
у/п (Χ([βη]+ΐ) - Яа) -* ξ ~ Μ (0, а(1 - а) /р2(ха)) при η -^ оо.
Для доказательства теоремы 2 потребуется
Лемма 1. Пусть φ(θ)— дифференцируемая функция, причем
φ'(θ) ф 0. Если ^/η{θη-θ)±>ξ~Ν(0,σ2) при η -+ оо, то
V* [φΦη) ~ φ(θ)] ±φ'№~Μ* (θ, σ V(*)]2) ·
Пояснение. При η —► оо распределение оценки 0П
приближенно нормально и концентрируется около Θ. Отображение φ
в малой окрестности θ практически является линейным
растяжением с коэффициентом φ'(θ) угла наклона касательной к графику
У = φ(β) у = φ(χ) в точке θ (рис. 8). Так как распределение оценки θη
в основном сосредоточено на расстоянии порядка 1/у/п от точки
0, то нормальность сохраняется (см. П9), а дисперсия умножается
на коэффициент [φ'(θ)]2.
Доказательство леммы 1. Разложим φ(χ) в точке θ по формуле
Тейлора: φ(θη) - φ(θ) = (θη — θ) [φ'{θ) + ζη], где для любого ε > 0
величина |£η| < ε при \θη - θ\ < δ(ε). Отсюда P(|Cn| < ε) ^
^ Ρ(\θη — 0| < ί) —► 1 при η —► оо, так как θη —» θ (см. вопрос 1).
ρ
Поэтому ζη —► 0. С учетом свойства сходимости 1 из П5
V» [ψΦη) - ψ{θ)] = WH (θ„ - θ)} (φ'(θ) + ζ„)^ξ· φ'(θ). Ш
Доказательство теоремы 2. Докажем ее сначала для выборки
(?7ъ?72> -- - Μη) из равномерного распределения на [0,1]. По лемме 3
гл. 4 порядковая статистика щь) ~ Sk/Sn+i, где Sk = η + ... + τ&,
г» — независимые показательные случайные величины с
параметром λ = 1, г = 1,... ,п+1. Поэтому у/п(щк) — ol) ~ y/n(Sk/Sn+i—a).
Проведем следующие простые преобразования:
v^ (Sfc/Sn+i - α) = >/ϊί [(1 - α) Sfc - α (S«+i - Sk)]/Sn+i =
= [η/5η+ι] · [bnYn - cnZn + dn],
где
bn = (1 - α) y/k/n, cn = a y/(n + 1 - fc)/n, dn = (A; - cm - a)/y/n,
Yn = № - fc)/Vfc, Zn = [(Sn+1 - Sfc) - (n + 1 - fc)]/Vn + l-fc.
ρ
В силу закона больших чисел (П6) 5η+ι/(η+1) —► Μτι = 1 при η —►
—► оо. Применяя свойства сходимости 1 и 3 из П5 для непрерывной
ρ
при χ > О функции </?(#) = 1/ж, получаем, что n/Sn+i —-» 1.
§ 4. Относительная эффективность
89
Заметим, что случайные величины ξη = bnYn и ζη = cnZn
независимы, так как являются функциями от независимых
векторов (τι,...,τ^) и (ть+1,... ,τη+ι) соответственно (см. лемму из
§ 3 гл. 1). Поэтому характеристическая функция вектора (£п»Сп)
(см. П9) в силу свойства 5 математического ожидания из П2 имеет
следующий вид:
Положим А: = кп = [απ] + 1. Тогда Ьп —* (1 — а)<у/а, Сп —► а>/1 — а.
Согласно центральной предельной теореме (П6) распределение
обеих случайных величин Υη и Ζη стремится к ЛГ(0,1). Отсюда
с учетом свойства сходимости 1 из П5 получаем, что
ξ„^ξ~^(0,(1-α)2α) и Сп^С~^(0,а2(1-а))·
Применяя теорему непрерывности характеристической
функции (П9), из приведенного выше представления для ^(£п,Сп)(^ь^2)
выводим, что (ξηιζη) —* (£>С)> гДе (£>С) ~~ нормальный. вектор
с независимыми компонентами. Свойство 3 из П5 (для непрерывной
функции <р(х,у) = χ — у) обеспечивает сходимость ξη — ζη —» ξ — ζ.
Здесь предельная величина ξ — ζ1 являясь линейной комбинацией
компонент нормального вектора, также имеет нормальное
распределение, причем Μ (ξ — ζ) = О и D (ξ — ζ) = Οξ + DC = α(1 — α)
ввиду независимости случайных величин ξ и ζ (Π2).
Чтобы установить сходимость распределения у/п (щ[ап]-\-1) — а)
к ЛГ(0,а(1 - а)), остается заметить, что dn —► 0 при к = [an] + 1,
и воспользоваться свойством 1 из П5.
Для выборки (Χι,... ,ХП) из закона F с плотностью р(х) в силу
метода обратной функции (см. § 1 гл. 4) порядковая статистика
X(k) распределена как F_1(r7(fc)). Производная обратной функции
d F-\a) = l l
da v ; p(F_1(a)) p(xa) '
Применение леммы 1 завершает доказательство теоремы 2. ■
§4. ОТНОСИТЕЛЬНАЯ ЭФФЕКТИВНОСТЬ
В качестве оценок мы использовали различные функции от
выборки: Х(п) = max{Xi,... ,ХП}, X, MED.
Λ ^ «. m ^ Любые непрерывные
Определение. Статистикой Τ будем называть произвольную функции η переменных
борелевСКую (СМ. П2) функцию ОТ выборки (Хи . . . ,Хп). являются борелевскими.
Определение. Статистика Τ = Тп называется асимптотически мет^^к^ео1?еРраций
нормальной, если найдутся такие числовые последовательности ап над борелевскими,
иЬ >0 что а также их суперпозиций
и ип ^ и, 4ΐυ и предельного перехода,
. - снова будут борелевскими.
при η —► оо.
90
Глава 7. Асимптотическая нормальность
Пример 2. Гипотеза случайности ([32, с. 133]). Такой
гипотезой называют предположение о том, что данные (#ι,... ,#п) — это
реализация выборки, т. е. случайного вектора (ΛΊ,... ,ХП) с
независимыми и одинаково распределенными компонентами. Допустим,
что Χι имеют непрерывную функцию распределения. Тогда из
соображений симметрии все п! вариантов расположений Χι
относительно друг друга равновероятны. Одной из статистик,
измеряющих степень «беспорядка», является Rn — общее количество
инверсий в выборке: говорят, что Χι и Xj образуют инверсию, если
г < j, но Xi > Xj. Крайние случаи, когда Χι < ... < Хп (Rn = 0)
и Χι > ... > Хп (Rn = (η - 1) + (η - 2) + ... + 1 = п(п - 1)/2)
естественно рассматривать как свидетельства «полного отсутствия
беспорядка». Слишком малые или слишком близкие к числу п(п —1)/2
значения статистики Rn служат основанием для того, чтобы
отвергнуть гипотезу случайности.
Известно, что статистика Rn асимптотически нормальна:
(Rn - MRn) /y/DRn~ 1+Z~ ЛГ(0,1) при η -> оо,
где MRn = п(п - 1)/4, DRn = п(п - 1)(2п + 5)/72 (см. [81, с. 271]).
Это позволяет при достаточно больших η проверить гипотезу
случайности, например, по «правилу трех сигм» (см. § 2 гл. 3).
Для асимптотически нормальных оценок параметров в
регулярных (см. § 3 гл. 9) статистических моделях типичным порядком маг
лости коэффициента Ьп является \j\fn. Условие асимптотической
нормальности для них представляется в следующем виде:
\/η(θη-θ)^ξ~Λ/ΧΟ,σ2(θ)) при η — оо.
Определение. Величина σ2(θ) > 0 называется асимптотической
дисперсией асимптотически нормальной оценки 0П.
Например, если 0 < DXi < оо, то согласно центральной
предельной теореме (П6)
Vn(Xr-MX1)^f~A/'(0,DA'i) при η -> оо, (1)
т. е. асимптотической дисперсией выборочного среднего X (как
оценки для Μ Χι) служит DX\. Теоремы 1 и 2 дают еще два
примера асимптотически нормальных оценок.
Замечание. Вообще говоря, асимптотическая дисперсия σ2(θ)
может не совпадать с пределом при η —► оо последовательности
сп = D(y/n(0n — θ)) = ηΟθη по той причине, что из сходимости
распределений не следует сходимость моментов (см. П5).
Так, условия теоремы 2 выполняются для выборки с функцией
распределения F(x) = 1 — (1/ In χ) при χ > е (и плотностью
р(х) = (жIn2x)~lI{x>e}) (это распределение встречалось ранее
§ 5. Устойчивые законы
91
в § 2 гл. 4). Легко видеть, что ΜΧι = оо. Покажем, что также
бесконечны и математические ожидания порядковых статистик
Х(Ь) для всех к = 1,... ,п.
Действительно, метод обратной функции показывает, что Х^к)
распределена так же, как F-1^^))- Согласно формуле (2) гл. 5
плотностью 77(*.) является рщк)(х) = nCkZ{хк~1(1 — x)n~kI{o<x<i}-
Применяя формулу преобразования с якобианом J = Ff(x) = р(х)
из П8, находим, что
pXw(x) = nCknZ\ F{x)k-\l - F(x))n-kp(x). (2)
Наконец, заметим, что при любом к (проверьте второе равенство!)
ОО °° 4-1
MX(fc) ^ MX(i) = хрх{1) (х) dx = η ί — J dx = oo.
—оо е
Асимптотическая дисперсия σ2(θ) характеризует точность
асимптотически нормальной оценки, вычисленной по большой
выборке.
Определение. Относительной асимптотической
эффективностью асимптотически нормальной оценки θ\ по отношению
к асимптотически нормальной оценке 02 называется величина
Почему относительная эффективность eg j определяется как
σ2/σϊι а не как σ<ιΙσ\ или σ|/σι? Пусть требуется оценить
параметр θ с заданной точностью £, причем за каждое наблюдение Х{
мы должны заплатить цену С. Тогда размеры выборок п\ и пг,
обеспечивающие заданную точность для оценок θ\ и 02
соответственно, определяются из соотношения δ = σι/^/ηΓ = аг/\/п2.
Таким образом,
е?ь?2 = σ2/σ1 = П2/П1 = КС)/(Щ(7),
т. е. относительная эффективность ej j представляет собой ога-
ношение затрат при использовании оценки 02 к затратам при
использовании оценки θ\.
Примеры вычисления е-§ j для некоторых распределений
приведены в задачах 1-3 и ряде задач следующей главы.
Вопрос 2.
При каких размерах
выборки будет конечна
дисперсия MED для
распределения Коши?
(Используйте то, что
для закона Коши
x{l-F{x)) -► 1/π
при ж—►Н-оо.)
§5. УСТОЙЧИВЫЕ ЗАКОНЫ
В определении асимптотической нормальности участвуют
константы: центрирующие ап и масштабирующие Ьп > 0. В связи
с этим возникает следующий вопрос: нельзя ли подобрать другие
а'п и Ь'п > 0 такие, что (Tn — a'n)/b'n сходилось бы к
невырожденному*) закону, отличному от нормального? Следующая лемма дает
отрицательный ответ.
*) Распределение случайной величины ξ вырождено, если Ρ (ξ = const) = 1.
На все свои законы есть.
Фамусов в «Горе от ума»
А С. Грибоедова
92
Глава 7. Асимптотическая нормальность
Лемма 2. Пусть (Тп - an)/bn —► ξ и (Tn - a!n)/b'n -» f', причем обе
случайные величины ξ и ξ' имеют невырожденное распределение.
Тогда существуют такие константы α и b > О, что b'n/bn —► Ь,
(с4 — an)/bn —> α и ξ' ~ a + bξ (т. е. невырожденный предельный
закон определяется однозначно с точностью до преобразований
Доказательство приведено сдвига и растяжения),
в [90, с. 371].
В § 2 гл. 4 в качестве предельных законов для порядковых
статистик (Х(п) — an)/bn, где Х(п) = max{Xi,... ,ХП}, возникали
так называемые распределения экстремальных значений.
Оказывается, и для 5η = Χι + ... + Хп (сумм независимых и одинаково
распределенных случайных величин) можно полностью описать
класс предельных законов для статистик (5П — ап)/Ьп. (Условия
сходимости приведены, например, в [82, с. 643].) Такие законы
(и только они) обладают свойством устойчивости.
Определение. (Невырожденное) распределение F устойчиво,
если для любых αϊ, 6ι > 0 и аг, 6г > 0 найдутся а и b > 0 такие,
что F(ai + bix) * F(u2 + b2x) — F(a + bx).
Другими словами, при сложении независимых случайных
величин, имеющих устойчивое распределение, получается снова тот
же закон, но, вообще говоря, с другими параметрами сдвига
и масштаба. Нормальный закон устойчив: если Χ ~ Ν(μι,σ{)
hF~ Ν{μ2, &%) независимы, то X + Υ ~ λί(μι + μ2> σ\ + сг§).
Согласно теореме Леви —Хинчина характеристические
функции устойчивых законов (с точностью до сдвига и масштаба)
допускают следующее представление:
<ψ(ί) =exp{-|t|Q(l + ιβ G(t,a) sign *)}, (3)
где а и β — постоянные, 0 < а ^ 2, — 1 ^ β ^ 1,
{ —lnltl, если а = 1,
tg 7> α, если α ψ 1.
Соответствующие распределения имеют непрерывные плотности,
которые вычисляются по формуле обратного преобразования
Фурье из П9. Явный вид плотностей известен для нормального закона
(а = 2, β = 0), распределения Коши (а = 1, β = 0) и законов
с а = 1/2, /3 = ±1:
р+(*) ^^e-W/^o,, p-(*) =*>+(-*).
Легко проверить, что функция распределения F+(#) закона с
плотностью р+(х) удовлетворяет соотношению F+(x) = 2 (1 — Ф(1/^/х))
Здесь * означает свертку
гэункций распределения
см. ПЗ).
П. Леви (1886-1971),
французский математик.
А. Я. Хинчин
(1894-1959), советский
математик.
Задачи
93
Рис.9
при χ > О, где Ф(х) — функция распределения случайной
величины Ζ ~ ЛГ(0,1). Иначе говоря, случайная величина 1/Z2 имеет
функцию распределения F+(x).
Закон F+(x) возникает в качестве предельного в задаче о
частоте возвращений в 0 симметричного случайного блуждания Sk =
= Χι +... + Хк, где Xi независимы, P(Xi = -1) = P(Xi = 1) = 1/2,
г = 1,2, — Обозначим через Zn время до η-го возвращения в О
(рис. 9).
Тогда Zn — сумма времен между последовательными
возвращениями. Интуитивно понятно, что эти времена независимы и
одинаково распределены. Поэтому предельный закон для Zn должен быть
устойчивым. В [82, с. 492] доказано, что P(Zn/n2 ^ х) —► F+(x)
при η —► оо. Иными словами, число возвращений в 0 растет не
пропорционально количеству шагов п, а как у/п. Это связано с тем,
что ΜΖι = оо, и закон больших чисел (П6) не применим к сумме
величин с таким распределением.
Пример 3. Гравитационное поле звезд. Представим, что
в шаре радиуса г с центром в начале координат расположены
наудачу η звезд единичной массы. Обозначим через Χι,... ,Хп
^-компоненты гравитационных сил, создаваемых в центре шара
отдельными звездами. Положим Sn = Χι + ... + Хп. Тогда при
таком стремлении г —► оо и η —► оо, что ^ пг3/п —► А, рас-
о
пределение случайной величины Sn стремится (с точностью до
масштаба) к устойчивому закону с а = 3/2, β = 0 (так называемому
распределению Хольцмарка) (см. [82, с. 252]).
Когда ж постранствуешь,
воротишься домой...
Чацкий в «Горе от ума»
А. С Грибоедова
Вопрос 3.
а) Какую
характеристическую функцию
имеет разность двух
независимых случайных
величин с функцией
распределения F+(x)?
б) Будет ли
соответствующий закон устойчивым?
в) Как ведет себя X
для такого закона при
возрастании размера
выборки п?
(Используйте свойства
характеристической
функции из П9.)
ЗАДАЧИ
1. Вычислите eMED^ для выборки из закона Λ/Χ0,1).
2. Пусть случайные величины X и Υ независимы и показательно
распределены с λ = 1.
а) Докажите, что разность X — Υ имеет распределение с
плотностью р(х) = ^ е-'*' (закон Лапласа).
б) Вычислите D(X — F), используя свойства дисперсии из П2.
в) Для выборки из сдвинутого на θ закона Лапласа найдите
eMEDjC'
Первое —это понять
правило, второе —
научиться его применять.
Первое достигается
разумом и сразу, второе —
опытом и постепенно.
Артур Шопенгауэр,
«Афоризмы житейской
мудрости»
94
Глава 7. Асимптотическая нормальность
3* Элементы выборки распределены согласно закону F(x — 0), где
F(x) = (1 - ε) Φ(χ) +εΦ(χ/3),
О ^ ε ^ 1, Ф(х) — функция распределения ЛГ(0,1). Другими
словами, F(x) — это омесъ (см. § 2 гл. 5) с весами 1 — ε и ε
законов Л/ХО, 1) и Л/ХО, 9) соответственно. Определите приближенно
значение ε, при котором MED становится эффективней X.
Указание. Линеаризуйте функцию ^ΜΕΕ>^(ε) в окрестности 0.
4. а) Найдите значение а, при котором достигается минимум
функции д(а) = М|£—а| для случайной величины ξ с плотностью
р(х) (ср. с задачей 1 гл. 1).
б) Определим в общем случае медиану га распределения
случайной величины ξ как любое число, удовлетворяющее
неравенствам Ρ(ξ ^ га) ^ 1/2 и Ρ(ξ ^ га) ^ 1/2. Пусть М|£| < оо.
Докажите, что функция д(а) = Μ\ξ — а\ имеет минимум при
а = га.
Указание. Установите, что д(а) — д(ш) ^ 0, если а ^ га.
5* Выборка размера η получена из распределения
Fe{x) = 1 - (1 - я/0)а при 0 ^ χ < 0,
где а > 0 — известный параметр. Каков порядок малости
величины θ — Х(п) при η —► оо? Сколько (с точностью до порядка)
наблюдений потребуется, чтобы оценить θ = 1 с погрешностью
0,1 при а = 5?
6. Докажите, что для максимума выборки из закона Коши
Ρ(πΧ(η)/η ^ х) —► 6_1/χ/{χ>0} при η —► оо (т. е.
предельным является распределение экстремальных значений И-го типа
с а = 1, появившееся в § 2 гл. 4).
Указание. Примените правило Лопиталя.
7* Пусть в эксперименте по локализации источника излучения из
§1а = 0, 6 = 0, с = 1. Будут ли независимыми
а) полярные координаты йи$ точки (Xi,Yi),
б) сами Χι и Yi?
Указание. Перейдите к полярным координатам (П8) и
используйте формулу площади поверхности вращения.
РЕШЕНИЯ ЗАДАЧ
1. Медиана Xij2 = θ в силу симметрии закона λί(θ11)1 причем
ρ(θ) = 1/V5UF. Теорема 1 дает σ^ = 1/[4р2(0)] = π/2.
Согласно формуле (1) имеем σ^ = DXi = 1. Отсюда εΜΕΕ>·χ =
= 2/π « 0,64. Таким образом, для нормального закона оценка
X эффективней MED примерно на 36%.
2. а) Так как Χ -Υ ~Υ — X = -(X - У), в силу следствия из П8
ρχ-γ(χ) = ργ-χ(χ) = Ρχ-γ(—х)·, т. е. эта плотность — четная
Решения задач
95
функция. Вычислим ее при χ ^ 0. Ввиду того, что р-у(у) =
= ру(—у) = eyI{y^o}i используя формулу свертки (ПЗ), запишем
оо О
рх_у(х) = | е-(-»)/{1,<в} еУ1{у<0} dy = е~' | e^dy = \ е~х.
—оо —оо
График плотности закона Лапласа приведен на рис. 10.
б) Из ответа на вопрос 3 гл. 4 имеем DX = l/λ2 = 1. Согласно _~2~Γι
лемме из § 3 гл. 1 случайные величины X и (-Υ) независимы.
Применяя свойства дисперсии 2 и 1 из П2, находим: D(X — Y) =
= DX + D(-Y) = OX + Dr = 2.
в) В силу симметрии ху2 = θ, причем ρ(θ) = 1/2. Теорема 1
дает σ\ίΕΌ = 1/[4р2(0)] = 1. С учетом пункта б) из (1) получаем,
что σ^τ = eMED-% = 2. Таким образом, выборочная медиана
MED вдвое эффективней выборочного среднего X как оценка
параметра сдвига закона Лапласа.
3. ЬЛХ\ = #ι/2 = θ ввиду симметрии функции распределения
F{x) , причем ρ(θ) = —= (1 — ε + ε/3). Дисперсия случайной
ν2π
величины Χι — смесь вторых моментов: DXi = J x2 dF(x) =
= (1-ε)$χ2άΦ(χ) + ε$χ2άφ(^) = 1 -ε + 9ε = 1 + 8ε. Отсюда
в силу теоремы 1 и формулы (1) имеем:
«И = «МИ>,Х = \ (1 + 8е) (l " | СУ =
-1(>+¥-¥«'+?«·)·
График этого многочлена приведен на рис. 11. Ближний к 0
корень εο уравнения β(ε) = 1 можно приближенно найти из pa- q
2 / 20 \
венства -(l-f-^-εΙ =1 (функция заменяется на касательную
в нуле). Получаем εο « 0,1. Отметим также, что преимущество
выборочной медианы MED максимально при ε = 5/12 и
составляет около 44%.
4. а) По формуле замены переменных из П2 запишем функцию
g(a) = Μ\ξ — α\ в виде
2АУ=Рх-у(х)
0 1 2
Рис. 10
g(a) = (α - χ) dF(x) + \ (χ - a) dF(x) =
—oo α
a
= 2aF(a)-2 xp(x)dx - a + Щ.
96
Глава 7. Асимптотическая нормальность
Дифференцируя правую часть по а, приходим к равенству
gf(a) = 2F(a) — 1. Поэтому g(a) имеет минимум при #ι/2·
б) ТаккакМ|£—α\ ^ М|£|+|а| < оо, то функция д(а) определена
при всех а. Используем для записи приращения Δ = д(а) — д(т)
формулу замены переменных из П2:
а +оо
A = (a-m)F(m)+\(a+m-2x)dF(x)- (a-m)dF(x).
Добавляя и вычитая интеграл /(а — га) dF(x), получаем:
Δ = (α - га) [2F(ra)
а
1] + 2 ί (а
x)dF(x).
Ha безрыбьи и рак— рыба.
Г. Лопиталь (1661-1704),
французский математик.
Оба слагаемых в правой части неотрицательны: первое — в силу
определения медианы га, второе — из неравенства а ^ га и
неотрицательности интегрируемой функции на области
интегрирования. Случай а ^ га рассматривается аналогично.
5. Найдем £п, убывающие к нулю при η —► оо, из условия, чтобы
вероятность Ρ(θ — Χ^η) ^ δη) сходилась к пределу, отличному
от 0 и 1. Из задачи 3 гл. 1 имеем Р(Х(П) < х) = [Fe(x)]n.
Следовательно,
P(x(n)>e-sn) = i-^-^i-^yj=i-^i-(^yj.
Поэтому величина (δη/θ)α должна убывать со скоростью 1/п.
Это влечет для δη порядок малости η_1/α. В частности, для
оценивания θ с точностью δη = 0,1 при а = 5 потребуется
примерно 105 наблюдений.
Причина столь большого значения необходимого размера
выборки кроется в гладкости при а > 1 функции
распределения Fq{x) в точке χ = Θ. В соответствии с методом обратной
функции (см. § 1 гл. 4) для близости Χ(η) κ θ нужна
«сверхблизость» к 1 одной из координат щ точек, взятых наудачу из
отрезка [0,1] (рис. 12).
Хотя Х(п) в этой модели и не является асимптотически
нормальной оценкой (это вытекает из теоремы 1 гл. 4 и леммы 2
текущей главы), она, по крайней мере, очевидно, состоятельна
при любом а > 0.
6. Применим для вычисления lim х[1 — F(x)] правило Лопиталя
χ—>+οο
(см. [45, с. 284]):
lim
:—►Ч-оо
Л , = lim ——*
l/x ж—+оо -1/аГ
zpW= lim 1/H1+/)]
ж-»+оо 1/аг
π
Решения задач
97
Чтобы установить для χ > О сходимость Ρ(πΧ(η)/η ^ х) —►
—► е_1/х при η —► оо, достаточно сослаться на теорему 1 гл. 4. Вывод:.
7. Без ограничения общности можно считать, что сфера имеет „* "закона Ко(ши *μη&Γ
радиус 1. Вычислим Fr^(v^) = Р(Д ^ г, Φ ^ φ). В силу порядок η при η->оо.
симметрии она, очевидно, равна ^- Sh/Si. Здесь S& — пло-
Ζ7Γ
щадь поверхности шарового сегмента («шапочки»), отсекаемого
плоскостью ζ = ft, где ft = ftr определяется из пропорции
(1 — ft) : 1 = 1 : л/1 + г2 (рис. 13). 5/j можно вычислить по
формуле площади поверхности вращения, образованной дугой
функции f(x) = у/1 — х2 (проверьте второе равенство!):
ι
Sh = 2π ί f(x)y/l + [f'(x)]*dx = 2π/ι.
(4)
l-h
Поясним происхождение формулы для вычисления площади
поверхности вращения (подробнее см. [45, с. 652]). Разобьем
отрезок [а, Ь], на котором задана вращаемая дуга у = /(х), на части
длины Axi (рис. 14). При малых Axi общая площадь поверхности
вращения приближенно равна сумме площадей поверхностей
усеченных конусов, получаемых вращением вокруг оси абсцисс хорд
длины
Ah = y/(AxiY + {Ayiy.
Для неусеченного конуса с образующей длины U и радиусом
основания уг (см. рис. 14) площадь поверхности Si = nyik.
Действительно, эту поверхность можно развернуть в сектор круга
радиуса U и длиной дуги 2куг (рис. 15). Тогда Si находится из
пропорции
2-пуг : 2nh = Si : πΐ2.
Следовательно, для усеченного конуса, образованного хордой
длины /i, площадь равна
π [(yi + Ayi)(h + Ah) - ydi] = π [yiAh + hAyi + AyiAh]. (5)
Подобие прямоугольных треугольников на рис. 14 влечет
пропорцию
Ауг : AU =уц1г <=Ф Ауг = (уг/к) Ah.
Подставив выражение для Ау% в (5), получим
2тгу* Ah + (yi/k) (Ah)2 = 2пуг Ah + o(Ak).
Отсюда видим, что главная часть интегральной суммы есть
У = /0*0
2пуг
(ф\
Рис. 15
2π Σ Уг AZi = 2π Σ Vi V1 + (Ayi/Axi)2 Ax^
При измельчении разбиения она стремится к 2π J* у у/1 + {у')2 dx.
98
Глава 7. Асимптотическая нормальность
Вопрос 4.
Как вычислить объем
тела вращения?
Бывает, что усердие
превозмогает и рассудок.
Козьма Прутков
Из (4) следует, что FR#(r,<p) = ^ h = ^ ί 1 - -j==\.
Поэтому R и Φ независимы. Плотность ριι,φ(τ,φ) =
= — г(1 + г2)-3/2 получается при замене координат на
полярные из функции рх1^у1(х1у) = — (1 + ж2 + у2)~3^2
Ζ7Γ
(двумерная плотность Коти). Интегрированием по у (см. П8)
находим маргинальную плотность
+оо
'*<*> = К ί ,i + t* - ~- V
ΔΈ J (1 +аг + yz
— oo
1 1
„2ϊ3/2
)3/2 2π1+χ2 ^1 + ^2 + ^2
+oo
—oo
πΐ +аГ
Таким образом, случайные величины Х\ и Υί имеют
распределение Коши, но они зависимы, так как ρχχух (ж,у) φ ρχλ (χ)ργλ (у).
ОТВЕТЫ НА ВОПРОСЫ
1. Представим (MED - Χι/2) в виде βηξ,η, где βη = —=
и ξη = y/n(MED - х1/2) -* ξ ~ λί(0,1/[4р2(ж1/2)]) при η -> oo.
ρ
Тогда MED —> Х\/2 в силу свойств сходимости 1 и 2 из П5.
2. Дисперсия порядковой статистики Х^) конечна тогда
и только тогда, когда МХ?к\ < оо. Так как для закона Коши
х2р(х) Fk~l(χ) —► 1 при χ —► +оо, то с учетом формулы (2)
заключаем, что J ж2 Px(fc) (ж) dx сходится и расходится
одновременно с интегралом J [1 — F(x)]n~kdx. Используя указание,
выводим отсюда, что МХ?к\ < оо при 3 ^ к < η — 2.
Следовательно, дисперсия выборочной медианы MED конечна
для η ^ 5.
3. а) По формуле (3) ψ~*~(ί) = exp{—^s/Щ(l + г sign ί)}. Согласно
свойствам характеристической функции (П9) разность таких
независимых случайных величин имеет характеристическую
функцию ψ+(ί) ψ+(-ή = е"2\/Й.
б) С точностью до масштабного коэффициента эта функция
совпадает с характеристической функцией устойчивого закона
при а = 1/2 и β = 0.
в) Очевидно, характеристическая функция суммы Χι +...+ХП
равна e~2nv'*', откуда X имеет характеристическую
функцию e~2v'nt', т. е. распределение X растянуто в η раз по
сравнению с распределением Χι.
4. Разрезая тело вращения на слои толщины Дж*, получаем инте-
ь
тральную сумму J2ny2 Дж», которая сходится к π jy2dx.
Глава 8
СИММЕТРИЧНЫЕ РАСПРЕДЕЛЕНИЯ
§ 1. КЛАССИФИКАЦИЯ МЕТОДОВ СТАТИСТИКИ
Согласно одному из подходов к классификации статистических
методов, их можно условно разделить на три класса (см. [84, с.21]):
параметрические, робастные и непараметрические.
Первые, как правило, обладают максимальной эффективностью
в рамках заданной модели Fe(x), θ Ε θ С Rm, т. е. на некоторой
т-параметрической кривой в пространстве всех функций
распределения (рис. 1а).
Так (см. пример 4 гл. 9), X — эффективная оценка параметра
сдвига μ закона Λ/Χμ,σ2). Здесь т = 2, θ = (μ,σ), θ = R χ (Ο,οο).
Однако, она весьма чувствительна к утяжелению «хвостов»
распределения, приводящему к появлению в реализации выборки
выделяющихся наблюдений («выбросов»).
Оценки, которые обладают высокой эффективностью для
заданной параметрической модели, и, кроме того, не боятся
небольших отклонений от нее, т. е. достаточно точны в некоторой
окрестности m-параметрической кривой (рис. 16), называются робаст-
ными (см. § 4).
Наконец, непараметрические методы успешно работают на
целом классе законов распределения (рис. 1в), скажем, на множестве
fic всех непрерывных функций распределения. В этой главе мы
обсудим поведение ряда оценок параметра сдвига на классе Ω8
симметричных гладких распределений.
Определение. Функция распределения F принадлежит классу
Ωβ, если существует такое с: 0 < с ^ +оо, что F(—c) = 0, F(c) = 1
и F(x) на (—с, с) имеет четную, непрерывную и положительную
плотность р(х) (рис. 2).
Обратим внимание на то, что\ распределение с плотностью р(#),
график которой приведен на рис. 6 гл. 7, не входит в класс Ωβ, так
как носитель*) этой плотности н£ является интервалом.
Симметрия является
той идеей, посредством
которой человек на
протяжении веков пытался
постичь и создать
порядок, красоту и
совершенство.
Г. Вейль
Нам нравится смотреть
на проявление симметрии
в природе, на идеально
симметричные сферы
планет или Солнца, на
симметричные кристаллы,
на снежинки, наконец,
на цветы, которые почти
симметричны.
Р. Фейнман
Robust (англ.) — крепкий,
надежный, устойчивый.
Рис. 1
у = ρ{χ)
*) Носитель — множество, на котором плотность положительна.
100
Глава 8. Симметричные распределения
Хотя условие симметричности распределения может показаться
искусственным и редко выполняющимся в точности на практике,
бывают задачи, где оно возникает довольно естественно.
Пример 1. Контроль и обработка. Пусть имеются два ряда
наблюдений: Χι,... ,ХП (так называемая «контрольная» выборка)
и Υί,... ,УП («обработка»). Это могут быть, скажем, размеры
растений на двух грядках, на второй из которых применялся
определенный вид удобрений, а на первой — нет. Нас интересует, есть ли
эффект, т. е. значимое увеличение размера растений, от применения
удобрения.
Рассмотрим следующую статистическую модель: Xi = μ + ε^,
Yi = μ + θ + ε^, где μ —средний размер растений, θ —
увеличение размера за счет удобрения, е^ и ε\ — случайные величины,
включающие в себя влияние неучтенных факторов на размер
конкретного растения. Допустим, что Με* = ЬЛе[ = 0, случайные
величины {ε*, ε^, г — Ι,.,.,η} независимы и одинаково
распределены с непрерывной и ограниченной на своем носителе (а,Ь)
(—00 ^ а < b ^ +оо) плотностью.
Образуем новые случайные величины Zi = Yi — Xi = θ + £*, где
Si = ε\ — Si. Зная плотность распределения ρει(χ)1 можно записать
плотность Ρδλ(χ) по формуле свертки (ПЗ), откуда вытекают ее
четность, непрерывность и ограниченность (убедитесь!).
Следовательно, получаем, что распределение Fsx(x)
принадлежит классу Ωβ.
Таким образом, мы приходим к модели сдвига симметричного
распределения. Как проверить гипотезу Η: θ > 0 и как оценить
параметр 0, если гипотеза Η подтвердилась? Проверке гипотез
посвящена часть III этой книги. Сейчас же мы познакомимся
с двумя оценками для параметра сдвига в распределении F(x) € Ω8
и обсудим их поведение с точки зрения эффективности и робастно-
сти.
§2. УСЕЧЕННОЕ СРЕДНЕЕ
На соревнованиях по некоторым видам спорта (например, по
прыжкам в воду, гимнастике) при учете оценок, выставленных судьями,
наименьшая и наибольшая отбрасываются, а остальные
усредняются.
Определение. Пусть О < а < 1/2, к = [απ], где [·] — целая
часть числа, an- объем выборки. Усеченным средним порядка а
называется
Ха = W=2k (X(fc+!) + · · · + Х(п-к)),
где Χ(!) ^ Χ(2) ^ ... ^ Χ(η) —вариационный ряд (см. § 4 гл. 4).
Вопрос 1.
Какой носитель имеет
плотность р$г (ж)?
Вопрос 2.
Останется ли верным это
утверждение, если
отказаться от предположения,
что носителем ре1(#)
является (а, 6)?
§2. Усеченное среднее
101
Предельные случаи α = 0 и α = 1/2 соответствуют оценкам X
и MED (рис^З).
Оценка X достаточно эффективна (в смысле точности) на
распределениях, близких к нормальному, но слишком чувствительна
к «выбросам». С другой стороны, на нормальном законе MED
проигрывает X в эффективности 36% (см. задачу 1 гл. 7), но весьма
устойчива: даже если «выбросами» окажутся почти половина #*,
она не почувствует их присутствие (не сместится в их сторону).
Изменяя значение α от 0 до 1/2, будем получать компромиссные
оценки Ха. Наибольшая доля «выбросов» в выборке, которую
игнорирует усеченное среднее Ха (так называемая толерантность,
см. § 4), определяется выбором а. А как ведет себя асимптотическая
дисперсия усеченного среднего Ха (см. § 4 гл. 7) при изменении а?
Ответ дает следующая теорема об асимптотической нормальности
Ха на Ωβ.
Теорема 1. Пусть элементы выборки Χι распределены согласно
закону F(x — 0), где F £ Ωβ. Тогда для О < а < 1/2 имеем
у/п(Ха - Θ) Д ξ ~λί(0,σ1) при η -* оо,
где
σΙ =
(1-2α)2
ί t2p{t)dt + ax\_c
Здесь p{t) — плотность, отвечающая функции распределения F,
χι-α — (единственное) решение уравнения F(x) = 1 — α, т. е.
(1 — а)-квантиль распределения F (см. § 3 гл. 7).
Таблица, полученная на основе приведенной выше формулы
для σ£, демонстрирует, как уменьшается с ростом а
асимптотическая относительная эффективность е^ -χ для нормальной модели
сдвига (F(x) = Ф(х) —функция распределения закона ЛГ(0,1)):
α
еха>х
0
1,00
1/20
0,99
1/8
0,94
1/4
0,84
3/8
0,74
1/2
0,64
В частности, при а = 1/8 (при защите от 12,5%-го «загрязнения»
выборки) потеря эффективности составляет всего 6%!
Варианты поведения асимптотической дисперсии σ\ на
некоторых других симметричных распределениях рассмотрены в задаче 2.
А что можно сказать об относительной эффективности оценок Ха
и X на всем классе Ωβ? Оказывается, верна следующая теорема.
Вопрос 3.
Чему равно точное
значение эффективности
в последней графе этой
таблицы?
а) Догадайтесь.
б) Вычислите.
102
Глава 8. Симметричные распределения
Теорема 2. Для всех распределений F € Ωβ справедливы
неравенства (1 - 2а)2 ^ е^а x(i^) ^ оо·
Доказательство. Первое неравенство немедленно вытекает из
того, что
Xl-at ОО Xl-ot ОО
\ DXi = I t2p(t) dt + J t2p(t) dt^ \ t2 p(t) dt + x\_a f p(t) dt =
t2p(t)dt + ax2_a = Ι σ2α (Ι -2α)2.
Бесконечная верхняя граница достигается на распределениях с
бесконечным вторым моментом (например, на законе Коши). ■
Несложно установить, что нижняя граница является точной,
рассматривая последовательность распределений, которые могут
быть произвольными внутри [#α,#ι_α], но лежащая вне этого
отрезка вероятностная масса которых все более концентрируется
около его концевых точек.
Приведем таблицу нескольких значений нижней границы:
α
(1-2α)2
0
1,00
1/20
0,81
1/8
0,56
1/4
0,25
3/8
0,06
1/2
0,00
Из нее видно, что, скажем, при α = 1/8 потеря эффективности
может составить 44% (сравните с 6% на нормальном законе). Это
слишком много. Таким образом, на всем классе Ω8 усеченное
среднее Ха не обеспечивает удовлетворительный компромисс между
точностью и робастностью. Следующая оценка справляется с этой
задачей существенно лучше.
Вопрос 4.
а) Зависимы ли
величины Υι,.,.,Υν?
б) Верно ли, что
W = MED{Zi,...,ZN},
rfleZfc = ±(X(i)+X(j)),
«J?
Вопрос 5.
А все-таки, чему равно
точное значение ew-^7
§3. МЕДИАНА СРЕДНИХ УОЛША
По выборке ΑΊ,... ,ХП построим N = п(п + 1)/2 новых случайных
величин Yk = л {Х% + Xj)i i ^ 3 (их называют средними Уолша).
Рассмотрим статистику W = MED{Yi,... ,Yjv}.
Теорема 3. Если Χι имеют функцию распределения F(x — 0), где
F е Ωβ, то
σ2ρ) при η —► оо,
где a2F = 1/E(F), E(F) = 12 (jp2(t) dt) , p(t) — плотность,
отвечающая функции распределения F.
Отсюда нетрудно подсчитать, что для нормального закона
ew~x *** 0>955, т. е. потеря эффективности всего 4,5%.
§4. Робастность
103
Более того, на всем классе Ωβ верна следующая оценка снизу.
Теорема 4. Для всех распределений F Ε fls справедливо
неравенство ew^(F) ^ 108/125 « 0,864.
Таким образом, используя W вместо X для оценки параметра
сдвига симметричного распределения, мы в самом худшем случае
потеряем только 14% эффективности! (Этот случай реализуется
3v/5
(см. [86, с. 86]) при плотности р(х) = — (5 - х2) /{W<v/5}·)
С другой стороны, ew~x может быть сколь угодно велика
(бесконечна, если ΏΧ\ = оо).
При сохранении высокой эффективности медиана средних Уо-
лша оказывается достаточно робастной оценкой: она «не боится»
даже того, что доля «выбросов» в реализации выборки достигнет
29% (задача 4).
В § 4 определяется одна из характеристик устойчивости
оценок — асимптотическая толерантность, и приводится пример,
Доказывающий, как резко может уменьшаться точность неробаст-
ных оценок даже при крайне малом возмущении модели.
40
35
30
25
20
15
10
5
0
| ®
t s'jb*
Ι ι ι ι ι ι ι ι
*Λ
ι ι Ι
012345678 910
Рис. 4
§4. РОБАСТНОСТЬ
В реальных данных доля «выбросов» (выделяющихся значений)
обычно составляет от 1% до 10%. Это происходит из-за большого
числа неучтенных факторов (в медицине, психологии), сбоев
оборудования, скажем, скачков напряжения в электросети (в
экспериментальной физике), ошибках при вводе с клавиатуры чисел
в компьютер и т. д. Даже в астрономических таблицах встречается
|до 0,1% ошибок.
Казалось бы, можно придерживаться такой стратегии борьбы
с «выбросами»: найти их и исключить, а затем применить
эффективные параметрические методы для анализа оставшихся данных.
Конечно, среди точек на прямой «выброс» хорошо заметен. Но
реальные данные, как правило, многомерные. На рис. 4 приведена
двумерная выборка, где обведенная кружком точка (очевидный
«выброс») не выделяется среди остальных ни по координате X, ни
по координате Υ. Однако, если попытаться формально подогнать
прямую под это «облако» точек, например, с помощью метода
наименьших квадратов (см. § 1 гл. 21), то ее угловой коэффициент
будет существенно искажен под влиянием «выброса».
Возможна ситуация, когда даже проецирование многомерных
данных на всевозможные двумерные плоскости не позволит
выявить выделяющиеся наблюдения. Вопрос 6.
Так что исключение «многомерного выброса» (или группы та^ое^Гб^ко^в^?
«выбросов»)—весьма непростая задача. По-видимому, лучше
использовать робастные методы, которые за счет небольшой, как
104
Глава 8. Симметричные распределения
Пусть во всяком деле
лучшим советником будет
умеренность. Хорошо
обрабатывать землю
необходимо, а превосходно —
убыточно.
Плиний Старший
правило, потери в точности по сравнению с параметрическими
процедурами автоматически уменьшают влияние выделяющихся
наблюдений и не допускают существенного смещения оценок
параметров модели.*)
Замечание. Анализ многомерных данных часто сопряжен с
большим числом подвохов и сложностей, возникающих из-за так
называемого «проклятия размерности». При вычислении объема к-
мерного шара в § 4 гл. 3 мы уже встречались с тем, что наша
трехмерная интуиция не помогает предвидеть результат с должной
точностью.
Параметрические методы, как правило, крайне чувствительны
(уже при к « 7) к возмущению модели (см. пример 2 в гл. 16). По-
видимому, чтобы не ввести себя в заблуждение, следует совместно
анализировать не более четырех—пяти столбцов таблицы данных.
Даже и для одномерного случая, как показывает следующий
пример, точность некоторых оценок может резко уменьшаться
при незначительном утяжелении «хвостов» закона распределения
элементов выборки.
Пример 2. Смесь нормальных законов (Дж. Тьюки, 1960,
см. [89, с. 10]). Пусть Х\ имеют функцию распределения
где Ф(х)— функция распределения ЛГ(0,1), а параметры μ € R,
σ > 0 и 0 $ е < 1 неизвестны. Данная модель —смесь законов
Λ/Χμ,σ2) и Λ/Χμ, 9σ2) с весами 1 — ε и ε соответственно (сравните
с задачей 3 гл. 7). Все наблюдения имеют общее среднее μ, а разброс
у некоторых из них (в количестве « εη) в 3 раза больше, чем
у остальных.
Рассмотрим задачу оценивания разброса. Сравним следующие
две оценки: среднее абсолютное отклонение Rn и среднее квадра-
тинное отклонение Sn: Rn = - Σ \%i ~ ^|» &n = ~~ Σ {%% ~ ~Щ ·
n i=l n i—\
Следует учесть, что Rn и 5П оценивают разные характеристики
разброса. Скажем, если ε = 0 (наблюдения имеют в точности нор-
р
мальное распределение), то 5П —► σ (см. пример 3 гл. 6), в то время
Р у
как Rn —► σγ2/π « 0,798 σ. Кроме того, эти пределы зависят
ρ ^________
от ε (например, 5П —► σ>/\ + 8ε). Поэтому необходимо уточнить,
как проводить сравнение эффективности этих оценок. Возьмем
в качестве меры относительной точности оценок при больших η
*) Для данных на рис. 4 молено применить, скажем, робастный метод Тейла из
§ 1 гл. 21.
§4. Робастность
105
предел отношения (не зависящих от масштаба) коэффициентов
вариации:
ёп с (f\ = lim DSnAMSn)2 = [3(1 + 80ε)/(1 + 8ε)2-1]/4
e«n.«nV ) n^ooORnKMRnj1 π(1 + 8ε)/[2(1 + 2ε)2]-1 '
Приведем таблицу некоторых значений этой функции из [89, с. 11]:
ε
eRnfnie)
0
0,88
0,002
1,02
0,01
1,44
0,05
2,04
од
1,90
0,5
1,02
1
0,88
За малым погнался -
большое потерял.
Как видно, функция очень быстро возрастает: 12%-ное
преимущество 5П при ε = 0 исчезает уже при ε = 0,002 (достаточно всего
двух «плохих» наблюдений на 1000 для того, чтобы оценка Rn стала
эффективнее). Если же доля наблюдений из распределения с чуть
более «тяжелыми хвостами» составит 5%, то среднее абсолютное
отклонение окажется точнее более чем в 2 раза!
Этот пример показывает, что малое возмущение моделей может
приводить к качественному изменению статистических выводов,
в данном случае — выводов о сравнительной эффективности Rn
и5п.
Робастные оценки, как правило, осуществляют компромисс
между точностью и защищенностью от «выбросов». Если
асимптотическая дисперсия — это характеристика точности
асимптотически нормальных оценок, то каким образом можно измерить
защищенность?
Одной из простых мер робастности является асимптотическая
толерантность (см. [86, с. 31]). Содержательно она выражает ту Tolerantia (лат.) —
наибольшую долю «выбросов» в выборке, которую «выдерживает» теРпение·
статистика, не смещаясь вслед за «выбросами» на —оо или +оо.
Дадим формальное
Определение. Пусть для оценки 0(#(i),... ,#(п)) найдется такое
целое число А:, 0 < к < п, что
а) если X(k+2)i- · · ιχ(η) фиксированы, а X(k+i) —► —оо, то
0(я(1),...,Я(п)) -+ -оо;
б) если #(ΐ),... ,^(n_fc_!) фиксированы, a X(n-k) —* +оо, то
0(ж(1),...,Ж(п)) -++00.
Обозначим через к^ наименьшее такое к (тем самым θ допускает
по крайней мере А£ выделяющихся наблюдений).
Асимптотической толерантностью оценки θ называется предел τ г = lim к* In
(если, конечно, этот предел существует). *
Очевидно, что т^ = 0, т^ = а и tmed = 1/2. Примеры
вычисления толерантности других оценок см. в задачах 3 и 4.
) Отметим, что толерантность основывается на поведении оценки θ как
функции от η переменных и (в отличие от относительной эффективности) не связана
с распределением элементов выборки Χι,... ,Χη·
106
Глава 8. Симметричные распределения
Главное, делайте все
с увлечением, это страшно
украшает жизнь.
Л. Д. Ландау
Ф. Гальтон (1822-1911),
английский психолог
и антрополог.
ЗАДАЧИ
1. Сравните W как оценку параметра сдвига распределения
Лапласа (см. задачу 2 гл. 7) с оценками X и MED.
2* Постройте график асимптотической дисперсии σ\ (см.
теорему 1) для модели сдвига закона Лапласа. Будет ли эта
функция монотонной? Найдите пределы при а—►Оиа—>1/2.
3. Вычислите асимптотическую толерантность оценки Гальтпона:
θ = ΜΕϋ
< 2 С*Х0 + ^(n-i+i)), г = 1,..., —2~ > ,
где [ · ] обозначает целую часть числа.
Найдите точное значение tw
Пусть величины Xi равномерно распределены на [Θ — ~,0 + «]·
а) Смоделируйте с помощью таблицы Т1 выборку размера
η = 5 для θ = ~ и сравните точность оценок W и θ =
= £ C^(i) + ^(п)) на этих данных.
б) Какая из этих оценок предпочтительнее при больших п?
Указание. Используйте результат задачи 3 гл. 1 и формулу (6)
гл. 3.
Рассмотрим модель сдвига F(x — 0), где F имеет четную
плотность р(#), причем р(0) ^ р(х) при всех х. Докажите, что
среди всех таких распределений наименьшую асимптотическую
эффективность eMED -^(F) = 1/3 имеет равномерное
распределение.
Усердный в службе не
должен бояться своего
незнанья; ибо каждое
новое дело он прочтет.
Козьма Прутков
РЕШЕНИЯ ЗАДАЧ
Вычислим σ\ (см. теорему 3) для закона Лапласа:
+оо +оо
Отсюда E(F) = Yll\ = 3/4 и σ\ = 4/3. В свою очередь, из
решения задачи 2 гл. 7 имеем σ^ = 2 и σ2ΜΕΌ = 1, т. е. оценка
W точнее, чем X, но проигрывает MED примерно 33%.
Интегрируя плотность Лапласа, находим функцию
распределения: F(x) = 1 — т>е~х при χ > 0. Следовательно, для
α ^ ~ квантиль х\-а = — 1η 2α. Дважды интегрируя по частям,
нетрудно получить, что
-In 2α
Η
t2 e"* dt = l-2a + 2a\n2a-a (In 2a)2
Решения задач
107
Из теоремы 1 находим асимптотическую дисперсию оценки Ха:
σ"=(1-22α)2(1~2α + 2α1η2α)·
Функция σ£ монотонно убывает от 2 до 1: для закона
Лапласа MED оказывается эффективней, чем любая из оценок Ха
(рис. 5а).
Любопытно, что у закона Коши, несмотря на более «тяжелые
хвосты», оптимальной долей усечения будет не 1/2, аао ~ 0,38
(рис. 56). При этом выигрыш в эффективности по сравнению
с MED составляет около 8%. (В примерах 11 и 12 гл. 9 появятся
еще более точные оценки для параметра сдвига распределения
Коши.)
"п + :
3. Всего имеется
— I пар вида (Х(^,Х(п_^+1)) (рис. 6а). Если
при некотором к + 1 значение статистики X(k+i) равно —оо, то
и у всех пар с г ^ к +1 первая координата — тоже — оо. Медиана
полусумм 2 PQi) + ^(n-i+i)), г = 1,..., [^-γ-\» «уходит» в -оо
при к + 1 ^ « П 2 * Деля на п и переходя к пределу, находим,
что толерантность оценки Гальтона равна д.
Аналогично (рис. 66), чтобы W не обращалась в — оо,
необходимо, чтобы (п — к — 1)(п — к)/2 ^ п(п + 1)/4 полусумм
порядковых статистик были конечны. Положив к ~ т^тг, получаем
отсюда, что (1 - rw)2 = 1/2 или rw = 1 - >/2/2 « 0,293.
а) Возьмем, скажем, из 3-й строки таблицы Т1 первые 5
псевдослучайных чисел: х\ = 0,08; #2 = 0>42^ хз = 0,26; х± = 0,89;
#5 = 0,53. Для этих данных W = 0,395 и θ = 0,485, т. е. значение
оценки 0 оказывается ближе к 1/2.
б) Равномерное распределение на — о' 2 пРинаДлежит классу
Ωβ. В силу теоремы 3 точность оценки W имеет порядок \/у/п.
С другой стороны, из задачи 3 гл. 1 порядок малости
дисперсии DX(n) равен 1/п2. Случайные величины θ — Хщ
а
а)
1/2
Эксперимент можно
считать удавшимся,
если нужно отбросить
не более 50% сделанных
измерений, чтобы достичь
соответствия с теорией.
(Следствие из законов
Мейерса.)
Χι
(1)
Х<
(fc+i)
L(n)
Χ,
(1)
χ,
(fc+1)
Рис. 6 а) Х(п)
— оо
— оо
— оо
— ОО
^ОС
—оо
— оо
— оо
— оо
— оо
— ОО
— оо
— оо
"ОО
— оо
—оо
— оо
—оо
—оо
— оо
с
с
о
с
— оо
— оо
-«,
с
с
с
с
-оо
— оо
с
с
(?ΐ
С
— то
— оо
С
°
\ С
С
*(1)
*(fc+i)
б) х(п)
Х(1)
-оо
— оо
— оо
—оо
—:оо
—о©
— оо
— оо
— оо
—во
~~ос
X(k+1)
— оо
— оо
— оо
—оо
~»оо
— оо
с
с?
с
С
-~
С
С
с
с
— оо
С
с
с
с?
Х(п)
— оо
С
С
С
с
108
Глава 8. Симметричные распределения
И в ком не сыщешь пятен?
Чацкий в «Горе от ума»
А. С. Грибоедова
и Х(п) — θ ввиду симметрии одинаково распределены. Поэтому
DX(!) = DX(n). В соответствии с формулой (6) гл. 3 стандартное
отклонение V D0 оценивается сверху величиной порядка 1/п.
Таким образом, при больших η для модели сдвига равномерного
распределения оценка θ = ~ PQi) + ^(п)) значительно точнее
оценки W.
Замечание. Распределение величины п(Х^— # + « ) согласно
задаче 4 гл. 5 стремится при η —► оо к показательному закону
с λ = 1. В силу симметрии величина η(θ + ~ — Х(п)) имеет
тот же предельный закон. Можно доказать, что случайные
величины Χ(ΐ) и Х(п) асимптотически независимы (см. задачу 7
гл. 6). Отсюда и из задачи 2 гл. 7 получаем, что имеет место
сходимость η ( 2 (^(ΐ) Η" ^(η)) — β) —* £, где ξ распределена по
закону Лапласа.
6. По теореме 1 гл. 7 и формуле (1) гл. 7 относительная
эффективность eMED j£ = 4p2(0) DXi. Причем она не зависит от
масштаба. (Действительно, если Υ = сХ, то согласно следствию
из П8 плотность ργ(χ) = \c\~lpx(x/c), откудару(0) = с~2р^(0),
а согласно свойствам дисперсии (П2) DY = c2DX.) Поэтому
можно считать, что р(0) = 1. Таким образом, в силу четности
плотности р(х)1 задача 6 сводится к следующей:
минимизировать no f функционал
±oXl
-I
x2f(x) dx
при выполнении условии
оо
<К/(*) < ДО) = 1, |/(x)dx = i.
Утверждение. Минимум
/*(*) ='[о,*]·
функционала достигается на
Доказательство. Оценим снизу приращение функционала:
оо 1/2 оо
lx2(f(x)-f*(x))dx = \x2{f{x)-l)dx + \x2f{x)dx>
1/2
П/2
>Λ
(f(x)-l)dx +
f(x)dx-l)=0.
Ответы на вопросы
109
Замечание. Эту задачу можно обобщить (см. [50, с. 321]): для
распределений F Ε Ωβ, плотность которых имеет максимум
в нуле,
ex x(F) > т-Л-
Αα,χν ι ' 1 + 4α
(сравните с теоремой 2). Минимум достигается при равномерном
распределении на отрезке — о' 2 *
ОТВЕТЫ НАгБОПРОСЫ
1. Носителем плотности Ρδλ{χ) является интервал (—с,с), где
c = b — a.
2. Нет. Скажем, для плотности с носителем (0,1) U (8,9) носителем
| Рбг(х) служит множество (—9, — 7) U (—1,1) U (7,9).
3. а) Точное значение равно 2/π (τ. е. асимптотической
эффективности MED относительно X).
б) Выражая асимптотическую дисперсию σ£ через квантиль
χ = χι-α и дважды применяя правило Лопиталя, находим:
]t2p{t)dt + {l-F{x))x2
ton <j*=2-lim£-
α->ι/2 α *->ο \2F{x) -1]2 4ρ2(0) *
4. а) Вообще говоря, зависимы, поскольку увеличение Χι
приводит к росту и Х\ + Хг, и Χι + Хз-
б) Верно, так как в обоих случаях пробегаются всевозможные
значения ~ (Xi + Xj), где 1 ^ г ^ j < п.
5. IF = — je~t2dt = —=, откуда ежХ = 12 Тр. = 3/π.
6. Например, «облако» сферической формы с «выбросом» (или
группой «выбросов») вблизи центра сферы.
Глава 9
МЕТОДЫ ПОЛУЧЕНИЯ ОЦЕНОК
Следует поставить перед
собой цель изыскать
способ решения всех задач
одним и притом простым
методом.
Ж. Даламбер
Занимаясь той или иной
научной проблемой,
лучше исходить из
ее индивидуальных
особенностей, чем
полагаться на общие
методы.
Д. Курант, Г. Роббинс
Вопрос 1.
а) Какое
распределение имеет случайная
величина 1{χί<χ}1
б) Как называется
последовательность
в) Что такое Fn{x)
по отношению к этой
последовательности?
г) К чему сходится
Fn{x) при η —► оо для
фиксированного xl
В этой главе рассматриваются несколько простых и универсальных
методов получения оценок параметров статистических моделей,
в том числе —метод моментов и метод максимального
правдоподобия. Прежде всего, познакомимся с графическим анализом на
вероятностной бумаге.
§ 1. ВЕРОЯТНОСТНАЯ БУМАГА
Построим по выборке Χι,... ,ХП случайную ступенчатую функцию
Fn(x), возрастающую скачками величины - в точках Хи\ (рис. 1).
Она называется эмпирической функцией распределения. Чтобы за-
Н-
У = Ргь(х\+^
Рис. 1
*<1>0
дать значения в точках разрывов, формально определим ее так,
чтобы она была непрерывна справа:
л ι τι ι η
Fn{x) = - Σ 7{Χ(ο^} = - Σ hxi^)·
n t=l n t=l
Проблема. Пусть элементы выборки Χι,... ,Χη имеют функцию
распределения F((x — μ)/σ), где F известна, а параметры сдвига μ
и масштаба σ > 0 — нет. Как их оценить?
Из ответа на вопрос 1 вытекает, что эмпирическая функция
распределения Fn(x) служит естественным приближением к
теоретической функции распределения F((x — μ)/σ). Среди функций
этого двухпараметрического семейства следовало бы выбрать
такую функцию F((x — /£)/σ), чтобы она «меньше всего» отличалась
от Fn(x)1 и взять соответствующие μ и σ в качестве искомых
оценок. Однако, в общем случае из-за нелинейности F это
сделать затруднительно. Идея метода оценивания, приведенного ниже,
§1. Вероятностная бумага
111
состоит в «распрямлении» графика F((x — μ)/σ) и последующей
подгонки прямой, сглаживающей соответствующее «облако» точек
плоскости.
Для простоты допустим, что F непрерывна и строго монотонна.
Тогда для нее определена обратная функция F-1. Посмотрим, во
что переходит график функции у = F((x — μ)/σ) при
преобразовании (я,у) -> (x.F^iy)):
(x,F((x - μ)/σ)) -> {x,F~\F{{x - μ)/σ))) = (χ, (χ - μ)/σ).
Значит, график переходит в прямую у = (χ — μ)/σ.
Отсюда вытекает следующий способ оценивания μ и σ:
преобразуем график эмпирической функции распределения у = Fn(x)
в у = F~1(Fn(x)) и подберем «на глаз» наиболее тесно
прилегающую к нему прямую у = (х — μ)/σ. При этом оценка μ —это
координата точки пересечения с осью абсцисс, а σ — котангенс угла
наклона построенной прямой.
Если функция у = F~1(Fn(x)) слишком сильно отличается от
линейной, то предположение о том, что выборка взята из
совокупности с функцией распределения F((x — μ)/σ), скорее всего не
выполняется.
Для реализации этого способа получения оценок нет
необходимости строить целиком график у = F~1(Fn(x)). Достаточно
отметить только точки (ж(ф^-1(г/п)), отвечающие скачкам функции
Fn(x), и подогнать прямую к этому «облаку» точек (это можно
осуществить с помощью метода наименьших квадратов или других
регрессионных (сглаживающих) методов из гл. 21).
Чтобы избежать неудобства, связанного с построением точки
(x(n),F_1(l)), когда случайная величина Χι не ограничена сверху,
обычно используют точки (ж(^), F_1((z — 0,5)/η)), ι = 1,... ,η.
Пример 1. Моделируем нормальную выборку с помощью таблицы
нормальных случайных чисел из [10, с. 371]. Взяв первые η = 10
чисел Ζχ из 3-й строки этой таблицы, преобразуем их в реализацию
выборки из распределения Λ/Χμ,σ2) по формуле хг= μ + σΖχ для
μ = 1 и σ = 2. Получим следующие значения:
3,97 0,29 -0,27 2,39 2,85 3,75 2,57 -0,93 -0,71 -2,73.
По таблице обратной функции Ф~1{у) к функции
распределения ЛГ(0,1) (см. Т2 или [10, с. 136]) вычислим Ф~1{(г - 0,5)/п),
г = 1,... ,п:
-1,65 -1,04 -0,68 -0,39 -0,13 0,13 0,39 0,68 1,04 1,65.
Точки (#(фФ-1((г — 0,5)/п)) и подогнанная к ним «на глаз»
прямая приведены на рис. 2. Отсюда находим, что μ « 1,2 и σ » 1,8.
Как видно, графический анализ позволяет в данном случае
получить довольно точные оценки параметров, несмотря на малый
размер выборки.
Рис. 2
Будто —тяп-ляп., да
и корабль.
112
Глава 9. Методы получения оценок
Рис. 3
0,1 +
Для сравнения: выборочное среднее X и стандартное отклоне-
ние 5, где S2 = - ^2(Х% — X)2, которые в этой модели являются
г=1
оценками максимального правдоподобия (см. § 4 и задачу 2), имеют
значения 1,12 и 2,16 соответственно.
Графический анализ удобно проводить на так называемой
вероятностной бумаге. Для ее изготовления строится неравномерная
шкала на оси ординат на основе преобразования у' = F~l(y).
Шкала на оси абсцисс остается прежней. В новых шкалах
непосредственно наносятся точки (#(г), (г — 0,5)/п).
Оцифровка новой оси ординат для нормального закона показана
на рис. 3.
Следует отметить, что рассмотренный метод применяется
исключительно к модели сдвига-масштаба и моделям, сводимым
к ней при помощи некоторых преобразований. (Так, логнормальная
модель с плотностью ρμ σ{χ) = -== ехр \ ^ (Inχ — μ)2 \ΐίχ>ο\
9 χσν2π Ι 2σ У х
при логарифмировании Х[ — \\хХ\ сводится к Λ/^μ,σ2).)
Излагаемые далее методы получения оценок можно
использовать для более широкого класса статистических моделей.
А. М. Ляпунов
(1857-1918), русский
математик.
Вопрос 2.
Как вывести неравенство
Ляпунова из неравенства
Иенсена (П4)?
§ 2. МЕТОД МОМЕНТОВ
Моментом к-го порядка случайной величины X называется
величина otk = MXk. Моменты существуют не всегда.
Например, у закона Коши математическое ожидание αϊ не определено
(см. § 2 гл. 1).
Из неравенства Ляпунова
(М\Х\к)1/к ^ (M\X\l)1/l upnk^l
и свойства |М£| ^ М|£| следует, что конечность М|Х|т гарантирует
существование всех моментов ctk для к s= 1,... ,га.
1 п
Положим Ак = - Σ Χ{· Если момент а& существует, то в силу
пг=1
ρ
закона больших чисел (П6) Ак —► &к при η —► со. Поэтому для
реализации #ι,... ,#п выборки достаточно большого размера можно
1 п
утверждать, что ак = - Σ xi w аь τ· е· эмпирические
η /г
моменты
г=1
к-ro порядка ак близки к теоретическим моментам од. На этом
соображении основывается так называемый
Метод моментов
Допустим, что распределение элементов выборки зависит от га
неизвестных параметров #i,...,0m, где вектор θ = (0i,...,0m)
принадлежит некоторой области θ в Rm. Пусть M|X|W < со для
всех θ Ε θ. Тогда существуют все од = од(0), к = 1,... ,га, и можно
§2. Метод моментов
113
записать систему из m (вообще говоря, нелинейных) уравнений
<*к{в)=ук, fc = l,...,m. (1)
Предположим, что левая часть системы задает взаимно
однозначное отображение д: θ —► В, где В —некоторая область в Rm,
и что обратное отображение д~г: В —► θ непрерывно. Другими
словами, для всех (j/i,... ,ym) из В система (1) имеет единственное
решение, которое непрерывно зависит от правой части.
Компоненты решения θ = (#ι,... ,0m) при у к = Ак называются оценками
метода моментов*^
Пример 2. Рассмотрим модель сдвига показательного закона,
в которой плотностью распределения величин Х{ служит функция
рв{х) = β-(χ-θ>>Ι{χ>θ} (рис. 4). Здесь
оо оо
αι(0) = ΜΛΊ= lxe-{x-e)dx= [(у + в)е~уау = 1 + Θ.
θ о
Из уравнения 1 + 0 = Αι = X, находим по методу моментов оценку
Θ = Χ-1.
гамма-распределение
θ2: соответствующая
Пример 3. Пусть величины Х{ имеют
с двумя неизвестными параметрами θ\ и
плотность имеет вид
Ρθ(χ) = е^х^-1е-^Ч(х>0} /Г(02).
Согласно формуле (2) гл. 4 находим αϊ = θ2/θ\ и а2 = θ2(θ2 + \)/θ\.
Решив систему (1), получаем в качестве оценок метода моментов
01 = Аг/(А2 - А\) = X/S2 и 02 = А\/{А2 - А\) = X2/S2.
Какими статистическими свойствами обладают оценки,
полученные методом моментов?
Их состоятельность вытекает из непрерывности
определенного выше отображения g~l и свойства сходимости 3 из П5.
Для гладких отображений g~l такие оценки будут также
асимптотически нормальными. Это следует из того что, во-первых,
в силу центральной предельной теоремы (П6) имеет место
сходимость
у/й (Ак - ак) -i ξ ~ ЛГ(0, а2к - а2к),
если а2к < оо. А во-вторых, справедливо обобщение на
многомерный случай леммы 1 гл. 7 (см. [11, с. 33]).
Однако обычно асимптотическая дисперсия (см. § 4 гл. 7)
оценок, полученных по методу моментов, довольно велика.
Поэтому в §§ 4-6 будут рассмотрены оценки с наименьшей
возможной асимптотической дисперсией для так называемых регулярных
(см. § 3) статистических моделей.
У = Рв(х)
) Величины 0fc случайны, так как Ак —функции от Χι,... ,Xn.
114
Глава 9. Методы получения оценок
§3. ИНФОРМАЦИОННОЕ НЕРАВЕНСТВО
Пусть f(x,0) обозначает плотность распределения случайной
величины Χι. Для дискретных моделей используем это же обозначение
для Ρ (Χι = χ). Допустим, что выполняются следующие условия
регулярности:
R1) параметрическое множество θ — открытый интервал на
прямой (возможно, бесконечный)';
R2) носитель распределения А = {х: f{x,6) > 0} не зависит
от параметра Θ;
R3) при любых χ Ε А и θ Ε θ производная — f(x,0) суще-
υθ
ствует и конечна;
R4) для случайной величины U\ = — 1η/(Χι,0) при всех 0 Ε θ
υθ
справедливы тождество MUi = 0 и неравенство 0 < Л(0) =
= DUi < оо.
Заметим, что условие MC/i = 0 верно для тех статистических
моделей, где производная по 0 правой части тождества 1 = J f{xfi) dx
А
может быть вычислена дифференцированием под знаком интеграла:
д . .
° = | h ί{χβ) dX = \ \χ,θ) ί(Χ'θ) άχ = Μίθ 1η^(Χι'«) = Μί/χ.
Α Α
Контрпримером может служить равномерное распределение на
отрезке [0,0], где 0 Ε (0, + оо). Носитель А = [О, 0] зависит от 0, и
θ \ θ θ
° = έ1 = ^
\dx)*\m{l)dx = -eidx=-i·
Для выборки X = (Χι,... ,Χη) совместная плотность
распределения (или вероятность Р(Х\ = #ι,... ,ХП = хп)) в силу независи-
п
мости компонент распадается в произведение: /(ж,0) = Π ί(χίβ)·>
где χ = (#ι,... ,#п). Рассмотрим случайную величину
ип = £ ынх,в) = ± ± ы/(хив).
Тогда применение свойств из П2 дает MUn = О и DUn = пД(0).
Р. Фишер (1890-1962), Определение. Информацией Фишера для случайного вектора ξ
английский статистик. с плотностью (в дискретном случае — с совместной вероятностью
компонент) /(ж,0) называется величина
ig(fl) = Μ
|Ш/(^)Г
§ 3. Информационное неравенство
115
Отметим, что содержащаяся в выборке информация Ιχ (0) =
= Ιη(θ) = DUn = ηΙι(θ) пропорциональна размеру выборки. Она
интересна тем, что участвует в следующем ограничении снизу на
дисперсии оценок в регулярных моделях.
Информационное неравенство (Рао — Крамер). Допустим,
что выполнены условия R1-R4, 0 — любая оценка с М02 < оо, для
которой производная по 0 от функции
α(0) = ΜΘ = θ(χ) /(ж,0) dx, где χ = (#ι,... ,#η),
существует и может быть получена дифференцированием под
знаком интеграла. Тогда
"" ^ Ιη(θ) п1г(в) *
В частности, для оценок, имеющих смещение 6(0) (т. е. для
α(0) = 0 + 6(0)), нижней границей служит [1 + Ь'(0)]2//п(0), а для
несмещенных оценок— 1/7п(0).
Доказательство. Дифференцируем под знаком интеграла:
α'(θ) = | θ(χ) ^/(χ,θ)άχ = J θ(χ) ί^1η/(χ,0)1 /(Ж,0)с*ж.
Справа стоит Μ(0£/η). Отсюда, поскольку MUn = ηΜ[/ι = О,
получаем представление α'(0) = М[(0 — Μ0)[/η]. Применяя теперь
неравенство Коши — Буняковского (П4), оценим [а'(0)]2 сверху:
[α'(θ)}2 < [М(9- ΜΘ)2] [Mt£] = (D0)/n(0),
что и требовалось установить. ■
Несмещенные оценки, на которых достигается нижняя граница
1/7п(0), называются эффективными.
Пример 4. Пусть случайные величины Xi имеют нормальное
распределение Λ/"(0, σ2), где параметр масштаба σ известен, а параметр
сдвига 0 — нет. Здесь
ίΊ = 4ΐη
ay/2w
0-ϊ(Χι-θ)2/σ*
д_
дв
{Χχ-θΥ
2σ2
=4№-ί)·
Отсюда Д(0) = Di7i = σ 4D(Xi - 0) = σ 2. Поэтому оценка X с
дисперсией σ2/η является эффективной в этой модели.
Информационное неравенство показывает, что для регулярных
моделей погрешность оценки ν D0 не может убывать быстрее,
чем С/у/п. Контрпримером служит Х(п) — максимум выборки
116
Глава 9. Методы получения оценок
Χι,...,Χη из равномерного распределения на [0,в], который
оценивает 0 с точностью порядка 1/п (см. задачу 3 гл. 1). Подобные
оценки называются сверхэффективными.
Замечание. Другие условия регулярности, обеспечивающие
выполнение неравенства Рао—Крамера, приведены в [11, с. 150].
§4. МЕТОД МАКСИМАЛЬНОГО ПРАВДОПОДОБИЯ
Метод получил распространение после появления в 1912 г.
статьи Р. Фишера, где было доказано, что получаемые этим
методом оценки являются асимптотически наиболее точными при
выполнении условий регулярности из приведенной ниже
теоремы 1.
Для знакомства с методом предположим для простоты, что
элементы выборки Х{ имеют дискретное распределение: /(#,0) =
= Ρ (Χι = χ) (здесь 0 = (0ι,.. .βτη) — вектор неизвестных
параметров модели). Тогда совместная вероятность выборки /(ж,0) =
= /(жι,0) · ... · /(#п,0) зависит от η + т аргументов (здесь
х = (χι,... ,#п)). Рассматриваемая как функция от 0ι,... ,0m при
фиксированных значениях элементов выборки #ι,... ,#п, она
называется функцией правдоподобия и обычно обозначается через L(0).
Величину Ь(0) можно считать мерой правдоподобия значения 0
при заданной реализации х.
Представляется разумным в качестве оценок параметров
01) · · · )0т взять наиболее правдоподобные значения 0ι,... ,0т,
которые получаются при максимизации функции L(0) (рис. 5).
Такие оценки называются оценками максимального правдоподобия
(ОМП).
Часто проще искать точку максимума функции lnL(0), которая
совпадает с 0 = (0ι,... ,0m) в силу монотонности логарифма.
Пример 5. Для схемы Бернулли Χι,...,Χη с вероятностью
«успеха» 0 имеем: /(я,0) = Р{Х\ = х) = θχ(1 - 0)1_а:, где χ
принимает значения 0 или 1. Поэтому функция правдоподобия
L(0) = 0s* (1 — 0)n_Sn, где sn = χι + ... + #η, представляет собой
многочлен n-й степени (рис. 6 при sn > 1 и η - sn > 1). Найдем
точку максимума In L(0) = sn In0+(n—sn) ln(l—0). Дифференцируя
по 0, получаем уравнение sn/9 — (η — sn)/(l — θ) = 0, откуда
0 = sn/n = χ. Таким образом, ОМП в схеме Бернулли — это частота
«успехов» в реализации #ι,... ,#п.
Как и в § 3, в случае непрерывных моделей будем использовать
обозначение /(#,0) для плотности распределения случайной
величины Χι.
Пример 6. Рассмотрим модель сдвига показательного закона
с плотностью /(#,0) = β~(χ~θΪΙ{χ·^β}. В этом случае функция
Likelihood (англ.) —
правдоподобие.
§ 4. Метод максимального правдоподобия
117
правдоподобия равна
Ηθ) = Π/(*<·*) = е-(11+-+х")е"в7{ж(1)^}.
г=1
Отсюда (см. рис. 7) получаем в качестве ΟΜΠ θ = хщ, которая
отлична от оценки метода моментов θ = χ — 1, найденной ранее
для этой модели в примере 2. Заметим также, что здесь L(0) не
является гладкой функцией, и поэтому ОМП нельзя вычислять,
приравнивая нулю производную функции правдоподобия.
В случае, когда L(6) гладко зависит от 0ι,... ,0m, оценки
максимального правдоподобия являются компонентами решения (вообще
говоря, нелинейной) системы уравнений:
J- ЫЦ9) = Σ\щ In/(ж,*) = 0, J = 1,... ,ш.
(2)
Иногда эта решение можно найти явно (см. задачу 2), но чаще
приходится вычислять его приближенно с помощью итерационных
методов (например, метода Ньютона из § 5).
Пример 7. Для закона Вейбулла—Гнеденко, используемого в
моделях, описывающих прочность материалов (см. § 2 гл. 4), с
функцией распределения Faip(x) = 1 — ехр{—χα/β} при χ > 0
(параметры α и β предполагаются положительными) система (2) после
некоторых упрощений приводится к виду
α η i=l i=l / i=l n i=l
В [50, с. 387] доказано, что первое уравнение системы
(следовательно, и вся система) при любых χχ,... ,#п (не равных
одновременно 1) имеет единственное решение.
Как показывают два следующих примера, функция
правдоподобия с вероятностью 1 может быть не ограничена сверху, т. е.
глобальный максимум L(0) на множестве θ может не достигаться.
Пример 8 [50, с. 391]. Рассмотрим (рис. 8) смесь плотностей
(см. § 2гл. 5) ^Ζΐ ρ (*=JH) + ± ρ (£^),Гдее 6 (0,1), σχ > 0,
V\ \ V\ J &2 \ &2 J
&2 > 0, p(x) — любая положительная при всех х плотность,
(скажем, стандартная нормальная р(х) = —= е"х /2). Тогда плотность
выборки
л/2тг
Ш^К^ИК^)}
118
Глава 9. Методы получения оценок
представляет собой сумму положительных членов, один из которых
равен
η—Ι η
1-ε
σι
K^)fe) π/(^)
Когда μι=#ιΗσι—►(), этот член стремится к бесконечности при
любых фиксированных значениях ε, μ<ι, σ<ι, х2,... ,#η. Стало быть,
L(0) неограничена и глобальной ОМП не существует. Однако
отметим, что для смеси нормальных плотностей выполняются условия
теоремы 1, приведенной ниже, и поэтому при достаточно большом η
функция правдоподобия будет иметь (с вероятностью 1) локальный
максимум в точке, которая находится как решение системы (2).
Пример 9 [61, с. 71]. Допустим, что у модели сдвига-масштаба
— ρ ( — 1, плотность р(х) такова, что χι+ερ{χ) —► оо при χ —► оо
σ \ σ J
для любого ε > 0 (например, годится р{х) = ^(1 Η- |α:|)—х[1 Ч- 1п(1 Ч-
+ |#|)]~2). Тогда для η > 1 глобальной ОМП не существует.
Доказательство. Как всегда, хщ ^ Х(2) ^ · · · ^ х(п)
—вариационный ряд, построенный по реализации χ = (ж ι,... ,#п). Возьмем
с φ О такое, что р(с) > 0. Положим μ = хщ — са. Тогда
/(χ,μ,σ) =
η η
= σ-ηΥ[ρ((χί - μ)/σ) = р(с) а~п]\р(с + (χ{ί) - χ(ΐ))/σ) =
»=1 i=2
Для η > 1 множитель, заключенный в фигурные скобки, стремится
к бесконечности при σ —► 0, независимо от того, равно ли х^
величине хщ или нет. Следовательно, /(χ,μ,σ) —► оо.
В [61, с. 72] доказано обратное утверждение: если
плотность р(х) ограничена и непрерывна, а функция |#|1+ερ(#)
ограничена при некотором ε > 0, то с вероятностью 1 глобальная ОМП
(μη,ση) существует при достаточно большом η и (μη&η) *> (μ,σ)
при η —► оо. ■
Для заданной статистической модели координаты точки
максимума функции правдоподобия L(0) зависят от реализации
#1,... ,#п, т. е. 9j = 9j(xi1... ,#n), j = 1,... ,ra. Подставив вместо
аргументов в эти функции компоненты выборки (Χι,... ,ХП),
получим случайные величины Oj(Xi,... ,ХП)· Какими свойствами
обладают такие оценки?
§ 5. Метод Ньютона и одношаговые оценки
119
Для простоты далее в этом параграфе ограничимся случаем
скалярного параметра (векторный случай рассматривается, скажем,
в [11, с. 237] или [50, с. 379]).
Предположим, что помимо условий R1 - R4 из § 3 выполнены
дополнительные условия регулярности:
R5) распределения Fq различны при разных θ Ε θ;
R6) плотность f(x,6) при каждом χ Ε А трижды непрерывно
дифференцируема по 0;
R7) §f(x,0)dx можно дважды дифференцировать по
параметру θ под знаком интеграла;
R8) существует функция h(x) такая, что при всех χ Ε А
д3
^зЬД*,0)
^ h(x) для всех θ Ε θ и Mh(X\) < оо.
Теорема 1. При выполнении условий R1-R8 для достаточно
большого η существует с вероятностью 1 решение θ = θη уравнения
правдоподобия
£pnf(Xi)9)=0, (3)
дающее сильно состоятельную оценку: θη п' н'> θ при η —► оо,
причем у/п{вп-в) Α ξ ~ Л/"(О,1/Д(0)), где h(θ)-информация
Фишера случайной величины Х\ (см. § 3). Доказательство этой
теоремы можно найти
m «π -ηι -по л* в учебнике [69, с. 205].
Теорема 2. Пусть выполнены условия R1-R8 и θ — некоторая
асимптотически нормальная оценка:
Vn(0n ~ Θ) -i С ~λί (Ο,σ2(0)) при η — оо,
где асимптотическая дисперсия σ2(0) непрерывно зависит от Θ.
Тогда
σ2(θ) ^1/Ιι(θ) при всех 0G Θ. (4)
Ле Кам в 1953 г. доказал,
На основании неравенства (4) заключаем, что ОМП (при вы- что для разрывных σ2(θ)
полнении условий R1 - R8) имеет наименьшую возможную асимп- нарушат™не бо^ееГчем
тотическую дисперсию, равную 1/Д(0). Это свойство называется на множестве лебеговой
г, /. η меры нуль. Соответ-
асимптотическои эффективностью. ствующий контрпример
приведен в задаче 7.
§5. МЕТОД НЬЮТОНА
И ОДНОШАГОВЫЕ ОЦЕНКИ
Для численного решения нелинейного уравнения φ(χ) = О можно
использовать метод Ньютона (метод касательных), который
состоит в следующем. Прежде всего, задается начальное
приближение #о· Затем вычисляются значения #&+ι, к = 0,1,..., по формуле
хк+\ = хк - ч>{хк)/ч>'(хк), (5)
120
Глава 9. Методы получения оценок
О ^ χ* Xfc+i Xk
Рис. 9
К. Ф. Гаусс (1777-1855),
немецкий математик.
Доказательство теоремы 3
приведено в [6, с. 107],
обобщение ее на
многомерный случай
можно найти в [77, с. 192].
Рис. 10
которая получается в результате проведения касательной к
графику у = φ(χ) в точке (xki<p(xk)) (рис. 9). Действительно, полагая
у = 0 в уравнении касательной у = <р(хк) + <£'(х&)(# — х*),
находим, что координата Xk+ι точки ее пересечения с осью абсцисс
удовлетворяет соотношению
откуда (при <p'(xk) Φ 0) следует итерационная формула (5).
(в)
Замечание. Для нелинейной системы уравнений φ{χ) = О
аналогом уравнения (6) будет линейная система (pf{xk){xk+\ — Хк) =
= — <р(хк), где <р'(х) = \\8φί{χ)/8χ^\\ — матрица Якоби. Решив
линейную систему методом Гаусса (см. [6, с. 137]), найдем очередной
шаг Aajfc+i = Xk+i - Xk-
Оценку скорости сходимости приближений Xk в скалярном
случае дает
Теорема 3. Пусть в ί-окрестности корня х* уравнения φ(χ) = 0
функция φ дважды непрерывно дифференцируема, 0 < α < |<//(ж)|,
\φ"(χ)\ ^ β. Положим ε = min{£/2,a//3}. Тогда, если \х0 - х*\ ^ ε,
то при всех к ^ 0 выполняются неравенства \xk+i — х*\ ^ |#fc+i ~хк\
и |a?fc+i - х*\ ^ $~1\хк - я*|2·
Первое неравенство позволяет оценить погрешность текущего
приближения через предыдущие.
Второе неравенство показывает, что при выборе начального
приближения х0 из достаточно малой окрестности простого тсорнл,
т. е. такого, что φ'{χ*) ф 0, метод Ньютона сходится квадратичпо
(существенно быстрее геометрической прогрессии). Это означает,
что на каждой итерации число верных знаков приближения
примерно удваивается.
Если xq взято достаточно далеко от корня ж*, процесс может
расходиться, в частности, могут возникать так называемые
«осцилляции» (рис. 10).
Приведем пример алгоритма, который является частным
случаем метода Ньютона.
Пример 10. Задачу численного извлечения квадратного корня из
числа а > 0 можно представить как поиск корня уравнения φ(χ) =
= χ2 — а = 0. Применим метод касательных. Здесь φ'(χ) = 2х
nxk+i = Xk — {x\—o)/(?Xk) = о(ж*+а/ж*)> т,е* получаем известный
алгоритм усреднения Xk и а/ж*.
Пример 11. Для модели сдвига закона Коши с
плотностью ί{χβ) = 1 /[π (1 + (χ — θ)2)] уравнение правдоподобия (3)
§ 5. Метод Ньютона и одношаговые оценки
121
имеет вид
Xi-Θ
»=1 ! +
(Xi-Θ)2
= 0.
(7)
+оо
В этой модели информация Фишера 1\{θ) = - J -( гТз ^х = о *
По теореме 1 асимптотическая дисперсия ΟΜΠ 0 равна
1/Л(0) = 2. Следовательно, относительная эффективность
её med = тг2/8 « 1,234. Другими словами, в этой модели ОМП
0 асимптотически точнее выборочной медианы MED примерно
на 23%.
При поиске решения уравнения правдоподобия (3) в качестве
начального приближения 0о нередко используется значение оценки,
полученной по методу моментов, или любой другой легко
вычисляемой оценки (желательно, устойчивой к выделяющимся
наблюдениям). Оказывается, для регулярных моделей справедлив
следующий интересный статистический результат: достаточно сделать
всего один шаг по методу Ньютона, начиная с любой
асимптотически нормальной^ оценки, чтобы получить асимптотически
эффективную оценку 01 (т. е. столь же точную, как ОМП). Сформулируем
его более строго.
Теорема 4. Пусть выполнены условия R1 - R8 из § 3 и § 4, а оценка
0о такова, что у/п(во — 0) —► ξ ~ ΛΓ(Ο,σ2(0)) при η —► оо. Тогда
одношаговая оценка 0ι = 0о — φ(θο)/φ'(θο)ι где φ(θ) = — lnL(0) =
Ου
П Q
= Σ оБт/(ж»,0), обладает асимптотической дисперсией 1/Д(0).
г=1 όθ
Пример 12. Возьмем для модели сдвига закона Коши из
примера 11 в качестве начальной оценки 0О выборочную медиану MED.
Из теоремы 4 и теоремы 1 гл. 7 имеем, что одношаговая оценка 0ι
с
ψ(θ) = -2 Ε
Xi-Θ
и φ'(θ) = 2Σ
I-(Xi-Θ)2
• £11+ (*-*)» " irv"/ "£i(l + (X<-*)aja
является асимптотически эффективной для параметра сдвига 0.
Пример 13 [50, с. 377]. Пусть случайные величины Х\ имеют
плотность /(#,0) = (1 — θ)ρι(χ) + Θρ2(χ)> где плотности pi и р2
известны, а вес 0 £ [0,1] — нет. Допустим, что у распределений
с плотностями ρι(χ) и Р2(х) математические ожидания μι и μ*ι
различны, а дисперсии — конечны.
Поиск ОМП приводит к уравнению степени п—1 относительно 0:
Α ρ2№)-ρι№)
Si (i-0)pi№) + 0p2№)
= ο,
Вопрос 3.
а) Всегда ли это
уравнение имеет хотя бы
один корень? 6) Какое
наибольшее число корней
может быть у него?
Доказательство теоремы
см. в [50, с. 375].
122
Глава 9. Методы получения оценок
решить которое при больших η довольно сложно. Применение
теоремы 4 позволяет, не решая его, асимптотически эффективно оце-
Благодарение Всевыш- нить Θ. Для этого достаточно использовать в качестве 0О оценку ме-
нему, что нужное Он ТОда моментов, которая находится из уравнения (1— 0)μι+0μο = X:
сделал нетрудным, ^ — ν ' ^
а трудное—ненужным. во = (X — μι)/(μ2 — μι)· При сделанных предположениях 0О асимп-
г. Сковорода тотически нормальна в силу центральной предельной теоремы.
§6. МЕТОД СПЕЙСИНГОВ
Познакомимся теперь с оригинальным методом, предложенным
Ченом и Амином в 1983 г. (см. [15, с. 90]). Оценки, полученные этим
методом, асимптотически эффективны при выполнении условий
регулярности и оказываются состоятельными даже для тех моделей,
где глобальной ОМП не существует.
Рассмотрим хщ ^ #(2) ^ ··· ^ х(n)~~ вариационный ряд,
построенный по реализации выборки из закона с функцией
распределения F{x,6) и плотностью /(#,0), 0 Ε θ, носителем которой
является некоторый интервал (μι,μ2)· Параметры μι и μ<ι могут
быть неизвестны. В этом случае их следует считать компонентами
вектора 0. Положим Х(0) = μι и #(η+ΐ) = μ2· Спейсингами
называются величины
Di= [ f(x,e)dx = F(x{i),e)-F(x{i_1)ie)1 г = 1,...,п + 1.
X(i-i)
Метод спейсингов рекомендует в качестве оценки векторного
параметра 0 взять такую статистику 0, которая максимизирует
п+1
произведение G(0) = ΓΙ ^ или> что то же самое, максимизирует
г=1
функцию Я(0) = lnG(0).
Мотивировкой метода служит то обстоятельство, что в силу
п+1
условия Σ Di = 1 максимум функции G достигается, когда все
г=1
Di одинаковы (задача 8). Выбор значения 0, которое «уравнивает»
спейсинги, является разумным ввиду того, что при истинном 0
величины А(Х(фХ^_!),0) представляют собой в силу метода
обратной функции из § 1 гл. 4 одинаково распределенные спейсинги
с равномерным распределением на отрезке [0,1] (см. § 4 гл. 4).
Пример 14. Для модели сдвига показательного закона с
плотностью f{xfi) = ε~(χ~θ^Ι{χ·^θ} из примера 6 легко установить, что
п+1
Η(θ) = In (1 - e*"^1)) + θη + Σ 1η (e"^"1) - e~x^).
i=2
Из уравнения Η'(θ) = 0 находим θ = Хщ — 1п(1 + -) =
= Х(!) Ь 0(п~2) при η —► оо. Сравнивая ее с ОМП ^(ΐ), видим,
Задачи
123
что смещение уменьшилось до величины порядка η 2 (см. решение
задачи 3 гл. 6).
Сопоставим поведение логарифма функции правдоподобия
η η+1
InL(0) = Σ ln/(X(i),0) и поведение функции Η(Θ) = Σ In Di.
На основании теоремы Лагранжа о среднем можно записать, что
1П А = ln/(X(i),0) + ln(X(i) - X(i_1}) + ДЛХ(г)Д(г-1),0).
В случае, когда μι и ^2 известны, остаточный член Ri хоть
и зависит от 0, но имеет величину О(Х^) — X(;_i)). Так как
р
Χ(ή — X(i-i) —► 0 при η -^ оо, вклад остаточного члена в InDi
становится пренебрежимо малым, и поведение dH/θθ не
отличается от д In L/θθ* Это приводит к асимптотической эффективности
оценок метода спейсингов.
Если же μι (или дг) неизвестен, то вклад ϋι (или ϋη+ι) уже
не стремится к нулю при η —► оо. Это приводит к различному
поведению In L и Н: In L может быть, скажем, не ограничена сверху,
в то время как Η ^ О, поскольку 0 ^ Д ^ 1.
Пример 15 [15, с. 92]. Для выборки из сдвинутого на μ
распределения Вейбулла—Гнеденко с функцией распределения FMja(#) =
= [l — e~^~^a] 1{χ>μ}1 где параметры μ и a > О неизвестны,
логарифм функции правдоподобия имеет следующий вид:
1η£(μ,α) = nlna + (a - 1) £ ln(X(i) - μ) - £ (X{i) - μ)<*.
г=1 г=1
При а<1ид—>Х(!) эта функция стремится к -f оо.
В свою очередь, метод спейсингов позволяет получить
состоятельные оценки параметров μπα; правда, решать систему
уравнений дН/θμ = дН/да = 0 приходится численно.
Другие примеры применения метода спейсингов встречаются
в задачах 4 и 5.
задачи
1. Вычислите информацию Фишера Ι\(θ) для случайной
величины Χι, имеющей распределение Бернулли с неизвестной
вероятностью «успеха» Θ.
Указание. Выразите U\ = (д/д0)1п/(Хь0) через Хг.
2. Пусть Xi ~ Λ/Χμ,σ2). Найдите ΟΜΠ μ и σ. (Почему найденное
решение —это точка максимума функции правдоподобия, а не,
скажем, седловая точка?)
Числом поболее, ценою
подешевле.
Чацкий в «Горе от ума»
А. С. Грибоедова
124
Глава 9. Методы получения оценок
= Ip-\*S
3. Случайные величины Χι имеют функцию распределения
F ί χ~Ρ\? где F(x) = (1 — е~х) 1{х^о} (модель сдвига-масштаба
показательного закона). Найдите ОМП параметров μ и σ.
Указание. Учтите, что плотность разрывна в точке μ.
4. Для равномерного распределения на отрезке [μι,μ2] вычислите
а) ОМП,
б) оценки по методу спейсингов.
5. Случайные величины Χι имеют плотность ρ(χ,θ) = к е~
(сдвиг распределения Лапласа). Как устроено множество, на
котором функция правдоподобия максимальна для
а) четного,
б) нечетного размера выборки?
Указание. Сравните с задачей 4 гл. 7.
6? Для логнормальной модели с плотностью
ρ"·*(χ) = i^mехр {" Ъ(1пж"μ?)1{х>0}
найдите оценки параметров μ и σ по методу моментов.
7* Для выборки из закона Ν(θ, 1) рассмотрим оценку
\ьх,
если \Х\ ^ αη,
если \Х\ < αη,
где |Ь| < 1, 0 < ап —► О, но апу^ —► оо при η —► оо. Вычислите
асимптотическую дисперсию этой оценки.
8. С помощью метода Лагранжа проверьте, что максимум функции
п+1 п+1
Π Di при условиях Σ D{ = 1, 0 ^ А ^ 1, г = 1,... ,п + 1,
г=1 г=1
достигается, когда Di = ... = £>η+ι = 1/(я--f l).
РЕШЕНИЯ ЗАДАЧ
Принимаясь за дело, , ,
соберись с духом. 1. Ux = Χχ/Θ - (1 - Χι)/(1 - θ) = (Χι - θ)/[θ(1 - θ)}. Отсюда
Козьма Прутков
/х(0) = MUl = [0(1 - θ)]~2ΟΧ1 = [0(1 - β)]"1.
Этот результат можно получить и без вычислений: согласно
примеру 5, частота X является ОМП в этой модели; в силу
центральной предельной теоремы у/п (Χ—Θ) —> ξ ~ ЛГ(0,0(1-0))
при η —► оо; наконец, согласно теореме 1, асимптотическая
дисперсия 0(1 — 0) равна 1/7ι(0).
1 Π
2. ΙηΙ,(μ,σ) = —nln\/27r — ηίησ g Σ№ ~~ А*)2· Необходимым
условием экстремума этой функции является равенство нулю
Решения задач
125
частных производных:
Первое уравнение дает μ = X. Подставив μ во второе уравнение,
находим, что σ = 5, где 52 = - Σ № ~~ ^02 ~~ выборочная
пг=1
Убедимся, что найденное решение является точкой
максимума функции L, а не, скажем, точкой минимума или седловой. Подробности малейшей не
Для этого вычислим производные второго порядка:
d2\nL
η
d2\nL _ η 3 A ,v x2
θμ2
__ = --, (Χ-μ).
Учитывая, что при η > 1 с вероятностью 1 статистика S2 > О,
эти производные в точке (μ,σ) = (X,S) будут иметь
значения —n/S2 < О, —2n/S2 < 0 и 0 соответственно. Поскольку
определитель (Θ21ηΖ,/0μ2) (02 InΖ,/0σ2) - (д2 InΣ/θμθσ)2 > О, то
выполняются достаточные условия максимума (см. [46, с. 195]).
3. В данной модели θ = (μ,σ) £ θ = R χ (0, + оо),
L = ехр j-ηΐησ - ± £ (Х< - μ) J /{*(1)>μ}.
При любом σ > 0 эта функция возрастает по μ до точки
Х(!) = min{Xi,... ,ХП}, а затем обращается в 0. Рассмотрим
поведение функции InL в сечении μ = Χ(ι)· Приравнивая
частную производную нулю, получаем уравнение
einL = -5 + ?£W-Jf(i)) = ol
да
решением которого является статистика σ = X — X(i)· Заметим,
что Χ(ΐ) оценивает сдвиг μ, а X служит оценкой для ΜΧχ = μ+σ
(рис. 11).
4. а) Функцию правдоподобия можно записать так:
η
^=(μ2-μι)"ηΠ/{μι<χ^μ2} = (μ2-μι)"η/{μι^χ(1)}/{χ(η)<μ2}.
г=1
забуду.
Чацкий в «Горе от ума»
А. С. Грибоедова
υ = ΡμΛχ)
μ Χ φ Χ
Рис. 11
Максимизация L приводит к ОМП (ДьДг) = (^(ΐ)^(η))·
126
Глава 9. Методы получения оценок
б) В этой модели функция Η имеет следующий вид:
Η(μΐιμ2) = 1п(Х(1) - μι) + £ ln(X(i) - X(<_i))+
г=2
+ 1η(μ2 - 1пХ(п)) - (η + 1) In (μ2 - μι) ·
Приравнивая частные производные нулю, получаем систему
дН = 1 п + 1 = Ш_ = _± п + 1 _Q
#μι Χ(1)-μι μ2-μι ' #μ2 μ2--Χ"(η) μι-μ\ '
решение (Дь/хг) которой нетрудно найти:
μι=Χ(ΐ)- ^—γ (Χ(η) -Χ(ΐ)), h =Χ(η) + —[ (Χ(η)-Χ(ΐ))·
В отличие от ОМП эти оценки не имеют смещения.
ϊδ &(η—1)δ «£
Действительно, среднее расстояние δ между любыми сосед-
ними из η взятых наудачу из [μι,μ2] точек, очевидно, равно
^ι Μ (η) ^2 (μ2 — μι) Ι (η + 1). Поэтому математическое ожидание размаха
Рис. 12 выборки Х(п) — X(i) есть (п — 1)£ (рис. 12). Следовательно,
(Х(п) —Х(1)) — это поправка, устраняющая смещение оценок
Х(1) И Х(П).
5. а) Для модели сдвига распределения Лапласа
1ηΖ,(0) = -η1η2- Σ \Χί-θ\·
г=1
Максимизация этой функции равносильна поиску такого
значения 0, при котором сумма расстояний от него до всех элементов
выборки Xi была бы минимальной. Пусть η = 2k. Покажем,
что в качестве решения годится любое θ из [X^)^X(k-\-i)]-
Минимизируем сначала сумму расстояний до Х^) и X(k+i)· Она
равна Δι = X(k+i) ~ X(k) Для θ G [X(fc),X(fc+1)] и больше
Δι для θ <£ [X(fc),X(fc+1)]. Добавим точки Х(к-\) и X(fc+2)
(рис. 13). Сумма расстояний до них при θ Ε [Χ(*._ΐ),Χ(*.+2)1
равна Δ2 = X(k+2) — X(k-i) и больше Δ2 вне этого отрезка.
_► Очевидно, что только θ из [X(fc),X(fc+1)] С [X(k-i),X(k+2)] ми-
X(k-i) Хм Х(к+\)Х{к+2) нимизируют обе суммы сразу. Далее рассуждаем аналогично.
Рис. 13 б) «Склеив» точки Х^) и Х(*.+1), видим, что в случае выборки
нечетного размера ОМП будет выборочная медиана MED.
Интересно, что функция Η метода спейсингов из § 6 имеет
единственную точку максимума MED = ~ (Х(к)+Х(к+1)) и в
случае выборки четного размера (убедитесь!).
6. Вычислим сначала момент к-ro порядка
+оо
Ответы на вопросы
127
Сделаем замену у = In χ и выделим полный квадрат:
+оо
—оо
—оо
Заметив, что справа стоит интеграл по всей прямой от плотности
распределения Μ(μ + σ2λ;, σ2), получим α& = βχρ{λ;μ + k2a2/2}.
Приравнивая первый и второй теоретические моменты
выборочным, получим систему уравнений
βχρ{μ + σ2/2} = Аи βχρ{2μ + 2σ2} = А2.
Нетрудно убедиться, что она имеет решение
μ = 21ηΑι-(1ηΑ2)/2, σ = (ΙηΑ2 - 21ηΑι)1/2.
7. В этой модели X ~ Л/Х0, 1/п). Поэтому при η —► оо
Р(|Х| ^ αη) = Ф(д/п (в - on)) + Ф(-д/п (в + αη)) - /{^0}
(Ф(ж) — функция распределения закона ЛГ(0,1).) Так как
Р(л/п(Θ - 0) < я) = Р(у/п(Х - 0) < я, |Х| ^ αη)+
+P(^(bX-0)^z,|X|<an),
то при 0 φ О и 0 = 0 имеем, соответственно,
>/n(9-9)i{~J\r(0,l) и ^0 Λξ'~ΛΓ(0,62).
При 0 = 0 асимптотическая дисперсия σ2(0) = Ь2 < 1 = Д(0),
и неравенство (4) нарушается, несмотря на гладкость модели.
8. Максимизируем Η = £)1ηΑ· Для этого составим функцию
Лагранжа (см. [46, с. 271]): F = Σ Ь А - λ (£ А - 1)·
Приравнивая нулю частные производные функции FT запишем систему
уравнений для поиска экстремальных точек:
|£ = 1/Д-А = 0, г = 1,...,п + 1; Ц=£А-1 = 0.
Из первых η + 1 уравнения находим, что А = Ι/λ. Подставляя
в последнее уравнение, получим λ = п+1, откуда А = 1/(п + 1).
ОТВЕТЫ НА ВОПРОСЫ
1. а) Случайная величина /{χ^χ} имеет распределение Бернулли
с вероятностью «успеха» F(x).
б) Схема Бернулли с вероятностью «успеха» F(x).
в) Для фиксированного χ величина Fn{x) есть частота
«успехов» — попаданий левее х.
128
Глава 9. Методы получения оценок
г) По усиленному закону больших чисел (П6) эмпирическая
функция распределения Fn(x) сходится с вероятностью 1 к
теоретической функция распределения F(x).
2. Положим г = l/k > 1, η = |£|fc. Применяя неравенство Иенсена
к функции φ(χ) = |#|г, находим, что |Мг/|г < М|г/|г, т.е.
(M|£|fcy/fc ^ М|£ |*, что и требовалось доказать.
3. а) Левая часть уравнения (7) — сумма непрерывных функций,
каждая из которых положительна при θ < Х^ и отрицательна
при θ > Х(п). Следовательно, хотя бы один корень всегда есть.
б) Если привести слагаемые к общему знаменателю, то в
числителе появится многочлен степени 2п — 1. Поэтому максимальное
число решений уравнения (7) равно 2п — 1.
Математика дает наиболее
чистое и непосредственное
переживание истины; на
этом покоится ее ценность
для общего образования
людей.
Макс Лауэ
Красивый результат для этой модели получил Дж. Риде
в 1980 г. (см. [50, с. 376]): если 2К + 1 есть число корней
уравнения (7), то К сходится по распределению к закону Пуассона
с параметром l/π при п —> оо (см. § 1 гл. 5).
Удивительно, но для более сложной модели, когда
присутствует не только параметр сдвига, но и параметр масштаба,
решение (μ,σ) системы уравнений (2) для закона Коши всегда
единственно. Это установил Дж. Копас в 1975 г. (см. [50, с. 387]).
Глава 10
ДОСТАТОЧНОСТЬ
§ 1. ДОСТАТОЧНЫЕ СТАТИСТИКИ
Некоторые статистические модели допускают сжатие
информации—замену выборки X = (Χι,... ,ХП) размера η на статистику
Т(Х), которая «эквивалентна» всей выборке в задаче оценивания
неизвестного параметра Θ.
Рассмотрим для примера схему Бернулли с неизвестной
вероятностью «успеха» Θ: Р(Хг = χι) = θΧί(1 — θ)ι~Χί, где χι = 0 или 1.
Выборка X имеет совместное распределение
По одной капле
воды... человек, умеющий
мыслить логически,
может сделать вывод
о возможности
существования Атлантического
океана или Ниагарского
водопада.
А. Конан Дойл, «Этюд
в багровых тонах»
ί{χ,θ) = θ\\-θ)η-\ где
χ = (а?ь... ,яп), t = Τ (χ) = X>t.
г=1
Как было установлено в примере 5 гл. 9, оценкой
максимального правдоподобия для схемы Бернулли является частота
X = Т(Х)/п — функция от Т. Найдем условное
распределение (см. П7) выборки X при условии {Т(Х) = t}1 t = 0,1,... ,η:
Р(Х = х\Т(Х) =t)= θ'(1 ΘΤ
οιηθι{ΐ-βγ
_1_
если точка χ такова, что Υ^χι = ί, иначе вероятность равна 0.
Заметим, что это условное распределение не зависит от Θ.
Определение. Статистика Т{Х) = (Τι(А"),... ,Тт(Х)) в
дискретной модели называется достаточной, если для всех θ Ε θ, χ £ Rn
и любых возможных значений t = (ίι,... ,£m) условная вероятность
Р(Х = χ | Г(Х) = t) не зависит от Θ.
Оказывается, достаточная статистика содержит точно такую
же информацию (см. задачу 6) о значении параметра 0, что и вся
выборка. Чтобы убедиться в этом, заметим, что моделирование
выборки можно разбить на следующие два этапа.
1) Розыгрыш значения £0 статистики Г, имеющей
распределение Р(Т(Х) = £). (В схеме Бернулли Τ распределена по
биномиальному закону: Р(Т(Х) = t) = С* 0< (1 - 0)η_ί.)
Это понятие было введено
Р. Фишером в 1922 г.
130
Глава 10. Достаточность
2) Розыгрыш положения реализации выборки X на множестве
{х: Т(х) = to} («линии уровня») (рис. 1) в соответствии с
условным распределением Р(Х = χ \ Т(Х) = to). (Для схемы Бернулли
на этом этапе надо случайно (равновероятно) расставить ίο единиц
в наборе из нулей и единиц длины η (рис. 2).)
При этом от того, какое значение имеет параметр 0, ввиду
достаточности статистики Τ зависит только первый этап — розыгрыш
линии уровня.
0,1,0,0,...,10,0,1,0
V
П
Рис. 2
Factor (англ.) —
множитель.
§ 2. КРИТЕРИЙ ФАКТОРИЗАЦИИ
Как для заданной статистической модели найти достаточную
статистику? Ответ на этот вопрос дает
Теорема 1 (критерий факторизации). (Векторная)
статистика Τ в дискретной модели достаточна тогда и только тогда,
когда существуют функции д и h такие, что совместная вероятность
/(χ, 0) выборки X представляется в виде
f(x,9)=g(T(x),9)h(x), (1)
т. е. распадается в произведение двух функций (факторизуется):
первая зависит от 0, но от χ зависит лишь через Т(х), а вторая от
параметра 0 не зависит.
(В частности, для схемы Бернулли можно взять функции
g(tfi) = 0*(1 - 0)η_ί и h(x) = 1, где t = Т(х) =хг + ... + хп.)
Доказательство [32, с. 55]. Если статистика Τ достаточна, то
при любом χ условная вероятность Р(Х = х\Т(Х) = Т(х)) не
зависит от Θ. Возьмем эту вероятность в качестве функции h(x).
Так как событие {X = х} С {Т(Х) = Т(ж)}, то совместная
вероятность имеет вид
/(х,0) = Р(Х = х) = Р(Х = х,Т(Х) = Т(х)) =
= Р(Т(Х) = Т(х)) Р(Х = х\Т(Х) = Г(х)),
где Р(Т(Х) = Т(х)) играет роль функции д в представлении (1).
Обратно, пусть имеет место разложение (1). Тогда при любом χ
таком, что Т(х) = t, запишем:
_ Р(Х = х) _ , .
p(T(X) = t) -Ηχ>ν>
Σ №,<>) =
x':T(x')=t
= g(tft)h(x)
Σ g(tft)h(x')=h(x)
x':T(x')=t ι
Σ Hx') ,
x':T(x')=t
т. е. условная вероятность не зависит от θ. Если же χ таково, что
Т(х) φ t, то, очевидно, Р(Х = χ | Т(Х) = t) = 0. Таким образом,
§ 2. Критерий факторизации
131
при любом χ условная вероятность Р(Х = χ \ Т(Х) = t) не зависит
от0. ■
Замечание. Если Τ достаточна, то таковой же будет и
статистика S = φ{Τ), где φ — взаимно однозначная (борелевская)
функция (отображение, когда Τ — векторная статистика).
Действительно, в этом случае существует обратная функция (отображение)
φ~ι: Τ = (ρ-1 (5), и из представления (1) имеем
/(χ,θ) = 9(φ-1(8),θ)Η(χ) = 9l(S,e)h(x).
Отсюда в силу теоремы 1 статистика S является достаточной.
Теперь определим понятие достаточности для непрерывных
статистических моделей. Обозначение /(ж, Θ) станем
использовать для совместной плотности выборки X = (Χι,... ,ХП).
Тогда для статистики Т(ж), непрерывно зависящей от ж, верно
равенство Р(Т(Х) == £) = 0. Корректное определение условной
вероятности Р(Х = χ \ Т(Х) = i) в этом случае выходит за рамки
математического аппарата, используемого в этой книге. Поэтому
вместо введения понятия достаточности на языке условных
вероятностей, ) примем критерий факторизации в качестве определения:
будем считать статистику Τ достаточной, если она факторизует
плотность /(ж,0) в виде (1).
Пример 1. Для нормальной модели ΛΓ(μ, σ2) с неизвестными
параметрами μ и σ (т. е. θ = (μ,σ)) плотностью выборки служит
/(*,«) = Π -4= е-^^-")2 = 1=- е-*Ы2>?-2мЕ*<+^2).
г=1
ал/2тт (ал/2тг)п
Из этого представления видно, что статистика Т(ж) = (^ #», Σ #?)
является достаточной. Так как компоненты Τ взаимно однозначно
выражаются через χ = -^ii и s2 = —J2xf — (χ)2, το вся
информация о значениях параметров μ и σ содержится в я и s2.
Пример 2. Для модели сдвига показательного закона совместная
плотность X факторизуется так:
f(x,9)=Πβ~(*,~*) w>=«·" w·) · e~Exi- „ ,
i=1 Вопрос 1.
Какая статистика
Таким образом, для оценивания параметра θ достаточно знать 6УДет достаточной для
г ,. . fv ν ί выборки из равномерного
значение статистики A(1) = minjAi,... ,An}. распределения на [0,0]?
*) С таким подходом (и доказательством критерия факторизации для него)
можно познакомиться по учебнику [11, с. 431].
132
Глава 10. Достаточность
Вопрос 2.
Принадлежит ли
экспоненциальному семейству
модель показательного
закона с неизвестным
параметром масштаба σ:
Γσ{χ) = 1-β~χ/σ при
х^О (рис.3)?
Рис. Э
§3. ЭКСПОНЕНЦИАЛЬНОЕ СЕМЕЙСТВО
Всегда существует тривиальная (векторная) достаточная
статистика—вся выборка. Важным является вопрос: для каких
статистических моделей существуют достаточные статистики,
размерность которых не зависит от длины выборки? Примером класса
таких моделей может служить так называемое экспоненциальное
семейство.
Определение. Модель принадлежит экспоненциальному
семейству, если найдутся такие функции <7ο>0ι> · · · )#т и статистика
Τ = (Ti,...,Tm), что совместная плотность (или вероятность)
выборки представляется в следующем виде:
/(*,*) = ехр ί90(θ) + Σ 9ά{θ)Τά{χ)\ h(x).
При этом статистика Τ, очевидно, является достаточной.
(2)
Так, нормальная модель из примера 1 удовлетворяет
условию (2), если взять
9ο(θ) = -η(]ησ+£^, 9ι{θ) = £, д2{0) = -±, Λ = (2π)""/2.
Некоторые другие распределения из экспоненциального
семейства приведены в задаче 2. Отметим, что равномерное
распределение на отрезке [О, Θ] и модель сдвига показательного закона из
примера 2 в него не входят.
Замечание. Как доказали Е. Б. Дынкин и Т. С. Фергюсон
(см. [50, с. 40]), среди моделей сдвига только нормальный закон
и распределение const·InX, где случайная величина X имеет
гамма-распределение, допускают представление (2) с т = 1.
В частности, модели сдвига законов Коши и Лапласа не входят
в экспоненциальное семейство. Более того: для этих двух законов не
существует достаточной статистики, размерность которой меньше
длины выборки (см. [50, с. 47]).
В каких еще семействах, помимо экспоненциального, есть
достаточные статистики фиксированной размерности? Ответ дает
следующая «пессимистическая» теорема из [50, с. 48].
Теорема 2. Предположим, что элементы выборки имеют
непрерывную по χ плотность /(#,0), носитель А = {х: f(x,0) > 0}
которой есть интервал, не зависящий от θ Ε θ. Пусть для
совместной плотности выборки существует непрерывная т-мерная
достаточная статистика. Тогда
1) если т = 1, то найдутся функции g0l 9\ и Λ, такие что
справедливо равенство (2);
§4. Улучшение несмещенных оценок 133
2) если га > 1 и f(x,0) имеет непрерывную частную
производную по #, то существуют функции Qj и Л, такие что равенство (2)
справедливо с га' ^ га.
Таким образом, среди гладких семейств распределений с
фиксированным носителем только экспоненциальное семейство
допускает сокращение размерности данных через достаточность. При
этом важным условием в теореме 2 является независимость
носителя от Θ. Если оно не выполняется, то, как показывает пример 2,
для любого размера выборки может существовать одномерная
достаточная статистика.
§4. УЛУЧШЕНИЕ НЕСМЕЩЕННЫХ ОЦЕНОК
Пусть 0 — несмещенная оценка параметра 0, т. е. Μθ = θ для всех
θ Ε θ. Допустим, что в модели существует достаточная
статистика Т. Тогда ее можно использовать для улучшения оценки Θ.
Теорема 3 (Колмогоров — Блекуэлл — Рао). Предположим,
что дисперсия ΟΘ < оо для всех θ Ε θ. Рассмотрим оценку θτ =
= Μ(Θ(Χ) Ι Τ) (см. П7). Тогда θτ также будет несмещенной оценкой
для параметра 0, причем Όθτ ^ ΟΘ при всех Θ £ θ.
Доказательство. Тот факт, что θτ = Μ(Θ(Χ) \ Τ) является
оценкой, т. е. не зависит от 0, следует из достаточности статистики Т:
распределение выборки X при фиксированном значении Τ от θ не
зависит.
Свойство 1 условного математического ожидания (П7) влечет
несмещенность оценки θτ'- Μθτ = ММ(0|Т) = ΜΘ = θ. Для
доказательства неравенства заметим, что
ΟΘ = Μ(θ-θτ + θτ-θ)2 =
= М(0 - θτ)2 + 2 М(0 - θτ)(θτ -θ) + Όθτ > D0T,
поскольку первое слагаемое неотрицательно, а второе равно 0.
Действительно, так как θτ — функция от Т, то согласно свойствам 1 и 3
из П7, имеем:
М(0 - θτ)(θτ - θ) = ММ \(θ - θτ)(θτ -θ)\τ\ =
= Μ [(0Τ - Θ)Μ(Θ- θτ | Τ)] = Μ [(0Τ - Θ)(Μ(Θ | Τ) - θτ)\ =0. Ш
Отметим, что попытка дальнейшего^улучшения оценки θτ при
помощи статистики Τ бесполезна: Μ(θτ\Τ) = θτ по свойству 3
изП7.
Замечание. Можно доказать (см. [15, с.73]), что операция
усреднения по достаточной статистике не приводит к увеличению риска
Every cloud has a silver
lining (Джон Мильтон).
« Нет худа без добра.
134
Глава 10. Достаточность
Щ(в) = Μ ρ(θ — θ) (см. § 3 гл. 6) относительно произвольной
непрерывной выпуклой функции потерь р. Поэтому хорошие оценки, как
правило, являются функциями от достаточных статистик.
Следующий пример показывает, что в качестве исходной в
теореме 3 может фигурировать даже оценка, не обладающая свойством
состоятельности.
Пример 3. Для выборки X = (Χχ,...,Χη) из закона Бернулли
с неизвестной вероятностью «успеха» θ попробуем улучшить оценку
θ = Χι с помощью достаточной статистики Τ = Σ,Χΐ- Проверим
несмещенность θ: ΜΧχ = 1 · Р(Хг = 1) + 0 · Ρ(Χχ = 0) = 0. С учетом
П7 выводим, что
Μ(β\Τ = ί) =
= ι · ρ (хг = 11 f: Xi = Α + ο · ρ (χλ = ο Ι Σ *i = t) =
P (xx = 1, Σ Xi = t) Ρ (Χι = 1, Σ Xi = t - l\
αθ\ι-θ)η-* = αθ\\-θ)η-* =
= θ . Сг~_\ θ'-1 {I - ΘΥ~1 = Сг~_\ = (n - 1)! tl(n-t)l = t
θΙθ\ΐ-θ)η~ι Cl (t-l)I(n-t)! n\ n'
Отсюда получаем, что θτ = Μ(Θ\Τ) = Τ/η = Χ. Дисперсия при
этом уменьшилась в η раз.
§ 5. ШАРИКИ В ЯЩИКАХ
Ниже в задаче 3 встретится частный случай так называемого
полиномиального распределения, возникающий при случайном
размещении шариков по ящикам.
Предположим, что шарики, занумерованные числами от 1 до η
раскладываются по N ящикам (рис. 4). Произвольное размещение
описывается набором ω = (ji,J2>- -- ,3η)·> где ji — номер ящика (от 1
csr\ ^ £~\ до ^)> кУДа попал г-й шарик. Всего существует Nn различных на-
4jJ\J. .ч!р. MJ боров. Говоря о «случайном» распределении шаров по ящикам, мы
имеем в виду, что все размещения имеют одинаковые вероятности
N~n. Вычислим в этой модели вероятности некоторых событий.
Пусть lj — неотрицательные целые числа (j = 1,... ,ΛΓ),
/ι + .. .-Μλγ = η. Случайная величина ι/j — количество шариков в j-м
ящике. Какова вероятность события А = {ν\ = /χ,... ,ζ/^ = /./ν}?
Событие {ι/\ = 11} происходит, когда среди номеров ji
оказывается ровно 1\ единиц. Расставить Ζ χ единиц по η местам можно С^1
способами. На оставшихся η — 1\ местах надо разместить 1<ι двоек
Cln-i способами и т. д. Перемножая все возможности и перекрестно
/\\
... j ... N
Рис. 4
§ 5. Шарики в ящиках
135
сокращая факториалы, получаем, что
Р(А) = С* ■ Cth ■■-θ£7ί-...-ΐκ-1*-η = ЩгЬ^ТΝ~η· <8>
Подсчитаем теперь вероятность того, что ровно к ящиков из N
окажутся пустыми. Для этого потребуется
Теорема 4. Вероятность события В&, состоящего в том, что
произойдут ровно к событий из Αι, Α<ι... ,Α/ν, вычисляется по формуле
Р(Дк) = Е(-1)'"*с?5,,
1=к
где
Si= Σ P{A3lA32...A3l), S0 = l.
Доказательство. Проверим, что индикатор 1вк представляется
в виде следующей двойной суммы:
ift = £(-!)'-*C-f[ Σ lAilAj2...Aj] ■ (4)
l^Ji<J2<».<ji^N
Действительно, пусть элементарное событие ω (см. ΠΙ)
принадлежит ровно га множествам из Αχ, Α<ι... ,Αν (см. рис. 5 для N = 3).
Если m < А:, то 1вк = 0 и все члены правой части выражения (4)
равны 0. Если га = к1 то 1вк = 1. В правой части равенства (4)
член, стоящий в квадратных скобках, равен 1, когда I = А:, и равен
0 в противном случае. Таким образом, правая часть также есть 1.
Пусть теперь га > к. Тогда 1вк = 0. Сумма в квадратных
скобках при / > га равна 0, а при I ^ га равна С1т (числу наборов
по I событий из га, содержащих ω). При этом вся правая часть
превращается в
Доказательство теоремы завершается взятием математических \£$/ ШШВ3
ожиданий от обеих частей тождества (4). ■
Следствием теоремы 4 является так называемая принцип
включения—исключения: вероятность того, что произойдет хотя бы
одно из событий Αχ, Α<ι... Αχ, равна
ρ (\Ja}) = ι - р(Во) = Σ (-iy-% =
Рис. 5
Ν
Σ
\Ν-1 ι
= Σ Ρ(^) " Σ P(AkAi) + ... + (-Ι)""1 Ρ(ΑιΑ2... ΑΝ).
3 к<1
Пример 4. Задача о совпадениях [81, с. 126]. Вычислим
вероятность наблюдать ровно к совпадений при случайном
сопоставлении двух одинаковых колод, состоящих из N различных
136
Глава 10. Достаточность
карт (или случайной раскладке N писем по конвертам).
Множеством элементарных событий (Ш) здесь будет пространство
перестановок из первых N натуральных чисел. Каждой
перестановке ω = (ii,z*2,... 4ν)> где ц φ im при Ι φ m, приписана
одна и та же вероятность 1/ЛП. Пусть Аш обозначает множество
перестановок, оставляющих m на своем месте: гт = га. Тогда
P(AhAh ... Αόι) = (Ν - l)\/N\ при 1 ^ ji < j2 < ... < ji < N.
Таким образом, Si = ClN(N - l)\/N\ = \/l\. В силу теоремы 4
p(**) = E(-i)'-fccf 1 = 1
Следовательно, P(Bk) —► e~l/к\ при Ν —► oo, т. е. предельным
законом для числа совпадений является распределение Пуассона
с λ = 1 (см. § 1 гл. 5). В частности, вероятность 1 — Р(#о) того, что
встретится хотя бы одно совпадение, стремится к 1 - е-1 « 0,632.
Точность приближения при небольших N видна из следующей
таблицы:
N
1 - Р(Д>)
2
0,500
3
0,667
4
0,625
5
0,633
6
0,632
Вернемся к вычислению вероятности pk того, что при случайном
размещении η шариков по N ящикам окажется ровно к пустых
ящиков. Обозначим через Aj событие {j-ft ящик пуст}. Чтобы для
заданных I номеров ящиков 1 ^ j\ < 22 < · · · < ji ^ N произошло
событие AjxAj2 ..-Ajn все шарики должны попасть в оставшиеся
N — I ящиков. Очевидно, вероятность этого равна (N — l)nN~n =
= (1 - l/N)n. Отсюда, St = ClN(l - l/N)n. Согласно теореме 4,
искомая вероятность задается формулой
Pk = E(-Vl-kctclN(i-±y. (5)
Изучим поведение р&, когда N и η возрастают так, что Ne~n/N —►
—* λ > 0. Нетрудно проверить, что это условие равносильно
соотношению
η = N In Ν - (In X)N + o(N) при N - oo. (6)
Теорема 5. Для k = 0,1,... при выполнении условия (6)
вероятность pk —► \ke~x/k\1 т. е. предельным законом для числа пустых
ящиков служит распределение Пуассона с параметром λ.
Доказательство. Элементарными выкладками правая часть
формулы (5) преобразуется к виду
11иГ1\(1.1)\1(1-1^1)(1.Ь1).....1]. (7)
1! ^ 2! 3! ^
..+
(-1)
N-k
(Ν - k)\
§ 5. Шарики в ящиках
137
Так как 1 - χ ^ е~х при О ^ χ ^ 1, то (1 - 1/Ν)ηΝι *ζ (Ne-n/N)1.
Таким образом, член в квадратных скобках в формуле (7)
оценивается сверху величиной (ЛГе"71/^) . Поскольку Ne~n/N —► λ,
каждое слагаемое в сумме выражения (7) по абсолютной величине
не превосходит (λ + l)l/(l — k)\ при всех достаточно больших N и п.
оо
Сходимость ряда Σ (λ + lY/jl обеспечивает законность перехода
j=o
к пределу под знаком суммы.
Проверим, что [(1 — x/N)Nex] —► 1 для всех χ > 0.
Действительно, раскладывая логарифм по формуле Тейлора, видим, что
InN [Nln(l - χ/Ν) + χ] = \ηΝ [(-χ - χ2/(2Ν) + ο^"1)) + χ] =
= ο(1).
Отсюда, поскольку при выполнении условия (6) In Ν — η/Ν —> In λ,
имеем
lim (1 - l/N)nNl = lim [(1 - l/N)Nel]n/N e^nN-n^1 = X1.
N—юо N—юо L J
Замена индекса j = 1 — k в формуле (7) завершает доказательство.
■
Пример 5. Неразличимые тары [81, с. 58]. Рассмотрим
варианты размещения η неразличимых шариков по N ящикам. На рис. 6
приведены для сравнения всевозможные варианты размещения при
η = 2 и N = 2 как различимых (занумерованных) шариков
(вверху), так и неразличимых (внизу). Для неразличимых
шариков каждый вариант описывается вектором ω = (ж1,Ж2>· ··>#//)>
где Х{ — число шариков в j-u ящике. Взглянем на него как на
последовательность символов, в которой «О» обозначает шарик,
а «|»—стенку, разделяющую два соседних ящика (рис.7). Так
как имеется N ящиков, то количество вертикальных черточек на
приведенной схеме равно N—1. Общее число позиций, занятых либо
ноликом, либо чертой равно η + N — 1. Причем η из них заняты
ноликами. Поэтому всего разных вариантов размещения будет
Сп+лг-1· Если считать, что все они равновероятны, то каждому ω
надо приписать вероятность 1/С^+ЛГ_1.
η = 2Ν = 2
|(Ш)| I
1®
1 (D
I ® 1
1 ® 1
1 £Ш
^ '
ιΟΟι ι
ιΟ
lOl
ι ιΟΟι
ч^ >■
Рис. β
100
Рис. 7
XN
Вопрос 3
Приведем небольшой отрывок из [81, с. 60], посвященный при- что^и^мме'шеним
менению этой модели в статистической физике.
«Рассмотрим механическую систему, состоящую из η
неразличимых частиц. В статистической механике обычно разбивают
фазовое пространство на большое число N малых областей или
ячеек, так что каждая частица приписывается ровно одной ячейке.
В результате состояние всей системы описывается как случайное
что при размещении
η неразличимых шаров
по N ящикам все ящики
окажутся занятыми?
138
Глава 10. Достаточность
размещение η частиц по N ячейкам. На первый взгляд кажется,
что (во всяком случае при подходящем выборе η ячеек) все Νη
размещений будут равновероятны. Если это так, то физики
говорят о статистике Максвелла — Больцмана (термин «статистика»
используется здесь в смысле, специфическом для физики).
Делались многочисленные попытки доказать, что физические частицы
ведут себя в соответствии со статистикой Максвелла — Больцмана,
однако современная теория, вне сомнения, показала, что эта
статистика не применима ни к каким известным частицам; ни в одном
случае все Νη размещений не являются примерно
равновероятными. Были введены две различные вероятностные модели, каждая
из которых удовлетворительно описывает поведение некоторого
класса частиц.
(...) В статистике Бозе—Эйнштейна каждому из
размещений приписывается вероятность 1/C£+N_V В статистической
механике показано, что это предположение справедливо для фотонов,
атомных ядер и атомов, содержащих четное число элементарных
частиц. Для описания других частиц должно быть введено третье
возможное распределение вероятностей. Статистика Ферми —
Дирака основана на следующих предположениях: 1) β одной ячейке
не могут находиться две или более частиц и 2) все различные
размещения, удовлетворяющие первому условию, имеют
одинаковую вероятность. Для выполнения первого предположения
необходимо, чтобы η ^ N. Тогда размещение полностью описывается
указанием того, какие из N ячеек содержат частицу, и, так как
существует η частиц, соответствующие ячейки могут быть выбраны
Cpf способами. Следовательно, в статистике Ферми—Дирака
существует Cft возможных размещений, каждое из которых
имеет вероятность l/C^. Эта модель применима к электронам,
нейтронам и протонам. Здесь мы имеем поучительный пример
невозможности выбора и обоснования вероятностной модели на
основе априорных соображений. Действительно, нет оснований
говорить, что фотон и протон не подчиняются одним и тем же
вероятностным законам».
Приведенные ниже результаты показывают, что размещения
неразличимых частиц (статистика Бозе—Эйнштейна) имеют
ряд существенных отличий по сравнению с размещениями
различимых частиц (статистика Максвелла—Больцмана).
Обозначим через т> вероятность того, что фиксированный
(скажем, первый) ящик содержит ровно к различимых шариков. Так
как остальные (п — к) шариков надо разместить по (N — 1)
ящикам, то
гк = Ck(N- l)n-kN~n = Ск (1/N)k(l - 1/N)n~k.
Это — биномиальное распределение с ρ = 1/Ν. Как было доказано
в § 1 гл. 5, при N —► оо и η —► оо так, что среднее число шариков
§ 5. Шарики в ящиках
139
на ящик η/Ν стремится к λ > 0, это распределение сходится к
закону Пуассона с параметром λ. Рассматривая отношение τ>+ι/τ>,
несложно установить (проверьте!), что максимум вероятностей г к
достигается при к* = [(п + 1)/ЛГ] « λ, где [ · ] — целая часть числа.
Пусть г^ — вероятность того, что фиксированный ящик
содержит ровно к неразличимых шариков. Рассуждая так же, как выше,
получаем гк = ^η"Λ)+(ΛΓ-ΐ)-ι/°ϊϊ+ΛΓ-ι = C^-kN_k_2/C^N_v
При том же предельном переходе, что и выше, для к = 0,1,...
имеем:
к /fc+l
г=1 I г=1
Это — геометрическое распределение с ρ = (λ + I)-1 (см. задачу 4
гл. 1). Поскольку ffc+i/ffc = 1 — (Ν — 2)/(η — к) (убедитесь!), то при
N > 2 вероятности т> монотонно убывают по к. Следовательно,
наиболее вероятным является то, что фиксированный ящик пуст.
В случае неразличимых шаров относительное преобладание
размещений с большим количеством пустых ящиков еще заметнее
проявляется при сравнении предельного поведения вероятности
события Вь обнаружить роено к пустых ящиков.
В случае различимых шаров вероятность рк этого события
задается формулой (5), а ее асимптотика приведена в теореме 5.
Для неразличимых шаров обозначим вероятность события Вк
через рк- Пусть Aj —это событие, состоящее в том, что j-ft ящик
пуст. Для заданных I ^ ji < J2 < - - - < ji ^ N события Ajx, Aj2,...,
Ajt означают, что I ящиков с номерами ji, j29 · · ·> ji пусты. Число
таких размещений равно числу способов, которыми η одинаковых
шариков могут быть распределены по N — I оставшимся ящикам.
Поэтому P(i4j1i4J2 ...Ajt) = С^+ЛГ_/_1/С^+ЛГ_1. В силу теоремы 4
Pk = Σ ("Ι)*"* С\ ClNCl+N_x_xICl+N_x. (8)
1=к
Приведем без доказательства предельную теорему для
вероятностей pfc·
Теорема 6. Распределение вероятностей рк1 заданное
формулой (8), сходится к закону Пуассона, если η, Ν —> оо так, что
N2/n - λ > 0.
В частности, чтобы при λ = 1 для достаточно большого N
с вероятностью р0 « 1/е « 0,368 не осталось ни одного пустого
ящика, потребуется случайно бросить ЛГ2 неразличимых шариков.
Это отличается по порядку от величины Ν 1η ΛΓ, которая (согласно
теореме 5) понадобится в случае различимых шариков.
140
Глава 10. Достаточность
ЗАДАЧИ
Достоинство человека
измеряется не той
истиной, которой он
владеет, а тем трудом,
который он приложил для
ее приобретения.
Г. Лессинг
С помощью критерия факторизации найдите достаточную
статистику для
а) равномерного распределения на отрезке [0ι,02]>
б) модели сдвига-масштаба F((x — 0ι)/02) показательного
закона с функцией распределения F(x) = 1 — е~х при χ > 0.
2. Докажите, что экспоненциальному семейству принадлежат
а) биномиальное распределение: /(#,0) = С^ θχ(1 — 0)m_a:, x =
= 0,1,..., m (в частности, при га = 1 — закон Бернулли),
б) гамма-распределение с неизвестным параметром 0: /(#,0) =
= ψτ-τ ^α~1^~θχΙ{χ>ο} (ПРИ α = 1 — показательный закон).
3. Пусть X — выборка из распределения Пуассона с неизвестным
параметром 0 > 0: f{xfi) = θχβ~θ/χ\, χ = 0,1,2,.... Найдите
а) распределение суммы ξ + г/, где ξ и η — независимые пуас-
соновские случайные величины с параметрами λ и μ
соответственно,
б) условное распределение X при условии Χι + ... + Хп = га.
4* Пусть величины ΛΊ,... ,ХП выбраны случайно (с повторением)
из множества {1,2,... ,ΛΓ}. Значение N неизвестно.
а) Докажите достаточность и найдите распределение
статистики Х(п).
б) Укажите такую функцию #, чтобы статистика д(Х^)
несмещенно оценивала значение N.
5? Элементы выборки имеют гамма-плотность из задачи 2 с a = 2.
а) Проверьте несмещенность оценки 0 = \/Х\.
б) Улучшите ее с помощью достаточной статистики (см.
теорему 3).
6? Рассмотрим Ιζ(θ) = Μ
ΙθΐηΜ,θ)
l2
информацию Фишера,
введенную в § 3 гл. 9. Докажите, что для выборки X из
произвольной дискретной модели
а) для любой статистики Τ верно неравенство /т(Х)(0) ^ ^х(0)
при всех 0,
б) для достаточной статистики неравенство в п. а)
превращается в равенство.
Пусть 77ι,... ,77п — координаты точек, взятых наудачу из отрезка
[0,1]. Точки разбивают [0,1] на (п + 1) частей, длины
которых Δ^ называются равномерными спейсингами (см. следствие
в § 4 гл. 4). Найдите распределение наибольшего спейсинга
Δ(η+ΐ) при помощи принципа включения—исключения из § 5
и следующего результата Б. де Финетти (см. [82, с. 57]):
Ρ (Δι > хи ..., Δη+ι > a?n+1) = (1 - χι - ... - ζη+ι)+
для произвольных х\ ^ 0,... ,#η+ι ^ 0 (здесь /+ = max{0, /}).
Решения задач
141
РЕШЕНИЯ ЗАДАЧ
1. а) ПЛОТНОСТЬЮ выборки X = (Χι,... ,ХП) служит Истинное знание
самостоятельно.
η
Π If ^α ι If ^α ι τ Л- W· ТОЛСТОЙ
_ Ht'{»<>«!> '{»«<«2> ^ /{g(1)>gl}/{g(n)^}
ЛЯ' j №-0i)n (02-0i)n
Стало быть, (Х(!),Х(П))—достаточная статистика,
б) Поскольку плотность величины Χχ равна θ21β~^χ~θι^θ2Ι[χ^01^
то
г=1
Следовательно, статистика Τ = (Χ(ΐ)Σ,Χί) является
достаточной. Отметим, что вектор оценок максимального правдоподобия
в этой модели (Χ^,Χ—Χ^) (см. задачу 3 гл. 9) связан со
статистикой Τ взаимно однозначным (линейным) преобразованием.
2. а) Совместная вероятность выборки X = (Χι,... ,ХП)
/(*»*) = (ПСт ) 0^>(1 -0)™-Σ*< =
= ехр\
exp jmn 1η(1 -θ)+ (in ^) £ **} Π <%'
Видим, что Τ = Σ*ΰ 9ο(θ) = runln(l - β) и 9ι(θ) = In ^.
б) Плотность выборки X из гамма-распределения имеет вид
f(xfi) = exp jnalnff - 0£я*} Γ(α)-η7{,(1)>0} Д*?"1·
Таким образом, Τ = X)Xi> 0о(0) = naln0 и <?ι(0) = -θ.
3. а) Используя формулу полной вероятности (П7) и
независимость случайных величин ξ и г/, получаем, что
m
Pm = Ρ (ξ + η = Ш) = EP(i + r/ = ^r/ = fc) =
fc=0
τη m
= ΣΡ(£ = ™"Μ = *) = Σ Ρ (ζ = m - fc) P(r/ = fc).
fc=0 fc=0
Вопрос 4.
Тем самым мы вывели дискретную формулу свертки из ПЗ. п^Ус^апо^едовате"ьно-
Далее с учетом бинома Ньютона находим, что _п ™ пк _
сти Сп=е п 2^ —(
Pm = Σ 1 7TT e ΤΓ e ι е , (Примените центральную
fc=o (m""k)· k· m! предельную теорему
(см. П6) к пуассоновским
т. е. ξ + η имеет распределение Пуассона с параметром λ + μ. случайным величинам.)
142
Глава 10. Достаточность
б) Согласно пункту а), сумма Χι + ... + Хп распределена по
закону Пуассона с параметром ηθ. Поэтому
P(X-x\X1 + ... + Xn-m)- 9{ΣΧί = πι) "
_ Р(Х\ = Χι,. . . ,Χη-1 = Χη-ΐ,Χη = m — Χι — ... — Xn-l) _
(пв)те-п9/т\
nS
θχ
e
Xi\
(ΠΘΓ с-пв
ml
ml
xi\x2\...xnl
Это — вероятность того, что при случайном размещении га
различимых шаров по η ящикам в ящике с номером г (г = 1,... ,п)
окажется ровно Xi шариков (см. формулу (3) из § 5).
4. а) Так как совместная вероятность выборки равна /(ж,ЛГ) =
= Ν~ηΙ[Χ(η)^Ν^ то статистика Х(п) достаточна в силу
критерия факторизации. Ввиду независимости случайных величин
Χι,...,Χη имеем Р(Х(П) ^ га) = Р(Х\ ^ га,...,Χη ^ га) =
= (m/N)n. Отсюда
Р(Х{п) =т) = Р(Х{п) ^ га) - Р(Х{п) < m - 1) =
= N-n[mn-(m-l)n].
б) Запишем условие несмещенности для функции д(Х(п)):
Σ д(т) N-n[mn - (га - l)n] = N,
т. е. Σ9{ηί) [тп - (га - 1)η] = ΛΓη+1, Ν = 1,2,.... Вычитая из
суммы до N сумму до N — 1, находим, что при всех N
g(N) = [ΛΓη+1 - Nn] J [Nn -(Ν- 1)η].
Нетрудно вывести, что g(N) « I 1 + - J ЛГ, когда N велико.
^ ^ оо
5. Проверим несмещенность оценки θ: ΜΘ = J (1/х) 92xe~9x dx = θ.
о
Согласно задаче 2 б), статистика Τ = Σ %г достаточна. В силу
леммы 1 гл. 4 она имеет гамма-распределение с плотностью
9n{t)- {2η_ιγ 0 t e I{t>0}.
η
Плотность вектора (Χι, Σ Xг) равна плотности вектора
г=1
η
(^ъ Σ ^г) в точке (x,t — χ) (см. формулу преобразования
г=2
плотности из П8):
P(xltT)(^t) = РхЛх)9n-i(t - χ) = —Х *_ е— I{o<x<t}·
Решения задач
143
Тогда условная плотность (П7) случайной величины Χι при
условии Τ есть
Р<Х!|П(*,*) = (2п - !)(2п - 2)*(* - ^)2n_3<"2n+1^o<x<t}·
^ ОО
Наконец, М(0|Т = *) = /(1/ζ)ρ(Χι|Τ)(:ζ,*)<£ζ = (2η - 1)/ί, τ. е.
^ J?
искомая оценка 0Т = М(01 Т) = (2п - 1)/(Χι + ... + Хп).
6. а) Положим Qe(t) = Р(Т(Х) = £) и введем случайные
величины f/ = d\nf(Xft)/M nV = d\nQe(T(X))/de. Рассмотрим
тождество
Μ(ί/ - V)2 = Ιχ(θ) + ΙΤ(Χ){Θ) - 2 M(UV). (9)
Распишем M(UV) из правой части формулы (9):
v f(pfi) Q'eJTjx)) .. , _ „ <#(t) v .,, βχ _
?75^'ог(т(=П/м)-?о^.:^м/(м)-
_ „<ye(t) a „ f r-r ^ - τ MM!-
= Σ
ο»(«)
2
<Ш = Μ
Q'e(T)
η2
<?·(Τ)
= Ιτ(Χ) (β).
Итак, правая часть тождества (9) равна Ιχ(θ) — Ιτ(Χ)(θ)· Так
как его левая часть неотрицательна, то неравенство доказано,
б) Для достаточной статистики Τ просуммируем правую часть
формулы (1) по таким х, что Т(х) = t. Получим
Qo(t) = g(t,e) Σ Η*)- (Ю)
x:T(x)-t
Подставляя соотношения (1) и (10) в левую часть тождества (9),
обратим ее в нуль.
7. Для произвольного χ ^ 0 положим Aj = {Aj > χ}, j =
= 1,... ,η + 1. Взяв в формуле Б. де Финетти одно из Xj равным
#, а все остальные — равными 0, получим, что P(Aj) = (1 — ж)+.
Таким образом, все спейсинги распределены одинаково (так же,
как Δι = r/(i)), но, конечно, зависимы: их совместная плотность,
найденная в следствии из § 4 гл. 4, не равна произведению
плотностей случайной величины Aj.
Ввиду очевидного равенства Ρ(Δ(η+ΐ) ^ х) = 1 — P(\JAj)1
для применения принципа включения—исключения
осталось вычислить вероятности P(Aj1Aj2...Ajl) для любых
1 ^ Зг < 32 < · · · < 3ι ^ п+1· Положив в формуле Б. де Финетти
Xjx,... ,Xjt равными #, а все остальные — равными 0, находим,
что P(AjxAj2... Ajt) = (1 — /#)+. Группу из I упорядоченных
144
Глава 10. Достаточность
Моделируйте задачу
с помощью таблицы Т1.
Сколько дуг
понадобилось?
индексов можно выбрать С1п+1 способами. Окончательно имеем:
рп(х) = Ρ(Δ(η+1) < *) = Σ! (-1)' Ci+i (1" te)+·
1=0
Придадим этому результату другую форму, известную как
теорема о покрытии (см. [82, с. 43]). Для этого свернем отрезок
[0,1] в окружность единичной длины и будем считать точки
0,771» · · · Мп серединами дуг длины х. Тогда с вероятностью рп(х)
дуги покрывают всю окружность.
Вот некоторые значения этой вероятности для χ = 0,2:
η
Рп (0,2)
8
0,040
10
0,134
15
0,493
20
0,766
25
0,903
30
0,962
40
0,995
50
0,999
Таким образом, вместо 5 дуг, достаточных для регулярного
покрытия, в среднем потребуется около 15 случайных дуг,
и не менее 30 дуг обеспечивают полное покрытие окружности
с вероятностью 0,962. Этот численный пример поясняет
причину медленного уменьшения с ростом η погрешности метода
Монте-Карло (см. § 3 гл. 3).
ОТВЕТЫ НА ВОПРОСЫ
1. Для выборки из равномерного на отрезке [0,0] распределения
η
f{xfi) = θ-ηΥ[ΐ{χί>0}Ι{χ^θ} = 0~П1{х(1)>о}1{хы^в}'
г=1
Взяв g(tfl) = 0-nJ{t<0} и h(x) = 1{Х{1)^о}> видим, что максимум
Х(п) — достаточная статистика.
2. Плотностью выборки из показательного закона служит
f{xft) =exp|-nln0-- έ^Μ{χ(,))θ}·
Таким образом, Τ = ^Хи 9ο(θ) = —nln0 и #ι(0) = —1/0.
3. Положим сразу N шариков по одному в каждый ящик.
Оставшиеся η — Ν шариков разместим C^Zn^-n-i = @η-ι способами.
Стало быть, искомая вероятность есть С^Ц1/C%+N_1.
4. Пусть Χι,... ,ХП — выборка из закона Пуассона с λ = 1,
5η = Χι + ... + Хп. Тогда 5П имеет распределение Пуассона
с параметром п, сп = Р(5П ^ п). Поскольку М5П = D5n = η
(см. вопрос 2 гл. 5), то в силу центральной предельной теоремы
= ρ (^-yJ^ < θ) -► Ф(0) = 1/2 при η
00.
Глава 11
ДОВЕРИТЕЛЬНЫЕ ИНТЕРВАЛЫ
§1. КОЭФФИЦИЕНТ ДОВЕРИЯ
Вместо того, чтобы приближать неизвестный скалярный
параметр 0 с помощью «точечной» оценки 0, можно локализовать его
иначе — указать случайный интервал (01,0г), который накрывает 0
с вероятностью близкой к единице (рис. 1).
Определение. Пусть а € (0,1). Две статистики θ ι и 02
определяют границы доверительного интервала для параметра θ с
коэффициентом доверия 1 — а, если при всех θ £ θ для выборки
X = (Χι,...,Χη) из закона распределения Fq(x) справедливо
неравенство
ρ(θ1(Χ)<θ<θ2(Χ))
>\-а.
(1)
Часто на практике полагают а = 0,05. Если вероятность в левой
части неравенства (1) стремится к 1 —α при η —► оо, то интервал
называется асимптотическим. Как правило, длина доверительного
интервала возрастает при увеличении коэффициента доверия 1 — а
и стремится к нулю с ростом размера выборки п.
Пример 1. Для модели сдвига показательного закона с
плотностью рв(х) = ε~(χ~θ^Ι{χ·^θ} оценкой максимального
правдоподобия согласно примеру 6 гл.9 является Хщ = min{Xi,... ,ХП}.
Поскольку 0 < ^(ΐ), можно взять Х(!) в качестве 02. Попробуем
подобрать константу са так, чтобы для в\ = Хщ — са (см. рис. 2)
при всех 0 выполнялось тождество
Ρ (Х(1) - са < θ < Х(1)) = Ρ (Х(1) -Са<0) = 1-а. (2)
Используя независимость и показательность величин Χι — 0,
перепишем условие (2):
а = Ρ (Χ(1) -в^са) =
= Ρ (Xi - θ ^ са, г = 1,... ,п) = ехр{-пса}.
Откуда находим, что длина интервала са = (— 1η α)/η. Отметим,
что са —► оо при а —► 0 и са —► 0 при η —► оо.
Касательно расстояния
от Земли до Солнца
можно заметить, что
каждое новое, более
точное определение этой
величины не
укладывается в доверительный
интервал, построенный по
старым наблюдениям.
В. Н. Тутубалин,
[79, с. 313]
н—У
01
0«0
Рис. 1
02
У = Рв(х)
О 01 0 Х(1) Хг
Рис. 2
Вопрос 1.
Какое са подойдет для
построения доверительного
интервала с помощью
статистики Х^ в модели
равномерного
распределения на отрезке [0,0+1]?
146
Глава 11. Доверительные интервалы
Рис. 3
В «Философском очерке
теории вероятностей»
Лаплас, определив
отношение массы
Юпитера к массе
Солнца, предлагает
пари, что будущие
поколения ученых не
изменят найденное им
число более чем на 1%
(вероятность того, что
это произойдет, согласно
Лапласу, ничтожно мала).
Но современное значение
отличается от найденного
Лапласом на 2%.
В. Н. Тутубалин, [79,
с. 313]
§2. ИНТЕРВАЛЫ В НОРМАЛЬНОЙ МОДЕЛИ
Пример 2. Допустим, что элементы выборки Χι распределены по
закону Λί(θ, σ2), причем параметр масштаба σ известен, а параметр
сдвига θ — нет. Эту модель часто применяют к данным, полученным
при независимых измерениях некоторой величины θ с помощью
прибора (или метода), имеющего известную среднюю погрешность
(стандартную ошибку) σ (рис. 3).
χ
Пусть Ф(х) = (2π)-1/2 J e~u l2du — функция распределения
—оо
закона Л/ХО, 1). Для 0 < a < 1 обозначим через ха так
называемую α-квантиль этого закона, т. е. решение уравнения Ф(ха) = α
(см. § 3 гл. 7). Приведем некоторые значения #ι_α/2 (см. также
таблицу Т2):
а
Xl-at/2
0,05
1,96
ИГ2
2,58
10"3
3,29
10"5
4,26
Согласно примеру 4 гл. 9, эффективной оценкой для θ служит
X. Известно, что ~Х ~ Μ{θ,σ2/η). Тогда у/п(Х - θ)/σ - ΛΓ(0,1).
Поэтому в качестве^ границ интервала с коэффициентом доверия
1 — а можно взять θ\ = X — σχι_α/2/\/η и θ2 = Χ - &ха/2/у/п:
а.
Ρ(0ι < θ < Θ2) = Р(ха/2 <yfii{X- θ)/σ < *ι_α/2) = 1
В силу четности плотности закона λί(011) верно равенство
ха/2 = — #ι-α/2· Таким образом, из приведенной выше таблицы
видим, что с вероятностью 0,95 истинное значение параметра сдвига
θ находится в интервале X ± 1,96 σ/γ/^ ~ X ± 2а/у/п (правило
двух сигм).
Замечание 1. В теории измерений обычно предполагают, что
наблюдения Χι = θ + ε^, где ошибки ε ι — независимые и одинаково
распределенные случайные величины (не обязательно нормальные)
с ЬЛбг = 0 и Dei = σ2 < оо. В силу центральной предельной теоремы
(П6)
у/п(Х-в)/а Д Z~JV(0,1) при η
00.
Значит, X ± 1,96 σ/\/п— асимптотический 95%-й доверительный
интервал. Если значение σ неизвестно, то на практике его заменяют
на состоятельную оценку σ = 5, где S2 = - Σ № ~ ^02» получая
приближенный 95%-й интервал X ± 2S/\/n.
Однако нередко на самом деле Χι = θ + Δ + ε^, где Δ —это
систематическая ошибка измерения. Попытка оценить величину
возможного отклонения X от θ лишь на основе разброса
наблюдений Xi вокруг X, вообще говоря, может приводить к ошибочным
выводам.
§2. Интервалы в нормальной модели
147
Другими причинами неверных заключений могут быть
зависимость наблюдений Х^ наличие которой не предполагалось
исследователем (подробнее см. § 4 гл. 15), или нарушение однородности
данных при слишком большом увеличении их количества.
Пример 3. Предположим, что элементы выборки Χι
распределены по закону ΛΓ(μ,β2), причем значение параметра сдвига μ
известно, а параметра масштаба Θ — нет. Такую модель можно
использовать для определения средней точности прибора (или
метода) путем многократных измерений эталона (рис. 4).
Чтобы построить доверительный интервал для 0, потребуется
следующее
Определение. Пусть случайные величины Ζι, ...,Ζ&
распределены по закону ЛГ(0,1) и независимы. Тогда распределение
случайной величины Щ. = Ζ2 + ... + Ζ\ называют распределением
хи-квадрат с к степенями свободы (кратко: R\ ~ χ|).
Отметим, что каждое слагаемое Ζ2 имеет гамма-распределение
(см. § 4 гл. 4) с параметрами а = λ = 1/2, т. е. Z2 ~ Г(1/2,1/2).
Отсюда согласно лемме 1 гл. 4 находим, что й£ ~ Г(А:/2,1/2).
Таким образом, плотностью закона хи-квадрат служит функция
рщ (х) = ск xk/2-le~xl2I{x>Q}, где ск =
Вопрос 2.
Как доказать это
утверждение?
2к'2Г(к/2)
Здесь Г(р) = J xp~le~x dx — гамма-функция Эйлера, график ко-
о
торой изображен на рис. 9 гл. 3. Дифференцируя pR2 (#), нетрудно
убедиться, что при к > 1 плотность имеет единственный
максимум в точке к — 2 (рис. 5). Закон χ2 дает пример распределения
с неограниченной плотностью.
Отметим, что МЩ. расположено правее точки максимума
плотности (так называемой моды распределения) из-за того, что правый
«хвост» плотности «тяжелее» левого, т. е. убывает медленнее.
Дисперсию ОЩ. легко подсчитать с помощью формулы (2)
гл.4. Она равна 2к (проверьте!). Поскольку R\— это сумма
независимых и одинаково распределенных случайных величин Z?,
согласно центральной предельной теореме имеет место сходимость
(Щ. — к)/у/2к —> Ζ ~ ЛГ(0,1) при к —► оо. Нормальное приближение
является довольно точным уже при к > 30. Значения некоторых
квантилей закона χ| для к < 30 приведены в таблице ТЗ.
Перейдем теперь к построению доверительного интервала для θ
η
по выборке Xi из распределения Λί(μ, θ2). Введем Όη=Σ (Xi-β)2-
г=1
η
Заметим, что величина Д^ = Dn/02 = J] [№—/Ό/0]2 распределена
%=ι
по закону \£. Обозначим р-квантиль этого закона через хр (рис. 6).
к = 1 У = РнФ)
Вопрос 3.
Чему равно МЯ|?
(Попробуйте догадаться
без вычислений.)
148
Глава 11. Доверительные интервалы
t V = PrI О)
^α/2 2l-a/2
Рис. β
ki<k2
Тогда для 0ι = \/Dn/xi-a/2 и 02 = y/Dn/xa/2 при всех θ > О
справедливо равенство
1 - α = Ρ (xa/2 <R2n< xi-a/2) = Ρ (θι < θ < 02) ,
т. е. (01,0г) — искомый интервал.
Пример 4. Пусть Χι ~ ^(01,0^), где оба параметра 0ι и 02
неизвестны. Для построения доверительных интервалов понадобится
Определение. Пусть случайные величины Ζ и Щ. независимы
и распределены согласно законам ЛГ(0,1) и χ| соответственно.
Тогда распределение случайной величины Тк = Ζ / у/Щ/к
называют распределением Стпьюдентпа с к степенями свободы или
t-распределением (кратко: Тк ~ £&).
При ^каждом А: случайная величина Тк имеет четную плотность
(см. [38, с. 58])
_zi._i.iwo Г./Л+1
-(fc+l)/2
где „fc =
-(ψ)
Рис. 7
Вопрос 4.
К какому распределению
стремится tk при к—>οο?
(Используйте закон
больших чисел (П6)
и свойства сходимости
(П5) или же найдите
предел последовательности
плотностей ртк (х).)
V^k г(|)
(3)
В частности, при к = 1 получаем закон Коши с плотностью ртг (х) =
= 1/[π (1+ж2)]. С ростом А: «хвосты» tk становятся «легче» (рис. 7).
Математическое ожидание случайной величины Тк не
существует при к = 1 (см. замечание в § 2 гл. 1) и равно 0 при
к > 1 в силу четности плотности ртк(х)- Дисперсия величины Тк
бесконечна при к = 2 и равна к/(к — 2), если к > 2 (см. [50, с. 315]).
Теорема 1. Для нормальной выборки Х{ ~ Λ/χβι,β!) выборочное
среднее X = - £) X* и выборочная дисперсия S2 = — Σ(Χί — X)2
независимы,*) причем nS2)в\ ~ χ2_ι, а \М — 1 (X — 6{)/S ~ ίη-ι·
Доказательство теоремы опирается на следующую лемму.
Лемма 1. Пусть (η χ п)-матрица С ортогональна: С-1 = Ст
(см. П10), случайный вектор Υ = (ΥΊ,.,.,Υ^) имеет независимые
Λ/ΧΟ, 1) компоненты. Тогда вектор Ζ = СУ распределен так же,
как и У.
Доказательство леммы. Заметим, что при ортогональном
преобразовании ζ = Су длины векторов в Rn не меняются:
|z|2 = zTz = (Cyf Су = (утСт) Су = ут (СТС) у = \у\\ (4)
*) Оказывается, что из независимости выборочного среднего X и выборочной
дисперсии S2 при η ^ 2 следует (как доказал Р. Гири в 1936 г.)
нормальность распределения элементов выборки Χι,...,Χη (см. [72, с. 198]). Однако,
для выполнения условия p(X,S2) — 0 достаточно, чтобы этот коэффициент
корреляции (П2) существовал и распределение случайных величин Χι было
симметричным.
§2. Интервалы в нормальной модели
149
Обратная матрица С 1 = Ст также будет ортогональной, причем
| det С | = 1. Вопрос 5.
Согласно условиям леммы плотность ру(у) = (2п)-п/2е~ъ М2. с ^омощью^свойств
По формуле преобразования плотности (П8) с учетом (4) получаем: из П10?
pz(z) = \detCT\pY(CTz) = (2π)-η/2ε-21°ΤΗ2 = (2π)-η/2β"ϋ*Ι8.
■
Другое доказательство леммы 1 немедленно вытекает из
формулы для преобразования ковариационной матрицы нормального
случайного вектора при умножении его на числовую матрицу
(см. П9).
Доказательство теоремы. Возьмем в качестве С
ортогональную (η χ п)-матрицу с последней строкой (1/у/п,... ,1/у/п).
Значения Cij при г < η не важны, лишь бы С была ортогональной
(можно, скажем, дополнить последнюю строку до ортогонального
базиса в Rn при помощи стандартного алгоритма Грама—Шмидта
(см. соотношения (9) гл. 21). Нетрудно проверить, что годятся
C{j —
[ 1/у/г(г + 1), если j < г,
-i/y/i(i + 1), если j = г + 1,
О, если j > г + 1.
В качестве Υ возьмем вектор с компонентами Yi = (Xi — 0ι)/02·
Рассмотрим Ζ = CY. При умножении последней строки матрицы
С на вектор Υ получается соотношение
Zn = -J=(yi + ... + yn) = VnF. (5)
η η
С другой стороны, из формулы (4) следует, что Σ Ζ? = Σ Υ?.
г=1 г=1
С учетом формулы (1) гл. 6 из этого равенства и соотношения (5)
выводим, что
=£ = Σ ^i^ = t(Yi- У)2 = ±Y?-nY2 =
&2 г=1 **2 г=1 г=1
г=1 г=1
В силу леммы 1 имеем nS2 jQ\ ~ Χη-ι· Из соотношения (5)
получаем, что у/п(Х — 0ι)/02 = y/nY = Ζη ~ ΛΓ(0,1). Так как
X — функция от Ζηι а 5 —от Ζι,...,Ζη_ι, то X и 5 независимы
(см. лемму о независимости из § 3 гл. 1). Наконец, случайная
величина
распределена по закону £η_ι согласно определению. ■
150
Глава 11. Доверительные интервалы
На основе доказанной теоремы построим доверительные
интервалы для неизвестных параметров θ ι и 02 закона //(θι,θ^).
Доверительный интервал для параметра сдвига θ\ выглядит
так:
р(х-^^<01<Х-^)=Р(уа/2<Тп_1<у1_а/2) = 1-а,
где ур— р-квантиль распределения Стьюдента tn-\ (см.
таблицу Т4). В силу симметрии закона уа/2 = — 2/ι-α/2·
Доверительный интервал для параметра масштаба 02 таков:
где zp— р-квантиль закона χ2_ι (см. таблицу ТЗ).
\y/Z\-a/2 y/zot/2 J \
Z*/2 < -ψ- < 2ΐ-α/2
)=ι-α,
Замечание 2 [32, с. 95]. Было бы неверным считать, что
двумерный параметр (01,0г) с вероятностью (1 — а)2 накрывается
случайным прямоугольником
Лу yi-a/2S у ya/2S \ χ ί VnS y/nS\
\ y/n-l ' y/n-l) \y/Z\-a/2 ' y/Z<x/2) '
так как случайные величины Τη_ι и 52, на основании которых
строились эти интервалы, зависимы (обе являются функциями
от 5).
Чтобы построить доверительную область для вектора (0ι,02),
используем независимость X и S2. Обозначим р-квантиль закона
Λ/χθ, 1) через #р, а р-квантиль распределения χ2_ι через 2р. Тогда
Ρ(να\Χ-θ1\/θ2< Χΐ-α/2, *α/2 < nS2/θ2 < Zl-a/2) = (1 - С*)2.
Соответствующее (случайное) множество точек плоскости
представляет собой трапецию, отсекаемую от угла 02 =
= \/п\Х — 0ι|/#ι-α/2 ДВУМЯ параллельными оси абсцисс прямыми
#2 = y/nS2/za/2 И θ2 = y/nS2/Zi_a/2 (рИС. 8).
Замечание 3. Величину Τη_ι, определяемую формулой (6),
можно представить также в виде
При сравнении этого представления с величиной у/п{Х — 0ι)/02,
имеющей стандартное нормальное распределение, замечаем, что
различие состоит в замене неизвестной дисперсии 0\ на ее несме-
щенную и состоятельную оценку Σ № — γλ2
п~ 1 г=1
из § 2 гл. 6).
На то, что при этой подстановке закон ЛГ(0,1) меняется на
ίη_ι, впервые обратил внимание в 1908 г. Уильям Д. Госсет,
работавший в то время в Дублине на пивоваренном заводе Гиннеса
X)2 (см. пример 3
§ 3. Методы построения интервалов
151
(см. [72, с. 122]). Условия контракта не позволяли Госсету
публиковать результаты под его собственным именем. Госсет выбрал
псевдоним «Student». С тех пор найденное им распределение стало
называться законом Стьюдента.
Сравним ряд квантилей Х\-а/2 закона ЛГ(0,1) с
соответствующими квантилями у\-а/2 распределения tn-\ при η = 10:
α
#1-α/2
Vl-a/2
0,05
1,96
2,26
ΙΟ"2
2,58
3,25
ΙΟ"3
3,29
4,78
ΙΟ-5
4,26
8,83
В частности, видим, что для выборки размера 10 длина
интервала для 01 с коэффициентом доверия 95% при замене неизвестной
дисперсии на ее оценку возрастает примерно на 2,26/1,96—1 « 15%.
§3. МЕТОДЫ ПОСТРОЕНИЯ ИНТЕРВАЛОВ*)
Метод 1. Использование центральной функции
Рассмотрим выборку X = (Χι,... ,ХП). Допустим, что найдется
такая функция #(ж,0) (называемая центральной), что
1) распределение д(Х,в) не зависит от 0 для всех 0 Ε θ;
2) при каждом χ G Rn функция д(х,0) непрерывна и строго
убывает (возрастает) по 0.
Скажем, для модели сдвига показательного закона из примера 1
можно взять д{Х,9) = Χ(ΐ± - 0 ~ Г(1,п). Для Х\ ~ Λ/"(0ι,02) из
примера 4 годятся у/η — 1 (X — 6\)/S ~ tn-i для параметра сдвига θ ι
и nS2/el .
' Υ2
Λη-
для параметра масштаба 02.
Обозначим р-квантиль распределения #(-Х",0) через хр. Возьмем
0 ^ pi < р2 ^ 1 такие, что р2 — pi = 1 — а. Определим Τι (ж) и Т^{х)
как решения относительно 0 соответственно уравнений
g{xfi) = хР1 и g{xfi) = хР2. (7)
Однозначность их определения гарантируется условием 2. Тогда
при всех 0 е θ для #(ж,0), убывающей по 0 (рис. 9),
Р(Т2(Х) < 0 < Γι(Χ)) = Р(хР1 < g(Xfi) < хР2) = 1 - α.
Когда pi = α/2, интервал называется центральным. При
помощи именно этого метода был построен доверительный интервал
в примере 1 (р\ = 0), а также центральные интервалы для θ\ и 02
в примере 4.
Нахождение р(св,0) для конкретной модели — отдельная задача,
не всегда имеющая решение. Однако, можно выделить класс моделей,
для которых такая функция существует: если функция
распределения F(xft) элементов выборки Χχ непрерывна и строго монотонна
*) Материал этого параграфа имеет более технический характер.
152
Глава 11. Доверительные интервалы
Рис. 10
<>ЛП
ПО 0, ТО МОЖНО ВЗЯТЬ
ff(X,0) = - Σ lnF(X4,0). (8)
t=l
Действительно, ее непрерывность и монотонность очевидны, а в
соответствии с методом обратной функции (см. § 1 гл. 4) случайные
величины г/» = F{Xi,9) равномерно распределены на отрезке [0,1]. Там
же установлено, что каждая из величин — In r/» имеет показательное
распределение с параметром λ = 1, т.е. — lnr/t ~ Г(1,1). Наконец,
η
в силу леммы 1 гл. 4 находим, что д{Х,9) = — Σ In г/» ^^(η,Ι).
t=l
(Пример применения формулы (8) содержится в задаче 1(a).)
Метод 2. Использование точечной оценки
Предположим, что имеется точечная оценка Т(Х) для параметра
0 с функцией распределения Ft(£,0), которая непрерывна и строго
убывает (возрастает) по 0.
Возьмем 0 < pi < р2 ^ 1 такие, что Р2 — Pi = 1 — α. Для
каждого θ £ θ определим ί*(0) как р^-квантиль распределения
^т(£>0), к = 1,2. Если функция Fr{t,0) убывает по 0, то обе функции
tk(0) возрастают (рис. 10).
Обозначим через Ga подмножество θ χ θ следующего вида:
Ga = {{θft'): ίι(θ) < θ' < ί2(θ)} (рис. 11). Определим Δ(0') как
сечение Ga при фиксированном 0': Δ(0') = {θ: {θβ') £ Ga}.
Так как функции ίι(θ) и ^(0) строго возрастают, то множество
Δ(0') является интервалом (возможно, бесконечным). Обозначим
его левый и правый концы через 0χ(0') и 02(0')·
Рассмотрим случайный интервал Δ(Τ(Χ)). Заметим, что
событие {0 € Δ(Τ(Χ))} происходит тогда и только тогда, когда
{Т(Х) € (^ι(0))^2(0))} и, значит, при каждом 0 G θ имеет
вероятность 1 — а, что и требуется.
Наглядный смысл метода состоит в том, что сначала строят
диаграмму по вертикали: для каждой абсциссы 0 находят
соответствующие квантили ίι(θ) и #2(0)> а затем для наблюдавшейся
ординаты t = Т(ж), где ж —это реализация выборки, «считывают»
по горизонтали значения 0ι(ί) и 02 (t). Другими словами, концы
интервала (01,0г) находят как решения относительно 0 уравнений
FT(T(x),e)=Pk, k = 1,2. (9)
Пункт б) задачи 1 дает пример построения доверительного
интервала с помощью этого метода.
Аналогичные рассуждения можно провести и для дискретной
модели. Отличие состоит в том, что из-за ступенчатости функции
распределения i*r(£,0) удается, вообще говоря, добиться лишь
выполнения неравенства P(ti < Т(х) < t2) = FT(t2 - ,0) - FT(ti,6) ^ 1 -a.
При этом вместо квантилей берут наибольшее t\ и наименьшее t2i
удовлетворяющие, соответственно, условиям
FT(tu9) Οι и FT(t2 - ,0) ^ Р2.
§ 3. Методы построения интервалов
153
Кривые Θ1 = tk(9) также будут ступенчатыми (рис. 12). При
«считывании» 01 и 02 следует взять крайнюю правую точку пересечения
горизонтальной прямой с левой кривой и крайнюю левую точку —
с правой кривой.
Вместо уравнений (9) надо решать относительно θ уравнения
FT{tft)=pi и FT{t-fi)=p2, где* = Г(ж). (Ю)
Пример 5. Построим доверительный интервал для неизвестной
вероятности «успеха» θ в схеме Бернулли длины п. В качестве
точечной оценки возьмем частоту «успехов» Τ = X. Случайная
величина Τ принимает значения k/η, к = ОД,... ,п, при этом
FT{k/nfi) = Р(пт < к) = Σ σηθ\\ - θ)η-\ (и)
г=0
Заметим, что правая часть соотношения (11) равна 1 — i^(fc+1)(0),
где rj(k-\-i) ~ (& + 1)_я порядковая статистика выборки размера η
из равномерного распределения на отрезке [Q, 1] (см.
утверждение 3 гл. 5). При к < η статистика Щк+i) имеет бета-плотность
nC*_!a?fc(l - x)n-k~l > 0 для 0 < χ < 1 (см. формулу (2)
гл. 5). Следовательно, Ет(к/п,0) строго убывает по Θ при к < п.
В соответствии с уравнениями (10), границы θ χ и 02 центрального
доверительного интервала находятся из соотношений
FT((ifc-l)/n,0i) = l-a/2 и FT(k/nfo) = α/2. (12)
В таблицах [10] они указаны для 1 — α = 0,9; 0,95; 0,99.
Пример 6. Пусть Χι распределены по закону Пуассона с
неизвестным параметром Θ: Р(Хг = к) = е~99к/к\, к = 0,1,... .
Построим доверительный интервал для θ с помощью метода 2.
Как и в предыдущем примере, в качестве точечной оценки возьмем
Г = X. Ввиду задачи 3 гл. 10 сумма Χι +... + Хп распределена по
закону Пуассона параметром ηθ. Поэтому
FT{k/nfi) = Р(пТ < к) = β~ηθ Σ (пву/г\. (13)
г=0
В силу формулы (1) гл. 5 правая часть (13) равна 1 — Fsfc+1(0), где
Sfc+i ~ Г(А: + 1,п) с плотностью nk+lxke~nx/к\ > 0 при χ > 0.
Следовательно, Frik/nfl) строго убывает по Θ. Границы
центрального доверительного интервала находятся из уравнений (12), где
Ft задается формулой (13).
Метод 3. Стабилизация асимптотической дисперсии
Допустим, что известна асимптотически нормальная оценка (см.§ 4
гл. 7): у/п (θη — θ)-+ξ~ ΛΓ(0, σ2(0)) при η —> оо. Потребуем, чтобы
асимптотическая дисперсия σ2(θ) была положительна и
непрерывна при всех θ € θ.
Построим асимптотический интервал для θ с помощью
преобразования, стабилизирующего дисперсию, основанного на лемме 1
154
Глава 11. Доверительные интервалы
гл. 7. Для этого подберем такую фушащю φ, чтобы
асимптотическая дисперсия последовательности φ(θη) не зависела от
неизвестного параметра Θ:
σ(θ)ψ'(θ)=ο,
т. е.
т=с\^у (14)
Тогда у/п (φ(θη) — φ(θ)) —► φ(ξ) ~ ЛГ(0, с2) при п —► оо. Отсюда, так
же, как и в примере 2, получаем:
Ρ (φ(θη) - X-^f- < ψ{θ) < φ(θη) + ^f) - 1 " α, (15)
где #ι_α/2 обозначает (1 — а/2)-квантиль распределения ΛΓ(0,1).
Ввиду предполагаемой положительности и непрерывности σ(0), из
формулы (14) видим, что функция φ строго монотонна. Тогда из
соотношения (15) очевидным образом находим асимптотический
доверительный интервал для самого параметра Θ.
Метод 4. Подстановка оценки параметра
Пусть выполнены предположения, сформулированные при
изложении метода 3. Тогда
у/п(0п-0) = ν^(θη-θ) χ σψ)_ m
σ(θη) σ(°) σ{θη)'
Распределение первого сомножителя в этой формуле сходится
к ЛГ(0,1). Из асимптотической нормальности оценки Θη вытекает
ее состоятельность (см. ответ на вопрос 1 гл. 7). Ввиду
непрерывности σ(θ) второй сомножитель в формуле (16) стремится к 1 по
вероятности (П5). В силу свойства сходимости 1 из П5 произведение
имеет в качестве предельного закона ЛГ(0,1), откуда
Ρ [θη - Χι-ο,/2σ(θη)/^/η < θ < θη + Ζ!_α/2е(вп)/у/п) -+ 1 - α,
где ^ι_α/2 —это, как и прежде, (1 — а/2)-квантиль распределения
JV(o,i).
Замечание 4. Используя разные асимптотически нормальные
оценки, будем получать различные доверительные интервалы.
Чтобы строить интервалы наименьшей длины (при заданном
коэффициенте доверия), следует выбирать оценки, имеющие
наименьшую возможную асимптотическую дисперсию σ2(0)
(асимптотически эффективные). Если для модели выполняются условия
регулярности, то годятся оценки максимального правдоподобия
(см. § 4 гл. 9).
Проиллюстрируем методы 3 и 4 на примере схемы Бернулли.
Задачи
155
Для применения метода 3, как и в примере 5, возьмем в
качестве оценки неизвестной вероятности «успеха» θ частоту X.
Она, согласно примеру 5 гл. 9, является оценкой максимального
правдоподобия с σ2(0) = 0(1—0). Условие (14) при с = 1/2 приводит
к функции φ(θ) = 9 ί β(* ~~ θ)]~ι^2άθ = arcsin \/θ. При этом в силу
формулы (15) интервал с границами
arcsin VX±%^
2 у η
накрывает arcsin y/θ с вероятностью, стремящейся к 1 — α при
η —> оо. Применив функцию φ~1(χ) = sin2 ж к его границам,
построим асимптотический доверительный интервал для самого
параметра Θ.
Метод 4, в свою очередь, приводит к интервалу с границами
а/2
x±Xl
\Jx(i-X)·
ЗАДАЧИ
1. В модели выбора наудачу η точек с координатами Χι из отрезка
[О, Θ] с неизвестным θ > О постройте интервал с коэффициентом
доверия 1 — a
а) на основе формулы (8),
б) при помощи метода 2 с использованием оценки Х^ =
= max{Xi,...,Xn}.
2. Элементы Χι выборки имеют функцию распределения F(x — 6).
Пусть F(0) = 0, а плотность р(х) такова, что с = р(0) > 0.
а) Найдите предельный закон для величины п(Х^ — 0), где
Х{1) =min{Xi,...,Xn}.
б) На его основе постройте асимптотический доверительный
интервал для параметра сдвига Θ.
3. Рассмотрим модель сдвига из предыдущей задачи, но потребуем
теперь, чтобы F(0) = 1/2 и F была непрерывной. Найдите
коэффициент доверия интервала, образованного парой порядковых
статистик (см. § 4 гл.4) (Χ^)^(ΐ))^ где к < I. Вычислите его
значение для к = 2, / = 5, η = 6.
4. Докажите теорему 1 при η = 2 непосредственно.
5. Для распределения Пуассона из примера 6 постройте
асимптотический доверительный интервал методами 3 и 4.
6. Пусть (Χ,Υ) — двумерный нормальный вектор (П9).
Неизвестный коэффициент корреляции его компонент
ρ = ρ(Χ,Υ) = ЩХ- ΜΧ)(Υ - MY) /VOX ΏΥ
оценивается при помощи выборочного коэффициента
корреляции
Нужно обращать острие
ума на самые
незначительные и простые вещи
и долго останавливаться
на них, пока не
привыкнешь отчетливо и ясно
прозревать в них истину.
Р. Декарт
Р. Декарт (1596-1650),
французский математик
и философ.
Заметим, что для α = 5%,
η = 100 и χ = 0,03
в качестве левой границы
последнего интервала
формально получаем
отрицательную величину
-0,0034.
Строили мы, строили и,
наконец, построили.
Чебурашка
Только сокровища
ума действительны.
Ими можно делиться,
ничего не теряя; они
даже умножаются,
когда ими делятся.
Чтобы приобрести такое
богатство, надо трудиться.
Демофил
156
Глава 11. Доверительные интервалы
Можно показать (см. [50, с. 391]), что распределение величины
\/п(рп — р) сходится при η —► оо к закону ЛГ(0, (1 — р2)2).
Найдите преобразование (впервые предложенное Р. Фишером),
стабилизирующее дисперсию рп.
Читать следует тогда
только, когда иссяк
источник собственных
мыслей, что нередко
случается и с самым
умным человеком. Но
спугнуть, ради книги,
собственную, неокрепшую
мысль —это значит
совершить преступление
против духа.
А. Шопенгауэр
Δ(Χ(η))
Рис. 13
Вопрос 6.
При каком значении р2
доверительный интервал
из задачи 16 имеет
наименьшую длину?
РЕШЕНИЯ ЗАДАЧ
1. а) Функция F{Xi,6) = χ/θ, О < χ < θ, убывает по θ при
θ > 0. Согласно формуле (8), д(Х,в) = ηΐτιθ — Y^laXi. Решая
уравнения (7) относительно Θ, находим границы интервала
/ » \ V»
Tfe(X)=fex**]p4 ' * = 1>2>
где хРк обозначает р^-квантиль закона Г(п,1), 0 < р\ < p<i ^ 1
и Р2 - Pi = 1 - ol.
б) Функция распределения статистики Х(п), равная (χ/θ)η при
О < χ < 0, убывает по Θ. Поскольку р-квантиль хр = ρλΙηβ,
множество Ga представляет собой угол между лучами θ' = ρλ θ
и V — Р2 θ, где Р2 — Pi = 1 ~ ol (рис. 13). Сечение Δ(Χ(η))
является интервалом уХ^р^ , Χ(η)ΡΪ /nJ.
2. а) Используем независимость величин Xi и формулу Тейлора:
Р(п (Х{1) -θ)>χ) = Ρ(Χ(ΐ) > θ + х/п) =
= P(Xi -θ> χ/η, i = 1,... ,η) = [1 - F(x/n)]n =
= [1 - F(0) - p(0) s/n + o(l/n)]n =
= [1 - p(0) я/п + o(l/n)]n —► ехр{-р(0)я} при η —► оо.
б) Осталось, как в примере 1, взять 02 = ^(ΐ) и #ι = Х^) — cQ,
где са = - In α / (ρ(Ο)η).
3. Рассмотрим случайные величины Yi = Xi — θ, имеющие
функцию распределения F(x). Для них Y^ = Х^ — θ и
P(X(fc) < 0 < Х(|)) = P(Y{k) < 0 < У(|)).
Поскольку P(Y(k) < Y(i)) = 1 при А: < Ζ, выполняется равенство
P(F(fe) < 0 < Y(l)) = P(Y{k) < 0) - Р(У(0 < 0).
Согласно ответу на вопрос 3 гл. 5 о распределении случайной
величины У(д.),
P(F(fe) < 0) = Σ ^^(Ο)^! - F(0))"-\
Учитывая условие F(0) = 1/2, находим отсюда, что
P(x{k)<e<x(l)) = 2-nlj:ci.
i=k
Решения задач
157
Для λ; = 2,/ = 5,η = 6 получаем значение коэффициента
доверия 2"6(С£ + Cg + С$) = 50/64 « 0,78.
Отметим, что в отличие от предыдущей задачи
доверительный интервал строится при помощи пары разных статистик, а не
за счет «подправления» одной статистики.
4. Для η = 2 имеем:
Х=\(Х1+ Х2), S2 = \ {XI + Х22) -Χ2 = \{Χγ- Х2)2.
Случайные величины Υι = Х\ + Х2 и Υ2 = Χι — Х2 нормально
распределены: Υί ~ Λ/Χ20ι,20^), Υ2 ~ ΛΓ(Ο,20|) (в частности,
ΜΥ2 = 0). Причем ковариация между ними равна
Μ(ΥιΥ2) - ΜΥι · MY2 = ЩХ* - XI) = ΜΧΪ - МХ| = 0.
Следовательно (см. П9 или [90, с. 322]), они независимы.
Поэтому независимы, как функции от них, X и 52. Наконец, так
какУ2/(^202) ~Af(O,l),To2S2/0| = [Г2/(^2 02)]2 ~ χ?.
5. В силу центральной предельной теоремы (П6) для выборки
из закона с конечной дисперсией у/п(Х — МХ\) при η —► оо
сходится по распределению к ЛГ(0, DXi). Из ответа на вопрос 2
гл. 5 для закона Пуассона Μ Χι = DX\ = θ. По формуле (14)
при с = 1/2 вычислим φ(θ) = i J θ~^2άθ = у/9. Таким
образом, асимптотические доверительные интервалы строятся на
основе сходимости к закону λί(0,1/4) (метод 3)
к закону Л/"(0,1) (метод 4).
6. Для с = 1 найдем
где arcthz — это функция, обратная к гиперболическому
тангенсу th# = (еж — е~х)/(ех + е"*).
При |р| близких к 1 и не слишком больших η распределение
оценки рп сильно отличается от нормального. Преобразование
Р. Фишера zn = arcthpn в этом случае существенно повышает
точность нормального приближения (на рис. 14, взятом из [13,
с. 381], изображены графики плотностей величин рп и 2П для
Ρ = 0,8).
В [10, с. 51] для статистики 2П приведены следующие
асимптотические формулы:
Μζη = arcthp + o(l/n), Dzn = Ι/(η — 3) + o(l/n) при η —* оо.
Б. Л. Ван дер Варден в [13, с. 41] пишет: «Вообще в
математической статистике часто оказывается, что 4 уже является большим
числом». В формуле для Dzn, во всяком случае, η ^ 4.
Рис. 14
158
Глава 11. Доверительные интервалы
ОТВЕТЫ НА ВОПРОСЫ
1. Так же, как и в примере 1, запишем:
1-а = Р(Х{1)-са<в) = 1-[Р(Х1-в>са)]п = 1-(1-са)п.
Отсюда находим, что длина интервала са = 1 — а1/71.
2. Обозначим через Ф(х) функцию распределения ЛГ(0,1). Тогда
при χ ^ О
P(Zl < χ) = Р(-у/х ^ Ζλ < yfx) = Φ(λ/χ) - Ф(-Vi).
Дифференцируя по х1 вычислим плотность случайной
величины Ζ ι:
2 --х/2_ 1 -χ/2
— i С· ,
γ2πχ
которая совпадает с плотностью закона М^^Ь поскольку
Γί 2) = л/тг- Этот результат можно получить и с помощью
общей формулы преобразования плотности из П8 (убедитесь!),
заметив, что Ζ\ = \Ζ\\2, где Ρ(\Ζ\\ < χ) = Ф(х) - Ф(-х) при
ж^Ои, следовательно, p\zx\(x) = 2Ф,(х) при χ ^ 0.
3. MAg = M(Z? +...+ Z2) = fcMZ? = fcDZi=fc.
4. В соответствии с законом больших чисел (П6) имеем, что
при А: —► оо. Функция 1/у/х непрерывна при χ > 0. В силу
свойств сходимости 3 и 1 из П5 предельным законом для tk будет
Λ/χο,ΐ).
Другой подход: очевидно, (1 + х2/к)~^к+1^2 —► е"-* /2 при
А: —► оо. Используя асимптотику Г(#) = \Ζ27Γ#χ_1/26_α:(1 + о(1))
при # —► +оо, обобщающую формулу Стирлинга на
действительные χ (см. [81, с. 84]), нетрудно проверить, что dk —► 1/\/27г.
Наконец, из поточечной сходимости плотностей κ плотности
вытекает сходимость по распределению (см. [90, с. 394]).
5. Во-первых, (Ст)-1 = (С_1)т = (СТ)Т. Во-вторых,
выполняются соотношения:
1 = det Ε = det(CT · С) = det CT · det С = (det С)2.
6. Длина доверительного интервала
*<»> (рГ1/п -ν*1/η) = ^(η)Ρ2-1/η {[ι - (1 -«)/р2]-1/п -1}
убывает по рг £ (1 — <*> 1]·
Часть HI
ПРОВЕРКА ГИПОТЕЗ
В этой части книги приводятся основные понятия теории
проверки статистических гипотез: статистика критерия,
критическое множество, ошибки I и II рода и др. Рассматриваются методы
проверки равномерности, показательности и нормальности
распределения элементов выборки. Устанавливается оптимальность
критерия Неймана—Пирсона. Обсуждается последовательный анализ
Вальда.
Глава 12
КРИТЕРИИ СОГЛАСИЯ
§ 1. СТАТИСТИЧЕСКИЙ КРИТЕРИЙ
Эксперимент. Предположим, что кто-то подбросил 10 раз
монетку, и в 8 случаях она упала гербом вверх. Можно ли считать
эту монетку симметричной?
Статистическая модель. Используем для описания
эксперимента схему Бернулли, т. е. будем считать данные эксперимента
реализацией выборки X = (ΛΊ,... ,Хю), где Х\ — 1 (выпадает герб)
с вероятностью θ и Χι = 0 (выпадает решка) с вероятностью 1 — 0.
Как проверить гипотезу Η о том, что θ = 1/2?
Правило, позволяющее принять или отвергнуть гипотезу Η на
основе реализации выборки #ι,... ,#п, называется
статистическим критерием. Обычно критерий задается при помощи
статистики критерия Τ (ж ι,... ,#п) такой, что для нее типично
принимать умеренные значения в случае, когда гипотеза Η верна,
и большие (малые) значения, когда Η не выполняется.
Для приведенного выше эксперимента в качестве статистики
Τ можно взять сумму χι + ... + хп. Тогда гипотезе Η: θ = 1/2
противоречат значения, которые близки к 0 или п.
При проверке гипотез с помощью критериев всегда
присутствует возможность ошибочно отвергнуть гипотезу if, когда на
самом деле она верна. Например, симметричная монета может
случайно упасть 10 раз подряд гербом вверх. Но вероятность
наблюдать такое событие равна всего лишь 2~10 = 1/1024. Если
мы готовы пренебречь возможностью осуществления столь
маловероятного события, то появление 10 гербов подряд следует считать
основанием для отклонения гипотезы Η: θ = 1/2.
В общем случае задается малое число а — вероятность, с
которой мы можем позволить себе отвергнуть верную гипотезу Η ι
(скажем, а = 0,05). Это число называют уровнем значимости. '
Исходя из предположения, что гипотеза Η верна, определяется
наименьшее значение #ι_α, удовлетворяющее условию I
Р(Т(Хи...,Хп)>Х1-а)<<*.
(1)
§ 2. Проверка равномерности
161
Если функция распределения статистики Τ непрерывна, то #ι_α
является, очевидно, ее (1 — а)-квантилью (см. § 3 гл. 7). Такое #ι_α
называют критическим значением: гипотеза Η отвергается, если
ίο = Τ(#ι,. ..,#η) ^ х\-а (произошло маловероятное событие),
и принимается — в противном случае.
При этом величина qlq = Ρ(Τ(Χι,... ,Xn) ^ to) задает ή6ακ-
тический уровень значимости. Он равен вероятности того, что
статистика Τ (измеряющая степень отклонения полученной
реализации от наиболее типичной) за счет случайности примет значение
ίο или даже больше. Фактический уровень значимости —
наименьший уровень, на котором проверяемая гипотеза Η принимается
(рис. 1).
Проверим для данных эксперимента гипотезу Η: θ = 1/2 на
уровне значимости а = 0,05 и вычислим а$. Известно, что сумма
Τ = х\ + ... + хп имеет биномиальное распределение:
Р(Т>к)=±Сгп0\1-в)п-\
г=к
Для θ = 1/2 правая часть этого выражения при к = 8 равна
(45 + 10 + 1)/1024 » 0,055 и при к = 9 равна (10 + 1)/1024 w 0,011.
Поэтому для α = 0,05 наименьшим #ι_α, удовлетворяющим
условию (1), будет 9. Поскольку полученное в эксперименте значение
ίο = Т(ж1, · · · ,#п) = 8 < 9, на заданном уровне значимости гипотеза
Η: θ = 1/2 принимается.
С другой стороны, фактический уровень значимости а$ =
= Р(Т ^ 8) « 0,055, что всего на 0,005 превосходит заданный
уровень: уже при а = 0,06 гипотезу Η следует отклонить.
На основе данных эксперимента нельзя уверенно принять или
отвергнуть гипотезу Η (хотя последнее представляется более
правдоподобным). Следовало бы еще несколько раз подбросить монетку,
чтобы прийти к более взвешенному заключению.
Вычисление фактического уровня значимости нередко
позволяет избегать категоричных (и при этом — ошибочных) выводов,
сделанных лишь на основе сравнения ίο с критическим значением
#ι_α, найденным для формально заданного а.
Если значение Τ попало
в область, имеющую при
выполнении гипотезы Η
высокую вероятность,
то можно заключить,
что данные согласуются
с гипотезой Н. Отсюда
происходит термин
«критерии согласия».
Рис. 1
Вопрос 1.
Чему приближенно равна
вероятность наблюдать не
менее 60 падений гербом
вверх при 100 бросаниях
симметричной монеты?
(Воспользуйтесь
табл. Т2.)
Не все стриги, что растет.
Козьма Прутков
§2. ПРОВЕРКА РАВНОМЕРНОСТИ
Пример 1. Орбиты планет и комет [72, с. 113]. В 1734 г.
Французская академия присудила Даниилу Бернулли премию за
исследование по орбитам планет, в котором он пытался показать,
что схожесть орбит является неслучайной. Если предположить,
что Солнце и планеты образовались в результате концентрации
вещества первоначального «волчка» (рис. 2), то согласно закону
162
Глава 12. Критерии согласия
Д. Бернулли
(1700-1782), швейцарский
математик (племянник
Якоба Бернулли (1654-
1705), установившего
в 1713 г. справедливость
закона больших чисел для
частоты «успехов» в
независимых испытаниях).
Д. Бернулли известен
своими результатами
в области механики
жидкостей и газов.
В 1778 г. им была
опубликована в изданиях
Петербургской Академии
наук работа «Наиболее
вероятное определение по
нескольким расходящимся
между собой
наблюдениям и устанавливаемое
отсюда наиболее
правдоподобное заключение»,
где впервые был высказан
и использован для оценки
неизвестного параметра
принцип
максимального правдоподобия
(см. [19, с. 419]).
Рис. 2
сохранения момента импульса J орбиты планет должны
лежать примерно в одной плоскости, что и наблюдается в
реальности.
В 1812 г. Лаплас исследовал схожую проблему: образовались
ли и кометы в общем «волчке» или же они —всего лишь
«гости», захваченные притяжением Солнца. В последнем случае углы
между нормалями к плоскостям орбит комет и вектором J должны
не концентрироваться вблизи нуля, а быть равномерно
распределенными на отрезке [0,π/2]. Проведя статистическую
обработку известных к тому времени астрономических данных,
Лаплас пришел к выводу, что гипотеза о равномерности не
отвергается.
Каким же образом можно проверить гипотезу равномерности?
Рассмотрим несколько разных методов.
Метод 1. Критерий Колмогорова
Статистикой критерия является величина
Dn= sup \Fn(x) - F(x)l
—oo<a:<oo
(2)
где Fn(x) = - Σ Ι{Χί^χ] ~это эмпирическая функция распреде-
п ;г
г=1
ления, встречавшаяся ранее в § 1 гл. 9, F(x) — функция
распределения элементов выборки (на рис. 3 изображен случай
равномерного распределения на [0,1]). Для любого фиксированного xq
согласно усиленному закону больших чисел значение Fn(#o), равное
частоте попаданий Xi левее #о, ПРИ η -+ оо с вероятностью 1
стремится к F(xo) = Ρ (Χι ^ хо). Теорема Гливенко утверждает,
что для произвольной функции распределения F(x) имеет место
сходимость Dn ——'■+ 0. (Доказательство этой теоремы приведено
в [19, с. 206].) Поэтому в случае, когда гипотеза равномерности
верна, значение Dn для выборки достаточно большого размера не
должно существенно отклоняться от нуля.
Как количественно характеризуется значимость отклонения от
нуля? В силу центральной предельной теоремы (П6)
уД (Fn(x0) - F(x0)) ^ ξ ~ ΛΓ(0, F(x0)(l - F(xQ)).
Поэтому в фиксированной точке xq величина \Fn(xo) — F(xo)\
имеет порядок малости 1/у/п. Оказывается, что и величина Dn
имеет тот же порядок малости, причем справедлив следующий
результат.
§ 2. Проверка, равномерности
163
Теорема Колмогорова. Если функция распределения элементов
выборки F(x) непрерывна, то для χ > О
lim Р(д/пDn < ж) = К(х) = 1 + 2 £ (-l)fce-2fc2*2.
n->°° fc=i
Быстрая сходимость к предельному закону позволяет
пользоваться этим приближением уже при η ^ 20.
Замечание 1. Особенностью статистики Dn является то, что закон
ее распределения оказывается одним и тем же для всех
непрерывных функций F. Он зависит только от размера выборки п.
Действительно, полагая в формуле (2) χ = F~1(y) = sup{#: F(x) = у},
0 < у < 1 (рис. 4), получаем Dn = sup |Fn(F_1(y)) - у\.
Согласно методу обратной функции (см. § 1 гл. 4) случайные
величины Yi = F(Xi) образуют выборку из равномерного
распределения на отрезке [0,1]. В силу монотонности и непрерывности
функции F(x) неравенства χ ^ F_1(y) и F(x) ^ у эквивалентны
(см. рис. 4). Поэтому
^ _1 1 п 1 п
Fn(F (у)) = - Σ I{Xi^F~4y)} = " Σ t{Yi<y}·
n i=l n i=l
Правая часть — эмпирическая функция выборки Υί,... ,Υη.
Приведем таблицу некоторых квантилей функции К(х):
a
X\-ot
0,5
0,83
0,15
1,14
ОД
1,23
0,05
1,36
0,025
1,48
0,01
1,63
0,001
1,95
Таким образом, для заданного уровня значимости α критерий
Колмогорова отвергает гипотезу равномерности, если для F(x) =
= χ величина у/пDn(x\,... ,хп) ^ #ι_α.
Так как функция распределения F(x) непрерывна и не убывает,
a Fn (x) — кусочно-постоянна, то sup в формуле (2) достигается
в одной из точек разрыва функции Fn. Отсюда получаем простую
формулу для вычисления значения Dn(x\,... ,#п):
Dn(xu...,xn) = max J I - F(a?w),F(a?(<)) - ί-=- \.
В задаче 1 критерий применяется для проверки качества
таблицы случайных чисел Т1. Задача 3 показывает, что условие
непрерывности функции F(x) в теореме Колмогорова необходимо.
А
1-
уф"
S~~\V = F(x)
ι
0' x = F~\y)
Рис. 4
Вопрос 2.
Как может выглядеть
эмпирическая функция
распределения Fn, для
которой Dn (χι,... ,#η) φ
Φ max --F(x(i))?
Метод 2. Критерий омега-квадрат
Статистика Dn измеряет отклонение эмпирической функции
распределения Fn от теоретической функции распределения F в
равномерной метрике. Если воспользоваться (взвешенной) квадратичной
164
Глава 12. Критерии согласия
метрикой, то получим статистику критерия омега-квадрат:
оо
"»М= J [Fn(x)-F(x)]24>[F(x)]dF(x),
—оо
где ψ(ν)— заданная на [0,1] весовая функция. Рассмотрим два
варианта: ^ι = 1 (критерий Крамера — Мизеса), ф2(у) = 1/[у(1—2/)]
(критерий Андерсона —Дарлинга).
Первый из них хорошо улавливает расхождение между Fn и F
в области «типичных значений» случайной величины с функцией
распределения F (часто он оказывается более чувствительным, чем
критерий Колмогорова). Второй же, благодаря тому, что ф^у)
быстро возрастает при у —► 0 и у —► 1, способен заметить различие
«на хвостах» распределения F, которому придается
дополнительный вес.
Так же, как и для статистики Dn, закон распределения
величины ω^(φ) один и тот же для всех непрерывных функций F.
При выполнении ряда условий относительно φ можно доказать,
что существует lim Ρ(ηω^ι(/φ) ^ χ) = А(х), зависящий от ψ. Для ψι
η—юо
и ^2 известны разложения в ряды соответствующих законов А\(х)
и Аъ(х) (см. [10, с. 83]). Приведем таблицу некоторых квантилей ур
и ζρ этих законов (А\(ур) = Α2(ζρ) = ρ):
а
Уг-а
Zl-a
0,5
0,12
0,77
0,15
0,28
1,62
ОД
0,35
1,94
0,05
0,46
2,49
0,025
0,58
3,08
0,01
0,74
3,88
0,001
1,17
5,97
Значения ηω^Ψι) и пи^ь('Ф2) вычисляются по следующим
формулам (первая из них выводится в задаче 4):
ιΊ2
η
ηωΙ(ψ2)=-η-2Σ
*Х*(г))-
2г-1
2п
г=1
«zibF(x(0)+(l-^)ln(l-F(xw))]
В гл. 18 появится еще один критерий (так называемый критерий
хи-квадрат), с помощью которого можно проверять равномерность
по сгруппированным данным.
Многие вещи нам
непонятны не потому,
что наши понятия слабы;
но потому, что сии вещи
не входят в круг наших
понятий.
Козьма Прутков
§3. ПРОВЕРКА ПОКАЗАТЕЛЬНОСТИ
Прежде чем познакомиться с методом проверки показательности,
введем формально понятие статистической гипотезы.
Напомним, что под статистической моделью в § 1 гл. 6
понималось семейство функций распределения {F(#,0), θ € θ}, где
θ — множество возможных значений параметра. При этом данные
§ 3. Проверка показательности
165
#1,...,жп рассматривались как реализация выборки Χι,...,Χη,
элементы которой имеют функцию распределения F(xflo) с
неизвестным значением θο € Θ.
Пусть выделено некоторое подмножество θο С Θ. Под
статистической гипотезой Η понимается предположение о том, что
#о £ Фо· Если множество θο состоит всего из одной точки, то
гипотеза Η называется простой, иначе — сложной. В последнем
случае задача заключается в проверке принадлежности закона
распределения величин Χι целому классу функций распределения
{F{x,0), θ € θο}·
Под гипотезой показательности понимается сложная гипотеза,
в которой этот класс образуют функции распределения вида
F(x,6) = (l — β~θχ) /{д:>о}, где θ > 0 (рис. 5). Рассмотрим методы
проверки такой гипотезы.
Метод 1. Исключение неизвестного параметра
Согласно лемме 3 гл. 4, вектор (5ι/5η,... ,Sn_i/Sn), где
Sk = Χι + ... + Xk, распределен так же, как вектор порядковых
статистик (?7(ΐ),. · · Л{п-\)) Для выборки размера (п — 1) из
равномерного распределения на отрезке [0,1].
Так как эмпирическая функция распределения строится по
порядковым статистикам, то данное преобразование сводит задачу
к проверке равномерности. Однако, за исключение «мешающего»
параметра θ приходится платить уменьшением размера выборки
на 1.
Пример 2. Следующие данные представляют собой количества
летных часов между последовательными отказами установки для
кондиционирования воздуха на самолете типа «Боинг-720» [40].
23 261 87 7 120 14 62 47 225 71
246 21 42 20 5 12 120 11 3 14
71 11 14 11 16 90 1 16 52 95
Считая времена между отказами независимыми, проверим
гипотезу их показательности. Вычислим Sk = х\ + · · · + ж*, к = 1,... ,30:
23 284 371 378 498 512 574 621 846 917
1163 1184 1226 1246 1251 1263 1383 1394 1397 1411
1482 1493 1507 1518 1534 1624 1625 1641 1693 1788
В результате деления на $зо = 1788, получим ряд значений
W*3(h к = 1,... ,29:
0,013 0,159 0,207 0,211 0,279 0,286 0,321 0,347 0,473 0,513
0,650 0,662 0,686 0,697 0,700 0,706 0,773 0,780 0,781 0,789
0,829 0,835 0,843 0,849 0,858 0,908 0,909 0,918 0,947
166
Глава 12. Критерии согласия
Построенная по этому ряду эмпирическая функция
распределения изображена на рис. 6. Максимальное отклонение Dn =
= 0,65 - 10/29 « 0,306, \/29 £>п « 1,65. Из приведенной выше
таблицы квантилей функции Колмогорова находим, что гипотеза
показательности отвергается на уровне значимости 1%.
Статистики ηω^ψι) и ηα^(^>2) критерия омега-квадрат равны,
соответственно, 0,627 и 3,036. Из таблицы квантилей А\(х) и ^(я)
следует, что первая значимо велика на уровне приблизительно 2%,
вторая —на уровне 2,5%.
Метод 2. Подстановка оценки параметра
Пусть θη — оценка максимального правдоподобия для параметра θ
(см. § 4 гл. 9). Рассмотрим модифицированные статистики
Колмогорова и Крамера—Мизеса:
Dn = sup
\Fn{x) - F{xfin) ,
οο
ώΙ= ί [fu(x) - F(x,en)]2 dF(x,en)-
(3)
Замечание 2 [80, с. 317]. Эти статистики, в отличие от их
прототипов Dn и ω\ (V>i), не обладают свойством «свободы от
распределения» элементов выборки, поэтому для каждого параметрического
семейства распределений нужны отдельные таблицы. Более того,
их распределения могут зависеть и от истинного значения
неизвестного параметра (параметров). К счастью, для семейств сдвига-
масштаба (к которым относятся, в частности, показательный
и нормальный законы) этого последнего осложнения не возникает.
Несложно проверить (см. задачу 3 гл. 9), что оценкой
максимального правдоподобия для параметра θ показательного закона
является θη = 1/Х1 где X = (Χι + ... + Хп)/п1 которая ранее
встречалась в замечании к примеру 1 гл. 6.
М. Стефенс (см. [35]) предложил вместо статистик y/nDn и mb\
распределение статистики использовать для показательной модели их несколько преобразо-
Dn не зависит от Θ1 ванНые варианты (^ + 0,26 + 0,5/^ (Dn - 0,2/п) и (п + 0,16) ώ2η,
распределения которых практически не зависят от п, начиная
с η = 5. Приведем таблицу соответствующих квантилей х\-а и yi-a
этих распределений (рассчитанную методом Монте-Карло):
Вопрос 3.
Почему в случае
показательного закона
α
#1-α
2/1-α
0,15
0,926
0,149
од
0,990
0,177
0,05
1,094
0,224
0,025
1,190
0,273
0,01
1,308
0,337
Еще один критерий для проверки показательности («Новое
лучше старого») рассматривается в § 1 гл. 13.
§ 4. Проверка нормальности
167
Рис. 7
§4. ПРОВЕРКА НОРМАЛЬНОСТИ
Б. Л. Ван дер Варден в [13, с. 84] пишет:
«Я до сих пор живо помню, как однажды, когда я был еще
ребенком, мой отец привел меня на край города, где на берегу стояли
ивы, и велел мне сорвать наугад сотню ивовых листочков. После
отбора листьев с поврежденными кончиками у нас осталось 89 целых
листиков. Вернувшись домой, мы расположили их в ряд по росту,
как солдат. Затем мой отец через кончики листьев провел кривую
и сказал: «Это и есть кривая Кетле. Глядя на нее, ты видишь, что
посредственности всегда составляют большинство и лишь немногие
поднимаются выше или так и остаются внизу».
Если эту кривую расположить вертикально (рис. 7) и в качестве
единицы масштаба на оси ординат выбрать отрезок, длина которого
равна высоте всей фигуры, то ордината /ι, соответствующая абсциссе
£, будет, очевидно, представлять собой частоту (или долю) тех ивовых л. А. Ж. Кетле
листьев, длина которых меньше t. И так как частота h приближенно (1796-1874), бельгийский
равна вероятности, то наша кривая приближенно представляет ρ = Чиолог
= F(x) — функцию распределения длины листьев.»
Как проверить сложную двухпараметрическую гипотезу
нормальности о том, что выборка была взята из совокупности
с функцией распределения ,Ρ(#,μ,σ) = Φ Ι χ~μ J с какими-то
неизвестными параметрами μ и σ > 0? (Здесь, как обычно,
1 Х 2
Ф(х) = —== Г е~и t2du — функция распределения стандартного
ν2π -оо
нормального закона.)
Прежде чем применять критерии, полезно посмотреть на
данные на вероятностной бумаге (см. § 1 гл. 9): если точки
ί#(ψφ-1 (г~ ' )) не расположены рблизи некоторой прямой, то
гипотеза нормальности скорее всего ошибочна.
Чтобы ее формально отвергнуть, можно использовать
Метод 1. Исключение неизвестных параметров
Пусть т — произвольное, но заранее фиксированное целое число от
1 до п. Положим
-ι
n + ^iti"1
Aj — Am,
Xj+i ~ Ami
l + ^"m'
если j = 1,...
если j = m,..
,m -
.,n-
-i,
-1.
Оказывается, случайные величины Υί,... Χη-ι независимы и
одинаково распределены по закону Λ/χθ,σ2) (ввиду нормальности
Yi,... ,Υη-ι достаточно (см. П9) проверить, что MYj = 0, DYj = σ2
и cov (Υ{ι Yj) = 0 при г ф j).
168
Глава 12. Критерии согласия
Переход от выборки Χι,...,Χη к набору случайных величин
Υί,... Χη-ι позволяет избавиться от неизвестного параметра сдвига
μ, однако при этом размерность данных уменьшается на 1. (Можно
было бы попытаться исключить параметр μ за счет следующего
простого преобразования: Х[ = Χι — X, г = 1,... ,п. Однако Х[ не
будут образовывать выборку.)
Для исключения оставшегося параметра σ совершим еще одно
преобразование:
Zk = Yk/y/~B~kl где Вк = J— "Σ Yf, * = l,...,n-2.
К. Саркади показал (см. [10, с. 57]), что случайные величины
Ζι,... ,Zn_2 также независимы, причем Z*., очевидно, подчиняется
закону Стьюдента £n-fc-i (см. § 2 гл. 11).
Обозначим через Fn-k-i(x) функцию распределения
закона tn-k-i- Если гипотеза нормальности верна, то (согласно
методу обратной функции из § 1 гл. 4) случайные величины
Fn-k-i(Zk) должны быть независимыми и равномерно
распределенными на [0,1]. Это проверяется с помощью одного из критериев,
рассмотренных в § 2.
Таблицы значений функций Fn-k-i для разных степеней свободы
приведены в [10, с. 174]. Для вычисления ее на компьютере можно
численно проинтегрировать плотность, задаваемую формулой (3)
гл. 11 (множитель Cn-fc-i в которой легко определяется из свойства
гаммагфункции Г(х + 1) = хГ(х) и тождества Г(1/2) = y/π), или
воспользоваться рекуррентными формулами из [20, с. 22, 51],
позволяющими выразить Fn-k-i через элементарные функции.
Метод 2. Подстановка оценок параметров
Согласно задаче 2 гл. 9, оценками максимального правдоподобия
параметров μ и σ являются соответственно X и 5, где X = — V Х^,
η
Статистики y/nDn и mb\, определяемые формулой (3) при
F{x,dn) = Ф((х — X)/S), сходятся при η —► оо к некоторым
предельным законам. М. Стефенс (см. [35]) установил, что для
нормальной модели распределения (сходящихся к тем же законам)
модифицированных статистик (у/п—0,01+0,85/ν^) Dn и (η+0,5) ώ\
практически не зависят от η при η ^ 5. Приведем таблицу
соответствующих квантилей х\-а и у\-а этих распределений:
α
Х\— α
2/1-α
0,15
0,775
0,091
од
0,819
0,104
0,05
0,895
0,126
0,025
0,955
0,148
0,01
1,035
0,178
Вопрос 4.
Зависимы ли
а) Х[ и ХГ при i#i,
б) Х[ и XI
Вопрос 5.
Применим ли к ним
критерий Колмогорова?
§ 4. Проверка нормальности
169
Замечание 3. Важно отметить, что предельные распределения
статистик y/nDn и шо\ отличаются от К(х) и А\(х). Дело в том,
что при вычислении значения θη используются те же самые
#1,... ,#п, что и при построении эмпирической функции
распределения. Поэтому Fn(x) и F{xfin) (в случае, если проверяемая
гипотеза верна) оказываются ближе друг к другу, чем Fn(x) и F(#,0O)·
При этом критическими становятся существенно меньшие
значения статистик, чем в случае простой гипотезы. Например,
сравнение £о,95 = 0,895 с медианой χι/2 = 0,83 и квантилыо #о,95 = 1,36
функции распределения К(х) показывает, что значения, типичные
для y/nDni оказываются критическими для статистики y/nDn.
Метод 3. Центральные выборочные моменты
Простые критерии (см. [13, с. 281]), которые несколько больше,
чем критерий Колмогорова, учитывают поведение «хвостов»
распределения, основаны на центральных выборочных моментах
п г=1
При помощи величин М2, Ms и М^ вычисляются выборочные
коэффициенты асимметрии G\ и эксцесса G2:
Gl=M3/M^/2, G2 = M4/M%-3.
Эти случайные величины можно использовать в качестве оценок
для (независящих от сдвига и масштаба) теоретических
коэффициентов асимметрии 71 = Мз/Мг и эксцесса η2 = /Wm! ~~ 3,
где μ\ζ = Μ (Χι — MXi)fc — центральные теоретические моменты.
(Для нормального закона 71 =72 = 0.)
При конечных η целесообразно заменить G\ и G2 на
Если истинное распределение является нормальным, то
математические ожидания величин G[ и G'2 в точности равны нулю,
а дисперсии задаются формулами
2_ 6п(п-1) 2_ 24п(п- I)2
σι ~ (п - 2)(п + 1)(п + 3)' σ2 ~ (п - 3)(п - 2)(п + 3)(п + 5)'
При этом статистики G[/ai и G2/a2 асимптотически нормальны
(см. §4 гл. 7): распределение каждой из них сходится к закону
λί(0,1) при η —► оо. Значимость их отклонения от нуля можно
определить по таблице Т2.
Замечание 4 [10, с. 56]. Как показал Э. Пирсон (1930 г.),
распределение статистики G[/ai довольно быстро приближается к ЛГ(0,1),
тогда как распределение величины G2/a2 даже при больших η
170
Глава 12. Критерии согласия
оказывается далеким от нормального. Р. Гири (1935 г.) предложил
заменить ее на статистику Сз = — Σ \Х% — X\/S, у которой
п LV π/ п \п /J
Распределение величины (G3 — MG3) /y/DGs удовлетворительно
аппроксимируется стандартным нормальным законом при η ^ 50.
Задача 2 показывает, что, как правило, нельзя надежно
проверишь сложную гипотезу по небольшой выборке (состоящей из
нескольких десятков наблюдений): критерии улавливают только
очень крупные отклонения, так как за счет варьирования
параметра (параметров) обычно удается достаточно хорошо подогнать
F{x,9) к эмпирической функции распределения Fn(x).
С другой стороны, для выборок большого размера (порядка
нескольких сотен наблюдений) трудно гарантировать одинаковость
условий при сборе данных (однородность наблюдений).
По-видимому, хороший способ разрешения этой проблемы —
использование статистических методов, не предполагающих строгую
нормальность наблюдений, для которых требуется лишь
непрерывность функции распределения элементов выборки. Именно
такие критерии рассматриваются в гл. 14-17.
Проверить нормальность по сгруппированным данным можно
также при помощи критерия хи-квадрат (см. гл. 18).
§5. ЭНТРОПИЯ
Обозначим через ξ некоторый эксперимент с исходами Αι,... ,Αν,
которые осуществляются с вероятностями pi,... ,рлг
соответственно. Энтропией этого эксперимента называется величина
H = Hti) = -jrPilog2Pi, (4)
г=1
где по непрерывности полагаем 0 · log2 0 = 0. Ясно, что Η ^ 0,
причем Η = 0 тогда и только тогда, когда все вероятности р^, кроме
одной, равны нулю.
Утверждение. Максимум энтропии Я, равный log2 N,
достигается при pi = ... = ρΝ = 1/Ν.
Доказательство. Поскольку вторая производная функции
φ(χ) = #log2# положительна при χ > 0, то эта функция
выпукла (П4). Записывая неравенство Иенсена (П4) для случайной
§5. Энтропия
171
величины г/, принимающей значения pi с вероятностями 1/ЛГ,
получим неравенство
/ 1 N \ ( 1 \ 1 1 N 1 N
которое равносильно доказываемому утверждению. ■
Энтропия может служить количественной характеристикой
меры неопределенности эксперимента. Если, скажем, pi = 1,
Р2 = · · · — PN = 0, то с полной уверенностью результатом
эксперимента будет осуществление события А\. Если же р\ =
= ... = pN = 1/iV, то такое распределение обладает максимальной
неопределенностью в том смысле, что нельзя отдать предпочтение
ни одному из событий А{.
График значений энтропии Η (ζ) = —plog2p — (1 —ρ) bg2(l —p)
для бернуллиевской случайной величины ζ при разных 0 ^ ρ ^ 1
приведен на рис. 8. Наибольшую неопределенность имеет опыт
с равновероятным появлением «успеха» и «неудачи».
Ценность понятия энтропии заключается в том, что
выражаемая им «степень неопределенности» является именно той
характеристикой, которая играет определяющую роль в реальных
процессах в природе и технике, связанных с передачей информации.
В конце XIX века психологами было установлено, что среднее
время реакции человека на последовательность беспорядочно
(равновероятно) чередующихся сигналов N различных типов с
увеличением N растет примерно как Η = log2 N. Приведем небольшой
отрывок из книги [92] на эту тему.
«На рис. 9, заимствованном из работы американского психолога
Р. Хаймана, кружками отмечены данные восьми опытов, состоящих
в определении среднего времени, требующегося испытуемому, чтобы
указать, какая из N лампочек (где N меняется от 1 до 8) зажглась.
Это среднее время определялось из большого числа серий зажиганий,
в каждой из которых частоты зажиганий всех лампочек были
одинаковыми, причем предварительно испытуемый специально
тренировался в подобных опытах. По оси ординат на рис. 9 отложено среднее
время реакции (в секундах), по оси абсцисс — величина log2 N; при
этом, как мы видим, все 8 кружков довольно точно укладываются на
одну прямую.
Исходя из этих данных, можно было бы предположить, что
среднее время реакции во всех случаях определяется энтропией
опыта ξ, состоящего в подаче сигнала. Из этого предположения
следует, что уменьшение степени неопределенности опыта путем
замены равновероятных сигналов неравновероятными должно на
столько же уменьшить среднее время реакции, на сколько оно
уменьшается при уменьшении числа используемых типов сигналов,
приводящему к такому же изменению энтропии Η (ξ). Это
утверждение допускает прямую экспериментальную проверку, полностью его
подтверждающую. Так, на том же рис. 9 квадратиками отмечены
i
0,6
0,4
0,2 <
'Т
"У
г
1
ri
f
«
2
^
Η
3*
Рис. 9
172
Глава 12. Критерии согласия
результаты восьми опытов (проведенных с теми же испытуемыми,
что и раньше), в которых N лампочек (где N равнялось 2, 4, 6
или 8) зажигались с разными относительными частотами pi,... ,рлг>
причем предварительно испытуемый некоторое время тренировался
на сериях зажиганий с такими частотами. Здесь снова по оси ординат
откладывалось среднее время реакции Т, а по оси абсцисс — энтропия
Η (ξ) = — pilog2pi — ... — pn log2 pn\ при этом оказывается, что
квадратики с большой степенью точности укладываются на ту же
прямую, что и кружки. Мы видим, таким образом, что энтропия Η (ξ)
действительно является именно той мерой степени неопределенности
исхода опыта, которая решающим образом определяет среднее время,
требуемое для определенной реакции на появившийся сигнал.
Причина изменения среднего времени реакции при изменении
относительной частоты различных сигналов, очевидно, кроется в том,
что испытуемый быстрее реагирует должным образом на более часто
повторяющийся (т. е. более привычный для него) сигнал, но зато
медленнее реагирует на редкий сигнал, являющийся для него
неожиданным. Разумеется, эти факторы носят психологический характер.
Тем не менее мы видим, что они могут быть количественно
охарактеризованы величиной энтропии Η (ξ) опыта £».
Понятие энтропии играет также важную роль в статистической
механике и в теории кодирования информации. Сам термин был
введен Р. Клаузиусом в 1865 г. в качестве меры «хаоса»
термодинамической системы (см. [72, с. 138]):
«Проблема обратимости-необратимости — это интересный
парадокс классической механики и термодинамики. Суть проблемы
заключается в том, что законы классической механики обратимы и
поэтому не могут объяснить, почему кусок сахара растворяется в чашке
кофе, но мы никогда не наблюдаем обратный процесс. Необратимость
нашего мира отражает второй закон термодинамики, впервые
сформулированный Л. С. Карно (первый закон термодинамики — это
закон сохранения энергии). Спустя сорок лет Р. Клаузиус ввел
математическое понятие энтропии, ставшее основным в теории необратимых
процессов. (Согласно Клаузиусу слово «энтропия» происходит от
греческого τροπή, означающего «поворот», «превращение». Клаузиус
утверждает, что он добавил «эн», чтобы слово звучало аналогично
«энергии».) Используя понятие энтропии, второй закон
термодинамики можно сформулировать следующим образом: в изолированной
системе энтропия не может уменьшиться, обычно она возрастает.
Л. Больцман пытался проверить этот закон с помощью кинематики
атомов и молекул. Он показал, что необратимость не противоречит
обратимой механике Ньютона: применение последней к большому
числу частиц с необходимостью приведет к необратимости, так
как системы, состоящие из миллионов молекул, стремятся перейти
в состояние, имеющее большую термодинамическую вероятность.
Это и есть «основная причина» распада, износа, старения (и, как
утверждают некоторые, упадка нравов или цивилизации)».
... а понял бы, уединясь,
Вселенной внутреннюю
связь,
Постиг все сущее в основе,
И не вдавался в суесловье.
И. В. Гете, «Фауст»
§5. Энтропия 173
Подробнее о проблеме необратимости можно почитать, скажем,
в пятом томе Берклеевского курса физики [67].
Рассмотрим теперь, следуя [69, с. 20], использование понятия
энтропии в теории кодирования информации.
При передаче сообщений по каналу связи их необходимо
записать в «двоичном коде». Если используется алфавит из N символов
(букв), то для кодировки каждого символа потребуется (с
точностью до 1) log2iV «двоичных» символов 0 и 1. Например, для
передачи текста на русском языке, состоящего из букв и пробелов,
можно (при объединении «ь» и «ъ») каждый символ закодировать
последовательностью из 0 и 1 длины log232 = 5. Для передачи
текста из η символов алфавита понадобится код длины η log2 N.
Для больших по объему сообщений можно существенно
уменьшить эту величину, используя то, что разные символы алфавита
встречаются в тексте с различными частотами (см. таблицу из
примера 3 гл. 1). Если pi,... ,рлг — вероятности их появления, то
в силу устойчивости частот среди сообщений длины η практически
будут встречаться лишь сообщения, в которых каждый г-й символ
алфавита будет появляться V{ « npi раз. Уточним это утверждение.
Допустим, что каждый символ сообщения появляется
независимо от других с соответствующей вероятностью р{. Для
δ > 0 обозначим через Anj множество тех сообщений, у которых
{\щ — npi\ ^ £, г = 1,... ,ЛГ}. Их станем называть типичными, так
как в силу закона больших чисел
N (\v Ι λ
Р(Ап,б)^1- Σ р \\--Pi \>δ -*1 при η-^оо.
г=1 VI п I /
Пусть Мп?<5 обозначает число «типичных» сообщений. При условии,
что все рг>0и0<$<1из теоремы Макмиллана (см. [90, с. 64])
следует, что - log2 Mnj стремится к энтропии Η = ~ΣΡί 1°ё2 Рг
при η —► оо. (Обобщение теоремы Макмиллана на стационарные
цепи Маркова можно найти в [12, с. 300], см. также задачу 5.)
Другими словами, число «типичных» сообщений не превосходит
2п(#+е)^ где £ > q сколь угодно мало. Каждому такому
сообщению можно присвоить порядковый номер, для записи которого
потребуется п(Н + ε) «двоичных» символов, и вместо сообщения
передавать эту запись. Тем самым, с вероятностью близкой к 1,
осуществляется сокращение длины сообщений с коэффициентом
сжатия 71 = Ηι/Η0 < 1, где Но = log2 N и Hi = Η. Для русского
алфавита на основе таблицы из примера 3 гл. 1 имеем Η « 4,35,
7ι «0,87 (см. [92, с. 238]).
Для независимо появляющихся символов невозможно
предложить способ кодирования (бесконечно большого текста), который
давал бы большую экономию, чем 71 (см. [92, с. 200]). Однако,
символы текста на русском языке, очевидно, зависимы: если оче-
Рассказывают, что
создавая свой код, Морзе
отправился в ближайшую
типографию и подсчитал
число литер в наборных
кассах. Буквам и знакам,
для которых литер в этих
кассах было припасено
больше, он сопоставил
более короткие кодовые
обозначения
Μ. Η. Аршинов,
А. Е. Садовский,
«Коды и математика»
174
Глава 12. Критерии согласия
редная буквой является гласной, то следующая вероятнее всего
окажется согласной; «ь» не может следовать ни за пробелом, ни
за гласной; за буквой «и» после пробела часто следует еще один
пробел; после сочетания «тс» естественно ожидать букву «я» и т. п.
Эти наблюдения подсказывают разбить текст на блоки длины к
и считать эти блоки символами нового алфавита.
Для подсчета частот двухбуквенных и трехбуквенных
сочетаний Д. С. Лебедев и В. А. Гармаш использовали отрывок из
романа «Война и мир» Л. Н. Толстого, содержащий около 30 000
букв (см. [92, с. 246]). На основе полученных данных были
получены оценки соответствующих энтропии: #2 ~ 7,9, #з ~ 10,9,
что приводит к коэффициентам сжатия 72 = Щ/Ц^Щ) « 0,79
и 7з = #з/(3#0) ~ 0>?3· Согласно [92, с. 245] коэффициент
сжатия (бесконечно большого) текста не может быть меньше, чем
7оо = Ит Hk/(kH0). Лингвист Р. Г. Пиотровский (см. [92, с. 268])
к—юо
оценил 7оо русских литературных текстов как 0,24, а деловых
текстов —как 0,17.
К. Шеннон назвал величину 1 — 7оо избыточностью языка.
Во многих случаях она полезна тем, что позволяет выявлять
опечатки и восстанавливать пропуски. (О кодах Хемминга,
умеющих исправлять подобные ошибки, можно почитать в [91, с. 288]
или [92, с. 392].) Последовательность независимых равновероятных
символов, имеющая энтропию Η = log2 ΛΓ, несократима. Поскольку
сильно сжатый текст похож на нее, практически невозможно
восстановить в нем пропущенный или искаженный символ. Это
обстоятельство нередко приводит к потере архивированных данных при
возникновении дефектов на дискетах.
На практике для кодирования неравновероятно появляющихся
символов используют, например, оптимальный метод Хафмана
(см. [91, с. 276] или [92, с. 206]). Он является самым экономным
в следующем смысле: если г-й символ записывается цепочкой из
0 и 1 длины /i, то код Хафмана имеет наименьшее
математическое ожидание Σ Upi длины элементарного кода среди всех кодов,
обладающих свойством префикса: никакая цепочка не является
началом другой, более длинной.
В заключение параграфа приведем утверждение, объединяющее
равномерный, показательный и нормальный законы как распреде-
Отыщи всему начало, и ты ления с наибольшей энтропией.
многое поймешь. Рассмотрим случайную величину £, имеющую плотность рас-
Козьма Прутков Пределения р(#) с носителем А = {х: р(х) > 0}. Тогда максимум
энтропии Η (ξ) = — $р(х) log2p(#) dx при одном из условий
а) А = (0,1),
б) А = (0, + оо) и Щ = 1,
в) А = (-оо, + оо), Щ = 0 и Df = 1,
Решения задач
175
достигается на плотностях /{о<ж<1}, е х1{х>о\ и —= е х /2 соот-
ν2π
ветственно. Справедливость этого утверждения в случае в)
предлагается установить в задаче 6.
ЗАДАЧИ
1. Примените критерий Колмогорова для проверки любого столбца
таблицы случайных чисел Т1.
2. Проверьте данные из задачи 1 на показательность. (Если тебе
дадут линованную бумагу, пиши поперек. — Хуан Рамон Химе-
нес)
3* Нарисуйте график плотности предельного закона статистики
y/nDn для выборки из распределения Бернулли.
4* Выведите формулу для вычисления ηω^{φ{) из § 2.
5. Установите, что lim — log2 Mn s = Η даже при δ = 0.
η—юо П '
Указание. Используйте формулу (3) гл. 10 и формулу Стир-
линга: ^2ппппе~п/п\ —► 1 при η —► оо (ее доказательство
см. в [81, с. 72]).
6* а) Докажите, что для произвольных плотностей р(х) и q(x) из
неравенства Иенсена вытекает неравенство
\p(x)\np(x)dx ^ \p(x)\nq(x)dx.
(5)
б) С помощью этого неравенства установите справедливость
последнего утверждения из § 5 в случае в).
РЕШЕНИЯ ЗАДАЧ
1. Выберем для проверки пятый столбец таблицы Т1: его
максимум равен всего лишь 74, кроме того, 6 из 20 чисел (30% данных)
попали в интервал от 29 до 35 (6% диапазона).
Эмпирическая функция этого столбца (рис. 10, а)
располагается целиком выше диагонали единичного квадрата и в точке
0,35 отклоняется от диагонали на величину Dn = 0,35. Значение
статистики y/nDn равно 1,57, что значимо на уровне с*о = 1,5%.
Еще к более категоричным выводам приводит критерий омега-
квадрат: ηωΚψι) = 0,85 (α0 < 0,01) и ηω^{φ2) = 5,1 (а0 < 0,01)
(при замене наблюдения 0 на 0,01).
Однако для четвертого столбца картина совершенно иная.
Отклонение эмпирической функции распределения от
диагонали Dn = 0,17 (рис. 10, б). Отсюда получаем, что y/nDn = 0,76.
Эта величина принадлежит области «типичных» значений
распределения Колмогорова: с*о = 61%. Хорошее согласие с
гипотезой равномерности подтверждается также критерием омега-
Если у тебя есть фонтан,
заткни его; дай отдохнуть
и фонтану.
Козьма Прутков
Недостойно многократно
опускать сосуд в пустой
колодец. Пахарь не
понесет зерна на голую
скалу. Согласившийся
легко примет выгоды, но
первым препятствием
устрашится. Поэтому
испытывайте
препятствиями.
Агни-Йога, 264
Если тебе дадут
линованную бумагу, пиши поперек.
Хуан Рамон Хименес
1 I I I I I I I I
0' 0,2 0,4 0,6 0,8 1
а)
1η
0,8 I
0,6-
0,4-
0,2-
1Ц7г
У* у = Fn(x)
I I I I I I I I 1 1
ПО Π Λ Г\£! ПО 1
0' 0,2 0,4 0,6 0,8 1
б)
Рис. 10
176
Глава 12. Критерии согласия
1-
0,8 "
0,6-
0,4-
0,2-
0
ΌηίϊΕ?
jjy = Fn(x)
ι ι ι ι ι ι ι ι Ι
0,2 0,4 0,6 0,8 1
a)
0,2 0,4 0,6 0,8
6)
Рис. 11
То, в чем нет
загадочности, лишено очарования.
А. Франс
квадрат: ηωη(ψι) = 0,103 (α0 = 57%) и ηωη(ψ2) = 0,723
(α0 = 54%).
Так можно ли пользоваться таблицей Т1? С помощью
компьютера была проверена вся ΤΙ (η = 300). Результаты
следующие: y/nDn = 0,981 (α0 = 29%), ηυβη(φ{) = 0,196 (α0 = 37%)
и ηω2η(φ2) = 1,98 (αο = 9,4%).
Кроме того, тест на случайность, основанный на количестве
инверсий Rn в выборке (см. пример 2 гл. 7) дал в качестве
значения статистики (Rn — MRn^/y/DRn величину —1,16. По таблице
Т2 находим, что фактический уровень значимости αο = 12,3%.
Таким образом, в целом Т1 пригодна для имитации выбора
наудачу из [0,1].
2. Применим метод исключения неизвестного параметра к
данным из четвертого столбца. На рис. 11, α по Yk = Sk/S2o
(к = 1,... ,19), где Sk = Χι + · · · + Хк, построена эмпирическая
функция распределения. Близость к диагонали
исключительная! Статистика y/nDn = 0,343. Согласно [10, с. 346] функция
Колмогорова в этой точке равна 0,002. Значение статистики
попало далеко в область левого «хвоста».
В чем же дело? Может быть, мала выборка? Применим
(с помощью компьютера) критерий ко всей таблице Т1. Получим
y/nDn = 0,656 (a0 = 79%). Неужели ΤΙ можно использовать
в качестве таблицы показательных случайных чисел? Это,
конечно же, не так, хотя бы потому, что все Х{ ^ 1.
Объяснение. Рассмотрим поведение случайной величины Yk
при к = [απ], где 0 < a < 1, [·] обозначает
целую часть числа. Для любых Χι > 0 с MIj < оо
в силу свойств сходимости (П5) и закона больших чисел (П6)
ρ
Yk = Sk/Sn = (\an]/n) · (Sk/k) · (n/Sn) —» α при η —► оо.
Используя монотонность Fn(x), отсюда так же, как при доказательстве
ρ
теоремы Гливенко (см. [19, с. 207]), можно вывести, что Dn —> 0.
Если DXi < оо, то в силу центральной предельной теоремы (П6)
и леммы 1 гл. 7 (φ(χ) = 1/х) отклонение \Yk — a\ имеет порядок
малости \/у/п. Поэтому величина y/nDn « const и вполне может
попасть в область «типичных» значений закона Колмогорова
(более аккуратное объяснение приведено в § 3 гл. 26).
Главная цель расчетов —
не цифры, а понимание.
Р. В. Хэмминг
Кроме опасности отвергнуть верную гипотезу Η из-за
случайности (обычно статистика критерия принимает с малой
вероятностью любые значения), существует опасность подтвердить
Η в том случае, когда она ошибочна (подробнее эта проблема
обсуждается в следующей главе).
Метод подстановки оценки параметра с поправкой Стефенса
для данных из четвертого столбца Т1 приводит к θ = 1,818,
Решения задач
177
Dn = 0,28 и (v/n4-0,264-0,5/Vn) (Z)n-0,2/n) = 1,308 (рис. 11, б).
Это значимо на уровне ао = 1%. *^
3. Функция распределения Ρζ{χ) бернуллиевской случайной
величины ζ (см. § 1 гл. 1) имеет два скачка: в 0 высоты q = 1—рив1
высоты р. Эмпирическая функция выборки Χι,... ,Хп из этого
закона отличается от нее лишь величиной скачков (рис. 12).
Поэтому Dn = \Х — р\.
В силу центральной предельной теоремы при η —► оо имеет
место сходимость у/п{Х — р) —> ξ ~ Л/Х0,рд). По свойству
сходимости 3 из П5 y/nDn —► |£|. Так как случайная величина \ξ\
положительна с вероятностью 1, то ее функция распределения
и плотность при χ < 0 равны нулю. При ж^Ов силу симметрии
закона ЛГ(0, pq) имеем
Fm(x) = Р(-х ζξ^χ) = Ft(x) - Ft(-x) = 2Fz{x) - 1.
Дифференцируя, находим, что при χ ^ 0 плотность
распределения величины |£| равна удвоенной плотности ξ (рис. 13).
(Отметим, что плотность предельного закона зависит от р.)
4. Сделав замену у = F(x), видим, что
ι
ω2η(ψ1)=Ιη = \(κ(ν)-ν)2άν,
Не все то волк, что серо.
1"
1-р
1-Х¥
V = Ft(x)
Рп\
y = Fn(x)
·+-*
Рис. 12
Рис. 13
где Fn(у)— эмпирическая функция наблюдений Yi = F(Xi)
(г = 1,... ,η) из равномерного распределения на отрезке [0,1]
(см. замечание 1). Упорядочим величины Yi по возрастанию:
Y(l) < У(2) < ··· < У(п)·
Положим У(0) = 0, Υ(η+ΐ) = 1· Разбивая отрезок [0,1] на части
[Y(i), У(г+1)]> г = 0,... ,п, представим интеграл 1п в виде
Ум
Поменяв индекс суммирования в первой сумме, запишем
Воспользовавшись тождеством (а + Ь)3 — (а — Ь)3 = 26 (За2 + Ь2)
ν 2г-1 , 1
для а = Y(i) ^— и о = —, окончательно получим
2п
1 п
2тГ
к2
3(y(i)"V) +a]=i^?+i|i(y«"Hki)
*) В примере 2 гл. 13 гипотеза показательности для этих же данных будет
отвергнута с помощью еще одного критерия.
178
Глава 12. Критерии согласия
5. Согласно формуле (3) гл. 10 Мп0 = . .. . ' , ., где U = ηρι. Из
l\\l2\ ...iNl
формулы Стирлинга имеем Inn! = η In η — η + ο(η). Отсюда
1 Ν
- 1ηΜη,ο = Inn - 1 - Σ \Pi lnnPi - Pi] + ο(1) =
П i=l
Ν
= -Y^Pi\npi + o(l).
i=l
Для примера рассмотрим симметричную схему Бернулли
(N = 2, р! = р2 = 1/2). Тогда М2п,о = С?п =
(2п)!/(п!)2-количество последовательностей длины 2п, у которых число нулей
совпадает с числом единиц. С помощью формулы Стирлинга легко
вывести (проверьте!), что Ρ (Агп.о) = 2~2пМ2П,о ~ l/y/πη —> 0
при η —* оо, в то время, как Ρ (Α2η,δ) —► 1 при любом δ > 0.
Поэтому сообщения из Лгп.о составляют пренебрежимо малую
часть множества «типичных» сообщений Λ2μ,<5, несмотря на то,
что lim — log2 M2n,o = Ит — log2 М^п.ь = Я = 1.
η—юо 2п п—>оо 2п
6. а) Неравенство (5) равносильно утверждению
оо
J р0*0 р(0
—оо
где случайная величина ξ имеет плотность р(х). Так как
функция 1η χ выпукла на (0,оо), то с учетом неравенства Иенсена (П4)
запишем
оо
Μ1ηϋ<1ηΜϋ=1ηί qMp{x)dx=lnl=0·
— оо
б) Возьмем в неравенстве (5) в качестве q(x) плотность закона
Λ/ΧΟ, 1) и используем то, что Μξ2 = Οξ + (Mf )2 = 1:
оо оо
- р(х) \пр(х) dx ^ — р(х) < — In >/27г - %- > dx = In л/27гё,
— оо —оо
причем верхняя граница достигается при р(х) = q(x).
^ ОТВЕТЫ НА ВОПРОСЫ
У = F(x)
1. По центральной предельной теореме (П6) при η = 100
► Р(5П ^ 60) = Ρ (SnZ^!2 ^ W-J^A ~ ! _ φ(2) ~ o,023.
ж \ yn/4 vW4 /
4 2. Например, может выглядеть, как на рис. 14 (п = 1).
Ответы на вопросы
179
3. Рассмотрим случайные величины Υι = ΘΧ{ с функцией
распределения (1 — е~у) I{y^o}i не зависящей от Θ. Выразим через них
Fn(x) и F(xft):
F(x,e) = (l - β-/*) /{ж>0} = (l - e-e*'Y) 1{θχ>0].
Когда переменная х пробегает значения от — оо до +оо, этот
же интервал значений пробегает и переменная у = θχ. Поэтому
sup
Fn(x) - F{xfi)
= sup
У
ktl{Y^v}-^-e-y/Y)l{y>0}
Распределение правой части равенства от θ не зависит.
4. Так как вектор (Х[1... ,Х'П) получается линейным
преобразованием из нормальной выборки (ΛΊ,... ,ХП), то он также является
нормальным (П9). Некоррелированность компонент такого
вектора эквивалентна их независимости (см. [90, с. 322]). Положим
Yi= Xi — μ. Тогда
cov [XI Xj) = M(Yi - Υ) (Yj - Υ) =
= -M(YiY)-M(YjY) + DY.
Поскольку MCYi Y) = - DYi = - σ2 и DY = - σ2, находим, что
η η η
coy^X^Xj) = σ2 < 0. Следовательно, величины Х[ и Xj
зависимы, т.е. набор Χ[1...1Χ,η не является выборкой. Более
того, все Х[ связаны линейной зависимостью: Х[ +... + Х'п = 0.
В свою очередь,
cov (Х<,Х) = Μ [(Yi - Υ)Υ] = Μ (YiY) - DF = 0.
Поэтому X не зависит от Хг', г = 1,... ,п. Согласно лемме о
независимости из § 3 гл. 1, видим, что X и выборочная дисперсия
52 = - Σ (Х{ — X)2 независимы между собой (см. теорему 1
гл. 11).
5. Нет, так как случайные величины Ζ& ~ tn-k-i1 к = 1,... ,п — 2,
имеют разные распределения (меняется число степеней
свободы).
Глава 13
АЛЬТЕРНАТИВЫ
Самый отдаленный пункт
земного шара к чему-
нибудь да близок, а самый
близкий от чего-нибудь да
отдален.
Козьма Прутков
Яр
tfi
θ() ta θ ι
Рис. 1
Полезно подчеркнуть,
что номинация ошибки
как I или II рода зависит
от того, какая из
возможностей принимается
за гипотезу, а какая —
за альтернативу. Если
поменять их местами,
то изменятся и названия
ошибок.
§ 1. ОШИБКИ I И II РОДА
Пример 1. Рассмотрим модель Xi ~ Λί(θ1σ2)1 где дисперсия σ2
известна, а математическое ожидание Θ — нет (см. пример 2 гл. 11).
Для проверки гипотезы Н0: θ = θο можно применить критерий,
основанный на статистике Τ (Χι,... , Χη) = X. Если Щ верна,
то X ~ М(во^2/п). Найдем критическое значение ta из условия
α = Ρθο(Χ^ία):
α = ρθο fy/n(X-0o) ^ y/n(ta-0o)\ =1_φ fy/n(ta-0o)\ ^
где Ф(х) — функция распределения закона Af(0,1). Обозначив
р-квантиль этого закона (т. е. решение уравнения Ф(х) = р) через
жр, получаем
ta = θο + σχι-a/Vn. (1)
Если значение выборочного среднего χ ^ ία, то гипотеза Щ
отвергается. Понятно, что если она верна, то неравенство X ^ ta
выполняется с вероятностью а. Отвергая в этом случае верную
гипотезу #о, мы совершаем так называемую ошибку I рода.
С другой стороны, может оказаться, что на самом деле верна не
гипотеза Я0, а ее альтернатива Н\: θ = 0ι, где, скажем, θ\ > 9q.
Если при этом случится, что χ < tai то мы примем ошибочную
гипотезу if о вместо if ι. Тем самым мы допустим ошибку II рода.
Найдем вероятность β ошибки II рода для рассматриваемой
модели. Когда верна альтернатива, выборочное среднее X
распределено по закону Ν(θ\,σ2/п). Поэтому из равенства (1) имеем
(2)
β=?θΛχ<^=φ(^-θι))=φ(χι-α-^φΙ-θο)).
Наглядный смысл вероятностей а и /3 показывает рис. 1, где
приведены графики плотностей распределения среднего X при гипотезах
Я0иЯь
В общем случае для параметрической статистической модели
{F(#,0),0 е θ} в множестве θ выделяются два непересекающихся
§ 1. Ошибки I и II рода
181
подмножества θο и θι. Предполагается, что компоненты выборки
X = (Χι,... ,ХП) имеют функцию распределения F{xfi), где θ
принадлежит одному из этих подмножеств. Гипотеза Щ заключается
в том, что θ £ θο, а альтернатива Н\—ъ том, что θ £ θ\. Когда
множество θο (θι) состоит из единственной точки, гипотеза Но
(альтернатива Hi) называется простой, иначе — сложной.
Чтобы задать критерий уровня а, укажем в Rn критическое
множество Ga такое, что Р#(Х Ε GQ) < α при всех θ Ε θο·*^
Вероятность ошибки II рода такого критерия β = β(θ) = Ρ θ (Χ φ Ga)
при θ Ε θ\. Функцией мощности критерия называется
W{9) = 1 - β(θ) = ΡΘ(Χ 6 Ga), θ 6 θχ.
Так, если критерий из примера 1 использовать для проверки
простой гипотезы Н0: θ = θ0 против сложной альтернативы #ι: θ > 0о>
то из формулы (2) с учетом симметрии функции
распределения Ф(х) находим (рис. 2)
W(0)
= 1_ф(Ж1_а_^(^
А
1-
w(ey
a 7
/ 1
/ 1
1
!
I
θο θ
Рис.2
Когда \¥(θ) ^ α при всех θ € θι, критерий называется
несмещенным. Несмещенность означает, что попадание в критическое
множество Ga (и, следовательно, — отвержение гипотезы Н0) при
справедливости любой из альтернатив не менее вероятно, чем
попадание в него при выполнении if о, т. е. правильное отвержение
имеет не меньшую вероятность, чем неправильное.
Если для любого θ Ε θι функция мощности \¥(θ) —► 1 при
η —> оо, то критерий называется состоятельным. Вопрос 1.
При непараметрическом подходе в множестве всех функций примераИ1 ^аГне^мещен-
распределения выделяются два непересекающихся класса: класс ным, 6) состоятельным
против сложной альтерна-
гипотез и класс альтернатив. тивы#1:0>0о?
Следующий пример содержит критерий для проверки сложной
гипотезы показательности распределения элементов выборки,
настроенный против непараметрических альтернатив определенного
вида.
Пример 2. «Новое лучше старого» (Холлендер—Прогиан),
см. [88, с. 260]. Допустим, что времена Χι работы прибора до г-го
отказа (г = 1,... ,п) образуют выборку из некоторого непрерывного
закона. Нас интересует гипотеза
Но: Ρ(Χι ^ х + у | Х\ ^ х) = Р(Х\ ^ у) для всех #,у ^ 0.
(3)
(Здесь Р(А\ В) — условная вероятность события А при условии
события В (см. П7).) Гипотеза (3) означает, что вероятность
отсутствия поломок за дополнительный период времени у при условии,
*) То есть формально статистикой критерия (см. § 1 гл. 12) является индикатор
множества Ga.
182
Глава 13. Альтернативы
Φ. Прошан (см. [88,
с. 262]) пишет:
«Тенденция к удлинению
интервалов, если она
выявлена, может быть
результатом опыта
эксплуатации, доводки
или смены поврежденных
частей, а тенденция к их
сокращению — напротив,
может быть результатом
износа, старения или
плохого технического
обслуживания».
что прибор уже проработал в течение периода времени #, равна
вероятности того, что новый (еще не работавший) прибор прослужит
начальный период времени у. Утверждение о том, что это верно
для всех #,у ^ 0 эквивалентно утверждению о том, что работающие
приборы любого «возраста» не лучше и не хуже, чем новые.
Гипотеза Щ равносильна сложной параметрической гипотезе
показательности: Р(Х\ ^ х) — е~9х при некотором θ > 0.
Легко убедиться, что показательности достаточно для выполнения
гипотезы Щ: при любых #,у ^ 0
Р(Хг >х + у\Х1^х)=е-в <*+*> /е~вх = е'9* = Ρ(Χι > у).
Необходимость доказать сложнее (см. [81, с. 475]).
В качестве альтернатив рассмотрим два класса законов.
а) «Новое лучше старого»:
Н1:Р(Х1^х + у\Х1^х)^Р(Х1^у) для всех ж,у ^ 0, (4)
причем хотя бы для некоторых #,у ^ 0 неравенство (4) строгое.
б) «Новое хуже старого»:
Н2: Р{Х\ >x + y\Xi>x)> P(Xi > у) для всех ж,у ^ 0, (5)
причем хотя бы для некоторых #,у ^ 0 неравенство (5) строгое.
Упорядочим величины Xi по возрастанию:
X(i) < Х(2) < ... <
^(госстатистикой критерия Холлендера—Прошана является величина
/,
Тп= Σ V>(X(i)>XC?)+X(*o)> где V>(<M>) = <
i>j>k I
I u« cum u s u.
V 7
(Суммирование здесь производится по всем п(п — 1)(п — 2)/6
упорядоченным тройкам (г j,fc), для которых г > j > к.)
Поясним, почему Тп можно использовать в качестве статистики
критерия для проверки гипотезы Н0 против альтернативы Hi (или
Яг). Положим
Г(х,у) = Р(Хг Ζ χ) Ρ(Χι > у) - Ρ(Χι > χ + у).
Заметим, что Т'(х,у) = 0 для всех #,у ^ 0 тогда и только тогда,
когда гипотеза Но (3) верна. Оказывается, (линейно связанная
с Тп) статистика Т* = 1/4 — 2Тп/[п(п — 1)(п — 2)] служит оценкой
для параметра A(F) = МТ"(Х',У), где X' и У' независимы
и имеют распределение (времени безотказной работы) F. Мы
можем рассматривать Т'(х,у) как меру отклонения от Но в точке
(#,у), a A(F) — как среднее значение этого отклонения.
Когда распределение F соответствует Hi (4) и непрерывно,
параметр A(F) положителен. Если выборка берется из такой
совокупности, величина Т* возрастает (что эквивалентно убыванию Тп).
1,
1/2,
0,
если а > Ъ,
если α = Ь,
если α < Ъ.
§2. Оптимальный критерий Неймана,—Пирсона,
183
В [88, с. 432] приведена таблица критических значений Тп для
η ^ 50. Для достаточно большой выборки можно воспользоваться
нормальным приближением: (Тп — MTn)/y/DTn —* ξ ~ ЛГ(0,1), где
ΜΤη = η(η-1)(η-2)/8,
DTn = |n(n-l)(n-2)
^(n-3)(n-4) + ^(n-3) + l
Известно (см. [88, с. 264]), что критерий состоятелен против if ι, #2·
Применим его для проверки показательности четвертого
столбца таблицы Т1 равномерных на [0,1] случайных чисел (см.
задачу 2 гл. 12). Для равномерного закона справедлива альтернатива
#ι (проверьте!), поэтому есть надежда отвергнуть Я0.
Прежде, чем использовать критерий «Новое лучше старого»,
рекомендуется убедиться, что величины Х{ образуют случайную
выборку из общей совокупности, т. е. проверить их независимость
и одинаковую распределенность. Одним из способов проверки этого
является критерий, основанный на асимптотической нормальности
числа инверсий Дп в выборке (см. пример 2 гл. 7). Значение
статистики (Rn — MRn)/y/DRn для четвертого столбца Т1 равно —0,389.
Ему соответствует фактический уровень значимости (см. § 1 гл. 12)
olq = 0,697. Следовательно, гипотеза случайности не отвергается.
Вычисленная на компьютере статистика Холлендера—Прошана
Тп приняла значение —3,16, что значимо мало на уровне а = 0,002.
§2. ОПТИМАЛЬНЫЙ КРИТЕРИЙ
НЕЙМАНА-ПИРСОНА
При сравнении двух критериев уровня а, заданных при помощи
критических множеств G'a и G£, лучшим будет тот, у которого
мощность больше. Если альтернатива сложная, то (как и при сравнении
точности оценок (см. § 3 гл. 6)) возникает проблема сравнения
двух функций W'{0) и Wn{9) (рис. 3). В случае проверки простой
гипотезы Н0 против простой альтернативы Hi ситуация проще:
существует наиболее мощный критерий и можно явно указать его
критическое множество G*.
Прежде чем строго сформулировать и доказать этот
результат ), обсудим подробнее проблему выбора критического
множества.
Для модели из примера 1 возьмем внутри диапазона
«типичных» значений статистики X при справедливости гипотезы Щ
маленький отрезок Δ такой, что Ρθ0(Χ G Δ) = α (рис. 4).
В свою очередь, если для критерия с критическим множеством
{х G Rn: χ ^ ta} сдвигать границу ta вправо для уменьшения
ι'
OL-
\
W\Q)y/y^
yyWn{Q)
►
00
Рис. 3
Вопрос 2.
Чем плох критерий,
задаваемый соответствующим
критическим множеством
{x€Rn: χ€Δ}?
*) Впервые он был получен Ю. Нейманом и Э. Пирсоном в 1933 г.
184
Глава 13. Альтернативы
Рис. 4
Ничего не доводи до
крайности: человек,
желающий трапезовать
слишком поздно, рискует
трапезовать на другой
день поутру.
Козьма Прутков
В. Гейзенберг
(1901-1976), немецкий
физик.
М. Планк (1858-1947),
немецкий физик.
Байка. Студент на
экзамене по физике,
записав формулу для
величины кванта энергии
света E = hi/, сообщил,
что ι/—это постоянная
Планка. На вопрос «Что
же тогда обозначает здесь
Н1у> был немедленно
дан ответ: «Высоту этой
планки».
Боюсь,... чтоб множество
не накоплялось...
Фамусов в «Горе от ума»
А. С. Грибоедова
H2>\Pi(*i)=Pi
Рис. 5
величины α ошибки I рода, то дополнение к критическому
множеству {х € Μη: χ < ta} будет увеличиваться, и соответствующая
величина ошибки II рода β будет возрастать.
Таким образом, не удается добиться того, чтобы α и β были
обе сколь угодно малы при фиксированном размере выборки η
(Тришкин кафтан).
Проблема напоминает принцип неопределенностей в квантовой
физике, сформулированный в 1927 г. Гейзенбергом: невозможно
одновременно сколь угодно точно определить положение и скорость
элементарной частицы (см. [14, с. 28]). Для погрешностей измерения
координаты Ах и импульса Ар выполняется соотношение
неопределенностей Ах · Ар ^ h, где h обозначает постоянную Планка
(Ь«6,626-10-34Дж-с).
Если за ошибку I рода приходится платить цену Са, а за
ошибку II рода —цену С/?, то критическое множество можно
постараться выбрать так, чтобы минимизировать «взвешенные» общие
затраты аСа + βΟβ (см. задачу 1).
Не всегда реальное значение ошибок сводится к величине
общих затрат. Например, в случае проверки на основе результатов
медицинских анализов гипотезы if о, состоящей в том, что пациент
болен, против альтернативы if ι, что он здоров, ошибка I рода
приведет к тому, что не будет оказана врачебная помощь больному
человеку, а ошибка II рода — к тому, что станут лечить здорового.
В этой ситуации более верным представляется следующий
подход: при заданной (достаточно малой) вероятности ошибки I рода
а постараться уменьшить вероятность ошибки II рода β насколько
возможно за счет подбора критического множества.
Для выборки X = (Χι,... ,ХП) и множества G Ε Rn положим
Pk(G) = Pek(X £ G) для к = 0 и 1. Тем самым, гипотеза
Но и альтернатива Hi порождают в Rn меры Р0 и Pi. В этих
обозначениях задача сводится к нахождению множества G* такого,
что Po(G*) ^ α, a Pi(G*) была бы как можно больше.
Пример 3 [38, с. 216]. Рассмотрим дискретную модель, в которой
при гипотезе Но мера Pq равномерно распределена на конечном
множестве из Μ точек {a?i,..., хм} в Rn, а при альтернативе Hi
j-ft точке приписана вероятностная масса Pi(xj) = Pj, j = 1,... ,Μ.
Тогда для а = k/N любое подмножество из к точек задает критерий
уровня а (рис. 5). Чтобы максимизировать мощность
(вероятностный вес) этого подмножества при альтернативе #ι, очевидно, надо
упорядочить величины pj по убыванию и набрать в критическое
множество к точек с наибольшими pj.
Немного усложним модель, предположив, что при
справедливости гипотезы Но точки Xj имеют вероятностную массу qj = rrijS.
Можно мысленно представить, что j-я точка («молекула») состоит
§ 2. Оптимальный критерий Неймана—Пирсона
185
из щ частей («атомов») массы δ при гипотезе Но и массы Pj/rrij
при альтернативе Hi. Оптимальное критическое множество из
«атомов» строится так же, как и раньше. Причем, поскольку
для «атомов» фиксированной «молекулы» отношение Pj/rrij одно
и тоже, можно считать, что при упорядочении они идут подряд.
В результате видим, что оптимальное критическое множество
«молекул» строится на основе включения в него точек с наибольшим
отношением — = — $, другими словами, — с наибольшим отноше-
rrij qj
нием вероятностей (правдоподобий) Pi(xj)/Po(xj)-
Для абсолютно непрерывной модели имеет место то же самое,
только отношение вероятностей заменяется на отношение
плотностей Pi(x)/po(x) выборки X при Hi и Щ. Для строгой
формулировки теоремы Неймана — Пирсона рассмотрим для с ^ О систему
вложенных множеств Gc = {х € Rn: Pi{x)/po(x) ^ с} (рис.6)
и определим функцию <р(с) = Po(Gc)·
Тогда φ(0) = 1 и <р(с) может только убывать с ростом с. Покажем,
что φ(ό) ^ 1/с —► 0 при с —► оо. Действительно,
1 ^ Pi(6?c) = pi(x)dx ^ с po(x)dx = cPo(Gc) = с<р(с).
(β)
Потребуем выполнения двух условий:
1) плотности ро(х) и ρι(χ) положительны при всех ж€Кп;
2) для заданного уровня значимости а € (0,1) существует
с = са, для которого v?(ca) = а (это всегда выполняется, если
функция <р(с) непрерывна).
Теорема 1 (Нейман—Пирсон). При сделанных
предположениях 1 и 2 наиболее мощный критерий уровня а задается
критическим множеством
G* = GCa ={xe Rn:Pl(x)/p0(x) ^ с*}.
(7)
Доказательство. Пусть G — критическое множество некоторого
критерия уровня а. Согласно определению множества G и
условию 2
P0(G) < а = P0(G*).
(8)
Обозначим через 1(х) и /*(ж), соответственно, индикаторы
множеств G и G* и рассмотрим функцию
/(х) = (Г (х) - 1(Х)) Ых) - СаРо(х)).
(9)
Покажем, что она неотрицательна при всех χ £ Rn. В самом
деле, при χ € G* оба сомножителя в формуле (9) неотрицательны:
первый —так как 1*(х) = 1, а второй —по определению (7). При
χ ф G* первый сомножитель в формуле (9) равен —1(х) ^ 0,
Товарищи ученые,
доценты с кандидатами!
Замучились вы с иксами,
запутались в нулях.
Сидите, разлагаете
молекулы на атомы...
В. Высоцкий
Рис. β
186
Глава 13. Альтернативы
а ввиду определения (7) и второй сомножитель неположителен.
Поэтому
(К \f(x)dx = \I*(x)pi(x)dx- \I(x)pi(x)dx-
I*(χ)Ро(х)dx - \I(x)po(x)dx\ =
-cQ
= Pi(G*) - Pi(G) - cQ [P0(G*) - P0(G)].
Отсюда и из неравенства (8) вытекает, что Pi(G*) ^ Pi(G). ■
В учебнике [38, с. 219] доказано, что если мера Лебега множества
{х: Pi(x)/po(x) = с} равна нулю, то G* является единственным
наиболее мощным критическим множеством критерия уровня a
с точностью до подмножества Rn лебеговой меры нуль
(контрпример см. в задаче 5).
Покажем, что при выполнении условий 1 и 2 критерий
Неймана — Пирсона является строго несмещенным.
Теорема 2. Для множества G*, задаваемого формулой (7),
справедливо неравенство Pi(G*) > a.
Доказательство. Если в формуле (7) константа cQ > 1, то из
соотношения (6) следует, что
Pi(G*) ^ cQP0(G*) = caa > a.
При ca ^ 1, поскольку pi (ж) < caPo(x) ^ Ро{х) при χ eG , имеем
Pi(G*) = l- \pi(x)dx>l- \po(x)dx= \p0(x)dx = a.
G* G* G*
Итак, в любом случае Pi(G*) > α, что и требовалось доказать. ■
Укажем множество G* для модели примера 1. Ввиду (7) найдем
Ρι(χ)/ρο(χ) = ехр |- ± Σ [(*» - 0ι)2 " (*i " 0o)2]} =
= expj^01-0o)x-i^(02-0o2)}.
Неравенство Pi(x)/po(x) ^ ca эквивалентно неравенству
χ^σ2 lnca/[n(0i - θ0)\ + (Θι + 0ο)/2. (10)
Отсюда заключаем, что критерий примера 1 является наиболее
мощным при ία, равном правой части неравенства (10). Из
формулы (1) можно найти соответствующее значение са.
Отметим, что граница ta в равенстве (1) не зависит от θ\.
Поэтому мощность рассматриваемого критерия максимальна при
любом θ ι > #ο· Другими словами, критерий является равномерно
наиболее мощным против сложной альтернативы Ηι: θ > 6q.
§ 3. Последовательный анализ
187
§3. ПОСЛЕДОВАТЕЛЬНЫЙ АНАЛИЗ
Приведем небольшой отрывок из [72, с. 120], посвященный истории
возникновения последовательного анализа.
«В классической теории математической статистики
предполагается, что элементы выборки (наблюдения) заранее известны. В основе
одного из важнейших направлений современной статистики лежит
понимание того, что не нужно фиксировать заранее объем выборки,
его следует определять в зависимости от результатов более ранних
наблюдений. Таким образом, о^ь^м аы<к*ркк сяучаек. Эта кдея
последовательного выбора постепенно развивалась в работах Г.
Доджа и Г. Ромига (1929 г.), П. Махаланобиса (1940 г.), Г. Хотеллинга
(1941 г.) и У. Вертки (1943 г.), но настоящим основателем теории
последовательного анализа в математической статистике является
А. Вальд (1902-1950 гг.). Его последовательный критерий отношения
правдоподобия (1943 г.) стал важным открытием, позволившим (в
типичных ситуациях) на 50% уменьшить среднее число наблюдений
(при тех же вероятностях ошибок). Неудивительно, что в годы
второй мировой войны открытие Вальда было объявлено «секретным».
Его основная книга «Последовательный анализ» опубликована лишь
в 1947 г. Год спустя Вальд и Дж. Волфовиц доказали, что методы,
отличные от последовательного критерия отношения правдоподобия,
не дают такого уменьшения числа элементов выборки.»
Рассмотрим последовательный критерий Вальда в случае, когда
элементы выборки Χι при гипотезе Н$ имеют известную
плотность ро(х) > 0, а при альтернативе Η ι — известную плотность
Ρι(χ) > 0. Определим случайные величины Ζι = 1η(ρι(Χ;)/ρο№))·
Потребуем, чтобы и при гипотезе Я0, и при альтернативе #ι были
выполнены два условия: 1) ΜΖι ^ 0, 2) 0 < DZi < оо.
Положим So = 0, Sk = Z\ + ... + Zfc, к = 1,2,.... Случайная
величина Sk представляет собой координату «блуждающей частицы»
после к независимых и одинаково распределенных «шагов» Zi
случайного блуждания по прямой. Пусть Sk — это наблюдавшиеся
значения величин Sk- На рис. 7 изображена возможная траектория
(развертка во времени) случайного блуждания — ломаная,
соединяющая точки плоскости с координатами (&,$&).
Последовательный критерий Вальда состоит в следующем.
Задаются константы со < 0 и ci > 0, и наблюдения продолжаются
до момента выхода ν блуждания s^ из интервала (co,Ci). Если
sv ^ со, то принимается гипотеза if о; если sv ^ Ci, то принимается
альтернатива Н\ (см. рис. 7).
Может ли блуждание продолжаться как угодно долго?
Теорема 3. При выполнении указанных выше условий 1-2 про- „
_ \ Доказательство теоремы
цедура Вальда с вероятностью 1 заканчивается за конечное число можно найти в [32, с. 149]
шагов ι/, причем моменты Мик < оо для всех к ^ 1. или Р8· с· 2321-
188
Глава 13. Альтернативы
Замечание 1. Первое утверждение теоремы интуитивно понятно
вследствие условия 1, приводящего (ввиду закона больших чисел)
к систематическому «сносу» блуждания и выходу его из интервала
(co,ci) за время порядка Ci/MZi при ΜΖι > 0 и порядка co/MZi
при ΜΖι < 0.
Как вероятности α и /3 ошибок I и II рода критерия Вальда
связаны с константами со и С\1 Ответ дает следующая теорема.
Теорема 4. Зададим о! > 0 и /3' > 0, удовлетворяющие условию
α' + β' < 1. Возьмем
О = In [/?'/(!-<*% с1 = In [(1 -β')/α'}. (11)
Тогда для вероятностей а и β выполняются неравенства
α ζ а'/{\ - β'), β ^ /37(1 - α')> α + β ^ ο! + /3'. (12)
Замечание 2. Эти неравенства показывают, что каждая из
вероятностей а и /3 может лишь незначительно превысить а' и β',
соответственно, когда последние малы. (Например, для а' = /3' = 0,1
граница сверху равна 1/9 « 0,111.) Кроме того, сумма а + /3
вероятностей ошибок не может превзойти задаваемую величину
а'+/3'.
Доказательство. Обозначим через А^ (А^) множество тех
результатов наблюдений (жι,... ,жп), для которых процедура
заканчивается на шаге η (у = п) принятием гипотезы #о (альтернативы
#ι). Например,
^п = {(^ь... ,хп): со < 5fc < сь А: = 1,... ,п - 1, sn < со}. (13)
При гипотезе Но в силу теоремы 3 справедливо равенство
оо оо
ΣΡο(^°)+ΣΡο(^) = ι. (14)
71 = 1 71=1
Так как в точках множества А^ согласно определению (13) вы-
71 71
полняется неравенство sn ^ со 4=> Πρι(^) ^ ^ο Π Ρο(#ΐ)> где
г=1 г=1
do = ехр{со} = /3'/(1 — &'), то из соотношения (14) имеем
оо оо / оо \
β= Σ Ρι«Κ<*οΣ Po(A°n) = do 1- Σ Po(4,))=do(l-a).
71=1 71=1 \ 71=1 /
Аналогично доказывается, что
a < (1 - /3)/db где di = exp{Cl} = (1 - β*)/a/.
Из этих двух неравенств, соответственно, выводим соотношения
β < (1 -α)0'/(1- α') ζ /37(1-00,
α<(1-/3)α7(1-/30<«7(1-/?0·
Складывая неравенства /3' — /З'а ^ /3 — Ыβ и —а + а/3' ^ —а' + а'/З,
получаем а + /3 ^ а' + /3'. ■
§ 3. Последовательный анализ
189
Замечание 3. Сравним критерии Вальда и Неймана — Пирсона.
Во-первых, у последнего заранее фиксируется число наблюдений п,
и решение отвергнуть гипотезу Н0 принимается в случае попадания
конечной точки блуждания sn в множество [1пса,оо) (рис. 8).
Во-вторых, для определения са по вероятности а ошибки I рода
надо знать распределение статистики критерия Неймана—Пирсона
при справедливости гипотезы Я0, в то время как для расчета
границ со и С\ критерия Вальда для заданных α и β не возникает
проблемы отыскания распределений. Информация о плотностях
Ро(х) и р\(х) требуется только для вычисления математического jnCa
ожидания числа наблюдений ν до принятия решения. Вычисление
опирается на теорему 5.
Теорема 5 (тождество Вальда). При условии конечности
величин ΜΖι и Μι/ справедливо тождество MSU = ΜΖι ·Μν.
Контрпример. Это тождество справедливо не для всякого
случайного момента остановки блуждания. Пусть Ρ(Ζι = —1) =
= Ρ(Ζι = 1) = 1/2, ι/ = min{n: 5n = -1}. Тогда Ρ(ι/ < oo) = 1, но
Mi/ = oo (см. теорему 2 гл. 14). Поскольку ΜΖι = 0, MS„/ = —1,
слева получаем —1, а справа — неопределенность вида 0 · оо.
Доказательство. Положим Yn = I{co<sk<cuk=i,...tn-i} = 1{ν>η}-
oo oo
Ввиду формулы 3 гл. 1 Mz/ = ΣΡ(ν ^ η) = J2MYn. Как функция
71=1 71=1
только от Ζι,...,Ζη_ι случайная величина Yn не зависит от Ζη.
Отсюда
оо оо η оо оо
ms„ = Σ м sni{u=n) = Σ Σ м zki{u=n} = Σ Σ Μ zki{v=n) =
η=1 η=1fc=l fc=ln=fc
oo oo oo oo
fc=l n=fc fc=l fc=l
Здесь первое равенство и перемена порядка суммирования
законны благодаря абсолютной суммируемости соответствующих
рядов (см. [41, с. 343, 365]):
оо оо оо оо
Σ Σм\zk\i{v=n) = Σм\zh\Yk = Σμ|ζ*|·мп =
fc=ln=fc fc=l fc=l
= Μ|Ζι|·Μι/<οο
в силу условий теоремы (ΜΖι конечно <==> Μ|Ζι| < оо). ■
Пусть заданы малые вероятности а и β ошибок. На основе
замечания 2 они примерно равны константам о! и β1 из теоремы 4.
Так как длина интервала (со, ci) при малых а' и /3' будет большой,
a MZi конечно, то можно пренебречь величиной «перескока»
случайным блужданием границы в момент остановки, т. е. считать, что
Sv « Cj, если принимается гипотеза ifj, j = О, 1. Эти рассуждения
Рис. 8
190
Глава 13. Альтернативы
Более точные
аппроксимации см. в [11, с. 360],
[12, с. 223].
приводят к приближенным равенствам
MS,, « со(1 — а) + cia, если верна гипотеза Я0,
MS„ « со/3 + ci(l — /?), если верна альтернатива Щ.
Применяя тождество Вальда, отсюда получаем
ЬЛ0и
ср(1 - a) + cia
bAoZi
Mil/ :
cq/? + ci(1-/?)
M!Zi
(15)
Выясним, насколько последовательная процедура Вальда
экономичней критерия Неймана — Пирсона для модели примера 1.
Прежде всего, выразим явно Zi через Х^.
z =]nM*i) = (Хг-е0)2-(Хг-
Po(Xi) 2σ2
Поэтому если верна Hj (j принимает значения 0 и 1), то
M*Zi =
01 — θο
L _ *°±*ιΛ = (_i)i+i №
-θο)2
2σ*
(16)
Для критерия Неймана — Пирсона (см. задачу 3) с теми же
вероятностями ошибок а и β необходимое число наблюдений п*
равно [σ(χα + χρ)/(θι — θο)]2 (с точностью до 1), где хр обозначает
р-квантиль закона ЛГ(0,1). Возьмем для простоты а = β. Из
формул (11), (15) и (16) следует, что экономичность критерия
Вальда равна
Е(а) =
ЪЛои ЬА\и
1 - 2а , 1 - а
2a£ а
(17)
Не во всякой игре тузы
выигрывают!
Козьма Прутков
Что ни толкуй Вольтер
или Декарт —
Мир для меня —колода
карт.
Жизнь —банк: рок мечет,
я играю,
И правила игры я к людям
применяю.
М. Ю. Лермонтов,
«Маскарад»
При a = 0,05 по таблице Т2 находим ха « —1,645. Подставив эти
значения в формулу (17), получаем £(0,05) w 0,49. Таким образом,
в данном случае для принятия решения с помощью
последовательного критерия Вальда потребуется в среднем примерно вдвое
меньше наблюдений, чем для оптимального критерия Неймана —
Пирсона с заранее фиксированным размером выборки (см. также
задачу 4).
Можно доказать, что критерий Вальда минимизирует средний
размер выборки по сравнению с любым другим последовательным
критерием, имеющим те же или меньшие вероятности ошибок I и II
рода (см. [11, с. 358]).
§4· РАЗОРЕНИЕ ИГРОКА
Представим, что два противника принимают участие в игре,
состоящей из большого числа независимых партий. Вероятность
выигрыша первого игрока в каждой из партий равна р, а второго —
q = 1 — ρ (ничьих не бывает). Плата за проигрыш в одной
партии равна 1. Начальный капитал первого игрока составляет А:,
§ 4. Разорение игрока
191
второго— (Μ — к). Игра прекращается, когда один из участников
проиграет все наличные.
Ход игры можно наглядно представить при помощи
поднятой на к единиц вверх траектории случайного блуждания 5П =
= Ζ\ + Ζ<ι + ... + Ζη, где «шаги» Zi независимы, Ρ {Ζι = 1) = ρ,
Ρ(Ζ{ =—l)=q (рис. 9). Величина (Sn+к) — капитал первого игрока
после η сыгранных партий. Считая суммарный капитал игроков Μ
заданным, найдем г к — вероятность разорения первого игрока.
Перенесем начало координат на рис. 9 в точку (О,А:). Обозначим
через и момент окончания игры (разорения одного из игроков).
Поскольку ΜΖι = ρ — q и DZi = 1 — (ρ — q)2 < оо, при
ρ φ 1/2 выполняются условия теоремы 3. Следовательно, Ми < оо.
Докажем, что в случае ρ = 1/2 (ΜΖι = 0) Ми также конечно.
Приведем, следуя [12, с. 90], доказательство для четного Μ = 2т.
Пусть Ζ = min{fc,M — k}. Тогда с вероятностью 2~l ^ 2~т игра может
закончиться за I партий. Поскольку в течение игры суммарный
капитал Μ не меняется, разбивая блуждание на независимые отрезки
длины т, видим, что Р(и > т) < 1-2"т,..., P(v > jm) ^ (l-2~m)J'.
Но вероятности Р(г/ > г) убывают с ростом г, а при г = jm
(j = 1,2,...) мажорируются членами геометрической прогрессии со
оо
знаменателем 7 = 1 — 2~т. Поэтому ряд JZ Р(и > *) сходится.
г=0
Согласно формуле (3) гл. 1 его сумма равна ЬЛи.
Конечность Ми обеспечивает законность всех переходов
доказательства теоремы 5 (тождества Вальда) из § 3. Запишем его при
ρ = 1/2 для со = -fc, ci = Μ - k, rk = Р(5^ = со):
Su = con + ci(l - rfc) = MZi · Mi/ = 0 · Mu = 0.
Отсюда находим т> = 1 — fc/M, т. е. шансы на выигрыш прямо
пропорциональны величине начального капитала.
Получим этот ответ другим способом — разложением по
первому тагу блуждания (рис. 10). С учетом формулы полной
вероятности (П7) интуитивно понятно, что вероятности г\~ должны
удовлетворять рекуррентным соотношениям
rfc=prfc+i-rgrfc_i, fc = l,...,Af-l, (18)
с граничными условиями г0 = 1, гм — 0 (строгий вывод
см. в [39, с. 39]). В случае ρ = 1/2 можно переписать соотношение
(18) в виде rfc+i — г& = г\~ — γ^_ι, из которого следует, что точки
плоскости (fc,rfc) лежат на одной прямой г к = А + Вк (рис. 11). Из
граничных условий вытекает, что А = 1, В = —1/М.
Прежде чем рассматривать случай ρ φ 1/2, обсудим аналогию
между соотношением (18) и краевой задачей для
дифференциального уравнения второго порядка
у"(х) = f(x,y), у(х0) = а, у(х\) = Ь. (19)
Рис. 9
Случай нечетного Μ
разберите самостоятельно.
Рис. 10
Ifc
Ifc+i
-1kk+ΙΜ
Рис. 11
192
Глава 13. Альтернативы
Я больше всего дорожу
аналогиями, моими
самыми верными
учителями.
И. Кеплер
Рис. 13
Вопрос 3.
Какое значение Z*.
представляется наиболее
правдоподобным при
ρ = 1/2 для к = 10
и Μ=20 (рис. 14)?
При малом h > 0 производную первого порядка у' (х) можно
приближенно заменить на так называемую конечную разность
[у(х + h) — y(x)]/h. Производная второго порядка у" (х)
аппроксимируется второй симметричной разностью
у(х + h)- у(х) _ у(х) - у(х - h)
h h у(х + h)- 2y(x) + у(х - h)
h h2
(20)
При р = 1/2 соотношение (18) имеет вид г&+1 — 2г& -f Vk-ι = 0,
аналогичный виду правой части равенства (20), если положить
ж = fc, у(х) = Гк и h = 1. Общим решением соответствующего
дифференциального уравнения у" = 0 является у = А + Вх.
Чтобы найти г к при ρ φ 1/2 (задача 6), можно использовать
основную идею метода стрельбы, применяемого для численного
решения краевой задачи. Предположим, что мы умеем численно
решать задачу Коши
у"(х) = /(ж,у), у(х0) = а, у'(х0) = с, (21)
например, методом Эйлера из § 6 гл. 2 или Рунге — Кутты
(см. [6, с. 439]). Фиксируем а и будем менять с. Обозначим через
д(с) значение решения задачи (21) при χ = х\ из краевого условия
задачи (19). Тогда численное решение краевой задачи (19) сводится
к поиску корня с* уравнения д(с) = Ь. Так как значения д(с)
мы умеем вычислять в пробных точках сп (рис. 12), то можно
приближенно найти с* с помощью деления отрезка пополам или
метода Ньютона из § 5 гл. 9. Рисунок 13 объясняет происхождение
названия «метод стрельбы».
Приведем ответ задачи 6: т> = (λΜ — Afc)/(AM — 1), где λ = q/p.
Устремляя Μ к бесконечности, видим, что предел г к равен 1, если
ρ ^ 1/2, и равен Afc, если ρ > 1/2. Таким образом, искусный
игрок может с положительной вероятностью 1 — \к никогда не
проиграть даже «бесконечно богатому» противнику. (Если он не
проиграл из-за случайности сразу, то в дальнейшем его шансы
уйти от поражения резко увеличиваются по причине «сноса» вверх
траектории блуждания.)
Найдем среднее время до разорения одного из игроков (среднюю
продолжительность игры) Ik = Μ ζ/, к = 1,... ,Μ — 1.
Рис. 14
10 20 30 40
50 60 70 80
Те же рассуждения, что и при получении соотношений (18),
приводят для Ik к уравнениям
1к =plk+i+qh-i + 1, к = Ι,.,.,Μ- Ι,
(22)
§ 5. Оптимальная остановка блуждалия
193
с граничными условиями ίο = 0> 1м = 0 (единица в правой
части уравнения (22) добавлена потому, что одна партия уже была
сыграна). Нетрудно проверить, что при ρ = 1/2 ему удовлетворяют
Ik = k(M — к). Следовательно, при больших Μ и k « olM среднее
время игры равных по силе противников имеет порядок М2. Этот
результат становится менее удивительным, если принять во
внимание центральную предельную теорему (П6), согласно которой
траектория симметричного случайного блуждания 5П колеблется
в среднем в пределах ±у/п.
Иначе дело обстоит при ρ φ 1/2 (см. замечание 1 из § 3).
§5. ОПТИМАЛЬНАЯ ОСТАНОВКА БЛУЖДАНИЯ
Проведем небольшой вероятностный эксперимент. Пусть в
начальный момент частица попадает с равными вероятностями в любую
из Μ + 1 точек с целыми координатами отрезка [О, М]. Если
частица оказывается в одном из концов отрезка, то выигрыш равен
0. В противном случае участник эксперимента должен принять
решение: остаться в данной точке и взять приз, равный высоте
столбика над этой точкой (рис. 15 для Μ = 7), или же подбросить
симметричную монетку и переместить частицу на 1 влево, если
выпадет герб, и на 1 вправо, если выпадет решка. После этого
снова можно или взять приз, или сделать еще один «случайный
шаг» и т. д.
Если в результате перемещения частица попадет в концевую
точку отрезка [0, М], то блуждание принудительно
останавливается, и выигрыш оказывается равным 0. Проблема состоит в
выборе стратегии, приносящей участнику эксперимента
максимальный средний выигрыш. Ответьте на вопрос 5.
Предположим, что в начальный момент частица оказалась
в точке с абсциссой 6 на рис. 15. Ответьте на вопрос 6.
Давайте проведем моделирование. Прежде всего, разыграем
начальное положение частицы. Для этого откройте какую-нибудь
книгу «случайным образом» и обратите внимание, скажем, на
вторую ) цифру справа номера правой страницы. Если эта цифра
окажется больше 7, то открывайте книгу до тех пор, пока она не
попадет в множество {0,1,... ,7}. Возьмите ее в качестве начальной
координаты частицы на рис. 15. Если частица оказалась в 0 или
7, то выигрыш равен 0, и моделирование закончено. В противном
случае надо принять решение: взять приз или начать блуждание.
Если выбрано второе, то снова надо открыть «случайным образом»
книгу и переместить частицу на 1 влево или вправо, в соответствии
с тем, оказалась ли вторая справа цифра номера меньше 5 или
нет. После перемещения надо или взять приз, или продолжить
Вопрос 4.
Чему равно Μι/
при р# 1/2?
(Используйте для его
вычисления тождество
Вальда.)
4
3
2Н
1
0' 12 3 4 5 6 7
Рис. 15
*) Первые справа — всегда нечетные, а третьи — слишком медленно меняются.
01 Μ
Рис. 16
Вопрос 5.
Стоит или нет
останавливаться, если частица
находится в точке,
указанной стрелкой
на рис. 16?
Вопрос б.
Какая из двух стратегий
в данной ситуации лучше:
сразу взять приз или
сделать ровно один
«случайный шаг» и взять
приз?
194 Глава 13. Альтернативы
случайное блуждание и т. д. Если при этом частица попадет в О
или 7, то моделирование прекращается с нулевым выигрышем.
(Повторите моделирование 4 раза, каждый раз разыгрывая заново
начальное положение частицы, и подсчитайте общий выигрыш.)
Давайте рассмотрим некоторые стратегии.
Стратегия «Никогда»
Если никогда не брать приз, то в соответствии с задачей о
разорении игрока из § 4, частица с вероятностью 1 рано или поздно
попадет в один из концов отрезка, где выигрыш равен нулю.
Стратегия «Сразу»
Очевидно, что средний выигрыш при немедленной остановке в
начальном положении составляет
(О+ 2 + 3 + 4 + 6 + 4 + 1 + 0)/8 = 20/8.
Стратегия «Все или ничего»
При использовании такой стратегии блуждание продолжается до
момента попадания или в точку 4 с максимальным выигрышем,
равным 6, или до «поглощения» на одном из концов отрезка с
нулевым выигрышем. Для подсчета среднего выигрыша воспользуемся
свойством 1 условного математического ожидания (П7), в котором
роль условия будет играть начальное положение.
Рассмотрим, например, случай, когда в начальный момент
частица оказалась в точке 5. Тогда блуждание до попадания либо
в 4, либо в 7 представляет собой задачу о разорении игрока при
ρ = 1/2, имеющего начальный капитал к = 7 — 5 = 2, в то время
как суммарный капитал двух игроков Μ = 7 — 4 = 3. В§4 было
доказано, что вероятность разорения игрока т> = 1 — к/М. Отсюда
1 2
находим условный средний выигрыш 0 · « + 6 · « = 4.
Аналогично, перебирая все возможные начальные положения от
0 до 7, легко подсчитываем безусловный средний выигрыш:
6'(0+ϊ+5+!+1+Ι+3+0)/8=21/8·
Наилучшая стратегия
В [24] в качестве оптимальной для данной задачи приведена
следующая красивая стратегия. Представим, что призовые столбики —
это картонные полоски, приклеенные на лист бумаги. Закрепим
кнопками резинку в концевых точках отрезка [0,М], оттянем ее
вверх и отпустим (рис. 17). При этом столбики разделятся на два
класса: такие, которые будут поддерживать резинку, и такие, над
Вопрос 7.
Чему равно среднее
время до остановки при
использовании стратегии
«Все или ничего»?
Вопрос 8.
Чему равен максимальный
средний выигрыш для
столбиков, изображенных
на рис. 15?
Решения задач
195
которыми резинка пройдет сверху, их не касаясь. (Мы наглядно
построили то, что формально называется выпуклой оболочкой
графика функции.) Оптимальная стратегия состоит в том, что нужно
останавливаться в тот момент, когда частица попадет в точку, над
которой располагается столбик из первого класса (на рис. 17 такие
точки обведены кружками).
ЗАДАЧИ
1. Каким следует взять ta для критерия из примера 1, чтобы
минимизировать сумму a + /??
2. Пусть выборка состоит из единственного наблюдения Х\ с
плотностью р(х — Θ). Что представляет собой при разных значениях
са критическое множество критерия Неймана — Пирсона для
проверки гипотезы Щ: θ = 0 против альтернативы Ηι: θ = 1,
если р(х) = [π(1 + х2)}~1 (плотность закона Коши)?
3. Докажите, что число наблюдений п*, обеспечивающее
заданные вероятности а и β для модели примера 1, равно
[σ(χα + Χβ)/(θι — θο)]2 (с точностью до 1), где хр обозначает
р-квантиль закона ЛГ(0,1).
4. Вычислите предел при а —► О экономичности критерия Вальда
Е(а), определяемой формулой (17), с помощью асимптотики
1 - Ф(х) ~ (ял/27г)-1 ехр{-я2/2} при χ —» +оо.
5? Дайте ответ на вопрос задачи 2 для модели сдвига
показательного закона с плотностью р(х) = е~х1{х^0}.
6* Найдите вероятность т> разорения игрока при ρ φ 1/2 методом
«стрельбы».
Неусыпный труд препят-
ства преодолевает.
М. В. Ломоносов
РЕШЕНИЯ ЗАДАЧ
1. В силу формулы (2)
а + β = 1 - Φ (ж1-в) + Φ (si-α - у/п (0ι - θ0)/σ). (23)
Положим для краткости с = у/п (θι — θο)/σ. Дифференцируя по
χ = χι-α правую часть равенства (23), получим уравнение
φ{χ) - φ{χ - с) = 0, (24)
где φ(χ) = Φ'{χ) = —■== е~х /2 —плотность закона Л/ХО, 1). Так
ν2π
как φ(χ) — четная функция, строго убывающая при χ > 0,
уравнение (24) имеет единственный корень х* = с/2. Подставив его
в соотношение (1), найдем оптимальную границу ta = (0ο+0ι)/2.
Другим доказательством может служить рис. 18, на котором
а + β превосходит минимальную сумму на величину η.
2. Очевидно, оптимальное критическое множество задается
неравенством ρι(χ)/ρο{χ) ^ с ф=ф (1 + х2)/[1 + (х - I)2] ^ с.
Меньше читайте, меньше
учитесь, больше думайте.
Учитесь у учителей
и в книгах только тому,
что вам нужно и хочется
узнать.
Л. Н. Толстой
Но Hi
θο ta θι
Рис. 18
196
Глава 13. Альтернативы
График функции у(х) = Р\{х)/ро{х) приведен на рис. 19, где
и = (л/5—1)/2 « 0,618 — «золотое сечение», ранее встречавшееся
при решении задачи 5 гл. 1.
Рис. 19
-3 -2 -1 0
1 + *г
щимпиципип»
Изменяя значение с от +оо до 0, видим, что критическим
множеством является
пустое при с > 2 + ус ,
точка при с = 2 + >*,
отрезок при 1 < с < 2 + ус,
луч при с = 1,
два луча при 1 — ус < с < 1,
прямая при 0 ^ с ^ 1 — ус.
3. В силу четности плотности закона ЛГ(0,1) для квантилей этого
распределения верно тождество х\-а = — #α· Поэтому
формулу (2) можно переписать в виде
β = Φ (-χα - yfti (0i - θ0)/σ). (25)
Применив обратную функцию Ф~1 к обеим частям
формулы (25), получим равенство хр = — ха — у/п{в\ — θο)/σ, из
которого следует доказываемое утверждение.
4. Выведем сначала саму асимптотику, следуя [81, с. 192].
Установим более сильный результат: для всех χ > 0 справедливо
двойное неравенство
(х'1 - х~3) φ(χ) < 1 - Ф(х) < χ~λφ(χ). (26)
Оно легко доказывается интегрированием по лучу [#,оо)
очевидного неравенства
(1 - ЗаГ4) φ{χ) < φ{χ) < (1 + х~2) φ{χ),
в котором участвуют производные с обратным знаком членов
неравенства (26).
Взяв натуральный логарифм от обеих частей равенства
1 - Ф{х) = х- V(x) (1 + о(1)) = -i= e-2/2 (ι + <,(!)),
χ\/2π
приходим к асимптотике
1п(1 - Ф(х)) = —х2/2 -In я - 1пл/27г + о(1) при χ —► +оо.
Ответы на вопросы
197
Теперь все готово, чтобы вычислить искомый предел:
-1п(1-Ф(ж)) _ 1
lim E(a) = lim 0 = lim
+о 2χί
χ—>+οο
2χ2
5. Для χ > 0 отношение плотностей l(x) = Pi(x)/po(x) =
= [e"x+1/{a;^i}] /[e~xI{x>o}] = el{x^i}' В частности, мера
Лебега множества {χ: l(x) = е} равна бесконечности, и
оптимальное критическое множество G* не определяется однозначно. Его
можно представить в виде G' U G": в случае α < 1/е множество
G пустое, G" —любое подмножество луча [1,оо) такое, что
Po(G") = α (рис. 20); в случае α > 1/е в качестве G' годится ^^.Т.?0^
любое подмножество интервала (0,1) такое, что Ро(С) = а— 1/е,
G" = [l,oo).
6. Аналогом производной у' (х) « [у (χ + /ι) — у (ж)]//ι является
приращение Ak = rfc+i — τν Запишем соотношения (18) в терминах
Afc: Ρ(η+ι ~ гк) = q(rk - rk-i) <=> Ak = λΔΛ_ι, где λ = q/p
и к = 0,1,... ,М—1. Начальным условиям задачи Коши у(хо) = α
и у'(#0) = с соответствуют го = 1 и Δ0 = с. Последовательно
выражая Δ& через предыдущие, находим решение дискретной
задачи Коши:
Гк(с) = г0 + Δ0 + ... + Δ^_ι = 1 + с + сА + ...+ cAfc_1 =
= l + c(Afc-l)/(A-l), если λ φ\.
В соответствии с методом стрельбы, подберем константу с так,
чтобы выполнялось второе краевое условие гм = 0. Получим
с = — (λ — 1)/(λΜ — 1), что приводит при ρ φ 1/2 к ответу:
rfc = 1 - (λ* - 1)/(λΜ - 1) = (λΜ - λ*)/(λΜ - 1).
ОТВЕТЫ НА ВОПРОСЫ
1. Критерий будет несмещенным из-за возрастания функции Ф(х)
и состоятельным, поскольку при θ > 0о
W(fi) = Φ (y/n (θ - θ0)/σ - χι-α) -► 1 при η -^ οο.
2. Критерий плох тем, что он имеет вероятность ошибки II рода
Пример наглядно де-
β — Ρ* (Υ Φ К\ « 1 монстрирует характерное
Ρ - Гвх [Л ψ Lb) ~ I. свойство азартных игр-
они обычно длятся
3. Рисунок 14 подсказывает значение 1к ~ 50. На самом деле, как намного больше, чем
доказано ниже, правильным ответом будет 1к = к(М-к) = 100. предполагалось.
В [81, с. 367] выведена явная формула (восходящая
к Лагранжу и многократно переоткрывавшаяся после) для
вероятности разорения 1-го игрока в n-й партии
υ. - _L Jn-k)/2 Jn+k)/2
Vk,n- M Ρ q
I--(s)-(s)-(^)·
198
Глава 13. Альтернативы
6-
5
4
3
2
1
7
/
/
/
/
4-
_
-1
к—
\
W
V
\
\
UiX
0 12 34 567
Рис. 21
На ее основе была вычислена таблица распределения времени
до окончания игры ν при ρ = 1/2, к = 10 и Μ = 20:
m
Ρ(ι/ ^ πι)
20
0,053
40
0,235
60
0,400
75
0,495
100
0,634
150
0,803
200
0,894
300
0,969
В частности, медиана распределения μ « 75, но (в среднем)
в каждом пятом случае ν будет больше, чем 150.
4. Mi/ = MSt//MZ1 = [-krk + (Μ - fc)(l - rfc)] /(ρ - q)> где rfc =
= (λΜ — \k)/(XM — 1), λ = g/p (см. решение задачи 6).
5. Надо продолжать блуждание, так как и слева, и справа есть
более высокие столбики.
6. Вторая стратегия в среднем вдвое выгодней, поскольку 4 · 1/2 +
+ 0-1/2 = 2.
7. Используя формулу Ik = к(М — к), получаем
(0+1·3 + 2·2 + 3·1 + 0 + 1·2 + 2·1 + 0)/8 = 14/8 = 1,75.
8. Аналогично подсчету для стратегии «Все или ничего» из рис. 21
находим
(0 + 2+[2.| + 6-|] +[2·| + 6.|] +
+6 + 4+ [4 · | + 0 · |] +θ)/8 =22/8.
Удалось ли вам набрать за 4 моделирования больше 11?
Часть IV
ОДНОРОДНОСТЬ ВЫБОРОК
Нужно различать понимающих и соглашающихся. Понявший
Учение не замедлит применить его к жизни. Согласившийся будет
кивать головой и превозносить Учение как замечательную мудрость,
но не применит эту мудрость в жизни. Согласившихся много, но
они, как сухой лес, бесплодны и без тени, только тление ожидает их.
Понявших мало, но они, как губка, впитывают драгоценное знание.
Е. И. Рерих, «Путями духа»
В эту часть книги включены наиболее простые и полезные методы
статистической обработки данных. Материал и стиль его
изложения во многом почерпнут из книги [88] —одного из лучших, по
мнению автора, руководств по непараметрической статистике для
исследователей и практиков — экономистов, социологов, биологов
и специалистов в других областях, использующих статистические
методы.
Один из моих друзей определил практика как человека, ничего
не понимающего в теории, а теоретика — как мечтателя, вообще не
понимающего ничего.
Л. Больцмап
Великая цель образования — это не знания, а действия.
Г. Спенсер
Руководство [88] особенно
ценно тем, что около
половины его объема
занимают таблицы,
позволяющие вычислять
фактические, а не
асимптотические, вероятности
ошибок при обработке
выборок небольшого
размера, которые часто
встречаются в
прикладных исследованиях.
Глава 14
ДВЕ НЕЗАВИСИМЫЕ ВЫБОРКИ
ίο
i
1-
-^
0
к
1-
У
0
i
1-
^
к
\F/i
OfG
С\
\ ·)
X
а)
к
^<л
F^P
/ G
6)
I
/^
^
в)
ι
р=
.
F/^
—►
г)
Рис. 1
§ 1. АЛЬТЕРНАТИВЫ ОДНОРОДНОСТИ
Данные. Два набора наблюдений #ι,..., хп и yi,..., ут будем
рассматривать как реализовавшиеся значения случайных величин
Χι,..., Хп и Υ\,..., Υ^.
На протяжении всей главы будем считать выполненными
Допущения
Д1. Случайные величины ΧΊ,... ,ХП независг/лш г/ гшетога общую
функцию распределения F(x).
Д2. Случайные величины Υί,... ,Υ^ независимы и имеют общую
функцию распределения G(x).
ДЗ. Обе функции F и G неизвестны, но принадлежат
множеству Ω0 всех непрерывных функций распределения.
Нас будет интересовать
Гипотеза однородности
Н0: G(x) = F(x) при всех #.*)
В качестве гипотез, конкурирующих с ifo> выделим следующие
альтернативы (рис. 1):
а) неоднородности Hi: G(x) Φ F(x) при некотором х (а в силу
непрерывности — и в некоторой окрестности точки х);
б) доминирования Я2: G(x) ^ F(x) при всех ж, причем хотя
бы для одного χ неравенство строгое (говорят, что случайная
величина Yi стохастически больше случайной величины Χι, поскольку
Ρ(Υί ^ χ) ^ Ρ (Χι ^ ж) при каждом ж);
в) правого сдвига Я3: G(x) = F(x — 0), где параметр θ > О (эта
альтернатива — частный случай предыдущей);
г) масштаба Н±: G(x) = F{x/0)1 где 0 < 0 ф 1.
*) Формально Но представляет собой сложную непараметрическую гипотезу
(см. § 1 гл. 13): в пространстве Ω0 χ Ω0 она задает «диагональ» {(F,G): G — F}.
§ 2. Правильный выбор модели
201
Причины, по которым следует рассматривать конкурирующие
гипотезы, отличные от #ι, таковы:
1) с практической точки зрения бывает важно уловить
отклонения от Но только определенного вида (скажем, наличие
систематического прироста у yj по сравнению с χ ι);
2) за счет сужения (по сравнению с Hi) множества пар
распределений (F,G), составляющих альтернативное подмножество,
обычно удается построить более эффективные (чувствительные)
критерии, настроенные на обнаружение отклонений от Но
конкретного вида.
Альтернатива доминирования Η2 встретится в§Зи§5.Вгл. 15
приведены два полезных критерия, применяемых против
альтернативы правого сдвига Н^. Методы анализа альтернативы масштаба
#4 (и ее обобщения, когда присутствует неизвестный «мешающий»
параметр сдвига) изложены в гл. 24.
§2. ПРАВИЛЬНЫЙ ВЫБОР МОДЕЛИ
При проверке гипотезы однородности двух наборов данных
х\,...,хп и 2/1,...,ут важно понять, с каким из двух случаев
мы имеем дело: двумя реализациями независимых между собой
выборок или парными повторными наблюдениями.
Примером первого случая может служить определение
влияния удобрения на размер растений. Здесь х\,...,хп
обозначают размеры растений на грядке, где удобрение не применялось,
Уь · · · > Ут — на соседней грядке, где оно применялось (см. пример 1
гл. 8). В этой ситуации можно предположить независимость
выборок Χι,..., Хп и Υί,..., Ym. Формально это выражает допущение
Д4. Все компоненты случайного вектора (ΛΊ,..., Хп, Υί,..., Ym)
независимы (см. § 3 гл. 1).
Пример второго случая — исследование эффективности
определенного воздействия (лекарства) на величину измеряемого
показателя (скажем, артериального давления), где ж ι,... ,#п — это
значения показателя (у каждого из η наблюдаемых больных) до
воздействия, a yi,... ,уп — после воздействия (га = п). Для
каждого фиксированного г (г = 1,... ,га) числам χ ι и у; в
вероятностной модели Д1—ДЗ соответствуют случайные величины Χι и Yi,
которые нельзя считать независимыми, так как χι и у^ относятся
к одному и тому же человеку.
Статистические методы, применимые ко второму случаю,
рассматриваются в гл. 15. Конечно, их можно использовать и для
независимых между собой выборок, отбросив, если тфп, лишние
наблюдения в одной из реализаций (их надо отбирать случайно,
скажем, с помощью таблицы Т1). Однако при этом игнорируется
важная информация о совместной независимости, что снижает
202
Глава 14. Две независимые выборки
чувствительность методов по сравнению с критериями,
рассматриваемыми в настоящей главе.
В свою очередь, использование приведенных в этой главе
критериев для данных, относящихся ко второму случаю, представляет
собой грубую методическую ошибку, нередко допускаемую
неопытными прикладниками, которые пытаются проверить однородность
Не все йогурты одинаково своих наблюдений при помощи первого попавшегося метода,
полезны. Рассмотрим три критерия проверки гипотезы однородности
Из телерекламы. в ПредпОЛОжении справедливости допущений Д1—Д4.
§3. КРИТЕРИЙ СМИРНОВА
Н. В. Смирнов
(1900-1966), русский
математик.
i
ΙΟ
k
аУ
Dn
^T^Gm
χ
Рис. 2
Для проверки гипотезы однородности #о против альтернативы
неоднородности #ι используется критерий Смирнова , статистикой
которого служит величина
Αι,τη = SUp \Fn(x) - Gm(x)\ ,
где Fn(x) = - Σ *{*<<*}> Gm(x) = — Σ Ι{Υ^χ}>
n i=i m i=i
т. e. Dny7n — расстояние в равномерной метрике между
эмпирическими функциями выборок (рис. 2).
Слишком большое расстояние противоречит гипотезе Щ.
В [10, с. 350] приведена таблица критических значений 2?n,m для
п,га < 20 и уровней значимости 1, 2, 5, 10%.
Для нахождения значения статистики на реализациях ац,... ,жп
и Уь... ,ут можно либо построить графики функций Fn и Gm и
визуально определить их наибольшее расхождение, либо произвести
вычисления на компьютере согласно формулам
Dn,m = max{D+m,Z?-m},
где
E>n,m = sup (Fn(x) - Gm(x)) = max f i - Gm(X{i))\ ,
D"m = sup (Gm(x) - Fn(x)) = ™*т{± ~ Fn(Yu))} ·
Здесь X(!) ^ ... ^ X(n) и У(!) < ... < У(Ш)—упорядоченные по
возрастанию элементы каждой из выборок.
Н. В. Смирнов в 1939 г. доказал, что если гипотеза Но верна, то
при выполнении допущений Д1—Д4 имеет место сходимость
оо, (1)
( у/пт/(п + m) J5n,m ^ Ж) —► К(х) При П, Ш
где UT(ж) —функция распределения Колмогорова, определенная
в § 2 гл. 12 (там же приведена небольшая таблица значений этой
функции). Доказательство сходимости (1) при условии
Д5. Размеры п,т —► оо так, что п/(п + га) —► 7 £ (0,1)
§ 4. Критерий Розенблатта
203
можно найти в [11, с. 428]. Контрпример в задаче 3 показывает,
что условие непрерывности ДЗ необходимо. Данное приближение
является довольно точным уже при n,ra ^ 20 (см. [32, с. 108]).
Расстояние от пункта А до пункта В равно 1 км. Пусть η —
скорость движения из Л в В, а тп — скорость движения на обратном
пути. Тогда 2/(1/η + 1/m) = 2nm/(n + m) —средняя скорость. Эту
величину называют средним гармоническим чисел пит.
На рис. 3 изображена верхняя половина окружности с центром
в точке О, построенная на диаметре PR длины η + m, \PS\ = η,
\SR\ = т. Перпендикуляр ST к диаметру PR пересекает окружность
в точке Т. При этом а = \ОТ\ = (п + т)/2 — среднее арифметическое
η и т. Из подобия APTS и ATRS следует, что Ь = \ST\ = у/пт —
среднее геометрическое.
Величина под корнем в формуле (1) представляет собой
половину среднего гармонического пит. Почему половину? Дело
в том, что Fn-Gm = (Fn - F) + (G - Gm), если G = F. При
сложении независимых случайных величин их дисперсии
складываются (П2). Поэтому для фиксированного χ дисперсия отклонения
Fn(x) — Gm(x) при т = η будет в 2 раза больше дисперсии
отклонения Fn(x) — F(x).
Замечание 1. В случае альтернативы доминирования (см. § 1)
вместо критерия Смирнова надо применять односторонний
критерий, основанный на следующей предельной теореме для
определенной выше статистики D+m: при справедливости гипотезы if о для
любого χ ^ 0 имеет место сходимость
Ρ [yJnm/{n + m)Dlm < ж)
1-е
-2хг
при п, т —► оо.
(2)
(Для случая т = п эта сходимость будет установлена в § 6.)
Согласно § 2 гл. 12 для правого «хвоста» распределения
Колмогорова справедливо разложение
1 - К(х) = 2 [е~
2xz
— е
-8х*
+ е
-18ж2
....].
Второй член заключенного в квадратные скобки ряда представляет
собой четвертую степень его первого члена. Пренебрегая им и всеми
последующими членами, из сравнения сходимостей (1) и (2) видим,
что фактический уровень значимости (см. § 1 гл. 12) данного
критерия примерно вдвое меньше, чем у критерия Смирнова.
Вопрос 1.
Как на этом рисунке
построить отрезок длины
с = 2пт/(п + т) так,
чтобы стало очевидным
неравенство а^Ь^с?
\а
pn>S Om R
Рис. 3
§4. КРИТЕРИЙ РОЗЕНБЛАТТА
Для проверки гипотезы однородности Щ двух выборок против
альтернативы неоднородности Н\ (см. § 1) можно воспользоваться
204
Глава 14. Две независимые выборки
также критерием типа ω2 из § 2 гл. 12. Статистика этого критерия
задается формулой
оо
<ш= | [Fn(x)-Gm(x)]2dHn+m(x),
где Нп+т(х) = Fn(x) Η Gm(x) представляет собой
η + т η + т
эмпирическую функцию, построенную по объединенной выборке
(Χι,... ,Xn,Yi,... ,У^п).
Согласно [10, с. 86], статистика ш^т зависит лишь от
порядковых номеров (рангов) выборочных элементов:
2 = J_
Шп>т пт
1 τι ι т
i/6+^E№-i)2 + jE№-i)2
-2/3,
где Ri — ранг Х(ф а 5^· — ранг Yyj в объединенном вариационном
ряду (см. § 4 гл. 4).
Положим для краткости Ζ = Zn m = ω2 . В 1952 г.
п + т п,Тп
М. Розенблатт доказал, что при условии справедливости
гипотезы Н0 и выполнении допущений Д1—Д5 имеет место сходимость
P(Z<aO-Ai(aO, (3)
где предельный закон Αι тот же самый, что встречался в § 2
гл. 12. Математическое ожидание и дисперсия этого закона равны,
соответственно, 1/6 и 1/45, в то время как
45 у n + mj |_ n + m 4 \n mJ'J
Поэтому при вычислении приближенных критических значений
рекомендуется вместо Ζ в формуле (3) использовать статистику
Ζ* = (Ζ - ΜΖ)/λ/45 ΏΖ + 1/6.*) Это обеспечивает
удовлетворительную точность приближения уже для n, m ^ 7.
§5. КРИТЕРИЙ РАНГОВЫХ СУММ УИЛКОКСОНА
Критерий ранговых сумм Уилкоксона применяется для проверки
гипотезы однородности Щ против альтернативы
доминирования if2 (см. §1), в частности, — против альтернативы правого
сдвига Н%.
*) Очевидно, MZ* = 1/6, DZ* = 1/45, причем из приведенных выше
формул для MZ и DZ из (3) с учетом свойств сходимости (П5) следует, что
Ρ(Ζ* ^χ)-+Αι(χ).
§ 5. Критерий ранговых сумм Уилкоксона
205
Вычислим статистику V критерия ранговых сумм Уилкоксона.
1. Обозначим через Sj ранг порядковой статистики Yyj
(j = 1,... ,га) в вариационном ряду, построенном по
объединенной выборке (ΛΊ,... ,Χη,Υι,... ,Ym) (рис. 4).
2. Положим V = Si + ... + Sm.
Критерий, основанный на статистике У, был предложен Ф. Уил-
коксоном в 1945 г. для выборок одинакового размера и
распространен на случай га ^ η X. Манном и Д. Уитни в 1947 г.
Суть критерия сводится к следующему: если верна гипотеза Я0,
то значения Y^ должны быть рассеяны по всему вариационному
ряду; напротив, достаточно большое значение V указывает на
тенденцию преобладания Yj над Xil что свидетельствует в пользу
справедливости гипотезы Я2. Таким образом, критическая область
выбирается в виде луча {V > с}, где с —некоторая константа.
Малые выборки. Критические значения статистики V для
n,ra ^ 25 приведены в таблице [10, с. 357].
Большие выборки. Рассмотрим статистику
η т
(4)
Вопрос 2.
Верно ли, что все
слагаемые I{xi<y.\
в сумме (4) независимы?
При отсутствии совпадений среди Χι и Yj справедливо равенство
(см. задачу 4)
l/ = V-m(m+l)/2, (5)
и, следовательно, критерии, основанные на V и С/, эквивалентны.
Предложенная Уилкоксоном ранговая форма V удобнее для
вычислений. С другой стороны, с помощью считающей формы С/, В [86, с. 143] сообщается,
изученной Манном и Уитни, нетрудно установить (задача 5), что статистиков "работе
в случае справедливости гипотезы Н$ имеем: Г. Дехлера, опубликован-
14тт ._ ^хт , ..ч /-л /лч ной в Германии в 1914 г.
MU = nm/2, DU = nm(n + m + l)/12. (6)
Когда гипотеза Н0 верна и выполнены условия Д1—Д5, имеет
место сходимость
u* = (u- mu)/Vdu Λ ζ - л/χο, ι).
Доказательство этого результата можно найти в [86, с. 145].
(7)
Поправка. К сожалению, нормальное приближение (7) не
обеспечивает достаточную точность при п,га < 50. Например, при
25 ^ η, πι ^ 50 (см. [88, с. 87]) в 40% случаев истинные
критические точки для статистики V отличаются от точек, полученных
на основе сходимости (7), более чем на 1. Существенно точнее
следующая аппроксимация, предложенная Р. Иманом в 1976 г. Она
использует полусумму нормальной и стьюдентовской квантилей.
Положим N = п + т. Критическим α-значением статистики
206
Глава 14. Две независимые выборки
служит ζα = (χι-α + 2/ι-α)/2, где Χ\-α и 2/ι_α обозначают,
соответственно, квантили уровня (1 — а) закона ЛГ(0,1) и распределения
Стьюдента с (Ν — 2) степенями свободы (см. таблицы Т2 и Т4).
Таким образом, если наблюдаемое значение статистики U* окажется
больше или равно ζαι то гипотеза Н0 отвергается.
Совпадения. Когда среди п + т наблюдений есть одинаковые,
статистику V следует вычислять с учетом средних рангов.*) При
подсчете U это соответствует назначению веса 1/2 нулевой разности
Yj — Χι. В приближении (7) надо заменить DU на
пт
~Ϊ2~
n+m+1- * uth(ll-l)
(η + m)(n + m — 1) fc=1
(9)
где д — число групп совпадений среди всех п + т наблюдений, Ik —
количество элементов в k-ft группе. Наблюдения, не совпадающее
с другими, рассматриваются как группы размера 1.
Оценка параметра сдвига. Для альтернативы правого сдвига
Щ в качестве оценки параметра θ можно взять
θ = MED{Yj - Xu 1 ^ г ^ п, 1 ^ j < m}. (10)
Известно (см. [86, с. 171]), что при выполнении условий Д1—Д5
имеет место сходимость
у/пт/(п + т)ф- θ)^ξ~λί(0,l/E(F)),
где E(F) = 12 ({ρ2(χ)dx\ , (11)
ρ(χ) — плотность, отвечающая функции распределения F.
(Отметим, что величина E(F) ранее встречалась в теореме 3 гл. 8.)
Доверительный интервал. Описание способа построения
доверительного интервала для параметра θ в случае малых выборок
приведено в [88, с. 96].
При больших η и га приближенный доверительный интервал
с коэффициентом доверия (1 — 2а) образует пара порядковых
статистик (W(fce+i),W(nm_fce)). Здесь W{1) ^ ... ^ tV(nm) —
упорядоченные по возрастанию разности Yj — Χι (1 ^ г ^ п, 1 ^ j ^ га);
ка — целая часть числа
пга/2 — 0,5 — xi-a \Jmn(n + га + 1)/12,
χι-α обозначает (1 — а)-квантиль распределения Λ/ΧΟ,Ι); 0,5 —
поправка на непрерывность, происхождение которой объясняется
в § 2 гл. 15.
*) Пусть, например, наименьшие 4 значения совпадают. Тогда всем им
приписывается средний ранг (1 + 2 + 3 +4)/4 = 2,5.
§ 5. Критерий ранговых сумм Уилкоксона
207
Численный пример применения критерия ранговых сумм
Уилкоксона— Манна—Уитни содержится в задаче 2. )
Комментарии
1. Как доказано в [86, с. 167], критерий ранговых сумм
состоятелен против альтернативы доминирования if2, в частности, против
альтернативы правого сдвига Яз.
2. Распределение случайной величины V = Si +... + Ьт можно
найти, пользуясь тем, что при справедливости гипотезы Но
вероятность каждого из С™+т возможных сочетаний Si,... ,5m
(соответствующих расстановкам У}, j = 1,... ,га, по η + га местам) одна
и та же. Вопрос 3.
3. Покажем, как оценка 0, определяемая равенством (10), свя- пе™% [^=27 ДЛЯ
зана со статистикой U. Ввиду формулы (4) при отсутствии
совпадений, U равна числу положительных разностей Yj — Χι.
Естественной оценкой параметра θ будет такая величина 0', чтобы
наборы (Υ[ = Yi — 0',..., Υ^ = Ym — θ') и (Χι,... ,Χη) выглядели
как выборки из одного и того же закона. Для таких выборок
распределение статистики U симметрично относительно среднего
пт/2. Таким образом, приходим к следующему уравнению
относительно 0':
η т η т
Σ Σ I{Y'-Xt>o} = Σ Σ I{Yj-Xi>9'} = пт/2.
i=lj=l 3 г=1 j = l
Когда величина θ' становится равной θ из формулы (10),
происходит «перескок» через уровень пт/2.
4. Точный доверительный интервал для малых выборок
строится с помощью метода 1 из § 3 гл. 11, примененного к
71 771
д(х>у,в)= Σ Σ J{w-**>*}·
i=lj = l
Когда известно, что наблюдения имеют нормальное
распределение (см. § 4 гл. 12), для проверки однородности можно использовать
критерии из примера 1.
Пример 1. Однородность нормальных выборок.
Проверим однородность двух независимых выборок (Χι,...,Χη)
и (Yi,...,ym), где Χι ~ Λ/Χμι,σ?), Yj ~ ΛΓ(μ2,^), причем все
параметры μι, μ2, 0Ί, σ2 неизвестны. Несмещенными оценками для
дисперсий σ\ и σ\ служат
ι τι ι т
(см. пример 3 гл. 6). В силу теоремы 1 гл. 11 (п — 1) Sf/af ~ Хп-и
(т — 1)51^2 ~ Xm-i> причем Si не зависит от X, а ввиду
независимости выборок — также и от Y. Это же верно и для S2.
*) Обобщение критерия для многомерных данных см. в § 3 гл. 23.
208
Глава 14. Две независимые выборки
Вопрос 4.
Что происходит с законом
^fci,fc2 ПРИ *ь k2-+oo7
Total (англ.) — общий.
Вопрос 5.
Какое распределение
имеет статистика Т2?
независимы.
Определение. Случайная величина ζ имеет F-распределение
(Фишера—Снедекора) с к\ и к^ степенями свободы (обозначается
C~*fci,fca)> если
Критерий Фишера. Если верна гипотеза
Η': σι = σ2, μι и μι — любые,
то в соответствии с приведенным выше определением статистика
Sf/Sf распределена по закону Fn_i>m_i. Ее критические значения
можно найти в таблице Т5.
В случае, когда критерий Фишера не отвергает гипотезу if', для
проверки однородности остается проверить гипотезу Η" \ μι = μ2·
Обозначим неизвестную общую дисперсию через σ2 . Так как
распределение хи-квадрат является частным случаем
гамма-распределения (χΊ ~ Г(А:/2,1/2)), из леммы 1 гл. 4 вытекает, что
α"2 [(η - 1) S2 + (m - 1) S2] ~ X2+m_2.
Поскольку математическое ожидание закона Хп+т-2 равно
ПтШ-2, статистика 5t2ot = [(η - 1) 52 + (m - 1) 5|]/ (п + т — 2)
несмещенно оценивает σ2 по объединенной выборке.
При справедливости гипотезы Нп ввиду независимости выборок
имеем: X — Υ ~ ЛГ(0, (1/п -f l/m) σ2). При этом X — Υ (функция
от X и Υ) не зависит от Stot (функции от 5ι и 5г) в силу леммы
о независимости из § 3 гл. 1. Отсюда согласно определению закона
Стьюдента tk с к степенями свободы (см. пример 4 гл. 11) имеем:
т-(х-ю/(*ч/571)-^<х-г)/*.~*
Это приводит к так называемому критерию Стьюдента, который
позволяет проверить гипотезу Я". Критические значения
статистики in+m_2 даны в Т4.
Несмотря на то, что критерий Стьюдента оптимален для
нормальных выборок, рассмотренная процедура проверки
однородности имеет скорее теоретическое, чем практическое значение.
Почему?
Во-первых, это объясняется тем, что критические значения
статистики 52/5| существенно изменяются даже при небольших
возмущениях модели (см. в гл. 16 задачу 6 и замечание 2 при
* = 2).*>
Во-вторых, эффективность критерия Стьюдента быстро
уменьшается при отклонении от строгой нормальности. (Относительная
асимптотическая эффективность двух критериев при
альтернативах правого сдвига определена, например, в [86, с. 76].) В частности,
п+т—2·
*) Устойчивая ранговая альтернатива критерию Фишера, не предполагающая
нормальности наблюдений, описывается в § 2 гл. 24.
§ 6. Принцип отражения
209
эффективность критерия ранговых сумм Уилкоксона—Манна—
Уитни по сравнению с критерием Стьюдента равна E(F) (см.
формулу (11)).
Рассмотрим для иллюстрации модель Тьюки смеси нормальных
законов из примера 2 гл. 8 (при д = 0иа = 1),у которой функция
распределения F выглядит так: F€(x) = (1 — έ)Φ(χ) + εΦ(χ/3)1
где Ф(х)— функция распределения ΛΓ(Ο,Ι), 0 ^ ε ^ 1. Следующая
таблица (из [86, с. 85]) показывает изменение эффективности E(F€)
в этой модели при небольшом утяжелении «хвостов».
ε
E(Fe)
0
0,955
0,01
1,009
0,03
1,108
0,05
1,196
0,08
1,301
0,10
1,373
0,15
1,497
В силу теоремы 4 гл. 8 эффективность E(F) = ew~x(F) ^ 0,864
при всех F £ Ω8 и может быть сколь угодно велика.
Отметим также, что у критерия cm φ η по сравнению
с критерием с га' = п' = (п + га)/2 эффективность уменьшается
в 1/[47(1 - 7)] > 1 Р93» 7 = п/(п + т) (см· [86, с. 171]), поэтому
желательно брать выборки одинаковых размеров (если, конечно,
есть такая возможность).
§6. ПРИНЦИП ОТРАЖЕНИЯ
Материал этого параграфа в основном заимствован из гл. III
замечательной книги [81], которую автор настоятельно рекомендует
прочитать заинтересовавшемуся читателю. В конце параграфа
некоторые из полученных результатов будут использованы для
решения двух задач из области проверки однородности выборок.
Рассмотрим случайное блуждание 5П = ξι + ... + £п, где
независимые «шаги» & принимают значения +1 и —1 с
одинаковой вероятностью 1/2. Траекторией (путем) блуждания длины η
будем называть ломаную, соединяющую точки плоскости с
координатами (г, 5г), г = 1,... ,п. Каждый из 2П возможных путей имеет
одинаковую вероятность 2~п.
Обозначим через ЛГП)Ш количество путей, ведущих из точки
(0,0) в точку (п,га) (рис. 5). Пусть для такого пути А: —это число
шагов вверх (& = +1), Z — число шагов вниз (& = —1). Тогда
k + I = η и к — I = т, откуда к = (п + ш)/2. Расставить к «плюс
единиц» по η местам можно С* способами. Поэтому
ДГ — Wn+m)/2
(12)
где подразумевается, что биномиальный коэффициент равен 0, если
(п + т)/2 не является целым числом между 0 и п.
Пусть а и Ь — положительные целые числа. Перенесем
начальную ординату блуждания из 0 в α и потребуем, чтобы в момент
η траектория приходила в точку с координатами (п,Ь) (рис.6).
Рис. β
210
Глава 14. Две независимые выборки
Рис.7
о' ι
Очевидно, что количество таких путей равно Νη^-α· Сколько из
них являются положительными^ т. е. лежат целиком над осью
абсцисс? Ответ на этот вопрос получим с помощью следующего
утверждения.
Принцип отражения. Число путей, ведущих из (Ο,α) в (п,6)
и касающихся или пересекающих ось абсцисс, совпадает с числом
путей, ведущих из (Ο,α) в (п, — Ь), которое равно Nnia+b-
Доказательство. Обозначим через г момент первого касания
или пересечения траекторией оси абсцисс (рис. 7). Отразим
относительно этой оси отрезок пути от (т,0) до (n, b). Присоединив к нему
отрезок исходного пути от (Ο,α) до (т,0), построим новый путь,
ведущий из (Ο,α) в (п, — Ъ). Очевидно, что по построенному пути
исходный восстанавливается однозначно. ■
Следствие. Количество положительных траекторий из (Ο,α)
В (П,Ь) раВНО Nnib-a ~ Νη,α+6·
Геометрическая задача. По всей ширине дороги рассыпано
зерно. Слева от дороги на заборе высоты α сидит ворона (рис. 8).
Она хочет поклевать зерна, а затем перелететь на забор высоты Ъ
(потому, что b > α), который находится справа от дороги.
Частным случаем следствия принципа отражения является сле-
1 дующий результат, полученный У. Уитвортом в 1878 г. и заново
Ж. Бертраном в 1887 г. (см. [81, с. 87]).
Задача о баллотировке. Предположим, что на выборах первый
кандидат набрал к голосов, а второй кандидат набрал I голосов,
причем к > I. Тогда вероятность того, что при последовательном
подсчете голосов первый кандидат все время был впереди второго,
равна (к — 1)/(к + /).
к _ / Доказательство. Траектория, удовлетворяющая условиям
теоремы, обязательно проходит через точку (1,1) (рис. 9). Согласно
^ следствию принципа отражения и формуле (12), число положитель-
к + Ζ ных путей из (1,1) в (к + Ζ,λ; — I) равно (п = к + 1 — 1, α = 1, Ь = А: — I)
Рис 9 Λη,*-ί-ι - JVn.fc-1+ι = Ct'l, - CfeVi·
Правая часть простыми преобразованиями приводится к виду
Nk+i,k-i(k - 1)/{к + Z), что и утверждалось. ■
Среди путей за время 2п выделим пути, приходящие в (2п,0):
и2п = Р(52„ = 0) = ЛГ2П)0 · 2~2п = С%п 2~2п («о = 1). (13)
Формула Стирлинга*) (п\ ~ у/2пппп е~п при η —► оо) позволяет
получить следующую асимптотику для U2n (убедитесь!):
^2п ~ l/y/πη при η —► оо. (14)
*) Простое доказательство этой формулы можно найти в [81, с. 72].
Вопрос 6.
В каком месте на дороге
надо приземлиться
вороне, чтобы общая
длина двух перелетов
была минимальной?
i^J1
Рис. 8
τ—ι—ι—г—г
§ 6. Принцип отражения
211
Другими словами, доля среди всех 22п возможных траекторий
путей, приходящих в точку (2п,0), стремится к нулю со скоростью
порядка 1/\/п (см. решение задачи 5 гл. 12).
Оказывается, что неотрицательных путей за время 2п ровно
столько же, сколько путей, приходящих в (2п,0).
Теорема 1. При всех значениях η справедливо равенство
P(Si^0,...,S2n^0) = U2n.
Доказательство. Э. Нелсон (см. [81, с. 115]) предложил
следующее оригинальное преобразование, взаимно однозначно
переводящее траектории, приходящие в 0, в неотрицательные.
Обозначим самую левую (если их несколько) точку
глобального минимума заданного пути, ведущего в точку (2п,0), через
Μ = (λ;,-га) (рис. 10). Отразим участок, ведущий из начала
координат в точку М, относительно вертикальной прямой у = к
и передвинем отраженный участок так, чтобы его начальная точка
совпала с точкой (2п,0). Примем Μ за начало новой системы
координат, в которой построенный путь ведет из начала в точку
(2п, 2т), а все его вершины лежат не ниже новой оси абсцисс. ■
Указание. Обратите внимание, что у такого пути обязательно
5ι = 1, а также S2n > 1> так как 2п —четное число.
Рассмотрим траектории, имеющие единственный глобальный
максимум в момент 2п (рис. 11).
Траектория блуждания, не возвращающегося в 0 за время 2п,
является либо положительной, либо отрицательной (не считая
начальной точки). Из симметрии и вопроса 7 вытекает, что
Р(А2п) = P(Si φ 0,... ,52η φ 0) = и2п.
(15)
Введем обозначения: В2п = {S2n = 0}, f2n = P(A2n-2B2n)
вероятность вернуться в 0 впервые в момент 2п. Ввиду (15)
hn = Р(А2п-2) - Р(А2п-2В2п) = и2п-2 - и2п.
(16)
С учетом того, что щ = 1 и и2п —► 0 при η —► оо, из
формулы (16) получаем, что вероятность вернуться в 0 когда-нибудь
h + /4 + · · · = 1· Из соотношений (13) и (16) легко выводится
тождество
i)m
Μ 2η
Рис. 10
Вопрос 7.
Как вывести, что
Ρ(5ι>0,...,52η>0) =
1 7
= 2ω2η?
¥\
S2n
2п
Рис. 11
Вопрос 8.
Чему равна Ρ(5ι<£>2η,
...,ί>2η-1<<ί>2η)?
hn = 2^ ^2η-2·
(17)
Асимптотика (14) дает для f2n порядок малости η 3/2. Поэтому
Σ 2η f2n ~cj] —= = 00, т. е. среднее время до первого возвра-
71=1 71=1 УП
щения блуждания в 0 бесконечно.
Пусть g2n-i — вероятность впервые достигнуть уровень 1 на
(2п — 1)-м шаге.
212
Глава 14. Две независимые выборки
Рис. 12
Рис. 13
Теорема 2. Имеет место равенство <?2η-ι = /2η·
Доказательство. Величина Кп = 22η_1ρ2η-ι совпадает с числом
отрицательных (за исключением крайних точек) путей, ведущих из
(1, — 1) в (2п,0) (рис. 12). Соединив точку (1, — 1) с началом
координат, получим траекторию, впервые возвращающуюся в 0 в момент
2п. Сопоставим исходному пути эту траекторию и симметричную
к ней относительно оси абсцисс. Так как исходный путь по этим
траекториям определяется однозначно, то 22п/2П = 2Кп. Ш
Из теоремы 2 вытекает, что среднее время до момента первого
достижения произвольного уровня h > О симметричным
случайным блужданием бесконечно.
Обозначим через ν<ιη момент последнего попадания β 0 за время
2п (рис. 13). Найдем распределение этой случайной величины.
Положим а2г,2п = Р(^2п = 2г), г = 0,1,... ,п.
Теорема 3. Справедливо соотношение с*2г,2п = ЩгЩп-2г-
ДОКАЗАТЕЛЬСТВО. Мы интересуемся путями, у которых S^i = 0
и i>2i+i Φ 0,... ,52η Φ 0. Первые 2г вершин можно выбрать 22гг/2г
различными способами. Взяв точку (2г,0) в качестве нового начала
координат, согласно равенству (15) видим, что остальные (2п — 2г)
вершин можно выбрать 22п~2ги2П-2г способами. Всего получаем
22nU2i U2n-2i вариантов. ■
Из теоремы 3 и асимптотики (14) следует, что предельным
распределением для случайной величины ^2п/(2п) является
распределение арксинуса с функцией распределения F(x) = (2/π) arcsin y/x
и плотностью р(х) = 1/(пу/х(1 — ж)), 0 < χ < 1 (график р(х)
приведен на рис. 8 в гл. 5). Действительно:
X
Ρ(^2η/(2η) < χ) = Σ a2i,2n ~ Σ Ρ ( ζ; ) ~ -Ч Р(У) dV-
г<хп г<хп \п/ п J
Рис. 14
Оказывается, что время, в течение которого траектория
блуждания находилась в полуплоскости у ^ 0, распределено так же,
как случайная величина ν<ιη (см. § 4 гл. 16). Но если ограничиться
только путями, приходящими в момент 2п в 0 (рис. 14), то условная
вероятность того, что в точности 2г (г = 0,1,... ,п) их звеньев лежат
над осью абсцисс, равна 1/(п+1) независимо от г. Это утверждение
известно как теорема о равнораспределенности.
§ 6. Принцип отражения
213
Доказательство. Рассмотрим отдельно случай г = п. Число
путей, приходящих в точку (2п, 0), все звенья которых лежат выше
оси абсцисс, совпадает с числом положительных путей из (0,2)
в (2п — 1,1). В силу следствия принципа отражения оно равно
&2η-ι ~ ^2η-ι = ~ ^2η· Это доказывает теорему при г = η
и, а в силу симметрии — также и при г = 0.
При 1 ^ г < η — 1 воспользуемся индукцией. Для случая η = 1
теорема очевидна. Предположим, что она верна для всех путей,
длина которых меньше 2п. Пусть первое возвращение в 0
произошло в момент 2г. Участок пути до 2г расположен либо в
положительной, либо в отрицательной полуплоскости. В первом случае
1 ^ г < г и участок после 2г имеет ровно 2г - 2т звеньев над осью
абсцисс. Согласно предположению индукции и ввиду формулы (17),
такой путь может быть выбран
ι 22п—2г 22п—2
о 2 Гhr * 7-; U>2n-2r = —, -77 ^2r-2 ^2n-2r (18)
2 η — г + 1 r(n — г + 1)
различными способами. Во втором случае конечный участок длины
(2п — 2г) содержит ровно 2г положительных звеньев и,
следовательно, η — г ^ г. Для фиксированного г число путей,
удовлетворяющих этим условиям, также определяется величиной (18).
Общее количество путей обоих типов получается суммированием
слагаемых вида (18)по1 <г^ги1 ^ г ^ η — г соответственно.
Во второй сумме заменим индекс г на j = η — г + 1. Тогда j
меняется от г + 1 до п, а слагаемые имеют вид (18) с заменой г
на j. Отсюда следует, что число путей, у которых г звеньев лежат
в положительной полуплоскости, получается суммированием (18)
по 1 ^ г ^ п. Так как г не входит в (18), сумма не зависит от г, что
и утверждалось. ■
Применим изложенные результаты к некоторым задачам,
возникающим при проверке гипотезы однородности Н0 двух
независимых выборок X = (Χι,... ,ХП) и Υ = (Yi,... ,Yn) одинакового
размера п. Допустим, что среди всех 2п значений обеих
выборок нет совпадающих (условие ДЗ гарантирует выполнение этого
с вероятностью 1). Упорядочим каждую выборку по возрастанию:
Χ(ΐ) < ... < Х(п) и У(1) < ... < У(п). Положим L равным числу
индексов г, при которых Х^ < Υ^ (г = 1,...,п). Близость этой
величины к η указывает на то, что альтернатива доминирования
#2 (см. § 1) предпочтительнее гипотезы однородности Щ. Чтобы
вычислить критическую границу, надо найти распределение
случайной величины L при условии справедливости гипотезы Hq.
Для этого переведем задачу на язык случайных блужданий.
Упорядочим по возрастанию все 2п значений обеих выборок в
вариационный ряд. Пусть £ь = — 1 или +1 в зависимости от того,
214
Глава 14. Две независимые выборки
21
2п
Рис. 15
элементом выборки X или выборки Υ является k-ft член
построенного ряда (к = 1,... ,2n), Sk = ξ\ + ... + £&. Полный путь длины
2п соединяет начало координат с точкой (2п,0).
Заметим, что событие Х^) < Y(k) происходит тогда и только
тогда, когда S2fc-i содержит по меньшей мере к «плюс единиц»,
т. е. когда S2fc-i > О· Это влечет неравенство S2k ^ 05 и поэтому
(2А:- 1)-е и 2к-е звенья траектории лежат выше оси абсцисс. Отсюда
следует, что равенство L = I верно в том и только в том случае,
когда в точности 21 звеньев лежат выше оси абсцисс. По теореме
о равнораспределенности вероятность этого события равна 1/(п+1)
независимо от /.
Статистика L впервые была использована для проверки
однородности Ф. Гальтоном при исследовании данных, предоставленных ему
Чарльзом Дарвином. Значения I и η были равны 13 и 15
соответственно. Не зная реальных вероятностей, Гальтон отверг гипотезу #о.
Однако в предположении Но вероятность того, что L примет значение
13 и более (фактический уровень значимости критерия,
определенный в § 1 гл. 12), равна 3/16. Другими словами, в 3 случаях из 16
будет наблюдаться такое же или большее превосходство элементов
Υ над элементами X при полном совпадении законов распределения
элементов выборок. У. Феллер пишет ([81, с. 88]): «Это показывает,
что численный анализ может быть полезным дополнением к нашей
не совсем надежной интуиции.»
В заключение получим с помощью принципа отражения
предельную теорему (2) для статистики одностороннего критерия
D+m = sup(Fn(:z) - Gm(x)) при га = η.
χ
Для этого заметим, что для любого 1(1 = 1,... ,п)
№,„ > Чп} *=* {^2nSk > l, S2n
В силу принципа отражения (рис. 15), а также формул (12)
и (13) имеем
-·}·
ρ (d+ > -Ί = Ν2η·21 -
Сп—Ι
9η
Множитель у/пт/(п + га) в утверждении (2) при га = η равен
yJn/2. Чтобы установить для произвольного χ ^ 0, что при η —* оо
P(VW2Dt,n>x)^e-2x\ (19)
остается применить формулу Стирлинга и разложение логарифма
ln(l + t)=t- t2/2 + o(t2) при t -+ 0 (задача 6).
ЗАДАЧИ
Ум заключается не только 1. Пусть х\,... ,#2о — реализация выборки из равномерного распре-
пРиНмен^ деления на отрезке [0,1], построенная по четвертому столбцу
Аристотель таблицы Т1 (см. решение задачи 1 гл. 12); yi,... ,У20
~~реализация выборки из закона с функцией распределения G(x) = χ3
Решения задач
215
на [0,1] (согласно задаче 3 гл. 1 ее можно моделировать, взяв
в качестве у\ наибольшее из трех первых значений в г-й строке
табл. Т1, деленное на 100). Проверьте гипотезу однородности
с помощью одностороннего критерия из замечания 1.
2. В условиях задачи 1 примените критерий ранговых сумм Уил-
коксона—Манна—Уитни.
3. При выполнении условия Д5 найдите предельный закон распре-
деления для статистики критерия Смирнова у/пт/(п + га) Dnm
в случае двух независимых выборок из распределения Бернулли
с одинаковой вероятностью «успеха» р.
Указание. См. задачу 3 гл. 12.
4. Выведите формулу (5), связывающую величины U и V при
отсутствии совпадений среди всех Х\ и У}.
5? Получите выражения (6) для MU и DU.
6? Докажите асимптотику (19).
РЕШЕНИЯ ЗАДАЧ
1. На рис. 16 приведены графики эмпирических функций
распределения Fn и Gn для реализаций #ι,... ,#п и yi,... ,уп (п = 20).
Значение статистики D+n равно 0,4. Отсюда получаем, что
хо = у/п/2 D+n = 0,4 \/ϊϋ « 1,265. Следовательно, фактический
уровень значимости с*о = е~2х° = е~3,2 « 0,04.
2. Вычисленная на основе данных задачи 1 статистика V равна
489 (для совпадений были взяты средние ранги). В соответствии
с формулой (5) находим U = V — 210 = 279. Согласно (6)
MU = 200. Подсчитанная по формуле (9) с учетом совпадений
DU « 1365,2. Поэтому нормированная статистика [/*,
определенная равенством (7), принимает значение 2,138.
Вычислив поправку Имана (8), получим, что U* = 2,192.
Для уровня значимости a = 0,025 по таблицам Т2 и Т4
(для к = т + η — 2 = 38) находим критическое значение
ζα = (1,96 + 2,024)/2 « 1,992. Поскольку 2,192 > 1,992, гипотеза
однородности Но отвергается на уровне 2,5%.
3. Эмпирическая функция распределения Fn выборки Χι,... ,ХП
из закона Бернулли имеет два скачка: в точке 0 высоты 1-Х
и в точке 1 высоты X. Аналогично устроена функция Gm,
построенная по выборке Yi,...,Y^. Поэтому Dn,m = \Х — У\
(рис. 17). Пусть q = 1 — р. В силу условия Д5, центральной
предельной теоремы и свойства 1 сходимости из П5
;
(
т
,Тг \ d
п + т
η
п + т
νΚ(Χ-ρ)^ξ~λί(0,(1-Ί)ρς),
η ~ Λ/"(0,7Ρ?)·
^ι(ρ-Υ)±
Леность всему (дурному)
мать: что человек умеет,
то позабудет, а чего не
умеет, тому не научится.
Владимир Мономах
Рис. 16
1-г
1-У
1-Х
\Dns
Fn
Рис. 17
216
Глава 14. Две независимые выборки
*—
J rn
щ
ulffl
Рис. 18
'JTI
И5^
О 1
Рис. 19
Следовательно, ввиду независимости X и У имеет место
сходимость у/пт/(т + п)(Х — У) -» £ + 77 = С ~ АГ(0,рд). Согласно
свойству 3 сходимости (П5) искомым предельным законом
является распределение случайной величины \ζ\ (его плотность
изображена на рис. 13 гл. 12).
4. Запишем ранг (т. е. номер в порядке возрастания) Sj статистики
Y(j) в вариационном ряду, построенном по объединенной
выборке (Χι,... ,Χη¥ι, · · · Хт), в следующем виде:
η т η
sj = Σ ^№<у(л} + Σ hy^Yu)} = Σ i{Xi<YU)y +j.
i=l fc=l i=l
Тогда статистика ранговых сумм Уилкоксона равна
т т
V= Σ S, = £7+Σ j = u4m(m +l)/2.
i=i i=i
5. Если гипотеза Hq верна, то случайные величины Xi и Yj имеют
общую непрерывную функцию распределения F(x). Введем
величины ξι = F(Xi) и щ = F(Yj). Они независимы в силу
независимости Х{ nYj и равномерно распределены на отрезке [0,1]
в соответствии с методом обратной функции (см. § 1 гл. 4). При
этом Uj = I{Xi<Yj} = I{b<Vj}- Отсюда
Mlij = Р(£ < η,·) = dxdy = ^.
0<х<у<1
Поэтому DJy = Μ/?· - (MJ«)2 = MJy - i = i - i = i
Поскольку Ρ=ΣΣ^ι Для вычисления D£/ воспользуемся
t=lj = l
формулой для дисперсии суммы (см. П2):
η т η т
г=1 j = l fc=l ί=1
Для фиксированных г и j разобьем слагаемые в двойной сумме
по А: и Ζ на четыре группы: А) {к = г,/ = j}, В) {к = г J Φ j},
С) {к φ г,/ = j}, D){k φ ij φ j} (рис.18). В группе А
cov (Iijilij) = D/ij = -. В группе В в силу независимости
случайных величин &, r/j и 7# имеем
M(lijlu) = Р(& < т^,& < г/г) = dxdydz = -,
0<х<2/<1
0<ж<г<1
так как интеграл равен объему пирамиды, основанием которой
служит грань единичного куба, лежащая в плоскости χ = О,
а вершиной — точка с координатами (1,1,1) (рис. 19).
Следовательно, cov(IijJu) = M(lijlu) - Mlij · М1ц = - - - = — · Из
соображений симметрии ковариация в группе С такая же, как
Ответы на вопросы
217
DU
= nmU + -T2- + ^2-J =
в В. Наконец, согласно лемме о независимости из § 3 гл. 1 и
свойству 5 математического ожидания (П2), ковариация в группе D
равна 0. Собирая все вместе, получаем
nm(n + m+l)
12 '
6. Пусть I равно целой части числа ху/2п. Чтобы установить
асимптотику (19), достаточно вывести, что
In (С?-1/С%п) = -12/п + о(1) при η -> оо, I = 0(у/п).
К этому результату можно прийти и без формулы Стирлинга
(см. [39, с. 58]), но с ней получается немного короче.
Действительно, 1η η! = η In η — η + - In η + In у/2к + о(1). Элементарные
выкладки показывают, что
- In (Су-'/СЗ^) = In (η + l)\ + In (η - /)! - 2 In η! =
= (n + 0b(l + ^)+(n-0b(l-^) + |b(l-^)+o(l).
Разложение в ряд 1п(1 -И) при t —► 0 с учетом условия / = 0(у/п)
позволяет завершить доказательство (проверьте!).
ОТВЕТЫ НА ВОПРОСЫ
1. Опустим перпендикуляр SX на ОТ (рис. 20). Тогда отрезок
ТХ — искомый. Это вытекает из подобия прямоугольных
треугольников Δ STX и Δ OTS, имеющих общий острый угол:
2 ι nm 2nm
c/b = b/a
с = b2/a =
(η + m)/2 n + m
Неравенство α ^ b ^ с верно потому, что катет короче
гипотенузы.
Ρ η s О m
Рис. 20
Можно строить и другие «средние», продолжающие это
неравенство. Для начала опустим перпендикуляр XY на отрезок
ST и положим d = \TY\ = с2/b = 4(nm)3/2(n + m)"2.
Затем построим перпендикуляр YZ к отрезку ОТ. Получим
е = \TZ\ = d2/c = 8(nm)2(n + m)~3 и т. д.
2. Например, 1{χ1<γ1} и 1{χλ<γ2), являющиеся функциями от ΛΊ,
очевидно, зависимы (строгое доказательство вытекает из
решения задачи 5). Однако для фиксированной пары индексов (zj),
подавляющая часть индикаторов, а именно nm — η — m + 1
(см. рис. 18), не зависят от 1{χί<γ.) в силу леммы о
независимости из § 3 гл. 1.
3. Из С™+т = С| = 10 возможных сочетаний трех «X» и двух «У»
только наборы «ΧΧΧΥΥ» и «ΧΧΥΧΥ» имеют сумму рангов
V ^ 8 (9 и 8). Поэтому P(V ^ 8) = 1/5.
218
Глава 14. Две независимые выборки
Рис. 21
1 +
Ич/\
А
2п χ
Рис. 22
4. По определению закона χ2 (см. пример 3 гл. 11)
Л\
х1
0
к
У\
/Ч X
>/
У
у'\
7.
U
1 К\
Рис. 23
έ Σ ζ1
(20)
где все Zi (г = 1,... ,fci + λ^) подчинены стандартному
нормальному распределению и независимы. Согласно закону больших
чисел (см. П6), делимое и делитель в формуле (20) стремятся по
вероятности к MZj = DZi = 1. Так как функция </?(#,у) = χ/у
непрерывна на множестве {х > 0,у > 0}, то по свойству
сходимости 3 из П5 распределение случайной величины ζ при
fci, Afe —► оо вырождается в 1.
По определению закона tk (см. пример 4 гл. 11)
Τ = ξ
п + т — 2
V
где ξ ~ Л/^О, 1), η ~ Xn+m-2» f и ^ независимы. Согласно
определению F-распределения имеем Τ2 ~ Fi,n+m-2·
Из рис. 21 понятно, что вороне следует лететь по траектории,
у которой «угол падения равен углу отражения», так как прямая
короче ломаной.
Перенесем начало координат в точку (1,1) и продолжим путь из
концевой точки еще на один шаг вверх или вниз (рис. 22). При
этом из одного положительного получим два неотрицательных
пути длины 2п.
Изменим систему координат так, как показано на рис. 23. В
новой системе траектория будет положительной.
Глава 15
ПАРНЫЕ ПОВТОРНЫЕ НАБЛЮДЕНИЯ
§ 1. УТОЧНЕНИЕ МОДЕЛИ
Методы этой главы предназначены для выявления неоднородности
реализаций выборок ΑΊ,... ,Хп и Υι,...,Υη одинакового размера,
которые нельзя считать независимыми между собой (см. § 2
гл. 14).
Прежде всего, уточним статистическую модель из § 1 гл. 14
применительно к данной ситуации. Вычислим приращения Zi = Yi—X^
г = 1,... ,η, и разложим каждое из них на две части: Zi = θ + ε»,
где θ — интересующий нас эффект воздействия — систематический
сдвиг, который мы будем считать положительным, е% — случайная
ошибка, включающая в себя влияние неучтенных факторов на Ζ{.
В дополнение к допущениям Д1—ДЗ из § 1 гл. 14 предположим,
что выполняется условие
Д6. Случайные величины ει,... ,εη независимы и имеют
непрерывные (вообще говоря, разные) распределения такие, что
Р(е< < 0) = Р(е< ^ 0) = 1/2, г = 1,...,п.
Это означает, что равны нулю медианы функций распределения
случайных величин е\ (см. § 2 гл. 7).
Замечание 1. Предположения Д1—ДЗ из § 1 гл. 14 не
обеспечивают одинаковой распределенности ε». Действительно, пусть
случайные величины Х\ и Х2 распределены по стандартному
нормальному закону ЛГ(0,1) (см. § 2 гл. 3) и независимы.
Положим Υ\ = Χι + Х2 и Υ2 = Х\ — Х2. Нетрудно проверить, что
Υ\ и Υ2 распределены по закону ЛГ(0,2) и независимы, так как
cov(Yi,y2) = 0 (см. П9). Но Zi = Υγ - Χγ = Х2 ~ ЛГ(0,1),
Ζ2 = Υ2 - Х2 = Χι - 2Х2 ~ Л/Х0,5). Отсюда ει = Ζλ - θ ~ Λ/Χ-0,1),
а ε2 = ^2 — θ ~ Λ/^—0,5). Кроме того, что ει и ε2 имеют разные
распределения, они еще и зависимы, т. е. нарушается условие Д6:
cov (ει,ε2) = cov (Χ2ιΧλ) - 2cov (X2lX2) = -2^0.
Итак, пусть выполнено предположение Д6. Рассмотрим задачу
проверки гипотезы Н'0: θ = 0 против альтернативы Щ: θ > 0
Да вместе вы зачем?
Нельзя, чтобы случайно.
Фамусов в «Горе от ума»
А. С. Грибоедова
220
Глава 15. Парные повторные наблюдения
(штрих указывает на то, что проверяемая гипотеза и сдвиговая
альтернатива задаются не для пары законов (F, G) (см. § 1 гл. 14),
а для распределений приращений Ζτ). Для ее решения используем
критерии знаков (§ 2) и знаковых рангов Уилкоксона (§3). )
§2. КРИТЕРИЙ ЗНАКОВ
Выполним следующие шаги.
1) Зададим уровень значимости (см. *§ 1 гл. 12) — малую
вероятность α ошибочно отвергнуть верную гипотезу Щ.
2) Положим Ui = /{Zi>0}> г = 1,... ,η.
3) В качестве статистики критерия знаков возьмем сумму
5 = Ui + ... + Un и подсчитаем ее значение s на реализациях
хи...,хп иуь...,уп.**)
Малые выборки. При η ^ 15 вычисляем фактический уровень
значимости, определенный в § 1 гл. 12 (см. рис. 1):
а0 = Р0(5 > а) = 2~η Σ0ί = 2_П Σ* <?«· (1)
i=s i=0
9ι
2П
Если ао ^ а, отвергаем гипотезу Щ, в противном случае—прини-
, _.,. - |_^ маем. В [10, с. 402] приведена таблица биномиальных коэффициен-
[■^Ι,ΙΊ,Μ,^, г тов, облегчающая вычисление а0.
On — s г
Рис· 1 Большие выборки. Для расчета ао при η > 15 можно
применить нормальную аппроксимацию распределения
стандартизованной статистики
5* = (5 - MS) /VOS =(S- n/2) J v/n/4 .
Если гипотеза Щ верна, то в соответствии с центральной
предельной теоремой (П6) распределение величины 5* при η —► оо сходится
к стандартному нормальному закону ЛГ(0,1) (см. § 2 гл. 3).
Пусть χι-α —квантильзаконаЛГ(0,1) уровня 1—α (см. § 3 гл. 7),
s*—наблюдаемое значение статистики S*. Если s* ^ #i-Q, то
отвергаем гипотезу #0» в противном случае — принимаем.
Поправка. Можно значительно улучшить качество
приближения дискретного биномиального распределения непрерывным
нормальным законом за счет введения поправки на непрерывность.
Рассмотрим «подправленную» статистику
<?* = (S - 0,5 - п/2)/у/ф . (2)
*) Их обобщения для многомерных данных приведены в § 2 гл. 23.
) Если значение г-го приращения Ζχ = ух — Χχ > 0, то это отмечают знаком
«+», если Ζχ < 0 —знаком «—». Отсюда происходит название критерия.
§2. Критерий знаков 221
Как показывает рис. 2, сдвиг влево на 0,5 позволяет точнее
аппроксимировать сумму площадей прямоугольников площадью под
графиком правого «хвоста» нормальной плотности.
Совпадения. Если среди значений Zi встречаются нули, то их
надо отбросить и соответственно уменьшить η до числа ненулевых
значений Ζ^
Оценка параметра. Когда гипотеза Щ отвергнута,
принимается альтернатива Щ. В этом случае представляет интерес
величина сдвига Θ. В качестве ее оценки θ можно взять выборочную
медиану приращений MED{Z^ г = 1,... ,п} (см. § 2 гл. 7).
Доверительный интервал. Определим номер ка как
наибольшее число слагаемых, при котором
2"nEQ^a. (3)
г=0
Тогда пара порядковых статистик (Z(fca+i),Z(n-fca)) (см* § ^ гл* 4)
образует доверительный интервал для θ с коэффициентом доверия
1 — 2а (см. § 1 гл. 11). Для нахождения ка можно также
воспользоваться таблицей из [10, с. 353].
При большом η значение ка с учетом поправки на
непрерывность приближенно равно целой части числа
п/2 — 0,5 — #ι-αλ/η/4> где х\-а — квантиль закона ЛГ(0,1).
Пример 1. Времена реакции [80, с. 123]. Числа Х{ и у ι
в приведенной ниже таблице представляют собой времена реакции
г-го испытуемого на световой и звуковой сигналы соответственно,
Ζ% =: Ух Х{1 % = 1, . . . ,ΙΖ.
г
Хг
У г
Zi
1
176
168
-8
2
163
215
+52
3
152
172
+20
4
155
200
+45
5
156
191
+35
6
178
197
+19
7
160
183
+23
8
164
174
+10
9
169
176
+7
10
155
155
0
11
122
115
-7
12
144
163
+19
Поскольку 2ю = 0, отбросим это наблюдение, уменьшив размер
выборки до η = 11. Статистика знаков 5 имеет значение s = 9. По
формуле (1) находим ао = (1+11+55)/2048 « 0,033. Следовательно,
на уровне значимости а ^ 3,3% гипотеза Щ: θ = 0 отвергается.
Хотя в нашем случае η < 15, подсчитаем для сравнения
значение статистики S* по формуле (2). Получим 1,809. В таблице
Т2 этому значению соответствует уровень значимости 3,5%.
Упорядочив Zi по возрастанию, вычисляем оценку параметра сдвига
θ = MED{zi,.. .,29,211,212} = 19. Наконец, для а = 0,05 из
неравенства (3) находим ка = 2, что приводит к интервалу (7,35)
с коэффициентом доверия 90%.
ί——г
/с + 1 к + 2
Рис. 2
222
Глава 15. Парные повторные наблюдения
Комментарии
1) Если потребовать, чтобы все величины ε ι в допущении Д6
имели одинаковое распределение, у которого нуль — единственная
медиана, то в силу закона больших чисел (П6) критерий знаков
будет состоятельным против альтернативы Н%: θ > 0.
2) В случае альтернативы Щ: θ < 0, очевидно, достаточно
поменять местами выборки ΑΊ,... ,ХП и Υί,... ,Υη.
3) Покажем, как оценка MED параметра сдвига связана со
статистикой 5 критерия знаков. Интуитивно понятно, что сдвиг
разумно оценить такой величиной 0', чтобы набор Z\ = Zi — θ'
(г = 1,... ,η) выглядел как выборка из распределения с нулевой
медианой. Для такой выборки S имеет биномиальное распределение
(см. § 1 гл. 5), симметричное относительно своего математического
ожидания п/2. Эти соображения приводят к следующему
уравнению относительно 0':
η η
Σ hz[>^} = Σ I{zi>o'} = η/2.
г=1 г=1
Когда величина Θ' становится равной MED, происходит «перескок»
через уровень п/2.
4) Нетрудно убедиться, что приведенный выше доверительный
интервал получается в результате применения метода 1 из § 3 гл. 11
к функции g(zfi) = £/{*<>*}.
5) Ходжес и Леман показали (см. [88, с. 66]), что при
оценивании сдвига с помощью MED следует использовать выборку четного
размера η = 2А:, поскольку выборочная медиана для выборки
размера 2к + 1 имеет ту же самую точность.
§3. КРИТЕРИЙ ЗНАКОВЫХ РАНГОВ
УИЛКОКСОНА
Пусть кроме допущения Д6 выполнено условие
Д7. Случайные величины ει,... ,εη имеют одинаковое
распределение, симметричное относительно нуля:
Fei (—χ) = 1 — F£l (χ) для всех х.
Для проверки гипотезы Н'0 против альтернативы Щ (см. § 1)
совершим следующие шаги.
1) Зададим уровень значимости критерия а (малую
вероятность ошибочно отвергнуть верную гипотезу Н'0).
2) Вычислим Zi = Yi — Xi, г = Ι,.,.,η, и упорядочим
|Ζι|,...,|Ζη| по возрастанию. Пусть R{ обозначает ранг
(порядковый номер) величины |Z<|.
3) Положим Ui = I{Zi>o}i г = 1,... ,η.
§ 3. Критерий знаковых рангов Уилкоксона
223
4) В качестве статистики критерия знаковых рангов возьмем
Τ = R\Ui + ... + RnUn и подсчитаем ее значение t на реализациях
хи...,хп иуь...,уп.
Малые выборки. При η ^ 15 отвергнем гипотезу Яд, если
окажется, что t ^ £Q, где критическое значение ta берется из
таблицы А А книги [88].
Большие выборки. Для η > 15 можно использовать
стандартизированную статистику
г = Г-МГ = Г-[п(п + 1)/4] (4)
уДУГ у/п(п + 1)(2п+1)/24*
распределение которой сходится к ЛГ(0,1) при η —► оо, если
справедлива гипотеза ifq и выполнены условия Д6—Д7 (задачи 4-6).
В случае, когда наблюдаемое значение этой статистики
t* ^ xi-ot, где х\-а — (1 — а)-квантиль закона ΛΓ(Ο,Ι), гипотеза Н'0
отвергается, иначе — принимается.
Поправка. В 1974 г. Р. Иман предложил следующую
аппроксимацию, обеспечивающую значительное снижение относительной
ошибки для критических значений. Она использует линейную
комбинацию нормальной и стьюдентовской квантилей (см. [88, с. 47]).
Положим
i' = if[l + V(«-l)/[»-(i?]]. (5)
С помощью таблиц Т2 и Т4 вычислим ζα = (#ι-α+2/ι-α)/2, где х\-а
и у\-а обозначают соответственно квантили уровня (1 — а) закона
Λ/ΧΟ,Ι) и распределения Стьюдента с (п — 1) степенями свободы
(см. § 2 гл. 11). Если ϊ* ^ 2α, то гипотеза Н'0 отвергается, иначе —
принимается.
Совпадения. Если среди значений Zi встречаются нули, то их
надо отбросить и, соответственно, уменьшить η до числа
ненулевых значений Ζ ι. Если среди ненулевых \Ζχ\ есть равные, то
для вычисления статистики Τ надо использовать средние ранги.
В формуле (4) дисперсию ΌΤ следует заменить на
1_
24
n(n + l)(2n + l)-i £/*(£-1)
1 fc=i
(6)
где д — число групп совпадений, Ik — количество элементов в к-й
группе.*)
) Не совпадающие с другими наблюдения считаются группой размера 1. Если
совпадений нет вовсе, то сумма в выражении (6) пропадает.
224
Глава 15. Парные повторные наблюдения
Оценка параметра. Когда гипотеза Щ отвергается, в качестве
оценки параметра сдвига θ можно взять медиану средних Уолша
(см. § 3 гл. 8)
W = MED{(Zi + Ζά)/2, l^i^j^n}.
Доверительный интервал. Построение доверительного
интервала для случая η ^ 15 описано в [88, с. 55]. При больших η пара
порядковых статистик (V(fca+i),V(M-fca)) образует приближенный
доверительный интервал с коэффициентом доверия 1 — 2а. Здесь
V(i) ^ ... ^ У(м) —упорядоченные по возрастанию средние Уолша
(Zi + Zj)/2 при 1^г^'^пиМ = п(п + 1)/2; ка — это целая
часть числа
п(п + 1)/4 - 0,5 - ζι_αλ/η(η+1)(2η + 1)/24, (7)
где х\-а обозначает, как и ранее, (1 — а)-квантиль закона Λ/^Ο,Ι),
а 0,5 представляет собой поправку на непрерывность (см. § 2).
Проверка симметрии. Прежде чем применять критерий
знаковых рангов, следует удостовериться в справедливости допущения
Д7. Простой графический метод проверки основан на сходимости
выборочных квантилей к теоретическим (см. § 3 гл. 7). Так как для
теоретических квантилей ζρ симметричного относительно медианы
Ζι/2 закона верно равенство Ζι/2 — ζρ = Ζ\-ν — Ζι/2ι то для
порядковых статистик Ζψ) можно ожидать выполнения соотношений
6 = MED - Z{i) ъщ = Z(n+1_0 - MED, i = 1,... ,[n/2],
(здесь [·] обозначает целую часть числа). Поэтому для выборки
Zi,... ,Zn из симметричного относительно медианы распределения
точки плоскости (£i»?7i) должны располагаться вблизи диагонали
У = х-
Замечание 2. Условие строгой симметрии относительно
медианы является почти столь же нереалистичным, как и
предположение, что распределение величин Z{ в точности нормально. Как
правило, надежно проверить симметрию можно лишь по выборке из
нескольких сотен наблюдений. Асимптотический критерий Гупты
для решения этой проблемы приведен в [88, с. 76]. Ссылки на
другие критерии см. там же на с. 81.
Предположение о симметрии иногда оказывается справедливым
в силу специфики получения наблюдений, приводящей к
одинаковым вероятностям отклонения на произвольную величину от
медианы как влево, так и вправо.
Симметрия распределения величин Zi довольно естественно
возникает в модели «контроль — обработка» (см. пример 1 гл.8).
Однако подчеркнем еще раз, что в случае совместной
независимости выборок Χι,...,Χη и Yi,...,y^ для проверки гипотезы
§ 3. Критерий знаковых рангов Уилкоксона
225
однородности следует использовать не критерии знаков и знаковых
рангов Уилкоксона, а методы, изложенные в гл. 14.
Пример 2. Для данных из примера 1 проверим гипотезу Щ: θ = О
с помощью критерия знаковых рангов. После отбрасывания Ζιο = О
в выборке останется η = 11 наблюдений. Упорядочим их:
Z(j) | -8 | -7 | 71 10 1 19 | 19 | 20 | 23 | 35 | 45 | 52
Видим, что MED = 19. Для визуальной проверки симметрии
построим точки (&,ту<), определенные выше. Проведем прямую у = χ
(рис. 3). Хотя выборка слишком мала для уверенного заключения,
построенная диаграмма, по-видимому, не противоречит допущению
о симметрии распределения случайной величины Zi.
Упорядочим по возрастанию величины |Z<| и присвоим средние
ранги совпадающим значениям:
\Zi\
А
Ui
7
1,5
0
7
1,5
1
8
3
0
10
4
1
19
5,5
1
19
5,5
1
20
7
1
23
8
1
35
9
1
45
10
1
52
11
1
Согласно приведенной таблице статистика критерия знаковых
рангов Τ = Y^R%Ui = 61,5. Учитывая, что среди величин \Ζχ\
есть две группы совпадений, по формуле (6) вычислим дисперсию
DT = (11 · 12 · 23 - 3 - 3)/24 = 126,25. Отсюда по формуле (4)
для нормированной статистики Т* получаем значение t* « 2,54.
Положив α = 0,005, из таблиц Т2 и Т4 (при к = η — 1 = 10)
находим ζα = (2,576 -f 3,169)/2 « 2,87. Согласно формуле (5) имеем
ί* = 3,14. Так как 3,14 ^ 2,87, то гипотеза Щ отвергается на уровне
значимости 0,005.
С помощью компьютера вычисляем значение оценки параметра
сдвига W = MED{(Zi + Ζ,·)/2, г ^ j} = 19,25. На основе
формулы (7) строим 90%-цый доверительный интервал (V(15),V(52)) =
= (15/2,31), который несколько уже интервала (7,35), полученного
ранее при применении критерия знаков к этим же данным.
0 10 20 30
Рис. 3
Комментарии
1) Если в условии Д7 все ει имеют одинаковое симметричное
гладкое распределение (см. § 1 гл. 8), то критерий знаковых рангов
будет состоятельным против альтернативы Щ: θ > 0 (см. [86,
с. 64]).
2) Покажем, что связь между статистикой Τ критерия
знаковых рангов и медианой средних Уолша W аналогична
рассмотренной ранее связи между статистикой S критерия знаков и
выборочной медианой MED. Согласно задаче 1 при отсутствии нулевых
значений и совпадений среди величин |Ζ*| статистика знаковых
226
Глава 15. Парные повторные наблюдения
рангов Τ равна Σ I{(Zi+Zj)/2>о}> τ·е· Τ есть число положительных
средних Уолша. ^Естественной оценкой параметра сдвига θ будет
такая величина 0, чтобы набор Z[ = Zi — θ (г = 1,... ,η) выглядел
как выборка из закона с θ = 0. Но при θ = 0 распределение
статистики Τ симметрично относительно своего среднего п(п+1)/4.
Тем самым, приходим к соотношению
Σ Ι{(ζΐ+ζρ/2>ο} = Σ 1{(zi^zj)/2>d] = n(n + l)/4.
Когда величина θ становится равной медиане средних Уолша,
происходит «перескок» через уровень п(п + 1)/4.
3) Построенный выше доверительный интервал получается
в результате применения метода 1 из § 3 гл. 11 к функции
9(*β) = Σ I{(zi+zj)/2>0}'
4) Сравним критерий знаков с критерием знаковых рангов по
их «чувствительности» к обнаружению сдвиговой альтернативы
Н'ъ: θ > 0. Их относительная точность при больших η (см. [86,
с. 77]) совпадает с относительной асимптотической
эффективностью (см. § 4 гл. 7) связанных с критериями оценок: выборочной
медианы MED и медианы средних Уолша W (доказательство
приведено в [86, с. 90]). Согласно теоремам 1 и 3 гл. 8 на классе fis
гладких симметричных распределений верно равенство
eMED^(F) = —Ά-Γ, (8)
3(}p2(x)dx)
где р(х) = F' (#) — плотность закона с функцией
распределения F(x). В частности, для нормального закона eMED,w = 2/3 < 1
(см. задачу 1 гл. 7 и вопрос 5 гл. 8), а для распределения Лапласа
£med,w = 4/3 > 1 (см. задачу 1 гл. 8).
Оказывается, чем «легче» хвосты у распределения F, тем
предпочтительнее оценка W по сравнению с MED. Для уточнения
этого утверждения приведем отрывок из [86, с. 122], в котором
обсуждается предложенное У. Ван Цветом в 1970 г. упорядочение
симметричных распределений по весу их хвостов:
«Пусть F и G из Ω5. Будем говорить, что хвосты F «легче»
хвостов G (или G имеет хвосты «тяжелее», чем у F), что обозначается
F ^ G, если функция G~l(F{x)) выпукла при χ ^ 0.**
Заметим следующее: 1) F ^ F, 2)F^GnG^H влечет
за собой F ^ Н. Следовательно, ^ — слабое упорядочение. Если
F ^! G и (? ^ F, то мы называем F и G эквивалентными.
Пусть F(x) = G(ax) при α > 0, тогда G~1(F(x)) = αχ, так что
F ^ G, также F~1(G(x)) = χ/а и поэтому G ^ F. Отсюда мы видим,
что распределения, различающиеся лишь по параметрам масштаба,
эквивалентны.
*) Определения выпуклости и строгой выпуклости функции приведены в П4.
§ 4. Зависимые наблюдения
227
Так как F и G из Ω5, то их плотности / и g положительны
в нуле. Далее положим /(0) = д(0) (общность при этом не
теряется), что достигается преобразованием масштаба: F(x) = F{x/a)
с σ = f(0)/g(0). Теперь допустим, что F ^ G, причем они не
эквивалентны. Тогда q(x) = G~1(F(x)) строго выпукла для некоторого х,
a q'(x) = f(x)/g(G~1(F(x))) строго возрастает для некоторых х.
Поскольку <j'(0) = f(0)/g(0) = 1, то q'(x) > 1 для некоторых χ и,
наконец, G~l(F(x)) > χ. Отсюда F(x) > G(x) и 1 - F(x) < 1 - G(x),
так что вероятность попадания наблюдения «на хвост» G больше».
Нетрудно проверить, что верно следующее упорядочение:
равномерное ^ нормальное ^ закон Лапласа =^ закон Коти
Можно доказать (см. [86, с. 137]), что для F, G £ Qs отношение
F *4 G влечет неравенство eMED,w(F) ^ eMED,w(G), где eMED,w
задается формулой (8).
§4. ЗАВИСИМЫЕ НАБЛЮДЕНИЯ
До сих пор мы предполагали, что приращения Zi независимы
(допущение Д6). Для иллюстрации того, что происходит при отказе
от этого допущения, рассмотрим следующий пример.
Пример 3. Влияние сериальной корреляции [86, с. 38].
Пусть компоненты нормального случайного вектора (Ζι,...,Ζη)
(см. П9) таковы, что Ζι ~ Λί(θ, 1), M(ZiZj) = ρ при ^ = г±1и0 —
в противном случае, причем коэффициент корреляции \р\ ^ 1/2.
(Корректность данного определения проверяется в задаче 2.) При
/9 = 0 получаем независимые Ζ ι, а при ρ φ 0 зависимы лишь
стоящие рядом случайные величины. Эта модель — частный случай
m-зависимой последовательности с га = 1 (см. П6).
Проверим гипотезу Щ: θ = 0 против альтернативы Щ: θ > 0.
При ρ = 0 равномерно наиболее мощный критерий Неймана-
Пирсона уровня значимости а задается критическим множеством
{z e Rn: yfn~z ^ #ι_α}, где χ ι _α — квантиль закона Λ/ΧΟ, 1)
с функцией распределения Ф(х) (см. пример 1 гл. 13). Выясним,
каков истинный уровень значимости этого критерия, если на самом
деле ρ φ 0, т. е. вычислим
при справедливости гипотезы Щ. Как линейная комбинация
компонент нормального вектора, статистика y/nZ распределена
нормально с параметрами M(y/nZ) = 0 и D(y/nZ) = 1 + 2р(п — 1)/п
(последнее равенство верно в силу свойств дисперсии 1 и 3 из П2).
Отсюда при больших η имеем
αρ(Ζ) = 1-Ф (Х1_а 1фЁ\ * 1 - Φ {χι-α /у/Т+Щ .
228
Глава 15. Парные повторные наблюдения
Вычислим для критерия знаков аналогичную характеристику
ap(S) = Ρ ((5 - η/2) /ν^/4 > *ι_α) .
Здесь S = Х)£/г> где £7^ = /{^>о}· При выполнении гипотезы Щ
находим, что
MS = n Mt/i = η Ρ (Ζι > 0) = η/2,
DS = η D*7i + 2(η - 1) cov (Uu U2) =
= n/4 + 2(n - 1) [P(Zi > 0, Z2 > 0) - 1/4],
поскольку D[/i = MJ7? - (MUi)2 = M^ - 1/4 = 1/4. Из задачи З
Ρ(Ζι > 0, Z2 > 0) = i + -^ arcsin p. (9)
Подставляя этот результат в предыдущую формулу, получаем
-.^ η . η — 1
D5 = — Η arcsin p.
4 π
Так как Μ |[/ι|3 = Μί7ι = 1/2 < οο, то выполняются условия
теоремы Хефдинга и Робинса из П6, согласно которой распределение
статистики (S— MS)/y/DS стремится к ЛГ(0,1). Отсюда при η —► оо
РК ' V VOS ) \νΊ + (4/π) arcsin ρ)
Наконец, приведем для сравнения аналогичную характеристику
для статистики Τ критерия знаковых рангов Уилкоксона (см. [86,
с. 99]). Из задачи 6 имеем ЬАТ = n(n+l)/4, DT = η(η+1)(2η+1)/24,
а (Τ) = ρ (Т^МГ \ к1_ф ί χι-α \
Μ ' V VDT V V >/1 + (12/ir) axc8in(p/2) /
В таблице указаны значения характеристик при а = 5%.
Ρ
Op(S)
Ор(Г)
-0,4
0,000
0,009
0,000
-0,3
0,005
0,018
0,006
-0,2
0,017
0,028
0,018
-ο,ι
0,033
0,039
0,033
0
0,05
0,05
0,05
ο,ι
0,067
0,061
0,067
0,2
0,082
0,071
0,081
0,3
0,097
0,081
0,095
0,4
0,109
0,092
0,107
0,5
0,122
0,101
0,120
Мы видим, что истинные уровни значимости всех трех
критериев довольно существенно отличаются от 5%. При положительной
корреляции далекие от нуля величины Zi как бы подтягивают
к себе следующие за ними наблюдения, что приводит к увеличению
дисперсии статистики критерия по сравнению с номинальной. Так,
если ρ = 0,4, то гипотеза Н'0 отвергается примерно в 10% случаев
вместо 5%.
Заметим также, что строка для ар(Т) почти идентична строке
для otp(Z). Это объясняется тем, что arcsin ρ = ρ + ρ3/6 + ... .
§ 5. Критерий серий
229
Поэтому
1 + — arcsin(/9/2) «1 + -/0«1 + 2/0.
7Г 7Г
Наличие корреляции для реальных наблюдений — скорее
правило, чем исключение. Б. Мандельброт и Дж. Уоллис исследовали
около 70 рядов геофизических данных: речной сток, количество
атмосферных осадков, частота землетрясений, годовые кольца на
деревьях, мощность геологических слоев, а также число солнечных
пятен (см. [84, с. 420]). В большинстве случаев была выявлена
значимая положительная корреляция.
Пример 4. Колебания уровня воды [90, с. 449]. Рассмотрим
(упрощенную) вероятностную модель, описывающую отклонения
от среднего значения уровня некоторого водного бассейна
(например, Каспийского моря), вызванные испарением с водной
поверхности и колебаниями в стоке. Обозначим через Нп уровень в бассейне
в п-м году. Запишем для него уравнение баланса
#п+1 = Нп — kS(Hn) +Tn+i,
где к — коэффициент испарения^ S(H) — площадь водной
поверхности на уровне Я, Τη+ι — величина стока в (п + 1)-м году.
Пусть Ζη = Нп — if, где средний уровень Η можно
считать известным из многолетних наблюдений. Предположим, что
S(H) = S(H) + c(H — Я). (Для гладких 5(Я) это приближенно
верно для не очень больших отклонений Η — Н.) Тогда величины
Ζη подчиняются соотношениям
Ζη+ι = θίΖη + εη+ι
с а = 1 — ск и εη+ι = Τη+ι — kS(H). Будем считать случайные
величины еп независимыми и одинаково нормально
распределенными с нулевым математическим ожиданием и дисперсией σ2. Как
установлено в [90, с. 448], указанные соотношения имеют при всех
целых η и \а\ < 1 единственное стационарное (П6) решение
Ζη = Σ α%εη-ί, причем cov (Z0, Zn) = σ2αη /(l - a2).
i=0
Интересным практическим выводом в данной модели является
то, что оптимальным (в среднеквадратичном смысле в классе
линейных функций) прогнозом на следующий год по результатам
наблюдений за предшествующие годы ..., Ζη_ι, Ζη служит просто
величина aZn (см. [90, с. 489]).
Законы математики,
имеющие какое-либо
отношение к реальному миру,
ненадежны; а надежные
математические законы
не имеют отношения
к реальному миру.
А. Эйнштейн
§5. КРИТЕРИЙ СЕРИЙ
Рассмотрим один простой метод, позволяющий обнаруживать
определенного вида корреляции наблюдений Ζ ι, который называется
критерием серий (см. [10, с. 91]).
230
Глава 15. Парные повторные наблюдения
Пусть h — некоторый заданный уровень. На практике обычно
в качестве h берут предварительно вычисленное значение
выборочного среднего, выборочной медианы или произвольную константу
между минимумом и максимумом наблюдений.
Положим ζι = I{Zi^h}- Если Ζι,... ,Zn — независимые
одинаково распределенные случайные величины, то ζι,... ,£п — схема
Бернулли (см. § 3 гл. 1) с неизвестной вероятностью «успеха»
p = p(ft) = P(Zi<ft).
Реализация случайных величин ζι,... ,£п представляет собой
последовательность из символов 0 и 1 длины п. Сериями назовем
цепочки символов одного вида. (Например, 111010 содержит 4
серии.) Обозначим число серий через Тп. Тогда
Тп = 1 + δι + ... + ίη_ι, где Si = /{Ci+i#Ci} = ICt+i ~ C»l-
(10)
Вопрос 1.
Чему в этом случае равны
ЬЛТП и DTn?
Вопрос 2.
Чему примерно равна
Р(Тюо>60)прир=1/2?
Вопрос 3.
Как доказать эту
формулу, используя
модель размещения
неразличимых шариков
по ящикам из § 5 гл. 10?
Здесь δί — индикатор перемены символа на (г + 1)-м месте. Если
Ci> · · · ιζη — схема Бернулли, то δι образуют стационарную га-зави-
симую последовательность (П6) с га = 1.
По теореме Хефдинга и Робинса (П6) при 0 < ρ < 1
распределение статистики (Тп - MTn)/\/DTn сходится к ЛГ(0,1).
Поскольку в общем случае вероятность ρ неизвестна, для
проверки независимости Ζ{ применим критерий, основанный на
условной предельной теореме для Тп. Пусть 5η = ζι + ... + ζη. Для
к = 1,2,... ,п — 1; га = 0,1,... ,η; Ι = η — га имеем
р(т -u\q -m)- 1 2^-i^-i lC™ ' А: = 2г,
(П~ ' П" J ~ I (C?r11Cj1_1 + ^.CSTiO/C-, * = 2i + l.
Заметим, что условное распределение Р(ТП = k\Sn = га),
к = 1,2,... ,п, при фиксированном га не зависит от неизвестного
параметра р. Для него верен следующий результат.
Условная предельная теорема. Пусть га, η —► оо так, что
п/(п + га) —► 7 € (ОД) (допущение Д5 из гл. 14). Тогда
Р(ТП < А: | 5П = га) = Ф((Л - Mm,n)^m,n) + о(1),
где
2/т
Доказать формулу для
Дт,п предлагается
в задаче 7.
//m,n = M(Tn|Sn = ra) = l +
„.2 _ п(гр ι Q _ ч _ 2/m(2/m - η)
στη,η - D(?n I ^n - ТП) - 2 -— ·
' η (η — 1)
Здесь Φ(#) — функция распределения закона ЛГ(0,1), I = η — га.
(П)
Этим приближением можно пользоваться при η ^ 20.
Критические значения для меньших η приведены в [10, с. 354].
Задачи
231
Для проверки независимости случайных величин Ζι,... ,Zn
против альтернативы их положительной коррелированности Я+
(отрицательной коррелированности #~), ведущей к относительно
малому (большому) числу серий, надо:
1) задать уровень h (скажем, равный ζ);
2) преобразовать реализацию ζι,... ,zn в последовательность из
нулей и единиц I{Zl^hy,... J{zn^h}l
3) подсчитать количество серий к и число единиц га в этой
последовательности;
4) вычислить дШ)П и σ^ η по формулам (11);
5) найти значение
t* = /^ + °'5 ~ Рт,п)/°туп в случае Я+,
[ (А; - 0,5 - μπι,η)Ιστη,η в случае Я";
6) определить по таблице Т2 приближенный фактический
уровень значимости
а0
= Γι-ΦΗ*)
в случае Я+,
в случае Я~;
7) отвергнуть гипотезу независимости случайных величин
Ζι,... ,Zn, если значение с*о достаточно мало, иначе — принять эту
гипотезу.
Пример 5 [10, с. 93]. Ниже указаны результаты проверки
правильности прогноза температуры воздуха на сутки вперед в течение
28 последовательных дней. Знаками «—» отмечены дни, когда
абсолютная ошибка прогноза была более 2°. В остальных случаях
результаты прогноза отмечались знаком «+».
++++++++++ + + + --+ + + + + - + +
Можно ли утверждать, что правильные и неправильные
результаты прогноза группируются случайно?
В данном примере к = 7, I = 20, га = 8, η = 28. По
формулам (11) вычисляем дт?п = 12,429 и σ^ = 4,414. Отсюда находим
t^ = —2,346, что согласно таблице Т2 значимо мало на уровне 1%.
Таким образом, гипотезу о чисто случайном расположении знаков
«+» и «—» следует отвергнуть.
ЗАДАЧИ
1. Докажите, что при отсутствии нулевых значений и совпадений Мозг гораздо чаще ржа-
\ Г7 \ т веет, чем изнашивается,
среди величин |Z»| для статистики знаковых рангов Т, опреде- ' "™ш" aci^
ленной в § 3, имеет место представление Кристиан Бови
Т= Σ/{(Ζ,+Ζ,)/2>0} = Σ/{(Ζ(ί)+Ζω)/2>0}·
(12)
232
Глава 15. Парные повторные наблюдения
2? Проверьте, что для всех η матрица Σ = ||σ^·||ηχη) где
(1, если j = г,
ρ, если j = г ± 1,
О в противном случае,
положительно определена при \р\ < 1/2.
Указание. Разложите главный минор порядка η сначала по
первой строке, затем —по первому столбцу для получения
рекуррентной формулы.
3* Выведите формулу (9) из примера 3.
Указание. Запишите формулу плотности нормального вектора
(Ζχ^) (Π9) и перейдите к полярным координатам.
4Ϊ* Убедитесь, что при выполнении условий Д6—Д7 случайные
векторы U = (J7i,... ,Un) ий= (ϋι,... ,Λη), определенные при
описании критерия знаковых рангов, независимы.
5? Определим антиранг Αι как такой номер, что IZ^J = 1^1 (г)
(т. е. Ai есть индекс того наблюдения, которое соответствует г-му
по величине абсолютному значению). Положим Wi = I{zA >o}·
Докажите, что при выполнении гипотезы Щ и условий Д6—Д7
случайные величины Wi,...,Wn образуют схему Бернулли
с ρ = 1/2.
6? Используя представление Τ = ^iW{, с помощью теорем Лин-
деберга (П6) и Лебега (П5) установите при справедливости
гипотезы Щ и условий Д6—Д7 сходимость распределения
стандартизованной статистики Т* = (T—MT)/y/DT к закону ΛΓ(Ο,Ι).
7ί Проверьте формулу для дт>п из соотношений (11).
Указание. Используйте представление (10).
РЕШЕНИЯ ЗАДАЧ
1. Пусть Z(ix) < ... < Z(i) —положительные порядковые
статистики. Тогда Τ является суммой рангов этих статистик
относительно их абсолютных значений.
Изобразим круг с центром в начале координат и радиусом
Z(ix) (рис. 4). Тогда ранг Z^j равен числу точек Zyj в круге,
включая Z(ix), поскольку мы ранжируем расстояния от 0. Во
второй сумме из (12) выделим слагаемые с г = %\. Заметим,
что полусуммы (Z(ix) + Z(j))/2 (1 < j < г) будут положительны
только для Z(j), попавших в круг. Перебор всех г = ή,...,ζρ
"р—τ——1*> завершает доказательство.
(i) (n) 2. Обозначим главный минор порядка η через J9n. Условием
положительной определенности матрицы Σ является
положительность всех Di, г = 1,... ,п (см. П10). Разложив Dn сначала по
первой строке, а затем —по первому столбцу, получим
рекуррентное соотношение
Dn+2 = Dn+l - p2Dn, (13)
Рис. 4
Решения задач
233
которое представляет собой разностное уравнение 2-го порядка
с постоянными коэффициентами (см. [42, с. 672]). Поскольку
Di = 1 и Дг = 1 — р2, выводим из (13), что Do = Di = 1
(начальные условия). Так как в уравнении (13) участвует р2, то
его решения при ри—р совпадают. Поэтому можно считать, что
Р>0.
Если 0 < ρ < 1/2, то характеристический многочлен /(λ) =
= λ2 — λ + ρ2 уравнения (13) имеет действительные корни
λι,2 = 2 (1 ^ λΑ ~~ 4р2), причем 0 < λ2 < λι < 1. Общее решение
уравнения (13) в этом случае представляется в виде а\™ + 6λ2,
где константы а и Ь находятся из начальных условий. Ответ
таков:
Dn = [(1 - λ2)λ? - (1 - Ai)AJ] / (λ! - λ2). (14)
Неравенство О < λ2 < λι < 1 влечет неравенства 1 — λ2 > 1 — λι
и λ™ > λ2. Поэтому правая часть равенства (14) положительна
при всех п.
Если ρ = 1/2, то λι,2 = 1/2. Общее решение уравнения (13)
ищется в виде (а+Ьп) \™ 2. Начальные условия выполняются для
Лп = (1 + п)2-п>0.
Отметим, что если ρ > 1/2, то при достаточно большом η
минор Dn станет отрицательным. Действительно, формула (14)
и в этом случае дает решение уравнения (13), только теперь
λι и Аг — комплексные числа. Записав их в тригонометрической
форме, используя формулу для синуса суммы, нетрудно вывести,
что
Dn = т£т sin[(n + 1) arcsin#(р)], где Н(р) = ^4^
Функция Н(р) монотонно отображает луч (1/2, +оо) на интервал
(0,1). Введем обозначение φ = arcsin Η (ρ). Тогда φ £ (0,π/2).
Очевидно, что при п*, равном целой части от π/<ρ, аргумент
синуса (η* + 1)φ впервые попадает в интервал (π,2π), где Dn
становится отрицательным.
3. Согласно формуле из П9, искомая вероятность равна
оооо
J J 2тгуТ^ Ι 2(!-Ρ) J
о о
Переходя к полярным координатам х = г cos φ, у = r sin φ
с якобианом замены г, получим
234
Глава 15. Парные повторные наблюдения
Вычислим внутренний интеграл и введем замену ψ = 2φ:
£ΞΖ\ ι #.
4π J 1 — ρ sin V>
о
Это табличный интеграл (см. [20, с. 66, 144]): при \р\ < 1
π
1
Φ
2 tg^"p
с?^ = / arctg
_ π Η- 2 arcsin p
l-psin^ у/1-ρ2 \Λ - ρ2 Ι у/1-Р2
о Ιο
4. Для [Ti = /{Х;>о} по лемме о независимости из § 3 гл. 1 имеем
η
P(l/i = ti<, Ι-ΧΓ.Ι < a*,» = 1,... ,η) = JJ Ρ(*7; = tu, |Х<| < Xi).
i=l
Покажем, что перемножаемые вероятности также распадаются
в произведения. Пусть щ = 1. Тогда в силу непрерывности
и симметрии относительно нуля функция распределения F(x)
случайной величины Xi имеем:
P(Ui = 1, \Xi\ < s) = Р(0 < Xi ^ х) = F(x) - F(0) =
= F^ -\ = \ (2FW -χ)= р(^ =*) р(№1 < *)■
Аналогично доказывается, что для любого χ верно равенство
P(Ui = 0, |Х*| < я) = Р(£7< = 0) Р(\Хг\ < ж).
Таким образом, U = (£/ι,... ,ί7η) и (|Χι|,... ,|-Х"п|) независимы.
Так как R = (ϋι,... ,ДП) — вектор-функция от (|ΑΊ|,... ,Ι-Χ^Ι),
toU и R также независимы.
5. Вектор антирангов А = (Αι,... ,АП) — вектор-функция от R.
Действительно, образуем (2 χ п)-матрицу из столбцов (г,Дг)
и переставим столбцы в порядке возрастания Д^. Тогда А —
первая строка в полученной матрице:
(1 ·· п\ (Аг ··· Ап\
\R! ·.· Rn) ~* V1 ··■ п)'
[Например, (j з 1 4) ^ (l 2 3 ί) ]
Ввиду задачи 4 случайные векторы U и А независимы.
Используя это и формулу полной вероятности (П7), запишем:
P(W = ν>) = Σ p(W = w\A = a)P(A = a) =
= Σ Ρ(^{ζα.>ο} = Щ, г = 1, · · · ,η) Ρ(Α = о) =
;ρ(Α = α) = 2-η,
что и требовалось установить.
-G)"?1
Решения задач
235
6. Согласно определениям статистики Τ и случайных величин Wi
имеем:
T=±RiUi = tRi I{Zi>0} = t i hzAi>o) = tiWi.
Другими словами, Т —линейная комбинация независимых
и одинаково распределенных бернуллиевских случайных
величин Wi. Отсюда по свойствам из П2 немедленно получаем, что
МТ = Σ iMWi = Ι Σ г = η(η + 1)/4,
ΏΤ = Σ ? OWi = \ Σ г2 = η(η + 1)(2η + 1)/24.
Для установления асимптотической нормальности статистики
Τ центрируем Wi (перейдем к & = Wi — MWi = Wi — 1/2)
и используем следующее утверждение.
Теорема 1. Пусть £ι,£2> · · · —независимые и одинаково
распределенные случайные величины, причем Μ£ι = 0, 0 < σ2 =
η
= D£i < оо. Рассмотрим Sn = Σ °i£i> гДе {ci} — числовая
г=1
последовательность. Если
max{|ci|,...,|cn|} Λ
rn = —/' ' "=Ц- —► 0 при η —► оо,
то 5П /VE£ Α Ζ - ΛΓ(0,1), где DSn = σ2(с? + ... + с2).
Доказательство. Проверим условие Линдеберга (см. П6):
1
2Гл2 Σ Μ
&'(ш>«Щ]
€
<^Σ Μ [οΗΪΗ\ξι\>εσ/νη)] = ± Μ [&Ι№ >εσ/τη)} .
При всех η случайные величины под знаком последнего
математического ожидания мажорируются величиной £2 с
М£2 = σ2 < оо. Так как εσ/τη —► оо, то они сходятся к 0 при
всех ω. Чтобы завершить доказательство, остается применить
теорему Лебега о мажорируемой сходимости (П5). ■
7. Ввиду одинаковой распределенности случайных величин δί
согласно формуле (10) имеем
МГП = 1 + (п - 1) Щбг | Sn = πι). (15)
236
Глава 15. Парные повторные наблюдения
Вычислим условное математическое ожидание (см. П7):
Μ(ίι | Sn = m) = Ρ(ίχ = 11 Sn = m) =
_ P(Si = l,Sn=m) _ Ρ(ζιφζ2,ζ3 + ... + ζη=τη-1) _
P(S„ = m) P(Ci + ... + <„ = m)
_ 2p(l - p) Cr-lV""1 (1 ~ P)'"1 _ 2 CZ-2 _ 11m
C?pm(l-p)1 C™ n(n-l)'
где I = n — m. Остается только подставить его в (15).
ОТВЕТЫ НА ВОПРОСЫ
1. Аналогично вычислениям в примере 3 из (10) имеем
МТп = 1 + (п - 1)Μίι = 1 + (η - l)P(Ci ^ C2) = 1 + 2И(п - 1),
где q = 1 — р. Согласно свойству 3 дисперсии (П2) запишем
ОТп = (п - 1) Dii -f 2(n - 2) cov (ib &). (16)
В соответствии с определением случайных величин δ{
Οδ1 = М£2 - (Μίι)2 = Mii - 4рУ = 2pq(l - 2pq),
cov (SUS2) = P(ii = l,i2 = 1) - (Mil)2 =
= P(Ci = 0,C2 = Us = 0) + P(Ci = 1,C2 = 0,Сз = 1)-
— 4p2q2 = q2p + p2q — 4p2q2 = pq(l — 4pg).
Подставляя в формулу (16), получим
DTn = 2pq[(n - 1)(1 - 2pq) + (n - 2)(1 - 4OT)].
2. При ρ = 1/2 по формулам, выведенным в предыдущем ответе,
МТП = (п + 1)/2 и DTn = (η - 1)/4. Для η = 100 и Тп = 60
величина (Тп - MTn)/>/DTn « 1,91. По таблице Т2 искомая
вероятность равна 0,028 (сравните с вопросом 1 гл. 12).
3. Условная вероятность любой последовательности из га единиц
и I = η — га нулей при условии {Sn = га} одинакова и равна
pmql/P(Sn = m) = 1/С™· Пусть fc = 2г + 1. Тогда имеется либо
г серий из «0» и г + 1 серия из «1», либо г + 1 серия из «0» и г
серий из «1». В первом случае разбиение I нулей на г (непустых)
групп можно осуществить C\Z\ способами, га единиц на г + 1
группу — Сгш_х способами (см. вопрос 3 гл. 10).
Глава 16
НЕСКОЛЬКО НЕЗАВИСИМЫХ ВЫБОРОК
В этой главе критерий ранговых сумм Уилкоксона—Манна—Уитни
из § 5 гл. 14 обобщается на случай, когда данные состоят из
нескольких рядов наблюдений (обработок), которые
рассматриваются как реализации независимых между собой выборок.
Исходная гипотеза Но говорит об отсутствии различия в обработках,
т. е. предполагается, что все наблюдения можно считать одной Не в совокупности
^ „ *» *. ищи единства, но
выборкой из общей совокупности. более —в единообразии
разделения.
§ 1. ОДНОФАКТОРНАЯ МОДЕЛЬ Козьма Прутков
к
Данные. Данные состоят из N = Y^rij наблюдений ж^·, по rij
наблюдений в j-ft выборке (обработке), j = 1,... ,fc. Будем считать
их реализацией случайных величин Xij, где
Xij = μ + pj + Sij, г = 1,... ,n,·; j = 1,... ,k. (1)
Здесь μ — (неизвестное) общее среднее, β$ — (неизвестный) эффект
от воздействия фактора для j-ft выборки, е^ — случайная ошибка.
Положим μ^; = μ + /3,.
Обработки
1
#11
#21
3?πχ1
2
Х\2
#22
Хг%22
к
Х\к
#2fc
#Hfcfc I
Допущения
Д1. Все ошибки ец независимы.
Д2. Все е^ имеют одинаковое непрерывное (неизвестное)
распределение.
Для проверки гипотезы однородности
Щ: μι = ... = μ\ζ
можно использовать критерий Краскела—Уоллиса (§ 2) или
критерий Джонкхиера (§ 3).
§2. КРИТЕРИЙ КРАСКЕЛА-УОЛЛИСА
Критерий Краскела—Уоллиса (см. [88, с. 131]) применяется для
проверки гипотезы Н0 против альтернативы
Hi: не все μ^ равны между собой.
238
Глава 16. Несколько независимых выборок
Выполним следующие шаги.
1. Ранжируем все N наблюдений вместе от меньшего к
большему Пусть Rij обозначает ранг наблюдения Х^ в этой совместной
ранжировке.
2. Положим для j = 1,... ,λ;
Sj = Σ -R»i> R-j — Sjln3'> R~ — ~jy Σ Rij = -^ ^ = 2 *
Таким образом, R.j— это средний ранг наблюдений Хц,
относящихся к обработке j, Д.. —общий средний ранг.
3. Найдем значение статистики критерия Краскела—Уоллиса
W, определяемой формулой
12 Л ,п п ,2_
^ = Щ^^пЛЯ,-Я^=[щ^0/п{
12 Д„2,
-3(ЛГ + 1).
Если гипотеза Я0 верна, то все к выборок берутся из общей
совокупности, поэтому величины R .j не должны сильно отличаться
от Д... Это объясняет, почему большие значения статистики W
противоречат гипотезе Щ.
Малые выборки. Гипотезу Н0 следует отвергнуть, если
наблюдаемое значение w статистики W окажется больше или равно к;а,
где критическая граница wa для заданного уровня значимости а
(см. § 1 гл. 12) определяется по таблице АЛ книги [88] (к
сожалению, только для к = 3 и 1 < η j < 5).
Большие выборки. Если гипотеза Щ верна, то при
min{ni,... ,rifc} —► оо
статистика W имеет в качестве предельного закона распределение
хи-квадрат с к — 1 степенями свободы (см. [86, с. 190J).
Приближенный критерий уровня а таков: отклонить гипотезу Но, если
w ^ zi-ot, где ζι-α — это (1 — а)-квантиль χ|_ ^распределения
(см. таблицу ТЗ); в противном случае — принять гипотезу Н0.
Поправка. Для выборок среднего размера точность
приближения может оказаться недостаточной. Например, согласно
примечанию переводчика на с. 132 книги [88], при а = 5% для к = 2
и πι = П2 = 4,5,6 относительная погрешность ошибки I рода
превосходит 33%. Следующая поправка статистики W, предложенная
Р. Иманом и Дж. Давенпортом (1976 г.), позволяет существенно
уменьшить эту погрешность (для указанного случая —в среднем
в 5-6 раз). Именно, в качестве статистики для проверки однород-
§ 2. Критерий Краскела—Уоллиса
239
ности к выборок возьмем
Й?=1 W[(N-k)/(N-l-W) + 1]. (2)
Приближенное критическое значение уровня α для нее равно
Wa = 2 [*1-α + (* " 1)Λ-α] , (3)
где ζι-α и /i_Q —(1 — а)-квантили, соответственно, закона χΙ_ι
(см. табл. ТЗ) и распределения Фишера—Снедекора Fk-i,N-k
(см. табл. Т5).
Совпадения. Если среди х^ встречаются одинаковые значения,
то для вычисления W надо брать средние ранги, а затем заменить
И^на
^\^ -1; m=i
д — число групп совпадений, lm — количество элементов
в га-й группе. Не совпадающие с другими х^ считаются группой
размера 1.
Сравнение обработок. Для того чтобы узнать, какие из
обработок отличаются друг от друга, О. Данн (1964 г.) предложил
следующий приближенный критерий уровня а: принять решение
Mr 7^ ββ> если
где ρ = 1 — а/[к(к — 1)], хр — р-квантиль стандартного нормального
закона ЩО, 1) (см. табл. Т2).
Оценка контраста. Для значимо различающихся обработок
с номерами г и s представляет интерес контраст АГ8 = μΓ — μ8.
В качестве первичной оценки для него возьмем оценку параметра
сдвига, задаваемую формулой (10) гл. 14:
Vrs = MED{Xir - Xl8, 1 ^ г ^ nr, 1 ^ I < ns}, r ^ s; Vrr = 0.
(Отметим, что достаточно подсчитать лишь А:(А: — 1)/2 значений
статистик V^s для г < s, поскольку Vsr = — V^.)
Далее, вычислим взвешенные суммы
к I к л к
Wr = Y,n8Vr8 Ση8 = -~ΣηθΚθ, г = l,...,fc. (5)
s=l / s=l iV s=l
Наконец, определим уточненную оценку контраста как
Ars = Wr-W.. (6)
ΛΓ(ΛΓ + 1)
12
ll/Z
(1/пг + 1/n,)1/2,
(4)
240
Глава 16. Несколько независимых выборок
Пример 1. Содержание влаги [83, с. 368]. Были взяты 14
образцов некоторого продукта, которые случайным образом разбили
на пять групп заданных размеров. Все группы хранились в разных
условиях, а после хранения у всех образцов определили содержание
влаги. Данные (в %) приведены в следующей таблице (в скобках
указан соответствующий ранг Rij):
Условия хранения продукта
1
7,8 (7)
8.3 (10,5)
7,6 (6)
8.4 (12)
8,3 (10,5)
Si =46
Д.1 =9,2
2
5,4 (1)
7,4 (5)
7,1 (3,5)
52 = 9,5
Д.2 = 3,17
3
8Д (9)
6,4 (2)
S3 = 11
R.3 = 5,5
4
7,9 (8)
9,5 (13)
10,0 (14)
£4 = 35
Д.4 = 11,67
5
7Д (3,5)
Ss = 3,5
Ft .5 = 3,5
Статистика Краскела—Уоллиса W для этих данных принимает
значение 8,39. Учитывая два совпадения, получаем W « 8,43.
Для закона χ| по табл. ТЗ линейной интерполяцией находим, что
приближенный фактический уровень значимости а0 « 8%.
Так как размеры выборок малы, сделаем поправку Имана и Да-
венпорта. В соответствии с формулой (2) статистика W « 12,51.
Зададим уровень значимости а = 5%. Найдем квантили ζι-α
и /ι_α, участвующие в формуле (3). Из табл. ТЗ для к — 1 = 4
берем ζι-α = 9,49. Для к\ = 4 и k<i — 9 согласно табл. Т5
имеем Д_а « 3,63. Отсюда wa ~ 12,01 < 12,51. Следовательно,
гипотеза однородности отвергается даже на уровне значимости 5%.
(Отметим, что относительная ошибка найденного ранее
приближенного фактического уровня значимости с*о = 8% составляет
(8 - б)/5 = 60%.)
Для выяснения того, какие же из способов хранения значимо
отличаются друг от друга, применим приближенный метод Данна
(см. формулу (4)). Поскольку rtj малы, зададим не 5%-ный, а
больший уровень значимости.*) Возьмем, скажем, а = 0,15. Тогда для
ρ = 0,9925 из [10, с. 116] извлекаем хр « 2,43. Все значения Сг8
(г < s) указаны в таблице:
Г, S
|Д.Г — R-s\
Ors
1,2
6,03
7,42
1,3
3,70
8,51
1,4
2,47
7,42
1,5
5,70
11,14
2,3
2,33
9,28
2,4
8,50
8,30
2,5
0,33
11,74
3,4
6,17
9,28
3,5
2,00
12,45
4,5
8,17
11,74
*) Когда данных мало, функция дискретного распределения статистики
|Д.Г — R-s\ растет большими «скачками». Поэтому неразумно устанавливать
слишком жесткие условия.
§2. Критерий Краскела—Уоллиса
241
Неравенство (4) имеет место только для пары (r,s) = (2,4).
Таким образом, при вероятности ошибочного решения 0,15 способы
хранения 2 и 4 различаются значимо.
S
1
2
3
4
5
Первичные оценки
Vki = 1,2
Vu = 2,5
Vis = 1,7
V44 = 0
Vie = 2,4
Wa = 1,38
V2i = -1,2
1^22=0
V23 = -0,85
V24 = -2,5
V25=0
W2 = -1,09
ns
5
3
2
3
1
Оценим контраст Δ42. Приведем значения необходимых для
этого первичных оценок Vr8 и их взвешенных сре^ших Wr. В данном
случае значение уточненной оценки контраста Δ42 = W^ — W2 =
= 2,47 мало отличается от значения первичной: V42 = 2,5.
Комментарии
1) Распределение статистики W при условии справедливости
гипотезы Hq можно получить из того, что в этом случае все
ΛΠ/(ηι!.. .rife!) возможных наборов по п\ рангов для первой
выборки, ..., Пк рангов для к-й выборки равновероятны (см.
формулу 3 гл. 10). На каждом наборе подсчитывается значение W
и заносится в таблицу.
2) Надо иметь в виду, что неоднородность некоторой пары
выборок может быть замаскирована присутствием других
выборок в таблице данных (см. [88, с. 135]). Как заметил К. Габриэль
(1969 г.), статистика W имеет тот недостаток, что ее значение w8Ub,
вычисленное для некоторого подмножества выборок, может
превзойти значение wtot для всех выборок. Например, пусть выборке
с номером 1 соответствуют ранги 8, 9,10,11; выборке с номером 2 —
1, 2, 6, 7; выборке с номером 3 — 3, 4, 5, 12. Тогда для выборок
с номерами 1 и 2 (к = 2) w8Ub « 5,333, а для всех трех выборок
Щоь ~ 4,769. (Отметим, что этот же изъян присущ и статистике
Фридмана из следующей главы.)
3) Приближенные критические границы Сг8 в формуле (4)
рассчитаны в предположении, что гипотеза однородности Hq верна.
Когда она не верна, способность метода Данна обнаруживать
значимо различные обработки резко уменьшается с ростом к. Это
хорошо видно из примера 1, где к = 5. Хотя на уровне 0,15
мы и приняли решение μ<ι Φ μ±, уже на уровне 0,1 (хр = 2,58
и С24 = 8,81 > 8,50) мы не смогли бы сделать этого. *) В защиту
*) Критерий ранговых сумм Уилкоксона—Манна—Уитни, примененный к
обработкам 2 и 4 для проверки гипотезы Но против односторонней альтернативы
№ < А*4, имеет фактический уровень значимости ао = 0,05.
Вопрос 1.
Чему равна P(W^2) при
к=т=П2 = 21
242 Глава 16. Несколько независимых выборок
столь консервативного подхода приведем (см. [88, с. 145]) описание
ситуации, где встречается другая крайность — тенденция различать
на самом деле неразличимое.
«Рекламируя по телевидению свое новое лекарство как панацею,
каждая фирма непременно заявляет, что при испытаниях оно
показало себя эффективнее всех известных препаратов. Целью таких
испытаний (если, конечно, они не откровенно подделаны) является
вовсе не помощь изготовителю в принятии решения, а лишь
предоставление ему возможности оптимистически объявить о проведенном
сравнении, дабы произвести впечатление на публику и увеличить
продажу. Правильнее было бы потребовать от него использовать для
статистического анализа метод множественных сравнений. Чем более
одинаково неэффективны были бы хваленые лекарства, тем труднее
было бы сделать убедительный вывод и тем большее число испытаний
пришлось бы провести, чтобы прийти к желаемому заключению».
4) При оценке контрастов с помощью первичных оценок Vr8
мы сталкиваемся с тем неприятным обстоятельством, что они не
удовлетворяют линейным соотношениям, которые выполняются
для самих контрастов. Так, Δ42 = Δ41 + Δΐ2, но в общем случае
V42 φ Vax + V12 (2,5 φ 1,2 + 1,2 = 2,4 в примере 1). На эту
несогласованность величин Vr8 обратил внимание^. Леман. Э. Спе-
тволль (1968 г.) предложил уточненные оценки АГ8 (см. формулы
(5) и (6)), которые не только согласованы, но и состоятельны, когда
пг и п8 стремятся к бесконечности, а остальные rij фиксированы.
Недостатком оценки Аг8 является ее зависимость от выборок с
номерами, отличными от г и s.
5) В случае, когда функция F£ распределения ошибок ец
в модели (1) является нормальной, асимптотическая
эффективность критерия Краскела—Уоллиса по отношению к оптимальному
F-критерию однофакторного дисперсионного анализа (статистика
которого задается равенством (9) в примере 2 ниже) равна величине
E(F£) из формулы (11) гл. 14.
Если справедливо допущение, что наблюдения Х^ имеют
нормальное распределение (или очень похожее на него), то можно
воспользоваться критериями из следующего примера.
Пример 2. Проверка однородности независимых
нормальных выборок. Пусть все Хц ~ Λ/Χμ^, σ|) (г = 1,... ,rij, j = 1,... ,λ;)
независимы, причем параметры μ^ и Gj неизвестны. Несмещенными
оценками для μ^ и σ| являются (см. пример 3 гл. 6)
х., = ±Ъхц и s^-^—YKXij-Xj)2- (7)
Положим Ν = Πι + ... + rife. Для проверки гипотезы
Я': σι = ... = σ&, μι,... ,μ^ — любые,
Статистика может
доказать что угодно, даже
правду.
Ноэл Мойнихан
§2. Критерий Краскела—Уоллиса
243
обычно используется критерий Бартлетта, статистикой которого
служит отношение взвешенных среднего арифметического и
среднего геометрического величин S%,... ,5£:
*-{*£*%)/Ш®14· (8)
Вопрос 2.
Если выполняется гипотеза Я' и все п5 > 3, то статистика в™$^%ч™ НП*™*
Β* = Ί->ΝΙηΒ, ΓΛβ7 = ι + _1_[(έ^)-έ].
приближенно имеет χ^_χ-распределение (см. [10, с. 47]). Можно
показать, что критерий Бартлетта обобщает критерий Фишера из
примера 1 гл. 14 (задача 6).
Когда гипотеза Н' принимается, для установления
однородности выборок остается убедиться, что верна гипотеза
#": μι = ... = Mfc.
Для ее проверки используется F-критерий однофакторного
дисперсионного анализа (см. § 4 гл. 21), основанный на
отношении
ι А ,„ „,а
Ση^Χ-ί-Χ-Υ
k-l Ά }К '3 "' 1 к п>
Д= Ί JIn, , weX.. = j-ZEXij, (9)
которое при справедливости гипотезы Н" распределено в точности
по закону Fk-i,N-k (см. пример 1 гл. 14) для любых п$ > 1.
Доказательство. По условию σι = ... = σ& = σ. Так как
статистика R не зависит от σ, то без ограничения общности будем
считать, что σ = 1. Для фиксированного j рассмотрим случайную
величину Sj из формулы (7). По теореме 1 гл. 11 имеем
(nj - 1) 5? = Σ (Xij - X.j)2 ~ X2nj_v (10)
г=1
Так как выборки независимы и хи-квадрат является частным
случаем гамма-распределения, из соотношения (10) и леммы 1 гл. 4
вытекает, что
vint = Σ Σ (Хц - x-if ~ XN-k- (и)
j=li=l Vint: от англ. variability-
изменчивость, interior —
Здесь Vint — мера общей изменчивости внутри выборок. внутренний.
С другой стороны, случайные величины X.j ~ Λ/Χμ^·, 1/ftj)
независимы между собой. Поэтому (см. задачу 4) при справедливости
244
Глава 16. Несколько независимых выборок
Vout- outside (англ.) —
внешний.
гипотезы Я" статистика
^=Егъ(Х,--Х..)2~х£_1·
(12)
Здесь Vout — мера разброса между выборками.
Ввиду независимости выборок и теоремы 1 гл. 11 Χι,... ,Х* не
1 k
зависят от 5ι,... ,5^. Поскольку X. = — J] njXji т. е. является
N j=i
линейной комбинацией Xj, из леммы о независимости из § 3 гл. 1
вытекает независимость Vint и Vout. Использование определения
закона Фишера—Снедекора завершает доказательство. ■
Замечание 1. Для любых Хц верно тождество (задача 3)
Vtot. total (англ.) —
общий.
Вопрос 3.
Как связана R при к = 2
с Τ из примера 1 гл. 14?
vtot =ΣΣ (Хц - х~Г = Уш + v«,t.
j=l i-1
(13)
Таким образом, общая изменчивость (разброс, дисперсия) Vtot
распадается на слагаемые, каждое из которых представляет свой
источник изменчивости данных. Отсюда и происходит название
«дисперсионный анализ».
Отметим, что статистика критерия Краскела—Уоллиса W
является нормированной величиной Vout для рангов Я^·, статистика
F-критерия R из формулы (9) — это отношение нормированных
величин Vout и Vint.
Замечание 2. Критерий Бартлетта весьма чувствителен даже
к небольшим отклонениям распределения элементов выборок от
нормального. Так, допустим, что все наблюдения распределены по
закону Стьюдента tj с 7 степенями свободы, которое очень похоже
на нормальный закон ЛГ(0,1) (см. рис.7 гл.11). В следующей
таблице приведены некоторые значения (взятые из [10, с. 114, 174])
функций распределения этих законов и разности Δ (χ) между ними.
X
*7
Λ/χο,ΐ)
Δ(χ)
0,0
0,5
0,5
0
0,5
0,683
0,691
0,008
1,0
0,825
0,841
0,016
1,5
0,911
0,933
0,022
2,0
0,957
0,977
0,020
2,5
0,980
0,994
0,014
3,0 I
0,990
0,999
0,009
Наибольшее отличие Дтах = 0,022 достигается при χ « 1,5.
Обозначим через Ьа критическое значение уровня α статистики
Бартлетта В, т. е. Р(В ^ Ьа) = а при справедливости гипотезы Н'.
Г. Бокс (1953 г.) установил, что даже для больших выборок при
замене распределения ЛГ(0,1) на закон ίη эта вероятность меняется
драматически (на рис. 1 изображен сдвиг плотности В при такой
§3. Критерий Джонкхиера
245
замене). Например, для уровня значимости α = 5% получаем
следующую картину:
Законы
Ι Λ/χο,ΐ)
Количество выборок
k = 2
17%
5%
к = Ъ
32%
5%
fc = 10|
49%
5%
Статистик, уверенный в том, что использует уровень 5%, в
действительности может иметь дело с уровнем 49%! Приведем цитату
на затронутую тему из [84, с. 38]:
й
ft
О1 6Q
Рис. 1
«Предполагалось, что отклонения от идеальных моделей можно
игнорировать как несущественные; что статистические процедуры,
оптимальные в строгой модели, останутся примерно таковыми
и в приближенной модели. К сожалению, оказалось, что такие
надежды зачастую не имеют под собой никакой почвы; даже
безобидные отклонения часто имеют следствием эффекты гораздо более
сильные, нежели это предвидело большинство статистиков».
§3. КРИТЕРИЙ ДЖОНКХИЕРА
На практике часто встречается ситуация, когда исследователь
пытается выявить значимое возрастание (или убывание) уровня
интересующего его фактора от выборки к выборке. В этом случае
надо применять не критерий Краскела—Уоллиса, а более
чувствительный критерий Джонкхиера ([88, с. 136]).*)
Он используется для проверки гипотезы однородности Н0
против альтернативы возрастания влияния фактора
Я2: μι ^ ... ^μ&,
(14)
где хотя бы одно из неравенств строгое.
Выполняются следующие шаги.
1. Вычисляются к(к — 1)/2 значений статистики Манна—Уитни
Ura, 1 ^ г < s ^ к (см. § 5 гл. 14), где
Urs=ti:i{Xir<Xu}- (15)
i=U=l
2. В качестве статистики критерия Джонкхиера берется
J=Eur8= Σ1 Σ иГ8. (16)
r<s r—1 s=r+l
*) Критерий был предложен в работах Т. Терпстры (1952) и независимо
А. Джонкхиера (1954) (ссылки на работы см. в [88, с. 140]).
246
Глава 16. Несколько независимых выборок
Малые выборки. Гипотеза Но отвергается, если наблюдаемое
значение статистики J окажется не меньше критической величины
tai которую для /с = 3и2^п7^8 можно найти в таблице А8
книги [88].
Большие выборки. Пусть J* = (J — MJ)/VDJ, где
ш = Емиг8 = \ Znrn8 = \{n2- jznf],
Г<8 Δ Г<8 4 \ j = l /
DJ = ^ \N^2N + 3) " Ση){2ηό + 3)1 , Ν=Σ4.
72 I j=i J j=i
Если верна гипотеза Hq, то статистика J* имеет асимптотическое
распределение ЛГ(0,1) при min{ni,... ,п&} —► оо (см. [86, с. 199]).
Обозначим через х\-а квантиль уровня 1 — а для закона ЛГ(ОД).
В случае, когда наблюдаемое значение J* больше или равно £ι_α,
гипотеза Н$ отвергается, в противном случае — принимается.
Совпадения. Для учета совпадений следует заменить
индикаторы в (15) на /{xir<xls} + - I{xir=xls], чтобы в случае равенства
значений сумма дополнительно увеличивалась на -.
Сравнение обработок с контрольной. Такая задача
возникает, например, при исследовании эффективности ряда новых
методов лечения (лекарств), предназначенных для улучшения
принятого ранее стандартного метода. (Разумеется, позже можно
сравнить друг с другом те обработки, которые оказались значимо лучше
контрольной.)
Пусть роль контроля играет обработка 1. Приближенный
критерий Данна уровня а выглядит так: следует принять решение
№j > Mi) если
v-lV2
\R.j-R.1\^Dj=xp
N(N + 1)
(Ι/η, + 1/щ)1/2, (17)
12
где ρ = 1 — a/(k — 1), хр —р-квантиль закона ЛГ(0,1) (табл. Т2).
Пример 3. Роль мотивации [88, с. 137]. П. Хандел (1969 г.)
исследовал влияние чистой мотивации (знания цели работы) на
выполнение монотонных производственных операций
(вытачивание металлических заготовок определенных форм и размеров).
18 мужчин были случайным образом разделены на 3 группы.
Рабочие, попавшие в контрольную группу А1 не имели
информации о требуемой производительности, в группе В они получили
лишь общее представление о том, что должны делать, наконец,
§3. Критерий Джонкхиера
247
в группе С рабочие имели точную информацию о задании и могли
контролировать себя по графику, лежащему перед ними. В таблице
приведены числа заготовок, обработанных каждым из рабочих за
время эксперимента (в скобках указаны ранги Rij)*^
Группа А
40 (5,5)
35(1)
38 (2,5)
43 (10,5)
44 (13)
41(8)
Si = 40,5
Д. ι = 6,75
Группа В
38 (2,5)
40 (5,5)
47 (17)
44 (13)
40 (5,5)
42 (9)
S2 = 52,5
Д.2 = 8,75
Группа С
48 (18)
40 (5,5)
45 (15)
43 (10,5)
46 (16)
44 (13)
53 = 78
Д.з = 13
Поскольку мы ожидаем таких отклонений от Но, при которых
производительность растет с осведомленностью, применим
критерий Джонкхиера. По формуле (15) с учетом совпадений получаем
U12 = 22, U13 = 30,5, и2г = 26,5.
Согласно (16) имеем J = 22 + 30,5 + 26,5 = 79.
По [88, табл. А.8] находим, что фактический уровень
значимости с*о = 0,023. Теперь применим приближение для больших
выборок и сравним с тем, что дал точный критерий. Значение
J* » 2,02. В табл. Т2 ему соответствует уровень 0,022.
Сравним группы В и С с контрольной. Из приведенной выше
таблицы имеем Д.2 — Д.ι = 2, Д.з — Д.ι = 6,25. Для a = 0,05
квантиль хр = 1,96, D2 = £>з ~ 6,04. Поэтому группа С значимо
отличается от контрольной, а группа В — нет.
Наконец, оценим контраст Δ31. Из таблицы данных находим,
что Vi2 = —1,5, Vis = -4 и V23 = -3. По формулам (5) и (6)
вычисляем Wi = -11/6, W3 = 7/3 и Δ31 = W3-Wi = 25/6 w 4,17 φ
7^31=4.
Комментарии
1) Нетрудно видеть, что величину J можно вычислить по
совместной ранжировке всех N наблюдений. Таким образом, хотя для
подсчета J и не нужна совместная ранжировка, зная ее и не зная
самих Xij, можно восстановить значение J. Поэтому распределение
случайной величины J при условии справедливости гипотезы Щ
можно найти тем же способом, что и распределение статистики
Краскела—Уоллиса W: все Ν\/(ηι\... п&!) возможных наборов
рангов при выполнении гипотезы if о равновероятны; для каждого из
них вычисляется значение J.
*) Ранжировка нужна для сравнения групп В и С с группой А на основе (17).
248
Глава 16. Несколько независимых выборок
2) Для обеспечения состоятельности критерия Джонкхиера
против альтернативы #2 (см. условие (14)) достаточно, чтобы
N —» оо и rij/N —► 7j, где 0 < η^· < 1, j = 1, — ,k.
ι
Рис. 2
§4. БЛУЖДАНИЕ НА ПЛОСКОСТИ
И В ПРОСТРАНСТВЕ
Материал этого параграфа продолжает тему поведения траекторий
случайных блужданий из § 6 гл. 14, только теперь частица будет
перемещаться по точкам с целыми координатами на плоскости или
в пространстве (блуждание по fc-мерной целочисленной решетке
рассматривается в § 4 гл. 17).
Случайным будем называть такое блуждание, при котором
частица переходит в одну из 2к соседних по осям координат точек
с вероятностью — независимо от своего положения (на рис. 2
приведена возможная траектория блуждания*) для к = 2). Пусть,
как и в § 6 гл. 14, U2n — это вероятность вернуться в начало
координат на 2п-м шаге, f<in — вероятность того, что первое
возвращение в начало координат произошло в момент 2п.
Лемма. При η ^ 1 верно равенство u<in — Σ h%^2n-2i
t=l
Щ = 1).
(здесь
Доказательство. Общее число путей за время 2п очевидно равно
(2к)2п. Попадание в начало в момент 2п может быть либо первым
возвращением, либо первое возвращение произошло в некоторый
момент 2г < 2п и далее через (2п—2г) шагов частица вновь вернется
в начало. Вероятность последнего события при фиксированном г
равна /2i^2n-2i> так как имеется (2А:)2г/2г путей длины 2г,
оканчивающихся с первым возвращением, и (2к)2п~2ги2П-2г путей из начала
в начало длины (2п — 2г). При разных г эти события несовместны.
Складывая их вероятности, выводим доказываемую формулу. ■
Установим ряд интересных результатов с ее помощью.
Теорема 1. Пусть к = 1. Обозначим через ^п время, в течение
которого блуждающая по прямой частица, совершая 2п шагов,
находилась правее нуля. Тогда при η ^ 1 /?2г,2п = Р(^2п = 2г) =
= и>2г u>2n-2ii i = 0,1,... ,п (см. теорему 3 гл. 14).
Доказательство. § 6 гл. 14.) Согласно теореме 1 гл. 14
/?2η,2η = ^2η· В силу симметрии имеем также βο,2η = Щп· Поэтому
достаточно доказать теорему для 1 ^ г ^ η — 1.
*) В отличие от терминологии § 6 гл. 14, траекторией (путем) теперь станем
называть не развертку во времени, а ломаную в Rfc, соединяющую
последовательные положения блуждающей частицы.
§ 4. Блуждание на плоскости и в пространстве
249
Пусть для такого г в течение ровно 2г из 2п шагов частица
находилась правее нуля. При этом первое возвращение в нуль
должно осуществиться в некоторый момент времени 2т < 2п, и
имеются две возможности: либо частица до этого момента частица
находилась правее нуля, либо она была левее нуля. В первом случае
1 < г ^ г, и на участке пути после 2г частица находилась правее
нуля в течение (2г — 2г) шагов из (2п — 2г). Всего таких путей
1 cfir £ <y2n-2r о
- Δ J2r ' * P2i-2r,2n-2v
Во втором случае на участке пути после 2г частица находилась
правее нуля в течение 2% шагов из (2п — 2г), откуда г ^ η — г. Таких
путей
1 с%2г £ с\2п—2г о
- Δ J2r · * P2i,2n-2r·
Следовательно, при 1 ^ г ^ η — 1 имеем соотношение
ι г ι п—г
&2г,2п =л Σ f2rP2i-2r,2n-2r + « Σ $2τβ2%,2η-2τ- (18)
Δ r=l Δ r=l
Применим теперь индукцию. Теорема, очевидно, верна при η = 1.
Предположим, что она справедлива для путей, длина которых
меньше 2п. Тогда формула (18) сведется к равенству
1 г ι п—г
$2г,2п = ό u2n-2i Σ hrU>2i-2r + « U2i Σ hr^2n-2i-2v
Δ r=l Δ r=l
С учетом леммы получаем, что первая сумма равна г/2г, тогда как
вторая сумма равна U2n-2ii поэтому теорема верна и для путей
длины 2п, что и требовалось доказать. ■
Рассмотрим степенные ряды с коэффициентами Щп и fc
2η·
U(z) = Σ U2nz2n, F(z) = Σ f2nz2n, 0< * < 1.
n=0 n=l
Связь между функциями U(z) и F(z) устанавливает
Теорема 2. Имеет место соотношение F(z) = 1 — 1/U(z).
Доказательство. Используем условие % = 1и лемму:
оо оо л / η \
ВД - 1 = Σ «2η ^2η = Σ *2П ( Σ Λ< "2n-2i =
n=l n=l \i=l /
— Vs f ~2г V* л, ~2п-2г __
= L·, J2i Ζ 2^ u2n-2i Z =
г=1 п=г
= (£/***) (Ё«2п22п) = F(*)tf(*).
Изменение порядка суммирования законно в силу
неотрицательности членов ряда. ■
250
Глава 16. Несколько независимых выборок
Так как U(z) и F(z) — степенные ряды с положительными
коэффициентами, то их пределы при ζ —► 1 (конечные или
бесконечные) равны, соответственно, Ση2η и Σίΐη (см. [33, с. 57]).
В силу теоремы 2 расходимость ряда Σ u2n равносильна тому, что
Σ /2η = 1· Последнее равенство означает, что блуждающая частица
рано или поздно вернется в начало координат с вероятностью 1.
Такое блуждание называют возвратным. Докажем замечательный
результат, впервые опубликованный Д. Пойа в 1921 г.
Д. Пойа Теорема Пойа. Случайное блуждание на прямой и плоскости
ский математикерИКЭН возвратно, а в трехмерном пространстве — невозвратно.
Доказательство. Исследуем сходимость ряда Ση2η в
двумерном и трехмерном случаях (возвратность одномерного блуждания
была доказана ранее в § 6 гл. 14).
Найдем U2n для блуждания на плоскости. Общее число путей
длины 2п равно 42п. Для того, чтобы в момент 2п частица снова
оказалась в начале координат, число шагов верх должно совпадать
с числом шагов вниз, а число шагов вправо — с числом шагов влево.
Поэтому, если г —это число шагов вверх, то число шагов вниз
равно г, а число шагов вправо так же, как и число шагов влево,
равно η — г (всего 2п шагов). Представим, что шаг —это шарик,
направление — ящик, и мы случайно раскладываем 2п шариков по
четырем ящикам. В соответствии в формулой (3) гл. 10 число таких
размещений шариков равно
iUl(n-i)\\n-i)\=C*a(C$ ■ (19)
Поскольку г может принимать значения от 0 до п, то
«а» = 4-2пС2"„ Σ (Сгп)2 = 4~2пС2п Σ С\ С:~' = (2-2"С£п)2. (20)
г=0 г=0
Здесь мы воспользовались тождеством
£.&пСГ* = С%п, (21)
г=0
вытекающим из сравнения коэффициентов при tn в обеих частях
раскрытого по биному Ньютона равенства (l+t)2n = (l+t)n(l+t)n.
(Другое доказательство формулы (21) будет получено в примере 4
ниже.)
Применение формулы Стирлинга к соотношению (20) (см.
формулу (14) гл. 14) дает асимптотику
ν>2η ~ (ΐ/λ/πη) = — ПРИ η -^ оо,
§ 4. Блуждание на плоскости и в пространстве
251
откуда следует, что ряд Σ u2n расходится, т. е. блуждание на
плоскости возвратно. Аналогично в трехмерном случае имеем
U2n = e-2" ^ М
o«+kn ili!j'!j!(n-i-j)l(n-i- j)!
2 (22)
= 2-2nc?n Σ
0<i+i<n
n!
^(n-i-j)!
Здесь в квадратных скобках стоят вероятности г^· наблюдать при
случайном размещении η различимых шариков по трем ящикам
в первом ящике i, во втором —j и в третьем — (n — i — j) шариков
(см. § 5 гл. 10). Поэтому
Σ rh < max rij Σ rij = max r^·. (23)
Вероятности г^ достигают своего максимального значения при
*о = jo ~ п/3 (задача 2). Используя формулу Стирлинга, получаем
с Зл/3 /0,ч
max r<?· ~ - , где с = ——. (24)
o^t+j^n ■'η 2π ν '
Так как 2~2пС2П ~ l/y/πη, из соотношений (22)-(24) имеем, что
в трехмерном случае г/2П по порядку не превосходит п~3/2.
Следовательно, ряд Ση2η сходится, и блуждание невозвратно. При
оо
этом вероятность возвращения когда-нибудь F(l) = ]Г f^n при-
п=1
ближенно равна 0,35 (см. § 4 гл. 17). ■
Приведем небольшой отрывок из [81, с. 374] о теореме Пойа.
«Прежде всего, почти очевидно, что из этой теоремы вытекает,
что в одномерном и двумерном случаях с вероятностью 1 частица
бесконечное число раз пройдет через каждое возможное положение,
однако в трехмерном случае это неверно. Таким образом, для двух
измерений в известном смысле справедливо утверждение «все дороги
ведут в Рим».
С другой стороны, рассмотрим две частицы, совершающие
независимые случайные блуждания, причем перемещения их происходят
одновременно. Встретятся ли они когда-нибудь? Чтобы упростить
изложение, мы определим расстояние между двумя возможными
положениями как наименьшее число шагов, ведущих из одного
положения в другое. (Это расстояние равно сумме абсолютных величин
разностей координат.) Если две частицы продвигаются на один шаг
каждая, то расстояние между ними либо остается тем же, либо
изменяется на две единицы, и поэтому расстояние между частицами
будет либо всегда четным, либо всегда нечетным. Во втором случае
наши две частицы никогда не смогут занять одно и то же
положение. В первом случае легко видеть, что вероятность их встречи на
п-м шаге равна вероятности того, что первая частица за 2п шагов
достигнет начального положения второй частицы.
252
Глава 16. Несколько независимых выборок
Следовательно, теорема Пойа утверждает, что в двумерном (но
не в трехмерном) случае две частицы наверняка бесконечное число
раз будут занимать одно и то же положение. Если начальное
расстояние между двумя частицами нечетно, то аналогичное рассуждение
показывает, что они будут бесконечно много раз занимать соседние
положения. Если назвать это встречей, то теорема утверждает, что
β одномерном и двумерном случаях две частицы с достоверностью
встретятся бесконечное число раз, однако в трехмерном случае они
с положительной вероятностью никогда не встретятся».
Пример 4. Гипергеометрическое распределение [81, с. 63].
В урне находятся Μ шаров черного цвета и (Ν — М) шаров белого
цвета. Случайным образом без возвращения извлекается группа из
η шаров. Тогда вероятность того, что в ней будет ровно т черных
шаров задается формулой
p{m,nW,N)=C%Cl-_mM/C%, m = 0,l,...,n. (25)
Доказательство. Занумеруем черные шары числами от 1 до Μ,
белые — числами от (М + 1) до N. Пусть черные шары появились
при извлечениях с индексами 1 < г ι < %2 < ... < гш ^ п. Эти
индексы можно выбрать С™ способами. Для фиксированного
набора индексов количество вариантов выбора номеров шаров равно
Ам Αν~™μ> гДе Ам = ЩМ-1) ...(М-т + 1) = т\С% обозначает
число размещений из Μ по т.
Так как количество всех элементарных событий равно А%1
находим, что
s^m дт лп—т
р(т,п,М,Ю = СпАм.пА»-м= (26)
ΛΝ
_ η rnl CM (η - m)\ CN_M _ CMCN_M
n\ Cpf Сдг
Поскольку сумма по всем га вероятностей (25) равна 1, взяв га = г,
N = 2п и Μ = η, получим еще одно доказательство тождества (21).
Название «гипергеометрическое распределение» происходит от
гипергеометрического ряда (см. [42, с. 279])
С(аМ») = 1 + f ζ + i a<a + W + ^ ζ2 + ■ ■ ■, (27)
который при а = 1 и Ь = с сводится к сумме геометрической
прогрессии. Нетрудно проверить, что
р(га,п,М,ЛГ) =
Ап
Лп
1 АМА%
га! -Ajv-M-n+mJ
где величина в квадратных скобках совпадает с коэффициентом
при zm ряда (27), у которого а = -М, b=-nnc = N-M-n + l.
Задачи
253
Любопытно, что многие элементарные функции выражаются
через функцию G:
(1 + z)n = G(-n, 1,1, - ζ), 1η(1 + ζ) = ζ G(l,l,2, - г),
arcsin г = ζ G (l/2,1/2,3/2, ζ2), arctg г = ζ G (l/2,1,3/2, -ζ2).
Модель случайного выбора без возвращения применяется при
выборочном контроле качества продукции. В партии из N изделий
дефектные изделия играют роль черных шаров. Их число Μ
неизвестно. Пусть в контрольной выборке размера η было обнаружено
т дефектных изделий. Формула (25) позволяет сделать выводы
относительно истинного значения М.
Еще одним примером использования данной модели может
служить оценка размера популяции по данным повторного отлова. Из
озера вылавливают Μ рыб, помечают их краской и выпускают
обратно. При повторном отлове η рыб га из них оказались
помеченными. Как оценить общее число N рыб в озере (задача 1)?
Наконец, отметим, что из формулы (26) вытекает сходимость
p(m,n,M,N) -> С™рт(1 -р)п-т
при N —► оо и M/N —► р, где 0 < ρ < 1. Другими словами, для
больших N и Μ практически нет различия между выбором без
возвращения и выбором с возвращением.
ЗАДАЧИ
1. Пусть единственное наблюдение Χι представляет собой число
помеченных рыб при повторном отлове из примера 4. Оцените
общее число рыб в озере методом а) моментов, б) максимального
правдоподобия (см. § 2 и § 4 из гл. 9).
2Ϊ* Проверьте, что г0 и jo» при которых вероятность г^
максимальна (см. пояснение к формуле (22)), принадлежат отрезку
[2_1 ϋ + ι1
[3 1э 3+1J·
Указание. Рассмотрите соседей точки (го Jo) по осям.
3* Получите тождество (13).
4? Подправьте доказательство теоремы 1 гл. 11 так, чтобы вывести,
что статистика Vouti заданная формулой (12), имеет
распределение x2k_v
5? Покажите, что наибольшее значение статистики критерия Крас-
кела—Уоллиса W равно (ΛΓ3 - Σ>?)/[ΛΓ(ΛΓ + 1)].
6* Установите, что критерий Бартлетта при к = 2 равносилен
двустороннему критерию Фишера из примера 1 гл. 14.
Если вы не добились
успеха сразу, попытайтесь
еще и еще раз. А потом
успокойтесь и живите
в свое удовольствие.
Уильям Клод Филдс
254
Глава 16. Несколько независимых выборок
РЕШЕНИЯ ЗАДАЧ
1. а) Вычислим момент ΜΧι = £ т CQ С£Г£ /Cfc:
т=1
т=1
Отсюда находим оценку метода моментов Ν = [ηΜ/ΛΊ], где
[ · ] обозначает целую часть числа. Доля т/п помеченных рыб
в выборке примерно равна их доле Μ/Ν в озере,
б) Рассмотрим отношение соседних вероятностей
р(т,п,М,Ю = (Ν-Μ)(Ν-η)
p{m,n,M,N - 1) (Ν -Μ -η + τη) Ν '
Простые выкладки показывают, что правая часть больше 1,
когда mN < пМ и меньше 1, когда mN > пМ. Поэтому
р(га,п,М,ЛГ) имеет максимум также при N = [пМ/т].
2. Обозначим через го и jo те г и j, на которых достигается
наибольшее значение функции
T(t,j)sTy = 3nry = 7nr
при 0 ^ г + j ^ п.
i\j\(n-i- j)\
Сразу можно выписать следующие четыре неравенства:
ϋ! <т . ϋ! <т. ·
(io-l)!jo!(n-io-io + l)!^ го30' (to + l)!jo!(n-t0-jo-l)!^ го'°'
п!
■<Ti
го
!(jo-l)!(n-to-jo + l)!^ г°'0' to!Uo + l)!(n-to-io-l)!^ г°3°
X. Гюйгенс (1629-1695),
нидерландский астроном
и механик.
Они сводятся к двум таким:
η - jo - 1 < 2t0 < η - jo + !>
η - г0 - 1 < 2j0 ^ η - г0 -f 1.
Подставляя в первое неравенство оценки сверху и снизу для jo
из второго, получаем для го искомые границы. В силу симметрии
они верны и для jo-
3. Для доказательства тождества (13) потребуется теорема
Гюйгенса. Прежде, чем ее сформулировать, дадим несколько
простых определений.
Пусть в Rk заданы точки (векторы) Ж; с приписанными им
массами га;. Положим га = J^m». Центром масс называется
точка с = — У] гПгХг. Для нее, очевидно, выполняется равенство
т
Σ7ηι(χι — с) = О. Величину Ια = Σπι^Χι — о|2 называют
моментом инерции относительно точки о.
Решения задач
255
Теорема Гюйгенса. Ia = Ic + т\с — о|:
Доказательство. Используем очевидные равенства (см. ШО)
\х\2 = χτχ и \х + 2/|2 = \х\2 + 2жт2/ + ll/l2· Пусть ^ = Ж; - с.
Тогда
/а = Σ ™ilVi + (с - а)|2 = /с + 2 (£ пцу^т(с - а) + ш|с - а|2.
Но Х^ш*2/г = О» так как с —центр масс. Следовательно, второе
слагаемое пропадает. ■
Примером применения этой теоремы может служить
вычисление момента инерции тонкого обруча радиуса г и массы га
относительно оси, проходящей через точку на ободе и
перпендикулярной к плоскости обруча (рис. 3). Согласно теореме он
равен 2mr2.
Докажем теперь тождество (13). Для этого запишем теорему
Гюйгенса отдельно для j-ft выборки, полагая га; = 1, га = η7·,
α = X.. и с = X.ji
%(Хц - х..)2 = Σ(Χα - x-i? + nj(x.j - х.)2·
г=1 г=1
Остается только просуммировать по j от 1 до к.
4. Возьмем pj = rij/N (j = l,...,fc), где ΛΓ = Ση3· Тогда, по
определению, X.. = Y^PjX.j- Если все щ = 1, то годится
доказательство теоремы 1 гл. 11. Обобщим его на случай, когда
есть щ > 1. Мы знаем, что X.j ~ Λ/Χμ^·, l/n^) и независимы
между собой, кроме того, мы предполагаем, что верна гипотеза
Η": μι = ... = μίς. Обозначим через μ это общее среднее.
Станем дополнять до ортогональной матрицы не строку
(1/у/к,... ,Ι/y/fc), а строку (\/ρϊ,... ,\/Pfc)· В качестве Υ
возьмем вектор с компонентами Yj = -y/n^ (X.j—μ). Тогда случайная
величина Yj ~ ΛΓ(0,1) и независимы. Рассмотрим Ζ = CY. При
умножении последней строки С на У получается равенство
Zk = y/piYi + ... + y/PkYk.
(28)
к к
Из формулы (4) гл. 11 следует, что Σ Ζ? — Σ Yj. В силу
.7=1 j=l
теоремы Гюйгенса (при rrij = rij, га = ΛΓ, α = μ, с = Χ.) имеем
Σ η,·(Χ,- - Χ.)2 = Σ njiX.j - μ)2 - Ν(Χ.. - μ)2.
j=l 3=1
(29)
Используя определение Yj и учитывая равенство (28), запишем
правую часть (29) в виде
к /к \2 к к-1
Σ*?- Σν^) =Σζ2-ζΙ=ςζ2.
3=1 \j=l / j=l j=l
Z^L
Рис. 3
256
Глава 16. Несколько независимых выборок
Согласно лемме 1 гл. 11 вектор Ζ имеет независимые ЛГ(0,1)
компоненты. ■
5. Подставим ранги Rij в тождество (13) вместо Хц·,:
Σ ηό{κά - д..)2 =ΣΣ(Κί- я··)2 - Σ E(Rij - Rj)2- (зо)
Поскольку первая двойная сумма не зависит от разбиения
рангов {1,2,... ,JV} на группы, минимизируем вторую двойную
сумму. Покажем, что ее минимум достигается на любом из
разбиений, у которых ранги, расставленные по возрастанию
в каждой группе, идут подряд. Для этого нам потребуется
Теорема о межточечных расстояниях (см. [64, с. 28]).
Пусть с— центр масс точек Xi в Rfc с массами га;. Тогда
Ic = Y^rrii\Xi - С\2 = — Σ ™>гЩ\Хг ~ Xj\21 ГДв πΐ = ΣΤηί·
г т i<j г
Доказательство. Обозначим через yi = xi — с. При этом
\xi - Xj\2 = \Vi - 2// = Ш2 + \уа\2 - 2yJyj.
Используя определение момента инерции относительно центра
масс с, запишем
ΣΣ™>ϊ™>3 (Ш2 + \уа\2) = Σ™ιΣ (™>з\Уг? + ™>э\Уэ\2) =
= ЕШг (т|2/г|2 + /С) = 2т/с.
г
С другой стороны,
Σ ς ™>i™>jyjyj = Σ тг2/Г (Emii/i) = о.
г j г \ j /
Отсюда получаем соотношение
2mlc = J2Ylmimj\xi — Xj\2 = 2 Σ rriimj\xi — Xj\2,
г j i<j
которое и требовалось установить. ■
nj
Рассмотрим j-ю группу. Сумма Σ (Rij—R-j) равна моменту
г=1
инерции относительно R.j точек Rij с массами 1. Убедимся,
что он минимален, когда ранги идут подряд. (Это интуитивно
понятно, так как только в таком случае rij точек с
целочисленными координатами образуют наиболее компактную группу.)
' У* 111 #\.' ' Действительно, для любого упорядоченного по возрастанию
φ ι ♦ φ ι φ ι ι ι φ набора из rij рангов соответствующие межточечные расстояния
Рис. 4 могут быть только больше, чем у набора, где ранги идут подряд
(рис. 4).
Ответы на вопросы
257
Вычислим это минимальное значение. Очевидно, что момент
инерции не зависит от выбора начала координат, поэтому можно
считать, что ранги равны 1,2,...,η,. Положим для краткости
η = Пу Тогда по теореме Гюйгенса для rrij = 1, га = η, α = О
и с = (п + 1)/2
г А/. 71+А2 " 2 fn+A2
= n(n + l)(2n + l)/6 - n(n -f l)2/4 =
= n(n -f l)(n - 1)/12 = (n3 - n)/12.
Остается только подставить полученные результаты в
формулу (30) и учесть, что N = п\ + ... + п&.
6. Элементарные выкладки показывают, что статистика F = Sf/S^
критерия Фишера и статистика В критерия Бартлетта при к = 2
связаны соотношением
В = [(nF + m)/N]NF-n1 где ΛΓ = η + га.
При любом Во > 1 (см. ответ на вопрос 2) это уравнение имеет
два действительных корня Fi < 1 и F2 > 1 (если Во = 1, то
Fi = F2 = 1). Таким образом, событие {В > Во} эквивалентно
объединению несовместных событий {F < Fi} и {F > F2}
(рис. 5).
ОТВЕТЫ НА ВОПРОСЫ
1. С точностью до перестановки столбцов возможны только 3
варианта распределения N = 4 рангов:
[2 А)' (з ψ [а з)·
Легко вычислить, что значения статистики W для них равны
2,4, 0,6 и 0 соответственно. Поэтому P(W ^ 2) = 1/3.
2. Заметим, что всегда В ^ 1. Действительно, применим
неравенство Иенсена (П4) к выпуклой вниз функции у = ех и случайной
величине ξ, принимающей значения #; = Ins? с вероятностями
Pi = πι/Ν:
Ы)
2\щ
(4Γ]1/Ν = βΧΡ{ΐ(
πι In s\ + ... + nk
h"2)} =
= exp{5>iM = eM* ^ Me* = 5>"р< = ±Σ*4*1
Таким образом, взвешенное среднее арифметическое не меньше,
чем среднее геометрическое с теми же весами.
Когда, скажем, s\ увеличивается, а остальные s?
остаются фиксированными, среднее арифметическое растет линейно
258
Глава 16. Несколько независимых выборок
по sf, а среднее геометрическое — как степенная функция с
показателем —^ < 1, т. е. медленнее. Если гипотеза Н' не верна
(одна из дисперсий σ? существенно больше остальных), то
соответствующая оценка s? также будет отличаться от других, что
приведет к значению статистики В, значимо превосходящему 1.
При к = 2 статистика Д, задаваемая формулой (9),
представляется в следующем виде:
1
_ Vout
R =
к — 1 Vout
Vint
Ν-2 "" η + τη - 2
В свою очередь, согласно примеру 1 гл. 14 имеем формулу
Τ2 = ^р , (31)
&tot
где Sfot обозначает несмещенную оценку дисперсии одного
наблюдения, построенную на основе объединенной выборки:
4 = ^b[(n-l)S? + (m-l)Sf] =
η + т — 2
- ^L·-, Ε № - x? + Σ И - ΤΠ = —L_ *«·
Следовательно, знаменатели уйиТ2 совпадают. Покажем, что
совпадают и числители. Величина V^t по определению равна
моменту инерции масс пит, расположенных в точках X и У,
относительно общего центра масс (см. решение задачи 3). В силу
теоремы о межточечных расстояниях из решения задачи 5 этот
момент равен числителю правой части равенства (31).
Глава 17
МНОГОКРАТНЫЕ НАБЛЮДЕНИЯ
В этой главе мы обобщим схему парных повторных наблюдений из Пять тысяч раз твердит
§ 1 гл. 15 на случай, когда данные представляют собой fc-кратные °АН0 и то же'
ПОВТОрНЫе Наблюдения, к > 2. Фамусову «Го^о^а^
§ 1. ДВУХФАКТОРНАЯ МОДЕЛЬ
Данные. В каждом из η блоков содержится по одному
наблюдению Xij на каждую из к обработок. Будем считать наблюдения
реализацией случайных величин Х^ в модели
Xij = μ + oti + Pj + 6ij, г = 1,... ,n; j = 1,... ,Α:.
(1)
Блоки
1
2
η
Обработки
1
#11
Х21
Хп\
2
#12
#22
Хп2
к
Х\к
Х2к
Хпк
Здесь μ — неизвестное общее среднее, а* — эффект блока г
(неизвестный мешающий параметр), /3, — эффект обработки j
(интересующий нас параметр), ец —случайная ошибка.*)
Пусть справедливы те же самые, что и в гл. 16,
Допущения
Д1. Все ошибки Sij независимы.
Д2. Все Sij имеют одинаковое непрерывное (неизвестное)
распределение.
*) Заметим, что параметризация (1) избыточна и не позволяет однозначно
восстановить параметры μ, α*, fij. Например, положив а\ = щ + с, β'· = β$ — с
при произвольном с, мы имеем тождество μ + cti + β$ = μ + α.\ + β'·.
260
Глава 17. Многократные наблюдения
§2. КРИТЕРИЙ ФРИДМАНА
Для проверки гипотезы
Я0:/?ι = ... = /?* (2)
против альтернативы
Hi: не все /3j равны между собой (3)
применяется Критерий Фридмана (см. [88, с. 155]). Выполним
следующие шаги.
1. Отдельно для каждого г-го блока (строки таблицы)
ранжируем к наблюдений внутри него от меньшего к большему.
Обозначим через Qij ранг Х^ в совместной ранжировке Хц,... ,Х^.
2. Для j = 1,... ,λ; положим
Ti = ±Qih Q-^Ъ/щ Q.. = ^.n.M*^l) = *+l. (4)
Здесь Q.j — это средний ранг по всем η блокам наблюдений,
относящихся к j-й обработке (столбцу таблицы), Q.. —средний ранг по
всей таблице.
3. В качестве статистики критерия Фридмана возьмем
'-чгпу £»'-«-''
к
пк(к + 1) ~ J
12 v-^2
-3n(ifc + l).
Если гипотеза Я0 верна, то все Q.j должны быть близки
к Q.. = (к + 1)/2. Если /3j не равны, то Q.j будут различаться
сильнее, а поэтому некоторые из (Q.j — Q..)2 окажутся больше
других, что приведет к большим значениям F.
Малые выборки. Гипотеза if о отвергается, если значение /
статистики F превысит критическую границу, определяемую по
таблице А15 из [88] (к = 3, η < 13; к = 4, η ^ 8; к = 5, η ^ 5).
Большие выборки. Если гипотеза Но верна, то статистика F
сходится по распределению при η —► оо к χ|_χ (см. [86, с. 203]).
Приближенный критерий уровня а таков: следует отклонить #о,
если / ^ 2ι_α, где ζι-α — это (1 — а)-квантиль закона χ1_1 (см.
таблицу ТЗ); иначе — принять гипотезу Н$.
Поправка. Для небольших выборок это приближение не
является удовлетворительным. Так, при а = 0,01 для к = 6 и η = 6
относительная погрешность ошибки I рода составляет 63% (см. [88,
с. 132]). Следующая поправка Р. Имана и Дж. Давенпорта (1980 г.)
значительно снижает эту погрешность (в данном случае —до 3%).
§2. Критерий Фридмана
261
Положим
/ = 0, га = 2, если 7 < к < 20, η > 12;
/ = ι, ш = к — 1, если А: ^ 7, η > 7;
/ = 1, га = (к - 1)(п — 1), если к > 5, 2 ^ η ^ 6.
Другие возможные случаи см. в [88, с. 12]. Введем статистику
F=(ZF + raG)/2, где G = [(п - l)F]/[n(k - 1) - F]. (5)
Для статистики F приближенное критическое значение уровня α
равно (hi-a + гаД_а)/2, где ζι_α и Д_а—это (1 — а)-квантили
соответственно распределения χ|_χ (табл. ТЗ) и закона Фишера—
Снедекора ^.^ <*._!)(„_!) (табл. Т5).
Совпадения. Если среди хц,... ,ж^ есть одинаковые значения,
то следует вычислять средние ранги, а затем заменить статистику
^на
F' =
12 Σ (Tj-nQ..)2
3=1
"**1)-гпШ&и)-''}'
«β»
где Qi — это число групп совпадений в блоке г, 1гШ — размер га-й
группы совпадений в блоке г, при этом х^, отличающиеся от других
внутри блока, считаются группой размера 1.
Сравнение обработок. Для определения, какие из обработок
отличаются друг от друга, применяется следующий приближенный
критерий уровня а: принять решение βηφ βν, если
(7)
\TU -Τυ\> Ск,аУ/пк(к + 1)/12,
где Tj определены в формуле (4), а Ск,а представляет
собой (1 — а)-квантиль распределения размаха ξ^) — £(ΐ) выборки
(£ъ · · · Лк) из ЛГ(0,1). Вот некоторые значения (7^>α:
к
α = 0,1
α = 0,05
α = 0,01
2
2,33
2,77
3,64
3
2,90
3,31
4,12
4
3,24
3,63
4,40
5
3,48
3,86
4,60
6
3,66
4,03
4,76
7
3,81
4,17
4,88
8
3,93
4,29
4,99
Более подробные таблицы см. в [10, с. 226] или [88, с. 340].
Оценки контрастов. Обозначим через Auv = βη - βν контраст
эффектов обработок u u v. В качестве первичной оценки контраста
возьмем
Zuv = MED{Xiu - Χίυ, 1 < г < n}.
(8)
262
Глава 17. Многократные наблюдения
Вопрос 1.
Чему равна P(F^4) при
Ь3ип=2?
Поскольку достаточно найти лишь k(k —1)/2 значений
Zuv для и < v.
Определим уточненную оценку контраста Auv так:
Auv = Zu. — Zv., где Zj. = -^ Ζβ, Zjj = 0.
Z=l
(9)
Уточненные оценки не менее эффективны, чем первичные, при
этом они еще и согласованы (см. комментарий 4 в § 2 гл. 16).
Их недостаток — зависимость Δωι> от наблюдений, относящимся
к остальным (к — 2) выборкам.
Пример применения критерия Фридмана к экспериментальным
данным содержится в задаче 1.
Комментарии
1) Распределение статистики F при условии справедливости
гипотезы Hq можно получить, опираясь на равновозможность всех
(А:!)п ранговых наборов.
2) П. Элтерен и Г. Нетер (1959 г.) установили, что
асимптотическая эффективность (для альтернатив сдвига) критерия Фридмана
по отношению к F-критерию двухфакторного дисперсионного
анализа (см. пример 1 ниже) равна
е*Ш = ^ ВД),
где F£ обозначает функцию распределения ошибок ец из (1), E(F£)
задается формулой (11) гл. 14. Некоторые значения E*(F€) для
закона λί(011), равномерного распределения и закона Лапласа,
приведены в следующей таблице из [88, с. 197]:
'—-——^ к
Законы (Fe) '—■—-^_
Нормальный
Равномерный
Лапласа
2
0,637
0,667
1,000
3
0,716
0,750
1,125
4
0,764
0,800
1,200
5
0,796
0,833
1,250
10
0,868
0,909
1,364
00
0,995
1,000
1,500
Пример 1. Деухфакторная модель для нормальных
наблюдений. Допустим, что ошибки Sij из (1) распределены по закону
Λ/Χ0,σ2). В этом случае оптимальным критерием для проверки
гипотезы Н0 (2) является F-критерий двухфакторного
дисперсионного анализа, основанный на статистике (см. [8, с. 160])
^Σ(χ,-χ,)2
*-А 7=1
(»-D(*-i) ££№j ~Xi- ~Xj+x)2
где
1 k ι η ι η fc
Xi. = -£ Σ Xij, Xj = — Σ Xiji Χ·· = ^ΣΣ Xiji
*itl
ni=
i=l
имеющей при условии справедливости гипотезы Hq распределение
Фишера—Снедекора Fk-i9in-1)ik-iy
§ 3. Критерий Пейджа
263
В задаче 2 предлагается доказать следующее тождество:
Σ E№i-х··)2 = кέ(χ, -χ.)2 + η J2(x.j -χ.)2+
(10)
Оно показывает, что общая изменчивость распадается на части,
обусловленные влиянием эффектов блоков и обработок, и часть,
связанную с изменчивостью самих данных (см. замечание 1 гл. 16).
§3. КРИТЕРИЙ ПЕЙДЖА
Нередко условия эксперимента таковы, что обработки
упорядочены естественным образом, например, по интенсивности стимулов,
сложности заданий и т. п. Приводимый ниже критерий Пейджа
(см. [88, с. 163]) учитывает информацию, содержащуюся в
предполагаемой упорядоченности (в отличие от критерия Фридмана,
статистика которого F принимает одно и то же значение для всех
А:! перенумераций обработок).
Для проверки гипотезы Н0 (2) против альтернативы
возрастания эффектов обработок
Я2:/?!<...<&, (И)
где хотя бы одно из неравенств строгое, вычисляется статистика
критерия Пейджа
£=ΣΉ=Γι + 2Γ2 + ... + *Γ*, (12)
где Tj задаются формулой (4).
Малые выборки. Для k ^ 8 приближенные критические
значения 1а статистики L при справедливости Н0 (2) даны в таблице
А16 из [88] (к = 3, η ^ 20; к = 4 - 8, η ζ 12).
Большие выборки. Пусть L* = (L — ML)/\/DL, где
ML = пк(к + 1)2/4, DL = п(к - 1)к2(к + 1)2/144. (13)
Если верна гипотеза if о, то распределение статистики L* сходится
при η —► оо к Л/ХО, 1) (см. [86, с. 207]). Обозначим через х\-а
квантиль уровня 1 — о; закона ЛГ(0,1) (см. таблицу Т2). Когда
наблюдаемое значение L* больше или равно #ι_α, гипотеза Но
отвергается, в противном случае — принимается.
Совпадения. Используйте средние ранги.
264
Глава 17. Многократные наблюдения
Сравнение обработок с контрольной. Допустим, что роль
контроля играет первая обработка. Приближенный критерий
уровня α устроен так: принять решение β$ > β\, если
Τά - 7\ > Dk9ay/nk(k+ 1)/6, (14)
где величина Tj задана формулой (4), Dk,a — (1 — а)-квантиль
распределения максимума из компонент нормального вектора
(ξι,...,&-ι) (см. П9), у которого ξj ~ Л/"(0,1) и М&£ = - при
i φ j (корректность этого определения проверяется в задаче 3). Вот
некоторые значения Dfc,a> вычисленные линейной интерполяцией
таблицы А13 из [88]:
к
a = 0,1
a = 0,05
a = 0,01
2
1,28
1,65
2,33
3
1,58
1,92
2,56
4
1,74
2,06
2,69
5
1,84
2,16
2,77
6
1,92
2,24
2,84
7
1,98
2,29
2,89
8
2,03
2,34
2,94^
Пример 2. Прочность волокон хлопка (см. [88, с. 165]).
В опыте, описанном в книге [93, с. 108], изучалось влияние
количества калийного удобрения, вносимого в почву (в расчете на
Кг О), на разрывную прочность волокон хлопка. При η = 3 блоках
использовалось к = 5 уровней удобрений. С каждой делянки
отбирался один образец хлопка, на котором производилось 4
измерения показателя прочности по Прессли. В таблице приведены
средние по этим четырем замерам, а в круглых скобках — ранги Qij
внутриблочного ранжирования.
Блоки
1
2
3
Калийное удобрение (кг/га)
163
7,46 (2)
7,68 (2)
7,21 (1)
Γι =5
122
7,17 (1)
7,57 (1)
7,80 (3)
Т2 = 5
82
7,76 (4)
7.73 (3)
7.74 (2)
Т3 = 9
61
8.14 (5)
8.15 (5)
7,87 (4)
Т4 = 14
41
7,62 (3)
8,00 (4)
7,93 (5)
Тъ = 12
Проверим с помощью критерия Пейджа гипотезу об отсутствии
влияния количества удобрения на прочность нити против
альтернативы убывания прочности с ростом количества удобрения.
L = Γι + 2Т2 + ... + 5Т5 = 5 + 2 · 5 + 3 · 9 + 4 · 14 + 5 · 12 = 158.
Для а = 0,01 из [88, таблица А. 16] при η = 3 и к = 5 находим, что
критическое значение 1а = 155. Поскольку 158 > 155, гипотеза (для
рассматриваемых уровней количества удобрения) отвергается.
Хотя число блоков η мало, посмотрим, что дает нормальное
приближение. По формулам (13) получаем ML = 135 и DL = 75.
§4. Счастливый билетик и возвращение блуждания
265
Отсюда L* « 2,66. В соответствии с таблицей Т2 эта величина
значимо велика при a = 0,004, т. е. гипотеза должна быть отвергнута
на еще меньшем уровне значимости.
Сравним обработку 4 с обработкой 1. При α = 0,01 согласно (14)
вычисляем границу Dfc)CK^/nfc(fc + 1)/6 = 2,77\/Ϊ5 « 10,7. Так как
Т± — Τι = 14 — 5 = 9 < 10,7, то на уровне 1% обработки не
различаются. Однако, 9 больше, чем граница 2,16 \/Ϊ5 « 8,37,
соответствующая уровню значимости a = 5%. (Вообще, для небольшого
количества данных при сравнении обработок не следует задавать
слишком малые уровни, чтобы не пропустить различие.)
Первичные оценки ]
Ζ4ι = 0,66
Z42 = 0,58
Z43 = 0,38
Z44=0
Z45 = 0,15
ZA = 0,354
Z11 = 0
Zi2 = 0,ll
Zi3=-0,30
Zi4="0,66
Zi5=-0,32 1
Zi. =-0,234
Вычислим по формуле (9) уточненную оценку контраста Δ41.
Значения необходимых для этого первичных оценок Zuv (см. (8)),
а^также их средних Z4. и Ζχ., приведены в таблице. Таким образом,
Δ4ι = Ζ4. - Ζν = 0,588 φ Ζ4ι = 0,66.
Комментарии
1. Распределение статистики L при справедливости
гипотезы Hq можно получить из равновероятности всех (А:!)п наборов
рангов.
2. Критерий Пейджа состоятелен против альтернативы
возрастания эффектов обработок #2 (см. (11)).
В заключение, заметим, что однородность нескольких выборок,
данные которых сгруппированы, можно проверить с помощью
критерия хи-квадрат, рассматриваемого в гл. 18.
§4. СЧАСТЛИВЫЙ БИЛЕТИК
И ВОЗВРАЩЕНИЕ БЛУЖДАНИЯ
Он улетел, но обещал
вернуться.
Из мультфильма
Покажем на трех примерах, как аппарат характеристических и про- «Карлсон вернулся»
изводящих функций помогает вычислять вероятности довольно Математика—дело
СЛОЖНЫХ событий. настолько серьезное, что
wiumnoiA ^v^oixjrijri. ей всегда нужно неМНОЖКО
Напомним, что характеристической функцией случайной ве- занимательности,
личины ξ называется ψξ(ί) = Me***. Основные свойства характери- Б Паскаль
стических функций приведены в П9. В отличие от
характеристических, производящие функции определяются только для случайных
величин, принимающих целые неотрицательные значения:
71=0
(15)
266
Глава 17. Многократные наблюдения
Как счастье своенравно!
Софья в «Горе от ума»
Отметим, что F(z) из теоремы 2 гл. 16 является производящей
функцией времени возвращения блуждающей частицы в начало
координат при k ^ 2, но не является вероятностной производящей
функцией при к = 3, поскольку в этом случае F(l) < 1 из-за того,
что время возвращения с положительной вероятностью бесконечно
(см. теорему Пойа в § 4 гл. 16).
Назовем шестизначный номер билетика (или талончика)
счастливым, если сумма трех первых цифр равна сумме трех последних.
Пусть щ обозначает j-ю цифру номера случайно выбранного
билетика (j = 1,... ,6). При этом случайные величины щ,...,щ
независимы и одинаково распределены: Р(^ = га) = 1/10, га = 0,1,... ,9.
Производящая функция
<Pm(z) = i:(l + z + ... + 2?) = ±(l-zw)/(l-z)
10
10
(16)
Нас интересует Р(щ + щ + щ = щ + щ + щ). Покажем, что число
таких номеров билетиков совпадает с числом номеров, у которых
сумма всех шести цифр равна 27. Для этого воспользуемся
«принципом отражения» (см. §6 гл. 14): номеру (ι/ι,.-.,ι/β) сопоставим
номер (г7ь772,?7з,9 — ^4» 9 — г/5,9 — щ). Очевидно, что это взаимно
однозначное отображение первой группы номеров на вторую.
Основным свойством производящих (а также
характеристических) функций является то, что они перемножаются при сложении
независимых случайных величин ξ и η. Действительно, в силу
леммы о независимости из § 3 гл. 1 и свойства 5 математического
ожидания (П2) имеем:
ψξ+η{ζ) = Μζ*+η = Μζξζη = Μζξ · Μζη = φξ(ζ) φη(ζ). (17)
Положим 5β = ηι + ... + щ. Из формул (16) и (17) выводим, что
Ψ!Ιλ(ζ) = 10Γ+(\-ζ™)*{\-ζ)
\-6
(18)
В соответствии с принципом отражения вероятность того, что билет
окажется счастливым, равна P(Sq = 27), а это есть коэффициент
при ζ27 в разложении функции <Psq(z) по степеням ζ. Для его
вычисления используем разложение бинома в ряд Тейлора
(1 + ^ = 1 + С^ + С^2 + ..., \ζ\ < 1, χ е R, (19)
где
ск = х(х-1)...(х-к + 1)
к\
обобщенный биномиальный
коэффициент. Тогда правая часть равенства (18) записывается в виде
10-*(l-Ctz10 + C%z*>-...)(l-Clez + C/lez2-...).
Перемножая почленно ряды, видим, что коэффициент при ζ27
равен 10"6 (-1 · С% + С\ · C}J6 - С\ · Cl6). Нетрудно подсчитать,
а. с. Грибоедова чт0 искомая вероятность есть 55252 · Ю-6 « 1/18.
§ 4. Счастливый билетик и возвращение блуждания
267
В качестве второго примера найдем вероятность
возвращения в 0 одномерного несимметричного случайного блуждания
Sn = ζι + · · · + £п> У которого «шаги» ξ* независимы и одинаково
распределены: Р(£& = 1) = ρ и Р(£& = — 1) = 1 — ρ = g, где 0 < ρ < 1.
Эта модель ранее появлялась в § 4 гл. 13 при рассмотрении задачи
о разорении игрока.
При ρ φ - в силу закона больших чисел (П6) случайное
блуждание имеет «снос» (рис. 1), вследствие чего интуитивно понятно,
что вероятность возвращения меньше 1. Вычислим, как она зависит
от р.
Как и в гл. 16, будем использовать обозначение u<in для
Р(#2п = 0) и /2п для вероятности вернуться в 0 впервые в момент
оо
2п. Очевидно, что u<in = C2npnqn- Пусть U(z) = Σ U2nz2ni
71=0
оо
F(z) — Σ /2η^2η, 0 ^ ζ ^ 1. Нетрудно убедиться в том, что φθρ-
7^1
мула, связывающая и^п и /2П> приведенная в утверждении леммы
из § 4 гл. 16, остается верной и для несимметричного блуждания.
Поэтому справедливо также и получаемое с ее помощью равенство
F(z) = 1 — l/U(z) (теорема 2 гл. 16). Вычислим U(z). Для этого
понадобится тождество (7£η = (—l)nC^1/24n (коэффициент С^1/2
определен выше).
Применяя разложение (19) с χ = —1/2, находим
Sk
μ=ρ-ς
(μ+ε)η
μη
(μ—ε)η
к п
Рис. 1
Вопрос 2.
Почему оно выполняется?
Щ*) = Σ (-l)nCT1/24npnqnz2n = (1 - Apqz2)
71=0
24-1/2
Следовательно, вероятность возвращения в 0 когда-нибудь равна
F(l) = 1 - 1/17(1) = 1 - χ/1 - 4pq = 1 - |1 - 2р\ = 1 - \р - q\.
В частности, при ρ = 0,9 имеем F(l) = 0,2. Заметим, что
F(l) = /2 + /4 + · · ·, но /2 = 2pq = 0,18 (рис. 2). Таким образом,
если блуждающая частица не вернулась в 0 сразу, то шансы на
возвращение в дальнейшем составляют всего лишь 0,02.
Наконец, вычислим вероятность возвращения в начало
координат для симметричного случайного блуждания по А:-мерной
целочисленной решетке (продолжение материала § 4 гл. 16). Здесь
потребуются не только степенные ряды U(z) и F(z), но и
характеристические функции.
Обозначим через Sn положение блуждающей частицы после η
шагов. Тогда Sn = £х + ... + £п, где fc-мерные векторы шагов £{
независимы и имеют вид (0,... ,0, ± 1,0,... ,0), причем каждое из 2fe
направлений равновероятно.
Вопрос 3.
Как вероятность
невозвращения 1—F(l) = \p—q\
связана с вероятностью
никогда не проиграть
бесконечно богатому
противнику (см. § 4
гл. 13)?
268
Глава 17. Многократные наблюдения
Прежде всего рассмотрим одномерный случай. Вычислим
характеристическую функцию (см. П9) шага ξι:
ψξι(ϊ) = Ме^1 = \ е~* + \ е" = cost.
Δ Δ
С учетом свойства 2 из П9 V>sn (0 = Σ е**' P(^n = 0 = cosn t. В силу
периодичности при / φ га функции e**(i-m) на [—π, π]
π π
Ρ(5η = m) = ^ J ^η(ί) e-itmd< = JL J cos" t,
-<tmA.
Аналогично в А;-мерном случае для векторов t = (ίι,...,ί/ь)
и m = (mi,... ,mfe) справедливы формулы
^(f) = Ме«Т* = ± Σ (е-«* + е«0 = ± Σ cost,,
о-* m
π π
P(Sn = m) = (2π)"* J ... | [i £ cost,
—7Γ —π
Положим в последнем равенстве m = 0. Тогда
«η = P(Sn = О) = (2*)"* J" ... J ί± Σ сое J dt.
—7Г —π
Суммируя далее под знаком интеграла геометрическую
прогрессию, получим следующее представление:
-1-1
Щг) = Σηηζη = (2π)~* J ... J [l - \ Σ cos J dt.
—π —π
Согласно теореме 2 гл. 16 возвратность блуждания равносильна
расходимости интеграла
7Г π
1/(1)
= (2π)~* J... J [l-i Σ οοβ*,·]
-1
dt.
(20)
—π —π
Подынтегральная функция непрерывна всюду внутри fc-мерного
куба [—π, π] χ ... χ [—π, π] кроме начала координат. Поэтому
расходимость интеграла (20) эквивалентна расходимости интеграла по
/.-мерному шару сколь угодно малого радиуса ε с центром в О.
Перейдем к полярным координатам (г,φι,... ,v?fc-i) по формулам (8)
>3,
гл. 3 с якобианом замены J = rk 1sin </?isin φ<ι.. . sin</?fc_2.
Разложение в ряд Тейлора функции cost = 1 — - t2 + o(t2) при
Δ
t —* 0 позволяет заменить подинтегральную функцию вблизи О на
Задачи
269
-ι-i
|(*?+···+Φ
1 2
2Г
-1-1
. Таким образом, интеграл по шару
эквивалентен произведёнию'одномерных интегралов
ε Г π π 2π
^— dr |sinfc_2v?i|dv?i... |sin</?fc_2|d</?fc_2 dy?fc_i
02Г
где выражение в квадратных скобках равно некоторой
положительной константе. Следовательно, сходимость или расходимость
кратного интеграла определяется поведением одномерного интеграла
ε
J rk~3 dr, который, очевидно, расходится при к < 2 и сходится при
о
больших к. Ш
Вероятность возвращения когда-нибудь F(l) = 1 — 1/U(1)
можно найти, численно подсчитав интеграл в правой части
формулы (20). Она приближенно равна 0,35 при к = 3 и 0,2 при к = 4.
ЗАДАЧИ
1. Д. Хэбб и К. Уильяме (см. [88, с. 171]) разработали тест
эстакадного лабиринта для сравнительной оценки
«сообразительности» животных. Он состоит из 12 заданий. В приведенной
ниже таблице даны средние числа ошибок при выполнении этих
заданий крысами, кроликами и кошками (в скобках указаны
ранги Qij внутри каждой строки).
Самое прекрасное, что
мы можем испытать, это
ощущение тайны. Она
есть источник всякого
подлинного искусства
и всякой науки.
А. Эйнштейн
Номер
задания
1
2
3
4
5
6
7
8
9
10
11
1 12
Животные
Крысы
1.5 (2)
1,1 (2)
1.8 (1)
1.9 (3)
4.3 (3)
2,0 (1)
8.4 (3)
6.6 (3)
2.4 (2)
6.5 (2)
2.6 (2)
6,5 (2)
Кролики
1.7 (3)
1.5 (3)
8,1 (3)
1,3 (2)
4,0 (2)
4.6 (2)
4.0 (2)
5.1 (2)
2,5 (3)
6,9 (3)
2,5 (1)
6.8 (3)
Кошки
0,3 (1)
1,0 (1)
3,6 (2)
0,0 (1)
0,6 (1)
5.5 (3)
1,0 (1)
ЗД (1)
ОД (1)
1.6 (1)
4,3 (3)
1,0 (1)
Есть ли животные, которые значимо различаются?
Докажите тождество (10).
270
Глава 17. Многократные наблюдения
3? Установите, при каких значениях коэффициента ρ G [—1,1]
матрица Σ = ||σ^·||ηχη, где
'"=ft
если г = 2,
если г ^ j,
неотрицательно определена (см. ШО).
Указание. Используйте представление Σ = (1 — р)Е + pi, где
Ε — единичная матрица, a J — матрица, все элементы которой
равны 1, и примените преобразование, приводящее I к главным
осям.
Вредно даже читать
о предмете прежде, чем
сам не поразмышляешь
о нем. Ибо вместе с новым
материалом в голову
прокрадывается чужая
точка зрения на него
и чужое отношение к нему,
и это тем вероятнее, что
леность и апатия внушают
избавиться от усилий
мышления и принимать
готовые мысли и давать
им ход. Эта привычка
затем вкореняется,
и тогда мысли все уж
идут обычной дорожкой,
подобно ручейкам,
отведенным в канавы:
найти собственную,
новую мысль тогда уже
вдвойне трудно. Это
в значительной мере
обусловливает недостаток
оригинальности у ученых
А. Шопенгауэр
РЕШЕНИЯ ЗАДАЧ
1. Применим критерий Фридмана. Суммы рангов по столбцам Tj
равны 26, 29 и 17 соответственно. Поэтому статистика критерия
F = 6,5. Согласно табл. ТЗ критическим значением ζι-α на
уровне a = 0,05 распределения хи-квадрат с к—1 = 2 степенями
свободы является 5,99. Так как 6,5 > 5,99, то гипотеза Н0 об
одинаковой сообразительности отвергается на данном уровне
значимости.
Поскольку число блоков η = 12 невелико, вычислим также
поправку Имана и Давенпорта. Новая статистика G = 4,086.
В данном случае к < 7 и η > 7, поэтому / = 1 и га = 2. Отсюда
F = - (IF + mG) = 7,336. Критическое значение Д_а закона
Фишера—Снедекора i*2,22 уровня a = 0,05, вычисленное
линейной интерполяцией по аргументу l/fc2 табл. Т5, равно 3,44.
Критическая граница - (Ιζι-α + гаД_а) = 6,435. Поскольку
F = 7,336 > 6,435, гипотеза Н0 отклоняется.
Проведем сравнение видов животных (обработок) на уровне
α = 5%. Тогда CkyayJnk(k + \)/\2 = 3,31\/l2 « 11,5. Так как
1^2 — Тз| = |29 - 17| = 12 > 11,5, то кошки сообразительнее
кроликов. Однако, |Т\ - Т3| = |26 — 17| = 9 < 11,5, поэтому
нельзя утверждать то же самое относительно крыс.
2. Представим левую часть соотношения (10) в виде
Σ Σ [Хц - χ? = Σ Σ (oi + bj + с,,·)2,
i=lj=l
i=lj=l
где a,i = X{. — X.., bj = X.j — X.. и Cij = X\j — X{. — X.j + X...
Для доказательства тождества (10) достаточно вывести, что
Μ
г,3
г ,3
г,Э
г,3
Ответы на вопросы
271
Проверим, что Σ aibj = Σ aicij = Σ bjCij = 0. В самом деле,
г ,3
г,3
г,Э
Σα^ = Σ<μΣ (x.j - х..) = Σ (Η
г,з
t=l 3=1
η к
<=ι Li=i
ΣΧ-з-ъХ"
= o,
J] сцс^ = Σ ai Σ №j - -X"-j - -^t- + X-) =
i=i Li=i j=i
= Σα{ [kXi. - kX.. - k{Xi. - X.)] = 0.
Аналогично проверяется равенство Σ^°ϋ = 0·
*>i
3. Собственному значению λ ι = η матрицы i" соответствует
собственный вектор (1,... ,1). Так как ранг матрицы J,
очевидно, равен 1, то все остальные собственные значения
\2 = ... = Хп = 0. Пусть С — ортогональная матрица
преобразования, приводящего I к главным осям: С71С = Л. Заметим,
что матрица
В = СТЕС = (1 - р) СТЕС + рСт1С = (1-р)Е + рЛ
подобна Σ (см. Π10). Поэтому согласно следствию 2 из Π10
Dn = det Σ = det В. Но В — диагональная матрица, у которой
Ьц = 1 — ρ + ρη1 Ь22 = · · · = bnn = 1 — р. Следовательно,
Dn = (1 — ρ + /οη)(1 — /θ)η_1 · Условие неотрицательности
всех миноров Di равносильно неравенству —
1
п-1
< ρ < 1.
Для неотрицательной определенности матрицы Σ при любых η
необходимо и достаточно, чтобы 0 ^ ρ ^ 1.
ОТВЕТЫ НА ВОПРОСЫ
1. Возможно (З!)2 = 36 ранговых наборов. Поскольку стати- Чтобы правильно задать
стика F не изменяется при перенумерации блоков и обработок, больш^чаТть ответа
достаточно рассмотреть только 6 вариантов: Р шекли
/1 2 3\ /12 3λ /1 2 3λ
\1 2 ЗУ' \1 3 2/' \2 1 ЗУ'
/1 2 3\ /12 3\ /1 2 3\
V2 3 iy ' V3 1 2,/' ^3 2 iy *
Легко вычислить, что значения статистики F для них равны 4,
3, 3, 1, 1, и 0 соответственно. Поэтому P(F ^ 4) = 1/6.
272
Глава 17. Многократные наблюдения
Рис. 3
2) Согласно определению обобщенного коэффициента
^-1/2 —
-1)η·1·3·...·(2η-1) =
2пп!
_ (-1)п(2п)! _(-l)w(2n)l , )п п п
2ηη!·2·4·...·2η 4n(n!)2 V ; 2n '
3. Совершим один шаг блуждания. Тогда частица окажется либо
в точке 1 с вероятностью р, либо в точке —1с вероятностью
q (рис. 3). Пусть для определенности ρ > 1/2. Тогда в
первом случае невозвращение равносильно неразорению игрока
с начальным капиталом 1 при игре против «бесконечно
богатого» противника. Его вероятность (см. § 4 гл. 13) равна
1 — λ = 1 — q/p. Во втором случае возвращение происходит
с вероятностью 1. Окончательно имеем, что вероятность
невозвращения есть р{\ — q/p) + q>0 = p — q.
Глава 18
СГРУППИРОВАННЫЕ ДАННЫЕ
Нередко данные, находящиеся в распоряжении исследователя,
представляют собой таблицу количеств попаданий наблюдений
в некоторые множества. В этой главе будут рассмотрены методы,
позволяющие анализировать такие данные. Все они имеют в
качестве предельного закона для статистики критерия распределение
хи-квадрат, определенное в примере 3 гл. 11.
Эти методы весьма универсальны, но одновременно довольно
грубы из-за потери информации при группировке. Их можно
рекомендовать для применения на предварительной стадии
статистического анализа.
Ба! Знакомые все лица!
Фамусов в «Горе от ума»
А. С. Грибоедова
§1. ПРОСТАЯ ГИПОТЕЗА
Пусть £ι,... ,£п — выборка (см. §1 гл.4) из закона с функцией
распределения F(x). Разобьем множество значений ξι на N
промежутков (возможно, бесконечных) Aj = (a^fy], j = 1,...,ΛΓ
(рис. 1).*) Положим pj = Ρ (ξι € Δ^·), а случайные величины Vj —
равными количеству элементов выборки в Δ j (ι/ι + ... + ι/# = η).
Функция F неизвестна. Проверяется гипотеза
Я0: F(x) = F0(x),
где F0 —заданная функция распределения. Если гипотеза верна, то
согласно закону больших чисел (П6) частоты попадания β
промежутки pj = i/j/n при достаточно больших η должны быть близки
к соответствующим вероятностям р® = Fo(bj) — Fo(aj).
В качестве меры отклонения от гипотезы Щ Карл Пирсон
в 1900 г. предложил статистику
_0Ч2_^(^-ПР?)2
i=i Pj
npj
(1)
Замечание 1. Первое представление в формуле (1) показывает,
что Х\ есть взвешенная сумма квадратов отклонений частот от
*) Если множество значений ξι является интервалом, то aj = bj-
274
Глава 18. Сгруппированные данные
Вопрос 1.
Почему число степеней
свободы предельного
закона не совпадает
с числом слагаемых
в суммах из (1)?
гипотетических вероятностей. Для фиксированного промежутка
в силу центральной предельной теоремы (П6) каждое
отклонение асимптотически нормально (см. § 4 гл. 7) и имеет порядок
малости \j\fn. Множитель η перед суммой необходим для того,
чтобы предельное распределение статистики не вырождалось в 0.
Поскольку складываются квадраты отклонений с весами, обратно
пропорциональными гипотетическим вероятностям (чтобы
«уравнять» слагаемые между собой), представляется правдоподобным,
что предельным законом будет распределение хи-квадрат — сумма
квадратов независимых и одинаково распределенных по закону
Λ/ΧΟ, 1) случайных величин.
Теорема 1. Если 0 < р!· < 1, j = 1,... ,ΛΓ, то при η —► оо
**-с-
Xn-v
Доказательство. Раскладывая независимые «шарики» &
(г = 1,... ,п) по «ящикам» Δ^· (j = 1,... ,ΛΓ) с вероятностями
ρ® попадания в j-ft «ящик» (см. § 5 гл. 10), получим
P(i/i = Ii,...,i/jv = In) =
(p°i)1i...(p°n)1n,
Ii!...Ijv!
если все lj ^ 0 и l\ + ... + In = n, иначе вероятность равна 0.
Используя известную формулу возведения суммы в n-ю степень
(αϊ + ... + αΝ)η =
*ι ··
ΛΝ >
Ιι+...+Ιν=π
находим, что характеристическая функция (см. П9) случайного
вектора ν = (ι/χ,... ,ι//ν) имеет вид
М*) = MeitT" = (p?ei4' + ... + p%eitN)n, t = (tu.. · ,tN). (2)
Нетрудно убедиться, что для преобразованного случайного вектора
ι/* = (i/J,... ,ζ/]^) с компонентами ι/? = (ι/, —np®)/y/n
характеристическая функция выглядит так:
W. (ί) = е-^*тР° [l + £ р° (е«''^ - 1)1", р° = (р?,... Λ) ·
Логарифмируя и раскладывая при ε —► 0 в ряды Тейлора функции
1п(1 + е) = ε - ε2/2 + 0(ε3) и eie = 1 + ie - ε2/2 + 0(ε3) (см. [82,
с. 573]), получаем:
In
φν. (ί) = -i V^tTp°+n Σ p° (e^/^ -1) -
2
-t[?ii$(^/VK-i)] +o(VVS) =
= -5E^ + 5(ep?*j)2+0(i/VS) = -5*T»+0(i/Vii).
§1. Простая гипотеза
275
где (см. П10)
г- и„ II „ jn\--P°i) npHfc = j,
Отсюда следует, что предел фи* (£) при η —► со есть
характеристическая функция ехр < — - tT Σί > многомерного нормального закона
Λί(0,Σ) (см. П9). (Неотрицательная определенность матрицы Σ
устанавливается в задаче 5.) По теореме непрерывности из П9
распределение случайной величины ι/* сходится к указанному закону.
Заметим, что ковариационная матрица Σ вырождена (ШО).
Причиной этого является линейная зависимость компонент
вектора ι/*:
ν*1 + ... + ν*Ν=0. (4)
Однако, ее подматрица А размера (N — 1) χ (Ν — 1) уже не
вырождена. Действительно, нетрудно убедиться, что обратной к ней
служит матрица
л-1-и-нь и h -{VpI + Vpn приА:==^
А = Ь - \\Ojk\\(N-l)x(N-l)> °jk - \ . о , , .
[1/р% при кфз.
Таким образом, для подвектора с = (z/J,... ,ι^ν-ι) предельным
будет невырожденный нормальный закон ЛГ(0, Л). Согласно
последнему утверждению из П9 и свойству 3 сходимости из П5
сВст —► ζ ~ χ2Ν_ι при η -^ оо. (5)
С другой стороны, из формул (1) и (4) имеем
^=e4w)2-E4w)a+3-w+...+^-i)a.
j=l /^ j=l Pj PN
Но правая часть совпадает с сВст1 что с учетом сходимости (5)
завершает доказательство теоремы 1. ■
Как отмечено в [32, с. 111], приближение распределения
статистики Х\ с помощью закона Xjv-i является достаточно точным при
η ^ 50 и пр® ^ 5 для всех j = 1,... ,ΛΓ.
Замечание 2. Последнее условие предназначено для того, чтобы
обеспечивать возможность попадания хотя бы нескольких
наблюдений & в каждый из промежутков Aj. Это необходимо для
пригодности лежащего в основе теоремы 1 нормального приближения для
распределения величин \/n(pj - р°): чем больше для заданного j
ожидаемое количество попаданий пр®, тем приближение точнее.
Поэтому число промежутков N не должно быть слишком большим.
Однако, его не следует брать и очень малым, так как в этом случае
276
Глава 18. Сгруппированные данные
набор вероятностей р?,...,р§/ недостаточно хорошо представляет
гипотетическую функцию распределения Fo(#). Обычно на
практике берут N « log2 n.
Когда N выбрано, возникает вопрос, каким образом задавать
промежутки Δ^· = (a^fy]. Если областью возможных значений
случайной величины ξι служит ограниченный интервал, то можно
разбить его на равные по длине части. Альтернативным
выбором (годящимся для неограниченных областей значений ξι)
является разбиение действительной прямой на равновероятные
промежутки, у которых aj = bj-i, а правые границы bj находятся из
уравнений F0(bj) = j/N, j = 1,... ,Ν.
Иногда N и р°л не выбираются исследователем, а определяются
самой изучаемой проблемой.
Пример 1. Генетические законы Менделя (см. [35, с. 563]).
В экспериментах с селекцией гороха (1856-1863) Мендель наблюдал
частоты различных видов семян, получаемых при скрещивании
растений с круглыми желтыми семенами и растений с
морщинистыми зелеными семенами. Эти данные и значения теоретических
вероятностей, определяемые в соответствии с законом Менделя
независимого расщепления признаков, приведены в следующей
таблице:
Тип семян
Круглые и желтые
Морщинистые и желтые
Круглые и зеленые
Морщинистые и зеленые
Частота pj
315/556
101/556
108/556
32/556
Вероятность р°
9/16
3/16
3/16
1/16
Проверим гипотезу Но о согласованности частот с
теоретическими вероятностями при помощи критерия хи-квадрат.
Статистика критерия (см. формулу (1)) Х\ « 0,47. Из табл. ТЗ получаем,
что это значение находится между квантилями уровня 0,05 и 0,1
закона χ§. Таким образом, согласие наблюдений с гипотезой Щ
очень хорошее.
§2. СЛОЖНАЯ ГИПОТЕЗА
Метод группировки наблюдений с последующим применением
критерия хи-квадрат применим и для проверки сложной гипотезы Щ
о принадлежности неизвестной функции распределения элементов
выборки некоторому заданному классу функций распределения
?={F(xft), 0евСМ*}.
В этом случае общая (при всевозможных θ € θ) область
значений ξι также разбивается на N промежутков Aj = (a^fy],
Г. И. Мендель
(1822-1884), австрийский
естествоиспытатель.
Вопрос 2.
Чем подозрителен датчик
псевдослучайных чисел,
у которого в промежутки
(404
(И]-(И
попали соответственно
504, 505, 492 и 499 точек?
§ 2. Сложная гипотеза
111
j = 1,... ,Ν. Как и ранее i/j обозначает число элементов выборки
в Δ^. Однако теперь вероятности Ρ(£ι € Δ^) при Hq уже не
будут заданы однозначно, а представляют собой функции от Θ:
Pj(0) = F(bj,e) — F(a,j,e) (рис.2). Из-за этой зависимости от
неизвестного параметра нельзя просто подставить Pj(0) вместо р°
в (1). Р. Фишер (1924 г.) доказал, что если подставить р^(0), где 1
θ — оценка максимального правдоподобия, основанная на частотах ,ЙЛ
(определяемая ниже), то при некоторых условиях на класс Τ 3 \
функций распределения (см. [32, с. 115]) статистика
Χ2η=Σ(^-ηρΛθ))2/[ηΡ^θ)]
7 = 1 '
(6)
О ajAjbj x
Рис.2
будет иметь в качестве предельного закона снова распределение
хи-квадрат, только уже с (N — 1 — к) степенями свободы, где к —
размерность вектора Θ. Доказательство этой
теоремы можно найти
Определение. Значением оценки максимального правдоподобия, в ι ·с *■
основанной на частотах Θ, служит вектор θ = (0i,...,0fc), на
котором достигается максимум вероятности
P(z/i =Ii,...,i/jv = In) =
n\
\Ρι(Θ)]1ι·-·\ρν(Θ)}1ν·
hl...lNl
Это равносильно максимизации по θ функции
3=1
(7)
или (для гладких моделей) решению системы, вообще говоря,
нелинейных уравнений
h j dem -и'
πι = 1,... ,k.
3=1
(8)
Пример 2. Критерий χ2 для пуассоноеской модели (см. [32,
с. 116]). Положим 7Гт(0) = е~в0т/т\, т ^ 0. Возьмем промежутки
Δ; = U ~ U), 3 = 1,...,ЛГ - 1; Δλγ = [Ν - Ι,οο). Тогда
оо
вероятностиρ3(θ) = 7rm_i(0), j = 1,... ,ΛΓ-1; ρΝ(θ) = Σ тгт(0).
m=N-l
Так как θ — скалярный параметр, причем (d/άθ) In 7rm(0) = πι/θ — 1,
το система (8) сводится к одному уравнению:
ΝΣΐΐ+ιϋ/θ-1) + 1Ν Σ (т/0-1)тгш(0)/ £ тгт(0) = 0.
j=0 m=N-l I m=N-l
Поскольку h + ... + In = η, отсюда получаем соотношение
1
θ =
Ν-2 оо / оо
Σ J 'i+i + 'ν Σ ™>πτη(θ) / Σ π™(0)
j=0 m=N-l I m—N-l
(9)
278
Глава 18. Сгруппированные данные
Первый член в скобках равен сумме всех значений &, меньших или
равных N — 2. Второй член представляет собой In M(£i | ξι ^ Ν-ΐ)
(см. Π7). Он приближенно равен сумме всех значений &, которые
больше или равны N — 1. Поэтому решение θ уравнения (9) близко
к среднему арифметическому £ — оценке максимального
правдоподобия параметра 0, построенной по всей выборке.
Применим критерий хи-квадрат к данным о падениях
самолетов-снарядов в южной части Лондона во время второй мировой
войны (см. [81, с. 177]). Опасность попадания в жилые дома вместо
военных объектов велика при низкой точности стрельбы (при так
называемой стрельбе по площадной цели).
Карта южной части Лондона была разбита на η = 24 χ 24 = 576
небольших участков, каждый площадью 1/4 кв. км. На карте
были отмечены места падения самолетов-снарядов (подобно рис. 3).
В таблице ниже приведены количества участков Ζ^+ι ровно с j
падениями, j = 0,1,...,7. Так как участков много, а вероятность
попадания самолета-снаряда на отдельный участок мала, то при
справедливости гипотезы о низкой точности стрельбы можно
воспользоваться законом редких событий (см. § 1 гл. 5), согласно
которому число попаданий на любой из участков есть (приближенно)
пуассоновская случайная величина с некоторым общим для всех
участков параметром Θ. Мы также предположим, что попадания
на разные участки независимы.
Общее число падений Μ = Y^jlj+i = 537. Возьмем в качестве
начальной оценки неизвестного параметра закона Пуассона среднее
число падений на один участок θ = Μ/η « 0,932. Тогда ожидаемые
количества участков ровно с j падениями примерно равны nnj(9).
3
ηπ,·(0)
П7Г/(0)
0
229
226,7
228,6
1
211
211,4
211,3
2
93
98,5
97,6
3
35
30,6
30,1
4
7
7,14
5
0
1,33
6
0
0,21
7
1
0,03
8,46
Прежде чем вычислять статистику критерия хи-квадрат, надо
объединить последние 4 столбца таблицы для того, чтобы
ожидаемое количество оказалось не меньше 5: U + ... + h = 8
и η(π4(0) + ... + тг7(0)) == 8,71.
Теперь заменим начальную оценку θ на 0, максимизируя по 0
функцию (7) на компьютере (удобно вычислять р$(0) по формуле
Рь(0) = 1 — Pi(0) — · · · — Р4(0))· Вероятно, проще всего уменьшать 0
с шагом h = 0,001 до тех пор, пока функция возрастает. Ответ
таков: 0 = 0,924 (отличие от 0 составляет всего-навсего 0,008).
Соответствующие ожидаемые количества приведены в третьей строке
таблицы.
Значение статистики Х\ (см. формулу (6)) для таких данных
равно 1,05. Поскольку N = 5 и к = 1, предельный закон должен
иметь N — к — 1 = 3 степени свободы. Из табл. ТЗ находим,
что значение статистики попадает в интервал (0,58; 2,37), обра-
Вопрос _3.
Почему ξ —ОМ Π для
пуассоновской модели?
Рис. 3
§ 2. Сложная гипотеза
279
зованный 10% и 50% квантилями χ| (с помощью таблицы из [10,
с. 140] уточняем, что фактический уровень значимости равен 0,79).
Поэтому гипотеза о низкой точности стрельбы принимается. В [81,
с. 177] отмечено:
«Большинство населения верило в тенденцию точек падения
скапливаться в нескольких местах. Если бы это было верно, то
следовало бы ожидать большую долю участков без попаданий либо с
большим числом попаданий и меньшую долю участков промежуточного
класса. Приведенная таблица показывает, что точки падения были
совершенно случайными, все участки — равноправными; здесь мы
имеем поучительную иллюстрацию того установленного факта, что
неискушенному человеку случайность представляется регулярностью
или стремлением к скоплению.»
Обратим внимание на необходимость объединения
маловероятных промежутков: если оставить N = 8, то θ « θ = 0,932
и Х\ = 32,6. Это значимо велико для χ| даже на уровне Ю-5
(см. [10, с. 144]). Причиной резкого роста значения статистики
является малая величина ηρ%{θ) « 0,03, придающая слишком
большой вес квадрату отклонения наблюдаемого количества /8 = 1
от ожидаемого количества ηρ%(θ).
Если данные предварительно группируются, то оценить θ
можно и до группировки наблюдений, например, методом
максимального правдоподобия (см. § 4 гл. 9). Однако, как показывает
следующий пример, в этом случае статистика Х\ будет сходиться,
вообще говоря, к другому предельному закону.
Пример 3. Проверка нормальности по сгруппированным
данным. Пусть & ~ ΛΓ(μ,σ2), г = 1,...,п, причем оба
параметра μ и σ неизвестны. Для разбиения прямой на промежутки
Ai = (aj>fy]> j = Ι,.,.,ΛΓ, оценим неизвестную функцию
распределения Ф((х — μ)/σ) при помощи Ф((х — 0/5), где ξ = -£)&
и 52 = — ΣΧ&-О2· Чтобы вероятности попадания ξι в промежутки
Δ^ были примерно одинаковы, возьмем в качестве bj решения
уравнений
4>((x-0/S)=j/N, j = l,...,N-l,
(см. табл. Т2 или приближение Хамакера для Ф-1 из § 5 гл. 4).
Далее подсчитаем i/j — количества попаданий в построенные
промежутки. Затем вычислим основанную на частотах оценку
максимального правдоподобия θ = (^1,^2) при помощи численного
поиска точки максимума функции (7), исходя из точки с
координатами (£,5). При этом для нахождения Pj(0) понадобится
запрограммировать приближенное вычисление у = Ф(#), например,
280
Глава 18. Сгруппированные данные
Δι Δ;
Рис.
-Ϊ—ЭЬ
-*-►
Рис. β
с помощью алгоритма Морана (см. [58, с. 282]):
s = 0
t = x * Sqr(2)/3
For г = 0 То 12
г = г + 0.5
s = s + Sin(2 * t) * Ехр(-г * ζ/9)/ ζ
Next г
у = 0.5 -f s/3.1415926536
(Он обеспечивает 9 точных десятичных цифр у Ф(х) при |х| < 7.)
Важно отметить, что сами оценки ξ и S использовать в
формуле (6) нельзя. В [80, с. 322] указано, что в случае нарушения
этого запрета статистика Х% не будет (асимптотически) следовать
распределению хи-квадрат с N — 3 степенями свободы: график ее
функции распределения пройдет несколько ниже графика функции
распределения закона χ#_3· Не будет она следовать и
распределению хи-квадрат с N — 1 степенями свободы (как было бы при
точно известных параметрах). График ее функции распределения
пройдет несколько выше.*)
В качестве иллюстрации на рис. 4 приведены графики
функций F7 и Fg распределения законов χ^ и χ| соответственно. Они
ограничивают полосу, в которой будет проходить график функции
распределения предельного закона для Х\ при N = 10, если для
вычисления Pj(0) использовать оценки £ и S. Согласно табл. ТЗ на
уровне 0,95 ширина полосы равна 16,9 — 14,1 = 2,8.
§3. ПРОВЕРКА ОДНОРОДНОСТИ
Допустим, что имеется к независимых между собой выборок
размеров щ из распределений F», % = 1,... ,к. Общее число наблюдений
η = πι + ... + η&. Проверим гипотезу однородности
Щ: Fi = ... = Fk
с помощью критерия хи-квадрат. Для этого сгруппируем данные:
разобьем общую для всех выборок область значений наблюдений
на промежутки Δ^, j = Ι,.,.,ΛΓ, и для каждой пары индексов
(г, j) подсчитаем величину щ$ — количество попаданий элементов
i-й выборки в 2-й промежуток (рис. 5). В результате получим kxN
таблицу (рис. 6), которую и будем анализировать в дальнейшем.
Иногда данные с самого начала имеют дискретную структуру:
в опытах наблюдается некоторый переменный признак,
принимающий конечное число N значений (см. пример 4 ниже).
*) Как показали Чернов и Леман в 1954 г. (см. [13, с. 284]), статистика Х\
асимптотически распределена как сумма ξ2 + ... + ξ%_3 + Ίιξ%_2 + 72^_!»
где ξι — независимые Λ/"(0,1)-случайные величины; числа 71 и 72 лежат между
0 и 1 и зависят от проверяемого закона и способа разбиения на промежутки
области возможных значений наблюдений.
§ 3. Проверка однородности
281
Если гипотеза Щ верна, то ожидаемое количество наблюдений
в ячейке с индексами г и j равно щр$, где ρ = (pi,... ,рлг)
обозначает (неизвестный) вектор вероятностей попадания в промежутки
Δ^ при справедливости гипотезы Щ. Естественной оценкой для pj
служит pj = (u\j + ... + Vkj)/n — общая по всем выборкам частота
попаданий в Δ^ (см. задачу 6). Тогда статистика
к N
^η=ΣΣ (Угз ~ Пфз) /(*4Pj)
=1.7=1
(10)
измеряет отклонение наблюдаемых количеств от ожидаемых. Если
справедлива гипотеза Щ, то, как доказано в [44, с. 483], статистика
Х\ сходится по распределению к хи-квадрат случайной величине
с (к — 1)(N — 1) степенями свободы при min{ni,... ,η*} —► оо.
Следующий любопытный пример из [72, с. 132] показывает, что
к выводам, основанным на применении этого предельного
результата, следует относиться с известной осторожностью.
Пример 4. Парадокс критерия хи-квадрат [72, с. 132].
Ниже приведены три таблицы, в которых отражено действие
некоторого лекарства (способа лечения) только на мужчин, только
на женщин и, наконец, на больных обоего пола (объединенные
результаты).
Факты — упрямая вещь,
но статистика гораздо
сговорчивее.
Лоренс Питер
Мужчины
л
А
в
700
80
В
800
130
Женщины
А
1 я
В
150
400
В
70
280 j
Вместе
А
1 я
В
850
480
В
870
410
Здесь А — принимавшие лекарство, А — не принимавшие
лекарство, В — выздоровевшие, В — не выздоровевшие.
Заметим, что среди принимавших лекарство мужчин доля
выздоровевших 700/(700 4- 800) » 0,467 больше, чем 80/(80 + 130) «
« 0,381—доля выздоровевших среди мужчин, не принимавших
лекарство. Такая же картина и у женщин: 150/220 w 0,682 >
> 400/680 » 0,588.
Статистики Х\ (см. формулу (10)) для таблиц данных
мужчин и женщин принимает значения 5,456 и 6,125. Из [10, с. 1411 двадцать процентов
/ * гг«о\ ι здоровья,
(см. также табл. ТЗ) для закона хи-квадрат с 1 степенью
свободы находим, что фактические уровни значимости равны
соответственно 0,020 и 0,013. Это говорит о существенности различия
вероятностей выздоровления между теми, кто принимал лекарство
и теми, кто его не принимал.
С другой стороны, как это ни странно, из таблицы с
объединенными результатами следует, что доля выздоровевших
больше среди тех людей, которые лекарство не принимали (!):
480/870 « 0,539 > 850/1720 « 0,494, причем статистика Х\ для
третьей таблицы равна 4,782, что значимо велико на уровне 0,029.
Рассчитано, что
петербуржец, проживающий на
солнцепеке, выигрывает
Козьма Прутков
282
Глава 18. Сгруппированные данные
В [72, с. 133] Г. Секей пишет:
«Аналогично, новое лекарство может оказаться эффективным
в каждом из десяти различных госпиталей, но объединение результат
Статистика — самая тов Укажет на то» что это лекарство либо бесполезно, либо вредно».
точная из всех лженаук. Причина парадокса заключается в непропорциональном пред-
Джин Ко ставительстве в разных категориях: мужчины выздоравливают
хуже, но лекарство испытывалось в основном на них.
Кроме того, число мужчин (210), не принимавших
лекарство, недостаточно велико: согласно таблице, приведенной в книге
Дж. Флейс « Статистические методы для изучения таблиц долей
и пропорций», вероятность β ошибки II рода, для таких данных
равна 50%. Чтобы обеспечить β = 10%, необходимо иметь не менее
475 пациентов в этой категории.
ЗАДАЧИ
Опыт—лучший учитель. 1. Проверьте первый столбец табл. Т1 на равномерность с
помощью критерия хи-квадрат.
2. В [10, с. 21] проводится анализ 2000 четырехзначных
псевдослучайных чисел из книги М. Кадырова «Таблицы случайных
чисел» (Ташкент, 1936). Первая цифра оказалась нулем у 160,
тройкой —у 247, шестеркой —у 191, девяткой —у 185 чисел
(остальные 1217 чисел начинались с других цифр). Стоит ли
пользоваться такой таблицей?
3. Ниже приведены данные о количестве студентов двух групп,
решивших в течение месяца занятий 0,1-7,8-15 и более 15 задач.
Проверьте гипотезу о том, что студенты обеих групп одинаково
активно решают задачи.
Число задач
Группа 1
Группа 2
0
9
3
1-7
8
5
8-15
5
9
>15
4
11
4. Выведите теорему 1 при N = 2 непосредственно из центральной
предельной теоремы (П6).
5* Докажите неотрицательную определенность матрицы Σ,
задаваемой формулой (3), а) вычислив главные миноры (см. П10),
б) установив, что она является ковариационной матрицей
случайного вектора ι/* из доказательства теоремы 1.
6* Покажите при помощи метода неопределенных множителей
Лагранжа (см. [46, с. 271]), что оценка pj из § 3 максимизирует
функцию правдоподобия сгруппированной выборки при условии
Pi + ...+Рлг = 1.
РЕШЕНИЯ ЗАДАЧ
Мало хотеть — надо уметь. 1. Поскольку длина столбца η = 20 возьмем N = 4 « log2n
промежутков. При справедливости гипотезы равномерности равные
Решения задач
283
по вероятностям попадания промежутки имеют одинаковую
длину 1/ЛГ =1/4. Ниже приведены подсчитанные по таблице Т1
значения i/j, j = 1,... ,ΛΓ. Все ожидаемые количества npj = 5.
Отсюда Х\ = (02+32+12+22)/5 = 2,8. Согласно таблице ТЗ
критическим значением закона χ2 на уровне a = 5% является 7,82.
Так как 2,8 < 7,82, то гипотеза равномерности принимается.
щ
0-24
5
25-49
2
50-74
6
75-99
7
2. XI = (402+472+92+152)/200+172/1200 = 20,816. В соответствии
с табл. ТЗ эта величина значимо велика для χ2 даже на уровне
0,001. Авторы [10] (с. 21) заключают: «Рекомендацию
случайных чисел М. Кадырова для статистических расчетов едва ли
можно признать оправданной».
3. Нетрудно по формуле (10) подсчитать, что X2 « 8,039. Согласно
табл. ТЗ 5%-ное критическое значение χ2 равно 7,82. Поскольку
8,039 > 7,82, проверяемая гипотеза отвергается.
Обратим внимание на то, что фактический уровень
значимости (см. § 1 гл. 12) в данном случае равен 4,5% ([10, с. 141]),
т. е. на уровне, скажем, 4% гипотезу пришлось бы принимать.
При внимательном просмотре данных, замечаем, что количества
i/ij в группе 1 убывают, а в группе 2 возрастают. Без всякой
науки различие групп представляется очевидным, в то время
как критерий хи-квадрат едва смог его уловить. Эта задача
демонстрирует недостаточную чувствительность критерия
(особенно для небольших выборок).
4. Положим q = 1 — ρ и представим статистику X2 в виде
(vi - пр)2 (у2 - nq)2 = (vi - пр)2 [(n-vi) -n(l-p)]2 _
пр nq np nq
= {у\ - пр)2 (np-vi)2 = (f^i - пр)2 _
пр nq npq
v\ —np
I y/npq \
В силу центральной предельной теоремы и свойства 3
сходимости из П5 правая часть сходится по распределению к χ2,
а) Вычислим detU для произвольных действительных
Ρ?>···>Ρλγ· Для этого заметим, что Σ = D(E — Ρ), где D —
диагональная матрица с элементами р?,... ,р% на главной
диагонали, Е — единичная матрица, Р — матрица, все строки
которой равны (р?,... ,Рлг)т. Согласно свойствам определителей
detI7 = detjD · det(E - Ρ) = ρ?.. .p°Ndet(E - Ρ). Чтобы
вычислить det(23 — Ρ), применим к Ρ преобразование подобия
с ортогональной матрицей С, у которой первым столбцом
284
Глава 18. Сгруппированные данные
является вектор (l/y/Ν,... Д/л/iV) (см. теорему 1 гл. 11):
К. Жордан (1838-1922),
французский математик.
СТРС =
Гр?л/ЛГ
0)
(перемножая Ст и Р, мы использовали ортогональность всех
строк матрицы Ст, кроме первой, вектору (1,... ,1)). Отсюда
СТ(Е - Р)С = Е- СТРС =
*
О
О
Поскольку матрица в правой части является
верхнетреугольной, то ее определитель равен 1 — Σρ?· Следовательно,
det Σ = (1 - Σ Ρ?) Π Ρ? Д·1151 любых действительных р9.
Если р? — это вероятности попадания в промежутки Aj
(pV > О, Σρ? = 1)» то все главные миноры Σ положительны,
за исключением последнего, который равен 0.
Так как матрица Ρ не симметрична, то нельзя сослаться на
теорему о приведении к главным осям (см. решение задачи 3
гл. 17). Однако ее можно с помощью невырожденного
преобразования Τ привести к жордановой нормальной форме: J = Т~1РТ,
у которой на главной диагонали стоят собственные значения
матрицы Р, над главной диагональю —0 или 1, а на остальных
местах — только нули (см. [49, с. 142]). Легко видеть, что Σρ° —
собственное значение матрицы Р, соответствующее собственному
вектору (1,...,1). Поскольку ранг матрицы Ρ равен 1, то все
другие собственные значения этой матрицы нулевые. Далее
рассуждаем аналогично.
б) Вычислим моменты первого и второго порядка компонент
η
вектора и = (ι/ι,...,ι/jv), где ι/,· = Σ/{^€дл, используя то,
1=1
что элементы выборки ξι (I = 1,... ,η) независимы и одинаково
распределены, а промежутки Δ^ не пересекаются:
М^ = Μ Σ'«,едл = Σ Ρ(ξι € Δ,·) = η Ρ(6 е Δ;) = ηρ%
Μί/? = Μ Σ 7{ίι€ΔΛ7{ί„,€Δ4} = Σ MI{(l€AjtU€Aj} =
Ι,τη Ι, τη
= ί Σ + Σ W € Δ^ € Δ,) = ηρ? + η(η - Щ)2,
\τη=ί τηφϊ/
Мчч = ( Σ + Σ ) Ρ(6 ε Ajtm e4) = o + n(n - 1)Рук.
\m=l τηφϊ/
Решения задач
285
Согласно определениям дисперсии и ковариации, находим
cov(i/j,i/fc) = Mi/ji/k - Mi/j · Mz/fc = -^PjPfc-
В силу свойств дисперсии и ковариации 1 и 4 из П2 матрица Σ
служит ковариационной матрицей случайного вектора ι/*.
Моменты компонент случайного вектора и также можно
получить дифференцированием характеристической функции φν(ί),
t = (ίι,... ,ijv), задаваемой формулой (2), на основании
следующего утверждения (см. [65, с. 165]).
Утверждение. Если у случайного вектора ζ конечны моменты
M|£j|m при всех j = Ι,.,.,ΛΓ, то существуют смешанные
моменты αί1ν..,ίΝ = Μ ξ1^ ... ξι$ для всех lj ^ 0, h + ... + In ^ rn.
В этом случае характеристическая функция ψξ(ί) имеет
непрерывные частные производные до порядка га включительно,
причем
αΐι,·.·,ΐΝ ι υ dh miN
οτχ ...στΝ \ti= =tN=0
Положим f(t) = pje'*1 + ... + p°NeitN. Согласно (2)
'Φvit) = /n(t). Вычислим частные производные
характеристической функции в 0:
2§р = тр° [(п - 1)Г-ЧРу<> + Г-Че^] |t=0 =
= -пр%п - 1)р° +1] = -пр° - п(п - 1)(р°)2,
^|gl = п{п - 1)/"- W гр°е«* \t=Q = -»(» - 1)Рук.
Поскольку \i/j\ < η, το M|z/j|m < оо для любого га.
Применяя утверждение, находим интересующие нас моменты первого
и второго порядка.
6. Раскладывая η = Πι +... + п& наблюдений по к χ Ν (г = 1,... ,Α:;
,7 = 1,... ,ΛΓ) ячейкам таблицы (см. рис. 6), видим, что функцией
правдоподобия сгруппированной выборки служит
Цр) = cJ\p7j = СП^> где с = п! /П^1 и ^ = Σ>ο·
Поэтому задача равносильна максимизации по переменным
Рь-..,ΡΝ функции
/(Ρ) = Σ h lnPj при условии g(p) = 1 - Σρά; = 0.
286
Глава 18. Сгруппированные данные
Составим функцию Лагранжа F(p,A) = f(p) + Xg(p) и запишем
систему уравнений для поиска экстремальных точек:
£^ = i-A = 0, j = l,..,N; °-ψϊ=9(ρ)=0.
Из N первых уравнений находим, что pj = lj/Χ. Подставляя их
в последнее уравнение, получим λ = ίι + ... + /# = п, откуда
Pj = /j/n, что и требовалось установить.
И сам я догадаюсь.
Чацкий в «Горе от ума»
А. С. Грибоедова
Рис. 7
ОТВЕТЫ НА ВОПРОСЫ
1. Поскольку v\ +... + ι/ν = η, то слагаемые в суммах из формулы
(1) зависимы между собой.
2. Во-первых, для качественной проверки равномерности 2000
чисел разбиение отрезка [0,1] всего на 4 промежутка явно
недостаточно: log22000«ll.
Во-вторых, статистика X2, определяемая формулой (1),
принимает значение (42 + 52 + 82 + 12)/500 = 0,212. Это значение
подозрительно мало: вероятность того, что X2 окажется таким
или еще меньше, согласно табл. ТЗ для χ2 примерно равна 0,025.
Понятно, что при несовпадении истинных вероятностей pj
попадания в промежутки с гипотетическими р° статистика X2
имеет тенденцию к росту (в [32, с. 113] доказано, что критерий
хи-квадрат будет состоятельным (см. § 1 гл. 13) против таких
альтернатив). Поэтому обычно обращают внимание только на
большие значения статистики.
Однако, иногда важно, чтобы датчик генерировал
псевдослучайные числа, которые больше похожи на реализацию
выбираемых наудачу из отрезка [0,1] точек, чем последовательности,
равномерные по Вейлю (см. § 5 гл. 3). У выбираемых наудачу
точек есть определенный случайный разброс. Нетрудно
предложить способы более регулярного заполнения отрезка [0,1]
(зависимыми) случайными точками, у которых частоты попадания
в промежутки будут меньше отличаться от соответствующих
вероятностей, чем при выборе наудачу. (Например, такой: первую
точку берем наудачу, вторую выбираем наудачу из большего
по длине из двух отрезков, на которые разбила [0,1] первая
точка, и т. д.) Для таких датчиков значения статистики X2 будут
попадать в область «левого хвоста» закона χ2 (рис. 7).
3. Функцией правдоподобия пуассоновской выборки служит
L(A) = λΣ^β-λη/Π
Xi\ (см. § 1 гл. 5). Уравнение
правдоподобия — In L(\) = -V^i-n = 0 имеет корень λ = x.
ал А
Часть V
АНАЛИЗ МНОГОМЕРНЫХ ДАННЫХ
Эта часть книги содержит базовые сведения по статистическому
анализу таблиц вида «объекты—признаки». В ней рассматриваются
методы классификации многомерных данных (гл. 19),
корреляционный анализ признаков (гл. 20) и модель линейной регрессии
(гл. 21).
Глава 19
КЛАССИФИКАЦИЯ
Навостри ум свой
математикой, если не
найдешь для этого
никакого иного средства,
остерегайся только
классификации букашек,
поверхностное знание
которой совершенно
бесполезно, а точное
уводит в бесконечность.
И не забывай, что число
фибр твоего мозга,
их складок и извилин
конечно. Там, где сидит
какая-нибудь история
бабочки, нашлось бы,
может быть, место для
биографий Плутарха,
которые могли бы
вдохновить тебя.
Г. К. Лихтенберг
Рис. 1
ьг Солнце
О ВAFGKM
Рис. 2
При статистическом анализе таблицы данных, состоящей из
нескольких столбцов (признаков), необходимо иметь в виду эффект
существенной многомерности, из-за которого к верным выводам
можно прийти лишь при одновременном учете всей совокупности
взаимосвязанных признаков. Так, точки и кружки на рис. 1 почти
не отличаются друг от друга по каждой из координат в
отдельности, но очевидным образом разделяются по новому признаку —
сумме координат.
Похожий случай приводится в [1, с. 15]: попытка различить два
типа потребительского поведения семей сначала по одному признаку
(расходы на питание), потом по другому (расходы на промышленные
товары и услуги) не дала результата, в то время как
одновременный учет обоих признаков позволил обнаружить значимое различие
между анализируемыми совокупностями семей. (См. также пример 1
в гл. 23.)
Рассмотрим еще один пример, показывающий, что удачная
классификация может даже привести к появлению нового
направления исследований (см. [4, с. 35]).
«С давних пор астрономы знали о различной светимости звезд,
т. е. о различной их «истинной яркости». В конце XIX в. были
открыты также различные спектральные классы звезд, попросту
говоря — различный цвет их излучения (от красного до голубого).
До 1913 г. эти характеристики существовали в представлении ученых
раздельно, но вот (независимо друг от друга) датский астроном
Герцщпрунг и американец Ресселл сопоставили их между собой
и построили двумерную проекцию объектов-звезд на плоскость
признаков спектр — светимость. Результаты оказались неожиданными
(рис. 2).
Астрономы увидели, что звезды не распределены в пространстве
этих признаков равномерно, а образуют несколько ярко выраженных
кластеров, причем стало возможным предсказать эволюцию звезд по
значениям их основных характеристик. С тех пор диаграмма Герц-
шпрунга—Ресселла стала одним из важных инструментов в работе
современных астрономов.»
§ 1. Нормировка, расстояния и классы
289
Если число признаков га > 3, то разбиение множества
объектов на компактные группы (так называемые кластеры)*^ может
оказаться непростой задачей. Данная глава посвящена знакомству
с некоторыми подходами к ее решению.
§ 1. НОРМИРОВКА, РАССТОЯНИЯ И КЛАССЫ
Разбиение объектов на классы может в значительной степени
зависеть от выбора единиц измерения (масштабов шкал) признаков:
килограммы или фунты, сантиметры или дюймы.
Пример 1 ([52, с. 26]). Студенты группы записывают свои вес (х)
и рост (у). По этим данным на плоскости строится диаграмма
рассеяния («облако» точек с координатами (#г»Уг)> г = Ι,.,.,η,
где п — число студентов в группе). Масштабы по осям задаются
произвольно. На рис. 3, а девушки (А) довольно четко отделяются
от юношей (В). На рис. 3, б шкала на оси веса сжата вдвое. При
этом более естественным представляется уже деление на высоких
юношей (D) и всех остальных студентов (С).
В приведенном примере при классификации не следует считать
расстоянием между объектами евклидово расстояние между
соответствующими точками (хг,Уг) на плоскости, так как признаки
имеют разные единицы измерения. Требуется предварительная
нормировка показателей, переводящая их в безразмерные
величины. Перечислим наиболее распространенные типы нормировки
одномерных наблюдений Ζι,... ,Zn.
Статистическая
однородность — понятие,
базисное для статистики;
общепринято, что
какую-либо обработку
статистических данных
(усреднение, установление
связей и т. д.) надо
производить только
в однородных группах
наблюдений.
И. Д. Мандель,
«Кластерный анализ»
60 65 70 75 80 85
а)
200
190
180
170
160
150 Lv
Φ
D
Типы нормировки
N1) Zi = (Zi — Zmin)/yZmax — Zmin).
N2) Z[ = (Zi — Z)/S, где Ζ = — J] Zi — среднее арифметическое,
S2 = - Σ(Ζΐ — Ζ)2 —выборочная дисперсия.
N3) Ζ\ = (Zi - MED)/MAD, где MED— выборочная медиана
(см. § 2 гл. 7), MAD**) — (нормированная) медиана
абсолютных отклонений от MED:
MAD=-^^MED{\Zi-MEDi,i = l,...,n},
где Ф~1 (х) — функция, обратная к функции распределения
закона ЛГ(0,1).***) Такое преобразование менее подвержено
влиянию выделяющихся значений Z^
60 70 80 90
б)
Рис. 3
*) Разные варианты уточнения этого понятия приведены ни лее.
**) Сокращение MAD происходит от английского наименования Median of
Absolute Deviations.
***) Множитель 1/Ф_1(3/4) « 1,483 обеспечивает для выборки из закона
λί(μ,σ2) сходимость MAD —► σ при η —* оо (см. П5).
290
Глава 19. Классификация
Помимо типа нормировки решающее влияние на результат
классификации оказывает выбор меры близости между ш-мерными
точками. Приведем основные способы задания расстояния dij от
ТОЧКИ Xi = {Xi\,Xi2, · · · ,#гт) ДО ТОЧКИ Xj = (Xjl1Xj2, · · · ,Xjm)·
Рис. 4
1>
ν
k
k <f
Δ
9
w
i*
Рис. 5
Вопрос 1.
Почему метрика Чебы-
шёва отвечает значению
р=оо?
Расстояния между объектами
т
D1) Метрика города (рис. 4)*^: dij = Σ \x%i—Xji\- При использова-
нии метрики города хорошо выделяются классы, имеющие вид
«облака», вытянутого вдоль оси некоторого признака.
В случае, когда координаты объектов принимают только
значения 0 и 1, это расстояние равно количеству несовпадающих
координат, т. е. длине пути по ребрам единичного ш-мерного
куба из одной вершины в другую (метрика Хемминга).
( т \ 1/2
D2) Евклидова метрика: dij = ( Σ (хи
\ι=ι
D3) Метрика Чебышёва: d^ = max \хц — Xji\.
Все три расстояния являются частными случаями
(соответственно при ρ = 1, 2 и оо) так называемого расстоянья Минковского
хл)2)1
1*3 = Ι Σ \ХИ ~ xJl\P )
1 /ρ
Известно (см. [90, с. 208]), что при любом ρ ^ 1 для расстояния
Минковского выполняется неравенство треугольника: dij ^ dik+dkj.
На рис. 5 изображены единичные «шары» В™ для ρ = 1, 2, оо
при т = 2. Отношение объемов рт = V(В™)/V(В™) = 1/т! при
увеличении размерности быстро уменьшается: рг = 1/2, р5 = 1/120,
р10 = 1/3628800 « 3 · ИГ7.
Иногда матрица расстояний (мер близости) d^ между
объектами задается непосредственно: например, как таблица экспертных
оценок сходства объектов или как матрица прямых измерений
близости (скажем, размеров межотраслевых поставок). В этом
случае снимается проблема выбора типа нормировки и расстояния.
(Однако, заметим, что для некоторых из рассматриваемых ниже
методов классификации требуются сами координаты объектов, а не
только расстояния dij между ними.)
На основе заданного расстояния между объектами можно
уточнить, какие множества называются группами однородных объектов
или классами. Выделим некоторые
Типы классов
С1) Класс типа ядра [60] (в [56, с. 235] такой класс
называется сгущением). Все расстояния между объектами внутри
*) Ее также называют метрикой city-block или манхеттенской.
§2. Эвристические методы
291
класса меньше любого из расстояний между объектами класса
и остальной частью множества объектов. На рис. 6
сгущениями являются А и В. Остальные пары множеств не
разделяются с помощью этого определения.
С2) Кластер (сгущение β среднем [56]). Среднее расстояние
внутри класса меньше среднего расстояния объектов класса
до всех остальных. Множества С и D теперь разделяются, но
у Ε (G) среднее внутреннее расстояние больше, чем среднее
расстояние между Ε и F (G и Я).
СЗ) Класс типа ленты [60] (слабое сгущение [56]). Существует
τ > 0 такое, что для любого Χι из класса S найдется такой
объект Xj е 5, что dij ^ τ, а для всех Хк φ S справедливо
неравенство dik > т. В смысле этого определения на рис. 6
разделяются все пары множеств кроме I и J, К и L.
С4) Класс с центром. Существует порог R > 0 и некоторая
точка х* в пространстве, занимаемом объектами класса S
(в частности, элемент этого множества) такие, что все объекты
из 5 и только они содержатся в шаре радиуса R с центром
в х*. Часто в качестве х* выступает центр масс класса 5,
т. е. координаты центра определяются как средние значения
признаков у объектов класса. Множества I и J являются
классами с центром, а Е1 F и G — нет.
Обратим внимание на то, что накладывающиеся множества К
и L не разделяются при помощи перечисленных определений классов.
Тем не менее, в примере 4 из § 5 предлагается способ проведения
разделяющей границы между подобными множествами на основе
статистической модели случайного выбора из одной из к многомерных
нормальных совокупностей.
Вообще, классификация (кластер-анализ) отличается от других
разделов статистики большой зависимостью результатов расчетов
от содержательных установок исследователя.
§2. ЭВРИСТИЧЕСКИЕ МЕТОДЫ
Подавляющая часть классификаций на практике проводится
именно эвристическими методами. Это объясняется относительной
простотой и содержательной ясностью таких алгоритмов,
возможностью вмешательства в их работу путем изменения одного или
нескольких параметров, смысл которых обычно понятен, и
невысокой трудоемкостью алгоритмов.
А1) Связные компоненты. Все объекты разбиваются на
классы типа ленты, или слабого сгущения (тип СЗ в § 1), где
задаваемый параметр τ G (тш dij, max dij). В этой постановке
задача классификации эквивалентна нахождению связных компонент
1 .Л .0\
w & 1
1-.·:.·-.·:.·-»:·£?
| и,:·.'.*: F
%**£
I .::/ J^
Ιί^-Μ:^
Рис. β
Научное исследование —
это искусство, а правила
в искусстве, если
они слишком жестки,
приносят больше вреда,
чем пользы.
Дж. Томсон, «Дух науки»
292
Глава 19. Классификация
Рис. 8
графа (вершины графа г и j соединены ребром, если ац < г).
(Алгоритм выделения связных компонент методом поиска в
глубину излагается в § 9.) Для выбора величины τ полезно построить
гистограмму межобъектных расстояний (высота прямоугольника
над промежутком Αι на рис. 7 пропорциональна количеству dij
в Αι). При хорошей структурированности данных гистограмма, как
правило, имеет два выделяющихся максимума: при dij « dint
(типичное внутриклассовое расстояние) и при dij « dout (типичное
межклассовое расстояние). Часто удачным выбором τ оказывается
значение (dint + dout)/2.
Рис. 7 0 min d
max djj
A2) Кратчайший незамкнутый путь (КНП). Его также
называют минимальным покрывающим деревом или каркасом.
Соединяются ребром две ближайшие точки, затем среди оставшихся
отыскивается точка, ближайшая к любой из уже соединенных
точек, и присоединяется к ним и т. д. до исчерпания всех точек.
Р. Прим в 1957 г. доказал, что построенный таким способом граф
имеет минимальную общую длину ребер среди всевозможных
соединений, связывающих все вершины (см. [28, с. 60]).
В найденном КНП затем отбрасывают к — 1 самых длинных дуг
и получают к классов (рис. 8).*) Метод позволяет выделять классы
произвольной формы.
Рис. 9
Заметим, что если разрешается добавлять в граф новые вершины
(точки Штейнера), то можно добиться меньшей, чем у КНП, длины
пути. Уже для трех точек Л, В и С на плоскости таких, что
наибольший из углов А АВС меньше 120°, существует точка О внутри
треугольника, для которой минимальна сумма \ОА\ + \ОВ\ + \ОС\.
Доказательство [64, с. 77]. Пусть О —некоторая точка внутри
А АВС. При повороте на 60Q вокруг вершины А точки О, В и С
перейдут в точки О', В' и С', соответственно (рис. 9). Так как
ААОО' равносторонний, то \АО\ = |00'|. Отрезок ОС переходит
в отрезок О'С. Поэтому \ОС\ = \0'С'\. Таким образом, сумма
\ОА\ + \ОВ\ + \ОС\ = \00'\ + \ОВ\ + lO'C'l, т. е. равна длине ломаной
BOO'С. Она минимальна, когда ломаная является отрезком.
Поскольку Ζ ΑΟΟ' = 60°, для этого необходимо, чтобы Ζ ΒΟΑ = 120°.
Другими словами, сторона АВ должна быть видна из оптимальной
*) Число к задает исследователь. На практике обычно 2 ^ к ^ 5.
§2. Эвристические методы
293
точки под углом 120°. Из симметрии то же самое должно быть верно
и для двух других сторон Δ ABC. Ш
Для произвольного расположения вершин графа на плоскости
и любого числа точек Штейнера эффективные алгоритмы
построения кратчайшего соединения неизвестны (согласно [28, с. 63]).
A3) Метод /с-средних*) предназначен для выделения классов
типа С4 («класс с центром»). Приведем два варианта:
(a) Алгоритм Г. Болла и Д. Холла (1965 г., см. [52, с. 110]).
Случайно выбираются к объектов (эталонов); каждый объект
присоединяется к ближайшему эталону (тем самым образуются
к классов); в качестве новых эталонов принимаются центры масс
классов. ) После пересчета объекты снова распределяются по
ближайшим эталонам и т. д. Критерием окончания алгоритма служит
стабилизация центров масс всех классов.
Вместо случайно выбираемых эталонов лучше использовать к
наиболее удаленных объектов: сначала отыскиваются два самых
удаленных друг от друга объекта, затем 1-й эталон (/ = 3,... ,к)
определяется как наиболее удаленный в среднем от уже имеющихся.
(b) Алгоритм Дою. Μακ-Кина (1967 г., см. [52, с. 98]). Он
отличается от метода Болла и Холла тем, что при просмотре списка
объектов пересчет центра масс класса происходит после
присоединения к нему каждого очередного объекта.
Отметим, что алгоритм Мак-Кина связан с функционалом
качества разбиения F2 из § 5.
А4) Алгоритм «Форель». Случайный объект объявляется
центром класса; все объекты, находящиеся от него на расстоянии не
большем Д, входят в первый класс. В нем определяется центр масс,
который объявляется новым центром класса и т. д. до стабилизации
центра. Затем все объекты, попавшие в первый класс изымаются,
и процедура повторяется с новым случайным центром.
Можно скомбинировать алгоритмы А4 и А2 ([52, с. 67)]: при
небольшом R по алгоритму А4 находят к' > к классов; их центры
соединяют КНП, из которого удаляют к — 1 самых длинных ребер
и получают к классов. При этом образуются классы более сложной
формы, чем m-мерные шары (рис. 10). Здесь важна идея двух-
этапности классификации: сначала выделить заведомо компактные
маленькие группы, затем произвести их объединение. Так можно
успешно классифицировать довольно большие массивы информации
(сотни объектов).
А5) Метод потенциальных ям. Предположим, что каждый
ООЪеКТ Х{ == ^Ж^1,. . . <i%im)
создает вокруг себя поле притяжения
*) Это название, ставшее популярным, введено Дж. Мак-Кином.
**) Считается, что каждому объекту приписана масса 1.
Вопрос 2.
Как построить
оптимальную точку О при помощи
циркуля и линейки?
(Постройте на стороне
ВС, как на основании,
равносторонний
треугольник и опишите вокруг него
окружность.)
Вопрос 3.
Где на плоскости
находится точка, сумма
расстояний от которой
до вершин выпуклого
четырехугольника
минимальна?
«Форель»:
Первоначальное название ФОРЭЛ —
ФОРмальный ЭЛемент.
Предложен В. Н. Елки ной
и Н. Г. Загоруйко в 1966 г.,
см. [1, с. 222].
Рис. 10
294
Глава 19. Классификация
Рис. 11
с некоторой весовой функцией, например, гладким квартическим
ядром
Wi(x) = [l-(ri/R)2]2I{riiR},
где Гг = \х — хг\, а параметр R > О задает эффективный размер
области притяжения. Все вместе объекты создают потенциальное
поле U(x) = — Y^Wi(x). Классам соответствуют потенциальные
ямы: объект Ж; относится к яме, в которую он «скатывается»
при свободном движении. Практически приходится, стартовав с а^,
запускать некоторый алгоритм (локальной) минимизации.
Одним из простейших методов минимизации функции т
переменных U(x) является циклический перебор 2т точек, соседних с
текущей по осям с шагом ±h (h — точность поиска точки минимума). Если
значение U(ев) в какой-то из них меньше, чем в текущей, происходит
перемещение в нее (противоположную по этой оси точку можно не
проверять) (рис. 11). Для ускорения полезно запоминать для каждой
оси знак успешного перемещения по ней во время предыдущего цикла
и сначала пробовать сдвигаться в том же направлении. Критерием
окончания служит отсутствие перемещений за время цикла.
Обозначим через yi конечную точку пути из Хг. Объекты Χχ и Xj
т
отнесем к одному классу, если Σ \yu—yji\ ^ 2kh (т. е. у{ и у- близки
1=1
в метрике города D1 из § 1). При этом число перемещений при поиске
локального минимума (длина пути) характеризует удаленность χ г от
«центра» класса (дна ямы).
Из-за необходимости проведения численной минимизации для
каждого Xi метод рекомендуется применять для классификации
небольшого числа (нескольких десятков) объектов.
Мне завещал отец:
Во-первых, угождать всем
людям без изъятья;
Хозяину, где доведется
жить,
Начальнику, с кем буду
я служить,
Слуге его, который чистит
платья,
Швейцару, дворнику, для
избежанья зла,
Собаке дворника, чтоб
ласкова была.
Мол чал и н в «Горе от
ума» А. С Грибоедова
§3. ИЕРАРХИЧЕСКИЕ ПРОЦЕДУРЫ
Общая схема этих процедур такова: сначала каждый объект
считается отдельным классом; на первом шаге объединяются
два ближайших объекта, которые образуют новый класс (если
сразу несколько объектов (классов) одинаково близки, то
выбирается одна случайная пара); вычисляются меры отдаленности
ρ (см. ниже)*) от этого класса до всех остальных классов, и
размерность матрицы межклассовых мер отдаленности сокращается
на единицу; шаги процедуры повторяются до тех пор, пока все
объекты не объединятся в один класс.
*) Мы не называем их расстояниями из-за того, что не для всех мер
отдаленности выполняется неравенство треугольника.
§ 3. Иерархические процедуры
295
Наиболее известны следующие две процедуры (рис. 12):
Р1) Метод «ближнего соседа»: pmin = min d^·,
Xi£Sk,Xj€Si
P2) Метод «дальнего соседа»: pmax = max d^.
&i€Sk,Xj€Si
Решение о том, какое из разбиений на классы, получаемых при
проведении иерархической процедуры, наиболее содержательно,
принимается на основе анализа так называемой дендрограммы :
по горизонтали откладываются номера объектов, а по вертикали —
значения мер отдаленности p(Sk1Si)1 при которых происходили
объединения классов Sk к Si.
На основе данных, представленных на рис. 13, а, построены
дендрограммы для процедур Р1 (рис. 13, б) и Р2 (рис. 13, в). Хорошо
видна следующая особенность метода «ближнего соседа» —
цепочечный эффект: независимо от формы кластера к нему присоединяются
ближайшие к границе объекты. Метод «дальнего соседа» не
приводит к подобному эффекту. Подробнее о сравнении разных методов
классификации см. в § 7.
Ртах
^—у Ртгп
Рис. 12
Dendron (греч.) — дерево.
8-
7-
6ι
5-
4J
31
%
ΙΟ
«2
•
•7
•6
.*
Λ
•3
ι ι ι ι ι ι ι
123 456 7
a)
Рассмотрим некоторые другие иерархической процедуры.
1
РЗ) Метод средней связи: pave =
Σ Σ dij (здесь
Пк и щ — количества объектов в классах Sk и Si).
Α. Η. Колмогоровым было предложено изящное обобщение
метода РЗ, основанное на понятии степенного среднего чисел
ci > 0,... ,сп > О
сг = ι - >; ci \ (ι)
·--(;&*)
Очевидно, а = —У2с%— среднее арифметическое. Устремляя г
η
к +оо, —оо и 0, получаем, соответственно, с+<х> = тахсг,
с-оо = minci, со = (Пс01/Лг —среднее геометрическое (проверьте!).
Таким образом, мера отдаленности Колмогорова
Ρκ(τ) =
ll/r
^Г Σ Σ 4
(2)
включает в себя в качестве частных случаев pmin, Pmax и paVe-
Р4) Метод центров масс: pcenter = \хк - ^|2, где хк и щ
обозначают центры масс к-το и /-го классов.
Недостатком этого метода является возможность появления
инверсий — нарушений монотонности увеличения уровня при
построении дендрограммы (т. е. объединение классов на некотором
шаге процедуры осуществляется при более низком значении меры
отдаленности, чем на более раннем шаге).
8
7Н
6
5
4
3-
2Н
1
8
7·
6
5
4-
ЗН
2-
1-
т
3 4 5 6 7 12
б)
д
3 4 5 12 6 7
в)
Рис. 13
Average (англ.) — средний.
Вопрос 4.
Может ли возникнуть
инверсия при
классификации методом Р4 трех
объектов?
296
Глава 19. Классификация
Р5) Метод Уорда*): pw = ПкЩ \хк - xi\2- Как вытекает
Пк +П1
из приведенной ниже теоремы 1, множитель —^— позволяет
Пк +Щ
предотвратить появление инверсий.
Замечание 1. Покажем, что верно равенство
Pw = Σ \xi-Xkti\2- Σ \хг~Хк\2- Σ кг-жг|2, (3)
VieSkUSi XitSk VieSi
где Xkj — центр масс SfcUSj. Таким образом, pw представляет собой
прирост общей внутриклассовой инерции Vint (см. формулу (6)
в § 5) при замене классов Sk и Si на их объединение.
Доказательство. В силу теоремы Гюйгенса (см. решение
задачи 3 гл. 16) правая часть (3) равна Пк\хк — Xk,i\2 + щ\хг — Xk,i\2·
Сгруппируем массы Sfe и 5/, поместив их в точки χ к и ~х\
соответственно. Общий центр масс Xk,i при группировке масс не
меняется (убедитесь!). Для завершения доказательства остается
воспользоваться теоремой о межточечных расстояниях из решения
задачи 5 гл. 16. ■
Для вычисления (на очередном шаге иерархической процедуры)
мер отдаленности между вновь образованным классом и всеми
другими оставшимися классами удобно воспользоваться общей для
методов PI—P5 формулой Г. Ланса и У. Уильямса:
/9(50, Si U S2) = CiPoi + C2P02 + Сзрп + C4|a>i — P02U (4)
где poi = p(SoiSi) и т. п. Коэффициенты С\—С± для процедур
PI—P5 приведены в следующей таблице:
Номер
Р1
Р2
РЗ
Р4
ι Р5
Название
Ближний
сосед
Дальний
сосед
Средняя
связь
Центры
масс
Метод
Уорда
Сг
1/2
1/2
щ
Πι+712
πι
П\+П2
ηρ+ηι+Π2
с2
1/2
1/2
П2
П\+П2
п2
П\+П2
П0+П2
Пр+П\+П2
С3
0
0
0
711712
(ni+7l2)2
710
710+711+712
с4
-1/2
1/2
0
0
0
Для методов Р1 и Р2 формула (4) вытекает из тождеств
min{a,/3} = Ι (α + β) - \ |α-/3|, max{a,/3} = \ (α + β) + \ \α-β\.
Для процедур РЗ—Р5 формула (4) выводится в задаче 1.
*) Предложен Дж. Уордом (J. Ward) в 1963 г.
§4. Быстрые алгоритмы
297
Замечание 2. При использовании меры отдаленности
Колмогорова, определяемой равенством (2), величина /0#(τ), очевидно,
удовлетворяет условию (4) с теми же коэффициентами, что
И pave = Рк(Х)-
Замечание 3. Формула Ланса—Уильямса (4) была обобщена на
более широкий класс иерархических процедур М. Жамбю:
/9(50, Si U S2) = Cipoi 4- С2Р02 + C3pi2 + C4IP01 - P02I+ ( .
+ C5h(S0) + C6/i(5i) + C7h(S2), [ j
где h(Sk) —значение меры отдаленности, при котором произошло
образование класса Sk (т. е. его уровень на дендрограмме). В
частности, при
С\ = (га0 4- mi)/M, С2 = (ш0 + га2)/М, С3 = (mi + га2)/М,
С± = 0, Съ = -га0/М, С6 = -mi/M, С7 = -га2/М,
где Μ = mo + mi 4- га2, получим меру отдаленности pj(Sk,Si),
равную моменту инерции объединения Sk U £г относительно его
центра масс (см. [30, с. 117]).
Следующие условия (Г. Миллиган, 1979 г.) обеспечивают
отсутствие инверсий у процедур, удовлетворяющих формуле (5).
Теорема 1. Пусть
а) коэффициенты Ci, C2, С5, Се, CV неотрицательны,
б) C4^-min{CiA},
в) Ci -f С2 + Сз ^ 1.
Тогда иерархическая процедура, задаваемая формулой (5), не
имеет инверсий.
Контрпример. Для метода центров масс Р4 нарушается
условие в):
Ci + С2 4- С3 = 1 - πιη2/(πι + п2)2 < 1.
§4. БЫСТРЫЕ АЛГОРИТМЫ
В 1978 г. М. Брюиношем было введено важное понятие редуктивно-
сти (сводимости) мер отдаленности. Оно заключается в том, что
для произвольного δ > 0 условия p{Si,S2) ^ δ и p(So, Si U 52) < δ
влекут выполнение хотя бы одного из неравенств р(5о, Si) < δ или
/p(So, £2) < δ (см. [52, с. 55]). Иными словами, (S-окрестность
множества, полученного объединением двух ^-близких классов (пунктир
на рис. 14), включена в объединение ί-окрестностей этих двух
классов (сплошная линия на рис. 14). Можно дать другую
формулировку свойства редуктивности: если /θ(5ι, S2) ^ δ, a p(Sq1 Si) ^ ί,
p(S0, S2) > δ, то р(5о, Si U S2) > δ.
Рис. 14
Вопрос 5.
Обладают ли свойством
редуктивности а) Ртгп,
6) pW?
298
Глава 19. Классификация
Для редуктивных мер отдаленности можно построить быстрые
алгоритмы (см. [1, с. 263]), позволяющие классифицировать
тысячи объектов. Разберем их принципиальную схему.
5-
3-
2
0
:
2
1
^
ι :
з
* ι
11
) ί
5
4
Τ
a)
1
2
3
4
5
1
0
2
Χ
0
3
4
a
0
4
7
6
5
0
5
9
8
5
:*
0
6)
3
4
5
6
3
0
4
5
0
5
5
'i
0
6
;з)
β
8
0
в)
3
6
7
3
0
6
а
0
7
5
6
0
7
8
7
0
8
5
0
г)
Д)
Рис. 15
При k-м шаге иерархической процедуры приходится искать
минимальный элемент в матрице мер отдаленностей классов, т. е. минимум
из Nk = (η — k + l)(n — к)/2 чисел. Ясно, что минимальный элемент
находится среди элементов, не превосходящих некоторый порог δ.
При соответствующем выборе δ массив таких элементов имеет размер
намного меньший, чем Nk. В этом и состоит основная причина
большой скорости работы алгоритмов и экономии компьютерной
памяти.
Обозначим через Us множество пар (г j) номеров классов таких,
что pij ^ £, а через Vs — массив из номеров классов, присутствующих
в Us.
На первом этапе попарно объединяются классы из Vs до тех пор,
пока текущее Us не станет пустым. Затем берется новое значение
порога δ' > δ и формируются множества Us' и Vs' и т. д. до полного
слияния всех объектов в один класс.
Рассмотрим работу алгоритма на примере данных рис. 15, а. В
качестве расстояния между объектами используем метрику города D1
из § 1, а мерой отдаленности классов будем считать ртгп- Зададим
δ = 3. Тогда Us = {(1,2),(2,3),(4,5)} и Vs = {1,2,3,4,5} (рис. 15,6).
После объединения наиболее близких объектов с номерами 1 и 2
в новый класс под номером 6 матрица межклассовых мер
отдаленности преобразуется к виду, приведенному на рис. 15, е. При этом
изменятся Us и VJ: Us = {(3,6),(4,5)}, Vs = {3,4,5,6} и т. д. На
шаге, соответствующем рис. 15, д, уже нет пар классов, для которых
pmin ^ 3. Поэтому приходится увеличить порог до δ' = 5, что
и позволяет завершить процедуру.
При выполнении свойства редуктивности рассмотренный
алгоритм строит точно такую же дендрограмму, что и обычная
иерархическая процедура (для присоединения класса 3 к классам 1,2 на
рис. 14 достаточно просмотреть окрестности 1 и 2, а не проверять
связь 1,2-4).
Эффективность алгоритма существенно зависит от выбора
последовательности порогов δ < δ' < δ" < ... . Если δ слишком
велико, то Us включает почти все пары классов, и мы практически
возвращаемся к традиционной иерархической процедуре. Если же
величина порога слишком мала, то придется часто формировать
множества Us и Vs. Обычно используют следующие два способа
выбора порогов.
Первый способ (на основе гистограммы р^). Порог δ находится
из условия достаточности выделенной компьютерной памяти для
хранения всех рц ^ δ.
Пусть, например, число объектов равно 100. Тогда на первом шаге
имеется iVi = 100 · 99/2 = 4950 пар классов. При этом задано, что их
количество в памяти не должно превышать 200. Предположим, что
первые четыре интервала гистограммы содержат 180 пар, а пятый —
§ 5. Функционалы качества разбиения
299
еще 40 пар. В таком случае можно поместить в память только 180
пар, причем порог δ будет равен наибольшему значению рц этих пар.
Второй способ (изменяющееся среднее). Вычисляется среднее
арифметическое всех р^. Пусть это будет δχ. Если возможно
размещение в памяти всех р^ ^ δ ι, то полагается δ = δι. Иначе удаляются
пары, у которых р^ > δι, а для оставшихся снова подсчитывается
среднее арифметическое 02 и т. д. до тех пор, пока все р%3 ^ ok не
уместятся в заданной компьютерной памяти.
Замечание 4. Е. Диде и В. Моро (1984 г.) показали, что если
слегка ужесточить условия теоремы 1, заменив неравенство в) на
неравенство в') С\ + Сч + тт{0,Сз} ^ 1, то меры отдаленности,
удовлетворяющие (5), будут редуктивными.
§5. ФУНКЦИОНАЛЫ КАЧЕСТВА РАЗБИЕНИЯ
Будем считать, что число классов к задано (случай, когда оно
неизвестно, обсуждается в § 6). Пусть щ обозначает количество
объектов (m-мерных точек) Xi (г = 1,... ,п) в классе Sj (/ = 1,... ,fc).
При разбиении на классы типа «класс с центром» (С4 в § 1)
в основе многих характеристик качества лежит формула
η к к
ΣΙ«<-«Ι2 = Σ Σ \χί-χι\2 + Σηι\χι-χ\2. (6)
i=l l=lXieSi 1=1
Здесь слева от равенства стоит Vtot — момент инерции
относительно общего центра масс χ всех объектов; первое слагаемое
справа, обозначаемое через Vint, представляет собой сумму
моментов инерции 1\ классов Si относительно их центров масс χι;
второе слагаемое Vout характеризует межклассовый разброс (это
момент инерции системы, у которой точки каждого класса стянуты
в его центр масс).
Перечислим некоторые функционалы качества F,
определенные на множестве всевозможных разбиений 5 объектов на к
классов (чем F(S) меньше, тем разбиение 5 лучше).
к
F1 = Σ h = Vint (общая внутриклассовая инерция).
Замечание 5. Как следует из замечания 1, метод Уорда (Р5 из § 3)
обеспечивает наименьшее увеличение функционала F1 при каждом
шаге процедуры. Однако, эта пошаговая оптимальность алгоритма,
вообще говоря, не влечет его оптимальности в том же смысле для
любого наперед заданного числа классов.
к χ
F2 = Σ — h (сумма внутриклассовых дисперсии).
1=1 п1
Материал этого
параграфа довольно сложен.
Формула (6) немедленно
вытекает из ее
одномерного аналога (13) в гл. 16.
300
Глава 19. Классификация
Основной результат Дж. Мак-Кина (1967 г.) состоит в
доказательстве того, что его вариант алгоритма fc-средних (A3 в § 2)
приводит к локальному минимуму функционала F2. Точную
минимизацию F2 с использованием динамического программирования
осуществил Р. Дженсен в 1969 г. (см. [26]).
F3=E Σ \xi-xj\2 = 2YlnlIl.
l=lXi,XjeSi 1=1
Последнее равенство здесь справедливо в силу теоремы о
межточечных расстояниях (см. решение задачи 5 гл. 16).
F4 =
1 ,г
int
η — к
vout
(сравните с формулой (9) гл. 16).
Ряд функционалов качества разбиения связан с обобщающим
формулу (6) матричным тождеством (задача 2)
Wtat = Wint + Wout. (7)
η
Здесь Wtot = Σ(Χί — x)(xi — х)т — общая матрица рассеяния;
г=1
к
Wint — матрица внутриклассового разброса: Wint = _} Wj, где
1=1
Wi = Σ (xi — xi)(xi — Χι)τ — матрица рассеяния 1-го класса;
Xi€Si
Wout = Σ ηι(χι—χ)(χι—χ)τ — матрица разброса между классами.
1=1
Формула (6) получается из тождества (7) применением к
участвующим в ней матрицам операции взятия следа (см. ШО). В частности,
Fl = Vint=tTWint.
F5 = detWint.
F6 = ti{WintW;Jt).
Fl = det {WintW;o\) = det Wint/ det Wtot.
Функционалы F6—F7 изучались Х. Фридманом и Дж.
Рубином в 1967 г. Они инвариантны по отношению к невырожденным
линейным преобразованиям координат объектов. Действительно,
если Xi = Вхг1 где В — невырожденная (т х т)-матрица, то
Wint = BWintBT и Wtot = BWtotBT (см. свойство 5 дисперсии
и ковариации из П2). При этом матрица
WintWtot = BWintBT (BT)_1 WTo\B~l = BWintW^B-1
подобна матрице WintW^0\, поэтому согласно следствию 2 из Π10
у них одинаковые следы и определители.
§ 5. Функционалы качества разбиения
301
В целях последующего применения к задаче классификации
нормальных совокупностей (пример 3) рассмотрим
Пример 2. Оценки максимального правдоподобия для
параметров многомерной нормальной модели [32, с. 66].
Предположим, что случайные m-мерные векторы ξ{ ~ Λί(μ,Σ)
(см. П9) и независимы (г = 1,... ,п). Пусть вектор средних значений
μ = (μι,.,.,μ™) и невырожденная ковариационная (га χ га)-мат-
рица Σ неизвестны, θ = (μ,Σ). Общее количество неизвестных
параметров с учетом симметричности Σ равно га + га (га + 1)/2.
Согласно П9 плотность случайного вектора £{ задается формулой
p{xfi) = (2тг)-ш/2 (det Σ)~1/2exp j- ± (χ - μ)τΣ~\χ - μ) j . (8)
В силу независимости случайных векторов ζ{ логарифм функции
правдоподобия (§ 4 гл. 9) имеет вид
1η£(0)=Σ>ρ(*<,β) =
+ const. (9)
ι "
2
η In det 17+ £ (χι- μ)τΣ~1(χί- μ)
Максимизация L(0) эквивалентна минимизации выражения в
квадратных скобках в формуле (9). Положим χ = (χι + ... + жп)/п.
Разобьем сумму в равенстве (9) на два слагаемых на основе
тождества, обобщающего теорему Гюйгенса (см. решение задачи 3 гл. 16),
которое предлагается проверить в задаче 3:
£(Χϊ-μ)ΤΣ-1(χί-μ) =
(Ю)
= п(х- μ)τΣ~ι{χ -μ)+Σ(χι~ χ)ΤΣ~1(χί - χ).
Первое слагаемое неотрицательно для любой Σ в силу положитель- Вопрос б.
ной определенности матрицы Σ~ι и равно 0 только при μ = χ. ι;-^положительно
Второе слагаемое от μ не зависит. Следовательно, достаточно определена?
минимизировать по Σ выражение
η In det 17+ £ (xi - χ)τΣ~1(χί -χ). (11)
г=1
Введем выборочную ковариационную матрицу
Σ = Σ(χΐ9...9χη) = -Σ (xi-x)(xi-x)T. (12)
п г=1
На основе легко проверяемого тождества уТВу = tr (yyTB) и
линейности оператора tr, получаем
Σ (xi-xfE'^Xi-x) = ntr^IT1). (13)
302
Глава 19. Классификация
Учитывая формулу (13), выражение (11) можно переписать в виде
Вопрос 7.
Почему условие
Αι = ... = Am =Д влечет
равенство Έ — Σ1
lndet!7 +
tr (Я1Г1)]
(14)
Минимизация суммы (14) по Σ эквивалентна минимизации
функции
ψ(Σ) = tr {ΣΣ~ι) - πι - In det (ΣΣ'1)
(постоянные га и In det Σ добавлены для дальнейших
преобразований).
Так как Σ и Σ — ковариационные матрицы, то (согласно
замечанию из Π10) они неотрицательно определены, а Σ даже
положительно определена в силу невырожденности. Обозначим через
λι ^ Аг ^ ... ^ Ат ^ 0 собственные значения пары матриц (Σ,Σ),
т. е. решения характеристического уравнения det {ΣΣ~ι — \Е) = 0
(см. П10). Тогда
т
^(^) = Σ(λ/-ι-ΐηλζ).
1=1
Поскольку λ— Ι — Ιηλ^Ο при λ ^ 0, из последнего соотношения
получаем, что ψ(Σ) ^0, причем равенство имеет место только при
Αι = ... = Am = 1, т. е. для Σ — Σ.
Таким образом, оценками максимального правдоподобия
параметров μ и Σ являются, соответственно, статистики χ и Σ.
Пример 3. Многомерные нормальные наблюдения и
функционалы качества разбиения на классы [1, с. 169].
Предположим, что каждое наблюдение ζ{ (г = 1,... ,п) извлечено из одного
из к нормальных законов ΛΓ(μ/, Σι) (Ι = 1,... ,Α:). При этом μι и Σ^
вообще говоря, неизвестны. Задача исследователя — определить,
какие Πι из η наблюдений извлечены из класса λί(μ11Σ\)1 какие
П2 из η наблюдений извлечены из класса Ν(μ2, Σ2) и т. д. Числа
щ в общем случае также неизвестны.
Введем векторный параметр разбиения 7 = (7ь· · · >7п)> где
7г~ номер класса (от 1 до А:), к которому относится
наблюдение £;. Тогда задачу разбиения на классы можно
сформулировать как задачу оценивания неизвестных параметров 7ь · · · /Уп
при «мешающих» неизвестных параметрах μχ и Σι (I = 1,...,fc).
Обозначим весь набор неизвестных параметров через 0, т. е.
θ = (7, Μι, · · · ,Mfc> Σ\,... ,Σΐζ)· Тогда логарифм функции
правдоподобия (см. формулу (9)) будет равен (с точностью до сдвига на
константу) величине
(15)
1 к
1 /=1
щ (7) In det Σ\+ Σ (x% -
a><€Si(7)
-μ,)τΙ7Γ1(*ί-
-Μι)
§ 5. Функционалы качества разбиения
303
Максимизируем выражение (15) по Θ. Пусть θ обозначает точку
максимума.*)
Рассуждения, аналогичные проведенным в примере 2,
показывают, что оценками максимального правдоподобия для параметров
μι при фиксированных 7> ^ъ · · · >27& являются центры масс
классов
Xl=Xl{j) = — Σ Xu (i = l,.-.,fc).
Подставляя их в формулу (15) и учитывая тождество (10),
получаем, что достаточно минимизировать по 271,... ,27& и 7 функцию
k Г 1
Σ mlndet27i+ Σ (*i - Χι)τΣ^\χί - Щ) , (16)
*=i L XieSi J
которая, принимая во внимание равенства (12) и (13), совпадает с
Σ U lndet 27* + щ tr (2,i27i"1)l , (17)
z=i L J
где Σι = — Σ (χί — Xi)(xi — xi)T — выборочная ковариационная
матрица класса Si. Отметим, что Σι = —W/, где Wi — это
т
матрица рассеяния класса Si (см. пояснение к формуле (7)).
Анализ выражений (16) и (17) в некоторых частных случаях
приводит к ряду интересных выводов.
Случай 1. 27^ = σ2Ε (Ι = 1,... ,&), причем параметр σ известен.
Тогда минимизация (16) по 7 равносильна минимизации
функционала качества разбиения на классы Fl = Vint.
Случай 2. 27ί = 27 (/ = 1,... ,Α:), где матрица 27 известна. В этом
случае минимизируемым функционалом является
™= Σ Σ Φ*,χι),
i=ixieSi
где под расстоянием между точками χ и у подразумевается
d(x,y) = (χ — у)ТΣ~ι(χ — у) {расстояние Махаланобиса). (18)
Случай 3. Σι = Σ (Ι = 1,... ,Α:), где матрица 27 неизвестна. Тогда
выражение (17) можно представить в виде
η
lndet27 + tr(i;int27-1)], (19)
ΐΛ ί, liTI7 1
где ΣΜ = ± Σ ηιΣι = -Ε^ = - Wint. (20)
71 /Ξι η ιΞ[ η
*) Оговоримся сразу, что состоятельность оценки θ остается под сомнением,
поскольку размерность вектора θ превосходит общее число наблюдений п.
304
Глава 19. Классификация
Точно так же, как и в примере 2, находим, что матрица Σμ
минимизирует сумму (19). Подставив ее в формулу (19), замечаем, что
второе слагаемое превращается в константу, а минимизация
первого по 7 равносильна минимизации функционала F5 = det Wint.
Замечание 6. Если матрицы ковариаций Σι (I = 1,... ,fc)
совпадают, то можно обобщить одномерный F-критерий однофакторного
дисперсионного анализа (см. формулу (9) гл. 16) на
многомерную нормальную модель, например, так: для проверки гипотезы
о равенстве средних Н$: μλ = μ2 = ... = μ}ζ в качестве
статистик критерия будем использовать монотонные функции от
Fl = detWint/detWtot- Положим для краткости L = F1.
Известно (см. [8, с. 49]), что при справедливости гипотезы Щ
ч п-к -1 1- л/Г „ п , . 0
а) к_х -т= F2k-2,2(n-k-i), если ш = 2и^2;
£*\ η — к — т + 1 1— L —, . - , 0
б) — ~ Fm,n_fc_m+i, если га ^ 1 и к = 2;
771 L
ч 71 — к — 771 + 1 1 — λ/Γ „ . i , 0
в) — -j= ^2т,2(п-)к-т+1), если га > 1 и А; = 3.
Для других значений т и к и больших η можно указать
хорошую аппроксимацию, предложенную М. Бартлеттом (1947 г.):
статистика
_(n_l_!^)lni
имеет приближенно %2-распределение cm(fc-l) степенями свободы.
Обобщение на многомерный случай F-критерия двухфактор-
ного дисперсионного анализа (см. пример 1 гл. 17) приведено в [8,
с. 160].
Случай 4. Матрицы ковариаций Σι не равны между собой и
неизвестны. Минимизируя отдельно каждое слагаемое в сумме (17),
находим, что оценками максимального правдоподобия для Σι
служат выборочные ковариационные матрицы Σι. Подставляя их
в формулу (17), превращаем вторые слагаемые в квадратных
скобках в константы. При этом минимизируемый по 7 функционал
приобретает вид
к
F9= Σnι\ndetΣι.
1=1
Заметим, что функционал F9 равносилен (взвешенному) среднему
геометрическому определителей матриц Σα,... ,17^, в то время
как функционал F5 эквивалентен определителю матрицы,
равной (взвешенному) среднему арифметическому этих же матриц
(см. формулу (20)).
§ 5. Функционалы качества разбиения 305
31
32
33
34
35
36
37
38
39
40
41
42
43
1
199
227
228
232
231
215
184
175
239
203
226
226
210
2
105
117
122
123
121
118
100
94
124
109
118
119
103
3
73
77
82
83
78
74
69
73
77
70
72
77
72
4
23,4
25,0
24,7
25,3
23,5
25,7
23,3
22,2
25,0
23,3
26,0
26,5
20,5
5
15,0
15,3
15,0
16,8
16,5
15,7
15,8
14,8
16,8
15,0
16,0
16,8
14,0
6
19,1
18,6
18,5
15,5
19,6
19,0
19,7
17,0
27,0
18,7
19,4
19,3
16,7
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
1
205
228
218
190
212
201
196
158
255
234
205
186
241
220
242
2
ПО
122
112
93
111
105
106
71
126
113
105
97
119
111
120
3
68
78
65
78
73
70
67
71
86
83
70
62
87
88
85
4
20,8
22,5
20,3
19,7
20,5
19,8
18,5
16,7
21,4
21,3
19,0
19,0
21,0
22,5
19,9
5
14,1
14,2
13,9
13,2
13,7
14,3
12,6
12,5
15,0
14,8
12,4
13,2
14,7
15,4
15,3
6
16,4
17,8
17,0
14,0
16,6
15,9
14,2
13,3
18,0
17,0
14,9
14,2
18,3
18,0
17,6
Рис. 16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1
129
154
170
188
161
164
203
178
212
221
183
212
220
216
216
2
64
74
87
94
81
90
109
97
114
123
97
112
117
113
112
3
95
76
71
73
55
58
65
57
65
62
52
65
70
72
75
4
17,5
20,0
17,9
19,5
17,1
17,5
20,7
17,3
20,5
21,2
19,3
19,7
19,8
20,5
19,6
5
11,2
14,2
12,3
13,3
12,1
12,7
14,0
12,8
14,3
15,2
12,9
14,2
14,3
14,4
14,0
6
13,8
16,5
15,9
14,8
13,0
14,7
16,8
14,3
15,5
17,0
13,5
16,0
15,6
17,7
16,4j
Пример 4. Разделение многомерных нормальных законов
(дискриминантпный анализ). В таблице на рис. 16 указаны
размеры челюстей и зубов тридцати собак (номера 1-30),
двенадцати волков (номера 31-42) и ископаемого черепа неизвестного
животного (номер 43), найденного в четвертичном слое (по
данным Де Бониса, приведенным в [30, с. 25]). Рис. 17 демонстрирует
измеряемые характеристики: 1 — длина черепа, 2 — длина верхней
челюсти, 3 —ширина верхней челюсти; следующие измерения
относятся к зубам: 4 — длина верхнего карнивора, 5 — длина первого
верхнего моляра, 6 —ширина первого верхнего моляра. Требуется
решить, к какому из классов (собак или волков) следует отнести
неизвестное животное.
Для того, чтобы это сделать, воспользуемся статистической
моделью случайного выбора единственного наблюдения из некоторого
многомерного нормального закона, причем заранее известно, что
этот закон является одним из к заданных законов Λ/Χμ^,Ι^)» гДе
J = l,...,fc.
В соответствии с принципом максимального
правдоподобия будем считать областью притяжения закона λί(μ^Σι)
(I = l,...,fc) множество таких точек χ € Rm, где плотность
распределения Ν(μι,Σ{) больше других. Это равносильно тому,
что величина
Ы(х) = lndet Σι + (χ- μι)τΣ^1(χ - μζ)
имеет наименьшее значение среди hi,...,ft* (см. формулу (8)).
Рис. 18 иллюстрирует получаемое при т = 1 и к = 2 разбиение
R на две области притяжения.
Рис. 17
ι
I
ι ЛК ι
))))))))))))))»))|<«Ш(ф)))))))|««««(«(Т«(«
μι μ2
Рис. 18
306
Глава 19. Классификация
Замечание 7. В случае к = 2 данный способ выбора между
законами с произвольными (известными) плотностями р\ и рг
минимизирует сумму α + β вероятностей ошибок I и II рода при
проверке гипотезы Н\: р(х) = ρι(χ) (см. § 1 гл. 13) против
альтернативы #2 · р(х) = Р2(х) по единственному наблюдению х0 Ε Rm.
Доказательство. Обозначим через G критическое множество
критерия для проверки гипотезы if ι против альтернативы #2.
Тогда
<* + β = \pi(x)dx+ P2(x)dx = 1+ (pi(aj) -рг(ж))dx.
G R™\G G
Интеграл в правой части принимает наименьшее значение в случае,
когда множество G состоит из всех точек, где подынтегральная
функция неположительна, т. е. рг(ж) ^ Pi (ж). ■
Отметим, что оптимальное множество G принадлежит (при
с = 1) семейству критических множеств из критерия Неймана-
Пирсона (см. § 2 гл. 13)
{ Pi(*) J
Для α + β можно получить оценку сверху (см. [90, с. 392]):
a + β < e_J5, где В = - In y/pi(x)p2(x)dx.
Здесь В = В'(рьрг) ~~ расстояние Бхаттачария (см. [1, с. 67]). Оно
инвариантно относительно взаимно однозначных преобразований
координат и обращается в нуль при р\ = Р2- Известно, что для
двух нормальных законов
B = lln-li 2 / +±(!ι2-μι)τ(Σι + Σ2>\ \μ*-μι).
2 ^/(det^Xdet^) 8 ^2 μι) \ 2 J ^2 μι)
В частности, при Σι = Σ% видим, что В = 6?(μ1,μ2)/8, где d(x,y)
обозначает расстояние Махаланобиса (см. формулу (18)).
Применим эти результаты к данным о собаках (I = 1) и волках
(/ = 2). Чтобы уравнять влияние размеров черепа и зубов
(первые на порядок больше последних), нормируем столбцы таблицы,
приведенной на рис. 16, с помощью устойчивого к выделяющимся
наблюдениям преобразования
Z' = (Z - MED)/MAD (нормировка N3 из § 1).
Так как истинные μι и Σι неизвестны, используем вместо них
оценки максимального правдоподобия ~х\ и Σ\. [Все
промежуточные вычисления (нормировку, подсчет средних и ковариаций,
§ 6. Неизвестное число классов
307
умножение матриц, нахождение обратных матриц и
определителей) удобно проводить с использованием встроенных функций
программы Excel.]
В результате подсчетов получим значения hi = —2,94
и /12 = 39,7. Поскольку h\ < /12, в соответствии с принципом
максимального правдоподобия неизвестное ископаемое животное,
скорее всего, было собакой. При этом значение В = 4,08, что
приводит к оценке суммы вероятностей ошибок I и II рода величиной
е~в « 0,017.
Этот вывод подтверждает и диаграмма рассеяния (рис. 19) —2
нормированных признаков 1 (длина черепа) и 4 (длина верхнего
карнивора). Первый откладывался по оси X, второй —по оси Y.
Волки обозначены треугольниками, собаки — точками, неизвестное
животное — крестиком. На основе диаграммы можно заключить,
что главным признаком, с помощью которого различаются собаки
и волки, является размер зубов.
•
|_! 1
ψ w
τ
•V.
τ
• ·. ·
ч/ vf* #
•#
§6. НЕИЗВЕСТНОЕ ЧИСЛО КЛАССОВ
В случае, когда число классов к заранее не задано, функционал
качества разбиения выбирают, чаще всего, в виде некоторой
алгебраической комбинации (взвешенной суммы, произведения) двух
функционалов F(S) и G(S). Первый, как правило, характеризует
внутриклассовый разброс и является убывающей функцией от к.
Второй сдерживает тенденцию к излишней детализации и
возрастает при увеличении к.
-4 -2 0
Рис. 19
Бабушка, а почему у тебя
такие большие зубы?
Красная Шапочка
Основываясь на общей концепции степенных средних,
разработанной А. Н. Колмогоровым (см. [52, с. 90]), можно взять F = ут
и G = l/zr (см. формулу (1)), где
-|1/т
dij
(i = Ι,.,.,η).
Здесь S(xi) обозначает класс, включающий объект cci, v(xi) — число
объектов в S(xi), η — общее количество объектов. Выбор параметра г
находится в распоряжении исследователя.
Величина JT называется мерой концентрации точек,
соответствующей разбиению S. Пусть щ — это число объектов в классе Si,pi = —
η
(Ζ = 1,... ,fc). Тогда нетрудно проверить, что ζ_ι = 1/fc, J+0o = maxpi,
Ξ_οο = mm pi, — log2 Jo = — Σ Pi 1°S2 Pi ~ энтропия разбиения (см. § 5
гл. 12),
(21)
*ι = -Σ* = -Σ( -^ Ι = — Σ щ = Σ ρι ·
nt=l n i=l \ η / η 1=1 1=1
Заметим, что при любом τ мера концентрации имеет минимум,
равный 1/п, при разбиении на η одноточечных классов, и максимум,
равный 1, при объединении всех объектов в один общий класс.
308
Глава 19. Классификация
Пример 5. Задача аппроксимации матрицы связей [1,
с. 173], [52, с. 103], [56]. Предположим, что данные представляют
собой матрицу связей А= \\а^\\пхп между объектами (чем больше
величина а^, тем связь сильнее). В качестве а^ могут выступать,
скажем, объемы межотраслевых поставок или коэффициенты
корреляции признаков.*^
Требуется найти такое разбиение 5 с булевой матрицей
В = \\bij\\nXni которое бы в наибольшей степени соответствовало
матрице А. Элементы Ь^ определяются так: Ъц = 1, если объекты
Xi и Xj принадлежат одному классу, bij = 0 — если разным.
Как сопоставить матрицы А и В друг с другом? Ведь ац —
действительные числа, а Ь^ — булевы переменные. Б. Г. Миркин
(см. [56]) предложил взвешивать Ь^, вводя некоторые
коэффициенты сдвига μ и масштаба σ > 0, и использовать в качестве меры
точности аппроксимации величину
Δ(5, μ, σ) = £ (ау - μ - σ^·)2. (22)
*ij=i
Минимизацию Δ(5,μ,σ) надо производить по 5, μ и σ. Для
упрощения задачи зафиксируем μ и σ. Тогда поиск минимума
функции (22) по 5 равносилен минимизации функционала
H(S) = - Σ (ay " P)bij, где ρ = μ + σ/2. (23)
Действительно, поскольку bf^ = ify, можно записать отдельное
слагаемое из суммы в формуле (22) в виде
(dij - μ)2 - 2a(a,ij - μ)^· + σ26^ = const -2σ(α^ - p)bij, (24)
что и доказывает равносильность.
Величина ρ играет роль порога существенности для величины
связей. В самом деле, чтобы минимизировать правую часть
равенства (24) по Ь^ надо, очевидно, положить Ь^ = 1, если ац > р,
и Ь^ = 0, если aij ^ р. Однако, сами Ь^ порождаются разбиением
5, поэтому мы не имеем права назначать им произвольные булевы
значения. Тем не менее, для уменьшения H(S) при а^ > ρ выгодно
поместить Xi и Xj в один класс.
Переходя к внутриклассовым связям (для которых Ь^ = 1),
имеем
h(s) = -Z Σ («у-р) = -Е Σ <Ηί + ρΣ»ι.
1=1 Xi,Xj£Si l=lXi,XjGSi 1=1
где щ — число объектов в классе Si. Это представление
показывает, что H(S) обеспечивает компромисс между общей суммой
*) Если заданы расстояния dij между объектами, то можно формально
преобразовать их в связи, например, по формуле ац; = 1/(1 + dij).
Элементами булевых
матриц служат нули
и единицы. Они названы
так в честь Дж. Буля
(1815-1864)-английского логика.
§ 7. Сравнение методов
309
внутриклассовых связей и (взвешенной) мерой концентрации z\
(см. формулу (21)).
Разбиение, минимизирующее H(S), обладает тем свойством,
что получаемые классы Si оказываются кластерами
(сгущениями в среднем) в смысле определения С2 из § 1: средняя связь
a(Si) = Σ aijln<i не меньше, чем средняя связь вовне a(Si^Si)
Xi,Xj€Si
и средняя связь между любыми классами a(Si,Sm). Точнее, для
любых / φ т имеем a(5j,Sj), a(Si,Sm) ^ ρ ^ a(Si) (см. [1, с. 174]).
Это оптимальное разбиение может быть найдено с
помощью иерархической процедуры, на очередном шаге которой
объединяются те классы Si и 5т, для которых сумма связей
Σ (aij — р) максимальна и положительна. Процесс объеди-
Xi€Sl,Xj€Sm
нения заканчивается, когда такие суммы для всех Ι φ т становятся
неположительными.
Смысл параметров μ и σ проясняет минимизация по ним
Δ(5,μ, σ) при фиксированном разбиении 5. Вычислив частные
производные по μ и σ функции
/(/*>σ) = Σ (aij - μ ~ σ)2 + Σ (αυ ~ μ)2,
получим систему уравнений относительно оптимальных μ и σ:
Σ (α0·-μ-σ)+ Σ (<*θ·-£) = 0, Σ (αίά-μ-σ) = 0.
(tfj): 6y =1 (tfj): 6<j=0 (ij): 6y=l
Подставляя второе уравнение в первое, находим, что μ равно
средней межкластерной связи. Из второго уравнения вытекает, что
μ+σ — это средняя внутрикластерная связь. При этом порог ρ — их
полусумма, σ — характеристика контрастности связей (ср. с рис. 7).
Недостатком рассмотренного метода является наличие единого
порога ρ для всех классов, что не соответствует ситуации, когда
присутствуют классы существенно различных размеров (о путях
его преодоления рассказывается в [1, с. 175]).
§7. СРАВНЕНИЕ МЕТОДОВ
Определяющее значение при выборе метода классификации имеет
общее число объектов п. Если оно велико (сотни или тысячи),
то необходимо применять эвристический алгоритм А4 («Форель»),
скомбинированный с А2 (кратчайший незамкнутый путь) (§ 2), или
быстрые иерархические процедуры для редуктивных мер
отдаленности (§ 4).
Для η ^ 200 в [52, с. 108-117] приводятся результаты
экспериментального сравнения нескольких методов классификации
310
Глава 19. Классификация
(в частности, A3 из § 2 и Р1—Ρ5 из § 3) путем их применения
к моделированным совокупностям объектов.
Объекты генерировались как точки в m-мерном единичном
гиперкубе (3 ^ т ^ 7). Задавалось число классов к (3 ^ к ^ 7)
и наудачу в гиперкубе выбирались центры классов ух (I = 1,... ,fc).
Для каждого класса с помощью датчика случайных чисел
моделировались т длин сторон гиперпараллелепипеда с центром в уь
в который затем случайно бросались щ точек (30 ^ гц ^ 50).
При фиксированных тик каждое разбиение генерировалось 50
раз и показатели усреднялись (всего было обработано около 2000
выборок).
Кроме того, генерировались «шумящие» объекты, равномерно
распределенные в гиперкубе. Их количество составляло заданный
процент ρ от η (10% ^ ρ ^ 30%). Эти объекты предназначались
только для того, чтобы «сбивать с толку» алгоритмы
классификации, но, естественно, не участвовали в расчете показателей качества
классификации (одним из таких показателей было расстояние Хем-
минга (см. метрику D1 из § 1) между моделированным разбиением
и разбиением, которое построил алгоритм).
Изложим кратко основные выводы. Наилучшей (почти
идеальной) по восстанавливаемости разбиения проявила себя
иерархическая процедура Р5 («метод Уорда»). Следом за ней идут
процедура Р2 («дальнего соседа») и алгоритм A3 (метод fc-средних Болла
и Д. Холла) (случайный выбор эталонов в алгоритме A3 показал
себя как крайне неудачный). Самой плохой оказалась процедура
Р1 («ближнего соседа»).
По уровню устойчивости к шуму лидерами стали алгоритмы A3
и Р5. Замыкает список снова Р1.
Всякий необходимо
причиняет пользу,
употребленный на своем
месте. Напротив того:
упражнения лучшего
танцмейстера в химии
неуместны; советы
опытного астронома
в танцах глупы.
Козьма Прутков
Не следует воспринимать эти результаты как приговор методу
«ближнего соседа», а также близким к нему «по духу» (имеющим
цепочечный эффект) алгоритмам А1 («связные компоненты») и А2
(«кратчайший незамкнутый путь») из § 2. Речь может идти лишь
о том, что на первичном этапе классификации, не обладая
информацией о структуре классов, лучше применять менее чувствительные
методы.
В случае, когда классы имеют сложную форму, скажем, относятся
к типу СЗ из § 1 («класс типа ленты или слабое сгущение»), именно
алгоритмы Р1, А1 и А2 позволят правильно произвести разбиение.
Г. Миллиган и М. Купер в 1985 г. опубликовали
результаты экспериментального сравнения в похожих условиях
тридцати методов классификации (см. [52, с. 157]), в число
которых вошли алгоритмы минимизации функционалов (см. § 5)
F4 =
п — к
tvW
int
fc-l
tiW,
out
(Калинский и Харабаш,
§ 9. Поиск в глубину
311
1974) и инвариантного функционала Fl = det Wint/det Wtot
(Фридман и Рубин, 1967). Первый оказался самым лучшим, а
второй — в группе самых плохих. Дело, скорее всего, в удачной
нормировке матриц рассеяния у F4 (сравните с формулой (9) гл. 16).
§8. ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ
После проведения классификации важно в удобной форме
представить ее результаты. Приведем список важнейших (согласно [52,
с. 159]) характеристик классификации.
1. Распределение номеров объектов по номерам классов.
2. Гистограмма межобъектных расстояний (подобная
изображенной на рис. 7).
3. Средние внутриклассовые расстояния.
4. Матрица средних межклассовых расстояний.
5. Визуальное представление данных на плоскости двух (в
пространстве трех) «наиболее информативных» признаков.
6. Дендрограмма для иерархических процедур.
7. Средние значения и размахи во всех классах для каждого
признака.
Последний пункт наиболее принципиален, так как в
подавляющем большинстве случаев интерпретация классов происходит по
средним значениям признаков в них. Сопоставление же средних
значений для заданного признака наиболее просто осуществляется,
если классы не имеют наложения проекций. Степень разделепности
классов по каждой оси можно охарактеризовать с помощью
коэффициента
где Яг—размах по заданному признаку 1-го класса, a Li,Z/2,...—
длины наложений проекций классов на ось признака (рис. 20). Если
7 = 1, то классы полностью разделимы. Чем ближе η к 0, тем больше
наложение проекций классов друг на друга.
Вред или польза действия
обусловливаются
совокупностью обстоятельств.
Козьма Прутков
R
R,
Li
Рис.
i
20
Дз
§9. ПОИСК В ГЛУБИНУ
Основой для выделения связных компонент графа в методе А1
из § 2 служит алгоритм обхода всех вершин неориентированного
связного графа G, именуемый поиском β глубину (сокращенно ПГ).
Изложим его, следуя [28, с. 323].*)
В процессе поиска в глубину вершинам графа G присваиваются
номера (ПГ-номера), а ребра помечаются. В начале ребра не
помечены, вершины не имеют ПГ-номеров. Начинаем с произвольной
*) В [28] приведены также подробные описания (с примерами) многих других
полезных алгоритмов поиска на графах, скажем, поиска β ширину (с. 37) или
метода Дейкстры нахождения кратчайшего пути между двумя заданными
вершинами графа (с. 342).
312
Глава 19. Классификация
W= (3,2,5)
ЛГ2 = (4,1,5)
ЛГз = (1,5)
ЛГ4 = (2,5)
ЛГ5 = (2,1,3,4,6)
N6 = (5)
2(4)Х\3(2)
Γ^5(3)
4(5)/б(6)
Рис. 21
вершины v. Присваиваем ей ПГ-номер ΠΓ(ν) = 1 и выбираем
произвольное ребро vw. Ребро vw помечается, как «прямое», а вершина
w получает (из г;) ПГ-номер ПГ(гу) = 2. После этого переходим
в вершину w. Пусть в результате выполнения нескольких шагов
этого процесса пришли в вершину х, при этом к — последний
присвоенный ПГ-номер. Далее действуем в зависимости от ситуации
следующим образом.
1. Имеется непомеченное ребро ху. Если у вершины у уже есть
ПГ-номер, то ребро ху помечаем как «обратное» и продолжаем
поиск непомеченного ребра, выходящего из вершины х. Если же
вершина у не имеет ПГ-номера, то полагаем ПГ(у) = к + 1, ребро
ху помечаем как «прямое» и переходим в вершину у. Вершина у
считается получивший свой ПГ-номер из вершины х.
2. Все ребра, выходящие из х, помечены. Тогда возвращаемся
в вершину, из которой χ получила свой ПГ-номер.
Процесс закончится, когда все ребра будут помечены и
произойдет возвращение в вершину v.
Для того, чтобы в пункте 2 узнать, из какой вершины получила
свой ПГ-номер вершина ж, надо запоминать список Q, в который
каждая вершина включается в момент получения ПГ-номера и
исключается, как только произойдет возвращение из этой вершины.
Включение и исключение вершин производятся всегда с конца
списка.*)
Пусть граф G задан списками смежности, т. е. для каждой
вершины χ приведен Nx — список всех вершин, соединенных с ней
ребрами.
На рис. 21 изображен граф и списки смежности, которыми он
задан, а также представлены результаты применения к этому графу
поиска в глубину из вершины ν = 1. Каждой вершине приписан ее
номер и ПГ-номер (в скобках). «Прямые» ребра проведены сплошными
линиями, а «обратные» — пунктирными.
Отметим, что по построению «прямые» ребра образуют
незамкнутый путь (дерево), соединяющий все вершины (связного) графа G.
Однако, этот путь, вообще говоря, не является кратчайшим (см. А2
из § 2): на рис. 21 выгоднее соединить вершины 4 и 6, а не 5 и 6.
Можно показать, что трудоемкость и объем памяти для поиска
в глубину составляют 0(п + га), где п — число вершин графа, га —
число ребер (см. [28, с. 325]).
Поиск в глубину используется в качестве составной части во
многих алгоритмах. В частности, с его помощью почти без
дополнительных вычислительных затрат решается задача выделения
связных компонент графа. Для этого достаточно один раз
просмотреть список вершин графа, выполняя следующие действия.
Если просматриваемая вершина г (г = 1,... ,п) имеет ПГ-номер, то
*) Программисты называют такой список стеком.
Решения задач
313
перейти к следующей. Иначе положить ν = г, ΤΪΓ(ν) = fc+1, где к —
последний присвоенный ПГ-номер, и применить поиск в глубину.
После его окончания (т. е. выделения компоненты, содержащей г)
продолжить просмотр списка вершин с г + 1. Различать вершины
разных компонент можно по их ПГ-номерам, если для каждой
компоненты запомнить последний ПГ-номер.
Замечание 8. После удаления к — 1 самых длинных ребер
КНП (алгоритм А2 из § 2) автоматическое разбиение на классы
можно произвести путем выделения связных компонент
оставшегося графа.
Рис. 22
Нить, которую дала Ариадна Тезею для блуждания по лабиринту
острова Крит, предназначалась не только для того, чтобы найти
обратную дорогу, но и позволяла избежать «петель» — бесконечного
хождения по замкнутой траектории. Для этого нужно просто
поворачивать назад, если нить пересекает дорогу (рис. 22). Петля
становится тупиком. На языке теории графов происходит возвращение по
«обратным» ребрам, которое разрывает циклы и превращает граф
лабиринта в дерево.
ЗАДАЧИ
1? Выведите формулу (4) Ланса и Уильямса для мер отдаленности Ну, между ими я, конечно,
иерархических процедур РЗ-Р5 из § 3. пГ^лТниГподумать
2* Проверьте, что Wtot = Wint + Wout (см. формулу (7)). ужас!
3. Получите ТОЖДеСТВО (10). Репетилов в «Горе от
__ _ w-,-1/2/ \ ума» А. С. Грибоедова
Указание. Введите вектор у = Σ ' (χ — μ).
4* Пусть ρι(χ) и р2(х) — плотности законов Λ/Χμ^ Σ χ) и Ν(μ2, Σ2)
(см. замечание 7), причем Σ ι = Σ2 = Σ (модель Фишера).
а) Запишите явно уравнение разделительной гиперплоскости
hi = /ΐ2·
б) Найдите вероятности ошибок I и II рода а и β при
классификации на ее основе.
РЕШЕНИЯ ЗАДАЧ
1. Для процедуры средней связи РЗ с учетом 5ι Π S2 = 0 имеем
[η0(Πι + П2)] Pave(So, Si U S2) = £ Σ dij =
XieSoxjeSiuS2
= Σ Σ dij + Σ Σ dij =
= ЩП1 pave(So, Si) + ЩП2 /w(#(b #2)·
Разделив обе части на ηο(πι + пг), получим требуемое.
В случае метода центров масс Р4 доказательство немного
сложнее. Рассмотрим систему из двух масс Πι и п2, которые
314
Глава 19. Классификация
находятся в центрах масс Χι и ж2 классов 5ι и S2 соответственно.
По теореме о межточечных расстояниях (см. решение задачи 5
гл. 16) момент инерции этой системы относительно общего
центра масс Ж152 равен
1х12 =П1|Ж1-Ж1,2|2 + п2|ж2-Ж1,2|2= ηι™2 |ж!-ж2|2. (25)
В силу теоремы Гюйгенса (см. решение задачи 3 гл. 16) момент
инерции относительно центра масс х$ класса So имеет вид
Ιχ0 = nl|#l _^о|2 +^2|^2 -Хо\2 = Ixlt2 + (п1 + ™2)|#ι,2 - Ж0|2.
Отсюда и из формулы (25) следует, что
ηι\Χι-Χο\2+η2\Χ2-Χθ\2- П1П2 |«1-Ж2|2 = (П1+П2)|Ж1 2-Ж0|2.
П\ +П2
Остается только разделить обе части на {п\ + п2).
Поскольку мера отдаленности метода Уорда Р5 задается
равенством pw = —^—^— \xi — ж2|2, формула Ланса—Уильямса
Πι Η- 7l2
ДЛЯ Нее ЛеГКО ВЫВОДИТСЯ ИЗ формулы ДЛЯ рcenter-
2. Достаточно доказать, что для фиксированного класса Si
выполняется матричное тождество
Σ (xi - x){xi -х)т= Σ (xi - xi)(xi - Щ)т+
XiESi &i€Si
+ nt(xi -x)(xi -x)T.
Для элементов на главной диагонали оно вытекает из
теоремы Гюйгенса. В противном случае оно следует из тождества
ab = [(a + Ь)2 — (α — Ь)2]/4 и линейности центра масс.
3. Положим у = Σ~ι'2{χ — μ) (см. ΠΙΟ). Ввиду дистрибутивности
матричного умножения у = Σ~1^2(χ — μ). В новых координатах
доказываемое равенство (10) имеет вид
Е\Уг\2 = п\у\2+£\Уг-у\2·
г=1 г=1
Оно справедливо в силу все той же теоремы Гюйгенса.
4. а) Уравнение разделяющей классы поверхности h ι = /ι2 в
данном случае эквивалентно условию
(х - μι)τΣ-\χ - μι) = (χ - μ2)τΣ-ι{χ - μ2). (26)
Сделаем замену у = Σ"ι^2(χ — μι). Тогда χ = Σx^2y + μχ
и Σ~ιί2{χ — μ2) = у + 6, где 6 = Σ~ι^2(μλ - μ2). При этом
условие (26) превращается в уравнение
\у + 6|2 - \у\2 = (у + 6)т(2/ + Ь) - у7^ = 26т2/ + |6|2 = 0.
Ответы на вопросы
315
Это уравнение гиперплоскости в координатах у. Подставив
в него выражения для у и 6, запишем его в координатах х:
Ьт(2у + Ь) = (Ml - μ2)τΣ~\2χ - Ml - μ2) = 0. (27)
Положив о = Σ~1(μ1 — μ2), перепишем (27) в форме
ατ(2χ — μι — μ2) = 0.
б) Пусть верна гипотеза #ι: Χ ~ λί(μ^ 27). Введем случайную
величину У = ατ(2Χ — μλ — μ2). Как линейная функция
от нормального вектора X, случайная величина Υ имеет
нормальное распределение (П9). Найдем МУ и ΏΥ при условии
справедливости гипотезы Н\\
ΜλΥ = ατ(2μ1 - μλ - μ2) = ατ(μ1 - μ2) = d,
где d = ώ(μ1,μ2) = (μχ — μ2)τΣ~1(μ1 — μ2)—расстояние
Махаланобиса между μλ и μ2 (см. формулу (18)); по свойствам
дисперсии из П2
Dtf = 4D!(aTX) = 4ατΣα = ΑατΣ[Σ~ι{μι - μ2)] = 4d.
Таким образом, Υ ~ Af(d14d) при выполнении гипотезы Н\.
Отсюда
где Ф(х) обозначает функцию распределения закона Λ/χθ,1).
Аналогично, при гипотезе Н2: Χ ~ Λί(μ2,Σ) находим, что
случайная величина У ~ ЛГ(—с?, 4с?) и
Чем более далекими в метрике Махаланобиса являются μχ и μ2,
тем меньше вероятность ошибочной классификации.
ОТВЕТЫ НА ВОПРОСЫ
1. Пусть вектор χ = (#ι,... ,#m) имеет ровно к компонент
величины Μ = max{|a;i|,... ,|#m|}. Тогда
{\x1\r + ... + \xmn1/p=:M[k + e{ + ... + epm_k)1/p,
где Si < 1. При ρ —► оо выражение в квадратных скобках справа
стремится к А:, а вся правая часть — к М.
2. Обозначим через D вершину равностороннего треугольника
BCD (рис. 23). Искомой точкой служит точка пересечения
окружности с отрезком AD внутри А АВС. Действительно,
Ζ ВОС = 120°, поскольку опирается на дугу ВС величины
240°. С другой стороны, ΔΒΟΌ = Ζ BCD = 60°, так как
316
Глава 19. Классификация
ч/З
А
О1 1 2
ш
ABC
Рис. 25
эти углы опираются на общую дугу BD. Отсюда ΔΑΟΒ =
= 1SO°-ZBOD = 120°, Ζ АОС = 360°-Z£OC-Z ЛОЯ = 120°.
3. Точка пересечения диагоналей О — искомая. Для любой другой
точки О' отрезки диагоналей заменяются на ломаные (рис. 24).
4. Может. Для вершин равностороннего треугольника со
сторонами длины 2 на втором шаге происходит объединение на уровне
у/3 < 2 (рис. 25).
5. а) Если pmin(S0,Si) ^ δ и /9min(5o,52) ^ £, то
pmin(So,Si US2) = min{pmin(5o,5i),/9min(5o,52)} ^ ί.
б) Пусть pw(Si,S2) < <*> а Pw(So,Si) ^ ί, PwOubft) ^ ί.
Воспользуемся формулой Ланса и Уильямса:
/0w(So,SiUS2) ^ [(no-f^i)i + (^o + ^2)^-%^]/(^o + ^i + ^2) = δ.
-1
х)т = (2гт)_1 = 27" \ то обратная
27 _1 является симметричной. Пусть
6. Так как (см. ΠΙΟ) (27
ковариационная матрица
С — ортогональная матрица, преобразующая 27 к главным осям:
СТ27С = Л. Тогда ΟτΣ~λΟ = Л~\ где Л"1—диагональная
матрица с положительными элементами на главной диагонали.
7. Согласно обобщенной проблеме собственных значений (см. Π10)
для пары Σ и Σ найдется такая невырожденная матрица D,
что ΌΤΣΌ = Л и ΌΤΣΌ = Ε. Если Л = Е, то Σ =
= (ХЯУЧО)-1 = (DD7)-1 = 17.
Глава 20
КОРРЕЛЯЦИЯ
После того, как (с помощью методов из гл. 19) объекты
разбиты на однородные группы (классы), возникает задача изучения
взаимосвязей признаков внутри отдельного класса. На практике
чаще всего встречаются следующие два вида зависимостей: а)
объекты образуют «облако» эллиптического типа (рис. 1, а), б)
объекты располагаются в окрестности некоторой кривой
(поверхности) (рис. 1, б). В случае а) оба признака являются
«полноценными» случайными величинами, и изучению подлежит уровень
зависимости (корреляции) между ними. Случай б) соответствует
«функциональной» зависимости между признаками, испорченной
шумом. Зависимости первого вида изучаются в этой главе
методами корреляционного анализа. Методы, позволяющие во втором
случае построить интересующую исследователя кривую
(поверхность), относятся к так называемому регрессионному анализу. Они
обсуждаются в гл. 21 и § 2 гл. 22.
§ 1. ГЕОМЕТРИЯ ГЛАВНЫХ КОМПОНЕНТ
Допустим, что каждый из η объектов описывается га признаками
(координатами), и представим данные (для отдельного класса
объектов) в форме таблицы X = ||ж^||пХтп. Вычислим для каждого
_ 1 п
признака (столбца матрицы X) среднее значение Χι = — Σ хи
п i=i
и центрируем данные: х'й = хц —Щ.*"* Далее в этой главе будем
считать хц уже центрированными:
Д1. χι =0 для / = 1,... ,га.
Обозначим через Σ = ||<7fci||mxm выборочную ковариационную
матрицу (центрированных) признаков: Σ = - ХТX (т. е. ды —
выборочная ковариация k-το и /-го столбцов матрицы X).
Поскольку Σ — матрица ковариаций, она неотрицательно
определена (см. ШО). Следовательно, существует ортогональная
матрица С, приводящая Σ к главным осям: С ΣΟ = Л.
Здесь Л —диагональная матрица с неотрицательными элементами
λι ^ ... ^ Хт на главной диагонали, которые являются корнями
уравнения det(57 — \Е) = 0. Они называются собственными
значениями матрицы Σ. Предположим, что все \ι положительны
а)
б)
Рис. 1
Сократ. А смог бы
ты, не глядя на скалу,
а рассматривая ее
отражение в воде, сказать,
как можно было бы
взобраться на самую
вершину?
А. Реньи. Диалоги
*) Это преобразование не искажает интересующую нас внутреннюю структуру
класса, характер взаимосвязей признаков.
318
Глава 20. Корреляция
и различны (для экспериментальных данных хц это условие
выполняется практически всегда). При этом столбцы Ci,... ,Ст матрицы
С (главные оси или компоненты) определяются однозначно с
точностью до выбора направления оси (одновременного изменения
знака всех координат вектора q). Они образуют новый ортонор-
мированный базис в Rm (рис. 2), обладающий рядом важных
свойств.
1) Проекции объектов на первую главную компоненту С\ имеют
наибольшую выборочную дисперсию среди проекций на
всевозможные направления ά в пространстве Rm.
Доказательство. Вектор проекций у на направление ά
(άτά = 1) задается равенством у = Xd. Ввиду допущения Д1
1 п 1 п гп га
Ι7=-Σ& = -ΣΣ xndi = Σ %idi = 0.
n i=l ni=ll=l 1=1
Тогда выборочная дисперсия проекций на направление d равна
S2(d) = ±Еу1 = ±УТУ=± (XdfXd = dTEd. (1)
П ,j = 1 П П
Тем самым задача сводится к максимизации по d квадратичной
формы dTΣά при условии d d = 1. Для ее решения применим
метод неопределенных множителей Лагранжа (см. [46, с. 271]).
Приравнивая нулю частные производные по переменным d\
функции Лагранжа
F(d,A) = dTEd - \{dTd - 1) = Σ Σ °kidkdi -ХЕ<% + \
k=ll=l 1=1
приходим к системе (линейных относительно c?i,... ,G?m)
уравнений
q m
£- F(d,A) = 2 Σ *kidk ~ 2λ* =0, / = 1,... ,m.
ddi fc=i
Ее можно записать в матричной форме:
Σά - Xd = 0 4=> (Σ - \E)d = 0.
(2)
Поскольку dTd = 1, нас интересуют только ненулевые решения.
Для них должно выполняться условие det(I7 — ХЕ) = 0, т. е.
искомое направление d обязано быть собственным вектором
Σ, отвечающим собственному значению λ. Умножая
соотношение (2) на dT слева, получим
d Σά = λ ά ά = λ.
Левая часть есть S2(a) (см. формулу (1)). Следовательно, λ
должно равняться наибольшему собственному значению λι
матрицы Σ, а ά = С\. Ш
§ 1. Геометрия главных компонент
319
2) Второй собственный вектор С2 характеризуется тем, что
выборочная дисперсия проекций объектов на ось С2 максимальна
среди всех направлений d, ортогональных вектору Ci, т. е.
таких, что dTCi = 0.
Доказательство. Функция Лагранжа в этом случае
выглядит так:
F(d,A,//) = dTEd - \(dTd - 1) - μ{άτοι - 0).
Вычисляя ее частные производные по dj, приходим к системе
Σά-Xd- μοι = 0. (3)
Транспонируем равенство (3), умножим на С\ справа и
воспользуемся тем, что С\ — собственный вектор с собственным
значением λι (т. е. Ес\ = AiCi), а также условием dTCi = 0:
dTEci - XdTCi - μο{αχ = 0 4=> λι·0-λ·0-μ·1=0.
Отсюда μ = 0. С учетом этого из (3) вытекает, что d —
собственный вектор матрицы Σ с собственным значением λ. Умножая
равенство (3) слева на d , выводим, что λ = Аг и d = c<i. Ш
3) При I ^ 3 аналогично устанавливается, что с/ — направление с
наибольшей выборочной дисперсией проекций объектов среди
направлений, ортогональных векторам Ci,... ,cj_i.
4) Сумма выборочных дисперсий исходных признаков (столбцов
матрицы Χ) ση + ... + дшш = tr Σ в силу подобия матриц Σ и
Л (см. П10) равна tr Л = λι + ... + \т = S2(c{) + ... + S^c™),
т. е. сумме выборочных дисперсий проекций объектов на (новые)
главные оси. Эта величина может рассматриваться как мера
общего разброса объектов относительно их центра масс.
Представляет интерес относительная доля разброса, приходящаяся
на к первых главных осей,
7fc = (Ai + ... + Afc)/(A1 + ... + Am), к < т.
Если эта величина при некотором к достаточно близка к 1, то
возможно уменьшение размерности пространства признаков за
счет перехода от т исходных признаков к к новым признакам —
первым главным компонентам. На практике нередко удается
ограничиться двумя или тремя компонентами без существенной
потери информации. Объекты описываются координатами в
новых осях, которым специалисты-прикладники, как правило,
могут придать содержательную интерпретацию.
Пример 1 ([30, с. 206]). Найдем и интерпретируем главные
компоненты для данных примера 4 гл. 19. Напомним, что
исходными признаками там были следующие: 1—длина черепа,
2 —длина верхней челюсти, 3 —ширина верхней челюсти, 4 —
Математика приводит нас
к дверям истины, но самих
дверей не открывает.
В. Ф. Одоевский
320
Глава 20. Корреляция
1
2
3
4
15
6
1
1
2
0,96
1
3
0,35
0,20
1
4
0,61
0,66
0,37
1
5
0,72
0,74
0,35
0,89
1
6
0,59
0,59
0,35
0,76
0,79
1 J
Cl
0,43
0,43
0,23
0,44
0,46
0,42
С2
0,23
0,38
-0,89
-0,07
0,02
-0,10
сз
0,53
0,39
0,38
-0,40
-0,27
-0,44
С4
0,11
0,01
-0,02
-0,52
-0,31
0,79
С5
0,05
-0,20
0,00
-0,58
0,78
-0,09
Сб
0,68
-0,69
-0,13
0,18
-0,09 ,
-0,01
Рис. 3 Рис. 4
длина верхнего карнивора, 5 — длина первого верхнего моляра,
6 — ширина первого верхнего моляра.
Очевидно, что при нормировке данных с помощью средних
арифметических и стандартных отклонений признаков (N2 из
§ 1 гл. 19) выборочная ковариационная матрица Σ совпадает с
выборочной корреляционной матрицей исходных признаков. [Ее
нетрудно подсчитать с помощью программы Excel. Результаты
вычислений представлены таблицей на рис. 3.]
Обратим внимание, что длина черепа (признак 1) и длина
верхней челюсти (признак 2) сильно коррелируют (j5i2 = 0,96),
поэтому целесообразно оставить в модели только один из них.
Признаки 4, 5 и 6, относящиеся к зубам, также очень тесно
связаны между собой, поскольку J945 = 0,89, /?4б = 0,76 и
Р56 = 0,79.
На рис. 4 приведены собственные векторы Ci,... ,св,
вычисленные степенным методом (см. § 3). Собственные значения
Afc, соответствующие им доли следа Xk/Y^^i (в %) и
накопленные доли 7fc (в %) указаны в следующей таблице:
Номера компонент
Собственные значения
Проценты от следа
Накопленные проценты
1
4,100
68,3
68,3
2
0,883
14,7
83,0
3
0,639
10,7
93,7
4
0,259
4,3
98,0
5
0,097
1,6
99,6
6
0,022
0,4 \
100,0
На первые 3 компоненты приходится 93,7% полной
дисперсии «облака». При этом первая компонента имеет смысл общего
размера. Это следует из того, что все координаты у с\ одного
знака и примерно одинаковы по величине, т. е. при
проецировании на эту ось координаты нормированных признаков просто
складываются.
Вторая компонента, по существу, отвечает за ширину верх-
ней челюсти (признак 3), поскольку третья координата у С2
по абсолютной величине равна 0,89 « 1. Эта ось отражает
различие в пропорциях челюстей и отличает удлиненные формы
от укороченных (гончих и колли от бульдогов и боксеров). На
§ 1. Геометрия главных компонент
321
вторую ось волки проецируются в основном рядом с немецкими
овчарками.
Третья ось противопоставляет размеры челюстей размерам
зубов: первые три координаты у Сз примерно равны по
абсолютной величине последним трем координатам, но
противоположны по знаку. Другими словами, третья ось отражает
относительную (по сравнению с размерами черепа) величину
зубов. Она позволяет отличить животных с развитыми зубами
(волки, немецкие овчарки, доберманы) от собак других пород
(сенбернары, мастифы, сеттеры).
5) Пусть Mfc — это подпространство, натянутое на главные оси
ci,... ,Cfc. Оказывается, при проецировании объектов на
произвольное подпространство Lk размерности к в Rm
геометрическая структура искажается в наименьшей степени, если этим
подпространством является М*. (см. [1, с. 350]):
а) сумма квадратов расстояний от объектов до их проекций
на Lk минимальна, когда Lk = Mk (в этом случае она равна
n(Afc+i + ... + Am) (доказательство см. в [76, с. 243]));
б) при проецировании на Mk наименее искажается сумма
квадратов расстояний между всевозможными парами объектов (для
Mk ее изменение составляет η2(λ&+ι + ... + Am));
в) когда Lk = Mk, в наименьшей степени искажаются
расстояния от объектов до их центра масс (совпадающего с началом
координат О ввиду допущения Д1), а также углы между
всевозможными парами прямых, соединяющих объекты с О.
Поясним последнее свойство. Рассмотрим матрицу скалярных
произведений G = ||<7ij||nxn = ХХТ. Нетрудно понять геометрический
то
смысл элементов этой матрицы: да = Σ хи представляет собой
1=1
квадрат расстояния от г-го объекта до О, а при i φ j величина
то
9ij — Σ xuxji пропорциональна косинусу угла между прямыми,
1=1
соединяющими г-й и j-й объекты с началом координат.
Обозначим через Υ = ||2/ii||nxm матрицу координат проекций
объектов на подпространство Lfc. Ей соответствует Η = \\hij\\nxn = УУТ.
Тогда при Lfc = Mk достигается
min|G-H|2=n2(A^+1+... + A^), (4)
где \А\2 = Σ a%j·,— квадрат евклидовой нормы матрицы А.
Замечание 1. Проецирование на плоскость двух первых
компонент часто применяется еще на этапе классификации (выделении
однородных групп). Авторы [4, с. 103] считают: «Гипотеза состоит в
том, что наибольший разброс данные будут иметь в направлениях,
«соединяющих» центры групп, а значит, проекции на старшие
главные компоненты обеспечат наилучшую «точку зрения» на данные,
322
Глава 20. Корреляция
когда группы видны на наибольших расстояниях и не закрывают
одна другую».
Замечание 2. Следует иметь в виду, что главные компоненты
вычисляются по выборочной ковариационной матрице Σ и поэтому
зависят от масштаба признаков. Скажем, если один из признаков
принимает значения от 0 до 100, а другие — от 0 до 10, то
независимо от структуры данных первый признак будет отождествляться
с первой главной компонентой. Чтобы избежать этого, обычно
перед вычислением главных компонент данные нормируют (см. § 1
гл. 19).
§2. ЭЛЛИПСОИД РАССЕЯНИЯ
Рассмотрим m-мерный случайный вектор £ с математическим
ожиданием М£ = О и ковариационной матрицей Σ$. (В частности,
годится эмпирическое распределение ) с нулевыми средними
арифметическими значений координат признаков (допущение Д1 из § 1)
и выборочной ковариационной матрицей Σ.)
В ШО доказано, что любая ковариационная матрица
неотрицательно определена. Потребуем дополнительно, чтобы матрица Σξ
была невырожденной. Это равносильно ее положительной
определенности, а также положительности всех ее собственных значений
λι ^ ... ^ \т. Обозначим соответствующие им собственные
векторы (направления главных осей) через Ci,... ,Ст.
Для произвольного направления d в Rm (\d\ = 1) случайная
величина ζ = dT£ представляет собой координату проекции
вектора £ на направление d. Найдем такое направление, для которого
дисперсия ϋζ имеет наибольшее значение. Запишем:
DC = M(dT£)2 = M(dT£)(dT£)T = Μ dTHTd = dT Σ^ά.
В точности так же^ как в § 1 для случая выборочной
ковариационной матрицы Σ, доказывается, что максимум дисперсии Οζ
достигается на направлении С\.
Аналогично устанавливается, что при I > 1 собственный
вектор ci является направлением с наибольшей дисперсией Οζ среди
направлений, ортогональных векторам Ci,... ,Q_i.
В силу того, что Σξ невырождена, существует обратная к ней
матрица Σ71, которая также положительно определена (см.
вопрос 6 гл. 19).
Определение. Эллипсоидом рассеяния распределения вектора £
называется m-мерный эллипсоид
χτΣξ1χ ^m-f 2.
*) У которого каждому набору (хц,... ,ж»т) координат г-го объекта (т. е. строке
таблицы данных X) приписана вероятность 1/п.
§ 2. Эллипсоид рассеяния
323
Он однозначно выделяется среди всех других эллипсоидов
следующим своим свойством (см. [44, с. 333]): если рассмотреть рае-
померно распределенный на нем вектор U (имеющий постоянную
плотность внутри эллипсоида и равную 0 вне его), то первые
(равные 0) и вторые моменты (т. е. ковариации компонент) вектора U
совпадут с моментами вектора £.
Осями эллипсоида рассеяния служат главные оси матрицы Σ ζ
(рис. 5 для Σ). Длины его полуосей пропорциональны ^Дь где
Χι — собственные значения матрицы Σ$, а m-мерный объем равен
константе, умноженной на (det Σς)1/2 = (λι... λ™)1/2.
В заключение параграфа познакомимся с одним из способов
сравнения «степеней рассеяния» многомерных распределений,
который связан с их эллипсоидами рассеяния.
Пусть m-мерные случайные векторы £ и η имеют распределения
с М£ = Μη = О и матрицами ковариации Σ ξ, Ση.
Определение. Будем говорить, что среднеквадратическое
рассеяние случайного вектора ζ вокруг начала координат О не больше,
чем рассеяние вектора г/, если для любого d G Rm верно
неравенство
M(dT£)2 < Μ(άτη)2
(5)
Неравенство (5) означает, что дисперсия случайной
величины dT£ для любого направления d не превосходит дисперсии
случайной величины άτη. Раскрывая скобки, очевидно, получаем,
что неравенство (5) равносильно неотрицательной определенности
матрицы Ση — Σς.
В [11, с. 102] доказано, что при условии невырожденности
матриц Σς и Ση среднеквадратическое рассеяние вектора £ вокруг
начала координат не больше рассеяния вектора η тогда и только
тогда, когда эллипсоид рассеяния вектора ζ целиком лежит внутри
эллипсоида рассеяния вектора г/.
Замечание 3. При т ^ 2 неравенство (5) устанавливает лишь
частичный порядок на множестве ковариационных матриц. Напри-
(2 0λ (Ь 0\
мер, матрицы I п о ) и Ι η ι ) не лУчше и не хУже одна другой,
поскольку в направлении d = (1,0) меньше дисперсия для первой
матрицы, а в направлении d = (0,1) —для второй (рис. 6).
В подобной ситуации для сравнения «степеней рассеяния»
многомерных законов обычно используют такие скалярные
характеристики ковариационных матриц, как след λ ι + ... + Am или
определитель λι... Am. При этом надо иметь в виду, что выводы
для разных характеристик (как и для выше приведенных матриц)
могут оказаться прямо противоположными (эту тему продолжает
задача 1).
Рис. 5
Рис. β
324 Глава 20. Корреляция
§3. ВЫЧИСЛЕНИЕ ГЛАВНЫХ КОМПОНЕНТ
Следующий простой алгоритм (степенной метод) позволяет
вычислить для симметричной (не обязательно неотрицательно
определенной) матрицы А несколько наибольших по модулю собственных
значений Aj и соответствующих собственных векторов с\ (см. [6,
с. 221], [16, с. 166]). Сначала разберем частный случай этого
алгоритма—вычисление λι и ci.
Возьмем произвольный ненулевой вектор Хо из Rm. Пусть
выполнены два условия: |λι| > |Аг| ^ ... ^ |Ат| и cjxo φ 0. Положим
х%+\ = Ах{ (τ. е. Х{ = Агх01 что объясняет название метода).
Тогда последовательность значений ii+i = xIxi+i/\&i\2 сходится
к Αι со скоростью геометрической прогрессии со знаменателем
7 = |λ2/λι|<1.
Доказательство. Обозначим через &i,...,bm координаты
вектора хо в базисе ci,... ,ο™, т. е. хо = b\C\ + ... + ЬтСт. Так как
Aci = А/с/, то Alci = Ajc/. Отсюда Xi = \\biCi + ... + А^Ьтсш =
= Ai(bici + Si), где δι = 62(λ2/λι)^2 + ... + ftm^m/AiJ'c™, причем
в силу первого условия \δ{\ —Ο (η%) —► 0 при г —► оо.
В частности, когда все А/ > 1, это означает, что при каждой
итерации длина вектора ж» увеличивается, но быстрее остальных
растет его координата по оси с\. При этом направление Ж;
приближается к направлению первой главной оси (рис. 7).
Формально это можно доказать с помощью известного из
линейной алгебры неравенства Коши—Буняковского—Шварца:
\хТу\ ^ |&||у|· Согласно второму условию алгоритма Ь\ =
= с?*о#0. Отсюда \χί\ = (χ'[χί)1/2 = \Χι\ψι\+0(Ίί)]; e, =
= Xi/\xi\ = (signAi^signfcOci + r<, где \п\ = 0(γ); ti+i =
= λ1 + 0(7<). ■
Замечание 4. Если |λι| > 1, то \xi\ —► оо, а если |λι| < 1, то
\xi\ —► 0 при г —► оо. При вычислении на компьютере в первом
случае возможно переполнение, во втором — исчезновение порядка.
Предотвратить эти ситуации позволяет нормировка векторов Xi на
каждом шаге.
Учитывая замечание 4, приходим к следующему алгоритму
для вычисления λι и с\.
1. Положим г = О, to = 0 и зададим произвольный ненулевой
вектор хо из Rm. Нормируем хо: пусть во = #ο/|#ο| (обычно
сразу берут е0 = (1,0,... ,0)).
2. Вычислим Xi+i = Ае^ и ί^+ι = eJxi+\.
3. Нормируем ж^+1: ен-1 = «t+i/|«t+i|·
4. Если |ii+i — ii| ^ ε, где ε —достаточно малое число, то
положим λι = U+\ и ci = ei+i и закончим итерационный
процесс. Иначе увеличим г на 1 и перейдем к шагу 2.
§ 3. Вычисление главных компонент
325
Замечание 5. Если при выборе х0 случится, что cjx0 = 0, то
через несколько итераций за счет погрешностей округления, как
правило, появится ненулевая координата у х\ в направлении Ci,
и процесс, хотя и с некоторым запаздыванием, выйдет на первое
собственное значение. Можно также стартовать с разных хо и
сравнивать результаты.
Пусть |λι| > |λ2| > ... > |Λλ| > |Afc+i| ^ ... ^ |Am|. Для
вычисления k > 1 первых главных компонент кроме умножения
на А и нормировки понадобится еще ортогонализация. Именно,
предположим, что Χι и с\ уже известны при всех I < к — 1. Чтобы
найти Ajfe и q, выполним следующие шаги.
1. Положим г = 0, ίο = О И зададим произвольный вектор х$ из
Rm (надо только, чтобы с£хо φ 0).
2. Проведем ортогонализацию Xi к векторам Ci,...,Cfc_i:
Уг = хг ~ (с1хг) с1 ~ · · · ~ (ck-lXi) Ск-1-
3. Нормируем у{: е* = у{/\у{\.
4. ВЫЧИСЛИМ 2Ci+i = Авг И ί^+ι = efxi+i-
5. Нормируем «i+1: zi+1 = «i+i/|«i+i|.
6. Если |ίί+ι — ίΐ| ^ ε, то положим λ& = ii+i> cfc = ζί+ι и
закончим процесс. В противном случае приравняем aji+i = 2г+ъ
увеличим г на 1 и перейдем к шагу 2.
В заключение обсудим, насколько следует доверять
вычисленным значениям Χι и q. Следующий пример показывает, что для
числа объектов η порядка нескольких десятков разброс этих
значений может оказаться достаточно большим.
Пример 2. Статистика главных компонент для
нормальной модели. Предположим, что объекты представляют
собой выборку размера η из закона ΛΓ(О, Σ) с невырожденной
матрицей 17, у которой все собственные значения Χι (I = l,...,m)
различны. Тогда:
1) собственные значения Αι,..., Am и отвечающие им собственные
векторы Ci,... ,2™ выборочной ковариационной матрицы Σ
являются оценками максимального правдоподобия для
соответствующих Αι,... ,Am, ci,... ,Ст (см. пример 2 гл. 19), и,
следовательно, обладают асимптотической эффективностью (см. § 4
гл. 9);
2) у/й (λι - λι) Λ ξ ~ Λ/ΧΟ, 2λ?) при η -* οο (см. [1, с. 354]);
3) y/n (ci — ci) —* ζ ~ ΛΓ(0, У) при η —► оо, где элементами матрицы
V служат vki = Xt £ |Q|2Afc/(Afc - λ*)2·
Построим на основе свойства 2 асимптотический доверительный
интервал (см. § 1 гл. 11) для Αι в примере 1. Так как свойство 2
равносильно сходимости yJn/2 (Χι/Χι — 1) —* ξ/(Χι\/2) ~ ΛΓ(0,1),
то при достаточно больших η приближенно с вероятностью 1 — а
326
Глава 20. Корреляция
выполняется неравенство
λΐ /(l + Х1-а/2>/Уп) <\l<Xl/(l- Χγ-*Ι2\Ρφ) ,
где Χι-α/2 — квантиль уровня (1—α/2) законаЛГ(0,1) (см. § 3 гл. 7).
Для а = 5% по таблице Т2 находим, что Х\-а/2 = 1,96. При η = 43
получаем 95%-ный доверительный интервал для λι от 2,88 до 7,1.
§4. ЛИНЕЙНОЕ ШКАЛИРОВАНИЕ
Предположим, что исходной информацией об η объектах служат
экспертные данные о различиях между ними, выраженных
числами dij (или о сходствах α^)·*^
Хотелось бы представить объекты в виде точек некоторого
координатного пространства Rm невысокой размерности (обычно
га = 2 или 3). При этом различия dij между объектами должны
быть как можно точнее переданы евклидовыми расстояниями Sij
между точками в Rm.
Каждый объект характеризуется координатами
соответствующей точки по осям (шкалам) построенного пространства. Сами
шкалы интерпретируются как новые признаки — те латентные или
скрытые факторы, которыми неосознанно руководствуются
эксперты, оценивая степень различия объектов. Процесс
представления объектов наборами координат в некоторых осях называют
шкалированием.
Линейное шкалирование Торгерсона.**) Метод полезно
связать с выделением главных компонент, для чего удобно начать с
нетипичного для приложений случая, когда объекты уже
представлены точками Xi = (хц1... ,Xim) в Rm, г = 1,... ,п, а различия dij
являются евклидовыми расстояниями между ними:
т
4 = 4 = Σ(^-^)2· (6)
1=1
Введем матрицу X = ||#^||nxm. Допустим, что ее элементы хц
центрированы по столбцам (см. Д1 в § 1). Зададим величины gij,
z,j = 1,... ,η, формулами
9α = -\(%-δ*ό-δΙ+δΙ), (7)
η,— mj ' η μ
ι J η i=ij=i
Процедура (7) перехода от матрицы Δ = \\δ^\\ηχη к матрице
G = ll&jllnxn называется двойным центрированием: нетрудно
*) Сходства можно преобразовать в различия, например, по формулам
dij = 1/(1 + a,ij) или dij = 1 - dij при 0 ζ ац ζ Ι.
> У. Торгерсон предложил этот метод в 1952 г., опираясь на работы Т. Юнга и
А. Хаусхолдера (1938, 1941). Его также называют методом главных проекций.
§ 4. Линейное шкалирование
327
убедиться, что средние значения каждой строки и каждого столбца
матрицы G равны 0.
Метод Торгерсона опирается на следующие две теоремы.
Теорема 1. Имеет место равенство G = ХХТ (т. е. G совпадает с
матрицей скалярных произведений, встречавшейся ранее в § 1).
Доказательство (см. также [25, с. 79]). Надо проверить, что
m
9ij = J2xuXjh i,j = l,...,n. (8)
1=1
Раскрывая скобки в правой части равенства (6), получим формулу
mm m
*a = Σ 4 + Σ 4 - 2 Σ χ*4ΐ· (9)
1=1 1=1 1=1
Далее, для любого фиксированного j в силу теоремы Гюйгенса
(см. решение задачи 3 гл. 16) имеем представление
Ι Σ (*« ~ хц? = ± Σ {xa ~ О)2 + (*Я " О)2·
п г=1 п г=1
(Здесь rrii = 1/п, m = 1, α = χ β и с = χι = 0 с учетом допущения
Д1 из § 1.) Суммируя по I = 1,... ,т, приходим к равенству
mm ι η
<^ = Σ^ + Σ4' гдех2г = ^4· (Ю)
1=1 1=1 п г=1
Точно так же, как формула (10), выводится соотношение
« = Σ>2< + Σ>2<· (и)
1=1 1=1
Припишем каждой точке (строке) х\ = (хц1... ,^т), г = 1,... ,п,
массу 1. По допущению Д1 их центром масс будет начало
координат О. Согласно теореме о межточечных расстояниях (см. решение
задачи 5 гл. 16) запишем:
/о = Σ Ы2 = ι- Σ \xt - xj? = ^ Σ Σ \х< - χ)?,
i=l n i<j ^i=lj=l
где Ιο — момент инерции точек относительно О. Последнее
соотношение эквивалентно равенству
л су η m m
ί.2 = ^ο^ΣΣ4 = 2Σ4 (12)
71 ni=ll=l 1=1
Подставляя соотношения (9)—(12) в формулу (7), получаем
равенство (8). ■
Теорема 2 (см. [8, с. 189]). Отличные от нуля собственные
значения μι у матрицы скалярных произведений G = ХХТ = \\gij\\nxn
и матрицы рассеяния W = ХтX = \\wij\\mxm одинаковы. При
328
Глава 20. Корреляция
этом соответствующие собственные векторы уг и ζ χ (Gyl = μ^yь
Wzi = μχΖχ) связаны простым соотношением
уДЙУх = Χζχ.
(13)
Поскольку выборочная
ковариационная матрица Σ
и матрица рассеяния
W отличаются лишь
постоянным множителем:
E = -W,
η
дают с собственными ^
векторами с; матрицы Σ,
а μί=ηλ|.
Заметим, что справа- в равенстве (13) стоит вектор координат
проекций точек на 1-ю главную компоненту ζχ. Таким образом, не
зная самих координат хц, можно на основе различий dij = 8ц
ζι совпа- восстановить конфигурацию точек в пространстве Rm с помощью
следующей процедуры шкалирования:
1. Двойным центрированием матрицы различий Δ вычислить
матрицу G.
2. Степенным методом найти для матрицы G первые га
отличных от нуля (положительных) собственных значений μχ и
соответствующих им собственных векторов yt.
3. Из (13) определить координаты точек в новом базисе
пространства Rm, состоящем из главных осей ζι,... ,zm.
Замечание 6. Сама матрица X не восстанавливается по
матрице G однозначно. Действительно, пусть координаты точек Xi
преобразуются в новые координаты по формуле х\ = Cxi, где С —
любая ортогональная матрица (см. ШО). Так как векторы Х{ — это
столбцы матрицы X , то X = СХ или X = ХС1. Тогда
G = ХХТ = (ХСТ)(СХТ) = Х(СТС)ХТ = ХХТ = G,
т. е. матрица G сохраняется при ортогональном преобразовании
координат.*^
С другой стороны, матрица рассеяния W = ХтX меняется:
W = ХТХ = (СХТ)(ХСТ) = С(ХТХ)СТ = CWCT.
Новая матрица W подобна W (см. ШО). Следовательно, их
собственные значения μι совпадают. Новые собственные векторы
ζ χ связаны с ζχ тем же преобразованием, что и координаты точек:
ζχ = Οζχ (рис. 8). В самом деле,
Wzi = (CWCT)(Czx) = C(Wzx) =
= Ο(μχζχ) = μχ(Οζχ) = μχΖχ.
При этом правая часть соотношения (13) сохраняется:
Χζχ = (ΧΟτ)(Οζχ) = Χζχ.
Подход Торгерсона состоит в применении описанной выше
процедуры шкалирования к произвольной симметричной матрице
Рис. 8
*) По этой причине исследователи иногда производят дополнительный
(субъективный) поворот системы координат, чтобы содержательно интерпретировать
признаки, соответствующие повернутым осям.
§ 4. Линейное шкалирование
329
различий D = \\dij\\nxn. Размерность т координатного
пространства задается исследователем. Обозначим через G* результат
двойного центрирования матрицы D. )
Замечание 7. В случае, когда различия d^ не являются
евклидовыми расстояниями, матрица G* может не быть неотрицательно
определенной. Прием, который обычно используется для
преодоления этого, заключается в переходе к модели с так называемой
аддитивной константой: d'^ = d^ + α, где α > 0. Наименьшее знаи-
чение а, обеспечивающее выполнение неравенства треугольника
для всевозможных троек ύζ ·, очевидно, определяется по формуле
а = max max {dik — d^ — djk> 0} . (14)
Но из выполнения неравенства треугольника еще не следует
неотрицательная определенность матрицы G*, вычисленной на
основе d^ (см. пример 3 ниже). Покажем, что, увеличивая а, можно
добиться того, чтобы а1^ оказались евклидовыми расстояниями
для некоторой конфигурации точек в Rm, если размерность га
также достаточно велика. Действительно, для любой размерности
к можно указать к + 1 точку в Rfc, которые находятся друг от
друга на одном и том же расстоянии h (они называются вершинами
правильного симплекса). Таковыми будут, скажем, щ = (0,... ,0) и
Щ = {щи... ,щк) (г = 1,... ,fc), где
(h(y/k + 1 + к - 1)/(ку/2), если г = j,
h(y/kTl - 1)/(W2), если г φ j,
(15)
(рис. 9 для к = 2). При очень большом значении а объекты будут
располагаться вблизи вершин правильного симплекса с ребрами
длины а в пространстве Rn_1, где п — число объектов.
С другой стороны, при увеличении а все более нивелируются
относительные отличия между d^ по сравнению с отличиями
между исходными dij. Кроме того, увеличивается число значимых
по величине положительных μι, τ. е. растет размерность т
пространства, в котором располагается конфигурация точек,
достаточно точно воспроизводящая d[j. Поэтому разумнее не добиваться
неотрицательной определенности матрицы (?*, а ограничиться тем,
чтобы несколько ее наибольших собственных значений μι были
положительными, а все остальные собственные значения — малыми
по модулю.
Пример 3. Проиллюстрируем вышесказанное на примере анализа
корреляционной матрицы, изображенной на рис. 3.
*) При умножении всех dij на с > 0 элементы и собственные значения G*
умножаются на с2, собственные векторы остаются прежними, а задаваемые
формулой (13) координаты объектов в построенных шкалах умножается на с.
Из-за этого шкалирование Торгерсона называют линейным.
Рис. 9
330
Глава 20. Корреляция
30-
20-
•3 10"
-60-40-20 .
-20-
Рис. ]
• 1
• 2
•5 40
L0
Положим dij = 100 χ (1 — Pij)· Вычисленные степенным
методом из § 3 собственные значения матрицы G* и приходящиеся на
них проценты от полной дисперсии (следа матрицы) приведены в
следующей таблице:
Номера компонент
Собственные значения
Проценты от следа
Накопленные проценты
1
3820
72,3
72,3
2
1321
25,0
97,3
3
317
6,0
103,3
4
-187
-3,5
99,8
5
12,5
0,2
100,0
6
0,0
0,0
100,0
Поскольку μ4 = —187, матрица G* не является неотрицательно
определенной. На рис. 10 показана конфигурация точек на
плоскости, возникающая при выборе т = 2. Таблица на рис. 11
показывает, насколько точно евклидовы расстояния между точками
плоскости (они указаны в скобках) соответствуют dij.
1
2
3
4
5
6
1
0
2
4(18)
0
3
65 (66)
80 (80)
0
4
39 (36)
34 (35)
63 (62)
0
5
28 (29)
26 (27)
65 (65)
11(8)
0
6
41 (41)
41 (39)
65 (64)
24(5)
21 (13)
0
Рис. 11
В целом точность хорошая за исключением расстояния 1-2
и расстояний между точкой 6 и точками 4, 5 (первое слишком
большое, вторые — слишком малые). Для объяснения этого факта
заметим, что для с?23 = 80, d<i\ — G?i2 = 4 и dis = 65 не выполняется
неравенство треугольника: 80 > 4 + 65. Чтобы его обеспечить,
пришлось увеличить расстояние между точками 1 и 2 до 18.
В свою очередь, точки 4, 5 и 6 должны находиться на расстоянии
примерно 65 от точки 3, при этом каждая из них должна быть
(почти) равноудалена от точек 1 и 2. Это означает, что точки 4,
5 и 6 обязаны располагаться рядом, а именно — вблизи точки
пересечения окружности с центром в 3 и радиусом 65 и серединного
перпендикуляра к отрезку с концами в точках 1 и 2. Получаем
противоречие с тем, что d^e = 24 и dse = 21.
По формуле (14) на компьютере была подсчитана наименьшая
аддитивная константа а = 11, обеспечивающая выполнение
неравенства треугольника для всех троек d^· = d^ + α. Таким d^·
соответствует матрица G* со следующим спектром:
Номера компонент
Собственные значения
Проценты от следа
Накопленные проценты
1
4958
63,5
63,5
2
2094
26,8
90,3
3
663
8,5
98,8
4
190
2,4
101,2
5
-93,3
-1,2
100,0
6
0,0
0,0
100,0
§ 4. Линейное шкалирование
331
Здесь уже положительны μ\—μ±, а доля следа, приходящаяся на
отрицательное собственное значение, уменьшилась с 3,5% до 1,2%.
Как показывает рис. 12, точки только слегка отдалились от
начала координат, конфигурация качественно не изменилась. Однако
на первые две оси теперь приходится всего 90,3%, а не 97,3% следа
матрицы G*, как раньше (дисперсия «размазывается» по спектру).
Это проявляется в плохом воспроизведении d!^ для признаков 4, 5 ·^
и 6 (см. таблицу на рис. 13).
30
20-1
НИ
1
2
3
4
5
6
1
0
2
15 (18)
0
3
76 (76)
91 (91)
0
4
50 (45)
45 (44)
74 (72)
0
5
39 (37)
37 (34)
76 (75)
22 (10)
0
6
52 (50)
52 (48)
76 (73)
35(5)
32 (14)
0
1
2
3
4
5
6
1
0
2
15 (19)
0
3
76 (76)
91 (91)
0
4
50 (50)
45 (46)
74 (74)
0
5
39 (38)
37 (34)
76 (75)
22 (13)
0
6
52 (52)
52 (52)
76 (76)
35 (35)
32 (29)
0
Номера компонент
Собственные значения
Проценты от следа
Накопленные проценты
1
5631
59,6
59,6
2
2568
27,2
86,8
3
904
9,6
96,4
4
335
3,6
99,9
5
7,3
од
100,0
6
0,0
0,0
100,0 J
-60-40-20 .
-20-
Рис. 12
Рис. 13
Преодолеть этот недостаток можно за счет увеличения
размерности га до 3. Как демонстрирует рис. 14, третья координата как
раз и отвечает за разделение признака 6 и признаков 4 и 5.
Соответствие пространственных расстояний и d!^ (за
исключением пары 4-5) довольно хорошее (рис. 15).
Рис. 15
Чтобы добиться неотрицательной определенности матрицы G*,
понадобится увеличить аддитивную константу α до 17. Спектр
выглядит так:
При га = 4 все расстояния между точками (при округлении до
ближайшего целого числа) совпадают с d[j = dij + 17.
Пример 4. Анализ межотраслевых связей [78, с. 47].
Данные были взяты из книги [34] известного американского
экономиста А. Картер. Они представляют собой подсчитанные на
основе межотраслевого баланса американской экономики
коэффициенты прямых затрат рц, равные отношению затрат г-й отрасли
на закупку продукции у j-й отрасли к общей величине затрат
1)
2)
3)
4)
5)
6)
5 40
(13,26,5)
(29,18,-1)
(-62,9,-1)
(5,-19,-15)
(11,-11,-6)
(4,-24,19)
Рис. 14
332 Глава 20. Корреляция
г-й отрасли. Симметризация г^ дает в качестве мер близости
o,ij = fij + Tji- Переход от α^ к различиям йц осуществлялся по
формуле dij = (maxdij — а^)/(таха^· — mina^·).
На рис. 16 представлена структура межотраслевых связей,
полученная методом многомерного шкалирования (чтобы не
загромождать рисунок, отмечены только отрасли, которые производят
значительные закупки или поставки). Сильные связи обозначены
стрелками.
Основу структуры связей составляет обеспечение первичными
ресурсами ресурсоемких отраслей. В первую очередь это поставки
аграрного, лесного и рыбного сектора (1) в пищевую (2),
табачную (3) и текстильную (4) отрасли. Пищевая отрасль (2) снабжает
обувное производство (5). Продукция текстильной
промышленности (4) нужна при переработке металлолома (6).
Вторую основную ветвь составляют поставки чугуна и стали
(7) в группу металлопотребляющих отраслей:
металлообрабатывающую промышленность (8), автомобильную промышленность (9),
железнодорожный транспорт и суда (10) и переработку
металлолома (6). Металлообрабатывающую промышленность (8) отдает
значительную часть своей продукции в строительство (11), которое
в свою очередь делает вклад в сектор недвижимости и помещений
(12). Еще две очевидные ветви —это связь добычи руд цветных
металлов (13) с обработкой цветных металлов (14) и
нефтедобывающей промышленности (15) с нефтеперерабатывающей (16).
§5. ШКАЛИРОВАНИЕ ИНДИВИДУАЛЬНЫХ
РАЗЛИЧИЙ
Во многих исследованиях, особенно в социальных и поведенческих
науках, данные получают от нескольких источников информации,
например, от нескольких субъектов или при разных
экспериментальных условиях. Недостатком метода Торгерсона является то,
что входной информацией для него служит единственная матрица
различий D = ||с?^||пхп (п —число объектов), полученная
осреднением данных всех субъектов. При осреднении теряется
информация, отражающая различие во мнениях субъектов, которая может
оказаться весьма ценной для понимания сути изучаемого явления.
Подход, учитывающий эти различия, называется анализом точек
зрения или шкалированием индивидуальных различий ([78, с. 85]).
Рассмотрим часто применяемую при таком подходе
Модель взвешенных факторов
Обозначим через X = \\хц\\пхт матрицу координат объектов
(стимулов), где хц — неизвестные параметры модели. Будем
называть ее групповой. Предполагается, что у каждого субъекта s
(s = 1,... ,λ;) существует своя, индивидуальная матрица координат
Рис. 16
§ 5. Шкалирование индивидуальных различий
333
объектов Х8 = ||#iZs||nXm> элементы которой связаны с элементами
групповой матрицы X следующим образом:
%ils —
(16)
где wis — (неизвестный) вес координаты / для субъекта s. Величина
у/Шй представляет собой коэффициент растяжения по 1-й оси
координат объектов в пространстве субъекта s по отношению к
групповым координатам хц (см. пример 5 ниже). Таким образом,
всего в модели имеется (пт + тк) неизвестных параметров: пт
групповых координат хц и тк весов wi8.
Иначе можно трактовать модель взвешенных факторов как
определение субъектами расстояний между объектами не на основе
обычной, а на основе взвешенной евклидовой метрики:
dijs —
1=1
1/2
η 1/2
Σ Wia {Хц — Xjl)
.1=1
Пример 5. Зрительное восприятие буке [78, с. 91].
Испытуемые оценивали степень сходства между 19 печатными буквами
русского языка. На рис. 17, α изображена полученная
конфигурация в групповом пространстве, а рис. 17, б дает представление
о расположении экспертов (субъектов) на плоскости весовых
коэффициентов.
Эксперты различаются по тому, какой вес они придают каждой
из осей. Одна часть экспертов (они находятся ниже диагонали на
рис. 17, б) придает больший вес первой оси, противопоставляющей
буквы с остроугольными элементами буквам с прямоугольными
элементами. Другая — второй оси, отвечающей за преобладание
круглых элементов букв над прямоугольными. На рис. 17, б такие
эксперты располагаются выше диагонали.
При этом для разных экспертов степень различия весов
неодинакова. Большинство экспертов группируется вблизи диагонали.
Для них различие между весами осей несущественно.
С другой стороны, для эксперта с номером 1 веса сильно
отличаются: первая ось для него намного важнее второй. Для эксперта
с номером 2 картина прямо противоположная. На рис. 18
представлены субъективные пространства восприятия для экспертов 1
(рис. 18, а) и 2 (рис. 18, б), получаемые растяжением или сжатием
групповой конфигурации с коэффициентами, равными квадратным
корням из соответствующих весов.
Кроме различия по отношению двух весов, эксперты
отличаются между собой по сумме обоих весов. Непосредственный анализ
исходных данных показывает, что экспертам, которые при
сравнении букв обоим факторам приписывают малые веса, соответствует
as
к
|у м
л и
А
НГ
у.
I д
Остроугольные -
прямоугольные
эл-ты
а)
Η
Прямые —
круглые эл-
Остроугольные
прямоугольные
б)
Рис. 17
» 2
3 3
i-
Остроугольные -
прямоугольные
эл-ты
а)
» 5>
3 3
as
я
к
уМ
ли
А
О
сз
в
РБ
¥
Π
АТ
Остроугольные -
прямоугольные
эл-ты
б)
Рис. 18
334
Глава 20. Корреляция
большое количество ответов «похожи», а экспертам, которые
приписывают обоим факторам большие веса, соответствует
наименьшее число ответов «похожи». Например, эксперт с номером 3 при
сравнении 153 пар букв ответил «похожи» 117 раз, а эксперт 4 —
только 3 раза.
Для каждого субъекта s введем диагональную (т χ т)-матрицу
W8 с элементами у/щ^ (I = l,...,m, s фиксировано) и запишем
соотношения (16) в матричной форме: Х8 = XW8. Тогда матрица
скалярных произведений субъекта s представляется в виде
&s = \\9г
Объекты
Рис. 19
гЭ8\\пхп
= X8Xj = XW28XT (т. е. gij8 = £ xuXjiwl8).
1=1
Все вместе матрицы Gs, s = 1,... ,Α:, образуют трехмерный массив
G (рис. 19).
С другой стороны, для каждого субъекта s можно двойным
центрированием (7) его матрицы различий Ds = \\dij8\\nxn вычислить
G* = ll^sllnxn- Объединяя все матрицы G*, получим массив G*.
Напомним (см. формулу (4) в § 1), что одним из свойств
оптимальности главных компонент является то, что матрица
скалярных произведений координат объектов искажается β наименьшей
степени при проецировании на подпространство, порожденное
несколькими первыми компонентами. Поэтому в качестве меры
соответствия параметров модели хц и w\a данным Ds (s = 1,... ,λ;)
возьмем
F = \СГ - G\
2 _
= Σ\<Ζ-β.\*=Σ(*φ
Σ XilXjlWls)2-
ι
Опишем алгоритм численной минимизации F, опирающийся на
разработанный в 1970 г. Дж. Кэрролом и Дж. Чанг
Метод канонической декомпозиции*) (см. [78, с. 96]).
Наряду с групповой матрицей X введем матрицы Υ = ||у^Нпхт
и Ζ = ||*ie||mXfc, где yjt = Χβ и ζΪ8 = wl8. Игнорируя совпадение yjt
с Xji, будем считать Χ, Υ и Ζ наборами независимых переменных.
В новых обозначениях минимизируемая функция F запишется так:
f = f(x,y,z) = Σ (atu
г,3,з
Σ XiWjizis)2-
I
(17)
Процедура минимизации включает следующие пункты.
1. В качестве начальных значений для X и Υ можно использовать
координаты Xmed> получаемые применением метода Торгерсона
к матрице
Dmed = MED{Dll...1Dk}.
*) Минимизация нелинейной функции F представляется как последовательное
решение ряда линейных систем.
§ 5. Шкалирование индивидуальных различий
335
(Медиана предпочтительнее среднего арифметического: она
уменьшает влияние на начальную оценку групповых координат
тех субъектов, чьи ац8 сильно отличаются от других.)
2. Фиксируем Х1 Υ и минимизируем F сначала по Ζ. Для этого
положим и = п(г — 1) + j (так что и = 1,... ,п2). Определяя
a>ui = xuVji и bus = 9ij8i перепишем функцию (17) в виде
F = Σ (bus - Σ вы zis)2 = \B- AZ\\
где А = ||α„(|| n2Xm, β — limits 11η2 χfc· Согласно методу
наименьших квадратов минимизирующие правую часть веса Ζ могут
быть найдены по формуле Ζ = (АТА)~1АТВ*^
Доказательство. Пусть Ь8 и z8 (s = 1,... ,fc) обозначают
столбцы матриц В и Ζ соответственно. Тогда
\B-AZ\2 = Z\ba-Azs\2.
8
Ввиду формулы (7) гл. 21, s-e слагаемое достигает минимума
при zs = (АТА)~1А Ь8. Остается объединить все векторы Ь8 в
матрицу В. Ш
3. Попытаемся улучшить оценку для Υ при фиксированных X и
Ζ. Положим ν = п(г — 1) + s (так что ν = 1,... ,nk). Определяя
Ply = xnzia и qjV = 9*j8, минимизируем
F = E(Qjv-EyjiPiv)2 = \Q-YP\2,
j,v I
где Ρ = ||pit;||mxnfc> Q =J\qjv\\nxnk' Оценка наименьших
квадратов для Υ имеет вид Υ = QPT(PPT)~1. Вопрос 1.
л л j_ т> Ъ * Почему верна эта
4. Аналогично, фиксируя Υ и Ζ, попробуем улучшить оценку для формула?
X. Вводя обозначения t = n(j — 1) + s (так что t = 1,... ,ηλ;),
R = ||nt||mxnfc> Η = \\hit\\nxnk, ГДе rit = yjiZl8 И /l^ = g*ja,
получим
f = Σ (hit - Σ *a nt)2 = \H- XR\2,
i,t I
что дает оценку X = HRT(RRT)~l.
Пункты 2-4 составляют о&ш шаг итерационной процедуры.
С каждым шагом функция F уменьшается. При этом
происходит точная минимизация по Χ (Υ или Z) при фиксированных
значениях остальных наборов переменных.**) Процесс
минимизации завершается, когда уменьшение F станет
несущественным.
Рис.. 20
*) Вместо вычисления (АтА) г быстрее решить методом Холецкого (см. ШО)
систему линейных уравнений (ATA)Z — АТВ.
**) По существу, осуществляется покоординатный спуск, только в качестве
координат выступают не числа, а матрицы (рис. 20).
336
Глава 20. Корреляция
Μ "Α
БВЛТГ
Бп ф Г
К
X
A3 3
цс
АЖ
Ж
ш
ч
Сибилянтность
а)
Α9χ
жш м
Сонорность
б)
Дрожащий
в)
Рис. 21
Так как переменные хц и Χβ были разделены, итоговые
матрицы X и Υ могут отличаться одна от другой. Для
преодоления этого несоответствия с содержательным смыслом хц
после завершения поиска минимума полагают Υ = X и еще раз
пересчитывают оценку матрицы весов Ζ.
Можно было бы приравнивать матрицы на каждой итерации.
В этом случае пришлось бы пересчитывать только две матрицы
вместо трех. Однако свойства такого алгоритма не изучены, и нельзя
утверждать, что он сходится хотя бы к локальному минимуму.
Исследования рассмотренного алгоритма канонической
декомпозиции с помощью моделирования по методу Монте-Карло
показали его высокую работоспособность ([78, с. 97]).
Пример 6. Восприятие на слух болгарских согласных [78,
с. 118]. В болгарском Институте обучения иностранных студентов
болгарскому языку Гергановым Е. Н., Терехиной А. Ю. и Фрумки-
ной Р. М. проводились исследования различий восприятия
согласных звуков между болгарами и иностранными студентами. Были
выбраны 4 группы испытуемых по 50 человек: болгар, испанцев,
вьетнамцев и арабов. Пары из 21 согласных звуков в сочетании
со звуком Ъ (БЪ—ВЪ) были записаны на магнитную пленку —
всего 210 пар. Испытуемые должны были внимательно слушать и
отмечать, похожи ли два звука в паре. В результате для каждого
испытуемого была получена матрица сходств. Совместный анализ
данных всех испытуемых позволил построить шестимерное сти-
мульное пространство, представленное на рис. 21.
Первая ось (рис. 21, а) делит все согласные на сибилянты (Ч, Ш,
Ж, ДЖ, Ц, С, ДЗ, 3) и остальные. Вторая ось разделяет сибилянты
по частоте: низкочастотные — шипящие (Ч, Ш, Ж, ДЖ) и
высокочастотные—свистящие (3, С, Ц, ДЗ). Третья ось (рис. 21, б)
выделяет среди всех согласных группу сонорных (Η, Μ, Ρ, Л). Четвертая
ось отвечает за место образования звуков: от губных (Φ, Β, Π, Б,
М) к зубным (С, 3, Ц, ДЗ), далее —к переднеязычным (Т, Д) и,
наконец, —к заднеязычным (К, Г). Пятая ось (рис. 21, в) выделяет
дрожащий звук Р. Интересной является шестая ось, она
соответствует признаку «глухость—звонкость», но «количество звонкости»
определяется как бы в относительной степени. Из рис. 21, β хорошо
видно, что противопоставление глухости—звонкости реализуется
попарно: 3 располагается выше, чем С; Ж — выше, чем Ш и т. д.
На рис. 22 представлены профили весов, с которыми учитывали
эти 6 признаков 4 группы испытуемых — носителей разных языков.
Все испытуемые, особенно группа испанцев, при сравнении звуков
наибольшее значение придавали признаку «сибилянтность». Для
испанцев характерен также большой вес для признака
«сонорность». Наиболее низкие веса у арабов, они в наименьшей
степени учитывали признаки «шипящие—свистящие», «сонорность»
§ 6. Нелинейные методы понижения размерности
337
Испанцы к
Арабы к Ч
Болгары f*^,^/v
Вьетнамцы
Рис. 22
Сибилянт- Шипящие— Сонор- Передне- Дрожащий Глухость—
ность свистящие ность язычные— звонкость
заднеязычные
и «глухость—звонкость». Болгары, в меньшей степени, чем все
остальные, учитывали признак «переднеязычные—заднеязычные»,
а ориентировались при сравнении в большой степени на признак
«глухость—звонкость».
По-видимому, различие в восприятии звуков носителями разных
языков объясняется различием фонетических систем, на которые
опираются их родные языки.
§6. НЕЛИНЕЙНЫЕ МЕТОДЫ ПОНИЖЕНИЯ
РАЗМЕРНОСТИ
Ортогональное проецирование на подпространство первых главных
компонент, осуществляемое при линейном шкалировании Торгер-
сона, хорошо передает структуру данных, когда множество точек
имеет большой разброс по одним направлениям и совсем
небольшой—по другим. Если же «облако» точек не похоже на
многомерный эллипсоид (его конфигурация существенно нелинейна), то
точки, находящиеся на разных концах конфигурации, могут при
ортогональном проецировании накладываться друг на друга.
Пример 7. Проецирование вершин многомерного
симплекса [78, с. 35]. На рис. 23, а изображены проекции на
плоскость двух первых главных компонент 16 групп точек по 4 точки
в группе. Каждая группа генерировалась с помощью датчика
случайных чисел вблизи одной из 16 вершин правильного симплекса
в Е15 (см. формулу (15)). Точки из окрестности одной вершины
обозначены одинаковыми буквами.
На первую (из пятнадцати) компоненту приходится 8,3% следа
ковариационной матрицы, на вторую —7,6%, на обе —лишь 15,9%.
Видим, что проецирование на плоскость двух первых главных
компонент не позволяет сохранить разделение на группы.
Для анализа подобных сложных конфигураций применяются
нелинейные методы понижения размерности. Они заключаются
в минимизации некоторой функции F, выражающей суммарное
Круговое движение
первее прямолинейного:
оно проще и более
совершенно.
Аристотель
' 1
0;
.5-
#Е
Б I I
Hff H F F
A " H F >
—ι—ι—ι—ι—г
4.2
в» в
—ι—ι—
-(
1 Π -,
0:
1 Π -
Ι,ΙΜ
-]
),3 0 0,5
a)
£ h * и
* *»ff
,0 0 1,
6)
Рис. 23
0
338
Глава 20. Корреляция
В мире не происходит
ничего, в чем бы
не был виден смысл
какого-нибудь максимума
или минимума.
Л. Эйлер
расхождение между заданными различиями объектов d^ и
расстояниями Sij между образами объектов в подпространстве небольшой
размерности.
Наиболее простой из таких функций является
*о = Σ №j - dij)2·
Широкое распространение получил метод Сэммона*):
Fi =
Σ №i
i<j
dij) /dij,
где d = Σ^υ,
(18)
который обладает свойством более точно передавать небольшие
различия и менее точно — большие, так как при отображении
больших расстояний допустимы большие ошибки. (Деление на
константу С\ нужно для инвариантности F\ к изменению масштаба
величин dij.)
На рис. 23, б изображен результат применения метода Сэммона к
данным примера 7. Значение F\ удалось уменьшить с 0,44 до 0,13.
Видим, что разделение точек на группы сохраняется на плоскости.
Для поиска минимума функции F прежде всего строится
начальная конфигурация точек в пространстве небольшой
размерности га. Это могут быть просто проекции в подпространство,
образованное какими-либо из га координатных осей, или в
подпространство га первых главных компонент, или, наконец, случайная
конфигурация, в которой пт координат получены с помощью
датчика случайных чисел.
Исходя из начальной конфигурации, отыскивается
конфигурация точек, на которой достигается (локальный) минимум
функции F. Для этого обычно применяется
Метод сопряженных градиентов (см. [6, с. 284]).
1. Определяется направление pt в пространстве Rnm по
формулам
Pi = -01 > Pt = ~9t + PtPt-i ПРИ * = 2A · ·.,
миними-
( dF dF \ c,
где gt = I -— ,..., - ) обозначает градиент
\OXii OXnmJ
зируемой функции F, pt-1—направление на предыдущем
шаге, коэффициент /?t = \gt\2/\9t-i\2'
[В задаче 2 предлагается проверить, что координаты градиента
функции Fi, заданной формулой (18), удовлетворяют
соотношениям
= — Σ ( -г- " 7" ) (Xil " х^ '
дхй d
(19)
&i
*) Предложен Дж. Сэммоном в 1969 г., см. [78, с. 35].
§ 6. Нелинейные методы понижения размерности
339
где г = 1,... ,η; Ζ = 1,..., т. Считается, что все объекты различны
(dij φ 0), а в случае совпадения образов объектов в М™ (Sij = 0)
соответствующее слагаемое полагается равным некоторой константе
с φ 0, чтобы образы могли «разойтись» в процессе минимизации.]
2. Производится перемещение до точки минимума по
выбранному направлению (например, с помощью рассматриваемого
ниже алгоритма золотого сечения)
«t+i = xt + Oitpt, где F(xt + atpt) = mmF(xt + apt).
3. Если |flft+1| ^ ε, где ε —достаточно малое число (скажем,
ε = 0,001), то поиск заканчивается, иначе t увеличивается
на 1, и происходит возвращение к пункту 1.
Впервые метод сопряженных градиентов был опубликован в
качестве численного алгоритма для решения системы линейных
уравнений Ах = Ь с положительно определенной матрицей А.
Эта задача равносильна минимизации по χ квадратичной
функции F{x) = - свтЛсв — ЬТх. Оказывается, что (при отсутствии
погрешностей округления) метод сопряженных градиентов
позволяет найти точку минимума F(x) не более, чем за к итераций,
где к — размерность χ (см. [18, с. 200]). При этом направления
одномерной минимизации рг,... ,рк являются взаимно
сопряженными относительно матрицы A: pjApj = 0 при всех г φ j, что
объясняет название метода.
При решении задач понижения размерности метод
сопряженных градиентов обладает по сравнению с другими
методами численной минимизации рядом преимуществ:
1) на каждом шаге осуществляется минимизация по
выбранному направлению, что ценно ввиду большого числа пт
оптимизируемых переменных;
2) в отличие от метода Ньютона (см. [18, с. 141]) не
требуется память для хранения и не расходуется время на
вычисление матрицы вторых производных размера пт χ пт;
3) в отличие от наискорейшего спуска (см. пример 8) метод
сопряженных градиентов обычно удовлетворительно
работает при минимизации «овражных» функций.
Пример 8. Критика метода наискорейшего спуска. Иногда
в качестве направления минимизации на очередном шаге
рекомендуют выбирать антиградиент —gt, поскольку в этом направлении
функция убывает быстрее всего (см. [45, с. 478]).*) Однако, эта
*) В частности, для поверхности («горы»), задаваемой гладкой функцией двух
переменных, антиградиент указывает направление (локально) наискорейшего
спуска.
340
Глава 20. Корреляция
Ш^
\Υ\^
ί
^/1
«)
v^
\\\V
Л
=^//i
6)
Рис. 24
Забросить ключ
от дома и уйти,
Не как изгнанник, что
бредет без смысла,
Но выбирая свой
маршрут разумно,
Меняя скорость, если
склон сменился.
У. X. Оден, «tr The Journey»
(1928)
Для заданных выше Fq
или F\ это обязательно
произойдет, поскольку
они стремятся к +оо при
Ы—►оо.
«жадность» метода приводит к огромному числу смен направления
при движении вдоль «дна оврага». Наглядный пример (см. [18,
с. 140]) дает поиск минимума функции Розенброка
F{x,y) = m{y-x2)2 + {l-x)2,
которая определяет в трехмерном пространстве поверхность типа
серповидного ущелья с точкой минимума (1,1). На рис. 24, а
показан процесс минимизации F(x,y) методом наискорейшего спуска
из точки (—6/5,1) (гладкие кривые —это линии уровня функции,
отрезки ломаной соответствуют шагам спуска). Алгоритм мог бы
надолго «застрять» вблизи начала координат, если бы не помогла
счастливая случайность — на одной из итераций процедура
одномерного поиска неожиданно нашла второй минимум по
направлению. Затем было выполнено еще несколько сотен шагов, но
ощутимого изменения целевой функции это не дало. Счет был
прерван после 1000 итераций вдали от искомого решения.
В свою очередь, метод сопряженных градиентов позволил дойти
до точки минимума за два десятка шагов (рис. 24, б). Хорошо виден
его циклический характер в случае двух переменных: движение
вдоль дна ущелья подправляется перемещением по антиградиенту.
Для полноты изложения приведем один из алгоритмов
минимизации по направлению, в основе которого лежит
Метод золотого сечения (см. [18, с. 120]).
Алгоритм включает следующие пункты.
1. Необходимо проверить, что pt — это направление убывания
F (определение pt см. выше). Для этого зададим малый шаг
δ > 0 (скажем, δ = 0,01) и вычислим при а = δ значение
φ(α) = F(xt + apt).
Если φ(δ) > φ(0), то заменим направление pt на
антиградиент —gt и будем уменьшать величину шага делением пополам
до тех пор, пока не добьемся убывания функции.
2. Определим отрезок [а, Ь], содержащий точку минимума
функции φ(α). Положим а = 0, а для нахождения b будем
увеличивать шаг вдвое до тех пор, пока функция не прекратит
убывать.
При поиске точки минимума а* (непрерывной) функции φ(α)
методом золотого сечения предполагается, что φ унимодальна, т. е.
строго убывает слева от а* и строго возрастает справа от а*. Для
такой функции положение точки минимума можно уточнить,
вычислив φ в двух внутренних точках отрезка [а, Ь]. Например, так как на
рис. 25 φ(τ) < <p(s), то α* обязана находиться на отрезке [a,s]. (Если
нет унимодальности, то в результате применения метода золотого
сечения будет найден один из локальных минимумов.)
§ 6. Нелинейные методы понижения размерности
341
3. На отрезке [а, Ь] возьмем две пробные точки r=a+ (1—x)(b—a)
и s = a+x(b—a)1 где χ = (л/5—1)/2 « 0,618 — золотое сечение
(см. решение задачи 5 гл. 1),*) и вычислим значения φ{τ) и
¥>(*)·
4. Если <£>(г) < v?(s)> то полагаем at = г, а' = а,
г' = а + (1 — x)(s — a), s' = г, ()' = s и вычисляем v?(r')·
В противном случае полагаем at = s, a' = г, г' = s,
s' = a + х(Ь - г), 6' = Ь и вычисляем </?($').
5. Если Ь' — а' ^ ε (скажем, ε = 0,01), то заканчиваем поиск,
иначе убираем у всех переменных штрихи и возвращаемся к
пункту 4.
*)
φ(α)
φΛ)
Замечание 8. В отличие от линейного шкалирования Торгерсона
(§ 4), метод Сэммона позволяет обрабатывать матрицы различий с
пропусками. Для этого суммирование в формуле (18) достаточно
проводить только для тех пар объектов, у которых различия
измерены. Экспериментально установлено, что качество восстановления
конфигурации будет почти таким же, как для полной матрицы,
даже если доля пропусков составляет около 30%.
э4с э4с эк \
Замечание 9. О заполнении пропусков. ' В таблицах реальных
данных, как правило, встречаются пропуски. Если обрабатывать
только часть таблицы, состоящую из строк без пропусков, то может
пропасть много важной информации.
С другой стороны, многим методам заполнения пропусков (сред-
невыборочными значениями, по регрессии (см. гл. 21) и т. п.)
присущи следующие два принципиальных недостатка.
1. Параметры алгоритмов заполнения обычно вычисляются по
присутствующим данным, что вносит зависимость между
наблюдениями.
2. Распределение данных после заполнения отличается от
истинного (возникает смесь истинного и вырожденных
распределений с вырождением на гиперплоскостях, на которых
располагаются предсказываемые значения). В частности,
заполнение средними приводит к искусственному увеличению доли
объектов со значениями признаков в центре совокупности.
Эти недостатки влекут смещенность и несостоятельность
оценок параметров моделей при обработке заполненной таблицы
данных.
*) Замечательно, что точки г и s осуществляют золотые сечения не только
отрезка [а, Ь], но и отрезков [a, s] и [г, Ь] соответственно. Это позволяет вычислять
всего одно значение φ при следующей итерации.
**) При каждом выполнении пункта 4 длина отрезка локализации точки
минимума уменьшается в 1 + κ « 1,618 раз. Всего за 10 повторов первоначальный
отрезок сожмется в(1 + >г)10«123 раза.
***) Материал замечания основан на дополнении Никифорова А. М. к переводу
книги Литтл Р. Дж. Α., Рубин Д. Б. «Статистический анализ данных с
пропусками»,—М.: Финансы и статистика, 1990.
φ{τ)
4
ч>(*)
Г S
Рис. 25
342
Глава 20. Корреляция
В качестве альтернативы рассмотрим
Метод локального заполнения
Пусть у г-й строки таблицы X = ||#^||пхт есть данные в столбцах
с номерами /ι,... ,/&, к < га. Обозначим через Si множество строк
X, не имеющих пропусков в столбцах /ι,...,/*. Для заполнения
пропуска в j-ft ячейке г-й строки выделим в Si подмножество Rij
тех строк, у которых нет пропуска в j-й ячейке. Если Rij пусто,
то заполнение невозможно (г-ю строку придется исключить из
обработки). В противном случае найдем в Rij строку, ближайшую
к г-й в смысле, скажем, евклидова расстояния в fc-мерном
подпространстве, порожденном столбцами с номерами /ι,...,/* (если
таких строк окажется несколько, то выберем одну из них случайно).
Заполним пропуск значением из j-й ячейки найденной строки.
Какими статистическими свойствами обладает этот метод?
Будем рассматривать строки таблицы как реализации
случайных векторов Χι,...,Χη. Пусть случайная величина Мц
—индикатор наличия пропуска в 1-м столбце г-й строки. Положим
Mi = (Мц,... ,M;m), г = 1,... ,η. Допустим, что
1. случайные векторы (Χι,Λ4"ι),... ,(Χη,Λ1"η) независимы и
одинаково распределены;
2. Μι не зависит от Χι (τ. е. пропуски не зависят от значений);
3. распределение Χι имеет m-мерную плотность (см. П8);
4. Р(Мц = 1) = pi < 1 для всех I = 1,... ,га.
Обозначим через F(x) = F(xi,... ,#т) функцию распределения
вектора Χι = (Хц,... ,Xim): F(x) = P(Xu ^ χι, Ι = l,...,m), a
через Fn(x) — эмпирическую функцию распределения, построенную
по полученной методом локального заполнения таблице X:
1 п
Fn(x) = - Σ I{Xu^xi, г=1,...,ш}·
Тогда при выполнении указанных выше условий 1-4
sup |Fn(aj) - F(x)\ п' н') 0 при η —► оо.
χ
Приведенное утверждение означает, что при неограниченном
увеличении размера выборки локальное заполнение обеспечивает
совпадение распределения заполненной выборки с истинным. Из него
вытекает, что оценки, непрерывные в равномерной метрике (см. [11,
с. 26]), состоятельные для полных данных, будут состоятельны и
для данных с пропусками после локального заполнения.
§ 7. Ранговая корреляция
343
§7. РАНГОВАЯ КОРРЕЛЯЦИЯ
Нередко на практике представляет интерес гипотеза
независимости признаков ξ и η:
Н0: F^(x,y) = F^(x)Fv(y) при всех я,у,
где F£iV(x,y) = Ρ(ξ ^ χ,η ^ у)—это функция распределения
случайного вектора (£,77) (см. П8), а ^(#) и i^ (у)—функции
распределения его компонент.
Для ее проверки применяют ранговые критерии. Они не зависят
от конкретного вида функций F$ и Fv при условии их
непрерывности. Кроме того, эти критерии робастны (устойчивы) (см. § 4 гл. 8)
к выделяющимся наблюдениям («выбросам»), которые обычно
присутствуют в крупных массивах реальных данных. Рассмотрим
сначала наиболее часто используемый
Критерий Спирмена
Обозначим через R{ ранг (т. е. номер в порядке возрастания)
наблюдения & среди ξι,... ,fn, а через S* ранг щ среди щ,... ,ηη. Таким
образом, наблюдения порождают п пар рангов (ϋι,5ι),... ,(ДП,5П).
Статистикой критерия Спирмена служит выборочный
коэффициент корреляции ps ранговых наборов (ϋι,... ,Яп) и (Si,... ,Sn),
определяемый формулой
Ps = E(Ri-R)(Si-S)
г=1 /
_ _ 1/2
Z(Ri-R)2E(Si-s)2i
г=1 г=1
(20)
1 п п +1
В этой формуле Д = S = — Σ г = —о—· С учетом легко доказыва-
п г=1 2
" 2 n(n + l)(2n + l)
емого по индукции равенства 2_^г = — ~ имеем
г=1 6
г=1 г=1 г=1 V * / ^
Переставив пары (ДгЛ) в порядке возрастания первой
компоненты, получим набор (Ι,Τι),... ,(п,Тп). Тогда статистика (20)
запишется в виде
-^si'-^H15-2*1)· (21)
Таким образом, ps — линейная функция от рангов Т{. Правую часть
равенства (21) можно также представить (задача 3) в виде
fe^-^Eti-^^l-^.I.nEtfl.-Si)2, (22)
— та- τϋ = ι -
n*-n£i г) n(n-l)(n+l)«ti
который наиболее удобен для вычислений.
344
Глава 20. Корреляция
Совпадения. Пример 9 показывает, что формула (22) пригодна
для подсчета ps только в случае отсутствия совпадений (т. е.
в случае, когда среди значений наблюдений fi,...,£n (vi,-- · >^n)
нет одинаковых). Если совпадения есть, то при ранжировании им
следует присваивать средние ранги*) и затем вычислять ps на
основе формулы (20).**)
Пример 9 ([2, с. 108]). Десять однородных предприятий были про-
ранжированы вначале по степени прогрессивности их
оргструктур (признак ξ), затем по эффективности их функционирования в
отчетном году (признак г/). В результате были получены
следующие две ранжировки: 1; 2,5; 2,5; 4,5; 4,5; 6,5; 6,5; 8; 9,5; 9,5 и 1; 2; 4,5;
4,5; 4,5; 4,5; 8; 8; 8; 10. Для этих данных правая часть равенства (22)
равна 0,921, а коэффициент ps, вычисленный по формуле (20),
имеет значение 0,917. С помощью табл. Т6 устанавливаем, что при
η = 10 критической границей для ps на уровне значимости 0,001
служит величина 0,879. Поскольку 0,917 > 0,879, корреляционную
связь между признаками ξ и η следует признать значимой.
Исследуем некоторые свойства статистики ps при
справедливости гипотезы #о· Множество рангов (Τι,... ,ТП) — это некоторая
перестановка множества (1,...,п). При выполнении гипотезы Щ
все п! таких перестановок равновероятны. Поэтому для любого
1 ^ г ^ п
MTi=±k Р(Ц = *)=£* ^^ = Ц± .
fc=l fc=l n! l
Из формулы (21) немедленно получаем, что Mps = 0 при
выполнении гипотезы Щ. Нетрудно установить, что Dps = 1/(п - 1)
(задача 4). Так как ps — коэффициент корреляции, то
согласно следствию из неравенства Коши—Буняковского (П4) всегда
—l^ps^l. Крайние значения достигаются: при полном соответ-
Почему верно последнее ствии наборов рангов (Д; = Si, г = 1,... ,п) имеем ps = 1, а при
утверждение? противоположных рангах (Т; = п — г + 1) получаем ps = — 1.
Достаточно близкие к 1 (или —1) значения ps противоречат
гипотезе if о· Критические границы при односторонней альтернат
тиве Ηι: ρ(ξ,η) > 0 на нескольких уровнях значимости для п ^ 50
можно найти в табл. Т6.
Для п > 50 годится нормальное приближение, основанное на
сходимости
Ps I у Dps -> Ζ ~ Λ/ΧΟ, 1) при п —► оо
в случае справедливости гипотезы Н0 (доказательство см. в [86,
с. 227]).
*) Так, для выборки 2, 5, 5, 7 получаем ранжировку 1; 2,5; 2,5; 4.
**) Для подсчета выборочного коэффициента корреляции ранжировок (20)
можно воспользоваться функцией «Коррел» из Excel.
§ 7. Ранговая корреляция
345
Поправка. Для небольших выборок это приближение не
является удовлетворительным. Р. Иман и У. Коновер в 1978 г.
предложили следующую поправку, значительно повышающую точность
аппроксимации (см. [88, с. 10]). Положим
Ps = \ Ps (sfc=l + yJ(n-2)/(l-p2sj) .
С помощью табл. Т2 и Т4 вычислим ζα = (#ι-α +2/ι-α)/2, где χι-α
и yi-a обозначают, соответственно, квантили уровня (1 — а) закона
Л/"(0,1) и распределения Стьюдента с (п — 2) степенями свободы
(см. § 2 гл. 11). Если ps ^ Ζα, то гипотеза Щ отвергается в пользу
альтернативы Hi: ρ(ξ,η) > 0, иначе — принимается.
Критерий Кендэла
Другую ранговую меру связи ввел в 1938 г. М. Дж. Кендэл. Будем
говорить, что пары (ξΐ,ηί) и {£j,ty) согласованы (1 ^ г < j ^ п),
если ξι < £j и r\i < щ или & > ξj и щ > щ (т. е.
sign {£$ — ξι) sign (r/j — 77;) = 1). Пусть S — число согласованных пар,
а Д —число несогласованных пар. Тогда превышение
согласованности над несогласованностью есть*)
Τ = S - Д = £ sign (ξ,- - &) sign (τ/, - ту<).
i<j
Значения Т изменяются от —п(п — 1)/2 до п(п — 1)/2. Например,
max Τ = п(п — 1)/2 достигается при идеальном согласии порядка
£ι,···,£η и Г71,...,77п. Для измерения степени согласия Кендэл
предложил коэффициент
т=_Т_ = 2Г = 2(5-Д) = 4_ , .
maxT n(n-l) n(n -1) n(n -1) ' v ;
так как 5 + Д = n(n —1)/2. Заметим, что величина Д — это
количество инверсий (см. пример 2 гл. 7), образованных величинами ηι,
расположенными в порядке возрастания соответствующих &.
Таким образом, коэффициент г (линейно связанный с Д) можно
считать мерой неупорядоченности второй последовательности
относительно первой.
Ввиду формулы (23) и асимптотической нормальности
статистики Д при справедливости гипотезы Щ имеет место сходимость
τ/ν^^Ζ~ΛΓ(0,1) при п —► оо,
где От = 2(2п + 5)/[9п(п - 1)].
Обсудим связь между коэффициентами τ и ps. Очевидно, стаг
тистика Τ представляется также в ранговой форме:
Г = Σ sign (Rj - Ri) sign (Si - S*) = Σ «** № - τ0· (24)
i<3 i<3
*) Предполагается, что среди ξι и среди 7ji нет совпадений.
346
Глава 20. Корреляция
Аналогично, R = Σ I{Ti>Tj}· С учетом соотношения (23) получаем,
ЧТО
Согласно задаче 5 для коэффициента ps верна похожая формула:
ps = l ~ ^з—" Σ U ~ *) Ι{Τι>τ& (25)
η -η iKj
показывающая, что в случае ps инверсиям придаются
дополнительные веса (j — г). Из-за этого возникает предположение, что ps
сильнее реагирует на несогласие ранжировок, чем т. Однако М. Кендэл
и А. Стьюарт в [35, с. 683] отмечают, что величины ps и τ при
справедливости гипотезы Но сильно коррелироеаны: коэффициент
корреляции между ними равен 2 (п + 1) /γ/2η(2η + 5). Он убывает
от 1 при η = 2 до 0,98 при η = 5 и далее возрастает до 1 при η —> со.
Замечание 10. Обобщенный коэффициент корреляции [36].
Для удобства реализации на компьютере системы алгоритмов
корреляционного анализа полезно вывести обобщенную формулу
для вычисления разных парных корреляционных характеристик
(таких, как г, /)§ и ^, где
p=t(Xi- x)(Yi - Υ) Ι \± (Xi - χ)2 · Σ (Xi - ϋ)2]
i=l I U=l i=l J
обозначает обычный коэффициент корреляции между выборками
X = (Χι,...,Χη) и Υ = (Υι,...,Υη)). С этой целью определим
некоторое правило, в соответствии с которым каждой паре (Х^, Xj)
компонент вектора X приписывается число («метка») с^ = с^(Х),
причем это правило будет обладать свойством отрицательной
симметричности: Cij = — Cji, сц = 0. Тогда обобщенный коэффициент
корреляции между X и Υ определяется формулой
/Г т1/2
г = Σ сц{х)сц{У) / E4-W · Е4-(у)
г<3 I li<j i<j
Убедимся, что коэффициенты j?, ps и τ могут быть получены
как частные случаи обобщенного коэффициента г при
соответствующем выборе правила приписывания числовых «меток» cij.
1) Установим для любых -ΧΊ,... ,ХП и Υί,... ,У^ справедливость
тождества
Σ № -х)(У< - F) = \ Σ № -**)«· - Υί).
При Χι=Υι оно следует из теоремы о межточечных расстояниях,
доказанной при решении задачи 5 гл. 16 (πΐι = 1, га = п). В
общем случае оно выводится из указанной теоремы с помощью
представления АВ = [(А + В)/2}2 - [(А - В)/2]2 (см. задачу 6).
Ввиду установленного тождества при выборе в качестве «меток»
Cij(X) = Xj — Xi коэффициент 9 преобразуется в jp.
§ 8. Множественная и частная корреляции
347
2) Положим Cij(X) = Rj — Ri, где Дг —ранг Х{ в выборке X.
С учетом предыдущих рассуждений и определения коэффициента
Спирмена (20) видим, что гв этом случае совпадает с ps-
3) Пусть Cij(X) = sign (Xj—Xi) = sign (Rj—Ri). Тогда делимым
в формуле для 9 служит определенная выше статистика Т, а
делитель равен п(п — 1)/2. Принимая во внимание формулу (23),
заключаем, что обобщенный коэффициент Ϋ превращается в т.
§8. МНОЖЕСТВЕННАЯ И ЧАСТНАЯ
КОРРЕЛЯЦИИ
Может представлять интерес задача измерения статистической
связи сразу между к ^ 3 выборками. С этой целью Кендалом был
предложен ранговый коэффициент конкордации (согласованности)
к (п -п) <=1 \j=1 2, )
где Rij —ранг (от 1 до п) г-го элемента в j-ft выборке (столбце).
Укажем некоторые свойства коэффициента W (см. [36, гл. 6]).
1) 0 ^ W < 1, причем W = 1 тогда и только тогда, когда все
к ранжировок совпадают. То, что W не принимает отрицательных
значений, объясняется тем обстоятельством, что в отличие от
случая парных связей для к ^ 3 выборок противоположность
согласованности утрачивается: упорядочения могут полностью совпадать,
но не могут полностью не совпадать.
2) Обозначим через ~ps среднее арифметическое
коэффициентов Спирмена по всем k(k — 1)/2 парам выборок. Тогда
W = [(k-l)ps + l]/k.
Таким образом, W и ~ps линейно связаны. В частности, при к = 2
имеем W = (ps + 1)/2, т. е. коэффициент конкордации W линейно
зависит от коэффициента Спирмена ps-
3) Сравнение с критерием Фридмана из § 2 гл. 17 (с точностью
до замены обозначений к ^ п) показывает, что при больших η
статистика к(п — \)W распределена приближенно по закону хи-
квадрат с (п — 1) степенями свободы.
Перейдем теперь к обсуждению понятия частной или
«очищенной» корреляции. Начнем с примера из [2, с. 64].
«Даже если удалось установить тесную зависимость между двумя
исследуемыми величинами, отсюда еще непосредственно не следует
их причинная взаимообусловленность. Например, при анализе
большого числа наблюдений, относящихся к отливке труб на
сталелитейных заводах, была установлена положительная корреляционная
Вопрос 3.
Будет ли значение
W = 0,09 значимо велико
на уровне 5% при к=20 и
п=15?
(Воспользуйтесь табл. ТЗ
критических значений
Х2-распределения.)
348
Глава 20. Корреляция
связь между временем плавки и процентом забракованных труб [3].
Дать какое-либо причинное истолкование этой стохастической связи
было невозможно, а поэтому рекомендации ограничить
продолжительность плавки для снижения процента забракованных труб
выглядели малосостоятельными. Действительно, спустя несколько лет
обнаружили, что большая продолжительность плавки всегда была
связана с использованием сырья специального состава. Этот вид
сырья приводил одновременно к длительному времени плавки и
большому проценту брака, хотя оба этих фактора взаимно независимы.
Таким образом, высокий коэффициент корреляции между
продолжительностью плавки и процентом забракованных труб
полностью обусловливался влиянием третьего, не учтенного при
исследовании фактора — характеристики качества сырья. Если же
этот фактор был бы с самого начала учтен, то никакой значимой
корреляционной связи между временем плавки и процентом
забракованных труб мы бы не обнаружили. За счет подобных
эффектов (одновременного влияния неучтенных факторов на
исследуемые переменные) может искажаться и смысл истинной
связи между переменными, т. е., например, подсчеты приводят к
положительному значению парного коэффициента корреляции, в то
время как истинная связь между ними имеет отрицательный смысл.
Такую корреляцию между двумя переменными часто называют
«ложной». Более детально подобные ситуации — обнаружение и
исключение «общих причинных факторов», расчет «очищенных»,
или частных, коэффициентов корреляции и т. п. — исследуют
методами многомерного корреляционного анализа.»
Определение. Частным коэффициентом корреляции между
случайными величинами X и Υ при исключении влияния случайной
величины Ζ называется
ρ(χ,υ\ζ) Ξ Ρχηζ = Pi**) - ρ(χ,ζμυ,ζ)
К этой формуле приводит попытка исключить зависимость от
Ζ, заменив X и Υ такими случайными величинами
X' = X - αΖ, Υ' = Υ- bZ,
которые некоррелированы с Ζ: ρ(Χ',Ζ) = 0 и ρ(Υ,1Ζ) = 0. Тогда
«оставшаяся» корреляция представляет собой обычную
корреляцию между X' и У.
Доказательство. Допустим для простоты, что MX = MY =
= Μ Ζ = 0. Для краткости введем обозначения σ$ = \/D£ и
ΡΖή = Ρ(ζ>ν)- Константы а и Ь нужно выбрать так, чтобы имели место
равенства
UX'Ζ = MX Ζ - aUZ2 = 0, MY Ζ = MY Ζ - bMZ2 = 0.
Отсюда находим
ΡΧΖ <τχ <?Ζ <?χ * ΡΥζσγσζ Λ <?Υ /олч
α = 5 = Pxz — » ь= 5 = Ρυζ — · (26)
σζ σζ σζ σζ
§ 8. Множественная и частная корреляции
349
(27)
Запишем обычный коэффициент корреляции между X' и У':
ЩХ - aZ)(Y - bZ)
Ρχ,γ, = .
<7X-aZ<7Y-bZ
Числитель в формуле (27) можно представить в следующем виде:
UXY -aUYZ -bUXZ + abUZ2 =
= Ρχγ σχ <τγ — αργζ <τγ <7ζ — bpxz <τχ <τζ + αϋσζ·
Заменив α и Ь в этом равенстве их значениями из соотношений (26),
получим
ЩХ - aZ)(Y - bZ) = (ρχγ - ρχζ ργζ) σχσγ.
Точно также вычисляются дисперсии
σχ-αζ = ЩХ -αΖ)2 = (1 - ρχζ)σχ,
σγ-ьг = ЩУ ~ bZ)2 = (1 - p\z) σγ.
Подстановка всех этих выражений в формулу (27) приводит к
равенству
Ρχγ - ΡχζΡυζ /2g\
ΡχΎ'
Ρχγ\ζ,
y/(l-PxZ)(l-pYZ)
которое и требовалось установить. I
Для получения оценки рху\х*^ для коэффициента ρχγ\ζ надо
заменить в соотношении (28) теоретические коэффициенты
корреляции выборочными (см. определение (20)):
<*> Р&у ~ PwzPyz
(29)
К этой формуле можно прийти точно так же, как и выше,
отталкиваясь от условия ортогональности реализации выборки ζ и
линейных комбинаций х' = χ — αζ и у' = у — bz. В этой интерпретации
Pxy\z представляет собой косинус угла между проекциями векторов
χ и у на подпространство в Rn, ортогональное вектору ζ (рис. 26).
Если дополнительно предположить, что X, У и ^ — выборки
из независимых нормальных законов, то (как доказано в [13, с. 370])
выборочный частный коэффициент корреляции ρχγ\ζ будет
распределен точно также, как и обычный выборочный коэффициент ρχγ,
но для выборок размера не п, а п—1. Отсюда и из задачи 6 гл. 11
вытекает сходимость распределения случайной величины у/п axcthpx\r\z
к закону Л/*(0,1) при η —► оо.
Пример 10 ([2, с. 85]). По итогам года у 37 однородных
предприятий легкой промышленности были зарегистрированы следующие
(среднемесячные) показатели их работы: χ — значения
характеристики качества ткани (в баллах), у — количества
профилактических наладок автоматической линии, ζ —случаи обрывов нити.
*) Здесь неслучайный вектор χ = (χι,... ,хп) обозначает реализацию выборки
X = (Χι,... ,Χη), где Xi независимы и распределены так же, как и случайная
величина X.
\
Ζ\
\
А^
i
X
/
v^
*/
Рис. 26
350
Глава 20. Корреляция
На основе этих данных были подсчитаны парные коэффициенты
корреляции: fixy = 0,105, fixz = 0,024, pyz = 0,996. Проверка на
статистическую значимость свидетельствует об отсутствии связи
между качеством ткани, с одной стороны, и числом
профилактических наладок и обрывов нити —с другой, что не согласуется с
профессиональными представлениями технолога.
Однако расчет частных коэффициентов корреляции по
формуле (29) дает значения pxy\z = 0,908 и fixz\y = -0,907, которые
вполне соответствуют представлению о естественном характере
связей между изучаемыми показателями.
В заключение отметим, что ранговый коэффициент Кендэла τ
(в отличие от коэффициента Спирмена ps) переносится на
случай частной корреляции с помощью формулы, аналогичной
формуле (29):
Taty ТдьхТух
>/(1 - т2.)(1 —rg.)
(см. [36, гл. 8]). Критерии значимости для тху\х можно отыскать в
журнальных статьях, указанных на с. 216 книги [86].
§9. ТАБЛИЦЫ СОПРЯЖЕННОСТИ
Рассмотрим задачу выявления статистической связи для
сгруппированных (разбитых на категории) данных. Если ранее
обсуждались случаи количественных (§§ 1-6) и порядковых (ранговых)
(§§ 7-8) переменных, то теперь переменные — качественные и
описываются номером группы, а данные представлены в виде таблицы
сопряженности (признаков) \\vij\\nxmi в которой ι/^—числа
объектов с признаками г, j.*)
Опишем три выборочные схемы, приводящие к таблицам
сопряженности ([2, с. 125]).
Схема I возникает в случае, когда строки (ι^ι,... ,^т) таблицы
данных (г = Ι,.,.,η) можно рассматривать как независимые
выборки из полиномиальных распределений (см. § 5 гл. 10 и дока-
т
зательство теоремы 1 гл. 18) с вероятностями q\j (Σ qij = 1) и
m
заданными числами наблюдений щ = Σ угу Такая организация
3=1
данных обычно возникает, когда хотят сравнить между собой
несколько одномерных распределений, представленных выборками
заранее заданного размера. Наиболее важной для схемы I является
гипотеза однородности
1 п
Я/: qij = q.j, где q.j = - Σ ftj,
ni=l
*) Таблицы с тремя и более входами анализируются в книгах [7], [47].
§ 9. Таблицы сопряженности
351
которая подробно обсуждалась ранее в § 3 гл. 18.
Схема II. Предполагается, что (ι/ц,. .. ,vnm) имеют
полиномиальное распределение с вероятностями (рп,... ,рПт) и
фиксированным общим числом наблюдений N = Y^Vij- Таблица сопряженно-
сти в этом случае является обычной двумерной гистограммой для
N наблюдений. Гипотезе Hj из схемы I в схеме II соответствует
гипотеза независимости, состоящая в том, что совместное
распределение есть произведение маргинальных (частных) распределений:
т η
Η π: pij = riSj, где r< = £ р#, Sj = £ pi<7.
Схема III возникает, когда в схеме II общее число наблюдений
рассматривается как случайная величина. Ее важным частным
случаем является случай, когда все уц независимы и распределены
по закону Пуассона с параметрами λ^·. Тогда их сумма N также
имеет распределение Пуассона с параметром с = ]Г А# (см. задачу 3
г,3
гл. 10). Гипотезам Hi и Hi ι соответствует гипотеза
мультипликативности
т η
Ηιιι\ Xij = Oibj/c, где α* = £) λ#> fy = Σ -Ч?·
i=i <=i
В качестве примера применения схемы III может быть
рассмотрена задача, в которой uij — число отказов (аварий) г-го вида на
установках j-το типа в течение заданного времени наблюдения.
Параметры Xij отражают ожидаемые количества отказов.
Можно доказать, что если в схеме III зафиксировать N, то
она переходит в схему II с р^ = Xij /с. При этом гипотеза Нщ
преобразуется в гипотезу Нц. Аналогично, если зафиксировать в
схеме II суммы по строкам щ = ι/ц +... + щт, то схема II переходит
в схему I с qij = Pij/ri, а гипотеза Η 11 —в гипотезу Я/.
Для проверки гипотез Ηι—Нш применяется вариант
критерия хи-квадрат, статистика которого имеет вид
2 " ™ (i/y _ mmj/N)2 ™ »
^ =^ΣΣ „ ' , где τα=Σ "Φ mj = Σ Чу
i=lj = l ni™>j j=l i=1
При справедливости проверяемой гипотезы при достаточно
больших N статистика X2 приближенно распределена по закону хи-
квадрат с (п - 1)(ш — 1) степенями свободы.
Для схемы II это утверждение вытекает из теоремы Фишера
(см. формулу (6) гл. 18). В этом случае имеется (т + η — 2)
неизвестных параметров п,... ,rn-i,si,... ,sm-b Методом Лагранжа
находим, что оценками максимального правдоподобия для них
будут величины η = щ/N и Sj = mj/N (задача 7). При
этом число степеней свободы предельного закона хи-квадрат равно
пт — 1 - (т + η — 2) = (η — l)(m — 1).
352
Глава 20, Корреляция
Пример 11 ([44, с. 481]). В приведенной ниже таблице
представлены результаты социологического обследования о связи между
доходом семей и количеством детей в них. Признак А означает
количество детей и принимает значения 0, 1, 2, 3, ^ 4. Признак
В указывает, какому из диапазонов (0-1), (1-2), (2-3), (^ 3) (за
единицу принято 1000 шведских крон) принадлежит доход семьи.
^ξ
0
1
2
3
^4
! TUj
0-1
2161
2755
936
225
39
6116
1-2
3577
5081
1753
419
98
10928
2-3
2184
2222
640
96
31
5173
^3
1636
1052
306
38
14
3046
Пг
9558
11110
3635
778
182
25263
Значение статистики X2 равно 568,6, что значимо больше
критической границы 32,9 уровня 0,001 закона хи-квадрат с
(5 — 1)(4 — 1) = 12 степенями свободы (см. табл. ТЗ). Поэтому
гипотеза независимости признаков А и В отвергается.*)
Помучишься — так
научишься.
ЗАДАЧИ
1. Пусть А, В и А — В — неотрицательно определенные матрицы.
Докажите, что
а) trA^trB; trA = trB«=» А = В,
Указание. Используйте приведение А — В к главным осям.
б) det A ^ detB; если detB > 0, то det A = detB <=ϊ Α = В.
Указание. Рассмотрите сначала случай В = Ε и докажите,
что тогда все собственные значения матрицы А—Е не меньше 1.
2? Выведите соотношения (19).
3. Получите представление (22) рангового коэффициента Спир-
мена ps-
Указание. Разложите Σ [(г - ?^-\ - Ы - rL^i)] ·
4? Докажите, что Dps = 1/(п—1) при справедливости гипотезы Щ.
71+1
Указание. Положим & = Ri —. В силу равенства Σ 6 = 0
имеем
0 = Μ (ft Σ fc) = Μξϊ + (η - l)Mfc6.
5? Проверьте справедливость для ps представления (25).
6. Проверьте, что для любых #ι,... ,#п и yi,... ,уп верно тождество
п _ _ 1
Σ (χι - х)(у% - у) = - Σ (хз - xi)(yj - Ух)-
г=1
г<3
*) Однако в [11, с. 412] отмечено, что более тонкий анализ этих данных
указывает на очень слабую зависимость между А и В.
Решения задач
353
7. Используйте метод неопределенных множителей Лагранжа для
нахождения оценок максимального правдоподобия неизвестных
параметров ri,... ,rn_i,si,... ,sm-i в схеме II из § 9.
Указание. См. похожую задачу 6 гл. 18.
РЕШЕНИЯ ЗАДАЧ
1. а) Так как матрица А — В неотрицательно определена, все ее
собственные значения λ^ неотрицательны (см. ШО). Поэтому
tvA - trB = tr(A - В) = ]£λ< ^ 0; если trA = trB, то
tr(A — В) = 0. Следовательно, все λ^ = 0, СТ(А — В)С = 0.
В силу невырожденности С получаем, что А = В.
б) При detB = 0 утверждение очевидно. Пусть detB > 0,
т. е. матрица В положительно определена. Сначала рассмотрим
случай единичной матрицы: В = Е. Пусть μ и с — собственное
значение и соответствующий собственный вектор матрицы А:
Ас = μα. Тогда (А — Е)с = (μ — 1)с, т. е. λ = μ — 1 — собственное
значение А — Е. Но А — Ε неотрицательно определена, поэтому
А ^ 0 <=ϊ μ ^ 1. Отсюда detA = \[μι ^ 1 = det 23. Если
detA = 1, то каждое μ» = 1, так что А = Ε (см. вопрос 7
гл. 19).
Теперь рассмотрим общий случай положительно
определенной матрицы В. В этом случае матрица
D = В~1'2{А - В)В~1'2 = В-1'2АВ-1'2 - Ε
будет неотрицательно определенной. Действительно,
xTDx = (хтВ~1/2)(А - В)(В"1/2ж) = ут(А - В)у > 0,
где у = В~1^2х. Следовательно, det(B~l^2AB~1^2) ^ 1, т.е.
det A det В-1 ^ 1, причем равенство имеет место тогда и только
тогда, когда В~1'2АВ~1'2 = 23, т. е. когда А = В.
2. Вычислим частную производную по х^т функции
Г m I 1/2
G = CiFi = Σ (Sij - dij)2/dij, где δ^ = Σ(χα - Xji)
i<j 11=1 J
Если г ф к или j φ k1 το Θ[(δψ — dij)2/dij]/dxkr — 0. Пусть
сначала г = к1 a j = г + 1,... ,п (рис. 27). Тогда
__ ^[№j ~dij) /dij] 2(Sij —dij) dSij
Подсчитаем отдельно Θδ^/θχ^
dxv
%2_ __
2δ*,
d
dxu
m
Σ fan
Li=i
Xjlf
Sij
Подставляя этот результат в предыдущую формулу, получим
0>j == **\Oij ("ij )\pGir ^Ejг)/\PijU'ij\^
Вопрос 4.
Почему условие det В > 0
необходимо?
к
г
Ц
к
к
ш
•
S
•ыч
ίΗ
ТЧ1
R
Рис. 27
354
Глава 20. Корреляция
Аналогично, в случае j = к и г = 1,... ,j — 1 имеем
Наконец, сложим ненулевые слагаемые и поменяем индексы:
σ*«ί j=t+l i=l j = l °гзагз
Зфг
3. Для краткости введем обозначения: А = ^(г — Т^)2,
* - Σ (< - ^)'· с - Σ (< - Η1) (*" ψ} т°™
('-^-(«-^'-e-ic+E^-Sii)'.
Поскольку последняя сумма также равна В, получаем равенство
А = 2В-2С^=>1-^ А/В = С/В = р8.
4. Дополним обозначения из решения предыдущей задачи еще
^ г, η + 1 ~ п + 1 π
двумя: & = Д; - —— и r\i = Si —. При этом
Bps = С = Х)^г^?г- Возводя в квадрат, получим соотношение
в2/4 = Σ i«fcw&· (зо)
Ввиду того, что при справедливости гипотезы Но случайные
величины ξι и щ независимы, из формулы (30) следует равенство
В2ЬАр% = B2Dps = Σ (Щ& ■ *Лтцъ).
Эта сумма содержит η слагаемых с индексами г = j, и так
как все индексы равноправны, то все эти слагаемые одинаковы.
Точно так же равны друг другу остальные п(п — 1) слагаемых с
индексами г φ j. Поэтому
B2Dps = ηΜξΙ · Щ\ + п(п - 1)М&6 * МГ71Г72. (31)
В силу тождества Σ & = 0, имеем
0 = Μ (ξι Σ6) = Μξ2ι + (η - 1)Μ£ι6,
Следовательно, Μ£ι£2 = τ Μ£?. Если взять математи-
η — 1
ческие ожидания от обеих частей равенства Σ£? = &·> то
найдем, что М£^ = В/п. Поэтому M£i^2 = —В/[п(п — 1)].
Аналогичные формулы верны, конечно, и для Mr/2
и Μ г/1 г/2· Подставив все в равенство (31), получим
B2Dps = В2/η + В2/[п(п - 1)] = В2/(п - 1). Остается только
сократить обе части на В2.
Решения задач
355
5. Пусть, как и прежде, А = Σ(ί — Т^)2. Ввиду формулы (22),
достаточно показать, что А = 2J9, где
D=EU-i)I{Ti>Tj}·
Добавим к правой части и вычтем из нее Ε = Σ j Ι{Τι>τό}'-
D=Y,3Цт&Ъ} ~ Σ *I{Ti>Tj) +E-E =
= Т.з1{ъ>т,} - Σ * [hr^Tj] + 1{Ъ>Ъ}] =
η η η—1 η
= Σ 3 Σ 7№>тл - Σ * Σ ΐ·
j=l г=1 г=1 j=i+l
η
Заметим, что Σ ^{Ti>TJ} равна числу тех Τί (г = Ι,.,.,η),
г=1
которые больше, чем Tj, т. е. равна n — Tj. Следовательно,
η=£ί(η-Τι)-ηΣί(η-ί).
j=l г=1
Заменяя в верхнем пределе второй суммы (п — 1) на η и приводя
подобные члены — суммы, получаем
η η
£>=Σ*2-ΣΉ,
г=1 j=l
Остается заметить, что А = Σ(ί — Т;)2 = 2 ^ г2 — 2 ^ гТ^.
6. Введем обозначения а\ = (#г + Уг)/2 и bi = (xi — yi)/2. Используя
тождество АВ = [(А + В)/2]2 - [(А - #)/2]2, запишем для левой
части представление
Σ (χι - *)(v< - у) = Σ (β* - s)2 + Σ & - &)2·
г=1 г=1 г=1
Аналогично для правой части получаем равенство
- Σ (ъ - *i)(vj - Vi) = - Σ («i - <*г)2 + - Σ (bj - bi)2.
n г<3 n i<j n i<j
Завершает доказательство применение теоремы о межточечных
расстояниях из решения задачи 5 гл. 16 для mi = 1, га = п.
7. Запишем функцию правдоподобия сгруппированной выборки
L(0) = с Π {risjYiJ — с Π ^ Π s J^» гДе параметр 0 является
г, 3 г j
вектором 0 = (ri,... ,r ), и с от него не зависит. Таким
образом, задача равносильна максимизации по 0 функции
/(0) = Σ щ In г ι + Σ mj m sj ПРИ выполнении условий
* з
#) = ι-Ση = ο, Λ(β) = ι-Σ^· = ο.
* з
356
Глава 20. Корреляция
Запишем систему уравнений для поиска экстремальных точек
функции Лагранжа ,Ρ(0,λ,μ) = /(0) + Хд(в) + μ/ι(0):
dF/dri = щ/гг - λ = 0, г = 1,... ,η;
dF/dsj = rrij/sj — μ = 0, j = 1,... ,ra;
&Ρ/0λ = 0(0) = 0, &Ρ/0μ = /ι(0) = 0.
Из п первых уравнений находим, что Т{ = щ/\. Подставляя
найденные г ι в уравнение д(в) = 0, получим λ = Σ щ = ΛΓ, откуда
Yj = щ/N. Аналогично из оставшихся уравнений находим, что
μ = Σ rrij = N и 'sj = rrij/N.
ОТВЕТЫ НА ВОПРОСЫ
1. Евклидова норма матрицы при транспонировании не
меняется: |Q — YP\2 = \QT — PTYT\2. Минимум достигается на
Υ = (PPT)~1PQT. Остается только транспонировать обе
части этого равенства с учетом свойств из ШО.
2. Подставим η — г + 1 вместо Т{ в правую часть формулы (21),
(. η + Λ
получим, что второй сомножитель равен — I г — I.
3. Поскольку 20 · 14 · 0,09 = 25,2 больше, чем 5%-ное критическое
значение 23,7 закона xf4, то, несмотря на малость числа 0,09,
гипотеза об отсутствии связи отвергается.
4. Необходимость условия detB > 0 показывает пример матриц
Глава 21
РЕГРЕССИЯ
К регрессионному анализу относятся задачи выявления
искаженной случайным «шумом» функциональной зависимости
интересующего исследователя показателя Υ от измеряемых переменных
Χι,... ,Xm. Данными служит таблица экспериментально
полученных «зашумленных» значений Υ на разных наборах х\,...,хт.
Основной целью обычно является как можно более точный прогноз
(предсказание) Υ на основе измеряемых (предикторных )
переменных.
Регрессионный анализ по
праву может быть назван
основным методом
современной математической
статистики.
Н. Дрейлер, Г. Смит
Predict (англ.) —
предсказывать.
§ ι. подгонка прямой
Термин «регрессия» ввел Ф. Гальтон в своей статье «Регрессия к
середине в наследовании роста» (1885 г.), в которой он сравнивал
средний рост детей Υ со средним ростом их родителей X (на основе
данных о 928 взрослых детях и 205 их родителях). Гальтон заметил,
что рост детей у высоких (низких) родителей обычно также выше
(ниже) среднего роста популяции μ « X « У, но при этом
отклонение от μ у детей меньше, чем у родителей. Другими словами,
экстремумы в следующем поколении сглаживаются, происходит
возвращение назад [регрессия) к середине. По существу, Гальтон
показал, что зависимость Υ от X хорошо выражается уравнением
γ - γ = (2/3) (Χ - Ύ) (рис. 1).
Позднее регрессией стали называть любую функциональную
зависимость между случайными величинами, даже в тех
ситуациях, когда предикторные переменные являются неслучайными. В
примечании переводчиков на с. 26 книги [23] высказано интересное
мнение по поводу «живучести» термина «регрессия».
«Можно предположить, что его удивительная устойчивость
связана с переосмыслением значения. Постепенно исходная
антропометрическая задача, занимавшая Гальтона, была забыта, а
интерпретация вытеснилась благодаря ассоциативной связи с понятием
«регресс», т. е. движение назад. Сначала берутся данные, а уж потом,
задним числом, проводится их обработка. Такое понимание пришло
на смену традиционной, еще средневековой, априорной модели, для
которой данные были лишь инструментом подтверждения.
Негативный оттенок, присущий понятию «регресс», думается и вызывает
психологический дискомфорт, поскольку воспринимается
одновременно с понятиями, описывающими такой прогрессивный метод, как
регрессионный анализ.»
Если кто-то способен
предсказать, чем
закончатся его исследования,
то эта проблема не
очень глубока и, можно
сказать, практически не
существует.
А. Шильд
358
Глава 21. Регрессия
Проиллюстрируем основные идеи регрессии на примере
подгонки прямой под «облако» экспериментальных точек (аздг),
полученных в соответствии с моделью
r\i = a + bxi + ει, ι = 1,... ,η.
(i)
Здесь коэффициенты прямой α и Ъ — неизвестные параметры, χι —
(неслучайные) значения предиктора X (для простоты допустим,
что Xi φ Xj), Si — независимые и одинаково распределенные
случайные ошибки, Mei = 0. Для нахождения оценок коэффициентов
α и b применим
г(Яг,Г7г)
X
Рис. 2
А. М. Лежандр
(1752-1833), французский
математик.
Некоторые детали спора
о приоритете между
Лежандром и Гауссом
приведены в примечании
переводчиков к с. 32
книги [23].
ι / (xwm)
р*
X
Рис. 3
yf f
(*i,Vi)
A(*i,r?i)
Χ
Рис. 4
Метод наименьших квадратов (МНК).
Естественным условием точности подгонки пробной прямой
у = α + βχ служит близость к нулю всех остатков
δί(αβ) = щ — а — βχί (рис. 2). Общую меру близости к нулю
можно выбирать по-разному (например, тах|й| или X)|u|), но
наиболее простые формулы для оценок а и Ь получаются, если в
качестве такой меры взять
Ρ{αβ)=ΣδΊ=Σι{ηί-α-βχί)2.
г=1 г=1
(2)
Минимум F(a$) достигается (см. задачу 1) в точке (а,Ь), где
2 й-к_^ (з)
^ п / п
ь= Σ(νί- Щхг - х) / Σ(χί ~ х)2 ι a = rj-hx.
i=l / i=l
Метод наименьших квадратов был впервые опубликован в 1805 г.
Лежандром в работе, посвященной нахождению орбит комет.
К. Гаусс утверждал, что использовал МНК еще до 1803 г.
Замечание 1. Прямая, подогнанная под «облако» точек МНК,
вообще говоря, отличается от первой главной компоненты (см. § 1
гл. 20). Дело в том, что при построении главной компоненты
переменные X и Υ считаются равноправными, и минимизируется
сумма квадратов длин отрезков, перпендикулярных компоненте, а
не направленных вдоль оси У, как в случае МНК (рис. 3).
Недостатком метода наименьших квадратов является излишняя
чувствительность МНК-оценок к выделяющимся наблюдениям
(«выбросам»), возникающая вследствие зависимости меры F не
от самих остатков $*, а от их квадратов. Стремление уменьшить
остатки в точках «выбросов» может привести к значительному
смещению оценок параметров. Так, если переместить вверх точку
(#ι,77ι) на рис. 4, то, чтобы уменьшить δ\, МНК-прямая довольно
сильно повернется.
Одной из устойчивых к «выбросам» (робастных) альтернатив
МНК может служить
§1. Подгонка прямой
359
Метод Тейла (см. [88, с. 215])
В этом методе оценки коэффициентов прямой задаются
следующими формулами:
Ъ = ΜΕΌ{(ηό - m)/(xj - а?<), 1 ^ % < j < η} , (4)
α = MED{ty — bxi1 i = 1,... ,n}.
Причина робастности метода Тейла кроется в том, что
одиночный «выброс» может исказить самое большее (п — 1) оценок
{Vj —Vi)/(xj —Xi) коэффициента наклона Ь, в то время как медиана
вычисляется по п(п — 1)/2 оценкам.
Пример 1 ([86, с. 234]). Закон Хаббла в астрономии гласит:
скорость удаления галактики прямо пропорциональна расстоянию до
нее. В таблице ниже указаны расстояния Υ (в миллионах световых
лет) и скорости X (в сотнях миль в секунду) для 11 галактических
созвездий (см. [66]).
Требуется подогнать прямую Υ = ЬХ к этим данным.
Созвездие
Дева (Virgo)
Пегас (Pegasus)
Персей (Perseus)
Волосы Вероники (Coma Berenices)
Большая Медведица (Ursa Major No. 1)
Большая Медведица (Ursa Major No. 2)
Лев (Leo)
Северная Корона (Corona Borealis)
Близнецы (Gemini)
Волопас (Bootes)
Гидра (Hydra)
Χ
22
68
108
137
255
700
315
390
405
685
1100
Υ
7,5
24
32
47
93
260
120
134
144
245
380
Υ/Χ
0,341
0,353
0,296
0,343
0,365
0,371
0,381
0,344
0,356
0,358
0,345
Имеется 11 χ 10/2 = 55 попарных наклонов, начиная с
наименьшего 0,187 для Льва и Северной Короны. Медиана наклонов
Ь = 0,359, оценка метода наименьших квадратов b = 0,353 « b.
Замечание 2. Интересно, что оценка b в формуле (4) связана с
ранговым коэффициентом Кендэла τ (см. § 7 гл. 20), причем эта
связь аналогична связи МНК-оценки b в формуле (3) с обычным
выборочным коэффициентом корреляции р.
Действительно, занумеруем наблюдения так, что χ ι < ... < χη.
Если из щ вычесть истинные значения Ьх^ то щ — bxi = a + Si
(г = 1,... ,η) образуют выборку (набор независимых и
одинаково распределенных случайных величин). Не зная Ь, будем
вычитать из г/г величины /?#г, где β меняется по нашему
произволу. Чем ближе β к Ь, тем больше щ — βχ{ будут похожи на
выборку. В противном случае, они будут проявлять тенденцию
к возрастанию (или убыванию) вместе с номером г (это зависит
Дистанции огромного
размера...
Скалозуб в «Горе от ума»
А. С Грибоедова
360
Глава 21. Регрессия
от знака Ь — β). В этом легко убедиться, записав щ — βχ{ в виде
ηι—βχι = ηi — bxi+Xi(b—β) = α+ε;+х;(Ь-/3), из которого понятно,
что в силу возрастания Х\ с увеличением i у ηι — βχ% появляется
положительный (или отрицательный) «снос».
Тенденцию к изменению щ — βχχ с ростом г (или ее отсутствие)
можно исследовать с помощью коэффициентов корреляции.
Возьмем сначала обычный выборочный коэффициент корреляции β(β)
между рядами (хи... ,хп) и (r/i - /?жь... ,τ/η - /?хп):
~/^ч = Σ(^* ~ *)[fo ~ Ю ~ β(χ* ~ *)]
ν/Σ(** - ^)VE[fe - 9) - /*(*< - П2
Наименьшей зависимости г/г — βχ% от ж» (г = 1,... ,п) соответствует
значение ρ = 0. По отношению к β это дает уравнение
п п
£ (а* - х)(гц -η)=βΣ(χΐ- *)2>
г=1 г=1
решением которого и является МНК-оценка Ь из формулы (3).
В случае коэффициента Кендэла τ заменим жг и гу< — /?#г их
рангами г и Тг соответственно. Тогда (см. формулу (24) гл. 20)
Правую часть можно переписать также в виде
'да-^ёЧ^-')·
Рассуждения, аналогичные проведенным в комментарии 3 к
критерию знаков из § 2 гл. 15, показывают, что решением уравнения
τ (β) = 0 является оценка 6, задаваемая формулой (4).
Какими свойствами обладают МНК-оценки? Как вытекает из
задачи 2, в случае, когда вектор ошибок ε = (ει,... ,εη) нормально
распределен, МНК совпадает с методом максимального
правдоподобия (см. § 4 гл. 9) и, следовательно, является наиболее точным
для больших выборок (асимптотически эффективным). Другие
статистические свойства МНК-оценок обсуждаются в § 3.
§2. ЛИНЕЙНАЯ РЕГРЕССИОННАЯ МОДЕЛЬ
Предположим, что (с точностью до случайных ошибок) целевая
переменная Υ есть линейная комбинация 0ιΧι+.. .+втХт предик-
торных переменных Χι,... ,Xm с неизвестными коэффициентами
#Ъ · · · βπι-
Измерения щ переменной Υ (г = 1,... ,п, где п ^ га),
отвечающие заданным (не обязательно различным) значениям хц,... ,#im
§2. Линейная регрессионная модель
361
предикторных переменных, имеют вид
где €{ — случайные ошибки.
Вводя для векторов и матриц обозначения η = (r/i,... ,r/n)T,
Χ = Ikiillnxm, 0 = (0ι,... Аг)т, е = (ει,... ,εη)τ, можно записать
модель в матричной форме:
η = ΧΘ + ε.
(5)
Матрицу X называют матрицей плана эксперимента.
Будем предполагать, что для модели (5) выполняется
допущение
Д1. Столбцы χι = (#и,· ·· ,Xni)T, I = l,...,m, матрицы X
линейно независимы. Иными словами, ввиду выполнения
неравенства п^т матрица X имеет ранг т (см. ШО).
Пример 2. Подгонка полинома. Рассмотрим х\ = (1,... ,1)т и
χι+ι = (и[,... ,и1п)Т, I = l,...,m —1. Здесь щ < ... < ип— так
называемые «узлы», в которых вычисляются значения многочлена
р(и) = ft + в2и + 03^2 + · · · + втит-1
и «зашумляются» случайными ошибками ε* (рис. 5 для га = 4).
Матрица X имеет вид
/1
1
\1
Ui
U2
«2
,.τη— Ι
\
..7П—1
/
Определитель подматрицы X, образованной первыми га
строками X (га < п), является известным из линейной алгебры
определителем Вандермонда: detX = П1<г<?<т(Ч? ~~ ui)- ®н отличен от
нуля, поскольку «узлы» различны. Поэтому ранг подматрицы X (и
матрицы X) равен га, а столбцы a&i,... ,жт линейно независимы.
В дальнейшем при изучении статистических свойств оценок
параметров 01,... ,0т (см. § 3) будем считать выполняющимся также
допущение
Д2. Случайные величины ει,...,εη одинаково распределены с
Мб{ = 0, Обг = σ2 (параметр 0 < σ < оо также неизвестен) и
некоррелированы: MeiSj = О при г φ j.
Оценим параметры 0ι,... ,0m методом наименьших квадра-
п
ТОВ, МИНИМИЗИРУЯ ПО θ фуНКЦИЮ F(6) = Σ (Ήί—θΐχί1 — - · -—^mXim)2·
^ г=1
Точка ее минимума θ называется МНК-оценкой, вектор δ с
362
Глава 21. Регрессия
^
/^W
Рис. 6
γ=θλν+θ2ν2
10 20 30 40
Рис. 7
компонентами Si = щ — в\Хц - ... — 0mXim, i = l,...,n,—
вектором остатков, а значение в точке минимума RSS = F(0) —
остаточной суммой квадратов.*^
Для нахождения оценки θ интерпретируем задачу
минимизации функции F(0) в терминах пространства Rn. Рассмотрим
в Rn подпространство L(X), порождаемое столбцами 2Ci,...,ajm
матрицы X. Очевидно, что вектор ΧΘ = 0i2Ci + ... + втхт
пробегает Ь(Х), когда θ пробегает Rm. Поскольку
Γ(θ) = \η-ΧΘ\2,
видим, что минимизация по 0 равносильна нахождению в
подпространстве L(X) вектора ΧΘ, наименее удаленного от η. Как
известно, таким вектором служит ортогональная проекция η на L(X)
(рис. 6). Следовательно, вектор остатков δ = η - Χ θ должен быть
ортогонален векторам ж ι,... ,жт, порождающим подпространство
L(X), т. е.
Χτ(η-Χθ) = 0 или (ΧτΧ)θ = Χτη. (6)
Соотношение (6) представляет собой систему линейных уравнений
относительно θ с положительно определенной (задача 3)
матрицей В = ХТX, которую называют информационной. Решить
систему (6) можно, например, методом Холецкого (ШО). Так как
ввиду положительной определенности матрица В является невы-
рожденнной, для МНК-оценки θ получаем представление
θ = Β~ιΧΊ
4·
(7)
Пример 3 ([2, с. 177], [27, с. 57]). На рис. 7 точками изображены
результаты эксперимента по изучению зависимости между
скоростью автомобиля V (в милях/час) и расстоянием Υ (в футах),
пройденным им после сигнала об остановке. Для каждого
отдельного случая результат определяется в основном тремя факторами:
скоростью V в момент подачи сигнала, временем реакции θ\
водителя на этот сигнал и тормозами автомобиля. Автомобиль успеет
проехать путь 6\V до момента включения водителем тормозов
и еще θ^ν2 после этого момента, поскольку согласно
элементарным физическим законам теоретическое расстояние, пройденное
до остановки с момента торможения, пропорционально квадрату
скорости (убедитесь!).
Таким образом, в качестве модели годится Υ = 6\V + 62V2.
Для экспериментальных данных по формуле (7) были подсчитаны
значения θι = 0,76 и 02 = 0,056 (график параболы Υ = в\У + 62V2
приведен на рис. 7).
*) В обозначении использованы первые буквы соответствующего английского
термина «Residual Sum of Squares».
§ 3. Статистические свойства МНК-оценок
363
Замечание 3. Удобно иметь дело с матрицей X, столбцы которой
ортогональны друг другу. В этом случае формула (7) упрощается:
так как матрица В оказывается диагональной с элементами \χι\2
(I = 1,... ,га) на главной диагонали, из представления (7) получаем
выражения
θι=χΙη/\Χι\2 , / = l,...,m. (8)
Если исходный набор линейно независимых векторов Ж1,...,жт
таким свойством не обладает, то его можно ортогонализировать
с помощью стандартной процедуры Грама—Шмидта, вводя новые
векторы
х\ = χι - α(ί_ΐ)ία?ί_1 - ... - αιιχ[, Ι = 1,... ,ra, (9)
где an = xfx'i/lx'il2 (подробнее см. [43, с. 111]). Выражая χι через
ajj,...,^, получим
χι = χ\ + αμ.ΐ)/»}.! + ... + ацх[, Ι = 1,... ,m. (10)
Соотношения (10) можно записать в матричной форме: X = Х'А,
где А — верхнетреугольная матрица с единицами на главной
диагонали (она, очевидно, обратима). Подставляя это выражение в
формулу (5), приходим к модели η = Χ'θ'+ε, где θ' = Α~1Θ. Исходный
вектор θ восстанавливается по Θ' с помощью формулы
θ = ΑΘ'. (11)
§3. СТАТИСТИЧЕСКИЕ СВОЙСТВА
МНК-ОЦЕНОК
МНК-оценки параметров в линейной регрессионной модели (5)
при выполнении допущений Д1 и Д2 обладают рядом важных
свойств.
Утверждение 1.
1) Оценка 0, задаваемая формулой (7), является несмещенной,
т. е. М0 = Θ.
2) Матрицей ковариаций Cov(0) = ||cov(0fc,0i)||mxm служит
матрица σ2Β~1.
3) Для любого вектора с Ε Rm несмещенной оценкой для
величины ст0 служит ст0, причем DcT0 = а2сТВ~1с.
Доказательство. Воспользуемся формулами из П2
ЩМ) = ^ М& Cov(A£) = A Cov({) AT, (12)
где £ = (£ι,..., ξπι)τ — произвольный случайный вектор, для
которого определены М£ и Cov(£), А —числовая (к χ т)-матрица.
364
Глава 21. Регрессия
Применим формулы (12) к (7) с учетом того, что для
вектора ошибок ε в модели (5) выполняются равенства Με = О,
Cov(e) = σ2Ε:
Μθ = Β~ιΧτΜη = Β~1ΧΤΜ(ΧΘ + ε) =
= Β~1ΧΤΧΘ + Β~1ΧτΜε = 0,
Cov(0) = Β~1ΧτΟο\(η)ΧΒ-1 = В-1ХтСоу(е)ХВ~1 =
= Β~ιΧτσ2ΕΧΒ-1 = σ2Β~ιΧτΧΒ-1 = σ2Β~\
Свойство 3 сразу следует из свойства 2 и второй из формул (12). ■
Замечание 4. В случае, когда столбцы ж ι,... ,жт матрицы X
ортогональны друг другу, из свойства 2 вытекает, что ϋθι = σ2/\χι\2,
I = l,...,m. Оказывается, что в общем случае Οθι ^ σ2/\χι\21
причем равенство при всех I достигается только для ортогональных
столбцов (см. [71, с. 62]). Тем самым, так называемое ортогональное
планирование эксперимента, при котором столбцы матрицы X
выбираются ортогональными, является в приведенном выше смысле
оптимальным.
Для получения более содержательных заключений о
распределении оценки θ предположим, что выполняется допущение
ДЗ. Вектор ε имеет нормальное распределение (см. П9).
Замечание 5. Если ветзны допущения Д1—Д2, то при любом
векторе с £ Rm оценка сТв имеет минимальную дисперсию в классе
линейных (вида άτη) несмещенных оценок для ст0, а при
справедливости также и допущения ДЗ этот класс можно расширить до
множества произвольных несмещенных оценок (см. [71, с. 54-55]).
Обозначим через Щ оператор проецирования (проектор) на
подпространство L в Rn (т. е. Щж — это проекция вектора ж на L),
а через dim L — размерность L.
В дальнейшем важную роль будет играть
Лемма 1. Пусть случайный вектор ξ ~ λί(01σ2Ε) (см. Π9), а
два подпространства L\ и L% в Rn ортогональны между собой
(Li i. L2)· Тогда векторы Щ^ и Щ2£ независимы и нормально
распределены, причем случайная величина a~2|IlLfc£|2 (k = 1,2)
имеет хи-квадрат распределение с n& = dim Lk степенями свободы.
Доказательство. Так как проецирование — это линейное
преобразование, проекция нормального вектора £ также будет иметь
многомерное нормальное распределение (П9).
Dimension (англ.) —
размерность.
§3. Статистические свойства МНК-оценок
365
Если ζ = С£, где С — ортогональная матрица, то согласно
лемме 1 гл. 11 ζ ~ Λ/Χ0,σ222). Это означает, что если в каком-
нибудь ортонормированном базисе случайный вектор имеет
независимые Λ/"(0,σ2) компоненты, то этим свойством он обладает в
любом таком базисе.
Для завершения доказательства леммы выберем в Rn ортонор-
мированный базис βι,... ,еп, у которого первые η ι векторов лежат
в Li, а следующие п^ векторов —в Z/2· Тогда
Π^£=Σ (eft)*, IIt2£= Σ (eft)*,
i=l i=ni+l
где коэффициенты β[ζ — это координаты ζ в базисе βι,... ,еп. ■
Для построения доверительных интервалов потребуется
Теорема 1. В случае выполнения допущений Д1—ДЗ для линейной
регрессионной модели (5) верны следующие утверждения.
1. Случайная величина a~2RSS = σ~2\η — Χθ\2 имеет
распределение хи-квадрат с п — т степенями свободы и не зависит
от оценки θ и, поскольку M(a~2RSS) = п — т (см. вопрос 3
гл. 11), статистика σ2 = RSS/(n — т) несмещенно оценивает
неизвестную дисперсию σ2.
2. Для любого вектора с £ Rm случайная величина
сТ(в - 0) / [σ у/стВ-1с\ (13)
распределена по закону Стьюдента tn-m с (п — т) степенями
свободы (определение tk дано в примере 4 гл. 11).
Доказательство. Рассмотрим проекции вектора η на
подпространство L(X) и на его ортогональное дополнение LL(X) до Rn.
Из определения МНК-оценки θ вытекает, что
UL{x)V = xd, nLx(x)77 = 5, (14)
где δ = η — ΧΘ — вектор остатков. Подставляя модель (5) в
формулы (14) и учитывая, что ΧΘ € L(X), получаем
Хв + Пцх)€ = Хв, (15)
Τ1^{χ)ε = δ. (16)
Умножая обе части равенства (15) на матрицу В~1ХТ слева,
приходим к равенству
0 + В-1ХтПцх)е = д, (17)
так как В~1ХТХ = В~1В = Е. Из формул (16) и (17) на
основании леммы 1 заключаем, что оценки δ и θ независимы. По-
366
Глава 21. Регрессия
Вопрос 1.
Является ли теорема 1
гл. 11 частным случаем
доказанной теоремы?
скольку RSS = |<5|2, в силу леммы о независимости из гл. 1 отсюда
вытекает также независимость RSS и θ (σ и θ). С учетом леммы 1
и формулы (16) видим, что случайная величина a~2RSS ~ Хп-т
(так как dimL±(X) = η — га).
Перейдем к доказательству пункта 2. Из формулы (17)
следует, что случайный вектор 0, будучи линейным преобразованием
нормального вектора е, сам является нормальным. Поэтому для
любого с Ε Rm случайная величина сТв нормально распределена.
В силу утверждения 1
cT(d-e)/\aVcTB-1c\ ~ЛГ(0,1)
и, как выше установлено, не зависит от σ. Следовательно,
случайная величина (13) имеет распределение Стьюдента tn-m. Ш
На основе теоремы 1 построим методом 1 из § 3 гл. 11
доверительные интервалы для σ, компонент вектора θ и значения целевой
переменной Υ в заданной точке (#?,... ,ж^).
Пусть ζρ обозначает р-квантиль закона х2_ш (см. § 3 гл. 7).
Тогда в силу теоремы 1
Ρ {ζα/2 < a~2RSS < 2ι_α/2) = 1 - a. (18)
Разрешая неравенство в формуле (18) относительно σ, получаем
для него доверительный интервал с коэффициентом доверия 1 — a
вида
[yRSS/zi_a/2, yRSS/za/2 J .
(19)
Пусть у ρ обозначает р-квантиль закона tn-m. В силу симметрии
закона Стьюдента верно равенство yi-a/2 = ~Уа/2- Взяв в качестве
вектора с вектор, у которого 1-я компонента равна 1, а остальные
равны 0, находим из (13) границы (1—а)-доверительного интервала
для θ ι:
θι ± yi-a/2$ y/<hh (20)
где du —диагональный элемент матрицы D = В~1.
Наконец, задавая с = (ж?,... ,#£JT, для θιχ\ + ... + 0m#™
получаем (1 — а)-доверительный интервал с границами
сгв±у1-а/2Э\/сгВ-1с
(21)
Пример 4 (упрощенный вариант из [63]). Данные в таблице ниже
представляют собой «зашумленные» значения линейной
зависимости Υ = а + ЬХ. Ошибки ει ~ ΛΓ(0,σ2) моделировались при помощи
датчика нормальных случайных чисел (см. § 5 гл. 4). В каждом
из «узлов» щ = — 1 — 1/10 + 1/Ъ (I = 1,...ДО) ошибки
добавлялись дважды. Поэтому матрица X состоит из двух столбцов
§ 3. Статистические свойства МНК-оценок
367
длины 20: Х\ = (1,..., 1)т и Х2 = (^1,^1,^2,^2, · · · ,^ю,^ю)Т· Кроме
того, одно из значений щ = α + bxi + ε^ было заменено на «выброс».
щ
W
Щ1
-0,9
0,94
1,03
-0,7
0,93
0,96
-0,5
0,75
0,84
-0,3
0,79
0,65
-од
0,40
0,64
0,1
0,44
0,44
0,3
0,42
0,21
0,5
0,17
0,21
0,7
0,23
0,46
0,9
-0,03
0,22
Задача состоит в вычислении МНК-оценок неизвестных
параметров а, Ь и σ, обнаружении «выброса» и построении 95%-ных
доверительных интервалов для параметров и значения прямой в
точке предполагаемого «выброса».
Прежде всего, обратим внимание на то, что, благодаря
симметрии расположения «узлов» относительно нуля, столбцы Х\ и χ<ι
ортогональны. Поэтому для нахождения оценок α и Ь можно
воспользоваться формулами (8). Получим α « 0,535, Ъ « —0,5. На рис. 8
построена подогнанная прямая у = a+bx. Нетрудно подсчитать, что v
RSS = £(т7г - a - bxi)2 « 0,23. Отсюда σ = y/RSS/(n - га) « 0,11
(η = 20, га = 2).
Из табл. ТЗ для χ(8 находим квантили ζ0,ο25 = 8,23 и _^
^0,975 = 31,5. Используя формулу (19), для параметра σ получаем
доверительный интервал (0,08; 0,17).
Из табл. Т4 берем уо,975 = 2,101 для ίι8. По формуле (20)
вычисляем границы 95%-ных доверительных интервалов (0,48; 0,59)
и (—0,59; —0,41) для α и b соответственно.
Наибольшую величину имеет остаток Sis = 0,46—0,18 = 0,28 (он
больше, чем 2σ « 0,22). С помощью формулы (21) получаем
интервал (0,10; 0,27) для значения прямой в щ (см. рис. 8). Поскольку
наблюдение 0,46 находится вблизи границы 0,27 + 0,22 = 0,49, то
оно, вероятно, является «выбросом».
Замечание 6^ Ответ на вопрос об асимптотическом распределении
МНК-оценки θ при увеличении числа наблюдений дает следующая
теорема.
Теорема 2. Потребуем, чтобы помимо выполнения
допущений Д1—Д2 ошибки ει были независимы. Тогда, если матрица
п~1В = п~1ХтХ при η —► оо стремится к положительно
определенной матрице Σ, то
ν^ (θ - θ) Λ £ ~ Af(0, σ2Σ~ι).
Выведем этот результат из теоремы 3, обобщающей теорему 1
из решения задачи 6 гл. 15.
Теорема 3. Пусть ε ι, ег,- · .—независимые и одинаково
распределенные случайные величины, причем Μει = 0, ϋει = σ2,
0 < σ < оо. Пусть А = \\ац\\пХ7П1 ε = (ει,... ,εη)τ. Положим
368
Глава 21. Регрессия
£п = п 1^2Ате. Если η ιΑΓА стремится к положительно
определенной матрице Л, то
£п ~* £ ~ ·Λ/"(0> σ2Λ) при п->оо.
Доказательство теоремы 2. Подставим модель (5) в
формулу (7):
θ = Β'ιΧτ(ΧΘ + ε) = θ + В-1*71*,
и перепишем результат в виде
Vn(fl - 0) = y/iiB-1XTe = η~ιί2Ατε,
где Ат = пВ"1Хт. Поскольку
п-1АтА = η (В"1ХТ)(ХВ-1) = пВ"1 -> Л = Ι7-1,
Доказательство теоремы 3
можно найти в [86, с. 308]. то остается воспользоваться теоремой 3.
Рис. 9
§4. ОБЩАЯ ЛИНЕЙНАЯ ГИПОТЕЗА
Напомним, что в модели (5) неизвестный вектор Μη = ΧΘ
принадлежит заданному подпространству L(X), порожденному
столбцами матрицы X. Более общим образом рассмотрим модель
77 = 7 + *, (22)
где (неслучайный) вектор 7 неизвестен, но известно, что он лежит в
заданном линейном подпространстве Lq С Rn размерности щ < п,
а случайный вектор ε ~ ΛΓ(0, σ2Ε).*^
Проверяемая гипотеза Η состоит в том, что 7 лежит в
некотором подпространстве L\ С Lo, dimLi = Πι < щ**)
Критерий для проверки гипотезы Η естественно строить,
основываясь на сравнении расстояний от η до подпространств L0 и L\
(рис. 9).
Введем обозначения Д> = \η — ΤΙ^η\21 D\ = \η — Πχ,1τ||2, где Щ0
и П^! — проекторы на подпространстве Lq и L\ соответственно.
Так как векторы η — TIl0V и ^l0V — П^гу ортогональны
(см. рис. 9), то по «теореме Пифагора»
An = |nLorj - ULlV\2 = Ζ* - D0. (23)
Теорема 4. При выполнении гипотезы Η статистика
Я" D0/(n-no) ηο"ηι,η"ηο' l j
*) Инвариантная (геометрическая) форма (22) модели (5) наглядна и удобна в
рассуждениях. На практике же требуется та или иная параметризация модели,
т. е. выбор векторов, порождающих пространство Lo-
**) Подчеркнем, что исходные предположения относительно модели (в
частности, что 7 принадлежит Lq) сомнению не подвергаются. Их иногда называют
основными предположениями.
§4. Общая линейная гипотеза
369
т. е. R распределена по закону Фишера—Снедекора с щ — п\ и п—по
степенями свободы (см. пример 1 гл. 14).
Отсюда получаем F-критерий Фишера, отвергающий
гипотезу Η на уровне значимости а, если наблюдаемое значение
статистики R превосходит (1 — а)-квантиль закона Fno_nijn_no
(см. табл. Т5).
Доказательство теоремы 4. Согласно модели (22) и условию
7 € Lq запишем
η - Щ0?7 = 7 + е - nLo(7 + е) = е - Щ0е,
т. е. вектор η — Щ0?7 является проекцией ε на ортогональное
дополнение Lq" к подпространству Lq (L0 θ Lq = Rn, dimL^ = n — no).
Поэтому согласно лемме 1 случайная величина g~2Dq имеет хи-
квадрат распределение с η — щ степенями свободы (независимо от
того, верна или нет гипотеза Η: 7 € L\).
В силу тех же условий (22) и 7 € -^о верно равенство
Πι,ο*7 = 7+Πΐ/0£· Если гипотеза Η справедлива, то П^ту = 7+П^е.
Тогда из равенства (23) получаем: £>οι = |Щ0е — П^ер.
Очевидно, вектор IIl0£ — П^е является проекцией вектора е
на ортогональное дополнение Lqi подпространства L\ до Lo
(Li Θ Ζ/οι = L0> dimLoi = щ — ni). Так как Lqi и Lq" ортогональны
(см. рис. 9), то в силу леммы 1 случайные величины Д>1 и Do
независимы, причем a~2D0i ~ Хпо-тц- Следовательно, согласно
определению распределения Фишера—Снедекора статистика R
распределена по закону Fno _П1 ,п_По. ■
Выведем из теоремы 4 несколько важных следствий.
1. Однофакторный дисперсионный анализ. Множество
наблюдений щ представляет собой совокупность групп наблюдений
Aj (j = 1,... ,λ;) по nj > 1 наблюдений в Δ^. Всего Ν = πι +... + η&
наблюдений. Мы предполагаем, что
Tfij = fij + Sij, I = 1, . . . ,?2j, (^5)
где параметры μι,... ,μ& неизвестны, а все ошибки ε^ независимы
и одинаково распределены по закону Λ/χθ,σ2). Тем самым, отклик
η зависит от фактора с к уровнями. Для оценки этого влияния
на каждом из уровней фактора проводится несколько независимых
наблюдений.
Рассматривая г\ц как компоненты вектора η (записав их в
порядке номеров групп Δ^, j = l,...,fc), приведем модель (25) к
370
Глава 21. Регрессия
(μι\
+
(26)
виду (5):
ί Vn \
r\vi
Vn22
Щк
\Vnkk/
Покажем, как с помощью F-критерия можно проверить
гипотезу однородности Η" : μι = ... = μ*, (см. пример 2 гл. 16). Ей
соответствует подпространство L\ в RN, порождаемое вектором
(1,.. . ,1)т, dimLi = 1.
Ортогональным базисом подпространства Lq = L(X),
очевидно, служат столбцы α&ι,...,α&& (Ν χ /с)-матрицы X из
формулы (26), dimLo = к. Найдем проекцию вектора η на L0:
/1 0 .
1 0 .
0 1 .
0 1 .
0 0 .
^0 0 .
. 0\
• °
. 0
• °
• г
■ ι/
е\2
£п22
£ik
\епкк/
к
Σ
UL0V = Σajxj> гДе аз = xJv/\xj\2 = Vj = ^7 Σ Vij·
1_
Величина Dq = \η — Щ0Г7|2 при этом представляется в виде
к Щ 2
А)= Σ Σ ivij-fjj) .
.7 = 1 г=1
Аналогично, нетрудно установить, что
к rij ^ _ 1 к nj
Όι = \η- nLlr7| = Σ Σ (Vij ~ V) , где г/ = — £ Σ
(27)
i=li=l
iV ^
i=u=i
%··
Сравнение с формулами (11) и (13) из примера 2 гл. 16 показывает,
что D0 = Vint·» Di = Vtot- Из формул (12)—(13) гл. 16 следует, что
An = Kut. Наконец, в силу теоремы 4 имеем
D_ W(fc-l) _ Doi/(fc-l) w
R ~ Vint/(N-k) ~ Do/{Ν-к) ~ F*-i.^-b
что было доказано непосредственно ранее в гл. 16.*)
2. Адекватность вида зависимости. Любую непрерывную
зависимость между Υ и X, где X принимает значения из некоторого
отрезка, можно, согласно теореме Вейерштрасса, сколь угодно
точно равномерно приблизить алгебраическим многочленом
подходящей степени (см. § 2 гл. 5). Аналогично, периодическая непре-
*) Схему двухфакторного дисперсионного анализа из примера 1 гл. 17 также
молено представить в виде линейной регрессионной модели (5) (см. [32, с. 205]).
§ 4. Общая линейная гипотеза
371
рывная функция аппроксимируется тригонометрическими
многочленами.
Обобщая пример 2, рассмотрим некоторую систему базисных
функций {φι(χ),φ2(χ),...} на [—1,1], скажем,
{1,#,#2,...} или {1, sinnx, cosnx, sin27nr, cos27nr,...}.
Ограничиваясь начальным набором из га функций, приходим к
исследованию зависимости вида
У = 9т(Х) + ... + 9Л(Х). (28)
Выбирая на [—1,1] «узлы» Uj (j = 1,... ,fc), произведем в каждом
из них по rij > 1 «зашумленных» измерений зависимости (28)
(всего Ν = Πι + ... + nk измерений). Для описания проведенного
эксперимента используем модель
Vij = 0iVi(tij) + · · · + θπιφπι(^) + Sij, i = 1,... ,η,·, (29)
где случайные ошибки ец независимы и одинаково распределены
по закону ΛΓ(0, σ2).
Составим из величин г\ц вектор η в порядке возрастания j от
1 до А: (см. левую часть (26)). Столбец с номером / (Z = 1,... ,га)
(Ν χ т)-матрицы плана эксперимента X будет выглядеть
следующим образом:
Χι = (φι(μι),... ,<pz(tii) ,..., <fi(uk),... ,<pt(uk)). (30)
s ν ' ч s/ '
Πχ Tlfc
Допустим, что «узлы» щ,... ,Ufc выбраны так, что для заданных
базисных функций </?ι(#),... ,</?ш(#) векторы 2Ci,...,ajm линейно
независимы.
Для проверки гипотезы об адекватности системы базисных
функций возьмем в качестве L\ подпространство 1/(Х),
порожденное векторами 2Ci,...,ajm, dimL\ = га. При этом, очевидно,
Г>1 = RSS.
В качестве подпространства Lq используем подпространство,
порожденное столбцами матрицы из правой части (26), dimLo = k.
Величина Dq Для него задается формулой (27). Вопрос 2.
При справедливости гипотезы адекватности в силу теоремы 4 т*<}$ С при
(RSS-D0)/(k-m) ( ,
R ~ Do/{Ν-к) ~ F*-"»,"-fc. (31)
Пример проверки гипотезы адекватности см. в задаче 4.
3. Понижение размерности модели. Гипотеза И'
допустимости понижения размерности состоит в том, что в модели (5)
компоненты 0m/+i,...,0m (га' < га) параметрического вектора θ
можно считать равными нулю. Покажем, что она также является
частным случаем общей линейной гипотезы.
372
Глава 21. Регрессия
Поскольку Με = 0 (см. Д2 в § 2), то η = Μη € L(X), где
L(X) = L(asi,... ,жш) — подпространство, порожденное столбцами
а?1,... ,жт матрицы X. Возьмем L(X) в качестве ϋ/ο> cUtyiLo — тп,.
Гипотеза Н': 0m>+i = ... = 0m = 0 означает, что 7 лежит в
меньшем подпространстве L\ = L(a&i,... ,жт>), dimLi = mf < m.
Вычислим Dq и Д)1· Из определения МНК-оценки θ следует
(см. формулы (14)), что
nLoV = xe=Y,b*i- (32)
Отсюда Do = |t| - Щ0^|2 = |П^|2 = \δ\2 = Л55.
Чтобы найти Α)ΐ, предположим, что векторы a&i,... ,жт
ортогональна.*^
Обозначим через L^ ортогональное дополнение L\ до Lq:
L\ Θ Lqi = Lo,dmiLoi = m — m'. Тогда L^ = L(acm/+i,... ,жт)
в силу ортогональности базисных векторов 2Ci,...,ajm. Из
формулы (32) вытекает, что
т' ^
nLlT7 = nLl (ULoV) = Σ Ъ *j- (33)
i=i
Подставляя равенства (32) и (33) в формулу (23), находим
|2
j=ro'+l
= Σ β/l^r (34)
Γ21
Таким образом, при выполнении гипотезы Hf (24) преобразуется в
ρ _ A)i/(ra - га;) „ ,„ ν
Л " RSS/(n-m) Fm-m''™ (35)
Примеры проверки гипотезы if' приведены в задачах 5 и 6.
Замечание 7. Дополнительным преимуществом ортогональной
модели является то, что в силу соотношений (8) при переходе
к модели размерности га' < т не надо пересчитывать оценки
параметров #ι,... ,0m>.
§5. ВЗВЕШЕННЫЙ ΜΗΚ
После оценивания параметров регрессионной модели (5) полезно
изучить поведение реализации вектора остатков δ = η — Χθ.
*) Бели это условие не выполняется, перейдем к ортогональному базису в Lq по
формулам (9). С учетом того, что ортогонализационная матрица А является
верхнетреугольной, в силу формулы (11) равенство в'ш,, χ = ... = в'ш — О
влечет 0m/+i = ... = 0m = 0. Так как А~г — также верхнетреугольная,
то верно и обратное. Поэтому гипотезу Hf достаточно уметь проверять в
ортогональной модели.
§ 5. Взвешенный МНК
373
В случае^хорошего соответствия данных и модели случайные
величины δ ι,... ,£п должны быть похожими на выборку из закона
распределения ошибок ε^. Однако нередко наблюдается увеличение
разброса значений δι с ростом г (рис. 10, а) или чередование серий
из положительных и отрицательных значений (рис. 10, б),
возникающая из-за сильной коррелированное™ соседних остатков (см. § 5
гл. 15).*)
В связи с этим рассмотрим два обобщения модели (5),
возникающие в результате отказа от допущений одинаковой
распределенности и некоррелированности ошибок ε г.
1. Неравноточные наблюдения. Допустим, что в модели (5)
Με = О, Cov(e) = ||сот(е<,е,-)Н»хп = σ2ν, (36)
где V —известная диагональная матрица с элементами Vi на
главной диагонали, σ — неизвестный параметр. Другими словами,
ошибки некоррелированы и Dei = σ2ν».
Положим Wi = 1/vi и, меняя масштаб с помощью
преобразования ήι = y/wlrfi, получим новую модель:
X
б)
Рис. 10
ή = Χθ + е,
(37)
где Xij = y/wlxij, Si = у/ще%. Из формул (36) и (37) следует, что
Мёг = 0, Dei = σ2, cov(ei,6j) = 0 при г φ j1 т. е. для новой модели
выполняется допущение Д2 из § 2.
МНК-оценкй параметров #]>... ,0т находятся (согласно § 2)
путем минимизации функции
F&) = Σ Wi " Mil "... " «mXirn)2.
i=l
А для исходной модели имеем (щ = у/щщ, х^ = у/щх^)
F(0) = Σ Wifa - Mil - ... - OmXim
i=l
)2·
(38)
Почти все величайшие
открытия в астрономии
вытекают из
рассмотрения того, что мы
уже раньше назвали
качественными или
численными остаточными
феноменами, иначе
говоря, они вытекают
из анализа той части
числовых или качественных
результатов наблюдения,
которая «торчит» и
остается необъясненной
после выделения и учета
всего того, что согласуется
со строгим применением
известных методов.
Дж. Гершель, «Основы
астрономии», 1849 г.
Выходит, что теперь мы «взвешиваем» каждый член суммы,
умножая его на Wi = 1/vi. Это придает больший вес наблюдениям,
дисперсии ошибок которых меньше, что интуитивно
представляется вполне разумным. Такая процедура называется взвешенным
методом наименьших квадратов.
Нетрудно видеть, что матрица X из формулы (37)
представляется в виде у-1/2χ **) Аналогично, ή = V_1'2t/. Подставляя эти
выражения в формулу (7), находим МНК-оценку
ν-1*Γ__
θ = (χ χ)-1 χ ή = {χτν~ιχ)-ιχτν
τ17-ιΛ
(39)
*) Подробнее об исследовании остатков см. [23, с. 186].
**) Здесь V-1/2 —диагональная матрица с элементами 1/у/щ на диагонали.
374
Глава 21. Регрессия
Это и есть значение 0, минимизирующее сумму квадратов (38),
которая в матричной записи имеет вид
F{fi) = (η- Χθ)τν~ι{η - Χθ). (40)
Согласно утверждению 1 из § 3, ковариационной матрицей
случайного вектора θ служит
Cov(0) = σ2{ΧΤΧ)-1 = σ2(ΧΓν1Χ)-1. (41)
Разберем несколько приложений рассмотренной модели.
Пример 5. Взвешенное среднее. Если модель (5) содержит
единственный неизвестный параметр θ (га = 1), то из формулы (39)
несложно получить, что его МНК-оценка с учетом допущений (36)
выглядит так:
^ η In
θ = Σ™ΐχΐνί / Σ™ΐχ1· (42)
В случае, когда все Х{ = 1, она представляет собой просто
взвешенное среднее наблюдений щ с весами wi.
Пример 6. Линейный закон — прямая, проходящая через
начало координат ([75, с. 404]). Пусть Y —потери тепла в
(стандартном) коттедже, а X обозначает разность между
внутренней и наружной температурой. Рассмотрим линейную модель
Υ = ΘΧ, при этом дисперсия наблюдений щ = θχ{ + ει (ι = 1,... ,η)
будет, скорее всего, возрастать с увеличением χχ. Простейший
вид такой зависимости — это Dei = с#г> т.е. дисперсия
пропорциональна разности температур. В этом случае из формулы (42)
при W{ = а2/(сх{) находим, что θ = Σνί/Σχί = ν/χ- Ввиду
соотношений (41) ΟΘ = σ2/Σ'ωίχί = °/Σχι- Если же допустить,
Вопрос 3. Л что Ώει = сх\, то приходим к оценке θ = — Σ (Vi/Xi)·
Чему равна дисперсия ΟΘ η
в этом случае?
Пример 7. Повторные наблюдения. Пусть ^ — среднее из ki
наблюдений, причем все они имеют одинаковое математическое
т
ожидание Σ xij^j и общую дисперсию σ2, г = 1,...,тг. Если все
3=1
наблюдения независимы, то D^ = σ2/&ΐ, так что в формуле (36)
надо положить V{ = l/k{.
2. Коррелированные наблюдения. Рассмотрим обобщение
модели (36), допуская, что наблюдения могут не только иметь
разную точность, но и быть зависимыми между собой. Для этого
матрицу V в формуле (36) будем считать известной положительно
определенной (см. П10) матрицей общего вида. Ковариации ошибок
связаны с ее элементами Vij равенствами εον(εΐ,ε^) = a2Vij.
§ 5. Взвешенный МНК
375
Для такой матрицы существует единственная положительно
определенная матрица V1/2, называемая квадратным корнем из
матрицы V, такая, что Vl'2V1'2 = V (см. ШО).
Умножая обе части модели (5) на обратную к V1'2 матрицу
V-1/2, приходим к новой модели ή = Χθ + е, где ή = ν~1'2η1
χ = V~1/2X. ε = ν~1/2ε. В силу формул (12) и симметричности
матрицы V-1/2 имеем:
Me = V"1/2 Me = О,
Cov(e) = V"1/2 Cov(e) V"1/2 = σ2 V~^2V V"1/2 =
= σ2 y-l/2(Vl/2Vl/2)v-l/2 = σ2^
т. е. видим, что для новой модели опять выполняется допущение Д2
из § 2. Нетрудно убедиться, что формулы (39)-(41) остаются без
изменений (благодаря симметричности V"1'2) и в случае любой
положительно определенной матрицы V.
Пример 8. Оценка параметров сдвига и масштаба с
помощью МНК. Пусть элементы выборки ΑΊ,... ,ХП имеют функцию
распределения F((x — μ)/σ), где F(u) — известная функция
распределения, μ G Ш и σ > 0 — неизвестные параметры сдвига и
масштаба соответственно. Рассмотрим стандартизованные случайные
величины Ui = (Х{ — μ)/σ, г = 1,... ,η. Тогда ί/i,... ,i/n — выборка
из закона с функцией распределения F(u). При этом порядковые
статистики (см. § 2 гл. 5) двух выборок связаны формулами
υ(ί) = (Χ(ί)-μ)/<7, г = 1,...,п, (43)
и так как функция распределения F(u) случайной величины Ui
известна, то в принципе любые вероятностные характеристики
порядковых статистик Е/ф могут быть рассчитаны. Положим
M[/(i) = аи cov (U(i),U(j)) = Vij.
Учитывая формулы (43), запишем соотношения
X(i) = μ + аЩ) = μ + σα* + а(Щг) - α<), i = 1,... ,η. (44)
Вводя обозначения ?7i = X\i) и ε^ = σ(£/(ΐ) — α^), представим (44) в
виде обобщенной линейной регрессионной модели:
ηι = μ + σαι + е», г = 1,... ,η,
где Мбг = О, cov (ε;, ε^) = σ2^, или в матричной форме:
\ηη/ \1 ап/ \εη/
Согласно замечанию 5, МНК-оценки параметров μ и σ в
равенстве (45), вычисляемые по формуле (39), имеют минимальную
376
Глава 21. Регрессия
дисперсию в классе линейных несмещенных оценок, построенных
по порядковым статистикам -ϊ(ΐ),... ,Х{п)- Приведем некоторые
результаты вычислений для равномерного и показательного законов
(подробности см. в [38, с. 89]).
Для f/i, равномерно распределенных на отрезке [0,1], в задаче 1
гл. 5 были подсчитаны щ = Mf/(^ = i/(n +1). В [38, с. 93] найдены
ълтт тт i(n—j + l) ...
ViJ = MU(i)UU)-aiaj = {η + ι)2{η + 2), К j.
Там же проверяется, что V-1 имеет элементы (η + 1)(η + 2)ρ^> где
Ра = 2, Pi,i-i = Pt-м = -1, Pij = 0 при \j - i\ > 1,
а МНК-оценки параметров масштаба и сдвига выглядят так:
σ-—(Χ(η)-Χ(1)), μ- -- η_χ .
Они (с точностью до репараметризации модели) совпадают с
оценками метода спейсингов из задачи 4 гл. 9.
Для показательно распределенных Ui (F(u) = (1 — e~u)J{u^0})
при решении задачи 5 гл. 4 было установлено, что
Zi = (η - г + 1)(C7"W - i7(i-i)), *7(o) =0, г = 1,... ,η,
независимы и распределены так же, как и ЭД. Поскольку MZi = 1,
fc=i η - * + 1 " ^ η - * + 1 " fctl η - * + 1 '
f Λ α*τ(Ζ«,Ζ,) ^mi^> 1
^ Йкй (»-* + !)(»-' + !) £ι (n-fc + 1)2*
В [38, с. 96] проверяется, что матрица V"1 имеет элементы ^, где
%г = (П ~ I + I)2 + (Π - г)2, ^i,i-l = tfi-l,i = "(п - г + I)2
fej = 0 при |j — г| > 1), а МНК-оценки параметров σ и μ таковы:
σ = п(Х - Χ(ΐ))/(η - 1), μ = X - σ = (ηΧ(1) - Χ)/(η - 1).
В случае нормального закона для моментов порядковых
статистик U^i) нет простых формул. Известно, что μ = X, однако для
вычисления σ приходится пользоваться таблицами (см. [70]).
§6. ПАРАДОКСЫ РЕГРЕССИИ
Существуют три вида Есть несколько типичных ошибок («тонких мест»), которые сле-
с^тистика намая ложь и дует иметь в виду, применяя регрессионный анализ. Сами по себе
Марк Твен они достаточно очевидны. Тем не менее, о них часто забывают при
работе с реальными данными и в результате приходят к неверным
выводам.
§6. Парадоксы регрессии
377
30 50
а)
70 X
800 X
Рис. 11
1. Неоднородность данных. Существенно исказить вид
регрессионной зависимости могут не только выделяющиеся
наблюдения («выбросы») по оси отклика У, но и аномальные значения
предиктора X.
Пример 9 ([2, с. 64], [54]). На рис. 11, о представлены данные о
числе телевизионных точек У (в десят. тыс.), установленных в
1953 г. в девяти городах США (Денвере, Сан-Антонио, Канзас-
Сити, Сиэтле, Цинцинати, Буффало, Нью-Орлеане, Милуоки,
Хьюстоне) и о численности населения X (в десят. тыс.) этих городов. У
Выборочный коэффициент корреляции между наборами 500
Ж1,...,жд и У1,...,уэ ? = 0,403, что при η = 9 свидетельствует 3оо
Ιο весьма малой степени линейной связи между X и У.
Если же к этим данным добавить соответствующие сведения о
Нью-Йорке (хю = 802, ую = 345), то пересчитанный для η = 10
коэффициент ρ = 0,995. На рис. 11,5 изображены в более мелком
масштабе точки с координатами (ж^Уг), i = 1,... ,10, и проведена
регрессионная прямая, по сути, соединяющая центр масс первых
девяти точек (ж, у) с (якьУю)·
2. Коррелированность предикторов. В случае, когда ре- ^
грессионная модель включает много предикторов, некоторые из
них могут оказаться приблизительно линейно связанными между
собой. Обсудим связанные с этим проблемы.
При подгонке полинома на отрезке [0,1] (см. пример 2) уже
для предикторов Хз = U2 и Х± = ί73, измеряемых в «узлах»
щ = г/20, г = 0,1,... ,20, выборочный коэффициент корреляции jo
между соответствующими столбцами матрицы X составляет 0,986
(рис. 12).
Сильная КОррелирОВанНОСТЬ предикторов Опасна тем, ЧТО при- Интерполяция — частный
* ,τττ/ ι случай регрессии при
водит к неустойчивости МНК-оценок, вычисляемых по фор- п=т.
муле (7), к малым возмущениях наблюдений щ. Дело в том, что
в этом случае столбцы матрицы X оказываются практически
линейно зависимыми, вследствие чего матрица В = X7X ста- 8 т;
новится почти вырожденной, а задача поиска решения линейной
системы (6) — плохо обусловленной (см. [6, с. 131]).
Рассмотрим подробнее влияние возмущений на интерполяцион- о
ный полином степени η — 1, проходящий через точки плоскости с
координатами (щ,т#), г = 1,... ,п. В форме Лагранжа он выглядит так:
0 0,2 0,4 0,6 0,8 1
Рис. 12
0 12345678910
а)
Р(и) = Σ ViLi(u), где Li
г=\
JUL щ - Uj
Зфг
То, что р(и) интерполирует заданные точки, вытекает из равенств
Li{ui) = 1 и Ьг(щ) = 0 при j φ г.
На рис. 13, а, заимствованном из [53, с. 32], построен полином
степени 8. На рис. 13, б продемонстрированы последствия добавления
новой (десятой) точки: график даже не поместился в окне рисунка.
0 123 4 56 78 910
б)
Рис. 13
378
Глава 21. Регрессия
Рис. 14
Другой пример: даже для полинома степени 6 удаление
точки с координатами (4,1) на рис. 14 приводит к значительным
изменениям — возникновению осцилляции.
В регрессионных задачах полиномы высоких степеней имеют
тенденцию сглаживать ошибки наблюдений, вместо того, чтобы
выражать истинный вид зависимости отклика от предиктора. На
рис. 15 десять точек, разбросанных вблизи прямой, сглажены для
иллюстрации МНК-полиномом степени 6. Если зависимость на
самом деле достаточно сложная, то для ее обнаружения могут
оказаться полезными методы непараметрической регрессии,
обсуждаемые в гл. 22.
Кроме вычислительной неустойчивости, коррелированность
предикторов приводит к затруднениям в интерпретации резуль-
2345678910 татов расчетов. Например, при исследовании зависимости веса Ζ
Рис. 15 студентов двух групп от их роста X и размера обуви Υ методом
наименьших квадратов (после предварительного выравнивания
масштабов данных) в первой группе было получено регрессионное
уравнение
Ζ - ~Ζ = 0,9 (Χ - Χ) + 0,1 (Υ - F),
а для второй группы зависимость оказалась сильно отличающейся:
Ζ -Έ = 0,2(Х -X) +0fi(Y -Т).
Как объяснить существенное различие коэффициентов этих двух
моделей? ^
На практике, подсчитав МНК-оценки 0i,...,0m в линейной
регрессионной модели, исследователь в первую очередь обращает
внимание на предикторы с самыми большими (по абсолютной
величине) 0j, так как именно их изменение сильнее всего
сказывается на отклике. Исследователь нередко хочет не только точно
предсказывать отклик для произвольных значений предикторов,
но и желает, задавая эти значения, управлять откликом, надеясь,
что регрессия отражает причинно-следственную связь между
откликом и предикторами. Понятно, что «нажимать» надо на самые
эффективные «рычаги».
В приведенном выше примере для первой группы важнейшим
предиктором оказался X, а для второй —У. Дело здесь в том, что
X и Υ сильно коррелируют друг с другом, вследствие чего общий
«весовой» коэффициент при (X — X) + (Υ — Υ) случайным образом
распределился между слагаемыми.
К счастью, рассмотренное затруднение нетрудно преодолеть.
Достаточно проверить предикторы на наличие тесных линейных
связей и каждую обнаруженную группу заменить в модели на ее
единственного представителя.
3. Неадекватность модели. Когда простейшая линейная
зависимость Υ = 0ιΧι + ... + 0тХт неадекватно описывает данные,
§6. Парадоксы регрессии
379
Τ
Υ
τ
Υ
Ύ
Υ
Ύ
Υ
1865
9,10
1877
14,19
1889
25,88
1901
41,14
1866
9,66
1878
14,54
1890
27,87
1902
44,73
Ш7
10 06
i£70
14,41
1891
26,17
i003
46,82
1868
10,71
i££0
18,58
1<9Р^
26,92
1904
46,22
Ш0
11,95
1881
19,82
1<Ш
25,26
i£05
54,79
1870
12,26
1<Ш
21,56
1894
26,03
i£0tf
59,66
i£7i
12,85
1883
21,76
i£05
29,37
1907
61,30
i£72
14,84
i*&f
20,46
1896
31,29
Ш*
48,80
1873
15,12
i££5
19,84
7^7
33,46
1909
60,60
1Я74
13,92
1886
20,81
1<Ш
36,46
iPii?
66,20
1875
14,12
1887
22,82
1Ш
40,87
i£7tf
13,96
Ш*
24,03
1900
41,35
для построения более сложной модели обычно пытаются отдельно
изучить влияние каждого предиктора Xj на отклик Y. Для этого
сглаживают двумерное «облако» точек при помощи некоторой
нелинейной функции. Список наиболее часто используемых
монотонных функций содержится в следующей таблице.
Поведение отклика
Очень быстрый рост '
Быстрый (степенной) рост
Медленный рост
Очень медленный рост
Медленная стабилизация
Быстрая стабилизация
Кривая 5-образной формы
Уравнение
у = еа+Ъх
у = еа+Ыпх
у = еа+Ыпх
у = а + Ып χ
у = а + Ь/х
у = а + Ъе~х
у = 1/(а + Ье~х)
Усл. на Ь
Ь>0
Ь> 1
0 < Ь < 1
Ь>0
ЬфО
ЪфО
Ь>0
х1
X
1пх
1пх
1пх
1/х
е~х
е~х
у'
In у
In у
In у
У
У
У
1/У
*) В [51, с. 46] содержится любопытная классификация углов из книги по
альпинизму (изданной около 1900 г.): «Перпендикулярно —60°, мой дорогой
сэр, абсолютно перпендикулярно — 65°, нависающе —70°».
[Последняя функция называется логистической кривой. При
а > 0, b > 0 она возрастает, имеет две горизонтальные асимптоты
У = 0, у = 1/а и перегиб в точке с координатами (1η(6/α),1/(2α)).]
Переход к новым переменным х' и у' (см. таблицу) сводит задачу
к подгонке прямой у' = а + Ьх' из § 1.
Пример 10. В таблице на рис. 16 для каждого из годов с 1865 по
1910 (Т—номер года) указано количество чугуна Υ (в млн. тонн),
которое выплавлялось за год во всем мире. Постараемся подогнать
регрессионную кривую к этим данным.
Положим X = Τ — 1864. На рис. 17, а изображена кривая
(ломаная), соединяющая точки плоскости с координатами (Χ^,Υί),
г = 1,... ,п, где η = 46. Ван дер Варден (см. [13, с. 179])
пишет: «Эта кривая поднимается вверх значительно быстрее, чем
прямая линия или квадратная парабола». Не соглашаясь с этим
мнением, попытаемся сгладить кривую с помощью параболы. На
рис. 17, α приведен график подогнанный параболы с помощью
МНК. При этом остаточная сумма квадратов RSS = 364,7 и
(согласно теореме 1) оценка стандартного отклонения ошибок
σ = yjRSS/{n - πι) = 2,91, где m = 3.
380
Глава 21. Регрессия
О н—ι—ι—ι—ι—ι—ι—ι—н
6 16 26 36 46
а)
6 16 26 36 46
б)
Рис. 17
О 4 8 12 16
Рис. 18
Поскольку заметна некоторая тенденция усиления колебаний
кривой относительно параболы с ростом X, применим, следуя Ван
дер Вардену, преобразование У = In У. На рис. 17,5 построена
кривая, соединяющая точки с координатами (Χ^,Υ/), i = Ι,.,.,η.
Она хорошо согласуется с подогнанной МНК-прямой, имеющей
уравнение у = а + Ьх1 где а = 2,203, Ь = 0,0413 (оценки
коэффициентов прямой вычисляются по формуле (3)).
Однако, если попытаться использовать последнюю
подгонку для предсказания (прогноза) Υι на основе формулы
Yi = ехр(а + bXi), то получим значение RSS = 381,8, которое
несколько больше, чем вычисленное ранее при подгонке параболы.
Справедливости ради отметим, что сумма модулей остатков для
параболы, наоборот, немного больше: 95,6 > 93,6. В целом, можно
считать подгонки примерно одинаковыми по точности.
Следует иметь в виду, что в случае ошибки при выборе типа
сглаживающей кривой результаты экстраполяции*"* могут
оказаться совершенно неудовлетворительными. Это наглядно
демонстрирует рис. 18, на котором зависимость у = log2 χ
аппроксимируется полиномом степени 3, интерполирующим точки с
координатами (1,0), (2,1), (4,2) и (16,4).
При построении модели нужно максимально учитывать всю
имеющуюся информацию о качественном поведении
регрессионной кривой: монотонность, выход на асимптоту и т. п. В идеале,
желательно опираться на законы (физики, химии, экономики),
лежащие в основе зависимости (как в примере 3). Следующий
пример показывает, что в случае формальной подгонки кривой,
взятой из некоторого класса функций, необходима перепроверка.
Пример 11 ([2, с. 177] по данным А. Я. Боярского). Рассмотрим
в качестве отклика Ζ вес коровы, а в качестве предикторов —
окружность ее туловища X и расстояние от хвоста до холки Υ.
Сравнительному анализу были подвергнуты три регрессионные
модели:
(a) линейная: Ζ = θ\ + Θ2Χ + Θ^Υ,
(b) степенная: Ζ = Θ[ΧΘ*ΥΘ3,
(c) учитывающая содержательный смысл задачи: Ζ = 9qX2Y.
Происхождение последней модели легко объяснить. Для этого
следует представить себе приближенно тушу коровы в форме
цилиндра с длиной образующей, равной У, и радиусом
основания, равным Χ/(2π) (рис. 19). Если р — средняя плотность, то вес
Ζ = ρπ[Χ/(2π)]2Υ = θοΧ2Υ с точностью до головы и ног («рогов
и копыт»).
Рис. 19
*) То есть восстановления значений отклика по значениям предиктора,
расположенным вне обследованного диапазона.
§6. Парадоксы регрессии
381
Вначале по всем (п = 20) имеющимся наблюдениям для каждой
из моделей была вычислена МНК-оценка θ векторного параметра
θ и оценка σ = y/RSS/(n - m) стандартного отклонения ошибок,
где RSS — остаточная сумма квадратов (см. § 2), га — размерность
вектора Θ. Результаты расчетов приведены в левой стороне
следующей таблицы из [2, с. 179].
Модель
1
2
3
По всем наблюдениям
θ
θι = -984,7
02 = 4,73
03 = 4,70
θ[ =0,0011
02 = 1,556
03 = 1,018
0о = 1,13· 10"4
σ
25,9
24,5
26,6
По части наблюдений
"тяж
01 = 453,2
02 = 0,62
03 = -0,22
0J = 266,4
02 = 0,203
θ3 = -0,072
0о = 1,11 · 10"4
0"лег
81
79
28
Из них как-будто следует, что формальные модели 1 и 2
оказались несколько точней содержательной модели 3. Однако, это
лишь кажущееся благополучие, что сразу выявляется при
перепроверке путем разбиения данных на обучающую и контрольную
подвыборки.
В качестве обучающей была взята подвыборка из 10 самых
тяжелых коров, а в качестве контрольной — из 10 оставшихся легких
коров. На основе обучающей подвыборки для каждой из моделей
была заново подсчитана МНК -оценка "тяж (см. правую сторону
таблицы). Видим, что модели 1 и 2 не выдержали испытание на
устойчивость коэффициентов (0з даже поменял знак).
Кроме того, при попытке предсказания веса легких коров с
помощью модели с такими коэффициентами, оценка стандартного
отклонения ошибок Элег увеличилась для формальных моделей
более чем в 3 раза!
Этот пример убедительно демонстрирует, что не следует
переусложнять модель, ориентируясь на минимизацию σ: за счет
трех управляемых параметров («рычагов») удалость «подогнать»
формальные модели к данным лучше, чем однопараметрическую
содержательную.
4. Скрытый фактор. Желание истолковывать регрессионную
связь как причинно-следственную может приводить к парадоксам,
подобным приведенным в двух следующих примерах (см. также
близкое к этой теме понятие частной или «очищенной» корреляции
из § 8 гл. 20).
Пример 12 (см. [57]). Во время второй мировой войны
англичане исследовали зависимость точности бомбометания Ζ от ряда
факторов, в число которых входили высота бомбардировщика if,
скорость ветра У, количество истребителей противника X. Как
382
Глава 21. Регрессия
и ожидалось, Ζ увеличивалась при уменьшении Η и V. Однако
(что поначалу представлялось необъяснимым), точность
бомбометания Ζ возрастала также и при увеличении X.
Дальнейший анализ позволил понять причину этого парадокса.
Дело оказалось в том, что первоначально в модель не был включен
такой важный фактор, как Υ — облачность. Он сильно влияет и
на Ζ (уменьшая точность), и на X (бессмысленно высылать
истребители, если ничего не видно). Сильные отрицательные причинно-
следственная связи в парах (Υ,Ζ) и {Χ,Υ) привели к появлению
положительного коэффициента при X в линейной регрессионной
модели для Ζ.
Пример 13 ([4, с. 171]). Если найти корреляцию между
ежегодным количеством родившихся в Голландии детей Ζ и количеством
прилетевших аистов X, то она окажется довольно значительной
[37]. Можно ли на основе этого статистического результата
заключить, что детей приносят аисты?
Рассмотрим проблему на содержательном уровне. Аисты
появляются там, где им удобно вить гнезда; излюбленным же местом
их гнездовья являются высокие дымовые трубы, какие строят в
голландских сельских домах. По традиции новая семья строит себе
новый дом — появляются новые трубы и, естественно, рождаются
дети. Таким образом, и увеличение числа гнезд аистов, и
увеличение числа детей являются следствиями одной причины Υ —
образования новых семей.
ЗАДАЧИ
Отложил на осень, а там 1. Докажите, что функция F(a,/3), определяемая формулой (2),
имеет глобальный минимум в точке (а,Ь) (см. (3)).
2. Проверьте, что если в модели (5) вектор ошибок ε нормально
распределен (см. П9), то МНК-оценки являются оценками
максимального правдоподобия (см. § 4 гл. 9).
3* Убедитесь, что при выполнении допущения Д1 из § 2 матрица
В = ХТХ в модели (5) положительно определена.
4. Установите адекватность линейной Υ = а + ЬХ и
неадекватность тригонометрической Υ = a+b sin(nX) зависимостей для
данных из примера 4.
5. Проверьте для модели Υ = а + ЬХ гипотезу И': Ь = 0 на
основе данных из следующей таблицы (подобной таблице из
примера 4).
щ
VI
Щ1
-0,9
0,55
0,49
-0,7
0,53
0,67
-0,5
0,72
0,49
-0,3
0,51
0,81
-од
0,45
0,55
0,1
0,45
0,67
0,3
0,47
0,42
0,5
0,54
0,33
0,7
0,51
0,53
0,9
0,33
0,47
Решения задач
383
Рис. 20
X
9,75
9,00
9,60
9,75
11,25
9,45
11,25
9,00
7,95
12,00
8,10
10,20
8,55
Υ
19
40
42
42
47
49
50
54
56
56
57
57
58
X
7,20
7,95
8,85
8,25
8,85
9,75
8,85
9,15
10,20
9,15
7,95
8,85
Υ
61
62
62
65
65
65
66
66
66
67
68
68
Χ
9,00
7,80
10,05
10,50
9,15
9,45
9,45
9,45
8,10
8,85
9,60
6,45
9,75
Υ
68
69
69
70
71
71
71
72
73
74
74
75
75
Χ
10,20
6,00
8,85
9,00
9,75
10,65
13,20
7,95
7,95
9,15
9,75
9,00
Υ
75
76
77
80
82
82
82
83
86
88
88
94
6. На рис. 20 представлены 50 пар наблюдений из
исследования докторов Л. Матера и М. Уилсона (см. [23, с. 87]).
Рассматривались переменные: X — длина «линии жизни» на
левой руке в сантиметрах (с точностью до ближайших 0,15 см),
Υ — продолжительность жизни человека (округленная до
ближайшего целого года). Верно ли, что Υ и X связаны
линейной регрессионной зависимостью?
Указание. Для вычисления оценок коэффициентов
используйте то, что £>i = 459,9, Σχ1 = 4308,57, Σ,ν% = 3333,
Σ,χ%η% = 30549,75.
РЕШЕНИЯ ЗАДАЧ
1. Частные производные функции F(a,/3) таковы:
£~»и*
OL-βχϊ),
dF_
δβ
= -2Σχί(νί -<*-βχ%).
Приравнивая их нулю, получим систему из двух линейных
относительно а и β уравнений )
(αη + βΣχί = HVh
\αΣχΐ+βΣχϊ = T,xiVi-
Выражая а из первого уравнения и подставляя это выражение
во второе, находим для решения β представление
ηΣ^^-(Σ^)(Σ^)
*Σ*?-(Σ*02
(46)
(47)
Убедитесь, что она является частным случаем системы (6).
384
Глава 21. Регрессия
После деления числителя и знаменателя на п2 получаем в
числителе выборочную ковариацию между χ и т/, а в
знаменателе — выборочную дисперсию набора χ (см. формулу (1) гл. 6).
Следовательно, дробь (47) совпадает с оценкой Ь из (3).
Чтобы найти а, удовлетворяющее (46), надо подставить Ь
вместо β в первое из уравнений системы. Разделив обе части
на п, приходим к оценке α из (3).
Проверим, что найденная точка является точкой (сначала —
локального, затем — глобального) минимума функции F. Для
этого вычислим частные производные второго порядка:
да2 ~ ' θαθβ ~Ζ^Χ" δβ2 Ь г'
Если не все ж* одинаковы* \ то
*? = 2n>0' d^W'{d^) =4ηΣ(^-χ) >o,
т. е. выполнены достаточные условия наличия в точке (2,6)
локального минимума (см. [42, с. 335]).
Так как F дважды непрерывно дифференцируема (в
данном случае вторые производные —константы), а гессиан V2F
во всех точках плоскости есть неотрицательно определенная
матрица, то F — выпуклая функция. Следовательно, минимум
является глобальным (см. [55, с. 24]).
Согласно П9 для нормального вектора ε допущение Д2 влечет
независимость компонент и их одинаковую распределенность
по закону Λ/"(0,σ2). Поэтому независимы и случайные
величины щ = μι + ει ~ Λί(μί,σ2), где μι = хц01 + ... + Х{Швш.
Положим у = (у1,...,Уп)т· Плотность случайного вектора
*? = (Чь · · · Мп)Т имеет вид
лм-П^Ч-^Ь'-Ч-г»^-*)·}
Максимизация этой функции по θ\,... ,0m при фиксированных
У ι > · · · ,Уп равносильна минимизации суммы квадратов остатков
в аргументе экспоненты справа.
Первое решение. Поскольку для любого у € Rm
утВу = утХтХу = (Ху)тХу = \Ху\2 > О,
матрица В неотрицательно определена (она, очевидно,
симметрична: (ХТХ)Т = ХТ(ХТ)Т = ХТХ). Из линейной
алгебры известно свойство (см. [8, с. 17]): ранг ХтX совпадает
*) В противном случае все точки (xi,Vi) располагаются на одной вертикальной
прямой, и по ним, очевидно, невозможно оценить коэффициент Ъ угла наклона
прямой.
Решения задач 385
с рангом матрицы X. Ввиду Д1 ранг X равен т. Поэтому В
невырождена и, следовательно, положительно определена.
Второе решение. В его основе лежит идея замены базиса из
столбцов X на ортогональный (см. замечание 3).
Воспользуемся тем, что существует невырожденная матрица А такая, что
X = Х'А, причем столбцы матрицы X' ортогональны между
собой (см. (9), (10)). Тогда
В = ХТХ = {Х'А)ТХ'А = АТ{Х')ТХ'А = АТВ'А.
Здесь В' = (Х')ТХ' — диагональная матрица с элементами
|a?j|2, где х[,... ,χ^ — столбцы матрицы X'. Очевидно, В'
положительно определена, т. е. утВ'у > 0 для любого у € Rm,
2/^0. Полагая ζ = A~ly, получаем
zTBz = yT(A-1)T(ATBfA)A-1y = ^Β'ι/ > 0
при любом ζ € Rm, ζ φ 0, что и требовалось установить.
4. Для линейной зависимости в примере 4 уже были найдены
оценки a = 0,53, Ь = —0,50 и подсчитана величина RSS = 0,23.
Для данных из таблицы примера 4 вычисляем к = 10
полусумм ординат точек с одинаковыми абсциссами и по
формуле (27) находим значение Д). Подставляя его в (31),
получаем R = 1,00. С помощью линейной интерполяции по
аргументу Ι/fci табл. Т5 вычисляем квантиль уровня 95% F-pac-
пределения cki = к — ш = 10 — 2 = 8ик2 = п — к = 20 —10 = 10
степенями свободы. Она приближенно равна 3,07. Так как
1,00 < 3,07, то гипотеза об адекватности линейной модели не
отвергается.
Аналогичные расчеты для тригонометрической модели
(также ортогональной) дают следующие результаты: a = 0,53,
Ь = -0,34, RSS = 0,70 (более чем в 3 раза превосходит RSS
линейной модели), R = 5,76. Поскольку 5,76 > 3,07, на уровне
значимости 5% гипотеза адекватности отвергается.
На рис. 21 приведены для сравнения графики подогнанных
методом наименьших квадратов прямой и синусоиды. Для
последней заметно, в частности, значительное рассогласование
с данными вблизи концов отрезка [—1,1].
5. Точно так же, как и в примере 4, вычисляем оценки a = 0,52,
Ь = —0,09 и RSS = 0,21. В силу ортогональности модели
для подсчета Дц можно воспользоваться формулой (34). Для
ш' = 1 она дает Д>1 = Ь2 \х2\2- Подставляя значение Д)1
в (35), находим, что R = 4,77. С помощью табл. Т5 определяем
квантиль уровня 95% F-распределения cki =m—ш' = 2—1 = 1
ик2 = п — ш = 20 — 2 = 18 степенями свободы. Она равна 4,41.
Так как 4,77 < 4,41, то на уровне значимости 5% понизить
размерность модели не удается.
5tei
386
Глава 21. Регрессия
-1
О
Рис.
22
На рис. 22 представлены данные задачи и подогнанная к
ним прямая. По-видимому, все-таки существует тенденция к
уменьшению ординат точек с ростом их абсцисс, т. е.
истинная линейная зависимость имеет небольшой отрицательный
наклон.
По формуле (47) вычисляем Ь = —1,367. Из (3) получаем
a = —79,23. На основе данных таблицы, приведенной на
рис. 20, подсчитываем (с помощью программы Excel) значение
D0 = RSS = Z(Vi - Vi)2 = 9608,7.
Так как столбцы матрицы X не ортогональны, для
вычисления величины D0i будем использовать ее определение (23):
An = Di — D0. Остается только найти D±. Для этого заметим,
что проекцией вектора η на одномерное подпространство Li,
порождаемое вектором (1,...,1)т, очевидно, служит вектор
(г/,... ,г/)т, где, как обычно, η обозначает среднее
арифметическое щ (сравните с однофакторным дисперсионным анализом
из § 4). Отсюда
2?i = |f|-nLl4|2=f:(fh-4)2.
г=1
Подсчитав с помощью Excel значение Ό\ = 9755,2, из
формулы (35) при п = 50, га = 2 и га' = 1 имеем R = 0,732.
Интерполяцией таблицы Т5 по аргументу l/fo (fci = 1, Afe = 48)
вычисляем квантиль уровня 95%. Она примерно равна 4,04.
Так как 0,732 < 4,04, то на уровне значимости 5% коэффициент
наклона прямой можно считать равным нулю. Иными словами,
для рассматриваемых данных нет значимой зависимости
продолжительности жизни Υ от длины «линии жизни» X (что
наглядно демонстрирует рис. 23).
ОТВЕТЫ НА ВОПРОСЫ
1. Да, является при га = 1 и х\ = (1,... ,1)т.
2. В Lq входят такие векторы из Жм (N = πι + ... + п&), у
которых первые п\ координат одинаковы, следующие п^
координат одинаковы и т. д. Столбцы ж/ (I = 1,... ,га) матрицы X
(см. (30)), очевидно, лежат в L0· Поэтому порождаемое ими
подпространство также содержится в Lq: Li = L(X) С L0.
Если dimLi = га < к = diraLo, то имеет место строгое
включение L\ С L0. ^
3. Так как Wi = a2/(cx2)1 то D0 = σ2/ J] id%x\ = c/n.
Часть VI
ОБОБЩЕНИЯ И ДОПОЛНЕНИЯ
В эту часть книги включен материал, дополняющий содержание
предыдущих глав. В гл. 22 рассматриваются ядерные оценки
плотности и функции регрессии (дополнение к гл. 21). Ранговые методы
из гл. 14 и 15 обобщаются на случай многомерных данных в гл. 23.
Глава 24 посвящена анализу двухвыборочной модели масштаба. В
гл. 25 обсуждаются свойства так называемых L-, М- и Д-оценок
параметра сдвига (углубление материала гл. 8). Наконец, в гл. 26
некоторые ранее установленные результаты выводятся из теоремы
о сходимости дифференцируемых функционалов от эмпирической
функции распределения к функционалу от броуновского моста.
Сократ постоянно указывал своим ученикам на то, что при
правильно поставленном образовании в каждой науке надо доходить
только до известного предела, который не следует преступать. По
геометрии, говорил он, достаточно знать настолько, чтобы при случае
быть в силах правильно измерить кусок земли, который продаешь
или покупаешь, или чтоб разделить на части наследство, или чтоб
суметь распределить работу рабочим. Но он не одобрял увлечения
большими трудностями в этой науке, и хотя сам лично знал их, но
говорил что они могут занять всю жизнь человека и отвлечь его от
других полезных наук, тогда как они ни к чему не нужны.
Л. Н. Толстой
Глава 22
ЯДЕРНОЕ СГЛАЖИВАНИЕ
§ 1. ОЦЕНИВАНИЕ ПЛОТНОСТИ
Из § 1 гл. 9 известно, что несмещенной и состоятельной оценкой
неизвестной функции распределения F(x) случайной величины X
является эмпирическая функция распределения
Fn{x) = ±ti{xw**}, (ι)
1 ν
которая возрастает скачками величины - в точках Λ (ψ где
Х(!) < ... < Х(п) — упорядоченные элементы выборки (график
функции Fn(x) изображен на рис. 1 гл. 9).
А как оценить плотность р(х) = F'(x) (если она существует)?
Так как Fn (x) — кусочно-постоянная функция, то ее производная
равна 0 всюду, за исключением точек скачков Fn(x), и не годится
в качестве оценки для р(х).
Основная идея состоит в предварительном сглаживании
эмпирического распределения за счет его свертки (см. ПЗ) с
распределениями, имеющими плотности и сходящимися к сосредоточенному
в точке 0 распределению. Точнее: рассмотрим случайную
величину Zn = X + hnY, где случайная величина Υ имеет (известную)
плотность q(y) и не зависит от X, а числа hn > О и hn —► 0 при
η —► оо.
Согласно следствию из формулы преобразования плотности
1 у
(П8), плотностью случайной величины hnY служит — q(-£-). С
tin tin
учетом формулы свертки (ПЗ) выразим плотность rn(z) случайной
величины Zn:
'Μ-±Ηϊϊγ)™-±Η!τγ)μ*· (2)
При hn —► 0 случайные величины Zn будут сходиться к X по
вероятности (П5), а плотности rn(z) — к плотности p(z) для почти
§1. Оценивание плотности
389
всех ζ при выполнении, скажем, условия 1 из приведенной ниже
теоремы 1.*)
Заменив F(x) в формуле (2) на эмпирическую функцию
распределения Fn(x)1 получим для p(z) оценку
«"-сИтсО'-ю-ж!;·^). (з)
которую обычно называют оценкой Розенблатта—Парзена
(Rosenblatt, 1956; Parzen, 1962). Какими статистическими
свойствами она обладает?
Теорема 1. Пусть выполнены следующие условия:
1) плотность q(y) непрерывна и ограничена, причем
<*= Q2(y)dy < оо;
2) hn —► 0 при η —► оо так, что nhn —► оо. Тогда
Pn(z) = rn(z) + ξη(ζ) J \pnh~n , (4)
где rn(z) —► p(z) при почти всех ζ, а случайные величины ξη(ζ) Доказательство этой
d теоремы можно найти
асимптотически нормальны: ξη(ζ) —► ζ(ζ) ~ «Л/(О, αρ{ζ)). в учебнике [11, с. 58].
Естественно, возникает вопрос об оптимальном выборе q(y) и
скорости стремления к нулю последовательности hn при η —► оо.
Ответ на него зависит от свойств гладкости оцениваемой
плотности р(х). Ограничимся классом плотностей, для которых верно
допущение
Д1. Носителем**^ р(х) является конечный интервал, на котором
р(х) дважды непрерывно дифференцируема с условием
ι2
=JVw
dx < оо.
Предположим также, что для q(y) справедливы условия
Д2. J" yq(y) dy = О (это всегда верно для четной функции q) и
β = у2я(у) dy < оо.
Совершив замену у = (z — x)/hn во втором интеграле в
равенствах (2), применим формулу Тейлора:
rn{z) = q(y)p(z - yhn) dy =
= \q(y) [p(z) - yhnp'{z) + \ y2hlp'\z) + o(y2h2n)
= p(z) + \hlp"(z)\y2q(y)dy + o(h2n).
dy =
*) Достаточно ограниченности плотности q(y) и выполнения при некоторых
О 0 и ε > 0 неравенства q(y) ^ с/|у|1+е (см. [21, с. 18]).
**) То есть множеством {х: р(х) > 0}.
390
Глава 22. Ядерное сглаживание
Подставляя результат в представление (4), видим, что
pn(z) - p(z) = - βΚρ"(ζ) + U*)/Vnhn + o(h2n),
Μ\ρη(ζ)-ρ(ζ)}2 =
§ β^ηΡ"(ζ)
2
+ cv(*)/(nftn) + o(ft£),
поскольку из формул (3) и (2) имеем Mpn(z) = rn{z), т. е.
Μξη(ζ) = 0.
Математическое ожидание во второй из формул представляет
собой квадратичный риск оценки ρη(ζ) (см. § 3 гл. 6).*) Однако
риск зависит от ζ через неизвестные значения ρ(ζ) и pff(z). Чтобы
избавиться от этого, усредним риск по всем ζ с помощью интеграла
JM[pn(z)-p(z)]2<fe,
главная часть которого (после отбрасывания ο(/ι*)) равна
АК) = \ β2ΊΚ + a/(nhn). (5)
При hn —► 0 первое слагаемое в сумме (5), отвечающее за смещение
оценки pn(z)i убывает. Второе слагаемое, отражающее дисперсию
(«разброс») оценки рп(ζ), наоборот, возрастает. Минимум функции
J(hn) достигается при /ι* = [α/(β2η)]1^ п~1^ъ (убедитесь!).
Подставляя h^ в формулу (5), находим минимальное значение
АК) =
!(а2/?)2/у/5
п"4/5. (6)
Таким образом, порядок малости оптимального h^ есть п-1/5. При
этом скорость сходимости ρη(ζ) κ ρ(ζ), определяемая величиной
y/J(h%), составляет лишь п~2/5 в отличие от скорости п-1/2,
которая имеет место для сходимости Fn(x) к F(x) (см. § 2 гл. 12).
Это можно объяснить тем, что в оценке значения p(z) при
фиксированном ζ принимают участие лишь Х^ находящиеся в некоторой
уменьшающейся окрестности точки ζ, а не вся выборка.
Теперь выберем оптимальную плотность q(y). Заметим, что
J{hn) в формуле (6) зависит от q(y) через а2/?. Эта величина
1 ν
инвариантна относительно преобразования Υ = аУ, q(y) = - <?(-),
(j σ
где σ > 0. Поэтому, не ограничивая общности, можно считать, что
β = Sy2Q(y)dy = 1. Тогда (ввиду Д2) приходим к задаче
минимизации а = $q2(y)dy при условиях $q(y)dy = $y2q(y)dy = 1,
$УЯ(у) dy = 0. Ее решением ([86, с. 86]) является функция
Зу5 /« 2\ г
loo I * ^{N<V5}'
*) Абсолютный риск Μ \ρη{ζ) — ρ{ζ)\ изучается в монографии [21].
§1. Оценивание плотности
391
ранее встречавшаяся в теореме 4 гл. 8. При выборе β = 1/5
оптимальная плотность q* имеет более простой вид:
В статистической литературе ее обычно именуют ядром
Епанечникова (Epanechnikov, 1969), хотя оно было еще раньше введено
Бартлеттом (Bartlett, 1963).
Насколько важно использовать именно такое ядро?
Конкуренцию ему могут составить ряд ядер, перечисленных в следующей
таблице (см. также рис. 1):
Ядро — это непрерывная
ограниченная четная
функция с единичным
интегралом jq(y)dy = l
(не обязательно
неотрицательная).
N
1
2
3
4
5
Ядро
Епанечникова
Квартическое
Треугольное
Гаусса
Прямоугольное
ч(у)
(3/4)(1-у2)/{,у,^1}
(15/16)(1-у2)2/{ы<1}
(1-М)'{|уК1}
(2π)-1/2βχρ{-2/2/2}
(V^JflyKi}
E(q)
1
0,995
0,989
0,961
0,943
Квартическое ядро, в отличие от ядра Епанечникова,
дифференцируемо в точках —1 и 1. В случае треугольного ядра можно
быстро производить пересчет оценки плотности pn(z) при
увеличении переменной ζ с заданным шагом Αζ. Это важно при
интерактивном построении графиков ρη(ζ) для «окон сглаживания»
hn разной ширины (см. пример 1 ниже). Ядро Гаусса (или
нормальное) бесконечно дифференцируемо на всей оси. Однако оценка
Pn(z) вычисляется медленно по причине многократного подсчета
значений экспонент. Достоинством прямоугольного ядра является
его простой вид. Формально эту функцию нельзя называть ядром
из-за разрывов в точках —1 и 1, но ее можно рассматривать как
предел последовательности ядер, имеющих форму трапеции.
В последнем столбце таблицы указаны эффективности
E(q) = [a(g)2/?(g)]-2/5[a(9*)2/?(9*)]2/5
ядер по отношению к оптимальному ядру Епанечникова q*
(см. формулу (6)). На основе этой информации приходим к
заключению, что выбор ядра мало влияет на величину
среднеквадратичной ошибки оценки pn(z).
Ядра —чистый
изумруд. ..
А. С. Пушкин, «Сказка о
царе Салтане»
Отметим, что если неизвестная плотность р(х) имеет
непрерывные производные более высокого четного порядка т > 2, то
можно добиться и большей, чем п~2/5, скорости сходимости за счет
использования ядер, принимающих отрицательные значения. При
выполнении условий $q(y)dy = 1, $ykq(y)dy = 0 при 1 ^ k < га,
Jymq(y)dy = с φ 0 прежние рассуждения приводят к задаче
392
Глава 22. Ядерное сглаживание
Рис.2
0,2 0,4 0,6 0,8
а)
0,2 0,4 0,6 0,8
б)
5]
4-
3
2
1
oJ
hn = 0,5
-н—ι—
—+—
—ь-
-Η—
0,2 0,4 0,6 0,8
в)
Рис. 3
минимизации функционала
\jq2(v)dyY^ymq(y)dy
решением которой на отрезке [—1,1] является некоторый полином
степени т (см. [85, с. 148]). В частности, для т = 4 (при с = —1/21)
получается ядро вида (15/32)(7з/4—Ю^/2-f-3) /{|y|<i} (рис. 2). Скорость
сходимости соответствующей ядерной оценки равна п~4/^9.
В общем случае погрешность оптимальной оценки имеет порядок
малости n-m/(2m+1> (см. [ц) с. 60]), который приближается к п"1/2
при увеличении т. Это объясняется тем, что для более гладких
плотностей к оцениванию значения р(х) привлекаются элементы
выборки, лежащие во все более широких окрестностях точки х.
Недостатком таких оценок является возможность появления у
них отрицательных значений, что противоречит тому, что р(х) ^ 0.
При практическом оценивании плотности р(х) по заданной
реализации выборки важен не столько выбор вида ядра, сколько
правильное определение ширины «окна сглаживания» hn.
Пример 1. С помощью таблицы случайных чисел Т1 была
моделирована выборка размера η = 100 из распределения с
плотностью ρ(ζ) = 2 (/[o,i;o,4] + ^[о,б;0,8])· На рис. 3 приведены графики
оценок j5n(^)> вычисленных на основе треугольного ядра для
следующих значений hn: 0,1; 0,02; 0,5.
Выбор слишком малого hn приводит к быстро меняющейся,
неустойчивой оценке, так как pn(z) опирается только на небольшое
количество наблюдений из узкой окрестности точки ζ (велико
второе слагаемое в формуле (5), отвечающее за дисперсию оценки).
С другой стороны, слишком большое значение hn влечет
чрезмерное сглаживание оцениваемой плотности, что не позволяет
выявить ее характерные особенности (такие, например, как наличие
нескольких максимумов). Оценка pn(z) в этом случае оказывается
сильно смещенной.
§2. НЕПАРАМЕТРИЧЕСКАЯ РЕГРЕССИЯ
Изучаемая в этом параграфе задача заключается в сглаживании
данных {(хг,Уг)}2=\ при помощи некоторой непрерывной кривой
у = т{х). Данные рассматриваются как реализация выборки,
описываемой одной из двух моделей.
Модель со случайным планом эксперимента
Пары (Xi,Yi) считаются независимыми и одинаково
распределенными. Кривая регрессии определяется как (см. П7)
m(x) = M(Y\X = x).
§2. Непараметрическая регрессия
393
Это определение корректно, если М|У| < оо. Если у вектора [Χ,Υ)
существует плотность р(х,у), то
т(х) = I у р(х,у) ay р(х),
где р(х) = J* р(х,у) dy — маргинальная плотность случайной
величины X.
Например, пусть (Χ,Υ) ~ λί(μ,Σ) (см. П9), где μ = (μι,μ2),
Σ = ||σ^||2χ2· Несложно подсчитать ([2, с. 167]), что в этом случае
т(х) = μ2 + — (х - μι),
σ22
т. е. кривая регрессии линейна.
В случае управляемой неслучайной предикторной
(предсказывающей) переменной X применяется
Модель с фиксированным планом эксперимента
В этой модели
Yi = m(xi) + ει, г = 1,... ,η,
где Xi — «узлы» (задаваемые значения X, в которых производятся
измерения отклика У), е% — независимые и одинаково
распределенные случайные ошибки, Με^ = 0, Dei = сг2.
Замечание 1. Если допустимы многократные наблюдения в
фиксированной точке X = х, то можно оценить т(х) с помощью
среднего арифметического соответствующих Υ^.
Однако, часто этому препятствуют финансовые ограничения:
слишком дорого проводить более одного измерения для каждого
фиксированного уровня χ предиктора X.
Возможно также, что условия эксперимента нельзя воспроизве- Если есть VBeDeHH0CTb
сти из-за разрушения объекта (например, при изучении безопасно- что т—гладкая кривая,
сти водителя при столкновении автомобилей) и т. п. точки^ж" должны ЛИЗИ
содержать информацию
В основе процедуры оценивания кривой регрессии т(х) лежит та^м^бразом8 гшед^ Х'
идея локального усреднения. ставляется возможным
использовать нечто вроде
~ . локального усреднения
Оценка определяется как взвешенное среднее близких к χ данных
для формирования
η In оценки т{х).
™(χ) = Σ m{x)Yi / Σ щ{х), (7) ρ- охбэнк
г=1 I г=1
394
Глава 22. Ядерное сглаживание
где веса Wi(x) велики для Xi, близких к точке ж, и малы для
остальных Xi.
Замечание 2. В соответствии с примером 5 гл. 21 величина т(х)
при каждом χ является оценкой взвешенных наименьших
квадратов, так как она служит решением задачи минимизации функции
Σ Wi(x)(Yi -Θ)2=Σ Wi(x)(Yi - m(x))2. (8)
Один из наиболее простых способов определения весов Wi(x)
опирается на использование некоторого ядра q(y):
Щ(х) = Qh(x ~ Xi), где qh(y) = h~lq(y/h). (9)
Здесь h = hn обозначает ширину «окна сглаживания». Для
многомерной предикторной переменной Χι = (Хц, · · · Am) можно взять
т
Wi(xi,... ,хш) = |J qh(xj - Xij).
Задавать веса можно и по-другому. Для одномерной
предикторной переменной Гассер и Мюллер в 1979 г. (см. [85, с. 328])
предложили
т(х) = qh{x - у) dy, (10)
где X(i) ^ X(2) ^ ... ^ X(n) — упорядоченные по возрастанию Xi,
n+l
X(o) = — oo, X(n+i) = -boo· Заметим, что Σ Wi(x) = 1.
В случае весов Wi (x) из формулы (9) правая часть равенства (7)
приобретает вид
fa(x) = f:Qh(x-Xi)Yi /£<ih(x-Xi). (и)
Выражение (11) определяет так называемую оценку Надарая—Ват-
сона (Nadaraya, 1964; Watson, 1964). С учетом формулы (3)
1 п I
™>(х) = - Σ Qh(x - Xi) Yi / Pn(x),
n i=\ I
где pn (х)— ядерная оценка Розенблатта—Парзена маргинальной
плотности р(х) переменной X.
В следующей теореме приведены условия, обеспечивающие
состоятельность оценки Надарая—Ватсона т(х).
Теорема 2. Пусть для модели со случайным планом эксперимента
и одномерной предикторной переменной
1) J\q(y)\dy <оо,
§ 2. Непараметрическая регрессия
395
2) уя{у) -* о при \у\ -* °°,
3) МУ2 < оо,
4) η —► оо, hn —► О, η/ιη —► оо.
^ Ρ
Тогда га(#) —► га(#) в любой точке непрерывности функций
т(#), р(#) И σ2(#) = 0(У|Х = х) такой, ЧТО р(х) > 0. Доказательство этой
теоремы приведено в [85,
Сформулированный результат показывает, что оценка т(х) из с 5Ч
формулы (11) сходится по вероятности к га(х) — истинной кривой
регрессии. Естественно поставить вопрос, какова скорость этой
сходимости. Одной из возможных мер точности оценки является
квадратичный риск R(x,h) = Μ [т(х) — т(х)]2.
Теорема 3 (Гассер и Мюллер, 1984). Рассмотрим модель с
фиксированным планом эксперимента*) для одномерной предик-
торной переменной X. Без ограничения общности можно считать,
что «узлы» Xi G [0,1]. Предположим, что
1) используется ядро q(y) с
<* = Я2(У) dy < оо и β = y2q(y) dy < оо;
2) q(y) имеет носитель (—1,1), причем q(—1) = q(l) = 0;
3) веса щ(х) задаются формулой (10);
4) т(х) дважды непрерывно дифференцируема;
6) Dei =σ2, i = Ι,.,.,η;
7) η —► оо, hn —► Ο, nhn —► оо.
Тогда
R{x,hn) =
\p2[m"(x))2h4n + aa2/(nhn)
(1 + 0(1)).
Видим, что так же, как и в формуле (5), квадратичный риск
состоит из двух частей: квадрата смещения и дисперсии, где
смещение (как функция от hn) возрастает, а дисперсия — убывает.
В. Хардле в [85, с. 41] пишет: «Это качественное соображение
раскрывает сущность задачи сглаживания: баланс между
дисперсией и квадратом смещения».
Пример 2. Обнаружение локального максимума кривой
регрессии ([85, с. 92]). На рис. 4 представлены моделированные
данные. Использовалась модель с фиксированным планом
эксперимента: η = 50, Xi = г/n, г = 1,... ,η. Точки порождены «зашумле-
нием» с помощью взятой из таблицы Т1 реализации ει ~ Л/"(0, 1)
кривой регрессии
т(х) = 1 - χ + ехр { -200 (х - 1/2)2 }
*) Для случайного плана эксперимента скорость сходимости та же, но с
другими константами (см. [85, с. 102]).
396
Глава 22. Ядерное сглаживание
0,2 0,4 0,6
Рис. 4
(т. е. на линейную функцию у = 1 — χ накладывается нормальный
«горб» с центром в 1/2 и шириной примерно равной 2σ = 1/10).
Из-за большой интенсивности «шума» локальный максимум
т(х) практически не различим. Однако, он хорошо заметен на
графике (пунктир) оценки т(х) из (11), для которой
использовалось гладкое квартическое ядро q(y) = (15/16)(1 — У2)21{\у\^1} и
был определен методом пропуска (см. ниже) оптимальный размер
«окна сглаживания» h = 0,09.
Методы ядерного сглаживания могут быть также применены
и для оценивания производных кривой регрессии. Так, первую
производную т!(х) можно оценить, используя веса
™*(х) = я'(*г) Σ q(zj) - Φ;) Σ q'(zj)i где * = (χ
Xi)/h,
получаемые дифференцированием правой части равенства (11)
по х.
Пример 3. Зависимость скорости роста от возраста
(см. [85, с. 46]). На рис. 5 представлены ядерные оценки кривых
средней скорости V (в см/год) роста Η (т.е. V = Я') в зависимости
от возраста Τ (в годах) для мальчиков (штрихованная линия) и для
девочек (сплошная линия).
У девочек наблюдается локальный максимум скорости роста
около 12 лет. У мальчиков аналогичный пик еще более выражен,
но происходит примерно на 2 года позже.
Применение метода непараметрической регрессии позволило
обнаружить и у мальчиков, и у девочек дополнительный локальный
максимум У, так называемый средний скачок роста, в возрасте
около 8 лет. Другие подходы, основанные на априорной фиксации
параметрических моделей, приводят к значительным трудностям в
обнаружении этого второго пика.
Так же, как и при оценивании плотности, решающую роль
играет не вид функции д(у), а правильный выбор ширины «окна
сглаживания» h. Часто в этом помогает
Метод пропуска или кросс-проверка.
η
Минимизируется по h функция S(h) = ΣΚ — ^г№)]2, где
/ i=1
nii(Xi) = Y^u)j{Xi)Yj J Y^u)j{Xi) представляет собой оценку для
m(Xi) по выборке, в которой г-е наблюдение пропущено. Здесь
S(h) — сумма квадратов ошибок предсказания Y{ (невязок) на
основе выборки без (Xi,Yj).
§2. Непараметрическая регрессия 397
Для данных из примера 2 был подсчитан ряд значений S(h):
h
S(h)
0,05
51,0
0,10
46,6
0,15
47,3
0,20
47,6
0,25
47,5
0,30
47,2
0,35
47,7
0,40
48,3
0,45
48,7
0,50
49,1
Заметим, что S(h) имеет два локальных минимума: при h « 0,1
и/ι» 0,3. Уточним оптимальное значение h, проводя вычисления по
сетке с меньшим шагом:
h
S(h)
0,05
51,0
0,06
48,7
0,07
47,4
0,08
46,7
0,09
46,4
0,10
46,6
0,11
46,7
0,12
46,7
0,13
46,8
0,14
47,1
0,15
47,3
Таким образом, с точностью до 0,01 функция S(h) имеет глобальный
минимум при h = 0,09.
Альтернативным методом, применяемым в случае, когда
Χι,...,Χη располагаются очень неравномерно («где пусто, α где
густо»), является модификация ядерной оценки, у которой h
зависит от х. В качестве такого h (x) часто берут расстояние от точки
χ до ее k-го (в смысле близости κ χ) соседа Х{ (см. [85, с. 54]).
Значение параметра к (1 ^ к ^ п) задается исследователем.
В заключение главы обсудим проблему уменьшения влияния
выделяющихся наблюдений («выбросов») на ядерные оценки
кривой регрессии. К сожалению, локальное усреднение,
осуществляемое этими оценками, имеет неограниченную возможность
реагировать на «выбросы».
Например, график оценки т(х) (пунктир) в правой половине
рис. 4 особенно извилист из-за необходимости компенсировать
квадраты остатков в точках с большими значениями ошибок е% (таких,
как ε35 = 1,73 и ε39 = -2,36).
Повышение устойчивости сглаживания может быть
достигнуто за счет уменьшения весов наблюдений с большими невязками.
Кливленд (Cleveland W. S., 1979) предложил следующий простой
алгоритм, реализующий эту идею (см. [85, с. 209]). Процедура
начинается с вычисления пробной оценки, итеративно пересчитываются
веса и несколько раз производится повторное сглаживание.
Алгоритм «LOWESS»
(модификация для m-мерных предикторных
переменных Х{ = (Хц,... Дгт))
1. Задается к (1 ^ к ^ п). Для каждого Xi вычисляется
расстояние h(Xi) до А:-го соседа в Rm и по формуле (9) определяется
соответствующий вес Wi(X{). Веса всех наблюдений запоминаются
в массиве.
В оригинале LOcally
WEighted Scatter plot
Smoothing (англ.) —
локально взвешенное
сглаживание диаграммы
рассеяния.
398
Глава 22. Ядерное сглаживание
2. В окрестности каждой точки Х{ строится локальная
линейная аппроксимация поверхности регрессии т(Х) на основе
взвешенного метода наименьших квадратов (см. § 5 гл. 21) путем
минимизации по θ = (0ι,... ,0m) функции
П 2
Σ Щ(Хг) (Уг — 0\Хц — ... — OmXim) .
г=1
3. Используя оценки невязок ei, вычисляется выборочная
медиана σ = MED{\£i\, г = 1,...,п} (оценка масштаба) и
определяются коэффициенты устойчивости С{ — ^(?г/(б5)), где
q(y) = (15/16)(1 - У2)2/{|У|^1} — квартическое ядро.
4. Строится локальная линейная аппроксимация, как в
пункте 2, но с весами CiWi(Xi).
5. Пункты 3 и 4 повторяются до стабилизации величин с\.
Пример 4. На рис. 6 из [85, с. 210] показано применение алгоритма
«LOWESS» к моделированным данным. Точки генерировались в
соответствии с моделью Y{ = (l/50)#i + £i (η = 50), ж* = г,
Si ~ ЛГ(0,1). Кривой регрессии является прямая с малым
коэффициентом наклона, причем дисперсия ошибок Dei настолько
велика, что систематический прирост Υ при увеличении X (так
называемый тренд) почти не заметен из-за интенсивного «шума»
(если оставить на рис. 6 только «крестики»).
Для к = 25, т = 2 и Χι = (1,Жг) на рисунке представлен также
0 10 20 30 40 50 Результат сглаживания после двух итераций алгоритма. Построен-
Рис 5 ная оценка уверенно игнорирует «выбросы», расположенные вблизи
границ рисунка, и довольно точно воспроизводит теоретический
линейный тренд.
4—I—I—I—1—1—I—I—h
Глава 23
МНОГОМЕРНЫЕ МОДЕЛИ СДВИГА
§1. СТРАТЕГИЯ ПОСТРОЕНИЯ КРИТЕРИЕВ
В этой главе одно- и двухвыборочные ранговые критерии из гл. 14 и
гл. 15 обобщаются на многомерный случай.*) Если в многомерной
модели участвуют р-мерные векторы, то нас будет интересовать
некоторая векторная р-мерная статистика S = (Si,...,Sp), у
которой каждая компонента Sj при нулевой гипотезе центрирована:
М5,=0, j = l,...,p.
При построении критериев станем придерживаться следующего
плана:
1. установим, что в случае справедливости нулевой гипотезы
при η —► оо распределение статистики n~l/2S стремится к
р-мерному нормальному закону ЛГ(0, V) с невырожденной
матрицей ковариаций V (см. П9);
2. найдем состоятельную оценку V для V (см. § 2 гл. 6);
3. исходя из этого, видим, что статистика критерия
S*=n-1STV~1S = ST(nV)-1S
распределена в пределе по закону χι (см. П5, П9).
В наше время накоплено
огромное количество
знаний, достойных изучения.
Скоро наши способности
будут слишком слабы,
а жизнь —слишком
коротка, чтобы усвоить
хотя бы одну только
наиболее полезную часть
этих знаний. К нашим
услугам полное изобилие
богатств, но, восприняв
их, мы должны снова
отбрасывать многое,
как бесполезный хлам.
Было бы лучше иногда не
обременять себя им.
И. Кант
Кто не понимает ничего,
кроме химии, тот и ее
понимает недостаточно.
Г. Лихтенберг
§2. ОДНОВЫБОРОЧНАЯ МОДЕЛЬ
Пусть данные представляют собой реализацию η
независимых и одинаково распределенных р-мерных случайных векторов
Χι,... ,ХП, каждый из которых обладает р-мерной функцией
распределения F(xi — 01,... ,жр — 0Р), где θ = (01,... ,0Р) обозначает
неизвестный вектор сдвига.
Данные можно представить в виде таблицы размера η χ ρ:
X и Χ
12
Χ
1ρ
ΧηΙ Χη2
χ,
ηρ
*) Изложение, в основном, следует гл. 6 монографии [86].
400
Глава 23. Многомерные модели сдвига
Здесь г-й строкой служит вектор Xi, j-ft столбец представляет
собой выборку размера п, взятую по j-ft компоненте векторов. (Такая
таблица обычно возникает при записи ρ измерений по каждому из
η объектов.)
Предположим, что выполняются следующие допущения.
Д1. Распределение F имеет плотность р{х\,... ,хр).
Обозначим через Fi(#),... ,FP(#) маргинальные (частные)
функции распределения, а через Fjk (j,k = 1,... ,р)—двумерные
частные функции распределения.
Д2. Для каждой из Fj{x), j = 1,...,р, единственным
решением уравнения Fj(x) = 1/2 является 0.
Другими словами, допущение Д2 означает, что 0 является
единственной медианой распределений Fj(x) (см. § 2 гл. 7).
Мы хотим проверить гипотезу
Но: θ = 0 против альтернативы Ηι: θ φ 0,
где 0 = (0,...,0).*) Без дополнительных предположений о виде
распределения F для построения критерия подходящей
представляется статистика S, компонентами которой служат знаковые
статистики (см. § 2 гл. 15). Мы будем использовать (более удобную)
симметричную форму знаковой статистики, имеющую нулевое
математическое ожидание при условии справедливости гипотезы Щ:
η
Sj = ^signX^^Et-EJ, j = l,...,p,
г=1
η η
где Et = Σ 1{х^>о}, Σ j = £ Ι{χίά<ο}, sign χ — знак числа х, ΙΑ —
г=1 г=1
индикатор события А. (Здесь предполагается, что нет наблюдений,
равных 0, что верно с вероятностью 1.) Поскольку Σ+ + Σ J = η,
получаем Sj = 2 Σ+ — η, т. е. статистика 5j и статистика знаков из
§ 2 гл. 15, равная Et, линейно связаны.
Многомерное обобщение критерия знаков
Чтобы сформулировать теорему, на которой основывается
обобщение, потребуются некоторые дополнительные обозначения. Так,
пусть X = (Χι,... ,ХР) — случайный вектор с функцией
распределения F. Для j,k = 1,... ,р положим
р++ = Р(Х,- > 0,Хк > 0), р+- = P(Xj >0,Xk< 0),
pjk+ = P(Xj <0,Хк>0), pjk- = P(Xj < 0, Хк < 0).
*) Для заданного вектора 0; гипотезу Н'0: θ = Θ' можно преобразовать в #о,
вычитая в' из векторов наблюдений.
§ 2. Одновыборочная модель
401
Теорема 1. При справедливости гипотезы Но и выполнении
допущений Д1, Д2 имеет место сходимость
n-l/2S Д Ζ „ tf(Qi у) при п _> <»,
где V = \\vjk\\pxp, Vjj = 1,
vjk=Ptk~ +P]k -Pjk ~Pjk~ в случая k£j.
Доказательство. Ввиду независимости Xij, г = 1,... ,n, согласно
свойствам математического ожидания и дисперсии (П2)
MSj = £ Μ signXij = η Μ signX,- = η (Ρ(Λ> > 0) - Ρ(Χό < 0)) = 0,
г=1
η
DSj = Σ DsignXij = nDsignXj = nM(signXj)2 = η,
г=1
откуда Vjj = 1. При А: ф j находим, что
η
cov (Sj,Sk) = Σ M(signXijSignXifc) = η Μ (sign X, sign Xfc) = m;jfc.
г=1
Теперь установим асимптотическую нормальность. Для
произвольного вектора λ £ Rp распределение случайных величин
ξη = n-^2\TS = η"1/2 £ Yu где У, = £ \ά sign J*^,
i=l г=1
Yi —случайные величины с MYi = 0 и ΌΥ{ = ATVA, сходится
при п-^оок закону Λ/χθ, \TV\) в силу центральной предельной
теоремы (П6). Согласно теореме непрерывности (П9) при всех t
характеристические функции Μ exp{it£n} —► ехр{—λ VXt2/2}.
Остается применить обратное утверждение теоремы
непрерывности, положив λ' = t\. Ш
Для построения критерия нам нужна состоятельная оценка
матрицы V. Поскольку Μ (sign Xj sign Хк) = Vjfc, в силу закона
больших чисел (П6) имеет место сходимость
1 п Ρ
Vjk = - Σ signXij signXifc —> vjk. (1)
ni=l
Определим матрицу V, полагая Vjj = 1, беря Vjk из формулы (1).
При нулевой гипотезе V — состоятельная оценка V, а статистика
5* = ^(nV)"1,» (2)
асимптотически распределена по закону χ2 при условии
невырожденности матрицы V.
*) Используя равенство маргинальной медианы нулю, нетрудно показать (про-
ъеръте\), что ν^ — 4pJ£ - 1.
402
Глава 23. Многомерные модели сдвига
При ρ = 2 статистику 5* можно записать в виде (убедитесь!)
-)2 (дг+- - jy-+)2
Ν++ + Ν— Ν+- + ЛГ+
(3)
где ЛГ++ = ζ /{х„>о,х«>о}» ^ = Σ ^{Хг1<о,х<2<о} и т. п.
г=1 г=1
Эти величины удобно представлять в форме таблицы.
Χι
<0
>0
Х2
<0
Ν—
Ν+-
>0
Я-+
Ν++
Приводимый ниже пример показывает, что многомерный
критерий имеет преимущество перед наивной стратегией применения
одномерных критериев по каждой из компонент.
Пример 1. Тест проверки способностей [86, с. 300]. Был
проведен выборочный опрос η = 100 американских студентов с
использованием университетского психологического теста проверки
способностей Scholastic Aptitude Test. Данные представляют собой
пары измерений (Vi,Qi), ... ,η, где Vi — сумма баллов, полученных
г-м студентом по вербальной (verbal) части теста, a Qi — по
количественной (quantitative) части теста. В таблице приведены числа
измерений, которые ниже (меньше) и выше (больше)
национального среднего по двум компонентам. Пусть 0' = {θγβ^) — вектор
национальных средних. Проверим на уровне значимости а = 0,05
гипотезу #о: θ = θ' против альтернативы Н[: θ φ &.
V
Ниже
Выше
Q
Ниже
34
8
Выше
22
36
В соответствии с формулой (3) имеем 5* = 22/70+142/30 « 6,59.
Эта величина превосходит 0,95-квантиль закона χ|, равную
5,99 (см. табл. ТЗ). Следовательно, гипотеза Щ отвергается на
уровне 5%.
С другой стороны, отдельно по компоненте V оказалось 56
измерений ниже θ'ν и 44 —выше θ'ν. Нормальное приближение
для критерия знаков с поправкой на непрерывность (см. § 2 гл. 15
и табл. Т2) дает для таких данных приближенный фактический
уровень значимости с*о =0,136 (для односторонней альтернативы).
Аналогично, для компоненты Q имеем 42 измерения ниже O'q и
58 —выше 0д. Для таких данных а$ = 0,069 > 0,05.
§2. Одновыборочная модель
403
Многомерное обобщение критерия знаковых рангов
(см. § 3 гл. 15)
Для получения этого критерия потребуется ввести
дополнительное допущение о центральной симметричности плотности
ρ{χι,...,χρ).
ДЗ. Плотность р{х\,... ,#р) при любых х\,... ,#р удовлетворяет
условию р(#ь... ,Хр) = р(—#ь..., — Хр).
Из ДЗ, очевидно, следует, что каждая из частных плотностей
Pj(x), j = 1,... ,р, является четной функцией.
На рис. 1, а изображена область, ограниченная характерной
(типичной) линией уровня некоторой (взятой для примера) двумерной
плотности, удовлетворяющей условию ДЗ, а на рис. 1, б— аналогич- а'
ная область для плотности, не удовлетворяющей ДЗ.
Рассмотрим вектор (центрированных) знаковых ранговых
статистик Уилкоксона Τ = (Τι,... ,ТР) с компонентами
♦
T^ = ^TT^^ijSign(Xij), j = l,...,p, (4) б)
Рис. 1
где Rij— ранг \X%j\ относительно |Xij|,... ,|Xnj|. Следующая
теорема дает нам предельное распределение вектора Τ при условии
справедливости гипотезы Я0.
Теорема 2. При справедливости гипотезы Щ и выполнении
условия ДЗ имеет место сходимость
η-ι/2 т Λ Ζ - ЛГ(0, V) при η - оо,
где V = ll^fcllpxp, Vjj = 1/3,
оо
vjk = 4 j ад Fk(y) dFjk{x,y) - 1 в случае к Ф j. АЖЗДЙТЗ!]2
—оо
Для построения критерия требуется состоятельная оценка
матрицы V. Учитывая, что sign(#) = 2 /{д;>о} — 1 при ж^Ои что сумма
η
Σ Rij = n(n + 1)/2, запишем правую часть равенства (4) в виде
г=1
Ъ = ^ Σ ^ Wo> - η/2 Ξ ^ Τ+ - п/2.
Статистика Т+ изучалась в § 3 гл. 15. В частности, при
решении задачи 6 гл. 15 было установлено, что ее дисперсия
ОТ* = п(п + 1)(2п + 1)/24. На основании этого возьмем
V" ~ ηΌ1>~ η (n + 1)2 m* " 6(η + 1) * (5)
404
Глава 23. Многомерные модели сдвига
120
ПО
100
90
80
70
6?
• г*· ·
00 120 140 160
Рис. 2
В [86, с. 291] объясняется, что в качестве состоятельной оценки для
Vjk при j φ к годится
Vjk =
n(n+l)a£i
Σ Rij signtXij) Rik sign(Xifc).
С учетом соотношений (5) и (6) положим V =
статистика
Т* = TT{nV)-lT
(6)
. Тогда
(7)
в случае справедливости гипотезы Н0 распределена в пределе по
закону Хр при условии невырожденности матрицы V.
Пример 2. Влияние высоты проживания на величину
артериального давления* В [86, с. 293] приведена таблица
значений давления крови у η = 15 перуанских индейцев в возрасте 21 год,
родившихся высоко над уровнем моря, родители которых также
родились в высокогорье. Обозначим через X величину
систолического давления, а через Υ — величину диастолического давления.
На рис. 2 изображена диаграмма рассеяния точек (хг,Уг),
г = 1,... ,п. Если не обращать внимание на два «выброса», то можно
предположить, что распределение случайного вектора (Χ,Υ)
Центрально симметрично относительно θ = (#ι,02)> где θ ι (Θ2) —
центр частного распределения систолического (диастолического)
давления. Проверим гипотезу Щ: θ = 0' против альтернативы
Н[: θ φ θ\ где θ' = (120,80) —стандарт для мужчин в возрасте
21 год в США.
Введем обозначения: Х[ = Х{ - 120, X? = rank(|X;|)sign(X|),
Y( = Yi-80, Y(' = гапк(|У^'|) sign(>7). В таблице на рис. 3 приведены
значения этих переменных.
По формуле (4) вычисляем Τι = 2,69 и Тг = —4,81. Из (5) имеем
vii = г?22 = 31/96 « 0,323. На основе последней строки таблицы
и формулы (6) находим г?12 = V21 = 0,096. Используя функцию
обращения матрицы из программы Excel, получаем
(nV)
1 = ( °'S
V-ο,ι
226
067
-0,067\
0,226/
По формуле (7) подсчитываем значение Т* = 8,605. Так как оно
превосходит 0,95-квантиль закона χ|, равную 5,99 (см. табл. ТЗ),
Рис. S
Гх
\Х*
\х"
Υ
у/
у»
170
50
15
76
-4
-3,5
125
5
5
75
-5
-5
148
28
14
120
40
15
140
20
13
78
-2
-1,5
106
-14
-10
72
-8
-8
108
-12
-8
62
-18
-14
124
4
3
70
-10
-9
134
14
10
64
-16
-12,5
116
-4
-3
76
-4
-3,5
114
-6
-6,5
74
-6
-6,5
118
-2
-8
68
-12
-10
138
18
12
78
-2
-1,5
134
14
10
86
6
6,5
124
4
3
64
-16
-12,5
114
-6
-6,5
66
-14
-11
§2. Одновыборочная модель
405
то на приближенном*) уровне значимости 5% следует отклонить
гипотезу #q, т. е. давление крови перуанских индейцев значимо
отличается от давления их американских сверстников.
Точечная оценка θ для вектора θ — пара медиан средних Уолша
(см. § 3 гл. 8). Вычисления дают θ = (126,73).
Замечание 1. Достоинствами обоих рассмотренных выше
критериев являются их устойчивость к «выбросам» и инвариантность
относительно преобразований масштаба координатных осей.
К недостаткам относятся асимптотический характер (для
конечной выборки они дают не точный, а приближенный уровень
значимости) и отсутствие инвариантности относительно вращения
осей.
При дополнительном предположении о многомерной
нормальности распределения наблюдений
Д4. Xi ~ Ν(θ, Σ) с невырожденной матрицей ковариаций Σ
(в этом случае распределение имеет плотность, см.
приложение П9)
для проверки гипотезы Щ используется критерий Хотеллинга,
статистикой которого служит
G=[(n-p)/p}XTE~1X, (8)
где X = (Хь... ,ХР), Σ = - £ (Xi - X)(Xi - Χ)τ - выборочная
пг=1
ковариационная матрица.
С помощью критерия Хотеллинга можно отклонить гипотезу
if о на уровне а, если наблюдаемое значение g статистики G
превосходит (1 — а)-квантиль распределения Фишера—Снедекора с ρ
и (η —ρ) степенями свободы (см. табл. Т5).**)
Этот критерий не имеет указанных в замечании 1 недостатков.
Более того, его статистика инвариантна относительно любых
невырожденных линейных преобразований координат.
Действительно, пусть Υ ι = GX%. В силу свойств ковариаций и
матричных операций (см. П2 и Π10) запишем
ΥΤΣу1 Υ = (СХ)Т (СΣxCT)~l (CX) =
= ХТСТ [{Οτ)-ιΣ~χΟ-λ] СХ = ХтЪхгХ.
Однако, критерий Хотеллинга не обладает устойчивостью к
«выбросам» (робастностью) ввиду того, что (как показывает
следующий пример) неробастны статистики X и Σ.
*) Критерий базируется на асимптотической нормальности статистики Т, а
применяется к конечной выборке размера η = 15.
**) О критерии Хотеллинга рассказывается в книге Андерсон Т. Введение
в многомерный статистический анализ, М.: Физматгиз, 1963. Также см.
монографию [8, с. 85].
406
Глава 23. Многомерные модели сдвига
Пример 3. Применим критерий Хотеллинга к данным примера 2.
С помощью Excel вычисляем X = (127,5; 75,3) и
~ /269,2 106,5\
^106,5 182,7j '
Для Θ' = (120,80) находим, что при п = 15ир = 2 статистика
С = [(п - р)/р) (X - ΘΤΣ'1 (X - θ1)
имеет значение 4,12. Согласно табл. Т5 0,95-квантиль
распределения Фишера—Снедекора с 2 и 13 степенями свободы равна 3,81. Так
как 4,12 > 3,81, гипотеза Щ: θ = 0' отвергается на уровне 5%.
Исключим теперь два выделяющихся наблюдения — точки с
координатами (170,76) и (148,120) (см. рис. 2). Для оставшихся
данных в количестве щ = 13 вектор средних Хо = (122,7; 71,8)
(как и следовало ожидать, средние значения уменьшились). В свою
очередь выборочная ковариационная матрица оставшихся данных
s, /116,2 33,2\
J° \ 33,2 44,67 "
Она совсем не похожа на прежнюю Σ. Новое значение статистики
G'0 = 13,0 превосходит даже 0,995-квантиль F-распределения с 2 и
11 степенями свободы, равную 8,91 (см. [10, с. 202]).
§3. ДВУХВЫБОРОЧНАЯ МОДЕЛЬ
Сравним две многомерные независимые выборки размеров η
и т. Пусть Χι,... ,ХП и Υ ι,... ,Ym — выборки из р-мер-
ных распределений с функцией распределения F(#i,.. .,#р) и
F(xi — Δι,... ,#р — Δρ) соответственно. Выборки представляются в
виде двух таблиц размеров пхритхр, которые удобно объединить
в общую матрицу данных D размера Ν χ р, где N = п + т:
/Хп ... ΧιΡ\
D =
пр
Χηι ... Х^
Yu ... Yip
^■* ml · ■ · *тр'
Предположим, что верно допущение Д1 из § 2, а также выполнено
условие
Д5. Выборки Χι,... ,ХП и ΥΊ,... ,Ут независимы между собой
(другими словами, строки матрицы D независимы).
§ 3. Двухвыборочная модель
407
Отметим, что допущения о симметрии закона F не делается.
Параметр Δ = (Δι,...,Δρ) задает величину сдвига
распределения Υ относительно распределения X. Мы хотим проверить
гипотезу
#о: Δ = 0 против альтернативы #ι: Δ φ 0.
Рассматриваемый ниже критерий известен как
Многомерное обобщение критерия ранговых сумм
Уилкоксона—Манна—Уитни
(см. § 5 гл. 14)
Пусть W = (Wu... ,иу, где
ι m
Щ = 5щЕД« - т/2, j = l,...,p, (9)
где N = η + га, Rij — ранг Yij относительно элементов j-ro столбца
матрицы D. (Для удобства вычислений удобно преобразовать D в
матрицу jR из рангов по столбцам.) Ниже мы покажем, что Wj —
это центрированная сумма рангов: MWj = О при
последующая теорема дает предельное распределение статистики
ΛΓ-1/2 W при справедливости нулевой гипотезы.
Теорема 3. Пусть верна гипотеза Но и выполнены допущения Д1,
Д5. Предположим, что n, га —> оо и η/Ν —► 7> 0 < 7 < 1· Тогда
n-v2w ±ζ~λί(ο,ν),
где V = ||vjfc ||рхр, Vjj = 7(1 - 7)/12,
vjk = 7(1 - 7)
оо оо
J J Fj{x)Fk{y)dFjk{x,y) - 1/4
при к φ j.
Доказательство теоремы 3
можно найти в [86, с. 297].
Покажем, что bAWj = О при справеливости гипотезы Но. В
соответствии с обозначениями из § 5 гл. 14 формулу (9), определяющую
статистику Wj, можно записать в виде
ИЪ=1У(ЛГ+1)-т/2, (10)
т
где Vj = Σ Rij· Согласно формулам (5) и (6) гл. 14 имеем
1=1
MVj = MU, + т(т+1) = ™ + то(т+1) = т(ЛГ + 1) . (11)
3 3 2 2 2 2
η т
Здесь ί/j = J J] /{xi7<yr} (см. формулу (4) гл. 14). Остается взять
г=11=1 %Э 3
математическое ожидание обеих частей равенства (10) и подставить
туда соотношение (11).
408
Глава 23. Многомерные модели сдвига
Для построения критерия (см. § 1) нужна состоятельная оценка
V для асимптотической матрицы ковариаций V. В силу (10) и
формул (5)-(6) гл. 14
птл/ — DT^f __ DUj __ nm(n + т +1) __ nm
j ~~ (W+1)2 " (Ν + Ι)2 " 12(iV+l)2 " 12(ΛΓ + 1) '
На основании этого возьмем
Далее, если в формулу, определяющую Vjk (см. утверждение
теоремы 3), вместо Fj(x)1 Fk(y) и Fjk(x,y) подставить одномерные
и двумерную эмпирические функции распределения, то получим
оценку
^ пт
ϊϊ Σ RtjRtk - Ν/4
(jv + iyfe--*-" "'-J" (13)
(Таким образом, потребуется вычислять скалярные произведения
столбцов матрицы рангов Д.) Используя формулы (12) и (13) для
определения элементов матрицы V, получим, что при
справедливости гипотезы Но статистика критерия
W* =WT(NV)~lW (14)
распределена в пределе по закону χ£ при условии невырожденности
матрицы V.
Пример 4. Обнаружение фальсификации данных.
Исследователю-медику требовалось провести статистическую обработку
данных из области диагностики пациентов, страдающих
мигренями. При этом таблица данных состояла их двух частей:
часть I составляли наблюдения, полученные самим исследователем,
часть II — заимствованные данные.
У исследователя имелись основания сомневаться в
добросовестности сторонней информации. Возникали подозрения, что данные
были получены следующим образом: реально были записаны хаг
рактеристики головной боли лишь небольшой группы больных,
затем они была многократно дублированы и немного искажены
(«зашумлены»), чтобы не было заметно периодичности. (Забегая
вперед, скажем, что проводимый ниже статистический анализ
подтверждает наличие фальсификации.)
Для обнаружения различия между частями I и II таблицы было
проведено исследование, состоящее из нескольких этапов.
1. Отбор больных и признаков. Из обеих частей таблицы
были отобраны (с помощью фильтра в программе Excel) пациенты с
диагнозом «Эпизодическая головная боль напряжения»: в группе I
оказалось η = 41 таких больных, в группе II — m = 58 больных.
§ 3. Двухвыборочная модель
409
Среди ряда характеристик головной боли (таких, как средняя
интенсивность боли, характер боли, ее локализация и т. д.) для
анализа были взяты два признака: X —средняя длительность
одного приступа (часы) и Υ — среднее частота приступов в месяц
(дни). Соответствующие данные приведены в таблице на рис. 4.
Группа I
X
7
й
2,5
7
1,5
2,5
5
3,5
! 2
2
5
4
5
3,5
11
7
4,5
7
3
4
Υ
10
4
10
11
8
5,5
8
8
1
10
8
4
8
10
8
4
10
4
10
6
Группа 11
X
3,5
2,5
2,5
5
2,5
2,5
3,5
1,5
3,5
3,5
1
2,5
3,5
2,5
2,5
12
12
9
5
2,5
Υ
2
8
10
10
8
7
8
6
7
10
4
4
5,5
3
8
12
3
4,5
10
6 |
| Группа II
X
3,5
3,5
3
3
3,5
3,5
3,5
4,5
5
5
5,5
6,5
5
5
5
3,5
4
3
4
3,5
Υ
8
12
12
10
10
8
12
11
8
8
10
10
10
10
10
8
10
8
8
10
Группа II
X
3
4
3
3
3,5
3
4
3,5
4,5
4
3,5
3
4
4
2,5
3
4
4
2,5
5
Υ
10
2
0
0
0
4
4
2
4
2
8
2
0
0
2
8
8
2
2
7
Группа II
X
3
2,5
4
3,5
4
3,5
3,5
3
4,5
3
4
3
3
3,5
4
4
4
Υ
8
8
10
10
8
ю
8
8
ю
10
ю !
10
8
8
8
8
8
Рис. 4
14
2. Визуальный анализ. На основе указанных данных была 12]
построена диаграмма рассеяния на плоскости (Χ,Υ) (рис. 5). Парам 10.
(Xi,Yi), относящимся к группе I, соответствуют черные точки, а
парам (Xi,Yi), относящимся к группе И —серые квадраты.
Рассматривая диаграмму, приходим к ряду выводов.
а) Центр «облака» серых квадратов смещен вверх по оси Υ
относительно центра «облака» черных точек.
б) Очевидно, что у серых квадратов разброс по обеим
координатам намного меньше, чем у черных точек.
в) «Облако» серых квадратов имеет округлую форму, в то время
как «облако» черных точек совсем не похоже на реализацию
выборки из двумерного нормального закона. Обычно такая
реализация (после исключения нескольких «выбросов») имеет
вид эллипса, густо заполненного точками в центральной части
и реже —по краям. В нашем же случае скорее наблюдается
уменьшение плотности точек (расширение «облака») при
увеличении значений обоих признаков, т. е. «облако» черных точек
имеет форму «веера» (см. рис. 1,6).
Рис. 5
410
Глава 23. Многомерные модели сдвига
г) Количество совпадений в группе II намного больше, чем в
группе I: для га = 58 представителей группы II на
диаграмме присутствуют только 21 серый квадрат (21/58 « 0,36),
а для η = 41 представителя группы 1 — 31 черный кружок
(31/41 « 0,76).
3. Статистическая проверка однородности. Вектор
выборочных средних (Χ, Υ) в группе I имеет значение (4,2; 7,1), в группе
II—(3,7;9,8). Средние заметно отличаются, особенно по второй
координате. Стандартные отклонения в группе I равны (2,7; 2,7),
в группе И—(0,8; 1,7). Видим, что разброс в группе II намного
меньше, чем в группе I.
Ввиду пункта в) приведенных выше выводов для исследуемых
данных неуместно применять критерии, опирающиеся на
предположение о нормальности распределения наблюдений (скажем,
критерий Хотеллинга). Более надежным подходом является
использование многомерного обобщения рангового критерия Уилкоксона—
Манна—Уитни. Вычисления дают N = 99, W = (1,305; 6,475),
νη = ν22 = 0,02, v12 = vzi = 0,0025,
<NV\-l - ( °'513 -°>06Λ
к } ν-0'064 °>513/'
Наконец, W* = 21,28, что превосходит 0,999-квантиль закона
χ|, равную 13,8. Таким образом, группы I и II нельзя считать
однородными на уровне значимости 0,001.
Замечание 2. Если применить одномерный критерий
Уилкоксона—Манна—Уитни к каждому из признаков отдельно, то будем
иметь следующие результаты: для признака X нормированная
статистика критерия (см. формулу (7) гл. 14) принимает значение
0,93, а для признака Υ — значение 4,6.
Первое из них (согласно таблице Т2) незначимо на уровне 5%.
Другими словами, критерий Уилкоксона—Манна—Уитни не
улавливает различия между группами I и II по первому признаку. Это
можно объяснить тем, что при переходе от самих наблюдений к
их рангам нивелируется очевидное визуальное отличие на рис. 5
черных точек группы I с большими значениями признака X от
серых квадратов группы II.
В свою очередь, для признака Υ картина иная. Статистика
значима велика даже на уровне 0,001, что подтверждает наличие
систематического сдвига вверх по координате Υ серых квадратов
группы II относительно черных точек группы I. По степени
разброса группы будут сравниваться в следующей главе.
Глава 24
ДВУХВЫБОРОЧНАЯ ЗАДАЧА О МАСШТАБЕ
В этой главе рассматриваются ранговые (и поэтому — устойчивые
к «выбросам») альтернативы F-критерию, не предполагающие
нормальности распределения наблюдений.**)
Данные представляют собой две независимые случайные
выборки, по одной из двух генеральных совокупностей. На основе
выборок мы хотим выяснить, есть ли различие в мерах рассеяния
(масштаба) этих совокупностей.
§ 1. МЕДИАНЫ ИЗВЕСТНЫ ИЛИ РАВНЫ
Статистическая модель
Имеется N = п + т наблюдений ΛΊ,... ,Χη, Υί,... ,Ym:
Xi = μ + σιε», г = 1,... ,η; Υ,- = μ + σ2ε^ j = 1,... ,m;
где μ — неизвестная общая медиана распределения наблюдений,
σι > 0 и σ^ > 0 — неизвестные параметры масштаба, ει и ε ^ —
случайные ошибки.
Допущения
Д1. Все ошибки {ε^,ε^} независимы.
Д2. Все {ε^,ε^} имеют одинаковое непрерывное (неизвестное)
распределение, медиана (см. § 2 гл. 7) которого равна 0.
Для проверки гипотезы Н0: σι = σ2 применяется
Свободный от распределения ранговый критерий
Ансари—Брэдли
1. Упорядочить N наблюдений от меньшего к большему.
2. Наименьшему и наибольшему из наблюдений присвоить
ранг 1, второму и предпоследнему по величине присвоить
*) Критерий Стьюдента (ί-критерий) и F-критерий для дисперсий приведены
в примере 1 гл. 14. Критерий хи-квадрат для проверки нормальности
рассматривался в примере 3 гл. 18. Проблема зависимости наблюдений обсуждалась в
§ 4 гл. 15, неробастность F-критерия —в замечании 2 гл. 16 (к = 2).
**) Изложение, в основном, следует главе 5 монографии [88].
Многие статистики
развивали своего рода
«логику», следы которой
можно найти во многих
прикладных книгах
по статистике и суть
которой можно свести
к следующему: прежде
чем применять двухвы-
борочный ί-критерий,
нужно сначала применить
критерий нормальности
к каждой выборке
(например, критерий
согласия хи-квадрат).
Если результат не даст
большой значимости, то
можно считать, что
распределения нормальны, и
применять F-критерий
равенства дисперсий.
Если же последний
также не выйдет за
уровень значимости,
то можно предполагать
равенство дисперсий и
позволить себе применить
ί-критерий. В этом
рецепте нет ни слова о
возможном отсутствии
независимости, (...) ни
слова о катастрофической
неробастности F-крите-
рия для дисперсий, ни
слова (или едва-едва
что-нибудь) о том,
что делать, если один
из предварительных
критериев превзойдет
уровень значимости. '
Из книги [84, с. 81]
412
Глава 24. Двухвыборочная задача о масштабе
ранг 2 и т. д. Если N четно, то расположение рангов будет
1,2,... ,ЛГ/2,ЛГ/2,... ,2,1; если же N нечетно, то расположение
рангов будет 1,2,... ,(ЛГ - 1)/2, (N + 1)/2, (N - 1)/2,... ,2,1.
3. Обозначив через Sj ранг Yj в указанной ранжировке,
вычислить значение статистики критерия Ансари—Брэдли
т
3 = 1
т. е. сумму рангов, относящихся к Υί,... ,Ym.
Поясним, почему слишком большие (или слишком малые)
значения Ζ противоречат Hq. Пусть, например, σι < σ2· Тогда значения Υ
будут проявлять склонность к большему рассеянию (разбросу), чем
значения X. Поэтому при ранжировке (по схеме 2-го шага метода)
наблюдения Yj, в большинстве своем, будут иметь малые ранги, а
Xi — большие. В результате величина Ζ окажется малой. (Примером
крайнего случая служит такое распределение представителей X и Υ
в упорядоченной объединенной выборке: ΥΥΧΧΧΥΥ.)
Малые выборки. Критические значения статистики Ζ для
п,т ^ 10 приведены в табл. А 6 книги [88].
Большие выборки. Если гипотеза Н0 верна, то статистика
Z* = (Z-MZ)/V0Z (1)
асимптотически (при min{n,m} —► оо) распределена по
стандартному нормальному закону ЛГ(0,1). Математическое ожидания и
дисперсия в (1) задаются формулами
MZ=m(^±2)) DZ=nm(N^){N-2)^ ^ N_четное;
MZ=rn(N+ll DZ=nm(N + l)(N>+3) _ ^^
4iV ' 48 Ν2
Обозначим через χι-α квантиль уровня (1 — а) закона ΛΓ(Ο,Ι) (§ 3
гл. 7), а через ζ* — наблюдаемое значение статистики Ζ*.
Односторонний критерий приближенного уровня а для
проверки гипотезы Но против альтернативы Ηι: σι < σ<ι таков: если
ζ* ^ — χι-α, то отвергаем гипотезу #о, иначе — принимаем.
Односторонний критерий приближенного уровня а для
проверки гипотезы Hq против альтернативы Н^: σι > σ<ι таков: если
ζ* ^ #ι_α, то отвергаем гипотезу Щ, иначе — принимаем.
Совпадения. Если среди N наблюдений есть одинаковые, то
для подсчета Ζ надо использовать средние ранги. Для больших
выборок следует также заменить DZ в формуле (1) на величину
пт
fc=l
[16 N(N - 1)], если N — четное;
§ 1. Медианы известны или равны
413
пгп
16NJ2hRl
к=1
(N-
+ I)4 / [16 N2(N - 1)] , если N- нечетное.
Здесь g — число групп совпадений среди N наблюдений, Ik —
количество элементов в к-й группе, Rk — средний ранг наблюдений в к-й
группе. Не совпадающие с другими наблюдения рассматриваются
как группы размера 1.
Пример 1. Продолжим анализ данных из примера 4 гл. 23.
Напомним, что критерий ранговых сумм Уилкоксона—Манна—Уитни
не позволил обнаружить сдвига по компоненте X наблюдений в
группе I относительно наблюдений в группе П. Поэтому можно
предположить, что выборки имеют одинаковую медиану. Исходя
из этого допущения, попробуем обнаружить различие в рассеянии
выборок с помощью критерия Ансари—Брэдли.
Для вычислений удобно использовать такие операции
программы Excel, как «Сортировка» и «Фильтр». В результате их
применения (для η = 41 и т = 58) получим следующие значения:
ζ = 1784,2 ΜΖ = 1464,6 и ΏΖ = 4955,7 (с учетом совпадений —
4623,7), ζ* = 4,7. Эта величина значимо велика даже на уровне
а = 0,001 (см. табл. Т2). Таким образом, приходим к заключению,
что выборки нельзя считать однородными, поскольку у наблюдений
в группе I рассеяние по компоненте X значимо больше.
Комментарии
1. При справедливости гипотезы #о вероятность каждого из
С™ возможных размещений У-ов по N местам одинакова.
Благодаря этому можно найти распределение Ζ при нулевой гипотезе.
2. Во многих двухвыборочных ситуациях интересно выявить
различие совокупностей в сдвиге или разбросе. Одно из решений —
применение критериев, предназначенных для более общих
альтернатив (например, критерия Смирнова или критерия Розенблатта из
гл. 14). Другой путь — совместное применение двух критериев:
одного для сдвига (например, критерия Уилкоксона—Манна—Уитни
из § 5 гл.14), другого —для масштаба (скажем, критерия
Ансари—Брэдли). Р. Рандлес и Р. Хогг в 1971 г. показали, что при
выполнении Н0 статистики последних двух критериев
асимптотически независимы. Отсюда следует, что если мы применяем
критерий Уилкоксона—Манна—Уитни на уровне αϊ и критерий
Ансари—Брэдли на уровне с*2, то вероятность отклонить гипотезу об
идентичности совокупностей X и Υ хотя бы одним из критериев,
будет приближенно равна а\ + ol<i — ol\Ol<2,.
3. Критерий Ансари—Брэдли можно применять исключительно
в ситуации, когда совокупности Χ πΥ различаются лишь в мерах
рассеяния, в частности, не имеют сдвига друг относительно друга.
В то же время требование равенства медиан не обязательно для
классического F-критерия, основанного на отношении выборочных
дисперсий. В следующем параграфе рассматривается (похожий на
Например, для η = 2
и т = 2 имеется
С\ — 6 размещений:
XJCYY, ΧΥΧΥ,
ΧΥΥΧ, ΥΧΧΥ,
ΥΧΥΧ, ΥΥΧΧ.
Набор соответствующих
значений Ζ таков:
(3,3,4,2,3,3). Отсюда,
скажем, находим, что
Р(£>4) = 1/6приЯ0.
Пусть, например, п = 3,
тп = 4 и все наблюдения
из совокупности X
оказались меньше
любого наблюдения из
совокупности Υ. Тогда
Ζ имеет значение 10 вне
зависимости от степени
разброса каждой из
выборок.
414
Глава 24. Двухвыборочная задача о масштабе
ранговый) критерий Мозеса, для которого равенство медиан также
не требуется.
§ 2. МЕДИАНЫ НЕИЗВЕСТНЫ И НЕРАВНЫ
Статистическая модель
Имеется две группы наблюдений: ΛΊ,... ,Хп и Υί,... ,Ym:
Χΐ=μι + σι Si, г = 1,... ,η; Υ,- = μ2 + σ2ε,·, j = 1,... ,m;
где μι и μ2 - неизвестные медианы совокупностей (мешающие
параметры), σι и σ2 — неизвестные (интересующие нас) параметры
масштаба, е» и ej — случайные ошибки.
Допущения те же, что и в § 1.
Для проверки гипотезы #0 · σι = σ2 используется
Свободный от распределения
похожий на ранговый критерий Мозеса.
1. Задать целое k ^ 2 и случайным образом разбить каждую
из групп наблюдений на п' = [п/к] и га' = [т/А:] подгрупп
размера А: соответственно.*) Все не вошедшие в подгруппы
наблюдения отбросить.
2. Обозначить через ΛΊΓ,...,Λ*Γ А: наблюдений, попавших в
r-ю подгруппу для X, г = 1,...,п', а через 1Ίθ,...,3^θ —
к наблюдений, попавших в s-ю подгруппу для У, s = 1,... ,га'.
3. Подсчитать Ci,... ,СП> по формулам
α-Σ^-^Σ**·) , r=i,...,n'.
4. Подсчитать £>ι,... ,£>т' по формулам
^=Σ^-ΗΣ^1 , e = l,...,m'.
5. Применить к Ci,...,Cn/ и J9i,...,J9m/ критерий ранговых
сумм Уилкоксона—Манна—Уитни (см. § 5 гл. 14).
Если Но не выполняется, например, σι < σ2, то величины Da
имеют тенденцию превосходить величины Сг- Это приводит к
увеличению рангов Ds и, как следствие, к большим значениям статистики
критерия ранговых сумм.
Оценка отношения коэффициентов масштаба. В случае
невыполнения Но представляет интерес величина η = σ<ιΙσ\. Для
ее оценивания Г. Шорак в 1969 г. (см. [88, с. 116]) предложил
следующую процедуру.
*) Здесь [·] обозначает целую часть числа.
§2. Медианы неизвестны и неравны
415
Группа I
3,5
3,5
5
2,5
2,5
3,5
2,5
9
Ci
33,5
2,5
2,5
4
7
4,5
7
3
4
С2
23,0
7
2
2,5
2,5
2,5
3,5
2,5
5
С3
20,7
7
1,5
3,5
5
1,5
1
12
2,5
С4
97,5
1,5
5
5
11
3,5
3,5
2,5
12
Сь
106,0
Группа II
5
4
4
4
3
4,5
3
3
Όχ
4,0
3,5
3,5
4
4
3,5
4
4
4
D2
0,5
4,5
4
3
3
3
2,5
4
3
D3
3,4
3,5
5
4,5
4
3
3
2,5
3,5
£>4
4,9
3
3,5
5,5
5
3
3,5
3
4
D5
6,5
3
5
3
4
5
4
3,5
3,5
А>
4,4
3,5
3,5
3,5
6,5
3
3,5
2,5
4
D7
ю,о
1. Вычислить п'га' отношений D8/Cr, г = 1,... ,п', 5=1,... ,га'.
2. Обозначить через Q(i) ^ ... ^ Q(n'm') упорядоченные
значения отношений D8/Cr.
3. Взять в качестве оценки
~ _ JfyY)2 ПРИ п'ш' = 21 + 1,
7 " \(Q(i)Q(i+i))1/4 при nW = 2/.
Пример 2. Применим критерий Мозеса к данным из примера 4
гл. 23. Сравним рассеяния измерений в группах I и II по
компоненте X без предположения о равенстве медиан совокупностей
(использовавшегося в примере 1 ранее).
Если задать fc = 8, то в первой выборке размера η = 41
потребуется отбросить всего одно наблюдение (п' = 5), а во
второй выборке размера га = 58 —два наблюдения (га' = 7). Для
выбора номеров отбрасываемых наблюдений используем таблицу
равномерных случайных чисел Т1. Будем считывать ее по строкам,
начиная с первой. Получим числа 10, 09, 73, 25, В соответствии
с ними отбросим в первой выборке элемент с номером 10, а во
второй —с номерами 9 и 25 (так как 73 > га = 58, то это число
игнорируем).
Далее, разобьем оставшиеся наблюдения группы I случайным
образом на подгруппы размера 8. Опишем, как это удобно сделать.
Продолжим считывание табл. Т1 со второй строки: 37, 54,
Обращая внимание только на первую цифру, отнесем первый элемент
выборки группы I к подгруппе с номером 3, второй — к подгруппе
с номером 5 и т. д. (ноль и цифры, большие п' = 5 игнорируются).
При этом полезно отмечать в соседнем столбце текущий размер
пополняемой подгруппы и вносить в момент заполнения подгруппы
(когда размер станет равным к = 8) ее номер в список номеров уже
заполненных подгрупп (скажем, записываемый на листе бумаги).
Когда подгруппа заполнена, ее номер, встретившийся в таблице,
также игнорируется.
Аналогично разобьем на га' = 7 подгрупп наблюдения группы И.
Результаты разбиения приведены в двух таблицах на рис. 1.
416
Глава 24. Двухвыборочная задача о масштабе
Также на рис. 1 указаны соответствующие Сг и Д,, г = 1,... ,5,
s = 1,...,7. Видим, что все Ст больше любого из Ds. Согласно
таблице критических значений статистики критерия Уилкоксона—
Манна—Уитни из [10, с. 358] вероятность этого при справедливости
гипотезы Но для выборок размеров г = 5 и s = 7 менее 0,001. Таким
образом, приходим к тому же выводу, что и в примере 1: рассеяние
в группе I по компоненте X значимо больше, чем в группе И.
Путем написания простой программы для процедуры Шорака
на Visual Basic в Excel было подсчитано значение оценки для
«отношения разбросов» 1/7 = σι/σ2, равное 3,112.
Комментарии
1. Г. Шорак рекомендует выбирать размер подгрупп к как
можно больше (но не более 10), однако не делая п' и га' настолько
малыми, что распределение соответствующей статистики критерия
ранговых сумм Уилкоксона—Манна—Уитни не сможет обеспечить
разумный уровень значимости. Размер подгрупп к надо выбирать,
учитывая только размеры выборок η и га. М. Холлендер и Д. Вулф
(см. [88, с. 114]) пишут: «Было бы неверным так подбирать
различные значения к, чтобы получились значимые решения. Такой
подход делает незаконными все выводы!»
2. У критерия Мозеса есть недостаток: два человека,
обрабатывая одни и те же данные, могут получить различные выводы
при одном и том же уровне значимости а. Эта возможность
возникает из-за случайности процесса разбиения на подгруппы.
Иными словами, повторное применение критерия Мозеса к тем же
данным, но с другим разбиением на подгруппы, может привести в
противоположным выводам. В связи с этим подчеркнем, что при
использовании критерия допускается лишь одна чисто случайная
группировка. Совершенно недопустимо манипулировать
группировками для достижения значимого результата!
3. М. Холлендер в 1968 г. показал, что при выполнении
гипотезы Щ и симметричности распределения статистика
критерия Мозеса и статистика критерия ранговых сумм Уилкоксона—
Манна—Уитни некоррелированы и асимптотически независимы.
Это влечет те же заключения, что и в комментарии 2 из § 1.
4. Известны и другие критерии для проверки гипотезы if о,
применимые для выборок большого размера. Так, в [88, с. 117]
приводится критерий Миллера, основанный на методе «складного
ножа» (jackknife). Он обладает более высокой эффективностью
сравнительно к критерием Мозеса, но свободен от распределения
лишь асимптотически.
Глава 25
КЛАССЫ ОЦЕНОК
8 1. L-ОЦЕНКИ ПУСТЬ Расцветают сто
° ' цветов.
Рассмотрим ВариаДИОННЫЙ ряд Хщ ^ Х(2) ^ · · · ^ Х(п) (см· § 4 Китайская мудрость
гл.4). L-оценками называются линейные комбинации Y^WiX^
порядковых статистик, где Wi — некоторые веса. Эти оценки
обобщают усеченное среднее (см. § 2 гл. 8)
*а = }T^2k (X(fc+1) + * * * + Х(п~к))> где 0 < а < -, А: = [ап]*\
у которого А: крайним с каждой стороны наблюдениям приданы
нулевые веса, а оставшимся (п — 2к) центральным наблюдениям —
одинаковые wi = 1/(п — 2А:). Чтобы изучить поведение L-оценок
при больших п, удобно задавать веса win (г = 1,... ,η; η = 1,2,...)
в виде
Win = lx(ud> (1)
где λ(t) — некоторая функция, определенная на отрезке [0,1].
Например, усеченному среднему Ха отвечает
λ(0 = ι_2α 7{«<*<ι-«}· (2)
Естественно рассмотреть более гладкое распределение весов.
Приведем условия (из [50, с. 328]), обеспечивающие асимптотическую
нормальность L-оценок.
Теорема 1. Пусть случайные величины Χι независимы и
одинаково распределены на интервале (а, Ь), —оо^а<Ь^оо, согласно
распределению F, у которого
1) существует положительная при а < χ < Ь плотность р(#),
2) MX? < оо.
Потребуем также, чтобы выполнялось условие
3) \{t) — ограниченная функция, непрерывная почти всюду
(ότι
носительно лебеговой меры) с § \(t) dt = 1.
о
*) Здесь [·] обозначает целую часть числа.
418
Глава 25. Классы оценок
Положим
ι
//(F,A) = IxtyF-^dt, a2(F,A) = \ϋ2{1)α4- ( [σ(ί)Λ
о о \о ί
где G(t) -любая функция с G'(t) = X(t) /ρ(F_1(*)).
Тогда при условии a(F,A) > 0 для статистики
(3)
справедлива сходимость
у/И (Ln - //(F,A)) -if- ЛГ (О, a2(F,A)) при η -+ оо.
Следствие. Пусть элементы выборки Χι распределены согласно
закону F(x — 0), где F симметрична относительно 0, а функция λ —
относительно 1/2. Тогда легко проверить, что μ(^,λ) = 0, и поэтому
VH(Ln-0)^£~A/-(O,a2(F,A)).
Для заданного распределения F наиболее эффективная
L-оценка параметра сдвига θ получается путем минимизации
дисперсии a2(F,A) по λ.
Теорема 2. Допустим, что плотность р(х) = F'(x) имеет две
производные р'(#), рп{х) почти всюду и что р(х) —► 0 при χ —► ±оо.
Положим
7(х) = -|/(»)/р(»). (4)
Тогда асимптотическая дисперсия a2(F,A) минимальна при λ = λ*,
которая пропорциональна функции 7'(^_1(0) (см. условие 3
теоремы 1). В этом случае
оо
a2(FX) = l/I(F), где /(F) = J [р'(х))2/p(x)dx (5)
— ОО
обозначает информацию Фишера, введенную ранее в § 3 гл. 9.
Другими словами, такая L-оценка является асимптотически
Доказательство этой эффективной (как и оценка максимального правдоподобия),
теоремы приведено
в * ' с' '' Пример 1. Нетрудно проверить, что для стандартного
нормального закона (F = Ф) функция η(χ) = χ. Отсюда оптимальная
А* = 1. Соответствующая Ln совпадает с ОМП X. Информация
Фишера 1(Ф) = 1.
В случае логистического распределения с F(x) = 1/(1 + е~х)
находим, что η(χ) = 2F(x) — 1 = th(#/2). Оптимальная
X*(t) = 6t (1 - ί), причем /(F) = 1/3.
§2. Μ-оценки
419
Для закона Коши с плотностью р(х) = 1/[π(1 + χ2)] получается
весьма своеобразная оптимальная функция
λ*(t) = 2cos(2nt)[cos(2nt) - 1],
которая отрицательна при
ч
> 1/4 (рис. 1).*) Здесь 1(F) = 1/2.
В случае «наименее благоприятного распределения» Хъюбера,
определяемого в примере 2 ниже, оптимальной L-оценкой является
α-усеченное среднее Ха (а = F(—b)) с весовой функцией,
задаваемой формулой (2). Таблица значений 1(F) для разных b содержится
в [89, с. 92].
Замечание 1. Помимо эффективности, важную роль играет
устойчивость оценки по отношению к выделяющимся наблюдениям
(«выбросам»). Если значения весовой функции X(t) вблизи концов
отрезка [0,1] малы по сравнению со значениями в середине, то
L-оценка относительно нечувствительна к «выбросам». Тем не
менее, для того, чтобы оценка имела положительную толерантность
(см. § 4 гл. 8) необходимо, чтобы носителем функции X(t) был
интервал (а, 1 — а) при некотором О < а < 1/2.
Рис. 1
§2. М-ОЦЕНКИ
Усеченное среднее Ха служит компромиссом между средним X
(а = 0) и выборочной медианой MED (а —► 1/2). Другой
компромисс подсказан тем фактом, что среднее и медиана суть величины,
минимизирующие, соответственно, Σ(Χι — 0)2 и £) \Х{ — θ\ (см.
задачу 1 гл. 1 и задачу 4 гл. 7). П. Хьюбер предложил
минимизировать меру «разброса»
Σ Pb(Xi ~ Θ),
i=l
где функция рь(х) при некотором Ь > 0 задается формулой
рь(х) =
\х2/2,
[Ь\х\-Ь2/2,
если \х\ ^ Ь,
если \х\ ^ Ъ.
(6)
(7)
Она пропорциональна х2 при \х\ ^ Ь, а вне отрезка [—6,6] заменяет
ветви параболы на две прямые линии. Эти куски графика
согласованы так, что ръ(х) и ее производная фъ(х) = Рь(х) непрерывны
(рис. 2). При увеличении b функция рь будет совпадать с х2/2 на
все большей части ее определения, так что оценка Хьюбера будет
сближаться с X. В свою очередь, при уменьшении b происходит
сближение с выборочной медианой. (В качестве компромисса
иногда предлагается значение b = 1,5.)
) Для неотрицательности λ*(ί) необходимо и достаточно, чтобы 7/(а0 ^ 0 при
всех х. Это эквивалентно выпуклости функции — logp(x). Такие распределения
называются сильно унимодальными.
i
b
-ρ/
K-b
Фь
ь χ
б)
Рис.2
420
Глава 25. Классы оценок
Подобно тому, как усеченные средние Ха (0 < α < 1/2) обрат
зуют однопараметрическое подмножество класса L-оценок, оценки
Хьюбера (0 < Ь < оо) образуют однопараметрическое
подмножество класса так называемых М-оценок.
М-оценка Мп параметра сдвига θ определяется для некоторой
функции р(х) как точка минимума по θ функции
Σρ№-*)·
г=1
(8)
Если р — выпуклая и четная, то можно показать, что значения 0,
минимизирующие сумму (8), образуют некоторый отрезок, а если
ρ строго выпукла (П4), то минимизирующее значение единственно
(см. [50, с. 57]).
Если функция ρ имеет производную φ = //, то оценка Мп
является решением уравнения
Σ Ф(Хг ~ Θ) = 0.
»=1
(9)
Доказательство (10)
можно найти в
монографии [89, с. 58], где
приведено детальное
изложение теории
М-оценок не только
для модели сдвига,
но и для более общих
параметрических моделей.
Пусть элементы выборки Х{ имеют функцию
распределения F(x — 0), где F обладает четной плотностью р(х). Тогда при
слабых предположениях относительно φ и F
V^ (Мп - 0) Л С ~ЛГ(0,a2(F,V>)) при п -> оо, (10)
где асимптотическая дисперсия a2(F,i/>) задается формулой
σ2(Ρ1φ)=\φ2{χ)ρ(χ)άχ Ι\\φ'(χ)ρ{χ)άχ\ . (11)
Если р(х) = — \пр(х)1 то φ = ρ' = η(χ) (см. формулу (4)). В
этом случае минимизация суммы (8) эквивалентна максимизации
произведения Пр№ ~~ 0)> т· е· ^-оценка параметра сдвига
совпадает с оценкой максимального правдоподобия (ОМП) (см. § 4 гл. 9).
Таким образом, М-оценки обобщают ОМП (ей они обязаны своим
названием). Известно, что при выполнении условий регулярности
(см. § 3 гл. 9) ОМП является асимптотически эффективной оценкой
с a2(i*Vy) = 1//(F), где 1(F) определена в (5).
Пример 2. Для закона ЛГ(0,1) функция η(χ) = #, поэтому
оптимальная оценка Мп совпадает с X. Нулевая толерантность этой
оценки (см. § 4 гл. 8) связана с неограниченностью функции ί(χ).
Для логистического распределения с F(x) = 1/(1 + е~х) имеем
'у(я) = th(#/2). В силу строгой монотонности и ограниченности η(χ)
(см. [89, с. 61]) толерантность решения уравнения (9) равна 1/2.
В случае закона Лапласа с плотностью р(х) = - е-'*' весовая
функция р(х) = \х\ не имеет производной в нуле. Полагая 7(0) = 0,
§2. Μ-оценки
421
получаем у(х) = sign χ. Соответствующая ΟΜΠ — выборочная
медиана MED, имеющая a2(F,y) = 1 и обладающая асимптотической
толерантностью 1/2.
Для распределения Коши с плотностью р(#) = 1/[тг(1 + х2)]
функция η(χ) = 2х/{\ + ж2) оказывается немонотонной (рис. 3).
Поэтому уравнение (9) может иметь несколько решений (см.
вопрос 3 в гл. 9). Коллинз (1976) и Кларк (1984) (см. [84, с. 137])
показали, что если а) брать ближайшее к выборочной медиане
решение или б) пользоваться методом Ньютона, выбирая в качестве
начального приближения MED (см. теорему 4 гл. 9), то оценка
будет асимптотически эффективной, причем от медианы будет
унаследована толерантность 1/2.
Наконец, рассмотрим случай «наименее благоприятного
распределения» Хьюбера с плотностью р(х), пропорциональной функции
ехр{—/0б(#)}, где рь{х) задается формулой (7). Для этого закона
η{χ) совпадает с фь(х) = Рь(х)- Толерантность оценки Хьюбера
также равна 1/2.
Пример 3. Минимаксный подход Хьюбера. Вместо того,
чтобы предполагать функцию распределения F известной, более
реалистично допустить, что она известна лишь приближенно.
Одной из таких моделей, предложенных Хьюбером, является
представление F в виде смеси
F(x) = (1 - ε) G(x) + ε Я(я), (12)
где функция распределения G(x) и 0 ^ ε ^ 1 заданы, а Н(х) — это
произвольная неизвестная функция распределения
(предполагается только, что GvlH симметричны относительно нуля (см. гл. 8)).
Обозначим через Ω((7,ε) семейство распределений,
удовлетворяющих (12) для фиксированных G и ε. (Легко видеть, что любое
распределение вида (1 — ε')ΰ(χ) + ε,Η(χ)1 где 0 ^ ε' ^ ε, также
входит в Ω((7,ε).) В соответствии с минимаксным подходом
представляет интерес нахождение М-оценки (функции ψ), на
которой достигается
min sup a2(F,V>). (13)
В частном случае, когда G совпадает с функцией
распределения стандартного нормального закона Φ с плотностью
φ(χ) = (2п)~1^2е~х /2, решением этой задачи (как доказано в
[50, с. 335]) служит оценка Хьюбера с ^ь(ж)> У которой Ь = 6(ε)
определяется из соотношения
1/(1 - е) = 2 Ф{Ь) -1 + 2 у?(Ь)/Ь. (14)
Рис. 3
422
Глава 25. Классы оценок
Некоторые значения Ь(е) приведены в таблице (взятой из [89, с. 92]):
ε
Не)
0
оо
0,001
2,630
0,01
1,945
0,05
1,399
0,1
1,140
0,2
0,862
0,5
0,436
1
0
В частности, видим, что 5%-му «загрязнению» отвечает b « 1,4.
По ходу доказательства в [50] устанавливается, что при
φ = фъ(#) наибольшее значение a2(F,Vb) достигается на
распределении F с плотностью р(#), пропорциональной ехр{—ръ{х)}, ввиду
чего его и называют «наименее благоприятным распределением»
Хьюбера.
Замечание 2 (см. [84, с. 149]). Дж. Тьюки в 1970 г. предложил
для параметра сдвига θ так называемую W -оценку 0,
представляющую собой решение уравнения
θ=ς *»№ -*)Xi/t, ™{Ъ - д). (is)
i=l / г=1
где w(u) — некоторая весовая функция. Правая часть (15) является
взвешенным средним наблюдений Х{ с весами
Wi = w(Xi — θ), г = 1,... ,η.
Для подсчета θ обычно прибегают к использованию итерационного
алгоритма. Начиная с 0о = MED, вычисляются величины
ej+i = f:xMXi-ej)/itw(Xi-ej), j = o,i,..., (ΐβ)
г=1 I г=1
до тех пор, пока не будет достигнута стабилизация 0j*^
Отметим, что W-оценки являются на самом деле М-оценками
специального вида, так как в силу (15) Σ № ~~ 0) w(Xi — θ) = 0, и
г=1
значит, Σ Ψιν(Χί — θ) = 0 с i)w (и) = uw(u).
г=1
Из-за простоты вычисления популярны одношаговые W-оценки
θ ι в (16), имеющие очень хорошие характеристики: они наследуют
толерантность 1/2 выборочной медианы и обладают
асимптотической дисперсией М-оценки с φ = фи)1 задаваемой формулой (11).
Замечание 3. Если для описания данных используется не модель
сдвига, а модель сдвига-масштаба, то прежде чем оценивать сдвиг,
надо оценить параметр масштаба с помощью какой-нибудь ро-
бастной оценки, например, (нормированной) медианы абсолютных
отклонений
1
MAD =
Φ"1 (3/4)
MED{\Xi - MED\,i = 1,... ,η},
*) Процедура итерационного перевзвешивания часто применяется в
регрессионном анализе (см., например, алгоритм «LOWESS» в § 2 гл. 22).
§3. R-оценки
423
где Φ~ι (χ) —функция, обратная к функции распределения ЛГ(0,1),
1/Ф_1(3/4) « 1,483 (она ранее встречалась в § 1 гл. 19).
Толерантность MAD равна 1/2.
Затем для некоторой φ оценка параметра сдвига θ находится
как решение уравнения
С другой стороны, можно также совместно оценить параметры
сдвига и масштаба при помощи обобщения М-оценок на случай
векторного параметра (см. [84, с. 269], [89, с. 141]).
§3. Я-ОЦЕНКИ
Так называемые Д-оценки ведут свое происхождение от ранговых
критериев для проверки гипотез о значении параметра сдвига θ
(см. гл. 14, 15).
Пусть Х(!) < ... < Х(п) обозначают упорядоченные
наблюдения, d\,... ,с?п — набор неотрицательных чисел. Рассмотрим
п(п + 1)/2 полусумм вида (X(j) + Х(&))/2 при 1 ^ j ^ к ^ η (при
j = к это просто сами порядковые статистики X(j))· Каждой такой
полусумме припишем вес
Wjk = dn-(fc-j) / Σ idi- (17)
/ <=i
Легко проверить (убедитесь!), что в сумме эти веса дают 1.
Рассмотрим дискретное распределение, присваивающее вероятности
Wjk значениям (Ху) + X(k))/2. По определению, R-оценка Rn есть
медиана этого распределения.
Отметим аналогию с L-оценками Ln = ^идХ^, у которых веса
ъу< ^ 0, £ гу< = 1. В этом случае Ln есть математическое ожидание
распределения, приписывающего вероятности Wi значениям Х(<).
Пример 4. Пусть d\ = ... = dn_i = 0, dn = 1. Тогда Y^idi = η,
Wjk = l/n при j = к и равны нулю в противном случае.
Дискретное распределение, по которому строится Д-оценка, приписывает
вероятность 1/п каждому из ^(ΐ),· · · ,Χ(η)·> τ· е· Яп —это просто
выборочная медиана наблюдений.
Возьмем, наоборот, d\ = 1, с?2 = ... = dn = 0. Тогда веса
Wjk положительны, лишь когда к — j = η — 1, т. е. когда j = 1
и к = п. Таким образом, полусумме (X(i) + Х(п))/2 присваивается
вероятность 1, и Дп представляет собой середину размаха выборки.
Когда c?i = ... = dn = 1, все величины (X(j) + Х(&))/2 имеют
одинаковый вес. Медиана Rn этих полусумм появилась в § 3 гл. 8
под названием медианы средних Уолта W.
424
Глава 25. Классы оценок
1 · · · к··· η
т
Напротив, оценка Гальтона, определенная в задаче 3 гл. 8 как
θ = ΜΕϋ{ (X(i)+X(n_i+1))/2, i = l,...,[(n + l)/2]}
(здесь [·] обозначает целую часть числа), не входит в число
R-оценок. Дело в том, что полусуммам вида (X(i)+ X(n-i+i)) /%
приписаны равные веса, а всем остальным — нулевые, но согласно (17)
полусуммы, находящиеся на одной диагонали k — j = const (рис. 4),
должны иметь одинаковый вес.
Kdn Для того чтобы получить асимптотическое распределение для
Рис. 4 ^> зададим di = c?in с помощью функции ΑΓ(ί),
определенной на (0,1), неубывающей и удовлетворяющей соотношению
К{\ — t) = —K(t) (т. е. график K(t) центрально симметричен
относительно точки плоскости с координатами (1/2,0)), полагая
*■-*(=£)-*(яЫ·
Для модели сдвига Χι ~ F(x — 0), где распределение F
предполагается симметричным с (четной) плотностью р(х)1 при некоторых
условиях регулярности на К и F имеет место сходимость
τ 2
^x{Rn - θ) Λ £ ~ЛГ(0,а2(ВД),
1 / Г оо
где a2{F,K) = [ K2{t)dt I [ K'[F{x)]p2{x)dx
О ' L-oo
Как и в случае L-оценок и М-оценок, для заданной функции
распределения F существует асимптотически эффективная оценка
Д-оценка. Она соответствует функции
^№ = 7 {F~l{t)) ι гДе 7 задается формулой (4).
Пример 5. Для логистического распределения в примере 1 было
отмечено, что η{χ) = 2F(x) — 1, так что оптимальная функция
K(t) = 2t — 1, и, значит, din = 2/(2п + 1) для всех г = 1,... ,п. Так
как Д-оценка в силу соотношения (17) не меняется, когда все din
умножаются на одну и ту же положительную константу, то
получающаяся в результате асимптотически эффективная Д-оценка есть
медиана средних Уолша W. Согласно задаче 4 гл. 8 толерантность
rw = 1 - л/2/2 « 0,293.
В случае закона Коши оптимальная K(t) = — sin(27r£).
Для стандартного нормального закона η(χ) = χ и,
следовательно, K(t) = Ф_1(£), где Ф"1—обратная к функции
распределения закона ЛГ(0,1). Соответствующая ей Д-оценка называется
оценкой с нормальными весами (или метками) и обозначается
через N.
§3. R-оценки
425
Оценка N из примера 5 интересна тем, что на классе Ω, гладких
симметричных распределений (см. определение в § 1 гл. 8) она
доминирует по эффективности над оценкой X (см. [86, с. 121]).
Теорема 3. Если Xi имеют функцию распределения F(x — 0), то
eNjc(F) ^ 1 для всех F € Ωβ,
где неравенство строгое, за исключением случая F = Ф.
Тем самым N улучшает нижнюю границу медианы средних Уо-
лша W: ewjf(F) ^ 108/125 « 0,864 для всех F € Ωβ, приведенную
в теореме 4 гл. 8.
В [84, с. 146] указана толерантность τχ = 2Ф(—л/1п4) « 0,239.
Однако П. Хьюбер в [89, с. 77] высказывает мнение: «Не следует
рекомендовать N для практического использования — показатели
ее количественной робастности*) возрастают очень быстро при
отклонении от нормальной модели, и оценка N очень быстро
становится хуже, чем, например, оценка W».**)
В заключение отметим любопытную взаимосвязь между М-,
L- и Д-оценками. Для заданной F € ils и нечетной φ обозначим
через λ^ функцию, пропорциональную ^/(F_1(£)), и положим
K+=il>(F-1(t)). Тогда
^(F,^)=ai(F,^) = oJ(F,^).
Другими словами, для всякой М-оценки найдутся
асимптотически эквивалентные L-оценка и Д-оценка.
В частности, при φ = 7 согласно примерам 1, 2 и 5 имеем
а) для нормального закона с F = Ф
М: ф(х) = х, выборочное среднее X,
L: \φ(ί) = 1, выборочное среднее X,
Д: UT^(i) = Ф_1(£), оценка с нормальными весами ΛΓ;
б) для логистического распределения с F = 1/(1 + е~х)
M:^(a0 = th(s/2),
L:A^(t)=6t(l-t),
Д: ϋΓ^,(ί) = 2t — 1, медиана средних Уолша W.
К рассмотренной взаимосвязи имеет отношение следующий
результат о применении к классу L-оценок минимаксного подхода
Хьюбера (см. пример 3).
Сначала покажем, что М-оценке Хьюбера с φ = фь (независимо
от вида F) соответствует в классе L-оценок усеченное среднее Ха,
где а = F(—b). Действительно, ф'ь(х) = ^{|х|<ь}· Тогда функция Хфь
пропорциональна
Фь (F-1®) = 1, если \F-X(t)\ < Ь,
*) Приведенные в [89, с. 21].
**) Быстрый рост показателей связан с неограниченностью K(t).
426
Глава 25. Классы оценок
и равна нулю в противном случае. Так как неравенство |F-1(i)| < Ъ
эквивалентно неравенству F{—b) < t < -F(b), то Хфь(Ь) постоянна на
интервале (а, 1 — а) и равна 0 вне этого интервала.
Отсюда ввиду (13) возникает вопрос: не является ли L-оценка,
минимизирующая для G = Φ
sup σ£(^,λ),
FeQ(G,e)
усеченным средним Xa с α = Ф{—6), соответствующим оценке
Хьюбера с константой 6, определяемой по ε из соотношения (14)?
Л. Джекел в 1971 г. доказал, что это действительно так (см. [50,
с. 339]).
§4. ФУНКЦИЯ ВЛИЯНИЯ
Обозначим через Ω± = {F} множество функций, представимых
в виде F = Hi — #2, где Hi и Яг —некоторые ограниченные
неубывающие функции. Это множество включает, в частности,
произвольные функции распределения (Яг = 0). Мы будем
рассматривать функционалы Т, заданные на Ω±, τ. е. отображения из
Ω± в R.
Нас будут интересовать оценки вида T(Fn), где Fn(x) —
эмпирическая функция распределения (см. § 1 гл. 9). Например, для
функции распределения F естественными оценками
математического ожидания Ti{F) = JxdF(x) и медианы T2(F) = F_1(l/2)
являются выборочное среднее Ti(Fn) = JxdFn(x) = η-1 ΣΧί = Χ
и выборочная медиана T2(Fn) = F~l(l/2) = MED (см. § 2 гл. 7).
Чтобы понять насколько такие оценки устойчивы к «выбросам»,
Ф. Хампель (см. [84]) предложил изучить влияние на функционал
«атома» единичной массы, помещенного в точку с «большой»
координатой у (функция распределения δυ(χ) = 1{х^у})· Степень
реакции на подобное «возмущение» выражается характеристикой
А(у) = lim Ш-*)Р + Ь6У)-Т(Е)
называемой функцией влияния. Если функция А (у) неограничена
при у —* ±оо, то оценка быстро смещается в сторону «выброса», и,
следовательно, неробастна (см. § 4 гл. 8).
Вычислим А(у) для определенного выше функционала Τχ.
Пусть Ft = (1 - t) F + tSy. Тогда
Τι(Ft) = xdFt(x) = xdF(x)+t \xdSy(x) - \xdF(x)
Отсюда Ai(y) = ^ Ti(Ft) = JxdSy(x) -$xdF(x) =y- Ti(F).
Таким образом, математическое ожидание Τι имеет неограниченную
линейную функцию влияния.
§ 4. Функция влияния
427
Дифференцируя тождество 1/2 = Ft(Ff 1(1/2)), нетрудно
установить (проверьте!), что функцией влияния функционала Т2
служит А2(у) = [1/2-δυ(χι/2)]/ρ(χι/2)ι где р(я) — плотность
распределения F, #i/2 = F-1( 1/2) —медиана F. В частности, при Χι/2 = О
имеем А2(у) = [2p(0)]_1signy. Следовательно, MED = T2(Fn)
робастна при условии ρ(χι/2) > 0.
Покажем, как функция влияния связана с асимптотической
дисперсией оценки T(Fn). При некоторых условиях на функционал
Τ для произвольной функции G Ε Ω± выполняется следующее
равенство, обобщающее (18):
Jim T((l-t)F + W)-T(F) = | Α{χ) dG{x) (19)
Из него при G = F вытекает, что
lA(x)dF{x)=0. (20)
Поэтому в формулу (19) вместо dG можно подставить d(G — F).
Далее, если функция F «близка» к F, то имеет смысл
воспользоваться разложением функционала Τ в «точке» F в ряд Тейлора
до члена первого порядка:
T(F) = T(F) + ί А(х) d(F - F)(x) + ... . (21)
В силу теоремы Гливенко (см. [19, с. 201]) при η —> оо
эмпирическая функция Fn стремится к F с вероятностью 1. Взяв ее в
качестве F в формуле (21) и учитывая равенство (20), получим
Vn(T(Fn) -T(F)) « yfc \ A(x)dFn(x) = -L £ Л№). (22)
Применяя к правой части (22) центральную предельную теорему
(П6) (с точностью до обоснования законности отбрасывания
остаточного члена из (21)), выводим сходимость
V^ (T(Fn) - T(F)) Л ξ ~ Я (θ, | Л2(х) dF(x)
Отсюда, в частности, немедленно находим асимптотическую
дисперсию выборочной медианы MED (см. теорему 1 гл. 7).
В заключение приведем результат Ф. Хампеля (1968 г.),
связывающий функцию влияния и Μ-оценки (см. [84, с. 151, 173]):
для нормального закона (F = Ф) решением задачи минимизации
задаваемой формулой (11) асимптотической дисперсии a2(F^)
М-оценки при условии ограниченности ее функции влияния:
sup|i4(y)| < с, служит оценка Хьюбера с Vb(#)> где Ь определяется
по с из соотношения с = Ь/(2Ф(Ь) — 1).
•
Глава 26
БРОУНОВСКИЙ МОСТ
§ 1. БРОУНОВСКОЕ ДВИЖЕНИЕ
В § 6 гл. 14 была введена модель симметричного случайного
блуждания. Допустим, что для заданного значения η выполнено
следующее преобразование графика траектории блуждания (рис. 1):
масштаб по оси абсцисс сжат в η раз, а по оси ординат — в у/п раз. При
этом кусок графика на [0, п] преобразуется в (случайную) ломаную,
заданную на [0,1]. Обозначим ее через Wn(t). Известно (см. [12,
с. 350]), что в пределе при η —► оо на [0,1] возникает случайный
процесс W(t), называемый стандартным броуновским движением
или винеровским процессом**^. Сходимость Wn(t) к W(t) можно
понимать как сходимость конечномерных распределений
процессов: для любых 0 ζ ti < t2 < **· < tk ζ 1 последовательность
(Wn(ti),... ,W»(*k)) 4 (W(h), ■ ■ ■ ,W(tk)) (см. П5).
Процесс W(t) характеризуется следующими свойствами:
1) W(0) = 0,
2) приращения Wfo) — W(ti),... ,W(ifc) — W(tk-i) независимы,
3) W(t) - W(s) ~ Щ0, t-s)upn0^s<t,
4) траектории W(t) непрерывны с вероятностью 1.
Однако траектории процесса W(t) нигде не дифференцируемы с
вероятностью 1 (доказательство приведено, скажем, в [87, с. 65]).
Этот факт соответствует физической природе процесса, а
математически объясняется разной скоростью сжатия в горизонтальном и
Физическое явление,
описанное Робертом
Броуном, состояло в
сложном и беспорядочном
движении взвешенных в
жидкости частиц
цветочной пыльцы. За многие
годы, прошедшие со
времени этого описания*),
броуновское движение
превратилось в объект
изучения как чистой, так
и прикладной математики.
Даже теперь продолжают
обнаруживать многие его
важные свойства, и, без
сомнения, остаются еще
не открытыми новые и
полезные аспекты этого
процесса.
Г. Хидэ, [87, с. 8]
Рис. 1
*) Наблюдения проводились в 1827 г.
**) Обозначение W(t) введено в честь Н. Винера, внесшего значительный вклад
в построение теории броуновского движения.
§ 2. Эмпирический процесс
429
вертикальном направлениях ломаной случайного блуждания,
вследствие чего каждый локальный максимум (минимум) траектории
становится с ростом η все более «острым».
Из свойств 1 и 3 вытекает, что MW^(i) = 0 при всех t.
Вычислим ковариационную функцию R(s,t) = MW(s)W(t). При s < t,
используя свойства 2 и 3, находим, что
R(a,t) = M[W(s) - W(0)][W(t) - W(s)} + MW2(s) =
= M[W(s) - 0] · M[W(t) - W(s)} + 3 = 5.
В общем случае, очевидно, Д(з,£) = min{s,£}.
§2. ЭМПИРИЧЕСКИЙ ПРОЦЕСС
Построим на основе W(t) новый случайный процесс.
Определение. Броуновским мостом называется случайный
процесс B(t) = W(t) - tW(l) при 0 ^ ί < 1 (рис. 2).
Название объясняется тем, что оба конца каждой траектории
B{t) закреплены: В(0) = В(1) = 0. Нетрудно проверить, что
cov (β(β), B(t)) = min{s,t} - st.
(1)
Броуновский мост B(t) возникает в качестве предельного
процесса при описанном выше преобразовании случайного блуждания,
из которого вычитается прямая, соединяющая начало координат с
точкой (п,5п) (см. рис. 1).
Другой путь, приводящий в β(ί), состоит в изучении условного
распределения траекторий блуждания, возвращающихся в нуль в
момент η (см. [39, с. 211]). На языке процесса W(t) это
соответствует переходу к пределу при ε —► 0 на множестве броуновских
траекторий, у которых |И^(1)| < ε.
Еще один подход, приводящий к появлению броуновского моста,
который мы обсудим подробно, основан на сходимости к B(t) так
называемого эмпирического процесса
Bn(t) = y/fi(Fn(t)-t), *€[0,1],
где Fn(t)— эмпирическая функция распределения (см. § 1 гл.9),
построенная по выборке r/i,... ,r/n из равномерного распределения
на отрезке [0,1] (рис.3). Можно доказать (см. [39, с. 235]), что
конечномерные распределения Bn(t) сходятся при η —* оо к
распределениям B(t). Однако нам потребуется более сильное утверждение
о сходимости непрерывных функционалов*) от Bn{t).
W(\)
*) Функционал — это отображение из пространства функций в R.
430
Глава 26. Броуновский мост
Рассмотрим для примера статистику Un = sup Bn(t). Верно
ли, что ип-Ъи= sup B(t) при η —► оо? Нетривиальность ответа
здесь связана с невозможностью представления U как функции от
значений Bn(t) в конечном числе точек.
К тому же траектории предельного процесса B(t) непрерывны
с вероятностью 1, в то время как траектории Bn(t) имеют разрывы
в точках скачков функции Fn(t).
Для преодоления указанных трудностей рассмотрим на [0,1]
два пространства функций: С[0,1] — множество всех непрерывных
функций, £>[0,1] — множество функций, непрерывных справа (в
точке 1 слева) и имеющих лишь конечное число скачков (см. [11,
с. 40]). Так как С[0,1] С Г>[0,1], то £>[0,1] (вместе с σ-алгеброй Ли
(Ш), порожденной цилиндрическими множествами*^) можно
считать выборочным пространством процессов Bn(t) и B(t). Положим
||у|| = sup |y(*)|.
Теорема 1 (функциональная предельная теорема для
эмпирического процесса). Пусть G — функционал, определенный
на D[0,1] и непрерывный в равномерной метрике в каждой точке
Эта теорема вытекает из У € £>[0,1]: для любых уп,у G £>[0,1] условие \\уп - у\\ -+ О при
Г^Ьс.Т2зГа3аННОГ° η - оо влечет G(yn) -> G(y). Тогда G(Bn) Λ G(B).
Очевидно, рассмотренный выше для примера функционал U
удовлетворяет условиям теоремы 1. При этом распределение
случайной величины U можно найти в явном виде (см. задачу 6 гл. 14):
P(U < х) = 1 - е-2*2 при χ ^ 0.
Далее в § 3 обсуждается ряд следствий более сильного
утверждения, справедливого для дифференцируемых функционалов от
эмпирической функции распределения.
§3. ДИФФЕРЕНЦИРУЕМЫЕ ФУНКЦИОНАЛЫ
Интересно, что такие, на первый взгляд, не связанные между собой
статистические результаты, как
а) предельные распределения статистики Колмогорова и
статистики омега-квадрат (§ 2 гл. 12),
б) асимптотическая нормальность выборочных квантилей
(теорема 2 гл. 7),
в) критерий хи-квадрат (§ 1 гл. 18),
*) То есть множествами функций y(t), удовлетворяющих условиям вида
{y(ti) ^ Άι» - · · ti/(*fc) ^ -Afc}» гДе Αι,... ,Л^ — произвольные борелевские
множества (см. П2) на действительной прямой.
§ 3. Дифференцируемые функционалы
431
на самом деле вытекают из приведенной ниже теоремы 2. Для ее
формулировки потребуется следующее
Определение. Функционал G, заданный на £>[0,1], называется
непрерывно дифференцируемым порядка к в точке уо € D[011],
если существует такой функционал д(уо&), что для любой
функции ν е С[0,1] и произвольной последовательности Vh Ε J9[0, l],
\\vh —v\\ —> О ПРИ действительном h —► 0, выполняются соотношения
Второе из соотношений
G(yo + hvh) - G(yo) / \ / \ / \ означает непрерывность
— ГГ —- -* 9{y0iV), g{yOiVh) —► ЯкУоР)- в равномерной метрике
η в точках из С[0,1]
функционала g{yo,v),
который можно называть
Пример 1. Рассмотрим функционал G(y) = \\у — уо\\. Он производной порядка к от
непрерывно дифференцируем по любому направлению, так как в Уо по напРавлению ν·
G(yo) = 0,
g(y0,v) = lim <?(» + *»> = lim |W| = |H|.
/ι—>U fi h—>U
Пример 2. Для любого натурального к функционал
1
G(F)= l\F-F0\kdF,
о
где F и F0 — функции распределения случайных величин,
принимающих значения только из [0,1], является непрерывно
дифференцируемым fc-ro порядка по любому направлению, поскольку
1 1
g(F0,v) = lim С(*Ь + ^) = lim [ W* dF = Г Н* dF.
0 0
Пример 3. Покажем, что для произвольного ρ Ε (0,1) функционал
G(F) = F~1(p) = mf{t: F(t) ^ p] непрерывно дифференцируем в
точке F0(t) = t, где t Ε [0,1], причем g(F0,v) = —v(p).
Доказательство. Введем обозначение
t* = G(F0 + hvh) = inf{*: t + hvh(t) ^ p}. (2)
Так как функционал G является непрерывным в равномерной
метрике в точке i*o, мы можем положить t* = р+£, где δ = δ(Η) —► 0
при h —► 0. Из ||vfc — v|| —► 0 и г; Ε С[0,1] вытекает, что при h —► 0
ВД = |vh(p+i)-v(p)| < |νΛ(ρ+ί)-ν(ρ+ί)| + |ν(ρ+ί)-ν(ρ)| — 0. (3)
В силу (2) и (3) имеем неравенство
Ρ < F0(i*) + hvh(t*) = ρ + £ + ΛνΛ(ρ + ί) = Ρ + ί + h[v(p) + 0Д(Л)],
где |0| < 1. Аналогично можно написать обратное неравенство:
ρ > F0(t*-)+hvh(t*-) =p+5+hvh(p+5-) = ρ+£+%(ρ)+01β1(/ι)],
432
Глава 26: Броуновский мост
Доказательство
см. в [11, с. 50].
где \θ\\ < 1, R\{h) = \vh(p + δ—) - ν(ρ)\ —* 0 при h —* 0. Поэтому
[G(F0 + hvh) - G(F0)]/h = (ρ + δ- ρ)/Λ = ί/Λ -► -ν(ρ). ■
Пример 4. Рассмотрим разбиение отрезка [0,1] точками
0 = t0 < t\ < ... < £/v = 1. Тогда для F0(t) = t функционал
G(F)-£ 7s~Fo '
где AjF = F(tj) — F(tj-i), AjF0 = tj — tj-ι, будет непрерывно
дифференцируем 2-го порядка, поскольку для него
Сформулируем предельную теорему для статистик, которые
можно представить в виде дифференцируемого функционала от
эмпирической функции распределения Fn(t), построенной по выборке
г/1,... ,τ/η из равномерного распределения на [0,1].*)
Теорема 2. Если Fo(t) = ί, ί G [0,1], и функционал G(F)
непрерывно дифференцируем порядка к в i*o, то при η —* оо
nV2[G(Fn)-G(Fo)]±g(F0,B),
где В есть броуновский мост.
Следствие 1. Рассмотрим статистику критерия Колмогорова
Dn = sup \Fn(t) —1\. Ввиду примера 1 из теоремы 2, примененной
O^t^l
к функционалу Dn(Fn), вытекает, что y/nDn —► ||В||. А. Н.
Колмогоровым для функции распределения случайной величины ||В||
получено представление в виде ряда:
К(х) = Р(||В|| < х) = 1 + 2 Σ (-l)fce-2fc2*2 при χ > 0.
k=l
Распределение статистики sup \Fn(x) — F(x)\ согласно замеча-
—οο^χ^οο
нию 1 гл. 12 оказывается одним и тем же для выборки Χι,... ,ХП из
закона с произвольной непрерывной функции распределения F(x).
Замечание. Дополним объяснение из решения задачи 2 гл. 12.
Пусть 0 < μ = МХи σ2 = DXU Si = Χλ + ... + Xu 5? = $ - χμ.
Рассмотрим
ίμ + Si ιμ
ζη = y/n max
l^i<n
—= max
у/71 l^i^n
Si_ _ i
Sn П
nS?-iSn
= \fn max
ημ + Sn ^M
ημ + SjJ
= σ
ημ + £η
max
l^i^n
5?
S°n
G\fn η ay/n
) Существуют статистики, которые не представляются в таком виде, скажем,
п-1
7/(n) = max{r/i,... ,ηη} или Τ = £ ЩЩ+г-
г=1
§ 3. Дифференцируемые функционалы
433
Здесь первый сомножитель сходится по вероятности к σ/μ в
силу закона больших чисел, а второй —по распределению к
sup |W°(t)| ~ К{х). В частности, для равномерного распределе-
0<*<1
ния на отрезке [0,1] имеем μ = 1/2, σ = 1/VT2, σ/μ = 1/л/З « 0,6.
Следствие 2. Распределение статистики Крамера—Мизеса ω\ =
= J [Fn(x) — F(x)]2 dF(x) также не зависит от функции рас-
—оо
пределения F в случае ее непрерывности. Для Fo = t, t € [0,1],
^ ι ^
функционал o;£(Fn) = J[Fn(i) — t]2 dt согласно примеру 2 непре-
о
d λ
рывно дифференцируем 2-го порядка. Поэтому ηω^ —* J^2(t) eft.
о
Для предельного распределения так же, как и для К(х), известно
разложение в ряд и составлены таблицы (см. [10, с. 83, 348]).
Следствие 3. Пусть Щ\рП]+1) обозначает выборочную р-квантиль
(О < ρ < 1) (см. § 3 гл. 7) для выборки r/i,...,r/n из равномерно
распределенных на отрезке [0,1]. Тогда 77([pn]+i) = F^1(p). Ввиду
примера 3 из теоремы 2 следует, что у/п (г7(Ь>тг]+1) ~~ р) "-* ~~ В(р) ПРИ
η —► оо.
Случайная величина В(р) = W(p) — pW(l), будучи
линейной комбинацией компонент нормального вектора (W(p),W(l)),
сама распределена нормально (согласно П9). Далее, МВ(р) =
= MW(p) — pMW(l) = 0. Из равенства (1) вытекает, что
дисперсия ΏΒ{ρ) = cov (В(р), В(р)) = р(1 - р), т. е. В(р) - Af(0,p(l - р)).
Очевидно, что случайной величины —В(р) распределена так же.
Тем самым установлена асимптотическая нормальность
выборочных квантилей для выборки из равномерного распределения на
отрезке [0,1].
Для того, чтобы обобщить этот результат на случай
распределения с заданной плотностью р(х) (т. е. доказать теорему 2 гл. 7),
остается лишь применить лемму 1 гл. 7.
Следствие 4. Для F0 = t положим pj = AjFo = tj — tj-u
j = 1,... ,iV (см. пример 4). Тогда статистика хи-квадрат
Χΐ = β(Ρη)=Σ(ΑιΚ-ρι)2/ρι,
3 = 1
где nAjFn представляет собой число щ в промежутке [tj-i,tj).
Согласно примеру 4 при η —► оо
3 = 1
434
Глава 26. Броуновский мост
Покажем, что ζ ~ χ^-ι· Для этого рассмотрим случайный вектор
£ = (£ь · · · ,Ы, где 0 = AjB. Так как AjB = AjW - pjW(l), то
£ —нормальный вектор. Вычислим его ковариационную матрицу
Σ = \\ajk\\NxN- Запишем:
bjB = AjW-PjJtbkW=JtajkAkW, j = l,...,AT, (4)
fc=l fc=l
где djk = Sjk — Pj*^ В силу свойств 2 и 3 броуновского движения
M(AjW)(AkW) = SjkPj. (5)
С учетом соотношений (4), (5) и равенства pi +.. .+рлг = 1 нетрудно
вывести (проверьте!), что
N
ajk = Μ(Δ,·β)(Δ*.Β) = Σ ajiukipt = ^-fcPj -p^Pfc.
i=i
Таким образом, ковариационная матрица Σ совпадает (с
точностью до обозначений) с матрицей, задаваемой формулой (3) гл. 18.
Дальнейшие рассуждения повторяют приведенные во второй части
Нажми, водитель, тормоз, доказательства теоремы 1 гл. 18.
наконец,
Ты нас тиранил три часа
подряд,
Слезайте, граждане,
приехали, конец...
Ю. Визбор, «Охотный
ряд»
*) Здесь Sjk = 1 при j = к и Sjk = 0 при j Φ к {символ Кронекера).
ПРИЛОЖЕНИЕ.
НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ
ВЕРОЯТНОСТЕЙ И ЛИНЕЙНОЙ АЛГЕБРЫ
РАЗДЕЛ 1
АКСИОМАТИКА ТЕОРИИ ВЕРОЯТНОСТЕЙ
Вероятностной моделью называется тройка (Ω, Л, Р), где
• Ω = {α;} — множество элементарных событий ω\
• Л — такой набор подмножеств Ω, что
1) Ω€Λ _
2) если А € Л, то и его дополнение А = Ω \ А € Л,
3) если А\,А2,... принадлежат Д, то и их объединение [J Ак € Л.
Совокупность подмножеств Ω, обладающая свойствами 1-3,
называется σ-алгеброй, а сами подмножества — событиями;
• Ρ — вероятность, т. е. такая функция от событий, что
1) Р(А) ^ 0 для любого А € Л,
2) Ρ(Ω) = 1,
3) для непересекающихся событий А\ ,^2,... P((J Ак) = Σ P(-Afc)·
Целью придумавших
систему было, очевидно,
скрыть, что в этих значках
содержится какой-то
смысл.
А. Конан Дойл,
«Пляшущие человечки»
Свойство непрерывности.
Для вложенных событий А\ D A2 Э ..
lim Р(АО = Р(П
доопределение. Функция ξ(ω) называется случайной величиной, если
для произвольного числа χ множество {ω: ξ(ω) ^ χ} € Λ (в таком случае
говорят, что ξ измерима относительно σ -алгебры Λ).
Набор ξ = (£i,...,£fc) случайных величин называется случайным
вектором.
РАЗДЕЛ 2
МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ
И ДИСПЕРСИЯ
Определение. Для случайной величины ξ ^ О
Щ =|ί(α») Ρ(Λ,) = Jim ["g 1^1 Ρ (l^i <ξ < ±) +ηΡ (Ο η)
Ω
436
Приложение
Эта формула означает, что если заменить ξ дискретной случайной
величиной ζ^ таким образом, что ξ^ = (г — 1) 2~п на множестве
{or. (г — 1) 2~η ^ ξ < г2~п}, то, вычисляя М£^ и устремляя η —* оо,
приходим к пределу, который и называется М£.
Определение. Для произвольной случайной величины ξ
Щ = М£+ - М£~, где ξ+ = max{£,0}, ξ~ = -min{£,0},
и хотя бы одно из математических ожиданий конечно. В случае, когда
М£+ = М£~ = +оо, М£ (интеграл Лебега) не существует.
Определение. Борелевской σ-алгеброй В называется наименьшая σ-
алгебра, содержащая всевозможные интервалы на прямой.
Определение. Функция φ(χ) — борелевская, если она измерима относи-
тельно В (в частности, такова любая непрерывная функция).
Теорема о замене переменных. Для борелевской функции φ
+оо
SKteST" м^) = Цн)Р(<М= J*«)Fe(cfc),
Ω -οο
где F$(x) = Ρ(ξ ^ χ) —функция распределения случайной величины ξ.
+00
Следствие. Момент k-го порядка M£fc = J xkF^(dx).
— оо
Свойства математического ожидания
1) М(£ + с) = М£ + с, Щс£) = сЩ.
2) М(£ + η) = М£ + Mr/, если нет неопределенности вида оо — оо.
3) Если ξ ^ г/, то Щ ^ Mr/.
4) |М{| ^ М|{|.
5) М(^г/) = М£ · Mr/, когда ξ и г/ независимы, а М£ и Mr/ конечны.
Для случайных величин ξ и г/ таких, что М£2 < оо и Mr/2 < оо
определены
• дисперсия ϋξ = М(£ - Щ)2 = Щ2 - (Щ)2,
• ковариация cov (£, η) = Μ (ξ — M^)(r/ — Mr/) = M(^r/) — M£ Mr/,
• коэффициент корреляции ρ(ξ,η) = cov (ξ, η) /y/ΰξΤϊη.
Свойства дисперсии и ковариации
1) D(£ + c) = D£, D(cO = c2D^.
2) Если ξ и η независимы, то Ό(ξ + η) = ϋξ + Όη.
3) Для случайных величин ξι,... ,£п с конечными М£2
D ft б) = Σ D6 + 2 Σ ewte,fc) ·
4) cov (αξ + 6, cr/ + d) = ac cov (ζ, г/) и ρ(α£ + 6, ст/ + d) = p(£,r/) при
ac> 0.
5) Пусть случайный вектор ξ = (ξι,...,&) имеет
ковариационную матрицу Σ = || cov (&,£,·) \\kxk, В — произвольная числовая
(т х &)-матрица (см. раздел 10). Тогда η = Βζ имеет
ковариационную матрицу ||cov (r/i,^·) ||mXTO = ΒΣΒΤ.
Раздел 4. Вероятностные неравенства
437
РАЗДЕЛ 3
ФОРМУЛА СВЕРТКИ
Рассмотрим независимые случайные величины ξ и г/, т. е. такие, что для
любых чисел χ и у верно равенство
Ρ«<*,4<ν) = Ρ(ίΟ)Ρ(»Κν)·
Если они распределены дискретно, то в силу независимости
Р(£ + η = Xi) = Σ Ρ(ί = Xi ~ Vj,V = Уз) = Σ Р(£ = *« " Vi) Р(^ = Уз)-
3 3
Если же у них есть плотности Ρζ(χ) и ρη(χ), то плотность суммы
Pt+v(x)= Ρί(χ ~ У) Pn(v) аУ-
— оо
В общем случае функция распределения суммы независимых случайных
величин ξ и η вычисляется по формуле
+оо
F€+4(x)= J Fi(x-y)Fr](dy).
—оо
Интеграл справа называется сверткой i^(x) и Εη(χ)
(обозначается Ft* Fr,).
РАЗДЕЛ 4
ВЕРОЯТНОСТНЫЕ НЕРАВЕНСТВА
1) Для случайной величины ξ ^ 0 и любого ε > 0 верно неравенство
Чебышёва
Щ
Р« > е) <
Следствие. Взяв г/ = (ζ — М£)2, получим Ρ(\ξ — М£| ^ ε) < ^
2) М|£ту| ^ ^/Μξ2Μ?72 (неравенство Коши—Бупяковского).
Следствие. Применяя его к случайным величинам ξ' = ξ — М£
и η* = η — ΝΙη и используя свойство 4 математического ожадания,
получаем, что для коэффициента корреляции верно неравенство
\р(Ш < ι.
3) Если ψ(χ) — выпуклая вниз функция и М£, М<р(£) конечны, то
<£>(М£) ^ Μ <£>(£) (неравенство Иенсена).
Для строго выпуклых*^ φ в случае ξ ^ const неравенство строгое.
Замечание. Для бернуллиевской случайной величины ξ неравенство
Иенсена означает, что график у = φ(χ) на [0,1] лежит под хордой,
соединяющей точки с координатами (0,<^(0)) и (1,<р(1)).
*) φ(ρχ + qy) < ρφ(χ) + q<p(y) для любых х фу, 0 < ρ < 1, ς = 1 - р.
438
Приложение
РАЗДЕЛ 5
СХОДИМОСТЬ СЛУЧАЙНЫХ ВЕЛИЧИН
И ВЕКТОРОВ
Определение. Случайные величины ξι ,£г, · · · сходятся при η —► оо
к случайной величине ξ
1) почти наверное (ξη η' Η'> ξ), если Ρ {ω: ξη(ω) —► ξ(ω)} = 1;
2) в среднем квадратическом (ξη ' **> ζ)? если Μ(£η — ξ)2 —► 0;
ρ
3) по вероятности (ξη —► ξ), если Υε > 0 Ρ(\ξη — ξ\ > ε) —> 0;
4) по распределению (ξη —> £), если функции распределения F^n(x)
Буква «d» происходит сходятся к F^(x) в точках непрерывности последней.
от distribution (англ.) —
распределение. d
Пример ξη = 1/га —* ξ = 0 показывает, что функции F^n могут не
сходиться к^в точках разрыва последней: F^n(0) = 0 φ F^(0) = 1.
Случайные векторы ξη сходятся к вектору ξ в смысле п* н' >, с* "">
Ρ
или —►, если в соответствующем смысле сходятся все их компоненты.
Определение. Говорят^ что £п —*■ ξ, если М<р(£п) —> ЪЛ<р(£) для любой
непрерывной и ограниченной функции φ на Rfc.
Критерием £п —► £ является сходимость линейных комбинаций
компонент Ат£п —> Ат£ для всевозможных А = (λι,... ,λ&).
Диаграмма зависимости видов сходимости
п. н.\
с. к. I =► Ι ρ I =► Гй"
Теорема о монотонной сходимости. Пусть ξι ^ £г ^
и Μ£ι > —оо. Если ξη п' "*> ζ при η —► оо, то М£п ΐ М£.
ρ
Теорема Лебега о мажорируемой сходимости. Пусть ξη —► ξ при
η —► оо. Если найдется такая случайная величина г/, что |£η| ^ ?7
и Mr/ < оо, то
М|£|<оо, Щп-+Щ и Μ\ξη-ξ\-+0 при η -^ оо.
Свойства сходимости
Пусть а, 6, с —константы, αη, /?η, £η, ζ —случайные величины. Тогда
1) otn —►α, βη —► 6, ίη —> ί => αη Η- /?η£η —► α + 6£;
2) ίη -^ с =» ξη -^ с
3) Для любых случайных векторов £п, £ и непрерывной функции φ
на R* £п £ € =*. *>(£„) Д *>(£) и £η Λ ζ =ф. „($„) Д „(€).
Раздел 6. Предельные теоремы
439
РАЗДЕЛ 6
ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
Пусть Х\,Х2,.. . — независимые одинаково распределенные случайные
величины. Положим Sn = Χι + ... + Χη-
Усиленный закон больших чисел. Если существует μ = ΜΛΊ (не
обязательно конечное), то Sn/n η" Η> μ при η -+ оо.
Из приведенной выше диаграммы зависимости видов сходимости
ρ
следует сходимость Sn/n —► μ (закон больших чисел).
Центральная предельная теорема. Если 0 < σ2 = DXi < оо, то
о* ^п — М5П Sn — μη d гт
Sn = —у==~ = 1= ► Ζ при η -» оо,
где Ζ — стандартная нормальная случайная величина с функцией
распределения
ад-тЬ£.
е-'"*.
Обозначим через Fn(x) = P(S£ ^ ж). Центральная предельная
теорема равносильна сходимости Fn(x) —► Ф(а?) при всех х. На самом
деле можно показать, что эта сходимость является равномерной:
sup \Fn(x) — Ф{х)\ —► 0 при η —► оо.
Следующая теорема позволяет оценить скорость сходимости.
Теорема Берри—Эссеена. Пусть Μ|Χι|3 < оо. Тогда
ил / \ л/ м ^ CM|Xi -μ|3
sup |i<n(x) — Ф(х)| ^ ' при всех η,
х aay/n
где С — постоянная. ^ (Доказательство см. в [12, с. 420].)
Приведем два обобщения центральной предельной теоремы на случаи
неодинаково распределенных и зависимых слагаемых.
Теорема Линдеберга. Пусть Х\,Х2,... —независимые случайные ве-
п
личины, μι = bAXi, 0 < of = DXi < оо, αη = Μ5η = Σ Vu
η
bn = DSn = Σσϊ> d,n = {ω- \Χΐ{ώ) — μι\ > ebn}. Тогда, если для любого
г-1
ε>0
lim Ι_ ΣΜ[№-μ02^,η]=0,
το (Sn - an)/bn i Ζ ~ A/*(0,1) при η —► оо (см. [90, с. 351]).
*) Берри утверждал, что С ^ 1,88, но его вычисления содержали ошибку. Эс-
сеен показал, что С ^ 7,59. В дальнейшем С удалось уменьшить до следующих
значений: 2,9 (Эссеен, 1956); 2,05 (Уоллес, 1958); 0,9051 (В. М. Золотарев, 1966);
0,7655 (И. С. Шиганов, 1982). Известно также, что С ^ l/ν^π « 0,3989. (см.
[90, с. 402]).
440
Приложение
Последовательность ΛΊ,Λ^,... называется стационарной, если для
любого η совместное распределение (ΛΊ+ί> · · · ,Χη+i) одно и то же при
всех г. Последовательность называется т-зависимой, если (ΛΊ,.,.,Λη)
и (Xj,ATj-+i,...) независимы при j > η + m.*^
Следующая теорема —частный случай результата В. Хефдинга
и X. Робинса (1948 г.).
Теорема Хефдинга и Робинса. Пусть случайные величины Х\ ,Хг, · · ·
образуют стационарную тп-зависимую последовательность; ΜΛΊ = μ,
Μ|ΛΊ |3 < оо. Тогда при η -* оо
Sn-μη d^^ ^ σ2)) где σ2 = 0χι + 2 j» coy (Xl) Xl+i) β
y/n
3=1
РАЗДЕЛ 7
УСЛОВНОЕ МАТЕМАТИЧЕСКОЕ
ОЖИДАНИЕ
Определение. Условной вероятностью события А при условии
события В {предполагается, что Ρ (В) > 0) называется
P(A\B) = P(Af\B)/P(B).
Формула полной вероятности. Если события ЛьАг,... не
пересекаются и (J Ak = Ω, то для любого события В
Р(В) = ZP(Br\Ak) = ZP(B\Ak)P(Ak).
к к
Пусть случайные величины ξ и η имеют дискретные распределения.
Определение. Условное математическое ожидание ξ при условии
события {ω: η (ω) = y-j} есть
Μ(ξ Ι ν = Уз) = Σm p(£ = m \v = Уз)-
i
Определение. Условным математическим ожиданием М(^|г/)
называется случайная величина, принимающая на множествах вида
{ω: η(ω) = yj} значения М(£ | η = yj).
Пусть случайные величины ξ и η имеют совместную плотность
Ρ(ζ,η)(χΜ) (см- раздел 8).
Определение. Условная плотность ξ при условии η есть
Р,Ф,У) = ^{Х'У)/Р^У)'
еслирг,(у) > 0,
еслир^у) = 0.
*) Примером могут служить щ = φ(ξΐ,... ,£i+m-i)> где & — независимые и
одинаково распределенные случайные величины, φ — произвольная борелевская
функция на Rm (например, линейная).
Раздел 8. Преобразование плотности случайного вектора
441
Определение. Условное математическое ожидание ξ при условии
события {ω: η(ω) = у] задается формулой
ΓΟΟ
М(£ \ν = у) =\ χρα\τι{χ,υ) dx.
J —oo
Определение. Условное математическое ожидание М(^|г/)
—случайная величина, принимающая на множествах {ω: η(ω) = у} значения
Определение М(£ | η) в общем случае приведено в [90, с. 231].
Свойства условного математического ожидания
1) М(М(£|т/)) = М£.
2) Если ξ не зависит от г/, то М(£ | η) = М£ (п. н.).
Для любой борелевской функции φ(χ) имеют место равенства
3) Μ(ψ(η)ξ\η)=φ(η)Μ(ξ\η) (п. Η.),
4) Μ[Μ(ζ Ι η) Ι φ{η)\ = Μ(ξ \ φ(η)) (π. Η.).
РАЗДЕЛ 8
ПРЕОБРАЗОВАНИЕ ПЛОТНОСТИ
СЛУЧАЙНОГО ВЕКТОРА
Случайный вектор ξ = (£ι,... ,ξ&) (его распределение) имеет плотность
Pt(x) ^ 0, где χ = (χι,... ,Xfc), если для любого борелевского множества
BeRk
p(teB) = \pt(x)dx.
в
В частности, совместная функция распределения компонент ξ
Xl xk
Ft(x) = Ρ(£ι < χι,.,.,ζη < Xk) = "· pt(x)dxi...dxk.
-oo —oo
Плотность р£ (х) можно найти из равенств (верных почти всюду)
dkFj(x) / ч = u Pfri < & < a?i + Д,. ■., a?fc < fa < a?fc + Д)
dxi...dxk δ№ Sk
Плотность подвектора (fa,... ,fa), 1 ^ j < fc, вычисляется
интегрированием pz(x) по координатам Xj+i,... ,х&:
оо оо
ei,- >tj)(xu - - - >х*) = '" Pt(x)dxj+i...dxk.
Ρ(€ι
-оо —оо
Допустим, что соотношения у% = φ%{χ\,... ,Xfc), i = 1,... ,fc, задают
взаимно однозначное дифференцируемое отображение у = φ(χ) некоторой
442
Приложение
области из Rfc на другую. Обозначим через φ ι обратное отображение,
/ДуГ1 ... д(Ркг\
dyi дуг |
— якобиан φ (см. раздел 10).
J {у) = det
ДуГ1 ... ДуГ1
\ #2/fc dj/fc '
Формула преобразования плотности. Плотность распределения
случайного вектора η = φ(£) вычисляется по формуле
Pf,(v) = \J(v)\Pt(v~4v))-
Следствие. Если η = a + ί>£, то pv(y) = 777 Р( ( —г— 1 ПРИ ЪфО.
\Ъ\ \ b )
РАЗДЕЛ 9
ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ
И МНОГОМЕРНОЕ НОРМАЛЬНОЕ
РАСПРЕДЕЛЕНИЕ
В этом разделе i обозначает комплексное число у/—1. Используемые
термины матричного исчисления определены в разд. 10.
Определение. Характеристической функцией (х. ф.) случайной
величины ξ называется комплекснозначная функция действительного
аргумента ψζ(ί) = Ши* = Μ cos(t£) + i M sin(^).
Например, для Χ ~ Λ/*(μ, σ2) характеристической функцией служит
фх(г) = ехр ίϋμ - \<r2t2\ (см. [90, с. 296]).
По ψξ(ί) функция распределения F^(x) определяется однозначно.
оо
В частности, если J \ψξ(ί)\άί < оо, то у случайной величины ξ есть
— оо
Ж. Фурье (1768-1830), плотность, вычисляемая по формуле обратного преобразования Фурье:
французский физик
и математик.
v*{x) = h \ e_toV€(*)*·
Свойства характеристических функций
1) *е(о) = 1, |Ve(*)| ^ M|e4te| = ι.
2) Если ξ и η независимы, то
Ψϊ+η(ί) = Ши^+Г}) = М(е** · eitri) =
3) Ψα+bd*) = Meit(a+b° = eitaMei(bt)* = еиаф^(Ы).
4) Если М|£Г < оо, то ^п)(0) = гпЩп. Обратно, если существует
и конечна ф$?п)(0), то Щ2п < оо.
Раздел 9. Характеристические функции...
443
Определение. Характеристической функцией случайного вектора ζ =
= (£ι,... ,£&) называется функция от t = (ίι,... ,tk)
Теорема непрерывности. Из сходимости ζη —► ξ при η —> οο (см.
раздел 5) вытекает, что ф$п(Ь) —► ^(t) при всех t € Rfc.
Обратно: пусть ф$п (t) —► ф(Ь) при всех t, где φ непрерывна в О, тогда
φ является характеристической функцией распределения, предельного
для распределений случайных векторов £п.
Определение. Случайный вектор ξ называется нормальным с пара-
метрами μ и Σ (обозн. £ ~ Λί(μ, Σ)), где μ = (μι,... ,μ&), матрица
Σ = ||a/j||fcxfc неотрицательно определена, если
it μ - 2 t JCtj = exp < г £ ^'Mi - 2 Σ Σ vijUtj > .
Для такого вектора М£, = μ^· и cov (&, £j) = σ^.
Некоррелированность компонент нормального вектора (aij = О при
Ι Φ j) эквивалентна их независимости.
Вектор £ является нормальным тогда и только тогда, когда для
любого λ = (λί,... ,Afc) линейная комбинация его компонент λτξ имеет
нормальное распределение (см. [90, с. 322]).
Если £ ~ Λ/*(μ, Σ) и В — произвольная числовая (m x &)-матрица,
то 7j = В£ ~ λί (Βμ, ΒΣΒΤ).
Когда ранг матрицы Σ равен г < ку распределение ζ сосредоточено
в г-мерной гиперплоскости μ + Σχ, где χ пробегает Rfc.
В случае невырожденности Σ (т. е., когда г = к) нормальный вектор
ζ имеет положительную на всем Rfc плотность
р((х) = (2π)-*/2 (det JE7)-1/2exp {-§ (χ - μ)τΣ~1(χ - μ)} ,
где det Σ и Σ'1 суть соответственно определитель и обратная матрица
матрицы ковариаций Σ.
В частности, для к = 2, μι = μ2 = 0, ση = σ22 = 1, 0Ί2 = 0"2ΐ = Ρ
Pg(X'y)=Wr^eXP(" 2(1-^) j'
где ρ — коэффициент корреляции между ξι и £г (здесь \р\ < 1).
С помощью этих свойств можно показать, что нормальности
компонент недостаточно для того, чтобы вектор был нормальным.
Действительно, рассмотрим случайный вектор
(Р,п,) = J^'M)' если ζ ^ 0,
{ \tt,-M), если^<0,
где ξ ~ Λ/*(0, 1) и η ~ Л/*(0,1) независимы. Нетрудно проверить, что
каждая из компонент ξ' и г/ будет стандартной нормальной. При этом
плотность вектора (ξ',η') равна удвоенной плотности (ξ,η) в I и III
координатных углах и равна 0 во II и IV координатных углах.
444
Приложение
fan
0,21
\flml
«12
«22
Cim2 ·
αΐη\
агп
CLmn/
Если ξ ~ Α/*(μ, -Σ7) и матрица JC невырождена, то £ = μ + Αζ, где
А = Σ1/2 и ζ имеет независимые Л/*(0,1) компоненты.
Из этого представления немедленно вытекает, что для
невырожденной Σ = ||aij||fcxfc квадратичная форма (ξ — μ)τΣ~χ(ζ — μ) имеет
распределение хи-квадрат с к степенями свободы.
РАЗДЕЛ 10
ЭЛЕМЕНТЫ МАТРИЧНОГО ИСЧИСЛЕНИЯ
Определение. Прямоугольная таблица действительных чисел ац (г =
= 1,..., m; j = 1,... ,η), имеющая m строк и η столбцов, называется
(τη χ п)-матрицей (обозначается А = ||aij||mxn):
А =
Определение. Матрица, чьи столбцы являются строками матрицы А
(при сохранении их порядка), называется транспонированной по
отношению к матрице А и обозначается Ат.
Во всех формулах, где участвуют матрицы, под вектором χ =
= (xi,...,xm)T мы понимаем вектор-столбец, т.е. (т χ 1)-матрицу
с элементами х%.
Матрицу можно умножать на действительное число b путем
умножения на Ь каждого ее элемента. Матрицы одинаковой размерности можно
складывать поэлементно.
Определение. Матрица, все элементы которой равны нулю, называется
нулевой и обозначается О.
Определение. Векторы cci,...,ccfc называются линейно зависимыми,
если найдутся числа ci,... ,с*, не все равные 0, что
ciCCi + ... + CfcCCfc=0 (здесь 0 — нулевой вектор).
Ранг матрицы А определяется как максимально возможное число
линейно независимых строк (или, что эквивалентно, столбцов) А.
Определение. Произведением С = АВ (т χ 1)-матрицы А на (Ι χ η)-
матрицу В называется (τη χ η)-матрица С с элементами
ι
dj = Σ aikbkj, i = 1,... ,m; j = 1,... ,η.
fc=l -
Свойства умножения матриц
1) (АВ)Т = ВТАТ.
2) (АВ)С = А(ВС) (ассоциативность).
3) (А + В)С = АС + ВС (дистрибутивность).
Однако, в общем случае умножение некоммутативно: АВ φ ΒΑ.
Раздел 10. Элементы матричного исчисления
445
Введем еще несколько понятий, имеющих смысл исключительно для
квадратных матриц.
Определение. Верхнетреугольной (нижнетреугольной) называют
квадратную матрицу, у которой все элементы a%j под (над) главной
диагональю ац,аг2, · · ·, аПп равны нулю.
Определение. Квадратная матрица, на главной диагонали которой
стоят единицы, а остальные элементы — нули, называется единичной
и обозначается Е.
Определение. Говорят, что (η χ п)-матрица А невырооюдена, если ее
ранг равен п.
В этом случае найдется (η χ п)-матрица Ό такая, что Ό А = Е. Она
называется обратной к Л и обозначается Л-1.
Когда обратные матрицы существуют, выполняются тождества
(А7)-1 = (A-'f и {ΑΒ)-ι = Β-λΑ-\
Важнейшими характеристиками (η χ п)-матрицы А являются ее след
tr А и определитель det А. Сокращения tr и det
происходят от английских
η „ * л терминов trace (след)
Определение. Следом называется сумма элементов А на главной диа- и determinant (определи-
гонали: tr А = ац + ... + αηη· тель).
Пусть ρ = (iiyi2, · · · ΛΟ — это перестановка длины п, т.е. числа
1,2... ,п, записанные в произвольном порядке.
Определение. Определитель матрицы А задается формулой
detA = Y^Z(p)aii1a2i2...anini Z(p) = JJ siga(ii-ik).
p l<fc<i<n
Здесь ρ пробегает все п\ перестановок, sign(x) —знак числа χ.
В частности, det А = аца22 — ^12^21 ПРИ w = 2,
det A = ana22«33+tti3Ci2itt32+tti2tt23tt3i —Λ13Λ22Λ31 —«цагзлзг—«12^21^33
при η = 3 и det A = аца22--лПп для (верхне-) нижнетреугольной
матрицы.
Условие det А ф 0 равносильно невырожденности матрицы А.
Иногда удается вычислить определитель с помощью следующей
формулы, называемой разложением по i-й строке:
det А = Σ (-ΐγ+> OijMij,
где Mij — определитель матрицы, получаемой из А вычеркиванием г-й
строки и j-ro столбца. Аналогично можно разложить определитель и по
j-му столбцу.
446
Приложение
Свойства следа и определителя
1) det Ат = det А.
2) tr(AB) = tr(BA) и det(AB) = det A · det В.
Следствие 1. Если А невырождена,, то det Л-1 = Ι/det А.
Следствие 2. Пусть Ό невырождена и В = D~lAD (такую В
называют подобной А). Тогда tr В = tr А и det В = det А.
Определение. Квадратная матрица А называется симметричной, если
АТ = А.
Определение. Матрица С ортогональна, когда СТС = Ε <=$> C~l =
= Ст. (Из свойств определителя следует, что | detC| = 1.)
Теорема о приведении к главным осям. Для любой симметричной
(η χ п) -матрицы А существует ортогональная матрица С такая, что
СТАС = Л, где
/λι Ο ... 0\
Л =
О λ2 ... О
\0 0 ... λη/
причем действительные числа |λι| ^ |Аг| ^ ... ^ |λη| являются корнями
характеристического многочлена n-й степени от X
det(A-\E) = 0.
Эти корни называют собственными значениями матрицы Л, а
задачу их нахождения — проблемой собственных значений. Каждому λ*
соответствует собственный вектор е.% (иначе называемый главной осью),
ДЛЯ КОТОРОГО Aei = λίβί И β^β* = 1. ЕСЛИ Аг φ Xj, TO вг И Bj
ортогональны, т. е. efej = 0. Когда все λ* различны, собственные
оси Вг определяются однозначно с точностью до выбора направления
(одновременной смены знака всех компонент вектора). В этом случае
в качестве е% можно взять столбцы матрицы С.
Для симметричной матрицы А имеют место очевидные равенства
tr А = Σ Xi, и detA = TTAi.
i=1 г=1
Определение. Симметричная матрица А называется неотрицательно
определенной, если хТАх ^ 0 для любого вектора χ € Rn.
Замечание. Ковариационная матрица Σ произвольного случайного
вектора ζ = (ξι,... ,ξη) обладает этим свойством. Действительно,
ι Π ~ п. п.
0< Μ
= Σ Σ XiXj сом fa, ξ^) = χ Σχ.
Неотрицательная определенность А равносильна неотрицательности
всех главных миноров
Di = аи
/ ч /an ... αΐη\
D2 = det(an ai2),...,Dn=det ,
Va2i a22/ I /
4 7 \ani · · · ann/
Раздел 10. Элементы матричного исчисления
447
а также — условию, что все собственные значения λ* ^ 0.
Для неотрицательно определенной матрицы А число положительных
Ai совпадает с рангом А. Если ранг равен п, то матрица называется
положительно определенной.
Теорема Холецкого (метод квадратных корней). Для положи- А.-Л. Холецкий
тельно определенной матрицы А возможно представление е ст с*5ранцузски
А = UTU,
где U — верхнетреугольная матрица, элементы которой последовательно
вычисляются по формулам
Щ\ = оц, u\j = aij/uii, j = 2,3,... ,η; ...;
Щг = ο,α- Σ uki, v>ij = — [aij - Σ ukiUkj I , j = г + 1,
fc=l UU \ fc=l /
. ,n;
2 _ V^ 2
unn — °"nn 2-/ ukn'
fc=l
Для вычисления uu приходится извлекать квадратные корни. Это
объясняет название метода.
Метод интересен тем, что позволяет решать систему линейных
уравнений Асе = 6 с положительно определенной матрицей А примерно
вдвое быстрее метода Гаусса (после представления А в виде UTU
требуется всего лишь провести дважды «обратную прогонку»: UTy = Ь
и Uχ = у). При этом метод Холецкого численно устойчив.
Отметим, что в классе невырожденных квадратных матриц X
уравнение ХтX = А имеет много решений: подходит любая матрица
X = CU, где С — произвольная ортогональная матрица.
Действительно,
ХТХ = (CU)TCU = (UTCT) CU = UT(CTC) U = А.
Среди этих решений только одна матрица симметрична. Она
называется квадратным корнем из Λ и обозначается А1/2. Ее можно
явно указать на основе теоремы о приведении А к главным осям: если
СТАС = Λ, то А1/2 = СЛ1/2СТ. Матрица А1/2 имеет наибольший
след среди всех решений X (см. [86, с. 22]).
Обобщенная проблема собственных значений. Для
неотрицательно определенной матрицы А и положительно определенной В
найдется такая невырожденная матрица D, что
Доказательство приведено
в [6, с. 159].
DTAD = Л
D1BD = E.
Здесь Л —диагональная матрица с неотрицательными элементами
λι ^ Аг ^ ... ^ λη на главной диагонали, которые могут быть получены
как решения характеристического уравнения
det(A-AB)=0 или det (АВ~1 - ХЕ) =0.
Числа Хг называются собственными значениями матриц А и В.
448
Приложение
Доказательство. Отметим, что матрица АВ~1 не обязательно
является симметричной. Однако S = В~1/2АВ~1^2, очевидно, симметрична
(здесь β"1/2 = (β1/2)-1). Она также неотрицательно определена:
xTSx = (ттВ-1/2А^2) (а1'2В~1/2х) = \а1'2В~1/2х\2 > 0.
При этом характеристическое уравнение
det [в1/2 (в-1/2ЛВ"1/2 - \е) В1/2] =0 «=* det (S - ХЕ) = 0.
Обозначим через С ортогональную матрицу преобразования,
приводящего S к главным осям: CTSC = Л. Тогда D = В~1/2С.
Действительно,
DTAD = CTB~l/2AB~l/2C = CTSC = Λ,
DTBD = CTB~l/2Bl/2Bl/2B~l/2C = Ε.
Из доказанной теоремы легко вывести, что выполняются равенства
η п
tr(АВ"1) = Σ Xi и det(AB~l) = J\Xi ■
ТАБЛИЦЫ
Таблица 1
Случайные числа*)
Равномерно распределенные
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
1
10
37
08
99
12
66
31
85
63
73
98
11
83
88
99
65
80
74
69
09
2
09
54
42
01
80
06
06
26
57
79
52
80
45
68
59
48
12
35
91
89
3
73
20
26
90
79
57
01
97
33
64
01
50
29
54
46
11
43
09
62
32
4
25
48
89
25
99
47
08
76
21
57
77
54
96
02
73
76
56
98
68
05
5
33
05
53
29
70
17
05
02
35
53
67
31
34
00
48
74
35
17
03
05
6
76
64
19
09
80
34
45
02
05
03
14
39
06
86
87
17
17
77
66
14
7
52
89
64
37
15
07
57
05
32
52
90
80
28
50
51
46
72
40
25
22
8
01
47
50
67
73
27
18
16
54
96
56
82
89
75
76
85
70
27
22
56
9
35
42
93
07
61
68
24
56
70
47
86
77
80
84
49
09
80
72
91
85
10
86
96
03
15
47
50
06
92
48
78
07
32
83
01
69
50
15
14
48
14
11
34
24
23
38
64
36
35
68
90
35
22
50
13
36
91
58
45
43
36
46
12
67
80
20
31
03
69
30
66
55
80
10
72
74
76
82
04
31
23
93
42
13
35
52
90
13
23
73
34
57
35
83
94
56
67
66
60
77
82
60
68
75
14
48
40
25
11
66
61
26
48
75
42
05
82
00
79
89
69
23
02
72
67
15
76
37
60 1
65 1
53
70
14
18
48
82
58
48
78
51
28
74
74
10
03
88
Нормально распределенные
1
-1,75
-0,29
-0,93
-0,45
0,51
2
-0,33
0,09
0,13
-0,24
-0,88
3
-1,26
1,70
0,63
0,07
0,49
4
0,32
-1,09
0,90
1,03
-1,30
5
1,53
-0,44
1,41
1,73
-0,27
6
0,35
-0,29
-0,88
-0,06
0,76
7
-0,96
0,25
-0,10
-1,49
-0,36
8
-0,06
-0,54
0,23
-0,08
0,19
9
0,42
-1,38
0,13
-2,36
-1,08
10
-1,08
0,32
0,37 1
-0,99
0,53
*) Фрагменты таблиц из [10, с. 366, 372].
450
Таблицы
Таблица 2
Вероятности верхнего «хвоста» стандартного
нормального распределения
у = 1-ф(х) = ^= J e~u '2du
ν2π χ
χ
ГсцГ
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1Д
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2Д
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3,0
0,00
0,500
0,460
0,421
0,382
0,344
0,309
0,274
0,242
0,212
0,184
0,159
0,136
0,115
0,097
0,081
0,067
0,055
0,045
0,036
0,029
0,023
0,018
0,014
0,011
0,008
0,006
0,005
0,004
0,003
0,002
0,001
0,01
0,496
0,456
0,417
0,378
0,341
0,305
0,271
0,239
0,209
0,181
0,156
0,134
0,113
0,095
0,079
0,066
0,054
0,044
0,035
0,028
0,022
0,017
0,014
0,010
0,008
0,006
0,005
0,003
0,003
0,002
0,001
0,02
0,492
0,452
0,413
0,375
0,337
0,302
0,268
0,236
0,206
0,179
0,154
0,131
0,111
0,093
0,078
0,064
0,053
0,043
0,034
0,027
0,022
0,017
0,013
0,010
0,008
0,006
0,004
0,003
0,002
0,002
0,001
0,03
0,488
0,448
0,409
0,371
0,334
0,298
0,264
0,233
0,203
0,176
0,152
0,129
0,109
0,092
0,077
0,063
0,052
0,042
0,034
0,027
0,021
0,017
0,013
0,010
0,008
0,006
0,004
0,003
0,002
0,002
0,001
0,04
0,484
0,444
0,405
0,367
0,330
0,295
0,261
0,230
0,201
0,174
0,149
0,127
0,108
0,090
0,075
0,062
0,051
0,041
0,033
0,026
0,021
0,016
0,013
0,010
0,007
0,006
0,004
0,003
0,002
0,002
0,001
0,05
0,480
0,440
0,401
0,363
0,326
0,291
0,258
0,227
0,198
0,171
0,147
0,125
0,106
0,089
0,074
0,061
0,050
0,040
0,032
0,026
0,020
0,016
0,012
0,009
0,007
0,005
0,004
0,003
0,002
0,002
0,001
0,06
0,476
0,436
0,397
0,359
0,323
0,288
0,255
0,224
0,195
0,169
0,145
0,123
0,104
0,087
0,072
0,059
0,049
0,039
0,031
0,025
0,020
0,015
0,012
0,009
0,007
0,005
0,004
0,003
0,002
0,002
0,001
0,07
0,472
0,433
0,394
0,356
0,319
0,284
0,251
0,221
0,192
0,166
0,142
0,121
0,102
0,085
0,071
0,058
0,048
0,038
0,031
0,024
0,019
0,015
0,012
0,009
0,007
0,005
0,004
0,003
0,002
0,002
0,001
0,08
0,468
0,429
0,390
0,352
0,316
0,281
0,248
0,218
0,189
0,164
0,140
0,119
0,100
0,084
0,069
0,057
0,047
0,038
0,030
0,024
0,019
0,015
0,011
0,009
0,007
0,005
0,004
0,003
0,002
0,001
0,001
0,09
0,464
0,425
0,386
0,348
0,312
0,278
0,245
0,215
0,187
0,161
0,138
0,117
0,099
0,082
0,068
0,056
0,046
0,037
0,029
0,023
0,018
0,014
0,011
0,008
0,006
0,005
0,004
0,003
0,002
0,001
0,001
Примечание. В силу симметрии распределения Φ(—χ) — 1 — Φ(χ).
Таблицы
451
Таблица 3
Распределение хи-квадрат с к степенями свободы
1 Zp к
F 2k/2T(k/2) J0
¥^
1
2
3
4
5
6
! 7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0,001
0,000
0,002
0,024
0,09
0,21
0,38
0,60
0,86
1,15
1,48
1,83
2,21
2,62
3,04
3,48
3,94
4,42
4,91
5,41
5,92
6,45
6,98
7,53
8,09
8,65
9,22
9,80
10,4
11,0
11,6
0,025
0,001
0,05
0,22
0,48
0,83
1,24
1,69
2,18
2,70
3,25
3,82
4,40
5,01
5,63
6,26
6,91
7,56
8,23
8,91
9,59
10,3
11,0
11,7
12,4
13,1
13,8
14,6
15,3
16,0
16,8
0,05
0,004
0,10
0,35
0,71
1,15
1,64
2,17
2,73
3,33
3,94
4,58
5,23
5,89
6,57
7,26
7,96
8,67
9,39
10,1
10,9
11,6
12,3
13,1
13,8
14,6
15,4
16,2
16,9
17,7
18,5
од
0,016
0,21
0,58
1,06
1,61
2,2
2,83
3,49
4Д7
4,87
5,58
6,30
7,04
7,79
8,55
9,31
10,1
10,9
11,7
12,4
13,2
14,0
14,8
15,7
16,5
17,3
18,1
18,9
19,8
20,6
0,5
0,46
1,39
2,37
3,36
4,35
5,35
6,35
7,34
8,34
9,34
10,3
11,3
12,3
13,3
14,3
15,3
16,3
17,3
18,3
19,3
20,3
21,3
22,3
23,3
24,3
25,3
26,3
27,3
28,3
29,3
0,9
2,71
4,61
6,25
7,78
9,24
10,6
12,0
13,4
14,7
16,0
17,3
18,5
19,8
21,1
22,3
23,5
24,8
26,0
27,2
28,4
29,6
30,8
32,0
33,2
34,4
35,6
36,7
37,9
39,1
40,3
0,95
3,84
5,99
7,82
9,49
11,1
12,6
14,1
15,5
16,9
18,3
19,7
21,0
22,4
23,7
25,0
26,3
27,6
28,9
30,1
31,4
32,7
33,9
35,2
36,4
37,7
38,9
40,1
41,3
42,6
43,8
0,975
5,02
7,38
9,35
11,1
12,8
14,4
16,0
17,5
19,0
20,5
21,9
23,3
24,7
26,1
27,5
28,8
30,2
31,5
32,9
34,2
35,5
36,8
38,1
39,4
40,6
41,9
43,2
44,5
45,7
47,0
0,99
6,64
9,21
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
27,7
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
0,999
10,8
13,8
16,3
18,5
20,5
22,4
24,3
26,1
27,9
29,6
31,3
32,9
34,5
36,1
37,7
39,3
40,8
42,3
43,8
45,3
46,8
48,3
49,7
51,2
52,6
54,1
55,5
56,9
58,3
59,7
452
Таблицы
Таблица 4
Распределение Стьюдента с к степенями свободы
m±mff1+
?)"' *
ΙΓ^^ρ
i
2
3
4
5
6
7
8
9
10
12
14
16
18
20
22
24
26
28
30
32
34
36
38
40
60
οο
0,9
3,078
1,886
1,638
1,533
1,476
1,440
1,415
1,397
1,383
1,372
1,356
1,345
1,337
1,330
1,325
1,321
1,318
1,315
1,313
1,310
1,309
1,307
1,306
1,304
1,303
1,296
1,282
0,95
6,314
2,920
2,353
2,132
2,015
1,943
1,895
1,860
1,833
1,813
1,782
1,761
1,750
1,734
1,725
1,717
1,711
1,706
1,701
1,697
1,694
1,691
1,688
1,686
1,684
1,671
1,645
0,975
12,71
4,303
3,182
2,776
2,571
2,447
2,365
2,306
2,262
2,228
2,179
2,145
2,120
2,101
2,086
2,074
2,064
2,056
2,048
2,042
2,037
2,032
2,028
2,024
2,021
2,000
1,960
0,99
31,82
6,965
4,541
3,747
3,365
3,143
2,998
2,897
2,821
2,764
2,681
2,625
2,584
2,552
2,528
2,508
2,492
2,479
2,467
2,457
2,449
2,441
2,435
2,429
2,423
2,390
2,326
0,995
63,66
9,925
5,841
4,604
4,032
3,707
3,500
3,355
3,250
3,169
3,055
2,977
2,921
2,878
2,845
2,819
2,797
2,779
2,763
2,750
2,739
2,728
2,720
2,712
2,705
2,660
2,576
0,999
318,3
22,33
10,21
7,173
5,893
5,208
4,785
4,501
4,297
4,144
3,930
3,787
3,686
3,611
3,552
3,505
3,467
3,435
3,408
3,385
3,365
3,348
3,333
3,319
3,307
3,232
3,090
Примечание. В силу симметрии распределения у\-р — —ур.
Таблицы
453
Таблица 5
Распределение Фишера—Снедекора с к\ и к2
степенями свободы
ki/2vP
(ё) р-'('+Н
-(fei+fe2)/2
dv
r((fc1+fc2)/2)
μ Г(*1/2)Г(*а/2)
Для каждой пары (&2,&ι) в таблице приведены значения трех
квантилей νρ: при ρ = 0,9 (верхнее), ρ = 0,95 (среднее) и ρ = 0,99
(нижнее). Левые границы доверительных интервалов находятся из условия
V\-P(k\,k2) = l/vp{k2,k\). Интерполяцию рекомендуется проводить по
аргументам 1/к\ и l/fe. (Более подробные таблицы см. в [8], [10].)
*2\
1
2
3
4
5
6
7
8
9
ю
11
12
1
39,9
161
4052
8,53
18,5
98,5
5,54
10,1
34,1
4,54
7,71
21,2
4,06
6,61
16,3
3,78
5,99
13,7
3,59
5,59
12,2
3,46
5,32
11,3
3,36
5,12
10,6
3,29
4,96
10,0
3,23
4,84
9,65
3,18
4,75
9,33
2
49,5
200
5000
9,00
19,0
99,0
5,46
9,55
30,8
4,32
6,94
18,0
3,78
5,79
13,3
3,46
5,14
10,9
3,26
4,74
9,55
3,11
4,46
8,65
3,01
4,26
8,02
2,92
4,10
7,56
2,86
3,98
7,21
2,81
3,89
6,93
3
53,6
216
5403
9,16
19,2
99,2
5,39
9,28
29,5
4,19
6,59
16,7
3,62
5,41
12Д
3,29
4,76
9,78
3,07
4,35
8,45
2,92
4,07
7,59
2,81
3,86
6,99
2,73
3,71
6,55
2,66
3,59
6,22
2,61
3,49
5,95
4
55,8
225
5625
9,24
19,2
99,2
5,34
9,12
28,7
4Д1
6,39
16,0
3,52
5,19
11,4
3,18
4,53
9,15
2,96
4,12
7,85
2,81
3,84
7,01
2,69
3,63
6,42
2,61
3,48
5,99
2,54
3,36
5,67
2,48
3,26
5,41
5
57,2
230
5764
9,29
19,3
99,3
5,31
9,01
28,2
4,05
6,26
15,5
3,45
5,05
11,0
3,11
4,39
8,75
2,88
3,97
7,46
2,73
3,69
6,63
2,61
3,48
6,06
2,52
3,33
5,64
2,45
3,20
5,32
2,39
3,11
5,06
6
58,2
234
5859
9,33
19,3
99,3
5,28
8,94
27,9
4,01
6,16
15,2
3,40
4,95
10,7
3,05
4,28
8,47
2,83
3,87
7,19
2,67
3,58
6,37
2,55
3,37
5,80
2,46
3,22
5,39
2,39
3,09
5,07
2,33
3,00
4,82
7
58,9
237
5928
9,35
19,4
99,4
5,27
8,88
27,7
3,98
6,09
15,0
3,37
4,88
10,5
3,01
4,21
8,26
2,78
3,79
6,99
2,62
3,50
6,18
2,51
3,29
5,61
2,41
3,14
5,20
2,34
3,01
4,89
2,28
2,91
4,64
10
60,2
242
6056
9,39
19,4
99,4
5,23
8,79
27,2
3,92
5,96
14,5
3,30
4,74
10,1
2,94
4,06
7,87
2,70
3,64
6,62
2,54
3,35
5,81
2,42
3,14
5,26
2,32
2,98
4,85
2,25
2,85
4,54
2,19
2,75
4,30
20
61,7
248
6209
9,44
19,4
99,4
5,18
8,66
26,7
3,84
5,80
14,0
3,21
4,56
9,55
2,84
3,87
7,40
2,59
3,44
6,16
2,42
3,15
5,36
2,30
2,94
4,81
2,20
2,77
4,41
2,12
2,65
4,10
2,06
2,54
3,86
40
62,5
251
6287
9,47
19,5
99,5
5,16
8,59
26,4
3,80
5,72
13,7
3,16
4,46
9,29
2,78
3,77
7,14
2,54
3,34
5,91
2,36
3,04
5,12
2,23
2,83
4,57
2,13
2,66
4,17
2,05
2,53
3,86
1,99
2,43
3,62
оо
63,3
254
6366
9,49
19,5
99,5
5,13
8,53
26,1
3,76
5,63
13,5
3,11
4,37
9,02
2,72
3,67
6,88
2,47
3,23
5,65
2,29
2,93
4,86
2,16
2,71
4,31
2,06
2,54
3,91
1,97
2,40
3,60
1,90
2,30
3,36 1
454 Таблицы
13
14
15
20
25
30
40
60
120
оо
1
3,14
4,67
9,07
3,10
4,60
8,86
3,07
4,54
8,68
2,97
4,35
8,10
2,92
4,24
7,77
2,88
4,17
7,56
2,84
4,08
7,31
2,79
4,00
7,08
2,75
3,92
6,85
2,71
3,84
6,63
2
2,76
3,81
6,70
2,73
3,74
6,51
2,70
3,68
6,36
2,59
3,49
5,85
2,53
3,38
5,57
2,49
3,32
5,39
2,44
3,23
5,18
2,39
3,15
4,98
2,35
3,07
4,79
2,30
3,00
4,61
3
2,56
3,41
5,74
2,52
3,34
5,56
2,49
3,29
5,42
2,38
3,10
4,94
2,32
2,99
4,68
2,28
2,92
4,51
2,23
2,84
4,31
2,18
2,76
4,13
2,13
2,68
3,95
2,08
2,60
3,78
4
2,43
3,18
5,21
2,39
3,11
5,04
2,36
3,06
4,89
2,25
2,87
4,43
2,18
2,76
4,18
2,14
2,69
4,02
2,09
2,61
3,83
2,04
2,53
3,65
1,99
2,45
3,48
1,94
2,37
3,32
5
2,35
3,03
4,86
2,31
2,96
4,70
2,27
2,90
4,56
2,16
2,71
4,10
2,09
2,60
3,86
2,05
2,53
3,70
2,00
2,45
3,51
1,95
2,37
3,34
1,90
2,29
3,17
1,85
2,21
3,02
6
2,28
2,92
4,62
2,24
2,85
4,46
2,21
2,79
4,32
2,09
2,60
3,87
2,02
2,49
3,63
1,98
2,42
3,47
1,93
2,34
3,29
1,87
2,25
3,12
1,82
2,18
2,96
1,77
2,10
2,80
7
2,23
2,83
4,44
2,19
2,76
4,28
2,16
2,71
4,14
2,04
2,51
3,70
1,97
2,40
3,46
1,93
2,33
3,30
1,87
2,25
3,12
1,82
2,17
2,95
1,77
2,09
2,79
1,72
2,01
2,64
10
2,14
2,67
4,10
2,10
2,60
3,94
2,06
2,54
3,80
1,94
2,35
3,37
1,87
2,24
3,13
1,82
2,16
2,98
1,76
2,08
2,80
1,71
1,99
2,63
1,65
1,91
2,47
1,60
1,83
2,32
20
2,01
2,46
3,66
1,96
2,39
3,51
1,92
2,33
3,37
1,79
2,12
2,94
1,72
2,01
2,70
1,67
1,93
2,55
1,61
1,84
2,37
1,54
1,75
2,20
1,48
1,66
2,03
1,42
1,57
1,88
40
1,93
2,34
3,43
1,89
2,27
3,27
1,85
2,20
3,13
1,71
1,99
2,69
1,63
1,87
2,45
1,57
1,79
2,30
1,51
1,69
2,11
1,44
1,59
1,94
1,37
1,50
1,76
1,30
1,39
1,59
00
1,85
2,21
3,17
1,80
2,13
3,00
1,76
2,07
2,87
1,61
1,84
2,42
1,52
1,71
2,17
1,46
1,62
2,01
1,38
1,51
1,80
1,29
1,39
1,60
1,19
1,25
1,38
1,00
1,00
1,00
Таблицы
455
Таблица 7
Односторонние критические значения
коэффициента Спирмена ps
P=P(ps ^ rP)i к — размер выборки
llT^^ii
4"
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
35
40
45
50
100
0,1
1,000
0,800
0,657
0,571
0,524
0,483
0,455
0,427
0,406
0,385
0,367
0,354
0,341
0,328
0,317
0,309
0,299
0,292
0,284
0,278
0,271
0,265
0,259
0,255
0,250
0,245
0,240
0,222
0,207
0,194
0,184
0,129
0,05
0,900
0,829
0,714
0,643
0,600
0,564
0,536
0,503
0,484
0,464
0,443
0,429
0,414
0,401
0,391
0,380
0,370
0,361
0,353
0,344
0,337
0,331
0,324
0,317
0,312
0,306
0,283
0,264
0,248
0,235
0,165
0,025
1,000
0,886
0,786
0,738
0,700
0,648
0,618
0,587
0,560
0,538
0,521
0,503
0,485
0,472
0,460
0,447
0,435
0,425
0,415
0,406
0,398
0,390
0,382
0,375
0,368
0,362
0,335
0,313
0,294
0,279
0,197
0,01
0,943
0,893
0,833
0,783
0,745
0,709
0,671
0,648
0,622
0,604
0,582
0,566
0,550
0,535
0,520
0,508
0,496
0,486
0,475
0,466
0,457
0,448
0,440
0,433
0,425
0,394
0,368
0,347
0,329
0,233
0,005
1,000
0,929
0,881
0,833
0,794
0,755
0,727
0,703
0,675
0,654
0,635
0,615
0,600
0,584
0,570
0,556
0,544
0,532
0,521
0,511
0,501
0,491
0,483
0,475
0,467
0,433
0,405
0,382
0,363
0,257
0,001
1,000
0,952
0,917
0,879
0,845
0,825
0,802
0,776
0,754
0,732
0,713
0,695
0,677
0,662
0,648
0,634
0,622
0,610
0,598
0,587
0,577
0,567
0,558
0,549
0,510
0,479
0,453
0,430
0,307
Примечание. В силу симметрии распределения P(|ps| ^ гр) — 2р.
ЛИТЕРАТУРА
Классика — это то, что все
хотели бы прочитать, но
никто читать не хочет.
Марк Твен
1. Айвазян С. Α., Бухштабер В. М., Епюков И. С, Мешалкип JI. Д.
Прикладная статистика: Классификация и снижение размерности. —
М.: Финансы и статистика, 1989
2. Айвазян С. Α., Енюков И. С, Мешалкин Л. Д. Прикладная
статистика: Исследование зависимостей. — М.: Финансы и статистика,
1985
3. Айвазян С. А. Статистическое исследование зависимостей. — М.:
Металлургия, 1968
4. Александров В. В., Алексеев А. И., Горский Н. Д. Анализ данных на
ЭВМ. — М.: Финансы и статистика, 1990
5. Амелькин В. В. Дифференциальные уравнения в приложениях. —
М.: Наука, 1987
6. Амосов Α. Α., Дубинский Ю. Α., Копченова Н. В. Вычислительные
методы для инженеров. — М.: Высшая школа, 1994
7. Аптон Г. Анализ таблиц сопряженности. — М.: Финансы и
статистика, 1982
8. Арене X., Лейтер Ю. Многомерный дисперсионный анализ. — М.:
Финансы и статистика, 1985
9. Березовский Б. Α., Гнедин А. В. Задача наилучшего выбора. — М.:
Наука, 1984
10. Большее Л. Н., Смирнов Н. В. Таблицы математической
статистики. — М.: Наука, 1983
11. Боровков А. А. Математическая статистика. — М.: Наука, 1984
12. Боровков А. А. Теория вероятностей. — М.: Наука, 1986
13. Ван дер Варден Б. Л. Математическая статистика. — М.:
Издательство Иностранной литературы, 1960
14. Вихман Э. Квантовая физика. — М.: Наука, 1986
15. Воинов В. Г., Никулин М. С. Несмещенные оценки и их
применения. — М.: Наука, 1989
16. Волков Е. А. Численные методы. — М.: Наука, 1987
17. Галамбош Я. Асимптотическая теория экстремальных порядковых
статистик. — М.: Наука, 1984
18. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. — М.:
Мир, 1985
19. Гнеденко Б. В. Курс теории вероятностей. — М.: Наука, 1988
20. Двайт Г. Б. Таблицы интегралов и другие математические
формулы. — М.: Наука, 1983
Литература
457
21. Деврой Л., Дьерфи Л. Непараметрическое оценивание плотности. —
М.: Мир, 1988
22. Демидович Б. П. Сборник задач и упражнений по математическому
анализу.— М.: Наука, 1990
23. Дрейпер Я, Смит Г. Прикладной регрессионный анализ: В 2-х кн.
Кн. 1. —М.: Финансы и статистика, 1986
24. Дынкин Е. Б., Юшкевич А. А. Теоремы и задачи о процессах
Маркова. — М.: Наука, 1967
25. Дэйвисон М. Многомерное шкалирование.— М.: Финансы и
статистика, 1988
26. Дюрап Я, Оделл П. Кластерный анализ.— М.: Статистика, 1977
27. Езекиэл М., Фокс К. А. Методы анализа корреляций и регрессий.—
М.: Статистика, 1966
28. Емеличев В. Α., Мельников О. И., Сарванов В. И., Тышкевич Р. И.
Лекции по теории графов. — М.: Наука, 1990
29. Ермаков С. М., Михайлов Г. А. Статистическое моделирование. —
М.: Наука, 1982
30. Жамбю М. Иерархический кластер-анализ и соответствия. — М.:
Финансы и статистика, 1988
31. Журбенко И. Г. Анализ стационарных и однородных случайных
систем. — М.: Издательство МГУ, 1987
32. Ивченко Г. И., Медведев Ю. И. Математическая статистика. — М.:
Высш. шк., 1984
33. Карлин С. Основы теории случайных процессов. — М.: Мир, 1971
34. Картер А. Структурные изменения в экономике США. — М.:
Статистика, 1974
35. Кендалл М. Дою., Стьюарт А. Статистические выводы и связи. —
М.: Наука, 1973
36. Кендэл М. Ранговые корреляции.— М.: Статистика, 1975
37. Кимбл Г. Как правильно пользоваться статистикой. — М.: Финансы
и статистика, 1982
38. Козлов М. В.t Прохоров А. В. Введение в математическую
статистику. — М.: Издательство МГУ, 1987
39. Козлов М. В. Элементы теории вероятностей в примерах и
задачах. — М.: Издательство МГУ, 1990
40. Кокс Д., Льюис П. Статистический анализ последовательностей
событий. — М.: Мир, 1969
41. Колмогоров Л. Я, Фомин С В. Элементы теории функций и
функционального анализа.— М.: Наука, 1989
42. Корн Г., Корн Т. Справочник по математике для научных
работников и инженеров.— М.: Наука, 1984
43. Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия.—
М.: Наука, 1986
44. Крамер Г. Математические методы статистики. — М., 1975
45. Кудрявцев Л. Д. Курс математического анализа, Т. 1. —М.:
Высш. шк., 1988
46. Кудрявцев Л. Д. Курс математического анализа, Т. 2. — М.:
Высш. шк., 1988
47. Кульбак С. Теория информации и статистика. — М.: Наука, 1967
48. Ламперти Дою. Вероятность. — М.: Наука, 1973
458
Литература
49. Ланкастер П. Теория матриц. — М.: Наука, 1982
50. Леман Э. Теория точечного оценивания. — М.: Наука, 1991
51. Литлвуд Дою. Математическая смесь. — М.: Наука, 1978
52. Мандель И. Д. Кластерный анализ.— М.: Финансы и статистика,
1988
53. Математика и САПР, Кн. 1. — М.: Мир, 1988
54. Миллс Ф. Статистические методы. — М.: Госстатиздат, 1958
55. Мину М. Математическое программирование. — М.: Наука, 1990
56. Миркин Б. Г. Анализ качественных признаков и структур. — М.:
Статистика, 1980
57. Мостеллер Ф., Тьюки Дою. Анализ данных и регрессия. — М.:
Финансы и статистика, 1982
58. Мэйндоналд Дою. Вычислительные алгоритмы в прикладной
статистике. — М.: Финансы и статистика, 1988
59. Никольский С М. Курс математического анализа, Т. 2. — М.: Наука,
1983
60. Орлов А. И. Некоторые вероятностные вопросы теории
классификации. Прикладная статистика. — М.: Наука, 1983.-е. 166-179
61. Питмен Э. Основы теории статистических выводов. — М.: Мир, 1986
62. Пойа Д. Математическое открытие. — М.: Наука, 1976
63. Практикум по математической статистике / Под
редакцией Н. С. Бахвалова, Ю. А. Розанова, И. Г. Журбенко, А. В.
Михалева. — М.: Издательство МГУ, 1987
64. Прасолов В. В. Задачи по планиметрии, Ч. 2. — М.: Наука, 1991
65. Прохоров Ю. В., Розанов Ю. А. Теория вероятностей. — М.: Наука,
1987
66. Рей Г. Звезды. Новые очертания старых созвездий. — М.: Мир, 1969
67. Рейф Ф. Статистическая физика. — М.: Наука, 1986
68. Розанов Ю. А. Введение в теорию случайных процессов. — М.:
Наука, 1982
69. Розанов Ю. А. Теория вероятностей, случайные процессы и
математическая статистика. — М.: Наука, 1985
70. Сархан Α., Гринберг Б. Введение в теорию порядковых статистик. —
М.: Статистика, 1970
71. Себер Дою. Линейный регрессионный анализ. — М.: Мир, 1980
72. Секей Г. Парадоксы в теории вероятностей и математической
статистике. — М.: Мир, 1990
73. Сидоров Ю. В., Федорюк М. В., Шабунин М. И. Лекции по теории
функций комплексного переменного. — М.: Наука, 1982
74. Соболь И. М., Статников Р. Б. Выбор оптимальных параметров в
задачах со многими критериями. — М.: Наука, 1981
75. Справочник по прикладной статистике, Т. 1 / Под редакцией
Э. Ллойда, У. Ледермана. — М.: Финансы и статистика, 1989
76. Справочник по прикладной статистике, Т. 2 / Под редакцией
Э. Ллойда, У. Ледермана. — М.: Финансы и статистика, 1989
77. Сухарев А. Г., Тимохов А. В., Федоров В. В. Курс методов
оптимизации. — М.: Наука, 1986
78. Терехина А. Ю. Анализ данных методами многомерного
шкалирования. — М.: Наука, 1986
Литература
459
79. Тугпубалин В. Н. Теория вероятностей и случайных процессов. — М.:
Издательство МГУ, 1992
80. Тюрин Ю. #., Макаров А. А. Анализ данных на компьютере. — М.:
ИНФРА-М, Финансы и статистика, 1995
81. Феллер В. Введение в теорию вероятностей и ее приложения, Т. 1. —
М.: Мир, 1984
82. Феллер В. Введение в теорию вероятностей и ее приложения, Т. 2. —
М.: Мир, 1984
83. Хальд А. Математическая статистика с техническими
приложениями.—М.: ИЛ, 1956
84. Хампель Ф., Рончетптпи Э., Рауссеу П., Штаэль В. Робастность в
статистике. Подход на основе функций влияния. — М.: Мир, 1989
85. Хардле В. Прикладная непараметрическая регрессия. — М.: Мир,
1993
86. Хеттманспергер Т. Статистические выводы, основанные на
рангах. — М.: Финансы и статистика, 1987
87. Хида Т. Броуновское движение. — М.: Наука, 1987
88. Холлепдер М., Вулф Д. Непараметрические методы статистики.—
М.: Финансы и статистика, 1983
89. Хьюбер П. Робастность в статистике. — М.: Мир, 1984
90. Ширяев А. Н. Вероятность. — М.: Наука, 1989
91. Яблонский С В. Введение в дискретную математику. — М.: Наука,
1986
92. Яглом А. М., Яглом И. М. Вероятность и информация.— М.: Физ-
матгиз, 1960
93. Cochran W. G., Cox G. M. Experimental Designs, 2nd ed. — New York.:
Wiley, 1957
ОБОЗНАЧЕНИЯ И СОКРАЩЕНИЯ
О книгах Жордана Ш,... ,Ш0 — ссылки, соответственно, на разделы 1,... ,10 прило-
говорили, что если
ему нужно было ввести
Дж. Литлвуд, [51, с. 46]
жения
'£3%ΖΖΖΖΤ С* = «!/(*!(» - fc)!) - где п! = 1 · 2 ·... · (п - 1) · п, 0! = 1
бГ^То они^'нег^' £ ~ — случайная величина ξ распределена по закону (рас-
получали обозначения а, пределена так же, как)
п„ /т..™.,- гк1 ^ αλί •Л/'СОД)? Ν{μ,Σ) — стандартный (§2 гл. 3) и многомерный (П9)
нормальные законы
χΙ —распределение хи-квадрат с к степенями свободы
(§ 2 гл. 11)
Fklyk2 — распределение Фишера— Снедекора с к\ и к%
степенями свободы (§ 5 гл. 14)
Γ(α,λ) — гамма-распределение с параметрами а и λ (§ 4 гл. 3)
Г(р), #(r,s) —гамма- и бета-функции Эйлера (§ 4 гл. 3)
—:—^, *>,—>, —» —символы сходимости почти наверное, в
среднем, по вероятности, по распределению (П5)
Ια —индикатор множества А (§1 гл. 1)
sign χ — знак числа χ (§5 гл. 4)
Ρ (А) —вероятность события А (Ш)
Ρ (А | В) — условная вероятность А при условии В (П7)
Fz(x), Ρξ(χ), Ψξψ) —функция распределения, плотность (§ 1 гл. 1)
и характеристическая функция случайной
величины ξ (Π9)
Μ ξ —математическое ожидание случайной величины ξ
(§ 2 гл. 1, П2)
Μ (ξ Ι ν) — условное математическое ожидание ξ при условии η
(П7)
D£ —дисперсия случайной величины ξ (§ 2 гл. 1, П2)
cov (£, η) — ковариация случайной величины ξ и η (Π2)
Обозначения и сокращения
461
Rn — n-мерное действительное пространство
£ = (£ъ · · · >£п) — n-мерный случайный вектор (набор случайных
величин)
Ft(xi,... ,#η), Ρζ(χι1... ,#п) — функция распределения, плотность
случайного вектора £ (Π8)
Cov(£) — матрица ковариаций случайного вектора ξ (Π2)
X = (Χι + ... + Хп)/п — выборочное среднее наблюдений
Х(!) < Х(2) < · · · < Х{п) — вариационный ряд выборки Χι,... ,ХП,
элементы вариационного ряда — порядковые
статистики (§ 4 гл. 4)
det A, tr А —определитель и след матрицы А (ШО)
А , А-1, А1'2 — транспонированная, обратная матрицы и
квадратный корень из матрицы А (ШО)
а>п = о(Ьп) — an/bn -+ О,
a>n~bn — an/bn —► 1
a>n = 0(bn) — последовательность an/bn ограничена
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютный риск 390
аддитивная константа 329
аксиоматика теории
вероятностей 435
алгоритм Дж. Мак-Кина
293
- Форель 293
- степенной метод 324
- быстрый 298
альтернатива возрастания
уровня фактора 245
- эффектов обработок
263
- доминирования 200
- масштаба 200
- неоднородности 200
- правого сдвига 200
анализ межотраслевых
связей 331
- точек зрения 332
антиградиент 339
антиранг 232
арксинус-распределение 61
асимптотическая
дисперсия 90
- толерантность 105
- эквивалентность оценок
425
-эффективность 119
асимптотически
нормальная оценка 90, 91
- статистика 89
Баланс между дисперсией
и квадратом смещения
395
бета-распределение 61
бета-функция Эйлера 36
биномиальное
распределение 58
блуждание возвратное 250
- случайное 248
броуновский мост 429
быстрые алгоритмы 298
Вариационный ряд 48
вектор нормально
распределенный 443
- остатков 362, 372
- ошибок 361
- равномерно
распределенный 12, 323
векторы линейно
независимые 371
вероятностная бумага 112
вероятность вернуться
в нуль впервые
в момент 2п 267
когда-нибудь 267
- невозвращения 268
- разорения первого
игрока 191
вершины правильного
симплекса 329
взаимосвязи признаков 317
взвешенная евклидова
метрика 333
- сумма 239
взвешенное среднее 374,
393, 422
винеровский процесс 428
влияние сериальной
корреляции 227
восприятие на слух
болгарских согласных
336
времена реакции 221
время возвращения
блуждающей частицы
в начало координат
266
выбор единиц измерения
289
- меры близости 290
- точки наудачу 9, 12
выборка 42
-, размах 261
выборочная дисперсия 74,
125
- проекций на
направление 318
- квантиль 87
- медиана 86, 423, 426
- приращений 221
выборочное среднее 73, 426
выборочные
коэффициенты асимметрии
и эксцесса 169
выборочный коэффициент
корреляции 343
выделение связных
компонент графа 312
выпуклая оболочка 195
Гамма-функция Эйлера 35
генетические законы
Менделя 276
гессиан 384
гипергеометрический ряд
252
гипергеометрическое
распределение 252
гипотеза допустимости
понижения размерности
371
- мультипликативности 351
- независимости 343, 351
- нормальности 167
- об адекватности 371
- однородности 237, 243,
304, 370
- показательности 164
- простая 165, 181
- равномерности 163
- симметричности
распределения 222, 224
- сложная 165, 181
гистограмма
межобъектных расстояний 292
главные оси или
компоненты 318
гравитационное поле звезд
93
Данные центрированные
317
датчики 19
Предметный указатель
463
двойное центрирование 326
двумерная плотность
Коши 98
двухфакторная модель 259
дендрограмма 295
диаграмма рассеяния 289,
307
диаметр разбиения 11
дискретная формула
свертки 141, 437
дисперсионный анализ 244,
262
- двухфакторный 370
дисперсия 12
длина «нисходящей серии»
45
доверительный интервал
асимптотический 145
- центральный 151
Евклидово расстояние 326
Зависимость наблюдений
227
задача аппроксимации
матрицы связей 308
- Коши 26, 192
- краевая 192
- наилучшего выбора 52
- о совпадениях 135
закон больших чисел 439
- Вейбулла—Гнеденко 45
- Коши 12, 419, 424
- Лапласа 93, 420
- показательный 42
- редких событий 59
- сохранения момента
импульса 161
заполнение пропусков 341
золотое сечение 17, 341
зрительное восприятие
букв 333
Избыточность языка 174
индикатор множества 9
- наличия пропуска 342
интерполяционный
полином 377
информация Фишера 114
Каркас 292
квадратичный риск 76,
390, 395
квартическое ядро 294
классы 290
кластер 289, 291, 309
код Хемминга 174
количество инверсий 90,
345
контраст эффектов
обработок 261
корреляционный анализ
317
коэффициент корреляции
выборочный 155
- Кендэла 345
- обобщенный 346
- обычный 346
- Спирмена 343
- частный 350
коэффициенты
асимметрии и эксцесса 169
кривая регрессии 392, 398
критерий Андерсона—Дар-
линга 164
- Бартлетта 244
- Данна 246
- Джонкхиера 245
- знаковых рангов 222
- Колмогорова 162
- Крамера—Мизеса 164
- Краскела—Уоллиса 237
- Лебега 41
- Мозеса 414
- несмещенный 181
- Пейджа 263
- равномерно наиболее
мощный 187
- ранговых сумм Уилкок-
сона—Манна—Уитни
205
- серий 229
- согласия 161
- состоятельный 181
- статистический 160
- Фридмана 260
- хи-квадрат 273
F-критерий двухфактор-
ного дисперсионного
анализа 262
- однофакторного
дисперсионного анализа 243
критическое значение 161
- множество 181
Логистическая кривая 379
логистическое
распределение 418, 420, 424, 425
логнормальная модель 112
локальное усреднение 393
Маргинальная плотность
393
математические датчики
21
математическое ожидание
10
матрица выборочная
ковариационная 301,
317
- внутриклассового
разброса 300
- , евклидова норма 321
- информационная 362
- ковариаций 363, 436
- плана эксперимента 361
- положительно
определенная 446
- разброса между
классами 300
- рассеяния класса 300
- связей 308
- скалярных произведений
321
- , собственные значения
317, 446
медиана (нормированная)
абсолютных
отклонений 422
- средних Уолша 224, 423
межклассовый разброс 299
мера концентрации 307
- неупорядоченности 346
- общего разброса 319
- общей изменчивости
внутри выборок 243
- отдаленности 294
- Колмогорова 295
- отклонения 273
- «разброса» 419
- между выборками 244
метод Дейкстры 311
- главных проекций 326
- наименьших квадратов
335
- наискорейшего спуска
339
464
Предметный указатель
- Ньютона 339
- (метод касательных)
119
- прямоугольников 30
- середины квадрата 21
- сопряженных градиентов
339
- степенной 320
- стрельбы 192
- суперпозиции 62
- Хафмана 174
- Холецкого 335
- центров масс 297
- Эйлера 26
метрика евклидова 290
- манхеттенская 290
- Хемминга 290
- Чебышёва 290
- city-block 290
минимаксный подход
Хьюбера 421
минимальный спейсинг 56
минимальное
покрывающее дерево 292
мода распределения 67,
147
модель сдвига-масштаба
110, 112, 124
- случайного выбора 253
- Фишера 313
модифицированные
статистики Колмогорова
и Крамера—Мизеса
166
модифицированный метод
Неймана (расслоенная
выборка) 65
момент выхода 187
- инерции 10
- объединения 297
моменты центральные
выборочные 169
- теоретические 169
мультипликативный
датчик 21
«Наименее благоприятное
распределение»
Хьюбера 421
нарушение однородности
147
независимость выборок 201
- случайных величин 12
нелинейные методы
понижения размерности
337
необходимость
объединения маловероятных
промежутков 279
непараметрические методы
99
неравенство Иенсена 437
-Ляпунова 112
- Коши—Буняковского—
Шварца 324, 437
- треугольника 329
неразличимые шары 137
нормальное распределение
242
нормированные полиномы
Бернштейна 63
носитель распределения
114
Область притяжения 305
обнаружение
фальсификации данных 408
обобщенный
биномиальный коэффициент 267
общая внутриклассовая
инерция 299
- изменчивость (разброс,
дисперсия) 244
- матрица рассеяния 300
однородность нормальных
выборок 207
односторонний критерий
203
оператор проецирования
(проектор) 364
определитель Вандермонда
361
оптимальная плотность
390, 391
орбиты планет и комет 161
ортогональная проекция
362
ортогональное дополнение
372
- планирование
эксперимента 364
основное свойство гамма-
функции 35
основные понятия теории
проверки
статистических гипотез 159
остаточная сумма
квадратов 362
относительная
асимптотическая эффективность
91
- доля разброса 105
отрицательная
симметричность 346
оценка асимптотически
нормальная 90, 91, 105
- взвешенных наименьших
квадратов 394
- Гальтона 106, 424
- максимального
правдоподобия 116
- метода моментов 113
- метода наименьших
квадратов 362
- Надарая—Ватсона 394
- , непрерывность в
равномерной метрике 343
- несмещенная 73, 364
-эффективная 115
- одношаговая 121
- параметров сдвига
и масштаба с помощью
МНК 375
- первичная контраста 261
- робастная 99
- Розенблатта—Парзена
389
-сверхэффективная 116
- с нормальными весами
(или метками) 424
- сильно состоятельная 119
- состоятельная 75
- уточненная контраста
262
- Ходжеса—Лемана 78
L-оценка 417
М-оценка 420
Я-оценка 423
W-оценка 422
ошибки I и II рода 180
Парадокс критерия хи-
квадрат 281
параметрическое
множество 114
Предметный указатель
465
первичная оценка
контраста 239
переменные
количественные 350
- порядковые (ранговые)
350
- предикторные 357
плотность Коши 54, 84
поверхность регрессии 398
погрешность метода
прямоугольников 30
подгонка полинома 361
поиск в глубину 311
покоординатный спуск 335
полиномиальное
распределение 134
полиномы Бернштейна 62
поправки на
непрерывность 220
порядковые статистики 48
последовательность вполне
равномерная 37
- равномерная по Вейлю
36
последовательный
критерий Вальда 187
постоянная Планка 184
прирост общей
внутриклассовой инерции 296
пробная прямая 358
проверка нормальности
по сгруппированным
данным 279
производные кривой
регрессии 396
процедура Грама—Шмидта
363
- итерационного
перевзвешивания 422
псевдослучайные числа 19
Равновероятные
промежутки 276
равномерные спейсинги 48
разделение многомерных
нормальных законов
(дискриминантный
анализ) 305
разделительная
гиперплоскость 313
разложение по первому
шагу блуждания 191
размах выборки 126
разность вторая
симметричная 192
- конечная 192
ранг 204, 343
- средний 344
распределение
- арксинуса 212
- Бернулли 10
- бета-распределение 61
- биномиальное 58
- гамма-распределение 47
- Коши 54
- нормальное 31
- показательное 9
- Пуассона 59
- равномерное 9
- сильно унимодальное 419
- Стьюдента 148
-хи-квадрат 147
- Хольцмарка 93
- экстремальных значений
44
^-распределение 148
расслоенная выборка
(выборка по группам)
33
расстояние Бхаттачария
306
- Махаланобиса 303
- Минковского 290
регрессионный анализ 317
регрессия 357
регулярные статистические
модели 114, 119
редуктивность
(сводимость) 297
риск абсолютный 76
- квадратичный 76
Свойства гладкости 389
свойство префикса 174
связь между
коэффициентами 346
сгущение в среднем 291
сдвиг распределения
Лапласа 124
середина размаха выборки
423
серия 230
символы равновероятные
174
симметричное случайное
блуждание 93
симметричные гладкие
распределения 99
система базисных функций
371
систематическая ошибка
146
слабое сгущение 291
случайная величина 7, 435
случайный вектор 435
смесь нормальных законов
104
- распределений 62
сообщения типичные 173
соотношение
неопределенностей 184
состоятельность 75
спейсинги 122
- равномерные 140
список смежности 312
способы выбора порогов
298
среднее абсолютное
отклонение 104
- арифметическое 203
- время до разорения
одного из игроков 192
- гармоническое 203
- геометрическое 203
- квадратичное отклонение
104
- число падений на один
участок 278
среднеквадратическое
рассеяние 323
средние Уолша 102, 224
средняя внутрикластерная
связь 309
- межкластерная связь 309
стандартное броуновское
движение 428
- отклонение 12, 34, 74
стандартный нормальный
закон 418
статистика 89
- асимптотически
нормальная 89
- Бозе—Эйнштейна 138
-достаточная 129
- критерия 160
- Ансари—Брэдли 412
466
Предметный указатель
- Джонкхиера 245
- знаковых рангов 223
- знаков 220
- Краскела—Уоллиса 238
- омега-квадрат 163
- - Пейджа 263
- Фридмана 260
- Максвелла—Больцмана
138
- Ферми—Дирака 138
статистическая гипотеза
164
степенное среднее 295
степень разделенности 311
стрельба по площадной
цели 278
сумма внутриклассовых
дисперсий 299
сходимость конечномерных
распределений 428
- в среднем квадратиче-
ском 438
- по вероятности 75, 438
- почти наверное 438
- по распределению 438
считающая форма 205
Таблица сопряженности
(признаков) 350
тауберова теорема 70
теорема Гливенко 162, 427
- Берри—Эссеена 439
- Гюйгенса 255
- Лебега о мажорируемой
сходимости 438
- Линдеберга 439
- Макмиллана 173
- непрерывности 443
- о вычетах 85
- о замене переменных 436
- о межточечных
расстояниях 347
- о монотонной сходимости
438
- о приведении к главным
осям 446
- Пойа 250
- функциональная
предельная для
эмпирического процесса
430
- Хефдинга и Роббинса 440
- Холецкого 447
- центральная предельная
439
теоретические
коэффициенты асимметрии 169
типичное внутриклассовое
расстояние 292
- межклассовое расстояние
292
тренд 398
Узлы 361, 393
- равномерной сетки 30
уменьшение размерности
319
упорядочение
симметричных распределений по
весу их хвостов 226
уравнение баланса 229
уровень значимости 160
усеченное среднее 100
условие строгой симметрии
224
условия регулярности 114,
119
условная предельная
теорема 230
уточненная оценка
контраста 239
Фактический уровень
значимости 161
формула Ланса—Уильямса
296
- свертки 437
- Стирлинга 175, 211
фрактал 25
функция весовая 422
- влияния 426
- Лагранжа 127, 286, 318
- мощности 181
-правдоподобия 116
- сгруппированной
выборки 285
- производящая 266
- равномерно непрерывная
63
- распределения 8
- риска 76
- Розенброка 340
- характеристическая 443
- центральная 151
- штрафа (потерь) 76
- эмпирическая
распределения ПО, 162, 342
Хвосты распределения 43
Центральная
симметричность плотности 403
центры масс классов 303
цепочечный эффект 295
Частная или «очищенная»
корреляция 348
частоты попадания
в промежутки 273
число инверсий 183
- серий 230
Ширина «окна
сглаживания» 392
шкалирование
индивидуальных различий 332
Экономичность критерия
Вальда 190
экспоненциальное
семейство 132
эллипсоид рассеяния 322
эмпирическая функция
распределения ПО
эмпирический процесс 429
эмпирическое
распределение 322
эффект воздействия 219
- существенной
многомерности 288
Ядро 391
- Гаусса 391
- квартическое 391
- нормальное 391
- прямоугольное 391
- треугольное 391
ОГЛАВЛЕНИЕ
Предисловие 3
К читателю 5
Часть I. Вероятность и статистическое
моделирование 7
Глава 1. Характеристики случайных величин 7
§ 1. Функции распределения и плотности 7
§ 2. Математическое ожидание и дисперсия 10
§3. Независимость случайных величин 12
§ 4. Поиск больных 13
Задачи 14
Решения задач 15
Ответы на вопросы 18
Глава 2. Датчики случайных чисел 19
§ 1. Физические датчики 19
§ 2. Таблицы случайных чисел 20
§ 3. Математические датчики 21
§ 4. Случайность и сложность 22
§ 5. Эксперимент «Неудачи» 24
§6. Теоремы существования и компьютер 26
Задачи 26
Решения задач 27
Ответы на вопросы 29
Глава 3. Метод Монте-Карло 30
§ 1. Вычисление интегралов 30
§ 2. «Правило трех сигм» 31
§ 3. Кратные интегралы 32
§4. Шар, вписанный в fc-мерный куб 35
§ 5. Равномерность по Вейлю 36
§ 6. Парадокс первой цифры 37
Задачи 38
Решения задач 39
Ответы на вопросы 41
468 Оглавление
Глава 4. Показательные и нормальные датчики 42
§ 1. Метод обратной функции 42
§ 2. Распределения экстремальных значений 43
§ 3. Показательный датчик без логарифмов 45
§ 4. Быстрый показательный датчик 46
§ 5. Нормальные случайные числа 50
§ 6. Наилучший выбор 52
Задачи 54
Решения задач 54
Ответы на вопросы 57
Глава 5. Дискретные и непрерывные датчики 58
§ 1. Моделирование дискретных величин 58
§ 2. Порядковые статистики и смеси 60
§ 3. Метод Неймана (метод исключения) 64
§ 4. Пример из теории игр 66
Задачи 67
Решения задач 68
Ответы на вопросы 69
Часть П. Оценивание параметров 71
Глава 6. Сравнение оценок 72
§ 1. Статистическая модель 72
§ 2. Несмещенность и состоятельность 73
§ 3. Функции риска 76
§ 4. Минимаксная оценка в схеме Бернулли 78
Задачи 79
Решения задач 80
Ответы на вопросы 83
Глава 7. Асимптотическая нормальность 84
§ 1. Распределение Коши 84
§ 2. Выборочная медиана 86
§ 3. Выборочные квантили 87
§ 4. Относительная эффективность 89
§ 5. Устойчивые законы 91
Задачи 93
Решения задач 94
Ответы на вопросы 98
Глава 8. Симметричные распределения 99
§ 1. Классификация методов статистики 99
§ 2. Усеченное среднее 100
§ 3. Медиана средних Уолша 102
§4. Робастность 103
Задачи 106
Решения задач 106
Ответы на вопросы 109
Глава 9. Методы получения оценок ПО
§ 1. Вероятностная бумага ПО
§ 2. Метод моментов 112
§ 3. Информационное неравенство 114
§4. Метод максимального правдоподобия 116
§ 5. Метод Ньютона и одношаговые оценки 119
§ 6. Метод спейсингов 122
Задачи 123
Решения задач 124
Ответы на вопросы 127
Глава 10. Достаточность 129
§ 1. Достаточные статистики 129
§ 2. Критерий факторизации 130
§ 3. Экспоненциальное семейство 132
§ 4. Улучшение несмещенных оценок 133
§ 5. Шарики в ящиках 134
Задачи 140
Решения задач 141
Ответы на вопросы 144
Глава 11. Доверительные интервалы 145
§ 1. Коэффициент доверия 145
§ 2. Интервалы в нормальной модели 146
§ 3. Методы построения интервалов 151
Задачи 155
Решения задач 156
Ответы на вопросы 158
Часть III. Проверка гипотез 159
Глава 12. Критерии согласия 160
§ 1. Статистический критерий 160
§ 2. Проверка равномерности 161
§ 3. Проверка показательности 164
§ 4. Проверка нормальности 167
§ 5. Энтропия 170
Задачи 175
Решения задач 175
Ответы на вопросы 178
Глава 13. Альтернативы 180
§ 1. Ошибки I и II рода 180
§ 2. Оптимальный критерий Неймана—Пирсона 183
§ 3. Последовательный анализ 187
§ 4. Разорение игрока 190
§ 5. Оптимальная остановка блуждания 193
Задачи 195
Решения задач 195
Ответы на вопросы 197
470 Оглавление
Часть IV. Однородность выборок 199
Глава 14. Две независимые выборки 200
§ 1. Альтернативы однородности 200
§ 2. Правильный выбор модели 201
§ 3. Критерий Смирнова 202
§ 4. Критерий Розенблатта 203
§ 5. Критерий ранговых сумм Уилкоксона 204
§ 6. Принцип отражения 209
Задачи 214
Решения задач 215
Ответы на вопросы 217
Глава 15. Парные повторные наблюдения 219
§ 1. Уточнение модели 219
§ 2. Критерий знаков 220
§ 3. Критерий знаковых рангов Уилкоксона 222
§ 4. Зависимые наблюдения 227
§ 5. Критерий серий 229
Задачи 231
Решения задач 232
Ответы на вопросы 236
Глава 16. Несколько независимых выборок 237
§ 1. Однофакторная модель 237
§ 2. Критерий Краскела—Уоллиса 237
§ 3. Критерий Джонкхиера 245
§ 4. Блуждание на плоскости и в пространстве 248
Задачи 253
Решения задач 254
Ответы на вопросы 257
Глава 17. Многократные наблюдения 259
§ 1. Двухфакторная модель 259
§ 2. Критерий Фридмана 260
§ 3. Критерий Пейджа 263
§ 4. Счастливый билетик и возвращение блуждания 265
Задачи 269
Решения задач 270
Ответы на вопросы 271
Глава 18. Сгруппированные данные 273
§ 1. Простая гипотеза 273
§ 2. Сложная гипотеза 276
§ 3. Проверка однородности 280
Задачи 282
Решения задач 282
Ответы на вопросы 286
Часть V. Анализ многомерных данных 287
Глава 19. Классификация 288
§ 1. Нормировка, расстояния и классы 289
§ 2. Эвристические методы 291
§ 3. Иерархические процедуры 294
§ 4. Быстрые алгоритмы 297
§ 5. Функционалы качества разбиения 299
§ 6. Неизвестное число классов 307
§ 7. Сравнение методов 309
§ 8. Представление результатов 311
§ 9. Поиск в глубину 311
Задачи 313
Решения задач 313
Ответы на вопросы 315
Глава 20. Корреляция 317
§ 1. Геометрия главных компонент 317
§ 2. Эллипсоид рассеяния 322
§ 3. Вычисление главных компонент 324
§ 4. Линейное шкалирование 326
§ 5. Шкалирование индивидуальных различий 332
§ 6. Нелинейные методы понижения размерности 337
§ 7. Ранговая корреляция 343
§ 8. Множественная и частная корреляции 347
§ 9. Таблицы сопряженности 350
Задачи 352
Решения задач 353
Ответы на вопросы 356
Глава 21. Регрессия 357
§ 1. Подгонка прямой 357
§ 2. Линейная регрессионная модель 360
§ 3. Статистические свойства МНК-оценок 363
§ 4. Общая линейная гипотеза 368
§5. Взвешенный МНК 372
§ 6. Парадоксы регрессии 376
Задачи 382
Решения задач 383
Ответы на вопросы 386
Часть VI. Обобщения и дополнения 387
Глава 22. Ядерное сглаживание 388
§ 1. Оценивание плотности 388
§ 2. Непараметрическая регрессия 392
Глава 23. Многомерные модели сдвига 399
§ 1. Стратегия построения критериев 399
§ 2. Одновыборочная модель 399
§ 3. Двухвыборочная модель 406
Глава 24. Двухвыборочная задача о масштабе 411
§ 1. Медианы известны или равны 411
§ 2. Медианы неизвестны и неравны 414
472 Оглавление
Глава 25. Классы оценок 417
§ 1. L-оценки 417
§ 2. М-оценки 419
§ 3. Д-оценки 423
§ 4. Функция влияния 426
Глава 26. Броуновский мост 428
§ 1. Броуновское движение 428
§ 2. Эмпирический процесс 429
§ 3. Дифференцируемые функционалы 430
Приложение. Некоторые сведения из теории вероятностей
и линейной алгебры 435
Раздел 1. Аксиоматика теории вероятностей 435
Раздел 2. Математическое ожидание и дисперсия 435
Раздел 3. Формула свертки 437
Раздел 4. Вероятностные неравенства 437
Раздел 5. Сходимость случайных величин и векторов 438
Раздел 6. Предельные теоремы 439
Раздел 7. Условное математическое ожидание 440
Раздел 8. Преобразование плотности случайного вектора . . 441
Раздел 9. Характеристические функции и многомерное
нормальное распределение 442
Раздел 10. Элементы матричного исчисления 444
Таблицы 449
Литература 456
Обозначения и сокращения 460
Предметный указатель 462
дело настолько серьезное
ι нужно немножко заниматгпьности
НИ na
с
VI
1И
1ЬШИНГТ
Д; ι πι яг
, j:
,л а
Я К^НТ|
IM ПРИ —
.№
нн
ны
HUI
н:
BN 978-':-сЧ774-996-0
785947П749960