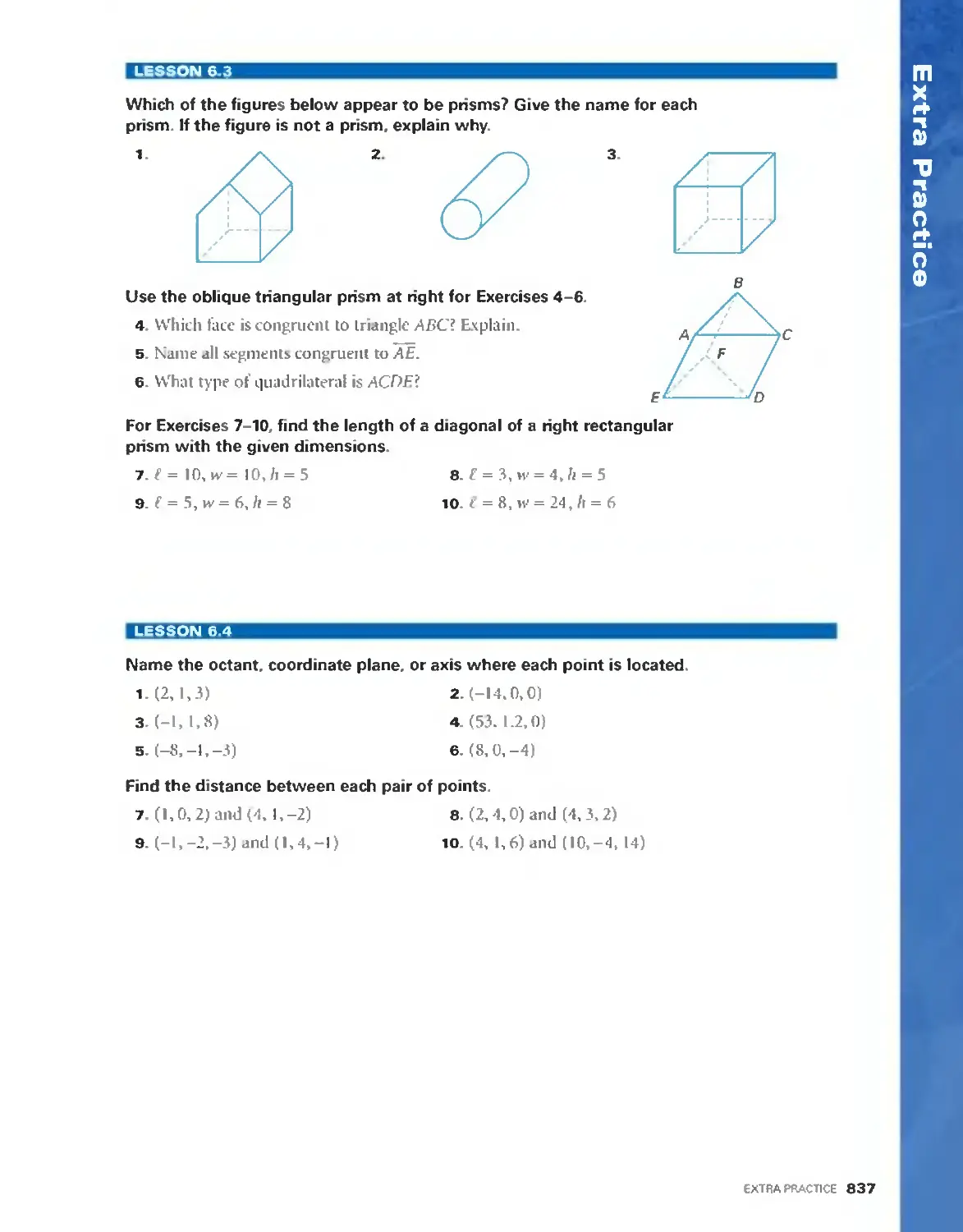
Текст
Lessons
1.0 0 Building Your
Geometry Portlolio
1.1 0 The Building
Blocks ot Geometry
1.2 0 Measuring Length
1.3 0 Measuring Angles
1.4 0 Exploring Geometry
by Using Paper
Folding
1.5 0 Special Points in
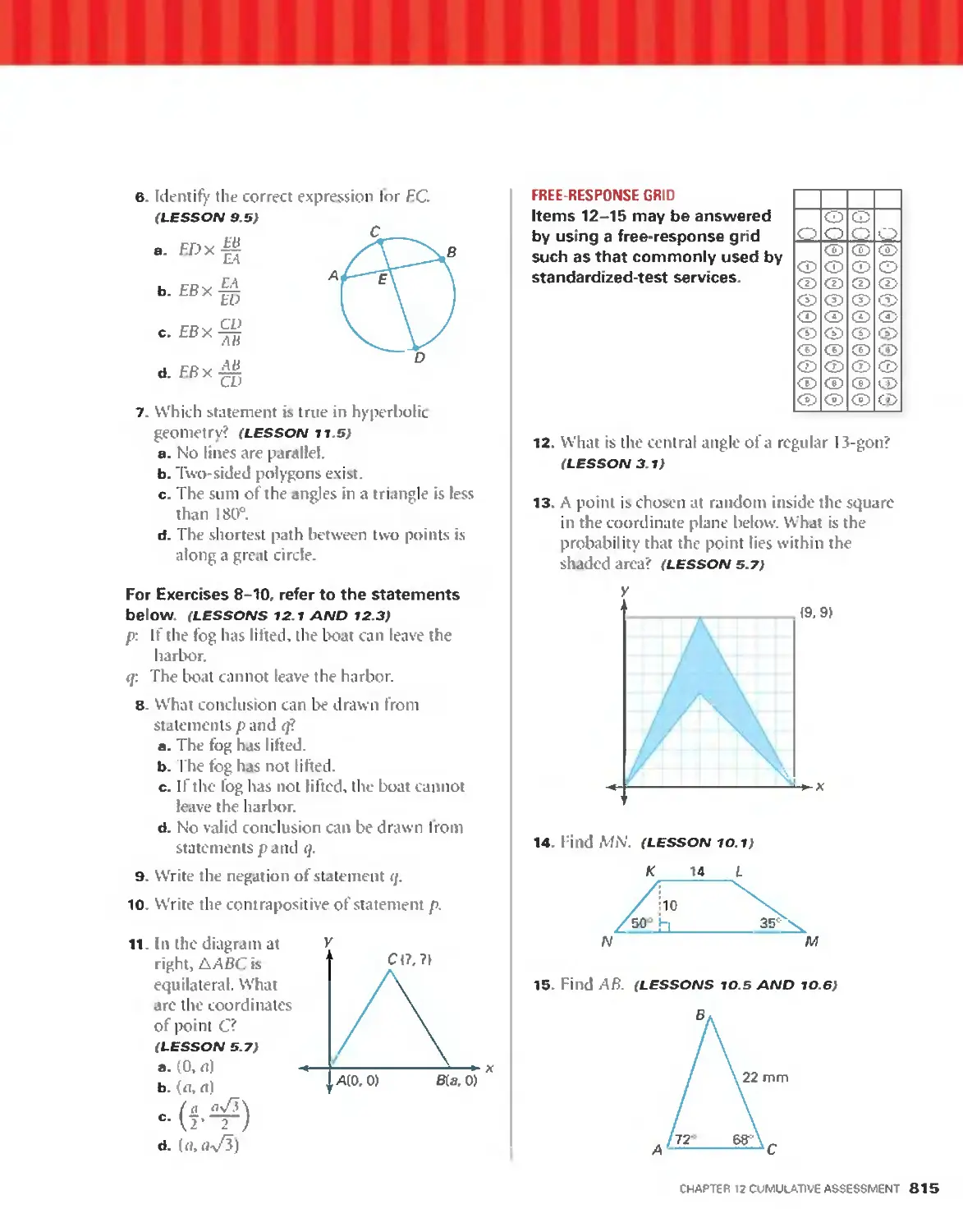
Triangles
1.6 0 Motion in Geometry
1.7 0 Motion in the
Coordinate Plane
chapter Proiect
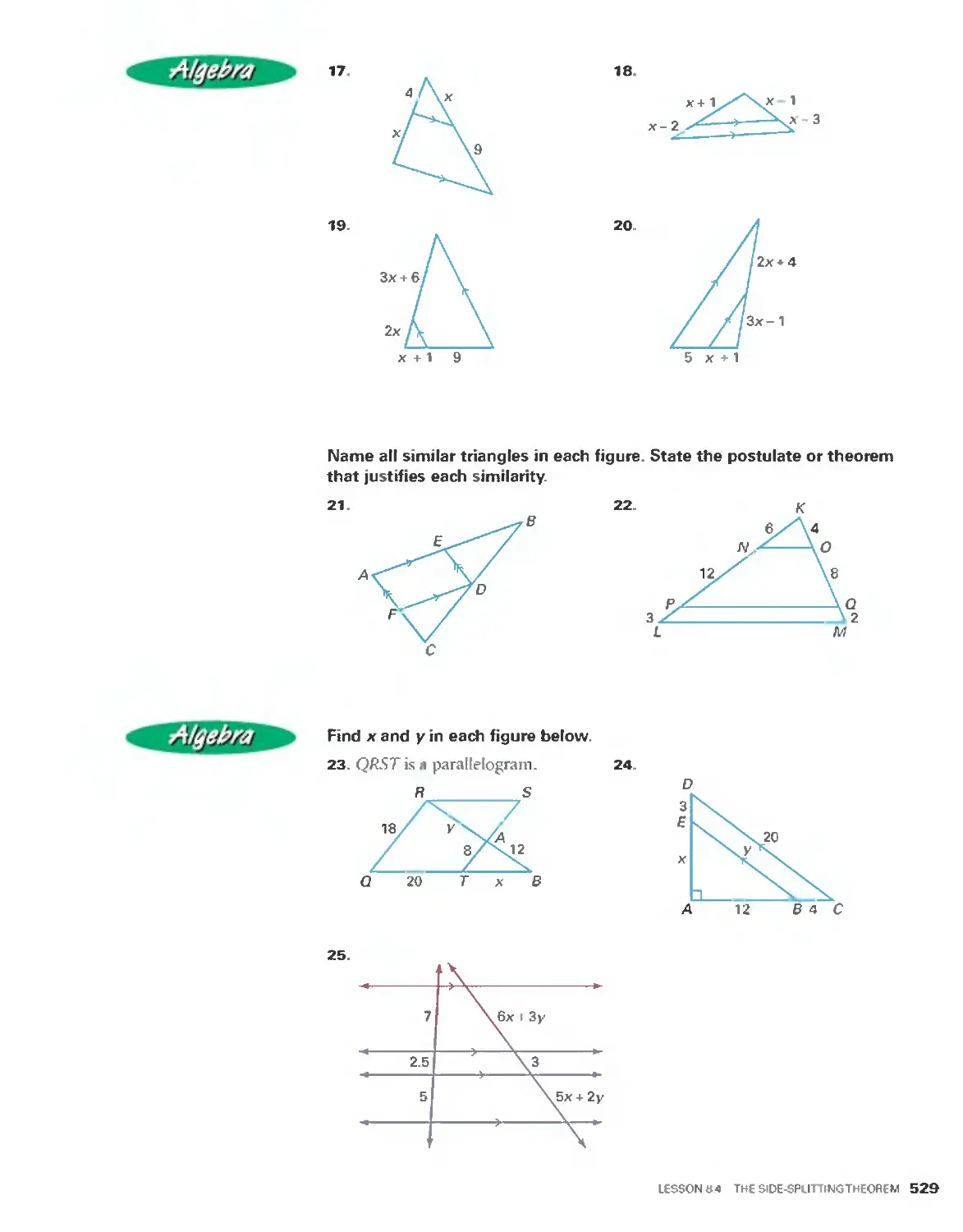
Origami Paper
Folding
Exploring
Geometry
GEOMETHY IS BOTH ANCIENT AND MODERN.
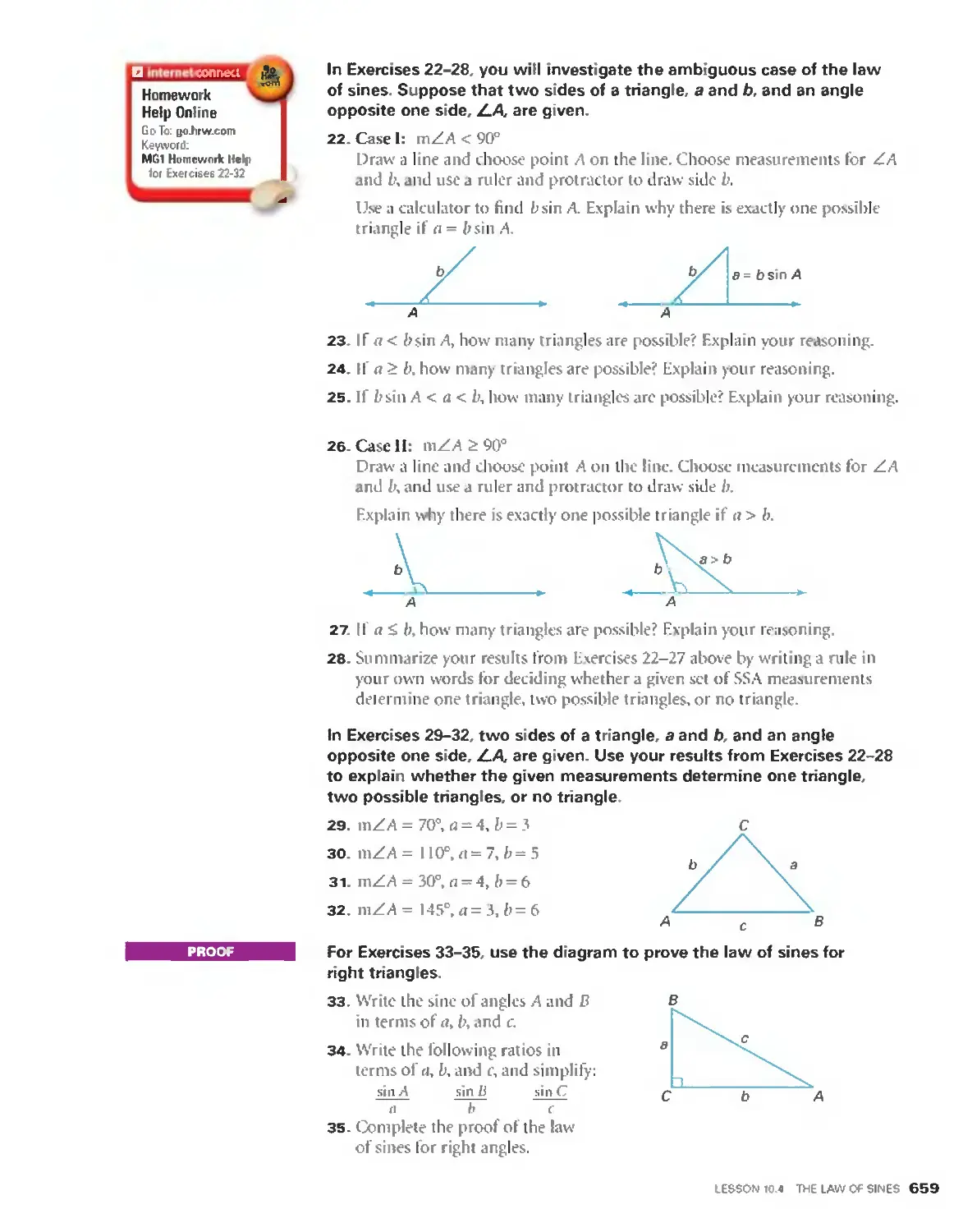
From its traditional beginnings as a systematic
study in the works of Euclid, through its
develpoment in the works of the French
philosopher and mathematician Rene
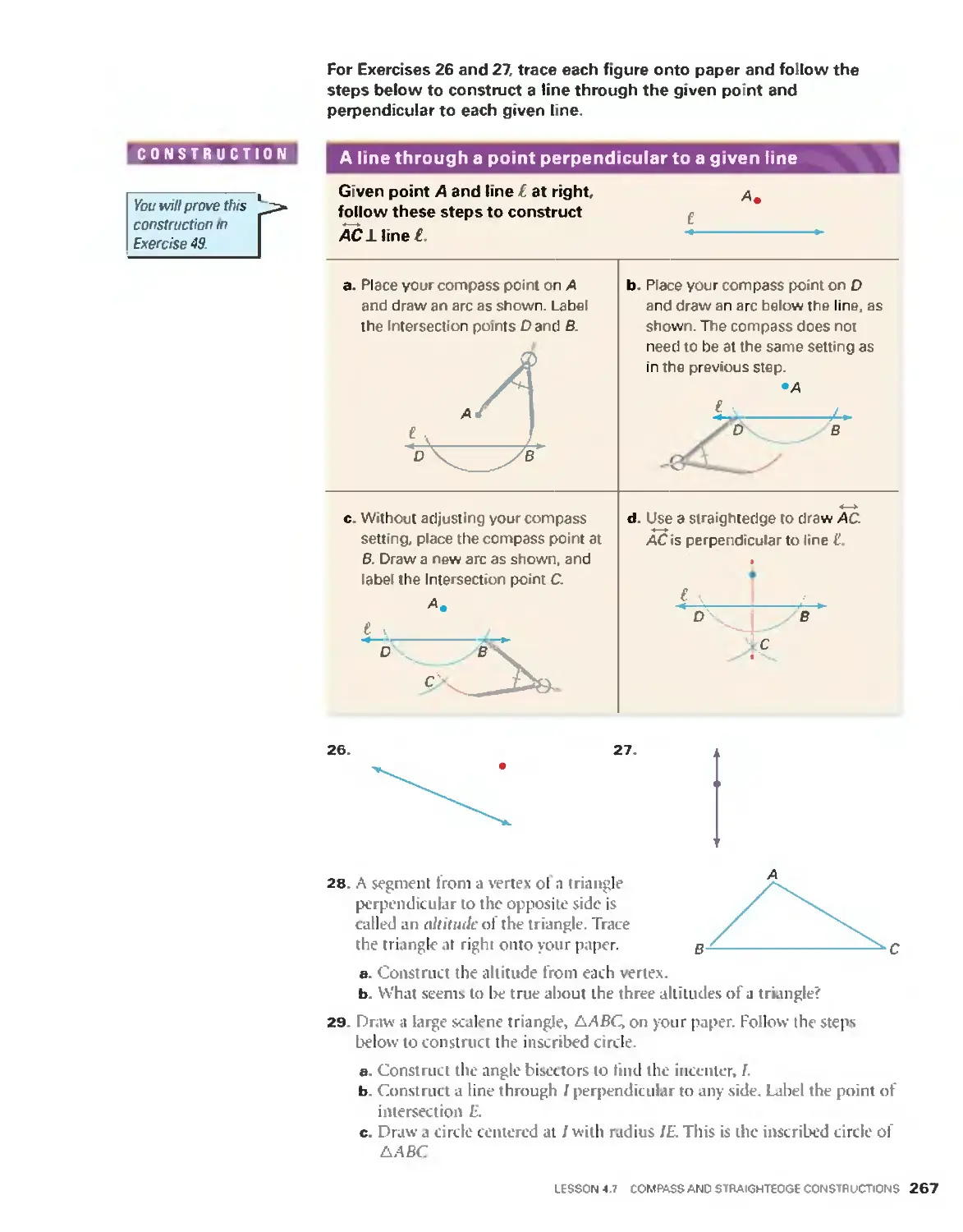
Descartes, to its present—day study using
sophisticated computers and calculators.
geometry has an unbroken tradition in the
West that spans well over two thousand years.
This first chapter is for you to get acquainted
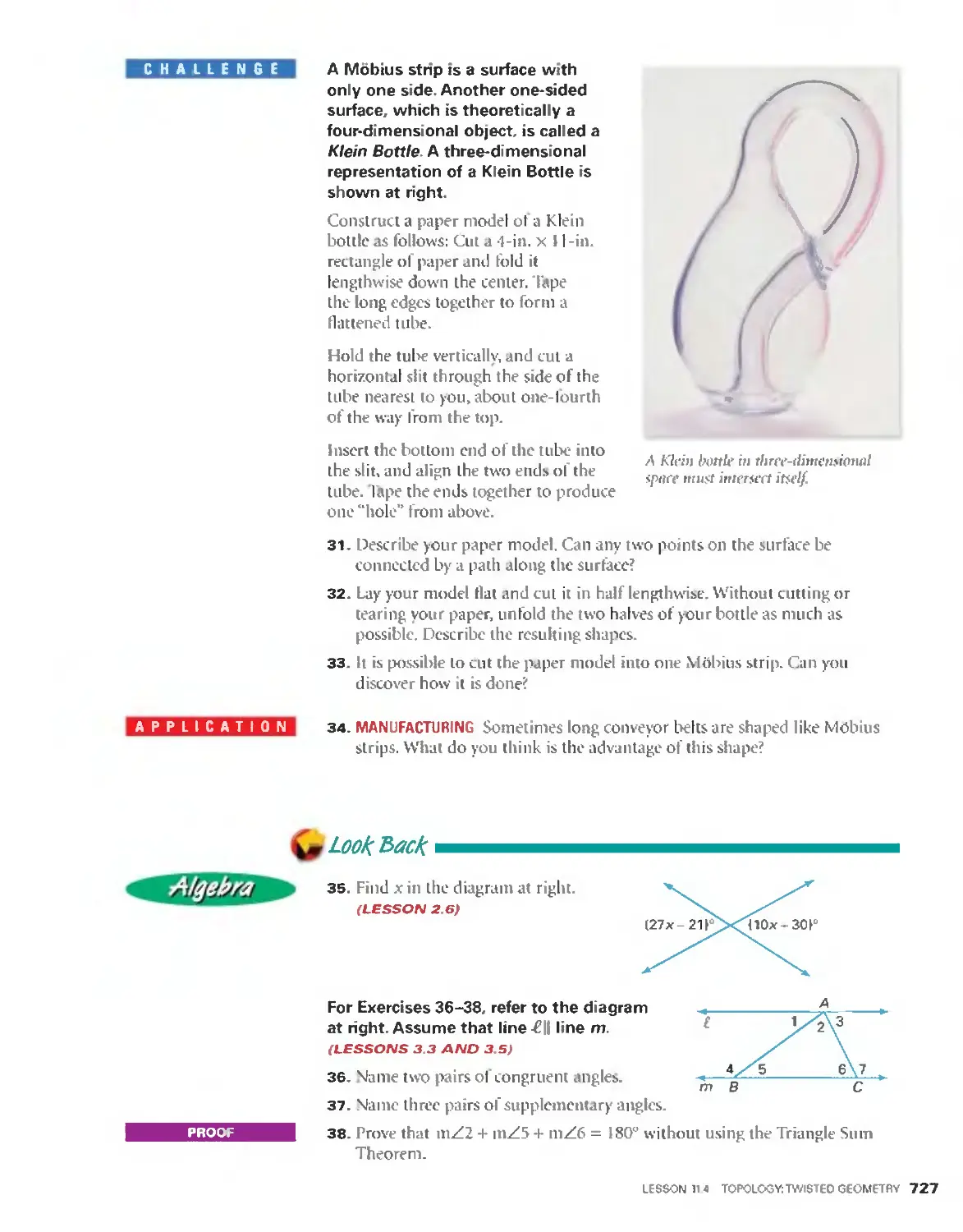
with geometry. You will be introduced to a
number of tools for exploring geometry, such
as paper folding. compass and straightedge,
and geometry drawing software. In this way,
you will discover what geometry is by experi-
encing it.
| I “III \\\\\\\\\\\\\\\\\\\\\\\\\\
Tr _
F’ F3
/ :=: r-7 F
, SF:
&
L
-1 .
_ l-¢1¥TEf'T'“-iTr_|‘l "‘thfm. -
“. u‘-t._.?.._~
1
._ j j
. 4(1)} Ni‘ ii.
." ‘ "i - ' ‘fir. : . \ --- \ I
.. __,. . - .
. \ ‘ I‘
l
0
9
I .’
\ ,. O
_ Q 0
I \
As you begin your study of geometry. set up your own port folio. The first
lesson of this book. l esson LO. tells you how to do this. Throughout this
book _vou will find many suggestions of things to include in your portfolio.
About the Chapter Project
Origami is an ancient art form that originated in
Japan. Using a few basic folds. masters of the art
have created elegant and intriguing lorms that
have become the classics of the tradition.
One of the most popular and enduring of the
origami classics is the paper crane, which you
will study in the Chapter Project. As vou fashion
the bird. notice how paper folding is used to
create the symmetry of the finished form.
After completing the Chapter Project, you will be
able to do the following:
0 l'old the classic origami crane.
0 .-\naly7.e the patterns lormed on the paper by
the folds of the crane.
About the Portfolio Activities
Throughout the chapter. you will be given
hands—on projects to do that will enhance and
extend your understanding of the material in
the lessons.
0 In the Portfolio Activity on page -12. you will
learn how to create a regular hexagon by
folding paper.
0 In the Portfolio Activity on page 49. the center
of mass ofa triangle is found by using the
midpoints of the sides of the triangle. I'he
triangle can be balanced on this point.
0 Two of the basic rigid transformations are
used to construct “snowflake” patterns in the
Portfolio Activity on page 53.
Objective
0 Begin to construct a
geometry portlolio that
will help you to
organize your work
throughout this course.
W" Artist and other
prolossionals often keep
portlolios ol their work.
Although you are probably
not yet a professional in
any area, the work you do
in school may help you
decide on your future work
and career.
4 CHAPTER I
Building Your
Geometry Portfolio
I ———«
I
\
I
1
\.I
.‘ _L
I 0 "“—
, no
¢4‘
‘\
- 0
"I
Building a portfolio will help you organize and display vour work. Design it to
show your work in a way that rellects your interests and your strengths. You
should concentrate on the things your enjoy; these will |‘tl'()l)di)i)' be the things
you Li0 best. You may want to create geometric constructions on a computer.
Study the geometry of beehives and spider webs, or explore the geometry
found in works of art.
Geometry in Nature
People have long been attracted to geometric
. _ _ .1
hgures In nature. such as the sptral shell of the . ‘ 1': \
chambered natttilus. The larger the shell grows. "Q ' \ _
the more closely its proportions approach the \
value of the golden ratio. which is a very
important number in mathem:ttics. The
underlying geometric principles of natural
objects often seem to he the reason for their
visual appeal. As you look around yourself, __.\,-W _
you will find many examples of '\- -'$‘.‘t 1;. .
' . ’. ".5 h ‘ ._- Q,‘ ‘.‘\.\\g.‘ ‘ ' he‘ .
geometric beattty tn nature. __ ‘ ’ Q '- I - '
i s \ “‘.-" ‘
| P . u
341 L t
.“ .. --
'_ - . E U ‘I ‘ "', ' 5 I .
A ’_ 4 ...‘v- _ A
\
Geometry in Art
Many artists create works of art by using pure geometric
forms. Tlte work of art at right. by a famous artist of tlte
Bauhaus School in Germany. uses rectangular solids and flat
surfaces. As the work illustrates. pure geometric forms have
their own beauty. Make your own collection of works of art
that use pure geometric forms.
2.‘) 1.[II L -t 6‘ '
ml: in lwisg, P
|tt;.:b:-:3. I" Inna;-3 O twa 11:: ['1 n.
hlls.
Geometry in Architecture
The dimensions of the Parthenon reveal the ancient ’ ‘*3?
Greeks‘ fascination with geometry. ‘l he ratio of the “‘ “—- -- ._ __ _ ‘ - _,
height of the original structure to its width is very 5- ‘ - ‘ . -' —. ‘- ;? _
‘close to the golden ratio. Geometry is still an _I .
important element in architectttre today. By ',-“
applying principles front geometry and physics. l
architects design structures that are both .;.‘ 4 ‘ -
strong and beautiful. ._-,,. _' r__?1.fi __‘::'.Dt.' ‘ ,-_‘ €).::_..__.____ __ _1- ‘ _
\ v - ' ,.“5.,T 5* '4‘ . l ~.=- -—' * '
E‘ ' *2: £3‘ \ S-""‘
N
LESSON 1.0 BUILDINGYOUR GEOMEYHY PORTFOLIO 5
Your Notebook and Journal
ix-lathelnaticiutis keep records
ol their theories and discoveries.
You. too. should keep :1 notebook
ufyour work. including tests.
homework activities, and special
activities such as research projects.
Your teacher might also want you
to keep at iournal.
'3 D
An”,
Hr. vim l.‘:_‘ -H I.
?::;‘.'...~- “-T~:‘~>_,\-."-9_l"“‘.*} '
.‘T'-,'__:\. _‘_ I .
“1 I
. '~‘‘._. 2%!‘ '=.t__,1
- _\ ‘fall
‘*"3_‘n"»'i7"»"-2“-'5". -.’:’.::.'§':.:‘.‘.‘”
"’ "1 '.""“" ‘ """"""'l-l-4-3.‘-'..:
-‘"1 --n -A.._.,.$
-"'*Iw,' .
§_
-
P‘W“‘\v~
.-I :. - L Iq
..'-l.-..u’‘.‘, .. £...,..“.'T.‘.'.‘ -.
_.,. -..'-o. —
'--’-| -23-» I“'* -1- 5 m ..|..u.. .i...... Jrdl‘ ils lrum -
—‘ Iwn pg: N lnnnnlu L1‘. 1': wirmlw.
Putting Your Portfolio Together
6 CHAPTER t
\-arious containers can be used for your portfolio.
File folders, accordion files, and even cereal bo\'es
will work very well. You mzw have at number of
string designs or physical models that will
not [it into your portfolio container.
These should still be ‘considered .1
part of your portfolio.
On the follmving pages are live
diiTerent things to include in your
portfolio. You should begin right aw'a_v
and continue to add to your portfolio )
throughout this course—d0n’t
wait until the last minute.
-. , J
u. I
L '
_..—-—--'2‘
_“' .......'~--'.—-''’'-’*''''
'2’! \——-4'
\
h’
You Can Begin Now
1. You can create a star with almost any ntlmber 1
of points bv using the following method: Start 1 K
by drawing a circle. Draw the desired number . ‘
of points spaced evenly around the circle. :3
Connect the points, skipping the same ‘ '
number of points each time. Experiment by 3 1
skipping different numbers of points. You
may wish to color your stars or draw two or
more stars in the same circle.
Try to determine when the star can be drawn
without picking up your pencil.
II
2. Circular designs known as nirtndulas (from "‘ ~ ' g.’ '
the Sanskrit word for “circle” or "center"] ..‘ " "‘ _ ‘ 0,3.
appearin the Hindu and Buddhist " . ‘ .' 1, 9
traditions as svmbols of the wholeness 9;’ _ _ . _ _
of the universe. The Aztec calendar. a ‘_,- -I ' - ‘ 9 —‘ ' >\ " ‘ 9"‘
huge carved stone lrom ancient 4,.‘ F, i _ .-. ""1: ‘- K ‘
Mexico. bears Striking resemblances , ,II ’ I
to the mandalas of the East. Write a \., ' ___-_ ,
report on mandalas-and their history. .‘i 1 . _.,_‘_'.-°" ._
and then try creating mandalas of 1}‘ M _ \ Qt?‘ ‘* 53- ’7___
your own. - ‘L’ \<- - "-
-gr ’ ’ "r§%* “' ‘-
3. Interesting designs can be created _J ' ' "Z"-"' ‘""l""‘f'"
bv using onlv straight lines One tvne ‘ '~' ~ ‘» '-' (mm ""l"r"'M""U
of line design is made from string and
is known as "string art." Make your own
design. using either string or pencil. paper,
and a straightedge.
Student project
LESSON 1.0 BUILDINGYOUR GEOMEYRY PORTFOLIO 7
I I O I I I 9 9 9
I I I I O I I I I 9 9 9 9
I I I I I I I I I 9 9 9
I I I I I I 9 9 9
I De’ I I IT-I I 9 9 9 9
I I I I I I 9 9 9
I I I I I I\ I I I 9 9 9
I I I I I I 9 9 9
I I I I I I I I I I I I
I I I o I I I 9 9
I I I I I I I I 9 9 9
4. A special kind of-art is the creation of Celtic “l<not"
designs such as those shown here. Experiment with
your own designs. ‘Study the diagrams alvove to help
you get started.
\_ C‘ ——.a-
3
5. Islamic culture is extremely rich in geometric and calligraphic
art. Collect examples of Islamic or other geometric art for your ;- . .- VT
portlolio. You may want to create some designs olyour own in - ‘Y-.. " _ "‘ . ' '.
. _ "- . -v- __
the style 01 Islamic art. ‘ ;'
. .’,"‘ 4 I7
Vy-1 . T.
2.
d ‘ . >y '
1 Q ‘ _ - ‘E...-
1 f I . I A
".QQQ§§ 25;.
. 3. ‘I
' - _It.':: m‘ _=m’€
8 CHAPTER I
The Building Blocks
of Geometry
Objectives ‘ -'-
o Understand and - ' ,
identity the undefined - - - - - - _
ggfloint line. and . -' - L 6_ I I _m_c nouns M” as
' .7.-, - points. lines. and planes can be used
0 Define segment, my. ,;. . ' to make madramatical I u -Is of
same. Collmear. . 1 .I:ysicaI obiects. The models can be
i"’9’59‘5 i"’9’59‘”°"- '9 ' used to solve roaI-worId : mblems. '.
and coplanar. - _ _ _ 1 '
.."'.- -'.‘. o
' L':"'(:":5“'l§’(‘)’i'"°t£‘:f[:g'S‘_"i‘i"fd The spiral galaxy M51 in the corrstellarion Amlromedzt is the
plane; companion gal:1.\;t-'ofour galrtyy, the .'\-‘l'llk_l' it-hy. ]ust_us a galaxy
is made up ofsmrs, n geonr¢'trrr_ftgm'e IS composed 0] p011llS.
Basic Geometric Figures—Undefined Terms
The most basic figures of geontetry are Imftzts. lines. and planes. They can he
thought of as building blocks for other geometric figures. Because they are so
basic. they are not defined in terms olother figures. In fact. they are often
referred to as umlefinerl terms. But even though points. lines. and planes are
undefined, they can be explained.
The first thing to re.tli7e about geometric figures is that they are not real-world
objects. Lines and planes have no thickness, and points have no size at all. l'his
book contains many illustrations. but the illustrations are not the same as the
geometric figttres they represent. Theoretically, geometric figures exist “only in
the mind.”
Points When you look at the night sky and ,. . . _. . . _ X
see the stars. the tiny dots of light seem like . > i'__-. ° -'
points. Points are often shown as dots. but a l _ - 3
unlike physical dots, geometric points have ._-, «_ . -'- . = -
no size. Points are named by capital letters I " .' - P°i"“‘ A “"d X
such as A or X.
Lines A geometric line has no thickness, is . __ I _ ._
perfectly straight. and E"(t€’l‘l(l$ forever. A line _ _ A _ _ 8' '.
can be named by two points on the line, with - ' ‘ .71
a double—headed arrow ( *—*] over the two - _ H -
letters. or by a single lowercase letter. ‘ - '7 ‘_ 153, m. .1", ,;.,
LESSON 1.1 THE BUILDING BLOCKS OF GEOMETRY 9
Planes A geometric plane extends infinitely _ _ __
in all directions along a llat surface. You , . - -t " '._
can think of any flat surface, such as the -'_. _: 3;
top of your desk or the front of this book. ,_'- -
as representing a portion of .1 plane. 55-’
In the figure at right. the llat sttrlace .',_ . O ._
represents a portion ola plane. A plane . : .
can be named by three points that lie in . -' ‘
the plane. such as M. and O. and that ; _ _ _-. __ . _ _ _
are not on the same line. A plane can also '. __PIa'ne M'Nt"_)_,'o'r5t _ . '. "
be renamed by a script capital letter. such "I ' - v' '-'* ‘ '
as ill.
an -'
Points are said to be collinear if a single line D
can contain them all. (Any two points are .
collinear.) In the figure at right, A, b’. and L, A E c
but not D, are collinear. Points are said to be
coplanar ifa single plane can contain them all. 905013 A» and 0
(Any zlnre points are coplanar.) am °°"'"°ar'
Defining Figures in Terms of the Basics
It is now possible to define three important geometric figures. Notice how each
oi‘ the following definitions builds on the lll1d€Fln€Ll terms point‘. lint’. and picnic".
Definition: Segment
A segment is .1 part of a line that begins at one point and ends at another.
‘I he points are called the endpoints of the segment.
1.1.1
A segment is named by its endpoints. A bar . :5 ' - '3' ' ' ' '
(_) is drawn over the two letters _, _ H .
representing the endpoints. ._ .1: I . _:
Definition: Bay
A ray is a part ot a line that starts at a point and extends infinitely in one
direction. The point is called the endpoint of the ray.
1.1.2
A ray is named by its endpoint and one other ._ . _ - - - .- . -
point that lies on the ray. The endpoint is ' ‘X " ' - Y _ __
named first. An arrow [—*] is drawn over the _‘ ' ~ ,.-_, _ _ - - .
two letters representing the points. . 37.‘; , ‘XV ' . '-' .
10 CHAPTER I
Definition: Angle
An angle is a figure lormed by two rays with a common endpoint. The
common endpoint is called the vertex of the angle, and the ravs are the
sides of the angle.
An angle divides a plane into two regions: the interior and the exterior
of the angle. If two points. one from each side of an angle, are connected
by a segment, the segment passes through the interior of the angle.
1.1.3
An angle can be named with the angle symbol (L) and three letters: one point
from each side of the angle plus the vertex. with the letter for the vertex in the
middle. If there is only one angle with a given vertex. the angle can be named
with the angle symbol and the single letter that represents the vertex. Angles
can also be named with a number shown in the angle’s interior.
- ..._..B'°.'-' . .
'- ACAB a-_-.-' ''
E X A M P L E 0\l-ante each figure.
X Y P O M N
3. 4-—ojo—>m b. To 0- QT-op d- 0 Y
P
e. f. g. h. .3 L, 7
T
3 X-T» O H Lg
G SOLUTION
<—> <—> : Z —_=~ _
a. XY, YX .or line in b. PQ or QP c. MN :1. point Y
9. L3 f. LX 9. LPQR. LRQP. or AC)
h. plane RST, plane RTS. plane SRT. plane STR, plane TRS, plane TSR.
or plane L
Intersections of Geometric Figures
When geometric figures have one or more points in common. they are said
to intersect. The set of points that they have in common is called their
intersection. in the Activitv that tollows. you will discover some fundamental
geometry ideas, or postulates. involving intersections of geometric figures.
Postulates are statements that are accepted as true without proof. Postulates,
like undefined terms, are building blocks of geometry. (Postulates are also
known as axioms.)
LESSON t.1 THE BUILDING BLOCKS OF GEOMETRV 11
I l L
no special tools
Cl-IECKPOINT 5/
H1
cuzcxpomr ./
cuscxpomr ./
CHECKPOINT 5/
CHECKPOINT V
12 CHAPTER 1
Dlscoverlng Geometry Ideas In a Model
The illustration at left may be thought of as at model of-.1 real—world object
such as a box or a classroom. Complete each postulate below.
1. Examine the illustration. Identify the places where lines intersect each
other. What kind of geometric figure is the intersection of two lines?
Postulate
The intersection of two lines is .1 ? . 1.1.4
How many lines intersect at each corner of the figure? Do you think
there is a limit to the number of lines that can intersect at a single point?
2. Identify the places in the illustration where planes intersect each other.
\-\-‘hat kind of geometric Figure is the intersection of two planes?
Postulate
The intersection of two planes is a ? . 1.1.5
3. Look at points A and B. How n1.tn\- lines pass through both of these
points? Could there be another line. different from the one shown. that
passes through both points A and B?
Postulate
Through any two points there is exactly one ? . 1.1.6
4. Look at points A, B. and C. How many planes pass through these three
noncollinear points? Could there be a plane, other than the one shown,
that passes through all three points?
Postulate
Through any three noncollinear points there is exactly one .
1.1.7
5 Pick any plane in the illustration. Then pick two points that are in the
plane. Name the line that passes through these two points. Is the line in
the plane that you picked?
Postulate
it" two points are in it plane. then the line containing them ?
1.1.8.
Exercises
. Communicate
1. Explain how geornetrit ligtires are Llifferenl from real-worlLl ohiects.
2. Examine the room vou are in. \lame some objects that could be
represented by points, lines, and planes.
3. Explain why one point is not enough to name a line.
4. Explain why two points are not enough to name a plane.
5. Why is the order ol the letters important in the name of a ray? You may
wish to illustrate your reasoning with a diagram.
0 Guided $4’///8 P/dft/'68
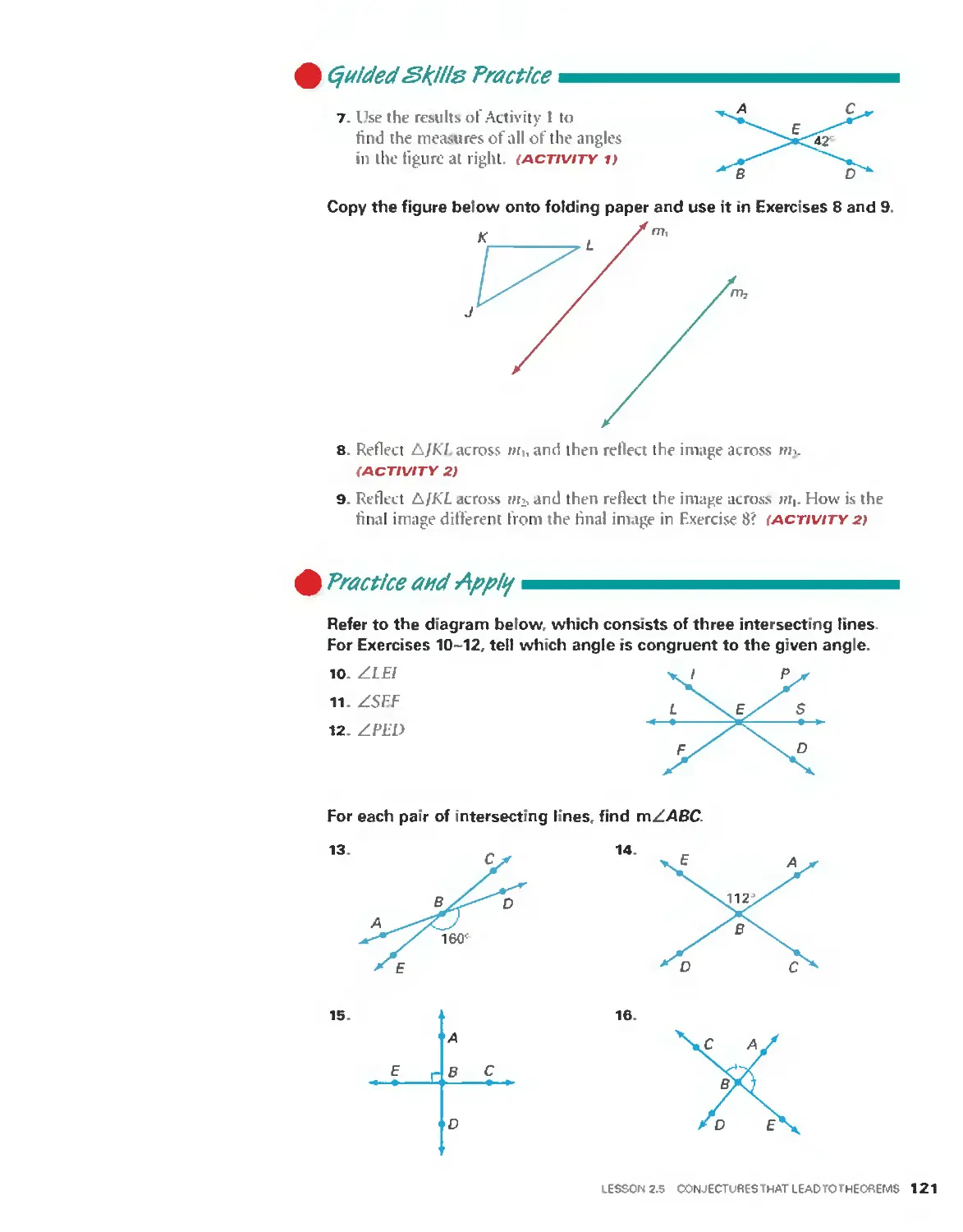
6. Refer to the figure at right. Name a
point. a line, a segment, and 21 ray
_ _ A 8
III the hgurc. (EXAMPLE)
P
7. Give lour names tor the angle in 0 1
the tigurc at right. (ExAMPLE)
R
8. Give three names for the R
plane in the figure at right. o
(EXAMPLE) M ' N
I
0
LESSON 1.1 THE BUILDING BLOCKS OF GEOMETRV 13
Practice dim’ flpp/y
In Exercises 9-12, refer to the triangle below.
9. Name all of the segments in the triangle. 3
10. Name eacl1 olithe angles in tl1e triangle
in three different ways.
11. Name the rays that form each side of the
angles in the triangle.
12. l\-ame the plane that contains the triangle.
A P P L I c A T I 0 N HOBBIES In Exercises 13-17, refer to the aquarium shown below.
State whether each object in the aquarium is best modeled by a point, a
line. or a plane.
13. an edge of the aquarium 14. a grain of sand
15. a side of the aquarium 16. the stirlaee of the water
17. .1 corner of the aquarium
- "3? _ l,
' 7 T, -
I
.. 4,
O‘ It _
-. ~- '
s I
we
\ " .. _ . ’
_ _. . ¢ _,
Q _ _ ' ' I
.. ' ' -.. “ A -1 ‘ t _ " "'
. l__ \ _ _ - . _
D Inhmctconnod .39, In Exercises 18-25, classify each statement as true or false. and explain
|0lT| .
Honrework YOUT TEBSOTIITIQ.
Help °"'"'° 18. l ines have endpoints.
Go lo: no lirw.conI
Kawmid: 1 _ h; .
Mm “mm” mp 9 Planes ne edges.
l°' 5*°'°'5°‘ "H5 20. Three lines that intersect at the same point must all be in the same plane.
‘ 21. Two planes may intersect a third plane without intersecting each other.
22. Three planes may all intersect each other at exactly one point.
23. Any two points are contained in exactly one plane.
24. Any three points are contained in exactly one plane.
25. Any four points are contained in exactly one plane.
14 CHAPTER 1
‘\
‘-.
Refer to the figure below for Exercises 26-30.
26. ?\J-ame a line in the figure. Give three other names for the line.
27. .\1-.une a point on line in.
28. _\l-tune the intersection of lines in and M.
29. .\lame an angle in the figure. Name the
vertex of this angle and the two rays that
form the sides of the angle. '7' E ”
30. Can an angle ll'I the figure he named LA?
why or why not?
In Exercises 31-40, refer to the figures below.
31. Name the intersection of planes IT’ and '3.’..
32. Name a line in plane Cl’.
33. Name d point in plane 1}’.
P. I ‘U 34. Namea point on KM.
_ f M. 35. Name the intersection of MU and MN.
K _
36. Natne three collinear points in the figure.
. 37. Name two coplanar segments in the Figure.
0 O O 5
I L N
3& Name the intersection ofline u and W.
Q "’ 39. Name the intersection of planes Q and
P MPT.
IT M _ - . -
— n 40. Name three eoplanar points in the hgure.
A 7 7
W R
I/
How many different segments can be named in each figure below?
Name each segment.
41. 42. 43.
A B A B C
<
ABCD
44. Write a general rule or lormula lbr finding the number ol segments that
can be named by a given number of points on a line. Can you explain why
the rttle works?
LESSON 1.1 THE BUILDING BLOCKS OF GEOMETRV 15
COl'lI'IOd
Activities
Online
Go 10: go.hrw.com
Keyword:
MG! Flatland
:33-.
CHALLENGE
16 CHAPTER I
How many different angles can be named in each figure below?
Name each angle.
45. 46. 47. A
A A B
B
V V
v B C C
D
48. Write .1 general rule or formula for finding
the number of angles that can be named by
a given number of rays with the same
endpoint. Can you explain whv the rule
works? { Assume that all revs lie on one side
of-.1 straight line. as shown.)
[_00,(' Back
Simplify each expression.You may wish to draw a number line.
49. 22+ (-6) 50. 7+ 15 51. ll — (-4)
52. -81 — (-30) 53. |— lI+ [—35)| 54. II.‘- — lO|
55. -123 — 4t 56. |2l + (—35)| 57. |— 54 + [—20)|
Look Beyond
58. You can make a diagram V
to find the answer to the
following, problem. Suppose
that -1 people are excltanging _ /A -
cards. Each person exchanges ‘
one card with each of the _
other 3 people. How tnamy sv-
exchanges are made? (Hint:
Draw -1 noncollinear points.
Then draw line segments -
between the points. l-low
many segments did you x , '
draw? How does this relate
to the exchanges of cards?) ‘
59. If 5 people exchanged cards
as described above. how -
many exchanges would
there be? lixplain how to
determine the number of
exthmtges when it people
exchange cards.
Objectives
0 Construct a geometry
ruler.
o Detme length and
congruent
0 Identity and use the
Segment Addition
Postulate.
Measuring Length
\ .i-aw.“ ;.:"3ll“.*:~ .‘
‘I
M
We ask questions such as: How tall
are you? and How far do you live from here?
Distance or length measure Is possible R ‘
‘ because of some basic nssu .- ‘oars.
A ruler in the‘ e}'t'pit't:L’ 0]-the ntiu'o.-'t.‘ope nmlcc-'.~: it pas_<il:lc-' ta ttiettsrtrr: in
miits 0f'om=-nrilliontlr ofn nmcr: l‘llt’$(’ units are known as microns.
The Length of a segment
in defining the length ol :1 segment. we will use a mmzlrrrlim’. which is like
.i rulcr. A number line is a line that has been set up to correspond with the
rezil numbers. A 3
4--
14-3-24 012$-Y
A geometry 'rutef'
The coordinate of a point on the number line is a real number. in the
illustration, -5 is the coordinate of point A and 4 is the coordinate of point B.
How would you find the distance between points A and 8? Try |— 5 — 4|. Also
try I4 — {—.’s)|. What do you notice about the absolute values? l'his leads to a
definition of the distance between two points.
Definition: Length of E
Let t and b’ he points on at number A 8
line. with ctitirdiilttes (1 and la. Then 3 b
the measure of AB, which is called Wfio, A3
its length. is |a— bl or H: — n|. |a— b or |b— a| 1.2.1
the measure. or length, of W is written as tumor. more commonly. as just AB.
LESSON 1.2 MEASURING LENGTH 17
E X A M P L E 0 Find the measuresllengthsl of T3, and Won tl1e number line below.
. '3 '1‘ 9
' £3 E 3 2 1 o i 2 3 E 5
Osotunou
ABtormE)=|—-1--il=|—3|=3orAB=|.t—(—4t|=lsl=3
.«tx(ormfi)=l-4-1|=l-5l=5ontx=lt-(~4‘!=|5|=5
XB[ot'n1X—Bl=It—4l=|-3|=3orXB=I4—l|=|3I=5
rnvnus FindST. _ 1 I § _
—.&—3—§1't'>123:5.Ee';
Fair Rulers
The rulers you will use in this bool<—with a few interesting exceptions [see
Exercises 4?—49 and the Portfolio Project on page 75)—-are "fair" rulers. ‘I hat
is. they have equal intervals from one integer to the next. In the Activity below.
you will use a compass and straighteclge to construct a simple lair ruler.
Constructing and Using a Fair Ruler
ou I 1. NEED 1. Use your straightedge to draw a line.
compass and Ciloose al'I_V point 0|‘! lite" line and
straightedge label it 0. Adjust your compass to an
appropriate spacing, and set the point
of the compass on the point labeled. ,
1
Use the pencil part of the compass to
draw a short mark that crosses the
number line to the right of (). label
the point of intersection l.
2. Set the point of the compass on the
new point. and draw another mark to
its right. Label the new intersection 2.
3. Repeat the previous step as many
times as desired.adding l to the
label each time.
4. Construct the negative numbers to
the left ol‘ 0.
5. 'l'he distance from 0 to l on a ruler is
known as the unit length. Two common
unit lengths are indies and rettriiimrrs.
Make up a name for your unit length.
0 2 3...
CHECKPOINT ./ 5. Use your ruler to measure an obiect in your classroom. Estimate the
fractional part of the measurement. Compare your measurement with
those of vour cl-assn1ates.What do you ohset we?
18 CHAPTER 1
congruent Segments
Congrucnt figures are
figures that are the same
sine and shape. ll" you \
move one of them onto
the other. they will A 8
match exactly. like the
segments in the figure I
at right. The segments
on the ruler that you C D
constructed in the
Activity were all
congruent because the
same compass setting
was usetl for each one.
3|’!
8|
The symbol for coIIgrtm_IIce is E. 5 l IS read as “Segment W is
congruent to segment }'Z."
In geometry. tick marks are used
to show which segments are known
to be congruent. Within a given The
illustration. segments that have a
single tick nmrk are congruent. E
Similarly. segments that have
two tick nutrks are congruent,
and so on. c D
From your exploration of a fair ruler. Which 999m9"lS 3'9 °°n9"J9m-7
the following important principle
should be obvious:
Segment Congruence Postulate
If two segments have the same length as measured by a fair ruler. then
the segments are congruent. Also. if two segments are congruent. then
they have the same length as measured by a fair ruler. 1.2.2
E X A M P L E the Segntent Congmence Postulate to completethe following:
lfX}' = rz. then ? . Irfi 2 W2. theII ? _
O SOLUTION
ll'Xl"= imhenfiafi. Irfiafinhen xi-' = tz.
CRITICAL THINKING What Could happen if the ll1tt:‘r\':llS on a ruler were not evenly spaced? Could
you be sure that segments with the sante measure were congruent or that
congruent seginents had equal Inettsurcs? Explain your answer.
LESSON 1.2 MEASURING LENGTH 19
CRITICAL THINKING
E X A M P L E oThe towns of Dycrsberg. Newton.and
A ' P ICATION
NAVIGATION
PROBLEM SOLVING
20 CHAPTER 1
Segment Addition
Look again at the ntttnber line in Example I. Notice tltat X is between A and B.
The relationships among the lengths .-L\', X5’, and AB depend on an important
assumption known as the Segment Addition Postulate.
Segment Addition Postulate
P R O
__
If point R is between points
P and Q on a line. then
PR + RQ = PQ. PR no
P0 1.2.3
What is being added in this postulate? In geometry, addition and other
arithmetic operations are defined for numbers. not for geometric figures.
A5’ + CD = 5
AB + CD = 5
m.-tb’ + inf = 5
Which of these statements make sense?
IW|N%IlI3lNI|'lfl(_’;
Saint Thomas are located along a straight ) nyeubug A
portion ol Ventura I~Iighway. I\'ewton is
between Saint Thomas and Dyersberg. lip
The distance from Dyersherg to Saint ‘
Thomas is 25 miles. The distance from I m-_
Dyerslaerg to Newton is I mile more than NM“ (“MW
3 times the distance from Newton to 3
Saint 'I homas. Find the distance from Sm ,_-
Dversherg to Newton and from I\'eu-ton Thom» ‘
to Saint Thomas. ”'“‘° i“°-We.
SOLUTION
Write an equation. First represent each town as a point on a line segment.
Let Dyersberg be A. let Saint Thomas be B. and let Newton be C Let xbe the
distance in miles from C to B, or C3. Then the distance from A to C, or AC.
is 3:: + I.
Since (" is between A and B.AC + CE = AB.
AC+ CB=AB A 3x+1 C X 9
(3x+I)+x=25 ' '
‘l.\"l:1l=§l';! I 25 :
x=_
x = 6 miles. the distance Irom Newton to Saint Thomas
The distance from Dyersberg to Newton is found as tollows:
AC= 3x+ I = 3(6) + I = l9miles
As a check. note that the total distance is 6 + I9 = 25.
Exercises
. Communicate
1. 'l'he ttnit length on a ruler can A Point:
be any desired size. Gix-“e SOIHC W Picas
commonly used ttnit lengths. '"‘h“
_ ./ centimeters N
2. lixpl-.tin why it is important for
a ruler to have equal intervals.
p-
3. Suppose that the centimeter
were the only unit ol measure
for length. What problems
would this create? Discuss‘ why
it is useful to have dillerent
units for measuring length.
4. Once you have constructed a
ruler, why might you want to
divide the ttnit length into
smaller intervals?
C ‘nmpure: sofrtmre often allows‘
you to .\'t'lecI the um’! ofrnemtue.
5. Explain why each of the following statements does or does not make sense:
13. mm + op: 50 b. MN + OP = 50 c. m MN + mm’ = so
0 61//‘dad 3k///3 P/fldt/6'5?
APPLICATION
In Exercises 6-8. find the lengths of the segments. (EXAMPLE 1)
'1" . L’
—é—1t—§—21't'>1'§345
6. MN 7. N
0701)
a.T\-T5
"J
9. Complete the statements below. (EXAMPLE 2)
a. II" E 2 F), then 2 . u. n‘ AB = co. then 2 .
10. NAVIGATION The cities of Bloomington. ‘-7 -. ._.
-,1 1
Forsyth. and Decatur are located on a D- . N ....
straigltt road from Bloomington to atoomington
Decatur. with Forsyth between them. v '
The distance from Bloomington to L. ' EL ’_
Decatur is -10 miles. The distame from T . '
Bloomington to Forsyth is 7 times the r -
distance from Forsyth to Decatur. Find ’ ,,., ;_
the distance from Bloomington to ,.,,,..._
Forsyth and from Forsyth to Decatur. _’ °°¢3"-"'
(EXAMPLE 3)
LESSON 1.2 MEASURING LENGTH 21
I1 inlemclcnnned
Homework
Help Online
Go To: an l1rw.com
Keyword:
MG1 Homework Help
lo: Exercises 20-21
22 CHAPTER 1
Practice dlid 34,0;/y
ln Exercises 11-16, find the length of 11-8‘ .
11. - '3 §
-3: -3 -2 -1‘ 6 1 2 3 H 5 6
12. A - - - 3‘ - 9
-7 -6 -5 4 3 2 1 0 1 2 3
13- A : : : é : Q
-2 -1 o 1 2 3 a 5 6 7 8
14. Q . . . Q .
-7 -6 -5 4 -3 2 1 o 1 2 3
15- - ; Q : : 3 1
-5 -4 -3 -2 -1 0 1 2 3 4 5
15- : : é ‘ 5 : ‘
5 4 3 2 -1 o 1 2 3 a 5
17. Find the length ol each segment deternfined by points A, B, and C on the
nu mbcr line below. Show that the order of the coordinates does not matter.
_ J . § . - . .
-54-3-2-161254’-3
0):.
9)
ln Exercises 18 and 19, name all congment segments.
13. A 3 19. F E
E F A B C D
In Exercises 20-22, point A is between points M and B on ITB. Sketch
each figure and find the missing lengths.
2o. MA = 30 AB = 15 M8 = 1
21. M11 = I5 Ab’ = ; M8 = 100
22. MA = ; AB = 13.3 ME = 29.6
Find the indicated value in Exercises 23-25.
23. PR = 25 x = ? 2-X 3*
— P 0 n
24. P0 = 25 PR = L - - 5* - 3* ,
P o n
25.PQ=2S PR=; 2*“ X
P o n
‘\
I.
\
\
Towns A, B, C. and X are located along a straight highway. Town Bis
between A and C. and the distance lrom A to C is 41 miles. BC is 2 miles
more than twice AB.
26. Write an equation and solve it to find AB and BC.
27. Town X is between A and 3.6 miles from A. Find XC.
In Exercises 28-33. explain why each statement does or does not
make sense.
23. ‘(Y = 5000 yd 29. E: 32 in.
30. mST = 6cm 31. \’Y+ X7 = 32 cm
32. n1I’—R=-46 cm 33. V-5: I2 cm
CULTURAL CONNECTION: AFRICA The Egyptian royal cubit (1550 B.C.E.) was
subdivided into 28 units known as digits or fingers. From this basic unit,
a number of others were created:
4 digits = I palm I2 digits: I small span
5 digits = I h.1ndsbreadth I4 digits= I great span
6 digits: I fist I6 digits = I foot (t’eser_]
8 digits: I tlouble palm 2-I digits: I short eubit
34. A digit is apprmzitnatelv L9
centimeters. Draw a line and '
use -.1 centimeter ruler to mark
a unit length of I digit. Then
ttse :1 compass to construct a
digit rttler.
35. A cubit is the distance from
the elbow to the tip of the
middle finger. Measure your
own cubit with your digit
ruler. How does it compare
with the Egyptian royal cubit?
[T
H
EI%F-='.'F§r.'. $31’? -E-=.?.l‘x’rl4l'"='
ti rm:-..~v.=¢'-. .'.?lnT*.‘:AI
mi |IlllllllIlllll' Imuu mmunlitn-Ii-I Ill
You can divide the unit length of a ruler by folding the paper. If you fold
the paper so that the points at 0 and 1 line up. the fold marks the point
2- on your ruler.
36. What point would be marked ifyou folded the paper again so that the
points at U and %line up?
37. Construct a ruler with tt fairly large unit length. Divide the interval from
0 to I to find the points tor and
38. What are some points on your ruler that you cannot find bv using this
method?
LESSON 1.2 MEASURING LENGTH 23
APPLICATION
24 CHAPTER 1
L00»? Back
Choose any two different positive numbers.
39. Add the two numbers together. Is the sttm positive or negative?
40. Subtract the smaller number lrom the larger number. What kind ol
number do you get? .\low take the absolute value of this number.
41. Subtract the larger number from the smaller number. What kind ol-
number do you get? .\low take the absolute value of this number.
42. Compare your answers from Exercises 40 and 4|. lixplain why they are the
same or why they are ditlerent.
Choose any two different negative numbers.
43. Add the two numbers together. is the sum positive or negative?
44. Subtract the smaller number from the larger number. What kind of
number do you get? \low take the absolute value of this number.
45. Subtract the larger number from the smaller number. What kind oli
number do you get? \low take the absolute \-'-alue of this number.
46. Compare your answers from Exercises -14 and 45. Explain why they are the
same or why they are different.
Look Beyond
GEOLOGY Here is one example of.) ruler that does not have evenly spaced
divisions. l'he Richrer' scale is used to measure the intensity of earthquakes. An
increase of I unit on the Richter scale indicates an increase in ground motion
by a factor of l0. You can represent this with an "unfair" ruler.
47. Draw part of a ruler to represent
values on the Richter scale. Start
with the distance from O to l as l
mm. The distance from t to 2 will
be IO mm. the distance from 2 to 5
will be ml] min. and so on. (You will
quickly rtm out of room on your
paper!) How far would the distance
be from 3 to 4? from 4 to 5?
48. How much more ground motion is
caused by an earthqttake with an
intensity ol‘8 than by one with an
intensity of 6?
49. liarthquakes can also be measured
by the amount of energy released.
An increase of I unit on the Richter
scale indicates an increase by a factor
of 32 in the amount of energy
released. How much more energy is
released by an earthquake with an
intensity ol‘8 than by one with an
intensity ofé?
Measuring Angles
Air speed Altitude -- - .
indicator indicator - ,,
I 0
_ ‘ ;u,.,o:/ Altimeter
_. ti , '3‘ '3:
‘\-\" 7.x. E: E ‘
§‘* - - l we .
Automatic ' °_ ' nsu‘:
direction I ' _ __ Q ‘i i _ Venice;
Objectives """9' -J3 on ‘.9, '5 W Sojedt
Y Ad‘ '17’? :" £5. I" ICE Or
0 Measure angles with a 9.-“‘~6‘ : Q _ K‘ 1, 1-0 '
protractoi. _=°°' .-- 300- - :_I -._ ‘ '-
W '3 I . é , ] \
0 Identity and use the J, ¢._§ I ' 4.5 9" i 2 ‘ '
Angle Addition 4: is -x I"-_;-..,;”‘ R.\““ ' .
posw|a[e_ .. _ h - ' Directional gyro
Anglo measure is used in many
:1’ “"°z;,F.:;::’t";e'P:'p"°”m’g'f‘;:r"9'e Thehmdingqftiiisizirplane, its imiimted by theilirectiomiigyro
in the photo above, is I66, (I rltrection that is It little east ofiltte
ai lane to navigate safety tlirougli the skies. _ _ _ _
'1’ south. 4' The imrltitgs on the dial must he nniittplied by i 0. J
Defining Angle Measure
A protr-actor is used to measure angles. As on a ruler. the intervals on a
protractor must be equal. Then you can be sure that if two angles have the
some measure. they are congruent. -and vice versa.
To understand how a protractor is used. study the following, exantple:
E X A M P L E ol.seaprotractor to find the measure of A013.
0 SOLUTION
1. Put the center of the prolrttclor at the
vertex. A B
_ —b
2. Align the protractor so that AB passes
through 0 on the protractor.
3. Read the measure o£}ACAB [in degrees]
at the point where AC intersects the
scale on the protractor.
The measure oI‘ACAB is l2l°.or
m.£.C/lb’ = l2l°.
CRITICAL THINKING Why isn’t the measure of ACAB 59° instead of L2 l°?
LESSON 1.3 MEASURINGANGLE5 25
CRITICAL THINKING
EXAMPLE
26 CHAPTER 1
Angles, like segments. are measured in standard units. The most common unit
ot angle measure is the degree. This is the unit of measure that results when a
ltaltlcircle is divided into I80 equal parts.
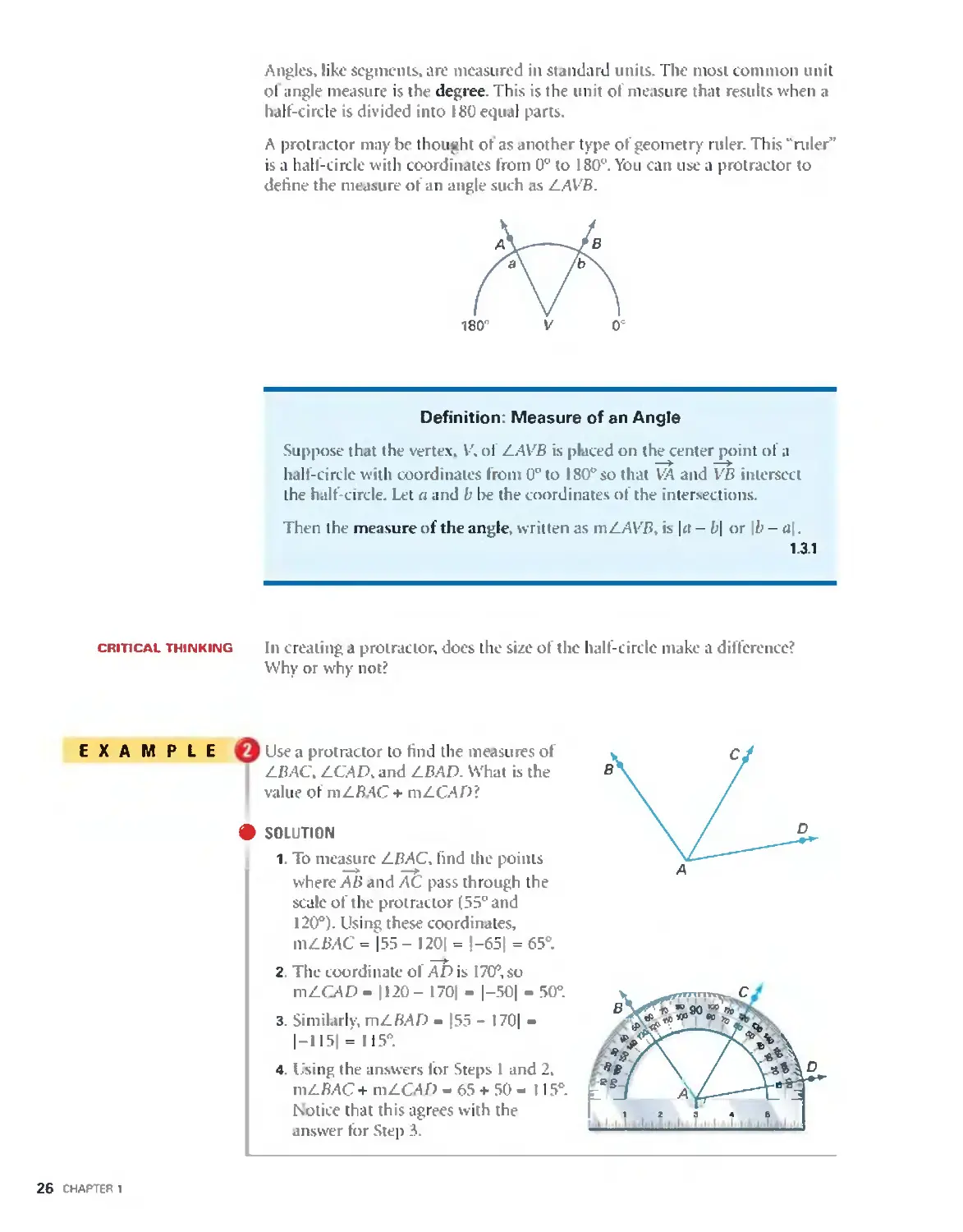
A protrnctor may be thought ot as another type of geometry ruler. This “ruler”
is u halt'—circle with coordinates from U“ to I80“. You can use a protraetor to
define the measure ofan angle such as AAVB.
180" V 0‘
Definition: Measure of an Angle
Suppose that the vertex. \-’. ol‘ A.—'l\-’B is placed on the center point of n
- . . . - d h .
hall—circle wnh coordinates lront 0° to I80” so that MA and VB intersect
the half-circle. Let rt and b be the coordinates oi" the intersections.
Then the measure of the angle. written as mé.-'-ll-"B. is |ct — b| or lb — a].
1.3.1
In creating a protr-actor. does the size of the haltlcirele make at difference?
Why or why not?
Use a protra1c.tor to find the measures of c
./_BAC. ACAD. and LEAD. What is the 3
value of n1Z_B4C + mLCAD?
O SOLUTION D
1. To measure ABAC. hnd the points
*5 —P
where AB and AC pass through the
scale of the protr-actor [55" and
120°). Using these coordinates,
mLb‘/tC = I55 — I20] = [-65] = 65°.
2. The coordinate 0|" A-5 is 170’, so
mA('.»tD - |t2O — t7o| - |—5o| - 50°.
3. Sintilarly, mLB.»lD - I55 - I70] -
|—ll5| = H5“.
4. Using the answers lbr Steps 1 and 2.
n1LBAC+ m£C-lD - 65 + 50 - l 15°.
l\otiv:e that this agrees with the
answer for Step 3.
congruent Angles
A B Atigles. like segments. are congruent ili one
can be moved onto the other so that thev
match exactly. Tick marks are used to show g
which angles are known to he congruent. ‘N F ’ G _‘-
C D Note: Angles are said to match if their sides
zA§ADandzBszC - . ._
match. The lengh ol the sides, Wl'llLl1 are rays [F __ £6
that go on lorever. does not matter.
From the discussion of a protractor. the following important geometry
principle should be obvious:
Angle Congruence Postulate
If two angles have the same measure, then they are congruent. If two
angles are congruent. then they have the same measure.
1.3.2
E X A M P L E 0 Complete the following statements by using the Angle Congruence Postulate:
I ll' mAABC = m£DEF. then ? .
IYAABC E ADEF. then ? .
O SOLUTION
ll mA~’lBC = n1.:.’DFF, then A-lBC':“ ZDFF.
I ll-(ABC S ZDEF. then m£.»lBC= m£DFF.
Angle Addition
Look again at Example 2. Step at shows that n1ABAC + mzC.»'«tD = mzBAD.
This suggests the following postulate:
Angle Addition Postulate
_ . . P 5
ll point 5 is In the interior ol ZPQR,
then mZPQS + mASQR = mZPQR.
0 1.3.3
CRITICAL rnmxmc. As with the Segment Addition Postul-ate. you should ask yourself. What is
really‘ being added—-angles or measures of angles?
4-1 + AB = ltiU°
Which statement makes sense? m LA + mil; = [80
LESSON 1.3 MEASURING ANGLES 27
Pairs of Angles
Sometimes it is important to consider pairs of angles.
Special Angle Pairs
Complementary angles are two angles whose measures have a sum of
90°. Each angle is called the complement of the other.
Supplementary angles are two angles whose nteasttres have a sum 0|‘
I80". Each angle is called the supplement ol the other.
1.3.4
E X A M P l. 0 Name all complementary and supplementary angle pairs below.
g ‘ 120/
A B c
O SOLUTION
AA and AB are complementary angles.
LA is the complement of AB. AB is the Complement oi AA.
AA and AC are supplementary angles.
AA is the supplement of At". LC is the supplement oli AA.
If the endpoint of a ray falls on a line
so that two angles are formed. then the
angles are known as .1 linear pair.
cnmcAL THINKING ll" two lines intersect at a point, how many linear pairs are formed? Explain
how this situation tits the definition of -.1 linear pair.
The definitions above lead to the following property:
Linear Pair Property
ll‘ twt) angles form ti linear pair. then they are supplementary.
1.3.5
You will use the Linear Pair Property to prove an important conjecture in
Lesson 2.5.
28 CHAPTER 1
Classification of Angles
Angles can be classified ttccordittg to their measure.
Definitions: Three Types of Angles
.-'1 right angle is an angle whose measure is 90°.
.-‘tn acute angle is an angle whose measure is less than 90°.
An obtuse angle is an angle whose measure is greater than 90° and less
than 180°.
1.3.5
The symbol for a right angle is a small
_.— Right angle symbol
square placed at the verte\' ol the angle. '
Extending Angle Measure
You ntay have noticed that so far the angle measures studied have been greater
than 0“ and less than I80”. One reason for this is that the definition of the
interior am_l exterior olian angle doesn't applv outside this range. [Try it
and see!)
However. it is sometimes necessary to talk about angles of 0° and less or of
l80"and greater. Compass headings, for example. range lrom 0° to 560°. You
can think of them as being based on a 360“, or circular. protraetor. .-‘tngles with
a measure of I80" are called straight attgles, and angles with .1 measure greater
than I80” are called l£'_fll.’.‘.' miglcs.
In Chapter l0. angles are studied in terms of rotation, in which case their
measures can be greater than 360° and can even be negative.
Exercises
. Communicate
1. A magnetic compass is used in navigation to determine which direction is
north. Once you know which direction is north, how could you use angles
to describe the direction in which you are traveling?
2. Think of-a memorv aid. or amt.-mtmie. to help you remember the
difierence between complementary and supplenientary angles.
LESSON 1.3 MEASURING ANGLES 29
30 CHAPTER I
3. Discuss the similarities and dilTerences between segment length and angle
measure.
4. Use an example to explain why the /\ngle Addition Postulate fails if point 3
is not in the interior oi" APQR.
5. Classify each of the following statements as true or false. and explain
your reasoning:
a. All right angles are congruent.
b. All acute angles are congruent.
c. All obtuse angles are congruent.
6. ljxplain why one of these statements in-altes sense and the other does not:
a. 111A.-'1 + mL2 = l90°
b. AX+ LY: l50°
7. Explain why the definitions of interior and exterior ofan angle do not
apply to straight angles and reflex; angles.
. qr//dad 8.6///3 Practice
8. Use the protractor in the
figttre at right to find the
measure ol‘ Ll’t"l-"X.
(EXAMPLE 1)
In Exercises 9-11, use the
protractor in the figure at
right to find the measures
below. (EXAMPLE 2)
9. mAQPR
10. mLRP.S'
11. m LQPR + n1LRPS
12. Complete each statement by applying the Angle Oongruence Postul-ate.
(EXAMPLE 3)
a. ll‘ 111 Al 'l-’W = mLX}"Z. then .
b. If AUl-’l1-’ E LXYZ, then
13. Mine a complementary angle pair and a supplementary angle pair in the
figttre l?I(-.‘lUW. (EXAMPLE 4)
40°
50
0 Practice film’ 74,20/y
Refer to the figure below. Find the measure of each angle.
14. m LAVB
15. m AAVC
16. n1L.vll/I)
17. n1.LB\-’C
18. m ABK-"D
19. m AC1/D
- mmtcnnnnd Use a protractor to find the measures of the indicated angles. You may
Homewom ‘ trace the figures or use a piece of paper to extend the rays if necessary
Help (mine 20 m AX 21 m LY
Go To: go.lrrw.cum ' '
Ke-_mwd:
MGI Homework Help
[or Exercises 2|] 26 X
J
Y
22. m AABC 23. m 42
1 \A
24. m.LRST
25. n1 ASRT
26. m ASTR R T
In the figure below. mzCED - 25° and zAEB and (BED form a linear
pair. Find the following:
27. m ABEC B
23. m 4.458 C‘
29. m AA FC
in E 5 ¥
In the figure. mzEDG = 70° and mzf-"DH = 60°. Find the following:
30. m 412
31. mi}
32. Ill Al
33. n1L4
34. n14£FD]
LESSON 1.3 MFASURINGANGLES 31
I..'/ I
CHALLENGE
32 CHAPTER 1
35. In the figure at right. n1A.»tLE = 31°
and m (Si F= 59°. What is the 5
measure oi" ZSLA? \'\-‘hat is the
relationship between ASLE and E
(ALF?
L
Find the missing angle measures in Exercises 36-38 Refer to the
figure below.
36. inzl-i-’ZX = 80° ni.£XZY = 34° ni.£WZY = _?_
37. m.£WZX = 21° m.£XZY = L 1n.{WZY = 43° 2 X
38. m A H-'7.\’ = L m .4 X’? Y = 34° in z l-'t’ZY = 52°
W
In the diagram below, mLKNM = 87°. mALNM= (Zx — 8)‘, and
mAKNL = (x + 50)°. N
39. What is the value of t?
40. What is m 1 KM ?
41. What is DIZLNIW? K M
In the diagram below, mLADC = (43 + x)“. Find the value of x. and then
find each indicated angle measure.
42. m (ADC
43. m (A DB
44. rnzBDC
45. What is the angle hetween the minute and hour hands on a clock at 3:00?
46. What is the angle between the minute and hour hands on a clock at 5:00?
47. Another unit of angle measure, used primarily in engineering, is called a
gmdian. There are I00 gradians in a right angle. is l gradian smaller or
larger than 1 degree? Why?
48. l\'-.nne all sets of congruent angles in the ligu re below.
NAVIGATION Exercises 49-56
involve compass headings.
Headings are numbered in
the clockwise direction from
000 to 560. starting at north. .'
The headings from 000 to _ ‘__, . 3-,,‘ 3
I80 are equal to the _ .13‘; "' "'3 I
measure of the angle .~ 4 3;
formed bv the compass -- ‘ V ‘._
needle and a ray that 3
points in the direction . \1
of travel. The headings \9" -. ‘ “ acre i
from ISO to 360 are --“‘ .
found by subtracting W
the measure of this 0‘ -
angle from 560.
.31‘-I1: .
new. . '
Find the heading for Zr’ % ‘AT
each of the following 7"“"7" ’ ' ‘F47
compass directions: ‘ ° _ - . ,_
J . I 3-}.-
49. \l ' \ ‘; _
\ \‘~ .
50_ E I{.'I7{- _ _ f I
51. S I ‘I’ - \ I ' 2-"2. '
52. W “Viv - dvf '
-ttz
53. NE g_
54. SW '
55. NNE _
. Chicago 56_ SSW —_‘
355 57. NAVIGATION A pilot is flying to Chicago on a heading of 335. Refer to the
diagram at left. would the pilot’s heading be greater or less than 555 if the
0X plane was traveling to Chicago from point X?
Pilot
58. SCUBA DIVING Scuba divers often navigate in a square pattern at a constant
depth. Examine the ligu re at right. If the diver starts out at a heading of
315. what compass headings are needed to navigate around the rest olthe
square? Other than using the headings. what else must a diver do in order
to navigate the square?
I
F
-c'
‘-''‘*!.on:
1'] 1
-'—.
L 'nderu-mar ctnrrrpasses. ‘~..
like this progrmnnmlrle ‘
to-mptm'r. are used by \r_
din-‘ens to rravigare.
LESSON 1.3 MFASURINGANGLES 33
n lutemetoomea ,3?‘
Activities
Online
Go To: go.ltrw.conI
Keyword:
MG! latitude
34 CHAPTER 1
Look Back
Refer to the figure below for Exercises 59-62. (LESSON 1.1)
59. Give .1 different name for Al.
60. ldentifv a line that is coplanar
with Al.
61. Name all lines that are formed hy
the intersection of two planes.
62. ldentifv three collinear points.
For each figure below, find the length of the indicated segment.
(LESSON 1.2)
63. 64.
+ >
9 -3 0 -6 D 10
65. ll" Ab‘ = 27, find AC and BC. (LESSON 1.2)
4x — 3 x
A C B
£00K’ Bet/om’
66. CULTURAL CONNECTION: ASIA Our Llnil
measure of degrees comes from the
ancient Bahyloni-ans. The B-abylonians
based the measurement ofan angle on
a circle di\"iLiL‘Li into 360 equal parts.
What are some advantages to using
this unit of measurement? (Hint: List
all of the factors of 360.)
67. Just as the units on a ruler are
subdivided. so are the units on
a protractor. Astronomers.
architects. and surx-'e_vors often
need angle ineasurernents that
are more precise than degrees.
A degree is often divided into
60 units called nn'rmre.<, and a
minute is divided further into
60 units called seconds.
a. How many seconds are in I degree?
b. How many seccmds are in L5 minutes?
c. I low many minutes are in L75 degrees?
Objectives
0 Use paper folding to
construct
perpendicular lines,
parallel llllBS, segment
bisectors, and angle
hisectors.
0 Define and make
geometry comectures
Geometry Using
Paper Folding
Paper folding can be used '«
to create precise geometric
Ilgures without me use 0!
special drawing instr
Origami, the rmciem Irtprmese art of paper folrlirig, relies on properties
ofgemnetry to pl'0(illt‘t’_filSt‘in(.lifflg and often beztirtiful shapes.
Paper Folding: The Basics
When created according to certain rules. a diagram is considered to be
mathematically precise. These types of diagrams are called constructions. In
this hook. you will learn to construct geometric ligures with paper folding. .1
compass and st raightedge. and geometry software.
The term fiilrling paper refers to any paper that is suitable to use for folding
geometric figures. You should use paper you can see through, such as wax
paper, so that you can match figures precisely when you told. “Patty paper”
is ideal hecause it makes white creases when folded and is easy to write on.
In the following activities. V\Ol'l< with a partner. Be sure both you and your
partner understand why the constructions work. Learning why things work
the way they do is one of the most important objectives of this course.
The terms defined below will be used in the Activities in this lesson.
Definitions: Perpendicular and Parallel Lines
Perpendicular lines are two lines that intersect to form a right angle.
Parallel lines are two coplanar lines that do not intersect. 1.4.1
LESSON u GEOMETRY usmc PAPER FOLDING 35
folding paper, and a
marker or pencil that
will write on lolding
paper
cuecxpomrr ./
CHECKPOINT ./
36 CHAPTER 1
Making Conjectures in Geometry
A conjecture is a statement that vou think is true. It is an "educated guess"
based on observations. l\.lathem.1tical discoveries often start out as conjectures.
In the .r‘\eti\-ity that follows, you will make conjecture: about perpendicular
and parallel lines.
' /
Perpendicular and Parallel Lines
1 Fold the paper once to make a
line. Label the line If’.
2 Draw a point on line I.‘ and
label it A. Fold the paper
through A so that line 1'
matches up with itself. Label
the newline m.
3. Measure the angles formed by lines E and in. What kind of lines are
formed?
4. Mark a new point on line E.
and label it B.
5. Fold the paper through B so
that line it‘ matches tip with
itself aagaain. label the new
line H.
6. \-\-hat kind of lines are F and u? what kind or lines are m and fl?
Complete the lollowing conjecture about parallel and perpendicular
lines:
lf two coplanar lines are perpendicular to the same line, then ? .
Measuring the Distance From a Point to a Line
How would you l'l1(-.‘ilhlll"c‘ the
distance from the tree to the
fence in the photo at right?
Would you use the segment
W. W’. or TC? _-
It
‘.
ln geontetry. the distance
4 er
from a point to at line is the /' 3 ‘~~._
length of the perpendicular ,x" “‘~~.~
segment from the point to /" ’ “‘~..
the line. Thus. the distance - ‘E.’
from the tree (point X] to
_ 4:) _
the _tgnee ( AC] is the length
of X3
CRITICAL THINKING Why do you think the distance from a point to a line is delined along a
perpendicular segment?
You can use paper folding to help you 11te;m1t'e the distance from at point
to a line.
Finding the Distance From a Point to a Llne
- - E) 1. Fold a line and label it I‘. 2. Fold the paper over so that I"
fuming ,,,,,,e,_ 3 m;,,ke,_ Choose a point not on the lines up with itselt. but do
and 8 Fl_I|9fl'0f line and label it P. not crease the paper yet.
measuring)
I
J’ ‘F
3. Slide the top edge of the paper. 1
keeping Flined tip on itself, until
P is on the fold. Carefullv crease
the paper. making sure that P is
on the crease.
cuecxpotm ./ 4. Use a ruler to measure the distance
from Pto if along the creased fold.
-P
LESSON :4: GEOMETRY usmc PAPER FOLDING 37
- E D
folding pa per, a marker.
and a ruler
CHECKPOINT ./
CHECKPOINT M
38 CHAPTER I
Segment and Angle Bisectors
In Activity 3 below. you will use the following definitions:
Definitions
A segment bisector is a line that divides a segment into two congruent
parts. l‘he point where a bisector intersects a segment is the midpoint of
the segment. A bisector that is perpendicular to a segment is called a
perpendicular bisector. An angle hisector is a line or rav that divides an
angle into two congruent angles. 1.4.2
' 3
Exploring Segment and Angle Bisectors
Part I
1. Fold line ti. Choose points .1 and 1
B on I’. Fold the paper so that A
matches up with B. l abel the °
resulting line ru. What is the
relationship between in and E?
Segment Bisectors
2. Choose a point on m and laltnel it
C. Measure TC and 77‘. Repeat.
choosing several dillerent locations
for C What do you notice?
- . _ '13
Complete the lollowing comecture:
l‘he distances from a point on the /
perpendiutl-ar bisector to the T?
endpoints of the segment are ? .
Part ll Angle Bisectors
3. Fold intersecting lines 1' and k.
Label the intersection P. Label a
point Q on k and a point R on j. j 0
Fold the paper through P so that -~—..
line j matches up with line k. Label
the new line n. W hat is the
relationship between it and AQPR?
4. Choose a point on n and label it 5. .
Measure the distance from S to j
and the distance from S to k.
Repeat. choosing several dillerent
locations for 5. What do you
notice? Complete the following
conjecture:
The distances from a point on the angle biscctor to the sides of the
angle are ? .
Exercises
. Comma”/rate
1. When vou folded line I’ onto itself
in Step 2 of Activity 1, which pairs
ofangles matched up? Use this to
state an alternative definition ol-
perpendicular lines.
2. When vou constructed parallel lines
In and n in Step 5 of Activity 1. how .
n1-any right angles were formed? Make
a conjecture about how you can
determine whether two lines are
parallel.
3. When you folded A onto b‘ in Step l o
of Activity 3. how could you tell
(without measuring) that the new
line divided /lb’ ll1[0 (W0 L'Ollgl'llEfll 711,);-, _\-mp};-, or_Qfu,-_- your fold,-_-d
segments? papers to your work. label the
PflPl'.'T$ in t'(L\'t' they conic Ofii
4. Explain how you measured the
distance from S to i and S to kin
Step -I of Activity 3.
0 6;/idea’ 5k///8 Practice
For Exercises 5-8, use the figures below and your conjectures from the
Activities to complete the following statements:
5. Lines {-2 and m are ? . 6. 'l'he distance fiom P to F
(ACTIVITY 1) is ? . (ACTIVITY 2)
P
:1 m f
B
7. .-‘tcand BC are ? . 8. B.\’.md CA’ are E‘ .
(ACTIVITY 3) (ACTIVITY 3)
C B
A X -?>
A B C
LESSON u GEOMETRY usmc PAPER FOLDING 39
fl luumotcomea
Homework
Help Online
Go To: gnJtrw.com
Keyword:
M61 Homework Help
lot Exercises fl—24
40 CHAPTER 1
.'?a
P/fl6‘t'IZ'6’ mm’ 34,0;/y
Use a separate piece of folding paper for each exercise. Attach the
folded papers to your homework, and be sure to label each piece.
Fold each figure below. Do not use a ruler or protractor. Trace over each
figure and label all relevant parts.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
a 90°ang|e
a 4S"angle
an acute angle
an obtuse angle
two complenientarv angles
two supplementary angles
two parallel lines
a rectangle
a square
a triangle
a right triangle (a triangle
with one angle ol 90°)
a triangle with two equal sides
a right triangle with two equal sides
Fold a line and label two pgfltts A and B on the line. Construct the
perpendicular__bi_sector__of AB and label it 6. Label a point Con E, and
fold or draw AC and BC.
22.
23.
24.
25.
26.
Using the first conjecture vou made in Activity 5, what can you conclude
about 16‘ and BC?
Write a conjecture about triangles in which the vertex of one angle is on
the perpendicular bisector of the side opposite that angle.
How could you use the conjecture from Fxercise 23$ construct a triangle
with three congruent sides? (1 lint: Start by tracing AB onto another piece
of folding paper.)
Suppose that t is the
perflndicular bisector
ot'AB and that AB = 10.
Find AC and BC.
Suppose that m is the angle
hisector of ./_DEF and that
n1LDE.‘t’ - I3°.
Find IHLFFX and IHLDFF.
Fold two intersecting lines, and label them as shown in the figure
27. Fold the bisector of Lxl-'Y and label it E.
What is the relationship between t? and
Lil-"VZ?
28. Fold the bisector of Ll-Vt-"X and label it
m. What is the relationship between t’
and m?
29. Repeat Exercises 27 and 28 with several
dit't'erent pairs of intersecting lines. Make
a conjecture about the l}lS'c‘Ll.(}l'S of angles
formed by intersecting lines.
For Exercises 30-32, fold or draw two perpendicular lines on a piece of
folding paper and label them If and m. Label the intersection of £3 and m
point A.
30. Fold the angle bisettor of one of the angles
formed by t" and m. Choo:sc -.1 point on the
angle l)lS€(.t()l' and label it B. Fold two lines
through B. one perpendicular to and one
perpendicular to m.
31. Make a conjecture about the shape you formed
in Exercise 30. Measure any sides or angles
necessary to confirm your conjecture.
32. E is called a diagonal of this shape.
Fold the other diagonal of the shape.
Make a conjecture about the diagonals
of the shape you constructed.
£00k Bflfk
Name the geometric figure that each item suggests. (LESSON 1.1)
33. the edge of a table 34. the wall of a classroom
35. the place where two walls meet 36. the place where two walls
meet the ceiling
Name each figure. using more than one name when possible.
(usssorv 1.1)
37. 38. 39.
M
._’l‘_l’_‘. ‘lei’
To»
A P
40 41. .0 1.; 42.
P S 13
.P ‘R
LESSON 14 GEOMETRY USING PAPER FOLDING 41
A
C
8 F
D
U hlnmetoonned .2?“
Portfolio
Extension
60 To: go.lIrw.conI
Keyword:
MCI Origami
Lao
0%‘
Q.
1.00.? Beyond
In Chapter 4, you will examine properties of triangles. ln Lesson 4.7, you
will use a compass and straightedge to construct a triangle with given
side lengths.You can also use tracing paper to construct such a triangle.
as directed below.
43. Trace each segment afift onto a separate piece of flcing paper.
Place the paper with .4801) top of the paper with CD. and line up A and
C. You may want to poke a pin through A and C to keep them aligned.
Place the paper with 7:7-"on top of the other two. line up E and B, and then
line up l-' with 1).
Trace the cotnplete triangle on the top picu: of paper.
44. Can you create .1 different triangle front these segrnents? Why or why not?
I A 1 0
_ ty y ’ ‘ V .0 sW J I
3' <1“ :Q‘>> l\)‘ J. ‘P :1; Z
i I \ 'v 1 p
L‘: V) ’A‘
> ‘‘‘<
T
A mzrtlrtr luuugon is a six—sided figure with equal sides and equal angles.
You can create one by following the steps below.
1. Fold a square piece of paper along one
diagonal.
2. Place your protractor on the center point of
the fold and mark off dashed lines at 60°
angles.
3. Fold the right and left portions along the
dashed lines.
4. 'lurn the figure over and mark a new dashed
line. Cut along this line.
5. Open the figure. The finished product is a
hexagon.
You can also create a snowtlttke pattern trotn
these folds. Do not open your figure in step 5.
lnstead. fold the ligure vertically through the
center another time. Cut notches into each side
ofthe folded figure. When you unfold the figure.
you will have a snowflake.
42 CHAPTER 1
Special Points
in Triangles
Objectives
0 DISCOVQI pouns ol -
concurrency in
triangles.
0 Draw the inscribed
and circumscribed , — _ _.
circles ol triangles.
;‘lrr'lmeologisrs at this site in Belize have mum-ereri part of
S ecial virus in . . .
, M9,; hawpmm, (J rircnlnr sn'm'mrc. In this lesson, you Will learn it method
gpprigggiggg, {mm gffm jbrfimliug the Center ofu circle when only it part is giwir.
rel: - nlcatlons
Triangles and Circles
In this lesson, you will discover some interesting facts about triarrglrs and
circles. When you study proofs. you will understand why they are true.
I
Some pecial Points in Triangles
- U L NEED In this Activity. you will discover some special points in triangles. Save
lolding paper vour triangles for the next Activity. It" you are using geontetry software.
\ on you can "drag" the vertices of the triangles to explore dillerent triangles.
geometry , - _ - ‘ 5 . _
Samara 1. Drtm or told .1 triangle. Thtn (.OI'l.5l.l'l.lLl.
the perpendicular bisector of each side of
the triangle. What do you notice about
the perpendicular hisectors?
2. Draw or lold another triangle. Then construct
the angle bisettor of each angle of the triangle.
what do you notice about the angle hisectors?
3. Share your results with vour class. Complete the conjectures below.
CHECKPOINT V The perpendicular bisectors of .1 trimtglc 2 at a single ? .
The angle bisectors of a triangle ? at a single ? .
LESSON 1.5 SPECIAL POINTS INTRIANGLES 43
o- - L
lolding paper
and compass
OR
geometry
sottware
CHECKPOINT V
EXAMPL
A-P IBM
ARCHAEOLOGY
Special Circles Related to Triangles
For any triangle. vou can draw an
inscribed circle and a rirr'untsrrilu'd
circle. An inscribed circle. as the
name stiggests, is inside the triangle
and just touches its three sides. A
circumscribed circle is outside the
triangle [circmn— means “-around")
and contains all three vertices.
Inscribed circ|e Circumscribed circle
Constructing the Special Circles
1. Use the triangles vou created in Activity l. Draw circles with centers at
the special points you discovered in Activity I. Can you draw the special
circles defined above?
2 Complete the conjectures below.
Inscribed and Circ umscribed Circles
The intersection point of the angle bisectors of the angles of a triangle is
the center of the ? circle or the triangle.
The intersection point ol the perpendicular bisectors oi the sides ot a
triangle is the center oi the '5 circle of the triangle.
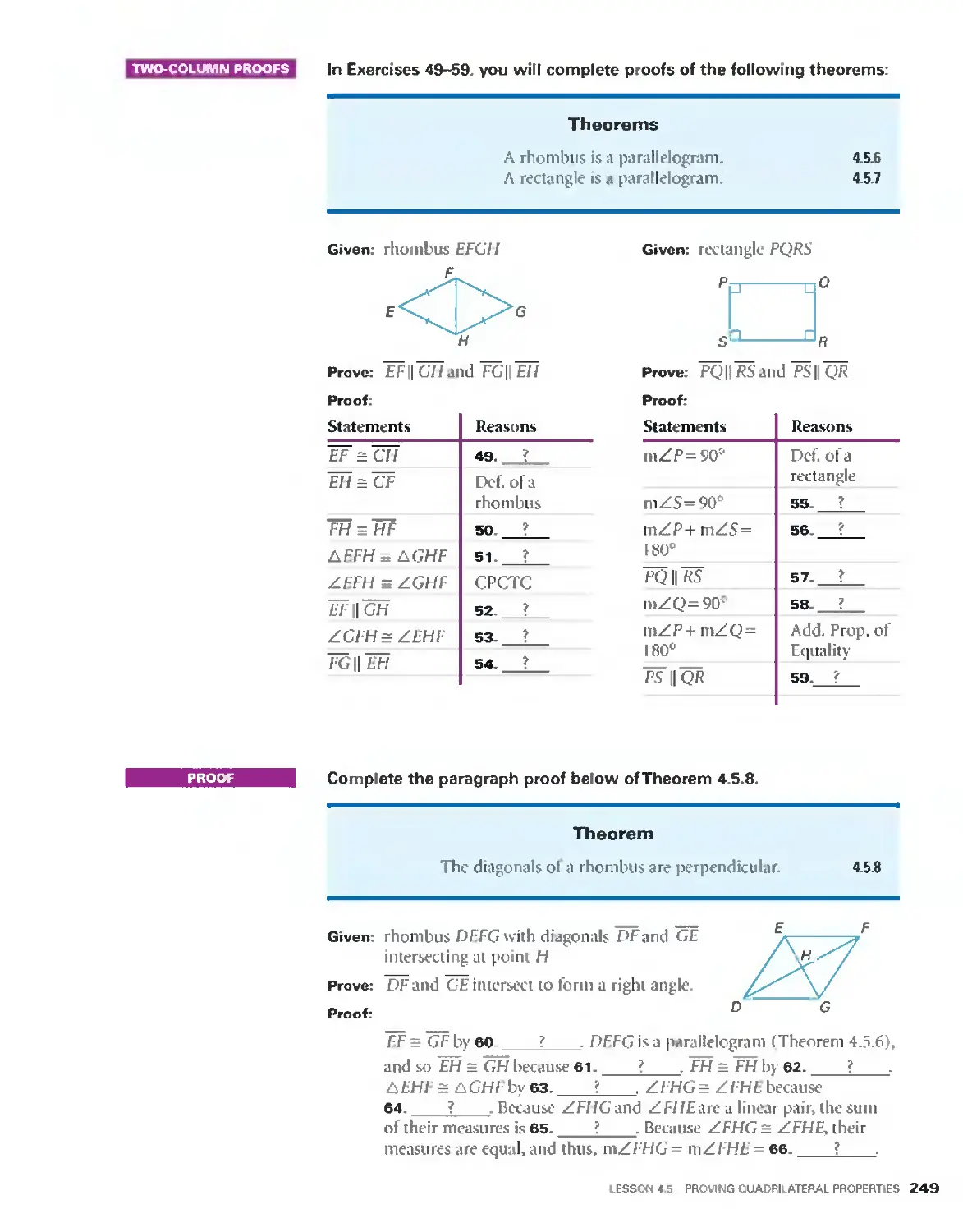
0 An archaeologist wants to find the original diameter of a broken plate.
How can she do this by applying one of the coniectures from Activity 2?
SOLUTION
lhe archaeologist draws an outline oi
the broken plate. Then she selects three
points on the circuniference oi" the
plate and connects them to form a
triangle. The intersection of the
perpendicular bisectors ol the sides ol
the triangle is the center of the plate.
[Only two hisectors are needed,
however, the third acts as a check.)
The radius of the circle is the distance
from the circles center. 0. to the edge
of the plate. By measuring this distance
and doubling it. the archaeologist can
find the diameter of the plate.
44 CHAPTER 1
Exercises
. Communicate
' ' "" ‘:~:1''-‘ —‘ " I. The lines you constructed
in Activity I are said to
I be concurrent. The word
)\ comes from the Latin _ __ '-__ .
\ words can f“togetl1er”) and "
‘ currere (“to run"). Why is
this word appropriate for
-— these lines!
2. The center of an inscribed
'- circle is called the incenter
ofa triangle. Can the
inccntc-r be outside the
triangle? Explain why or ..——
why not.
L’
//T ‘I
s,
0 3. l'he center of at circuntscribed
A: _‘ circle is called the
circtlmcenter of a triangle.
(_‘,;tn the circtnnccntcr be
outside the triangle? Explain
why or why not.
Gmrrmry gmphirs $(1ftll"tJJ1’ has rmmy
trstjlirl lltrznrrrs [hr cretuirtg r.‘mlS!rm'!ltm.i.
Using gcmrmry graplrirs
.<o_ftwure, you am “dmg"
the poirtrs in n figure to
exmrmte diffisrent cases.
0 6/1/'ded.S,('///3 P/fltt/66
4. What is the result when you fold or draw the perpendicular ltisectors ol'
the three sides of .1 triangle? (ACTIVITY 1)
5. What is the result when you told or draw the angle bisectors of the three
angles of a triangle? (ACTIVITY 1)
For Exercises 6 and 7, use your conjectures about inscribed and
circumscribed circles to complete the table. (ACTIVITY 2)
Inlersecting lines Type ol circle formed Name of center
6. perpendicular bisectors ? ?
7. angle bisectors ? ?
8. Trace the portion ofa circle
shown at right. Choose three
points on the circle and draw a
triangle to connect them. Then
Construct the circttmscribed
circle around the triangle to
complete the figure.
(EXAMPLE)
LESSON 1.5 SPECIAL POINTS INTRIANGLES 45
Practice mm’ 34,0;/y
It hum-teamed ,:g_ Draw each of the triangles below onto a separate piece of folding paper
"omewmk ‘°"' or draw them by using geometry software. Triangles are named by the
Help Online symbol A and the names of the vertices. such as AABC.
E§J:;?;'”"°“ Find the following:
":2 9. the perpendicular bisectors of 10. the angle bisectors of each
each side of AABC angle of ADEF
E
8 :
A / C D F
11. the circumscrilaed circle of AG!!! 12. the circumscribed circle of AIKL
H
13. the inscribed circle of A.\-'I.N'O 14. the inscribed circle of APQR
N
O
. ,\2\J R
M O
15. the perpendicular bisectors of AST U
16. the angle lJl$€CI01'.\ 0fASTU
17. the circumscribed circle of .£\STU'
18. the inscribed circle of ASTU
46 CHAPTER I
CHALLENGE
In Exercises 19-23, draw or fold three triangles:
° an acute triangIe—a triangle with all angles less than 90°
° an obtuse triangle—a triangle with one angle greater than 90'
' a right triangIe—a triangle with one angle equal to 90°
19.
20.
21.
22.
23.
Construct the circumcenter of the acute triangle. is it inside or outside
the triangle?
Construct the circumcenter of the obtuse triangle. is it inside or outside
the triangle?
Where do you think the circumcenter of-a right triangle should be?
Construct the circumcenter of the right triangle to test vour conjecture.
Use the circumcenter of the right triangle to draw the circumscribed circle.
How does the longest side oI'the triangle divide the circle?
Based on your answer to Exercise 22. make a conjecture about the
circumscribed circle of a right triangle. Draw several diI'I'erent right
triangles and test your conjecture.
Draw or fold two acute triangles and construct the midpoint of each
side. Use one in Exercise 24 and the other in Exercise 25.
24.
25.
26.
Connect the midpoints to form another trianglc. Your drawing should
now contain four small triangles inside the original one. Cut out the four
small triangles and compare them. \-\-‘hat do vou observe?
Draw a segment from each midpoint to the I.
opposite vertex. These segments. called the
n1c't.llrl.lI:, are shown in the Iigu re at right.
Label point C where the medians intersect.
Measure the following segments in your
triangle and complete the table:
CK=? CL
CY=? CZ=?
CM=?
CX=?
-.a
What is the relationship between the lengths in the nrst row of the table
and the lengths in the second row? Make a conjecture about point C.
which is known as the cemroid.
In the triangle at right. t" is the
perpendicular bisector ol‘
Suppose that X is a point on I".
What can you Say about AX
,. ‘1
and B)\!
What can you say about anv _'— H
point on the perpendicular .
bisector of of EC’
Explain why the intersection
of the perpendicular
bisectors is the center of the
circumscribed circle.
LESSON 1.5 SPECIAL POINTS INTRIANGLES 47
c It A L L E N G E 27. In the triangle at right. m is the angle II
bisector of 1 F. Suppose that Y is a point
on m. W hat can you say flnut the_
distance from Y to sides DE and EF?
What can you say about any point on the
angle bisector of AD? of .«*_''I-? Explain
why the intersection of the angle biscctors
is the center of the ln5Ll'llJé‘t'.l circle.
APPLICATION 28.CONSTFlUCTl0N
.-\ contractor is
installing a round
air-conditioning
duct. The duct must
pass through a
triangular opening.
as shown in the 92 in.
figure at right. Trau; 68 in.
the figure onto
folding paper and
construct the largest
circle that will fit
inside the triangle.
38 in.
L001? Bfltk
Complete the statements below. (usssorv 1.1)
29. Points that lie on the same line are said to be 2 .
30. Points or lines that lie in the same plane are said to be ? .
In Exercises 31-33, you may wish to include a diagram to illustrate your
answer. (LESSON 1.1)
31. Is it possible for two points to be noncollinear? Wlw or why not?
32. Is it possible for three points to be noncoplanar? Why or why not?
33. Is it possible lor two lines to be noncoplanar? Why or why not?
'4: I / ln Exercises 34-37, refer to the figures below, in which WY- 48 and
ABACE ACAD. Find the measures listed below. (LESSONS 1.4 AND 1.5)
34-XV dx—3 3x+2
35. w.’ w R v
36. m A BAC
37. n1 .«*_"C/ti)
48 CHAPTER I
1.001? Beyond
Another special point in a triangle is angmde
formed by the altitudes of the sides. An
altitude is a perpendicular line segment
from a vertex of a triangle to the line
containing the opposite side.
38. Draw or told an acute triangle and laibel_the vertices A. B. and C. How
would you lind the distance from A to BC?
39. Construct the altitude for each vertex of AABC What do you notice?
40. Draw or fold an obtuse triangle. Construct the altitudes of this triangle.
(I lint: Extend the sides of the triangle.) What do you notice? How is this
different from the construction you did in Exercise .39?
A median of a triangle is a line segment from mama“
a vertex to the midpoint of the opposite side
(see Exercise 25]. In addition to the property
of medians that you already examined, there
is another interesting feature of medians.
I. (“tit out a triangle from still" cardboard. Draw one median of the
triangle. 'l'ry to balance the triangle on the line you drew. Make a
conjecture about the part of the triangle on each side of the median.
2. Draw the other two medians of your triangle. Try to balance the triangle
on the point where the medians intersect. known as the centroid.
Explain in your own words why the centroid is called the center ofnuzss.
3. According to a law of physics. a free-lallin g body should rotate around
its center of mass. Test this theory by tossing your triangle like a Frisbee.
What do you observe?
You will confirm your conjecture from Step I when you examine areas
of triangles in Chapter 5.
LESSON 1.5 SPECIAL POINTS INTRIANGLES 49
Motion in Geometry
9 Every motion can be
\ modeled in terms at three
matliarnatlcal ‘motions.’
or tra- - - ations.
v
Objective \
0 Identity and draw
the three basic rigid
transformations: \
translation, rotation,
and rellection.
' I
This photo illustrates the basic F \ C
rnrttltenmtmti "motion" or n'rtn::jhrrrmti0n
lcnown (IS l.l'i1i‘lSldl.l0l‘l. The skier is moving in
(1 straight line, without twisting or turning. ‘\
Rigid Motion
Compare the two “snapsltots" above of the same skier in motion. The picture
on the left has been rrrtrzslnml in the direction of the arrow. Notice that the
two pictures are the same size and shape. If you (.ll| one of them out, it would
fit onto the other exactly.
As with segments and angles. planar figures that match etnctly are said to he
congruent. l'ranst"ornmtions that do not change the size or shape ofa figure
are known as rigid transformations.
In geometry. the terms preitnztge and
image refer to .1 shape that undergoes
a motion or transformation. Points
on the image ofan obieet are usually
named by adding at prime symbol (’)
to the original name of the point.
You can easily draw d rigid
transiorntation by tracing the same
obieet in two different positions on ‘.1 \
piece of paper. I nbel the first tracing \
as the preimage and the second one as
the image. The only real trick in
drawing the hasic transformations is
to locate the image properly. You will
learn how to do this in the Activities
that Iollow.
50 CHAPTER 1
o E D
tracing paper
CHECKPOINT 5/
I Ill. ED
tracing pa per
CHECKPOINT 5/
Translations
In a translation. every point nl a
figure moves in a straight line. and
all points move the same distance
and in the same direction. The
paths of the points are parallel.
' I
Drawing a Translation
1. Trace both the ol:-iect and the line at
right onto .1 piece of tracing paper.
Do not move the paper yet.
2. Slide vour paper so that your
drawing of the line atavs on the line
in the diagram. Trace the object a
second time.
3. Label vou r first and second drawings
of the object as preimage and inmgc.
respectively.
Drawlng a Rotatlon
Rotations
In a rotation. every point of a figure
moves around a given point known 11>
the center of rotation. All points nttwe
the same angle measure.
1. Trace both the object and the point
at right onto a piece of tracing paper.
Do not move the paper yet.
2. Place the point of your pencil on the
point, and press down to hold the
tracing paper in place at that point.
Turn the paper around the point as
tar as you wish. Trace the object a
second time.
3. Label your Iirst and second drawings
oi‘ the curved object as preirnage and
image, respectively.
Center of rotation
LESSON L5 MOTION IN GEOMETHY 51
I. E -
a pointed ubiect. a ruler,
a protractur, and
scissors
52 CHAPTER 1
cmacxpomr ./
Reflections
Hold a pencil in front ofa
mirror and locus on the
pencil point. P. The
reflection of that point.
called the reflection
image of the point.
P’. will appear to be
on the opposite side
side of the mirror
at the same distance P
from the mirror as P. 7
In a nmthentatical
rcllcction. a line plays
the role of the mirror,
and every point in a
geometric figure is
"flipped" across the line. ‘
In Part I of Activity 5.
paper folding is used
to produce the appropriate
motion of .1 reflected point.
V
4;.
' H».
"Mirror"
line .
Preimage
Drawing a Reflection
Part l l‘he Reflection of a Point
1. Drmv line 1:‘ and .1 point. P, not on line (1.
P
O
t
2. Reflect point P across line t:' as follows: Fold your paper along line I".
Use a pointed object such as .3 sharp pencil or a compass point to punch
a hole through the paper at point P. Unfold the paper and label the new
point P’.
3. l)r;1w-Pl_3".e1tul label the intersection ot -Pfiand line I’ as point X.
a. Measure the length ot')\"—P and
b. Measure the angles formed by PP’ and line F.
4. What do you notice about the relationship between and line F?
Complete the statement below. and then use your results from the
Activities in Lesson L5 to explain win‘ it is true.
The Reflection of a Point Across a Line
lfa point is reflected across 21 line. then the line is the ? of the
segment that connects the point with its image.
CHECKPOINT 5/
TRY THIS
Part ll lhe Reflection of a Friangle
1. Draw line t’ with AABC on one side.
2. Fold your paper along line if and
punch holes through points A. B. and 3
C to obtain image points A'.B'. and C'.
Connect the image points to form
AA’B'C'. the reflection of AABC.
3. Cut out AABC. Place it face down
on Ar-1'B'C'. Do the two triangles
match exactly? t‘
4. Form a conjecture about a triangle
and its reflected image. Complete the
statement below.
1‘he Reflection of a Triangle
if a triangle is reflected across a line. then the reflected image of the
triangle is ? to the original triangle.
Reflect each figure below across line i’ . Do your conjectures about the
reflection of triangles and segments seem to be true when the figures touch
the retlection line?
A
Summary: Three Rigid Transformations
The facts that you discovered by doing hands-on translations. rotznions,
and reflections in the Activities can be developed into the formal
lTldtl'l'c‘n1dtlCdl definitions given helow.
A translation is a transforrnation in which everv point of the preim-age is
moved the same distance in the same direction. 1.6.1
A rotation is a transformation in which every point of the preimage is
moved bv the same angle through a circle centered at a given fixed point
known as the center ofromtion. 1.6.2
A reflection is a transformation in which every point of the preimage is
moved across a line known as the mirror fine so that the mirror is the
perpendicular hisector of the segment connecting the point and its
image. 1.6.3
LESSON 1.6 MOTION IN GEOMETHY 53
Exerc/ses
Q Comm://1/mte
In Exercises 1-6, determine whether
each description represents a translation.
a rotation, a reflection, or none of these.
Explain why.What is the direction of
motion, center of rotation, or line of
reflection in each case?
1. a canoe drifting straight ahead
2. .1 ball rolling down a hill
3. the image of -.1 building in a lake
4. hands moving on .1 clock
5. a pair of scissors opening and closing
6. a slide projected onto a screen
7. Of the (W0 figures below. which is the best illustration
of a refleuion across :1 line? Explain your reasoning.
fit//dad .5/Q///3 Practice
n internetoomea ,3‘ ln Exercises 8-10. trace the figures onto folding paper.
“°'“"W°_'k 8. 'l‘r.anslaue the ligure along the given line. (ACTIVITY 1)
Help Onhne
Go To: go.hrw.com
Key-maid:
MG! Hornewurk Help
lor EIGICISBS 8-23
9. Rotate the figure about the given point (ACTIVITY 2)
V .
10. Reflect the ligu re across the given line. (ACTIVITY 3)
7
54 CHAPTER 1
. Pratt/ce and Apply
ln Exercises 11-19, trace the figures onto folding paper.
Translate each figure along the given line.
11.
.... "\D
13. I
Rotate each figure about the given point.
14. 15. 16.
I
Reflect each figure across the given line.
18. 1
M we
Copy the figures below onto tracing paper. Fold the paper along the line
and trace the reflection of the figure on the back of the paper.
20. 21.
.+llll4El.
A
22. The word MOM has some unique chnrttcteristics when reflected across
different lines. Rellect the word across each line.
a. b. c.
M M MOM MOM
23. Write your name in capital letters on a piece ol folding paper. Reflect your
name across at vertical line. Do any of the letters stay the same? Relleet
your name across a horizontal line. Do any of the letters stay the s.1n1e?
24. In the diagram at right. A/lBCl1as
A A.
been translated to i A'_B'_ C. Copulie
figures and draw A.-1', BB’. and CC’.
What two things can you say about the B 3,
relationship among these segments? C C’
LESSON 1.5 MOTION nu GEOMETHY 55
56 CHAPTER I
25. ln the ligure at right. ADEF has 9
been rotated to AD’F"F". Copy the SE
figure and draw ADCD’ and Al.-‘CHI
Measure these angles. What do you F D»
think is the measure ol AFCF? E fl
F’ E’
26. ln the figure at right, AGHI has been 5
reflected to AC’ H'1'. Copy the figure
and draw (T7. TH’, and TI’. \-\-‘hat is I
the relationship bc-tween these: H
segments and the line of retlection?
GI
27. While visiting the beach,Teresa __
saw the two pairs of footprints ;_
shown at right.
a. \'\'hich pair represents a rellection?
b. which pair represents a translation? "
28. What translbrmation describes the _: . _ r .
relationship between the picture _ _ _ '- —' I._,.-..
on the wood block and the one on . .1 mt ‘<4;
the print? Which is the preimage '~ '3‘
and which is the image? / _'‘'-‘
_ ‘II ‘ ' P
Wood Mar}. Print
The shape below, called a net. can be cut out and folded to create a
cube. Refer to the figure for Exercises 29-31.
29. Explain how to draw the net by starting
with one square and applying translations.
30. Fxplain how to draw the net bv starting
with one square and applying rotations.
. , i i
31. E'(|)l'.lll'l how to draw the net by starting D A F
with one square and applying reflections.
A fourth type of transformation is a glide reflection. A glide reflection is
a combination of a translation and a reflection.
32. The lbotprints shown below represent a glide rellection. Copy the figure.
draw an arrow in the direction of the translation, and draw the line ol
reflection. What do you notice?
D $1‘
Activities
Online
Go 10: go.hrw.cnun
Keyword:
M BI Rigid
33. The figure below shows a shape that I1-as been transfonned by two glide
rellections. How could you continue applying glide rellections to form a
pattern? Copy the figure and draw two more images of the shape.
Preimage Second
image
First
image
Look Back
For each triangle in Exercises 34-36:
a. Name all sides and angles of the triangle. (LESSON 1.1)
b. Measure the lengths of the sides in centimeters. (LESSON 1.2)
c. Measure the angles of the triangle. (LESSON 1.3)
A
K
2%
34. A 35.
E
D
C
37. In the triangle at right. two angle
bisectors have been constructed.
l'race the figure and draw the third
angle bisector. (LESSON 1.5)
38. In the triangle at right. two
perpendicular bisectors have
been constructed. Trace the figure
and draw the third perpendicular
hisector. (LESSON 1.5)
Look Bet/om’
Sometimes you may want to translate a figure a given distance or
rotate a figure by a given degree measure.This can be done with
tracing paper. a ruler, and a protractor.
39. l'race the figure and the line below onto apiece oltracing paper. l'hen
translate the figure so that point Ton vour paper matches up with point 5
in the diagram. \-\'hat distance has the figure been translated?
T S
40. Use the method from Exercise 39
and a ruler to translate the figure
at right 5 centimeters along the
given line.
Moé/M
LESSON 1.5 MOTION nu GEOMETRY 57
41. Trace the figure and the angle at right onto
a piece of tracing paper. Then rotate the
figure so that Vfion your paper matches
up with VW in the diagram. Bv what
angle has the figure been rotated?
42. Lse the method lrom Fxercise 4| and a
protractor to rotate the triangle at right
3 ,, Nomad £5 cottnterclockwise |)t_.'¢l5° about point X.
Portfolio
Extension
(30 To: go lIw.cnm
t<i:vvmtd-
MG! Snow
$0.110
oé
Q
Snowflakes You may wish to use geontetry software to complete this activity.
1. Draw .TBt
2. Draw several more
segtnents attached to A8.
all on the same side of
the segment. as shown.
3. Reflect the segments
across Ab‘.
4. Rotate the entire ligttrc
60° about A. Then rotate
the image 60° about A.
Repeat until you have 6
images. including the
preintage.
5. Create other snowtlalces
with this method. If you
are using geometrv
graphics Softvm re. try
dragging the points of the
snowflake to see how
your design changes.
58 CHAPTER 1
Motion in the
Coordinate Plane
0- :7, 1; r- ; : ssos :1: +- x: - '"
tn 3-; ;’ 800"‘ *9: g N ST § GZOTH N T:
E E E l I lbulrl N .5;
-2 o 8 ‘room it 51 st :7, 9
Q n (V) - --
n N PlONEE:5°TH N S1 l l 6001 52°“ " 57
. H N sr
. MUSEUM --— —— SGOYH N 51’
.1’ HOLLY AV
~°”h P°'k l" SOOTH N sr " 8 5
.. .. '5 _ on O u
U -r
E 5 '5 5 5 m_ 5 400m N 51 “-32!” " I E
- - _ l 1 I 3 ssorn J? «I
Oblectwes T i i_ I [ _i 3001-” N 5' —— E L 300%
0 RQVIQHI the algebraic 3 3 3 3 “J '“ " 3 U)
concepts of coordinate fj ,5 ,I_ E E ‘,5 I 202_TH N 51 " —c
plane, ofigin,x- and g_ o o 8 m m ,",', U, ,_ 3 L5;
y—coorrlinotes. and o ‘ N N _F£ Em 3 N room N sr W I-'_-"
ordered pair. V’ W, mug iu "4 ‘ m In 3:‘ 0 mm g
1’ usl i ’ CENTER 1 I I z. I I .,, ‘°"'°
0 Construct translations, — ' ‘-' co 1 *5 *5 is *5 I PU‘ i
reflections across axes . I . '0 $001” 5 8 o O Q o 5°” 5 T5’. 2
and rotations about the — ay,¢ - D”',’cEs Q msT"° I‘ .501“ S In E
origin ona - ten ._ $1, an 1: ;'
coordinate plane. 5 l 2007“ 5__l__ l 57 l M’ '6 § 3
51' 3001115 sr "‘. 3:‘
1'! -— 3:
‘ST. A Opk-U9 350;
A coordinate plane ‘ ST ' 7 ' 5 I —‘ 2‘: ';—'
enables you to dascnha L . I SOOTH S 3 ST ‘S
geometry ideasbyusing ._l ’_ .1 1 l ‘ 1 Pg?‘
algebra Foroxamplo, :— tn In In ._,_ ___ .5901“ 5. 5T L .= ,_ .. f!
you can use algebra to
mm M‘ """"°m"u"" The rlrnvntmvrr area of Provo, Umh. is laid out as a coorrlirmte
0'0 Mme "mom “mg grid Furl: lllork is our’ lurnrlred urriti on I! ride
special construction tools. ~ ' ' ‘ ‘ ' '
Operations on the Coordinates of a Point
Y By applying nlgebrnic operations to the coordinates of 21 point, you can relocate
. it on the coordinate plane. For example, if you add 2 to the x—coorclin:ite and 4
3 to the }-'-coordimtte of the point All 3]. the result is .1 new paint. A'[-1. 7].
O
5 A14. 7) _ _
image Prermage Translormation Image
N2. 3) A'l4. 7}
4
O . . . . .
2 Am 3, This operation. which is known as .1 tnmsform-.1t1on, can be expressed as a rule
Preimage by using trnnslormation notation.
+1? - - _ ' -
2 4 6 X Tlx.yj=(_\+2.}-+4)
l
The letter Tst-ands for the transforination. but any other letter could be used.
As you may notice. the tr'.1nsl'ormation in the example zibove is a jimctirm.
tesson 1.7 MOTION INYHE COORDINATE Pt.-we 59
The Three Rigid Transformations
In the Activities that follow. you will discover rules tor the three basic rigid
transformations of geometry in a coordinate plane.
' I
Translations
I I I H) 1. Copy .e’_\ABC onto graph paper.
97339“ D399‘. 8 F|-|l9'- 2. Pick a number between -10 and
3" 3 ”'°"°°'°°' +l0 ( except 0]. Then choose
either x or y.
3. Depending on your choice, add
the number you picked to either
the x- or the )'-coordinate of
points A. b‘. and C. l'he other
coordinate remains unchanged
in each point.
Plot each of your new points. and then connect them to form a new
triangle. Does your new triangle seem to be congruent to the original
one? Measure the sides and the angles of each triangle.
PROBLEM SOLVING 4. Look for a pattern. The original figure has been translated to a new
position. In what direction has it moved and by how much? Draw an
arrow to show the translation. Compare your results with those ot
your classmates.
CHECKPOINT ./ 5. Explain how to translate a figure horizontally or vertically in the
coordinate plane. What would you do to the coordinates of each point
in the figure? Fvpress your method as a set of rules for moving points in
the original figure h units horizontally or v units vertically.
Horizontal and Vertical Coordinate Translations
Horizontal translation of It units: H (X. ,1-') = (_§_._:_)
\"e-rtical translation ol V units: V (x, y] = (i.i) 1.7.1
A - p I C A 1- I 0 N Refer to the map at right. Suppose
NAWGA-"ON that you are driving from point A
’ at the intersection of 500 W and
200 S to point B at the intersection
ol'30U 15 and 400 N. l'he rule for
the horizontal movement is
H[.\'. y) = (x + 800, y]. The rule for
the vertical movement is
\/tx, J») = [x, y + 600). These rules s§§;';3§§§§‘§_§~駧§§-g-§~é~é’
can be combined to show both the 3g g E § § ‘§” ‘t_§ ' " "
horizontal and vertical movements: E
5
T(x, y) = [x + 800. y + 600].
60 CHAPTER 1
' Z
Reflectlons Across the x- or y-axis
- - E - 1. Copy AABC onto graph paper. y
graph paper. a ruler. 2. Multiplv the x-coordinate ol 3
3" 3 p'°"‘m°' each vertex by -l . Leave the
)'-coordinate unchanged. 6
3. Plot each of the new points. and 4 A42. 4)
connect them to form the new
triangle. Does the new triangle
seem to be congruent to the Bis. 2}
original one? Measure the sides 1 I I X I X I X
and the angles of each triangle. £ 2 4 6 3
4. Repeat Steps 2 and 3 for the
)'—coordinates. leaving, the
x—coordinates unchanged.
CD. 61
5. 'l he original triangle is reflected in each case. What are the litres of
reflection. or the “mirrors" of the reflections?
CHECKPOINT V 6. Explain how to rellect a figure across the x- or y-axis. What would you
do to each point in the figure? Express vour method as a set of rules for
reflecting points in the original figure across the x- or y-axis.
Reflection Across the x- or y-axis
Rellection across the x-axis: M (x, y) = (
Rellection across the y-axis: N (x, y] = { . , ? )
1.7.2
TRY nus Experiment with figures in other positions. such as those below. Do your rules
seem to work for all positions?
3 ) AB, 5)
CRITICAL THINKING How would you write a rule for translating a point and then rellecting it
across an axis?
l.E$SON17 MOTIONINYHE co-onorrmre Pt.-we 61
' .3
180° Rotations About the Orlgln
- l.I NE 1. Copy AABC onto graph paper. y
gran“ vaper. aruler. 2. Multiply the x- and y-coordinates
and 8 “mum” of each vertex by — l. 6 cm’ 6,
3 Plot each new point. and connect
them to form the new triangle.
Does the new triangle seem to be
congruent to the original one? 3“. 21
Measure the sides and angles of - y 3 , : : : ; , X
each triangle. 1 2 4 5 3
4. The original figure has been
rotated. Where is the center of
the rotation? By how many degrees has the figure been rotated? Draw a
curved arrow to show the rotation.
CHECKPOINT .1 5. Explain how to rotate a figure 180°-about the origin. lispress your
method as a rule for rotating points in the original figure about the
origin.
180° Rotation About the Origin
Rtx, y) = (_?_._?_) 1.7.3
mv nus Use your rule trom Activity 3 to rotate the triangle with vertices at [1, 5),
[-2, 4), and [-5. -2) by ISO“ about the origin.
CRITICAL THINKING You can think of the figure at
right as being formed by two \
rellections of the upper left
panel. First the original
panel is reflected across —
the y—axis. l'hen the _ _
resulting ligure is
rellected across the
x—axis. \_
Explain why a 180° rotation can be
thought of as a combination of these
two reflections. Do you think this
idea could be extended to describe
any rotation as a combination of
two reflections?
62 CHAPTER 1
Exercises
. Communicate
1. Explain how you would find
the x- and )'-coordinates of A
points A and B on the
coordinate plane at right.
2. Plot the points (I. 5] and ~
(5. I). Do you think that the _& -_é - 2» - A - X
order of the coordinates
matters? Why do you think *2’
the coordinates ofa point are '3 4'
called orderedpr'1ir:5.'
3. What are some advantages to
using the coordinate plane
for transforniations?
4. What happens when you rellect a figure across the .\'-axis and then rellect
the image across the y—axis? Explain the result in terms of a single
transforination in a coordinate plane.
0 6/rided SK’///3 Pratt/6'49
5. Plot the points (2. 4]. [—l. 4]. and (2. l). and connect them to form a
triangle. What rule would you use to translate the triangle 5 units to the
right? Write your rule in the form Htx, y) = [L _?_J. Draw the translated
figure and label its coordinates. (ACTIVITY 1)
6. Plot the points (I. 3], [-2, 5], and (O, 0), and connect them to forth a
triangle. What rule would you use to reflect the figure across the y—axis?
Write your rule in the form Nix. y) = (L, L). Draw the rellected figure
and label its Coordinates. (ACTIVITY 2)
7. Plot the points (2. 2), [4, 4). and (2, 4]. and connect them to form a
triangle. What rule would you use to rotate the ligure I80‘ about the
origin? Write your rule in the form Rix. y) = (L L]. Draw the rotated
figure and label the coordinates. (ACTIVITY 3)
LESSON 1.1 MOTION INYHE COORDINATE Pt.-we 63
P/d6‘tIZ‘6’ 4/14 App/y
In Exercises 8-17, copy each figure onto graph paper, and then use the
given rule to transform the figure. Identify the type of transformation
given by each rule.
- -umuoomad 8. H[x,y) = (x+ 3.;') 9. H[x.yJ = [x- 2.)’)
Homework
Help Online
Go To: go.lIw.conI
Keyword:
MGI Homework Help
fol Em.-Iclscs B-3|]
11. V[x.yJ = (x,y— I)
12. M{x.)') = (x. -y] 13. M(x.y) = (x, -y]
V V
15. -\'l'.\'. y) = [—x. y]
64 CHAPTER 1
" I
I
In Exercises 18-22, use graph paper to draw the transformationlsl of the
figure as indicated.Write the rule(s) you used below each transformed
figure.
18. Retlect the figure across the x—axis.
19. Reflect the Figure‘ iicrnss the y-axis.
20. Rotate the figure 180'’ about the origin.
21. Rellect the figure across the x—a~:is. and
then reflect the image across the y-axis.
How does this figure relate to the
tr-ansl’ormed figure from Exercise 20?
22. Retlect the figure across the y-axis. and
then reflect the image across the x—axis.
How does this figure relate to the
transf0rmer.l figures from Exercises 20
and 2|?
ln Exercises 23-30, describe the result of applying each rule to a figure
in a coordinate plane.
23. F[x.y) = [x+ 7,y)
25. Atx, y) = (x— 6, y+ 7']
27. C(x.,vJ = (x.y+ 71
29. Z[x.y_] = (x-7.)’)
24. T(.\'. y] = (—x. y)
26. Fix.» = (X. ;'—4J
28. Wtx, y) = [—.\'. —,v)
30. K[x.,v_) = (x.y+ 2)
31. Copy the figure below onto graph paper. Apply Rule I to the figure. then
Rule 2 to its image, and so on. Draw each image that results.
Rule 1: A(x, y] = (x. —y] y
Rule 2: Btx, y") = [—x, y)
Rule 3: Ch", y} = (x. -y}
Rule 4: Dix, y] = (—x. y)
What is the final result of
applying Rules I--1?
ln Exercises 32-35. you will use the idea of the slope of a line. Recall
from algebra that the slope of a line is the change in the y-coordinates
divided by the change in the x-coordinates for any two points on the line.
Graph the triangle with vertices Km, 0). U1, 2). and MW, 3).
32. Apply the transformation i'[x, y] = (x+ 4, y+ 5) to the triangle. Label the
new vertices K’. L’. and M’.
33. Draw a line through K and K’. \-\'hat is its slope? Draw a line through l.
and L’. What is its slope? Draw a line through M and M’. What is its slope?
34. How do the slopes of the lines relate to the transformation rule The, y)?
35. Based on your results from Exercises 32-3-1. make a c()niecture about
the slope of the line through K and K’ when the transform-.ttion
T(x. y] = (x+ It. y+ k) is applied to point K.
LESSON 1.1 MOTION INYHE COORDINATE Pt.-we 65
‘\
\
\
CHALLENGES
66 CHAPTER 1
ln Exercises 36-43. you will discover another rule for transforming an
object.
36.
37.
39.
41.
42.
43.
On graph paper. graph the
line y = X. Complete the
table of values at right to
get started.
What angle does the line -1
form with the x-axis?
. Plot each ofthe following points on the graph, and connect them to form
:1 triangle:
A(2. 1) B(5. 2) CI6. 4‘
Reverse the x— and y—coordinates of points /1. b‘, and C to create new points
A’. B’, and C’. Plot these points on the graph with A, B, and C, and connect
them to form a new triangle.
. What is the relationship between the figures you drew?
Write a rule in the form Rlx, ,1’) = (L. ?_l for the transformation. (Hint:
The rule should use only the letters xantl y, with no signs or numbers.)
Draw segments connecting A to A’. B to B’, and Cto C'.Wh.1t is the
relationship between these segments and the line y = :5’
Choose a point (x, y]. where x < y. ls this point above or below the line
y = :3 Apply the transformation rule you wrote in Exercise 41 to this point.
Is the image of the point above or below the line y = A? Repeat this exercise
for points where x > yand x = y.
In Exercises 44-47, you will explore glide reflections in a coordinate
plane.
44.
45.
47.
What two transl'ortn-ations
would you apply to A/LBC
to get ADE!-‘f Express
these trnttslbrnnttiolts with
a single rule of the form
T(xJ = (L. 1.1- V
Apply the transformation
rttle you found in Exercise 44 - - i t v 7 - "
to ADEF. What is the result? “ E
Apply the translormation to
the resulting image three or 4__ 0
four more times. Describe
what happens. 8 _6‘_ F
. Write a general rule tor a glide ‘
rellection with the y—;1~:is as the A 3“
line of reflection ttnd with a C
vertical motion of I‘.
Write a general rule for a glide
reflection with the .\‘-axis as the
line of reflection and a
horizontal motion ol‘ lt.
APPLICATION
COMPUTER PHOGHAMING The Postscript computer language is designed to
communicate between computers and primers. A page in the PostScript
language is laid out as .1 coordinate plane with the origin at the lower left—hand
corner of the page. The following Postscript code draws a segment from a
point located at [l-14, 72] to (M4. -132).
newpath ' ‘ I-
144 72 moveto
144 432 llnoto
stroke (
showpage
48. Each unit in the - ' 3.. I
PostScript coordinate - -- -
system is %in. long. 3
What are the coordinates, 1‘
in inches, of the endpoints ,-
of the segment clrawn by
the code above? Sketch the
segment on .1 graph with A
axes labeled in inches. \
49. Rewrite the code above to draw a segment between points whose
coordinates, in inches. are ( l. I l and (3-. -1.5].
L001? B463‘?
Give the compass heading for each direction below. (LESSON 1.3)
50. W 51. NW
52. SW 53. SSW
Tell how you would find each point of a triangle. (LESSON 1.5)
54. circumcenter
55. incenter
Describe or draw an example of each type of translation below. if you
make a drawing, label the preimage and image. (LESSON 1.6)
56. translation 51. rotation
58. reflection S9. glide reflection
L001? B65/011d
60. Plot the points (I. 2]. H, 2). and (I. 8) in a coordinate plane, and connect
them to lbrtn a triangle. Apply the transformation Qlx. y) = (—y. x) to the
triangle. What type of translorimttitiit is this? Try applying the same
transformation to several different triangles to conlirm your answer.
61. Based on your results from Exercise 60. write a transformation. R(x, y), for
the rotation ofa figure 90° about the origin in the cloc'kwise direction.
LESS-ON 1.1 MOTION INYHE COORDINATE PLANE 67
Rmitl Qrlgaml
0-N <o 790:9/4 F0/ding
Origami, the ancient Japanese art of paper folding. prodmes intriguing
figures from simple paper folds. In this project. you will use paper
folding to create -.1 paper crane. l-'irst follow Steps 1-6 to make the
crane base. Then continue with the final folds to finish your crane.
Use a 6- to 8-inch square of paper.
C A
5 A0
‘- F0” ‘hf P3P" "‘ h“" 35 5'‘°“'"- 2. Fold point 1 forward and down to point b’.
Fold point C backward and down to point B.
3. Open the paper at
point Band
lay it rm. -F D":
05 D B
I
G G
4. Crease the paper by folding points D and B
inward to point F on the center line.
5- Open the figure and pull G upward. reversing the 6. Turn the paper over and repeat Steps 4
folds you made in Step -1. and 5.
You have now completed the crane base. Continue with the steps below to complete the crane.
K L
0 0}
H ‘J I
K <—L (underneath)
7. From the crane base. fold points H and I upward 8. Pull points K and L outward and reverse the
into point I on the center line. Turn the paper over folds. These will become the tail and neck of
and repeat. the crane.
9. Fold the neck to lorm the head. and bentl the
wings down as shown. You can blow into the
base of the figure to inflate its body.
Your crane is finished.
10. l'nlbltling a paper crane will reveal a pattern of
creases. Trace over and label the geometric figures
formed by the creases. Are any of the figures
congruent with one another?
11. The crane base can be used to create many origami
figures. Can you figure out how to fold a frog or a fish!
12. Find an origami book at your library and expand
your collection of origami figures.
Chapter Review and Assessment
VOCABULARY
acute angle . . . . . . . . . . . . . .. 29 exterior . . . . . . . . . . . . . . . . . .11 plane . . . . . . . . . . . . . . . . . . . . 10
angle . . . . . . . . . . . . . . . . . . ..11 image . . . . . . . . . . . . . . . . . . . . 50 point . . . . . . . . . . . . . . . . . . . . . . 9
angletrisector............38 incenter........... ..... ..ll5 postulate
center ol rotation . . . . . . . . . . 51 inscribed circle . . . . . . . . . . . M prelmage . . . . . . . . . . . . . . . . . 50
circumcenter ............ . . 45 interior ................. . . 11 ray ..................... . . 10
circumscribed circle ..... . . 414 intersect ................ . .11 reflection ............... . . 52
collinear . . . . . . . . . . . . . . . .. lo intersection ............. . .11 right angle . . . . . . . . . . . . . . . . 29
complement . . . . . . . . . . . . . . . 28 length .................. . .17 rigid translormatr on ...... . . 50
complementary angles . . . . . 28 line . . . . . . . . . . . . . . . . . . . . . . . 9 rotation . . . . . . . . . . . . . . . . . . . 51
concurrent . . . . . . . . . . . . . . . . 45 linear pair .............. . . 28 segment ................ . . 10
congruent . . . . . . . . . . . . . . .. 19 measure ol an angle ...... . . 26 segment laisector . . . . . . . . . . 38
coniecture . . . . . . . . . . . . . . . . 36 midpoint . . . . . . . . . . . . . . . . . . 38 sides ol an angle . . . . . . . . . . 11
construction . . . . . . . . . . . . . . 35 number line ............. . . 17 supplement ............. . . 28
coordinate of a point ..... . . 17 ohtuse angle ............ . . 29 supplementary angles . . . . . . 28
coplanar . . . . . . . . . . . . . . . . . . 10 parallel lines . . . . . . . . . . . . . . 35 translation . . . . . . . . . . . . . . . . 51
degree ................. . . 26 perpendicular trisector . . . . . 38 unit length . . . . . . . . . . . . . . . . 18
enrlpolrrt . . . . . . . . . . . . . . . . . . 10 perpendicular lrnes ...... . . 35 vertex ol an angle . . . . . . . . . . 11
POSTULATES
Lesson section Postulate or Theorem
1.1 1.1.4 Postulate The intersection of two lines is a point.
1.1.5 Postulate The intersection of two planes Is a llne.
1.1.6 Postulate Through any two points there is exactly one and only one line.
1.1.7 Postulate Through any three noncollinear points there is exactly one plane.
1.1.8 Postulate If two points are in a plane, then the line containing them is In the plane.
1.2 1.2.2 Segment If two segments have the same length as measured by a given fair ruler,
Congruence then the segments are congruent. Also. il two segments are congruent,
Postulate then they have the same length as measured by a given ruler.
1.2.3 Segment Addition If point Ris between points Pand 0 on a line, then PR H0: P0.
Postulate
1.3 1.3.2 Angle Addltron
Postulate If point S is in the interior of APOR, then m4POS— m4'SOR= mzPOR.
1.3.3 Angle
Congruence If two angles have the measure, then they are congruent. If two angles
Postulate are congruent, then they have the same measure.
1.3.5 Linear Pair If two angles form a linear pair, then they are supplementary.
Property
70 CHAPTER 1
Key Skills 81 Exercises
LESSON 1.1
Key Skills
Identify and name geometric figures.
In the figure below, A, B, and C are points. (A-5 is
j. j —'9 %’ —}
a line. ABund AC are segments. AB. AC und CA
are rays. and ABAC is an angle.
LESSON 1.2
Key Skills
Determine the length of a given segment.
ln thfligure below. find the lengths of (-75. WT,
and FF.
C D E F
10 5 0 5 10
CD=|-3—{-2]|=6
DF=|—2—3| =5
L‘:-'=|3—7|=4
Determine whether segments are congruent.
In the figure -.1bo\~'c. are E), E, und E—Fco11grttettt
segments?
None of the segments are congruent.
Add the lengths of segments.
In the figure below. AB = I-'.tnt.l BX = 15. Find AX.
Z 3 x
AX:/lB+BX=7+l5=22
Exercises
Refer to the figure below.
1. N-.m1e all segments J
in the figure.
2. Nillllt: all dllglcb
in the figure. K L
Refer to the figure below.
:4
~-;
R M C
K \o\
3. Name-.1ll lines
in the figure.
4. Name all rays
in the figure.
Exercises
Refer to the figure below.
C H J ___K
v ...v—r
-3 : : '0 ' ' 5 ' 10
5. Find the length of ever)’ segment in the figure.
6. Name all congruent segments in the figure.
ln Exercises 7 and 8. point A is between
points R and Pon a line. Sketch a figure for
each exercise and find the missing measure.
1. R.-t=25.AP=13,RP=;
s. R.«‘t=';..»‘lP=7,R!’=|3
CHAPTER 1 REVIEW 71
LESSON 1.3
Key Skills
Determine the measure of a given angle
For the ligure below, lind the measure of ./_Al-"B
and ./_Bl-‘C
m /_Al-’B = |-10° - 2U°| = 20°
m.’_Bl/C _—_ |60° — -1U"| .—_ 20°
C
. in ‘m‘°-1;
eiégiiwfl “in ac“ 8"
.9¢'£ ,;$ A
93 9.
E V 3%“
Add measures of angles.
For the figure above. find m./_Al-’C.
m ./_Al-’C = nn'_Al-’B + n1./_BVC = 20° + 20° = -10°.
Determine whether angles are congruent.
In the figure above, are ./_A\-’B and LBVC
congruent angles?
’es; L/ll-"B E ./_B\-"(' because they have the sanie
measure.
LESSON 1.4
Key Skills
Use paper folding to construct geometric
figures.
For the figu:e_ below. construct the perpendicular
bisector of AB, th_e; angle bisector of {_ABC', and a
line parallel to A8 that passes through C.
C
B A
‘lo construct the perpendicular bisector of /(hi
fold the paper so that A matches up with B.
To construct the angle hisector of AABC, fold the
paper so that BA matches up with BC.
. ‘j.’ «
To construct a line parallel to A8 through C, told
the perpendicular bisector of ABonto itsell’ so
that C is on the fold. ,
lLO
<—aé/—»->—»
3 l
A
72 CHAPTER I
Exercises
Refer to the figure below.
9. Find the measure ol—e\-'er_y angle in the figure.
10. Name all congruent angles in the figure.
In Exercises 11 and 12, find the missing
measures.
11. n1LH<'.'vl = l3°
m.v_.w<.\.' = 25° L
nt.’_LKN = L K
M
12. m./_u<.u= ;
n1AMKN = 75° N
mLLKN = 90°
Exerclses
Trace each figure onto folding paper and
construct the given figure.
13. a line parallel to Al’
§
Y
14. -.1 line through Pperpendicular to t’.
P.
?——»—¢—
15. the perpendicular bisector of MN
o
M N
16. the angle bisector 0|" ./_QRS
H,//*5"
\\
LESSON 1.5
Key Skills
Construct the circumscribed
circle of a triangle. '
The center of the circtnnscribed
circle of a triangle is the
intersection of the perpt-:nr.licul;ir
bisectors of the triangle.
Construct the inscribed circle of a triangle.
The center of the inscribed circle ofa triangle is
the intersection of the angle bisectors oi" the
triangle.
LESSON 1.6
Key Skills
Identify translations, rotations. and
reflections.
Q4 Q4
€34 K9
Translate a figure along a line.
flfl
Rotate a figure about a point.
fl
Translation
Reflecrion
6
Reflect a figure across a line.
vlv
Exercises
Use geometry software or folding paper and a
compass to construct the following;
17. the angle bisectors oi an acute triangle
18. the perpendicular bisectors ofan obtuse
triangle
19. -.1 right triangle circumscribed by a circle
20. a triangle with two congruent sides and its
inscribed circle
Exercises
21. Identify the following as being best
represented by a translation. rot-.ttion. or
reflection.
a. ge0n1etry tularrtosg
b. .1 child on a slide
c. a Ferris wheel
22. Translate the figure along the line.
V
23. Rotate the figure about the point.
24. Rellect the Figure across the line.
CHAPTER 1 REVIEW 73
LESSON 1.7
Key Skills
Use the coordinate plane to transform
geometric figures.
Plot the points (2. 3], [—l , 2). and (D, 0). ant.)
connect them to form a triangle.
Give the rules for translating the figure 5 units
down and lot’ rellecting the figttre across the
y-axis, and draw the transformed figures.
To rellect across the
the y—a.\is. use the rule
Nfx. ,1’) = (-x, y).
to translate 5 units
down, use the rule
V(x.y) = (X. y- S).
V Y
M.
.x 41
Applications
Exercises
Plot the points (1, 1). l3. 3). and (2, 4). and
connect them to form a triangle.
25. Translbrm the triangle by using the rule
T[x,y) = [x+ 2,y— 7].
26. What rule would you use to translate the
triangle 3 units to the left?
27. Translorm the triangle by using the rule
S(x.,v) = (.1: —,v).
28. W hat rule would you use to rotate the triangle
l80°a1lmut the origin?
29. TRAVEL Smitltville is between Bastrop and Lafirange on a
straight highwzty. The distance from Bastrop to Smithx-ille
IS 22 kilometers. The distance from Bastrop to L-.t(3range is
5 kilometers more than 3 times the distance from Bastrop \
to Smithville. Write an equation for the distances, and then __
solve it to lind the distance from Smitlwille to La(_'.rangc
and l'r0m Bastrop to l..aGrange.
30. ENGINEERING Jenny has a piece of a broken gear from an
antique clock. She needs to find the original size of the
gear in order to get a replacement part. Trace the part of
the gear shown at right. and construct the complete circle. \
74 CHAPTER 1
Chapter Test
Refer to the figure below.
1. Natne the intersection of planes A and B.
2. .\l.tme three coplanar points in the figure.
3. NA\"l(iA'll()h The towns ol I inton. Rocky
Ford. and Titnpas are located along a straight
road. Rock)’ Ford is between Limon and
Tintpas. The distance from I imon to Rocky
Ford is I3 miles more than 5 titnes the
distance from Rocky Ford to Ti mpas. The
distance from I imon to Timpas is I03 miles.
Find the distance from Litnon to Rocky Ford
and from Rocky Ford to Timpas.
Point 0 is between points 8 and F on B75‘. Sketch
each figure and find the missing measure.
4. BC=42 CF=i BF: 60
5. BC=§ ('F=2.3 BF=5l
In the figure below, mzRPS = 32° and ZOPS and
ASPT fonn a linear pair. Find the measure of
each angle.
0 P T
6. IIIZQPR 7. IHZSPT 8. IHZRPT
Use a separate piece of paper to fold each figure
below. 00 not use a ruler or protractor. Trace
over each figure and label all relevant parts.
9. two parallel lines
10. a right triangle
11. Use folding paper to construct the angle
bisectors ofa right triangle.
Refer to the figure below for Exercises 12-13.
Suppose that a is the bisector of zxwz and that
mzYWZ= 18° Find the measure of each angle.
X
V W
12. n1£Xl‘l-'1’ I3. n1£,\'WZ
14. ART A potter wants to reconstruct a broken
ceramic base. He needs to find the original
size of the base. Trace the part of the base
shown below and constntct the complete
circle.
3
Trace each figure below onto folding paper.
15. l'rans|-ate the figure along the line.
ID
16. Rotate the figure about the point.
5.
17. Reflect the figure across the line.
[2
Plot the points (5, 1), (7, -1), and (3, -3), and con-
nect them to fonn a triangle.
18. Transfornt the triangle by using the rule
Tfx, y] = [x— 2,y+ 3).
19. What rule would you use to translate the
triangle 4 units to the right?
CHAPYER 1TEST 75
C 'PER
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Questions I-3. write the
letter that indicates the best ginswer.
1. Find NB on the line below. (LESSON 1.2)
2. \-\’hi_ih expression states that E—l-' is congruent
to HG? (LESSON 1.2)
a
b.EF= HG
c.Ff‘=‘F(=i
d.E = MG
3. Refer to the ligure below. If WZ bisects
A X W Y. which of the following statenients is
[met (LESSON 1.3)
W
r
a. n1.£XWZ > m./_’ YWZ
b. n1AXW7 < n1AYW7
c. In A X WZ = n1ZYl\-‘Z
cl. m£XWZ at In./_’YWZ
76 CHAPTER I
D intemet connect .5i'in
Standardized
Test Prep Online
Go To: 9o.hrw.com
Keyword: MM1 Test Prep
Name each figure. (LESSON 1.1)
4.
A
B
5.
r
C
6
o
E F
7.
G H
For Items 8-11. trace each diagram onto
folding paper and construct the given figure.
(LESSONS 1.4 AND 1.5)
8. the perpendicular hisector
."”___,,4
9. the angle bisector
<
10. the circumcemer
(Draw the circumscribed circle.)
11. the incenter
(Draw the inscribed circlc.)
For Items 12-16, identify each transformation
as a translation, rotation, or reflection.
(LESSONS 1.6 AND 1.7)
12.
G
13.
A
15. S[x.y) = [x — Ly)
16. T(x.)'J = (x. —y)
FREE-RESPONSE GRID
_ CD 7
Items 17 20 may . C.) QGQ
be answered by using @ ‘(E @
a free-response grid q) q) q) (9
such as that commonly G) <3 <3 <3
used by standardized- g 8 3 (3
test services. G) Q) Q) Q)
(E) (E) (E) (E)
G CD CD (D
(E) (D (E) (D
® (D ® ®
For Items 17 and 18, refer to the figure below.
(LESSON 1.2)
. *3 Q . . Q
-5--4—§—2—io123Z5
17.AB= ?
13..-1C= ?
19. Refer to the figure below. If n1 AAVD = 85°.
what ism Am-‘C! (LESSON 1.3)
20. Refer to the figure below. What is IHAMON?
(LESSON 1.5)
CHAPYEH 1 CUMULATIVE ASSESSMENT 77
78
Lessons
2.1 0 An Introduction to
Prools
2.2 0 An Introduction to
Logic
2.3 0 Definitions
24 0 Building a System
of Geometry
Knowledge
2.5 o coniectures that
lead to Theorems
Chapter Proiect
Logic Puzzles and
Games
Reasoning
in Geometry
REGARDLESS OF WHO YOU ARE OR WHAT YOU DO,
there are times when you must reason clearly.
Whether you are scaling a cliff. or playing a
game of nim with a friend, or—like Sherlock
Holmes—trying to solve a mystery, the basic
principles underlying your reasoning process-
es are similar.
Geometry presents a unique opportunity for
studying the processes of reasoning. Since
ancient times, geometry has been for
many people the foremost example of
a fully reasoned system of knowledge.
7%
ll"
-3-"."_3
About the Chapter Project
In this chapter, you will investigate the principles
of logic and apply them to proofs of geometry
conjectures. But logic is useful lor more than
in-atliematical proofs. As you will see, it is also
useful in everyday life and in recreational gantes
and puzzles. ln the Chapter Project. I ogir Puzzles
and Gctnres, you will try your hand at the
mathematical game known as "sprouts" and two
different logic pu77les.
After completing the Chapter Project, you will be
able to do the following:
o Analyze certain games and devise strategies
lor play.
0 Solve logic puzzles by using reasoning.
o Solve a tvpe of logic puzzle by setting up a
table that displays information in an orderly.
structured way.
m ~»*. ‘.3-' e ..
' i h!7f4‘:g:$k~ ’ . ‘t w‘‘'
in. ¢- . ,_ . - - ,_ _ '
R‘ 3.l_?l§.i-‘ s v | I gt’; I q‘ '
i 'f_ 3 it : I
t ' ,-3'
.4
! T‘
_ J I 1
..' 5' ;
\_ \ .-~. .
3“; "' -’c.-.-'-at at-.5
_ - 73.‘: (3\ .
-Q \ 1 - v
x‘ 2‘ 1 . ‘-19 Ex’ 3':
' -. * _ ' ‘ . I
x ‘L ‘ .‘f%. ‘ K.‘
.. ._ ' ‘ \ _\ J" ; .
r :‘ .x;>%“,*fi'§’_.i§
. 3 ‘ .-.
\:. 5%:
\ _ .
\ \.‘.\
‘Q _ \ §\ ‘ ‘the game of nim is played
“‘ by two persons. who take
7 turns. twelve counters are
arranged in rows of 3. 4,
“ i ‘ and 5. as shown. On a
‘ \ players turn, he or she
must remove one or more
counters from any one of
l the three rows. The object
of the game is to take the
last remaining counter.
About the Portfolio Activities
1 h roughout this chapter, you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The rules of the game of nim -are given above.
The game can be analy7ed to develop a strategy
for winning. After you have played the game a
few times. you will be ready to begin your
analysis.
0 One of the basic winning patterns for the
game of nim is given in the Portfolio Activity
on page 87. A second version of the game is
also introduced.
0 Three different patterns that lead to the
winning pattern of the first Portfolio Activity
are given in the Portlolio Activity on page I I4.
79
An Introduction
to Proofs
1
Objectives
0 Investigate some
interesting proofs
of mathematical
claims.
0 Understand the
meaning olthe __
term proof.
5 ._
l
~'I
-\~_
lv
J
1
WII \ ‘I: 2 L
Have you ever \ I :2}-"f
needed to prove sonmbing \ \ _\. __ , _
You said? I! you used a ‘ - Z.» "3 -’ no
Iogical argument. you were ‘ ‘ \
probably able to make you! b " _
case. Logical arguments 1 1' - x
"M ”"""" 5 def’-""9 7°’-"' A rhessbomd has 64 squarc-.~‘. so it can be rmriplerely corcwd by 32 appropriately
arvknownasproofs. _. . _ . _ . . - _ _ __
sized dmrnnmss. This setup is the lmszs of two fimrous muthermitiuil questions.
Proving You r Point
pnoor Suppose that two squares are cut from opposite
corners ol’ a chcssboard. Can the remaining
squares be completely covered by 5| dominoes?
If your answer is yes, can you ofler a method
l'or showing that it is possible? lfyour answer
is no. can you explain why it cannot be done?
In either case. you would be giving a proofof
your answer.
I
Here is a proof that the altered chessboard cannot be covered by 3| dominoes:
Be-:ause of the pattern of a chessboard. each domino must cover one dark
square and one light square. Thus. any arrangement of dominoes must
cover the same number of dark squares as light squares.
Notice that the squares which were cut off are the some color. leaving more
squares oi" one color than the other. Therefore. it is not possible to cover
the altered board with the 3| Llominoes.
80 CHAPTER 2
PROOFS
no special tools
cnscxpomr V
/ I /
r
PROBLEM SOLVING
CHECKPOINT V
CHECKPOINT V
Three hallenges
Part I
Suppose that you change the chesslmard
problem so that you cut on one dark
square and one light square anywhere on
the board.
Use the diagrant at right and your own
explanation to prove that the altered
board can be covered by 31 dominoes.
Part [I
How could you find the sum 0|" the
first 11 odd -:mtt1ting numbers without
actually adding them? Make a table
like the one below. and see if you can
discover the answer.
Sum of the
First it odd first :1 odd
:1 numbers numbers
1 I 1 1
2 I 1, 3 I 4
3 I 1, 3. 5 I 9
4 I 1, 3. 5. 7 I 16
5 I 7 I 7
6 I 7 I
n I 7 I ?
The diagram to the right of the table is a
“proof without words" of the algebraic
result that you may have discovered.
F xplain in your own words how the
diagram proves the result.
Part III
You are given the ligure at right. which
is built entirely of squares. The area of
square C is 64, and the area of square D
is St.
Use the above inI’orm-ation to determine
whether the overall ligu re is 21 square.
{Recall that all four sides of a square
must be the same length.)
The prulm-ny through
the maze suggests a proof
LESSON 2 1
AN INYHODUCTION T0 PROOFS 81
What Is a Proof?
A proof is a convincing argument that something is true. But before you allow
yourself to be convinced by :1 supposed proof, you should make sure that it is
sound.
In niatheinaties. a proof starts with things that are agreed on (called postulates
or axioms]. Then logic is used to reach a conclusion.
There are many different styles of proofs in mathematics. Some proofs follow
a prescribed form and are called formal proofs. For example, the calculations
below are a formal proofthat. for the given equation, x = 4.
Sx+ 4 = 24 Given
5x = 20 Subtraction Property of Equalrty
x = 4 Dft/lSf0l'l Property of Equ-mty
As you can see, a definite form is followed in this proof. Each statement on
the left is given a justi'/Italian in the column on the right. But this is not always
the case. The prools you did in the Activity did not follow any particular form.
but they are just as mathematically sound (if they are correct!) as formal proofs.
In addition to the free—form proofs used in this lesson. volt will learn the
following styles for proofs:
° two-column proofs. Lesson 2.4
° par-agrapli prools. lesson 2.»!
° flowchart proofs. Lesson 4. l
' coordinate proofs. lesson 5.? ‘- —"
' table proofs, Lesson 9.3 _ ‘ °
' 0
I
Exercises
. Cam»/my/mte
n tgggmgmgmga la} 1. In your own words. describe what a proof is. p "..| .
Ill 5
Activities 2. ll‘ the indicated squares were removed from ' .I' .
O"'"‘‘’ the chessboard at right, explain why you could '. |'.
Go To:9o.hrw.cotn _ , h ,- - . . .' h 3] . °
Kcymm not cover t e remaining squares mt .
M81 Alice dominoes.
4 3. In Part II ofthe Activity, a geometric
solution is given for an algebraic problem. I
What do you think might be a advantage for
a geometric solution over an algebraic one? _
82 CHAPTER 2
4. Consider the following argument for proving that the figure in Part III of
the Activity is a square: I measured the sides and they were the same, so it
is a square. Is this a proof? Why or why not?
5. Explain how you proved whether the overall figure in Part [ll of the
Activity "as a square. Could anyone find a llaw in your argument?
0 fit//dad SK’///8 P/'d6‘t/6'8
PROOF
6. Suppose that tour squares were removed from a chessboard. What would
need to be true about the colors ol these squares in order for the
remaining squares to be covered with 30 dominoes? (ACTIVITY)
7. According to your answer in Part ll
of the Activity. what is the sum of the
lirst [0 odd numbers? of the lirst I00 9
odd numbers? (ACTIVITY)
8. The diagram at right is built entirely of |
squares. the overall ligure is also a square.
II" the area ol’ square A is Gal and the area
of square I is 4. what are the areas of the
other squares! What is the area ofthe
overall square? (ACTIVITY)
0 Pract/ca dlfd App/y
PROOF
For Exercises 9-11, consider a variation of the chessboard problem
(pages 80-81) in which the chessboard is covered with square tiles. each
the size of 4 squares on the board.The board can then be completely
covered with 16 tiles. You may wish to draw diagrams on graph paper.
9. ll’ one square were removed from each corner of the board. could the
altered board be covered completely with IS tiles? Why or why not?
10. ll‘ four squares were removed lroni the top row ol the board. could the
altered board he covered completely with 15 tiles? Why or why not?
11. State a rule for removing four squares so that the altered board can he
covered by I5 tiles. How would you prove your rule?
12. Copy the diagram at right and label each area.
Use the diagram and your own explanation to
prove the following:
[x+aJ[x+b]=a2+nx+bx+nh 13
The following procedure is a shortcut for squaring a number that ends
in 5: Multiply the number formed by the first digits (all digits except the
final 5) by the next consecutive number. Then put 25 at the end of the
product. For example, to square 35, multiply 3 x 4 and then put 25 at
the end of the product. 12, to get 1225.
13. Use the shortcut to square 25. 3'5, and I05. 30 5
Does it work?
14. Explain how the diagram at right illustrates
how the shortcut works for squaring 35. 3°
15. Use the diagram and your own explanation
to prove that this shortcut works For squaring 5
any number ending in 5.
LESSON 2: AN INYRODUCTIONTO PROOFS 83
I ' I / Use the table below to answer Exercises 16-21.The numbers in the
table are perfect cubes: 1’ = 1, 2‘ = 8, 3“ = 27, 4’ = 54, . . .
A B C
1 8
64
?
?
n mg.-ngmmeq ,3 16. Sttppose that you wanted to know which column contains the number
Homewmk “"" l,O{J(),UO0,[]()[) (one billion]. One method is to fill in the table until you
Help online rt-acli |,000,000.000. What is one disadvantage of this method?
Go To: 9o.l'trw.cot'n
Kwmm 17. Another method is to atnztlyze the pattern of the numbers in the table.
M01 Homework Help One billion [l.0O0.000.0(l0) is the cube ol what number? (Hint: IO" = I000.
lor Exercise I6-2l 1001 = -, _ I i )
18. Look at the columns in the table. Notice that column A contains the
numbers I’, 4-‘. 7‘, . . . What numbers occur in column B? in column C?
19. What is true of every number in column C? ls this true of any number in
column A or B?
20. In what colutnn does the number 999‘ occur?
21. Prove that l.O0(),OO0.00U occurs in column A.
I ; I / Exercises 22-28 involve partial sums of the infinite sequence
%. 71-. . . . , in which the denominator of each tem is doubled
to obtain the next term.
22. what are the next four terms ol the sequence?
23. Are the terms getting larger or smaller? Explain your answer.
24. Complete the table below. in which terms of the sequence are added
together.
Number of terms Terms Sum of terms
1 % or 0.5
2 -} §-. or 0.75
3 %. —},g 17;. or 0.875
4 %,.},%,% I orO.9375
5 2 I 2
6 7 I 7
7 7 ?
8 ? ?
25. What number do the sums in the table seem to be approaching?
26. Because the sequence has infinitely many terms. you c.annot add them all
with your calculator. l‘l()W€\'€’l’_. it is still possible to find the sum til‘ the
infinite sequence. Start by drawing a square with an area ol l square unit.
label the lengths of the sides of the square.
84 CHAPTER 2
PROOF
27. Divide your square into pieces
with areas equal to the terms oi
the sequence. Use the diagram
at right as a guide.
J_
28. Explain how the diagram 1 "l
indicates the sum of the %
infinite sequence. What is
the sum oi" the sequence? 1 l
I-r -I
Suppose that you know the square of a positive integer n and you want
to find the square of n + 1. in Exercises 29-32. you will discover a
method.
29. Draw a square array of dots with
5 rows of 5 dots, as shown at right.
Explain how the array represents
the square oi 5, or 53.
30. Increase the side lengths oi your
square to represent the square
of the number [5 + l . or 63.
Use your diagram to show that
6-'=5’+5+6.
31. Use your diagram to prove that
the square ofthe number 12+ 1 is
found by adding 1: and 71+ l to
the square oi" H.
32. Use this method to find the square
of 21 . given that the square of 20
is 400.
Exercises 33-37 refer to the following conjecture:
1 + 2 + 3 + 4 + - - - + n = where n is any positive integer
33. Verify that the conjecture is true for values
of n from I to 5.
34. The triangle at right represents the sum 0
l+2+3+-i+5+6. Count the dots to ' '
fi d I I O I
n tie sum. . . . .
35. Find the sum ofthe integers l throughé ' ' ' ' '
O O O O O O
by using the formula in the conjecture.
Does the result agree with your answer
to Exercise 5-1?
36. A second triangle is added to the original
figure. as shown at right. Find the number
oi dots in the resulting rectangle. [H 1 = 7
37. How does the number oi" dots in one of
the triangles relate to the number of dots
in the rectangle? Express this relationship
as a formula in terms oi" n and n + 1.
Explain how this proves the conjecture.
LESSON 2: AN INTRODUCTIONTO PROOFS 85
CHALLENGE
APPLICATION
86 CHAPTER 2
38. The positive integers are written in 1
a triangular array. as shown at right. 2 3
Use the conjecture given for Exercises 4 5 6
33-37 to prove that the number I000 7 8 9 10
occurs in the 45th row.
11
39. GAMES In a popular mystery game. players try to solve a murder. The
‘‘murder" is represented by three cards: the murderer. the place, and the
weapon. The cards are placed in an envelope and kept concealed until the
end oi" the game.
To solve the murder, you must use logic. Suppose you have determined
that the crime was committed in the study with the candlestick by either
Colonel Mustard or Professor Pluni. Then you learn that one of the other
players is holding the Professor Plum card, which means that the murderer
cannot be Professor Plum. You should now be able to solve the murder.
What is your full conclusion?
Your conclusion about the identity ol‘ the murderer involves a special kind
ol‘ argument known as -.1 rlisfimctire syllogism. Explain in your own words
when you can Lise this kind of an argument.
Look Back
40. Draw a plane and label it Q. Draw three noncollinear points in plane 0.
and label them A, B, and C. (LESSON 1.1;
41. In the ligurc you drew for Exercise -10. draw E, B—C, and X. What shape
is formed? (LESSON 1.1)
Use the diagram below for Exercises 42 and 43. (LESSON 1.2)
42. ll‘ LN = 18, find the value ol'x. _ “+3 - 4“ ,
43. ll'LM = 7. lind LN. L M N
In the diagram at right, mAKIT = 80°. (LESSON 1.3)
44. Find the value of x.
45. Find mzKl Y and mzTll’.
£00k B6!/0IId
' _/ ,- / / The triangular array of numbers shown below is commonly known
as Pascals triangle, named after Blaise Pascal (1623-1662). Pascal's
triangle has applications in geometry lsee Lessons 11.1 and 11.7),
algebra, and probability.
46. How would you find the entries for the 1
next row in the triangle? 1 1
47. Write out the first eight rows of I 2 1
Pascal's triangle.
1 3 3 1
48. For each of the lirst five rows. add the
entries in the row. \-\'h.at is the pattern
in the sums? 1 5 10 10 5 1
49. What other interesting patterns can
you find in Pascal's triangle?
CULTURAL CONNECTION: ASIA
The illuslrrllinrl at right is the
earliest known 1’¢'I'$f0lI of "‘Pn.<ra!
trr'mtgle." it isfmm (I ("ltitIe.»'e
book primed nromtrl l303 CE.
I lmemetconnecl pg‘
Portlolio
Extension
Go To: ga_l1rw.com
Keyword:
MG! Niml 1:
VAO
Oqs
°~ ln the game of nim [see page 79). the
object is to take the last remaining
counter. In a second version of the
game. the object is to force your
opponent to take the last counter.
° Pl-av a few games of both versions .
of nim with a friend. How is your .
strategy for the second version (
different from your strategy for the
original version of nim?
PROOF ' If you are able to leave two rows with
two counters each, you can alwavs I
win. Show that this is true for both
versions of the game.
LESSON 2: AN INTRODUCTIONTO PROOFS 87
Math Problem, Long Baffling, Slowly Yields
l)_\ (iina lxolntn. .\"t'w lirrlt l'imr'.\'
A century-old math problem of notorious difiiculty
has started to crumble. Even though an exact
solution still deties mathematicians. researchers can
now obtain answers that are good enough for most
practical applications.
The traveling salesman problem asks for the
shortest tour around a group of cities. It sounds
simple—just trv a few tours out and see which one is
shortest. But it turns out to be impossible to try all
possible tours around even
a small number of cities.
Companies typically
struggle with traveling
salesmen problems
involving tours of tens
of thousands or even
hundreds of thousands 01
points.
For example, such
problems arise in the
fabrication of circuit
boards. where lasers must
drill tens to hundreds of
find the best one. By I980. they got so good that they
could solve a 3l8-city probletn. an impressive feat but
not good enough for many purposes.
Dr. David Johnson and Dr. Jon Bentley of AT&T
Bell laboratories are recognized by computer
scientists as the world champions in solving problems
involving about |0D.000 cities. Bv running a fast
computer for two days. they can get an answer that is
guaranteed to be either the best possible tour or less
than 1 percent longer than the
best one.
In most practical situations.
an approximate solution is good
enough. Dr. Johnson said. By
iust getting to within about 2
percent of the perfect solution
of a problem involving drilling
holes in a circuit board. the time
to drill the holes can usually be
As if 1908. the compmcr saltmcut for thr shortest route Cut m ham he ‘did-
rmmectmg 5.32 rim: with /1I‘é-Fcctttnwl affirms looked
like this. it was ti:-riri1,g-‘est me}: problem miudm -of up
to that tum-'. Now. rt mute‘ for 2.392 :lt'.stir:rttiaIt.¢ has
lirrtr cot-uptm-xi, and Jnuthrmntia irms are working cm a ones thin can be attacked one by
The researchers break large
problems into tnany smaller
thousands of holes in a _s,a,rs..»n,-pr..t,t.-in. |'.'5<turct':t\lt'v.'Yttrk L."niI't'r_\ttyanr‘l one.and give these fragments to
board. Vliltal happens is bnririm-jersyatrnr .-ti-ml;-si.<)
that the boards move and
the laser stays still as it drills the holes. Deciding
what order to drill these holes is a traveling
salesman problem.
Very large integrated circuits can im-olve more
than a million laser-drilled holes. leading to a
traveling salesman problem of tnore than a million
“cities.”
In the late l970s. investigators were elated to solve
30-city problems, using clever methods that allow
them to forgo enumerating every possible route to
8 CHAPTER 2
A
fast computers that can give
CKHCI '¢ll‘ISW(‘t'S.
For example. Dr. Bentley said.“lfl ask you to solve
a traveling salesman problem for 1,000 cities in the
U.S., you would do it as a local problem. You might go
from New York toward Trenton and then move to
Philadelphia.” he explained. Then the researchers
would repeat this process lrom other hubs. like
Chicago. and combine the results. “We end up
Calculating only ct few do7en instances per point," Dr.
Bentley said. “if you have a million cities, you might do
only 30 million calculations."
1 ~ ‘\I I‘
: 1. \ ‘ “:
~ ~...~ .;
°~ .“
‘-st‘...-.-
9“
fl
Cooperative Learning
The most obvious way to solve a "trave|ing—salesinan” probleiri is to try all 3.
possible routes and determine which is the shortest. How m-any routes would {'7
_vou need to consider? One way to find the number of possible routes is to A, _ .0
multiply the ntimber ofehoices liir each city along the route. Suppose that a \
route contains four cities: .4. B, C, and D. One ofthe cities will be the starting
and ending point. I-'rom that city, there are 3 possible choices for the lirst city D
to visit. then from that city there are 2 remaining possible choices for the One way to visualize the
second city to visit. then froth that poim there is 1 remaining possible choice number of routes is by
lor the third city to visit. lhus. the number of possible routes is "SW9 9 "99 dl39"9"“ like
the one below.
l X 3 )( 2 X I = 6 C _ D_ A
starting choices choices choices number of B ‘
citv to visit to visit to visit possible D_ C- A
(given) first second third routes A_ C B —- D-- A
In order to reduce the number of coniputatioiis needed to liiid the shortest \ \D‘ B—A
route. notice that a route traveled in reverse order has the same length. B — c—A
ABCDA has the same length as ADCBA. ‘C — B — A
ABDFA has the same length as ACDBA.
ACBIJA has the same length as A DBCA.
Thus. it is necessary to compute the lengths of only three routes.
1. Copy and complete the table below.
Number of Multiply factorial Evaluate Divide by 2
cities form
-I 3 x 2 x t 3! o 3
5 7 9 7 9
6 7 7 7 7
7 7 9 9 7
,, 9 9 9 7
Based on the table above. complete the lbllowing formula:
The number of routes. N. that must be calculated to determine the
shortest route for visiting it cities is N = ? .
I 1' rs____ ._,.,
2. L'se the formula above to determine the following: How many routes must
be calculated to determine the shortest route through l0 cities? through 15 H
Ill '
cities? through 20 cities? through 50 cities?
3. Suppose that a computer could calculate the length of I billion routes
per second. How long would it take to find the shortest route through 20 fit‘
. . _ . _ _ _ _. . NA
cities! through 2| cities? through 50 cities? (rl\"E your answers in seconds. ‘ F“ 0
days. and years.
4. Compare your answers to Exercise 3 with the estimated age of the “mu ;
universe. about 15 billion years. Do you think the traveling—salesinan 5 AND C‘ . Cl
problem is really “too tough for computers”? Why or why not? r_~i=. \ '3 " 7
CHAPTER 2 EVEWITNE 6 MA 89
An Introduction
~ to Logic
«if
V L
0
_ \‘\ .
Y
4
Objectives
0 Define condirfonals \
and model them Wllll
Euler diagrams. npmomnnyfwm
0 Use conditional: in requires Ioglcalraasaulng.
logical arguments. logical reasoning ensures ‘
0 Form the converses of "M the cmcmsmns you '
. reach are !rue—iI the rest ‘ ~
condmonals. onhesmemensmme
0 Create logical chains 5'HW"W"5'9W9-
trom conditionals.
A - p L | c A 1- | 0 N Orgmii.tm.\' am he ('liLs.~'ijir'il rtrcorrling to their strticrtirc. For example, all oftlle
BIOLOGY jlowcrs shown above belong to the orchid fmnily. Class organization, whirl: nL~'o
e.x-remis to nmnnfizcmml things, is the basis oflogiml reasmiing.
Drawing Conclusions From Conditionals
The force of logic comes from the way chewolets
inlormation is structured. For example. all
Corvettes are Chevrolets, .1 fact! which can
be represented by an Euler (pronounced
“(Ji|er"} diagram like the one at right.
Note: Euler diagrams are often called
Venn diagrams.
From the Euler dizigr-am. it is easy to see that the following statement is true:
If :1 car is a Corvette. then it is a Chevrolet.
“IF-then" statements like this one are called conditionals. ln logical notation,
condition-.1ls are written as follows:
If p then :1
or
1; => q (Read as "p implies q.")
In .1 conditional. the part following the word i_fis the hypothesis. The part
following the word then is the conclusion.
If 21 car is a Corvette, then it is a Chevrolet.
Hypothesis Conclusion
90 CHAPTER 2
_ _ _ Chewolets
l\ow consider the following, statement:
Sus-.ui’s car is a Corvette.
. . . Co ettes
By placing Susans car into the Euler W
di-agram,)~'ou can see that it is .1
Chevrolet. (Anything inside the
circle is also inside the rectangle.)
oSusan‘s car
l'he complete process or drawing the conclusion that Sus-an’s car is at Chevrolet
can be written as a logical nrgmnem. This particular .1 rguntent. which is known
as a syllogisin (see Lesson l2.I ), has three parts.
1. If a car is a Corvette. then it is a Chevrolet.
2. Susan’5 car is at Corvette.
3. Therefore. Susan's car is a Chevrolet.
The process of drawing ltrgicrtlly certain conclusions by using an argument is
known as deductive reasoning, or deduction.
E . A tll P L E oRecal| the following tlefinitions from your earlier studies:
Au equilateral tmmgle is a triangle with three congruent sides.
An isosceles triangle is a triangle with at least two congruent sides.
PROBLEM SOLVING :3. Draw an Euler diagram that b. What conclusion can you draw
conveys the following inl'orn1:ition: about triangle ABC?
3 It" a triangle is equilateral,
then the triangle is isosceles.
Triangle ABC is equilateral.
A c 0 SOLUTION
a. ,s°sCe,e5 triangles b. Triangle ABC is isosceles.
Equilaterat
triangles
0 .";ABC
LESSON 2.2 AN INTRODUCTIONTO LOGIC 91
Reversing Conditionals
When you interchange the hypothesis and the conclusion of a conditional. the
new conditional is called the converse of the original conditional.
Conditional: It a car is a Corvette. then it is a Chevrolet.
Converse: |l'a car is a Chevrolet. then it is a Corvette.
The original conditional is true. But what about its converse? ll there is an
example of a Chevrolet that is not a Corvette—and there certainly is—then
the converse is lalse. An example which proves that a statement is false is called
a counterexample.
E X A M P L E 0 Write a conditional with the hypothesis “.1 triangle is equilateral"'and the
I conclusion “the triangle is isosceles." Then write the converse ol vour
conditional. Is the conditional true? is the converse true?
0 SOLUTION
Conditional: lfa triangle is equilateral, then it is isosceles.
Converse: lfa triangle is isosceles, then it is equilateral.
The original conditional is true, according to the definition or" an equilateral
triangle. (If a triangle has three congruent sides. then it has at least two
congruent sides.) M
The converse is false. however. as the
counterexample at right shows. [AMNO
is isosceles but not equilateral.) N O
TRV THIS Write a conditional with the hypothesis “an animal is a snake" and the
conclusion “the "tninial is a reptile." Then write the converse of your
conditional. Is the conditional true? is the converse true?
Logical Chains
Conditionals can be linked together. The result is a logical chain. In the neu
ewarnple, three different conditionals are linked together to form a logical
chain. (It does not matter whether the conditionals are actually true.)
E X A M P L E 0Consider the following silly conditionals:
If cats freak, then mice frisk.
If sirens shriek. then dogs howl
It dogs howl, than cats freak.
Prove that the following conditional follows logically from the three given
conditionalsz
It sirens shriek, then mice Irish.
92 CHAPTER 2
O SOLUTION
Identify the hypothesis of the conditional /
you are trying to prove: or ~‘ _ 00
If sirens shriek, _ , _ ‘ all
C
I \ .9
Look for a conditional that begins with l 1 -)
“il' sirens shriek.”
It sirens shriek. then dogs howl.
Look for -.1 conditional that begins with '
"if clogs howl." .
If dogs howl, then cats freak.
Look for a conditional that begins with '
"if cats freak out."
‘ \‘
If cats freak, then mice frisk.
l'here is a zigzag pattern in the steps ol‘
the logical chain. \
If sirens shriek, than dogs howl.
X ~
If dogs howl, then cats freak
/
k, then mice frislt
Finally. by linking the hrs: hypothesis and
the last conclusion. You can conclude:
If sirens shriek, then mice lrisk
mv ‘nus Working individually or in groups, create logical chains of your own.
CRITICAL THINKING Notice that Example 3 does not prove that mice frisk. What is proven instead?
What is lacking in the argument that is t1ecessar)' to prove that mice actually
frisk?
The proof of the conditional in Example 3 relied on the lollowing property:
If-Then Transitive Property
Given: You can conclude:
ll"A then B, and Il A then C.
if B then C. 2.2.1
Notice that the same property is used repeatedly in long chains of
conditionals.
LESSON 2.2 AN INTRODUCTIONTO LOGIC 93
Exerc/ses
. Com»/my/care
A P P L l C A T l O N 1. WEATHER Look at the satellite "
photo at right, which shows a
cloud cover over .-‘tnisterdalm, “ _ '-
the capital of the Netherlands. I.‘
Can you conclude that it was - — -3 ‘
raining in Amsterdam at the ""‘ _.._
time the satellite photo was ‘ _ ‘.9 -
taken? \ ' -‘fin. ‘
. ‘\ I ..
n humctoonned ,fo 2. Draw an Euler diagram to - <4} _ 'a_
no - _ - - .. ~ ’ a. _ _ - , ' 1
Acfivifies illustrate the conditional ll _ — *__ ._‘,:_-T .
Onlina it rains, then it IS cloudy. _ ;..,5_____gr..— _ _‘t_,.;, - K
Go To.9o.hrw.com , .K ‘ x ' ‘E? =.'‘ - ‘ ' .
K,.,y“,,,,,,. 3. VH1-at is the converse of the H ' _
Mm logic cundmflnal given in Exercise (.lond.~‘ over the .M'rl'tL'_rlar|d.«'. lt>0_kutg
‘ 2? use Your Fuler diagram south. The N()l‘Ht Sm t.\' on the right.
to illustrate whether the
converse is true.
4. Fxplnin how to write the converse ofa given conditional.
6. Explain how to disprove a given conditional.
0 611/764’ SK’/'//8 Pfdft/68
6. Consider the following statements:
All United States Postal workers are Federal emplovees.
John is at United States Postal worker.
Write the first statement as a conditional and use deduction to show that
John is a federal employee. Draw an Euler diagram to illustrate the logic
of your deduction. (EXAMPLE 1;
u immgcmrm 7. Write a conditional with the hypothesis “two lines are parallel" and the
Homewow conclusion "the two lines do not intersect." Then write the converse of
Help Onlina your conditional. Is the conditional trite? Is the converse true?
Go To. 9o.lnw.com (EXAMPLE 2)
Keyword.
MG! Nnmnwurlt Help
'0! Exerctses 7. 17-1“ 8. Consider the three eonditionals below. (EXAMPLE 3)
If a number is divisible by 2. then the nutnber is even.
[1 a number is even, then the last digit is U, 2. 4, 6, or 8.
ll’ .1 number is divisible by 4. then the number is divisible by 2.
Prove that the following conditional follows logically Irom the three
conditionals above:
ll'a number is divisible by 4. then the last digit is 0. 2, 4, 6. or 8.
94 CHAPTER 2
0 Practice mm’ 74,20/y
For Exercises 9-12, refer to the following statement:
All people who live in Ohio live in the l'nitetl States.
9. Rewrite the statement as a conditional.
10. Identify the hypothesis and the conclusion of the conditional.
11. Draw an Euler diagram that illustrates the conditional.
12. Write the converse ofthe conditional.
For Exercises 13-16, use the Euler diagram to write a conditional.
13' Flowers 14' Supplementaryangles
Linear
pairs
15' Musicians 16' -Snarks
Booiums
For Exercises 17-20, identify the hypothesis and conclusion of each
conditionaI.Write the converse of each conditional. If the converse is
false, give a counterexample to show that it is false.
17. If it is snowing in Chicago, then it is snowing in Illinois.
18- ll two angles are complementary. then the sum ol their measures is 90°.
19. ll'the measure of each angle in a triangle is less than 90°. then the triangle
is acute.
20. If a figure is rotated. then its size and shape stay the same.
For Exercises 21-23, refer to the diagram below, and write a conditional
with the given hypothesis and conclusion.
21. Hypothesis: AAXB and ABXD form a linear pair.
Conclusion: LAXB and .LBXDare supplementary.
22. Hypothesis: LAXB and LBXD-are supplementary.
Conclusion: mL.»Ut'B+ m.LBXD = I80’
23. Hypothesis: I'll/_BXC+ m/_('XD - 90°
Conclusion: HILAXB = 90° A X D
LESSON 2.: AN INTRODUCTION TO l.0GlC 95
APPLICATION
96 CHAPTER 2
In Exercises 24-29, use the given statements to draw a conclusion.
Then draw an Euler diagram to illustrate your conclusion.
24. If an animal is a mouse. then the animal is a rodent. Mikey is a mouse.
25. If someone is human. then he or she is mortal. Socrates is human.
26. If Jennifer goes to the beach, then she will get a sunburn. Jennifer is going
to the beach tomorrow.
27. llsomeone lives in Norway. then he or she lives in Scandinavia. lngrid
lives in .\lorxvay. A B
28. Ifa figure is a square. then the figure is a
rectangle. Figu re ABCD is .1 square.
29. If two points are in plane ‘.1’. then the line D C
containing them is in plane T. Points Sand Tare in plane IF.
In Exercises 30-33, arrange each set of statements to form a logical
chain.Then write the conditional that follows from the logical chain.
30. II’ it is cold. then birds lly smith.
ll‘ the days are short. then it is cold.
If it is winter. then the davs are short.
31. If the police catch Tim speeding. then Tim gets a ticket.
ll‘ Tim drives a car. then Tim drives too fast.
If Tim drives too fast. then the police catch Tim speeding.
32. If quompies plaun. then romples gleer.
If ruskers bleer. then homblers frain.
lf homhlers frain. then quompies plaun.
33. ll‘ you go to a movie, then you will spend all of your money.
If you clean vour room. then you will go to a Inovie.
If you cannot buy gas for the car. then you will be stranded.
ll" you spend all of your money. then you cannot buy gas for the car.
34. HUMOR Can logic be used to prove the impossible? Consider the following
logical chain:
l'he independent farmer is disappearing.
That man is an independent farmer.
Therefore. that man is disappearing.
Write the above argument using a conditional statement. How would you
criticize the argument?
CHALLENGE
APPLICATIONS
PROOF
35. The following is an old saying dating back to at least the fifteenth century‘:
For want ol'a nail. the shoe was lost.
l-‘or want of a shoe, the horse was lost.
For want of a horse. the rider was lost.
For want of a rider. the battle was lost.
l-‘or want ol the battle. the war was lost.
Rewrite the saying as a logical chain of eonditionals. Then write the
conclusion that lollotvs from the logical chain.
FINE ARTS People have different opinions about what constitutes a work of art.
Consider the objects below. Use one of the conditional statements below or
one of your own to present a logical proof that each work is or is not a work
of art.
ll'an object displays form, beauty. and unusual
perception on the part of its creator. then
the object is a work of art.
If an object displays creativity on the
part of the person who made it. then
the object is a work ol‘ art.
36. 37.
Two Open Morlulrtr Culu':i1'Hrtl_f Ojj‘.
Sol lfwlfl. I972
>
Four! Immc,
Alexander Calder, I972
38. MUSIC Write a conditional with the given
hypothesis and conclttsion.
Hypothesis: A person performs
classical mttsic.
Conclusion: l'he person dislikes jazz.
Write the converse of the conditional.
Yo-Yo Ma is a famous classical cellist who
also loves j-.177. Is this a counterexample
to the original conditional or to the
converse? is either the conditional or
the converse true?
LESSON 2.: AN INTRODUCTION ro LOGIC 97
CONNECTION
APPLICATION
98 CHAPTER 2
Look Back
39. A floor is best modeled by what geometric Iigure? (LESSON 1.1)
40. With folding paper. construct a segment and its perpendicular bisector.
(LESSON 1.4)
41. With folding paper. construct an angle and its bisector. (LESSON 1.4)
Complete the statements below. (LESSON 1.5;
42. lhe perpendicular bisectors of-.1 triangle meet at the ?
43. The angle bisectors of a triangle meet at the ?
44. The center oi" the circumscribed circle of a triangle is outside the triangle
ifthe triangle is ? , is inside the triangle ifthe triangle is ? , and is
on the triangle it" the triangle is ?
45. I\'-ame the three basic types of rigid transformations. (LESSON 1.6)
46. Rellect the word YAM across a vertical line. (LESSON 1.6)
L004’ 3670114
PATTERNS IN DATA In this lesson. you learned about deductive reasoning.
Another kind of reasoning is called inductive reasoning. Inductive reasoning
is based on the recognition of patterns.
For Exercises 47-50, use inductive reasoning to find the next number in
each sequence.
47. 5.8, 11. I-1.;
49. 2.6. l8. 54.;
4a. 20. 27. 3-6. -17.60. ;
5o.3.I_.%.%.;
51. The beginning of the Fibonacci sequence given below. The numbers of this
sequence are known as Fibonacci numbers. What are the next five
Fibonacci numbers?
I. 1.2. 3.5. 8.
52. Which terms in the Fibonacci sequence are even? Describe the pattern of
even and odd numbers in the sequence. and explain why this pattern
occurs. ,
53. Which terms in the Fibonacci
sequence are divisible by 5? _ \
by 5? Guess a pattern for the \ ‘
multiples of 3 and off». and \ j \
check your answer by
examining the sequence.
BOTANY In m'ricltoke5 and other
plants. the number of spirals in each
directitm rm‘ cften Filrorirtcci Jmmlrt-‘rs. &
This artichoke has 5 cIockwi.i'e spirals '
and 8 cotrnter:'!oc!;ivi.<e spirals.
Definitions /\\\
O
'9.
) s. bfler:
Objectives .
0 Use Euler diagrams to
study delitll‘ll0l'tS of In -
objects.
0 Use principles oi logic
to create definitions ot
objects.
line you ward‘. -_v --r with someone.
only to find out that you and the other person is .
had different definitions oi the same terms? in l -
mathematics it is especially important to know .3;,
the definitions of the terms you are studying.
Definitions and Euler Diagrams
Which of the figttres in card 3 above are lloppers? Simply by observing the
dillerences between the figures in the card I and card 2. it is possible to write it
definition of-a flopper.
A llopper is El figure with one “eye" and two "tails."
Using this delinition. you can see that tigu res d and o are tloppers.
Definitions have a special property when they are written as conditional
statements. For C.\'tlt'ltplC:
It a figure is a ilopper. then it has one eye and two tails.
You can also write the converse of the conditional by interchanging the
hypothesis and conclusion:
ll. ".1 figttre has one eve and two tails, than it is :1 tlopper.
l\otice that both the original conditional and its converse are true. i'ln's special
property is truefor all definitions. The two true eonditionals can be combined
into a compact Form by joining the hypothesis and the conclusion with the
phrase “if and only it." which is represented by p 4:; q.
[1 if and only if q or p ¢> q
The resulting“if-attd-ottly-if"stalctttcttl is known as .t biconditional.
LESSON 2.3 DEFINITIONS 99
Bv combining the conditional and its converse. you create the following
definition ol -.1 flopper, expressed in logical terms:
A figure is a flopper il'.1nd only if it has one eve and two tails.
Euler di-.tgr.nns can be used to represent the two parts of the definition:
1 eye and 2 tails Floppars
1 eye and
Flowers 2 tails
CRITICAL THINKING Can you create -.1 dingrain to represent the fact that both the original statement
and its converse are true? How would the parts of the diagram be related?
' I
Captur ng the "Essence" of a Thing
' l E0 1. l ook at the figure at right. Suppose that
no special took it is -.1 geometrical object you want to study.
Make up your own name for the object.
Then answer the question. \'\-‘hat must be
true oI'.t geometrical ligure in order for it to
be a f\-‘our name lot‘ the ohiectl ?
2. According to your concept of a [vour name
, which of the objects below
woultl you consider to be one? (There are no
set rules for this. The conditions are up to you.)
cnzcxromr ./ 3. Write your own definition of a fivour name for the object) . B-use
your definition on your .1n.~.wer to Step I or any other conditions you
place on the object. lest your definition of the object to be sure that it
is ncttiatlly true.
1 00 CHAPTER 2
Create your own object. and then give it a name and a definition. Your obieet
does not have to be geometrical or even mathematical, but it should be
something you can draw. ‘lest your definition to be sure it is valid. Share your
TRY THIS
definition with others.
2
Adjacent Angles
o I II. n
no special tools
An important concept in geometry is that 0|" adjacent angles. By examining
the figures in the boxes below, you should be able to form an idea about
what adjacent angles are—and also what they are not. This information will
enable you to write your own definition of adjacent angles.
ADJACENT ANGLES
/ 4 5
2 2
1 1 3 1 2
/3
.41 and .42 £1 and £2 41 and .42
.42 and .43 42 and 43
.44 and .45
(There are others also.)
NOT ADJACENT ANGLES
A
1 2
I
41 and 42 41 and 43 C
D
l2 : \ .4ADB and .4ADC
I ‘2
.41 and .42 .41 and .42
Can they overlap?
CHECKPOINT J
1. List the adjacent angles in the figure at right.
2. What do adjacent angles have in common?
3. Angles that do not overlap have no
interior points in common. Use this fact
and your answers from Steps I and 2 to
write a definition ol adjacent angles.
Definition: Adjacent Angles
Adjacent angles are angles in a plane that have their ?
? in common but
and one
:-
LESSON 2.3 DEFINITIONS 101
Exerc/ses
. Co/rm/mrimte
1. Explain how a definition is different from a conditional statement.
2. Choose a definition from a dictionary anrl write it as u biconditionnl. Is it
a valid definition?
3. Explain why the following statement is not at delinition:
A tree is a plant with leaves.
4. l'he following are hlopsz The following are not blops:
CD
‘ 4/ |\ I
\\
_ O _ \ ..
% Q = © =
///
write :1 definition ofa blop and identity which ol the following are blops:
9 ‘t “i
ll 4
5- Recall from Leasoll l.l that points. lines. and planes are referred to as
undefined terms. \'\'h_v do you think it is necessary to have undefined
terms in geometry?
-——
0 fit//ded 3k///8 Pmc 1’/6'6
6. Use the figure at right to write a definition
of-a glosh. Write your definition as precisely
as possible.
Fxzunine the shapes below. According to your definition, which (ifany) ol
the figures are gloshes? (ACTIVITY 1)
. b. § 1:. d. o. f.
7- List all pairs ofadjacent angles in
the figure at right. (ACTIVITY 2)
1 02 CHAPTER 2
ll lnumctconnoct
Homework
Help Online
Go To‘ Do hrw.com
Keyword:
M61 Homework Help
lot Exercises ll—lE
APPLICATIONS
0 Pmct/ca mm’ 74,20/y
In Exercises 8-16, use the following steps to determine whether the
given sentence is a definition.
a. Write the sentence as a conditional statement.
b. Write the converse of the conditional.
1:. Write a biconclitiottal statement.
d. Decide whether the sentence is a definition, and explain your reasoning.
8. A teenager is :1 person who is I3 years old or older.
9. A teenagtr is at person front I3 to 19 years old.
10. Zero is the integer between -I and l.
11. An even number is divisible by 2.
12. An angle is formed by two rays.
13. A right angle has a measure of 90°.
14. GEOLOGY Granite is a very hard, crystalline rock.
15. CHEMISTRY Hydrogen is the lightest ofall known substances.
16. BIOLOGY An otter is -.1 small furry mantntal with webbed feet that are used
for swimming.
17. \lame all pairs of adjacent
angles in the figure at right. X Y
W V 2
For Exercises 18-22, explain why the indicated angles are
not adjacent.
18. \] 19. 20.
— ‘2
1 : __\L2é 1
A1 and £2 .41 and .43 .41 and .42
21. 22. A
B
K. c
.41 and .42 D 4’ADB and (ADC
23. The lbllowing are llishes: The lhllo\t'ing are not llishes:
l \l
s: v 1 § 9
\\ 4’
A s> <“'* O A V >"
/\\ &|§ I? § “
Which ol the following are flishes?
a. b. C. / d.
// /
A \\* Q’ <l=
m\ ‘ ’/ \
LESSON 2.3 DEFINITIONS 103
1 04 CHAPTER 2
24. The following are cobbles: The following are not zobblcs:
A”@z@: |j=@)’°
Which of the following are 7olJbles?
.,. .,_d@
25. The following are The following are not
parallelograins: parallelogr-anlsz
E <> [1000
Which of the following are pzmlllelograms?
cl
26. The following are polygons: The following are not polygons:
A ‘>X<>§
Write a definition of a polygon.
27. The following are regular The following are not regular
polvgons: polygons-
AO mo D>00©
Write a definition of :1 regular polygon.
c It A L L E N G E 28. Examine the figures below. Choose two or more Iigures with sortie features
in common. Then choose a name and create 41 definition lor the figures
you chose. 'lell which of the other figures below are examples of the object
A Q Q
/A\ A /-h
0 ©
A P P L I c A T I 0 N 29. BIOLOGY Scientists who study birds are known as ornitho1ogists.'lhey
classify birds into 29 different orders. Eaeh order has a number of delining
characteristics. Read the descriptions of the three orders below, and classify
each of the six birds shown according to their order.
I
l‘ :1\.
Greater Rondmmrer
\ _
/.""’i
.¢'«’'.' 5':
l-I-'Iu'te-Thrtmred -—"“: ::é"’ ' Rub;»'- I71 roared
Swijt ‘\ Hutmuingbird
/K " Yellow-Iiilled
' Cuckoo
L
1 l /l
\ \
I
~ \ .
Great Blue __ Rnsmlc’ .
Heron " Spoonbill
Cimniifornms: long—legged. long—neel~:ed birds that wade in shallow water
or. in some cases. feed on open ground
(‘uculifimnes small-to mediun1-sized. slender. ttsually long-tailed birds
with zygodactyl feet tzygodrtetyl means that the toes are arranged in pairs,
with two in front and two in back.)
Apodiformes: small or very small birds with tiny leet, e.\:tren1e|y short
humeri, and long bones in the outer portion of the wing (Hmnezi are the
bones of the upper arm part of the wing extending from the “shoulder" to
the “elbow."J
LESSON 2.3 DEFINITIONS 105
106 CHAPTER 2
Look Back
30. Point B is the midpoint of A—C. Find xand AB. (LESSON 1.2}
-2x+1 x+1D
E 3 c
Refer to the figure below for Exercises 31-34. (LESSON 1.6)
31. Retlect the triangle across the given line.
32. Draw W. b‘—B’, and E. A
33. What is the relationship among the three
segments you drew in Exercise 32?
34. What is the relationship between the line
of reflection and each of the segments you C
drew in Exercise 32? 5-
Refer to the figure below for Exercises 35-38. (LESSON 1.6)
35. Translate the triangle 5 units along
the given line. A
36. Draw bl’. TH.tltld CC.
37. What is the relationship among the three
segments you drew in Exercise 36?
38. What is the relationship between the C
given line and each of the segments
you drew in Exercise 36? 0 1 2 3 4 5
Look Beyond
3 t’ m
39. Copy the Figure at right onto folding
paper. Reflect AABC across line t’. and
then rellect the image across line in.
40. What is the relationship between A C
AABCand the Final image (after two
rellections)? What single trnnslbrmation
would produce the same image?
41. Copy the figure at right onto folding
paper. Reflect ADEF:tLross line it.
and then rellect the image over line p.
-:2. What is the relationship between
ADEF-and the final image (after
two reflections,i? What single F
transformation would produce p
the same image?
Objectives
0 Identity and use the
Algebraic Propemes ol
Equality.
0 Identity and use the
Equnralence Properties
ol Equality and 0t
Congmence.
0 Link the steps at a
prool by using
properties and
postulates.
Building a System of
Geometry Knowledge
F
D
- x
C
vi
div '3‘ t
l .
'6.,i.,\_..y...s _ . ..et..;.,.»;..-,.:»'~142-_n‘..\.,.
1,...‘ .. _'..o. "3: -...t»,»-_-ti-,¢---_'a.-L._.n,.-:
AF slvi-_-n I 4-91-4-'qL_-iv.-sént-vvrvr-‘r-'
V5» ;?.‘..\».L II‘-lv§I1uI.r;.nn¢.[ 144.31-I _.'.w6i.y-My K
?* '”2<‘' -~!‘¢‘rv:'-v.-‘rv‘1-'-rt -rr*i_-Aw‘
" -mu» 5
In algebra you used tire Properties at ?_"g‘.*_ _?L"2.-
Equalftyta rrnmampsara. .. .Each rm :1“-,’;:;‘;}T - 1’
is a iusrification which guarantees that each -21; kah-
statamant you write In a proof is - = mlng L
that the smtements you start with are true. _
‘gun.’ .. .l I
The first georm-‘try "tt’xrlrool:_.” The Flements, was written by Furlirl, a
(Ire *k rrltrtlierrmririart who lived in Alexmldr in. Egypt, urormd 300 B.C.E.
,u'-\,. .u',.(‘, . .
Algebraic Properties of Equality
The intporlance of Euclid's work lies not so much in what he discovered as
in the way he organized the existirtg knolvledgr 0fgt’ometr_v of his time. Starting
from simple beginnings. he built up a large system of geometry knowledge.
Euclid began I he L-'lemeur.~' with five basic postulates. or statements that are
accepted as true without proof. In addition to the postulates. Euclid included
twentgx-tltree definitions and live statements he ca|led“con1mon notions."
'l'he second common notion reads as follows:
if equals are added to equals, then the wholes are equal.
You may recognize this from your study of algebra as the Addition Property of
Equality. This propertv is used to solve equations, as in the example below.
x- 5 - 5
x — 5 + 3 = 5 + 5 Addition Property 0/ Equality
x = S Simplify
Notice that eqrmls (the 35) are added to eqrutls ("the sides of the equation} to
give two wlltrles [the sides of the new equation]. which are themselves equal.
LESSON 2.: BUILDING A SYSTEM or GEOMETRY KNOWLEDGE 1 07
y4-/:/ /
CRITICAL THINKING
Algebraic Properties of Equality
Let a. b, and c be real numbers or expressions representing real numbers.
Addition Property If it = b. then u + C = b + t‘. 14.1
Subtraction Property If :1 = b, then u — c = (2 — r. 14.2
Multiplication Property If :1 = b. then at‘ = bc. 2.4.3
Division Property If u = b and c at 0. then % = 14.4
Substitution Property ll :1 = b. vou may replace it with I) in
any true equation containing a and the
resulting equation will still be true. 2.4.5
In the figure. the lengths of K3 and E are equal. What can you conclude
about the lengths of the two overlapping segments. AC and BD?
It is easy to see the following:
‘ AC
2.22%: ..___...<~ an 4
‘ ‘ + 4 ’ A B c D
l'hus. AC = BD.
BD
How does the conclusion illustrate the Addition Property of liqualitv? In terms
of Euclid‘s second common notion. what equals are added to what other equals?
Linking Steps to Prove a Theorem
The following example illustrates how each step in a proof can be linked to the
information that is given. ‘Hie proof is a continuation of the example about
overlapping segments. The result is called a theorem.
E X A M P L E 0 In the figure,AB = CD. Prove that AC = BD.
1 08 CHAPTER 2
O SOLUTION
A ' E E ' 5
You are interested in the lengths AC and BD. Because B is between A and C
and F is between B and D. the Segment Addition Postulate can be used to
write an equation for each length.
AB+BC=AC BC+CD=BD
You are given AB = CD. Notice what happens when vou add BC to both sides
of the equation.
The two sides of W = C“ 55V?"
the new equation AB + RC = BC + C D Addmon Property of Equat.-ty
express "79 lengths AC B0 Seams-rt Addltwn Postulua
AC and BD.
Now you can substitute l(" and BI) into the equation to get the conclusion
you want; lC = BD.
TWO-COLUMN PROOF
You can use boxes and i
colors to make the proof ’
easier to understand.
The result that was proven in Example I. along with its com-erse. can be stated
as at theorem. You will be asked to prove the converse in Exercise 2|. in
mathematics, a theorem is a statement that has been proved deductively. In
your future work in geometry, you can use a theorem to justify a statement
without writing out the whole proof.
Overlapping Segments Theorem
Given a segment with points A, B. C, and D arranged as shown, the
following statements are true:
1. If AB = CD. then AC= ED.
2. If AC: l3D. then AB = CD.
A
14.6
Two-Column Proofs
The proof in Example I might be written out as shown below. A two—column
format has been used. This format is especially convenient for many of the
proofs you will do in your study of geometry.
As you ntay notice, the steps in the final form of a proof n1-av not be in the
same order as the steps you followed to discover the ideas.
Statements Reasons
1. .-‘iB= CD Given
2. AB+ BC = BC+ CD Addition Property ofFqua|it_v
3. 1‘-lB+ BC = AC Segment Addition Postulate
4. ‘C CD = BD Segment Addition Postulate
5. AC = BD Substitution Propertv ol‘Fqu-ality
PROOF
Paragraph Proofs
An alternative to .1 two-Column proof is a paragraph proof. An advantage of a
paragraph proof is that you have a chance to explain your reasoning irt your
own words. A paragraph proof of the Overlapping Segments Theorem might
read as follows:
You are given AB = CD ‘\dd BC to both sides of the equation, resulting in
AB + BC = l3C+ CD. In the ligure. AB+ BC: ACand BC+ CD: BD by the
Segment Addition Postttlate. The expressions on the left of these equations
match the expressions in the previous equations. so you can substitute the
equivalent expressions, ACand BD. The result is AC = BD.
LESSON 2.: BUILDING A SYSTEM or GEOMETRY KNOWLEDGE 109
‘\
I
\
\
The Equivalence Properties of Equality
lll addition to the Algebraic Properties of Equality, there are three important
properties known as the Fquimlenrr Propern'e.< of!-‘quality. They are so 0l)\-‘lOllS
that you probably don't think of them when you use them. In geometry,
however, they are often used to justify steps in a prool'.
Equivalence Properties of Equality
Reflexive Property For zinv real number rt. :1 - (1. 2.4.7
For all real numbers a and b.
if (1 = ll. then I: = a. 2.4.8
Symmet ric Property
For all real numbers 11,12. and c.
if a = band b = C, then u = :1 7.4.9
Transitive Property
There are also equivalence properties for relations other than equality. as you
will learn in the next section.
The Equivalence Properties of Congruence
CRITICAL THINKING
1 10 CHAPTER 2
Congruence, like the relation of equality. satisfies the equivalence properties.
The congruent shapes helow illustrate this fact. Any relation that satisfies these
three equivalence properties is called an equivalence relation.
Equivalence Properties of Congruence
Reflexive Property
figure A E figure A 1 2.4.10
A
Symmetric Property __
If figure A E figure B. -4—
then figure B E figure A. A B 2.4.11
Transitive Property
lf figure A E figure l3 —’ —’
and figure B '—_‘ figure C, __A B V C
then figure As figure C _____________________ 2.4.12
ln Lesson l.-1 you used a eontpass to draw ’/T‘
congruent segments on at line. What property
oleongruence guar-.mtees that the segments
are actually congruent? (Hint: Imagine a
segment that connects the points of
the compass.) A 3 c
E X A M P L E 0The first stamp pictured at right
,A'PLlC"l'ION
HOBBIES
TRY THIS
measures 3 centimeters by 6 centimeters.
I'he second stamp is congruent to the
tirst. The third stamp is congruent to
the second.
From the given information, what can
you conclude about the first and the
third stamps? State your conclusions
by using geonwtr)-' terms. What property
discussed in this lesson justifies your
conclusion?
SOLUTION
The first stamp is congruent to the third
stamp [and so the measurements of the
stamps are equal}. The justification for
this conclusion is the Transitive Propert_s-
of Congruence.
9!
)4. _ _ Ease’? :
17:1}-;&, My
09
" I-on-.. .
8.: a''K"''’-'_’‘*'-‘'
-/ .,n'_‘.;-. . _
> ~A. L.- I
#425“ ’ Elfisltj E
267-} 1)f
Russian stamps ctmmrcnun'nt‘ing
the Russian .lmt-ricrm Company
Create examples of your own that illustrate the Equivalence Properties of
Congruence. Share your answers with your classmates.
Exercises
. Communicate
1. Why is it necessary to use postulates in geometry?
2. Explain the difference between .t postulate and a theorem.
3. Rephrase F.uc|id’s second common notion in your own words. Give an
example that uses this notion.
4. Euclid's first common notion reads as follows:
Things which are equal to the same thing are also equal to one another.
Rephrase this statement in your own words. How is Euclit-l's first common
notion related to the Fquivalence Properties of Equality?
Guided 347'//3 Practice
For Exercises 5 and 6, refer to the diagram below. (EXAMPLE 1;
W X Y
afisfi
WX = 8
l-‘l"'l' = 19
Find XZ.
Z
6.
WX = 30
W} = 75
Find 't'Z.
LESSON 2.: BUILDING A SYSTEM or GEOMETRY KNOWLEDGE 1 1 1
For Exercises 7 and 8, refer to the diagram below, in which
ACDE 5 AC’D’E’ and AC’D’E’ 2 AC"D"E". (EXAMPLE 2)
7. What conclusion cam you draw
ahout ACDE and AC"U'E‘"?
. . . C’
8. What property yusnhes your C C"
conclusion? N
D D’ D
E
. Practice mm’ App/y
1 .- z r In Exercises 9-12, identify the Properties of Equality that justify the
indicated steps.
9. x+ 6 = 14 Given to. 2x— 3 = l7 Gwen
x+6—6= H-6 I;Propeny .Zx—3+5= l7+5 '_rPropeny
x = 8 2x = 20
2x + 2 = 20 + 2 ; Property
x = 10
11. rr+ b = c + (1 Given 12- A8 + CD = X)" Given
t‘ + d = c + f Given CD + DE = ‘(Y Given
a + b = c + } L Propeny X Y = CD + DE 1 Property
AB+ CD = CD+ DE iPropony
PROOF In Exercises 13-19. you will complete and prove the Overlapping Angles
Theorem.
Overlapping Angles Theorem
Given AAOD with points )3 and C
in its interior as shown, the following
statements are true:
1. ll’ ml;-‘lOB= mACOD, then ?
2. ll" mi/lOC = mz_’BOD, then ?
2.4.13
,. . . .. . . £7“
Homework Refer to the figure at right to answer
He'll‘ OW"? Exercises 13-‘I9.
Go To: yo.lrrw.com
Keyword: 13. ? + ? = ml.-\-[LP
M61 Homework Help _ _
lor Exercises 13-20 14. f + .’ = l'l‘I£.Ni Q
and 30-6
15. What postulate justilics your answers
to Exercises l3 and I4?
1 12 CHAPTER 2
‘\
.
Part 1: Let mAMLN = mAPLQ.
16. Use the Addition Property of Equality to add nréNLPto both sides of the
equation.
17. Use the Substitution Property ol’ Equality. the Angle Addition Postulate,
and your conclusions to Exercises 13. I4. and 16 to write the conclusion
for the first part of the Overlapping Angles Theorem.
Part 2: Let mAMLP = mANLO.
18. Use the Subtraction Property ol’ Equality to subtract ntANLP from both
sides ol' the equation.
19. Use the Substitution Property ol Equality, the Angle Addition Posttilate.
and your conclusions to Exercises I3, l«l.and Is to write the conclusion
for the second part of the Overlapping Angles Theorem.
20. Prove the second part of the Overlapping Segments ‘I heorem (see page
109], which is the converse of the lirst part. Draw and label your own
diagram. (Hint: Use the Subtr-.iction Property of Equality.)
Refer to the diagram at right, in which
WX = YZ. Use the Overlapping Segments W X Y 2
Theorem to complete the following:
21. WA’: n, W)’: I5. XZ= ?
22. H/Y=9. Xi'=2¢t+ I, Y7=u‘,
rl= ?, l-‘VJ: ?
Refer to the diagram at right. in which
mAEDF = mAHDG. Use the Overlapping 5 G
AnglesTheorem to complete the following:
23. m.'_’L-‘D!-‘= 25°. rn.v_’L-DG = 85? m.'_’HDl'= L
24. n14EDG= (9x— 81°. niAFDG = [6x+ 8)”. m4GDH = (2x— 1 ‘'°.
2: = _?_, m.éHDF = _?__, mAHDG = 3.’
Refer to the three triangles below for Exercises 25-28.
B D H
A Qt)“ 30" C E,60" 30° F 6 60° 30' >, I
25. Complete the conclusion below. 26. Complete the conclusion below.
AB = DF ml.-‘lBC = n1AFDF
DE = CH m4EDF= IIIAGHI
AB = ? in.£z‘lBC = ?
27. Which property iustifies vour
answer to Exercise 25?
28. Which property justifies your
answer to Exercise 26?
LESSON 2.: BUILDING A SYSTEM or GEOMETRY KNOWLEDGE 1 13
{See E.rerci.~:e 29.)
PROOFS
CHALLENGE
1 14 CHAPTER 2
29. loAnn wears the same size hat as April. April wears the same size hat as
Lara. Will lzmfs hat fit lo.~\nn? What property of congruence justifies your
answer?
Given: m.éBAC+ ml/iCB = 90°
mADCF+ m£DFC = 90°
im_’ACB = m.£DC£-.'
Prove: n14BAC = m4DEC
Proof:
Statements
A
8
Reasons
m.£B.»\C + m.£ACb‘ = 90°
nv_’DCL' + m/_’D!;'C = 90'”
Given
3o. ?
m4BAC+ m4ACl3 = mA DCE+ m4DEC 31. ?
n1AACl3 = mADCE
Given
m4l3AC+ m4ACl3 = ml.-\Cl3 + m4DEC 32. ?
33. ?
mil + ml-1 + n1/_’5 = |80°
m.£4 = m.'_’2
m.é5 = mA3
mil + 11142 + in/_’3 = l8tl°
Given:
Prove:
Proof:
34. 1! by 35. ?
m.éCBD = ITIACDB
mA.riBD = 90°
ml LDB = 90”
m.«*_’Al3C = m4EDC
Given:
Provo:
Proof:
Statements
Subtraction Property
Since 111.54 = m.»_’2, you can replace mg.’-4 with m.»_’2 in the equation
.SiIIIii:.ll'i)‘, you can replace m.é5 with
38. ? , giving 37. ? .
B D
Reasons
m4ABD= 90°
mAABC + méCBD = ml.-'iBD
39. m.é.riBC+ HIACBD = -{
mAEDB = 90°
41. ?
mz CDF+ mz("DB = 90°
mzABC+ m./_"CBD = m4CDF+ n1£CDB
n1/_"CBD=n1/."CDB
m.£Ab‘C + mz_’CBD = mz_’CDL‘ + m.£CBD
46. ?
Given
38. '{
Transitive [or 5Lli)§IlIL|li0lI)
Property
40. ?
Angle Addition Postulate
42. ?
43. ?
44. ?
45. ?
Subtraction Propertv
CHALLENGE
APPLICATION
Examine the relationships below. Determine which of the following properties
each relationship satisfies: the Reflexive Property, the Symmetric Property, and
the l'r-ansitive Property. l'hen state whether the relationship is an equivalence
relation. Ila property is not satislied by a given relationship, giye a
counterexample.
4‘). ti < l1. where rt and b are real numbers.
48. u 5 12. where (I and l: are real numbers.
49. u is divisible by b. where a and E: are real numbers.
50. Figure A is a retleetion of figure B.
51. Figure A is a rotation of Figure B.
52. A is a sister of B. where A and B are people.
53. A has the same last name as B. where A and B are people.
Look Back
Recall the five postulates about points, lines, and planes that you
discovered on page 12 and refer to the figure below to answer
Exercises 54-59. (LESSON1. 1)
54. \i-ante three points that determine plane 32.
55. Which postulate justilies your answer
to Exercise 5-1?
56. \lame two points that determine line I".
57. which postulate justifies your answer F.
to Exercise 56?
58. .\lame the intersection of plane IR and
plane M.
59. which postulate justilies your answer
to Exereise 58?
60. PHOTOGRAPHY .-’t tripod is a three-
legged stand used by photographers
to hold their cameras steady. Why
do you thinl: tripods provide more
stability than four-legged stands?
which of the live postulates
justilies your answer?
(LESSON 1.1)
LESSON 2.: BUILDING A SYSTEM OF GEOMETRV KNOWLEDGE 1 15
Longitude
circle \
'\
I
Latitude
circle
Equator
APPLICATION
D lntametoonnect .29.,
mm
Portfolio
Extension
Go To: 9o.hrw.corn
Keyword
MGI Nirn2
«£0
Look Beyond
Because the system of logic \ve use in geometry is hased on the postulates ol
Fttclid, it is commonly known as Fm'lirlt'mt getnrtetry. It is possible to have
geometries in which one or more of ljuclid's postulates do not hold. Geometry
on a sphere. such as Earth's sttt'laL'e. is known as spl'teriml geometry. In
spherical geometry, a line is defined as a circle that divides the sphere imo two
equal halves.
61. l_.'sing this delinitiott ofa line. which of the following are lines?
° lines oflatitude
' lines of longitude
° the equator
62. Explain why lines are defined this way in spherical geometry. (Hint: Pick
two points on a globe and stretch :1 string between them to lind the
shortest distance from one point to the other.)
63. Explain why the following postulate is not true in spherical geometry:
Through any two points. one and only one line passes.
64. NAVIGATION Pilots navigating long distances often travel along the lines of
spherical geometry. called great circles. Using a globe and string. determine
the shortest route for a pilot traveling from Washington. D. C., to London,
lingl-and. What do you notice?
T
<2»
«:9
These are wntrrirtg
corrrliirtrttiom.
In a game of nim. if yott leave two rows of two counters each. then you can
always win, in either version of the game. {See pages 79 and S7.)
The following strategies allow you to achieve this winning combination—or
an even quicker win. depending on your opponent's moves.
° On your turn. leave two rows with the same number of cottnters
in each row.
or
° On your tttrn. leave three rows with one. two. and three counters.
in any order.
Fxplain how these combinations can be Converted to eventual wins. no
matter what your opponent does. in either version of the game.
In either version ol‘ mm. the person who ntoves first cart alwavs win. Try to
discover the first move that will allow you to always win. Explain the
strategy behind this move.
1 16 CHAPTER 2
Conjectures That
Lead to Theorems
1 region 2 regions
Objectives
0 Develop theorems ) qg :-
lrom conjectures. - _
o Write two-column and - - ___ -
paragraph proofs. ' L
A FGQIODS 8 regions 16 regions
basedithnen W_" make Do you 5(’(’ (1 pattern in the niunlier of regions in
p’ ' 7°" 9 the circles? Do you think the pane: I! will continue?
inductive reasoning.
A Need for Proof
From the pattern of circles above, vou might make this conjecture:
True I
or ? - The number ol regions doubles eztch time a point is added.
false. I
This c0n_iecture can he tested by drawing
pictures. \-\-‘hat do you notice about the
ligure with 6 points? 6 points
7 regions
As you can see, the number of regions for 6 points is not 32 but 3|. Thus. the
conjecture is false. For a conjecture to be considered true by mathematicians it
must first be proven detluctively. as in Activity 1.
The Vertical Angles Conjecture
Vertical angles are the opposite angles
formed by two intersecting lines.
A pair of scissors suggests ‘
(approximately) the idea of
ruler and
prutractor
OR
geometry
Somme vertical angles. with the blades
making one of the angles and the
handles forming the other.
LESSON 2.5 CONJECTURES THAT LEADTO THEOREMS 1 1 7
CHECKPOINT 3/
TWO-COLUMN P‘ 0 I
1 18 CHAPTER 2
1. Draw several pairs of intersecting lines.
I11 the Iigure at right. Al and 42 form
one pair ol vertical angles. a11d £3 a11d 4
4’-I forn1 another. 3
2. Measure each pair or vertical angles.
\'\'l1at do you notice?
3. Make a co11_iecture about vertical angles.
4. \-\"hat is the relationship between A3 and £1? betwee11 A3 and A2?
5. Complete the follotvittgz
mzl + mA3 = ? n1é2 + mA3 = ?
6. \-\-‘hat Property ot Fquality leads to the Iollowing co11clusion?
mzl + nu‘_'3 = 11142 + mé3
7. \-\'l1at Propertv of Equality leads to the conclusion that 1n.«_’l = 11142?
Inductive and Deductive Reasoning
Inductive reaso11i11g is the process of forming co11jectt1res that are based on
observations. As you have seen. a conjectu re can turn out to be false; thus,
inductive reasoning is not accepted in mathematical proofs.
Activity I began with inductive reasoning and concluded with deductive
reasoning. I11 Steps I-3. you used inductive reasoning to make -.1 co11_iecture
based on observations. I11 Steps 4-7, you use deductive reasoning to complete
an informal proof. The conjecture 1011 made in Activity I is stated and proved
lo1'111ally below.
Vertical Angles Theorem
If two angles form a pair of vertical angles. then they are congruent.
2.5.1
Given: Al a11d A2 are vertical angles. 4
Prove: Zl 1-112 1 3 2
Proof:
Statements I Reasons
1. Al and A2 are vertical angles. Given
2. 1111! +1114? = I80”
11112 + I11.£3 = l8U°
3. 11141 + 11143 = 11142 + m4}
4. m.«_’l = 11142 (Al E 42)
Linear Pair Property
Substitution Property of Equality
Subtraction Property of Equality
In Activity 2. vou will explore another example oi" an inductive result that is
proven as at theorem.
I ' |. D 1. Draw two parallel lines. t‘,.Ind fl.
pipe,‘ rum and A IBC as shown in the figure B
and protractor at right.
Esme“ 2. Rellect AABCaero:.s 6.. Label its
sohwuarg ililtlge A:4'B'C. A C
3. Rellect AA'B'C' across £3. label its ‘I
itnage z‘_\./l"b"'C".
4. Study the relationship between
AA BC and AA"B"("'. What single
transformation do you think would 8,
produce AA"B"C" from AABC?
5. Measure the distances AA". BB’! and CC'.Wh;1t do vou notice?
6. Measure the distance between E’, and £3 Ilow does this distance relate
to the distances vou measured in Step 5?
7. Do all of the points on the triangle seem to have moved in the same
direction? Explain your answer.
CHECKPOINT ./ 8. Complete the following theorem. which is proven below:
Theorem
Rellection across two parallel lines is equivalent to a ? of
? the distance between the lines and in a direction
? to the lines. 2.5.2
CRITICAL THINKING What must you prove about the reflection of a point across two parallel lines
in order to show that the theorem you completed above is true?
PROOF The diagram at right Sllggfils a prool 7
of the result in Step 6 of Activity 2.
1. Which ol the indicated distances 91
are equal? Wliy? x '
2. What is the distance between
if. and E2? D?
3. What does the expression 2D. + .‘'.D_- ‘— i
represent in the diagram? How does D I i
it compare with the distance between ' ;
t-'. and £3? ;
CRITICAL THINKING Do you think the result from Step 6 of Activity 2 is true for any point on the
figu re? How could you prove that each point moves in the same direction?
LESSON 2.5 oomectunes THAT LEAD TO THEOREMS 1 19
The Importance of Theorems
Con_iectures. like the prediction about the regions of a circle at the beginning
of this lesson. may turnout to be false. l'h is is because they are based on a
finite ntnnber of observations or measurements. You should always ask
yourself whether there is a case that might prove your coniecture to be false.
Theorems are different from conjectures. In the Vertical Angles Theorem. the
measures of the angles in the diagram do not matter. They could be any size
at all. and the proof would still work. |'his is why the theorem is true for all
possible pairs of vertical angles.
Exercises
. Co»//mm/mte
n Iuumotoonnaa ,?,-3.,
tom
Activities
Online
Go To‘ no.hrw.coI11
Keyword:
M61 Prool
APPLICATION
120 CHAPTER 2
1. Consider the following statement: Every integer is less than l.0O0.000.000.
Does the statement seem true for integers you use in everytlay life? Is it
really true?
2. Explain the difference between inductive and deductive reasoning.
3. Why is deductive reasoning the only type of reasoning allowed in proofs?
4. Explain the difference between theorems and conjectures.
5. Describe how you can translate a given figure by using only reflections.
6. ENTERTAINMENT If you have enjoyed all of the films by a certain director
that you have seen so far, does this mean that you will enjoy the next film
of his that you see? Explain your answer.
0 fill/d€d'5k///3 Fido?/6'9
7. Use the results oi".-’tLti\'ity l to A C
find the measures of all of the angles 42-‘
in the figure at right. (ACTIVITY 1)
B D
Copy the figure below onto folding paper and use it in Exercises 8 and 9.
[771
K L
8. Reflect AJKI across m.. and then rellect the image across rm.
(ACTIVITY 2)
9. Reflect AIKL across ml, and then reflect the image across In.. How is the
final image dillerent from the final image in Exercise 8? (ACTIVITY 2)
0 Pfdc‘ 1'/6'8 dim’ 34,0]/y
Refer to the diagram below, which consists of three intersecting lines.
For Exercises 10-12. tell which angle is congruent to the given angle.
10. ALE]
11. ASFF
12. AP}.-‘D
For each pair of intersecting lines. find m.£ABC.
1 .
4 E A
D C
15. 16.
A
E 8 C
D
LESSON 2.5 OONJECTURES THAT LEAD TO THEOREMS ‘I 2 1
‘ /;/ /
f
D imemetcomed .39
um‘-
Homework
Help Online
Go To: 9o.hrw.com
Keyword
M61 Homework Help
lot Exercises l7—20
122 CHAPTER 2
For Exercises 17-20, find the value of x and méABC.
17.
19. 20.
i~12x+ 13)
C
(—21x+ 2|"
l3x + 5}"
Tell whether each argument is an example of inductive or deductive
reasoning. Is the argument a proof? Why or why not?
21. Fvery time John eats strawberries, he breaks out in hives. Therefore, John
is allergic to strawberries.
22. If Erika did not turn in her homework. then she made .1 bad grade.
Erika did not turn in her homework. Therefore. Erika made :1 had grade.
23. Angles that form :1 linear pair are supplementary.
Therefore. Al and A2 are supplelnentary.
1 2
‘me’.
24. 'I'he number of blac.k—footed ferrets has increased each year since I985.
Therefore. there will be more black—l'ooted ferrets next year than there are
this year.
PROOF
PROD‘
in Exercise 25-27. complete the two-column proof of the following
theorem:
congruent Supplements Theorem
If two angles are supplements of congruent attgles, then the two angles
are congruent.
2.5.3
Given: 4: 5 45, .41 and 42 /
are supplementary.and A3 1 2 _._
and 44 are supplement.try. /4
Prove: £2 E .14 31h
Proof:
Statements I Reasons
mzl + ind}. = 130" Definition ofsupplementary
m£3 + mé-4 = 180° angles
mil + m£2 = mz_’3 + ind-'1 25.__?__
4| 5 43 [m4] = 11143} 26. 3.’
mil + m£2 = mél + 11144 Substitution Property
m.£2 = m.£4 (£2 ‘=:- A4) 27. ?
28. Write a pararzraph proof of the Congruent Supplements Theorem.
ln Exercises 29-34. refer to Activity 2 and the proof outlined on page
119. Refer to the figure below. Suppose that AMNO is reflected across
line m, and then its image is reflected N
across line n.What is the distance from
AMNO to AM"N"O" if the distance
from m to n is
29. 5 cm? M
30. 10 cm?
31.xcm?
0
«eat
on
m||n
Refer to the figure below. Suppose that you wish to use two reflections
to translate the figure in the direction of the arrow.
32. ll'vou wish to translate the ligurc 10 em.
how far apart should the parallel lines
used in the retlections be?
33. How can you determine the location
¥____
of the parallel lines?
34. Is there more than one pair of parallel
lines that will give a translation of 10 cm?
Use diagrams to illustrate your ansu.-er.
LESSON 2.5 oomectunes THAT LEAD TO THEOREMS 1 23
CHALLENGE
124 CHAPTER 2
You may want to use
geometry graphics
software for Exercise 40. I
For Exercises 35-38. copy each figure onto folding paper. Reflect each
figure across (3., and then reflect the image across (2. Draw an arrow
that represents the direction and distance that the figure has been
translated.
35. 5, 36.
A
f1
D
«T» {'52
37. £2 £1 38. £2 E‘
Q 4
Exercises 39-43 refer to the pattern in the number of regions in the
circles on page 117.
Draw circles with 6 and with 7 points, and connect the points in each
circle with segments. To be sure that you have the maximum number
of regions. make sure there are no points where three segments
intersect inside the circle. (Hint: Do not space the points regularly on
the circle.) How many regions are possible for a circle with
39. 6 points!
40. 3' points?
One way to find a pattern in a sequence is by subtracting each term
from the next.This gives a new sequence, called the first differences.
This method can be continued to find second differences, third
differences, etc., until the pattern is clear.
41. Complete the ch.iit below. {Work from the bottom up to fill in the chart.)
Numberofregions 1\ 2 4 8 16 7 7 ?
_ _ \ \ \ \ / \ / \
First differences 1 2 4 7 7 7
_ \ \ \ \ \ \ /
Second differences 1 2 7 ? 7
_ \ \ \ / \ / \ /
Third differences 1 3 4 7
42. Using the pattern, what conjectti re would yoti make about the mi mber ot
regions in a circle with 8 points? with 9 points? with 10 poiiits?
43. If yoti found that the pattern in the chart above was correct for 100. I000.
or even more points on :1 circle, would yoti have proven that the pattern is
correct for any number of points? Why or why not?
V
" Eivée §;*_'.§
V b N I “fly 4032
‘ _ ' U __ J.
\/'
(Sec Extrrristr 49.)
£00k Back
Refer to the figure below for Exercises 44-46. B C
(LESSON 1.1) A I D
44. .\l-ame four points in the figure.
45. Name fottr segments iii the figure. 6 l H
46. .\lame four planes in the figure. E
F
Exercises 47 and 48 refer to the statements below. (LESSON 2.2)
if I ant well rested iii the afternoon. then I atu in a good mood.
lfl sleep until 8:00 .-\.M.. then I am well rested in the afternoon.
if it is Saturday, then 1 sleep until 8:00 .>'\..\-l.
47. Arrange the statements to form a logical chain.
48. Write the conditional statement that follows from the argument formed by
the logical chain in Exercise 47.
49. Draw an l:.uler diagram to illustrate the argttment below. (LESSON 2.2)
Every member of the Culver High School football team goes to Culver
High School. Brady is a member of the Culver High School football team.
Therefore. Brady goes to Culver High School.
50. Below is a chain of conditionals. Construct an Euler diagram for these
statements. and complete the concluding statement. (LESSON 2.2)
If vott are taking geometry, then vou are developing good reasoning
skills.
If vou are developing good reasoning skills. then you will be able to
succeed in many dilferent careers.
lfyott are able to succeed in many different careers. then you will be
able to choose your profession.
l'herefore, if you are taking geometry, then ? .
Look Beyond
51. Copy the figure at right. Reflect AABC 8
across t',, and then reflect its image across
1'}. Label the linal image .oj.A"B"C".
52. What single transformation would
produce the same final image as the
two reflections?
53. What seems to be special about the
intersection point, D?
54. Use a protractor to measure 1./tDA".
LBDB". and LCDCZ What seems to be
the relationship between the measures E2
of these angles and the measure of Al?
55. Write a conjecture about the reflection of a figure across two intersecting
lines. Include Your results from Fxercise 54 in your conjecture.
LESSON 2.5 OONJECTURES THAT LEADTOTHEOREMS 1 25
~zJ"P?E9‘
0'‘ K ‘
. EU Lngic Puzzles r
Q A and
. . V
Activity 1J
l he game of sprouts was invented by mathematicians lohn Conway
and Michael l"aterson. The object is to he the lust player to make :1
legal move.
Rules of the Game
Start by drawing three spots on a piece of paper.
The game is played by two people. who take turns.
to make a move. draw a curve joining two spots or stat ting and
ending at the same spot. and place a new spot on the curve.
' No curve can cross another curve.
' No spot can have more than three curves coming from it.
Not Iegalmoves
with a friend. Trv to figure mg " mm "kw" "' "ml ("'°"" '" "-“‘l-
oul '.t strategy that will 0
enable TQJLI to .nlw-a)-‘s win if r. 0
you have the tirst turn. 0 0
" 39
, ll i - —.-.——.—
\'ou can vary the game by
I
-T--' starting with four. live. or
any other number of spots. <3 5
L F\ fix &
Play a few gatnes ol sprouts \
E
E
2 \‘ §
\ s
. . j i _
Activity 1 \
In the following puzzle. each letter represents a tliflereiit digit. ll
Use the clues given to determine the digits, and then arrange ‘ t
the letters in numerical order to solve the puzzle. ,..‘ l ~
O+O=E HAT TxV=OL
o x o = E + MAT J
LEVE M)-<M=OM H><|=| -
O
. . V I
Activity 3‘ ,\
. _ _ _ _ _ _ V, .
The following puzzle is by the British writer known as “Calilian.
Accomplishments
"i\ly four graiiddaughters are all accomplished girls." Canon -
Chasuble was speaking with evident selflsatisfactioii. “Each
of them." he went on. “plays a different musical instrument
and each speaks one European Iaiiguage as well as—if not
better th:1ii—a native." 0 G "
"What does Marv plav?" asked someone.
"The cello." \. o»
"Who plavs the violin?" \
"D‘yo1i know." said Chastilile. "I've temporarily forgotten. Anno ‘-. \'
Domini. alas! But 1 know it’s the girl who speaks |-‘rench."' ' '\
. . . . . . . 5-: _“
'1 he remainder ot the facts whi-:li I elicited were ot a somewhat lfl
negative cliaracter. l leariied that the organist is not Valerie; that , -
the girl who speaks German is not I orna; and that Mary knows
no ltaliaii. Anthea doesn’t play the \' iolin: nor is she the girl who \
speaks Spaiiish. Valerie knows no French, Lorna doesn't play the
harp, and the organist can’t speak ltalian. B
I
W’ hat are Valerie’s accomplishments? '
C .2
0 5 5 Q '5 E S 2
= 3 at I. 5 - ; as
3 5 5 e E as :2 .5: D‘
Maw i \
Valerie
4 _ _:~
Lorna ‘l “
Anthea l _ -'
French
German -1‘
Italian _
‘ 4‘
_ "1.’
Spanish
Chapter Review and Assessment
VOCABULARY
adjacent angles . . . . . . . . . . 101 deduction . . . . . . . . . . . . . . . . . 91 paragraph proof . . . . . . . . . . 109
bicondirlonal . . . . . . . . . . . . .99 deductive reasoning ..... .. 91 prool ................... . . 82
conditional .... equivaiencerelation ......110 theorem
converse . . . . . . . . . . . . . . . .. 99 hypothesis . . . . . . . . . . . . . . . . 90 two-column prool . . . . . . . . . 109
counterexample . . . . . . . . . . . 92 inductive reasoning ..... . . 118 vertical angles . . . . . . . . . . . 117
conclusion . . . . . . . . . . . . . . .. 9] logical chain ............ . . 32
SUMMARY OF POSTULATES AND THEOREMS
esson umber eorem or Postuiate
2.2 2.2.1 if-Then Transitive Given: ”|fA then B, and if Bthen C."
Property You can conclude: ‘'If A then C."
2.4 2.4.1 Addition Property if a = b, then a+ c = in c.
2.4.2 Subtraction Property
lfa=b,thena-c=b-c.
2.4.3 Multiplication Property
if a = b, then ac: bc.
2.4.4 Division Property
lfa=b andc1=0,then-g:
alu-
2.4.5 Substitution Property
if a = b. you may replace a with b in any true equation
containing a and the resulting equation will still be true.
2.4.6 Overlapping
Segments Theorem
Given a segment with points A, B, C. and Dtin order) the
following statements are true:
1. if AB = CD. then AC = BD.
2. if AC= BD. then AB: CD.
2.4.7 Reflexive Property
of Equality
For any real number a. a = a.
2.4.8 Symmetric Property
of Equality
For all real numbers a and b. if a = D, then b: a.
2.4.9 Transitive Property
of Equality
For all real numbers a. D, and c, if a = b and D: c. then 3 = c.
2.4.10 Reflexive Property
of Congruence
figure A 5 figure A
2.4.11 Symmetric Property
of Congruence
if figure A 2 figure B, then figure B 5 figure A.
2.4.12 Transitive Property
of Congruence
if figure A E figure 8 and figure 8 5 figure C, then
figure A E figure C.
2.4.13 Overlapping Angles
Theorem
Given zAOD with points 8 and C in its interior. the following
statements are true:
1. if mzAOB = mCOD, then mzAOC= mBOD.
2. if m£AOC= mBOD. then m£AOB = mCOD.
128 CHAPTER 2
2.5 2.5.1 Vertical Angles
Theorem congruent.
if two angles form a pair of vertical angles, then they are
2.5.2 Theorem
Reflection across two parallel lines is equivalent to a translation
of twice the distance between the lines and in a direction
perpendicular to the lines.
2.5.3 Theorem
Key Skills 8: Exercises
LESSON 2.1
Key Skills
Give a proof of a conjecture.
©®:”.
The following table shows the number oi‘ points
and the corresponding number oi segments:
Points 2 3 4 5
1 3 6 10
Segmenu;
Conjecture: For it points on :1 circle. the number oi"
. . - I
segments needed to connect all points is
Proof: For each point. a segment connects it to
every other point, giving ri - I segments.
therefore, the total number of segments should
be ii( ii - l). However, H-3is same segment as
so each segment is counted twice. Thus. the total
must be divided by 2, giving
i.EssoN 2.2
Key Skills
Draw a conclusion from a conditional.
What conclusion follows lrom these statenients?
lian animal is a cat. then it has four legs.
Dinah is a cat.
Conclusion: Dinah his tour legs.
State the converse of a conditional.
Converse of the conditional above:
ll'an animal has four legs. then it is a cat.
Reflection across two intersecting lines is equivalent to a rotation
about the point of intersection through twice the measure of the
angle between the lines.
Exercises
The horizontal line intersects the curve at
three points and divides it into four pieces.
/\ F
1. into how many pieces will the curve be
divided by two horizontal lines that each
iiitersect the curve at three points each? by
three horizontal lilies?
2. Complete the table below, subtracting to find
tltc lirst dilfereiices.
Lines 1 2 3 4
4 ? ? ?
\/ \/\/
First dilierences 7 7 7
Sections
3. Based on the table, make a coniecture about
the pattern in the number of sections.
4. write at proof of voiir conjecture.
Exercises
Refer to the following statements:
if a “star” doesn't flicker. then it is a planet.
The evening star doesn't llicker.
5. Give the concliision that follows from the
statemeiits above.
6. Write the converse of the conditional above. is
the converse true?
CHAPTER 2 REVIEW 129
Arrange statements into a logical chain and
draw a conclusion.
a. If John gets his driver’s license, then he will
buy a car.
b. If John buys a car, then he will not have any
money.
c. lfjohn passes his driver's license exam. then
he will get his driver's license.
The order of the logical chain is c. a. b. The
conclttsion is "If John passes his driver's license
exam, then he will not have any money."
LESSON 2.3
Key Skills
Write a definition of an object.
These objects are trapezoids.
EDGE
These objects are not trapezoids.
_l l_
A \X/ 1 F
Which of the following objects are trapezoids?
a./\ b. c. l/‘ d. ,:
Write a definition of a trapezoid.
Objects b and c are trapezoids. A trapezoid is a
lour—sided hgu re with exactly two parallel sides.
Determine whether a statement is a
definition.
is the following statement a definition?
A right angle measures 90°.
lfa statement is a delinition. then the conditional
form and its converse are both true.
Conditional: lfan angle is a right angle.
then it measures 90°.
If an angle measures 90°,
then it is a right angle.
Since both are true. the statement is a definition.
Converse:
130 CHAPTER 2
Exercises 7 and 8 refer to the following
statements:
a. If lune tells Andrew a secret, then Andrew tells
Tina the secret.
b. lfCharles tells June a secret, then lune tells
Andrew the secret.
c. If Darren tells Charles a secret. then Charles
tells June the secret.
7. Arrange the statements into a logical chain.
8. \-\'hat conditional statement does the
argument formed by this logical chain prove?
Exercises
These objects are tori (singular, torus).
These objects are not tori.
9. \-\"hich of the following objects are tori?
a. b. c. d.
10. Write a delinition of torus.
Determine whether the following statements
are definitions:
11. A square is a figure with four sides.
12. A point that divides a segment into two
congruent parts is the midpoint.
LESSON 2.4
Key Skills
Use the Properties of Equality and
Congruence to write proofs.
In the ligure below. il '—_“ if». Prove that i2 E i4.
1
2
3
4
Two-column proof:
Statements I Reasons
mil + mi2 = l80°
mi3+ mi4 = l80°
Linear Pair Property
Linear Pair Property
mil + mi2 = Substitution Property
mi?» + mi-1
mil = mi} Given
n1i2 = mi-1 (i2 5 i4) Subtraction Property
Paragraph proof:
By the Linear Pair Property. mil + mi2 = 180°
and mi’: + mi4 = l$0°. By the Substitution
Property. mil + rni2 = mi} + Inivl. You are
given mil = mi3. so by the Subtraction
Propei'ty, mi2 = mi-4, or i2 .=. i4.
LESSON 2.5
Key Skills
Use deductive reasoning to prove a
conjecture.
Make a conjecture about the angle formed by the
angle bisectors of a linear pair, and prove your
conjecture.
By measuring the angles, you can make the
lollowing conjecture: The angle bisectors of a
linear pair form a right angle.
Exercises
In the figure below, mi1 = 90‘?
13. \r\-"hat property would you use to prove that
mi2 = 90°?
14. What property would vou use to prove that
mi4 = 90°?
15. What theorem would you use to prove that
mifi = 90°?
16. Use your answers from Exercises 15-] 5 to
write a two—column or paragraph proofol’ the
following conjecture:
If two lines intersect to form a right
angle. then all of the angles formed are
right angles.
Exercises
Three numbers, a, b, and c, are called a
Pythagorean triple if 82 + b2 = c’.
17. Show that the numbers 3. 4. and 5 are a
Pythagorean triple and that the numbers
5. l2. and I3 are another Pythagorean triple.
CHAPTER 2 REVIEW 131
Four numbers. a. b, c, and d, are called a
Pythagorean quadruple if 32 + b2 + c"’ = d2.
18. Show that the numbers 3, -I, I2. and I3 are a
Pythagorean quadruple.
Given: the figure below. in which fibisects
*>
AAOC and OD bisects IBOE
19. If (1, I1, and care a Pythagorean triple and c, ii.
and e are another Pythagorean triple, make a
conjecture about rt, 1:. (I. and e.
prove: mg; + "113 = 90° 20. Use_Properties of Equality to prove the
proof. comecttire you made in Exercise 19.
Statements Reasons
mil = mil Definition ofangle
bisector
n1.«:'3 = in.«;’4 Definition of angle
bisector
ml I + 11142 + Linear Pair Property
H113 + IIIZ4 = 180°
mg}. + m.«;’2 + Substitution Property
111113 + nu13 = 180°
2(nw_’2 + m£3] = I80” Distributive Property
m.«_"2 + mz3 = 90” Division Property
Applications
21. COMPUTER PROGRAMMING The following is part ol a (.()n‘lplll.t-.’l'
progmni used to evaluate the quadratic formula:
INPUT A
INPUT B
INPUT C
IF B2 — 4*A'C < 0
THEN
DISP "NO REAL SOLUTIONS"
END
Suppose that A = I. B = 3. and L": 4. Can you determine
what the program would do?
22. BIOLOGY In biological classification. animals are grouped
into categories according to physical characteristics.
Consider the following definitions:
."vl¢tnmml.~' are animals that have hair and produce milk.
Mormtrenzes are mammals that lay eggs.
Suppose that 21 biologist is examining a platvpus and finds
that it has hair, produces milk, and lays eggs. is a platvpus
a monotreme? Why or why not?
132 CHAPTER 2
Chapter Test
1. What are the next four terms in the sequence?
l I l l
T‘ I’ 7;" TE‘
2. W hat conjecture can you make about the
sequence of terms in Exercise l?
For Exercises 3-4, refer to the following
statement:
If a quadrilateral is a square, then it is a
rectangle.
3. Identify the hypothesis and the conclusion of
the conditional.
4. Write the converse of the conditional. ll‘ the
converse is false. give .1 counterexample to
show how it is false.
For Exercises 5-6, refer to the following
statements:
a. If Brett flies his kite, then it is cool.
b. If it is cool, then it is autumn.
c. If it is windy, then Brett flies his kite.
5. Arrange the statements to form .1 logical
Cilalin.
6. What conditional statement results from this
logical chain?
For Exercise 7, use the following steps to deter-
mine whether the sentence is a definition.
a. Write the sentence as a conditional
statement.
b. Write the converse of the conditional.
c. Write a biconditional statement.
d. Decide whether the sentence is a
definition, and explain your reasoning.
‘I. An obtuse angle has a measure of lUO°.
8. Use the figure in which rniADl3 = (8x— 311°.
miBDC= (3.x'+ 9)"‘, and miAD('= l lO° to
find ntiBDC.
Complete each proof.
N
Given: mil + mil = 90 4
mi} + mill = 90° K
mi2 = mi} L M
J
Prove: mil = I'ni4
Statements | Reasons
mil + mi2 = 90° 9. 7’
mi3 + mid = 90°
mil + n1i2 = mifl + mi-1 10. _2_
miz = mi} __'{_
mi I + mil = mil + mi-‘l 12. L
mil = mi4 13. L
Given: ii and i2 are supplementary
mil = l45°
_.i
Prove: mil = 35°
Statements | Reasons
it and ii! are supplementary M _t_
mil = l45°
mil + mi2 = l8[]‘ 15 L
miz = 55° — 11 __.?_ _
CHAPTER 21157 133
-- E-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Questions l—4. write the
letter that indicates the best answer.
1. Refer to the figure below. Which of the
following statements is true? (LESSON 1.3;
e. AABC is an acute angle.
b. (ABC is art obtuse angle.
c. £ABCis at right angle.
d. AABC is a complementary angle.
2. What are the first four terms in the sequence
for the rule "“'_,+ H. where n is a positive
integer? (LESSON 2.1;
11.0, I,3.6.... b. I.5.2.5,3.5.Il.5....
c. I. 25.5.8.5. d. l, 3,6. I0,
3. which process is used to form conjectures?
(LESSON 2.5;
e. deductive reasoning
b. inductive reasoning
c. tr-ansllorntation
d. indirect proof
4. Reler to the figure below. Which ot the
Following statements is true? (LESSON 2.5)
9. Al and 12 form a linear pair.
b. [I and A2 are parallel.
c. mil = mzl
d. mzl > 111.42
134 CHAPTER 2
0
I intemet connect
Standardized
Test Prep Online
Go To: go.hrw.con1
Ke-/word: MM1 Test Prep
A square is divided into regions by pairs of
perpendicular lines as shown. (LESSON 2.1)
V
5. How manv regions are formed by three pairs
ol" perpendicular lines? by four pairs of
perpendicular lines?
8. \-\-‘rite a conjecture about the number of
regions formed by n pairs of perpendicular
lines.
7. Write a proofol’ the conjecture you made in
[tent 6.
A triangle has vertices at (4, 1), (2, 2), and
(3. 0). What are the vertices of the image after
the following transformations? (LESSON 1.7)
8. rellection across the .\:—a»<is
9. translation 3 units to the left and I unit down
10. Write-.1 conditional statement based on the
Euler diagram below. (LESSON 2.2)
Rectangles
Squares
11. The figures below are splorts.
\'/ 41/
7,\‘1v3Cl l
The figures below are not splurts.
>I<>3/:A2&
Write a definition of splon‘. (LESSON 2.3)
For Items 12-15, refer
to the diagram at right.
(LESSON 1.1)
12. l\‘-ame five points in the figure.
13. l\'-ante three lines in the figure.
14. Name four rays in the figure.
15. l\ame eight angles in the figure.
16. Which of the following is a definition?
(LESSON 2.3)
a. The midpoint oi" a segment is .1 point that
divides the segment into two equal parts.
b. An acute triangle is a triangle that has an
angle of less than 90°.
c. Two points determine exactly one line.
d. An equilateral triangle is an isosceles
triangle.
FREE-RESPONSE GRID
The following Items may G) C)
be answered by using a C)
- \.' - o (-
free-response grid such as G) G) CO CD
that commonly used by (3 ® _® ®
standardized-test services. (3) G) 5;. Q
(E) (Z) G) G
G) G) 6) C5“
(E) (E) (E) (E)
G) ® 6) G
G) (E) (D G
® ® <3) @
For Items 17 and 18, refer to the figure below.
(LESSONS 1.3 AND 2.5)
130’
1 2
3
17. n1/_’l = f
18. m./_’.’» = ?
For Items 19 and 20, refer to the information
and the figure below. (LESSON 1.3)
mzQP'I‘= 140°
niAQPR = (2x— 5)°
n1éRP5=[4x+ l0)°
mzSPl = [.1.\:J°
19. x = ?
20. m£RPS = ?
CHAPYER 2 CUMULATIVE ASSESSMENT 1 35
136
Lessons
3.1 0 Symmetry in
Polygons
3.2 0 Propertiesof
Ouadrilaterals
33 0 Parallel Lines and
Transversals
3.4 0 Proving That Lines
Are Parallel
3.5 o The Triangle Sum
Theorem
3.6 o Angles in Polygons
3.7 o Midsegments ol
Triangles and
Trapezoids
3.8 0 Analyzing Polygons
With Coordinates
Chapter Proiect
String Figures
Parallels
and
Polygons
RECTANGLES, TRIANGLES. AND HEXAGONS ARE
examples of polygons. Patterns of polygons
are often used for decorative purposes. The
tiling pattern at right below is from the
Alhambra, a famous Islamic fortress in Spain.
The interplay of parallel beams and polygons
in the photograph of the Thorncrown Chapel
below suggests the theme of this chapter.
As you will learn, parallel lines and their
properties provide a basis for classifying
and exploring four-sided polygons known
as quadrilaterals.
I -5‘-
, \_r.
- 1 N‘.
1 *4!’ \
I .-- —‘ \ \ \
A e
' . ' ‘I
t , 'r 1‘ Q0
.0 I I
\
.- .. _ \‘
r"~'f. * D C
'- . 0
‘ -._ 2 :>:_::
A‘, \\ :4
,5 .c. t I , §~ ~_:.;_?_«'.:_‘
tr 1 _ -} . . K‘ ‘Y: “
: rz "E ‘ i I §
1 .
__.\,\,V
IA .
/I:/
I
.4 1.
.
I—v.
Thorrrcmwn
(impel. Eureka
Sprirrgs. .»trkurr.\‘ns
Llesigrrcrl by E.
my [nuts
1)
I IF
-I
3'-
_.‘£:::v AV
2'':
39'.
552
3:2.‘
-°§°': '
. ..
§9"= "' 4
WI : 4“
'59‘ 49 '9‘
0 4 pl‘
3‘ 5. '
it I ‘O 0.
,*24v«‘‘”c
$35.,‘ 9‘
it ¢Wa\"
About the Chapter Project
in this chapter. vou will investigate the
properties of polygons. The kev that unlocks the
study of polygons is found in the properties of
parallel lines, which you will explore in Lessons
3.3 and 3.4. In the Chapter Project, String
I-'igm'e.~‘, vou will learn to make one of the world’s
most popular string figures. which is known in
the United States as “Jacob's ladder." The figure
consists of polygons between two (roughly)
parallel lilies.
After completing the Chapter Project. you will be
able to do the following:
0 Make popular string figures by following a set
of instructions.
0 Appreciate the skills and ingenuity of the
ancient peoples that created such figures.
:;"
T?‘
Pic: Mtmdrian. Composition
with Red, Blue and Yellow.
1930. Oil on Cmrwts. 20" X 20 "
About the Portfolio Activities
Throughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
Chapter Proiect is geometric art.
0 In the Portfolio Activity on page I-17'. yott will
study artful ways of forming the surface of a
quilt with patches. The repetition of the
individual shapes often results in intriguing
overall designs.
0 Tessellation. the art of covering a surface with
congruent shapes that fit together without
gaps or (wt-:rl.tpping. is the subject of the
Portfolio Activity on page I54. Translation
tessellations are studied in depth.
0 Rotation tessellations are the subject of the
Portfolio Activity on page I97‘.
137
Objectives
0 Define polygon.
0 Define and use
rellectronal symmetry
and rotational
symmetry.
0 Define regular
polygon, center of a
regular polygon,
central angle 0! a
regular polygon, and
axis of symmetry.
Symmetry in Polygons
:73 1. --~r-
i " W 1
:57’ 1 ""-
-—~4 _ ?D For ‘V x
E E ‘ "
Polygons appear all around you in man-ma I -
oblects. Understanding the mathematical properties
olpo _- : as will help you understand how to use .
them for artistic and practical pu ~ -5»
‘E
Synnnerricnl polygons give this Native American blanket (l(’.\lgll an nmmtii-e.
rtppertrrtm'e. They also how.’ l'ntere'sn'ng rmtthenzntical prnpcrtits.
1 38 CHAPTER 3
Defining Polygons
In Lesson 2.5 you learned how to use examples and “nonexamples" to write
definitions. Use the following, figures to define .1 polygon:
A C) Q 2
O . .9
These are polygons.
Compare your definition ol' .1 polygon with the definition below. Docs vonr
definition have -all the requirements it needs? Does it have more than it needs?
Polygon
A polygon is a plane hgure formed from three or more segments such
that each segment intersects exactly two other segments, one at each
endpoint. and no two segnients with a common endpoint are collinear.
The segments are called the sides of the polygon, and the common
endpoints are called the vcrticcs of the polygon. 3.1.1
‘l
Equiangular
Equilate ral
A polygon is named according, to the number of its sides. Familiarize yourself
with information in the table below.
Polygons Classified by Number of Sides
Triangle 3 Nonagon 9
Ouadrilateral 4 Decagon 10
Pentagon 5 1 ‘I-gon 11
Hexagon 6 — Dodecagon 12
‘ Heptagon 7- -13-gon 13
ioctagon 8 n-gon n
An equiangular polygon is one in which
all angles are congruent. An equilateral
polygon is one in which all sides are
congruent. A regular polygon is one that
is both equiangulnr and equilztteral.
Central angle
The center of a regular polygon is the
point that is equidistant from all vertices
of the polygon. A central angle ola
regular polygon is an angle whose vertex is
the center of the polygon and whose sides Center
pass through two consecutive vertices.
Reflectional Symmetry
Lay your pencil on the pliotogruph of the blanket on page I38 so that the part
ofthe photo on one side of your pencil is the mirror int-age of the part on the
other side. The line of your pencil is an axis of.cymrm'try.
Reflectional Symmetry
A figure has rcllectional symmetry ifand only if its rellected image
across .1 line coincides exactly with the preintage. The line is called an
axis of symmetry. 3.1.2
Imagine reliecting each of the following ligu res across the lines shown. As you
can see, tl1e retleeted image will coincide e.\".tt.tly with the preimage. Therefore.
each figure has rellectional symmetry. and each line is an axis of symmetry.
LESSON 3.1 smmernv IN POLYGONS 139
For Activity I. recall the following classilication scheme for triangles:
Triangles Classified by Number of congruent Sides
Three congruent sides: equilateral
At least two congruent sides: isosceles
No congruent sides: scalene
Equilateral isosceles Scalene
' /
Reflectional Symmetry in Triangles
0|! ED 1. Draw an example of each type
fahjing paper, ru|g[' Oi triangle Sh0\5'Il '<1b0V'e. and
and prolfaclor lind am‘ axes ol'svtnn1etri'
that exist. How many axes ol 3 (_
symmetry does each type of
triangle have?
2. Fold each triangle along its
axes of s_vn1nietr_i', if it has
any. After folding, which
angles seem to coincide? \ ‘
3. Complete a table like the one ‘
below.
":.";';::::.:.’;°‘ c.,..“:::;‘.::;:::..es
equilateral ? ?
isosceles ? ?
scalene ? ?
CHECKPOINT / 4. Study the relationship between each axis ol'si_.'mmetry and the side it
intersects. Use your ruler and protractor to make measurements.
Complete the lollou-ing conjecture:
Triangle Symmetry Conjecture
An axis ofsyninietry in a triangle is the ? ? of the
side it intersects, and it passes through the ? of the angle
opposite that side of the triangle.
1 40 CHAPTER 3
Rotational Symmetry
Rotational Symmetry
A figttre has rotational symmetry il' and only if it has at least one
rotation image, not cotmting rotation images of 0° or multiples of 560°.
that coincides with the original image. 3.1.3
A p p I c 1 0 H The flower at right has approxitnate rotational
BOTANY symmetry. \lotice that it will coincide with
itself 5 times if it is rotated completely about
its center ol‘ rotation. which is also known as
its center of symmetrv. l'h us. the figure of the
flower is said to have 5-fold romfimml symnurtry. ' -
l\ote: All geometric figures have 0'’ and 360°
rotational symmetry. A figure that has only 0°
and 360° rotational symmetry is said to have
only Irit-'ial rotational symmetry. For such
a figure in a plane. any point in the plane of
the figure is a center of rotation.
/ ' Z
Rotational Symmetry In Regular Polygons
- ll lI.I. NEED 1. Draw or trace a regular pentagon such as the
tracing paper one in the illustration. Label the center’ P and
the vertices Q, R, 5, T, and U. Draw PQ. Then I
copy the figure onto a sheet ol‘ tracing paper.
2. Use a pencil point to anchor the traced ligu re
on top of the original at their centers so that
the figures coincide. 5‘ . U
3. Rotate the top figure counterclockwise until
point Q on the traced ligure coincides with
point R on the original. Continue to rotate 5 T
point Q. stopping at each point—S, I‘. U.
and linallv Q. How many rotations did you
make in all?
cnecxpomr ./ 4. Do the central angles ol .1 regular polygon seem to be congruent?
{You will prove that they are congruent in Lesson 4.2.)
Assuming that the central angles of a regular polygon are congruent.
Complete the rule below for finding the meastt re ol a central angle of
a regular polygon.
The Central Angle of a Regular Polygon
‘I he measure. 8, of a central angle ol a regular polygon with n sides is
given by the lollowing formula: 6 = ? .
LESSON 3.1 SYMMETRY IN POLYGONS 1 41
E X A M P I. E .4-\ windmill is-.1devieelbrptnnpiug I
A ' P L I C ATI 0 N
AGRICULTURE
Exercises
Th} Mnhnl. India
1 42 CHAPTER 3
water by using energv from the wind. If
you connected the tips of the blades with
segments. what figure would be formed?
What is the measure of .1 central angle ol
the figure? For what degrees of rotation
does the rotational image of the figure
coincide with the preinr-age? What is the
rotational synnnetry of the figure? ; ‘
SOLUTION
The windmill has 4 blades, so the
segments connecting, the tips of the blades
will form a regular 4—sided polygon. that
is, -.1 square. Use the formula to find the
measure of central angle:
(-.’=36(l+4=90°
With each rotation of the figure through 1‘ central angle. the image of the
figure coincides with its preimage. 'l his happens for rotations of 90'’. I80“,
270”. and 360°. At 3-60°, the figure is at its original position again. Counting
the numbers of rotations‘ in the list. the figure has 4-fold rotational symmetry.
. Comm”;/cute
1. Describe the position ol all the axes of synrnietry in the picture at left.
2. Explain how the picture at left illustrates the definition of symmetry.
Identify a point and its preim-age. \-\'hat is the relationship between the
point and preimage and their axis of svmmetr)'?
3. Why are 0° and 560° rotations 113
not used to define rotational 3;» " __
symmetry? -5 l
4. What kinds ol'syn1n1etry does “'_. '
a regular hexagon have? ‘ ' 'i. Y’ \lI>~
, .
Deserilme all possible rotations
and rellections ol‘-a regular *«
hexagon. ‘ _r _-_"' '
5. Identify regions of the Escher K ' A‘
woodcut at right that have jdé
rotational syrmnetry. Where
are the centers of rotation?
in L2 |'.xln""h'5lI||||L IV I.'r nun; Ens‘ cl-M.-A
<.--n|-- .11 tk \'. ?~£.I'1I IIr- I All rI;.lns reserml
. qt//dedsk/'//3 Practice
:1 Inhmqtconnoct ,3-3.‘ 6. Draw the axis ofsymmetry in the
com - - _ - _ -
Acfivmes triangle at right. Does this triangle
Online conhrm your COl'l]t"CIlll’€ lrom Actmtv I?
GoTo'nol1nn.cnm Why or why not? (ACTIVITY 1)
Keyword:
M61 Rouluaux
‘ 7. Find the measure of a central angle for each regular polygon below.
(ACTIVITY 2)
9.0
A P P L I C A T l 0 N 8. AGHlCULTURE What is the romtional wmmetry ofa windmill with 4
blades? with 6 blades? (EXAMPLE)
0 Practice dlfd 74,30/y
For Exercises 9-12, copy each figure and draw all of the axes of
symmetry.
II mlmotcnnmct
Homework
9. 10. 11 . 12.
Help Ontine
Go To‘ no.l1rw.com
Keyword:
M6! Homework Help
for Exercises 9-12. 18-21
4
13. How many axes of syminetry does a circle have? lixplain your answer.
Each figure below shows part of a shape with reflectional symmetry,
with its axis of symetry shown as a black line. Copy and complete
each shape.
5. 1 6.
17. which of the completed shapes Irom Exercises 14-16 also have rotational
synnnetry?
LESSON 3.1 smmemv IN POLYGONS 143
1 44 CHAPTER 3
If a figure has n-fold rotational symmetry. then it will coincide with
itself after a rotation of (3—’6;i)}a. For example, an equilateral triangle
has 3-fold symmetry, so it will coincide with itself after a rotation of
(3% = 120"
3 .
Each figure below shows part of a shape with the given rotational
symmetry. Copy and complete each shape.
18. 19.
s
4-fold 2-fold
6-fold 3-fold
20.
22. which of the completed shapes lrom Exercises l8—2l also have
retlectional symmetry?
23. Draw a figure with exactly 1 axis of symmetry.
24. Draw a figure with exactly 2 axes of symmetry.
25. Draw a figure with exactly 5 axes of symmetry.
26. Draw a tigure with 5-fold rotational symmetry.
27. Draw a figure with 8-fold I'()tdll()l'lill symmetry.
For Exercises 28 and 29, copy the figure at right.
28. Draw an axis of symmetry for /TE that
passes through E at a single point. ATE
What is the relationship between 17
and the axis of symmetry?
29. Rellect E over the axis of symnietry.
What point is the image of A? What point is the image of B?
What segment is the image of AB?
For Exercises 30 and 31, copy the figure at right.
30. Draw an axis of symmetry for 1.-QBC that C
passes thrnuglt [ABC at a single point.
What is the relationship between AABC
and the axis of symmetry? A 3
31. Retlect 44 BC over the axis of symmetry.
What ray is the image of El?
What ray is the image of BC?
What angle is the image of AABC?
32. Describe how to draw an axis of symmetry for any given angle.
‘I311
APPLICATIONS
Figure ABCD below is equilateral. Determine whether each of the
following could be the result of a reflection. a rotation, or either:
33. mis the image of W.
34. E is the image of E. ‘
35. fl is the image of E).
36. Lb’/IX is the image of LBCX.
37. LDCX is the image of ABCX.
38. LDAX is the image oi‘ LBCX.
39. LCXD is the image of LAXD. '
Graph each equation below on a graphics calculator or graph paper
Then write an equation for the axis of symmetry of each graph.
4o.y=(x—l)3+3 41.y=2[x—-113+}
42.y-—[x+2]3+3 43. y-—2(x+5)3+3
44.)’-|x]+3 45. y-|x+3I
46. What is the measure ol a central angle of a regular chihagon { I000 sides)?
What is the measure ofa central angle of :1 regular m_vri-agon (l0.000 sides)?
47. Draw a quadrilateral that is equilateral but not equiangular.
48. Draw a quadrilateral that is equiangular but not equilateral.
49. FURNITURE A table is in the shape
of a regular octagon. The table can
be extended by putting in a leaf. as I ' l ’
shown. Is the extended table
regular? equilateral? equ iangular?
50. RECREATION The Ferris wheel
shown at right has I6 cars. Imagine
a polygon formed by connecting
the cars. What is the measure oi"
a central angle of this polygon?
CULTURAL CONNECTION: AFRICA The designs below are taken from Egyptian
bowls dating back to 3500 B.c.E. Describe the symmetries in each
design.
51 . 52. 53. 54.
I
:/— \_ H .;.',"._:.-'5.-
LESSON 3.1 SYMMETRY IN POLYGONS 145
APPLICATION
APPLICATION
146 CHAPTER 3
TRAFFIC SAFETY Euuninc cacli road sign below. Identify the type of polygon.
Is it regular? Describe all of its s}'n1ntetries (ignore any figures or words on
the sign).
55. 56. § 57. 58.
Look Book
Refer to the diagram at right for Exercises 59-61.
(LESSON 1.1) A
_ _ _ (—I0 (—I0
59. l\'.tmL‘ thc IIIICTSCCIIOII of and AB and MN.
60. Maine three points that determine plane ‘J’.
61. lxznne the intersection of planes 8 and '.T. ,3
Refer to the diagram at right for Exercises 62-64. A
(LESSON 1.1) C
62. mt.-IBD - 80°, mLABC- 3-D”, m./LCBD - L
63. mLrlBC= 25°. n1LCBD = 60'’. mt mm = L 5’
64. mLABC= IIILCBD, niLABD = 88°. ni.I;ABC = L
Look Beyond
0 ' * * ' R‘ 7 A
— 7
France Japan Syria United Kingdom St. Lucia
-1:
4: 2+ * I
I I '1 K5
Qatar Micronesia Canada Macedonia Israel
United States Guyana Russia Ethiopia Iceland
GEOGRAPHY Name all of the countries listed above whose flags have the
type of symmetry given below.
65. reflectional, with a horizontal axis of symmetry
66. rcllcctional. with .1 vertical axis of svmmctrv
67. rot.ttit)n.Il syntntelry of I80”
68. no symmetry
OUILTING The ltillmving designs are called 9- patch quilt ltlocks lrecztuse they
are based on a grid of?) congruent squares.
n human wmad .?,°_., “ l E
_ mm . \,
Portfolio 1
Extension _
Go To: go.Itrw.com _ '-
Kc-n-mid:
Mm Ouilts _ _
Ohio Star Shoo Fly CardTrIck
Star Cross Friendship Star
1. Describe all of the types ()l- symmetry . .
in each quilt block shown above. '°
2. The quilt design at right consists of u )4
Ohio Star blocks. Copy one of the K]: 3;}
9~patch blocks shown above or create "X "1
your own. Design your own quilt by
using the block you cliosc. It may
he helpful to use graph paper. _).lv ' a
- - fir " ‘yr
3. Describe the symnietry ot your overall
quilt design. Did arty interesting ,. _ . ,_
patterns occur that were not part ()l- ' ‘ ' ' ' '
the original block?
LESSON 3.1 smmernv IN POLYGONS 147
Objectives
0 Define quadrilateral.
parallelograni,
mambus. rectangle,
square, and trapezoid
0 Identity the propenies
at quadrilateials and
the relationships
among the piopenies.
Properties of
Quadrilaterals
Abasetialldrls -m is
actually a square. The names
of i - - other quadrilateral:
also describe (lie figure.
p
The lerigili n_fmrh side ofii tiiisetiiill iliiiniorril is 90_fcet, and the pi'tclii*r’s moiirid
(it's on the di(igr1rztrl_fnJrrr harm‘ platf to stmml base‘ at it paint about 6fi'et t‘!0st'r
to liomc plum than to secorrd base.
148 CHAPTER 3
Special Quadrilaterals
Any four—sidcd polygon is ii qtiadriliitcral. Quiidriliitcrals that liaw: certain
properties are called spei:iul qrmilr'r'lrilt-'ra!s. Study the definitions below. [In
the figiires, arroii-heads are used like tick in-.ii-ks to indicate that two lilies,
scgmciits. or rays are pzirzillcl.)
mfl r.71// F7<>
A parallelogram is a
quadrilateral with two
pairs of parallel sides.
A rhombus is a quadrilateral
A trapezoid is a _ _
with four congruent sides.
quadrilateral witti
one and only one
pair of parallel sides.
1 l""1l 1,r'
A rectangle is a quadrilateral
with four right angles.
A square is a quadrilateral with
four congruent sides and four
right angles.
CRITICAL THINKING Which of the quadrilaterals seem to have rotational synnnetry? Which have
rellectional symmetry? What can you learn about quatlrilaterals from their
symmetries? Keep this in mind as you do the Activities that follow.
' /
Parallelograms
1. Draw a parallelogram that is not a rhombus.
fmer and a rectangle. or a square. Measure the angles
wotractor and the sides of the figure. Which angles and
0“ sides appear to be congruent?
9ED|'l1EIly _ _
graphics 2. Draw diagonals to connect the vertices.
software Measure the diagonals. Which parts of the
Iiqure appear to be congruent? If you are
using geometry drawing software, see it" the
coniecture holds when you vary the shape ()l
your figure by dragging one of the vertices.
3. COll$(.’t'H!lI'(.’ tuigIt’.~' of a polygon are angles that have a side in common.
What do you notice about consecutive angles in a parallelogram?
CHECKPOINT V 4. What conjectures can you make about the sides. angles, or other parts
of the figure? Complete the conjectures below.
Coniectu res: Properties of Parallelograms
Opposite sides ofa parallelogram are ? .
Opposite angles ot'a parallelogram are ? .
Diagonals ofa parallclogranl ? .
Consecutive angles ofa parallelogram are ? .
Rhombuses
1. Draw a rhomlaus that is not a square.
Draw diagonals to connect the vertices.
. . . A
Make measurements as in Activity l.
cuecxpomr V 2. Do the coniectures you tirade about 0 3
parallelograms in Activity I seem to
be true for your rhombus? Discuss why c
they should or should not be true for
rhombuses. Complete the conjecture
below.
Conjecture: A Property of Rhombuses
A rhomlius is a ? .
3. What new coniecture can you make about rhonrbuses that is not true
for all parallelogrants? Fill in the blank in the conjecture below.
Conjecture: A Property of Rltontbuses
The diagonals of a rltonrbus are ? .
LESSON 3.2 PROPERTIES OF QUADRILATERAL5 149
ruler and
protractor
OR
geometry
gra phlcs
software
CHECKPOINT ./
.><
CHECKPOINT ./
Parallelograms
Rectangles
Squares
E7
Rhombuses
1 50 CHAPTER 3
Rectangles
1. Draw a rectangle that is not tsquare. Draw diagonals to connect the
verticcs. Make measurements as you did in Activity I.
2. Do the conjectures you made about par-allelograms in Activity I seem to
be true for rectangles? Discuss why thev should or should not be true
for rectangles. Fill in the blank in the conjecture below.
Conjecture: Property of Rectangles
A rectangle is a ? .
3. What new conjecture can you make about rectangles that is not true lbr
all parallelograms? Fill in the blanks in the conjecture below.
Conjecture: Property of Rectangles
'l'he diagonals ofa rectangle ? .
Squares
1. Draw a square with diagonals connecting the vertices. Make
measurements as in Activity I.
2. What coniectures that you made in the preceding Activities seem to be
true for squares? Discuss why they should or should not be true lor
squares. Fill in the blank in the conjecture below.
Conjecture: A Property of Squares
A square is a ? . a ? , and a ? .
3. l'i|| in the blank in the conjecture below.
Conjecture: A Property of Squares
The diagonals of a square ? each other.
are ? . and are ? .
The Inheritance of Properties
Is a square a rectangle? ls a square a rhoml_ms? ln the Activities, you may have
made some conjectures about these questions. ‘I he liuler diagram at left shows
relationships among the classes of quatlrilaterals. You will be asked to prove
these relationships in Chapter 4.
Certain regions of the Euler diagram "inherit" properties from the larger
regions in which they are located. Explain what is meant by the inlterimnrc of
properties. Illustrate your answer with examples from the conjectures you
made in the Activities.
Exercises
. 60/mm//zimte
1. Explain the relationship between a rhomhu: and a square.
2. Explain the relationship between a rectangle and a parallelogram.
A P P L I C A T I 0 N 3. DPTICALILLUSIONS l'hc‘ drawing at right.
composed of three rltombuses, forms an
optical illusion. What does the drawing
" '“"""‘°°"‘°“ 5%?“ appear to be? Can you see the illusion
Activities more than one way? Try drawing your
00'1"‘? own optical illusions with rhomhuses,
Go To" no.hrw com . . . . '
Ku__w°m_ parallelogratns. or trapezotds.
M61 Btidge
4. An alternative definition ofa trapezoid is “a quadrilateral with at least one
pair of parallel sides." How would this definition afl'er.t the cldssificatitan of
qttadrilaterals?
0 611/464’ 5k///8 P/dd‘ 1'/6'8
5. Use your conjectures from Actit-ity I
and the diagrant at right to find the
l"l'l(:‘i.lSl.ll"(:‘l1I(:‘l1l.S l)(:‘l0\%'. (ACTIVITY 1)
an. AB b. m£.4BC
c. .-U5 d. mAb’CD
_ . . . 30
6. Use your C()l‘I]E:‘Cl.l1l"€h lrom Activity 2 J
and the diagram at right to find the
measurements below. (ACTIVITY 2) I
1!. FG b. ml!-"CH
c. m£GHl d. n1£F]G
12cm H
7. Use your conjectures from Activity 3
and the diagram at right. in whiLh KO i.s
2 ft, to find LN. (ACTIVITY 3)
8. Use vour conjectures front Activity 4
and the diagram at right to find n1x_’PTQ
and mAQl'R. (ACTIVITY 4)
s ’ R
LESSON 3.2 PROPERTIES OF QUADHILATERAL5 1 51
/.:z'/
D snternetoomect
Homework
Help Online
I30 To: 9o.htw.corI
Keyword.
M61 Ilomeworlt Help
for Exetcises 35--ll
1 52 CHAPTER 3
pile.
I01T|
0 Practice dim’ Apply
For Exercises 9-32, use your conjectures from Activities 1-4 to find the
indicated measurements.
In parallelogram WXYZ, WX= 10, W2: 4, WY= 13, and
mzWZY= 130°
9. Y7 10. XI" W X
11. WV 12. VY
13. rm." I1"Xl" 14. mzxwz
15. tnx_’XI’Z Z V
In rhombus FGHI, FG= 21, FH= 15, and mzFGH= 70°. F
16. GH 17. H1
18. F] 19. [H , G
20. mdl-IH 21. mZGI’I
22. nt£F]G 23. mil!!! H
In rectangle ABCD, AB: 6. AD = 8. and AC: 10. A D
24. CD 25. BC
26. BI) 27. AF 5
28. b’!.- B C
In square KLMN, KL - 50 and KM-- 70.7. K ‘-
29. LM 30. LN
31. m£KOL 32. mALO.-\-I O -
N ‘ M
33. In parallelogram PQRS. mAP= (2x}"" and mAQ = :6’. Find x and the
measure ole-.tch angle in PQRS.
34. In rectangle WXYZ, diagonal WY= x— 2 and diagonal XZ = \l;. Find x
and the length of the diagonals of WXYZ.
Use the definitions of quadrilaterals and your conjectures from Activities
1-4 to decide whether each statement is true or false. II the statement
is false. give a counterexample.
35. Ila figure is a parallelogram, then it cannot be a rectangle.
36. Ila figure is not a parallelogram. then it cannot be a square.
37. Ila figure is at parallelogram. then it cannot be a trapezoid.
38. Ila figure is a trapezoid. then it cannot be a rectangle.
39. Ila figure is a sqttare. then it is a rhomhus.
40. Ila figure is .1 rectangle. then it cannot be a rhombus.
41. lfa figure is a rhombus, then it cannot be a rectangle.
APPLICATION
For Exercises 48 and 49, refer to the
figure at right. (LESSON 3.1)
48. List all nontrivial degrees of the
49. Copy the figure and draw all oi its
42. ltt Activity i. you made the following coniecturc: Tlte opposite sides of at
parallelogram are congruent. What is the converse of this statetnent? Do
you think that the converse is true?
43. Use your answer frottt Exercise 42 to explain whether the following,
statemettt is true or false: [fa figure is a rhomhus. then it is a parallelogram.
44. GARDENING Susan is making
a shelter for her tomatoes by
stretching plastic over :1 wooden
frame. Fach wall of the lrante is
a rectangle. with diagonal braces
added for support. as shown. If the
brace connecting points .a'l and C has
at length of 73 in.. how long is tlte
brace connecting points B and D?
A ~ ' '
£00k Bdflk
Write each statement as a conditional and then write the converse of
the conditional. Is the statement a definition? (LESSON 2.3)
45. All whales are tttatntttals.
46. All squares are four~sitletl polygons.
47. All squares are rectangles.
rotational s_vntmetr_v for the figure.
ZHCS of syttttttetry.
£00k Bel/Md
50. ltt Activitv 2. you made the following conjecture: The diagottals of a
rhotnbus are perpendicular to each other. What is the converse of this
statement’! Do you think that the converse is true?
51. A figure with two pairs of congruent adjacent
sides and opposite sides that are not congruent
is called a kite. l)raw a kite with diagonals
connecting the vertices. l low does this figure
relate to your answer for Fxercise S0? Kite
52. In Activity 3, you ntade the following conjecture: The diagonals of a
rectangle are congruent. What is the converse of this st-atentent? Do you
think tltat the cottverse is true?
53. A trapezoid in which the nonparallel sides are
congruent is called an isosceles trapezoid. Draw
an isosceles trapezoid attd the diagonals connecting
the vertices. How does this figure relate to vour
answer for Exercise ‘S27 lsosceles "anezoid
LESSON 3.2 PROPERTIES OF QUADHILATERAL5 1 53
The tessellation pattern by M. C. Escher shown below is an e.\ample ofa
translation tessellatinn. Each of the repeating figures is d translation of other
figures in the design. You can make your own translation tessellation by
following the steps below. You rnay have adjust your cu rt es to get .1 pattern
that you like.
Draw your figures on graph paper or tracing paper. or use geotnetr}-' or
tessell-anon sonware.
1. Start with a square, rcetaiigle. 2.Tr-anslate the curve to the opposite
or other pttrallelogram. Replace side of the parallelogram.
one side of the parallelogram
with a curve. as shown.
c o C D
3. Repeat Steps l and 2 for 4. Your figttre will now lit together with
the other two sides ofyour itselfon all sides. You can add details
pttrallelogram. to your figure or divide it into two
or more parts. as shown below.
translate the entire Iigure to create
an interlocking design.
2- _i_ - __ L.‘
3 o’£ 05:: 0% ‘IE _
£s5‘\ 5 -_ \ -\—§
3 ‘.13 L_ \.|,.. \o)3 _ \..3
at. 0| ._. ' \ L 3 LE
'9 I.—-‘.E x ‘.]Q ‘.)3 I.‘ \.,6 :_;_
§\ k m\\ -L \ }$
-" ' ' G '-
~’)3 1 “J3 ~°lQ" ‘
ea ' .4
It-.. -win" " F :' 3...
'-I L2 EHIIITII Sylllmmv l‘r.1uIn;El2I"¢I9°=I' r-.'a n An II.‘-'. llnrn-I!a Iml hll H5343 l\t1ll'Vl\5.
1 54 CHAPTER 3
Parallel Lines and
Transversals
For practical as well as artistic reasons, parallel
' lines are alton used In architecture and engineering.
.‘ The stfking appearance 0! the parallel cables diet
support the strap - - - portions of the Golden Gate
Bridge contribute to tire beauty 0! the structure.
._x \-
Objectives I ' i
\\
o Define transversal, l l l \
alternate Interior
angles, alternate
exterior angles. same- I
side interior angles, I
and corresponding I '
angles
0 Make conlectures and , - 73
prove theorems by ' ",5-* 3
using postulates and ' - -‘ ' W43"
properties ol parallel " _
lines and transversals. ta .
Transversals and Special Angles
When parallel lines are taken by lllClllSL‘lH.‘5.
it is hard to imagine how they can be studied.
Look, for example, at the parallel lines at right.
What conjectures could you he expected to -”‘°"3 is "°" ""”°“ "° 5‘”dV-
make about them?
Now look at the ligure with a third line
intersecting the given parallel lines. There are
now many discoveries to make. The line that
intersects the two parallel lines is known as a The trans-Vgrgal changes um
mznsversal. picture.
Definition: Transversal
A trans»-ersal is a line. ray. or segment that intersects two or more
coplanar lines. rays. or segments. each at a different point.
3.3.1
Notice that. according to the definition, the lines,
rays. or segments that are Clll by the transversal
do not have to be parallel. This will be important
in l 855011 3.4.
LESSON 3.3 PARALLEL LINES ANDTRANSVERSALS 1 55
paper. ruler.
and pratractor
OR
geometry
graphics
software
1 56 CHAPTER 3
CHECKPOINT ;/
Special Angle Relationships
In each step ol this Activity, the terms interior
and exterior will be used as shown at right. E"t°"°'
«Tu
Start with two parallel lll‘lL‘S. (ll you are using
lined paper. select two horizontal lines on the
paper.) Then draw a third line that intersects
both of the lines. l\'umber each of the eight
angles that are formed, as shown at left.
Interior
<
Extanor
There are traditional names for certain special pairs of angles in the figure
you drew. Measure each of the angles in the special pairs defined below. In
Step 5. vou will make a con_iecture about each pair ofangles.
1. Angles 3 and 6 are alternate interior \? ‘ ‘L.
angles. as are angles -1 and 5.
2. Angles I and 8 are alternate exterior
angles. _\lan1e another pair of alternate
exterior angles. 3 4
‘T 5 6
7‘ 87
3. Angles 3 and S are same—side interior 3 14 2——>
angles. \lan1e another pair of same-
side interior angles. 5 6
7 8
1 2
4. Angles I and 5 are corresponding ——>
angles. \lame three other pairs of
<.orresponding angles.
34
.__/56a?.
78
5. Fill in the blanks in the conjectures below using words from this list:
congruent. Complementarv. supplementary.
Coniectures
l-‘or two parallel lines cut by a transversal:
Alternate interior angles are ? .
Alternate exterior angles are '5 .
Same-side interior angles are ? .
Corresponding angles are ? .
E X A M P L E .lndicate whether the pairs below are alternate interior. alternate exterior.
TRY THIS
same-side interior. or corresponding angles.
a. Al and L8 ;
b. L7 and :13
c. 45 and L4
d. 43 and L5 ‘ 2 ,,,
3 4
a. alternate exterior angles
b. corresponding angles
c. alternate interior angles
d. same—side interior angles
List three special pairs of angles not mentioned in the Example above.
One Postulate and Three Theorems
In the Activity on the previous page. one of the
four conjectures you may have made is that
corresponding angles are congruent. Notice what
happens ifyou slide [translate] one olithe parallel
lines closer to the other. ljventually. the indicated
corresponding angles will overlap. Do you think
the corresponding angles will match exactly? Does
this diagram seem to support your conjecture?
Move the parallel lines together.
'l'he conjecture about corresponding angles will
not be proven in this book. but because it seems
obvious. it will be given as a postttlate.
Corresponding Angles Postulate
If two lines cut by a transversal are parallel. then corresponding angles
are congruent. 3.3.2
Because the corresponding angles conjecture has been given as a postulate, it
can be used to prove theorems. ln pat ticular, you can use it to prove the other
three conjectures that you made in the Activity about parallel lines and
transversals on the previous page.
LESSON 3.3 PARALLEL LINES ANDTRANSVERSALS 1 57
TWOCOLUMN PROOF
The symbol II means ‘is L_
parallel to. '
for the reasons. For
example, an abbreviation
for the reason in Step 2
is "us —>corr. As
1 58 CHAPTER 3
To prove your con_jecture about alternate
interior angles, begin by drawing a figure E
in which two parallel lines are cut by a
tran$\-‘ersal. Show that two alternate 1
interior angles. such as Al and A2, are
congruent. p
Given: l"||m
Line p is a transx-ersal.
Prove: Z l E .._/.2
Plan: Study the figure for ideas, and plan vour strategy.
The Corresponding .43 and 42 are vertical
Angles Postulate tells angles, so 43 5 42.
you that 415 43.
r A 3 —
/7/Ly
,/1 7
From the information in the figure you know the following:
Al E .43 and £3 E .12
U7‘
l'hus. 41 E .42 (the desired result).
What postulate or property allows you draw the final conclusion? (Recall
the properties of congruence.)
Now you can write your proof. ln proofs ol" this nature. you may lind it
convenient to use a two-column format.
Proof:
Statements I Reasons
__ _ 1. l ine E1 is parallel to line m. Given
'" "”””’g "’°°'5 ’" _ Line p isa transx ersal.
geometry, you may wish _ _
m devefop 3j,j,,e,,,—,-,1-,-0,,5 :__;.-. 2. A l 5 .13 ll parallel llll(‘b are cut by a
transversal, then corresponding
angles are congruent.
3.15512
4.11542
Vertical angles are congruent.
Transitive Property of Congruence
The con_jecture can now be stated as a theorem.
Alternate Interior Angles Theorem
If two lines cut by a transversal are parallel. then alternate interior angles
are congruent. 3.3.3
In the exercise set, you will be asked to prove the two remaining conjectures
from the Activity.
Exercises
. Communicate
A P P L I C A ‘l’ I 0 N 1. ARCHITECTURE Describe all of the transversals that you can find in the
photo of the John Hancock building at left.
' _ 2. In the diagram at right. what type of angle
pair are Al and 42? What can you say about
them? Name three more angle pairs of this
I type. What type of angle pair are Al and 4-1?
‘-7 1 What can you say about them? Name three
more angle pairs of this type.
3. in the diagram above, what might you call angles LI and 47? What do
you think is true of this angle pair? .\lame another angle pair of this tvpe.
_ 4. For each diagram below, describe all of the transversals or explain why
‘j_,.___- .. there are no transversals.
I a. b. c. d.
The’ John I ianrorl. Center. g m
('liiL'ugt.1. Illirmis. is H27 I k
feet mil. ,-T’
u
p c: r 5 t
0 6///dfidsk///8 P/dflt/6'8
For Exercises S-8, refer to the diagram below. List two angle pairs of
each indicated type. (ACTIVITY AND EXAMPLE)
5. alternate interior angles
6. alternate exterior angles 13 2
Te.
7. same—si(.le interior angles
8. corresponding angles 5 6__,,.—-'
4-"""'—7 3
0 Practice 4/14 7‘lp,0/y
n tnmmetcannect In the figure at right, lines m and n are parallel.
. l 2
Homewofl‘ 9. List all angles that are congruent to Al. ‘T 3 4 —” "7
Help Online _
so To:'o_hyw,coq-n 10- l ist all angles that are congruent to L2. 5 5
Keyword: _ , 7 8 "
MGI Hcmtwmvltllnlp 11. Are there any angles in the figure that are
l‘‘' E"°'°l3“5 9'” not congruent to Al or to L2? Explain.
5
12. ll‘ mu - |30°. lind the measure of each angle in the figure.
LESSON 3.3 PARALLEL LINES ANDTRANSVERSALS 1 59
1 60 CHAPTER 3
For Exercises 13-17. refer to the diagram below. Lines p and q are
parallel. Name all angles congruent to the given angle, and give the
theorems or postulates that justify your answer.
13. AI 14. .12 15. 4’?-
16. the angle lormed by Al and £2
17. the angle Iormed by A2 and 215
Refer again to the diagram at right.
Determine whether the indicated line
is a transversal. If so, identify two lines
that it intersects.
18. line p 19. line 4}
20. line r 21. line 5
In AABC. D—l:'_ || fig, and LADE E LAED. Find the indicated angle
measures. A
22. maps 23. mzasn 30\\
24- mzmss 25. m..£BDE D
26- mZCDB 27. mAABD 50¢ 25.:
em 1:, Ell c 3 '3
In the diagram below, l31|| £2, m.«_’2 = x°. and m.r_’8 = (3x — 60)’. Find the
indicated angle measures.
28. m£2 29. m./_’l (_ 1 2
30. mzfl 31. mA5 1 3 ‘
32. m.£7 33. mass 82 «A758 ‘Le.
Write a two-column or paragraph proof for each theorem below.
34.
Alternate Exterior Angles Theorem
ll" two lines cut by at transversal are parallel. then alternate exterior
angles are eongruent. 3.3.4
35.
Same-Side Interior Angles Theorem
ll‘ two lll1L‘S cut by -.1 transt-ersul are parallel. then s-.une—side interior
angles are supplementary. 3.3.5
36. In the diagram at right. lilies £":1nt_l mare
parallel. Write a two-column proof that the 2 E
measure of each angle in the figure is 90“. 3 ‘
— =3 2 — m
APPLICATIONS
CARPENTRY In the diagram of a partial wall frame, the ceiling joist, F0,
and soleplate. R5, are parallel.
37. How is corner brace firelated to ITQ-and E? P . I
38. How are x’_RTPand LQPTrel-ated? ' 1
39. How is P—7‘related to the vertical beams I ' 2 I
that it crosses?
40. llowarc /_| and /.2 related? H T
NAVIGATION A periscope is an instrument used on submarines to see
above the surface of the water. A periscope contains two parallel mirrors
that face each other.
41. Identify a transt-t:rs'.1l in the diagram A
at left. What does this line represent? — .p .. _ .p — — ..
42. Are Al and L4 alternate exterior
angles? Why or why not? ,
43. The angle at which light rays are
reflected from a mirror is congruent
to the angle they form with the
mirror. For example. Al I /_2.
Prove that At a 44.
44. Suppose that mail = -15°. Find \J
the measures of L2, L3. and 44. ‘
\—-¢
Look Book
45. A ? is .1 part of a line that starts at a point and extends without
end in one direction. (LESSON 1.1)
46. Two lines that intersect to form a right angle are ? . (LESSON 1.4)
47. Two coplanar lines that do not intersect are ? . (LESSON La)
48. ? are the opposite angles formed by two intersecting lines.
(LESSON 2.5)
49. A ? is a plane figure formed from three or more segments such
that each segment intersects exactly two other segments, one at each
endpoint. (LESSON 3.1)
50. A ? is a quadrilateral with exactly one pair of parallel sides.
(LESSON 3.2)
51. A ? is a quadrilateral with tour congruent sides. (LESSON 3.2)
Look Be;/om’
In the diagram at right, A—B “Ex
52. Write a two-column proof that the sum of the
interior angles of trapezoid A BCD equals 360°.
53. Write a paragraph proof that the sum of the
interior angles of any trapezoid. parallelogram.
or rectangle is 360°.
LESSON 3.3 PARALLEL LINES ANDTRANSVERSALS 161
Objectives
0 Identify and use the
converse ol the
Corresponding Angles
Postulate.
e Prove that lines are
parallel by using
theorems and
postulates.
Suppose that you
needed to create a n- -I -
of parallel lines or that you
lied to be sure the: certain
given lines were parallel.
The converse: ol the
trensversel properties that
you learned in Lesson 3.3
will enable you to do
these things.
Proving That Lines
Are Parallel
‘>-
. . \
‘F -.
--_s=:
.' ,§_"¢‘-- '
u ‘ \-‘:3.
A :3‘ |. 1 ’ 7 . ' “O.
— - -1
r||I‘. T 3 _ s
_, \ I " ( ~-‘s
‘\ ' .1
Ll: .
7 ' - .5,
» do
The pnrnbolir mirrors in rmrorroiuiml telescopes
gather pnmllel rays of light jinn: dismnr stars and
direct them :0 ti cenmtl point. In the plmmgrriph.
terlriiir:itrii.n' are inspecting the mirror oftlie Hubble
Space 'l‘t’.k!scopt2.
The Converses of the Transversal Properties
In Lesson 3.3. you studied a postulate and three theorems about parallel llllL‘S
and transversails. In each of these. the parallel lines and it tranwers.il were
given, and conclusions were drawn about certain special angles. In this lesson,
the process is reversed in order to write the converscs ol' the postulate and
theorems.
E X A M P L E Write the converse of the Corresponding Angles Postulate.
O SOLUTION
1 62 CHAPTER 3
Identify the hypothesis and the conclusion ofthe Corresponding Angles
Postulatte. Then interchange the hypothesis and the conclusion to form the
CO l‘l\"E PS9.
Original statement: it" two lines cut by a transversal are parallel. then
corresponding angles are congruent.
Converse: It" corresponding angles are congruent, then two lines cut by a
transversal are parallel.
Another wav of Stating the converse is as follows:
Theorem: Converse of the Corresponding Angles Postulate
ll‘ two lines are cut lay a transversal in such a way that corresponding
angles are congruent. then the two lines are parallel. 3.4.1
Notice that the converse is labeled as a theorem. This is because it can be
proved with the theorems and postulates you already know. However. the
proof will be given later because it involves a special form ot reasoning known
as indirect proof. which vou have not yet studied [see Lesson I2.-I).
E X A M P L E Ofiuppose that m.Ll = 6-1” and 11142 = 6-1”
Using the Converses
In addition to the Converse of the Corresponding Angles Postulate. the
converse of each of the other transversal theorems is also true. You will be
asked to prose these converses in Exercises 18-25 by using Theorem 3.4.1.
/
SOLUTION
LI and /.2 are corresponding angles.
l'he Converse of the Corresponding Angles Postulate states that if
corresponding angles are congruent. then the lines are parallel. You can
conclude that lines I’ and m are parallel.
in the figure at right. What can you
conclude about lines t‘ and m? m
E X A M P L E oGiven line I" and point P not on the line. draw a line through Pthat is
parallel to t‘.
SOLUTION P‘/<
Draw a line through point P and line 2.
Label and measure LI. 5-
I
Using a protractor, draw a new line through /
P such that the new angle corresponds to
/_l and has the same measure as Al . By the Converse of the Corresponding
Angles Postulate, the new line. m. is parallel to line t‘.
Note: You can also do this as a construction with a compass and a straightedge
(see lixercises 32 and 35 in Lesson -1.7].
LESSON 3 4 PROVINGTHAT LINESARE PARALLEL 1 63
Exercises
. Communicate
For Exercises 1 and 2. state the converse of each theorem.
1. ll‘ two lines cut by a transt-ersal are parallel, then corresponding angles
are congruent.
2. If two lines cut by a transversal are parallel. then s-.une—side interior angles
are supplementary.
3. lixplain how a theorem that is used to prove that lines are parallel am he
used to develop a method for drawing parallel lines. as in the photo at lelt.
4. Explain why the lines in the diagratn below are not parallel.
my
80'
7?’
0 Guided 3/U//8 Practice
5. Write the Conver.~;e of the Alternate lnterior
Angles Theorem. (EXAMPLE 1)
6. Are lines m and n in the figure at right
parallel? Why or why not? (EXAMPLE 2)
A
7. Copy the figure at right and draw a line
a is through point A that is parallel to
"""‘°°""'d (EXAMPLE 3)
Homework 8 C.‘
Help Online
Go To .h .cmI ,
KBl-‘”0l9l:- M 0 P/flfltlte film’ 74,0;/y
M6! Homework Help
for Examines B-15 _ _ _ _
For Exercises 8-15, refer to the diagram at left, and fill in the name of
‘ the appropriate theorem or postulate.
8. If mzl = m47, then I . ll I; by the Converse of the ?
9. if 11112 = m.»_’8. then ti’. II I) by the Comerse of the f
10. lfn1.r_’=i = 11116. then fill C; by the C()ll\»'€l':>€ ofthe ?
E‘ 4132 11. ll‘ m4?» = 11115. then t:'.ll C": by the Converse of the ?
12. If m.»_’2 = 11146, then full (9.: by the Converse of the ?
€*‘_’3"5 -7&1?" 13. ll" m.r_’3 = 11117. then (ill €~ by the Converse ol' the ?
M. If mg»: + mzi = 180‘ . then ft ll 63 by the Converse of the i’
15. If 11113 + m./16 = 180°. then f." (1 by the (".onver.se of the ? .
1 64 CHAPTER 3
TWO—COLUMN PROOFS
16. Write it two-Column proof that Trill?!-‘I.
F E
17. Lines m and n in the figure at right are R m
parallel. Write a two-column proof that 1
qttadrilateral RSU I‘ is a parallelogram.
T n
For Exercises 18-24, complete the two-column proof of the following
theorem:
Converse of the Same-Side Interior Angles Theorem
ll" two lines are cut by a transversal in such a wav that 3-ame—side interior
angles are sttpplcmcntary. then the two lines are parallel.
3.4.2
Given: ./_’l and 12 are supplementary. 13 1-‘
Prove: F. "P1 2
«T — j- £9
Proof:
Statements I Reasons
Al an-.| A2 are supp|ementar_v. 18. ?
mzl + m£2= 180° 19. ?
mzl + m£3= l8U° 20. ?
mzl + m£2= mél +n1A3 21. ?
mZ2 = 11115 (.42 E 13) 22. ?
Etllfg 23. ?
Write two-column proofs of the indicated theorems.
24. Converse of the Alternate Interior Angles Theorem
If two lines are cut by a transversal in such a way that alternate
interior angles are congruent, then the two lines are parallel.
3.4.3
25. Converse of the Alternate Exterior Angles Theorem
ll" two lines are cut by a tranwcrsal in such a way that alternate
exterior angles are congruent. then the two lines are parallel.
3.4.4
LESSON 3 A PROVINGTHAT LINES ARE PARALLEL 165
PARAGRAPH PR0053
APPLICATIONS
1 66 CHAPTER 3
For Exercises 26-37. complete the paragraph proofs of the theorems in
the boxes below.
Theorem
If two coplanar lines are perpendicular to the same line. then the two
lines are parallel to each other. 3.4.5
Given: ml. F and pl. P fm fp
Prove: p||m ‘A . 8
Proof: Jl rl
Line 5 is a 26. ? of m and p. I ‘C. ID T5- .5?‘
by definition. A UK} 2 LEE!) because 6 H
27 1.’ . Therefore, 28 ? is 1
parallel to 29. ? hy 30. 7.‘ .
Theorem
If tuo coplanar lines are parallel to the same line, then the two lines are
parallel to each other. 3.4.6
Given: flln, mlln. and p is a transversal
of t‘, m. and H.
Prove: m
Proof:
Because Ellu, /_l a 31. ? by
32. ? .Because m||u, then
A3 I 33. 7.‘ ht-' 34. ? .
'lhus, LI -2 35. ? by 38. ? ,
and £"||m by 37. 3.’ .
I‘ m
38. DRAFT ING A T square and a triangle —>
can be used to draw parallel lines.
While holding the T sqtture in place.
slide the triangle along the T square as
shown. [low Catt you prom: that the
resulting lines. P and m. are parallel?
39. CIVIL ENGINEERING Suppose that you are painting lines for angled parking
in a parking lot. How could you make sure that the lines are parallel?
APPLICATION
Plmnb bolt
APPLICATIONS
40. CARPENTRY A plumb hub is a weight hung Roof
at the end ofa string, called a plumb line.
'l'he weight pulls the suing straight down ‘X120
so that the plumb line is perfectly vertical. . J
Suppose that the angle fornted by the wall 120°
and the roof is 120° and the angle formed Wall
by the plumb line and the roof is 120°.
Explain why this shows that the wall is
vertical.
Plumb bob
Look Back
For Exercises 41-45, refer to the following statement: Every rectangle is
a parallelogram. (LESSON 2.2)
41. Rewrite the statement as a conditional.
42. Identify the hvpothesis and conclusion ol'the statement.
43. Draw an Euler diagram that illustrates the statement.
44. Write the comerse of the statement. and construct its Euler diagram.
45. Is the converse true or false? If it is true. write a paragraph proof of it. If it
is false, disprove it with a counterexample.
46. NAVIGATION ‘I pilot is flying at .1 compass heading of I55. What is the
heading ofa pilot llving in the opposite direction? {LESSON 1.3)
47. NAVIGATION A pilot is flying at a compass heading of 255. What are the
two possible headings of a pilot flying perpendicular to the first pilot?
(LESSON 1.3)
L001? Bet,/and
Exercises 48 and 49 refer to the photo of railroad tracks shown below.
48. How could you prove that the
railroad tracks are parallel?
49. In the photo, the lines appear to
meet at the horizon. \-\"h_v? Some
people ttse the expression “meet
at infinity" when referring to
parallel lines. What does this
mean? Does it make sense?
50. The drawing at right represents a cube.
What is true of the lines that contain the
edges shown in red?
51. What would happen if the red edges in
the drawing were extended?
LESSON 3 A PROVINGTHAT LINES ARE PARALLEL 1 67
1 68 CHAPTER 3
»===~z"-P
..~‘.i
99 °V°'AIbena
by Paul Hojfmzm
The town leaders of Ve-greville, Alberta. contacted Dale Resch, a
computer science professor. for a special project—to build a 3-l—foot
Faster eg.
The problem Resch faced was that no one other than a chicken had
ever built a chicken egg. With no formal training in mathematics.
Resch relied on his ability to pl-av with geometric abstractions in his
mind, then with his hands or a computer. to turn those abstractions
into physical reality.
Resch assumed that someone had developed the mathematics ‘I
ofan ideal chicken egg. He soon found. however. that
there was no formula for an ideal chicken egg.
After four months of contemplation and simulation.
Resch realized that he could tile the eg with 2.208
equilateral triangles and 524 three-pointed stars
(equilateral but non—regular hexagons) that
varied slightly in width. depending on their
position on the egg.
VV
I-‘or si\' weeks. Resch led a team of volunteers
in assembling the egg. Residents were afraid ‘
it might blow down. I ong after the egg was
finished. Resch used a computer to analyze
the eggs structural integrity and found that
it was ten times stronger than it needed to be.
Cooperative Learning
Lse folding paper and a compass or geometry graphics
sol'tware for the following £.“(|‘.|l()l'illl()l'I5.
4-;
A‘: Xxy
\\
. fit;
_ Al
1. The tiles on the Vegreville egg have two shapes;
equilateral triangles. and three-pointed stars. which are
equilateral, but not regular, hexagons. The three—pointed
stars maybe created as follows:
Draw or told an equilateral triangle. Fold
the perpendicular bisectors or the sides
to find the center of the triangle. Place
the point of your compass at the center
of the triangle and draw a circle that
completely encloses the triangle. The
radius of the circle should be at least
twice the distance l>l'0lTI the center
to a vertex of the triangle.
Draw segments from each vertex
to the points where the
perpendicular bisectors ofthe
sides intersect the circle to form
an isosceles triangle on each side
of the equilateral triangle. The
ligure lormed by the equilateral
triangle plus the three isosceles
triangles is a three-pointed star.
Explain why the three—pointed star
is equilateral.
2. What are the axes of symmetry of
the three-pointed star that you created
in Step I? What type of rotational
symmetry does it have?
3. Draw an equilateral triangle on each side
of your three-pointed star. Draw three
new three-pointed stars in the gaps
between the equilateral triangles. Draw
an equilateral triangle on each side nf
these three-pointed stars. and draw
three—pointed stars in the gaps between
these triangles. Continue drawing three-
pointed stars and equilateral triangles
in this way until you understand the
pattern at" shapes in a plane. How is
your pattern like the pattern of tiles on
the Vegreville egg? [The pattern of tiles
is easiest to see near the top and lmttom
of the egg.) l low is it different?
1?
§
169
Objective
0 Identify and use the
Parallel Postulate and
the Triangle Sum
Theorem.
W“ Euclidean 9- n -07
was loumled on live
postulates or axioms.
Ono 0! them. the Parallel
Postolate, has been
thoroughly investigated by
-- r-- mar -ticians.
The Triangle Sum
Theorem
1-‘ _, 3': fil
. -' I'll‘:-.v.u-'0 W /‘IE ‘£3;
' ‘ ” ‘ , T’!
‘L’; - ...':..I um-‘V.-. -“:1 ’-‘l
Ire‘ ----‘-—._3a?r' " -
-_e.- E -
——— 1
Three rli_fj"t'l'r:nl _r.{e'mnt'-‘(lies apply to the rrz'rm_qle's dmwn on the three tlij]l:'re'llr
s1rr_fru't*5. Hit’ d{l_Ii°r't’ltt‘c's in the georm’lr'it*s are l1tl_\‘t’d on the Pnmllel Postulnte.
of’
«T» E
There is one and only am‘
line rlrrouglr palm P that
is parallel to line I".
1 70 CHAPTER 3
The Parallel Postulate
The following postulate is a modern equivalent of Euclitl‘s filth postulate:
The Parallel Postulate
Given a line and a point not on the line. there is one and only one line
that contains the given point and is parallel to the given line.
3.5.1
In l_.t~:5at)ll 3.4 you drew a line through a given point and parallel to a given
line. You probably never questioned whether such a line actually existed, or
whether there could be more than one such line. The ussunzptitzn that there is
in fact exactly one such parallel line is known as the Parallel Postulate.
The Parallel Postulate is used to prove a theorem about the angles of a
triangle. Before ,V‘0u look at the theorem. try the Activity below.
The Triangle Sum Theorem
I L D 1. Cut out a triangle from a piece
scissors and paper 0' P'<‘P"-
2. Tear two corners oil the triangle.
3. Position the two torn-oll corners ‘~
next to the third angle as shovt n .
at right. ’ .-—>
CHECKPOINT ./ 4. Make a conjecture about the sum
of the measures of the angles of
a triangle.
5. In the diagrant below. line i’ has been drawn through a vertex of the
triangle so that it is parallel to the opposite side. How does the Parallel
Postulate relate to this figure?
6. Fill in the table below for a figure like the one above. Use geometry
theorems, not physical measurements, to find the answers.
ma l m£2 m.¢3 m£4 m£5 mz3+mz4+m.¢5
40° 30° 7 7 7 7
20° 30° 7 7 7 7
30° I 100 7 7 7 7
7. Does the table support the coniecture you made in Step 1? Explain.
CRITICAL THINKING Does your work in the itctivity prove your conjecture? Why or why not!
The conjecture from the Activity is stated below as a theorem. and it is proven
on the following page.
The Triangle Sum Theorem
The sum of the me-asttres ol the angles ofa triangle is l80°. 3.5.2
LESSON 3 5 THE TRIANGLE SUMTHEOHEM 1 71
TWO-COLUMN PROOF
Proving the Triangle Sum Theorem
To prove the theorem. begin by drawing line L’ through a vertex of the triangle
so th-at it is parallel to the side opposite the vertex.
Given: AABC
Prove: mil + mil + mi}: = 180°
Plan: Study the illustration. which is
related to the Actit-itv in which
you tore oil the corners of a
triangle. You can ttse what you
discovered in the Activity to
write a two-column proof of
the "triangle Sum 'l'heorem. 2 3
Proof:
Statements
1. (H717!
I Reasons
As drawn (justification: the
Parallel Pnstulate)
2- mil + mitt + mi5 = 180° The angles fit together to form a
straight line.
3. i2 E i-I (ntiz = 111,14‘ Alternate Interior Angles 'l'heorem
i3 5 i5 lmi_'- = ntiS)
4. mil + nti2 + nti3 = l80° Substitution in Step 2
A'P ICATION
GEOGRAPHY
CRITICAL THINKING
1 72 CHAPTER 3
Another Geometry
ll is possible to create geometries in which the Parallel Postulate is not true.
On the surface of a sphere. for example. lines are delined tlilTc-rently front the
way their are defined on llat surlltces. and there are no parallel lines.
On the surface of a sphere. a litte is
defined as a great circle, which is a -:3‘.
circle that lies in a plane that passes
through the center of the sphere. _Q«>‘
(A great circle divides a sphere into ‘I
two equal parts.) l'he equator is a LARK‘
great circle on the surface of Earth. ,‘ ‘J
I ines of longitude. which run north I,
and south. are also great circles.
Notice that any two distinct lines
[great circles) intersect at two points.
Thus, there are no parallel lines on
a sphere.
Discuss the following statement: On the surface ol a sphere, the shortest path
between two points is not a straight line. What is the shortest path?
Exercises
APPLICATION
D - connect
Activities
Online
Go To: go h.tw.t:aa1
Kewmid:
MG1 Hypercao
6:14
'0
£
Communicate
1. Explain how the torn—triangle Activity
is similar to :1 proof of the Triangle
Sum Theorem.
2. Explain why the torn-triangle Activity is
not a proof of the Triangle Sum Theorem. ‘}
3. What role does the P-.1rallel Postulate ‘~
play in the proof of the Triangle Sum
Theorem?
\ .
4. NAVIGATION You can use a globe and ' ‘L
a piece oi" string to d}?I}]l‘0.‘(illl'dlC the
distance of the shortest route between
two points on Earth. Estimate the
shortest route from New York City to
Bangkok, Th-.ti|-and. What might be some
difficulties in traveling along this route?
6/¢/dad 3k///8 Practice
For Exercises 5-7, refer to the diagram below. (ACTIVITY)
C
5. .\l-.une two pairs of alternate 1 3
interior angles in the diagram.
6. What is the sum ot mzl. mA?., and 11113?
7. If mA4 = 65" and mé5 = 50°, what is mA2?
A B
Practice and Apply
For Exercises 8-12, two angle measures of a triangle are given. Find the
missing angle measure, or state that the triangle does not exist.
8. mil = 85°. n1.v_’2 = 45°. nil} = ?
9. mi:-A = 45°. n1.dB = ? , m.dC = 90°
10. mAK = ? , mzL = 60°, mzM = 60°
11. IIIAX = 90°. nili’ = ? . mAZ = 90°
12. n1£F= lO5°, m£G= 80°, m£H = ?
l~_‘o_r Ex_e;rcises 13-20, refer to the diagram below, in which W II B—C,
AB ll FC. m4'ADE = 60°, and m£ACB = 50° Find the following:
13. mil} 14. mil-t A
15. n11:-QED 16- n1£EDB A E F
17. mil")!-"C 18. m£FFC
19. IIIAECF 20- n1AF B C
LESSON 3 5 THE TRIANGLE SUMTHEOREM 1 73
A’/,..I /
F @111! C0l'|l'lOd
Homework
Help Onlino
Go To po.|rrw.r;orI
Keyword‘
MG! llomuworlr Help
lor Exercises 24-39
CONNECTION
1 74 CHAPTER 3
D
fin
Find the indicated angle measure for each triangle.
21. mzl 22. 11142 23. mA3
60°
140"
Find x and the measure of each angle of the triangle.
. int.-1 = ? ,
mAC= ?
25. x: E’ . rn£D= ? ,
IILCI: = ? ml!-' = ?
24. x: ?
mAB= ?
a
tax’ — 10l
(X7 I 2xr 10)”
E F
In Exercises 26-44, you will have an 3
opportunity to discover and prove an 2
important geometry theorem related
to the figure at right. Begin by copying 1 3 4
and completing the following table: A ' C—"
mzt mzz mm + mzz mz3 mzl
30“ 70° 26. ? 27. ? 28. ?
30‘ 80° 29- ? 30- ? 31. ?
40‘ 80 32. ? 33. ? 34. ?
40" 90° 35. ? 36. ? 37. ?
38. An angle such as 14 that forms a linear pair with an angle ol‘ a polygon
is called an exrer ior mrgle of the polygon. How many exterior angles are
possible at each vertex til‘ at given polygon? Are the exterior angles at a
given vertex congnrent? Fxplain your reasoning.
39. For an exterior angle of a polygon at a given vertex. the angles of the
polygon at the other vertices are called remote interior angles of the
exterior angle. in the diagram above. A I and A2 are remote interior
angles of 44. Use the table above to complete the following theorem:
Exterior Angle Theorem
The measure of an exterior angle of a triangle is equal to ?
. 3.5.3
40. TECHNOLOGY Use geulnetry graphics software to draw the figure shown for
Fxercises 26 -3-? so that you can slide point C along the ray, displaying
mzl + mil’. and mitt. Describe your results.
TWO-COLUMN PROOF
APPLICATION
CHALLENGE
Complete the two-column proof of the Exterior AngleTheorem below.
Given: AABC with exterior angle A4 and 3
remote interior angles ii and i2
Prove: mi4 = mil + mi2
Proof: A E.
Statements I Reasons
AABC with exterior angle i4 Given
mi4 + mi3 = 180'‘ 41. ?
mil +n1i2+mi3= I80° 42. ?
mi4 + n1i3= mil +n1i2 + mi3 43. ?
mi4 = mil + mi2 44. ?
45. NAVIGATION lbwns A, bland C form a triangle in which AA 2 AC. A pilot
flies from town A to town B at :1 heading of 350. then to town C at a heading
of 260. At what heading should the pilot fly‘ to return to town A? (Hint:
Draw vertical [nurth—soulh) lines through each ofthe points. Use same-
side interior angles.)
Heading 260 B
c /\
Heading 330
\
A
N
/.004’ B464’
46. l'he set ol'c.ommon points ofn-.0 figures is their 2' . (LESSON 1.1)
47. ? points determine a line. (LESSON 1.1)
48. ? points Llclcrlnim: a plane. (LESSON 1.1)
49. Adjacent supplementary angles form a ? . (LESSON 1.3)
LESSON 3 5 THE TRIANGLE SUMTHEOREM 1 75
APPLICATION
APPLICATION
1 76 CHAPTER 3
50. SPORTS The diagram at right shows
the layout of a baseball diamond.
Suppose that the line from home
plate to the third basemzm forms a
l0° angle with the third-base line
and that the line from home plate
to the shortstop forms 'a 30° angle
with the third-base line.
if the batter hits the ball so that the path of the ball bisects the angle
formed by the shortstop. home plate. and the third baseman. what angle
does the path otthe ball make with the third-base line? (LESSON 1.3)
3 Home plate
Look Bet/and
CARTOGRAPI-IV A map that is commonly used in navigation is the Mercator
projection. shown below. All straight lines on this map. called rlmml: lines.
have :1 constant c0n1pa.~:.s heading.
51. Do any rhurnb lines correspond
to great circles on a globe? If so.
which ones?
52. Suppose that you draw a rhumb
line that is not .1 latitude or
longitude line. Trace this line
[with your linger") on a globe
and describe its path.
Cmlidtts Mtrrrmor ( l5l2—l 59%|)
‘-7
Objective
0 Develop and use
formulas for the sums
of the measures of
interior and exterior
angles of a polygon.
Angles in Polygons
<.“'.~i ‘_"5{-K ,- ' ‘.
D».
a
.‘
This human polygonal structure required careful
planning and design in order for all of the pieces to fit
together properly. How do you think the designers of
the figure achieved the final result’
- ll
calculator Iopfonall
Angle Sums in Polygons
A convex polygon is one in which no
part ofa line segment connecting '.-any
two points on the polygon is outside the
polygon. A concave polygon does not
have this characteristic. In this book,
the word polygon will mean a convex
polygon unless otherwise stated.
Convex polygon Concave polygon
I
Sums of Interior Angles
Pentagon ABC DE has heen divided into
three triangular regions bv drawing all
possible diagonals from one vertex.
1. Find each of the following:
niAl + niL2 + niA3 = ?
mA4 + mA5 + mA6 - ?
n1./.7 + m./.8 + nt./.9 = ?
2. Add the three expressions.
in./_I + m./_?. + nt./.3 + m./.4 + - - - + mL9 = ?
LESSON 3.6 ANGLES IN P0-LYGONS 177
1 78 CHAPTER 3
CHECKPOINT ./
cnscxpomr ./
3. Use the diagram and the result lrom Step 2 to determine the stun
of the measures of the interior angles of pentagon /lb‘CDL' [that is,
mAEAB + mil} + m£BCD + mACDE + mAE = ? J.
4. You can form triangular regions by drawing all possible diagonals from
illustrate your answers.
a given vertex of any pol)-‘gon. Complete the table below. Use sketches to
Number Number of Sum oi measures
Polygon of sides triangular regions 0! angles
triangle 7 1 180'
quadrilateral ? .7 ?
pentagon 7 3 540
hexagon ? 7 ?
n-qon 7 ? ?
of the number of sides. n. Complete the formula below.
5. Write a lormula for the sum of the interior angles of a polygon in terms
Sum of the Interior Angles of a Polygon
The sum of the measures of the interior angles of a polygon with n
sides is ? . 3.6.1
Recall that a regular polygon is one
90- 90°
in which all the angles are congruent
and all the sides are congruent.
Fquilateral triangles and squares are 90 90° 60’
examples of regular polygons. In an
eqttilateral triangle. each angle has <1 50-: 500
measure ol 60°. In a square, each angle
has a measure of 90”.
Complete the chart below, l'hen complete the formula beneath it.
Regular Number sum 0! measures Measure ol one
polygon 0! sides of interior angles interior angle
triangle ? l 130' ?
quadrilateral 7 l 7 90'
pentagon 7 l 7 7
hexagon 7 l 7 7
n—gon 7 l 7 7
The Measure of an Interior Angle of a Regular Polygon
The measure ofan interior angle ofa regular polygon with :1 sides
is ? .
3.6.2
' Z
Exterlor Angle Sums In Polygons
Lt. ED 1. Draw a triangle and extend each side in
pmlmlo, and one direction to_lorm an exterior angle
Scissors at each vertex. Find the sum ol the
03 measures of the three exterior angles
9°°'"9"‘/ that vou formed. Record your results.
graphics ' '
soltware
2. Cut out the exterior angles and Fit them together. Record your results.
3. Repeat Steps 1 and 2 for a quadrilateral.
4. Repeat Steps 1 and 2 for a pentagon.
5. Make a conjecture about the sum of the measures ol the exterior angles
of a polygon [one at each vertex]. You will prove your conjecture in
Steps 6-10.
6- \-\-'hat is the sum of the measures Interior
of all interior and exterior angles a"9',,°\3
of the triangle at right?
Exterior angles
7. What is the sum of the measures of
all interior and exterior angles of the
quadrilateral at right?
8. Using your results from Steps 6 and 7. write a lormula lor the stlm of
the measures of all interior and exterior angles of an n—gon.
9. Complete the table below.
Sum of Sum of Sum of
Number exterior and interior exterior
Polygon of sides interior angles angles angles
triangle 3 540 180‘ 360
quadrilateral 7 7 7 7
pentagon 7 7 7 7
hexagon 7 7 7 7
n-gon 7 7 7 7
CHECKPOINT ./ 10. Use the torintila from Activity l and the formula from Step 8 aboxe to
write an t-_“(|]l‘€:>Sl()ll for the suln of the measures of the exterior angles of
an n—gon. Use algebra to simplify the expression. Complete the theorem.
Theorem: Sum of the Exterior Angles of a Polygon
The stun of the measures of the exterior angles of a polvgon is ?
3.6.3
LESSON 3.5 ANGLES IN P0-LYGONS 179
Exercises
. Communicate
1. Explain how to tell how many triangular regions can he formed in tt
polygon by drawing all possible diagonals from one vertex.
2. is it possible to draw a quatdrilateral with three interior angles that
measure 60° each? Explain your reasoning.
3. The figures dt left can be a “proof without words" of the result you may
have discovered in Activity 2. A polygon has its sides extended as ray. 5.
Imagine that you are looking at the figure from farther and farther away.
Fxpluin why the sum of the exterior angles is 360°.
0 6///dee'.—Sk///3 Plfltt/[8
4. Find the sum of the measures of the interior angles of an octagon.
(ACTIVITY 1)
5. Find the sum of the measures 0|" the interior angles ufa l3—gun.
(ACTIVITY 1)
6. Find the sum of the measures of the exterior angles ofa heptagon.
(ACTIVITY 2)
7. Find the sum of the measures of the exterior angles of an I I-gon.
(ACTIVITY 2)
Practice and Apply
8- Refer to the figure at right to
find the indicated measures.
a.x= ?
b.v= ?
c.z= ?
12. 13. 14.
‘ 110"
‘ ‘ 100
1 80 CHAPTER 3
I Inhmuoomod .1?“
I9
Homework
Help Online
Go To: gnJ1rw.cnm
Keyword:
MGI llomewurli. Help
for Exercises l5-2-I
‘\
.
\
CHALLENGE
For each polygon, determine the measure of an interior angle and the
measure of an exterior angle.
15. a rectangle 16. an equilateral triangle
17. a regular dodecagon 18. an equiangular pentagon
For Exercises 19-21, an interior angle measure of a regular polygon is
given. Find the number of sides of the polygon.
19. 135° 20. 150° 21. l65°
For Exercises 22-24, an exterior angle measure of a regular polygon is
given. Find the number of sides of the polygon.
22. 60° 23. 36° 24. 24°
For Exercises 25-37, find the indicated angle measure. C
25. uni.-1 26. mAB t4xi°—t32—<)"
27. m£C 28. m£D
A 8
29. ind}; 30. ml!
31. m£G 32. mill
J
33. ml! 34. ml]
35. mzlx’ 36. mil.
37. mAM
Q" ' ‘ll (5x + 15)"
38. What is the maximum possible number of acute angles in a triangle?
Can <1 triangle have no acute angles? Explain your reasoning.
39. What is the maximum possible number of acute angles in a quadrilateral?
Can a quadrilateral have no acute angles? Explain your reasoning.
40. What is the maximum possible nu mher of atute angles in a pentagon?
Can a pentagon have no acute angles? Explain your reasoning.
41. Pint] the sum of the measures of the numbered vertex angles of a
5—pointed star polygon. (1 lint: First find the measure of the exterior angle
indicated by a question mark in each diagram below.)
LESSON 3.5 ANGLES IN P0-LYGONS 181
APPLICATIONS
APPLICATION
APPLICATION
1 82 CHAPTER 3
42. GEMOLOGY Precious stones are often cut in a brilliant! cm‘ to llltlltlllllit‘ the
amount of light reflected by the stone. The angles of the cut depend on
the refractive properties of the type of stone. 'l'he optimal angles for a
diamond are shown in the cross section below. The cut has rellectional
symmetry across the a\'is shown. Find the measures of the indicated angles
in the figure.
Crown angle
main
angle
......-.a.... .-.
5 Axis of symmetry
43. GEMOLOGY A brilliant cttt topaz should have a pavilion main angle of
40“ and a crown angle of 57°. Sketch a cross section ol" such a gem and
lind the other angles in the cross section.
£00K’ Bdfik
44. How is the distance lrom a point to a line determined? (LESSON 1.4)
45. List all pairs of supplementary angles in the photo below. What are these
types of angles called? (LESSON 1.3;
46. TRANSPORTATION Due to zoning regulations.
the measure of-an angle at an intersection
cannot be less than 75". lt mz I = 75°,
what is ntzvl? (LESSON 1.3) \
47. List all pairs of congruent angles in the 1 .
photo. What are these types ol'an_s,v|es \ t.- .
called? (LESSON 2.2)
£00k Beyond
Some regular polygons fit together around a single point with no
overlaps or gaps. For example, four squares fit together at a point, as
shown at left.
48. What is the measure of each angle at the
indicated point? What is the sum of the measures ~'
of the angles at this center point? 0
49. For a regular n—gon to form a pattern like the one
described above, the measure of its interior angles
must be a factor of 360°. Explain why this is true. _“' "\
50. What other regular n—gon5 will fit together around ._. . . -
a point? How can you be sure that you have found ._-
all of the wossilmle 11- (ms? -
I . .g \ 1 5K
51. BIOLOGY A beehive is constructed lrotn regular -”"'m‘> ~
hexagons. as shown. What do you think are some A -3* _ ...
advantages of using hexagons? ' '
Midsegments of
Triangles and Trapezoids
o
X - W‘
cu‘:
I ""1,"
‘ -- can you think of a way to estimate
the width of the pyramid halfway up the
‘-' . ' _ -_ - stairs witltoutmoasurlngltattbat
- 1 I point? This lesson suggests a way.
L . ' . -xv.
. 6» ~ ~ -
,.- l , ° . .. gs
: ' . . '. ‘I _ _ _ _ ' I .5“ I I
Obgectwes - -. _ F ' ._ _ _ ‘ ‘ . ‘- 2-‘. _ ‘
. I . . ‘ ‘ ' Ir . ' .
0 Define midsegmentof - M. - _ , tj . '
a mangle and . . | ' - ' ~._
midsegmantof a l . I‘ 'i_ '.‘_ _ ’ i‘ T _ —' W W 2' u ‘L
trapezoid. ' i . ll : ._ _ "
. 4 . l
0 Develop and use . ._.. ‘ -—".' . ' 1’ __
tormulas based on 5*‘ - — - ._ '
the properties at *‘ 3C _u.' .:' -' -' “ " "‘ ..
1 I [l '0 . . .
,,?i%:g:,::n;'apez°| The Mil}-‘mt Temple of the Gum!‘ lngtmr m Ttkal, Gtmtetmtlrt. has four
npprtrxinmrely trapezoidal fllt‘L’$. A stairway rises J Utlfeet along one side.
Midsegments of Triangles
Definition: Midsegment of aTriangle
A ntidsegtnent ofa triangle is u segment whose endpoints are the
midpoints of two sides. 3.7.1
Triangle Mldsegments: A Conjecture
1. Draw AABC. Find the ntidpoints. M and N, of sides
ruler and 1—b’ and E. Then draw MN. the mldsegment.
protractor
on 2. Measure and b’—C. W hat is the relationship
gwmwy between their lengths?
g;?t'w,(':“;: 3. Measure /_l and /.2. Measure /.3 and /_-1. _
What do your measurements suggest about BC
and A-IN? What postulate or theorem allows you
to draw this conclusion?
CHECKPOINT ./ 4. Complete the coniecture below.
Triangle Midsegment Conjecture
.-\ midsegment ol 3 triangle is 3.’ to a side of the triangle and
has .1 measure equal to ? of that side.
LESSON 3.7 n-uosesmemrs or tntmetes ANDTRAPEZOIDS 1 83
E X A M P I. E 0 lose is on his school swim team. __ A
During the sum mer. he en joys training " ,1. K»
at a small lake near his house. To
‘ ' P ' C A T ' 0 N evaluate his progress. he needs to know .
SPORTS the distance across the lake. Xi". How \ "" """"" --- --------- __
can he use the conjecture from Activity . - .
l to find this distance? '_ . J
‘-
. SOLUTION
lose can select a point, A, from which he cafiieasure segments H and
Then he can tind the midpoints ot‘.='tX and Ar’ and llN.:§_l:lrt'.‘ the distance
between them. Since this distance is half the length of Xl’. Jose can double the
distance to find his answer.
Midsegments of Tra pezoids
Definition: Midsegment of aTrapezoid
A midsegment or a trapezoid is :1 segment whose endpoints are the
midpoints of the nonparallel sides- 3.7.2
' Z
Trapezoid Midsegments: A Conjecture
mm 1. Draw trapezoid ABCD. Find the niidpoints. A B
/3 6!
fu|e|' and M and N, ofthe nonparallel sides. Draw MN,
nrotractor the midsegment.
°“ M‘ hl tn;--T-.1? 1 M2 5N
\ gwmgtw 2. ieasuret e engtto asesxban Cant
, 9'3!-""°9 of midsegment MN. 1 4-
software 0 C
3. Find a relationship between MN and the
lengths of the bases. AB and DC. .llint: Find A8 + DC).
4. Measure Al and L2 and then 44 and L5. What do you_r_
measurements suggest about the relationship between DC and MN?
5. Measure L2 and L5. What do you notice? Also measure L5 and L6._
W hat do vour measurements suggest about the relationship between ‘ll:
and MN ?
6. Complete the conjecture below.
"I mpemid Midsegment Conjecture
cuscxpomr ./ A midsegment of-.1 trapezoid is ? to the bases of the trapezoid
and has a measure equal to ? .
184 CHAPTER 3
E X A M P I. E The base of the pyramid of the Temple ofthe Giant Jaguar is a square that is
ISO feet on a side. The top is .1 square that is 40 feet on :1 side. What is the
A _ P 1 C A T I 0 H width of the pvramid at a point midway between the base and the top?
ARCHAEOLOGY ‘ H
' ..t.
-- 1
. LLL
‘L _ 51;‘ . “|(‘.:.-5?". _
I ‘l ‘L: — Y‘.-‘ ‘\ .
I _* '- r-T ' “" “*
O SOLUTION
Use the trapezoid midsegment con_ieL.ture:
Length oi‘ midsegment = %(base I + base 2)
' ( 40 + 150)
-3
Making the Connection
1. Draw trapezoid ABCD. which may be any A 3
ruler and shape or size, with midsegment MN . Then
"'°‘”’°‘°' fill in a table like the ()l_1£l)€l0w by gradually
0" reducing the length ol'AB. (Choose your N
gfgmég own measurements tor Ab’ and DC.)
30 Mare
DC AB MN 9 C
6 5 ?
You can use the table
3 4 feature of a graphics
5 3 7 calculator to find the
' ‘ — 1 values of MN asA8
6 2 ? ' approaches zero.
6 1 ? : Enter the function
6 D5 ? Iasy=l6+x]:2.
6 0.1 ?
2. As lb’ approaches 0. what type of figure does the trapezoid become?
CHECKPOINT ./ 3. Write at formula for the length of the midsegntent of a “trapezoid” with
one base length equal to 0. How does your formula relate to the Triangle
M idsegment Conjecture?
LESSON 3.7 MIDSEGMENTS OF TFHANGLE5 ANDTRAFEZOIDS 1 85
Exerc/ses
APPLICATION
APPLICATION
1 86 CHAPTER 3
. Commmrimte
1. In the figure at right. the horizontal segments
across the large triangle are all midsegments
of smaller triangles. \-\-'hat is the ratio of the
base ol the red triangle to the lower base of
the blue trapezoid? Explain your reasoning.
A
2. II" the length of the lower base of the blue
trapezoid in the figure at right is I. what are
the lengths of the midsegments in the figure?
Describe the pattern in the sequence of lengths
you just lound.
3. In Activity 3, vou saw how a triangle can be considered a hmirr'ng (‘use of a
trapezoid. Wliat do you think liniiling case means?
4. Consider the following method for linding the length of the midsegment
of-.1 trapemid: First subtract the length of the shorter base from the length
of the longer base. l'hen take half the dillerence, and add it to the length of
the shorter base. Does this method work? Why or why not?
fit//ded 3k///3 Practice
For Exercises 5-9, refer to the conjectures you made in Activities 1-3.
5. What is the length of the
midsegment of a triangle with -
a base of I2? (ACTIVITY 1) ' 7 mi
6. SPORTS A swimmer is practicing in _ ' I
the lake shown at right. The red line . ‘_ __ _ ‘ .
is the midsegment of the triangle. A 3
What is the distance from point A to
point B? (EXAMPLE 1)
7. What is the length of the midsegment
ofa trapezoid with bases of? and I5?
(ACTIVITY 2)
8. ARCHAEOLOGY 'l he structure shown at right
has four congruent sides that are trapezoids
with a height QF96 ft and bases of 180 ft and
48 ft. What is the width of the structure at a
point midway between the bottom and the
top? (EXAMPLE 2;
9. Write the l'riangle Midsegment Conjecture
and the Trapezoid Midsegment Conjecture 130
as formulas for the length ol‘ :1 midsegment
in terms of the length of the baselsl. How
are the two formulas related? (ACTIVITY 3)
D tnhemetconnect A?-
M
I-lomewotk
Help Online
Go To. nn.lmv.corI
Keyword.
MGI I|oI11ewor'.. Hob
for Exercises In-I5
. Practice dlfd Apply
Use the conjectures you made in Activities 1-3 to find the indicated
measures.
1o..='lB 11 I] 12.PQ
c F K 40_);_
, _#
G 50 H
14. DL‘ 15. F6
A F
S
-‘- D but 5
jw J
' 5x 5
T B C
In Exercises 16-20, refer to the diagram of AABC at right below.
16. Find DE. F0. and H! in AABCM right.
17. Describe the relationships among the lengths
you Found in Fxercise I6.
x’+x-2 G
’ x’+3x-12 H
18. The midsegment of it triangle divides two sides
of the triangle into two congruent segments.
Make a conjecture about the lengths of parallel
segments that divide two sides of .1 triangle into
four congruent segments.
8
19. What do you think is true about parallel segments that divide two sides of
a triangle into three congruent segments? into eight congruent segments?
into n congruent segments? Draw several triangles and test your
conjecture.
20. Are the conjectures you made in Exercises I8 and l9 also true for
trapezoids? Why or why not?
21. Segments and TQ(ll\’ld? two sides of AJKI.
into three congruent segn1t?n_ts, as shown. Write a
conjecture about MN and PQ. Draw several other
triangles and test your conjecture.
22. In the figure at right, the three red segments are
midsegments ol' the large triangle. Find the length 16
of each midsegment.
Add the side lengths of the outer triangle. Then
add the side lengths of the smaller triangle formed 25
by the midsegments. What is the relationship
between the two sums?
LESSON 3.7 MIDSEGMENT5 or TRLANGLES AND TRAPEZOIDS 187
CHALLENGE
APPLICATIONS
1 88 CHAPTER 3
ln Exercises 23-26. write informal arguments based on your conjectures
about triangle midsegments and quadrilaterals.
23. Draw a scalene triangle. Draw any two midsegments of the triangle. What
type of quadrilateral liaving these midsegments as adjacent sides is
formed? Explain why.
24. Draw an isosceles triangle. Draw the midsegments that connect the two
equal sides to the third side. What type oi‘ qttadrilateral having these
midsegments as adjacent sides is Formed? F.xpl-ain why.
25. Draw a right triangle that is not isosceles. Draw the two midsegments that
connect the legs to the hvpotenuse. What type oi‘ qu:n.lrilateral having
these midsegments as adjacent sides is Formed? Explain why.
26. Draw an isosceles right triangle. Draw the two misdegments that connect
the legs to the hypotenuse. What type of quadrilateral having these
midsegments as adjacent sides is Formed? Explain why.
27. In Exercises 2|-27 oi‘ Lesson 2.l. you examined the sum oi‘ the inl'*inite
sequence % + % + % + fi + - - - hy using areas ol‘ squares and rectangles.
Another way of determining this sum involves the Triangle Midsegment
Conjecture.
Figure A is a square with a side length ot‘ l. and each hori.sontal segment is a
midsegment ofa triangle. Find the length of each midsegment in figure A.
Then use figure B to explain why the stun of the inlinite sequence is I.
Figure A Figure B
28. ENGINEERING ls F—Cthe midsegment oftr-ape7oid ABDF in the figure at
left? Explain your answer.
PAINTING A painter is using a 20-h ladder whose base is 5 ft from the
wall.
29. Determine the distance from the ladder to y
the wall at a point ltallway up the ladder.
30. Determine the distance from the ladder to
the wall at a point three—quarters ol‘ the ‘
way up the ladder.
31. The painter can reach the wall lirom 2 It
away or less. Fstim-ate the percent oi" the
ladder from which the painter can reach
the wall.
APPLICATION
APPLICATION
32. MUSIC A ltar;rnt¢'rt'd dulcimer is an ancient
trapezoidal stringed instrument. The bases
of the trapezoid are approximately 17 in.
and 38 in. Estimate the length of a string
at the center of the dulcimer.
Look 346*
33. BIOLOGY Draw an Fuler diagram to illustrate
the relationships below. (LESSON 2.3)
A squirrel is a rodent.
All rodents are mammals.
All mammals are animals.
Use the conjectures you made in Lesson 3.2 to classify each statement
as true or false. Explain your reasoning. (LESSON 3.2)
34. All rhomhuses are squares. 35. All rectangles are parallelograms.
36. All squares are rectangles. 37. All paral|elo§.Itan1s are rhombuses.
For Exercises 38-40, find the unknown angle measure in each figure.
(LESSON 3.5)
39. 40.
86°
1 20 45-: X 9
Look Beyond
41. Draw a triangle and all ol‘ its midsegments, as shown at lelt. Cttt out the
four triangles that are fornted. and compare them with each other. Write a
conjecture about them.
42. Test your conjecture from Exercise 4 I by using several other triangles.
Based on your conjecture, what is the ratio of the area of each of the four
triangles to the area of the original triangle?
43. The figure at left is Formed by drawing the midsegments of the three outer
triangles in the figure above. l'he large outer triangle is equilateral and has
a side length of I. Find and add the side lengths of all of the shaded
triangles.
44. Is the total area of the shaded triangles in the figure more or less than the
area of the outer triangle?
45. II‘ the midsegments of each shaded triangle were drawn and the resulting
center triangle of each was “unshaded," would the shaded areas of the new
ligure be more or less than the shaded areas above? Would the sum of all
the side lengths he more or less? Explain your reasoning.
LESSON 3.7 MIDSEGMENT5 or rntmetes AND TRAFEZOIDS 189
Objectives
0 Develop and use
theorems about equal
slopes and slopes of
perpendicular lines.
0 Solve problems
involving
perpendicular and
parallel litres in the
coordinate plane by
using appropriate
theorems
Analyzing Polygons
With Coordinates
_‘~.
_. W
- ti
I . \
\ —L 5‘ D
1,, ' __.' \ \
W _ _ I _ _ _ _ . o ‘ . r
Gm -tarsus-eamarhematical _".
erhadta Indicate steepness. This - - _ ------ "
=--dtwhllenolascolorfulasdia Q, .- ‘_
names of roller coasters, is more precise. , ' ~\
I
.-‘tnrtlseinml parks o_ftr'n lItll’t" rlr’sTr'iptit-'r’ names for their r'ollr'ri'or1sters. Nmm’.~'
such as “.Shovker" or “Wild Thing" git-e rirlers nu irlm about the sreepiress of the
frills they will experiem'r:.
Hypotenuee
r’
/'
L°9L/‘
EXAMPLE
190 CHAPTER 3
O SOLUTION
Slope: A Measure of steepness
‘I he slope of a line or surlace tells you how steeplv it rises or falls in terms of
:1 ratio. This ratio is lound by using a right triangle. Recall that the sides of a
right triangle that are adjacent to the right angle are called the legs of the
triangle and that the remaining side is the hypotenuse oi" the triangle.
Consider a right triangle in a Coordinate plane with hori7ontal and vertical
legs. The slope of the hypotenuse is the ratio of the length of the vertical leg.
the rise. to length of the horizontal leg. the full. If the hypotenuse rises from left
to right, the slope is positive; if it Falls lrom lelt to right. the slope is negative.
Find the slope oi‘ the segment with (B. 6)
endpoints at (2. 5) and [3, 6).
rise = 3
l2, 3)
Draw a right triangle as shown. By run = 6
counting squares. you can see that the
rise is3and therun is6.Thus.the * 7 7 7 7 7 7 7 7 7 X
slope is = 1. or 0.5.
Note: in Example I. you found that the slope ol'the segment with the given
endpoints is 0.5. To Lise this method to find the slope of :1 line, choose anv two
points on the line and find the slope ofthe segment with those endpoints.
LESSON 38 ANALYZING POLVGONS WITH COOHDINATES
To find the slope of a line with two given points without drawing a picture.
use the definition below.
Definition of Slope
The slope ofa nonvertical line that contains the points (x.. y.) and
(x3. y3) is equal to the ratio 3.8.1
— : " — I
cnmcm. THINKING in the case of a vertical line or segment, the slope is undelined. Explain why
the slope of a vertical line or segment is undefined.
E X A M P I. E 0 Find the slope of Ev.-ith the endpoints AIS, -3] and B(2. 3).
O SOLUTION
)'.")' 3—[—3] 6
lSl0pc?=$= T_-_T-=_—3y=-2
Parallel and Perpendicular Lines
; . I / Recall from algebra the s|ope—intereept Iorin ol'a line:
y = mx + ll.
V where 11: represents the slope and b represents the It-'-intercept
y = 15,, + 2 . The two lines in the graph at left have the same slope, 1.5. As you can see. thev
seem to be parallel. The theorem below. which will not be proved formally in
x this book, follows from the algebraic concept of slope.
l0. -3) _—_ _ -3 _
V I 5” Parallel L|nesTheorem
In a coordinate plane. two nonvertical lines are parallel it and only if they
have the same slope. Any two vertical lines are parallel. 3.8.2
The slopes of perpendicular lines also have a special relationship to each other.
This relationship is stated in the following theorem. which can be proved
using the coordinate proof methods described in Lesson 5.7.
Perpendicular Lines Theorem
in a coordinate Plane. two nonvertical lines are perpendicular ifand only
if the product of their slopes is —l. Any vertical line is perpendicular to
any hori.I.ontal line. 3.8.3
LESSON as ANALYZING POLVGONS WITH COOHDINAYES 191
The fact that the product of the slopes of pcrpcndicular lines is -1 can be
stated another way. In order lor the product of two numbers to equal —l , one
number must be the negative reciprocal of the other. ‘thus. if the slope of a
line is then the slope ofany line perpendicular to that line must be
You can ttse this relationship to test whether lines are perpendicular withottt
multiplying their slopes.
E X A M P I. E 0 Draw quadrilateral QUAD with vcrticcs
I at Ql I1 4]. U(7.8).A[9. 5?. and DH. I].
What type of quadrilateral is Qtvtt)?
O SOLUTION
Based on the figure. it appears that QUAD
is :1 parallelogram and perhaps a rectangle.
You can test these coniecturcs by linding
the slope of each segment.
—— 8—I -1 2 —- 5-1 -1 2
slo1)eotQU=.I.—_-T=E=_3 slopeotD.»l=E—§=3=§
, , -—_4—t_—_a . , -—_5—3_—3
biO}1L0iQ —l_‘!—T 5i0[Jt.0i
Because the opposite sides ol. the quadrilateral have the same slope. the
figure is a parallelogram.
Because the slopes of the adjacent sides or the quadrilateral are negative
reciprocals. the angles in the figure are right angles. Thus. the figure is a
rectangle.
Midsegments in the Coordinate Plane
Coordinates mav be used to verilv the conjectures about triangle and
trapezoid miclsegmcnts that you made in the previous lesson.
I J I I Recall the following formula from algebra for the midpoint ofa segment in a
coordinate plane:
Midpoint Formula
The midpoint ofa segment with endpoints (x.. y.) and (X1. yg) has the
following coordinates:
3.8.4
7 ‘ )
l
lg
Notice that the coordinates of
the midpoint are the averages of
the coordinates of the endpoints.
(1']+.Y: )'l+y2)
1 92 cum-Vren 3
E X A M P L E 0 Draw AABC with vertiees .»l[2. 6].B(O, O). and CH, O), and use this triangle to
test the triangle midsegment conjecture.
O SOLUTION
The midpoint (HE is (3 *2’ O. 6:0) = (l. 3-]. and
the midpoint ot'Ft'C" is (3:;". "30) = (3. 31.
Thus. the slope of the midsegment is
3-3 _ 9 _
3T1 ‘ 2 ‘0'
The slope off is —?:g = g = 0. so the
midsegment is parallel to a side of the triangle.
Because W and the midsegment of the triangle are horizontal. you can_
determine their lengths by counting squares on the grid. ‘I he length ol'BC is 4,
and the length of the midsegment is 2, so the length of the ntidsegntent is halt"
ol the length ol‘T3Ti. This confirms the Triangle Midsegmenr Conjecture.
TRY nus Draw trapezoid DE!-"G with wertices DH. 2). Eli’. 2), H9. 0], and Gto. 0], and
use this trapezoid to test the Trapezoid Midsegtnent Conjecture.
CRITICAL THINKING Are the cases above proofs of the Triangle and Trapezoid M idsegment
C()t1jeLtttt'es? Why or why not?
Exercises
. Communicate
1. Describe lines with the following:
a. a positive slope b. a negative slope
c. a zero slope d. an undefined slope
2. Explain the meanings of the tertns rise and run.
3. Suppose that nonvertical lines I". and (3 are perpendicular and that the
slope of E. is m. What is the slope of 8;? Explain your answer.
4. In the diagram at right. the two lines
have slopes ol l and —l. but they do
not appear to be perpendicular.
Explain why.
5. In Example 4 and the Try This that
lollows it, one side of the triangle
and trapezoid is on the x-axis.
What is a possible advantage to
placing, the ligu res in this position?
LESSON as ANALYZING POLVGONS wma CC-ORDINATES 193
0 614/dedsk/‘//3 Practice
6. A segment has endpoints at [ l. 2‘) and (3. 8}. Plot the points and draw a
right triangle with this segntent as the hypotenuse. Use the right triangle
to find the slope of the segment. (EXAMPLE 1)
In Exercises 7-9. use the definition of slope to find the slope of the
segment with the given endpoints. (EXAMPLE 2)
7. [0, O) and [4, -l" 8. [—l, 3] and (4. 5] 9. (2, I) and [4, -6]
10. Draw a quadrilateral with vertiees at (0. 2], (I, -1‘), (5. l]. and (4, 4']. W hat
type of qu:1dril:iter.rl is this? Fxplnin your answer. (EXAMPLE 3)
11. Dr-.1wa trapezoid with vertices at (0.01. (0.4). (5. 4]. and (5. O).and use this
trapezoid to test the Trapezoid .\lidseginent Conjecture. (EXAMPLE 4)
0 Pfdft/68 and 24,0]/y
' te et ea °.
D II rn cnnn %
Homework
Help Online
Go 10 no.hrw.t:urn
Kewiord
M61 Ilornswork Help
for Exercises 2022
PROOFS
1 94 CHAPTER 3
ln Exercises 12-15. the endpoints of a segment are given. Determine the
slope and midpoint of the segment.
12. (O. O) and (4. .2}
14. (-3.—l) and (3. 3:)
13. [—l. I] and (l.—l)
15. (-5, 2] and (I. -3)
ln Exercises 16-19, the endpoints of two segments are given. Determine
whether the segments are parallel. perpendicular, or neither.
16. [—l. l] and (2. 5]: (2. 2) and (5. 4')
17. [-2. I] and (l. -2); (—I. —l).md (5. 3]
18. (-2. 2) and (5. 2); (2. -ll and (2. 4]
19. (—l. 2] and (l,—2):(l.—2) and [2.—l]
Refer to the diagram at right
for Exercises 20-22.
20. liind the slope oi
21. Find the slope of TB.
22. Is 41 .1 right angle?
Fxplain your answer.
For Exercises 23-28, the vertices of a triangle are given. Use slopes to
determine whether each triangle is a right triangle.
23. (—l.tl).(-l.?-].(l. I) 24.(l.3l.[2.U),(—?-.2)
25. [-2, 3). (3, —l J. (-2, —l} 26. (I, 0). [0, I}, (-1. 0]
21. (I, 21. (.1, 3). (4.01 23. [9, 51. (2.~6]. (~l.—l)
Draw the quadrilateral with the given vertices on a graph. Identify the
type of quadrilateral and prove your answer.
29. (0,—2l. (5.—2}. (5.61. (0.6) 30. (0, tn. (2, 5}. (5. 3). [7, 0)
31. to, 3»). (-1. I), t2,o1,(.1. 2) 32- (I, 51. (-2. I). (-1. -3}. (2.—n
33. (0. 6). (3.9). (9. 3). (6. 0) 34- (I. 0'). I5. I). (-1. 4). (-1. U
PROOFS
‘\
.
\
CHALLENGE
APPLICAYION
For Exercises 35-37, the vertices of a rhombus are given. Draw the
rhombus and use slopes to prove that the diagonals of each rhombus
are perpendicular.
35. (-2. l). ( l. 5]. (5, 2). (2. -2’)
36- 3): (6, 5)! _l J: [-21
31. (0. 0]. (0, :1). (cl, :1]. (fl. 0)
For Exercises 38-41, the slope and one endpoint of a segment are
given. Give the coordinates of the other endpoint. More than one
answer is possible. (Hint: Start by drawing a right triangle with the
given point as one of its vertices.)
38. slope = %; (0. O) 39. slope = 2; (6, —l)
40. slope = —g; [—l, 4] 41. slope = —l; [2, 5)
42. l'he vertiees ofa triangle are NO, 8]. B(2, 0}. and 013», 4). Find the
midpoints of the sides and prove that each midsegment is parallel to a side
of the triangle.
43. The vertices ofa trapemid are K[(), 0), MD. 7}, A-{(4, O], and NH, 9}. Find
the endpoints of the midsegment and prose that it is parallel to the bases.
44. Parallelogram ABCD has verlices at A(—l. x—l ), B[x. x+ l), CI3. l), and
D(x -2. —l ]. Use the slopes of Hand 7) to find .\'.
For Exercises 45-49. draw a quadrilateral that fits the given conditions.
Label the vertices. and give the slope of each side. More than one
answer may be possible.
45. trapezoid ABCD with vertices .-l(3, 5] and B[8, 5}
46. parallelogram FFGH with vertices H3. 2] and FT—l, 5}
47. rectangle IKLM with vertices It 1.6] and Klfl, 2)
48. parallelogram NPQR with vertiees N(-2, l) and Qt-pl. -2)
49. rectangle STU V. in which the midpoint of §7' is (S. 5], the midpoint of
T is (10. 5]. the midpoint offiis (7. l).and the midpoint ol'T‘is (2. l)
50. CONSTRUCIION According to the Americans with Dis-.tbi|ities Act, 21 ramp
is a route with a slope greater than The maximum allowable slope of
a ramp is L and the maximum rise is 30 in. What are the minimum
I2 ‘ , . _ _
and maximum runs tor a ramp with a rise of 30 m.?
l_a%t,,«_«
._j
. - ‘ - ,_ ' fl -
"""‘ ' 33;: “ '
__:__.—— arm‘ '-
LESSON as ANALYZING POLVGONS WITH C0-ORDINATES 1 95
A P P L I c A T I O N 51. CONSTRUCTION A house is 25 ft wide. and
has a peaked roof, as shown at right. City
building codes require the pitch (slope) of the
roof be at least 0.3 and no greater than 0.7.
Use the given coordinates to show that the
roofofthis house does not meet the building
codes. How could the height of the roof
be adjtisted so that it does meet the codes?
Look Back
52. Iixplain the dit'ferenc.e between :1 postulate and a theorem. (LESSON 2.2)
Refer to the figure at right, in which 3, 4‘ :
€1|l £2, and find the indicated angle W 4 145.
measures. (LESSON 3.5) 92 < /F50“ 2 :
53. méj 54. méz
55. ll‘lé'l 56. mél 1;"
A P P L I C A T I O N 57. CONSTRUCTION |'he diagram at right
shows a house whose roof has a pitch
of Find the angle that the roof
forms with the walls. (LESSON 3.6)
£00k Beyond
CULTURAL CONNECTION: AFRICA An ancient
Egyptian drawing l'rom 2650 B.C.E. shows
a rounded vault. The mimbers, which are
the marks on the diagram, give the height,
y. of the vault at horizontal intervals. x. of
I cubit.
58. Given that l palm is equal to 4 lingers
and I cubii is equal to 7" palms. copy
and complete the table below.
' ' “H ed xlin lingers) Height (from drawing) i y(in fingers)
P M l' _ _ . .
Egelfsggn 0 cubit = 0 fingers 3 cubits, 3 palms. and 2 fingers 98 fingers
50 T01 IDJIIW-00!“ 1 cubit = ? 3 cubits, 2 palms, and 3 fingers I ?
Ke-wrord:
MGI Escher 2 cubits = ? 3 cubits ?
4 3 cubits = ? 2 cubiis and 3 palms ?
4 cubits =? ‘I cubit, 3 palms, and 1 finger ?
5 cubits =? 0 ?
59. l'se the x- and y-coordinates lrom the table to plot the points on a graph.
Then draw a smooth curve throtigh the points.
1 96 CHAPTER 3
QOLIO
0+‘ —
0.
In addition to translation tessellalititis ("see page
I54), another pattern used by M. C. Escher is
known as a rotation tessellation. iou can make
your own rotation tessr:llati0n liy following the
steps below. As in the Portfolio Activity for
Lesson 3.2. you may have to make adjustments
to \-‘our curves in order to get a pattern you lilce.
Draw your figures on graph paper or tracing
paper, or use geometry or tessellation software.
1. Start with a regular hexagon. Replace one
side of the hexagon. with a curve, as shown
below. Rotate the curve about point B so that
point .-‘l lies on point C.
A M l' ‘-35"‘: N_rI1I:Ia:Il'-‘::vt1|I‘[I"."0I')wCnn|o¢ \..tl.\’. Flam llni I
all rights. rescind
F 8 _ \. — . _
3. Replace side EF with a new utrve. and __
rotate it around point F to replace side FA.
E c If
F ‘ ~.
0 \> _3
2. Replace side fihvith a new curve, and _
rotate it around point D to replace side DE. E -. ,. '6
5
4. Your figure will now lit together with itsell
on all sides. You can add details to your
figure. if desired. Rotate the figure to create
an interlocking design.
2 ii 3 ,
i:_. ‘. ' ‘
J ' I.
i‘ ' ‘ ‘ i(“‘\
_ it I
‘ — ‘.’_t—_:___- .
LESSON as ANALYZING POLVGONS wnn co-oat:-rNArEs 1 97
.§;fi§i;tt
rage‘
'I he string activity below ' .";'-
and the resulting net have ' '
appeared in many parts of
the world under different
names: Osage diamonds ,
among the Osage Indians of
North America. the Calabaslt
net in .\frit.t. and the Quehec
bridge in Canada. In the
United States. it is commonly
known as Jacol.1's ladder.
‘I. Start with .1 piece Ol
string 4 to 5 feet in
length. Tie the ends
together. loop the string
around your thumbs and
little fingers as shown.
\\
1 98 CHAPTER 3
2. Use your right index
finger to pick up the left
palm string from below.
In a similar way, use your
left index finger to pick
up the right palm string.
/'.‘
.’
gtring (357 ‘acres
. Let your thumbs drop
their loop. turn your
hands so that the lingers
face out. With your
thumbs. reach under all
the strings and pull the
farthest string back
toward you.
4. With your thumbs. go over 5. Drop the loops from your 8. Drop the thumb loops. Pass
the near inde‘<—fiuger string. little fingers. Pass your little your thumbs over the index-
and then reach under and lingers over the index—linger linger strings. get the near
pull back the far index string and get the thumb little-finger st ring from
finger string. string closest to your little below. and return.
lingers front below.
A!
7. Loosen the left index-finger 8. Each thumb now has two 9. Bend yottr index Fingers and
loop with your right hand, loops. Using vour right insert the tips into the
and place the loop over your hautl. lift the lower loop of triangles that are tteur the
thumb. Do the same with the left thumb up and over thumbs.
the right index—finger loop. the thumb. Do the same
with the lower loop of the
right thumb.
{\
. ‘R:
L§"“\.\ ~
A
3101 A
V
10. Gently take your little fingers out of
their |O0p5— Turn your hands so that
your palms l"-ace away from you. The
iudex—liuger loops will slip off your
lznuckles. Straighten your index fingers.
1 he finished net will appear.
CHAPYER 3 PROJECT 1 99
Chapter Review and Assessment
VOCABULARY
alternate exterior angles . . . I56 equiangular polygon . . . . . .139 regular polygon . . . . . . . . . . . 139
alternate lnterior angles . . . I56 equilateral polygon ..... . .139 remote lnterror angle . . . . . . 114
axis of symmetry ...... . . . .139 midsegment ol a rltomhus . . . . . . . .. ...... ..148
center of a regular “B9319” - - - - - - - - - - - - - - - '33 rotatlonal symmetry . . . . . . . 141
polygon . . . . . . . . . . . . . . . . 139 niidsegment ot a trrangle . . . I83 sanwsme imam,
central angle of a regular parallelogram . . . . . . .. . . . . 148 angles . . . . . . . . . . . . . . . . . 156
p°'V9°" ' ' ' ' ' ' - - - - ' ' ' ' -' '39 polygon . . . . . . . . . . . . . . . . .138 slope . . . . . . . . . . . . . . . . . . . .191
°°"°3"° l’°'V9°" - - - - - - - - - - "7 quadrilateral . . . . . . . . . . . . .148 square . . . . . . . . . . . . . . . . . . 148
'3°'“’°" P°'V9°“ --------- -- "7 rectangle . . . . . . . . . . . . . . . . 148 transversal . . . . . . . . . . . . . . . 155
correstwndino angles - -- --155 reflectional symmetry .. . . . 139 trapezoid .............. . . 148
POSTULATES AND THEOBEMS
Lesson Number Postulate or Theorem
3-3 3.3.2 Corresponding If two lines cut by a transversal are parallel, then corresponding
Angles Postulate angles are congruent.
3.3.3 Alternate Interior If two lines cut by a transversal are parallel, then alternate interior
Angles Theorem angles are congruent.
3.3.4 Alternate Exterior If two lines cut by a transversal are parallel, then alternate exterior
Angles Theorem angles are congruent.
3.3.5 Same-Side Interior If two lines cut by a transversal are parallel, then same-side interior
Angles Theorem angles are supplementary.
3-4 3.4.1 Theorem: Converse If two lines are cut by a transversal in such a way that
200 CHAPTER 3
of the Corresponding
Angles Postulate
correspondlng angles are congruent, then the two llnes are parallel.
3.4.2 Converse ofthe
Same-Side Interior
Angles Theorem
If two lines are cut by a transversal in such a way that same-side
interior angles are supplementary. then the two lines are parallel.
3.4.3 Converse of the
Alternate Interior
Angles Theorem
If two lines are cut by a transversal In such a way that alternate
interior angles are congruent, then the two lines are parallel.
3.4.4 Converse ot the
Alternate Exterior
Angles Theorem
If two lines are cut by a transversal in such a way that alternate
exterior angles are congruent, then the two lines are parallel.
3.4.5 Theorem
If two coplanar lines are perpendicular to the same line, then the
two lines are parallel.
3.4.6 Theorem
If two lines are parallel to the same line, then the two lines are
parallel.
Lesson Number
3-5 3.5.1 The Parallel
Postulate
Postulate orTheorem
Given a line and a point not on the line. there is one and only one
line that contains the given point and is parallel to the given line.
3.5.2 Triangle Sum
Theorem
The sum of the measures of the angles of a triangle is 180°.
3.5.3 Exterior Angle
Theorem
The measure of an exterior angle ot a triangle Is equal to the sum
of the measures of the remote interior angles.
3-5 3.6.1 Sum of the Interior
Angles of a Polygon
The sum, s, of the measures of the interior angles of a polygon
with n sides is given by s= (n- 2)180".
3.6.2 The Measure of an
Interior Angle of a
Regular Polygon
The measure, m, of an Interior angle of a regular polygon with n
sides is m: 180"-
360"
ll '
3.6.3 Sum of the Exterior
Angles ofa Polygon 360°.
The sum of the measures of the exterior angles of a polygon is
3.8 3.8.2 Parallel Lines
Theorem
in a coordinate plane. two nonvertical lines are parallel if and only
if they have the same slope.
3.8.3 Perpendicular Lines
Theorem
Key Skills 8: Exercises
LESSON 3.1
Key Skills
Identify reflectional symmetry of figures.
Draw all of the axes of sylnlnetry ol ‘.1 regular
hexagon.
Identify rotational symmetry of figures.
Describe the rotational syntnletry 0|‘ a regular
hexagon.
A regular hexagon has (1-fold rotational symmetry.
The image will coincide with the original figure
after rot.ltiuns of 60°. I.-20°. l8U°. 240°. 300°. and
360°. After a rotation of 560“. the figure is
returned to its original position.
In a coordinate plane, two nonvertical lines are perpendicular if
and only If the product of their slopes is -1.
Exercises
Copy each figure below.
1. Draw all axes of symmetry of the figure above.
2. Describe the rotational symn1etry ol"the hgure
3bO\€.
4$‘vflVAv'.‘
§
7
3. Draw all axes of symmetry of the figure above.
4. Describe the rotational symmetry ol'the figure
above.
CHAPTER 3 REVIEW 201
LESSON 3.2
Key Skills
Make conjectures about the properties of
quadrilaterals.
In a parallelogram. the opposite sides and angles
are congruent. and the diagonals hisect each other.
In a rhombus. the diagonals are perpendicular to
each other. In a rectangle. the diagonals are
congruent.
LESS-ON 3.3
Key Skills
Identify special angle pairs.
In the diagram below. A’-‘l and A5 are alternate
interim angles. .42 and A7 are alternate exterior
angles. £4 and A6 are same-side interior angles,
and A2 and £6 are corresponding angles.
100-=
2
3 4 "’
m||n
—2:—~
Find angle measures formed by parallel lines
and transversals.
For the diagram abow e.
m.é4 = m.£5 = m.é8 = l0O° and
mA'2 = nu./_’3 = n1A'6 = nil? = 80°.
LESS-ON 3.4
Key Skills
Use the converses of transversal properties to
prove that lines are parallel.
Are lines t‘. and ("'1 parallel?
£1
f’ w X
The angles A’ WXUand A'XUl/are congruent
alternate interior angles. By the converse of the
Interior Angles Theorem. the lines are parallel.
202 CHAPTER 3
Exercises
ABCD is a parallelogram, EFGH is a rhombus.
and JKLM is a rectangle. Find the indicated
measures.
5. mA'r‘lBC= 48° 6. AX = 7
mA'ADC= ? At. = ?
3% B
D C
7. mA'El"F= ? 8. IL: I3
E = (
J K
G M L
Exercises
Refer to the diagram below.
9. Name a pair ofcorresptinding
angles.
10. Name a pair ofalternate f
interior angles. 3 ‘
8
11. Name all angles that are 1 2 7
congruent to Al. 5 6
12. Suppose that mil = I30”.
Find the measure of each
angle in the figure.
Exercises
Refer to the diagram below.
13. Is 1'' parallel to m?
Explain yottr answer.
14. Is In parallel to M?
Explain vour answer.
15. Is [2 parallel to q?
Explain your ans\.\-er. p q
16. Prove that the opposite sides of a rectangle are
parallel.
LESSON 3.5
Key Skills
Use theTriang|e Sum Theorem to find angle
measures.
Find the measure oi" (F.
F
D E C
[DEF and A'(“EF form a linear pair.
so mAF= l80°— I I0” = 70.
By the Triangle Sum Theorem.
ml D + m4 F + m.£DEF = 180°.
so mA'DEF = l80° — 30° — 70° = 80°.
LESSON 3.3
Key Skills
Find interior and exterior angle measures of
polygons.
ln .1 regular octagon. what is the measure of an
interior angle? What is the measure ol an exterior
angle?
The sum of the interior angles of an octagon is
I080”. The measures of all the interior angles are
equal. so the measure of each interior angle is
I080” + 8 = l35°.
The sum of exterior angles of any p0l_vg0n is 360°.
so the measure of each exterior angle is
360° + 8 = -15‘ .
LESSON 3.7
Key Skills
Solve problems by using triangle and
trapezoid midsegments.
A trapezoid with one base of ID has a midsegment
of I7. What is the length of the other base?
The midsegment is the average of the bases. Let x
represent the unknown length.
“3j;*"=17
l0+x=.’i-1
x=2-1
Exercises
Refer to the diagram below. mAPRO = 90 .
mAPTO = 125", mAPOR = 57“, mAPSO = 83°,
and mARSO = 30°
17. Find all angle
measures in O
ARST. P
13. Find all angle
measures in
APST S R
19. Find all angle
measures in APQR.
20. Find all angle
measures in APQT.
Exercises
21. Find the missing
angle measure in the
diagram at right.
22. What is the measure
oi" an interior angle
ol a regular pentagon?
23. What is the measure ofan interior angle ofa
regular 17-gun?
24. What is the measure of an exterior angle ofa
regular dodecagon?
Exercises
25. What is the length of the midsegment of a
triangle with a base of I2?
26. What is the length ol‘ the base of a triangle
with a midsegment ol‘ 45?
Find the indicated lengths in trapezoid KLMN.
27. Rb K 30 L
28. TU
2—|:.u\-J.
50
CHAPTER 3 REVIEW 203
LESSON 3.8
Key Skills
Use slope to determine whether lines and
segments are parallel or perpendicular.
A triangle has vertiees at All). 0), BM. 1]. and
Q3. 5). ls AABCa right triangle?
W3 has .1 slope of W: has a slope of -4, and TC
has a slope of Because 1' - (-4) = -1. TB is
perpendicular to B_(_-T. Therefore. A,-‘lBC is a right
triangle.
Applications
33. CRAFTS Ruth is making a quilt with the block
design called Bow Ties. shown at right. Describe
all lines ofsyntntetry and all rotational
symmetries for the block.
34. ART An artist is making a wooden frame
for stretching :1 canvas. To make sure that
the frame is rectangttlar. he measures the
diagonals. If the frame is a rectangle. what
will be true of its diagomls?
35. ENGINEERING The grade of .1 road is its slope
expressed as a percent. For example, a road
that rises 6 ft 0» er :1 horizontal run of I00 it
has a slope of or a grade ol'6%. What is
the grade of each section of the road represented
by the graph at right?
204 CHAPTER 3
Exercises
29. AFGH has vertices at HI. I], GR. 0). and
H[—l. -1). Is Al-‘CH a right triangle?
Match each type of special quadrilateral with
the correct set of vertices. Explain your
reasoning.
a. trapezoid
b. parallelogntm
c. rectangle
30. (U. 2). (2. 5]. (5. 2). (5. ll
31. (2. ll. (1. 3). t'5.5).(6.3)
32. (0. ll. (3. 31. (7.3).(l.—l]
-*.=.~*:.~'-'«.
I. n- '=.~?3:-.v-
- A
‘K
‘
1/
3° 460.30)
10 135,10). _//"“
X
lO'Oll 10 2b 30 40 50.60
Chapter Test
Copy the figure for Exercises 1 and 2.
1. Draw all axes of
symmetry of the
figure.
. Describe the rotational
synnnetry of the ligu re.
3. DESIGN A square table is extended by
putting a leaf in the center of the table. 15 the
extended table regular? equilateral?
equiangular?
For Exerclses 4-9, refer to the diagram.
In rhombus ABCD. AB = 38. BD = 43, and
mABCD = 75°. Find the indicated measures.
B
4. BC 5. Fr)
6. mADL'(_, 7. n1ADAB A c
8. m.4ADC 9. m.4AEB
D
10. GRAPIIIC ARTS To set the frantic for a
rectangular painting, Jason uses diagonal
braces as supports. If the brace connecting
points Qand in the diagram below is 25
inches, how long is the brace connecting R
and F?
2:
T S
For Exercises 11-13, refer to the diagram below.
11. Name .1 pair of alternate exterior angles.
12. f\ame all angles that are congruent to £2
13. Find the measure of each angle in the figure.
Complete the paragraph proof.
Given: m .L I and n L l"
S
Prove: m n A, E3 3 In
F 3
4r D 0
Proof: T
Linc ("I is .1 14. E’ of m and n. by definition.
45133 E AEFD because 15. ? . Therefore.
16. ? is parallel to 17. ? by 18. ?
For Exercises 19-24, refer to the diagram.
0-H I E, P_o .l r_n, mATOR= 70°, and
m.£T$U = 50°. Find the indicated
measures.
19. rn£R
ml T
mA'S UT
mZQPU
m£PQU
m£Pl."Q
20.
21 .
22.
23.
24.
For each polygon, determine the measure of
an interior angle and the measure of an
exterior angle.
25. at square 26. .1 regular ()cl(1g0n
For Exercises 27-Z9, refer to the diagram of
AJKL below. Find the indicated lengths.
OP
QR
MN
27.
28.
29.
30. Draw a ligure with vertices at A[—3. 5].
H2. 4}. CI—l. 2). Identify the figure and prove
your answer.
CHAPTER 3TEST 205
-- E-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTlPl.E-CHOICE For Questitms l-3. write the
letter that indicates the best answer.
1. Refer to the regular pentagtm helnw. What is
mg l! (LESSON 3.5)
B
a. lO8°
b. l20°
1:. 540°
d. 72"
2. Refer to the Figure below. Which of the
following statements is true if land m are
parallel? (Lesson: 3.3)
m
a. .4 I and £2 are parallel angles.
b. mil > 11112
c. .41 and £2 are vertiml angles.
d.n1£| = ntA2
206 CHAPTER 3
O
D intemet connect
Standardized
Test Prep Online
Go To: go.hrw.com
Keyword: MMI Test Prep
3. Refer to the figure below. Which ofthe
following statements is true? (LESSON 3.5)
A
sec
a. tnézl + ntAB= mAC
b. AA. AB. and A C are adjacent angles.
c. m£A + m£B+ m£C= 360°
d. tndzl + n1£B + n1AC= 180°
Complete the statements in Items 4-7.
(LESSONS 1.1, 1.4. AND 1.5)
4. The ll]t€l‘S€(.ll('.ll‘l of two lines is a ? .
'l'he intersection of two planes is a ? .
5. ll" two points are in a plane. then the line
containing them ? .
6. 'l he dist.-tnce from a point to a line is the
length of the ? from the point to
the line.
7. The intersection ol the perpendicular
biseetors of -.1 triangle is the center of the
? of the triangle.
For Items 8-11, write the rule for each
transformation. (usssorv 1.7)
3.
9- Y
D‘ ‘: D
E.
2--Ed
' F
-l—|1i—f—i—:-—i—4—i-D-X
-4 -2 2 4
1o. ,,
11- ,,
L
4-|:.:|?j*i:4?.?9-D-X
-4 -2 ._ 2 4
L’ M-
2._
K’ 4,
For Items 12-16, r_efer to the diagram
below. in which DE ||F—G, DE = 3, FG = 8,
m£EGF = 34°, m£EGD = 30°, and
mAEJH = 42°. (LESSONS 3.3, 3.5, 3.6.
AND 3. 7)
D E
G F
12. Name three angles that are mngruent to
A’ FGF.
13. What is the ratio of II to F6?
14. H] = ? . I II = ?
15. m£GFE = ? , m£H]F= ? ,
m£G!] = ? . mdGF] = ?
16. m£H!E= ? , mAGHI = ? .
m.£GDE= ? . m.£DH! = ?
FREE-RESPONSE GRID Items 17-20
may be answered by using a (3 (3
free-response grid such as C3 C?’ C3 C‘
that commonly used by G g (C?) g
standardized-test services. (3 ® ® ®
17. The measure of an angle is g g g 3
25°. What is the measure of its (3 (E (3 (3
complement? (LESSON 1.3) (9 (9 Q) (9
13. The measure of an angle is 3 g g g
7'5”. \'\''hat is the n1e.isure (If its (3, ® (3
supplenient? (LESSON 1.3)
19. An angle is its own complement. What is its
measure? (LESSON 1.3)
20. An angle is its own supplermmt. What is its
measure? (LESSON 1.3)
CHAPYEH 3 CUMULATIVE ASSESSMENT Z07
208
Lessons
4.1 o congruent Polygons
4.2 0 Triangle
Congruenoe
4.3 0 Analyzing Triangle
Congruence
4.4 0 Using Triangle
congruence
45 0 Proving
Ouadrilateral
Properties
4.6 0 Conditions for
Special
Ouadrilaterals
4.7 0 Compass and
Straiglrtedge
Constructions
4.8 0 Constructing
Translomrations
Chapter Project
Flexagons
Triangle
Congruence
ALL AROUND YOU—lN NATURE, ART, AND HUMAN
technology—you find things that are the same
shape and size. Such things are said to be con-
gruent. In the photos on these pages, notice
that there are many congruent triangles.
Triangles have the property of being rigid,
which makes them useful in building bridges
and other structures. Also, since any polygon
can be divided into a number of triangles, the
properties of triangles can be used to study
polygons in general.
Buchrrirlstcr Fuflcr
I'l895—l983}
J_. - _ _
X‘ if“ --v~~t ‘ “'7
>;« xi, _ -.n,z»1I
‘ ‘ml-
11l7l""'
. y.
...v"'v"'-" .
I
,-v-.
.'_‘_-5"
,1:
I
ll
About the Chapter Project
In 1939 an American graduate student at
Princeton made an interesting discovery. He
folded strips of paper to form an object called a
tlexagon.
/
Flexagons have an interesting mathematical
property. The hexalle\:-agon, for example, has
three faces, but only two are visible at anv given
time. All flexagons ha\-'e at least one hidden face.
1- :.. To lincl the hidden face, the llexagon must be
5:" folded. or “flexed.” a certain way.
I ' 7
After completing the Chapter Project. you will be
able to do the following:
0 Create a he\'aflesagon and a hexahexallexagoii.
0 Describe the patterns in the order of faces ofa
fletagon.
Mmilmrrnu Britlgc.
New Yorl.
'. l
Vl'.i:p!ii l
About the Portfolio Activities
Throughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
Chapter Project is congruent polygons.
0 ln the Portfolio Activity on page .325. vott
will use a strip of paper to fold a series of
triangles. The more triangles you told, the
closer they become to a set of congruent
equilateral triangles.
o Tessellations involve covering a surface with
congruent shapes that fit together without
gaps or overlapping. In the Portfolio Activity
on page 252. you will explore tessellations
with congruent. nonregular quatlrilaterals.
o In the Portfolio Activity on page 28l , you will
explore tessellations with congruent hes-agons
that are not regular but that have one pair of
parallel and congruent opposite sides.
209
Congruent Polygons
. \ T r
O \ ‘:3? {A
\
"\ . j
-.- '- -\' ._ ')
'— \ ,,g.‘\\. _ ‘uZi‘——\\
_ _ \\ X
Obyectives ‘\ 5
_. J
o Define congruent x ‘*1 ~_
polygons. \ 424?’ -
o Solve problems by
using congruent
polygons.
- "
V Q 7 \ V;¢v \ V‘ ‘_
VI 1 5 V 1 5* H 1
‘I ~ i
‘ i .. I
s 3 VII ‘ L 4 i
V “ \v V 5 -I v ‘
, l , t 4 “., L
_ \ 5 ‘ r I 1 A p. 5
Retpeatnrg . 1 I 1 vfi 1 I V . 1 V I
» 0
In earlier lessons you ‘ " Q ‘
learned about congruent ' I‘, , I ‘ I I ‘ I
segments and angles In [30 ’ 50'” ‘W ‘9‘ ‘ ‘V . § “.9‘ -
ms “man W" W”, jrrqiieittlp ‘xv ' ‘ ‘ ‘V. ‘ ‘ “V.
develop e definition of ¢'’’'P’0_)'*’d '" ‘C .1. V; L .4‘p L
¢,-ongmgm polygons. Islzianrr an. \ 1 y Q ‘ p I y j 9; j
Polygon congruence
Polygons I and 2 at right are congruent.
If you slide one on top of the other. you
will see that they mzttch exactly’. Can you -
think old way to determine whether two /
polygons are congruent without actually
moving them? What nieasuremenls would
you need to make? Pfilvg-fin 1 Polygon 2
If two polygons are congruent, then their respective angles and sides are
congruent. l'he converse is also true: ll" the respective angles and sides ol'a
polygon ntzttch. then the polygons are congruent. These facts will be stated
later as .1 postulate [see page 212], but first you will need to learn some
terminology and notation.
2 ‘I0 CHAPTER I
E X A M P L E flwhat are all of the possible names forthchcxagon
PROBLEM SOLVING
TRY THIS
Naming Polygons
When naming polygons. the rule is to go around the figure. either clockwise or
counterclockwise. and list the vertices in order. It does not matter which vertex
you list first.
at right?
. SOLUTION
Make an organized list. You can approach the question F
systematically. as follows: \ 0
Pick a letter lrom the figure, such as A. then write 5
the letters of each vertex of the figure. going first in
one direction and then in the other.
ABCDEF AFEDFB
Then use each of the other letters in the figure as starting points.
b'CDL-'l".'l b‘/‘l l"L'DC
CDEF.-U3 CB.»-’lFED
DFFA BC DCBA FE
EF/'lb'CD EDCb'.-°‘l!-'
FABCDE FEDCBA
In all. there are 12 possible names for the he.\'-agon.
_ _ L
What are all of the possible names
for the pentagon at right?
Corresponding Sides and Angles
ll" two polygons have the same number
of sides. it is possible to set up a
correspondence between them by
pairing their parts. In quadrilaterals
ABCD and FFGH, for example. you can
pair angles A and B and I-'. C and G.
and D and H. Notice that you must go
in the same order around each of the
polygons.
The correspondence or the sides follows
from the correspondence of the angles.
ln this case. side E corresponds to side
T‘!-‘, and so on.
LESSON 4 1 CONGRUENT P0-LYGONS 21 1
cnmcAL rumxmc How many different ways are there ofsetting up a correspondence between
the vertices of the two quadrilaterals on the previous page if they must go in
order?
When you write 21 congruence statement about two polygons. you mttst write
the letters of the vertices in the proper order so that they correspond.
E X A M P I. E The polygons at right are congruent. G
Write a congruence statement about 7 H
them.
0 SOLUTION
Write a name tor one ol the polygons. A
followed by the congruence symbol. 5
Then imagine moving the other polygon
on top of the first one so that they match e\;act|y. Finally, write the name
of the second polygon to the right of the congruence symbol. with the
corresponding vertices listed in order.
ABCD 2 EFGH
cRmcAL THINKING There is more than one wav to write 21 congruence statement for polygons
ABCD and EFGI I above. Complete the congruence statements below. and then
write all of the other possibilities as well.
BCDA =_- ? CBAD 2- ?
You should now be ready to state the Polygon Congruence Postulate.
Polygon congruence Postulato
Two polygons are congruent if and only if there is :1 correspondence
between their sides and angles such that:
° Each pair of corresponding angles is congruent.
° Each pair of corresponding sides is congruent.
4.4.1
E x A M P I. E flea»-e that AREXEAFEX.
O SOLUTION E
List all of the sides and angles
that are given to be congruent.
/_R 2 LF E2 E
/_REX I /_FEX RX an FX
¢’_l-I)\fR =_= LLIXF H X F
21 2 CHAPTER 4
Exercises
I connect .19..
: - - ‘ad
Activities
Online
Go To: go.hrw com
Keyword.
MCI Panto
I lntemelconnect 1%,?“
Homework
Help Online
Go To: go.hrw.com
Kq/wold"
MCI Homework Huh
lot EIEICISES 9. 3|]
Six congruences are required for triangles to be congruent—threc- pairs of
angles and three pairs of sides. Thus. one more pair of congruent sides is
needed for these triangles.
Notice that -1:? is shared by the two triangles. L se the Rellexive Property ol
Congruence to justify the statement that L-‘X ’=‘ L'X. This gives the sixth
congruence.so you can conclude that AREX E AFEX.
. Communicate
1. Sketch a triangle and label the vertices A. B. and C. List all of the possible
names for this triangle. Does the order of the vertiees matter in naming a
triangle? Explain your reasoning.
2. Suppose that quadrilaterals MNOP and QRST are congruent. l ist all ol the
pairs of corresponding sides and angles in the two polygons.
3. When are two segments congruent? Explain.
4. When are two angles congruent? Fxplain.
5. Explain the difference between the statements .-47 E C. and AB - CD
6. Does AB 5 CD make sense? Explain.
0 fill/ded 3k///3 Practice
7. Give all possible names for the pentagon at right. P
(EXAMPLE 1)
O T
R S
8. Use notation to write a congruence
statement about both pentagons at right. V
(EXAMPLE 2)
Z W
Y X
9. Prove that A/IBC E ADBC. (EXAMPLE 3) 3
A D
C
LESSON -H CONGRUENT F0-LYGONS 213
2 14 CHAPTER 4:
Practice mm’ 34,0;/y
For Exercises 10 and 11, consider a pentagon, ORSTU.
10. Give three other names for pentagon QRSTU.
11. Name the interior migles oi pentagon QRSTU. using three letters for each.
Suppose that ORSTU E VWXYZ
12. I is: all pairs oi corresponding angles.
13. Name the segment that is congruent to each segment below.
a.$l mm
Determine whether the pairs of figures below are congruent.
Explain your reasoning.
14. 15.
\cm
6cm
16. 17. AABC.1nd ADBC
d l B
7cm
C
18. 4 19.
_i ‘ 1. /
-1 a '—5—°:—>
_, : I. 50’-
4
For Exercises 20-25, refer to the figures at right and complete the
statements.
A E
20.8. ? bu ? B D
c. ACE ?
21. a. A735 ? b. B_C 2 ?
c. T35 ? C F
AABCE AEDF
22. a. ZMLQ E ? b. ALMP E ? L M N
c. AMPO -=« ? d. ANOPE E‘
23. a. P—Q E E‘ b. T) E E‘
""" ___ """ O P O
c. -' N 5 ? d. N05 2' LMPQ E i\=lNOP
CHALLENGES
APPLICATIONS
24.a..LA§_?_ MEL 3 F
c..LC§ ? d.LGE 7 A 7C 6
mile; _ :0 J H
25.a./Ilia; b.IIz ? E
mms ;_ a.B_‘s_;_ ABCDEE FGHII
e.fil§__?__
Given: 4L 2 AP, AM 2 40, AMOL azonp, D171 5%, W 2%,
LR=5, OR=3,and OP=5
M O
M
L R-OjP
26. LQ = E‘
27. RP = ?
28. Is £tl.MQ E APOR true?
Why or why not?
Use the figure of rhombus ABCD A
at right for Exercises 29 and 30.
29. ll’ l1ILBD;'l = A". what is mLD.-tb’? \-\-‘hat is mz1DCb'!
30. Write a two-column proof that AABDE ACBD. D 3
Given: AXYZ E ABFGH and .-SFGH E AJKL
31. What must be true about ABX Y4 and AIKL?
32. Name a property that justities your conclusion from Exercise 31.
C
33. Given .f.=.AB(’ E AACB, what can you say" about AABCE Explain your
reasoning.
34. Given AABC E ABCA, what can you say about AABC? Explain your
reasoning.
35. CARPENTRY A shop makes house- c
shaped mailboxes like the one shown
at right. The walls opposite each other 0 A
are congruent. as are the two slanted
portions of the roof.
a. Name 6 pairs of congruent .
polvgons on this mailbox. .—- '
b. Name 5 pairs of congruent angles F
on this mailbox. 7-
c. Name 5 pairs of congruent
segments on this mailbox.
36. OUILTING The quilt shown at right L
was assembled lrom 12 identical
“Balkan Puzzle" blocks. Make a sketch
of one of these blocks. l~low many ‘
different congruent shapes can you
find in the quilt? Describe them.
LESSON -1 I CONGRUENT F0-LYGONS 2 15
APPLICATIONS
CONNECTION
2 16 CHAPTER 4:
37. FASHION Janet is making a pair of
earrings out of polymer clay. She
wants the left and right earrings
to be congruent. Draw a diagram
of both earrings and label the
vertices. Write a congruence _ I
statement for the two triangles
and find the measure ol each
angle in both earrings. ’
38. FASHION Janet cuts a triangle out \ \‘
of paper and traces it onto the clay ‘
twice to make the two earrings. -
Will the earrings be congruent?
What property of congruence
justifies your answer?
£004’ 346*
A 8
DE,
41. Ll3AC':“ LDCA
Given: ABCD is a parallelogram. Justify each
statement below with a theorem, property, or
definition. (LESSONS 3.2, 3.3, AND 3.4)
asfinfiv 4o.H9||B_c
42. /_D/ICE /_B("A 43. H‘ 2 c‘_A
Determine whether each of the following statements is true or false.
Explain your reasoning. (LESSON 3.2)
44. A square is a rhombus.
45. A parallelogram is a trapezoid.
46. A parallelogram is a rhombus.
47. A rect-an le is a warallelo ram.
I
1.00.(' B870}/d
COORDINATE GEOMETRY Plot the following points on a graph and connect
them to form a rectangle: A(1, 2), Bil, 4). CM, 4), and DH, 2).
48. Use the rule F(.\'. y) = (x+ 5. y- 3) .
to transform the Iigure. Is the image
congruent to the preim-age? Why or I.
why not!
49. Use the rule l-‘(x. y) = (3x. -2)’) to
transform the figure. Is the image
congruent to the preim-age? \-\-'l1y or
why not?
Objectives
0 Explore triangle
rigidity.
o Develop three
congruence postulates
for triang|es—SSS.
SAS. and ASA.
Triangle Congruence
g The framework of the
'- Eifiei Tower contains
Architects and engineers use '3' thousands of m-angles.
triangular braces because triangles . 1- .
edd rigidity to e smrcture. The __I
rigidity of triangles has important
consequences in geometry.
r _' '9
- ‘l ED
drinking straws, string,
a ruler. and scissors
Triangles in Physical Structures
A physical triangle is rigid. As long as the sides do not change or break loose.
the shape of the triangle will not change. The rigidity oi‘ triangles contributes
a postulate to geometry. which you will investigate in Activity l below.
' I
Triangle Rigidity
1. Construct each triangle described below
from drinking straws and string. when
you pull the strings tight, your triangles "
will be rigid. '
AABC: I | \
r‘lB= 8 in..BC= 9 in.. CA = ID in. .
AXYZ:
XY = 6 in.. Y7 = 8 in.,7X = 10 in.
2. Compare your triangles with those "
made by other members of your class.
Are vour triangles congruent to theirs?
3. Given the lengths of the sides ofa triangle, can the triangle have more
than one shape? How does your answer to this question relate to the fact
that triangles are rigid?
4. Do you need to know the angle measures ol :1 triangle to make ‘.1 copy oi
it? Fxplain.
LESSON 4 2 TRIANGLE C0-NGRUENCE 21 7
CHECKPOINT ./ 5. Your work with the triangle in Steps I-4 should suggest the important
CRITICAL THINKING
geometry postulate that is partiallv given below. Complete it by filling
in the blanks.
SSS (Side-Side-Side) Postulate
It" the ? ot one triangle are congruent to the ? or
another triangle, then the two triangles are ? . 4.2.1
Are anv polygons other th-an triangles rigid?
lfyou repeat Activity I with quadrilaterals
instead of triangles. would your results be _ . -
similar? It‘ the corresponding sides of two ' V
quadrilaterals are congruent. must the 6
quadrilaterals be congruent?
6 pieces at tracing paper
and a straighredge
21 8 CHAPTER 4
Useful Geometry Tools
If you use the Pol_vgon Congruence Postulate on page ll}. to show that two
triangles are congntent. you must show that three pairs of sides are congruent
and three pairs of angles are congruent. Postulate «L2. I. which you discovered
in Activity l, provides a shortcut for showing that two triangles are congruent.
You need to show only that three pairs ol sides are congruent. ln Activity 2.
you will discover two more shortcuts for proving triangle congruence.
' 2
Two More congruence Postulates
Part I
1. Trace each tigure at right onto
a separate piece 0|" tracing paper
near the center of the paper.
ATE
Av C
2. Arrange the pieces of paper on top
of each other so that point A of each
segment is over the vertex of /_A and
the segments fall along the two rays
of the angle.
3. On the top piece ot paper, draw a
segment connecting points B and C. 4-
Trace the rest of AABC.
4. Compare your triangle with those ot othe.r members or your class. Are
the triangles congruent?
5. In a triangle, an angle formed by two sides ot the triangle is called the
irtdtnlerl angle of the two sides. (informally. it is the angle "between" the
two sides.) ll‘ two sides and their included angle are fixed in a triangle. is
the size and shape of the triangle fixed?
Cl-IECKPOINT ./ 6. Your work with the triangle in Steps I-5 should suggest the important
geometry postulate that is partially given below. Complete the postulate
by filling in the blanks.
SAS (Side-Angle-Side) Postulate
If two ? and their ? in one triangle are congruent
to two ? and their ? in another triangle. then the
two triangles are ? . 4.22
Part H
1. Trace each figure at right onto A B
a separate piece of tracing paper
near the center of the paper.
2. Arrange the pieces of tracing
paper on top of each other so
that the. vertices of the angles
are over the endpoints of the
segments. one side of each angle
lies along the segment. and the A 3
other sides of the angles are on
the same side of the segment.
3. On the top piece of paper, extend the sides of the angles so that they
meet to form a triangle. Trace the rest of A/lb'C.
4. Compare your triangle with those of other members of your class. Are
the triangles congruent?
5. In a triangle. a side that is part of two angles or the triangle is \,3.llC'd the
included side of the two angles. (lntormallv. it is the side “between” the
two angles.) If two angles and their included side are fixed in a triangle.
is the size and shape of the triangle fixed?
CHECKPOINT V 6. Your work with the triangle in Steps I-3 should suggest the important
geometry postulate that is partially given below. Complete the postulate
by tilling in the blanks.
ASA (Angle—Side-Angle) Postulate
If two 7.‘ and the ? in one triangle are congruent to
two ? and the ‘t in another triangle. then the two
triangles are ? . 4.2 3
LESSON -1 2 TRIANGLE C0-NGRUENCE 219
Using the New Postulates
The triangle postulates you discovered in the activities of this lesson allow you
to save steps in proofs (compare with the proof on pages 212-213). But much
more important is the fact that they allow you to determine triangle
congruence from limited inlormation.
E X A M P I. E ln each pair below, the triangles are congruent. Tell which triangle
congruence postulate allows you to conclude that they are congruent, based
on the markings in the figures.
a. b. c.
O SOLUTION
a. $55 b. ASA
o
m
:-
m
Exerc/ses
Communicate
1. What is the advantage of using the SSS. SAS. and ASA Triangle
Congruence Postulates instead of the Polvgon Congruence Postulate given
in lesson 4.l"
2. Given LA at right, describe how you would create
AABC in which AB = 2 inches and AC = 3 inches.
3. When using the ASA Triangle Congruence
Postul-ate. does it matter which two angles are
given? Why or why not?
A P P l. I C A T I 0 N 4. ENGINEERING \-\-‘hat is meant by triangle rigidity?
How does this property of triangles make
them especially useful for building
structures such as hridges
and towers?
220 CHAPTER 4
. qt//‘dad 3k/'//3 Practice
For each pair below, tell which triangle congruence postulate allows
you to conclude that the triangles are congruent. (EXAMPLE)
. Practice mm’ Apply
Determine whether each pair of triangles can be proven congruent by
using the SSS, SAS, or ASA Congruence Postulate. If so, write a
congruence statement and identify which postulate is used.
3- G H i J 9 F W
B X
n Y
F K
10. M n. G
0
N F H
L
P D
12. T R 13- L
c n
s 0 H
For Exercises 14-19, some measurements of a triangle are given.
Is there exactly one triangle that can be constructed with the given
measurements? If so, identify the postulate that applies.
14. AABC: AB = 5, AC = 7. BC= I0
15. ADLYE DL' = I4, L-‘I-' = 12. m/_l.-' = 75°
16. AGHI: mLG = 60° . in/_H = 60°. In/_l = 60"‘
17. AIKL: JK = 3. m/_] = -15°. m/_K = 90°
18. AM-\i'O .'t-IN = 8, mi.-W = 50°. mLN = I10”
19. AUVW: mLU= 40°, UV = l0, VW = 7
LESSON -1 2 TRIANGLE C0-NGRUENCE 221
n .. .
mm is
Homework
Help Online
Go To: go.hrw.corn
Keyword:
MGI Homework Help
for Exercises 23-31
CHALLENGE
APPLICATION
222 CHAPTER I
In Exercises 20-22, you will create a triangle from three given sides.
20. Draw a segment the same length as one of the
segments shown at right. Then set your compass to
the length of one of the other segments. Place the
compass at an endpoint of the first segment you
drew, and construct a circle. Wltat is true of any
segment that connects this endpoint of the first
segment to a point on the circle? Wlty?
21. Set vour compass to the length of the third segment.
Place the C()l‘llp21SS at the other endpoint of the first
segment you drew. and construct a circle. What is
trtte ol'an_v segment that connects the endpoint of
the first segment to a point on the circle? Why?
22. Connect both endpoints of the First segment to one ol‘ the points where
the circles intersect. What is true of the figure you created? Why?
For Exercises 23-29, complete the two-column proof below.
Given: rectangle ABCD A B
Prove: Diagonal Wfidivides rectangle
/tb’CD into two congruent
triangles.
Proof: 0 C
Statements Reasons
mat = mz D = 90° Definition of rectangle
E: n E) 23. 2
ZABD 5 (CD8 24. ?
mzxl = tn.£B = 90° Definition of rectangle
E)“ EC 25. ?
ZADB ‘=‘ ZCBD 26. ?
"DE 2 F5 27. ?
AA DB 5 23. L 29. ?
30. Refer to the definition of the center of a regular polygon on page I59.
Write a paragraph proof that the central angles ol'a regular polygon
are congruent.
31. Prove that a diagonal of at rhomhus divides the rhomlms into two
congruent triangles.
32. Suppose that two congruent triangles share a common side. Is the tigure
Formed by the two triangles sometimes. always. or never a parallelogram?
Fxplain your reasoning.
33. CARPENTRY A carpenter is building
a rectangular l)ookshell'and finds that \
it wobbles from side to side. To stalnili7e
the bookshelf. he nails on a board
that connects the top left corner to the ‘
bottom right corner. Why does this
diagonal board stabilize the book-shell? ,
A P P L I C A T I 0 III S 34. CONSTRUCTION In I'r.iming -.3 home.
certain triangles in the roof structure
must be congruent. How can you be
sure that the triangles are congruent
without i11e:1st1rir1gnr1yangles? which
triangle congruence postulate would
you use?
A B
35. QUILTING A quiltcr is making .1 quilt out
of regular liexagons that are Lmnposerl \\ /
of triangles. as shown at right. , \
a. Is AI-‘Oats ACOD? 0
Why or why not? F C
b. Is ABOAE .«3COD? -'
Why or why not? __ ‘
c. Explain two wa_vs to prove that
flFOF E flCOB.
E D
RECREATION In Exercises 36-39, pairs of triangular boat sails are shown.
Based on the congruences shown, are the sails in each pair necessarily
congruent?
36. 37.
/.
1 u
38. 39.
/\
I
J
1.
’ ‘—Ii - CONGRUENCE 223
3-» "
:2... '‘‘';..‘''.q.— _ _-_J! -___E
Look Back
Complete the two-column proof below. (LESSON 3.4;
TWO-COLUMN PROOF Given: 1’. I’; and £2 E [3
Prove: I’; I’-
Proof:
Statements Reasons
Given: quadrilateral JKLM 5 quadrilateral WXYZ (LESSON 4.1)
45. Identify an angle that is congruent to AK.
46. Identify A ssegmettt that is congruent to H.
47. Is it impossible. pOS$ibl£’, or definite that AW 5 Al ?
£00k Bfiyfllfd
Use straws or geostrips to create four segments—two that are 3 inches
long and two that are 5 inches long.
48. Form a quadrilateral from these segments. is tour quatlrilateral rigid?
PROBLEM SOLVING 49- Make a model. What type of qtltldrilalerztl do you seeln to get when the
congruent segments are opposite each other? What type of quadrilateral
do you seem to get when the congruent segments are atdjacent to each
other?
§
L
.5
.
‘..
_, .'
_———— "0, R3
K-A
224 CHAPTER I
CREATING EOUILATERAL TRIANGLES
Use folding paper. geometry graphics software. or a ruler and protractor to
draw each figure.
1. Draw two parallel lines, I’ and 2. Bisect the obtuse angle formed
m. and a transversal. p. by lines in and p. Label the angle
ltliseclor q.
P p Q
f
m m
3. Bisect the obtuse angle formed p (I
by ti and .3. Continue biseeting EX f / / / / _
angles as shown, alternating
between lines I’ and m. What m
seemstol)etrueal)outthe \« \ \ \ \ \
triangles that are created?
4. Use a long strip of paper with parallel edges. l'o|d the paper to create a
transversal. and then unfold the paper.
To l)lS'c‘(.l the obtuse angle formed. fold the paper so that one edge
matches evactlv with the crease from the first fold. Alternate folding
the strip up and down to create a long row of triangles.
I umotoonnect .29.,
am
Portlolio '
Extension
Go To: gn.l1Iw.cotI
Keyword:
MCI Triangle
5. l'he triangles should become more regular as you go. Keep making
triangles until you get a row of nine equilateral triangles. Cut off
the irregular triangles from the beginning. Using the row of nine
equilateral triangles (without further cutting), how can you make
a regular hexagon?
WORKING ON THE CHAPTER PROJECT
You should now be able to complete Activity I of the Chapter Project.
LESSON 4 2 TRIANGLE CONGRUENCE 225
Analyzing Triangle
Congruence
. t L 2
\ ' H. -\
\-
I‘. ~! ‘- _ \
Objectives \— -~
0 Identify and use the
SSS, SAS. and ASA .
congruence Postulates
and the AAS and HI.
Congruence Theorems. in me pmgws (9,-Sm rm,
discovered three different three-
e Use counterexamples _ _ _
to move In at other part conrlnneuons afsrde end angle
slde and a“g|e l"Q3$UTU$ M3‘ UOMIMINO M9 shape
combinations cannot W!’ Size of 8 triangle. In this lesson,
be used to prove you will learn two more.
mangle congruence.
A - p L 1 c A 1 1 9 N In the method of rrittrtgrtltttirnr. observers at two
FORESTRY different places each take note of their line of
sight to an object. The location of the object is
the point where their lines of sight cross. By
plotting the lines of sight on '1 map. the location
of the object can be found. Why do you think
this method is called trmrtgttltttiotz? Think about
this question as you continue your imrestigation
of triangle congruence postulates and theorems.
Three New Possibilities
You may have realized that the three-part combinations ofsides and angles
you studied in the previous lesson are not the only combinations that are
possible. In fact. there are three others. Which of the following combinations
do you think can be used to establish triangle congruence?
1. AAA combination—three angles
Valid
Omar? 2. AAS combination —two angles and a side that is not between them
3. SSA cornbination—two sides and an angle that is not between them (that
is. an angle opposite one of the two sides)
You can rule out the AAA combination by finding a L'0l.ll1t€l"c‘\tdlllpif;‘. and a
simple proof will show that the AAS combination is a valid test tor triangle
congruence. A counterexample can also be found for the SSA combination.
226 CHAPTER 4
E X A M P L E oshow that theAAAc0mbi.nation is notavalid test for triangle congruence.
O SOLUTION
In order to get a clear idea ol what you need to disprm-'e. state the combination
in the form of -.1 coniecture. as given below.
Conjectu re: If the three angles of one triangle are congruent to the three
angles of another triangle. then the triangles are congruent.
Counterexamples to this statement are
easy to find. in the triangles at right.
there are three pairs of congruent angles.
but the two triangles are not congruent.
Therefore, the conjecture is false.
AAA cottntetexatnple
E X A M P L E Oshow that thcAAS combination isavalid test for trianglccongrucncc.
O SOLUTION
The A.-XS combination can be N07,-c;h‘;h6,_g,-yen
converted to the ASA combination. 5,-des 3,9 "0, bem,ee,,
the given angles
The triangles at right are an AAS __
combination. To com'ert this to N ' 0
an ASA combination. lind the
measures of the third angle in
each triangle. Remember that the
sum of the measures of the angles fi 60° .7
ofa triangle is 180°. M 3 0 P 3 R
AAS example . . .
mA0 = I80 — [60 + 75) = 45°
m.£R = I80 — £60 + 75) = 45°
The measure ol the third angle
is the same in each triangle. so N O
40 E AR. The given side.
measuring 3 units. is the included
side ofthe 45° and 60° angles in
each triangle. Therefore, the two 60“\ 45° 60“ _ 45°
triangles are congruent by the ASA M 3 0 P 3 R
Congruence Postulate. . . . can be convened to ASA.
CRITICAL THINKING 'l'he two triangles at right represent a The missing angle
version of AAS. but the triangles are /measure is 75"-
not congruent. There is an important ‘
dilTerence between the two triangles. 3
What is it? E
® 45 5
Is this an example of AAS?
LESSON 4.3 ANALVZINGTRIANGLE CONGRUENCE 227
TRY THIS
For an AAS combination to be used. the congruent parts must correspond.
Notice carefully the wording of the following theorem:
AAS (Angle-Angle-Side) CongruenceTheorem
lf two angles and a nonincluded side of one triangle are congruent to the
corresponding angles and nonincluded side oi another triangle. then the
triangles are congruent. 4.3.1
The three combinations you studied in Lesson 4.2 are postulates. but the AAS
combination is a theorem. You will be asked to prove this theorem in the
exercise set.
Which pairs of triangles below can be prox-en to be congruent by the .-'—\.v‘\S
Congruence ‘l'heorem?
E<(>\\ :<Q\ dr ;
%>\
&
E X A M P L E oshow that the SSA combination is notavalid test for triangle congruence.
228 CHAPTER 4
O SOLUTION
It is a little more ditficult to find a
counterexample tor this conjecture.
but the figures at right provide one. 3
The sides and angles are congruent. A
but the triangles are obviously not
congruent. Therefore, the conjecture
5
SSA counterexample
is false.
When you try to draw :1 triangle for
an SSA combination. the side opposite
the given angle can sometimes pivot like
:1 swinging door between two possible
positions. This “swinging door" ellect ,_ __ ,
show that two triangles are possible tor "swinging door“
certain SSA information.
The “swinging door” etlect, which invalidates certain SS.-\ information as a test
for triangle congurenee. does not always pose .3 problem—-as you will see in
the next section. (See also Exercises 38-39.)
A Special Case of SSA
ii‘ the given angle in an SSA combination is
a right angle. then the “swinging door" side
cannot pivot to touch the ray in two different
places as in the illustration in Example 3.
Thus. if the given angle is a right angle. SSA
can be used to prove congruence. In this case,
it is called the Hvpotenuse—l/eg Congruence
Theorem. You will be asked to prove this
theorem in the exercise set for Lesson 4.4.
The perpendicular segment
touches the line at just one
point because iris the shortest
segment that can be drawn
from the point to the line.
HL (Hypotenuse-Leg) Congruence Theorem
ii" the hypotenuse and a leg of a right triangle are congruent to the
hypotenuse and a leg oi" another right triangle. then the two lrlallglcs
are congruent. 4.3.2
E X A M P L E When \-'em1s rises before the Sun it is known
PROBLEM SOLVING
as a morning star. When it sets alter the Sun, VOW’
it is known as an evening star.
Venus rising ahead of the Sun l
as a morning star: E
The diagram shows why \-'en us can be both
a morning star and an evening star. Note:
The daily rotation of the Earth and the orbits
ofthe planets are both counterclockwise.
viewed from above t_ from the north].
Venus as
evening
star
Venus as
morning
star
Venus is a morning star when it is to the
right of the dashed line in the diagram. it
is an evening star when it is on the left
‘_.
I’
The orbits of Earth and Venus are nearly circular. The radius of F2-.n'th"s orbit is
about l.S x i0" kilometers. while the radius of Venus’s orbit is about l.l x 10“
kilometers. Make a scale drawing of the positions of the Sun. Earth. and Venus
when Venus rises as :1 morning star 30° ahead of the Sun.
‘Earth
SOLUTION
Make a diagram. There are two possible positions
for Venus for :1 given position ol‘ Earth. This is an
SSA combination, with the Sun. Earth. and Venus
at the vertiees of a triangle. The side connecting
Venus and the Sun is the “swinging door.”
LESSON 4.3 ANALVZINGTRIANGLE CONGRUENCE 229
Exemses
. Com»/my/mte
1. Think of a memory aid. or nmemonic device. to help you remember that
SSS, SAS, ASA. and A.-XS are all valid tests For triangle congruence and that
AAA and SSA are not valid tests.
For Exercises 2 and 3. is the given information sufficient to determine
whether the triangles are congruent? Why or why not?
2. Any two corresponding angles and one corresponding side are congruent.
3. .-my two corresponding sides and one corresponding, angle are congruent.
4. Explain why any two corresponding sides are sulficient to determine
congruence for right triangles.
A P P L I c A T I 0 N 5. FOREST RY In the method of triangulatioma triangle has one vertex at the
object being observed and one at each observer. Vt-'hieh angles and sides
are known in this triangle? \'\"i1lCh postulate or theorem guarantees that
the triangle is “uniquely determined"—that it is the onlv possible triangle
with the given measurements?
0 Q/I/4'64’ SK’///8 Practice
For Exercises 6-8, is it possible to prove that the triangles are
congruent? Explain your reasoning. (EXAMPLES 1, 2, AND 3)
6. 7. 3.
A P P L I c A T I 0 N 9. ASTRONOMY Copy the diagram of the positions ofthe Sun, Earth, and
Venus on page 229. Use the diagram to estimate the distance from Earth to
Venus for both positions of Venus. (EXAMPLE 4)
230 CHAPTER I
D lnhmolcnnnect 9‘!
3&4
Homework
Help Online
Go To: uo.ln1w.r:um
Kay‘/mid:
MOI Homework Help
for Exercises 10-19
. Practice 4114' Apply
In Exercises 10-19, detennine whether each pair of triangles can be
proven congruent. If so, write a congruence statement and name the
postulate or theorem used.
10. B X ‘I1. D K5
A K G F
A C 2 Y
12. J
13.p QU
K
"s 7
‘I4. D W X 15. L E
F E Y M F
16. B C 17. X
W Y
A F E D Z
18. 19.
N P J
0
O
M G H I
For Exercises 20-24, refer to axvz below, in which W 2 E. Copy the
figure and mark the congruent sides.
_ — X
20. Draw a segment perpendicular to Yd
with one endpoint .11 X. Label the other
endpoint W.
21. ldentilv the two right triangles formed by
W1’ and name the hypotenuse of each. Y z
22. W hat can you about the hypotenuse: of the two right trizmgles?
Explain your reasoning.
23. Which properly proves that W'X '=' WX?
24. What can you say about the two right triangles in the figure?Wl1ich
theorem or postulate justifies this conclusion?
LESSON 41.3 ANALVZINGTRIANGLE CONGRUENCE 231
CHALLENGE
TWO—COLUMN PROOF
CHALLENGE
232 CHAPTER 4:
For Exercises 25 and 26. refer to the diagram below.
25. Given: LA E LD, -A‘? ETJC-: and A _B C
41354 2 LECD ‘ 2
Prove: A.-’lFB E ADCE 3 4
26. Given: 4: 2 44, TF5 IT; and 4.4 E LD F E o
Prove: AAFBE ADCE
For Exercises 27-29, refer to the diagram below.
27. AJKL 2 r_\.M1<L bv ? K
23. AMKI. 5 AMNI by ?
29. AIR’! 2 r_\..x.-mi b} 2 M
J N
L
For Exercises 30-34. determine whether the given combination of
angles and sides determines a unique triangle. If so, identify the
theorem or postulate that supports your answer.
30. AABC: .-’tB= 6, mLB= 70°,and l'I1.fi.-*'l = 40°
31. ADEF. DL‘ = 5, L‘!-‘ = 7, and mLl-' = 30°
32. AIKL: nnfil = 50°. mils’ = 75".a1nd m.LL = 55°
33. £tM.’\'O. MN: 8. M0 = lU.und m./_N = 90°
34. APQR PQ= I2, mLP = 45°. and m.iLR = 100°
For Exercises 35 and 36, copy equilateral triangle ABC below.
35. l)r-aw the angle bisector of LA, and label the
intersection with l’:—Cas D.
a. What can you s-.1y-.ibout AA BD and AACD?
\-\-'hich postulate or theorem justifies your answer! A
b. \-\-'hat.1re in/_ADB-.1nd IIILADC? Explain your
reasoning.
36. Draw the bisectors of LB and LC, labeling the
intersections with the opposite sides as E and F. 8 C
respectively. VV rite :1 paragraph proof that AD.
and _C_!-‘divide A/tb‘C into six congruent
triangles. llint: Use your results from Exercise 35.
37. Write .1 two-column proof of the AAS Congruence Theorem.
ln Exercises 38 and 39 you will further explore SSA combinations. if
two sides and a nonincluded angle of two triangles are congruent. then
the triangles are not necessarily congruent. However, if certain
restrictions are placed on the side lengths or angle measure, it is
possible to show that the triangles are congruent (see Lesson 10.4).
38. Try to draw AABL with each set ofside and angle measures below. How
many different triartgles can you draw for each set of ttleztsttrenients?
a. .48 = 4, BC = l_. and tmfii-’t = 75°
b. AB = 3-. BC = 2. and in/_i-‘t = 60°
c. AB= 5. B('= 4. and IIIL.-*'l = l0O°
39. Trv to draw AABC with each set of side and angle measures below. I low
many dilferent triangles can you draw lor each set of measurements?
a. AB = I, M}: 4, and inzzl = 75"
b. AB = 2. BC = 3. and Inz.-‘X = 60°
c. AB= 4, BC= 5, and nnf.-‘X = lU0°
d. Complete the following, conjecture:
SSA Conjecture
In an SSA combination. if the given side opposite the given angle is
E’ the other given side. then the triangle is uniquely determined.
Under these cond it ions, SSA can be used to establish congruence.
Test vour conjecture by making up some triangles ol your own.
A P P L I C A T I 0 N S 40. ARCHAEOLOGV A student is estimating the height ofa pyramid. From a
certain distance, the angle of elevation of a point on the highest part of the
structure is 25°. From a distance of I90 feet closer, the angle of elevation of
the point is 30°. Draw a triangle with the point at the top of the structure
as one vertex, and the points where the measurements were made as the
other vertices. Which postulate or theorem can be used to show that this
triangle is uniquely determined?
The 'Tt'mplc of Ktlkuikuri or Chicken I121: The lveigln of the structure can be
estinmred by a rutrtlvod that involves cieatiilg rt triangle (is described in E.xert‘ise' 40.
The nmmi coinpurutions involve ti-igommierry. which you will srmly in (Vmprrr I0.
41. ARCHAEOLOGV Make a drawing of the triangle for Exercise 40, using the
scale IO-D feet = I centimeter. Use your drawing to estimate the height of
the pyramid.
42. ENGINEERING An emhankment rises at an angle of 20° from horizontal. On
the embankment, two l0—foot vertical poles are each anchored by a guy
wire to the ground directly uphill from each pole. If the guy wire of each
pole makes an angle of 60° with the embankment. must the wires he the
same length! Which postulate or theorem justifies vour answer!
43. NAVIGATION Towns A. B. and C are connected by straight roads. For each
set of measurements given below. draw a possible map. and determine
whether AA BC on your map is uniquely determined. if so, state which
theorem or postulate supports your answer.
an. AB = l2 miles. BC: 7 miles. and AC: 8 miles
b. Ab‘ = 6 miles, m.«£BAC = 40°. and mm BC = 60°
c. m.£BAC = 75°. IIIZABC = 50°. and tn.£ACB = 55°
LESSON 41.3 ANALVZINGTRIANGLE CONGRUENCE 233
Look Back
44. Draw three lines that intersect at a point. (usssow 1.1)
45. Draw three lines that do not intersect. (LESSON 1.1)
-:8. Draw two lines th-at intersect at third line without intersecting each other.
(LESSON 1.1)
In the diagram at right, £ ll m.
47. Identify all congruent angles in the diagram
at right. (LESSON 3.3)
48. Identify a pair of supplementary angles that
are not a linear pair in the diagram at right.
What is this type of angle pair called?
(LESSON 3.3)
49. The angles of a triangle measure (2x]°. [3x)°. and (»txl°. Find each angle
measure. (LESSON 3. 5;
‘\
V.
\
\
50. What can you say about the interior angles oi a triangle th-at has two
congruent exterior angles? (LESSON 3.6)
L004’ Bel/0/rd
51. Consider two regular pentagons. Are they necessarily congruent? What
information would you need to have in order to show that two regular
polygons are congruent?
A P P L I c A ‘I’ I 0 N 52. SPORTS A soccer ball is composed of regular pentagons and regular
hexagona. Are all of the regular pentagons congruent? Are all of the regular
ltexagons congruent? Fxplain your reasoning.
234 CHAPTER 4
Using Triangle
Congruence
‘ srswe *
. J __ 5 . z
—~ at __n .
‘I3. _ .‘ s _ _' ,QE-''.- .2
._ .. _ - . was
w . r-~ \ '
:. s ‘ )§_;§ »« 4; at
Q. . ‘ . . _ - . \ '1.
1.6-. _ . , . ~ ._
§‘_ #3? «i € ‘/44 '._, t
Objectives . - ——_ /E \ . . .
‘is. ._. _ -h _ '_‘</ )>__-: - )
0 Use congruence of '5?‘ '\\._ '7‘: E 5 ' ~.}'
triangles to conclude , - " V \ ‘
congruence ol 3;. " 3‘ ’ R ' ' ‘Q -_ wi
corresponding pans. ” - -
0 Develop and use the
Isosceles Triangle
Theorem.
Ll I2 I'I-.hv'i 'Sq|un- ’imi" OWW -Inn! III In
It \' Lam ll -hr-J. ‘tllrlyjm t¢5d'\¥\l.
The design elements of this woodcut by
M. 0. Escher are metbouratically related. llra
size of one part determines the size of another
By using chains of matltentatlcal - — rnlng
you can deduce things about one part of a
figure from lnlormatlon about another part.
CPCTC in Flowchart Proofs
It follows from the Polygon Congruence
8 E
Postul-ate (given in Lesson AM) that if
two triangles are congruent, then their
corresponding parts are congruent.
l'herefore. if A_\BCE_A DL-‘l-‘. you can A D
conclude that AB E DE What other pairs
of sides and angles must be congruent? C F
This idea is often stated in the following It AABCE ADEF, then H; 5 E, . .
form: Carrespmuling parts o_ft'on_qrm'rzt
triangles are congruent. abbreviated as Cl-‘C I‘ C. In each proof in this lesson.
you will use a triangle congruence postulate or theorem to establish that two
triangles are congruent. Then you will use CFC TC.
In the following, examples, the flowchart proof is introduced. This type of
proof will be especially useful for undersanding more complicated proofs that
occur later in the book. but it is best to begin with simple examples.
LESSON 4 I USINGTRIANGLE CONGRUENCE 235
E x A M P L E oGiven: Kc’7s§r‘).?:Ts‘rfi.-.:ndzc:szr.> C
is
FLOWCHART PROOF
CRITICAL THINKING
Point X the midpoint of TB.
Use eo__i_1gru_e_nt triangles to show A X 3
that AX E BX {and thtI$..-XX = BX),
l'hen use the definition ofa midpoint.
Prove:
Plan:
D
O SOLUTION
Arrange the information as .1 flowchart, with the given information in l)-t).'(e‘s
on the left (or at the top]. The goal is for each ol your ho.\'es to lead to the
desired conclusion. which is usually in .1 box on the right side [or at the
bottom) of the chart. Write the justificdtion lor each statement below its I1-ox.
_ AACXEABDX }—
WEW __ Xis the midpoint]
iAX= Bxl Of
SAS 1
CPCTC Def. of midpoint
Given
You can also write the statements in the boxes and their jtistitications as a two-
column proof. which way is easier for you? which way do you think is easier
for another person to read and understand?
Why can vertic.-al angles A/IXC and Ab’ ND not be used in this proof in place of
AC and AD?
E x A M P L E oGiven: .Tt§sfi,.TtTs?T»,zAszr) E F
FLOWCHART PROOF
236 CHAPTER 4
Prove: '=“
Plan: Use the Overlapping Segments
l'heorem to show that A—C '=“ W
and thus. AACE E ADBF by the A 8 C D
SAS Congruence Ptusttildtflhel
use CPCTC to show that LL‘ E FB.
0 SOLUTION
E =- W‘ AC = D8
(A3 = DC} (Tc 2 EB)
Given Overlapping
Segments Theorem fr
AACEaADBF ]— .\_ Ezfi ]
Given SAS CPCT C
Given
CRITICAL THINKING
TRY THIS
FLOWCI-{ART PROOF
The lsosceles Triangle Theorem
An isosceles triangle is a triangle with at least
two congruent sides. The two congruent sides
are known as the legs of the triangle. and the /
remaining side is known as the base. The angles L99 ” "‘- L99
whose vertices are the endpoints of the base are / 3359 3.19195
4-
Base
Vertex angle
known as the base angles, and the angle opposite
the base is known as the vertex angle.
is an equilateral triangle an isosceles triangle? Explain.
the following theorems. which vou may have already conjectured, are among
the great classics of geometry:
Isosceles Triangle Theorem
If two sides of a triangle are congruent. then the angles opposite those
sides are congruent. 4.4.1
Converse of the isosceles Triangle Theorem
If two angles ofa triangle are congruent, then the sides opposite those
angles are congruent. 4.4.2
Using the plan provided below, write a flowchart proof of the isosceles
Triangle Theorem.
Given: C
Prove: LAE LB
Plan: Draw the bisector ol the vertex angle and
extend it to the base as shown at right.
Show that the two triangles that result arc
congruent by SAS. I'hen use CPCTC. A
D
W
Two corollaries
A corollary of a theorem is an additional theorem that can easily be derived
from the original theorem. Once the theorem is known. the corollary should
seem obvious. .-\ corollary can be used as a reason in a proof, just like a
theorem or a postulate.
There are a number of corollaries to the lsosceles Triangle Theorem that you
will be asked to prove. The corollaries on the next page are two of the most
important ones. You will be asked to prove them in the exercise set.
LESSON 4 I USINGTRIANGLE CONGRUENCE 237
Corollary
The measure ol each angle ol an equilateral triangle is 60°.
4.4.3
Corollary
The bisector ol the vertex angle Qt‘ an isosceles triangle is the
perpendicular bisector of the base. 4.4.4
E X A M P L E 0A resort owner plans to install a gondola ride across a small canvon on her
property. study the diagram below. What is the distance across the canyon?
‘ ‘ '1 '° ” 0 SOLUTION
CONSTRUCTION The 30° angle is an e\‘terior angle.
,4 ye, , By the Exterior Angle Theorem: . v *
mex + 40° = 30° '
mLX = -10” l
Because two angles of the triangle
are congruent. the sides opposite
them are congruent. by the Converse : .- "1
of the Isosceles Triangle Theorem.
‘I herefore. the distance across the
canyon is 350 feet.
fxerc/ses
Cfllfilfilllf/'6'dt'€
1. What is C PCT C? I-low would vou use it in .1 proof?
2. What is a corollary? How is a corollary related to a theorem?
3. lfa triangle has three congruent angles. is it necessarily equilateral? Why
or why not?
4. Can .1 right triangle he isosceles? Cm a right triangle be equilateral?
Explain your reasoning.
238 CHAPTER 4
FLOWCHART PROOFS
APPLICATION
. 6;/idea’ Ski//3 Practice
Complete the flowchart proofs below. (EXAMPLES 1 AND 2)
Given: ABC DE is .1 regular pentagon. A
Prove: .fl.r’lCl') l5 i$0SCE'lE5 l.*lC= AD]. E 8
Proof:
I AB=AE Lm.éB=m.éE BC=ED D C
Def. of reg. Def. of reg. Def. of reg.
polygon polygon polygon
5. ? '
SAS
I
AC = AD
6. ?
Given: QRSTis a rectangle, TU = V3. and Qt" = RU. O R
Prove: .fl.QTV E .fl.RSl'
Proof:
T U V S
mfg:-Vflj ZOTV ZRSU
Def. of act. '“ = m 2
r tzorv 5 znsu) ‘OW ‘ MS“
i 7
"V-’R5U = 9° Transitiwty 8' '
or
Def‘ of ram‘ Substitution
Given
9. CONSTRUCTION lemme wants _ - -
to estimate the distance across 1
a river from point A to point 8.
Starting at point A and facing
directly opposite point 8, he
turns 50” to his right and walks
in .1 straight line to point C,
where the angle between the
lines of sight to points A and B
is 25°. How does he know that
the triangle formed by points
A, B, and C is isosceles? If
Ierome walked lO0 feet from
point A to point C, what is the
distance across the river?
(EXAMPLE 3)
LESSON 4 I USINGTRIANGLE CONGRUENCE 239
‘x
\
\
PROOFS
- - conned .?,';’I‘
10
Homework
Help Online
Go To: go.lnw.corn
Keyword:
MG! Ilnrncwork Help
for Exercises 20-22
240 CHAPTER I
Practice mm’ Apply
Find each indicated measure.
10. mAZ X
V4
2
o
11. KL
K
g
M L
12. QR 13. ml!‘ E
G
1-1. mz.=1BD 3 15. CI! F
65 ” J 12 G
A C
D
18. PR P 17. mm, L
//\-"X + 3 I
‘ X
(x+1i O M
iv"39X+4D)°
R \
Ni
For Exercises 18 and 19, write flowchart proofs.
18. Given: [A E Jr). .-’lB= DE. 19. Given: \"'W' = WX and
and AF= DC VY = XZ
Prove: £3 E ZE Prove: E. W'YZ is isosceles.
w
A F c 0 V Y 2")‘
For Exercises 20-22. refer to the diagram below and write a flowchart.
paragraph, or two-column proof.
20. Given: H3 1| FE, and Cis the midpoint of 'B—E.
Prove: E E E B D
21. Given: AABCE ADEC
Prove: II E" C
22. Given: E E WE-and E 1| W A '5
Prove: C is the midpoint of
FLOWCHART PROOF
TWO-COLUMN PROOF
PROOFS
CHALLENGE
Complete the flowchart proof below of the Converse of the lsosceles
TriangleTheorem.
Given: AX E Al’and T2 J. W Z
Prove: E E T2
Proof:
Given
i mZXWZ = 90'
Given
m£Xl/l-‘Z = mzYWZ
IAXWZ = AYW27
‘>:AXM’ZEAYlr’lr'ZJ—-[W572]
25. ? 26. r
23. 7
Complete the two-column proof below.
Given: E 2 B_c-and AABX 2 4cm 3
Prove: E FTC
Proof:
Statements I Reasons A X C
/Tb‘ E b’—C Given
AABX E ACBX Given
[TX 5 B—X 27. ?
AABX E ACBX 28. E‘
H 2 FX 29. ?
Based on the two-column proof above, complete the following
statement, which you can use in your proof of Corollary 4.4.4 in
Exercise 33.
The 30. E’ of the vertex angle of an isosceles triangle 31. 7.’ .
32. Write a paragrapli prool ol'Coro|l;1ry4.4._’» on page 253.
33. Write a paragrupli proof of Corollary -l.-1.4 on page 23-8.
34. L15»: the diagram below to prove that T E GH.
J I
B C E F
l.E$SON -I I USING TRIANGLE CONGRUENCE 241
APPLICATIONS
APPLICATION
CONNECTION
PROOFS
242 CHAPTER I
35. SURVEYING A surveyor needs to
measurelthe distance across a pond V 30 m ‘D m T
from point I to point B. Descnbe
how the measurements shown in 3‘ "‘ X
the diagram at right enable him to 40 m 30 m
determine the distance. 2 3
36. ROAD SIGNS A yield sign is an equilateral
triangle. What can you say about the angles
YIELD
of the triangle? Fxplain your reasoning.
L001? Back
Determine the sum of the interior angles and the sum of the exterior
angles for each polygon. (LESSON 3.8)
37. square 38. hexagon 39. dodecagon
40. ROAD SIGNS A stop sign is a regular
(equilateral and equiangular) octagon.
Are all equilateral octagons equi-angular?
Are all equiangular octagons equilateral?
Fxplain your reasoning. {LESSON 3.1)
STOP
CDORDINATE GEDMETRY Points AIO, 0) and B(3. 6) are endpoints of AB.
Point CI3, 1) is an endpoint i CD. For each point D given below,
determine whether 15 and CD are parallel, perpendicular, or neither.
{LESSON 3.3)
41. DH, 2)
42. DH, 4) 43. D[2,—l}
1001? Beyond
Another proof of the lsosceles Triangle Theorem was “discovered" by a
computer. |'his proof had been done by the Greek geometer Pappus of
Alexandria (320 C.E.) but had not been known to ntathematicians for
centuries. It is much simpler than Fuc|id's prooliol the same theorem (which
is quite complicated) and even simpler than the one given in this chapter.
DlSC(Wf;‘l' it for yourself below.
44. Given: A.-SBC is isosceles, and K ’=" 17?. C
Prove: LA E LB
Plan: Show that AABC 5 Ab‘ ‘IC.
45. Use the plan given for Exercise 44 to prove the
Converse of the isosceles Triangle Theorem.
Proving Quadrilateral
Properties
V
Objective \ 5
. l
0 Prove quadrilateral
coiuectures by using
triangle congruence h
flfgfgfifif and In Chapter 3 you made coniectures about
- - .- properties of quadrllaterals. Now. with
dte help of the trisnyle cr - 3 -nce postulates
and theorems. you are in a position to - I -
your cooi9ctums—i! they are two.
A - p i c | o N A property of rhomhuses explains why this lamp asseittlily stays perpendicular
ENGMEENNG to the wall as it moves. You learned this property as a conjecture in Lesson 3.2.
Do you know which property it is?
An Important Conjecture and Proof
In the Activity below. you will make it conjecture about an important property
of parallelogranm. The proof of the conjecture is given on the following page.
Rotational Symmetry in Parallelograms
1. Trace the parallelogrmn at right onto P L
two sheets of tracing paper.
2. Place one figure over the other so that
.‘ they match. Place the point ol your
\ . . - . - .
' pencil at point C. and hold ll hrmlv in
place. Rotate the top piece ol paper M G
\ l80°. Describe the result.
‘ 3. Does APLM seem be congruent to AGML? Fill in the blank to complete
the conjectu re below.
Conjecture:
CHECKPOINT V A diagonal of a parallelogram divides the parallelogram into ? .
LESSON ¢.5 Pnovin-3 OUADRILATERAL Pnoeermes 243
CRITICAL THINKING
E x A M P L E .Given: parallelogram PLGM with
CRITICAL THINKING
244 CHAPTER 4
In the diagram below. the diagonal ML IS a tr.ms\-ersal to two dtllcrent pairs
of parallel lines. Name those parallel lines. List the alternate interior angles for
each pair of lines.
diagonal W
Prove: ALCJU E ANIPL
0 SOLUTION
Proof A (paragraph format):
Proof B (two-column format):
Statements
./
%
L
/G
E and are parallel. .ILC()l'Cllng to the delinition of a parallelogram.
Therelore. A3 and A2 are congruent alternate interior angles.
Sitnilarly. .41 and A4 are congruent because W and W are also
parallel. Finally. diagonal LM is congruent to itself. 1 hus, two angles
and the included side are congruent in &.I.G.-\-l and AMPL. Therefore,
the triangles are congruent by the ASA Congruence Postul-ate.
Reasons
1. Parallelogr-amfl.GM
has diagonal LM.
2.fi.||E.7
3. £35 £2
4.W||§l:
5. Al 5 .44
6.mE
7. ALCM 5 AMP}
Given
Def. ofa parallelogratn
|| lines = alt. int. angles 5
Def. of a pa rallelogram
|| lines =3 alt. int. angles 5
Rellexive Prop. ot'Congruence
AS.-\ Congruence Postulate
This result is stated as a theorem on page 217. In Exercises 24-30, you will be
asked to complete a flowcliart proof of this theorem.
How can you use the result from the Iixample to prove that opposite angles of
.t p.tr.tllelt)gr;tm are congruent? You will be asked to write this proof in the
exercise set.
A System of Geometry Knowledge
With the theorems. postulates. and definitions you now know. you can prove
all of the conjectures you have made about the properties of parallelograms
and the other special quadrilaterals. It is best to start with the simplest ones
first. As you progress. you will find that it is often possible to ttse a previously
proven result as part of a proof ofa more complicated theorem In this way,
you are building .1 system of knowledge.
l'he exercises in this lesson and the next will guide you through at series of
proofs of the conjectures about quadrilateral properties that you made in the
Activities in Lessons 3.?» and 3.4. The earlier exercises will give you the most
guidance. but in the later exercises you will be on your own.
Exercises
. Communicate
. 6/ridedski//s Practice
APPLICATION
1. As you proved in this lesson. .1 parallelogram has I80” rotational
symmetry. Describe all oi" the types of symmetry of rectangles. rhomhuses.
and squares.
2. For parallelogram PQRS. state all pairs P 0
of congruent triangles that are formed [
l)y diagonals a and Eintersetting
at point X. S R
3. Is ‘theorem 4.5.2 on page 247 true tor
rectangles? Why or why not?
4. is Theorem -1.5.3 on page .248 true for rhombuses? Why or why not?
Find the indicated measures for W x
parallelogram WXYZ. (EXAMPLE)
5. tnAWXZ 6. mz W 7. XY
8. CONSTRUCTION lfa ramp has a rise of more than 6 incl'tes. handrails that
are parallel to the ramp are required on both sides. lfthe upright post at
the bottom of the ramp is 36 inches tall. how do you know that the upright
post at the top of the ramp is also 36 inches tall?
36 in.
LESSON 4 5 FROVING OUADRILATERAL FROFERT|ES 245
In Exercise 9-16, find the indicated measures for each parallelogram.
9- (‘D 10. DA 3 7 C
11. m.ZC 12. mzf) % ;
50'
A "TD
13. mAQ 14. m.4RPQ P 0
15. m.4sPR 16. mzPRQ 5
60" 40°
3 7.7 H
' 5 . / In Exercise 17-22, find the indicated measure for each parallelogram.
17- S\-' 18. ml:-S
3 T
a + 7 43 " 2
V U D
19. QR R 20. CD
C D
a 10 V
6 -2
X S x — 7
T x + 4
21. m.(N 22. mZG
M N F
0 E
(Gar + 16)°
.4 Ix‘ 4) 27
P O H G
23. State vshcthcr each pair of lri-angles could fit together to form .1
parallelogranl (without reflecting). Justify your answer.
A VXVQQ
246 CHAPTER I
In Exercises 24-71, you will be asked to prove theorems about
quadrilaterals.
Fill in the blanks below to complete a flowchart proof of Theorem 4.5.1
(refer back to the Example on page 244).
Theorem
A diagonal ofa p-.1r.1||clogran1 divides the parallclogr-tun into two
congruent triangles. 4.5.1
_ . . — A B
FLOWCHART moor Gwen: par-.1|le|ogr.un1 A BCDwnh diagonal BD
Prove: QABTJE &.CDB
Proof: 0 C
E I W) Z >
24. ?
26. ? V . ? -T * ABDE D8
.28 —J _ A M
27. ? 29. 9: 31. ?
Reflexive Property
of Congruence
Complete the proof below of Theorem 4.5.2.
Theorem
Opposite sides of it p.tr.tllelogr.tm are congruent. 4.5.2
TWO-COLUMN PROOF Given: p;1ra|le|ogr.nn ABCD with diagonal B—D A B
Prove: ms T)-and E E Tb‘
Proof: D C
Statements Reasons
ABCD is it parallclograin. 32. ?
33. ? A diagonal oh parallelogram
divides the par.lllelt)gran1 into
two congruent triangles.
A—I3sC—i);1ndA—I)*='fi3 34. ?
LESSON 4 5 Pnovmc OUADRILATERAL PFl0FERTtES 247
TWO-COLUMN PROOF
£9
flhlemau -
Homework
Help Online
Go To: go.lrrw.corrr
Keyword:
MGI Hun-rcworlt Help
for Exercises 41-48,
60 66. 69-1|
248 CHAPTER 4
Complete the proof below of Theorem 4.5.3.
Theorem
Opposite angles of a parallelogram are congruent. 4.5.3
Given: parallelogram ABCD with diagonals filand A B
Prove: Ab’/ID 2 ADCB and 4 WC ’=' ACDA
Proof: 0 C
Statements
ABC D is a parallelogram. Given
AABDE 35. j?_ 36. 3.’
AB.-tr 5 37. L 33. =3
39. 3'
I Reasons
and 40. ? CPCTC
41. Write a paragraph proof of Theorem 4.5.4. Begin by drawing an
appropriate diagram and writing out what is given and what is to be
proved. [Your proof should be very short.)
Theorem
Consecutive angles of a parallelogram are supplementary. 4.5.4
Complete the paragraph proof below ofTheorem 4.5.5.
Theorem
The diagonals otia parallelogram bisect each other. 4.5.5
Given: par-alliogranr ABCD with diagonals K‘
and BDinterseLting at point E
A B
Prove: Point F is the midpoint of Iaand E ~
Wand H)-are parallel by 42._ ? so ABDC and ADBA
are congruent 43. ? angles. AIs£);_zAQ') and ZCAB are
congruent alternate interior angles, and A32 CD because
44. ? sides ofa parallelogram are 45. ? .
AABF E £sCDFb_v 46. ? . TF2 W7bec-arise 47. ?
so point E is the midpoint of -E'—L'-)l))' definition. Also. 1-‘TEE ("—E
because 48. ? , so point E is the midpoint of A—Cb_t' the
definition ofa midpoint.
Proof:
TWO-COLlW|lll PROOFS
In Exercises 49439. you will complete proofs of the following theorems:
Theorems
A rhombus is a parallelogram. 4.5.6
A rectangle is a parallelogram. 4.5.1
Given: rhombus EFGI I
.<]>.
Given: rectangle PQRS
Tfi.
H SCLC R
Prove: fi?||fi.md F_c;||fi Prove: P_QnR_s.md fiufi
Proof: Proof:
Statements Reasons Statements Reasons
F 5 T 49. ? ml P: 90* Del". of-a
E 5 W‘ Del". ol‘:1 "“‘”‘"?'~|“
rhombus mAS= 90° 55. ?
W5? 50. ? mAP+ mZS= 56. 7.’
AFFH 5 &.GHF 51. 2 ‘fly’ _
AFFH 5 AGHF CPCTC "Q ll R3 57- ?
Ellfifi 52_ ? mzQ= 90‘ 58. ?
AGFH E 41.-HI: 53_ ? mzl’ + m£Q = Add. Prop. of
_—‘ _— I80” Equality
I-c. || LH 54- ? __ __ ,
PS || QR 59. 4
Complete the paragraph proof below of Theorem 4.5.8.
Theorem
The diagonals ol a rhombus are perpendicular. 4.5.8
E F
Given: rhombus DFFG with diagonals fi‘and '(-if
intersecting at point H
Prove: Wand H‘ intersect to form -.1 right angle.
Proof: D G
F—F 5 FT by 60- ? . DFFG is a parallelogram (Theorem 4.5.6),
and so EH E (-774. because 61. ? . T-'fi ’=' E by 62. ? .
&.EH!' 5 &.GHI- by 63. ? . Al-‘HG E A!-'HL because
64. ? . Because AFIIG and .£FHEare -.1 linear pair, the sum
of their measures is 65. ? . Because ZFHG E ZFHE. their
measures are equal, and thus, mzi-‘HG = ml!-'HL' = 66. ? .
LESSON 4 5 Pnovmc OUADRILATERAL PFl0FERT|ES 249
PROOFS
PARAGRAPH PROOFS
250 CHAPTER I
67. Write a two-column. flowchart. or paragraph proof of 1 heorem 4.5.9.
(Hint: A rectangle is a parallelogrant; therefore, it has the properties ofa
parallelogram.)
Theorem
The diagonals of .1 rectangle are c()ngru':‘nt. 4.5.9
Given: rectangle RSTU with diagonals R—7'.Ind F] R S
intersecting at point V
j : V
Prove: RI‘ 5 US -
U T
68. Write a [W0-L‘Oll.ll11n, llowchart. or paragraph proot of Theorem 4.5.10.
Recall that a kite has two pairs of congruent adiaeent sides and that
opposite sides are not congruent.
Theorem
The diagonals of a kite are perpendicular. 4.5.10
Given: kite l-V.X'1’Z with diagonals W and .7
intersecting at point A
Prove: EWLX7
ZX
‘IV
Y
Write a paragraph proof of each theorem below.
Theorem
69. A square is a rectangle. 4.5.11
Theorem
70. A square is .1 rhomhus. 4.5.12
Theorem
71. The diagonals of .1 square are congruent and are the perpendicular
bisectors of each other. 4.5.13
CHALLENGE
APPLICATIONS
72. Draw a parallelogram and find the midpoint of each side. Connect the
midpoints to form a quadrilateral within the parallelogram. Prove that
two pairs of congruent triangles are formed. Use this to prove that the
quadrilateral formed by connecting the lill(lpOllllS is a parallelogram.
(Hint: Connect one pair ol‘ opposite ntidpoints in the original figure.)
73. ART An artist cuts tour congruent right triangles of stained glass. Show
how the four triangles can be put together to form each quadrilateral
listed below.
a. a parallelogram that is not
a rhombus or a rectangle
b. a rhombus
c. a rectangle
d. a trapezoid
e. a kite
74. SPORTS Because a baseball diamond is a square. it is also a rectangle, a
rhomhus. and a parallelogram. Which of the following must lie true, hasetl
on the properties of special quadrilaterals? Explain you r reasoning.
a. 'l he distance from tirst base to third base equals the distance from
second base to home plate.
b. The center of the pitcher's mound is on the diagonal lront first to third
base. (Note: The tnotmd is on the diagonal from home plate to second
base at a point 3- feet from the midpoint of that diagonal.)
c. The path from first base to second base is parallel to the path from
third base to home plate.
L001? Back
75. Suppose that the angles in one triangle are congruent to the angles in
another triangle. Are the triangles necessarily congruent? \~\'hy or why not?
(LESSON 4.3)
Write a congruence statement for each pair of triangles below. and
name the postulate or theorem to justify it. (LESSONS 4.2 AND 4.3)
76. C 77.
G 73- M O
I
A
N
8 H p
J
5 O
K
F
D L R
LESSON 4 5 FROVING OUADRILATERAL FROFERT|ES 251
;4-/,/ 1
.
I llilruotconncd
Portfolio
Extension
Go To: go.hrw.con1
Keyword:
MGI Regular
79. Given AKLM 5 ARST. lind the values of xand y. (LESSONS 3.8
AND 4.4)
5' l3x— yl“
L004’ B€70I1d'
80. Recall that an isosceles trapezoid has congruent A 3
legs. In the diagram at right, two segments
perpendicular to the bases have been added F .1
to form a pair of right triangles. D E F C
Use the information given in the diagram to pro\-e that the base angles ol
an isosceles trapezoid are congruent. '.l lint: First prove that ABFE is a
rectangle and therefore a parallelogram.)
81. Use your result lrom Fxercise 80 to prove that the diagonals of an isosceles
trapezoid are congruent.
Tessellations With Quadrilaterals
ln Chapter 3. you explored several dilTerent types of repeating patterns.
or tessellations. The only regular polygons that can he used to form
tessellations are equilateral triangles, squares. and regular hexagons. [Why-?}
However, if you use nonregular polygons. there are many more possibilities.
1. Draw a nonrcgular quadrilateral. D C
such as A BCD. Find the midpoint
ofone ol'the sides and label it
B
A
2. Using tracing paper or geometry graphics D
software. rotate ABCD about point E. C
3. Repeat Step 2 for the midpoints ol A 3
each side of ABCD. 'l'hen continue
the pattern by rotating the images
about the nridpoints of lhe.ir sides.
4- Try creating tessellations with
dillerent quadrilaterals, including
special quadrilaterals and concave B
quadrilaterals. Do all of the
quadrilaterals that you chose work?
Can any of them be used to form
tessellations in more than one way?
252 CHAPTER I
Objective
0 Develop conjectures
about special
quadrilaterals—
parallelograms.
rectangles. and
rltomhu ses.
How can you tell
whether a given figure is a
parallelogram, a rectangle,
a rlrornbus. or a square? In
this lesson, my will
discover some the: - - ~
that provide answers to
this question.
Conditions for Special
Quadrilaterals
'fi'.‘~qn-"_
'I
=".:.‘..5_ ‘I - ‘ '.- -
"2 J \ I-4, LE.” ‘u . ‘t
_ 1 _ _ o _ . 1. —_
_"’_' 5 1! I ‘ _
I
. I _‘ -
'-_ 3 '. r4.- ‘ '
.. , _ - -
'‘s‘._- ': ‘T’. ‘F '— ‘
‘a.-. :' ~“
‘ - "1' ‘Q... -_ -. ‘ ' Q‘ 91'
A perflwlly rrrtnrigtllar jbtuidmion i5 n'q1.iired finr the proper c0n5trru'tion of many
modern lmildirrgs. Herc’ workers are applying an impor mm gmrrzerr)-' principle to
ensure that a portion ofrhefimm.lnIicm is u rmanglc.
Visitors to non—western cultures as far away as lklozambique. in southern
Africa. have reported observing local workers employing the technique shown
above to ensure that :1 foundation ofa house is .1 rectangle. According to their
reports, l'Il€dSl|I'€l1l€lllS'¢lI'€ made bv using long poles [see page 255].
The Conditions That Determine a Figure
llyou are given a quadrilateral. how can you tell which oithe special
qmdrilaterals. if any. it is? One may to try is to check the given information
against the definitions of the special figures. However, the inform-.1tion you are
given nmy not match the information referred to in the deliuitions. This does
not mean that the figure is not one of the special quadrilaterals.
LESSON 4.6 conomoms FOR SPECIAL OUADHILATEHALS 253
uncooked spaghetti or
another maternal lsuch
as soda straws or
tuothprcltsl to serve as
the sides of model
quadrilaterals, a ruler,
and a protractor
CHECKPOINT M
CHECKPOINT M
CHECKPOINT M
254 CHAPTER 4
What I oes It Take to Make...
In each part of this Activity. decide whether the conjectures listed are true
or false. ll" you believe that a coniccturc is false. prove that it is false by
giving a counterexample. Make sketches of your cottnterexamples. ll" you
believe that a conjecture is true. consider how you would prove it.
Part I: What does it take to make a parallelogram?
State whether the following conjectures about parallelograms are true or
lalse:
1. If one pair of opposite sides ol‘a quadrilateral are congruent. then the
quadrilateral is a parallelogram.
2. It" two pairs of opposite sides ot a quadrilateral are congruent, then the
quadrilateral is a parallelogram.
3. If one pair of opposite sides oli a quadrilateral are parallel and
congruent, then the quadrilateral is a parallelogram.
4. if two pairs ofsides of a quadrilateral are congruent. then the
quadrilateral is a parallelogram.
5. If the diagonals ofa quadrilateral bisect each other. then the
quadrilateral is .1 parallelogram.
Part ll: What does it take to make a rectangle?
State whether the following conjectures about rectangles are true or false:
1. llonc angle of a quadrilateral is a right angle. then the quadrilateral is a
rectangle.
2. If one angle ol a parallelogram is a right angle. then the parallelogram is
a rectangle.
3. It" the diagonals ol'a quadrilateral are congruent, then the quadrilateral
is a rectangle.
4. ll’ the diagonals of a parallelogram are congruent. then the
parallelogram is a rectangle.
5. If the diagonals of .1 Parallelogrant are perpendicular, then the
parallelogram is a rectangle.
Part lll: W’hat does it take to make a rhombus?
State whether the following conjectures about rhombuses are true or false:
1. If one pair of adjacent sides of a quadrilateral are congruent. then the
quadrilateral is a rhombus.
2. Ifone pair oladjacent sides ol a parallelogram are congruent, then the
parallelogram is a rhombus.
3. If the diagonals ofa parallelogram are congruent. then the
parallelogram is a rhon1hus_
4. It the diagonals of parallelogram hisect the angles of the parallelogram.
then the quadrilateral is a rhombus.
5. It" the diagonals of a parallelogram are perpendicular. then the
parallelogram is a rhombus.
The "Housebuilder" Theorem
A - p L c A 1 0 N Carpenters have long used diagonal measurements to determine whether the
CARPENTRV sides of a house's foundation formed a rectangle. The building method has
been used throughout the world. including the African countries lklozambique
and Liberia. where people use long poles instead of measuring tapes to
compare lengths. in Activity 2 below, you will apply an important theorem.
which you may have conjectured in Activity I.
' 2
Building a Rectangular Structure
- I ' D 1. Break oft" two pairs of sides T
uncooked spaghmi 0, ol two cltilerent lengths lrom
anflthdet "'BtE"a' l5l|€h your modeling material. let
assoastrawsor ‘ _ \ \ \ - ‘. _
mmpicks, ,0 Serve as lllLS(. he the pairs oi Oppobllt.
the sides of model sides lor yottr model
°”ad"'m°'a's lotlndation.
2. Model the diagonals oi‘ the
foundation with two more
pieces 0! your modeling
material. Break off the
pieces for the diagonals at
the correct length.
cuecxpomr ./ 3 Compare the lengths ot the diagonals. Are they equal? it they are. then
yottr foundation is rectangular. according to one of the conjectures you
made in Activity L State that conjecture. (This conjecture, when proven.
will be called the Housebuilder Theorem.)
4. If the diagonals are not the same length, adjust the sides of your figure
until they are. Note: it may be easy to make a reasonably good first
guess at a rectangle when you are working with a small model. but it is
much more dillicult when you are trying to create a large rectangle such
as a foundation.
CRITICAL THINKING The head of the lamp in the picture I
remains vertical as it moves up and
down. Which of the conjectures you
made in Activity l explains‘ why this
is true?
LESSON 4.6 conomoms FOR SPECIAL OUADHILATEHALS 255
Adding to Your System of Geometry Knowledge
The following theorems are based on your work in Activity I. You will have
the opportunity to prove these theorems in the exercise set.
Theorem
ll two pairs of opposite sides ol'a quadrilateral are congruent, then the
quadrilateral is a parallelogram. 4.6.1
Theorem
If one pair of opposite sides ofa quadrilateral are parallel and Longruent.
then the quadrilateral is a parallelogram. 4.6.2
Theorem
lf the diagonals of -.1 quadrilateral lwiseet each other. then the tpiadrilateral
is :1 parallelogram. 4.6.3
Theorem
lf one angle of a parallelograin is a right angle, then the parallelogram is
a rectangle. 4.6.4
The HousebuilderTheorem
if the diagonals of a parallelogram are congruent, then the parallelogram
is a reet-.1 ngle. 4.6.5
Theorem
lf one pair of adjacent sides of a parallelogram are congruent, then the
parallelogram is a rhombus. 4.6.6
Theorem
if the diagonals ot a parallelogram bisect the angles of the parallelogram,
then the parallelogram is a rhomhus. 4.6.7
Theorem
If the diagonals of a parallelogram are perpendicular. then the
parallelogram is a rhomhus. 4.6.8
256 CHAPTER I
Exercises
. 60/mm//1/‘mtg
1. The definition of a parallelogram is a quadrilateral with two pairs of
parallel sides. Consider the lbllowiiig alternative definition:
A pm'ufli’Iogi'am is rt qutidi'iIrit¢'i'ui ti-'ht7.~'e tipposite .~'1't.les in IL? cmigriiem.
Does this dcliiiitioii work? I low many other dcliiiitioiis for a
n ' mm“ .'?.t parallelogr-.ini can you think of!
Activities _ _ _ _ _ _
ontine 2. Choose at coiiiecttire from Part I of Activity 1 that turned out to be lailse.
sore; go_hrw_com and explain why it IS false.
Keyword _ _ _ _ _
MGI Swing 3. C‘hoo.se a coiiiecttire from Part ll of Activity l that turned out to be false.
and explain why it is false.
4. Choose a conjecture from Pam Ill ol'i\ctivity I that turned out to be false.
and explain why it is false.
0 6///48454’///8 P/dd‘?/'68
For Exercises 5-8, determine whether each quadrilateral is necessarily a
parallelogram, a rectangle, a rhombus, or none of these. Give all of the
names that apply to each quadrilateral. (ACTIVITY 1)
9. l'he figure at right is a pair-allelogram.
What must be true about the figure in
order for it to be a rectangle also?
(ACTIVITY 2)
O P/ddt/£8 dlid 74,40/y
Exercises 10-13 refer to quadrilateral ABCD with diagonals AC and
% intersecting at point E. For each set of conditions given below.
determine whether the quadrilateral is necessarily a parallelogram.
If so, give the theorem that justifies your answer.
1o.fiaET3,7iZ‘a'l§fi 11.}W?=TEW=.-aT5T?
tzfia/T2 Hi||(.‘—D 13.T’a(.TD. Hi||C—D
LESSON 4.6 conomoms FOR SPECIAL OUADHILATEHALS 257
PARAGRAPH PROOF
PROOFS
258 CHAPTER I
Exercises 14-19 refer to a parallelogram FGHI with diagonals FH and GI
intersecting at point J. For each condition given below, determine
whether the parallelogram is a rhombus, a rectangle, or neither. Give
the theorem that justifies your answer.
14. W E W 15. T75 G—H
17. F—G E W 13. m.4F]G = 90°
16. n1..’.’l-'GH = 90°
19. m.4FHG= 90°
For Exercises 20-25, refer to the diagram of parallelogram KLMN at left.
State whether each set of conditions below is sufficient to prove that
KLMN is a square. Explain your reasoning.
2o. m.4:<L.u = 90°. m/_'l'\'PN = 90° 21. E 5 Hi, Ki 5 MN
22. mg“ N = 45°. n14’l,NK = 45° 23. 7:7? 5 MN. 753' 5 TN
24. JLKM 5 .r_’LMK, ALK.-\-I E .4.'l-{KN 25. &NKL 5 m'\L.-\-1
Use the diagram at right to complete the following two-column proof of
Theorem 4.6.1:
Givan:H3sE'5-.1ndX'f>s'c".T3 A 1 3 °
Prove: ABCD is a parallelograni. 4 2
B C
Proof:
Statements I Reasons
:4—l3ETI-l3a11d§T3E?flT>’ 26. 1'!
ET) 5 'l>'_D 27. ?
A./lb'D 5 ACDB 23. ?
-9
L’! 5 4'2 and £3 5 £4 29.
ATJIIWS and Tb‘|| C—D
ABCD is aparallelogr-.1m. 31.
N
P
9
unq-
Use the diagram below to complete the paragraph proof of the
HomebuilderTheorem below.
Given: panillelograni EFGI I with TIE !'—H E F
Provo: EFGH is a rectangle.
Proof: H G
Opposite sides of a par-allelograni are congruent, 50 TI? E 32. ?
and W? E ?T1[Rellexive Properly). Became E E W (given).
AFHG E AFGH by 33. I’ . KFHG E AFGH becenlse 34. ? ,
and AE! {G and AFGH are supplemcnlar_v because they are 35. I
angles. AEHG2md AFGH are right angles l>ecau.se 36. ? .
'l'herefore. /_’I-'l;'H and 4'}.-'FGare also right angles because 37. 7.’
Thus. EFGH is a rectangle by 38. _§__
Write a two-column, paragraph, or flowchart proof for each of the
following theorems:
40. Theorem 4.6.3 41. Theorem 4.6.4
43. Theorem 4.6.7
39. Theorem -1.6.2
42. Theorem 4.6.6 44. Theorem 4.6.8
CHALLENGE
FLOWCHART P‘ I I
Recall the following conjecture from Lesson 3.7, which you will now
prove as a theorem:
The Triangle Midsegment Theorem
A niidsegmenl ofa triangle is parallel to 21 side of the triangle and has .1
measure equal to half of the nieasure of that side. 4.6.9
Complete the flowchart proof below.
Given: In AABC. D is the midpoint ol'.»'l—C. and E is the midpoint ME.
\
I Extend segment 0? L
to fon11_ W such that 3. I,
I EFE DE |
A
Prove: ITE um and or = _-LAB
Proof:
ofiafi I ozzaza
T0565 45' ‘If
Def. of midpoint
\. !_ ./
0 ACED 5 ABEF
46. ?
/ N.
I 0 <4 5 z1 | L0 EEBE
(33%: fi—]
As constructed
CPCT C 47
1
. ?
I
1
|oA_c B_F ] ofiafi | |@DE+£F=DF
48. ? 52. ?
Trans. Prop. .
/ 1
ABFDisaparallelogram
49.: Substitution
\ ‘A
la» D—£|uA—a | @JF=AiJ
50: i 51 .—2
[9D£_'=%*:J
53. ?
@135: %AB
54. ?
LESSON 4 5 couomoms FOR SPECIAL OUADRILATEHALS 259
A P P L l c A T l 0 N S 55. ART An artist is making a frame for stretching a canvas. She cuts two
boards that are 2 feet long and two boards that are 3 feet long. How can
she pttt the boards together to make sure that the frame is rectangular?
56. CONSTRUCTION In a ladder. all of
the rungs are congruent and the
two side pieces are congruent. E
What else is necessary in a ladder Z‘-.3
in order to ensure that the rungs
are parallel?
Corner braces may be used to W——
stabilize the ladder. Explain how r
corner braces can be placed to
ensure that the rungs are l
perpendicular to the side pieces.
How many corner braces are
needed? Explain your reasoning.
1001? Back
For Exercises 57-59, consider a regular polygon with a central angle of
72°. Find each value below. (LESSONS 3.1 AND 3.6)
57. the number of sides of the polygon
58. the measure ofan interior angle
59. the measure ol'an exterior angle
60. Explain the differenee between a postulate. a conjecture. and at theorem.
(LESSONS 1.1, 1.4. AND 2.4)
PROOF 61. Given: 5 [TC-and [T3 E B
Prove: AADC 2 ACEA
(Hint: AABCis isosceles.) D E
(LESSON 4.4)
Look Bet/Md
Draw a general quadrilateral and find the midpoint
of each side. Connect the midpoints to form another
quadrilateral. Label the figure as shown at right. W X
62. What type of qttadril-ateral appears to be formed L
by the midpoints? Test your eonjeetu re by drawing N
several quadrilaterals or, if you are using geometry
graphics software. by dragging the vertices to 3
dil-lerent positions.
M
63. Draw diagonal W to form tr_iangles Al‘l"XYand Al-S-7}’. What part of
these triangles are segments KL and MN, respectively?
PROOF 64. Use the Triangle Midsegment Theorem to prove that KL-\-IN is a
parallelogram.
260 CHAPTER I
Compass and
Straightedge
Constructions
Va
Ԥ
Objectives
0 Construct congruent I!
Comes °' 5e9'.“°'“5' The use of a compass and stmig - - I -
angles, and triangles. . . .
to cansauct figures Involves the pr uciplas of
. construct an 3ng|e triangle congruence. As run will learn,
bisector. comp. . .- are uselul for much more than
drawing circles.
A Classical Mathematical Game
For centuries, malh€maliCLlllS have enjoyed a sort olg-an1e. 'l he “gan1e"
requires .1 conip-ass and a Slrdighlcdgt. By using just these tools, you can create
preci.se geometric figures.
., consmucnou Given A-3 at r_ig,_ht, fol_low Steps 1-4 A B
\ COMPASS and to construct CD 2 AB.
STRAIGHTEDGE
1. Using .1 straightedge. draw line E. 2. Select a point on E and label it C.
Note: A straightedge is
t? if‘
not a ruler. It has no mam
marks on it and cannot
be used to measure
3. Set your compass to the distance 4. Place the point of your contpass
AB in the given figure. on C and draw an are that
intersects line 1'. label the
intersection ofthe arc and the
line as point D.
distances.
LESSON 4.7 commss AND STRAIGHTEOGE CONSTHUCTIONS 261
Three Important Assumptions
Three important assumptions were involved in the construction in Activity I.
Keep these assumptions in mind as you do Activity 2.
1. You can place the point of your compass or the edge of your straightedge
precisely on a given point or line [or circle).
2. Given two points, you can set your compass so that the distance between
the point and pencil of the compass is equal to the distance between the
two given points; you can also set your straightedge precisely on both
given points.
3. The distance between the point and pencil ofthe compass does not change
once it has been set—until you reset it. (This is why a compass can be used
to draw a circle.)
Copying a Triangle
A Triangle congruent to a Given Triangle
ONSTRUCTION Given AABC at right, follow Steps l— 5 C
COMPASS and to construct AMINO E /_\.ABC.
‘q STBAIGHTEDGE
A B
1. Llsing a straightedge, draw line I’. 2. Set your compass to the distance
Select a point on line 6‘ and label AB in the given triangle. Place the
it M. the point of your compass on .-\-I,
F and draw an arc that intersects
no line 1''. Label the intersection N.
M
i’.
M N
3. Set your compass to the distance 4. Set your compass to the distance
AC in the given triangle. Place the BC. Place the point of your
point of your compass on .\'I. and compass on N and draw an arc
draw an are above MN. that intersects the first are you
drew. l abel the intersection
‘GK : as point 0.
-—>
E M N
\|o
LOT ?D-
M N
s. Connect points M. N. and O. _0
Result: /_\.M.'\’OE AABL. E i :
M N
262 CHAPTER 4
Justifying a Construction
The steps in the construction of a figure can he justified by combining the
assumptions ol compass and straightedge constructions with geometry
theorems you already know. The proof below justilies the construction in
Activity l.
TWO£0I.UMN PROOF Glven: AABC, with AMNO constructed as in Activity 2.
Prove: AMNOE AABC
Proof (refer back to Activity 2):
Statements Reasons
1. MN E E Comp-ass set at distance AB
was used to construct MN.
2. MO E 4-TC Compass set at distance AC
was used to construct MO.
3. E 5 £73 Compass set at distance BC
was used to construct W.
4. AMNO E AABC‘ SSS
Bisecting an Angle
I ' 3
Angle = isector
I TRUCTION Given /_A at right, follow the steps
COMPASS and below to construct its hisector.
\ STRAIGHTEDGE A
1. Place your compass point at A 2. Place your compass point first
and draw an arc through the at B and then at C. Using one
rays of the angle. Label the compass setting. draw arcs that
intersection points as B and C. intersect in the interior of AA.
Label the intersection as Draw
a ray front A through F. AF is the
C bisector of 4B 1C.
A B?’
TRY ‘nus Write a proof to justify the construction of the angle bisector in Activity 3.
LESSON 4.7 commss AND STRAIGHTEOGE comstnucnows 263
Exemses
. Comm/I//'mte
1. Explain the difference between a straightedge and :1 ruler. Why is at ruler
not used in constructions?
n - oomect 2. in Step I of the construction in Activity 5. which of the construction
Activities assuntptions were used? Explain.
2:330 hm cm 3. In Step 2 of the construction in Activity 3. which of the construction
K..,,.,.§,.d;' ' assumptions were used? E.\'pIain.
MGI American
4. Describe how you would do the eunstrttctioils from the activities with
folding paper or on .1 computer. Name some advaiittiges or disadvantages
of one of these methods.
0 qt//dad 5k///8 Pldtt/6'8
Trace the figures below onto paper, and construct a congruent copy of
each. (ACTIVITIES 1 AND 2)
_ _ _ B
For Exercises 7-9. refer to the diagram at right.
Trace the figure and construct the angle bisector
of the indicated angle. (ACTIVITY 3)
A C
7. LA 8. /.8 9. LC
0 Practice dlld flpp/y
Construct a congruent copy of each figure below.
../
1: n : A
A L
264 CHAPTER II
Trace each angle below onto your paper and construct the angle
bisector of each.
16. 17.
For Exercises 18-21, trace each angle onto paper and follow the steps
below to constmct a congment copy.
°°"'5“‘“°“°“ An anglecongruenttoagivenangle
_ _ I Given AR at right, follow these steps /
Y0" ""'”"’°"'e ""3 to construct A3 a AR.
construction in
Exercise 47.
3:.
a. Using a straughtedge, draw a ray b. Place your compass point on R
with endpoint B. and draw an arc. Label the
Intersection points 0 and S.
I
-D 0
R S
c. Without adjusting your compass. d. Set your compass equal to the
place the compass point at 8. distance 08 in zfi.
Draw an are that crosses the ray.
and label the intersectlon polnl C.
8%: +C —»
e. Without adjusting your compass. f. Draw 32 to form 43. AB is
place the compass point at C. congruent to /19.
Draw an arc that crosses the lirst
arc and label the intersection A.
3%
Bo—?&-c—> 3'j’t'_"
18- L. 1s./\
20. ! 21. V
LESSON 4.7 commss AND STRAIGHTEOGE comstnucnows 265
For Exercises 22 and 23. trace each segment onto paper and follow the
steps below to construct the perpendicular bisector and midpoint.
CONSTRUCTION
The perpendicular bisector of a given segment
and the midpoint of a given segment
You will prove this
construction in "
Exercise 48.
Given /T at right, follow these steps to _
construct line the perpendicular bisector of AC.
ATOC
a- Set your compass equal to a
distance greater than half of AC.
ATOC
b- Place your com pass point on A
and draw an arc as shown
,.4_.
c. Without adjusting your compass
setting, place the compass point at
C. Draw a new arc as shown and
label the intersection points of the
two arcs B and D.
d. Use a straightedge to draw 55.
Label the intersection with Iéas
point E. fi Is the perpendicular
bisector of R, and E is the
midpoint.
23.
Trace the triangles below onto paper and construct the perpendicular
bisector of each side. Using the intersection of the perpendicular
bisectors. construct the circumscribed circle of each triangle.
24.
266 CHAPTER 4:
25.
For Exercises 26 and 2'], trace each figure onto paper and follow the
steps below to construct a line through the given point and
perpendicular to each given line.
C 0 N 5 7 3 U 3 7 ' ° N Aline through a point perpendicular to a given line
You will prove this ' fGoll‘ll::v'::::e:;nd ime £ at right’ A’
construction in <- . ps 0 construct 6
Exercise 49. Ac ‘L ‘me A
a. Place your compass point on A b. Place your compass point on D
and draw an are as shown. Label and draw an are below the line, as
the intersection points D and 8. shown. The compass does not
need to be at the same setting as
in the previous step.
-A
E -. :
<-
D B
\,
. 4—)
c. without adjusting your compass d. Use a straightedge to draw AC.
setting, place the compass point at Acis perpendicular to line ii.
5'. Draw a new an: as shown, and .
label the Intersection point C.
A‘ F o‘ I e
L‘ 1} _ C
c \
26. 27.
O
. I _ A
28. A segment lrom at vertex ol :1 trnmgle
perpendicular to the opposite side is
called an rlltitmle of the triangle. Trace
the triangle at right onto your paper. 3 C
a. Construct the altitude from each vertex.
b. What seems to be true about the three altitudes of a triangle?
29. Draw a large scalene triangle, AABC, on your paper. Follow the steps
below to construct the inscribed circle.
a. Construct the angle bisectors to tind the incentcr. I.
b. Construct a line through I perpendicular to any side. Label the point of
intersection
c. Draw a circle centered at lwith radius IE. This is the inscribed circle of
LtAB(
LESSON 4.7 commss AND STRAIGHTEOGE CONSTRUCTIONS 267
For Exercises 30 and 31. trace each figure onto paper and follow the
steps below to construct a line through the given point and parallel to
the given line.
CONSTRUCTION
Given point M and line If at
right. follow’ these steps to
construct AC ll line 2.
You will prove this
construction in
Exercise 44.
Aline through a point parallel to a given line
M
i
‘T.
e. Use a straightedge to draw a line
through M that Intersects 8. Label
the intersection point P.
M
b. Place your compass point on Pand
draw an arc as shown. Label the
inte rsection points R and T.
M
E
<-
PT
c. without adjusting your compass
setting, place the compass point at
M. Draw a new arc as shown and
label the Intersection polnt N.
N
8'?‘
PT
d. Set your compass to the distance
RT. Place your compass point on N
and draw an art: as shown. Label
the point of intersection 0.
N
‘—’ - 1
e. Use a straightedge to draw MO. Lme A715 IS parallel to llne 8.
30.
31.
Construct each of the following special quadrilaterals with a compass
and straightedge:
32. traptzoid
34. rettaltgle
36. square
268 CHAPTER 4:
33. par.1llclog,rant
35. rhombus
37- lzite
u mm‘; ,:,9, Refer to the construction. shown at right. of an
Homework '°"‘ angle congruent to a given angle Complete the
Help onnne two-column proof that L3 5 LR.
E,':v1-:;?;éh'w‘c°m Given: ZB. as constructed
MGI Numewn* Huh PmVe_ 1 B = A R
Proof:
Statements I Reasons
E E @ Same compass setting used
[TC 5 E 38. ?
TC; 35 39. ?
Ar‘-IBC E QQRS 40. ?
AB 5 1R 4:1. ?
42. Refer to the construction. shown
at right. of the perpendicular
bisector of a given segment.
f-—'§ .:_
EEVB that BDJ. AC and that
Bf} hisewtts R.
43. Refer to the construction. shown
at right. ofu line through a point
perpendicular to a given line. Prove
that .-‘-\(.J_l1ne E.
44. Refer to the construction. shown _
at right, of a line through it given " T»
point parallel to a given line. Prove R
th-.uK-TE)||1ine .t_ ,
P T
A P P I. I C A T I 0 N 45. MAP READING A geologist
is at point X near Croton c,.,..,..
Peak in Big Bend ”'="‘
National Park. He wishes X,
to go back to the road
by the shortest path. \
Make your own sketch \
of the map and use a
compass and straightcdge
to construct his path.
(You may assume that the ,. _ .’ " "
road is perfectly straight.)
Cwlon
Spring
Demif o_fI0pographicaI map
LESSON 4.7 commss AND STRAIGHTEOGE CONSTRUCTIONS 269
CHALLENGE
270 CHAPTER 41
46. Draw a large scalene triangle. and construct at least two of each of the
following:
- Perpendicular bisectors: these meet at a point called the rircmnremer.
- Altitudes: these meet at a point called the orrhmrcnter.
0 Medians (a segment joining a vertex to the midpoint of the opposite
side]: these meet at a point called the reutmid.
11' your constructions have been done Carefully. these three special points
should be collinear. Draw the line through the three points.
Look Book
Identify the type of transformation shown in each figure below.
(LESSON 1.6)
47. \ 48.
1 0
49.
-a— r
Classify each quadrilateral below as a parallelogram, rectangle, square,
rhombus. kite, or trapezoid. List all terms that apply to each figure.
(LESSONS 3.2 AND 3.3)
50. 51. 52. 53. J . L
S '1 . 1‘
Look Beyond
54. Trace segment Kgonto paper and construct equilateral A‘ '3
triangle AABC as follows:
Place your compass point at A. and adjust the compass
so that its pencil point is at 8. Draw an arc as shown. A 8
Without adjusting the compass setting. place the
compass point at B and draw another _.Ec. Labcl_the
intersection point C Draw segments AC and BC.
55. CULTURAL CONNECTION: EUROPE The French general
1\'-apoleon [1769-1821] was an amateur mathematician.
l\'apole0n discovered the following construction:
A6 T08
Draw any triangle. Construct an equilateral triangle
along each side. as shown. Construct the perpendicular
hisectors of each equilateral triangle to find the
circumcenters, and ioin the circumcenters to form a
triangle. What seems to be true about this triangle?
Constructing
Transformations
’
Objectives
0 Translate, rotate, and
reflect figures by using
a compass and ;
straughtedge.
o Prove that translations.
rotations, and Wh
'9"9C"°"5 W959“ All olthe mmslomratlons you have
°°"9""?"°° and °me' studied so far have been rigid. That is, the
pmpemes‘ 8129 and shape oftho ablectx that are _ I _
. Use file Bewveenness not change_ You can now Flt-lug i" “g n _fl'lr’"N"U"_.
postmate to Establish . . - [fmukese transloymauans pyesejve tht. t plum more it rt
the Triangle Inequality congruence and otlrorpmperties as well. rigid georm tric mm.
Theorem.
Translating Segments and Polygons
Recall from Lesson [.6 that at tnmslation is .1 trttnslorntation that moves every
point 0|-‘an object the same distance in the some direction.
Translating a Segment
- ll ' ED Make your own drawing like the one at right. 3
compass. straightedge. The arrow. known as a tr-.mslation vector. shows
3”" '”'°' the direction and (.llSidllCt‘ of the translation you
are to construct. The distance is the length of A
the vector. T»
cuecxporm ./
1. Construct a line. 6... through point A and pantllel to the translation
vector. Construct another line. E3, through point B and parallel to the
translation vector. Are lines ti. and t.,»_ parallel? E.\'plain.
2. Set vouL:ontpass to the length, x, of the translation vector. On the right
side of AB, construct points A’ and B’ that are the same distttncc. x,
from points A and B on lines fl and t”';, respeCti\'el}'.
3. Connect points A' and B’. Measure 71-9. and A"B'. Are the two segments
congruent?
LESSON 4.8 CONSTBUCTING TRANSFORMATIONS 271
The following Example gives a proof that .717? and .-1'3’, as con.<.tructed in
Activity I. are congruent: '
E X A M P L E Given: Hand .~l'B’. as
constructed in
Activity I
Prove: T1‘ 5 /Vb"
Proof (refer to Activity 1, page 271):
PARAGRAPH ' ' I IF
ZEFHW because they lie on lines fl and F3, which were constructed
to be parallel. (For the method of constructing a line through a given
point and parallel to a given line. see page 268.) 33-’ E E37 because the
same compass setting [the distance x] was use to construct them.
Quadrilateral A,-‘t'B’B is a parallelogram because a _pa_i_r of opposite
sides are congntent and parallel. Therefore, AB 5 A'B' because
opposite sides of a parallelogram are congruent.
' 2
Translating Polygons
1. If you translate each of the three sides of C
no speciamoys AABC as indicated by the translation
vector. will your new figure be congruent B
to the original one? State the theorem or
A
postulate that jtlstifies your answer.
2. If you translate each of the lour sides of
quadrilateral ABCD as indicated by the B
translation vector. will vour new ligurc be
congruent to the original one? State the D
theorem or postulate that justities your
answer. (I lint: Divide the figure into two A
triangles by drawing a diagonal.)
an
CHECKPOINT M 3. Show how anv polygon can be divided
into a number ol triangles by connecting
the vertices with segments. Include both
convex and concave polygons in your
illustration. What can you conclude convex concave
about the translation ol a polygon? polygon polygon
4. W hat can you conclude about the
translation ofan open ligure composed
of segments. such as the one shown at
right? Can you apply your conclusion
from Step 3 to this figure?
cRrncAL THINKING Do you think your conclusion about translations of segments and polygons
can be applied to translations of curves? (1 lint: I low can you use a number of
segments to approximate a curve?)
272 CHAPTER 4
Preservation of "ABCD"
The rigid transformations. which are also known as isrmtetrie‘. preserve Angles.
Bet tvt't’rtrtt’s5. C0iiirtr’rlI'il‘_)", and l')ismm'e (“ABCl')"}.
CRITICAL THINKING How do Activities t and 2 show that translations preserve angles and distance?
|t'A. B, and X are collinear points, how can you he sure that their image
points, A’, B’. and X’, will be collinear in a translated image ot‘ the figure? If X
is between A and B, how call you he sure that X’ will be between A’ and B’?
To answer the above questions. you will need a mathematical t-.-ay to
determine which of three given points is between the other two (ifany) from
information about the distances between them. The postulate below gives a
method. It is the converse ofa postulate you have already studied.
Betweenness Postulate
(Converse of the Segment Addition Postulatel
Given three points P. Q. and R, if PQ + QR = PR. then P. Q. and R are
collinear and Q is between P and R. 4.8.1
THY THIS You are given the points R. S, and T. where R5 = 9.8. TR = 9.6. and T5 = I9.-1.
Assuming that the given distances are exact. are the points collinear? If so,
which point is between the other mo?
Colllnearlty and Betweenness
You are given segment AB with
poittt X between A and 8. Points
A. B. and X have been translated
as shown at right by the translation
vector and connected bv segments.
Are A’. B’. and X’ in the translated
image collinear? Does X’ lie between
A’ and B’? How can you prove your
answers ntathematicztlly? Follow the
steps below.
1. What do you know about distances AB and A'B’? about distances t.\’
and A’X’? about distances BX and B’X’? Explain your reasoning.
2. Frotn the Segment Addition Postul-ate you know that AX + X1? = AB.
What can you conclude about A’X' + X’B'? Explain your reasoning.
CHECKPOINT ./ 3. Is X’ collinear with A’ and B’? Is X’ between A’ and 3’? Do translations
preserve collinearity and betweenness? l.'xpl.tin your reasoning.
no special tools
B
LESSON 4.3 CONSTRUCTINGTRANSFORMATIONS 273
CRITICAL THINKING
274 CHAPTER 4:
TRY THIS
The Triangle Inequality Theorem
What seems to be true about 3
AB+ BC:ts comp-.tred with AC?
Suppose that point B is relocated so
that AB+ BC = AC. What happens T
to AABC? A C
The answers to the questions above suggest the following theorem:
Triangle Inequality Theorem
The sum of the lengths of any two sides ol'-.1 triangle is greater than the
length of the third side. 4.8.2
This theorem can be argued inlormally by considering the two other
possible causes.
Informal Argument
Case 1
Given three segments, if the
sum of the lengths ofany two
oi‘ them is less than the length 8 b_
ofthe third segment, then no 9
triangle can be formed lJ_\ 17 ‘% H + b< 0
connecting their endpoints. H
The endpoints of two ol‘ the 0
segments eannot be connected.
The endpoints cannot
be connected.
Case 2
Given three segments. if the
stun of the lengths ol'.m_v two
of them is equal to the length
ofthe third segment. then no 3 1,
triangle can be formed by
connecting their endpoints.
The endpoints. and hence the
segments themselves.
are collinear (justification:
the Betweenness Postulate).
The endpoints
are collinear.
Tints, ifthree segments form at triangle. the sum of the lengths of any two
segments must be greater than the length olthe third. This is the only
remaining possibility.
Which of the l'ollo\-.'ing are possible side lengths of at triangle?
a. l4,8,25 b. l6,?,23 c. l8,8,24
Exercises
. Communicate
1. How does the Betweenness P().\>tl.llilt(-.‘ justify the translation of the segrnent
in Activity I?
2. What does “ABCD" refer to? Explain in terms of the translation of .1
triangle.
3. In the word isomrtry. the root -mt"'IT)"l]1€dl'lS ‘‘measure.'‘‘ what do you think
the prefix 550- means? Check your dictionary. How does this help explain
the term isometr)-'?
4. ln A.-1B(". AB = 9 and AC = 6. What can you say about BC? Does it have a
minimum possible \-alue? Does it have a I‘lT.1‘(ilItll m possible value? ljxplain
your reasoning.
. q/4/dedsk/7/3 Practice
Trace the figures below.Translate each figure as indicated by the given
translation vector. (ACTIVITIES 1 AND 2 AND EXAMPLE)
5. / 6.
.
7. Trace the figure at right. Translate the angle as
indicated by the given translation vector, and
measure both angles. W hat do vou notice?
(ACTIVITY 3)
Practice and Apply
ll mtemetconnect .39, Trace each figure below and translate it as indicated by the given
Hgmewmk ‘um translation vector.
Help Online 8 9
Go To: go.luw.cam ' K‘ '
Kuwmid:
MG! Homework Help fie \
for EXEICISES 8- I9
4
10. 1 1 .
P
.
LESSON 4.3 CONSTRUCTINGTRANSFORMATIONS 275
CONSTRUCTION
You will prove this L-
construction in
Exercises 26-29.
276 CHAPTER 4:
A rotation about a point by a given angle
Given 2TB‘. point P, and AR shown at right.
follow the steps below to construct the
rotation of 35 about Pby mzR.
H4» 'P \BA
a. Place your compass point on P.
Draw an arc through A and an arc
through 8.
R4»
b. Draw W. Construct an angle
congruent to /R with W as
one side. as shown. Label the
intersection with the arc through
A as A‘.
14.
c. Draw P—B. Construct an angle
congruent to AR with F5 as
one side, as shown. Label the
intersection with the are through
B as B’.
L
\
.1’.
cl. Draw A‘B'. A‘B‘ is the rotation of
1? about Pby mzfi.
Trace each figure below and follow the steps above to rotate the
segment about the given point by the angle below it.
13.
CONSTRUCTION
T]. .
You will prove this —
construction in
Exercises 30-37.
L
A reflection across a given line
Given IE and line f shown at right.
follow the steps below to construct
the reflection of IE across £2.
3
eA-/.
>
e. Construct a line, rn, through A and b. Set the compass point on the
perpendicular to I’, and another intersection of E‘ and m and the
line, n, through 8 and perpendicular pencil point at A. Draw an arc that
to (Z, intersects m as shown. Label the
B intersection point A’.
d. Draw A’B'. A'B’ is the reflectlon of
E across line 8.
c. Set the compass point on the
intersection of 1' and n and the
pencil point at B. Draw an are that
crosses n as shown. Label the
intersection point B’.
«jap-
A.
Bf
I Y) H
Trace each figure below and follow the steps above to reflect the figure
across the given line.
17.
16.
/ o— —o
18. 19.
e1 /V
Which of the following triangles are possible?
20. .-lb‘ = 7, BC: IO, AC = I2 21. DE = 6. E!’ = 5,1)!-' = I4
22. CH: l7. lii=9. Gl=8 23.]K= l0.KL= l0.]L= l0
LESSON 4.3 CONSTRUCTINGTRANSFORMATIONS 277
TWO-COLUMN PROOF
PARAGRAPH PROOF
CHALLENGE
278 CHAPTER 4:
Refer to the diagram below for Exercises 24 and 25
24. Complete the following inequalities:
a. ? + '5 > x 10 8
b. x+ ? > In
c. x+ ? > 8 "
25. Solve the inequalities in Exercise 2-1 and complete the following statement:
? <.c< ?
Refer to the rotation of a segment about a point by a given angle (page
276). Complete the two-column proof below.
Given: /Vb" is a rotation of Eabout point P.
Prove: NB’ 5 E
Proof:
Statements I Reasons
El‘ 5 W Same compass setting used
W; 2 T’? 26. 3:
[A PA’ 5 48173’ By construction
AA PB 5 .4’A’PB" 27. 5
AA PB 5 £\A'P8' 28. 7.‘
THE E 29. ?
Refer to the reflection of a segment across a line (page 277l.Two lines
are added to the figure: one through A and parallel to ‘ and one through
A’ and parallel to ‘, as shown below. Complete the following proof.
: _ _ _ 3
Given: /Vb" is a reflection of zlliacross line 8. P <:"‘—;—’;’C.~'—>
. X 5 5Y
{ -———-er-—->
Provoz ‘A7 5 X 3 D7 _._
A’ :'B'
Proof: By construction. Hand W are perpendicular to E‘. fl E E and
W E W [ BY = KY]. .7 is perpendicular to p and q. and Wis
perpendicular to p and q because 30. ? .Therefore. ACDA’
is a rectangle by 31. ? ,and F E 32 ? because
opposite sides ofa rectangle are congruent. By definition. ACYX
and A’DYXare rectangles, so E E fl; and We F37’ hecause
33. ? .Thus, ‘(T 5 ‘IT’ t CY = on by 34. 2 and
E2 B’D t BC = B’Dl by 35. ? .Then AACB 5 AA’DB’ l)\r'
36. 3.’ . and A’B' 5 H3l)ecause 37. ? .
38. Lse a compass and straightedge or folding paper for the following:
- Draw a triangle and label the vertices R. L, and M.
- Rotate the triangle I80” about point K. Labg|__{\_’_f. L’. and M’.
- Reflect the rotated image, AK’l’M', across !.'-\l'. I ahel K”. I ”, and M".
- Construct the perpendicular bisector of L"M'C and reflect AK"L”M”
across the perpendicular bisc-ctor. Label K'”. L"'. and M"’.
- Draw a translation vector from i\-1'” to M, and use it to translate
Af4.'"L"'.-\-'1'". W hat happens?
A P P L I c A T I 0 N S 39. MARCHING BAND During a nntreltittg-band X X’
show. a group of band members moves in
a triangular formation. as shown at right.
Band members X. Y. and Z are the section
leaders. What must the section leaders do to Y Y
ensure that AXYJ E AX'Y’£? \-\"h.tt must
the other band members in this fornmtion z 2"
do to ensure that .£sXY.7 E AX’Y’.7’? T’
40. DESIGN Trice the design at right and translate it
by using Alias at translation vector. 'l'ra1nsl.tte the
image several times. using the same tnmslution
vector, in order to create a border pattern. If you
were to use this pattern as .1 border on at page.
describe what translation to use to go around a A M B
C0l'l1€l'.
Look Back
Describe all of the types of symmetry in each letter and symbol below.
(LESSON 3. 1)
G
41. A 42. N 43. O0 44.
L4 0
LESSON 4.3 CONSTRUCTINGTRANSFORMATIONS 279
PROOFS
APPLICATION
PROBLEM SOLVING
280 CHAPTER 4:
45. which of the following are true for every equilateral triangle? Choose all
answers that apply. (LESSON 4.4)
a. /\ segment joining a vertex to the midpoint of the opposite side divides
the triangle into two congruent right triangles.
b. The angle bisectors are the same as the perpenclicular bisectors.
c. 'l'he inscribed circle is the same as the circumscribed circle.
d. All of the angles measure 60°.
Write a two-column, flowchart, or paragraph proof for Exercises 46
and 47. (LESSONS 4.5 AND 4.6)
46. Given: ABCD is an isosceles 47. Given: PQRS is a
trapezoid; VHF); parallelogram;
EEEC; b’—XLxTD. cTs,fi. and TY
(‘YJ_.-1D intersect at Z.
O X R
P Y S
Prove: E W
Prove: LA 5 LD
48. NAVIGATION The edges 3" 1 _ -
of-a parallel ruler. shown ' ' ,- -. _ _ _
at right. always remain ‘ ' :- . " _ J. _ I‘ '
parallel as the ruler is '5‘ 3 -
opened and closed. Use — '
a geometry theorem to
explain why this istrue. '_;- _ V _
(LESSON 4.6) - — 3'“ 7 ,.
Look Bet/om’
For Exercises 49-52, refer to the diagram at right.
49. Draw a large equilateral triangle. Connect
the tnidpoints of the sides to form a second
triangle inside the first. .\lext. draw a third
triangle by connecting the midpoints of
the sides of the second triangle. Continue this
pattern. drawing as many triangles as you can.
50. Are all of the triangles formed equilateral? Why or why not?
51. Suppose that the length ofa side of the original triangle is 1 unit. What is
the perimeter of the original triangle? of the second triangle? of the third
triangle?
52. Look for a pattern. Add the perimeters of the second. third. fourth. and
lifth triangles. l low does this compare with the perimeter of the lirst
triangle? What happens as the perimeters of additional triangles are added
to this sum?
TESSELLATIONS WITH HEXAGONS
Any hexagon with one pair of opposite sides that are parallel and congruent
cant be used to create a tessellation. Use a compass and straightedge or
geometry graphics software to create the following constructions:
1. Construct a hexagon with one A 3
pair of opposite sides that are p
parallel and congruent, and label 5-
the vert ices A, B. C. D. E. and F. E 0
where A—l3.ti1d fiiare the sides
that are parallel and congruent.
A B
2. Translate the liexagon so that A'B' F /'
coincides with ED. (Hint: Draw a C
translation vector from A to E.) E D
3. Locate the midpoint, M. of RI.
Rotate hexagon .~‘lBCDF I80“
about point M.
4. By continuing the translations
and rotations. vou should be
able to continue this pattern
intlcfiuitely. Try experimenting
with different hetagons. If you
used geometry graphics software,
try dragging the vcrtices to
different locations.
This design was created
with concave hcwagorrs.
LESSON 4.3 CONSTRUCTINGTRANSFORMATIONS 281
‘*“"?F"" F PM 0":
“ In l939. a l.llll\CI'Sll._Y mathematics student named Arthur ll.
Stone was playing with a strip of paper trimmed from a
F... notebook. He discovered something interesting—fleVagons.
Flexagons are polygons made lrom folded paper that show
different faces when “tlexed." l'he instructions below will give
you a chance to play with two of these unique figures yourself.
For your first flexagons, it may be helpful to use paper with
one color on the Front and another on the back, as shown.
Later, you can get creative by drawing designs on the llexagons.
which have a kaleidoscopic effect when flexed.
Activity 11
HEXAFLEXAGON A hexallexagon has three laces, but only two are visible
at a time. Be sure to make your cuts and folds as precisely as possible
to ensure that your Hexagon will flex smoothly.
1 First cut a strip of paper divided into I0 2. Fold the strip so that the triangles
equilateral triangles. Label the front and labeled I face each other.
back of the strip as shown.
-1 t 3 A 5
\ a A 3 I
B A .5
Front ts A 3 4
Back
3. Fold the strip so that the triangles labeled 4 Fold the strip so that the triangles marked
2 face each other. 3 face each other. Carefully glue together
the triangles labeled 4, and let the glue dry.
9 \
B B
5 B
5. Now you are ready to flex your
liexallexagoit. Pinch together two triangles
and push in the opposite side so that the
flexzagon looks like a Y shape when viewed
from above. Open the flexagon from the
center. Repeat. How does the arrangement
of the laces change as vou lle\: the llexagon?
282 CHAPTER 4
Activity
HEXAHEXAFLEXAGON A hexahexaflexagon has twice as many faces as the
hexaflexagon. It is also more complicated to construct, so follow the
directions below carefully.
1. First cut a strip of paper divided into I9 equilateral triangles. Label the
front and back of the strip as shown.
2 l 3 2 I 3 z I 3
3 Z l 5 ;_ l 3 1
Front
Back
2. Fold the strip so that each pair 3. Fold the strip so that each pair
of adjacent 4s, 5s. and 6s lace of adjacent 35 lace each other.
each other. The strip should coil
around itself and look like the
one shown below.
4. Tuck one end of the strip under the other so that the remaining pair of 3s
face each other. Fold down the flap, and carefullv glue the unlabeled
triangles together.
.\~. \.
5. Flex your hexahexatlexagon in the same way as you did the first llev.-agon.
Can you get all six faces of this llexagon to show?
Extension
1. What are the Front-back face Combinations?
2. Are any combinations of faces not possible?
3. Is there a pattern to the order in which the faces are revealed?
CHAPTER 4 PROJECT 283
Chapter Review and Assessment
VOCABULARY
base angle ............. .. 237 CPCTC . . . . . . . . . . . . . . . . .. 235 legs ol an isosceles
base ol an Isosceles corollary .............. .. 237 ‘"3"l!'° -------------- --237
triangle . . . . . . . . . . . . . . . ..Z37 isosce|es mangle _ _ _ 237 vertex angle . . . . . . . . . . . . . 237
POST ULATES AND THEOREMS
Lesson Number Postulate or Theorem
4.1 4.1.1 Polygon Congruence Two polygons are congruent if and only if there is a way of setting
Postulate up a correspondence between their sides and angles, in order, such
that {1} all pairs of corresponding angles are congruent, and {2} all
pairs of corresponding sides are congruent
4.2 4.2.1 SSS (Side-Side~Sidel If the sides of one triangle are congruent to the sides of another
Postulate triangle, then the two triangles are congruent.
4.2.2 SAS (Side-Angle- If two sides and their included angle in one triangle are congruent to
Side) Postulate two sides and their included angle in another triangle, then the two
triangles are congruent.
4.2.3 ASA (AngIe-Side- lf two angles and their included side in one triangle are congruent to
Anglel Postulate two angles and their Included side In another trlangle, then the two
triangles are congruent.
4.3 4.3.1 AAS (Ang|e—Angle— If two angles and a nonincluded side of one triangle are congruent
Side) Congruence to the corresponding angles and nonincluded side of another
Theorem triangle, then the triangles are congruent.
4.3.2 HL lHypotenuse—Legl lf the hypotenuse and a leg of a right triangle are congruent to the
Congruence hypotenuse and corresponding leg of another right triangle, then
Theorem the two triangles are congruent.
4.4 4.4.1 Isosceles Triangle lf two sides of a triangle are congruent, then the angles opposite
Theorem those sides are congruent.
4.4.2 Converse of the ll two angles of a triangle are Congruent. then the sides opposite
Isosceles Triangle those angles are congruent.
Theorem
4.4.3 Corollary The measure of each angle of an equilateral triangle ls 60°.
4.4.4 Corollary The bisector of the vertex angle of an isosceles triangle is the
perpendicular bisector of the base.
4.5 4.5.1 Theorem A diagonal of a parallelogram divides the parallelogram into two
284 CHAPTER 4:
congruent trlangles.
4.5.2 Theorem
The opposite sides of a parallelogram are congruent.
4.5.3 Theorem
The opposlte angles of a parallelogram are congruent.
Lesson
Number Po=‘ulate orT‘1eorer1
4.5.4 Theorem Consecutive angles of a parallelogram are supplementary.
4.5.5 Theorem The diagonals of a parallelogram blsect each other.
4.5.6 Theorem A rhombus is a parallelogram.
4.5.7 Theorem A rectangle is a parallelogram.
4.5.8 Theorem The diagonals of a rhombus are perpendicular.
4.5.9 Theorem The diagonals of a rectangle are congruent.
4.5.10Theorem
The diagonals of a kite are perpendicular.
4.5.11 Theorem
A square is a rectangle.
4.5.12Theorem
A square is a rhombus.
4.5.13Theorem
The diagonals of a square are congruent and are the perpendicular
blsectors of each other.
4.6 4.6.1 Theorem if two pairs of opposite sides of a quadrilateral are congruent, then
the quadrilateral is a parallelogram.
4.6.2 Theorem if one pair of opposite sides of a quadrilateral are parallel and
congruent. then the quadrilateral is a parallelogram.
4.6.3 Theorem if the dlagonals of a quadrilateral blsect each other, then the
quadrilateral is a parallelogram.
4.6.4 Theorem if one angle of a parallelogram Is a right angle. then the
parallelogram is a rectangle.
4.6.5 Housebuilder if the diagonals of a parallelogram are congruent, then the
Theorem parallelogram is a rectangle.
4.6.6 Theorem if one pair of adjacent sides of a parallelogram are congruent, then
the quadrilateral Is a rhombus.
4.6.7 Theorem if the diagonals of a parallelogram bisect the angles of the
parallelogram, then the parallelogram is a rhombus.
4.6.8Theorem If the diagonals of a parallelogram are perpendicular. then the
parallelogram is a rhombus.
4.6.9Triangle Midsegment A midsegmenl of a triangle is parallel to a side of the triangle, and
Theorem its length is equal to half the length of that side.
4.8 4.8.1 Betweenness Given three points P, O, and R, if PO+ OR: PR. then 0 is between
Postu late
Pand Ron a line.
4.8.2 Triangle lnequalitv
Theorem
The sum of the lengths of any two sides of a triangle is greater
than the length of the third side.
CHAPTER I REVIEW 285
Key Skills 8: Exercises
LESSON 4.1
Key Skills Exercises
Identify corresponding parts of congruent In the diagram below, £tKLM E APOR.
polygons. Complete the following statements about
Given: ABCDE E FGHI! A B G F °°"9fl°"°°° R
ldentifv all 3- ' l‘ ‘- 1-” E j? K
. _ talrs 0 E J _ O
congruent Sidc> D C H I 2. RP E ? D
and angles. 3_ L P E ? L ([4 P
332%,-lf'§_(=;Tl,-CTJEFI.-I7‘;-I7,-I-‘.7127?’ 4-IEQPRET?
LAELF, LBELG. LC§LH.LDELI, LFEL]
LESSON 4.2
Key Skills Exercises
Use SSS, SAS, and ASA postulates to Are the triangles in each pair below
determine if triangles are congruent. A congruent? State the postulate or theorem
which triangles below are that s"pp°ns V°"' answer‘
‘ * AABC?
Longrucnt to B C 5_ 5_
£1 £6
E F H I
J M
f S : 7 7 8.
K L N 0
ADL1-‘s A \b’Cby ASA. AGH! s A ’lb’Cby SSS.
AIKL cannot be provcn congruent to AABC from
the given inlorlnation. £t.\I.'\'O E AABC by SAS.
LESSON 4.:-.
Key Skills Exercises
Use AAS and HL Theorems to determine Are the triangles in each pair below
whether triangles are congruent. congruent? State the postulate or theorem
In the ligurc at right is 5 mm s"pp°"s V°"' answer‘
Al.-'1-’W 2 :3! ‘ST.’ U 9. 10.
:3 UV I" 2 «A US I'by A-‘XS. so
11.
Al.-'l-'18-'; AI 'STby the
Transitive Property‘ of Congruence. V W
286 CHAPTER 4:
LESSON 4.4
Key Skills
Use triangle congruence in proofs.
In the ligure below, E '=" D—C and B7) 5 fl. Prove
that .44 s .40. 3 C
A D
AABC E £xDCb’ by 585. so AA 5 AD because
CPCT C.
Use properties of isosceles triangles in proofs.
QRSTis a kite. Prove that 0
Q5 bisects TR. T R
Because AQYR is isosceles, zone 5
ZQRT. Also. AQTS E AQRSl1_v SSS.
so 4 TQS E [ROS because CPCTC. Then
aour 2 AQUR bv ASA. so [U 2 W because
CPCTC.
LESSON 4.5
Key Skills
Prove properties of quadnlaterals.
Quadrilatcr-iEFC_;‘_l_l is a rhombus.
Prove that EDE GD. F V G
)'
Because E!-‘GH is a rhombus. it is also a
parallelogram. so the diagonals biseet each other.
Tlierelore, EDE GD.
LESSON 4.8
Key Skills
Classify quadrilaterals from given information.
If quadrilateral ABCD has two parallel sides and
AB E CD, is ABCD .1 parallelogram?
The information given is not enough to determine
whether ABCD is a parallelogram. For example. if
the parallel sides are AD and B(‘, A BCD could be
an lSOSC.t"lc5 trapezoid. as shown below.
B/C1‘:
Exercises
Complete the proof below. M
Given: quadrilateral .’\-INOP with
AMPN. .é.\-INP. AOPN. p N
and .(ONPall congruent.
Provo: M MOP is a rhombus. 0
Proof:
L\.M NP and AONP are isosceles by
12- ? . so .717’ 5 TN and
W’ E EV7 by 13. ? . Also.
AMPN 5 AOPNby 14. '6 ,
so ET‘ 5 —O—}"and MN E Cwbecause
15. ? . Because all ofthe sides
are congruent, MN OP is a rhombus.
Exercises
16. In parallelogram RSTU. prove that A Rand
AS .1 re supplementary.
17. In rectangle CDEF with diagonals intersecting
at G. prove that .r3.CDG E AEFG.
18. In rhombus NOPQ, prove that
z.\'(_)Q E 4POQ.
19. In square VWXY. prove that
Al-’l1"X 2 Al-1"Xl’.
Exercises
Classify each quadrilateral according to the
given information. List all terms that apply to
each quadrilateral. (You may wish to draw a
diagram of each quadrilateral.)
20. In PQRS, Wzllfiatid P—Qz R—S.
21. In KL.\-IN, mm. mum, and FL 2
22. l_n__l_VX£Z_, T1?’ -,\7_l)_is€ct each other.
W‘/J. X73, and WX J. X Y.
23. In EFGH. EIICTH, E 5 and n1zL' = 90°.
CHAPTER I REVIEW 28‘)
LESSON 4.7
Key Skills
Construct figures by using a compass and
straightedge.
Construct an angle with A '2’
.X
Y
X
twice the measure ol‘ LA. R
LESSON 4.9
8 C
/
\
L»
8 C
Key Skills
Translate, rotate, and reflect a figure by using
a compass and straightedge.
Rotate APQR about point P.
Draw and construct
LCBX 5 LA.
Using fit. construct ./_,\'m' 2 LA.
By the Angle Addition Postulztte
and the Substitution Property,
IIILCBY = 2 x mLA.
p _:
Construct arcs centered at P through points Q and
R. Choose a point on the are through Q. and label
it Q’. Construct LQ'PR' as LQPR, and connect Q‘
and R' to form L\.PQ'R’.
:
\
u
n
n
1
Applications
Exercises
Use a compass and straightedge to complete
the following constructions:
24. Construct an isosceles triangle.
25. Construct the perpendicular hisector ol' the
base of the isosceles triangle.
26. Construct a rectangle.
27. Construct the angle bisector oi" any angle ofa
rectangle.
Exercises
Refer to the diagram at J
right.Trace the figure ‘
onto paper for each K L
exercise.
T»
28. Translate AIKL as indicated by the translation
\"t':‘Cl0l'.
29. Rotate .é.]I<L about point K.
30. Reflect AIR’! across the translation vector.
31. Reflect £xlKLacross KL
32. SURVEYING Refer to the figure at right. What measurementtsl
would you need to make in order to determine the distance across
the lake? (Assume that the distance cannot be measured directly.)
33. DESIGN Trace the figure shown below. Construct at congruent copy
oi" the figure by using a compass and struightedge.
K
288 CHAPTER 4:
Chapter Test
In the diagram below, ABCD 5 EFGH. Complete 15. SL‘R\-' F.Yl\1G A surveyor needs to measure
the following statements about congruence. the distance across a field from point I to
5 point K. \-\"h.1l is the distance? Justify your
D C H -.1nswer. J
.70 “
Z ; F 85 ft /\ Q
A B L -
-1 G alzfl 705 \.K
1 b’ E_?_ 2. DC5_?_ 3 I'L‘E_'{_
4 AC: , 5 Z H 2 7 6 CB“): , Find the indicated measure for each parallelogram
16. RU 11. n1z,\’i-7
For Exercises 7-12, are the triangles in each pair
congruent? State the postulate or theorem that
supports your answer.
R S X Y
2x+ 10 -1x—24
7. 8.
_/ 35
U 15 T W Z
9.
Given: ABCD is a parallelogram
and E '=- f
Provo: ABCD is a rhombus. D c
10.
Statements Reasons
ABCD Is a parallelogram. Given
5 E c—o, .13 _ E 13. _?_
IE 2% 19. L
Find each indicated measure. ,5 2 B—Cs C—Ds E 20. L
11. mzi’ 12. 11110 ABCD Is a rhombus. 21. _e_
X 0
Construct each of the following with a compass
and straightedge.
22. a trapezoid 23. 21 rhombus
P R
W y is each of the following triangles possible?
13. LA: 14. 11118 " “°‘- WW “°t-7
A {2x)° 24. AB= I7. BC= 2(1,.r‘lC= 22
M
25 DE=25. El-'= 10, 1:17:40
3 2e. c11=9.m=1:1.G1=9
L O 15 N
Bx 20)., 27. X)’: 13. YZ= ll, X2: 24
CHAPTER .1 TEST 289
-- e-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For QLl':‘$ti()n> I-8. write the
letter that indicates the best answer.
1. What is the slope utfi with endpoints
D(—7, 7) and E(—.%, —3)? (Lesson 3.8}
"J
8- ‘z
b- -%
.5.
°' 2
u. -1
2. Refer to the diagrams below. Find the values
of x and y. (Lesson 4.1;
N Pv: j :0
%‘I\ l2x+y 1)°x[(2y+1-1)”
.. .\_ .. l3x—2l
M 60_56 O R
AMNOE APOR
a. x= 20%.y= l9%
b. .\'= l8,}'= 25
c.x=l9%,y=lB%
d.x= 20%,y=23
3. Which congruence statement indicates that the
two triangles are congruent? (Lesson 4.3)
Y U
2 V
X T
a. AXYZE f\.TVL-', S.-\S
b. rfl-.X£l'E fit I l-’U. HL
c. AXZYE L-.Tl-’U, SSA
d. AA Y7: .-"‘\TU\I’. SAS
290 CHAPTER 4:
£19-
fl intemetcon - - to"
Standardized
Test Prep Online
Go To: go.hrw.com
Keyword: MM1 Test Prep
. Which pair of points defines a line Y
perpendicular to MN?
(Lesson 3.3)
a- (0. 7), (8, —4)
b.(4.—7L(-4,4)
c. (-7, O), (4, 8]
d. (7. -4). (-4, -1)
. \-\-‘hat is the measure of AACE’ (Lesson 4.4)
a. 42° 3
b. I 26°
c. 63-” 5"
d. cannot be determined
A C
. What is the unknown angle measure?
(LESSON 3.5}
a. l20°
b. l8U°
c. I50”
d. I00”
. \-\"hich pmlttltlte or theorem justifies the
congruence statement AQD/l ‘—_' AU,-‘lD?
(Lessons 4.2 AND 4.3;
a. SSA O U
b. 585
c. HL
d. SAS
D A
8. Which is not a leztture of every rhombus?
(LESSON 4.6)
a. parallel opposite sides
b. congruent diagonals
c. four congruent sides
d. perpendicular diagonals
9. Write the converse of this Stzltememt It trees
bear cones. then the trees are conifers.
(LESSON 2.2)
10. Use the rule Tu‘. y) = (x+ 2, y — 2} to
transform the figu re below. What type of
transformation results? (LESSON 1.7)
Y
11. Lines 1’ and m are parallel. Find 11112.
(LESSON 3.3)
m
130'
12. Are the triangles below congruent-.’ which
puslttlale or theorem iustifies your answer?
(LESSONS 4.2 AND 4.3)
13. Which of the following measurements do not
del'ine a possible triangle? Choose all that
apply. (LESSONS 3.3 AND 4.3)
a. mAA = 50°, 11148 = 85°, n1zC= 45°
b. /‘lB= l2, BC= 7..-‘lC=9
e. mix! = 90°, m.£B = 65°, m£C= I3°
d. AB= I8, BC= 6. .AC= I0
FREE-RESPONSE GRID
Items 14-16 may be answered (3: C9
by using a free-response grid '3 C? Q R ‘
such as that commonly used Q’) (33 “'3'
. . G) (D (D G
by standardized-test services. (9 C3 C9 Q)
C) (E) (E) (3
CD C4‘) C?) G‘
G) G) {D (E
(D G) <1?) CD
{D (D {D G‘
G) G) (D C?
(E) (E) (E) G
14. QUAD is a rectangle. Find x. (LESSON 4.5)
0 U
OC=x C-
DC=3x—8
D A
15. Find the measure of an interior angle ollthe
regular polygon below. (LESSON 3.6)
16. Point A is theflidpoint ot Point D is the
midpoint of CE Find BC. (LESSON 3.7;
CHAPTER 4 CUMULATIVE ASSESSMENT 291
Perimeter *
and Area
THE IMPORTANCE OF THE IDEAS OF PERIMETER
AND AREA is suggested by the images on these
pages. How long is the oval track around the
playing field? How long is the Great Wall of
China? How much grain can be grown on a
given field?
Sometimes, people require information about
area for strange reasons. When the conceptual _ __ —«
anist Christo devised his plan of surrounding i
islands by pink plastic, he needed to know ' _ ‘. .
how much material would be required for the
Lessons proim
5-1 ° P°'i“'°‘°”"‘“ A'°° You may already be familiar with formulas for
52 . Areas “Triangles. perimeter and area. In this chapter, you will
P8r8||e|09f8mS. and deepen your knowledge of them by develop
Trapezoids . .
mg and proving them.
53 o circumferences and
Areas of Circles
5.4 0 The Pythagorean
Theorem
5.5 0 Special Triangles
and Areas ol I _ " ~
Regular Polygons , " .‘k __ ' '1
'4? 3 ' '- ‘ .
5.5 o The Distance «:3 ' ‘ _.,.--2? ¢ '
Formula and the '3 ?",."'-*3} 3'
Method at _ ‘ ' _. l 'gf__ -
Quadrature ' " "_;J3'..“ "5 . ' ‘Q’ P
" :3» ’'--‘5.-.*- -1:41.
5.7 0 Proofs Using ,,,rt‘.‘‘' '4' J5 - 3»
Coordinate '-*"r_'_ - -..' -.
Geometry v ' . '- "J -—r
. a ‘-2 ='
5.8 o Geometric _ _A ~- - ‘ x 5: 2-33..-
Probability ' «r. ~ ,,,«_' ~ -_ *j7~',¢‘ ‘“
. °"‘ - . . .I~‘:'*:*.‘-753-“'5‘*'
Chapter Protect .- ._..__‘-v‘__b,_Jr3,: 3"
Area olaPoIygon r‘ -34- _ _
.. _ ‘l
292
About the Chapter Project
ln this chapter. you will stttdgr formulas for the
area of common shapes such as rectangles,
triangles. and circles. But there are many other
shapes that cannot be included in these
categories: stars. crescents. and irregular shapes
that do not even have names. much less formulas
for their areas.
in the Chapter Project. you will study polygons
drawn on square grid paper in such a way that
every vertex is at at grid point. By determining
the area of the figures and searching for at
pattern. you will derive the formula for the area
of such figures discovered by George Pick in l899.
After completing the Chapter Project you will be
able to do the following:
0 Find the areas of certain C01TIple.\' figures
without using traditional area lhrnmlas.
nu-llll Jill
Chri.s'tt>'.\‘ Surrounded Islands. l3i.\‘u1yrIrBrzy.
t\firmti. Florida. I980-I983
About the Portfolio Activities
Throttghoul the Chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
Chapter Proiect is the area of ligures in a plane.
0 In the Portfolio Activity on page 320. you will
find areas of irregular polygons h_v dividing
them into rectangles and triangles.
o In the Portfolio n‘\Cl.i\"ii_Y on page 546, you will
lind the area of a crescent-shaped figure called
A ftlllf.
o In the Portfolio Activity on page 359. you will
use a calculator to generate random points on
a grid and use them to test the theoretical
proltaltility that at point chosen at random lies
within a given area on the grid.
293
Perimeter and Area
_ -—— _ _ .0’ _
. u fie’) ' -.
Q ' }' j‘ ', -:
J . ‘I _. ' _ - _' ' —
6 . ' 7 .5 Q ‘J. 4-’... 3'2‘,
/ :7 ,.
DGHB Of _ ., '0 : _-F’ "'~‘-I
the Nile
4 > 1. .
1¢ ‘ ,
. I‘ 4
Objectives N_"9 . ."’." ‘ .
River int» - ' , ,
0 Identity and use the \ *' - ’ I . ,. -
Area at a Rectangle _ .,’ ~\ ‘ f
and the Sum of Areas . -' 1 " __, i '
Postulates. _ 1
\ .
o S0lv|e pr0:]-IGIES h [1 l"r_ll ‘ I...‘ l
nwo ving Ixe -“IE9 . |§:_“ I
Derimeters and fixed "W" {'"'apm.°"aM‘ how “my ' ' ‘fl II
mag Ieetollencing wouldrrtaketaenclose I‘ _ r-~ K I I ' . _
it? Hownurclt carton could you plantar: " ’ . F: l I "
it? These questions involve the ideas of .- H.‘ g T’ I 1
perlnteter. circumference. and area. ' -7 ‘
A . p U c A I 0 N III ancient Egypt, the vearly flooding of the Nile Riser was beneficial for crops,
SURVEYING but it damaged and even destroyed property boundaries. This forced the
l;'g,\-‘ptians to devise methods for redetermining bound-.Iries after each flood.
The later development of such methods by Greek mathematiei-ans led to the
science oi‘ “ Earth measure" for which geometry is named.
Perimeter
Perimeter
The perimeter of a closed plane figure is the distance around the Figure.
5.1.1
A
E
3 For a polygmt. the perimeter is the sum of the lengths of its sides.
D The perimeter of a polygon can he used to appro.\'imate the perimeter of a
closed figure in a plane. For example, the perimeter of the irregular FIg1II’e at
C left is approximately equal to the perimeter of polygon .IlBCDL.
cnI'ncAL THINKING How could you redraw the polygon in the figure at left above to get a better
estimate of the perimeter of the irregular ligure?
294 CHAPTER 5
E X A M P L E Find the periinizter ole-ach ligiire.
a. pent:.tgt)n ABCDE
B,.7.}C2
2 >0
A __ 5
5 E
b. parallelogram WXYZ
W X
0 SOLUTION
a. The perimeter is the sum of the sides of the peiitagoii.
perimeter = 3 + 7 + 2 + 5 + 6 = 23 units
b. The figure is at parallelograni. so opposite sides a re ol equal length.
H-’X = l"Z = 5 4' W = Xl" = 3
The perimeter is the sum of the sides.
perimeter = WX + Xlr’ + YZ + ZW
= 5+_’»+S+3= I6 units
Figures are non-
averlapping if they
have no points in l-
common {except for
boundary points).
Area
The area of a closed plane figure is the number of non—o\-erlaipping
squares of-.1 given size that will exactly cover the interior of the Figure.
5.1.2
In the lloor tile illustration at right. there are 3 rows
oftiles with -I tiles in each row. You can find the
total number 0|‘ tiles by llllllll]Jl)«'lllg. .
3 X 'l = 12
Number of rows I iJNumDer of tiles
in each row
T
nvelve Ix I tiles
will exactly cover
a 3 x 4 rectangle.
l'he following postulate is used to find the areas of nonrectangular shapes.
[See Example 2 on page 296.)
Postulatez The Sum of Areas
If .i figure is composed of non-overlapping regions A and B, then the area
of the figure is the sum of the areas of regions A and 8. 5.1.3
LESSON 5.1 PEHIMETERANDAREA 295
Area and Perimeter of Rectangles
The perimeter and area oi a rectangle can be found easily bv using the
definitions on the previous pages. However. it is often more convenient to use
the following formulas:
The Perimeter of a Rectangle
The perimeter ofa rectangle with
lzoase b and height It is given lay:
P = 2b + 2h. ’'
_l l_
Postulatez Area of a Rectangle
The area of a rectangle with
base band height it is given by:
A = bit. h
_l L
*1 r 5.15
E X A M P L E 0 Find the area of each figure below. Explain your method in each case.
0 SOLUTION
a. Multiply the base and the height.
The area is I5 square units. g
6 3
L0
b. Divide the Figure into separate
rectangles. One way of doing this
is Shown at riglm (2.5 x 6) ‘ (3 x 8i = 15 + 24
= 39 square units
c. Select an appropriate grid and place
it over the figure. ljstimztte the area by
counting the nutnber of squares inside
the Figure. One method is as follows:
Take half the number of squares that
are only partially inside the tigure
[these are identified with dots]. Add
this to the number of squares that are
entirely inside the ligtt re. Tltere are
I8 partial squares and I6 complete
squares. The area is -.tpproximatel,v
%(l9) + I6 = 25_l—!squ'.1re units.
cRmcAL THINKING How is Postulate 5.l.3 [on page 295] used in E‘(dlll[JlL‘ 2?
296 CHAPTERS
' I
Flxed erlmeterlMaxlmum Area
v D A gardener has 24 feet of fencing for a . ~.r -- . - _
9,39,. nape, garden. What are the dimensions of the “ ' of.
I : on ' rectangle that will enclose the greatest area? _ J‘. i 661
""::‘- 9'39"“ 1. Sketch three different rectangles with a - - ,,.'}4r ""- -
" calculatol . . . . £3, :5-
perimeter ol 24 units. What IS the area ’ .,
of each? - ..
A ' P I c I 0 H 2. Show that h = I2 — b for a rectangle '
GARDENING with a perimeter ol 2-1.
'I
3. in 3 table lht? One «N right. hfll. b h: 12 _ b A: bh
do you observe about the area values?
,4 1 I 1 4. Plot the values forband/I from the table 2
on a graph. with I1 on the horizontal axis
and A on the \rertical a\'is. 3 7 7
_a
11 11
5. W hat are the dimensions of the rectangle that has the ma.\'imum area
for the given perimeter? If you have a graphics calculator. graph
A - b( I 2 — b) by entering Y = xnz — X). Trace the graph to find the
maximum.
cuzcxpomrr ./ 6. What kind of rectangle is your result from Step 6? Do you think this
would he the result for any fixed perimeter?
W Z
Flxed rea/Mlnlmum Perimeter
- ' D A larmer wants to enclose a rectangular area of 3600 square leet with the
9,39,, papef minimum amount of fencing. What should be the dimensions of the
on rectangle?
' '_. graphics - . . = 3600 - . .
‘ calcumm 1. show that h b tor a rectangle. 3600
with an area of 5600. b h = T P=2b+ 2"
2. Fill in a table like the one at right. 10 350 740
‘ ' P "3 '9 " let I; range from l0to I00. 20 7 ?
AGRICULTURE 3. Plot the values lor b and P lrom the 30 7 ?
table on a graph. with b on the . .
‘ {ex 1 horizontal axis and P on the vertical
axis.
4. What are the dimensions ol the rectan le that has the minimum
8
periine er or re given area. ' vou ave a grap tics ca cu a or. grap I
t I ll ? It h I I I t I
P = 2b + % by entering Y = 2x + 7-2)-(°—°. Trace the graph to lind the
minimum.
CHECKPOINT ./ 5. What kind of rectangle is your result from Step 5? Do you think this
would he the result for any lixed area?
LESSON 5.1 PERIMETERANDAREA 297
Exerc/ses
Q Co»/mm/cate
A P P L I c A ‘I’ I 0 N S 1. RECREATION Explain a way to 2. AVIATION Explain a way to estimate
estimate the perimeter of the the area of .1 wing of the airplane
swimming pool shown below. shown below.
I\i_\.
‘I 1'.
fllntemetoonnw °
. . . M
Activities
Online . - _ . .
Go To. 90 M, M, 3. L se the hgu res below to e.\'pI.=un the following statement:
§fg:'§::;s,hm area of figure A + area of ligun: B at area of figure C
C
4. lVl;tm_.' applications in Y
m.1then1.ttir:s involve
finding the area under a
curve. How Could you
estinmte the sltaderl area
in the. figure at right?
. qt/idea’ Sk///3 Practice
5. Find the perimeter of the Figure at right.
(EXAMPLE 1) 2 2_5
1.5 2-5
. . . 2
6. Find the area ofthe hgure at right. 1'5
(EXAMPLE 2} 5
298 CHAPTER 5
D lntumetoonnect .12
«mi
Homework
Help Ontine
Go To: no.hrw.com
Keyword
M61 I-lomewtr‘ Huh
Ior Exercises 8-1|!
PARAGRAPH PROOF
I‘! /
1
7. What is the maximum area of-a rectangular garden with a perimeter
of -18 feet? (ACTIVITY 1}
8. What is the minimum perimeter of a rectangular region with an area ot
900 square square feet? (ACTIVITY 2)
0 Practice and 74,0’?/y
For Exercises 9-18, use the figure and measurements below to find the
indicated perimeters and areas:
AD: IS in. AC: I3 in. 8D: l0 in.
DL = ll in. E! = 3 in. CH = -'l in.
9. the perimeter of rectangle ADU
10. the area of rectangle ADH A_i 8 CL: i_D
1 1. the perimeter of rectangle CD! K
12. the area of rectangle CDLK G -I I. “
13. the perimeter of hexagon GHCDLI
14. the area of hexagon) GHCDL] E T: F
15. the perimeter of rectangle BCHG 1 '1 1‘
I J K L
16. the area of rectangle BCHG
17. the area of r:~.BHG tllint: Use your answer to Exercise I6.)
18. If points I and D were connected by a segment. what would he the area of
AADI?
19. Write a paragraph proof of the formula for the perimeter of a rectangle.
In Exercises 20-23, find the area of the rectangle with vertices at the
given points.You may find it helpful to sketch a graph.
20. (O. O). (0. 2). (5. 03. (S. 2]
21- (3. ll. (3, 7).(9. 1). (9. 7]
22. (—2, -5). (-2. 5). H. -5). (4. 3-)
23- (0. 0]. (3. 3-). (6. U). (3.-3]
24. The perimeter of a rectangle is 72 centimeters. The base is 3 times the
height. What are the dimensions of the rectangle? What is the area?
25. 'l'he area of a rectangle is 27 square feet. 'I he base is 5 more than twice the
height. W hat are the dimensions of the rectangle? What is the perimeter?
26. The perimeter of a rectangle is 80.1‘. The base is 7 times the height. In
terms of x, what are the dimensions of the rectangle? What is the area?
27. The perimeter of a rectangle is equal to its area. l'he height is 3 more than
the base. What are the dimensions of the rectangle? What is the area?
28. For a rectangle with a lived perimeter of I00, 2b + 2!: = I00. Solve this
equation for b or hand graph the resulting ftmction. What type of
function represents this relationship? What values of In and la do not make
sense in the equation?
LESSON 5.1 PEHIMETERANDAHEA 299
CHALLENGES
APPLICATIONS
300 CHAPTER 5
29. For a rectangle with a lixed area of I00, bl: = I00. Solve this equation for b
or h and graph the resulting function. What type of function represents
this relationship? What valties of band it do not make sense in the
equation?
30. The squares in the grid below
measure 0.5 centimeters on
each side. Estimate the area of
the shaded Figure.
31. The squares in the grid below
measure 0.5 centimeters on
each side. Estimate the area of
the shaded figure.
CONSTRUCTION A house has a roof with
the dimensions shown at right. Both
rectangular halves of the roof will be
covered with plywood.
4211 We
32. If plywood comes in pieces that measure
3 feet by -1 feet, how many pieces of
plywood are needed to cover the root?
Assume that both halves of the roof are
the same.
33. Show a possible arrangement of the plywood pieces on one hall" of the
ro0l'. Try to make as few cuts as possible. How much scrap plywood is lel't
over after covering the entire root?
34. SOLAR ENERGY Eric uses solar power to heat his home. He wants to provide
lS.0O0 BT1 1s of heat from 2 solar panels. Eric wants the panels to be equal
in size and l0 feet long. ll‘ 6 sqtiare feet of panels provide I000 BTL‘s, what
should be the dimensions of the panels that he uses?
APPLICATIONS
Barn
35.
36.
37.
38.
39.
40.
AGRICULTURE You haw: 200 feet '
of fencing material to make a
pen for livestock. lfyou make
a rectangular pen, what is the
maximum area you can fence
in? Extend the table at right to
determine the answer.
AGRICULTURE Suppose that you
need an area of 5623 square feet
for grazing livestock. Wh-at is the
minimum amount of fencing
needed for a rectangular pen
with this area? Extend the table
at right to determine the answer.
AGRICULTURE Repeat Exercise
35. but suppose that one side
of the pen can he left out by
placing the pen against the wall
of the barn, as shown at left.
AGRICULTURE Repeat Exercise
36. but suppose that one side
of the pen can be ten out bv
placing the pen against the wall
of the barn. as shown at left.
LANDSCAPING Rudy is buying
sod for the lawn illustrated at
right. Given the dimensions,
estimate the number ofsquare
feet of sod that he needs.
Assume that all angles shown
are 90°.
LANDSCAPING Dian wants to
plant a rectangular vegetable
garden that measures 10 feet by
lt'-: feet. She will plant the
vegetables in rows that are IO
feet long. Dian wants an equal
amottnt of space for lettuce.
tomatoes. carrots, zucchini, and
peppers. In addition. she wants
one IO-foot row of marigolds
that will be I foot wide. How
much space will Dian have for
each tvpe of vegetable?
Base Height Perimeter Area
1 ? 200 ?
2 7 200 ?
5 ? 200 .7
20 ? 200 ?
Base Height Perimeter Area
1 .7 ? 5625
? ? 5625
5 ? .7 5625
20 ? ? 5625
Base Height Perimeter Area
1 ? 200 ?
2 ? 200 ?
5 ? 20D ?
20 ? 20D ?
Base Height Perimeter Area
1 ? ? 5625
2 7 7 5625
5 ? ? 5625
20 ? 7 5625
40 ft
21 ft
15 fr .}‘{1:d.
30 ft
LESSON 5.1 PEHIMETER AND AREA 301
APPLICATION
CHALLENGE
302 CHAPTER 5
41. HOME IMPROVEMENT Brenda wants
to paint her room. which measures
I4 feet x 16 feet x IU feet. as shown.
The room has -.1 6 foot x 4 foot
window and a 3 foot X 7 loot door
that will not be painted. She will give : ‘
the walls and ceiling two coats 3 6
of paint: a base coat and a final coat. to I
One gallon of the paint tor the base
coat costs $10 and covers 500 square
feet. One gallon of the paint for the
final coat costs $20 and covers 250
square feet. The paint is sold only in
I-gallon cans. If the sales tax is 7'9’ _. how
much will it cost to paint the room?
16
14
£00k B464’
42. Draw an Euler diagram to illustrate the relationships among
parallelograms, rectangles, rhombuses, and squares. (LESSON 3.2)
43. Find the measure of an exterior angle of an equilateral triangle.
(LESSON 3.8)
44. If the sum of the measures ol'3 angles of a quadrilateral equals 300°. find
the measure of the fourth angle. (LESSON 3.6)
45. Find the sum of the measures of the angles of-a polygon with u sides.
(LESSON 3.6)
46. Find the measure of an interior angle 0! a regular hexagon. (LESSON 3.6)
47. Find the slope of the segment connecting the points [2, 5) and [4, -1].
(LESSON 3.8)
48. Find the slope of a line perpendicular to the segment given in Exercise -17'.
(LESSON 3.8)
49. What is the slope ofa horizontal line? (LESSON 3.3)
50. What is the slope ofa vertical line? (LESSON 3.3)
51. Find the midpoint of the segment connecting the points (—-1.6] and (6. -1].
(LESSON 3.8)
Look Bet/0/rd
52. Which has a greater area, a square with a side length of 4 inches or a circle
with a diameter of 4 inches? Explain your answer.
/\
K/
53. The square at right has I-inch sides.
How could you estimate the area of
the circle inside the square?
Areas of Triangles,
Parallelograms, and
Trapezoids
Objectives '
0 Develop formulas for
the areas ol triangles, \ .
parallelograms, and . f ‘
trapezoids. -
:: ‘
0 Solve problems by
using the formulas lot
the areas of triangles.
parallelograms. and
trapezoids.
Design: on graph paper, such as this V I _
knitting pattern, .- I :5! a method [or 2. .. -_;_—-rt
estimating areas of geometric figures. but it is " ' J-U
often more convenient to use exact Iormulas.
Areas of Triangles
Parts of aTriangle
Altitude
For each possible
choice of the base
of a triangle, there is a
corresponding altitude
and height.
I Any side ofa triangle can be called the base of
the triangle. The altitude of the triangle is a
perpendicular segment from a vertex to a line
containing the base of the triangle. The height Base/
of the triangle is the length of the altitude.
5.2.1
The Area Formula for Triangles
Part l: Derit. ing a Formula for the Area of a Right Triangle
1. Draw a rectangle on graph paper. Calculate its area.
2. Draw .1 diagonal ofyour rectangle to form two right triangles. What do
you know about these triangles from your stuclv 0|‘ special
quadrilaterals? Based on this, what is the area of each triangle?
- ll Ill. 0
graph paper
LESSON 5 2 AREAS OFTRIANGLES. PARALLELOGRAMS. ANOTRAPEZOIDS 303
CHECKPOINT V
in terms of its base, b, and its height. it.
2. Draw an altitude of the triangle from the
top vertex to the base of the triangle. is
the altitude parallel to the sides of the
rectangle? What theorem justilies your
answer?
these statements?
1. Copy the (lraning at right onto graph paper.
3. H you are given :1 right triangle. can you always
form a rectangle by fitting it together with a copy
of itself? Illustrate your answer with examples.
4. Write a formula for the area, A. of a right triangle
Part ll: Deriving a Formula for the Area of Any Triangle
h
h
b
3. The altitude divides the rectangle into two smaller rectangles. Each
rectangle is divided into two congruent triangles. Wltat theorem justifies
4. What is the relationship between the area of the rectangle and the area
of the shaded triangle? Explain your answer.
CHECKPOINT M 5. Write a formula for the area. A. of a triangle in terms of its base. I}. and
its height, lt.
CRIUCAL THINKING How can you use the method from Activity 1
to derive the formula for the area of an obtuse
E x A M P I. E oYou are buildinga triangular llat.
A ' PLICATION
THEATERABTS
triangle with base It and height lt. such as the
one at the right? (See Exercise 52.] 5
_______ __t‘_l
b x
In Activity I. you det ived the following forntttla:
Area of aTriangle
For a triangle with base It attd height it. the area, A. is given by:
t = ébh 5.2.2
U
as shown at right, for a dance .\ 6
perl'ormance. "I be flat needs to .
be covered with cloth. What is 1' ,
the area you need to cover? ‘ :
\ r‘ _
II I
35 in. 29 in. -
\ .
I (.
48 in.
O SOLUTION a
A = ya = %(-181(21): 50-: in.‘
' -
304 CHAPTER 5
-cu.-;r
-3
Areas of Parallelograms
Parts of a Parallelogram
Any side of a parallelogram can be called the Almude
base of the parallelogram. An altitude of a
parallelogram is a perpendicular segment : "
from a line containing the base to a line _5
containing the side opposite the base. The ‘xgase
height of the parallelogram is the length
of the altitude. 5.2.3
' 2
The Area Formula for Parallelograms
- I D 1. Copy the drawing at right onto _ _
graph paper and graph paper. Draw an altitude in
S°'“°'S the parallelogram from point A to
the base so that a right triangle
is lorrned. ‘ ’
2. Cttt out the parallelogram. Cut otT the right triangle. translate it to the
opposite side. and fit it to the tigu re.
What kind of quadrilateral is formed? What is the area of the ngure in
terms or b and In or the original paral|e|o_s_:ram? How does the area of the
parallelogram relate to the area 0|" the tigure formed by the translation?
CHECKPOINT M 3. Write a formula for the area olia parallelogram in terms of its base, 1:.
and its height. 11.
4. How do you know that the ‘ _____r ____ __A D___ _
triangle will always tit, as in Step 2? i
To answer this question. tirst prove 5 5
that AAEB E ADFC. Then prove ‘ _
that ADI-‘L’ is a rectangle. E C F
in Activity 2, you derived the following formula:
Area of a Parallelogram
For a parallelogram with base b and height ii. the area. A. is given by:
A = M1 5.2.4
E X A M P I. E Find the area of parallelogram ABCD. A D
7
A = bh = 5[l_’a] = 65 square units 3 13 C
LESSON 5 2 AREAS OFTRIANGLES. PARALLELOGRAMS. ANOTRAPEZOIDS 305
Areas of Trapezoids
Parts of aTraPhzoid
The two parallel sides of a trape7oid are
known as the bases of the trapezoid. 1 he Leg
two nonparallel sides are called the legs of X‘
the trapezoid. An altitude of a trapemid
is a perpendicular segment from a line
containing one base to a line containing
the other base. The height of a trapezoid
is the length of an altitude.
1. Make two copies of the trapezoid at right on bi
graph paper and cut them out. The bases of the
graph paper and
scissors
trapezoid are la. and E13, and the height is h.
2. Find a wav to fit the two copies of the
trapezoid together to form a parallelogram.
Sketch the parallelogram. D1
cuscxpomr M 3. Write a formula for the area of the parallelogram involving the
expression (b, + b3). Use the formula you wrote for the parallelogram
to write a formula For the area ol the original trape7oid.
In Activity 3:. you derived the following formula:
Area of a Trapezoid
For a trapezoid with bases in and b3 and height h. the area, A, is given by:
A = §(b.+t:-1):: 5.2.5
a bare trapezoidal region of the lawn
in front of his house. The dimensions
of the region are shown at right.
E X A M I. E or-\ homeowner needs to buy sod for T‘ N
l \
A ' P ICATIO N
LANDSCAPING
What is the area of the region? n n . 1
ll 0.! "' '"'
0 SOLUTION 50*!
A = éw. + bah ;
; 23 R;
A=3[3O+50](23) : 32“
A = 920 it =
son
306 CHAPTER 5
E X A M P I. E 0 Lise the diagram and inc-asurernents given below to tind the areas of the
indicated figures.
a. At-"1-1-’Z b. AWXl
c. parallelogram VWXY cl. trapezoid WXYZ
W 9 X
Z 6 V Y
0 SOLUTION
a. area of AH-lr'Z = gm. = %t6)(s) = 24
u. area of m-vxr = gm = %t91ts;= 36
c. area of parallelogram l='WX Y = bl: = (9](8] = 72
d. area of trapezoid W'Xl"._’. = -%-[b. + l2_,J!t = %[9 + l5){S) = 96
Exercises
. Communicate
1. Draw :1 parallelogram and one of its diagonals. What can vou say about
the two triangles formed by the diagonal? Draw the other tliagonal to form
four triangles. Are any or the four triangles congruent? which postulates
and theorems can you use to prove your answer?
2. Catt two triangles have the same base and height and not be congruent?
Can two trapemids have the same base and height and not be congruent?
Explain your reasoning.
3. In the parallelogram shown at
right. which is longer, AB or It? A 0
Use your answer to explain why
the parallelogram with a given h
base and height that has the ,-
smallest perimeter is a rectangle. B C
4. In a trapezoid. what is the average ol' the lengths of the bases? How is this
quantity related to the area ofthe trapezoid?
5. Suppose that you are given a rectangle. a triangle. :1 parallelogram, and a
trapezoid. each with a base of 16 and a height of l 1. Which figures must
have the same area? Which area cannot be determined? Explain
your reasoning.
LESSON 5 2 AREAS OFTRIANGLES. PARALLELOGRAMS. ANOTRAFEZOIDS 307
0 Guided 3k/'//3 Practice
6. Find the area of the sh-aclccl triangle.
(ACTIVITY 1 AND EXAMPLE 1) 15
40
7. Find the area of the shaded purullclogrann. (ACTIVITY 2 AND EXAMPLE 2)
7
8. The two congruent trapezoids shown fit together to form -.1 paralleltngram.
Find the area of each trapezoid. and find the area of the pnrallelogrtmi.
(ACTIVITY 3 AND EXAMPLE 3)
7
10
9. Lise the diagram below to lind the arnras of the indicated figures.
(EXAMPLE 4)
A 20 B
a. £3./‘DE
b. par-ullclograin ABCE 25
c. trapezoid ABF D D 17 E C
. Practice mm’ Apply
II Intemecoomea For Exercises 10-12, find the area of each triangle.
Homework 1o_ 11_
Help Online
Go To: go.hrw.I:om 5
Keyword: 7
MGI Homework Help
lor Exercises 10-30
4
For Exercises 13-15, find the area of each parallelogram.
13. 14.
24
For Exercises 16-18, find the area of each trapezoid.
16. 17. 18. 25
308 CHAPTER 5
CONNECTIONS
For Exercises 19-30 use the diagram and measurements below to find
the area of each figure.
T" ll TL E II E A B C
E II E ITC II E
BK - 14 K1. - 14 D E F G H
IL = 32 DH = 25
FK = 7 EH = I?
)1 - 8 DG - I8 I J FK L
19. AKCL 2o. ABIK 21. ABCK
22. ADI] 23. B(‘K] 24. EGK]
25. ABFD 26. ACKI 27. FHIJ
23. BCHL 29. BCLI 3o. ACL!
COORDINATE GEOMETRY For Exercises 31-34, find the area of a triangle
with vertices at the given points. You may find it helpful to sketch
a graph.
31. (0. 0). (0. 3). (4.0)
33. (I. 0). [3, 0). (U. 6)
32. U. -7-). (5. 3). (3. 7)
34- (-2: 1]: (4: I]: [la
COORDINATE GEOMETRY For Exercises 35-38, find the area of a
parallelogram with vertices at the given points. You may find it
helpful to sketch a graph.
35. (0. O). [4, 0). (6. 2). (2, 2
36. (0, II. (0. 3), (3. 5). (3, 3)
37. (2.3), (3.—lJ. (—l.—l]. (-2. 3)
38. (4. I], (5, I), (2. -2], [l.—2)
COORDINATE GEOMETRY For Exercises 39-42, find the area of a trapezoid
with vertices at the given points. You may find it helpful to sketch
a graph.
39- 2]) (5: -2)) UL (_l)
40. (Z. I], [4, I),(6,~I), (-I, -1]
41. (1. 0]. (5. 0). (5. 5). I I. 3-)
42.(3.IJ.t6.—lJ.t—I.—1I.(—2.I)
43. Find the base ofa triangle with -.1 height ol ll) cm and an area of I00 cm}.
44. Find the height of a parallelogram with at base of IS cm and an area of
I23 cm’.
45. Use the diagram at right ofa trape7oid and
its m idsegment to determine a formula for
the area of a trapezoid that uses only the
height ofthe trapemid and the length, m.
of its midsegment.
LESSON 5 2 AREAS 0FTRlANGlE$. PARALLELOGRAMS. AND TRAFEZOIDS 309
c 0 N N E c I I 0 N s 46. MAXIMUM/MINIMUM The triangles below have the same perimeter. which
has the largest area? Make a conjecture about the triangle with the largest
possible area for a given perimeter. llxplain your reasoning.
8
47. MAXIMUMIMINIMUM The parallelograms below have the same perimeter.
which has the largest area? Make a conjecture about the parallelogram
with the largest possible area for a given perimeter. Explain your
reasoning.
48. Write out a two-column or paragraph proof of the formula you derived
in Activity I.
49. Write out a two—colum n or paragraph proofof the formula you derived
in Activitv 2.
50. Write out a two-coltunn or paragraph proof ofthe formula you derived
in Activity 3-.
51. A kite is a quadrilateral with e'<actly two C
pairs ofadjaeent congruent sides.
Given: The diagonals ofa kite are
perpendicular. 3 D
Prove: The area is equal to one—half
of the product of the lengths of the
diagonals.
[l lint: Lise the formula for the area of A
a triangle.)
)4 b
52. l'se the diagram at right to prove P 0
K
that the formula for the area of a
triangle works for an obtuse triangle. h
The longest side of the shaded triangle
N
AK} M divides the rectangle into two
congruent right triangles. What is the
area of each of these triangles?
Right triangle &.k’l.N is divided into two triangles, AKLM and AKMN.
What is the area of AK.-1-1.'\'2
Prove that the area of AKL.-X-l is —;bfl.
M L
3 1 0 CHAPTER 5
APPLICATION
‘\
I.
\
\
53. FARMING In order to fertilize a
held. a larmer needs to estimate —
its area. listimate the area of the
field outlined in the photo at
right. lf an acre equals -13,560
square feet. how many acres is _ §°
the field? If it takes 435 pounds “ . ' ' '5
of fertilizer to cover I acre, how
much fertilizer is required to
cover the field?
£00k Back
54. Construct an Euler diagram to illustrate the relationship between sealene.
isosceles, and equilateral triangles. (LESSON 2.3)
55. Refer to the diagram below. Prove that A/IBC 2 ADL-‘I-'. (LESSON 4.4;
B E
A ‘ F c ' D
56. Find the area of a square with a side length of ::+ y. (LESSON 5.1)
57. Find the area ofa rectangle with a base of .\'+ 2 and a height of 2.-— 3.
(LESSON 5. 1)
Look Be:/0/rd
CULTURAL CONNECTION: AFRICA lleron’s formula. named after .1 matlteniatici.tn
who lived in Ale\'-andria in around I00 C.I-‘., can be used to find the area ofa
triangle from the lengths of the sides. The formula is
A = \."$(5— a)(s— b}(s— (I.
where 5 is the serriiperimen.'r—that is, hall'ol'the peritneter—and a, la. and c are
the lengths of the sides.
58. Find the setniperinteter of a triangle with side lengths of 7, 8. and 9.
59. Find the area of the triangle described in Exercise 58.
60. TECHNOLOGY Set up a spreadsheet to rind the area ofa triangle using
Heron's formula when the lengths of the sides are given. l'ind the areas of
the triangles with the sides given below.
=.5'lA2 4- B2 + C2)
is I B I C I D .//[ E I
I 3 D c 3 A
2 7 8 9 ? .?
3 3 4 5 ? ?
4 2 1 O 1 O ? ?
S x x x ? ?
|:snnrtn2-*tn2—A2rtD2-B2t*tn2—c2n |
LESSON 5 2 AREAS 0FTRlANGlE$. PARALLELOGRAMS. AND TRAFEZOIDS 3 ‘I ‘I
The ancient Chinese book The Nine Chapters on the Mctthcnmtirztl Art is the
collective effort of mathematicians over hundreds of years that may have
begun long before Euclid compiled his famous work. The Elenmns. The
version that rVlSlS today has been significantly edited and annotated by many
people.
The Nine Ch£lprt’t’.\' on the Mathentrttinrtl Arr has only recently received attention
in the West. This ancient text contains algebraic and geometric proofs that are
commonly credited to other mathem-.1ticians who didn't discover them until
hundreds of years later.
On the following page. you will e\'plore how to simplify comp|e\ problems by
using a ‘‘patchwork‘’ method of cutting up figures and rearranging the pieces.
Cooperative Learning
l'he following problems and methods are the work of Lit‘: Hui . who wrote a commentary
for the hook around 2.36 (“.l'.. The commentary. which is now considered to be a part of
the book. contains explanations of solutions given in the earlier version.
1. You can begin your exploration of The Nine Clmprers on the .'t'h1r!termtriral Art with
the following problem:
Find the side length ola square that is 5 D
inscribed in a right triangle.
a. Draw a square inscribed in a right triangle as shown C S 3 a a
at right. Make two congruent copies of the square
and triangle and fit them together to lorm a
rectangle. A b C b
b. Cut each triangle into three pieces and reassemble
them to form a long rectangle as shown at right. 3
.< —b—+v< —a— +-
c. What can vou sav about the area ol‘ the rectangle that you formed in part is
compared with the area ofthe one that you found in part b?
d. Write an expression in terms ol‘ (1 and I; for the area of the rectangle in part a.
Write an e\'pression in terms ol‘ :1. b, and s for the area of the rectangle in part b.
e. Set the two expressions from part d equal to each other to lorm an equation in
terms of rt. b. and 5. Solve the equation For 5 to lind the side length of the square.
2. \low try a harder problem liront The r\r'ine Chapters on the .'t~farltenrariml Art.
Find the radius ofa circle that is inscribed in a right triangle.
a. Refer to the diagrams at right. Two congruent copies A D a A
ol the triangle fit together to lorm a rectangle. The V‘
rectangle is divided into triangles and squares, which
are reassembled to form a long rectangle. Explain c b b / b
why EH in the long rectangle‘ is equal to r, the radius
of the inscribed circle.
B a C B a C
b. ln rectangles ADBC and EFGH. E F
explain why the lengths labeled ‘ :
a, b. and c are the same as the H.. _3_ .;. :9: ..,. C G
side lengths :1, b. and c of AABC.
1:. Write an expression in terms of n and l: tor the area ol-
rectangle ADBC. Write an expression in terms of :1, b, r, and r
for the area of rectangle EFGI I.
d. Set the two €‘€])l'€b.sl()l‘|S from part 1: equal to each
__ other to form an equation in terms ol'u, Ir, 1;
._._ * and r. Solve the equation for r to lind the
radius of the circle.
Circumferences and
Areas of Circles
S '-:= e
-.;ll -t'_[l[L\_-
objectives L: H U ':’\.'ll.L’ 't’tS luttcittig _ _
\ .\. -
0 Identity and apply A it'_1t!-k'f \ ‘Ad, . -' - 7‘ , ' '\ -__ _ ‘.._ e_
tormulas tor the ‘‘ H. nus — - _ _-‘_ , - _£'-‘ 6‘ LU ;$é' '._‘-'3"
circumlerence and ‘ _ - '2. _ _" ' " - ‘-. .-,-. _ -
area otattircle. . ' ._ , _ . «- _ _ '-, ‘ "-436 "8 '3' “-
.---_.‘I‘ _‘ : 4%.. Hippar-‘mus -.- . -_‘ ‘ *‘x"5-t,-5 er... - -- a-._ -
0 Solve ntohlems using '
the lormulas lor the Howdatlte areas ofthelaryercr: -
circumlerence and v the Moon cr -- re with the area olymt
area of a circle. -wn orstate7A detailedplwtograplt can
I : - r (4 . f : : I : It I .
The dianieter of the Moot: is about I077 miles. lim can use this
t'i.t_forrmttt'ott to tletermine the scale oftliis phomgt'aph. liteti you
can estimate the areas of the craters that are visible.
The Definition of a Circle
When you draw a circle with a
compass, the distance from the
point of the compass to the pencil
or pen does not change. Therefore.
every part of the circle you draw is
the same distance from the center '
oi" the circle. the point where the a
compass is fixed. This leads to the
following definition:
Definition: Circle
A circle is the set of all points in J.
plane that are the same distance. r,
from a given point in the plane
known as the center of the circle.
The distance r is known as the radius
of the circle. The distance d = 2r is
known as the diameter of the circle.
5.3.1
3 1 4 CHAPTER 5
circumferences and Areas of Circles
You are probably already familiar with the lormulas lor the circtiiiiferences
and areas of circles from your earlier mathematics studies. The following
activities will lead you to an understanding, of these l'orniul-as.
The Circumference of a Circle
0 I I) 1. The distance around a circle is called Obie“ C d Ratio: 5'
smng and ,._.IE, ,3, mpg its circumference. Measure the "
measuw and Calculator circumferences and diameters of seteral 1- °3"' 3"-4 1° 7
circular objects. Record the results in a 2. 2 ? .7 7
table like the one at right. _3_ 2 7
2. ‘l he ratio -31- is known as It, pronounced
"pie.” What do you notice about your values for this ratio? Find the
average of the values.
3. Compare your result with the results of your classmates. How close are
the results to 3. I4. an approximate value of It? Press the 11: key on your
calculator. Iollowed by ENTER. What value does the calculator show?
cuscxromr ./ 4. \-\'rite a lormula for the circumference. C. ofa circle. Begin by
expressing It as a ratio. Then solve for C and write the formula in terms
of the radius. r.
In .-\.ctivit}r I. you discovered the following formula:
Circumference of a Circle
The circumference. C. of a circle with diameter d and radius r is given by:
C = mi or C = Zitr 5.3.2
E X A M P L E Find the circumference ol each circle below. Give your answers exactly, in
terms of 1:, and rounded to two decimal places.
a. b.
O SOLUTION
a. C= 7rtr= 21r[4) = 31: ea 25.l3
b. C: mi = 1ttl0_‘J= I01: == 3|.-l2
LESSON 5.3 CIHCUMFEREWES AND AREAS OF CIRCLES 31 5
' Z
The Area of a Clrcle
- - El) 1. Draw a circle. I abel its radius r.
,u|e,,c0m,,,,55, Using anv method you like. such as
nrotraqhorlontionall. paper folding. divide the circle into
ml S°'5S°'5 eight congruent pie-shaped parts.
or sectors.
2. Cut out the sectors and reassemble
them into a single figure, as shown at
right. It‘ the curved parts of your figure
were segments instead of curves, what
kind ol figure would you have?
3. Divide the circle into I6 congruent sectors by cutting each sector trom
Step 2 in half. ‘I hen reassemble the sectors as in Step 2. As the number
of sectors incrcases, do the curved parts seem straighter?
4. \-\'hat geometric figure do your sector assemblies in Steps 2 and 3
resemble? The height of your figures is approximately equal to r. the
radius of the circle. What happens to this approximation as the number
of sectors increases infinitely‘?
5. The base of your assembled figure is approximately equal to half oi‘ the
circumlerem:e of your original figure. (\-‘v'liy?] Write an expression tor
the base of the figure in terms of It and the radius, r. of the circle.
CHECKPOINT ./ 6. Write an expression tor the area of the Iigure in terms of 1: and r.
Area of a Circle
The area. .4. of a circle with radius r is given by:
A = m-' 5.3.3
cnmcm. THINKING Why does the method you used in Activity 2 become more realistic as you
increase the number of sectors?
E X A M P I. E 0 Find the area ol each circle below. Give your answers exactlv. in terms ot TE,
and rounded to two decimal places.
a. b.
O SOLUTION
a. A = nr’ = n(3=) = 9:: 23.27 units:
b. r=rl+2—‘ +2=3.5units
7
A = m’ = n(3.5-’) = 12.25:: .~. 33.48 units’
31 6 CHAPTER 5
Exercises
. Communicate
1. Suppose that you have I00 feet of fence to make a play area for your dog.
Does .1 square or a circle provide more area? What other factors might you
take into consideration in designing the play area? . \
2. There are many dilTerent approxintations
for 1:. Two commonly used values are .’».l4
and Compare these values with the A
value your calculator gives for .1. (_ii\-'c a H I '
reason you might choose either .3.l4 or ‘—‘.
Why is it necessary to estimate 3! when 1
calculating the area and circumference
of a circle?
3. When the cassette in the photo is e» . ‘
rcwinding. which moves taster, point A ' 3
or point 8? Explain your reasoning.
0 Q1//0'84 3k///3 P/dflt/6'8
In Exercises 4-1 give your answers exactly, in terms of it, and rounded
to two decimal places.
4. Find the circumference of a circle with a radius of 3. (EXAMPLE 1)
5. Find the circumference of a circle with a diameter of 25. (EXAMPLE 1)
6. Find the area ofa circle with a radius of 5. (EXAMPLE 2)
7. Find the area ofa circle with a diameter of 28. (EXAMPLE 2)
Practice dlfd 74,20/y
In Exercises 8-13. find the circumference and area of each circle.
Use 3.14 for 1:. Round your answers to the nearest tenth.
8.r=6 9.r=l0 1o.d=ls
Use g for 1:. Leave your answers in fraction form.
11.r=6 12. d=2l 13. rl=3§
‘ _/ . r 1 Find the radius of the circle with the given measurement. Give your
answers exactly, in terms of 1:, and rounded to the nearest tenth.
14. C- I2 15. C- 62.8
16. C-Stht 17. A-314
18. A = 50 19. l = l00:r
LESSON 5.3 CIHCUMFERENCES AND AREAS OF CIRCLES 31 7
In Exercises 20-2'I. find the area of the shaded region. Give your
answers exactly, in terms of 1:, and rounded to the nearest hundredth
20. 21. 22.
_l |_
I I-
01
23. g 24.
/ \ .2
20
26.
V V \L
"K 60/\ J
28. What happens to the circuniference ot a circle when the radius is doubled?
/\
_l
29. What happens to the area of a circle when the radius is doubled?
A P P L I c A T I 0 N S 30. MEAL PLANNING lI'a l0—inch pizza is enough to feed 2 people. will an
I8-inch pizza be enough to feed 5 people? Why or why not?
31. MEAL PLANNING [fa I0-inch pizza costs $5 and an I8-inch pizza costs $1 5.
which is the better deal? Explain your reasoning.
W --.r:-"‘:_"..’4-k-
“_.;..'..I-— 10!:
O ‘K '.-°.'3““;a- '-. ..-. \\
’ 1, \ ‘M... _sf. _ \ ‘
~‘ ‘ ' -e -' ‘VI
« ‘ :3;- . - 1"’
f .. yg U
.1
C __ ,
C
32. IRRIGATION Cemer pivot irrigmion is __ _ _
——n..'4—
a method of agricultural irrigation —— -
using a long, wheeled arm with
man)’ nozzles that pivots about the
center of a circle.
If the area inside the square is one
square mile. what is the area. in
square feet, ol‘ the irrigated circle?
(Note: I mile - 5280 feet)
3 1 8 CHAPTER 5
Di_fl'ererIrirI! gear
a lnoemoloonnoct
Homework
Help Online
Go To: uo.hrw.corrr
Keyword:
MG! llomcworlt Hahn
for Exercises 33-31
Utrmil of the Maori?"
SlII'li'l(‘e, showing the
H ippnrclrus Crater
I't'ir'dedJ
AUTOMOBILE ENGINEERING Tires are tested for traction by driving around a
small circular track. Refer to the diagram below for Exercises 33-37.
33. What is the circumference of the circle
formed by the inside tire tracks?
34. What is the circumference of the circle \
formed by the outside tire tracks? 7 ft
35. Based on your answers to Exercises .‘.-3
and 34, what can you say about the
speed of the inside tires compared
with the speed of the outside tires?
I
123::
The tires ofn mr need to turn at
differerrr speeds on rt curve. 111
nmke this passibfe, :1 device called
(I dillcrcnlial gear is used.
Suppose that the tires have a radius
of 15 inches.
36. How many revolutions will the inside
tires make in one lap around the circle?
37. How many revolutions will the outside
tires make in one lap around the circle?
38. ASTRONOMY At left is a detail of the photo of the Moon from page H4.
l'he diameter of the Moon in the photo is l2.2 cm. Lise your own
measurements and the I'act that the actual diameter of the Moon is I077
miles to estimate the actual diameter of the indicated crater.
Use your estimate ol the diameter to find the approximate area of the
crater. is it closest in size to New York City (309 miles"). Los Angeles
(469 milesl), Delaware [I955 nrilesz). Lake Superior [3l.7OO miles:),
or 'l‘e.\'as (261.9!-I miles”)?
Look Back
Recall from algebra that a radical can be simplified by taking the square
root of any factors that are perfect squares. For example:
zafi = 2. 23 x 3 = 2 x 5./5 = l0—\/3
Simplify each expression below.
39. 3,-’§ 4o. 16x/52
Find the Positive solution for x.
42. x*+|6=25 43.x’+l-I-l= I69
45. Given parallelogranl ABFD with diagonal RT, 5 C
prove that AABC '=“ ACDA. (LESSON 4.5)
41. 3e‘.00
44. xi + 12.25 = 13.59
46. Find the area ofa triangle with a base of
9 in. and a height of 7 in. (LESSON 5.2) A D
47. Fintl the area ofa parallelogram with a base ol- 3 cm and a height of
3.5 cm. (LESSON 5.2;
48. Find the area of a trapezoid with a height of 3 cm and bases oI‘6 cm and
5 cm. (LESSON 5.2)
LESSON 5.3 CIHCUMFERENCES AND AREAS OF CIRCLES 31 9
PROOFS
8
1.004’ Beyond
49. in the diagram at left. the centers of all the circles are collinear. Prove that
the sum of the circumferences of the small circles is equal to the
circttrnference of the large circle.
50. Show that the result you proved in Exercise 49 is true for any number of
smaller circles.
51. CULTURAL CONNECTION: ASIA A yin-yang syn1bol is composed ofcircles and
semicircles, as shown below. Yin and yang represent the two
complementary forces. or principles. that make up all aspects and
phenomena of life.
Which of the three indicated paths from point A to point B in the diagram
is the longest? Explain your reasoning.
B tmomctconnect
Portfolio
Extension
Go To: go.hrw.com
Keyword
M01 Square!”-aot
Ea
You can find the areas of some irregular polygons by dividing them into
rectangles and triangles and adding the areas of these figures.
1. Find the areas of the figures below. The first one has been divided into
two rectangles and a triangle to help you.
2. Sometimes it mav be easier to subtract areas than to add them. Find the
areas 01’ the ligures below by subtracting areas‘ from the area of a larger
rectangle. The lirst rectangle has heen drawn to help you.
WORKING ON THE CHAPTER PROJECT
You should now be able to complete z\c.ti\-‘ity I of the Chapter Project.
320 CHAPTER 5
Objectives
0 Identity and apply the
Pythagorean Theorem
and its converse.
0 Solve problems by
using the Pythagorean
Theorem.
A I I I year-old
clay table! from ancient
BabyIon—la what Is now
lraq—ravoltm‘ont'zed our
knowledge of ancient
mathematics.
The Pythagorean
Theorem
". A"Lu_|_” .Mfl€l \ QIiz\tn_ - _ ‘LN/I’
kflmu‘. IlHllA.\ \
M ' ?‘\wI:.w.|f It V 'Q"M E
' _ AK! A It.
llU\( '
¥\K‘mLA- 5.,“ am” ‘KIl0ltll\MAI1Itfl I R A N /A
. 1
E’ Mum“ K!R.\tINt. ‘U ‘ . I
ANCIENT “*“:l'm" .5-um ‘
Cm or _.Q,£u.,\,, ~
— \_ \
5 U r , ‘£1 , N t _ ‘ _ \ 1
I.
‘ U": "1 .7, 7.‘ ,‘ 1 ".5 l _t . JJHL -‘
I
o . i; ,- IT I ’; - " " 7’
/
-1 I 3-0 IT " '. ' .
4f - " Arum tn
. ' I
I #' ‘\ 5(1)
A fifl , I ‘ . -
n.{r I. I ‘ }
' , / ..
- I , 1- J; r , - ii F1
¢ ;v- __
% I 0."; n 1 0 _:__IP -—-jsnwh
tr’, {I 14.’ I 0 :1» u -Kila-an
. M. M. '
- ' t..t-- Culuvulf -. two...
When tht-'rr1bler known as Plimpton 322 was fitsrfiumd. no one ttndersmml the
significrtttre of the strrmg ’ columns ofmtrubers until (I nmr.'temrtrit‘t'an who
looked at it made an exciting rli.s‘t‘ot'ery.
Plimpton 322
CULTURAL CONNECTION: ASIA At the height of its power, according to Greek
historian llerodotus [«l85—-127 ll.C.E.). Babylon was the world’s most splendid
city. It was surrounded by walls almost 85 feet thick with eight bronze gates.
the main gate and its walls were decorated with figures composed of glazed
colored brick that depicted dragons. lions. and bulls.
l'he tablet in the illustration above, known as Plimpton 522, comes from a
mttch earlier period known as the Oltl Babylonian Empire, which included the
reign of King l lammurabi, who ruled from i792 to I750 It.C.t-I. and became
famous for his wise and fair code of laws.
Plimpton 522 is a piece ofa larger tablet. Part of the larger tablet, including at
least one column of numbers. has broken off and is lost. On the part that
remains. there are columns oi‘ numbers. incltltling the two columns shown on
the next page, with four apparent errors corrected.
LESSON 5.4 THE PYYHAGOREAN THEOREM 321
calculator
Solving the Puzzle
1. Work in pairs. Fach person should pick two numbers at random lrom
50 to 5000. Lise a calculator to square each number. Subtract the smaller
square from the larger square. Take the square root of the difference. Is
the result an integer? -L
2. Repeat Step I at least nve times. How otten. 119 '
if ever did vou obtain an integer as the 3367 169
_ _‘ ' 4601 ‘1825
result.’ 12709 5549
3. Square the numbers in each row of the 65 13541
tablet at right. Subtract the smaller 319 97
square from the larger square and take 2591 3:81
the square root of the dillerence. How ;\ 4:19 12:97
often is the result an integer? 4'9“ 759
4. Do you think the Babylonians knew 4.5 8151
which sets of integers were related 1679 kg
in this way? Fxplain. 161 2929
I771 289
(‘olrmms II and Ill 55 3229
ofPlirnprr:m 52.2 x 10
In the Activity. you discovered that Babylonians knew about the sets of numbers
now called Pythagorean triples —that is. sets of positive integers u. b. and r
such that ll‘ +l1l = C2.
It is also clear, from other evidence on the tablet. that the B-abylonians knew
that right triangles have the property known today as the Pytlrrrgomrrr
relrrtiorrslrip. But surprisingly. Plimpton 322 was created over a thousand years
before the teacher Pythagoras (569—-500 li.(‘.l-..), the person to whom the
relationship is traditionally attributed.
At present there is no direct evidence that the B-abvlonians could prove the
Pythagorean relationship.
Proving the Relationship for Right Triangles
lilt-
‘I’
as / -= is
I —L ,
3; s _ ::
!L">fi;2j§-} it
F] 1 if
‘in am Em!
Chirrese dirIgnmr_
322 CHAPTER 5
CULTURAL CONNECTl0N: EUROPE The Pythagoreans were members of a set ret
society of followers of Pythagoras in ancient Greece. According to tradition.
Pythagoras said. “\lumber rules the universe." We do not know how
Pythagoras actuallv proved the theorem that now bears his name. or whether
his particular proof-—there are many others—originated with him.
CULTURAL CONNECTION: ASIA One very early illustration of the Pythagorean
Theorem is found in an ancient Chinese source known as Chou pei smm rhing.
The source does not give details of a proof. but it does include the diagram
shown at left. which stlggests a proof of the theorem [see page 323). According
to some scholars. the date of the diagram is at least as early as Pythagoras.
PARAGRAPH PROOF in outer part of the Chou pei smm thing diagram. four congruent right
triangles form a large square with a smaller square in the center. The area
of the larger square can be found by squaring the length of its sides, which
are equal to n + b. or by adding the individual pieces that make up
the figure.
8
By setting these two expressions equal
to each other and simplifying, you
obtain the famous result.
(n+Z1l2 = 4(-la») + r’
(11 + 2nl1+ I12 = 2:11) + ('2
‘I
f+E=r
CRITICAL ‘IHINKING Does the shape ot‘ the right triangles matter in the proof above? How do you
know that the central ligure is in fact a square? [See Exercise 39 for another
proof of the Pythagorean Theorem based on the Chou pea" smmg (‘hing diagram.)
Pythagorean Theorem
For any right triangle, the sum of the
squares of the lengths ol the legs is 3 as
equal to the square of the length of the
hypotenuse. b
a’ + Ir‘ = c’ 5.4.1
E x A M P L E 0 The following is a rule or thumb
for safely positioning a ladder: The
. distance from bottom of the ladder
' ' P C A T I 0 N to the wall should be one—l'ourth of
SAFETY the length of the ladder. Thus. the ‘l
bottom of-a l6—t'oot ladder should be
4 feet from the wall. llow tar up the
wall will the ladder reach? 16“ I
1 ‘J
tr + D‘
‘ll + b1
ll
I“:
Id
:-
.
II II
to to to —
-is U‘! as
O O Isl
I
5?
3
+
2"
.
ll
'J|
-3‘
C‘
I‘.
ll
\/240 se 15.5 it 4“
?‘
ll
LESSON 54 THE PYYHAGOREAN THEOREM 323
The bracketed
numbers In the right
margin refer to
propositions proven
earlier in The
Elements.
324 CHAPTER 5
The Converse of the Theorem
The converse of the Pvtltagoreatt Theorem is also a true theorem. It is useful
for proving that two segments or lines are perpendicular.
Converse of the Pythagorean Theorem
If the square of the length oi one side ol a triangle equals the sum of the
squares of the lengths of the other two sides, then the triangle is a right
triangle. 5.4.2
CULTURAL CONNECTION: AFRICA The following, proof of the Converse of the
Pythagorean Theorem is taken directly from Euclidis The Elements, Book I,
which was translated from the original Creek by Thomas l leath. You will
notice that some of Euelid’s notation and use of terms are different from our
own. Exercises 52-64 will help you follow the proof and put it into a modern
form.
PROPOSITION 48
lf in it trimtgle the sqmm’ on one ofrlte sides be equal to the squares on the
remaining two sides oftht’ triangle. the angle contained by the rermtining
two sides of the ttfnttgle is right.
For in the triangle ABC let the square on one sitle BC
be equal to the squares on the sides BA, 10,
I say that the angle BAC is right.
For let A!) be drawn from the point A at
right angles to the straight line AC. let AD
be made equal to BA. and let D(" be joined.
Since DA is equal to Ab‘.the square on DA 0 A 3
is also equal to the square on A8.
Let the sqttare on AC be added to each:
therefore the squares on l)A. AC are equal to the squares on BA. AC.
But the square on DC is equal to the squares on DA.
AC, for the angle DAC is right‘. [l.47[
and the square on BC is equal to the Squares on BA. AC, for
this is the hypothesis;
therefore the square on DC is equal to the square on BC,
so that the side l)C is also equal to BC.
And. since DA is eqttal to AB,
and AC is common.
the two sides DA. AC are equal to the two sides BA. AC:
and the base DC is equal to the base BC;
therefore the angle DAC is equal to the angle BAC [1,8]
But the angle DAC is right;
therefore the angle BAC is also right.
Therefore etc. Q.E.D.
E X A M P L E A plowed lield is in the shape Old triangle. If the sides have the lengths shown
in the figure. is the field n right triangle?
A'P IC ION
AGRICULTURE ; _
_ 3.7 ' — _ - .
T‘? _ _ _ H
_ 3 _ 1|-
:‘ ' ,9)
. SOLUTION
It the lield is a right triangle. then :21 +l13 = (2, where ti, b. and c are the lengths
of the sides. lhe longest side on right triangle is the hypotenuse, so it" the
field is .1 right triangle. the hypotenuse, C. must be 3.7.
.13 +123 = (1.211 + (5.5):
= 13.69
Since e= ,1 13.69 = 3.7 miles, the lield is a right triangle.
The following helpful inequalities can be derivecl from the Pythagorean
relationship:
Pythagorean Inequalities
For AABC. with c as the length (it the longest side: 5
ll’ r’ = :1’ + Ir’. then AABC is a right triangle.
ll c’ > a3+ Zr’, then AABC is an obtuse triangle. A n C
If C2 < :1’ + if‘, then A/lb‘C is an acute triangle.
5.4.3
E X A M P L E 0A triangle has side lengths ol'7inches.8 inches. and t2 inches. is the triangle
right. obtuse. or acute?
O SOLUTION
129 ; 7''+s’
|4=I> H3
Therefore, the triangle is obtuse.
TRY nus A triangle has side lengths of 8 inches, 8 inches. and ti inches. Is the triangle
right, obtuse. or acute?
LESSON 54 THE PWHAGOREAN THEOREM 325
Exerc/ses
0 Com»/my/mte T — ' "-‘Ij
1. State the Pythagtirean Theorem
in your own words.
n hmmmmm #3. 2. What are some practical uses of
Amivmes ‘°"' the Pythagore-.tn Theorem and
amine its converse?
E:vT_:j,§’,j';""""°°” 3. Explain how something called the
MGITl1corum "3-4-5 rule" could help carpenters
_ create square corners.
4. t-‘xplain how the Greek postage stamp
shown at right illustrates the
Pvthagorean Theorem.
0 qt//dad 3k///8 Pfdft/60
5. A right triangle has one leg with a length of -48 and a hypotenuse with a
length of 80. What is the length of the other leg? (EXAMPLE 1)
6. A triangle has side lengths of 7. I0. and I2. is the triangle a right triangle?
(EXAMPLE 2)
‘I. A triangle has side lengths offl. I5. and I8. is the triangle right, au:ute, or
obtuse? (EXAMPLE 3)
Practice mm’ Apply
‘ 5 . x / For Exercises 8-13. two side lengths of a right triangle are given. Find
the missing side length. Leave your answers in radical form.
n, _.mmEd_ |7._ 8.{1=3,b=4,('=i 9. a=l0,l)=l5,t'=L C
vom 3
Homework 10.rl=46,b=7-,t‘=i 11. rl=i,b=6.tT=8
Hel Online _
G°TE:m_hrw_wm 12. rJ=27. b=_?_. (‘=33 13. (J: l. l): Lt'.'=l b
Keyword:
MG! Homework Help _ _ _
1°, gmc.m 9.30 Find the perimeter of each tnangle. Round your answers to the
‘ nearest tenth.
14. 15.
3 5 24
50
16. 17.
17 10
326 CHAPTER 5
CONNECTIONS
Each of the following triples represents the side lengths of a triangle
Determine whether the triangle is right, acute, or obtuse.
18. 5.9. I2 19. l3. l5. I7 20. 7. 241.25
21. 7. 24. 26 22. 3. 4, 5 23. 25. 25. 30
Find the area of each figure. Leave your answers in radical form.
24. 25.
10 ‘:1 . r
26. What is the length ofa diagonal ol a square with at side length of 5?
27. What is the side length of a square with a diagonal of to?
Find the area of the shaded region in each figure. Round your answers
to the nearest tenth.
28. 29. 30.
X 3 3
3.6
x 29
5 9
2.4
21 ,_
NUMBER THEORY Mathematicians have long been fascinated with
techniques for generating Pythagorean triples. For each method below,
generate five sets of triples. Then use algebra to show that the method
will always work.
32. Method of Plato
let M be any integer greater
than l.
31. Method of Pythagorean:
Let in be any odd number
greater than t.
33. NUMBER THEORY Test the lollowing conjecture lor [0 different Pythagorean
triples: ln each Pythagorean triple. at least one ol’ the numbers is divisible
by 3. and at least one is divisible by 5.
34. NUMBER THEORY If you multiply (.‘llL'.l'1 number of a Pythagorean triple by
the same constant. you get another Pythagorean triple. For example,
(3, 4, 5] is a Pythagorean triple. Multiplying each number by 2 results in
(6. 8. I0"). another Pythagorean triple.
Use algebra to show that it’ (x, y. z] is a Pythagore-an triple. then tux. try, :12]
is also a Pythagorean triple for any positive integer (1.
LESSON 5.4 THE PYTHAGOREAN THEOREM 327
328 CHAPTER 5
PROOF
PROOF
35. CULTURAL CONNECTION: ASIA
The Sulbrz.mtms were ancient 7
Indian mathematical manuals
[or the design and construction
of Vedic altars.
lhe diagram at right, from the ,_- G
Sulbasmms. demonstrates a
methotl for constructing a
square with an area equal to the _ _
sum ol'the areas of two given
squares. Use the Pythagorean
l'heorem to prove that this
construction works.
Given: ABC D, EFGH, and BRSTare squares.
AR = FH
Prove: area of BRS'l'= area of ABCD + area of U-‘CH
36. Explain how to use the method from the $rrlba5utm~' to construct a square
with twice the area of a given square.
There are over 100 different proofs of the Pythagorean Theorem.
Exercises 37-39 present three of them.
37. President James Garfield (l8.’»l—l88l l,
a president of the United States.
devised a proof of the Pythagorean
Theorem that uses a trapezoid. b
3
Using the ligure at right. write two
different expressions for the area of
the trapezoid. Set the two expressions
equal to each other to discover
Garfield's proof. 3
38. i5.‘<plain how the diagram below is a “proof without words” ol the
Pythagorean Theorem. You may wish to draw the figures on a separate
piece of paper and cut them into pieces to help E‘\:pi;tin the proof.
b H
e C 3
b b
c
b 3
CHALLENGE
APPLICATIONS
2nd base
I
l
Catcher (home plate)
/:1 I
39. The diagram from the Chou per’ smm sttggests at least two different proofs
of the Pythagorean Theorem.
a. Write an expression for 8, the area of A s
sqttare EFGI1. by adding the areas of the I-
lbttr inner right triangles and square UKL.
r'=;
b. Write an expression for r’, the area of
a
square L‘!-‘CH. by subtracting the areas of
the four outer right triangles from the area 3|
of square ABCD.
1' D
r=;
Simplify each equation to prove the Pythagorean Theorem.
40. PUBLIC SAFETY if the base of the ladder
in the photo at right is 8 feet oil‘ the
ground. how far up the wall will the
ladder reach?
41. TRAVEL Starting from his house. Jesse
drives north 6 miles and then turns east
and drives 2 miles. He turns north again __ I
and drives 4 miles and then turns east -
and drives 7 miles. l-low far is he from '
his house? (Hint: You may wish to draw 1- "E.
a map.) . Illa” "
42. SPORTS A baseball diamond is a
square with 90-foot sides. What is the ‘
approximate distance of a catcher’s
throw from home plate to second base?
I!
E b B
a C 3
b
J F
K c D
G a C
1.001? Bdfk
Recall from algebra that a fraction with a radical in the denominator can
be simplified by multiplying by a fraction equal to 1.This technique is
known as rationalizing the denominator. For example:
A = L X Q = 4"/5 = -*-v’5
V/-E V/-E V/-E V/-E >< t/E 5’-
Rationalize the denominator in each expression below.
4 I3 «'5
43. — 44. — 45. —
J5 J3 J?
For Exercises 47-48, classify each statement as true or false. If true,
explain why. If false, give a counterexample. (LESSON 4.6)
46. Every rhombus is a rectangle.
47. Every rhombus is a parallelogram.
48. llia dittgonztl divides ".1 qtladrilaterttl into two congruent triangles, then the
quadrilateral is a par-allelogrant.
LESSON 5.4 THE PYYHAGOREAN THEOREM 329
FLOWCHART PROOF
330 CHAPTER 5
L004’ Beyond
In Exercises 49-64, you will examine Euclid's proof of the Converse of
the Pythagorean Theorem. Read through Euclid's proof on page 324.
49. What is the hypothesis of Proposition 48! What is the c.onc.lusion?
50. Draw a triangle and label the vcrticcs A, B. and C. Use Euclid‘s directions
to construct the triangle A-.DACas in the proof.
51. In your diagram for Fxercise 50. can you be sure that the figure connecting
D to b‘ is really at single segment? (Hint: Don’t assume what you are trying
to prove.)
Complete the flowchart proof based on Euclid's C
proof of the Converse of the Pythagorean Theorem.
Given: (BA)? + (/tc)’-’ = (802
Prove: £-ABC is right.
Proof:
D A B
0 DA = A8
Winn Ll’ the rru-nstm:
By construction Hf 43,-tap
l
(9 52. L J [ 0 ADAC is right. J
Square both sides 54. _?_
of equation 0.
I
[0554 J (W: 1
Add lACl’ to both Pythagorean Given
sides of equation 9. Theorem
I 0 lDCJ’= «sci? ',«
57. _?_
I
l
Iosa; [eDA=Ae J [®AC=AC J
Take the square 59. L 60. ?
root of both sides |
of equation a. K /
‘I (1161. ?_ [‘
SSS Postulate
Q3 mABAC= mADAC
e2. 1
@ m.£BAC= 63. ?_
Substitutioln Property
1
to
| Q AABC IS right.
64.;
Special Triangles and
Areas of Regular
Polygons
\,_ “ti Tat
.‘| I“-‘.1 ‘I M I .3 /‘
\ l
Objectives — y _
0 Identity and use the _ ' I
45-55-90 Triangle ' ‘ cg
Theorem and the .
was-so Tnangle ml"? """"""'."
1-he°rem_ me man! drawing inc .3
Tsquare and two special
0 Identity and use the triangles. one of the triangles
formula for the area of has 59919; megsupmggofi 50-, _ .
8 |’99l||8f DDYYQOH and 90°. The other lies angles
mensuring 45", 45°, and 90°. The ‘
properties oi’ these triangles '
make them especielly useful in
geometry as well as in drawing.
This rlmfrsrmm uses her T square to esmblisir rm irmtgimtry
lint’ parallel to the luisc nfher page. Then, using a speriul
ll imigle. site dr'aw.~: a segment at n 30" angle to this line.
45-45-90 Triangles
If you draw ‘.1 di'.1gon.t| of a square. two congruent
isosceles triangles are formed. Because the diagonal
is the hypotenuse of a right triangle. its length can
be found by using the Pyth:1gt)rean Theorem.
E X A M P L E otse the Pvthagore-an Theorem to find the length oi" the hypotenuse of AABC.
what is the r-atio ofthe hypotenuse to a leg? ,4
' _I.- r" I O SOLUTION h
if =10! +103 = 200 1°
1.: V/200: dnoox J": not/5
. — C 0 B
I he ratio or the hypotenuse to a leg is '0‘/2, or \/5. 1
I0
CRITICAL THINKING What is the length of .1 diagonal ofa square with 21 side of length 5? What is the
ratio of the diagonal to the side?
LESSON 5.5 SPECIAL tntaNGtEs AND AREAS OF REGULAR P0-LYGONS 331
Notice that a diagonal of a square forms a right triangle with two 45° base
angles. This triangle is known as .1 43-45-90 triangle. Because this is a right
triangle, the hypotenuse can be found by applying the Pythagorean Theorem.
45-45-90 Triangle Theorem
In any-15-45-90 triangle, the length of the lwpotenuse is \/5 times
the length of a leg. 5.5.1
30-60-90 Triangles
It" you draw an altitude of an equilateral
triangle, two congt'ttent right triangles are
formed. The measures of the acute angles 30*
of each right triangle are 3-0” and 60”. This
triangle is known as :1 30-60-90 triangle.
‘the length of the hypotenuse ofa 50-60-90
triangle is twice the length of the shorter leg. I 60°
E X A M P L E orind the unknown lengths for the
30-60-90 triangle shown at right.
0 SOLUTION
In a 320-60-90 triangle. the length of the [W
hypotenuse is twice the length of the g
shorter leg. Thus, the length of the
hypotenttse is I0.
my
I : 2 I Use the Pythagorean Theorem to find the 1
length of the other leg. 5
S1 + 1.3 I03
25 + 3-‘ = mo
JF1 = 100 — 25
:8 = 75
x=\/7‘—5=5~/323.06
332 CHAPTER 5
30-so-go Triangles
- - - 1. Use the Pythagorean Theorem to fill in a table like the one below Ior
no special ‘no.5 several 30-60-90 trianglts. Write your answers in simplest radical form.
Shorter leg Hypotenuse l Longer leg
1 2 .7
2 ? ?
3 ? I 2
2. Look fora pattern in the lengths ol the longer leg and make a
generalization.
3. Let x be the length of the shorter leg.
a. What is the length of the ltypotenuse? 30
b. What is the length of the longer leg? ? 7
CHECKPOINT ./ 4. Use your results to label a general 50-60-90
triangle like the one at right. Then complete 59-:
the theorem below. )4’
30-60-90 Triangle Theorem
In an)‘ 30-60-90 triangle. the length of the hypotenuse is ?
times the length of the shorter leg. and the length oi" the longer leg is
? times the length of the shorter leg.
5.5.2
. I P L E 0 lake is measuring the height of-a tree that his grandfatlter planted as a boy.
lake uses a special instrument to find a spot where a 30° angle is formed by his
line oi sight and a ray parallel to the ground. lake’s eve level is 5 feet above the
ground. How tail is the tree if Jake is standing 80 feet from the base?
. SOLUTION
The line of sight to the tree is the hg,-potenuse of a right triangle. The lengh of
the longer leg 01 the triangle is 80 leet. The length, x. of the shorter leg of the
triangle is equal to the height of the tree above lake's eye level.
‘ _/ .' I I 80 = xx/3
so so J3 80‘/5 -
a. = — = — — = , or about 16.2 teet
V5 #6 Va 3 _,v"'
hon. find the height, h. of the tree.
ll -= 46.2 + 5 = 51.2. or about 51 leet 5 f‘.la.Q.§
LESSON 5.5 SPECIAL rntmctes AND AREAS OF REGULAR P0-LYGONS 333
Areas of Regular Polygons
To find the area of a regtllar hexagon. divide
the hexagon into 6 congruent. non-
overlapping equilateral triangles. Find the
area of one triangle and multiply by 6 to
find the area ofthe hexagon. i\ote that the _
altitude of the equilateral triangle is the Nmude
longer leg of :1 30-60-90 triangle. The I
altitude is g or the length or the side of the
hexagon multiplied by V/3.
E X A M P L E Find the area of a regular hexagon with sides of 20 centimeters.
. SOLUTION
Divide the hexagon into 6 equilateral
triangles. Because the altitude of one of
the triangles forms the longer leg of a
30-60-90 triangle and halfof the side of
the hexagon forms the shorter leg, the
length of the altitude is l0\/3 centimeters.
20 cm
Use the area formula to find the area of
one of the triangles. "nude _ wv,Ǥ cm
10 cm
A = §(2o)(toc/E‘;
A = l0U\/3 '*’°°'“
Because the hexagon is composed of 6 congruent triangles. the area of the
hexagon is found as follows:
A = 6[l(J0\/3) = GUOV/3 = 1039 square centimeters
The method of dividing a regular hexagon into
congruent triangles can be applied to find the
area of any regular polygon.
An n—sided regular polygon can be divided
' into n non—overl-apping congruent triangles.
Each altitude of a triangle froin the center of
the polygon to a side of the polvgon is called
The Can_ml’i{nr dollar min. :1 I1 apmhem of the p0|).g0n_
tvr "lutum‘.’ is (J rcgrrlm
ll-tgtm.
I Apothem
Area of a Regular Polygon
The area, A, of a regular polygon with apothem u and perimeter p is
given hy:
A = éup 5.5.3
334 CHAPTER 5
E X A M P L E 0Find the area oitlte regular pentagon
shown at right.
O SOLUTION
The perimeter, p. is 5 x ID. or 50 units.
A = fiap
A = %(6.88')[50) = 172 square units
Exercises
. Co»//rm;/'mte
u mumnm 1. Describe how two I5-45-90 triangles fit together to form a square.
Acfivmes Describe how four 45-45-90 triangles lit together to form .1 square.
0"“'‘° 2. An equilateral triangle is in regular 3-sided polygon. Describe its apotliem.
Go To: go.hrw.com
Kevword 3. A square is a regular l—sided polygon. Describe its apothem.
MG! Carpentry _ _ ‘ _ I
4. Can the lengths or the sides of a 45-45-90 triangle or :1 30-60-90 triangle
ever be .1 Pytlmgore-an triple? Wliy or why not?
. Guided Ski//3 Practice
5. Find the length of the hypoteimse 8. Find the missing lenghs for
of .’_\RST. (EXAMPLE 1) at-t-’Xi’. (EXAMPLE 2;
‘ H Wl\
7 so
X 1 Y
7. How tall is the tree in the diugrrmt at left? (EXAMPLE 3)
. 60° ‘.
8. Find the area ofa regular liexugoii with
sides of 12 inches. (EXAMPLE 4)
9. Find the area of the regular decagon at
right. (EXAMPLE 5)
LESSON 5.5 SPECIAL rntmctes AND AREAS OF REGULAR P0-LYGONS 335
D hnernetoonnect .1”
cuff‘
Homework
Help Online
Go To: go.htw.com
Keyword:
MG! Homework Help
for Exercises I0-I3,
l8-2|
336 CHAPTER 5
Practice mm’ App/y
For each length given below, find the
remaining two lengths. Give your
answers in simplest radical form. 300
10. X = 6 2 Y
11. y = 6
12. - = I4 60. I
1ay=4Ǥ X
14. p = 6
15. r = 6
16. q = 4x5
17. r= I0
18. 1;‘ = 3.4 h
19. K = 6wG 30
m4m7 g *
60‘
21. h = 206
Find the area of each figure. Round your answers to the nearest tenth.
22. 23.
73 5.4
I
24. 25.
J _L
15
60"
5 "- F
26.
12 12
12
Each of the following triples represents the side lengths of a triangle.
Determine whether the triangle is a 45-45-90 triangle. a 30-60-90
triangle, or neither. Explain your reasoning.
28. -1, 4. 4d? 29. 6. 3~/Z 3t/3
mmfizs ngmfi
niwhfi 31fiAflfi
CllALl.ENGES
x 10 “x
APPLICATION
APPIJCATION
For Exercises 34-39. find the perimeter and area of each figure. Give
your answers in simplest radical form.
34. .1 30-60-90 tri.1ngle with .1 hy potenuse oi" I8
35. :1 45-45-90 triangle with .1 l'l)"|1(Jl.t-.’l‘Il.lS€ of 24
36. an equilateral triangle with sides of length 8
37. .1 regular hexagon with sides of length 13
38. a square with a dialgonal of M
39. .1 regular hexagon with an apothem of 5
For Exercises 40-43, refer to the figure at left of a regular octagon inside
a square.
40. From the diagr.1m at left. what can you say about the triangles formed by
the corners ofthe square, outside of the octagon? Find the value of x.
41- Find the length of the apothem of the octagon.
42. Find the area of the octagon.
43. It" the sides of a regular octagon have length 5. vthat is the area of the
octagon?
CIVIL ENGINEERING An engineer is in
charge of attaching guy wires to a
tower. One wire attaches to a point on
the ground 60 feet from the tower.
44. lfthe angle that the wire forms
with the tower is 45‘! what is the 5°.‘
length oi" the wire?
45. It‘ the angle that the wire forms ‘5_
with the tower is 60‘! what is the
length of the wire?
Look Back
ORA!-TING In drafting, aT square is used to align drawings.TheT square
is held against the side of the drawing board, and the straightedge
stays perpendicular to the side of the drawing board. (LESSON 3.4)
46. An artist makes a series of horizontal lines with the straightedge of the
1' square by moving it up I inch for each new line. What is the relationship
between these lines? \-\-'h_v?
47. With the 30-60-90 triangle positioned
.15 shown at right, the artist uses the
hypotenuse to draw .1 line that forms
an angle of 60° with the straighledge. K
Without moving the '1' squ.1re. she slides
the triangle 1 inch to the right and draws
another line the same way. \*\"h:1t is the
rel.1tionship between the two lines? Whv?
LESSON 5.5 SPECIAL tntmstes AND AREAS OF REGULAR P0-LYGONS 337
calculator is in
degree mode.
338 CHAPTER 5
Be sure your
L
48. Find the smallest possible area for a rectangle with at perimeter of I00 and
side lengths that are whole numbers. Then find the greatest possible 'trea.
State the dimensions of each rectangle. (LESSON 5. 1)
B 7.5 cm D
49. Find the area of the triangles in
_ _ 3 cm
the hgure in right. (LESSON 5.2)
A dcm C
50. Find the height of a trapezoid with an area of 10.5.5 ft’ and base lengths of
17.5 ft and 5.3 ft. (LEssoN 5.2)
51. The base ofan isosceles triangle is 8 m and the legs are 6 m. Find the area
and perimeter. (LESSONS 5.2 AND 5.4)
52. In APQR. tind PR. (LESSON 5.4) no
100
P H
53. Find the area and perimeter ol a right triangle with legs ol lengths ti and lr.
(LESSONS 5.2 AND 5.4)
1.004’ Beyond
Refer to the diagram at right.The
ratio {of the lengths of the legs of
a right triangle is called the tangent V
of £A.The £~_j button on your
calculator is used to calculate A
tangent ratios.
X
54. Use your calculator to tind the tangent of 45°. Does your answer agree
with the ratio of the corresponding sides ofa 45-45-90 triangle? Why or
why not?
55. Use your calculator to lind the tangent of 3-0”. Does your answer agree
with the ratio ol'the corresponding sides ofa 30-60-90 triangle? Why or
why not?
56. In the regular pentagon at right,
with its center at A. what is the
measure of LA? y
57. Use your calculator to find the
tangent of LA.
58. If the side length of the regular
pentagon is 12, what is y?
59. Use your results from Exercises 57 and 58, and the fact that the tangent of
LA is fito find x.
60. Use your results from Exercises 56-59 to lind the area of a regular
pentagon with a side length of I2. (Him: What is the ap0thent?]
61. Lse the method above to find the area of a regular 9—gon with aside
length ot"4.
The Distance Formula
and the Method of
Quadrature
qr -
Objectives ; ' \~ “ ; “ , ~ ‘ Q
0 Develop and apply the ' Q ,_, r
distance lormula. I -
0 Use the distance ' _‘
formula to develop ' Q
techiques for ' _- . '
estimating the area _ . i . ' F" ' ‘
under a curve '
The abllltyto campurathadlsranco C
between two points is important in many
situations. In some cases. an estimate
basedonmaasummentissufliciontln _ ._ . . _ . _ ._ .
me, cases, Weaterprecism is mcessam to reach In: destrmanorr 0) qrmtkiy ms po.-.:«rb_l¢' u heiuopter prior
trm-'t’i.~‘ the .~'horrt’.<I dr_~'tmu‘£ be‘.twt’t’I1 two pomrs.
The Distance Formula
The distance between two points on the same lroriwrrtal or vertical line can be
found by taking the difference of the x- or }’-\.I'.)0l’(ii|"iZlt€S.
The vertical distance between points A and B V
is AB - |7 —:=-| - [3 —7| - 4.
The horizontal distance between point; B and
Cis BC- I5 -2! - I2-5| - 3.
Became AC is the h_vpotenuse of right triangle
is/l BC, its length can be Found by using the
Pythagorean Theorem.
(Ac)! = (AB): + <_b'C)’
- 4’ + 33
- l6+9
= 25
AC - 25 - 5
l'he Pythagorean l'heo1'em can be used to find the distance between any two
points in the coordinate plane.
LESSON 5.5 me orsmuce FORMULA ANDYHE METHOD or OUADRATUHE 339
Distance Formula
In a coordinate plane. the distance, d, between two points (x., y.) and
(x_., ,v_.) is given by the following fortnula:
d = J (X3 - xi): + (y; — y.)3 5.6.1
A proof ol the distance formula is given below.
Given: points Am. )3] and B(x_.. y;]
. . - . - f-’_""""':—":
Prove: the distance between the two points is \,- Ix: — 95.)? + ()5. — y.)3.
Proof: Draw -.1 riglttiiangle with V
hypotenuse AB and .1 right
angle at point Cl-‘:3, y.). Let 5 gm. ,2;
d be the distance between 4
points A and B. d
AC = l-V2 - Nil 2
= |)'-_. — yll A(X,, M ‘ .C(x2l Yilx
Use the Pythagorean Theorem.
dz - |x~ — x.t* + I» — ml’
J You can drop the absolute-
value symbols because the
quantifies are being squared.
fl! ' (X2 — xi]! + (F1 — I'll?
Solve for rl.
fl = \/ (X3 — xi): + U’: — ft)!
E X A M P I. E Q A helicopter pilot located I mile east V
and 3 miles north of the cnntnmnd center ‘
must respond to -tn emergency located 7 10
miles east and II miles north of the the
center. How far must the helicopter travel 8
to get to the emergenqt site? 6
O SOLUTION 4
Let (0. 0] be the coordinates of the
command center. with the positive part of 2 “v 3)
the }"-d.\llS representing north. Then the Helmopter
helicopter‘s current coordinates are (I, 3). . , .
\\2 4 6 8
The coordinates ol the emergency site are V Command Center
[7, I I]. Use the distance formula.
d- \.f'(7- l)’+ [It -31’
d= \"62+3: = \-‘56+6=l = V‘ l0U= l0
The helicopter must travel I0 miles to get to the entergency site.
340 CHAPTER 5
The Method of Quadrature
The area of an enclosed region on a plane can be approximated bv the slim of
the areas of a number of rectangles. This technique, called quadrature, is
particularly important for linding the area under a curve.
Estimating the Area of a Circle
- ' I. D Part 1: Method A [Left-Hand Rule) |
g;‘|’g:|§’t‘;E°' and 1. Draw a quarter of a circle i' K ., 9 D ‘
Wlll'I a radius ol 5 tinits Pr’ ‘\ .“
centered at the origin. [0, 0). it t \ _,
Draw rectangles as shown. l‘ g
with the upper left vertex “ , \
of each rectangle touching \
the curve. This method is \ -’
called the lcft—hmid rule.
2. Find the )'—coordinate of each point. A. B.
C. D, and F. The segment connecting each
point to the origin is the ll)-'pOlt.‘llllSt.‘ of a
right triangle. Because the radius of the
circle is 5 units. this is the length ol the
liypoteiiusc of each triangle. for point C.
the y-coordinate is found as shown below.
y I \:‘5Z- .23 I \,/E
The y-coordinate ot each point is the
height of a rectangle.
3. Find the area of each rectangle. ('l'his is simplified by the fact that the
base of each rectangle is l.]
4. Find the sum of the areas of the rectangles by completing the pattern
below.
v‘53-0-’+~.-’5-'-l3+\/5’-21+----
\/g+\/E+\/3+----=5.’
CHECKPOINT / 5. Multiplv your sum by 4. The result is an estimate of the area of a
complete circle with a radius of 5 units. Does this method overestimate
or underestimate the area of the circle? Explain why.
6. Calculate the true value of the area ofa complete circle to four decimal
places by using A - arr’. Find the relative error ol your estimate by using
the following l'ormtila:
E_@x]0Q
l.
where V, - estimated value. V, - trtie value. and E - percent of error
LESSON 5 5 me DISTANCE FORMULA Amonie METHOD or OUAORATUHE 341
Part II: Method B (Right—Hand Rule)
CHECKPOINT ./ Repeat Part I with the rectangles
arranged as shown at right. Here. the
upper right vertex of each rectangle
is touching the curve. This method
is called the right-ltaml rule. Does
this new method overestimate or 1*
underestimate the area of a complete
cirele? Explain why.
Part lll: Combining Methods
CHECKPOINT / Averxtge your estimates for the area of the circle lrom Parts I and ll. What
is the relative error of your new estimate?
CRIUCAL THINKING Do you think that the average of the results from methods A and B will always
give more accurate results than either method by itself? Explain your answer.
Exemses
. Comm////cute
1. Fxplain the relationship between the distance formula and the
Pytlmgoreaii ‘l heorem.
2. When using the distance formula. does it matter which point is (x.. yr]
and which point is [x;. ,1-'1)? Why or why not?
Y
3. Describe two methods of estimating
the shaded area under the curve at right.
4. For each method you deserihed in
Exercise 3. how might you make your
estimate of the area more accurate!
. fit//dad 8k///5 Practice
Find the distance between the indicated points. (EXAMPLE)
5. V
342 CHAPTER 5
For Exercises 7 and 8, estimate the area of the quarter-circle with a
radius of 4 by finding the areas of the given rectangles. (ACTIVITY)
7.
. Practice and Apply
g . . mm 1 ,3?“ Find the distance between each pair of points Round your answers to
Homewmk '° the nearest hundredth.
"°'P °"‘""= 9. (0. 01 and (5,8)
Go To: 9o.hrw.com
Kcv1\-out 10. (I. 2) and (‘L 6)
MG] Homework Help
lor Exercises 9-20 11 . (L 4) and (3. 9)
‘ 12. (-3. -3) and (6. I2]
13. (—l, 4]z1nd(-6. I6)
14. (-2, —3);1nd (-6. -I 2]
' '4: z / Refer to the diagram below for Exercises 15-23.
B
C
I
18. Find the perimeter of Al-‘JH. A. _ .
3:-
II
15.
to
II
16.
?
?
?
0
‘I7.
19. Find the perimeter of A/lb‘!-I " J
20. Find the perinwter of 1 _ _ _ _ _ I X
qualdrilulerai FGHI. ‘ 2 2 5
21. is ABCD isosceles? Why or ‘2 ’
why not? 5 '
22. is AAIE istisceles? Why or 0
why not?
23. is AB}.-TH cquihncral? Why or
why not?
For Exercises 24-26, use the converse of the Pythagorean Theorem
to determine whether the triangle with the given vertices is a right
triangle.You may wish to plot the points and connect them to form
the triangle.
24. ('2. I). (6, 4),and [-4. '9)
25. (l. 5], (6. 0). and [-2. 2)
26. (I. 4]. (4, 2), and (6.6)
LESSON 5.5 me DISTANCE FORMULA moms METHOD OF OUAORATUHE 343
344 CHAPTER 5
PROOF
For Exercises 27-30. give your answers in simplest radical form.
27. Suppose that the endpoints ofthe hypotenuse ol'a -I5--IS-90 triangle are
(3, 3-) and (9, 2), What is the length of the legs?
28. Suppose that the endpoints of one leg olia 45-45-90 triangle are (0. 5] and
(4. -l ). What is the length of the hypotenuse?
29. Suppose that the endpoints of the hypotenuse ol a 50-60-90 triangle are
('4. -2) and U’. 2). What is the length oi‘ the shorter leg? of the longer leg?
30. Suppose that the endpoints of the longer leg ofa 30-60-90 triangle are
(-3-. S) and (2. I]. What is the length ofthe shorten leg? ofthe
hypotenuse?
In Exercises 31-34, you will use coordinate geometry to explore a
property of right triangles.
31. Find the midpoint of the hypotenuse of the right triangle with vertiees at
(0, O). (6, 0}. and (0. 8]. What is the distance from this midpoint to each
vertex? What do you notice?
32. Repeat E\tCrL‘istI 3|. using a right triangle with \’L'l'l.lLt.‘S at (0. O), (-l. O}.
and (0. 7).
33. Based on your results from Fxercises 3| and 32. make a conjecture about
the distance from the midpoint of the hypotenuse ofa right triangle to
each vertex of the triangle.
34. Prove your conjecture from Exercise 33 by using a right triangle with
vertices at [0, 0). (x, O] and (0, y).
35. l'se the method of quadrature to estimate the shaded area under the curve
shown below. Lise both the left-hand and right-hand rules. and then
average your results.
36. l'se the method ofquadrature to estimate the area between y - .3 and the
:.'-axis for 0 s x s 4.
37. Use the method of quadrature to estimate the area between y = .x-' + 2 and
the .\'-axis for 0 s x s 2.
38. ['56: the method of quadratu re to estimate the area between y - -A3 + 4
and the x—a.'tis for -2 s x s 2.
APPLICATIONS
39. ENVIRONMENTAL PROTECTION m ‘i p '',;s_;. «.3;
An oil pipeline runs through ‘
part ofa national torest. '_;‘..__- i:"1" Q5‘ 4'4‘ ‘- '
Because of the danger to the ,v_, .
forest. an environtental group _ T‘ '
wants to know the length of 011- I '. :_§,‘’'.-‘ '’
the pipeline that lies inside ; "* .-J ‘._. .~--- ' - . __.-
the boundaries of the lorest. . ' J--“I 3; '. -'-‘M
Use the map at right to find ‘ ’ M“ '’‘l‘ ‘ :.-_. ; "
the desired length. Each M i ' 3452:!‘-'§;‘
square of the grid represents “ -A I ._ , a' ’ -
I square mile.
40. CIVIL ENGINEERING A dam has been built on a river. and the rix-er has
begun to back up to form a lake as shown in the “in.ip" at right. Each
square on the map represents I0,IJ00 sq ft. Use the method ot quadrature
to estimate the area of the lake.
I I
I
I
I !
I
-' I
'__
!
I
I
A lake formed by a dam, viewed from above, will usually have a flat side.
Explain why. This makes it convenient to use the method of quadrature.
What else must be true about the shape of the lake in order to ttse the
method of quadrature as explained in this lesson?
L00.(’ Bdtik
41. Prove that the quadrilateral with vertices at .-\(-I, I], B(7, -5], C(lO, -I ),
and D[2. 5') is a rectangle. (LESSON 3.8)
42. Suppose that a circle and a square both have .1 perimeter of 100 meters.
Which has the larger area? (LESSON 5.3)
43. Suppose that a circle and a square both have an area of 225 square
centimeters. which has the larger perimeter? (LESSON 5.3)
44. The legs of -.1 right triangle are 4.5 centimeters and 8 centimeters. What is
the length of the hypotenuse? (LESSON 5.4)
45. The hypotenuse oI'a right triangle is 5 centimeters and one of the legs is
4 centimeters. What is the length of the other leg? (LESSON 5.4)
46. Each side ol‘ an equilateral triangle measures 8 inches. Find the area and
perimeter. (LESSON 5.5)
47. Each side of an equilateral triangle measures 5 units. Find the area and
perimeter. (LESSON 5.5;
LESSON 5.6 THE DISTANCE FORMULA ANDTHE METHOD OF CIUAORATUHE 345
Qsvflo
.9
Look Beyond
The area of an enclosed region can be approximated by using shapes
other than rectangles. In the figure below, the area of the quarter-circle
is approximated by the areas of four trapezoids and one triangle.
48. The quarter—cirele in the ligu re has a
radius of 5 units. Use the y- values you
found in the Activity on page 541 as
the bases of the trapezoids and use l
as the height to estimate the area
under the curve.
49. ls your answer an overestimate or
underestimate of the actual area
under the curve? Why?
50. Compare your answer to Exercise 48 to
your 'an.swer to Part Ill of the Aetivity.
What do you notice?
51. The area found bv using trapezoids is
equal to the average of the estimates
found by using the left-hand and
right—hand rules.
Use the diagram at right y.
and the formulas for the
area of a rectangle and the
area of a trapezoid to prove
this fact algebraically. it
)1 mg jut
The figure below contains a -l5—<l5—90 triangle. Three semicircles have been
constructed. with their centers at the midpoint of the hypotenuse and the
midpoint of each leg. l'he shaded crescents in the figure are called ltme.~'.
4
1. Find the area ofthe 45-90-45 triangle.
2. Find the total area of the small senticircles.
3. Find the area of the large semicircle.
4. Find the total area of the lunes.
5. What other area in the figure is equal to the total area of the Iunes?
346 CHAPTER 5
Proofs Using
Coordinate Geometry
cnecxpomr ./
1. Use the coordinates of the triangles given in the table to test the following
theorem: The midsegment of :1 triangle is parallel to :1 side of the triangle
and has .1 nreasure equal to half the measure of that side. (Theorem 4.6.9]
Draw the first two triangles in the coordinate plane, and complete the
5 : J- “"‘
\ "
‘* Q!‘ h In
4;‘ " _\ ‘ ‘ '-' ‘ s _
_ \ ’ ,2“ .
. . -Gr
"1 1 .v-. 5 W
s L . ‘3
Objectives
9 Develop coordinate _-._ "1
proofs for the Triangle — -
Midsegment Theorem. \ t
the diagonals ol a __ .- '
parallelogram, and the I ' _ 1
retlection of a point ' ' ‘Kt;
across the line y: x ~ ‘
The essential amibotes of ,- - - - ‘c figures -1" ‘y
o zlggrttjlzfiactgllcrzlgfi :1; an be captured in a coordinate drawing. For this
solve pmblgms omhe -ason. coordinate gea- -: can be usedtopmv; ‘ I .
coordinate plane ' " ' ””'°°'°'”5'
v '3
A - p L I c . I 0 N Meteorologists use latitude and longitude readings to track hurricalles on
MHEOROLOGY a map of Farth. \le-ar the equator. these coordinates are very similar to
xy—eoordinates.
Three Coordinate Proofs
' ' - The Triangle Midsegment Theorem
graph paper
table below.
Coordinates oi
Veffices of midpoint M and S Slope Length
"'°"9'° E ac Ms l 716 Ms l AC
Al0.Dl.B(2.6l.CT8.0] M0,?) 347.?» l? I? 7 I 7
Al0.0l. Bl6.—8l. 0:10.01 Ml7.7] Sl?.?l I7 I7 7 I 7
General case
lsee Steps 3 8t 4} M(?, ?] S{?, 7} ? ? ? ?
LESSON 5.‘! PROOFS USING COORDINATE GEOMETHV 347
2. In each triangle you drew in Step I. one vertex was at the origin and
another was on the x—axis. These vertices were chosen to keep the
calculations simple. Do you think it is possil.1le to create a triangle ol
any shape and size that fits these same conditions? Explain your answer.
Y
3. The figure at right represents the
general case of the Triangle
M idsegment Theorem. The triangle
could be of any shape and size. and
it could be in any quadrant of the
coordinate plane—so don’t take the
drawing too literally.
B420. 20)
Sl?, ?)
AW. 0) C(2r. 0)
The number 2 has been used as a multiplier to keep the calculations
simple. Notice that the numbers 2p, 2:}, and Zr can represent any desired
real number. Explain vthy this is true.
cuecxpomrr ./ 4. l-‘ill in the third row of the table on the previous page. Based on_th is
information. what have you proven about the relationship of MS and
AC? Explain why this proves the Triangle Midsegment Theorem.
CRITICAL THINKING Compare this proof of the Triangle Midsegment Theorem with the one that
appears in Lesson -1.6. Which proof seems easier to you? Explain why.
' Z
The Dlagonals of a Parallelogram
v I U. H In 1. Use the coordinates of the parallelograms given in the table below to
l mph paper | test the following theorem: the diagonals ofa parallelogram bisect each
other. ( Theorem 4.5.4‘ Draw the lirst figure in the coordinate plane.
Three vertices oi’-a parallelogram are given. Find the fourth vertex and
fill in the blanks of the table.
Three vertices of a _ _ _
parallelogram Fourth vertex Midpoint of BD Midpoint ol AC
AID. O). B(2. 6}. Dim. O) C(?. 7) l?. 7) (7. 7)
General case (see Step 2) Q7, 7) [7, 7) I (7. 7)
CHECKPOINT ./ 2. fhe figure at right represents the Y
general case of the theorem. Use the 342 , 2 p ca, 7)
coordinates of the ligure to fill in the
blanks of the table. Based on this
information, what have you proven
about the diagonals of a parallelogram?
Explain your answer.
D(2r. Ol
CRITICAL THINKING How can you prove this theorem without using coordinate geometry? which
proof seems easier to you? Explain why.
348 CHAPTER 5
' 3
Reflection Across the Llne y = x
- I - You may recall that the effect ot
graph nape, reversing the x— and y—eoordin-ates
0l'a point is to rellect the line
across the line y = x. You can use
"'00" coordinate geometry to prove this
result.
Y
1. If you know the x—coon.linate ol
a point on the line ,1’ = x, what
cart you conclude about the y-
coortlinate? (Filling in a table
like the one at right will reveal
Sufi the pattern.)
5.,‘ 2. Find the midpoint between the
”’ S -34- points P.(rr, b] and Pauhlll by
using the midpoint formula.
Does this point lie on the line
y = x? Fxplain your reasoning.
3. Pick two points on the line y = x .
and use them to find the slope of
this line. Record yottr result.
n
4. Find the slope of the line that passes through the points P.[a. b] and
P3(b. :1). Record yottr result. Hint: You can rewrite la — (I as —[n -11].
5. Compare your results in Steps 5 and -I. \'\"hat can you conclude about
the relationship between the two litres?
CHECKPOINT / 6. Recall the definition ofa reflection from Lesson 1.6. Explain how your
results prove that the result ot reversing the coordinates of a point is a
reflection of the point across the line y = x.
Exercises
. Com/mm/mtg
1 . In coordinate geometry proofs, why is it possible to place one vertex of the
figure at the origin and one side along the x-axis?
2. ln a coordinate geometry prool about triangles, could you place one vertex
at the origin. one on the x—.1xis. and one on the y—axis? Why or why not?
3. ln a coordinate geometry proof. what do you need to show to prove that
two lines are parallel? that two lines are perpendicular?
4. In a coordinate geometry proof. what do you need to show to prove that
two segments bisect each other?
LESSON 5.‘! PROOFS USING COORDINATE GEOMETHV 349
0 Guided 34’///3 P/dtt/68
Find the length of the segment with the given endpoints. (ACTIVITY 1)
5. (O. O) and {_u. 1;) 6. (p. q) and [r. 5)
Find the midpoint of the segment with the given endpoints.
(ACTIVITIES 1 AND 2;
7. [0, 0) and [2p. 21]) 8. [2p, 2q) and [Zn 25)
Find the slope of the segment with the given endpoints. (ACTIVITY 3)
9. (O, O) and (p. q) 10. [p, q) and [r_. 5)
0 Practice and /1,0,0/y
Determine the coordinates of the unknown vertex or vertices of each
figure below. Use variables to represent any coordinates that are not
completely determined by the given vertices.
11. rectangle ABCD 12. isosceles triangle DP F
Alt}. 0). B(U. pl. DIU, U). L'[p. ql. I-'(i,?j)
C(-?_» .2» DUI» 0)
13. parallelogrzim CHI] 14. square KLMN
G(U.0). Hlp. q). K[U.Ol. LI ?_ . ? l.
{L ? . E‘ }. K130) :\~1{ E’ , E‘ J..'\'[P.U)
Y
M
L
K v ‘X
15. trapezoid PQRS 16. rhombus I'Ul-’W
PUL0]. QUI. Ill. T(0. 0), UUA I1).
350 CHAPTER 5
PROOFS
fl- ntetn --
Homework
Help Online
Go To: go hrw.com
Keyword:
MG! Homework Heb
lor Exercises 27-30
CHALLENGE
ln Exercises 17-20, you will prove theTrapezoid MidsegmentTheorem
by using coordinate geometry.
17. Trapezoid ABCD at right has
vertices at A([], U), B[2p. 2qJ,
C(2r. ). and D(2s, ? ].
18. Find the eoonl_i'i1ates of M. the
midpoint of and N. the
midpoint of CD.
19. Find the lengths AB. BC. and MN.
Prove that the length of the
midsegment is the average of the
lengths of the bases.
20. Find the slopes of AT). B—C. and
Prove th-at the midsegment is parallel
to the bases.
In Exercises 21-23, you will prove that the center of the circumscribed
circle for a right triangle is the midpoint of the hypotenuse.
21. Find the midpoint. M. of the
hypotenuse of AIKI at right.
22. Show that the midpoint otithe
hypotenuse is equidistant from
the three vertices.
23. Explain why point M must be
the center of the circumscribed
circle for AIKL.
ln Exercises 24-26, you will prove that the midpoints of any
quadrilateral are the vertices of a parallelogram.
24. In quadrilateral EFGH at right. V
find the coordinates of the
midpoints of the sides.
25. Copy the diagram and connect
the midpoints ol' the sides.
26. Prove that the quadrilateral
formed by connecting the sides
is .1 parallelogram.
Use coordinate geometry to prove each of the following theorems:
27. The opposite sides ofa par-allelograni are congruent.
28. The diagonals ol .1 square are perpendicular to each other.
29. The diagonals of a rectangle are congruent.
30. ll'thc diagonals of a parallelogram are perpendicular. then the
parallelogram is a rhombus.
31. The medians ofa triangle intersect at a single point. [Hint: Find the
equations or the lines containing the medians.)
LESSON 5.1 Peo-ors uswe COORDINATE Geo-Mernv 351
APPLICATION
CONNECTION
352 CHAPTER 5
32. CIVIL ENGINEERING Points A and B are y
on opposite sides of a straight portion ,3
of a river 50 meters wide. Point Bis 100
meters downstream from point A. An Aw‘ 391- ‘-
engineer is desivning a road from point
A to point b‘. To find the lowest cost
road between the points. the engineer
positions points A and B on a
coordinate plane as shown. 'l'he road costs more to build over the river, so
part of the road will be built on land. leaving the river bank at point X. as
shown.
a. L.|se the given coordinates to find db the length of the road that lies on
land. and (I...-, the length of the road that lies over the water.
1:. MAXIMUM/MINIMUM Suppose that the cost of building the road is $1000
per meter on land and $2000 per meter over the water. Write an
equation for the cost {in thousands of dollars] of the road in terms of
A; Use a graphics calculator to graph the cost function, and trace to find
the coordinates of X for the lowest cost road.
— O-——->X
XIX. OI EH00. OI
L004’ Back
Given square .4800 with AB = 5, and diagonals H3 and W) intersecting
at point E, find the indicated measures. (LESSON 3.2, 4.5, 5.4)
33. BC 34. CD 35. AD
36. AC 37. BD 38. A15
39. EC 40. BE 41. ED
42. mLBEA 43. mLBEC
You_are given trapeziod .4800 with bases E and ‘(E and midsegment
MN, where AB = 5.7, CD = 8.5, and the height, h = 3.5. Find the
indicated values. (LESSON 3.7, 5.2)
44. .-\—IN 45. Area of trapezoid ABCD
L004’ Beyond
46. Draw a scalene triangle. AA BC, and construct median KW. Prove that the
area oi (LARA.-1 is equal to the area of r_'sAC:\-I.
47. Lstng AA BC from Exercise 46. construct the centroid (the intersection of
the medians) of L\.A£__?_.i_\;l and label it D. Construct the cctttr_g_idot' .i:\._;_4__(:‘r\-'1
and label it F. Draw DF. What is the reltttio_rts,hi;) between AM and DI‘?
What is the relationship between b'Cand DI.-7! If you are using geometry
graphics software. try dragging the points to different locations to see it‘
your results still hold. Otherwise, draw several diflaent triangles to test
your results.
Geometric Probability
Objective —. 3
VUOATAN
0 Develop and Gulf of Mexico PENINSUIA
apply the basic
formula for
geometric '
probability. -
p . .
some scientists Ocean UATEMA -
believe that an asteroid l HONDURAS
or comet caused the
extinction oi the dinosaurs. . - n a
What is use likelihood that \
one particular such obloct
would have struck land? According in the fossil i'ccm'd, Earth cxpcrieiiccci i'l smidcn and drastic change
You can use geometric about 65 million years ago that l’(;'$llil’i.’t’i in the extittt firm of dirmsiturs like
P'0b3_W"1}’_'0 ’l9’_P 90-SW9’ Tvr:u1nosaurus res. Sonic scieiitists i)(.'iiL’I’¢’ that this tipltmwil was caused by
q"°‘"°"5 "*9 ms‘ an asteroid striking Earth near the l’m‘imin Peiiinsrilti.
The Probability of an Event
Consider the following question:
The surface of Earth consists of about 30 percent land and 70 percent
water. Assuming that a comet or asteroid would be equally likely to strike
anywhere on F.arth. what is the probability that such an object would
strike land instead 0l'watcr?
Mathematical intuition should tell you that there is a 50 percent chance, or
probability, that the object would strike land. Probability is a number from O
to l (_ or from 0 to 100 percent) that indicates how likely an event is to occur.
-A probability oI’O [or 0 percent) indicates that the event cannot occur.
-A probability ol’ 1 tor I00 percent) indicates that the event must occur.
For many situations, it is possible to define and calculate the theoretical
prolmbiliryol an event with mathematical precision. 'l he theoretical
prnbalaility that an event will occur is a fraction whose denominator
represents all equallv likely outcomes and whose numerator represents the
outcomes in which the event occurs.
LESSON 5.3 GEOMETHIC PROBABILITY 353
Theoretical Probability
_ __ Consider the following two probability experiments:
' ' a. There are 30 marbles in a
PROBABIUTY bag. and 3- of them are red.
A marble is drawn at random B
from the bag. The probability
ofidrawing a red marble is:
3 _
P=3a—0.l
b. A point in the figure at right is
selected at random. The
probability that the selected
l‘0l|'|l l5 “Om 379%‘ A l55 Figm'e B im'lm‘lt-‘5 Figure A (the inner circle).
= area A
area B
In cases like a. which you are prol)abl)' already lltmiliar with trom your
algebra studies, the number of possible outcomes can be cotmted. In cases
like b, however. the number of possible outcomes is infinite. in these cases.
the areas of the figures are used as measures of the sets of outcomes.
E X A M P L E 0 its dart lands in the blue part of the board below.a prize is givcn.What is the
probability that a dart that hits the board at random will win?
0 SOLUTION
'l he area of the blue part of the
board is 60 square units. The area of
. . . 6 8
the entire board is 96 square umts.
'l he probability that the dart will to
land in the blue part is E, or 3.
96 8
I2
E X A M P L E In a gante, pennies are tossed onto a Penny covers
grid of squares whose sides are equal an intersection.
to the diameter of a penny. To win, a
penny must touch or cover an
0 intersection of the grid. What is
the probal)ilit_v oi" winning on a
randont toss?
0 SOLUTION
- Imagine that circles are drawn
around each intersection on the
grid. as shown on the following
page. It" the corner oi"-.1 penny falls
within one of these circles. the
penny itself will touch or cover an center of penny
ll'll.Cl'5CCl.lOll. inside circle
354 CHAPTER 5
The diagram at right represents a single
square of the grid. if the center oi‘ the
penny lands irt at shaded region. the toss
will be -.1 winning toss.
Let a unit be defined as the radius ofa penny. Then the width oi" a square (and
the diameter of a penny) will be 2 units.
Area ol'a shaded region: A_. - J‘! x I3 - Jr units‘
Area ol'a square: A. = 2 x 2 = 4 units:
l he area of each quarter ol'a circle is § units}. so the area of the shaded
regions is rt. unitsz. i'he theoretical probabilitv. P. oi" the penny touching or
covering a \'ertex—and oi‘ the player winning—is lottnd below.
aret of shaded rtgiotts
II
p __. j._____._.._ = _
area or square -1
Experimental Probability
In the following Activity, you will use exp:-2 imenml pmlmtnliry and the result
Irortt Example 2 to estimate tlte value oist.
/ .
A "Monte Carlo'' Method for Estimating TE
- u I. D 1. Toss a pertrty randomly onto the grid paper. \l0tiCe whether tlte coin
9,-M paperwlh squams touches or covers an intersection of two lines. Repeat for a total of 2.0
equal-nwldthtorhe tosses. Record the number ol tosses that touch or cover an intersection
dia'"°'°' °f 3 pennv and tire rturnber that do rtot.
2. Share your results with tlte rest of your class. Find the totals for the
entire class. To find the experimental proabability that the penny will
touch or cover an intersection, calculate the ratio of the number of
tosses that touch or cover art intersection to the total number of tosses.
Call this number R.
3. For a large number oi tosses. you may assume that the value of the
experimental probability. R, will be close to the theoretical probability,
P. that you euleulated in Example 2. Using this assumption. calculate art
estimate for It-.
R ~ g [assumed to be true lor large numbers)
m~Rx4
4. Compare your estimate with the known value of J1’-. Determine the
relative error of your estimate by using the fortnula below.
E-W"%xl0O
where E - percent of error. V, - true value. and V, - estimated value
LESSON 5.3 GEOMETHIC PROBABILITY 355
Exemses
. Comma”/care
‘I. Why does a prt)l)al)ilily always have to be a number front 0 to I
(or 0% to I009-bl?
2. What does it tnean for an outcome to have a probability of O?
3. What does it mean for an outcome to have a probability of I?
4. Assign a pmbaltility to each of the following words:
often seldom usually
never maybe frequently
sometimes always rarely
Rank the ‘words in order from lowest probability to highest. Compare your
list with those of yott r classmates. \-\-'hich words do you agree on? Which
words do you disagree on?
5. In the /\ctivity, how did your estimate of It from 20 tosses compare with
the estimate of It from the total tosses for the entire class? How do you
think you could improve your estimate of .1?
0 fill/ded 3:?///8 Practice
10
6. Find the probability that a dart tossed
at random will land in the blue area of |
the figure at right. (EXAMPLE 1) 4 5
7 I
7. If the area of the shaded region at
right is :r square units and the area
of the square is 4 square units. what
is the area of the unshaded region?
What is the probability that a penny
tossed onto a grid with squares
equal to the width ofa penny will
not touch or LO\"CI' an intersection?
(EXAMPLE 2)
8. Fxplain how you could use a grid with squares equal to the width ofa
penny to estimate 11:. (ACTIVITY)
. Practice and Apply
Find the probability that a dart tossed at random onto each figure will
land in the shaded area.
9. 10. 11.
_l O
356 CHAPTER 5
D tntentetconnect
Homework
Help Online
Go To: 90 hrw.com
Keyword.
MG1 Homework Help
lot Exercises 15-23
4
»{<'
CHALLENGE
For each spinner below, find the theoretical probability that the arrow
will land on red.
12. 13. 14.
PROBABILITY Convert each probability to a percent.
15. 0.75 16. i 11.
'.HIl-J
PROBABILITY Convert each percent to a decimal probability.
18. 60% 19. 50% 2o. _i::%9*o
PROBABILITY Convert each percent to a fractional probability. Write your
answers in lowest terms.
21. 45% 22. 8(l% 23. <as%9«o
For Exercises 24-27. refer to the spinner shown at left.
24. What is the probability that the arrow will land on S?
25. What is the probability that the arrow will land on an odd number?
26. What is the probability that the arrow will land on an even number?
27. Add your results from Fxercises 25 .1 nd 26. What does this result represent
in terms of probability?
28. Design a dartboard in which the probability ola dart landing in a red
circle is U.5.
29. Design a dartboard in which the probability of a dart landing in a red
triangle is
In the dartboard shown at left, the radius of the inner circle is half of the
radius of the outer circle.
30. What is the probability that a dart thrown at random will hit a red region?
31. What is the probability that a dart thrown at random will hit a black
region?
32. What is the probability that a dart thrown at random will hit a white
region?
33. l'he squares in the grid at right
are exactly the width ol'a penny.
What is the proliability that the
center ofa penny tossed at random
onto the grid will land within a
white square, with no part of the
penny touching an intersection?
Ll:5$UN 5.3 Gl:OMtlHtC PHUBABILIIY 357
APPLICATIONS
358 CHAPTER 5
34. METEOROLOGY The weather forecaster predicts an 30% chance of rain.
Express this as a probability in decimal and fractional forms.
35. METEOROLOGY The area ol Oklahoma is 69,956 square miles. the area of
its capital. Oklahoma City. is 625 square miles. ll" a tornado touches down
at random in Oklaltnnta, what is the probability it will touch down in
Oklahoma City?
SKYDIVING A skydiver jumps from an airplane and parachutes down to
the rectangular field shown below. Assume that she is equally likely to
land anywhere in the field.
36. What is the probabilitv that
she will land on target A? 25 m
37. What is the probability that c
she will land on target B?
10 m . 25 m
33. What is the probability that :20 m
she will land on target C? :
39. What is the probability that 20 m A
she will miss all three of the 10 m
targets?
100 m
40. TRANSPORTATION At a sttbway stop in New York City. a train arrives every
5 minutes. waits l minute. and then leaves. Suppose that you go to the
stop at a random time. Use the diagram below to determine the
proltability that you will wait 2 minutes or less for a train to arrive.
| Ill
5 min
|<- T «v
1 min
Look Back
In Exercises 41-46, three lengths are given. Classify the lengths as sides
of a right triangle, an acute triangle. an obtuse triangle, or no triangle.
(LESSONS 4.5 AND 5.4)
41. I6. 50, 34
44. ll. 60. 61
42. 2?. 56. 50
45. IU. 24, 25
43. l6.63.8?.
46. 8. I5. 25
Find the area of each figure described below. {LESSONS 5.2 AND 5.3)
47. a triangle with a base oi" -l and a height of 7.5
48. a parallelogram with a base of l and a height of 7.5
49. a trapezoid with bases ol 20 and 50 and a height of l2.6
50. a circle with a radius of l6 (Note: Use % l'or rt.)
1_oo.('BeyoI1d
APPLICATION
RECREATION The dimensions of a standard
dartboard are given below.
,2oi
outside edge of double ring to center = I70 nim
outside edge of triple ring to center = I I7 mm
outer bull's—eye diameter = 5| mm ,_ _ ’ §
inner bull"s-eye diameter = I2.7 nini 000019 3"?!) '
double and triple rings inside width = 8 mm M &
Suppose that a thrown dart is equally -m-pye R,-Hg
likely to land anywhere on the board. | , .
51. What is the probability that the dart ‘ Q
will land in the double ring? \ ‘ ‘
52. What is the probability that the dart
will land in the triple ring?
Eacli sector‘ of the litirird has (1
riiiiiilierfroiii I r020.
fllI'IhmIiO0nned % 53. The higliest scoring section ol' the board is in the 20 sector ol' the triple
pomoiio ring [60 points). What is the probability of hitting this section?
fifgijgfwm 54. 'l'he inner buIl’5—eye [50 points) is the small red circle in the center of the
Keyword; board. What is the probability of hitting the inner l)till's-eye?
M618 II _ _ _ ’
u M 55. The outer buIl’s-eye [25 points) is the black ring around the inner bull 5-
‘ eye. \-\-‘hat is the probability of hitting the outer bull's—eye?
56. When playing darts. wliy might the actual results be dil't'ei-eiit from the
theoretical probabilities?
Qgtfio
41°
TECHNOLOGY Most scieiitilic and graphics
calcul.itoi's have random-number generators. V
which generate a number betweeii O and l. 10 —
8
1. Use your calculator to generate two random
numbers. Multiply each number by IO to get
a number between 0 and I0. and use the
results to create an OI'LlC‘l‘C'('.l pair. Round to
three decimal places.
For example: 0.698402-'1 365 and
0.3.30fi8I29II —> [(5.98-'1, 3.307]
2. Use this iiiethud to generate 20 orderetl pairs.
It a point chosen at random is on the It) x I0
grid shown at right. what is the probability
the point will be in the shaded region?
You will use the points generated in Steps 1
and 2 to test this probability.
3. Copy the IO x I0 grid at right, including the
shaded region. Plot the ordered pairs on your
grid.
4. HOW niany points 5
are inside the
shaded region?
Divide this number 2
by 20 to estimate
the probability. 2 4 6 8 10 X
5. Was your estimate close to the probability
you calculated? Compute the relative error by
. i-. — v.
using the Iormula F = % x IOU, where
V, is the estimated lexperiiiieiitali value and
V, is the true (theoretical) value.
WORKING ON THE CHAPTER PROJECT
‘i'ou should now be able to complete Activity 2
of the C‘hapter Project.
LESSON 5.3 GEOMETHIC PROBABILITY 359
This project cliallcngcs you to lind a formula
lor the areas of polygons drawn on dot paper
with all of the vertices on dot.~—surprisingl_v. one
l'ormul'.1 will work for all of them! Work with a team
of three or four classniates. You will probably find it
helpful to divide the work among your team members.
. . W
Activity 11
Compute the areas for the figures in each group below.Then, on a
separate piece of paper, complete a table like the ones given for each
group. For each figure, N‘, is the number of dots on the boundary, N
is the number of dots in the interior, and A is the area.
GROUP A Group A
Nb N,‘ A
7 6~;-
2
360 CHAPTER 5
GROUP C
Activity
To help you determine the formula. Notice that all the figures in each
group of Activity 1 have the same number of boundary points.
1. What is the pattern for calculating the area?
2. Write the pattern as -.1 formula in terms of N_:, and N,
3. Test your tormula by creating new figures on dot paper and calculating
their areas.
The formula you have just di.«>co\"ered was originally found b\-' George Pick
in H599.
Activity 3]
Refer to the figure at right.
1. Calculate the probability that a point chosen at
random in the grid will be inside the shaded region.
2. Use a random-number generator to create 20 ordered
pairs. Copy the figure onto graph paper and plot the
ordered pairs on the figure. Divide the number of
points that fall inside the shaded region
by 20. is your qesult Close to the — ‘
prolmltility you calculated in Step I? T
T
l’ /
1° - — - .~ %
B —%_..-’~—-/
'I-uI' 7
6 ' l \
‘ I. %
2 I ‘I
2 -I 6 8 ‘ID X \
Chapter Review and Assessment
VOCABULARY
area .................. .. Z95 circle . . . . . . . . . . . . . . . . . . . 314 probability . . . . . . . . . . . . . . . 353
altitude of a parallelogram . 305 circumference . . . . . . . . . . . . 315 Pythagorean triple . . . . . . . . 322
aititiide of a trapezoid . .. . . 315 diameter . . .... . . . ...... . . 314 quadrature . . . . . . . ...... . . 341
altitude of a triangle ..... . . 303 height of a parallelogram . . 305 radius . . . . . . . . . . . . . . . . . . . 314
apothem ............... . . 334 height of a trapezoid .... . . 306 sector ................. . . 316
base of a parallelogram .. . . 305 height of a triangle ...... .. 303 30-60-90 triangle . . . . . . . . . . 332
base of a triangle ....... . . 303 legs of a trapezoid ...... . . 306 45-45-90 triangle . . . . . . . . . . 332
bases of a trapezoid ..... . . 306 iioiioverlappiiig ......... . . 295
center ................. . . 314 perimeter . . . . . . . . . . . . . . . . 294
POSTUIATES. FORMULAS, AND THEOREMS
Lesson Number Postulate or Theorem
5.1 5.1.3 Postulate: Sum of If a figure is composed of non-overlapping regions A and B, then
Areas the area of the figure is the sum of the areas of regions A and 8.
5.1.4 Perimeter of a The perimeter of a rectangle with base band height his P= 2b + 2n
Rectangle
5.1.5 Postulate: Area of a The area of a rectangle with base to and height h is A = bh.
Rectangle
5.2 5.2.1 Area of a Triangle The area of a triangle with base b and height h is A : -5-bh.
5.2.2 Area of a The area of a parallelogram with base b and height his A = bh.
Parallelogram
5.2.3 Area of a Trapezoid The area of a trapezoid with bases b, and b,and height h is
A =,1,(b,+ b2)h.
5.3 5.3.2 Circumference of a The circumference of a circle with diameter d and radius r is C= rid
Circle or C - Zrtr.
5.3.3 Area of a Circle The area of a circle with radius ris A = 1'EI'2.
5.4 5.4.1 Pythagorean For any right triangle. the square of the length of the hypotenuse is
362 CHAPTER 5
Theorem
equal to the sum of the squares of the lengths of the legs; that is
c’ = a‘+ 13'.
5.4.2 Converse of the
Pythagorean
Theorem
if the square of the length of one side of a triangle equals the sum
of the squares of the lengths of the other two sides, then the
triangle is a right triangle.
5.4.3 Pythagorean
inequalities
For any triangle ABC. with c as the length of the longest side:
if c’ = a’+ b’. then AABC is a right triangle.
if c’ > a'+ b’, then AABC is an obtuse triangle.
lf c?< 37+ b’. then AABC is an acute triangle.
Lesson Number
5.5 5.5.1 45-45-90 Triangle
Theorem
Postulate or Theorem
In any 45-45-90 trlangle, the length of the hypotenuse is J5 tlmes
the length of a leg.
5.5.2 30-60-90 Triangle
Theorem
In any 30-60-90 triangle, the length of the hypotenuse is 2 times
the length of the shorter leg. and the length of the longer leg is J5
times the length of the shorter leg.
5.5.3 Area ofa Regular
Polygon A = -5-ap.
The area of a regular polygon with apothem a and perimeter pis
5.6 5.6.1 Dlstance formula
Key Skills 8: Exercises
LESSON 5.1
Key Skills
Find the perimeter of a polygon.
Find the perimeter of polygon ;lb’!’CDL' below.
4 (_:m 3
3cm 5cm
E 2.3 cm F
o ’ c
Polygon ABCDF F has a perimeter of
_’v+4+5+5+4+3=2-I cm.
Find the area of a rectangle.
Find the arezl of rectangle .-’lBCD abtwe.
The base of the rectangle is -1 alld the height is 2.3.
so the area is -l X 2.5 = 9.2 cm}.
LESSON 5.2
Key Skills
Find the area of a triangle.
Find the areal of it triangle with a base off: and a
height ol'8.
The area is % x 6 x 8 = 24.
Find the area of a parallelogram.
Find the area 0| :1 parallelogram with a [wise of6
and at height ofs.
The area is 6 x 8 = -18.
On a coordlnate plane, the distance between two points (X1: V1)
and (X3, V7} is d = V-’lx,— x.)’+ ty, — yd’.
Exercises
Find the perimeter of each polygon.
1. 2.
23 13 33
2.0
Find the area of each rectangle.
3. 4.
Exercises
For Exercises 5-8, find the area of the given
figure.
5. a triangle with a base oil and a height of l2
6. a triangle with a base of 7 and a height ol‘5
7. at parallelogram with a [ruse of -1 and a height
ol'9
CHAPTER 5 REVIEW 363
Find the area of a trapezoid.
Find the area oi a trapezoid with bases of 6 and I0
and a height of S.
The area is as + IO} x 3 = st.
LESSON 5.3
Key Skills
Find the circumference of a circle.
Find the circumference of a circle with a diameter
of 8 inches.
The circumference is II’. x 3 ~ 25.l2 inches.
Find the area of a circle.
Find the area ofa circle with a radius 0t‘ 3 meters.
the area is .1. x 32 ~ 38.26 square meters.
LESSON 5.4
Key Skills
Find the lengths of the sides of a right
triangle by using the PythagoreanTheorem.
Find the missing leg of a right triangle with a leg
of 40 and a hypotenuse of «t I .
if the missing leg is (L then :1’ + 40‘ = 4] ‘. or
cr' +1600 = t68l.Thus. :1" = 8l.and .n= 9.
Determine whether a triangle is right, acute,
or obtuse by using the Pythagorean
inequalities.
A triangle has side lenghs of 28. 45. and 50.
Classify the triangle as right. acute. or obtuse.
502 - 2500 and 28" + 452 — 2809
Since 2500 < 2809, the triangle is acute.
LEssoN 5.5
Key Skills
Find the side lengths of 45-45-90 triangles.
The hypotenuse ofa 45-45-90 triangle is l8. Find
the length ol the legs.
The hypotenuse is \/E times the length of a leg. so
the legs have lengths of
£.=.l§£=9 2
J5 2 f.
364 CHAPTER 5
8. a trapezoid with bases of 3 and 5 and a height
of 6
Exercises
9. t-'ind the circumference ofa circle with a
diameter of ll.
10. Find the circumference ofa circle with a
radius of 2.5.
11. Find the area ofa circle with a radius of IO
12. Find the area of a circle with a diameter of l
Exercises
Two side lengths of a triangle with
hypotenuse c are given. Find the third side.
(2-21 47-;
b=99 c=t0I
13. a - 20
14. ct =
Three side lengths of a triangle are given.
Classify the triangle as right, acute, or obtuse.
15. 48, 63, and 65
16. 48. 55. and 73
Exercises
11. 't he hypotenuse ofa 45-45-90 triangle is I00.
Find the length of the legs.
18. The length of each leg ofa -‘l5-45-90 triangle is
34. Find the hypotenuse.
19. ‘t he longer leg ofa 50-60-90 triangle is 27.
Find the lengths of the shorter leg and the
hypotenuse.
Find the side lengths of 30-60-90 triangles.
The longer leg of a 30-60-90 triangle is I2. Find
the shorter leg and the h_vpotenuse.
The longer leg is times the shorter leg. so the
shorter leg has .1 length of L2‘ - '2:/3 - 4w./5.
The hypotenuse is twice the length of the shorter
leg, or Sc/3.
LESSON 5.8
Key Skills
Determine the distance between two points
on a coordinate plane.
Find the distance between the points (-4. l}
and [2, 3).
d=.n2—4F+t3—i'=¢§=2¢3
Estimate the area under a curve by the
method of quadrature.
Use the method ol quadrature to estimate the area
between the curve y = 2.’ and the x—axis from
.x'= I to .\'= -l.
V The area can be estimated by
12 three rectangles with .1 base of
8 I and the following heights:
J \
X fi=I 2=4 i=9
1 2 3
Thus. the area is approximately I + -1 + 9 = H.
LESSON 5.7
Key Skills
Prove theorems by using coordinate geometry.
Prove that ilithe diagonals ol‘ a rectangle are
perpendicular to each other. then the rectangle is .1
square.
A general rectangle can be Y
drawn with vertices .1t (0, 0).
(:1, 0). (rt. (1), and [0, 11). The lo‘ bl la’ b’
slopes of the diagonals are Ti
and —g. if the diagonals are _,_ X
la, 0)
perpendicular to each other.
I I. 1' , - . .
then = -1. so IT’-..\Al1ICh means that
l) - rt [or (J - —tt]. Thus. the lengths of the sides oi"
the rectangle are the same, so the rectangle is a
square.
20. The hypotenuse of 21 30-60-9(l triangle is I6.
Find the lengths of the shorter leg and the
longer leg.
Exercises
Find the distance between each pair of points
21. [0, O} and (6. 8)
22. [3, 3) and (7, 2)
23. [-2, -'l) and (.*,—lJ
24. Use the method of qu-.1dr.1ture to estimate the
area between the curve y - .1" and the .1‘-axis
Irom x= I to :.'= -I.
Exercises
ln Exercises 25-28, you will prove that if the
diagonals of a parallelogram are equal. the
parallelogram is a rectangle.
25. Draw .1 general parallelognun in .1 coordinate
plane with three vertices at B{0. 0), Ma, 0).
and Cd». L‘). Give the coordinates ol'the fourth
\'erte\t. D.
26. Write expressions for the lengths ofthe diagonals
oi" the parallelogram you drew in Exercise 25.
27. Assume the Ll i.1gon-.1ls are the same length. Set
the expressions from Exercise 26 equal to each
other and prove that u or I: must equal 0.
28. Use your result from Exercise 27 to complete
the proof.
CHAPTER 5 REVIEW 365
LESSON 5.8
Key Skills Exercises
Find the probability of an event. Find the probability that a dart tossed
randomly onto each figure will land in the
\'\-‘hat is the probability that a randomly generated
shaded area.
point with 0 5 x 5 5 and O 5 ,1-' 5 5 will land in a
circle with radius 2 centered at [3, 3]? 29. 30.
The diagram below represents the points with
O 5 2: 5 5 and 0 5 y 5 fraud the circle with a /»
radius of 2. y /I
5 \ ‘
C
(3, 3) 31. 32.
5 > x
w 5
The area of the circle is =l."t. and the area of the
stluare is 25. so the pl'()l)'tll)llll.}‘ is -=- 0.50.
Applications
33. SAFEW You have a 20-foot ladder to climb onto a wall that is 16 8! lflasl
feet high. Due to safety considerations. the ladder must extend at — 3 '1
least 3 feet past the top of the wall. and the bottom of the ladder
must be placed away from the wall at a distance of %ol the length
of the ladder from the ground to where the ladder rests against * ft '5
\
ff ft
the roof. Use the diagram at right to find x, the length of the
ladder from the ground to the wall. is the ladder long enough?
How lar will the bottom ol‘ the ladder be from the wall?
34. SPORTS A running track has straight sides and semicircular ends.
The outer radius of the semicircles is 80 meters. the inner radius
is 40 meters, and the straight sides are I60 meters long. What is
the perimeter of the outside edge of the track? What is the " '5 <3
perimeter of the inside edge oi. the track? What is the area of
the track?
#1‘
366 CHAPTER 5
Chapter Test
Use the labeled figure below to find tl1e indicated
perimeters and areas.
C D
'1'5°‘° 6 cm
3 _ F
4 cut _1 I.
A G 6 cm E
-1
. the perimeter of pentagon ABCDI;
. the perimeter of hexagon ABFCDE
. the areal oi" rectangle ("DEG
. the area of hexagon A BFCDF
h6\)N
Find the area of the given figure.
5. .1 triangle with a base ot'9 and height of IS
6. .1 par-.tllelogr.1m with .1 height of 8 and base
of I2
7. .1 trapezoid with bases of S and 9 and a height
of 7
Find the circumference and area of each circle.
Use 3.14 for 1:.
8. r= 3 9. r= 26 10. d= 30 11. d= 42
12. COl\'SUMl;'R ECONOMICS Which is the
better deal: .1 l2-inch rottnd pizza that costs $8
or a I2-inch square pi77zt that costs $8?
Explain.
Find the area of the shaded region. Use 3.14 for -z.
13. \
24
12
For Exercises 14-17, two side lengths of a right
triangle are given. l’-“Ind tl1e missing side. Leave
your answers in radical form.
15. r1=lU,l1=_2_.t?=26
16. t1=i.l)=l2,r.'=l6 17. rJ=6.lJ=6,t'=i
14. a=7,b= 24.c=_§_
18. The hypotenuse of -.1 -45--15-90 triangle is 80.
Find the lengths of the legs.
19. The length ol'«.-.1ch leg of:1 '15--15-90 triangle is
28. Find the hypotenuse.
20. The longer leg ofa _*U—6U—90 triangle is 15.
Find the lengths of the shorter leg and the
hypotenu.se.
21. The hypotenuse of a 50-fit)-90 triangle is 24.
Find the lengths of the shorter leg and the
longer leg.
Find the distance between each pair of points.
Leave your answers in radical form.
22. [-3. -3] and L5. 3) 23. [2, 3] and (5. 7)
24. (O. O).1nd (—l. -3) 25. (—6. 3] and (4. 9)
In Exercises 26-30, prove the Trapezoid
Midsegment Theorem by using coordinate
geometry.
26. Tmpezoid IKLM .1bove has vertices at [(0. 0}.
K{2p. 2q), !(2r.Ll. and .\-'l[2$.L).
27. Find the coordinates of Ehe midpoint of TE,
and D. the midpoint of UH.
28. Find the lengths of W. and it
29. Prove that the length of the midsegment is the
average of the lengths of the bases.
30. Find the slopes oi]-ilfi. E. and E. Prove that
the midsegment is parallel to the bases.
I-“ind the probability that a dart tossed randomly
onto each figure will land in the shaded area.
31. 32. 2
CHAPTER STEST 367
-' E"S CUMULATIVE ASSESSMENT
College Entrance Exam Practice
o
I: Internet connect
MULTIPLE-CHOICE Fnr QlIt';‘5ll()l1b I-3. write the standmdized
letter that indicates the best answer. Test Prep onnne
Go To: go.hrw.com
1. Which of the lbll()\s'ing are possible side KGYVIUWIMM1 703* FWD
lengths of a triangle? (LESSON 4.8) _
a- 8. I3. 24
b. 8. I6. 27
c. 8, I2, 20 Give the most specific name for each figure.
d. 8. 8. 2t It may help to draw a possible example.
(LESSONS 3.1, 4.6, AND 5.3)
2' RSTU 15 a p‘"dlMOgra'“' Find ST" 4. quadrilateral ABCD. in which AB = CDand
(LESSON 4.5)
AD = BC
9 s _
f 12 5. polygon MNOPQR
3n — 20
U 7 6. quadrilateral FGHI. in which FG = HI,
Eflm. and F1"?
a. I6
b. 37 ‘I. a plane figure in which all [mints are
c. 28 equidistant from point P
d. II)
For Items 8-12, refer to the diagram below.
Complete the proof that AABD is isosceles.
(LESSON 4.4)
3. Find the area of the circle l)elmv. (LESSON 5.3) I
C
a. 25H
b. 6.25:: ‘
c. IOII ‘\
A B
d. lOO:r E
8. KCABE (CB/l by ? .
a. CPCTC
b. ASA
c. lsosceles Triangle 'l heorem
d. ("nnverse of the ls0.s'cele:~. Triangle Theorem
368 CHAPTER 5
9- AACDE L~.BCDby 2 .
a. Isosteles 'li'iangle 'l'heorem
b. SAS
c. ASA
d. Angle Addition Postnlate
10- !_('AD“:‘ .f_CBDl)}' ? .
a. CPCTC
b. .f\S.'\
c. lsosceles Triangle Theorem
d. definition of angle bisector
11. AD/IE 2 .LDb‘L' by ?
a. lsnsceles Triangle Theorem
b. Converse of the Isosceles Triangle Theorem
c. Angle Addition Postulate
d. SAS
12. AABD is isosceles by ?
a. delinition of isoseeles triangle
b. CPCTC
c. Isosceles Triangle Theorem
d. Converse of the isosceles Triangle Theorem
In Items 13-16, suppose that AABC has
vertices at A (-1, 8), B (4, 3), and CH, 2).
13. Find the slope of each side of AA BC.
(LESSON 3.8)
14. Prove that AABCis .1 right triangle.
(LESSON 3.8)
15- Find the midpoint ofeach side of AABC.
(LESSON 3.3)
16. Find the length ol'e.n:h side of AA BC. Round
your answers to the nearest hundredth.
(LESSON 5.6)
FREE-RESPONSE GRID
Items 17-20 may be answered by using a free-
response grid such as that commonly used by
standardized-test services.
@®®@®G®@@ O
@@@@@G@@@@O€*
@{=3@@@G@@£-)@OG*
’="-‘l|'~“’=}"-‘@‘3E°)£-WK)
For Items 17-19, refer to the figure below.
(LESSONS 5.2 AND 5.4)
17.
18.
19.
20.
W15X
XZ- ;
I-VJ = L
'.treaol"tr-.1pe;t.oid WXYZ = _?_
Find the length of ti side ofa square with the
same area as a circle with at radius of IO.
Round your answer to the nearest tenth.
(LESSONS 5.1 AND 5.3)
CHAPYEH 5 CUMULATIVE ASSESSMENT 369
370
Lessons
6.1 0 Solid Shapes
6.2 0 Spatial
Relationships
63 0 Prisms
6.4 0 coordinates in
Three Dimensions
6.5 0 Lines and Planes in
Space
6.6 o Perspective
Drawing
Chapter Project
Polyhedra
Shapes
in Space
WHAT GIVES THE PICTURE ON THE FACING
page such a dramatic effect? Even though it is
printed on a flat, two—dimensional surlace, the
French Concorde jet has the illusion of depth.
In this chapter, you will find out how to give
drawings this three—dimensional quality.
As you study geometric figures in space, you
will discover that three-dimensional figures
have properties similar to those of two-
dimensional figures. In this chapter, you will
apply what you already know about points and
lines in a plane to points, lines, and planes in
space.
.r:¢J’{ '
DNA rnoltttrh’
5' :
_ _q.
I I
I I
'l'iu'¢*e—drmeusiomri -I
compmer rllmtrmious
;
ofit r hr3_§-n if-" 3; .t'
"1t*:Jr'ejrr1rnr " 4.
_n._
l I
- ' -- - ‘ - I - » - r ' . . . . . jr
, earlier Grcelt !_1h1losopher Plato also Lnevt this . In the Pomoho ACM“), on page 387’ you “.1”
l ha’ and the _h""° r‘_’g"l‘" Pollrhedm ‘ll? One" lmild the five Platonic solitls from patterns
called Platonic solids alter lum. called m.l5_
I “‘ Ill“ Cl"=1Pl°T PTf3.l'3‘3l= Y0" Will 9-‘Pl0T¢‘ “’h)' 0 In the Portfolio r\ctivity on page 395, you
1 ‘her? ‘"9 '3-‘“lClll" ll"? reglllilr P0l}'h"dT'-‘- will create two nets that "pop up" to form a
After L-Omplfling the Chapter larojeu you will be dotlccaltcdron with the help ofa rubber band.
able to do the lollowillgz o In the Portfolio Activity on page 408, you
0 \-'isuali7.e and understand the relationships “"” €733‘? 5""‘"‘:%“l"‘_r l‘°l.V'h°d“‘- 3'50 Glued
among Polygons in 5P.dce_ Archlntedean solids. lrom nets. I
I i 1 f I 1 l
I
' ' -_. _L
About the Chapter Project
Solid ligures that are bottnded by polygons are
called polyhedra. Mathematicians have long been
interested in regular polyhedra, which are
bou ntled by congruent regular polygons.
The last book of Fuclid's Flrmrms contains a
proof that only live regular polyhedra exist. l'he
About the Portfolio Activities l __
Throughout the chapter. you will be given
opportunities to complete Portfolio Activities
that .1 re designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
Chapter Project is polyhedra.
_..q__
— -—w
u
4 ——i
Objectives
0 Use isometric dot
paper to draw three-
dimensional shapes
composed of cubes.
0 Develop an
understanding at
orthographic
|)l’O|8CllOll.
0 Develop a basic
understanding ol
volume and surface
area.
' P I O N
MECHANICAL DRAWING
372 CHAPTER 5
Solid Shapes
Architects.
any nears, and many
other prolossionals
must be skilled in the
an of dra wing three-
dimensional shapes.
In tlrls lesson. you
will lean: some of
the fundamental
conceps 0! this art.
An isometric drawing is one in which
the horizontal lines of an object are
represented by lines than form 30° angles
with -.1 hori7ontal line in the picture.
Drawing Cubes
A type of graph paper called isometric dot paper
can be helpful in drawing solid shapes such as
cubes. This paper has diagonal rows of dots
that form ".1 30° angle with horizontal lines.
Connect the dots as shown to draw a cube.
On a solid cube. at most three faces are visible
at a time; however, sometimes you may wish
to represent the hidden faces of-.1 cube. This is
done by using dashed lines. as shown in the
second drawing.
In the first and second drawings. the cube is
viewed from above. In the third drawing, the
cube is viewed from below.
30°
.30“
' I
Uslng Isometric Grid Paper
- - - 1. 1’)r-aw each solid figure below on isometric dot paper. Then redraw the
;5o,,,et,.,, do. papa. hgu res with the red cube or cubes removed.
2. Draw each solid figure below on isometric dot paper. Then add a cube
at each red face and draw the new figure.
CHECKPOINT ./ 3. Describe how the drawings change as vou add or subtract cubes.
' 2
Using Unit Cubes
- I ' ED 1. Use unit cubes to build the three figures below. Are your hgures the
uni‘ cubes and same as those of your classmates? ll not. how are they different?
ISOITIEUIC dot paper
2. Build three solids of your own with at least six unit cubes in each. Draw
your solids on isometric dot paper.
cnecxpouxrr ./ 3. Could any of the drawings you made in Step 2 represent more than one
solid figure? Fxplain your reasoning.
LESSON 6.1 souo SHAPES 373
Orthographic Projections
An orthographic projection is a View ofan object i It which points of the
object are “projected” onto the picture plane along lines perpendicular to the
picture plane.
'l_vpic-ally, a solid may be drawn front six dilterettt
views: from. back. left. right. top. and bottom.
For the solid at right, all six’ orthogr-.tpltic views
are shown below. Edges that cannot be seen itt a .
particular View are represented by dashed lines. g -- -
[:11 ____:::i'
Top
Front Right
Left Back
Bottom ...... --
You may find it helpful to think of the different "J 3 i‘-,
views ot an object on an ttnlolded bo\' that has fl
‘.1 dillerettt view on each face. B '1' B
n 3 '
Volume and Surface Area
1. Use 7 unit cubes to build a model of
unit cubes and the solid shown at right._Then drtttt .
uravh 0390' six orthograpltic. projections of the
object on graph paper. representing -
the views from the back. Iront. left.
right. top. and bottom. '
CHECKPOINT ./ 2. The volume of a solid Iigure is the
number of uttit cubes that it takes
to Completely fill it. How can you
determine the volume of the Iigure .
that you built?
Front
CHECKPOIN1’ ./ 3. The total area of the exposed surfaces ofan object is called its surl-"ace
area. How can you use the ot thographic. projections of the object to
determine its surl-ace area?
CRITICAL THINKING In the orthographic projections you drew itt Activity 3. each exposed lace ol"
the object appeared in exactly one view. [)0 you think this would be true for
any object you might build? Use drawings or models to explain your reasoning.
374 CHAPTER 6
Exercises
. Communicate
1. A solid built from cubes has the top view shown at right.
Draw two possibilities for this solid.
2. A solid has the right view and front view
shown at right. \-\"hat is :1 possible top view
for this solid? Front Right
3. Why do you think an isometric drawing uses angles of 30° from -.1
horizontal line? (Hint: Draw a cube on isometric grid paper and measure
its edges.)
4. Describe the difference between volume and surface area. lnclude units in
your description.
0 Q/I/ded Sk///3 PI‘d6'f/6'8
Use isometric dot paper for Exercises 5 and 6. (ACTIVITY 1)
5. Draw the solid below with 6. Draw the solid below with a
the red cube removed. cube added at the red face.
\
in
Use unit cubes for Exercises 7-10. Refer to the figure below.
(ACTIVITIES 2 AND 3)
7. Build a model ofthc figure out of unit cubes.
Then turn the figure and draw a dillerent view
on isometric dot paper.
8. Draw si\' orthographic projections of the solid.
9. Find the: solids \-rolurne in cubic units.
10. Find the solids sttrlace area in square units. \Fmm
. Pmct/ca and Apply
For Exercises 11-16, refer to the isometric drawing of a cube shown
below. Identify the letter of the indicated face.
I) ' ' d
. . 2’ .
11. from 12. right \i‘ "
c
13. top 14.lcl't 8 9
c f u
15. bottom 16. back 9 .
Front f
LESSON 6.1 SOLIDSHAPES 375
376 CHAPTER 5
17. What litres would you add to the drawing \.
at right to indicate the hidden faces?
18. Draw an orthographic projection ofthe cube.
For Exercises 19-23. refer to the isometric drawing below.
19. Give the solid's volume in cubic units.
20. Give the solids surface area in square units.
21. Draw six orthographic views of the solid.
22. Draw the solid on isometric dot paper
from a different viewpoint.
23. Draw the solid on isometric dot paper "Hon!
with a cube added at each red face.
Refer to the drawing below for Exercises 24-27. Assume that there
are no hidden cubes.
24. Each flat area of the solid is a lace. How \.
many faces does this solid have?
25. Draw the front face. I
26. Is -my other lace of the solid congruent to
the front face?
“<.
27. All‘ any two faces of the solid congruent? F'°'“
Fxplain your answer.
The three solids below each have a volume of 4 cubic units.
a. b. c.
‘\
Front ‘Front
28. Find each so|id's surface area in square units. Which has the smallest
surface area?
29. Draw six orthographic projections of each st)lid.
30. Draw two other solids with -a volume of-4 cubic units that are different
solids from those above [not just different views).
Refer to the solid below for Exercises 31 and 32.
31. Draw six orthographic projections of the solid.
32. Are there any exposed faces of the solid that do
not appear in any of the orthographic views you
drew in Exercise 5]? Explain.
33. Use isometric dot paper to draw two solids that have the same volume but
dilferent surface areas.
34. ['54: isometric dot paper to draw two solids that have the same surface area
but dillerent volumes.
flh0anet-- -
Homework
Help Online
Go To: gajiiwxzom
Kcvwoid
MG! Homework Help
lot Exercise 35
:3.
CHALLENGES
APPLICATIONS
35. The solid at right is made up of 3 tinit cubes.
Draw a solid with a smaller volume btit a larger
surface area.
36. Draw two dilTc-reiit solids that have the same
orthographic projections from the top and
bottom views.
37. Draw two diITerent solids that have the same orthographic projections
from the from and back views.
38. How many unit cubes does it take to build a 2 x 2 x 2 cube?
.1 5 x 5 x 3 cube? a 4 x 4 x 4 cube? an n x H x ll cube?
39. What is the surface area in square units ofa 2 x 2 x 2 cube?
.13 x 3 X 3 cube? a 4 x 4 x 4 cube? an n x 1'! x ll cube?
40. The hgure at right shows a 3 x 3 x 3 cube
built from unit cubes. Suppose that the
exposed laces of the cube were painted
red and then the solid was disassembled
into unit cubes.
How many tinit ctihes would have
a. 5 red faces?
b. 2 red faces?
1:. l red face?
d. no red faces?
_<_/
41. Repeat Exercise 40 for -.1 4 x 4 x 4 cube.
42. ARCHITECTURE Draw orthographic
projections that represent the top.
front. and right views of the
building shown at right. Assume ‘
_ _
that the lront laces are the ones on --
the right, in sunlight. "' 5 ‘
43. RECREATION The isometric drawing of a tent. shown at left. can be used to
show how the tent will look when it is assembled.
Draw si\' orthographic views of the tent. Vt hat might these views be used
for?
._ \ '
.— _ \' i
5 " _ __ ;
\,' 3 ‘ p ‘
LESSON 6.1 SOLIDSHAPES 377
APPLICATION
‘*9
50
'5'
378 CHAPTER 5
600ft
L00»? Back
Find the area of each figure. (LESSONS 5.2 AND 5.3)
44. 45.
6 8
V 2.9 m :,».-2-3 "1
__l_.._\
ICL7 m
10
46. 47.
Find the unknown length in each right triangle. (LESSON 5.4)
48- 49.
3 cm ?l 315 Y‘;
6 cm
265 yd
50. ARCHAEOLOGY The top ofa p}'l'i1lTllLl has
been destroyed. Lse the diatgrani of .1
cross section at left to cstini-.1tc its original
height. (LESSONS 3.7 AND 5.4)
A’
Look Bet/and
Use the orthographic projections Top
at right for Exercises 51-54.
51. ['54: isometric dot paper
to draw two diiTe-rent
views of the solid. —-
52. Are any Cubes hidden Len :Front Right [Back
in your drawings! I I I l I - : I
53. How many faces does
the solid have?
54. How many congruent -
faces does the solid have?
Explaiin your answer.
Spatial Relationships
Objectives r
0 Define polyhedron.
0 Identify the ‘
relationships among J
points. lines, segments. i‘ .
planes, and angles in ' -‘
three-tlunensional -
space.
0 Delme dihedral angle.
‘~ Bun 9.
The interplay of lines and planes is apparent In real-
warld abiects such as this quartz crystal. Understanding the
relatlanslrlps among llnes and planes in three dimensions -
essential to understanding the structure of matter.
Figures in Space
A Closed spatial ligu re made up of polygons is Ldll(.‘Cl a polyhedron (plural.
polylierlrrl or p0lylte¢'lrnn5]. Closed spatial figu res are also known as solids.
Definition: Polyhedron
A polyhedron is a closed spatial €998
figure composed of polygons. called
the faces of the polyhedron. The
intersections of the faces are the ’
edges of the polyhedron. The V°”°" ‘K Face
vertices of the laces are the vertices
of the polyhedron. 6.11
The polyhedron you are proliably most familiar with is a cube. A cube is an
example of-a regular polyhedron. In a regular polylredmn, all of the laces
are Longruent regular polygons, and the same number of polygons meet at
each vertex.
LESSON :3: SPATIAL RELATIONSHIPS 379
Lines and Planes in Space: A Step-by-Step Procedure
0!! L ED
no special tools
CHECKPOINT ./
cuecxpomr ./
I I L ED
no special tools
380 CHAPTER 6
ln the Activities that lollow. vou will discover and develop ideas about how
lines and planes relate to each other in space.
' I
Parallel Lines and Planes in Space
Part I
1. Sketch a cube and label its vertices
as shown. ldetitily the segments that :
form the vertical edges. -4 0
Do E and E seem to be coplanar?
Do they seem to be parallel? Do you F
think that they would meet if they
were extended infinitelv?
2. Which edges of the cube seem to E H
be parallel?
3. Are there edges of the cube that are not parallel and yet would never
meet if they were extended infinitely in either direction? Explain how
this can be. These segments [or lines or rays) are said to be skew. Make
a list of four pairs of skew edges in the cube.
Part ll
1. How many laces does it cube have? \-\-'l1ich faces seem to be parallel to
each other?
2. Write your own definition of parallel planes by completing the
sentence below.
3 C
Definition: Parallel Planes
Two planes are parallel il and only if ? . 6.2.2
Note: Two plane figures are parallel iii and onlv if they are contained in
parallel planes.
' Z
Segments and Planes
Part I
1. Each edge ofa cube is perpendicular
to two different laces. For the cube at
right, make a list of edges and the faces
to which they are perpendicular.
2. What do yott think it means lior a
segment or a line to be perpendicular
to a plane? Draw .1 line, I". on 2! piece
ol paper and label a point. P, on it.
Hold your pencil so that it is
perpendicular to the paper. and
place the tip on point P. ls the
pencil perpendicular to line I"? l
3. Is it possible to tilt your pencil so
that it is still perpendicular to line E
but not to the paper? Make a sketch
illustrating your answer.
4. Draw a new line. m. through point P. Place your pencil on P so that it is
perpendicular to I’ and m at point P. \-\'hat is the relationship between
the pencil and the plane of the paper?
5. Draw several other lines through point P. when you place your pencil
on P so that it is perpendicular to the paper. is it -also perpendicular to
these other lines?
Cl-IECKPOINT ./ 6. Write your own definition ol a line perpendicular to a plane by
completing the sentence below.
Definition: A line Perpendicular to a Plane
A line is perpendicttlar to a plane at .1 point P if and only if it is
perpendicular to every line in the plane that E’ . 6.2.3
Part ll
1. Each edge of a cube (see Step I of Part I)
is parallel to two different laces. Make a
list of edges and the laces to which they O
are parallel. What do you think it means
for a segment or a line to be parallel to -.1
plane?
_ _
2. l')r-aw a line, 9'. on a piece of paper. Hold
your pencil above ti so that it is parallel
to the line. Does the pencil seem to be A
parallel to the plane of the paper?
3. Turn your pencil so that it is still parallel to the paper but not to the
line. Do you think that you could draw another line on the paper that is
parallel to the pencil in this position?
CHECKPOINT ./ 4. Write your own definition olia li.ne parallel to a plane by completing
the sentence below.
Definition: A Line Parallel to a Plane
A line that is not contained in a given plane is parallel to the plane if
and only ill it is parallel to ? . 6.2.4
LESSON 5 2 SPATIAL RELAYIONSHIP5 381
Angles Formed by Planes
A half-plane is the portion ol-a plane that lies on one side oi at line in the
plane and that includes the line. The angle between two hall‘-planes is known
as a tlihtftlral tingle.
Definition: Dihedral Angle
A dihedral angle is the figure formed by two hall'—pl-anes with a common
edge. Fach half- plane is called a face of the angle, and the common edge
of the haltlplaites is called the edge of the angle.
Edge,
‘Faces
\
‘ \
Ha|f-pIane Dihedral angle 6'25
Measuring Dihedral Angles
- L - ED 1. Some of the laces ofa cube form right dihedral B C
scissofs and 9ith9[ iingle5 l5_u the faces arfi pel'p'c‘ndlCl.'ll'<]l' to each
St"? *0|d5n9 Better or other]. Each face of the cube is perpendicular to D
an '"d°" card how many other faces of the cube? F G
2. Draw :1 horizontal line. I’. on a piece of paper. 5 H
Mark and label points A. B. and C on the line,
with point 8 between A and C. Make a crease
through point B so that line I" lolds onto itself.
\'\-‘hat is the relationship between line if and
the line of the crease?
3. Open the paper slightly. The angle formed by
the sides oi‘ the paper is a dihedral angle. l'he
measure of the dihedral angle is the measure
of /_.r‘lBC. A 5"
- . 3"=T"’
CHECKPOINT ./ 4. Write your own dehnition oi the measure of _
a dihedral angle by completing the sentence
below.
Definition: Measure of a Dihedral Angle
l'he measure of a dihedral angle is the measure of an angle formed
by two rays that are on the faces and that are ? to the edge.
6.2.6
382 CHAPTER 6
5. Open the paper and llatten it.
Add points X and Y on the line
of the crease. Draw two rays
from each point, with one ray
on each side of the crease. as
shown.
6. Fold the paper again along the
same crease. Cut out pieces of
paper that lit neatly into the
angles lormed by the different X_----~v
ravs. Compare the shapes of the B
pieces of paper. Do the angles ___,
that are formed by the new rays
have the same or dil'l'e-rent
measu res than that of LABC?
CHECKPOINT ./ 7. By measuring the angles formed by different rays in Step 6, you can get
a variety of results. W hat is the smallest angle that vou could measure?
What is the largest? Use your results to explain why a dihedral angle is
measured along rays that are perpendicular to the edge.
Exercises
. Communicate
1. ll’ two lines in space are perpendicular to the same line. are the two lines
parallel to each other? Why or why not?
2. It" a line not in a plane is perpendicular to a line in the plane, is the first
line perpendicular to the plane? Why or why not?
3. ll :1 line is perpendicular to two intersecting lines in a plane. is the first
line perpendicular to the plane? Why or why not?
A P P l I C A T I 0 N CHEMISTRY Use the model of a I}
sodium chloride crystal, which has a .
cubic structure, for Exercises 4-6.
4. Describe a pair of parallel segments. .3!
and explain why the segments are
parallel. I
5. Describe a pair of parallel planes. and
explain whv the planes are parallel.
6. Describe a pair of perpendicular
planes. and explain why the planes (ry,-ml fmrim qt _s-orliiun cMorid¢-
are perpendicular. (table salt)
LESSON 5 2 SPATIAL RELAYIONSHIPS 383
fl - conned ,?.9_.,
_ _ _ IBM
Activities
Online
Go To: nc.hrw.cnm
Keyword:
MGI 3-0
384 CHAPTER 6
. q/4/ded 3.6///3 Practice
Use the figure of the cube at right for Exercises 7-11. (ACTIVITY 1)
7. l\'t1me two pairs of parallel edges.
8. Name two pairs ol skew edges. G
9. Mine two pairs ol parallel laces. H K
10. List two edges and the planes to M
which they are perpendicular. N
11. List two pairs of parallel edges that do L 0
not lie on the same l'-ace of the cube.
12. in the ligure at right. line p is
perpendicular to plane R. What is the
relationship between line 1: and line
:1? line 1: and liner? (ACTIVITY 2)
IT)
13. In the figure at right. line in is parallel 8
to plane S.What can you conclude about
a certain line in plane 8? (ACTIVITY 2)
14. What is the measure ot the dihedral angle
in the tigure at right? (ACTIVITY 3) E
G
. Practice mm’ Apply
to
15. in the ligure at right. line p is parallel to
line q. What can you conclude about the
relationship between line p and plane M?
18. ln the figure at right, line Mr is not parallel
to line n. Can you draw a conclusion
about the relationship between line m
and plane Q? Fxplain your answer.
17. In the figure at right. line [3 is perpendicular
to line r but not to line 5. What can you
conclude about the relationship between
line p and plane IR?
fl Inceruteonnoct
Homework
Help Online
Go To: no.hrw.com
Keyword:
MGI Ilomcworlt Help
lot Exercises III-22
APPLICATIONS
For Exercises 18-422. indicate whether each statement is true or false for
a figure in space. Explain your answers by making sketches.
18. ll" two lines are parallel to a third line. then the two lines are parallel.
19. II‘ two planes are parallel to a third plane. then the two planes are parallel.
20. II‘ two planes are perpendicular to a third plane. then the two planes are
parallel.
21.II'two lanes are we wendieular to the same line. then the wlanes are
I I
parallel.
22. II’ two lines are perpendicular to the same plane, then the lines are parallel
Use your model from Exercise 23 to answer Exercises 24-26.
23. Fold an index card in l_1_alfand_l131rlt
it \i'itl1_t\~'o segments, AB and CD, so
that /tBis perpendicular to the folded '3
edge and E5 is not. Cut along each -a
segment from the folded edge. ~
Insert two more index cards to model
intersecting planes, as shown at right.
24. Which inserted card forms a plane
that is not perpendicular to the edge?
25. Which inserted card can be used to
measure the dihedral angle formed
by the folded card?
26. Which of the two angles formed by
the inserted cards is larger?
Ships navigate the surface of the ocean, which can be modeled by a
plane. Airplanes navigate in space. Exercise 27-30 concern the
navigation of ships and airplanes.
27. NAVIGATION Ship A is traveling south. Ship B in the same \-'icinity is
traveling southeast. 'I'heir lines of travel ? .
28. NAVIGATION Airplane A is traveling south at an altitude oi’ 23,000 feet.
.\Iearl)y. airplane B is traveling southeast at an altitude oi" l8.000 feet.
Their lines of travel are ? .
29. NAVIGATION Two airplanes flving hori.oontalIy at the same altitude are
flying in the same i’ .
30. NAVIGATION An airplane
takes oIT from a runway.
The airplane's nose and
wingtips define the piam
a_fflig!n. Sketch the
dihedral angle formed hy -
the airplanes plane ol
flight and the surface of
the runway. Is the angle ~
acute. right. or obtuse?
Explain.
\
_
LESSON :3: SPATIAL RELATIONSHIPS 385
CHALLENGES
fllnhnunconnun &%
Portfolio
Extension
Go To: gc.hrw.corn
Keyword:
MG! Platonic
336 CHAPTER 6
Look Back
ln Exercises 31-34, use a compass and straightedge to construct each
figure. (LESSON 4.7)
31. Draw an angle and label it LABC. Construct a copv of LABC.
32. Draw a segment and label it Construct its perpendicular bisector.
33. Draw segment and label it F—(J. l‘~Lt_rk a point. H, not on E1 Construct a
line through point H parallel to F6.
34. Draw a triangle and label it /_‘~.]Kl . Construct a copy ol' AIKL.
Find the area of each polygon below. (LESSONS 5.1. 5.2. AND 5.5)
35. square 36. trapemid 37. parallelogram
22
21
I4 32 23
38. right triangle 39. equilateral triangle 40. regular hexagon
9
28 53 15
Look Beyond
42. .-‘lrrattge the figure helow into
exactly three squares by moving
only three tootltpicks.
41. .-‘lrnmge the figure helow into
exactly three triangles by
moving only two tootlrpicks.
\ _ board or cardboard.
’ Tetrahedron
He:-tahedron lcube]
I Q _
omhedr n 2. Cut out the nets and told along all
0 of the dotted lines. You ntay wish
to color the faces or decorate them
in some way.
‘ Octahedron
. \'L “
t ‘ 3. Use tape or glue to assemble
' 6 each polyhedron. -'
clodecaheclron
Dodecahedron
/ wonxmc on me CHAPTER PROJECT V\
\ _ You should now be able to complete
" Activity l ol- the Chapter Project.
"' icosaheclron
Icosaheclron
BUILDING PLATDNIC SOLIDS
A regular polyhedron has congruent regular polygons as laces. with the
same number of laces meeting at each vertex. There are exactly live ditlerent
convex regular polyhedra. shown below. Because the Greek mathematiciatn
Plato proved that only these five exist. they are also known as the Platonic
solids. Poly-hedra are named for the number of faces they have.
5 \
‘ - Tetrahedron Hexahedron lcubel Octa hedron
- [4 faces) [6 faces) (8 faces}
.\ \
tetrahedron
Dodecahedron Icosaheclron
(12 faces} (20 faces)
1. 'l'he patterns at right are nets
Cube for the Platonic solids. Enlarge
and copy the nets onto a
sturdy material such as poster
LESSON e2 SPATIAL RELAYIONSHIPS 387
Prisms
Many Ianuliar objects are
shaped like polyhedra known
asprismans you . n - I .
you will apply your knowledge
of congruent segments. angles.
and polygons _ _
, , I
Objectives
0 Define prism, right . ' .
prism, and oblique '
prism.
0 Examine the shapes of
lateral faces ol prisms.
0 Solve problems by
|1S|"§J "l9 df'3§l9":l A {riser l}l;'(lIiI is bent as it passes through the rrimigniur gins: prism
;?SanS]"'e ° 3 "9 t in r.hi.~' experinirnr. laser light consists ofonr pure color, so it is not
refracted into it .\pt'.-’L‘l‘Tflm as ordinary light would be.
Prisms
The figures shown below ztre prisms. A prism is named lay the shape of its base.
Triangular prism Rectangular prism Pentagonal prism Hexagonal prism
A prism is -.1 polyhedron that consists of a polygonal
region and its translated image on .1 parallel plane, with ' -'
quadrilateral liices connecting corresponding edges. ' - _.'
n.,_
3 _ .
833 The laces formed by the polygonal
, region and its iinage are each called
Lateral Lama] :i base Olvllie prism. the rem-tuning
face ,._...---* edges laces. which are quadrtlaterals. are
called lateral faces ol the prism. The
‘ edges of the lateral lliccs that are not
Lateral edges of either hase are called lateral
/ .
Base face edges of the prism.
383 CHAPTER 6
CRITICAL THINKING
uncooked spaghetti
and miniature
marshmallows
CHEC KPOINT /
C HEC KPOINY M
What type of quadrilateral are the lateral l"-aces of a prism? (l lint: which edges
are parallel? Which edges are congruent?)
The Lateral Faces of Prisms
Part I
Use uncooked spaghetti and miniature :
marshmallows to build a model ol‘a rectangular
prism. The lateral edges should be vertical. as
shown at right. .-I
/-l
1. What type of quadrilateral is each ofthe =
following? Explain.
a. BASE b. B'L'.'Eb' c. L'S'SE
2. List all pairs of congruent polygons in this model.
3. Translate the upper base in the direction ol'a
slide arrow pointing from B to E, as shown at ' E H
right. What type of quadrilateral is each of the ”
following? Explain. It
a. BASE b. B'E'EB c. E'S'SE ' ‘ --
4. Which of the pairs ol. polygons that you
listed in Step 2 are still congruent after the
translation of the upper base!
Part ll
Return your prism model to its original shape.
1. Rotate the upper base to the right or left, as _,
shown at right. ls your new figure still a prism? .
Why or why not? .
2. Are the segments that formed the correspontling
edges of the bases of your original prism still ,-
coplanar?
3. Why do you think prisms are delined so that
one base is a translation of the other?
4. ls it possible to manipulate your prism so that
it is still a prism but none of its lateral faces are
rectangles? Explain.
In the Activity. you discovered that all lateral laces of a prism are rectangles or
nonreetangular parallelograms. This gives an additional classilieation for
prisms.
An oblique prism has at least
one nonrectangular lateral face.
A right prism is a prism in which
all of the lateral laces are rectangles.
Lessonsa PRISMS 389
The Diagonals of a Right Rectangular Prism
A diagonal of a polyhedron is a segment .
whose endpoints are vertices of two
dillerent faces of the pOl}"l'lL‘Lll'Oll.
Diagonal
Diagonal of a Right Rectangular Prism
In a right rectangular prism with dimensions L" X it-'>< II. the length of a
diag,oI1al is given by
d = vliz + w-' + k3. 6.3.1
Given: rectangular prism with dimensions E‘ x wx la
/ I
h
d
m
W
F
Prove: d =
Proof:
Statements I Reasons
m3 = ti’ + W2 Pythagorean Theorem
dz = nag + It" Pytllagorcaln Theorem
cl-' = £3 + W! + if Substitution Property of Equality
cl = J F3 + w3 + IF Take the square root of each side.
E X A M P L E 0 Iron atoms form lmdy—t'eutered cubic
structures. The atoms form cubes with
one atom in the center and one at each
vertex. as shown at right. The tube, 0 0
called a unit cell, is the smallest unit '
ol a repeating pattern.
A ' P l 0 N
CHEMISTRY
The atoms along the diagonal may be ’ " ‘
thought oi as touching each other. ll‘ .' . '
a unit cell measures 291 pieometers
( l picometer = l X I0"! meters] on
each edge, what is the approximate 5.7;]. v¢'m:‘_\‘ of (hi: dm-kc-d cube is
radius of an iron atom? at the remer of one ofthe atoms.
390 CHAPTER 6
O SOLUTION
First Find the lrrngth of the diagonal of the unit cell
:1 = x/E3 + is»! +113
:1 = «’291= + 2913 + 2913 = ,/3(2911) = 291d?
:1 == 504 picometers
lhe diagonal is the length of four radii. so
divide lay -1.
r = 504 + 4 -- I26 picometers
The radius of an iron atom is approxiinately
I26 picometers. or 0000000000 l 26 meter.
fxerc/‘ses
. Communicate
1. Why is a prism with rectangular lateral 5
faces called at "right" prism? A ; D
2. In the right rectangular prism shown
at right. which faces are congruent? ;: G
Would they still he congruent if the prism pg
were oblique? Fxplain your reasoninq. E H
3. in the rectangular pi ism shown at right
above. could more than one pair of faces
be called the bases? Explain your
reasoning.
4. Identifv some re-.il—wor|d objects that Q,‘
are prisms. including oblique prisms
and prisms that do not have . ~s
rectangular bases. ‘x.
A rare exrmtplt’ of
rm oblique prism -
0 Guided 34’///3 Pmc 1'/6'8
Refer to the oblique rectangular prism with 8 ._ C
base EFGH shown at right. Classify each A 0
quadrilateral named below. (ACTIVITY)
5. EFGH 6. ..-'lDH!.' 7. IBFE
E H
A P P L I C A T I 0 N 8. CHEMISTRY Sodium has a body—centered cubic structure with a unit
cell that is -130 picometers wide. Estimate the radius ol'a sodium atom.
(EXAMPLE)
LESSONE3 PRISMS 391
392 CHAPTER 6
Practice and App/y
Which of the figures below appear to be prisms? Give the name for each
prism. if the figure is not a prism. explain why not.
9. 10.
11. 12.
I 1.
W
13. ‘I4.
Use the right triangular prism below for Exercises 15-20.
15. Which face is congruent to AABC? Explain.
16. Nanne all segments congruent to
17. What type ofquadrilatcral is ACFD? 8
18. l\".|me all segnients congntent to E—I-'. \
19. l\ame two congruent lateral faces. .-
20. List all right angles in the prism. A‘ C
Use the oblique rectangular prism below for Exercises 21-25. In the
prism. m4GKN = 60° and m4GKL = 80°.
21. l\an1e all segments congnient to ,
22. What type ofquadrilateral is G}.'\'l<? G ' J
23. What type ofqutulrilatcral is H.-\~ll\F!
24. Name‘ all pairs of congruent faces.
H I
25. l isl all obtuse angles in the prism. K N
Find the length of a diagonal of a right rectangular prism with the
given dimensions.
26. t"'=-1, w= l2. ll= 3
28. E" = 7'15. w = 8, h = 8.5
27. t’ = l0. w=5. h= I2
29. E = a, w= (I, .lI= a
D rnotconnect
Homework
Help Online
Go To: 9o.hrw.com
Keyword
MGI Homawur‘ Heb
lor Exercise 34-!!!
CHALLENGE
APPLICATION
For Exercises 30-33. refer to the right
rectangular prism shown at right.
30. I’ = ? , iv: 3. lr= 2-‘l. (l: 26 '1
31.('-7,w- 2 ,h-l0.d-l5 0'
32.£:-¢1.w-a,lr-2¢1.:l- ?
33.I"=x,w=x.lt=.7«'.tl=l0.x= ? r W
For Exercises 34-38, complete the table below.
34.
35.
36.
37.
38.
39.
40.
41.
42.
Number of Number of Number of
Type of prism faces vertices edges
triangular ? ? ?
rectangular 7 7 7
pentagonal 7 7 7
hexagonal 7 7 7
n-gonal 7 7 7
Use the pattern from the table abote to determine how many l‘-aces.
vertices. and edges a 20-gonal prism has.
CULTURAL CONNECTION: EUROPE bwiss mathematician Leonhard Euler
(l707—l783) proved a relationship between the faces. vertices. and edges
ofa polyhedron. Let I-' represent the number of l"-aces. V represent the
number of vertices. and E represent the number of edges of a prism. For
each prism in the table above. calculate V - E + F. What do you notice?
The base of the right hexagonal
prism shown at right is a regular
hexagon with a side length of a
and a height of Ir. Find the length
ofthe indicated diagonal in terms
of u and h.
PACKAGlNG A manufacturer wishes to
package a candy bar in a box" shaped like
a right triangular prism with equilateral
triangles for the bases. The unfolded
pattern for the box’, called a net, is
shown at right. Explain how the net
should be folded in order to produce
the desired shape. Draw a net lor a box
shaped like a right hexagonal prism. x
LESSON 53 PRISMS 393
APPLICATIONS
CONNECTION
APPLICATION
394 CHAPTER 5
43. CHEMISTRY A given substance has a bodv—centered cubic structure. like that
of iron and sodium. II‘ the radius of one atom of this substance is u. find
the length ofa side, in terms of tl. of at unit cell of the substance.
44. CHEMISTRY Another type olatotnic
structure is called jitce-centered mhic. . ._
lhis strticture is a cube with one atom
at each vertex and one in the center of 0'
each face. as shown at right. Calcium -
has a I‘-ace—centered cubic structure and
has an atomic radius of I97 0 ...
picometers. Find the dimensions. ,
including the diagonal. of a unit cell
of calcium.
Each vertex ofthe drtslted cube is
at the center ofmte of the atoms.
L004’ Back
Classify each statement as true or false and explain your reasoning.
(LESSON 4.5)
45. lhe diagonals ofa rectangle that is not a square bisect each other.
46. The diagonals of at rectangle that is not a square bisect the angles of
the rectangle.
47. The diagonals Ola rectangle that is not a square are perpendicular to
each other.
48. The diagonals ofa rectangle that is not a square divide the rectangle into
four congruent triangles.
COORDINATE GEDMETRY For Exercises 49-51, find the length and midpoint
of the segment connecting each pair of points. (LESSON 5.8)
49. (3. 4). [3.—4J 50. [4.—2], [-2. 3) 51. [2.—2]. (5. 6)
52. OPTICS When white light
passes through a glass
prism, it is separated into i
a spectrum of different ' |
wavelengths, as shown ' I
at right. In the diagram.
the light hits the prism
at an angle oi‘ 36°. Use
the information in the
diagrant to determine the
angle between the red and
violet light rays leaving
the prism.
ll imunetconned EH
Portfolio
Extension
Go To: goJtrw.com
Keyword:
MG] 4-D
F;-{O
Look Bel,/0114'
The Spider and the Fly Suppose that
a spider and a lly are in at room shaped
like at right rectangular prism. The fly
can travel directly to any point in the
room by flyinn, but the spider must 8 ft
walk on the walls. floor, or ceiling.
'Y‘I
53. What is the shortest distance 3
that the fly can travel to get
from point A to point C?
E H
-
G
A. D
TH
ion C
54. What is the shortest distance that the spider can travel to get ll'0l't't point A
to point C? (Hint: think of the room 215;: box. Unfold the box so that it
lies Hat. and the path traveled by the spider will he -.1 straight line.)
\
525
a.
\ V
POP-UP DOOECAHEORON
I ollow the steps below to create a
model 0i‘ :1 regular dndecahedron.
1. Make two copies of the
pattern at right out of
cardboard. Fold along
the. dotted lines.
2. Holding the two pattern
pieces together, place a
rubber band around them
as shown.
3. Release your hold on
the pieces to Form the
dedecahcdron.
LESSON 6.3 PRISMS 395
Coordinates in Three
Dimensions
Objectives ,
0 Identify the features of
a tliree-tlimensioiial . .
coordinate system,
including the axes. -
octants. and _ .
Coordinate wanes" Byus ng a I - . -dimens one coordinate . .
0 Solve problems by - it is posible to locate obiects anywhere
using the distance ‘n space. one method used by as. . . . . er; in
l9""Ul3_i"lhfEE dent‘ -zinmin . I-O8i8b8SGd0l1Uli- : - em. ‘ ‘
dimensions.
By using the x— and y—axes in a coordinate plane, you can give the location of
any point on the plane. Only two ntinibers are required to do this. so ii plane
is said to be rii'o-diniensiomil. By adding a third axis, called the :'-axis. that
intersects the x— and y—axes at right angles, you caii give the location of any
point in space. Three ntinibers are required lor this. so space is said to be
rlii'ee-iiimeizsioital.
The Arrangement of the Axes
Fxaniine the x- and y-axes at left. There are two ways 2
y to add a third axis. The positiie direction of the z--axis
tan point either straight up [out ofthe page) from the
origin or straight down [into the page). In the most
coninion systein. the z—axis points straight tip. To
"’ represent the three axes on .1 page. turn the axes so that
the x-axis points down and to the lelt. the )'-axis points
to the right. and the z—axis points straight up. as shown
at right. imagine that the x—axis points straight out
lrom the page.
7719 arrows on
the axes point
in die positive
dnmon This arrangement ol the axes is called a right-handed
system. With your right hand. let your index finger
represent the x—.ixis. your middle linger. the y—.nis. - y
and your thumb. the 2-axis. Hold these fingers at
right angles to each other. as shown. liacli finger \
points in the positive direction of the axis.
396 CHAPTER 5
CRITICAL THINKING
\-’iew your right hattd from different
perspectives while keeping your
lingers in the same positions to see
different views of the rigltt—ltanded
system. Do the axes shown at right
represent right—hand systems? Z
x!
X
Y
. I‘ P L E 0 Locate the point P( I, 2, 3) in a three—dimensional coordinate system.
SOLUTION
1. Starting at the origin.count I unit in the
positive direction along the x—axis. Make
a mark on the x—-axis at this position.
2. From your mark on the x—a.\is. count 2
units in the positive direction along the
y—a.\'is. drawing a dashed line to represent
the distance. Make 2! mark at the new
position.
3. From tlte new position, count 3 units
in the positive direction along the
z-axis, drawing a dashed line to
represent the distance. Label vour
final position as point P[ l . 2. 3).
,mLzm
CHECKPOINT y’
The Octants and the Coordinate Planes
Just as the x- and y-a.\'es divide the plane
ittto four quadrants, the x-, y- and z—axes
divide space into eight octants. The octant
in which all three coordinates ofa point
are positive, abbreviated f+. +, +). is called
the first acmm.
The remaining oct-ants are descrihetl by the
words top. lmrrom, frmtt, lmrlc. lift, and right.
For example. the top—l'ront—leI't octant is
the octant in which each point has positive
x- and 2-coordinates and a negative
y—coordinate. or [+. —. +].
' - lane
2-plane *2 p
Y X
Y
L
/ " ‘
X first octant
xy-plane
What are the signs for the coordinates of points in each of the other si.\' octantsr
Each pair of axes also determines a coordinate plane. |'here are three
coordinate planes. each named by the pair ofates that determines the plane:
the xv-plane. the xz-plane, and the ,1-'2-plane.
' In the \'y-plane, the z-coordinate of every point is 0.
' In the xz—p|-ane. the )'—coordinate ofevery point is O.
' In the yz-plane, the x-coordinate ol'everi_.' point is 0.
CHECKPOINT ./ What can you say about the coordinates of a point on the x—axis? on the
y-axis? on the 2-axis?
LESSON 6-! C0-OHOINATES INTHREE DIMENSIONS 397
E X A M P L E 0 Draw a right rectangular prism
in the first octant so that three
of its faces are in the three
coordinate planes. Label the
coordinates of each vertex.
0 SOLUTION
One possible solution is shown in
| the figure at right.
The Distance Formula in Three Dimensions
Recall lrom Lesson 6.5 that the length of the diagonal of a right rectangular
is
prism with dimensions 8 x wx la is given by d = x-' E3 + w‘ + h’.
To Iind the distance between two points in three-dimensions. construct a right
rectangular prism with faces parallel to the coordinate planes and with the
given points as vertices. The segment jointing the two points is a diagonal ol
this prism. The dimensions of the prism are t" = II; — x.| , w = I)’: — y.|. and
It = I22 — z,|.
'l herefore, the distance between two points in space is given by the following
forntulzt:
Distance Formula in Three Dimensions
The distance. (I. between the points [x.. y., 2.) and (x_», yg. 2;) is given by
(‘l = \'(x; — x;)3 'l'' (_I’g — _}"|)3 + [Z3 — .'-31):. 5.4.1
E x A M P L E ofind the distance between the points RH, s. -9) and s<—3. 2,—s).
O SOLUTION
R5 = f(—3 — 41-’ + [2 — 61% + [-5 — (-9; 12
\/
= J77: 2 8.6
mv nus Find the distance between the points CB, -4, -5) and Dt2.0. —I ).
398 CHAPTER 6
Exercises
. Communicate
1. What can you say about the location of-.1 point in space that has one
coordinate equal to 0? two coordinates equal to 0?
Exercises 2 and 3 refer to the coordinate axes A2
and point Pat right.
2. is it possible to determine the coordinates of . P
point P from the diagram? Explain your
reasoning. It" not, what inform.ttion is needed!
3. Is it pussibit? to determine the octant in which
point P is located from the diagratn? If not. is
it possible to determine an oct-ant in which P -“
could not be located?
4. In the distance formula in three dimensions. why is it not necessary to use
.tl)solttte-value signs on the lengths ol‘ the sides?
5. llllflgille that your Ci:ISSl'OOl'l1 is in .1 three-dimensional coordinate S\’SIE‘l'l1.
Choose a point in the room to represent the origin. and describe the
coordittates oi‘ some ohiects in the room.
0 Guided SK’///8 Practice
Locate each point in a three-dimensional coordinate system.
(EXAMPLE 1)
6. ('2.0.—l] ‘Lt-l.-2.-3:] 8. (32.-l.4]
9. A right rectangular prism in the lirst oct-ant of -.1 threc—diincnsion-al
coordinate system is positioned so that three of its faces are in the
coordinate planes. The prism has a length of 2, width oI’7. and height of 6.
Find the coordinates of each vcrte.\'. (EXAMPLE 2)
Find the distance between each pair of points. (EXAMPLE 3)
10. (0. 0, 0] and [3, 6, I) 11. (3. l, 0) and [:'».-3. l)
12. (-4, 7. -2) and [2, 3. -5)
0 P/fl€t/66 and Apply
Locate each point in a three-dimensional coordinate system.
13. (4. l, 5) 14. [0, -3. O) 15. (0. -5. 2) 16. [-3. —l . 3)
Name the octant, coordinate plane, or axis in which each point is located.
17- (3. I, 7) 18. [—2. l0.—4J 19. (4.0. -2) 20. [O,—5, O)
21. (-3, I. 7*] 22. [—l. 3, 0) 23. (4.0, 0] 24. [-8. —I.—5)
LESSON 5 -1 C0-OHOINATES INTHREE DIMENSIONS 399
$3":
I! - conned
Homework
Help Online
Go To: go.hrw.cnm
Keyword:
MGI Homework Help
lot Exercises -13 AB
400 CHAPTER 5
Give the coordinates of a point in the given octant.
25. first oct-ant
27. top—b.tck—|el't
26. bottom—l'ront—right
28. L1otton1—b-.1ck—|c-ft
Find the distance between each pair of points.
29. (I. I. I) and (—I.—l.—I) 30. (2. L3) .1nd(3.—2.7)
31. (2. O. I) and (-5. -6. -5) 32. (7, -6. 5) and (6. 4. 3)
For Exercises 33-42, refer to the diagram below of a right rectangular
prism.
Determine the coordinates of each point.
33. point F 34. point H 2
35. point C 36. point E E ' T F
6 G
Find each measure. 7 W 1 %H
37. AD 33. AG A ! ‘V
39. AH 40. DF D 10 C
X
41. area ol‘ FGDA 42. area of A BCD
The midpoint of a segment in a three dimensional coordinate system is
given by the following formula:
Midpoint Formula in Three Dimensions
’l'he midpoint of a segment with endpoints at (x,, y., 2,) and (x_., )1, .1)
Xr 'l‘.\';§ y] +}’? 21+ 2‘
—, f —) 6.4.2
isthepoinr( 2 _ . 2
Find the midpoint of the segment with the given endpoints.
43. [5, -2. 3] and [6, -7, 4] 44. [3, 2. I) and (I, 2, 5]
45. [—I,—4,—5J and [6, I,0) 46. [2,—l.0J and [0,0, I)
47. (I, I, I)-.1nd(—l,—l.—l) 48. ta, b,c) and [—u, —b,—cJ
49. Give the coordinates of a point that is not on an axis or in a coordinate
plane and that is :1 distance of I unit from the origin.
50. GRAPHICS A white I
sphere is illuminated 1 /‘
by two different light
sources. one red and
one blue. Where the
red and blue light
mix, magenta light is
produced. Examine 4. T. _, y
the illustration at
right. Where are the
light sources located
with respect to the X
coordinate ewes?
‘\
Q
\
\
APPLICATION
APPLICATION
L004’ Back
Find the slope of the segment with the given endpoints. (LESSON 3.8)
51. [(9.0) and (6.41 52. {L3} and 3]
53.(3. Hand [2.—5l 54. (-3. I] and [6,-4}
Graph each line and find the x- and y-intercepts.
55. y: 2x+ I 56. 2x+3-y= 6
57.y—3=4l.\‘+I] 58. 3-x—)'=5
59. PHYSICAL SCIENCE The relationship between Celsius and Fahrenheit
temperatures can be represented by-.1 straight line. Suppose that the
x—eoordin.tte represents Celsius temperature and the y—eoordin.tte
represents Fahrenheit temperature. Then the freezing point of water is
the point [0, 32] and the boiling point is (I00. 2l2].
1:. Find the slope of the line through the given points.
b. Find the equation of the line through the given points.
100:? Bel/and
ASTRONOMY The table below gives the x-. y-. and 2-coordinates of points
in a three—dimensional coordinate system with the Sun at the origin.
The \‘—.tVis points in the direction of Earth's position at the first moment of the
spring, or \-'ernal, equinox. The xy-pla ne is the plane ol‘ F.-.u'th's equator at the
time of the equinox.
An astronomical unit is a measure or length that is equal to the mean distance
from Earth to the Sun, about 92,960,000 miles or I-l9.600.000 kilometers.
2
Ean_h's x
°'b't Sun-Centered Coordinates of Major Planets
on August 17, 1990 (in astronomical unitsl
v
Planets x y z
I''‘'' T I Earth 0.319 -0.546 -0.237
I Mars 1.389 0.145 0.029
Position of Earth i _
at Verna] equinoy I JUDIIET -2.238 4.328 1.910
L Saturn 3.935 -3.443 -3.656
.‘nurrr. Tlv -I-Imuumml A.lnuIur,I1r n\: ymr n-xi:
60. Calculate the distance from Farth to Jupiter on August I7, I990. Then
comert from astronomic-.1l units to miles.
61- Calculate the distance from hrlars to Saturn on August I7. I990. Then
convert from astronomical units to kilometers.
62. Calculate the distance from the Sun to Mars on August I7. I990. l'he
mean distance from the Sun to Mars is 227,940,000 kilometers. [low close
to this value is your calculation? Why do you think there is a dil'lerence?
63. Of the planets in the table, which is closest to the Sun?
LESSON 5 -1 co-onoiNATEs INTHREE DIMENSIONS 401
Lines and Planes
in Space
j—.—:_
) _
Objectives
0 Define the equation 0! X
a line and the equation
of a plane in space.
0 Solve problems by
using the equations
of lanes and planes
in space.
Planes W space can - \
fonn: --aimnsiami ‘ \
shapes, as in these ‘ ‘~
computer drawings. Each \
plane in the drawings can ‘i ‘
be described \ '
mat - : tically.
The Equation of a Plane
Recall lrom algebra that the standard form of the equation ol a line in a plane is
Ax+ By - C,
where A, B, and Care real numbers, A is nonnegative, and A, B, and C are not
all zero. The standard equation of a plane in space resembles the equation of a
line. with an extra variable for the added dimension of space:
Ax+ By+ Cz - D.
where A, B, C, and D are real numbers, A is nonnegative. and A, B, C, and D
are not all zero. for example.
2x+ 5y— Zz = 9
is an equation of a plane where A = 2. B = 5, C = -2, and D = 9.
402 CHAPTER 5
Using Intercepts in Graphing
In the coordinate plane. a line that does not lie entirely on an axis crosses the
x- and y-axes at one or two points called intercepts. ln coordinate space,-.1
plane that does not lie entirely on an axis has one. two. or three intercepts.
E X A M P L E 0 Sketch the graph ofthe plane defined by the equation .2x+)'+ 32 = 6.
O SOLUTION
Find the intercepts where the plane crosses each axis. 1 he x—interccpt. for
example. is the x—coordinate of the point where the plane crosses the x-axis. At
this point. the y- and :-coordinates are 0. To find the x-intercept. set y = 0 and
z = 0 and solve the equation lor x.
2x+0+3[O)=6
2r=6
x=3
The x-intercept is (3, 0. 0]. Similarly. the
y—intercept is (0. 6, OJ, and the
z—intercept is [O. O. 2). Plot the
intercepts as points on the axes. These
three noncollinear points determine
the plane. To sketch the plane. connect
the points with segments and add
shading. NOTE: Intercepts are often
written as single numbers.
What Happens to the Equation of a Line in Space?
In a coordinate plane. 2x + 4)’ = 8 is the equation of a line.
Y
In a three dimensional coordinate
space. the equation 2x + 4y = 8 is the
equation ofa plane in which the
coefficient of z is equal to 0.
Notice that this equation ol a plane
is unaffected by the values ot z.
l'hus for anv values 0|"): and y that
satisfy the equation. any value of 2
will also work. Thus every point
directly above and below the line is
in the graph of the plane.
-2xtdyt0z 8
The equation of the
line In the xy-plane
is 2x + dy = 8.
' 1’
LESSON 5.5 LINES AND PLANES IN SPACE 403
Lines and Planes in Space: A Step-by-Step Procedure
Imagine that you are able to plot one point of a graph in space every
minute according to a given set of instructions. Your instructions have
one rule for the x—-coordinates. another for the y—coordin.nes. and another
lbr the 2-coordinates. These rules are called parametric equations.
Let r = 1, 2. 3. . . . represent the time [in minutes) at which you plot ench
poim. Your rules tor each coordinate would have the following torm:
x = [an expression involving rl
y = Ian expression involving (I
z = Ian expression involving II
Note: t can also be 0 or negative.
E X A M P I. E 0 To plot .1 graph in a 'L'()()l‘(.lllldl.t':‘ plane. you will need just two rules. Use the
rules below to plot at line in .1 Coordinate plane lor I = l. 2, 5, 4...
x = 2!
y = 3! + I
O SOLUTION
Fill in .1 table like the one helow. Then
plot the points in the xy-coordinate plane.
I
1
E X A M P L E Use the rules below to plot 1 line in a coordinate system fort = I, 2. 3, 4...
x=2x+l
y=3r—3
z=-11‘
O SOLUTION
Fill in a table like the one below. Then plot the graph
in a three—dimensional coordinate systein.
ts. 1. 8)
y 2
-2
404 CHAPTER 5
Exercises
(Icbmwmwflw¢e
1. What is the standard iorm lor an equation olia plane? How is it similar to
the stamlard equation of a line? How is it different?
2. Describe the characteristics of a plane defined by an equation in which the
coefficient of x is O.
3. Describe the characteristics of a plane defined by an equation in which the
cociTicii:nt of z is 0.
4. Describe the characteristics of a plane defined by an equation in which the
coeihcients of y-and 2 are U.
5. Can 3 line in J thr<:c-diincllsional Coordinate systcili pass lhrough exactly
one octunt? exactly lwo oettilits? emctly three octdnts? more than lhree
octants? F..\:plain \-‘our reasoning.
0 fil/I'd€d§.('///3 Practice
Sketch the graph of each plane. (EXAMPLE 1)
6. 3.x‘+6y+-1z=l2 .’x+5y—z=2
Using t = 1. 2. 3. . create a table of x- and y-values for the equations
be|ow.Then graph each line in a coordinate plane. (EXAMPLE 2)
8.x=!+2 9.x=r-l
y-41‘ y-2r+3
Using t = 1. 2, 3. , create a table of x—, y-, and z-values for the
equations be|ow.Then graph each line in a coordinate system.
(EXAMPLE 3)
1o..x=r 11.x=5r—2
y-2r y-(+6
z=r+l z=—t
0 P/flfif/£8 4/14 74,0]/y
Use intercepts to sketch the plane defined by each equation below.
12. 3_x'+2y+7z-4 13. 2_x'—4y+z--2
14.x-2)’-22--4 15. -3x+y-4
16.x—2y=2 17.x=-4
Plot the line for each pair of parametric equations in a coordinate plane.
.’ ’ ’ 1s..x-=r+3 19.x=2r—i
y=i—r y=—r
2o.x=5x 21.x=2
y-5 y-—m+6
LESSON 5.5 LINES AND PLANES IN SPACE 405
Plot the line for each set of parametric equations in a coordinate system
"-” ’ 22.x=r 23..x'=r+l 24.x=r 25.3.-=3:
y=2: y=2r+l y=r y=4
z=5t z=0 z=l—r z=4r—7'
The trace of a plane is its intersection 1
with the xy-plane. To find the equation
of the trace. set the z-coordinate equal
to 0 lall points in the xy-plane have a - 2"," V: 6
z-coordinate of 0). For example: \ J’,
2.1: + y + 32 = 6 Equation of the plane ___,. V
2.x'+y+ 3(0) = 6 Serzequalroa
2x + y = 6 Eqirman or the mica X
. . mm“ ,73__ Find the equation of the trace for each plane defined below. Sketch the
Homewmk plane and indicate the trace.
Help °““"° 26. .\'+3y—z= 7 27. 5x—2r+z= 2
Go To: uo.hrw.corn '
Keyword: 28. 2x+ 7r+ 32 = 2 29. 4x — 2y + 22 = l
MCI Homework Help '
lot Exercises 26-29
30. VV rite parametric equations to describe the line that passes through the
‘ points (0. U. 0) and (2, 4. I). (Hint: Start with the rule for the x—coordinate.
The equation will be of the form x = at + Lt, where at and bare constants.
31. Write parametric eqtrations to describe the line that passes through the
points (-2. I. 5) and [6, -4, 7).
In a coordinate system, plot the pair of lines described by each set of
parametric equations below. Determine whether the lines are parallel,
intersecting, or skew. Explain your reasoning. (Note: Let t = 1, 2, 3,
and s = 1, 2. 3, ...l
32. .t'=l x=l 33.x: .x'=3 34.x=l x=3
J-‘=2 y:_\' y: }I=2 }P:5
z=r z=3 z= z=5 z=r z=s
C H A L L E N G E 35. Do the lines described by the parametric equations below intersect?
How can you tell? ll" they intersect. lind the point of intersection. ( l lint:
Set the x-coordinates equal to each other to form an equation. Repeat with
the y— and z—coordinates to get ar system of three equations in s and r, and
then solve the svstem.]
.\I=l—l .t=s—3
y=2t+l y=s
z=—r z=2s—7
A P P L I C A T l 0 N 36. HOUSE PAINTING You agree to pay a friend 55 per hour 10 help paint your
house. ‘I he paint costs $25 per gallon, and the equipment [l-adder, brushes.
etc._] costs $200. An equation representing the cost. 2. of painting for x
.. hours and using y gallons of paint is 2 = 5:: + 25;’ + 200. Write this
equation in the standard form for an equation of-a plane. and sketch a
l graph of the plane.
406 CHAPTER 6
APPLICATIONS
CONNECTION
PROOFS
37 HOBBIES Delia rented a booth at a craft fair for $50. She is selling earrings
at a profit of 5? per pair and bracelets at a profit OI‘ $4 each. Her profit, Z.
for selling .1: pairs of earrings and y bracelets is represented by the equation
2 = 7x+ -Iy — 50. Write this equation in the standard form for an equation
of a plane. and sketch a graph of the plane. Find the trace of the plane.
What is Delia's profit for points in the trace?
38. NAVIGATION Suppose that an airplanes initial path at takeoff is described
by the following parametric equations:
x = —r
.1’ - I
2 - 0.52‘
Plot the line described by the given equations. II‘ the positive x-a.\:is points
north, in which direction did the airplane take off?
L001? Back
COORDINATE GEOMETRV For each pair of lines below, state whether the
lines are parallel, perpendicular, or neither. (LESSON 3.8)
39. y-3x+3 4o.y-x+2 41._v-2.x'—l 42.2x+3_v-6
y=3x—? y=2—x y=—2x+='I 3x—2y=6
43. Given: _L_I 2_L2 and E 2 Ti 1 E 2 F
Provo: EF nu HG (Lesson! 3.3)
H G
44. (_'.iven rectangle ABCD with diagonals Tend B—IIJ. prove AADC 2 ABCD.
(Lesson: 4.5;
45. Given rectangle A BCD with diagonals i-IT:-and fi'3that intersect at point F,
prove AAED E ACEB. (LESSON 4.6)
46. Given quadrilateral PQRS in which P—Q 2 R_S and P-15 2 E prove that
PQRS is a parallelogram. (LESSON 4.6)
LESSON 5.5 LINES AND PLANES IN SPACE 407
I r
Porttolio
connect
Extension
Go To: gu.hrw.com
Keyword;
MGI Solids
623
Q.
\"°_Uo
:’:‘;.x
L00:(' Béyfllfd
Symmetric equations for a line in space are in the form
";"' = LEE = ”cz‘, where tx., y,, 2.) is a point on the line and a, b.
and c are constants.
The relationship between the parametric and symmetric forms is shown
below.
"‘_"‘.'=——”_"=:'3_z' <-—> t=x_"' <—> x'=ur+t'
n I) c n ' "
r=y_y| y-br+y.
ll Z=l'.'f+Z]
1,:-3—2|
Write each set of symmetric equations in parametric form.
:c—2 )"‘5 2+! 48 ‘._-,_,V*“_z—5
"' 3 -1 4 2 —<
Write each set of parametric equations in symmetric form.
‘ 49. x=2r+l 50. x=t—4
y - -3: + 6 y - 2:
2- 4! 2-6r+2
AHCHIMEDEAN SOLIDS
Archimeclean solids. or semiregular polyhetlra. are named alter Greek
mathematician Archimedes. All of the Faces ofan Archimedean solid are
regular polygons. but two or more types of polygons are used. In addition.
every vertex must have the exact same arrangement of laces d.l'()lll'l(l it.
There are exactly 13» Archimedean solids.
1. Enlarge and copy the net at right. You
may wish to acld tabs at some of the
edges to help in assembling the
polyhedron. This solid is called a
1'homl7icul7ocmlretlron. It has 8
equilateral triangular faces and I8
square laces. Three squares and one
triangle meet at every vertex.
2. Fnlarge and make two copies of the net
at right. the net forms hall of the solid
known as a mrmmed icosrilreclroir. If
you truncate. or cut oil. the vert ices of
a regular icosahedron {refer back to
the Portlbliti Activity on page 379].
this shape is lormed. A truncated
icosahedron has I2 regular pentagonal
faces and 20 regular hexagonal faces.
You may recognize the truncated
icosahedron as a eommon object a
soccer ball.
408 CHAPTER 6
Perspective Drawing
Youkuawrllatoblectsthataralaraway ' \ it “i
--poarsmllertliantheywouldiltheyware _?,—.- ‘ t -
lose to you. In studying perspective drawing " ' ' 5
I will learn the rules for making things V . _
.- ppaar in proper relationship to each other.
I‘ ‘I
I'D
Objectives ,
0 Identity and define the
basic concepts ot I \
perspective drawing.
0 Apply these basic "‘ 5 % .
concepts to create | 3
your own perspective '— _ * I
drawings | 1 3 — _ ——
Ertrnpenrt Rermrssarree rlr'ii$l.\' in the fmrrrcerrrh rlrrmrgh sixreenrlr
eertrttries i"t‘£llSL'(Wi.’l'l;'[l, fi'mrt clrtssiml Greek and Rontmt arr. how to
create the illnsiorr of depth in drawings rzml pnirzrings. Notice the
rtflrttit-'trly flat rtppt’(lrmtt‘£ ofrlttr pit’-R('tlfllSSlJl’lL‘t’ WOI'l\‘ on the right
r:0rrtpm'ed Ivitlt tire RL'il(ll5S£lilt:‘£-' prtirttiitg to the lefi.
Perspective Drawings: Windows to Reality
Modern perspective drawing methods.
discovered by the Italian architect
/l picture-plmte "wr'rtdow" Fillip Brunelleschi (l377—l 146). are
*-‘°""“"""’£ “ P'°l9"""‘ "”"‘.‘-’*’ based on the idea that 21 picture is like
at wintlow.
~ An artist creating a picture. or a
person looking at the finished picture.
is rlrortgin‘ oi‘ as looking through the
; picture to the realitv it portrays. (The
=.-v-" word per'spet'tive comes from the Latin
,__ words meaning "looking through")
3 W hen someone looks at an olajecl.
there is at line of sight from every
Q3 point on the object to the eye. imagine
a plane. such as an empty catwas. that
intersects the lines of sight. The points
of intersection on the plane make up
the image of the object. and the image
0 _. is said to be projecteri onto the “picture
plane."
LESSON 5.5 PERSPECTIVE DRAWING 409
Albrecht Durcr(n7I—i52s). ,- «-u.“;.~;.+._T""'.' --*-'—'_".;“'-1"’
. . . ' . - ' — .'gl"
:1 German artIst,visIted Italy --’-‘-l -*4 .3‘ " .1‘ ' '-
to learn the techniques of \s'- ~r-_ " f ,_
perspective drawing. llc - _ . . I . . -_ "
I‘
produced a number ofworks ‘ _ _ ‘it-_ -4.‘ L: .. ,..J— '3'
that showed artists employing ‘ ‘
. . .__._ ‘ -_‘-~ - ‘ l ‘W ." _
these techniques. as in the ":_-—;-s-.‘ "‘ .t \,-3 L
woodcut at right. - . __- ~T--:7 -—-‘-'Z —- - _,_
I l - . A I '1.
Two rlrlms pmdiicmg mt nnnge
nfn lute. mm point at a lime
cnscxpomrr ./ How does the technique used by the artist in Dtirer’s woodcut illustrate the
projection ofan object onto a picture plane?
Parallel Lines and Vanishing Points
Have you ever noticed how the rails Ola
railroad track or the sides ofa highway seem
to meet as they recede into the distance? ——.———-
The point where parallel lines seem to meet. / ' ' . .
which is often on the horizon, is known in H \
perspective drawing as the vanishing point.
.«Tb‘-and cTDon the sidewalk in the picture below are actually the same length.
but when they are projected onto the picture plane seen by the student. the
image oi‘ AB is longer than the image of CD.
1 '-v‘
‘a.
nu‘: ‘ -X ‘ —
‘ 0- . 1*‘-n "-. w ‘L ‘
.3. . :, 3' _
n 5 | ‘
.‘ ' ,1-wfpr
- C’ n
c D , -
A 3' __
A B
‘ I
s “ 5
4 1 0 CHAPTER 6
Principles of Perspective Drawing
The two theorems on this page provide the basis for an understanding of how
perspective drawings are made. Thev can be demonstrated by studying the way
parallel lines project onto the picture plane of a perspective drawing.
Theorem: Sets of Parallel Lines
In a perspective drawing. all lines that are parallel to each other, but
not to the picture plane. meet at a single point known as a vanishing
point. 6.6.1
CRITICAL THINKING Do you think that the point where a set 0|" parallel lines seem to meet has to be
somewhere in the drawing? Use illustrations in your explanation.
Theorem: Lines Parallel to the Ground
In a perspective drawing, a line that is in the plane ol' the ground in the
drawing and is not parallel to the picture plane will meet the horizon of
the drawing. Any line parallel to this line will meet the horizon of the
drawing at the same point. 6.6.2
CRITICAL THINKING Parallel lines that are parallel to the picture plane of at perspective drawing are
usually represented with no vanishing point. In most cases this procedure
causes no problems. Can you think ol‘ situations in which it would result in
unrealistic drawings?
LESSON 6.5 PERSPECTIVE DRAWING 41 1
41 2 CHAPTER 6
In a perspective drawing. the concept of varnishing points applies even when
no parallel lines are actually shown in the drawing. in the row of telescope
dishes shown below. for example, there are imaginary lines that pass through
points at the tops and at the bottoms of the rellectors. These lines meet at
CHECKPOINT V the h0ri7on. Explain why.
\ .
' u C I
\\. x‘: \‘\.4. ‘ _
Much of the subject matter of early perspective drawings was architectural.
Buildings and houses are ideally suited to the development of the theories of
perspective drawing because they usually contain many lines that are parallel
to each other and to the ground.
llventually, perspective drawing began to inlluence architecture, as illustrated
in the Church of San Lorenzo in Florence, Italy. shown below. Brunelleschi
used the principles of perspective drawing in his design for this church. The
vanishing point of the structural elements appears to be at the altar.
I
l
I ,.r—-... :..——_,,.....
l..3..t.~;-.El‘_—‘.-.11".
' \‘ t-.JL71
s t§.;*3~e‘T
E :_u..‘J ..'a"
L . -1 ' I-&I \
1-
‘ l
“ t t I‘;
. .4”
, 'JJ_ 1) F 4 9?’
up I ‘Tr
Church of San Lorenzo in l-'forertct', lmfy
Exercises
. Comm/Irimte
E - I H connect 17'?"
Activities
Online
Go To: 9o.hrw.com
Kcvwold.
M61 Perspective
4
CRITICAL THINKING
1. Explain what is meant by a vanishing point in a perspective drawing.
2. Assume that any two lilies in a perspective drawing that are parallel to
each other but not to the picture plane meet at a point. How is this
statement extended to apply to sets ol‘ parallel lilies in Theorem 6.6.l?
What theorem or postulate justities this extensioli?
3. Lxplain why a line that is in the plane 01 the ground and is not parallel to
the picture plane must end at the horizon. Make a sketch to explain your
answer.
4. Explain why drawings of buildings and houses are ideally suited to the
development of perspective drawing. Make a sketch to explain your
EIIISWFI’.
5. in a perspective drawing. the horizon is usually represented by a
horizontal line that is assumecl to be at eye level. Why do you think this
assumption is made?
6. What is the dillerence between a perspective drawing and an isometric
d rawing?
7. The images of the two
pol-ar bears in the picture
at ri ht are actuallv the .-- — .-.. - __ - =".
. g .' . . ‘ 3* ‘L _._=-_j-us. ?:-‘
same size (measure them]. - - - j; _;_-e -
but one appears larger than “ —
the other. Explain why.
“Q -
IE
0 fit!/dedtgki//3 Practice
8. The drawing at right is a perspective drawing of B
a U.ll)f;‘. What do you know about the lilies that A /2.‘ D
contain 47. E and E? about the lines that
contain AC, BD, and GF? (THEoREM 6.6. 1; C
9. In the drawing of the cube, the lines that G E
Contain the vertical segments will not meet
at a vanishing point. Use the principles
of perspective drawing to explain why. F
(THEOREM 6.6. 1)
10- imagine that the drawing of the cube represents a cube-shaped building
on level ground. Where will the lines that contain the nonvertical sides of
the building meet? (THEOREM 8.8.2)
LESSON 5.5 PERSPECTIVE DRAWING 413
4 1 4 CHAPTER 6
P/fl6‘t'IZ'6’ dim’ 34,0;/y
The exercises below give the steps that are used to produce various
types of perspective drawings.
11. A drawing that has just one vanishing point is said to have one—point
perspective. Follow the steps below to produce a one—point perspective
drawing or" :1 cube.
a. Draw a square. 'l'hen draw a horizontal line to represent the horizon.
Mark a vanishing point on the horizon.
. j . j -
b. From each corner 01 the square, lightly draw dashed lines to the
vanishing point you marked in part a.
- T . T .
c. Lightly draw the sides oi a smaller square whose vertices touch the lines
you drew in part b.
- T . T p
d. Erase the perspective lines that extend “behind” the smaller (.l,li}€. The
dashed lilies that remain indicate the edges of the cube that are hidden
from view.
_
12. Repeat the steps in Exercise 1 I. but place the vanishing point to the left or
right of the square.
13. Repeat the steps in Exercise I I, but place the hnrimn line and vanishing
point below the square.
14. What happens ifvou place the vanishing point in the interior or on an
edge of the square?
For Exercises 15 and 16, trace the figure below onto your paper.
1
u
I
15. Locate the vanishing point for the figure.
16. Draw the horiron line.
17. A drawing that has two vanishing points is said to have two-point
perspective. Follow the steps below to produce a two point perspective
drawing of a cube.
a. Draw a vertical segment. This will be
the front edge ofyour cttbe. Draw a .— g T u —-
horizon line above the segment. Place
two vanishing points on the horizon
line as shown. with one on either side |
of the vertical segment.
1:. Lightly draw lines back to each *— 0' ' —’
vanishing point from the endpoints ‘ '— -
of the vertical segment
as shown. -. -
c. Draw vertical segments to complete ' ' 0 '
the front sides of the cube.
d. Lightl_v draw lines from the endpoints -— o 0 —-
ol‘the segments you drew in step c to ' ’ ’ " "
each vanishing point. Draw a vertical .
dashed line between the two
intersection points of the light
perspective lines.
e. Erase the perspective lines that extend
bevond the edges of the cube. Use
dashed lines to indicate the edges ol
the cube that are hidden from view.
18. Repeat the steps in Exercise 17. but place the horizon line and vanishing
points below the vertical line.
19. Repeat the steps in Exercise I7. but place the hori7on line so that it
intersects the vertical line.
20. What happens to a two-point perspective drawing ofa cube as the
vanishing points are moved closer together? farther apart?
21. What happens to a two—point perspective drawing of a cttbe if both
vanishing, points are moved to the same side of the original vertical line?
if one vanishing point is directly‘ above the vertical line?
For Exercises 22 and 23, trace the figure below onto your paper.
22. I ocate the vanishing points for the figure.
23. Draw the horizon line.
LESSON 6.6 PERSPECTIVE DRAWING 415
24. Follow the steps below to create .3 perspective drawing of your name in
black letters.
a. Draw “flat” block letters
and -.1 horizon line with at
vanishing point, as shown. J @ I
b. Draw lines from all corners .\
and ztppropriute curved edges
of the letters. as shown. / KJ
c. Fill in the edges as shown. J _]
Erase the perspective lines 6
to complete the drawing.
I htemel connect
Homework
Help Online
Eglggfg-“M-°W 25. Use one—point or two—point perspective to dr-.1w a city view. Start with
Ms; n.,.'..w.,,i. neg, boxes for the buildings and then add details.
for EXEICIEE 25
Tiling was particularly intriguing to the artists who first explored
perspective studies.The pictures below suggest a technique for
creating a tile pattern in a perspective drawing. Study the pictures to
answer Exercises 26-28.
a. P b.
l
4 1 6 CHAPTER 5
26. A method for finding the lines parallel to W? is suggested by the diagonals.
Explain how the diagonals can be used to determine these parallel litres.
27. Explain how the tile pattern could be viewed from at corner by applying
two-point perspective. How would the intersecting lines be determined?
28. Create your own one— or tv.-o—point perspective dr'awing of a square tile
pattern.
£00k Bdtk
29. A solid composed of unit cubes has the top view shown :
at right. What are two possibilities for the solid? Make
an isometric drawing of each. (LESSON 6.1) E
30. A solid composed of unit cubes has the front
and right views shown at right. W hat might
the top view look like? (LESSON 6.1)
Front
Locate and sketch each point in a three-dimensional coordinate system.
(LESSON 6.4)
31. (5.—l.-2) 32. (13.0.0) 33. (-2.0. 5)
Find the distance between each pair of points with the given coordinates
in a three-dimensional coordinate system. (LESSON 6.4)
34. (4. 3, 2]1nt‘l [-5. 2,—l) 35. (—|.U. l}and (I5. 5,—2]
Find the midpoint of the segment with the given endpoints in a three-
dimensional coordinate system. (LESSON 6.4)
36. (5. 5. 5] and [-3. -3, -3) 37. (0. 0. O) and {—l. IO. 9)
L004’ B6‘70I1d'
38. The artist in the photograph
at right is using an image
produced by a projector to K ,
create a mural. Draw a diagram - __ __;‘“ _
showing how an image on a . _ _ _ ‘~
slide is projected onto a screen -_ 1 . .
or wall. Assume that the light ‘ ,_ _. ,, . ‘
source is a single point of _. . M
light. (The lens arrangement
of the projector makes this _.
assumption appropriate.)
39. I low is the projection process
of the slide projector like the *
projection in perspective
drawing? [low is it different?
‘I
LESSON 6.6 PERSPECTIVE DRAWING 417
418
:3:
E3
‘E9:
..-—-\
Activity
The Small Stellated Dodecahedron
A stellared polyhedron is formed from an existing polyhedron by extending the
plane of each face until the planes meet, forming a new polyhedron, which is
larger and has a star shape.
' Enlarge and copy the net below to create a regular
dodecahedron out of cardboard.
l l ' Enlarge and make I2 copies of
the net below. The base should
be the same length as an edge of
the dodecaheclron. 1 he triangles
are lSOSCClC‘a. with a vertex angle
of 36° and ti lmse angle of 72°.
Color the triangles. if you wish.
° Fold the I2 nets above to
form I2 pvratnids that are
open at the bottom. Use
glue or tape to attach one
pyramid to each face of
the clotlecahedron.
L.
4!
Activity
Why AreThere Five?
The live convex regular polyhedra. known as the Platonic solids. have been
stttdied e\'tensively since the time ol the ancient Greeks. To see why there are
only live, consider a single vertex of each one. Since all vertices of a regular
polvhedron are identical. the shape of the polyhedron is uniquely determined
by one vertex.
1. l'he patterns below are possible arrangements of equilateral
triangles at a vertex. Copy the patterns and cut them out.
Glue or tape the red edges of each pattern to form a single
vertex.
~ Which Platonic solid has 3 triangles at each vertex? K-\-'hich has
1 triangles at each vertex?
Iohmmes Kepler |_'l57l -I650) lvelievcd
that the orbits ofrhe planets were
2. Try some other arrangements of equilateral triangles at .1
vertex. \-\-‘hat is the minimum number possible? \-\-‘hat is the
maximum number possible? Explain your reasoning.
described by riested reguIm' polyliedra.
3. l'he pattern at right is a possible arrangement
of squares at a vertex. Copy the pattern and cut
it out. Glue or tape the red edges to Iorm a
single vertex.
Which Platonic solid has 3 squares at each
vertex? Are any other arrangements oi" squares
possible at a single vertex?
4. What arrangements of regular pentagons are
possible at a single vertex? Which Platonic solitl
has an arrangement of pentagons at each vertex?
5. Can any other regular polygons be arranged at a single vertex? Explain
your reasoning.
Extension
\ 1. In each vertex arrangement above, what is the stun of the angles at the
vertex?
2. As the sum of the angles increases. what happens to the sharpness of the
vertex? What do you think is the maximum possible sum of the angles?
3. How do vou think it would be possible to prove that there are exactly I5
Archimedean solids?
CHAPYEH 5 PROJECT 41 9
Chapter Review and Assessment
VOCABULARY
base ol a prism ......... .. 388 lateral edge of a prism . . . . . 383 parametric equations .. . . . 404
coordinate plane . . . . . . . . .. 391 lateral lace ol a prism . . . . . 388 polyhedron . . . . . . . . . . . . . . . 319
diagonal ol :4 polyhedron... 31!) line parallel to a plane . . . 381 prism ... . . . . . . . . . . .. . . . . 388
dihedral angle . . . . . . . . . . . . 382 line perpendicular to right-handed system . . . . . . . 396
edge oi as polyhedron . . 319 3 P'a"° - - - - - - - - - - - - - - - --33' right prism . . . . . . . . . . . . . . . 389
edge ol a dihedral angle . . . 382 ”‘°35“'° 0' 3 d"'°d""' skew lines ............. . . 380
lace 01 a polyhedron .... . . 319 angle ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' ' 38' solid . . . . . . . . . . . . . . . . . . . . 319
lace ol :4 dihedral angle .. . . 382 ohuque Wsm ' ' ' ' ' ' ‘ ' ' ' ' ' 339 trace ol a plane . . . . . . . . . . . 406
hall-plane . . . . . . . . . . . . . .. 382 “mm ' ' ' '_' ' ' ' '_' ' '_ """ ' ' 397 vanishing point . . . . . . . . . . . 410
intercept .............. . . 4103 mhogmphlc Plowman ' ' ' ' 3" vertex ol a polyhedron . . . . . 319
isometric drawing . . . . . . . . 312 parallel planes ' ' ' ' ' ' ' ' ‘ ' ‘ 330
POSTULATES AND THEOREMS
Lesson um - .r Postu ate or Theorem
6.3 6.3.1 Diagonal of a Right
Rectangular Prism
The length of the diagonal. d. of a right rectangular prism is given
by d: -’l"~’+ w‘-’+ h2.
6.4 6.4.1 Distance Formula in
Three Dimensions
The distance, d, between the points (x.. y., 2,) and (X2, y,, 2,) in
space is given by d = \."(X; — x.)’+ (y-2 — y.)’ +12, — 2.)’.
6.4.2 Midpoint Formula In
Three Dimensions
The midpoint of a segment with endpoints at lx. , y., 2,) and
lxz. V2, 22) In space ls glven l)y("'-_?"2._
6.6 6.6.1 Theorem: Sets of
Parallel Lines
In a perspective drawing, all lines that are parallel to each other, but
not to the picture plane. will seem to meet at a single point known
as a vanishing point.
6.6.2 Theorem: Lines
Parallel to the
Ground
In a perspective drawing, a line that is on the plane of the ground
and is not parallel to the picture plane will meet the horizon of the
drawing. Any line parallel to this line will meet the horizon at the
same point.
420 CHAPTER 5
Key Skills 81 Exercises
LESSON 8.1
Key Skills Exercises
Create isometric drawings of solid figures. Refer to the isometric drawing below. Assume
A solid figure is that no cubes are hidden in the drawing.
composed ol seven
cubes as shown. - -
Nldkt-.‘ .3 drttwing of ' '
the solid on ' '
isometric dot paper. . .
. ' . 1. Make an isometric drawing ofthe solid from
a tlit"t"e1'ent angle. (You may wish to create a
model of the solid bv using unit eubes.]
' 2. Draw the six orthographic views of the solid.
3. Find the volume of the solid.
_ _ _ 4. Find the surface area of the solid.
Draw orthographic protections of
solid figures.
Draw six orthographic projections of the
solid above.
Back
Left Front Flight
Bottum
Find the volume and surface area of solids
that are composed of cubes.
Find the volume and surface area ofthe
solid above.
The solid is composed of seven cubes. so its
wolunie is 7 cubic units. There are 30 exposed
cube faces. 50 the surface area is 50 square units.
CHAPTER 6 REVIEW 421
LESSON 6.2
Key Skills Exercises
Identify relationships among lines and planes Refer to the right hexagonal prism below.
in space. H G UVWXYZ is a regular hexagon.
In the cube. name a set of 5. Name two pairs of T S
parallel faces. perpendicular E ' F parallel faces. 0 ' R
laces. and Ekew 'l‘hen D C 6_ Name a pair of P O
Mme an ‘'3 ge ‘m_ '3 ‘KB perpendicular laces.
that are perpendicular. _
A 3 7. Nan1e .1 pair of U 2 Y X
Faces .»\DHL' and BCGI-‘ are parallel. I‘-a-is ADHI.-' skew edges‘ V W
and ALE-1:‘ are perpendicular. El I and BF are skew 8. Name an edge and a
edges. ABis perpendicular to BCGF. face that are perpendicular.
LESSON 5.3
Key Skills Exercises
N
Identify parts of a prism. , Refer to the prism below.
In the pentagonal prism at A 0 9. Name a base. A B
. _ _ _ I - \
right. name a lmse. a lateral H L J 10. Name 3 me”! lhcel \ C
lace, and a lateral edge. P
11. Name a lateral edge.
G K
- ; - I - D
Pentagon (JHUIK 1s_ab;1se, par-allelogram GLPR IS
a lateral face. and I. ‘is a lateral edge. F
Find the length of a diagonal of a right 12. \'\-‘hat is the length of -.1 diagonal ofa right
rectangular prism. rectangular prism with a length of 24. width
A right rectangular prism has a length of 20, :1 0‘ 8' ‘md hag“ °l 6-'
width of IO. and a height of 24. What is the length
of its diagonal?
The length nl‘ .1 diagonal is given by the formula
d= Jr-' + we + h-'.
d: ~.r‘2D3 + I03 + 243 = V‘ lU76 =6 52.3
Lesson 8.4
Key Skills Exercises
Locate points in a three-dimensional Locate each point in a three-dimensional
coordinate system. coordinate system and name its octant.
13. (5. 3.4}
14. (-6. l. -2]
Locate the point (3. —l. 7)
in a three—dimensional
coordinate system. l\ame
the octant ofthe point. /'
ex’
(3, 1, 7} is in the
top—front—left octant.
l3, -1. 7l
0
422 CHAPTER 5
Find the distance between two points in
space.
Find the distance between the points (3. —l . 7)
and [2.U,—5).
d= /(_x2—Xt)"+U’2‘}’|}3+(Z:‘Z113
{(2-5)-’+I0-t-I)F+{-5-7)‘
\,l+l+l44=v‘rl-T6=l2.l
LESSON 8.5
Key Skills
Sketch planes in space.
Sketch the plane defined by the equation
x+ 2y- 5: = I8.
First. [ind the intercepts.
x-intercept: .x'+ 2(_0] + 3(0) = I8. so x= I8
y-intercept: 0+ 2y+ 3(0) = I8. so y = 9
z—intercept: O + 2(0) + 32 = I8, so 2 = 6
Plot the intercepts as
points and sketch the
plane.
Plot lines in space.
Plot the line represented by the parametric
equations below.
x=2t
y= t+|
z=—t
When t= 0. the point
defined by the equations
is (O. |.O]. When I = I.
the point defined by the
eqtuttions is (2. 2. —l ].
Locate these points and
sketch the line.
Find the distance between each pair of points
in space.
15. [2.4.5)-.1nd(D. 7.—I)
16. (-1, 6. -2) and (-5. 2, 4)
Exercises
17. Sketch the plane defined by the equation
2x+ y — 2 = ID.
18. Sketch the plane defined by the equation
-x+ -1y+ 2 = 8.
19. Plot the line represented by the parametric
equations below.
x=t+3
}'= t—l
z=2t
20. Plot the line represented by the parametrir.
eqtmtions below.
x=—1+2
y=t—-‘l
z=—3t+l
CHAPTER 6 REVIEW 423
LESSON 6.6
Key Skills Exercises
Use vanishing points to make perspective 21. Make a une—point perspective drawing of a
drawings. right rectangular prism with the vanishing
Make .1 one-point and a two-point perspective 90"" to the "El" 0' the Pnsm‘
drawing of the letter T. 22. Make a one-point perspective drawing of at
right rectangular prism with the vanishing
point below the prism.
«To». 4.. * 23. Make a two-point perspective drawing of
"' ‘ ‘ -- -- a right rectangular prism with the hori7on
above the prism.
24. Make a two-point perspective drawing of
a right rectangular prism with the hori7on
One point Two DOIHIS below the prism.
Applications
25. GEOLOGY (.'rystals are classified by the
diflerent axes. called erysmllugrapltic an‘ .
that passes through the center of the crystal.
Topaz has a crystal structure called
ortltorhombit‘. In topaz. t|1ree axes of tl1ree
dil'l'erent lengths all meet at right angles.
Draw the three axes for topaz. Suppose that
tl1e endpoints of the axes are vertiees of-.1
crystal. Draw an outline of the crystal
around your axes.
26. FUND-RAISING The school band is raising l'l'l(Jl1L‘)‘ to buy new
uniforms. The band members will wash cars in a space donated
by a local business. The supplies for the car wash cost $20. 'l'he
charges are $3 for a regular car wash and $5 for a deluxe car
wash. The amount of money. 2, raised by at regular washes and
ydeluxe washes is given by z = - x + 5y — 20.
Write this equation in the standard form and sketch the graph
of the plane. Indicate the trace of the plane on your graph.
What does the trace represent?
Top
27. DESIGN The diagrams at right are three orthographic views
0|‘ a table. Use the diagrams to make a perspective drawing :1
ol the table.
F ront Side
424 CHAPTER 6
Chapter Test
Refer to the \
isometric drawing
et right. Assume
that no cubes are ~
hidden in the
drawing.
1. Make an isometric drawing of the solid from .1
different angle.
2. Draw the six orthographic views of the solid.
3. Find the volume oi‘ the solid.
4. Find the surlace area of the solid.
Refer to the cube below.
5. Name two pairs of parallel faces.
6. Name a pair ol skew edges.
7. Name an edge and a lace that are
perpendicular.
3. lwo pencils lying on the same table are lying
in the same ;.
Refer to the prism below.
J x
9. Whiclt face is congruent to AQLM?
10. Name a lateral face.
11. Name a lateral edge.
12. Name two right angles.
13. DESIGN Students want to hang balloons
along tl1e diagonal of a gym area tl1at is a
rectangular prism with .1 length o|' 12 feet.
width ol'9 feet. and height of 5 feet. How long
will tl1e balloon display be?
Name the octant, coordinate plane, or axis in
which each point is located.
14. {2.5.9) 15. (-1.5. -3)
11. [O.—4.0) 13. (—6.6.0}
16. (I. 0, -3}
19. (2.0. 0)
For Exercises 20 and 21, find the distance
between each pair of points.
20. ll. 0, 0] and [0, l. l
21. (-*1. O. l} and (3. -2.1)
22. Sketch the plane detincd by the equation
x+ 2y + 42 = I 2.
23. Sketch the plane defined by the equation
3-x+ 3-y+ 22:18.
24. Plot the line represented by the parametric
equations below.
.\:=!+l
y=2(
z=I-3
25. AVI.-\ I'lON Suppose that an airplane’s initial
path at takeoff is described by the following
parametric equations:
.\.‘=!
y=—O.5t
2=2r
Plot the line described by the given equations.
lithe positive x—-axis points north. in which
direction did the airplane take off?
26. Make a one—point perspective drawing ofa
cube with the tarnishing point to the left of
the cube.
21. Make a one—point perspective drawing ofa
cube with the vanishing point below the
cube.
28. Make a two-point perspective drawing of a
cube with the horizon below the cube.
29. Make a two—point perspective drawing ofa
cube with the hori7on above the cube.
CHAPTER BTEST 425
-- E-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Questions I— I0. write the
letter that indicates the best answer.
1. _R__el'er to the triangle below. Find the length of
A 8. (LESSON 5.5)
A
60
B 2 C
a.2\/3
b.2
c.-4
¢2fi
2. Find the distance between (I5. 0. I9) and
[6,9, 10]. (LESSON 6.4)
a. x/2-3?
b. 9
c. 90’;
¢9fi
3. Refer to the figure below. Find the area of
L‘!-‘GH. (LESSON 5.2)
a. I I?’
b. 23-1
c. 34
426 CHAPTER 5
O
intemet connect .531
Standardized
Test Prep Online
Go To: go.hrw.com
Keyword: MM1 Test Prep
4. Find the area of the Iigurc bclow.
(LESSON 5.5)
a. 4.5
b. I8
c. 9fi
d. 20.25
. \\-‘hat is the measure of an interior angle of at
regular nonagun (9-gun)? (LESSON 3.6)
a. 40°
b. 100°
c- H0"
d. l60°
. The area of a circle is 154 square inches.
A],1pru:<i1nate its circumference. (LESSON 5.3)
‘P? in.
b. 4-1 in.
c. 51 in.
d. 77 in.
. \-\"hat is the midpoint of .1 segment with
endpoints at (9. I2) and (—l 2. 9]?
(LESSON 5.6)
a. (-1.5. 10.5)
b. (v1.5.6)
c. [-6. -4.5)
d. (10.5, -10.5)
8.
10.
11.
12.
13.
14.
15.
What is the midpoint ofa segment with
endpoints at (2, I0, 0) and (l I. I0, -6)?
(LESSON 6.4)
a. (6.5. 0. -3)
b. (-1.5, 10, 3)
c. (6.5. 10. -3}
d. (5.5. 5, 3]
. In the oblique rectangular prism shown below,
find x. (LESSON 2.2)
a. 60
b. 80 X‘
c. IOU
d. I20 80°
Find the surface area of the solid shown
helow. Assume that no Lubes are hidden.
(LESSON 6.1)
a. 34 square units
b. 45 square units
c. 54 square units
d. 66 square units
ls the statement below a definition? Explain
your reasoning. (LESSON 2.3)
Skew lines are not parallel and do not intersect.
A circle and a square both have an area of -14]
square inches. Find the circumference and
perimeter. respectively. (LESSONS 5.1
AND 5.3)
A qtiatlrilateral has vertices at (3. —l J. (9. -5].
(7. -8]. and (I. 4‘. Use slopes to prove that
the quadrilateral is a rectangle. (LESSON 3.8)
Find the area of the regular hexagon below.
(LESSON 5.5)
Draw a rhombus and construct a reflection 01
it over a horiaontal line. (LESSON 4.5)
FREE-RESPONSE GRID
Items 16-19 may be answered
by using a free-response grid
such as that commonly used
by standardized-test services.
®@3@G@G@G@3@
®@®@G®®®G@D®
®@®@®@@®G@b
@OG@®®®®G D
16. Find the area ol L~.PFC. (LESSON 5.2)
G
sftl
'4"n' P 12ft
17. Find the total area ol‘ the three rectangles
below. (LESSON 5.1)
6
10 I
18. Refer to the diagram below. Find the value of);
(LESSON 3.6)
19. A point. P. is selected at random on the
segment below. What is the probability
that 2 -5 P <_-'. 2.5? (LESSON 5.7)
CHAPYER 6 CUMULATIVE ASSESSMENT 427
Lessons
7.1 0 Surface Area and
Volume
7.2 0 Surface Area and
Volume of Prisms
7.3 0 Surface Area and
Volume of Pyramids
7.4 0 Surface Area and
Volume of Cylinders
7.5 0 Surface Area and
Volume of cones
7.6 0 Surface Area and
Volume of Spheres
7.7 o 'l'hree-Dimensional
Symmetry
Chapter Project
A Three-
Dimensional
Puzzle
Surface
Area and
Volume
Kugel Ball, at the
Houswn Muselnn
FOR SEVEN DAYS, 120 WORKERS AND 90 ROCK
climbers worked to cover the Reichstag build-
ing in Berlin with shiny silver fabric. A million
square feet of fabric and over 10 miles of plas- Q
tic cord were required for the feat.
Why would anyone want to wrap a huge build-
ing? This is a question that conceptual artist
Christo, who conceived of the project 24 years
before he was allowed to do it, has heard
many times. What do you think? Is it art?
'5!
In this chapter, you will investigate the
surface area of solid objects. Christo *
certainly needed to determine the
surface area of the Reichstag to
prepare for the project.
Quartetby '_‘f' '1; _ '_
Barry Lelia , ' ,
at
x . ‘ J‘ ‘ ~-
- ., . _
~ _ -5.
a[Na:uml Science
'_a.
Pine Circles.
Cone Sphere
by On-is Drury
,‘ "' . . .._ _ _
. I1 q . _- “ I
. “El: "-1 ‘f g’ “-‘I’ 4 “f u __ ,4
‘\ ‘v ‘P u , - 5 1. I \
(\
l
Concepnmlurrist On-ism l
explaining his project '
~ *—- 1. 1 ul ll
1”‘ ' I I
L ~ ' "
- A . I‘
About the Chapter Project About the Portfolio Activities
Models of solid figures can be very useful in Throughout the chapter. you will be given
studying the properties of these figures. opportunities to complete Portfolio Activities
‘ Throughout this chapter. you will use nets for that are designed to support your work on the
solid figures to determine surface area. Chapter Project.
In the Chapter Project. you will create a three- The theme of each Portfolio Activity and of the
dimensional puzzle based on the tangram. Chapter Project is modeling solid figures.
After completing the Chapter Project. you will be 0 In the Portfolio Activity on page 452, you will
able to do the following: build three oblique pyramids that lit together
_ _ _ to form a cube.
0 Assemble three-dimensional 0lJ_|€ClS
{mm nets 0 In the Portfolio Activity on page 459, you will
_ _ _ examine the lateral surface of an oblique
0 Understand the volume ot a three—dimensional Cylmd,_.,_
object in terms of the sum of its parts. _ _ _ _ _ _
o In the Portlolro Activity on page 48:». you Will
create a solid of revolution by using cardboard
and thread.
429
Objectives
0 Explore ratios of
surface area to
volume.
0 Develop the concepts
of maximizing volume
and minimizing suilace
Surface Area and
Volume
BT93.
A ' P L I CA
BIOLOGY
ION
4 t
_. _\ __ .
. —‘ it _ 7: ..
.= ' _.=‘ 5 ‘es
-s. .5 .- -‘J )4: h _I .. __
ifi I E '| -. I
r- I |
g‘ 5) _ 1» ; Fl ' 3%"
“j - I .~ it . .
- 2' ' I - .
r _ ' | .' {Ii
nmshapasandsltes olpianrs .-an ,: _ .‘ ._- , U
and animals are partly determined by ' ' E '. _:::§~%>-
the necessary ratia alswface area to ' ‘ .1 _.§. ..\ 3 ___~-_ .‘fl.,;‘_
volume. Somef - ': a lame rafio is . ' ‘.‘._“‘.'- ~.
advantageous. while otlter times a - ‘_, J _R_;§_':"!‘\_.'_ " -'.3s"1;i°
smallnnioisbemrr ‘ . . -f-'a_ ‘:'s=:
«air.-‘v:s*a.f= 3‘ 3;; -‘ .
Desert plants must conserve water but have .1 lot of light. Tropical plants
receive .1 lot of water but must often compete for light. Leaves with .1 large
surface area collect more light than leaves with a smaller surface area, but they
also lose more water through evaporation.
430 CHAPTER 1
Surface Area and Volume
The surface area 0|‘ an object is the total area of all the exposed surfaces ol‘ the
object. The volume ol‘ .1 solid object is the number of nomwerlapping ttnit
cubes that will exactly till the interior of the figure.
Surface Area and Volume Formulas
l‘he surl-ace area, 5. and volume, V, 01 a right
rectangular prism with length t’, width w. and
height h are
S = 2£’w+ Zwh + 21°]: and V = Ewh. I’ 7.1.1
The surlace area. S. and volume. V. of a culie
with side 5 are 5
S = 652 and V = 5‘. 5 7.1.2
In Activity I below, voti will explore the relationship between the voltiiiie and
surface area of right rectangular prisms.
' I
Ratio of Surface Area to Volume
- ' D Part 1
isoiiigtiiic 310! P3139! 1. Draw or build Several rectangiilar prisms with a width
or uni cu es,ai‘t _ . - . ,_
sp,ead5he_e,som.,fl,e and height ot I unit and a length I — I. 2. 5. . . .
or a graphics Copy and complete the table below, or use a
calc ulator luptionali
spreadsheet to generate
a similar table.
‘ / I /
. Surface area = .
Length, E “W + 2”” zwh Volume = Ewh Ratio of ——r-%°”
1 6 1 7
2 ? ? ?
3 .7 ? ?
n .7 ? 7
2. If E = IUD. what is the ratio of stirllice area to volume? What happens to
the ratio ol" surface area to volume as the value oft’ increases? Is there a
iitiiiiber that the ratio approaches?
Part II
1. Draw or build several tubes with side 5 = I, 2, 3, . . . Copv and
complete the table below, or use a spreadsheet to generate a similar
table.
/ - . . .
' I / Side. s Surface area = 65‘ V0'U|'|1e= S3 I Ratio of "':;f:;%35
1 6 1 ' ?
2 ? ? I .7
3 ? _v I ?
n 2 2 | ?
CHECKPOINT V 2. lfs = I00. what is the ratio of surface area to volume? What happens to
the ratio ol‘ stirlace area to volume as the value of s iiiereases? What
conclusions can vott draw about the surface-are.i-to~vo|ti me ratios oi
smaller cubes compared to those of larger cubes?
By extending your tables from Activity I. you can discover another important
result: For it gii-mi voliniie greater Hum I, the cube in Part II will have a smaller
surlace-area-to-volume ratio than the long rectangular prism in Part I.
Compare. for example. the ratios for a cube and a long prism. each with a
voltiiiie ol' 8. [For the cube, 5 = 2. and for the prism. t’ = 3.}
LESSON 1.: sunmce AREA AND VOLUME 431
CRITICAL THINKING
L ED
graphics calculator or
graph paper
C r
W‘
MAXIMUMIMINIMUM
432 cum-Vren 7
CHECKPOINT V
In general. a "bunched—up" object (like a cube or a sphere) will have a smaller
surface-area—to-volume ratio than a long, thin object with the same volume.
Also. a large object has a smaller surface—area—to—volu me ratio than a small
obiect of the same shape [compare the ratios for cubes with different side
lengths].
These observations have important consequences itt the sciettces. in biology
and physics. many important processes happen at the surface of a solid body.
For example, an animal‘s loss of body heat to
the atmosphere occurs at the surface.
If its body is large and the surface area
is small. the rate of heat loss will be
low. If its body is small and the
surface area is large, the rate ol
heat loss will be high.
On sunny days. a snake
may stretch out in the sun
to absorb heat. At night,
a snake may coil its body
to retain heat. Why does
this strategy work?
‘ Z
Maxlm zlng Volume
1. Create an open box trom .1 standard
8.5 x l I inch piece of paper by cutting
squares from the corners and folding
up the sides. as shown. Copy and
complete the table below.
\
Side of square, 1:’ I Length. 3 I Width, w Height, h Volume, ("wh
1 9 5.5 1 58.5
2 7 7 7 7
3 .7 ? 7 7
x .7 7 .7 .7
2. \-\-‘hat side length of the square will maximize the volume of the box?
3. L159 a graphics calculator or graph paper to graph the volume as a
function of the side length of the square. Let x be the side length of the
square. and let y be the volume of the open box.
4. Use the trace function oi‘ your <.alculator or estimate trom your graph to
find the following:
a. the side length that produces the largest volume
b. the largest volume
A cube has a larger volume for its surface area than any other rectangular
prism. However, it is not possible to make a cubic box from an 8.5 x I I inch
piece of paper by using the given method. l'he shape you determined in
Activity 2 is the closest shape to a cube that can be created by this method.
E X A M P L E D.-X cereal comp-anv is choosing
A P P I C A T I 0 N
MANUFACTURING
CRITICAL THINKING
between tvro box designs with
the dimensions shown at right. __ ..-.-"' in
Which design has the greater _ «gt; .; Povagfr
surface area and thus requires Pf”(£ - Fl} 10 in
more material for the same _ =2 5 = I‘ _ :4 _ _
volume? 8 '"- . ' - . -
SOLUTION _ ‘~ _
Both boxes have a volume of I60 4 in. 5 '"' 2 in. 8 '"'
cubic inches. The surface area of box
A is 2(8)(5] + 2(4][5] + 2[4](8) = I84
square inches.
The surlace area of box Bis 2(lO]l_8) + 2(2)[8] + 2(2][ I0] = 232 square inches.
Box B has the greater surtace area.
Most cereal boxes use a design that is more like box B than box A. What
considerations other than surface area might be important in choosing a
box design?
Exercises
. 60/:1/mm/‘mtg
APPLICATION
1. Explain why the surface area of a right rectangular prism is given I)» the
formula 3 = Ztw + 21'}: + Zwli.
2. What can you say about a solid whose surface-area—to—volume ratio is
greater than ti’ What can you say about a solid whose surt'ace~area-to-
volume ratio is less than I?
3. Explain why the surtace—area—to—s-olume ratio of a rectangular prism with
t_limensions of I" x l x l approaches 4 as I‘ increases. (Hint: Which Idt.t'.\ of
the prism have the same area as t? increases?)
4. In Activity 2. you discovered that the surtace—area—to—volume ratio of a
cube approaches 0 as the side length increases. C an this ratio ever equal 0?
W h_\' or why not?
5. BIOLOGY SingIe—c.elled organisms
are able to absorb all of their
oxygen and food through their
surt'-ace. Use surf-ace—area—to—
volume ratios to explain why
this is not possible for larger
animals.
LESSON 1.: SURFACE AREA AND VOLUME 433
APPLICATIONS
Homework
Help Online
Go To: uo.hrw.cnm
Keyword:
MCI Homework Help
for Exercises l2-SD
CONNECTIONS
434 CHAPTER 1
‘Ms’
0 Guided 34’///3 Practice
Determine the surface-area-to-volume ratio for a rectangular prism with
the given dimensions. (ACTIVITY 1)
6.S><l><l 1.l0xl><l 9.l0><lU><lU
10. HOBBIES Teresa is selling vegetables from her garden at a l'armer‘s market.
She has some rectangular pieces of cardboard that are 42 X 48 inches. What
is the maximum volume for a bow made I)_\,-' cutting squares out of the
corners of these pieces and folding up the edges? What siae squares should
be cut out to make a box with this volume? (ACTIVITY 2)
8.5X5X5
11. MANUFACTURING A company is choosing between two bow designs. The
dimensions (in inches) of box A are 4 x 2 x 6 and of box B are 5 x 2 x 8.
Which has the smaller surllice area? (EXAMPLE)
0 P/flct/68 dlld
Copy and complete the following table for rectangular prisms:
Length Width Height 522:9 Volume .~°;|""l::l‘|=;;::’°_B.
2 2 1 1 2. ? 1 3. -I 1 4. ?
4 4 1 1 5. 7 1 6. 7 1 7. 7
7 3 5 1 3. 7 1 9- 7 20. 7
4 2 1 . 7 3 22 . 7 34 23 . 7
2 5 24. 7 104 25. 7 25- 7
Find the surface-area-to-volume ratio of each of the following:
27. a cube with a volume ol 64 cubic units
28. a cube with a volume of 1000 cubic units
29. a rectangular prism with dimensions of ix x n x l
30. a prism with a square base. where the lateral edge is twice the length of a
base edge
MAXIMUMIMINIMUM For each situation below, determine whether you
should maximize the volume or minimize the surface area. Explain your
reasoning.
31. building a storage bin with a limited amount of lumber
32. designing soup cans that will hold 15 ounces of soup
33. mailing a package with dimensions whose sutn is less than 72 inches
34. building a tank that must hold I00 gallons of water
35. MAXIMUMIMINIMUM Compare the surtace.-—area—to—volume ratio ofan
nx n x l rectangular prism with that ofan n x u x n rectangular prism as
n increases.
36. MAXIMUMIMINIMUM Based on your answer to Exercise 35, make .1
conjecture about what type of rectangular prism has the smallest surl‘-ace
area for a given volume.
CHALLENGES
APPLICATIONS
37. Find the side length oI'a cube with a surI1tee—area—to—-uolunie ratio of I.
38. A prism with a square base has a lateral edge that is twice as long as the base
edges. II" its surlace—area—to—volume ratio is I. find the length of a base edge.
39. BIOLOGY Flatwonns do not have _ o -I
gills or lungs. They absorb oxygen \ 5 ‘
through their skin. Use surI'ace-are:a~ - ' j ‘
1
to—\-olume ratios to explain how the
('. _ ., .9
1 tn. «
Q \ _ ’ V
shape ola llatworm helps it absorb \
enough oxygen.
Mmim:
flatworm
40. PHYSIOLOGY I luman lungs are subdivided into thousands of air sacs. The
total surface area of an average person's lungs is about I00 square yards.
Use sutI11ce—area—to—volume: ratios to explain why such a large surface area
is necessary.
41. BOTANY l'se surlace-area-to-volume ratios to explain why tall trees with
large, broad leaves do not usually grow in deserts.
42. COOKING A roast is Iinished cooking when the internal temperature is
l60°F. l'se sttrlace-area-to-volume ratios to explain why a large roast takes
longer to cook than a small one of the same shape.
43. CHEMISTRY Lise surlaee—area—to—volume ratios to explain why a large block
of ice will melt more quickly if it is broken up into smaller pieces.
44. PHYSIOLOGY Use surficearea-to—volume ratios to explain why
chewing your food thoroughly makes digestion easier. _
45. BOTANY A barrel eaetus has a short. squatty lorm. \‘_ _ ' -$2»
Use surlace—area-to-volume ratios to ' '- .
explain how this form helps the
cactus conserve water in
desert conditions.
Look Back
46. Show that AAA ittforniatitin cannot be used to prove that triangles are
congruent. (LESSON 4.3)
Find the area of each figure below. (LESSONS 5.1 AND 5.2)
47. IT: as.
15 45 28
not
29 53
5o_ 33
16
45
LESSON 7.1 SURFACE AREA AND VOLUME 435
436 cunt-Vren 1
51. If two triangles have the same area. are they necessarily congruent? If not.
give a counterexample. (LESSON 5.2)
52. If the perimeter of a rectangle is 20 inches. give five possible areas and the
dimensions for each. (LESSON 5.2)
53. What is the area ofa circle with a circumference of ION? (LESSON 5.3)
54. The legs of an isosceles triangle measure I5 feet and the base is I6 feet.
Find the area. (LESSON 5.4)
55. The legs of an isosceles right triangle measure 6 centimeters. Find the
length of the hypotenuse. (LESSONS 5.4 AND 5.5)
/.004’ Beyond
Ratios of surface area to volume play a part in determining how big a
person can be. As the size of a person increases, the weight increases in
proportion to the volume, while certain other measurements increase in
proportion to the surface area.
56. Estimate the total area of the bottom
of both of your feet in square inches.
One way to do this is to trace your
feet onto a piece of graph paper and ‘
count the squares.
57. Divide yottr weight in pounds by .
the area of the bottom of both of “ '
your feet. This gives the pressure.
in pounds per square inch, on the
bottom of your feet.
58. Suppose that the size of yottr body
increased while keeping the same
shape. If the length and width ol
your feet were doubled, the area of
your feel would increase by a factor
of ? . Estimate the new
area of the bottom of your feet. If
your lengtp. width, and height were
doubled. your weight would
increase by a factor of ? .
What would be your new weight?
59. Divide the new weight by the new
area to find the new pressure on the
bottoms of vottr feet. Fxplain what
happens to the pressure on your feet
as your size increases. How does this
limit the size of the human body?
Objectives
0 Define and use a
formula lor lilltllllg the
surface area of a fight
prism.
0 Define and use a
formula lor finding the
volume of a right
prism.
0 Use Cavalierfs
Principle to develop a
formula for the volume
ol a right or oblique
prism.
Surface Area and
Volume of Prisms
\
Many : - - rs are packaged in boxes " "-
that are prisms. You can use sudaoe area to
estimate the amount of material used in each
box or use volume to estimate the amount 0!
the product in each box.
You can use (hr: strt'fitt'r: rrrea oft: box to e'st‘imrm.' the rtmomtt
ofwmpping papm you will need to cover the box.
Recall trom Lesson 6.3 that a prism has two parallel congruent faces called
bases and that the remaining laces. called lateral faces. are parallelograrns. In a
right prism. all of the lateral laces are rectangles.
An altitude of a prism is a segment that /A"i‘”d°5
has endpoints in the planes containing ‘ J
the bases and that is perpendicular to
both planes. The height ol'a prism is
the length ofan altitude. __l
Right prism Oblique prism
Surface Area of Right Prisms
The surlace area of a prism mav be broken down into two parts: the area ol
the bases. or base area. and the area of the lateral faces. or lateral area.
Since the bases are congruent. the base area is twice the area ol one base. or
28. where B is the area of one base.
LESSON 7.2 SURFACE AREA AND VOLUME OF PRISMS 437
CRfl1CAL11flNKHHG
EXAMPL
438 CHAPTER 7
To lind the lateral area of a right prism. you may find it helpful to use a net.
Because the net folds up to form the prism. the area ol the net is equal to the
surface area of the prism.
If the sides of the base are 5.. s;., and st
and the height is h. then the lateral area
is given by the lbllowing lormulaz
L = s.lt + 53!: + S\h=h[51 + 53 + 55]
Because s. + 53 + 5'. is the perimeter of
the base. we can write the lateral area
as I = lip, where p is the perimeter of the
base.
5:4
How can you show that the formula for lateral area. I. = lip, is true for right
prisms with bases that are not triangles?
'l he surlace area 01 a prism is the sum of the base area and the lateral area.
Surface Area of a Right Prism
I'he surface area, S. ofa right prism with lateral area L. base area B.
perimeter p. and height la is
S=l+2B or S=lip+2B. 7.2.1
The net for a right triangular prism is below. What is its surl'aee area?
SOLUTION
The area of each base is
B‘: gmtzn = 21.
F42
'l he perimeter of each base
isp= l0+21 +17:-I8.
so the lateral area is
1 = :.p= so¢_4s1= 1440.
30
10 21 17
Thus, the surface area is
.3: L+2b’= l440+2(Zl)= 14-'lO+42= I482.
Volumes of Right Prisms
Recall from lesson 7.! that the volume of a right rectangular prism with
length I". width w. and height It is given by V = Fwli. Because the base area. b‘.
of this type of prism is equal to he. you can also write the formula for the
volume as V = Bit.
Does this formula work for right prisms with bases that are not rectangles?
The discussion that follows begins by considering a triangular prism with a
height of l.
The prism at right has :1 height of l. The number
of unit cubes needed to fill the prism is equal to
the number of unit squares needed to cover the 4
base. which is equal to the area of the base. 1
A prism with a height of It can be made by
stacking !t prisms with a height of I on top of
each other. The volume of this prism is It times
the volume of the prism with a height of l. or Ii
times the area of the lmse. Thus. the volume of
any right prism with a base area of B and height
of It is 1-" = Bh.
E X A M P L E 0 An aquarium in the
shape of a right
rectangular )l'iS|'l'l
A I P l c l 0 N has dimensibns of
’‘°”’“““'“5 1 I0 x 50 x 7 let-t. Given
that I gallon = 0.134
cubic feet, how many
gallons of water will the
aquarium hold? Given
I gallon ol water as 3.35
pounds, how much will
the water weigh?
O SOLUTION
The volume of the aquarium is found by using the volume formula.
V = Bit = (‘wit = (I l0][50)(7J = 38,500 cubic feet
To approximate the volume in gallons, divide by 0.134.
V = 38.500 —:- O.l 34 3 287,313 gallons
To approximate the weight. multiply by 8.33.
weight 2 (287.31 3)(8.33) 2 2,395.31? pounds
. _z— -
E X A M P L E 0 An aquarium has the shape of at right regular 14'” ' 7”3 '"'
hexagonal prism with the dimensions shown ’
at right. Find the volume of the aquarium.
O SOLUTION 48 '"'
The base of the aquarium has a perimeter of
[I-41(6). or 84. inches and an apothent of
7»/3 inches. so the base area is found as follows:
B = %up = %[84][7vG5 = 294x/G = 509.22 square inches
l'he volume is v = Bl: = {294\/3)t48) = l4l I 2‘/.' 2 24,443 cubic inches.
LESSON 12 SURFACE AREA. AND VOLUME 0: PRISMS 439
440 CHAPTER 1
Volumes of Oblique Prisms
In an oblique prism. the lateral edges are not perpendicular to the bases. and
there is no simple general lormula for surface area. However, the formula for
the volume is the same as that for a right prism. To understand why this is
true. consider the e.\:planation below.
Stack a set of index cards
in the shape ofa right
rectangular prism. If you
push the stack into the
shape of an oblique prism,
the volume of the solid
does not change because
the number of cards does _ _
not change.
Both stacks have the same number or cards, and each prism is the same height.
Also. because every card has the same size and shape. they all have the same
area. Any card in either stack represents a cross section of each prism.
The prisms above illustrate an important geometry concept.
Cavalieri's Principle
If two solids have equal lleigltls‘ and
the cross sections formed by every
plane parallel to the bases ol both 2
solids hav * equal areas, then the . .
two solids have equal volumes. —
7.2.2
The solids will have equal volumes if they are the same height and all cross-
sectional areas are equal.
Every oblique prism can be compared with a right prism with the same base
and height. As the stacks of cards suggest. every cross section of a prism is
congruent to its bases. so all of the cross sections of the oblique prism are
equal to the cross sections of the right prism. Thus. by Cax-alieri's Principle.
they have equal volumes.
The formula for the volume of anv prism is given below.
Volume of a Prism
The volume, V, ofa prism with height hand base area B is
V = b‘h.
7.2.3
Exercises
. Communicate
1. Explain how to find the surliice area of a right prism.
2. F.X|)l'.lll1 the formula lor the volume of'a right prism.
3. Explain C.walieri’s Principle and how
it can be used to lind the volume of an
n hmuammm #3 oblique prism. ) ,
_ __ «ml . . ., . ‘. .. "
Aclwmes 4. Can Lavalieri s Pnnuple be used tor 1
Online two prisms of the same height if the I
3° T05 9°"'V'-°°'" base of one is it triangle and th: l‘
Keyword; l f I I h . ' | ‘
Mm A,,,,,,,,_,,, vase o t_1:. or er IS a - ‘1
hex-.igon:' Vt hy , r
Or why not! __—_—_.
0 Guided 34’///3 Practice
Determine the surface area of the prism formed by each net.
(EXAMPLE 1;
5. 5 6.
22 9
10 16 10
Find the volume of each prism. (EXAMPLES 2 AND 3)
7. right rectangular prism 8. right regular octagonal prism
,.—e+st.-'5
=~ ‘l.
12 40
7 12
LESSON 7.2 SURFACE AREA AND VOLUME OF PRISMS 441
I tncemetcomea "9.
9.
air!
Homework
Help Online
Go To: go.lrrw.com
Keyword:
MGI Hemcwerlt Help
lot Exercises 13-20
442 CHAPTER 1
P/fl6‘t'IZ'6’ mm’ 34,0;/y
Draw a net for each figure named below.
9. cube
10. right rectangular prism
11. right equilateral triangular prism
12. right regular hexagonal prism
Find the volume of a prism with the given dimensions.
13. B= 7 sq cm. in = 5 cm
14. B: 9 sq m, h = 6 in
15. B: I7 sq in.. It = 23 in.
16. B= 32 sq ft. h= l7 ft
Find the surface area and volume of a right rectangular prism with the
given dimensions.
17. i"= 5. 1v: 7, II = 2
18. t’: 16, w=9. l1: l0
«-1 .=£ =
19-£—2,n 3,11 l
20. L’ = L3, 14': 4. h= 0.5
21. Find the height of a rectangular prism with a surface area of 236 in.’ and -.1
base measuring 7 x 9 in.
22. The height Ola right regular ltexagonal pristn is 25 cm. and the sides of its
base measure I8 cm. Find its surface area.
23. The height of a right regular he\'agonal prism is 20 cm, and the apothem
of its base is 4‘/Ecru. Find its surface area.
24. If a cube has a volume of 3-13 yd}, what is its surface area?
25. l'he figure at right is a net for 2 .— 3 _
an oblique rectungttlar prism. _ _
The 3 x 2 rectangular faces are 2.8:" 3 2.8
the bases of the prism. Find its 3
volume and surface area. It ' ‘ "1
may help to copy the net and 1
fold it to form the prism.
26. The figure at right is a net
for an oblique triangular
prism. Find its volume and
surface .1 rea. It may help to
copy the net and fold it to
form the prism.
CHALLENGE
APPLICATIONS
27. Find the volume of a right trapezoidal prism if the bases of the trapezoid
tneasure 6 In and 8 In. the height ofthe trapemid is 7 In. and the height of
the prism is IS in.
28. Find the voltune ofa right triangular prism whose base is an isosceles
right triangle with a hypotenuse of IO cm and whose height is 23 cm.
29. Find the sttrlhce area and volume of a right triangular prism whose base is
an isosceles triangle with legs measuring -1 in. and a base oI‘6 in. and
whose height is L5 in.
30. II‘ the height ol‘ a prism is doubled and the bases are unchanged, what
happens to the volume of the prism?
31. If the edges of a cube are doubled, what happens to the surface area? What
happens lo the volume?
32. If the edges ofa cube are tripled. what happens to the surface area! What
happens to the volume?
33. The height of a right regular hexagonal prism is equal to the side length of
its base. Ifthese side lengths are doubled. what happens to the volume?
What happens to the sttrI'-ace area?
34. What happens to the side length of a ctthe if its volume is doubled? What
happens to the surface area?
35. MANUFACTURING Find the surface area and volume of each box of cat food
shown below.
«-!..?::.=--
0”’) /—’;"’ ‘,3’?! ‘
§:’-5. \k\TTg
{ \ I 5
9In A 3 I ' /fix 7} 9m
i ‘I s.,~« »
€f*_“l' :" \’u\_§
beast "' ‘_g.uN¢"“‘-5
_ 3in- 2in.
6In.
7in.
36. RECREATION I'he swimming pool shown below is a right prism with
concave hettagonal bases. Use the given dimensions to find the volume in
cubic feet and in gallons (I gallon = (LI 54 cubic foot}.
24 It
20 it
an
an L
10ft _E
10 ft
37. RECREATION Find the surface area oi‘ the sides and bottom of the
swimming pool shown above. If I gallon of paint covers 400 square feet.
how many gallons of paint will be needed to paint the inside of the pool?
LESSON 12 SURFACE AREA AND VOLUME or PRISMS 443
A P P L I C A T I 0 N S 38. RECREATION The tent shown \I_
at right is a right triangular I
prism. l'he bases of the prism 35;.
are isosceles triangles. Find
the surface area of the tent,
I
-\l‘‘---..
including the floor. ‘:/ 7 0 h>
39. ARCHITECTURE Use the lateral
area of the building shown at
right to estimate how much I it
glass was used to cover the l
outside walls of the building.
Each story is l2 feet high. and «H
the base of the building is a
square with sides ol'4t-‘. feet. - ll_
._'_
i
1.00.‘? Back
‘ .4; 2' / Simplify each radical expression. Give answers in simplified radical
form. (ALGEBRA REVIEW)
40. V/2_0 41. (V/filtx/it
42. tsfite 43. (2../Etta»/2?}
3 _
44. 75- 45. ‘/27 + \/lfi
Exercises 46 and 47 refer to a 30-60-90 triangle with a hypotenuse of
10 inches. (LESSON 5.5)
46. Find the length ol the shorter leg.
47. Find the length ol the longer leg.
/.00k B670/Id
C O N N E C T I O N COORDINATE GEOMETRY A prism in a three-dimensional coordinate system
has one base with its vertices at Al0. 0. O). Bl0. 5. 0). CM. 5. 0). and
DH, O. O).The second base has its vertices at EIZ, 2. 2), H2, 7, 2),
Gl6. 7. Zl. and Hi6. 2. 2).
48. Draw the prism on a set of coordinate axes. Name the type of prism.
49. Find the volume of the prism.
C II A I. L E N 8 E 50. Find the surface area ofthe prism.
444 CHAPTER 1
Surface Area and
Volume of Pyramids
1! AA;
_ ‘ ‘-up .
. .. ,5. '1 __ _ _
{ ~ _I_ T ¢
- - I-. i l I ' ‘ - - :, 4 -
Obyectnres ' ‘ '- . _ .
0 Define and use a " ‘ ‘ ‘___ L
lormula lor the surtace . ..._ ._ A cultures’ the pyramid ms
area of a regular ,
Wramm , an enduring appeal. From ancient
' - ' E: - Farr tombstathe Trans: - ‘cs
0 Define and use a Pyramid In San Francisco. a pyramids
lormula lor the volume shape pm my .m and . ,1; beauty,
of a pyramid. _
Pyra mid 3
A pyramid is a polyhedron consisting of a base. Vfiflflx
which is a polygon. and three or more lateral
faces. ‘I he lateral faces are triangles that share a : 4 Lateral
single vertex. called the vertex of the pyramid. \ edge
F'lCl1 lateral l‘-ace has one edge in common with :———— Altitude
the base. called abasc edge. l'he intersection of ‘ .. _K‘ Lama,
two lateral laces is a lateral edge. E faces
The altitude of a pyramid is the perpendicular W 4. Egg:
segment from the vertex to the plane of the base. i
The height ofa pyramid is the length of its 383,,
altitude.
A regular pyramid is a pyrarnitl whose base is
a regular polygon and whose lateral faces are I _
congruent isosceles triangles. In a regular pyramid. ."i : ‘°‘""'-'d°
all of the lateral edges are congruent. and the ' _ fiéénat
. . . ‘-
altitude intersects the base at its L(.'IIl.Cl'. The length _] '9
ofan altitude of a lateral lace ofa regular pyrarnid
is called the slant height of the pyramid.
Pyraniids. like prisms, are named by the shape of their base.
Triangular Rectangular Pentagonal Hexagonal
pyramid pyramid pyramid pyramid
LESSON 1.3 SURFACE AREA AND VOLUME or Pvr-wmos 445
The Surface Area of a Pyramid
To analvze the surface area ofa pyramid. it is helplul to use a net. The area of
the net is the same as the surface area of the pyramid. For |1_Vl'dl‘l'll(lS that are not
regular, the area of each face must be calculated separately, and then the areas
must be added together. For regular pyramids. however, there is an easier way.
E X A M P L E Find the surface area oi" a regular square pyramid whose
slant height is I" and whose base edge length is 5. e
O SOLUTION s
The surface area is the sttm of the lateral
areas and the base area.
Area of each l _ t.
S = L + B triangle = 35:‘
. _l s L
S = 4 £38 + 5‘
(2) g ¥‘_._.;. at
This can be rewritten as lollows:
_ ' , "1 s r
.s = ;t%(4.»-} + .<- f
Because 45 is the perimeter ot the base.
5 = %Ep+ 52.
'l he lateral area of any regular pyramid is equal to -1-£"p. ‘I he surl'ac.e area is
found by adding the base area. B. l() this value. -
Surface Area of a Regular Pyramid
The surlaee area. S. of a regular pyramid with lateral area L. base area B.
perimeter of the base p, and slant height I” is
5=I+B or S=%t'p+B. 7.3.1
E X A M P L E 0 The roofofa gazebo is a regular octagonal pyramid
with a base edge of 4 teet and a slant height of 6 feet.
Find the area 01 the roof. ll" roofing material costs
$3.50 per square foot. lind the cost of covering the
roof with this material.
0 SOLUTION
The area of the root" is the lateral area of the
pyramid.
L = %t'p = §(6)(3 x 4) = 96 square li:et
91: square feet x 53.50 per square foot = $336.00
446 CHAPTER 7
The Volume of a Pyramid
The volume ol a pyramid has an interesting relationship to the volume of a
prism with the same base and height as the pyr-aiiiid.
Pyramids and Prlsms
ll Ll. D 1. Using construction paper, make a right square prism and a regular
5.33 w,,s_,,l,ct-on square pyramid with the same base and the same height. Seal the lateral
D-‘4t19I.$CISS0fS.IatJB. edges with tape. (Do not seal the base edges.)
and dry cereal or _ _ .
packing material 2. Fill the pyramid with dry cereal or
packing niatei’i.il. Pour the contents
into the prism. Repeat as necessary to
l'ill the prism completely. How many
times did yoli have to fill the pyramid
in order to till the prism?
‘ho
//
CHECKPOINT ./ 3. Make a conjecture about the relationship a.
ol- the volume ofa pvraniid to the volume _
of a prism with the same base and height. r’
Express your conjecture as a l'ormul-a for -
the volume ofa pyramid.
This relationship between triangular prisms and pyramids can be verified by
dividing a triangular prism into three triangular pyramids, as shown below.
The pyramids are not congruent to each other, but they each have the same
volume.
D F D F F
E E E E
\
h
A A
C A C A C
8 8
Triangular prism Pyramid I Pyramid ll Pyramid lll
Consider the pyramids in pairs, as follows:
Pair A: Pyramid I has base DEF and height Ii.
Pyramitl ll has base ABC and height li.
Notice that the bases are congruent and the heights are equal. it can he
shown. using Cavelieriis principle. that pyramids with congnient bases
and equal heights have equal volumes.
Pair B: Pyramid II has base EBC.
Pyramid lll has base EFC.
l'he bases of these pyramids are congruent because E is a diagonal
ol'BEFC. The heights are also equal because both pyramids include
vertex A. Therelore, these two pyramids have equal voluines.
LESSON 7.3 sunmce AREA. mo '-"0LUME or Pm.-ximos 447
By the Transitive Property. the three pyramids all have equal volume, so each
must be one-third of the original prism. This suggests the following formula:
Volume of a Pyramid
The volume. lrfi of a pyramid with height It and base area B is
v = %Ba. 1 32
cnmcm. THINKING Once you know that the above formula works for all triangular pyramids. how
would you show that it works for pyramids with other bases?
E X A M P L E 0 CULTURAL CONNECTION: AFRICA 'l'he pyramid of Khufu is a regular square
pyramid with a base edge of apprmzilnately 776 feet and an original height
of -181 feet. The limestone used to construct the pyramid weighs apprcwiinately
I67 pounds per cubic foot. Estimate the weight ofthe pyram id of lxhufu.
[Assume the pyramid is solid.)
' P - Tl I "
ARCHAEOLOGV
O SOLUTION
'l he volume ofthe pyramid is found
as follows:
.: _ 1
l — 3B1:
==_l.(7763)f-'18!)
== 965348.885 ctlbic feet
The weight in pounds is
96,548,885 cubic feet x 167 pounds
per cubic foot s= I6.l23-.663.850
pounds. or 8,061.83] tons.
£xerc/'5es
. Com»/my/cute
1. Define pynmiid. Is there any type of pyramid in which more than one face
could be considered the base?
2. Fxplnin how to find the surface area of a regular pyramid.
3. Explain how to find the volume of a pyramid.
448 CHAPTER 7
u . _,..,¢q,....,d ,g_o,_ 4. Ina regular pyramid. which is larger.
Aciiiiiiies "M the height or the slant height? Explain
ontine your reasoning.
hmmm 5. Explain the relationship between the
M61 Pyramids volume of a pyramid and the volume
, ofa prism with the same base and
height.
Tht'.'$€ strirrgs trflighrs form the
I(1rt'rrtIt'dgt'€ of n 39-gtmnl pyrrmtiri.
0 Guided Ski"//3 Practice
Determine the surface area of each regular pyramid. (EXAMPLE 1)
6. 7.
10 8
I
7 e
A P P L I C A T I 0 N 8. CONSTRUCTION l'he roof ol'a gazebo is a regular decagonal pyramid with a
base edge of 4 It and a slant height 0|" 7 lit. Find the surface area 0|" the
roof. (EXAMPLE 2)
9. CULTURAL CONNECTION: AFRICA The pyramid of Khafre is a regular square
pyramid with a base edge of 708 ft and a height of/l7l lit. It is constructed
of limestone. which weighs approximatel_y 167 pounds per cubic l't)t)t.
Estimate the weight of the p)-Tumid. (EXAMPLE :1)
0 P/46¢/Ce film’ flpp/y
Draw a net for each regular pyramid named below.
10. a square pyramid 11. a triangular pyramid
12. a pentagonal pyramid 13. .1 hexagonal pyramid
g humgqconinq igg__ Find the surface area of each regular pyramid with side length s and
iiomewoiii ‘°'" slant height € given below.The number of sides of the base is given by n.
""9 °"""° 14. s = 3 15. s = 6 16. .< = IO
fi§v‘[3;,:',;’_"'"‘°"‘ 2 = 9 2 = 7 P = 12
M61 Homework Hob H = 3 H = 4 H = 6
tor Exercises 14-23
Find the volume of each rectangular pyramid.
17. 18. 19.
/3'11 l
/7'6"" ;_ »9In.
. _.-..‘..-.-._
fl.----.i._..--
7|
3'.” 9'.” l2m.
4m 7 m 13 in.
LESSON 7.3 SURFACE AREA. mo '-"0LUME or Pvrt.-umos 449
ln Exercises 20-23, draw a diagram of each pyramid and label the base
edges and the altitude. Find the volume of each pyramid. Give exact
answers.
20. a rectangular pyramid with a 5 x 7 base and a height of I l
21. an octagonal pyramid with a base area ol 16 and a height of H
22. a right triangular pyramid with base edges of 5. I2, and I3, and a height
of if]
23. a square pvr-amid with .1 base edge 0H and a height equal to the diagonal
of the base
Use the diagram of the pyramid below for Exercises 24-30.
24. Find the area ofthe base. BCDL-'.. A .'2
3
Find the area of each lateral face. E \ xi l 8
25. AABC _______ 4
3 .
2e. AACD 3
27. AA or
D C
28. A ll.-‘B
29. Find the surface area ofthc pyramid.
30. Find the volume of the pyramid.
;4 g; I / Find the height of each pyramid described below.
31. I.‘ pentagonal pyramid with a base area of 24 square units and a volume of
I04 cubic units
32. a regular square pyramid with a base edge of IO units and .1 volume ol
SUO cubic units
33. a regular triangular pyramid with ‘.1 base perimeter of 12 units and a
volt: me of 8 'LlIl)l(.' units
34. a regular he\:a,r:onal pyramid with a base edge ol 2 units and a slant height
of 2 units
Copy and complete the table below for the vertices, edges, and faces of
pyramids. For each entry in the last row, explain your reasoning.
l Number ol Number of Number of Number of
sides of base, n vertices, V edges. E laces, F
3 4 6 4
4 35. ? 36. 7 37. ?
5 38. ? 39. 7 40. ?
II 41. ? 42. 7 43. ?
TABLE PROOF 44. Use the last row of the table above to prove that V - F + F - 2 for
all pyramids.
450 CHAPTER 1
CHALLENGE
APPLICATIONS
45. Find the volume and suri':1ce area of the rectangular pyramid below.
46. CONSTRUCTION The entrance of the Louvre museum in France is .1 square
pyramid with a base area of 225 ml and a height of I5 in. What is the
volume of the pyramid?
47. CONSTRUCTION How much glass would it take to cover the pyramidal
entrance ofthc Louvre? (Ignore the ll':1pL‘z.'0iCI;tI doorway and do not
include the floor.)
Look Back
48. An angle measures 51". What is the measure of its complement? What is
the measure oi" its supplement? (LESSON 1.3)
Quadrilateral /1300 has vertices at AIO, 0), BIS, 0), CI7, 6), and DI2, 6).
(LESSONS 3.5 AND 5.6)
49. What type of special qtmdriluterai is ABCD? Prove your answer.
50. Find the perimeter of the quadrilateral.
51. Find the area of the quadrilateral.
52. Give the vertices ofa quadrilateral with the same area as A BCD but a
different perimeter.
Find the area of the shaded region in each figure. (LESSONS 5.1 AND 5.3)
Q
Li
\ J1‘
LESSON 1.3 SURFACE AREA AND VOLUME OF PVRAMID5 451
53. 54.
Qt
B lnternetconnect
Portlolio
Extension
Go To: go.hrw.corn
Keyword:
MGI lso'l’at
452 CHAPTER 1
5:3
1.004’ Beywm’
In Exercises 56-60, write a conjecture for each question. If a theorem
you know supports your reasoning, state the theorem.
In the proof of the tormula tor the volume of a pyramid. it was stated that it"
two pvramids have the same height and bases of the same area. then they have
equal volumes. F.xamine the illustration below.
56. In the illustration, the intersecting plane is parallel to the plane of the
bases of the pyramid. and it intersects each altitude at its midpoint. How
does the intersecting plane seem to divide the lateral edges of the
pyramids?
57. How do you think the lengths of the sides of the red triangles compare
with the lengths of the sides of the bases in each pyramid?
58. How do you think the areas of the red triangles compare with the areas of
the bases? How do yott think they compare with each other?
59. Do you think the results from Exercise 58 would be the same if the
intersecting plane intersected the altitudes at points other than their
midpoints?
60. How do your results show that the pyramids have equal volumes?
NETS FOR oauous PYRAMIDS Adjacent edges of
E the pyramid must
The net at right is for an be 9003' in '9"9“"-
oblique square pyramid. 1
1. Find b‘l.-'. which sides
are congruent to BE? H A ,1 3 ‘ F
2. Find Ff. \‘hfl1iCl1Llf.lL I L4 1 J
is congruent to 1-0 1 1
3. Make three copies of the
net and fold them into 1 1 [-
three congruent square D -1 C
pyramids. I-‘it the three
pyramids together to
form a cube. How does
this illustrate the
formula tor the volume
of a pyramid?
WORKING ON THE CHAPTER PROJECT
You should now be able to complete
Activity I of the Chapter Pro_iec.t.
Objectives
0 Define and use a
formula for the surtace
area of a right cylinder
0 Deline and use a
formula for the volume
ol a cylinder.
hv Many everyday
abject: are cylindrical in
shape. You can use the
volume of these objects to
find how much liquid they
will hold.
A ' P l. I II A T10 N
ENGINEERING
Surface Area and
Volume of Cylinders
I _ ::. .::::.
\ ' 1’r‘i - -
/\
I .
j
_-.4‘ &n
IL
..,-—r~ L. . .-
-vi ’ I V '
.' 1
' N .39.;
-- .:
" ' -'-. ' ‘L
- 1'» _-' . -
_,“,', ‘-. .5 Y’ ‘
‘ . u ‘-
ff .‘. - ‘ Vs.‘
I’ '~.‘’-"’'.: . . . . -
' ”.'—”‘ 32'' _.-~' '.'-In’. "."'-a -e«.‘._:" ' "-‘~.'- '3.» "..i ~"~ -3: ".;.,_J
The gasoline you buy at a pump is stored in underground tanks. How could
you use the dimensions oi an underground gasoline tank to estimate the
number ol'c.iir tanks that could be filled from it? (See |;'.\'ample 2. page 455.)
\-
Altitude - ,-
-Axis
Cylinders
A cylinder is a solid that consists oi" a circular
region and its translated image on :1 parallel plane.
with a lateral surlace connecting the circles. 83585
The faces formed by the circ:ul.ir region and its .
translated image are called the bases of the cylinder.
An altitude of a cylinder is a segment that has endpoints in the planes
containing the bases and is perpeiidieiilar to both planes. The height ol'a
cylinder is the length of an altitude.
The axis ofa cylinder is the segment joining the centers of the two bases.
lithe axis of a cylinder is perpendicular to the bases. then the cylinder is a
right cylinder. If not. it is an oblique cylinder.
LESSON 1:: SURFACE AREA Anovot UME or cvtiiuoens 453
Cylinders and Prisms
As the number of sides of a regular
polygon increases, the figu re becomes
more and more like a circle.
Similarly, as the number of lateral
faces ofa regular polygonal prism
increases. the figure becomes more
and more like a cylinder.
This fact suggests that the formulas
for surface areas and volumes of
prisms and cylinders are similar.
The Surface Area of a Right cylinder
'1 he surface area ofa right cylinder with a A
radius of r and a height of It can be found . —A nr’
by using a net. The net for a right cylinder, ° if
shown at right. includes the two circular
bases and the lateral surface. which h +
becomes a rectangle. The length of this
rectangle is the circumference of the base .
of the cylinder. or lrtr. The height of the I
rectangle is the height of the cylinder, or It. ° A 2mh
211:r To It
Thus. the lateral area of the cylinder is lttrh. and the area of each base is rtrz.
‘I he surface area of a cylinder is the sum of the lateral area and the base areas.
Surface Area of a Right Cylinder
’l'he surface area, S, ofa right cylinder with lateral area L, base area b‘,
radius r. and height h is
S = I + 2B or S = Zrtrh + Zrtri. 7.4.1
E X A M P L E 0 A penny is a right cylinder with a diameter
of l9.05 millimeters and a thickness of L53
A _ P L 0 N millimeters. Ignoring the raised design,
l estimate the surface area of a penny.
COINS
0 SOLUTION
The radius of a penny is half of the diameter,
or 9.525 millimeters. Use the formula for the Pt'm1ie.~=, at one time madeof
surface area ofa right cylinder. PW“ ‘¢’Pl'l"- ‘"1" "OW ”Wll" Of
cnpper—plrrt¢'rl zinc.
S = Zrtrh + 2m"
5 = 2n('9.525Jt l .55) + 2n(9.525)3 = 663.46 square millimeters
454 CHAPTER 7
ll L I.
no special tools
CHECKPOINT ./
CRITICAL THINKING
Volumes of Cylinders
For the lollmving Activity. recall the methml you used in Lesson 5.3 to find the
area ol a circle.
Analyzlng the Volume of a Cylinder
I he tormula tor the area ot a /.7‘ 7
circle was found bv dividing
the circle into sectors and
fitting them together to form
a shape that was close to that
of a rectangle. The same idea
can be used to find the volume
of a cvlinder.
1. Refer to the figure above. What geonwtric >0ll(.l does the cylinder
approximate when the sections are arranged as they are at right above?
2. Use the length. width. and height ot this arrangement to write a lormula
for the volume of a cylinder in terms of its radius and height.
How would _vou show that the lormula tor the volume of an oblique cylinder
is the same as the formula for the volume oi" a right cvlinder? Use sketches to
illustrate your answer.
Volume of a Cylinder
l'he volume. V. of a cylinder with radius r. height !1. and base area B is
V = Bil or V = Itfvl. 7.4.2
E X A M P L E 0The tank in the illustration on page -153 has a length oi"?-I I'eet 6% inches and
A ' P I‘: l 0 N |
ENGINEERING
Note: 1 cubic foot ,
~ 7.48 gallons. r
an ottlcr diameter oi" 8 l'eet 0 inches. Assuming a wall thickness oi" about 2
inches. what is the volume of the tank? At l5 gallons per car. how many car
tanks could be filled from the storage tank it" it starts out completely lull oi"
gasoline?
SOLUTION
The tank is not perfectly cylindrical, because ol‘ its hemispherical heads. but
you can approximate its volume by a slightly shorter cylindrical tank. say. 29
feet long. Subtracting the wall thickness from the dimensions of the tank.
v = m-‘h 2 i:t3.s33',F(2s.cac»7) 2 1323 cubic feet
Convert from cubic feet to gallons.
I3-23 cubic feet x 7.48 gallons per cubic‘ foot s== 9896 gallons
Thus the tank could deliver about ¥?’. or sex 660. l5—ga|lon lill—up5.
LESSON 74 sunmce AREA AND VOLUME or cvtiruoens 455
Exemses
. Cohm/:0/icate
n . mm.“ ;},g_‘ 1. Explain the difference lretween an altitude and the axis of a cylinder.
10111
Activities 2. Is -.1 cylinder :1 polyhedron? Wlw or why not?
Dnline _ _ ' _ _
Go To: uo.hrw.cnm 3. Explrnn how to find the surface area 0| 21 right cvlmder.
,'f,°.1,’;“,‘§,','f;,,,.,,,,g 4. Write the formula for the surface area ofa right cylinder in factored form.
Which form do you prefer. and why?
5. How are cylinders and prisms alike? How are they different?
0 614/dad 3k///8 Practice
A P P L l I: A ‘I’ I 0 N COINS The dimensions of various coins are given in the table below.
Coin Diameter Thickness
nickel 21.21 mm 1.95 mm
dime 17.91 mm 1.35 mm
quarter 24.26 mm 1.75 mm
Find the surface area of each coin. (EXAMPLE 1)
6. nickel 7. dime 8. quarter
Find the volume of each coin. (EXAMPLE 2)
9. nickel 10. dime 11. quarter
O Pratt/ce and App/y
Draw a net for the right cylinders shown below. Label the dimensions of
the net.
12. 13.
'\_
4 I5
5
O - .“4
- - connect
Homewmk Find the unknown value for a right cylinder with radius r, height h, and
Help Online surface area 5. Round your answers to the nearest tenth.
E2,‘_'Sj,§‘d‘Z'“'“"°°'“ 14. I = 5, ll = 4, 3 = ? 15. r = 4, ll = 15, 3 = ?
MGI H rk H I _
y.,,5,:T.,}':;:u.;gp 16. 1 = Ii = I, S= ? 17. r = 3-. ii = ? . S= /Z1
4 18.r-7,li- ?.S-550 19.r- ?,li-2.5-70st.
456 CHAPTER 1
CHALLENGE
CONNECTION
Find the unknown value for a right cylinder with radius r. height h, and
volume V. Give your answers in exact form.
21. r= -1. fl = I5. V = ?
23.r-8,fl- ? .V-l536
25.F- 7.‘ ,fl-9, V-803!
20. r=5. fI="l. l/= ?
22. r-2. !t- ?, V- IZII
24. r- ? ,1:-6, V-543:
26. '|'he surface area ofa cylinder is 200 cm’. The diameter is equal to the
height. Find the radius.
27. The volume ofa cylinder is 360:: mm‘ and the height is 10 mm. Find the
circumference of the base.
28. ‘\ semicircular cylinder is formed by cutting a solid cvlinder with a radius
ol'8 ft and height of IO ft in half along a diameter. Find the volume and
surface area of the semicircttlar cylinder.
29. How does doubling the height of a cylinder alfect the volume?
30. I low does doubling the radius ofa cylinder affect the volume?
31. How does doubling the height and radius of a cylinder affect the volume?
32. How does doubling the height and radius of a cylinder atlect the
surface area?
33. The volume ofa cylinder is equal to its surface area. Prove that the radius
and height must both be greater than 2.
34. MAXIMUMIMINIMUM A right cylinder has a volume of l6Jt culiic units. To
find the minimum possible surface area, first solve the volume equation
arr-'h = I631. for hand substitute the expression for it in the surface area
formula.
Graph this formula for surface area on a graphics calculator, using .\: for
the radius. (1 lint: Use a viewing window with O s x s It) and 0 s y s 200)
Use the trace function of the calculator to estimate the radius for a
cylinder with the minimum sttrface area. What is the height ofthe
cylinder? What is the surface area?
35. CULIUBAL CONNECTION: ASIA In ancient Mesopotamia, cylinder seals were
used to make impressions in clay talilets. These seals. which were shaped
like cylinders. had carved designs and were rolled on soft clay to create a
repeating pattern. Suppose that an archaeologist discovers an impression
from a cylinder seal that is 4.7 cm wide. W hat was the radius of the
cylinder seal?
LESSON 1:: surtmce AREA Anovot UME or cvtiruoens 457
APPLICATIONS
458 CHAPTER 1
36. MARINE BIOLOGY The Giant Ocean
Tank in Boston’s \lew England
Aquarium. shown at right. is a
cylinder that is 23 ft high and has
a volume of 2(l{J.()U0 gal. Find the
diameter of the tank.
(Note: 1 gal ss 0.13-1 ft‘)
37. PUBLIC HEALTH A scientist
researching the health risks of
cigars and filtered cigarettes
wishes to compare the amount
of tobacco in each. A cigarette
is a cylinder with a diameter of
().l6 in. and a length {without
the filter) of 2.56 in. A cigar is a I
cylinder with a diameter of 0.75
in. and .1 length of 7 in. How
many times more tobacco is , -
contained in the cigar than in
the filtered cigarette?
38. MANUFACTURING A processing plant needs storage tanks to hold at least
half :1 million gallons of waste water. How many cylindrical tanks must be
built to hold the water if each tank has a diameter of 50 ft and a height of
25 It? (Note: I ti‘ = 7.43 gal]
39. PRODUCT PACKAGING A ntanul'-acturcr is designing a can that will hold 6-'l
fluid ounces. or ll5.3 in.'‘, and that uses the least amount of materials.
Use the method described in Exercise 54 to find the can with the
minintum surface area.
Look Back
Copy each symbol. Draw all of the lines of symmetry and describe all
rotational symmetries of each symbol. (LESSON 3.1)
.3. §
40. ® 41. (2) 42. R
Find the surface area and volume of each solid. (LESSONS 7.2 AND 7.3)
44. right rectangular prism 45. cube
gj
7.5
10
46. right triangular prism
5 \ .13
- p’
12 ' X
47. regular square pyramid
£00k Bet/0;/a’
A P P L I I: A ‘I’ I 0 N CARPENIRY The cross section of the strongest
beam that can be cut from a cylindrical log is g
shown at right.
The diameter is divided into three equal segments, h
and ])€l'p(’.l1(‘llClllt1l‘ segments are drawn as shown.
l'he points where these segments intersect the circle
are the vertices of the beam.
win.
win.
48. Use the Pythagorean Theorem to write an
equation relating the quantities h. w, and d for
the shaded triangle at right.
49. Use the Pythagorean Theorem to write an
equation relating the quantities W. 11. and x for
the shaded triangle at right.
50. Use the Pythagorean Theorem to write an
equation relating the quantities h, II. and x for
the shaded triangle at right.
' r ; z / 51. Use the equations you found in Fxercises 48—S() to find the height. it. and
width. w. of the strongest beam that can be cut from a log with a diameter
of 18 inches. Round your answers to the nearest tenth.
“£0 \ _
NETS FDR OBUOUE CYLINDERS
.-\ net for the lateral surface of an oblique cylinder
has an interesting shape. Io examine this. construct 6..
an oblique cylinder from a right cylinder. ‘-.
° Create a right cylinder by rolling up a rectangle
of heavy paper. Tape the edqes together. Your
diameter should he at least 3 inches.
' Use a pencil to mark two parallel circles at an
angle to the bases. Cut along the circles to ~
form an oblique.
' Unroll the paper to see the net. What do you
notice about the sides of the net?
LESSON 1:: sunmce AREA Anovot UME or CYLINOERS 459
Surface Area and
Volume of Cones
' v I ‘ -. 3'5. .
: ,3 .‘ ' . ~ -; - T. ." j:
. 1.‘!
x V. ':
ea . 2
Objectives " I _,- -'
" In
0 Define and use the
formula lor the surlace
area of a cone. _
0 Define and use the _ |
formula for the volume The propenies a! cone: can be used to _ _ \3_
of a cone. model the physical properties alreal-world ____ 2-3 _._ ;j.:;__~;_
objects tlmthave approximately conic shapes. N , __,__..p. ‘ _. ‘ _‘— ‘ “— "
As at volcano erupts and deposits lava and ash over 21 period of time, it forms a
cone. Volcanic cones may be different shapes and sizes. depending on factors
such as the rate at which the lava and ash are deposited. how fist the lava
cools, etc.
A cone is a three—dimensional figure that
consists of a circular base and a curved ‘ —\.a9n9,(
lateral surface that connects the base to a |_m,,,g
single point not in the plane of the base. surface ~.. ‘_
called the vertex ._H _
‘W Altitude
The attitude of-.1 cone is the perpendicular
segment from the vertex to the plane of the
base. The height of the cone is the length V ‘B399
of the altitude.
P.
if the altitude of at cone intersects the base oi the cone at its center, the cone is
a right cone. if not. it is an oblique cone.
Right cone Oblique cone
460 CHAPTER 1
lust as a cylinder resembles .1 prism. a cone resembles .1 pyramid. As the
number of sides of the base ol -.1 regular pyramid increases. the figure becomes
more and more like a right cone. The illustrations below suggest that the
formulas for the surface areas and volumes of prisms and cylinders are similar.
C ---- “.3 \'’.;m 2
The Surface Area of a Right Cone
' I
The Surface Area of a Right Cone
0 I D "I he surtace area or a right cone IS found
no special was by using a method similar to the one used
for .1 right pyramid. The net for a right
cone includes the circular base and the
flattened lateral surface. which becomes a ‘\
portion of a circle known as :1 sector. The \
1'.‘
Slant height. C Base
I.’
radius, t’. of the sector is the slant height
Lateral surface
of the cone. - '
__ E = 8 The surface area of a right cone can be
\ ' found by adding the area or the lateral
- surface and the area of the base. Use the
steps below to find the surface area of the
cone at left.
1. The lateral surface ofa right cone 4 C'r°U"1'_°'°"°°-0
r- 3 occupies a part of a circle. The arc A ’ tsma" ewe)
lrom A to B matches the -
circtnnterence of the base of the F _—'L’°'r'g‘£ ‘::;'°
cone. The length, c. of this arc is __ 0 ' 6
equal to the circumference of the Lateral surface
base. Find c for the given cone by B
using the radius of the base [r = 3). “"‘- fiircumfer|Br;ce. C
arge clrc 8
2. Find C. the circumference of the larger
circle. for the given cone by using the
slant height [6 = 8) as the radius.
3. Divide c by C. |'his number tells you what fractional part the lateral
surface occupies in the larger circle.
4. Find the area of the larger circle for the given cone by using the slant
height" (F = 8]. Multiply this number by the fraction from Step 3. The
result is the lateral area, L. of the cone.
CHECKPOINT V 5. Find B, the area ot the base, for the given cone by using the r.1dius
[r = 3). Add this to the lateral area. L. of the cone from Step 4. What
does your answer represent?
LESSON 1.5 SURFACE AREA AND VOLUME as cones 461
E X A M P I. E oFind the surface area ofa right cone with the indicated measurements.
80 LUTI ON
‘I he circumference of the base is c = 210 = Mn.
The lateral area is a sector of a circular region
with circumference C = 2m''' = 501:.
.4
'l he portion of the circul;
‘ ‘ If
1 1 '~ L = j =
lltc sector is C 50” I
Calculate the area ofthe sector ( lateral area].
r region occupied by
._,.|-4
its-'3 = 2251:
7. - 225:: = 1051:
I:
L =
Calculate the base area and add the lateral area.
b’ = rt!” = -191:
B+ l, = 4% + IDSII: =l5-11'! = 485.8
._Jon-n-n--nu--nu-u
no special tools
462 CHAPTER 7
CHECKPOINT /
' Z
The Surface Area Formula for a Right Cone
way and save vour work in vour nott-:l)00k.
Fxplain.
1. l-ollow the steps In l;xample I above and ttt z'\CIl\-ll}-' I on the previous
page to lind the surface area of a general right cone. That is. use the
variables r, it. and E instead of numerical measures. Your answer will be
a formula for the surface area of a right cone.
2. Use algebra to simplify vottr formttla. Show your steps in an organized
3. Compare vuur results with the formula given ht-:l0w. Are they the saute?
radius r, and slant height I‘ is
Surface Area of a Right Cone
S=L+B or S=r[rt‘+Jtr3.
The surface area. 5, ol a right cone with lateral area I . base of area B.
7.5.1
The Volume of a cone
in Lesson 7.3. you lound that a pyramid
had one-third of the area ofa prism with -
a congruent base and equal height. Now Ԥ
imagine performing a similar experiment
wilh a cone and a cylinder. The result ol
the e\'periment should be the s4me—you
can try it—he'cause cones and cylinders
are like many—sided pyramids and prisms.
l his similarity leads to the formula for the volume of a cone.
Volume of a Cone
'[ he volume. V, of a cone with radius r. height h, and base area B is
V = %Bh or v = %Jtr*’h. 7.5.2
cnt1'tcAL THINKING is the formula for the volume of an oblique cone the same as the formula for
the volume of a right cone? What principle justifies your answer? lllttstrate
your answer with sketches.
E X A M P I. E A volcanologist is studying a violent eruption ol'a eone—shaped volcano. The
original volcanic cone had a radius of 5 miles and a height of 2 miles. The
eruption removed a <:one—sh-aped area from the top olithe volcano. This cone
had a radius of 1 mile and a height olé mile. What percent of the total
volume of the original volcano was removed by the eruption?
A‘P lc ION
GEOLOGY
. SOLUTION
Find the volume of the original volcano.
v = l‘m'-‘I. = ls:5’)(2) = 52.4 cubic miles
Find the volume of the destroyed cone.
v - %nr’Ii - %[I3](0.5] -- 0.52 cubic miles
Find the percent of the original volcano
removed by the eruption.
(LS2 -
“J0 3'
LESSON 1.5 SURFACE AREA AND VOLUME 0; comes 463
Exemses
. Comma»/care
1. Explain how to find the surface area of a right wne.
2. Explain how to Find the volume of a right Cone.
3. In a right cone, which is longer, the altitude or the slant height? Explain
your reasoning.
4. Slant height is not defined for an oblique cone. Explain why.
5. What happens to the volume of a cone if the radius is doubled? if the
height is doubled? if both are doubled?
0 fill/ded SK’///8 Practice
6. The diagram below represents a net for a right eone. Find the surf-.1ee area
of the cone. (ACTIVITY 1)
v‘\ ‘*5
f=13*"’
7. Find the surface area of a right cone with the measures shown below.
(EXAMPLE 1)
_ \8
8. A formula for the surface area of a right cone is
3 (surface area) = L (lateral area] + B (base area].
Explain how to rewrite the formula by sulistituting values for L and B in
terms of 1:, r, and t’. where r is the radius of the base of the cone and t‘ is
the slant height of the cone. (ACTIVITY 2)
9. Find the volume of the oblique Lune shown below. (EXAMPLE 2)
27
464 cum-Vren 1
D lnhrnctconned
Homework
Help Online
Go To. 9o.l'urw.com
Keyword:
MG! Homework Huh
Io: Exercises 10-15,
18-29
0 Practice dlld 74,20/y
Find the surface area of each right cone.
10.
13.
_ 5cm 11.
E /’
E1 4cm
' ' ‘K
h
3cm
14.
1.3
u
n
u
I
:<—3
u
n
71.
10 cm
/
-8 cm
.‘..
6cm
12.
15.
2 in.
.4";
1.6 in.
1.2 in.
16. A right cone has a radius of .* in. and a height oi 4 in. \'\"l1.at is the slant
height of the cone?
17. A right cone has. a radius of 3 in. and a height ol'6 in. What is the slant
height of the cone?
Find the surface area of each right cone.
‘I8.
21.
Find the volume of each cone.
24.
_ 19.
‘-— -24
\-
1
,\ 22.
;-:23
’ 20
25.
-~-'- — 13.3
n"V:~15o
: an
‘*9
f-— -5.0
:n. .
~1.1
E-— -45
-.1___,§_\_‘7
20.
23.
26.
‘I2
fJ__ _.__
\‘1.6
33.2
. .. I.-
‘6.0
LESSON 7.5 SURFACE AREA AND 'J0tUME OF (ZONES 465
CONNECTIONS
466 CHAPTER 1
27. 28. . 29. .
._. _42 ‘-65
.3‘ _ ___i1 . ___rt
‘21 ‘*1: 9
30. ll‘tri-anguar region A BC below is rotated in three dimensions about
(—} _ _ _ _
AB. what solid hgure is formed? Find its surface area.
C
20
A 30 B
31. A right triangle has sltles of IO, 24. and 26. Rotate the triangle about each
leg. and lind the volume of the figures formed.
32. A regular square |'.l_Vl'ElTllLl is inscribed in a right cone of the same height.
l'he radius of the base and the height of the cone are each 10 cm. What is
the ratio of the volume of the pyramid to the volume of the cone?
33. A right cone has a radius of 5 in. and a surface area of 180 in.’ What is the
slant height of the cone?
34. Find the surface area ot'a right cone whose base area is 251: cm’ and
whose height is I3 cm.
35. An oblique cone has a volume ot I000 cm‘ and a height of IO cm. What is
the radius of the cone?
MAXIMUMIMINIMUM A right cone has a slant height of 10.What are the
radius and height of a cone with the maximum volume? Copy and
complete the chart for Exercises 36-42.
Radius Height Volume
1 V.-._T9 %rrx1’x JST9 ::1o.4
2 V.-E 36. 7 10
3 37. 2 33. 7 "E
4 39. ? 40. 7
5 41. 2 42. 7 °'
TECHNOLOGY Use a graphics calculator and the information from
Exercises 36-42 to graph the values of the radius on the x-axis and the
values of the volume on the y-axis. Set the viewing window so that
Ymax is at least 410.Trace the graph to find the following:
43. the radius (::-value] that produces the largest volume
44. the largest volume
A P P L I c A T I 0 N S 45. RECREATION An oblique conical tower is to be built at
an amusement park, as shown in the architect's sketch
below. l'he vertex is to be directly above the edge of
the circular base. The tower is l50 ft tall, and the
diameter of the base is 60 It. What is the volume ol
the cone’!
C
.,,‘ \\ _
l V ‘ ‘ l “ an "
c2‘ .1 \ ’- J’ I
_/‘ N.‘ \‘ x .
I H .
E - -r ‘us . :.‘_lr-;g_ 1 "
- 4‘-I" I " . ._ 0" g
7.5 cm
I
\ o
,_.‘I.2cm
46. SMALL BUSINESS A ' .
businesswoman is selecting \ '
glasses for her new ice—cre.nn
parlor. Estimate the volumes T
of the two glasses shown l 18-4 cm
at right. 145 cm
_r_ 1
',__ -
MANUFACTURING Cone-shaped paper cups can be manufactured from
pattems shaped like sectors of a circle.The figures below show two
pattems. The first has a straight angle (‘l80°l.The second has an angle
of 120°. Use the information provided in the diagrams for Exercises
47-49.
C ll A L L E N G E 47. ll" each sector has :1 radius of6 cm. what will be the area of each sector?
I Hint: What fraction ol'the circle is included in the sector?)
48. Find the volume of the cup formed by the sector with the straight angle.
(Hint: The length of the arc of the sector is equal to the ciruttnlerence of
the base of the cone.)
SS 49. Find the volume of the cup formed by the sector with a I20“ angle.
6 cm ,-
120'
6 cm
I I‘
, ~ —_ 21/
q‘-."'7" 6 cm h 6 cm
LESSON 7.5 SURFACE AREA AND 'J0l.UME OF (ZONES 467
CONNECTION
APPLICATION
468 CHAPTER 1
L00»? Back
Refer to the graph below for Exercises 50 and 51. (LESSON 3.8)
50. If is perpendicular to what
4%’
is the slope of AB?
_ _ (—> _
51. ll is parallel to CD, what IS the
slope of
52. Prove that a diagonal divides a parallelogram into two congruent triangles.
(LESSON 4.6)
53. Find the distance between (2,4) and (-5, 8) in a coordinate plane.
(LESSON 5.6)
54. MAXIMUMIMINIMUM A manufacturing
company makes cardboarcl lmxes of v-.1r_ving .
sires by cutting out square corners from
rectangular sheets of eardbo-.1rd that are
I2 in. wide and I8 in. long. The cardlmard
is then folded to form a box. It"-a customer
wants a box with the greatest possible
volume for the given sheet ofcardlaoard,
what should be the dimensions of the
squares that are cut from the corners? What
will be the dimensions of the box? What
will be the volume of the box?
(LESSON 7.1)
£00k Bet/0;/d
55. SCALE MODELS An “I I0 gauge" model train engine is #of the size of a
real train engine. If the model’s width is 1.5 in. and its length is 5.5 in.,
what is the length ofthe real engine?
Objectives
0 Define and use the
lormula for the surtace
area of a sphere.
0 Detine and use the
formula for the volume
oi a sphere.
How much cloth do you drink is needed to
make a not-alr balloon? You can use the formula
for a sphere to estimate the balloons surface area.
Surface Area and
Volume of Spheres
The brrlloolr is beilrg inflated by fmrlring
hot air in lo the cloth “envelope,”
The Volume of a Sphere
A sphere is the set of all points in space that are the same distance, r, from a
given point known as the center ol the sphere. To find the formula for the
volume of a sphere, we first show that a sphere has the same volume as a
cylinder with a double cone cut out of it. Then, by using the formulas for
cones and cylinders. we derive the formula for the volume of each figure. The
discussion that follows begins with a numerical calculation before moving on
to the general case.
e'''''''_
g___
: : _ j_ d
The height and diameter of ' ' |
the cylinder are the same ‘
as the sphere '5 diameter.
fl
Suppose that the sphere has a diameter of 50 units and that the cylinder has a
height and diameter of 50 units. Assume that a blue plane cuts through the
sphere and the cylinder I0 units above their centers. You can prove that the
two red cross sections—the circular region in the sphere and the annulus l the
ring-shaped figure) in the cvlindt-:r—are both equal to SZSJI square units.
djdjp I1 jdjp
LESSON 7.6 SURFACE AREA AND VOLUME OF SPHERES 469
There are three red right triangles in the figure below: one in the sphere and
two in the cylinder with the cones removed. The triangle in the sphere can be
solved lor b, the radius of the disc. ‘I he two triangles in the cylinder are
isosceles and have known side lengths, as you can convince yourself by studying
the figtt re. ( The blue cutting plane is parallel to the bases of the hollow cones in
the cylinder.) The inlormation from the triangles is used to calculate the areas
of the cross sections.
25 - 4- 25-
'“ 10
‘ Q‘?
ln the cylinder, the acute b /gt ‘
angles of the large red L l
triangle are cangment. You __ 25 - _ ‘ 25
can show that the acute """ l 10l ‘\—- 25 I‘! 10 . '
angles of the small triangle '
are congruent, as well.
L
Area of the circle in the sphere Area of the annulus
be + I0’ - 25' area of large circle — area of small circle
ll-'l+ I00-625 -1252-3103
tr’ = 525 = nus? — 10°)
1, = = «[625 — I00)
2 - .1: 525
are“ ' Elf‘ - area = Slin gquare units
= 5253. square units
PROOF Thus. the areas are equal. Next. generalize the procedure to get the formulas
for £1 sphere and a cylinder of radius r. I et r be the radius of the sphere and
y be the distance from the centers of the ligures to the blue cutting plane.
Area of the circle in the sphere Area of the annulus
Zr’ + y1 = F’ area of large circle — area of small circle
1 ‘D ‘I I "I
lr=r—y‘ =:rr*—:ry‘
. ._ ,-‘2 ,v_2_ ‘ " . ._ 2 7)
are.1—7t\.r—} —J'E[f"—y') area—7tlr—y‘
This shows that the formulas are true for all planes parallel to the hases ol
each figure and for all values of y.
.113)
The corresponding I
cross sections have ’
equal areas.
Therelbre, the conditions of Cavalieri's Principle are satisfied. The volume ol
the sphere equals the volume of the cylinder with the double cones removed.
l-"(spltercl = l-’{cylinder] — Vlcones)
Wsphere] - :itr’(2r) — 2(%Jt.")[r]
= 2.-tr‘ — ism ‘
- .-:i'II!'l
470 CHAPTER 1
CRITICAL THINKING
Volume of a Sphere
The volume, V. ofa sphere with radius r is
V - itltr“.
; 7.6.1
When the cutting plane in the proof of the volume formula cuts through the
center oi the sphere and the center of the cylinder, what happens to the
annulus? How does this affect the calculations? Explain.
E X A M P I. E The envelope of -.1 hot—-air balloon has a radius of 27 teet when fully inflated.
Approximately how inany cubic feet of hot air can it hold?
- P I b N
CARTOGRAPHY
O SOLUTION
V = énr‘
- i$n.(27)-‘
- ét i9.os3)ar
i6.2«MJr cubic feet -= 32,433 cubic feet
The Surface Area
In previous lessons. you analyzed
the stirt-ace areas of three-
dimensional tigures by unfolding
them to form a net on a flat
surface. But, as mnpmakers know,
a sphere cannot be unfolded
smoothly onto a Hat stirface.
The most common map of the
world uses a Mercator proiection
of Earth's surface onto a flat
plane. On this kind of map, the
landmasses near the North and
South Poles. such as Greenland
and Antartic-.1. itppcur to be
much larger in relation to other
landm-asses than they actually are.
l he formula for the surface area
of a sphere can nevertheless be
derived by using some clever
techniques.
of a Sphere
i’ Z" I 1'
\ -- 4
’ .
1. g. ' 1
‘A ,' - (' 5
. \
‘Utx
This map is n i\-fermmr proiet"rion. You
will learn more about prqiecririg n splxere
(mm a flm silrfnte in Lesson l M‘.
LESSON 7.6 SURFACE AREA AND VOLUME or SPHERES 471
To derive the formula for the
surface area of a sphere, begin with
an approximation. imagine the
surt'-ace ofa sphere as a large number
of polygons. as in the geodesic dome
in the photo at right. the smaller
these polygons are. the more closely -10
they approximate the surface ofa ,. 7: — - —
sphere.
Consider each polygon to be the 3,5‘: I
base of a pyramid with its vertex i
at the center of the sphere. The " "
volumes of these pvramids added / ‘
together will appro.\'imate the
volume oi the sphere. The height :(,_t\ .
of each pyramid is the radius of _ \ F’ '
the sphere. Therefore. the volume ‘
ofeaeh pvramid is %b’r. where
b‘ is the area of the base of the
pyramid and r is the radius of D0m,;‘.,. Md“, M“,
the sphere.
Volume of a sphere as ';B.r + '.l;B_>T + - - - + —;—B,_.r
~l,'r[b'.+B_-+---+b',..)
If the total area of the bases of the
pyramids is assumed to equal the
surface area of the sphere. S. then
the volume, V, of the sphere can be
written as
The larger the number
of pyramids, the closer
the approximation will V _
be to the actual volume }
ofthe sphere. The solve for 5 .0 get \
approximation is said to 1 ‘I, R _____,_,,.-
be exact "in the limit.” - 7
r[S). -—— """" " " "“"--—-.
.__,_,|_
\
\
I
You now have a formula for the surface
area ofa sphere in terms of its volume.
Now substitute in the formula for
volume from the previous page.
31/
3-T
I’
= -111’!
Surface Area of a Sphere
The surface area. S, of a sphere with raditts r is
S = 4.-cr’. 1.62
472 CHAPTER 1
E X A M P L E The envelope of a hot—-air balloon is 51
feet in diameter when inflated. The Cost
A _ P ‘C '0 N I ofthe fabric used to make the envelope
is St .31 per square foot. Estimate the total
HOT-AIR BALLOONING
cost of the fabric for the balloon envelope.
0 SOLUTION
First estimate the surface area of the
inflated balloon envelope. The balloon is
approximately a sphere with a diameter
of 5-1 feet. so the radius is 27 feet.
.5 = 41:1’:
= =t1r{27]3
= 4( 72931:.
= 291611: ss 9160.9 square feet
l\ow multiply‘ the surface area of the
fabric by the cost per square foot to
find the approximate cost of the fabric.
9160.9 square feet x $l.3l per square foot s= 3112.000
Exercises
. Com;//m/rate
1. How does the formula for the surface area of a sphere with a radius of r
relate to the formula for the area ofa circle with a radius of r?
2. lf the area of a circle is approximately 39 ftz, what is the surface area of a
sphere with the same radius as the circle? Explain your answer.
‘ 3. What happens to the area ofa circle when the radius is doubled? when it is
tripled?
ti 4. What happens to the surface area of a sphere when the radius is doubled?
. 1 when it is tripled?
5. W hat happens to the volume of a sphere when the radius is doubled?
when it is tripled?
0 6://'ded.Sk///3 P/’d6‘t/6'5
6. Find the approximate volume ofa sphere that has -a radius of l0 tt. Round
your answer to the nearest whole number. (EXAMPLE 1)
7. Find the surface area ofa sphere that has a diameter of IS fL Find the cost
of constructing the sphere if the cost for materials and labor is $1.50 per
square foot of surface area. Round your answer to the nearest whole dollar.
(EXAMPLE 2;
LESSON 7.6 sunmce AREA AND VOLUME or SPHERE5 473
llh- rnctoonnect ,Z,3‘
Homework
Help Online
Go To: go.hrw.com
Keyword:
MG! llornoworlt Help
lot Exercises 8-3|
Area of cross section, A
CHALLENGE
APPLICATIONS
474 CHAPTER 1
P/’d6‘t'IZ‘6’ dlid 34,0;/y
In Exercises 8-19, find the surface area and volume of each sphere.
where r is the radius of the sphere and d is the diameter. Express your
answers in two ways: (a) as an exact answer in terms of It, and lb) as an
approximate answer rounded to the nearest hundredth
8.r=4 9. r=8 10. r=4l
11. r= 33 12. r= I3.-ti 13. r= I222
14. d= I8 15. d: 16 16. d: 22._’»l
17. d: H.418 18. 1': l2.33 19. r= 99.98
In Exercises 20-25, find the area and volume of each sphere with the
given radius or diameter. Give exact answers in terms of 1: and a
variable.
20. r=x 21. r= 2y 22. d= tzx
23.rl==ty 24.:-==2‘-' 25.:-=4;-'
In Exercises 26-31. find the surface area of the sphere at left based on
the area, A, of a cross section through its center. (Hint: See Exercise 1.)
26. A = 225 27. A = 125 28. A = 32.30
29. .4: 11.22 30. A = l61t 31. A = 22_'m:
32. What is the volume of the largest
ball that will fit into .1 cubical box
with edges of 12 in.?
33. A cube and .1 sphere both have -.1
volume of I000 cubic units. What
are their surface areas?
34. A cube and a sphere both have -.1
surface area of 864 squa re units.
What are their volumes?
35. The ligures shown at right are a
hemisphere, i] right circular cone,
and .1 right circular cylinder. Each
has the same volume. and each has —
a base with a radius ol‘ 10 in. Find
the atltitutle of each.
’ .4
Radius of bases = to ih.
In Exercises 36 and 37.
round your answers to the
nearest tenth.
36. SPORTS Find the surface F’ ‘*3-5 i"- . >' '_ 5;?
area and volume of the ' ' 5: _ 5;}
softliall at right. ,_—2-9 '"-:7 ‘J
: I’
37. SPORTS Find the surface S
area and volume of the "- ____ "
baseball at right. soflbsn basebau
APPLICATIONS
CHALLENGE
38. SPORTS A can of tennis balls has 3 balls stacked tightly in it. The
appro\'imate height of the stacked balls and of the interior of the can
is 9 in. How much space to do the tennis balls occupy! Approximately
what percent of the space inside the can do the balls occupy? Round your
answers to the nearest tenth.
39. GEOGRAPHY ljartlfs radius is approximately 4000 mi. lftwo—thirds oi
Earth's surl'-ace is covered by water and one—third is land. estimate the land
area on Earth.
FOOD Hosea buys an ice-cream cone.The ice cream is a sphere with a
radius of 1.25 in.The cone has a height of 8 in. and a diameter of 2.5 in.
Round your answers for Exercises 40-42 to the nearest hundredth.
40. What is the volume of the ice cream?
41. What is the volume of the cone!
42. ll" the ice cream sits in the cone so
that it forms a hemisphere [a half ol‘
a sphere) above the rim of the cone.
what is the total surface area of the
hemisphere oi" ice cream and the cone?
43. METALWORK A metal sculptor has a
solid bronze sphere with a radius of
IO in. She melts the sphere and casts a
hollow sphere with an inner radius of
10 in. What is the thickness of the
shell of the hollow sphere?
L001? Bdtk
Find the surface area of each figure. (LESSONS 7.2, 7.4, AND 7.5)
44. right rectangular prism: E‘ = 3 in.. w: l0 in.. it = 5 in.
45. right cone: r= 15 cm. slant height = 45 mi
46. right cylinder: r= 9 m. It = 10 In
Find the volume of each figure. (LESSONS 7.3. 7.4, AND 7.5)
41. rectangular pyramid: base length = l5 ti, base width = 7 ft, altitude = l2 ft
48. right cone: r: 5 in.. It = ID in.
49. oblitpte cylinder: r = 7.5 m, It = 20 m
L001? Bet/and
50. What is the ratio of the volume of a sphere to the surface area of the same
sphere? Express your answer in terms of the radius. r. oi" the sphere.
51. Write a formula for the volume ol .1 sphere in terms of its surlace area. S.
52. If the radius of a sphere is 4.5 units, by what number can vou multiplv the
surface area of the sphere to lind the volume?
53. A sphere with a diameter of 2r is contained in a cube with edges of lr.
What is the ratio of the volume olithe cnbe to the volume of the sphere?
LESSON 7.6 suarace AREA AND VOLUME or SPHERE5 475
M _,.;, '1: R e s U 3 E.
of K ng Tut 5 Tomb
GEM-STUDDED RELICS AJIAZE EXPLORERS
Special (fable to the New York Times
LOt\[>ON.Nov.30. 1-2zz—The Cairo correspondent of the London Times.
in a dispatch to his paper, describes how Lord Carnan-‘on and
Howard Carter unearthed below the tomb of Ramses Vl. near Luxor,
two rooms containing the funeral paraphernalia of King
Tutankhamen, who reigned about i350 b.c.
A sealed outer door was carefully opened. then a way v.-as cleared
down some si\'teen steps and along a passage ofabout twenty-live
—-— feet. A door to the chambers was found to be sealed as the outer door
an had been and as on the outer door. there were traces of re-closing.
l \
'3 E5 The excitement ol‘ unearthing the tomb was followed by three
years of hard work. Unpacking a bo\' ol‘ priceless relics took three
painstaking weeks. ‘I he items. which had been stored for thousands of
years. could have been easily damaged if not handled with great care.
A crumpled robe in Box 21 presented a dilemma for 1 toward Carter.
. Should he preserve the garment as is and lose the chance to learn its
'6.‘ -‘~‘.'-" full design? Or should he handle it and sacrifice the cloth in order to
(H ‘_,.* examine the complete robe?
Excerpt from Howard Carter’s notes _ -
. . . by sacrificing the cloth. picking it carefully away piece by
to, - piece. we could recover, as a rule, the whole scheme of decoration. ./
‘ Later. in the museum. it will be posuible to make a new garment
of the exact size, to which the original ornamentation—head-
work, gold Flt-'qllll1.‘l, or whatever it may he-can be applied.
Restorations of thin kind will be far more useful. and have much
.- greater archaeological value. than a few irregularly shaped pieces ' "-1'
.. - - of cloth and a collection of loose heads: and sequlnei. _~_"_,_
.)€\ -"‘]- . i. . a I . -- - . I _ -
: ,;.~' -__ Men build a Sin Ie track railway through the _- e " ,
1* _ . Valley of Kin sfor transporting cases of relics ; - V
L x _' from Tutank amen’s tomb in Luxor,1922. ' ' .2‘ -' -— __ ,,- . ‘ -
t - . . "~ - I - . 1-: \
' ",‘) ‘ ¢’'._ _ .. 1 _ . \ A - ' \
- ""'Z?3+ '~':}--. "’ i-fix'.i;T‘-53.‘. ‘M4 :‘.- ‘. ' ' “ I" ‘ I... ** l\
‘_t ' .. . \ L '1-; 1 _ _- at _ _‘ -II
4.7.6 we J». u» ~ - ‘* ====''='‘‘‘=—e -e - »\
ugfmfi _ _."._fi, \'\ -..-‘W3 .*-‘gt ¢"‘__‘____.v -- "fl. \ I. I -5 -
I-‘.._. . ‘'_J“ .-l -1' _v _" -_V.’_, ‘ - ' — ‘ 1 ~ ’- ' - 3 ‘
‘uh
~"=.r. - ‘F«:'..'*2- «-"'~“'“ » . -'.‘~ -' a . .
~~= _ .k‘i?-'.:_g’-.- 3?! t.-ei. ' ~ ,1 t
I .‘-‘ .‘ if‘ I‘ I . ‘f 1-‘ \.t
H . (4,, - $"§_ . .
«.-.-:.«r’ _ . ,._- - .1 -.
-. ’. _ g_ ‘X’ ah K
i‘ l l‘ ‘ «"5
"4 We
a . ' ° I """.-gag
_ u ‘I . __ _
~ 5 ' -
Coo erative Learnin l a’ . Ti
_ -.- ,5 .
*8 I
The robe in Box 2| had the shape of the lateral . , - f -
surface ofa cylindrical shape. which was laid flat to ._ _ \ i
form two l'L‘ClillIglll&ll' layers. Bv estimating the height l 3; _ -
and width of the rectangles. Howard Carter was able (at. .1, }‘_‘h'
to determine the size of the garment. The robe was , -_ . ' ' 1* ' 2‘ ,..a‘-]
co» ered by n repeating pattern of glass beads and _-:5" ¢
gold sequins. with :1 lower band of beaded fringe. or * fl‘ ' - r
pendant strings. in the following \ctivity, some ofthe . , _ _.i__‘ ’ '
data has been removed from his notes. _ y ’ ‘ . .» . \‘ .' ‘v
'( =4: ".7. "es . -. ‘*4. g
:fi,_\_r‘ A, "'A\ ‘ '_- .1; Quit '_ ,'
" - ‘= ‘ x~ "fa-0"’
. ‘ '- ‘ - .¢;'-'*"r\V,'
We know the distance between the pendant strings of the lower band to ' .. ._" 1’-‘E ,_ V— ."_‘ '.“.
have averaged 8 mm. There are 137 of these pemlztnts. Therefore the _‘ -..;_‘..a‘ $‘_4',‘:'j" . '5...‘
circumference of the lower part. of the ganm-nt mmt. have been - ' '-‘. , 7' 4,: ‘X; ‘_’-.'{-'=?‘‘
. . . r u . o i‘ . ‘ I .1
f which would make one width about f . - .i,.{ .-‘- ,o_ “ '5: ’_'l
-'v':"‘, ‘ ‘E’,-_,.i:}.{,l__a \"“(1
Now there are 305-! gold steqnin-1. three aeqtunca in the pattent require 9 - - '. , ‘ ‘D ,~‘ _ I‘, ‘
square centimetres. Therefore total area of network = ? . As Y” Q’ 519'
clrctunference was ? , this: would make the height work out at ,
about ? .
Thus size of garment would work out at about ? X ? . 1, I
5. u T l
1. Determine the missing information in llov.-.1rd \ - - - -‘ i
. 1 ‘ - - _ .1, I’ It - _' ‘H l
Carters notes. and explain how you lound . , _ l ‘ K _ _ 1 _I_ _
each value. lnclude units in your answer. You _ _ '3' ,- ' ' '
may wish to convert all the me-asurentents to _ _ ~* .- ‘ \
the same units lirst. .I ' \ ‘t ‘ \
2. Use a tape me21.~.ure or ruler and string to f7 ‘Y i \
compare the size of the robe to that ol‘ ., ‘\, ~
your own clothes. How do they compare? - "\
K - \ '
British archeologist and Egyptol ist ~
Howard Carter (left) and Callem er
_ (right) opening the entrance to the fourth
.. ' ' ' ,_ chamber of Tutankhamen’s tomb, I 923. .
' ‘ .-«A - ‘ “F
§ K ' .
- , -I
.. _ ‘ _
' - . I
I. - xl ‘ I
"' _I ‘I I I
‘ ‘I '4 I .
- .::.;
‘_ \ CHAPTER 7 EYE‘.-.'n'NESS MATH 477
" “F .5 V. C‘ ‘ v
v ~ ,4. .. -
Three-Dimensional
Symmetry
Objectives
0 Oetine venous
transiurmatnons m ‘
mrae-dimensional
space. .
o Solve problems by : '- .. ~ ._
using transtormations . ‘ _. " I
in three-dimensional . " ‘ ’
space. '
I so far, me definitions '~.
olsynunelry have been
limited to a plane. Bur '3
three-dimensional figures.
like the tiger in the photo. "
may also have symmetry.
Tiger.’ Ti_;,{c'r.' burning bright
In t!I(?]orc’SI.~' ofme m'ghI.
I-1-‘hm immormi hand or eye
Cr)uMfrmm.' rhyferrrful symmetry?
—Wr'Iham Blrrkr’
Three-Dimensional Reflections
A three dimensional figure may
be rcflcclcd across a plane, just ___
as a two-dimensional figure can
be reflected across a line. What ‘
happens to each point in the
preimage of .1 figure as .1 result
of a rellection across a plane?
You will irwc-s1ig:1tc this
question in Activity 1.
478 CHAPTER 1
-- I Partl
no snecialtools 1. Graph the poim At t, I. I) in a three-dimensional 2
coordinate space. Use dashed lines to make the
location of the point in space evident. A“, L “\
2. Multiply the x-coordinate of point A by —l
and graph the resulting point. Label the _, +y
new point A’. ;------- '
3. Point A’ is the image of point A rellectcd x’
across a plane. Name this plane. If you
connect points A and A’ to liorm AA’.
what is the relationship between this segment
and the plane of reflection?
4. Write your definition For the reflection of
a point across a plane in a three—dimensional
coordinate space.
R
5. Experitnent with other reflections oli point A.
What happens if you multiply the x-coordinates
by —l? the z—coordinatcs?
6. Now study the rellection of an entire segment,
such as /71 across -.1 plane. (For example,
multiply the x-coordinates 0|" points A and
B by —l and connect the resulting points.)
Experiment with the reflections of other _____ __
ligurcs. such as cubes. I
z
AH. ‘|.1l\i_N
I
Bl1.1.0l
CHECKPOINT V 7. Write your own detinition for the reflection
ol a figure in a three-dimensional coordinate
space across a plane.
Part II
1. Fill in the table below. Use the terms fiom. lmch. left, right. mp. and
bottom to describe the octant oli a point.
Coordinates i
Octant of image of image
Reflection across the xy-plane front—right-bottom (2. 3, -4-)-
At2. 3. 4| Reflection across the xz—pIane ? ?
Reflection across the yz-plane ? ?
Reflection across the lry-plane ? ?
Bl-4, 5. 6) Reflection across the x2-plane ? I
Reflection across the yz-plane ? ?
CHECKPOINT ./ 2. Generali/e your findings for point P(x. y. z].
a. Vt hat are the coordinates of the reflection of P across the xjl-plane?
b. What are the coordinates of the reflection ol P across the xz—plane?
c. What are the coordinates of the reflection ot‘ P across the yz—plane?
LESSON 71 THREE-DIMENSIONAL smmernv 479
CHECKPOINT ./ The tln-cc—dimensional figures below have reflectional svnnnetry. Explain why.
Where is the reflection “mirror" in each case? Create vour own definition of
reflectional symmetry in space. (Use the earlier definition of reflectional
symmetry in a plane as a model.)
L! r
_ _,... . .|
V.‘ ‘ ‘ 3"h:\n' _,‘- ‘A '1".
‘"2 I has-t.-9.1.‘ '-' *1 xv -1
I ‘ l I i ' _ ' 1
. é a 3 .3 (‘Vii |' a i‘ ii
"" I. “‘ ' l ' . .~
. .' 9 "._ ET” I‘ ' 1'.”
“ —*-..E_ ‘ '1» \ .-
'”!;§ T ' ‘ 5 p‘ L it
_ -ti*_ I” Q‘ T“ 1 . 1;
- —— .n -1
a v. mm ~
1 §" .
1 r _-
I I _ _
Rotations In Coordinate Space
~ - I 1. Graph E in a three—dimensional
no spam. [0015 coordinate space. Use dashed lines 2
to make the location of the segment
evident. A(—1, 1. 1l
2. Multiply the x- and 1'-coordinates of
points A and B by —l and graph the EH’ 1' 0)
resulting points. A’ and B'. Connect
the new points to form /l’B'.
j _ _ x’
3. A'B' is a rotation image oi AB about
the z-axis. About what point on the
z—axis has point t been rotated?
4. ltnagine the segment rotating about I
the z-axis. as suggested by the picture. ‘
Does it seem to you that each of the I
rotation images of point A is in the 1_
same plane? of point B? What is the
relationship between these planes and
the z—axis?
CHECKPOINT ./ 5. Write your own definition of the
rotation ofa figure about an axis in
coordinate space.
480 CHAPTER 7
CHECKPOINT
./ The three—dimensional figures below have rotational symmetry. Explain wlt)-'.
What is the axis oi rotation in each case? Create your own definition of
rotational symmetry in space. [Use the earlier definition of rotational
symmetry in the plane as a model.)
E X A M P L E ‘You are givenfiwitli endpoints
TRY THIS
Revolutions in Coordinate Space
ll‘ you rotate a figure about an axis. a spatial figure is tormed. The spatial figure
is the set of points through which the original figure passes in one complete
revolution.
_ , Bio. 5, 5}
.4(0. 3. O] and BIO, 5, 5). Sketch.
describe. and give the dimensions
of the figure that results when
a. E is rotated about the z—axis.
Am. 5. Ol
b. E is rotated almut the y-axis.
O SOLUTION
i_--
:-y
the lateral surface of a cylinder with a
radius of 5 and height of 5.
y-axis, {arming a circular
{V7}? is rotated about the z-axis, forming
region With 3 radius 0! 5.
Describe or sketch the spatial
figure that would be formed
by rotating each of these plane
figures about the red line.
LESSON 77 THREE-DIMENSIONAL swmernv 481
Exemses
. Comma»/care
1. Describe the similarities and differences l)':‘l1\5":‘E€l1 three-dimensional
rellectional s_yn1metry and two-dimensional reflectioml symmetry.
2. what spatial figure is formed by 3. What spatial figure is formed by
rotating rectangle ABCD about Er? rotating AFFG about PT}?
A 3 5
D C
G F
4. List some objects in your classroom that lldt-‘t'.' thn:c—dirncnsional rotational
symmetry.
0 qt//W80’ 3.?///3 Practice
Graph the point A(2, 1, -1) in a three-dimensional coordinate space.
Give the coordinates of the image if point A is reflected across each
coordinate plane listed below. (ACTIVITY 1)
5. x}-'-plane 6. .\‘Z-Pl..ll'lL 7. yz-plant-3
8. Graph E with endpoints A[ l , 3. -2] and B[ I, 3. 0) in .1 three-dimensional
coordinate space. Multiply the y— and z—coordinates of points A B by
—l and graph the resulting points. A’ and B’. Almut what axis is AB rotated
to get .Il'b"? (ACTIVITY 2)
9. Sketch the: spatial ligurc that results when H. with endpoints All, 2, U)
and B( I , 2, — t). is rotated about the 2-axis. (EXAMPLE)
0 Practice dim’ flpp/y
Draw three-dimensional coordinate systems and graph segments with
the given endpoints. Reflect each segment by multiplying the
y-coordinates by -1.
10. (4. -2. 3) and [-2. -3. 2) 11. (-5. 2. I) and (I. I. I)
12. (I. -2, -3-) and (—|, 5. 2) 13. [3, 2. -3) and [-4. 3. -2)
14. [5, 3, 2) and (_—I, —I, —l) 15. (I, 2, 3) and (I, .5. 3]
What are the coordinates of the image if each point below is reflected
across the xy-plane in a three-dimensional coordinate system?
15. [6, 5, 8) 17. (-2. 3,—l} 18. (I, 1. H
19. (4, -2. 3) 2o. [-5, 2. I) 21. (I,—2.—3)
482 CHAPTER 7
- - connect ,1!
I9“
Homework
Help Dnline
Go To: gaJuw.com
Keyword:
MG! Horncworlt Hob
lor Exercises 2B-3-l
CONNECTION
CHALLENGE
APPLICATION
What are the octants and coordinates of the image if each point below is
reflected across the xz-plane in a three-dimensional coordinate system?
22. (6. -2. 8] 23. (—vt,—«t.—l] 24. (1.0, I)
25. (1, I. O) 26- (4. -4. I] 21. (2. 2. -8]
In Exercises 28-31, AP has endpoints A(5, 0, 10) and B(5, 0, 0).
28. What spatial figure is formed by rotating .73 about the x-axis?
29. What is the area of the figure formed by rotating /TB about the x—axis?
30. What spatial figure is lormed by rotating H about the z—axis?
31. What is the volume of the figure formed by rotating E about the z-axis?
In Exercises 32 and 33, CD has endpoints CM, 0, 0) and D(0, 0, 4).
32. What spatial figure is formed by rotating E about the z—axis?
33. What is the volume of the figure formed by rotating 5 about the z—axis?
34. MAXIMUM/MINIMUM I he area ofa right triangle with a fixed perimeter is
maximized when the triangle is a 35-45-90 triangle. Suppose that you
rotate a 45-45-90 triangle about one leg to create a cone. Does the cone
have the maximum volume for the given slant height? Why or why not?
(See Exercises 43-44 in Lesson 7.5. page 466.]
POTTERY A potter is making pots according to certain patterns. For each
half of a pattern given below, sketch what the complete pot will look
like. (Rotate about the dashed red line.)
35. 36. - 31.
38. 39. : 40.
Look Back
Find the volume and surface area of each prism. (LESSON 7.2)
41 42.
7 5
11
12
15
Hl9hH'l8"9U'fir prism Regular hexagonal prism
LESSON 77 THREE-DIMENSIONAL SYMMETRY 483
APPLICATION
APPLICATION
APPLICATION
CHALLENGE
484 CHAPTER 1
43.
44.
45.
TRANSPORTATION A lrucl-CS
storage space is shaped like -.1
reetangttlar prism that measures
7 lt IE] in.x8 I1 2 in.x 2'1 it.
What is the volume of the
storage space? (LESSON 7.2)
Find the surface area and
volume of a regular square
pyratttid with a base area, b‘.
of 36 cm-' and .1 lteight. h. of
5 cm. (LESSON 7.3)
HOBBIES Seeing barbecue
srnokers displayed next to bags
of potting soil. Dolores decides
to change her old smoker at “
home into a planter. The center -, \ ‘
of her smoker comes up to her - '-. _ :n.,3’\
waist and is thus ltalfof her -_—,, ’
height ol'5 it. Use this
inforntation to estimate other '
dimensions in the photo. and - . l
then determine how much soil ' '
it will take to Fill the smoker to
the centerline of the barrel '/
from wltieh it is made.
(LESSON 7.4)
L00’? Bet/and
OPTICS A spinning fan creates the illustion of being solid. A strobe light.
which emits a flash at certain time intervals, can "freeze" the motion of
the fan.
46.
47.
Suppose that a fan with four equallv spaced, identical blades is turning at
I2 revolutions per second. How often will the strobe need to flash to make
the fan appear to be frozen?
If the strobe tlashes 36 times per second. at what speeds (in revoltttitins
per second} can the fan move and still appear to be frozen?
It
‘J
9
P
’\
75..
.
I
II ltmrnotoonned #3.,
UCTI
Portlolio
Extension
Go To: go.hrw.corI
Kewlord:
MOI Solllev
CREATING SOLIDS OF REVOLUTION
If a region in a plane is rotated about an axis that lies in the same plane, the
resulting figure is called a solid of revoltrriori. Follow the directions below to
create your own solids of revolution with cardboard, foam core board, a
needle and thread.
1. On a piece of graph paper, draw a shape that has
at least one vertical edge. such as the one shown at
right. Th is edge will he the axis ()l'reyt)Iuti(1n 0|‘ your
solid. Your shape should be at least to units high.
2. Number the intersections of the grid lines with the
edge of your figure. as shown. For each intersection.
set your compass to the width of your figure, and
draw a circle on a piece of cardboard. Number the
circle according to the number of the intersection.
. L
\
\
\ \
\.-~—.....
.1 t
/'
3. Cut the circles out of the cardboard. These circles represent cross—sections
of your solid of revolution. (‘ut IO small pieces oi‘ loam core board that
are approxirnately the thickness of the squares on your graph paper to use
as spacers.
4. Using a small needle. thread the
circles of cardboard in order.
alternating with the pieces of
foam core. Secure the string at .
the bottom with a small piece
of tape. Tie a loop in the string
at the top for a hanger. -
LESSON 77 THREE-DIMENSIONAL SYMMETRY 485
lgfifii '‘=' ‘ W :7 ‘
This puzzle is a three-dimensional version of the ancient Chinese puzzle
known as the tangram (see page 359).
Activity 1
THE PUZZLE Copy the nets shown below and
on the next page onto heavy paper and
assemble them to form six solids.Then see
if you can fit them together to make a cube.
4 The measurements are given in centimeters.
Make two copies
of this DIBCG.
486 CHAPTER 1
2.
4————j- —.
2 1 2 2 2
___"j_ _
\
\
2
V \ 2.
\
2 2
C/\
4 -I 4 4 2 _‘2
2. 2 2 2
2 2. 2, 2.
“ /\ /\
Activity
Describe each piece in as much detail as possible. What shape is it?
What are the lateral faces and bases? Find the lengths of all edges that
are not given.Then find the volume of each piece.
Extension
1. What are the dimensions 0|‘ the
cube that is formed when the
pieces are usscmblord? Does the
sum of the mlu mes of the
individual pieces equal the
volume of the cube? -
2- Can vou assemble the ..
pieces to form any other
interesting solids?
’ cwmsn 7 mo set 487
Chapter Review and Assessment
altitude of a cone ....... . . 460
altitude oi a cylinder .... .. 453
altitude ol a prism . . . .. . . . 437
altitude oi a pyramid .... .. 445
annulus ............... . . 469
axis of a cylinder ....... . . 453
base ol a cone .......... . . 460
base ol a (Minder ....... . . 4%
base ol a pyramid ....... .. 445
base etige oi a pyramid .. . . 445
cone . . . . . . . . . . . . . . . . . . . . 460
VOCABULARY
cylinder . . . . . . . . . . . . . . . . . 453
height at a cone . . . . . . . . . . 460
height of a cylinder ..... . . 453
height ol a prism . . . . . . . . . . 437
height ol a pyramid ...... . . 445
lateral edge of a pyramid . . 445
lateral lace ol a pyramid 445
lateral surlace of a cone . . . 460
lateral surlace of a cylinder 453
oblique cone . . . . . . . . . . . . . 460
oblique cylinder . . . . . . . . . . 453
POSTULATES AND THE I ‘I MS
pyramid . . . . . . . . . . . . . . . . . 445
regular pyramid . . . . . . . . . . 445
rightcone......... .... ..460
right cylinder . . . . . . . . . . . . .453
slant height of a cone .. . . . 460
slant height of a cylinder .. .453
sphere ................. . .469
vertex of a pyramid ...... . .450
vertex of a cone ......... . .445
Lesson um- . Postulate or Theorem
7.1 7.1.1 Surface Area and The surface area, S. and volume, V, of a right rectangular prism
Volume of a Right with length L’, width w, and height h, are S= 2 t“w+ 2wh + 2t-‘h and
Rectangular Prism V — (."wh.
7.1.2 Surface Area and The surface area, S, and volume, V, of a cube with side length 5
Volume of a Cube are S= 6s’and V- 5’.
7.2 7.2.1 Surface Area of a The surface area, S, of a right prism with lateral area L, base area
Right Prism B, perimeter p, and height his 8 = La 2B or S: hp+ 2B.
7.2.2 Cava|ieri's Principle If two solids have equal heights and the cross sections formed by
every plane parallel to the bases of both have equal areas, then the
two solids have equal volumes.
7.2.3 Volume of a Prism The volume, V‘, of a prism with height h and base area B is V Bh.
7.3 7.3.1 Surface Area of a The surface area. S. of a regular pyramid with lateral area L, base
Regular Pyramid area B, perimeter of the base p, and slant height (3 is 5‘: L — B or
s = %t'p + 3-
7.3.2 Volume of a Pyramid The volume, V, of a pyramid with height hand base area Bis
v = ,}ah.
7.4 7.4.1 Surface Area of a The surface area, S. of a right cylinder with lateral area L, base
488 CHAPTER 1
Right Cylinder
area B. radius r, and height h is S: L‘ 2B or S: Zrtrh + 2-itr’.
7.4.3 Volume of a Cylinder
The volume, V, of a cylinder with radius r, height h, and base area
Bis V= Bh or V-rtr’h.
Lesson Number Postulate or Theorem
7.5 7.5.1 Surface Area of a The surface area, S, of a right cone with lateral area L, base area 8,
Right Cone radius r. and slant height f‘ is S: L + 8 or S = ttrf + -arr’.
7.5.2 Volume of a Cone The volume, V, of a cone with radius r, height h, and base area B is
v = %Bh or v = %1:r?n_
7.6 7.6.1 Volume of a Sphere The volume, V, of a sphere with radius ris V = %Jrr’.
7.6.2 Surface Area of a
Sphere
Key Skills 8: Exercises
LESSON 7.1
Key Skills
Solve problems by using the ratio of surface
area to volume.
A cube has a volume of 27.000 Clli.)iL millimeters.
What is its ratio of surface area to volume?
The length of each edge of the cube is
€r‘27,0(}t'J = 30 millimeters. so the area ol
each face is 3-0 x 30 = 900 square millimeters.
There are 6 laces. so the surface area is
6(9()0) = 5400 square millimeters. Thus. the ratio
oi" surlaee area to
volume is $3383 = 0.7.
LESSON 7.2
Key Skills
Find the surface area of a right prism.
Find the surface area ol'the right triangular prism
below.
The lateral area is hp. or
l00(_36 + 77 + 35} = 19.300. N
_L
The area of each base is 3 77
L,(_s6)(77) = I536.
09
The surface area is ‘°°
S: L+ 2B. Or
I9.80O + 2(l386] = 22.572.
The surface area, S, of a sphere with radius ris S— dxr’.
Exercises
1. Find the ratio of surface area to volume for :1
Cube with a volume ol'64 uthic inches.
2. Find the ratio of sttrface area to volume for -.1
cube with -.1 volume of I00 cubic inches.
3. Compare the ratios of surface area to volume
lot .1 cube with an edge length 0H and lor a
right rectangular prism with the dimensions
4x7x1
4. A right rectangular prism has a square base.
and its height is triple the base edge. Find the
ratio of its surface area to volume.
Exercises
Refer to the right hexagonal prism with a
regular hexagonal base below.
5. Find the lateral area
of the prism.
6. Find the surface area
of the prism.
CHAPTER 1 REVIEW 489
Find the volume of a prism.
Find the volume ofthe prism on the previous
page.
The area of the base is I386, so the volume is
V = Bh, or l386(l0'D) = l38.60'D.
LESSON 7.3
Key 5|-(Ills
Find the surface area of a regular pymmid.
Find the surl-ace area ol the regular square
pyramid below.
The lateral area is %t"p. or
%(2s)(5e») = 700. .. /25
The area of the base is 24 I
I41 = I96.
H
The surlace area is
S = L + b‘, or 14
700 + I96 = Q96.
Find the volume of a pyramid.
Find the volume of the pyramid above.
The area of the base is 700. so the volume is
v = am. or §(7oo)(24) = 5600.
LESSON 7.4
Key Skills
Find the surface area of a right cylinder.
Find the surface area of the right qrlinder below.
The lateral area is Znrh.
or 21t(I2)[7] = l68n:. '12
The area of each base is
nr’, or EH23] = l4471:. 7
The surface area is
S = l. + 28. or
l(»81t + 2(l'l*l.'t) = 4561:.
Find the volume of a cylinder.
Find the volume of the right cylinder above.
The area of the base is l<l4rt. so the volume is
V = Bin. or I-147:0’) = I0t)8rt.
490 CHAPTER 1
7. Find the volume of the prism on the previous
page.
8. Find the volume of the prism on the previous
page if the dimensions are doubled.
Exercises
Refer to the regular pyramid below.
9. Find the lateral area of
the pyramid. 1 ,“ 2
10. Find the surface area of
the pyramid.
11. Find the volume of the 5
pyramid.
12. l'ind the volume ol the
pyramid it" the height is
doubled.
Exercises
A right cylinder has a radius of 4 and a
height of 9.
13. Find the lateral area of the cvlinder.
14. Find the surface area of the cylinder.
15. Find the volume of the cylinder.
16. Which increases the volume ofa cylinder
more, doubling the height or doubling the
radius? Explain your reasoning.
LESSON 7.5
Key Skills
Find the surface area of a right cone.
Find the surface area of the right cone helow.
The lateral area. L. is rtrf. or
rE(6.l( l0.9l = 65.41I:.
The area of the base, B. is H14: 9.1 -_.
or M63] = 361:. mi 1&9
The surface area is '
5 = L + b‘, or H 6'
65.-tn: + 361: = 101.-11:.
Find the volume of a cone.
Find the volu me of the cone above.
The area of the base is 36ft. so the volume is
v = §B1i. or %361I:(9.l] = lO9..2rt.
LESSON 7.6
Key Skills
Find the surface area of a sphere.
Find the surl'-ace area ofa sphere with a radius ol'9.
The surface area is S = -17:1". or 416% = 5247:.
Find the volume of a sphere.
Find the volume ofa sphere with a radius ol'9.
‘l he volume is V = %1tfi or -T-:-1:9’ = 9721:.
LESSON 7.7
Key Skills
Reflect a figure in a three-dimensional
coordinate system.
Reflect the segment with endpoints at (5. 5. 2) and
(5. 5. -2) across the J.-z—plane.
The image has
endpoints at
(5. -5. 2) and
(5. -5. -2).
Exercises
Refer to the right cone below.
17. Find the lateral area ol
the cone.
18. Find the surface area of 21
the cone.
5.: 2.0.
19. Find the volu me of the
cone.
20. Find the volume of the
cone ifthe height is
doubled. Round your
answer to the nearest
hundredth.
Exercises
21. Find the surlace area of a sphere with a radius
0|‘ 5.
22. Find the volume ol a sphere with a radius of 5.
23. Find the radius of a sphere with a volume of
3671:.
24. What is the side length oi"-a cube that has the
same volume as a sphere with a radius of I?
Exercises
A segment has endpoints at A(0. 0, 0) and
BIO, 4, 6).
25. Draw a retlection of the segment across the
xy—plane. Give the coordinates of the
endpoints 0|‘ the image.
26. Draw a reflection ofthe segment across the
yz—plane. Give the coordinates of the
endpoints of the image.
CHAPTER 1 REVIEW 49‘!
LESSON 7.7
Key Skills, continued
Sketch the spatial figure formed by rotating in
figure about an axis.
Sketch the spatial figure formed by revolving the
segment with endpoints at (5. 5. 2) and (5. 5. -2}
about the z—axis.
>—N
*5.
Applications
29. PRINTING A roll of paper used in printing has
a diameter of 3 feet. a hollow core of 4 inches.
and a width of 5 feet. If the thickness of the
paper is 0.0015 inch. what is the length of the
paper on the roll?
30. SPORTS A basketball has ‘.1 radius of
approximately 4.75 inches when filled. H0“
much material is needed to make one? How
much air will it hold? if the basketball is stored
in a cubic box" whose edges are 9.5 inches long.
what percent of the box is not tilled by the
laaskethall? [Rottnd your answers to the nearest
hundredth.)
31. PHYSICS A spherical soap bubble with a radius
ol'5 centimeters lands on a Hat surface and
becomes a hemisphere. \-\"hdt is the radius 0!
the hemisphere?
492 CHAPTER 1
A triangle has vertices at l0. 0. 0). (2. 0. Ol. and
(0. 0. 5).
27. Sketch the spatial ligure formed by rotating
the triangle about the y-axis.
28. Sketch the spatial figttre formed by rotating
the triangle about the z—axis.
- Chapter Test
Find the surface-area-to-volume ratio for each of
the following:
1. a cube with -.1 volume oi" I25 cubic units
2. a rectangular prism with dimensions it X l X l
3. a right rectangttlar prism with -.1 square base
and a height that is quadruple the base edge
4. Pl IYSICS Use surl'ace—area—to—volume ratios
to explain why solar panels are shaped like
large thin rectangular prisms.
Find the surface area and volume of a right
rectangular prism with the given dimensions.
6. l= 6, w= 4, h= 0.25
7. Find the volume Ola right triangular prism
whose base is an isosceles right triangle with a
leg of I2 centimeters and whose height is l5
centimeters.
3. CAMPll\'G The tent
shown is .1 right
triangular prism. The
bases of the prism are 5.0 ft
isosceles triangles. Find _l.
the surf-.1-:e area of the
tent, including the lloor.
5. l=5,n-'=t$.h=7
/5.0 it
—+ -1.5 ft -1*‘
For Exercises 9-12, refer to the regular square
pyramid below.
_ 26
:10"-“ ._
24
9. Find the lateral area of the pyramid.
10. l'ind the surface area of the pyramid.
11. Find the volume of the pyralllid.
12. Find the volume of the pyramid if the height
is doubled.
A right cylinder has a radius of 6 inches and a
height of 8 inches.
13. Find the lateral area of the cylinder.
14. Find the surface area of the cylinder.
15. Find the volume of the cylinder.
16. 'l he volume ol"a cylinder is IUOII cm‘ and the
height is -1 cm. Find the circumference oi" the
base.
Find the surface area and volume of each right
cone.
17. _ 18. :
: _‘/15 E ’/.13
CL..‘;;:9 EL ‘;\5
19. Find the surlltce area ofa sphere with a radius
oi‘ I2.
20. Find the volume ofa sphere with a radius of
I2.
21. Find the surface area and volume ofa sphere
with a diameter ot'6.t'. Give an exact answer in
terms of It and the variable.
22. Find the stlrface area and volume of a kickball
with a diameter ol'9 inches. Round your
answers to the nearest hundredth.
What are the coordinates of the image if each
point below is reflected across the xy—plane in a
three-dimensional coordinate system?
23. {I,5.9) 24. (-3. 2. -5) 25. (6.—I,—4)
3!? has endpoints Jl3. 0, 6) and K (3. 0, 0). What
spatial figure is formed in each case?
26. rotating -jK' about the x-axis
27. rotating T‘? about the z—av<is
CHAPTER 1- TEST 493
-' E'S CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Questions I— I0. write the
letter that indicates the best answer.
1. Find the volume of the figure below.
(LESSON 7.5}
G!
u..-.-.....-
a. 3631 b. ltsrr
c. 541: d. 72::
2. Refer to the triangle below. which of the
l'()llowing statements is true? (LESSON 3.5)
A
C B
a. AA and A8 are adjacent to .«_’C.
b. min + mzti = I80
c. Ind;-l + man = mic
d. AA and K8 are complements of AC.
3. Refer to the prism below. Find the area of
RSTU. (LESSON 8.3)
S T
R U 2
W X
1.5
V
3.5 Y
a. 7' units: b. 5.25 units?‘
c. 3 units3 d. 10.5 units‘
494 CHAPTER 1
0
D internet connect uxiiri
Standardized
Test Prep Online
Go To: go.hrw.com
Keyword: MM1 Test Prep
4. Refer to the figure below. What can be
concluded about the measures of Al and A2?
(LESSON 3.3)
a. m.»;'l = mA2
b. mél + n1./12 = l80°
c. ml] + ml}. = 90“
d. No conclusion can be drawn.
. Verticatl angles are ? . (LESSON 2.5)
a. complementary
b. supplementary
c. congruent
d. obtuse
. lflines are parallel. then same-side interior
angles are ? . (LESSON 3.3)
a. complementary
b. supplementary
c. congruent
d. obtuse
. Which of the lollovring is valid for proving
that triangles are congruent?
(LESSONS 4.2 AND 4.3)
a. :'\r\/\
b. ASA
c. SSA
d. none of the above
8. The diagonals ofa rhombus are 7.’ .
(LESSON 4.5)
a. congruent
b. parallel
c. perpendicular
d. convex
9. The dia,r:onals ol‘ a rectangle are ? .
10.
11.
12.
(Lesson: 4.5)
a. congruent
b. parallel
c. perpendicular
d. convex
Find x in the diagram below. (Lesson: 3.7)
4.8
7.2
11. I2
b. 5.6
c. 6
d. 3.4
Write the conclusion. if any, that follows from
the given statements. (Lesso~ 2.3)
lf .1 person exercises regularly. then that
person is in shape.
Vaness-.1 is in shape.
Complete the Euler diagram below.
(LESSON 3.2)
Parallelograms
Rhombuses
Recta ng Ies
13. What is t|1e area of a circle with a radius of
Give an exact answer. (Lesson: 5.3 )
7?
14. What is the raditts ol'a circle with an area of
7? Give an €‘((ICt answer. (Lesson: 5.3 ;
15. Draw six orthographic views of the solid
below. (Lesson: 6.1)
’>
FREE-RESPONSE GRID
Items 16-18 may be answered T
by using a free-response grid C‘ C‘-3 O ‘:3
such as that commonly used G '3 g 5
by standardized-test services. (3 ® ® (-9
® ® G) is‘)
CD CD ® 03
(E) (E1 @ *3
CD (9 ® ©
CD CD ® (3
GD CD Q) €53
(E) (E) ® Q7
18. Find the length of the diagonal ofthe right
rectangular prism below. Round your answer
to the nearest tenth. (Lesso~ 6.3)
Ln)
8
17. Find the surface area of the right rectangular
prism above. (LESSON 7.1)
18. Find the volume of the regular hexagonal
pyramid below. Round your answer to the
nearest unit. (Lesson: 7.3)
—I
0
.L.
O
CHAPYER 7 CUMULATIVE ASSESSMENT 495
Lessons
8.1 o Dilalions and Scale
Factors
8.2 0 Similar Polygons
8.3 0 Triangle Similarity
Poslulates
8.4 0 The Side—Sp|itting
Theorem
85 0 Indirect
Measurement and
Additional
Similarity Theorems
8.6 0 Area and Volume
Ratios
Chapter Project
indirect
Measurement
Similar
Shapes
IN 1948 KORCZAK ZIOLKOWSKI (1908-1982)
began work on the world's largest sculpture,
the Crazy Horse Memorial, in the Black Hills of
South Dakota. The sculpture is 563 feet high,
more than 9 times the height of the sculptures
on Mount Rushmore. The completed lace of
Crazy Horse is nine stories tall.
In the photo on the page facing, a scale model
of the finished statue stands in front of the
actual work, which is 1 mile behind it. The
model is if the height of the mountain carving
in progress. Such figures are known as similar
ligures. You will be studying similar ligures
throughout this chapter.
l
\
korrznk Ziolkowski
with scale model
.. \|
L
. _. "-~,?=~
_‘r_ .
, '-re.‘ 1 _. y l.
. -\ -
‘\ ‘~\‘."~‘.'
.' I. - ' \
_ ‘V
M:_. Q _ ‘ ,_
Prt'rr'sirm ¢'.tplosr'v¢'.s' w¢'1'¢’ u.~r'r1m ,_ (- ~_'7" ‘ /‘ _ "
Crr‘a!¢'tlrr‘0r1tlil1(’O} thcrform F l - V E
- , '>_ v_
.5‘ I‘ . ’
_" int ' _
-. g" ' _
-Q1} ' ‘E9:
.I- ;_ . ‘f ‘ ,,_
54". ‘ \ £1, - .
'_‘ I 1
‘ . 2 _ 1!‘ . 3
. ‘ J . h‘ . .0
\ " 5' “aft *7 ' t
I ‘ “ I
- -' . l 4 I
- o 4
D
$
%~f~.:;
‘ _-
rt‘ " L
I. .
.1, -‘~
.' 3" _ —
3? n
‘_.
_‘ \
._ ‘
s L.‘
I ‘ ~ -
C
\
‘T’
M “G _I
C ~ ‘ ' '\..
\ ‘ ‘ '
._ .'
\ ‘5 i f ‘H
‘ \
T — ' L . g.‘
VI .
.1
Erin Ilr-rsc I M‘ Sill: N aid
0 i<<'IR|.[.\l2.:r;:ui§mr
About the Chapter Project
Similarity is a term used to describe objects that
are the same shape. but not necessarily the same
size. One application of similarity is a scale
model, which is an object built in the exact
shape of another obiect. but usually smaller.
Scale models are olten used to get an overall
View of a large object or area.
Throughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Proiect.
The theme of each Portfolio Activity and of the
Chapter Proiect is scale ntodels.
o In the Portfolio Activity on page 506. you will
In the Chapter Project. vou and your classmates enlarge a design by using grids»
build a scale model of your or school. starting _ _ _
with 3 map‘ 0 In the Portlolro Activity on page 5-12, you will
_ _ _ _ _ use indirect measurement to find the
Alter completing the_(.hapter PTOJCCI you WI“ be dilmmsions or 3 building
able to do the lollowtng:
0 Work as -.1 team to apply the techniques of
measurement to real—world objects.
0 Create maps and models of large structues
that cannot be measured directly.
497
About the Portfolio Activities ~_ _
Dilations and Scale
Factors
Objectives
0 Construct a dilation of
a segment and a point
by using a scale factor. I . g
0 Construct a dilation at l. ,
a closed plane figure.
I
Acamara-:~ rapmiectsan 3‘
inverted image through a small
I I It wont. DI! . . .
gfinbéig mo, zizmfin the "E: Tin’ prmrzple of the tTttm(’l‘ll obsruru, the forerumter of the modern
camera, was distrowred by pit)-sittist Hm :Il— Huithum (5165-1039 C.E.).
- p L I 0 N The cttmerat obscure was used to draw accurate images of an ohject or a scene.
PHOTOGRAPH The artist traced the image that was projected through a pinhole onto it
dmwing surllacc. In a modern cantcra, the pinhole has been replaced by -.1 lens
and the drawing surface has been replaced by light-sensitive plmtogruphic film.
Dilations
50 Int you have studied three types of
transforntattions: translations. rotations.
and reflections. These tr-.tnsl'orm.1tions
are called rigid because they preserve
size and shape.
A dilation is an L’.\£:tIl'lplE' of .1 trans-
formation that is not rigid. Dilations
pre.«»er\re the shape of an object. hut 1 51¢‘ 553!‘ Offilt‘ f_igNI_'t‘ is
they nm}, change its 5i7_e_ rltrlngcrl by rt dilation.
A dilation of :1 point in a coordinate plane can he fottnd by multiplying the
x- and ,v~coordin-ates ol it point bv the same number, n.
Dtx. y] = Inx, ny)
The number n is Called the scale factor ol the trztnslorntalion.
498 CHAPTER 3
E X A M P L E What is the image of the point [2,3] transformed by the dilation
D(x. y] = (tlx, -1y]? What is the scale factor?
0 SOLUTION
The image is the point D{2. 3) = [4 - 2. -I - 3) = (3. l2_) . The scale Ilactor is
I the multiplier. 4.
Dilations in the Coordinate Plane
' L D 1. Plot AL‘-. «ll on a coordinate plane. Use the distance formula or .3 ruler
gmph page,’ to find the distance. OA. from O[0. 0) to A. ['56 dilutions with the scale
2|-iI3||£::l»|c':_":‘|;lr lactors given below to translorm point 4, and then copy and complete
U 1 ._
on lhc table.
geom_et.ry _
\ Glanhtcs A 0A Scale factor Image. A’ 0A’ Ratio -0‘
software 04
ta. 4) 7 2 t7, 7» l 7 7
ta. 4) 7 o 5 t7, 7» I 7 7
13.4» 7 1 1?. 7» | 7 7
ts. 4) ? n 1?. 71 7 7
2. Plot point A and its image. A’. for each dilation above. Vt hat is the
simplest geometric figure that contains all of these points? Add this
Iigure to your graph.
3. Complete the following coniecture:
Conjecture
c|-|Ec|(PomT ,/ The distance from the origin to the image of a point transformed by a
dilation with scale factor n is ? the distance from the origin
to the preimage.
4. Plot point A again and a new point, 86. 6}. on a new coordinate plane.
Use the distance formula or a ruler to find the length olfi. Use
dilations with the scale factors given below to translorm points A and B,
and then copy and complete the table.
8 AB Scale lactor Image, 8' A'B’ Ratio %'
(5, e) ? 2 (?.-?l— 7 2
__[5, 6) ? 0.5 Q, ?j ? ?
(5, 6) ? -1 (.7. ?l 7 7
(5, ea 7 n ' (7. 7) 7 7
z ; I / 5. Find the slope of each dilated segment, W.
6. Complete the following conjecture:
Conjecture
CHECKPOINT ./ The image of a segment transformed by a dilation with a scale factor
of n is ? the length of the preimage, and the slopes of the
image and preimage are ? .
LESSON 81 DILATIONS AND SCALE FACTORS 499
OPTICS
CRITICAL THINKING
I.
ruler and
calculator
OR
Q I
geometry
graphics
software
CHECKPOINT M
CRITICAL THINKING
500 CHAPTER 3
In a dilation. each point and its image lie on a straight line that passes through
a point known as the center of dilation. ln Activity I, that point was the
origin. livery dilation has a center of dilation.
The colored portion of the eve. known as the iris. Changes shape to let in more
or less light. when the iris is relatively open it is said to be diluted. A similar
device in a camera. also known as the iris. is placed hehind the lens to let in
more or less light to accommodate dillerent lighting conditions.
I 0
In the plant) on the Itjft. the r-ye is comrm red for relatively bri_t,-In ligln.
In the pllttm on the iigln. it is dilumljor less ti:-iglii conditions.
You may have noticed that the size of images of segments that have been
dilated varies according to the scale factor. II" the size of a figure is reduced by a
dilation. the dilation is called a contraction. If the size of a figure is enlarged
by a dilation, the dilation is called an expansion. For a dilation with a scale
factor 0|‘ II:
If |n| < I. the dilation is a contraction.
If |n| > I. the dilation is an expansion.
How is the image or a point ()I' segment affected In’ a negative scale lactor?
Drawing a Dilation
1. Draw a polygon. such as a triangle. and
a center ol dilation. Draw lines that pass
through each vertex of the figure and the
center of dilation.
Prenmage
C
. Decide on a scale factor n for your C:i?atg:Jfif
dilation. Choose one of the vertices and
measure the distance, x, from the center
of dilation to the vertex. Multiply this
distance by n to obtain a new value, x‘.
On the line containing the chosen
vertex. plot a point that is a distance of
x’ from the center of dilation. This new
point is the image of the chosen vertex.
—é
/
. Repeat for each of the other vertices
of vottr figure.
. Connect the images ol the vertices
to form the dilated image of the
ftgu re.
How could you draw an approximate dilation of a curved plane figure!
E X A M P L E The students shown below ttrll using a pinhole to observe .3 solar eclipse. The
process l'l'Ifl_\" be understood as a dilution. with the pinhole as the center of
A _ P I C I 0 N diliitioti. 'l:he tlianieter ofthe Sun is app_roxiiii-.it_ely 87(_3.0t]0 mi. lfthe iiii-age is
0.25 inch in di-.inieter. what is the scale lactor ol the dilation?
ASTRONOMY
In
H
0 SOLUTION
The diagr-.1m at right { not to scale) shows Sun /.
the path of rays of light from the edges of the ._
Sun its seen lrtim Earth. The .s<.'ale factor is '-_
negative because the image is on the opposite '-.
side 0|" the center oldilation (the pinhole].
The ratio 0|‘ the image to the preimdge is ‘-_
0.25 inch _ —l£ . .
5S.l2.5.200.0fl0 iltfit 4'5 " '0 '5" the P'""°'9 \\.__
scale factor is .ipproxiiii-ately -4.5 x 10'”.
LESSON 3 i DILATIONS AND SCALE FACTORS 501
Exemses
. Comma»/care
1. What is a dilation? How is a dilution different from other tr.1|tsf0rn1ati()ns
n _ we #0 you ll-ave studied?
l'l metoonnect ,
Acmmies '°"‘ 2. What is a scale l'-actor? How can you determine the scale factor ofa
amine dilation by looking at a segment and its image?
Go To: qo.hrw.corn
Keyword: Explain how the image of a figure transformed by a dilation would be
M" D"“‘‘'’''‘ affected by the following scale factors:
‘ 3. 2 4. 0.5 5. -1 e. 1
0 fill/dad SK’///8 Practice
Find the image of each point transformed by the given dilation. Plot the
point and its image on a coordinate plane. (EXAMPLE 1 AND ACTIVITY 1)
7. (I. 5): Dix, y] = (3.\'. 3)’) 8. (—l, 4]: Dtx. y) = [2x. 23')
9. (6. -2]: Dix. yl = |.’0.25.\'. 0.25;‘) 10. (2. 3); D(x. y] = (-2.7.‘. -2);)
Copy each figure below and draw a dilation with the given scale factor
(ACTIVITY 2)
11. scale factor of .2 12. scale factor 0l'—l
13. The figure at right slmws a seglnent ‘~--
and its inn-age under a dilation. What 35 cm , :"'i].,.8 cm
is the scale I-actor ol the dilation? ‘
(EXAMPLE 2) Preimgge | ‘"1393
Center of
dilation
0 Practice and App/y
For Exercises 14-17. the vertices of a figure and a scale factor, n, are
given. Use the dilation Dix, y) = (nx, ny) to transform each figure, and
plot the preimage and image on a coordinate plane.
14. u,3_). [2.5).(4..>.-1 15. (-3. 5;. (8. 9). (2. -6)
n = 2 =
16. (0, O). [6, U). (4. 4]. (2. 5) 17. (Li J. [5, —l). [-2. -5)
n = —% n = 1.6
502 CHAPTER 3
- umctoonnoct .2,
O
oin
Homework
Help Dnline
Go To‘ go luw.t:ua1
Keyword:
MGI Homework Help
for Exercises 18-21
In Exercises 18-21, the blue figures represent the preimages of
dilations, and the red figures represent the images. Find the scale factor
of each dilation.
13. , )1 M33) 19.
l- T ll. ‘ll
l__l :7
1
20. y 21. V
.0
~§7 (6 4)
_(6.0)
" 4-2.0} "
t—s.—4)
Copy each figure below and draw a dilation with the given scale factor, n.
22. H = _’r 23. M = 24. M = -2
25. Copy the figure below. Draw three dilations of the triangle with -.1 scale
factor of 2, using the three given points as centers of dilation. How are the
images alike? How are they dillerent?
4»
AI 30
26. Copy the figu re below. l.oc-ate the center 0|" dilation and find the scale
factor.
Pfein-gage
Image
LESSON 81 DILATIONS mo SCALE FACTORS 503
CHALLENGE
APPLICATION
‘L
Cuber! lattice
504 CHAPTER 3
For Exercises 27-30, the endpoints of a segment and a scale factor n are
given. Show that the dilation image of the segment has the same slope
as the preimage.
27. (I, O) and (5. 3); n = 2
29. (-2, 4) and (-1, 8); ll =
28. (-2. 3) and (3. I); H = 5
—% 30. (I. I) and [2, I); n = L?"
For Exercises 31-34, a point and a scale factor are given. Find the line
that passes through the preimage and image, and show that this line
contains the origin.
31. (5, I); H=-=1
33. [_’»,—5]; n = -3
32. (-2, 3); M = ‘
34. (-1, 7); n = 2.
The figure below shows a right rectangular prism in a three-
dimensional coordinate system.
35. Draw the image 0|" the prism 2
transformed by the dilation (0. 0. 5}
D(x, )2 z) = (2x. 2}’. 22). Label
the coordinates of the image's
vertices.
(0. 3, 5}
(4, 3. 5)
36. What is the ratio of the lengths
of the edges in the image to
the lengths or the edges in the
preimage? ‘O’ 0' 0)
"(/1 DD)
4..
l0. 3. Ol
—- —>
37. What is the ratio of the surface
area ol the image to the surlace
area of the preimage?
l4. 3. D)
38. What is the ratio of the volume
of the image to the volume ol-
lhe preimage?
39. An example of a dilution that is not centered at the origin Ufa Coordinate
plane. is Dix, y} = (2,\' — 4. 2,1-'— 3). l'se this dilation to transform the
segment with endpoints (2, 5) and (5. 5). Plot the preimage and the image
on a coordinate plane. Determine the scale factor and locate the center ol-
dilation. Write the rule tor a dilation with a center of (2, I) and a scale
factor of 4.
40. HOBBIES A quilter has a pattern tor a
-1—in. square quilt block and wishes to
enlarge it to a l2—in. block. What is
the scale factor ot the enlargement?
l'he pattern is traced onto a grid ot
l—in. squares. as shown at left. One of
the shapes in the pattern has vertices
at (U. I). [1, I). (2. 2), and (1. 2].
What are the coordinates of the image
of this shape in the I2 in. block?
APPLICATIONS
APPLICATIONS
OPTICS The diagram below shows a part of a camera obscura.The
image is projected through a small hole into a dark room or chamber.
This projection is an example of a dilation.
41.
43.
What part of the camera 3'
0lJ5Cl.II'd EELS 33 l.l'I€ CCITLCT A
of dilation?
. Is the scale factor positive
or negative? Ftplain your
answer.
Explain why the projected
image is inverted. 3 A’
. GRAPHIC ARTS An artist is using a photocopier to reduce :1 design. The
original design is 5 in. wide. The copy should be 2 in. wide, \-\-‘hat is the
scale factor of the dilation?
L00:(’ Bdfti’
45.
46.
47.
49.
50.
The base ot an isosceles triangle is 6 m and the legs are 8 m each. Find the
perimeter and area of the triangle. (LESSONS 5.2 AND 5.4)
A leg of a 45--15-90 triangle is 7 cm long. What is the length of the
hypotenuse? (LESSON 5.5)
ENGINEERING A spherical gas tank has an outer diameter of 40 It. The tank
is made with I—in. thick steel. Find the dilierence between the surface area
of the outside and 0| inside of the tank. (LESSON 7.6)
. ENGINEERING Suppose that I gal of paint covers 400 it}. How many gallons
of paint are needed to paint the inside and outside of the tank described in
Exercise 4?? (LESSON 7.6)
EARTH SCIENCE The circumference of a great circle of Farth is about
40,000 km. \-\-‘hat is the radius of Earth? (Lrsssorv 7.6)
EARTH SCIENCE The height of Earth's atmospltere is about 550 km. Use this
information and your answer to Exercise 49 to find the volume 01- Earth
and its atmosphere. (LESSON 7.6)
Eurrlfs rrnrmsphertt. as plrntographed by n Rtissirrn ctvsrnonnur
LESSON 8 I
DILATIONS AND SCALE FACTORS 505
506
1.004’ Beyond
Another type of transformation that is not rigid can be described in a
coordinate plane by T(x, y) = (mx, ny), where the x- and ywalues are
multiplied by two different scale factors.
51. Draw a triangle with vertices at (I. 5}. (5. I], and [5, 3) in a coordinate
plane. Transform the figure hy using the transformation
T(x, y) - (2x. 4}-').
52. How are the preimage and image alike? How are thev ditterent? How is
this I) pe of transformation like a dilation? How is it different?
53. [sing the segment with endpoints [ l. 3] and (5. I). what is the ratio of its
slope to the slope of its image?
54. Lise the transl'orm-ation Tix. y] = (M. —y] to transform the figure at left.
D lntnnntconnect
Portfolio
Extension
Go To: no.hrw.cnm
Keyword
MOI Scale
L001
USING GRIDS TO ENLARGE A DESIGN
Choose a design, cartoon. or photo that you wish to enlarge. You may wish
to photocopy the design so that you do not damage the original.
1. Using a ruler, draw a gritl of
;—cm squares on the design.
2. Draw a grid with the same
nu mher of squares on a larger
piece of paper. I hese squares
should be at least twice as big.
3. Copy the pattern that appears
in each square of the first grid
onto the corresponding square
in the larger grid. It may help
to cover all but one square of
the design as you copy it.
Be sure rt! copy om‘ sqrmre at
H rimr‘—do not try to draw
!m‘gt’r parts of flu’ tit’.-iigrr.
Once all the squares are copied. you will have an accurate enlargement ol
the design.
WORKING ON THE CHAPTER PROJECT
You should now be able to complete Activity I of the Chapter Project.
Similar Polygons
Objectives
0 Define similar
polygons.
0 Use Properties of
Proportions and sc ale
factors to solve
problems involving
similar polygons.
scale m- musedby
architects. clty planners. movie
set designers. and hobbyists To
create a scale model. ~ I - -nies
of similar figums are needed.
If
.'.1 ;'
‘it
I! ’.'
I‘
Similar Polygons
When a ligure undergoes a dilution (Lesson 8.1 i. the preimztge and image have
the same shape but are not necessarily the same size. They are said to be
similar.
Definition: Similar Figures
Two figures are similar ifand only if one is congruent to the image of the
other bv a dilation. 8.2.1
The symbol -
means st'mi!ai:
AABC — AA’B’C’
In the dilation at right. the
corresponding angles of the
triangles are congruent. and
the ratios of the lengths ol
the corresponding sides are
all equal to the absolute
value ofthe scale lactor of
the dil-.ttion—whieh is 2 in
this case.
8’
£85 48' AC 5 4C’
-gig: = %’g = 7%?’ = 2 <: Sc—aIe_factor |
LESSON 3 2 SIMILAR P0-LYGONS 507
ZAE ZA’
CRITICAL THINKING
E X A M P L E ofitre thetriangles at right similar?
508 CHAPTER 3
when the ratios of corresponding sides of two polvgons are equal [as in the
illustration on the previous page), the sides are said to be proportional. A
statement of the equality oi‘ two ratios is called a proportion. 'l he concept 0!
proportion is important in the Polygon Similarity Postulate.
O SOLUTION
Polygon Similarity Postulate
Two polygons are similar ifand only if there is a way of setting up a
correspondence between their sides and angles such that the following
conditions are met:
- Each pair of corresponding angles is congruent.
- Each pair of corresponding sides is proportional. 8.2 2
In a similarity statement. as in a
congruence statement. the letters
oi the \-ertices must be written in
corresponding ordei.
V)
AABC — ADFE
HID E
ls either condition in the Polygon
Similarity Postulate. taken separately.
enough to guarantee that two polygons -1
are similar? Use the figures at right to
explain your answer. 2
lt is given that AP 5 AS. AQ 5 AT. 26 57
and AR E AU, so the first condition 33
of the Polygon Similarity Postulate is R U
satisfied. To see whether the second 20
condition is satisfied. check each ratio 30
of corresponding sides. 7-
ELLE--3
QR‘2o‘2 i>‘E‘2o‘2
Because the ratios are equal, the corresponding sides are proportional. and the
second condition of the Polygon Similarity Postulate is satisfied. Therefore.
APQR ~ ASTU.
TRY THIS
CRITICAL THINKING
EXAMPLE
0 In the figure at right. pentagon
Properties of Proportions
When working with similar figures. it is often helpful to know the following
Properties of Proportions:
Properties of Proportions
Let u, b, c. and d be any real numbers.
Cross-Mult iplication Property
ll‘ % - fiend l1 and d nu 0, then mi - bc. 8.23
Reciprocal Property
If % = fiend II. b. L. and ti =2 0. then 3 = 8.2.4
Exchange Property
ll ‘-' - 5 and tab, 1'. and rl us 0, then - Q. 8.15
(1 d l. d
“Add—One” Properly
- _r_ ,u+b_'+d
ll %— Hand banddae O.thtn b — ‘ d . 8.2.6
Verify each property for the proportion % = %.
Why do you think the last property in the list above is called the “Add—One"
Property‘? (Hint: Separate each side of the equation into two separate
fractions.)
ABCDE ~ pentagon FGHU. Find AB. 3
. SOLUTION 6
Because the pentagons are similar, the D 15 C
Polygon Similarity Postulate states that
the sides are proportional; thus.
AB_ BC _Q_g_£»1
FG OH H! U IF" 20
Btitdllbe illl the ratios of the sides are equal. 8
any two ratios are equal. l'or example: ; 20 H
fig): CD
FG H I
A13‘ _ I‘?
I6. 20 SUDSIIIUIL’ the known lengths mto the propomon
. 243 _ l_
'6 I6 ‘ 20
A3 - E - 1.1
- I6 To solve, mumply both sides by 16
LESSON 3 2 SIMILAR P0-LYGONS 509
A ' P I C A T I 0 N
ARCHITECTURE
Consider the two similar rectangles WJ X
shown at right. By the Polvgon J |_ L L
Similarity Postulatc,
Kl. _ I_.'t-1 _ .-'u.\ _ .\'K _I '_
wx ‘ XY ‘ Yl ‘ 7w‘ '1 "
N M Z T
You can form .1 proportion with any two of these ratios, such as =
Notice that each ratio in the proportion contains a side length from each
rectangle. By using the Exchange Property. you get =
'l hus, the ratio of the long side to the short side is the same in each rectangle.
This provides another way of thinking about simihtrilv: the ratio ofany two
sides in one polygon is the same as the ratio of the corresponding sides in at
similar polygon.
E X A M P L E 0 .-‘linlt-er and Adrianne are making at scale model ol .1 building with :1
rectatigular foundation, as shown below. if the long sides of the model
are 24 inches, how long are the short sides?
0 SOLUTION
Because the scale model is similar to the
original building, the ratio of the shorter Building 13 ft
side to the longer side is the same in
each rectangle. 32 ft
A = LE
24 ?-2 Model xin.
: o 4!. — -1.31 I '
2| 24-32 24 24in.
._ -132 — - -
.v. — 32 . or l3.n inches.
5 .
' \ .
\
§ n \
{L |
5 ' ‘ - '
~? - .~ _ he
\ Q ‘~\.\ “. §"\:.~ .,
\ -‘ “ \ 50.
l K O \ w.
‘> 0 ¢ ‘
\\ L .’ 5‘, .\
510 CHAPTER 3
Proportionality Within a Figure
Exercises
. Communicate
Classify each statement as true or false and explain your reasoning
g . nqggnmcg 1. ll A.-lB(" ~ ADEF. then ADEF ~ AABC.
Smiéies 2. n AABC ~ .«:~.r)EF. then AABC ~ £~.F.FD.
Go To; no hrw.com 3. If two figures are congruent. then they are similar.
4. If two ligurcs are similar. than they are congruent.
4 5. Any two regular polygons with the Saint‘ number of sides ztre similar.
0 67';/idedski//3 Practice
Determine whether each pair of figures is similar. Explain your
reasoning. (EXAMPLE 1)
6. 7.
25
35 27
30 24 ~, ,_ 32
20 28
In Exercises 8 and 9, the polygons in each pair are similar. Find the
missing length. (EXAMPLE 2)
8.l.IH SJK
20 B
A M
5 12 F J
r 24 40
33 45 -7| 127 25-/_ l?
H\l L K N P
D 13.2 G 20 32
22
c
A P P L I c A T I 0 N 10. ARCHITECTURE A scale model ol a building has the dimensions shown
below. Find the length of the actual building.
I ""°d°' 3'5 °'" Building 42ft
7.5 cm
LESSON 3 2 SIMILAR P0-LYGONS 51 1
n tnumetconnect 1‘-.19.‘
Homework
Help Online
Go To: go.hrw.cor11
Keyword:
M61 Homework Help
for Exercises 16-19
51 2 CHAPTER 3
Practice 4114 34,0;/y
..‘ 5(;_(',1'_T5. ._
11. (men the proportionality 5l.llLt11Lt)l—_|\’l_", — TR — T4 tor two snmlar
triangles. write a similarity statement that shows the correct
C()TTE‘S[)()F|d€HC€.
12. Given the proportionality statement = = E = 1 for two similar
rectangles, write a similarity statement that shows the correct
C()l'l'E‘.Sp()l‘|l'.]€flC€.
13. Given AABC ~ AXY7. write a proportionality statement for the ratios
between the sides.
14. Given qttadrilateral EFGH ~ quadrilateral I-"'1-VX Y. write .1 proportionality
statement lor the ratios between the sides.
15. Given pentagon IKLMN ~ pentagon PQRS7, write a proportionality
statement for the ratios between the sides.
For Exercises 16-19, determine whether the polygons are similar.
Explain your reasoning.
16. 17.
A B M
[_ E F 15 2025
20 27
3'6 2'4 P 22.5 N
J
D 5.4 c H 3'6 G J so L
P
18. 19.
K 25 25
O T 30 U 18 18
22.1 T O
10.4
16 J L
S 19.5 R 34 20 20 30 30
V 1.
N M
20 S 28 R
20. Verify the C1'oss-Multiplication Property tor the proportion - 5%.
21. \-'erifi' the Reciprocal Property lor the proportion -
22. \-'eriF_v the Exchange Property for the proportion =
'..~|1v
~-. 5 - J.’ 5
23. (men 4 8, find 9.
For each pair of similar figures below, compare the ratio of the sides of
the figures with the ratio of the areas of the figures.
24. J L 25.
51 ‘I7
3 6 24 ®.
'1 I‘ 15
45
CHALLENGE
For Exercises 26-29, the given polygons are similar. Find x.
26. 27.
16 x
A 1-8 3
1.8
33.5 3
23. 29.
8
I x
4 x
X _l L2
_| F
‘I F 4.8 x+1
30. Use the diagram below to determine whether quadrilateral GHU ~
qttattlrilateral KLMN. Explain your answer.
H l
L M
G J K N
Solve each proportion for x.
r.- 27 -l.8_(
31. %_7 32.
3 1
;-I_0 6-;
33' 8 — 1' 34 1 _ I50
4 _ 7 5—?.x_3_t-t-l
35 kl H4 36. 8 — I
37. In general. what do you think is true alxout the ratio of the sides and the
ratio of the areas of two similar polvgons?
For real numbers a, b, c, and d, where b at O and d at 0.% =
Detem1ine whether each proportion is true for all values of the
variables for which the proportion is defined. If a proportion is not true,
give a numerical counterexample.
38 flzfl 39 “+-t='-*4‘
' J ' lr+x d+x
u-I-b__i.+rf rt _ L‘
40' b _ ti 41'a+b—:'+rl
42. Verify that the following proportion is true tor all real numbers :1, (1. tr, :1‘. 1-’.
andfl where b. d.and f at 0: ll"I—: = [if = 177, then‘-I: =
LESSON 3 2 SIMILAR P0-LYGONS 51 3
A P P L I c A T I 0 N S 43. WILDLIFE MANAGEMENT A method used to estimate the size oI'wiltl—animal
populations uses proportions. Suppose that a scientist catches 500 fish from
a lake and then tags and releases them. After a short time, the scientist
comes back. catches I00 fish, and finds that 8 oi" them are already tagged.
Assuming that the proportion of tagged fish in this catch is equal to the
proportion of tagged fish in the entire population, estimate the number oi"
fish in the luke.
44. WILDLIFE MANAGEMENT On the map of the Aransas National Wildlife
Refuge shown below, the scale is I em = 3.5 mi. Estimate the area of the
refuge in squztre centimeters. and then use that value to estimate the area oi
the refuge in square miles. I Iow many acres are in the refuge? (Note:
I square mile = 640 acres)
I -as
\I.':l(lI'ifl
“r o O
.Austwell
3 ~
I T’! 2940
_ Reftrge
‘ l:'nmmu.
San Antonio
an I '\'S 15 my
N \TIO.\'. IL
IV]! I HJH"
IIEFUOL
A
I d _\’t\'\"\
V g}
\ ~\
-' ($‘l3s’|‘¢
I _ ' I 5 QEV3."
I . \ . ~..\} P‘
I - u_O()S£_' ISL IND '
\I ' - srtn P.-IRA __ Gulf of
— I m_kp()n \ (’ I it 0
,¢ 0 5 ID muss
3 l
0 5 I0 KJLOMETERS
_ \
\-‘\. -t- -
\ =4.-I
lhe .-it'ar:5.u5 Mrtiotta! I-t’."!dhTe Refuge on the Iems roast romm'rt5 important nesting sites
for ehdmrgered whooping cmrtes. I he dehatte salt-trntrsh em't'rormtem‘ must he mre_fnlly
rrmt'mnihet'l in order to help this and other species ofwildli}'e sttrvive.
514 CHAPTER 3
A P P L I c A T I 0 N S 45. LANDSCAPING In the landse.tping diagram below. the scale is I em = I5 ft.
Measure the diagram and use the given scale to determine how far apart
the trees should be planted.
H." _
46. FINE ART Brenda is attempting
to paint a reproduction of the
Maui: Lisa from a print that is
If» in. by 24 in. If her canvas is
15 in. wide. how tall should it be
in order for the reprodttction to
be proportional to the print?
47. FINE ART In the prim OI‘ the i\-lomt
Lisa described in Fxercise 46, the
face is 6 in. tall and 4 in. wide.
What should be the dimensions of
the Face in Brend-a’s reproduction?
48. INTERIOR DECORATING Fernando is drawing .1 lloor plan of his house
to help him in arranging furniture. His dining room is a I2 it x I5 ft
rectangle, and his table is a regular octagon with 2 It 3 in. sides. It" the
room on the floor plan is 8 in. X IO in.. how long should the sides of the
table in the floor plan be?
LESSON 3 2 SIMILAR P0-LYGONS 51 5
‘x
'.
\
\
APPLICATION
51 6 CHAPTER 3
Look Back
49. The angles of a triangle measure ix + 51°. ('51- + l2)‘’. and (2.1: + 3]". Find
the measures of the angles. (LESSON 3.5)
Which of the following can be used to prove triangle congruence?
(LESSONS 4.2 AND 4.3)
50. ASA 51. A.-'\:\. 52. SAA 53. SAS
54. Find the measure of a base angle ofan isosceles triangle whose vertex
angle is 92°. (LESSON 4.4)
55. A right triangle has legs of 5 cm and 7 cm. Find the length of the
hypotenuse.
56. A right triangle has a leg ot'5 em and a hypotenuse of? cm. Find the
length of the other leg.
L004’ Bflyfllfd
INDIRECT MEASUREMENT Anthony uses the following method to estimate
the width of a river:
Anthony stands at point N and adjusts the visor of his cap until it is in his line
of sight to point R on the opposite shore. Without changing the position oi" his
cap. he turns and sights along the visor to point A on his side of the river.
57. Explain how Anthony Can Find the width ol the river.
58. Which segment in the figure has the same length as W?
59. Which postulate can be used to prove that ASNR '=“ .£tS.'\'A? Llxplain
_YOl.ll' i:lllS\’\'Cl'.
60. What are some possilyle problems with using this method ol indirect
measurement?
Triangle Similarity
“ “ U
A \ a
3
5
Objective i l L
0 Develop the AA wh "
Triangle Slmllaltly Similar triangles
Postulate and the SSS have interesting
and SAS Triangle mafl|9nHffca[p(opgrfi9g_
Similarity Theorems. _ _
Triangle Similarity
Activities l, 2. and 3 suggest some shortcuts lor determining triangle similaritv.
AA Triangle Similarity Postulate
_ u "L NEED 1. Draw AABC with mm = 45° and mzB = 65°. What is n1.((“? .\-leasure
mm and the sides of AABC.
urotractor 2. Draw .CtDEF with mzD = -15° and m.(E = 65“ such that DE is longer
03 than AB. What is mZF? Measure the sides of ADEF.
enmet
graphic? 3. Use your measurements to complete the table below.
software
Sides I Angles
AABC AB=7 ac=7 AC=? ImAA 45°mAB 65" mAC ?
rosr DE=? EF= ? or: 7 ImAD 45° mAE 65° mAF 7
Rah-O —é%=7 %_I;:
4. What is the relationship between corresponding sides? between
corresponding angles? Are the triangles similar? Explain vour reasoning.
cmscxporur V 5. Based on your results, complete the postulate below.
AA (Angle-Angle) Similarity Postulate
if two ? of one triangle are congruent to two ? oi
another triangle. then the triangles are ? . 8.3.1
Lesson 8 3 TRIANGLE SIMILARITY 51 7
E X A M P I. E 0.-\re the triangles at right similar?
J
P 55“
SOLUTION
By the Triangle Sum Theorem. I ‘
m4; = 130° — 90° — 55“ = 55°. so K L M N
m4! = m.(P (.415 AP) and
IIIZK = m£M [.(K E (M).
Thus. by the AA Similarity Postttlate. ILJKL - APMN.
ruler,
protractor, and
compass
OR
geometry
graphics
software
cnacxpomr ./
E X A M P I. E oitre the triangles at right similar?
1. Draw AABC with AB = 2 cm. BC = 3 cm. and AC = 4 un. Measure the
angles of AABC to the nearest degree.
. Draw ADEF with DE = 6 cm. EF = 9 cm. and DF = l2 cm. Meztsure the
angles of ADFF to the nearest degree.
3. Use your measurements to complete the table below.
Sides Angles
«A30 A8: 2 BC: 3 AC: 4 mAA- .7 mAB 7 mAC .7
t\DEF DE: 6 EF= 9 OF: 12 m.:D- .7 mAE ? mAF- .7
Ratio 1% = 7 5% = 7 %E =
. \-\-‘hat is the relationship between corresponding sides? between
corresponding, angles’! Are the triangles similar’! Explain your reasoning.
. Based on your results, complete the theorem below, which you will be
asl<ed to prove in Exercises 25-27.
SSS (Side-Side-Side) SimilarityTheorem
It the three ? ol one triangle are proportional to the three
:1; of another triangle. then the triangles are _:?_.
33.2
Ft’
T
SOLUTION 4 7 2.4! E“
The ratios of the three sides are U 4 2 V
as follows: 0 7 S
%=;=: 15-1-5 Q5 L 2
UT 2.4 3 TV ' 4.2 ‘ 3 L'\-' .2
Thus, the sides of the triangle are proportional and. by the ' ' ‘ "
Theorem. AQRS - AUTV.
51 8 CHAPTER 3
' 3
SAS Tr angle Slmllarlty Theorem
- - U. D 1. Draw £:ABC with A8 = 3 cm, 13C: -1 cm. and 11118 = 60°. Measure the
,,,|,_., and sides and angles ol A/tb‘C.
protractor
on 2. Draw .CkDFF with DF = 6 cm, FF = 8 cm, and mzF = 60°. Measure the
geometry sides and angles of ADEF.
graphics
sohware 3. Use your measurements to complete the table below.
l Sides Angles
AABC AB: 3 BC: 4 AC: 7 mAA=? m.zB=60° mAC=?
‘LDEF DE: 6 E!-'= 8 DF= ? mAD= ? m.«_E 60 mAF= ?
Ratio 333:? ‘SE:-7 %=7
4. What is the relationship between corresponding sides? between
corresponding angles? Are the triangles similar? Explain your reasoning.
CHECKPOINT V 5. Based on your results. complete the theorem below. which you will be
asked to prove in Fxercises 28-30.
SAS (Side-Angle-Side) Similarity Theorem
If two ? or one triangle are proportional to two ?
ol another triangle and their ? ? are congruent.
then the triangles are 2 . 8.3.3
E X A M P I. E am? the. triangles shown below similar?
2m 3 5.4
Y 2
F H
O SOLUTION
l'he ratios of the given sides are as follows:
Q _ .-1 EL‘. = _ 2
KY — 2 X2 3.6 — 2
Thus, the sides of the triangle are proportional. and the included angles of
these sides are congruent. By the SAS Similarity Theorem. AQRS ~ AU H’.
CRITICAL mmxrms Why are ASA and AAb not included in -.1 list of triangle similarity theorems?
LESSON 8 3 TRIANGLE SIMILARITY 51 9
Exemses
. Com»/my/mtg
1. In the figure below. the midsegments divide the large triangle into four
smaller triangles. How would you show that each ot the smaller triangles is
similar to the large triangle?
luwumdoomect
Activities
Online
Go To: go.lIrw.cotn 2. Recall the HL Congruence l'heorem from lesson -1.5. Could there be an
"°>""°."“_ _ I IL Similarity Theorem? Why or why not?
MG! Similarity
3. Use a counterexample to explain why there is no AAA Similarity Postulate
tor quadrilaterals. That is. it" three angles ofone quadrilateral are
congruent to three corresponding angles of another quatlrilateral, Cxpltlill
why the qtttldrilaterttls are not necessarily similar.
4. Use .1 countere.\:ample to explain why there is no 5838 Similarity Postulale
for quadrilaterals. l'h-at is. it" tour sides of one quadrilateral are congruent
to four corresponding sides of another quadrilateral. explain why the
quaclrilaterals are not rrecess-ar-il_v similar.
0 fill/dad 54'///8 Pfdtt/6'6’
Each pair of triangles below can be proven similar by using AA, SSS, or
SAS information. Write a similarity statement for each pair. and identify
the postulate or theorem used. (EXAMPLES 1, 2, AND 3)
5.
A L
12 15
20 B 25 K
24 30
'3 J
6.
7- G
M
7
f 14 H 0 ‘ID A
520 CHAPTER 3
. Prdct/ce and Apply
a - rntoonnect Determine whether each pair of triangles can be proven similar by
Homework W using AA, SSS, or SAS similarity. If so, write a similarity statement, and
Help Dnline identify the postulate or theorem used.
Go To: no hrw.com
Keyword: 3- T 9- F
MG1 Homework Hob 2-5
lo: Exercises 8-I5 I Z
,. 1 60 _ 45
X G
K
1.6
J
10
A
10.
11.
W
L
3
4
6
8
12.
24
Q
H
D
E
12
1 K
8
13
15
27 C
13.
M
R 3
3° 25 20 £ 4-5 5'75
3 4
35 _
L N
X W P O
In Exercises 14 and 15, can the pairs of triangles be proven similar? Why
or why not?
In Exercises 16 and 17, indicate which figures are similar. Explain your
reasoning.
"3- 1 20 s K 40 J ‘7- A
15 10 cm
0 Fl 36
_, x c '1 3
z 36 Y H 1 ‘4 '3'“ r
12cm Fl .. *8
27
“I I
W X Z 16 cm Y T 3
LESSON 8 3 TRIANGLE SIMILARITY 521
522 CHAPTER 3
For Exercises 18-21, refer to the diagram below Is the given
information enough to prove that AABC ~ AADE? Explain your
reasoning.
A E
— — E _ E c
18. BFIIDE 19. AD Ab
. . _ E _ K
20. AD - DB and AE EC 21. AD DE 8
For Exercises 22-24, refer to the diagram below.
22. Draw ANOP in which each side is twice L
as long as each side of AKLM. ls
QNOP ~ AKLM E‘ Why or why not?
23. Draw AQRS in which each side is l cm
longer than the corresponding side of
£tI‘\'L.-\-I. ls £rQR.S ~ £~.KLM? \-\-'11) or
why not?
24. Draw ATUV .. §KL.'t-f such that
= = = What is the K
ratio of the perimeter of ATUV to
the perimeter of A-.I\’L‘\"l?
5 CH’! 4 cm
3cm
A
3
$
E F
u
ii
v
A
v 2
In Exercises 25-27 you will prove the
SSS SimilarityTheorem. In the diagram at
right, the sides of AABC are proportional
- A8 _ E _ 91
to the sides of ADEF, and -[TE — EF — FD .
Also, W has gen flied such that
A6 = DE and GH || BC.
25. Use the A/\ Similarity Postulate to prove
that AAGH ~ AABC.
26. Use the result of Exercise 25 to prove that
£tAGH E ADEF.
27. Use the results of Exercises 25 and 26 to
prove that AABC ~ ADEF.
C
In Exercises 28-30 you will prove the SAS
SimiIarityTheorem. In the diagram at right,
two sides of AUVW are proportional to two
sides of axvz, -% = and /_u '—: /_x.
Also ST has been added such that US = XY
and W || VT. W
28. Use the AA Similarity Postulate to prove
that £tU.S'l ~ AL.-'l-'1-‘l-’.
29. Use the result of Exercise 28 to prove that
IAUST E A-.Xl"Z.
30. Use the results of Exercises 28 and 29 to
prove that AUVW -- AXYZ.
PROOF
CHALLENGE
APPLICATIONS
Recall from Lesson 2.4 that a relationship is called an equivalence
relation if it satisfies the Reflexive, Symmetric, and Transitive
Properties. Exercises 31-33 establish the fact that similarity is an
equivalence relation.
31. Prove that AABC ~ AABC (Reflexive Property).
32. Prove that if &Ab‘C ~ ADE!-'. then ADI.-"F ~ AABC (Symmetric Property].
33. Prove that if AABC ~ ADEF and ADEF ~ AGHI. then AABC ~ £t(_il”
(Transitive Property].
34. Refer to the diagram at right. Suppose that X
there is a quadrilateral STU V with ./_T E /_X
and ./_V E ./_Z and that all four sides ol'STUV
are proportional to all four sides of I-VXYZ. W
Show that the two quadrilaterals are similar.
Generalire your results from this case to make 2
a conjecture about a set of conditions that can
be used to prove similarity in quadrilaterals.
In Exercises 35-38, refer to the following situation: Four artists are
copying a design to a larger scale.The design contains a triangle, and
the artists need to make a triangle that is similar to it.
35. GRAPHIC DESIGN Tony Iirst draws one side of his triangle and then copies
the angles from the original triangle at the endpoints of that side. He then
extends the angles until they meet. \-\"ill 'lony’s triangle be similar to the
original? Explain your reasoning.
36. GRAPHIC DESIGN Biata measures the sides of the original triangle and then
multiplies each length by 5 to get the sides of the triangle in her design.
Will Bi-ata‘s triangle be similar to the original? Explain your reasoning.
37. GRAPHIC DESIGN Miki copies one angle lrom the original triangle. then
measures the two sides adjacent to that angle. and multiplies the lengths
by 5. She then draws sides with these lengths adjacent to the copied angle
and connects the endpoints to form a triangle. \\" ill Mil-ci’s triangle be
similar to the original? F\:plain your reasoning.
38. GRAPHIC DESIGN George measures two sides of the triangle and multiplies
the lengths by He draws one of the sides and copies the nonincluded
angle at one ol‘ the endpoints. He extends the angle and then draws the
remaining side from the other endpoint so that it intersects the side of the
copied angle. Will George’s triangle be similar to the original? Explain vour
reasoning.
LESSON 8 3 TRIANGLE SIMILARITY 523
524 CHAPTER 3
‘\
>
Look Back
Refer to the diagram at right.
A—B=‘.:' B—C and line] I] line k.
Find each angle listed below.
(LESSON 3.3)
mi’ C
k A x” A O
39. x 40. y
41. 2 42. I’
l ‘7t5°/ B\
Plot point A(3, 5) on a coordinate plane and draw a line through this
point and the origin.
43. What is the slope of this litte? (LESSON 3.9)
44. What is the distance from the origin to point A? (LESSON 5.6)
45. Draw a right tri-angle with point A as one vertex. tlte origin as one vertex.
and one side on the x-axis. Find the ratio of the length of the longer leg to
the length of the the shorter leg. (LESSON 3.2)
46. Choose another point .m_vwhere on the original line and label it B. Draw it
right triangle with point B as one vertex, the origin as one vertex, and one
side on the x—axis. Find the ratio ol'the length of the longer leg to the
length of the shorter leg. (LESSON 8.2)
47. Are the triangles in Exercises 45 and 46 similar’! lixplain your reasoning.
(LESSON 3.2)
L004’ Bflyfllfd
In the diagram below, the three triangles are similar, and AC, DF, and
5 are parallel.
D A
4]
EF
8 C
All
H I
48. Copy the dtugratu and draw lmes AD. BE . and CF. Label the point ol
Intersection X.
49. Draw lines AG. BH. antl (J. Label the point ol Il]teI'St‘(.tl()l‘l l.
_ ¢—'P I-—> <—! _ _ _
50. Draw lines DG, EH. and F]. I ttbel the point of Intersection 7.
51. What do you notice about points X. Y. and .4?
Objectives
0 Develop and prove the
Side—SpIutung
Theorem.
0 Use the Side-Splitting
Theorem to solve
problems
when you hear the
p - - ‘side spmztug. " you
may think of laughter. In
geometry, it refers to 0
mm! theorem
The Side-Splitting
Theorem
l
¢u—'
The capital letter A rmiy be t:ml)elli.<!IL'rl in emllrsss H-'£l)'S for reasorts ofbeuuty
and style. But in its most lJ:1sit'j0r'm, it sItgg('.\'!.s :1 gt‘oruetr)' theorem.
The Side-Splitting Theorem
As you will see in F.x-ample 2, people have been solving problems about
proportions in triangles since ancient times. One useful result is the Side-
Splitting Theorem.
Recall from the 'l'ri-angle Midsegment l'heorem in Lesson 4.6 that the
midsegment of -.1 triangle is parallel to one side of the triangle. The following
theorem applies to any segment that is parallel to one side ofa triangle.
Side-Splitting Theorem
A line parallel to one side of the triangle divides the other two sides
proportion-allv. 3.4.1
LESSON 84 THE SIDE-SPLITTINGTHEOHEM 525
TWO-COLUMN P‘ 0 0
CRIHCAL THINKING
Given: TTF. II E A
Db EC
Prove: — = —'
AD AE D E
Proof:
8 C
Statements Reasons
1. Elli Given
2. mzb‘ = mzl ll" || lines are cut by at tr:1nsvcrs-.i|.
m./_’C = mzz corresponding angles are E.
3. AABC - AADE AA Similarity Postulute
4. % = Polygon Siiuilarity Postulutc
5. AD+ DB =1-SB Segment Addition Postulate
AE + EC = AC
6. ”%?B = Substitution Property
7. -;’;‘—g + % = g-E + Addition ot'fn1«:tions
DB _ EC .. .-,
8 l+ W - I + Sllllpllly.
9. ii = Slll)l.l'£.lCtl()n Property of Equality
What other proportions can you find in AABC by using the Side—Sp|itting
Theorem?
The diagram at right man‘ help
you remember the proportions in
a triangle with a segment parallel
to one side. The following are
Whole
left
Whole
right
some of the proportions resulting l-0W9‘ WW6‘
from the Side—Splitting Theorem: km
upper left _ upper right upper Iclt _ |0we,- H1
lower left - lower right upper right - lower right
upper Ielt _ upper right |(,w-‘.1-|€i't _ lower right
whole lefi _ whole right whole left — whole right
E X A M P I. E ollse the Side-SpIittingTheorem to findxinthe triangle below.
526 CHAPTER 3
O SOLUTION
Choose a proportion that includes x as a single term.
upper left _ upper right
lower left _ lower right 12 15
L3 = '_5
'5 X 16 x
IZX = 240
r = 20
The following is a corollary of the Sidc—Splitting Theorem:
Two-Transversal Proportionality Corollary
Three or rnore parallel lines divide two intersecting trattsversals
pr0pOrti0n'.Ill\-'. 8.4.2
_ _ _ s t
In the dragratn at right. lHlL‘S I’. m. A‘ X,
and H are parallel. with transversals ’ 1'
s and t. A 3\ Y! m
One proportion that results trom
- - 9 '-L“ =
Corollary 8.4.- . BC Y2. C 2 n
D
CRITICAL THINKING How can you tell that AADX ~ ABDY?
E X A M P L E 0 CULTURAL CONNECTION: AFRICA Students in ancient F.g}'pl studied geometry to
solve practical problems involving the pynunids. This problem is based on a
|]l'0l)lt‘lI‘l in a papyrus copied in 1650 B.(‘..E. by the scribe Ahrnes from a source
that m:I_v date back to 2000 B.C.E.
F 3.5 B
In the diagram al>ove,l_J—I3. and F5 are parallel, AD = AI.-' = 7 cubits,
DF = FB = 3.5 cubits. and DE = 2.25 cubits. Find the rcnmining lengths.
. SOLUTION
Use the l‘wo— l‘ransvers.al Propoi tionality Corollary:
AD _ fl L = L =
DF ‘ EG =” 5.5 EG :’ EG “'5
and
LP _ E5 = ' '=
I-'b‘ ‘ or: =’ %.5 cc =” (‘C 3'5
Use the definition ofsiniilar triangles:
AD _ DE 7 _ 2.25 . =
F ‘ I-‘G =’ 10.5 " G1-' =” OF H75
AD _ E L _ Eé ' = '
AB ‘ BC =" 14 ‘ L =’ bc 4'”
LESSONS: THE SIDE-SPLITTINGTHEOHEM 527
Exerc/ses
Q Co»/mm/cate
1. Use the exutnplcs on page 526 to tndkc D
.1 list of proportions in the figure at right. f
2. Are all isosceles triangles similar?
Explain or give a counterexample. C d
3. Are all equilateral triangles similar? Explain or give a C0llt'tlt.‘l‘L‘xtll't1plC.
4. Are all right triangles sinrilur? Explain or give at cotlnterexantple.
5. How does the capital letter A relate to the Side-Splitting Theorem? If the
cross bar is ll0I’ll.Ol1l1ll, what is true of the places when: it intersects the
sides of the letter? Would this he true ofan italic (sl-unted) A. as well?
Q///dad’ 5;?///8 Practice
Use the Side-Splitting Theorem to find x. (EXAMPLE 1)
6. 2 3 7. 8. 4
10 9
X 5
x
L:
4 6 x
Find the indicated measurements. (EXAMPLE 2)
9. D!-‘ B
F
10. FB 9
4
11. FG
12. BC A 5 E G C
0 Practice and Apply
ll Inumuoomm {.53 In Exercises 13-20, use the Side-Splitting Theorem to find 2:. In some
flfll . .
Homewom exercises, there may be more than one possible value for x.
Help Online
60 lo: uo.hrw.com
Keyword:
MG! Homework Help
for Exercises 13-20 24 20
13. X B 14.
15. 16.
528 CHAPTER 3
‘ I r I 17. 18.
x+1 X 1
x_2 )«-3
19. 20.
2x~4
3x+6
2x 3x—1
5 x+1
x+1 9
Name all similar triangles in each figure. State the postulate or theorem
that justifies each similarity.
21. 2
B
E
A
D
F
C
Find 2: and y in each figure below.
23. QRST is .1 parallelogram.
R 8
‘I8 Y A 2 20
8 1 X Y
O 20 T x B
,\
7 ya,»
;L \3
5 &x+2y
l ’ \
2- K
24.
25.
LESSON 34 THE SIDE-SPLITTINGTHEOHEM 529
CONNECTION
530 cum-Vrea s
The Side-Splitting Theorem can be used to divide a segment into any
number of congruent parts using a compass and straightedge.
26. Draw a segment and label its :1 T ‘'3
endpoints A and B. Using your
straightedge, draw a ray extending
from point A to form an acute
T 4
angle with E. A
27. Set yottr compass to some small
length (such as I cm) and mark
off several lengths along the ray.
as many as the number of parts
you wish to divide the segment
into.
In
28. Connect the last mark to point B
with a segment. Construct lines .
parallel to this segment through A
each mark of the compass.
8
/—:~
8
M.’
B
29 Explain why the parafl lines in
the last figure divide .46 into five
C
congruent segments. It 3
30. Draw a segment that is 15 cm long. Use
the method described above to divide the
segment into seven congruent segments.
COORDINATE GEOMETRY The distance between two parallel lines is
measured along a line perpendicular to both. In Exercises 31-34, you
will explore the distances between parallel lines in a coordinate plane.
31. Graph the lines y - x. y - x + 2. and y - x — 3 in a coordinate plane. How
can you verify that these lines are are parallel?
32. Graph the line y = —x in the same plane. How can you verify that this line
is perpendicular to the lines)‘ = x. y = x + 2. and y = x — 3?
33. Give the coordinates of the points where the line y - —x intersects the lines
y = .1: and y = Jr + 2. Find the distance between these parallel lines.
34. Graph the horizontal line y = 3 in the same plane. Use the Two-
Transversal Proporlionalily Corollary to write a proportion. and solve it to
find the distance between the lines y - x and y - .1: - 5.
35. Prove the converse ot the Side-Splitting Theorem: It a segment divides
two sides of a triangle proportionally, then the segment is parallel to the
third side.
C it A L L E N G E 36. In the diagram at right.;L€. = l.3.—. = 2.2.
and AD = i0 cm. Find AB.
A P P L I c A T I 0 N S 37. MUSIC A simple stringed instrument
can be created with parallel strings
on an isosceles trapezoidal frame, as
shown. lithe note for the first (lowest)
string. with a length ofcifl cm. is an F.
then a string with a length oi‘ 20 cm 3
would be one octuvc higher. also an F.
ii" a string for the note C is% of the
length oi the string for the lower F, where
would you place the string on the frame?
38. MUSIC For the instrument above, the string lor the note G is % ol the
length of the string for the lower F. Where would you place the string on
the frame?
39. BIOLOGY An orb spider web consists of a spiral of straight segments
attached to a series oi radial segments that meet at the center. Fach sector
19.5 cm of the web can be modelled by nested similar triangles. Suppose the
outside ofa spider web is approximately a regular I6-gon with a side
length oi 19.5 cm and the 9 inner segments are spaced at equal intervals.
The riiugrnrrt n'prt'$¢'m'$ Use the diagram to estimate the length of silk used to build the web.
P J =,\\ _
ll ll":
i
\‘~
I
I
Notice the spiral ofstirziglit segments in this orb spider welt. Though spider ll’t.'l)5 in
nature are not peifectly syntmetricul. or the spacing of their spirals even. you can model
a web mrulremrttimlly and get at good estirmzte of the lmgtli of the sill; in its spiral.
F30 cm
LESSONS: THE SIDE-SPLITTINGTHEOHEM 531
APPLICATION
CONNECTION
532 CHAPTER 3
Look Book
40. ENGINEERING Find the height ofthe
stack ol pipes $hown at right. The
diameter ofeach pipe is 8 ft. (Hint:
Connect the centers of the circles to ‘gr’ I 1 ,
form an equilateral triangle.) . _ v—_ “.5
-4‘
.z'r .
1;. Y ‘—
;t '-’-‘-'‘'a'
> I ‘ 5
- If x.» ;—L ' A
COORDINATE GEOMETRY For Exercises 41-47, refer to AABC with vertices
A(3, 5), BIG, 1), and C{—2. -7) in a coordinate plane. (LESSON 5.6)
41. Draw AABC in a coordinate plane.
42. Find the perimeter of AABC.
43. Find the midpoint of each side. Label them D. E. and F.
44. Find the perimeter of ADEF.
Recall that the median of a triangle is a segment that connects a vertex
to the midpoint of the opposite side. (LESSON 5.6)
45. Draw the median of AABC from A. and find its length.
46. Draw the median of AABC from B, and find its length.
47. Draw the median oi’ £1-..»’lb'C from C, and find its length.
Look Beyond
48. Are the triangles similar? Why
or win; not?
Refer to the figures below for Exercises 48-49.
49. Find the ratio of the length of
the shorter leg to the length
I
2
ot the hypotenuse for each
triangle. What do you notice? 5
30'
50. The shorter leg of -mother right triangle with a 30° angle has a length oi
I7. What is the ratio of the length of the shorter leg to the length of the
i‘I_V[‘.>0tv‘:‘nliSt;‘ for this triangle?
Indirect Measurement
and Additional
Similarity Theorems
C
Mtmumcm Valley in trizomz
Objectives - I 0_ -5‘ f
I
0 Use triangle similarity i_' 1 __
to measure distances ’ g
indirectly. 1 '
T
0 Develop and use I I ‘ '
similarity theorems for ~_~. __ __
altitudes and medians * . _ : - _
of triangles. '*' ' " "
‘ {
Directly measuring the dismnce across a ‘--‘-' . -*‘—.__ __ _
lake or me nargm ala mountain can be dmrcun .- ‘: - w*_. :L“‘‘‘*._-_ 5 E
or even i . . . - ibla. A more practical method ~ <_. sag;
was similar triangles to estimate the desired ‘ W 2
nr : . amour. _. ~—.“x
‘:-;‘l¥~
Using Similar Triangles to Measure Distances
EXAMPLE
inaccessible distances can often be measured by using similar triangles.
Suppose that .1 military engineer needs to
know the distance across a river in order to A
build a temporary bridge. Using a point on
the opposite side of the river as at reference X
point, the engineer sets up right triangles
along the bank of the river. Use the diagr-.nn
at right to find the distance across the river.
B 72m C
40m
0 SOLUTION 0
Using the right angles and vertical angles. t'_‘.ABL ~ £1-.Dl.-"C bv AA Similarity, so
AB BC
T)?‘ = ”'|€l'Ci-()l'€I
x _ 72 x _ l_2
4—n ‘ .Tn‘ °' m - 5
.1 = '2 - 40 = 96 meters
LESSON 3.5 INDIRECT MEASUREMENT AND ADOITIONAL SIMILARITYTHEOREMS 533
E X A M P I. E 0The diagram at right illustrates another
CRITICAL THINKING
E X A M P I. E olfim wants to know the height ol
534 CHAPTER 8
method oi setting up right triangles A
along the rit-er bank. Use this diagram
to fund the distance across the river. X
-60 m
D SOLUTION 3' 5
Because L.«‘lb’L-‘ E ACD and LA 5 LA, 32 m
.-BABE ~ £~.ACD by AA Similarity. and 80
sofl. = Therefore: C m D
AC, CD
I _ éfl A‘ _ 2
.1‘+32 " 30' ‘" x+32 ‘ -1
4x= it + 96
x = 96 meters
Why do you think the engineer used 90° angles? Could other angles be used?
a basketball hoop. 'l he regulation
height is I0 feet. Use Kim's height
and the length ot‘ the shadows in X
the diagram at right to find the Q‘ 9-’ 70.
height of the basketball hoop. ls " ‘
the hoop at regulation height? '-
1 85" 2
SOLUTION 50"
Because the Suit is so far away, the
sun’s rays are essentially parallel,
and AI = 42. Both Kim and the
post of the basketball hoop are
perpendicular to the ground, so
the two triangles are similar by
the AA Similarity Postulute.
A = E
70 30
70- 7% = - 70
.2: H9 inu:hes.or9 Ieet
and II inches.
The hoop is I inch below regulation
height.
PARAGRAPH PROOF
CRITICAL THINKING
E X A M P I. E l'he trianglesinthe diagram-are similar.Sol\-'el'or x.
Additional Similarity Theorems
As you know. the sides of similar triangles are proportional. As you will see
below, other parts of similar triangles are also proportional.
Proportional Altitudes Theorem
it" two triangles are similar. than their corresponding altitudes have the
same ratio as their corresponding sides. 8.5.1
Recall that an altitude ol'a triangle may be inside the triangle. outside the
triangle. or a side of the triangle.
The following proof shows the case of an altitude inside the triangle. You will
be asked to prove the Case ofan altitude outside the triangle in Exercise 26.
Given: mac ~ AXYZ; H7 x
is an altitude of AABC
and )4’!-V is an altitude
ol‘AXt"Z.
Pmw lf) = M5
‘ xw xi‘
pm": 8 D c Y W 2
Because £s.«tb’C ~ £s,\’t’£, Lb’ 5 Al by the Polygon Similarity
Postulate, and LBDA and L}'l-V,’ are right angles by definition of
altitude. Thins. AABD ~ AXYW by the AA Similarity Postulate. and
= by the Polygon Similarity Postitlate.
How would vou prove the case of an altitude that is a side of the triangle?
. SOLUTION
L = |_6 2?
l2 20
I2 - -“ = E « I2
I2 20
I = - 15
These are
corresponding
sides.
LESSON 8.5 INDIRECT MEASUREMENT AND Aootrlot-1:tL SIMILARITY THEOREMS 535
Recall that at nu-diam of .5 triangle is at segment that joins a vertex to the
midpoint of the opposite side.
Proportional Medians Theorem
If two triangles are similar. then their corresponding medians have the
same ratio as their corresponding sides. 8 52
You will be asked to prove this theorem in Exercises 35-41.
E X A M P I. E 0The triangles in the diagram are similar. Solve for x.
C SOLUTION
i — 3_-2.
6 _ .1:
4).‘: l9.2
x = 4.3
Exam/zses
. Com/mm/cate
1. Fxplain how triangle similaritv is used in indirect measurement.
2. Are the triangles in the 5
diagratn at right necessarily
similar? Why or why not? 26 39
3. How could vou Find the height of an object from the length of its shaclow?
4. Suppose that the shadow of the object is not visible.
Describe another method of linding the height
ofthe object with indirect measurement.
536 CHAPTER 3
0 6/¢/‘dad SK’///8 Practice
5. Use the diagram at right to esliinalc the
width of the lake. Justify your answer. EXT
(EXAMPLE 1) 5,; km
3 km
10 km
6. Use the diagram at right to csxiinau: the
width of the lake. Justifv }.'our:1I1swer.
(EXAMPLE 2)
10 km
1:: km
7. Tranh wums to know the Iiciglu of -.1
streetlight in his ileighlaorhuml. He
measures his shadow and the po|e’s
shadow -.11 the same time ofday. Tranh
is l?0 cm tall. Find the height olithe .
stree-(light. (EXAMPLE 3) 840 cm 310 cm
In Exercises 8 and 9, the triangles are similar. Find x. (EXAMPLES 4
AND 5)
8' 2 4 9' 1.5 2 E1
3 3
3.6
7.2
. Practice dlfd Apply
ll Imematcnnnecx For Exercises 10-13, use the diagrams to find the height of each
Homework ‘ building-
Help Online 10 11
Go To: go.Inw.com ' '
Keyword:
MGI Homework Help II I I I I
let Exercises I|]—2|]
12 ft
‘ 22.5 ft ,. 110 ft
81 ft 27 it 20 h
12. I , . . 13.
I I I I I
18 fl I I I I I I
9 ft
12 ft 20 11 6 ft 1:: fl
LESSON 3.5 INDIRECT MEASUREMENT AND ADDITIONAL SIMILARITY THEOREMS 537
For Exercises 14-17, the triangles are similar. Find x.
14. 15.
1 5.6
13
115
17.
In the diagram at right, AADE -- ARVW,
A0 = CD, and RT = TV.
18. RH-’ = E‘ 19. L-‘B = ?
2o. wt-’ = ?
21. Are AIKL .tnd AA-[K] similar? Explain.
22. Find the length 0! the h'_p'pOlt?l'IlISt.’ of AIR’! and of AA-IKI.
23. Find the area of AIKL and of :15.-‘K.’-[K].
24. Find the lengths of the dashed altitudes of AIKL and of ./_‘u\-[K].
25. is the ratio of the altilttdes 0| Alf-{L and A.-UK] the sanie as that (ii the
corresponding sides of AIKL and AMKI? Explain your reasoning.
26. Use the diagram below to prove the Prnportiotul Altitudes Theorem for
the case when the altitude is outside the triangle.
X
A
E rt.
Y Z
538 CHAPTER 3
PROOFS
CHALLENGE
Complete the proof of the following theorem:
Proportional Angle Bisectors Theorem
ll’ two triangles are sitnilar. then their corresponding angle bisectors have
the s-ante ratio as the corresponding sides. 8.5.3
Given: mac ~ ./_xxt7.Tr‘) X
Eds ABAC. and K
Kw’ bisects AYX7. Y W Z
Prove: =
Proof: 3 D C
Statements Reasons
AABC ~ AXY7 27. ?
AB 5 ll’ 28. ?
m.{BAC = n1£l"X.7 29. ?
E5 bisects ABAC; Given
bisects AYXJ.
30. L: 2 - in.4b’AD Definition of angle bisector
L: 2 - mAlXl-\-’
31 . ? Substitution Property and
Division Property
32. ? .-\A Similarity Postulate
33. ? Polygon Similarity Postul-ate
34. Prove the following theorem:
Proportional Segments Theorem
An angle hisector of a triangle divides the opposite side into two
segments that have the same ratio as the other two sides. 8_5.d
Glven: In .«_\.1t:L, W bisects AKIL.
Provo:
flit: First construct a fie parallel to
]M through R. Extend [L to intersect
KB"! _ [K
WW7
this line at point N.
LESSON 3.5 INDIRECT MEASUREMENT AND ADOITIONAL SIMILARITY meoet-:tt-is 539
FLOWCHART PROOF
APPLICATION
5ft
3ft \:
Mirror
12ft
The film ofoprirs gmtrnmee
!Im( the t'ndt't:zm’d rtngfes
are titmgl near.
540 CHAPTER 3
For Exercises 35-41, complete the proof of
E
the Proportional Medians Theorem. 3
Given: AEFG ~ ./_xsIt_J.fi is the median or
AEFG. and Si-’ is the median of .-SSTU. F T
V
Prove: ET = ST H G U
mg;
Proof:
1 I AEFG~ASTU I
[TSP is the median} [3V is the median
of AEFG. of ASTU.
Given Given Given
I I I
1 v 1
His the midpoint Vis the midpoint _Eg_ _ E t
ofE—I-J. «W U 5’ [area]
35. ? Def. of median Polygon 38. ?
| | Similarity
FG=2'FH ITU=2'TI/
Def. of midpoint 36. ?
37. ? 39. ?
| 40. 2 - —
SAS Stmtlanty
.7
| 41. 2 I
Polygon
Similarity
r \ -
42. PALEONTOLOGY You can use a mirror
to estimate the height of an object, . '
as shown in the photo. According .‘
lo the laws of optics. the light \
reIIects on 21 mirror at the same
angle from which it strikes the , ‘-
mirror. Use the diagram to ‘- _ 1 ‘
estimate the height of the ? '
dinosaur skeleton.
-1
\ " 11- 1 ‘V .. ~...
v 2.:-v
APPLICATION
OPTICS The diagram at right shows
a convex lens, which is thicker in
the middle than at the edges. A
convex lens bends light rays to
form an image of an obiect on the ""399
opposite side of the lens. Light 5
rays through the center of the lens Object
are not bent, so BB’ and C0’ are
straight segments. Thus, AABC and
- - __8c = A2 2'
AAB’C’ are similar and 8,6,, Ac”
object distance
image distance'
obiect size
image size
43. Prove that AABC -— .-'_‘~.AB’C’.
44. ll‘ an object 6 cm from a convex lens forms an image IS cm from the lens
on the opposite side. what is the ratio of the size of the object to the size
of the image?
45. Rosa placed a lens 25 cm from an object 10 cm tall. An image was lbrnted
5 cm from the lens on the opposite side. I-low tall was the image?
46. How could you arrange an object. a lens. and an image so that the ohiect
and the inmge are the same size?
47. How could you arrange an object. a lens, and an image so that the image
is 20 times taller than the object?
Look Back
Find the shaded area of each figure. (LESSONS 5.2, 5.3, 5.4, AND 8.4)
48. 49.
2 1
..l
2
I‘
I-—3—>-t
50. 51.
3
4
2 3
‘ I‘
5
Find the volume of each solid. (LESSONS 7.3 AND 7.5;
52. 53.
:7
" — 5
3v
‘l
LESSON 8.5 INDIRECT MEASUREMENT AND ADDITIONAL SIMILARITY THEOREMS 541
1.00,(' Beyond
CULTURAL CONNECTION: AFRICA Eratosthenes, a Greek astronomer who
lived in northern Africa, used indirect measurement to estimate Earth's
circumference in approximately 200 B.C.E. Eratosthenes knew that the
Sun was directly above the city of Aswan at noon on the summer
solstice, so a vertical rod would cast no shadow. He measured the angle
that the Sun's rays formed with a vertical rod in Alexandria at the same
time and found it to be 75°.
54. Explain why Al 5 A2 in the diagram below. Remember that the Sun's rays
are considered to be parallel.
55. The distarrce from Aswan to Alex-.mdria is 5000 strrrles, or about 5?5 mi.
_ -r cl 7 _ _ _ ,
Complete the proportion = 3 and solve it to hnd l;r.rtosthenes
estimate of Earth's circttritlerertce.
56. Given that ha rth‘s circumference is approximately 24.900 mi. find the
relative error in Eratosthenes‘ estimate.
' 75$
ATLANTC :
,0“-AN - nloclrlorranetrn Sea
'1'‘ 3‘ Alexandria
ll ntnmctconnect "_. . sun-5 my I '
Portfolio mm ' r‘ ' _ ‘N ,l_ 7 5 F cam’ '
Extension - m‘ ‘ ‘ Alexandria
Colo‘ ohrwcom EGYPT
41 ' ' A andrra ' I - 55'-
K*Y“'°"-‘: . Center “ o—--“ ' F»
MCI Indirect or __.._;-";:_-5°°° Aswan u_~_
-Aswan E ‘ ‘ stades
arth _ \ _
‘ |TI£2= 7 Aswan
QELUO
°Q~
4 TECHNIQUES FOR |NDlRECT MEASUREMENT
Lse proportions and at least two or the
methods listed below to lind the dimensions
of a building or other structure at your
school or in vour neighborhood.
' .\-leasure the shadow ol‘ the building and ~_ ' " _ hi’
the shadow ofa person or object with a - Z -.-_ ‘7
known height. « .5‘
' Use -.1 mirror to create similar triangles. |
as shown in Exercise -13. t
- . . . " 1
' Take a photograph ol the building with a ,. z-— -2
person or object of known height standing V.
in front oi it. Measure the building and 1
the person in the photograph.
WORKING ON THE CHAPTER PROJECT
You should now be able to complete Ar:tivit~_,' 2 of the Chapter Project.
‘
542 CHAPTER 3
Area and Volume Ratios
C
1.-.
-7
Objectives ,'
0 Develop and use ratios ‘J
lor areas ol similar ,-'
figures. I‘
_ 4
0 Develop and use ratios _;v
lor|_w(.r]olumes of similar "one ‘We,’-ca, mm
5° ' S‘ has twice the diameter of ;
9 Explore relationships 0"‘-W9’: WW ""9" ‘"0’? Wm ’
betvfee" °'°S5‘ . U" my". mm mm? TM‘ Sp.’rer|'m! trmks are best for storing i.'0Mtt’lHS
sectronaIarea,wer9ht, Iesstm wrllshowynuhowta d, __ _ _ _’ I. H‘ I
and hem” answefquesfimsh-kc mesa rm rrprr:~.~m_e, am. 1 as rqm mrrme am I
whtml drmnmrls like butyIrrrr' and bumdrem’
Changing Dimensions of Figures
ll’ the diameter of the spherical container in the photo is doubled. what would
happen to the volume? In the Activities that follow. you will answer this and
related questions.
Ratios of Areas of Similar Figures
- I LL N in For each pair of similar ligurcs below, the ratio ofa pair of L‘ort'L‘5ponding
calculamr measures is given. Find the ratio of the areas for each pair.
1. Two squares 2. Two triangles
side of square A _ 3 side of triinglc A _ 2
side 01' square Li — I side ol triarngle B _ I
area of sqtmc A _ 3 arm of triangle A _ 3
area of square ll _ ? area of triangle ll _ 3
3 10 Triangle A
I 1 5| _\Triang|e B
Square A Square 8 8 :3
LESSON as AREA ANDVOLUME nmros 543
3. Two rectangles 4. Two circles
aide of Iwcmsle A _ 3 tadius olcitcle .~\ _ 4
sicle of tectangle B 2 radius col‘ circle 13 3
area of rectangle .-\ _ 3 “-34 0; Chat A _ 3
area of rectaitgle B ? area cl‘ circle 13 ?
9 Rectangle A
18
Circle A
6 Rectangle B
12
Circle 8
5. Use the results of Steps I-4 to complete the following conjecture:
Conjecture
cuzcxpomr ./ Two similar figures with corresponding linear measures in the ratio 2-:
have areas in the ratio ? .
Solids are similar if they are the same shape and all corresponding linear
dimensions are proportional. For example, two rectangular prisms are
similar if the lengths and widths of the corresponding laces and bases are
proportional. In Activity 2. you will explore the ratios of the volumes ol-
similar solids.
' Z
Ratios of Volumes of Simiiar Figures
0 I. E For each pair of similar solids below, the ratio ot a pair ol corresponding
ca|cu|3m, measures is given. Find the ratio ol the volumes for each pair.
1. Two cubes 2. Two rectangular prisms
edge of Lulac A _ 3 edge of prism A _ _;
edge of cube ll _ l edge at prism B _ 2
volume ol'uIl.tc A = _'{ \’°l”'“¢ 0'. I-“ism A =
volume of cubc B ’ volumc ol prism ll ?
' 8
' 1
Cube A Cube 8 Prism A Prism B
544 CHAPTER 3
CHECKPOINT ./
CRITICAL THINKING
TRV THIS
3. Two spheres 4. Two cylinders
radius ot cylinder A _ 2
radius of sphere A _ 2
radius 0! cylinder B _ I
radius ul sphere B _ T
\,o|um¢ Of‘-ube A = 3 volume olicvlindcr .-\ = 2
volume of cube B ? volume ol cylimler B ?
(“"12
/1° 10 3
. j 5 5
sphe.e A sphem 3 Cylinder A Cylindei B
5. Use the results of Steps l—I to complete the following, coniecture:
Conjecture
Two similar solids with corresponding linear measures in the ratio -11,
have volumes in the ratio ? .
Are all cubes similar? Why or why not? Are all spheres similar? Why or why
not? Are all cylinders similar? Why or why not?
a. '|'he corresponding sides of two similar triangles are in the ratio What is
the ratio 01' their areas?
b. The surface areas of two similar rectangular prisms are in the ratio What
is the ratio of their corresponding sides?
1:. One sphere has a radius ot' 5 meters. Another sphere has a radius 0|"
I5 meters. What is the ratio of their volumes?
Cross-Sectional Areas, Weight, and Height
l'he amount of weight that a structure
can support is proportional to its cross-
sectional area. For example. column A.
whose radius is 3 times the radius of
column B. can support 9 times more
weight than column B. This is because
the cross—sectional area ol column A is
9 times that olcolunm l3.
3
F r r
Column A Column B
In Example I and :\ctivit_v 3. you
will investigate the mathematical
conseqttences of some animals’ support
requirements.
The Itmd-lterlrhtg crtpucities of
the (‘OIIININS depeml on their
cross-sectxbmtl rtrens.
LESSON 86 AREA ANDVOLUME RATIOS
545
E X A M P I. E or-xyoung elephant that is -1 ft tall-at the
A'Pl.lCATl0N
BIOLOGY
shoulder has a leg bone whose Circular
cross section has a radius of-1 cm. How
much thicker would the leg bone need
to he to give the same support to an
elephant that is 8 ft tall at the shoulder?
Bv what scale factor does the original
radius need to be multiplied to provide
a sufficient c.ross—sectional area?
O SOLUTION
The height ot the elephant increases by a factor of 2. However. the volume ol
the elephant increases by a factor of 3. l'hus. the larger elephant would need a
leg bone with a cross—sectional area 8 times larger than that of the original
elephant.
Thus. 8.11‘: is the required cross-sectional area-
Let R represent the radius of the leg bone of the larger elephant.
KR) - 8.111
R2 = 8r’
R = \."El'
Thus, the radius of the larger bone must be J5, or about 2.8. times the radius
of the smaller hone.
calculator loptionall
546 CHAPTER 3
CHE CKPOINT 5/
Have you read stories of giants hundreds ol feet tall? Do you think giants like
this could be real? The elephant example shows how increased linear
dimensions aITect the structures that must support the increased bulk. Think
about the question of giants as you do the next Activity.
' 3
Increasing Height and Volume
1. Complete the chart to determine the necessary scale factors for the
cross-sectional radius of leg bones of animals.
Height scale [actor Volume scale factor crossggffgxzrdius
2 8 \- 8
3 27 J?
4 64 7
5 7
100 .7 ?
2. If a normal-sized horse requires a leg hone with a cross-sectional radius
ol 2.5 cm, what must the cross-sectional radius of a leg bone be for a
horse that is 20 times taller? 50 times taller? I00 times taller?
3. What eITect does increasing the size of the horse have on the relative
proportions of the legs? Would the legs of a larger horse he
proportionally thicker or thinner than those Ola normal-sized horse?
Exercises
. Communicate
1. What is the relationship between the ratio of the edges of two cubes and
the ratio of their volumes?
2. Why are all spheres similar? Why are all cubes similar? is this true for
other three-dimensional figures? If so. name or dest.ril)e them.
3. Ifyou know the surface areas of two similar prisms, explain how vou can
find the ratio of their volumes.
4. What happens to the volume ola
cylinder if the radius is doubled
but the height stays the same?
5. l low does the eross—seetional area 1’
of a bone relate to an animal’s
. . . Cl
wetglit and height-.‘
:4‘
611/764 34'///8 P/flit/[E
6. Of two similar parallelograms. one has a base of 8 and a height oi‘ 3. "l he
linear dimensions of the other parallelogram are one—half the linear
dimensions of the lirst. Find the ratio of the areas‘. (ACTIVITY 1)
1. Of two similar pyramids. one has a square base with each side equal to 6
and a height of-1. The linear dimensions oi" the other pyramid are one-half
the linear dimensions of the Iirst. Find the ratio of the volumes.
(ACTIVITY 2)
8. The leg bone of an animal has a circular
cross section with an area of about -in cm".
if the animal's height were tripled without
changing the proportions ol its -
measurements. how would the
volume of the animal he J
allected? How would the
cross—sectional area of
the leg hone be affected?
(EXAMPLE 1 AND
ACTIVITY 3)
LESSON as AREA ANDVOLUME RATIOS 547
Homework
Help Online
Go To: no.hrw.cnm
Keyword:
MBI Hulncworlt Help
for Exercises 11-21
548 CHAPTER 3
Practice d/Id App/y
D
3cm
E C
In the figure at right, Fc n E.
9. Find the ratio of the perinieters ol-
AABD and AECD.
10. Find the ratio uli the urcas 0|‘ AABD A B
and AECD.
L X
K M W Y
Jam N
V *2
5m
13. In the figure at right. 5 o
ABCDEF- PQRSTU. ABCDEF
has a perimeter of -12 m and an
and area 0|‘ PQRSTU. p O \
In the figure at right.
JKLMN ~ VWXYZ. JKLMN has
a perimeter ot2-1 m and an area of 50 m’.
11. Find the perimeter of lI'l‘l-"\’l"Z.
12. Find the area of l-'1-‘I-'Xl'7.
area or 96 ml. Find the perimeter
The ratio of the corresponding edges
of two similar pyramids is Find the
ratio of the following: \
14. the pcrimctcrs 0|" their lnascs
15. the areas of their lmses
16. their volumes
Two spheres have radii of 5 cm and 7 cm.
Find the ratio of the following:
11. the circumterences of their great circles
18. their surface areas
19. their volumes
The ratio of the heights of two similar cones
is %. Find the ratio of the following:
20. their radii
21. their volumes
22. the areas of their lmses
The ratio of the base areas of two similar
cylinders is g-. Find the ratio of the following:
23. their heights
24. the circumlerences of their bases
25. their volumes
APPLICATION
The ratio of the surface areas of two spheres is 143- Find the ratio of the
. 169'
following:
26. their radii
21. their volumes
28. the circuntlerenccs of their great circles
29. Two similar cylinders have base areas 0|‘ I6 cm? and 49 cm2. It the larger
cylinder has a height of 2| cm. find the height of the smaller cvlinder.
Two similar cones have surface areas of 225 cm’ and 441 cm’.
30. if the height of the larger cone is I2 cm. find the height of the smaller cone.
31. ll‘ the volume of the smaller cone is 250 cm’, find the volume of the
larger cone.
The ratio of the volumes of two prisms is Find the ratio of the
following:
32. their surface areas 33. the perimeters of their bases
34. corresponding base diagonals 35. the areas of their bases
The small cone is fomted by cutting off the
lower part of the larger cone. Use the figure at
right for Exercises 36 and 37. 2 cm
36. ll" the larger cone has a volume of 288 cm‘
find the volume of the smaller (.'()l"ltL. 6 cm
31. It‘ the base of the smaller cone has an
area of 5.6 cm’, find the area of the
base of the larger cone.
38. A cross section of the leg bone of a horse is a circle with an area of I9 cm’.
What is the diameter of the leg bone?
39. What should the diameter of the cross section in Exercise 38 be to support
a horse twice as tall?
40. A l0U—t"t tall cylindrical tower has a cross—sec.tional radius of 26 ft. What
would he the ratlius of a 350-It tall tower that is similar to the I00-ft tall
tower?
41. ASTRONOMY The circumferences of Earth and the Moon are about -10.200
km and l0,0l'J(l km. respectively. Find the ratio ol their diameters and the
ratio of their volumes.
LESSON as AREA ANDVOLUME RATIOS 549
APPLICATIONS
550 CHAPTER 8
42.
43.
44.
45.
46.
47.
F000 A new pizzeria sells an 8—in. diameter pizza for 334.00 and a l6—in.
diameter pi77a for $8.00. Which pi77a is the better deal? Fxplain.
PACKAGING A l2—oz box of noodles is a rectangttlar prism that measures
I5 cm x 20 ctn x -1 ctn. To make 2-t—o.r. box. should [lie company double all
of the dimensions of the 12-02 box? Explain.
PACKAGING A toothpaste company packages its product in -1 tube that
has a circular opening with a radius of 2 mm. The company lllCl'C;1SL::
the raditts of the opening to .5 mm. Predict what will happen to the
amount ol toothpaste used it" people continue to ttse the same length of
toothpaste on their toothbrushes.
BUSINESS The area of the parking lot at lerome's Restaurant is 400 ml.
Jerome buys some adioining land attd expands the parking lot to L5 times
as wide and l.75 times as long as the original lot. Find the area of the
expanded lot.
SPORTS ‘l he diatneter of a standard basketball is about 9.5 in. A company
that makes hasketballs is contracted to make promotional baskethalls with
a diameter of 5 in. The materials for a standard—si7.ed basketball cost $11.40.
How much will the materials cost for a promotional basketball made of
the same materials?
STORAGE A city stores rock salt tor winter road maintenance in a dome-
shaped building that is 82 ft in diameter at the base. ‘I he building holds
3366 tons of salt. Because the city is growing. the city planners decide to
build a second. smaller dome. The linear dimensions ol the new dome
will be three—fourths the linear dimensions of the old dotne. Estimate the
storage capacity of the new dome.
CHALLENGE
£00k Bdfk
48. The measure of each interior angle of-.1 regular polygon is I65". I low
many sides does the polygon have? (LESSON 3.5)
49. The exterior angles of a regular pnlvgon each measure -10°. How many
sides does the polygon have? (LESSON 3.6)
50. Which of the lines below are parallel? (LESSON 3.8)
a. 5x + 4y = I8
b. —lOx+ Sy = 21
c. 30x — 2-1)’ = -15
51. Write an equation for the line that is parallel to 5x + 4y = I8 and passes
through the point (3. 8). (LESSON 3.8)
52. Write an equation of the line that is perpendicular to 5x + -ty = I8 and
passes through the point (3. 8). (LESSON 3.8)
Solve each proportion. Give all possible values of x. (LESSON 8.2)
x+l_3_.\
53. 4 -8
.2 _.\‘-I
54';-+2‘ 2
55 .\—l=.\'+2
iv
x+l 2x+
56. In a rectangle, the ratio of the length oi the long side to the length oi the
short side is If the short side has a length of 9, what is the length ol‘ the
long side? (LESSON 8.2)
51. in the triangle below, fiflfi. Solve for x. (LESSON 3.4)
A
x_1 x+‘I3
D E
x—9 x'2
B C
Look Bet/and
ABCD is a square with side lengths of 1.The squares inside ABCD are
tamed by connecting the midpoints of the larger square.
58. What happens to the perimeter of D c
each successive square? Using a
calculator. add the perimeters of the
lirst eight squares. Keep track of the
sums as each perimeter is added. Do
you think the sum of the perimeters
of all the squares generated this way
will ever reach I4? Explain.
A 8
LESSON 86 AREA ANDVOLUME RATIOS 551
‘Q
ln this project, you will build it st-.i|e model of your school and possibly the
urea atround it. You and your class should use any methods you know. both
direct and indirect, to find the dimensions you will need to build your
model. Be creative! 3
S‘ ‘-
' ' r I ,\ - .. L:
‘ .1 I I F I '
I ‘ I: __-lnnnnul ' ‘II III -6
II I‘II I I IIIIIIIIII :"
* ‘. ‘*7 " - ’ ‘ IIIII .- : '
I -_|]'' IIIIII a. II: I7, ]. - 4
- av _. ----- II -I I _ —.~ .
3‘ ‘J n J . __.__ I
‘ I '1 1-
\
_:
i
ll
Pltotogrztpltfc .\ lethod .'l!t'r.tstu't'rrg :1
Direct .-\-'l('nsm'ement
smd(’Ht'.< sn'irle
Activity 1J
THE MAP To give context to your model. you will need a mztp of the area you
are modeling. One possibility is to enlarge the portion of your city map in
which your school is located. Draw the map on -.1 coordinate grid and locate
one or more physical Idndlndrlts on it to serve as reference points for the
measurements you make. l\I.tke as many measurements as you will need to
model and locate the Ieatu res of your school.
__..__ vv ~(<'
§7/ e ”g°"3 ;5_ L, ..
C
4; W ‘ E
E
Q
4% 9,, . ‘*
0 § 5 '9 \
552 CHAPTEHB
‘s"”$"””f DRIVE
my
‘iv? ., \— ~’ .
1- 1! .,.xx
I, ' .5‘ '3 M‘ . 1, n v — h ‘.5
' " '~;r ‘ | _~. -_.) - '- ' ‘
I e. I « -u . .
. _‘__l 4:-.' \ll".LLM .. ;.’~._ K: ~ ‘_
* l—— - _l HIGH cuoo - 1—, =' j.“3~’--\-.t .§$.~;2
| ' ; *'.-'r‘~-' as
- .. -' _ =_ ‘-’ “" ’.2..c#
.x - « «r .1 w .- x , - -~ '
- __t- I‘ ___ ' If .
_. -_. .-
1 'g'_ art‘ ' :—-I
TI u i \,
-’ \' revs "’ .
-:-. 4 I _\_ 5- __ _ ' I. - J "''i
T "
Activity
l_..1_v out a coordinate grid on the area where your model will be built. UM.’ the
grid to give 0rgani7ati0n and Structure to the measurement$ you took in
Activity I. Create pliysical models of the buildings and other structures on
your campus and place them cm the grid.
I
\ \
\
' \
9
4
—" I.
\‘ I \ '—»a"’ f
— I s
'\ \ / .‘\i‘—'\ X
* — 3! '“r‘r\§
I r F "‘
I
Chapter Review and Assessment
VOCABULARY
center of dilation ....... . . 500 expansion . . . . . . . . . . . . . . . 500 scale factor . . . . . . . . . . . . . . 498
contraction . . . . . . . . . . . . .. 500 proportion . . . . . . . . . . . . . . . 508 similar . . . . . . . . . . . . . . . . . . 507
dilation........ ...... ....498 proporlional...... ...... ..503
POSTULATES AND THEOREMS
Lesson Nu - - Postu ate or Theorem
8.2 8.2.2 Polygon Similarity Two polygons are similar if and only if there is a way of setting up a
Postulate correspondence between their sides and angles such thar
- Each pair of corresponding angles is congruent.
- Each pair of corresponding sides is proportional.
8.2.3 Cross-Multiplication For real numbers a, b. c, and (1 such that b, d at 0, it -E =
Property then ad = bc.
8.2.4 Reciprocal Property For real numbers a. b, c, and (1 such that 3, b, c, d afi 0. if % = 5,
then g =
8.2.5 Exchange Property For real numbers a, b. c, and dsuch that a, b, c, d an 0, it = g,
_ b
then % —
8.2.6 "Add—0ne" Property For real numbers a, b, c. and d such that b. d 35 0, if -3 =
then T“ ' " = 7-“ d.
8.3 8.3.1 AA (Angle-Anglel if two angles of one triangle are congruent to two angles of another
Similarity Postulate triangle, then the triangles are similar.
8.3.2 SSS (Side—Side—Sidel if the three sides of one triangle are proportional to the three sides
Similarity Theorem of another triangle, then the triangles are similar.
8.3.3 SAS lSide-Angie- if two sides of one triangle are proportional to two sides of another
Side) Similarity triangle and their included angles are congruent, then the triangles
Theorem are similar.
8.4 8.4.1 Side-Splitting A line parallel to one side of a triangle divides the other two sides
Theorem proportionally.
8.4.2 Two-Transversal Three or more parallel lines divide two intersecting transversals
Proportionality proportionally.
Corollary
8.5 8.5.1 Proportional if two triangles are similar, then their corresponding altitudes have
554 CHAPTER 3
Altitudes Theorem
the same ratio as their corresponding sides.
8.5.2 Proportional
Medians Theorem
if two triangles are %imllar. then their corresponding medians have
the same ratio as their corresponding sides.
8.5.3 Proportional Angle
Bisectors Theorem
if two triangles dre similrlr. then their corresporlding angle blsectors
have the same ratio as their corresponding sides.
8.5.4 Proportional
Segments Theorem
An angle bisector of a triangle divides the opposite side into two
segments that have the same ratio as the other two sides.
Key Skills 81 Exercises
LESSON 8.1
Key Skills
Draw a dilation on a coordinate plane.
Find the image of a segment with endpoints at
(I, 3) and (4, 0] that is transtormed by the
dilation D(x, y] = (2x, 2y).
The endpoints of the image are (2. 6) and (8. 0].
Draw a dilation in a plane.
Draw an equilateral triangle and dilate it about
one vertex by a scale l'-actor of .2.
Pretmage
LESSON 8.2
Key Skills
Image
Determine whether polygons are similar.
Are the rectangles in the diagram below similar?
Why or why not?
_I
‘I
L
1
F 8
48
II" the rectangles were similar, the proportion
E - E would be true. Cross—ntultiplying gives
30 ‘ 72
I8 - 72 = 30 - 48. or 1296 = I440. so the rectangles
are not similar.
_l
‘I
L
I-
72
Exercises
Find the image of a segment with endpoints
at (-2, 1) and (3, 4) that is transformed by the
given dilation.
1. D(x. y) = (3x. 3y)
2. D0‘. y] = (—x. —y)
Copy each figure below and dilate the figure
about the given point by the given scale
factor.
3. H = 3
O
4. H = %
Exercises
Determine whether the polygons in each pair
are similar. Explain your reasoning.
5.
1
30 36 18 2
f 24
46
B _l t._
_l L
4.2 5-4
1 F
5'6 7 2 F
CHAPTER 8 REVIEW 555
Use proportions to find the side lengths of The figures in each pair below are similar
similar figures. Find x
The triangles in the diagram below are similar. -,_
Hm X" %
53 3_ _l L
_l
, 18 9
%-(A—‘_‘—->56;--24-63 *1 “
— '5 '2 or -12 1 x F 18
3 ‘ .36 ’
LESSON 3.3
Key Skills Exercises
Use the AA Similarity Postulate and SSS and For each pair of triangles, name the postulate
SAS SimilarityTheorems to determine or theorem that can be used to prove that the
whether triangles are similar. triangles are similar.
Name the postulate or theorem that can be used 9_ 21
to prove that the triangles are similar. 24
A D 28 18
11
A ‘IO. 22
E F 20 10
B C Q
22
LB E LE and LC E LF. so the tri.mg,l«.-5 are
11.
similar by the AA Similarity Postul-ate.
12
28
Lesson 3 4
Key Skills Exercises
Use the Side-Sp|ittingTheorem to solve Use the Side-Splitting Theorem to find x.
r blems inv l ' tri n les.
9 ° _ °‘""9 _“ _ 13. ,5 X 14.
In the triangle below. DE||B(.. Find 1'. 13 7
20 16
A 21
20 18 X
W
D E
10 X 15 12 15 16.
C 12 8.4 do
' 20.: = 130 x = 9 x X 14
-[IQ
D D
II
>< Is;
556 CHAPTER 3
Lesson 8.5
Key Skills
Use similar triangles to measure distance
indirectly.
A right square pyramid has a b-ase edge of 40 It. II
the pvr-amid casts a shadow 60 ft long at the same
time that a yardstick casts a shadow 6 ft long. what
is the height of the pvramitl?
Because the sun’s rays f‘--.
are considered parallel.
the triangles formed by
the pvramid and the
yardstick are similar.
The horizontal side of _
the large triangle is 60 ft 3
plus 20 ft, or 80 ll. 5 f‘
g = 6.\' = 240 x = 40
The height of the pyramid is -10 ft.
x
,....---..
M
0
33
_.
I.
Use similarity theorems to solve problems
involving altitudes and medians of triangles.
The triangles below are similar. Find .\:.
xi
6.4 5-5
Because the triangles are similar. their altitudes are
proportional.
L = 5;
L2 5.1
1 3 - .-‘E. = 53'. . I 2
' L2 6.4
2:: L05
LESSON 8.6
Key Skills
Find the ratio of the areas of similar figures.
"I he ratio of the sides of two similar
quadrilaterals is 3. Find the ratio of their areas.
3
The ratio oftheir areas is =
Exercises
17. Catherine is L6 in tall and casts a shadow ol
3.5 m. At the same time. a house casts a
shadow of 17.5 m. Find the height of the
house.
Refer to the diagram below.
18. A sun-'e_vor made the measurements shown
below. T is parallel to W.\’. Find the distance
across the base of the hill.
The triangles in each pair below are similar.
Find x.
Exercises
21. The ratio olithe sides of two similar
triangles is What is the ratio of their areas?
22. The ratio ol the sides of two similar
parallelograms is What is the ratio of their
areas?
CHAPTER 3 REVIEW 557
Find the ratio of the volumes of similar solids. 23. The ratio of the edges of two similar prisiiis
The ratio ol the edges ol two similar p)"l'kll'l1ldS I5 m- Whdl IS the T-!lI0 09 lhflr V0llI|'|1€'S?
. ‘.3 . _ . _ _ _
is =,. Find the ratio of their volumes. 24. The ratio ol the radii ol two similar spheres
. . _ ‘ ' - 1 .' ' - . ' ' ' \
Thu ratio 0, mm voiumw is = %_ is 2. \'\ hat is the ratio ol their voluiiits?
Applications
25. GRAPHIC DESIGN An artist uses a photocopier to enlarge a design by 120%.
It" the area of the original design is IU in:. what will be the area of the
enlarged design?
26. LANDSCAPING Brian needs to cut down \‘
a tree that is 30 in away from his house. -
To estimate the height ofthe tree. he \
places a mirroi on the ground 15 in \
from the base of the tree and stands I ‘s x ' .,_8 m
in away from the mirror. in which he --------------- --J- --|--- —‘—
can see the reflection of the top of the ,1
tree. Brian's eyes are 1.8 in above the
ground. ll‘ the tree falls toward Brian"s
house, will it hit the house.’
15m 1m
27. FINE ARTS The sculpture Battolmim
by ("Lies Oldenburg and Coosje van
Brtiggen is a giant replica ol‘-a
baseball bat and is 100 ft and 9 in.
tall. What is the ratio ol'the volume
of this sculpture to the volume of a
real baseball but that is 35 in. long?
558 CHAPTER 3
L Chapter Test
Find the image of a segment with endpoints at
(6. -1) and (-4. 2) that is transfonned by the
given dilation.
1. Dix, y,J = (—2.x.—2y) 2. Dix. y) = (0.5x. 0.5}-')
3. Copy the figure at
right and dilate the
figure about the given
point by a scale factor
of 2.
Determine whether the polygons in each pair are
similar. Explain your reasoning.
J K
4- ..1 l..
A D
_, ,_ 5.4
2.3
"1 I‘ _l r
B 1.3 C M 7.8 L
5. K
30 38 ”
mm
35 L O 17.5 S
The figures in the pair below are similar.
Find x.
6. 29
23 23
4_sfi4.6
x 29
7. Clair is enlarging a rect-angular flag from ti
diagram that is 3 inches hy S ln(,i'IL.5. ll she
wants the llag to be 18 inches long, how wide
should the flag be?
For each pair of triangles, name the postulate
or theorem that can be used to prove that the
triangles are similar.
“V A
10_ 1 5
346° 12
1/10
For Exercises 11-12, use the Side-Splitting
Theorem to find x.
13. SCALE DR.-‘-\Wll\‘(_i And} is l.2 lllL‘lL‘rS tall
and casts a shadow of L5 mt-.'ters. At the same
time, a lamppost casts a shadow of 25 meters.
Find the height of the lanippost.
ln Exercises 14 and 15, the triangles in each pair
are similar. Find x.
14. 5
185
16. 'l he ratio of the sides ol" two similar triangles
is What is the ratio of their areas?
17. the ratio of the edges ol two similar pyramids
is What is the ratio of their volumes?
18. The ratio of the heights oi two similar cylinders
is What is the ratio of their volumes?
CHAPTER sTEsT 559
" E‘S CUMULATIVE ASSESSMENT
College Entrance Exam Practice
0
D internet connect
MULTIPLE-CHOICE For Questions I— 10. write the standardized
letter that indicates the best answer. Test Prep ontine
Go To: go.hrw.com
1. Find the sum ol'.A(' and BD. (LESSON 1.2) I K8vW0rd:MM1Te8| Prep
A B C D ‘
—§—é—ic')"|§3a§6
3- 3 4. Find the lateral area of the cone below to the
5- 9 nearest hundredth. (LESSON 7.5)
1:. H
d. 5 5
1; \ 1
2. What is the sum ol the first l5 positive odd '11-
numbers? (LESSON 2. 1)
a. 4.41
8- 335 b. 7.53
b‘ 240 c. L05
°- '30 d. -H9
d. 255 I
I _ _ _ 5. ll' line 1’ has a slope of 5 and line in has a slope
3. \i\-hat Is the sum oi the number nl lateral oi-0___)_‘ [hm the line) are :, _
edges and the number of Faces of .1 hexagonal (LESSON 33)
prism? (LESSON 5.3) ,_ p_m,||,_.|
b. perpendictllar
c. vertical
d. none of the above
6. If pentagon ABCDE ‘=‘ pentagon .-\-LNIKL,
which ofthe following is true? (LESSON 4.1)
3. l2
b. 14 A B "
c. 26 N K
d. 24 C
E L
D M
:1. AC E ZR’
1:. 4._A_ 2 AM
o. AE ‘=‘ MN
d. cannot be determined from the given
information
560 CHAPTER 3
10.
‘I1.
12.
13.
14.
. Which of the following quztdrilatemls has
congruent diagonals? (LESSON 4.5)
a. trapezoid
b. rectangle
c. parallelogram
d. rhomhus
. Which ol the following quadrilaterals can have
exactly two right angles? (Lesson: 4.5)
a. trapezoid
b. rectangle
c. parallelograni
d. rhomhus
. Find the midpoint ofa segment with
endpoints at ('5. I) and (I. -3}. (LESSON 5.5)
a. (6. -2)
b. (2, 2)
c. (3. -l_]
d. ,1,-2)
The point (3. —l. 2) is in which octant ofa
three—diniensional coordinate system?
(LESSON 6.4)
a. first oetunt
b. top-right—back
c. top—l'ront—lel't
d. bottom-front-right
Find the y-intercept ol the plane dehned by
the equation 5x + 2y - z = 6. (LESSON 5.5)
Solve the proportion for x. (LESSON 8.2)
2 + .x' _ x
3 2
which of the following is not valid for
proving triangles similar? (LESSON 8.3)
a. SSS
b. AA
0. SSA
d. 53.3
Find the ratio of the volumes of-.1 sphere with
a radius of 3 and a sphere with ‘.1 radius of6.
(LESSON 8.6)
FREE-RESPONSE GRID
Items 15-18 may be answered
by using a free-response grid
such as that commonly used
by standardized-test services.
oaoeooeoe D
®e®®®®wo®oDo
®@@@0®®®G@Dv
ooeeeeeoeep
15. What is the sum of the interior angles of the
Iigure below? (LESSON 3.5)
16. What is the sum ol the exterior angles of the
figure above? (LESSON 3.5)
17. Find the value of): in the figure below. Round
your answer to the nearest tenth.
(LESSON 5.4)
36
54
18. In the figure bEl0\\',fi|I-1?. Find Bf).
(LESSON 8.4)
24 32
20
CHAPYEH s cumuumve ASSESSMENT 561
Lessons
9.1 0 Chords antlllics
9.2 0 Tangenls IO Circles
9.3 0 Inscribed Angles
and Ilics
9.4 0 Angles Formed by
Secants and
Tangenls
9.5 0 Segments of
Tangenls. Secanls,
and Chords
9.6 0 Circles in the
Coordinate Plane
Proiect
Tangent Curves
562
Circles
GREEK GEOMETERS AT THE TIME OF EUCLID
believed that circles have a special perfection.
With the rediscovery of Euclid's Elements by
English philosopher Adelard (twelfth century),
this way of thinking made its way into the
European world. The designs in many early
chtird1es were based on geometric principles
learned from Euclid.
Among the most famous; works of an based on
the geometry of the circle is the north rose
window in the Notre Dame Cathedral in Paris
(thirteenth century).
The circular structures In the aerial photo of
the Pueblo mins at Chaco Canyon are known
as kr'vas.The circular design of these cere- 4
monial structures reflects the Pueblo
belief, suggested by the recurrence
of celestial phenomena that time
is ciicular in nature.
-‘I ' I '_
o‘ ‘i:_
' . ‘I \‘
..- __
1' 5
'f_ ‘u - . -‘ .3‘
." -'3 . . l Q j 05',‘ II ‘ . .2
I ' _.‘! . _
- - . 1
R134 wfmlnw,
Nolrs 1.Jmm: Curl: -dml
This selection cannot be included in this
publication because the copyright holder
has denied permission andlor has
electronic use restrictions with which we
Clium Cmiyou
‘L
.4.
.-1‘ ..
cannot comply.
. L.
a- .
¥ '1-.
‘ I Q -
5, .. V .
I
_ .
1 , II ' ‘
"' .- O .
n ‘\
? _ _ .
l9 - ‘ —
- 1
‘H I
. . K ‘ _‘
. N-'.' '
‘I, ‘A
Natural well or mime
at ( ‘Iiicliéir [mi
About the Chapter Project
The art of constructing, elegant egg shapes from
curves of different radii is an ancient art that
goes back to prehistoric
times. Certain principles
of geometry in this
chapter will enable
you to construct
objects like
the egg shape
shown at right.
After completing
the Chapter
Project. you
will be able to
do the following:
0 Construct .lrtlStiL
eggs from given examples.
0 Create your own designs by using reverse
curves.
About the Portfolio Activities
Throughout this chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Proiect.
o The basic construction for circle flowers is the
topic of the Portfolio Activity on page 572.
o A method tor creating a single smooth curve
from two curves of different radii is shown in
the Portfolio Activity on page 579. With this
method. you can construct the egg shapes in
the Chapter Project.
0 The method of creating a reverse curve, or
“S—eurve." by connecting two arcs smoothly is
given in the Portfolio Activity‘ on page 609.
This principle. which is important in art,
engirieering. and architecture. will enable you
to construct the figures in the Chapter Project.
as well as figures of your own design.
563
Objectives
0 Define a circle and
its associated parts.
and use them in
constructions.
0 Define and use the
degree measure ol
arcs.
0 Deline and use the
length measure of
arcs
o Prove a theorem about
chords and their
intercepted arcs.
Chords and Arcs
\ \ K K ‘\)x‘
\.>;\1l,
: 7‘,%:<i , \\ ' \ ‘
~edi‘?“ “g
x \
W
Tostudytlte - -» -tryol
circles. you will need to know some
basic definitions and ideas. with
these. you can qulckly learn to malts
interesting constructions.
The mnth(’mm‘t'r‘aI Iiwrttrcs oftirc'sr'
attractive dcsigrts, which were crmred with
getmtetry graphics soft»-ttt't', can easily be
uru.im'tood from the ideas in this lesson.
564 CHAPTER 9
Circles: A Formal Definition
A circle can he named by using the symbol 0 and the center of the circle. The
circle in the illustration below is GP. or circle P.
. ch_ords_
AB. DE
D
- P, or circle P
Definition: Circle
A circle is the set ofall points in a plane that are equidistant lrom a given
point in the plane known as the center of the circle. A radius (plural,
radii) is :3 segment from the center of the circle to -.1 point on the circle. A
chord is a segment whose endpoints line on a circle. A diameter is .1
chord that contains the center of a circle. 9.1.1
In Activit r I below. vou will use concc :15 from the detinition ofa circle to
)
perlorm and an-aly7e a construction.
' I
Constructing a Hexagon in a Circle
L D 1. Draw .1 urcle with a compass. Label a
compass and the center P. Choose a point on the
5‘”"9h“"d9° circle and label it A (figure a‘.
A
2. Without changing your compass
setting. place the point of your
compass on point A. Draw an arc
that intersects the circle at a new
point. Lalael the new point B
[figure b‘.
3. Em chord 37?. Draw radii Filand
Pb‘(figut'e cl.
CHECKPOlNT ./ 4. What kind oltriangle is AABF?
What are the measures of its angles?
lixplain vour reasoning.
c.
5. Without changing your conip-ass A
setting. place the point of your A
compass on point B. Draw an arc
that intersects the circle at a new
point. Lalael the new point C
[figure d‘.
6. Draw cli_<)rd b‘—Car1d the new
radius PC.
7. Continue drawing new points.
chords, and radii until you have
completed a figure like the one
shown in figure e.
ls polygon .»lb‘CDl;'l-' a regular
hexagon? Explain your answer.
cnecxpomr ./ 9. An angle such as LAPB is
known as .1 central angle ofa
circle. [ See page 566.) Are all
the central angles in the figure
congruent? Does the sum of
their measures equal 360"?
Explain your reasoning.
LESSON 9.: ct-Ionos AND ARCS 565
Major and Minor Arcs
An arc is an unbroken part ofa circle. Atty two distinct points on a circle
divide the circle into two arcs. The points are called the endpoints of the arcs.
N J /'\ /\
0 ~1_ MON and MLN are
fig‘; (my) ,-5 | semicircles ofG>P.
a minor arc
ale? 1 ?
M10 (blue) is a
I major arc of GP.
A semicircle is an arc whose endpoints are endpoints of a diameter. A
semicircle is informally called a hall‘-circle. A semicircle is named by its
endpoints and another point that lies on the are.
A minor arc ofa circle is an arc that is shorter than a semicircle of that circle
A minor are is named by its endpoints.
A major arc ofa circle is an are that is longer than a semicircle ol'that circle.
A major arc is named by its endpoints and another point that lies on the arc.
Central
angle
566 CHAPTER 9
I
I nte ice pted
arc
Degree Measures of Arcs
Certlml rmgles of R A
circles are used to RS IS the
rind the measures i‘ iniefceflied
of an-5_ S are of central
angle (RPS.
Definitions: Central Angle and lntercepted Are
A central angle of a circle is an angle in the plant. of a circle whose vertex
is the center of the circle. An arc whose endpoints lie on the sides of the
angle and whose other points lie in the interior of the angle is the
intercepted are of the central angle. 9.1.2
An orange may consist of nine wedges,
seen in cross section here. Thus, an
average wedge would form -a central
angle of about one—ninth of the full
circle, or -40°. ( When you look at a
typical orange wedge, does it seem to
be about 40°?)
Central
angle r
._“
"-.~ v.
\
lntercepted
arc
Arcs can be nieusu red A
in terms 0| degrees. ~\l mA’§= 50'
B
/'5
:1 InACB =360° -50" =3l0’
D
Definition: Degree Measure of Arcs
The degree measure of a minor arc is the measure of its central angle.
'1 he degree measure of kl lll<1_l0l'dl‘C is 560° minus the degree measure
of its minor £ll'(.'. The degree nieasure of d semicircle is |80°. 9.1.3
E x A M P L E Orind the nie-.-isuresofér. ’f§..md ET}. 7
n G
O SOLUTION
The ll1Ctl5llrL‘S of §7' and T3 '.1l‘C‘ found
from their central angles. 3
miz? = 100° mi? = 90°
it?’ and 7:5. which have just one endpoint in coininon. are called .idjacent
ares. Add their lI1C'.1SllrL‘S to Iiiid the iiiezisure ol R15.
l1'l§i§=ll'll§T+lll7§= lU0"+90°= 190°
Arc Length
A second w.s_v to measure an arc is in lerins (if its length. To Find the length of
an arc. you need to know the radius of the circle of which the arc is a part.
E x A M P L E 0Find the length ofthe indicated are.
Express your answer to the nearest
P P I C A T I 0 N millimeter. (There are -0 equal "R “
sectors on :1 dartlm:ird.J -
GAMES _ \
r _ 170 mm‘ ~
0 SOLUTION in} \
The length of the are is ,—l0ol'the .\ .
circumference of the circle. 0- O
Remember that C = Em". I
= 17K as 55.4 3 53 mm
LESSON 9.1 CHORDS AND ARCS 567
TRY THIS
CRITICAL THINKING
compass and
stra ightodgo
CHECKPOlN'I' ./
PARAGRAPH PROOF
Cl-IECKPOINT ./
568 CHAPTER 9
In general. the length of an arc can be found by using the formula below.
Arc Length
If r is the radius of a circle and M is the degree measure of an arc oi the
circle. then the length. L. of the arc is given by the following:
_ 1‘! _
L — 9.1.4
B
3
Find the length of Round your answer to
the nearest hundredth.
Is it possible for two arcs to have the same degree
measure but different lengths? Fxplttin why or why not.
' 2
chords and Arcs Theorem
1. In the figure. chords '1fi3and El_')are congruent. A D
The minor arcs AB and CD are called the
arcs of the chords. Do you think that 33
and CD have equal measures? ‘lo lintl the
answer. make your own drawing of the figures
and construct central angles [APB and 1 CPD. 3 C
2. Prove that A/'lPb‘ and ACPD are
congruent. \-\'h.tt can you conclude Z
d _
The diagram does not contain
about central angles AAPB and
/5 /T
4039? ‘‘l’‘’”' A3 '*'“d CD ? any specific features other
3. It two chords of a circle are Sf’: ‘(hi 94:9” l':'""”,:"i:’,:’7
congruent, what can you conclude 9 9 0 9" rep 9”’ S 9
general case.
about their arcs?
4. How can you extend this Activity to
congruent chords of two or more
different congruent circles? Explain
and include appropriate diagrams.
In the process of discovering
your result, Vhu have proved
a theorem.
5. Present your discovery as a
par-agrapli proof. Complete
the theorem below.
Chords and Arcs Theorem
In a circle, or in congruent circles, the arcs ol congruent chords
are ? . 9.1.5
Exercises
. Communicate
In Exercises 1-5. classify each statement
as true or false and explain your
reasoning.
1. Every diameter 0|‘ -.1 circle is also
a chord 0|‘ the circle.
2. Lvery radius ofa circle is also a
chord of the circle.
3. Every chord of a circle contains
a #3 exactlv two points of the circle.
- rnteonncct . _ _ _
. . . M‘ 4. ll two chords of a circle tire
Activities h h_ . _ __ _
online congruent.t en t eir arts are
Go To: no.hrw.con-i also congruent.
Keyword. . .
m;1c..,.;g5 5. It two arcs of a circle are \
congruent. then their chords
are also congruent.
6. l low can you show that two
arcs of-.1 circle are congruent?
Is there more th-.iii one way?
Discuss.
7. Are all semicircles 0|-as circle ‘_
congruent? Explain. g
. 6/ridedski//s Practice
Use the figure below for Exercises 8 and 9. A
8. Find the degree nieasiires of 75?. $
/'3 /\
BC.a1l1d CA. (EXAMPLE 1) B
9. Find the length of Round C
)'0llr answer to the nearest
hundredth. (EXAMPLE 2)
PARAGRAPH moor 10. Write a palralgrtlpll proof of the Chords and Ares Theorem for the case in
which the congruent chords are in (lll-l-€l't‘l'lt congruent circles. Use the
d iagrani below to begin your proof. (Acrivrrv 2 AND THEOREM 9.1.5;
B
N
LESSON 9.! CHORDS AND ARCS 569
flhterneloo -
Homework
Help Online
Go To: gn.hrw.t.-on
Kawnord:
MG! Homework Help
for EIEICISBS 23-30
570 CHAPTER 9
PROOF
17::
Practice and Apply
Use the figure of GP below for Exercises 11—22.
11. Name the center of the circle.
12. l\nme a radius ol the circle.
13. Mme :1 chord ofthe circle.
14. l\‘-.1me :1 diameter of the circle.
15. l\‘-.|n1e 2! central angle of the circle.
16. l\'.tn1e -.1 semicircle ol the circle.
17. l\-.1me two minor arcs ol the circle.
18. l\‘-.1me two major arcs of the circle.
Identify the given part of GP.
19. X13 20. "E7? 21. "F5
Find the degree measure of each arc by using
the central angle measures given in 00 at right.
23. ‘fl? 24. T51} 25. T27‘
25. 27. 28. (E
(\ /'\
29. SUV 30. l-’lR
Determine the length of an arc with the given central angle measure,
m£P, in a circle with the given radius. r. Round your answer to the
nearest hundredth.
31. m.éP= 90"; r= I0 32. m.éP= 60°; r= 3 33. m.éP= 30°; r= I20
Determine the degree measure of an arc with the 3
given length, L, in a circle with the given radius. r. /
34.L=l-l;r=7O 35.L=20;r=lO0 A
36.L=3;r=l5 37.L=5;r=25 V
38. In OR at right, it m.{AR8 = 43° and AB= 5, /
find Xl’. lixplain your reasoning. X
Suppose that ABCDE is a regular pentagon inscribed A
in Q0 and that A0 = 2. Find the following:
39. m.v;’/lQb‘ 40. ntfli; 41. m.«lCi.- E B
_ x‘\ _ A
42. length ol AE 43. length ol ACE
D C
44. Complete the converse of the Chords and Arcs Theorem below and
prove your result.
The Converse of the Chords and Arcs Theorem
In a circle or in congruent circles. the chords of congruent arcs
are 5 9.1.6
APPLICATIONS
APPLICATIONS
45. LANDSCAPING Sixty tulips are planted
around the base of-a circular tountain. If
the fountain is 20 ft in diameter and the
tulips are placed 1 it away from the base.
what is the length of the arc between
consecutive tulips?
46. DEMOGRAPHICS Smith High School has 450 freshmen, 575 sophomores.
400 juniors. and 325 seniors. Create a pie chart that shows the distribution
of students. First Find the percent of the total student body for each class.
'l'hen multiply each percent by 560° to find the measure of the central
angle for each section ol'the chart.
47. CIVIL ENGINEERING A cloverleaf I
intersection consists of four ramps -—-
that are roughly circular. Use the
measurements and objects in the
photo to estimate the length
of the section of road §_-_~. V _ _ _
indicated by the dashed arc. 5% ‘s_ R. T-Sf“-*—‘
4.‘ _
It‘
To estimate, use I — — ’ "
I car nu I6 feet. .
Look Back
48. What effect does doubling the radius of a sphere have on its volume?
(LESSONS 7.1 AND 7.6)
SPORTS Find the volume of each obiect. (LESSONS 7.2 AND 7.6)
49. 'a,,» so. _ J H‘ "Q15! -‘. F = 59 m
P‘ _ I - . III/= ITI
{{(((((///‘-£?'_!!‘: ‘ _ _ - I. 1.; _ h = 2 m
’%z. .-; tn" -
N1‘ - I "'Ih ‘hi ‘(LII It‘-‘II. Ix‘. xi‘
... -‘,-_. ,_ .._\
' ‘at: :2:-r,;‘3 ;:: 1.1.; -;c-:.
SPORTS A bicycle tire has a diameter of 26 in. (LESSON 5.3)
51. Find the circuntlerence of the tire.
52. II" the Iiicvcle travels so that the wheel nrakes IUO complete turns. how far
does the bicycle travel?
LESSON 9.: cnonos AND ARCS 571
CONNECTION
flluerndu - &'“
Portfolio
Extension
Go To: go.liiw.i:mii
Keyword:
MG! Sqrcirclc
Look Beyond
TRIGONOMETRY The circle with its center at the origin and a radius of 1 is
called the unit circle. You will study functions defined on the unit circle
in trigonometry. 3
53. What are the coordinates of A. B, C, and D
on the unit circle shown 1t right? (3 A
54. Wh-at is the circumference of the unit circle?
Use the graph of the unit circle to find the following: 0
55. nifi and 56. mABC and 57. mABD and
length ol fl length of AB(‘ length ol ABD
v°_'-Io
oqf‘
O. 9
A
CONSTRUCTING A CIRCLE FLOWER A circle flower is formed when three or
more circles meet at the center of another circle. forming "petals." A six-
petal circle flower has a construction that is similar to that of the regular
hexagon in Activity 1.
B . . . .
1. First draw a circle with a coinpass or geometry graphics
software. Choose a point on the circle and label it A.
Draw another circle coiigrueiit to the lirst with point A
as its center.
2. Choose one of the points where circle A intersects the
original circle and label it B. Using this point as a center.
draw another circle congruent to the First. Repeat. going
around the circle in one direction, until you have
completed the flower.
3. How is the flower related to the hexagon in Activity I?
Think about why the petals meet at the center of the
flower. You may wish to consider the measures of the
arcs and central angles in the figure.
WORKING ON THE CHAPTER PROJECT K ~.
You should now be able to ‘ ' \ -
complete Activity I of the g c ‘ T 'l ‘ .- '
Chapter Project. ' \ _ P ' -I 1 «ill '_ I \‘
l g -«F- ‘ , -
Mriii;.' orlicr iiiterestiiig cii'clt' i_
ptmcriisrirept>ssilrlt' Thi_~"'qiIilt" 5 -“~c_ ' -
was asscriililerl lJ_l’ ti coiii,nirtcrfi'rini '
(I prmerii (Ill prrge 223 oftiiis liotik.
572 CHAPTER 9
Objectives
0 Define tangents and
secanrs at circles.
0 Understand the
relationship between
tangents and certain
radii ol circles.
0 Understand the
geometry ol a radius
perpendicular to a
chord ot a circle.
Tangents to Circles
' shutuo‘s_o_r9"_‘
or shuttle ‘ ' ' ' '
Momentum
“ t
1'bom--r-tumolanabiacl f
revolving amund Earth in a circular
orbit is in the direction or a line
tangent to the orbit of the object. You
will encounter such Ihws Imquenuy,
both in the sciences and the arts.
1
Pull of
the Earth
This pirotogmph was trtkett by an rrsltmmtrt during a sprtrr’ wrrik. The space
shuttle is mbitittg L‘m'rh from right to left. if it were notjbr the gmvitariottrri puii
ofthe Earth, the simtrie would comimue in :1 straight line in the (iil'£‘4.'!i0M ufit:
momermmt. it would quite literrriiy "go 0,0001 rt rrrngr’nt."'
CRITICAL THINKING
Secants and Tangents
A line in the plane of a Circle may or may not intersect the circle. There are
three possibilities.
P Tangent
Secant ""3
line
2 points of intersection 1 point of intersection 0 points of intersection
Secants and Tangents
A secant to El circle is :3 line that intersects the circle at two points. A
tangent is a line in the plane of the circle that intersects the circle at
exactly one point. which is known as the point of tangency. 9.2.1
The word trtrtgettt comes from the Latin word meaning "to touch." The word
secunt comes from the Latin word meaning “to cut." Why are these words
appropriate minutes for the lines they describe?
LESSON 9 2 TANGENTSTO CIRCLES 573
- - ED 1. Draw OPwith radius
comniiss. 2. l ocate a point R on the circle and draw
ruler, and _
protractor QR. Mcasti re LPQR.
0“ 3. Repeat Step 2 with point R closer to point 3
gfgglgég Q. but still on the circle. If vuu are using
software geometry graphics sottware. drag point R
toward point Q. What do you observe
about mLPQR as point R tum-es closer to 0
Q? What happens when R coincides with Q?
CHECKPOINT ./ 4. Make a conjecture about the relationship between a tangent to a
circle and a radius drawn to the point of taiigency. Based on your
observations, complete the theorem below. which you will be asked
to prove in Exercises _%l—34.
Tangent Theorem
lfa line is tangent to a circle. then the line is ? to a radius of
the circle drawn to the point ol‘ tangency. 9.2.2
' Z
Radii Perpendicular to Chords, Part 1
- - ED 1. Draw 0P with chord Tb’.
colmnassé 2. Coiistrtict a radius perpendicular to chord
ru er, an "— - - - _ - .
prmracm, AB. Label the point of intersettiun A.
0“ 3. Measure AX and BX. What do you observe?
l . . .
\ gffglfclsv 4. Repeat Steps I-3 with different circles and
505W-‘"9 chords. if you are using geometry graphics
softwaie. L‘.\pL‘l'llI'lL‘lll. by chaiigiiig the size of
the circle and by dragging the chords to different
locations. Make a conjecture abotit radii that
are perpendicular to chords in circles. Based on
your conjecture, complete the theorem below.
Radius and Chord Theorem
CHECKPOINT V A radius that is perpendicular to a chord of a circle 2 the
chord. 9 Z3
TWO-COLUMN PROOF 5. Draw Wand W3 in one of your circles. Using this diagram. write a two-
column prool‘ ol‘ the Radius and Chord Theorem.
574 CHAPTER 9
E X A M P L E O0Ph:1sa radius of5in. and P,\’is3in.F§is perpendicular to Eat point X.
Find AB.
1
.’ ' ’ ’ . SOLUTION
By the Pytltagoreart I heorem:
(AX? + 31 - 53
(Ax)! - 53 — 53
(Ax)? - re
.1): = 4
Bv the Radius and Chord Theorem, W bisects A—B, so BX - AX - 4.
'l'herefore. AB = AA’ + BX = -1 + 4 = 8.
Radii Perpendicular to Chords, Part 2
- ' L ED 1. L'xplain how this diagram is like
compass, the Ont‘ in ."'\‘.[iVil.}' 2.
ru|er,anr:| A _ — — .
prommor 2. Imagine ntovtng point \ to
03 point R. What happens to
\ geometry i Ill.Cl'SL‘Cl.lOIl points A and 8
graphics as X gets closer to R? What
sohvvare '
happens when X touches R?
What conjecture does this
suggest? l'se vou r answer to
complete the theorem below,
uhich is proved on the
CHECKPOINT V iUllt)\s'ing pllgf.
Converse of the Tangent Theorem
[fa line is perpendicular to .1 radius of-.1 circle at its endpoint on the
circle. then the line is ? to the circle. 9.2.4
CRITICAL mrrurunc The proof on the following page uses the fact
that the hypotenuse is the longest side of -.1 right c
triangle. How could you argue that this must b
be true?
a
c > a and c > 1)
Why?
LESSON 9 2 TANGENTSTO CIRCLES 575
The Converse of the Tangent Theorem
The following proof uses the definition of it circle in an interesting way. When
you understzind the proof, you should be able to summarize it quickly in your
own words [see Exercise IS).
PARAGRAPH PROOF Given: Point Pis on O0, and O—Pis pcrpcndicul-.ir to
Prove: Es tangent to (30:11 point P.
Proof: Choose anv point on 3-153 other than
point Pand label it Q. Draw right triangle
OPQ. Since Tjis the liypotenuse of at
right triangle. it is longer than 55, which
is a radius of the circle. Therefore. point
Q does not lie on the circle. This i.s true
f;_);-all points on except point P. so
.48 touches this-_c)ircle at just one point. A P O B
By definition. AB is tangent to OO'.1t
point P.
Exercises
. Comm//1/mte
1. Eitplain the three possihle relationships £3‘? =~'=_ ___-A -
between a line and a circle in a plane. ’_ ' ' _
uin oomed 2. Explain how u secant intersects a circle. A‘ V.
A°‘l"i“°5 3. How many line: are tangent to tl circle? ’ . -
Online E,‘ ‘lain \ . \ ‘ ‘
Go To: go.hiw.com I" ' ,
Keyword: . ' . . ‘ ' . -.
Mcnmem 4. How rnany lines are tangeiit to 1 CITLIC \_
at tl given point? E\Lpiall't. _
4 _ _ . .
5. Describe a point of tangency in the _ ._-
- 73
photo at right. ’f —— .—
I _l -_,
1"‘ I ‘
0 fill/déd r3:(’///8 PI’d6‘t/6'8
e. 75’ is tangent to on at K. it 1. In an OR = 3. Find RS.
K.-\-I = I and LM = 2. tind KL. (Acnvrrv 2 AND THEOREM
(ACTIVITY 2 AND THEOREM 9.2.3)
9.2.2)
as
K L
576 CHAPTER 9
PARAGRAPH PROOF
CONSTRUCTION
3. ex l_i_a£a rtlgitls of l 3. xn-' = 5.
and X1/_L YZ. Find YZ. (EXAMPLE
AND THEOREM 9.2.3)
4E—‘.o
9. \-'eril'y that AB is tangent to (DC
at B. (Ac'nwTY3 AND
THEOREM 9.2.4)
2'
L.
Y A 5 B
Practice and Apply
E Ex_er'cises 10-12, refer to GR, in which
RY.LXZ at W.
10. 2 7.’
11. ll RY - 7and RW - 2, what is X11-"? X
What is WA! ’ 2
12. ll‘ RY = 3dl'lLl RH" = 2, what is X11-"? Y
What is W2?
13. In the diagram at right. what is the
radius of (DO?
7'9:
D
14. In (DN. verify that line F is a tangent
by using the Ct)|1\'erse of the
Tangent Theorem.
Q
15. In /\L‘ti'.'itv 2 you proved a theorem about a radius that is perpendicular to
a thord. Writes .1 pflrttgrdpli proof of the following related theorem:
Theorem
The perpeltdicttlar hisector of .1 chord passes through the center of
the circle. 9.2.5
16. Use Theorem 9.2.5 above to construct a circle through any three
noncollinear points. |‘irst_dr;i\v tlfie points not on a straight line. Label
them A. B. and C. Dmw .4Band BC. Construct the perpendicular hisector
of each segment. Where is the center of the circle that contains A. B. and
C? Complete the construction. How does this construction relate to
Actix-itv 2 in Lesson 1.3?
17. Use the Converse of the Tangent Theorem to constnict a tangent to a
circle at a given point. First draw a circle '.1I'l(iillJ€'l the center P. Choose
any point unit: circle and label it A. Draw AP. How is the tangent line at
A related to AP? Complete the construction.
LESSON 9 2 TANGENTSTO CIRCLES 577
PARAGRAPH PROOF
' g." I /
I intometoonn - .2,
fill!
Homework
Help Online
Go To: uc.hrw.com
Keyword:
MGI Homework Help
for Exercises 19-23
578 CHAPTER 9
._'ununarize ie two 0 1 ' nvcrseo e '1 ‘en ecr in run
18\ tl} l'l'tle(.o l'thTai tThwe fw
page 576 in your own words.
Use the diagram of (-“B to find the indicated lengths. Line r is tangent
to (5-8 at T, BT = 2, B5 = 1, and WT = 5. Round your answers to the
nearest hundredth.
19. BA = L
20. 5.4 = L
21. SN = __z_
22. Bit’ = _?_
23. XT = L
24. COMMUNICATIONS A radio station installs
a VHF radio tower that stands I500 ft
tall. What is the maximum ellective signal
range of the tower? the diagram suggests
a way to use tangents to solve the problem.
Use the Pythagorean Theorem to find d.
(The diameter of Earth is approximately
8000 mi.)
25. SPACE FLIGHT The space shuttle orbits at
I55 mi above Earth. How far is it from
the shuttle to the horizon? t l'he diameter of
Earth is approxiiiiatcly 8000 mi.)
26. DESIGN An artist wants to draw the
largest circle that will lit into a square.
She uses the following method:
Draw square /tb’CD. Connect the
midpoints of sides Hiand H) with a
segment. Connect the midpoints of D C
sides E and b’—C with another segment.
Construct the desired circle. How can you pl’0\(‘ that this is the largest
circle that will lit in the square? How can you prove that no part of the
circle lies outside the square?
L004’ 546*
27. A triangle has a perimeter of 24 cm and an area of 24 cm3. What are the
perimeter and area ofa larger similar triangle if the scale factor is $4?
(LESSONS 3.1 AND 8.6)
28. A rectangle has a perimeter of 22 It and an area of 22 ft"; W hat are the
perimeter and area ofa larger similar rectangle it‘ the scale factor is g?
(LESSONS 3.1 AND 8.6)
‘\
.
\
\
29. A rectangular prism has dimensions t’ = 12 in.. w: 8 in.. and It = 15 in.
What is the volume of-.1 larger similnr rectangular prism if the scale factor
is (LESSONS 8.1 AND 8.6)
A P P L I C A T I 0 N 30. ENGINEERING A cvlindrical water tower has a radius of 30 ft and a height
of I00 ft. What is the volume of a larger similar water tower if the scale
factor is %? (LESSONS 8.1 AND 8.6)
L004’ 5670/14
c H A L L E N G E Answer the questions below to prove theTangentTheorem.
PARAGRAPH PROOF 31. Suppose that the 'l'-angent Theorem is 18215:.
That is. suppose that line m is tangent to 00
at point A, but that line m is not perpendicular
to E. If this is true. then there is some
segment with endpoint O, ditTerent from m,
that is perpendicular to line m. Call that
se ment 573. Then AOB.-‘t is J ri ht trinn le. ~. In
E5 E5 8
Wlmt is the hypotefie of_A()Bzt? Which A 8
segment is longer. 0.4 or OB?
g immgmma fig‘ 32. Point 8 mttst be in the exterior of the circle because m is a tangent line.
pomom, M What does this intply about the relative lengths of OA and OB? Explain.
Ezténggamom 33. Compare your answers to Exercises 3| and 32. What do you observe?
mryvusiiiiim 34. lfan assumption leads to a contradiction. it must be rejected. This is
the basis for a type of proof known as an imiiiect pmofor a prooflry
contradiction. Explain how the argument above leads to the desired
conclusion.
CONSTRUCTING SMOOTH CURVES A curve may be made up of arcs of more
than one circle. ln order for arcs from two different circles to join smoothly
at a point, they must have the same tangent at that point.
1. Using a compass and straightedge or geometry
graphics softw:1re. draw (E)Pwith radius ii
Construct line t’ tangent to OP-at R; that is,
construct a line perpendicular to Wat R [refer
to Exercise I7}. For another circle to have the
same tangent, t’, its center must be on the line
(I3-E. Why?
2. Choose a point on 7372' that is not Por R and
label it Q. Construct at circle centered at Q
with radius GP and GO will have the
same tangent at R.
3. Try tracing part of your construction in a
different color. Starting on OP near R. trace
nnfil y-nu gel to R, and [hen confinue tracing YL:lU ShOl.lld I'lO\'t' l_7C illJlC l0 COl'l'l]JlClL‘ ACll\"ll.V 2
on OQ. The curves should join smoothly at R. "l ‘he ‘7h=1l“3T l’F0i€C1-
WORKING ON THE CHAPTER PROJECT
LESSON 9 2 TANGENTSTO CIRCLES 579
Inscribed Angles
and Arcs
».\
Objectives
0 Define inscribed angle "
and intercepted arc. ‘
¢ - ‘ u
o Develop and use the __ . "'
Inscribed Angle Theorem ~..-.“-" "‘
and its corollaries.
You can find the center of a circular
ollrecl. such as the tabletop shown here.
by using a carpenter: square. The
pmcess involves inscribed angles.
- p g o N A carpenter‘-.« square is used both for creating right angles in structures and for
CARPENT-Ry testing whether angles in structures are right angles. It can also he used to find
the center ofa circle. l'he method for finding the center ofa circle relies on an
important gcomctrv corollary [see the application on page 58-1).
The Inscribed Angle Theorem
An inscribed angle is an angle whose
vertex: lies on a circle and whose sides
are chords ol the circle.
L.-‘Ii-’C is inscribed in GP.
/‘N
AAI-’(' intercepts AC.
ll" you know the measure of the inscribed angle, you can determine the
measure of its intercepted arc. How do you think this can he done? ln the
activities on the following pages. you will discover the answer.
CRITICAL THINKING In the illustration above. what is n1Al-’(" + 1113?”? Would a similar result be
true for all possible inscribed angles in 2.! circle? Explain.
580 CHAPTER 9
Angles and lntercepted Arcs: A Conjecture
- - ll. I) 1. l’)raw three ditTerent figures in which
C0|'"_Das5, inscribed angle 1/WC intercepts an A
SUBIGNBUG9. arc ol the circle. Include one minor ,_Min0r
3': prommor arc, one major arc. and one semicircle. V C arc
ggomguy 2. Measure the inscribed angle and
9'3P“'°5 the intercepted are in each tigu re.
soltware
_ A
(You will need to draw central
angles to determine the measures
of the arcs.) _‘_Major
. - V are
3. Coinpare the niea-sures ol the
inscribed angle and its intercepted
C
are in each case.
CHECKPOINT 1/ 4. Make a conjecture about the A
relationship between the measure
ol an inscribed angle and the _ I
measure of its intercepted arc. V S°'"'°"°'°
/ ' Z
Proviné the Conjecture
- I ' I) To prove your conjecture from Activity I. you will need to consider three
no Special tools separate eases.
Part I
1. In the figure at right, one side ofthe
inscribed angle contains the center of
the circle. What is the relationship
between mzl and mil?
2. Notice that 43 is an exterior angle of
The center of the circle is
AAVP. What is the relationship among on one side of me an9.e_
m43. mAl.and mél?
TABLE PROOF 3. Complete the table below. For each entry in the last row. give a reason.
mm m.»:2 m£3 mi?
20° ? ? ?
30-: 7 7 7 As you justify each entry
n ? ? ? ofrhe table for the
40 general case, you are
x° ? 7 ? -‘-’-""' also proving a theorem.
CHECKPOINT u/ 4. Wl’i% does your table show about the relationship between ni.«;'l and
nut ?
LESSON 9.3 mscnieeo ANGLES AND ARCS 581
Part II
1. In the figure at right. the center
of the circle is in the interior of The center
the inscribed angle. What is the i"Sii‘7:‘fh‘;"°'°
relationship between ml] and interior or
"‘-p . . ’»‘-7 the angle.
ntA)4. between m4»: and lIl}\C. .
2. Complete the table below. For each entry in the last row of the
table, give a reason.
TABLE PROOF _ _ A
m41 rnAX rnz4 mCX rn..»:AVC mAXC
20 ? 20 ? ? ?
As you justify each 9
entry of the table for the 30 ? 2L. ? 7 ?
general case, you are do 7 50 ? 7 P
also proving a theorem. --;_ xu 7 yo 7 7 7
TI“
cuzcxvomr ./
CHE CKPOINT |/
3. \'\"h.lt does your table show about the relationship between mAA\-"C
and mAXC?
Part III
One more case remains to be proved.
In this case. the center of the circle is
in the exteiinr of the inscribed angle.
Draw your own figure for this case
and prove your conjecture for it.
(You may want to make :1 table.)
The center of
the circle is in
the exterior
of the angle.
Create your
own figure.
Conclusion
Complete the theorem below. which your work in this Activity" has proven.
Inscribed Angle Theorem
|‘he measure of an angle inscribed in a circle is equal to ?
the measure of the intercepted arc. 9.3.1
E X A M P L E 0 Find the measure 0| ZXVY. X
0 SOLUTION
45L
A.X'l-"Y is inscribed in OPand
intercepts XY. By the Inscribed
Angle Theorem:
mzxt-’Y= %ntX)"
582 CHAPTER 9
E x A M P L E Ga person's effective field or
A'P
Two Results of the Inscribed Angle Theorem
ICATION
OPTICS
"553--
In the figure at right. AA is inscribed
in a semicircle. Therefore, the are it
intercepts is also a semicircle. Thus,
the measure of the intercepted arc
is I80° (why-'?), and the measure of
44 is 1 x l80°. or 90°.
2 A
This calculation illustrates the following important corollary to the Inscribed
Angle Theorem:
Right—Angle Corollary
If an inscribed angle intercepts a semicircle. then the angle is a right
an gle. 9.3.2
ln the figure at right. the measure
of is twice the measure of AD.
or 2 x 50° = It)0°. The measure of
Z8 is one-half the measure of X6.
or%'><lOO°=50°. A
These calculations illustrate an important principle. Notice that ADand AB
intercept the same arc. As‘ you found, they have the same angle measure. This
leads to another corollary of the Inscribed Angle Theorem.
Arc-Intercept Corollary
If two inscribed angles intercept the same arc. then they have the
same measure. 9.3.3
vision is about 30°. In the
diagram of the amphitheater,
a person sitting at point A can
see the entire stage. What is
the measure of £3? Can the
person sitting at point B view
the entire stage?
SOLUTION
Angles A and b’ intercept the same arc.
By Corollary 9.3.?-. the angles must have
the same measure, so m£A = 11148 = 30°.
The person sitting at point B can view
the entire stage.
LESSON 9.3 mscnleeo ANGLES AND ARCS 583
E x A M P L E em OPwithdian1eler:-‘-173.
ma: llO°.and m§B= I30°. C 110
I Find the measures of Al, .42, .43,
[-1. (AFC .éADl3lt1I1d £C.'-1D.
A B
O SOLUTION
Copy the figure and add infornmtion
130
as you work through the solution.
Begin by labeling as many all
l'll(.‘&1:sll res as you can. Since AB is
. /5 /\
:1 drametcr. ACE and ADB have
a measure of l80°. Therefore.
/K‘ O /\ U
m.»lC = 70 and m.»lD= 50 .
Al and 42 intercept Thus. mél = 11152 = %[l I0] = 55°.
4.’: and £4 intercept |'hus. m1} = méel = -i-(50) = 25“.
.4.-‘lPCis n C€l1ll'di angle. Thus, m4.-'tPC = n1Ar(f'= 70”.
[A178 is inscribed in .1 seniicircle. Thus, mAADB = 90°.
AC.»lDintercepts Thus. mACAD= %[l |0+ I30} = l20°.
. P - , I 0 N A carpenter needs to Find the center
CARPENTRV of a small tabletop. How can she do
this by using .1 carpenter's square?
The carpenter inseribcs two right angles,
[ABC and ZDEF. in the circle. She then
draws the hvpotenuses of the triangles by
connecting points A and C and points D
and F. The il1l(:‘l’5€\.'ti()l1 of Rand -51-"is \
‘ the center of the table.
You will be asked to perform \ B
a similar construction in "*-
Exereise 49. D '
,\ E
-. A I
584 CHAPTER 9
Exercises
. Comma:/‘mtg
Refer to G0 in the photo for Exercises 1-5.
1. .\l-.une an inscribed angle in 00.
_ A
2. Explain how to hnd In§5. ‘ B ‘
nlmamotoonnea .12 _ _ W»
. . . '°"l 3 Explzun huw to find mxil. 1
Activities
Online 4. Explain how to find mfi. C 0
Go To: uohrw.com _ _ _
Ke,,...o..1; 5. l:.xpl'.'iln how to hnd m.L2.
MG: IAT
I
" 6. Explain why two inscribed ‘ -’
angles that intercept the same
arc have the same measure. " ~‘
. quidedsk/’//3 Practice
A P P L I c A I I 0 N PHOTOGRAPHY A person standing at a point /M on the edge of a circular
gallery takes a photograph. Suppose that QP represents everything that
is included in the photograph and that m0P = 70”. M
7. What is IIILO.-\-IP, known as the pI't'mI'c
mIglI—-of the camera? (ACTIVITIES 1 AND 2,
THEOREM 9.3.1, AND EXAMPLE 1) 0
8. What is IIILONP? (COROLLARY 9.3.3 AND
EXAMPLE 2;
In or, HK is a diameter, m@ = 50°, and mil? = 90°. Imeonem 9.3.:
AND EXAMPLE 3) G H
9. Find the measures of LG!-‘H.
LGKH. LIFK. and LKH].
10. Find the measure of LKGH. J
K
. Practice mm’ Apply
a uumamnnee :3“ In ow, m)??? = 60°; mL vyz = 40°, and W is a diameter. Find the
Holnewo k
"'3'P °“""'3 11 n1LX‘l’l'l-’ 12 mLl-VXY X
l3oTo:9ohrw.com I ' Z
K°V“'°'d- 13. n1L.\'l'lv’Y 14. HILXWJ
MCI Homework Help /\
‘°'E’‘°'°i5°5 "'13 15. IIIYXZ 16. IILL Y1-"Z
“ 17. mi? 18. nil-"'2 Y V
19. in -''Y 20. mm/ZY
LESSON 9.3 mscnleeo ANGLES AND ARCS 585
TABLE PROOF
As you iustify each
entry of the table for the
general case, you are
also proving a theorem. I...
APPLICATIONS
586 CHAPTER 9
For Exercises 21-28, refer to GP with diameter AC. Find the following:
22. mzb’
24. tuft?
21. mz/l
23. m4BCA
25. mAP(‘ D
27. .1163
26. m4 CPD
/\
28. m.-'lD
For Exercises 29-32. refer to the circle below.
29. n1.-fl‘? = 68°
30. m1 D = 50“
/'3
31. mCD = 87°
32. méB = 11°
mAC=
HIKE =
?
?
11145 =
mFB=
?
?
mAl')= L
mAC = ?
1114.4 = ?
mAA = ?
A
D
D
V C
Quadrilateral OUAD is inscribed in a circle. as shown below. Copy and
complete the following table. For each entry in the last row, give a
reason.
xx /\
rn£U rnODA rnOUA rn.¢:D m..»:U+rn£D rn..»:O+rn£A
100“ 33. 7 34. 7 35. 7 36. 7 37. 7
38. 7 160 39. 7 40. 7 41. 7 42. 7
x 43. 7 44. 7 45. 7 46. 7 47. 7
48. Based on the inl'orm-ation in the table,
state a theorem about the angles col" .1
quadrilateral that is inscribed in a circle.
U
q
0 D
In Exercise 49. you will use a piece of paper with right-angle corners to
model the use of a carpenter's square to find the center of a circular
object, as described on page 584.
49. CARPENTRY Draw a large circle on a sheet of paper. Place one right-angle
corner of a sheet of paper on the circle so that both sides of the angle cross
the circle. Mark the three points where the right angle at the corner of the
paper touches the circle. and connect them to form a triangle. Repeat these
steps to form another triangle in the circle. Identify the point where the
longest sides of your triangles intersect. Explain why this point is the
center of the circle.
50. STAINED GLASS An artist is
creatinq a circular stained-glass
window with the design shown
Center of circle
\ — I
1 l r
A
_v
3* I
at right. The artist wants the arc
intercepted by A.-‘l and 18m
measure 30°. W hat should the
measures be of AA and AB?
FLOWCHART PROOF
APPLICATION
This map of tin:
l'm'!t'rl Smms uses
only four colors.
Look Back
For Exercises 51-61. complete the
flowchart proof below.
Given: Line 6 is the angle hiscctor of
ABXC, and line m is the angle 5 5 ‘
bisector of ACXD. D C
Prove: Line F and m are perpendicular.
Proof:
/3 " /d
(m..»:3-m..»:-1'1
F is the angle bisector of ABXC.
/5 ‘ /5
(m..»:6-m..»:5}
53. 7 H m.£2+mz3=m.£4+m.£5J
Transitive Property 54_ 3
of Equality |
/2 B /6
(m.»:2 - m..»:6}
52- Z
‘V
m..»:MXL - m.»:MXN
m.£2 + m.»:'3 = m.»:'MXl.
mz-1 + m£5= m.£MXN
55. 7 56._?_
M Cum
57. ? 59. ? 61. '2
Look Beyond
CARTOGRAPHY A famous theorem in ntathenmtics is related to mapm.1|<ing.
Tl1cjEmr—mlor rlmtwrem states that any map in .1 plane can be colored with a
maximum of four colors so that no two adjacent areas are the szlme color. The
first "proof" of this theorem, by Appel and Hnken in 1976. was controversial
because parts of the proof used a computer and could not be vcrilicd by hand.
62. Explain why the “nmp" below cannot be colored with fewer than lbur
colors.
63. Makc up your own map and try to color it with only four colors.
LESSON 9.3 mscnleeo ANGLES AND ARCS 587
Objectives
0 Define angles tonned
by sec ants and
tangems of circles.
0 Develop and use
theorems about
measures of arcs
intercepted by these
angles.
A ' P L I C I 0 N
NAVIGATION
Angles Formed by
Secants and Tangents
The print: pies ale role geometry are
used by navigators at see. For example.
the "ban'zomal angle of danger‘ enables a
navigator to stay 1! safe distance from it
dangerous region.
llll
A mwigatur on board a ship can measure the angle between two lines of sight
to lighthouses on the coastline. This nteasurement tells the navigator whether
the ship is inside or outside a circle ofdunger that contains hazardous rocks or
shdllotvs. The technique is based on secant lines that intersect the circle of
danger.
588 CHAPTER 9
Classification of Angles With Circles
Angles formed by pairs of lines that intersect a circle in two or more places can
be studied systetttatically. There are three cases to consider. according to the
|1LtC:"ntEnl of the vertex of the angles.
Case 1:Venex is on the circle. Case 2:Vet1ex is inside the circle.
6'6
b. c.
V
Two
seca nts
120" 120' 30 7 60
As you mstity each _,
entry of the table for the 100 ? ? ? ?
general case. you are 80' ? 7 ? 7
also proving it theorem. — ____ X ? .3 ? ? V C
2.7‘ .1AVCis an acute angle.
CHECKPOINT 3/ Complete the following statement:
'I he measure of an acute secant—Iangent angle with its vertex on
a eircle is ? the measure of its intercepted are.
3. The seczttlt-tattgettl angle is obtuse.
Copy and complete the following table:
f‘.
rnAXV mz1 mz2 m./_PVC méA VC
200° 160" 10° ? 100"
220° ? ? ? ?
240° ? ? ? ?
V C
X ? 7 ? 7 AAI/Cis an obtuse angle.
CHECKPOINT / Complete the following statement:
Vertex on Clrc|e—Secant and Tangent (Case 1a)
- - I In this r\CIIVIl)’, you will examine three
no spam] touts Conltgurtttions ol seeant—tangent angles.
1. The scctttlt-tatlgettt angle is '.t right angle.
. . . Se t
(The secant contains the center ol the circle.) £35"
m/_'.»‘-lV(' = 2 mfii? = 2 “’"9e'“
CHECKPOWT 1/ How does this relationship compare with
the one between an inscribed angle and V C
its intercepted arc? 4AvCis a right angle.
TABLE PROOFS 2. The secant-tangent angle is acute.
Copy and complete the following table:
m/fl-I7 m.£1 m/2 m.4'PVC m AVC
The measure ol'an obtuse secant-tangent angle with its vertex
on :1 circle is ? the measure of its intercepted arc.
CHECKPOWT 1/ 4. Based on tour results. complete the following theorem:
Theorem
[fa tangent and a secant (or a chord) intersect on a circle at the point
of tangent)’. then the measure of the -angle formed is ? the
measure of its intercepted arc. 9.4.1
CRITICAL THINKING Case lb (vertex on circle. two secants] has already been studied in this book
Where? What theorem corresponds to this case?
LESSON 9.4 ANGLES FORMED av SECANTS ANOTANGENTS 589
Z
Vertex Inside CircIe—Two Secants (Case 2)
no special mots
TABLE PROOF
As you justify each
entry of the table for the
general case, you are
also proving a theorem. «x___
..._j_?_J"'
CHECKPOINT M
1. AA!/C‘ is an exterior angle of AA DV. \-\/hat
is the relationship between the measure of
./_Al-’(" and the nteasttres of /_l and /.2?
2. Copy and complete the lollowing table:
mic‘: rnB‘B m.«’_1 I mL2 m.LAVC I m4DVB
160° 40° 30° I 20° 100° I 100 T“'° Secam
180° 70° 7 I 2 2 I 7
200° 60° 7 7 7 7
x" x° 7 7 7 7
3. Based on your results, complete the theorem below.
Theorem
The measure of an angle formed by two sec-ants or chords that
intersect in the interior of a circle is 7.’ the 7.‘ of the measures
9.4.2
of the arcs intercepted by the angle and its vertical angle.
TAKE PROOF
As you justify each
entry of the table for the
general case, you are
also proving a theorem. ‘-
cnecxeomr ./
I .3
Vertex Outside Circle—Two Secants (Case 3b)
1. Al is an exterior angle ol AB\='C. What is
the relationship between the measure of
/_l and the n'l(:‘dStll’t:‘S of /.2 and LAVC?
2. Copy and complete the following table:
mg?) I n1A—Z‘ m .1 m./:2 mLAVC
200 40° 100° 20° 80'
— — —: : Two secants
250 60" .7 ? ?
100° 50 2 ? ?
-" x,° X,‘ 7 7 ?
3. Based on your results. Complete the theorem below.
Theorem
The measure of an angle formed by two secants that intersect in the
exterior ofa circle is ? the ? ol" the measures of the intercepted
9.4.3
HTCS.
You will e‘<p|OrE' cases 3.1 and 5:: in Fxercises 27-3;
590 CHAPTER 9
A - p L . c . , 0 N The illustration below shows a ship at point F and two lighthouses at points A
NAVIGA-"ON and B. Thecircle encloses a region olidangerous rocks. The measure of‘ an
angle Inscribed In AGB. such as AC Is known as the horizontal angle ol
danger. l\a\-'igation charts contain information about horizontal angles ol
danger for different regions.
l'he ship’s navigator measures AF. the angle formed bv his lines of sight to the
two lighthouses. He knows that he is outside the circle of danger because mzF
is less than the hori7onta| angle of danger for the area. Why does this method
work?
- , .3» .
F E.
D _. .
; 1
. Q: Q - _1
pi la .' . .
at danger - -
. ‘c a -
Notice that .4 C is an inscribetl angle and that it intercepts 71-3 l'hus. if the
ship were on the circle, AF would equal AC. Therefore. it should be obvious
that if mAFis less than m£C. the ship is outside the circle.
camcAL THINKING How can you use theorems from this lesson to prove the ‘‘obvious‘’ fact
mentioned above? How can you prove that if m.{ F were greater m.£C, then
the ship would be t'n.~'i:.le the circle!
E X A M P L E oFind in.£;'-‘ll-"Cineacltfigure.
a. b.
0 SOLUTION
an. AA\-''(" is formed lw a secant and a tangent that intersect on the circle.
By Theorem 9.3.1. mzAvC= §mfi\7 = ét 150°) = 75°.
b. .4.»-ll-‘C is formed by two sec-ants that intersect inside the circle.
BY Theorem 9.3.2. mzavc = $(mE+ m§B) = §(9.n° + 40°) = 60°.
c. A/ll-"C is formed bv two sec-ants that intersect outside the circle
/‘K.
By Theorem 9.3.3. n1zAl/C = %(m?t?'— mam = 530° — 20°: = 30°.
LESSON 9.4 ANGLES FORMED BY SECANTS ANOTANGENTS 591
‘i n 1
E X A M P L E 0 Given: TU is tangent to OPat point T. R
mi)? = 90° 9°
lllfi = l50° / 150
in6§= 50° 0
Find the following: ‘
5 1 i‘
U
. SOLUTION
a. mASIU b. mzt c. mzz V 2
Makt-: your own sketch of the figure. As you obtain new information. add it to
the figure.
a. Because the vertex of 48 IL‘ is on
EJPand ASTI ‘is formed by a tangent
and .1 SCCi19LiillC, DIZSIU = lgltgf.
To find mST. note that -
50° + 90° + 150° + mfi = 350°.
Thus, mg? = 70° and
mzsw = §(7o°) = 35°.
b. Because the vertex of Al is in
the interior of OP-and is formed
by two intersecting chords.
mzt = %(m6§+ mm = §(9o° + 70°) = 30°.
c. Because the vertex of A2 is outside the circle and is formed by two
secants, 111.42 = %(ntfi'— n16§) = %(l50° — 50°) = 50°.
50°
Exercises
. Co/rmrz//1/care
1. 'l'he meusu re of an acute sec.ant—
tangent angle with its vertex on
a circle is ?
2. the measure of an obtuse sec-ant-
tangcnt angle with its vertex on { .
.1 circle is ? -
3. The measure of -.1 secant-secant /
[or chord—chord) angle with its \
vertex inside .1 circle is ?
4. Thf l1k"i'lSlll'€ Of Fl SL’Cdl]I'$f'Ci'll1l \ //
angle with its vertex outside a
circle is 7 In (In: figure, every chard aftlte army’
circlr: is tmtgent to the inner rinle.
592 CHAPTER 9
. 61¢/‘dad 3,6///3 Pmct/ce
5. ln oz mfi»?- = 13391:‘ W 6. ln (30. 111.73 = 50° and
is tangent to OZ-at Y. find m@ = l50°. Find mLl.
in; Wl",\'. (THEOREM 9.4.1 (THEOREM 9.4.2 AND
AND EXAMPLE 1) EXAMPLE 1)
N
M J.
P
Y V
7. ln (DA, mfié - 84° and 8. H is tangent to 0G at B.
mfTE = 40°. Find mLBFC. mfifi = 70°, mi? = 100°. and
(THEonEM 9.4.3 AND mfi‘ - 130°. Find the follow.-ing.
EXAMPLE 1) (EXAMPLE 2)
a. m.£ABC
b. n1L|
c. mL2
d. mLD
A
A P P I. I C A T l 0 N 9. NAVIGATION Lighlllcmses are located _ - '
at poinls A and B on the circle of Q‘ - - r- "
danger. ll" a ship is lomlcd at point X '’ - '9"
(not shown) and IHLBXA - .27". is ‘
the ship inside or outside the circle
ofdangcr? Explain. (APPLICATION) ‘
50"
. Prdct/ce and Apply
Dlnhmltmnnea. In ox, ml/73: 36, mfl7= 148", and ml’J-l7= 70'’. W is tangent to OX
Homewofk at Y. Find each of the following:
Help Online 1o_ mLS}.'v
Go To: go lnw.com
Kewmrd: 11. mi VS)’
M61 Horlewotk Hulp
lav Em.-rcnsus Ill-26 12_ m; S\-’)’
LESSON 9.4 ANGLES FORMED av SECANTS ANOTANGENTS 593
ln the figure. 718 and CD are
chggls, m 55 = 60°; and
mAD = 110‘. Find each of the
following:
13. um! 14. mzz
15. mi?» 18. mz-1
‘ / ; 2 / In the figure, V2 is tangent to GP at V
17. ll" inl’-'3: I50", find mz tt-"C.
18. n‘ mzavc = 30°. find mfrff.
19. ll’ mi-7(“= 2;-+ 4. Find mzavc
20. ll’ IHAAVC = 3x— 1. find mfif.
Refer to 00 for Exercises 21-26. {IE3
is tangent to (30 at A, mCD = 105“,
m’BE = 47': and mAB = m55. Find
the following:
f\- ..-o'‘\
21. mAB 22. m U)
23. mz.»-tED 24. m4CAF
25. mA('QD 26. mABQ(‘
In Exercises 27-37, you will explore
cases 3a and 1-30 from page 588.
Case 3c: A secant and a tangent
intersect outside the circle.
lfleler to GP for Exercises 27-30.
VC is tangent to GP at C.
27. What is the relationship between the
measure of A l and the measures of
A2 and AA\-’(.?
TABLE PROOF 28. Copy and complete the table. For eaclt entry in the last row. give 3 reason.
/-~. rm
mBXC mAC m/1 m/2 m/AVC
250 60 a. 7 b. ? c. i'_—‘
200 40 d. ? e. 7 I. ?
:30 40 g. 7 h. 7 i. 7
70“ 30 j. 7 It. ? I. 7
x.” x,° m. ? n. 7 o. 7
29. Write an equation that describes Ind.-«ll-"C in terms of 1:152 and mfii.
594 CHAPTER 9
CHALLENGE
30. Lloniplete the following, theorem:
Theorem
The measure ofa secant-taltgent angle with its vertex outside the
circle is '
-1
9.4.4
Case 3a:Two tangents intersect outside the circle.
Refer to GM for Exercises 31-37. V5 and V5 are tangent to GM at A
and C. respectively.
31. What is the relationship between the
measure of Al and the me-.i.«.ures of
A2 and AA!/C?
32. The measure ot Al is half the measure
of its intercepted arc. _\l-.nne the arc.
33. The measure Ol 12 is half the measure
of its intercepted arc. \l-ante the arc.
34. Given nirt,\’E‘= 260‘? find 111775.
TABLE Pnoor 35. Copy and complete the table. For each entry in the last row.
give a reason.
P i f f‘\
mAXC mAC mA1 m£2 mAAVC
300° 3. ? b. ? c. ? d. ?
250° 9. 7 r. 7 9 7 . 7
Asyou justify each 220. . 7 . ? k 7 I 7
entry of the table for the " ' ' ' '
general case, you are 200" m- 7 "- 7 0- 7 9- 7
also provingethearem. ~ -._ X q. -; ,_ 7 s_ -; 7
36. Write an equation that describes niéxtl-’C in terms of in txli and mfié.
37. Complete the following theorem:
Theorem
The nieastire of-.1 tangent-tangent angle with its vertex outside the
circle is '
-\
9.4.5
38. Justify the following statement algebraically by using the cliagrani of OM
above:
/3 ;-s.
mAXC—mAC _ ’ »>«_
——-—2——-——- — mz-UK, |80°
(1 lint: um‘ ,\'c+ m§iE= ? 1
39. Use the statement in Exercise 38 to write an alternative iersion of
Theorem 9.-1.5.
LESSON 9.4 ANGLES FORMED BY SECANTS ANOTANGENTS 595
In Exercises 27-37, you completed the investigations of angle-arc
relationships in circles. In Exercises 40-55. you will summarize the
angles studied. Complete the table below.
SUMMARY OF ANGLE-ARC RELATIONSHIPS
Location sides Formula for
Diagram of vertex of angle mz/WC
A
central angle: A
center of circle sides formed mzAVC— mAC
by 2 radii
C
Via the center of the circle.
A
C
40. ? 41. ? 42. 7
D B
A inscribed angle:
V 43_ 3» sides formed 44_ 7
by 2 secants or
C chords
1—)
VC tangent
at V 45. ? 46. 7 47. 7
. sides formed
48. ? exterior of ClI'CI9 by 2 tangents 49. L
50. ? 51. ? 52. ?
53. ? 54. ? 55. ?
A W tangent
‘ at C
596 CHAPTER 9
APPLICATION
APPLICATIONS
56. COMMUNICATIONS The maximum distance that a radio signal can reach
directly is the length of the segment tangent to the curve of Farth's surface.
It" the angles formed by the tangent radio signals and the tower are 89.5“.
what is the measure of the 893 ‘E 895:.
intercepted arc on Farth? — "N ‘
Given that the radius of Earth
is approxitnately «I000 mi. to
estimate how far the signal _’
can reach. - ‘ - -7 .
Look Back
Find the indicated angle measures. (LESSON 3.6)
57. 58.
1 20°
80° 84"
60. ARCHAEOLOGY 'l he Great Pyramid of Giza in Egypt, built bv Khufu
(Cheops in Creek). is considered by some to be the greatest structure ever
. -_.__ K .- .
btnlt. its rottghly square base measures an average ol 1'1’? :7 it on a side.
and its original height. before erosion. was 48! %t"t. I-‘ind the volume olthe
original structure. I5otIrrr': Ftrqw'lopt’rlia Britmmiml (LESSON 7.3)
DESIGN A photocopier was used to reduce AABC by a factor of 0.75.
61. Are :2. tBCand :‘.‘t.«l’b"C' similar-.’ A
Explain your reasoning. (LESSON 8.2) 12 20
62. Find the following ratios: % £4.
(‘'8' " L C 16 3
and (LESSON 3.5; A-
_ I 15
63. Find A C’. (LESSON 8.6) 7
5' 12 3'
Look Beyond
A conic secriimr is the intersection of a right double cone and a cutting plane. In
the diagram below. the intersection of the plane and the cone forms a circle.
Other geometric figu res are formed when the angle at which the plane cuts the
double cone is adjusted.
Dest.ril)e how the cutting plane should be adjttstecl
in order to produce each conic section listed below.
You may use a sketch or a verbal description.
\
64. ellipse O 65.parttl)ola V
66. one point 0 67. two intersecting lines X
68. hyperbola 69. one line 4?-
/\
LESSON 9.4 ANGLES FORMED BY SECANTS ANOTANGENTS 597
EEITN sfi
' E-Lfiillfl .!|Ji ~“= \j)
_:i_|tS1_'.|fl|‘« :
Imagine that you are a geologist in ' -
the Los Angeles area. You have
records from three ditTerent .
stations (A, B. and C) of waves
produced by the earthquake. I-‘rom
these seismogmrns you must \
pinpoint the epicenter. the place X ,
on the earth’s surface directly - _ __,u‘~‘
above the origin of the '
earthquake. To find the epicenter,
you will use two tvpes of seismic . ~\
waves. 5 \A-ayes and P waves. ''
Becatise S waves and P waves ".5: s‘ \-
travel at different speeds, you can
use the difference in their travel _' Q
times to determine how far *‘ "
they have gone. You are now _ -
ready to begin. '
5 - AFTER - v
\
\
I
‘ W
' \ WAVE
‘ SPEED VALUES
Speed of P wave
- { V, = 6 KTTVS
Speed of S wave
\ v, - 3.5 kmfs
' i
I
5
STATION DATA
I D. (seconds)
Station A 4.4
Station B 5.5
Station C 6.3
-‘S:
\ .
I‘. :_-J $7 ,r\_‘
‘ '5'
oh’ \‘
\
“§ It ' ‘ -
- ' rrs sersrrroqrrzrrr
Qficv shows 5' -waves
‘ .N and P rmvcs
1'
1
~ -u
u
§
. x l l.
. ‘ .'_ 1
Cooperative Learning
1. First you will examine how the time difference between the arrival of the
S and P waves depends on the distance from the station to the epicenter
of the earthquake. let ri represent the distance from the station to the
epicenter.
a. S waves travel at 3.55 kilometers per second (kmlsl. Write an equation in
terms of d for r_t-. the time [in seconds] for the S waves to travel to the
station.
T5 = ?
b. P waves travel at 6 kmls. Write an equation in terms of d for tit the
time [ in seconds} for the P waves to travel to the station.
fp =
c. Use the equations from parts a and b above to write an equation in
terms of d for D, the ditference in time between the arrival of the S
waves and P waves.
E-)=f_g—T;I= ?
d. Solve your equation from part c for d to find an equation in terms ol D
for the distance from the station to the epicenter.
tl= ?
Use your equation from part d above to find the distances in kilometers
from each staion to the epicenter.
Station D d
A 4.4 7
B 5.5 7
C 6.3 7
Make a scale drawing of the locations of
the three stations. with I lcm = I cm. Draw
three circles centered at the three stations.
using the distances you calculated above as
the radii of the circles. The epicenter is in
the region where the three circles overlap.
For more precision. draw chords connecting
the intersections of each pair of circles. The
epicenter is the intersection of these chords.
Label the epicenter on your drawing.
B
/\
53‘
56.0 km 63.4 km
54.4 km 5
All of the seismograph readings used to locate the epicenter of the 1994
Los Angeles earthquake came lrom stations that were southeast of the
epicenter. How would that make finding the location of the epicenter
more diificult?
CHAPTER 9 Evswrmess MATH 599
Segments of Tangents,
Secants, and Chords
_ it "-=_‘ "‘
. lélmted ' -?‘L~§'~ I lrirhfir: It"-‘I ¢-¢-n.-m-
tates ‘-=~ ..
u ‘R L:
. ~ \,.
-t’!
The ¢'m.'cr:nt'mrr'or.' of ‘._
a (mores is grmtfir along ‘ ‘5_
5 rt s:nr.it‘r'rrulara:r. " _\
I
' Clrrrlrirl ltzrl .
n n ‘I.
Objectives 4, ..,~ L
0 Define special cases - -
ol segments related
to circles, including J _
secant-secant, secant- I ,
tangent. and chord-
chord se ments.
9 ‘~ YUCATAN
0 Develop and use Mexico _I - .
theorems about ,- - ‘s .4’
measures of the Belize .9
segments. _
l ' T('nl!rl( of Kirk.-rlkan
Gualemala Honduras at cm’.-.. lr:d
A theorem In this -» - will
extend ynur list of techniques for El Salvador N.
finding the center of circular oblacts. ' “rag "3
A - p L c . 1 0 N A semicircular arc of natural wells icenotesl like the one at Chichén ltzj
GEOLOGY stretches across the Yucatan peninsula. Some scientists believe that the cenote
are is evidence of an impact by an asteroid or comet. perhaps explaining the
extinction of the dinosaurs (see page 353). The center of the arc would be the
point where the asteroicl or comet actually struck Farth.
600 CHAPTER 9
Exploring Segment Relationships in Circles
In the previous lt.sS0l'I. you imestigated special angles and ares formed by
secants and tangents of circles. As you will see. segments formed by secants
and tangents ofcircles also have interesting relationships. The terms in the list
below are used to elassifv such segments.
in the illustration. is a tangent line and is a secant line.
W is a tangent segment.
fiis a secant segment.
TC is an external setaut segment.
b'—C is a chord.
' I
Segments Formed by Tangents
d . . +-,-+
?,j’.';‘,""“‘ an 1. Construct OPwith tangent lines AA and
0“ 2. Measure the lengths of Wand Ti
geumet _
graphicrsy 3. Make a comecttire about the lengths oi
3°*“”3"-‘ two segments that are tangent to a circle
from the same external point.
PARAGRAPH PROOF 4. Add segments .31-I3, PT’, and Yfito your
figure. Write a paragraplt proof of your
conjecture.
5. Complete the theorem below.
Theorem
CHECKPOINT ./ If two segments are tangent to a circle from the sa me external
point, then the segments ? . 9.5.1
- - Ll. D Part I
‘H I I éj‘
:=|:3|';‘rD355 3'10‘ 1. (.ons‘t_r_t,1ct OP\\'l[h secant lines X/t
on and XB.
geonaetrv 2. Construct A—L)and B—(Iand label their
qrap ics - . - - -
Samara llllt"l'S€(.ll0n point 0.
3. Name the two large triangles in your figure that have at vertex at X.
What can you conclude about them? (Hint: Use Theorem 9.3.3.)
Complete the following similarity statement:
AAXD - ?
' /‘ . 2 /‘ 4. Complete the proportion below. _ _
’ Cross multiply and state your result I" we process 0' dlswvenng
' X» W) ‘ ' your result, you are proving
8 H190! em.
? 7
PARAGRAPH PROOF 5. Present your discovery as -.1 paragraph proof. Complete the theorem
below.
Theorem
cuscxpotm M If two secants intersect outside a circle. the product of the lengths of
one secunt segment and its external segment equals ?
(Whole x Outside = Whole x Outside) 9.5.2
LESSON 95 SEGMENYS 0F TANGENTS, SECANTS AND cuonos 60 1
cnecxpomr ./
compass and
ruler
OR
geometry
graphics
software
PARAGRAPH PROOF
602 CHAPTER 9
CHECKPOINT /
Part ll
1. imagine moving point B-along the
(--'>
circle so that XB becomes a tangent
line. Points 1:‘ and D will coincide at
the point 0|" tartgettcy. \'\-‘hat is the
relationship between X8 and XI’)?
2. Substitute XB for Xi”) in your
result from Step 5 of Part I.
B and D (relocated)
3. Based on your result, complete the theorem below, which you will be
asked to prove in Exercise 38.
Theorem
ll :1 secam and a tangent intersect outside :1 circle, then the product
of the lengths of the secant segment and its external segment equals
2
(Whole x Outside = Tangent Squared) 9.5.3
1. (Z_<>ttstrtrct -.1 circle with chords T;-and
DB intersecting at point X. A B
2. Draw '.»t_E'Jand PE. l\ame the two
triangles lormed.
3. Name two angles of the triangles that D
intercept the same are of the circle. What C
can you conclude about these angles?
4. What other angles of the triangles can you show to be congruent? What
can you conclude about the triangles?
5. Complete the proportion below by
relttting two sides of one triangle
to two sides of the other triangle.
Cross multiply and state your result.
DA’ g
XA -5
6. Present your discovery as a paragraph proof. Complete the theorem
below.
l In the process of discovering
your result, you are proving
a theorem.
Theorem
it two chorcls intersect inside a circle. then the product of the lengths
of the segments of one chord equals ? . 9.5.4
Applying the Segment Theorems
E X A M P L E 0 Global positioning satellites are used in _ .
navigation. If the range of the satellite. A _ X
AX. is 16,000 miles. what is BX? ' '
NAVIGATWN 0 SOLUTION _
and are tangents to .1 circle ,
from the same external point. By _ I ‘ 3
Theorem 9.5.! , they are equal.
AX - BX - l6.0UO miles
E x A M P L E elnthefigure.E.’- l.3|.GX-0.lS. ? G
and FX - 1.46. Find HA. Round your
answer to the nearest hundredth.
O SOLUTION F
EX and FX are secants that intersect outside the circle.
By Theorem 9.5.2. Whole x Outside = Whole x Outside.
I-‘X’ GA’ - FX° HX
l.3l 'D.4S - l.-I6 ' HX
l.-46 ' HA’ = 0.5895
HX ~ 0.40
E X A M P L E 0.-\n eagle is released from captivity at a 50 ,
ranger station near an approximatelv __06t 4.,
circular lake, and it builds a nest in a - -tio
A'P lC- ION
tree on the opposite shore. The distance
WILDLIFE MANAGEMENT
from the station to the lake is 500 yd
along a road tangent to the lake, and
50 yd along a line straight to the nest.
How far is the nest from the ranger station? ' - = -
00y-I
O SOLUTION
The road is a tangent and the line to the nest is a sec-ant. ‘I hey intersect outside
the circle. Let cl be the distance from the ranger station to the nest.
By Theorem 9.5.5. Whole x Outside = llangent Squared.
d x 50 - 300’
tl x 50 - 90.000
d= I300 yd ~ 1 mi (l mi = lF6O yd)
LESSON 95 SEGMENTS OFTANGENTS, SECANTS AND cnonos 603
E x A M 9 L E Om the figure. AX=O.26. XC=0.9l.and
DX - 0.27. Find X8. 3
A3" I / O SOLUTION :3
.—‘t'(_', 'l.')—.‘\;. and :\T3are chords that intersect C
inside a circle. By Theorem 9.5.4:
AX' \'C- DX-XB
0.26 ' O.9l = 0.27 ' XB
0.27 - XB - 0.2366
XB -= 0.88
E X A M P L E The map shows the Yucatan peninsula, where A and Bare points on the cenote
ring. Assuming that the cenote ring dc-lines the outer edge of an impact crater
ofan asteroid or comet. where did the object hit the Earth? Use a ruler and the
A ' P l c A T l 0 N map with the given scale to find the point of impact.
GEOLOGY
I 1). \
0 "* ‘ Zr
(_ Progreso .
' YUC TAN
O SOLUTION Maids’ FEM SULA
A
Construct F. the perpendicular T
bisector of Ab. Label Q the Canon;
midpoint of ,Tr'.and D, the Ring
intersection of I" with the _ Chichén ttzé
cenote ring. Some“ here on ,.:_ jl
line I" there exists another ‘’ “' '°°'‘''°”""‘*‘
point, E. such that I-if is a
diameter of the circular "' 1 -? .,
crater. [Why?) “-
The diagratn below Shows the position
of points A. B, and D on the circle.
Bv measuring the map. AC - BC - L7 cm. and CD - 0.9 cm.
E
By Theorem 9.5.4:
CD- C}.-'= AC- BC
03' CE- L7‘ L7
CE -= 3.2 cm
__ _ A 1:
DE [Si d rameter ol the circle, 3
and DE - 0.9 + 3.2 - 4.1 cm. 0
For the given map scale. the actual diameter is about I80 km. Using a radius
of 2.05 ctn for the cenote ring. you can locate the center point on t". This point
is 0.35 cm southeast of Progreso on the map. Using the given map scale. the
center of the possible impact crater is a little over 15 km southeast of Progreso.
This would be where the comet or asteroid actually hit the Earth.
604 CHAPTER 9
Exercises
. Cowman/‘mtg
For Exercises 1 and 2, explain the meaning of the statement and state
which theorem is related to it.
1. Whole x Outside = Whole >< Outside
2. Whole x Outside = Tangent Squared
3. Suppose that two sccants or chords intersect on a circlc. Can you
determine anything about the lengths of the segments formed? \-\"hy or
why not?
4. Suppose that a tangent and :1 M.'Cdl'll intcrscct on u circlc. Can you determine
anything zthout the length of the segment formed? \‘\-'h_\' or why not?
5. l ist as many methods as you can for finding the center of a circle. How
much of the circle must be known for each method?
. qu/‘dad Ski//3 Practice
6. and arc tangent to 7. In OQ. AX = 16, CX = 9.
OPand AX = 7. Find BX. and BX = I8. Find DX.
(THEOREM 9.5. 1 AND (THEOREM 9.5.2 AND
EXAMPLE 1) EXAMPLE 2)
8. is tangent to OR at B. 9. In the diagram. AX = 6,
AX = 8. and CA’ = 2. Find BX. BX = 5. and DX = 8. Find CX.
(THEOREM 9.5.3 AND (THEOREM 9.5.4 AND
EXAMPLE 3) EXAMPLE 4)
LESSON 95 SEGMENTS OFTANGENTS, SECANTS AND cnonos 605
‘\
COI'I'lEd
Homework
Help Online
Go To: go.hrw.cMn
Kcy-void:
MGI Homework Help
lor Exercises I8-2|
606 CHAPTER 9
‘\
v
11?;
. Practice and Apply
10. in the Cllitgmln at right. is the
perpendicular bisector of E;
FG - I3, and DF - 48. Find the
diameter of the circle: that contains
points D. E. and G. (EXAMPLE 5) E
E is tangent to OR at C.
Identify each of the following:
11. a tangent segment
12. a secant segtnent
13. All L“{l.Cl'll3l SL‘Cdl'll SCt.’,lllClll
Identify each of the following
in the figure at right:
14. two pairs of congruent anglcs
15. .1 pair ofsimilttr triangles
Find x in each circle below.
16. Q 17. 9%
D
In the figure below, W and are tangent to GP, the radius of GPis
3 cm, and VA = 6 cm. Find the following:
18. VB 19. AP
20. PV 21. XV
22. l\:tme an angle congruent to ./_A\-"P.
23. l\;'tll1E an angle congruent to ./_AP\-’.
24. l\'-.1mc an arc congruent to
Use the figure below for Exercises 25-27. (Hint: You may need to use
the quadratic formula.)
25. Given WA - 4, WE - lO,.1nd l-'l-’C- 5. B
[ind CD.
A
26. Given WB - .\', WA - 6, WD - _x'+ 3. W
and WC - 5. find x.
27. Given Wb’ = x, l-'0"/l = x— 16. W1) = 3, C
and WC = S, find x. D
‘ _/32 / Use the figure at right for C
Exercises 28 and 29.
28.Given AF=x, BF=.\'—2. CF=3-, A B
and DE = 8. find 3:.
CHALLENGE 29.GivenAB=l0.CE=2.ztnd CD=l2.
find AF. D
In Exercises 30-37, you will summarize the properties of segments
formed by secants, tangents. and chords.
SUMMARY: SECANTS TANGENTS AND CHORDS
Location Types of
I iogra of vert .egmonts More
*9
VA tangent
at A exterior 2 tangent AV = CV
V of circle segments
I/C’ tangent
at C
30. .7 31. 7 32. 7
1 secant segment
33. ? °""3"°' and 1 tangent 34. ?
T of circle segmem j
A
C
35. 7 36. 7 37. 7
D B
ALGEBRAIC PROOF 38. Prove Theorem 9.5.3 h)’ using the
diagram at right. (I lint: Dram
segments fihtnd B—C. Then set
up a proportion with the
quantities in the theorem.)
LESSON 95 SEGMENTS 0F TANGENTS, SECANTS. AND CHORDS 607
APPLICATIONS
APPLICATION
FLOWCHART PROOF
608 CHAPTER 9
39. LUNAR EXPLORATION The diameter of
a lunar crater, from measurements
made on Earth. is known to be
32 km. How far is it from the lunar
lander, located at l., to point X on
the far rim of the crater, where a
rock sample is to be taken?
40. ENGINEERING Jeff is restoring .a
clock and needs a new gear drive 0
to replace the broken one shown
at right. l'o make a new gear. he
must determine the diameter of
the original drive. In the picture.
I-‘ is the midpoint of H). Use the
product of the chord segments to
find the diameter of the drive.
BD= l0.l cm FF= 2.5cn1
BD= 10.1 cm
EF= 2.5 cm
L002? 3676*
PACKAGE DESIGN A manufacturer is considering the three potential
package designs shown below. Draw a net for each one.Then
calculate the surface area and volume for each.
(LESSONS 8.1, 7.1, 7.4, AND 7.5)
41. _, cm 42. 43.
16cm
16 cm
:J.....
lo
3
I0 cm
10cm
A flowchart proof of Theorem 4.5.2 is shown below. In Exercises 44-49.
state the reason for each step of the proof. (LESSON 4.5)
Given: parallelogram /IBCD with diagonals intersecting at point X
Prove: AX = CX and DX = BX
Proof:
— -1 ACADEAACB ]
7
46
':
LADB:.£CBD AX: CX
47. ? DX = BX
Look Bo:/o;/o’
/ .- / 50. The drawing below suggests a visual proof of the P_vth;tgorean Theorem.
Use chord—segment products to expl-.1in how the proof works.
Artist’: coiweptiort o!'Pythrtgora5, with
relrlterl images. See Lessoil H. I.
REVERSE CURVES In the Portfolio Activity for I esson 9.2. you constructed
smooth curves by using arcs of different circles with the same tangent. It"
the center of one circle is outside the other circle. the direction of the curve
is reversed. creating an S shape.
1. Using a compass and straightedge or womum; on me cup-[53 pRoJEc'|'
ge°"‘e‘_'igmp""5 5°m"'a“" draw OP “ml You should now be able to complete Activity 3
radius PR. Construct line t" tangent to Pat of the c|mp;,_~, projcu
R [that is, a line perpendicular to W at R].
2. Extend We past R. choose :3 point on W in
the exterior of GP. and label
it Q. Construct -.1 circle \
eentere_d_-.i_t Q with '
radius QR. oPand CZIQ /
have the same tangent at R.
O
n’
4 \/
3. Trv constructing a “snal<e" of reverse
curves like the one shown at right.
The lines of construction have been
left in the picture to help you.
LESSON 9 5 SEGMENTS or TANGENTS, SEEANTS_ AND cuonos 609
Circles in the
Coordinate Plane
0
9’ I
Objectives { Dir!‘
0 Develop and use the
equation ot a circle. J
o Adjust the equauon , 4
tor a circle to move
the center in a
coordinate plane. /”F
/
/
Wh jg I-_
: - -utor graphics sonwara can /-'/ ,,
create a variety olgeometric objects, - ‘
such as points. lines. and circles. To \\ j
do this, the software has subroutines __...—-
that use algebraic representations of
these obiocts—tIiot is. equations.
Graphing a Circle From an Equation
In your work in algebra, you may have investigated graphs of equations such
as y = 2x — 3 (a line), y = x3 — 3 [a parabola], and y = 5 - 2*" (an experiential
curve]. in this lesson. you will investigate equations in which both xand y are
squared.
E x A M P I. E oGiven: .\-’+fi=25
Sketch and describe the graph by finding ordered pairs that satisf)' the equation.
I Use a graphics calculator to verify your sketch.
0 SOLUTIDN
/ .- x / When sketching the graph of a new type of equation, it is Qtten helptul to
locate the intercepts. To find the x—intercept(s), find the va|ue(s) ot".\' when
y = 0. (When a graph crosses the .\‘-:.t\:is. y = 0.)
x’+o’=25
.\:3=25
x=:i:5
Thus. the graph has two .\'—intercepts. [5, 0) and [-5, 0).
6 1 0 CHAPTER 9
To find the y—intereept[s). find the value[s] ofy when x = 0.
01+y3=25
).3=25 .
yn 1-5 I
Thus. the graph has two ' ‘?
y-intercepts. (O. 5] and [0, -5). ,
Now set x to some other value.
such as 3.
33 +_)'2 - 25 J
y1 = 16 §
y = :4
Thus, there are are two points with an x-value of 3: (3, 4) and (3, -4].
Similarly, by chtmsittg other
convenient values for x, a table
like the one below is obtained.
0
y Points on graph
=4 (3, 4). 13. -4)
-3 =4 1-3. 4). 1-3, -4)
4 =3 (4. 3). 14. -3)
-4 :3 1-4. 3). l—4. -3)
Add these new points to the graph.
The graph ofa circle with a radius of5 and its center at the origin. (0. 0).
begins to appear. Sketch the I.'.lIl'\-‘E.
CRITICAL THINKING How does the graph change if 25 in the equation is changed to -19? to 81? to 5)?
You can also graph the cun-‘e on a graphics fir
_ Lu} TEc“N°l°5V calculator or a computer with graphing mu no.2 n..3:"*
‘.'::°_l‘_ GMPWCS soltware. You can use the trace function of the
_ CALCULATOR . . .
':_‘;‘;.. calculator or software to hnd the coordinates -V3=
_..ss . . . . . '-V-a=
u-v oi llldlvldlldl points on the graph. $5:
\ Q-
Graphing technologv norm-allv requires an W"
equation to be in the form y = _ .‘r'ou
will need to solve the circle equation for y.
For exantplez ffi
/.r I x3+y3=.2S
yl = 25 — X’
y = :t: 25 — x3
Thus, you will need to graph two separate cu rves:
Using Graphing Technology
y=\/25—x3 y=—\/25—.\'3
LESSON 9.6 CIRCLES nuns COORDINATE PLANE 61 1
‘of’
G I I
coonommz ceommv
cmacxpomr ./
Deriving the Equation of a Circle
In a circle, all of the points area y
certain distance. 1', from a fixed point.
In the simplest case. that fixed point
is the origin, as shown.
lx. V‘)
I IVI
For any point (x, y) on the circle that
is not on the x— or y—axis. you can
draw a right triangle whose legs
have lengths of |x| and |y|. The
length of the hypotenuse is the
distance. r, from the point to the
origin. For any such point:
x3 + y! = r3 Equation I
By substituting 0 for x or y in the
equation. you can that it is also
true for any point (X, y) on the circle
that is on the x— or y—axis.
lfa point (_x.. y. is not on the circle. then its distance from the orgin is some
value not equal to r, and the equation will not be true for it. That is, for any
point not on the circle:
x.’+J-':’== F’
Fxplain why this is true.
Notice that eqttation l satisfies the lollm-.'iItg two conditions:
-lt is true oliall points (x, y) that are on the circle.
-lt is not true ofany point (x.. )5] that is not on the circle.
Thus, equation I is the equation ofa circle.
CRITICAL THINKING
61 2 CHAPTER 9
Moving the Center of the Circle
To find the smndrtrrl form ofthe V
eqmuimt ol" a circle centered at a
point Ur. Is] that is not at the origin.
study the diagram at right. For such
a circle:
(x- II)? + [_y - k): - 1'1 Equation? A
It should be clear that the equation
is not true for a point that does not
lie on the circle, so equation 2 is | |
the general equation of the circle. a
I low can you show that the relationships shown in the diagram are the same
For points U1, 3:) in Quadrants II. III. and IV?
E x A M P I. E amen: tx—7)1+(y+3)Z=36
Find the center of the circle and its radius.
0 SOLUTION
Comparing the given equation with the standard form of the equation of
the circle. ,V'QnI find the following correspondences:
The standard form The given
of the equation equation
[x — h)’ l x — 7)‘
[y—k)’ ly+3l‘orly—l—3ll'
r‘ 36
From this vou can conclude that
II = I". k=—3..tnd r= 6.
That is. the center 0|" the circle is [7, -3). and the radius is 6 units.
mv ‘nus For each equation below, tind the radius and the center of the circle
represented. Graph the equation and compare the graph with your values
for the radius and the center of the circle.
a.(x+3»)*+(y—3t*=49 b.(x—3J’+(y+3)*=49
c.(x—4)3+ty—sF=30 d.(x+2]3+(y—5]2=:'n(J
Exercises
. Co/mum//‘mtg
1. Explain how to Find the x- and y-intercepts of A2 + y: = 4.
2. Explain how to Find the Jt- and y~intercepts of (Jt'— 2)‘, + [y+ 2]! = -1.
3. Is it possible for a circle to have no x— or y—intercepts? What would the
graph look like?
4. TECHNOLOGY Most graphics calculators will graph only
equations of the form y = . How would
you solve the standard equation of
a circle for yi‘ ‘
5. Use the distance formula .35 vi
(Lesson 5.6] to write an it _
expression for the distance _ ii’!
\
_ _ _ n €3-
trom point (it, It) to point n909§§O%
(_x, y). 1 low does this 0
expression relate to the
standard equation ofa circle?
LES-‘-or 9.6 ctnctesmme co-oaomnre PLANE 613
0 Guided 3:?///3 P/dtt/66
For Exercises 6-8, refer to the equation x’ + y’ = 100 (EXAMPLE 1)
6. Find the x- Ltllti y-itttercepts.
7. Contplete the table below.
2: y Points on graph
0 2 2
2 2
6 . 2
-5
3
-3
8. Plot the points from the table in a coordinate plane and sketch the circle.
For Exercises 9-11, refer to the equation lx — 4)” + ty — 3l2 = 25.
(EXAMPLE 2)
9. Find the x— and y—intcrccpt>.
10. ("tmtplete the table helow.
x y Points on graph
2 2
11- Plot the points from the table in a coordinate plane and sketch the circle.
0 Pldft/'66 d/1d >4,0,0/I’!
Find the x- and rintercepts for the graph of each circle.
nhumotaomact 12-x,+y..=64
Homework ’
Help Online 13. .\* + y’ = 50
E:‘I:;1'_;I:.iII‘Vl.C0fll 1‘. X3 + (y _ 4]! _ 25
N61 Homework Help _ _ 1
lorExerciseal2-32 15- (v\ ' 2), + Y ' 9
. 1e.(x—6)“-’+[;»—s)*= I00
6 1 4 CHAPTER 9
‘\
‘\
Write an equation for the circle with the given center and radius.
17. center: (0, 0]; radius = 6
19. center: (0. 0]; radius = \/I-5
21. center: (0, 6]; radius = 5
23. center: (I. -3’); radius = IO
18. center: (0, 0]; radius = 2.5
20. center: (2. 3]; radius = 4
22. center: (-1. -5); radius = 7
24. center: (4. -3); radius = -/7
Find the center and radius of each circle.
26. 3.2 + y: = 36
28. {.\‘—6)3+y3 = 9
30. (x+513+ (y— 213 = I6
32. (x+ n-’+ (y+ 3}” =19
25. .r1+y3= I00
27. r"+y3= 10]
29. .v'+(y—3:)1=4
31.y'+[x+3)“ =49
Write an equation for each circle.
33. V
(0. 4)
35. V
Draw a circle on graph paper with the given intercepts and find its
equation. Some exercises may have more than one possible answer.
x-interceptls) y-interceptlsl
35- 3. -3 3. -3
37. 2, 6 none
38- 0 0. 8
39- none 5
40- none none
LESSON 9.6 cmctes INYHE COORDINATE PLANE 61 5
CHALLENGE
APPLICATION
APPLICATION
6 1 6 CHAPTER 9
Write an equation for the circle with the given characteristics. It may be
helpful to sketch a graph.
41. center: [2, 3]; tangent to the x—axis
42. center: (2, 3): tangent to the _)'-a\:is
43. center: (0, I]; contains the point [4, 4)
4:4. center: (2. 3»); contains the point [8, 5)
45. center: (2, 3): contains the point [8, ll)
46. has ii I . 3] and (5. 3] as endpoints ofa diameter
TECHNOLOGY Use geometry graphics software or graph paper for
Exercises 47-53.
47. Sketch the graph of {x— 3]’ + (y — S)” = 4. Rellect the graph across the
x-tutis, and sketch the image. Write an equation for the image.
48. Sketch the graph of [x— 4]! + (y— 2)’ = I. Reflect the graph across the
y-axis. and sketch the image. Write an equation for the image.
49. Sketch the graph of [x— 2]! + f = 9. Translate the graph 6 units to the
right. and sketch the image. Write an equation for the image.
60. Sketch the graph of [x— 6]: + (y— 4): = 9. Translate the graph 2 units to
the right and I unit down. and sketch the image. Write an equation for the
image.
51. Sketch the graph of [x— SF + (y— 4‘; = 9. Rotate the graph l80° about
the origin. and sketch the image. Write an equation for the image.
52. Find the equation ol'the line tangent to the circle x3 + )3 = I00 at the
point [-6. 3}.
53. Draw a triangle with vertices at (O. 0}. (0. 6]. and [8, 0). Find the equation
of the circle that circumscribes the triangle.
54. COMPUTER GRAPHICS A computer screen is a coordinate plane in which
each pixel is one unit. A typical computer screen measures 640 pixels
horizontally and -180 pixels vertically. The origin of the plane is the upper
left corner of the screen. so all ;-coordinates are negative.
A computer programmer wants to create a circle that is as large as possible
for a typical screen. What is the equation of the circle? ( More than one
answer is powilale. depending on your choice of the center.)
Look Back
55. Suppose that a dart is tossed at random onto the graph of xi + y3 = 100.
What is the probability that it will land within the graph ol'the circle
.\.-’ + yl = 25? (LESSON 5.7)
56. ASTRONOMY You can view an eclipse by
using a pinhole camera. If the image of
the Sun measures x mm in diameter
when the distance from the image to
the pinhole is 50 cm. how large will
the image be when the distance is
I00 cm? 25 cm? -15 cm?
(LESSON 8. 1)
A P P l I c A ‘I’ l 0 N STRUCTURAL DESIGN A manufacturer is designing a wheelchair to
use in wheelchair basketball.The wheel diameter is 24.5 in.
(LESSONS 5.3 AND 9.3)
57. If the wheels rotttte through 45°, how far will the wheelchair travel?
58. A b:ts|<etb:tll court is 94 ft long. How mrmy rotations ofthe wheels will
it take to get from one end ol‘ the court to the other?
‘J 1 y
- ‘J
1 .h— -my - ' I ‘[4
M — _ \_ 5-J
4' l - wk
_ ‘ . .
‘I-=2.‘ ’ _|-- r’ V‘
. oi‘ . \ .-
.- ' "=1-
_ I
“ \
\
l‘|.’h¢'elchm'r lmskerlmll is a highly mmp¢'tirivt-‘ organized sport. I he plrt;»'er5'
chair‘: are often ¢'u5rorn-made.
59. Find DF. (LESSON 9.5) 50. Find DF. (LESSON 9.5)
D
. G
C
F
Look Bet,/and
/ . r / ln Exercises 61-63, you will prove that an angle inscribed in a semicircle
measures 90 . Refer to the diagram below.
61. Use the equation for a circle with radius r
centered at (O. O] to explain why the coordinates
ofa point on the circle are (p. ‘fr! — [:3].
52. Find the slopes of the segments that lorm the
inscribed angle in the diagratn.
63. Prove that the inscribed angle I]lC:.lSll res 90°.
(Hint: ll" two lines are perpendicular. the
product of their slopes is ? .1
LESSON 9.6 CIRCLES mme COORDINATE PLANE 61 7
The theorems you studied in this chapter will help
you construct the figures in this project. You can use
a compass and straightedge or geometry graphics
software.
Activity 1‘
Make your own circle—llower designs. Begin by drawing
a simple circle flower, as in the Portfolio Activity on
page 572. Then extend your flower as shown at lefi by
adding another level ofcircles. Write a paragraph to
describe how you created the new level.
Make your figure more elaborate by adding chords and
perhaps additional circles and arcs.
Activity
An egg shape can be constructed by connecting an art
with a relatively small radius (at one end of the egg)
and an arc with a relatively large radius [at the other
end] with a smooth curve or curves.
Geometric egg shapes can be classified according to the
number of different radius measures involved. The egg
shown at left is a three—radius egg. '1 hat is, it uses three
different radii——one for each are at the ends of the egg
and one for the connecting curves. See if yott can
construct it. tllint: identify the pie—sh-aped sectors that
fit together as in the illustration on page 579.)
618
fhe egg below is a lbur-radius egg. See if you The egg below is J five—r-udius egg. See if you can
can construct it. It may help to work from an construct it. The principle of the circle flower was
enlarged photocopv of the illustration. used to construct the interior of the egg.
. . W
Activity 31
There are :1 number of reverse curves in the drawings below [see page 609).
How many can you identily? l'ry constructing
figures of your own that use reverse curves.
_—_ C
\ _
. _.
I
\
\ ,J/
\ "I >\‘%;_-‘-
CHAPTER 9 PROJECT 61 9
Chapter Review and Assessment
VOCABULARY
arc . . . . . . . . . . . . . . . . . . . . . .566 diameter . . . . . . . . . . . . . . . . 564 radius . . . . . . . . . . . . . . . . .. 564
arc length . . . . . . . . . . . . . . . .568 external secant segment . . .600 secant ................. . .513
are measure .. . . . ....... . .567 inscribed angle . . . . . . . . . . .580 secant segment . . . . .... . . 600
center . . . . . . . . . . . . . . . . . . .564 intercepted arc . . . . . . . . . . .566 semlclrcle . . . . . . . . . . . . . . . .565
central angle ........... . .566 major arc ............. . . 566 tangent ................ . .513
chord . . . . . . . . . . . . . . . . . . . .564 minor arc . . . . . . . . . . . . . . . .565 tangent segment . . . . . . . . . .600
circle . . . . . . . . . . . . . . . . . . . .564 point of tangency . . . . . . . . . 513
POSTULATES AND TIEOREMS
Lesson Number Postulate or Theorem
9.1 9.1.5 Chords and Arcs In a circle, or in congruent circles, the arcs ot congruent chords are
Theorem congruent.
9.1.6 Converse of the In a circle, or in congruent circles, the chords of congruent arcs are
Chords and Arcs congruent.
Theorem
9 2 9.2.2 Tangent Theorem If a line is tangent to a circle, then the line is perpendicular to a
radius of the circle drawn to the point of tangency.
9.2.3 Radius and Chord A radius that is perpendicular to a chord of a circle bisects the chord
Theorem
9.2.4 Converse of the If a line is perpendicular to a radius of a circle at its endpoint on the
Tangent Theorem circle, then the line ls tangent to the circle.
9.2.5 Theorem The perpendicular bisector of a chord passes through the center of
the circle.
9.3 9.3.1 lnscribed Angle The measure of an angle inscribed in a circle is equal to one-half the
Theorem measure of the intercepted arc.
9.3.2 Right Angle Corollary If an inscribed angle intercepts a semicircle. then the angle is a right
angle.
9.3.3 Arc-Intercept If two inscribed angles intercept the same are, then they have the
Corollary same measure.
9.4 9.4.1 Theorem If a tangent and a secant (or a chord) intersect on a circle at the
point of tangency, then the measure of the angle formed is one-half
the measure of its intercepted arc.
9.4.2 Theorem The measure of an angle formed by two secants or chords that
Intersect In the Interior of a circle ls one—ha|l the sum of the
measures of the arcs intercepted by the angle and its vertical angle.
9.4.3 Theorem The measure of an angle formed by two secants that Intersect in
the exterior of a circle is one—hall the difference of the measures of
the intercepted arcs.
620 CHAPTER 9
Lesson Number Postulate or Theorem
9.4.4 Theorem The measure of a secant-tangent angle with its vertex outside
the circle is one-half the difference of the measures of the
intercepted arcs.
9.4.5 Theorem The measure of a tangent-tangent angle with its vertex outside
the circle is one-half the difference of the measures of the
intercepted arcs. or the measure of the major arc minus 180*.
9.5 9.5.1 Theorem If two segments are tangent to a circle from the same external
point, then the segments are of equal length.
9.5.2 Theorem If two secants intersect outside a circle, then the product of the
lengths of one secant segment and its external segment equals
the product of the lengths ofthe other secant segment and its
external segment. (Whole x Outside — Whole x Outsidel
9.5.3 Theorem If a secant and a tangent Intersect outside a clrcle, then the
product of the lengths of the secant segment and its external
segment equals the length of the tangent segment squared.
(Whole x Outside = Tangent Squaredl
9.5.4 Theorem If two chords Intersect Inside a circle, then the product of the
lengths of the segments of one chord equals the product of the
lengths of the segments of the other chord.
Key Skills 8: Exercises
LESSON 9.1
Key Skills Exercises
Identify pans of a circle. Refer to GP below.
in 0M.:>'and (.—Darc A A 3 4° 0"“ 3
chords. CD is also a diameter. V
WT; and I-1T)are radii. C D A
Central allglc 4Ct'l/IE,“ V W
intercepts minor arc CE. 0
C
Find central angle measures. 1. Name a chord. at radius. a central angle. «ind .1
ln find n.h£(‘)'y\[p. lTldj()T EITC.
90:’: + 600+ 900+ n,|A(-DIN-P: 2. Find ITIAAPB.
mzotxlp = l 20° 3. Find m’lE.
4. Find the length of SEE. Round your answer to
the nearest centimeter.
Find arc measures and lengths.
in ON,lind n1@-and the length ol OP.
m@= mzowp = 120°
length of (fi= x 2‘.lti_2i cm) 2 -M cm
CHAPTER 9 REVIEW 62']
LESSON 9.2
Key Skills
Use properties of secants and tangents to
solve problems.
In the figure below, is tangent to (DC at F.
BF= I0, CG= 5. and FF= I2. Find AD-and FG.
By the Wthagorean Theorem:
(CG): + (AC)! = (.-'tG)3
31 + (.403 = 53 3
AC = 4
By the Ch(flS and Ari
Theorem, BGbisects AD.
so AD= 2° AC=8.
BECall5€;—i? E-angent E F
[0 OG. Gf'_l_L'f-'.
(G:-‘)3 + (L-'1-‘)1 = (L'G)3
121 + 53 = (EGF
EG = I3
LESSON 9.3
Key Skills
Find the measure of an inscribed angle and its
intercepted arc.
I-‘ind unit?)-.1nd m,£C. 3
Z‘-
mAD = 2 X m/_’B = IOU" q
A
/5..
/_’Band AC both intercept A
so m£C= mzB = 50°.
LESSON 9.4
Key Skills
Use the angles formed by secants and
tangents to solve problems.
In OX. m./_’ YUZ = 66".
in/_’ VZU = 35". and
IIIW = 80‘? Find mfg, V 2'
lllfi mzYT7.', and
um VYW. U
M!
622 CHAPTER 9
Exercises
ln CM below. is tangent to GM at N,
NP = 24, M0 = 5, and NL = 31.2.
5. |'ind the radius of GM.
6. Find NIL.
'N L
In OP, PS=7, ST=10, PT=12, OX=6,and
RX = 6. Classify each statement as true or
false and explain your reasoning.
7. 173 L fi
8. fiis tangent
to OP;u 5. p.
Exercises
In on below, mfi = 40° and mzt-"HG = 25°.
Find the following:
9. m.£F E
1o_ 11173,-(T; H A G
12. mzr ’
Exercises
In (36 below, is tangent to O6 at H,
77.} || NP, mHP = 136‘; and mKN = 42°. Find
the following:
13. IHAR.-UN
14. mAKH]
6‘.
15. mRH
f-\
16. mNP
LESSON 9.4
Key Skills, continued
mi’? = 2 x rn4l"UZ = 2 x 66° = 132°
m6? = 2 x mz vzu = 2 x 55° = 70"
.v-A f\
mg)-'T7= EZLV = E? = 51°
im:‘l/YW = %x ml-’?= % x 80° = 40°
LES8ON 9.5
Key Skills
Use segments formed by tangents, secants,
and chords to solve problems.
In 0/l, BI-'= 24, CF: 52.and DI": 48. Find Lil-'.
C
1!’ ‘’
By Theorem 9.5.4:
BFX DI-'= CFX EF
24x4s=3-2x£F 8
EF = 3-6
s
LE58ON 9.8
Key Skills
Sketch a circle from its equation.
Sketch the circle [x+ 3]: + (y— 4}. = I6
center: [-3, 4]
radius = -l
-3
Write the equation of a given circle.
Write the equation of a circle with center (5. U)
and radius 6.
(x— hF+ (y—kF= r? h: 5, }:=0, r=6
(x- 5): + )3 = 36
Exercises
G)P has a diameter of 75,
SO and ST are tangent to
GP at O and T, and R3 = 60.
Find the following:
17. SQ
18. ST
In OX. SY = 12. S2: 18.
SV=4, VW=8, WZ=6,
and WT = 5. Find the
following:
1 9. 5 L:
20. WT
Exercises
Sketch the following circles:
21. r’ + y’ = 49
22. (x— I)3 + (y+ 2)! = 25
Write the equation of the circle with the given
center and radius.
23. center: (0. 0); radius = I
24. center: (6, -2]: radius = 8
CHAPTER 9 REVIEW 623
Applications
25. SURVEYING A simple \--'a}-' to get a rough estimate of property boundaries is to use
a measuring wheel. Attach an 8—in. diameter wheel to a long handle. put a marker
on the edge of the wheel, and count the number of rotations the wheel makes as
you walk along the property line, rolling the wheel. llthe wheel makes 42.5
rotations, how long is the property line?
26. COMMUNICATIONS A radio station wishes to locate
its broadcasting tower an equal distance from
three small towns. I‘race the figure shown and Keystone
locate the center of the circle that passes through °
the three points in order to find the location of
the tower. 5,,,a",,me O
oopal City
27. NAVIGATION A lcayaker is rowing toward .1 lighthouse. ll‘ the light is 85 ft above sea
level, how far away is the kn}-alter when he first sees the light? Assume that the
water is calm and visibility is good. [I mi = 5280 ft. radius of Earth = 4000 mi)
28. AGRICULTURE A Iieltl is irrigated by a pipe that extends from the center of the field
to its outer edge and sweeps around in an arc. The corner of the field is blocked by
the farmer’s house and yard. If the area of the square field is I mi‘. what is the area
of the irrigated sector? To find the area of the
sector, use the following formula:
area of sector = ,‘—6C-0; x area of circle,
where C is the degree measure of the arc that
bounds the sector
What percent of the entire
field is the irrigated sector?
4
624 CHAPTER 9
Chapter Test
For Exercises 1-4, refer to OC.
1. Name a chord. a
radius. a central
angle. and a major
arc.
2. Find m.£QCR
. f‘.
3. Find mR5
_ r\
4. Find the length 0| RS . Round your answer to
the nearest centimeter.
(—>
F6 is tangent to OE below at F. _
5. ll‘ EF= 6 and
EG= I0. find FG.
6. If K] = 6, find H].
llOCitrigl1t.
CE .1. AD at B.
7. E5;
8. If CF= 6 and C8 = 4,
what is AB?
9. ll. CB= 7 and AD= 48,
what is the radius?
15
In em, mKL = 30°, K
mzMJN= 25°, and E ‘-
is a diameter. Find the
following: J ‘V
/'\
10. mAKlL 11. mllx’
/\ /\
12. mLN 13. mj.'\'
14. DESIGN A jeweler is making at circular pin
with the design shown below. She wants
the arc intercepted by
A C and A D to measure
I20”. If C is the center of
the circle. what should D
the measure of each
angle be?
Use the drawing below for Exercises 15-18.
.33 is tangent to 00 at A, mzADF = 52°,
m.£BFD= 36°, and mil} = 130°. Find each
rneasufe.
/‘s /‘s
15. mAF 16. mBl')
17. inA.»‘lEl-‘ 18. 11148/lG
Find x In each circle below.
19. 20.
4 .
5 5:
1 ) 1 D E
21. ("E and CF are tangent
to OH. GH has a radius
0|‘ 9 centimeters. and C
CE= I2 centimeters.
Find HC. F
Sketch each circle.
22. 3:‘ +y- = 36
23. J:' +y’= 64
24. {x+ 2)-'+ (y— .‘»}-= 9
Write the equation of the circle with the given
center and radius.
25. center: (0. O); radius = 2
26. center: (I, -5]: radius = 4
CHAPTER 9-TEST 625
-- E-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Question» I-6. write the
letter that indicates the best answer.
1. Find the sum 0|" the surface areas of figure A
and figure B. (LESSON 6.1)
Assume that there are no hidden cubes.
a. 38 units’
b. 78 units:
c. 76 unilsz
d. 86 units"
2. What is the ratio of the area ofcircle A to the
-.1 red of circle B? (LESSON 5.3)
so
8.
.,.
5
C.
125
"- ifi
626 CHAPTER 9
. r'il‘-’-'.
D intemet connect ..or‘n
Standardized
Test Prep Online
Go To: 9o.hrw.com
Keyword: MM1 Test Prep
4
3. Refer to the ligure h-i.‘l0w. What can be
Luncluded about the slopes of lines land in?
(LESSON 3.8)
a. The slope of line lis greater than the slope
of line in.
b. The slope of line Iis less than the slope of
line in.
c. The slope of line lis |S° greater than the
slope of line in.
d. The slope of line I is 1% times the slope of
line in. '-
4. Refer to the di.1gr-ain below. Find the area of
triangle ABC. (LESSON 5.2)
E
C
49370
a. .25 units’
b. 63 units"
c. l|.4 units!
d. 3| .5 units:
5. Choose the most complete and accurate
description of the two polygons below.
(LESSON 4.6)
5.
a. quadrilaterals
b. trapezoids
c. similar trapezoids
d. congruent trapezoids
6. In (30. which angle or
are measures 60°?
(LESSON 9.3)
a. Z:-‘lBD
5.4306 0
/5-.
c. AD
A
«LEE C
7. The oblique pyramid has a rectangular base.
Find its volume. (LESSON 7.3)
B
7.81 ‘ 75
2
8. The ratio of the volumes of two spheres is
27: l . ll‘ the smaller sphere has a radius of
IS in.. what is the radius of the larger sphere?
(LESSONS 7.1 AND 7.9)
For Exercises 9-10, refer to the figure below.
Y
(4, 3}
(O. O}
9. Construct a rotation of the segnteltl. Rotate
the segment |8[]° eou nterelockwise about the
endpoint ('0. 0]. (Lesson: 4.9)
10. Give the coordinates of the endpoints of the
rotated segment from ltem 9. (LESSON 1.7)
11. Write a paragraph proof that :’_\.Pl’W
and APYX in 0!-’beloware congruent.
(LESSONS 4.2 AND 4.3:
12. An equilateral triangle is inscribed in a circle
with a radius of 3 units. If a point is picked at
random anywhere inside the circle. what is the
probability that the point will not be inside the
triangle? (LESSON 5. 7:
FREE—RESPONSE GRID
Items 13-15 may be answered
U
me
by using a free-response grid
such as that commonly used
by standardized-test services.
‘:
J
6968689990
@®@@@@@@®@L”JG
'EJE}@(:‘;@8@@@(s.
moogmgagmmn
13. Find the volume of a cylinder with a radius of
2 and a height ol‘7. Round your answer to the
nearest tenth. (LESSON 7.4)
14. Find the slope of a line that passes through the
points (2. 6) and (9. I2). (LESSON 3.8)
15. Find the area of the parallelogram below.
Round your answer to the nearest hundredth.
(LESSON 5.5)
4
CHAPYER 9 CUMULATIVE ASSESSMENT 627
628
Lessons
10.1 o Tangent Ratios
102 0 Sines and Cosines
10.3 0 Extending the
Trigonometric
Ratios
10.4 o The Law of Sines
10.5 o The law of Cosines
10.6 0 Vectors in
Geometry
10.1 0 Rotations in the
Coordinate Plane
Chapter Project
Plimpton 322
Revisited
Trigonometry
HAVE YOU EVER WONDERED HOW HIGHWAY
engineers are able to make sure that a section of
a freeway or overpass will correctly match up
with a section that is under construction a con-
siderable distance away? Accurate measure-
ments and calculations are necessary to ensure
success. In this kind of work, trigonometry is an
indispensable tool.
Trigonometry, like much of geometry, depends on
triangles. The simple study of the ratios of the
sides of right triangles quickly leads to more
sophisticated calculation techniques that are
widely used in surveying, navigation, and the
sciences.
W
‘\"‘ ‘i-N A \
on
._—#.w—
About the Chapter Project
Plimpton 322. the Babylonian clay tablet that
you studied in Lesson 5.4. contains some very
sophisticated trigonometry.
In the Chapter Project, Plimpron 3.2.? Revisited.
you will study the arrangement of the numbers
in the table and the meaning ufthe values in the
remaining column.
After completing the Chapter Project, you will be
able to do the following:
o Read and write numbers in r:mu'r]orm, at
svstem used in ancient Babylon.
0 Use the Bulwlonian number systent to analyze
it cuneiform tablet.
.-1'3... - _ , ‘
\'I 'F "
§t""' ' 3 -
‘ I
. r- ‘ \ .
-‘ah! .
r . I;
t I at’, \
t;_’ It‘
\ 1'.‘
' l
About the Portfolio Activities
l'h roughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
("lmpter Prqiect is the Plimpton 322 tulrlet.
0 ln the Portfolio Activity on page 638, you will
examine the reason for the order of the vnltres
in the table.
0 In the Portfolio Activity on page 646. you will
discover a trigonometric identity that you will
use to in emmine the tablet.
629
Objectives
0 Develop the tangent
ratio by using right
triangles.
0 Use a chart or graph to
find the tangent of an
angle or the angle tor
a given tangent.
0 Solve problems by
using tangent ratios.
Tangent Ratios
Trigonometry is an
essential tool at - n
One Iamous survey was
the Great Trigonomelric
Survey at India. which
began in 1802
Mount Everest is nrnned jbr Sir Gt'or‘ge El't'fL':Ti. who was the 5rrpc'rintc'trrit'irt‘ oftlre
Great I'rigmtorm'trir Survey oflmiia jrom 1823 to 1843. I he mounmin's heigln,
rtlront 5.5 miles. was conrprueri by using rrigorronretry.
ruler,
protractor, and
calculator
OR
geometry
graphics
software
CHECKPOINT M
630 CHAPTER 10
Tangent Ratios
In the Au:tivities that lbllow, you will examine one ofthe three important
ratios of trigonometry, the lrmgrmt ratio.
I
A Familiar Ratio
1. Draw an angle between 50‘-and 5U"5uch
that one side of the angle is horizontal. Le
. Hypotenuse 9.
Label the vertex A. Draw a vertical opposite
segment to create a right triangle. A
2. Measure the leg of the triangle opposite A. A Le
. _ _ 9
3. Measure the leg oi the triangle ad;-a-:ent to A. adjacent
ZA
4. Divide the length of the opposite leg by
the length ol' the adjacent leg.
5. Repeat Steps I-4. using the same angle but different side lengths.
What do vou notice?
CRITICAL THINKING
It is common in
trigonometry to use the
Greek letter 0 (them) to
represent the measure
of an angle.
Recall that the slope of-a line is its rise divided bv its run. How is the ratio vou
calculated in Acti\-'it_v I related to the concept of slope?
5‘
Examine the triangles at right. LA N
is congruent to LM, and LCand /A
LO are right angles. Thus. by AA g
Similarity. AABC ~ AMNO. A C M 0
_1_'£_L‘«2
AC — MO. llns leads to the lollowing
By the Polygon Similarity Postulate.
definition:
Tangent Ratio
For a given acute angle L A with a measure of
6°. the tangent of L 1, or tan 0. is the ratio of
the length of the leg opposite LA to the length
of the leg adjacent to LA in any right triangle 0
lnwing A as one vertex. or A Adjacent
= opposite
adjacent’
Opposite
tan 6 10.1.1
Note: ln trigonontetry. the letter of the vertex of an angle is often used to
indicate the measure of the angle. '[ hus, the tangent of LA can also be written
as tan A.
E X A M P L E ohleasurc the legs of the triangle below to Iind tan 0.
0 SOLUTION
The leg opposite the angle is 2.9 centimeters.
and the leg adjacent to the angle is
3.8 centimeters.
TRY THIS
CRITICAL THINKING
l'se the given measurements to find the tangent of the other acute angle in the
triangle from F.\.'ampIe I.
What is the measure of an angle with a tangent of I? Explain your reasoning.
LESSON 10.1 ‘IANGENT RATIOS 631
ruler,
protractor, and
graph paper
OR
geometry
graphics
software
CHECKPOINT J
ruler. protractor. and
your tangent graph
lrom Activity 2
PROBLEM SOLVING
CHECKPOINT V
632 CHAPTER 10
Graphing the Tangent
1. Draw five triangles as shown. with angles ol I5” 50°, 45°. 60°, and 75°.
4a Q
15° 30»
M
2. For each triangle, measure the opposite
and adjacent legs to lind the tangent of
the angle. Copy and complete the table
below.
9 tan 9
1 5 ?
_3’On_ T
-457 7
60 ?
75 if
3. Plot the ordered pairs (0. tan Bllrom the
table above. Connect the points with a
smooth curve.
4. Does vour graph increase or decrease?
Describe its behavior.
' 3
Using the Tangent
In this Activity you will model the calculations of a surveying crew
nteasttring the distance across a canyon. Make a scale drawing, and
let I centimeter = IO meters.
1. Make a diagram showing the sides
ol" a canyon. and draw a line across A
the canyon representing a line of
sight from point X to point Y. e”a,.%’_>
2. Draw a lme through Yperpendicular '\ ,
In--v)
to X Y. Choose a tuoiitt_<>it this line ‘WWW ,’
and label it Z. Draw XZ. jg/g,l'[z //
3. Measure /_Z and 72. (Remember. / /’
X Y and X2 span the canyon. so
thev cannot be measured directly.) x
Use your graph from Activity 2 to
estimate the tangent of /_Z T
4. Substitute the values for tan 7. and Y2 into the equation below.
tan 7 -
Solve to find XY. the distance across the canyon.
5. Compare the value you calculated for .\'Y with the actual distance on
your drawing. How accurate is your answer? What could be some
possible sources of error in your estimate?
Calculating Tangent Ratios
So far. you have measured the sides of triangles to find tangent ratios.
However. since measurements can often be inaccurate. volt will usuallv use a
scientific or graphics calculator. or a table such as the one in the infobank in
the back of this book.
Lise the JA1] function key on your scientific or gr-apltics calculator to find the
tangent ol an angle. (Be sure your calculator is in degree mode.)
E X A M P L E a calculator to find tan 45°.\-’eriF_v y'our.tnswer by usingaright triangle.
. SULUTION
Lising the UN‘ function key on a calculator. tan 45” = I.
ln the triangle at right, ni/_A = 45°. Bv the
Triangle Stim Theorem and the Converse of
the lsosceles Triangle Theorem. the triangle is
isosceles. so the opposite and adjacent legs are
equal. Thus. the ratio of the opposite leg to
the adiacent leg must equal I. A
Sometimes it is n'e‘Cc>>.tl')' to lind the angle measure for
a given tangent ratio. To find the angle with a tangent
of you can draw a right triangle with legs of length 7
rt and b. and measure the angle. b
To find the angle using a calculator. use the 1'11] key. For any positive
number r. the 1flj, key gives the measure oi an angle between (J"and 90“
whose tangent is r. The tan" Function is calletl the inverse tangent function.
Notice that the input and output for the tangent and inverse tangent functions
are reversed.
Function and key Given linputl Want to find (output)
tangent rm I angle measure tangent ratio
inverse tangent TAN-‘ tangent ratio angle measure
E X A M P L E Lise your calculator to find an angle that has a tangent of Round your
answer to the nearest degree. Verify your answer using a right triangle.
0 SOLUTION
l sing a calculator. tan" % = 33.69 2 34°.
The triangle at right has a leg of2 cm and 2 cm
a leg of 3 cm. The measure of the angle is
approxiinately 34°. 3 cm
LESSON 10.1 TANGENT RATIOS 633
Exemses
. can/mm:/mte
1. Where do you think the word rrigom)me'rrycomes from? (Him: What
could be another name for a tri-gon?)
2. Does the tangent ratio increase or decrease as -an angle gets larger? Explain
your answer.
3. What happens to the tangent ratio
as an angle approaches 0“? Use your
calculator the lind the tangent of 0°.
Does your answer make sense?
Why or why not?
4. What happens to the tangent ratio as
an angle approaches 90°? Try to lind
the tangent of 90°bv using your
calculator. What happens? Explain
why in terms oi" right triangles.
5. When measuring the sides of a
triangle to lind the tangent ratio. 1“
does it matter what units you
use? What happens to the units
in your answer? L
‘s
0 6!//d€dr3.('///8 P/‘dtt/6'6
Measure the sides of the triangles below to find tan A. (EXAMPLE 1)
6- 7. ;
A
A
Use the graph you created in Activity 2 to estimate the tangent of each
angle.Then find the tangent by using your calculator. and compare your
answers. (ACTIVITY 2 AND EXAMPLE 2)
8. 20° 9. 40° 10- 70"
11. Lise your calculator to lind an angle that has a tangent of Round to the
nearest degree. Verify your answer by using a right triangle. (EXAMPLE 3;
634 CHAPTER 10
n tnoeruetconnect
Homework
Help Online
Go To: 9oJlrw.com
Keyword:
MG! Homework Hahn
for Exercises I2-17,30-3d
4
CHALLENGE
0 Practice and 74,0,0/y
Find tan A for each triangle below.
12. 13. 14.
18.03
12| : 24.19 32 3 : I10
21 A A 15
A 1.2
15. 16. 17.
5 8
26 24
J5
10 A
A
A
Use a scientific or graphics calculator to find the tangent of each angle
below. Round to the nearest hundredth.
18. 25° 19. 67°
21. 53° 22. 75°
10
2o. l9°
23. 89°
Use a scientific or graphics calculator to find the inverse tangent of
each ratio below. Round to the nearest degree.
24. 1 25. 3 26. 3
8 :-
27. 9.5 23. I 29. 0
For Exercises 30-34. use the definition of tangent ratio to write an
equation involving x. Find the tangent of the given angle by using a
calculator, and solve the equation to find the unknown side of the
triangle. Round your answer to the nearest hundredth.
30. 3 1.
37° .
32. 33.
12
34. Use the tangent ratio and the
Py'Ih'¢'lg0rc‘al1 Theorem to find
x and yin the triangle at right. Y
Round to the nearest tenth.
LESSON 10.1 TANGENT RATIOS 635
A P P L I c A ‘I’ I 0 N S 35. SURVEYING Use the diagram at right
to determine W173, the distance across. 3
the lake.
A 530 m C
36. ENGINEERING l'he steepness.
or grade. 0|‘ a high-wag.' or
railroad is expressed as a
percent. In the photo of the 1 . - .~'
cog railway at Pike's Peak. in F - -~ « l’ "
Colorado, the grade is I8 ‘ i‘. ‘
percent. I'hus, for every I00 ft _- - _ " _ . ,. ._
of horizontal run. the train A _ R ~:‘;.-§f“§_:.i
rises I8 ft. Find theangle of , . _ ___ .« '3 .-. "‘- UR" “
inclination of the railway. 2 _ - ‘_ ' - _“ __
37. ENGINEERING The maximum grade of the railway at l’il<e's Peak is 25
5 5 percent. Find the angle of inclination ol‘ the railway at this point.
’ S 33. INDIRECT MEASUREMENT Use the figure at left to estimate the height of the
Ilagpole. Round to the nearest meter.
42+ _ _ _
«' 39. SURVEYING In the photo below ol Glen Can_von_. Utah. point P is on the
2° '“ north rim. point Q is on the south rim. PR = 300 It, PQ J. PR, and
m4’ R = 75°. Find PQ. the width of the canyon.
‘ _‘
|f"\~_
. 1 I‘ \ Q.
_ i._-_ __ \ . ‘ j
V? 3“ ,1 ‘r . __.‘ _.
. ‘S ,‘ ‘g " ‘ i
x ‘V: ._fi _. V ‘ Kt . ‘
I-'\""\‘ .- _,_ Q
'~ 5 -t
I "_:%'-“‘\(
-IV I h’.
0 .1
»‘.~
4 ' ‘ ‘C
'3.
— /-4
636 CHAPTER 10
1.00.? Back
Find the volume and surface area of each solid.
40. right prism 41. cvlinder 42. cone 43. sphere
(LESSAON 7.2) (LESSON 7.4) (LESSON 7.5) {LESSON 7.5)
I :
h=1d.2'« ,_' ,r=25
‘D h = 14 E _
d 10 . -'7
6 _ r= 7
Use G-P, with MNJ_PR for Exercises 44-46. (LESSONS 9.4 AND 9.5)
44. = ?
45. PR=8, PQ= 3
MQ= 2 Q.~.'= ? 43
46.PR=I2.PQ=<l M I N
MQ = ? QN = ? ”’
Look Beyond
,5 ' _ my __~I£{: 53' 7931)}2115.19-T;U:~—3-;_\j;t;,A;,1;i:‘mI'CI°}I
34.233 tuft‘--l ,Il°é<t.1f.,’§a-v~j5;‘3s_1n,_;gl:‘:,_§a,t»,-.—:§f7=‘.4-.'<'
3:», _ _ i\n_1* 1 -is I\ q€3l‘t|-:_..,.\....., -.2: _l'[-1'_'.'.,_'_L"[-r£_‘-lg ~ -a .-...¢{,‘.:°I.v
‘I ' ‘
CULTURAL CONNECTION: AFRICA Trigonometry has been used by many
cultures for over 4000 yaars.Tha following problem is taken from an
ancient Egyptian papyrus:
[fa pyrmnid is 250 cubits high and the side ofits base )5 360 cubitts
long. what is its sc'kc'rI? —Proh|em S6 of the Rhind pztpyrus
A cubit is 1‘. measure of length equal to about 21 inches. and the scked is :1
l‘I‘lE".lSlll'E of stc-‘e|)ness.
47. In the diagram at right. what is
the ratio of the run to the rise of
the pyramid? (Notice this is not
the same as the slope.)
rise = 250 cubits-
. . . . I
48. How IS tl1e ratio ol run to rise
related to the concept of the run = 180 cubits
tangent ratio?
49. The selted is the ratio you computed in Exercise 47. converted into palms
per cubit. Since I cubit = 7 palms, this is found by multiplying the ratio
by 7. Find the scked of the pyramid.
LESSON 10.1 TANGENT RATIOS 637
06‘
‘I.
TRIGONOMETRY IN BABYLONIAN MATHEMATICS
Recall from the Plintpton 322 tablet (see
Lesson 5.4) that two columns represented .1
leg and the hypotenuse of Pythagorean triples. 169 1 19
‘I he arrangement of the numbers may seem
random. but the reason for the arrangement
becomes clear when you consider the angles 5'
formed in the right triangles. '20
1. Complete the table below. What do you notice about the arrangement
of the values of the angles? Why do you think this table might have
been useful?
Column ll Column Ill
Opposite leg Hypotenuse Adjacent leg tan 0 0
119 169 120 ? ?
3367 4825 3456 ? ?
4601 6649 4800 ? ?
12,709 18,541 13,500 ? ?
ll lntemotconnect fig; 65 97 72 ? ?
Purfiuliu 319 481 360 ? ?
Extension
Go To: 9o_h,w_c°m 2291 3541 2700 ? ?
:fg;";'i‘l’m3 799 12419 960 ? P
_ 481 ‘I69 600 ? ?
4961 8161 6480 ? ?
45 75 60 ? 7
1679 2929 2400 7 7
161 289 240 7 7
1771 3229 2700 7 7
56 106 90 7 7
2. The lirsl angle is almost equal to 45". Is it possible to lind a Pythagorean
triple that corresponds to a 45°angle? Why or why not?
WORKING ON THE CHAPTER PROJECT
You should now be able to complete Activitv I of the Chapter Project.
638 CHAPTER 10
Objectives
0 Explore the
relationship between
the measure of an
angle and its sine and
cosine.
o Solve problems by
using sine and casino
ratios
0 Oevelop two
trigonometric identities.
Sines and Cosines
Wh , _ _
Sure and cosine ratios can be used to
solve many - :» olproblams. For example, I
i! you know the length and the approximate
angle of the rope. you can estimate the ,_
height of a parasailor above the wars:
Trigonometric Ratios
in Lesson I0.l, you learned that the tangent ofan angle is the ratio of two
sides of a right triangle containing the given angle. However. there are other
trigonometric ratios that can be formed by using different sides of the Sdl‘l‘le
triangle. l'he three most important ratios are the tangent, the sine. and
the cosine.
Sine and Cosine Ratios
For .1 given angle /_A with 1‘. measure of 0°.
the sine of AA, or sin 0. is the ratio of the Hvpotenuse _
. . _ . Opposite
length ol the leg opposite A to the length ol
the hypotenuse in a right triangle with A as A idlacem
one vertex, or
. os'te
sin (9 - en)‘, I . 10.7.1
hypotenuse
l'he cosine of LA, or cos 0. is the ratio of the length of the leg adjacent
to A to the length of the hypotenuse, or
adjacent
—-j—. 10.2.2
lwpotenuse
cos 6=
LESSON 102 SINESANO COSINES 639
scientific or graphics
calculator and graph
paper
In this sequence of
triangles, the adjacent
legs stay the same.
I/Wmt happens to the "
other sides ?
CHECKPOINT V
89 sure your calculator l -
is in degree mode. |
CRITICAL THINKING
EXAMPLE 0
' P I 0 W
RECREATION
I
Sines and Coslnes
1. hsamlne the triangles In the diagram below. As (-1
inereasts. what happens to the value of sin 6? DOLS it
increase or decrease? What happens as (9 gets close to 0°?
to 90‘? Write a conjecture about the sine of 0°and ol 90°.
HV"' Opp-
H .
Hyp Hyp. 0 VP Opp.
‘ 0 PP-
ge 99- e _1j a Leg_
Adi. Adj. Adi. Adj.
2. Repeat Step I for cos 0.
3. Compare the behavior of the sine and cosine ratios as the measure ol’
an angle increases from 0°to 90°.
4. Copy and complete the table below. [Use the 5*‘ I and C03 I kevs on
vour calculator.) Round your answers to the nearest hundredth.
e l 0” 10° 20 30 no 50° 60‘ 10° 80“ so
sin 0 2 2 2 2 2 2 2 2 2 2
cos 0 ? 7 ? ? ? ? ? ? ? ?
5. Plot the pairs [8 sin (9) lor the angles in the table. Draw a smooth
curve through the points. Repeat for the pairs (6! cos (9). Do your
graphs verify the conclusions you made in Step 3?
Could the sine or cosine of an angle ever be bigger than I? Explain your
answer in terms ol' right triangles.
A paraglider is towed behind a
boat by -l(J()—ft ropes attached
to the boat at a point I5 it above
the water. The spotter in the boat
estimates the angle of the ropes
to be .*5"above the horizontal.
Estimate the paraglitlefs height
above the water.
400 ft
15ft
SOLUTION
Label the hypotenuse and the opposite and adjacent legs for the given angle.
The hypotenuse is -100 it. Since the height is the opposite side. use the
sine ratio.
sin 35° = = Using a scientific catculamr, sin 35° : 0.5736.
_ E
— L
0.5736 — we
x = -'l00(0.5736) :: 229 it
'l‘hus, the height of the paraglider is approximately 229 + I5 = 24-1 ft.
640 CHAPTER 10
E X A M P L E aCi'tarlL‘$, an amateur astroiionier.lias been keeping records ofthe position of
the sunrise each day as viewed from a fixed point, A. I le marks the position
1; - p I c 3 g ,4 of the sunrise on the autumnal equinox and the winter solstice. (On the
ASTRONOMY autuinnal equinox. there are equal hours of daylight and darkness. and on the
winter solstice. there are the fewest hotirs of daylight.) What is the measure of
(A. the angle between the positions ofsunrise on these two days?
0 SOLUTION
C1111.‘-IL-S uses ropes to mark the lines of l _
. . . . . 35 ft Equinox.
sight lrom point A in the direction of the Adjacent C gem 21
A
sunrise on the two days. I Ie uses another
rope to make a line perpendicular to the
equinox line as shown. and measures the
distances from point A to this rope.
D pposite
To find the tingle whose cosine is 0.788.
use the inverse cosine, or 005"] key on
your seientilie or graphics calculator.
cos" 0.788 = 38"
An identity is an equation that is true for all values of the variables in the
equation for which all terms in the equation are defined. For exaiiiple. the
equation [it + b][u — b] = rri — 1:1 is an identity. Iiecaiise it is true for all values
ofu and ii. In Activity 2, you will discover two trigonometric identities.
Tvvo Tr gonometric Identities
' ' I. II} Part I
Sfiieltfiifi OI‘ Graphics 1. Copv and complete the table lielow by using a scientific or graphics
C8 C“ “Or calculator. l P:l\"€ at least three digits after the decimal point for each
valtie.
. L19.
0 sin 0 cos 0 cos 9 tan 9
20" 7 7 7 .7
40° 7 7 .7 .7
60" 7 7 7 7
CHECKPOINT V 2. What do you notice about the values in the tangent coluinn? Write a
trigonometric identity involving the sine, cosine, and tangent ratios.
3. What happens when you simplify the right side of the equation below?
opposite
sin 9 _ hypotenuse
C0? _ adjziceiit
hypotenuse
Does the equation prove your identity from Step 2? Explaiii.
Lt-Zssoiu ioz SINESANO COSINES 641
This tabie will help you I__
discovers Pythagorean /
identity {see page 646}.
CHECKPOINT g/
PROOF
642 CHAPTER 10
Part II
1. Copy and complete the table below by using a scientific or graphics
L'alt.'ulator. Leave at least three digits after the decimal point for each
value.
cos 9 (sin 0]’ + [cos 9)’
8 sin 0
2D ? ? ?
an 7 7 ?
60 ? 7 ?
2. What do you notice about the entries in the last row of the table? Write
a trigonometric identity involving sine and cosine ratios.
3. The following is a partial proof oi‘ the identity lrom Step 2. For each
step in the proot, give a reason.
(%)’+(%)2
+
(sin 9 )1 + (cos 9 J’
C
°..|=t..
let:
A
r’
(I3 + D7 A
6
Compare the numerator and denominator of the fraction in the last step.
I low could you complete the proof of the identity?
b
Summary
As you saw in Activity 1. the sine of
an angle increases from 0 to l as the
measure of the angle increases from
0° to 90". while the cosine of an angle
deueases from I to D as the angle
increases from 0'’ to 90°. The graphs
are shown at right.
In Activity 2. you discoxered and proved the following, two important
trigonometric identities:
Two Trigonometric Identities
9 (sin (9)9 + (cos 61" =
tan 9 = Egg-0;
10.2.3 10.2.4
Mathematical ideas often have intriguing connections like these, which is p-art
of the fun of mathematics. In you r later studies. you will see these identities
often—they seem to pop up everywhere!
Exercises
. Communicate
1. Think of :1 mnemonic [memory aid’) to help you remember the parts ol
the tangent. sine. and cosine ratios.
0 ) msite . o 3 msite ad'acent
tanflzk J; cosgz;
adjacent hypotenuse hypotenuse
2. Describe three ways vou could find
9 in the triangle at right. Do your
answers agree for the three ways? 5 3
H J
4
3. In Activity 2. you found that tan 9 = Lise the behavior of sin Hand
cos 9 to explain the behavior of tan (9 tor values of Bclose to {)‘’and close
to 90°.
4. Which of the following equations are identities? Explain your reasoning
in each case.
a. 2.‘: + 5 = 7
b. 11+ 2n = 311
c. :13 + (13 = F’
d. sin 6: tan 6- cos 6
0 fill/dad 5/?///8 Practice
Determine the height of each triangle Round to the nearest foot.
(EXAMPLE 1)
5. 6. 7.
25 ft 3 ft
” h 32 ft
A h
34° 50
Find 6 in each triangle. Round to the nearest degree. (EXAMPLE 2)
8. 9.
32 ft
37 fl
4 I
72 fl
42ft
LESSON 102 SINESAND cosmes 643
I -- oomecz .73,
VON‘
Homework
Help Online
Go To: go.hrw.cMn
Kcy-void:
MGI Homework Help
for Exercises 30-35
644 CHAPTER 10
Practice 4114’ 34,0;/y
For Exercises 10-17, refer to ACDE.
Find each of the following: C
10. sin C 11. sin D 5 13
12. cos C 13. cos D
14. [an C 15. ton D E 12 D
16. n1ZC 17. 111.40
_ Y
For Exercises 18-23, refer to .&.XYZ.
Find each of the following:
- _ E - _ ii
18. Slni— I7 19. CO5: — I7 17 15
20. sin';=-1% 21. cosi=-F;
— 2 = 12 - ' = A
22. tan; 3 23. tan ; '5 X 8 Z
TECHNOLOGY Use a scientific or graphics calculator to find the following.
Round your answers to the nearest hundredth.
24. sin 35° 25. cos 72° 26. sin 57°
27. cos 52° 28. sin 45° 29. C05 45'’
Round your answers to the nearest degree
30. sin" 0.3 31. sin" 0.875 32. cos" 0.56
33. cos '0.I25 34. sin" 0.5 35. C05" 0.95
Use trigonometric ratios to find the area of each figure.
36. triangle ABC 37. parallelogram KL.-UN
B
5 K L
5 i ;7
40
A D C
ujw +1 N 15 M
TECHNOLOGY Use a scientific or graphics calculator to answer Exercises
38-40.
38. Choose an angle between 0° and 90'’. Find the sine of your angle. then find
the inverse sine of your answer. Repeat for four more angles. Based on
your 0l)servation. complete the lblltwvilig identitv:
5in_'($in 9] = ?
39. Repeat Exercise 38 for the cosine and inverse cosine. ("omplete the
following identity:
cos"[cos 6‘) = ?
40. Repeat Exercise 33 for the tangent and inverse tangent. Complete the
following identity:
l:1n '[l.tn 9] = ?
‘\
-.
\
\
CHALLENGE
APPLICATIONS
The prefix co- in cosine indicates a certain relationship of the cosine to
the sine of an ang|e.The exercises below develop this relationship.
41. In AABC below, fintl sin A and cos 8. Using the right triangle, explain why
these ratios are the same.
42. Complete the following, statements. You may wish to draw right triangles
to help determine your answers.
sin 30° = cos ?
sin ?
sin 65° = cos ?
= cos 40° sin ? = cos 45°
43. What is the relationship between the pairs of angles in Exercises -ll
and -12? Use your answer to complete the following identities:
sin 6 = cos ? cos 6 = sin ?
Use the identities tan 0 = 53;‘; and (sin 0l2+ (cos 0)’ = 1 to simplify
the following expressions:
44. tan 6 - cos 6 45.
.- 2 I _
46. I [Mn 6} 47. (L050): I
48. Use the identity (sin 6 )" + (cos 6 )" = I, together with factoring and
substitution. to prove the l‘bllowing identity:
[sin (9 1" — (cos 6 )' = Ztsin 6)’ — l
49. FORESTRY A spruce tree is /_.§_
approximately the shape of a ~ '- h
cone with a slant height of 20 It. 20 fl ,‘ '
The angle fornied by the tree ."_‘_{
with the ground measures 72“. ,"-:4; '_
Estimate the height of the tree. ‘/'72. . ‘
Round to the nearest foot.
50. RECREATION A water slide is a straight ramp 25 in long that starts from the
top of-.1 tower 2| in high. Find the angle the slide forms with the tower.
51. CONSTRUCTION According to “pl ..
the Aniericans With Disabilities
Act, a ramp can rise no more
than l ft for every l2 ll of A
horizontal distance. W hat is the !
niaximum angle that the ramp
can form with the ground?
LESSON 102 SINESAND cosmes 645
Look Back
For each length given, find the remaining two lengths.
(LESSON 5.5)
52. x = 7 y = ? z = ? 60' Z
53. x = ? y: l I z = ? "'
54.x= 2 y= 2 z= 3 V 3”
55. [1 = l q = ? r = 7.’
56. p= 2 q = 3 r = 2 " P
57. p: ? q= ? r= 16 45' 45“
I’
For each arc length, I‘, and radius, r, given below, find the measure of
the central angle. (LESSON 9.1) :3
53. £:'= l2:r,r=20 59. t:= l0JI.r=lU'(J
oo.t’=5It,r=25
L00}? 3870/14’
The three ratios in a right triangle that we have explored are tangent
sine, and cosine.There are three other ratios to be considered.
cotangent secant cosecant
_ adiacent _ h tenusa _ h otenuae
COT9— sec9— CSC9—
61. How are the ratios above related to the tangent. sine. and Cosine ratios?
I1 tnmaatconnect 62. ln Exercises 4l—43. )"§\u discovered at rekttionship between the sine and
Portfolio cosine in the form of two identities. Is there :1 similar relationship between
Extension tangent and cotangent? between seeant and Losecant? Explore. using right
EEYTQI:-“W-°°“ triangles or your c-alcttlator. and then complete the following identities:
I ‘ :
“'5' "'°"““°5 a. tan 6 = cot ? b. cot (9 = tan ?
. c.sect9=esc ? d.cscl9=see ?
Q$T_Lu0
Q0 PYTHAGOREAN IOENTITIES
The identity {sin 6)’ + (cos 6)’ = l is otten called .1 Pythagorean identity
because it is derived from the Pytltagoream Theorem. l'ltere are two other
Pythagorean identities that can easily be derived lirom this identity.
1. Divide each term in the identity 5l“‘PmV' 45 "“‘Ch «'5 l‘055lbl€- F-3<l“'k’55 V0“"
[sin 6]: + (cos (9)1 = l by {sin (9)3, and identity using one of the ratios in Exercises
simplify as much as possible. Express your 51 3nd 62-
identity using one of the ratios in Exercises
61 and 62. WORKING ON THE CHAPTER PROJECT
2_ Divide each term in the identity You should now be able to complete Activity 2
(sin 9]-' + (cos 9)-' = l by (cos 6):. and of the Chapter Project.
646 CHAPTER 10
Extending the
Trigonometric Ratios
Objectives
0 Use a rotaung ray in
a coordinate plane to
define angles measuring
greater than 90° and
less than 0°.
0 Delme SIIIE, Cosme,
and tangentfor angles
ol any size.
so far, trigonometric ratios have been defined in
terms of acute angles of right triangles. But it is important
to - - - e the trigonometric ratios for other angles. In this
lesson. you will learn how this can be done.
i
.'r:. ‘ .‘
tH'i . '
.3! |_l_:--- . _
.- ‘ y.-"
_r-‘p’.
IO’
/— .
_3
.
The curve sham: on the osrillosrope is a graph
of the souml wave gerrerrrtcd by the synrlresizer.
Strch (I L'llt'|’t' it kmm-‘rt ris rr sine curve.
Extending Angle Measure
lmngine a ray with its endpoint at the origin of a coordinate plane and
extending along the positive x—axis. Then imagine the ray rotating a certain
nu miner of degrees, say 0. counterclockwise about the origin. As the
illustration shows. 6 can be any number of degrees, including numbers greater
than 360”. A figure formed by a rotating ray and a stationarv reference ray.
such as the positive x-axis. is called an angle of rotation.
CRITICAL THINKING
Angles of Rotation
9: ~* 9 45°
405“
How do you think an angle of rotation could have a neg-atix-‘e n1easure?
LESSON 10.3 EXTEND-INGTHETRIGONOMETRIC RATIOS 647
The Unit Circle
To define the trigonontetric ratios for all possible rotation angles you can use
the mu’: cirrle. The unit circle is a circle with its center at the origin and a
radius of l. in the lzmguuge of transforntations, it consists of all the rotation
images of the point Pt I. 0] about the origin.
/
E X A M P L E oFind the coordinates ot‘PIthe image of P11?) _P“ 0}
| point P[ l. 0] rotated l‘S0°'.1l7out the origin. ' “ I '
O SOLUTION
PROBLEM SOLVING Use a graph. Draw :1 perpendicular segment
from P’ to the \'-axis as shown. Ldik-_‘i the
intersection Q. Since ¢’P’OQ is supplenientary to AVOP, its measure is 30°.
Thus. L\.P'OQ is a 30-60-90 triangle with its hypotenuse equal to l.
Q0 = and F!) = 'l he x—c.oordinate of P’ is -‘,5 or as -0.866.
= 0.5. Thus. the coordinates ol‘ P’ a re (-0.866. 0.5).
The y-coordinate ol P’ is %
' /
Redefining the Trigonometric Ratios
- - ED 1. Let 1-’ be the 5U" rotation nnage
scjemjfic 0, graphics ot P[ l. 0) ‘-about the origin. Use
Cfilculamr the rules from the 30-60-90
Right Triangle Theorem to
find the coordinates of H
2. Let P' ’ be the 2l0° rotation
image of P[ l, 0) about the
origin. Find the coordinates
of P".
3. Let Pwis the 330° rotation
image of P[ I, 0) about the
origin. Find the coordinates
of V".
CHECKPOINT ./ 4. 1:. Use the results of Steps I-3 to complete columns .2 and 3 of the table
below.
b- L86 the ._*'''“J and Performance Assessment
columns 4 and 5 o te tl e.
Rotation x-coordinate y-coordinate
angle, 9 of image point of image point cos 9 sin 9
30* I 7 7 7 7
rSe:ExampIe 1-‘; 150' = -0.865 % = 0.5 ? 7
210 I 7 7 7 7
330- | 7 7 7 7
648 CHAPTER 10
CHECKPOINT |/
CRITICAL THINKING
5. \-\- hat relationsliips do you see in the table?
6. Complete the lollowing definition tor the sine and cosine of an angle.
Unit Circle Definition of Sine and Cosine
Let (9 be :1 rotation angle. Their sin 0 is the ? —coordinate of the
image of point P[ l, 0) rotated 9° about the origin. and cos Bis the
? -coordinate.
l\'eg-ative rotations are represented by clockwise rotations ofthe point Pt 1. 0}.
Test the unit circle delinition of sine and cosine as follows:
a. Sketch the image point P’ of P( l, O} as a result ol'a -50° rotation [clockwise]
about the origin.
b. Find the coordinates of the image point P'and use this information to give
the sine and cosine of —.’~0°_
Check your answers by using a scientilic calculator.
E X A M P L E 0A wheel witha l—lt radius isturning slowly at
A P P II: AT l 0 N
ROTARY MOTION
.1 constant velocity of 1° per second and has
a light mounted on its rim. A distant observer '
watching the Wl'll.'L'l from the edge sees the
light moving up and down in a vertical line.
Write an equation for the vertical position, It,
oi" the light starting from the horizontal
position at titne 1' = 0. What will he the
vertical position of the light after l min? after
5 min? alter 24 hr?
,1
~tr
\_lcos t. sin t)
1% \n -
jfiasition
at time t
\
SOLUTION
imagine a coordinate system with the origin at the center ot the wheel as
shown. After tseconds have elapsed, the value of 9 is P. The coordinates of
the light are [cos t. sin 1']. Notice that sin r. the second coordinate. is the
vertical position of the light. Thus, at time t the vertical position. It, of the light
is given by the equation
It = sin 1'.
At t = l min, or 60 sec. It = sin 60° as 0.86? units.
At t = 5 min. or 300 sec. h = sin 500'‘ = -0.86? units.
At 1’ = 24 hr, or 86.400 sec, h = sin 86. 400° = 0 units.
LESSON 10.3 EXTENDINGTHEYRIGONOMETRIC RATIOS 649
scientific or graphics
calculator and graph
paper
CHECKPOINT |/
' Z
Graphing the Trlgonometrlc Ratios
1. Extend the graphs ofeach of the V
trigonometric ratios below For
values of Bfrom 0"to 560'’ by
plotting points at intervals of 30°.
y=sint9
9o°18o-=' 270° 360*"
2. Use your graphs to determine the
intervals in which the sine and cosine
are positive and those in which they are
negative. Complete the table below.
Quadrant of Sign ol Sign of y = cos 0
image point sin 9 cos 9 1
I l0“to 90 1 + 7 9
II t90'=- to 180*} l + 7 SW‘ 130” 270 3é0 ’
m n8o=- to 270°: l — 7 1
IV l270° to 360°l | 7 7
Using a Calculator to Find an Angle
lu Activity I. you saw that sin 30°and sin 150° both equal 0.5. There are, in
fact. inlinitelv many angles for which sin (9 has a given value from 0 to l, but
in working with triangles, you will want to find angles between 0°-and l80°.
The example which follows illustrates how to use your calculator along with a
graph to fintl the desired angles.
E X A M P L E 0 Find two values otflbetween 0°and l80"sueh that sin 9 =0.9397.
PROBLEM SOLVING
SOLUTION
Use the SEQ] [inverse sine) key to find the measure ol'an angle whose sin is
0.9397. The calculator will give you approximately 70°. Note: For a given value
from D to l. the sin ' lttnctit)n of a calculator will always return an angle
measure from 0° to 90'’.
Draw a graph of the sine function.
You can see that there is another
angle that has the same sine value.
To find that angle, subtract the
first angle from 130".
180°-70°: ll0°
Thus. the values are 70"and I l0°.
70"90“1 10' 180"
K 4
\ 1'
70° and 110"‘ have
the same sine value.
TRY THIS
650 CHAPTER 10
Find two values of (9 between 0°-and l80°such that sin (9 '«= 0.5736.
Exercises
APPLICATION
. Communicate
1. Explain how a rotating ray is used to extend the definition of an angle.
2.
How is the unit circle used to extend the trigonometric ratios bevond 90°?
Explain how to use the unit circle definition of sine and cosine to find
each of the following:
3. sin 90°and cos 90°
4. sin l80°and cos l80°
Explain how to use the unit circle definition of sins and cosine to find
the sign of each of the following:
5.
cosine in Quadrant Ill
6. sine in Quadrant ll _ i
7. ENGINEERING The drive mechanism of
the oil pump converts the circular
motion of point X to vertical motion in
a straight line at point Y. Explain how a
trigonometric function can represent the
vertical component of the motion ol‘
point X.
0 qu/dedsk///5 Pratt/ce
8. l-‘ind the coordinates of P’. the
10.
11.
12.
9. use the unit circle to find
the sine and cosine ol' Hlirom
the coordinates of the given point.
(ACTIVITY 1;
image of point P(l. 0] rotated
210° about the origin.
(EXAMPLE 1)
Y
l0.7660. 0.6428)
1
TL.
X
A wheel with a radius ol l unit turns
at a rate of 1° per second. Write an V \1 ' Der
equation for the vertical position of \‘e°°"d
Xi 1, 0]
point X starting, from the horizontal
position shown at r = 0. What is the ; X
vertical position of point X alter
l0 min? 20 min? l hr? l2 hr? v
(EXAMPLE 2)
Use the graph of the cosine ratio to determine the sign of the cosine in
Quadr-ants I through IV of the coordinate plane. (ACTIVITY 2)
Find two values of Qbetween 0°and l80°such that sin 9 2 0.7071.
(EXAIWPLE 3)
LESSON 10.3 EXTENDINGTHETRIGONOMETRIC RATIOS 651
ll .- connect ,?,°.,
IOITI
Homework
Help Online
Go To: uo.hrw.com
KE’)'n\‘DldZ
MGI Homework Help
for Exercises 37-45
652 CHAPTER 10
Practice mm’ 34,0;/y
TECHNOLOGY In Exercises 13-20, use a calculator to find each of the
following. rounded to four decimal places:
13. sin 65°
17. cos 65°
16. sin 295°
20. cos 295°
15. sin 245°
19. cos 245°
14. sin |l5°
18. cos I IS‘’
ln Exercises 21-28, use graph paper and a protractor to sketch a unit
circle and a ray with the given angle H with the positive x-axis. Find
the coordinates of the point on the ray at a distance of 1 from the
origin, rounded to four decimal places. Use these values and the unit
circle definition of sine and cosine to give the sine and cosine of each
angle, rounded to four decimal places.
21. 45° 22. I35” 23. 225° 24. 315°
25. 50° 26. l50° 27. 2l0° 28. 330°
TECHNOLOGY In Exercises 29-36, use a calculator to find the sine and
cosine of each angle. Use these values to give the x- and y-coordinates
of a point at the given angle on the unit circle. Round your answers to
four decimal places.
29. 50° 30. 60°
33. 180° 34. 2l()°
32. t20°
36. 560°
31. 90°
35. 300°
ln Exercises 37-44, give two values of H between O‘’ and 180“ for the
given value of sin H. Express your answers to the nearest degree.
37. 0.707] 38. 0.8660 39. 0.5000 40. 0.9659
41. 0.32] 7' 42. 0.9900 43. 0.9990 44. 0.9999
45. If sin (9 = 0.4 756, what are all the possible values of (9 between 0°-and 560°,
rounded to the nearest degree?
46. If cos 9 - —0.7500. what are all the pryssible values of 9 between 0°:md
360°. rounded to the nearest degree?
47. ASTRONOMY An astronomer observes a
satellite that is moving around a planet
at the rate of I” per hour. Assuniing
that the radius of the satellites orbit is I
unit, v\h.il is the horizontal position of
the satellite after 2 days? after 5 davs?
Y
Satellite
\
/ \
4-? fl; EarthI;‘>
Starting position
(1.0)
View of planet from above
APPLICATIONS
CHALLENGES
£00k Back
Use AABC for Exercises 48-55. (LESSONS 10.1 AND 10.2)
48. sin A = 49. cos B =
50. tan A = 51. cos A =
52. (sin.-n=+;= I 53. ‘ii =;
cos;-1
54. sin A = cos;
Look Beyond
55. cos A = sin 1
ASTRONOMY 'l'he graph shows the positions
of the tour “Galilean” moons 0|’ lupiter as
seen from Earth at midnight on April 1-16.
I993. l'he parallel lines in the center of the
graph represent the visible width of lupiter.
56.
57
58.
Galileo was able to observe lttpiter’s four
largest moons with his small telescope.
When viewed lrom Farth, they appear
to moxe back and forth in an
approximately straight line through the
center of the planet. The names of the
four moons are listed below.
1. lo
ll. Europa
Ill. Ganymede
IV. Callisto
Use the graph to sketch the positions of
the planet lupiter and its four Galilean
moons as thev would appear to a person
with a small telescope or a pair of
binoculars on [at] April 4. [_b) April 8,
and (c] April I2. Use dots for the moons
and a circle for Jupiter.
Use the graph to estimate the orbital
periods of each of the four Galilean
moons of Jupiter.
What kind ol curve do the lines for the
moons‘ orbits appear to be? Explain why
they have this shape. (Note: The orbits of
the tour moons are nearly circul-.1r._)
B
C a
A b C
Cmtjigurrttirm ofsrtrellires I-Ivjbr
April 1-16. 1993 at midnight
(.‘r'eenwirl'| Mean Time (GMT)
DAY WEST
0.0
EAST
1.0 _
2.0
/‘
3.0
[\
to Ill
\
/‘_\
\\
/E
5.0
6.0 j
7.0
5
I
8.0
9.0
Y
\\_
10.0
11.0
12.0
« YA
0C/‘
\
/
13.0
/X\
14.0
.L
15.0 F
ll
94/!‘
16.0 l_é
F
Scrum: TAr.{m--uu-urnl ‘tlnmm tn the liw I9"
653
The Law of Sines
‘I a ‘ -I I.’-E.‘-.h.3" .7‘ _ 1- _ 1 ,. F. .11
~ _ ‘ I _ 54' ~ _ - 7 ' n-..
J - I ‘V "Iii L" .1 '
A-‘ *2‘ -2'-- ’_ —-9 -
. :‘ «’~':’;- '
_ _ _ l -luL'-c...-
' “ ‘ '‘ _;_' 4,-‘__‘ ,. 3
\ . - . _S- ‘ _» -=P".'\ ~ 3 o
1 ""°'~‘( " 2:
- >5? _
' y -w- A ‘fig?’
0 _ _ 2; . .5 _ ' - " .1. » ' '-‘
‘ - - .' - -. ' . -54 ,
biectives .:.._-.p. -6; J J F ’ . . _ _ _.:,_W .
0 Develop the law of ' _ '5“- '5" - V '- '-gIF._5»":- .
sures. , - =5 ,5-' f 3 -’‘‘-‘'~‘5‘ ' '
0 Use the law at sines to ' '9' ' 2,
solve triangles. ' _ R /-
f ‘I
C - — p ‘- -5.
"V ..4-q f ' ' ) "
The triangle formed by the three points ~._ -.,-~ '_ _ . -'7.
an my satallitp photo is not a right trianglp. ‘_ ,.-. _ - ' .-.
however. the diktances between the - :' - “'
can be town! by using trigonometry.
Smcllitt photo ofSmr Frmiciscu Bay area
The Law of Sines
The trigonometric ratios you have studied all relate to right triangles. In the
lollowing Activity. you will r:‘\q.1lore the law olsineb. .1 theorem involving sine
ratios that applies to all triangles.
Law 0 Sines
1. Draw an acute triangle. a right A
geometry graphics triangle. and an obtuse triangle. C 8
software or ruler and l abel the sides and edges as b
protractor, and _ _ __ _ ‘ ‘ .‘ _‘
scientific or graphics Salli)“ ll. i\_lLJ!sll K ‘ht Slkltb dlld 3
calculamr angles ol each triangle. C
2. Copy and complete the table below. using your Ineusurenwnts lrom
Step l.
‘— ——'-B -—'-C-
mAA mAB mAC 0 b c 5"":-‘A Iris ‘ flic‘ '
acute ? ? ? ? ? ? ? ?
right ? ? ? ? ? ? ? ? ?
obtuse ? ? ? ? ? ? ? ? ?
CHECKPOINT g/ 3. Write a conjecture using the data in the last three columns of the table.
654 CHAPTER 10
PROOF
Your conjecture from Activity I can be stated as the following theorem:
The Law of Sines
For any triangle AABC with sides ii. 11. and (2 A
c
sin A = sin B = sin C 5
cl I! C B
(; .9
10.4.1
The proofof the law of sines is divided into three cases: acute. right. and
obtuse triangles. The following is a proof of the acute case: you will prove
the reniaining cases in F.xercises 33--19.
Given: zieute AABC with sides :1. l}. and C C
Prov? sinA = sin B = sin C D:
' it (i i. Q 3
Proof: b
Draw the altitudes from B and C Lahel
the intersections of the altitudes with
Hand A—C;is D, and D_». with lengths A D: 0 3
Ii. and II}, respectively. l'hen sin t= %
and sin B = Solving each equation
for li.. Ii. = bsiii A and Ii. = ii sin B. By
substitution. 1: sin A = (1 sin B. Dividing
both sides of the equation by ab gives:
ab {ll}
55;‘ = EWVLB
(I b
. . . I - . I, . . . .
Similairly, sin A = and sin C = so [‘Sll't A = a sin C, which gives:
it i‘
Therefore. STIA = =
b I‘
Solving Triangles
The law of sinus um be used to find the ineusures of sides and angles in a
triangle, ii" the measures of some sides and angles are given. You can use the
law of sines to solve at triangle if you are given the ineiistires of
1. two angles and one side
01'
2. two sides and an angle that is opposite one of the sides.
LESSON 10.: THE La’-‘N OF SINES 655
E x A M P L E oFind band (in thetriatnglc at right.
. SOLUTION
Set up a proportion using two ratios
from the law ofsincs. Start with the
known angle whose opposite side is
also known, in this case, AA and u.
Then by the law of sines:
AM = §i_n_C = §i_I1£
(1 t‘ (I b ,
Sin = §in4l° Si" 720 _ Si“ mZB= —I72"+4l:‘)
2() r T ‘ T =57‘
"Si" 73° = 70 Si" ‘Ho lisin 72” = 20 sin 6?”
. 20 " Ill” ,, — ' "-3
¢=%~l-*-3 l:= =l9.4
mv nus Given AABClron1 Exainple l with a= I5. mzrt = 70°. and n1zC = 50°.
lind I: and C.
E x A M P L 0 Find mAfQin the triangle at right. 0 r= 34 5
O SOLUTION
. = 27
sin R = sin Q q
1 q
siu82" = sin 0 ”
3-1 27
34 sin Q = 27 sin 82”
sin Q = —--——z7 Si" 820 = 0.786
34
Q = sin" 0.786 = 52°
mv nus Given AQRS from Ex-.nnple 2 with q = 18, r = 26. and mAR = 75°.
find n1AQ.
Note: When solving triangles by using the law ofsines where two sides and 21
nonincluded angle are given. it may be possible to have two dillerettt answers.
This is known as the umltiguous ((15? of the law of sines.
In the L‘X'.llll})lC. sin" was used to find the angle in question. llowcver. the
inverse sine function will only give values of angles less than 90°. To find the
possible obtuse angle. subtract the value from ISO“.
Ambiguous case of the law of Sines
cRmcAL THINKING Is the situation in Example 2 ambiguous? Why or why not?
656 CHAPTER 10
E x A M P L E Os boater travels regularly from _ _, -
San Mateo to Alameda across ‘ .. - ‘-
San l-'rancisco Bay, a distance of = -- =-all II " * -
I2-3.8 mi. Suppose that one day I ‘
he needs to stop at the baseball X __‘
park. If the angle formed at
the baseball park is 95°and the . _ : . , ' ‘-
angle formed at Alameda is 53°.
how far does the boater have to
travel to get to Alameda via
the baseball park?
19
O SOLUTION
Use the law ofsines
= til =
I23 I: 12.8 b
1: sin 95” = l2.8 sin 53” 1: sin 95° = l2.8 sin 32°
c= =iti.5 ¢-= =6.a
The total distance to Alameda is approximately lU._’o + 6.8 = l?'.l mi.
Exercises
. Communicate
1. Explain why the law of sines
cannot be used to solve AABC
D 24 E
U Cl DOC! ° . .
A can -‘E5 2. Explain why the law of slnes
0::::"'g'°s cannot be used to solve ADFF. 30 33
Go To: go!nw.com
Keyword:
MGI Sines F
- G
30
3. Explain why the law of sines ,(55;
cannot be used to solve .r_~.c.1 II.
28
H
4. Explain how the ambiguous case ofthe I-an ofsines relates to the SSA
combination and the "swinging door" effect (see Lesson 4.3].
LESSON 10.l THE La!-‘N OF SINES 657
658 CHAPTER 10
0 611/480’ 34’///3 Practice
5. Find band cin AABC. 6. Find mAQin AQRS.
(EXAMPLE 1) (EXAMPLE 2)
C Q
7 b /
58 36:: 50"
B C A R q S
7. How much greater is the distance from point X to point Yto point 7thnn
the distance from point X to point Z? (EXAMPLE 3)
0 Practice fllfd App/y
C
In Exercises 8-15. find the
indicated measures. Assume 3 b
that all angles are acute. It may 3
be helpful to sketch the triangle 0 A
roughly to scale.
8. m.£A = 56” 111.48 = 24° b = l.22 cm I.‘ = ?
9. mil? = 29“ a = ‘3-.l2cm b = 3.28 cm 1114.4 = ?
10. mzb' = 29° cl = 5. l 2cm 1: = 3.28 cm 1' = ?
11. ml}? = 6}” I1 = 7.36cm c= 2.l.‘.l cm mAC = I’
12. m£B = 67° 11 = 7.36 cm L‘ = 2.13 cm {I = ?
13. mAB = 73° m.éC= 85° (1 = 3-.M cm b = ?
14. m.»_’ l = 3-5“ 11148 = 44° c= 2.4 cm a = ?
15- n1.v_’A = 53° mZC= 72” L‘ = 2.34 cm I: = ?
Find all unknown sides and angles in each triangle. if the triangle is
ambiguous. give both possible angles. It may be helpful to sketch the
triangle roughly to scale.
16. n1zP= 30°. n1AQ= 40°, (1: i0
17. mzQ= 60°. mAR = 80°. r= 7 I q
18. mAP = 72°. mAR = 36”. q = 12 K :
19. m.»_’P= 60°. p= 9. q = 7
2o. n1zQ= l20°. q= l2, r=8
21. n1£R= 45°, p= ll. r=8
D connect fig‘
Homework
Help Online
Go To: go!nw.com
Keyword:
MGI Homcwnrlt Hub
for Exercise: 22-32
PROOF
In Exercises 22-28. you will investigate the ambiguous case of the law
of sines. Suppose that two sides of a triangle. a and b. and an angle
opposite one side, LA. are given.
22. Case I: m.éA < 90°
Draw a line and choose point A on the line. Choose measurements for :SA
and b. and use a ruler and protr-actor to draw side b.
Use a calculator to find l) sin A. Explain why there is exactly one possilile
triangle if (1 = bsin A.
b
A
23. If rz < bsin A, how many triangles are possible? Explain your reasoning.
24. it’ a 2 in. how many triangles are possible? Explain your reasoning.
25. If bsin A < a < b. how many triangles are possible? Explain your reasoning.
26- Case H: mm 2 90°
Draw at line and Clioose point A on the line. Choose Ineasuremcnts for AA
and I1. and use a ruler and protrauor to draw side 1).
Explain why there is exactly one possible triangle if a > ll.
bl bl. :a>b
27. ll‘ :1 S b, how many triangles are possible? Explain your I'e:Isol'ling.
28. Summarize your results from Exercises 22-27 above by writing a rule in
your own words for deciding whether a given set of SSA measurements
determine one triangle. two possible triangles. or no triangle.
in Exercises 29-32. two sides of a triangle. a and b, and an angle
opposite one side. LA. are given. Use your results from Exercises 22-28
to explain whether the given measurements determine one triangle.
two possible triangles. or no triangle.
29. inzrl = 70°. r1: 4. in = 3 C
30. IIIAA = ll0°, rt= 7. l)= 5
31. méxt = 30°, n=-1, l:= 6
32. n1AA=l45°.cr=.l,b=6 A C B
For Exercises 33-35. use the diagram to prove the law of sines for
right triangles.
33. Write the sine ofangles A and B B
in terms of :1, I1, and C.
. . . . . C
34. Write the lollowrng ratios III ‘E’
terms of a. b. and c, and simplify:
sin A sin 13 sin C C b A
rt l.v t
35. Complete the proof of the law
of sines for right angles.
LESSON 10.l THE La!-‘N OF SINES 659
TW0—C0|.U|V|N PROOF For Exercises 36-49. use the diagram at right to
prove the law of sines for obtuse triangles.
Given: obtuse AABC with sides a. b. and c
fig = = E
Prove:
(I it 4'
Proof:
Draw altitudes from b‘ and C. label
the intersections of the altitudes with
“‘”‘ T .
AB and AC. as D. and D3, with
lengths ll. and 113. respectively.
Statements Reasons
sin A = % sin B = Definition ofsine
II. = 36. 9, ll. = 37. ? 38. ?
39. ? Substitution Property
sing = sin B 40- if
a b
. ’) .
sInA= stnC=41. ? 42. ?
ln = 43. ? In = 44 ? 45. ?
csinA=n.sinC 46. ?
47. ? Division Property
as. ? 49. ?
C H A L L E N G E 50. Lise the lawofsines to prove that the identity below is true for any triangle
AABC.
rt — b _ n + b
sinzi —- sin )3 _ sin A-l- sin B
A P P L I c A T l 0 N 51. WlLDtll-‘E MANAGEMENT Scientists are tracking polar bears that have been
lined with radio collars. The scientists have mo stations that are 9 km
apart along a straight road. At station I. the signal from one of the collars
comes from a direction -19° from the road. At station 2. the signal from the
same collar comes from a direction 65” from the road. I low far is the polar
hear from station 2? What is the shortest distance from the road to the
bear?
Station 1
Road
9 km Polar
bear
Station 2
660 CHAPTER 10
APPLICATIONS
52. ARCHITECTURE A real—est.nc ,~ ; __ ' /
developer \5‘€ll1I$ to build an /
office building on a triangular , “_
lot between Oak Street and 3rd - r'
Avenue. The dimensions of the r -
lot are shown at right. Use the , " -
diagram to find the measures
of the angles lormed by the
sides of the lot.
53. FORESTRY A plume of smoke is
spotted from two dilTerent ti re
towers that are 5 mi apart. From
tower A. the angle between the
smoke plume and tower B is 80°.
From tower B. the angle between
the smoke plume and lower A is
70°. Which tower is closer to the
smoke plume? How far is the
smoke from the tower!
Smoke
plume
SURVEYING Suppose that you are driving toward a mountain.You stop
and measure the angle of elevation from your eye to the top of the
mountain, which is 11.5". You then drive 5 mi on level ground.You
stop again and measure the new angle of elevation. which is 27.5]?
Lines of sight 3
F \ h
11.5
A 5 mi C D
Hi-hW8
u
54. Determine the measure of .».’ABC.
55. Find BC.
56. Use your result from Exercise 35 to determine the height of the
mountain.
LESSON IOJ THE La!-‘N OF SINES 661
CONNECTION
A good window to use:
0 _< 6 _< 360
with 6 step = I
-1.5 S x 5 L5
-1 S y S l
662 CHAPTER I0
Look Back
57. Find the surface area and volume of a sphere with a radius of 15 meters.
(LESSON 7.6.)
58. What happens to the volume and surface area ol a sphere if the radius is
tripled? (Lsssorvs 7.5 AND 8.8)
Find x in each diagram below. (LESSONS 8.3 AND 8.4)
59. GO. A
51 x+ 2 2x
B C
45 ‘ 2x- 1 dx— 4
24 "
D E
Use a scientific or graphics calculator to find the following. Draw a
triangle to illustrate each angle. (LESSONS 10.1 AND 10.2)
J3
63. cos"
61. tan" J3 2
L004’ Bet/o/rd
POLAR COOHDINATES In a rectangular
coordinate system. a point is
represented by x and y, the horizontal
and vertical distance from the origin.
In a polar coordinate system, a point
is represented by a distance from the
origin, r, and an angle from the
positive x-axis. 0.
64. Point A has coordinates [2, 30°} in a polar coordinate s\-‘stem. Plot point A
on a graph and find its rectangular coordinates.
65. Point B has coordinates (3. 3) in a rectangular coordinate system. Plot point
B on a graph and find its polar coordinates.
66. Use a graphics calculator with a polar graphing mode to graph some ol
the following functions. Draw or describe the graphs.
,_..—=- r= sin 6 r= sin (20) r= sin [39]
r=cos0 r=cos(26} r=cos(50l
In polar ronrdiririrtxc. me sirnplesr graph is n rirrle. Mrmy graphs in polar t'oordinnte.< lmve
the shapes offlnwers'. s'mrs', or spirals.
Objectives
0 Use the law ofcosines.
together with the law
of sinus. to solve
triangles.
0 Prove the acute case
ol the law oi cosines.
of Cosines
n_r
'-'~..
The law of casines can be used
to determine whether three « I I -s ol
campers can conrrmrnicrlte from their
campsites by using two-way radios.
I ' " #
At a campground there are three groups of campers at three different
campsites. The Campers carry t\t'O-\‘h';ly‘ radios with a range of about I mile.
What information is needed to determine whether the three groups can all
communicate directly with each other?
The Law of Cosines
In the previous lesson. you used the law of sines to solve triangles given two
angles and a side or two sides and an angle opposite a given side.
Suppose that you have it triangle with two known sides in which the included
angle is known. By S.-\S congruence, the triangle is uniquelv determined.
However. the triangle cannot be solved using the law of sines because every
possible proportion in the law 0|‘ sines will have two unknowns.
You can use the law of cosines to solve .1 triangle if you ure given the measures of
1. two sides and the included angle or
2. three sides.
The Law of Cosines
For any triangle AA BC with sides o, b, and r: B
if = b’ + (.3 — 21):‘ cos A '’ ""
bl - tr’ + L: — 20¢‘ cos B
L"-n3+lf-’-Zabcos C A b 0
10.5.1
LESSON 105 THE LAW OF COSINES 663
E X A M P I. E oFind bin thetriangle at riglIt.
. SOLUTION
Using the second equation in the law ofcosines,
b'' = :1’ + 5 — Zarcos 8
Ir’ = 23'-' + 323 — 2r28)t321cos=I_>.°
I‘ 2 «I97.-I
b 2 22.3
rav nus Given AABC from E‘LdlI'l]Jl(‘ I with :1: 17, c: 23. and m.£B = 55°. Iind D.
CRITICAL THINKING Explain why you cannot use the law ofsines to solve the triangle in lixample I.
D
Find the measures of .51.’), AE, and AF in the
triangle at right. f_ 14
I2: 15
O SOLUTION
Step I E
Use the law of cosines to lind the first angle. F d: 7
It is convenient to start with the largest angle.
which is opposite the longest side. e.
e2 = d3 +_{’ — Zdfcos I.-
I53 = 73+ I-I3 — 2{7)[|-Dcos F
223 = 245 — 196 Los E
-20 = -I96 cos E
E = cos '(__|3906) 2 84"
Step 2
Use the law of sines to find the second angle. Since the remaining
angles are acute (why?J. you do not have to worry about the
ambiguous case.
sin !- = sin 84°
I5
1
sin F = 2 0.93
I
Step 3
Use the Triangle Sum Theorem to lind the third angle.
ml!) 3 180° - (84° + 68°) N 28°
rav THIS Given AIDEF from Example 2 with d: I0. t’‘—' 18. and f= ll. find the
measures of 1 D, AF, and .£F.
CRITICAL THINKING Could the law of cosines have been used in Step 2 of Example 2? Why do you
think the law of sines was used instead?
664 CHAPTER Io
E X A M P L E 6Suppose three campsites are '— ‘ ..
TRY THIS
positioned as shown. The
campers com mun ic-ate bv using
l\v0-w:1_V radios with a range \ \' ‘g _
of about I mi, or 528() It. Will __ . -gt. _:
the campers at sites I and 3 be ' ' ‘5; .. 5 _ 4'
able to communicate directlv
with each other? __
"Vic . ‘ ‘Iv; .
SOLUTION I _.._. " it
. . .2-‘5. ~ ‘
Lse the law ot costnes. 14‘ "' '
— ~ 5‘ ‘j ~£_ ~;_ . 1- .
IF = (1? + L2 — Zaecos B
I1‘ = 5900’ + 3400‘ — 2(5900l(34[]()lcos 86'’
If 3 245320.058
b = -1992 ft
'l'he campers at sites I and 3 will be able to communicate directly by using the
two-way radios.
If the distance lrom site I to site 2 is 3600 ft, the distance from site 2 to site 3
is 4000 ft. and inzt? = 8-'t°,will the campers at sites I and 3 be able to
communicate directly with each other? Why or why not?
Proof of the Law of Cosines: Acute Case
PROOF
The following is at proof of the acute case of the law oi. cosines. You will he
asked to prove the obtuse case in Fxercises 26—3l.
C
Given: acute AABC with sides rt. l1. and C
Prove: (12 = (J3 + (T1 — 2lJC COS A b 3
Proof:
Draw the altitude from C with height h, .
which divides '/Tl-3 into two segments, c. A C B
and l.'_:_-. l'hen. by definition of cosine,
cos A = 3
I:
(we) c.os."l = %(2bc)
21);‘ cos A = Zcc.
Multiply both sides by 20::
Srmplify
From the Pytlmgoreaii Theorem:
‘I ‘P ‘J
w=k+q
‘I 1 ‘J
:r=lr+(c—r.)' c’=c—c.
:13 = it’ + r’ — 241'. + cf Distribute.
(I3 (
= _It1 + cl!) + (3 — Zccl Rearrange terms.
b: = h‘, 1' C[?
3 = liq‘ + L’ — 211:‘ cos A Subs!!!-m0.':
LESSON I05 THE LAW OF COSINES 665
Exemses
. Comma»/care
B
1. Suppose that AABC is a right
triangle. Use the law ofcosines to C 3
Find L2. and simplify as much as
possible. What do vou notice?
A D C
n ' '_ _f'°°"'"’“ 1131 Which rule should you use, the law of sines or the law of cosines. to
3°:!""'°5 find each indicated measurement below? Explain your reasoning.
I] IIIE
Go To: go.hrw.com 2- 3- 32
Keyword:
Mm cosines ? P17
15
‘ 40° 50° 7 38
12
4. Suppose that three angles ofa triangle are given. Could you use the lztw of
sines or the law ofcosines to solve the triangle? livtplain your reasoning.
. qz//dad Skills Practice
Use the law of cosines and the law of sines to solve each triangle.
5. (EXAMPLE 1) 6. (EXAMPLE 2)
A
D
3° 45
50
B 36 C E 28 F
1. Suppose that three Campers have two-\w'zty radios with -1 range ol 7920 ft.
The distance between sites i and 2 is 5750 ft, the distance between sites i
and 3 is 6690 ft. and the angle formed with site 1 at the vertex: is 82°. ("an
the campers at sites 2 and 3 commumicate directly? Why or why not?
(EXAMPLE 3)
. _ J‘ "
-.x .v_
4 A» ‘ ., ‘F ' ‘L
'- ‘:. '7
1., é ' ' -"’
ff‘. ' Y‘:
_
( L
666 CHAPTER 10
0 Practice and 7450/y
u - connect For Exercises 8-13, find the indicated measures. It may help to sketch
Homework the triangle roughly to scale.
Help Online
.-..
..
II
\
..
I
_.
~.1
G°TO:w"w_c°m 8. at: 12 . t— 11148: 55°
K Ii: _ _ I . _ ‘ _ 0
h:g;“;;;mwn-M 9. a _ 2.2 it _ 1.3 1 _ 2 mgr. _ 52
'°' E*"'°‘5‘-“"9 1o. 11 = ? l: = as 7 c= 7% 5 mm = 87°
I m -" ' A
“ 11. u=lO t:=7 C=8 m.4,1= ?
12. u = 3.6 II = 3.6 C = 2.5 mAC= ?
13. a=27 b=-1l c= I5 mAB= ?
Solve each triangle.
0 14
14. 15. 5 16.
D 3.7
h 8.8
3.5 J
F I g H
17. M 18. P 19. r
18 25 7 <1
‘DA 30
N {Tl O R
B
C
B
b
C
l.
k
2
2 K
36
S
28
U
Exercises 20-25 summarize the methods of solving triangles by using
the law of sines and the law of cosines.
SUMMARY OF TRIANGLE-SOLVING PROCEDURES
Glven Example Theoremlsl
1-D.?§5..7
three angles cannot be solved
fl /
800
two angles and one side 1° 20. ?
60°
24
. 50'
two sldes and included 21 ?
angle 16
22. 7 23. 7 layv of slnes
(ambiguous case)
three sldes 24. 7 25. 7
LESSON I05 THE LAW OF COSINES 667
PROOF
CHALLENGE
APPLICATIONS
668 CHAPTER 10
In Exercises 26-31, you will prove the obtuse case of the law of cosines.
Refer to the diagram at right.
26. I3}; delinition of cosine, cos 9 = _?_. C
27. Multiply both sides of the equation
from Exercise 26 by l1, and sintplify. .
28. Lise the identity
cos (I80 — A") = —cos A to rewrite
your equation from F.\'eru:ise 27 in
terms of cos I. A c B
29. By the Pythagorean Theorem. :1’ = I’
+
30. By the Pythagorean Theorem. bi = f + C’
31. Expand the square of the binomial in the equation from F\'ercise 29.
Substitute the results of Exercises 28 and 30 into this equation and
simplify to complete the proof of the law of cosines.
32. Using the law of cosines. prove the Triangle c
Inequality ‘theorem: For £..«tb’C with sides :1, b,
and e. (1 + l1> 1'. Also prove that C > rt - it lor
rt > (1. b
C
33. SPORTS On a standard baseball field. the bases form a square with 9U—ft
sides. ‘I he pit-eher’s mound is 60.5 it from home plate on a diagonal from
home plate to second base. Find the distance lrom the pitcher's mound to
first base.
34. NAVIGATION Mark and Stephen walk into the woods along lines that form
a 72°-angle. If Mark walks at 2.8 mph and Stephen walks at -1.2 mph. lt0v\
far apart will they be after 3 hr?
35. NAVIGATION The distance from U
Greenfield to Brownsville is 57 km,
and the distance from Greenfield to
Red River is 25 km. The angle B'°W"5""'°
formed by the roads at Greenfield is . 37 km
42°. The state highway department ‘,
plans to build a straight road from ‘\ 42 ‘Greenfield
Brownsville to Red River. How long Red River,’ 25 km
will the road be. and what angle will
the new road lorm with the road /
from Greenfield to Brownsville? "
36. INDIRECT MEASUREMENT From point A. the
distance to one end of a small lake is 300 yd.
the distance to the other end is 500 yd. and
the angle formed by the lines of sight is lO5°. __________________________ .__,.
Fstintate the width of the lake. “~._ _,.-"'
300 yci‘-.‘1o§..-"'500 vd
'A
37. LANDSCAPING Nina wants to use three long boards as a border for a
triangular garden. The boards have lengths of IO ft. I2 ft. and I5 ft. Find
the angles at the corners oi" the garden.
CONNECTION
CONNECTION
1.00.? Back
COORDINATE GEOMETRV For Exercises 38-41.
draw the image of AABC under the given
transformation. (LESSONS 1.7 AND 8.1)
38. T(x.yJ = (3x, 3y)
39. T[.x'.y) = (.x'— 2.}-'— 2]
40. T[_t. y) = '—:y)
41. T[x.y) = (2x+ I. 2}-'— 3}
42. The perimeter of a rectangle is 80 cm. The ratio of its width to length is
Find the length and width of the rectangle. (LESSON 8.2)
U1
Determine whether the triangles in each pair can be proven similar.
Explain your reasoning. (LESSON 8.3)
43. 44.
1o 5 2o 10
1 15"
5
4
40° 1 1 5"
8
10
45. In the diagram at right. ER is tangent
to GP. Find radius PQ. (LESSONS 9.2
AND 10.1)
40‘ 3
O 15 Fl
Look 3670110’
TRIGONOMETRV You can use right triangles to simplify expressions
involving inverse trigonometric functions. For example, consider the
expression coslsin" xl.
46. sin" x is an angle that has a sine ratio
of This angle can be represented by
represented by drawing .1 right triangle X
with a hvpotenuse of I and a leg of length
x. Use the Pythagorean Theorem to find '
an e\:pression for the length of the sin 9: 31‘-
adjacent leg. 3 = sin—1 X
47. Use the clelinition of cosine and your result from Exercise -17 to write an
expression for cos 9. which is equal to cos(sin ' Jr).
Simplify the following expressions:
48. tan(5in" x) 49. sinlcos" x) 50. sin(tan"x}
LESSON I05 THE LAW OF COSINES 669
r.-1/nurse cu:
unrvenses
AGE
~s*“°3.2.2s::nAsA
June 2, I999
Web posted at: 9:28 P..\i. PDT (GI 25 GMT]
CHICAGO ( .\P) -- A new r'a1'lio-tclcscopt‘technique has established 1 “golden
ruler" for measuring cosmic distances -and raises doubts about the claim th.1r
N.-\S.-\ ttstrononrcrs had detcrnrincd the age and gspansion rite of (hi: urrix-rrse.
lint Hertnstein ol' the National Radio Astr-orromt Observatory said his method
produces "the most precise distance ever measured to a remote g-a|axy" and
suggests .1 I": percent to 20 percent rnargin of error in the technitrtre used by the
astronomers sponsored by the National .-\eron.1trtics and Space .-\drnin'rstr:1tion.
New neasururg L
techniques l
'''Ours is a ditLr_t tt1e'tsun:ment, using getatttetry. trtd is independent of all other
methods ofdtternrining cosmic distances.” Herrnstein said “l'uesd-av at a national
rrrecting ofthe :'\n1er'ican Astronomical Society.
I lhe NASA team concluded that the universe is I3 billion to I3 billion years old
and is expanding at tn accclcratirrg rate of 70 kilometers per second for eve-r'_v 3,5
rttillion ligltl-years ill Llislattce limit the Earth.
Earlier
measurements
(by NASA}
‘Golden ruler’ for measuring cosmic distances
Herrnstein said this calculrttion was offbv as much as 2D percent. He based his
untclusion on the dililet'enr.e in calculaletl distance to .1 specific g'.1l't:c_y' when
comparing his technique with the method used by the NASA group.
lletrnslein used .1 galamy called NGC 4258- to establish what he called .1 "golden
rulet" for measuring cosmic distances.
MBsers_ t_ NGC 4258 is surrounded by a rotating cltrud ol gas. \‘\"ithin this gas dnud is
. ' water vapor. which tends to amplifv radio signals. This creates radio “hot spots"
Radio hot spots _ '
called rnasers.
The orbital speed of masers between NGC 4.258 and Earth was nre.1sured in
I99-l_. and again every few months over the lollowing thrcc ye trs. After
cletcrtnirting the speed at which the tnaset's wen: mnvittg. the astrtrnonters
created a triangle with a rn.1ser position at one angle, its latest position at .1
secottd angle. and Earth at the third .1nglr:. Measuring the angles gives the
distance. "It is tery simple and direct." said Herr nstein.
llelrnslein conducted his studv using the Very Long Baseline Arra_5-. which is a
series of radio-telescope antennae that are scattered across the United States,
from the Virgin lsl.-tnds to Hawaii.
The antennae operate as a single unit and are able to measure tr-atural radio
sigrrals to tn ac-;'trr'.1r:_r' 500 times t.'_,t'e.ttcr than the Hubble I(‘l($»C0pt: can mr:.1surc
visible light.
Tl.
fire world 5
la ryesr telescope I
G.rp_t'J'igltl I999 The /lS.\'r'JL'it'Il’r:'(l Press. All riglm r¢'s1'1 v1'.'.rl.
E] E
V
I unel loruntd lane scant Prtrt! Mop g
D 1-.‘ D
Cooperative Learning
O I
Refer to the diagratn at right. ‘I he angle, (2 orbit of maser 1' .
between two positions of a given maser in in NGC 4258 '
NGC 4258 was measured by the Very l ong P. .-
Baseline Array, or VLBA. ‘I he two positions ' ‘ '._
. . _ — .1
ol the maser lorm two vtrttces ol an Position of position or
isosceles triangle, and the position of masar in 1997 maser in 1994 _ .‘
Earth forms the third vertex. °
1. 'I'he maser in galaxy NGC -1253 rotates
at about I I00 km per second. Use this
to determine the distance that the _
maser traveled in 3 years between the
two indicated positions in the triangle. d d -’
l'se l yr = 31336000 sec. ‘
C
2. For extren1eIy small vertex angles. such as --
9, the altitude ot'an isosceles triangle is very
nearly equal to the lengths of its legs. Thus
the altitude can be used to approximate the /9 = °-000000025
lengths. :3, of the legs of the triangle in the '
diagram. Find the altitude as an estimate oi" cl.
3. According to Herrnstein's measurements, NGC
-1258 is about 23.5 million light-
years away. A light-year is ;_‘
approximately 9.46 X IO” km. Earth _*--Q. | IL‘
I low close is your answer to '-"'9'-"7' k '~ I - I‘ ‘ll *-
_ _ _ (J mfltascmln . u‘ my _ ..
llerrnstern s. - Dig: W 151))‘
_ J . . I ,at\¢',~4 Ml \
I’, - ' ill I .‘l“,A‘ .
' ‘ I I ' _ ‘
" J ‘ V I
. -‘Q’ ".031 I:-'’’' ’
\ - y i ,\ 11¢ .)_A.‘_ .._.
‘\_ -‘ \ -\ ‘| '$.' 'b:6,p' ' '
~ - _ . ._,--.3 ~ '-l-L.,v.Vf'
‘ v ’\ .-'\‘“§*'l—‘ -l“ ‘:3:
Am» ..~.3é'= L_$te‘-.5-I .-‘: \: ‘s it"
4;‘ :I ':.;_§'t '.-§._,--.__,~_;_-\- ~
Q! ‘._\'*v _._ -'_1'._,?‘.‘- ' "
'§% ;§\‘:‘‘ .-J.“-
. . ‘V . \ ‘ ‘ .
[rm _l'-Ierrrr5teu_1. K‘; _-_J _
.N'anwml Radio ~ \ . '-
Asrrontnny Olrservrrtory '’ ‘U--.. ‘G -,
1" 1
3 t K V! I‘ . I
. .1 .
,~ ."g.f 1.-
I
s ‘ 5; 5. .
, ' 4 ‘
’_ __ -1
, .
' « ‘I J , *&
.. ’ c
‘ ‘tr
&—F'' ' ‘Q__(‘ J I 5 _ . ‘J
.4‘ - '
' “ ,1 4‘ - _ "CHAPTER. .EvE\'.'ITN SMATH \
5-‘ ' ' - \ _ ' . \ 5‘_
I I
Vectors in Geometry
Objectives
0 Define vector.
0 Add two vectors.
0 Use vectors and vector
addition to solve
problems.
Wh _
The path on ball In n
spans event is allected by
the wind. For this reason,
stadium: for certain I - -
have days that give a
visual indication of the
winds direction and Its
rnagnirude. Because wind
has these two properties It
can be represented by a
vector.
672 CHAPTER 10
A...‘ S:
I_|
WI.
What Is a Vector?
A vector is a m.ttltc-m.itiea| object that
has lmth .1 magnitude (.1 numerical
measure) and at direction. Arrows are
used to represent vectors, because
arr()\-is have both magnitude and
direction. l'he length of at vector
arrow represents the magnitude of
the vector.
A lowercase letter with .1 vector
arrow over it nmy be used to
indicate .1 vector. '1 he symbol
|_t7_Ldenotes the magnitude
of V .
- -::+ ~—«=' —-—~ -
- -- ———-“E —— E
?.+—-—— ————~-:”——?-»———
\ 2.‘ __
:1‘ =: - ,9
—-— 3 .~ - ,.
:: .‘ u ‘
__ _,‘
:: --
:: .>
r‘: "I ‘-
_:-I
."-.93. 4 ‘ar-
9: 5 - §’\_'
/ I \'K ‘..
—...-
"-14-"
K b '0
Ti b, and -6 are vectors.
Magnitude of Tr‘ = IT/"|
Magnitude of W = |W|
A - p . 3 A 1- . 0 ,4 Anything that has both magnitude and direction can be modeled by a \C‘ClOl'.
Pmsms In the examples below, vectors are used to represent a velocitv, a lorce. and a
displacement (a relocation].
CHECKPOINT ./ Describe the magnitude and direction ofthe vector in each.
|
‘,9
-. I
Velocity The wind sod; inrlimtes the Force The titgliom‘ appfig-5 a force on the
strength and dirt-ctitm of the wind. lmrge in the dirt‘-‘mien the hinge is pointed.
XI
Dis-plncenmn The t'ttr spec-d.\' down the
qttm‘t¢.'J'-tttiitt mick.
To describe the direction of a vector, you need a direction to ttse as a reference.
On a coordinate grid this is usually the positive x—axis direction.
cuscxpomrr ./ What are the reference directions in the three pictorial examples?
Vectors fiith the same direction. such as vectors Y _. /"
T1‘-and (J in the illustration. are said to be parailri. ‘(Y5
Vectors at right angles are perpendirtdai'. 3”
X
Vector Sums
In many situations it is appropriate to combine vectors to get a new vector
called -.1 resultant. ‘I he process of combining vectors represented in the
example below is called vettar addition.
A . p . 0 H A hiker travels 3 miles northeast. then 3 _ 1 mi E
' - ' . , , ml 0'
RECREATION I mile east. the resultant sector [red] NE 135
is the total distance traveled in a specitic
direction from the starting point.
- p . 1- g 5 ,4 Two tractors pull on a tree stump
AGRICULTURE with the iorces and directions shown. 259° lb ’;
The combined force exerted by the
tractors in the direction shown is the
resultant \-ector. 2500 lb
LESSON 10.5 vecroas IN GEO-Metnv 613
The Head-to-Tail Method of Vector Addition
In the hiker example. each vector represents a displ-acement——that is. a
relocation of the hiker from a given point. In sttch cases. the ltcml-to-rail
rnerhod is a natural way to do vector addition.
E X A M P I. E oI‘ind the sum ot vectors"r'2‘-aitdlzi. 1m_| E K
I 9
j_':— *
O SOLUTION 3m';|E .5. b
To use the head-to-tail method of /
vector addition, place the tail of one
vector at the head of the other. The
vector sum is a new displacement 1 mile F
vector from the tail of the Iirst vector x X
to the head of the second vector. 3 mile
NE
Resultant
vector
(sum!
TRY THIS Use the head-to-tail method to Find the sum oi. two parallel vectors.
The Parallelogram Method of Vector Addition
In manv cases. the pnrrtlh-'iog7'mn trtethorl is a natural way to think olicomlaining
vectors. This is especiallv true when two forces act on the same point, such as in
the tractor e:<amplc on the previous page.
M 0 Find the sum of vectors Tfiand Ti?
0 SOLUTION _
To find the sum ofthe vectors. complete K
a parallelogram by adding two segments
to the tigurc. The vector sum is a vector
along the diagonal of the parallelogram. 7,‘ ‘-._
starting at the common point.
mv nus W'h.tt is the vector sum it two equal forces are applied to a point in opposite
directions? \-\-‘hat happens to the sum if two such forces are unequal?
CRITICAL THINKING The par-allelograni method and the
he-ad—to—tai| method are equivalent
since they produce the same resultant.
How does the diagram at right show
that the methods are equivalent?
674 CHAPTER 10
E X A M P L E 09. swimmer heads perpendieularto a 3—mph eurrentin -.1 river.ller speed in
A'P IC
SPORTS
still water is 2.5 tnph. Find the actual speed and direction of the swimmer.
SOLUTION
Because the vectors are at right angles. the
parallelogram method for addition
gives a rectangle. Thus, vou can solve
for x by using the Pythagorean Theorem.
1
X‘
—-2
3
||
L.»
'-“ to
.
3+
I5.2
.x'= v‘ 15.25 2: 3.9 mph (the actual speed of the swimmer)
There is more than one way to find H. For example:
— 3i ..
tan 0 — J 0 ~ 0.833
9 z uin-'(u.833) -. 40°
The swimmer swims at an angle ol 40° with the current of the river.
E X A M P L E The .s\-.-immer in Example 3 changes the direction of her elTort so that she is
PROBLEM SOLVING
heading at an angle of 4U°with the direction of the current. What is her actual
speed and direction?
SOLUTION
Draw a diagram. One way to solve
such problems is to draw an accurate _ __
vector diagram and measure the -, - " '
resultant vector and its angle (9. '
ll'}'0u wish to solve the problem using
trigonometry, begin by labeling the
sides of a triangle as shown below.
Then use known properties of
parallelograms to find n14’ C. which
is I-10°. Then use the law ofeosines.
c“=u"'+lr’—2ubcosC
51 + 33 _ 2[2_5)(3m COS I 400 If you are usmg graph paper
= 2' _ you can make a ruler from 9
S + 9 — = offhe same paper.
t‘ 2 \/26.74 3 5.l7
Lise the law of sines to tind m£BAC.
which is the same as méfl. """""" " 3
_" '5 /a = 2.5 mph
‘ill'|;" 3 .. 3- ,I
2.5 SJ? — Z :5!’
sin/l= 0.3109 A b=3.0 mph 0
_ _l lcurrentl
sin ((13109) 3 l8°
lhe swimmer’s actual speed is 5.l7 mph at angle of IS“ with the current.
LESSON 10.5 vecroas IN GEOMETRV 675
Exemses
. Cohm/imitate
1. What is the magnitude Ufa vector? Explain.
2. What is the direction olizt vector? Explztin.
- - oomect
nofn
Activities Describe the magnitude and direction of the vector or vectors in each ot
Oflllfle the following:
Go To: go.hrw.cocn _ _
Keyword: 3. an airplane llytng northwest at 175 knots
MGI Vaclota _ _
4. 21 boat going t5 knots upstream against a current of 3 knots
5. two equal tug—of—w.tr teams pulling in opposite directions on a rope
. qt//dad 8.4’///5 Pratt/ca
6. Find the sum of vectors Valid it by using -5
the head-to-tail method. (EXAMPLE 1)
7. Find the sum ofwectors ?and it by using T9“
the parallelogram method. (EXAMPLE 2)
A P P L I c A T I 0 N S 8. SPORTS A swimtner heads perpendicular
to the direction of .1 current whose speed
is LS mph. ‘l he speed of the swimmer in
still water is 2 mph. Find the switnmer's 2 mph
actual speed and her direction angle. 9.
with respect to the direction of the current.
(EXAMPLE 3) 1-5 m ph
9. SPORTS A swimmer heads in a downstream
direction at an angle of IS" with the direction
ofa 2-mph current. The speed of the
swimmer in still water is 2.5 mph. Find the 2'5 mm/v
swimmer's actual speed and her direction £15:
angle. 6. with respect to the direction of the 2_o Fph
Cllffflll. (EXAMPLE 4)
676 CHAPTER 10
. Pratt/cs and Apply
n connect Copy each pair of vectors and draw the sum 7:‘ + 77'-by using the head-
Homework to-tail method. You may need to translate one of the vectors.
Help Online 10 11
Go To: uo.hrw.com
Keyword.
MGI Homuwulk Hob
lol Exercises ll]-I7
ml
trl
12. 13.
3* __ 8' _‘
. b b
A b
Copy each pair of vectors and draw the sum "5 + ?by using the
parallelogram method.You may need to translate one of the vectors.
14.
3
16. 17.
-5/' _
-5 /’
For each given pair of vectors _§and 7;in Exercises 18-23, use the
parallelogram method to find the vector sum 1:’. Use the law of cosines
to find |_¢?|, the magnitude of 7:‘. Use the law of sines to find the angle
that -1? makes with
13. 19. 20.
~ 3
8 _-a.
—~ _. so
kl a 65" b __
b
r7|= |= -
b -8
15.
cl
b
6 |‘a‘ 45 F-a‘|=3.75
F$|=a |"‘|— |b|=7.5
21. 22. 23.
7*" 7;
. ——_.-—-.—:—>
70-I fio
_». N209 b
b 7:
|a‘|=e |:=:|=6 |a‘|=2.5
|bl=1o.s |b|=7.5 fi;|=3_5
LESSON 10.5 vecroas IN GEOMETRV 677
APPLICATIONS
- o~s
II
in ‘dead reckoning, ‘pilots
use visible landmarks to
check their course.
678 CHAPTER 10
24.
25.
AVlA'l10N Mina. a student pilot. is
making her first solo llight from Austin
to Llano, lexas. Using a plotter and an
aeronautical chart. she determines that
her true course direction should be 505.
According to the weather report. the
wind at her cruising altitude of 4300 ft
has a speed ol‘ I0 knots and a heading
oi'22O [the direction fiom which it is “
blowing). The trtle air speed of her
plane. at cruising speed, is 1 l0 knots.
-K
Lsing a mechanical
computer. Mina determines
that she must hold a heading
of 293 to achieve her desired
true course. According to the
computer, her ground speed
will be a little over I08 knots.
True course is set
under the index.
Wind correction angle
(—5"'l is read under the x.
' .n -'-'
Ground speed is read under '-" ' W, _;.>” - ‘~.,_.. *....'.'.'
the center of the wheel. ' --» .. ' t:°"“7{"'"-it»
1:. Use trigonometry to check the tomputer‘s values for Min-a’s ground
speed and heading. Round your answers to two decimal places.
b. Mina has established a visible """ __" u" 3," "‘
landmark at the bend ofa river, °
14 nautical miles front her point ' :_ K ‘°,g J 3 ‘<-
ol‘ departure. Alter how many _ ‘U 1--(J "*3
minutes into her flight should she ' - '“ :3 - -~''. ' _
be over this landmark? [1 knot = ' _ :21 ,. we . \] I
l nautical mile per hour} ~ . ' —.— I .. -«:3
SCUBA DIVING Dan is investigating a boat sunk at the mouth ofa river. to
reach the wreck. D-an must swim against the current ol'2.7 mph. Suppose
Dan dives and starts swimming downward at 4.! mph [still water speed} at
a 15“ angle with the water’s surface. Find the actual speed D-an will swim
as a result of the current.
APPLICATION
‘\
.
\
\
CONNECTION
26. NAVIGATION A boat leaves port and sails in still water at 5.6 mph for 3.5 hr.
The boat then turns at a 57°angle and sails at 4.9 mph for 4.25 hr.
at. If the boat turns and heads directly for port at 6 mph. how long will it
take it to reach port?
b. At what angle will the boat have to turn to head directly back to port in
part a?
Look Back
Use the figures at right for Exercises 27-33. (LESSON 9.5)
21. Given: I-S4 - 5; VB - 3; 0
VC = 6. Find CD.
28. Given: VB = x, MA = 7;
VD - x— I: \*'t’‘- 9. Find x. B
29. Given: VB - VA - x- 6: C
Vl) = 9; VC = 5. l'ind x.
30- Given: VY - 9; VA’ - 4.
Find vw. X
31. Given: VW - 8; VX - 4.
Find 1-’ Y.
32. Given: A)’ - X; YB - x— 2;
l"(" - 4, YD - 6. Find x. 3
33- Given: Ab’ = 9; CD = 4;
DY - l2. Find AY.
£00K’ B€70IId
COORDINATE GEOMETRY Vectors? and Tihave theirtails at the origin,
(0, 0). on a coordinate plane. The head of vector rri is at point MM, 5).
and the head of vector Tfis at point Nl—3. 8).
34. Find the magnitude of the vector sum
35. Find the angle 6 that Timakes with the positive x-axis.
36. Find the coordinates of the head ot‘
37. What do you notice about the coordinates of the head of 7;? Given the
coordinates of the heads of two vectors that have their tails at the origin,
write a rule for finding the coordinates of the head of the vector stun ot
the two given vectors.
38. Write .1 paragraph proof for your rule from Exercise 37. Use diagrams to
illustrate. (Hint: Use the he.td—to—tail method ol vector addition.)
39. Given the coordinates of the head ofa vector that has its tail at the origin.
write a rule for finding the angle 6' that it makes with the positive \‘-axis.
LESSON 10.5 vecroas IN GEOMETRV 679
Objectives
0 Use transformation
equations to rotate
points.
0 Use a rotation matrix
to rotate points or
polygons.
Rotations in the
Coordinate Plane
J 1 r
'1] .
WI ‘
computer: use
geometric tmnslormations '3
ta show moving objects.
In ms lesson. you will \ . ~ - r
explore mtarions in a - '
coordinate plane. \ |
\_,\
V’ \ “t-'.\ rm.
Astrmmurs prepared for the Hubble Spam Iflesmpe repair niission
by studying computer sinmlrttiolrs oftlre plmrrrerl ew.-‘m.
r
.\*‘
CRITICAL THINKING
0|! LN D
scientific or graphics
calculator. graph pa per.
ruler. and prorractor
680 CHAPTER 10
Transformation Equations
In earlier lessons. you studied translations. reflections. and dilations in a
coordinate plane. You also studied the special case ofa rotation by 130“ about
the origin. Using trigonometry. it is possible to rotate a figure in a coordinate
plane by any angle measure.
The transformation Rfx. y = la’. y'), where
.1’ - .\' cos 6' — ysin 9 and
y' - xsin 6 + ycos 6,
is :1 rotation by 6’°about the origin. The above equations are known as
transformation equations above.
What happens to the point (0,0) under a rotation? Explain. using the
transformation equations above.
Rotating a Point
Part I
1. Draw coordinate axes on graph paper and choose a point P on the
graph. label the x- and y-coordinates ol point P.
2. Choose a value of 6 between 0°and 180°.
rotation relate to the value 0|" 6?
Part II
1. Copy and complete the table below.
3. Use your values for x, y, and 0 in the transformation equations to find
P’. Plot P'on your graph. Draw segments connecting Pand P’ to the
origin and measure the angle of rotation. How does the angle of
CHECKPOINT /
to complete the following transformations:
O°rotation: R(x.yJ =( ? , if )
90°rotation: R(x.y) = (;,i)
I80"rotation: R(x.y) — ( ? . ? )
2'/'0°rotation: R(.\'.}') = ( ? . ? )
360°rotation: R(x.y) = (L, 7 ‘
Describe your results.
9 0° SD‘'’ 180" 270° 36D
sin 9 7 7 7 7 7
cos 9 7 7 7 7 7
2. Substitute the values of sin Hand cos 6 into the transformation
equations for each value of (9. and simplify. Use the resulting equations
3. Fxperiment with negative values For 6, and values greater than 360°.
E X A M P L E 0 According to the treasure map below, some iewels are ~
buried at a point 60 paces east and 55 paces north
ofa well. Suppose that the direction of north on
the map indicates tnle north and that you are
are using a magnetic compass. which points
in a direction 5.5” west of true north.
How wottld you find the location
of the jewels? ‘ -
$45
of'// PA“;
..:'-—--.~--.4
to pom
Detail of map
0 sownon
/‘
__.l
r U.-,,-"-
Assume the map is on a coordinate plane, with the well at the origin. If true
north is represented by the y—-axis. then point X is at coordinates (60. 3-5}.
B€CE!ll>L true north is 5.5° east of the value of north on your compass. the
point must be rotated about the origin clockwise by 5.5°. (Recall that
clockwise rotations are negative.) Use the rotation equations.
x’ = xcos 6 — ysin H = 60 cos[—5.5°) — 35 sin[—5.5°) = 65 paces
y’ = xsin 49 + yeos 0 = 60 sin(—5.5°l + 35 eos(—5.5"] =1 29 paces
Using your compass, walk 6.’: paces east and 29 paces north to find the jewels.
LESSON 10.1 BOTATIONS mme COORDINATE Pt.-we 681
EXAMPLE
682 CHAPTER 10
TRY THIS
Rotation Matrices
Recall from algebra that :1 matrix is it set of nu mhers arranged in rows and
columns and enclosed in brackets. Matrices are a convenient way to
manipulate and display data.
A rotation in a coordinate plane can be represented in terms of the 2X2 matrix
cos0 —sin0 . . . .
. _ . called a rotation matrtx. When using matrices to transform
suit? L050
points in a coordinate plane. each point is written as a column matrix [ V].
The image is the product of these lV\O maitrices. *
l‘o multiply two matrices. each row in the first matrix is multiplied by each
column in the second matrix. The product of a row and a column is found lw
multiplying the terms in the row by the terms in the column and then adding.
I'—''’' -7
For example. [4 IJX ; = 4lZ)+ |l3l= 1|.
For the image Ola point transformed bv a rotation matrix, the first row
multiplied by the column is the entry in the first row of the product matrix.
and the second row multiplied by the column is the entry in the second row of
the product matrix.
The expressions in the product
x cos 9 — y sin 0 _i_.- matrix agree with the
I _.,-in 9 + y cos 9 transformation equations at
the beginning of the lesson.
cost? —sint9 x
sin9 cos!) x y
Rotate :i~..»4lBC with vertices A(0. 0). B[5, 0}. and CB, 4) by 60°
lcotinterclockwisel about the origin.
SOLUTION
When rotating more than one point. it is convenient to represent the
coordinates in a single matrix with several columns. The matrix representing
the vertices of AABF can be written as 3
—sin 60° = 0.5 -0.366
cos 60° 0.866 0.5 '
Multiply this matrix by the matrix representing AABC.
0.5 -0.866 0 5 3 _ 0 2.5 —1.9e4
0.866 0.5 0 0 4 ‘ 0 4.33 1.598
C A’ B’
C05 60“
Th t t" ‘t .
E ['0 d I()l‘l l'l'ld l'I\ IS 5'” 60°
C’ L 303. 4)
x
A’ 60h \_
Bl5. or
Rotate ri~.DFFwith vertices DIO, I), H2, 0], and Fl l, 3) by 30°
(counterclockwise) about the origin.
Plot points A’, BC and CI and COHHCLI them to
form a triangle.
Exercises
. 60»/hm/imte
1. Give examples of two rotations, one counterclockwise and one clockwise.
that produce the sarne result. Use either transl'orm-ation equations or
rotation matrices to show that the results are the same.
2. (“house two supplementar}-' angles and Find their rotation matrices. How
are they alike? How are they diffetent?
3. Choose two complementary angles and find their rotation matrices. How
are they alike? How are they different?
4. Find the rotation matrices for 6' - 0°. 90°. l80°. 270°. and 360°l)}' finding
the sine and cosine values. How do the matrices compare with the
rotations you found in the Activity?
qt/I'd'€d'.»3/fl"//S P/46¢‘/6'3
Use transformation equations to rotate the point (5. 4) by the given
angle. (EXAMPLE 1)
5. l0‘’ 6. 90° 7. —30°
Find the rotation matrix for the given angle, and use it to rotate AABC,
with vertices A(1, 1), B(3, 0), and C(2, 2). (EXAMPLE 2)
8. 45" 9. 72" 10- -60°
0 Pldfl‘/6'8 and 74p,0/y
n connect For Exercises 11-16, a point. P, and an angle of rotation, 6 are given.
Homework Determine the coordinates of the image P’.
Help Online _._ _ - _
Gomgmwmm 11. Pm. 3,. 6 — 45° 12. Pt-l. I), 6 — 30°
$g;":::Wm_ My 13. P[—3. -2), 49 = 30° 14. P[2. 0). 49 = I40°
'°' 5"°'°"°‘ "'22 15. M5. 5}. 6 - 20° 16. H2. 6). 0 - 400°
For Exercises 17-22, the coordinates of a point Pand an image P’are
given. Determine of the angle of rotation. 0.
17. pt4.2). P'(—2.4} 13. no.7). p'(—3. -7)
19. pt—1o.—9,\. H-9. 10) 20. ms. -2). PL?-. -2)
' V‘: I \-'/Q-
21. P[\/§;\/E): No.2) 22. P(T".;:
Find the rotation matrix for each angle below by finding the sine and
cosine values. Round your answers to the nearest hundredth.
23. 45° 24. 30°
25. 120° 26. 320°
LESSON 10.1 BOTATIONS mme COORDINATE Pt.-we 683
CHALLENGE
APPLICATION
684 CHAPTER 10
Find the image of the polygon with vertices represented by the given
matrix, rotated by the angle 0 Draw the polygon and its image on the
same coordinate axes. You may wish to use a graphics calculator for
the matrix multiplication.
0 3 2 _ . -2 I 3 _l
z7.[| 2 5].9—90’ 28.[ I 2 _4:|,0— 10°
2 1 7 4 _ 0 2 4 6 _..r.
z9.[5 3 l 2].t9—225° 3o.[ 2 l O].0—;0
31. Find the rotation matrix for a 3D°anglc and the rotation matrix for a 40°
angle. Show that their product is the same as the rotation matrix for a 70°
angle. Explain why in terms of the rotation ol'a point.
32. One sertex ol'a regular pentagon centered at the origin is (-1. 0). Describe a
procedure lor finding the coordinates of the other l'our vertices. Carry out
your procedure and plot all five vertices on a coordinate plane.
33. A point that is rotated by 0°stays in the same place. Find [Ra]. the rotation
matrix for a O°ang|e. This is called the idemii}-' imnrix. Choose any rotation
matrix and multiply it by the identity matrix. What do you notice?
34. let IRIIII denote a 6U°rotauon matrix. Use a graphics calculator to
multiply [Rm] X IR,.;.] X |RujIl X |Ru::i X |Rm| X |RL.r,|. Show that the
product is the same as IR.,I (see F..\'ercise 3-3]. Fxplain why in terms of the
rotation of a point.
35. A point that is rotated by 0°, then rotated by —9"\s'ili end up at its original
position. Find the rotation I'natri\: for a .’~5°angle and the rotation niatm
for a -35“ angle. 'l hese matrices are called invt=rsr nzcm'ic¢-s of each other.
Mtlltiply the two matrices together. W hat do you notice?
36. L'se the translormation equations on page 680 to prove that for any point
A and any rotation about the origin. the distance 0 l is equal to OA’.
[l lint: Label the coordinates of A(x. y]. Then (O.=l)*' = ? and
(OA’)3 = ? . Simplify the expression for (O.=1’J3 to show that the
distances are equal.)
37. ARCHITECTURE A restaurant atop a tall building revolves 3-60"e-aeli hour to
give patrons a panoramic view. ll" a certain table has a location of
(.’~0’, -42’) relative to the center, find its coordinates:
a. after 20 minutes
b. after t minutes
CONNECTION
APPLICATION
CONNECTION
£00k Back
COORDINATE GEOMETRV Graph each line and use the inverse tangent to
determine the angle formed by the line and the x-axis. (LESSON 10.1)
38. }'= 2x 39. y= 0.5.2‘ 40. y: _’»x+ I
Find the sine. cosine. and tangent of each angle below. Round to the
nearest hundredth. {LESSONS 10.1 AND 10.2)
41. 37° 42. 90° 43. 250° 44. —I0‘’
Find the angle Obetween 0° and 90° for each trigonometric ratio given.
Round to the nearest degree. {LESSONS 10.1 AND 10.2;
45. tan 9 = 2.75 46. cos 9 = 0.36 47. cos 9 = 0.3l 48. sin 9 = 0.77
49. PUBLIC SAFETY A slide in a
playground must have a
m;1\:iinum average angle of
elevation of 30°. The dimensions
of a slide are shown in the
diagram at right. Does the slide
meet the salicty requirements?
(LESSON 10.1)
J
)
G3
.3‘
_-'
-—'
—-'
Look Beyond
TRIGONOMETRV So far you have used degrees
to measure angles. Another common unit of
angle measure is called a radian. A radian is
the central angle measure of an arc in a circle
with a length equal to the radius of the circle.
m/0 = 1 radian
50. llow many radians arc in 3-60"’? (I lint: Find
the circuiiifereme of the circle.)
Find the radian measure for each angle below.
51. l30° 52. 90° 53. 60°
LESSON 10.1 BOTATIONSINTHE COORDINATE Pt.-we 685
686 c~iAP1=n so
'_.
.. . -v wt:-f'*’ .... -.
,:__ 4', . _ r _-_.'.- ': ''.:_
" ‘on L... n’ 0 .
. -.4 ‘ l .. Q
J" 4’-:D“\\
In this project, you
will re-examine the
Babylonian tablet
known as Plimpton 322.
Activity 1}
THE BABVLONIAN NUMBER SYSTEM The Babylonians used a base 60 number
system. Some remnants of this system that still survive are the 360
circle and our units of time, 60 minutes per hour and 60 seconds per
minute.The following are the symbols for some of the Babylonian
numerals written in the Babylonian alphabet, called cuneiform.
1 V 6 3; 11 (Y 16 (Ill so («
2 YT 7 :5 12 (ll 17 (:3 40 *3‘
3 HT 3 {ill 13 (in 13 431: so <5;
4 ‘:1 9 ‘:‘-3 14 <':' 19 (E35 60 :22
5 10 < 15 ('.'.‘ 2o «
Nu mhers greater than 60 \s'ere expressed by using these same numerals in
differeiit positions. All digits but the last position are multiplied by -.1 power of
60. For cxaniplc. the i3'.1b}‘iOl1i:.1ll number T(33i‘i" or I. I6. -11. is expressed in
our number systeni as l X 603 + l6 x 60 + 4! X l = 4601.
In order to ntake the numbers easier to read. commas are used to
separate the digits and a semicolon to represent the equixralent of
the decimal point. I lowever, the Babylonians did not use gaps or
punctuation marks. but relied on context to determine the
positions of the digits.
A number with a fractional part. such as l; 38. 33. 36. 36. is
expressed in our number svstem as
58 33 36 . 6
I+—+——,+-—+-—= l. 42 6.944444...
60 no’ 60' so‘ 6 6
The table below contains the transcription of the numbers on
Plimpton 322. Some ol‘ the damaged numbers have been 3
supplied by researchers. Compare the values in the transcription ‘
with columns II and Ill on page 638. Four entries in columns I]
and Ill below are errors. Can you find them?
Column I Column ll Column Ill Column IV
1;59,D, 15 1.59 2,49 1
1:56, 56, 53.14. 50.6.15 56,7 3,12,‘! 2
fi.'55, 7, 41. 1:33, 45 1.16.41 1,50. 49 3
‘I; 53, 1D. 29, 32, 52, 16 3. 31, 49 5. 9. 1 4 .
'I;48,54,1,40 1.5 1.37 5
1.'47,6,41.40 5.19 3.1 6
1:43. 11. 56. 23. 26. 4D 38. 11 59. 1 7
1; 41, 33, 59, 3, 45 13.19 20, 49 3 '
1.’ 38, 33, 36. 36 9. 1 12. 49 9
1; 35, 1D, 2. 28, 27, 24. 26. 40 1. 22. 41 2.16.1 10
1:33, 45 45 1.15 11
1.‘ 29, 21, 54. 2,15 27. 59 48, 49 12
‘I;27.D, 3. 45 7.12.1 4,49 13 '
1,‘ 25, 48, 51. 35. 5. 4D 29. 31 53, 49 14
1; 23, 13, 46. 40 56 53 15
Activity
THE FIRST COLUMN Use the table above to find the values of the entries in
the first column of Plimpton 322. Use as many digits after the decimal
point as you can find.
Square the entries in the tan 9 column on page 638. Compare them to the
values in column I of Plimpton 322. What do you notice? Use the second
Pythagorean identity that you found on page 646 to
identify the ratio described in column I.
CHAPTER 10 PROJECT 687
-_.
Chapter Review and Assessment
VOCABULARY
angle of rotation . . . . . . . . .. 647 inverse tangent . . . . . . . . . . . 633 tangent . . . . . . . . . . . . . . . . . 631
cosine . . . . . . . . . . . . . . . . . .. 639 magnitude of a vector . . . . . 672 transtomtation equations . . 680
direction of a vector . . .. . . . 672 rotation matrix . . . ...... . . 682 unit circle . . . . . . . . . .. . . . . 648
ldentity . . . . . . . . . . . . . . . . .. 641 sine . . . . . . . . . . . . . . . . . . . . . 639 vector . . . . . . . . . . . . . . . . . . . 672
POSTULATES AND THEOREMS
Lesson Number Postulate or Theorem
10.2 10.2.3 ldentity tan 6 = 5%
10.2.4 ldentlty lsm 01’ + (cos 9)’ = 1
10.4 10.4.1 The Law of Sines For any triangle AABC with sides .9, b, and c:
*J%—‘1 = #9:“ = ”'%£
10.5 10.5.1 The Law of Coslnes For any triangle .\ABCwith sides a. b, and c:
a’=b’+c’—2bccosA b’=a’+c’—2accosB
c’=e’+b?—2abcosC
Key Skills 8: Exercises
LESSON 10.1
Key Skills
Use right triangles to find tangent ratios.
Find the tangent of -15“.
The triangle at right is a
-l5—«l5—9O right triangle.
so the opposite leg and
adjacent leg are equal.
Thus,
tan 45° =
Find an angle that has a given tangent ratio.
0 » aosite
‘F = 1. A
:!(.l_|dt.Cl1l
Find an angle with a tangent of
Using a calctilator. tan '
688 CHAPTER no
Exercises
Use the given right triangle to find the
tangent of each angle.
1. tan A = ?
2. tan B = ?
. . . 8
Use a scientific or
graphics calculator to 3
I find the measure of
each angle. A 7 c
3. 111.4’/t = ?
4. m£B = ?
% = 26.365 == 27°.
LESSON 10.2
Key Skills
Use right triangles to find sine and cosine
ratios.
Find the sine and cosine of 30°.
The triangle at right is .1
30-60-90 right triangle with 2
a hypotenuse of length 2. so '
the opposite leg has length A I
_ I-
I and adjacent leg has "3
length
§in%O°= opposite = 1
‘ ‘ hypotenuse 2
COS 30°: tld_|d\.Cl1l = 33
liypotentise 2
Find an angle that has a given sine or cosine
ratio.
Give an angle with a cosine of 3.
Using a calculator. cos" % = 60°.
LESSON 10.3
Key Skills
Find the coordinates of a point on the unit
circle corresponding to a given angle.
Find the coordinates (x. y}
of point Pon the unit circle
at right.
Point P has L.0Ol'dil]3l€S
(cos 40°. sin -10°) = (0.77. 0.64).
Find the measures of angles with a given sine
or cosine.
Find all angles between 0”and 360°with a sine
ol'0.7'.
Using a calculator. sin" 0.7 = 414.43” s= 4-1°. From
the graph ol sin 9. you can see that there is
another angle with the same sine value. namely
|80° - -14" = I36".
360°
J -M“ 135 V 9
Exercises
Use the given right triangle to find the sine
and cosine of each angle.
5.sinA= ? cosA= ?
B
6.sinB= ? cosB= ?
Use a scientific or graphics 73 55
calculator to find the
measure of each angle.
7. mm = 7.‘ A 48 C
8. mdb‘ = ?
Exercises
For Exercises 9-12. use a sketch to illustrate
your answer.
9. Find the coordinates ol'a point on the unit
circle corresponding to a 70° angle of rotation.
10. Find the Coordinates of a point on the unit
circle corresponding to a l.’»U“angle of
rotation.
11. Find all angles between 0°-and .’~fiO°with a sine
of 0.2.
12. Find all angles between 0°and 360"with a
cosine of 0.8.
CHAPTER 10 REVIEW 689
LESSON 10.d
Key Skills
Solve triangles by using the law of sines.
Use the law of sines to solve the triangle below.
M
30 37
36
m L
"'j.:5,”“3 = ’'_;}f. 50 sin L = 3c»(’%‘‘‘) : 0.477.
Thus. mAL = bin '().47'.'’ = 28°. 50 by the
Triangle Sum Theorem,
m.»_’M = I80" — (3c»° + 23°) = I 16°.
(Note: Because AM is obtuse. (L must he acute,
30 the triangle is not ambiguous.)
Then sin 36° = sin l|6°
37 m ’ so
_ 57 sin 116° _
m — jsi" 36,, -— 56.6.
LESSON 10.5
Key Skills
Solve triangles by using the law of cosines.
Use the law ofcosines to solve the triangle below.
8
A 32 C
if = (:3 + r’ — Zbc cm A = 709. so a = 27.
Use the law of sines to find THZB.
= so 11141? s= 76°
By the Triangle Sum Theorem,
l“AC= 180° — (55" + 76°] = -19'.’
690 CHAPTER 10
Exercises
Refer to the diagram below.
0
£0
16
115
P a R
13. l'ind the unknown angles in APQR.
14. l'ind the unknown side of APQR.
Refer to the diagram below.
U
l 5
2 4 °
5 18 T
15. Find the unknown angle in ASTU.
16. Find the unknown sides in ASFU.
Exercises
Refer to the diagram below.
F
23
.49.
D 20 E
17. Find the unknown side in ADEF.
18. Find the unknown angles in ADEF.
Refer to the diagram below.
G
2% 3‘
LX
IIBH
19. Find the largest unknown angle in AGHI.
20. Find the reniaining unknown angles in AGHI.
LESSON 10.8
Key Skills
Find the sum of two vectors by using the
head-to-tail method and the parallelogram
method.
é
Find the sum of vectors a and 1: below.
/
Head-to-tail method:
79‘
_n
LESSON 10.7
Key Skills
Rotate a point in a coordinate plane by a
given angle.
What is the image of the point [3, 2} under at 90°
rotation?
The traiisforiiiatioii equations are
at’ = xeos90" —ysin90° = x[O) — y[l) = —y
;/ = xsin 90°+ yeos90° = xii) + y(0) = x
so the image is the point (-2. 3}.
Rotate a polygon in a coordinate plane by a
given angle.
What is the image of AABC with vertices A(O. O),
B( I, 2). and CT I, 0) under :1 60" rotation?
Multiply the rotation matrix by the triangle
matrix".
0.5 -0.866 0 I I = O -L232 0.5
0.866 0.5 0 .2 0 0 L866 0.866
The image L\.A’B'C'l1as vertiees A’t'0. O],
B'(—l.23.-7., 1.866). and C(0.5. 0.866).
Exercises
Copy vectors T): and 7 below.
To‘
21. liind the sum of Tiancl Tfby using the head-
to-tail method.
22. Find the sum ol 7; and '?I))- using the
head—to—t.ail method.
23. Find the sum of Taiand Tfby using, the
parallelogram method.
24. Find the sum of and T-by using the
paralielogrtnn method.
Exercises
25. ‘\v\-'h:1t is the image of the point (I, 5) under a
27'0"rot;1tion?
26. What is the image of the point (4. -3) under a
4.'>°rotation?
27. Find the image of ADFF with vertices M0. 0).
EB, I). and F13. 2) under :1 30"rot;1tion.
28. Find the inmge of AGHI with vertices G( I, I),
H[—I. I]. and I( l,—l] under a l35"rotation.
CHAPTER 10 REVIEW 691
Applications
29. INDIRECT MEASUREMENT Estimate the height ,3’ g u u
ol the building in the diagram at right. ,.",I'
I I I I I I
/"1 3°‘ /3 5° I — | |.
- -1
35 m
30. NAVIGATION Two planes set off from an
airport. one with a heading oi‘ 045 at
I00 mph. the other with a heading ol
ISO at ll5 mph. llow l':1r apart will the . .
planes be after 40 min? ‘E " J‘
31. ENGINEERING A truck weighing 6000 lb
is parked on :1 ramp that forms a lO°.Ingle
with the ground. 'l'o find the force required to
mowe the truck uphill, the vector representing .
the trucks weight (pointing straight down)
is broken down into two perpendicular
vectors, one parallel to the ramp. l‘.Il}<:‘lt'.‘I'.l rt .
and one perpendicular to the ramp. labeled b.
The stun T? + 1: equals the vector representing
the weight. Find the magnitude of 7?. the lbrce
required to push the truck uphill.
al
10
soon lb 75
32. ASTRONOMY The diagram at right ( not to scale) A
shows Alpha Centauri. the closest star to the
Sun. and two positions of Farth. A and B. at |
six months apart in its orbit around the Sun. 186 000 000 [I
Use the law ofcosines and the information in ' '
the diagram to estimate rl, the distance lrom
Earth at position A to Alpha Centauri.
0.0004222"
/
Alpha
Centauri
692 CHAPTER 10
Chapter Test
Use the diagram below for Exercises 1-4.
A
.
C 3 3
Find the tangent of each angle.
1. tanA=_7_ 2. tan B=_§'_
Use a scientific or graphics calculator to find the
measure of each angle.
3. 11141-l=i 4 m£B=;
Use the diagram at right 3
for Exercises 5-8. Find
each of the following.
_ 34 30
5. sin A=; r.osA=;
6. sin B=_:_ cos b‘=_:_ A 15 4::
Use a scientific or graphics calculator to find the
measure of each angle.
7. I111.-1=_?_ B. n1£B=_3,'_
9. Find the coordinates of a point on the unit
circle corresponding to :1 36° angle oi" rotation.
10. Find the coordinates ol'a point on the unit
circle corresponding to a I IS'''‘ angle of rotation.
11. Find all angles between 0° and 360° with a
sine of 0.6.
12. Find all angles between 0"‘ and 360° with a
cosine ol'0..’».
For Exercises 13-1 -1, refer to K
the diagram at right.
13. Find the unknown angle in 1 ,-
AIKL.
14. Find the unknown sides in 59¢ 102°
AJKL. J 10 L
For Exercises 15-16, refer to the diagram
below.
15. Find the unknown angles /’5\
in ADFF. :106 : 15
16. Find the unknown sicle
ol'ADEF. D 25 F
For Exercises 17-18, refer to the diagram
below. 5
17. l'ind the unknown side
in AQRS. 12
18. Find the unknown
angles in AQRS. 0 15 R
19. NAVIGATION" Nathan and Julia are walking
along lines that form a 38° angle. ll‘ Nathan
walks at 5.6 miles per hour and Julia walks at
-l.l miles per hour. how far apart will they be
after 2 hours?
For Exercises 20-21, copy vectors 5‘, H and E.
20. l’ind_the sum Ofl-I
and b by using the 3 / /
head-to-tail method. b 77'
21. Find the sum offi
and F by using the
parallelogram method.
22. SPORTS A swimmer heads perpendicular to
:1 2—tuiles—per—hour current. I lis speed in still
water is L8 miles per hour. Find the actual
speed ofthe swimmer and his direction angle,
0. with respect to the direction of the current.
23. What is the image olithe point [.3.—l,l under a
90° rotation?
24. Find the rotation matrix for a 150° angle.
CHAPTER 10l'EST 693
-' E’S CUMULATIVE ASSESSMENT
College Entrance Exam Practice
. t'i'u‘»’-'.
D mtemet conne- torn
Standardized
Test Prep Online
Go To: go.hrw.com
Keyword: MMI Test Prep
MULTIPLE-CHOICE For Qttestions I— ll). write the
letter that indicates the best answer.
1. Refer to the figure below. Suppose that :1 point
is chosen randomly in the large circle. What is
the probability that the point is inside the
shaded area? Round your answer to the
3. Refer to the figure below. Find the tan E to the
nearest hundredth. (LESSON 5.3)
nearest hundredth. (LESSON 10.1)
D
10.8 12
16.14
a. O.7l 5- 0-74
.,_ L... c. 0.90
c. 0.50 d- 0-67
a. 4.93
4. 'l'he value of sin 6 is given by which ratio?
2. Find the surfitce area of the prism below. (LESSON 10.2)
(LESSON 7.2)
'5 in‘ . adiacent
26"" 3' lt\'].HJl€ltuS€
.1dj.n:cnt
a. 2743 in: °”‘°‘5"
_ , 0 mos te
b. ll]. c’ diiiacel.-H
u '.| '
C. ll'I_ d onlmsifc
d_ 130 in’ ' hvpotenusc
24 in.
5. 'l he transformation l'(x, y) = [—.\'. ,v) is a
? . (LESSONS 1.7, 3.1, AND 10.7)
a. translation
b. rellection
c. rotation
d. dilation
694 CHAPTER 10
6. The transformation T(.\', y] = (—x. —y) is a
? . (LESSONS 1.7. 8.1. AND 10.7)
a. translation
b. reflection
c. rotation
d. dilation
7. Which theorem cart be used to find 11144 in
AABC? (LESSONS 10.5 AND 10.8)
a. law of Sines
b. law ofcosines
c. Pythagorean Theorem
:1. none of the ahtwe
8. Suppose that AA 5 zBand AB 5 AC. 'I'hen
AA 2 zcby ? . (LESSON 2.4 1
a. Reflexive Property
b. Symmetric Property
c. Transitive Property
d. Addition Property
111.14 = ? (LESSON 3.5)
1 3 4
. mzl + 11142
. mzl + ml.’-
. n1£2 + 1114’?-
. mzl + 11142 + 11113
9.059
10- The lilies y = ?_\'+ 3 and y= —%.x'— l are
? . (LESSON 3.3)
a. parallel
b. skew
c. vertical
:1. perpendicular
11. A point with coordinates (3-. S] is rotated by
45° about the origin. Give the coordinates of
the image point. (LESSON 10.7)
12. The magnitude ol‘ T1‘ is 6 and the magnitude
of b is ID. If 7and b are parallel. what is the
magnitude of 7:‘ + 1:? (LESSON 10.6)
13. Give the number ofvertices, edges. and faces of
an oblique pentagonal prism. (LESSON 6.3)
14. The rectangles at right
are similar. Find x. 2,,
(LESSON 8.2) X
36
15. Find kin AKL.-\-I at right.
(LESSON 10.4)
‘I
K ‘I 2 M
FREE-RESPONSE GRID
Items 16-18 may be answered
by using a free-response grid
such as that commonly used
by standardized-test services.
@@@@@@®@® O
@@@@®@@E)®@C}®
@)@@@®@@@’:}@LxO
W=T>f~‘C=)'?n"-‘(Mr-‘tt’="I[}
16. Find the radius ofa circle that has the same
area as a square with a side length off-.
(LESSON 5.3)
17. Find the radius of a sphere that has the same
volume as a cube with an edge length of 5.
(LESSON 7.6)
18. Find an angle 0° < 6 < l80°such that
sin 6 = —cos 6. (LESSON 10.3)
CHAPTER 10 CUMULATIVE ASSESSMENT 695
696
Lessons
11.1 0 Golden
Connections
11 2 0 Taxicab
Geometry
11 3 0 Graph Theory
11.4 o Topology:
Twisted
Geometry
11.5 0 Euclid
Unparalleled
11.6 0 Fractal
Geometry
11.7 0 other
Translonnations
Projective
Geometry
Chapter Project
The Tower ol
Hanoi
Taxicabs,
Fractals,
and More
CAN YOU IMAGINE A SYSTEM OF MATHEMATICS IN
which a coffee cup is the same as a doughnut?
Or one in which there are no such things as
parallel lines? You will explore many strange
ideas like these in this chapter.
By questioning commonly held assumptions
or taking imaginative leaps, mathematicians
create entirely new areas of mathematics that
often turn out to be rewarding lields of study.
Before branching out to more recent discover-
ies in mathematics. you will first study an idea
that goes back to classical times—the golden
ratio. This ratio appears again and again in
mathematics and nature. As you will see, the
sunflower on the facing page has an interest-
ing connection to the golden ratio.
'-.-4‘
5| ‘F
C
_.;c..
._ 5
.5"
-"'. .5’ -15-‘
0 ' S» J
. ,_ ‘,5
‘P
:Y [3 ‘$1-
'- -.3 ‘
GE: ’ ‘a I
. ‘~-
. -tr
:' . 4'_
es 3 - ‘~
-'7 £7 . ,','°',~"¢-
is“. ,. "3’
‘ i3"-- V
. “ 2*!’
9.: 3.
.' II
5
I
". -.
-.-
1 -El‘
‘_ ': '.
"(ts ‘-5
.._.
. II‘ ._
.-Io ' 5.
0 :0 _, 7‘,
r "_ .
.- - .-
.. “ '.'.§'/
9'‘
c
'J -O
‘u ..l
About the Chapter Project
You may be familiar with the puzzle known as
the tower of l lanoi. invented by Edouard Lucas
in 1883-. In the pu77le, a stack ofdisks in order
from smallest to largest rests on one of three
pegs. The object of the puzzle is to move the
disks. one at a time. to another peg without ever
placing any disk onto a smaller disk.
In the Ch-apter Project. you will study both the
number of moves required for a given number
of disks and the puzzles relationship to the
fractal known as the Sierpinslj gasket.
After completing the Chapter Project. you will be
able to do the following:
0 Determine the fewest numher of moves
required to solve the tower of l lanoi puzzle
with a given number of disks.
0 Use a graph to represent the possible states of
the tower of Hanoi puzzle and to lincl a
solution.
~0
About the Portfolio Activities
['h roughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of each Portfolio Activity and of the
Chapter Project is the tower of I lanoi.
0 In the Portfolio Activity on page 720, you will
study how puzzles can be represented
graphically and how solutions can be found
by using graphs.
0 In the Portfolio Activity on page 7-16, you will
generate ti lractal shape by using random
processes. such as rolling a number cube or
generating random points on a graphics
calculator.
697
Objectives
0 Discover the
relationslup known as
the golden ratio.
0 Solve problems by
using the golden ratio.
Wh _
The golden ratio can
be used to find the
dimensions at the golden
rectangle, which has been
considered for centuries
by artists and architects to
be the ‘ideal’ rectangle.
Golden Connections
l
. I
[I ll I ='
l l
l| ‘
l I -I l
,. 2- ___ 3- .-
-‘ _-‘.'-L"_,,z"._l.,t__:_-.-,'l‘;q-._ ‘ I 4‘ _
_ ..=fl<| if ' ft‘ ,__‘_‘ (iI"' P. .-
.,.___",:..:.~v‘-__-' -e,_~': ' '— _ -
-is‘-—i.~ -"‘ — ‘ «L. ‘- ' '-= ' .-
»- ‘ -. :~ ‘- 1
7' , ~ "" '- "
-'3‘; L J‘ " _____..m-
.?
4 - -‘A .I.r.&- - ‘
. _ ‘*3 -
.2 l‘. q
‘ \
' .
n'| I‘ -
‘Q ‘. _ . _ :4.
' - 1
\ . .. I‘ \"i
. ' \..k
The Ptttflteitmt is an mtciertl Greek temple tletlict'tri:tl to the godtlr.-'55 Atltemt.
Viewed from the jmm, the proportions nftltr rcmple siiggm the golden ratio, a
lltrttlterrttlticttl idea Whit'h t‘r1plm't’1.l flit.’ inmgiuation 0f('lrts$tt'r1l G1't?t’k lllittkcrs.
698 CHAPTER tt
Golden Rectangles
A golden rectangle is a rectangle with the v<— TE T ~>I
following property: lfa square is cut from
one end oflhe rectangle. the remaining piece
is similar to the original rectangle.
S S
If the long side ofthe large rectangle has .1
length of I" and the short side has a length
of s. then the sides of the smaller rectangle s _ E - s
are 5 and E — 5.
The ratio of the long side to the short side of The sm3;;er,ec,a,,g;e
a golden rectangle is called the golden ratio. is similar to me
Since the large and sm.tll rectangles are similar, entire rectangle.
the relationship between their sides can be
expressed by the proportion below.
if 5
("-5
.,_'
. “L “H, The Dimensions of a Golden Rectangle
h d . . .
§;?§u.::,':era" 1. Orient vour graph paper horwont-ally and draw a vertical segment IO
units long at the left edge. This will be the short side of your golden
rectangle.
PROBLEM SOLVING 2. Make a table. Your rectangle tnust satisfy the proportion = E, 5 .
.‘ ‘ 3
Copy the table below and experiment with different possible values for
t‘ until the values in the third and fourth columns match up to two
decimal places.
E s - 5’ = 7
20 10
? 10
10
? 10
? ‘I0 . ?
3. Complete your drawing, of the golden rectangle with the correct value
for 1'.
CHECKPOINT ./ 4. Complete the following statement: The golden ratio. is ? .
Seashefls
' _ D 1. Label vour golden rectangle 2. Draw square AEGH. Use your
ruler. compass. and ABCD and draw square FBCF. compass and the squares on
yuurgulden rectangle A E 3 the graph paper to make vour
‘"3"’ A°“"'W 1 squares as accurate as possible.
A E B
D F C H G
D _ F c
CHECKPOINT ./ 3. Repeat this process three more 4 Use a compass to make a
times. Do the rectangles that are quarter-circle in each square,
formed seem to be golden rectangles! as shown below. ‘i he resulting
l'ind the ratio for each rectangle ‘”"""~‘_ 3l‘l-‘l’0-‘“'_“=1195 '-l_
. "' . ior,'m'rthmrr spiral, which
by measuring the sides. k .
models the growth pattern of
A: E j 3 seashells such as the
chambered nautilus.
"ii ° /
D J F C I
LESSON I1 1 GOLDEN CONNECTIONS 699
;4/,'/ /
CRITICAL THINKING
700 CHAPTER ii
Computing the Golden Ratio
The proportion for the golden ratio can be solved algeliraically to find the
exact value for You must first notice that in a golden rectangle. the
proportion must be true for any value of 5. For convenience. let the value of 5
be I. and find a valtie of I" that satisfies the proportion.
f._ = .
5 E — 5
E = _|__
l E — l
("(9 — I) = 1 Cross multiply
£3 — F = I Distribute
#—£—i=o
Notice that the resulting equation is a quadratic equation of the form
ax" + l).\‘+ (‘ = 0, where (I = I. b = —I. and c= -1. To solve. substitute these
—l.J i ~
values into the quadratic Formula. A‘ = . Because F is a length.
. . . ‘la
consider only the positive value.
4—i+- —l--ll -I l+ 5
E: . J tmi] [J( J = 2‘/'3 W3
Next, substitute the values ol 8 and 5 into the ratio.
E = L 2 ‘L13
S I l
This is the value of the golden ratio. lt is often represented hy the Greek letter
dl( hi):
' P ia='—"_,"—l‘§ =i.6iso5_i9s9...
Do you think you would get the same value for t; ifsome value other than I
is tised for 5? Try several other values for 5. What do you discover?
- U D 1. Construct a square and label the vertices ABCD. Let the length of TBl)€
compass and 2 units. Extend side AB as shown.
straightedge D C
OR
geometry
graphics
software
A 8
ONSTRUCTIDN 2. Construct the midpoint of Eand label it M. Draw Since ABCD is
COMP‘-55 and a square. BC = ? units. Since M is the midpoint of Ab‘, M8 = ?
. SIRAIGHIEDGE . _ _ _ . . _
units. By the Pythagorean Theorem. Mt" — ! units.
' 3
Constructlng a Golden Rectangle
C
3. Set the point of your compass at M. and draw an are through C that
—>
intersects ABat E.
cHEc|(po|N1' ./ 4. Extend W; and construct a perpendicular to Eat E. Label the
intersection F. How do you know that rectangle AEFD is a golden
rectangle? Complete the following, statements:
= 2 -= 7 £39.: 7
AD . AL . AD .
D C F
D: —
A M 3 E
CRITICAL THINKING In the diagram for Step 4 01' Activity 3. AEFD is a golden rectangle. Name
another golden rectangle in this diagram. How do you know it is golden?
LESSON 11 1 GOLDEN CONNECTIONS 701
Exemses
. comm//1/mte
1. The golden rectangle is said to be se{f—replit‘rtri:zg. Use your results from
Activity 2 to explain what this means.
a H-n‘__ __ #3 2. Explain the construction ol"the golden rectangle. How is the Pythagorean
Acmmes Theorem used in this construction?
Online 3. Measttre the sides of several rectangles around you. such as a sheet ol-
ggyljmf-“'W-°W paper or .1 poster. Find the ratios of the long side to the short side. l\ame
Mm .;.,.}g.,., some that are close to the golden ratio.
4 4. Find the ratio of your total height to your height up to your navel. Is your
answer close to the golden ratio?
0 fill/dedgk///8 P/dtt/£6
In Exercises 5 and 6, determine the unknown side length of the golden
rectangle with the given side length. (ACTIVITY 1)
5.5=lO E‘: ?
6.s= ! E=9
7. Use the rectangle and spiral that you created in Activity 2. or construct a
new one. Draw AC and DE. What seems to be true about the intersection
of these segments? (ACTIVITY 2)
8. Use the method from Activity 5 to construct a golden rectangle whose
short side has a length of l in. (ACTIVITY 3)
0 Practice dlfd 74,0;/y
Determine the indicated side length of each golden rectangle. Round
your answers to the nearest hundredth.
9. 10.
11. _ 12. 5
702 CHAPTER 11
CONSTRUCTION
The value of the golden ratio, (0, has some interesting properties. Refer
to the diagram below for Exercises 13-15.
<
0
—>
1 ¢—1
13. Set up a proportion involving the side lengths of the two golden rectangles
in the figure.
14. Enter the value of gain your calculator, using as many decimal places as
your calculator will hold. and find 49‘. Compare this value with (,3. What do
you notice? Using your proportion from Exercise 13, explain why this is
true.
15. Enter the value oi‘ (Din your calculator. using as many decimal places as
your calculator will hold. and find go“. Compare this value with (:4 What
do you notice? Using your proportion from Exercise l3. explain why this
IS true.
Regular Pentagon ‘
a. Drawr3A and diameter 8—C.
Construct M, the midpoint of HE.
b. Construct line 8 ' E5 through A.
Choose either point where E
intersects GA and label it D.
BC
1:. Place your compass point at M
and draw an are through Dthat
intersects 55. Label this point P.
d. Set your compass to the length
DP. Mark off length DP around G:-A.
Draw segments to connect the
arcs, forming a regular pentagon.
16. Use the directions above to construct regular pentagon DEFGH in a circle
with a radius of-at least 3 cm.
17. Draw Measure F.-‘and L-'—Hto the nearest millimeter.
18. Find How close to ¢'Jis your answer?
LESSON 11 1 GOLDEN CONNECTIONS 703
For Exercises 19-21, refer to the diagram of the regular 0
pentagon at right. You will use trigonometry to verify
that the ratio 5-'1 is equal to ¢. E H
DE
19. Use the fact that DEFGH is a regular pentagon
to linil mLD.
20. ADEH is isosceles. so mLDFH - mLDHF - ? . F G
n lnumoccomoct ,7?“ 21. Use the law of sines and properties of proportions to write an expression
Q .
Homewofk for the ratio Iivaluate this expression on your calculator. \~\-‘hat do
Help Online .0“ if:
i 8'» -
Go To: i_;o.hrw.t:om
Keyword: h .
MG, ,,mmo,k Help If you extend t e sides of a regular pentagon,
fol Exercises 21 you get a five-pointed star known as the
"d 2‘ star of Pythagoras.This star was the M
4 symbol of the followers of Pythagoras.
22. Construct a regular pentagon and extend the
sides to form a star of Pythagoras.
23. Compute tlte measures of the angles in ADE]. L
E
_ _ ms
25. Measure H. and IF to the nearest millimeter. Find
What do you notice?
26. Measure l—F.ll1d F-Zto the nearest millimeter. Find
What do you notice?
24. l'se the law of sines to find What do you notice?
Recall from Lesson 2.2 that the Fibonacci sequence is a sequence of
numbers in which each term is the sum of the two terms preceding it.
The following is the beginning of the Fibonacci sequence: 1. 1, 2, 3, 5,
8, 13, 21,...
27. Find the next five terms ol’ the Fibonacci sequence above.
28. Copy and complete the table below by dividing each term in the sequence
by the preceding term.
Term 1 1 2 3 5 8 1 3 21 ? ? ? ? ?
Ratio — } % 7 7 7 7 7 7 7 7 7 7
Value — 1 2 7 7 7 7 7 7 7 7 7 7
29. What number do the ratios approach? Write a conjecture about the ratios
of consecutive terms of the Fibonacci sequence.
30. The 28th term ofthe Fibonacci sequence is 3l7,8l l, and the 29th term is
514,229. Find their ratio. Does this agree with your conjecture?
.. I — ' . . . .
:4 / . I 31. let in = the m-gative solution to the quadratic equation on page
‘ on — ldfl"
«E '
Use this expression to find the 20th term of the Fibonacci sequence.
700. Then the nth term of the Fibonacci sequence is given lily
c H A L L E N 6 E 32. Use the expression for the nth term ofthe Fibonacci sequence from
Exercise 3| to explain why the ratios in the table for Exercise 28 approach
ch (Hint: What happens to [d')'' as 71 increases?)
704 CHAPTER i1
APPLICATIONS
CONNECTION
33. PHOTOGRAPHY A photography studio offers prints in the following sizes:
3 x 5, 5 x 7, 8 x I0. I l x 14, and 16 x 20. Find the ratio ot the long side
to the short side for each of these rectangles. Which is closest to the
golden ratio?
34. MARKETING A manufacturer wishes to make a cereal box in the shape of a
golden rectangle, based on the theory that this shape is the most pleasing
to the average customer. It‘ the front of the box has an area ol‘ I04 in.-'.
what should the dimensions be? Round to the nearest inch.
35. FINE ARTS An artist wishes to make a canvas in the shape ofa golden
rectangle. I le only has enough training material for a perimeter of 36 in.
What should the dimensions of the calwas be?
1.00:? Bdtk
COORDINATE GEDMETRV Find the distance between each pair of points
below. Round your answers to the nearest tenth. (LESSON 5.5)
36. (D. 0] and (4. 7) 37. (I. 3) and (4. 21
38. (-6, 0} and (5. -2) 39. t—t,—3) and (3, -5]
40. Write an equation for the set of points in a coordinate plane that are a
distance of 3 from the point [2, I). (LESSON 9.5)
41. Find the coordinates ofa point on the unit circle that is the image of the
point (I, 0) under a 50° rotation about the origin. (LESSON 10.3)
42. l'he point (-0.645, 0.766) is the image of the point ( I . 0] under a rotation
about the origin. What is the angle ol' rotation? (LESSON 10.3)
43. Vector Tfin a coordinate plane points front the origin to (2. 5) and
vector b points from the origin to (3. 2]. What is the sum of these two
vectors? Sketch a diagram to illustrate your answer. (LESSON 10.6)
1.00:? Beyond
Fibonacci numbers, which are
. . . 1 -
numbers in the Fibonacci sequence, \ . ‘ I
occur frequently in nature. For -~ ‘ . * _.
. . a an .
example, the numbers of spirals in .9 ‘.0 J. n. -
. . I -
pinecones, artichokes, sunflowers, and o ' ago. . ‘ .0: o 0;‘.
. . . - ‘
other obiects are often Fibonacci ‘"9’ 3 Iigoglg -
numbers ‘:32 . " ’ ' J 5, '3.
. . ~
_ _ _ p gaii :9 :3 , .
44. Examine the photo of the sunflower . p:::'.‘.E3‘ N,‘ .5
at right. Notice that the seeds form -.1
two sets of spirals in opposite
y K -
directions. Try to Count the number g‘. " H I'J:'\\‘§ . $9 ’
of spirals to the left and to the right. ' ‘ v/J ' .12
Both numbers should be I-'ibonacci ' ‘' '_, ,0‘ -
numbers. What are they? “g ‘,5’, , O’! a
45. The numbers of petals of many types ‘I ‘ E a’ - ‘
of tlowers are l-‘ibonacci numbers. . _ ' q,
Find some pictures ol‘ Flowers and I - ‘ ‘ "\.’.
count their petals. Wliich ones are } ‘ , ~ V “\‘ \
Fibonacci numbers? - - _ \ ‘K5 \
LESSON 11 1 GOLDEN CONNECTIONS 705
Taxicab Geometry
I - '.
u ' . I - 3;-.5 . 1-" " '
i _ ' .
* P->%~1'~fe '- ...
g.‘‘._. as ' .
. - ctr - \
I ‘ I 4-
K. r‘
'3’? \ o;
__—=’— - ‘ ‘J
"“'-' - ’ ~I_. - '
3 ~- t
5 _ ., r ‘ _ V
' ‘ -HI‘ - .9
. . ' - J7
Obiectives - ' - ~ \
0 Develop a non- I ' it ‘_
Euclidean geometry, 2.
known as taxicab _:‘_
geometry. based on a —f- . -]
taxicab's movements - ‘
on 3 street grid. - ,'
I. I . _ i
0 Solve problems within - '-. .___z_. _ ' I" _
a taxicab geometry 1 __- ' - ' ‘ ‘_‘_
system. ,§~ - ‘ “ -\
\ ‘ ' n (
' , “ Z / , 3 ‘I
Agaomau-ysmdontwourd. § -3-1} ,
(Ire Pythagorean Theorem to find the distance V - ; - ,
bemoentwopoirrtsonacltynrapfli .- .r. -— - _1_____, . "'
a taxicab driver rnigm have a very tfrfferem‘ .—~- '3'’ ’ ‘E --'- ‘
idea. In this lesson, you will study a .. - - etry ‘ _,-P... -33- -‘ \
based on a taxicab drive/s definition ol the ' - - _. ,. .
distance -- ~nt‘wapor'nt$. -it-N ' ' ' x ,
Taxidistance
In taxicab geometry, points are located on .1 special kind of map or
coordinate grid. The horizontal and vertical lines of the grid represent streets.
Unlike points in .1 traditional coordinate plane. points in a taxicab grid can be
only at intersections of two “streets." Thus, the coordinates are always integers.
In tznticnl) geometry. the distance y
between two points. known as the
taxidistance. is the smallest number 6
of grid units. culled blocks. that .1
4
2
O
taxi must trnx-‘el to get from one point . 513' 4'
to the other. On the map shown.
the tutidistance between the two A“ H
points is S. '
I ‘ 3 ‘ I X
2 4 6 3
in this trixicrrir grid, the mxirii.~ranct'
from point A to poirit B is 5
706 CHAPTER 11
- I LL
graph paper
PROBLEM SOLVING
CHECKPOINT V
PROBLEM SOLVING
CHECKPOINT M
' I
Explor ng Taxidistances
Part I: The taxiclistancc from a central terminal
Assume that all taxis leave for their destinations front a central terminal at
point O(D. D].
1. Draw the si\ destination points y
in a taxicab grid. as shown in
the diagram at right. Label the _
points A through F and give 0 ._ 5
their coordinates. 2..
2. Make a table. Find the C
ta.\'idistance from O to each ol ' ‘ ' ‘
the six destination points.
(Make sure that you have found .5 -2:
the smallest number of blocks _4.. .
in each case.) Copy and F
complete the table below.
Point Coordinates I Taxidistance from O
A n, V; I 7
(7, ?l I 7
c n, 7» _ 7
o 4?, ?l l 7
E t?. ?) l ?
F 4?, 7» | 7
3. Based on your results. c.omplete the following conjecture:
'l he taxidistance between the points [0, O) and (x, y) is ? .
Part ll: The taxidistance between any two points
1. Make a table. Use the diagram lrom Part I to find the taxidistance
between the pairs of points given in the table below. Copy and complete
the table below.
(x., y.) lxz. yel x. X, y. y, Taxidistance
A 18 ‘I T ‘I 4 5
A D ? ? ? ? ?
A E ? ?
C D 7 ? ? ? ?
D E ? ? ? ? ?
E F ? ? ? ? 7
8 F ? 7 ? ? 7
2. Based on vour results. complete the following conjecture:
The taxidistance between the points (x.. y,) and (X2. yg) is ? .
LESSON 112 TAXICAB GEOMETRV 107
CRITICAL THINKING
I
l are-vh new I
PROBLEM SOLVING
CHECKPOINT M
708 CHAPTER it
Two Points Determine. . .?
For any two given points in Euclidean geometry. there is just one minimum-
distance wathwav between them. Is this true in taxicab aeontetrv? Consider
a C‘ -
points A and B below. In both arrangements. A and B are 3- taxicab units apart.
In the second arrangement. there is more than one minimum—distance
pathway between them.
B B .8
3 3 —
A. L .8 A. _I J’ Is
A A
First arrangement" Second arrangement:
one pathway three pathways
Under what conditions is there just one minimum-dist.tnce path between two
points in taxicab geometry? L.|nder what conditions is there more than one?
Taxicab Circles
In Fuclide-an geometry, a circle is the set or points that are a fixed distance
from a given point. What happens when this definition is applied to
taxicab geometry?
1. Plot a point P on graph paper. Then plot
all the points that are located I block from
point P. l'he very uncircul-ar—looking result
is a taxicab circle with a radius of I. ,/P
2. Draw additional taxicab circles with 0 0 0
O
radii of 2. 3, 4, and 5. Count the
number of points on caLl) circle. Find
the circumference oi" each circle by
adding the ta\:idistances between the
points on the circle. A raximb (frt‘I(' with a rmiius of I
3. Make a table. Copy and complete the table below to lind expressions for
the number of points on a taxicab circle and the circumference in terms
of its radius.
Number oi
Radius points on circle Circumference
1 4 8
2 7 7
3 7 7
4 7 7
5 7 7
r 7 7
4. Use the information in the chart to determine a taxicab equivalent for .1.
(I “m_ n = circumlcrcncc)
' diameter
Exercises
. Communicate
1. Why is the geometry studied in this lesson called taticah geometry?
2. Explain how to determine the distance between two points in taxicab
geometry.
3. Why is 1: not used in taxicab geometry? What is the taxicab equivalent
for It?
4. What are some practical applications of taxicab geometry?
5. What are some factors other than distance that a taxicab driver might take
into consideration when planning a route?
0 6///d€d3t(’///3 Pl'd6‘t/6‘€
For points MO. 1). Bl2, 3). and Cl—2. 1). find the taxidistances below.
(ACTIVITY 1)
6. AB 7. BC 3. AC
Plot the taxicab circle with the given center and radius. (ACTIVITY 2)
9. center: (3. 2]; radius: 2 10. center: (—I. 4); radius: -1
0 Pfdflt/£6 dlfd 5,0,0/y
Find the taxidistance between each pair of points.
11. (0. 0) and (7, 5) 12. (5. -3) and (-2, 4)
13. (1. 5) and [-2. -3) 14. (-9. -3) and (-3. —l)
15. (-11. 4] and (-3. 9] 16. (-129. L5] and (I52. 236)
Find the number of points on the taxicab circle with the given radius.
17.r=2 18.r=4 19. r=l2
n Intern tconnecl Find the circumference of the taxicab circle with the given radius.
g:$e3~;l<|>i':e 2o. r= I 21. r = 5 22. r = no
figggfgm-“°" Plot the taxicab circle with center P and radius r.
'1§}g::j;:;D'_§2'F 23. P[O. O"); r = 3 24. PIS. -2]; r = 5 25. Pt"-l. 3]; r = 2
26. ldentifv two pairs of points in a ta\:icab grid that have a ta.\:idistanCe of 4.
One of these pairs should have only one minimum—distancc pathway
between them. and the other should have several minimum-distance
pathwavs.
27. Sketch all of the dilierent minimum—tlistance pathways between the points
(1. 2] and (4. I) in .1 taxicab grid. How many pztthways are there?
28. Sketch all of the dil'l'erent minimum-distance pathways between the points
(3, OJ and (5, 2) in a taxiczab grid. How many p-.1thw.t_vs are there?
LESSON n2 TAXICAB GEOMETRY 709
CHALLENGE
APPLICATIONS
710 CHAPTER II
Shop (5. 4}
0
Recall from Chapter 4 that a point lies on a segment's perpendicular
bisector if and only if it is equidistant from the segment's endpoints.
Use this theorem in Exercises 29-33 to discover the taxicab equivalent
of a perpendicular bisector.
29. a. On a taxicab grid, plot points /\(0, 0) and BH. 2). Locate all points that
are a taxidistance of} from both A and B.
b. On the same diagram. locate all points that are a taxidistance of 4 from
both A and b‘.
c. Continue locating points that are the same taxidistance from both A
and B until you understand the l'orm of a taxicab perpendicular
bisector.
30. llow is the perpendicular bisector you constructed in Exercise 29 similar
to a perpendicular bisector in Euclidean geometry? How is it different?
31. Use the method lrom Fxercise 29 to construct a taxicab perpendicular
bisector for the points (5. 5) and [-4. U). l low is it like the taxicab
perpendicular bisector you constructed in Exercise 29? How is it dillerent?
32. Use the method lrom Fxercise 29 to construct a taxicab perpendicular
bisector for the points (I. 2) and (5. 2). What do you notice?
33. Lise the method from Exercise 29 to construct a taxicab perpendicular
bisector for the points [2, O) and [3, 2), What do you notice?
34. Use your formula from Activity I for the taxidistance between two points
to derive an equation for a taxicab circle with a radius of r.
35. For the points AID. O) and B(2. 2). lind the set of all points P such that the
sum ol the taxidistances -l P and BP is equal to 6. Describe your results.
36. PUBLIC SAFETY l'he mayor of a city wants to install police call boxes at
intersections around the city so that from cvcry point in the city there will
he a maximum distance of two blocks to a call box. Describe a way this
can be done. l'ry to find a way that uses the minimum number of boxes.
(l lint: Draw a pattern of taxicab circles with a radius of 2.)
37. COMMUTING lenny works at an office during the day and then works in a
retail shop in the evenings. Because she plans to ride her bicycle to work.
she would like to live within I0 blocks of her day job and within 8 blocks
of her night job so that she does not have to ride as far in the dark. Use the
taxicab grid at left to determine all of the possible
locations where Jenny should look for an apartment.
Look Back
Find y for Exercises 38 and 39. (LESSON 9.5)
39.
4
7
1 5
38.
9
40. Let BC= 5. AC= 21. 41. Let MP: I8 and .'t.-1N= 7.
and CD: 6. Find DE. Find MR.
(LESSON 9. 5; (LESSON 9. 5)
C‘
R M
‘ §N
P
Refer to the triangle below. Find the value of
each expression. (LESSONS 10.1 AND 10.2) 53 28
42. tan 6 43. cos 6 44. 6 a
1.004’ B€70lfd
b
'71
W
D
The following is a geometric "proo " that O = 1.Trace the steps and try
to find the error in the proof.
45. a. On graph paper, draw an 3 x 8 square.
Divide it into three regions. A. B. and A
C, as shown.
C
b. Cut out the pieces and fit
them together to torm a 5 x I5
rectangle. as shown. A C
B
c. The area of the square is 8 X 8. or 64. The area of the rcctattglt: is
5 x 13, or 65. However. since both areas are the sum of the 1re.ts of
A. B. and C. the areas must be equal, so 64 = 65. Subtracting 64 from
both sides of the equation gives 0 = I. \-\-‘hat is wrong with this proot?
LESSON 112 TAXICAB GEOMETRY 71 1
Objectives
0 Determine whether a
given graph has an
Euler path.
0 Use Euler paths to
solve problems
lllV0l\lll'Ig graphs.
Graph Theory
l\C\'l.\'(‘r.>'bLllGA
. -'r_ In
..'-' -''.| ‘-~._
‘ H‘. ‘M ' , _-“H
. I ' .. '-'-
.1‘fl.3.El‘5=TIl.':?r.®"» '&f_95'_:--
. _&v:au3q_.§33
’:- 3- .
','w‘\rfi '-5 ' ‘ta.
Wh ln 17.‘:|‘i. Leonhard Euler (pronounced "oIlar")
published a famous paper in which he solved a '
popular puzzle. Hls solution lntmducod a now my
branch of mathematics known as graph theory.
..4... - -
A local pasritnc in the city oflmnigslrerg. Prussia (now l\’nlirringratl, Russia) was
to try to wrtll: t'll.l‘tl55 Erich nftlrt: SE1-'t'll lnizlges over the river tvirltottt crossilrg any
bridge rwtrt’.
*\Z/
7 1 2 CHAPTER 11
D
The Bridge Problem
The following is an excerpt from Euler's paper. “The Solution to a Problem
Relating to the Geometry ofP0siti(1n":
The prolrlern, which lam told as
witlel y lcrrown, is trs_fbllrm*$: hr
K('lIllg.\'lJt!rg in Prussia, tlieze is
an islaml .4, called the Kneiplzofi}
lltt’ river wltirlr surrounds it is
tlivitierl into two branches, and
tltcst’ brariclzes are cros.~‘et.l by
seven bridges, tr, lz, c, d, r’, j; and
g. Concerning tliesc bridges, it
was tJslcer.l ivltotlter tm_vone could
arrange a route in Sttrlr a way
lllat he would cross each brirlgc t'lllt'(’ and only once. l was told that some people
tt5st'rt£’rl that‘ this it-'tI.~' illlpOS3ilJlt?, it-'ltr'l¢' otlwrs were in doubt; but nobody wortlrl
actually zrssrrr that it could be done.
730.; /
Euler's analysis olthe problem can be visualized by using a diagram called a
graph. A graph is composed of points, called vertices. and segments or curves
linking the vertices, called edges. In the graph at left. each land area (refer to
the map above] is represented by a vertex. and each bridge is represented by an
edge. The bridge problem now becomes that of finding an Euler path —a
continuous path that travels along each edge exactly once.
Odd and Even Vertices
You may have tried to Find an Euler path in the graph of the seven bridges and
decided that it was impossible. The people of Konigsberg thought so. but no
one had proved it inatheniatically until Euler presented his proof.
Euler's proof was based on the number of times each land area would have to
be visited in a solution of the problem. which is related to the number of
bridges to the land area. A graph makes his reasoning easier to understand.
In a graph. the number of edges at each vertex is called the degree of the
vertex. In the graph of the bridge problem, the degree represents the number
of bridges connected to each land area. Even verticcs have an even degree anti
Odd vertices have an odd degree.
_R
In the graph at right. Q has degree 4. so it is an /I \
even vertex. R and 5 both have degree 3. so they 0. .
are odd vertices. I’ has degree 2, so it is an even \ 5
vertex. Does the graph contain an Euler path? ‘_
T
In the lbllowing Activity, you will explore the relationship between the degree
of the vertices ol'a graph and whether the graph contains an Euler path.
Euler Paths
PROBLEM SOLVING \-\’hicIi ol the graphs below contain an l;uler path-.‘ Make a table like the
one below and see if you can discover the relationship.
O O O Q C D
a. l b. c. I \ . | §
I O
o
0 j o 0 o 0 L 0 \ OJ
0. f. ' 9. h.
In some graphs, edges ' ' / \ __ o \ \f
I o 0 O T .
may Intersect at a paint I X I I . I \ .
that is not a vertex. o o o \-
Number of Number of odd Number of even Is there an
vertices vertices vertices Euler path?
8. ? ? 7 ?
b. 7 | 7 7 7
c. 7 I 7 7 7
cuscxpomr ./ Make a conjecture based on your completed table. ['93 your conjecture to
complete the following theorem:
Theorem
A graph contains an Fuler path ii and onlv if there are at most ?
odd vertices. 11.3.1
LESSON 11.3 GRAPHYHEORY 713
E X A M P I. E oDoes the graph ofthe bridges of Konigsberg contain an Euler path?
PROBLEM SOLVING
CRITICAL THINKING
O SOLUTION
All lour vertices in the graph are
odd. so there are more than two odd
vertices. Tl1erelore. by Theorem I l.3.l.
the graph does not contain an Euler
path. That is. there is no route that
crosses each bridge (each edge of the
graph) exactly once.
C
0' —Degree
Degree //
5 \‘
AC
h
B
\\
/‘o
'< - Degree 3
0 Refer to the lloor plan ofa house given
at right. Is it possible to walk through
all the doors in the house by going
through each door exactly once?
0 SOLUTION
Make a model. A graph can be used to
model the lloor plan, with a vertex for
each room and for the area outside the
house and an edge for each doorway.
The graph has only two odd vertices
[Q and R). 50 it contains a Euler path.
'l hus, it is possible to walk through
all the doors in the house by going
through each door exactly once.
0
P O R
%T%j
I-
6
S
*5
\{
How could you find an Euler path in the graph above?
7 1 4 CHAPTER 11
Starting and Stopping
The following problem may provide some insight into Theorem ll.3.|:
While hiking on a snowy dav, you startle a
rabbit. It runs from bush to bush, hiding under
each one. It covers all paths between the bushes
[see the diagraml without following the same
path more than once. ’l'hen it stops. which
bush is the rabbit hiding under?
After trying a few routes, you should see I " l‘
that the rabbit always ends up under bush A x I,’ : “~._
F, an odd vertex’. The only other odd vertex ‘. ’ 3 ’, I --_
is the woods, where the rabbit began its C ' "
Journey. 0
CRITICAL THINKING
Suppose that there is an even vertex in a
graph and you do not start from it. You will
never get stuck at this even vertex for the
following reason: If:-lierc is an unused edge
lendirig into the even vt’rIt’x_. tlwrt’ must‘ he an
unused edge leading our of it.
even vsrmcss
\ /" _\
/ \
>
/\
On the other hand. suppose that there is an O00 VERHGES
odd vertex in the graph and that you do not \ I
start from it. ll" you are ahle to get to this .<; \ ' /4
vertex and keep coming back to it. then you
will eventually get stuck at it. There will be no
mmserl paths leazlirtg rtwrtyfronr it.
/ \
Notice that if you start at an odd vertex, it becomes. in ellect. an even vertex
once you have left it; therelore, you will never get stuck at it.
ll" there are exactly two odd vertices in a graph_. you can start at one and try to
end at the other. But il there are more than two odd vertices in a graph, there
is no chance of finding an l.'uler path through the graph.
'l'hus, the “only if“ part of Theorem 1 L3. I , which states that there is an Euler
path through a graph only ifthere are at most two odd vertices. has been
proven informally. And as vou can see. the two odd vertices must he the
starting and ending points of the graph. In the rabbit puzzle, one odd vertex
(the woods]. is the starting point. and the other odd vertex tbush E], is the
ending point.
The "if" part of the theorem. which states that there actually is such a path
when there are at most two odd vertices, has not been proven. However, in
Exercises 49-51 ol this lesson, you will learn a method. known as I-'lenry’s
algorithm. for finding such a path when the conditions are right.
Do vou think it is possible for a graph to have just one odd vertex?
Euler Circuits
A graph with only even vertices contains an Euler path that can start at any
vertex. There is another important feature of such a graph: 'l'he vertex that is
the starting point of the Euler path is also the ending point of the path. An
Fuler path that starts and ends at the same vertex is called an Fuler circuit.
E X A M P L E 0:\ street sweeper is cleaning the area
PROBLEM SOLVING
shown at right. is it possible to sweep
lmth sides of every street exactly once
and end at the starting point?
SOLUTION
Make a model. Model the problem with a
graph. using an edge to represent each side of
each street. The vertices represent intersections.
§::::n:z3
Because every vet te.x is even. the graph must
contain an Euler path. The street sweeper will l
L.’ L.’
be able to pl-an the desired route. '
LESSON 11.3 GRAPHYHEORY 715
Exercises
. Communicate
1. Exzplain the K("1nig.sl)ergl1ridge problem in your own words. \-\"h_v is there
no solution?
2. Suppose that the residents of Kotngsberg decided to build more bridges
until there was a way to cross each bridge exactly once. Discttss several
ways this could be done.
3. Explain the dilference between an Euler circuit and an Euler path.
4. Why do you think Euler called the Konigsberg bridge problem “a problem
relating to the geometry oi‘ position"?
6/r/dad 34'///3 Pratt/ce
Determine whether each graph below contains an Euler path.
(EXAMPLE 1)
5. . \ . 6. . 7. \
fl go
8. Draw .1 graph to represent the lloor plan
at right. with a vertex for each room and
the area outside the house and an edge for
each doorway. Does the graph of the floor
plan contain an littler path?
(EXAMPLE 2)
9. A truck is collecting materials for recycling.
The driver's route must cover both sides of
every street exactly once and end at the
starting point. In the map area shown at
right. is such J route possible? Use .1 graph
to illustrate your answer. (EXAMPLE 3;
. Practice and Apply
In Exercises 10-15, determine whether each graph contains an Euler
path. an Euler circuit, or neither.
_ l
\T/‘
10. 12.
11>» M.
7 1 6 CHAPTER n
. ‘I4. . 15.
o
'\\¢' \ \/
13.
o
For each floor plan below, draw a graph with a vertex for each room
and the area outside the house and with an edge for each doorway.
Determine whether the graph contains an Euler circuit.
17.
16.
l 1
A B C D
Fb 3 —t >—[—-4 l-Tl
E D C A F ‘ E
._L _l:l%
For Exercises 18-20, refer to the diagram below, taken from Euler's
paper, "The Solution of a Problem Relating to the Geometry of Position."
._D'/ E
(I
(K
/. e . ,,
‘ C
18. Draw :1 graph representing, the land areas and bridges in the diagram.
19. Does the graph contain an Euler path? an Euler circuit?
20. lfyou wanted to wall»: across each bridge in the diagram exrittly once.
where would you start? \-‘-‘here would you finish?
In Exercises 21-29. you will explore some simple concepts of graph
theory. Copy and complete the table below.
Sum of degrees of
Graph Number of edges vcrtices
\\ 21. 2 22. ?
23. 7 24. 7
o—-o
I — Q
l
0 o 25. 7 26. ?
\
LESSON 11.3 GRAPHYHEORY 717
CHALLENGE
- - - connect {(3,
Iflfll
Homework
Help Online
Go To: go.hrw.corn
ltem-ord:
MG! Homework Help
for Exercises 34-35
«'2»
O
;>
718 CHAPTER II
27. Make a conjecture based on your results from Exercises 2l—26. Use your
conjecture to complete the following theorem:
l'he sum of the degrees of the tertices of a graph is ? the number of
edges.
28. l'se the fact that each edge of a graph has two endpoints to explain why
the theorem in Exercise 27 is true.
29. An immediate corollary of the theorem in Exercise 27 is that the sum of
the degrees of the vertices ofa graph must be even. Use this fact to prove
that the number ol‘ odd vertices in a graph must be even.
Determine whether each figure below can be traced completely without
lifting the pencil from the page or retracing any part of the figure.
30. 31.
32. CULTURAL CONNECTION: AFRICA A popular
game of children in the Shongo tribe in Zaire
is to trace networks. like those shown at right.
in the sand with a linger. The networks must
be traced in a single stroke, without retracing.
Can the network at right be traced in this way?
llso. how could it be done?
33. tn the diagram at right.
is it possible to draw a
continuous curve that
intersects every segment
exactly once? {The attempt
shown intersects all but two
segments.) if it is possible.
draw the curve. ll‘ it is not
possil)le. explain why.
I-
I
;
LAW ENFORCEMENT Refer to
the diagram at right. A police
officer is checking parking
meters lrepresented by the : ' ' ' ' : : ' ' ' ' :
red dotsl along the streets. : . . _ . : : . . . _ :
The officerwishesto go ____ __ ._ ______
down each rowof meters , , , . , . . , . . . .
exactly once and return to : : : : :
thestartingpoint. 0000-0300000-
3-:. Draw a graph that represents I .
hi
this situation.
35. Determine whether the ol'licer
can complete the desired route
APPLICATIONS
CONNECTION
36. WILDLIFE MANAGEMENT A naturalist
observing a pack of wolves comes
across a set of trails on the ground, -
shown at right. Could the trails be ‘' ' '
traveled by a wolf in one trip. starting -
at the den and not retracing any of D;
the trails? Why or why not?
37. FUND-RAISING J0 and 'TaIm1r:1 are A
trying to raise money for .1 school trip _, \
by selling magazines door to door. lo 53;, c,c.i.%°""’ F” =
decides to cover each side of every 3 "°’ -;=';',
street separately, while llunara wants " I E
to alternate from one side of the street |§ 7* E“‘“"*“‘ T‘
to the other, covering it in one trip.
Refer to the map at right. Draw a
graph for ]o‘s route. Is there an Euler
path for Jo's route? Draw :1 graph for
l2tnmra's route. Is there an liuler path
for T;1m:1ra‘s route?
Look Back
Copy each figure and reflect it with respect to the given line.
(LESSON 1.6)
38. 39.
/'
In Exercises 40-“, write each statement as a conditionaI.Then write its
converse. (LESSON 2.2)
-:0. All people who live in California live in the United States.
41. Every square is .1 rectangle.
-:2. A sqti-are is a parallelogram with tour congruent sides and four
eongruent angles.
-:3. A dodecagon is a polygon with IS! sides.
-:4. TRIGONOMETRV For any angle 6 < 45°. sin 6 <2 cos 9.
Each solid below has a volume of 100 cubic units. Find h or r for each
figure. Round your answers to the nearest tenth.
45. 46. 47. 48.
LESSON 11.3 GRAPHYHEORY 719
L004’ Beyond
In Exercises 49 and 50, you will learn about bridges, which are another
A feature of graphs. In Exercise 51, you will apply Fleurys algorithm, a step-
'\ by-step procedure that uses bridges to find an Euler circuit in a graph.
01 0 B -:9. An edge in a graph is called a lnidge if removing it would split the graph
\ ' C into two separate pieces. Identify a bridge in the graph at left.
50. Draw a graph that cont-ains an Fuler circuit. ls any edge a bridge? Can a
graph that contains an Euler circuit have a bridge? Wh_v or why not?
/-E\ 51. Henry’: ulgorirftm. given below. is a procedure that uses bridges to find an
H. , F Euler circttit in a graph that has no odd vertices.
\-. Fleury’s Algorithm
G step a: Veril'v that the graph contains an Euler circuit. Choose a
starting vertex.
Step b: Travel any edge that is not a hridge in the untraveled part of
n '“t"'°“°""°d the graph.
P°'"°'§° step c: Repeat Step 1; until you have completed an Euler circuit.
Extension
5010; g,,_h,w_.;.,m Note: In Step b. consider only the untraveled part of the graph. If a bridge
:‘=g';~';$=m is removed lrom this part ol the graph, there will be edges that you are
unable to get back to. B’ C
l'se Fletm_."s algorithm to Find an Euler \\ ,.__ _ \
ciruit in the graph at right. I ist the A'\ '5 ' H'\ /‘D
vertices in the order they are traveled. F. T .E/
«FLUO
62*
Q USING GRAPHS TO SOLVE PUZZLES
Suppose that vou have three bottles. One holds 8 quarts. one holds 5 quarts,
and one holds 3 quarts. The 8—quart bottle is full of water. [low can you get
exactly -1 quarts oliwater in both the 5-quart and 8-quart bottles?
Problems like this can be solved with the aid of 1. The lirst level of the . (3, o, o)
a graph. The amount of water in the huttles at graph for this problem
any given time can be written as an ordered is Shown 3|! right.
triple. For example. the initial state in the puzzle Exlllilin how I0 get *3‘ 5- 0" "'5' °' 3’
can he “rn'|_[en as [8, O_ n]-eaning 8 [|u;"'[5 in ITOITI IIIC illiilili SUITE (0 (.‘llCi'l of Tilt‘ hl.2ll.CS
the 8—quart bottle, () quarts in the 5-quart bottle, Tellresenlfd b)’ ‘’9”iC‘’5 "1 ‘he 8r'<‘Ph-
lllld 0 L]|.lllnS ill TIN.‘ 3'qI.l'tlI'i. bouilf. EJCIT Sldle T5 2_ \‘Vha[ m()ve§ are pogsihle frgnj [he p()5i[i()n
represented lw a vertex in the graph. and two (3, 5_ 0}? what mo“-5 an: pgggiblc fmm the
vertices are connected by an edge if it is possible position (5, 0, 3]? Complete the next level of
to move from one vertex to the other in one the graph.
step‘ The fllegfil mow“ c(.ms"“ 0‘ the f°”,(M'"g: 3. Extend the graph until you find the position
pouring all ol the water lrom one bottle into M‘ 4‘ O)_ Dt.'5mL,L. how [D pm” me Wm
another bottle. or pouring as much water as from the homes to get exactly 4 quarts in
possible from one hottle to another bottle. bmh the 8_qmm and 3.-,_qu.(‘n bOme5_
WORKING ON THE CHAPTER PROJECT
You should now be able to complete Activity 2
of the Chapter Project.
720 CHAPTER n
Objectives
0 Explore and develop
concepts of topology.
including knots,
Mtlbius strips. and torn
0 Use theorems of
topology to solve
problems
Topology: Twisted
Geometry
Topology Is an axclrlng top c and
. - - as the basis for many riddles
and puzzles. It also has many important
applications. such as robotics.
Tm nsjhrining :1 cqljee (up into ll rlrmghnur
- P I 6 N
BIOCHEMISTRY
.'trlt'Jbitrs molectrle
Knots, Pretzels, Molecules, and DNA
topology is a branch ol‘ mathematics that studies the most basic properties ol
figures. In topology, it is important to know whether a point is inside, outside,
or on the boundary’ ol'a figure. but the distance between two points or
whether they are on d straight line is not significant.
In topology. figures are deformed by stretching and
squashing. as in the coliee cup exantple above, but
cutting or tearing is not allowctl. Do you think it is
Jossible to unlink the rinvs of the “ iretzel" at rivlit —a
l D I D
by deforming it without cutting or tearing it?
The shape at right is known as a Milbius strip.
1‘ classic topological figure with intriguing
properties. (You will explore Moliius strips in
Fxercises 25—3n().] The m.tthematical .lltdl_$'SlS ol
such objects has proven useful in other fields.
such as chemistry and biology.
David Walba and his co—\-.-orkers at the University of Colorado have
synthesized a molecule in the shape ofa Moi:-ius strip. Such structures can
help researchers understand why’ certain drugs with the same molecular
structure can have vastly different effects.
Researchers have also used a branch of topology called knot tlreory to study the
structures of complex. tangled structures such as DNA molecules.
LESSON IN TOPOLOGY:TWlS‘lEO GEO-METRY 721
Topological Equivalence
Two figures are topologically equivalent if one oli them can be stretched.
shrttnk, or otherwise distorted into the other without cutting, tearing. or
intersecting itselfor compressing a segment or curve to a point. In a plane,
all of the shapes below are topologically eqttivalettt.
OA $30913
A shape that is topologically equit-alent to a circle is called a simple closed
curve. A simple closed curve does not intersect itsell". l'he curves below are not
topologically equivalent to a circle; thus. they are not simple closed Lttrves.
U00 @4000
CRITICAL THINKING Are any of the shapes alum-e topologicallyequivalent to each other? Explain.
Jordan Curve Theorem
A fundamental theorem in topology was first stated by French mathematician
Camille lord-an (l85S—l922) in the nineteenth century.
Jordan Curve Theorem
Fvery simple closed curve in a plane divides outside
the plane into two distinct regions. the inside
and the outside. Every curve that connects a
point on the inside to a point on the outside
must intersect the curve. 8
11.4.1
The theorem. which is very difficult to prove mathematieallv.
seems obvious for the curve above. But for some curves it
is not so simple. Are points Pand Q on the inside or the
outside of the simple closed curve at left? For curves like
the snowllake at right. which are called jitirtnls (see Lesson
l I.7]. it can be very difficult to determine the region that
contains points near the curve.
The lordan Curve Theorem is also \
true for simple closed curves on a O
sphere, but not for those on a
douglmut—shapcd surface called a ' '
torus (plural. tori]. Thus. a torus is
not topologically equivalent to a sphere. Sphere Torus
722 CHAPTER n
Invariants
Properties that stay the same no matter A
how a figure is deformed without breaking '
are called invariants. For example. if the
pentagon at right is distorted into some
other curve, as shown, the order ol‘ the
points stays the same. Thus. the order of .
the points is an invariant. D
0):-
/33“
\ E.
E0 08
O! D
j C
One important invariant in topology comes from Euler’s formula for
polyhedra. which you may recall from lessons 6.3 and 7.3.
Euler's Formula
For any polvhecl ron with Vvertices, F edges, and F t-aces.
V - F+ F - 2. 11.4.2
The number V - F + F is an invariant of a surfice and is called the Fuler
cltaracteristic [or Euler number). Thus. if a polyhedron is deformed into a
surface that is topologically equivalent to the polyhedron.
the Euler characteristic remains the same.
For example. imagine that a tetrahedron is deformed
into a sphere. as shown at right. The number of .
vcrtices. edges. and faces are the same. although the -
edges are no longer straight and the laces are no
longer flat. Thus. the F.uler characteristic of a sphere
is the same as that ofthe tetrahedron. 2.
However. consider the figure at left, which is
topologically equivalent to a torus. It has l6 vcrtices.
32 edges, and I6 laces, so its Fuler characteristic is
V — E + I-' = l6 — 32 + l6 = 0. Thus, the Euler
characteristic ola torus is also 0. A simpler ligure for linding the Euler
characteristic of a torus is shown below, with I vertex, 2 edges. and I face.
Again. V — E + l-' = l - 2 + l = 0. l'he edges and vertices can be drawn in any
way. as long as each face is topologicallyequivalent to a disk; that is. it can be
flattened out and deformed to a filled-in circle without holes in it.
4 ' ‘s.
Finally. considering everything you have learned about topology. it may not
surprise you to learn that the “pretzel” shown at the beginning of this lesson
can indeed be unlinked.
6 Ml «OD
LESSON IN TOPOLOGY:TWlS‘lEO GEOMETRY 723
Exemses
. Com»/M//rate
1. E‘(|‘.|li1lll what it means for two shapes to be t0p0l0giL.tlly equivalent.
Are the shapes below topologically equivalent? Explain your reasoning.
2. 3.
- connect .1,-3.,
_ _ _ mm
Activities
Online
Go To: uo.hrw.cnm
Keytvord:
MG! Topology
4 4. E-«plain two methods of proving that a sphere and a torus are not
topologically EL]lll\'dl€lll.
5. Why do you think it might be easier to prove that figures are not
topologically equivalent than to prove that Iigures are topologically
equivalent?
0 614/den’ 3k///8 Practice
6. Which of the figures below are simple closed curves? (TOPOLOGICAL
EOUIVALENCEJ
a. b. c. d.
7. which of the figures below are topologically equivalent to O0?
(TOPOLOGICAL EOUIVALENCE)
Verify Euler's formula for the polyhedra below. (EULER'S FORMULA}
8. cube 9. octahedron
724 CHAPTER n
0 Pratt/ce and 74,20/y
For Exercises 10-15, refer to the simple
closed curve at right.
10. ls point P on the inside or the outside
of the curve?
11. ls point Qon the inside or the outside
of the curve?
12. Draw a rav from point P in any direction. How many times does the ray
intersect the curve? ("Points where the ray is tangent to the curve do not
count as intersections.)
13. Repeat Exercise l2 for several rays in different directions. Vt-‘hat can you
say about the numher of times each ray intersects the curve?
14. Draw several rays from point Q in several dillereltt directions. What can
you say about the number of times each ray intersects the curve?
15. Complete the following conjecture: A ray from a point on the inside ola
curve intersects the curve an ? number of times. and a ray from a point
on the outside of a curve intersects the curve an ? number of times.
16. Use your con_iecture from Exercise I5 to
determine whether the point is on the
inside or the outside of the simple closed
curve at right.
The following is a famous graph theory problem: Can three houses be
connected to three utilities (gas. water, and electricity) without any
intersecting lines?
17. Draw vertices A. B. and C to
represent the three houses and A 3 c
vertices G. W, and E to represent
the three utilities.
18. Connect both A and B to both C and
l-'l-’ with edges that do not intersect. G W 5
(Remember that edges do not have
to be straight.) The edges should Cm: the houses be minm'n.~d in the
form a simple dosed Cm-\.e_ utilities without any iittt'i'.~‘ecriii_q lines?
19. Use your graph from Exercise l8 to explain why C and E must be both
inside or both outside the simple closed curve.
20. ll necessar_v. move vertices C and F outside the simple closed cun-‘er.
Connect C to G and W with edges that do not intersect any existing edges.
Use the Iordan Curve Theorem to show that either A or 8 cannot l)':‘
connected to F without any intersecting edges.
21. Repeat Exercise 20 with C and L‘ inside the simple closed curve. Explain
why all the houses cannot be connected to all the utilities without any
intersecting lines.
LESSON IN TOPOLOGY:TWlS‘lEO GEOMETRY 725
726 CHAPTER n
Suppose that a polyhedron is deformed into a sphere and then all the
edges and vertices are moved to the top half of the sphere. The vertices
and edges form a graph, which can be drawn in a plane. Each region in
the graph is a face, and the region outside the graph is also a face.
"I 2' (‘I-'.'
. 3}
22. For the graph above. count the number of vertices. edges. and faces. Verify
that V— F+ F-2.
23. Verify that V— L‘+ I-‘= " for the graph at right. 0 T 0
Remember to cottnt the region outside the graph . T!
as a l"-ace. Based on the number of faces. wh:tt . . _
polyhedron do you think the graph represents? ' ' \
Fuler's lornntla. Make your graph so that no two
, ‘ 9 1
24. Draw a graph ol your own and use it to verify ' '\ '
\ I
edges intersect except at a vertex. .
In Exercises 25-30, you will explore the properties of the Mobius strip.
You will need paper, tape, scissors, and a pencil. Cut a strip of paper
about 1 in. wide and 11 in. long. Bring the ends of the strip together to
form a loop. but flip one end over to form a hall-twist before joining the
ends.Tape both sides of the seam securely.
25. Starting at the tape. use your pencil
to draw the path of an imaginary bug
crawling along the center of your Strip.
Continue until you reach the starting
point. Vt-‘hat do you notice!
26. Create another Mobius strip. and draw a
path about one—third of the way in from
the edge ol‘ the strip, continuing until you
reach the starting point. Describe your
results.
27. L'se your scissors to cut along the path
that yott drew on the Mobius strip in
Exercise 25. Describe your results.
28. L'se your scissors to cut along the path
that you drew on the Mobius strip in
Exercise 26. Describe your results.
Construct a double Mobius strip as follows: Hold two strips of paper
together and put a half-twist in one end.Tape the ends on both sides
to form two nested Mobius strips.
29. Run your linger along the inside of the two strips. keeping them nested.
What do you notice? Do the strips seem to be separate?
30. Pull the strips apart. What do you notice? As a challenge. try to nest the
strips back together again.
CHALLENGE
APPLICATION
PROOF
A Mobius strip is a surface with
only one side. Another one-sided
surface, which is theoretically a
four-dimensional object. is called a
Klein Bottle. A three-dimensional
representation of a Klein Bottle is
shown at right. \
Construct a paper model ol at Klein \
bottle as follows: Cut a -l—in. X ll—in.
rectangle of paper and fold it ‘t_
lengthwise down the center. Tape .
the long edges together to form a
flattened tube.
Hold the tube verticallv. and cut a
horizontal slit through the side of the
tube nearest to y-ou, about one—lourth -
of the way from the top.
Insert the bottom end of tlte tube into
the slit. and align the two ends ol' the
tube. l'ape the ends together to produce
one “ltole" from above.
A Klein: bottle in thrt't’-tlirrtemiomtl
.\'PfIt"t' mu.\'r llll(’f.\'t'(‘l' t't‘.<t'lf.
31. Describe your paper model. Can any two points on the surface be
connected by a path along the surface?
32. Lay your model Hat and cut it in half lengthwise. Without cutting or
tearing your paper, unfold the two halves of your bottle as much as
possible. Describe the resulting shapes.
33. it is possible to cut the paper model into one Miibius strip. Can you
discover how it is done?
34. MANUFACTURING Sometimes long com-'eyor belts are shaped like Mobius
strips. What do you think is the advantage of this shape?
L004’ BJM’
35. Find xin the diagram at right.
(LESSON 2.6)
For Exercises 36-38, refer to the diagram A
at right. Assume that line Ell line In. 3 1 3
(LESSONS 3.3 AND 3.5)
36. \l-ame two pairs ol congruent angles. m ‘B E
37. .\l-ante three pairs of supplementary angles.
38. Prove that tnél + |n.é5 + [1146 = ISO” without using the Triangle Sum
Theorem.
LESSON IN TOPOLOGY:TWlS‘lEO GEOMETRY 727
APPLICATION
CONNECTION
728 CHAPTER it
39. FOOD Suppose that you have a recipe for fruit salad that calls for one large
grapefruit and that you wish to substitute an equal amotint of‘oranges. ll a
large grapefruit is about 6 in. in diameter and an orange is abottt -I in. in
diameter. about how man 'oran es will on need?
) }
Use the law of cosines and AABCfor Exercises A
40 and 41. (LESSON 10.5) D
40. Given ii = 25. C = 20, and ml./‘l = 55? find n. c
41. Given rt = I04. c = -17. and n1.»:B = 92°. lind 1:.
L004’ Bet/and
KNOT THEORY In the branch of matheniatits ["79 50"“ -9'6‘ '9P’959"TS
called knot theory, -a knot is a continuous loop: that "79 5"3”‘“’73' ‘-5 9” '00-
is, the ends are joined so that it cannot be untied. '‘
A knot can be represented by a knot diagram.
which indicates crossings with a solid curve and a
broken curve. ‘two knots are equivalem if one can
be deformed into the other in three—dimensional
space without cuttinrr. Km" diagram
One way of determining whether two knots are equivalent is by tising the
Reideiireisrw moi-'r’.~‘. Kurt Reidemeister [l893—I97l] proved that iftwo knots
are equivalent. the diagram of one can be transt'ormed into the diagram of the
other by a combination of the three moves shown below‘.
0 _i/_
a /\ -/K-
42. The following is a sequence of knot diagrams. liach diagram results from
performing a Reidemeister move on the preceding diagram. showing that
the knots are equivalent. For each diagram. identify which ofthe
Reideineister moves was used.
_.... _e.. 5‘?
°/¢\ °z\“/x
l
43. Draw a knot diagram and transform it by a sequence of at least two
dillerent Reidemeister moves.
44. Lise a strip of paper about I in. wide and I? in. long to lorm a loop. Betore
joining the ends. put three half-twists in the strip. Then tape the ends
securely. lfyou cut the strip down the middle. you should get a knotted
loop. I latten your shape down as much as possible. and arrange it as
simply as you can. Draw a knot diagram for your shape. ignoring twists in
the paper. This knot is Called a trefoil knot.
Objectives
0 Explore and develop
general notions tor
spherical and
hyperbolic geometries
0 Develop inlormal
prools and solve
problems by using
concepts of non-
Euclidean geometries.
Many remlutionary
concems in math begin by
quosmming traditional
asumptions. For exemple.
a n - -.-rolnau-Euclidean
geometries reject Euclid’:
assumption about parallel
lines, with interesting end
useful results.
Euclid Unparalleled
M II IJIII 1':
'1 Ilill LL. I \"'Jl"°9
C. c LC Lt t!.V lluan
ll .nu..i. xmiglm .....md
lnmgine that you live on this rwo—dinmxsimml stu;lzu'e. As you nzove uutwzml
from the center, t.’VL’l'}’!lllll_t.{ gets smttller—i;tclucling yoursc'l_f. Woulrl you ever
l'(’t'lfll the etlge of your "tttziI-'t'r_~':’"? This W0O{lt'lll by M. C. F5L'llt’l', known as
Circle Limit 3, is the m tist’s eottceptioit ofu mm—£ucli:imu georiwtry.
Non-Euclidean Geometries
Euclid's geometr)-' is based on live tl:'>5Llll'l]\ll0l'lS or postulates:
1. A line ntay be drawn between any two points.
2. Any segment may be extended indefinitely.
3. A circle may be drawn with any given point as
the center and with any given radius.
4. All right angles are equal.
5. lltwo lines are met by another line
and if the sum of the internal angles
on one side is less than the sum of
two right angles. then the two lines
will meet.
If mg’ l + mz 22-180’
the lines will intersect.
LESSON us EUCLID UNPARALLELED 729
730 CHAPTER II
Because the tifth postulate in the list seemed less obvious than the others,
many mathematicians wished to prove it in terms of the other four. No one
ever succeeded in doing so. but along the way. a number of discoveries were
made. In particttlar. several statements were found to be logically equivalent to
the fifth postulate. Two statements are said to be logically equivalent if each
can be derived from the other. Some examples of statements that are logically
equivalent to the fifth postulate are as follows:
° If a line intersects one of two parallel lines. it will intersect the other.
- Lines that are parallel to the same line are parallel to each other.
- Two lines that intersect one another cannot be parallel to the same line.
- In a plane, if line t‘ and point P not on t‘. are given. then there exists one
and only one line through Pthat is parallel to E.
The last statement is perhaps the most useful of the four and is the version
that many mathematicians refer to as the Parallel Postulate. [See Lesson 3.5,
page 170.)
l'or years, mathematicians tried to prove the Parallel Postulate. tmtil it was
tinally shown that it was impossible. Many even wondered whether the Parallel
Postulate is in fact true in the real world.
If the Parallel Postulate is rejected. then any theorems that depend on it must
be questioned. One such theorem is the Triangle Sum Theorem. (Recall that in
the proof of the theorem. you mttst construct a line through one vertex that is
parallel to the opposite base.)
The great mathematician Karl Friedrich Gauss [1777-1855] went so far as to
measure the angles ofa triangle formed by the points of three different
mountain tops about 50 miles apart to see if the measures added up to l80°.
(Within the limits of the accuracy of his measurements. they did.)
Does m I + mzz + mz3 = 130°? 1 2
\ i 3 ii‘ .3
I‘ if ‘” ‘ * " ti.
“\ Q ‘N 5;"-ja " _-,_ ‘ .
!_,_ \
Q‘ ‘ch —.\ ‘ ‘ ‘ a _ I
-. \' ~ . - . {.
- \ \. '- -- . .
‘*5 \. .. \ .\.3‘ ~. 577*‘ -
v . ' -‘ .- R} I
_ . _ v. \. ' , . i
.y . X ‘
.\\ " “ 0
‘vs: ~ ’ ' '
Some mathematicians adopted a different attitude. They found that they could
develop entirely new svstems of geometry without using the Parallel Postu late.
Systems in which the Parallel Postulate does not hold are examples of non-
Euclidean geometries.
Euelide-an geometry is based on figures in a plane. The figures in the non-
Euclidean geometries that you will study here are in curved surfaces. Thus, the
concept of a straight line no longer applies. in these geometries, a line will be
delined as the shortest path between two points along the surt'-ace.
CRITICAL THINKING
Spherical Geometry
Geometry on a sphere such as Earth's surface. or spherical geometry. is an
example of a type of non-Fuclide-an geometry known as Riemannian
geometry. after its discoverer. G.F. B. Riemann [l826—l866).
In spherical geometry. a line is defined as a great
circle of the sphere; that is. a circle that divides
the sphere into two equal halves. The shortest
distance between two points in a sphere is always
a path along a great circle. in this geometry. as in
any Riemanni-an geometry, there are no parallel
lines at all because all great circles intersect.
\
All great circles intersect.
Imagine two superhuman runners who start
running at the equator. Their paths form
right angles with the equator. What happens to
their paths as they approach the North Pole?
How does this dilTer from the result you
would expect in a plane? 4
To the I
North Pole
Equator
4'?
Theorems that depend on the Parallel Postul-ate
for their proof may actually be false in spherical
geometry. On a sphere. for example. the sum of
the measures of the angles of a triangle is always I
greater than l80°, as in the spherical triangle at V
right.
In this triangle. the
sum of the measures
of the angles is 270°.
Do Fuclid's first four postulates seem to be true
on the surface of a sphere? If so. should all the
theorems that follow from them be true on a
sphere?
Hyperbolic Geometry on a "Saddle"
Imagine that vou are standing on the surlace of a sphere. In
every direction. the surface curves away from you. On the
\ surface of a saddle. the surface curves away from you in some
Ck .
Lines 1' and m are parallel
to line n but not to each other.
directions and toward you in other directions. On such a
surface. there is more than one line through a point that is
n parallel to a given line. In fact. there are infinitely many.
The geometry of a saddle is an example of hyperbolic
geometry. or lxolaachevskian geometry. Nikolai l,olaachevsl:y
( I77-'.’»—l3S6] was one of two ntathematicians who discovered
this type of geometry independently. the other being Janos
Bolyai [l802—l860l.
In hyperbolic geometry. just as in the other geometries you have studied. a lint
is defined as the shortest path between two points. in the illustration. lines 12'
and m pass through point P. and both are parallel to n (because they will
never intersect line H).
Once again. the Triangle Sum Theorem does not hold. On a saddle. the sum of
the angles in a triangle is always less than 180°.
LESSON us EUCLID UNPARALLELEO 731
732 CHAPTER II
Poincaré's Model of Hyperbolic Geometry
The “universe” in the Escher woodcut on page 729 is a representation of a
three-dimensional universe imagined by the French mathematician Henri
Poincare (1854-1912). Poincare. whose many interests included physics and
thermodynamics. imagined physical reasons for the geometric properties of
his imagined universe.
In the model ol Poincare's universe below. the
surlitce is not curved. but the measurement ol
size and distance is delined in a diflic-rent way
from Fuclidean geometrv so that it represents
a curved surlace.
Poincaré's universe can be represented by a circle.
'1 he temperature is greatest at the center of the
circle and drops to absolute zero at the edges.
According to Poincaré's rules for his universe,
no one would be aware 01' temperature changes.
ln Poincaré"s universe, the sire ofan object is
proportional to its temperature. An object would
grow smaller as it moved away from the center.
Because everything, including rulers. would
shrink in size, there would be no way to detect
the change. In fact, distance measures would
keep shrinking, so you would never get any
closer to the edge of the uniwerse. no matter
how long you traveled.
The arcs in the circle represent the paths that rays
of light would travel in Poincare's universe. These
are defined as lines in this system. Light rays that
stay close to the edge of the universe appear more
curved than those that pass close to the center.
Lines through the center are diameters of the
circle. Another feature of these lines is that they
'11‘? orthogonal to the circle; that is, they form
right angles with the circle at the intersections.
ln Poincaré's system. a line segment connecting
two points is a part of the are that is orthogonal
to the circle. This is the shortest distance hetween
the two points. If you wanted to walk from A to
B. the curved line would be shorter than the
straight line connecting them because your steps
would get larger as you approached the center of
the circle. You would cover more distance with
each step as you moved toward the center than
you would by walking directly to the point.
9
Temperature and size
are greatest at the center.
1_ .
x. _
Everything shrinks as you
move toward the edge of
Poincaré's universe.
Orthogonal arcs
Notice also on the previous page that more
than one line can be drawn through a point
that is parallel to a given line. For example.
I(—-) 1%: _ _‘
DF and F(- pass through the point L, and
(+5
both are parallel to AB. Thus. the geometry
of Poittcaré's universe is an example of a
hyperbolic. or Lolaachevskian. geometry.
Finally, notice that the sum of the measures ol mi‘ + m-’—’2 + m-43 < 130°
the angles in a triangle in Poineare‘s universe
is always less than I80? just as it is on the
surface of a saddle.
Years Later—AppIications
ln Einstein's general theory of relativity.
space is non-Euclidean. In fact. due to
the influence of gravity or—equivalently
—acceler-ation. space is curved. 'l he
non- Euclidean geometries Lliscovered
years earlier proved to be both an
inspiration and a useful tool
to Einstein in formulating his
fundamental laws of the
universe.
fxe/rises
E .
Activities
Online
Go To: go hrw.com
Kcvwotd:
MOI Poincare
mg --
1?;
. Communicate
1. Which postulate of Euclid was questioned by matliematici.ms? State it in
your own words.
2. What are the alternatives to the Parallel Postttlate that have yieldecl two
non—Euclidean geometries? Complete the following statements and explain
your l"c‘i.|S()l‘lil‘lgI
a. In a sphere. ifline E‘ and point P not on 1:’ are given, then there exist(s)
? linetsl through Pparallel to t’.
b. in a hyperbolic surface, if line ti and point P not on E are given. then
there e~<ist(s) 7.‘ line(s} through Pparallel to it’.
3. in spherical geometry, how does a line extend indefinitely?
4. in Poincare‘s universe. how does a line extend indefmitely?
LESSON n5 EUCLID UNPARALLELED 733
734 CHAPTER 11
. Practice and Apply
0 Guided 34’///3 Practice
5. What can you say about the sum of the measures of the angles ofa
triangle in spherical geometry? in hyperbolic geometry? Fxpress your
answers as inequalities. (SPHERICAL GEOMETRY AND HYPERBOLIC
GEOMETRY)
. . A '
Refer to the diagram of a sphere at right. 0 ,'£,E.%'tude
Determine whether each figure below is a E. - 4 _ F L _ d
line in spherical geometry. (SPHERICAL ‘ 6
GEOMETRY) c. D
4-» 4-; »,
6. AB 7. AC ‘Equator
-(—.> (—.¥
8. EF 9. F D
B
Refer to the diagram of Poincaré's model F,
at right. Determine whether each figure J 4
below is a line in hyperbolic geometry.
mvpenaouc ceorwernv)
-(—.> ¢.'—> .
10. F6 11. F] H ‘
-(_—.o -:—> \.. -I
12. on 13. ll! 06
14. Suppose that you cut an orange in half around its
“equator” and then cut each hall‘ twice at right 1
angles through the poles. You would have
divided the orange peel into S congruent
triangles. if you were to add the measures
of the angles ofone of these triangles.
what would be the result?
\
15. Draw a 2—gon. or a polygon with two edges, on a sphere. (Note: 'I he edges
ol‘a polygon must be segments. as they are in a plane.) What can you say
about the vertices of the 2-gun?
16. In spherical geometry, what can you say about the sum olthe measures ot
the angles of a 2—gon? Express your answer as an inequality.
17- Draw a quadrilateral on a sphere. Include one diagonal in your drawing.
13. What can you say about the sum ofthe m£"<1Slll'(’S ol'the angles of the
quadrilateral from Exercise I7? How do you know? Express your answer as
an inequality.
D connect
Homework
Help Online
Go To: 9oJtrw.com
Keyword:
MGI llomewnrlt Huh
lot Exercises I9-2?
iii
In Exercises 19-27. you will explore constructions in Poincaré's system.
Part I: Constructing a line through a given point
19. Cottstruct GP and choose a point. A. on the circle. To Construct a line
through A in Poincaré's systetn. first construct line 6 tangent to GP at A.
Choose a point, C, on line E’. Place your C0lTtp.ISS point at C and draw :1
circle through A. The are oithe circle that lies inside 0!-’is a line through
A in Poincaré's system.
20. Repeat Exercise I9. placing C at several different locations on line B. What
happens as C gets larther and farther away from A? What would happgn it
(' were infinitely far from A?
21. Explain why the center of an arc that is orthogonal to a circle at a point
must lie on the line tangent to the circle at that point.
22. Construct OQ and choose a point. B, inside the circle. To construct a line
through B in Poincaré's system. hrst choose a point, E. on OQ. Construct
ling: tangent to OQ at and construct line it. the perpendicular biscctor
of 51:‘. Place yottr compass point at the intersection of lines in and N and
draw a circle through B. The arc of the circle that lies inside DC) is a line
through B in |’oincare‘s system.
23. Repeat Exercise 22. placing E at several different locations on OQ. Explain
how the line varies as the location of E changes.
Part ll: Constructing a line through two given points
24. Construct GP and choose two points.
A and B. on the circle that are not .,.'
endpoints ofa diameter. To construct
a line through A and Bin Poincaré's
system. construct line ti tangent to GP
at A and line in tangent to OPat 8.
Place yottr compass point at the i
intersection oflines I’ and m, attd draw
a circle throttgh A and B. The arc of
the circle that lies inside OP is a line
through t and B in I’oincare's system.
25. Why would the construction in Exercise 24 fail if A and B were the
endpoints of a diameter? What would be the line through A and B in
this case?
26. Construct GQ and choose two points. C attd D.
inside the circle. To constrttct a line through C
and D in Poincare’s system. lirst dfzlflt;
Construct line it perpendicular to CO at C. Line
n intersects the circle at two points. Construct
lines p and q tangent to G0 at these points, and
label as C’ the intersection of pand q. Construct
a circle that passes through points C. D, and C'.
The arc ofthe circle that lies inside GQis a line
through C and D in l’oincaré's system.
27. Draw a line t’ and a point A not on line t’ in Poincare’s system. [low many
lines can you draw through point A that do not intersect line t‘? How is
this illustration related to the Parallel Postttl-ate?
LESSON its EUCLID UNPARALLELEO 735
736 CHAPTER n
In Exercises 28-33, you will explore polygons in Poincare’s system.
28. Draw three lines that intersect to form a triangle in Poinc-are’s system.
Measure the angles of the triangle.
29. What is the sum of the angles of the triangle from Exercise 28? How does
this compare with the sum of the angles ola triangle in Fuclidean
geometry and in spherical geometry?
30. Draw a right triangle in Poincare's system. (Hint: The diameter of the
circle is a line in Poincaré's system.) What can you say about the acute
angles of a right triangle in this geometry? Express vour answer as an
inequality.
31. Draw four lines that intersect to lorm a quadrilateral in Poinc-are's system.
Measure the angles of the quadrilateral.
32. What is the stun of the angles of the quadrilateral from Exercise 3|?
33. Write a conjecture about the sum of the angles in a polygon with M sides in
Poincaré’s system. (Your conjecture should involve an inequality.)
You can use equilateral triangles to build models of surfaces in
spherical, Euclidean, and hyperbolic geometries. Construct an equilateral
triangle with a side length of about 3 cm. Copy the triangle carefully
onto heavy paper or cardboard and cut it out. Make at least
20 copies of the triangle.
343. Tape 5 triangles together at a single
vertex. as shown. This is a model of
part of a surface in spherical geometry.
Describe your model.
35. Tape 6 triangles together at a single
vertex. as shown. This is a model ol‘ .
part of a surface in Euclidean geometry. __‘:___
Describe _vour model. -
II
36. Tape 7 triangles together at a single
vertex. as shown. This is a model of
part ofa surface in hyperbolic geometry.
Describe your model. a
37. How are the models you made in
Fxercises 34 -56 alike? How are they
different? Explain how the surfaces
model the different geometries.
38. Wh-at happens it‘ you extend the model in Fxercise 34 to create a surface
with S equilateral triangles at every vertex? (ll? you are not sure, make more
triangles and experiment with them.) Could the model for spherical
geometry extend to infinitely many triangles? \'\-'hy or why not?
39. What happens if you extend the model in Exercise 35 to create a surface
with 6 equilateral triangles at every vertex? Could the model for Euclidean
geometry extend to infinitely many triangles? Why or why not?
40. What happens ifyou extend the model in Exercise 56 to create a surface
with 7 equilateral triangles at every vertex? Model a surface in hyberbolic
geometry with at least 20 triangles. Could this model extend to infinitely
many triangles? Why or why not?
1.00.(’ Back
In Exercises 41-43, you will construct a regular octagon. (LESSONS 4.7
AND 5.4} A 8
41. (‘£r1strtrc:t_sqtrare A BCD. Draw diagonals
AC and BD-and label their intersection E.
Place your compass point at .-lind drzfl
an arc through E intersecting /lb'and AD. 5
42. Place your compass poim at B and draw
an arc through E in a similar fashion. D C
Repeat at C and D. Connect the eight
points where the arcs intersect the square
to form an octagon.
43. Prove that the octagon you constructed in Exercises 4| and 42 is regular.
44. Draw a floor plan for your house or apartment. Draw a graph that
represents the circulation of tr-aftic in it. Remember that the rooms are the
vertices and the doors are the edges of the graph. (LESSON 1 1.3)
45. Does your graph from Exercise rl-1 contain an Euler path? an Euler circuit?
Why or why not? (LESSON 11.3)
In Exercises 46 and 47, you will explore topological properties of letters
of the alphabet.
ABCDEFGHIJKLMNOPORSTUVWXYZ
46. Identity all letters of the alphabet (drawn as shown above) that are
topologically equivalent to the letter 2. (LESSON 1 1.4;
47. Are the words SIDE and CLOT topologically equivalent? Are LAST and
COZY? Explain your reasoning. (Lesson: 11.4;
L00)? Beywid
The area of triangle ABC on a sphere with a radius of r is given by the
formula
_ 2 _mAA+mAB+mAC _
A _ ntr (——--:—mo,, 1).
48. Verify the formula for the triangle on the
sphere shown at right. [Hint: W hat fraction 5‘
of the surlace area of the sphere is covered
by the triangle?)
49. in spherical geometry, the sum of the angles ofa triangle is always greater
than I80”. What can you say about the area ofa triangle in which the sum
of the angles is very close to I80”?
50. l'he area of a triangle on a sphere can not be greater than the surf-ac.e area
of the sphere. Use this fact to complete the following inequality involving
the sum of the angles of a triangle on a sphere:
l80° < In/_A + m/_B+ m/_C < ?
LESSON us EUCLID UNPARALLELEO 737
Fractal Geometry
Objectives
0 Discover the basic ‘ . . ~‘~ ”= -
propemes ot lractals, - '_ - v‘ -
including sell-similarity - - '
and iteration.
0 Build fractal d9Slg|'lS by ,
using iterative steps. 7 | .
WI _ _ _
The sell-smtrlarrry of
Iractals: nosac» ---= -_
programmer to write a
relatively short program Iar
drawing such structures. I
A fractal, suttlt as the computer-generrttcrl_Ii'rrt ultove, is u self—sirm'iar sn'm'mre.
Norirc that car}: subdivision ofrhe lem-es qftlteferiz has basimlly the smite
$mn'tur(' as the lerzves tItr'rrtselves—all the way down to the rurving tips.
Self-Similarity in Fractals
A fractal. like the Menger sponge at lelt. is a geometric
object that exhibits some type of selllsimilarity. '1 his
means that the structu re of the object alw.t_vs looks the
same, whether seen in a highly magnified view, lrom a
moderate distance, or from far away. If you were to cut
offa small cttbe-shaped portion of the Menger sponge
and examine it, you would find it to be a miniature copv
ol' the entire sponge.
ln m.tthentatic.tl|y created tract-als like the Menger
sponge, this process can theoretic-allv be continued
forever. and the sell‘-similarity will always be evident.
Fractals can be Ll'€£llE.’t.l by repeating a simple procedure over and over. The
Menger sponge, for example, is created by starting with a certain shape
[a cube] and changing it according to a certain rule (removing a part of the
tube]. This same rule is applied to the newlv changed shape. The process is
then continued. This repetitive application of the same rule is called iteration.
738 CHAPTER n
How Long Is a Coastline?
x
\ . .
K. I ‘ §
I
I" ‘,
. u ' |_ U
- _'. \ ‘~ . . 7
- Ir 1'‘
\_ :53" ' v . I ‘
.. _
I I‘ " ‘ ‘-
:5 ' I *
I
f.‘ I 4\.
I . " " _ - A ‘S. :
I-_ |I (
u ‘ I...‘ I - ."
Q -‘B-''‘ E ~_—-:.,_ ‘~?... ,'
J" F ' ‘’'~'‘
; ‘ H 4 \ 0 .»o
\ ‘ \. . ‘: 11., ‘..’‘L,‘_
4 , _., 35;; .
"‘ r ;:
_:t_§ ._. - _
f I 5.
" ‘ - \. .
In a theoretical fi'rt('t¢llC(N1StHrJ£’, where
the depth ofsel_f—similurity is endless, the
leugrh is rnm'idm'd to be infinite.
- p g c I 0 N A coastline is a good example of a self-similar structure in nature. Jagged
GEOGRAPHY irregularities such as luvs. capes, and inlets can be seen from an orbiting space
shuttle. The same basic structures are evident over .3 smaller section of the
coastline viewed from an airplane and over even smaller sections viewed
during .1 drive or a walk.
How long is a coastline? Unlike ordinary geometric segments or curves. which
can often be readily measured. the “length” of-a fractal coastline depends on
how closely you move in to measure it.
During the American Revolution. the British Royal Navy attempted to
blockade the Anlerican coastline. Although fairly successful. the l)|0L'kade was
not able to prevent shipping in and out ofn1-any harbors. What does a close
examination of the coastline reveal about its “length” that explains the
dilliculty faced by the British to completely blockade it?
\
\~' "_
is‘ “-\-
Mrmy objects found in mmire lmve some of
the properzies offracmfs Notice, for exmnple.
the self-sinrilnrity of the broccoli at right.
LESSON n.s FRACTAL GEOMETRY 139
' I
Creating the "Cantor Dust"
- - Ell One of the simplest Fractals was discovered by Georg Cantor ( l8-l5—l9l8)
a _ruler and pencil years before lractals were defined and studied. As you will see. Cantor‘s
Wm‘ 3" 9'35” fractal is a one-tlimensional version of the Menger sponge.
1. Draw a line 27 cm long.
2. Erase the middle third ol the
segment. You should now have t K
two segments that are 9 cm long, \
with a 9-cm gap between them. ‘
I
3. Frase the middle third ol‘ each of )
the two 9—cm segments. You will
now have four segments. each
3 cm long.
4. Continue erasing the middle third of each of these segments until vou
are left with a scattering of point—like segments. known as the Cantor
dust.
27 cm
1 iteration 9 0'“
2 iterations EL _3i‘_
3 iterations _ _ _ _ _ _ _ _
aiterations __ __ __ __ __ __ __ __
PROBLEM SOLVING 5. Calculate the number of segments and their combined length after each
iteration. VI-ake a table like the one below.
Iteration 0 1 2 3 4 5 It
Number of 1 7 7 7 7 7 7
segments
Combined
length lcml 27 7 7 7 7 7 7
CHECKPOINT ./ 6. -'\S the number ol" iterations increases. what happens to the number of
segments? W hat happens to the combined lengths of the segments?
cRt11cAL THINKING Describe the result if the process were repeated infinitely many times.
How many‘ segments would there be? What would be their combined length?
A - p L c . I 0 N When an electric current transmits data over a wire. a certain amount of
TELECOMMUNICATIONS “noise” occu rs, which can cause errors in transmission. The noise seems to
occur in random bursts, with “clean" spaces in between the bursts. Benoit
l'\-‘landelltrot, the discoverer oi‘ l'r'.tct'.tl geontetry. showed that the noise patterns
closely matched the pattern of the Cantor dust. This geometric representation
allowed the development of new strategies for reducing the transmission noise
to a minimum.
740 CHAPTER u
The Sierpinski Gasket
The Sierpinski gasket. like the Menger sponge and the Cantor dust. is created
by repeatedly applying a single rtile to an initial shape. The rules are as follows:
1. Start with a solid triangle. Find
the midpoint of each side.
2. Connect the midpoints of the
sides to form tour congntent
isosceles triangles in the interior
of the original triangle. Remove
the center triangle. This is one
iteration.
A
3. F.-ach new iteration is performed
on the remaining triangles. AA
A A
AAAA
Mathematical ideas often turn out to have surprising connections to seemingly
unrelated fields. In .-tctivity 2, you will learn about .1 connection between the
Sierpinski gasket and Pascal's triangle.
/ - I 2
Pascal and Sierpinski
0 ' ll Recall that Pascal s triangle is a triaiigtitar array
graph paper beginning with I at the top. Each number is 1 1
the sum of the two numbers directly above 1 2 1
it. The pattern is repeated endlessly.
1. Build a Pascal's triangle with at least 1 5 '0 5 1
2-4 rows of squares. as iriditated in
the diagram. As the sums get large,
you in-ay wish to add only the
final digits of the numbers.
The more rows you can
complete. the more
impressive the result
will be.
CHECKPOIN1’ ./ 2. Shade each square that
contains an odd number.
and leave the other
squares unshaded.
Describe your results.
LESSON “.5 FRACTAL GEOMETRY 741
Exemses
. Comma»/care
1. What is meant by self-similarity’? You may wish to use .111 object to aid in
your e.\:pl.1nation.
2. Name an object from nature that has some type of self—similarity and
describe how it is self-similar.
3. Mimi, Arnold, and Roberto -"‘ *
measure a section of '
co-.1stline by counting paces. _,_ -‘._,.-_\—"\‘
Arnold's stride is 3 ft long, _. __~- ,.,"'-- " "’ ‘-.. --. Q ;_
and he counts 2-l paces. ' _ _ '
Ruberto's stride is 2.5 ft Mm"
long, and he counts 36
paces. Mimi's stride is 2 ft
long. and she counts 47 ,—. .__.
paces. I-low long is the __, ii‘ '5 ii‘ -- -‘~
coastline for each person's Ame”
set Of l'l1(‘.'¢l$lll'"t‘l'l1E’niS?
4. Fxplain how a fractal '
coastline could be _ _
considered to have an ,_ .. "' "‘ _' ., '‘ ., ,—_, _
‘ '5 flfi
inhnite length. "'
Roberto
Three different n1ea.<uren1ent5 of II ctm~'tlim'
0 61//Wed 3k///3 P/dtt/68
5. Draw an equilateral triangle and divide the sides into thirds. Draw
s-egntents connecting the sitles to the base. forming two smaller equilateral
triangles. Repeat as shown. How is the resulting fractal related to the
Cantor dust? (ACTIVITY 1)
AAA
I iteration 2 iterations
6. Use the following rules to explain the shading pattern in Pascal's triangle
from Activity 2:
I
I even + even = even odd + Odd = even even + odd = ()LlLl
1 l...''- Based on these rules. devise a method for shading the squares without
I I I calculating the values in Pascal"s triangle. (ACTIVITY 2)
7. Build -.1 Pascal's triangle with at least I2 rows ofsquares. Shade each square
that contains .1 number divisible by 3. and leave the other squares
unshaded. How is the resulting pattern like the pattern from Activity 2?
How is it diflerent? (ACTIVITY 2)
742 CHAPTER 11
. Practice and Apply
ln Exercises 8—-18, you will explore the area and perimeter of the
Sierpinski gasket. Copy and complete the table below.
L :.
E =‘-
L xxx; :.:.:.:.
8
Iterations 0 1 2 3
Shaded area 8. ? 9. ? 10. ? 11. ?
Perimeter 12. ? 13. ? 14. ? 15. ?
16. Use the terms in the table to complete the following statement: At each
iteration. the area is multiplied by ?
17. As the number of iterations increases. what happens to the area? Does it
seem to have a limit as the number of iterations approaches infinity?
18. As the number ol iterations increases, what happens to the perimeter?
Does it seem to have a limit as the number of iterations approaches
infinity?
ln Exercises 19-23, you will construct a fractal called the Koch snowflake
and explore its properties.
19. Construct the lirst iteration of the Koch snowllake 75'l"”"'l°"
by following the directions below.
\/
a. Construct an equilateral triangle with a side length of IS cm.
b. Divide each side in thirds. and construct an equilateral triangle on each
side of the triangle with the middle third as the base.
1:. Fraser the base of each new triangle. You should now have a six-pointed
star. This is the lirst iteration.
20. Continue the construction ol' the Koch snowflake.
Repeat the steps above to complete at least three
iterations.
21. Find the perimeter of the Koch snowllake after the
lirst two iterations. Remember that the snowllake
starts with a perimeter of 3 x 13 cm, or 54 cm.
22. Does the perimeter increase or decrease? Does it increase or decrease by a
greater amount or a smaller amount from each iteration to the next? What
does this tell you about the perimeter?
23. Look at your snowllake and consider how it would change if you
completed many more iterations. Would the area of the snowflake increase
or decrease as the number of iterations increase? Would the area ever
become inlinite? (l lint: Can the snowflake always be enclosed by a circle?)
LESSON “.5 FRACTAL GEOMETRY 743
CHALLENGE
APPLICATION
744 CHAPTER n
In Exercises 24-27 you will explore a fractal known as the dragon curve.
24. 'lake at long strip of paper and fold it in half and then in half again (in the
same direction). repeating as many times as possible. Open each fold to
90°. The result. when viewed from the edge of the paper, is a dragon curve.
Draw your dragon curve on paper.
25. The following is an algorithm for drawing a dragon curve: Start with two
segments that intersect at a 90°angle. For each iteration. replace every
\/ with lJ_, as shown below. Draw a dragon curve with at least five
iterations.
1
‘t.
\
t.
t.
‘t
1 Iteration
3 iterations
2 iterations
26. Suppose that the dragon curve in Exercise 25 starts with a length of 2
tmits. What is the length after the first iteration? after two iterations? after
three iterations? Divide your results from succesive iterations to complete
the following statement:
The length of a dragon curve after n + l iterations is ___?_timcs the
length alter tr iterations.
27. How does the area covered by the dragon curve change after each
iteration? Do you think the area covered by the curve approaches infinity
as the number of iterations increases? Explain your reasoning.
28. Refer to the drawing of the Menger sponge at the beginning of this lesson
Describe the construction of the sponge. ll the volume before the first
iteration is I cttbic unit, what is the volume after one iteration? after two
iterations?
29. HOBBIES A kite may be made in the shape of
a tetrahedron. with paper or Fabric covering
two ofthe faces. l'our of these kites may be ‘
joined at the corners to form a larger ltite.
also in the shape ofa tetrahedron I the lirst
iteration). Four of these units may be joined
at the corners to form at larger tetrahedral kite
(the second iteration). As the units are joined.
the kite will begin to resemble a three-
dimensional Sierpinksi gasket. How many of
the Ol iginal kites are required for the second iteration?
How many are required for the third iteration?
100:? Back
Find the distance between each pair of points. (LESSON 5.6)
30. (4. -2}. (2. —I) 31. (5. -10). (-2. 3) 32. (I5. 2}. H», 5)
Find the distance between each pair of points in a three-dimensional
coordinate system. (LESSON 6.4)
33. (4. 3. 2J.(2.-3.5) 34- (I8. l.0_l.(0.-1.5) 35- (5. l.-5). I2.-l2.U}
36. Find the measure of the diagonal of a cube in the top—l'ront—t-igltt octant.
with a vertex at (0. O, 0}, and with a side length of 8. (LESSON 6.4)
£00k B6’!/flild
37. CULTURAL CONNECTION: ASlA
For centuries. women of India
lrave used fitscinating curve
patterns known as Kolams for
ritual and decorative purposes.
A fm-:.tal known as the Hilbert
curve inuv remind you of the
Kolams of India. Steps for
creating a Hilbert curve are
given below.
a. Start with a three—sided
“sqtiure" with no lmttom
edge.
b. Draw 4 new (smaller) three-
sided figure at each vertex.
Be sure your new figures are
oriented as shown.
c. Connect the new figures as
shown to form a single
continuous line. ljrase the
original ligure. This is the j
first iteration.
d. For each new three—sided
figure that you just created ]
in part b, create a new
(smaller) figure at each vertex.
Connect the new ligtttes‘ and :l
erase the original figures, as in
part c. This is -.1 new iteration.
38. l'he resulting curve is known as a sp-.1c.e—filling curve or a “monster curve."
If you were to continue this process indefinitely, what would the result
9&5
look like?
123 Egtaaggaéggg sfiggggaggfigs-2
#33 ‘:3 2“
£323 iiiggaes T? 7525533
%m.;*« 1% ._‘._b%-'3‘.E’;.‘:._.T‘2.t':'.E.‘’t9‘§
- I171 41' I-\ ,‘b
H ‘-
°«5f=?5§Bi
3 ll-:
:
ti-‘:5
=5“. §‘ii~e”JE%E;a
n E . '|. .. .
E?%%f%":3r~2.”?§:3 =‘=B3hg.5’f5.3%:
:'.I:1;-I.
dr[:-.!
3
‘T3533
%
Fa
4:5
3%
sin?
LESSON 11.5 FRACTAL GEOMETRY 745
fl lmtmctconned ,2£_.,
_ wm
Poniolro
Extension
60 To: no.hrw.com
Keyword:
M61 Fractals
746 CHAPTER it
THE CHAOS GAME
Can there be order in a
random process? The
following “chaos garne"
may lead you to ask
some deep questions.
1. Draw equilateral triangle A.-'1B(" with a side
length of IO centimeters. Roll a number cube
../’q
\\\\
Second Q“ Initial
seed 4' ‘. seed
or use some other method to randomly select Doiql ,-’ X‘ point
vertex A, B. or C. You can let I and 2 represent t.’ \‘ Third
A. let 3 and 4 represent B. and let 3 and 6 /’ ‘. seed
represent C. Mark the selected vertex. which is " '\P°i"‘
called the seed point. 8: ———————————— ——'—~c
Roll the number cube again to select another
vertex. This time. mark the point hallway
First vertex selected: A
Second vertex selected: 8
Third vertex selected: C
between the seed point and the selected vertex.
This point becomes the new seed point. Repeat
the process several times. using the new seed point each time.
If you were to repeat this pr0<.ess several hundred times. a pattern would
start to emerge. Combine your results with your classmates‘ results and
see if you can guess the pattern. The program below. which will work
with a graphics calculator. simulates the chaos game fora triangle with
vertices at (0, O}. (0.5. l). and (l. 0] and an initial seed point at (0.0) for
I500 repetitions. Study the program to see how the simulation works.
‘then rttn the program and describe the result.
PROGRAM: CHAOS
:FnOff :ClrDraw
:PlotsOff :AxesOff i
:0—>Xmin :1—>Xmax
:0—>Ymln :1—>Ymax }
:0—>X :0—>Y
For lK,1,1500) :rand—>N
:lf N51/3 :Then
:.5X—>X :.5Y—t»Y
:End
: If 1I3<N and NS 2/3 :Then
:.5(.5+Xl—t»X :.5l1+Yl—rY
:End
zlf 2/3<N :Then
:.5(1+X)—t»X :.5Y—>Y
:End
:Pt-OnlX,Y)
:End
These commands clear the screen of any
previous graphs.
These commands set the viewing window.
This locates the seed point arm, 0).
This generates I500 random numbers
These commands assign one of
the venices to each random
number and then locate the
seed points.
This shades the seed point on the graph
Other Transformations
and Projective Geometry
Objectives
0 Understand the
concepts of alhne
transformations and
geometric projection.
o Solve problems and
make congectures by
using the Theorem of
Pappus and the
Theorem of Desargues.
When you stretch or otherwise deform
a figure. will you sllll be able to - I -nlza
it? In what ways will it be the same? Those
are questions that are considered in the
study olproiectiro geometry. —
Nonrigid Transformations
The three rigid traitslbrittatioits reflections. rotations, and tr:msl.ttions—
preserve the shapes and sizes of objects. Dilations. on the other hand. preserve
shape but not size. There are types of transforntations that shrink, expand. or
stretch an obiect in different directions so that neither shape nor size an
necessarily preserved. One of these types of nonrigid transformtttions is called
an ajffirte trnrtsfonmttiou and is defined as follows:
Definition: Affine Transformation
An affine transformation tratnsfmttts each preintage point P in a plane to
an int-age point P' in such .1 way that
1. collinear points are tmnsfornted into collinear points.
2. straight lines are transformed into straight lines.
3. intersecting lines are tr.tnsformctl into intersecting lines, and
4. parallel lines are transformed into parallel lines. 11.7.1
LESSON n 1 OTHEHTRANSFORMATIONS AND PROJECTWE GEO-METRY 747
graph paper and
compass
CHECKPOINT /
CHECKPOINT g/
748 CHAPTER n
' /
An Affine Transformation
Part I
1. Draw a -1 x 4 square and a I x 4 parallelogram on graph paper as
shown below. (Use more than one grid square for ettclt unit squurc lll
order to make the figures large enough to work with.)
2. inscribe .1 circle in the square. Draw -.1 square and its diagonals inside
the circle.
3. Mark the points ol intersection of the circle with the grid lines. Mark
the vertices of the inner square.
4. Mark the same points in the parallelogram grid. The first Few are marked
in the diagram below.
. I
5. To draw the image oi‘ the figure under an alhne transformation. connect
the image points of the square with segments I including the diagonals)
and draw a smooth curve through the image points of the circle.
6. How does the resulting figure illustrate each olithe four conditions in
the definition of an -alline transftirniation?
Part ll
Aifine translorinations can be represented by using coordinates. For
example. multiplying the x— and y—coordinates ofthe points olia ligure by
two dililierent scale Factors is an example of an affine translbrmattit)n.
Multiply x by 2 and y by 3.
:>
Image point
(2):: 3,l’}
Preimage point
(x. y)
1. Draw a square and its diagonals in the first quadrant of a coordinate
plane.
2. Multiply the x—coordin-ates of the vertices ol'the square by 2 and the
y—coordinates by 3. Plot the resulting points and connect them with
segments (im:luding the diagonals]. Describe the resulting figure.
3. Multiply the x-coordinates of the vertices ol the square by 3 and the
y—coordinates by 2. Plot the resulting points and connect them with
segments (including the diagonals). Describe the resulting ligure.
4. 1 low do the resulting figures illustrate each of the four conditions in the
definition of an affine transl’orin-ation?
/ rs ._
xx. ~; _jx’;I.-\
.j. ".:;1;.
. ‘ R‘
_ =. y 2
.4! '.
.a-
Projections and Projective Geometry
In the photograph at the beginning ol' this lesson. the image of the apple is
distorted by a translornration. ls it an alline transformation? Study the two
images below.
as
l ' I
As you can see. the sides of the grid are parallel in the original image but not
in the translbrmetl image. TherelbI'e. parallel lines do not transform to parallel
lines, as required by the definition of an affine transformation. Thus. it is not
an alline transformation.
The transformation of the image of the apple is an example of a class of
transfornrations known as central projections. In such transformations, there
is a central point known as the center of projection. and the projected points
lie on rays containing the center of projection and the original points.
The diagram at right shows a projection
between two lines in the same plane. The
points on line I" are projected onto line m
from the center of projection. point 0.
The rays drawn lrom the center of the
projection are called the projective rays.
These rays intersect line L‘ at points A. B.
and C. The intersections of the rays with
line Mr determine the projected points. A’.
Bland C
:9‘
, .
ll
To ninke the mmp a Mercator projecrimi. its vertical
dirrtmsioiis must be adjusted. {See page 176.)
The surface of a sphere can be
projected onto a plane by means
ofa cj'lim.lrit'al pro_jem"ou. Notice
that it is impossible to proiect the
points at the North and South
Poles onto the map. and that it is
impractical to project points near
the poles.
Geography teachers have long
pointed out that Greenland is
really much smaller in relation to
other countries than it appears to
be on cylindrical projection maps.
l)et'ormities like these arise because
it is impossible to flatten Earth’s
spherical surface into a rectangle
without some distortion of size.
shape. distance. and direction.
LESSON n 1 OTHEHTRANSFORMATIONS AND PROJECTWE GEO-Mernv 749
st: aightedge
OR
geometry
graphics
software
PROBLEM SOLVING
750 CHAPTER n
cuscxpomr ./
For years. artists used the conc.ept of projection to given their works realism
and depth (see I esson 6.6). On the other hand, mathematicians used
projections to develop an entire system of geometry. l'he chart below
Summarizes its features.
Main Features of Projective Geometry
1. Projective geometry is the study of the properties of figures that do
not change under a projection.
2. There is no concept of size. measurement. or congruence.
3. Its theorems state facts ahout such things as the positions of points
and the intersections of lines.
4. An unmarked straightedge is the only tool allowed for drawing
ligures. 11.7.2
Two Projective Geometry Theorems
Part I: A Theorem of Pappus
CULTURAL CONNECTION: AFRICA Pappus was a mathematician who lived in
Alexandria. Egypt, in the fourth century C.E. His work was very important
in the developrnent of projective geometrv many centuries later. In this
Activity, you will discover one of his theorems.
1. Make a diagram. Orient your paper horimntally. Mark a point, 0,
toward the left edge ofthe paper. Draw two rays from point 0. C‘
2. Mark A). B.. and C. on one ray. 31. Z.
In the same order, mark A... B3, A‘ ,
and C» on the other ray. on < *
._:. ..__._ _ _ _ A2 T Q‘. _._
3. Draw A133 and A_-B1. Label their Intersection X. 8? C,
Draw AK‘; and Agfi. Label their intersection Y.
Draw B.C2 and B;C.. Label their intersection Z.
4. What appears to be true about X. Y. and Z 2‘ Make a conjecture. and
compare it with those of your classmates. ( If you are using geometry
graphics software. drag the rays in various ways to see whether your
conjet.ture still holds.} Based on your conjecture. complete the
following theorem:
The Theorem of Pappus
If A“ 13,. and C; are three distinct points on one line and A5 B1. and
Q are three distint.t points on a second line. then the intersections of
A113; antl A;B.. ol /MC; and AICI, and of B,C3 antl B;C, are ? .
11.7.3
Part II: A Theorem of Desargues
Girard Desargties (I593-I662) was a French mathematician whose ideas
are a mong the most basic in projective geometry. Follow the steps below to
discover one of his most important theorems. (Use as large a piece ol-
paper as is practical.)
PROBLEM SOLVING 1. Make a diagram. Draw AABC near the center of the paper. This can be
any type of triangle. but it should be small so that the resulting
construction will fit on your paper.
2. Mark .1 point outside AABCantl label it 0. This will be the center of
. . :’ Z) :’
protection. Draw 024. OR. attd OC.
_, _
3. Mark a random point. A‘, as the projection of A on 0A. [For clarity ol
construction, it should be farther from point 0 than from point A.)
_ _ -9‘ _ —>
Repeat tor BI a random pomt on Ob, and C a random pomt on OC.
Draw AA'B'(.'.
4. Extend mam] .-'l'B' until they intersect. and label the point of
intersection X. ( If the extended segments are parallel or intersect at a
point past the edge of your paper. reposition the image points.)
5. Extend A—Ca1rid A'C’ until they intersect. and label the point of
intersection Y.
6. Fxtend Whmd B’C' until they intersect. and label the point ot
intersection Z.
CHECKPOINT V’ 7. What appears to be true about points Y. Y. and 1? Make a conjecture.
and compare it with those of your classntates. (If you are using
geometry graphics sofiware. drag the rays and points in various ways to
see whether your conjecture still holds.) Based on vou r conjecture.
complete the following theorem:
'l'heTheorem of Desargues
If one triangle is a projection of another triangle, then the intersections
of the lines containing the corresponding sides of the two triangles are
? . 11.7.4
.
'v
LESSON 1! 1 OTHEHTRANSFORMATIONS AND PROJECTWE GEOMETRY 751
Exemses
. Cfllfilfil/II/Zdfe
1. Describe Whitt an ttlfine transforniation is. W hieh of the following are
special cases of affine translornnttiotis? Fxplain your reasoning.
a. dilutions
b. t1'Jl1Sl'.tti()l'lb
c. reflections
d. rotations
2. Describe what a central projectitm is. Which oi‘ the following are special
cases of central projections? Fxplnin your reasoning.
a. dilutions
b. translations
c. reflections
d. rotations
3. Explain how pmjeetive geonietry is dillierent from the other types of
geometry" you have studied.
4. In a Mercator projection, why do countries near the equator seem less
distorted than countries near the North and South Poles?
0 qt//ded 3k///S Plat’?/68
5. Copy the grids at right. [)rat-.- a \ \ \ \ \
right triangle on the square grid. _' \ \ \ \
and use the parallelogrant grid
to tr-unsform the triangle. _. 5 § 5 E
(ACTIVITY 1)
6. Draw a square in a coordinate plane with vertices at [0. 0), (0. l], (I. I],
and (I, 0). Use the affine transforniation fix, y) = I-ix. 3y) to transform
the square. What is the resulting tigure? (ACTIVITY 1)
7. Draw two parallel lines 1"’ and In. On line €.m'.1rk points A.. B.. and G.
On line in. mark points A1, B1. and C3. Find the intersections of A.B; and
/t_-B..ot' :‘l.C-_.. and i_»C., and ol B.C3 and B_-C.. Are the three points of
intersection collinear? (ACTIVITY 2)
8. Copy AABC and point 0 below and draw the image. AA'B'C'. translbrmetl
by a projection centered at O. Fxteml the corresponding sides of the
triangles until they i nterseet. and draw the line through the three points
of intersection. (ACTIVITY 2)
A
752 CHAPTER II
0 Pldfl‘/6'8 and 74,20/y
Sketch the preimage and image for each affine transformation below.
9. preimage: square [0, O]. [4. U}. (4. 4]. [0, 4)
truttslbrttlatiotl: T(J:, y) = (3x, -2)’)
10. preimage: rectattgle (0. 0), (5. 0). (5. 8]. [0, 8)
trtinsformation: S(x, y) = (2x. O.5y)
11. preitttage: triangle (-1. 7}, (-1. —| J, (0. 8}
tr-.1nsl"ormation: R(x, y] = (gar, Sr)
On a coordinate plane, draw a circle with a radius of 5 centered at the
origin. Use the parallelogram grids below to transform the circle.
13.
< / I
/
For Exercises 14-16, refer to the figures below. For each projection,
identify the following:
a. the center of projection
b. the projective rays
12.
14. projection of points on I’. onto £2 15. projection of points on H]; onto ml
16. projection of points on "13 onto rm
0 I773 N
0 """
. "‘ . _,.—> ‘G
P —-"" PA’ A R
,.
T" ,‘B -— ._ _‘> TH"‘—>
C F
C’ ~. ll \;
T ‘
£1‘,
Copy the diagram below and draw each projection.
17. Using 0 as the center of proicetion. I 6, 1":
project points A. B, C. and D onto line £1‘
£"_.-. Label the projected points /1’. Bi C: -P .A
and L7.
08
18. Using Pas the center of proj'et.tion. '0 ‘C
project points A’. Bi CI and D’ onto D
line (‘L Label the projected points A'(
B". CC and U5
LESSON n 1 OTHEHTRANSFOHMATIONS AND PROJECTWE GEOMETRY ‘I53
For Exercises 19-21. use the figure at right. A
19. ll" point A is the center of projection. then
the projt-:t.1it)n of B (into FK is ? ,
the projection of 1 onto FK is 1.’ ,
and the pi'ojec.tion of I onto I-‘K is ? .
20. ll" point L is the center of projection. then the
projection of H onto i\-M is ? , and the
projection of Jonto MA is. ? .
21. ll‘ point 1-‘ is the center of proiection. then the projection of ?
onto AG is 1. and the projection of ? onto AG is G.
In Exercises 22-29. you will explore the converse of theTheorem of
Desargues. The following construction begins where Activity 2 ended.
By working backward, you will locate the original center of projection.
22. Draw I’ and label X and Y-at arbitrary
locations on it.
and mark a random point, A. on it.
—>
24. Choose a point. b", not on 63. Draw X8’
I
23. ("liotise a point. B. not on 1”. Draw H3 \ i '3'
c'\1 B /
A‘ ,A,
and mark a random point. A’. on it.
if
25. Draw YA and mark :1 random point, C,
on it.
<7‘: . . . 47> <—— 0 I :4
26. Draw CB. Label the intersection ol CB X Y
and F .7.
27. Draw ‘M and 23’. Label their point of intersection C.
28. Asstiiiiiiig the converse of Des-.irgue’s Theorem. what can you conclude
alitiut AAB('anLl AA’B'C'.
_ _ _ _ <—>' 1-‘r (—r
29. |.oc-ate the center of projection, point 0. by drawing AA. BB’, and CC.
£001? 346*
30. Arraiige the statemeiits below to form a logical chain, and write the
conditional that follows from the logical ch-ain. (LESSON 2.2)
If the wind liltiws. then the trees shake.
If the apple fails. then the worm squirms.
If the trees shake. then the apple lalls.
.: ;,
Vi
‘£3
1
C
I‘ _
*
CI‘ \¢
754 CHAPTER it
For Exercises 31-33. tell whether each
argument is an example of inductive or
deductive reasoning. (LESSON 2.5)
31. All squares are rectangles. ABCD is a
square. '|'herelbre. A BCD is a rectangle.
32. There has never been .1 freeze recorded
in Florida in August. Today is August
12th. Therelore, it will not freeze in
Florida today.
33. Debra likes ever}-' type of fruit. Mangoes
are a type of fruit. Therefore, Debra
likes mangoes.
34. Describe what is meant by the golden ratio. (LESSON 11.1)
Find the taxidistance between each pair of points. (LESSON 11.2;
35. (4.5). (2. 1) 36. (—3.2).(1. 1) 37. (1.3).(5.5)
38. Does the figure at right contain an Euler path?
an Euler circuit? Why or why not? (LESSON 11.3)
39, In spherical geometry, how many lines are parallel to -.1 given line through
.1 point not on the line? (LESSON 11.5)
1.001? Bel/0IId
40. The Nine-Coin Puzzle In the picture of the nine coins below. you can
identify eight rows with three coins each. C an you rearrange the coins to
form ten rows with three coins each? (Hint: You can use the Theorem of
Pappus to solve this puule.)
-3:3‘
\ .
\'.
\ .
LESSON n 1 OTHEHTRANSFOHMATIONS AND PROJECTWE GEOMETRY ‘I55
°lPm\ W Towev
@
‘i’\9-ll“ @<F\His21te@‘i
£Lia\I‘c‘‘ % -
1-
- ~.
In this project, you will examine .1 puzzle, called the tower of Hanoi,
that was invented in 1883 by French mathematician Edouard Lucas.
Activity 1
THE PUZZLE The putzlc begins with three pegs, one of which has .1 stack of
disks that increase in size from the top of the peg to the bottom. The object
is to move all of the disks to another peg, following these rules:
' Only one disk Ind)’ be moved at -.1 time
° A disk must be placed on -.1 larger disk or on an empty peg.
1. \-\-‘hat is the least possible number Numbe, 0, pewes‘ numbe,
of moves needed to solve the pu7zle disks of moves
for 1 disk? for 2 disks? Complete the 1 7
table at right.
2 ?
2. Can you lind a formula for the number 3 ,
of moves in terms of the number of '
disks? l;'\'tend the table if necessary. 4 ?
3. According to a popul-(tr story, 64 gold disks on 3 diamond pegs are attended
by priests who move the disks according to the rules above. When they have
completed the puulc. the world will end. I low in-.inv l'l10\'CS are required?
If the priests can lTIO\"€ one disk per second, how
long will it take them to complete the puzzle?
756 CHAPTER n
‘H
“on...
A B
A B
A 8
ea.
c ,1-ALL;
Activity
STRANGE CONNECTIONS A graph may he used to represent the states of the
tower of Hanoi. When the vertices of the graph are arranged in a certain way,
the graph forms the same pattern as the Sierpinski gasket.
Start with the simplest case, a lower A
of Hanoi with only one disk. The pegs in '
the pu77le are labeled A, B, and C. Thus,
the initial state can be represented by a
vertex labeled A. it is possible to move the B0 T 0C
disk to either 8 or C in one move. so the
graph for the puule can be drawn as
shown. Notice that it is also possible to
move the disk from B to C (or C to B).so
B and C are connected by an edge. (A-fl
For the case with two disks, the states
can be represented by ordered p-airs. For (5 Al’
(C. Al
example, if the smaller disk is on peg B
[B7\ /(\(:,3t
and the larger disk is on peg A. the
position can be written as (B, A). The
graph for this pu71le is shown . . g .
at right” (C. (A. (A, Bl (3, Bi
1. Which states in the graph tor
two disks represent solutions to
the puzzle? Describe .1 possible
solution to the puz7le.
2. For the case with three disks, the (A Al
states may be represented as ordered
triples that describe the positions of
the disks in order from smallest to I '-
largest. l'ill in the states in the graph
at right. [Remember that if two \
vertices are connected by an edge. '\ i'\
you must be able to move a disk , _ _ , _ .
from one to the other in a single \ \
move.) Then describe a solution '\ '\ '\ '\
to the puzzle.
\
(B. A, Ali — I{C, A, Al
CHAPTER u PROJECT 75']
Chapter Review and Assessment
VOCABULARY
affine transfonnation .... .. 747 golden rectangle . . . . . . . . . . 699 projective rays . . . . . . . . . . . .749
blocks . . . . . . . . . . . . . . . . . . . 7tl5 graph . . . . . . . . . . . . . . . . . . . 712 sell-similarity . . . . . . . . . . . . 738
Cantor dust . . . . ...... .. . . 740 great circle . . . . . . ..... . . 731 Sierpinski gasket . . . . . . . . . 741
center o1 projection ..... . . 749 hyperbolic geometry . . . . . . 731 slmple closed curve . . . . . . . 722
central projection . . . . . .. . . 749 invariant . . . . . . . . . . . . . . . . . 723 spherical geometry . . . . . . . . 731
degree ol a vertex ...... . . 713 iteration ............... . . 738 taxicab circle .......... . . 108
edges . . . . . . . . . . . . . . . . . . . 712 logically equivalent ..... . . 730 taxidistanco . . . . . . . . . . . . . . 706
Euler characteristic ..... . . 723 Menger sponge ......... . . 738 taxicab geometry . . . . . . . . . 706
Euler circuit . . . . . . . . . . . . . . 715 Mobius strip . . . . . . . . . . . . . 721 taxicab radius . . . . . . . . . . . . 708
Euler path ............. . . 712 non-Euclidean geometry . . . 730 topologically equivalent . . . 722
even vertex . . . . . . . . . . . . . . 713 odd vertex . . . . . . . . . . . . . . . 713 topology . . . . . . . . . . . . . . . . . 721
lractal ................. . . 738 orthogonal ............. . . 732 torus . . . . . . . . . . . . . . . . . . . . 722
golden ratio . . . . . . . . . . . . . . 698 projected points . . . . . . . . . . 749 verticas o1 a graph . . . . . . . . 712
POSTULATES AND Tl-IEOREMS
Lesson section Pos u a - or Theorem
11.3 11-3-1 71190791“ A graph contains an Euler path if and only if there are at most two
odd venices.
11_4 11.4.1 Jordan Curve
Theorem
Every simple closed curve divides the plane into two distinct regions,
the inside and the outside. Every curve that connects a point on the
inside to a point on the outside must intersect the curve.
1 1.4.2 Euler's Formula For any polyhedron with Vvertices, E edges, and F faces, 1/ — E + F = 2.
11_7 11.7.3 The Theorem oi
Pappus
If A,, 3,. and C, are three distinct points on one line and A,, B2, and
C, are three distinct points on a second line, then the intersections of
AB, and A3,. of A.C-, and A,C.. and ot B.C, and B,C. are collinear.
11.7.4 The Theorem of
Desargues
If one triangle is a projection of another triangle, then the intersections
of the lines containing the corresponding sides of the two triangles are
collinear.
Key Skills 8: Exercises
LESSON 1 1.1
Key Skills Exercises
Determine side lengths of golden rectangles. 1. A golden rectangle has a short side length 013
A golden rectangle has .1 short side length ol‘5 ""113 Fmd ‘he Iwgth OM16 ‘("13 Side‘
units. Find the length of the long side. 2. A golden rectangle has .1 long side length of!)
. . . . . - u 1‘ts.F‘1dtlrlct th oftlr ‘ho tsidc.
the ratio ol the long side to the short side ol at I 1 H L 1 g L 1 r
golden rectangle is the golden ratio. 1}) e= 1.618.
758 CHAPTER n
Construct a golden rectangle.
Given square ABCD. construct A- D
a goldelrectangle whose short
side is All
B ->— C
Extend side Locate M. the
midpoint of BC and draw an art.
*?‘
centered at M that intersects BC A D
at E. Construct a line
—)
perpentficular to BCat E and
extend AD to intersect the B
perpendicular at 1-‘. /lBL‘l-' is a
golden rectangle.
30
"'3
LESSON 1 1.2
Key Skills
Find the taxidistance between two points.
Find the ttuidistance between (3. I) and (5, 2).
The taxidistemce between (an, y.)and (x3, y-_.J is
IX» - xil + I)’: -ril =
|5—3|+|2— l| =3.
Draw a taxicab circle with
a given center and radius.
Draw the taxicab circle
centered at [l, —l] with
a radius of 3.
LESSON 11.3
Key Skills
Determine whether a graph contains an Euler
path, an Euler circuit, or neither.
Does the graph below contain an Euler path. an
Euler circuit. or neither?
The graph contains 7 even vertices and 2 odd
vertices. Since there are odd vertices, the graph
docs not contain an Euler circuit. I l()\‘.'L‘\'L‘l'. there
are not more than 2 odd vertices. so the graph
contains an Fuler path.
3. Draw square W/YZ with a side length of 3
centimeters. and collsiruct a golden rectangle
whose short side is X)".
4. Identify another golden rectangle in the
diagram you ctmstructed for Exercise 3.
Exercises
Find taxidistance between the following pairs
of points:
5. [6. l) and (4. 5)
6. [7, 2) and (—l, 0]
Draw the taxicab circle with the given center
and radius.
7. center: [0, 0); radius: 2
8. center: [2, 3); radius: 4
Exercises
For each graph below, determine whether the
graph contains an Euler path, an Euler circuit,
or neither.
9. — 10. ’ '
. \|
. I
0 R X /
11. .&?Q. 12. . — C\.
\‘.;\.’/ \. _.
CHAPTER II REVIEW ‘I59
LESSON 1 1.a
Key Skills
Determine whether two figures are
topologically equivalent.
Are the figures below topologically equivalent?
The Iigure on the left is a simple closed curve. It
encloses -.1 region of the plane. The figure on the
right does not enclose any area. There is no way
to deform one into the other without cutting the
figure on the left. Thus. the figures are not
topologically equix-'alent.
Find the Euler characteristic of a figure.
Find the Euler characteristic of the figure below.
The figure is topologically equivalent to the figu re
below, which has 28 vertices. 56 edges. and 26 faces.
' T T ? °
0 I /_ o 0 l
O r I I .
. | |.
O I I I
I
The Euler characteristic is
l/— I.-+!-= 28—56+26=—2.
Lesson 1 1.5
Key Skills
Identity lines in spherical geometry.
Which of the following is a line in spherical
geometry?
A B
By delinition. a line in _
!spl'le‘l'lC;ll geometry is C D
-.1 great circle—a circle
that divides the sphere
into two hemispheres.
Thus. figure CD is a line. but figure AB is
not :1 line because it does not divide the
circle into two hemispheres.
760 CHAPTER n
Exercises
Determine whether the figures in each pair
below are topologically equivalent. Explain
your reasoning.
13. % S
14.
15. Find the Fuler characteristic ol the figure
below.
16. Use the Euler L‘l‘I'¢'trtlL'[t'.'l'lSIlL' to prove that the
figure above is not topologically equiv-.1lent to
El sphere.
Exercises
Refer to the basketball below.
17. Describe at curve on
the basketball that
is a line in spherical .
geometry.
18. Describe at curve
on the basketlmll
that is not at line in
spherical geometry.
Identify lines in hyperbolic geometry.
Which tigures in the diagram below are lines in
Poincaré's model of hyperbolic geometry?
According to Poincare‘s model, Y,
lines are defined
as diameters of the
outer circle or arcs
that are orthogmtal
X7 '
to the outer circle. M
Thus, ligu res X Y, YZ. and
YU are lines, bttt figure VW
is not a line because it is not
orthogonal to the outer circle.
LESSON 1 1.8
Key Skills
Create fractals by using iterations.
To form the Sierpinski carpet, start with a solid
square. Divide the square into .1 grid ol'9 squares,
and remove the center square. Repeat on the
remaining squares. Draw the first three iterations
of the Sierpinski carpet.
1 iteration
2 iterations 3 iterations
‘U geometry.
-1 P 20. Draw a curve in
Refer to the diagram of Poincare's model of
hyperbolic geometry below.
K
.Qi,.\
that is not :1 line /
in hyperbolic I‘.
geometry, and N
explain why it is
not a line.
19. Name three ligures in
the diagram that are
lines in hyperbolic
L
the diagram M
Exercises
The original figure and first iteration of a
fractal are shown below.
21. l’)r-aw the second iteration ol" the fractal.
22. Draw the third iteration ofthe fractal.
23. Does the area of the fractal above increase or
decrease with sttccessive iterations? ll" it
decreases. does it approach 0? If it increases.
does it approach inlinity?
24. Does the perimeter of the frut:tal above
increase or decrease with SllCC€S$i\-'6' iterations?
II" it decreases. does it approach 0? If it
increases. does it approach infinity?
CHAPTER n REVIEW 761
LESSON 1 1 .7
Key Skills Exercises
Transform figures by using affine Draw the preimage and image of the figure
transformations. with the given vertices under the given
Draw the preint-age and image of the rectangle t'a"5f°'mat'°"'
with vertiees at (0, 0). [0, 6), (3. 6]. and (3. 0) 25. (1. 3). (2, I). U. 0); Rfx, y) = (2x. 5y]
"-"m5f°rm€d by Tu’ y) = [3x’ ::'y)' 26- (2. -1). [3.U). (2. 2]. (L U; SIX. J’) = (I. 1-3)’)
TIO. OJ = (0. U) 24 ‘S 2“ 27. fJraw a central projection of AK! Mcentered
115, 6J=(9. 24) ' 1'6: K
T[.’.-. 0) = (9. O) _
3 M
. rl ta. 09 . X ' P
(0. '01: 3 ‘ is ' L
Transform figures by using central projections. 28. fJraw a central projection of points D. F. and
Draw a central projection of A 1'-°'"° “"6 '" c°'"”ed at Q‘
AABC centered at point 0. m
0- f-‘
C B 9 D E
_ _ :D- :> :)
Draw pl'0|€Ltl\"€ rays O.-‘l. OB. and OC and choose F
points A’, B’, and C’ on the rays. Draw A..«'l'B’ C’.
Applications
29. ARCHITECTURE An architect is designing an office
building, whose front face is to be in the shape ofa
golden rectangle. If the building will be -15 ft tall,
how wide should its front face he?
30. GEOGRAPHY A pilot is flying from Tokyo to London.
Use spherical geometry [0 describe the path the pilot
should take in order to tly the shortest distance.
31. GEOGRAPHY Tani and Alex are trying to measure
the coast of Oregon. Tani measures the coast from
a satellite photo and finds that it is 490 km long.
Alex uses a set of aerial photos and finds that
it is 560 km long. Explain the difference in
their results.
762 CHAPTER ll
Chapter Test
Given one side length of a golden rectangle,
find the unknown side length to the nearest
hundredth.
1. s = 15
l=L
l= 8
3. Draw square A BCD with a side length of
2 inches. and L‘0ItSIrl_.£l a golden rectangle
whose short side is BC.
2. s=;
4. l'JESlG\l A designer wants to make :1 sign in
the shape ofa golden rectangle. If the width of
the sign is 2| inches. what should the length
be? Round to the nearest inch.
Find the taxidistance between the following
pairs of points:
5. (4.61 and (1,5) 6. [3,2] and (-3-,—l)
Draw the taxicab circle with the given center
and radius.
7. center (0. 0); radius 5
8. center (I. '1); radius 3
For each graph below. determine whether the
graph contains an Euler path. an Euler circuit, or
neither.
0.
1 V
C
0'
11. WII lJl.lFF. M.-\NAGFl\-'iF.NT A park ranger
comes across a set of valley bear trails. Shown
l)':‘l()W. Could a bear travel all of the trails in
one trip, starting at the river and not retracing
any of the trails? Why or why‘ not?
3 Q-
I
12. \-’eril'y l3uler’s lormula for a rectangular prism.
13. Find the Euler
characteristic of the
figure at right.
For Exercises 14 and 15, determine whether the
figures in each pair are topologically equivalent.
Explain your reasoning.
"too £3:
.: Q
For Exercises 16 and 17, refer to the diagram of a
sphere below. Determine whether each figure is
a line in spherical geometry.
:l
K
16.17? L_' ' M
17.71! 4
J
13. Can a triangle it1 spherical geometry have two
right angles? Explain.
19. Draw three lines that intersect to form a
triangle in Poincare's system.
The original figure
and first iteration of
a fractal are shown
at right.
20. Draw the second iteration of the fractal.
21. Draw the third iteration of the fractal.
22. Does the area of the fractal increase or
decrease with successive iterations?
23. Does the perimeter ofthe fractal increase or
decrease with successive iterations?
Draw the preimage and image of the figure with
the given vertices under the given transformation.
74. [0, U}. ( l . 4]. I5. 2]; Six. }’.l = [233 0.5)’)
25. (1.0). ( I. 31. (5. 0). (5. 3); Rtx. y) = (-2:-. 3)’)
CHAPTER II TEST 763
-' E’S CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CH0lCE For Questions I-8. write the
letter that indicates the best answer.
1. Refer to the figure below. ll‘ mzl = 11112.
which statement is true? (LESSON 3.4)
/2 5
(TV
/1
a. Al and 4?. are alternate interior angles.
I). Al and A2 are vertical angles.
c. Line I is parallel to line m.
d. Line Iis perpendicular to line m.
2. Refer to the figure below. Which statement is
true? (LESSON 5.4)
A
c=8 D 3x-"3
3 a=6 C
a. C1 >z1’ +1):
b.r:3=a3+b3
‘ } )
c.C‘<;1'+b'
d.c>a+b
764 CHAPTER II
0.
D intemet connect t5r‘r'r
Standardized
Test Prep Online
Go To: go.hrw.corn
Keyword: MM1 Test Prep
3. If the length ofa side ofa regular hexagon is
2. what is the area of the hexagon to the
nearest tenth? (LESSON 5.5)
2
I 2.0
IO -1
3. 5
2U
coup
.8
4. The ligu re below is a right rectangular prism.
Find AG. (LESSON 6.3)
B C
A ' D 4
F 8 G
E 10 H
a. 61.4%
b.-l\.f'§
c. 2x’/i_§
d.4\-'4]
5.
Find the .\'-intercept of the line given by the
parametric equations below. (LESSON 6.5)
x = 4r — 8
y = 2! - 5
2=l+4
a. (0. 2.6]
I). (U. l.6.l
c. (U. 0.0]
d. none of the above
. .-\s the side length ofa cube is increased. the
ratio of surface area to volume ?
(LESSON 7.1;
a. increases
b. remains constant
c. is equal to l
d. decreases
if the radius of a sphere is doubled. the
volu me is increased by a Factor of L
(LESSON 8.6)
a. 2
b. l
c. 6
d. S
The value 0|" sin 0 is given by the ratio ?
(LESSON 10.2)
opposite
adjaecril
- fipotcnllst hypotenuse
opposite
opposite 9
' hypotenuse adjacent
hypotenuse
opposite
_ For the two similar quadrilaterals below, write
a proportionality statement by using the ratios
between the sides. (LESSON 8.2)
A
D
O
10. Determine whether the graph ‘ ’
at right contains an Euler . )i
path. an Euler cirutit. or
neither. (LESSON 11.3) _ .
FREE-RESPONSE GRID
Items 11-15 may be answered
by using a free-response grid
such as that commonly used
by standardized-test services.
ssaseesseeoo
asmeeeeeeao
@@@@@@®@@ 0
@@®@@G@@®@O®
11. How many dies of symmetry does the liglire
below have? (LESSON 3. 1)
12. Find the slope of the segment with endpoints
at (2.41 and (3, —l). (LESSON 3.3)
13. Find x in the triangle below. (LESSON 4.4)
14. Find sin the golden rectangle below.
(LESSON 11.1)
SI
C=12
15. Find the tawtidistance between the points ( I, -1]
and [7, I0]. (LESSON 11.2)
CHAPTER 11 CUMULATIVE ASSESSMENT 765
766
Lessons
12.1 o Trullt and Validity
in Logical
Arguments
12.2 0 And, Dr, and Not
in Logic
12.3 o A Closer Look at
lt-Then Statements
17.4 o indirect Prool
12.5 0 Computer Logic
Chapter Project
Two Famous
Theorem
A Closer
Look at Proof
and Logic
CAN A MACHINE THINK? AT TIMES IT CERTAlNLY
seems as if they can—as when the computer
Deep Blue beat the world chess champion Gary
Kasparov in a chess match. Whether they can
actually think or not, machines can clearly follow
rules and make "decisions" based on given
conditions. The decisions made by chess-playing
computers and other "smart" machines are made
possible by formal logic.
Formal logic reduces logical procedures to their
essential elements, which can be implemented
by computers or other machines. For example, the
following rule in chess can be programmed into
a chess computer.
If my king is in check. I must
° move out of check,
° capture the attacking piece.
- interpose a piece between the attacker
and my king, or
° resign.
..'7~ wrl ‘
‘\
Q ‘ h _ I
, . 0 - :4
Q
- \ -
J‘
I
‘ 3
wzmuzy an
‘II
About the Chapter Project
Number theory is a branch of nr.itheni.ttics that
is at least as old as Euclid. In fact. three books of
I.-'uclid’s L-‘Iemems are devoted to number theory.
In the Elerttents. Euclid uses segments of
different lengths to represent positive whole
numbers and proves theorems about numbers
geometric.tlly.
In the Chapter Project. you will study two
famous theorems from number theory. The first
is that then: are inlinitely many prime numbers.
and the second is that the square root of.-2 is
irrational.
After completing the Chapter Project you will be
able to do the following:
0 Have a deeper understanding of the
techniques of proof.
0 Understand the need for it class of nttmbers
that are not r'.ition.tl.
c -,"invI
. I;
About the Portfolio Activities
1 hroughout the chapter. you will be given
opportunities to complete Portfolio Activities
that are designed to support your work on the
Chapter Project.
The theme of cttch Portfolio Activity and of the
Chapter Proiect is nttmber theory.
0 In the Portfolio Activity on page 775, you will
explore the Euclidean algorithm for finding
the greatest common divisor (gcd) of two
numbers
0 In the Portfolio Activity on page 797. you will
learn how to prove the l.'uclidean algorithm.
767
Objectives
0 Define and use the
valid argument lorms
modus potions and
modus tollens.
0 Define and illustrate
the invalid argument
forms at affirming
the consequent
and denying the
antecedent
Truth and Validity in
Logical Arguments
Newspaper reporters. politicians.
lawyers, and even bueball managers
may use logic to canvinoe others of their
views. Recognizing valid arguments as
wall as invalid ones will help you to
think clearly in confusing site: i‘:
768 CHAPTER i2
Valid Arguments
in logic, an argument consists of a sequence ol‘ statements. The linal statement
oi‘ the argument is called the conclusion. and the statements that come before
it are known as premises. The following is an example of a logical argument:
lfan .anim.al is an amphibian, then it is .2 vertebrate.
Frogs are amph iiJi:.lIlS. Premises
lheretore, frogs are vertebrates. Conclusion
In this argument, the conclusion is said
to follow logically from the premises. The
premises force the conclusion. An argument
of this kind is known as a valid argument.
and the conclusion of such an argument is
said to be a valid conclusion.
A valid argument makes the following
“gu:irantee": lfrlie prr'mi5r'5 are all true,
then the conclusion is (me. In the valid
argument above. both premises are true.
Tl1erelore.the conclusion must be true.
Invalid Arguments
l\()w consider a different argument:
Some vertebrates are warm—blooded.
T1. .
Invalid argument * Frogs are vertebrates. Premises
(Don 't use one like this!) |
Therefore. frogs are warnt-blooded. Conr:Iusron(7l
This new argument is invalid. Both of the premises are true. but the
conclusion is false. This is rzever the case in it valid rwgrurterzt
CRITICAL nnmunc Consider the second argument. Suppose you did not know that :1 frog is not a
warnt-blooded animal. Would you have questioned the conclttsion anyw"ay'7.' ls
there something basically wrong with the argument? If you think there is. try
to describe what it is.
Tnv ‘nus write your own e.\'-amples of valid and invalid arguments.
A Valid Argument Form: Modus Ponens
Logicians can tell whether an argument is valid or invalid without knowing
anything about the truth of its premises or conclusion. l'hev are able to do this
by analyzing the form of the argument. The valid argument on the previous
page. for e\'-ample. has the following form:
Noteipandq mpmsem Argument Form: Modus Ponens
statements: that is.
sentences that can be
true or false—not
questions, commands etc.
If p then 1;
p Premises
Therefore, :1 COI'lCItlSi0n 1Z‘l.1
l'his argument lorm is sometimes referred to by its Latin name, modus
ponens. or the “proposing, mode." Any argument that has this form is valid.
regardless of the statements that are substituted for p and q. The following
nonsense argument. for example. is valid because it has a valid form:
If tliwers twiddle, then bokes malk.
F|i\-'\-'ers twiddle. Premises
Therefore. bokes malk. Conclusion
This argumenfs Form guarantees that if the first two statements should
somehow turn ottt to be true, then the third statement [the conclusion) would
be true as well.
LESSON 12.1 mum ANDVALIDITV IN LOGICAL ARGUMENYS 169
Another Valid Argument Form: Modus Tollens
Consider the following argument:
If 3 shirt is a De Morgan. then it has :1 blackbird logo.
This shirt does not have a l)l£tCl{l)il’(.l logo. PI'l:‘fflJSL'S
Therelore. this shirt is not a De Morgan. Conclusion
Does this argument seem valid to you? If you knew that the premises were
true. W()lIl[l you be certain that the conclusion was true? The argument above
has the lollowing form:
Argument Form: Modus Tollens
The symbol ~ If p then :1
means ""01" l ~13 Prelrrises
Therefore. ~ p Conclusion 12.! 2
This is a valid argument form. It is sometimes referred to by its Latin name.
nmdus tollens, or the “removing mode.” In more recc-nt times. it has come to
be known as the law of indirect reasoning.
False Premises
if the premises of an argument are fiilse. then there is no guarantee that the
conclusion is trite. even though the argument might be valid. The following
nmdus ponens argument is valid. but its conclusion is false.
lfan animal is an amphibian. then it can fly.
A frog is an amphibian. Premises
l'herelore, frogs can fly. Conclusion
‘the conclusion, though false. is at valid conclusion of the argument because
the form of the argument is valid. Remember. a valid argument guarantees
that its conclusion is true only ifirs prernises are true. There is no guarantee if
one or more of the premises are false.
cRI‘ncAL THINKING The valid argument above has a false premise and a false Conclusion. Do you
think it is possible for-.1 valid argument to have a false premise and a true
conclusion? lfso. give an example. If not, explain why not.
770
Invalid Forms
You should be careful not to confuse the morlus portens form with the
following irwnlid form:
Invalid Form: Affirming the Consequent
The consequent is the - It pthcn q
COHCIUSI-DI"), Q, 0’ the {I Pfemfses
conditional.
Therefore. p Not a valid conclusion 12.1.3
Form 12.1.3 is the tortn of -.1 common logical ntistake, or fallacy, known as
“allirnting the consequent." Tlte conclusion does not follow logically from the
pretnises even if it is .1 true statement. Be sure that you understand the
dillerence between this lorm and the mocius ponens form, which it closely
rescmbles. An exzunple ofallirntittg the consequent is as follows:
If Sancho is having plum pudding for dessert,
then he is happy. Premises
Sancho is happy.
Therefore. Sancho is having plum pudding for dessert. Conclusion {7}
Clearly, the argument doesn’t work. because Sancho mav be happy for some
other reason.
Another important invalid form that you will need to retognize c|o.st-zly
resembles the modus tolierts form.
Invalid Form: Denying the Antecedent
The antecedent is the l [t pthen q
NYPDWTESJ-S P. W319 ~ p Prernises
conditional.
Therefore. ~ q Not a valid conclusion 12.1.4
An example of denying the antecedent is as follows:
If Susan overslept. then she la running late.
Susan did not oversleep. Premises
Therefore. Susan is not running late. Conclusion 1'?!
Again. the argument isn"t valid because Susan might be running late for any
number of reasons.
LESSON 12.1 TRUTH ANDVALIDITV IN LOGICAL ARGUMENYS 771
Exerc/ses
772 CHAPTER 12
. Commozicate
ln Exercises 1-4, determine whether the argument is valid. Explain why
or why not.
1. If today is Wednesday. then the
cafeteria is serving beef stew.
Today is Wednesday. Premises
Therefore, the cafeteria is serving Conclusion fr‘)
beef stew.
2. if pigs ll_v, then todzlv is February 30.
Today is Febru-.1 ry 30. Premises
Theretore, pigs ily. Conclusion (7)
3. If Jan is a man. then Jan is mortal.
Ian is not .1 main. Premises
Therefore_. Ian is not mortal. Conciusion (7)
4. Ify- x, then a - b.
(1 as I! Premises
Therefore. )1 an .\.'. Conclusion f?)
5. Is it possible for .1 valid argument to have a false conclusion? Explain
your reasoning.
fifl/J64 3&7’//3 P/dc‘?/6'6
in Exercises 6-9, analyze the form of each argument and give its
traditional name.Then state whether it is valid or invalid.
6. If the weather takes a turn for the worse. then the local fan mers will suffer
.1 loss of income.
The weather takes d turn for the worse.
Therefore. the local farmers will suffer an loss of income.
(ARGUMENT FORM 12.1.1)
7. If Stokes was in top form. then he won the competition.
Stokes did not win the Competition.
Therefore. Stokes was not in top form.
(ARGUMENT FORM 12.1.2;
8. lfthe car is a Dusenberg, then it is a classic.
The car is ‘.1 classic.
Therefore, the car is a Dusenberg.
(ARGUMENT FORM 12.1.3)
9. If Sean stuffed himself at lunch, then he is feeling slr3ep_v now.
Sean did not stufl himself at lunch.
Therefore, Sean is not feeling sleepy now.
(ARGUMENT FORM 12.1.4)
J 1'1"’:
La“ ,.
J‘ baa.
‘ S
9 .,‘
I N
V
(See E.\'t'rt‘i.\'t’ l 4. )
\
In Exercises 10-11, write a valid conclusion from the given premises, and
identify the form of the argument.
10. lithe team won on Saturday. then the team is in the playofls.
The team is not in the playoffs.
11. ll‘ Sabrina finished her assignment on time, then she did a stupendous
amount of work at the last minute.
Sabrina Finished her work on time.
in Exercises 12-15, arrange the sentences to fonn an argument. Identify
the argument form, and state whether the argument is valid or invalid.
12. Therefore. Santantha is ill.
Samantha is absent.
ll" Samantha is ill. then she is absent.
13. Sims is not a man ofgood moral character.
If Sims is a man of good moral character, then he is innocent.
Tlterefore. Sims is not innocent.
14. Hedgehogs are tone deaf.
l'herefore. hedge-hogs will seldom be seen at symphony concerts.
ll" hedgehogs are tone deaf. they will seldom be seen at symphony concerts.
15. There were unpleasant surprises.
ll‘ the plan was loolpmof. then there were no unpleasant surprises.
Therefore. the plan was not foolproof.
In Exercises 16-19, use the following conditional: If the building was of
sound construction, then it survived the storm.
16. Write a mmltrs prmens argument. using the given conditional as one of its
premises.
17. Write a modus (aliens argument, using the given conditional as one of its
premises.
18. Write an invalid argument in the form of affirming the consequent. using
the given conditional as one of its premises. Label the argument as invalid.
19. Write an invalid argument in the form of denying the antcedent. using the
given conditional as one of its premises. Label the argument as invalid.
You are given the following premises:
If a student studies, the student will succeed.
Eleanor studies.
Tamara does not study.
Jose will succeed.
Mary will not succeed.
which of the following conclusions are valid?
20. Eleanor will succeed. 21. Eleanor will not succeed.
22. Tamara will succeed. 23. Tamara will not succeed.
24. Jose studies. 25. lose does not study.
26. Marv studies. 27. Marv does not study.
LESSON 12.1 ‘mum ANDVALIDITV IN LOGICAL ARGUMENY5 773
In Internet conned 3°;
Homework
Help Online
Go To: go.hrw.r:nrn
Keywu-rd:
MEI Homework Help
for Exercises (Q3-l
CHALLENGE
774 CHAPTER 12
In Exercises 28-31, consider the following argument:
If a quadrilateral is a parallelogram. then its diagonals are congruent
Quadrilateral PORS is a parallelogram.
Therefore. the diagonals of quadrilateral PORS are congruent.
28. Is the argument valid? Explain your reasoning.
29. Is the first premise true or false? Explain your reasoning.
30. ll" quadrilateral PQRS is a rectangle or .1 square. is the conclusion of the
argument true or false? Fxplain your reasoning.
31. It’ quadrilateral PQRS is not a rectangle or a square. is the conclusion of
the ttrgumcnt true Or false? Explain your reasoning.
A valid argument has premises a, b, c, and dand conclusion r.
32. Does the validity of the argument guarantee that the premises and
conclusion must be true? Explain your reasoning.
33. If the lour premises are true. does the validity of the argument guarantee
that r is true? Explain your reasoning.
34. Under what circumstances might r be false?
in Exercises 35 and 36. use two of the given premises to write a valid
conclusion. Identify the form of the argument that you used.
35. SPORTS ln footlrall. ifa team does not move the ball If] yd in 4 downs,
then they lose possession of the ball.
The Mammoths did not lose possession of the ball.
The Voyageurs ntoved the ball If] vd in 4 downs.
l'he Cheetahs did not move the ball I0 yd in 4 downs.
36. LANDSCAPING ll" tulips are not planted in the fall. then they will not llower
in the spring.
/\drianne’s tulips did not ilower in the spring.
i\'una‘s tulips flowered in the spring.
Geraldo planted tulips in the fall.
Look Back
Can each pair of triangles below be proven congment? Why or why not?
(LESSONS 4.2 AND 4.3)
For Exercises 40-42. refer to the figure below, in which
A x
m£1 = 20°, m£2 = 35’, and mSR = 80". 0
(LESSONS 9.3 AND 9.4)
40. mi)? = ? H
41. mP. = ?
/‘\ _ S
42. m PQ = .’
9 is an angle in the first quadrant with a tangent of J3. (usssorv 10.3)
43. Find 9. sin 6. and cos 6.
44. Can an angle in the second quadrant have the same tangent n56 3.‘ Why or
whv not?
45. (Jive the measure ol'-an angle in the third quadrtmt with the same
tangent as 9.
L001? Bet/and
Recall the If-Then Transitive Property from Lesson 2.2:
If p then q
If q then r
m _ I _ mm“ '19 Therefore, if p then r
Pottlolio M List all conclusions that can be drawn from the premises given below.
E:‘;_"::1v'cDm 46. lfx then y 47. ll" n then m
xe,w},,¢_ If ythen k liq then r
“'3' E”°'”°°“ ~k ll m then q
A H
ego
525
Q.
THE EUCUDEAN ALGORITHM
An algorithm for finding the greatest common divisor (gcd) of two
numbers is found in Book VII of Fuc|id's Flr'rm’ur.s'. Trace the steps in the
following example of finding the gal of I520 and 546:
I320 = 546(2) + 228 _ _ To find the numbarsmtins row,nota
,/ if that l320+546=2remainder22E
546 = 228(2) + 90
225' = 90(2) + 48
90’ = 4su) + 42
48‘ = 42(1) + 6 The last nonzero entry in this column
‘ _ is the gcd.
42" at?) + 0
1. Follow the steps used in the example to find the gcd of 630 and I65. of
280 and I50. and ol--lol and l20.
2. Two numbers are reluliwly prime iftheir gcd is l. Lise the Euclidean
algorithm to show that 330 and 9| are rel-ativelv prime and that 560 and
429 are relatively prime.
LESSON 12.1 mum ANDVALIDITV IN LOGIC.-at ARGUMENYS 775
Objectives
0 Define conjunctron,
disjtttrcttan. and
negation.
0 Solve logic problems
by USIDQ conjunction.
disjunction. and
negation.
And, Or, and Not
in Logic
L ~2‘ , l
\ E
§
P . p I I v‘
\ "\
f’ \‘
h .
The - -. and. or. and not are used -- amly
it everyday situations. - - - words have precise .
mathom- us In logical arguments. I
In logic, a statement is a sentence that is either true or false. The sentence
“Belinda ordered pepperoni on her pizza" is a sttttentent l}€C'tlllSt.' it must be
either true or false. A compound statement is formed when two or more
statements are connected. The sentence “lohn had :1 soda. and Belind-.1 had tea"
is a compound statement. A compound statement. like at simple statement, is
either true or false.
776 CHAPTER 12
conjunctions
A compound statement that uses the word and to connect simple statements is
called tt conjunction.
Sentence pi lbt'lt1)- is Tuesday.
Sentence q: Tonight is the first varsity track meet.
Conjunction p Al\D q: Today is Tttesda}-, and tonight is the first varsity
track meet.
A conjunction is true if and only ifboth of its statements are true. If one or
both of its statements are false. the conjunction is false. The four possibilities
for a conjunction can be illttstrutecl in a truth table.
All possible combinations of truth values for the
two statements that form the conjunction are
placed in the first two columns. ‘I he last column
indicates the truth values for the coniunetion. In
the first combinzttion. for example, both of the
statements that make up the conjunction are true.
In this case. the conjunction is true.
pAND q
T
F
F
F
E X A M P L E Determine whether the following conjunctions are true:
a. George Washington was the first president of the United States, and lohn
Adams was the second.
b. The sum of the measures of the angles of a triangle is 200°. and blue is
a color.
0 SOLUTION
a. The coniunction is true because both of its statements are true.
| b. The coniunction is false because one of its statements is false.
Disjunctions
Two statements may also be combined into a single compound statement by
the word or. This type of compound statement is known as a disjunction.
When used in everyday language. the word or often means "one or the other,
but not both." For example, if a waitress says, "You may have soup or salad
with your dinner," she means that you may choose just one of the two. This
use of or is known as the exclusive or.
In tnathematics and logic. or means “one or the other, or both.” This use of
or is known as the inclusive or. If someone asks how lohn will spend his
Saturday afternoons. the answer might be, “He will go swimming or bowling.”
This sentence can be written in logical form as p OR :1. where p and q are
identilied as shown below.
’ ‘ l le will go swimming or [he will go] bowling.
5.’) P on Q
The statement is false only if John does
neither one. There is nothing about the
statement which implies that lohn won't do
both. Notice that in the truth table. only
the fourth combination gives a value of
false for the disjunction. ll‘ lohn goes
swimming or bowling or both. the
disjunction is true, as the values for the
first three combinations show.
E X A M P L E Determine whether each disjunction below is true.
a. A square is a rectangle. or a pentagon has five sides.
b. Dogs can pl-av golf. or S — 3 = 2.
O SOLUTION
a. The disjunction is true because both of the statements are true.
I b. The disjunction is true because one ol the statements is true.
LESSON :2 2 AND. 09. AND NOTIN LOGIC 777
I no special tools l
CHECKPOINT ./
CRITICAL THINKING
778 CHAPTER 12
Negation 9.
Consider each of the following statements:
It is raining outside. It is not raining outside.
‘I he second statement is the rieguzioiz ol'the first one. If p is a statement. then
NOT p is its negation. The negation of p can also be written as ~p.
It is raining outside.
P
It is not raining outside.
.-up
Examine the truth table for the negation. P Np
Notice the following: When a statement. p. is
true, its negation. -«p, is false. When a T
statement. p. is false. its negation. ~p. is true. F T
ln the following Activity. you will explore one of De Morgan's laws, which are
named after British mathematician Augustus De Morgan (lS06—l87l }.
The Negation of a Conjunction
1. Copv and complete the truth
table for the negation of a
conjunction. Notice that the
fourth column represents the
negation of the third column.
pANDq ~lpAND q)
7 7
'|'I'|'I-I-I'D
‘H-(TI-t-D
7 7
7 7
7 7
Copy and complete the truth
table fora disjunction of two
negatiotts. Notice that the
values for -«p and -«q are used
to determine the truth values
for -up OR ~q.
. Compare the last column in the first table with the last column in the
second table. Explain what you observe.
. \-\-‘hen two logic statements have the same truth values, they are said to
he truth functionally equivalent. Complete the statement below. which
is one of De Morgan's laws.
~[ p AND :3) is truth functionally equix-alent to
In the two truth tables in the Activity. why should the combinations of T and
F be listed in exactly the same order in the first two columns of each table? lf
you list ‘I’ and l‘ values for the three statements p. q. and r, how many different
combinations of T and F will there be? What is a good order for listing these
combinations?
Exercises
. 60»/h/I/I//‘mtg
1. Explain the eonditions necessary for a conjunttion to be true.
2. Explain the conditions necessary for a disjunction to be true.
3. Explain the difference between an ll'lC.lllSi\-'c‘ orantl an exclusive or.
4. Give three different ways for the statement “Kiinba likes pizza and Lin likes
spaghetti" to be false.
0 qt//'fl'€fl'rSk/'//3 P/46¢‘/'68
Indicate whether each compound statement is true or false. Explain
your reasoning. (EXAMPLES 1 AND 2)
5. -l+5=9and -l-5:9
6. All triangles have three angles. or all triangles have four angles.
7. Three noncollinear points determine a unique plane,.1nd :1 segment has
two endpoints.
8. All squares are hexagons. or all triangles are squares.
Write a statement that is truth functionally equivalent to each
statement below. (ACTIVITY)
9.~rOR~s 1o.~[i.-\NDu)
0 Practice dlld 74,40/y
Write a conjunction for each pair of statements. State whether the
conjunction is true or false.
11. A carrot is a vegetal)Ie. Florida is a state.
12. A ray has only one endpoint. Kangaroos can sing.
13. l'he sum of the measures ofthe angles ofa triangle is 130°. two points
determine a line.
Write a disjunction for each pair of statements. State whether the
disjunction is true or false.
14. Triangles are circles.
Squares are parallelttgrants.
15. Points in a plane equidistant
front a given point form a circle.
The sides of an equilateral
triangle are congruent.
16. An orange is at fruit.
Cows have kittens.
LESSON :2 2 AND. 09. AND NOTIN LOGIC 779
Write the negation of each statement.
17. 'l'he figure is a rectangle. 18. My client is not guilty.
19. Rain makes the road slippery. 20. Triangles ha\-"C six sides.
21. a. Copy and complete the truth table for-»(~p).
P ~ P ~l~pl
T ? 7
F ? ?
b. \-\-' hat statement is equivalent to the statement ~ [-up)? Explain your
reasoning.
For Exercises 22-29. write the statement expressed by the symbols,
where p. q. r. and 5 represent the statements below.
p: AABC is isosceles.
x}: AA BC has two equal angles.
r: Al and .52 are adjacent.
3: Al and A2 are acute angles.
22.-vp 23. q0Rp 24.pAND r} 25.-wt]
26. ~s 27. rOR 5 28. 5A.\lD~ r 29. (1 OR ~s
For Exercises 30-32, construct a truth table for the given compound
'3 ' mm” statement. When is the compound statement false?
Homework
WP °"““° 3°‘ [F AND ‘3’ ‘ND ' p q r pAND q (p AND 11) AND r
G T 1 . .
xgyiollll mmm 31- [POE ‘l1 0R " T T T ? 2
“1E!éi.:T..':::";o'?;l° 32- Ur AND «I 0R 1 T F ? 2
‘ (T 5) T F 1' ? 1
T F F
US-E;-fills table I F T T
for Exercise 30. F 1' F
F F T ? ?
F F F ? ?
33. Fxplain all of the logical possibilities that would make this sentence true:
Flora will cook or wash the dishes. and Vernon will vacuum or wash the
windows.
A P P L I C A T I 0 N 34. ADVERTISING An advertisement for a set of holiday lights contains the
following statement: “Not all bulbs go out when one bulb burns out."
is this the same as "When one bull) burns out. all of the remaining bulbs
continue burning"?
ml
WM;
0-?
//m
\\‘l.‘~‘
(Q
/ .
Ida];
780 CHAPTER 12
A P P L I c A T I 0 N 35. COMPUTER DATABASES Computer database software can perform AND and
OR operations on stored data. Study the sample database printout below.
which contains IU records with 5 fields each.
Last name First name State Year of birth Annual income
Craighead Alicia TX 1955 S 25,000
Nrcar Bill MN 1942 S 45.000
Tuggle Lawrence LA 1972 S 20.000
Mallo Elizabeth TX 1956 8 50.000
Torres Ernest AK 1940 S 38,000
Tong Jun TX 1952 3 18,000
Jurek Chandra AZ 1944 3 31.000
Brooks hier Mary OH 1960 5 62.000
Lamb Charles TX 1951 S 41.000
Flaamsch Martin OK 1965 5 32.000
a. List all the records in which the individual was born alter I950 .-‘\l\'D
the annual income is greater then 5130.000.
b. List all the records in which the individual lives in Tetas OR the annual
income is less than S3t),U-00.
Look Book
Can each pair of triangles below be proven similar? Explain why or why
not. (LESSONS 3.3 AND 8.4)
36. ej 37. 33.
3 : ls
4 13 7
9
£ _U'
15 35
Find the indicated ratios for the triangle below. (LESSONS 10.1 AND 10.2)
39. sin A 40. cos B A
41. tan B 42. cos A 91 \-
C 12 3
Look Beyond
43. Can you determine whether the sentence below is true or false? Explain
your reasoning.
This scntenL‘c is false.
44. A woman is on an island and is trying to determine whether she should go
east or west in order to get back to the mainland. Two dit"ferent groups of
people live on the island. One group always tells the truth. The other group
always lies. The groups dress differently. but the woman does not know
which is which. She approaches two islanders who are dressed differently to
ask the direction to the mainland. What one question can she ask one of the
C H A L L E N G E islanders to determine the correct direction?
LESSON :2 2 AND. 09. AND NOTIN LOGIC 781
e 3
. MESSAGE OF THE MAYA
_ In Modern Translation
.1- I I - by Greg Stec
Special to the Cliristimi Science Monitor
Discovering the titles of Mayan royalty. the names of their gods and their food.
' t‘ V the dates ofimport-ant events, and all the other things great and small that
make up an advanced society has taken more than a hundred years of digging
and probing. At last. though, most of the M-aya's intricate writing is yielding to
* modern techniques of linguistics and computer technology.
__ ‘ So many dates are involved in Mayan inscriptions that at one time
. . . ~ ' - archaeologists theorized that the Maya worshipped time and numbers. The
' ‘ current thinking holds that the Maya were slaves to ritual and ‘ceremony. B)
3 dating an elite's birth, acconiplishments. and death with unimpeach-able
accuracy. the person's position and rank would be permanently established.
Computer programs wade through a sea of Mayan dates, saving investigators
h effort that can be used to examine other translations.
Q
- '_\ imagine having two calendars on your wall. with a different number of days
L . — -- .
. _ in each year. Every day would have two dates. usually dillerent. Your birthday.
“ ' ‘ -“ ~ .\ 5 ‘ for exam ale. mi ht be Au ist 4 and A iril 29.
I‘ \ l' g l
‘ ‘ ‘\' . The Ma 'an system was similar to this in that
§ \..§¥ .. . . . l . .
X T -‘ E it had two different calendars, one of
I _ Q}: -"' _ ., Vt‘ — them 260 days long and the other 365
‘-~. ‘ ‘ ‘ ' 5 days long. To get a better idea of how it
_ ‘ \‘‘}\ ' worked, you can use the diagram of
'7." .\‘ @_{.’ three wheels at left.
/33? ‘U ~ --" -\ ,"
v ‘ '\
"‘ . .3’ V . sf? 9 qfi\ E
“vs s . ‘£3 flgjk Em, Cooperative Learning
. u ‘ ' l _
""5, "_ ‘me The Mayan ceremonial calendar. or
__. en, _ 10 (39) izolkin, was 260 days long. it was
_‘ . _ _: rr ' composed of two independent cycles. a
__ A ‘. ' I3-day cycle and a 20-day cycle. The days
* I . \ ‘ ?@i _ _ \ iii the l3-day cycle were numbered from l
= _ -' .i-11 , 33$ ' to I3. and the days in the 20-day cycle were
, . '~{ ‘ ' named. like our days of the week. The two smaller
t ‘IE6 - wheels in the diagram can be used to explain the order
, \ of the days. As the wheels turn. each cycle advances
~ ' ' -\ by one dav. much like our calendar going from
.2 '-
Monday the lst to Tuesday the Ziid. and so on.
For convenience. let the days in the 20-day cycle be represented b_v letters instead of
the Mayan names. Then each day has a date composed of a number from I to 13
followed by a letter from A to T. For example, the first day of the year would be IA.
1. How tnany possible dates are there? Explain your
reasoning. _ -‘
2. The date shown in the diagram below is 7G. What
would be the date one day later? 13 days later? 20 . ‘ -_-
days later? - '*_ _ _,, '
3. To help you understand the arrangements of the dates.
consider some "calendars" with fewer da_vs.
a. Suppose that a calendar has cycles of 8 days and 5 '
days. The days in the 5-day cycle will be represented - - ' J .
b\-' letters from A to E. How many dates are possible? '
To find the order of the dates. repeat the numbers as
from l to 8 in one row and the letters from A to E in
another. as Follows:
l234S678|234S678l2...
AHCDF ‘\BCl)EAHCDF \HC...
Continue until the date [A repeats. Does every possible date occur? . ,
b. Suppose that a calendar has cvcles ol'6 da_vs and 4 days. The days in the \
1-day cycle will be represented by letters trom A to D. How many dates '
are possible? To lind the order of the dates. repeat the numbers from I l -
to 6 in one row and the letters from A to D in another, as follows:
l23456l234S... .
ABCDABCDABC... '
Continue until the date IA repeats. Does every possible date occur?
c. For every possible date to occur, what mttst be true of the number of ' ‘-
days in the cycles! (Hint: Look at the lactors of the number of days in
each cycle.)
The .\-layan solar calendar. or lmab. was ?-65 days long. It was .
composed ol ta months ol’2O days each (numbered from O to 19) ‘
and one month ol"5 days; the days of the 5-day month were
considered unlucky. The order of dates in the solar calendar was 3.
similar to our calendar. Using lowercase letters to represent the
names of the tnonths. the dates would start at Oa. then la. 2a. and
so on. The solar calendar is represented by the large wheel in the
diagram.
4. ln the diagram. the date on the solar calendar is l5a. The
combined date is 7G I3-a. What will be the combined date I
day later? 20 days later? 260 days later? 365 days later?
5. How many possible combined dates are there? Based on your
results from part c of Step 5, do you think every possible date
will occur? How many years will it be before the date 70 l3a
occurs again? .
,.
_ -' AFTER 12 EYEW -. -it
Objectives
0 Create truth tables to:
contlitxonals anti tor
conversas, int-erses,
and contraposttwes ol
conditionals.
0 Use il—tl1en statements
and fonns of valid
argument tor problems
involving logical
reasoning.
A ' P ICATION
CHIMINALLAW
A Closer Look at
If-Then Statements
4 .. -- ,
v ' ' 1
- Inca an Jsineverytlaylife,
‘ 4 ~ _ If-than statements are a very Important
7 4‘; "' - ‘ part of language. They are also used in
- matbantazlcal reasoning.
‘
Lawyers use logic when pmeming their cases to juries. For exnniple. (l iawyer
might argue, "lft‘he dejendmtt‘ committed the crime, then he could not hm-'e been
at the north shopping mall between i0 AM. and 10:50 A.M. ” How do you think
the argument would continue?
784 CHAPTER :2
The Truth Table for a Conditional
Various lorms of il‘-then statements have been used throughout this book. You
may recall from Lesson 2.2 that itlthen statements are called condition-als. You
can think ol':t conditional as :1 promise. in logic. if the “promise" is broken. the
conditional is said to liilse. Otherwise. it is said to be true.
Suppose that vour neighbor makes the Following promise:
lfyou mow my lawn, then l will give vou $10.
I’ ‘I
Four possible situations can occur.
1. You mow the lawn and your neighbor gives you 310.
the promise is kept. Therefoie, the conditional is said to be true.
2. You mow the lawn and your neigltbw does not give you $10.
The promise is broken. Therefore. the conditional is said to be false.
3. him do not mow the htwu. ibur rzfighbor gives you $l0.
l'he promise is not broken. 'l'herel'ore. the conditional is said to be true.
4. You do not mow the lawn. Your neighbor does not give you $10.
The promise is not broken. Therefore. the conditional is said to be true.
The truth table below sununarizes the truth values for the conditional p => q.
Recall that the logical notation l'or“il' p then :1" is p :5 q (read as "11 implies If].
P 0
The lirst two columns of the truth table list all possible LUlUlJll'|dl.l0llS of T and
F for the two .~.t.-ttements [7 and q. The third column list the truth values of the
conditional p =:~ q. \lotice that the only time p = q is false is when p is true
and q is false that is. when the promise is broken.
The Converse of a Conditional
Recall from lesson 2.2 that the converse
of a conditional results from interchanging
the statements following iftthe hypothesis}
and than [the conclusion). Consider
the following conditional and converse:
Conditional
ll‘ Tamika lives in Montana. then
she lives in the United States.
cuscxpomrr ./ ls this statement true?
Converse of the conditional
ll‘ l‘amik-.1 lives in the L'nited States. then she lives in Montana.
cnscxpomr ./ lsthis statement true?
The truth table below suntmarizes the truth values for the converse of the
conditional p => q.
1II1I|--t -I'D
-nl-1|-n —tn
-4 -n -1 -1 1|
cnmcm. THINKING Recall that two statements are truth functionally equivalent it" and only if they
have the same values in their truth tables. ("ompare the trttth values for the
conditional -Ind its converse. Are they truth functionally equivalent‘.' Explain)
your reasoning.
LESSON :2 3 A CLOSER LOOK Al’ IF-THEN SYATEMENTS 785
The Inverse of a Conditional
The inverse of a conditional is formed by negating both the hypothesis and the
conclusion. Below is the inverse of the conditional in the previous example.
Inverse of the conditional
if Tamika does not live in Montana. then she does not live in the
United gitates.
cnscxpomr ./ ls this statement true?
The truth table below represents the inverse of the conditional p => q. Notice
that extra columns are required for the negations of p and q.
p ~p ~a ~p= ~a
T
T
T
F
F
T
F
T
cnmcAi_ THINKING Are a conditional and its inverse truth t'unctionall_v equivalent? Is the converse
ofa conditional truth functionally equivalent to its inverse? Explain your
reasoning.
The Contrapositive of a Conditional
The contrapositive of a conditional is formed by interchanging the hypothesis
and the conclusion of the conditional and then negating each part. Below is
the converse of the original Conditional.
Contrapositive of the conditional
ll" l'amil<a does not live in the United States, then she does not live
in Montana.
cuscxpouvr ./ ls the st.itement true?
‘I he truth table below stnnmarizes the truth values lor the contrapositive of
the eontlitional p => q.
p a ~q —p ~q =9 —p
T T F F T
T F T F F
F T F T T
F F T T T
Notice that the final columns for the truth tables of the original conditional
and those of its contrapositive are the same. thus. the two statements are truth
l'unetion-ally equivalent. [fa conditional is true. its eontrapositive must also be
true. Moreover. ifa conditional is false. its contrapositive must also be lalse.
Thus, every theorem or postulate that can be written in if—then form can be
rewritten in contrapositive form—which will also be true.
786 CHAPTER :2
Summary of Conditionals
THREE RELATED FORMS OF AN IF-THEN STATEMENT
OR cONDl11ONAL
Conditional If p then q p =9 q
Converse If qthen p q => p
Inverse If -12 then ~q -p =9 ~q
Contrapositive If —q then —p —q =9 -p
‘rm! THIS Write the converse. inverse, and contrapositive of each conditional below.
Determine whether the original statement and each new statement are true
or false.
a. ll a triangle is equilateral, then the triangle is isosceles.
b. If a quadrilateral is a rhombus. then the quadrilateral is a square.
Exercises
. Co/rm//M/mte
In Exercises 1-4, write the converse, inverse, and contrapositive of each
conditional.
1. ll‘ today is February 30, then the moon is made ol green cheese.
2. If all three sides ofa triangle are congruent. then the triangle is equilateral
3. ll'l do not go to the market. then l will not buy cereal.
4. lf the car starts, then I will not he late for school.
- motaonned .195
IN"!
Acfivifies 5. Describe the circumstances that would make the statement “If a then 1:”
Online false.
60 To: no.hrw.cnm
Keyword.
MG‘lTrutl1Tbl -
- 0
Nfll
s‘.gg'IIrl( D _-_
THE Mon
5 0‘ :7:
cu££5E 5"
(See Fxer-rise l .]
LESSON :2 3 A CLOSER LOOK Ar IF THEN STATEMENTS 787
0 Guided 34’///3 P/dtt/68
6. Complete the truth table 7. Complete the truth table for the
for the conditional p => q. converse of the condtional p => q.
(TRUTH TABLE or rcorvvsnss or A
A CONDITIONAL) CONDITIONAL)
q p = q P 0 0 =9 P
T _7 T T 7
F T F ?
T F T ?
F F F ?
8. ("omplete the truth table for the 9. ("omplete the truth table for the
inverse of the conditional p => q. contrapositive of R1 conditional.
mvvsnss or A CONDITIONAL) (CONTRAPOSITIVE or A
CONDITIONAL)
p a -10 -0 ~11 = ~p
T T ? ? ?
T F 7 ? ?
F T ? ? ?
F F ? ? ?
0 P/dtt/68 mm’ flpp/y
For each conditional in Exercises 10-15, write the converse, inverse.
and contrapositive. Decide whether each is true or false and explain
your reasoning.
10. ll" -.1 figure isusqu-.1re.tl1cn it
is at rectangle.
. .. corned . 11. ll’ a= b. then :13 =11’.
3.
iflfll
H0meW0fl< 12. ll" :4 < E1, then 41’ < 12’. ;
Help Online _ _ _ .
G010: g,,_,,,w_c,,,,, 13. ll three angles ol at triangle l
:‘¢g;\';'d= H. l are congruent to three angles
,0, Ex'::;::',,_,';"’ of: another triangle. then the
u. and 25 triangles are congruent.
4 14. lfp and q are even numbers.
then p+ q is an even number. .‘ I‘
A P P L I G A 1’ I 0 N 15. PHYSICS lfwatcr is frozen at \ -
normal atmospheric pressure.
then its temperature is less
than or equal to 32"F.
788 CHAPTER :2
16. (jiven: if p then q. Write the contrapositive of the statement. Then write
the contrapositive of the contrapositive. What can you conclude about the
contrapositive of the contrapositive of an if—then statement?
17. Suppose that the following statetnettt is true:
lf the snow exceeds 6 in., then school will be
canceled. Which of the lollowing statements
mttst also be true?
a. lf the snow does not exceed 6 in., then
school will not be canceletl.
b. If school is not canceled. then the snow
does not exceed 6 in.
c. If school is canceled. then the snow
exceeds 6 in.
18. State the Pythagorean Theorem and its
converse. inverse, and contrapositive.
Determine whether each is true or false.
and explain your reasoning.
19. Choose a postulate or theorem from Chapter 3 that is written in if-then
form. W rite its com erse. inverse, and contrapositive. decide whether each
is true or false. and explain your reasoning.
20. Choose a postulate or theorem from Chapter 9 that is written in if-then
form. Write its converse. inverse, and contrapositive, decide whether each
is true or false, and explain yottr reasoning.
Some statements that are not written in if-then form can be rewritten in
if-then form. For example. "Every rectangle is a parallelogram" can be
rewritten as "If a figure is a rectangle. then it is a parallelogram." ln
Exercises 21-24. rewrite each statement in if-then form.
21. All seniors must report to the attditorinm.
22. A point on the perpendicular bisector of a segment is equidistant from the
endpoints of the segment.
23. She will call me if she is going to be late.
24. Doing mathematics homework every night will improve your grade in
mathematics.
25. The statement “p ifand only if q.” written as p 4: q, is equivalent to the
following two statements:
If p then :1
and lfq then p
Suppose that the statement rc:.> s is true. which or the following must also
be true? Explain your reasoning.
a. If rthen s
b. lfs then r
c. If --r then ~5
d. lf-«s then ~r
26. Statements using “ifand only if” are known as biconditionals. Based on
your results from Exercise 25. what can you conclude about certain
theorems in this book? Fxplain your reasoning and give two examples.
LESSON :2 3 A CLOSER LOOK Ar IF-THEN STATEMENTS 789
APPLICATION
790 CHAPTER :2
27. ACADEMICS Consider the following statement: You will make the honor
roll only if you get at least a B in mathematics.
Which of the following statements appear to convey the same meaning as
the original statement? Explain your reasoning.
a. If you make the honor roll. then you must have gotten at least a B in
mathematics.
b. If you get at least a B in mathematics, then you will make the honor roll.
c. lf you do not make the honor roll, then vott did not get at least a B in
mathematics.
d. If you do not get at least a B in mathematics then you will not make the
honor roll.
Look Back
Use the triangle below and the law of sines to find each missing
measure. (LESSON 10.4) C
28. Given mLl3 = 37°. tnLA = 50’.
and b - l0D. find c.
29. Given mLC - 65°, mLA - 47°,
and r: = 3.-15, [ind b.
8 c A
Copy the vectors below and draw the resultant vector by using the
head-to-tail method. You may need to translate one of the vectors.
(LESSON 10.7;
/\ \/ \\
Look Beyond
33. Suppose you know that statement p is true and you want to prove that
statement I; is true. You begin by proving that the conditional p => q is
true, which leads immediately to the conclusion.
Write an outline ol the argument in terms of what is given. what is to he
proved. and the logical principles that allow you to draw your conclusion.
34. Suppose that. as in Exercise 3?-, you know that statement p is true and you
want to prove that statement q is true. You are unable to prove directly that
the conditional p =:~ q is true. so you prove instead that its contrapositive.
---q ='.» -vp. is true. If the contrapositive is true. can --q possibly be true?
(Remember that you know p is true.)
Write an outline ol" the argument in terms of what is given, what is to be
proved, and the logical principles that allow you to draw your conclusion.
You will study this type of-argument in the next lesson.
Objectives
0 Develop the concept oi
indirect prooi (reductio
ad absurdum, or prooi
by contradicttoni.
0 Use il|dIfeCl proot Wm]
problems involving
logical reasoning.
Lewis Carroll. the
author of Alice in
Wonderland and Through
the Looking-Glass, was a
Ioglcian who was land 0!
absurdity as a form of
entertainment. But does
5:. -ityhava anyroal
place in logic or
mathematics? In this
Iessun, you will see that it
can. in fact. be quite
useful.
Indirect Proof
‘gt ..c-u-.133 I
'. - ..__—_—- -——.—~
\ .. n_._-it-g_na~:r_':1".-'-._. --
The time has cmm-',' the 11-‘kzirzzs srtid,
‘To mik ofnmny things:
0} 5lmes—and sltips—nnd sealing-wrv.'—
Of¢‘nbbngc’s—unrl kings-
And why flit’ ml is boiling hot-
Ami u-'I1crIterpigs have wings.’
—l.£wis Carroll. Through the Lrmking-Glass
Modus Tollens Revisited
You may have heard expressiotts such as “If he's twenty-one, then pigs have
wings!”
The speaker, perhaps without re;1|i7ing it, is inviting ml to use the law oi
indirect reasoning (modus rolieus). which you studied in Lesson l2.I. It is
certainly not true that pigs have wings. so the statement in question
(the hypothesis of the conditional) must be false.
If he's lwent_v-one. then pigs have wings. {If p then q}
Pigs do not have wings. (-0!
Therefore, he's not twenty-one. (Therefore, -pi
LESSON I2 4 INOIHECT PROOF 791
Indirect Proofs
A form ofargtnnent closely related to modus rolferls is known by its Latin
name reductin ad ahsnrdmn —|iterall}r, “reduction to absurdity." In this form,
an assumption is shown to lead to an absurd or impossible conclusion. which
means that the assumption must be rejected.
ln formal logic and matliematic s. certain proofs use the strategy of reductio
(1r'ft'lf1.\‘lH'r'fl.Ul'l. but with an important twist. In such proofs. you assume the
opposite or, in logical terms, the negation of the statement that you want to
prove. lfthis assumption leads to an impossible result. then it must be
concluded that the assumption was false. I hence. the original statement was
true. Such proofs are known as indirect proof: or proofs by contradiction.
792 CHAPTER 12
Using a Contradiction to Prove Your Point
What is meant by an “absurd" or “impossible" result? In logic. a trorinziriitrriou
is such a result. A contradiction has the following form:
p AND «-p
‘that is, a contradiction asserts that a statement and its negation are both true.
The following compound statement is a contradiction:
A horse is a vegetarian, and a horse is not a vegetarian.
ln tormal logic and in mathematics, an assumption that leads to a
contradiction must be rejected. Thus. contradictions turn oLtt to be very useful.
Proof by Contradiction
To prove a statement is true, assume that it is false and show that this
leads to a contradiction. 12.4.1
An Indirect Proof
The following proof uses a contradiction to prose the converse of the
Corresponding Angles Postulate. Recall that the converse of this postulate
[which is itself a theorem] states the following:
If two lines are cut by a transversal in such a wav that corresponding
angles are congruent. then the two lines are parallel. ( Theorem 5.4.]
‘lb prote Theorem 3.4.1. use the “if” part of the theorem as the given.
INDIRECT PROOF
Given: Line E‘ is a transi-ersal that
intersects lines at and n,
and AI ’=' Z2.
Prove: m|| :1
Proof: Assume that m is not parallel to n.
By assumption, in is not parallel to n. so the two lines will meet at
some point. C. as shown in the redrawn figure above.
Because £1 is an exterior angle of AABC. mzl = tm;’2 + m£3. But
this means that inzl > m.42 [because 111.43 > 0°). Therefore. Al is
not congruent to .42. Thus. the assumption that m is not parallel to n
has led to the following contradiction:
(.41; 42) Al\D [Al as .42)
Therefore. the assumption must be false. The conclusion is m|| n.
TRY THIS
Alibis and Modus Tollens
Arguments using the law of indirect
reasoning t modus mllens) are more
common than you might think. In a
Court of law. for example, a law_ver
might want to show that a statement
made by the prosecutor contradicts
the accepted evidence, or the given.
.-Krguments such as the following, are
(]LllN:‘ C0lTll'l1()l'|Z
"If the defendant set the tire. then
she must have been at the restaurant
between 7:30 I’.M. and l l:()[] I’.M. But
three witnesses have testilied that the
defendant was not at the restaurant
during those hours—she was in fact
at a party on the other side of town.
Therefore, the defendant did not set
the tire.”
Cmrrrrvnm artists nmkt"
.<lt¢'rd1¢'.~ of trial scemxs
The form of this argument can be represented as follows:
1. If the defendant set the fire. then she was at the restaurant between 7:30 PM.
and H230 HM. (Ifp then q)
2. |'he defendant was not at the restaurant between 7:30 PM. and l 1:50 PM.
(~ q)
3. Therefore‘. the defendant (lid not set the tire. (Therefore. -p)
Show how the argument above could be made into a proof by contradiction.
LESSON I24 INDIRECT moor 793
Exemses
. Comma»/care
1. What is a contradiction? Give the logical form and explain what it; means.
Are the following statements contradictions? Explain your reasoning.
2. A tiger is at cat, and 11 tiger is :1 mainmal.
3. A crocodile is it reptile. and .1 crocodile is not at reptile.
4. Some insects are butterllies. and some insects are not hutterllies.
5. Some dogs are not pets, and some pets are not dogs.
6. Summarize the steps for writing an indirect prooli.
ll - connect .30
Activities M
Online 61//ded 54’///8 Practice
Go To: 9o.hrw.com
:f£‘;’;"."’I"‘]‘:miW Form a contradiction by using each statement and its negation. (USING
A CONTRADICTION)
4
‘I. Lines 1'' and m are parallel. 8- /_\ABCis isosceles.
9. All sqtiares are rectangles. to- ABCD is a square.
A Suppose that two lines are cut by a transversal in such a way that the
n same-side interior angles are supplementary. Complete the following
proof that the lines are parallel. (INDIRECT PROOFS)
3 Suppose that 11. ? . Then lines If and m must meet at some point, C.
I. "7 forming AABC. The sum of the measures of the angles of :1‘./lb‘C must be
180°. However. this is a contradiction because 12. E’ . Thus. lines t" and m
must be parallel.
0 Practice and App/y
For Exercises 13-17, determine whether the given argument is an
example of indirect reasoning. Explain why or why not.
13. ll‘ it were snowing. there would be snowllakes in the air. l'here are no
snowflakes in the air. Therefore. it is not snowing.
14. ll-you were not ill. then \-‘mt would eat a large dinner. You did not eat a
large dinner. Therefore. you must be ill.
15. Ill see my sli-.idow. the sun must be shining. I see my shadow. Therefore.
the sun is shining.
16. Ill am not in the United States, then I am not in \lew York. I am in the
L'nited States. ’l'hereiore,| am in New York.
17. II" the dog knocked 0H.'l' the trash. then he would look guilty. The dog does
not look guilty. Therefore, the dog did not knock over the trash.
794 CHAPTER 12
INDIRECT PROOF
INDIRECT PROOF
CONNECTION
l.'I - connect &;
Homework
Help Online
Go To: 9o.hrw.cotn
Keyword;
MG! llomcworiz Heb
lot Exercises 34-37
APPLICATION
The following indirect proof, based on Euc|id's proof of Proposition 6 in
Book I of the Elements, has the classical reductio ad absurdum form.
From a certain assumption an absurd result is produced namely. that a larger
triangle is congruent to a smaller one contained in it. No contradiction is
stated formally.
Proposition 6 If in a triangle two angles equal one another. then the sides
opposite the equal angles also equal one another.
Given: lll AABC. LB 5 LC. A
Prove: E3 5 F D
Proof: Suppose that 18. ? . l'hen one ol the
two sides A—I3cL 1-?" must be longer than
the other. Let ABbe the longer side. Then
there exists a pofl, D, on ABstIL_h that_ B C
19. ? .Since BC’=' 2o. ? , DB EAC.
and A8221. ? . QABCE 22. ?
by 23. ? , which is absurd. Therefore.
24. ? .
Complete the indirect proof below.
Given: bisects um. and W is not .1 median or AIKL.
Prove: i E
Proof: Suppose that 25. ? .'l hen AIKL J
is 26. E’ . By the lsosceles Triangle
‘theorem. 27. ? .Sinc.e I.-‘vi bisects
LKIL 28. ? ,ani'.l so 29. 7.’ by
30. ? .'l‘hus. 31. ? because
CPCTC. This gives a C()l1Il'd(.llLIl()I‘I
because 32. ? .'l'hereI'ore, 33. ? .
K M L
NUMBER THEORY Write an indirect proof of each of the following:
34. There is no largest integer. [Hint: ll‘ n is an integer. then M + I is an
integer.)
35. There is no smallest positive real number. (_ Hint: %x < x for all positive
values of x) H
36. For two integers in and n. if m3 does not divide II: with no remainder, then
m does not divide II. with no remainder. (Hint: II" in divides n with no
remainder. then u can be factored into I: - m for some integer A.)
37. ll. .1 l-rattion has a terminating decimal é“{]?|8I‘I$I()l’I. then the denominator
divides some power of IO (I0. I00. IUOU. etc.) with no remainder. I Hint:
ll"-.1 decimal terminates alter it places, then multiplying it by l0"gives an
integer.)
38. LAW A defense attorney’ begins an argument with the following words:
“Suppose that the delendent is guilty of the crime. Then he was capable of
carrying a heavy load up a steep hill for nearly a mile..." How might the
attorney continue the argument? Explain how this would be an example of
an indirect prool'. State what the contradiction would be.
LESSON I2 4 INDIRECT PROOF 795
APPLICATION
796 CHAPTER 12
L00»? Back
39. Solve for x in the figure below. (LESSON 3.3)
ln Exercises 40-43, state whether the given side lengths determine an
acute triangle, a right triangle, an obtuse triangle, or no triangle.
(LESSON 5.4)
4o.a=l0.b=l2.c=l-I 41.rt='r'.l:=9,c=l5
42.a=4,l:=7,c=I2 43.a=8.l:=l2,t'=l'r'
Find the sine, cosine, and tangent of each angle below. (LESSONS 10.1
AND 10.2;
44. 72° 45. -15° 46. I40“ 47. 5°
48. TELECOMMUNICATIONS Suppose that you wish to
measure the height of a radio tower. From point .-'
A, you measure the angle ol elevation to the it"
top oi" the tower to be 55°. Then you walk 4 I
90 feet toward the tower to point B and
measure the new angle ofeleyation.
which is 68". Estimate the lreiglit ol'
the tower. (LESSON 10.4)
I .'
, \
-I I
:55 88 ' ‘ ' '
A so 3
L00»? Bel/and
Mathematical lnduction:The principle of mathematical induction is
useful in many proofs.The principle can be stated as follows: Suppose
that 5,, is a statement in tem1s of n, which can be any positive integer.
Suppose that the statement is true for n = 1 and that if the statement is
true for n, then it is always true for n+ 1.Then the statement is true for
all values of n.
49. Show that the statement "5"— l is c.livisil)le by 4" is true for n = l.
50. Assunie that "5" — l is divisible by 4" is true for some value of H. Show that
it must be true for n+ I; that is. show that “5"" — I is divisible by -1.”
(Hint: Ilia number is t'.ll\'lSll)l€ by 4. then it can be written as 4k for some
positive integer it‘. Since 5" — I is divisible by I, write 5" in terms of some
positive integer k.)
51. According, to the principle of mathematit'.tl induction. what lrave you
proved?
MORE ON THE EUCLIDEAN ALGORITHM
The Euclidean algorithm you studied in the Portfolio Activity in
Lesson l.?..l can he proved by using an indirect proof. There are two
parts to the proot'—the first part is to prove that the result is a divisor
of both numbers, and the second is to prove that it is the largest such
number.
Fx-amine the steps ofthe Fuclidean algorithm on page 775. The
process for linding the ged ofany two numbers a and b. where n > D.
can be written as follows:
ct = x + r a —- b = x remainder r
lln . connect #3., I] bi} 1)) I I '
_ Wm - r x + r.
Portfolio I 3 '
Extension '1 = T2(«\‘-3) + ’.1
Go To: gn.l1rw.com
Keyword‘ - - -
Itlct F - .
“'°" r,, _ 3 - r,,_ .(x,,) + r,, r 18 the get! of a and b.
‘ r.-i=r..(_x...i)+0
Note: Since the ren1ain«'.lers are a|w.tvs nonnegative integers. and the
remainder gets smaller at each step. the sequence of remainders will
always end in U.
1. Use the lust equation above to explain why 1",, must be rt divisor ol
r,, _ I. l'se the next-to-last equation to explain why r,. must he a
divisor of r,,_ 3. (l lint: Is the right side of the equation divisible by
13.?) Use the entire sequence of equations to explain why :3. must be
a divisor of both ri and la.
2. Suppose that there is a number r > 1;. which is a divisor of both (1
and D. Use the first equ-.1tion above to explain why r must be a
divisor of r.. Use the entire sequence of equations to e.\:plain why r
must be a divisor 0|" r,, How does this lead to a contradiction?
LESSON I2 4 INDIRECT PROOF 797
Computer Logic?/_
- J l i
. - .1
« J‘
\ _ _ ‘ _ _ _ , . .-.;- _
- _ .. L’ _'_l’______,_,. '
.2 if , ' '4 i‘ '
\‘i I -. - 9' . -
1‘ -" ' 3 Z.
- . . -‘ I -_
1 L‘ ‘l .
ti b . ‘ " :.
_ ‘ .‘ :q[ 2'
Objectives -- ' 3'!” - - I "5 '
_'_ [.0916 provides tire foundation for
0 IE(]i<$)il?3:]t(;t;oa:‘:jabIes. thaari -fc and decisioii-nuking‘ ' I
*'"::.7.::;‘.::°"'° on e -- ... +-
netwotks. _ ‘ _ _ _ _ 1" ‘"_ __j ‘ "
logical CIICUI8 are Iogicgates. which I l -T7 ,; .-. ; -
0 Solve prohlemsby lunctlonllka Ioglcaloperalorssuclias _ -I l,.‘_-
using computer Iotllc. “ AND. OR. andNOT. -' "-In-t.‘.-‘ ~ "2 _"OWE'
I ' ' .' t - . ‘
Q ‘—r..—. i l I‘ ll
' ' ;" “ii __-Jl
g - p L c . I 0 N A single computer chip in this“motherboard" contains hundreds of thousands
COMPUTER ARCHITECTURE of logic gates like the one shown greatly nugnified here.
The Binary Number System
Computers use the binary number system. Binary means “having two parts."
and the binary number system is based on the two numbers I and 0. You can
think of a computer as .1 system olielectrical switches that can be in two
possible conditions, on and off: A switch that is on is represented by .1 I, and
-.1 switch that is olT is represented by ‘.1 0.
On-Off Tables
- In new The tables in this Activity simulate the working of three different devices.
no 5pe¢;3| [9915 l'he colunms of the tables represent the difierent states of the devices and their
components. Let I = O.\l and 0 = OFF. Work in pairs to complete each table.
Part l
Pushing the power button on .1 TV remote control will turn the TV on
if it is offand turn it oll’ if it is on. Determine whether the TV will be
on or oil’ after pressing the power button. and till in the blanks in the
table below.
CHECKPOINT g/ TV before pressing POWER button TV after pressing POWER button
1 ?
0 ?
798 CHAPTER I?
cuacxeomrr ./
CHECKPOINT ./
CRITICAL TPHNKING
Part ll
To record on a particular video recorder. the user must press both Pl .-\‘t'
and RECORD. Determine whether the video recorder will record or not for
each combination of buttons listed in the table below. and fill in the blanks.
PLAY button RECORD button
1 1 ?
1 0 .7
1 7
0 ?
Video recorder
0
0
Partlll
the student driver car at Dover High School has been equipped with two
brake pedals so that either the student driver or the instructor can stop
the car. Determine whether the car brakes will be on or oft‘ for each
Combination of pedals listed in the table below, and fill in the blanks.
Student pedal Instructor pedal Brakes
1 1 7
1 0 ?
1 ?
0 0 ?
How do the tables in the Activity compare with truth tables?
Logic Gates
Fach table in the Activity above corresponds to a p-.1rticular type ol’ electronic
circuitry called a logic gate. Logic gates are the building blocks ot“‘sn1-art"
electronic devices. Eztch logic gate is named for a special logical litnction. such
as .\lOT. AND, or OR.
j _ — _
In the diagram below. [1 represents the electrical input. The input—output table
shows the resulting output for the given input. If the input, p, ofa NOT gate
has a value ot I. the output, NOT p. will have a value of U—and vice versa.
Notice that the iIIput—output table corresponds to the table in Part I ol-
the Activity.
NOT Logic Gage Input-Output Table
Input Output
9 NOT p 9 NOT p
1 0
Input Gate Output
0 1
Lesson 12.5 COMPUTER LOGIC 799
An AND logic gate needs two inputs. which are represented by p and q in the
diugr-.un below. \lotice that in order to get an output value of I. both inpttts
must have a value of I. ‘the input—output table corresponds to the table in Petrt
ll of the Activity.
Input-Output Table
AND Logic Gate ‘"9"’ °“‘P“‘
1 p q 9 AND 0
3’: AND)— DANDQ 1 1 1
1 O 0
Input Gate Output 1
0 1 O
o I o 0
An OR logic gate is represented below. along with its input—output table.
Notice that the input-output table corresponds to the table in P-.1trt Ill ot
the Activity.
Input-Output Table
Input Output
OR Logic Gate 9 f q 9 OR 0
1 l 1 1
g on — pOR q 1 | 0 1
Input Gate Output I 1 1
o | o 0
Network of Logic Gates
Logic gates can be combined to form networks. You can use input—output
tables to determine how a network operates.
E X A M P L E oConstruct.1ninput—output P
I table torthe network at right. 0 NOT
0 SOLUTION
Read from left to right. The first gate is p OR q. Determine the output from
this gate. Then perform the NOT operation: NOT (p OR 1;). To construct the
input—output table, consider all possible input L'0ml1in.lti0n5. I-' ill in the values
as you would for it truth table. where l is T and 0 is F.
Input-Output Table
Input Output
p q p OR q NOT ;OFl q)
1 1 1 0
1 0 1 0
0 1 1 O
0 0 0 1
800 CHAPTER 12
E X A M P t. E oCl'L‘dlCi1loglcfll(‘Xpl'C5Sl0l1ll1dl
corresponds to the network at right. P — 1&0 M
Q
_
AND
L
J‘
0 SOLUTION
Read from left to right. one braineh
at -.1 time. Combine the results of the
branches when they flow together.
1. .\lOT rippears First: NOT p.
2. l'he 1\\lD gate gives [NOT p} Al\D q.
3. The bottom branch gives _\l0T r.
4. The OR gate combines the output from Steps 2 and 5:
((\lOT pl .-\\lD q) OR {NOT r)
TRY nus llow in-.iny rows and how m.ui}- columns would be in an iiiput—output table
for the network in Example 2? Explain your reasoning.
Exercises
. Co/ii»////1/rate
1. Wlrat is a logic gate? What do logic gates represent?
ll - connect fig‘ 2. Does the OR logic gate represent an incltisive or exclusive or? How can
U0
Activities YOU tell?
°"l'"° 3. How are input—outptit tables for networks of logic gates related to
l3oTo: go.hrw.com I L I i Q
Kavwonf lflll. 1 [cl 7 (.5.
MG! B' - . . . .
may 4. In a network ol logic gates with two inputs. there are four possible
" combinations of input valties. How many combinations are possible with
three inputs? with four inputs? Explain your reasoning.
. ciaided Ski//3 Practice
Complete the input-output table for each network. (EXAMPLE 1)
5' :5 6'31“
Input-Output Table Input-Output Table
Input Output Input Output
p q NOTp NOTpOFl q p q pANDq NOT (p AND qt
1 1 ? ? 1 1 ? ?
1 0 ? ? 1 0 ? ?
1 .7 .7 0 1 .7 ?
0 .7 ? O 0 .7 ?
Lesson 12.5 COMPUTER LOGIC 801
- conned .73..
Iflfli
Homework
Help Online
Go To: go.hrw.I:orn
Keyword:
MCI Homework Help
lol Exercises 20-27
802 CHAPTER 12
. Practice and Apply
Create a logical expression that corresponds to each network.
(EXAMPLE 2 )
7.: . E9 3. g::@
1-
Draw the symbol for the gate that corresponds to each of the following:
9. l\OT 10. AND 11- OR
Use the logic gates below to answer each question.
13. If p = l.wh'.1t is the output?
9
15. ll’ p = l and q = 0, what is
the output?
12. if p = I. what is the output?
p-
14. if p = l and q = 0. what is
the output?
§’@- 3:-
. L _
.,.J
For Exercises 16-19, complete the
input-output table for the network
of logic gates at right.
p q NOT p NOT q {NOT pl OR (NOT 11)
16.! ‘I ‘I 7 7 7
17.! 1 0 7 ? 7
18.. O ‘I 7 7 7
19. O 7 7 7
For Exercises 20-27. complete
the input-output table for the
network of logic gates at right.
EATON
r
r— NOT
r NOT P (NOT p) AND q NOT r HNOT pl AND 11) OR (NOT rl
7 ? ? ?
? ? ? ?
? ? ? ?
Create a logical expression that corresponds to each network below.
23. 29. D“
P I to NOT
ca q IIN/%o_
30. 31. :\
2 : 1 D We like
' 49 _ 2 _ AND I
Construct a network of logic gates for the following expressions:
32. p AND (NOT q) 33. NOT (p OR q)
34. (p AND NOT q)) OR r 35. (pOR :1) OR (NOT r]
Two logical expressions are functionally equivalent if, given the same
input, they produce the same output. For Exercises 36 and 37, identify
the two expressions in each list that are functionally equivalent.
36. a. l\O’l' {p .-wt) q} 31. a. pOR N01‘ q)
b.(l\'OTp) AND ('NOTq] b. NOT [p on (1)
c. (l\OT 1:) OR [NOT 1}) c. (NOT p) AND [NOT :1}
c H A L L E N G E 38. Create a network of logic gates that corresponds to the input—output table
below.
Input Output
p 7
1
1
1
1
1
0
-I-IO-I-I-I-Id
0
0
0
0
A P P L I c A T I O N 39. ELECTHICFIY In electrical circuit diagrams, a switch is represented as shown
below. An open switch does not allow current to flow through the circuit.
/. _,_'.
open switch closed switch
In the circuits at right. the bull) will light up 8-
if there is a closed path through the circuit. —
'l'ell what logical function is represented by
each arrangement of switches. Explain how
switches A and B work together to form a
logic. gate in each case.
battery: —ll|l— bulb: —@—
LESSON 12.5 COMPUTER LOGIC 803
APPLICATION
804 CHAPTER 12
Look Book
40. ENVIRONMENTAL SCIENCE
The aerial photograph at
right shows workers
cleaning up an oil spill.
Use objects in the photo *3 -2 vi
to estimate the size of the "
squares in the yellow grid.
Then estimate the area of
the Spill. (LESSON 5.1)
41. .-‘t 50—ft pipe carries water
from a well to a house.
Suppose that the pipe
springs a leak. If the leak
is equally likely to occur
at any point along the
pipe, what is the
probability that the leak
will be within 5 ft of the
house? russsorv 5.8)
42. A point is chosen at random in the diagram
at right.What is the probability that the point
lies inside the shaded triangle? (LESSON 5.8)
In Exercises 43 and 44, determine whether the conditional is true for all
values of the variables for which the proportions are defined. If the
conditional is false, give a numerical counterexample. russsorv 8.2)
43. If'—‘' = i_, then 1 =
J’ -‘ )’ -‘
45. II" the perimeters of two similar triangles are I8 cm and 25 cm. what is the
ratio of their corresponding sides? (LESSON 8.6)
’_‘=v"""_""'_’"
*£___£
44. It y _\, then Y y+’+m.
Look Beyond
In Exercises 46-48. you will discover a network of logic gates that is
functionally equivalent to the statement ''If p then q."
46. Create a truth table for the statement "If p then q." Use I for true
statements and O for lalse statements.
47. Create an input—output table for each network below.
vp AND ~ it:
Q
48. Which of the networlzs in Exercise 47 is functionally equivalent to the
statement “If p then q”? Create a logical expression for this network.
\ I O - ‘
In ( ' ‘
. I
I
I " V3“ '
WE ,
I
Two of the most lllmous theorems in mathematics come from classical
times. Both of them involve indirect proof, which you studied in Lesson
l2.«l. Both of them also involve the prime factorization theorem. which is
known as the Fundamental Theorem of ‘slumber Th€0l'_v. It is not difficult
to prove. but here it will be assumed true.
Ever)’ number has a unique prime factorimtion.
l'he lnlinity of the Primes
l£uclid’s proof that there are infinitely many primes has captured the
imagination of people over the ages. To help you understand the proof.
which is actually very brief, a numerical example is given First.
The proof will assume that there is only .1 finite number of primes. Suppose.
for example. that there are only 5 primes, and that l l is the largest prime
number. Then the list of all the prime numbers would read:
2. 3-. 5. 7', l I
Now form a new number. m, by multiplving
the prime numbers together and adding I.
m= (2){3’J(5)t7){1 I) + I = 2311
The new number m must
be composite, atcotdmg to
the assumption. which
states that I I is the largest .— \{ ;
prime number. Therefore, ‘Q:
m must be faetorable into
a combination of prime . !
numbers, which (according _ ‘A. l
to the assumption] range e]
from 2 to I l. However.
none of the numbers in
the list of primes will
divide the number ev-actllv
because you will always
get a remainder ol‘ I.
CHAPTER 12 PROJECT 805
—é.—n_-
-— 306
9-}:
For example: 462 R I
5l23l I
If 23! l is not divisible by one of the pritnes in the list. then it tnust be either
prime. or divisible by some other prime greater than I l. which contradicts the
assumption that I l is the largest prime.
Once you understand this example. you should be able to follow the
generalization of it. which is given below.
Prove: There are infinitely many primes.
Proof: Assume that there are a finite number of primes. say. PI of them. Then
the list of the primes would be pr. pl. pt. . . . .1)... Form a new ntunber.
m = [pr.l{p~)(pal - - - (Pu) + I-
By assumption, in must be composite. However, in is not divisible by any of
the numbers in the list of primes. so there must be a prime larger than p.
which contradicts the assumption. Thus. there are infinitely many primes.
The “lncommensurability" of the Square Root of 2
In the early history of mathematics, it seems to have been widely believed that
any number could be represented as a fraction—that is. as 3 ratio of two
integers. |'his was certainly believed by the early Pythagoreans. lhus. the proof
that the square ro-ot of 2 cmmot be represented by such a ratio (which means
that it is irrational or irtcomnieusimiblr) came as a profottnd shock to them and
shook the foundations of their beliefs.
Before studying the incommensttrability theorem, yott will need to know three
simple theorems from number theory. The three theorems. given below. ttse the
prime factorization theorem.
Prove: The square of an even number is even.
Proof: lfa number is even, then 2 is one of its prime factors. When the
number is squared. the number 2 will appear at least twice in the
prime factorization of the square. Therefore. the square is divisible by
2, which mums that it is an even number.
Prove: l'he square of an even number is divisible by 4.
Proof: The proof is left as an exercise for you in Activity 2.
Provo: The square of an odd number is odd.
Proof: l'he proof is left as an exercise for you in .-\ctivity 2.
You are now ready to tackle the incommensurability theorem.
Prove: The square root of 2 cannot be written as a ratio of two integers.
Proof: Assume that the square root of 2 can be represented as the ratio of two
numbers—that is, as a fraction. If this fraction is not in lowest terms. I
then there is a fraction in lowest terms to which it can be reduced.
Thus. the assumption can be written in the following way, which is
equivalent to the original statement: Assume that the square root of 2
can be represented as a fraction in lowest terms.
—_j,_.__
,/-’°
“ /
,’>
/
Let p be the numerator and :1 be the denominator of the fraction that is
assumed to exist.
p and (1 have no common factors.
Square both sides of the equation.
Multiply to clear the fraction.
The last equation implies that [:3 is an even number and so p is an even
number. (Why?) 'l'herel'ore. p’ is the square of an even number. l'h is implies
that p-' is divisible by «I. But if p-' is divisible by :1, then if must be an even
number. ( Why ?) Therefore. :1 is even. as well.
if p and q are both even. then they must have a common lactor of 2. which
contradicts the original assumption. Therefore, the assumption must be
false. and the theorem is proven.
Activitv 1] The Infinity of the Primes
1. Repeat the numerical example in the proof for different numbers of
primes. Explain why you always get a remainder of I when you divide
m by one (or more) of the primes in your list.
2. lfvou subtract I instead of adding I to obtain the number m in the
proof. how would the proof be affected?
3. Do some research on number theory and learn about some of the
unproven conjectures such as the GtJiril)(l(.'ll (" mtjecture and the Twin
Primes Conjecture. Explain them in your own words and give numerical
illustrations for each one.
1 The "lncommensurability"
Activity of the Square Root of 2
1. Prove that the square ofan even
number is divisible by -"l.
*?’;J7iZ
l‘%(2- :2“
’b_
2. Prove that the square of an odd
number is odd.
3. In the incomntenstlraifilitv proof.
there are two points at which the
reader is asked to explain why a
certain result occurs. Write these
explanations in your own words.
‘-0
v4
V
\
—§_‘ n c
I crmprea :2 PROJF 807 ;—I
Chapter Review and Assessment
VOCABULARY
affirming the consequent . . . 771 disjunction . . . . . . . . . . . . . . . 777 proof by contradiction . . 792
argument . . . . . . . . . . . . . . . . 768 exclusive or . . . . . . . . . . . . . . 777 reductio ad absurdum . . . . . 792
binary number system . .798 inclusive or ...... ..777 statement .. . . . . . . . . 769
compound statement .... .. 776 indirect prool . . . . . . . . . . . . . 792 truth lunctlonally
conclusion ............. . . 768 inverse ol a conditional . . . . 786 equivalent . . . . . . . . . . . . . . 778
coniuuction ............ .. 776 logic gate .............. .. 739 lrulh table ............. .. 776
contradiction . . . . . . . . . . . . . 792 modus ponens . . . . . . . . . . . . 769 valid argument . . . . . . . . . . . 768
contrapositive of a modus tollens .......... . . 770 valid conclusion . . . . . . . . . . 768
conditional . . . . . . . . . . . .. 786 negation . . . . . . . . . . . . . . . . . 778
denying the antecedent . . . . 771 premise . . . . . . . . . . . . . . . . . 768
ARGUMENT FORMS
Lesson ion - rgumont orm
12.1 12.1.1 Argument Form: lfplhen G
Modus Ponens P
Therefore. q
12.2.2 Argument Form: lf pthen q
Modus Tollens ~61
Therefore. -«p
12.1.3 Invalid Form: lfpthen q
Affirming the Q
Consequent Therefore, p
12.1.4 Invalid Form: If pthen q
Denying the ~P
Antecedent Therefore, ~q
12.4 12.4.1 Proof by To prove statement s. assume -s. Then the lollowing argument form
Contradiction is valid:
If ~sthen HAND ~11
Therefore. 5
808 CHAPTER 12
Key Skills 81 Exercises
LESSON 12.1
Key Skills
Determine whether an argument is valid or
invalid.
Is the following, argument valid or invalid?
If the Memorial Day parade passes the house.
then the house is on Main Street.
The Memorial Day parade does not pass the house.
Therefore. the house is not on .\i.tin Street.
'1 his argument is invalid. it contains the invalid
argument form known as denying the antecedent.
Use the law of indirect reasoning lmodus
tollensl.
Give a valid conclusion based on the following
premises:
lithe oven is on, then the oven door feels mtrtn.
The oven door does not leel warm.
Using indirect reasoning [nmdus tullens). the
statement “The oven is not on" is a valid
conclusion.
LESSON 12 2
Key Skills
Write the conjuction and disjunction of two
statements.
Write the conjunction and disjunction of the
lollowing statements:
The sky is green.
Your pants are on fire.
Conjunction: The sky is green. and your pants are
on fire.
Disjunction: ‘I he sky is green, or your pants are
on lire.
Exercises
Determine whether each argument is valid or
invalid.
1. lfa polygon has 5 sides, then it is a pentagon.
Polygon ABCDE has 5 sides.
Therefore. polygon ABCDF is a pentagon.
2. If the car is out of gas, then the car will not
start. The car will not start.
Therefore. the car is out oi‘ gas.
Use the law of indirect reasoning to give valid
conclusions based on the following premises:
3. lfan animal is it rodent. then it has incisors
that grow continuously.
A cat does not have incisors that grow
continuously.
4. Ifa number is divisible l1y6. then it is divisible
by 3.
25 is not divisible by 3.
Exercises
For Exercises 5-8, refer to the statements
below.
luhn is my brother.
I7 is prime.
5. write the conjunction of the statements
above.
6. Write the dis_iunction of the statements above.
CHAPTER 12 REVIEW 809
Create a truth table for a compound
statement.
Create a truth table for the conjuction of the
statements above.
Let p represent the statement “The sky is green”
and let q represent “Your pants are on Fire." Then
the truth table for the conjunction p A\lD q is
shown below.
P a PAND a
T T T
T F F
F T F
F F F
LESSON 12.3
Key Skills
Create a truth table for a conditional.
Create a truth table for the following conditional:
If it is l:O0 I-'.M.. then Jill is in geometry class.
The conditional Catt be separated into its
hypothesis, p,“lt is l:(J0 I'.M.," and its conclusion.
q.“]ill is in geometry class.” ‘I he truth table is
below.
P 11
=
T
F
T
T
Write a converse, inverse, and contrapositive of
a conditional.
Write the converse, inverse. and contrapositive of
the conditional above.
Converse: If Jill is in geometry class. then it
is l:00 P..\l.
Inverse: ll" it is not 1:00 ItM., then Jill is
not in geometry class.
Contrapositive: If Jill is not in geometry class.
then it is not 1:00 l’..\-l.
810 CHAPTER 12
7. Create a truth table for the compound
statement from Exercise 5.
8. Create a truth table for the compound
statement from Exercise 6.
Exercises
For Exercises 9-12. refer to the following
conditional: If it is raining, then the ground is
wet.
9. Write the converse. inverse. and contrapnsitive
of the given conditional.
10. Create a truth table for the converse oi the
given conditional.
11. Create a truth table for the inverse of the given
conditional.
12. Create a truth table for thc contrapositive of
the given conditional.
LESSON 12.4
Key Skills
Use indirect reasoning in a proof.
lL£xPQlflwoit1t S is on Wand point Tis on
Q5 and PTintcr.~'.ect at point X inside APQR.
Prove that -CT$ancl T’7"do not bisect each other.
.r\>sLll1'le that 6.-§-arid 7’-Tlwisect each other. Since
§Sand P—7'arc diagonals of qtmdrilatctal PQTS,
if they bisect each other, then PSTQ is a
pmullelogrttm. If PSTQ is a parallelogrant. then
P_Sat1d were parallel. But P—S;1r1d were not
parallel because tliey lie on intersecting linis.
'1 his gntradiction proves indirectly that QS
and PTdo not biscct each other.
LESSON 12.5
Key Skills
Write a logical expression for a network.
Write a logical expression for the network below.
P — NOT —| .
AND
a TI‘
(Norm AND q
Create input-output tables.
Create an input—output table for the network above.
p q [NOT pl AND q
1 1 0
1 0 0
1 1
O 0 0
Exercises
Given: AABCis a scalene triangle, and K5,
the bisector of [A intersects BC at
point D.
B D C
\
Prove: :45 is not perpendicular to -135.
Proof:
_. Then /_ADBaL1§l
/_/lDC both measure 90°. Since AD is the
bisector of LA, LEAD 5 LCAD and
AD I 35. so 14. fly ASA. Thus.
15. ; becattsc CPCTC. However.
this C0lllI".tCllClS_l6. _?_, thus proving
ll‘It'.l£‘L‘ll)r' that AD is not perpendicular
to BC.
Assume 13. ?
Exercises
For Exercises 17 and 18, refer to the diagram
below.
ps
q|N\yQ|—
17. Write a logical expression for the given
network.
18. Create an input-output table for the given
network.
19. Write at logical expressiott for the network
below.
3:—
.- -
20. Create an input-output table for the network
from Exercise I9.
CHAPYER 12 REVIEW 81 ‘I
Applications
21. LAW l')etermine whether the argument helow is valid or invalid. Explain
your reasoning.
If Mr. Smith committed the crime. then he would have been at the
bank on Tuesday morning.
Mr. Smith was not at the bank on Tuesday morning.
Therefore. Mr. Smith did not commit the crime.
22. ELECTRICITY Imagine that you are planning your dream house
and you want certain appliances to work in an interconnected
way. Suppose that you want the living room IV to be off and
the kitchen radio to be on ifand only if the coffee maker and
toaster are on or the kitchen light is on. Draw a network of
logic gates to illustrate this situation.
p
r I ~
l 1' I‘. q —— ———' ‘ _
_ -p‘ m I In
1
812 CHAPTER 12
j-2
Chapter Test
Determine whether each argun1ent is valid or
invalid.
1. if today is Tuesday. tl1en i\'-at-.1lie l1as softball
practice.
l'oda_v is ’l'uesda_v.
Therefore. Natalie has softball practice.
2. If the car is .1 Subaru. then it has four—wheel
drive.
l'he car has four—v.-heel drive.
Therefore, tl1e ear is .1 Subaru.
3. If the switch is off, then the video game will
not play.
Tl1e switch is o11.
Therefore. the video game will play.
Use the law of indirect reasoning to give valid
conclusions based on the following premises:
4. It a parallelogram is a square. then it is a
rectangle.
A rhombus is not a rectangle.
5. If a 11u111ber is a multiple of8, then it is a
multiple of l.
The number 50 is not :1 multiple of 4.
For Exercises 6-10, refer to the statements
below.
A dolphin is a mammal.
Circles are polygons.
6. Write the con_iunc.tion of the statements
above.
7. State whether the conjunction is true or false.
8. Write the disiunction ofthe statements above.
9. state whether the disjunction is true or false.
10. Create a truth table for the disiunetion p OR q.
11. Write the converse, inverse. and contrapositive
of the following conditional:
If QRSTis :1 trapezoid. then QRST is a
quadrilateral.
Create a truth table for the following:
12. the converse of the conditional p :5 q
13. the inverse of the conditional p :5 q
14. the eontrapositiwe of the conditional p ='.> q
15. CHi3MlS'iRY Write the converse. inverse. and
(.‘(Jl1tl'd|'J()Sltl\"E of the conditional below.
Decide whether each is true or false. F.xplain.
If water boils at normal atmospheric pressure.
then its ten1perature is greater than or equal to
l00°C.
Complete the Indirect proof below.
Given: If-5 bisects Ab‘/\C; A
E is 11ot a niedian
of /\ABC.
Prove: }1—B' $ .-TC.
Proof: Suppose that 16. L. Then A.-'-'lBC is 11;.
By the isosceles Triangle Theorem. 18. _3_. Since
1713 bisects 4b‘.»\C. 19. _2_. and so 20. _f_ bv 21. j_.
Thus. 22. L l1ec:1use CPCTC. This gives 21
contradiction because 23. Tl1erefore. 24. L.
B D C
25. Write a logical expression for the network
below.
3-
26. Create an input—output table for the network
above.
27. Write a logical expressioii for the network
below.
D‘ AND
0 NOT l
or
28. Create an inpt1t—output table for the network
above.
CHAPTER 12 t£sT 813
-- E-s
CUMULATIVE ASSESSMENT
College Entrance Exam Practice
MULTIPLE-CHOICE For Questions I-8. write the
letter that indicates the best answer.
1. Refer to the hgure below. Which coordinates
are the result oI'a I80‘? rotation ofthc triangle
about the origin? (LESSON 1.7)
I 9. I4)
(-16. Tl
a. (1-16). (I 1. -9), (3. -3)
b. (-16. -7}, (-9. -14). (-3,-3.1
c. (l6,—7]. (9,—I4). (3,—3)
.1. (I6. 7). (9. M]. (3. 3)
2. Refer to the ligurc below. Find AF.
(LESSON 3. 7)
C X2+3X-14 D
3 5 E
A F
x2+x—4
a.8
b.3
c.4
d. I6
814 CHAPTER 12
. t?r9-.
I Internet connect ..oin
Standardized
Test Prep Online
Go lo: go.htw.com
Keyword: MMI Test Prep
3. Find the approxitnatc perimeter of the
triangle below. (LESSON 5.4)
D
5.4
F 3.7 5
a. 52
b. I6
c. l0
d. 35
. Which ofthe following statements is a
definition? (LESSON 2.3)
a. A monarch is an orange btttterfly.
b. A line segment is the shortest path
between two points.
c. A pile of loose rubble is a hazard.
d. A rhombus is a parallelogram.
. .-Ifihas endpoints at (l5, l5) and (9. -_‘-'0). The
endpoints ol. :1 segment parallel to fiare at
? . (LESSON 3.8)
a. (0, O) and (25. I6)
b. H5. I3) and (20.9)
c. [-1. —6} and (8, —l)
d. [-1, -3) and (l2. -l3)
6. Identify the correct expression lor FC.
(LESSON 9.5) C
a. FDx 3
[A
b. EBX
CD
C. EBX E
.1. FB ><
7. Which statement is true in hyperbolit
geometrv? (LESSON 11.5)
a. No lines are parallel.
b. Two-sided polygons exist.
c. The sum ofthe angles in a triangle is less
than 180°.
:1. The shortest path between two points is
along a great circle.
For Exercises 8-10, refer to the statements
below. (LESSONS 12.1 AND 12.3)
p: It" the fog lt-as lifted, the boat can leave the
harbor.
q: The boat cannot leave the harbor.
8. What conclusion can be drawn from
statements p and q?
a. The log has lifted.
b. The fog has not lifted.
c. If the log has not lifted. the boat cannot
leave the harbor.
d. No valid conclusion can be drawn lrotn
statements p and q.
9. Write the negation of statement I}.
10- Write the contrapositive of statement p.
11. In llte diagram at Y
right, A.-'-‘lB(" is
equilateral. What
are the coordinates
of point C?
(LESSON 5.7)
a. (0. ti]
b. (rt, rt]
«=-
d. [(1, M5]
FREE-RESPONSE GRID
Items 12-15 may be answered C) G
by using a free-response grid C7’ QEEQ.
such as that commonly used by (D g g g
standardized-test services. (3 <3 @ G}
G) C9 C9 Ii?‘
(1) (E) G) (E)
Q) (=2! (9 G)
{D (E) G) K D
G3 G3 G) G
{D t’)
(3) 6) CD CD
12. Wlt-at is the central angle of a regular l3—gon?
(LESSON 3.1)
13. A point is chosen at random inside the square
in the coordinate plane below. What is the
probability that the point lies within the
shaded area? (LESSON 5.7)
Y
l9. 9)
’\
X
14. Find MN. (LESSON 10.1)
K 14 L
Em
so 1-, 35°;
N M
15. Find AB. (usssorvs 10.5 AND 10.6)
B
CHAPTER 12 cumuurnve ASSESSMENT 81 5
Extra Practice
Extra Practice
CHAPTER 1
LESSON 1 .1
In Exercises 1-3, refer to the rectangle at right.
1. l\-ame all of the segments in the rectangle. 1 2
2. I\’-atne the plane that contains the rectangle.
3. Name the ravs that form each side of the
angles in the rectangle. D
In Exercises 4-6, classify each statement as true or
false, and explain your reasoning.
4. Two planes intersect in :1 line.
5. Two lines are contained in exactly one plane.
6. Any three points are contained in exactly one line.
Refer to the figure at right for Exercises 7 and 8.
7. Name the interseetion of lines I" and m.
8. l\ame an angle at the intersection ol lines t’ and
m. l\'-ame the vertex ofthis angle and the two
rays that form the sides of the angle.
LESSON 1 .2
In Exercises 1-3, find the length of AB.
‘- A 3 2- A B
4'l*.1l1Zl:l—.—l:-P- 4—.>
—4—3—2—1 o 1 234 -3-2-1012345
3- A B
—4'—a_2_1 o 1 E 3 4
In Exercises 4 and 5. point C is between points A and B on E
Sketch the figure and find the missing lengths.
4.AC=l2;CB= ? ;.-’lB=3-‘I
5./‘lC=ll;CB=|8;lb‘= 6
Find the indicated value.
. . 3v 3v—4
. I = ; '= .
6 ‘I Y 20 I: ’ >
In Exercises 7 and 8. explain why each statement does or does not
make sense.
7. Tb‘ + BC = I 5 cm 3. m vw = 3 in.
81 8 INFO BANK
LESSON 1 3
Find the measure of each angle. Refer to the diagram
at right.
1. in.«IAVB
2. |1‘I.:’L*W'C
3. m.{BVC
In the figure at right, m£BVC = 55° and ZAVB and
ABVD form a linear pair. Find the following:
4. mzCl-’D
5. n1.£AVB
6. mZAVC
In the diagram at right. m.{WXY = (7x + 14)°. Find the
value of x, and then find each indicated angle measure.
7. mzwxz
8. mzZXl'
9. mzl-l-"(Y
LESSON 1 .4
"1
X
#
‘
U
‘U
‘
U
0
'1".
O
Q
B
C
A V D
Y
12/
9,1 ~;‘[3x— 1)
Use folding paper to construct the figures described in Exercises 1-4. Do
not use a ruler or protractor. Trace over each figure and label all relevant
parts.
1. a 135° angle
3. a p:1r;1llelugran1 that is not :1 rectanglr. 4. a rh(1ml1L1.\
For Exercises 5-7, suppose that F is the angle bisector of
AABC, line k is perpendicular to £, and mAABD = 35°.
5. Find ind.-lBC and m.£DBC.
6. Find m.£EBC.
7. If ZFBC and z_’CB.-1 are supplementary
.mglL-5, lind mzl-'b‘I:'.
2. a I l2.S° angle
EXTRA nuance 81 9
LESSON 1.5
Trace each of the triangles at right onto a separate piece of folding
paper or draw them by using geometry graphics software.Triangles
are named with the A symbol and the names of the vertices, such
as AABC.
Find the following:
. the perpendictllar hisectnrs of AABC A
Extra Practice
1
2. the angle bisectors of L\ABC
3. the circumscribed circle OFAABC
4. the inscribed circle of A/tb‘C
5
6
Q
P‘)
. the mitlpoints ofeach side of ADEF 5
. the Inetlians 0| ADEF
LESSON 1 .6
For Exercises 1-4, trace the figures onto folding paper.
Reflect each figure across the given line.
Y X
Rotate each figure about the given point.
3. Q U
5. Make 21 list of capital letters that stay the same when reflected across a
vertical line. What is the longest word you can write with the letters in
Your list?
820 INFO BANK
LESSON 1.7
In Exercises 1-4, use graph paper to draw the transfomiations of the
figure as indicated
V
1. Rotate the figure I80” about the origin.
2. Reflect the figure across the ,v—-axis. P
3. Rellect the figu re across the x—a.\is. X
0
4. Rellect the figure across the .\'-a\is and then rellect the
image across the y—a\'is. How does this figure relate to
the transforined figure in Exercise I?
In Exercises 5-8, describe the result of applying each rule to a figure in
the coordinate plane.
5. H(x. y] = (x. y—3)
6. £[_x, y) = (x+ 2, y)
7. G[x, y) = [-x, y — 5)
8. F(x, y) = (y. 3:)
CHAPTER 2
LESSON 2.1
Use the table below to answer Exercises 1-4. The numbers in the table
are perfect squares: 1* = 1, 2’ = 4, 3‘ = 9, 4‘ = 16,
1. Suppose you vmut to know which column A B C D E
coutains the number l0.20l. Ten thousand
two hundred one (10.20!) is the square of 1 9 16 25
what number? 36 49 64 81 100
2. Look at the numbers that occur in each column
of the table. What is true of every number in
column E?
3. In what column does the number I00: occur?
4. Prove that 10,20! occurs in column A.
Suppose that you know the square of a positive integer n and you want
to find the square of n+ 2.
5. Draw a square of dots to represent the square of the number N.
6. Increase the side lengths of your square by 2 to represent the square of the
number n + 2.
7. ['54: your diagram to prove that the square of H + 2 is found by adding 221
and 211+ 4 to the square of n. Your proof should work for all values ol :1.
EXTRA PRACTICE 821
eogaoead enxa
Extra Practice
LESSON 2.2
For Exercises 1-4, refer to the following statement:
All animals that live in the Everglades live in Florida.
‘I. Rewrite the statement as .1 conditional.
2. ldentify the hypothesis and the conclusion ol the conditional.
3. Draw an Euler diagram that illustrates the conditional.
4. Write the converse of the conditional.
For Exercises 5-8, identify the hypothesis and conclusion of each
conditional. Write the converse of each conditional. lf the converse
is false. give a counterexample.
5. ll" two angles are supplementary. then the sum of their measures is ISO‘’.
6. ll. your transportation is a nmttircycle. then vou ride on two wheels.
7. It" you live in Baltimore, then you live in Mar_vland.
8. If you have a rose. then you have a flower.
LESSON 2.3
ln Exercises 1-5, use the following steps to detemtine whether the
given sentence is a definition:
a. Write the sentence as a conditional statement.
b. Write the converse of the conditional.
c. Write a biconditional statement.
d. Decide whether the sentence is a definition. and explain your
reasoning.
1. Mercury is the planet closest to our Sun.
2. School is the place where kids learn mathematics.
3. A multiple ol ten has a ones digit of zero.
4. The set ol points in a plane equidistant from a given point lorm .1 circle.
5. An equilateral triangle is a closed figure with three congruent angles.
6. The following are pentagons:
9009
Which of the figures at right
are not pent-agons?
The following are not pentagons:
a.CI 13.3 CD (LD
822 INFO BANK
LESSON 2.4 "1
ln Exercises 1 and 2, identify the Algebraic Properties of Equality that E].
iustify the steps. 3
1. x - 7 = l5 Given 2. -1x+ 6 = 38 ("liven
x—7+7=l5+7 ? «lx+6—6=3-8—6 ? 3
x=22 4x+4=;l2+4 " N
x = 8 3
II
Refer to the diagram at right, in which A 3 E 8
mAABC = mAEBD. Use the Overlapping
Angles Theorem to complete the following: C D
3. m.«:'.«lBC = 75° mA.e’lb’D = llU° m.«:'Cb‘D = ?
4. in4ABC = [3x + 4_J° m4'CBD = (x - 51° inx_’CBE = 67°
x = ? n1A'ABD = 7.’ mA'EBD = 7.’
LESSON 2.5
For Exercises 1-4, refer to the diagram at right,
which consists of three intersecting lines.
1. Which angle is congnient to AFBC?
2. ‘Which angle is congruent to £GBC?
3. Which angle is congruent to Al.-'b‘D?
4. Find the measure ofz.-lBC. A E
5. Find the nieasures ofull the angles in *5"+17lfl
the diagrann at right.
l8x— 23?\{
/%
Tell whether each of the following is an example of inductive or
deductive reasoning. ls the argument a proof? Why or why not?
6. Every 5dl.lll'I'.l:l}' for the last six weeks. it has ruined.
Tomorrow is S.1(urda_v.
Therefore. it will rain tomorrow.
7. Multiples of 3 are not prime.
The number 3-5 is a multiple ol 5.
Therelore, 55 is not prime.
EXTRA PRACTICE 823
Extra Practice
CHAPTER 3
LESSON 3.1
For Exercises 1-3, copy each figure, and draw all axes of symmetry.
..© .% .
B
Each figure below shows part of a shape with reflectional symmetry.
Copy and complete each figure.
k .3
./
7. which of the completed figures from Exercises 4-6 also has rotational
sytntnctry?
8. Graph }-' = llx — 3]! + I on u graphing calculator or graph paper. Then
write an equation for the axis of symmetry ol the graph.
LESSON 3.2
For Exercises 1-8, use your coniectures from Activity 2 in Lesson 3.2 and
the diagram below to find the indicated measurements. ln Ihombus
PORS, P0 = 5, PR = 6, and mAPOR = 74°. P
1. QR 2. RS 5
3. PT 4. n‘t£P5R
5. m,»‘_’QPS 6. mzPTQ H
7. ln rectangle KLMN. diagonal KM = x + 4 and diagonal LN = 3x. Find the
value ofx and the length of the diagonals of KL -\-‘IN.
Use the definitions of quadrilaterals and your conjectures from Activities
1-4 in Lesson 3.2 to decide whether each statement is true
or false. if the statement is false. give a counterexample.
8. [fa figure is not at rectangle. then it is not a square.
9. Ila ligure is a rhombus. then it is a square.
10. lfa figure is not a parallelogram. then it cannot be a rhombus.
824 INFO BANK
LESSON 3 3
ln the figure at right, lines k and f are parallel.
1. List all angles that are congruent to £3.
2. List all angles that are congruent to £4.
3. Are there any mtgles in the figure that are
not congruent to A5 or A4? Explain.
_ _ - V k
4. ll nil} = M0”. hnd the n'lEdSl.ll'(-2 of each 7 3
angle in the figure.
e/'
%~
eogoead aux;
5. If n1.«;’2 = 2.x” and mA6 = [_’t::— 503°, find
the measure ofeaeh angle in the figure.
In AFGH, lJ||HG and ZFIJ E AFJI. Find the indicated
angle measures. F
6. m.«:'HIG 7. m.«:'l-‘U
8. nh£FH 9. IIIZIGH
10. m.£GU 11. m.£FGI
LESSON 3.4
For Exercises 1-4, refer to the diagram below, and fill in the name
of the appropriate theorem or postulate.
t. It‘ nt.«:En3 = m£DB(", then Fn'||FC by the A
converse of the .
2. If tttmen = m4ABc, then Eur?‘ by the
converse of the . 5 D
3. |fn1ADFB + tttzrsc = 130°, then T=‘r3|tFC
by the converse of the T 3 c
4. n‘ m¢4DE = tttmcn. then Enfi by the
converse of the .
5. If m.«:'DEC = mAl:TCb‘, then EIIFC by the
converse of the T .
e. If m£EDC + m£DCB = l80°. then EMT
by the converse of the .
7. Given m4'Cb‘E = 43° and n1£BLI) =_I57°,
write at twt)-column prt)0l' that ED||BC.
EXTRA PRACTICE 825
Q LESSON 3.5
-3 For Exercises 1-3, two angle measurements of a triangle are given. Find
0 the missing angle measure, or state that the triangle does not exist.
9 1. m/_’A = 20° n1AB = 70° mzc = ?
Q 2. imizl = 50° m.«:'B = ? m.«:'C = 160°
(3 3. m.«:'zl = ? m.«:'B = 66° m.«:'C = 66°
5 4. ln the Figure at right. L_]||m. Wm.
X nv‘_’GK] = 20°. and n1£GlH = 55°. Find the L K J
III measures of the other 8 angles in the figure. vm
H I
In Exercises 5-7, find the missing angle measures.
5. 6. 7.
23-‘
I
76
LESSON 3.6
ln Exercises 1-3, find the unknown angle measures.
‘I. 2. 3. /\
95
160., 3 105'‘
150*
7 100'
ln Exercises 4-6, an interior angle measure of a regular polygon is
given. Find the number of sides of the polygon.
4. I08” 5. 156° 6. 140°
ln Exercises 7-9, an exterior angle measure of a regular polygon is
given. Find the number of sides of the polygon.
7. ?2° 8. 45° 9. 30°
10. In qtlzldriluteral FGHI. mAF = (2.\')‘’, m£G = Jr”. Infill = (x + l6]°. and
mil = (2.\'+ 201°. Find the value olx and the merasure of each angle in
the quadrilateral.
826 INFO BANK
LESSON 3 7
Use the coniectures you made in Activities 1-3 in Lesson 3.7 to find the
indicated measures.
1.DF= E‘ 2.GF= ? 3 N'O= 7
C J 25 K P 10 0
I "K
30 N ' T 0
D E H I .|: E
L M
80
A 60 B F G
A young girl is using a 15-ft ladder to rescue her kitten from
the branches of a tree. The ladder's base is 6 ft from the base
of the tree.
_ _ _ _ 15 ft
4. DCt(‘l'Illlll(‘ the distance lrom the ladder to the tree at -.1 point
lmllwav up the ladder. 6 ft
5. Determine the distance from the ladder to the tree at -.1 point
three—quarters of the wtty up the ladder.
6. The little girl can reucli the tree from I it .1\Nay or less. Estimate
the percent of the l:irlder’s height that the little girl must climb
to reach the tree.
LESSON 3.8
ln Exercises 1-4, the endpoints of a segment are given. Determine the
slope and midpoint of the segment.
1. (L lJ'.1m.l (3.2)
3. (I. -2) and (-2. 5]
2. (-2. l) and (2. 3-)
4. (0. -4] and [3.—l)
ln Exercises 5-8, the endpoints of two segments are given. Determine
whether the segments are parallel, perpendicular, or neither.
5. (4, I] '.1m.l [7, 6): [2, 5) and (I2. —I) 6. (—l, 2] and [2, 4); [-3. Hand (—l,—?.)
7. (2. 3]:1ntl (6. 2); (O. 5) and (-1, 9] 8. (-2. -2) and [5, 2); (4. 3) and (l I. 7)
For Exercises 9-12, the vertices of a triangle are given. Use slopes to
detemmine whether each is a right triangle.
9. (1.2). (3. l}.(2.4] ‘I0. (0. ll. (4. 2). (-3. 1}
‘II. (-3, —l}. (—I, I]. {-2. —-1] 12. (—I. 3]. (2. l}.(l.6]
EXTRA PRACTICE 827
eogxomd enxa
CHAPTER 4
LESSON 4.1
ln Exercises 1-6, determine whether the figures in each pair are
congruent. Explain your reasoning.
1. 2. 3.
3 120°
/ 4/ \
4 5 4.2 3
120-‘
3 3
Extra Practice
6.
4' V M 5' J ‘i J ‘ L r I
-1 _. r -1 : r 60;.
X — Z O - N
Suppose that heptagon LKJMNOP 5 heptagon AEFXWCB.
7. Name the segment that is congruent to each segment below.
a. fit? b. c. 777 d.
8. List all pairs ol congruent angles.
LESSON 4.2
ln Exercises 1-3, determine whether each pair of triangles can be proven
congment by using the SSS, SAS, or ASA congruence Postulate. If so,
identity which postulate is used.
1- A B 2- 3 F 3- F K
E7 & ‘<7~V*
D c H G E J L
T
ln Exercises 4-9, some measurements of a triangle are given. ls there a
unique triangle that can be constmcted with the given measurements?
If so. identify the postulate that applies.
4. APQR: PQ= 3. PR = I. n1x‘_’P = 30° 5. AEFG: FG = 1. EG = 7. mA'E = l.2°
6. AABC: BC = 4. m£B = 15°. n1A'C = l00° 7. ARST: mA'R = 20°, m.«£S = I00”. mA'T = 60°
8. £u\-INC: .'L-IN = 2, N0 = 2. M0 = 3 9. AIKI :]K = 6. m/_’] = l5°. nn.€K = 30°
828 INFO BANK
LESSON 4 3
For each pair of triangles given in Exercises 1-10, is it possible to prove
that the triangles are congruent? If so, write a congmence statement
and name the postulate or theorem used.
‘I.
OMNQM9
10.
M 2. 3.
: F J X
Kg : K
. AABC and APQR with AA '—.: 1!’, £8 5 AQ. and THE P—Q
. M57 and Mia with .«:R -=- AL.R—S 5 1T, .int1 E 5 K
. Ali-"XY and AERG with ix 2 412. 4')’ 2 .»_'G. dlld 2 FE‘:
. AAIA‘ and ABMK with AA 5 AB. 4’! 5 AR’, and A5 5 AM
. AMP and AL-‘MU with AK :—: .«:'M. W E and '="
. isiwxio and giant with .\-T 2 W. W 5 5, and W 2 W
mevu and AOLP with AR 2 11.. Av 2 AP. and Tu s W
LESSON 4.4
Given the following infomiation about a triangle, find the missing
measure.
8¢DmNO5Ul9UN-I
. shins: E E, mA'S = -1O°.n1.«*_’i\-I = L
. ciuvw; WV 5 mzu = 85°, m,«_’w = L
. mac: zit 2 Ab’, AC = 12, ct: = L
. gnu: D—] 5 IT. IHZD = 15°,iiiz1= 4
. £tKXQ: E 5 W, nigx = 50°, m£Q = 2
..CiRST: AR 5 £T. R5 = 5,57 = 4
. c.i)L1-am 2 0-}-‘. m.«;’L' = 45", that) = '4
. .r_~.t.\.-mi: AM 5 gm‘. LM = 13. LN = 4
. Am,-‘D: F0 5 E. mA'R' = (3.\‘)°.n1£U= 90°, 1‘ = 4
..c.Co1.; zc 5 41 , CO= 25. OL =;
EXTRA PRACTICE 829
eogxomd enxa
Extra Practice
LESSON 4.5
For Exercises 1-6, use the parallelogram shown at right.
Find the indicated measures. A 3
1. Given n1AA = (3x)° and n1.£D = (x+ I00)”, find mzf).
2. Given Ab‘ = land CD = (9 — 2!), find CD.
3. Given mACDb‘ = -10°. lind mi/l.
4. Given IIIAB = 50°. m.4C = [2x)°. and BD = (x — 4]. find BD.
5. Given m.éABC = l5° and m.éA('D = 45°, find m.4CBD.
6. Given n1.éC = 80° and mzf) = X“, find mz.-s.
Determine whether each pair of triangles could fit together to form a
parallelogram, and justify your answer.
7. 8. 9. ;:
K N O B L
A :*
M D E
J L
A C M N X 2
LESSON 4.6
Exercises 1-4 refer to quadrilateral WXYZ with diagonals WY and X—Z
intersecting at point P. For each set of conditions given, determine
whether the quadrilateral is a parallelogram. If so, give the theorem that
justifies your answer.
1. E P—l. 5 P—Z
3. ‘—_- 5
2. 2 E
4. X'l"||iE, 5 W
Exercises 5-10 refer to parallelogram ABCD with diagonals ‘A-6 and Bi)
intersecting at point P. For each set of conditions given, determine
whether the parallelogram is a rhombus, a rectangle, or neither. Give
the theorem that justifies your answer.
5. mm BF = mzcsp, mzscp = n1ADCP a. TC 5 173
7. E 3 E 8. mz/lb‘C = 90°
9. E 2 E 10. m.4DPA = 90°
830 INFO BANK
LESSON 4 7
Construct a figure congruent to each figure below.
L \,~ 2. X 3.
Trace each triangle below, and construct the angle bisector of each
angle. Using the intersection of the angle bisectors, construct the
inscribed circle of each triangle.
4. E 5. j 6.
Trace each triangle below, and constmct the perpendicular bisector of
each side. Using the intersection of the perpendicular bisectors,
construct the circumscribed circle of each triangle.
7. : 8. 9.
eogxomd enxa
7
LESSON 4.8
Trace each figure below and translate it by the direction and distance of
the given translation vector.
.1 .A. I
/ H \_/
Which of the following triangles are possible? Explain your reasoning.
4. WX = LX) = 2, H-‘V = 3 5. MN = l4,NO= I7, OM = 15
6.PQ=3.QR=vl.RP=5 7.AB=lO,BC=5,CA='l
8.GH=l-1.HI=20.G1=2<l 9.DE=l2.EF=5.DF=28
EXTRA PRACTICE 83 1
Extra Practice
CHAPTER 5
LESSON 5.1
In Exercises 1-5, find the area of the rectangle with vertices at the given
points.You may find it helpful to sketch a graph.
. [3, 0]. [0, 0). (3. -1], [0, 4)
- (4. 0). (4. -5]. (0. 0). (0, -5)
. (2, 5]. (6. 4). (2. -1]. (6, 3]
.(—l. 2). (—l.—-'1), (2, 2]. [’2.—tl]
. (—F'. -3}. (-2. 0), [-7. D). (-2. -3)
. The perimeter of .1 rectangle is -12 in. The length is twice the width. Vi hat
are the dimensions? What is the -.n'e.a?
Gfllfiwlfl-I
7. The area ofa rexmmglu: is 36 cm3. The width is 4 times the length. What are
the dimensions? What is the perimeter?
8. The area of a rect.ingle is 6-lxl. The length is -4 times the width. In terms of x, what are the
dimensions? What is the perimeter?
LESSON 5.2
In Exercises 1-3, find the area of each triangle.
1. 2. 3.
21
o-.I|-
‘:4. _
4 4 9
In Exercises 4-7, find the area of a parallelogram with vertices at the
given points You may find it helpful to sketch a graph.
4. (3.4). [8,-l).(l. ll. (6. I] 5. (—5.—l).(~.’v.—|). [5, l).(5. I]
6. (—l.—3). (7.—7]. [7.3).(—l.—7i 7. (2.—|]. [O.—5). (5.—l]. [.’-.—5)
In Exercises 8-11, find the area of a trapezoid with vertices at the given
points.You may find it helpful to sketch a graph.
8. (-3. 2). (2. 5}. (6. 2]. [|. 5) 9. (2. 5]. (6. —| I. (6. 6]. (2. 5]
10. (4. 3-). IL-1 1. (8.-I). I6. 3} 11. ('1. 0]. (4. 4). l7.—l J. (7. 5)
832 INFO BANK
LESSON 5 3 [11
In Exercises 1-8, find the circumference and area of each circle whose E].
radius or diameter is given. Use 3.14 for re. Round your answers to the W
nearest tenth. m
1. r = 3 2. r = S ‘U
1
3.d=M 4.11:3-6 9)
22 - - 0
Use -7- for re. Leave your answers In fractional form. 'J‘_
s.r=2n 6.d=32 0
¢
7. r = I2 8. d = I5
Find the radius of the circle with the given area or circumference. Give
your answers both in terms of 1: and rounded to the nearest tenth.
9. A = 201: 10. A = 628 11. C = 24
12.C=2Jt 13..-i=lI7 14..-i=l7'.-1
LESSON 5.4
For Exercises 1-5, two lengths of sides of a right triangle are given
Find the missing length. Leave your answers in radical form.
1.n=5.b=l2,r= ? 2.a=?',b=9.c= ?
3.tI=l0,b= ?.t‘=25 4.rl= ? b=6.C=|O
.11‘
Each of the following triples represent the sides of a triangle. Determine
whether the triangle is right, acute, or obtuse.
5.l5.I7..‘i 6.6.8.lU 7.ll.|0.|.i
8. 5. 12. I3 9. 13.23.40 10. 7.9, I]
Find the area and perimeter of each triangle. Round your answers to the
nearest tenth.
11. 12. 13.
12 5 8
25
EXTRA PRACTICE 833
Extra Practice
LESSON 5.5
For the given length, find the two remaining lengths. Give your
answers in simplest radical form.
2. b = 5
4. 1» = éxffi 60°
‘HI
‘I. ll =
3. C = 4
In Exercises 5-10, find the perimeter and area of each figure. Give your
answers in simplest radical form.
5. an equilateral triangle with side lengths of 22
. .1 square with a diagonal of 6
. 3 30-60-90 triangle with a hypotenuse of I6
. a regular hexagon with side lengths of IO
(DDVIO5
. a 45--15-90 triangle with leg lengths of 3
10. a regular octagon with side lengths C-f6
LESSON 5.8
Find the distance between each pair of points. Round your answers to
the nearest hundredth.
1. (I, 3]'.~1I1d [2,—l)
3. (3. 4] ttnd [0, 0)
5. [6, 3] and (2. I)
7. (O, I) and (4, SJ
2. (-5, 6] and [3, -2)
4. (2. 2] and (5. ll)
6. (-5. -7) and (-1. 7]
8. (I. -2] and [I2, 3}
In Exercises 9-14, use the converse of the PythagoreanTheorem to
determine whether the triangle with the given vertices is a right triangle.
You may wish to plot the points and draw each triangle.
9. (I, 5], (2,-I ]. and (7. 61 10. (—|. 3], [4,—2), and (-4, 0)
11. (2. 5]. [4.—2]. and (—-1, 0) 12. (2. 3]. (8, 4l.a1I1d(l. 7)
13. (2. IO). (I2. 0}. and (—-1. 4) 14. (—I6. I8). [4. 2). and H2. 8)
834 INFO BANK
LESSON 5 7
Determine the coordinates of the unknown vertex or vertices of each
figure below. Use variables to represent any coordinates that are not
completely determined by the given information.
1. isosceles triangle ABC with F3 5 K 2. par-a|lelogr.un UL’!-"G
Am, 0). mo. 2:1). cu. 2) pro. 0). E(?. 2). Fm. 2:). 01?. ?)
V Y
81
A‘="' D
For Exercises 3-8, refer to right triangle ABC
shown at right with vertices at Mo, 0), B(b, 0),
and C(0, cl. Using the coordinates of A, B, and
C, find the following lengths:
3. AB 4. AF 5. B(‘
B. (AB)-’+(A(‘)3 1. (BCF
8. Using the results from Exercises 3-7, draw in conclusion about right
triangle A BC.
LESSON 5.8
Find the theoretical probability that a dart tossed at random onto each
figure will land in the shaded area.
1. 10 2. 3.
I . G3
4
Convert the following probabilities to percents. Round your answers to
the nearest tenth of a percent.
4 3
4. 0.61 5. 6. 5 7. l
Convert the following percents to decimal probabilities:
8. 40% 9. 29% 10. 73% 11. 9%
12. l.2% 13. ().l% 14. 5.8% 15. 45.3%
Convert the following percents to fractional probabilities. Give your
answers in lowest terms.
16. IO% 17. 25%
20. 2% 21. 9I%
18. 50%
22. 44%
19. 75%
23. 28%
EXTRA PRACTICE 835
eogoeed enxa
Extra Practice
CHAPTER 6
LESSON 6.1
For Exercises 1-5, refer to the isometric drawing at right.
1. Give the volume in cubic units.
. Give the surlac.e area in square units.
. Draw six orthographic proiections of the solid.
. Draw the solid on isometric dot paper lrom a different viewpoint.
UIOUN
. Draw the solid on isometric dot paper with a cube added at each
shaded face.
The three solids at right each have a volume of 5 cubic units.
8. Find the surface area ol each solid in square units. Which a_
has the least surface area?
7. Draw six orthographic proiettions of each solid.
LESSON 6.2
In the ilglfl at right, W, Z—Y, and E are perpendicular
to f, and BC is not perpendicular to 6.
1. Is nté.-lB(" the measure of the dihedral angle formed liy
planes M and N?
2. is m4 \'l'Z the measure of the dihedral angle formed by
planes Ni and N?
In the figure at right, line m is perpendicular to plane LP.
3. ls line m perpendicular to line H? Explain.
4. What is the relationship lwztween line m and line r?
5. Indicate whether the statement below is true or false lbr at
ligure in space. Explain your answer by using sketches.
ll two lines never intersect. then they are parallel.
836 Mo BANK
LESSON 6 3
Which of the figures below appear to be prisms? Give the name for each
prism. lf the figure is not a prism, explain why.
‘I. I 2 3.
Use the oblique triangular prism at right for Exercises 4-6. B
4. which lace is congruent to triangle ABC? Explain. A L C
5. I\'.tme all segmc-:nts congruent to AE.
6. What type ol'quzIdri|'.1ter:1l is ACDF? E D
For Exercises 7-10, find the length of a diagonal of a right rectangular
prism with the given dimensions.
7.('=l0.w=l0.h=5
9.('=5,w=6.h=8
8.£’=3.w=4.lt=5
10.£=8,w=2-'l,h=6
LESSON 6.4
Name the octant, coordinate plane. or axis where each point is located.
1. (2. I,3) 2. (—I4.0.0)
3. (-I, L8) 4. (53. l.2,0]
5. [—S,—l.—3] 6. (S. 0. -4}
Find the distance between each pair of points.
7. (I, 0, 2) and H, l. -2] 8. (2, 4, 0) and (4. 3-. 2)
9. (-l,-2.—3J and (I,-l,—l) 10. (-1. L6) and (l0.—-'1, I4)
EXTRA PRACTICE 837
eogxomd enxa
LESSON 6.5
Use intercepts to sketch a graph of the plane represented by each
equation.
1. 5x—6y—6..=—l.-2 2.2x—2y—22=8
3.—=l\:—2y+8z=l6 4.x-_’»y=3
In a coordinate plane, plot the lines represented by each pair of
parametric equations.
Extra Practice
5.x=t+l 6.x
y= t )' 3
II
+ [v
1‘
Recall that a trace of a plane is its intersection with the xy-plane. Find
the equation of the trace for each equation of a plane below.
7.7x+.2y—z=l 8.2x+~ly—|8z=2
LESSON 6.6
In Exercises 1-6, locate the vanishing point and horizon line for each
figure.
1. 2. 3.
I
4 5. 6
7. Make a one-point perspective drawing of a triangular prism.
838 INFO BANK
CHAPTER 7
LESSON 7.1
Detem1ine the surface-area-to-volume ratio for a rectangular prism with
the following dimensions:
1.7><lxt 2.3><2><5
3. 6 x 6 x 6
5.57x2)<I8
4. l2xl2xl2
8.51 X9-1x95
Find the surface-area-to-volume ratio for each of the following:
7. .1 cube with at volume oi" I25 cubic units
8. a (.lll)E with ".1 stlrface area of 96 square units
9. a rectangular prism with dimensions I x n x Zn
For each situation, determine whether you would want to maximize the
volume or minimize the surface area.
10. designing -.1 howl out of -.1 limited amount of clay
11. building :1 carton with a fi\'ed amount ol cardboard
LESSON 7.2
Find the volume of a prism with the given dimensions.
1. B = 6 in}. it = 4 in.
3. B= lOn13.h = I3 I11
2. B = l-1cm3.h= 3 cm
4. B=42ft3,h= to in
Find the surface area and volume of a right rectangular prism with the
given dimensions.
5.E=4,w=l2.h=5 6.t"=l3.w=l6.h=3.l
7.t'=-12,w=3n0.h=l 8.£=0.05.w=l.l,li=2
9.(‘.=2l.w=2l.h=2| 10.(’=-1.3,w=3.7".lz=6.8
11. Find the height ofa rectangular prism with :1 surface area of 2880 in.’ and
.1 base measuring 5 in. lay 8 in.
12. Find the width ofa rect.rngu|.|r prism with :1 volume of I44 cm’ and .1
base measuring 3- cm by 6 cm.
EXTRA PRACTICE 839
eogoesd enxa
Extra Practice
LESSON 7.3
Find the surface area of each regular pyramid with side length 5 and slant
height I given below.The number of sides of the base is given by n.
1.n=6,s=4.("=-1 2.n=4.s=2,l:'=3‘.
3.n=3.s=5.l’=lO 4.n=6.s=l4.t’=7
Find the volume of a rectangular pyramid with height h and base
dimensions E and w.
5. h= 4,6 = 7.2. w=6.8 6. h= l2,£’= l8.w= I0
7.h=l0.P=24,w=20 8.h=l7,(’=l.’l..w=5
9. l!=-'l2.E = I5.W= 20 ‘I0. lt= 25.1"": l9,w= I2
Find the height of each pyramid described below.
11. a regular triangular pyramid with it base area of I6 square units and .1
volume of 48 cubic units
12. a regular square pyramid with a base length of 2-1 units and a volume or
H.400 cubic units
LESSON 7.4
Find the unknown value for a right cylinder with radius r, height h, and
surface area 5 given below. Round your answers to the nearest tenth.
1.r=6.h=3.5= 7.‘ 2.r=l4.h=7.5= 7.‘
3.r=O.5.h=l.2,$= ? 4.r= ? ,.'t=3,$=L6'=r
5.r=2.h= ? ,S='/'2 6.r= ? ,.'i=_’v,.\=|40r.'
Find the unknown value for a right cylinder with radius r. height h, and
volume V. Round your answers to the nearest tenth.
7.r=4.5,h=3.2.V= ? 8.r= ?,.'i=l2.V=l50
9.r=l5,.'i=25.\-’= ? 1o.r'=4.h= ? .V=24Jt
‘l1.r= ? .h=20.V=I80rt 12.r=lO.h=8.l"= ?
13. A cylilider with a diameter of -'l in. and a height 0t‘8 in. is replaced by a
cylinder that has the same volume. The new cylinder has 21 diameter ol
6 in. What is its height?
840 INFO BANK
LESSON 7 5
|'l1
Find the surface area and volume of each right cone Express your E].
answers in ten11s of 1:. B
2. 3.
‘D
20.2 B
O
H-
II
8
4 5. 6
23 17.9
7. 8. 9.
10. A right cone has a radius of I? in. and a height of I2 in. \-\"hal is the slant
height ol‘ the cone?
LESSON 7.6
Find the surface area and volume of each sphere, with the given radius
or diameter. Round your answers to the nearest hundredth.
1.r=5 2.d= I.-I 3. d=66
4.r=2.8 5.r=2.9 6.rf=2<l
7.d=4.02 8.r=62 9.d=l6
ln Exercises 10-15, find the surface area and volume of each sphere with
the given radius or diameter. Express your answers exactly in ten11s of 1:
and a variable.
10. r= 3.: 11.d=7y 12. d=x
13. r= l.ly 14. r= 2}-' 15. if =
|'~.aI>-t
EXTRA PRACTICE 841
Extra Practice
LESSON 7.7
What are the coordinates of the reflection image when each point
below is reflected across the xy-plane?
1.(l.|.2) 2-(3.|.-2.5.—7)
4. (4.—4, L2} 5. (-2. l5.0]
3.(2.|.—3l
e.L42,—A—6)
What are the coordinates of the reflection image when each point
below is reflected across the xz-plane?
7. (32, 32, 32) 3. (0. -5, -6) 9. (I4, I, 6.2)
10. (L3, 5.2.—4) 11. (—l2.l.—3, 6) 12. (—55,—64,—U.2]
What are the coordinates of the reflection image when each point
below is reflected across the yz-plane?
13. (IS. IS. IS) 14. (-2. .3. 3)
16. [3, -6. 8.9] 17. (2, -2, -2)
15. (-7.8. -7.8, —l())
18. -4, 3)
CHAPTER 8
LESSON 8.1
Find the image of the point transfon11ed by the given dilation. Plot the
point and its image on a coordinate plane.
1. (3.4): D(x. y} = (2x, 2y) 2. (4. I}: Dlx. J’) = (-1x. -4)’)
3. (—2,—6); D(.r. y] = (0.5.r. 0.5y) 4. (-5. 35); Du‘, y) = (—x. —y)
For Exercises 5 and 6. the dashed figures represent preimages of
dilations and the solid figures represent images. Find the scale factor
of each dilation.
5. y 6.
{-6. -8)
For Exercises 7-10, a point and a scale factor n are given Find the line
that passes through the preimage and image, and show that the origin
is on this line.
7. (—l,—.'-); n = 8. (-1. I); n = -3 9. (l.—5); n = 2 10. (2. 3]; n= -1
842 INFO BANK
LESSON 8 2
ln Exercises 1 and 2, determine whether the polygons are similar
Explain your reasoning. lf the polygons are similar, write a similarity
statement.
1. A 5 B 2. P
«flat:
DL8 C 1%
R
5 7.5 F 3 0
X
6 7.5
H 12 G 5 10
Z
3 Y
ln Exercises 3-6. solve for x.
I I
3-9 3 — 1 1-E 2-5-3
3‘;-‘9 4't+2_r-I 5;-‘9 6'x"Is.r.
LESSON8.3
Determine whether each pair of triangles can be proven similar by using
the AA, SSS, or SAS Similarity Postulates and Theorems. If so, write a
similarity statement and identify the postulate or theorem used.
‘I. 3 2. J
K L
35"
H 5!
3. lndicate which figures are similar. J;'\'plain your reasoning.
r 5 J
E 4 F
A 1’ B 5 (31.25
2 =3 3
"l
D C H G L 7.5 K
EXTRA PRACTICE 843
eogxomd enxa
LESSON 8.4
Use the Side-Splitting Theorem to find x. Some exercises may have
more than one possible answer for x.
1. 2. 3.
x 3 3 X
5 2
9 x 9-2
4 6 "
10
Extra Practice
Name all of the similar triangles in each figure. State the postulates or
theorems that iustify each similarity.
4. 3 5.
D F
A F '_ c
LESSON 8.5
ln Exercises 1-3, use the diagrams to find the height of each rectangle.
1. 2. 3.
60ft
6ft
.~. H A
12331 5 11 12 ft 2.5 rt
«30ft-I
'< —4»3ft - >1
ln Exercises 4-6, the triangles are similar. Find x.
844 INFO BANK
LESSON 8 6
ln the figure at r1'ght,D—E||A—B. B 3 5 4 c
1. Find the ratio oflhc pcrimctcrs 0|" AABC and ADEC.
2. Find the ratio of the areas. of AABC and ADEC. D
A
The ratios of the sides of two similar hexagons is Find the
ratio of
3. their pcrimclcrs.
4. their areas.
The ratios of the sides of two similar triangular prisms is
Find the ratio of
5. the pcrimclurs 0|. their lriallgular lhcus.
ll-IOJ
6. the areas of their triangular llices.
7. their \-'n|umes.
CHAPTER 9
LESSON 9.1
Determine the length of an arc with the given central angle measure,
m£P, in a circle with radius r. Round your answers to the nearest
hundredth.
1. ml!’ = 40°; r = 6 2. mzP = 20°; r = 8
3. m.£P = 75°; r = 20 4. mAP = 100°; r = 16
5. ml!’ = 55°; 1' = I3 6. mz_’P = ll8°; r = 30
7. mzP=66°;r=-40 8. n1ZP= 130°: r=6l
9. mzP = 80°; r = 59 10. mzP = 82°; r = 5
Determine the degree measure of an arc with the given length, L, in a
circle with radius r.
11.1 =52;r= I-I
13.L=35;r=ll
15.L=8;r=2
17.L=25;r=23
12. L= ?.7;r'= 5
14. L = 5b; r = 30
16. L = 2.3:r= 85
18. L = I00: r = 79
EXTRA PRACTICE 845
eogoerd enxa
Extra Practice
LESSON 9.2
For Exercises 1-6, refer to circle J, in which fiJ.K—L at S.
1. E E L
. if [L = -I and IS = I. what is KS? What is 5L?
. if]! = IO and IS = 3, what is KS? What is SL?
. if}K = 26 and IS = I 1, what is KS? \'l'ht1l is SL?
. IUK = 60 and IS = I2, whal is KS? What is SL?
. if [P = 42 and [5 = 30, what is KS? What is SL?
QUOWN
LESSON 9.3
ln circle P, mALPJ = 30° and mAKMJ = 45°. Find the following:
1. m.£LMP 2. IHAIPK
3. n‘I£.*\UK 4. n‘|ZLP.H
5. m.?U e. mA\-IPK
7. m.£!}\P 8. Inf?
/5
9. mKM 10. IHAPLM
11. ml’)? 12. mAK]P
13. mil? 14.n1APK.'i-1
846 INFO BANK
LESSON 9.4 [11
_ r-\ _ 0 .I-\ _ O r\. _ ° 4—¥ _ x
In circle E, mBD — 20 , mDF — 180 , and mAF — 45 . GA IS ,4.
tangent to circle E at A. Find each of the following: 3
1. n1.£C-AG C .u
2. mA(_yCA B
3. n1A(_GA 0
.s—.» H-
ln the figure, XY is tangent to circle Zat X. 6'
4. If m SW = 95°, find mzvxu-'. w
_ _ _ .f_'\ Y
5. ll n1£i",\ W = lO0°, llnd m,\W.
e. If m = x + 15. find unzrxw. ..
X W
LESSON 9.5
W and are tangent to circle R, XY = 4, and the radius of
circle R is 2. Find the following:
1. X2 Y
2. YR
3. OX X
4. RX
5. I\-nine an angle congruent to .5 YX R. z
6
7
. I\'-.unc an angle congruent lo .5 YRX.
. I\-EHTIE‘ dl'l 2ll'C C(Jl'lgl'U€l'lt ICI fa.
Find the value of xin each figure.
8. 9.
A
EXTRA PRACTICE 847
LESSON 9.6
Find the x- and y-intercepts for the graph of each equation below.
¢
0
II
a 1 , 1 I
U 1.x +) =49 2x-i+y=l2
E 3. (x— I)1+y3= I6 4.x-’+(y+2)1=36
Q s.(x—3)’+(y+4)’=s1 6.(.i.’-7}2+(}'+l}2= I2!
E Find the center and radius of each circle.
‘i 7.x3+;'=«I 8.x3+y’=6«l
II" 9.(x+l)-'+y3=l4 1o.x?+(y—l)2=27
11. (x+.’~)Z+(y—5)Z=3l 12. (.r—7)3+(y+I)3= I2
Write an equation for the circle with the given center and radius.
13. center: (1. 2); radius = 4 14. center: (-1. -6); radius = I2
CHAPTER 1 0
LESSON 10.1
Find tan A for each triangle below.
1 2. 4
8.08 3 A
/ 2
2 /S
A 7.5 ”
3. 4. 3
1 8 §3 3 23 "2
A 8.54 \
A
Use a scientific calculator to find the tangent of each angle below.
Round your answers to the nearest hundredth.
5. l5° 6. 23° 7. -II-'°
8. 69° 9. 42° 10. 54°
848 INFO BANK
LESSON 10 2
I'll
For Exercises 1-6, refer to AX YZ. Find each of the following: y 5;.
. . 3 . 9 1
. *- 5 = -_ 2. ~ ~ 5 = -_
1 smj V!” msj V!“ Jfi 2 m
_ 3 _ 3
3. cos ? — 4. tan ? — 5 X 3 Z 3
5. Ian ? = 3 6. sin ? = 4 g
— I — .43 ,_,
Use a scientific calculator to find the following. Round your answers to 6'
the nearest hundredth. w
7. sin 15° 8. cos 23° 9. tan |7°
10. cos 69° 11. sin 42° 12. Ian 47°
LESSON 10.3
Use a scientific calculator to find the following. Round your answers to
four decimal places.
1. sin 55° 2. sin I69” 3. sin 540°
4. cos 55° 5. cos I69“ 6. cos 340°
ln Exercises 7-9, use a scientific calculator to find the sine and cosine of
each angle. Use these values to give the x- and y-coordinates of a point
at the given angle on the unit circle. Round your answers to four
decimal places.
7. 20° 8. 160° 9. 200°
ln Exercises 10-15, give two values for angle 9 between 0° and 180° for
the given value of sin 0. Round your answers to the nearest degree.
10. 0.2250 11. 0.6157 12. 0.8746
13. 0.3907 14. 0.3090 15. 0.5150
EXTRA PRACTICE 849
Extra Practice
LESSON 1 0.4
For Exercises 1-4, find the indicated measures. 3
Assume that all angles are acute. It may be helpful
to sketch the triangles roughly to scale. C B
1. max = 52° m.£b' = 68” b = 4.2 cm :1 = ? C
2. m/.4 = 72° m.£C = 32° a = M cm c = ? A b
3. m.£B = 64° u = 2.34 cm I) = 3.5 cm m.£A = ?
4. mm = 25° mAC = 65° c = 5 cm :1 = I’
Find all unknown sides and angles in each triangle. If the P
triangle is ambiguous, give both possible angles. It may
be helpful to sketch the triangles roughly to scale. r a
5. mZP = 36° n1zQ = 68° 1} = 7 R
6. m.£R=7'5° p= I0 r=l-1 Q P
7. m.£Q = 40° rn.£P = 25° :1 = I2
LESSON 10.5
For Exercises 1-4, find the indicated measures. It may be C
helpful to sketch the triangles roughly to scale. Bound to
scale. Round your answers to the nearest tenth.
1.u=l b=|5 c= ? mAC=20°
b
2.u= I2 b=5 c= ? mzC=68° 8
3.a=-1 b=7 (=5 m.£C= E’
4.tl=9 b=.’.- c=8 m.£C= ?
B c A
Solve each triangle.
5- 9 3.8 5- G
E
2.5 '
6.4
,A4L H
7_1 3.2
F
850 INFO BANK
LESSON 10 8
Copy each pair of vectors below and draw the vector sum, -3’ + by
using the head-to-tail method.You may need to translate one of the
vectors.
1. 2.
‘T %
Copy each pair of vectors below and draw the vector sum, '5' + by
using the parallelogram method.You may need to translate one of the
vectors.
3. 4
ml
4
LESSON 1 0.7
For Exercises 1-8, a point, P, and an angle of rotation. 9. are given.
Determine the coordinates of the image, P’. Round your answers to
the nearest tenth.
1. P((). 5]; 6 = 48°
3. P(I.4]: 6= 17°
5. P(2.—2]; 9 = 50°
7. P(3.0]: 9 = 90°
2. H4, 2); 6 = 270°
4. H-2. -51; 9 = 05°
:5. H-1. 2); 6: 150°
3. H-3. -21; 9 = 200°
Find the rotation matrix for each angle below by filling in the sine and
the cosine values. Round your answers to the nearest hundredth.
9. I35“ 10. 215”
11. 35° 12. 3«l5°
13. 40° 14. 180°
15. 300° 16. 120°
EXTRA PRACTICE 851
eogxomd enxa
Extra Practice
CHAPTER 1 1
LESSON 1 1.1
Determine the indicated side length of each golden rectangle. Round
your answers to the nearest hundredth.
1. 2.
7 4.3
4 7
3 4
7 3
1o .7
5 6
7 1.5
32 .7
LESSON 1 1 .2
Find the taxidistance between each pair of points.
1. (2.«l]:1nd[l.6‘J 2. f—5,8] and [O.—2)
3. (—9.—5) and (-4. -7) 4. (—l0. IO] and (l0. —l0)
Find the number of points on the taxicab circle with the given radius.
5.r=3 6.r=7 7.r=l0
8.r=S 9.r=5 1o.r=2O
Find the circumference of the taxicab circle with the given radius.
11.r=3 12.r=6 13.:-=8
14.r=9 15.r=lI 16.r=2O
852 INFO BANK
LESSON 1 1 3
Determine whether the graphs below contain an Euler path, an Euler
circuit, or neither.
L
P O N
_ 3
s
E‘ o
_ c
3
o
A
5
F
3_ Y
fig
W
1. Which, if any. ol the following figures are topologically equimlent?
an b‘ C.
Verify Euler's formula for each polyhedron below.
2. tetrahedron
1. A 2.
4
LESSON 1 1 .4
3. dodecahedron
EXTRA PRACTICE 853
eogxomd enxa
Extra Practice
LESSON 1 1 .5
Refer to the diagram of a sphere at right. Determine N
whether the following figures are lines in spherical
geometry:
4.—> 4-.5
1. X Y 2. NL X
3. .'t~l‘}’ 4. LM
Refer to the diagram at right. Determine whether
the following figures are lines in hyperbolic geometry:
(-4 %5
5. AF 6. AB A
7. ‘R? 3. ‘I53
LESSON 1 1.8
Using the technique shown in the construction of the Sierpinski gasket.
construct a Sierpinski gasket with the following triangles:
1. 2.
3. Build Pasc;1|’s triangle with -at least I2 rows. Shade around each number
that is divisible by 2, and leave the other numbers unshaded. How is the
pattern dillcrcnt from the pattern you found in Activity 2 0|" Lesson l I .6?
How is it the same?
854 INFO BANK
LESSON 11 7
Draw a circle with a radius of 3 centered at the origin on a coordinate
plane. Use the grids of parallelograms below to transform the circle.
1. 2.
50'’
Copy the diagram at right and draw each projection. 0 p
3. [sing O as the center oi‘ projection. project points X. Y. _
and 7 onto line £3. label the projected points X’. Y’, and ' X’ y' '2 ' "1
Z’.
4. [Bing P as the center of projection. project points X’. Y’.
and 70mm line t".‘;. l abel the projected points X”, Y”. and £2
.5". 3
CHAPTER 1 2
LESSON 12.1
In Exercises 1-4, write a valid conclusion from the given premises.
Identify the form of the argument.
1. If the baby is hungry. then he cries. ‘I he baby is hungry.
2. ll" the baby is hungry. then he cries. The baby is not crying.
3. If the baby is not hungry. then he throws his cereal on the floor. The baby
did not throw his cereal on the floor.
4. ll" the baby is not hungry. then he will play in his playpen. l'he b.i|.>y is not
hungry.
For Exercises 5-7, refer to the following premises:
If Harry is a purple hippopotamus, then Larry is a blue dinosaur.
lf Larry is not a blue dinosaur, then Barry is a pink alligator.
Larry is not a blue dinosaur.
State whether each conclusion below is valid. Explain.
5. Harry is not a purple hippopotamus.
6. Harry is a purple l'lipp0p0IdmuS.
7. Barry is a pink alligator.
EXTRA PRACTICE 855
eogoead enxa
Extra Practice
LESSON 12.2
1. Write a conjunction for the pair of statements below Determine whether
the conjunction is true or false.
Some tlowers are red. Cucumbers are vegetables.
2. W rite at disjunction for the pair of statements below. Determine whether
the disjunction is true or false.
Parallel lines intersect. All rectangles are sqttures.
For Exercises 3-8, write the statement expressed by the symbols, where
p, q, and r represent the statements shown below.
p: ll.1rr_v is older than Larry.
:1: Larry and Barry are twins.
r: Harry is younger than Barry.
3. ~p 4. -4] OR -r 5. -q
6.p.-\ND -q 7. -tpAI\'D r) 8. -[p OR -r)
LESSON 1 2.3
For each conditional in Exercises 1-3, write the converse, inverse, and
contrapositive. Decide whether each is tme or false and explain your
reasoning.
1. If Harry and Larry are twins. then they are the saute age.
2. If two triangles are congruent. then they are similar.
3. lfm x n = 0. then m = O.
For Exercises 4-6, write each statement in if-then form.
4. All blue pigs can play the banjo.
5. l\o odd numbers are divisible by 2.
6. I will buy you at cantera if they go on sale.
856 INFO BANK
LESSON 12 4
In Exercises 1-4, determine whether the given argument is an example
of an indirect reasoning. Explain why or why not.
1.
Complete the indirect proof below.
. If Juan eats strawberries, then he breaks out in hives. Juan did not break
. l was in an accident. Ill was in an accident. then I must have been driving
If Bobby ate some cookies trom the cookie jar, then the cookie jar is not
full. l'he cookie jar is not full. Therefore. Bobby ate some cookies from the
cookie jar.
out in hives. l'hereI'ore. he did not eat strawberries.
eogoead enxa
my car. Therefore. I was driving my car.
. If the alarm rings, then the dogs bark. The dogs did not hark. Therefore,
the alarm did not ring.
Given: AABC. mi,-1 < 30°. and m.£B < 45°
Prove: AC is obtuse.
. . . . A B
Proof: suppose that 1C is 5. ? . lhen mzC S 6. ?
Thus InAA + 111.513 + In.£C S 7. ? + 8. ? + 9. ? = 10. ?
This contradicts the property of triangles that 11. If _ Therefore, 12. 7.’
LESSON 12.5
Use the logic gates below to answer each question.
1.
ll" p = 0. what is the output?
2. lfp = l and q = I. what is the output?
2:
For Exercises 3-10. complete the input-output p t—\
table for the network of logic gates at right. 0 AND} —L
S-°9°.“!”!»‘P!-9
--p AND q
(-p AND :1) OR r
‘P
EXTRA PRACTICE 857
ions
Postulates, Theorems, and Defini
Postulates, Theorems,
and Definitions
Def 1.1.1
Def 1.1.2
Def 1.1.3
Post 1.1.4
Post 1.1.5
Post 1.1.6
Post 1.1.7
Post 1.1.8
Def 1.2.1
Post 1.2.2
Post 1.2.3
Def 1.3.1
Post 1.3.2
Post 1.3.3
Def 1.3.4
Thm 1.3.5
858 INFO BANK
Segment A segment is a pan of a line that begins at one point and ends at
another.The points are called the endpoints of the segment.
Ray A ray is a part of a line that starts at a point and extends infinitely l|'l one
direction.The point is called the endpoint of the ray.
Angle An angle is a figure formed by two rays with a common endpoint.The
common endpoint is called the vertex of the angle, and the rays are the sides of
the angle. An angle divides a plane into two regions: the interior and the exterior
of the angle. If two points, one from each side of an angle, are connected by a
segment, the segment passes through the interior of the angle.
Postulate The intersection of two lines is a point.
Postulate The intersection of two planes is a line.
Postulate Through any two points there is exactly one line.
Postulate Through any three noncollinear points there is exactly one plane.
Postulate If two points are in a plane, then the line containing them is in the
plane.
Length ofA—B Let A and B be points on a numbgline, ._.—’3—._._.—-—§—-
with coordinates a and b. Then the measure of AB, which 5 mm or A5,:
is called its length. is |a—b| or |b— a. la_ bl or b_ 3'
Segment congruence Postulate If two segments have the same length as
measured by a given fair ruler, then the segments are congruent. Also, if two
segments are congruent, then they have the same length as measured by a given
ruler.
Segment Addition Postulate If point F? is between points Pand O on a line, then
PR + R0 = P0.
Measure of an Angle Suppose that the vertex, V, of AAVB is placed on the center
point of a half-circle with coordinates from 0° to 180° so that VA and VB intersect
the half-circle. Let a and b be the coordinates of the intersc-ctions.Then the
measure of the angle, written as mzAVB, is |a — b| or |b —- a|.
Angle Addition Postulate If point 8 is in the interior of APOR, then
m.£POS + m.£SOH = mzPOR.
Angle Congruence Postulate if two angles have the measure, then they are
congruent. If two angles are congruent, then they have the same measure.
Special Angle Pairs
Complementary angles are two angles whose measures have a sum of 90°. Each
angle is called the complement of the other.
Supplementary angles are two angles whose measures have a sum of 180°. Each
angle is called the supplement of the other.
Linear Pair Property If two angles form a linear pair, then they are
supplementary.
Def 1.3.6
Def 1.4.1
Def 1.4.2
Def 1.6.1
Def 1.6.2
Def 1.6.3
Def 1.7.1
Def 1.7.2
Def 1.7.3
Post 2.2.1
Def 2.3.1
Post 2.4.1
Post 2.4.2
Post 2.4.3
Post 2.4.4
Post 2.4.5
Thm 2.4.6
Post 2.4.7
Post 2.4.8
Post 2.4.9
Three Types of Angles
A right angle is an angle whose measure is 90‘.
An acute angle is an angle whose measure is less than 90°.
An obtuse angle is an angle whose measure is greater than 90° and less than 180°.
Perpendicular and Parallel Lines Perpendicular lines are two lines that intersect
to form a right angle. Parallel lines are two coplanar lines that do not intersect.
Bisectors and Midpoint A segment bisector is a line that divides a segment into
two congruent parts. The point where a bisector intersects a segment is the
midpoint of the segment. A bisector that is perpendicular to a segment is called
a perpendicular blsector. An angle bisector is a line or ray that divides an angle
into two congruent angles.
Translation A translation is a transformation in which every point of the
preimage is moved the same distance in the same direction.
Rotation A rotation is a transformation in which every point of the preimage is
moved by the same angle through a circle centered at a given fixed point known
as the center of rotation.
Reflection A reflection is a transformation in which every point of the preimage
is moved across a line known as the mirror line so that the mirror is the
perpendicular bisector of the segment connecting the point and its image.
Horizontal and Vertical Coordinate Translations
Horizontal translation of h units: H(x, y) = (X + h, y)
Vertical translation of v units: Vlx. y} - lx, y + V)
Reflection Across the x- or y-axis
Reflection across the x-axis: MIX, 1/} - (X, -54
Reflection across the y-axis: Nlx, y} - l-x, yl
180° Rotation About the Origin Rtx, yl - 1-x, — y}
lf-Then Transitive Property Given: "If A, then B, and if B, then C.'You can
conclude: "If A, then C."
Adiacent Angles Adjacent angles are angles in a plane that have their vertex and
one side in common but have no interior points in common.
Addition Property If a = b. then a + c = b + c.
Subtraction Property If a - b, then a - c - b — c.
Multiplication Property If a - b, then ac - bc.
Division Property If a - b and c :2 0, then % - %.
Substitution Property If a = b, you may replace a with b in any true equation
containing a and the resulting equation will still be true.
Overlapping Segments Theorem Given a segment with points A, B, C, and D (in
order), the following statements are true:
1. If AB - CD, then AC - BD.
2. If AC - BD. then AB - CD.
Reflexive Property of Equality For any real number a, a - a.
Symmetric Property of Equality For all real numbers a and b, if a = b, then b = a.
Transitive Property of Equality For all real numbers a, b, and c, if a = b and b = c,
then a = c.
POSTUL-KTESJHEC-REM5, AND DEFINITIONS 859
suogrtgugaa pue 'su1a.toaq_|_ 'sa:te|n1sod
ions
Postulates, Theorems, and Defini
Post 2.4.10
Post 2.4.11
Post 2.4. 12
Thrn 2.4.13
Thm 2.5.1
Thrn 2.5.2
Thm 2.5.3
Def 3.1.1
Def 3.1.2
Def 3.1.3
Def 3.1.4
Def 3.3.1
Post 3.3.2
Thrn 3.3.3
Thrn 3.3.4
Thm 3.3.5
Thrn 3.4.1
860 INFO BANK
Reflexive Property of Congruence figure A 2 figure A
Symmetric Property of Congruence If figure A I figure B, then
figure B -1 figure A.
Transitive Property of Congruence If figure A =_= figure 8 and figure 8 5 figure C.
then figure A 2 figure C.
Overlapping Angles Theorem Given LAOD with points B and C in its interior, the
following statements are true:
1. If m/_AOB - m/_COD, then m.aLAOC- m.a£BOD.
2. If m./_AOC - m./_BOD, then m./_AOB - mLCOD.
Vertical Angles Theorem If two angles form a pair of vertical angles, then they
are congruent.
Theorem Reflection across two parallel lines is equivalent to a translation of
twice the distance between the lines and in a direction perpendicular to the lines.
Theorem Reflection across two intersecting lines is equivalent to a rotation about
the point of intersection through twice the measure of the angle between the
lines.
Polygon A polygon ls a plane figure formed from three or more segments such
that each segment intersects exactly two other segments, one at each endpoint,
and no two segments with a common endpoint are collinear. The segments are
called the sides of the polygon, and the common endpoints are called the
vertices of the polygon.
Reflectional Symmetry A figure has reflectional symmetry if and only if its
reflected image across a line coincides exactly with the preimage.The line is
called an axis of symmetry.
Triangles Classified by Number of Congruent Sides
Three congruent sides: equilateral
At least two congruent sides: isosceles
No congruent sides: scalene
Rotational Symmetry A figure has rotational symmetry if and only if it has at
least one rotation image, not counting rotation images of 0° or multiples of 360°
that coincides with the original image.
Transversal A transversal is a line, ray, or segment that intersects two or more
coplanar lines, rays, or segments. each at a different point.
Corresponding Angles Postulate If two lines cut by a transversal are parallel,
then corresponding angles are congruent.
Alternate Interior Angles Theorem If two lines cut by a transversal are parallel,
then alternate interior angles are congruent.
Alternate Exterior Angles Theorem If two lines cut by a trdnsversal are parallel,
then alternate exterior angles are congruent.
Same-Side Interior Angles Theorem If two lines cut by a transversal are parallel
then same-side interior angles are supplementary.
Theorem: Converse of the Corresponding Angles Postulate If two lines are cut by
a transversal in such a way that corresponding angles are congruent, then the
two lines are parallel.
Thm 3.4.2
Thm 3.4.3
Thm 3.4.4
Thm 3.4.5
Thrn 3.4.6
Post 3.5.1
Thrn 3.5.2
Thm 3.5.3
Thm 3.6.1
Thm 3.6.2
Thm 3.6.3
Def 3.7.1
Det 3.7.2
Def 3.8.1
Thm 3.8.2
Thrn 3.8.3
P051 4.1.1
Post 4.2.1
P081 4.2.2
Converse ot the Same-Side lnterior Angles Theorem It two lines are cut by a
transversal in such a way that same-side interior angles are supplementary, then
the two lines are parallel.
Converse of the Alternate Interior Angles Theorem If two lines are cut by a
transversal in such a way that alternate interior angles are congruent, then the
two lines are parallel.
Converse of the Alternate Exterior Angles Theorem If two lines are cut by a
transversal in such a way that alternate exterior angles are congruent. then the
two lines are parallel.
Theorem If two coplanar lines are perpendicular to the same line, then the two
lines are parallel.
Theorem If two lines are parallel to the same line, then the two lines are parallel.
The Parallel Postulate Given a line and a point not on the line, there is one and
only one line that contains the given point and is parallel to the given line.
Triangle Sum Theorem The sum of the measures of the angles of a triangle is
180°.
Exterior Angle Theorem The measure of an exterior angle of a triangle is equal
to the sum of the measures of the remote interior angles.
Sum of the Interior Angles of a Polygon The sum, 5. of the measures of the
interior angles of a polygon with n sides is given by s - {n — 2l180°.
The Measure of an Interior Angle of a Regular Polygon The measure, m, of an
interior angle of a regular polygon with n sides is given by m = 180° —
Sum of the Exterior Angles of a Polygon The sum of the measures of the exterior
angles of a polygon is 360°.
Midsegment of a Triangle A midsegment of a triangle is a segment whose
endpoints are the midpoints of two sides.
Midsegment of a Trapezoid A midsegment of a trapezoid is a segment whose
endpoints are the midpoints of the nonparallel sides.
Slope The slope of a nonvertical line that contains the points lxi. Vii and [x,, yzj
is equal to the ratio
Parallel Lines Theorem In a coordinate plane, two nonvertical lines are parallel if
and only if they have the same slope.
Perpendicular Lines Theorem In a coordinate plane, two nonvertical lines are
perpendicular it and only if the product of their slopes is -1.
Polygon Congruence Postulate Two polygons are congruent if and only if there is
a way of Setting up a correspondence between their sides and angles, in order,
such that (1) each pair of corresponding angles is congruent and [2] each pair of
corresponding sides is congruent.
SSS (Side-Side-Side) Postulate If the sides of one triangle are congruent to the
sides of another triangle, then the two triangles are congruent.
SAS (Side-Angle-Side) Postulate If two sides and their included angle in one
triangle are congruent to two sides and their included angle in another triangle,
then the two triangles are congruent.
POSTUL-\TES.THEO-REM5. AND oenurnoms 861
suogguuaa pue 'su1a.Ioaq_|_ 'sa;e|n;sod
ions
Postulates, Theorems, and Defini
Post 4.2.3
Thm 4.3.1
Thm 4.3.2
Thm 4.4.1
Thm 4.4.2
Cor 4.4.3
Cor 4.4.4
Thm 4.5.1
Thm 4.5.2
Thm 4.5.3
Thm 4.5.4
Thrn 4.5.5
Thm 4.5.6
Thm 4.5.7
Thm 4.5.8
Thm 4.5.9
Thm 4.5.10
Thm 4.5.11
Thm 4.5.12
Thm 4.5.13
Thm 4.6.1
Thm 4.6.2
Thrn 4.6.3
Thrn 4.6.4
862 INFO BANK
ASA (Angle—Side-Angle) Postulate If two angles and their included side in one
triangle are congruent to two angles and their included side in another triangle,
then the two triangles are congruent.
AAS (Angle-Angle~Side) Congruence Theorem If two angles and a nonincluded
side of one triangle are congruent to the corresponding angles and noninrluded
side of another triangle, then the triangles are congruent.
HL (Hypotenuse-Leg) Congruence Theorem If the hypotenuse and a leg of a right
triangle are congruent to the hypotenuse and corresponding leg of another right
triangle, then the two triangles are congruent.
Isosceles Triangle Theorem If two sides of a triangle are congruent. then the
angles opposite those sides are congruent.
Converse of the Isosceles Triangle Theorem If two angles of a triangle are
congruent. then the sides opposite those angles are congruent.
Corollary The measure of each angle of an equilateral triangle is 60°.
Corollary The bisector of the vertex angle of an isosceles triangle is the
perpendicular bisector of the base.
Theorem A diagonal of a parallelogram divides the parallelogram into two
congruent triangles.
Theorem The opposite sides of a parallelogram are congruent.
Theorem The opposite angles of a parallelogram are congruent.
Theorem Consecutive angles of a parallelogram are supplementary.
Theorem The diagonals of a parallelogram bisect each other.
Theorem A rhombus is a parallelogram.
Theorem A rectangle is a parallelogram.
Theorem The diagonals of a rhombus are perpendicular.
Theorem The diagonals of a rectangle are congruent.
Theorem The diagonals of a kite are perpendicular.
Theorem A square is a rectangle.
Theorem A square is a rhombus.
Theorem The diagonals of a square are congruent and are the perpendicular
bisectors of each other.
Theorem If two pairs of opposite sides of a quadrilateral are congruent, then the
quadrilateral is a parallelogram.
Theorem If one pair of opposite sides of a quadrilateral are parallel and
congruent. then the quadrilateral is a parallelogram.
Theorem If the diagonals of a quadrilateral bisect each other. then the
quadrilateral is a parallelogram.
Theorem If one angle of a parallelogram is a right angle. then the parallelogram
is a rectangle.
Thm 4.6.5
Thm 4.6.6
Thm 4.6.7
Thrn 4.6.8
Thm 4.6.9
Post 4.8.1
Thm 4.8.2
Def 5.1.1
Def 5.1.2
Post 5.1.3
Thm 5.1.4
Post 5.1.5
Def 5.2.1
Thrn 5.2.2
Def 5.2.3
Thrn 5.2.4
Def 5.2.5
Housebuilder Theorem If the diagonals of a parallelogram are congruent, then
the parallelogram is a rectangle.
Theorem If one pair of adjacent sides of a parallelogram are congruent, then the
quadrilateral is a rhornbus.
Theorem If the diagonals of a parallelogram bisect the angles of the
parallelogram. then the parallelogram is a rhombus.
Theorem It the diagonals of a parallelogram are perpendicular. then the
parallelogram is a rhombus.
Triangle Midsegment Theorem A midsegment of a triangle is parallel to a side of
the triangle. and its length is equal to half the length of that side.
Betweenness Postulate Given three points P, O, and R. if PO 1» OR = PR, then 0
is between Pand Ron a line.
Triangle Inequality Theorem The sum of the lengths of any two sides of a
triangle is greater than the length of the third side.
Perimeter The perimeter of a closed plane figure is the distance around the
figure.
Area The area of a closed plane figure is the number of non-overlapping squares
of a given size that will exactly cover the interior of the figure.
Postulate: Sum of Areas If a figure is composed of non-overlapping regions A
and B, then the area of the figure is the sum of the areas of regions A and B.
Perimeter of a Rectangle The perimeter of a rectangle with base b and height h
is P = 213 + 2h.
Postulate: Area of a Rectangle The area of a rectangle with base b and height h
is A = bh.
Parts of a Triangle Any side of a triangle can be called
the base of the triangle.The altitude of the triangle is a
perpendicular segment from a vertex to a line containing
the base of the triang|e.The height of the triangle is the
length of the altitude.
Base-"
Area of a Triangle The area of a triangle with base b and height h is A = %bh.
Parts of a Parallelogram Any side of a parallelogram Altitude
can be called the base of the parallelogram. An ,7
altitude of a parallelogram is a perpendicular segment _J:
from a line containing the base to a line containing the ‘Base
side opposite the base.The height of the parallelogram
is the length of the altitude.
Area of a Parallelogram The area of a parallelogram with base b and height h is
A = bh.
1,, Base
‘x/—‘fi|ti:ude\ f _I_eg
LL
D2 “Base
Parts of a Trapezoid The two parallel sides of a
trapezoid are known as the bases of the trapezoid. L39
The two nonparallel sides are called the legs of the
trapezoid. An altitude of a trapezoid is a perpendicular
segment from a line containing one base to a line
containing the other base. The height of a trapezoid
is the length of an altitude.
POSTUL-\TES.THEO-REM5. AND t)EHNrnoNs 863
suogguuaa pue 'su1a.Ioaq_|_ 'sa;e|n;sod
ions
Postulates, Theorems, and Defini
Thrn 5.2.6
Def 5.3.1
Thrn 5.3.2
Thrn 5.3.3
Thrn 5.4.1
Thrn 5.4.2
Thrn 5.4.3
Thrn 5.5.1
Thrn 5.5.2
Thrn 5.5.3
Thm 5.6.1
Def 6.2.1
Def 6.2.2
Def 6.2.3
Def 6.2.4
864 INFO BANK
Area of a Trapezoid The area of a trapezoid with bases b. and b2 and height h is
A - gin. + ban.
Circle A circle is the set of all points in a plane that
are the same distance. r, from a given point in the |
plane known as the center of the i:ircle.The distance C,
r is known as the radius of the circIe.The distance I
d = 2r is known as the diameter of the circle. Ceme’
I
Circumference of a Circle The circumference of a circle with diameter d and
radius ris C = 1rd or C = 2Jl’l'.
Area of a CircleThe area of a circle with radius r is A = ztr’.
Pythagorean Theorem For any right triangle. the square of the length of the
hypotenuse is equal to the sum of the squares of the lengths of the legs: that is,
c’ = a” + D“.
Converse of the Pythagorean Theorem If the square of the length of one side of
a triangle equals the sum of the squares of the lengths of the other two sides.
then the triangle is a right triangle.
Pythagorean inequalities For any triangle ABC, with cas the length of the
longest side:
If c" - a’ + b’, then AABC is a right triangle.
If c‘ :- a’ + b‘, then AABC is an obtuse triangle.
If c‘ < a2 + b’, then AABC is an acute triangle.
45-45-90 Triangle Theorem In any 45-45-90 triangle, the length of the hypotenuse
is J5 times the length of a leg.
30-60-90 Triangle Theorem In any 30-60-90 triangle, the length of the hypotenuse
is 2 times the length of the shorter leg. and the length of the longer leg is J3
times the length of the shorter leg.
Area of a Regular Polygon The area of a regular polygon with apothem a and
perimeter p is A - —%ap.
Distance Formula On a coordinate plane, the distance between two points
(xi. V1] and lxz. V2} is d - \.-"(X2 - X1]! + iv; - vi)'=.
Ed e
Polyhedron A polyhedron is a closed spatial figure ;’ Q
composed of polygons, called the faces of the
polyhedron.The intersections of the faces are the 4\
edges of the polyhedron.The vertices of the faces Vertex Face
are the vertices of the polyhedron.
Parallel Planes Two planes are parallel if and only if they do not intersect.
A Line Perpendicular to a Plane A line is perpendicular to a plane at a point Pit
and only if it is perpendicular to every line in the plane that passes through P.
A Line Parallel to a Plane A line that is not contained in a given plane is parallel
to the plane it and only if it is parallel to a line contained in the plane.
Def 6.2.5
Def 6.2.6
Thrn 6.3.1
Thrn 6.4.1
Thm 6.4.2
Thm 6.6.1
Thrn 6.6.2
Thrn 7.1.1
Thrn 7.1.2
Thm 7.2.1
Thm 7.2.2
Thm 7.2.3
Thrn 7.3.1
Thrn 7.3.2
Thrn 7.4.1
Dihedral Angle A dihedral angle is the figure formed by two half-planes with a
common edge. Each half-plane is called a face of the angle. and the common
edge of the half-planes is called the edge of the angle.
r’ Half-plane Diliedral angle
Measure of a Dihedral Angle The measure of a dihedral angle is the measure of
an angle formed by two rays that are on the faces and that are perpendicular to
the edge.
Diagonal of a Right Rectangular Prism The length of the diagonal, d, of a right
rectangular prism is given by d = (.9 + w’ + W.
Distance Formula in Three Dimensions The distance. d, between the points
{x., y., 2.) and (x2, y2, 2-,) in space is given by d - \,-"ix; — x1)? + (ye — y.]'¢ + (22 — z.)2.
Midpoint Formula in Three Dimensions The midpoint of a segment with
endpoints at (24,, y.. z.) and [x«,, y»,, 22) in space is given by
x.+x;. y.+y, 2.4-:
EE I I’ ‘
Theorem: Sets of Parallel Lines in a perspective drawing, all lines that are
parallel to each other, but not parallel to the picture plane, will seem to meet at a
single point known as the vanishing point.
Theorem: Lines Parallel to the Ground In a perspective drawing, a line that is on
the plane of the ground and is not parallel to the picture plane will meet the
horizon of the drawing. Any line parallel to this line will meet the horizon at the
same point.
Surface Area and Volume of a Right Rectangular Prism The surface area, S. and
volume, V, of a right rectangular prism with length t", width w, and height hare
S - 2E'w + 2wh + 21!) and V - rwh.
Surface Area and Volume of a Cube The surface area, S, and volume, V, of a
cube with side length s are S - 659 and V - s3.
Surface Area of a Right Prism The surface area, S, of a right prism with lateral
area L, base area B, perimeter p, and height his S - L + 28 or S - hp + 28.
Cavalieri's Principle If two solids have equal heights and the cross sections
formed by every plane parallel to the bases of both have equal areas. then the
two solids have equal volumes.
Volume of a Prism The volume, V, of a prism with height h and base area Bis
V - Bh.
Surface Area of a Regular Pyramid The surface area, S, of a regular pyramid with
lateral area L, base area B, perimeter of the base p, and slant height 5' is 5 = L + B
orS= %-tp+B.
Volume of a Pyramid The volume, V, of a pyramid with height h and base area B
- _ 1
IS V —
Surface Area of a Right Cylinder The surface area, S, of a right cylinder with
lateral area L, base area B, radius r, and height his 5 = L + 28 or 5 = 2:trh + Znr’.
POSTUL-\TES.THEO-REM5. AND DEFINITIONS 865
suogaguuaa pue 'su1a.Ioaq_|_ 'sa;e|n;sod
ions
Postulates, Theorems, and Defini
Thm 7.4.2
Thm 7.5.1
Thm 7.5.2
Thm 7.6.1
Thm 7.6.2
Def 8.2.1
Post 8.2.2
Thm 8.2.3
Thm 8.2.4
Thm 8.2.5
Thm 8.2.6
Post 8.3.1
Thm 8.3.2
Thm 8.3.3
Thm 8.4.1
Cor 8.4.2
Thm 8.5.1
Thm 8.5.2
Thm 8.5.3
Thm 8.5.4
866 INFO BANK
Volume of a Cylinder The volume, V, of a cylinder with radius r, height h, and
base area B is V - Bh or V - Itr3h.
Surface Area of a Right Cone The surface area, S, of a right cone with lateral
area L, base of area B, radius r, and slant height r is S - l. + B or S - ztrt + rrrz.
Volume of a Cone The volume. V. of a cone with radius r. height h. and base area
Bis v - -5-Bh or v . .}m=h.
Volume of a Sphere The volume, V, of a sphere with radius r is V - gar“.
Surface Area of a Sphere The surface area, S, of a sphere with radius ris
S - 4Jtr7.
Similar Figures Two figures are similar if and only if one is congruent to the
image of the other by a dilation.
Polygon Similarity Postulate Two polygons are similar if and only if there is a
way of setting up a correspondence between their sides and angles such that the
following conditions are met:
1. Each pair of corresponding angles is congruent.
2. Each pair of corresponding sides is proportional.
Cross-Multiplication Property of Proportions For real numbers a. b. c, and d such
that band (1 =2 0, if % = -3}, then ad = bc.
Reciprocal Property of Proportions For real numbers a, b, c, and (1 such that a, b,
b d
c, and d =1 0, if% = then -5 = 7.
Exchange Property of Proportions For real numbers a, b, c, and dsuch that a, b.
c,and d-¢O,if-E - -3,then-E -
“Add-One" Property of Proportions For real numbers a. b. c, and d such that b
andd=o,if-§=.3.,tl1en£""£'Tb=-"%’.
AA (Angle-Angle) Similarity Postulate If two angles of one triangle are congruent
to two angles of another triangle, then the triangles are similar.
SSS (Side-Side-Side) Similarity Theorem If the three sides of one triangle are
proprtional to the three sides of another triangle. then the triangles are similar.
SAS (Side-Angle-Side) Similarity Theorem If two sides of one triangle are
proprtional to two sides of another triangle and their included angles are
congruent, then the triangles are similar.
Side-Splitting Theorem A line parallel to one side of the triangle divides the
other two sides proportionally.
Two-Transversal Proportionality Corollary Three or more parallel lines divide two
intersecting transversals proportionally.
Proportional Attitudes Theorem If two triangles are similar, then their
corresponding altitudes have the same ratio as their corresponding sides.
Proportional Medians Theorem If two triangles are similar, then their
corresponding medians have the same ratio as their corresponding sides.
Proportional Angle Bisectors Theorem If two triangles are similar, then their
corresponding angle bisectors have the same ratio as the corresponding sides.
Proportional Segments Theorem An angle bisector of a triangle divides the
opposite side into two segments that have the same ratio as the other two sides.
Def 9.1.1
Def 9.1.2
Def 9.1.3
Thm 9.1.4
Thm 9.1.5
Thm 9.1.6
Def 9.2.1
Thm 9.2.2
Thm 9.2.3
Thm 9.2.4
Thm 9.2.5
Thm 9.3.1
Cor 9.3.2
Cor 9.3.3
Thm 9.4.1
Thm 9.4.2
Thm 9.4.3
Circle A circle is the set of all points in a plane that are equidistant from a given
point in the plane known as the center of the circle. A radius lplural, radii) is a
segment from the center of the circle to a point on the circle. A chord is a
segment whose endpoints line on a circle. A diameter is a chord that contains the
center of a circle.
Central Angle and lntercepted Arc A central angle of a circle is an angle in the
plane of a circle whose vertex is the center of the circle. An arc whose endpoints
lie on the sides of the angle and whose other points lie in the interior of the angle
is the intercepted arc of the central angle.
Degree Measure of Arcs The degree measure of a minor arc is the measure of its
central angle.The degree measure of a major arc is 360° minus the degree
measure of its minor arc.The degree measure of a semicircle is 180°.
Arc Length If r is the radius of a circle and M is the degree measure of an arc of
the circle, then the length, L. of the arc is given by the following: L = 3%-;(2nr).
Chords and Arcs Theorem In a circle, or in congruent circles. the arcs of
congruent chords are congruent.
Converse of the Chords and Arcs Theorem In a circle, or in congruent circles, the
chords of congruent arcs are congruent.
secants and Tangents A secant to a circle is a line that intersects the circle at
two points. A tangent is a line in the plane of the circle that intersects the circle at
exactly one point, which is known as the point of tangency.
Tangent Theorem If a line is tangent to a circle, then the line is perpendicular to a
radius of the circle drawn to the point of tangency.
Radius and Chord Theorem A radius that is perpendicular to a chord of a circle
bisects the chord.
Converse of the Tangent Theorem If a line is perpendicular to a radius of a circle
at its endpoint on the circle. then the line is tangent to the circle.
Theorem The perpendicular bisector of a chord passes through the center of the
circle.
Inscribed Angle Theorem The measure of an angle inscribed in a circle is equal
to one-half the measure of the intercepted arc.
Right Angle Corollary If an inscribed angle intercepts a semicircle, then the angle
is a right angle.
Arc-Intercept Corollary If two inscribed angles intercept the same arc, then they
have the same measure.
Theorem If a tangent and a secant (or a chordl intersect on a circle at the point of
tangency, then the measure of the angle formed is one-half the measure of its
intercepted arc.
Theorem The measure of an angle formed by two secants or chords that
intersect in the interior of a circle is one-half the sum of the measures of the arcs
intercepted by the angle and its vertical angle.
Theorem The measure of an angle formed by two secants that intersect in the
exterior of a circle is one-half the difference of the measures of the intercepted
arcs.
POSTUL-\TE$.THEO-REM5, AND DEFINITIONS 867
suogguuaa pue 'su1a.Ioaq_|_ 'sa;e|n;sod
ions
Postulates, Theorems, and Defini
Thm 9.4.4
Thm 9.4.5
Thm 9.5.1
Thm 9.5.2
Thm 9.5.3
Thm 9.5.4
Def 10.1.1
Def 10.2.1
Def 10.2.2
Thm 10.2.3
Thm 10.2.4
Def 10.3.1
Thm 10.4.1
Thm 10.5.1
Thm 11.3.1
Thm 11.4.1
Thm 11.4.2
868 INFO BANK
Theorem The measure of a secaiit-tangent angle with its vertex outside the circle
is one-half the difference of the measures of the intercepted arcs.
Theorem The measure of a tangent-tangent angle with its vertex outside the
circle is one-half the difference of the measures of the intercepted arcs, or the
measure of the major arc minus 180°.
Theorem If two segments are tangent to a circle from the same external point,
then the segments are of equal length.
Theorem If two secants intersect outside a circle, then the product of the lengths
of one secant segment and its external segment equals the product of the lengths
of the other secant segment and its external segment. [Whole x Outside -
Whole x Outsidel
Theorem If a secant and a tangent intersect outside a circle. then the product of
the lengths of the secant segment and its external segment equals the length of
the tangent segment squared. (Whole x Outside = Tangent Squared]
Theorem If two chords intersect inside a circle. then the product of the lengths of
the segments of one chord equals the product of the lengths of the segments of
the other oliord.
Tangent Ratio For a given acute angle LA with a
measure of 6", the tangent of AA, or tan 6, is the ratio
of the length of the leg opposite ./_A to the length of
the leg adjacent to ./_A in any right triangle with A
o osite
as one vertex, or tan 6 - a lace"! .
Opposite
6
A Adiacent
Sine Ratio For a given angle LA with a measure of
6°, the sine of LA, or sin 6, is the ratio of the length of
the leg opposite A to the length of the hypotenuse in a
. . . - o osrte
right triangle with A as one vertex, or sin 6 - . A
Hypotenuse
Opposite
Adiacent
Cosine Ratio The cosine of AA, or cos 6, is the ratio of the length of the leg
adjacent to A to the length of the hypotenuse, or cos 8 = .
Identity tan 0 = 552%
Identity (sin 0]’ + (cos 0)’ - 1
Unit circle Definition of Sine and Cosine Let 0 be a rotation angle.Then sln 9 is
the y-coordinate of the image of point PH, 0} rotated 9’ about the origin, and
cos 9 is the x—coordinate.
The Law of Sines For any triangle AABC with sides a, b. and c:
EA - E - E
a b c
The Law of Cosines For any triangle AABC with sides a, b, and c:
a’=b3+c"—2bccosA b"=a’+c‘—2accosB
c‘=a‘+b’-2ab cos C
Theorem A graph contains an Euler path it and only if there are at most two odd
vertices.
Jordan Curve Theorem Every simple closed curve in a plane divides the plane
into two distinct regions, the inside and the outside. Every curve that connects a
point on the inside to a point on the outside must intersect the curve.
Euler's Formula For any polyhedron with Vvertices, E edges, and F faces,
V - E + F - 2.
Def 11.7.1
Def 11.7.2
Thm 11.7.3
Thm 11.7.4
Thm 12.1.1
Thm 12.1.2
Thm 12.1.3
Thm 12.1.4
Thm 12.4.1
Affine Transformation An affine transformation transforms each preimage point
Pin a plane to an image point P’ in sud1 a way that
1. collinear points are transformed into collinear points,
2. straight lines are transformed into straight lines,
3. intersecting lines are transformed into intersecting lines, and
4. parallel lines are transformed into parallel lines.
Main Features of Proiective Geometry
1. Projective geometry is the study of the properties of figures that do not change
under a projection.
2. There is no concept of size. measurement, or congruence.
3. Its theorems state facts about things such as the positions of points and the
intersections of lines.
4. An unmarked straightedge is the only tool allowed for drawing figures.
The Theorem of Pappus If A,, B1, and C, are three distinct points on one line and
A2, B2, and G are three distinct points on a second line, then the intersections of
A.B-, and A28“ of A.C-, and A26}, and of B.C2 and B26‘. are collinear.
The Theorem of Desargues If one triangle is a projection of another triangle, then
the intersections of the lines containing the corresponding sides of the two
triangles are collinear.
Argument Form: Modus Ponens
If p then q
F‘
Therefore, q
Argument Form: Modus Tollens
If p then q
~17
Therefore, ~p
Invalid Form: Affirming the consequent
If p then q
(7
Therefore. p
Invalid Form: Denying the Antecedent
If p then q
~13
Therefore, ~q
Proof by Contradiction To prove statement 3, assume —»s. Then the following
argument form is valid:
If ~s then it AND ~n
Therefore, 3
POSTUL-\TE5.THEO-REM5. AND DEFINITTONS 869
suogsguuaa pue 'su1a.roaq_|_ 'sa:te|n:tsod
16°
26°
36°
41°
870 Mo BANK
sin
0.0000
0.0175
0.0349
0.0523
0.0698
0.087 2
0.1045
0.1219
0.1392
0.1735
0.1908
0.2079
0.22%
0.2419
0.2588
0.2756
0.2924
02.256
0.3420
0. 3584
0.3746
0.3907
0.4067
0.4226
0.4384
0.4540
0.4695
0.4848
0.5000
0.5150
0.5299
0.5592
0.5736
0. 5878
0.6018
0.6157
0.6293
0.6428
0.6%1
0.6691
0.6820
0.6947
0.7071
Table of Trigonometric Ratios
005
1.0000
0.9998
0.9994
0.9986
0.9976
0.9962
0.9945
0.9925
0.9903
0.9877
0.9848
0.9816
0.9781
0.9744
0.9703
0.9659
0.9613
0.9563
0.9511
0.9455
0.9397
0.9336
0.9272
0.9205
0.9135
0.9063
0 8988
0.8910
0.8829
0.8746
0.8660
0.8572
0.8480
0.8387
0.8290
0.8192
0.8090
0.7986
0.7880
0.77 71
0.7660
0.7547
0.7431
0.7314
0.7193
0.7071
tan
0.0000
0.0175
0.0349
0.0524
0.0699
0.0875
0.1051
0.1228
0.1405
0.1584
0.1763
0. 1944
0.2126
0.2309
0.2493
0.2679
0.2867
0.3057
0.3249
0.3443
0.3640
0.3839
0.4040
0.4245
0.4452
0.4663
0.4877
0.5095
0.5317
0.5543
0.5774
0.6009
0.6249
0.6494
0.6745
0.7002
0.7265
0.7536
0.7813
0.8098
0.8391
0.8693
0. 9004
0.9325
0.9657
1.0000
Angle
45°
46°
47°
48°
49°
50°
51°
52°
53°
54°
55°
56°
57°
59°
60°
61°
62°
63°
64°
65°
66°
68°
69“
70°
71°
72°
73°
74°
75°
76°
77°
78°
79°
80°
81°
82°
83°
84°
85°
86°
87°
88°
89°
90°
sin
0.7071
0.7 193
0.7314
0.7431
0.7547
0.7660
0.7771
0. 7880
0. 7986
0.3192
0. 8290
0. 8387
0.8480
0. 857 2
0.8660
0.8746
0.8829
0.8910
0.8988
0.9053
0.9135
0. 9205
0.9272
0. 9336
0.9397
0.9455
0.9511
0. 9563
0.9613
0.9659
0.9703
0.9744
0.9781
0.9816
0.9848
0.9877
0.9903
0.9925
029552
0.9976
0.9986
0.9998
1.0000
005
0. 7071
0.6947
0.6820
0.6691
0.6561
0.6428
0.6293
0.6157
0.6018
0.5878
0.5736
0. 5592
015299
0.5150
0.5000
0.4848
0.4695
04334
0.4226
0.4067
0.3907
0.3746
0. 3584
0.3420
0.3256
0.3090
0. 2924
0.2756
0.2588
0.2419
0.2250
0.2079
0.1908
0.1736
0.1564
0.1392
0.1219
0.1045
0.0872
0.0698
0.0523
0. 0349
0.0175
0.0000
tan
1.0000
1.0355
1.0724
1.1106
1.1504
1.1918
1.2349
1.2799
1.3270
1.3764
1.4281
1.4826
1.5399
1.6003
1.6643
1.7321
1.8040
1.8807
1.9626
2.0503
2.1445
2.2460
2.3559
2.4751
2.6051
2. 7475
2.9042
3.0777
3 .2709
3.4874
3.7321
4.0108
4.3315
4.7046
5.1446
5.6713
6.3138
7.1154
8.1443
9.5144
11.4301
14. 3007
19.0811
28.6363
57.2900
Glossary
0
autte angle An angle whose measure is less than
90°. (29)
autte triangle A triangle with three acute angles.
{(15-1}
adjacent angles Two angles in a plane that share a
common vertex and 1 common side btrt have no
interior points in common. ( IDIJ
affine transformation .\ translormation in which
all preimage points are mapped to image points itt
such a way that vrolline.-tr points. straight lines.
ll'll( rsecting lines. and parallel litres are transformetl
as such. [7-l7)
alternate exterior angles Two non.-uljacent exterior
angles that lie on opposite sides of r tI'ans\'crs.1l.
i I56)
alternate interior angles l'wo nonadjacent interior
angles that lie on opposite sides of 1 tratrsvcrstl.
(I56)
altiludc ol'a cone A segment front the vertex
pcr'pemlicttlat' to the plane of the base. (-160)
altitude of a cylinder A segment that has endpoints
in the planes containing the bases and is
perpendicular to both pl.rnes. (-15.51
altitude ol'a parallelogram A segment from a line
containing the base to a line containing the side
opposite the base that is perpendicul-ar to both litres.
(305)
altitude ofa prism A segment that has endpoints in
the planes containing the bases and is perpendicula r
to both planes. H3?)
altitude of a py ramid A segment from the vertex
perpendicular to the plane of the base. (-145)
altitude of a traperoid A segment from a line
containing one base to the line containing the other
base. which is perpendicular to both litres. (306)
altitude of a triangle A segment from a vertex
perpendicular to the line containing the opposite
side. (303)
angle A figure formed by two rays with a common
endpoint. il l)
angle bisector A ray that divides an angle tnto t-no
congruent angles. [38]
angle ol rotation A ligute formed br -a rotating rat
and a stationarv reference ray. [6-£7)
annulus The region between two circles in a plane
that have the same center but ditferent radii. L469)
apothcm A segment from the center of a regular
polygon perpendicular to a side at the polygon.
(334)
/Ltessota
arc An unbroken part ofa circle. I566)
arc length lhe measure ot'the arc of a circle in
terms of linear units, such as centimeters. (567)
arc measure "fire measure ofan arc in a circle in
terms ol degrees. 1' 567)
area The number of IIO|l0\'t-!Il'elpping unit squares of
a given size that will exactly cover the inter ior ol a
ligute. l 295)
argument .-\ sequence or statements that lead to -a
logical conclusion. ('/‘(>81
axis ot cylinder The segment joining the centers of
the two bases. (453)
axis of symmetry A litre that divides a planar ligure
into two congruent tellected halves. (I39)
0
base angles ol an isosceles triangle The tngles
whose vcrlices are the endpoints of the base of an
isosu:lcs triangle. [237]
base edge ofa pyramid An edge that is part ‘M the
base ofa py ram irl; each lateral lace has one edge in
cotntnon with the base. (445)
base of a cone The circular face of the cone. { I60)
base of a parallelogram Anv side of a
parallelogram. [305]
base of a prism The faces formed bv the pohrgonal
region ind its image. {.588}
base of a pyramid The polrgonal face that is
opposite the vertex. (-1-I5)
bases Ola trapezoid The um parallel sides of a
trapevoid. (306)
base of a triangle Atty side of a triangle. (303)
base of isosceles triangle ’Ihe side opposite the
vertex angle. (237)
bases of a cylinder I he faces formed by the circular
region and its translated image. (453)
betweenness Given three points. A, B. and C. if
AB+ BC = AC, then A. B. and C are collinear and B
is between A and C. (2731
biconditional A statement using “if and only if."
[99]
binary number system A number system based on
the digits 0 and I. [798]
GLOSSARY 871
Glossary
blocks The grid units in truticab geometry. (706)
(‘antor's dust .-\ one-dimensional lractal created
from a segment by removing the center‘ one-third ol
segments at all levels of the slnrcture. (740)
center of a circle The point inside r circle that is
equidistant from all points on the circle. [fit-4)
center ol a regular polygon The point that is
equidistant from all vertices oli a polygon. l I39]
center ol dilation The point in a dilation thmugh
which every line connecting a preirnage point to an
image point passes. (500)
center of projection The central point in a class of
trartsliwrnrttions lznown as central projcctiorts. (7-19)
central angle of a circle .-\n angle lormcd by two
rays originating lrom the center of a circle. (566)
ccntral angle ot a regular polygon An angle whose
vertex is the center otithe polygon and whose sides
pass throtrgh .r\l_i.rcent vet't ices. [ I39]
central projections A cl.rss ot'transt'orm.rtions in
which every proiected point ot'an image lies on a ray
containing the center of projection and a point in
the image. (7-19)
centroid The point where the three medians of a
triangle intersect. ( I7)
chorrl .-\ segment whose endpoints lie on A circle.
(564)
circle The set ofpoints in .1 plane that are
equidistant from a given point krrmnn as the center
of the circle. [.1 l-1)
circumcentcr The center of a circumscribed Lll'Cl¢‘;
the point uh ere the three perpendicular lr'rsector's of
the sides of 1 triangle intersec'.t: it is cqrridistant from
the three vert ices ofthe triangle. HS)
circumtercncc The distance around a circle. (EH5)
circumscribed circle A circle that is dr.rwn around
the outside a triangle and contains all three verticcs:
a circle is c.ir'curnscrilted about a polygon it‘ each
vt rtetr of the polygon lies on the circle. ( t1)
collinear Lying on the sanre line. H01
complementary angles l'wo angles whose nreasures
have a sum ot 90°. (38)
compound statement A statement formed when
mo statements are connected by AND or OR. (776)
concave polygon A polygon that is not convex.
{I77}
conclrrsion The phrase following the word they in a
conditional statenterrt; the hrr-al statement ol an
argurnent. [90]
872 rnro BANK
concurrent Literally. “running together”; of three or
more lines, intersecting at a single point. (4:1)
conditional statement A statement that can be
written in the form “If p. then q." where p is the
hypothesis and q is the conclusion. (90)
cone .-\ tlrr'ee—dirrrerrsiorr-al ligure that consists ot'a
circular base and a curved lateral surface that
connects the base to a single point not in the plane
or" the base. called the vertex. (460)
congruence The relationship between rigures having
the same shape and same size; congruent segments
‘H1’ segments that match exactly. 1'19‘!
congruent po|_vgons Two polygons are congruent it‘
.rrrd only it" there is -a cor resporrderrce between their
sides and angles such that each pair of
corresponding angles is congruent and each pair of
cor responding sides is congruent. (213)
conjecture A statement that is believed to be true.
(36)
corrjrrnction A compound statement that uses the
word A ND. (776)
contraction A dilation in which the preirnage is
reduced in site. (500)
contradiction A contradiction asserts that a
st-aternerrt and its negation are both true. (79.21
converse ofa conditional The statement formed by
interchanging the lrypotlresis and conclusion ot a
conditional statement. (92)
convex polygon A polvgon in which any line
segment connecting two points ol the polvgon has
no part outside the polygon. ( I77)
coordinate ofa poi.trt The real number represented
by a point on a number line. [ 17]
coordinate plane A grid lirnned bv two or more
coordinatizcd litres. known as tL1'£1'S. that intersect at
right angles at a point known as the orig-irr. (397)
contrapositive ot a conditional The statement
lorrned bv interchanging the hypothesis 'll'tt.l
conclusion ofa conditional statement 'lllt.l negating
each part. (786)
coplanar Lying in the same plane. ( l0}
urrrespontling angles Two rrun-a.l_iau:rrt angles. one
interior and one exterior. that lie on the same side ol
a tr'ansver'sal. [ L56]
corresponding angles ol a polygon .-‘tnglcs ol a
polygon that are matched up with angles ofanothcr
polygon with the same number ol’ angles. [21 l )
Corrrzsportdirrg sides of a polygon Sides of a
polygon that are matched up with sides oli another
polygon with the satire number of sides. (ll l]
corollary ol a theorem .-\ theorem that tollows
directly trorn rrrother theorem and that can easilv be
proved from that thcorern. (237)
cosine In a tight triangle. the ratio of the length of
the side adjacent to an acute angle to the length of
the ht-potenuse. (6391
(OlInl(’”r(“<atttplE‘ An ex-antple that proves that a
statement, otten a conjecture, is talse. (92)
CP(_Tl'C Abbreviation for “cot responding parts of
congt uent triangles are congruent." (235)
cylittder A solid that consists ot a circular region
and its translated image in a parallel plane with a
lateral suttace connecting tlte circles. (453)
0
deductive reasoning The process ol drawing
Lonclttsions by using logical reasoning it1 an
argument. (9!)
degree In a graph. the number ol edges at a vertex’.
l:7l3'
degree measure of arcs The measure ol a tnittor are
is the n'te'tsure of its central tngle. The degree
tneasute ot a major ‘In. is 360° minus the degree
tneasure of its central angle. (56?)
diagonal oft! polygon .-\ segment that joins two
nonadjacettt vertices of a polygon. (390)
diagonal ot a polyhedron .-\ segment whose
endpoints are vertices ol two dillerent faces of the
polvhedron. (390)
diameter A chord that passes through the center of
a circle; twice the length of the radius ol'the circle.
(314)
tllht.‘(ll'tll angle An angle formed be two hall"-planes
with a common edge. (.582)
tlilation A tran5form.ttion in which every point P
has .tn image point P’ such that tline connecting
the two points passes throttgh a point 0, l:nov.n as
the crtm-r oftfilariott, and OP' - k o OP, where k is
the scrtlefm1m' ol' the dilation. l-I93)
dirt.-v.tion ot vector The orientation of a vector.
generally indirtted by an trrotvheatl. ((02)
tlisjumtion A compound statement that uses the
word OR. (777)
displacement vector .-\ vector that represents the
change in position of an objett. [67 ll
distance formula In a coordinate plane. the
distance. it, between two points, l t:i.-rt} and (31. )2),
is given by the lottttula ti = p’(.\'- — .t:. l-" + [ye — yd‘.
(340)
edge Segments or cun es tltat co nnea vertices of a
graph. (7l2l
edge of a dihedral angle The common edge of the
halt‘-planes ofthe tngle. (382.1
edge ot a polyhedron the segment formed by the
intersection of two faces of a polyhedron. (379)
endpoint A point at an end of a segment or the
starting point of a ray. (I0)
/Ltessota
equiangttlar polygon .-\ polygon in which all angles
are congruent. [ U9)
equilateral polygon A polygon in which all sides are
congt uent. (I39)
equilateral triangle .-\ triangle in which all tlttee
sides ate congruent. (I96)
Eqttitalence Properties of Equality or Congruettce
The Rellesi-re, Symmetric, attd Ttattsitive Properties.
(H0)
eqttlvalettce relation Any relation that satisfies the
Reflexive. Symtnettic. and Ttansiti-.-ie Ptopetties.
[I I0)
Fuler characteristic The Euler number V — E + F;
an ittvariant ol a sutt-ace. (723)
I-‘uler circuit .-\n Euler path th.tt starts and ends at
the same vertex and passes through all venices ot the
grtph. [7 I5)
Fuler path .-\ continuous path that travels along
each etlge of .t graph ex tctly once. (H2)
et en vertices The vertices ol a graph that have an
even number ()fcdges leading to them. [7l3)
e:tclusi\'e OR Indicating either one or the other. but
not both. (TT7)
e.\pansion A dilation in which the preitnage is
enlarged in size. (500)
e.\terit)r angle .-\n angle l’iJt'mct.l between one side of
polygon and the extension of an atljacent side. [ I74)
external seeant segment The ponion of a secant
segment that lies outside the circle. (600)
0
face of a dihedral angle One of the halt"-planes of a
dihedral angle. (382)
face of a polyhedron One ofthe polvgons that form
a polyhedron. [379]
face of a prism Each flat surface of a ptism. (388)
trattal A stt uctute that is sell-similar; eatlt
subdivision has the same st ruetute as the whole and
the structure of the object looks the same from any
view. (738)
GLOSSARY 873
Glossary
0
glide reflection A combination ot'a translatron and
a rcllecrion. [56]
golden ratio the ratio of the long side to the short
side of a golden rectangle. (6981
golden rectangle A rectangle in which the length 2'
and the width w satisf;.- the proportion i. (698)
graph A diagram ofvertices and edges. (712)
great circle A circle on a sphere that divides the
sphere into two equal parts. (I72)
0
hall-plane The portion of a plane that lies on one
‘il\lC ot a line in the plane and includes the line. {S82}
head-to-tail rnellrud In vector addition. finding the
sum of two vectors lav plan ing the tail of one vector
rt the he'rr.l ot the other: the vector \lr'avvrr lrom the
tail of the first vector to the heacl ol’ the second is the
vector sum. (6?-ll
height The length ol an altitude ufa polvgon. UD3]
ll_V['ICl’l)l)llC geometry The geometr_v ol a surface
that curves like a $'e'l\l\llC. l73l'I
lrypotenuse The side opposite the right angle in a
right triangle. (l9Dl
lrypothesis The phrase lollowing the word if in a
conclitional statement. (90)
identity An equation that is true for all values of the
variables in the equation for which the terms in tltr
equation are defined. (64!)
image A shape that results from a tr'anst'orm-ation of
a figure Lnown as the preirrrnge. (SD)
indirect proof A proof in which the statement that
vou want to prove is assunred to be false and a
contradiction or other “absurdity rs shown to follow
from the assumption. (793)
incenter The center ofan ins -rbed circle; the point
where the three angle bisectors of a triangle intersect:
it is equidistant from the three sides of the triangle.
(45)
inclusive ()1! Indicating either one or the other or
both. (777.1
inductive reasoning Forming conjectures on the
basis of observations. (I I8)
inprrt-orrtprrt table A table that gives the outputs of
a logic gate for dit't'erent input combinations. (799)
874 Mo BANK
inscribed angle .-\n angle whose vertex lies on the
circle and whose sides are chords ot the circle. (S80)
inscribed circle An inscribed circle in a triangle is
inside the triangle and touches each side at one
point; a circle is inscribed in .r polygon it" each side of
the polvgon is tangent to the circle. (-14)
intercepted are An arc whose endpoints lie on the
sides of an inscribed angle. [S66]
intercepts The points where -a line in a coordinate
plane passes through the .r- and y-as-es or where a
plane in a three-dimensional space crosses the .\'-. y-.
rnd z-a\tes. { t03)
intersect To one or more points in common. [ l I)
intersection point A point that two or more
geometric figures have in common. [I I)
invariant Properties ol‘a ligure that stay the same
regardless ot hon the tigure is delorrned. (723)
Inverse of a conditional The statement for med bv
negating both the hypothesis and conclusion of a
conditional statement. (780)
inverse tangent The t'unc‘tion used to tind the angle
with a given tangent ratio: abbreviated tan". (633)
isometric‘ drawing .-\ tvpe ol three-dinrensional
drawing. (372)
isusccles triangle A triangle with at least two
congruent sides. (23?)
iteration The repetitive rpplication ol the same rule.
(753)
kite A qrr.-rdrilateral with exactly two pairs of
.rd_i.rccntcongrrru1t sides. [3 I0)
0
lateral area The sum of the areas ol the lateral faces
ul'a |.H)l_Vl‘tCdlUn. H37)
lateral edge The intersection of two lateral laces ol'a
polyhedron. (-145)
lateral edges of a prism The edges ol the l-ateral
laces of a polyhedron that are not edges of either
base. (383)
lateral faces The laces of a prism or pr-rarnid that
are not bases. (338)
lateral surl'ace The curved sur lace of a cvlinder or
cone. ( t:'n3]
legs of a right triangle "fire sides -acliacent to the
right angle. (2291
legs ol a trapezoid The two nonpar allel sides of a
trapezoid. (300)
legs of an isosceles triangle I he two congruent
sides of an isosceles tr'i-arrgle. (23?)
length The length of a segment is the measure of
the distance trom one endpoint to the other. [I7]
line An undelined term in geometrv. a line is
understood to be perfectly straight. contain an
irrlirrite number of points, es-tend inlinitelv in two
directions, and have no thickness. (9)
linear pair ofangles The two angles formed by the
endpoint ol a ray when the endpoint falls on a line;
mo adjacent angles whose noncommon sides are
opposite rays. (28)
logic gate An electronic circuit that represents not.
and, or or. (799)
logical chain A series of logically linked conditional
statements. (92)
logically equivalent statements Two staterrrurts.
e-ach ol which can be logic-allv derived horn the
other. (7-'30}
magnitude The numerical tneasure ofa vector.
(GT2)
major are An arc ol a circle that is longer than a
semicircle ol that circle. (566)
matrix Data rrranged in rows and columns and
enclosed in l1I‘acl-:els. (682)
median .\ segment from a vertex to the midpoint ol
the opposite side in a triangle. (-1?)
Menger sponge A three-dimensional fractal crerted
from a cube in’ removing cubes from the centers of
cubic structures at all levels. (7.33)
midpoint ofa segment The point that divides a
segment into two congruent segments, { ,5-19)
midsegment ofa trapemitl A line connecting the
nridpoints ofthe two nonparallel segments of a
trapezoid. (.309)
midsegment of a triangle .-\ segment whose
endpoints are the midpoints of two sides. l I83‘)
minor arc An arc ot'a circle that is shorter than a
semiciT(‘le of that circle. (5136)
Mobius strip A one—sided surface for med by taLing
a long rectangular strip and joining the ends together
after giving it halfa twist. (72 I)
modus patterns In logic, a valid argument of the
following form:
If p then q
I’
Therefore. 1? (769)
modus tollens In logic. as valid argument of the
following form:
It’ p then q
\lOl q
lherefore Not p (7701
/Ltessota
negation lfp is a statement. then not p is its
negation. (7?l-‘J
non—Euclider-in geometry A system or geometry in
which the l"trallel l~"0:~:tul'tte does not hold. (729)
nonoverldpping Having no points in common
[except lor common boundary points]. Q95]
number line A line whose points c()|'responcl with
the set of real numbers. [ l7}
oblique cone A cone that is not a right cone. (4601
oblique cylinder A cylinder that is not a right
cylinder. (-53)
oblique prism A prism that has at least one
rronr-ect-angular lateral face. (339)
obtuse angle .-\n angle whose measure is greater
than 90" and less than 180'’. [29]
obtuse triangle A triangle that has one obtuse angle.
(654)
octant One of the eight spaces into which a three-
dirnensional coordinate system is divided by the ::.y-,
yz-. and .\z-planes. (39?)
odd vertices The vertices of a graph that have an
odd number of edges leading to them. (3913)
orthogonal Pertaining to right angles. (732)
orthographic projection A view of an object in
which the line ol sight is perpendicular to the plane
olthe picture. (374)
paragraph proof A form ofproof in which ones
reasoning is explained in paragraph form. as
opposed to flow chart or two-column prools. (I09)
parallel Of coplanar lines or .tny two planes in
space. that they do not nreet. no matter how far they
might be extended. (35)
parallelogram A quadrilateral with two pairs of
parallel sides. [I I8)
parallelogram method A method of adding vectors.
two vectors are represented as acting on a common
point. and a parallelogram is formed by adding two
sides to the frgttrc. The vector‘ sum is a vector along
the diagonal of the parallelogram. starting from the
common point. ((17-1‘)
GLOSSARV 875
Glossary
parametric equations Rules tor the coordinates ot
poims in a coordinate system, given in terms of a
certain prH'rlI'flt."l't."l", such as the time. I. ('40-!)
perinteter "I he distance around a closed plane
figure. l 294)
perpendicular blsector A line that is perpendicular
to at segment at its tnidpoint. (38)
perpendicular lines Lines that intersect to tour:
right angles. (35)
plane .-\n undefined ternt itt geornetr y; at plane is
understood to be a Ilat sur lace that extends infinitely
in all directions. [I0]
point An undefined term in geometry; a poitn can
be thought of as a slut that represents a location on a
plane or in space. Geometric points have no size. (91
point of tangency The point of intersection ol‘ a
circle or sphere with a tangent litre or plane. (573)
polygon A closed plane figure formed ttont three or
tnore segments such that each segment intersects
exactly two other segments. one at each endpoint.
and no two segtnents with a common endpoint -are
collinear. f. 138]
polyhedron A geometric §0|l\.l with polygons as
faces. { 379)
postulate A statetttettt that is accepted as true
without proof. {I 1)
preimage A shape that undergoes a motion or
transformation. [50]
premise .-\ statetrtenl which is given or accepted as
true in a logical argument and is used to establish a
conclusion. (7681
prism .-\ polyhedron that consists ofa polygonal
region and its translated image in a parallel plane.
with quadrilateral faces connecting the
correspottcling edges. (388)
probability .-\ nutnher lmtn [l to l [or lmnt 0 to
lD0'huJ that indicates how likely an event is to oc-c ur.
(353)
projected points ln projective geometry. the points
that lie on rays contaittittg the center ol projection
attd the original points. (7-49]
projective geometry The study or the properties of
hgures that do not change under projection. (749)
projective rays Rays drawn from the center ol .-l
projection. (749)
proul A convincing argument that uses logic to
show that .1 st ttement is true. £82}
proof hy contradiction An indirect prool in which
the statentent that you want to prove is assumed to
he lltlse: the asstttnptiott is shown to lead to a
contradiction. which indicates that the original
statement tnusl he true rather then l’a.lsc. (792!
876 INFO BANK
proportion .-\ statement of the equality of two
ratios. L508)
proportional sides The sides ot two polvgons are
proportional if all of the ratios of the corresponding
sides are equal. (508)
pyrantid A polyhedron in which all but one of the
polygonal faces intersect at a single point known as
the vertex of the pyramid. (4-IS}
Pythagorean triple A_ set ol‘ positive integers rt. iv.
and t" such that tr‘ +11‘ = r‘. (322)
quadrilateral A polygon with tour sides. ( l-It-I J
radius A segment that connects the center ot‘ a circle
with a point on the circle; one-half the diameter of .1
circle. (.51 tjt
ray A part ot'a line that starts at a point and extends
infinitely in one direction. (10)
rectangle .-\ quadrilateral with Your right angles.
ll-48')
rerluctio ad alJsur'rlum A form ofarguntent in
which an assumption is shown to lead to an absurd
or impossible conclusion so that the assumption
tnust be reiected: literallv "reduction to the absurd.”
I792}
reflection .-\ transfortnation such that every point of
the preimage may be connected to its image point by
a segment that [a] is perpendic.ttlar to the line or
plane that is the “mirror” ofthe retlection and lb)
has its midpoint on the mirror of the reflecrion. (53)
rellectional symmetry A plane figure has
retlectional symmetry if its rellection image across a
litre coincides with the preitn-age. the original figure.
{l39l
reflex angles .-\ngles with measures greater than
I80’. ('29)
Reflexive Property of Equality For am’ real number
ma =u.(|l0)
regular polygon .-\ polygon that is both equilateral
and equiangular. (I39)
regular polyhedron A polyhedron in which all faces
are congruent and the satne number of polygons
meet at each vertex. l33'9'I
regular pyramid A pyramid whose base is a regular
polygon and whose lateral faces are congruent
isosceles triangles. (4-15)
remote interior angle An interior angle ot a triangle
that is not adjacent to a git en extet ior angle. { I74)
resultant vector lhe vector that represents tlte sum
of two given vectors. [6733
rhombus .-\ qtr.1dril.1ter.1l with four congruent sides.
(148)
right angle An angle with -.1 measure ot'9D". (29)
right corte .-\ corte in which the altitude intersects
the base at its center point. (460)
right cylinder A cylinder whose axis is
per perrclicular to the bases. (453)
right-handed system A tltree-dimensional system or
coordinates, rtarned trom .1 mnemonic device
irtvolvirtg the lingers of the right hand. €396)
right prism A prism in 1vhiclt all ot'the lateral races
are rectangles. £389]
rigitl transformatittn A trattstorntalion that does
not change the size or shape ol .1 ligute. [50]
rise The vertical distance hetween two points in a
coottlinate pl'tne. (I90!
rotation A tr.tnsIorn1atior1 ir1 which every point ol
the preimage is rotated by a given angle ah-out .1
point [in two dimensions) or a line [in three
dintensiottsl. [SI]
rotation matrix A n1.1lri\t used to rotate .1 figure
about the origin through a given angle. [t':8.7.i
rotational s_y mntetry A ligure has rotational
symmetry if and onlv it" it has .11 least one rotation
irttage. not counting rt)l.1tion images of 0° or
multiples oi 3130”. that r.oit1t'.ir.les with the original
ligure. ( l-1|]
run The horizontal dis-t.1nce hetween two points in .1
crtotclinate plane. {I90}
srrntc-sitle interior angles Interior angles th.1t lie on
the same side ofa lrutnsrersal. ( I56]
scale factor In .1 trartsforrnation. the number by
which the distance of the preintage from the center
ol' dilation is multiplied to dttemtine the distance of
the image point from the center. ( I98]
secant A lir1eth.1t intersects a circle at two points.
(573)
secant segment A segment that contains .1 chord of
.1 circle and has one endpoint exterior to the circle
and the other endpoint on tlte circle. [(100)
sector ofa circle A region or a circle bounded by
two r-adii .1nd their intercepted arc. (3161
segment A part of -.1 line th.1t begins .1t one poirtt
and ends .1t .1nother; .1 segment of .1 line h.1s two
endpoints. ( ID)
segment bisector .-\ line tlt.1t divides .1 segment into
two congruent segments. [38]
sel.l'-sint'1l;rrity l'he propertv. possessed by Ir'.1ct.1ls.
that every subdivision of the l'r.1ct-.1l has .1 structure
similar to the structure of the whole. (7381
semicircle lhe .1rc of .1 circle whose endpoints are
the endpoints ot .1 diameter. (566)
sides of an angle The two rays that form an angle.
(1 11
Sierpinski gasket A two-dimensional fr-actal created
from a triangle bv removing triartgles from the
centers oli tr iatrgular structures at a.ll levels. [?-l I)
luessora
similar figures Two ligures that hat-e the satire
shape. but not trecessarily the s.tme size: two ligures
are similar if and only if one is congruent to the
image ol’ the other by a dilation. [5073
simple closed curve A shape that is topologically
equivalent to a circle: a shape that does not intersect
itselt. (F22)
sine In a right triangle. the ratio ol the lertgtlt ofthe
side opposite .1 It acute angle to the lengtlt of the
ltvpotenuse. (639)
skew lines Litres that are not coplanar and do not
intersect. £330]
slant height In at regular pyrarttid, the length ofart
altitude ol" a lateral lace. [-I-I5)
slope The ratio or rise to run for a segment; the
slope ofa tronvertical line that contains the points
[.r..y.) and (Jr-.y_-] isthe ratio (19!)
solid Closed sp.1tia.l ligutes. [379]
Solid til revolution .'\ll ttltject Iornted by rot.1ting .1
plane ligure about an axis in space. (45!)
sphere The set at points irt space that are
equidistattt from it given point known as the center
(‘ti the sphere. H139)
spherical geometry Geometry on tspherc; .1
gcomettr in which lirte is defined as a great circle
and there are no parallel lines. (73!)
square .-\ qtr.n:lril.1teral with four congruent sides
1nd tbLtt' right angles. {I-45)
straight angle An angle with a measure ol lH0°. [29]
supplerttentary angles Two angles whose measures
have a sum of I80”. [18]
srrrfacc arca ofa prism The sum of the 1re.1s oi all
l.1r:es of .1 prism. -. U8]
Symmetric Property of Fquality For .1ll real
numbers 11 and 1.1. it}: — b. then it — .1. (I In]
tangent In .1 right trr-angle, the ratio ofthe length or
the side opposite art .1cute angle to the length of the
side .1di-.1cer1t to it. (63!)
GLOSSARV 877
Glossary
tangent segment .-\ segment that is contained by -.1
litre tangent to a circle and has one of its endpoints
on the circle. (6-OD]
tangent to a circle .-\ line in the plane of a circle that
intersects .1 circle at .1 exactly otre point. [:'-73)
ta_\'lcztlJ geometry A geometry in which points are
located on a special kind of map or coordirrate grid
whose lrorizorttal and vertical lines represent streets
and whose coordinates are always integers. U06)
taxicab radius "fire distattce between the cettter of a
tauicab circle and .1m- point on the tauicab circle.
(706)
t-.1.\idist-ance In taxicab geometry, the srnarllest
number of gt id units that must be traveled to move
lronr one point to .1notlrer point. (706)
tlteoretn A statetnetrt that has been ptoven to be
true deductivel}-. (I09)
topology A branch ot ntatltematics that studies the
most basic properties of ligures. [7-'2! '
topologically equivalent .-\ble to be stretched.
shrunk. ot otlterwise distorted ittto atnother figure
willtottt cutting. tearing, or intersecting itselfor
compressing .1 segment or curve to -.1 point. [722)
torus .-\ three-clinrension-.1l donut-shaped surt'ace.
(?23)
(race ofa plane The llll<.'l'SCLllOl| of ii plant. with tlte
xy-plarte irt .1 thr'ee-ditnension-.1l coordinate st-stem.
(406)
transformation The tnor-entent of a ligure itt a
plarte lronr its origin-.1l position. the preimage. to .1
ttew position. the image. £50]
transtortnation equations The equations
3:’ - .1 cos 6 — ysin 6 and y’ - .1 sin 6 + )' sin 6 are
ltnown as tr.1rtsfortr1atiott equations. (630)
'l‘r-ansitive Property ul Equality For all real
trumherrr tr. b. and c. ifrr - lv and it - t. then rt - r.'.
(I10)
lrarnslattion A tr rrrslormation itr which every point
of the preitmtge nroves in the same direction lry the
-;.-rtne arrrotrrrt to limit the image. [fill
trarrsvcrsal .-\ litre. ray. nr segment that intersects
twtr» or more coplanar litres. rays. or segments. e'tch
it a dillerent point. (I55)
traptmitl A quaclrilateral with one and trrrlv otte
pair of parallel sides. ( l-I8]
45-I5-90 trlttngle :\ right triangle whose lrase angles
have nrcasttre-5 ol 45°. L332]
30 60-90 triangle .-\ right triangle whusc acute
angles have measures of 30° and t':0°. (33.2)
878 INFO BANK
triangle rigidity A property ol'tt'i-artgles which states
that ifthe sides of .1 triangle are fired, the triangle
can have onl_r one shape. (2l7]
trttth fttnctionally eqrtivalent When two logic
st-atenrents l1-ave the same trtrth tables. (73'8]
truth table A table that lists all possible
cotrtbittations of truth values for .1 givetr statentent
or co mbirtations of statements. (776)
two column proof A pr-ool in which the statenrents
are written itt the lelt-hand column and the re-.1scrns
are given in the tight-harrd ccrlurnn. (109)
unit circle A circle with .1 rrdittrr ol l (.Cl'|ICl'Ct.l at the
origin ol the coordinate plane. (648)
valid argument .\rr trgtrnrcnt in which the prcrrriscs
lorcc .1 conclusion: if the premises .-tr-r: true. then the
conclusion is true. (7681
Valid conclusion The corrclttsion in .1 valid
argtrnrerrt that follows logic.-tlly from the prrrnises.
(768)
vanishing point In .1 perspective drawing, the point
at which par.rllt-I scgtrrcnts of a depicted ohirsct will
meet if they are C\'ICl‘t<‘l(‘tl. [4 10)
Vector A nrathematical quantity that has both
rrragtrittrde [a numerical meastrre} and direction.
(672)
rector addition lhe process of combining two
vectors to create a resultant vector. (673)
vertex angle of art isosceles triangle l'he angle
opposite the base of the tt i-angle. [237]
vector sum The resttlt.tnt vector created by vector
addition. (V6?-ll
vertex A point where the edges of .1 figure intersect;
plural. 1-t-'rn'rc'.-'. [379]
vertex of at cone l'|1e point opposite the base of the
corte. ( I60]
vertex of an angle The poittt irt cutnntott ofthe two
rays that lortn .tn angle. [ I I]
vertical angles The opposite angles for tried by two
intersecting lines. [ I I7]
Selected Answers
Chapter 1
LESSON 1 .1
Exercises
6. Sample aI1:.wcr: point A: ‘A-3: . H. E 7. Ll. (Q.
AF-‘QR, or ZRQP 8. Sample .1ns1\-er: plane MNO.
plane NO-\-I. 0! plane iii. 9. fi.R"..T(_" 11. .»_’A:
A1’a.AC‘; 23-. Bit. BC‘; AC: E‘.»’t.Ct': 13. line
16. plan: 17. point ‘I9. False. Planes arc infinite.
cwtcmling witlmut bound .-llltl h.1ving no edges.
21. True. For euan1ple, two opposite sides of :1 box
inlet'sc<.l the lmllont plane of A l:u0\', but thcv tlt)n'I
ittttrsmt 1‘.-tch other. 23. F.-Ilse. There are an infinite
number of planes tltrough any two points. 25. False.
Three l'l(1l'lCr.'IllIl'tC¢ll' pnints .111: mntained iI1 ct.-tuly
one plant. but the Iourth point might be in .1 dill'cru1t
plane. 27. Sample at1s1\-er: point. E. A. or C
29. Sample answer: 1_’D/1('_: [\11it1l /1; A-5. If:
31. line L‘ 33. point M 35. point M 37. Sample
dll.S\\'t:I:fi) and 39. line In 41. I: E 43. 6,
E.zT‘.E.K.E.@ 45. t;A.»tt-‘B 47. 6;
ZAVD. .4 WC, [Bl/D. Z/ll-‘B, (Bl-‘C, and (Cl-’D
49. It") 51. I5 53. I9 55. —Ib-‘I 57. 74
LESSON 1 .2
TRY THIS (p. I8;
7
Exercises
6.5 7.13.9 9.a..»tB=(‘D b.}fi7'=-E
10. FD: 5 miles and BF = .35 miles 11. -1 13. .5
15. S 17. AB = 2; BC= 4; AC = 6; lhe order of
the u1ot1;linates does not n1.ntcr it1 sLtl1Iru.liut1.
bccattsc of the absolttte \'.1lllC signs. For cx.1n1ple.
|—3— t—ttI = I —t —[—3J| =2. 19. Tie H3;
F—(.'‘ 2 E‘; IT‘ 2 E; R‘ a '55"
21. '00
_1s
M A B
.‘lB=85
23.5 25. 37‘ 27. XC = 35 miles
29. l)ot‘:s not n1.1ke sct1sc;P—(2 is not .1 number.
31. .\-la|»zes sense; Xi’. X1. and 32 are .1ll nun1be1s.
33. Does not nmkc scnsc; and art: not
numbers. 35. S.tn1plc.mswcr: The Fgypti.u1 royal
cubit is longet. 39. positit-e 41. neg-.=tti1-e; l'he result
is .1 positive number. 43. negative 45. negati1'e;'l'l1e
rvrsult is .1 positive number.
LESSON 1 3
Exercises
3. 60° 9. 25° 10. 20° 11. 15°
12. I1. /_’UVl‘l-' E .r_’)t')'Z b. 111./_’L-‘Vii-' = n1.r_’X i2
13. Con1ple1t1et1l.tt'y angle pain 1_’C..-ID and 1_’DAE.
Sttpplctm-11t.1ry .tn}:l1: pair: ABA D IIIII ZDAE or
.r_’B/1C-.1I1d ./_’CAE 15. 85° 17. 10“ 19. 33° 21. I20"
23. 30° 25. 32° 27. 25° 29. I55° 31. 30° 33. 40°
35. 111ASl.;l = 90’; (S! F and (Al E are
conipletnentary angles. 37. 22° 39. I5 41. 22"
43. 30° 46. 90° 47. A gradian is stnallet-Ih.u1 l
degree since one gradian is 1 of one degree. 49. 000
to
51. I80 53. 045 55. 022.5 57. Less than 35S.'l'l1e
pilot would have to fly nmtc lo the west. 69. 1_’Cr‘lR
61. Lines I‘, m. and n 63. 6 65. AC: *1; BC: 6
LESSON 1 .4
Exercises
5. pantllel 6. PB 7. equal 8. equal
9. . 11.
I .
I I’
I I’
I ”
: 90, ‘,1 Acute angle
‘ I
I I’
I ll
. .
I ,’
I I
I
I
13. Al and £2 15. Lines I’ and m ate
are co11Iplet11et1t-.1r_1'. parallel.
I I
: ...... ..l ..... -.".'
I I
I ,- I
I ,- I
I 5‘ 1
I1!’ 2 I ’
-"I I
: :
-' I I
I I
I I
I I
I I
‘I7. 19.
I I , ‘\ I
---.5l ----:;I ---- B?“
I ” I I \‘
I , I I .,
I II I I \\
AL’ :3 A1 ~_c
/'1‘ I I ‘~
SELECTED ANSWERS 879
saemsuv passages
Selected Answers
21. \
\ I "I
All \\ ,’
I \
I V,
I \‘
Ci,’ \ B
I
23. Triangles that have il t-ettes: located on the
|T|Cl'pCl'kliLUl':!l' l)i:~:cctor til one ol the siclcs‘ have “ll
least two sides of equal length. 25. 1C - BC - S
27. bisectot 29. I'll: bisectots 0|-the angles lbnned
lav intersecting, lines are perpendicular. 31. The
shape appears to be a square. 33. line 35. line
37. V5.0: line!‘ 39. amp; mam; .r_~1
41. Plane 17. Plano PQR. Plane QRP. or Plane RQP
LESSON 1 .5
Iixcrciscs
4. The perpendicular bisectots meet in a single
point. 6. The angle l:Ii'it‘.‘Cl0l'S meet in a single point.
Type 0! :1-ch
intersecting Inns formed Name of coma:
6. perpendrcularbnsectors circumscribed cucumcentar
of AD is the same distance lrcnn 51-’ as it is from
W: Any point on the perpendicular bisector 0! AF
is the same distance from ‘b-F as it is from [Ti-. The
intersection of angle bisectot: is the same distance
from all .5 sides ofthe tn'an;:_.lc. 29. Collin -It 31. No.
Fhmugh any two points there is exactly one line.
33. Yes. lftwo non-parallel lines do not iltletsctl.
they are not in the same plane. 35. 25 37. l.’v°
LESSON 1.8. PAGES 50 ‘-
mv nus tp. 53)
The figures are congruent. The line of reflection
is the |‘t‘I’pcI'tr.liCltl ll’ bisectot of the st-,:n1cnt
connecting each point with its image. not including
points on the line of rcllcction.
Exercises
8. 9.
Prrimngt: Image hnage
7. ‘male bisnclnrs Iscribed incenler
19. Inside the triangle 21 . On the triangle 23. l'he
center of the circumscribed circle at at right triangle
is the midpoint of the longest side of the triangle.
25. S-ample answer: ‘Hie distance from a vertex to the
cent to l\.l is twice the distance lrum the centroid to
the opposite side. 27. l" is tl'It‘ same distance from
lJ—b as it is from E7: .-\ny point on the angle bisector
880 INFO BANK
V
10. 1 1 .
F'°'"‘°9° Frenmage Image
trnane
‘I3. ‘I 5.
Image
Preimage , ,4
1' \
fl \
Image '1‘ . ':
-' “ 1.1
Pre mane
I 7. ‘I9.
Ptcirn 19:: Image
Pie mane
2 ‘I .
23. lhe letters that stay the same in a rellection
tr.n:)s-4 a vctlical line are A. II. I. M, O. T. U, V, \'5v'. X.
and Y. The letters that stay the same in a rellertion
across at horizonntl line are B. C, D. E. H, l. K. O, and
X. 26. The mglcs all measure 70°. 27. a. F0r.1t|.1|'inls
m.t-zlc luv the I'i;.;ht and left foot. the pair on the left
In. Footprints made bv the same foot. the pair on the
right 29. Tt.tnsl.tte squdn: ABC D from its prcitnage
position one unit up. one unit down. .-ind one unit to
the left. Then tr.rnsl.rte the square twice to the right
lw um: unit. 31. Rellcu square .‘1B(_.Dfl'0l‘l'| its
prcinmge position across CT. CT’). W. and W. Then
rellect the square at BE!-‘A across E‘.
33. 'l'r.tnsform the second irmtge. then the third. and
50 (In.
Second Fourth
Prrimnnr image irn'tqt'
eeea
fifi
Ftrstt Thrrtl
rrnage Image
35. .. rTF.n—F,fi, £D,.«:F,.«£F r.. DE: 7.2 cm,
DF = 3 cm. EF = [.6 cm c. m.¢’D= 33",
m£E = ll]?!-°. m£F = -14“
A
.'
i
LESSON 1.7
TRVTHIS (p.t'»l]
ll rules do not wot'k. LhCi.k vour answers to the
Activities.
Exercises
5. H[.t.y') = [(x+ 5].y'J:
Y
PI'l‘II'n:I_]r-
M 4; image
l'r‘,4|
Ill]
6. N(x,y) = (-1.)-);
SELECTED ANSWERS 88 1
s.teMsuV pezoeres
Selected Answers
17. I80“ mtation;
v
Nlx. y) = (—.\'. y)
21. The result is a I8D° rotation about the origin as
in Ex. 20. 23. tmnslatimt 7 units In the right
25. tmnslation 6 units to the left and 3' units up
27. tr.msl'.tlion up 7 units 29. tr-anslation
7 units to lhc left
31.
v v
'\ .‘
' ‘ x . /t I : x
‘*2 K“
2‘ ~.
llulc I Rule 2
v r
. X . . X
I’
Rule 3 Rule -1
The trimglc ends where it started.
33. %. 36. ll’ K’ is the rcsull of lhc
lr.1nsform.1tion ol K under T(r.y] = l_x+ 11.); + k]
then KN’ has slope 37. -I5”
882 INFO BANK
41. Rtx. yjl = (y,.t:] 43. above the line; below the
line: below the liltc: dlmvc the line: on the line; on
the Iim:
46. It Ilips lmcl: and forth .1cross the __V-.-IVIS and
moves up to form .1 pattern.
v
144
12"
10"
4 e-»
47. Glx. y] = I.\'+ Ii, —y]
49. newpatlt
72 72 mnvctu
ZI6 32-I linelo
5| Iulie
shmx-page
51. 315 53. 202.5 55. Find the point where the
angle blSCLlOl'$ meet. 57. In .1 |ot.nion,.1 figure turns
¢ll'()LII'u.l a givcn point utllcd lhc umtcr of mh1Ii0n_
59. In .1glidetmnslbnnation. .1 figure is reflected
across at line. while being tmmlated in -.1 direction
par lllcl In that line.
CHAPTER REVIEW AND ASSESSMENT
:.IT1.TL'.H’ 3.§_Q'.iT:._7:-T\'r 5.(‘H=4;C]=S;
CK=I(v:H]= I:HK= I2:}K=8
7.
25 13
R A P
RP: 38
9. n1éPVT = I25°; IIIZQVT = 95°; m£Rl.-‘T = 65°;
IIIZSVI = 30°; n1£P\-"S = 95°; n1.cfQl-‘S = 05°;
IHARI-'5 = 35°; m.cfPl-’R = 60°: m.£QVR = 30";
IHZPVQ = 30° 11. ml! l<'.\' = 58°
‘I3. ‘I 5.
17. Sample answer:
19.
'. ' .
'. ' C7
' I
21. a. reflection b. tr.msl.ttion c. rotation
K A
Image Prat mane
29. It is 49 l<ilun1etcrs lmtn Sntithville In LaGr Inge
and 7| kilometers from I5.-tstrol‘ to I .!Crlng(‘.
chapter 2
LESSON 2.1
Exercises
6. Two squares ml each color need tu be remuvecl.
1. I00: lC|.0[H] B. .\rv:t of}? = 36: dl'l‘.-I OFC = I6: arm
of D= I6; med ofb’ = 36: area oi"!-' = 16: illtzl of
G = -1; area of H = 4; overall area = I96 9. No The
squares must be removed in 2 X 2 groups of four
(tlte same shape dllcl size as tlte tiles]. 11. ‘.1-.nnple
answer: ll’. lhc lmard is contpletcly L0\'Cl'C\l hv the I6
tiles. thctilcs will form 1 Ix I grid. The I retrieved
ChtS.sl.NJaIld squares must all come from just one of
the squ trcs in the -I x 4 grid. 13. 625: ‘>625: I L025,
yes 15. Sample dnS\vel': l'lte shortcut .~..tys that
(Ion + 5): = n[n + I] - 100 + 25. The di.tgr.nn can be
rc.trrangecl as a rectangle which is I011 by I0(n + I]
and .1 square which is 5 by 5. 17. I000‘ 19. Every
entry in column C is the cube of .1 multiple ol‘ 3.
No. columns A and I} do not contain dnv utlrcs
of multiples of}. 21. Because 999‘ will occur in
column C. the cube of tlte number immedi.ttel)'
l'nllnwing 999 must occur in column A. Therclote,
I000‘ must occur in column A 23. I he numbers
in tire sequence are getting smaller. The nutttemtot
of the fraction rem.1ins I. while the numbers in the
denominators are getting larger, me-aningth-.11 I is
being divided into more and more parts. lhe value
oi the sequence lr.u.tinn is therelhrc dect-easing.
25. The sums scent to be getting closer and closer
to I. lfthe sum were continued infinitelv, the sum
would he I.
27.
.l.
T»:
_. ...--.......-..-.-..-.......
P
29. The number of dots is found by ntultiplving the
number of rows [51 by the number ofcolurnns (51.
so the nuntber ol clots l'eprc:~:et1Is the number 5'.
31. A square .trr.ty of dots with in rows of n dots
represents the number n: . When the square is
ll1L'.I’C.!${‘(l to n + I rows ofyr + I dots. in n + I dots
will have been added to the number of dots in the
original square.
—t t:
33.Forn=l:I=l.1ndm, l:lT'=l.
3f_2 I 23'
Forn=2:l+.2=3atnd ,+'='—,=3.
.'Il.‘l- 1.) 5|-II
Forrr=.%: l+l+3=t':.1ncl—7
For n=-I: l+2+3+4= I0-and
36. 2|; yes 37. The mrmber ol dots in the tri.=tngle
is one-lmlfthe number ol riots in the rectangle. The
\lidBI'II.n'| suggests that the sum oi the integers lmrn I
to n can be related to the pattern ofthe dots in the
ttinrtgle. This triangle encloses hall" the number of
(lots in the rectangle with (.lllI‘lCl‘lSll)nS rt rtntl rt + I.
therefore it contains dots. 39. The ntutdet
was contmitted in the st-udy with the cdncllcsliclt by
Colonel l\'1ust.trd..-\ disjunctive syllogism can often
be used when at least one of two things must be true
SELECTED ANSWERS 883
s.reMsuV pezoeres
Selected Answers
If one of the two can be shown to be false, then the
other niust he tiLte.
a triangle
43. 23 46. mAK!l" - 45°. n1ATlY — 35°
LESSON 2.2
TRY THIS tip. 92)
If an animal is a snake, then the animal is a reptile.
Converse: It" an animal is a reptile, then it is a snake.
The conditional is trite: the converse is fals-:.
TRYTHIS lip. 93)
Your answer should show connections between
several “ll'.. .then" statements to prove an “ll. ..then"'
statement.
Exercises
6. If -a worl.er is a United States Postal worker, then
the person is a tederal employee. John is a United
States Postal workt r. Therelore, lohn is a federal
employee.
Ft-rlcr I employees
U .5. Postal
Workers
I John
7. CtJni.lition.i.l: ll two lines ‘ire parallel. then the
two lines do not it‘tlCl‘$t\l. Converse: If two lines do
not intersect. then the two lines are parallel. The
contlitional is true. The comerse is not trite.
8. Form a logical ch.-iin: ll'.1 number is divisible hi-
4, then the iiuinbei is divisible bv 2. If at number is
divisible by 2. then the number is even. If a number
is even. then thi: last digit is CI. 2.4. 6. or 8. Therefore,
if at number is divisible by -1. then the last digit is O, 2.
4. 6. or 8 hy the If-Then Transitive Piopeny. 9. li a
person lives in Ohio. then the person lives in the
United States.
‘II .
Poopli-who live III the USA
People who
live in Ohio
884 INFO BANK
13. lfa pl.mt is a tulip. then it is a llower. 15. If a
person is a lhiiist. then that person is a n'|U'iiLi'll'|.
I7. Hypothesis‘ it is snowing in Chic igo
Conc.lttsion: it is snowing in Illinois
Converse: If it is snowing in lllinois. then it is
snowing in Chicago. The converse is false. Sample
coiiiiterexainple: It is snowing in bpiingtield, Illinois.
but not in Chicago, lllinuis. ‘I9. llvpothesis: the
nieasure of each angle in a triangle is less than 90°
Conclusion: the triangle is acute Converse: lt'a
ttiangle is acute. then the measure (it e"tch angle is
less than 90°. The converse is tnie. 21. lf.L.rl\’B and
AB ‘(D form a linear pair. then L-tXB and ABXD are
supplementary. 23. ll‘m4B.\'(' + in.LCXD — 9-l]°.
then n1L2lYB - 90°
26. Conclusion: Socrates is a mortal.
Mortals
Human Beings
a Socrates
27. Conclusion: Ingrid lives in scandinavia.
Scandinavlans
Norwngi an:
o Ingrid
29. ('oiii'.lus-ion: The line containing points 5 and T
is in the plane.
Lines in plane I
Lines containing
pairs of points l'|
plane 'I'
o The line containing
points: S 1nd T
31. ll-Til“ drives a car. then Tim drives too fast.
ll"l'tm izltives too last. then the police catch Tim
speeding. lt'the police catch l'ini speeding. then Tim
gets a ticket. Conditional: ll-Tllll drives a cat. then
"Fm gets .1 ticket. 33. If you clean your room. then
you will go to the movie. If you go to the movie.
then you will spend all ol'youi money. ll’ you spend
all at your money. theit _voti cannot buy gets lor your
car. lfvou cannot buy gas for your car. then vou will
be stranded. Conclusion: If you clean your room,
then you will be stranded. 35. lfa nail is lost. then
the shoe is lost. It a shoe is lost, then the horse is lost.
ll" a horse is lost. then the iitler is lost. II’ a rider is
lost, their tlte battle is lost. If a battle is lost. then the
war is lost. C0t'tt.lllsi0t't: ll" 1 nail is lost. then the war
is lost. 37. Using the first conditional to lay the
foundatio ns, your argument should include
statemertts that support the claim that the object
displays lbrtn. be ruty. and rrntrsual perception on the
part of its creator. Lfsirrg. the second corrditiorral to
lay the foundations. your argument should include
statements that support the claim rh.-rt the object
displays creativity on the part of its creator. 39. a
plane 41. Fold over one side nfthe angle until it
meets the ulge of the opposite side of the angle. The
line l'ornre.l is the bisector ot'the angle. 43. incenter.
or center ot the inscribed Lircle of the triangle
46. reflection. rotation. and translation
LESSON 2.3
TRVTHIS tp. tot)
Your tlelinition should accurately rzlescrilrc the olr_iet.t
in cletr -and concise terms.
Exercises
6. Sample tnswer: A glosh is .1 figure which has 6
sides, 2 of which are parallel. and the rem.rinin_u, 1
sides are eqttal in length. According to this definition,
rt. C. cl. and fare gloshes. 7. Z1 and Z3; Zl and Z2;
Z2 and A I: 41.5 and it 9. a. Conditional: If a
person is a teenager, their the person is from I3
to l9 '_t'e"tt':~: olr.l. b. Converse: ll a person is lrotn
I3 to 19 ye.-rrs old. then the person is .1 teett.rger.
o. Biconditional: A person is a teenager it" and only
it the person is lrot'n l3 to l9 years old. d. The
statement is a definition becttrse the conditional and
the converse are both lrtte. 11. a. Cortdilional: II" a
numlrer is even. then it is divisible by 2. b. Cotwerse:
It" a number is divisible by 2. then it is even.
c. Biconditional: A rtumber is even if artd only it it
is divisible by 2. d. The statement is .1 definition
because the condiriotral and the converse are both
true. 13. I. Conditional: lfan angle is a right artgle.
lhert it has a measure ol’ 90°. b. Cotwerse: ll an
angle has a metsttre of90°. then it is .1 right angle.
c. Bicorrditional: An angle is a right angle ii and ortly
it it has .1 measure of 90°. d. The !tl¢llClTlCI'“ is ‘t
detinitiotr bwause the conditional and the converse
are both true. 15. a. Conditiorral: If a substartce
is hydrogen. then it is the lightest of all knowtr
substances. b. Converse: If a sttbstance is the lightest
of all known substances, then it is hydrogen.
1:. Biconditiottal: A substance is hvelrogert it and only
it" it is the lightest of all known substances. d. the
statetnent is a definition because the conditional and
the converse are lroth true. 17. ZWVX and ZXVY;
Zxl-'Y atttl Z Yl-’Z; Zllr'l.- l" and Z l VZ: Z l‘l"l-‘X and
ZXK-"Z 19. They do not share a Lomntnrt side.
21. They do not share .1 common vertex. 23. shapes
It and rt 25. shapes it and c 27. Sample .-\r'r.w.er: A
polygon is A regul"tr polygon il' arid only it all of its
sides and angles are congruent. 29. Cicorriitbrnres:
Great Blue Heron. Roseate Spoorrbill; Cuctrliforrrtesz
Greater Roadrunner, ‘{C"0\\'-Blllfkl Cuclcoo;
Apodilbrmes: ‘A hite-Collared bvrifi. Rttby-Throated
Huntntingbird
31 .
A A’
5 g C C' E E
3 B’
33. they are parallel.
35.
A 11'
DB P8’
C C’
53?‘
37. They are parallel Ind the sante length.
LESSON 2.4
TRVTHIS (p. t I 1)
Sample answer: Litre segments 7. —C. a d CD such
that :13 = 10“? 5 K. and B—C 2 E5. .7? 5 .—B by
the llelletive Property. Since H 5 E. ETC 5 E
by the Sytnnretric Propertv. Since E = E and
EC‘ 5 E5. then 717 a @ by the Trarrsitit-e l'r-operty.
Exercises
6. I9 6. .50 7. ACDF 5 C"D"F" 8. Transitive
Property of Congruence 9. Subtraction
11. Transitive 13. n1Zr\-{LN + tnZNLP 16. Angle
Atlclitiort Poslttlale 17. ntZMl P: mZr\'lQ
rs. tttZ."r-'lLr\' = rrrz!’LQ 21. I5 23. 83° 25. GH
27. Trtnsitive Property 29. Yes; 'l'r-ansitive Proper Ky
31. Transitive Property 33. tnZB/IC = ntZDFC
35. Substitutiorr Property
37. mZl + ntZ.7. + ntZ3 = ll"r0° 39. 90°
41. mZ(T)F + n1ZCDB = ntZI-"DB 43. Trartsitiw.‘
[or Substitution] Property 45. Substitution Proper-tr
47. Transitive: the relation is not an equivalence
relation. Cortnterexanrple to the Reflexive Property:
5 K 5. Counteresarrrple to the Synrrrretric Property:
2 < 3 bttt 3» if 2. 49. llellexive and Transitive;
the relation is not an equivalence relation.
SELECTED ANSWERS 885
saervtsuv pezoeres
Selected Answers
Counterex.unple to the b}'ll\nl€ll'iC l'ropert)-: I0
is clivisilrlc by 5. but 5 is not divisilrlc by ID.
61. Rtllcxivc. Symnwtric. and Tr 'tl15lll\'C; it is .m
equiv-.tlence relation. [ Note: Any figure is .t rotation
of itscll". by "Ill amuunt of 3{r0°]. 63. Rellcxivc.
Symntetrit. and Transitive; it is an cqtriv.-tlctnzc
rel.rtion. 55. Postul-ate I.l.7: Through -.nn- thu.-e
rmncollincar points then: is exactly one: plane.
67. l"O5[llldt(‘ l.l.(r: Through my two points then: is
exactly one line. 59. Postulrtte l.l.S: The intersection
of twu pl.rncs is‘ a line.
LESSON 2.5
Exercises
9.
K" L”
(flu
K L
J’ "F
J L
K.
J.
lhe first set of reflections tr-.ursl.tte5 the figure right
alnd doxxvrlwurd. The sccurltl set Ol l'Cllc'L'llUDS
translatctz the figure lcli and upward.
11. ZLEP 13. I60'’ 16. 90° 17.x= I5;
rnz.-'lB(‘ = 60° 19. x = -5; nil.-‘MC = 75°
21. Inductive redsonitrg; not 21 proof; it has not been
-thuwn lbr'1ll C tses. 23. Dcdueliw |'crt<tmit1g; =1
proof: The rnglrs in thc di.-rgnrnr form at linmr
pair. 25. Transitive [or Substitution] Property
27. SUl)lI'r.l(.ll0I1 Property 29. I0 un 31. Exun
33. The p.=u'.tllcl lines altould be dr.-mn pcrpv;ndio:rrl.rr
to the direction ol the arrow.
886 INFO BANK
35
39. .5]
4|.
Numberolfieaicms ‘I 2 I 8 ‘I6 31 57 Q3
1sldIft‘erenr:-as — » I 2 4 8 I5 26 -12
2nd r.|Ilterenoea—— 1 2 4 7 I1 1_§
31a dine-rencea A — 1 2 3 4 6
43. No, an induction proofcannot be .1 proof lbr all
(. 'tsc'~:. 45. Sample .’ll'l\\\'CI'Z .-I-1-5. E E5. Fifi 47. ll
it is Sattrrd.1y'.thcn I sleep until 8:00 AM. It I slnp
until 8:00 A..\l., then I am well rested during, the
tlternoon. II I am well rested in the dllCl'l'I(J0l'l. then
I am in .1 good mood.
49.
Culver H5 Students
Fnnlhrlll
Tr-:Im
Mt-mbr-rs:
0 Brady
CHAPTER REVIEW AND ASSESSMENT
1. 7‘; l0 3. The curve is divided b\- n lrorizotrtal lines
into I + 311 ~aeLtiun<. 5. The averting star is .-t planet.
7. c, b, 0 9. r and if 11. no. The centers: is not true
because a ligure with four sidec is not '¢ll\\"¢'l\‘& .1
square. 13. Linear l"1ir l-‘r'npert-r 16. \"ertiL.1l Angler:
Theorem 17. Leta: .3, in = -1, c: 5. lhen
11: + it: = L" gives: 3: + -I" = 5:. which is true. so 3. I
and 5 lorm .1 l-‘\'thrtgor'e.tI't triple. Let rr = 5, I1 = I2.
r = I3. Then :1’ +1»: = t" gives: 5’ + I2‘ = I3’, which
ls true. so 5. I2. and I3 form .1 Pythagorean triple.
19. Conjecture: ll rr. [1, "tl'tLl t are .1 l-‘}'lhrrgorc.1n triple
such that 41" + lr‘ = r‘ and r, d and e are another
P_t'thngoreart triple such that r" + :1: = 9:, then
£l"‘l'l}'.‘l'("=L'2. 21.3’—-Ix I X-l=9— lt3=-3'.
The prograni would di.5pl.n- “'l\O Rl-.'.-\L SULU1 IONS."
Chapter 3
LESSON 3.1
Exercises
6. Yes. the axis ol's\'n1tnr:trybisccts lsoth the side .-tnd
the angle through which it patées.
7. square: 90°. pcnta-C-,t)n: 72° hexagon: 60°
8. -1 blades: 4-fold. 6 blades: t"--fold
‘II.
13. A circle has an inlinite number ol'.t\'es 0|"
symmetry‘. Any line through the center of the circle is
an Mis ol's;.'mn1etr\-; an infinite number of such
lines can be dr'.t'n'tt.
15. I
I
“
I
I
17. Excrtjscs H and I6
"@ is
23. Sample answer: an isosceles triangle that is not
equil.ttet.1l. 25. Sample .msn.-er: an equilateral
tti.m-glc. 27. S tmplc "tnswcr: a regular oct 1g,on_
29. point B is the inmgc of point .«'t. point A is the
itnage of puinLB,E-T is the itlmgc ofil-'3 31. H6 is
the intage ol BA. BA is the image of BC. ZFBA is
the inmgc ol [ABC 33. either 36. l‘D[.-'tllOl'|
37. rellcclion 39. rellection
4|
[0
-I
Axis ofsyn1mctt_y':,\' = l
43.
/\
/ \
/Wis ol'symn1ett'j.': .x' = -5
u
1
45.
‘U
V
-lt-
-5
/Wis of sytnn1ett'j.': .x' = -3
47. Sample .-tnswcr:
49. The extended table is not l'C1.',ulal. It is not
equihtteral hut it is cqui.tn-gular. 61. The Egx-ptidn
bowl has no rdlcction symn1(tr_t' axes. There are
nontii-.-ial rot-.ttion-al svmntetries for notations ol'72",
l-H”. 216°. and 288°. 53. The Egyptian lmwl h is 2
axes of symmetry-—vertic.1ll;.- and horizontally
thro ugh the centet. There is at nontt ivial rotatio l'|i1l
symntetry for a notation of I80”. 66. The sign is a
tegul-.1 r octagon with B axes of ~'\-mmetu-—-l lines
thtough the n'Il\lPUII1IS ofopposite sides and 4 lines
through opposite vcrticcs. it has ttuntriviatl rtalattiotml
symmetries for rot.1tions of-15°. 90°. I35”, l80°. 225°.
270" and 315". 57. The sign is it tegulzn ttiangle OI
cquihttcral triattglc. It hllli 3 ates of syn'tmctry—e.tch
axis passes through .1 vertex and the midpoint ofthe
opposite side. it lld.S nontri\-‘ial rotational sytntne1_£x_3s
for rotation: of 120° and 210°. 69. point O 61. Ill?
63. 83°
LESSON 3.2
Exercises
5. a. 3 in. b. 50" c. l in. d. I30“ 6. a. I:-!(.l‘l] I). 30”
c. l50° d. 90° 7. Hi 8. m£P’TQ= m£QTR = 90°
SELECTED ANSWERS 887
s.teMsuV pezoetes
Selected Answers
9. to II. 6.5 I3. l3[r° rs. 50° 17. 21 19. 7.5
21. ll[l° 23. 90° 25. B 27. 5 29. 5031. 90°
33. ,1‘ = (10, mAP= n'r£R = ll-‘.C|°,
mzQ = rnzS = 60° 35. l-'-alse; rectangle 37. l'rue
39. True 41. False; square 43. llia ligure is a
rhombus. then its opposite sieles are congruent. so
it must be a pzrr'allelogr'arrr. The statement is true.
45. ll the creature is a whale. then it is a nr rrnmal.
Converse: It‘ the creature is r mammal. then it is
a whale. This is not a delinitiorr bCi.i:IUSC not all
rnarnm.-tls are whales. 47. ll .-t figure is a square. then
it is a rettangle. Converse: lfa figure is a rectangle.
then it is a squerre. 'l1tis is not .1 clelinition because
not all reuangles are squares.
49. _
I
I
.‘\ : I’.
. I
‘\ I ,1
\‘ | II
\-'*r
1’ I "V.
,1 I N‘
I I \
r I
I ' V.
J’ ‘I
I
I
LESSON 3.3
mvnrrs ([1. I37]
Sample answer: alternate exterior angles 2 and 7,
alternate interior angles 3 and 6. and sarne-side
interior angles -4 and 6
lzxcrciscs
5. A3 and (Gal-1 and £5 6. Al and £8; £2 and
£7 7. £3 and £5; £4 and do 8. Sample arrswer:
Al and £5: £2 and £6 9. £4, £5, [8 II. No.
L'\.-ery angle either is vertical to. corresponds to. or
is vertical to a corresponding angle of A l or .52.
Hence every angle is eorr_I.:r'trent to Z I or £2.
13. Z I E (6 by the Vertical Angles lheorem.
Z l E 19 by the Corresponding Angles Postulate.
£9 5 Al-1 by the Vertical Angle Theorem. so
.41 E AH by the Transitive l’roperty ol'Congruence.
‘I5. [3 E Z l by the Vet'tit.al Angles Theorem.
43 E :18 by the Corresponding Angles Posttrl.-rte.
£8 = A I l by the Vertical Angles lheorem, so
[3 '=" [I l by the Trtnsitive l-‘rtrpert}' (Jl Ctrngmenee.
17. lly the \"ert ical Angles Theo rem. the angle
formed by (2 and (3 is congruent to the angle
lirrmed by A4 and 5; and by the Corresponding
Angles I-'ostulate. is congruent to 110. By the
Vertical Angles Theorern. 110 = .413 , so by the
Transitive Property nl'(T0ttgr'uettce. Z l.l is
congruent to the angle formed by 112 and £5.
19. trarrsversal; intersects litres r and 3- 2|. transversal:
888 INFO BANK
intersects lines p and q and lines q and r 23. 50°
25. 25° 27. 25° 29. H4)” 31. 150° 33. I50”
35. Given: line I: || line rrr. Line p is a trrrts\'er's.rl.
Prove: nr£2 + rnzl = I80’
0
3
F
2 E
I D)
{statements Reasons
Line (7 || line m Given
l inc p is a tr.tnsversal.
m.£'_’ -9- ml?» = l80°
nil} = rnzl
Linear Pair Property
Cot responding
Angles Post ul.rte
m.£2 -9- ml l = l80° Substitution Prtrpcrty
31. It is a transversal to them because it intersects
them at two tlillerent points. 39. It is a transversal
to them lrecrusc it intersects them at two slitlerent
points. 41 . is a transversal since it intersects
the parallel tnirrurs. It is the path that light tr tvels
between the periscope ntirrors and it represents
the line of sight of the periscope. 43. By optics,
ll ’—_' £2. £2 '=' 13 because they are altenrate
interior angles. Al E 11.3. by the Transitive Property
ol-Corrgruence. Br optics, £3 E .54. Thus. 1 l E A4.
by the Transitive l-’r0pert_v of Cotrgruettee. 45. ray
47. parallel 49. polygon 61. rhombus
LESSON 3.4
Exercises
5. ll" alternate interior angles are congruent. then the
two lines cut by the tmrts-.'ersa.| are parallel. 6. Tire
irtdicaterl angles are cor'rcsPOhelirrg .-'tl'|(.I congruent.
so the Converse of the Corresponding Angles
Pcrstulate states lines nr IIII\l n are parallel.
9. Alternate E'(teriur Angles Theo rent 11. Alternate
Interior Angles Theorem 13. CQl'l'CSPOI't(Iln_L; Angles
Postulate 15. Sanre-Side Interior Angles lheorem
17. Gwen: m II n; n1zRSL' = tnz.’R'1 U = 70°
l’rovc: RSI "T is l |mr.tlleltJgI.tn'I.
Statements
Reasons
m I n;
nt4RSU = m4RI'U = 70°
ZRSUE ZRTU
ZRFUE .51 where (I is
its alternate interior angle
with tr.-tnsvcrs.-tl
ZRSUEZI
fium
RSTL-' is at p.=u'r|lelogl'.tn1.
Given
A ngle Co nyruencc
Postulate
Alternate Interior
A ngles Theorem
Transitive Property
ofCongrur.-ncc
Com-crsc (ml the
Co: responding
Anglesl’ostul.tte
definition of
|)dl'r.lllClI:)gI'}.Iln
I9. Definition of supplement try angles
21. Transitive [or Substitution 2- Property
23. C0nvcr:~:c olithr: Corresponding Angles llustulatc
25. Given: Al 5 A2; Prove: £1 | f'_.
Statements Reasons
Al E .42 Given
[2 E Z l \"enic.tl Angles Theorem
[I 5 £4 Transitive l’r0pe|t},' 0|
Cong: uenee
1.‘, || Cg Converse ofthe Corresponding
.-\ ngles l’ostul.=ttc
27. both are right angles 29. line p 31. A3 33. £2
35. £2 37. Converse of Corresponding Angles
l’0slul.tlc 39. l’.-tint lines that have c.oltgrucnl
correspomling angles to the first line. By the
Converse of the Corresponding Angles Postulate.
catch ol these littcs will he pnrallel to thc lirst. 41. ll’ L‘.
figure is .1 rechtngle. then it is .3 p.=trt|lelogr.nn.
43.
Parallclugrartts
46. It is false. For e.\‘.-nnple. at rhombus is .-1
par-.tllelogr.tnt, but it is not necessmily .1 rechntgle.
47. HS and 525
LESSON 3.5
Exercises
6. AI .tn-.l Z-1;£3 and £5 6. I80” 7. 65° 9. 15°
11. No such tri-angle exists. 13. 60° 15. 50° 17. l3D°
I9. 70° 21. 30" 23. I00" 25. S. 90”. 45°. 45" 27. 30°
29. IlO° 31. I10“ 33.60” 36. I30” 31. 150°
39. the sum oftlte measures ofthe remote interior
angles 41. Linear Pair Ptopertv 43. 'l'tansitive l_ or
Substimtioni l’ropenv 45. H5 47. 2 49. line.1rp.tir
LESSON 3.6
EXCl'Li9C\
4. loan” 5. I980" a. 560° 7. 360° 9. H0” 11. llD°
I3. 120° ‘I5. 90"; 90° ‘I7. 150"; 30" 19. 3 21. 24
23. I0 25. MI” 27. l(ll’u° 29. 70° 31. 50°
33. l4[i° 35. 71° 37. 58° 39. 3; Sample answer: .1
qu.u.li ilatet at] with angle tneatsures 60". 7'0". 70°, I60"
hits 3 d.(.UIC¢l|"l'c',lC‘i. hnl il 4 quar.ltil.tteral had -I mule
angles. then the sum oftheir measures would be less
than 360“. Yes: for example, a rectangle has -I right
angles.
41. I80’
-_-_-.I.--- -_---
rhxis or symmetry
.1‘: I-‘-l3_.y= I00
45. ll andél. £2 .nn.l £3. £3 and £4. And 14 and
Al: line.tr pnirangles 47. Al and £5. £2 and £4:
vet tical angles
SELECTED ANSWERS 889
s.reMsuV pezoetes
Selected Answers
LESSON 3.7
Exercises
6. 6 6. I4 miles 7. ll 8. 1H leet 9. Length of
triangle ntitlsegtnettt = "",’°: Length of tr.-tpeznitl
midsegment = the formula for the length
of the trztpezoitl ntidsegntent can be used to tind the
length of a triangle mitlsegtnent by letting the short
base = 0. 11. 25 13. 80 15. I0 I7. the lengths of
the segments are multiples ol the length at DE.
19. If pantllt-l st-gtnents divide two sides of I tri.=tn_-.:le
into three congruent segments. the length ofthe
shortest segtncnt is-I; ut the length of the base and
the length ofthe other segtnent isi: ol the length of
the base. lfp1tr.lllel segments divide two sides of .1
triangle into eight congruent segments. the length at
the shortest segtnt-nt isfi ofthe length of the base
and the length ot each ofthe l'en'tatinil'tg segments is
E at the lettgth oftlte hast: where m = 2. 3.4. 5. 6, T.
If par.tllt~l segtttcnts divide two sides of.) trian_-.:|e
into n congruent segtnents,the length ol'e.tt;h
-iegntent i-t '7'} oi the length of the lmse where m is
the segment ntttnher. from I to It — l. 21. By the
ztt-guntent of Exercise I9. each successive decreases by
-Il; = -: ifthe lmse length XL is l¢lliCl'I as one unit.
Th.-t-t-row MN = —§r<t and I-‘Q = ém .
23.
’ttt'atllelDgratttt; The two sides DI‘ the figure ate
triangle m id segments matlzing opposite sides p.1r.tllel,
therefore .t p.tt'.tllelogrant is formed inside the
triangle.
25.
Re-:t.tngle; Two sides of the figure .-trc tri.tnglr:
midsegments m.tking opposite sides p-.tr.tl|ei.
therefore at pat allelogrttnt is formed. Cottseeutive
ittterior angles are sttpplentent.-try. so .tll tngles
meastt re 90“.
27. Midsegment lengths .tre %, - -- Looking .11
the bottom edge of the box, we can figure out the
lengths of the segments ‘tlong the lmttom by the
lengths ofthe midsegments. l‘he first segment is
l — % = The 2nd segment isl — 1| = The 3rd
7
' - I l_l -
segment tsT—§ — iandsoon. lhtts
890 INFO BANK
-l-+ % + % + - -- must add up to the length oi
bottom edge ofthc sqtt.-tre. or I. 29. 2.5 ll 31. t0‘}t.
33.
Anim1|s
Mammals
Rodents
-1
35. 1': tie; all rectangles have two sets of parallel sides,
thus all re-cmttgles are par-allelogrztttts. 37. False;
pttr tllelogramr. need not hLl‘('C Ll” tour sicls
congruent. 39. 70
LESSON 3.8
TRY mus lp. 19.5}
E tnidpoittt: (2. l).fi tnidpoittt: i8. I l. DE = 3.
CF = 9. It ngth of tnidscgntent = 6. 50 the length ofthe
tnidsegtttettt is %(DE+ on = gm + 9) = I2] = o.
Ltmlirmittg thelntpeztaid ntitlsegtnent Lonjeu_tttt'e_
Exercises
3?. 8]
rise = 6
(1. 2t“~mn = 2
This is .-1 p.tr.tl|Llogr.-tn1 bec.-tttsr: the slopes of
opposite sides are equal, so opposite sides -.1 re
parallel.
‘vlidsegntent from (0. 2] to (4. 2] has length 4.
Using the bascs. the midpoint length
= %[base I +b.1se 2) = H3 + S) . Also, since the bases
ztttil midsegment are all-hori..:ontal, thev dlé p-.tral|e|.
13. —I; (0, 0) 15. —;i_: (*2, -1,) I7. perpent.licul-.u
19. neilhct 21. 23. Yes 25.12:: 27. N0
29.
V
Lfi___J
Rectangle; l'he slopes ofl_"._l3 and Ill are 0 and the
-slopes nffi-l ‘Incl .ttc uttclclittnl. Tltcrclott the
opposite sides ofthc polygon lI't‘ pamll-:l. \-'cI'tic ll
lines have undefined slopes and horizontal lines have
zero slopes. Thus a¢l_im:c|tt sides are pcrpcncliculatr
and .-'lBCD is .1 rectangle.
l’.1t'.tllelogr-mat; Sides IE and E5 have slope 2, hence
ate p.n-allel. Sides H7 and 'B—C have slope 7-5‘-, hence
are parallt I. Since it has two pairs of parallel sides.
ABCD is .1 p-arallelogntm.
Rectangle; Sides and 373 have slope —I. hence
"ll'C parallel. Siclcs HE and 6 have slope I. hcnu: arc
pamllcl. There are two sets ol'p.=u-.tllcl sides. and
the adjacent sides have slopes whose ptoduct is —I,
thcrelorc the rllllj.-lLCl'll sides are pcrpcnt.liLul.—tr. .-lB(" D
is .1 rectangle.
‘I .
' ‘ = 4. the slope ol
I
-2-’:
l'he slope of di.1gon.1l T =
diagonal W = ‘ ' "
,\ I _
I — 7. htncc the product oi the
two slopes is -l. the tlingtattals arc pcrpeltnliulldr.
37.
Y
‘K
_‘ F G
_, "E H.
1 Q x x ' x x X
l
The slope of the diaguttal = = = I. zlltd
. . -t_ r|_ _ _ _
the slope or the dt.tgon.tl 1;} — H — f — -1.
Saints the product ofthc slopes is -1. the di.-igotmls
tre perpendicular.
39. l'wo possibilities are (7, I] and [4, -S"). 41. Fwo
possibilities are (3, -11 and (5, 2). 43. The endpoints
ofthc ntidsegnicnt In) (2.0) and [2, 8). The
tnidsegment is vertical. as are the bases, hence it is
parallel to them.
Sample Answers. 45-49
45.
A (3. 5: an}. 51
.«SlO[)9
‘undefined
Clfi. 0)
DID. 0|
-9-l-l>x
‘I0
Jll.Gl
slum: - -2
KC3. 2]
- slope ={-
(1.1)
SELECTED ANSWERS 891
s.teMsuV pezoetes
Selected Answers
51. The root rises 23.0 — [05 = I2.5 It over at run ol
-1-; = I15 It. The slope nrpileh is then = l.[l.
the house violates the building codes. Saiitple
zlttswet: .-\d_iust the roofso that = .7‘
rise = .7( I15] = 8.7’! Adjttsl the peak ol the rool
to t I25. l9.25'). 53 20° 55. 35° 57. 108*‘
CHAPTER REVIEW AND ASSESSMENT
6. l8° 7. 90° 9. Sample .-'tI15\\'CI'! £2 and £4
11. A3, A6. A8 13. Yes; by the Converse ofthe
Corresponding Angles l‘ostu|.tte they ate parallel.
16. No; bec.-ittsr: if so. then s.tmv:—sidc exterior
.1 ngles would be sttppletnenmry, but
ll5' + 70° = I35‘ 1=l80°. I7. IIIZTRS = 25°.
m£RST = .l[l°, IIIZSTR = l2S° I9. IHZQPR = 33°,
HIZPQR = 57°, IIIZQRI’ = 90° 21 . 35°
23. ( %]° su lS8.8° 25. r. 27. to 29. was
3|. 1:. reetanglez Slopes of opposite sides are eqttttl
and slopes ofcotiscttttivc sides have prodttct —l.
33. l'he block has 2 axes of syntmetr_v—-2 lines
through the center alnng the tlittgot'tals_ It has L‘.
nontrivial rotattional s'_rtmnctr\- for at rot.tt ion of
ISO". 35. 28.6%, 40 2-1»
Chapter 4
LESSON 4.1
mv1'msip.2tn
KLMNO ONMLK
LMNOK KON ML
.-'th\'OK L LKOi'V'.\-I
NOKI M Ml KON
OKLMN NMLKO
892 INFO BANK
Exercises
7. QPTSR. QRSTP. PTSRQ. RSTPQ. TSRQP.
STPQR. SRQPT, TI-‘QRS. RQPTS. PQRST
8. Sample answer: l’QR.\ I‘ = V.».’l".\’ l1- 9. It is given
that [fl =' AD. AABC E ZDBC. [AFB E ZDFB.
W E W. and F E By the Rcllui-.'c Propcrtv
ofcongruence, Ft‘ 5 ETC. so AAHC E ADHC by the
Polygon (_.4Jl'tl_:l‘uCl'lCC Poslulttte. II. ZQRS. in ‘Q.
znsr, AUQR. zsru I3. .. b. fl 1:. W
I5. Yes; the segments have the same length.
I7. AABC E ADBC: All colt‘:-.'pot1dittg, angles and
sides are congruent. 19. Yes: the moisture ofthc two
angles is equal. 21. a. E b. E‘ 1:. El‘ 23. a. W’
em em d.W> 25. em bfi a3
a. W e.B—C 21. 8 29. (l8[l— 2;-3°; ll8[i- 2.x'J°
31. M12 5 AIKL 33. mac is isosceles. .'-E
and R an: Lorrespon:'.ling sides. so E E
35. n. ARNO E .t1t.»1KC, FRNT E B.alK3\'.
FR.-lB E TNKX. FBYT E RAKN. R.-'lCU E NKCO,
FRONT E B.-l("K.X' b. S.-imple ztnswcr:
AORN 5 £CAK_ ZONE E £CK.’l , (RON E A-‘lCl<',
ARFT E A/IBX, ARFB E ZNTX c. Satntple answer:
fiEfi.fi'=‘fi.fiEfi.fi"=“fi.fiEfi
37. S-.ttnple .tns-tver:
A
55 as 5
40
C
AABC E AIJEF
39. definition of p.u'.tllelogt'-an: 41. .-\ltern.tte
Interior Angles Theorem 43. Retlexi-re |'ropen\' of
Cotigmcnu: 45. False: pat'allclogt'atns have two paitzs
of parallel sides but trttpezoids onlv have I p.tir 0|"
parallel sides. 47. True. every rect-.tng_le isa
qutultilttterttl with two pairs of parallel sides.
LESSON 4.2
Exercises
6. S \S 6. S58 1. AS.‘ 9. AFDR E All-'Xi’: AS.-\
I1. Lil-GH E AFDH; AS.-K 13. C.tn’t be proven
congruent I5. 't'cs; SAS I7. Yes; .-’tS.r\ I9. No. more
than one triinglc ran he ('0n§tI'llClCt‘l.
21.
Any segment that connects this endpoint to a point
on the cin.lc ls congmcnt to the third scgtnent.
bccattsc the compass setting ttscd to create the circle
was the length of the third segmun.
23. Converse ot'S.tn1e-Side Interior Angles lheorem
25. Cottvctsc of Sitntc-Sitic ltttcriur Angicx: Theorem
27. Rciicxivc Prop;-t'ty 0fCOI1gI'll(‘l'|Ct‘ 29. AS.-\
31. Gi-.-en: rhombtts ABCD
Prtwc: Diagonal! W divides rhornlaus ABFD into two
congntrnt lrinnglcs.
A
D 9
c
Statentcnts Reasons
E 5 E dcfinitintt oi Ll rhotnhus
E 2 FE
E = W ltefle-rive Property of
Congruence
{'5 H30 5 t"‘.\CDB 535
33. "I he diagonal bo.trd ruins the rectttngle into two
wngmcnl. rigid Itiattglcs. 35. a. Yes; Bcuausc
\"l'li(li tnglcs .trc congrttt-nt, .'.’FO\ E AFOD. It
is given th.tt E _=_ and 53 = 55. By SAS.
AFO.-\ E AFOD. b. Ycs: Because it is at rcgular
hf."(.|g0ll,m =' E It is given that ITO 5 CT.)
and 6»? 2 0-12. t;;,- 555. AHOA = acop.
c. AFOE 2 ACOB by either SAS or $55. 31. ‘Its,
by 855 39. Yes. by ASA 41. Civctt 43. Trattsitivc
Propctty of Cottgtuence 45. AX 47. Possible
LESSON 4.3
rnv ms ([1. 223)
at .-ind c
Exercises
6. No. AAA is not at valid test lot congtuence. 7. Yes,
‘\.-‘.5 is .-1 v.tlit| tcst For COl'|_t;l‘llCnL‘-C. 8. ‘~10. SS.-\ is
not .1 valid test for congrttence. 9. 2 X 10'' km
"ll'lLi 0.5 X I0" km 11. ADEF E AFGD; S55
13. APQR '=‘ ."sT$U; SAS 15. C.tn't bc pro-.'('n
congruent I7. e’_\.W,\’i’ E Al-VA"; AS.-\ I9. Gin‘: be
[woven congruent 2|. AY1-VY has hypotcnuqc W:
A)\ W? has h}'[‘D((‘I1ll$l‘fi 23. llcflvtivc Propcnv of
Congruence
25.
A 1 c
2’
F E D
Statements Rvsasnns
AA = AD Given
F 2 D—C
ABFA 5 (ECU
AA!-B = ADCE ASA
27. [MS 29. Transitiw: PfD['*t‘l‘[_V'DI’-COI1gI‘l.l¢llC(‘
31. No
33. Yes; HL 35.
M
d 10
N o 3
D C
a. AABD ‘=' A.-HCD by s.=ts_ b. ZABD 5 ZADI"
becattse CPCTC. Bccttttse they fotnt ti linear pair and
are congruent, A-KDB and LI-IDC are right angles, so
tné/IDB = tn.£.*1D(" = 90°.
37. Given: .414 2 .45. 4A 2 .49, E = 57
Pruve: :5.-'iBC 5 ADEF [AAS is it \'diit.i tlteutcmi
A O
I-
9 - ‘ c E F
Slalcmcnia RLas't)ns
ABEZE [m£B= n1z‘.'F) Givcn
Z.-\ =- [D (nil;-i = mZD]
{TC ‘.5 F
mzf = 180° — m.( E — mil) Triangle Sum
m£C= 180° - 11118 —- ml/H Thcorcm
tn£C= l80"— m£E— nt£D Substitution
I’ropertg.'
m£C= m£F (ACE [F] Sttbstittttion
Pt'opcr1)'
AC E if Attgie Congruence
Postttiatc
flu-\B(" ’=' ADEF ASA
39. n. I b. l o. I d. longer: than
190 rt
Height = 461 ft
451 H
SELECTED ANSWERS 893
s.teMsuV pezoetes
Selected Answers
43. n. b.
B
B
12 ml. 6 H1!
7 ml.
A C
A 8 ml. C
't'cs: 555 Yes; ASA
c. 9
A c A c
No. AAA is not a valid cnngmencc pmtulate.
45. Szunple answer:
'i 1':
a7.AI 5£3Ez.’SE£7_.£2E£l'='£6‘=*£8
49. -l0°,6[l°. 80°
LESSON 4.4
‘mv nus tp. 237)
-i'E7«=v—w°D 3-
H9f1E\'Xl\lIly SAS CPCTC
CD bismcta: / C
5. AABC E AAED 6. CPCTC
7. Ovetittpping Segments Theorem 8. IIL
9. AA is sttpplctttcntary to an .tngl¢- tttcasttritig 30°
so ind/1 = lBO"— 50*‘ = I30”. By the Triangle Sum
Theorem m£B = 180° — mi.-l — n't£C.
l80° — I 30° - 25°
= 25°
By the C(Jl'I\.'Cl‘St: ol’ the lsosccics Triallgle Theorem
and the definition ol .in isosceles triangle. A IBC is
isosceles; I00 feet. 11. KL = 23 13. mzt- = 60°
‘I5. OH = 24 17. ml}. = 40'’
894 INFO BANK
‘I9.
.9. livxv la isosceles
Deli Iiliun ol
lsuscrtlcs Triangle
lsoacelea Triangle Given
Theorem
.'.*.WYl/‘ E .':.WZX
SAS
\|
.'_*.bW2 Is iaowalea
Di-liniliun of
laoscalea Triangle
2 I .
( -Aec=.-.o£c ,4:/D AB 05)
Given CPCTC Converse ol the
Altnrnatc Interior
Angles Theorem
23. Refle-(ire Property of Congruence 25. .-HS
27. Reflexive Propert-.- ofcongruence 29. CPCTC
3|. bisects the side opposite the angle 33. Lot lBC
be an isosceles triangle with AA E (C and 5 lie
the bisector ol .58. By the proof in Exercises 27-29.
1Tx'l_')i5CCl.SE and A/IBX 5 A('B.\'. Thus. by
CPCTC, AAXB E ZCXH. Since A.-L\’H and ACXH
lot In at linear pair. iiizi-LXB + niAC.\’B = 180". Since
IHZAXB E ZCXB. ml.-UCB = m£CXB = 90”. Thus
1-7 is the perpendicular bisector off. 35. l'he
sun-eyur constructs L~.Zl"( E ATB.-\’ by SAS. Because
CPCTC, thc slln-cyor knows lhl“ Y7 = TB. Thus. by
l'|\€t\5lll ing 72. he can determine the distance across
the pond. 37. Sum ul interior angle‘. = 36.4)" Sum uf
e'<tu'ior angles: 360° 39. Sum of interior .1ngie< =
1800'“; Sum of exterioi angles = 360°
41. l‘l:lTlCI'lI'.ii(.lliilI' 43. p.n.tI|cI
LESSON 4.5
Exercises
6. 25° 6. 50° 7. 2.2 8. The ramp. h.tndr.ti|.~:. and the
two upright posts form .1 p-ar.1llelogi'.tn1. Opposite
sides of at patallelograiii are congruent. 9. 5 ‘ll. 50’
I3. 60° I6. 80° 17. l0 ‘l9. 6 21. 20° 23. a. Yes;
l11e opposite sides are parallel by the .-\ltern.tte
Interior Angles Tlieoieni. Ii. No: The triaiigles lit
together In form it kite. c. No: The sides 0|’ the
triangles will not nratch up. 25. .-\ltern.tte lntei ior
Angles Theorem 27. Definition of-a parallelogmtit
29. Alternate |ntt‘ri0l' .-\nglcs Theorem 31. A5.-\
33. AAHD2 ACDB 35. .-'_\.CDB 37. .-‘_\.DC.-1
39. AB.-1D '=' ZDCB
41.
A B
D 1:
Given: .-lBCD is .1 p-.u.rllelogr.nrr.
Prove: AA and AB. AB and (C. [C and AD. and
(D and AA .1re supplen1ent.u'\-. Proof: By definition
of -.1 p.1r-allelogr-.1r1r. E || ‘B-5 and E | K . [iv the
Same-Side Interior Angles Theorem. AA and AB.
AH and AC, AC and (D. and (D and LA are
suppIer1rurtnrv. 43. alternate interior 45. congruent
47. C PCT C 49. Uefirtition of a rhomlnrs 51. S58
53. Cl’CI'C 55. Definition of-a rectarigle
57. Converse of the S.urre-bide Interior Angles
Theorem 69. Converse ofthe S.-1n1e-Side Interior
Angles lheorenr B1. di.1gon.1ls of .1 p-.1r.tllelogran1
biseu e-.1-.h other 63. S55 65. 180°
67. Given: rectangle RSTU with diagonals W and
irrteresting at V; Prove: T67 E E
Statements R(".1‘i0n§
RSTL-' is .1 recl.1ngle. Given
RS! L’ is .1 p:1r.1|lelogr.rn1. Theorem 4.5.?
E E Theorem 4.5.2
TUE TU Retleeive Property
of Co ngr Lrence
111.4 R UT = 90° delin it ion of
m£STl.-' = 90° rectangle
n1.£RUI'= n14$!U
(ZR UTE ASTU7 Substitution Prop.
.L1RTU E ASL? T S.-\S
E1‘ a su cvcrc
l'r.1nsit ive 0 r
69. Theorem: A squ.rre is a rectangle. A square is a
qu.tdril.1ter.1l with the property that all of its sides are
equal and every angle is 1! right angle. Since every
angle is .1 right angle. .1 square is .1 rev:t.1n_x-,l1- by the
definition ol'.1 rectangle. 71 . l'l1eoren1: l'l1e
cli.rg,or1.1ls of .1 square are congruent and .rre the
['*£‘l'[‘.'l.‘l1\lll.'lllal' lrisectors ol'e.1ch other. A squ.-1re is .r
rlrombus .111d hence a par‘.1llelogr.1n1 by theorems
4.S.l_’ and 4.5.6. l'e-epectively. Therclorc its clidgorr.-rle.
are perpenr.liv:u|.-1r bisectors of each other by
Theorems 4.5.8 and 4.5.5. A square is also .1 rectarrgle
by Theorem -1.5.l I and thus its .li.rg0n.1ls are
congrn ‘nt by Th<‘0r1‘n1 l.5.9.
73. a. b
76. No. A.-\A does not in1plytl1.1t triangles 1re
congruent. 77. AGH! E AHCL, HL 79. \' = I5;
y = 20
LESSON 4.6
Exercises
5. none 6. p.rr1llelog,r.u11 7. p.1r'alleIogr.1r11. l'CLl."ll'll{lC
8. p.tr.1llelogr.1n1, rhornbus 9. lhe di.1gon.1ls must be
congruent. 11. Yes. Theorem -1.6.3 13. Yes, Theorem
|.6.2 16. Rhombus. Theorem 1.6.6 17. Neither
19. Neither 21. No, KLMN is .1 rhombus by
Theorem 4.6.6. Bul suppose ZKLA-l 2*.» 90°. KL."t-'r7r\' is
r1ot r1eu:ess.1rilya squ.rre. 23. K! MN is .1 rhomlnrs by
lheorem 4.6.6. KLMN is a rectangle by l'heorem
1.6.5. Tlrerefore R'L..\lN is a square. 25. KL.\-IN is a
rlrombus by Theorem 1.6.6. sin-:1‘ W '=- E by
cvc rc. Also by cm: rc,m a '-FIT, so KL.\1N is ..
rect-.rngle bv The-urern 4.6.5. KL.\-{N is 1! square by
deliniliorr. 27. Rel'le'<ir'e Property 29. CPCT C
31. definition ol'p.1r.tllelogr'-.1n1 33. 558 35. Same-
Side Interior Angles Theorem 37. Opposite angles
of a p.1r.tllelogr.rm .1r'e congrtrcnt.
39. or.-...; qu.1dr 11.1..-.1 asap. RE 5 ET). FE || ET:
Prove: ABCD is .1 p.trallelt:g,r.1n1
A E
SELECTED ANSWERS 895
s.reMsuV pezoeres
Selected Answers
btatcmcnts
TH||TJ. HsC—D
Reasons
Given
ZYAB E ZXCD AlIcl'n'ttc Interior
4' ‘(BA E /_’XDC Angles Tlteutem
AAXB E ACXD ASA
W 5 E CFC TC
AAXD E ZBXP Venical angles
A ix!) 5 ABXC S.-\S
ZDAX '=' ZBFX CPCTC
H7 I -B-6 CUlIVc'l$t.' ul'lht-:
.-'~.Itet'n-ate lnteriot
Angles Thcnrcln
.-‘IBCD is at p-.u.tI|eIor-.tut. Detinition of-.t
p.tr.tllelogr.tnt
41. Given: p.-1r.tI|c|o_gr.tm ABCD with ml/‘l = 90°
Prove: ABCD is-.1 l'€CI1lllglE’
A
8
_l
[%I.?%]—[
definition of
parallelogram
mxfll 90
Gwen
m4A4-rn.£H-I80 _ m.£B=90
m/A I m/D- I80
S1mc-Sim: lI'lll‘l'lDI'
Angles Theorem
rn/D-90
Suhlrnction
Property
m.£C-'90 -
The measures in!
the angles at 9
quadrilateral and
In 350 .
ABCD is a
rectangle.
definition of
rectangle
43. Given: AB('D is .1 p'tr.1||t:Iugr:tm and K‘ biscus
AA and AC and ITD bisects 4'3 .-ind LT).
Prove: ABCD is -.1 rltombus.
A B
Statements
Reasons
ABCD is .1 p.tr.tlle|ogr.tm.
mZB = mZD
W bisects £8 and [D
mzssp = émzs
n1.£'lDB = mAD
lu|-— I'-
mzsps = émzs
ml lBD= ml/IDB
E -=- .75
ABFD is .1 rhumhus.
Given
Opposite angles 0|
:1 p:u.t|Ielog,t.uu are
Cong: ucnt.
Given
Dclinition of
zutglc b iseclo r
Substitution
Substitution
Converse oi" the
lsosceles l'ri.tng|e
T'hcorcn't
Theorem 4.5.0
45. Vcrtical .-‘utglcs Tltcorcm 47. CPCTC
#9. Theorem 1.6.2 51. Opposite sides of .t
p.ll".lllElO§_§l’all‘l are congruent. 53. Division Property
55. Thu: '2-ii bonds must he opposite each mhcr. and
thc 3-ft boards must be opposite ct-sh otltcr, She
must also matke sure the diagonals lmve the same
lllCiI5llI‘C. 57. 5 sides 59. 72° 61. Simc El 2 R",
A lBC is isoscclts. so {BAG 5 ABC:-l by the
Isosccles Triangle Theorem. Also. since F5 E B—b. by
tht: Scgttlcnt Adtlitiun l’osIu|.ttc E ’—_‘ By thc
Rcllcxivt‘ Property‘ of Co n_grut‘ncc 5 E, so
A4-UDCE ACEA bv .‘_\AS.
LESSON 4.7
mvnus (p. 263}
896 INFO BANK
hlatcntcnts I Reason-.-
E E A-8. S-atne compass selling used
7 E W Santc compass sctl in_-.; used
H‘ 5 W7 Rt?llEtl't'E property of congruence
AACF E AABF SS5
AC/\F 5 fill.-\F CPCTC
Exercises
5. B.
F
‘ i I
29. a.
39. {same compass setting, Usftl 41. CPLTC
43.
Statements Reasons
E E Sums: conlpass
55 E '(.‘—D setting
ABCD is .-1 kite. Definition ofkitc
F _E Di.I}_.'.0r|.|Is of 1 kit:
_L line C axe perpendicul-an.
47. notation 49. mlnslznioll 51. p.u.dIelog,|.1n| and
rhombus 53. p.Ir.-1llclogran1. rcrt.Ing|c:. square, Ind
rhombus
LESSON 4.8
TRYTHIS (p. 27.5)
R is balm-en T and S. and the points .-uc collinear by
Fheorem 4.9.|.
SELECTED ANSWERS 897
s.IeMsuV pezoeges
Selected Answers
TRYTHIS [_p, 274]
a. not possible. since l-l + 8 < 25
b. not possible. since 16 + 7 = 2.’.
1:. possible. since I8 + 8 > 2-!
Exercises
5. 6.
The angles have the
same measure.
‘II 13
B B‘
C . —_ C
I
A A'
‘I5. ‘I7.
.'b
898 INFO BANK
21. ADE} is impossible since DE + EF < D!-.
23. AIKL is pussihlc.
25. t+8> I0=:>.x->2
1+ l0>3 ::o-_t>—.'-! 792414 '3
lO+8>.\:=>.t< I8
27. Ovei'l.1pping Angles I heo ram 29. (‘PC IL"
31. definition of-.1 iecmiigle 33. Opposite sides of
a imtailglc are v:on_:ruc|1t. 35. Scgiiicnt .-\ddi|ion
l’osiuI.1te 31. Cl’C l'C 39. sample .mswer: 'l’he\- have
to walk llu-: same dist-.mce in the sainr: direction.
41. llcflcc1ion.I| S_Vl'I'In‘ll‘ll'_V across .1 vcrtic 1| axis
43. lleflectional syinnielry across .1 vertic.1l and
l1OI'|.ct.1l'Il‘.ll.L\1lS and ISO“ rot.uim1a1l s\-mmelry
415. .1. b. and d
47. hove: Xi = i2
0 X R
P V s
Statements Reasons‘
[X20 5 £Y7S Vcnical z\ ngles Thcorcm
ZXQZ ‘=' ZYSZ Alternanc lntcrior Angles
The{.u em
W E E Diagonals of .1 p.1r-.1llelogram
laiscu much other.
AQXZ E ASYZ ASA
if 2 E (X2: Y2] czvcrc
CHAPTER REVIEW AND ASSESSMENT
1. E 3. AK 5. Yes: SAS 7. Yes; 558 9. Yes; A.-\S
11. Yes: A45 13. Dcllniliun of isosceles tlizmgle
15. CPCTC
17. Given: CDEF is .1 rectangle and E and T15
imcrscct 4| G. l’rovc: ACDG '_—' AEFC
c 0
6
F E
at-atentents l Reasons
CDEF is .1 iect-.ing,le. Given
CDEI-' is .1 p.u'allelogr.1n1. l'h-eorem 4.5.?
E E fi Thcorcm 4.5.5
E -=- fi
C-13 = 2-T l'heorem -1.5.2
ACDG 5 Al-1-‘Xi’ SSS
19. L-wen: i-'W'Li is .1 squ-are.
Prove: AX-’H"X E A“".\'}'
V . A-'
Y X
Statements Reasons
\~'WXY is a square.
TX E W
\~"l.-i"}\'i" is a rcct tngle.
m.£W= 90"
n1./_’.\’ = 90°
mé W = m£X
Ai-"I.-VX E All/Xi
Given
Definition of-a squ.ue
Theorem -1.5.] I
Deiinit ion of-.1 rectangle
Transitive or Substitution
l’r1.\pen}'
SAS
21. p.1r.-tllc|ogr.1n1 by definition: rhombus by
Fheorem 4.6.6 23. p.tt'-allelogr-ant bv HL and
Theorem -1.6.2: re1_t.tng|el)_v Theorem 1.6.4 or 4.6.5
Chapter 5
LESSON 5.1
Exercises
5. 2| units 6. I635 units: 7. ll-'1 sq. ft 8. I20 Ft
9. 52. in. 11. 25 in. 13. .12 in. 15. 2-: in. 11. I6 in-'
19. Let 1: be the base and it be the height at .1
rcctanglrs. Since opposite sides ofa rcu:t.1n;.;|e are
the same length, two Sidfi have length It and two
sides have length it. The pet itnetet is
I1+ b+ h + I1 = 7i:n+ 2h. 21. 5(1units” 23. lsunits
25. II: 3cn1,b = 9cm, P: 24 cm 27. in = 3.}: = 6.
A = I8 units"
29.i.=#.o.-: =m
.1 J:
D h
80» -
ac» -
'20
' :::::::h :::::::h
L 2-168 2-163
(solved for bl
8832
{solved for h)
The relationship is a nonlinear function. Any value
which causes division by zero will make the function
undefined. and .1 negative v-.1luet'orb 0| 1: doesn't
make sense for .1 side lengtl:—th-at is. tr 5 0 or It 5 0
are sets of values that do n‘t make sense in the
equation.
31.-:7.5cn1’ 33. Izfi’ 35. 2500fi‘ 37. 5000 Ii"
39. (190 I1 41. $lO7.00 43. I20" 45. [n— ZHBO"
47. -2 49.0 51. (L5)
LESSON 5.2
Exercises
6. 500 units‘ 7. 55 units" 8. SI units‘; I02 units
9.11.204 units‘ b. 430 units-' o.b8=1units3
11. I2units" 13. 312 units’ 15. -lSunits"
17. 6 units’ 19. 98 units" 21. 70 units‘
23. Hounits’ 25. 56 units? 27. I-11:‘-units’
29. 233 units" 31. 6 units: 33. It units: 35. 8 units:
37. I6 units: 39. ‘)units’ 41. Ifiunitsi
43. it = 20 cm 45. A = b.J1;b_.,. = midsegment
47. The pamllelogtam with the Iaugest area is the
rectangle. Conjecture: Fol" p.tr.1IIclogr.tn1s with .1
given perimelet. the pamllelogmttt with the largest
area is a rectangle. S.|n1pIe answer: The shunetit
distance between .-1 point Ind .1 line is .-tinny, a
pet pemliculat. This perpendicular distance is large:
in the rCL‘£IllBlC than in the other two parallelogruns.
SELECTED ANSWERS 899
saemsuv pezoetes
Selected Answers
49. Given .1 pat-.tllelogr.1n1 ABCD with base it and
height it. let 3? be I segment pCI]1Cll(.lit.‘I.ll:lr to the
base. so that A/'lFD is for-nted. Translate {'1 lFD by
1: units so th.1t points D and C coincide. forming a
rectangle with lmsc ln tttd height lt. ltii area is NJ. so
the area ofthc parallelogram is Mr.
A B
51. Prove: Area ABCD = §(Bn)r_AC)
Statements Rcitstttm
.i'iBCT.l is .1 kit: with E .L B—D (_iiven
Arc-,1 kit: ABCD Sum at .‘tt'ea:i
= Area AABD+ Area ABC!) |’0-Slulilte
\l'L.1 kite lB(‘D Area ofa
= étsopmx + .\'c} Triangle
‘I Formula
Area kite ABCD Distributive
= §mx}tnD1+ §t.x'r:)u3r:; l’ropct't1
Arca kite ABCD Segnient
= %(BDllAC) Addition
Postulate
53. A = -l.9[l0.0'00 li =3 l l_’.:'.\ ‘:l(.l't.‘S; -18.9375 ll) ol
fertilizer
55.
Statements Reasons
L4 '=' AD. Given
ZEFD E ZBCA.
F 5 E
F—C 5 F—C Rcllmtiw: Property ot
Congrttencc
.717" 2 ‘IT? Overlapping Sv:','.tt1 ents
Theorem
AABC E ADE!‘ ASA
57. A3 — .1: - 6
LESSON 5.3
Exercises
4. (an -3 lS.8S units 6. .351! =4 78.54 units
s. 251: = 73.54 units‘ 1. I967: = C1 l‘.'1.7‘.'1 units’
9. (12.8 units; .l-I-1units' 11. units; ttnits‘
l“.|
i units' 15. v: to units
-3-‘: .
13. T Ul'Il(.S. us
900 INFO BANK
17. V %1 = ID units 19. to units
21. 651: = 204.20 units‘ 23. 4:: — 7.34 = 4.73 units"
25. 360 + I I2.Stt =« 713. I3 units‘
27. 56 — 81: -= 30.87 ttnit<’ 29. the area is multiplied
by -1 31. The I8-iuclt pizza is the better deal. The [B-
itt1.h pizza gives 5.41! in’ per clullar, while the I0-inth
pizza gives 511: in‘ per dollar. 33. -14 ft 35. [he inside
tites do not have to go as fat, so llltft‘ ate not moving,
as list. 37. ll] l'CVDluIi0lls 39. 6‘/i 41. 3[h;’§
43. .1‘ = S
45. Sample .-tttswcr:
Statements I Reasons
ABCD is .1 p.1rit|Ielogriun. (ii\-en
Opposite sides of .1
par-allelogt -am are E.
E E A—C Rv:llc\ti\-e l"I‘0pcl[}'
AABC 5 ACDA S55
47. ITS cm"
LESSON 5.4
TRYTHIS (p. 515]
8‘ < 8- + :1‘ so the triangle is ilfllll‘.
l-‘xcrciscs
5. 64 6. No 7. obtuse 9.5Jfi 11. zfi 13. V5
15. I295 units 17. 63 units 19. acute 21. obtuse
23..1-:u1c 25. 72uni1s" 27. lI.3t units 29. l5?.|
units‘
31 . l't'iples: 3, <1. 5; 5. I2. I}; 7. 1-1, 25: 9. -10, -II:
I I. 60. 6|: .-\lgel1t' tic proof:
in" + (—"' ' I I = tn‘ + (em "2"" +1)
2 I
_ -‘lt:r' + tn‘ — 2m: + I
_ 4
= rt!‘ + 2m" + I
-I
ti""-|t
I
=
Since the sum of the squates 0|" the lengtlts of two
sides equals the square of the longest side. any triple
generated with this method will represent the sides
(‘ll I‘ right ttiangle. 33. Answers may vary. 35. Let
AB = (I. RR = FH =l1. and BR = r. Thcn .1r-:.t
ABCD = (I1. area bl-‘CH = I1". and area BRS 1' = c‘.
Sinu: triangle BAR is ‘I right lriattgle. :1‘ + II" = L),
showing that BRST is the square v.hosv: area is equal
to the sttm of the areas of the two given squares.
37. F5: the formula lot the area ol I‘ tr.t[.\t:-zoitl,
A =%l1l_l1 + h_-) = %l'a‘I + Mitt +b] = gill!-17-)2.
Find the sum 0| the area at the thtee right ui-angles,
A = E"-l1b‘l' énll + -1-4.‘ = ab-r 1"-L‘. Then set the clrcllfi
equal-to one anoth-er and simt-slify.
%I_u + b]-' = ab + —;r’
[42 + bl‘ = Znb + L2
ll-+1’-I + .2.-tit = 2411: + LJ
1!: 1‘ it: = fl.
which is the Pt. thagorcan Theorem. 39. a. The area
of catch inner right triangle = %fll! ind. by segment
subtraction, the side of squ.tre.!]KL is (b — n). B\' the
Sum offlreats postulate. area EFGH = area UKL + 4 X
{1rv:.t oi" one inncr right triangle]:
t" = (l: — mz+ etflnis) = f.lv— u]" + 2:11»
I). The area oi eat-h outer right triangle = -'_-ab and
the side ofsquare ABCD = {it + 1;). By the-Sum of
Areas postulate. area ABCD = -‘I X {area of one outer
right triangle) + area EFGH. Thus. ‘ll'Cd EFGH = area
ABCD— -1 X (are: of one outcr right triangle).
r\Ig,ebt.tiLa||y', :7 = [07 + ill" — -l[%alr] = (.1 + b)" — 24111.
Simplifying each: .
Part .1.
t.*' = (i: — at"): + 2.1!:
= b" — lulu + ta’ + 2.1!:
= II" + :12
50 c; = :1‘: + l)
I’.-trt I).
c" = {:1 +11)? — Zul-
= n" + Zalv + b" — ‘ab
= rt‘. + if
So t" = 43: + 1:’
41. |3.5 miles 43. 335 45. "(.17 47. line. Opposite
sides ofa rhnmbuzi have equal lengths. Therefore. the
rhombus must be at p.trallclog,r.-mt.
LESSON 5.5
Exercises
5. 7../5 8. I4; 7‘/3 7. 34.6 ft 8. 37-1.I2im:lt.:s‘
9. 276.9 units" 11. .t = 2V-"3: z = 4e/3 13. .t = -1;
2 = 8 15. p: 3\.r'.5__:q = 3J5 17. p: S\.5:q = Sufi
19.»: I8;_t,v= 12¢? 21.k=2;g= I
23. 25.3 units-' 25. II2.Sunits‘ 27. I418 units’
29. 45-45-90 31. ncithcr 33. 30-60-90
35.!’ = £.‘l\I{i + 24 units: A = 144 units-'
31. P = 73 units; A = 253.5‘/3 units‘
39. P = 20./3'1 units; A = 50.5 units"
41. 5fi+5 units 43. A = 2.-'t../5+ I} 45. (19.28 ft
47. The lines are parallel because they both for m 60"
angles with the same line. 49. 6 units"; I L25 units?‘
51. 8‘/::1ttnits": 20 units 53. A = Sub:
P=u+b+ v'n +lr-'
LESSON 5.6
Exercises
5. J75 mm 1. 13.93 units-' s.9.9s units‘
9. 9.1.1 llnits 11. 5.3‘) units 13. I3 units 15. (1.08
units 17. 3.6l units 19. 22.37 units 21. The triangle
is l!i0S(.ClC!i. 23. The triangle is not equilateral.
. . . . 2'-_ _
25. The tttaugle is a tight triangle. 27. ‘ " unns
}
29.; unit<:;§ - x/iunits 31. The midpoint ofthe
hypt-Jtcnuse (3. -I]. The clistanccs ‘Ire the same.
5 units. 33. Conjecture: l'he distances from the
midpuint 0|" the hypotenuse to any \'e|'le.\t of a tight
tlianglc are equal. 35. Sample answer: l(:.37:'.\ units;
31. S.unple answer; 61; units: 39. 9.85 miles
41. I at W = (—I. I]. X = [7, —5], Y = t'Io_.—t).
J = (2.51
slope/TB: = T6 =—%
slot>eBC=—:—__‘%“— 5%--E;
:.::: — -;-
slopei—£_J= 1'‘ 5: = -'1 — %
Since slope E = -tlnpc E) and slupt: R = slope E).
W || and E W and AHCD is .1
|,'tal"¢lllElOj_.',l':llII. Since [slope EH slope E) = —l ,
H? L F and ABCD is a rectangle.
43. The square has the gteater perimeter. 45. 3 cm
47. i = §\.-Gttnits : P = 35 units
LESSON 5.7
Exercises
5- 6- 7- (Mi
8. (p+ r.q-t-5] 9.% ‘I0. 11. C(q_.p)
13. l(r+p.q] 15. Rlu.q); S(l!.0| 17. C[2r. 241] and
Df_2L<,O] 19. AD: 2s;BC= 2r— Zp; MN = 5+ r—p
Ht)+Bt| _ I2‘ I 2r 2;-I
— )
__, __ =s+r—p=MN
21. M(%, 23. M is equidistant front the three
vertices. Therefore. a circle can be dr.-twn through
I, K, and L and its radius is 1.-‘tr! = KM = LM.
27. Let ABCD be .1 p-.trallelogr.m1 formed by the
following, \et tices: M0. 0), Bl_p. q]. C(r,q]. and
D(.~', 0} where W and E are opposite sides and B73
SELECTED ANSWERS 901
saemsuv pezoetes
Selected Answers
and AD are opposite sides. Slopes of opposite sides
are equal:
q_ if
TE
p-1-—s
AB "
ct: = =.
U3 - CD
sc = - =
AD = J?
Bf" - ll)
29. Let ABCD IN: 11 rclitttnglt.‘ fornvtxl by AU]. 0}.
B(0. pl. Clp. q). and D(q. 0).
diagonal AC = V-
‘
di.-13:on.1I an - V.-
' y’???
I hus, the cli.1gon.1ls of .1 rect-.1ngle are congruent.
31. Let 1''» WC be at triangle formed by Alt). 0),
Bilp. 21]]. and C(2r, 0]. Then the mitlpoints of
the sides of the triangle are Mf_p. ql.1\'(p + r. q),
and l’[r,0].
The slope of medi.tn /IN is m -
rt
‘J ‘W TI
q-(l _ II
pt-r-[I p+r'
The equation 0|‘ .-l1\" is y -
17 — (l q
+r—tt p+r‘
The slope of n1cdi.tn is n.' - P
The equation of is y - " (x — Zr}
_ [I -.‘.r
The slttpc ofmcclittn ‘la’. is m - —
_ .o—-. _ 1
l‘he equation at BP is y — 2:1, ix — r)
Set the first two equations equal and solve for r.
‘I . _ ‘I .
P "1 — p_‘,'rL\.— Zr).
qxtp — Zr) = q[.\' — 2r)(p + r)
xp — 2r.\' = xp + xr— 2rp— 21"
2:‘ + Strip - Jrx
.\' - %[p + r]
Substitute into the first equation to find y:
‘I 2 2
J" ;T:_1(!”"1 - -1'1
So tl1e litst two equations intersect at
(%<P+ rt‘ ‘#1)-
902 INFO BANK
bubstitute these values into the third equation to
verify that the three lines i11re1'scu_t .1t 21 single point:
‘I 2
_fq- Zll':'[_%(p+ r]—r]
_ 21; 2p+1r-1:
ST
Zq Zp—r
_$:.T
)
=§q
Since this results in .1 true st.1tement. the three
1nedi.1ns intei sect .1t -.1 single point.
. - /— ~\-"3 Se’? 9
33.5 35.: 37.:-~.-2 39.T 41. , 43. 90
45. 24.35
LESSON 5.8
6. 1-: or 0.56 7. H'CLI. 0fI.tn$l'l1l(.lC(.l region:
«I —-n units‘; probability of penny not touehing
intersection: " I‘ = I — -- O.2l 13. Sample answer:
The width ollthc penny is L()ll‘il(.lCl'C\l I unit. so the
shaded arm is :11. 1nd the square his area I. The
probability that the penny will cover .1 vertex is
theoretic tlly. Repeated tosses should pl'0(lULC a
number close to The more tosses. the more
‘¢‘lC(lll'.lIE’ the estim-.tte should be. Multiply lav -t to give
“ 11. 13. 15. 75%
1
4.
an ctitimttte for J12. 9. 3-
17. 6(»%% 19. 0.5 21. 23% 25. or 0.6
27. 0.6 + 0.4 — 1.0. There is 1 l0()'.'tt1 1-h.111cc ot
Lntdittg on either an odd or .111 even number.
29. sample mtswer:
31.; 33. '1')" -»0.ll 35. 0.(K‘I89 31. 0.039
39.0.7l7 41.1ight 43. 1101.1 triamgle 45. acute
47. I5 units 49. 3|‘-Dllnltli:
CHAPTER REVIEW AND ASSESSMENT
‘I. 90 units 3. H20 units: 5. 2-‘! units‘ 7. 36 units:
9. H31 ttnits 11. I003: units 13. 29 15. J\ll[C
17. 50\/‘E units 19. 9‘/3 units: I8‘/3 units 21. I0
23. 5‘/E 25. D[1t + b.cl
21. B1) = AC
= »'::lvT)1*«.~'
(:1 + b)" +t" = {b—n)" +5
[:1 + b)’ - (I: — rt):
:1‘ + 241!’ + 1:’ - 1:’ - Enb + (1:
‘Mi’ ‘ 0
fl = 0 or I: = 0
29. 0.25 31 . 0_l875 33. -I(:_52 icct; ycs; -:4. I 3 ice!
Chapter 6
LESSON 6.1
Exercises
5. 6.
I I N ‘\' o o \ . I
. . . \ .
I . \ .
”‘ as
Top
Left From Right Back
Bun-Ilnm
9.6units-‘ 1o.26units’ 11.u 13.: 15.1’
17.
19. 5 units‘
2' E!
Top
Left From H am Back
Bolmvn
23. 25
27. Yes, the top view has 2 distinct faces which are
congl ucnt bcunusc they have the Sdlllc size and
sh ape. They are also congruent to one I‘.-tcc on the
back view and one face on the right view. l'he\- are
l'C(.I‘:lllglCS “hi-.h are I unit by 2 units.
29. a.
Top
L-_-fl Frunl Righl Back
[:1
Bottom
b.
Top
I_J |_l |_l |_l
L-_-fl Frunl Righl Back
B-Ofllillh
5' ._
I
Tap
Lnfi ‘ Front ‘Hinhl B1I:k
I
.B:ttom
SELECTED ANSWERS 903
snemsuv pezoeges
Selected Answers
31.
Bottom
33. Sample answer: 35. S.In1ple answer:
xx I I K. I
./. .
39. .24 units‘: S-‘I units‘: ‘J6 uniteal: bu’ units‘: 41. 8:
3-1: 2-1; 8
43.
Top
Left Front Right Back
I
I
I
I
Bottom
l'hese views might be used when writing instructions
on how to a.ssemble the tent.
-15. 2-1.6! nr -17. = 78.54 m" -19. = l}‘0.29 ml
LESSON 8.2
Exercises
7. Sznmple answer: W and E5: Hi and W4:
8. Sample -tnswcr: W and W and IT."-
9. Sample .ms\\-er: HIML and KCNO: HKOL and
IGNM 10. F! and Ki1\'.'H: FL and NICK
904 INFO BANK
11. .‘.~'ample answer: -H7 and T: E and T5
12. pcrper1dicul.1r; pcrpo.-ndicnlar 13. There exists at
line in S that is parallel to line m. 14. l'I1e me.tsure
oI'the dihedml angle is m./_’EFG. 15. Line p and
pI.tnc .7\'[.1rc parallel. 17. 1 inc (2 is I10! posrpchdicul.-Ir
to plane 3!.
19. line
25. l'he angle formed by the insert in .78.
27. intchcct 29. plan:
35. I96 units‘ 37. 50-! units’ 39. ae 97.! units}
LESSON 8.3
Exercises
5. rectangle B. p.tr-.1llelogr.tm 7. recungle
8. =I86 pm 9. hexagottal prism 11. not :1 plism:
prisms do not I1.“-c ctrrx-ed edges 13. not at prism;
no translated bases 15. A/{BC E ADE!-: in .1 prism.
the bases are II':lllSlillc1.l images 01 Cli.l'I other.
17. rectangle 19. ABFD and BCFF 21. W
23. p.tr.1||eIogr.tn1 25. AKIN’), AJGA, ZLMI, AIHL,
ZNH. £!.\-LN. £KGH. ZHLK 27. =- I6.-‘IO 29. Il\/(5
31. -v8.72
33. =«5.77
Number ol Number nl Number of
faces verlloes edges
35. 6 8 12
37. 8 12 I8
39. faces: 20 + 2 = 22; venlices: 2:20) = 40;
edges: 5:20) = on 41. .1: -13.
45. True becausr: lhr: diagonals of .1 p:u.1Ilclogmn1
biccct each other.
47. Fdltsc
49. 3: (3.01 51. = s_54:(
l~4I'\-I
.2)
x-inlelcept: (—l,.0) .\'-intercept: (-%.0)
LESSON 6.4 . ‘ '
y-unezcepl: [0, I]
59. L8; y = l.B.\ + 32
y-inlclccpt: (0. 7)
TRY THIS l_p. 398]
\/E = 5.74
LESSON 6.5
Exercises
5_ Exercises
6. 1
8.
X
(3. -1.4!
7. Z
t ’-°}
X 0”‘? y
ll ,ol
9. (0. 0. 0); (.1. o, 01: (0, 7. 0:»; (2. 7. 0'): <0, 0, 6]; ,0 _ ,,
(2.0. 6]; (0. 7. on: 12.7.51 10. ../E = 6.78
11.‘/ET-s 1.5812.‘/Fl-n7.8l "
13. ,
4
(-1 1.5)
? 2
l
E ' 2 4 V
1/?
17. 1op—I'ront-right 19. .l:£-p|.lnc 21. top—l1.—1ck-rigln
23. x-zuis 25. lxamlple answer: ( I, 2, 3] 27. Sample
1n1wcr:(-I.-2. 3] 29. JE as 1.4:» 31. ll
33.10.143.71 3s.(e. 10.0) 31.6 39. \/F» l3.(1
41.=13uni1s’ 43. 45. (5 -3
47. [0, 0. 0') 49. Sample .xnswer: ( '7,
51. 53. 6
SELECTED ANSWERS 905
s.IeMsuV pezoeges
W.-Q>>flC< 10900-0“
906 INFO BANK
23.
27. trace: 5.t— 2y = .2 29. trace: —uLr — 2;; = I
33.
P.-ll'.l"Cl. Th: lines d.l'C both vcnicdl. pct pt:ndit.ul:-tr
to the .\'}-'-pl.tnc .-tt (1. 2. 0] and I3. 5. 0).
36. ‘I've. set the coordinates of the two lines equal
to etch other and solve the system of equations.
(0. 3. —l )
37. 7x+-4y—: = 50
7.15 + 4}: = 50: $0
39. [umllcl 41. ncithcr
43.
Statements Reasons
412.42; $5?-T} (iiw.-It
TH || C0n\'ct"~:c at the
Corresponding,
Angles Po-‘\m|.itc
EFGH is .1 p.tml|c|ogr.tm. Tltcnrcm 4.6.2
E? 5 #6 Theorem 4.5.2
45.
A B
E
D C
Matentents Rc-mtons
ll3CD is .1 I'ect.-tnglc. Given
AB? D is .1 pantllcltzgnttn. Thcorcm 4.5.6
I-T5; E
\FE IF
BE EDE
MED; aces 3-55
Theorem 4.5.2
Theorem 4.5.4
LESSON 8.8
Exercises
8. l’.1r.t]lel to ea-;h other but not to the picture plane.
Parallel to t:.|:.'h ulhcr but nut in thc |'|l\'.hll'C plane.
9. The lines containing the \'l':l'IiC.1l scgntcnts will not
meet because they are parallel to each other and
|1hll'.I"l:l to lhc piuurc plant. 10. The lint: containing
the nonvcrti-all sitlcs of the bllilding meet at the
horizon ofthe dntwings. 11. Follow the steps to
prmlucc .1 one-paint pcl'spccti\"c t.lr.twing of .1 cube.
E
V: tislti .g point
SELECTED ANSWERS 907
s.reMsuV pezoetes
Selected Answers
17. Follow the steps to produce .1 l\\'0-point
pcizspcuivc drawing of .1 LLIIIC.
.
21. Th: cube bccomoss disrortcd.
19.
23.
W
27. S-annple answer: Make a perspective drawing of .1
squane wilh horizon:-al.1nd vex tical diagonnals. Divide
the horizontal diagon.-ll cqu.all)'. Pass lin<.‘$ from thv:
vanishing points through the division points.
V
29. E-'un1ple answer:
>{>
35 ~I7.0.$ 37. (—%, 5.
u| .=
)
CHAPTER REVIEW AND ASSESSMENT
1. Sample .1115»-en:
3. I I unil.s 5. Samph: .mswc1: OPQR5T.u1d
908 INFO BANK
m-'wx3-'2, PQwvand T552 7. Sample mswerz E
and WK 9. ‘3.:mplv: .mswcr: DI-"F 11. Sample answer:
E 13. lop-l'ronl-riglll 15. 7
‘I7.
I
19.
27.
Chapter 7
LESSON 7.1
Exerclses
e. 1.4 7. 1.2 a. 1.2 9. 0.6 10. (mt-‘12.?.'!i11’:
7.45 in. x 7.45111. 11.l1ox.-\ 13. 4 15. 48 17. 3
19.105 21. 7 23.1.45 25.110 27.1.5 . 2 +7‘,
31. Sample a11sw1:r: M.-1tin1i71: the volume; .155un1i111,;
1-ou use -all available lumber, the surface area is fi\'ed.
You want to create the m.uimum an1ou11t ol-storage
spacer. 33. °-ample a11s\w:r: Minin1i7rth1: surface
area; .1.<su111ing the item(s) to be mailed have .1 fixed
volume. you would want to minimize t|1e amount
of packaging to 11.-dttcvs the weight ofthc Package.
35. 2 + '1'; f 37. 6 39. Sample anst-ier: l'he tlat
shape of the worm maxitnizes the surlitee area :11
its body exposed to the air which m.-1.tin1izv:s the
amount ofoxygett it can take in through its $l\ll‘:
41. Sample answer: Tall trees with large. hro id leaves
h.-wt: .1 large stlrlitct‘ area exposed. The large sttrfacc
a1'e.1 is in1po1ta11t ifthere is competition for light, but
it also inereases water loss. In desert comlitions there
is plenty of light but little watcr. so -:onse1'\-'.-1tio1I ol
water is important; broad-leated nees would soon
die. 43. Sample answer: When hraken into smaller
pieces. .1 block of ice will have .-1 l.1I’}:('l' 5t1rface-.11'c.1-
to-volume ratio which 111axi111i.1es he-at e.\ch-ange.
45. Simple answer: The short. squat form ntaxiinizcs
the volume of the cactus and thcrcfon: this amount
of water it can hold. Also the surface area is kept to
a minimum whieh tninimizes water loss through
transpiration .-ind c\~'.1[\orat ion. 47. -1.35 units.
49. 6?.l units"
51. N11. Sample answer:
2
These two triangles have the stmc a1'1:.-1. but are not
congruent.
53. 25'. units 55. =8.-19 cm
LESSON 7.2
Exercises
5. 333 units‘ 6. 1715 units‘ 7. 340 units’
a. 27.31 1.74 units‘
9. Sample aitswer:
Ill
11 . :1-atttple a11s1\-er:
l I
13. 35 cm’ 15. 391 in‘ 17. 113 units-'; 70 units-‘
19. 3 units‘:-Q; units’ 21. "1 in. 23. l.792.S5u11}
25. l6.S units‘; -11.2nni1s-' 27. 332.11‘
29. I918? inl; l03.l8in' 31. The surface area is
multiplied by 2" = - , and the volume is multiplied by
2’ = 3. 33. The volume is multiplied bv 2‘ = 3,and
the sttrlltu: area is ll'|Ulll|'|llt.\l by 2" = -1. 35. Feline
Feast: st11'taCc area = l98i11';vc1lt1n1c = l(12 in’: kitty
K1unchies:su1t'ace area = l90in'; \'0lt.I1ne = l26i11‘
37. 89611"; 1.24 gal 39. .?..i.0401'1" 41. -1.» 43. .7-1 45.
541? 47. 8.66 i11.
LESSON 7.3
Exercises
5. 1.75.2.7 units’ 7. l.Lunits' 3. 14011
9. l3,l43.6-40.826 pounds
11. 13.
15. l2O units: 17. 30.4111‘ 19. -168 in‘
21. 23.
alliludc
_ attitude /
1 I.‘ A
I. p '1' r'
. ' :
\
K i l .1) ‘
base edges Luise edges
. /5 .
371-‘ units’ 34-}: units’
25. 17.5 units 27. =-=1-1.85 units‘ 29. 111.58 units-
31. I3 units 33. =3.=t6units 35.5 37.5 39. I0
41. 11+ l 43. 11+ l 45. 8-1C|011nits":3lS0 units:
47. 50.1.! 1115' 49. parallelogram 51. 50 units:
53. 21.-in units-' 55. 3.29 units‘
SELECTED ANSWERS 909
saemsuv passages
Selected Answers
LESSON 7.4
Exercises
6. 836.53 mm’ 7. 5?9.32111I11 8. l0S7.% 111111
9.1.3393 mm‘ 10. .1-10.11 mm‘ 11.xn3.9.xnun‘
‘I3.
15. -477.5 units-' 17.9 units 19. 5 units
1"
1.‘
21. 1-i|J1:t1nits‘ 23.3—: units 25. ' units
27. .37.?‘ mm 29. It clt1ul1lt:s the volume oi tht:
ct-limlcr. 31. It multiplies the volumc by 3.
33. S = V
Zrtr’ + 2Irrh = Itr-it
2r+ 2!: = 111
11 + 171
St = I
n‘:
2 2 _
E + r — 1
If either It or r is less than or equal to 1, then% 2 I
01 -E 2 I. and so i—‘ + > I. so both i1.u1d r must be
grc.1tc1' than 2.
35. =O.75 cm 37. f.u0tin1es111u1e 39. r = 2.64 i11.,
S >'= l3l.29in’. I1 =1 5.23 i11.
43.
1 A
."
..... .....
l
The symbol has 180“
rot.1i in ml syn1n1ctry.
The symbol has l80°
rot.1tion.1l §j'l'l'Il‘l'IL‘I|'\'.
45. 337.5 I.1nits::-$21.88 units" 47. 360 units}:
400 units‘
LESSON 7.5
Exercises
6. 232.74 unita‘ 7. £123.32 units" 8. S = 1:11" + Itr‘
9. 1809.56 units‘ 11. 301.59 cm-' 13. 2.3.5 units’
15. 133.54uni1s-' 11.7.31 in. 19. 1-113.72uni1s’
21. t1:«1.:r2uni1_<‘ 23. -1o.72uni1s‘
25. 2339.07 unit.’ 27. 19,393.19 units-‘
29. 3593.32 unit.-‘ 31. 6031.86 units‘; 2513.27 units‘
33.1.».-16i11. 35. 9.77 cm 37. J'9_l 39. J1?
41. \/7-5. 43. 3.1 units 45. 141,372 ft"
91 0 INFO BANK
47. 56.55 un:: 37.70 L111’ 49. 23.70 cm‘ 51. -Q
53. 8.06 units
LESSON 7.8
Exercises
a. 233,033 1:‘ 7. 7233.231'1": $10,357
9. a. 25t'1It units"; unii~;'\ to. $104.2") units‘-;
2144.33 units-‘ 11. a. 43515:: units"; 47.91111: units‘
b. I3.68-4.73 units"; l50.532.5S units
13. a. 597.s1.<t»ru1ni1s'; 2 1.1.1.01»: uniis“
1.. l3?6.52 u11iIs3;?643.6-8 units 15. a. 2511-. units‘;
-'—‘-f.l’i1: units‘ 1.. 3114.25 units-‘.214.-1.ms units-‘
17. 3. I3 I .790-1.‘: u11its:; 252.l{1It units'
1:. I I-1.03 units"; "9118 units‘
19. a. ..¥9.984.0Dli‘.1It uniisz; l._t_.L5..¥.t.49Ir11ni1:.’
1.. 125.313.-15 units-';4.13(»,277.-13 units-‘ 21. lby‘Ir;
. u . " I" _ . .~
%;-'1: 23. I6)-'1t;%y 1: 25.'—l1r;4—..1t 27. :1DOun1ts'
29. -1-1.83 units" 31. 2317.43 units’ 33. 300 unitsz:
|8.5.(vDl1nits‘: 35. I0 in.; 20 in.;(1.('>I-' in.
37. 2-1.».-1.?.in‘; 12.7? in’ 39. (>3-'.0_7iJ.(>-1.’: mi‘
41. 13.39111‘ 43. 2.60 in. 45.1327.-13011’
47. 1211 fr‘ 49. _15.s:1.29 m-‘
LESSON 7.7
TRYTHIS [p. 431)
sphere; cone; doughnut
Exercises
5. (2. i. ii 6.{2.—i.—l) 7. [-2, l.—i) 8. about the
x-axis
17. {-2. 3. I) 19. :.4.—?., -3) 21. [l.—2, 3}
23. b.1cl;-rigln-bottom. (-4. 4. —l) 25. in the xy-
pl.-1nc_. [l. -I, O] 27. front-lch-bottom. (2, -2. -8]
29. I he an:-a ofthis circle = Id I0)‘
= IOOH
-V .H4.lf.1 units‘-
31. 2501: == 735. Iounirs’ 33. ‘$1: -= 67.02 units‘
36. 37.
I I
I I
-A -A
I
I I
39.
i
I
41. 445.43 units‘; 456.08 units' 43. 1335i‘ 1:’
45. About 3 I1
CHAPTER REVIEW AND ASSESSMENT
'l.% 3. cube.-.%; pl ism. 2-1; The mic is langer fo: the
cube. 5. 38Suni|.~:‘ 7. 718.25 units' 9. l8units"
11. 5.20 units‘ 13. 72:: =226.l9 units-'
15. 144:: = 452.39 unius-‘ 17. 580:: -— I322.I2 units"
19. zsom » 379(v.lf»u11'II<' 21. 100:: r .u Ll(1unit53
23. 3 units
27. :
I
m
29. ~55, 35011 31. 6.30 (In
Chapter 8
LESSON 8.1
Excrciics
7. (3. I5)
Ir
Y
3
“ -:2,31
.3 '.a '; 8 X
4
0
(-4,-0.9
SELECTED ANSWERS 91 1
s.IeMsuV pezoeges
Selected Answers
‘I1.
Pre mane
Prelmaue
91 2 INFO BANK
25
Preimaue
Path of thv: thrcc inmgcs is twin: .15 large as its
con responding image. l'he ditference is that each
iinzige is placed in a different p0siIiDI1 relative to
the pn:in1.-1_L',c.
27. m = 33-3 = Endpoints ofinmgc .1rc(2.0)
and (l0.f.x). So. m = :l’’__'’_, = = 3:-
_ 3--a _ 2_ - -
29. m — 4 _ P2, - 3. Eliclpoizim of 1:11.15: ale (l.—2)
.1nd{—2.—4].So.m= = 5% = :1;
31.y= -121.0 =1_{o1= 0 = 0. So. the oligiu is on
this line. 33. y = 0 = —§[0) -> O = 0. So, the
origin is on this line.
35.
I
1 1:0, 0, 10': I0. 8, lo)
10
B-
8-
:" 0
l8.0.I0 ". ( H
[0.G.D)
PreImaue~ —- - , ; ; ; ; V y
4 > B In
2
" image
8
,0 |8.0,0l (a.e,m
X
37.4
39.
l’
5‘ I6. 11
_ Image
(0. 31 (5. 5)
Aimnpn
Stile [actor is 2. Cetttcr of dilation is (-1. 3).
D[.t.y) = H.t— 2.4y— I].
41. The small opening in the center plate. 43. The
itnngc is invertccl bcutttsc the light lmm point A
travels in a straight line to /1’; the light from point B
travels in a straight line to point B’; and so on for
each point on the preitttagc. 45. Pet imctcr = 2.7 n1:
/\rt‘.t 5 22.25 n1: 47. (vUl9.29 in:
49. 6306.2 km
LESSON 8.2
Tnvmts [[3, SI I)
Cross-.\-‘lttltiplication Property
3:t0.6¢D.(l]l_h)= l_2]t.%) = (1:15
Rec ip meal Property
I ¢o..s=eo.2¢0.c»=eo.%=% =>3=J
Escltange Property .
l :t0...¥:t0.2:t0.t.~:tD.-1-=
“Add-one" l’rope1't_v -
3z0.t:¢0.'L;fl'='3;"=.*»-‘;-=%=:~:‘:-=
lixerciscs
6. Yes. Corresponding angles are tong: uent, and
u)r1'csp01tt.ling sides are proportional: = =
- 17 12 _ - . ' '
7. N). -1-6 at 4-“, Letttespotttltttg suits are not
prnportionttl. B. FH = I9}! 9. JK = l5 10. 90 ft
11. ASST - AMWR 13. = =
£_fi..ffi.._-"5-‘~_"‘_'1 —
15' Pu ’ on ‘ Its ‘ M ‘ u= '7"a‘=‘{P'
AK E AM. and AL E AN. so corresponding angles
'll'C Longlucnt. 31% = %- = $1. so C[)I'l€Sl"l)I'l\llI'lg
sides are proportional. Titus. AIKL — APMN.
19. §—g :t %. so cm'rcspanr.li11g sides are not
proportional. l'hus. petttttgon KLMN! :5 pentagon
1 _ I 2 _ 3 - _ I -
PQRST. 21.3 .. E => 3 _ -5- 23. § _ 3 2'5. Rana
ol sides: 3 Ratio Ul .ne.ts: 9 Oltserve that Bl‘ = 9.
27. L2 29.5 31..t:= I2 33..t:= H 35.1‘: ll]
37. lfthc ratio ofthe sides is n.th1:nlhc rttio of
the '¢lI€¢lS is 11:. 39. False. It is true that 1% = '—};. but
5+1 6+l_1 - .‘i+l l1-l
-lot noI—9'm'loI ll-I‘
41. l'rue. lt"y—: = then
-1
— ;and
mi = lit‘ => alt‘ + ml = at‘ + lit‘ =? n{ L‘ + ti] = (U! + if)
I’! l
m - _
43. 3750 Fish 45. 25.5 ll 47. 5% in. tall -.ma 3;‘ in.
wide 49. 23°. ll2°. and -13° 61. vtlid 63. valid
55. -3.6 cm
LESSON 8.3
Exercises
5. AABC -- ALKI; SS5 .‘.\intila1ilyTlte01etn
6. AEFD ~ AQPR; .-‘M Simil.u'it_y Postulttlc
7. AGHJ - ./\.'WO.rl:5A5 Similarity lheorem
9. AGHF - AECD: U1 Sintilalilv Postulate
11. ALIK - AFB;-l: SSS Sin1il.t1it_v Thcnrcnt
13. ARTS - AN! M; 358 or S.-\S Sin1ildrit\'1ll€Df€t1I
15. Yes. by the SAS Similarity Theorem
17. AXYZ -« ARST; by the Angle-Sum Thct::n'cn1.
mAS = 32°. Also. AA > A 1' since both are right
angles. Then, apply the AA Similarity Postulate.
19. Yes. AB and AC arc pmpt)rtirm.tl to AD and AI.
respectively. Also, the included angle. AA , is shared
by both Lt.-'lBC and AADE. 31.) by the S.-\:a Sitttilatitv
Theorem, AABC - AADE. 21. not enough: I‘ll.TI.‘l
AD E AB to ensute that AABC — AADE 23. No,
because AQRS is not at rigln ll iangle. Tlterefm'e.
AQR5 is not similiar to AKLM. 26. Corresponding
tngles are congruent: since CTH | K, it lbllems that
AAGH '= AABC. Also. A.-‘I is sltat-ed by both
tri tngles. so by the AA Simil.-trity |’o.stnl.1tc.
AAGH — AABC. 27. Since AAGH E ADE!-', then
Lu-lGH — ADEF. But A.-'lGH - A.-'lBC. so that
t".ABC - ADFF. 29. -RUST — /\['l."l’|": this mc-Ins
that 'U_Sand U7 are propottional to El? and [-17
respectively. l'h-at is. = —(.r
i _ (‘W Q Us
“W. But it is given that
U. — ‘V ...o,fi = But US = )(l' wlticlt “‘€¢llls
that UT = XZ. Alsn, AU E AX. S0 .£~.U.ST E A.\'l'Z
l1yS.-'~\S. 31. AA E AA and AB = AB by the
Symmelrit: Ptupcrty ol Cungruence. so by the
A.-\ Similarity l’ostul.tte, AABC — AABC. 33. If
AABC ~ ADET. then AA 5 AD and AB 5 AZ
by the Polygon Similarity l’ostul.1te, and it"
ADE)" ~ AGHI. thcn AD 2 AG and AE 5 AH. '50.
it follows that AA E AG and AB 5 AH by the
Transitive Property of Ctzngrucnce. Thus. by the A.~\
Similarity l’ostul-ate. AABC — AGHI. 35. Yes. Since
Tony copied two anglvss li'on1 the origin.tltri.1ngle.
then by the AA Similarity l‘ostu|.ne. the two tti.tng,|es
are similar. 37. Yes. Since Nliki L'.0[)lCr.l an angle that
is atljacent to two sides of her tt iangle, ol which the
lengths an: 5 times the lengths oftwo sides ofthv:
original ttiangle. then by the .‘.~A5 Sintilatity
SELECTED ANSWERS 91 3
saervtsuv passages
Selected Answers
Fheorem. the two triangles are similar. 39. 135
41. 60 43. 45.; 47. Yes: both have at right .-utglc
and share .1 non-right angle. lhus, bv the AA
Sintihtrity Postuhtte. both Ire similar.
LESSON 8.4
Exercises
6. t5 7. (1 3.15 9. 1o. 11.
I3 4:3 = 9.6 15. -¥- = l0.5 17. it 19. I or 2
21. \ and ABFF.-D 1l'C congruent corresponding
angles and AB is in both .=_.BAC and .-EBED, so
ABED ~ £3.-iC by the .-‘M Sintiletrity Postuhtte.
Simil trI)'. AACB — .r"1FCD. Then. by the Tmllsitive
Prupelly, £.EBD - £.FDC. 23. x = 16:}-' = IS
25.x:-_::-.1nt.iy=2
12. 3.1-‘-
27. Sample .1111.»-.-er:
A B
29. By the 'l'\-so-1'1‘-.1ns\'er:s.t| I’1uportion.1|it_v
Corollary. the Arruwed lines divide and the my
pt'D|?Drtion.1|lj.'. But the my w.-15 divided into
congruent parts. so AB is divided into c.ongrI.Ient
parts. 31. Each line have at slope at L 33. (0. 0)
.1nd(—l. l);w/E -— LH
36. Given: AABC with [TE such that -ITJIQ =
Prove: E || K
I’rm)f: Since 13-; = 11:. by the A\ld'(,l‘C Pmpert_v
NH O JD _ FCC .1!-
ID _ ‘ll _
|’0.SlIIi.ll€ :7", = Also, AA 5 AA, so
AABC — AADF by SAS Simil.trit\'. By the |’oI)'gon
SiIl'IiidIiI}' Postulate. AADE E AAHC. so DI: II BC by
the Ctinversa: ol the Cnrrespnnding Angles P0.stul.tte.
37. The st: ing for the note C should be placed
I31. cm from the string For the higher P. 39. 2316 cm
If
. so by the Scgnunt Addition
91 4 INFO BANK
\"
9: ll.9.i
'.‘
LESSON 8.5
I-‘xcrciscs
5. The ttianglec .me ‘iill‘lii¢ll' by the AA Similarity
Postnl.1tc.%', = t = 13 km 6. The tri.-1n;;lcs
Jl'€ similar by the AA Similatity Postul-ate.
fi = -3-‘; .1‘: I8 km 7. -460.(15cm 8. 4.8
9. 2.1 11. Itaéft 13.2! h 15. tn 17.25 19. 1-1.4
21. vcs.';—';l = = g and Alt-IKI - AJKL, since
both are iight angles: su the u ianglec are similar by the
S.\S Similarity Theorem. 23. AIR’! : 3-1; A UK] : 90
25. 't'es.;-‘if = = 27. Given 29. Poiygpn
Similttnty l’ostul-ate 31. nizl-MD = n1.£Y)\W
33. -'12 — -'-u1 35. Definition I2)‘-I1'tt.\iiiln
M1" — .\1
37. Substitution l'1'opcrt\' and Division Ptopeity
Ht _ t._I
39. Substiltlliml Property 41. — SI
43. Since vertical tmgles are congruent.
zB.»t<' -=~ 43',-tc'_ Since B7: J. B'—c" zsca mu
£B'C'.’i are both right angles, AB?/I 5 AFC’ L
l'hus,l1y the AA Sintil.u ity Postul-ate.
AABC ~ A.-lB'C’_ 45. 2 un 47. .-irntttge them
so th.-tt the t.‘llSl.il'lL'.1.‘ from Il11.‘lm.1;:_C to the lens is
20 times greater than the distance from the obiect to
the lens. 49. -1 units-' 51. 13 units: 53. 10 units‘
I
LESSON 8.8
TRY THIS [p, 5-35]
25 .
8. H b. 3‘ C. %
Exercises
6. -l'- 7. 3} 8. The vulume would be multiplied lty
2}‘. while the Cl'O$>-St?CIl0I'ldlE1lrZ'¢1 would only be
multiplied bv 9. 9. '—i' 11. 30 nt
131’: Z3m;A =-12.67 m-' 1533-: 17.2, 19.1%";
.141 at P21: _ '
21.5 23% 25.l'2—5 27. 2'”, 29. llmi
31. 6S(1<t11‘ 33. 4 35. :—f__' 37. 57.6 cm" 39. I U l cm
?
s -. .
. 43. l\o. Doubhngnll the
dimensions would increase the volume of the box
bv .1 Iitctor o1'2' = B. To double the volume. all the
dimensions would be in creased by .1 I".-nstor 01
.7’ = 1.1:». 45.1050 m-' 47 =l-13010115 as. 9
_ __j_ . _t; ._ ._ ._
51.}-'— _:.x+ 4 53..x—2 55..1—-I 57.3-17
41
CHAPTER REVIEW AND ASSESSMENT
1. Th: endpoints ofthc inmgc are [-6, 3) tnrl 1'9. ll).
5. If the triangles were similar. the propottion
§ = would be I] ue. By u'oss-nutltiplying. we
obt.un .50 - 21 = .16 - 18 or 6.10 = (1-13. so the tri tnglt-s
are nursimilar. 7. 5.4 9. SAS Simihtriry |'heoren1
11. A5. Similatitg; Pnstulatte 13. I2 15. 9.6 17. 8 m
19. 2-1 21. 23. 25. 1-1.4 in.‘
1.71.."-.1723:-.1
‘ll.-‘El?
27-OT
Chapter 9
LESSON 9.1
1111' T111 s, (p. 563}
I = ET" r: 7.33 units
Exercises
3. ?0°; 160°; 110° 9. 3.67
10
R N O
0
It is given that ' P and ' M are congrttcnt. and that
fi and E are congruent. Form mo IllilIIgl1'3$ lI)':'
adding the r.1tlii!’—R. W, E and Then APQR
and AM.\'O aue Conglutrm by $55. Thus. AQPR and
zi\'MO .irc congiucnt and hence the «res 63 .1111!
1 ' ) are congruent. 11. point P 13. E and EC
15. Sample .utsv1cr: ABPC 17. Sample .Inswcr: W
and E3 19. Radius 21. Chord 23. 130° 25. 1211"
21. 116° 29. 211" 31. 1531 33. 62.8.1
35 =11.-16' 37.57“ =11.46" 39. 3'2“ 41.233”
43. lg! 9‘ l[l.0S 45. QT‘ =- l.l5l1 47. S.tmple
answer: 240 11 49 =t2.77in' 51. 261: = 3l.63in.
LESSON 9.2
Exercises
1;. ./3 1.3 3. 24
9. to’ = 3‘ + 6’
me)’ = inc}-‘ + mm-‘
Thus, A/IBC is .1 right triangle and B—C .L W. Thus
:15 is tangent to ' C by the Ootwerse o1'the Tangent
Theorem. 11. .3‘/lg; 3J5 13. I0 15. Let E be at
chord in - M and consider the llnl.‘ 1'. which is the
perpendicul.n' bisector o1'P—Q intersecting E at
point X. Let In: the r tdius 0| ' .U. which is
perpendicul.tr to E. By the Radius and Chord
Theoretn. 371-57 bisects E so W also passes
through puinl Thus lmlh W J. E .—u1r.l L‘ J.
Since both 1' and T p.1;~stltrottg,h point X and are
both J. 'F’_Q . titer ntust coincide. Thus. the
|?Cl'[.\Cl|t.lltLUldl' hiseetor (Wm E‘. passes tllmugh the
center of the circle, M.
17. Sample .l1'ISVW.‘l'!
SELECTED ANSWERS 91 5
ssemsuv pezoetes
Selected Answers
l'he tan tent line .1! the int A must be
is
pet'pemliLulat' to the radius AP.
19.2 21. V/§= 1.73 23. I 25. .1: Ill-l.29nti|es
21. P = 48cm; A = 9CH.l‘|'I: 29. 6fié6% in-'
LESSON 9.3
Exercises
1. 55° 8. 35° 9. n1AGl'H = 50"‘. IHZGKH = 25°.
mzfl-K = 90°. n1.’.'KH} = 45° 10. mzKGH = 90°
11. 30"‘ I3. I2D° I5. lSD° I1. l.ZD° I9. I00"
21. 29° 23. GI“ 25. 50° 21. 80° 29- 31°: 34°
3:. -135°; 43.5“ 33. 200° 35. 80° 31. l80°: The
sum of the measures of the inter ior angles of a
qu.'tdril.1ter.tl is 3(10°. 39. 200° 41. I303 43. (I-'_\."l°;
l'he measure of an inscribed angle is one-half the
measure of the intercepted arc. 45. H80" -30‘; The
n1e.tsurt‘ of the inscribed angle is one-halt" the
measure of the intercepted arc. 41. I8D"; l'he sum of
the measures of the interior angles of a quaclrilateml
is 560°. 49. The longest sides of the triangles
intersect at the center of the circle. Both t'igltt angles
intercept an an". that measures lS0°. so the
inltI‘CCplI:d arcs 1re semicircles. Thus. the longest
sides of the triangles are diameters of the circles.
\\'l'ti1.h intcrsea at the center at the circle. 61. litre m
is the .-mgle hisertor of ACXD. 53. m/.'?. = mzi
55. Angle Addition l’ostul-ate 51. Linear pair
pt't1l\t:r1v 69. Llivi-:it:-II l’mpert_\' ullfqualitv
6|. Dcfi nition of perpcntliv:ul.1r.
LESSON 9.4
Exercises
5. 69° 6. ID3° 1. 22” 8.3. 35° b. IOD° 0. 80° :1. 20°
9. The ship is outside the circle ol'cl.tnger since
mZB.\'A < mABC.*l. II. I?” I3. 35° I5. 33°
11. 75° 19. tx+ 21° 21. I09“ 23. 28° 25. 105“
21. mil = mA?. + ntfi.-IVC
29. nté/ll-"C = %(t1l§E — lllrlit }
3|. mzl = ml/WC + mA2 33. If
35. a. 60° b. l50° c. 30° d. l20° e. ll0°
t. 125° 9. 55” h. 70° I. I 10° 1. 110'’ 1:. 70°
I. 40° in. I60” n. lDlJ° o.n80° p. 20° q. 360°-32°;
trill’? = 360 - tn.t{A?T r. if "141 = —',-n1rl?l:.‘?
3. l8ll°- ‘Ti; m4? = émfi t. r‘‘— lat)”;
nté.-WC =-mzl — tn-Z2 31. one-Intlftlte difference
of the tnettsutrs of the intcrcqvted arm‘ 39. The
n1e.tsurc ol'.1 t.titgcttt-t.1Itp.et1I mglc with its vertex
outside the circle is the tne.1sure ol the major arc
minus ISO”. 41. Two sccants or chu-rcls 43. On the
circle 45. On the circle 41. tnzzll.-’C = %l'|I.fi\?
91 6 INFO BANK
49. tn/.'AVC = %(n1.'4’,‘?C— llbflzj = n1rf/‘E — I80"
51. Tm) secants 53. Exterior of .1 circle
55. nizztl-'C = §(_n1§(:"'— ml?) 51. 70° 59. 95'‘
6| . Yes: t:\'er_vthing was t'educt:d In’ it commu-n lactur.
G3. 9
LESSON 9.5
Exercises
6.? 1.8 8.4 9.4 10.60 Infiorfi 13.17
15. Satnplt: answer: ASVR and L~.Tl"L-'; AUSIV and
ARTW I1. 6 I9. 5 cm 21. ~ 3.71 cm 23. ABPV
25. 3 21. —.'‘'*,‘‘'‘'° 9: 15.193 29.——-'°*,‘@;2.:-'6 or
7.34
31. Tvm secant segments
35. II'lICl'i()l'(Jf(ll'1.lC 31. AV - VB = ('1-’ - VD
39. 15.22 km 4:. 2101: ~ (59.1; k'l'Il";
4001: = I2.‘-6.64 cm‘
43. Srtc/3317+ Zsrt as 3-41.85 cm’;
-“—’f—“ = llS.8Sctn 45. Delinilionol-.1
p.ira|le|ogr.tn1. 41. .\|tern.1tt‘ Interior .-\n;.:les
l'heorem 49. C|’Cl'C
LESSON 9.6
mvmts. (p. on)
a. Center t—3. .3): 1:. Center (3. -3):
radius Ir‘ nnlius 7
:1. Center (-2, 5);
raclius \/ii = 7.07
a. Center (4, S];
radius 9‘ 30 = 5.43
V
Exercises :5. {5.o1;(—1,o1.{o../§};(o, —\/5}
6. .1"-intcI'¢q.1r:~::(l0. 0) md (-10. 0] 11_ x3 + J.-’ = 36 19_ 1-‘ + y: = [3
_v-int-::r-:v:1\ts: ID. ID] 1nd (0. -ID) 21, _\—‘+ (y _ 6)-" = 35 23, f__\-_ |]-' + [_y+7}-' = 100
1_ 25.(o.o:;:=1o 21. [D.DJ;r= ».e"Io‘| 2940,31;
J: y Polntsongraph I’ = 7 31. (-3. 0); I’ = 7 33. .\‘I +y" = I6
0 no (0.101. 10. 101 35. [x + 2}’ + (y — 3}’ = -4
5° 0 (‘°- °1-l"°- 5' 31. Sample .ms\~.-er: 39. Sample .1nswer:
6 :b8 (B.6).lB.—8l [_\--4]-‘+’.1=.4 [_x_ |}5+(y_5f=|
6 [B (6.3].( B. B]
8 16 (8.5).l8.—6l
-8 t6
(-3. 5]. F8. -6]
8.
Y
A
F-
((1.\|(§5\.\
8: '3- 3| 1 1 2 : -
s_ 4l.[x—2)+(y—3) =9 43..\ +(y—l) =2)
“W (8-6) as.(x—2',‘+<y—3}‘= mo
". 41. (x-3)‘+<y+5)'=-a
2
A I I I - no. 9:
'—é'—€'—-’I—iQ 5'-5'é'B' X
-2-
I.
[-3, 5) _6_ (8.-5)
‘I-5,-5] (B. -8]
\_ [~
>-
9. .\-intercepts: (8. D], (0. D]
_v-inrcrccprs: (0. 6). (0. 0)
'I~0
X y Points on graph
0 3, O (U. B). (D. O)
B. O O (B. O). (D. O)
I 7,—l H.7).(1.-II
-1 3 (-1, 3|
4 B. 2 (4, B). M. 2|
7 7. -I (T. 7). (7. 4|
B 3, O (B. B). (B. O)
9 3 :9. 3)
1:. [Ni 0); (—5\/E. 0}. (o. 5‘/2'); (_o. — 5‘/5] 51% 51. 3.001: in. = 9.0 in. 59. 9
SELECTED ANSWERS 91 7
s.IeMsuV pezoeges
Selected Answers
CHAPTER REVIEW AND ASSESSMENT
. -1: -- - (\
1. sample answer: B(.,A!’ AAPC, CDA 3. 72°
6. I3 1. True: AQPX ’=' ARPX 9. 20° 11. 25° 13.
-"l?‘° 16. 94° I1. 90 I9. 6
2|.
23. .1‘+}-VI: I 26. .H0It 9- I008 in. 21. lI._’rS mi
Chapter 1 0
LESSON 1 0.1
mv THIS tp. o3 I]
Let f)’ be the other angle. I hen tan ;3 = ' '
35' a
.: 1:
ll
'51
Exerclses
6. 0.62. Answers will vary due: to itmceuracics in
l'I'It.‘.l5lll(‘|TI(‘ll[. 1. I. IS. /\ns\vcr$ will V.-'lI'\' due to
irmccuracies in measurement. 8. 0.36 9. 0.8-4
10. 2.75 11. 37° 13. 2.5 16. 2.4 11. l 19. 2.36
21. 1.33 23. 57.29 25. 54° 21.8-1° 29. 0°
3:. Ian 45'’ = g; .t— = 2 33. ton 23" = ‘-3; x = 22.57
35. 194.2 m 31. 1-1.0“ 39. lIl9.6 ft
41. V = l099.5b units‘; 5 = 596.90 units:
43. V a 55.4-19.35 units‘; 5 =» 1353.93 units’
45. MO = 112 units;
QN = 7.42 units
LESSON 1 0.2
Fxercises
a. 141cc: 6. 7 rm 1. 13 feet 3. 34° 9. 59° 11. fi
13. 15. 11. 22.62” 19. 1- 21. X 23. Y
25. 0:31 21. 0.62 29. 0.71 31. 6|” :3. 83°
36. I8-° 31. 67.5 units; 39. cos"lcos 9] = 9
III. sin 70° = 0.9397; cos 20° = 0.9397;
sin 70° = curs 20°; they are the same be: 1115!: tht: side
opposite the 70° .tnglc is the side .1tlja-zcnt to [he 20°
angle. 43. (90— 19]: (90 — 6) 45. cos 19 41. (tan Bf
49. I9fee1 51.4.8“ 53.x= 1 = Lf; =
V"?
91 8 INFO BANK
65.p=q= l;r=\/.5. 61.q=£=S\/3;
p=q=8v’3 59. 18°
In!
LESSON 10.3
TRY ‘nus (p. 650]
.<in"(0.57.i(3} '5 35°
The second angle is I80“ — 35° = 145 '.
Exercises
(-
8. (——‘-'2-1, —%) 9. sin 19 = 06128; cos 8 = 0.7660
10. y = sin I2.-\llc'1 10 minutes (600 sec]: -0.866.
After 20 minutes: 0.906. After I llI.lrlll'2 0. .-\l'tc1' ll
hours: 0. II. In Qu.aslr.ants I and IV cosine is
positive. In Quadmnts II and ll|,cosine is neg-.ni-1-e.
12. 15°; 135° 13. 0.9063 15. -0.900}
11. 0.4226 19. -0. I226 21. sin 15‘ -=- 0.7071;
cos -I5“ = 0.7071 23. sin 225° = -0.3-'07l;
cos 225° D-= -0.70I"l 26. sin 30° = 0.5;
cos 50° -= 0.8660 21. sin 2l0° = -0.5:
cos 210° = —0.S(>(10 29. x = cos 30" = 0.8660;
y = sin30° = 0.5 31. .1: = t.t)s90° = 0;y = sin90° =l
33. .\'= cos 180° = —l;_v = sin 180° = 0
35. .\' = cos 300" = 0.5; y = sin 300° = -0.8660
31. 45°; I.’.l5° 39. 30°; I50" 41. I9”; l6l° 43. 37°;
93° 45. 28°; I52“ 41. [he horizont-.1l position is
given by cos 1. where I represents the number ol
hours. .-‘Liter 2 days (415 hrs]. lht: hurizuvnlal position
is 0.6691. After 5 days, the horizontal position is
-0.5. 49.11 51. b 53. mn A 55. B [or 90° — A)
LESSON 1 0.4
TRYTHIS [p. 656. Ex. I]
In
(.
TRYTHIS lp. 656. Ex. 2]
Q = 42°
3
2.
van
Exercises
a.b=- l0.I:r=- I13 5. lIl.7-1° 1.=a .?..59h 9.27.46“
11. l5.-$5“ 13. 8.02 cm 15. 2.02 cm
11. mil’ = 40°; 1} = 6.16; p = 4.5?
19. HIZQ 9-‘ 42.3!»-1°; mZR -3 77.06“; r as I0. I5
21. C1151.’ l: mil’ = 76.48; m£Q = 58.52°; q = 9.65
Cns¢'2: IIIZP = l03.52°; HIAQ =- 31.-I8"; q -— 5.9I
23. S.-lmple .mswcr: ll'rr < Ir sin/L than side at is [00
short to form .1n_vtii.1ngle. so no triangle is possible.
25. Sample answer: ll" bsin,-l < n < b, there are 2
triangles possible. one l1y“swinging" side :2 to the
left and the other by "swinging" side it to the right.
27. Sample .rns\\-er: lln S b then no tritmgle is
possible since: for an oblust: or .1 right lri.-1nglc.thv:
side across from Elk‘ obtuse or right angle must be
the Itmgcst side ul thc tri.-tnglc. 29. I trI'uq._',Ic
possible 31. 2 triangles possible 33. sin.»‘I = 'I—‘_;
sin B = 35. E = in = since then-
r. rt b I
all ll'C equal to the same quantity. 31. a sin B
39. Iasin.-I = a sin B All. 43. I. sin .-I
45. Multiplication Property of Equality
41. = 49. Tmnsitivc or Substitution
Property of Equality 51. 7.44 km; 6.7-1 km
63. Tm\'t:I'A is closer to the smoke plume. The
smoke is 9.10 miles from the tower. 55. 3.62-‘. mi
51. S = 282?.-'l m"; V = I-$.|3?.2 n1‘ 59. =I I.3 units
81.6-5.9I° 63. 45°
65.91
LESSON 1 0.5
mv ‘nus (p. 604, Ex. 1)
Ir 9:20.65
TRY THIS lp. em. Ex. 2)
mil? =~l l7.9°: ml!’ =- 32.7°; mAD =~ 29.4”
TRY nus tip. 665]
b :4 5094.07 mi
Since 5091.07 < 3280 It. campers at Site I 1nd 3 will
be able to communicate directly with each other.
Exercises
5. II = 28.42; C = 53.97°; Ind.-‘I = 76-.03°
6. E as I I9.66°: F 13 27.6I°; mZD 9-‘ 32.73”
1. C-unpcrs at sites 2 and 5 cannot comnumic.atc
direclljr since their two-way mclius luwc in range of
only 7920 lirct. and lht: ‘list.-rncc between them is
about 8-I92 feet. 9. r x» 1. ll units 11. mil » 8.5.3.3”
13. méB = l53.8-1° I5. ntéG = }'2°;g = 8.8;
I1 =« 5.44 11. 111.40 -=- 2157"; n1z.\-I as lI2.-13°;
m »= 55.95 19. mil! 2: i'6.t';5°: 111.13 K 5-I.I7"’;
m£T = 19.18" 21. law ofcosines
23. Sample answer:
3
5
25. law of co<ines 21. It cos 9 = c.
29. :1’ =11’ + (c, + c]-
3l. :1: = Ir‘. + [L] + ()2
G: = Ir‘. + cf + Znr + 43
.r'= I:-'+2(-lncos/ll - r+.—’
tr" = II‘ — llrc cos,-I + c"
:1‘ = If + L” — Zbc cos .-1
33. 63.32 feet 35. The road will be 21.33 km long,
and the angle Ibrmt-d is 12.2-1°. 31. mm = -Il.(u5°;
m£B = 52.89”: m4C = 8?-. ln°
43. Yes. SAS similatih 45. PQ = I?...‘.i9
LESSON 1 0.6
TRYTHIS lp. 6754. Ex. I J
75
R
esultam
_, Vedor
TRY THIS (p. 674. Ex. 2]
If two equal forces are applied in opposite directions,
the resultant vector would have magnitude 0. If the
forces are unequal. then the resultant vector would
lmve a nmgnitude which is the difterence of the
tnagnilutlc at the two vectors.
Excrciccs
6. 7.
‘:7
35+?‘
.3‘
8. 2.5 mph; 5.$.I.3° 9. 1.16 mph; 8.3-1°
I3.
II.
71'
. A _. .
-3
D
_. _.
a-b
SELECTED ANSWERS 91 9
U‘
B
I
E
saemsuv pezoetes
Selected Answers
19.
I
23|
‘r‘| ~ Io.7I:22.:.9° 2:. |?‘| ~ I3.76;21.I9"
?‘| = 6.78; I35-‘|°
25.
2.7
4.1
1.65 mph
21. I2% 29.;-=9 31. lo 33. AI’ 2- I528
LESSON 1 0.7
mv nus Ip. 682]
v:ns3[I° —:~:in 30° X 0
sin 30'’ cos 30° I
_ -0.5 1.73 -0.63
‘ 0.8? I 3.I0
The new vcrticcs arc: D’ = (-0.5. 0.87].
E’ = (L73. II. I-" = (—0.63.3.IOJ
OI-J
.__,_
on
Exercises
5. 1': L23-:y'= LSI e_x'=—4;y’=5
1. x’ »= 6..I.I;y' x» 0.5m s. /I’ = (0. 1.41).
B’ = (2.12. 2.12). C’= (0,2.a3J
9. A’ = (-0.54. I36). B’ = (0.93. 2.35].
C’: I-1.23.252) 10. I’=(I..s7, -0.37).
B’ = (1.5, - 2.60],C’ = (2.73, -0.73] 11. (-3.54.
3.541 :3. I-mo.-3.2.3] 15. (2.99. 6.41) :1. 90°
0.7: -0.7:]
19. 270° or -90° 21. 45° 23. |:0JI OJI
-0.5 -0.87
25' [M7 -0.5]
920 INFO BANK
-4
I-°-7‘:-3 '31,. 11.41. -2.33:
‘ I
(2.12.-4.95)
C—-
(-1.41, -4.2d|
sin 30° Luv; 30" sin 40° \'.()S 40°
_ 0.3-4 -0.9-1 _
‘ 0.9-4 0.3-4 '
[cos7D° —sin7D"] = [034 -0.94]
3‘ |:Los 30° - sin 50°] [cos 40° - sin 40°]
sin 70° cos 70° 0.9-! 0.34
A rotation ol'3D° l'0I|o\\-cd b\- d |'ol.iIi{In of-I0" is
equivalent to .a rotation of 70°.
_ cos0° -sin 0° _ I 0
33'iR"i_[siI10° cos0°]—[0 I]
The product at any rotation matrix Ind thc idcntitv
matrix givc-5 the rotation nmtrivc. 35. The product of
two inverse man-ices gives the idenlitv matrix.
[R ]_ 0.82 -0.57
-‘-‘ ‘ 0.5? 0.82
[R ]_ 0.32 0.57
"" ' -0.57 0.32
['<«]><['L~-»]=[.'I ‘.’]
31. a. (2I.3}‘, 46.98] b. I he coordinates are
[30 cos[6t"] + 42 sinI6t°). 30 sin(6I°] — 4.2 costar")
.lI'tcr running Iur I‘ minutcs. 63.-L3”
41. ran 37° = 0.75; sin 37° = 0.60: cos 3?“ = 0.80
43. I ‘III 250° 9» 2.75: sin 250° as -0.94:
:05 250'’ x» -0.34 45. 70° 41. 56° 49. No. The slope
is too steep. 9 = 30.96°
CHAPTER REVIEW AND ASSESSMENT
1.% 3. 23.2“ 5. sin .-1 = cos,-1 = 11-’: 1. -483°
9. (0.34. 0.94) 11. I154"; I68.-16°
sinfl
I
133.5 130
13. m£R = 2l.26°; m£Q= -13.7-1° 15. l07°
11. lH.0b 19. mil = lD7.24°
21.
el
25. 03,-!)
21. D'[D,D), E'(2.l. 2.4). and F'(I.b,3.2]
Y
F'{1.6. 3.2)
29. 59.2 m 31. .\ force of IO-11.9 lb is n-quircd to
push the mxck uphill.
Chapter 1 1
LESSON 1 1 .1
Exercises
5. I6. I8 8. 5.56 1. Sample -.1115»-er:}K= J. TE; 1 he
intcrscuiun scclns to In: thc Lcmcr of the spiral.
8. The long side orthc rectangle should be I 618
inches. 9. 4.85 11. 5.26
¢_ 1
‘3-T-T.
I1. bample answer: In a circle of mdius 3 cm,
DE a 33 and E}! as 5.7. 19. 103°
= l.6l8035989 = :1:
21.
fl = 1\lI'| [I18
I)!‘ ill! 36'
23. mam; = 72°; mAlbD= 72°; ml! = 36°
25. g. -as L62 a. go 21. 34.55.39. 141. 23.3 29. The
ntios sv:v:n1 to .-1ppro.1\ h ¢.
31.6765
33. gs-1.67
7_
3-. 1.4
%=l.25
M _ —.
lT— 1.2!
20_
“-1.25
3x5
3
LESSON 1 1.2
Exercises.-
6.4 1.6 8.2
is closul ID the golden ratio. 35. I-‘ in. X H in.
1. 5.2 39. -1.5 41. (0.6-I28. 0.7660}
11. I0 13. II 15. I3 11.3 19. -18 21.10
23.
SELECTED ANSWERS 92 1
s.IeMsuV pezoeges
Selected Answers
21. -I p.1thw-a}-s
.1
‘[3. 3|
I
2 .‘
*.
04, -1
The bisectcnr has .1 bend in it. l‘lOW("n'Cr. the bend
consists ot'onl\- two points, rather than the three
fortncd in Exercise 29.
33. Because the tanicab distance between (2. O] and
(.3. 2} is odd. at perpendiv:u|.n' bisector -:'tnnot be
l'otn1ed.
35. The points Ire: 1-1. 0). H. 1), 1-1. 2), 10. -1 ),
(0. 3}. (I. —l J. (I, 3). (2, —l J. (.2. 3]. (3. 0]. (3. I].
ind (.3. 2].
Szttnplt: answer: The points forni two sets ()1 parallel
line segments oflengtlt 3: or .1 square -nitlt side
length 4 which has its corner points deleted.
31. The set of points Lt, y) will be the intersection ol
the circle all lddius I0 u:ntere1.l about (0. 0] and its
intt rior and the circle of r.-idius 8 centered about
(5. -I] and itsittte|'i01.lt-:n1ty should luck for places
within the region Sl'l(lrWll. intluding the edge paints
and sides.
922 INFO BANK
39. '-"-‘ = 8.57 4:. true = 11.22 43. = 0.85
LESSON 1 1.3
[Exercises
5. Yes 6. \lo 7. Yes
8.
A B
O
c
The graph docs not contain in Fttler path since
vertices B. C. D, and O are odd.
9. Yes
A 3 c 1::
G I
II. neithet I3. Euler path and circuit 15. Euler path
and circuit
17.
E : D
O
A = 1'.-'
Tl'1eI'e is no Euler circuit.
19. Euler path: no Euler 1.ir1.uil 21. S 23. 6 26. 8
21. The sum c1l'the degrees of the vcrtiecs cnfa graph
is twice the 11u1t1be1' ofedges. 29. Let S, be the sum
ol the degrees all the even v1:rtiL'1:5 .m1.l let 5,. he the
sum ot the degrees ol the odd veniccs with F the
number 01 edges. Then S.+ S_ = 2E. l\'ute that S, is
even sinte the sum ol'ew:n numbers is even. Then
S . = 7F - S, is even, since the difference of two
even numbers is even. T|1erel'ore.S_. is an even
number. that is. the sum of degrees at odd ven ices
is an even numbet. But the only way a sum cnfodd
lll.llTllJt:lS is even is it there cut: an even number 0|‘
those odd numbers. Therefcnn: the number of odd
vertiees must be even. 31. Yes
33. Sample answer: It is not possible. Consider each
bot and the outside to be a vertex and each segment
between two boxes as an edge.
OUIBIOE
The vertices representing the three larger boxes will
have degree 5, so there can be no Euler cinuit
35. Yes; all vcitices of the graph are even.
37.
Graph for Jo
In lo's graph, everv venex is even, so there is an Euler
path.
Graph tor Tamara
In 'l'amara's graph. there are two odd vertiees, so
then: is an Euler path.
39.
/
M. II" it shape is a square. then the shape is a
rectangle. Converse: It".-1 shape is a rectangle. then the
shape is a square. 43. If a shape is a do-decagon. then
the shape is a polygutt with I2 sides. Converse: ll 1
shape is .-1 polygon with l2 sides. [hen the shape is a
dodecagon. 45. 8.3 41. 4.4
LESSON 1 1.4
Exercises
6.a.l.).\l 7.l).c 8.8- II-2+6-2
9. 6 — I}. + 8 — 2 11. outside 13. The number of
times the ld\' liom P crosses the Llll't'C is always odd.
I6. mld: esen
I7.
0}
B
0
on
C I I
G W E
19. If one were inside and one were outside. there
would be no way to connect C to F. without
intersecting the simple closed cut"-'e.
2|.
bantple answer: note that B can be conneeted to G.
But then BGAW I'm ms 3 simple Lluscd t.LIn't: with
C on the inside and E on the outside. Everv cutve
connecting C to E inlet Stffils an already Ll.\llll|‘.'LlC(l
utility line. [The other eases lnllnw for similar
reasons}. 23. 20 — 30 + 12 = 2; the polyhedron h is
I2 I‘-aces, so it is a dodecahedmn. 25. The path
\'.()\"CI'S both sides of the Miilius strip. 21. The result
is a loop of papet with four |ta|f~twists. 29. Yes
31. Yes 33. Cut the bottle "diagonally." Start at any
point on the surface and return to it without
crossing itself. By avoiding the toined edges entirely.
this produces .1 surface without dividing it into n‘I(I|E
than one piece. Then cut around the sell"-
intersection. 35. Jr = 3
31. Sample answer: Al and L4. L3 and L7. L6 and
L7 39. .55‘ orattges 41. la .. I 15.6
LESSON 1 1.5
Exercises
5. |t'.I-1, B and C ire tngles of a triangle.
tnL.»‘l 1» mil? + mLC :- I80" in spherical geoinel 1:.‘
and n1.-LA + mLB + n1LC < I80“ in l't_\'l'|t:I'l._1()li(.
geome1rj.'. 6.Ye< 1. No 8. No 9. Yes 10. Yes
11. No I2.Yes 13. No
SELECTED ANSWERS 923
saemsuv passages
Selected Answers
15. Sample answer:
2-qon AB
/lsolidl
Q
The 1't:rtict:s must ht: opposite each other on the
sphvsre.
11. Satrtplt: answer‘:
The diagonal is B—D.
19. Santplt: answer:
2|. l|':1n arc is ortltogorial to .1 circle at .1 point. then
the tangent oftht: dI'L' is petpentliLular to the tttngcnl
of the circle at that point. By the llingent Theoretn,
the ta1ngent of the arc is also p€r['I<.'lltllCul¢1|’ to .1
r.1t.lius of the circle drawn to the paint of tangettqr.
l'he ttmgent of the circle at the given point must
contain the radius ofthe arc, and so it must contain
the center til the arc.
As Egcts (.l(JSCI' tn the lint: tht: ratlii til’ the arts
gt‘! VCl'_Y large.
924 INFO BANK
25. It",-l and B are endpoints of a diameter. then
if m and they never inttzrsed. In this case the lint:
through l and B is the circle P itself. 21. Infinitely
main‘ lines can be drawn thmugh A that do not
itttet'st:t.t E. This 1l'l(lr\\“3 that the l"1I.tllt:l l-‘nstulatt:
does not hold in l’oin-:.1ré's systern. because there are
intinitely ntany lines through .-1 that are parallel to 8.
29. The sum (‘ll tht: tneasures of the angles in the
triangle is less than I80". [Mcasurc the angles with a
pt'otrt1ctor to get .1 lltirlv accurate re.1dittg.) In
ELIt.lit.leatt Gt:t_1ntt:tr\'. the sum of the angle mt:ztsurt::~:
ol'.a tritngle is I80”. while in sphcti-:.1l gcotttetry it
would be greater than 180".
31 .
Q
A»
Cluadrttat:-rat ABC!)
33. ln hyperbolic geornetry. the sum of the angles
ol an rt - gm: -c (rr - T1130" 36. The triangles ltit m d
tlat sttrtitce. 31. Sample .-tnswcr: The mcndvzls are all
composed ofa number ofequtlateral triangles about
El given 'g'CI'It:.‘(. But in tht: lirst ITlCl\|Cl. the angle
nicasures of the triattgles about the vertex add to less
than 360°, so the model will not lay llat: it is convex.
In the SCC(Jll(.l mnt.lel the sum (ill the angle mt:ztsurt:s
cqtnls 360°. so the ntcndcl will lay ll.tt. In the third
model the sum ofthe angle measures is greater than
360°. 50 it will nnt lay flat: it "liunt.hcs up." 39. .-‘L
Fuclitleatt plane will be fcn'rncd. This is ctlled .1
tessell-at ion of the plane by equila1ter:tl triangles and
will t-:ttt:ntl to inlinitclv nmny triangles.
41.
A B
F
D C
43 .
A H ‘ 3
L J
E
G J
D K M C
ABCD is .1 square, so AB = BC = CD = D31 and
AA 2 AB 2 if 2 AD. Also. the same compass
setting was used to draw all four arcs, so
.‘1E=.-’lF=AG=BH =Bl = C}= CK=DL= DAL
lly the Overlapping Scgnit-nts Tl1v:cIrt-n1.
AH = I'B = B} = IC = C."-W = KD = DG = LA. By the
Segtnent .-‘Lc.l(litinn l’us1t.tl.-tte. HF = II = A-{K = GL
ny s.-15, M H! 5 z'_\B.lF 5 aca-11=— /\r:cx'_. so
HI. = H = M1 = KG because CPC |'C. Let
AB = 1 unit. Sime AABE is 4 -IS--15-9Otri.1nglc.
.-IE = AF = BH = By the Segment .-‘tdclition
l’ostu|.tte.Al- + BH — HF = AB = I, so
HF: 1- - %: = 1- x-5..-\|solt_1't|1e Segment
_!'
\ddition Postulatc. AH = I — A.-tHl isa
45-45-90t1'i-attgle, so HI. = \/§(l — = I —
so All = UL. Thus. all sides ul HFIIMKGI. are
congruent. Also. because Cl’Cl'C, ZAHL. = AALH =
éBF] = BLF = CIM = CM] = DKG = ZDGK. By the
Lincar Pair 0|‘ l’rupt:ny. ZLHT -'-' [HT] 2- IF” =
é]I."»l - 4l.‘.lK = (MN; = AKGL = AGLH. Since
all of the sides and angles are congr uent. HFJIMKGL
is .1 rvztgular octagon. 45. S.-tmplc .-ll'IS\\'t:l': the graph
has four odd 1.-ertices, so no Euler path or circuit
exists. 41. SIDE and CLOT are topologically
cqui1.-alcnt. I AST and CO7Y 'IfC not topologically
equivalent since A is not topologically equimlettt
to 0.
LESSON 1 1.6
Exercises
6. The points where segments conned to the lztast:
form the Cantor dust. 8. lfthe two boxes above a
box are both shaded ot unsltaded. tlten the box is left
unshadcd. Ilowever. it one oi‘ the lmxcs is shaded
and one is unshaded. the box beneath them is
shaded. 1. The shaded areas ate inverted p\'l'<Il'tlldS
with increasingly longer l.>.ases arranged in 1 self-
simil.u' patterns. as in Activity 2.
I1 [9|35]a4|1ze|1zels4|3s|9|1 |
| 1 Ito[45l12o[21o[252[21ol12ol45lin-I 1 |
I 1 In I5s]1es|a3a|41s2l41s2[3ao|1es|:.5I11I 1 I
[ 1 [also ]22o|49s|192|924[792|41.=s|22o]eaI12I 1 |
9. I8 11. lO.l25 I3. 36 16. 81 11. The 'tre.1
decreases, and its limit is 0.
2|. P=3)< lB= 54 Step 0
P: l_’><6=72 Step I
P=18><7=9{1 Step 2
23. The area oi the sttuuwllalcc is .-tlwdys inert: tsing.
The area never becomes infinite because the
siiuwllakc can always be enclosed in .1 circle of radius
ID. I cm.
A
T
25. l.‘I¢lll'l[.1|C .-ut:~:\\-ers:
283“ 5??”
‘- iterations
I iterations
21. The 'll'C¢l increases as iterations intrease. but not
without bound,bcc.1usc thc -tI'l'I0ul1t it incn:.is<~s by is
.1l\v.n-s less than Italfoftlte lltLl‘<;tM: oi‘ the previous
iICI'dtl('Il1S. 29. l(1;f14 3|. l-3.8 33. 7 36. I-L2
LESSON 11.7
Exercises
1: x
6. The resulting figure is at iectangle with vertices [0,
0). (0.32). (-4.3). and [-4. 0).
SELECTED ANSWERS 925
saemsuv pezoetes
Selected Answers
8. The points or intersection should be collinean.
9.
V
B t
I. Prntmnuc
,0. . ‘ k x
—-1
-8
Image
‘I3.
t5.a..\'
17.
19. C; H; K 21. B; D OI‘ E
926 INFO BANK
z A" Y r
31. deductive 33. deductive 35. -I 37. E: 39.0
CHAPTER REVIEW AND ASSESSMENT
1. 4.85
3.
x w B
Y 2 A
9. Eulet path; no Euler circuit 11. neither 13. Yes.
Both are qimplc clnscd r.ut'vcs. 15. -4 17. The two
ctuves that intersect at the endpoints ot'.1 diatneter
of the ball are bullt lines in spherical geoundty.
19. KL. KN. MN
21 .
H
3h
rF
U: 3”
:P
I‘
23. The area otithe nth iteration is r tnot'e than
the area ofthe l_fI' — l)st iteration. The area ofthe
fractal increases, but it is bounded.
26.
16
12
B
&
40
27.
29. 73 ft on 28 ft 31. The photos wete taken tiom
(lilTerent l1eights. .-\let's phuts have nmre detail.
so his metsuren1ents may include small inlets or
peninsulas th-at ate not visible in the satellite photo.
Chapter 1 2
LESSON 1 2.1
mv mus, (p. 769)
bample answer: Valid argument: If an animal is
an aniphilsiatt, then it is a vertebrate. Frogs are
atnphiliiatts. Theretore. frogs are vcrtehrttes. Invalid
argument: Sc-n1e reptiles are venomolts. Chanuleons
are reptiles. l‘heret'ore. Chameleons are venomous.
Exercises
6. Argument lurm: tmnlns pmtem {valid}
7. Argument Totm: nmdus wlletts [valitl' 8. Invalid
form: allitming the consequent 9. Invalid form:
t.lenying the antecedent 11 . By the PHD{lll't' prmens
argument form: |'herel'ore, she did .1 stupendous
amount ol" work at the last minute. 13. lt'Sims is .1
man ofgood moral char.-it ter. then he is innocent.
Sims is not a man ofgood moral character.
Therefore. Sims is not innocent. Argument lot In:
denying the antecedent; inv.-tlid 16. It the plan was
foolpmof there were no unpleasant surprises. [here
were unpleasant sut pt ises. Therefore. the plan was
not Toolproof. Argument Form: mmln.\' l‘0llt‘l'£.\'.' ‘t-'.1litl
17. If the building was olisound construction, then it
survived the storm. The building did not stm-iv: the
storm. Therefore, it was not of sound construction.
19. If the building was of sound construction. then it
survivet.l the storm. The lauilding was not at snuntl
construction. 'lT1eretort‘. it did not survive the storm.
Invalid 21. Invalid 23. |n\-alid 25. Invalid 27. \'alid
29. False 31. False 33. Yes, sinec a v tlitl argument
guarantees that its conclusion is true if its premises
are true. 35. Sample answer: In football. if a teatn
does not move the ball ll] vards in 4 dawns, then
they lose possmsion ofthe ball. 'lT1e Mammoths
did not lose possessiott of the ball. Thetefore. the
Mantnwths moved the ball at least I0 yarcls in l
dow ns. (mmlns rollettsl 37. Yes. using the SSS
Postulate 39. Yes, using the SAS Postulate 41. I 10°
43. 6' = 60°; sin6' = % = 0.3m; cosb‘ = 0.5
45. 240° -
bl
LESSON 12.2
Exercises
5. False. because only one of the statements is true.
6. True. because one olithe ~:taten1eItt is true.
7. True. because both of the statements are true.
8. False, because both statements are false.
9. ~[r.-\l\'Ds) 10. - 1‘ OR -vs 11. A eartm is a
veget.1ble,at1t‘l Florida is a state. The coninnction is
ttue because both statements ate ttue. 13. The sum
at the measures ofthe angles of a triangle is I8lJ°.
and two points dz terntine a line. The conjunction is
nue because both statetnents are nue. 15. Points in
a plane equidistant from a given point turtn a circle.
or the sides of an equilater 1| triangle are congruent.
The disiunction is ttue because both of the
statements are true. 17. The figure is not a redattgle.
19. Rain does not make the road slippery.
21 . a.
:13 P -l-IT-
T F T
F T F
b. ~[~p) is logieallv equivtlent to [J l)c<.ause they
both have the same truth values. 23. A/WC has two
equal angles, or AABC is isosceles. 25. A.-1BC does
not have two equal angles. 27. A l and .42 are
adjacent. or Al and 42 are acute angles. 29. AABC
has two eqltatl angles. or A I and £2 ate not acute
angles.
SELECTED ANSWERS 927
saemsuv passages
Selected Answers
pofla lpofiatofl
T T
-n-n-n-t-t-t-ta
-n-n—(—('n'I't—l—la
r
T
F
T
F
T
F
T
F
‘I!
‘tll three sttttentents must be false in order for (p OR
-1) OR r In lac lltlsc.
33. Flora .u'n;l \"crnun must c.tt.h complete at least
one chorc for thc sutcmvznt to be true. There are 9
combinations that will make the statement true
35.
Lost name First name Stats Year 0| btnh Annual Income
I Malia Elilabdtlt TX 1958 I 60,000
' Brooltshirr Mary on 1960 62.000
Lamb Charles TX 1951 41.000
Em-.-t1t::t:lt Martin OK 1965 32,000
I
Lnstnatne First name State Vearollnrlh Annual Income
Cratgln.-:t.l Alicia TX 1955 25.000
-Tuggll: L.1wrcnt:I: LA 1972 20.000
Metlo Elizabeth TX 1966 50.000
Piny Jun TX 1952 18,000
Lamb Clnrlrs TX —1's5i'——2t.ooo_-'
37. Yes.l.w the AA Sintilattity Postul-ate. as} 41.§
LESSON 1 2.3
TRY THIS. ( p. 787i
a. Original statement: ll" a triangle is equilateral. then
the ttiangle is isosceles. (true) Converse: Ila triangle
is isuscclcs. then the triangle is cqttilatcntl. (l.-tlsfl
lll\'(‘l'5L‘.! ll‘ at triangle is not cquil.1tt'r1l, then the
triangle is not isosceles. (false) Contratpositive: If the
triangle is not isosceles. then the triangle is not
equilateral. [true]
b. On iginal statement: It a quatlrilateral is .1
thumhus. then the qtt.ttlril.ttcr.tl is a square. {false}
Converse: ll" a quadrilateral is at square, then the
quadrilttteml is il tltombus. (true) Inverse: Ila
qtt.tt.lriLttct'.tl is not .1 rhutnhus, then the qtt.tt.lriLttct'.tl
is not a square. .true] Contrapositive: Ifa
qu.tdri|atei.t| is not a square. then the qu.tdril-.tteu.tl is
not a rhumhus. llalsc]
928 INFO BANK
Exercises
6.
F
T
T
11. ('onu;litiun.tl: True. since sqtntrittg both sides
maintains cqn ility due to thc Multiplintion
Property of Equality. Cum-erse: Ilia: - It: then :1 - b.
F.1lsc;il n- -3 and lv - 3. then [-3]: - (3)5 but a
and 17 are not equal. Inverse: ll'«t :2 it, then u" =2 b‘
False; if .1 - -3 and It - 3. they illl: not equal. bttt
{-3)" - [ii]: CDlllI'<l[‘I.):~illi\'C: ll ll‘ -0 I!‘ then a v la.
l'rue: ifa as b then taking the sqttare root ole-ach
side will not yield the same number. so ti o- b.
13. Condititinal: False. sirtu-. AAA clots not guctr tntcc
triangle congruence. Converse: ll" two triangles are
congt uent, then the three angles of one lIiulI|1.',lt" are
congt ucltl to the three ttnglcs all the other triartglc.
l'rue; given that two triangles are congruent. their
(.01 responding angles are congt uent by the Polygon
Congrtnzncc Postttl.-ttc. lnvcrscz If the three anglts of
one triangle are not congruent to the three angles
of another ll iangle. then the II iangles are not
congruent. True; it all the corrcsponcling angles are
not congruent, then the triangles are not congi uent.
Contnipositive: ll" two It inngles are not congt uent.
then the lhl'L‘.(‘ ang|c< of one triangle are not
congruent to the three angles of the other ti i-angle.
False; it" the triangles are not congluent they ntay still
h.n.-e congruent corresponding angles. Thcy could be
similar. 15. Conditional: True, by the laws of
physics. Cotwcrsc: II the writer tcm|\cr¢1lttrc is less
than or cqutl to 52°F, thcn it will lrcczc at normal
atmospheric pressure. line. by the laws of physics.
lnvcrsc: ll \VsltCr docs not li'cc1c at nurtrntl
at mosphcric pressttrt. then its tcntpcratnrc is grtater
than 32°F live. by the laws of physics.
Cuttlrttposititrcz ll w.ttct"s tcmpcraturc is grcsttcr than
32°F. then it will not freeze at normal atmospheric
[?|l'e'~:s'ulc. True. by the laws of physics. 17. l) is true
because it is the contrapositivc of the original
conditional. Since the statement is true. the
Ln»ntt'rtpo~;iti\'e is .-tlso trt.te. The other two could be
false l.‘rCI3-Illst‘ school could be canceled for other
reasons besides snow. 19. Sample answer: Theorem
.’r_l-‘r_.Z: llitwn ltonvertical lines are parttllel. then they
have the same slope. Conw:rsv:: ll‘ two nonvcnical
lines have the satire slope. then they are parallel.
Ttue; sinee Theorem 3.3.2 is at.ltt.tlly an if-anc.l—t)nlv—
if statement. the converse is true. lnverse: If two
non-r-ertical litres are not parallel. then they do not
have the same slope. True. ltecausc the inverse has
the same truth value as the converse. Contrapositive:
It" two nonyertical lines do not have the same slope.
then they are not parallel. True. because the
contrapositiye has the same truth value as the
conditional. 21. If you are a senior. then you must
report to the auditorium. 23. If she is going to be
late, then she will call me. 25. All ofthem are true.
1' it" and only its can be written as r c> s. In other
words. r implies‘ 5 and 5 implies r. 50 ilithe staterneltt
r it" and only its is true then: a. It" r is true then 2:
must also be true, because r implies .~'. h. The
statement is lt'ue ltvecau-:e 5 implies r. 1:. The
statement is true because it is the contrapositi-re of
a.. and since a. is titre. then this statement is -also
true. :1. The statentrrnt is true lie-:.1trse it is the
contrapositiye of b., and b. is true. 27. a. Same
rneanirtg: implies that getting at least a B in
mathematics is rt requirement to make the honor
role. is. Different meaning: this is the converse of the
original statement. c. Sznne meaning: implies that
getting at hast 1 ll in m.rr|n~m.rtics is a requirement
to male the honor roll. :1. Same meaning implies
that getting at least -a B in math is at requirement to
make the honor roll. 29. 5.5.‘ units
31.
rmttrltnnt
LESSON 1 2.4
Tnv rurs [p. 7931
r‘\ssumc that the detr-ndaru set the tire. Then the
delertd-ant was at the restaurant between 7:30 P.M_
and I I:30 P.M. But three witttesses have testified that
the clcl'cndant was not at the rcst.tur.tnt during those
hours. Thus the assurnpt ion that the deterrdamt set
the fire leads to the following contradiction:
(The delendrtnt was "It the restitttraltt between 7:30
PM. and I I:30 P.M.) r\l\lJ (thc delencl.-int was not at
the rest-aurartt between 7:30 l-‘..‘vl. and I I:30 I-'.M.).
Therefore. the assumption must be false. The
conclusion is the dcl'enr;lant did not set the lire.
Exercises
7. [Litres E and m are parallel) AND (lines I‘ and m
are not parallel}. 8. (AABF is isosceles) AND
[AABC is not isosceles). 9. [All squares are
rectztngles] AND [all squares are not rectangles‘.
10. ( KBCD is 1 squ.u'el .-\N|) (ABCD is not 3 sqttarc].
11. lines f’ and m are not parallel 12. the same-side
inter'ior angles are supplemc-ntar y 13. Yes. The
at‘.-zttntent has mndtrs rnllrrzs lbrnt: ifp then q: ~q;
therefore, —-p. 15. \lo. |'he argument has the nrodus
pmrrms form: ifp then q: yr. therefore. q. 17. Yes. The
argument has the nmdus mllr*u.c form; ifp then q: —q;
tlrer'efore, ~p. 19. E = E 21. L.-‘ICB 23. 5A5
l-’o:~.lulrtte 25. IT as ]—L 27. AK as LL
29. MUM = ALIM 31. KW = 33. 17 g’ ]—L
36. Suppose that there is a sntallest positive real
number x. llut {c < x, so A‘ is not the smallest
positive real number. Ihis is a contradiction.
Therefore there is no smallest ]'N.)'ii|lVt: real number.
31. Given: a fraction Vt ith rt decimal c.\'p.tnsion that
terminates after it places. Suppose the denominator y
does not cli\rir;le any power of ll] with no remainder.
Then ydoes not cliviclc IO“. ltut l0"(1_) - m an
integer. and so ltJ"x = my. Then y divides my so y
\ll\'itlCS IO".t. But y does not cliyicle .>;. so y clivislcs
I0‘ . a contrarliction. The-t'et"ore y divides I0" for sc-Int‘
rt. 39. it = l2 41. obtuse 43. obtuse
as. sin 45° -o 0.707: cm -IS“ ~ 0.7-‘tJ';'; tan 45° - I
47. sin 5° - 0.087; cos 5° -= 0.996; tan 5° -= 0.087
LESSON 12.5
TRYTHJS lp. 8()Il
An input-output table would require 8 rows because
there are three inputs: the table \\-ottlsl require seven
columns: three tor the inputs and four for the
combinations.
l- xerclses
5.
Input-Output. Table
Input Output
q Not p Not p OR q
l 1 O l
1 D O O
O I 1 I
0 o t l t
SELECTED ANSWERS 929
saemsuv passages
Selected Answers
8.
Input-Output Tabla
Inpul Output
p q p AMTNZ: lp- AND 1;)
1 1 1 0
1 O O 1
0 1 0 1
O O O I
7. p .-\|\'D (NOT ql 8.1.]: AND q) OR r
9. 11
—
13. 1 15. I
p q NOTp non; mot ql on [NOT an
17. I 0 O I 1
19. D D I I 1
I I ' [lNOTp) AM) :11
p q r NOT p (NOT pIAND 11 NOT r OH [NOT fl
- .
21. IF.‘ 0 O D I 1
23. 1 0 O O 0 1 1
25. O 1 O 1 I 1 I
27. o o o 1 o 1 1
29. [.\lOTp) AND (NOT 1]]
31. NOT ([NOTp) on [q.-\ND m
.3 -
3’?
37. NOT (p on 1;) and (NOT p] AND [NOT cf)
39. a. The .i1'r.mgcmcnt corresponds to the logic
function AND. Both A and B have to be closed for
the bulb to burn. b. The .1r1.u1gen1e111 C0In:S|.'I0llL1S
to the Iogiu. lumlion OR. Either A or B must be
closed foi the bulb to bum. 41. l0'.'-ix 43. False;
E
}__1 .2+II 1'-1+!) _ 1, ;
cxaniplc. 3- — E but T at T-lrcmusc 1 at E
7-’. - . .
45. lg (11 ='- = the r;1tu1- (11 Ihc pcnmctcrs
21 Hi
% or 1-: = the ratio of the sides. The ratio of the
pcrimclcrs is cqu.-1| to lhc ratio of the sides in similar
tri.'l ngles.
CHAPTER REVIEW AND ASSESSMENT
1. \-'.1lid 3. 'l11erefore. .1 (.11 is not a rodent. 5. John
is my brother and I7 is piime.
930 INFO BANK
9. Couvcrsc: Iflhc ground is wet. then it is mining.
|nveI'se: If it is not rainiiig, then the ground is not
wet. Co11u.1posi1ivc: If the giound is not wet. than it
is not raining.
11.
13. A711 K 15. E 2 H 17. p Oli I.N0’l'q)
19. (p OR q) AND (NOT r] 21. I1 is a valid
.u'gumcm. It h.1s1|11: modus mllms lbnn.
Extra Practice
CHAPTER 1
Lesson I.I
1. ERR . EB, -15.: 3. .-1-3 .111d lnrm angle 1.
E1 Ind EC’? iorm nnglc 2. and form angle .1,
and DC" and Dzi form .1113]: -1. 5. False. The two
lines Inight not be (.op|.1na1': they u.JLI|d he skew
linrs. 7. poinl
Lesson [.2
1. 5 3. S 5. .29 7. Does not Il'h|i\'C sens: bcunlse 171.5
11-lcrs 10 (hr sq.-.n1<n1. not the mcuurc of the
segment.
Lesson L3
1. -12° 3. 57° 5. 70° 7. .7.‘ = 5.5. mzW.\'Z = 35°
9. nizi-1"Xi' = 525°
Lesson IA
1 . 3.
135
1 . 3.
A A
i;;?l§o.
1'3 c 5 C
5.
E
=
lesson [.6
1 . 3.
{:3 .
[:1
5..-‘-\H IMO l'L.|VWX\",
Sample .1nswer: YM IOO
lesson I.7
1. 3.
v y
A 4
-1 ‘ 2 to ‘ ’ ‘ 4 .\' 1 r 1 yo 1 I X
-4 -4
5. vertic.1l shiti t.lL)'H 11 3 units 7. rellecrion across the
V-axis, \'ertit..1l shilt eluwn 5 units
CHAPTER2
Lc.~.son2.I
1. lol 3. column [5
6_..... CIIIIDD
..... ooooooo
..... oololoo
..... OOIICOO
----- 3333333
0000000
7. The represent.1tio11 of ()1 + 2)’ has .111 :1t.l1'litional
2» dots directly lJelo\v the origin-.1l rl columns and
2» + 4 dots added to tl1e right of the or iginal square.
The total dots in the new arrav is then
1:" + 211+ [2rr+ -1).
Lesson 2.2
1. ll "111 anirrtatl lives in the Evergl.1tles. then it lives in
FlOl'lLl.-‘I.
3.
Anrmals In Flonde
AIIIIHBIE
an
Everglades
5. H)'ptJll‘lESi:s: Two angles .1re supple1neut.1r_1-.
Conclusion: The sum of their 1nv:ast11'es is 180'’.
Converse: ll" the sum of the n1e.1sut'es of two angles
is ISO°. then the .1ngles are supplelttcntary. Com-erse
is true. 7. Hypothesis: You live in l1.1ltimore.
Concltrsionz You live 1n M.11_vl-.111d. Converse: It’
you live in M.1rylanr.l. then you live in Baltimore.
Converse is lhlseg you m.1_v live in .-\nnapolis.
Lesson 2.3
1. a. Ila pl-.tnn.t is Merctrn-. then it is the planet
closest to our sun. h. ll :1 planet is the one closest to
our sun. then it is Mercury. o. A planet is the closest
to our sun ili.1nd onlv it‘ it is Mercury. d. Delinition:
The l)icnnt.lition.1l is true.
3. a. ll .1 nurnher is .1 multiple at ten. then it has it
o111‘.s digit of zero. b. If .1 number has a ones digit of
zero, then it is :1 multiple of ten. 1:. A uurnber is .1
multiple ol ten if 1nd only if it has .1 ones digit of
zero. d. Dc finition: The bivsortditional is true. 6. a. If
.1 closed figure is .111 eq11i|.1te1al tri-.tngle. then it has
three congruent angles. b. "'51 1.luser.l figure l1.1s
three congruent .tnglcs. then it is an eq1til.=tter.1|
t1i.1ngle. c. A closed ligure is .In equilateral triangle
il .111r.l only if it has 3 congruent .1ngles. d. Not .1
definition: A pentagon n1:1y contain 3 congruent
angles and two other .u1g|es.
Lesson 2.4
1. Addition Property ot'Equ:1lity 3. 35°
Lesson 2.5
1. AGBF 3. £.’lB(" 5. 1111/(BF = n1£t"BD = l3T°:
1111211-BC = rn£bHD = 43° 7. Ded11c.tive reasoning;
is .1 prool: The argument is true for all n111l1i|\lcs of
D.
SELECTED ANSWERS 931
s.reMsuV passages
Selected Answers
CHAPTER 3
Lesson 3.!
1. 3.
\J
83
7. The figure i11 E.‘(Cl'(.i!iC ('1 has 180° t'0t.ttiot1.t|
symntclry.
Lesson 3.2
1.5 3. 3 5. I06” 7. .\'= 2;6 9. Falseuttltonthus
l‘l‘l.I_V h.-we interior Angles at 90°.
Lesson 3.3
1. £2. £6. and Z? 3. No: all the angles .ue listed in
either EKCl'\'.iSC I or Exercise 2. 5. mil. ml-I. 111.45.
and mz8 = 80°; m£2, 11113. mzfi. and ml?" = I00°
7. ?0° 9. ?0" 11. 35°
Lesson 3.4
1. ‘sltcrnatc interior /\ng|t‘s Theorem 3. S.1mc-Sidv:
Interior Angles lheorem 5. Alternate Interior
Angles Theorem
7.
Proof Stalcmcltts Reasons
n1.£CBE = -13° Given
n1.éBFD= l.5?'°
mZCBF -O n‘I£BFD F\\iditi0n
= I86?
ACRE and ABFD are Definition of
supp|cmcnt.an_r. Sttppletttentaty Angles
F1!) || ITC CCIl'l\'l.‘l'5C or S.-tn1c-Side
Interior ,I\ng|es Theorem
Lesson 3.5
1. 90° 3. -IS" 5. 55" 7. 76°
14:5.-st)n3.6
1.S0° 3. IS[}° 5.15 1.5 9.12
932 INFO BANK
Lesson 3.7
1. 30 3. -ti 5. I3 fcct
Lesson 3.8
1. %; [2, 1.5) 3. -3; (-0.5. L5} 5. |’cI'pendicLt|-at
7. Neithet 9. Right triangle 11. Not .1 night triangle
CHAPTER 4
Lesson -8.!
1. Not <.t1ngt'uenl. They are diftcrent lengths.
3. Not congruent. lhey lta-.-e dil’fet'et1t side lengths.
5. Congt uent. All conespomling pants are congruent
1.a.W h.tT «LE «LT
Lesson 4.2
1. S85 3. ASA 5. No 7. No 9. ASA
Lesson 4.3
1. ACMQ 5 ADFB by $51: 3. AABD a AFBD by
SAS 5. ARSTE M H». by SAS 7. \lo
9. AMNOE AGHI by SSS
Lesson-1.4
1. 10° 3. I2 5.50” 7. 90° 9.15
Lesson 4.5
1. ISO” 3. l0‘' 5. 30" 'l.£-JKL is congtuettt to
.D.O.Mt\' lav ASA. so they um be put ttagclher to lorm
a p.1r.1llelogr.1n1. 9. /~..\'Y7 is congluent to .r’\DEF by
555. so they can be put together to form .1
p.tr'.t||e|ogr.un.
Le.\son 4.6
1. WXYZ is .1 pat'.tl|e|ogr.m1. It the diagonals ol'.1
t|u.tdrii.ttctu| Itisect each other. then the qtt.tdri|.ttct'a|
is .1 p.=tr.t||t‘|o;.:I'.tm. 3. H-"Xi"? is .1 p.tr.I||e|ogr.tn1. If
two pairs of opposite sides of at qu.tdril.uer.1| Mt‘
m11g1Ltcm. then the quatdt'i|ater ti is it |‘.lldiici()glt|n'l.
6. iBCD is at rhotnbus. If the di.tgon.t|s of a
p.u'-allelogr-.mt bi.-sect the angles of the p.u'a||elogr-ant,
then the p.tmi|c|og1.1m is .1 rhon'IiJu:~:. 7. ABCD is
it t'hon'tl_>us. lfonc pair of .tdi.-tccnt sides of .1
p.tr-allclogt-.tm are congt uent. then the p-.tt.t|lelogr.nn
isa rhombus. 9. Neither
Lesson 4.7
1 .
5. Possible uiangle. The sum 0! the lengths ol any
two sides is grc.-ncr than the Ivsngth oflhc third side.
7. Not possible. since BC + CA < AB 9. Not
possible, since DE + EF c DF
CHAPTER 5
Lesson 5.!
1. I2 3. 4 5.15 7.]: - 3cm, 12- |2cm.P - 30cm
Lc.~4iun 5.2
1. K-21 3. I-75.5 5. \--I 7. \=I2 9. \=l8
11.A=l:'-
Lesson 5.3
1.('- 18.8.44 -28.3 3. C-44.0..-H - I519
-_}i.._<al) _8HII) __=-i _3I[»s
5.L— ,A——7' 7.C— 7A——7
9. r= 2../:7.-:5 11. r = 3.3 13. r — V-"%7.o.1
lesson 5.4
1. I3 3. Bu’?! 5. obmsc 1. acme 9. ohms:
11.)‘ = I0.8, I’= I5 13. A = 17.1. P ‘ 24.4
lesson 5.5
1.1:-7.5.;--14 3..-1-_1,b-2./.'1'
s.A- l2lv‘§.P-66 7.A—32.;‘3.P-_J4+B¢'.i
*3
9. \- l.5,P-6+3
L;-.~.-son 5.6
1. LIZ 3. 5 6. I.-17 7. 5.06 9. vcs 11. no 13. yrs
Lesson 5.7
‘V
1.C(b.n) 3.1: 5. \/b="+r.‘-' 7. b:+t"'
Lesson 5.8
1. P= ,1. 3. P— 5 5.30% 1. won»... 9.0.29
11.0.09 13. 0.001 15.0.-I:'.\3 11.1‘ 19.% 21.-;::—..
23.
CHAPTER 5
Lesson 6.1
1. 4 units’
3.
V Top
Kb :9: ED :13
Lcfl From Righl Back
Bmtnrn
5.
7. a
lilllllll
L:-I’! Frnnl Righl Back
SELECTED ANSWERS 933
s.IeMsuV pezoeges
Selected Answers
Lesson 6.2
1. N11. 3. Ycs. Sim: li11c m is [T|Cl'|?CI]\|iLl.||'Il' to plane
1‘. line n1 is pc1'pc11di1:ular to all lines in .Pth.1t it
imersflts.
5. I-alse. "I113 two lines could be skew. I-‘or e\.1n1pIe. i11
this ske1cl1,the lines E and m lie in p.11.1llel planes.
Z
X
Lesson 6.3
1. pcnmgoinil prism 3. 1'c1.l111gu|.1r prism 5. W .1n1.|
E 1..1- 15 s..1—st/E
Lesson 6.4
1.1‘nstoc1ant 3.1op—b;1ck-Iigi1l0cl;lnl 5.bot1om-
[rick-Ich (M12111! 1. J26 9. 2x1“'l—l
l.c.ss4111 6.5
1 .
7.7.t+2y-I
934 INFO BANK
Lesson 6 6
1 .
IVOIIZEIII
1: \
1 \
, 1
1 \
I \
I \
3.
4,7
."/I
_— Ill
r’ "
-I’ I’
I
a
5.
horizon
.«
"ax
4 I
I
I
7.
I11.1ri11.1n
--":‘I
'_—' ‘.4’:
__r'' ’r
If I‘,
.-
I
I
CHAPTER 7
Lesson 7.!
1.4.29 3.1 5.1.15 7.1.2 s.'*‘T3" 11.M.1\'imizc
vo|un1e.
Lesson 7.2
1. 24 in‘ 3.130111 5. S - 256; V - 2m
7. J - 266-I; V - 1260 9. 5 = 2616; 1-’ - 926!
11. I016? in.
Lesson 7.3
1. 89.0 3. 85.8 5. 65.3 1. I600 9. 4200 11. 9
Lesson 7.4
1. 339.3 3. 5.3 5. 3.7 7. 203.6 9. l7.67l.5 11. 3
13. in.
LC\'§0ll 7.5
1. S - l9.I'-.71; V - ‘).':'92It 3. 5 - 3-1.3.2‘-.11;
V - 685.6711 5. .5 - 2072.11; V - 34 |.3-3.1
7. S = 49.8815: V = 36.3611 9. .5 = 78.96112:
V = 66.901‘!
Lesson 7.6
1. 5 = .31-tlfi; V = 52.3.60 3. 5 = U158-1.78;
V = I50.532.55 5. S = I05.f-S: V = |02.l6
7. S = 5037; V = 34.0.? 9. S = 804.25: V = .2 I-I-4.66
11. S = -19ity";l' = %-1;«*‘ 13. S = -1.8ury";
V = Lil‘ II:y' 15. .5 = %It.\"': V = firtv‘
1/esson 7.7
1. {L I.-2] 3. I2. I. .5] 5.(-2.15.0] 7. (3-2, -.32, 32]
9. (I4. 4. 6.2] 11. (—lZ.|. 3.6] 13. (—IS, IS. 15]
15. (7.8.~7.S.~IOJ 17. [~?.,—2.-2)
CHAPTER 8
Lesson 8.!
1. (6. -2)
5. 3 7. y = 3);; Plugging in OID, 0) givcs D = 0.
which is lruc. Thus. the origin is on this lint.
9. y = -5.1‘; Plzlgginlg in 0(0. 0] gi-1-cs 0 = 0. whi1h
is true. Thus. the origin is‘ on this line.
Lesson 8.2
1.Yes.A/155,135 1-“.402 H.1nd£C=C.
ll) _ 11-: _ r11 _ D1‘ _;
U§0.fi'i—'fi'—*-
r1; ‘ if ‘ 3'
qu11driL1lcI11| ABCD - qu:1d1i|.1tcr.1l EFGH
3. .1‘ = 3 5. X = I2
Lesson 8.3
1. Yes, since 111.43 = 111zE 111d since = = 5,
AABC ~ ADEF by SAS Siu1iLu'il)' Theorem.
3. Qu.-1dri|.1lcr.-1| \BCD — qL1.1d1'il.1tcI'.1|!]}\"I since
corresponding angles axe congn uent and
U? — EE — J12 — BE — 3 _ ' - ‘
—"- — IX — " — H — 3. Qu.11|r1|.1tcm| EI'GH1s
not simil.u 1o quadrilatelals ABCD and HKL since
"3 — 1 A2 — 3 L
TF‘:"”'1.n‘ 3'°1'
Lesson 8.4
1. .1- = $ :1. .1- = 1 5. mint: - AIJBF [1,-1hc $115
Sin1il.1ri1y Fheorem.
Lesson 8.5
1. I1 = 37'.5I't 3. h = 28.8 F1 6. .1‘: 2.2
Lesson 8.6
1.1 3. 5.
2
-J
7.
HI Id
3. '1
I
'?~
1
CHAPTER 9
Lct1‘on9.l
1. 4.19 3. 2.6.l8 5. I2.-18 7. -16.08 9. 54.45
11. 212.8" 13. 132.3" 15. 229.?‘ 17. S}'.3°
Lcx-son 9.2
1. T5 3. 9.s~1.9.5-1 5. 5819.58.79
Lesson 9.3
1. I5" 3. 45" 5. I80“ 7. -15" 9. 90' 11.90‘' 13. |S0°
Lcs.11'on9.-1
1. I22.S° 3. -55° 5. I(10°
Lesson 9.5
1. 4 3. 2.47 5. AZXR 7. ZQ 9. -1
Lesson 9.6
1. .\'-i1m'1'1'q1ts: (T-', 0]. (-7. 0); y-inlo:r1' pts: (0. 7].
{0.—7] 3. _\'-intercepts: (5. 0). (-3. 0); y-intercepts:
[I]. 3.87). (D. -3.87) 5. .1‘-intercepts: ( I L06, 0).
(-5.06. 0}; y-intercepts: (0. 11.19]. (.0, -12.19)
1. center: [0, 0), r = 2 9. cemer: (-1, 0), r = 1/E
11. ccmcr: [-3. '3]. r = VG?
13.[.1-—1)~' + [y— 2)"=l(1
CHAPTER 1 0
Lesson l0.l
1. 1.1.1.4 = 3' = 0.4 :1. 1.11111 = g = 0.375 5. 0.2?
7. 1.07 9.0.90
Lesson 10.2
1. X 3..\’ 5.X 1.0.26 9.0.31 11.0.6?
Lesson 10.3
1. 0.8!‘): 3. —()..'-420 5. —0.9Slf.~ 7. [0.939?. 0.3420)
9. If—0.9.597. —0.3«I.7.0I- 11. 58° and 1-12” 13. 2.$°.1nd
|S}‘° 15. 3l°-and I-19°
SELECTED ANSWERS 935
s.1eMsuV passages
Selected Answers
Lesson [(3.4
1. 3.5? cm 3. 36.9” 5. m..»'_’R = 715°; r -‘—< 7.33:
p r: l.-I l 7. m£R = llS°: r '4 |6.92;p *4 189
Lesson l0.5
t. l2.l 3. -44.4“ 5. mzfl = 8-1.1“; mzf = 63.7"’:
n1..»'_’F as 32.2"
Lesson |0.6
‘I .
2|
cl
7+5
Lesson lO.7
t. (-3.7. 3.3) 3. (-0.2,-Ll) 5 0.7.43.7) 7. (0,3)
=»[“::: ::::]
u [:23 if]
1
2
.77 -.6-I
13 i: .64 .77
.5 .37
'5 l—.s7 .5]
CHAPTER 1 1
Lesson ||.l
1. 3.47 3. 6.l8 5. 5.0?
Lesson ll.2
1.3 3.2-‘ 5. ll 7. -to 9. 20 11.14 13.64 5. 88
Lesson ||.3
t. Euler circuit 3. Euler path
lesson HA
1. .1. and h. «I re ttalmlngiutlly equivalent.
3. l."—F+F=2;20-50+l2=2
Lesson ll.5
1. Xi rsaltne. 3. Mi IS not a line. 5. AF tsnot a
line. 7. E(" is not a line.
Lesson I L6
1 . 1.1 Y‘? V‘V v‘v I-I v
I 1' ‘V v
V‘? uv
T V
936 INFO BANK
[1|elaelsaltzeltzelaalaalaltI
I I [to]-ts.Itzolztulzszlztoltzol-zslto] ‘I I
| 1 I11I55l'tE5I3’30l-18?I4ci2|J3Dl1Ml§5I11l I |
The shaded boxes in '\t.tivity 2 are ttttsh.tde-:l in this
Pascal Triangle. 11te unshatded hosts in .-\ctivilv 2 ate
shaded in this l’asLal Triangle. In each case. a
Sierpinski gasket is suggested.
Lesson I L7
‘I .
CHAPTER 1 2
lesson l2.l
1. Therefore. he cries. [Irtodirs pmuws] 3. Therefore.
he is ht1tt;.;t'y. {nmrfus toflrrtsl 6. \-'.tlid by ruodus
I'D":-‘((5. 7. Valid by modrrs pa-rmrs.
Lesson 12.2
1. Some flowers are red. and t.ut.uml)crs alt:
vegetaltles. Ti'uc. since both statements are true.
3. Harry is not older than Latrrv. 5. Lztrtv and Bath-
are not twins. 7. It is not the case IITII llarrv is both
older than l..1rr)' and vottngcr than llarry.
Lesson I23
1. Corrdiriorrrtl: Tt ue. Twins are always the saute age.
Cont-:'rsr: ll" H.trrv and l trry are the same age. then
they are twins. False. l'he\' can be the same age
without t.'t.'t:n being t'eLttcd. Irrrcr-u.': ll llarr_v and
l..1rryare not twins. then they are not the same .t;:,e.
False: l'he_v could be the same age without being
twin-t. Gtttrrrtp¢)sitit'c.' If Harry and Lat ry are not the
stntc age, then they are not twins. Ti'ue. To be twins.
they must be the same age. 3. Comiitimml: False. It
could be the use that m at 0 and H = 0. ("rmt-'ersr:: If
m = 0. then m x u = 0. hue. lxro multiplied by any
number is zero. Im-‘r.'r.sr:: ll m X rt -0 0 then m - 0.
True: If m wt‘l'l‘ rcro, m x u would be zero.
Cmtrrttposirim If m s 0, then m x n at 0. False. If
H - fl and m u 0. m x u would still equal zero.
6. If a nurnbcr is odd, then it is not divisible [W 2.
Lesson I2.-1
1. No. To prove that Bobby ate same cookies bv an
ittdircct argument. it should first be assumed that
Bobbv did not eat some cookies from the cookie i.tr.
Also. the argument '¢IS>ulIlCS that the converse of
a conditional has the saint truth vtlur: as the
conditional, which is not the case. 3. No. The proof
doe; not stain by .munting the t'Jppuall€ of the
smtcnu-til to be pt'ovctl. 6. not obtuse L-tctitc or
right] 7. 30” 9. 90" 11. 'l1ie sum of the tneasures of
the tluee angles is ISO‘
1.;-win I25
1. l
-p l-p) A_ND q (—p AND ql OR r
3. 0 D ‘I
6. D D ‘I
7. I ‘I ‘I
9. 1 D I
SELECTED ANSWERS 937
s.IeMsuV pezoeges
Index
INDEX
0
AAA ( Attgle-A ngle—:\n_t:lc}
Contbitmtion, 216-22?‘
A.-\ t.-\ng|e-.-\t1gIe) Sitttilarity,
SIT. 55-1. 556
/\.-\S (Angle-Angle-Side)
Congruencc Theorem.
.7_2(i—.Z2h'. 28-1. _-‘Sti
ABCD (Angles. Bettvecrtttess,
Collittettritv. «Incl Distance]. 273
activities
Adjacent .-‘tttgle-s. IOI
Allinc TI'tl|"I§luI'll'l'eIlll)ll. T-I8
Angle l3iset.tor. 263
Angles and lntert.e['-tetl Arcs.
".\t.ll—.".\P.l'_7
Arett Fornntl.-1 tor
l"tll‘dllCl0gl'¢l|TIS. 305
Area Fm nntltt lot‘ Trttpezoicls.
30!)
Area Fottnul.t tor Tt i-angles.
303-30-I
Areal of-.1 Cittle. 3l6. 3-I I-3-I2
Building 5! Recungul-.u
Structure. 2:"-:3
Cantor Dust. I-'-I0
Chords and .-\tcs Tlteotent, 563
Cit-ctttnferettce of at Circle. 315
Collineatitr .tnd Betweettttess.
273
Cong: uettu: I’ustttl.ttcs.
2 l B——2 l9
Cungt uent Ttiattgles. 262
Diatgonals of .1 I’ar.1lle|ogr.tm,
3-13
Dihedrttl Angles. 382-383
Diltttions in the Coordinate
I’I-.tne. 499
Dimensions of .1 Golden
Rectangle. 699
Dtunving .1 Dilatiott, 500
"Essence" of .t l'hing. I00
Euler I’.tth.s. 713
I:'xterior Angle Sums in
|’olyg,on.s, I]-79
Fair Rulers. I8
F'II'I‘tlllJI' Ratio. 650
Fi red A II .-I! M ini mtt m
I-’erimetet'. 297'
FlVCLl Pet in‘tcten'.\-I.-tV<itnttnt
'\rca. 297
Ciconietry ltle.ts In .t .\'l0('ll‘l. I2
Golden I{ect.tngIes. 70!
Graphing the Titngent. 632
l‘lC‘<.1llCK«l_l{0nS_. 282
HC‘(.lgOI1S in Circles. 565
Heuthex.1fle.\'.-tgons. 28.3
938 mro BANK
Incon1ntensur.tbilit},- of the
Square Root of 2. 80?
Increasing Height and Volume.
5-16
Infinity of the Primes. B0?
Isometric Grid Paper. 373
L.tter.t| Faces of Prisms, 389
Law of Sines, 654-65?
Making the Comte-:tion. I85
M.txinti7ing Volttme. -1.52
Negatiott of t Conjunction,
778
On-OIT Tables. ':"J8—}'9‘J
I-’.traIIcI Lines and Planes in
Space. 380
P.trallclogr.tnts. I-I9
I-’.tst'.tl .tntl Si<‘t'pinsl<i. 7"-II
Pet'pentlicul.1r and P.tr.tlle|
l.it't(‘$. .’v6—.':'r'
Projectix-e Geometry
Tlteorcnts. 750-75!
l-’rot:I's. 8 I . S3
l-’yrtttnit.ls and Prisms. -H7
Raclii and Ttttgettts. 57-1
Rtttlii Perpendicular to Chords.
57-I-575
Rtttinndl Sytnmelt'}' in
Pttntllelogranis. 243-2-I-I
Ratio t)fSttrl.tce Arett to
\-'olun1e. 43I
Rtttius t)l' .-\re.ts ol Similar
Figures. 5-1.S—:'.\44
Rtttins of Volumes at Similar
Figu res. 5-1-l—:'.\-15
Rectztttgles. l:'-0
Redelittittg the 'l'i'igonontettit:
Ratios, 6-IB-(":50
Rellectiun A-.toss the Line. 349
Retlectional Syttttttetty itt
Triztngles. I40
Rellettiotts. 52, {ml
Retleetiotts Across I’-.n-ttllel
Lines. II9
Retleetiotts lll Coordinate
Space. -179
Rliutnbuses. I I9
Rc>t.tting 21 Point. 630-68|
Rot.ttion:tI Symmetry in
Regular I’oI;-gons, I4 I
Rotations, 51
I80“ Rotatiotts About the
Origin, 63
Rotatiotts in Coordin.tte Space.
480
SAS I'ri.tngIe Simil.ttit_r
I'l1eorern, 519
Seashells. t-99
Segment and Angle Bisectots.
38
Segment Congruent to .1 Given
Segment. 36!
Segments and I’I.tnes. 380-331
Segments Formed by Sec.tnts
and Iltngents. 601
Sines and Cosines, 6-I0
Solving the Puzzle, 322
Special Circles. -14
Special Points it1 Tri.tngle$. 1.5
Squares. I50
535 Tri.tngle Similttrity
Postulate. SI8
Sums of Interior .-\ngles.
|77—l78
Sttrface .\ret of .t Right Cone.
-lftl. 162
Tiixi-:.al'I Circles. 7'08
T.l3(lI.llSl.’lnCCS. 702-‘
30-60-90 Triattgles. .553
Tntttslating .-t Scgntenl.
27"l—2'r'2
'l"t':ttt.<.l.tting Polygmts. 272
Trttnsltttiuns. SI. 60
Ti'iangle Midsegments. ll-53
Triangle Midsegment
Theorem. 3-19-350
Triangle Rigidity. 217-215
Ti'iangle Sum Theorem. l7I
Two Trigottnmelric Identities.
(I4 l—li-12
Unit Culles, 373
Using the Tangent. 632
Vertex on Circle. :'\l-59-590
Vertical Angles Conjecture.
I l7—l IS
Volutne and Sulliltie Area. 37-1
Volume of -.1 Cylinder. -155
Wlmt Does It Take to .\'l.tl<e....
25-!
acute angles. 29
dilI.llli0I'I
single. 2?
propetly. I07—l03. I28
segment. .10. 70
vectot. 673-675. 69]
Addition Property of Equatlitr.
l07—l03
Add-One I’ropert_r. S09
Adelard. 56?.
adjacent angles, I01
afline transformations,
3"-17-7"-18. 7'62
algebra. 20
Alhambra. I36
alibis, 793
Alternate lixterior Angles.
I60. 200
AItet'tr.tte Interior Angles, I58. 300
of rotation. 642-648
special, l55—I:'-7. 202
rising calctrlators lo find. 650
vertex, 237
altitudes
of cones. 460
of cylinders. 453
of parallelograms. 305
computer .u'c|riteclure. F98
computer tI.rt.rb.tses, 78]
computer‘ graphics. 6 I 6
computer progntmming.
xepur
ol'prisms,437 vertic.tI, ll?‘-I18. I20, I29 67, I32
proportionality. 535, 554. Arrgle—Side-Angle (ASA) design. 279. 288. 424. 578
557 I’ostuI.tte‘. 2l9. 284. 286 dr'.tI'ling. I66, 337
oI'pyr.rmids, 445 angle sums. I70—I?2, I?7—I79. environment.tI protection,
of traperoids. 308 20!. 203 345
of U'I:ll1gI.€5. 49, 267. 303, 554. in polygons. 203 fine .1115. 97. 5 I5, 553. 705
557 annulus. 469-470 graphics, 400, 505. 523, 558.
altituclcs of triangles. 267, 30.! arttecedertls, F7]. 308 616
ambiguous use of the law of apothems. 3.51 humor. 96
sincs. 656. 659 Ipplications indirect ntc.tstrrcn1cr1t. 5 I6.
Angle-.-\ngIe (AA) Similarity.
SI7. 55-1. 556
Angle-.-\rtgIc-.-\r1gIc l_ .-\/\.-\I
combination. 226-227
‘lnglc-Angle-Sitle I.\.-\S)
Congrucncc Theorem.
226-228. 23-1. 286
angle nmtstrrcs. See also arrglcs;
trignnometr_v
centr .II. 62 I
(ICfil'IIlI(JI'l. 25-26
p.rr IIIel lines .rtu.I trains-.-r:rs.rIs.
.202
Triangle Sum Themem. .203
units. 26. 34
angles. See also angle measures;
trignnometn_r
acute. 29
acltlition. 27. I70—I72.
l77—l7'). 20I. 203
atljucent. IOI
base. .237
bisectors. 33. 263. 266. 554
bisectors. 38. 263. 266, 539.
554
u:ntt.tI, I39. 565-566. 62I
classilicatiorr of. 29, 533-592
congr uent. 27, 72. I23. 265
consecutit-e, I49
cotrespondirrg, I57. I62-I63,
200. 2| I-2 I3, 792-793
oI' d.rnger. 59 I
definition. I I
tliltedml, 332-333
exterior. II. I56. I60. I65.
I74-I75. I79, 200-ZOI
formed bv secants and
tangents, 588-592. 622
included. 2I9
inscr ibed. 580-584. 620. 622
inter'ior, I56, I58. I60, I65.
I77-I78. 200
measuring. 25-29
naming, ll
overI.tpping. IOI, I12, I28
p.!il'5 of. 28
rel.rlionship to arcs. 596
busir1css_. 550
rnaImI'.1cttrrir1g. 352. 133, LI-1.
I13. -158, I67. 727
m.aI'ktting, 705
p.tcI:.1_r;ir1g. 393. 158. 550. 608
prinlin;.:. 492
small busim:-ss. I6?
langtmgc arts
oommuni-:.ttions. 528.. 59?.
62 I
telewmmunicatinns. 740. 796
III: skills
c.trpenlr)'. I6]. I67. 2|-'5. 222.
255. 459. S80. 58 I. 586
Lnmmutirtg. 710
collstrllcticall. 43. I96. .223. 238.
239. 245. 260. 300. 449. -I5 I .
6-I5
mokirtg. 435
Iarming. 3| I
hrshion. 2 I 6
Irmd. 475. 550. 728
Iund rzrising. 424. 7I9
l'urrtiture. I45
gatrt-.lening. I53. 297
home intprovernent. 3412
home wiring. B12
house painting. 406
inlet ior decoratirtg, 515
irtigation. 3|S
I-.rntIsc.rping. 3DI. 306, 5 I5. 558,
57 I. 668. 774
rnup reading. 269. 345
meal pl.1nning. 3I8
moving and storage. 484
road signs. 242
s.rt'ety. 323, 329. 366, 685. 7 I0
storage, 550
miscellaneous
.u:.rdemics. 290
aquariurns, 439
.u'c|1itecture. 159, 37-7. 4 I2, 444.
5IO. 5| I, 66]. 684. 762
.1 rt. 204, 251. 260
.wi-.ttion. 298, 678
c.n'togr.tphv. I76, 4? I . 58?
coins, 454. 456
‘INIJ in logic. 7'76, 799-800 business and cv.'.onomics 636. 668. 692
Anclromeda _r;alav<y. 9 .rdvcrtisin_-.1_. 780 marching l>.mcI. 279
mcchttni-:.tl dr.twing_. _I-72
optic II illusions, ISI
pI‘tOlOgI'.lpI'I)’, I I5. 498, 585,
705
rotary’ motion. 6-I9
sun'c_vin;.'.. 212. 288. 62-1. 636.
(I6I
tcchnology. 3! I
the.-itre .1 rts. .I-04
tr'.trrspnrt.rtinn. I82. 358. 453,
455
s<.ir:nr:c
.-tgrir.uItur'e. I42. I43. 297. 301.
3| I. 325. (124. 673
.rrr.I1c0logy. -I4. I85. I86. 233.
373. 597
.|strnr'r0In)'. 229. 234]. 3|‘). IDI.
SOI . 549. 55'). fill’). (VII. (:52.
692
.tutun10l)iIc engineering. .'I I9
l)inIugy.‘J0. ICI3. I05. I32. I30.
I39. -‘-I30. -I33, 435. 531. 546
botany. 98. H I. 435
chetnislr )'. I03. 383. 390, 394.
435
civil engineering. I66. 337. 352..
57I
earth science. 505
electr ic it y. 803
engineering. 24. I88. 204, 220.
233. 243. 505. 532. 533. 579.
603. 636, 692
envirornnentatl science. 304
Ibrestt y. 226, 230. 645. 66!
genrology. I82
genetics, 721
geography. 146. 172,475.
739-740. 762
geology, 24. I03. 42 I. 463.
600
lunar explonttion. 603
m-.trine biology, -I53
meteorology. 358
n.t-vigation. 33. 60, H6. I6l,
I67. I73, I75. 233, 385. -‘-I07,
583. 1709i, 593. 603. 624. 668,
678. 679, 692
INDEX 939
Index
optic.-5. 394, 484. 505, 5-1 I. 583
paleontology. S40
pliysic-.\I science. -‘-IOI
physics. 49).. 673
pliysiology. -13.5
solar energy, 300
space flight. 578
st: uctural design, 6 I 7
weather, 9-I
wildlife mamgement. 51-1. 603,
660, ':'I9
social studies
criminal Lnv. 78I
drmogr.-iphics. 57]
law, 795. SI2
I.-nu cntorccment. FI8
public health. 458
traffic snfctv. I-I6
sports and leisure
crafts. 20-I
enlul.-iinmcnt. I20
g.1n1cs. 86. 567
hobbies, II I. -107, I34. 184.
504. 744
hot-.1ir b.-tllu-oning. 473
metttlwork. 475
music. II-I9. S3I
painting. I35
pottery. -IEI3
quilting. I47. 204. .715. 223.
572
rccre.ttion. I45, 223. 293. 359.
377. 443. 444. M17. 640. 645.
673
scuba diving. 33. 678
sl<yeliving__ 353
sports, I76. ISI. I86. 234. 2:'\l.
32'). 3136. 474. 475, -I92. 550.
57 l. 668. 675. 676. 774
sI'.|il|ei.I glass. 586
travel. 74. 329
Ar-.ms;is N.tIion'.1I Wildlife Refuge.
514
Aicliiniede-an Solids, ID8
Ara:-Intercept Corol|.try. 583. 620
arc length. 507-568
are measures. 5043-567, 621
arcs
angles and. 596
cenotes, 000
eongi uencv, 568
degree measures, 566-567. 621
in hyperbolic geonietry. I-'32
intercepted. 566, 5BI—SB-I, 630.
on
ioining, 579
length, 567-368
maior and minor. S66
areas
of ainnuli. -170
of circles. 3 It-, 3-I I-3-12. 362,
364. 470
under curves, 3-1 I-3-:2. 36:"-
940 INFO BANK
definition, 39:’-
oI' irregular polygons. 330. 362
lo.1d-bearing C.!p'.lClI\' and.
543-546
of P¢ll‘3ll€IOgl'ill'|'|S. 30:"-,
362-363
ratios of. 543-546, 557
of rect-.ing,Ies. 296-297. 362,
363
of regul-.=tr polygons, 334-335.
363
sum of, 295. 362
of ll’-l]‘£‘7-Olds. .506-I-07.
.l-62—_':6.\
ot Iri in;,-Ics. .l-0.!--30-I. 362-563.
737
arguments. See also logic
dciitiitioll. 9|
II"-'I11en smtelnctits. 90-93. 99.
I29. 7'8-I-787. 8 IO
invalid. 7'6‘). Til. SCI8-80‘)
mmius pmzrns. 769, 303
nmrius mII¢'n.~ "'70. 79I. 803
valid. 768-770. 809
art. geometry and. 5, 7
ASP. (Angle-Side-Angle)
Postulate. 2 I9. 284. 286
Assessinettts, 70-74. l28- I 32.
200-204. 284-286. 3t»2—3(i6.
420-424. 488-492. 554-558.
620-624. 688-692. 758-762.
S0.'~‘.—8I2.
'cISIClUl\l itnp.ii.ts. 353
astronomical! units. 40!
d‘€II.'JlIl5. See also pos1uL1tes.
Jefinitimi. I I
axis
.1rr.1ngcment (III, 39(>—397
er 1.-smllograpliic. 42-:
of {\'llll('.lClS. 4:13
of sx-ninietry. I39. -19.1
0
l3aI)\'luni'.|ns. 3-1. 32 I. 32.2. 633.
6$I'1—I.‘\I'i7
ballcmning. -I69. 473
l).1selmll dianmnds. I45. I76. 3.29
Imses
angles. 23?
area. 437
nl u'linder.~.'. 453
edges. 4 I5
ul parnllelograms. 305
DI prisms. 338. -137-438
of Irnpcmixls. 303
0| tii.tt1gles._i-03
of triangles. 237. 303
bases of triangles. 303
Brmmlmtm (Oldenburg and van
Bruggen]. 558
betweenness, 273
biconditioimls. 99. 789
hinzir_r number system. 798
blocks, 706
bocl_v-centered LlIl.)l(S, 390
Bolyai. Janos, 731
Izwidge problem. F12, 7 I6
bridges, I55, 720
Brunelleschi. Fillip. -109, 412
O
Calztbash nets. I93-I99
C-.\Iib.in (game). I2?
calnem obscura. -I98
Cantor. Georg. 740
Cantor dust, .7‘-10
Cat let‘. HO\\"¢Il'tl. 476-477
C-.wnIieri's Principle. 440, -*-I70.
I88
Celtic I.notworI;. 8
cenotes. 600
center of dilation. SDI]
center of mass. -19
center of projection, 7-19
center ol rotation. SI. 53
centers, I39. 314
centml angles. I39. 565-566, 62!
centml projections. 7-19, 762
centroids. 47. 49. 369
Chaco Canyon, 562
Challenges. I6, 32, 86, 97.
ll4—l I5, I81. I83. I95, Zlfl.
222. 232. 2-1|. 25'. 269. 278.
300. 329. 337. 3:"-l. 377. 386.
393. I00. I06. -‘I57. I67. 471.
I75. 434. 504. 5|}. 52.5. SM,
539. SSI. 579. 593. 607. M6.
(135. 660. Clfsfi. (384. 704. "HO,
7-14. 77 I. 780. 78I_. 80.3
ch.-inihenxl nautiltts. 5
Chaos Game. 7-16
Chapter Projects
'\rc.a of a Polygon, 360-36!
Flemgons, 282-283
lnclirca .\-Icasurcnicnt and
Scale Models. 552-553
Logic Puzzles "Ind G.une:i.
|2h—I.Z7
Origami P.1per Folding. 68-69
Plimpton 322 Revisited.
636-687
Polyhedra. I IB—I I9
String Figures. I‘J8—I99
Tangent Curves. falfl-I'\I9
Three-Dimensional Puzzles.
436-I87
Tuwer 0| llanoi. 756-757
Two Fantous Theorems.
805-307
Chaplet‘ Reviews. 70-74. I28-I 32.
200-204. 234-288. 362-366.
420-124. 438-492. 554-558.
620-624. 633-692. 753-762.
803-812
chessl>o.n'ds. 80-8 1. 83
chords. of circles
clelinition. 564
segtnents. 600. 602
theorems. 568. 574-575. 577.
602. 620
Chords and Arcs l'heorem.
568. 6.7.0
Chou pa smm thing, 322-323,
339
Christo. -I28
circle Ilowcrs. 7. 6 l 8
circles. 562-62-I
arcs. 566-568
ccntcr. 6l2—(>I_i
ciI'cttt'nfr:rcnccs In-;I .-trc I5.
3-l5—3I6. 54 I-342. 362. 36-1
classifi-ration ofattglcs with.
583-592
concentric. 367
of -:I.-1n_s;cI'. 588. 59]
definition. 3 M. 564-565
dcgrcr: measures. 3(>6—S67
cqn ttions. (ill. G23
gmphittg. 6l0—6 I I
great. I I6. |7.2. 73!
parts tJI'. 3H. 56-}. til
scxants and tattgcttts. 573-576.
583-592
segments in. (rfJ0—(»O4
t;Ixiu..1IJ. TITS. 759
H iattglc-t and. -13-4-1
unit. -372. (SIT. 6-18-650
circumu.-nlcrs. 269
t;irt.untIcrr.nu:s. 3I5. .362. 364
uircumwrilxd circles. -I I. 73
Cluc (game). I-If»
mastlittcs. 739-7-I0
coin toss and probabilitv. 354-355
College Entr.m.:e Exam Pmctices.
76-77, l34—l35. 206-207.
.29D—29I. 368-369. 426-427.
-‘-I9-I—-I95. 560-545 I . 626-627.
694-695. 764-765. 8|-I-8I5
coIline.trity. 273
collinear points. I0
compass and st: aiglnedge
constructions, .26I—2b3.
265-203. 276-277. 238
compass Imulings. 2:‘-. 29, 33
complementary angles. 28
compound st-atentents. 776-777.
8l0
computer logic. 798-80!
concave polygons. I77
conclusions, 90-91, I39. 768.
769-770
conctn rent lines. 45
conditionals, 90-93. 99, I29.
784-737, 810
cones
conic sections. 597
pants and I3, pes of. 460-46]
sut'l'.tce are-.1, 461-462. -188, 49l
volume. -163, 488. -19l
congruence
angles. 37, 72. I33. 265
arcs. 563
eqttivalettce properties of.
Il0—III. I28, I31
of figures, 50
of p.tr-allelograms. 247-248
of polygons, 210-313, 286
ofsegments. I9. 70. 7!. Nil
ol'tri.1ngle.s, 217-220. 226-229.
235-238. 262. 286
congruent polygons. 2 l0—2 I .5
congruent scgntcnts. 70. 7|
conic sections, 597
-Ionjcctures
Angles and Inter-rcptcd Arcs,
58l—5B2
dcfittition, _I-6
Goldbach. BU?‘
It.-lv.‘IIl'Ig to theorems. I I7—I20
proofs of, I29
Tri.tng|c Midscgntcnts. I83
Twin Primes. 807
t.onjunction~:. 776-778. 809
C0t'mct.tiuns
Algcbnt. I5. It». 20. 2 I. 22. 23.
3.2. 48. 65. (3-6. SI. 83. 8-1. 35.
87. I07. I08. I I0. l|.2. II3.
I22. I3 I. I-‘-IS. I52. I60. I74.
ISI. I87. I9l. I92. |95.2I:'>.
23-1. .233. 2-10. .246. 278. 297.
299. 309. 3 I 7. 3|‘). 3.26. 327.
3.29. 33 I . 332. 333. 3-13, 344.
37?. 393. 400. 4UI. -I05. -I06.
-I08. -13 I . 434. -142. 4-H. -150.
456, 457. 459. 47-3. 499. 504.
513. SI6, 52-1. 55 I. 570. 575.
573. 579. 59-1. 595. 59?. MIDI.
602. 604. 606. 607. 609. M0.
61 I. 6|=I. 6I5. 6I7. 635. (H5.
(167. 634. 700. 704. 710. 727.
7'96. 804
Coordin-.1te Geometry, 216.
2-12. 3419. 39-1. -107, 4-14. 530.
532. 6L2. 669. 679. 685. 705
Knot Theory, 728
MauintuntIMinitnum. 3 I D.
352. -13.2. 43-1. -157. 466. -I83
Nutnbet 'I'Ite0r_v. 327. 795
Polar 0Jordinates. 662
Plobatbility. 357
Technology, I74. -125, -I66
'I‘rigonon1etrv. S73, 61?‘. 669,
685. 7I9
consequents. 77]
construction. See also dt.min_g
compass and st migltteclge,
261-263. 265-268. 276-277.
288
expl-.=m.ttion of. 3:"-
justification of, 263
tr.tnsl'orm-ations. 271-274
Vegrex ille egg tiles, I69
t.'OnIl‘.l<II0l'lS. 500
contradictions. 792, S08
contrapositives of conditionals.
F86»-7'87. BIO
converses
of alternate exterior angles. I65
ot'.1|tern.tte interior angles, I65
ofthe Chords and Arcs
l'heorem, 570. 620
ofconditionals. I29, 785. 737,
BIO
of the Corrcspondittg Angles
Postulatc. I63. 200. 792-79.‘
in definitions. 99—|0[l
of the lsosccles Triangle
Fhcorcm. 237. 28-!
of the Pg.-th.tgorc.m TI'|I.‘OI'( m.
.52-I-325. 3.50. .562
reversing. 92
of the unto:-side interior
angles. I65
ofthc Segtncttt .-\ddit ion
Postulatc. 27.5
at the Tattgcnl Thcurcm.
575-576. 620
at the TI'Icnn:m of Dc~:.tt'gttcs.
75-!
of II'd|"l5VCl'!iilI pt‘-npcrtics.
I62—|f.~3. .202
use ul, I63
UJIIVCX lens. 5-! I
ct‘n1\'cx polygons. I77
Con\v.t\'. lnhn. I36
courdimle planes. 397-395
ctm|'din.tlc prtml. Sat: prool‘
C()Ul'dIl1dI€S. SL1‘ rtl.-.0 CtJl'll1CLIIt)lI'i
iIIlillI0lIS. -I99
distattce fottnula in three
dimensions. 393. -‘-I20. 423
Ini.I~;r.g,tnettts. I92—l93
oct-.1 nts. 397-398
operations on. 59-62. 74
pannttettic equal ions. -:04
ofa point. I7
polar. 662
prisms. -I-H
proofs, 3-19-35]
reflections. -179
revolutions. 48!
rotations in. 480, 680-682
in three dimensions. 396-398.
4.22
coplanar points, I0
cm'oll.n ies
Arc-Intercept, 533. (320
deiinil ion, 237
to the lsosceles I'ri.tng,le
Fheorem, 237-233. 284
Right-Angle. 583. 620
I'wo- l'r-.tn.s\'ets.t|
I’nopottion.1Iity, 527. 554
INDEX 941
xepug
Index
corresponding angles, 15?.
I62-I63, 200. ll I-313,
7'92-793
Corresponding Angles Postulate,
I57. I63—I63. 300
corresponding sides. 2| l-313
cosec-.1 ms. 646
cosincs. 639-642, t--19, 663-665.
683-690
conmgents, t--:6
counterexamplcs. 92
(_‘.PC.TC, 2,!-5-2.!-6
Cravy Horse .\-Icmorial. 1915
Critical Thinlzittg. I9. 20. 25. 26.
28. 37'. 6|. 62. 93. I00. I08.-
IIO.Il‘J_.II‘1.l7I.I9I.|93.
ZIZ. 2l8. 227. 236. 257. 2 I I.
255. 272, 273. 271, 294. 296.
304. SI6. .I-2.5. SJ-I. 3-12. 348.
I74. 389, 397. -II I, -I I 3. -LI-2.
I33. -I38, I55. -I53. 500. 508.
509. SI‘), 3213. 527. 534. 53-5.
545. 563, 373. 575. 530. S89.
59I. 6| I, (III. 6.II. 6-IU. 647.
649. 656. 664. 674. 630. 700.
70]. 7'08. 7|-I. "HS. 722. 73l,
7-I0. 7'69. 770. 7'78. 785. 736.
799
Cross-.\'IuItipIic.ttiun Property.
509. 55-1
crystal lattices, 383. 424
r.uI)e-.-
crystal Iattice. 390
drawing. 372-373. 380—38l
ratio of surl Ice area to volume.
I3 l—432
as regular polyltedron. 379
surface area and volume.
I30-43.3.. -I89
utt it. 373
cubils. 23. I96. 637
Cultural Connections
AIi'i4:aI. .13. I45. I96. .194. 31 l.
324. 448. 449. 527. 542. 637.
7 I 3
Asia. 34. 37. 312. 320, 32!. 322.
367. 457. 745
Europe. 270. 322. 393
cuneiform. 636
cu: ves
dragon. 7-1-1
Hilbert. 745
level. 425
monster, 7-15
simple closed, 722
sine, G-17
smooth. 579
tangent. 618-619
cylinders
nets of, 459
oblique. 43
parts and types of, 453
seals. 45?
942 INFO BANK
surl'.tce area, 45-1. -188, 490
volume. -155, 488. -190
0
dead reckoning, 673
dedttctive reasoning. 9!. I I8-l I9.
l3l. See also ar'gtttttettts; logic
delinitionc, properties of, 99. I34]
degree measure ot arcs. 567‘
degrees. 26. 3-1. 566-567, 713
De Motgattt. Attgustus. 778
density. -139. 4-13. 449
Desatgues. Girard. 75]
diagonals of polyhedrons. 390
diameters. of LII'CIC$. 5 H. 564
digits (unit of measure), 23
dihedral angles, 382-383
dilations. -198—S0l. 306. 507. 555
direction, 672
disjunctions, 777. 809
disiunctive syllogisrtt. 86
displacement vectors. 673
distance
cosmic. 670-6? I
lbrttttll.t for. 339-340, 363. 3-65
lonmtla in three dimensions.
398. -I20, -I33
indirect measurement ol.
533-533. 542. 557'
from a point to a line. 5?
segment addition. 20
taxidistance. 7l]G—7l]7. 759
Divisiott Property of Fqttality.
I08
DNA mOI(‘CllIC5. 72!
dodec lI'I(‘-.Il'O ns. 38?, -I IS
dragon L'.ttrv(‘5. 7 M
clrawing. See also constru-:t ion
-sttbcs. 372—.I7.l-. 380—.i8I
Fulcr diagt';tn1s. 9|
ison1L‘II'iL'.. 372. -Ill
mcchani-:.tI, .l-72
perspective. 409-H2. II I-Ilfi
l.)i.'It'er. Albrecht. -IIO
6
Earth. circumference of. 5-12. 5-19
ca rtlrqttakcs. 2-1. 398-59‘)
edges
0|" I1.-1ses_. I-15
of dihedral angles, 582
in graph lheona 7"l2. 7l5
0|" polyhcdrnns. 379
ol prisms, .l-88
egg design. l68—l6‘J
FiITel Tower. 2 I7
Finstein. .-\ll1crt. 7.3.3
cndpoints. l0—l I. 555
enlargements t_diI-ations),
—-I93——50I. 506, 507. 555. See also
translbrtnations
equality. properties of. l07—l08,
I I0. I28. I31
equiangular polygons. I39
equilateral polygons, 139
Equivalence Properties. I l0—l I 1,
I31
eqttiralence relations. I I0, 523.
3"?"
Eratosthenes. S-:2
Fschcr. M.C.. I5-1. 2.55
I
775
Fu-slidcan algoritlun, 775. 797'
Fut:lidr:an gconietry. I I6. 729-730
Fttlcr. l<‘on.trd. 393. it'll. 7| 7
Euler LIlBl'dLIt'.‘l‘ISIIC. 7'25, TM]
liulcr LIILUIIS. 7 I5. 720. 7'5‘)
Fulcr tliag.:ran1s_. 90—‘J I , 95. I00
Euler paths. 7"l2—7l S. 738-759
Fulcr's Formula. 723. 758
Fu|cr's number. 72.5
evcn verticcs. 7| .3
Everest. Mount. 634]
Exchange l’rt)perI}' (JI
Proportions. 509. 554
exulusix-e OR. 777
expansions. SOD
exterior angles. ll. I56. I60. I65.
l7~I—I75. I79. 200-20!
external seeant segment-;. (:00
Eyewitness Math
Age ol Universe. 670—67l
An ‘UILICIII \'\"onu.Ier. jI1—.i I3
Egg Over .r\II)erta. If}I1'—I69
I-’0it'tt of Disaster. 598-599
Too Tough to: Computers.
38-39
Treasure ot King Tut's Tomb.
-I7b—I77
The Wlteels of Time. 782-783
laces
at dihedral angles. 332
0| polyhet.I|'ot'ts. 379
(‘II prisms. 338. 437-433
ol pyldnllxlfi. I-IS
IopuIug}' and. 726
lair rulers. ll-I
lallacics. 77 l . See also logic
laI:~:e premises. 770
Fibonacci sequence. 98. 704-705
fingers (unit of measure}. .23. I96
lirst dit'l'etem:es method. 124
F|eury's algorithtn. 715. 720
llexagotts. 232-283
flowchart proofs. See proof
45--15-90 triangles. 33 I-332. 346,
363-364
I'our-color theorem. 587
fractals. 727., 738-74 I. 761
I'r-.1ction.s. 329
functions, 59
Fund-.unent.tI I'heorem of
Number Theory. 805
0
Galileo. 653
gallons. -I39
gdtllcs and puzzles
Babvlonian, 322
Chaos. 7-I6
compass and straiglttedge.
Zbl
graphs in. 720
logic. I26-127
networks. 718
nim. 87, I I6
Nine Coin. 755
three-dimensional, 486-487
Gauss. l..1rl I-'t iedrich. 730
gcd [greuttest common divisor}.
775
geometric probability, 353-355.
366
geometry
in architecture, 5
Euclidean. I I6. 729-730
fractal, 738-71 I
hyperbolic. 73 I-733. 735. 76!
in nature. 5
projective. 7-I9-75I
properties ofcqu IIIl)'. I07—l08.
I I0. I23. I3I
sphcrir II, I I6. 73I, 760
system oI'knowlcdge, 2-15. 256
t.tt<ic,.Ib. 706-708. 759
undcfine-zl terms in. 9-H)
vcc.tor.s. 672-675
glide rellcctiom. 56-57
Goldlmch COl'I_it‘(IllI'(‘. 807
golden ratio. 5. 698. 700—70I .
703
golden rectartglc-.. 698-699. 70I.
758-75‘)
golden rulers. 670
grades. 204. See also slope ol .1
line
graphics t..IIc.ul.-tmrs. -166. 6| I. M3.
633. 650. 7-16
graphittg
circles. f.~|0—fi| I. 623
intercepts in. 403
to solve puzzles. 720
teclmologx-, 6| I. 6 I3. 6l6
ttigonomett ic ratios. 632, 650
graph theory. 712-715. 725
great circles. I I6. I72. 73l
greatest common divisor tgcdl.
775
h.t.tb. 783
half-plancs, 382
hammered dulcimers. I89
he.1dings. comp.-1 ss. 25, 29
Itcad-to-tail ntcthod OI" vector
addition. 67 I_. (u9I
heights
ofconcs. 164.1
oI crlinclers. 15.3
Io.-td-bearing capacitv .-incl.
545-546
ul parallelograms. 305
(III prisms. 43-?
0| pyramicls. -I-I5
slant. 4-I5. -Ifal
of Irapevoids. 308
at Iriartgles. 30.5
llcrotfs Iurmul.t, 3| I
I lcrrnstcin, lim. f.~7CI—67l
hcmtllcxagons. 282
hcxaguns. 41. 53-1. 5155
hcxahcclruns, 337'
hcxahcuilctagolls. 283
Hilbert curves. 7-I5
H L [Hypotenuse-Leg)
Cong: uence 'I1teorem. 229.
EN. 236
Homebuilder Theorem. 25!)
horizontal angle of danger. 59l
Hubble space Telescope, I62
hyperbolic geometry. 731-733.
735. ?6I
ltypotenuses. I90, 229. 331-333
hvputhcscs. 90. 791
ices.-ihcdrotts. 387. -I03
identities. in I I-642. 658
iclcntity ITI.-lII'I‘(, (>8-I
lI'-Then stalctncnts. 90-93. 99.
I19. 784-737. SIO
ii‘-then IIJIISIIIVC propctlv, 93
images. 50—5I
incenters. 45
inclusive OR. 777
Incommeusurahilitv of the square
Root of .1. 306-807
index of rulers. 75
indirect me.tsurement. 5 I6.
533-536. 542, 55.1. 557. 692
indirect proofs. 579. 79!-793.
79?. BI I
induction. lIliIll'I€lIl.1lICdl. 796
ind uctire reasortirtg. I IS-I I9
inequalities. 27-1, 325. 367., 364
Infinity of the Primes I'heorem.
805-807
inhet itance of proper ties, I50
input-output tables. 80D—80I.
81 I
inscribed angles, 580-584, 6.20.
622
Inscribed Angle l'heorem.
580-584. 620
inscribed circles, <14. 73
‘intercepted arcs, 566. 58 I-58-1.
630, 62.7.
intercepts. 403
interior of an angle. I I
intersections. I I
inv.tIid .-1 rguntcnts. 769. 77'l.
303-80‘)
invariants. 723
inverse sines. 630. 669
inverse: of conditionals,
'F8t'i-—7'87. 8 I0
inverse tartgcnts. 633
irmtional nun1bcrs_. 806
Isl.-tmic art. 8
I'i0|'I‘Il.‘II'I(. (Ir.twit'tgs. 372. -I2 I
isometries. 273. 275. tire nlco
tr.tnsI'ormations
isosceles tr.tpc7oicl.s. I53
isosceles triangles. 9|. I I0.
237-238. 342. .234. 237
Isnscclcs T|'iangIc Thcurcm. 2-I2.
2‘!-I
iterations. 738. 71%|
0
].u:ob'5 I.-udder { string .trtI. I37,
I98
lord.-tn. C.-tmille. 722
Iordan Curve Theorem. 722, 758
_i0ttn1.1ls. S
lupitcr. 65.5
instification ofconstrttction. 263
0
Kepler, Johannes, -I19
kites. I53, 250. 285, .310. 74-1
kivas, 562
Klein bottles. 77.7
knot theory. 72 I, 728
Koch snowflakes, 7-13
KoI.tms. 7-I5
Kfitiigsbetg bridge prol.>It:m. 7|l.
Flt’:
laser light. 388
lateral edges, 445
lateral faces, 389. -I45
lateral surfaces. -153
law of cosmes. 663-665. 668. 683.
690
xepug
INDEX 943
Index
law of indirect reasoning, ?70.
793. 309
law of sines, 654-657‘, 688. 690
left-hand rule. 34 I
legs. 237
legs of trapezoids. 303
length
are. S67-568, e-2]
coastlines, ?39—?-10
definition. I?
measurement of, lF—20, 7|
unit. I8
Ien.v:s_. S-II
letters. 737
Ix.-wilt. Sol. 97
limestone elensity. -148. M9
limiting, eases. I86
I inear Pair Property. 28
linear pairs. 28
lines. See also parallel lines
concurrent. 15
eopl.-1nar_. I66, 200
in hyperbolic geon-n:-try. ':'.l-2.
7"6I
mirror. 53
(Jl'tI‘llJgi'IlhlI. 732
overview. 9- I D
panllel. II9
parlllel to planes. 3-SI
perpendi<.uI.1r. 3-3-37. 267, 38!
rhumh. I76
sl-(cw. 380
slope of. 65
in space. 330. 402-104.
422-423
in spherical geomeIr_v. II6
Lit’: llui. ..Il_l
I|.'Jd(I-I)C':ll ing C tpztcities. 545-546
Lobacltex-sk\', Nikolai. 73 I. 733
Iogaritluui-; spirals. 699
logic
computer. 798-SDI
conditionals. 90-92. 99
coniunctionc, 7711-773. 309
equivalence. I-'30
gates. 799-801
ll‘-Then statements. 90-93. 99.
I29. 784-787, 810
indilecl proof. 579. 79I-793.
797
iltdtlctive and deductive
reasoning. 91. I l8—l I9. 13!
invalid atguments. 769, 7?I.
808-80‘)
law oi" indireu reasoning, ?70.
809. BI I
logical chains, 9.7.-93
modus pt‘mt‘H.\‘. 7'69, 808
morlus roflcns. ?70. 79 I _. 808
negation. 718
puzzles and gatnes, l36—l37
valid arguments, 768-770.
809
944 INFO BANK
logical chains, 92-93
logieallv equivalent. 730
logic: gates. 799-80]
Lucas. Edouard, 756
lunes, 3:16
CD
magnitude. 6?‘:
maxjor arcs, Sbb
tnzmdatlas. 7
Mandelbiot. Benoit, 7-1]
muse: S. 670-67I
mathetuatical induct ion. 7'96.
Sift: also indmlive teasollillg,
matrices. (182. 63%. 691
Mayan calendar. 732-733
M.1_v.1n 'l'en1 ple of the Giant
Jaguar. I33. I85
measurement
of distances, 533-53-I
int‘Iil'e{.t, 516. 533-536, 5-12.
952. 557. 692
interior angle. 30l
oi" length, 17-20, 71
medi.I.ns, -I7, 532, 536. 539, 35-1,
557
Menger sponges. 738. ?-I0
Merc.nor projections. 749
micmns. I’?
mitlpoints. .58. I92—|9_l-, -I00.
I20
n1idsegn1t:nls
in the eoortlinate plane.
I9:-!—I 93
of trapcmitls. I8 l—I85. 205
of triangles. I8}-I3-1.
|‘J2—l 93, 20.3, 259. 285.
3-19—.I-S0
minor arcs. 566
minutes. angle units. 3-!
Miro. Jean. 97
mirror line. 53
Mtibius «trips, 72 I, 726-727
mmlus potterts. M9. 308
ntmlm mllens. 770. 79 I . 808
Mondtian. Pier. 5
l1'l()n:sI¢.'l'Clll'VC\'. 7-I5
Monte Carlo method. 355
Moon. 3|-I. 3I9. 54')
motion
in the coordinate pLtne. 59-62
reflections. 50. 51-53. 56-57.
(:0. 73, I I9
rigid. '30. 60-62
l‘DI.-III(Jl'lS. 50-5 I . S3. 62. 73
translations. 50-5 I . 53. 60. 73
multiplication. I28
Multiplication Ptopetly ol
Equality. I03
0
Mpoleon. 270
nautilus, 5
negation. 778
nels
for cubes. S6
for cylin-zlers. I59
for oblique prisms, M2
for Platonic solids. .387
for pyr.-tmid 5,. I-I6. -I52
tangrams as. l8{»—l8':'
IIE'I\VOI'I\"i. game of. 7" I S
|Ietwo|'Ics of logic gates. El-lJ0—u"lUI.
SI I
nim I_g.-Intel. 87. H6
Nita‘ (‘k.-tprcrs on the
Mmlu:rnm.iutl Art. The.
3 I 2-} I3
Nine Coin Puzzle. I-'55
non-Euulitlean geometry.
729-730
l‘llJICI)(JOI($, keeping. 6
NOT in logic, 770. 799, SI I
Notre Dame cathcdml (I-’aris_I. 562
numI\er lines. l7—IS
number theuty. 327, 795. 805
0
oblique cuncs. 160
oblique cylinders. 43
oblique prisms. 3-89. 440. 442. -15.2
obtuse mgles. .29
mt Igons. 737
mtahexlmns. 357
ouanls. 393-‘-3-9:-5
odd vcrtiees. 7|}
one-point perspective. -II4. I2-I
on-oll I tbles. 798-799
optical illusions. ISI
origami paper lulding. 3. 35-3:-‘..
42. 68-69
OR in ltagic. 776—T?7. 799-800
0| lltocenters, 269
orthogonal. 732
orthographic projections. 32-51
at llu.-rltombic structures. -‘-ll-I
Osage ('.II'¢IlI't0llLIS, l9B—l 99
Overlapping Angles Theorem.
I I2. I28
Overlapping Segments Theorem.
I09. LN. 236
O
palms [unit ol measure). I96
paper. IS»(Jl‘l'lCIl'I\. grid. 372-373
paper Ibldillg. 3. 35-38. -12. 68-6‘).
7.2. 252-233
Pappus OI Alexantlria. 2-12. 7'50
parabolic minors. 162
paragraph proofs. Sc-'¢' proo1'
parallcl lines
constructing, 268
delinilion. 35
paper lolding, 36
parallel postulate, 170-171.
730-731
in perspective d raw i ng.
*1 10-41 1
proofs of, 162-163. 202
rcllcctions across, 119
slopcs. 191-192. 20-1
ll'h':OI'v:‘ms. I19, I29. 166.
191-192. 200, 111. -I20
Ir.-1nsvcI's.t1s_. I55-I38
parallelogram method. 674-675.
(191
[1dl"d11L logra ms
arms of. 303, 362-363
conditions for. 25-I
congt ucnw theorems on.
247-218. 284-285
definition. 1-18
clidgoltals. 3-18
parts 01'. 305
properties, I-19. .202
r.Iti0n.|1 symmetry in.
.2-13-2-I-I
vcctor addition by.
67-I-675
parallel planes. 380
parallel vectors. 673
parametric.‘ equations. -I1]-1
Pttrlltcnon. 5
Past |1's triangle. E17. 741
1’.-ttcrwn. Michael. 126
pcmaguns. 703
perimcters
deliniliou. 294
of polygons, 294-295. 363
01' tcuautglcs. 296-297. 362
semiperimeters. 31 1
peris-copes. 161
perpendi<.u1.u' biscctors. 33. 266.
577. 620
perpeiidicuhit lines
constructing. 267
i1C11l'11l101l. 35
distances. 3?
paper folding. 36
slopes, 191-192. 204
theorems. 191-192. 201
perpendicul-.1 r vectors, 673
perspective dnming. 409-412,
414-416
pi. 315_. 355
1’ike’s I’€.l1\' I'ai1\\'a\'. 636
planes
coordinate, 397-398
cliltedral angles and. 332-383
equation 01', 402
o1" flight. 385
half, 382
overview. 9-10
parallel, 380
reflections across, 478-481
rolation of. -185
in space. 402-404. -122-423
traces. -106
Plato. 327, 371
platypus. 132
Plirnpton 322. 321-322, 638,
686-1187
plumb bobs. I67
1’oin::.tré. Henri. 732, 735.
761
point of tangcnqr. 573-57 1,
389
points
coordinates 01. I7‘. 39
ovcrvicw. 9-1 0
[1l'O_iCL'lC(‘l. 7 19
1'£‘I1CL'll01I across a linc, 52.
I 1‘)
rotations. 680-681
vanishing, -110-112. -‘-1 14-1 15.
4.24
polygons. 139-199. Sec also
parallclogrants; tri.-inglcs
angle sums in. 177-179. 201.
203
.11\utht:n1s. 334
areas. 295, 320. 334-335. 362.
363
U.'Jll¢.d\.'c. 177
mngrucm. 210-213. 235. 28-1.
2%!»
(.I.'JllVcX. 17?
cor responding, sides and
angles. 21 1-213
definition, I33-139
equi:mg,u1ar. 139
equilateral. I39
interior angle measurement.
201
nmniug. 21 1
perimeter of. 29-1, 363
in 1'oincaré’s system. 736
regular‘. 139. 173
rotations. 691
sitnil.u. 507-510
syimnetry in. 138-1-I2
tt.tns1.1ting, 272
1’o1yg,on Similarity Postulate.
508
polyhedrons
definition, 379
diagonals. 390
1:uIer's formula, 723
prisms. 388-391
regular, 379. 3137
1’ortt'o1io Actix ities
st‘n1iregtI1ar, -108
stellated, I 18
Archimeclea n Solids.-108
Areas of Irregular 1’o1\-gons.
320
Chaos Game, 746
Circle Flowers. 512, 618
Equil.ner.tl 1'riangles. 225
Euclidean Algorithm, 775,
797
-15--15-90 Triangles, 3-16
Ciamv: of Nim_. 87, 1 16
Cicontctry 1’0I'1101i0. -1-8
Graphs to Solve Puzzles. 720
Grids to Fnlargc a Design.
501"
Indirect .\-lcasurcmcnt. 5-12
Medians ofTri.tn;.:1es. -‘-19
Nets 1orOb1iquc Cylinders.
I39
1\v:ts for Oblique 1’yr.1n1id5_.
-152
Platonic Solids. 38?. I19
Pop-Up 1Jodu‘.a1tc-.‘1ron. ,1-95
Pr01)a1)i1i1ics. 359
Pylhagorcdlt Identities. 6413
Quilting. 147. 572
Rcvcrsc Cunrcs. 609
R01.t1ian TC'~:SC11ill1l)I‘IS. 197
Slntmth (‘urvc-.'. S79
Snowflakes. 58
Solids ofRm't)1t|1imt. 435
Tcsscll.-11 i-ans \\’ith llcxagnns.
231
Tcsscllaliuns \\’itl1
QudL1l11dICI'd1S. 252
T1'illIS1dt10n Tcsscilations. 15-1
Trigonomeuv in Babylonian
1\-lathetnutics. 638
xepug
POST&-CR11‘T computer lamgu-age.
67
postulates
AA [Angle-.-\ngle] Silnilaritv.
517. 55-1. 556
angle addition. 27. 70
angle congi uence. 27. 70. 72
Area of a Rectangle. 296
ASA [.-\ng1e-Side-.-\ng1e]. 219.
28-1. 286
Betweeiiiiess. 273
corresponding aligles. 157,
162-163. 200, 792-793
definition, 11-12
1’.tr.tIIe|. 170-171. 201.
730-731
Perimeter of a Rxtangle. 297,
362
Polygon Cong: uence. 212-213.
235. 28-1
INDEX 945
Index
Polygon Siniil-arit_v, 508, SIO,
55-!
SAS \'Side~.-Xngle-Side}. 2I9.
28-1, 286
segnient addition. 20. 70
segment congruence. I9. 70
$53 I Side-5ide—SideI. 218. 284,
286
$55 I Side-Side-Side) Sim ilaritv.
518, 522. 55-1, 556
sum of areas, 295. 362
surface .u'ea5 and volumes. -‘I88
undefined terms. 70
preinuigcs. 50—5l. 5.5. 500. 555
premises. 768-770
prime factoriration. 805
Principle of IX-Iathen1atic.1I
Induction. 796
prisms
0; |inde1's and. -‘I 54
di Igonals. .59[I—_59I. -I20. I22
oblique. .589. -140. H2. -152
parts ol, 558, -I22
pyramids and. I-17
right. .589. -120. 422. -no.
—I_57—4_59. -I38-I89
surlau: area ‘and volume.
I374!-10. -I38-I89
types of. 338-391
prolnilaility. .553-355. 366
pruhlem solving
draw an Euler .li.1gram. 91
look Inr .1 pattern. 60. 280
make .1 diagratn. I6. 229. 632.
675
make .1 model. 2.24. 7H. 715
make an organized list. 2II
make .1 table. SI. 699. 707. 7l3.
7-‘-I0
use :1 graph. 648. 650
write an equation. 20
projected points, 7-19
projections. 409. 749-751. .'\'c'e:1l_~‘4J
perspective dr:1win;'_.-,
projective rays. 3‘-I9
l’ro_iects. See Chapter Projects
proofs
.1.lg.ebr.1ic. 327. 470. 607. 655.
659. 660. 665. 0438.
of a coniecture. I29
by contradiction, 579. 792. 808
ofthe Converse of the
I’}'thagorean I heorem, 32-1.
330
coordin-.1te, 3-10, 344. 3-15.
347-352. 365. 6-I7
definition. 82
ofthe distance formula, 3-I0
llowc.hart, 82. 235. 236, 239.
2-10. 241, 2-17, 250, 258, 259.
280, 330, 5-10, 587, 608
formal, 82
946 INFO BANK
of the 1ncommensur.1bility' of
the square root of two. 806,
807
indirect, 579. 79l-793, 797. 8| I
of the infinity of the primes.
805. 806
uf the law of cosines, 665, 668
of the law of sines, 655. (259,
(160
logical reasoning. 90-93
need for, II7—I I8
overview. 80-82. I08-I09
p.tragr.-iph. 82. IO‘). LII. I60.
I66. 2 H. 218. 2 I9. 250. 258.
272. 278, 280. 299. .5“). 323.-
52-‘I. -‘I70, 535. 568. 569. 576.-
577. 578. 579. fifll. (102. (127.-
(155. (365
parallel lines. l(i-—l(i.5. 202
of the I’_y'thagorean Identities.
(.1-‘I2. I}-I6
of the Pythagorean Theorem.
.522-.52-I, .529—.5.50
table. .595. -‘I50, 58l. 582, ,68fi.
589. 590. 59-1. 593
ol the Triangle Inequality
Theorem. (:63
Triangle Mirlsegmeni
Theorem. .54‘)
Triangle Sum Theorem. I72
two-t.olumn. 82, I09. I12. II—I.
lll'I. I23.l.5I. l58.l(>0.I(15.
I72, I75. 222. 22.5. 232, 241.
24-1. 247. 249, 250. 253, 269,
278. .780. 3l0. 390. 526. 539.
57-1. M10
ol the voltllne of .1 sphere. -$70
wit huut words [visual]. SI.
323. 009
properties
.-Xdd-One. 509
Cross-Multiplicalion. 509. S54
OI‘ Equality. I07-I03. IIO. I23.
l_5I
Equivalerrce l’|'operIieS-. IIO
E.u:l1-artge. 509. SS4
if-then transitive. 93. I28
inhei itance of. I50
Linear Pair. 25
of proper tionality. 508-509,
556
Reciprocal, 509. S54
reflexive. IIO, I28
s_vmmet1ic. IIO, I28
transitive. 93, Ito. 128
proportional, defin it io n, 508
proportionality
I
of angle bisectors, '39. 55-1
within a Figure, 5I0
of media 115, 540. 554, 557
pI'Dp€l'[l<.’:S of, 508-509. 556
oI' segments, 539
Side-zaplitting Iheorem.
525-527. 55-4, 556
l'1-.o-'l'r.1n:wer.<al. 527, 55-1
Proposition -18 {Euclid}, 32-1, 330
protractors, 25-26. 72
puzzles and games. Set games and
puzzles
Pyramid of Giza, 597
Pyramid of Khafre. -I-I9
Pyramid of Khufu, 4-I8
pyramids
height. 233
II-‘la_v'an. I83, I85
nets for. H6. -152
I'elation§l'lip to cones. 461
surface area. -1413. -‘I88. I90
types of. H5
volume. I-17-I-I8. I88. I90
I-’_y'th.-tgoras. 522
Pythagorean identities. (1-I6
Pj.'th.-tgorean ineq11.1lities.325.
.562. .56 I
P_y'th.-tgoream Fheorem, .52 I-325.
339-310. .562. .564
Pythagorean triples. .522. .527
0
quadratic formula. 700
quadrature. method of, 3-1I—3-I2.
.565
quad rilatenils
conditions tor gpecial,
255-256. 287
conjecttlnss about. 202
inheritance of properties, ISO
rational symntetry in. 2-1.5-2-I-I,
287
simiI.1rit}'. 520
special. lIIfl—l5U
tesscllations with. 252
Quebec bridge. I98—I99
quilting. I I7. 20-I. 2I5. 223. 504.
572
radicals. 329
radius. of a circle, 3 I-I. :'-(rt, 57-I
Radius and Chord Theorem.
574-575. 620
random number generators. .559
rationaliring the denominator.
.529
ratios. S:-r .rl--.1 tI'igon01nctt')'
of are Is. 5-1.5-5-I-I. 557
goltlen. 5. 698. 700-701. 703
surface area to volume.
‘I .'5l—-I33. -‘I89
tangent. 6.5[l—(w3.5
of volumes. 5-‘I-I-5-I5. 558
rays. I0, 749
Reciprocal Property of
Proportions, 509, 554
rectangles
area and perimeter of,
296-297, 362, 363
in buildings, 253. 255, 256
conditions for. 25-1, 2 5
definition, 1-18
golden. 698-699
properties, 150. 202
theorems. 249-250
rectangular prisms. 451
retluuin ml nbsurdum. 792
rcllottinnal s}-mmc-Ir)‘. 139-1410.
201. -191
rclleuinns
fl\l'DSS a line. 7.5, 277, .11‘)
across parallel lines. 1 19
drawin_L:. 52-53. 56-57
thrco:-dimvsnsional. 478-181.
191
reflex angles. 29
Rt-llcxivc Property. 110. 128
regular licxagons. -12
regular polvgons. 139. 178
regular pyramltls. —l-15
Rt.'l(l(‘l'l'lClS1Cl'. Kurt. 728
relativity. general. 73.3
llcsch. Dale. l(}8
rcsultants. (>73
rcw-'olutions. solids lro m. 481. -185
rl'|nml)iuulaottahetlmns. -108
rlmmhuscs. 148-149. 202. 249.
25-1. 285
rhuml) lims. 176
l\licl'|lcr scale. 24
Riemann. G_l‘-.13.. 731
Right-Angle Cornllan_r. 583. (>20
right angles. 29
right cones. 400-402
right q linders. -153-15-I
right-handed system of axes,
396-397
right hand rule. 342
right prisms. 389. 420. 422. -I30.
437-139. 488-489
light triangles. 190-191, 303-304.
322-323. 331-333. 36-1. See’ also
tr igonomett _v
rigid transformatlons. 50. 60-62
rise. 19D
roller coasters, 190
rotational S_\'l'l'In1£'ll'_V, 141-142,
201, -$80, -192
rotation matrix. 682, 691
rotations
about a point. 73, 276
180° about the origin. 62
in the coordinate plane,
680-682. 691
definition, 53
drawing, 51
negative, 649
tessellations, 197
royal cubit, 23
rulers. I8, 24-26, 75, 670
run. 190
same-side interior angles. I60
S.-1.5 (Side~.-‘.ngle-bide] Postulate.
219. 234, 286
S.-1.5 (Side-.-\ngle-Side] Similarity
Theorem. 519. 522. SS4. 550
scale factors, 493. 507
scale models. 507. 552
scalene triangles. 140
Sears Tower. 59
seashells. 699
secants
angles tormecl by, 583-592
to circles. 573-575
cosecants, 6-16
segments, 600-601. (>07, (122.
633
seconds. angle units. 34
sectors. 316
seed point, 746
segment hiscctors, 266
segments
addition. 20. 70
lJiS(’CIOl'S. 38, 206
in circlcs.(100—60-l. 62.‘
C0l'lgI'll(‘l'll. I9. 70. 71. 261
definition. 10
length. 17-18. 71
overlapping. 109, 128
pl 'll'Il.‘,S and, 381}-.181
proportional, 5.19. 551
translating. 271-272
sckccls. 6.57
scl 1'-rt plic lting. 702
scll-si mil trity, 7'3-El-73‘)
semicircles‘. 566
scmipcrimtters. 31 I
scqrtcnccs. 84
Side-Angle-Sidc (SASI Pnslulatc.
219. 284. 2.. ‘u
Siu.lc-Angle-Sidc (S.-"\S] Similarity
Tl'lC[Jl'Cl'l1. 519. 522. 55-1. 556
Side-Side-Angle (SS.-\_l
t.(Jl'l1l)ll'ldl ion. 226. 228-229
Sidc-Side-Si-tlc (SSS) l’ostul.lIc.
218. 284. 281')
Sidc-Sidc-Sitlc (SSS) Similarity
l-’u:-lulatc. 518. 522. 554. 556
Sitlc-Splitting Theorem. 525-527.
‘"354. 556
Sierpinski carpets. 761
Sierpinski gaskets. 7-11. 743, 744.
757
similar hgures. 496-338. See also
congr uence
tlelinitiort. 507
dilations. 498-501, 506, 507.
:1):-
equivalence relations. 523
to measure distances. 533-534,
557
polygons, 507-510. 554. 555
ratios of areas, 5-13-5-1-1,.
557
ratios of Volumes. 544-545
sell‘-similaritv. 738-739
theorems about, 535-536
triangles, 517-519
simple closctl curves. 722
sincs. 6.59-(‘>42
curves. 6-I7
graphing. 650
law oi", (15~l—('aS7. 689. 690
unit Circles. 6-49. 689
1lsin_-.'.. (189
slccw lines. .180
slant heights. ‘l-15, I61
slope 01'.-1 lint‘, (>5. 190-192.
20-1
snowllakc patterns. -12. 713
soccer balls. 108
solids. Sift.‘ also pnlyl'|ct.lmI1s
.-Xlthilnctlcan. -103
ulln-:~:. 372-373
orthogr1pl1ic projedions. 37-1.
-121
Platonic. .187. 419
01 revolution. -135
spatial rclatitatiships. 379-383
volumes and surlacc areas. 37-1.
421
spam: shuttle. 573
spatial rclalinnsltips. 379-383.
391-1, -103. 120. -123. See: also
coordinates; polyliedrons
splieres. 469-473. 439. 491
spherical geometry. I lb. 760
Spider and the Fly. The. 395
spirals. 699. 705
sprouts (game). 121»
square roots. S06-S07
squares. 148, 150. 250
SS.-\ (Side-Side-Angle]
combination. 226. 228-229
555 -(Side-Side-Side) l‘0sttIlate.
218, 234. 28b
s1-.u of Pvtliagoras, 70-!
starting and stopping. 714-715
statements. See also arguments;
logic
argument forms, 768-771
compound. 776-777, 810
ll'- l'hen, 90-93, 99, 129.
784-787. 810
‘stella. Joseph. 155
Stone, Arthur H.. 232
straight angles. 29
straightedges, 261
string art. 7, 137. 198-199
xepu|
INDEX 947
Index
substitution, I28
Substitution l’ropert_v of Equality.
ID8
subtraction. I28
Subtraction Property of I;'qualit}'.
ID8
supplementary angles. 28
sun face area, -I28—=I‘)5
in biology. -I30, -I32, -I33. 436
of cones. 461-462, 483. 491
ofcvlinders. -154, -I88. -190
definition. 130
of prisms. -I_‘7—-I38. 188-I89
ofpynmids. -'1-I(1, ‘I88. -190
ratio to volume. 131-133, 189
ofsolitls, .571. 121
ofsphvsres. 171-473. 189. -I91
swinging door ellect. 228—229
syllogisnts. 9|
Symmetric Property, IID. I28
sylnntetry
.'t\'IS 01'. 13‘)
rcllectional. 1.5‘:-\—I 10.201. 191
rotatioml. I-tl-I-12.201. 180.
-I92
three—tlintensionaI. 473-I31
table proof. See proof
tangents
angles I‘-OITIICCI by. 583-592. 622
to circles, 573-576. 579
curves. 618-619
graphing, 632
identity‘ telation. 6-12. (188
inverse. (1.53
segments. 600-601. 607. (12.5
trigonometric ratios. .538.
630-635. 638
Tangent Theorem. 57«l—57(>. 379.
(120
tangrams. -I86-187
taaicah clrcles. 703. 759
ta.\i¢.aI) gemnetry. 706-708
ta.\idistance.s. 70fi—7[t7. 759
teclinolugv. 171. 425.466. 613.
(>16. 64-1. 652
temperature scales. -‘I01
tessellations. I5-1. I97. 152. 281
tetrztheclrons. 387
Theorem of Desaigues. 751. 75-1.
758
Tl1em'em ol Papptts. 750-751. 733
tlieorems. Set: also r.on\-'erse~:
A 4.5 l.-\ngIe-Angle-Side)
Cong: uence. 226-223. 284.
28!)
Alternate Exterior Angles, I00.
I05. 200
Alternate Interior Angles. I53.
I65. 200
948 INFO BANK
angle formed by secants or
chords. 590. 621
Chords and Arcs. 568, 620
Congruent Supplements, I23
conjectures and. I 17-120
Converse of the Alternate
I;'\'terior Angles. 200
Converse of the Alternate
Interior Angles. 200
Converse of the Corresponding
Angles, 200. 792-793
Converse ol' the Same-Side
Interior Angles. 200
coplanar peI'pendictIlar lines.
I136. 200
Correspontling Angles. I57.
I6-2-163. 200. 792-793
definition. 109
of l)esargues. 751. 75-1. 758
Fttlcr paths. 71.5. 715. 758
F..\'terior .-\ngle, I60. I65.
I7-I-175. 201
l_'v--‘i5—‘J0 Triangle. 3.52-3.53,
36.5
Iour—c.olor. 587
Fundamental Theorem of
Number Theory. 805
I IL [I I_vp-otenuse-Leg)
Co11g1'Lte|1ce. 2.7.9. 23-1. 286
lI(JI'nCIJlIIIt.ICI'. 256
importance oI'. I10
Infinity ol the I-‘rimes, I-105-307
Inscrilaccl Angle. 330-584. 620
intersecting Lhnrds. 602. 60-1
intersecting secants. 601. 603.
620. (>21
intersecting ttngent incl
secant. 602. 604. (>20. 621
Isosceles Triangle. 237-233.
242. 23 I
lotdan Cut re, 722. 758
on kites. 250
Law 01' Sines, 654-657
Lines Parallel to the Ground.
41 I. -120
measure of a secant » tangent
angle. 595. 621
measure of at tangent-tangent
angle. 595, 621
Overlapping Angles. I12. I23
Overlapping Segments. I09.
I23. 236
of Pappus. 750-751, 758
l’ar-allel Lines, 166. 191-192,
20D
parallel lines parallel to same
line, 20D
on parallelograms. 347-249.
256. 384-285
pet pendicular bisectors ol
chords. 577. 620
Perpendicular Lines. 191-192,
201
Proportional Attitudes. 535,
55-1. 557
Proportional Angle I’»isec1o1's
539. 554
Proportional Medians. 5-10.
55-1. 557
Proportional segments. 539.
55-1
proving. I08-I09
Pythagorean. 321-325,
339-340. 362, 36-1
on quadrilatenls. 356
Radius and Chord. 57-‘I-575.
62D
on rectangles, 219-250. 256
rellection across two
intersecting lines. 119, 129
reflection ICFOSS two parrllel
lines. I19. 129
on rhombuses. 219-250. 256
rotation about a point. 276
Same-Sitle Interior .-\ngIes. I60.
I65. 200
I-SICII.‘-.'\I1gIt"SICICI
Similarity‘. 519. S22. S31.
5'-3ft
segments tangent to .1 circle.
601. (>03. 621
Sets of I-‘alallel Lines. -1 I I. 420
Side-Splitting. 525-527. 55 1.
Sift
on squares. 25D
Sum of the I:‘€ICI'I[Jl' Angles nl a
Polygon. 179
Sum oI'tl1e Interior Angles oil a
Polygon. I75. 301
Tangent. 574-576. 579. [120
tangent IIILI sennt
intersection. SS9. 620
30-60-90 TI iangle. 333. 363
Triangle Inequality. 274
Triangle Midsegment. 259. 285.
349-350
Triangle Sum. 170-172. 201.
203, 730
30-60-90 triangles, 332-333.
36_I—3EHI
Tliorncrown Chapel. 1316
3- 1-5 rule, 326. See also
I-’)-tltagotean Theorem
tick marks. 19. 27
topologically equivalent, 722. 760
topology. 721-723. 760
tori. 722-723
torus, 732-723
lower of Hanoi, 756-757
traces. -I06
transformation equations,
680-681
transI'ormations
atfine. 747-748. 762
central pro iections. 7-19. 762
constructing, 271-27-I
dilations, -198-501, 506, 507.
3:»:-
equations. 680-681
non-rigid, 7'-17-7-13
not.llio n, 59
rigid, SD, 6|)-62
transitive Property. I I0, I28
translations
definition, 50-51, 53. 73
horizontal and vertical. 6D
polygons, 272
segments. 271-272
translation tessell.-itions. I5-I
transvcrsals. I55-I57. l(12—l6J.
ZDZ. 527.. 354
trapezoids
arms of, 306-307, 362-363
definition, I-18
iSO5I.‘I.‘I0:S_. I53
midsegments. 184-185. 20.5
traveling s.tlesn1.1n problem.
88-89
trefoil knots, 728
Triangle lnequ.i|ity' Theon ni. 27-1
TI ittnglc .\'Iitlscgmcnt Theorem.
25‘). 235. 3-l9—3S0
triangle rigidity. 2 I 7-2 I 3
triangles. Ste uh-'0 polygons:
ll ignnonietn_r
a\'.UIC. 325, 304
allitutles, -19, 267. 303. 554, 357
areas, 303-304, 362-363, 737
lJ¢l‘it.‘S ol‘, 237'. 303
circles and. -I3. 73
(.las'iiFl\'.1ll(Jl'l ol‘, l-I0
congrucnec. 2 l 7-220. 226-229,
2.35-2.33. 113).. Q36
copying. 162
equilateral. 91, I-10. I78, 22-.
736
—lS--15490, 33 I-332, 346.
363-364
hypotenuse, 190
incenters. 45
inequ-a.lity theorem. 2.7-:
isosceles, 9|, I-10. 237-233, 242,
28-1. 237
medians. -I9, 532. 536, 5-10, 554,
557
niidsegments. l83—l8-1.
I92—I93, 203. 259. 255.
349-350
non-Euclidea n, 737
obtuse. 325, 36-1
’.1sc.\l’s. 87
in ph}'$iC.1l structures, 2 I 7-218
rellectional symmetry in. 1-10
rellections of, 53, 6|
fit-:l'll. 190-191, 303-304,
322-323. 331-333, 364
rigidity. 2l7—2l8
rotations, 62. 73
scalene, I-10
semipet itnelers, 31 I
Side-Splitting lheoreni,
525-527. 554, 556
simil.u. S l7-SI9
sol» mg, 655-657. 667
30-60-90 [I iangles, 332-333,
363-364
Triangle Sum fheorem,
I70-I72. 20l, 203
triangulation. 226, 230
trigonometric identities, 641-642.
688
trigono metrv. 623-692. See also
sines: tangents
angles or rot.ition. 6-'17-G-'18
cosec.-1 ms, («-16
C0.<ines.(13‘:‘-(1 l2. 6-1‘).
663-665. 688-690
cot ingents. (-46
l..tw of Cosines, 663-6(>5
I M oFSines. 65-I-657
origin of word. 6.54
rot.nions in the coordinate
plane. 680-682
tlnit circles. 572, GI7. (1 I8-65D
ve¢.tors, 672-675
triseetiuns. 289
tntncncd iun‘aI1c¢.lr0n.~:, -108
truth functionally equivalent.
778
trutlt lttlales. 776. 784-785. BIO
Tr_v This, IS, 53, 6|. 92. 93, IOI.
I ll. I57. I93. 2| I. 228, 237.
.363. 273, 325. 393. —IBl. 509.
545. 568, 6l3-. 63 I , 650, 656.
664. 665. 674. 682. 76‘). 787.
793. 80!
T squares, I66, 337
Tut-.tnl<hamen. King. 476-477
Twin Primes Conjectttte. S07
two-column proofs. See proof
two-[Joint [,'|CL‘.sPELll\r'€. -1l5. -I2-I
tzolkin. 782-783
0
undefined tcnns. 9-H)
unit circles. 57).. 617. 648-650
unit Lubes. 373
unit length, I8
units
ol angle measure. 26, 3-1
ttstrunolnicll. -IOI
ul length. I8
0
valid arguments. 768-770. 809.
See also arguments; logic
valid conclusions. 768
vanishing points. I10-I12.
II l—-II5. -ll-‘I
vector addition, 673-675
vectors, 672-675. 691
vector sums, 673-675
‘v'enn [E.uler) diagrams, 90-91, 95.
IOD
vertex
angles. I I, 588-590
of cones, 460
degrees. 7l3
in graph theory, 712
odd and even. 7l3—7l5
ofa polygon, I35
ol'.1 polyhedron. 379
of a pyramid. 145
ch triangle. 237
vertical angles. I l7—l I8. I20.
I29
Vertical .-\ ngles Conieeture,
I I7-I 18
Vertical Angle Theorem, I18. I20.
I29
Very I ong Baseline Array t’\-'l.l1.-\ I.
67I
vole ln0C5. -160.. I63
volumes. l28—’l9'S
ul \'.(Jl'lt."s'. I63. -183, -l9l
ol tylinr.Ier:~:. -I55. -I83. -I90
(lcfinitio n. 430
maximizing. -I32
ofolnliquc prism-4. 440
of [.1\'fdl1"lII‘.lS. 447-143, 488.
490
ratios of. 544-545. 553
ratio to sutlau: area. -131-433,
489
at right prisms. -$38-l.’.~9,
488-I89
ofsolitls. 37-1, -‘Ill
ofspltetes. 469-471, -139. 491
0
W.-idlow. I-loliert. 436
W.1ll_m, I).w id, 72l
water. density and volume ul,
I39
weight. lo.u.l-bc'Iring cttpauity and.
545-546
xepu|
yin-yang srmbol. 320
O
£ioll.owski, Korczak, 496
INDEX 949