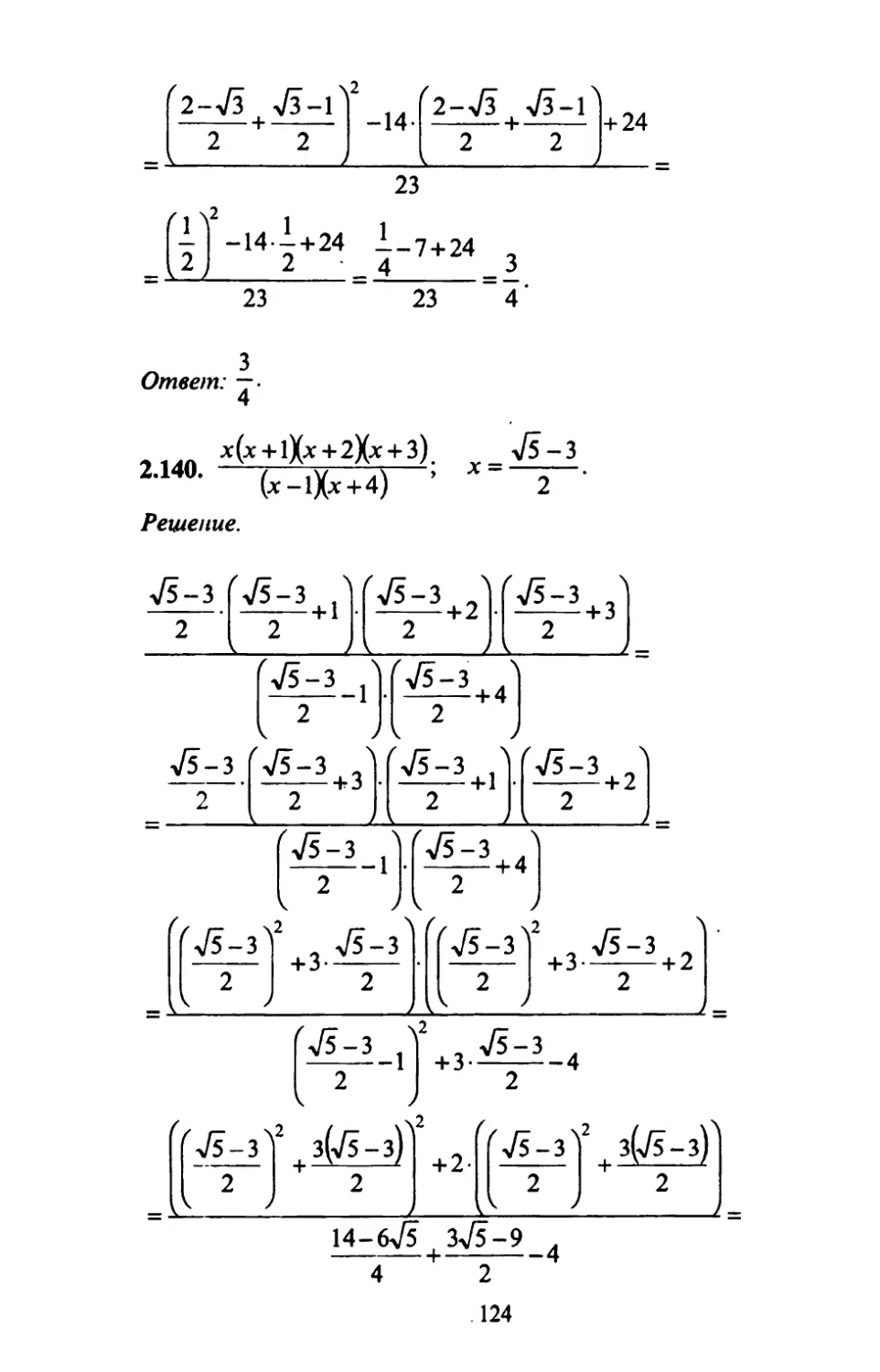для ntnuH
в ты
ГРУППА А
полный
СБОРНИК РЕШЕНИЙ ЗАДАЧ ПО МАТЕМАТИКЕ
для поступающих в вузы
ГРУППА А
Под редакцией М. И. Сканави
Москва Мир и Образование Астрель
УДК 51(076.1)
ББК 22.11
П51
Все права защищены.
Перепечатка отдельных глав и произведения в целом без письменного разрешения владельцев прав запрещена.
Полный сборник решений задач по математике для
П51 поступающих в вузы. Группа А / Под ред. М. И. Сканави. — М.: ООО «Издательство «Мир и Образование»: ООО «Издательство Астрель», 2012. — 912 с.: ил.
ISBN 978-5-94666-634-3 (ООО «Издательство «Мир и Образование»)
ISBN 978-5-271-37256-8 (ООО «Издательство Астрель»)
В помощь абитуриентам публикуется полный сборник задач по математике с решениями под редакцией М. И. Сканави по всем группам сложности.
Условия и нумерация всех задач полностью соответствуют изданию «Сборник задач по математике для поступающих в вузы» под редакцией М. И. Сканави, 6-е издание (М.: Оникс, Мир и Образование).
Пособия помогут при подготовке к выпускным экзаменам в средней школе, сдаче ЕГЭ и вступительным экзаменам в вуз. Книги адресованы школьникам старших классов, абитуриентам, репетиторам и преподавателям.
УДК 51(076.1)
ББК 22.11
ISBN 978-5-94666-634-3
(ООО «Издательство «Мир и Образование») ISBN 978-5-271-37256-8
(ООО «Издательство Астрель»)
ISBN 978-985-18-0106-6 (ООО «Харвест»)
© Суходский А. М., Маслова Т. Н., 2011
© Ничкова Н. Б., Фохт О. Б., наследники, 2011
© ООО «Издательство «Мир и Образование», 2011
© Оформление переплета. ООО «Харвест». 2011
Решения к главе 1
Вычислить (1.001—1.040):
1.001.
(7-635): 6,5+9,9
13:36+13:035-1— —
16 J 24
Решение.
(7-635): 63+93 * 16
13:36+13:035-1^1:^
16 I 24
0,65:63 + 9,9 = 0,1+93 1 24 _ 21А 24 ~ 169 24 30 + 5 16 j 169 48 169
2
= 20.
Ответ: 20.
1.002.
ГГ2_47\^5+Г6_17Л
I 9 72	7 28 ,
1	10
: (0358-ОД 08) 1,6-
Решение.
Yi-47'' I9 72 >
=[^|+^:035}13-^=(0Д+1М,б-§<7б-0>7б=1.
17 Л	A	io
: 135+ ~^ : (0,358-ОД08) 1,6-^ 72 J ^7 28 J	J	25
I	7 4 3 1
0,5:1,25 + -: 1-- — -3 , л I	5711
1.003. v>-1,5 + — :18-4	3
Решение.
7.4	3 ]	(2	49	Зк
0,5:1^25 + —:!-----3	- +--------3
5 7	11 J	( 5	55	11 J	168
55
1
1 1 1
1,5+- :18-
4	3
4
7 _3
4 55
— • — = 32. 7 3
Ответ: 32.
1.004.
(2,7 -0,8)-21 ---------^- + 0Д25
(5^-1,4):^
: 2-+0,43. 2
Решение.
(2,7 -0,8)-21
:2- + 0,43 = 2
19 7 ю'з
38 70
10' 3
. +0Д25
1 2	1
-----+ —+0,43 = 0,02+0,05+0,43 = 0,5.
20 5 20
1
8
2
•-+0,43 = 5
Ответ: 0,5.
1.005.
г^ц+з- . [21+4,5)0,375 4	3 . 5 _ (6	)
1’7	1
2,5-0,43- 1 *	2,75-1-
3	2
Решение.
22;i,i+31 . [21+4,5)0,375 5+1°.
4	3 . 5 _ (6 J = 2 3. Z
17	1	5 4 5
2,5-0,4 3- 1	2,75-1 -	Э
3	2	2 3
Ответ: 5.
20 3
-1_1 = 7_2 = 5.
U5
1.006.
13,75 + 9— Ц
6)
(	1 А 5
>03-8- -
6,8-3- |-5-
;---ф*-271.
з|-з|-56	6
Решение.
рз,75+91)12 (б^-зЩ (т+у)| (т-тН
)_______6 J _________5 J 6	1 _ V 4	6 J 5	5	5 J 6
(1O.3-81V Гз—-3-1-56	* (2,3-0,5)1	(1-11-56
I	* 1 2 3J 9 ( 3 6J	9	(6 6j
11(1+11 11.11
163 =	Г 2)	5 6	163 55 2 163	169 163	)
6	18 5 + 28	6	2+3	6	6	6
10'9 •
Ответ: 1.
1 + 0Д + —|:(1+0Д- —1-2,52
,6	15 J [,6	15 J
1	1W	1А 7
О,5--+ОД5-- : 0,25-- —
3	5	6 13
1.007.
Решение.
1 + 0,1 + —|:(1 + 0Д-— 1-2,52
6	15 J (6	15 J
fl 1 П
—Ь---1--
16 10 15
1+_L__L\63 6 + 10 15 J 25
0,5-1 + 025-
Т_
13
1_1 1_11(1_11L
2 3 + 4 5 Д4 6 J' 13
1.5-11
3	25 ^21 5 =
"11.12.2’5V-
60	13
Ответ: 3.
1.008.
3-+2,5 3
2,5-1-3
0,05
1-------+5’7
--0Д25
Решение.
Ответ: 1.
1.009.
Г	5 А	1
0,4 + 8 5-0,8- -5:2-"	8)	2
( 1	(	2Y1 '2
11.8-8,9-2,6:- -34-8	I	3 1	5
к V	//
•90.
Решение.
(	5^1	1
0,4+8 5-0,8- -5:2-
7---- г... " V\ 2 90 =
1--8-^8,9-2,6:-11-34-
I8 I 3jJ 5
I	2 1
0,4+40-4-5— -90
(15 о 89 13 ЗА 172
8	10 5 2) 5
34,4 90	344-9
<150_89 + 391.172 2-172 к 10 10 +10 ) 5
Ответ: 9.
5±-4> :5А
1010 U* 3 * 5 6 *
1.U1U. / 2	\	9	7	70	7
4—+0,75 -3 — 3	13
Решение.
(с 4 л 1) . 8	f229 25 83
I 45	6 I 15 ,.2	0,3:0,01	2	45	6 I 15 240	30 2
(ЛП,<М 7	70	7	<14	3^48	7	70 7
3 J 13	3 4 J 13
83 15 90 83 240	5	1	240 5	2	5	.
65 48 7	7	6-20 7	7	7	7
1213
Ответ: 1.
1.011. 1
3	1
|+0,425-0,005 :0Д
зо^+|+з| о 3
26:3^
-0,05.
Решение.
-+0,425 - 0,005 |:ОД б-+5-
---------j-YL+-4	2-o.o3 =
30,5+4 + 3^	26:3^
6	3	7
= (0,6+0,42)-10
61 1 10
2 +6+ 3
12--26
-^77" °’0-5 = 26-7
10,2	7	1	3	7 1	х
—ч------= —।--------= 2.
34	4	20	10	4	20.
Ответ: 2.
1.012.
1	1	2	2
3-1,9+19,5:4- 3,5 + 4- + 2 —
3	2 .	3	15
62	' f 1 'l
--0,16	+
Решение.
J ,П me J „2 ~ 2	10 19 39
3-1,9+19,5:4- 3,5+ 4-+ 2—-----------+ --
3	2 .	3	15 _ 3 10 2
— -0,16
75
( 1
0,5 1 —+4,1 20
2
2 62__4_
75 25
J/21 4Г 2[ 20 +10 ;
7 14 32
—। 4. — 2 3 15
19 13 103
_ 3 + 3 40 - 16-/|
2	103 4
3	10
Ответ: 4.
1.013.
(17
- + 0,6-0,005
^40
5+ll-l^
6 3	30
4,75 + 7-
+-------:0,25.
33:4-
7
Решение.
(17
-+0,6-0,005
^40
5 1 23 - + 1-1 —
6	3	30
4,75 + 7------Л0,25 =
33:4 — 7
6/17 + 3_МП 19 15	6 51 17
= ^ЬЦ1^Ьо+Л^.4 = 1^1О+Л9_.4 = 5 + 7 = 12.
- + i-—	33-1	-	47
6 3 30	33	5
Ответ: 12.
(4,5 1|-6,75 j-1	1^.0,22:0,3-0,96
1.014. / ।	i i \ 2 + 7 зУ
3-0,3+5--- :2-	0,2- — 1,6
( 3	38	3	40 J
Решение.
^4,5-11-6,75 j	1^0,22:0,3-0,96
( i	i i Л 24	7 ГУ
3- 03 + 5- - :2—	0,2- — 1,6
3	3 8 J 3	1/40 J
(9 5_27>l 2 [2’3 4 J 3 10 2 16 V 3 3 10+ 3 8J 8
15 И.10_24	,24
11'50 ’ 3 25 _ И 4 J 3 1 25,1 8 1
(1 _ 3/ 8	Л 2V	1.8 2 5 5
[5 40 J 5	[3 J 8	8 5
Ответ: 1.
3 13
1,88+2 — —
25 J 16
26 9
1.015. д-------гт
0,625- — 18
0,216
, 0Д5
3 2 'I
7,7:24— + — -4,5
4 15
+ 0,56 :0,5
Решение.
7 з
1,88+2 —
3_
16
0,625-
13.26
18' 9
oai6+o,56:0,5
Lai5 j_________
7,7:24- + —У 4,5
4 15
(1,88+242)-^
513 9_
8 18 26
f 216 56 V 3	(72 28 V
(150 100	4 16	150 50. J
77 4 V9"5_l + fll AV
10 ’ 99 +15 J 2 8 4 [45 + 45 ) 2
. 3 8 4 = 4------------------+ -
16 3 2
= 4.
Ответ: 4.
1.016. Г16—-13—У —+2,2(— 2	9 J 33 ^33
Решение.
f16l_13Z\H+2>2fA_l\l=f”_124H+ 2	9 J 33	1^33 11J 11	2 9 J И
22 f 8	3^2	49 6 1 2 49 17 „
—-----н— —----ч—I— = —I— = 2.
10 33 33	11	18 11 3 11 33 33
Ответ: 2.
(32 13^1 1—- — -3,6
I 63 21J
0Д28:3,2 + 0,86 5	2
^12 + 0,8	0,505-j-0,002
Решение.
1.017.
(32 13 1 1--— -3,6 0428:32+0,86	63 21J 0,04 + 0,86
| -12 + 0,8	0,505-|-0,002	1+0,8
J 8 18 _8 18 9 02 5
Ответ: 8.
95_39\18 163 63 j 5 0202 - 0,002
1.018.
1	I11 Ии
3^:10+0475:0,35	77-77 :1,4
3	( lo 1j ]
1,75-1—•— 17 56
0,5-- |-3 9
Решение.
1	(11
3-:10+0Д75:035	77 ,,
3	I 10 1J
1 1:1,4	1 + 1
_ 3 2
49 5 ____________.	__________90 7 = fw_n3 Л! ’.3'
17 56 I 9j 4 17 56 18
5	718 -10 1 .-з
18-7-3 3 3
6 ---
4 2
1 +
7
Ответ: 3.
1.019.
9
0Д25:0,25+1—: 2,5 ,17	>.
7-----------------+ —+1,9 • 0,5.
(10-22:23) 0,46+1,6 ^20	1
Решение.
0Д25:0,25+1—:23 , ч ____________16____। I _ +19 1.0 5 = (10-22:2,3)-0,46+1,6 I 20 ’ 1 Р
М 2 8
17 19
10 220 А 114 40+20
23 50 5
9
8	17 38 5 11 „
1 8 40 40 8 8
5 5
Ответ: 2.
(( 1 23А 22 (	3^1	1 )
1.020. 1--— : — - 0,6:3 — -2-+3,75:1- :2Д.
Ц 7 49 ) 147 4	4)2	2)
Решение.
((Л 23Л
22
147
(311	1
- 0,6:3— -2—+ 3,75:1— 4	2	2
:23 =
((8 23)147	(33 147 ... .) _
= ((?‘49"0J6'W + W;22 = (49 22 "°'4 + У22 =
= (4,5-0,4 + 2,5) ^ = 3.
Ответ: 3.
1.021. 2:3| +
f3l:i3U+f2A_E\18U. .4 J 3 ^ 18 36) 65 J 3
Решение.
(	1 Г 1	^2
4 :3 5+4 4 :13/3 +
"г—' I 18’36 J
18) 1
65 ]’3
(. 5 1 3 65 18 Л 1 (5 3 4)1
2 • —• н— —I— * — I* — = 1 —I— + —  —
( 16 4 2 36 65) 3 4 8 8) 3
= 03.
2
Ответ: 0,5.
1.022.
0,5 + - + -+0,125 (3,75-0,625)—
4 6	।	425
1+0,4+—	12,8-025
Решение.
0,5 + — + -+0,125 (3,75-0,625)— ^+-+-+- a]0<
4 6	+ v	425 = 2 4 6 8 + 3J25-48 =
l+04+—	12,8-0,25 l + 2+ll ЗД-125
3	’	15	3 5 15
25 3 12
= — •- + ^=- = 0,625 + 0,375 = 1.
24 5 32
Ответ: 1.
1.023.
2	1 (	5 1
26-:6,4 • 192:3- -3	9
8-:2 —
7	77
2 0,5:18-11
3
18’
Решение.
81-2^
f26?;6,4Ul^:3’L2LV.l = [S0.AU96 И
l * 3 * JI 9 J 0,5:18—11 18 I 3 32 J I 5 32 J
3 60 77
7 180 1 _25 27 11 112 1 _ 45 112 1 _
1.Л.Ц 18~ 6 * l 5 3-33 18“ 2	9 18"
2 56
= -l(45-9-112-2-l)=10.
Ответ: 10.
1.024.
7 11
0,725+0,6 + — + — 40 20
0,128-6—-0,0345 : —
4	25
•025.
7 И 0,725 + 0,6 + — + — ------j-----40 20, • 0,25 = 0,128 6—-0,0345: —
4	25
= 1325 + 0,725	305
0,8-0,2875	0,5125
Ответ: 1.
1,325 + — ---------------------0,25 = 0,128 -635-0,0345: ОД 2
1.025. | (520-0,43):036-217-2—1-(з1,5:12 —+114-2-+61 — .
к	к	3	2>
Решение.
^(520-0,43):036-217-21- ™:12^ :’.У. 2* = ^223,6:036-217 — W— • —+114-+—1 t	7 J 2 63	3 2 J
-	123^	„„л ,
2 I
17>
- 31,5:12 —+114-2 —+61— =
= (860-527)- -+266+ — 1=333—330 = 3.
2
7
1
2
Ответ: 3.
1.026.
(3,4-1375)—
A-fi-L+611
18 85	17 J
Решение.
(3,4-1375)-^
2
18
(7	2
1 —+6 —
85	17
+ 03 2 +
12,5
5,75 + -2
2Д25 — 17
12,5 ]
—7---------\ "I— 2 +---- =
5 (92 104Л 2	635
— — +------
18 85 17
17 16
=^Й+1+1'1+2=3-
18 85
1.027.
( 1 3,75+2 —
J 2
2--1,875
I 2
2-+1,5 4
2,75-1-2
10 if
Решение.
S’75*22	2 4 +1,5 1() / 375+2,5 _ 2,75+1,5^ 10
21-1,875 ’ 2,75 -1 * ’11 = I2’5 -1’875 ” 2’75 J 11
I 2	2 J
( 6,25	4,25^ 10(	17 A 10 _ 33 10 _ 6
1^0,625 1,25 J11 [	5 J 11 5 11	\
Ответ: 6.
1.028. ((21,85:43,7+8,5:3,4): 4,5): 11 +11|.
Решение.
2 ,11
((21,85:43,7 + 8,5 :3,4): 4,5): 1 =+1	= (0,5 + 2,5): 4 i
=Гз I"15
"I 9
Ответ: 2.
5	21
32 10 32 _42 =2 7 21 "21 + 21 - 21 -
1 |.7+11
2 ’ 5 + 21
1.029.
11 + 3,5:111:21 + 3,4:21-0,35.
I5 4J 5	8
Решение.
(2	1 >	2	1
1—+ 3,5:1— :2- + 3,4:2--0,35 =
5	4 J	5	8
= (1,4+3,5:1,25): 2,4 + 3,4: 2Д 25 - 0,35 = (1,4 + 2,8): 2,4 + +1,6 - 035 = 43:2,4 +1,25 = 1,75 + Ц5 = 3.
Ответ: 3.
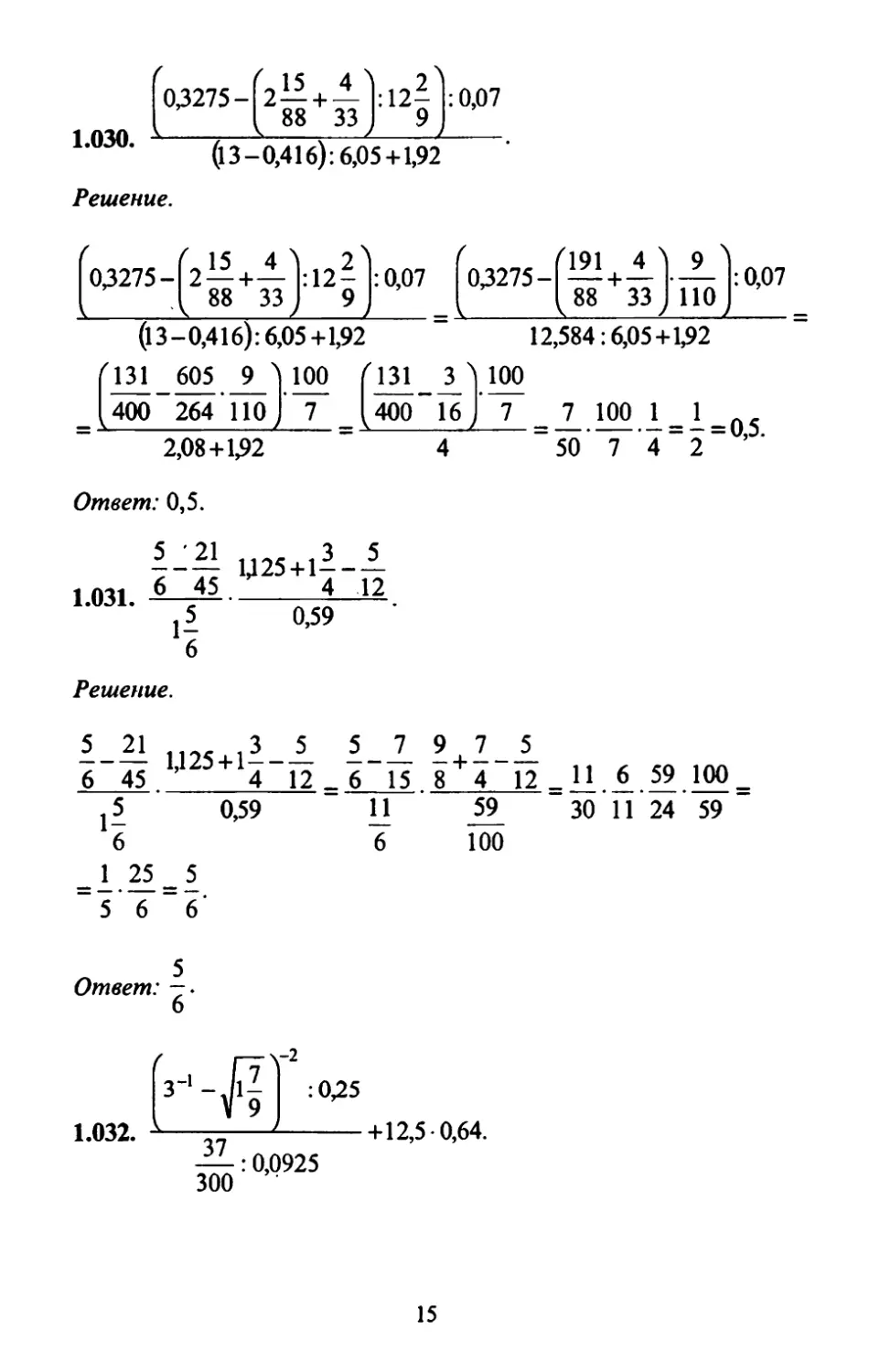
1.030.
f Г 15 4 Л 2 Л 03275 - 2— + — :12—
I 88 33 J 9 J
:0,07
(13-0,416): 6,05+1,92
Решение.
(15 4
03275 - 2 —+—
I 88 33
2 I :12- :0,07
9
(13-0,416): 6,05+1,92
(191 4 19 1 03275- —+— •— :0,07 ^88 33) 110) 12,584:6,05+132
г131 605 _9_) ЮР f 131 3 А 100
400 264 110) 7	^400 16) 7 _7 100 1 _ 1
2,08+132	”	4	~ 50 7 4 ”2
Ответ: 0,5.
1.031.
5_ 21
6 45
1-6
3 5 1Д25+1—- —
4 12 0,59
Решение.
5_21
6 45
059 И
9 7_2_
8 + 4 12 _ 11 6 59 100
59	30 11 24 59
100
±25 = 5
5’ 6	6’
Ответ: 7
6
з_|
1.032. *—

+12,5 0,64.
—: 0,0925 300
i----—-------------+12,5 • 0,64 =
0,0925
300
37 400
+ 8 =
300 37
у-------+ 8 = 3(-1)-2 +8 = 3 + 8 = 11.
Ответ: 11.
1.033. х'л „
1,3 + —
<5	17 А
-+2—- :2,5
I8 247_____
- 23+±1112
30 + 11 I 401
•0,5.
Решение.
3+2И :2,5	* + *ф1
( 8	24) л е _ ( 8 24 ) 5 2
-23 4 >11()U’
,3+ 30 +11 401
10 £
3 5 -2.2_!
"в 23	421.110 з'з
10 + 30 + 11 401 165 401
Ответ: 1.
((7 - 6,35): 6,5+9,9)-—-
1.034.
1	5> 1
1,2:36+1-: 0,25-1- 1-
5	6	4
: 0,125.
Решение.
((7-6,35): 6,5+9,9)-^
1	5^1 1
1^:36+12:025-1- 14
5	6 J 4
:0Д25 =
(0,65:6,5 + 9,9) ^-8
_______________64
(6 1 6 л 11> 5
-----+ -.4------
(5 36 5	6 ) 4
(OJ+9,9) | __________о
J_ + 24_ll | 5
30 + 5 6 4
90	3
30
1.035.
45 15.
Решение.
fl —- —113- + 3—•—	25 9 198 26
I 45 15/ 9	65 99	9 125+ 65 99
fl8l_137\l	’	f37 1241 * 2
1/2	9 J 85	[2 9 J* 85
1 52
_ 5 65 _ 1 _9
85 2. 1
18 85 9
Ответ: 9.
2:3-5
2a_iz 118
218 36 j 65
Решение.
3^2 Г3.15А5 f8_23A 147 5 , 33 147 4 3 (2 4 J~2 (7 49 J 22 = 2 +1+ 49 ’ 22 2 —+ (— 13) 2_f£LlZ) A l + 3_A.ll 16/4 ' J 2 (18 36J 65 8 8 36 65
Ответ: 16.
53
1.037.
((	13 9 A 9
4,625- ——:	'
18 26 J 4
- - 0,375 |: 0Д 25 +1 - - — I: (0358 -1,4796:13,7)
2 I 6 12 I
:- + 2,5:135:6,75 :1—
4	’ J 68
68
Решение.
13 9 19
4,625-— — :
18 26 I 4
9	I 53
:-+2,5:135:6,75 :1 —
4	68
|-0,375 j: 0Д25 +
/ <	7 \
--— : (0358-1,4796:13,7)
^6 12 J
• — +2:6,75 • — 9	Г’
68	(35	27^ 68
121	118+2’ 4 121
((37 1
0Д 25: 0Д 25 + 035: (0358 - 0Д08)	1+035:035
121 68 1 = 17
54 121’2 27'
Ответ:
17
27 ‘
1.038.
7	11	1 'I 5	3 ( 1 5 Y
з/-2^+2Л lYz-Zr 3- + -
<. 2 6Л 2__1 i 27 3 9
7 .И
5
12	18	24
19 /13	13
84 ‘ Г 42 2S:
31 52
l-ll I 13
13 A
42 "28 + 24
/12 218 + 224j Si 52/2 + 6j 4з 19:Г5В_213+АЪ2.-1Л 84 ^ 42	28 24 J 27 3 9
Y*3_^ + ^\36__3j7 + 5Y| 20 <217 36 3 13 20 [12 18 24 J 31 52^2 + 6 j] 13 _ [*72~ 31 52 T J 13
19 /223 69 t 5	29 4	” IZ-lZl + ZZ
84 /42 28 + 24/ 27 27	84 ' 56 27
(2 4 J 13 13 20
_2_ + 25	4 13
27 27
Ответ: 5.
1.039.
/ x	fl — -1,5|1,5
(32-1,7): 0,003 [20 J
(29 3 A (	14 A 1
— -•4:0,2 |2,44+1— -
35 7	25 8
62^+l,364:0J 24.
Решение.
(32-1,7): 0,003
<29 3 A
— -- -4:02
35 7
62 4-+1364:0Д24 =
3 3'
1,5:0,003 20 2 .1241	<500 9 A 20
14 4 5 4 1 20 + [в 40 2 j 1241 35 ’	’ 8 J
125_±\20_+11=1241.20_+11 = 12
2 20 J 1241	20 1241
1.040. 5-: 7
8,4-- 6-7
23 + 5:6,25)-7 8-0,0125+6,9
-20,384:1,3
Решение.
39
7
(2,3+5:635)-7 8 0,0125+6,9
-20,384:13
/ >
<42 6Г (2,3+0,8)-7Л	39 <ЗбГ ЗД-7А
[5 7^ ОД + 6,9 )	] 7 Щ 7 J
39
(73-2,9-15,68) = у
(20,88-15,68)=
39,7_ 39.26_15
7	7’5 14 ‘
15 Ответ: — •
14
Найти У из пропорции (1.041 —1.045):
Г Г 1 1 4-3,5- 2--1-I____"I 7 5
1.041. А----------------
:0Д6 32__3.1
„ 7 14'6
~41—-40 —
84	60
Решение.
( 1	1	( 23	49 А
4-33- 2--1- :0,16 41—-40—
Ц 7 5 JJ	I 84	60 J
32__3..1
7 14'6
7 33 А _4_ 16
4 2 35 I 25 35
7 7
(д-З-И-А.АЁ 2_ 25 16
I 10 J 25 35 10 4 35
2	2
, л 12:0375 - 02 0,016: ОД 2 + 0,7
1.042. —-------------------------
6—:15- + 0,8 Х 25	5
Решение.
(0,016:0,12+0,7)(б-:15-+0,8^ { —• —+—Y—•—+ -. v	у 25	5 J (125 25 10 } 25 5 5
1,2:0,375-0,2	3,2-0,2
(2 7Y2 4А 5 6
( 15 10 1 5 5 ) 6 5 _1 3	3	3’
1 Ответ: — •
1.043.
0Д25У 19_21\82 24 40 J 16
63
0,675-2,4-0,02
Решение.
fl^LLZ) 07 (— - —1 8—	±125
 Д бЗ 21J ,У'(24 40j°16 (63 21/10 15 16
(0,675 • 2,4 - 0,02)- ОД 25	(1,62 - 0,02)- ОД 25
40 63
63 40	1 5
1,6-0Д25 02
Ответ: 5.
9|1П-0^45:0,9 Л	I
1 Q44 ----------------= _i------------
103 024-15Д5:7,5	ij__42.7
40	8
9| 1 - 0,945:0,9 j-(10,5 0,24 -15,15:7,5)
-1-42;
9^“1П(2’52 2’02) 9 -~ -[20 20 j________ 2 2_4
43_35.7	43_5 9
40 8 ’	40 8 20
Ответ: 5.
[13_ 2._£.21 [11
15,2-0,25-48,51:14,7	44 И 66 2 J 5
1.045.	у	*	7—.	>~
3,2 + 0,8 5--3,25
Решение.
(15,2-0,25-48,51:14,7)- 3,2+0,8 5
13_A_J_-211.11
44 11 66 2) 5
(3,8 - 3,3)- (3,2+0,8  2,25) 0,5 - (3,2+1,8) _ 0,5 - 5
Г_5__^_.5^6
|^44 66'2 / 5	1^44 33 /5 12 5
Ответ: 25.
Вычислить наиболее рациональным способом (1.046 —1.048):
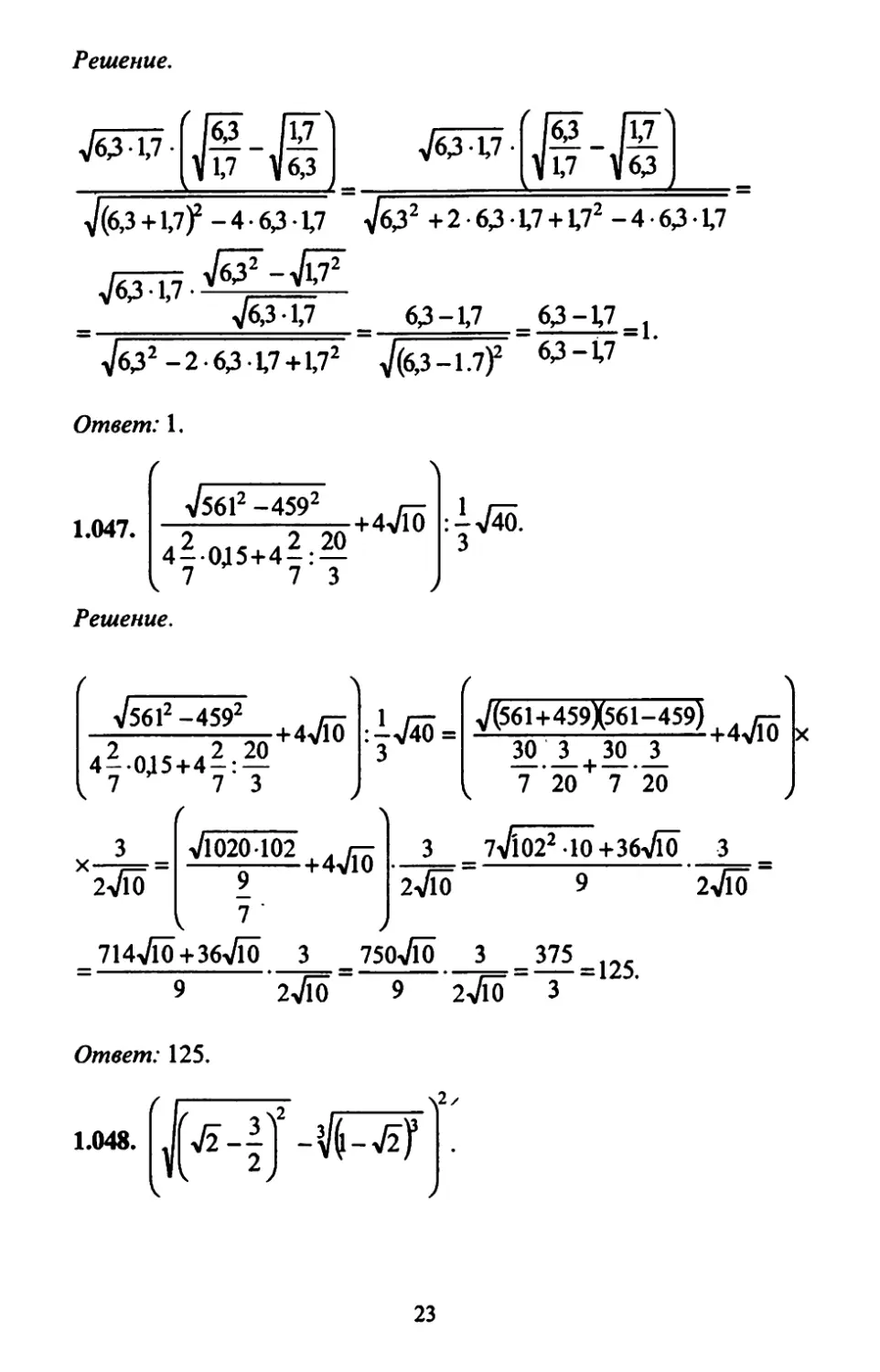
763-1,7-
1.046. -f=
V63-1.7-
1,7
te + lj)2-4-63-1,7 V632 +2-63-l,7 + L72-463-l,7 763-1,7
76,3 1,7	= 63-1,7 = 63-V = 1
7б32 - 2-63 1,7 + 1,72 J(6,3-l 7)2 6)3
Ответ: 1.
1.047.
V5612 -4592
4-0Д5+4 —: —
t 7	7 3
+4710
/
Решение.
75612 -4592
2	2 20
4 —-0Д5+4 —-
( 7	7 3
7(561+459X561-459)	/-
30	so.2.
7 20+ 7 20
3
/ \
71020 102 t 3 7TiO22 10 + 36710 3
9	2710	9	2710
I 7 J
714710 + 36-Л0	3	750710	3	375
9	2T10- 9	3
Ответ: 125.
1.048.
5-|Т-ОУ
--V2-1+ 2
.2
Ответ: -7 4
Вычислить:
2-2+5°
1.049.-------------------—
(0,5)-2-5(-2)-2 +[|
+ 4,75.
Решение.
2‘2+5°
+4,75 =
(0,5)”2-5(-2)-2 +
?+|
-----2------г+4,75 =
1____5 т2
(0,5Г(-2)2+Ы
- + 1
1	.	5
--—	1-2
, f	+4,75 = -±- +4,75 = —+4— = 5.
J______5	9	4+1	4	4
0,25 4 4
Ответ: 5.
1.050.
(0,б)° - (од)'1
3
Решение.
(0,6)°-(О,!)-1
1-10	=__z2_^-9^-9^ 3
3 Ответ: --
Решения к главе 2
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
ПОНЯТИЕ АЛГЕБРАИЧЕСКОГО ВЫРАЖЕНИЯ. ТОЖДЕСТВО И ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ
Алгебраическим выражением называется совокупность конечного количества чисел, обозначенных буквами или цифрами, соединенных между собой знаками алгебраических действий и знаками последовательности этих действий (скобками).
Алгебраическое выражение, в котором указаны только действия сложения, вычитания, умножения и возведения в степень с натуральным показателем, называют целым рациональным выражением. Если кроме указанных действий, входит действие деления, то выражения называют дробно-рациональным.
Целые рациональные и дробно-рациональные выражения вместе называются рациональными. Если входит еще и действие извлечения корня, то такое выражение называют иррациональным.
Числовым значением алгебраического выражения при заданных числовых значениях букв называют тот результат, который получится после замены букв их числовыми значениями и выполнения указанных в выражении действий.
Областью допустимых значений (ОДЗ) алгебраического выражения называют множество всех допустимых совокупностей значений букв, входящих в это выражение.
Действия над степенями
Действия над степенями производятся по нижеследующим правилам: атап = ат+п; ,	(2.1)
„т . п „т-п . а : а =а ; (а")'” = атп;
(а-ЬУ =ап Ьп-,
f \П п
I £
Ijj ~ ьп
(2.2)
(23)
(2-4)
(2.5)
Одночлен
Одночленом называется алгебраическое выражение, в котором числа и буквы связаны только двумя действиями—умножением и возведением в натуральную степень.
Многочленом называется алгебраическая сумма нескольких одночленов.
Одночлены, из которых состоит многочлен, называются его членами. Одночлен есть частный случай многочлена.
Формулы сокращенного умножения
(a+b)2 =а2+2ab+b2 ;	(2.6)
(a-b)2 =а2-2ab+b2 ;	(2.7)
(а+Ь^ = а3+3a2b+3ab2+Ь3;	(2.8)
(a-bf = а3 -3a2b+3ab2 -Ь3 ;	(2.9)
(a-b\a + b)=a2 -Ь2;	(2-Ю)
(a-b^a2 +ab+b2)=a3 -Ь3;	(211)
(a+b/a2 -ab+b2]=a3 +Ь3;	(2.12)
(a-bfa3 + a2b+ab2 +63)=а4 -b4 ;	(2.13)
(a-bja4 +a3b+a2b2 +ab3 +b4)=as -bs;	(2.14)
(a + bfa4 -a3b+a2b2 -ab3 +b4)=a5 +b5;	(2.15)
(a-bjifi5 + a4b+a3b2 + a2b3 + ab4 +as)=a6 -b6;	(2.16)
(a-b^a6 + a5b + a4b2 + a3b3 + a2b4 +ab5 +2>6)=a7-b1; (2.17) (a+ft)(a6 -asb+a4b2 -a3b3 +a2b4 -ab5 +b6)=a7 +b7; (2.18) +an~2b + an"3b2 +an^b3 +... + bn-')=an-bn , (2.19) где n — любое целое число;
(a + b^-1 -an~2b + an~3b2 -an~4b3 + ... + bn~[)= an +bn , (2.20)
где n = 2k+1, к — натуральное число;
(a+b + cf =a2 +b2 +c2 +2ab+2ac+2bc;	(2.21)
(a+b-c^ =a2 +b2 +c2 +2ab-2ac-2bc',	(2.22)
(a+b+c+ctf =a2+b2+c2+d2 +
+2ab+2ac+2ad+2bc+2bd+2cd;	(2’2^
(fl+b-c-d^ =a2 +b2 +c2 +d2 +
+2ab-2ac-2ad-2bc-2J>d+2cd-,	.	(2'24)
a(x~xx\x-x2)=ax2 +bx+c,	(2.25)
где xpx2 — корни квадратного трехчлена ax2 +bx + c .
Формулы (2.16) — (2.24) остаются верными, если вместо одночленов а, Ь, с, dподставить любые выражения.
Многочлен Рл(х) относительно переменной х вида
Pn(x)=aQxn + «1хл-1 + а2хп~2 + ... + алЧх + «0, где а0, al9 а2, ... ап — действительные числа и л0 *0, называется многочленом, расположенным по убывающим степеням х, или многочленом, представленным в каноническом виде.
Числа а0, ах, а2,... ап называются его коэффициентами, одночлен а^хп — его старшим членом, aQ — свободным членом, число п — степенью многочлена (п — натуральное число).
Корнями многочлена Рп(х) будем называть такие значения переменной х, при которых многочлен Рп(х) превращается в нуль.
Разделить многочлен Рп (х) на многочлен Qm (х) (т < л) значит найти два
таких многочлена 5я_т(х) и Rk(x), чтобы Pn(x)=Qm(x)sn_m(x)+ Rk(x) и степень многочлена Rk(x) была меньше степени делителя 2Л1(х), т.е. к < т . При этом многочлен Sn_m (х) называют частным, а многочлен яДх)—остатком.
Для любых двух многочленов Рп(х) и Qm(x) (т<п и 2w(x)#0) всегда найдется, и притом единственная пара многочленов Sn_m (х) и Rk (х)> удовлетворяющая тождеству
Л (*) = Qm №п_т (х)+ Rk (х)	(к < т),
т.е. если делитель не нуль — многочлен, то действие деления многочленов всегда выполнимо.
Теорема Безу. Если многочлен Pn(x)=aQxn +а}хп~} +а2хп~2 + ... + ап разделить на двучлен х - а, то в остатке получим число R, равное значению данного многочлена при х = а, т.е. R = Рп (а).
Схема сокращенного деления многочлена на двучлен. При делении многочлена Рп(х)=апхп +ап_{хп~х +ап_2хп~2 +... + а0,расположенного по убывающим степеням х, на двучлен х - а применяется метод сокращенного деления, называемый схемой Горнера.
Имеют место следующие формулы для нахождения коэффициентов частного , b2,..., 6лЧ и остатка^:
= О} + аа0,
Ьп-1 - ал-1 + а^п-2 >
Практически вычисление коэффициентов частного блЧ(х) и остатка R проводится по следующей схеме (схеме Горнера).
Пусть требуется разделить многочлен Рл(х)=ялхл + ал_1хл"1 +ал_2хл-2 + +... + я0 на двучлен х-а.
Значение а двучлена, коэффициенты многочлена (Ьп_х, Ьп_2,..., ) и остаток запишем в следующей форме:
ап	ак-1	ЛЯ-2	• ..	а\	ао
ftn-l ~	Ьп-2 = ап~1 + +а6л-1	ftw-З = ап-2 * + ^л-2		+ ab\	R = ao +aft0
Отсюда записываем частное
е„-1 W =*„-!* "* +bn_2xn~1 +... + blx+b0,
если R = 0, и результат деления
Pn(x).(x-a)=Qn_l(x)+-^- или Р„(х)= (х - а)вп_{(х)+R, х-а
если R*0.
Понятие корня. Основные свойства корня
Алгебраические выражения, содержащие операцию извлечения корня, называются иррациональными.
Корнем л-й степени из числа а называется такое число ft, и-я степень которого равна а (п > 2 ). Обозначается tfa , где а — подкоренное выражение (или число), п—показатель корня (п > 2; п g N).
По определению у[а = Ь, если Ьп = а , или (>/л )" = а.
Основные свойства корня
Если корни рассматривать в множестве действительных чисел, то: а) корень четной степени из положительного числа имеет два значения, равные по абсолютной величине и противоположные по знаку;
б)	корень четной степени из отрицательного числа в множестве действительных чисел не существует;
в)	корень нечетной степени из положительного числа имеет только одно действительное значение, которое положительно;
г)	корень нечетной степени из отрицательного числа имеет только одно действительное значение, которое отрицательно;
д)	корень любой натуральной степени из нуля равен нулю.
Действие, посредством которого отыскивается корень и-й степени из
данного числа а, называется извлечением корня п-й степени из числа а, а результат извлечения корня в виде tfa называют радикалом.
Таким образом, множество действительных чисел не замкнуто относительно извлечения корня четной степени, а результат этого действия (корень) не однозначен.
Заметим, что множество действительных чисел замкнуто относительно извлечения корня нечетной степени, а результат этого действия однозначен.
Арифметический корень и его свойства
Арифметическим значением корня или арифметическим корнем степени и(л>2;л€ДГ)из положительного числа а называется положительное значение корня. Корень из нуля, равный нулю, также будет называться арифметическим корнем, т.е. >fa =Ь есть арифметический корень, где а>0,6>0 и Ьп =а.
Множество неотрицательных действительных чисел замкнуто относительно извлечения арифметического корня, а результат этого действия однозначен. Это значит, что для любого неотрицательного числа а и натурального числа п (п > 1) всегда найдется, и при том только одно, такое неотрицательное число Ь, что Ьп = а .
Правила действий над корнями
Для любых действительных чисел а, Ь и с и натуральных пик имеют место следующие правила действий над корнями:
2п+у/а • 2пУ[Ь  2п+у[с = 2n+^abc >	(2.26)
2n+^abc = 2n+tfa  2n+4b  2n+-l[c ,	(2.27)
=	(i^o) 2n+№ vft	’	(2.28)
2a+J^ = y^ (ь*о) Nb 2n+tfb	(2.29)
(^)к=2П^>	(2.30)
2п+^Г = (2п+^)*:,	(2.31)
2тч^2л4у^ _ (2m+lX2«+lj^ ,	(2.32)
(2т+1Х2л+1|^ _ 2»14^2л^ ,	(2.33)
2^а=2tiabc (а^0,6>0,с>0),	(2.34)
2y/abc = 2^[о| • 2^|й[ • 2^Й (pbc > 0),	(2.35)
^ = 2Л (a>O,Z»O),	(2.36)
2лЕ = _^1[ 2л^|	J’	(2.37)
2^ = 2nVa (а>0),	(2.38)
2пу[а =2ffia (а>0)>	(2.39)
fcfaf = 2tfa* (а>0),	(2.40)
2у/а2к = ^^a\fk (а —любое действительное число).	(2.41)
Во множестве действительных чисел рассматриваются корни нечетной степени из любых действительных чисел и корни четной степени из неотрицательных чисел, причем берутся арифметические значения корней.
Замена дробного выражения, у которого числитель или знаменатель (или оба) иррациональны, тождественно равным ему выражением с рациональным числителем (знаменателем) называется исключением иррациональности из числителя (знаменателя) дробного выражения.
При исключении иррациональности из числителя (знаменателя) дробного выражения числитель и знаменатель этого выражения умножают на множитель, сопряженный с числителем (знаменателем).
Сопряженным множителем относительно иррационального выражения А называют всякое не равное тождественно нулю выражение В, которое в произведении с Л не содержит знака корня, т.е. Л В рационально.
Рассмотрим основные случаи исключения иррациональности из зна менателей дробных выражений (аналогично выполняется исключение иррациональности из числителей):
А
1. Дроби вида пг~г , где п> к, а> 0, Я — некоторое выражение; в каче-На
стве множителя, сопряженного со знаменателем, можно взять	, так
как	• ylan~k = а.
Умножив числитель и знаменатель этой дроби на ylan~k , получим
А	Апу[^ (
-г= = ~7=	,---=---------
п4ак	4ак -4ап~к а
2. Дроби ввда -т=—т=.
ja+Jb
Выражения 4a+4b и 4а -4b взаимно сопряженные, так как ra+ 4b\4а - 4b)=а - Ь, поэтому
A. а(4^-4ь) AUa-4b)
А _ Aja _ Ajb
~г=—/г - -----, е£ли а > 0, а - b;
Ha+y/b 2а	2Ь
A A{ja+jb]	A[ja+jb)
л-л”(Х-Ж^)=	"р"020-'’20'»’*4-
Выражения Ja+Jb и Уа2 -Jab + vb2 , а также Ja-Jb и
(а - b) рациональны. Поэтому исключить иррациональность из знаменателей указанных дробей можно следующим образом:
где а и b — любые действительные числа, причем а+b Ф 0.
где а и b —любые действительные числа, причем а # Ь •
где а и й—любые действительные числа, причем а+b # О.
гдеаиб—любые действительные числа, причем а*Ь. 	д
4.	Дроби вида ^7^ и
Для выражения tfa-tfb сопряженный множитель можно определить из тождества
(х-у)(х"_| +хп~2у+...+хуп~2 +у"_|)=х" -у" .
Если принять х = >[а, y = >[b , то получим
+ ^an~2b + ... + ^abn~2 +^b^^=a-b. Следовательно,
33
2 М. И. Сканави, группа А
где a*b ( а £ О, А £ 0, если п — четное; а, b — любые действительные числа, если п — нечетное).
Для выражения yfa+tfb сопряженный множитель можно определить из тождества
(х+/)(хл_1 -хл“2/+...+х(-у)п~2 +(-^)л_1)= хп +(-1)л уп.
Если принять х = у[а, у = tfb , то
fa+n4b ^4^ - 4^Ь +...+ (-l)"-2 4аЬп~2 + (- О"'1 4b^y а + (-I)”1 Ь. Следовательно,
л	А(24а2к~^-24a2k~2b+...+24аЬ2к~2 -2$^П
____= _к___________________________________________ 24а+24b	a—b
при а 0,6 О,а*Ь‘,
А
fa2k^b+...-2k^b2kl
а + Ь
где а и b—любые действительные числа и а+b # 0.
А
5.	Дроби вида I- гт I- .
Умножив знаменатель на
(jfl + 4b + 4с jfa+4b - 4с ) = а+b - с+2 Jab .
Умножив последнее выражение на а+b - с - 14аЬ, найдем ^a+b-c)+24ab^a+b-c)-24ab}=(a+b-cf -4ab-
Таким образом, множителем, сопряженным со знаменателем данной дроби,является fai+4b-4c)x(a+b-c-24ab)-Следовательно,
A A(4a+4b-4cta+b-c-24ab)
4a+4b+4c	(a+b-cf -Aab
где a S 0, b S 0, с > 0, (a+b-с)2 -4аЬ # 0.
Аналогично исключают иррациональность из знаменателей дробей
А	А
Г~ П~ Г и Г" гг г • yla+y/b-ylc ^Ja-yjb ~yjc
Если знаменатель дроби — сумма четырех квадратных корней
у/a + y[b + 4с +Jd
, причем ab = cd, то исключить иррациональность из
знаменателя этой дроби можно так:
_____А________ A^yla +jb)-[jc _ A^Ja+ylb-y[c-y/d)
-^Гс+Jdf " а+ь-c-d
где a^0,b>0,c^0,dZQ,a+b*c+d.
A
6.	Дроби вида зГ^зГГ.зП  у] Cl + у] О + yJC
Найдем сопряженный со знаменателем множитель. Для этого воспользуемся тождеством
(х + y+zjp2 +у2 +z2 -xy-xz-yz)=x3 +у3 + z3-3xyz.
Если принять х = у/a, у = y[b, z = y[c ,то
fya + 3y[b +3Jc^/a2 -^yfb2 -^-ylc2 -y[ab -y[ac -y/bc	a + b + c-£[abc .
Умножив полученное выражение на
В = (а + 6 + с)2 + 3(а + 6 + cfilabc + 9у](abtf , получим
(а+Ь+с-Зу/аЬс^ В -(a + b+c)3 -27abc .
Следовательно,
^ylb2	-y[ab-у[ас-ylbc^В
у[а +y[b +yfc	(а+6+с)3 -21abc
при у/a +y[b +у[с *0, (а + 6 + с)3 *21abc .
Преобразование сложного квадратного корня (радикала)
Выражения вида J j + .Jg называются сложными квадратными корнями (радикалами). Для их преобразования пользуются формулой
V 2 V 2
где Л > О, В>0 и Л2 - В > 0; знаки берутся либо только верхние, либо только нижние. В правильности этой формулы можно убедиться, возведя обе части формулы в квадрат. Эта формула упрощает сложный радикал, если А2 -В —точный квадрат.
Упростить выражения и вычислить их, если даны числовые значения параметров (2.001—2.124):
х
2.001. —7=	г'-~Т Ху/Х+Х + у/х х- Решение. ОДЗ:0<х#1. yfx+1	1	_ Xifx+X + уГх х2-yfx (Vx+lVx-l) у! = Д+^+1)(У7-1У х^*Рх-1)=х ! 1 Ответ: х -1. 2.002. pVp-47?)'2+(Vp Решение. ОДЗ: р#?.	-у[х 4х +1 4х{ху[х -1) Vx(*+Vx+1)	1 5c(xVx-l)	X—1 1	Д.Л-1)* ) р-я
Jp+Jq = i | i
P-g = fe/p+l/7)2 +typ-ffl. (Vp-TilVp+Ti)=
Jp+Jq {jp-4q^	4p+4q
ylp+2^pq+4q+Jp-2^pg+4q _2(ylp+4q)^
Jp-Jq	4p-y[q
2(jp+y[g\jp+4q)_ ^p+4qf (Jp-JqUp + yfq)	P~q
Ответ:
2(у[р+4д^ p-q
Тогда
(a-bi^Ja + Jbf _ (a-bj^+^bj
((Л-ЛКЛ+Л))2
I»-*)2
(л^У
a-b
Ответ: л-----*—.
а-Ь
2.004.
((а+Ь)-п/4 с1'2 У/3 а2-пЬ-3'4
(	а3~4
о с
Ца+dJ а
6 = 0,04-
Решение.
ОДЗ: а #-6 =-0,04.
Пусть
f(a + 6)-"/4-Л2 а2~пЬ~у4
\4/3
(а+Ь)~п!3 с2!3 _ Ьсуз a^^b-1	a^^ia+b^3'
( b3c4 f6=	6V2-c2/3
Ja + ft)2^'6-8" J (a+bY/3-a^^'
Ь.с2/3	b^c2'3
Т°ГДа X'Y~ a^3 (a+6)^ : (а+б)я/3 й(8-4"Уз
= by2 = (0,04 )V2 = 70Д4 = 0Д.
b e2'3 {a^bY3 a^3
a^3 \a+b)n/3-bV2-c2li
Ответ: 0,2.
2х~^3	х2^3	х+1
2Л05. x2/3_3x-V3"x5/3_x2/}-x2_4x + 3-
Решение.
ОДЗ:
х#0, х#1, х#3.
2Х-1'3	х^3	х+1	2х-*/3
х^3-Зх~^3 х5'3-х*3 х2-4х+3 х~У3(х-3) _	Х2^3______Х4-1	_ 2______1____Х4-1
х^3(х-1) (х-1Хх-3) х-3 х-1 (х-1Хх-3)
_ 2х-2-х-ьЗ-х-1 _	0
=	(х-1Хх-3)	-(х-1Хх-3) = 0-
Ответ: 0.
Решение.
а*Ь,
ОДЗ:  а > 0, Ь>0.
Ofr
и^-шр\ :шээшо
’O< u
‘u ш
эпиэтэд
{и-шу
'LWZ
‘O < ш r
qv
_ . ШЭ8ШО
I
qo _ (q£-qvj^. + qvp-^ _
T“ q£-q^-z+t’ q^ ^qpi+^)yy{qr+qp -
+3-j2tfy-2
Ответ: у2.
Решение.
ОДЗ:0</*1.
/ 1 1-2/+/2	4t+l-2t+l2
V 4 t____________ у 4t
I ! 1 1-2Z+/2" 1 1-t	l4t+l-2(+t2 1-t
4 t	2 4t	N 4t	241
Ответ:
2.010. t.
Решение.
/+4>0,
Г*0.
Ответ: -4.
Решение.
ода:{
1 + х>0, х £ О, <=> 1-4х ф о
Гх >0, |х *1.
4х _ 4х((1-ух) ~(1 + Vx) ) (Vu7(i-V7))2 (Vm(i+V7)(i-V7))2
4х(1-2л/х + х-1-2-Ух-х) _ -16xVx _ 16xVx (1+X)(1-X)2	(1 + X)(1-X)(1-X)
Ответ:
16xVx
(l-x2)(x-l)’
2.012.
x-1 x + x'/2 + l
x°’5 + l 2
x’’5-l+x-0>5‘
Решение.
x-1	x°’5+l	2 =(x1/2-l)(x1/2+l) (x1/2)3-l	2
x + x>/2+l\h5_1+x-O,5- x + xl/2+1	‘ x!/2+1 + J_
-1X* + X"2 +D+2xl/2	,/2 _1)2 +2x./2 =х_2л./2
x + x,/2 + l
+ 1 + 2x1/2=x + 1.
Ответ: x + 1.
Решение.
a>0,
ОДЗ:
r- ,----- |a>o,
\a > 1
a + 1 a-1
Пусть %— выражение в первых скобках, Y— во вторых:
Ответ:
Х-у xl/2jI/4+xl/4^/2	х1/4г1/4
х3/4 + х1/2/,4 ’	Х1/2 + j,/2	' х1/2 -2х1/4//4 +у[12 ’
Решение.
(х>0,
ОДЗ:
[х Фу,
х-у x,/2j1/4+x,/4j1/2	x1/4j"l/4
х3/4+х1/2/4’	х1/2+у1/2	 х,/2-2х1/4//4+у1/2
Ответ:
I п I ----
2.015.
Решение.
т * +п,
ОДЗ: 5У*0,
у > 0 при т = 2к.
I (лг-л)2+4/лл 2л т2~2тп+п2+4тп у т2-п2 =уп(т~п^:у »1(т+п)(т-п)
2	т2+2тп+п2	2	(т+п)2	2 т+п
=	. ^ш(л1+л)(т-л) =	. ут(т+п)(т-п) = у^ . ут(т-п) =
2 т+п 2т-т-п т-п 1 _ут-п т(т-п) _yin(m-n) _ т(т-п) _
Ответ: п1/у.
2.016.
((z^P+z^4)2_4z2/P+2/g (z^P_z^4)2+4zyp^4
\1/2
7
Решение.
ОДЗ: z ф 0, р 0, q Ф 0.
(гг,Р +z2/4)2 -4z2/^+2/« Y/2 _((z2lp)2 +2z2/p+2,4 +(z2lb2 -4z2/^2/’ (z1/p_z1/9)2+4z1/^1/<? J -^(zl/p)2_2zl/p+l/9+(zl/9)2+42l/p+l/9
\jlp?-2jlp*2lq+(?lq)2
^zVp)2 +2zXlp+xlq +{zXlq)2
[ (z2lp-z2lq V/2
z2lp_,2lq

Ответ: |z1/₽ -zxlq\
x-
3/4 + x
Решение.
ОДЗ: x>0.
x-1 xX'2+xU4 1/4	(x1/2-l)(x1/2+l) x2/4 + x1/4 1/4
x3/4+x1/2‘ x1/2+l	x3/4+x2/4	‘ x1/2 + l '
1/2-I
x2/4(xl/4 + l)
J/4zJ/4.n
-----------x,/4 + 1 = xl/2 -1+1 = xx 2 =
1
Ответ: ^Jx.
2.018.
Z	9	9 X“ 1
1+x+x	, 1-x+x
------9“ + 2----Г 4 2x+x 2x-x y
(5-2х2);х = Д92?
Решение.
1 + x+x2 _ 1-x+x2 ---------+2	 x(2 + x)-x(2-x)
•(5-2x2) =
(2-х)(1 + х+х2) + 2х(2+х)(2-х)-(2+х)(1-х+х2Й 1 x(2 + x)(2-x)
•(5-2x2) =
2+2x + 2x2-x-x2
(. _ 21 (10x-4x3) /. „	(2х(5-2х2Ь (.
*V~2x h -n—n	P-2x2)= Г 2\'	(5
I A4’* ) J I *(4-* ) )
_ (4-x2)(5-2x2) 4-x2
2(5-2x2)	2
-2x!)=
Отсюда при x = -J3,92 имеем
4 -(Д92 У _ 4-3,92 _ 0,08
2	2	" 2
Ответ: 0,04.
64.
Решение.
ОДЗ: z = VP~ + Vx2J3 -ylx3y2 -tfy* *0.
3/ 2 3/— ЗГ 2 3/— 3/ 2 3/ Т 3L л2
= >1х +у]*У + ]/У ~УХУ ~уУЛ - чх =з/64 =
,3Л“.42-16.
Ответ: 16.
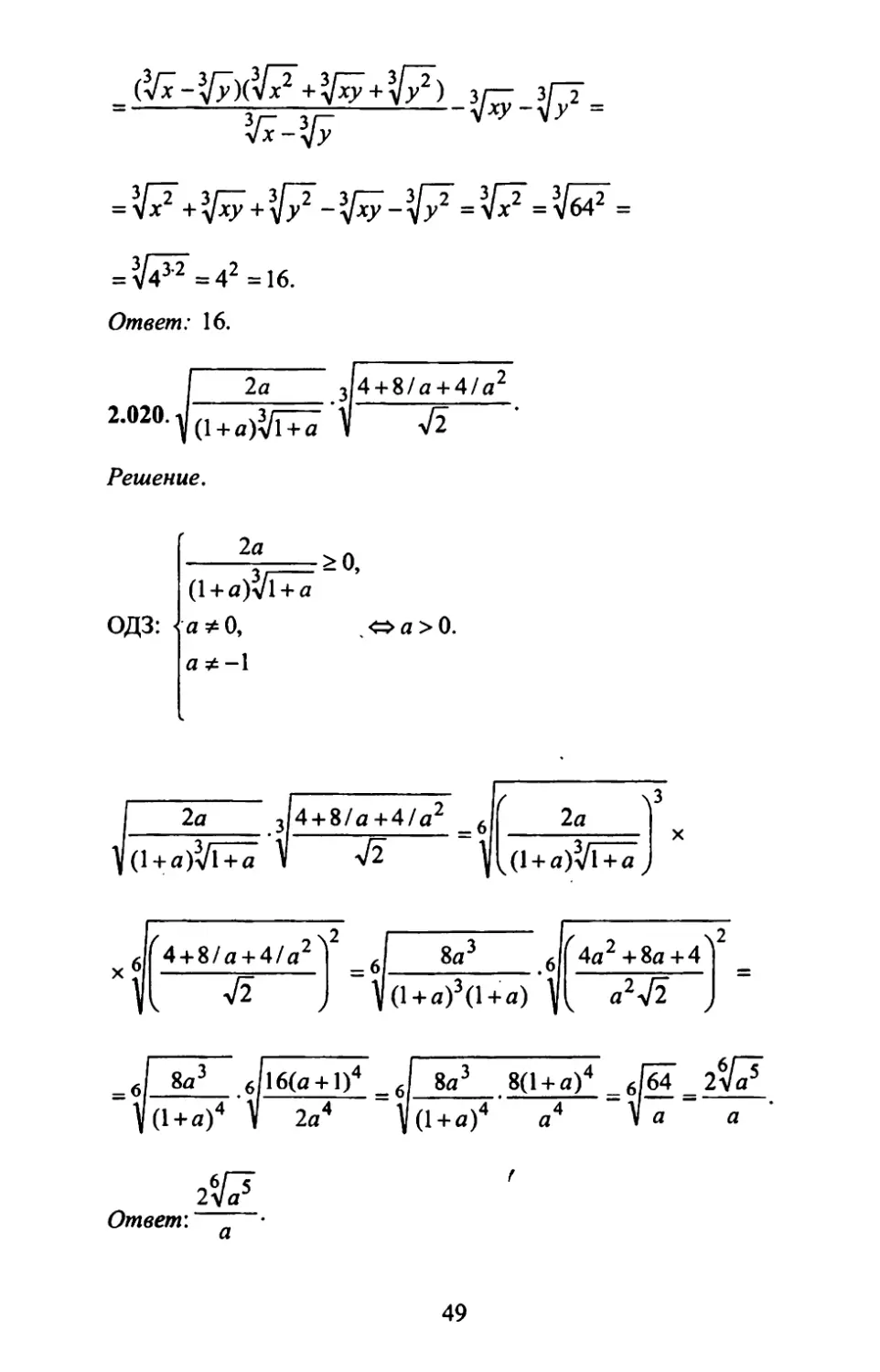
2.020.
314 + 8/д + 4/д2
V V2
Решение,
ОДЗ:
а 0,	Оа>0.
а
| 8д3	J16(a + 1)4 = J 8д3	8(1+ д)4 61б4 = 2^
(1 + д)4 V 2д4	у(1 + а)4 д4 Ь а
2^ Ответ: д

ТСх + 2)2 -8х
2.022.
Решение.
ОДЗ: 0 < х * 2.
7(х+2)2 -8х _ у/x2 +4х+4-8х _ Jxyjx2 -4х-4 _
-А = ~(Ж^ =	х~2
Jx	г~
у/х
_ Jx^2-if _ у[х -|х-2|
=	х^2	х-2	’
Отсюда:
1)для x<2,-Jx;
2) для х е (2;+°о), 4х .
Ответ: -Jx для хе (0;2); 4х для хе (2;<«).
2.0	23. ^6х(5 + 2>/б )• 7з>/2х - 2>/Зх.
Решение.
ОДЗ:х>0.'
^6х(5+2>/б) • у/Зу12х-2>/Зх = ^6х^ + 2>/б) • 7>/бх(УЗ-^) = = ^6х^ + 2л/б)^(Уб^(>/3-^))2 = ^/бх(5 + 2 л/б ) • ^/бх(5 - 2>/б) = >/бх^ + 2л/б)-6х^-2л/б) = ^36х2(25-24) = у/збх2 = Тбх.
Ответ: у[бх,
2.0	24. ^4xj 1 + 4>/б ) • ^4>/2х - 2л/Зх'.
Решение.
ОДЗ:х>0.
^4х(11+4>/б) • ^4>/2х-2>/Зх =	• ^2л/х(2>/2->/з) =
= ^4х(1+4Тб)-^Vx^-Vs))2 = ^4xJ 1+4-Уб) • ^4х(11 - 4^6) = = ^4х(н + 4>/б)-4х(11-4л/б) = ^16х2 (121-96) = ^400х2 = V20x.
Ответ: V20x.
2.025.
' а3 +а2 +ab + a2b	b \
а2-Ь2	+ а-Ь
\ /
д = 23;6 = 22.
Решение.
а3 -а-2Ь-Ь2/а
Д+А|(д+ЛГ \а а2
7
a4-a2 -2ab-b2
а3 + а2 + ab+a2b
__________ Ь__ а2-Ь2 а-Ь
1-J—z- \а + у/а + Ь
1 a J
а4 - (д2 +2аЬ+Ь2) .(а(а +1Ха+
д2(а + 1)+а/>(д+1) Ь
(a-b\a+b) а-Ь
а-Ь
а
_а4 - (а+ Ь^ /а(а+1) ; Ь
a2-a-b \ a-b a-b J
_ (a2 - a-bjp2 + а + б) а2 +а + Ь _
а2-а-Ь а-Ь
= (д2 +Д+^-1) = а_/> = 23_22=1
„2 . л . L
Ответ: 1.
Решение. [а >0, °®Uo. / 		\3/2 ( / 3ГЧ~У ^4/У. а» V 	Z— —	3		}у/2 ^/дд2/3-61/3	д(4/15)(з/2) 7 ^у	“W!” У'»)4	и-,», a(W46llf6>4
(д^-б1/8)6	«12/5 «6/4*6/8 10/3 А 2/3 = а-10/5 	2— = а-2 ,fl10/3-3/2 ,62/3-3/4 = - д3/2-63/4 !	л(-12+11Уб = д’2  д11'6 -ft-*/12 = д-2+11/6 —L =		= /,1/12	61/12 1 1 Ъ'!'1 ^Ь 1 Ответ: 	 12/^21. yja о ^jx + yll-х2 -^l-xyll-x2 2-027-	VT-x2 Решение. ОДЗ: 1-X^2-X 1-x2 #0.	a3/2 -b3^ 2 ,fl(20-9)/6 ,^(8-9)/12 = д-1/6 _ ’ bl/l2 /
Ответ: - при Vl-x2 < 0; V1 при Vl-x2 > О.
х(х2 -а2)~^2 +1 a2-Jx + a 1 2-0М- .{х-^+(х-аГ
Решение.
ОДЗ:
х2 -а2 >0, х-а >0, х*0, х-7х2 -а2 £0
х>а, х^О, а #0.
л	2
Ответ: —z--7.
х -а
Решение.
г# О,
ОДЗ:
г £-2.

аг 2^-2-а^	+	г'^а1'2 •(>-23'4)_
a3/2.2V2_23/4.fl	2^2а^2-2х/4)
o+7i
а1/2 -2^	^а-^-У4}	а^2 ^4
(а*/2-2^+2^-а1/2+21/2) a + 2V2 а+У4-а*2 а1/2^4^2-21>4)	ах>2^4	а^2^4
а + 2^а 2'/4.а'/г 2>/2 =2'/4.а'/2 = а^-У4	ах'2-2'14
Ответ: Л.
Решение,
[а >0,
Ответ: —• а
abc + 4 A be
V-------+4Л —
2.032. V	fl * a
Jabc +2
Решение.
ОДЗ: be >0.
a = 0,04.
Ответ: 5.
, n,,	+ +V(2j>-1)3
^4p + 2yj4p2 -1
Решение.
ОДЗ:р^|-
(72p+l + 72p-l
^2p+l+2y/4p2 -I +2p-l
(j2/>+l + j2p-lY2p +1 -^4p2-I + 2p-1
<^2p+\f +2y/4p2 -1 +(j2p^tf
(J^+J^x^-^p2 -i) _
(Тг^ТТ+Тг^Тхдр-^р2-!) _ г~т~
^+^~i =4р~^р -1 Ответ: 4р-^4р2 -1.
Решение.
ОДЗ: а>\.
7^7Т-У(а-1Хд + 1) j _ (1-7а2-1)У(а+1Ха-1)
•^(а-1Ха + 1)(л/а-1 -л/а + 1)	Va-l(Va-l ->/а + 1)
Ответ:
^а2 -1.
2.035.
а + 2 а 2 л/2а V2a+2 а->/2а
'а-У2 а + 2
Решение,
ОДЗ:
а > 0, а #2.
2.036
Решение.
ОДЗ:
inn > 0, пр о, т * О, р *0, тр > 0.
Зопт2р -Зтп-2у9тп2р -Зпр = -Зп(т + р).
Отверг -Зп(т + р).
2.037. ^1/2	*3/2 + *1/2 _х-1/2 ’
Решение.
[х>0, ОДЗ: j ,
хг + х2 х_____2 = (1-х)4х_______2
(V7)2-l	43 ~ х-1 ,Сз
Ответ: -
Решение.
ОДЗ: 0<а*1.
(g-l)2 а-24а+\-а-24а-\ _ (а-У)2{-44а) = _ д-1 1-д
4о	д-1	4д(д-1) 4а 4а
^~а
Ответ: -т=->1а
2.039.	°	—---------------;
4а3'2Ь~2	+9b^ «3/4-ЗЙ5/3
Решение.
а312	Ь2 -а3'2
Ь2	Ь2 _ ь2
у1а3/2Ь-2+6а3>4Ь-У3+9Ь4/2 ^4-ЗЬ3'3 \ Ь2 + й+1/3 +
Ответ: -4.
___1
2.040. S Ь+с • f 1 + б2—-'— "I: а~^~с; 1	1	2bc abc
— + -  \	7
а Ь + с
а = 0,02; Ь = -11,05; с = 1,07. Решение.
1	1	Ь+с-а
а Ь + с । | Ь1 +с2 -а2\а-Ь-с _ a(b + c)
1	1	2bc abc Ь + с + а
а Ь+с	a(b + c)
2Ьс + Ь2 +с2 -а2 ----------------х
2Ьс
abc (b+c-a)a(b+c) (fr2 +2bc+c2)-a2 abc _ a-b-c a(b+c\b+c+a) 2bc a-b-c _b+c-a (b+c)2 -a2 ab _ -(а-Ь-сУр+с+а$р+с-а)а b+c+a 2 a-b-c 2(b+c+a\a-b-c) = -(b+c-a)a = (a-b-cfr = (0,02+11,05-1,07)0,02 =
2	2	2	” 4‘
Ответ: 0,1. 1	1 a2 +2
X04L ^)+^T7-
Решение.
ОДЗ: 0£a*l.
1	1	д2+2 1-Va+l+Va a2 +2 _ 2
2^+Va)+ 2^-Va) 1-a3 2^ + Jafa-Ja) 1-a3	2(1-a)
a2+2	1 a2 +2	_ 1+a + a2-a2 -2 _
(l-a)^ + a + a2) 1 - л (l-a)^+a+a2) (l-a)^+a + a2)
(l-a^l+a+a2) a2+a+l
-1
Ответ: “5	7
a +a+l
2.042.
a = 0,32; x = 0,08. Решение.

-Jax _ - 70,32 0,08 _ -0,16 _ j 2x-a ~ 2 0,08-0,32 “ -0,16 ”
Ответ: 1.
(mn-lY” +	(mn + lj1 m
n2m ' mnm (тп-1/(пин1)п (mn-tfn"n
2n ”__
(/мл-1/” (п?и + 1)л m2n nm~n	nn
[mn-tf1 (mn+iy1 n2m mn ^2m mm
Ответ:
Решение.
x> a > 0.
Ответ: 1.
Решение.
ОДЗ:0<х#1.
Ответ:
2.046.
Решение.
(х #0, °Д3: [—1<S JC <1.
Ответ: -1,
2.047.
a-b a2+b2+а
i 24~Ь 1а2ЛЬГЬ? \i2 +b+ab+a).. (46 4 +4ab2 + a2): fab2 +a)
Решение.
ОДЗ:
a#+-“2’
• 2д2 + ab-b2 Ф 0, <=> a*0, 6*0
a * -b, a *0, 6*0.
a-b _ a2 +b2 +a	a-b _ a2 +b2 +a
l	^ + <,b^).2‘-b/‘, + bl2‘-b'>x
[4b4 +4ab1 +a2):l^b2 +a)	^2 +af
2b2 + a (a-b\a+b)-a2 -b2 -a
x(f>2 +& + a£ + a)=-
r	2b2 + a	'	’
2,2	2/2
a -b - a -b -a
(a + b)(2a - b)(2b2 +a)
(b(b + V) + a(b + V)) =
=_	(;,+1)(0+6)=z«±i). ±ll.
(а + b)(2a -b)(2b2 +a)	2a-b b-2a
b +1 Ответ: ----.
b- 2a
2048 Qp-9^y -3m:f,=Oi78;,=7;2S.
2p + q	2 +pq
Решение.
(2p-q)2 + 2q2 -3pq 4/;2 -3pq _ 4p2 -4pq + q2 + 2q2 -3pq
2p~'+q2	1 + Pq2	~ + q2
P
X 2 + Pc!2 = ^P1 -Ipg + ^bp. 2 + /X/2 = (p-q)(4p-3q) p(4p-3q)	2 +pq2 p(4p-3q)	4p-3q
7
= p - q = 0,78--= 0,78 - 0,28 = 0,5.
25
Ответ: 0,5.
/	3	_	\ (	2	2A
РЧ________2/ </-_ pg . p___________p g
2'049' [(p + f/)5/2 (p + <?)3/2 Jp + q) \<p + q)511 <P + q)V2, Решение.
ОДЗ: P + q > 0 <=> p > -q.
(	3 o2	\ (	2	2 A
___pq ipq , pq . p____________________p q
Sp+ч)5 2 (p+q)312 ylp+qj l(p+?)5/2 (p+^)7/2>
pq j q2	2</ iij- p2	fi g 1
(p+«7)1/2 {(p+q)2 p+q ) (p+q)5/2 I p+qJ
РЧ	(ч2 ~^ч(р+ч)+(р+ч? 1 Р2 . (Р+Ч-Ч
(р+ч)'12 [	(р + чУ	) (р+ч)5/2 I P + q
РЧ^Г -'-РЧ-~Ч2 +р2 +2-РЧ + Ч2} (р+ч)5/2 (р+ч)__ (р+чУ2-(р+ч)2	Р2Р
(р+Ч)	P
Ответ: q(j> + q).
2(х4 + 4х2 -12)+ х4 + 11х2 +30
2.050. ----------/----------------
х +6
Решение.
2(х4 + 4х2 -12)+х4 +11х2 +30 2(х2 + б)(х2 -2)+ (х2 + б)(х2 +5)
х2 + 6	х2 4- 6
(х2 + б)^(х2 — 2)+Х2 +5)	->	2 с о 2 1 1 о 2
= -^-------------------t = 2x~ -4 + х2 +5 =3х2 +1 = 1 + Зх2.
х“ + 6
Ответ: 1 + Зх2.
Oy/b+aja-by[b-ylab2 ay[b-yla3b2 -yfb^ + aja a = 4,91; b = 0,09. Решение,
= a + b = 4,91 + 0,09 = 5.
Ответ: 5.
Решение.

1-х2 >0,	1-1<х<1,
х # 0 [х # 0.
Ответ: 1 - х2.
Решение.
ОДЗ:-1<р<1.
л 2
Ответ:---т-
1-/
2.054.
За2+2ах-х2 ах-Зх2
(Зх + а\а+х) + а2 -9х2
Решение.
ОДЗ:
а х#±—, 3 хФ-а.
За2 +2ах-х2 1П ах-Зх2 ~(х+а\х-За} о (Зх+аХа+х) + а2 -9х2	(Зх+а)(а+х)
, 1Л.	х(а-3х)	_-х+За_*	10х _
(а-ЗхХа+Зх) Зх+а Зх+а
_ -х+За-6х-2а + 10х _ Зх+а _ Зх+а	Зх+а
Ответ: 1.
Решение.
ОДЗ: х*+у.
Ответ: l]x + y -ljx-y.
2.056.
а +1 b(abc + а + с) а b
1	4
Решение.
а+—
*> + -с
ОДЗ.
b(abc + а + с) * 0.
4	. b__________4
д + _£_ ab + \ b(abc+a+c) < bc+l	j
f 4bc+4 ab+1________4
la^c+a + c b b(abc+a+c)
4ab2c+4bc+4ab+4	4
b(abc+a+c) b(abc+a+c)
r4b(abc+a+c) b(abc+a + c)
1 Ответ: —•
2.057.
(x + yf-4xy x2 -xy
Решение.
I x Ф ±y,
ОДЗ: ।	°’
1^*0.
“2
X (x+?) -4xy x4 y-xj x2-xy x2y2-y4
x4 (y2-2xy + x2 x2-2xy+y2>
X/p-y2) [ X2 x(x-y)
y2(y-x)2 x4	(x-j)2 X-y
x*	y2\^c2-y2)~ {x-y\x + y)~ x + y‘
„ x~y
Omeem x + y
2.058.
Y i t i A ja+*+c,
1 1 Yl
1+ к
b2+c2-a2\ 2bc
a = I — ;b = 0,625; c = 3,2.
40
Решение.
2 , „2
1+_L_1[1___i_
a b+cfl a b+c
2bc
_ f a+b+c -a+b+c \ 2bc+b2 +c2-a2 _
I a(b+c) a(b+c) J	2bc
_fa+b+c a(b+c) (b2 +2bc+c2)-a2 _
^a(6 + c) -a+b+c	2bc
_ a+b+c 2bc _ 2(a+b+c)bc _
-a+b+c (b + c)2 -a2	(-a+b+c\b+c-a)(b+c+a)
- 2bc -	2 0,625 -3,2	_	4 -l-i
"(-a+Z,+c)2"r ЗЗ	У“(-1,825+3,825)2 "4_ '
— 1 F ILoZO + J,Z 40
Ответ: 1.
7x2 i'
Х059-
X 1	1
— — + -у2 У х
(х-у)2 + 4ху 1 + у/х
Решение.
ОДЗ:
х * О, у # О, х*-у.
х+у
2	2
х -ху + у
х + у 1	_ 1
у (х+у)х ху
1 Ответ: —• ху
f 3	2	1 4
2.060. 2х-у 2х + у 2х-5у
Решение.
ОДЗ:
С 3	2	1 \ У2	= (3(2х + у)-2(2х-у)	1
^2х-у 2х + у 2x-5yj4x2-y2	(2х-у\2х + у)	2х-5у
у2 _ (6х + 3у-4х + 2у _	1 'j 4х2-у2 _
4л2-J2 [	4x2-j2	2x-5j J у2
2x + 5j>	1	^4х2-д>2 (2x + 5^X^v-5>J-4x2 + у2
°	J'—/— =	(4л= !К-5.г)	х
4х2 -у2 _ 4х2-25у2-4х2 +у2 4л2 - у2 -24у2
З'2	{^х2-у2\2х-5у)	у2	(2х-5у)у2
-24 _ 24
2х - 5у 5у - 2х
24
Ответ: 7 т~ 5у-2х
2.061.
л-2 +2х-
11х-2
Зх + 1
х+1-
% = 7,(3)
Решение.
х2 +2х-
Их-2
Зх + 1
2х2 + х + 2
Зх + 1
Зх3 + 6х2 + х2 + 2х-11х + 2 Зх2 +Зх + х + 1-2х2
Зх + 1	Зх + 1
= Зх2+7х2-9х + 2	Зх + 1 _ Зх3+7х2-9х + 2 _
Зх+1 х2+Зх-1	х2+Зх-1
_ Зх3 +9х2 -Зх-2х2 -6х+2 Зх(г2 +Зх-1)-2(\2 +Зх-1) х2+Зх-1	х2+Зх-1
= fe_t?AlZ.!^3-5~2) = 3x_2 = 3-7,(3)-2 = 37--2 = 3-7--2 =
х2+Зл-1	9	3
22
= 3-—-2 = 22-2=20.
3
Ответ: 20.
1 с 1 п + 4^ 2.062. 6я“ +5tf-l +-----
\	я +1
Решение. ОДЗ: r/*-l.
За-2 + ——
а + 1
6а2 + 5а -1 +	: (за - 2 +	1 =
а + 1 J V a + lj
(д + 1)(6д2+5д-1)+д + 4 (д + 1)(Зд-2) + 3 = 6д3 + 11д2+5д + 3* д+1	’	д+1	д+1
д+1	6д3 + 2д2 + 2д + 9д2 + Зд + 3
'	2	о
За + а +1	За + а +1
2д(3д2+д + 1) + 3(Зд2+а + 1) (Зд2+д + 1)(2д + 3)
Зд2 + д + 1	Зд2+д + 1
Ответ: 2д + 3.
х 6-64 х2 4х2(2х + 1)
2,°63' 4 + 2х-1+х~2'4Л+J_'	1-2х
х X2
Решение.
ОДЗ:
х*0,
1 х*—.
2
х 6-64 х2 4х2(2х + 1)_- х6 6 х2
4 + 2х-1 + х-2 4_.1 + J_	1 -2х	4 + 2 + X 4х2 -4х + 1
X X2	X X2 х2
1-64х6
4х2(2х+1) =	/________х4 * 4х2(2х+1) =	1-(4х2)3
1-2х ~ 4х2+2х+1 (2х-1)2	1~2х	х4(4х2 +2х+1)
х4 _ 4х2(2х+1) _ (1-4х2)(1+4х2+ 16х4) _ 4х2(2х + 1) = (2х-1)2	1"2х	" (4х2+2х + 1)(1-2х)2	1“2х
_ (1-2х)(1 + 2х)(1+4х2 +16х4) 4х2(2х + 1) _ (1 + 2х)(1+4х2+16х4)
(4х2+2х+1)(1-2х)2	1-2х	(4х2+2х+1)(1-2х)
4х2(2х + 1) = (1 + 2х)(1 + 4х2 +16х4) - 4х2 (2х + 1)(4х2 + 2х +1)
1-2х	(4х2+ 2х + 1)(1-2х)
(1 + 2х)(1 + 4х2 + 16х4 - 16х4 -8х3 -4х2 (4х2 +2х+1)(1-2х)
)	(1 + 2х)(1-8х3)
.(4х2 +2x+ljl-2x)
(1+2хХ1-2х)(1+2х + 4х2) (4х 2 + 2х +1)(1 - 2х)
= 1 + 2х.
Ответ: 1+2х.
4а2 -Ь2
2.064.	-----Sb-toV.ab’
Ь3+2аЬ2-За2Ь а2-Ь2
Решение.
ОДЗ:
6*0,
Ь -Зя, b Ф +а.
4а2-b2	2аЬ-а2-4а2 +62
26 + а---__ fl3f>_2fl2fc2+afc3	...
Ь3+2аЬ2-За2Ь	а2-Ь2	б(б2+2а6-3а2)
аб(а2 -2а6+62)_ (а2 +2ab+b2]-4а2 ab(a-b)2 _ (а-бХа + б)	аб(б+ЗаХб-а) (а-Ь^а+Ь)
_ (a+b)2 -4а2 _ (а+b-2а\а+b + 2а) _
-(б+ЗаХ«+б)	~(b + 3a\a+b)
_ (b-a\b + 3a) __Ь-а _ а-Ь
-(б + ЗаХа+б)	а+b а+Ь
а-Ь Ответ:----
а + Ь
Решение.
ОДЗ:
х > 0, у >0, X * у.
(Vx -V7xVx +V7)
Ответ: x + y.
2.066.
Решение.
ОДЗ:
х >0, j>0, X * у.
y/у^ +yjx4y -ijxy4	(V?+^lx4y)-(^jxy4 +
Jx(4x^ + -/^)-у[у(4х^ +	_ 4х(х + у)-у[у(х + у)
‘\[y(tfy4 + >[x4)-Vx(tfy4 +^Х4) л[у(х +y)-Vx(x+у)
(x + y)(Jx-Jy) _ (л/х-^Хл/х+^/7) (x + ^X^y-Vx) -(4у/х-4у[у)
=-(4^+4V7).
Ответ: -($fx + ^[у).
a^1 +ab 1	а
2 067- a-V3_e-V6ft-VJ+r2/3"3^-
Решение.
b*0,
ОДЗ:
а>0,
b* -aV^ +aV3 #0.
Ответ: а5^6.
2.068.
1	1	2	4с2 ’
a2+b2+ab a2b2
a = 1^b =—.
Решение.
f-)a+6+2c) a+b (a+b+2c)
(a b ab )_________ gb v_______
1	1	2	4c2 ” a2 +2ab+b2 -4c2 ~
a2 b2 ab a2b2	a2b2
(a+b-2c\a+b+2c)
________ab_________(a+b-2c)(a+b + 2c)a2b2
(a+b)2 ~(2c)2	~ fa+b)2 ~(2cf)ib
a2b2
_(a+b-2c\a+b+2c\ib	J_=37 A = 1
(a+b-2c\a+b + 2c)	~ ’37	5 37 * 1
Ответ: 1.
a^-laV+ab4/3 V3 2.069. a5/3 _ a4/3bU3 _ ab2/3 + a2/3b  a
Решение.
a*0,
°ДЗ: a5/’ - a'W - ab2'3 + a2'3b # 0.
a3'3-la3^3 +ab^ w a3/3(a^+Ь4'3)
_aWbV> _abW + aWb •a a^P -a^bV3 _aVbW +^/3)X
1	H-fe2^)2
(aV3 -a^b'l3)-^3 -b3'3) a2'3^-b^}-b2l3^-b»3)
(^-/7	_^-^Jgv?-^P+^)_aV3 +fcl/3
(а'/’-б'/зрз.^л) а>/з_51/з aV3_fei/3	•
Ответ:	.
Решение.
ОДЗ: a*±b.
(а2 -Ь2)(Уа - Vfr)(а + 1>Ха-б)(Уа -V&)
(а^Ха-4^-^)_а (a+Z>)(Va-V^)
Ответ: a-b.
(m-l)Jm-(n-l)Jn
2.071. i 3	2
vw n + mn + m -m
Решение.
w>0,
ОДЗ:<и£0,
Jmn +n 4-w-l#0.
m -yjn
Ответ:
m
2.072.
Решение. ‘
ОДЗ: а^О.
Ответ:	- ylb^.
2-073- (й+йй-й)’
Решение.
у15-2у[б	_ 73-2л/Г2 + 2
Л-Л
ДЛ-Л)2 ..Уз->/2_1 Л-Л Л-Л
Ответ: 1.
,a\/m _aVny2 + 4д(т+л)/(тл)
2.074. ~------------- „I „I ’•
Решение.
а > 0, если т и п — четные числа,
ОДЗ:
’ а Ф О, а Ф 1.
^1/т _а1/л^2 +^д(т+л)/(тл)
(a2/m -а2/л)('”7^Т+'^Т)
а2/т -2а|/л1а1/л +а2/" + 4а(л|+л^/('лл^ " (ах'т -аХ1п\ах,т + «1/л)(а('л+|)/,л + а(л+1>/л)
_ a2/>”-2a<1/”,^1/")+a2/"+4fl(i;",KI/',)
(J/m -a1/")(a,/m +a1/”)(a1+I/m +a1+,/")
a2lm +2а(Х1т}^1п}+аг1п ~ (ax,m-axln)(ax/m +aX/n)(a al/m +a-ax/n) ~
___________(aX/m+aX,n)2___________ 1	1
(ax/m-ax/n)(aVm +ax,”)a(ax/m +ax/n) ~ a(ax,m-alln) aC^-Va
Ответ:
1
2/™-9x2/")(wJ7^3;
2.075. ^2,m-9xzln)(^x'-m-?:\lxx-n) (х1/,"+Зх1/”)2-12х(т+")/('”л)
Решение.
x > 0, если т и п — четные числа,
ОДЗ:
х 2тп/^т~п^
(х2/л< -9х2/л)(7х|-Я1 -зУх'~л
(х1/т+3х,/л)2-12х('п+л)/('лл)
= ((х1/л>)2 -(3x(1/w))2)(x(1-w)/,n -Зх(1~л)/л) = х2/”' +6?/л,г1/л +9Г2/" -12х(|/л')+(1/л)
(х1/л> -Зх1/л)(х|/,л +3х'/л)(х(|/л|)~' -Зх(1/лН
2/т_6х(1/т)+(1/Я)+9х2/и
1/m о 1/и
(х1/ш -Зх,/л)(х1/'л + 3х|/л)(----——
X X
(х|/л,-3х1/л)2
(Х^т _3х1/й)(х1/т +Зх1/Л)-—(х1/,Л -Зх1/Л) xVm +3jf
(x1/m-Зх|/Л)2	X
х1/л'+3х1/л
Ответ:
X
2.076.
'45-4V3
Решение,
V45-4V3
+3) =
6__
Т5-4
6(715+4)
= 6(V15-+^ + 30 + 6л/й = -бТ?5 - 24 + 30 + 6-У15 = 6.
15-16
Ответ: 6.
a~* l -b~' a2b2
2*077- а-3+Ь-3 '(а + Ь?-Заь[ ab ,
а = 1-л/2;й = 1 + >/2.
Решение. i 1	1
-1	A-'	„2.2	(z.2 A2 V ------7	„2t2
a —b a b a — b _ a b	a b
a"3 + b~3 (a + b)2-3ab I	. 1 a2 +2ab+b2-3ab
♦ v	7 zJ дЗ
a b
b-a
ab _ ab a2 -ab+b2 ab _	(a-b}a3b3
a2-b2 a3+b3 a2b2 a2-b2	ab(a + bffi2 -ab + b2)
~7b3~
a2-ab+b2 ab = _ ab = _ (l-JlKl + J?) 1 a2b2 (a+b\a-b)	(a+b)2	(1-V2+I+V2)2 4
1 Ответ: — •
4
2.078. ----------+ -5-------+ -5-------
^/“+3r + 2 Г+4/ + 3 / +5/ + 6 J
(t-3f+\2t 2
Решение.
ОДЗ:
t * —3,
t *-2,
r 1	2/	1 V (/-З)2 +12/ =
J2 +3/ + 2 +12 +4/+3 r2+5/ + 6j 2
_(	1	2t	1 f /2-6/+9 + 12/_
<(/+2X/+l)+(/ + 3Xr+l)+(z+3X/ + 2)J ’	2
_ f t + 3+2l(t+2)+l + l V t2 +6/+ 9 _ f 2(t+2)+2t(t+2) Y (/ + 3)2
\ (/ + 1X/ + 2X/ + 3) )'	2	_[(/+lX/+2X/ + 3)J ‘ 2
_ ^(/^Х/пУ^з)2 _^гН^П+з)2 _2
 2M/+2X/ + 3))2 ~2(t + 2nt + \nt + lT 
Решение.
ОДЗ: т > 3.
Ответ: V2(w4-3).
(а - b)2 + ab а5 +Ь5 + а2Ь3 + а3Ь2
2.080.-----\: —о--------;---з-----5---;---Г
(a+b)2-ab (а3 + b3 + a2b + ab2)(a3-Ь3)
Решение.
(я Ь,
ОДЗ: 5 А
[а ф —о.
(a-b)2 +ab а5 + Ь5 + a2b? + a3b2 _ a2 -2ab + b2 +ab t (a + b)2-ab (a3 +b3 +a2b + ab2)(a3-b3) a2 +2ab + b2 -ab
(a5 +a2b3)-^(a3b2 +b5) a2 ~ab + b2
((а3 + Ь3) + (a2b + ab2 ))(а3 -b3) a2 ±ab + b2
((a + b)(a2 -ab + b2) + ab(a + h))(a-h)(a2 +ab + b2) _
а2(а3 4-63) + 62(а3 4-Z?)
_ (°2 -С1Ь^Ь2)(а+Ь))(а2 ^b2)(a-b) _а_^
(a^b)(a2 -ab + b2)(a2 +Ь2)
Ответ: а — Ь.
2.081.
Решение.
ОДЗ: t > 2.
Ответ:
2-082, b(abc + a + c) .	1	’ Г
'	' а ч-------а ч—
b + l/c	b
Решение.
ОДЗ:
abc + а ч- с # О,
Ьс Ф —1, ab * -1.
b
ab + \
6 # О,
1_______6с+ 1	ab + \ = l-frc+QH+l)
b(abc+a+c} abc + a + c b	b(abc + a + c)
_ 1 -ab2c-ab-bc-1 _ -b(abc + а + с) _ b(abc + а + с)	b(abc + а + с)
Ответ: -1.
2.083.
2-х+4х2 +
5х2 -бх+3 Л. . 2х А --------- : 2х+1+--- .
х-1	х-1 I
Решение.
ОДЗ:х#1.
(_	, 2х )
: 2х+1+---- =
1	х-1 J
2—х + 4х!
Х-1
(х+Цх-1 + х)
4х3 -Зх+1 х-1	2х2+х-1
2х — 1	2х-1
Ответ: 2х-1.
а-1 . _ 2-Ь\ 6-1 ’ "а-2 ’
(2-Ь	а-1) (, а-1
2.084. Н~Т+2 “—у 1: Ь-—+а-I о — 1	а —2
a = V2+( Решение.
(2-b ^,a~L\(h.E—L	2~b^ (2-b\a-2)+2(a-l\b-l)
^6-1+ л-2; b-l+a а-2J (Ь-1Ха-2) Ь(а - 1\а - 2)+ a(2-b)(b -1) = ab-2 (b-l\a-2)	=
(b-l\a-2)	~ (b-l\a-2) a2b-ab2 -2а + 2Ь
_ ab-2 _ ab-2 _ 1	1
ab(a-b)-2(a~b) (a-b\ab-2) a-b 72 + 0,8-72 + 0,2
, .... - f «V <’ + b/b	Г--'j [ V<7 + 4b
2.085.	I—  [—	у ab •	.
Ju +yjb J a-b J
Решение.
ОДЗ-J/’>0,
f _ 4i t \lb \(4a ч jb)(4a -4b),
(%G -4b)2
Omnein: I.
2.086.
e~~,~ a - Va~ —b~
+	-b~
a i- у/a~ -b2 Wa4-a2b2
T-7a^^) W2
Решение
ОДЗ:
2 12 a ~b
b^-0.
>0,
/2	>2
-b
4yla4-a2b2 (5b)2
I 2 ”/ 2 a - V a - b J
(а~Уа2 -62)2 ~(а + 7а2-Z>2 )2	25b2
(а + >la2 -b2 )(a -7a2-b2)	4^а2(а2-b2)
_ а2-2а^а2-b2 +a2-b2 -a2-2a^a2 -b2 -a2 +b2	25b2
a2-a2+b2	4-|а|-7а2-*2
_ 4a^a2-b2	25b2	_ _ 25а _ (- 25, если a > 0,
b1 4-\a\-yla2-b2 ~ H " [25, если а < 0.
Ответ: -25, если а > 0; 25, если а < 0.
2.087.
л/3(а-Ь2)+ 736^8^ J2^-J2c ^2(a-b2)2 +(2bj2a)2
Решение.
а >0,
ОДЗ:
• о 0, 2(a-b2)2 +(2bj2a)2 *0.
J3(a-b2) + j3b^ ^(a-b2)2 +(2b42a)2
у[2^-у/2с- V3(a-62)+2V3/>2
42{4а-4с)	4з(а-Ь2 + 2Ь2)	y/2(J^-Jc)Jac
^2.-^1. J2>la2 -2ab2 +b4 + 4ab2	4i(4c-ja)
4a 4c
_	a + b	-Jac _-(a+b )-Jac _-(a + b yjac
-\la2 + 2ab2 +b4	*	^/(a + Z>2)2	a + b2
Ответ: - Jac.
i ». ин. ite.
ОДЗ:
Omee n:
Реше tue.
. и * ±8, °да „«о.
Ответ: 2.
2.090. (a-b)3(4a +4b) 3 + 2a4a +b4b 3(4ab-b)
a4a+b4b	a-b
Решение.
a*b,
ОДЗ:
a > 0, 6>0.
(a-b)\4a+Jb)~3+2a4a+bjb ! 3(7oK-6)
a-ja+bjb	a-b
(A-Tti3___________' з4ь[4^-4ьу
ayfa+bjb (4a -4b)(4a + 4b)
(a-b)3 +(2a4a +b4b)(4a +4b)3 t 14b
(4a+4b)3(a4a+b4b)	4a+4b
За3 + 9a2b + 9ab2 + 3b3 + 9a24ab + 9b24ab +6ab4ab a3 +3a2b + 3ab2 +b3 + 3a2 4ab + 3b2 4ab + 2ab4ab
_3(a3 +3a2b + 3ab2 + b3 +3a24ab ^3b24ab ^2ab4ab) _ a3 + 3a2 b + 3ab2 +b3 + 3a2 4ab + 3b2 4ab + 2ab 4ab
Ответ: 3.
2.091
x'^+x'V6' ^'V'3-*1'2?2'3	’
Решение.
ОДЗ:
x *0, у #0, X *±у.
х^-у^	(x>/3+?Z3)2-^	2/3 1/6	;;
xl/2+xI/3jI/6- х5/6>,1/3 _х1/2у2/3	У х3/6+х2/6д,1/6
(х2/6+>>2/6)_4х2/6>,2/6	2	=
Х у5/6„2/6_ г3/б„4/6	+ „2/3 „1/6	2/6/J/6 . „1/6чХ'
л у л у	л у л	т у J
х4'6+2х2У'6+//6-4х2у/6	2	л-'/6-/6
Х х^у^^-у2/6)	+ х^у'Р v2/6(x,/6+JV,/6)X
x4/6-2xy6/'6+/'6	2	х1'6-/6	(х2/6-уУ6)2
Х х^у^х^-у2!6) + x4V6 л%1/6 +3',/6)'х3/6?2/6И6 ~Г/6Т
2	х1/6-/6	х^-^6	2	= (х|/6-/6)
+ x4V6 х2/6(х'/6+/6)' х3'6.Л6 +xV%|/6'_P/6(x|/6+/6)X
2	Jx1/6-/6)2	2
Х х’/61Л6	+г4/М6'	y5/6v2/6 ~+ ЛМ6
•Л у	Л у	I	•'V у
_ X2/6 -2х116ух>6 +y2/6+2x'l6y'l(> _ х2/6 + V2’11' _ х1'3 +у'>2
Х^у^ 	= А.^//6 =	•
XV3 + yV3
Ответ:
2.092.
Решение.
ОДЗ: х*±1.
1
Ответ:	Г
х -1
Решение.
Г > О,

14*	t.141-2 ijllf+lji-l) 2к
' 4i i.i4i-2
Ответ: 2-Уз.
т4^3 -21т^3 п тУ3 + Зу[тп + 9п2!3
Решение.
ОДЗ: ш#0.
-21т^3-п (. v[7] зГ~2 _	m^3(m-27n)	.
m2/3 + 3& + 9„2'3 \ К Р™ ‘ т*	+9п^
К-M „	т»
}[т	т2^3 +5т^3пУ3 ^9п^3 т^3 ~Зп^3
_ т^3(т^3-Зп^3\т^3 + Зт^3пУ3 + 9л^3) тУ3 т213+Зтх13пх13+9п213	тУ3-ЗпУ3
= т2^3 -т2^3 =0.
Ответ: 0.
р-3	12	3
2.095. zp2+3p :z9~p2 -z3p~p2.
Решение.
ОДЗ:
0 < z * 1, р*0, р * ±3.
р-З 12	3	р-3	12	3
zp2+3p :z9~p2 'Z3p~p2 =zp2+3p 9~p2 3p~p =
p-3 t 12	3	(р-ЗУ+12р-3(р+3)
_zpG>+3) 0>-ЗХр+3) p(p-3) _z pG^+3)(p-3)	_
p2 -6p+9+12 p-3 p-9	P2+3p	p(p+3)	1
_ z p(p+3Xp-3)	_ z p(p+3)(p-3) _ z p(p+3\p-3) _ z p-3
1
Ответ: z p~3.
2.096.
Решение.
x>0,
ОДЗ:
a *0.
2	2
a _ a 4(x-a2) 4(a2-x)
a2
Ответ:----z-----
4(a2 -x)
2.097.
Решение.
ОДЗ: x>0,x*2.
4 M. И. Сканави, группа A
97
= 2.
Ответ: 2.
Решение.
1>0,
ОДЗ:
Ответ: 1.
2.099.
Решение.
• [х*0,
ОДЗ.
у * 0, х * 8 у.
(х2|/3+2^/ху + 4у2^3) С /7) х2/3+2х1У3+4у2/3 ( 3jT_
М (x4/3-8>-x,/3):x1V3| V7/
= ^+2xV+4/J 2^?-V7 Jp3 + 2х[У3 +4У2/3 V3
*1/3(*-8Л ' V7 =	W-fc/3)5 Х
х'/^’/з
2V7-V7 _	(х^3 +2x'/3yV3 +4//3У3	2у‘/3 -х‘/3 _
Х з/7	^3-2у^3+2х113у^3+4уУ3)'	у*3
у''3	2/3-х''3 =
2у'13-х1/3'	у'/3
Ответ: -1.
I-+2-2^)4+^ rFTZZ
2.100.		f—5------L-zVzJ- + 4+z.
z-2+-	Vz
Решение.
f-^A.Az + z2 z2-2z + l	ZV V z
, ) О-гЖгЬ fe-if ' fr-tf
- z(2 + z)= (z + if z - z(2 + z)= (z+2)z(z+2 -1)=z(z + iXz+2).
Ответ: z(z + iXz + 2)
2.101.
' 1 a2 +4 \Га 1 • 1 Y' <a + 41 a3 +2V2 Д2 V2 a J
Решение.
ОДЗ:
a 0, а Ф -42.
/	п\/	\— \ f
1 a2+4	__L + ll =	1 a +4
a + V2 a3 +2V2 ^2 4*2 a J a + 42 a3-^^42^
fa___1_ fl_f 1_____________g* 2 + 4	a2-42a + 2
y/2 a) ^a + ^2 (a 4-	~~>f2a + 2)^ 2л
a2-42a + 2-a2-4 a2-41a + 2 _ -42a-2 1 =
(a + V2 )(a2 - Via + 2) 2a ” a+ 41 2a
„ V2
Ответ:-----
2a
2.102. f(^_(1_a)-.li^z2) . p л	J a -a+1 |(a +
Решение.
ОДЗ:
a *0,
а * ±1.
"(o-l)'1 (1 a)-i1 1+0(0-2) I 1	a-l
a~3	J a2-a + l y(a + l)2	_L
I a3
l + g2-2a__1 _Г a3 , 1 "j a2-2a + l_1 _a3 + l
a2-a + l |« + 1| ^0-1 a-1) a2-a + l |« +1| a-l
(a-I)2	1 = (a+ l)(a2-a + l)(a-1) = (a + l)(a-l)
a2-a + l |a + l| (a2-a + l)-|a + l| la + l|
(a + l)(a-l)
2---------- = 1 -а, если a +1 < 0, или a < -1;
-(0 + 1)
(a + l)(a—1) _ _ j, если a +1 > 0, или, учитывая ОДЗ, a + 1
a > -l,a *0 и a * 1.
Ответ: l-а для a e(-oo;-l); a -1 для a e(-l;0)U(0;l)(l;oo).
2.103.
Решение.
ОДЗ:
ab > 0, а^Ь.
Ответ:
а
2’
2.104.
Ь4 -4а9
&2 -2а3 Ь2
Решение.
\а #0, °да »«о.
а ,1,	4а6	2-,1~Ь	4~	2 з/	3,4	9
b---Г ~а I ~Т—r+ — Vab* —4а
И	b3 Ъ6	Ь3	ab
34b2^3 Ь2
'ajb4-4a6
ЬЧ Ь3
Ь4 -4а6 а6Ь3
а2У^47|2аУ^47>| Ь2
b2	a2b	ab ^2 _2аз
з/Л а 1 2) b2 ty2 -2a3fy2 +2a3\a+b) I*2 b b)W-2a3	Ь
х .	—----- = (а+b^lb2 +2а3.
34ь^
Ответ: (a+b$b2 +2а3.
Ответ: -1.
II
н н н н н Q Q Ч * К
ОДЗ:
3
.	.	,	1	а+х+1
1+(а+х)1 i 1 —^?2+x2)	+ a+x 2ax-l+a2+x2 _ a+x x
l-(a+x)‘* [ 2ax J j 1	2ax a+x-1
a+x	a+x
a2 +2ax+x2 -1 _ a+x+1 (a+x)2 -1 _ (a+x+lXa+x+lXa+x-1) 2ax a+x-1 2ax	(a+x-l)2ax
.	2	( 2	i i \2
(	1 у a -a+l+a-1
_ (a+x+1)2 _ (	a-1 j _ [	a~^ J _
2ax	2a	2a
a-1	a-1
_ a4 a-1 _ a3
~(a-lf'l^~2(a-iy
a3
Ответ: ~Z7—
b
(a b
2.108. k + ~
a+b ~2a~
b a+b
h2 a+2b + — ’ a
a a+b a-b
a = 0,75; 6 = 4/3. Решение,
a b (a+b b -+-+2 • —------- :
b a 11 2a a + b I
b2 a+2b+— •
a
a [ b a+b a-b
a2+2ab+b2 a2+2ab+b2-2ab _ (a2+2ab+b2 a2-ab+ab+b2'\ ab	2a(a+b)	a (a+b\a-b)
(a+b)2ifl2 +b2) (a+b)2{fl2 +b2)_ (a+b)2^2 +b2) a(a+b\a-b) 2a2b(a+b) a(a+b\a-b) 2a2b(a+b)	(a+ft)2^2 +b2)
075-*	1-1 -2
’	3_43__________12..2.
2 0,75-1 2-1-1	2	24
3	4 3
Ответ:	•
4
а = 3 —;х = 0,28.
7
Решение.
ЮО--72 — I25 7 = 2500 1800 - 700
7	7 V 7 *25 “ 7	7 “ 7
Ответ: 100.
2.110.
yjc-d c2yflc
c-d с2+cd
---7 +	---- c + d \c2-cd
c = 2;d = l/4.
Решение.
dc-d c2J2c
Ответ: -7
3
(ah * 1 + a~lb+l^a 1 -b~lJ 2’11L a2b~2 +a~2b2 -](ib~l +a~lb)
Решение.
[a # 0, од3:(ь#о.
(aZ>~*+a ‘fc+lYa '-6 ‘j2 a2b~2 +a~2b2 -(afe-1 +a-lZ>)
a2 +b2 +ab (b-aY (a2 +ab+b2\b-a)2
ab 1	a3b3
a4+b4 a2+b2 a4 +b4 -a3b-ab3
a2b2 ab	a2b2
(р2+аЬ+Ь2\а-Ь)2	a2b2
a3b3 '^-а^ьУ^-Ь4) ip2+ab+b2\a-b)2	(p2+аЬ+Ь2\а-Ь)2
ab[fi3(a-b)-b3(a-b)) ab(a-b^fi -b3)
ip2 +ab+b2\a-b)2	1
abifl-b^a-b^2 +ab+b2) ab
1
Ответ:
ab
2.112.
V^2 J \ 4-4t + t2 \	7
Решение.
|z>0, o«*U2.

,з, J<3g2+2r+4)~> V (2-02
Ответ:
х^Р-х^ч	хУр
2Л13- (х1/р + х1/<?)2-2x'/q(x}/q+xVp) +	+1 
Решение.
Р*0,
ОДЗ:
9*0, х > 0,
x3/p-x3/q	х"р
(XVp +х,л?)2-2x{l\xxl4+xVp}+ x{q-p)lpg+\~
= {xVp-x'/q)(x2/p+x'/px',q +Х2/<?) ! Х1/р
(xi/p+xllq)(xl/p+xl/q-2xl/q) +xl/p~llq + l
_ (xl/p -x1/?)(x2/₽ + xl/pxi,<l +x2,g)	x1/₽
(xl,p +x1/?)(x1/₽-x1/?) x1/p J/?4
Vp + xVpxUg + x2lg хНРхМЧ _
xx'p+x"< V'+x17’"
2/P+2x1/px1/g+x2/g (x^+x17*)2
Mp + J'q
------"Р+х^^ + ЧГх.
Up + rU<l
Ответ: Р4х +
1 + a 1 -6д'2
9-4д-2
Зд-,/2+2д-3/2 д-1/2+Зд-3/2 Решение.
2.114.
ОДЗ:
a *0,
2
3
9-4д-2	1 + д-|-6д-2>|4
Зд-,/2 + 2д-3/2 д-,/2 + Зд’3/2
3	2
1/2 +аЗ/2
, 1	6
+	2
а а1
1	3
1/2 + „3/2 д а 
д2+д-6^
9д2-4 д2
Зл+2	а + 3
3/2	“372
а	а
9а2-4 а2
„3/2	„2 ,„ А „3/2 Y*
а	а + д —о а
За+ 2 а2 а + 3
1(Зд + 2)(Зд-2) (д + 3)(д-2)
[ д1/2(Зд + 2)	д1/2(д + 3)
I =(2д1/2)4 =16д2.
Зд-2 д-2У*
„1/2	1/2
a a J
[ 3a - 2 - a + 2
~l T72
Ответ: 16д .
2.115. 4ai +
. 2b^ J a + Jab'
^+4bV 2aJb
(ь+4Гьу 2 \	7
Решение,
fa >0, ОДЗ: [Z>>0.
«W a + b
2b4a + 2ay/b
- 4ab + +	-ab+b2)_ 2y/ab[Ja +y[b)^
a + b	4a + 4b
= a2 +3ab+b2 -ab = a2 + 2ab + b2 =(a + &)2.
Ответ: (a + bf.
Решение,
т >1, ОДЗ: п > О, Ш*П,
1 Ответ: ?• т
2.117.
1
Решение,
ОДЗ:
а *Ь, а >0, Ь>0, -1<а<1.
= (а+Л'Р +6-a-2a'^V2 _b),l+l_a2 =
=	.-1—+1-а2 = -1+1-а2 = -а2.
а1/2Ь1/2
Ответ: -а2.
Решение.
г(Уз+1)	з(Тз+2)	15(34-5/3) 1
Д73-1)(7з+1) (ТЗ-2)(Уз+ 2)+	) Тз+5
'2(73+1) 13(73+2) 115(34-5/3)^ 1 =
2 + -1	6 J 734-5
-473-10+15+57з 1 Тз+5 1 = 1
2 Тз + 5	2 Тз+5 2
^7754+157128
2 П9‘ 7^32+V^‘
Решение.
77754+157128	77727-2+15764-2	7?-372+15-472
^4732 + 797162 74716^2 + 79t^b2 ^4-2^2 + 79-з72 = 72172+60^ =	78172	= 3$2	= 3‘Т2 = 3
7^/2 + 72772 27^ + 377^ 21^+3‘72 5’72 5*
5747192 + 7718781
Решение.
5747192 + 7718781 _ 5^4^641 +7718Т2ГЗ
712724 + 67375	712^3+671253
574-473 + 7718-3^ 571673 +?7547з 712-27з+6-57з	7247з+307з
5^8 2^3 4-7^27 -2^3 5 2^2^3 4-7 3^2^
Ответ: — •
2.121.
Решение.
^32^4 4-^64^ - З^Ж = V25 -22/3 4-^26-2-|/3 - 3^2-21/4 = = 217/12 +217/12 -3-25/12 =2-2I7/i2 -3-25/12 =25/12(4-3)=25/|2 = = ‘^2? = 1^2.
2.122.
Решение.
- 22^7^2 = 24>/V18 - 22JV18 = 24V18 - 22^18 = 2^18.
Ответ: 2^18.
2.123. 2740-712 + 3^5748 - 2^75 - 4715^7.
Решение.
2^40712 + 3^748 - 2^75 - 4J15V27 = = 2740>/Гз + зТ^Аб^ -21/25~3 -4^157^3 =
= 2^40-2Тз + з75 -4>/з - 2772^3 -4^15-Зу/з = = 2^80-73 + 3 • 2у[з4з - 2у1^3 - 4^4573 = = 2^16 -5<УЗ + 6у[^/з - 2у[^/з - 4-^9-5-Тз = = 2 • 4^5^ + 6- 2>/s/3 - 4 • 3	=
= 8>/?7з+б7^-2>/^-127^ = 14^573 -14^573 = О. t
Ответ: О.
2.124. 5^бТ32 - 3^97162 -11718 + 2^75>/50.
Решение.
537б7И - 3^97162 -11718 + 2^75^50 = = 5^67162 -3^97812 -11^92 + 2^7572^2 = = 5^6-4-72 -3^9-942 -11VV92 + 2^75-5-72 = = 5^24-72 - 3^8172 -1 $1з42 + 2^375-72 =
= 5^8-3<Л - з427 -з42 -1	+ 2^125-372 =
= 5-2ll^-3-33у/з42 -111/з42 +2-53у/з42 = = 10^372-20^3^+10^^ = 0.
Ответ: 0.
Проверить справедливость равенств (2.125—2.134):
2.125.
4:
Решение.
Преобразуем отдельно левую и правую части равенства:
а) 4:
3
5
32/3 Т
= 20-3"2/3;
б) 10^5: (0,25^21679 )=10*||:• $23-З3-32/3 j=
= 1О.зУ4 -23/4.2^4-3"/12 = 5-31/4-23/4-22 =	2/3
2	22	23/4-311^12
Получили, что 20 • 3 -2/3 = 20 • 3 -2^3.
2.126. (4 + 715)(Л0 - Тб)-74-715 = 2.
Решение.
Возведем обе части равенства в квадрат. Тогда
(4+715 У (710-76^-715)= 4,
(4+715 ){* - 715 )(4 + 715 0 - 2ТбО + 6) = 4,
^42 -(V15)2 ^4 + Л5^6-2Тбо)=4,
(16-15)(4 + 715)-2.(8-7б0)=4, (l+715^8-7445)= 2,
(4+ 715 )(8-2715)= 2, (4 + 715)-2 (4-71?)= 2,
+	42-(Т15)2=1, 16-15=1, 1=1.
2.127. 7з - 75 • (з + 75 )• (710 - ^)= 8.
Решение,
Возведем обе части равенства в квадрат. Тогда
(7з - 75 J + 75 У (72 (75 - 1)У =64,
^-V^J + Vs)2 2(75-l)2 =64,
(3 - V5 )^ + >/5)(з + >/5 )(5-2л/5+1)= 32,
(З2-^ J? + V5)(6-2V5)= 32,
(9-з/з + Л)-2-(3-V5)= 32, 8^+ Т5)(з-7?)= 32,
8^32 -(75)2 )=32,
8(9-5)=32, 8-4 = 32, 32 = 32.
2.128.
УТз+Тё-79-672-Vis = эд 72-1
Решение.
Преобразуем левую часть равенства:
Итак, -7з = -7з.
2.129.
25-72+275 1^2 5
7250 + 5^8 V 5 +72 +
Решение.
Положим
25-72+275 , Т^г+Уб2 ^4 л^50 + 578 7s6-22 + 754-23
t/5^2
2^ + _5_+2= Ь+2-5>/2+25 5 +>/2+ V 5Л
Отсюда
_у = 5-У52 2 +У2 _ 5 + 72 = 5-V52-2+72-5-72 V52 -2	V52 -2	V52 -2
-*4^2 __ .
4^2
Получили -1 = -1.
2.130.
Решение.
Возведем обе части равенства в квадрат. Тогда
= 2,
У27-7зТЗ-7з+1 = j ^27-72-73+1 = j j _ j 727-7273+1	’ t/27-7273+1
Решение.
---16-----[	= 2^61 + 247?, 9-6-75+5 Тб-5 >
—^-=-6 = 27б1+2475, —^-=-6 = 2761+2475, 14-6-75	7-3-75
—^-=-3 = 761+2475, 4~21'ф^ = 7б1+2475, 7-3-75	7-3-75
7-3-75	(7-3V5j7+3V5)
12^-+14-=761+2475, 12^+i6=761+2475, 72^(зТ5)2	4
з75+4 = 7б1+2475.
Возведем обе части последнего равенства в квадрат. Тогда (3V5 + 4)2 = 61+24-75 , 45 + 24-75+16 = 61 + 24-75, 61 + 2475=61 + 24-75.
2.132.
Решение.
Умножая числитель и знаменатель каждой дроби на выражение, сопряженное ее знаменателю, имеем
Л + Уб _з(Уб4-Уз) 4(Л-Уз) 7-6 ~	6-3 +	7-3
V7+V6=V6+V3+V7-V3,
7б=>/б.
3	5	2
iA33- 45-42* 41+42 41-45'
Решение.
Умножая числитель и знаменатель каждой дроби на выражение, сопряженное ее знаменателю, имеем
V7+V5 =>/7+>/5.
4iJ10-7V2
2134'
Решение.
Умножая числитель и знаменатель каждой дроби на выражение, сопряженное ее знаменателю, имеем
^/2 -1^2 -l)Jho-142^Q-141) (Л-1У _ 3^0 - 742f
(Л+1р2-1) ЦО+142^0-742)’	2-1 V 100-98
2 -242 +1 =	3-242 = 499-7042.
V 2
Возведем обе части последнего равенства в куб. Имеем
(з-2<^У = 99-70-72, 27-54л/2+72-16^ = 99-70-72,
99 - 7042 = 99 - 7042.
Сделать указанную подстановку и результат упростить (2.135—2.145): x^-a-^-b-^+b^ + b^	2/31-1/2
2-135.----------ь* х2 ----------; х=а •
Решение.
(а *0,
ОДЗ: |6*0.
(а^-./2у _fl2/3 ,ь-|(д2 +b2^3b-l/2 +bl/2
b^.^b-t/2f
_a2b~3^2-a0b~3^2^i2+b2)+b1^2 _ ь^ь-'
а2 а2+b2 Ц2 а2 -а2 -Ъ2 +Ьг
= Ь3'2	Ь3'2 +	=	Ь3‘2	= 0
61/2в4/3	^2^3
Ответ: 0.
2.136.	Ц=- *2 ~2х+ •'/*; х= ^Г-
>[ь	1-4ь
Решение.
ОДЗ: 0<Л#1.
Ответ: 0.
(x+2b х+2а\х 4аЬ 2Л37, \х-2Ь + х-2а / 2’ X~7+b' Решение.
ОДЗ: а Ф -Ь Ф 0.
( m 4aZ> п
—г + 2^ —г + 2а	A L
a + b	a + b .
4ab 2b 2a 2(a+i) ^a + b	a + b >
a + b
> |a+b_ ' 2b(b-a))~2ab~
(4ab+2ab+b2 4ab-2ab-2b2 4ab + 2a2+2ab 4ab-2a2-2ab
—		♦---------------------1---------
a+b	a+b	a+b
a+b (2b$a+b) a+b 2b(3b+a) a+b
2ab I a+b 2b(a-b) a + b
(За + b 3b+a\ a+b (За + b 3b+a\a+b
—	I---.	|.	.. — — I	—---— |.	-
\a-b b-a I lab \ a-b a-b j lab
3a+b-3b-a a + b la-lb a + b l(a-b\a + b) a + b a-b lab	a-b lab	l(a-b)ab ab
x
a + b Ответ: — ab
2.138. (x + lXx + 2Xx + 3Xx + 4>
x =
41-5 1
Решение.
'12-lOjl 5/7-25?
4	+	2
+ 10.p2-l(b/7+52/7-2S'l 24, 4	2
к	/
3 Ответ:
4
11ад (г-1Хг + 2Хг-ЗХг + 4),
Решение.
23
23
3 Ответ: — •
4
2.140.
х(х+lX-х+2\х + 3).
(х-1X^+4)
Решение.
14-6V5 Зл/5-9
14-6-J5 зЛ-9
-1-4
7-3V5+3-J5-9 л -------------4 2
£ 5
1 Ответ: —
2-141- /G+i)2
Решение.
1
1
j3 + x-Jx+2 73-х-7х-2.
2.142.	1	1
73 + x • у/х+2 73 —х • у/х-2
Решение.
1 t 1
7з+7б • >/>/б + 2 5/З—7б • 77б —2 _ 1 1
5/3+Тб • ^у/б + 2 5/3—5/6 • 5/5/6— 2 7з—7б • 5/76— 2 + 7з+7б • 75/6 + 2 _ 7з+л/б • 5/л/б +2 • 5/3—7б • 5/76— 2 5/3—5/6 • ^у/б — 2 — 7з+7б • 5/5/6 + 2 7з+7б • y}Jf> + 2  д/З-л/б • у/у/б -2
(>/55/6-12 J - (5/55/6+12 у
5-J6-12+25/(5>/б-12^Уб+12)+5Уб +12
5>/б-12-5л/б-12
Юл/б+гдаб)* 2 -122 = 576+7150-144 = 57б+7б _ Тб
-24	”	-12	-12 " 2
л 76
Ответ: - —
2
2.143.
2bjx2-l х — Vx2 -1
а > b > 0.
Решение.
a2 + 2ab+b2 ZOJ-----------1
__V 4ab_______________ a+b la2 + 2ab+b2
-1 2jab 1 tab
la2-2ab+bz
2bi-----------
a+b a2 +2ab+b2 -4ab a+b a2-2ab+b2
2jab V tab	2y[ab V 4ab
(a-b)2	2b-^-
a+b a-b .Jab 2-Jab 2-Joi
2b.--------
V 4ab a+b l(a-b)2 2-Jab 1
_ b(a-b) ' a+b-a+b^ _
~ ' 2jdb Г
^ab 2b
Ответ: a — b.
2.144.
2aVl + x2 x + yll + x2
a>0,b>0.
Решение.
a2-2ab + b2 4ab
a-b , a2-2ab+b2 --7= +111 +------- 2jab I 4ай
„ 4ab+a2-2ab+b2 2a.--------------
V______4ab_______
a-b l4ab+a2-2ab+b2 2jab 1 ^ab
_ la2 +2ab+b2	. (a + b)2	2a(a+b)
2a J--------- 2a>  ---------—	---/=
V 4ab___________ V 4ab _ 2<Jab
a-b la2 +2ab+b2 a-b	l(a + b)2	a~.^ + g +
2Vai+’ 4ab 2jabi 4ab
a(a+b) (a-b + a + b Job 2jab
a(a + b) 2a _a(a + b) y/ab Jab 2jab Jab a
Ответ: a + b.
\ + bx t \-bx'
2.145.
1 +ax
1 \2a-b x = — • J---;
a V b
a b
0< — <a<b.
2
Решение.
1. I2a~b а У b
2a-b N b l2a-b N b
x
1+1. М2(2а-^>) j 42a-b al b _ Jb
1 i_l. Ib2(2a~b) j ! V2a-f>
I a 1 b	4b
a+4b(2a-b)
a _ 4b —42a—b a-Jb(2a-b) ~ 4b+42a-b
a
Ja+4b(2a-b) (4b-42a^b\4b-42a-b a-4b(2a-b) (4b + 42a-b\4b-42a-b l(a + y/b(2a-b')J(i + y/b(2a-bjJ _ b-24b(2a-b)+2a-b у ip~4l42a-b)Jp+4b(2a-b)') b-2a+b
y]b(2a-b)f 2a-2-Jb(2a-b) (?+4b(2a-b)f -b(2a-b) ~	2b-2a	1| a2-2ab+b2
a~4b(2a~b) Га+у/Ь(2а-Ь) a-y/b(2a-b) a+y/b(2a-b) b-a u a-b	b—a	b-a
H	7
a2 -b(2a-b) = a2-2ab+b2 = (b-a)2 = 1
(b-a)2	"	(b-a?	~(b-a)2
Ответ: 1.
Освободиться от иррациональности в знаменателе дроби (2.146—2.151):
14 2146- 43^/2-Решение.
$ М. И. Сканавн, группа А
129
=2(®-й)(7з+У2)(з+72).
Ответ: 2^/3 -’Л^З	+
4
2.147.	_4^9
Решение.
Ответ: (1/13 +1/9 )(-Лз + з)
Решение.
(з+(У2+Уз))(з+(У2+Уз)) (з+(У2+УзУ ..
(з-(У2+УзДз+(У2+Уз)) 32-(У2+Уз)2
_9+б('/2 + >/з)+('/2+'/з)2 _ 9+б(У2 + Уз)+2+2Уб + 3
9-(2+2>/£ + з) "	9 - 5 - 2 Тб
14+б(У2 + Уз)+2>/б 7+з(У2+Уз)+Уб =
4-2>/б	” 2—Уб
_ (7 + з(У2 + Уз)+ Уб)(2 + Уб)_ (2-Уб)(2+У^)
= 14+б(У2+Уз)+2Уб + 7Уб+з(У12 + У18)+б^
4-6
14+бУ2+бУз+9Уб + 6'/з+9^2+6 20+12-Уз+15-^2+9-Уб -2	-2
^+з42^+з4з) 2
п ^+з42^+з4з)
Ответ:	------L.
2
2.149.
6
Решение.
п 2л/з + з72-л/30 Ответ:---------------.
2
Решение.
Представим заданную дробь в виде
• Умножимэтудробь
на
(74+л/2 + л/з)(|+2-3-24^2} и,
применив равенство
с—24аЬ)=(в + Ь + сУ —4аЬ,	где
а>0,6>0 ис>0,получим
-42-4з\Д+42+43^4+2-3-24^2.) {44+42-4з\44+42+4з\4+2-3-244^2)
(4+2-3)2-4-4-2	9-32
(гТё-иКз-ФУг)
23
_	(>л/б+1)(?-4л/2)
Ответ:	a------L.
23
Решение.
ОДЗ: 0 < a * L a-1
a
2.152.	Показать, что если z = \a + 4a2 + А3 -vVa2 + 63 -а , то z3 + 3bz-2a = 0 •
Решение.
Тогда z3 + 3bz-2а = 2а~ 3bz + 3bz - 2а = 0, что и требовалось доказать.
2.153.	Если л/8-а + j5 + a = 5 , то чему равен ^(8-0^5 +a) 1
Решение.
|8-а>0, ОПЗ-(	<=>-5<а<8.
Д |5 + а>0
Возведя обе части равенства в квадрат, имеем
8 - а + 2-J(8 - а\5 + а) + 5 + а = 25 , или V(8-«X5+a) = 6.
Ответ: 6.
2.154.	Чему равна сумма 725 - х2 + 715 - х2 > если известно, что разность 725 - х2 - 715-х2 = 2 (величину х находить не нужно) ?
Решение.
ОДЗ:
Умножив обе части равенства на 725 - х2 + 715-х2 > имеем
[725-х2 -715-х2 ^725-х2 + 715-х2
= 2f725-х2 + 715-х2
откуда 725-х2 + 715-х2 = 5.
Ответ: 5.
2.155.	Преобразовать (a2 + b2\c2 + rf2) так, чтобы получилось (ас + bclf +(ad- bc^ .
Решение.
Раскрывая скобки, получим а2с2 + a2d2 +b2c2 +b2d2 .Прибавими вычтем выражение labcd. Тогда
а2с2 +2abcd+b2d2 + a2d2-2abcd + b2c2 = (ac+bd)2 ^(ad-bcf => => (a2 +h2)(c2 + d2]=(ac + bd)2 +(ad-bc)2.
2.156.	Вычислить сумму кубов двух чисел, если их сумма и произведение соответственно равны 11 и 21.
Решение.
Пусть a + b = llnab = 21. Тогда
а3 + Ь3 = (а + b/a2 - ab+Ь2 )= (а +. b^(a+bf - 3ab)= 11(112 - 3 21)=
= 11(121-63) = 638.
Ответ: 638.
2.157.	Вычислить значение выражения:
3	_____
a)— -z, z = VV3+^+VV3-V2;
3
б) х3 + Зх, х = Va/5+2 -VV5^2.
Решение.
б) X3 + Зх = ^V5 + 2 - Va/5-2 ) + 30/V5 4- 2 - VV5-2 = 45 + 2 - З3^ +2^ (V5 -2) + 3^45 + 2\45-2f -45+2 +
+ 3^75 + 2 - 3^75-2 = 4 - 33J(45 + 2\j5-2y5 + 2) +
+ 3^(45+2145-2^5-2) + 3^45 + 2 - 3^45-2 =
= 4 - 3^(5-4)(75+2) + 3^5-4^45-2) + 3^45+2 - 3^75-2 =
= 4 - 3^45 + 2 + 3^45-2 + 3^45 + 2 - 3^45-2 = 4.
Ответ: а) —; 6)4.
Решения к главе 3
ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ОСНОВНЫЕ ФОРМУЛЫ
Соотношения между тригонометрическими функциями одного и того же аргумента
sin2 a + cos2 a = l>	(3.1)
*	sina	tl\	~ tga =	, a#— (2л+11 neZ;	(3.2)
cosa	2	
. cosa	_ ctga =	,	neZ;	(3.3)
sina	
ЯЛ tgactga = l, a*—, n&Z-,	(3-4)
l+tg2a =—, a*—(2n+l)t neZ-	(3.5)
cos a	2	’	
l+ctg2a =—, a* ли, neZ	(3.6)
sin2 a	
(здесь и в дальнейшем запись п е Z означает, что п — любое целое число).
Значения тригонометрических функций некоторых углов
Для некоторых углов можно записать точные выражения их тригонометрических величин (табл. 3.1).
Таблица 3.1
Аргумент (а, градусы, радианы)			Функция			
			sin а	cos а	tga	ctga
О’(О)			0	1	0	00 (не определен)
15°	гп ' J2>		Уз-1 2У2	Уз+1 2У2	2-УЗ	2 + УЗ
18° I	.10 J		У5-1 4	л/з + Уз 2^2	У5-1 ^0+2У5	710+2У5 У5-1
30°			£ 2	Уз 2	1	Уз
			2У2	У?4-1 4	У10-2У5 У5+1	Уз +1 У10-2У5
45°	ы л,		1 •Ji	1 Л	1	1
54°	^Зл То		4	V5-V5 2У2	710-2У5	710-2У5 У5+1
(?)			Уз 2	£ 2	Уз	1 Уз
			Уз+1 2У2	Уз-1 2У2	2 + УЗ	2-УЗ
90°	f ^2,		1	0	(не определен)	0
Знаки функций по четвертям
Таблица 3.2
Четверти	Функция			
	sin а	cos а	tga	ctga
I	+	+	+	+
п	+	—	—	—
III		—	+	+
IV	—	+	—	—
Формулы сложения и вычитания аргументов тригонометрических функций
sin(a + p)=sinacosp + cosasinp;	(3.7)
sin(a - p).= sinacosP - cosasinp;	(3.8)
cos (a + p) = cos acos P - sin a sin p;	(3.9)
cos(a - p)=cos acos P + sin asin P;	(З.Ю)
tg(a + P)= 8	a,p,a + p* +7w, neZ- 1-tgatgP	2	(3.U)
tg(a ₽)=.*	«Д« ₽*,+*»» 1 + tgatgP	2	(3.12)
ctg(a + P) = c*£actsP J (х,р,а + р#лп, neZ-v ’ ctga + ctgP	(3.13)
ctg(a - P) = ctgactgP+*} а,р,а-р*ли, neZ ctga-ctgP	(3-14)
Формулы двойных и тройных аргументов
sin2а=2sin a cos а;	(3.15)
cos2a = cos2 а - sin2 а=2 cos2 а -1 = 1 - 2 sin2 а;	(3.16)
tg2a=	a# — + ^-,ke Z,a#-^+nn,«e Z .
* l-tg2a 4 2	2
ctg2a = Ctg ——a* — ,ke Z,a* ян,ne Z; 2ctga 2
sin3a = 3sina-4sin3ai
cos3a = 4cos3 a-3cosa1
tg3a= 3tga~tg.ct.> a*^(2n+l),n€Z. l-3tg a 6
, 3ctga-ctg3a , 7W „
ctg3a = —-----, a * —, ne Z
l-3ctg2a	3
Формулы Ьоловинного аргумента
. 2 a 1-cosa sin—=--------
2	2
2 a 1 + cosa cos — =-------
2	2
* > a 1-cosa	_
tg* —=------, а*л(2и + Цие Z ;
2 1 + cosa
. 2 a 1+cosa »	™
ctg — =-----, а*2лл,neZ;
2 1-cosa
a tg— =
2 1 + cosa
sina 1-cosa	™
-----, a*Jtn,«GZ; sina
a 1 + cosa Ctgy =
sina	_
-----, a#wi,neZ;
sina 1-cosa
(3.17)
(3.18)
(3.19)
(3.20)
(3.21)
(3.22)
(3.23)
(3.24)
(3.25)
(3.26)
(3.27)
(3.28)
Формулы преобразования суммы и разности тригонометрических функций в произведение
. о . . а+Р а-р sma + smB = 2sin	-cos   ♦ н	2	2 ’ . „ _ а+Р . а-р sina-smp = 2cos	-sin		  2	2	(3.29) (330)
о „ а+Р а-р cosa + cosP=2cos -cos-—- ; 2	2	(3.31)
а _ . а+Р . а-р п . а+Р . Р-а cos а - cos В = -2 sin	—sin - = 2 sin	-sin  	; 2	2	2	2	(3.32)
cos a + sin a = 41 cos(45° - a);	(3.33)
cosa-sina = V2sin(l5° -a);	(3.34)
, a sin(a+p)	„ л/»	<7 tga+tgP = —i—4-, a,P#-(2«-l|«eZ; cos a cos p	2	(3.35)
tga tgp= (	a,p#-(2n-l}neZ; cosacosp	2	(3.36)
„ sin(a+P) a	- ctga+ctgP = —-—а,Р*лл, neZ-sinasinP	’	(3.37)
4	„ o sinfe-a) -	„ ctga-ctgP= .	. ' а,Р#ли, neZ- sin asm p	’	(3.38)
n cos(a-B)	n , . _ o	„ tga+ctgP = —*—a* — + idc,ke Z,p*nn,ne Z  cosasinp	2	’	(3.39)
o cos(a + B)	n	* . tga-ctgP =	*—г-Цг, a* —+itk,ke Z,p*jw,ne Z • cosasinp	2	’	(3.40)
2	mt	„ tga+ctga =	, a*—, neZ; sin 2a	2	(3.41)
itn tga-ctga = -2ctg2a, a*—, neZ;	(3.42)
	1	? a l+cosa = 2cos“ — 2		>		(3.43)
	l-cosa = 2sin — 2				(3.44)
	l+sina = 2cos2	45° - I	2 ;	1 ?	(3.45)
	l-sina = 2sin2	45°-	K»| ft	ч	(3.46)
l + tga =	sin(45° + a) _ sin (45е	’+«)	a	л * — + nn, 2	neZ ; (3.47)
	cos45°cosa	cos a				
l-tga =	sin(45° - a) _ Vi sin(45	•-a)	л а* — + ли, 2		neZ; (3.48)
	cos45°cosa	cosa				
l+tgatgP= cos^a -61 a,P*-^+nn, neZ; (3.49) cosacosP	2
,	o cos(a + B)	0	.	r? l-tgatgp =	*—a,P* —+ лл, neZ- cosacosP	2	’	(3.50)
„ , cos(a-p)	„ ctgactgB + l= .	.^77, а,р*ли, neZ- sin a sin p	(3.51)
1-tg2 a= cos^a, а*^ + ли, neZ;	(3.52)
cos a 2
, j cos 2a	™
l-ctg2a =-----z—, а* ли, neZ;	(3.53)
sin a
tgz«-tg?p=Sin(ct+;^)sin(<^-^-,	»eZ; (3.54)
cos acos p	2
c,O-a8-f..s"ll“7la'ji;“1 "eZ; (3.55) sin asm p
tg2a-sin2a = tg2asin2a, а*у + ли, neZ; (3.56)
ctg2a-cos2a = ctg2acos2a, a# ли, ne Z ;	(3.57)
Формулы преобразования произведения тригонометрических функций в сумму
sin a sin p = ^-(cos(a - p)- cos (a + p));	(3.58)
cos a cos p = 1 (cos(a+p)+cos(a - p));	(3.59)
sin a cos p = i (sin (a + p)+ sin(a~P));	(3.60)
sinasinpsiny =
= -(sin(a + р-у)+ sin(p + у-a)+sin(y+ a-p)-sin(a+P+y)); (3.61) 4
sinacospcosy =
= (sin(a+p - y)- sin(p+у - a)+ sin(y+a - p)+sin(a+P+y)); (3.62)
sinasinPcosy =
= - (- cos(a + p - y)+cos(p + у - a)+ cos(y+ a - P)-cos(a + P+y)); (3.63) 4
cosacosPcosy=
= - (cos(a + P - y)+ cos(p + у - a)+cos(y+ a - p)+cos(a+ p + y)). (3.64) 4
Формулы, выражающие тригонометрические функции через тангенс половинного аргумента
2tgy
sina =----а*л(2и+1), neZ; •	(3.65)
l+tg2y
1-tg2 —
cosa =----а*я(2л+1), neZ;	(3.66)
1+tg2I
2tg— tga=	2 a, # (2«+l) neZ; l-tff 2 2	(3.67)
ctga =	a # ли, n e Z . *«7	(3.68)
Формулы приведения
sin ^±a^=cosa, sin(K±a)=Tsina, sin^-| n ± a j = - cos a, sin(2n ± a) = ± sin a;	(3.69)
cos^ ± a = ± sin a, cos(rc ± a) = - cos a, ГЗ A cod “n±a	cos(2rc±a)=cosa;	(3.70)
tgl ^±а j= + ctga, а*т, neZ,
tg(n±a)=±tga, a#-^(2n+l), neZ, tgl — я±а l=Tctga, a#Jtn, neZ,	(3.71)
tg(2jc±a)=±tga, а*^(2л+1), neZ; ctg| ^±а |=Ttga, а*^(2л+1), neZ,
ctg(n±a) = ±ctga, a#m, ne Z, ctg^-|n±a)= + tga, а#^(2и + Ц ne.Z, ctg(2m ± a)=± ctga, а Ф im, neZ. 144	(3.72)
Обратные тригонометрические функции
sin(arcsin х) = х, -1 < х < 1;	(3.73)
sin(arccos х) = 71 - х2, -1 х 1;	(3.74)
	(3.75)
эШ1 dlUgX) —	1	
7i+x2	
1	(3.76)
Vi+x2	
cos(arccos х) = х, -1 < х 1;	(3.77)
cos(arcsin х) = 71 - х2, -1 < х < 1;	(3.78)
Z	ч	1	(3.79)
Vi+х2	
cos(arcctg х) = •.	; 71+х2	(3.80)
tg(arctg х) = х;	(3.81)
tg(arcctgx) =—, х*0;	(3.82)
X	
Z	.	X	X	.	1	(3.83)
71-х2	
71-х2 tg(arccosх) =	, -1 < х < 0, 0<х<1;	(3.84)
X	
ctg(arcctg х) = х;	(3.85)
ctg(arctgx) = —, х^О;	(3.86)
X	
71-х2 ctg(arcsinx) 		, -l^x^O, 0<х£1; X	(3.87)
ctg(arccosx) =
arcsinx = <
arccosvl-x2, если 0<х<1,
- arccos v 1 - x2, если -1 < x <
(3.88)
i
(3.89)
0;
x
arcsinx = arctg-7==, -1 < x < 1;
Л7?
(3.90)
	д/l — x^ arcctg	, если 0 < x < 1,
arcsinx = ’	Л77	<191) arcctg	л, если -1 < x < 0; X
arcsinv 1 - x2, если 0 < x < 1,
arccos x =
л-arcsinvl-x2, если -1<х<0;
(3.92)
	7i-x2 arctg	, если 0 < x < 1,
arccosx = -	k? „ (W) л + arctg	, если -1 < x < 0; x
X	1	1 arccos x = arcctg -r-	, -1 < x < I; Vl-?	(3.94)
x arctgx = arcsin -r—	, -oo < x < oo; 7i+x2	(3.95)
arccos-7= I , если x>0, 7l + X2 arctgx = ! - arccos —7=, если x < 0;	(3.96)
arctg х =
arcctg—, если x > 0, x
arcctg—- я, если x < 0;
(3.97)
arcctgx =
arcctg x =
arcsin-. — —, если x > 0,
1
я - arcsin  -----j- , если x < 0;
(3.98)
arccos—=====, если x > 0, Ji^x2
X
- arccos	j , если x < 0;
(3.99)
arcctgx =
arctg—,еслих>0, x
л+arctg—,если x < 0; x
(3.100)
(3.101)
arctg x +arcctgx = —, -<»<x<oo;
(3.102)
sin x+arcsin у =
arcsin^x^l-J2 + ja/1-х2 J, если xy S 0 или x2 + y2 < 1;
n - arcsin^ x-Jl-j2 + y>ll-x2 естлх>0,у>0их2 +y2 >1; - л-arcsin^x^/l-y2 + jVl-x2 еслих<0,у<0их2 +y2 >1;
(3.103)
	arcsin^x-Jl - у2 -уу/\-х2 если ху > 0 или х2 + У < 1;
	л-arcsinf xJl- у2 -yVl-x2
arcsinx-arcsin^ = ’	к	)	(3.104)
	если х > 0, у < 0 и х2 + у2 > 1;
	_	’ (	/1	2	/1	2 Л
	- л - arcsin х-\/1 - у - у v 1 - х L
	если х < 0, у > 0 и х2 + у2 > 1;
	arccos^xy -	- х2 J1 - у2)), если х + у > 0;
arccos х + arccos у = <	Z	п	у	(3.105)
	2n-arccosl xy-yl^-x2 Jl-y2) |, если х + у < 0;
если x > у; arccos х - arccos у = «
(3.106)
arccos
если х < у;
	. х+у arctg	—, если ху < 1; 1-х^
arctgx + arctg^ = <	х+у л+arctg	=Чеслих>0иху>1; (3.107) 1-ху х + у - л+arctg	—, если х < 0 и ху > 1; 1-ху
arctgx -arctgy =
X — у
arctg----—, если ху > -1;
1 + ху
я + arctg ———, если х > 0 и ху < -1;
(3.108)
X — у
- п + arctg---если х < 0 и ху < -
Доказать тождества (3.001—3.062): 3.001. ^+cos_|2a + tg2a)(l-cos_|2a Решение.
(1+cos_| 2a + tg2a)^-cos_| 2a + tg2a)= 2 tg2a =
(,	1 sin2a Y. 1 sin2a'I
cos2a cos2aj^ cos2a cos2a J
_ cos2a+l + sin2a cos2a-l+sin2a
cos2a	cos2a
_ ((cos2a + sin2a)+lX(cos2a+sin2a)-l) (cos2a+sin2a)1 2 cos2 2a	cos2 2a
cos22a+2sin2acos2a+sin2 2a-l _ l+2sin2acos2a-l
cos2 2a	cos2 2a
2sin2acos2a 2sin2a -
=------=-----=----— = 2 tg2a.
cos2 2a cos2a. ,
-1
Получили 2tg2a=2tg2a.
3.002.
cos ’2a+ctg -я+2а
=1.
Решение.
5
_1	(5 н (5
cos 2a+ctd -я+2а ctd -я-a
12	‘
4
1	.J 4я+я _ ] ]
-----+ ctfl---+ 2а -ct] cos2a 1 2 I
4л+л ------а
1 cos2a
I	л
+cts2tt+ —+2a 4	2
( л
•ctg я+ —a 4
1	. J K n I d n
-----—+ctfl —+2a *ctg —a l-tg* 2a \2 J \4
J + tg2a
l+tg2a 1-tg2 a
-tg2a
Я 1+tg-tga 4 tgj-tga 4
1-tg2 a J 1-tga
1+tg2 a 2tga 1 + tga l + tg2a-2tga 1+tga 1-tg2 a 1-tg2 a, 1-tga l-tg2a 1-tga l-2tga+tg2 a 1+tga _	(1-tga)2 1+tga
(1-tgaXl+tga) 1-tga (1-tgaXl+tga) 1-tga
Получили 1=1.
3.003.
cos(3n-2a)
. /5л
2 sin —+ a 4
( 5л = t® a---
4	4
Решение.
cos(3n-2a)
. . гГ5л 2sin —+a
4
-cos2a
i (i .
1—cos —+2a	1-cos
1 2
-cos 2a
4л+л _
----+2a
2
-cos2a
-cos2a
7C
1 —cos 2n+ —+ 2a 2
1-cos —+2a 2
-cos 2a
1+sin 2a
Получили tg а-
tg2a+ctg3p _ tg2a
3.004. ctg2a + tg3p tg3p
Решение.
sin 2a cos3P sin 2a sin 3p + cos 2acos 3p
tg2a + ctg3p _ cos 2a sin3P  ________cos 2a sin 3P_____
ctg 2a + tg 3P ~ cos 2a sin3P ~ cos 2a cos 3p+sin 2a sin 3p
sin 2a cos 3p	sin 2a cos 3P
_ sin 2a sin 3P 4- cos 2a cos 3P sin 2a cos 3P_ cos 2a sin 3P	cos 2a cos 3p + sin 2a sin 3P
= sin2acos3p = sin2a cos3p = .ctg3p = tg2a,_Ь = ^. cos 2a sin 3p cos 2a sin3p	tg3p tg3p
tg2a _ tg2a
Получили
3.005. cos a+cos 2a+cos 6a+cos 7a = 4 cos—cos—cos4a.
2	2
Решение.
cosa+cos2a+cos6a+cos7a = (cosa+cos7a)+(cos2a+cos6a)= =2cos4acos3a+2cos4acos2a=2cos4a(cos3a+cos2a)=
.	. . 5a	a.	a	5a	.
= 2cos4a • 2 cos— cos— = 4cos— cos—cos4a 2	2	2	2
„	. a 5a .	. a 5a .
Получили 4cos—cos—cos4a = 4cos —cos—cos4a.
3.006. sin 9а+sin 10а+sin 1 la+sin 12а=4 cos—cos a sin-.
2	2
Решение.
sin 9a+sin 10a +sinl la+sinl 2a =
= (sin9a+sinl2a)+ (sinlOa+sinl la)=
„ . 21a 3a ~ . 21a a „ . 21a ( 3a a
= 2sin--cos—+2sm---cos — = 2sin- cos —+cos—
22	22	2^2	2
- . 21a . a . a . 21a
= 2 sin-2cosacos—= 4cos—cosasin-.
2	2	2	2
Тождество доказано.
7a 2
3.007. cos2a -cos3a -cos4a+cos5a = -4sin—sinacos
2
Решение.
3a
(cos2a+cos5a)- (cos3a+cos4a)=
* 7a	3a	- 7a	a	, 7a (	3a
= 2 cos—cos--2 cos—cos— = 2 cos— cos—
2	2	2	2	2	2
a
—cos—
2
2
7a
a
„ 7a f _ .	.a]	..a. 7a
=2cos—• -2 sin asm— = -4sin—sinacos—.
2 I	2	2	2
2
2
Тождество доказано.
3.008. sin 4a - sin 5a - sin 6a+sin 7a = -4sin—sin asin	.
2	2
Решение.
sin4a+sin7a-(sin5a+sin6a)=
. . Ila 3a - . Ila a . . llaf 3a a
=2 sin—cos----2 sin—cos— = 2 sin— cos---cos—
2	2	2	2	2	2	2
_ . Ila ( - .	. a ]	, • a . .Ila
=2sm—• -2 sin asm— =-4sin—sinasin-—.
2	2 1	2	2
Тождество доказано.
3.009. cos a + sin a + cos За + sin За = 2>/2 cos a sin ~+2a ^4
Решение.
cos a + cos — a + cos 3a+cos — 3a
I2 J I2
я
4
я COS cos 4
+2cos —cos —3a
4	1^4
л
= 2cos —
4
я cos —a
4
f я
+ COS-----
4
За
л/2 (я '
= 2-----2c0s —2а cosa =
2
п
4
cosacosf --2а |=2>/2 cosacos -- — -2a j= 14	1241
= 2V2cosacos — - —+2a =2-72 cos a sin —+2a . 2	4	4
Тождество доказано.
„	- 8cos2 2a
3.010. tga+ctga+tg3a+ctg3a =------.
sin 6a Решение.
sina	cosa	sin3a	cos3a	sin2a+cos2a	sin23a+cos23a
------1- —.-1------1-----=---------------p-------------
cosa	sma	cos3a	sin3a sinacosa sin3aco$3a
= 1 + 1 = 2 + 2 = sinacosa sin3acos3a 2 sinacosa 2sin3acos3a
_ 2	2 _ 2sin6a+2sin2a _ 2(sin6a+sin2a) _
sin2a sin 6a sin2asin6a sin2asin6a
_ 2-2sin4acos2a _ 4sin4acos2a _ 4-2sin2acos2acos2a _
sin2asin6a	sin 2a sin 6a	sin2asin6a
_ 8 sin 2a cos2 2a _ 8 cos2 2a
sin2asin6a	sin6a
Тождество доказано.
3.011. (sina)* 1+(tga)1 =ctgy.
Решение.
(sina)-1 + (tga)1 = -Д- + —— = —J— sin a tga sina
1 sina cosa
1 cosa
-----1----- sin a sin a
1	»	2 « , n 2 O-
_ „„ l+2cos —1	2 cos — +cosa_ 2	_	2
sina - • a	a ~ . a	a
2	sin—cos—	2sin —cos—
2	2	2	2
a cos—
2	. a
---— = ctg—
.a 2 sm —
2
Тождество доказано.
3.012.
. л .
sm - + 3a
U J
l-sin(3a-n)
= ctg
5 3 -л+-а
4 2
Решение.
sin[^ + 3aj	cos|2-|a| Cos2 * — -sin2 —
12 J _ cos3a _ I 2 j _	2______2
l-sin(3a-n) l + sin3a . .	3
v 7	1 + sin 2--a	l + 2sin — cos —
I 2	2	2
(	За	. 3a Y	За	. За (	За	. 3a Y	За	. 3a
cos---sin— cos— + sin— cos-----sin— cos—+ sin —
I	2	2 I	2	2 J Д	2	2 1	2	2
2 3a . 2 За . За За	(	Y
cos y+sin — + 2sin — cos —	cos^ + sin^
За За .3a cos--sin— 1-tg—
2	2	2
За .За .3a cos — + sin— 1 + tg— 2	2	2
A п , я За 164 ~'84 '6T  _
л За (п 3a ,8r18T ,8k+T
За ж (5л За т]=с1<т+т}
Тождество доказано.
„	sin2a-sin3a + sm4a , ,
3.013. —---------------— = tg3a.
cos2a - cos 3a+cos4a
Решение.
(sin2a+sin4a)-sin3a _ 2 sin 3a cos a-sin 3a _ sin3a(2cosa-l)
(cos 2a+cos4a)- cos 3a 2cos3acosa-cos3a cos3a(2cosa-l)
sin 3a
= —i- = tg3a.
cos 3a
Тождество доказано.
3.014. 2 sin2 (Зл - 2a)cos2 (5 л+2a) = — -—sinf - л - 8a |. 4 4	12	1
Решение.
,	. 2 х 1-cosx
Применяя формулы понижения степени sin — = —-— и
2 X 1 + cosx
cos — = —-—, представляем левую часть в виде
2 (l-^-tofecostlte^a))_ 1 (1 __4q))(1 t+4a))=
= (1 - cos 4aXl+cos4a) = (1 - cos2 4a)= f 1 - ^+<^s^a
If, 1 1	o )
= — 1-------cos 8a =
2	2 2
1(1 1	_ 1 1 1 . (5л _ )
- T-Tcos8a =---siri ——8a .
2 2 2	4 4 12 I
Тождество доказано.
3.015. sin 2a(l+tg2a tg a)+ 1 + s'na = tg2a+tg2f — + — 1-sina	^4 2
Решение.
Обозначив
j ! sin2a sinal cos2a cosa I
X = sin2a(l + tg2a tg a)=sin2
_ sin2a(cos2acosa+sin2asina) cos 2a cosa
и применив формулу cos х cos j + sin xsin у = cos(x - у), представим это выражение в виде
sin 2а cos a sin 2а
X =----------=--------= tg2a.
cos2acosa cos2a
Пусть Y =
1+sina
1-sina
1+sinf 2-—|
V 2 J
l-sinf2-l
I 2J
Поскольку sin2x = 2sinxcosx,TO
--.a a occ . ? a - . a a 1-ь2 sin—cos— cos" —+ sin" —+2sin—cos —
=	2	2 _	2	2	2	2 _
1/4.a a ? a . 2 a . a a l-2sin—cos— cos" — + sm —2sin—cos—
2	2	2	2	2	2
a ( . a V ( a	a Y
cos—+sin — cos—4-sin —
2	2 J 2	2
COS----Sin—	7 Э
2	2)	\ z 2 7
Разделив числитель и знаменатель выражения в скобках на cos у * О
и применив формулу +	= tg(x + ^)} где у, х + у — + пп, п е Z,
1-tgxtg.y	2
запишем
°2 l-tg?
Тогда X + Y = tg2a + tg —+ — ^4 2
Тождество доказано.
3.016. l-sin4a+ctg
:os4a = 0.
Решение.
l-sin4a+cti
cos 4a =
(Зл ' cost — - 2a
= cos2 2a + sin2 2a - sin(2 • 2a)+
—7^.---r-cos(2-2a)=
sin----2a |
I4	J
Зл -	. 3л . -
cos—cos 2a + sin—sin 2a = cos* 2 2a - 2 sin 2a cos 2a+sin2 2a + —x4--------x
• Зя	_ 3л . „
sin—cos 2a - cos—sin 2a
4	4
x Los2 2a - sin2 2a)= (cos2a - sin 2a)2 + cos^a+s*n^a x '	cos2a+sin2a
x (cos 2a - sin2aXcos2a + sin 2a) = (cos 2a - sin 2a)2 -
(cos 2a - sin 2aXcos 2a - sin 2aXcos 2a + sin 2a) _
cos 2 a + sin2a
= (cos 2a-sin 2a)2 -(cos2a-sin2aX =0.
Тождество доказано.
,	•	«a 6a sin2a-4
3.017. sin —cos — =-----------cosa.
2	2	4
Решение.
Пусть X = I sin2 — I - cos2 — j
2	2 I
„	,	. 2 x 1-cosx
Используя формулы понижения степени sin	—-—
> X 1+cosx cos' — = —-—, получаем
Y_( 1-cosa Y (1+cosa V _ l-3cosa+3cos2 a-cos3 a
2 J2 J	8
l+3cosa + 3cos2a+cos3a 17 ,	-	3 \
--------------------= -1- 6cos a - 2 cos a )= 8-------------------8		’
2cosa/ ,	2 1 cosa/ , /. • 2
= —-— 3 - cos a3 -11 -sin aj)=
cosa/ , ,  2 \ = ——-l-3-l+sm a)
4
sin2 a-4 4
cosa.
Тождество доказано.
f 3	1
3.018. cos -rc + 4aj+sin(3n-8a)-sin(4K-12a)= = 4 cos 2a cos 4 a sin 6a.
Решение.
cos - л 4-4a j+ sin(3n - 8a)- sin(4л -12a)=
= sin 4a+sin 8a 4- sin 12a = 2 sin 6a cos 2a 4- 2 sin 6a cos 6a =
= 2 sin 6a(cos 2 a 4- cos 6a)=2 sin 6a • 2 cos4a cos 2a = = 4 cos 2acos 4a sin 6a.
Тождество доказано.
3.019.
cos -л-6а 4-sin(n4-4a)4-sin(3n-a)
___L?________z______________________
= tga.
Решение.
cosf ^-л-ба |4-sin(n4-4a)+sin(3n-a)	...
|^ 2___J ________________________ sin 6a-sm 4a 4-sin a
. (5 x /.	/ - \ cos6a4-cos4a4-cosa
sm -л4-6а 4-со8(4а-2л)4-со5(а4-2л)
_ 2 cos 5a sin a 4-sin a _ sina(2cos5a4-l) _ sina _tga 2cos5acosa4-cosa cos a(2 cos 5a 4-1) cosa
Тождество доказано.
l+ctg|2a-|n |ctg(\ + a I
3.020------1___2 ) k2_______I = 1 tg2a.
ctga + tga	2
Решение.
l+sin2asma cos2acosa+sin2asina l+tg2atga_ cos2acosa  ________cos2acosa_____
ctga+tga cosa sina	cos2 a+sin2 a
sina cosa	sinacosa
cos2acosa+sin2asina sinacosa _ cosasina cos 2a cos a cos2a+sin2a cos2a
2cosasina _ sin2a 2cos2a	2 cos 2a
= |tg2a.
Тождество доказано.
. ( • 14 ] . (	8 I A
3.021. sin a+sum gl +—k +sin а--л =0.
Решение.
. (14	) . (8	. (15л-л
sina+sin —л+а -sm -л-а = sin a+sin-----+a
13 J I3 J 1 3
. (9л-л	( л
-a =sma + sin 5л+ a—
-sin
л
3
3
-sin 3л- a+— 3
= sina-sii
n ]	л
a+— = sina-sinacos--+cosasin
3	3

л . n 1 . V3 1 . V3 -sinacos—cosasin—= sina—sina +—cosa—sina-----cos
3	3	2	2	2	2
= sina-sina = 0.
Тождество доказано.
3.022. ctg2 a-ctg2 [3 =
cos2 a - cos2 p sin2 asin2 p
Решение.
cos2 а _ cos2 P _ sin2 Pcos2 a + cos2 fl sin2 a _
sin2 a sin2p	sin2asin2p
_ (sin p cos a - cos fl sin aXsin fl cos a + cos Psin a) sin2asin2p
= sin(p-a)sin(p + a) = ‘-(cos2a-cos2p) sin2asin2p sin2asin2p
^-bcOS2a-l-2cOS2p + l) 2„ 2ft
_ 2 '	' _ cos a - cos p
sin2asin2p	sin2asin2p
Тождество доказано.
3.023. (cosa-cosp)2 +(sina-sinp)2 =4sin2 „A.
Решение.
cos2 a - 2 cos a cos p+cos2 P+sin2 a - 2 sin a sin P+sin2 P = = (cos2 a+sin2 a)+(cos2 p+sin2 p)-2(cosacosp + sinasinp)= =2-2cos(a-p)=2-2cos^2~^^=2-2^1-2sin2^y^^= =2-2 +4sin2 -	=4sin2 ——
2	2
Тождество доказано. (tga+cos”1 alcosa-ctga) . 3.024. /	~	ч )“ 1 *
(cosa+ctgaXtga-cos a)
Решение.
(sina 1 Y cosa^ / .v	4	-+--- cosa------
(tga+cos ajcosa -ctga) _ cosa cosa j______sina J _
(cos a+ctg a)(tg a - cos“l a)	f cos+ cosa Y s*na _ 1
sina cos a cosa, sina+1 (sina-l)cosa
__ cosa_____sina
cosa(sina+l) sina^T sina cosa
Тождество доказано.
3
— л-a 2
sin 4a	cos 2a
3.025. j+cos4a i+cos 2a
Решение.
2 sin 2a cos 2a cos 2a	2 sin 2a cos 2a cos 2a
l+2cos22a-l l+cos2a 2cos22a l+cos2a _ sin 2a cos 2a _ sin 2a
cos2a(l+cos2a) l+cos2a
Тождество доказано.
3.026. cos2(a-90°)+ctg2(a-270°)=	cos2 (a+180°)
Решение.
cos2 (a - 90°)+ ctg2 (a -270° )= sin2 a+tg2 a = sin2 a + S*P,a = cosa
_ sin2 a cos2 a+sin2 a _ sin2a(;os2a+l) _ (l - cos2 afa+cos2 a ”	2	~	2	2
cos a	cos a	cos a
l-cos4a 1	2	1	2/ , „„.1
=.---*— = —*-------cos a = —\ - cos la+180 I.
cos2 a cos a	sin2 |a+90° J
Тождество доказано.
3.027.
l-tg(90° +a)	tg(180° +a)+l
l+ctg(s60° - a) ctg(z70° -a)-l
Решение.
l-tg(90° +a) _ 1+ctga _ ^ + tga _ tga+1 _ tg(180° +a)+l l+ctg(160°-a) 1-ctga j______1 tga-1 ctg(270° -a)-l
tga
Тождество доказано.
tg2acos l2B-tg2Bcos *2a	/ o\
3.028. -------1-	-1------= tg(a-p).
cos 2a+cos 2P
Решение.
sin 2a	1 sin2p	1
tg2acos~12p-tg2pcos~12a _ cos2a cos2p cos2p cos2a _
cos"12a+cos"12p	1	+ 1
cos 2a cos2p
sin 2а-sin 2Р
_ cos2acos2p _ sin2a-sin2p _ 2cos(a+p)sin(a-p) _ cos2a+cos2p cos2a + cos2P 2 cos(a + p)cos(a - p) cos2acos2p
cos(a-P)
Тождество доказано.
(	Г 7 я	и
3.029. 2 sin-l4a-tg —+4a + tg(5re+a)=ctga.
Решение.
2
1	|
----------tg sin 4a----|
1
= 2| —-----tg Зл+ —+4a |+tga =2
I sin 4a 2	)
( 1	A
= 2 -----+ctg4a + tga = 2
I sin 4a	)
2(l+cos4a) „	*
sin 4a
+tga =
1 sin 4a
1 cos4a ------1----- sin 4a sm4a
	+ tga = —	+ tga = 2tga---------------tga
l-tg2a
= l-tg2a+tg2«=_l_ = ctga
tga tga
Iя Л I 1 .
-tg -+4a + tga =
Тождество доказано.
.->[15	* ]	2
3.030. sm vrt-2a Fcos l О	)
cos 4a
4i
Решение.
. 2 X 1-COSJC
Используя формулы понижения степени sm — = —-— и
2Х 1 + COSX cos — =-------
2	2
, представляем левую часть равенства в виде
Тождество доказано.
3.031. (cos a-cos
рУ -(sin a-sin
P J2 = -4 sin2	& cos(a + p).
Решение.
(cos a - cos p)2"- (sin a - sin p)2 =
= cos2 a - 2 cos acos p+cos2 p - sin2 a+2 sin asin p - sin2 p =
= (cos2 a-sin2 a)+ (cos2 p-sin2 p)-2(cosacosp-sinasinp)=
= cos2a+cos2p~2cos(a+p)=
=2 cos(a+p)cos(a - p) - 2 cos(a + P)=
/	/ ot —В
= 2 cos(a+pXcos(a - p) -1) = 2 cos(a + PI cos 2 • p
-1
= 2 cos(a+P П - 2 sinI 2 * —-11=-4 sin2 a cos(a + p).
Тождество доказано.
3.032. sin2
fZl-2a'|_5tozf»!'-2aL
I8 J I8 J
sin 4a
V2
Решение.
.	( In . ]
1-cos-----4a
I 4	)
2
Г8л-л . ---------4a
4--------
2
cos
£______
2
( 9л 1-cos------4a
[ 4
2
(8л+л . cos------4a
1 I 4
- + —----------
2	2
( Я cos 2П - — + 4a Гн
2
i-> I Л Л 2л + —4a
I4 *
2
л
л
1	( (n . }\  L. (n .
= cos 2л + —4a -cos 2л- —+4a 2
4
4
1 (	(n , A (n .
- cos — 4a - cos — + 4a 2	4	4
-2sin^sin(-4a)
4
V2 . л sin 4a
=—sin 4a = —t=-
2 Jl
Тождество доказано.
3.033. cos4a-sin4actg2a = cos2a-2cos2 a.
Решение.
cos4a - sin4actg2a = cos4a - sin4a •
cos2a sin2a
_ sin2acos4ot-cos2ctsin4a sin(-2a) _ - sin2a sin2a	sina sin2a
= -1 = 2 cos2 a -1 - 2 cos2 a = cos2a - 2 cos2 a.
Тождество доказано.
• a
a^  г( In a A sm2
3.034. sin2 — + — -sm —+— =—7^-I 8 4 I I 8 4 I
Решение.
1
2
„ f a я cos 2я+--------
2 4
_ Ia K
-cod 2n+\ — + —
I 2 4
2 2
I a n ] (an cos-------cos —+ —
I 2 -4 I 2 4
If a n . a . n	a я. a. я
- cos—cos—+sin—sin—cos—cos—+sin — sin— 2	24	24	24	24
. a
i	~	-	/o	^sin —
1	* .	a	.	я	v2	.	a о
= --2sin—sin—=—sin—= —=£-.
2	2	4	2	2	^2
Тождество доказано.
3.035. cos4atg2a-sin4a= 2*8?. . tg2a-l
Решение. . sin2a . . sin2acos4a-cos2asin4a cos4a-------sin4a =-------:-------------
cos2a	cos2a
и
sin(-2a) sin2a x _
= —i=-------------= - tg2a =
cos2a cos2a
Тождество доказано.
2tga tg2a-l
3.036. sin2 2a-cos| — -2a pinf2a-— |= i 4 3 Г 6	4
Решение.
sin2 2a-co!
l-cos4a 1 . (. л ----------sin 4a-—
2	2 I 2
1 . n	1	cos4a	1	. (л	. ) 1
—sin— =--------+ -sin — 4a —
2	6	2	2	2	2
Тождество доказано.
1 _ 1 cos4a cos4a _ 1
4~4	2~+~~2	4
2
„	-2	I Л I I Л 11
3.037. sin a+cos ---a fcosl j+a = д-Решение.
Используя формулы
. 2 х 1-cosx sin — =-------
2	2
cos х cos у = у (cos(x - у)+ cos (* + >0), представляем левую часть равенства в виде
l-cos2a if - 2л ) 1 cos2a cos2a 1 1 --  +- cos2a+cos— =-  — + —  - = -
2	2 •	3	22	244
2
Тождество доказано.
tg3a
3.038. tg23a_j
1-ctg2 3a ctg3a
Решение.
tg3a 1-ctg2 3a _ tg3a________tg23a
tg23a-l ctg3a tg23a-l _J_ tg3c
_ tg3a tg23a-l t . = tg3a tg23a-l tg23a-l tg23a tg23a-l tg3a
Тождество доказано.
3.039. cos4a-sin4actg2a = -l.
Решение.	‘
cos4a-sin4actg2a = cos4a-sin4a-	— =
sin 2 a
_ sin2acos4a-cos2asin4a _ sin(-2a) _ -sin 2a _
sin 2a	sin2a	sin 2 a
Тождество доказано.
3.040.
1-cos4a ! 1 +cos4a cos-2 2a-1 sin-2 2a-1
Решение.
l-cos4a l+cos4a l-cos4a l+cos4a
---15-----'----15----=---i------'----i-----=
cos 2a-l ‘ sin 2a-l 1 j 1 j cos2 2a sin2 2a
_ (l-cos4a)cos2 2a (l+cos4a)sin22a _ (l-cos4a)cos22a
1-cos2 2a	1-sin2 2a	sin2 2a
(l+cos4a)sin22a _ (1 - (1 - sin2 2a))cos2 2a + (1+2 cos2 2a - l)sin2 2a cos2 2a	sin2 2a	cos2 2a
2sin22acos22a 2cos22asin22a *	• 2->
=-------j------+---------5------= 2 cos 2a+2 sin 2a =
sinz 2a	cos 2a
=2(:os2 2a+sin2 2a)= 2.
Тождество доказано.
3.041.
tga-cos *a cosa-ctga
= tgacos 'a.
Решение.
sina 1	sina-1
_j	------ — ——	
tga-cos	a _ cosa	cosa _ cosa
cosa-ctga	cosa	cosa	cosa(sina-'TJ
sina	sina
sin a-1	sina	sina sina 1	_]
=------------r-------r =---------=-----------= tga cos a.
cosa cosa(sina-l) cosa cosa cosa cosa
Тождество доказано.
3.042. cos2(45° - a)-cos2 (б0° + a)-cos75°sin(75° -2a)=sin2a.
Решение.
Используя формулы
?x 1 + cosx
cos — =------
2	2
sin xcos у = ~ (sin(x - j>)+ sin(x + >>)),
представляем левую часть равенства в виде
l + cos(90°-2a) l + costao0 +2a) 1/. / ~ \ • lien* о
-----1----------------------*--|sm(-2a)+sin|J50 -2a))=
= — (1 + cos(90° - 2a)-1 - cos(l 20° + 2a)+ sin 2a - sin (l 50° - 2a)).
Так как
cos(90° -2a)=sin2a, cos(l20e +2a)=cosl20°cos2a-sinl20°sin2a =
= —cos2a-----sin2a
2	2
и
sin(l50° -2a)=sinl50°cos2a-cosl50°sin2a = -cos2a +—sin2a , v 7	2	2
TO
2
sin 2a + - cos2a +—sin 2a+sin 2a—cos 2a-sin 2a
2	2	2	2
= — - 2sin2a = sin2a. 2
Тождество доказано.
l-2sm2a 1-tga
3.043.	= ;—— •
l + sin2a 1 + tga
Решение.
Используя формулы l-2sin2x = cos2x, sin2x+cos2x = l
и
sin2x = 2sinxcosx, представляем левую часть равенства в виде
____________cos 2a_______ cos2a
cos2 a+sin2 a+2 sin acos a (cos a+sin a)2
Применяя формулу cos2x = cos2 x - sin2 x, имеем
%. _ cos2 a-sin2 a _ (cosa+sinaXcosa-sina) _ cosa-sin a
(cosa+sina)2 (cosa+sina)2 cosa+sina
Разделив числитель и знаменатель этой дроби на cos a * 0, получи
y l-tga
1 + tga'
Тождество доказано.
sin2a+sin5a-sin3a - .
3 044. ------------;--= 2sma.
cosa+i-2sin22a
Решение.
sin2a+(sin5a - sin3a) _ 2sin'acosa+2cos4asina cosa+ |)-2 sin2 2a)	cosa+cos4a
_ 2sina(cosa+cos4a) _
cosa+cos 4a
Тождество доказано.
ctg22a-l -	. a о
3 045 —---------cos8actg4a = sin8a.
2ctg2a
Решение.
ctg2 2a 1	_ tg 2a-----cos8actg4a =
2 ctg 2 a	2
tg2a
l-tg22a tg2a o , . l-tg22a o .
= —г------=-----cos8actg4a = — ------cos8actg4a =
tg22a 2	2tg2a
= —----cos8actg4a = — ---cos8a —-
tg4a	tg4a tg4a tg4a
= Ц-  (1 -cosSa) =	= sinta
l-cos8a	l-cos8a
cos 8a
Тождество доказано.
1
3.046.
cos4a+l 1 . . ----------=—sin4a. ctga-tga 2
Решение.
cos4a+l _ cos4a + l _ cos4a + l _ (cos4a+l)sinacosa _ ctga-tga cosa sina cos2 a-sin2 a cos2 a-sin2 a
sina cosa	sin acos a
_ (cos4a +1)2sinacosa _ (cos4a+l)sin2a _ cos4a + l	? _
2(cos2a-sin2a)	2 cos 2a	2
cos4a + l sin 4a	sin 4a 1 . .
=---------------— = —-— = -sin 4a.
2	l + cos4a	2	2
Тождество доказано.
3.047. c<g(l5-+2«)=-^. l+sin4a
Решение.
Пусть X = ctg(l5° +2а)=
1
„	(	\ ,	X 1-cosx
Применяя к выражению tg(45° +2a) формулу tg—= $	, где
х*л+2ял, ne Z, имеем
x ________1_____ _ sin(9O0 +4a) _ cos 4a
l-cos(90° +4a) l-cos(90° +4a) 1 +sin 4a
sin(90° +4a)
Тождество доказано.
(sin* 1 * 2 a+tg2 a+l)(cos2 a-ctg2 a+1 (cos2 a+ctg2 a+ljsin2 a+tg2 a-1
Решение.
3.048.
=1.
iin2 a+tg2 a+lkos2 a-ctg2 a+l)_ x>s2 a+ctg2 a+ljsin2 a+tg2 a-1)
Y	2
,,	2 cos a
+1 cos a------5—
sin a
2
. 2 sin a sin a+—5— cos a
[2 cos2 a . I . 2 sin" a .
cos a+—j—+1 sin a+—,----1
sin a I cos a
cos2 asin2 a+sin2 a+cos2 a sin2 acos2 a-cos2 a+sin2 a
•2
• 2
• 2
________cos2 a_________________sin2 a_______i
.2 о	2	. 2	2*2	*2	2	*'
sm acos a+cos a+sm a cos asm a+sin a-cos a
cos2 a
sin2 a
Тождество доказано.
3.049.
ftga+^ctga sina+cosa
\2
2 sin 2a
Решение.
sina+cosa
sin2 a+2sinacosa+cos2 a
sina
cosa
__ cosa sing sin2 a+2sinacosa+cos2 a
1	2
sin2 a+2sinacosa+cos2 a
________sinacosa_________ sin2 a+2sinacosa+cos2 a
2
sin 2a’
sinacosa 2sinacosa
Тождество доказано.
3.050. sin2(45° + a)-sin2(30° -a)-sinl5°cos(150 +2a)=sin2a. Решение.
sin2(45° + a)-sin2^0° -a)-sinl5°cos^5° +2a)=
l-cos(90o + 2a) l-cos(60e-2a) 1/. / ~ \ . /,л. ~ \\
=-------------1-----(sin(-2a)+sin(30 +2a>
cos(90°+2a)	cos(60° -2a) sin2a sinfco*+2a)_
”2	2 V 2	+ 2	2
= ^(-cos(90° +2a)+cos(60e -2a)+sin2a-sin^0° +2a))=
= i(sin2a+cos60ecos2a + sin60°sin2a+sin2a-sin30’cos2a-cos30’sin2a)=
2V	7
1C. „	1	о Vi . „ 1	л
2l	2	2	2	2 I
1	„ . „
= -’2sin2a = sin2a.
2
Тождество доказано.
3.051. sin6 a + cos6 a + 3sin2 acos2 a = 1.
Решение.
sin6a+cos6a + 3sin2 acos2 a =
= (йп2аУ +(:os2 a/ +3sin2 acos2 a =
= (sin2 a + cos2 a)(sin4 a-sin2 acos2 a+cos4 a)+3sin2 acos2 a =
= ((sin4 a + cos4 a)- sin2 acos2 a)+ 3 sin2 acos2 a =
= ^(sin2 a + cos2 a)2 -2sin2 acos2 a^-sin2 acos2 a^+3sin2 acos2 a =
= (l - 3sin2 acos2 a)+ 3 sin2 acos2 a = 1.
Тождество доказано.
tg3a _ 3-tg2a
3-052* tga l-3tg2a
Решение.
tg2a + tga
tg3a _ tg(2a + a) _ l-tg2atga _ tg2a + tga _
tga tga tga (l-tg2atga)tga
2tgg_+tga 1-tg a
1—tga tga
2
tga ----2“
(1-tg a
f, 2tg2a '
1-tg2 a
tga
2 =
2+l-tg2a
1-tg2a _ 3-tg2a l-tg2a-2tg2a 1 - 3 tg2 a
1-tg2 a
Тождество доказано.
 (	\ • t( x	• 2 x
3.053. sinasin(x-a)+sin l у-a l=sin —.
Решение.
Используя формулы
sin A sin В = j(cos(^4 - /?)- cos(z4+В))
. э A 1-cosJ sin — =-------,
2	2
представляем левую часть равенства в виде
.. 1 / м \	\ l-cos(x-2a) cos(x-2a) cosx
X = - (cos(2a - x)- cosx)+-------= — -------------+
2	2	2	2
. 1 cos(x-2a) lz,	\ if, Л, xYl
2	2	2V	7	\ 2JJ
ifi fi • 2 * if. i . a • 2 X 'I 1 A . 2 X . 2 X = - 1- l-2sm — =— l-l+2sin — = — -2sin — = sin —.
• 2^	2JJ 2l	2 J 2	2	2
Тождество доказано.
3.054. cos2a-sin22a = cos2acos2a-2sin2acos2a. Решение.
cos2 a - sin2 2a = cos2 a - (sin2a)2 = cos2 a - (2 sin acosa)2 = =cos2 a-4sin2 acos2 a = cos2 all-4 sin2 a)=
= cos2 a(l-2sin2 a-2 sin2 a)=cos2 a(cos2a-2sin2 a = cos2 acos2a-2sin2 acos2 a.
Тождество доказано.
3.055. S--n?a —2(cos2a + cos4a + cos6a)-1 = 0.
sina
Решение.
S*n?a - 2(cos2a+ cos4a+cos6a) -1 = sina
sin(6a+a) ~ n ~	.
= — ------- - 2 cos2a - 2 cos 4a - 2 cos 6a -1 =
sina
_ ( sin(6a+a) _ 2 cos 6a 1- 2 cos2a - 2 cos4a -1 =
I sina	J
pin6acosa+co^sina_2cos6aL2cos2a_2cos4a_1 = sina	)
sin6acosa+cos6asina-2cos6asina ~	_ A .
----------------------------2 cos2a - 2 cos4a -1 =
sina sin6acosa-cos6asina _ n n A . ---------------------2cos2a-2cos4a -1 =
sina
s*n5.a - 2 cos 4a 1- 2 cos2a -1 = ( S^-a- - 2 cos4a 1 - 2 cos2a -1 = sina	)	I sina	)
sin4acosa + cos4asina	. A _	~	.
---------------------2cos4a |-2cos2a-l =
sina	J
sin4acosa+cos4asina-2cos4asina л ~	,
----------------------------------2cos2a-l =
sina
sin4acosa-cos4asina n n . sin3a n ~	.
=---------------------2 cos2a -1 =-----2 cos2a -1 =
sina	sina
fsin(2a + a) _	~	. fsin2acosa+cos2asina -	.
= 1 —ь---^-2cos2a 1-1 = 1---------------------2cos2a 1-1 =
sina	)	sina	j
_ sin2acosa + cos2asina-2cos2asina _ sin2acosa-cos2asina _
sina
sina
sina
Тождество доказано.
3.056. sin2 a - sin2 P = sin(a+p)sin(a - p).
Решение.
sin2 a-sin2 p = (sina-sinpXsina + sinp)=
. a+p . a-p * .a+p a-p = 2 cos--- sin---- • 2 sin-- cos--- =
2	2	2	2
C . a+P a+pY_ . a-p a-P'i = 2sin----cos----- 2sin----cos-—- =
I 2	2 1 2	2 J
= sin(a+p)sin(a - p).
Тождество доказано.
3.057. cos4 x+sin2 у +—sin2 2x -1 = sin(y+x)sin(y - x). 4
Решение.
cos4 x+sin2 y+^sin22x-l = cos4 x + sin2 y+i(sin2x)2 -1 =
= cos4x + sin2y+^(2sinxcosx)2 -1 =
4	. 2	1 j • 2	2	«
= cos x + sm y + ~4sin xcos x-l =
4
= cos4 x + sin2 у + sin2 xcos2 x -1 =
= ^os4 x+sin2 xcos2 x)+sin2 y-1 =
= cos2 x(cos2 x + sin2 x)— (1 - sin2 y)=
= COS2 X -cos2 у = (cOSX -COSyXcOSX + COSy)=
_ . x + y . x-y - x + y x-y
= -2sin---—sin--— 2cos----—cos----— =
2	2	2	2
. x + y	Х + уУл • X-y	X-y^
= - 2sin---cos _ z 2sin-----—cos---— =
I 2	2 A 2	2 J
- -sin(x + y)sin(x - y)=sin(x + y)sin(y - x).
Тождество доказано.
3.058.
ctg ^ + a tg(2n-2a)
<3
ctg -л-2а -tga
-2>/3sin —+a sinl —-a = 2sin|2a-—
.4	4	3
4
4
Решение.
Используя формулу sin xsinу = ±(cos(x- у)-cos(x + у)) и формулы приведения, перепишем левую часть равенства в виде
tgatg2a tg2a-tga
,	2 tga
tga-;;-%—
T cos2a-cos—|= *£аЧ»2а—yf^cos2a = 2 J tg2a-tga 2tg2a
/з cos 2a =----J—tg a _—_ cos 2a _
1-tg2 а
2 tga t
-—5-----tga
1-tg a
21 a	(1	л/з	A
= ——-J? cos 2a = sin 2a--Уз cos 2a = 2 —sin2a---cos2a =
l + tg2a	12	2
—	* /4 7C	7C I I 7C
= 2 sin2acos—cos2asin — =2sin 2a —
3	3	3
Тождество доказано.
л+а
3.059.
tg2a-tga
+2coi
Решение.
+а
-2а .
Используя формулу cos х cos у = (cos(x - у)+cos(x + у)) и формулы приведения, перепишем левую часть равенства в виде
tg2a(-tga) * я tg2atga , X =	\—2—L+cos 2a+cos — = ——--—+cos 2a =
tg2a-tga	2 tga-tg2a
2tga 4
—4~~ tga
= ——я------+ cos 2a =-+ cos 2a = - sin 2a+cos 2a =
tga.2^_ l+tg2a
1-tg a
= cos 2a - sin 2a = cos 2a-cos —2a =-2sin —sin 2a —
2 I 4 I 4
•2t-
л sin —2а
4
4
Тождество доказано.
~	.	-1. cos2a+sin2a
3.060. tg4a+cos 4a =----------
cos2a-sin2a
Решение.
A -i л sm4a 1	l + sin4a
tg4a+cos 4a =----— +--------=---------=
cos4a cos4a * cos4a ________(cos2a+sin2a)2________ cos2a+sin2a (cos2a+sin 2aXcos2a - sin2a) cos2a - sin 2a
Тождество доказано.
lga + t^+l8«Zl|P+2tg!„ = 2C0S-2a. tg(a+P) tgfa-Й
Решение.
3.061.
~	.	sin(x + у)	* sin(x-y)
Так как tgx + tg.y =—*—— и tgx-tgy =—*—— , где cos х cos у	cosxcosy
л	_
х, у * у + ли, п € Z, то левую часть равенства можно записать в виде
sin(a + р) sin(a-p)
cosacosB+ coSacosB +2tg2a = cos(a + p) + cos(a - p)	2 ц fa
sin(a+P) sm(a~P)	cosacosp cosacosp
cos(a + p) cos(a-p)
cos(a + p)+cos(a-p) _ 2 2cosacosp _ 2 Л . 2 \ = —ч----r/--2—+ 21g a =------------ + 2tga = 2ll + tga)
cos a cos p	cos a cos p
2 о -i
= —5—=2 cos a.
cos a
Тождество доказано.
3.062. 1-—sin22a + cos2a = cos2 a + cos4 a. 4
Решение.
1 - sin2 2a + cos2a = 1 - (sin2a)2 + cos2a =
= 1 - - (2 sinacosa)2 + cos2 a - sin2 a = 1 - - • 4sin2 acos2 a+ 4	4
+cos2 a - sin2 a = 1+cos2 a - sin2 a(l+cos2 a)=
= +cos2 a)(l - sin2 a)= (1 + cos2 ajcos2 a = cos2 a+cos4 a.
Тождество доказано.
Упростить выражения (3.063—3.113):
»1 • (« ~ 1 2а . 2 а
3.063. l-sin—Зя -cos — +sin —.
I2 J 4	4
Решение.
1 . f а . А 2 а( • 2 а 1-sin—Зя -cos — + sin — 12	2	2
. .К а 1	2 а . 2 а
= 1 + 81ПЗя— -cos —+ sin —
12	4	4
. 2 а . а . 2 а .(-(Х]-.2<х^-а а = 2sin — + sin— = 2sin —+sin 2 — =2sin —+2sin—cos—=
4	2	4	4 J 4	44
- . af . a	al	. af . a
= 2sin— sin—+ cos— = 2sin— sin—4-si
4	4	4	4	4
x	/	X
. a _ . я f а я 1	~ /т . a fa я я
= 2sin—-2 sin—cos-=2v2 sin—cos — 4--
4	4144	41442
_ o /т . a . f а+я Ответ: 2V2sm—sin —-—
4 I 4
l+sin2a
+cos2 a.
3.064.
cos(2a-2n)ctg
Решение.
2	l + sin2a
—r + cos a =---------------у--------------
cos(2a - 2rc)ctgl a - - л j	cos(2 л - 2al - ctgf n - a
l + sin2a
+ cos2a =
______1+sin 2a____
_	( 4л+л
-cos2actd-------a
4
1+sin 2a
2	i+sinza	2
+ cos a =---------—---------rr+cos a =
M .	Л	I I
cos2actg Л+ —a
4 J
•	2	2
l + sin2a	2 cos a+sin a+2sinacosa 2
--------7----г+cos a =--------------7-----x---+ cos a =
~ J я cos2actd —a
1 4
CO!
cos2a —
• i л sin —a
14
- (cosa + sin a^
-a
+ cos2a =
n i я I cosOcos —a
14 j
- (cos a+sin a)2 ~(cosa-sina)
+ cos2 a = - 1+cos2 a = (cos a + sin aXcos a - sin a)- — (cos a+sin a)
5 a—л
4
-sin2 a.
Ответ: —sin2 a.
Решение.
2 a cos —
. 4
• 2 a sin —
4
2 3a cos —
4
3a 4
2 a a cos —cos— 4	2
sin2
3a ~4
. ? 3a ,	2 3a
sin----1-cos —
4	4 a
----“-------—’COS—
. 2 3a	2
sin — ______________4__________
. 2 3a 2 a 2 3a . 2 « sin —cos —cos —sm —
4	4	4	4
2 a cos —
4
. 2 a • 2 3a sm — sin —
4	4
•2^.2 sin —sin
4
3a 4
. 2 3a 2 a 2 3a . 2 a sm —cos —cos —sm —
4	4	4	4
2 a a . 2 « cos — cos—sm —
4	2	4
. 3a a 3a . a
sm—cos—cos—sm—
4	4	4	4
га	a.2« л	• 2 a	2«	a	. 2 a	a
cos —cos—sm — 4sm —cos —cos— sm —cos—
4	2	4 =	4	4	2 =	2	2	=
sin—sina 2
4sin—sina	4sin—sina
2	2
.a	a » . a	a
sm—cos— 2 sin—cos— • „	,
2	2 _	2	2 _ sma _ £
4sina	8 sin a	8sina 8
Ответ: -• О
. a	a	a
sin—ctg—cos— 4	о	4
a A a —cos—ctg—
a . a
-sin— 4
a cos— . a 8	a
sm-------o__cos_
4 . a	4
sm— 8 a cos— a я . a cos------— 4-sin —
‘ . a 4 sm—
8
4
.a a	a . a
sm—cos-cos—sm—
4	8	4	8
.a	. a a a . a
sm—	sm—cos—cos—sm—
8=	4	8	4	8	_
a	a.	a.	a	a	a.	a.	a
cos—cos — 4- sm—sm —	cos— cos— + sm—sm—
4	8	4	8	4	8	4	8
. a sm—
8
Ответ: “tg—.
о
3.067. cosa^+cos *a+tga)^-cos *a+ tga) Решение.
cos a^ 4-cos”1
(л 1	sinaYi 1	sina
I	cosa cosa 1	cosa cosa
cosa4-14-sina cosa-14-sina = cosa---------------------------=
cosa	cosa
((cosa+sina)+lX(cosa+sina)-l)_ (cosa + sina)2 -1 cosa	cosa
cos2 a+2sinacosa+sin2a-l 2sinacosa . 	=	= 2sina. cosa-------------------------cosa
Ответ: 2 sin a.
3.068. sin2 a(l+sin"1 a+ctg afa - sin"1 a+ctg a Решение.
sin2
. 2 (i 1 cosaYi 1 cosa
= sina 1+-—+------11-----+----
sina sinaj^ sina sina
. 2 sina+l+cosa sina-l+cosa = sin a-----------------------=
sina	sina
= ((sina+cosa)+lX(sina+cosa)-l)=(sina+cosa)2 -1 = = sin2 a+2 sin acos a+cos2 a -1 = 2 sin acos a = sin 2a.
Ответ: sin 2a.
l-cos(8a-~3rc) 3069‘ tg2a~-ctg2a
Решение.
l-cos(8a-3ft)_ l-cos(3it-8a) _ (l-cos(3w-8a))sin2acos2a
tg2a-ctg2a ~ sin2a cos2a ~	sin2 2a-cos2 2a
cos2a sin2a
_ (l-cos(3re-8a))2sin2acos2a _ (l+cos8a)sin4a _
2 (cos2 2a-sin2 2a)	2cos4a
_ (l+2cos2 4a-l)sin4a _ 2cos24asin4a _ -2sin4acos4a _ 2cos4a	2cos4a	2
_ sin 8a
“	2~
л sin 8a
Ответ:------—
Решение.
1 f 1	Vai.al.a	l.a
= - -+cosa sm—= — sm—+—sm—cosa = —sm—+
2^2	J 2 4 2 2 2	42
l(.( a} . 3^1. a l.a 1.3	1.3
+ — sm— +sin-a =—sin-sm —+ -sin-a = -sin-a.
4^	2 J 2J4	24	24	2	4	2
1 . 3 Ответ: —sin—a.
3.071. sin2(j+2pj-sin2^y-2p).
Решение.
sin2f «+2B)-sm2f“-2pl= l-^(a+4p)_l-coS(a-4p) =
^2 J 1^2	2	2
. 1 _cos(a+4p)_ 1 cos(a-4p) _ 1 ( ( _4p)_cos((I +4₽))= 2	2	2	2	2
= -sin asin(- 4p)=sin asin4p.
Ответ: sin a sin 4₽.
cos”12x + sin 2x tg2x
3.072. l+cos4x
1
л . 21 4snr —x
4
— x
Решение.
cos l2x + sin2xtg2x l+cos4x
л . 2 П 1 | Я 4 sin —x ctfl —x
4 И4
1
1	. _ sin2x
------+sin 2x_ cos2x-cos2x
l+cos4x
1 + sin1 2 2x cos2x l+cos4x
l+sin22x cos2x(l+cos4x)
1__________l+sin22x ,	1
cos2x(l+2 cos2 2x -1) 2cos2x
4 J
l+sin22x 1	_ 1+sin2 2x+cos22x _ 1 + 1 _
2cos32x 2cos2x 2cos32x 2cos32x
-----,— = —т— = cos-3 2x.
2 cos 2x cos 2x
Ответ: cos 3 2x.
3.073. cos2((x+2p)+sin2(a-2p)-l.
Решение.
cos2 (a+2p)+ sin2 (a - 2p)-1 = ^+cos(^a+4P)+ t l-cos(2cx-4p)	1- cos(2a+4p) [ 1 cos(2a-4p)
+	2	2+	2	+2	2
= i(cos(2a+4p)-cos(2a-4p))= -sin2asin4p.
Ответ: — sin2asin4p.
3.074. sin2 (a + 2p)+sin2(a-2p)-l.
Решение.
sin2 (a+2p)+sin2 (a - 2p)-1 = * cos(2(X + 4p) +
l-cos(2ot-4p) _ । _ X _ cos(2a+4p)	_ cos(2a-4p)
+	2	2	2	+2	2
= - ^ (cos(2a+4p)+cos(2a -4p))=~ • 2 cos2acos4p = -cos2a cos4p.
Ответ: -cos2acos4p.
3.075. (cosa-cos2p)2 + (sina+sin2p)2.
Решение.
(cosa-cos2p)r+(sina+sin2p)2 =
= cos2 a-2cosacos2p+cos2 2p+sin2 a+2 sin a sin 2p +sin2 2p =
= (cos2 a + sin2 a)+ (:os2 2p+sin2 2p)-2(cosacos2p-sinasin2p)=
= 2 - 2(cos a cos 2p - sin a sin 2p)=2 - 2 cos(a+2p)=
= 2-2fl-2sin2^^l 2
= 2-2cosf2-^&> \ 2 >
= 4sin2^. 2
A . 2 a + 2p Ответ: 4sm —-—.
2
(1 - cos2a)cos(450 +2a)
3*076»	2 л . >
2sin 2a-sin4a
Решение.
= 2-2+4sin2	=
2
(l-cos2a)cos(45°+2a)	a) 22 fcoS2tt-s,n2а)
2sin2 2a-sin4a	2sin2 2a-2sin2acos2a
_ 41 sin2 a(cos2a - sin2a) _ 41 sin2 a _ 72 sin2 a	72 sin a
-2sin2a(cos2a-sin2a) -2 sin 2a 4 sin a cos a	4 cos a
V2 Ответ:-----tga.
,	2(3	(Х^	2^11
3.077. cos -я— -cos — л+ —
I8 4J I8 4)
Решение.
_	-J2 . а
Ответ: -—sin—. 2	2
3.078. ctg 45° -у +ctg 135° -у
Решение.
Ответ: 2tga.
3.079.
l+ctg2actga tga+ctga
Решение.
U^-'-elga l+ctg2actga _ 2ctga__________	2	_ 1+ctg a x
tga+ctga " L+Ctga	1+ctg* 2 a	2
ctga	ctg a
y ctga	ctga
l+ctg2a 2
ctga Ответ: ——•
2
_ cos ma- cos na
3.080. --------:---•
sinna-sinzna
Решение.
—2 sin---asin-----о
cos ma-cos ла _ cos ma-cos ла _2 2
sin ла-sin ma	sin ma-sin ла	™ + л -.т-л
2 cos--asm--------a
2	2
. т + л sin------a
2
т + л cos------a
2
ж т + л =tg—
a.
Ответ: tg
т + л ------a.
. of	3ft | •	2 х I Л	I	-'ll Л
3.081. sinz a---(l-tgza)tg — + a cos —a
\	2 )	\4	/	\4
Решение.
. 21	3л ]z, A 2	| Л	|	-21 Л I
sin a-----1(1 — tg a)tg —+ a cos —a =
V	2 J	14	у 147
1
' /a \A2	(	\
. I J I /,	2 x I Я I
sin —л —a (l-tga)tg — + a •
12	J)	14	J 2(n
> 4	7	4	z cos —-a
14
x 1-cos b^ + 2a
1-cos2a ]	^2 J ___________1_____
14-cos2aj . (л ~ A . , (n ' y sin — + 2a 1 + cos — 2a
12	J l<2	)
_l + cos2a l + cos2a-l + cos2a l + sin2a 2
2	1 +cos 2a cos 2a 1 +sin 2a
Ответ'. 2.
3.082. 1-
Решение.
	1 i 1 j 1 j	cos 2 a !_________________________________________1	! t 1 cos2a + l ~ cos2a+l
-cos 2a cos 2a cos 2a
cos2a4-1-cos2a _	1	_	1	_	1
cos2a4-l cos2a + l 2cos2a-14-l 2cos2a
1
Ответ :---ч—
2 cos a
cos 1 a+cos-1 В
3.083. -----ift . й--— •
tgacos p+tgpcos a
Решение.
1	1	cosa+cosp
cos-1 a+cos-1 p ,  ____cosa cosp_______ cosacosp
tgacos-1 P+tgpcos-1 a " sina 1	sinP 1 sin a+sin p
cosa cosp cosp cosa	cosacosp
a+p	a-p	a+p
cosa+cosp	2cos-^cos^	cos^ a+p
sina+sinp	^„a+P^a^P	sin«+P	Ctg 2 ’
2	2	2
_	. a+P
Ответ: ctg—
3.084.
Решение.
(3	A	3( л	A
tg -л-a +tg3 -+a ___Lz----I----kr--L
.3^5	A	t (3
ctg -л-a +ct81 2 Л+а ctga-ctg3a
ctg a-ctg3 a ctg3
3 я
ctg 2л+ —a -tga
(4л+я	A t
_ ctga-ctg3 a _ tg3a-tga
ctga-ctg3a _
1______1_“
ctg3 a ctga
л
2
, ,g ^ = ctg4a. 1-ctg2 a
ctg3 a
1
3.085. 1-
Решение.
, • -п л 1-sin —+а
2
cosa-1
• (л sm] - + а
V
cosa-1 cosa-1
cosa-1 l-2sin2 —-1 2sin2 —
2	2
Ответ: 0,5 sin
l-tg(%-2a)tga
3.086. ~7j-----'
td г л-а +tga V )
Решение.
(	\	1+ 2t^ ~tga
l-tg(re-2a)tga _ l+tg2atga _ 1-tg a _ . (3	A 4	ctga + tga	1 ..ял,
tg -я-а +tga	&	----+tga
\2	)	tga
l-tg2a+2tg2a
- l~tg2 a _ l+tg2a tga _ tga _ 2 tga l+tg2a 1-tg2a l+tg2a 1-tg2a 2^1-tg2a)
tga
= 1. 2te_cL- = ltle2a = ^ 2 l-tg2a 2 8	2 ’
tg2a Ответ: ——•
3.087.
Решение.
sin2 а	. ?	sin4 а
tg asm a	Cos2a	CpS2a
tg2a-sin2a sin2 a . 2 sin2 all-cos2 a)
cos" a	cos" a
sin4 a cos2 a _ sin4 a __ sin4 a _ 3	2 S 1 \ ~ -2	• 2	~ • 4	~
cos" a sin all-cos" a) sin asm a sin a
Ответ: 1.
ctg(27O° - a) ctg2 (360° - a)-1
1088- l-tg^-180")
Решение.
ctg(?70° - a) ctg2 (збО° - a)-1 _ tg a ctg2 a-1 _ 2tga l-tg2(a-180°) ctg(180° +a) l-tg2a ctg a l-tg2a x—- a * = tg2actg2a = 1.
2 ctg a
Ответ: 1.
cos2 (а-270е)	sin2 (a+270°)
3'089’ sin’2 (a+90°)-1+ cos'2 (a- 90°)-1'
Решение.
cos* * 2 (g-270°) sin2 (g+270°) _ (:os^70°-a))2 sin-2(g+90°)-l cos-2(g-90°)-l	1_______i
(ип(?0°+д)У
^in(27O° +g)f _ sin2g cos2 g _ sin2g cos2g
______?	।	1	।	1	। l-cos2g l-sin2g (jos(90°-g)jf________________________«>s2«	si“2« cos2g sin2g
. 2 о	2	• 2	. 2	2	2	• 2
- sm acos a + cos asm a _ sin acos a cos asm a _ 1-cos2 a l-sin2a sin2 a cos2 a
= cos2a+sin2a=l.
Ответ: 1.
3.0,0. ^‘82к7”')К!(°-г70-)-.).
(1+ctg2 (g+270° ))cos-2 (g+90°) Решение.
6+tg2 (g - 90° )Jkin’2 (a - 270’ )-l) (1+ctg2 (a+270° ))cos-2 (g+90°)
1
. 2 sin a
f 2 A 1	2
, cos g 1-cos g
1+——---------—
sin g cos g
\ /
\ sin2 a	1
2	2
cos a J sin a
sin2 a+cos2 a sin2 a 1
sin2 a cos2 a _ cos2 a _ sin2 acos~ a _ ^2 a
cos2 a+sin2 a	1	1	cos2 a
cos2 a sin2 a sin2 «cos2 a
Ответ: sin2 a.
3.091.
Л |	?! ft
tg 2+“ FCtg a-2
Решение.
)	>(	л')
-cos' a— J Г 2J
-ctg a--
2	♦ *>	?	• 7	2	-2
cos a - siir a _ cos~ a - sin a _ cos a-sin a ctg2 a - tg2 a cos2 a sin2 a cos4 a - sin4 a . 2	2	• 5
sin a cos a cos“asin"a
(cos2 a - sin2 ajcos2 a sin2 a _ (cos2 a - sin2 ajcos2 a sin2 a cos4 a - sin4 a	(cos2 a - sin2 alcos2 a+sin2 a
cos2 a sin2 a 2 • > 4cos2asin2a sin2 2a
—z------5— = cos asm" a =---------=-------
cos a+sin'a	4	4
Ответ:
sin2 2a ~~4
3.092.
a a tg—— Ctg —
.a .a tg—+Ctg —
Решение.
. а	а
sin— cos— _L 2
. 2 а 7 а sin —cos“ —
2	2
ос , а tgI”CtgI х (х х а tgI+Ctg2
а cos—
2
. а sm — __2_-
. а а sm— cos—
2^-2
а cos—
2
. а sm—
2
а . а cos—sin—
2	2
. 2 а 2 а sm —+cos —
2	2
а . а cos—sin—
2	2
2 а
= sm —cos
2
a
I
(	2 а . 2
-ч cos —sin — = -cosa.
I 2	2 J
Ответ: -cosa.
cos2 a-ctg2 a+1 3>093‘ sin2 a + tg2 a-1 Решение.
2	♦ 2	< cos a-----x—+1
cosza-ctg a+l_sin2a sin2a + tg2a-l . 2 sin2a -
cos a
• 2	2	2	-2
sin acos a-cos a+sin a
= —------2	=ctg2 a.
sin acos a+sm a-cos a sin a
cos2 a
7
Ответ: ctg a.
cos2 fca-90°)+ctg2 (90* +2a)+l 3'094, sin2fa -270°)+tg2(z70° +2a)+l ’
Решение.
cos2 fe a-90*)+ctg2 (90° +2a)+l _ sin2^a-270’)+tg2(i70°+2a)+l ~
(cos(90° - 2g))~ + (ctg(90° + 2а))~ +1	sin2 2а+tg2 2а+1
(-sin(270‘ -2а))2 +(tg^70° +2a))* +1 cos22a + ctg22a+1
. >„ sin2 2a , sin22acos22a+sin22a+cos22a sm' 2a + -—z—+1 ------------------------5-----
________cos 2a ____cos 2a________________________
2 cos2 2a , sin22acos22a+cos22a+sin22a
cos 2a + —j—+1 -------------------------2-----
sin 2a	sin 2a
Ответ: tg22a.
3.095.
. ?(. л sin 4a— ________L_ 2J_____: (з	> (3
ctg -n-2a +tg -n+2a 12	2
Решение.
•2л sin 4a—
л-|	|-sin| — -4a |i
2 )	[ I2 J)
f 3	А	С з	А	Сз	А	(з
ctg -n-2a +tg -ic+2a ctg -л-2а +ta -л+2а
\2	J	I2	J	I2	J	Д2
_ cos2 4a _ cos2 4a _ cos2 4a _ “ tg2a-ctg2a ~ sin2a cos2a ~ sin22a-cos22a ~
cos 2a sin 2a sin2acos2a
cos2 4asin2acos2a _ cos2 4asin2acos2a cos2 2a - sin2 2a	cos 4a
cos4a 2sin2acos2a _ cos4asin4a _
"~2	2
2cos4asin4a _ sin8a
4	4~ ‘
Ответ: —-sin 8a. 4
3.096.
1
l-cos(4a-7t) sin3 2a
Решение.
1| l-cos(4a-Jt) n sin3 2a 2tg —л-a cos a —
2	2
3-1	<3	Y (n	St
о 2tg -я-a cos —a
2 J	|^2	1 V2	JJ
1
Г 3 > '> j 3 2ctg^a + -u sin2|a- —л
l-cos(n-4a) sin3 2a
<3 Y M
2ctg -я+a -sin -я-а Д2	2
2
1	+1+cos 4a______1__________1_______
2 ctg a sin2 a sin3 2a -2tgacos2a 2 cos a sina
l+2cos22a-l 1	1 2cos22a
-I-------------1- ---------=-----------1-------p
sin 2a 2sma	2smacosa sin 2a
* Uuo (JC cosa
1	1	. 2 cos2 2a	1 2sin22a+2cos22a
-----------=	. .		-	1	=	------------- 2 sin a cos a sin 2a	sin 2a-sin 2a-sin 2a
2^in2 2a + cos2 2a) _	2
sin3 2a sin3 2a
Ответ:
2 sin3 2a
3.097.
cosl 2 a+2sin2(a-7t) cos2 a + 4 sin a + sin2 (a + я) cos3 (a - 4я)	cosa(4sina+l)
Решение.
cos2 a+2 sin2 (a - я) cos2 a-ь 4 sin a-ь sin2 (a + я) _
cos3 (a - 4я)	cos a(4sin a+1)
_ со82а+2(-8т(я-а))2 со82а+4$та + (5ш(я-ьа))2 __
(со8(4я -a))3	cos a(4 sin a+1)
_ cos2a + 2sin2a ^cos2 a+4sina+sin2a _ cos2 a+2sin2 a cos3 a	cos a(4sin a+1)	cos3 a
l + 4sina _ cos2 a+2sin2 a 1 _ cos2 a+2sin2'a+cos2a
cosa(4sina+l) cos3 a cosa	cos3 a
_ 2cos2a+2sin2a _ 2(cos2a+sin2a)_ 2
cos3 a	cos3 a cos3 a
( 3i	(	8 i 2	1
3.098. sin 2d — л + cos 2a—я +cod -я+2а .
2	3 J 13
Решение.
Пусть
(	3 i	f	8
y = sin 2a—я +cos 2a—я
I	2 J	I	3
(2
+ cos -я+2а =
I 3
( 3
= -sin -я-2а 2
I	(i	(2
+cos -я-2а +cos -я+2а
I	3	3
l 3	1
-sin -я-2а =cos2a;
(2)2	2	1 V3
cos —я+2а =cos—7icos2a-sin—nsin2a = —cos2a-sin 2a.
3	3	3	2	2
1	V3	1	V3
X = cos 2 a—cos 2a +—sin2a—cos2a-sin2a = 0.
2	2	2	2
Ответ; 0.
4 sin* 2 * (a - 5я)~ sin2 (2a+я)
3.099. --7---7-^-
21 о 3 cos 2a—я
2
-4+4sin2a
Решение.
4 sin2 (a - 5я)- sin2 (2a+я) _ 4(- sin(5rc - a))2 - (sin(ff+2a))2 _
/	3 '
cos 2a—я
I	2
-4+4sin2a
4+4sin a |со8|-я-2а I ^2
4sin2a-sin22a _ 4sin2a-4sin2acos2a
sin2 2a - 4+4 sin2 a 4 sin2 a cos2 a - 4+4(1 - cos2 a)
4sin2 a(l-cosz a)___________4sin2asin2a_______
4(1 -cos2 a)cos2 a -4+4 -4cos2 a 4cos2 a-4cos4 a-4cos2 a
4sin4 * * *a
4cos4 a
= -tg4a.
Ответ: - tg4 a.
‘ 2| 9	| . 2[ 17
3.100. sin -я+а -sin —я-а I8	J I8
Решение.
со/--2а cosf —+2а 11=-| -2sin—sin(-2a)
2	14	14	2	4 v 7
= —- (- sin 2a) =—sin 2a = -U sin 2a.
2	2 Ji
Ответ: -=sin2a. V2
3.101. ctg(4a-7U cos4f - я-2a sin4(-тс-2a
Решение. ctg(4a-7t)| cos4| - 1 I 1 = -ctg(n-4a^c< Г/ = -ctg(n-4al cc = ctg 4a cos4 —- I \ x л ff 2(n = ctg 4a cos , A  Гл л = ctg4acos —-4i Ответ: cos 4a.	< И JI4 )) 5	A	(9	Y -	л-2а -sin4 -Tt-2a = *	J	V	)) (4л+л	Yj* f . (8л+л 0 Ylj* I 4	)) И 4 )) j (	(n	yY	(	(	(n yiYl >	s л+ —2a	- sin 2л+ —2a	= 4	4 v	к V	V) ? 1	fir	M 2a -sm —2a = J	I4	JJ \Y ( (к Y2>l -2a - sin2 —2a	= JJ	))) cos4a . . a	— sin4a = cos4a. J sin4a
3.102.
i(5	1	>( 5
cos — л-2а -sin —я-2а
___I4	J I4
а .а I (_ а (ла cos— +sin— cos 2л— +cos — + —
2	21	2	[2 2
Решение.
/5	у	2(5
cos — л-2а -sin
14	I
-л-2а 4
a
a . a j (- a | cos —+ sm — cos 2 л-+cos
2	2 12
2
л a
2 + 2
sina
sina
(5 A cos -л-4а
I 2
cos
a	. a Y a	.ah	(	2 a	• 2 a 1	.
cos—+ sin — cos — sm— sma cos-sm — sma
2	2 12	2 1	I 2	2 1
~	(л .
cos 2л + —4a
2
cos a sin a 4sin2acos2a A n ----:------= 4cos 2 a. sin2a
2 cost	4a j л . л
[2 J_2sm4a 2cosasina	sin 2 a
Ответ: 4 cos 2a.
3.103.
I 5 о cos -л-2а 2
Решение.
cos 2л4- --2a 2
tg Я+ -
cos —2a I 2
. f л n sm —2a
2
tg ^-a j(l + sin2a) l + cos y-2aj
sin 20
(4	/
sin 2a
cos 2a л ----:----(1 +
__ 1 +sin 2a
sin 2a
cos 2a , _
— = ctg2a. sin 2a
Ответ: ctg 2a.
tg2a
tg4a-tg2a
Решение.
tg2a _ tg2a	_ tg2a(l - tg2 2a) _ 1 — tg2 2a
tg4a-tg2a ' 2tg2a _ t	~ tg2a(2-l + tg2 2a)” 1 + tg2 2a
1 - tg2 2a
j _ sin2 2a	cos2 2a - sin2 2a
_ —£os 2a _----- cos 2a ----_ cos2 2a _ sjn2 2a = cos 4a.
, sin2 2a cos2 2a + sin2 2a
1 +—->— ---------5-------
cos- 2a cos 2a
Ответ: cos 4a.
„ „л, sin 6a cos(6a-jc)
3.105. —— +  l.
sin2a cos2a
Решение.
sin6a cos(6a-n) _ sin6a | cos(n-6a) _ sin6a cos6a _ sin2a	cos2a sin2a cos2a sin2a cos2a
_ sin6otcos2a-cos6asin2a _ sin4a _ 2sin4a sin2acos2a	sin2acos2a 2sin2acos2a
_2sin4a _2 sin4a
Ответ: 2.
3.106.
1+cos(4a - 2 n)+cos^ 4a - j / j l+cos(4a+Jt)+cos 4a+—л
Решение.
l+cos(4a- 2л)+ cos| 4a--
3 A -rc+4a
2
l+cos4a+sin4a _ l + 2cos22a-l+2sin2acos2a 1 - cos 4a+sin 4a 1 - (j - 2 sin2 2a)+ 2 sin2acos2a
_ 2cos2 2a+2sin2acos2a _ 2cos2a(cos2a+sin2a)_ cos2a _ctg2a 2sin22a+2sin2acos2a 2sin2a(sin2a+cos2a) sin2a
Ответ: ctg 2 a.
sin(2a+2л)+2sin(4a - n)+sin (ба+4л)
сов(бл - 2a)+2 cos(4a - л)+cos(6a - 4л)
Решение.
8т(2а+2л)+28Й1(4а-л)+5ш(ба+4л)
cos(6n - 2a)+ 2 cos(4a - л)+cos(6a - 4 л)
_ 8т(2л+2а)-28т(л-4а)+8П1(4л+6а) sin2a-2sin4a+sin6a сов(бл - 2a)+2 cos(n - 4a)+cos(4n - 6a) cos2a - 2 cos4a+cos 6a
_ 2sin4acos2a-2sin4a _ 2sin4a(cos2a-l) _ sin4a _ t 2cos4acos2a-2cos4a 2cos4a(cos2a-l) cos4a
Ответ: tg4a.
3.108.
4sin -я + а
_________12	J	 aA__________________a
tg' -я-- —ctg j -я+-2	2	2	2
Решение.
4cosa	4cosa
4 cos a
2 a x 2 a Ctgy-tgy
2 a . 2 a 4 a . 4 a cos — sin —	cos —sin —
2 1	2	2
. 2 a	2a	.2» 2a
sin — cos — sin —cos —
2	2	2	2
л 2 a 2 a 4cosasin —cos —
;______________2	2
2a . 2 aY 2a .2a cos —sin — cos — +sin —
2	2	2	2
cosasin* 2a . 2 =----------= sin a.
cosa
Ответ: sin2 a.
sin(2a+p)+sin(2a-p)-cosf | я-2a
3.109. ------------------------Jy------
cos(2a + p)+cos(2a-p)-sin -n+2a
Решение.
( 3 sin(2a+p)+sin(2a-p)-cos -л-2а
_______________________________J _ 2sin2acosp+sin2a _ cos(2a+p)+cos(2a - p)- sin -л+2a 1 2cos2acosP+cos2a
I2 J
_ sin2a(2cosp+l) _ sin2a _ cos2a(2cosp+l) cos2a
Ответ: tg2a.
cos3a+cos4a+cos5a
3.110. -7-T--—A---------——.
sin 3a + sin 4a + sin 5a
Решение.
cos3a+cos4a+cos5a _ 2cos4acosa+cos4a _ cos4a(2cosa+l) _ sin 3a+sin 4a + sin 5 a	2 sin 4acos a+sin 4a sin 4a(2cosa+1)
cos4a x A
= -- — = ctg 4a. sin 4a
Ответ: ctg4a.
/7
3.111.
-(5	)	,f7	A
cos -л-2а +4cos -л-a -4 2	,	2
2
1+cos(4a - re)-8 sin2 (5 л - a) Решение.
,(5	A	,(7	)
cos -л-2а +4cos -л-а -4 12	I	12
1+cos(4a - тс)- 8 sin2 (5л - a)
Гл	W2 Г Гс
(4л + л	J f 6л+л ]] A
cos------2a +4 cod--------a -4
12 J 4 2 J
2л+1 ^-2a
1+cos(n - 4a)- 8(sin(5n - a))2
' 44x2 ( (	(^
+ 4 cod Зл+ —a 1	2
-4
1+cos(n - 4а)~ 8(sin(5n - a))2
l-cos4a-8sin2a
sin2 2a+4 sin2 a-4 l-cos4a-8sin2 a
4sin2 acos2 a-4(1-sin2 a) 4sin2acos2a-4cos2a _ l-^-2sin22a)-8sin2a 2sin22a-8sin2a
4cos2 a(sin2 a-1) _ -4cos2acos2 a _	-4cos4 a
8sin2acos2a-8sin2a 8sin2 alcos2a-l) -8sin2asin2a
cos4 a 1	4
=-----;— = -ctg a.
2 sin4 a 2
1	4
Ответ: —ctg a-
3.112.
5	1 . ( л a
cos — л-a sin —+—
2	2 2
2f Jt-aY, . л-a (3 cos --- 2sin----+соя -л-а
I 4 1	2	12
Решение.
a :os—
2
хч .	a
2sinacos— _______2
In a)	L . aY^ a
—z	x 14-sin— 2 cos—sina
2 2 I f n a ) I 2 1	2
----A 2cos—sina	v л
2 I 2
CO!
- ♦ a 2 sin a cos— ___________2. \ . aY-i a a a n a(t . a Yi • a) 1 + sin— 2cos—2sm—cos— 2cos— 1+sin— 1-sin—
2 1	2	22	2	2 1	2 J
2sin0 cos— 2
_ . a a ~ . a sina 2sm-cos- 2sin-? a cos**— 2
- . ? a 1-sm** — 2
a
a tg 2 ’ cos—
2
Ответ: 2tgy.
1+cos a + cos 2a+cos 3a cosa4-2cos2a-l Решение.
3.113.
14- cos a 4- cos2a 4- cos 3a _ 14- cos2a 4- (cos a 4- cos 3a) _ cos a 4- 2 cos2 a -1	cos a 4- 2 cos2 a -1
_ 14-cos2a4-2cos2acosa _ 14-2cos2 a-14-2^cos2a-l)cosa
cosa4-2cos2 a-1	cosa4-2cos2 a-1
=2cosa. cosa+2cos a-1
Ответ: 2 cos a.
Преобразовать в произведение (3.114—3.147):
3.114. sin 4a - 2 cos2 2a+1.
Решение.
sin 4a - cos 4a = sin 4a - sin(90e - 4a)= 2 cos45e sin(4a ^45° )=
= 2 — sin (4a
2 v
3.115. tgy+ctgy+2.
Решение.
.	a	a
_	_	sin—	cos—
tg—+ ctg—+2 =----—	_l--1
b2	2	a
cos— 2
. a sin—
2
. 2 a ? a sin — +cos~ —
2	2
a . a cos —sin—
2	2
+2 =
1	-	2	-	2	_ 2+2sina
---------+2 =------------+2 =-----+2 =--------- ♦ a a----Э a a-----------Sin<X Silla
sin—cos —	2 sm — cos—
2	2	2	2
(it A —+a	—a
2(1.sina)_fmrsing | = 2-2sin^-oos^— sina	sina	sina
A . (n aVfn a А л • 4П4+1П4^| sina	sina
A . 21 Я « = 4 sin — + —
4 2
sin"1 a.
>
~ л • 2i л <* Ответ: 4sm — + — 14 2
a.
3.116. cos'4a-sin"4a.
Решение.
sin4 a-cos4 a
—4	—4	1
cos a-sin a = —-------------4 ~------т----—-
cos a sin a cos asin a
a - sin4 a	s2 a - sin2 a%:os2 a + sin'
sin4 2a
16sin4 acos4 a
•4
1
-16cos2a	cos2a 1
=----2----= -16 —--------,— = -16ctg2asin 2a.
sin 2a	sin2a sin 2a
Ответ: -16ctg2asin 32a.
tg4a-tg6a
3.117.	—4-----“г—-
ctg a-ctg a
Решение.
tg4a-tg6a _ tg4a-tg6a = tg4a(l-tg2a)
ctg4 a-ctg2 a 1_______L_ 1-tg2 a
tg4 a tg2 a tg4 a
.tg«a=tg>a
1-tg2 a
Ответ: tg*a.
3.118.	l-3tg2(a+270’).
Решение.
l-3tg2(a+270’)=l-3(tg(270’ +ajf =l-3ctg2 a=4||-|ctg2a
/1 7з
=4 rTctga
! V3 t .1
-+—ctga =4 --2 2	2
cosa sina
cosa
2 2 sina
2 2
1 . V3 1 . V3 -sma----cosa -sma+—cosa
= 4.2	2	.2	2
sina	sina
4|sinacos60° -cosasin60° Asinacos60° +cosasin60‘l J sin2 a
4sin(a-60* Jsin|a+60°) sin2 a
Ответ: 4 sin (a - 60’ )sin(a+60’ )sin“2 a.
3.119.	l-3tg2(a-180’).
Решение.
l-3tg2(a-180’)=l-3(-tg^80r -а)У =
(1 3
= l-3tg2a = 4---tg'a =4tga - + — tga =
14 4	2 2	2 2
4 4
2 2
/ 1 -Уз sina Y1 >/з sina
= 4------------ +------------
2	2 cosa 2 2 cosa
1
. 1	V3 .	1	V3 .
4-cosa----sina -cosa + — sina
2	2	2	2
2
2
cos'a
__ 4(sin 30° cos a - cos30° sin a)sin 30° cos a + cos 30° sin a cos2 a
_ 4sin(30° -ajsin cos2 a
Ответ: 4sin(30’ -a)sin^0° +a)cos 2 a.
/	3 A ,(	3 A
3.120.	tg a-—л -ctg a + jit .
Решение.
2f 3 )	,( 3}	3
tg a—я -ctg" а+-я = -tg -n-a 2	2	2
f (3 W - ctg ^я+а
2	’2	4	-4
x 2	.2 cos" a sin a cos a-sin a
= ctg2 a - tg" a = —--------= —----------—
sin" a cos a sin" acos" a
_ 4(:os2 a-sin2 a)(cos2 a + sin2 a) _ 4cos2a
4 sin2 acos2 a	sin2 2a
Ответ: 4cos2asin 2 2a.
3.121.	3sin2 (a-270° )-cos2 (a+270°).
Решение.
3 sin2 (a - 270’)- cos2 (a+270’ )= з(- sin(?70’ - a))r - (cos^70’ + of = 3(sin(270° - a)^ - (cos^70’ + a))” = 3cos2 a - sin2 a =
'3 .... 1 .
3	2	1  2 1 J V3 1 .
-cos a—sin a =4|—cosa—sina 4	4
V3	1 .
—cosa+-sma
2	2
/к 2	2 ” л
= 4(x>s30’ cosa - sin 30’ sin a)(cos30’ cos a+sin 30’ sin a)=
= 4cos($0’ +a)cos(30° - a).
Ответ: 4cos(30’ +a)cos^( 3.122. sin2(a+90’)-3cos2 Решение.
Г1	3
= cos2 a-3sin2 a = 4 —cos2 a—sin2 a 14	4
. i	V3 . T i	V3 .
= 4 —cosa-----sina — cosa +—sina =
2	2	12	2
= 4(sin 30’ cos a - cos 30’ sin a')(sin 30’ cos a+cos 30’ sin a)= = 4sin^0’ -a)sin(30’ + a).
Ответ: 4 sin(30‘ - a)sin(30’ + a). /	/ о A
3.123. sin2 p— -cos2 a—я . 2	2
V 2 Решение.
sin2[p~^ -cos2
3 I I • я n a—-я = -sin —В
2	.2
71 3 H
2 II
( Зя cos------a
I 2
2
= sin
л2	(	Гъг	W2
I Jic	1	2	о • 2
- cos —-a =cos p-sin a =
I 2	J
7	\	к	))
_l+cos2P l-cos2a_l cos2p 1 cos2a_
~2	2	2+ 2 -2+~l
= i (cos2a+cos2p) = | - 2 cos(a+p)cos(a - p)=cos(a+p)cos(a - p)
Ответ: cos(a + p)cos(a—p)
(a \
3.124. 3-4cos2 -я-а .
12 >
Решение.
. .	>(3	.	l+cos(3re-2a)
3-4cos* -я-a = 3-4--------------  -	=
I2 J 2
= 3-2-2 cos(3k - 2a)= 1 - 2 со$(3я - 2a)=
= l+2cos2a = 21— + cos2a =2 cos —+cos2a =
I2 . „ (n	(n = 2-2cos —+ a cos — I6 J I6 _	.	(я ) Ответ: 4 cos — + a cos I* J 3.125. 3-4sin2| —-a I2 ) Решение. 	A cin 21  ry j— Э  A .	3 /V	/ Г Л a =4cos —+ a cos —a . ) I* J I6 ) (n 'I —a . I6 J l-cos(rt-2a)_
l2 J = 3-2-b2cos(K-2a)=l+2 fl	A f	Д = 2 —cos 2 a =2 cos — I2	J I	3 п Г . Гя V (n = 2- -2sm - + a sin — I I6 J I6 A . (n Y f = 4sin —+ a sin a— . I6 J I 6 J A • ГЛ V ( Ответ: 4sm —+ a sm a 1 6	) I	2 cos(u - 2a)=1-2 cos2a = cos 2a ^= a • (n	V (я a |= —4sinl - + a sin —a JI	16 j I 6 n ” 6 r
(п А (3
3.126.	1+cos —+ 3а -sin —я-За
V 2
(5 +ctd -я+За
2
Решение.
,	(я , ] . (3	. 1 J 5	- 1
1+соя —+3а -sin -я-За +cta -я+За =
12	112	12
. . ,	,	. ,	, • ,	, sin3a
= 1 - sin За+cos За - tg За = 1 - sin За+cos За-=
cos За
_ (cos За - sin 3a)cos За + cos За - sin За _ (cos3a - sin 3aXcos За+1) _
cos3a	cos3a
cos За
_ /Т j За . Г я « ।
2V2 cos —sin — 3a
„	2	14 J
Ответ:--------------1------1.
cos 3a
3.127.	l+cos(2a+270’)+sin(2a+450°).
Решение.
1+cos(ia+270°)+ sin(za+450° )= 1+cos(270° + 2a)+sin(450° + 2a)= = 1 +sin2a+cos2a = cos2 a+sin2 a+2 sin acosa+cos2 a -sin2 a = = (:os2 a+2 sin a cos a+sin2 a)+ (cos a - sin aXcos a + sin a)=
= (cosa+sina)2 + (cosa-sinaXcosa+sin a)=
= (cos a+sin aXcos a+sin a + cos a - sin a)=
= 2(cosa+sin a)cosa = 2 (cos a+cos(90° - a))cosa =
= 2 • 2cos45° cos
(a-45’)c
A osa = 4---cos
2
la-45’)cosa =
= 2л/2 cosacos(a-45’)=2V2 cosacosl45° -a
Ответ: 142 cos a cos(45’ - a).
3.128.	l-cos(ia-270’)+sin(2a+270’).
Решение.
l-cos(2a-270’)+sin(2a+270’)=l-cos(270’ -2a)+sin(270’ +2a)=
= 1+sin2a - cos2a = sin2 a+cos2 a+2 sin a cosa - (:os2 a - sin2 a)=
= (sina+cosa)2 +sin2 a - cos2 a = (sin a+cosa)2 +
+ (sina+cosaXsina-cosa)=(sina+cosaXsina+cosa+sina-cosa)=
=2(sin a+cos a)sin a—2 ^in a+sin(90’ -a))sina =
= 2 ♦ 2 sin45° cos(a -45* )sin a = 4	sin acos(a - 45° )=
= 2^2 sinacos(a-45* )= 2^2 sinacos(45* - a).
Ответ: 141 sin a cosW5* - a
3.129.	sinf—я - 2a |+ 2 sin2
2 I
и 3 I 1 2a—я -1.
2
Решение.
sin
-я-2а |+2sin2 2
(5	1	0Г3 i
2a—я -l = sin -я-2а +2sin -я-2а -1 =
2 J V JI2 J
=cos2a+2cos22a-l =cos2a+cos4a = 2cos3acosa =
= 2cosacos3a.
Ответ: 2 cos a cos За.
3.130.	1 -cos(2a - я)-cos(4a + я)+cos(6a - 2я)
Решение.
1 - cos(2a - я)- cos(4a + n)+cos(6a - 2я)=
= l-cos(n-2a)-cos(n+4a)+cos(2rt-6a)=
= 1+cos2a+cos4a+cos6a = 1+2cos2 a -1+cos4a+cos6a =
=2cos2 a+cos4a+cos6a = 2cos2 a+2 cos5acos a =
=2 cos a(cos a+cos 5 a)=2 cos a  2 cos	cos
= 4cosacos3acos2a = 4cosacos2acos3a.
Ответ: 4cosacos2acos3a.
i3 i Г 5 i
3.131.	1+ctgI—n-4a l+sin"1 -n+4a L
Решение.
. f3 A A . V5 . V J3 A 1 1+ctd -л-4а +sin -rc+4a =l+ctd -rc-4a +—7-------
Д2	)	12 I 12	1.(5.
\	7 к 7	\	7 siri-rc+4a
V
, A 1	, sin4a 1 cos4a+sin4a+l
= l+tg4a+--— = 1 +—— + — =-----------A----=
cos4a cos4a cos4a cos4a
_ cos2 2a - sin2 2a+2 sin2acos2a+cos2 2a+sin2 2a _
cos4a
(cos2a - sin2aXcos2a+sin2a)+ (cos2a+sin2a)r _ cos4a
(cos2a+sin2aXcos2a-sin2a+cos2a+sin2a) _ 2(cos2a+sin2a)cos2( cos4a	cos4a
2cos2oJ cos2a+cod "2a 2cos2a-2cos-cos| 2a--
cos4a	cos4a
2V2 cos2acos 2a - ~ 1 2^2 cos 2a cosl — - 2a I
__________ 1	4)= И /
cos4a	cos4a
2V2cos2acos( —2a 14 Ответ:------------—--------
cos 4a
sin a - 2 cos 3a - sm 5a
3.132.	--------------------—
cos a - 2 sin 3a - cos 5a
Решение.
sina-2cos3a-sin5a _ (sin a-sin 5a)-2 cos 3a __ cosa - 2 sin 3a - cos 5a (cosa - cos5a)- 2 sin 3a _ 2 cos 3a sin(- 2a) - 2 cos3a _ - 2cos3a sin 2a - 2 cos3a _ - 2 sin 3a sin(- 2a) - 2 sin 3a 2 sin 3a sin 2a - 2 sin 3a -2cos3a(sin2a + l) A o sin2a + l A o l + sin2a 2sin3a(sin2a-ll)	sin2a-l l-sin2a
Ответ: ctg3actg2
3.133. 2cos2
Решение.
2 cos21 —
.	2(3lt a\ c (5	,
= 2cos-------+V3cos -тс-a -1 =
12 2 J \2 J
= 2sin2 — -V3sina-l = l-cosa+V3sina-l
Ответ: 2 sin а— .
I 6 J
_____ sin 4а+sin 5а+sin 6а
3,134.		.
cos4a4- cos 5a+cos 6a
Решение.
sin 4a+sin 5a 4-sin 6a _ (sin4a+sin6a)+sin5a _ cos 4a+cos 5a+cos 6a (cos4a+cos 6a)+cos 5a _ 2sin5acosa+sin5a _ sin5a(2cosa+l) _ sin5a
2cos5acosa+cos5a cos5a(2cosa+l) cos5a
Ответ: tg5a.
3.135.	-cos5acos4a-cos4acos3a+2cos2 2acosa. Решение.
- cos 5acos 4a - cos 4a cos 3a+2 cos2 2a cos a =
= - cos 4a(cos 5a + cos 3a) 4- 2 cos2 2a cos a =
= - cos 4a - 2 cos 4a cos a+2 cos2 2 a cos a =
= -2 cos2 4a cos a+2 cos2 2a cos a = -2 cos a(cos2 4a - cos2 2a
= -2 cos a(cos 4a - cos 2aXcos 4a+cos 2a)=
=-2cos a(-2 sin 3a sin a) • 2 cos 3a cos a =
= 2 cos a(2 sin acos aX2 sin 3acos 3a)=2 cos a sin 2a sin 6a.
Ответ: 2cosasin2asin6a.
3.136.	sin 1 Oa sin 8a+sin 8a sin 6a - sin 4a sin 2a.
Решение.
sin 1 Oa sin 8a 4- sin 8a sin 6a - sin 4a sin 2a. =
= sin 8a(sin 1 Oa 4- sin 6a) - sin 4a sin 2a =
= 2 sin 8a sin 8acos2a - sin 4a sin 2a =
= 2 sin* 2 8acos2a-sin4asin2a =
= 2sin2 8acos2a-2sin2acos2asin2a =
= 2sin2 8acos2a-2sin2 2acos2a = 2cos2a^in2 8a-sin2 2a)=
= 2 cos2a(sin 8a - sin 2aXsin 8a + sin 2a)=
= 2 cos 2 a • 2 cos 5 a sin 3 a • 2 sin 5acos3a =
= 2cos2a(2 sin 3acos3aX2 sin 5acos 5a)=2 cos2asin 6a sinl Oa.
Ответ: 2cos2asin6asinl0a.
_____cos7a-cos8a-cos9a+cosl0a
3-137. ——----—------—-----r-TT—-
sm 7a - sm 8a - sin 9a+sin 1 Oa
Решение.
cos7a-cos8a-cos9a+cosl0a (cosl0a+cos7a)-(cos9a+cos8a) sin 7a - sin 8a - sin 9a+sin 1 Oa (sin 1 Oa+sin 7a)- (sin 9a+sin 8a)
_	17a	3a	0	17a	a 2coJ7afcos^_“>|
2cos-cos---2cos--cos—	2cos-r~	C0S^T	V
2	2______2	2 _ 2(2 2 J
- .	17a	3a	-	.	17a	a _ . I7af 3a a
2sin-cos---2sin--cos—	2sm--- cos----
2	2	2	2	2	2 2
17a
cos----
_____2
. 17a sm----
2
. 17a = ctg—•
л . 17a
Ответ: ctg-у-.
3.138. sin5a-sin6a-sin7a+sin8a. Решение.
sin 5a - sin 6a - sin 7a + sin 8a = (sin 8a+sin 5a)- (sin 7a+sin 6a)=
* . 13a 3a ~ . 13a a - . 13af 3a a^ =2sm---cos---2sm---cos— = 2sin- cos--cos— =
2	2	22	2(2	2)
» . 13af » . a'l . . a .	.13a
= 2sin- -2sinasin— =-4sin—sinasin—-.
2	2 I 2	2
a .	. 13a
Ответ: -4 sin
—sinasin----.
2	2
3.139. cos3a-cos4a-cos5a+cos6a.
Решение.
cos 3a - cos4a - cos 5a+cos 6a = (cos 6a+cos 3a)- (cos 5a+cos4a)=
_ 9a 3a _ 9a a . 9af 3a a A
= 2 cos—cos-2 cos—cos— = 2 cos— cos-cos— =
2	2	22	2^2	2 J
* 9a f . .	. a^ 4 . a • 9a
=2 cos— -2smasm— = -4sin —sin acos—.
2	2	2	2
л	. a . 9a
Ответ: -4sin—sinacos—.
2	2
sinl3a+sinl4a+sinl5a+sinl6a
3.140. —---------------—--------—
cosl3a+cosl4a+cosl5a+cosl6a Решение.
sinl3a+sinl4a+sinl5a4-sinl6a
cos 13a+cos 14a+cos 15a+cosl 6a
(sinl6a+sml3a)+(sinl5a+sinl4a)
(cosl6a+cosl 3a)+(cosl 5a+cosl4a)
29a	3	29a a о • 29af 3 a
2sin—cos-a+2sin—cos- 2sm— cos-a+cos-
2	2_______2	2	_	* 2	(	2	2
.	29a	3	_	29a	a	~	29a	f	3	a
2 cos——-cos—a+2cos—-cos— 2 cos  cos—a+cos—
2	2	2	2	2	2	2
« . 29a
2smT_t 29a
,	29a tg 2 ’
2 cos——
2
, 29a
Ответ: tg-y--
3.141. sin2a+sin4a+sin6<x.
Решение.
sin 2 a 4- sin 4a+sin 6a. = (sin2 a + sin 4a)+ sin 2 (3 a)=
= 2 sin 3acos a+2 sin 3acos 3a = 2 sin 3a(cos a 4- cos 3a)= = 2 sin 3a ♦ 2 cos 2a cos a = 4 sin 3acos 2acos a.
Ответ: 4sin3acos2acosa.
3.142.	sin 5a+sin 6a+sin 7a+sin 8a.
Решение.
sin 5a + sin 6a+sin 7a+sin 8a = (sin 5a + sin 6a)+ (sin 7a+sin 8a)=
„ . Ila a * . 15a a - af . Ila . 15aA
= 2 sin—cos—+2 sin-cos—= 2cos— sm—+sm-- =
22	22	2^	2	2 J
. a ~ . 13a	. a . 13a
= 2cos—-2sin-cosa = 4cos—cosasin—.
2	2	2	2
л . a	13a
Ответ: 4 cos—cos a sin—-.
2	2
3.143.	cos5a+cos8a+cos9a+cosl2a.
Решение.
cos 5a + cos 8a+cos9a + cosl 2a = (cos 5a + cos 8a)+ (cos9a + cosl 2a)=
.	13a 3a _	21a 3a „ 3af 13a	21a
= 2cos-—-cos— + 2 cos—- cos—- =2cos— cos-+cos- =
22	22	2^2	2 J
- 3a .	17a	.	. 3a	.	17a
= 2 cos — 2 cos-cos 2a = 4 cos—cos2acos—.
2	2	2	2
_	. 3a -	17a
Ответ: 4 cos—cos2acos .
2	2
3.144.	3+4cos4a+cos8a. Решение.
3+4cos4a+cos 8a = 3+4^2 cos2 2a -1)+ 2 cos2 4a -1 =
= 3+8cos22a-4+2(2cos2 2a-l)” -1 =
= 8cos2 2a+2(4cos4 2a-4cos4 2a+1)-2 =
= 8cos2 2a+8cos4 2a-8cos2 2a+2-2 = 8cos42a.
Ответ: 8 cos4 2a.
3.145.	-Jtga+sina --Jtga-sina, 0 < a < j.
Решение.
7tga+sina - ^/tga-sina = 7tga(l+cosa) - ^tga(l-cosa) =
= 7tga + sina - y/tga-sina = 7tga(F+cosa) - 71ба0"со$а)=
= 7tga • 71 +cos a - 7tSa' 71-cos a = 7tga (71+cos a - 71-cos a
_	~ I---- f n a
Ответ: 2^/tgacos — + — .
^4 2 )
3.146.	l + sin2a-cos2a-tg2a.
Решение,
1 + sin 2a -cos2a - tg2a = 1 + sin 2a - cos2a -	-
cos 2a
cos2a - (cos2a-sin2a)cos2a-sin2a _
cos2a
_ (cos 2a - sin 2a)- (cos2a -sin2a)cos2a _ (cos 2a - sin 2aXl - cos 2a)
cos 2a	cos 2a
-cos 2a)
cos 2a
-2sin — sinl 2a-— I-2sin(7C+a)sin(7C-a))
_____4	4 J _____________________
cos 2a
- 2 •—sinf 2a - —	2 sin2 a) 2^2 sin2 a sin2( 2a “
2 у 4 ___; =к 4
cos 2a	cos 2a
2>/2 sin2 a cos — + 2a
______________у 4
cos 2a
• 2 I 71 n I
sm acos — + 2a
I 4	)
Ответ: -------------------------.
cos 2a
3.174.	sin 2a + sin 4a-sin 6a.
Решение.
sin 2a + sin 4a - sin 6a = sin 2a + sin 4a - sin 2(3a) =
= 2 sin 3a cos a - 2 sin 3a cos 3a = 2 sin 3a(cos a - cos 3a) =
= 2 sin 3a • (-2 sin 2a sin(-a)) = 4 sin 3a sin 2a sin a.
Ответ: 4 sin 3a sin 2a sin a.
Доказать справедливость равенств (3.148—3.152):
3.148.	(sin 160° + sin 40°)(sin 140° + sin 20°) + (sin 50° - sin 70°) x
x(sin 130°-sinl 10°) = 1.
Решение.
(sin 160°+sin40°)(sin 140° + sin 20°) + (sin50° - sin 70°)(sinl 30° - sin 110°) =
= (sin( 180° - 20°) + sin 40°)(sin(l 80° - 40°) + sin 20°) +
+ (sin 50° - sin 70°)(sin(l 80° - 50°) - sin( 180° - 70°)) =
= (sin 20° + sin 40°)(sin 40° + sin 20°) + (sin 50° - sin 70°)(sin 50° - sin 70°) =
= (sin 20°+sin 40°)2 + (sin50° - sin 70°)2 = (2 sin 30° cos 10°)2 +
/	.	\2	/	-	x2
+(2cos60°sinl0°)2 = 2—coslO0 + 2-sinl0° =cos210°+sin210° = l.
I	2	J	V	2	J
Равенство справедливо.
3.149.	(cos34°)-1 +(tg56°)~’ =ctg28°.
Решение.
(cos34°)"' + (tg56°J-' = —L-+ctg56’ =	/  -4+ctg56’ =
cos 34	cos|pO -56 )
=	1 cos 56° = l+cos56° = l+cos2(28°) = l+2cos* 2 28° -1 _
sin56° sin56° sin56° sin2(28°)	2sin28°cos28°
2cos228° cos28° 4 oo0
=--------------=---------= ctg 28 .
2sin28° cos28° sin 28°
Равенство справедливо. cos28°cos56° cos2°cos4° V3sin38° 3 150 -------------+------------=-------------.
sin 2° sin28° 4sin2°sin28°
Решение.
cos28°cos56° cos2°cos4° sm28ocos28ocos56o +sin2°cos20cos4,>
-------------4	— — 	-—— — sin2° sin28°--------------------------sin2°sin28°
4sin28° cos28° cos56° 4-4sin2ocos2ocos4° __
4sin2°cos28°
2sm56°cos56° 4-2sin4° cos4° sinll2° 4-sin8° _
4sin2°cos28o	4sin2°cos28°
= 2sin60°cos52° = 2'T cos(90° ~38°) = V3sin38° 4sin2° cos28° 4sin2° cos28° 4sin2° sin28°
Равенство справедливо.
3.151. l-2sin50° =0,5cos’l160°.
Решение.
'	. cno (1 - 2 sin 50° )• 2 cos 160° 2cos 160°-4 sin 50° cos 160°
2cosl60°	2cosl60°
= 2cosl60°-2^in(-110°)+sin210°)=
2 cos160°
i ° J-2sin50o)-2cosl60o 2cos 160°-4sin50°cos 160°
2cosl60°	2cosl60e
_ 2 cos 160°-2(sin(-1 l(P)+sin210P) 2cosl60°+2sinl lQP-2sin21QP _ 2cosl60P	”	2cosl60p
= 2cos(l 80° - 20°) + 2sin(90° + 20°) -2sin(l80°+30°) _
2 cos 160° .
2 — _ - 2 cos 20° + 2 cos 20° + 2 sin 30° _	2 1
2cosl60°	” 2cosl60° “ 2cosl60°
Равенство справедливо.
3.152. (cos 70° + cos 50°)(cos 310° + cos 290°) + (cos 40° + cos 160°) x
x (cos 320°-cos 380°) = 1.
Решение.
(cos 70° + cos 50°)(cos 310° + cos 290°) + (cos 40°+cos 160°) x
x(cos 320° - cos380°) = (cos70°+cos 50°)(cos(360° - 50°)+cos(360° - 70°)) +
+(cos(90° - 50°)+cos(90° + 70°))(cos(270° + 50°) - cos(450° - 70°)) =
= (cos70°+cos50°)(cos70°+cos50°)+(sin 50° - sin 70°)(sin50° - sin 70°) =
= (cos 70° + cos 50°)2 + (sin 50° - sin 70°)2 = (2 cos 60° cos 10°)2 +
, (	1	)	(	1
+ (2cos60°sin(-10°))2 = 2—cosl0° + -2—sinl0°
I 2	i	к	2
= cos210° + sin210° + l.
Равенство справедливо. Вычислить (3.153—3.166): . 2 Л 2 Зл . 2 $Л 2 7л 3 153 sin* —+ cos— + sin*— + cos —.
8	8	8	8
Решение.
. 2 Я 2 Зл . 2 5л 2 7л sin* — + cos* — + sin — + cos* — = 8	8	8	8
1-cos— 1 + cos— 1—cos— 1 + cos—
------4+------4+------4+-------4 =
2	2	2	2
. п 4л-л 4л+л 8я-л
4 - cos—+cos-----cos----+ cos----
4______4________4_______4_
2
I.	/V	I A JV
-COS—+ COS Л-----COS Л+ — +cos 2л—
4	( 4 J ( 4 J (	4
2
4-cos—cos—+cos—+ cos— .
4	4	4	4 _4_?
2	2
Ответ: 2.
3.154. tg435° + tg375°.
Решение.
. «с» . к» cosl5’ sinl5’ cos* 215’+ sin215'
= ctgl5 +tgl5 ---------+--------=----------------
sinl5’ cosl 5° sinl5’cosl5’
2	2	2.
----;--------=--------= -7- = 4.
sinl5’cosl5’ 2sinl5’cosl5°	sin30°	j.
2
1
Ответ: 4.
3.155. tg255°-tgl95°.
Решение.
tg255° -tgl95’ = tg(27O’ -15’)-tg^8O’ +15’)= . ic« . к» cosl5" sinl5’ cos215’-sin215’
= ctgl5 -tgl5 =----------------=------------------=
sinl5 cosl5° sinl5°cosl5’
cos30’ 2cos30’	2cos30’ „	... _ /г
=-------------=---------------=---------= 2ctg30 = 2V3.
sinl5’cosl5’ 2sinl5°cosl5’	sin30°
Ответ: 2у/3.
(3	4
3.156. sml-«-2arctgj
Решение.
. (3	.	4>
sin -я-2arctg— =
2	3 I
-cos 2 arctg—
„ A 4 1 i
2 cos" arctg— -1
= 1-2 cos arctg—
18=2_
25 25’
7 Ответ: —
13	5
3.157. ctg—л-ctg—я.
Решение.
t 13	5	12я+я	5	( я 5я
ctg—я-ctg—n = ctg-----Ctg—Я = С1Я Я+— -ctg— =
612	12 Б 12	*12	\	12)	*12
х я 5я
= ctg--ctg— =
12	12
я 5я . 5я я 5я . я cos— cos— sm—cos-----cos—sm —
12 12	_	12	12	12	12	=
. 5я sm—
12
. я sm —
12
. я . 5я sm — sm —
12	12
1
2
. 4я sm—
12
4я	6я
cos----cos —
12	12
2sin-______3__
л я cos—cos—

Ответ: 2>/з.
3.158. sinf 2а + - п I I 4 1
2 если tg а = -
3
Решение.
.С 5 1 . [ 4л+я ~	к
sin 2а + -л =sm-----+2а =sin л + 2а + —
4	4
я
4
4
= — sinl 2а + -
4
. ~ л _ . я V2 V2 _ = -sm2acos—cos 2 a sin— =-sin 2 a-cos2a =
4	4	2	2
= —— (sin 2a+cos 2a) =——
2	2 ^1 + tg a
! 1-tg2 a' l + tg2a?
V2 tg2 a-2tga-l _ <J2 9 3	17^/2
2 l + tg2a 2 j + £	26
9
Ответ:-----
26
I 7 ) 3.159. cos 2a + —я L если
4 I
2. ctga = -.
Решение.
cos 2а+-л =cos 4
8л-я 4
*	я
+2a = cos 2л + 2a—
I 4
л А - л . _ . л V2 _ V2 . _ = соя 2a— =cos2acos—+sm2asm —= — cos2a+—sin2a = 1	4	4	4	2	2
V2 1-tg2a 2tga 2 |j + tg2a l + tg2a,
V2 fl+2tga-tg2 a^_ V2 ctga ctg2a
2 [ l+tg2a j" 2	1+ 1
ctg a
V2 ctg2 a+2ctga-l V2 9 + 3	_ 7-J2
2 ctg2a+l	2	4 j 26
9
Ответ: —r-26
3.160. , „ . „ , если tga = 0,2.
6 + 7sin2a Решение.
5	_	5	_	5+5tg* 2a____
6+7sin2a 61 14tga 6+6tg2a+14tga
l	+ tg2a
5+5 0,04	= 65
6 + 6 0,04+14 0,2 113’
65 Ответ: —.
2
3.161. -—----если tga = 0,2.
3+4cos2a
Решение.
2	=	2	=	2+2tg2a	= 2+2tg2a
3+4cos2a 4-4tg2a 3+3tg2 a + 4-4tg2 a	7-tg2a
l + tg2a
_2+2 0,04_26
7-0,04	87'
Л 26
Ответ: —.
3.162. sina, если sin —+ cos—=1,4. 2	2
Решение.
.a	a	,,
sin —+ cos—= 1,4 =>
2	2
, 2«	Л	.	a	a	2®
=>sin	— + 2sin — cos— + cos	— = 1,96, sin —+cos — + sin a
2	22	2^2 2j
1 +sin a = 1,96.
Тогда sin a = 1,96 -1 = 0,96.
Ответ: sina = 0,96.
1,96,
3.163. sin2a, если sina-cosa = p.
Решение.
sina-cosa = p =>
=> sin2 a-2sinacosa + cos2 a = p2, l-sin2a = p2, откуда sin2a=l-p2.
Ответ: 1 - p2.
3.164. 2-13cos2a+sin"12a, если ctga = -y.
Решение.
<	ю -	1	~ 13-13tg2a
2 -13cos2a+sin 2a = 2 -13cos2a+---= 2--------— +
sin2a l+tg2a
2	2	13----Ц- 1 + —1-
+	1	= 2- 13~13t8 a + l + tg a _2_	ctg tx + ctg a
2tga	l + tg2a	2tga 11	1	2
l+tg2a	ctg2 a ctga
12 _n ±4.1
=2- 13ctg2a-13 + ctg2a+l = 2_ 25 _ + 25	=
ctg2a+l 2ctga ±+i	--
25	5
13-325 _ 1+25 . 312 26	13_57
1+25 2-5	26 10	5 5
57 Ответ: — •
3.165. l+5sin2a-3cos“*2a, если tga = -2.
Решение.
1+5 sin 2a - 3cos-12a = 1+5 sin2a-1— = 1+-------±—
cos2a 1+tg a 1-tg a l+tg2a
j IQtgct _ 3+3tg2q = j +10(-2) _ 3 + 3(-2)r l + tg2a l-tg2a 1+4	1-4
Ответ: 2.
( 5л
3.166. ls y + a
если
(in ) 9
tg — + 2a = —
2	11
-ос ,
Решение.
sin 2a
2 sin 2a _ 2 sin 2a
n	cos 2a
cos — + cos 2a
2
= 2tg2a =
2 ctg2a’
(7л -	(6л + л
tg|j- + 2aJ=tg|—
9	9
= -ctg2a = —, ctg2a = -—;
2 _ 2 __22 ctg2a _ 9	9
11
22
Ответ: ---• 9
[ л	]	12
3.167. Найти число a€ , если известно, что tg2a = —— \	j	5
Решение.
2 tga __12 1-tg2a 5 ’
1-tg2 a 5
=>6tg2a-5tga-6 = 0, откуда (tg a)] = ^, что не подходит к решению задачи, так как по условию угол принадлежит 2-й четверти и его тан-
2
гене отрицателен, и (tga^ = - у .
Отсюда,
а =-arctg-4-ял, ле Z . Так как
то
2
a = -arctg j + тс
Ответ: я-arctg—.
3.168. Доказать, что если АиВ — острые углы некоторого прямоугольного треугольника, то sin 2 А+sin2В = 4 sin A sin В.
Решение.
sin 2 А + sin 25 = 4 sin A sin В =>
=> 2 sin A cos А + 2 sin В cos В = 4 sin A sin В.
Сумма острых углов прямоугольного треугольника равна 90°.
Отсюда А 4- В - 90°, В = 90° - А, и
2 sin A cos A 4-2sin(90° -j)cos(90° -л)= 4 sin A sin(90° - а) => => 2sinЛ cos A 4-2cosЛбш A = 4sin Acos A,
4sinAcos Л =4sin Acos A,
что и требовалось доказать.
Р < я j, если известно, что tg(a 4- р) = и
। я
3.169. Найти число В — <
I 2
tga = -4 .
Решение.
ч(а+Р)=ч“±йЬ_1
1-tgatgp 19
Так как tga = -4,
то l+4tgp "19’	откуда
P = -arctg5 + nn,ne Z. С учетом того, что Pe
л A , получим
J
p = л-arctg 5.
Ответ: p = л-arctg 5.
3.170. Найти sin4 a+cos4 a если известно, что sin a - cos a = - .
2 Решение.
sin4 a+cos4 a = ^in2 3 4 a+cos2 af -2sin2 acos2 a = 1-2 sin2 acos2 a.
„ 1
Возведя обе части равенства sin a-cosa = - в квадрат, получим
2	2	1
sin a-2sinacosa+cos a = — , 4
откуда
3 . 2	2	9
sinacosa = - sin acos a = —. 8’	64
Подставив это значение sin2 acos2 a в исходное равенство, получим
• 4	4	1 о 9	,	9	32-9	23
sina + cos a = 1 - 2 — = 1-=--= —
64	32	32	32
23 Ответ: —
3.171.	Дано: ctga = ^,ctgp = |,0<a<^,0<p<p Найти a + p. Решение.
о 3 1 ctga + ctgp = - + -, 4 7
cosa cosp _ 25 sina sinp 28’
sinpcosa+cospsin a _ 25
sinasinp 28
_	3 cosa
По условию ctg a = ----
4 sina
3 cos2 a 9 l-sin2a 9
= 77^—2— = —’ОткУДа
4 sin a 16 sin a 16
• 2	16
sm а = 25 И’ТаК КаК ае
4	„ 1 cos2 Р 1 l-sin2p 1
5	7 sin2 p 49 sin2 P 49 ’
откуда
sin2 P = 7^ и, так как Pe I I, to
50	\	\
. „	7	7
SinP = -^=- = —T=
V50 5V2 ’
Подставляя полученные значения, получаем
sin(a + p) 25 . / а\ m(o+D)=-,
5 5>/2
откуда а + Р = (-1)" + ли, пе И;иучитывая ограничения на а, р,име-
а Зя ем а+Р = — 4
Л	О Зя
Ответ: а+Р = — 4
3.172.	Найти ctg2a, если известно, что sin
и
270’< а < 360° • Решение.
sin(a-90’)=-p -sin (90°-а)=~-, sin(p0°-a)=—, 3	3	3
2	2	4
cosa = -, cos a--, 3	9
.	• 2	-2	5
1-sm a=—, sin a = —.
9	9
С учетом того, что х е (270°; 360°), имеем sina = --^-. Учитывая
найденные значения, получим
ctg 2a = —1— tg2a
j _ sin2 a
1	_ 1 - tg2 a _ cos2a _ cos2 a-sin2 a
2 tga 2 tga 2sina	2 sin a cos a
1-tg2 a	cosa
4_5
9 9
'5
2- - —
3
3
„	*5
Ответ:----
20
3.173. Доказать, что если a и P удовлетворяют неравенствам
л Л Л _ Л	7	„	1	Я
0<а<—,0<В<—и cosa = —tgB = —, то а + 2В =—.
2 Р 2	V50	3	4
Решение.
sina 2tgP
tg(a+2Р) = tga + tg2P = COSa 1-_tg2J3 = l-tgatg2p । sina cosa
2tgp l-tg2p
_ sina(l-tg2 P) + 2tgPcosa cos a(l - tg2 Р) - 2 sin a tg р
Так как ае 0;— , то
I 2J
7	2	49 .	. 2
cosa = —т=, cos а = —, 1 — sin а
>/50	50
49 . 2	1	1
—, sin a = —, sina =-?=
50	50	V50
1	7	1
Учитывая значения sina = —?=, cosa =-7= и tgB = —, имеем V50	V50	3
9	-F= 1-- +2----7==
sina(l-tg P) + 2tgPcosa _ V5Q < 9 J 3 V50 cosa(l-tg2p)-2sinatgp 7 (। О 2 * *
V50l 9J TV50
Отсюда tg(a + 2P) = l,T.e. a + 2p = ^ (при 0<a<— и 0<p<~), что и требовалось доказать.
3.174.	Найти tg2a, если известно, что cos(a-90°) = 0,2 и 90°<а<180°.
Решение,
cos(a - 90°) = cos(90° - а) = sin а = 0,2, sin2 а = 0,04,
*>	о	24
1 — cos 2 а = 0,04, cos2 а = 0,96 = —, 25
cosa =
при а е (90°;180°).
„	- sin 2а	2 sin a cos а
Далее, tg2a =-----—- =—5-----------—
cos 2а cos а - sinz а
2 1 (. 24бУ
5 I 5 J = 4л/б
24_J_	23 '
25 25
Ответ:-------.
23
3.175.	Доказать, что если а и Р удовлетврряют неравенствам
0<а<—, 0<р<— и tga = 5, ctgp = —, то а + р =—.
2	2	3	4
Решение.
CtgB=- C0SP^2 cos2P = 4 1~sin2P = 4 sin26 = 2.
3 sinP 3 sin2p 9 sin2p 9	13
л
откуда при 0 < P < у имеем
2	2
. а 3	sina sin a 1-cos а г 1
sinP = -₽=; tg а = 5;--= 5; —x— = 25;------= = 25; cos a = —
V13	cosa cos2 a cos2 a	26
Отсюда при 0 < а < — находим cosa = -7=. Тогда 2	V26
»	2 с 13
ctgp-tga = --5 = -y,
cosp _ sina _ cosacosp-sinasinp _ cos(a+p) _ 13
sinp cosa sinpcosa sinpcosa 3
Использовав найденные значения sin p = -7= и cosa = -7=, имеем 713	V26
cos(a+p) _ 13
3	1 ~~T’
713 726
13>/2cos(a+p) _ 13 j	_ _у> откуда
cos(a + р) = —у, отсюда a + Р = у, что и требовалось доказать.
3.176. Дано: ctga = 4, ctgP = |, 0 < a < у 0 < р < у Найти a + р. Решение.
.	. cosa . cos2 a l-sin2a
ctg a — 4, -— = 4, —5— = 16,---5— = 16,
sina sin a sin a
• 2	1-	n л
откуда sm a = —, отсюда при 0 < a < — имеем
1 a cosP 5 cos2p 25 l-sin2p 25 sma = -=; ctgP = -£ = -,—=	,-----£ = —
717 sinP 3 sin2 P 9 sin" p 9 ’
9	л	3
откуда sin p — следовательно, при 0 < p < — имеем sinP = -т= 34	2	V34
Тогда ctga + ctgP =
cosa cosP _ sinPcosa + sinacosp _д + 5 sina sinP sinasinP	3
17
3 ’
sin(a + p)_ 17
sinasinP 3
Использовав найденные значения sin а = —= и sin В = —/=, имеем л/17	у/34
sin(a+p)_17	17-У2 sin(a+p)_ 17
1___з_ з ’	3	" 3 ’
V17 >/34
откуда sin(a + p)=^y-.
п а< —
2
Отсюда a + р = у для 0 < 4
иО<Р<^.
О Я
Ответ: а + р = —.
4
3.177. Вычислить (1 + ctgaXl + ctgр), если а + р = -р Решение.
(1 + ctg аХ1 + ctg р) = (1 +	Y1 +
I sina 1 smp
sin а + cos а ------------х
sina
^sinp + cosp _ cos acosp + sin asin p + sin acos p + cos a sin p _ sinp	sin asin p
cos(a - P)+ sin(a + p) |(cos(a-p)-cos(a + p))
/9
2 cos(a-p)+ —
---------л~2=2‘ cos(a-p)+y-
Ответ: 2.
3.178. Вычислить (1 + tgaXl + tgp), если a + p = ^.
Решение.
(l + tgaXl + ЧЙ-
i cosa 1 cosP I cosa
cos P + sin p _ cos acos P + sin a sin P + sin acos p+cos a sin p _ cosp	cosacosP
(
2 cos(a-p)+^-
cos(a - 0)+sin(a + р) - 1 . .
2...................
(	=2.
у (cos(a-p)+cos(a + p)) Cos(a-p)+^y-
Ответ: 2.
V21	V21
3.179. Доказать, что если sina = —sinP = -^- иа,Р —острые
углы, то a + Р = 60°. Решение.
V21 . ,	21 t 2	21 i 28
sina =--,sm"a = —,1-cos a = —,cos"a = —
7	49	49	49
так как aa — острый угол, то cos a =
. п V21 .	21 ,	21	175
sinp =----, sin" P = —, 1 -cos" P = —, cos" p =-;
14 H 196 H 196 И 196
так как РР — острый угол, то cosp =
. Тогда
sin(a + р) = sin acos Р + cos asin p =-------+-----------= —
K H 7	14	7	14	2
Следовательно, a + р = 60°, что и требовалось доказать.
sin a + tga
3.180. Показать, что выражение cosa+ctaa неотрицательно в об-
ласти определения.
Решение.
sina + tga _ sina + tga _
cosa + ctga „ , 1 b cosa +-------------
tga
(	\2
8tg2|	Vitgf
=----:H------------7 = 7---------v2------г >o,
H2! 1+,8i
2 j 2) \A	J J
Что и требовалось доказать. 2	• 2
3.181.	Исключить а из равенств х = tg а, у = sm а.
Решение. 2 sin2 а у у 2
x = tg а = —z— = —— и — = cos а. cos2 а cos а *
Отсюда
у . 2	2	У
у + —= sin а + cos а, _у + — = 1, ху + .у = х, х-у = ху.
X	X
Ответ: х-у-ху.
3.182.	Доказать, что cos 2 - cos 8 < 0.
Решение.
cos 2-cos 8 = -2sin5sin(-3) = 2 sin 5 sin 3.
Так как -^<5<2л, то sin5<0;3<n, поэтому sin3>0. Тогда 2sin5sin3<0 и cos2-cos8 < 0, что и требовалось доказать.
3.183.	Величины а, р, у в указанном порядке составляют арифметиче-_	sin a-sin у	_
кую прогрессию. Доказать, что----------= ctgp.
cos у-cos а
Решение.
Согласно свойству членов арифметической прогрессии
ак =а*-1+°Аг-И ( * = 2, 3,.... п -1, поэтому
н 2
Тогда
~ а+у . а-у 2 cos--sm-----L
sina-siny _	2	2
cosv —cosa ♦ a + y . a —у
'	2 sin-Lsin----L
2	2
= ctg^|^ = ctg0,
что и требовалось доказать.
3.184.	Дана дробь — .	Преобразовать подко-
1 +у32со5415°-10-8>/з
ренное выражение к более простому виду, после чего дробь сократить. Решение.
___________5___________=____________5_____________
1 + ^32сов415°-10-8->/з 1 + ^32(cos215 )2-10-8-Уз
5(1-^4+У16)	= 5(l-^4+Vl6) = j _ 3/4 + 3/jg
+ 1+4
Ответ: 1-^4 + l/l6
3.185.	Выразить tg4 a+ctg4 а черезт, где m = tga+ctga.
Решение.
tg4a+ctg4a = ((tga+ctga)2-Itgactga^ -2tg2actg2a = = ((tga+ctga)r -2^ -2 = ^и2 -2^ -2 = m4 -4m2 +4-2 = = m4 -4m2 +2.
4 о л Ответ: m -4m +2.
Решения к главе 4
ПРОГРЕССИИ
ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ
Арифметическая прогрессия
Арифметической прогрессией называется последовательность, у которой задан первый член av а каждый следующий член, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом d, называемым разностью прогрессии.
Если заданы первый член ах и разность арифметической прогрессии d, то и-й член арифметической прогрессии вычисляется по формуле
ап +<7(л-1),	(4.1)
Формула (4.1) называется формулой общего члена арифметической прогрессии.
Свойства членов арифметической прогрессии
1. Каждый средний член арифметической прогрессии равен полусумме равноотстоящих от него членов:
ак = ак-\+^ак+\ , к = 2> з,п _ j.	(4 2)
2. В конечной арифметической прогрессии суммы членов, равноотстоящих от ее концов, равны между собой и равны сумме крайних членов:
Д| + ап = а2 + а„_х = ... = ак + ап_к^} =... = 2а, + d(n -1).	(4.3)
Сумма п первых членов арифметической прогрессии
Сумма п первых членов арифметической прогрессии равна
Sn=^-n.	(4.4)
Учитывая (4.3), т.е что ах +ап = 2а{ +</(л-1), формулу (4.4) можно записать в виде
Sn = 2ai+d2{n~^n.	(4.5)
Геометрическая прогрессия
Геометрической прогрессией называется последовательность, у которой задан первый член bv а каждый следующий член, начиная со второго,равен предыдущему члену, умноженному на одно и то же постоянное для данной последовательности число q, называемое знаменателем прогрессии.
Если заданы первый член и знаменатель геометрической прогрессии д,то л-й член геометрической прогрессии вычисляется по формуле bn=bl4n-1.	(4.6)
Формула (4.6) называется формулой общего члена геометрической прогрессии.
Свойства членов геометрической прогрессии
1.	Квадрат каждого среднего члена геометрической прогрессии равен произведению равноотстоящих от него членов, т.е.	'
(4.7)
2.	В конечной геометрической прогессии произведения членов, равноотстоящих от ее концов, равны между собой и равны произведению крайних членов:
*1 A = *»2 А-! =byb„_1=... = bk-bM..^qn-\ (4.8)
3.	Произведение п первых членов геометрической прогрессии с по
ложительными членами равно корню квадратному из л-й степени произведения ее крайних членов:
Рп=^ьп)п.	(4.9)
В общем случае
Сумма п первых членов геометрической прогрессии
Сумма п первых членов геометрической прогрессии вычисляется по формуле
S„=b>~n4	(4.10)
1-9
Учитывая (4.6), т.е. что bn -b^qn~x, формулу (4.10) можно представить в виде
Сумма членов бесконечной геометрической прогрессии
Бесконечный числовой ряд, образованный из членов геометрической прогрессии Ь} + Ь2 + &3+ ...+ Ьп +... , при |<?| < 1 сходится, и его сумма 5 равна
S =-^~.	(4.12)
1-9
Формулу (4.12) называют также формулой суммы членов бесконечно убывающей геометрической прогрессии.
4.	001.3а изготовление и установку самого нижнего железобетонного кольца заплатили 2600 руб., а за каждое следующее заплатили на 200 руб. меньше, чем за предыдущее. Кроме того, по окончании работы было уплачено еще 4000 руб. Средняя стоимость изготовления и установ-
4
ки одного кольца оказалась равной 2244 — руб. Сколько колец было уста
новлено?
Решение.
Пусть = 2600 — первый член арифметической прогрессии, d = -200— разность этой прогрессии, п — количество членов.
Тогда по формуле (4.5) получаем
Z-ZOOCC-IX-ZOQ) --------г-------------= 2244, п---------------------9
2	40
9п - 41л - 360 = 0, откуда п\ = 9; л2 = _ ~ (не подходит).
Ответ: п-9.
4.002.Сумма первого и пятого членов арифметической прогрессии равна 5/3, а произведение третьего и четвертого ее членов равно 65/72. Найти сумму 17 первых членов этой прогрессии.
Решение.
Имеем
5 а1+а5
65 43-4<=^
Используя формулу (4.1), находим
а, +а( +4d = |, (a1+2rf)(a1+3<Z) = ^
2а.+4</=-,
1	3
(a1+2rf)(a1+3J) = ^
a,+2d = —,	al+2d-~,
6	О
(a1 + 2<Z)((a1+2J) + </) = ^|	=
72 [O\O 7
По формуле (4.5) получаем =
2- + — 16
3 4
2
•17 = 1”
3
119
Ответ:
4.003. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, а за каждый последующий — на 1/2 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?
Решение.
Пусть ах = 1 — первый член арифметической прогрессии, d = ± —
ее разность, Sn = 7 — сумма п членов этой прогрессии, где п — количество членов. По формуле (4.5) имеем
--------—-л = 7, л2+Зи-28 = 0,
2
откуда пх = -7 (не подходит); п2 = 4 . Отсюда: стрелок попал в цель 21 раз.
Ответ: 21 раз.
4.004. Найти три первых члена аьа2, аз арифметической прогрессии, если известно, что Л] + а3+а5 =-12 и аха3а5 =80.
Решение.
\а{ + а3 +д5 =-12,
Из условия имеем s
[oj ^3 ^5= 80.
Используя формулу (4.1), получим
(ах + ax+2d + ax+4d = -12,
[aifo + Id \ax + 4rf)= 80
Ja1+2rf = -4,
+2rfXai +2d + 2J)= 80
ar(-4X-4+2</)=80
al=-4-2J, at(d-2) = -10**
|a|=-4-2rf, Ц-4-2^-2)=-Ю**
(at = -4-2d, (rf = ±3.
Я| =-4-2б/, d2 =9
[л = -4-2rf, \ax = -4-2J, Отсюда s ,	или i
[d = -3	|// = 3,
т.е.
= 2, d = -3
или
aj =-10, d = 3.
Тогда
ax = 2,a2 = 2-3=-l,a3 = 2-6 = -4;
или
a{ =-10, a2 =-10 + 3 = -7, a3 =-10+6 =-4.
Ответ: 1) 2, -1, -4; 2) -10, -7, -4.
4.005. Найти число членов арифметической прогрессии, у которой сумма всех членов равна 112, произведение второго члена на разность прогрессии равно 30, а сумма третьего и пятого членов равна 32. Написать три первых члена этой прогрессии.
Решение.
f(ai +d)d = 30, И3^СЛ0ВИЯИМееМ [(a,+2</)+(a, + 4rf)= 32 =>^=16-34/, (16-2</)rf = 30, 2d2 -16t/ + 30 = 0 или
rf2-8rf+15 = 0=>
/ = 3,	p' = 5
=> z ИЛИ 5 » ax =7	[ai =1
Для каждого из решений воспользуемся формулой (4.5).
1) При ах = 7, d' = 3 получим
14 + 3(«- 1)	о 2 it	л
П2 =----------л, Зп +11и-224 = 0,
2
32
откуда п} = 7 , п2 = —— (не подходит). В этом случае имеем
«I =7, а2 = Ю, а3 =13 •
2) При ц =1 сГ = 5 имеем 112 = ^-—^——л, 5л* 2 * *-Зп-224 = 0,
откуда п = 7 , п = -6,4 (не подходит). В этом случае три члена таковы:
= 1, а2 = 6,а3 =11.
Ответ. 7; 1)7, 10,13; 2) 1,6, 11.
4.006. Турист, поднимаясь в гору, в первый час достиг высоты 800 м, а каждый следующий час поднимался на высоту, на 25 м меньшую, чем в предыдущий. За сколько часов он достигнет высоты в 5700 м?
Решение.
Пусть ц=800 — первый член арифметической прогрессии, d = -25 — разность, Sn = 5700 — сумма п членов этой прогрессии. Используя формулу (4.5), получим
п = 5700, п2 -65и + 456 = 0,
2
отсюда п{ = 8 , п2=57 (не подходит).
Ответ: за 8 часов.
4.007. При делении девятого члена арифметической прогрессии на второй член в частном получается 5, а при делении тринадцатого члена на шестой член в частном получается 2 и в остатке 5. Найти первый член и разность прогрессии.
Решение.
{а9
«13 =2«6 + 5-
Используя формулу (4.1), получим
Гц + 8rf = 5(ц +rf) Г4ц =3J, Ш = 2(а} + 5d)+ 5 ** [а, = 2d - 5, **
'4(2J-5)=3< ‘ aj=2J-5
d = 4,
a( =3.
Ответ: 3; 4.
4.008. Найти четыре числа, образующих геометрическую прогрессию, у которой сумма крайних членов равна -49, а сумма средних членов равна 14.
Решение.
+Z>4 =-49, Из условия имеем < =14.
Используя формулу (4.6), получим
Ь + b,q3 = -49,	(1 + q3 )= -49,
b\q + bxq* 1 2 = 14	|б19(1 + ^) = 14
[a(i+?)J-?+?2)=-49>
[/w(l + $)=14.
Разделив первое уравнение системы на второе, получим
®=0 1V+359+14=o.
biq^ + q) 14 q 14
2?2+5?+2 = 0 т.е. q = -2, / =	=7, />, =-56.
Тогда получим:
1) bi' = 7, b2 = -14, b3 =28, b4' = -56 *
2) Z>j" = -56, b" = 28, b" = -14, />/ = 7 •
Ответ: 1) 7, -14, 28, -56; 2) -56, 28, -14, 7.
4.009. Найти третий член бесконечной геометрической прогрессии со знаменателем |<?| < 1, сумма которой равна 8/5, второй член равен -1/2.
Решение.
к
Используя формулы S = —- и bn — bxqnA , получим -
bi _8 \-q 5’ , 1 ^ = -2
—	, 16g2 -16g -5 = 0, откуда найдем Ч\ =	, Чг = — > 1 (не
7	(
подходит). Тогда ^з = Ь\Ч~ =
1У_ п
2 Л Л
8’
Ответ: -
О
4.010. Найти три первых члена бесконечной геометрической прогрессии со знаменателем |^| < 1, сумма которой равна 6, а сумма пяти первых членов равна 93/16.
Решение.
Используя формулы 5 = —— и (4.11), получим
1-^
У^ = 6,	р>!=б(1-д>	р!=б(1-д>
“м—й	16	2
t , 1 3 t , 1 3
Тогда Ь2 = 3- = -, Ь3 = 3 - = -.
Z7	, 3	3
Ответ: 3,—,—.
2 4
4.011. Сумма трех чисел, образующих арифметическую прогрессию, равна 2, а сумма квадратов этих же чисел равна 14/9. Найти эти числа.
Решение.
ах + а2 + л3 =2,
Из условия имеем
д|2
2	2 14
а2 +а3 =у
+
Используя формулу (4.1), получим
+О|+2t/ — 2,	в|+</	,
а2+(а, +J)'+(a1+2J)'= —	2,4 ,/2	_14
[ 1 9 [3	) 9
3 Отсюда имеем: 1) За2-4o,+1=0.
Тогда
,	, 2	' 1	" 1	"2	",
1) at =1, a2 =-, a3 = -;2) at =-, af = -, a3 =1.
,21	12,
Ответ: 1) 1,	2)	1.
4.012. Сумма третьего и девятого членов арифметической прогрессии равна 8. Найти сумму 11 первых членов этой прогрессии.
Решение.
Из условия имеем а3+О9=8. По формуле (4.1) получаем a1+2rf+a14-8rf = 8> 2^410^ = 8, а по формуле (4.5), находим SH = 2а1^—.11 = 44
Ответ: 44.
4.013. Сумма трех первых членов возрастающей арифметической прогрессии равна 15. Если от первых двух членов этой прогрессии отнять по 1, а к третьему члену прибавить 1, то полученные три числа составят геометрическую прогрессию. Найти сумму 10 первых членов арифметической прогрессии.
Решение.
Из условия имеем: av -1, ^+</-1, ах +2^41 --три последовательных члена геометрической прогрессии. По формуле (4.5) находим 53 =	t-—-3 = 15 или ^+^ = 5. По формуле (4.7) получаем
=(^-1X01+26/+!). Подставляя в это уравнение значение
ax =5-d , получим 16 = (4-d\() + d\ d2 +2d-8 = 0. Отсюда J,=-4, d2 =2 . Тогда ax =9, a2 =5, a3 =1; ax =3, a2 =5, a3 =7. Учитывая, что по условию «] < а2 < а3, получим а, = 3, d = 2. Тогда
Slo = 2’3+2'9 10 = 120.
Ответ: 120.
4.014. Известно, что при любом п сумма Sn членов некоторой арифметической прогрессии выражается формулой Sn = 4и2 -Зп. Найти три первых ч лена этой прогрессии.
Решение.
Пусть л=2 и п-3. По формуле (4.4), находим
5, =^-|^-2 = 4 (2f-3-2 = 10, =а±£1.3 = 4.(з)2_3.3 = 18
или по формуле (4.1) получаем
(а, + а, + d = 10,	[2а + d = 10,	[а=1,
+«! +2 J =18	[aj+rf = 9	|d = 8.
Тогда a2 = ax + d = 9, a3 = +2d = 17 .
Ответ: 1,9, 17.
4.015. Вычислить
(l+З2 +52 +... + (2n-tf +...+1992)-(г2 +42 +62 + (2nf +...+2002).
Решение.
Из условия имеем
l + З2 +52 + ... + (2л-1)2 +...+1992 -22 -42 -62 -(2л)2 -...-2002 =
= (1 - З)2 + (з2 - 42)+ (s2 - 62)+... + ((2л -1)2 - (2л)2)+...+(1992 -2002 )= = (1-2Х1+2)+(3-4ХЗ+4)+(5-бХ5 + б)+...+(2л-1-2лХ2л-1 + 2л)+ +...+ (199-200X199+200)=-3-7-11-...-(4л-1)-. ..-399.
Отсюда =-3, J = -4, ап =-399 . Используя формулы (4.4) и
ап ~ а\ 1
п = ——- +1, получим
Sn =
-3-399
2
-399 + 3 Л
-------+ 1
-4	)
= -20100.
Ответ: - 20100.
4.016. Найти четыре числа, образующих геометрическую прогрессию, у которой второй член меньше первого на 35, а третий больше четвертого на 560.
Решение.
Из условия имеем
£>!-*2=35, by - 64=560.
По формуле (4.6) получаем
*1-% = 35,	f*1(l-^) = 35, i-g _ 35
%2-*,93=560	|*i<72(l.-g) = 560	92(1-^)~560
=> </2 = 16,<?| = -4,<?2 = 4. Подставляя qx = -4, получим
*1 =7,*2 =~28,*з =112,*4 =-448. Подставляя qy = 4, получим
"	35 , "	140 . "	560 . "	2240
61 ’’Т'*2
14^7 оо 11. лло 35	140	560	2240
Ответ: 1) 7, -28,112, -448; 2)--,---,-----,-----.
3	3	3	3
4.017. Найти четыре числа, образующих геометрическую прогрессию, у которой третий член больше первого на 9, а второй больше четвертого на 18.
Решение.
IZh-fy =9, Из условия имеем <
1^-64=18.
По формуле (4.6) получаем
*1<72-*1=9, b^q-b^q* = 18
*!(<?2-1) = 9,	_	?2-1	_9_
-blq(q2-l) = lS -?(?2-1) 18
9
=> q = -2. Подставляя q = -2, получаем bx = —z— Я -1
9
=----= 3. Тогда
4-1
*2 =—6,*з =12,*4 =—24.
Ответ: 3, -6,12, -24.
4.018. Знаменатель геометрической прогрессии равен 1/3, четвертый член этой прогрессии равен 1/54, а сумма всех ее членов равна 121/162. Найти число членов прогрессии.
Решение.
Из условия имеем
ь4 =—,
4 54’
S
. ” 162
По формулам (4.6) и (4.11) получаем
.	, з .fiY bi i , i
о4 = ад = 6, - ; — =—, Oi= —
4	1 3 I 27 54 1 2
= —=>24з(з"-1)= 242-3”
162 V ’
=> 3” =243, n = 5.
Ответ: n = 5.
4.019. Найти первый член и знаменатель геометрической прогрессии, если известно, что Ь4 -Ь2 =-45/32 и 56 -64 = -45/512 .
Решение.
Из условия имеем
45
32’
-b4=-
45
512
^4 “ ^2 - “

Используя формулу (4.6), получим
[, 3 ,	45	32’	g(y2-l) 512 32
2	1	I	1 „
=> q = —,	= ~7>	= 7 • Подставляя эти значения qt и q2, найдем
16	4	4
= -6 и = 6 •
Ответ: 1) - 6, - —; 2) 6, - .
4.020. Найти первый и пятый члены геометрической прогрессии, если известно, что ее знаменатель равен 3, а сумма шести первых членов равна 1820.
Решение.
Из условия имеем q = 3, S6 = 1820 .
По формуле (4.11) получаем
^——^ = 1820, ^=5. 1-3	1
Используя формулу (4.6), найдем Ь5 = £^4 = 5 • (з)4 = 405.
Ответ: 5, 405.
4.021. Арифметическая прогрессия обладает следующим свойством: при любом п сумма ее п первых членов равна 5п2 . Найти разность этой прогрессии и три первых ее члена.
Решение.
Пусть л = 2 и и = З.Поформуле(4.5)находим
^а\	7 - S 72
7 Э ’	[2a1+t/ = 20, R = 10,
2ax+2d у1	=	(/*1=5.
2
Тогда a2 =15, a3 =25 .
Ответ: 10; 5, 15, 25.
4.022. Произведение трех первых членов геометрической прогрессии равно 1728, а их сумма равна 63. Найти первый член и знаменатель этой прогрессии.
Решение.
fa Л А =1728, Из условия имеем 5,	7	.
J	+b2 + Ь3 =63.
Используя формулу (4.6), получим
bi-btf-biq2 =1728,
' >
4	+	= 63
M = 1728,	(*W = 12,
1} + l\q + (bfl )j = 63	[^+12+12^ = 63
*W = 12, 6j+12^ = 51.
=> 4<?2-17<?+4 = 0,
<7 = 4 или q = —. 4
\q = 4, Отсюда получаем s или «
4=48.
Ответ: 1) 3, 4; 2) 48, ~ .
4.023. Решить уравнения:
а)	2х + 1 + х2 -х3 + х4 -X5 +... = 13/6, где |х|<1;
б)	—ьх + х2 + ... + хл + ... = —, где |х| < 1.
х	2	’ 1
Решение.
а) 2х + 1 + (х2 -х3 +х4 -х5 + ...)= 6
По формуле S =	получаем
1-9
X2	13	17
2х+1+-----= — =>18х2+5х-7 = 0 =>*!=-> х2=~а’
1 + х	6	2	9
б) —+ (х + х2 + ... + х" + ...)=
По формуле (4.12) получаем
Ответ: а) Х| = -, х2 = --; б) х2 = - .
4.024. Первый член арифметической прогрессии равен 429, разность ее равна -22. Сколько членов этой прогрессии нужно взять, чтобы их сумма была равна 3069?
Решение.
Из условия имеем at = 429, d = -22, Sn = 3069.
По формуле (4.5) получаем
2-429-22(и-1) п = 3069, (429_j= 3069
п2 -40л+ 279 = 0 => п{ =9, п2 =31.
Ответ: 9 или 31.
4.025. Сумма бесконечной геометрической прогрессии со знаменателем |<?| < 1 равна 16, а сумма квадратов членов этой же прогрессии равна 153,6. Найти четвертый член и знаменатель прогрессии.
Решение.
Из условия имеем
Ь\ + ^2 + 63 + • • • = 16, l^+l^+bl +... = 153,6,
По формуле (4.6) получаем
5, +biq + l\q2 +... = 16,	^(j+9 + 92 +...)=16,
Д2 + b2q2 + bfq4 +... = 153,6 J + q2 + qA +.. .)= 153,6.
По формуле (4.12) получаем
^—=16,
&2—Ц- = 153,6 1"?
=> b[ =16(1-9) => (1б(1-9))?——г = 153,6, откуда 9 = — . Тогда
1~9	4

= 12. По формуле (4.6) получаем b4 = bfq3 = 12 • — = 64
3
16
3 1
Ответ:	—
16 4
9 М. И. Сканави, группа А
257
4.026. Найти натуральные числа, образующие арифметическую прогрессию, если произведение трех и четырех первых ее членов равны соответственно 6 и 24 .
Решение.
[«!(«! + rf)(«2 +^) = 6 условия имеем < z , z Л , z
+ 2rf)(«j + 3J) =
^1 (#| + ^)(«2 + tZ)	6	J A A 1 J
=>-------------------------= — =>«i + 3d = 4,«, = 4-3tZ.
a1(a1+6/)(a2+t/)(a1+3rf) 24	1	1
Получаем уравнение
3d3 - lid2 + 48</ - 29 = 0 <=> 3d3 - 3d2 -19d2 +19d + 29d - 29 = 0 <=>
о(d-l)(3d2-\9d + 29) = 0 =>di =1,J23 =	(не подходят).
’	6
d = 1 => «] = 1, «2 = 2, «з=3, «4=4.
Ответ: 1,2,3,4, ...
4.027. Сумма третьего и девятого членов арифметической прогрессии равна 6, их произведение равно 135/16. Найти сумму 15 первых членов этой прогрессии.
Решение.
Из условия имеем
«3 +«9=6,
135 а3п9= —
По формуле (4.1) получаем
«I + 2J +«i +8</ = 6,	(«j +5J = 3,
*	135	135
(«J + 2rf)(«! + 8rf) =	(«! + 2tZ)(«l + 8J) = —
16 I	16
=> a, = 3 - 5d => (3 - 5 d + 2</)(3 - 5 d + 8<7) =
,2	1 .	1 .	1
16	1	4	2	4
	. 17	.7
Тогда «j =— и «| =—. 4	4
По формуле (4.5) получаем
17	1 .л	7	1 «л
,-------14	„ - + --14
S15 = -^—-----15 = 37,5 или 5,5 = -2—4--15 = 52,5.
Ответ: 37,5 или 52,5.
4.028. Найти число членов конечной геометрической прогрессии, у которого первый, второй и последний члены соответственно равны 3, 12 и 3072.
Решение.
Из условия имеем Ьх = 3, b2 = 12,..., Ьп = 3072.
По формуле (4.6) получаем
*1 =3, q=4, 4'"1 =1024
5
/»!=3,
% = 12,
б,?”’1 * =3072
Ответ: 6.
4.029. Найти сумму всех положительных четных двузначных чисел, делящихся на 3 нацело.
Решение.
Из условия имеем ах = 12, ап = 96, d = 12 .
По формулам (4.4) и (4.5) получаем
H = q"~a| +1; n = —~12+1 = 15, S„ = —9^-15 = 810.
d	6	”2
Ответ: 810.
4.030. Найти знаменатель q бесконечной геометрической прогрессии (|^| < 1), у которой каждый член в четыре раза больше суммы всех ее последующих членов.
Решение.
Из условия имеем Ь} = 4(5-^).
По формуле (4.12) получаем
/>, =4f-A—U *, =
U-? I
1 л 1
, 1-<7=4?, q = -
1~<7
1
Ответ: —
4.031. Известно, что внутренние углы некоторого выпуклого многоугольника, наименьший угол которого равен 120°, образуют арифметическую прогрессию с разностью в 5°. Определить число сторон многоугольника.
Решение.
Из условия имеем а\ = 120°, d - 5°. Используя формулы суммы членов арифметической прогрессии (4.5) и суммы внутренних углов л-уголь-ника Sn = 180°(л - 2), получим
240°+ 01-1)5-. и _ j 8qo^w _ 2)эи2 _ 25и +144 = 0 =>
=> Л| = 9,л2 = 16 (не подходит, так как в этом случае
=> а16 = 120° +5° -15 = 195°, а внутренний угол выпуклого n-угольника всегда меньше 180° ).
Ответ: 9.
4.032. Произведение третьего и шестого членов арифметической прогрессии равно 406. При делении девятого члена прогрессии на ее четвертый член в частном получается 2, а в остатке 6. Найти первый член и разность прогрессии.
Решение.
Из условия имеем «И3 °6	По формуле (4.1) получаем
= 2я4 +6.
(a1+2t/)(a1+5t/) = 406, Uj +8d = 2(fl| +Зб/) + 6.
=>at = 2d-6 и 14rf2-33d -185 = 0, откуда найдем
37	'	( 37 1	79
d, =----,d? =5. Тогда a, =2-------6 =------(не подходит) или
1	14 2	I 14 J 7
ai"=2-5-6 = 4.
Ответ :4 и 5.
4.033. В бесконечной геометрической прогрессии с положительными членами и со знаменателем |#| < 1 сумма трех первых членов равна 10,5, а сумма прогрессии 12. Найти прогрессию.
Решение.
По формулам (4.6) и (4.12) получаем:
bl + bxq + Ьд1 = 10,5,	k (1 + q + q1) = 10,5,
A = 12(l-9)	=12(1-9).
Отсюда 12(1-^)(1 +</ +02) = 10,5, 12(1-?3) = 10,5, ? = 0,5.
Тогда bi = 12(1 -0,5) = 6, b2 = 3, by =
3
Ответ: 6,3, — ,....
2
4.034. Найти три первых члена арифметической прогрессии, у которой сумма любого числа членов равна утроенному квадрату этого числа.
Решение.
Пусть и = 2 и л = 3. Из условия имеем
а\ +а2 =3-22,
<
+ а2 4-я3 = З-З2.
По формуле (4.1) получаем
fa} +ai + d = 12,	j2aj 4-rf = 12, fd = 6,
[al+al+d + ai+2d = 27 [a14-rf = 9	(aj=3.
Тогда a2 = 9,a3 = 15.
Ответ: 3, 9, 15.
4.035. При делении тринадцатого члена арифметической прогрессии на третий член в частном получается 3, а при делении восемнадцатого члена на седьмой член в частном получается 2 и в остатке 8. Определить разность и первый член прогрессии.
Решение.
[^13 “ За3,
Из условия имеем S ~
1^18 ~ 2^7 4- 8.
Используя формулу (4.1), получим
п, + 12</ = з(а1+24	(at=3d,	1а,=12,
п, +17d = 2 (а, + 6J)+ 8 (а, = 5d - 8 ** [d = 4.
Ответ: 4, 12.
Решения к главе 6
АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ
ОСНОВНЫЕ ФОРМУЛЫ
Для любых а, b и с верны равенства:
(a + bf =а2 + 2ab+b2	(6.1)
(a-bf =а2 -2ab + b2 ;	(6.2)
a2 —b2 = (a-b\a+b)‘,	(6.3)
(а + bf = а3 + За2Ь + ЗаЬ2 + Ь3(6.4) (a-b)3 =а3-За2Ь + ЗаЬ2-Ь3;	(6.5)
a3 +b3 =(a+b^a2 -ab+b2);	(6.6)
а3 -Ь3 = (a-b/a2 +ab + b2)',	(6.7)
ах2 + Ьх + с = а(х - Xj X* - х2), где %i, х2 — корни уравнения
ах2 +Ьх + с = 0 •	(6-8)
РЕШЕНИЕ УРАВНЕНИЙ С ОДНИМ НЕИЗВЕСТНЫМ
Уравнением с одним неизвестным называется равенство /|(*)=£|(*)	(6-9)
где fx (х) и gj (х) — некоторые заданные функции переменной х над числовым множеством М,
Решением (корнем) уравнения (6.9) с одним неизвестным называется такое численное значение неизвестного, взятое из множества чисел,
указанных в условии уравнения, которое обращает данное уравнение в тождество (верное равенство).
Решить уравнение — это значит найти множество всех его решений или показать, что решений нет.
Областью допустимых значений неизвестного (ОДЗ) уравнения (6.9), называется множество всех значений, взятых из числового множества, над которым задано уравнение, при которых существуют обе фун-кции(части уравнения) /(х) и gjx).
Пусть в результате преобразования уравнения (6.9) получено уравнение
(6.10)
Если все решения уравнения (6.9) являются решениями уравнения (6.10), то уравнение (6.10) называется следствием уравнения (6.9).
Два уравнения (6.9) и (6.10) с одним и тем же неизвестным называются равносильными (эквивалентными), если уравнение (6.10) является следствием уравнения (6.9) и, наоборот, уравнение (6.9) является следствием уравнения (6.10) или если оба уравнения решений не имеют.
При преобразованиях уравнения область его допустимых значений может изменяться, полученное уравнение в общем случае неравносильно данному. Если при некоторых преобразованиях ОДЗ уравнения расширяется, то полученное уравнение может иметь корни, посторонние для данного уравнения.
Если обе части данного уравнения возвести в одну и ту же степень, то все его корни будут корнями полученного уравнения, т.е. полученное уравнение всегда будет следствием данного, обратное утверждение не всегда имеет место.
Всякое целое рациональное алгебраическое уравнение п-й степени с одним неизвестным может быть записано в виде
апхп + an_xx'l~{ +... + ajX + a0 =0	(6.11)
где ап, ап_х,..., а0 — заданные числа (коэффициенты уравнения), х — неизвестное, п — натуральное число.
Коэффициенты ап и а0 называются соответственно старшим коэффициентом и свободным членом уравнения (6.11).
Уравнение первой степени с одним неизвестным
Целое рациональное алгебраическое уравнение первой степени называют просто уравнением первой степени.
Любое уравнение первой степени с одним неизвестным может быть приведено к каноническому виду •
пх + 6 = 0 (а*О}	(6.12)
Уравнение (6.12) является частным случаем уравнения (6.11), если в последнем положить п = 1, а, = 1 и а0 = b.
Уравнение ах + 6 = 0 (а^0)в множестве действительных чисел всегда имеет решение, и притом только одно:
Ь х =—. а
Уравнение второй степени с одним неизвестным
Целое рациональное алгебраическое уравнение второй степени называется уравнением второй степени, или квадратным уравнением.
Всякое квадратное уравнение с одним неизвестным можно привести к каноническому виду
ах2 +6х + с = 0 (а*О)	(6.13)
Уравнение (6.13) является частным случаем уравнения (6.11), если в последнем положить п = 2 , а2 = а , а{ = b п а$ = с .
Квадратное уравнение (6.13), записанное в канонической форме, называется неполным, если хотя бы один из его коэффициентов, кроме старшего а, равен нулю.
Если все коэффициенты квадратного уравнения, записанного в каноническом виде, отличны от нуля, то оно называется полным.
Полное квадратное уравнение, старший коэффициент которого равен 1 (а = 1), называется приведенным квадратным уравнением', оно имеет вид
х2+рх + ^ = 0.	(6.14)
Формулы корней полного квадратного уравнения
Если D = Ь2 -4ас > 0 (дискриминант уравнения), то уравнение (6.13) в множестве действительных чисел имеет два и только два действительных корня, которые определяются по формулам
(6.15)
- b - 4 b2 -4ac	-b + >lb2 -4ac
Xi =--------------, x7 =------------
1	2a	2	2a
Если b2 - 4ac > 0, то xl Ф x2, а если b2 - 4ac = 0, то xx=x2, Если b2 - 4ac < 0, то уравнение (6.13) действительных решений не имеет.
В частном случае, когда b — четное число, т.е. Ь = 2к , уравнение (6.13) принимает вид ах2 + 2кх + с = 0, а формулы (6.15) преобразуются в следующую:
(6.16)
-к±\к -ас
xi 2 _ а
Если уравнение приведенное, т.е. имеет вид х2 + рх + q = 0, то для определения его корней получим
Х^~ 2 * V 4
(6.17)
Разложение квадратного трехчлена на множители
Выражение ах2 +Ьх + с при а Ф 0 называется квадратным трехчленом.
Выражение D = b2 -4ас называется дискриминантом квадратного трехчлена.
Если D > 0, то квадратный трехчлен разлагается на множители с действительными коэффициентами:
ах2 + Ьх + с = а(х-хх\х-х2\	(6.18)
где Xj и х2 — корни квадратного трехчлена, определяемые по формулам нахождения корней полного квадратного уравнения.
Биквадратные уравнения
Биквадратным уравнением называется целое рациональное алгебраическое уравнение четвертой степени, которое может быть приведено к каноническому виду
ax4 + bx2 +c = 0 (a#0).	(6.19)
Заменив x2 на Z, получим at2 + bt + c = 0, из которого находим _-b- ylb2 -4ас _ - b + 4 b2 -4ac ‘l~ 2a 't2~ 2a
Если Zj >0 и Z2 >0	(a>0,c>0,b2 -4ac>0,6<0 или
a < 0, c < 0, b2 -4ac > 0, b > 0), то биквадратное уравнение имеет четыре действительных корня
J-b-ylb2 -4ас , l-b + ylb2 -4ас ------э	’ хз,4 =	-z-• 2а---------------------------------1 2а
Уравнения, содержащие взаимно обратные выражения
Уравнения, содержащие взаимно обратные выражения и имеющие вид
решаются с помощью подстановки
(6.20)
(6.21)
Тогда ** t и относительно z получается уравнение
aZ + & —= <?или д/2_с/ + £ = о (z*0).
Теорема Виета
Корни уравнения апхп +ап_1хп~} +... + а1х + а0 =0 (дл*0) сего коэффициентами связаны следующими соотношениями:
ап-\
Х1 + х2 +‘-- + х„ =----—,
ап
ап^
х!х2 + Х1Х3+... + Хл_1Х// = “^>
ап-3
{Х}Х2Х3 +х{х2х4 +... + Хл-2х,1-1Хн =-------->
ап
Х^Ху.-.Х^Х^^^-. ап
Например, для уравнений четвертой степени ах* + bx3 + сх2 + dx + е = О (а * 0) теорема Виета имеет вид
X] +Хэ +х3 +х4 =---,
а с
Х}Х2 + XjX3 +Х)Х4 + х7х3 +х7х4 +х3х4 = —, а d
Х1Х2Х3 +Х1Х2Х4 + Х1Х3Х4 +Х2Х3Х4 =--,
а
е ххх2х3х4 = —; а
для кубического уравнения ах3 + bx2 + сх + d = 0 (а Ф 0):
Х1 + х2 + хз =--,
а
с
< XjX2 +XjX3 +Х2Х3 = —, а
d xtx2x3 =---;
а
для квадратного уравнения ах2 + Ьх + с = 0 {а 0):
b %i+x2 =—, a
c
Xl%2 =-• a
Иррациональные уравнения
Иррациоиалънымуравнением называется алгебраическое уравнение, если хотя бы один из членов которого иррационален относительно неизвестного, т.е. это есть уравнение, содержащее неизвестное под знаком радикала.
Общий метод решения иррациональных уравнений заключается в следующем: сначала изолируется один радикал, затем обе части уравнения возводят в степень, потом снова изолируют радикал и т.д. При возведении обеих частей уравнения в одну и ту же степень получается уравнение, в общем случае неравносильное данному; поэтому проверка найденных значений неизвестного по условию исходного уравнения обязательна, т.е. является составной частью решения.
Если обе части уравнения /|(х)= /2(х) возвести в четную степень л, то корнями полученного уравнения (/j(x))n = (/2(х))л будут все корни исходного уравнения (х) = /2 (х) и уравнения fx (х) = -/2 (х).
При переходе от уравнения Л(х) = /2(х) к уравнению (yj (х))" = (/2 (х))л потери корней не произойдет, но могут появиться посторонние корни, а именно: корни сопряженного с исходным уравнения
Если обе части уравнения /i(x) = /2(х) возвести в нечетную степень к, то получим уравнение (х))* = (f2 (х))*, равносильное исходному в множестве действительных чисел.
При возведении в нечетную степень обеих частей уравнения, рассматриваемого в множестве действительных чисел, посторонние корни не появляются.
Приступая к решению иррационального уравнения, целесообразно предварительно определить ОДЗ, так как может оказаться, что это уравнение не определено в области действительных чисел.
При решении иррациональных уравнений следует иметь в виду, что не принадлежащие к ОДЗ значения неизвестного всегда посторонние для решаемого уравнения; их можно отбросить без проверки по условию. Найденные значения неизвестного из области допустимых обязательно следует проверить по условию уравнения, так как они также могут оказаться посторонними.
СИСТЕМЫ УРАВНЕНИЙ
Системой п уравнений с т неизвестными называется п уравнений, в каждом из которых неизвестные, обозначенные одной и той же буквой, означают одну и ту же неизвестную величину.
Решением системы п уравнений с т неизвестными называется всякая упорядоченная совокупность из т таких чисел, которые, будучи подставлены в систему вместо неизвестных, обращают каждое уравнение системы в тождество.
Решить систему уравнений — значит найти множество всех ее решений или показать, что она решений не имеет.
Если система не имеет решений, то ее называют несовместной или противоречивой, в противном случае — совместной.
{а}х +Zm’ = q,
может либо иметь единственное решение, а2 х + Ь2 у = с 2
либо иметь бесконечно много решений, либо не иметь решений. При графическом способе решения каждому уравнению данной системы ставится в соответствие некоторая прямая на плоскости ХО У; таким образом, данной системе на плоскости соответствует пара прямых. Две прямые на плоскости могут либо пересекаться в одной точке, либо совпадать, либо не иметь общих точек.
При пересечении прямых данная система имеет единственное решение; при совпадении прямых данная система имеет бесконечно много решений; если прямые не имеют ни одной общей точки, то данная система решений не имеет.
Решить уравнения (6.001 — 6.066):
6.001.	1 = 23.
х - 4	л* + 3
Решение.
ОДЗ: х * -3, х # 4.
х2+1 х2-1 „	16х2-25х-275 п
х-4 х + 3	(х — 4Хх + 3)
=> 16х2-25х-275 = 0 => х. =	, х2 =5.
1	16	2
55 Ответ:	, х2 =->.
16
6.002. ----
х~а
Решение.
ОДЗ: х*а,
Ь —^—=2. х-Ь
х*Ь.
Ь । а х-а х-Ь
2х2 - 3(а + б)х + (а + б)2 _ ^-а\х-Ь)	=°^
а+Ь ~2~
а + Ь
Ответ:	, х2 = а + о.
X2 6Л03. —
3*	4 Л
-2---------+ 4 = 0.
2 . v с
Решение.
_ 1 + V21
ОДЗ: х Ф 0, х Ф у
х2
Пусть —
= z, тогда z + — + 4= 0 => z
=^z2 +4z + 3 = 0, =» zj =-3, z2 =-1.
Чтобы найти х, решим два уравнения:
х2+х-5	~2
--------= -3 или
= -1.
Решая каждое из них, находим:
%! = -5, х2 *з =-1->/б, х4 =-1 + >/б.
Ответ: х, = -5, х2 =1, х3-4 = -1±>/б.
4	50	..
6.004. х -	=14.
2х4 -7 Решение.
„	„ 4	Z+2 50
Пусть 2х - 7 = z, тогда —--— = 14 =>
Чтобынайтих, решим два уравнения 2х4 - 7 = -4 или 2х4 - 7 = 25,
решив которые, получим х, =
, х3 = -2, х4 =2.
Ответ: х12 = ±Я—, х3>4 = ±2.
б-°°5- х(х + 2) (х + 1)2 12’
Решение, ОДЗ: х * 0, х * -1, х Ф -2.
1________1	= J_ 1_______________1	= J_
х(х+2) (х + 1)2 ~12^х2+2х х2+2х+1 12'
Пусть х2 + 2х = z, тогда
z2+z + 12 Л 2	л -5
—7----г— = 0=» z +z + l2 = 0=»Zi =-4, Zo =3.
z(z + l)
Чтобы найти х, решим два уравнения: х2 +2х = -4 или х2 +2х = 3.
Решая их, находим: хх1 е 0 (р < 0} х3 = -3, х4 = 1.
Ответ: хХ 2 е 0, х3 = -3, х4 = 1.
6.006.
1	?	2
l _ m + n “ ~	2	2 *
x m — n
Решение.
ОДЗ: x * 0, т * ±п. .	7	2	7	2
1 ~т+п 2	+ л 1 л
х + - = 2—----<=>х2 -2—--х + 1 = 0,
х т~-п~	т~-п
корни Х| =
т + п	т-п
----, х2 = ——• т-п-т + п
л	т + п	т-п	। ।
Ответ'. х1 =-, х2 =----, где т * л
т-п	т + п	1
Решение.
ОДЗ: х * 0, а * 0.
х2 Ъ3 Ь Ь2	х4 -{a2b + ab2\c2 + а3Ь3
— □----= — + — <=>----------------£--------
а3 х2 а а2	а3х2
или х4 - (я 2 6 + ab2 )х2 + а3Ь3 =0, ах Ф 0.
Уравнение является биквадратным относительно х. Пусть х2 = j тогда наше уравнение принимает вид
у2 - [a2b + ab2 )у + а3Ь3 = 0,
откуда
a2b + ab2 ±\(a2b + ab2\-4а3Ь3 --------------------------=
a2b + ab2 +JaAb2 +2а3Ь3 +а2Ь4 -4а3^
2
b2 -2a3b3 +a2b4 _a2b + ab2
~2	Г"
a2b+ab2±\
; yi =ab2, у2 -а2Ь.
Чтобы найти х, нужно решить два квадратных уравнения: х2 = ab2 или х2 =а2Ь.
х12 = tTofe2" = ±bja , где с учетом ОДЗ а > 0;
х3 4 = +т]а2Ь = +ch[b , где Ь > 0 ♦
Ответ: хХ2 = ±bja , где а > 0; х3 4 = +ajb , где Ь > 0 ♦
6.008.
х-3 х + 3 х + 6 х-6 -----1--=-----1----.
х -1	х+1 х + 2 х-2
Решение,
ОДЗ: х Ф +1, х Ф +2.
х-3 х + 3 х + 6 х-6	2х2-6 2х2 -24
----+------=-----+-----<=> —----= —------<=> х —1 х + 1 х + 2 х-2 х2-1 х2-4
х2-3 х2-12	6х2
х2 -1 х2 -4	(х2 -1)(х2 -4)
отсюда х = 0.
Ответ: х = 0.
5а 4а За о
6.009. ——+ ~+ ~= 8 у + а у + 2а у + За
Решение.
ОДЗ: у Ф -а, у Ф -2а, у Ф -За.
-g8-У3 +36лу2 +38а2^
у + а у + 2а у + За	{у + а)(у + 2ajy + За)
или
j>(4j>2 +18ау+19а2)=0,
у Ф -2а, уФ-За
>=>;> = 0 или 4^2 + 18яу + 19а2 =0.
-9а±78к?-76а2 -9a±aV5 a(-9 + >/3 ’	4	4	4
„ л a(-9± Уз)
Ответ: У| = 0, у2 з = —5-1.
4 1 1 1
6.010. з . з . . • х3 +2 х3+3 12
Решение.
ОДЗ: х # -V2, х * -7з.
1_____1_ = ±	х6+5х3-6
х3+2 х3+3 ^^^х’+г^+з)	**
1хб+5х3-6 = 0, [(х3+2р+з)*О.
Пусть х3 = у. Получаем квадратное уравнение относительно у: уг + 5 у - 6 = 0. Отсюда yt = -6, у2 = 1.
Отсюда х3 = -6 или х3 = 1 и X! = -Тб, х2 = 1.
Ответ: х1 = ~7б, х2 = 1.
6.011.
х-2 х + 2 х-4 х + 4 28 ----h----—----F-------. х-1 х + 1 х-3 х + 3 15
Решение,
ОДЗ: х#±1,х*±3.
Из условия имеем
----+
Iх-1
х + 2] / х-4 х + 4 ]	28
----I— ---------1=----
х + 1 1 I х-3 х + 3 1	15
х2-2 х2-12	14	2х2+6	14 .
х2 +3	7	»2+3	7 .
°(х._фГ5)-нв^_1р-9)+1з=0<=>
7х4-55х2+108 = Ьх4 -55х2 +108 = 0, (х2 - 1)(х2 - 9)	[(х2 - 1)(х2 - 9) * 0.
2
Пусть х = у, откуда
Ту2 - 55у +108 = 0;	= 4, у2 = у.
Чтобы найти х, решим два уравнения: х2 = 4, Х] 2 - ±2 или
Ответ: Xj 2 =±2,х3 4 = ±^у.
6.012. (х- 1)(х2 - 3) + (2х - 1)(х2 + 2) = 3.
Решение.
ОДЗ: хе Л.
Имеем
х3 -х2 -Зх + 3+2х3 -х2 +4х-2 = 3<=>
<=>Зх3-2х2 +х-2 = 0<=>Зх3 -Зх2 +х2-х + 2х-2 = 0<=>
<=>Зх2(х-1) + х(х-1) + 2(х-1) = 0<=>(х-1)(Зх2+х + 2) = 0
х-1 = 0,Х| = 1 или Зх2 +х + 2 = 0,Х2з 6 0 (D<0).
Ответ: х = 1.
6.013. 3| x+-V|-7| 1 + —| = 0. к х2)	\ х)
Решение.
ОДЗ: х#0.
зГ, + 'L7f,.£|.о« Хх^1>-7<»')х = о«
I	X2 J V х)	X2
3(х + 1)(х2-х +1)-7(х+1)х .	(х + 1)(3(х2-х + 1)-7х)
<=>-----------------------0<=>----------2	и
Xх	х“
^(x + l)(3x* 2-10x + 3) Q
Имеем (х+1)(Зх2-10х+3) = 0. Отсюда х + 1 = О, X] = -1 или , 1
Зх - 10х + 3 = О, х2 =—, х3 = 3.
Ответ: xt = -1, х2 = у, х3 = 3.
4	5
6.014.	---+ ~5----= 2.
•х2+4 х2+5
Решение.
ОДЗ: хе Л.
4	2
t9*----= о<=>2х4 * 6 7 * +9х2 = 0 <=>х2(2х2 +9) = О,
(х2+4)(х2+5)
х2 = 0,Х| = 0 или 2х2 +9 = 0, х2 3 е0.
Ответ: х = 0.
7(х-2)(х-3)(х-4) _ 2
6’015' (2х-7)(х+2)(х-6)
Решение.
7 ОДЗ: х * у, х # -2, х * 6.
11х3-93х2 + 190х
Из условия получаем -------------~ = СучетомОДЗэтоурав-
(2х - 7)(х+2)(х - 6)
нение равносильно
11х3 -93х2 + 190х = 0 <=> х(11х2 -93х + 190) = 0 =>
,	38
=> Xi =0 или 11х -93х +190 = 0, х2 =5, х3 = —
Л	А	с	38
Ответ: х> = 0, х2 = 5, х3 = —
2 -’ll
Х* 2+1 X лл 6.016. ------+ — = 2,9.
X X2 +1 Решение.
QJXS: х * 0.
Пусть — = у, тогда J <---2,9 = 0 <=> —-—----0 <=>
х	у	у
_	х2+1 5
Отсюда-----= — или
X 2
х2+1 2
Первое уравнение имеет корни *i = 2, хг = —, а второе уравнен решений не имеет (D < 0).
Ответ: Х| =2, хг = ^.
х + п т-п х + р т-р
6.017.----------=-----------~-
т + п х-п т + р х-р
Решение.
ОДЗ: х Ф п, х Ф р, т Ф -п, т * -р.
Из условия получаем
¥п\х-п)-(т-п\т + п) _ (х +р\х-р)-(т-р\т + р)
(m + n^x-n)	(т + р\х - р)
х2-п2-т2+п2 х2 -р2 -т2 + р2 (т + п)х - п(т + п) (т + р)х - р(т + р)
2	2	2	2
х -т	х -т______
(т + п)х - п(т + л) (т + р)х - р(т + р)
х2-т2	_	х2-т2	= о
(т + п)х - п(т + п) (т + р)х- р(т + р) (г2 - ж21 (___1______________1______1=о
' I (т + и)х - п(т + л) (т + р)х - р(т + р) I
Отсюда получаем х2 - т2 = 0 <=> х2 = т2, х12 =	, или
_______t____________________________ о
(т + п)х-п(т + п) (т + р)х - р(т + р)
(ш + р)х - р(т + /?)- (т + п)х + п(т + п) _
((ди + п)х - п(т + и)Х(ап + р)х - р(т + />))
или с учетом ОДЗ
(т + р)х-(т + п)х- р(т + р)+л(т + и)=0<=>
<	=> (w + p)x-(pi + п)х = р(т + р)-п(т + п)<^>
<	=> (pi + р-т-п)х = рт + р2 -тп-п2 <^(р-п)х = р2 -п2 + рт-тп <=>
<	=> (р- п)х = (р-п\р + и)+ т(р-п)^> (р-п)х = (р-п\р + п + т)
Отсюда:
1)если р-п-0, р = п, то, учитывая ОДЗ, хе Я, кроме/? и л;
2)если />-и^0, р^п.то х3= р + п^т.
Ответ: если п = р, то хе R, кроме пир; если п Ф р, то jq = т,
х2 = -т, х3 = т + п + р.
6.018. х2 4-х + х”1+х-2 =4. Решение.
ОДЗ: х 0.
Из условия имеем х
1 W 1 "I А л + — 1+1 х + - -4 = 0.
х J I х)
Пусть х + —= j=>x2 +2 + -^- = у2 илих2 +Д- = у2 -2.Нашеурав-х	X1	X2
некие принимает вид у2-2 + j>-4 = 0<=>у2 +у-6 = 0, откуда
у{ = -3, у2 =2 . Относительно х получаем два уравнения: х + — = -3,
откуда Xj 2 =
±>'5	1	ч	1
----или х + — = 2, откуда х34 = 1.
2	х
Ответ: xi 2 =-----,х34
21	> л <
6.019. i-;—— - х- + 4х = 6.
х -4х + 10
Решение.
ОДЗ: хе R.
Из условия имеем +	- 4х +1 о)+ 4 = 0.
?	21	v2 -4v-21
Пусть х~-4х+ 10 = j>*0:---j> + 4 = 0 <=> —-----= 0.Урав-
У	У
некие у~ —4у -21 = 0 имеет корни yt = -3, у2 = 7 . Относительно х получаем два уравнения: х2 - 4х +10 = -3 , х2 - 4х +13 = 0 (р < 0) или х2 -4х + 10 = 7, х2 -4х + 3 = 0, xj =3, х2 =1.
Ответ: Xj = 3, х2 = 1.
6.020. ---- +----= 2,5.
х-b х-а
Решение.
ОДЗ: х Ф Ь, х * а.
„ х-а	1 Л. у2 -2,5^ + 1 п
Пусть------ -у: У + — 2,5 = 0, -------= 0.
х-Ь	у	у
, 1
Уравнение у1 -2,5д> + 1 = 0 имеет корни Л = Уг=2 • Получаем
два уравнения относительно х:
х-а 1
Т^Т“2 ’
откуда Xj = 2а - b, или
---г = 2 откуда х2 = 2Ь - а .
х-Ь
Ответ: если а Ф Ь, то Xj =2а-Ь9 х2 -2Ь-а\ если а = Ь , то корней нет.
6.021. 8х4+х3+64х + 8 = 0.
Решение.
ОДЗ: хе R.
Из условия имеем (8х4 + х3) + (64х + 8) = 0 <=> х3(8х +1)+8(8х +1) = 0
<=> (8х + 1)(х3 + 8) = 0 <=> (8х + 1)(х + 2)(х2 - 2х + 4) = О.
Отсюда 8х+1 = O,Xj =-^-, или х+2 = 0,х2 = -2, или х2 -2х+4 = 0, х3 4 60 (£><0).
Ответ:
1 , х,--,х2 = -2.
6.022. (х + З)3 - (х +1)3 » 56.
Решение.
ОДЗ: xeR.
Из условия имеем
(х+3-х-1)((х+3)2 +(х+3)(х + 1)+(х + 1)2) = 56 <=> <=>2(х2 +6х+9+х2 +4х+3 + х2 +2х + 1) = 56<=> ох2 +4х-5 = 0,Х[ = -5,х2 =1.
Ответ: jq = -5,х2 = 1.
,	* + 2 х + 6 х + 10 ,
6.023. ----+—— +------= 6.
х + 1 , х + 3 х + 5 Решение. ОДЗ: х*-1,х*-3,х*-5. Из условия имеем:
(x + D + l t (х + 3) + 3 t (х + 5) + 5 _ 6 х+1	х+3	х+5
,	13	5,	Зх3+18х2+23х
х + 1 х + 3 х + 5	(х + 1)(х + 3)(х + 5)
С учетом ОДЗ получаем Зх3 +18х2 + 23х = 0 или х(3х2 +18х+23) = 0, откуда Xj =0, или
„ ,	-9 + V12	-9-V12
Зх2 + 18х + 23 = 0> х2 =---,х3 =------
Ответ: Х| = 0, х2
-9 + V12
-Г-^з =
л 1	1-	12	4 л_
6.024. 4х'+12х + —+ —= 47.
х х"
Решение.
ОДЗ: х 9*0.
Группируя, получаем:
+(12х + —
-47 = 0 <=>
х2 +-^ |+12
-47 = 0.
Пусть х + — = у=> х2 +2 + Дг = у2 или х2 + Д- = у2 -2 • Тогда
Х	X2	X2
4(у2-2)+12у-47 = 0, 4/+12у-55 = 0, yt=~,y2=^.
Относительно х получаем два уравнения: х +
1	5
или х + — = —, X 2
корнями которых ЯВЛЯЮТСЯ Xj 2
_	-n±Vio5 1
Ответ: х12 =--------, х3 = —9 х4 =2.
6.025. (х-а)2-(х-Ь)3 =Ьг-а3.
Решение.
ОДЗ: хе А.
Левую и правую части уравнения разложим на множители как разности кубов:
{x-a-x^bj^x-af +(х - а\х -б)+(х-b^ )=(b-a^)2 +Ьа + а2\
(b-a^c2 -2ax + a2 + x2 ~(a + Z>)x ++ x2-lbx + b2 )-- (b - afy2 + ba + a2 )= 0,
(b~afex2 -3(я + b)x + ab + а2 +62)-(й-а)(б2 +6а + д2)=0<=>
<=> (Z>-a)(x2 -(a + Z>)x)=0.
Отсюда:
1)если b -a = 0, b = a, to xgR;
2)если b-a*0, Ь*а,то x2 -(a + Z>)x = 0,или x(x-(a+ Z>)) = 0,откуда x{ = 0, x2 = a + b.
Ответ: если a = b , to xe R; если а Ф b, to Xj = 0, x2 = a + b.
6.026. — = (a+\f. x-1
Решение.
ОДЗ: x *1.
Приводим уравнение к общему знаменателю:
дх2-(д + 1)2(х-1) = 0дх2-(д + 1)2х + (д + 1)2 = 0 х-1	х-1
С учетом ОДЗ дх2 - (д+1)2 х + (д+1)2 = 0, откуда
(д+1)2 ±-4a(a + lf (д+1)2 ±^/(д+1)2((а+1)2 -4д) = 2а 2а '
_ (д+1)2 ±7(а+1У(д2 +2д + 1-4д) _ (д+1)2 ±^(a+iyCa-l)2 _ 2д	2д
(д+1У±(а-1У. 2д
_ (д+1)2 -(д-1)2 _ а2 +2д + 1-д2 +1 _ д+1
1	2д	2д	а '
(д+1У+д2-1 д2+2д+1 + д2-1 2д2+2д	,
х2 =  ---—-----=-----------------= — -----= д+1.
2д	2д	2д
л а+1 ' Ответ: х1 =----,где л#0; х2 =д+1.
(х-а)2 + х(х -л)+ х2 19
6.027. 7----v---7---ч--Г = Т’
(х-л; -х(х-а)+х	'
Решение.
ОДЗ: (х-л)2 -х(х-л)+х2 ^0.
Из условия получаем
б(х — л)2 -13х(х-л)+6х2 Л	\2 1 о /	\ , 2 а
---'—2---1---1----у = 0=>6(х-лу-13х(х-л)+6х =0.
7((х - а у - х(х - л)+ х2 ;
Разделим обе части последнего уравнения на х2 * 0:
„ х-л ?
Пусть----= у: бу -1 Зу + 6 = 0. Корнями полученного квадрат-
2	3
ного уравнения являются У\ = —, Уг - ~
Имее л два уравнения:
х-л 2	х-л 3
	= — или -= —, откуда X. = Зл , X-------------3	X-2	1
х2 = “2л . Сделав проверку по ОДЗ, получим ответ.
Ответ: если л # 0, то Xj = Зл , х2 = “2л ; если л = 0, то корней нет.
6.028. ---- +----------
а + Ь а-b х
Решение.
ОДЗ: л +Ь, х 0.
Из условия имеем
х 2л-х а + Ь , л ----ь-----------1 = 0»
а + Ь а-Ь х
(a-b)x2 +(2a-x\a + b)x-(a + b^(a-b)-(a + b\a-b)x __
~	{а + Ь\а-Ь)х
(а - b)x2 + 2а(а + b)x — (д + b)x2 — (а + Z>)r (п - />)- (я2 - Z>2
°	pQjr
((g-&)x2 - (fl+ fe)x2)+(2fl(a+ Z>)x -(fl2 -b2\]-(a + b^a-b) (a2-62>
(a-b-a-b)x2 +Ь,а2 +2ab-a2 +b2)x-(a+bf(a-b) л
~—------------------------------------------=Oe
-2bx2 +(a2 +2ab + b2pc-(a+bf(a-b)_n
СучетомОДЗ -2bx2 + ^i2 + 2а6 + 62}с-(д + б)2(а-б)=0 или 2bx2 -(a + bj x + (a + bf (a-b)=0, откуда
(a + bf ±-J(a + b^ -Sb(a + bf(a-b) _
“	4b	~
(р+ьУ ±7(д+&)2((д+^)2-8б(д-б))_
4b	~
_ (a+bf ±(a + b)Ja2 +lab + b2 -%ab + ib2 _
4b
_((i + b^ ±(a + b)Ja2 -6ab + 9b2 _(a + bf ±(a+b)J(a-3b^ 4b	4b
_ (a+b^ ±(a + b\a-3b)_ (a + b)((a+b)±(a-3b))-
4b	4b
(a + bXa+b-a+3b) _ (a + b)4b _а + ^
4b	4b ° ’
(a+bXa + b + a-3b) _ (a+bX^a-2b) _ (a+bXfl-b) _ a2 -b2
4b	4b	26	2b~'
a2 -b2
Ответ: если b Ф 0, то Xi = a + b, x2 = ———; если b = 0, to x = a. 2b
6.029.
2
a -1 a-x л ----+-----= 1.
ax-1 a
Решение.
ОДЗ: a#0,х/-. а
Из условия имеем:
ах~\ а
ах-\ а
д2-1 а х -----1----- ах -1 а а
с учетом ОДЗ ах2 - х - [а2 -1)2 = 0, откуда
= 1± 71+4д2(д2-1) = 1±>/4д4-4д2+1 = l±-J^fl2-lj
1,2 “ 2д “ 2а ~ 2а 1±(гд2-1).
2д
*1 =
1-2д2+1 2а
1-д2	1 + 2д2-1
-----> *2 =	«---- а---2а
= а.
1~л2	Л
Ответ: х, =----, х2 = а ПРИ a * 0.
а
6.030.
' х2 +6>2 _Г 5х Y ^х2-4_>	^4-х2 J
Решение.
ОДЗ: х Ф ±2.
Перепишем это уравнение в виде
/ 2 х V /	\2	2 х I/ ~е
х +6 f 5х |	х +6 _ If 5х |
^х2-4^	^х2-4у	х2-4 v[x2-4J
х2 +6
Р^4
5х х2 -4
х2 +6 5х	х2 +6 5х
=> “5--=----5---или —7 - “5—
х2-4	х2-4	х2-4 х2-4
С учетом ОДЗ получим уравнения х2 + 5х + 6 = 0
или х2 - 5х + 6 = 0,
откуда jq = -3, х2 = -2, х3 = 2, х4 = 3; х2 = -2 и х3 =2 не подходят по ОДЗ.
Ответ: Xj = -3, хг =3.
6.031- 73х + 4 + Jx-4 = 2>[х.
Решение.
ОДЗ: Зх + 4 >0,х-4 >0,х>0=> х>4.
Возводя обе части уравнения в квадрат, получаем
Зх + 4 + 27(Зх + 4^х - 4) + х - 4 = 4х <=> «27(Зх+4Хх-4) = 0.
Ещераз возводя в квадрат, получаем: (Зх+4Х* -4)=0 .Отсюда имеем
4	4
Зх + 4 = 0 илих-4 = 0,	= --,х2 = 4; х{ = _у не входит в ОДЗ. Про-
веряя х = 4 непосредственной подстановкой в исходное уравнение, имеем: Ответ: х = 4 •
6.032. -Jx +Vx + И + 7x-Vx+7T = 4.
Решение.
Пусть 7х + 11 = >0 или х + 11 = >>2 ,т.е. х = у2 -11 .Тогда
^У1 + «У—11 + ^У2 “У“П = 4 или ^у1 +_у-11 = 4-^у1 -у-11 • Возведя обе части уравнения в квадрат, получим
/ +>--11 = 16-8// -J'-ll + / - J-11» 87/-у-11=16-2у
или 4-J/ - у -11 = 8 - у. После возведения обеих частей уравнения в квадрат, найдем
1б/-16у-176 = 64-16>'+/, 0<j<8=*
15/ =240,	.
=> z	или у = 4.
0<^<8
Отсюда получаем Vx + 11 =4 или х + 11 = 16, х = 5. Проверкой убеждаемся, что это корень йсходного уравнения.
Ответ: х = 5.
6.033. ^/15 — л* + у/з — x = 6.
Решение.
|15-х>0,	[х<15,
°Д3: 3-х>0 ~ х<3,
Из условия имеем:
У15-х = 6->/3--х =>15-х = 36-12>/3-7х+3-х, 12>/з^х =24.Уз^7 = 2.
Отсюда 3 - х = 4 или х = -1. Проверкой убеждаемся, что это корень исходного уравнения.
Ответ: х = -1.
6.034. 1 + 71 + х7х2 -24 = х.
Решение.
Запишем уравнение в виде V1 + х>1х2 -24 = х-1. Возведя обе части уравнения в квадрат, получим
14-хл/х2 -24 = х2 -2x4-1, ху/х2 -24 = х2 -2х, х-1>0	|х>1
7х2 -24 = х-2, х>1.
=> х2 -24 = х2 -4x4-4 или 4х = 28; х = 7.
Проверяя х = 7 непосредственной подстановкой в исходное уравнение, имеем:
Ответ: х = 7.
(x-a)ylx-a 4-(x-ft)vx-fe , /	,\
6.035. 1\ —-------------------= а~Ь (а>Ь).
у!х-а л-yjx-b
Решение.
Из условия имеем
у/х-а +у!х~Ь
Разложим на множители числитель левой части уравнения как сумму кубов:
х-а
- yl(x-a\x-b) + (х/х-й j2
+ <Jx-b
а-Ь.
Так как jx-a + Jx-b # 0. то
(л/х-аУ -<J(x-a\x-b) + (y/x-b\ = а-Ь<^>
& х-а- J(x-a\x-b) + x-b = a-b<^>
<=> 2х - 2а = ,](х-а\х-Ь) о 2(х - а) = <J(x-a\x-b) =>
=>4(x-af = (x-a\x-b)<^4(x-af -(х-аХх-б)=0<=>
<=> (х-а%4х-4а-х + b)& (х-а/Зх-4а + б)=0.
Из последнего уравнения следует, что либо х - а = 0, откуда Х| = а,
либо Зх - 4а + b = 0, откуда х2 = —-— .
Подставляя Xj и х2 в начальное уравнение, убеждаемся, что это действительно корни.
„	4а-Ь
Ответ: х( = а; х2 =---.
6.036. V3x + 7-Vx+T = 2.
Решение.
ОДЗ:
Зх+7>0, х + 1>0
<=$> х>-1.
Возведя обе части уравнения в квадрат, получим
Зх+7-27(Зх + 7Хх+1) + х+1 = 4 <=>4х+4 = 27(Зх+7Хх+1) <=>
<=> 2(х+1)=V(3x+7Xx+l) => 4(х+1)2 = (Зх+1\х+1) <=>
<=>4(х + 1У -(Зх+?Хх + 1)=0«> (х+1Х4х+4-Зх-7)=0<=>
<=> (х+1Хх-3)=0 или ,х + 1 = 0,Х| =-1 или х-3 = 0,х2=3.
Непосредственной проверкой убеждаемся, что это корни начального уравнения.
Ответ: х, = -1, х2 = 3.
6.037. Vl + Vx +V1-V* =2.
Решение.
ОДЗ: х>0.
Возведя обе части уравнения в куб, получим
1 + Vx + 3^ +Vx^-Vxj+S^ + Vx^-Vx)2 + 1-Vx =8<=>
Так как у/1 + у[х + у! - 4х = 2, то уравнение принимает вид:
3^ +Vx)(l->/x) 2 = 6 <=>	+Vx^-Vx) = 1 <=> Vl-x = 1 <=>
<=> 1 - х = 1, х = 0.
Ответ: х = 0.
6.038. 2>/7^ : 0,63/- = 10^5 :-^216^9.
V 3	4
Решение.
ОДЗ: 7-х>0<=> х<7.
Будем упрощать исходное уравнение:
2Л^5^3 40^3 /г
<=>--------=----- <=> V /
3	2'^3"
Очевидно, что х = 3 есть корень этого уравнения и других корней нет.
Ответ: х = 3
6.039.
2	2
х + 5^2 л( х V -----+4 ---------- х ) х + 5 >
= 4.
Решение.
- Из условия имеем
|х + 5 . Г х . л /х + 5	4	. п
J-----+4J-------4 = 0<=> J----+  —- -4 = 0.
V х Vx + 5	V х х
V х + 5
Пусть
,|Х + 5 = у. >0: у + — -4 = 0<=>у2 -4у + 4 = 0<=>
V х	У
«(у-2)2 = 0<=>у-2 = 0<=>у = 2.
/х + 5	„
Тогда J =2 .Проверкой убеждаемся, что это выражение удовлетворяет условию.
х+5	.	_ .	5
Отсюда------= 4 <=> х + 5 = 4х, х = -.
х	3
5
Ответ: х = — •
6.040. ^24 + >/^-^5 + Тх =1.
Решение.
ОДЗ: х>0.
Возведя обе части уравнения в куб, получим
24 4- Vx - 3^(24 + Vx^(5 +7х)+3^44->/х)(54->/хУ - 5 - у[х = 1 <^>
<=> -3^4 + Vx )(5 + у[х^24 + 4х - y[s + y[x ^=-18.
Тах как ^24 +Vx - ^5 + >/х = 1 по условию, то получаем
V(24 + Vxfc+Vx) = 6 <=> (24+4х J5 + 4х )= 216,
(л/х)2 +29л/х-96 = 0.
Откуда у[х = 3, 4х = -3 (не подходит). Отсюда х = 9.
Ответ: х = 9.
6.041. Vx + 34-Ux-3 =1.
Решение.
Возведя обе части уравнения в куб, получим х + 34-х + 3- $](х + 34\х-3) (Vx + 34 - Vx -3) = 1.
Так как Vx+34 - Vx-3 = 1 > то имеем следующее уравнение:
37 - 3 V(x+34Xx-3) = 1 <=> Щх+34\х-3) = 12-» <=>(х+24Хх-3)=1728<=>х2+31х-1830=0; xt =-61,х2 =30. Проверкой убеждаемся, что это корни исходного уравнения.
Ответ: jq = -61, х2 = 30.
6.042. х2 + Зх -18+4>/х2+Зх-6 = 0.
Решение.
Пусть Vx2 + 3х-6 = у > 0. Тогда х2 + Зх -6 = у1 или
х2 + 3х = ^2 +6
и уравнение принимает вид:
у2 + 6-18 + 4у = 0 <=> у2 + 4^-12 = 0,	=-6 (неподходит), у2 = 2 .
Тогда
>/х2 + 3х-6 =2 <=> х2 + 3х - 6 = 4 <=>
<=> х2 +Зх-10 = 0; Х|=-5, х2=2.
Проверкой убеждаемся, что это корни заданного уравнения.
Ответ: Х| = -5, х2 = 2.
6.043. 7х2 + 32-2^х2 +32=3.
Решение.
Пусть Vx2 +32 =)>>0. Относительно у получаем уравнение у2 - 2у - 3 = 0, откуда yt = -1 (не подходит), у2 = 3 . Тогда
а/х2 +32 =3»х2+32 = 81 »х2 =49.
Это выражение удовлетворяет заданному уравнению. Отсюда |х| = 7
ИЛИ Xj 2 = ±7.
Ответ: = -7, х2 = 7.
6.044. У(5х+2)3 —-----= 6.
№х + 2?
Решение.
ОДЗ: х#-|.
Пусть ^(Sx + 2)3 = у, у 0 • Относительно у имеем уравнение:
у- — = 6 (у * 0) <=> у2 -бу-16 = 0, откуда у, = -2 , у2 =8. Тогда: У
и v^=-^,=4^=z#±i);
2)	V(5x+2)3 =8; х2 = 6.
-2(У4 + 1)
Ответ:	, х2 = 6.
6.045. хТх -4^? + 4 = 0.
Решение.
Пусть 7х = у, тогда х = у3, х2 = у6. Относительно у имеем уравнение
у3 у-4у2 +4 = 0 <=> у4 -4у2 + 4 = 0 <=> (у2 -2^ =0t=>
<=>у2-2 = 0, у2 =2,
откуда у12 = ±72 . Тогда Vx = -72, х1 = -78 и 7х = 72, х2 = 78.
Ответ: = -2-Л, х2 = 2у/1.
6.046. Зу[х -5у1х 1 = 2х"1.
Решение.
Из условия имеем З^х -	~ •
Ух х
Пусть Vx = у, у Ф 0, и уравнение принимает вид
Зд>---4- = °1г#0)оЗ/-5г-2 = 0«з(у2)2-5(г2)-2 = 0) у У
откуда у2 = 2; у2 = -1 (не подходит). Тогда у12 - ±71 => 7х = -2 или Vx = 71, х( = —Ji, х, = 78 •
Ответ: х, = -2у/2,х2 = 272.
6.047. х2 +7х2 +20 =22.
Решение.
Пусть 7х2 +20 = у > 0 , тогда х2 +20 = у2, х2 = у2 -20 и уравнение принимает вид у2 - 20+у = 22 <=> у2 + у - 42 = 0, откуда найдем У|=-7, у2=6; у1=-7<0 не подходит. Тогда 7х2 +20 =6 или х2 +20 = 36> х2 =16> *1,2 =±4-
Ответ: х( = 4, х2 = -4.
4 7х +3 -
6.048. 57=-— + —Г~ = 2-7х +2	5
Решение.
ОДЗ: yfx + 2 * 0,7х # -2, х * -8.
Пусть >[х + 2 = у, у 0. Относительно у уравнение принимает вид — + ^^ = 2 (у*0)<=>у2-9у+20 = 0,откуда у( =4, у2 = 5.
У 5
Тогда: 1) у/х + 2=4; х, = 8 ; 2) у[х +2 = 5; х2 =27 .
Ответ: Xj = 8; х2 = 27.
6.049. V778+47P78=6.
Решение.
ОДЗ: х3 + 8 > 0 <=> х3 > -8 <=> х > -2.
Пусть ух3 + 8 = у, у > 0, и уравнение принимает вид у2 + у = 6 <=> <=> у2 +у-6 = 0, откуда у, = -3, у2 = 2; = -3 не подходит. Тогда
Vx3+8=2, х3+8 = 16, х3=8, х = 2-
Ответ: х = 2.
(5 - х)>/5 - х +(x-3)Jx-3 »
6.050. 1---le I ’--------= 2.
V5-x +Vx-3
Решение.
[5-х >0, °«3:U-3>0o3fixS5'
п	(л/5-х)3 +(>/х-зУ
Перепишем уравнение в виде -Ь— . /_—\_ / = 2 и разложим
у15-х+у1х-3
числитель левой части на множители как сумму кубов:
(л/5-х + л/х-З“хХх”3) + 7(х“З)2
л/5-х + 7х-3
Учитывая, что знаменатель положителен, получаем
7(5-х)2 -	- х\х -3) + у}(х -3^ =2<=>
<=> 5 - х - ^/(5-хХх-З) + х - 3 = 2 <=>
<=>7(5-хХх-3) = О, (5-хХ*-3)=0,
откуда 5 - х = 0, Xj = 5, или х-3 = 0, х2 = 3. Проверкой убеждаемся, что это корни исходного уравнения.
Ответ: х} = 5, х2 =3.
6.051. 7х + 1 -у/9-х = >/2х-12.
Решение.
х+1>0,.
ОДЗ: < 9-х > О, 2х-12>0
Возведя обе части уравнения в квадрат и приведя подобные члены, получаем 7(х+1Х9-х) = 11 - х, откуда
(х + 1X9-х) = 121-22х + х2 <=> х2 -15х + 56 = 0; Xj = 7, х2 =8.
Проверкой убеждаемся, что это корни заданного уравнения.
Ответ: Xj = 7, х2 = 8.
6.052. ---7=т=--------П= =
x-vx-x х + ух -X
Решение.
х2-х>0,	[х(х-1)^0,	/ ,г ч
х Ф 0 |х Ф 0
Из условия получаем
Возведя обе части уравнения в квадрат, получаем —-— = 3 или х = 4 . Проверкой убеждаемся, что х = 4 является корнем последнего уравнения с радикалами.
Ответ: х = 4.
Решение.
ОДЗ: х#±1.
Пусть Vx = у, у * ±1 • Относительно у уравнение принимает вид
/-	(уг-|р->1)
у2-1	у+1	у2 -1	у+1
<=> у2 +1-у+1 = 4 <=> у2 — у—2 = 0,
откуда найдем у( = -1, у2 = 2 . Тогда vx = -1, х( = -1, или Vx = 2, х2 =8; X] = -1 не подходит по ОДЗ.
Ответ: х = 8.
6.054. 75 + V^ +	= V^.
Решение.
ОДЗ:
5+Vx>0, 5-Vx^0
<=>-125<xS125.
Возведя обе части уравнения в квадрат, получаем уравнение
5 +Vx+27(s + VxJs-Vx)+5-Vx = V? <=>
2д/25-Vx7 = Vx7 -10 => 100 - 4tfx2 = Vx7 - 20Vx7 4-100 <=>
Vx7-leVx7 = 0 <=>
откуда Vx7 =0, Xj = 0, или Vx7-16 = 0, Vx7 = 16, x2 =64. При
проверке х1 =0 не удовлетворяет исходному уравнению.
Ответ: х = 64.
6.055. Jxtfx + VxVx = 56.
Решение.
ОДЗ: х>0.
Из условия имеем
— —	( — Y —
xi°-х'о =56<=> х10 -х10-56 = 0.
2
Пусть х10 = }>>0. Относительно у уравнение принимает вид у2 - у - 56 = 0, откуда = -7 или у2 = 8;	= -7 < 0 не подходит.
1	12 ю
Тогда х10 =8 . Отсюда х = 8 3 , х = (г3)з , х = 210 =1024 .
Ответ: х = 1024.
6.056. 7х2 +9-Vx2 -7 = 2.
Решение,
ОДЗ. X2 -7>0.
Перепишем уравнение в виде 7х2 +9 = 7х2 - 7 + 2 . Возводя обе части уравнения в квадрат, получаем
х2+9 = х2 -7 + Vx2-7+4<=>Vx2-7 = 3 <=> х2-7 = 9 <=>
<=> х2 =16, х12 =±4.
Проверкой убеждаемся, что это корни заданного уравнения.
Ответ: Xj = 4, х2 = -4.
6.057. 710-х2 + 7х2 +3=5.
Решение.
ОДЗ: 10-х2 >0.
Возведя обе части уравнения в квадрат, получаем
10 - X2 + 27(ю-х2)(х2+з)+X2 + 3 = 25 <=> ^0-х2\х2+з) = 6 <=>
<=> (10-х2 )(х2 + з)=36<=>х4 -7х2 +6 = 0, х2 =1илих2 =6;
Х| 2 =+1, Х3 4 =+л/б.
Ответ: хХ2 - ±1, х34 = ±л/б.
6.058. т£| + ^р1 = 2.
V х + 3 V 5-х
Решение.
(х Ф -3,
ОДЗ:
|х*5.
_	75”х
Пусть 4/-т ~z>
J Vx+3
z Ф 0. Относительно z уравнение принимает вид
z + - = 2 <=> z2 -2z + l = 0<=> (z—1)2 = 0<=>z-l = 0, z = l. z
i 5-x	1	,
Тогда Zl—— =!<=>----- = 1; x = l.
Vx + 3	x+3
Ответ: x = 1.
J 16z Jz -1
6.059. 5J—-+( — =2,5.
V z-1 V 16z
Решение.
Пусть
J 16z
V z-1
= у, у *0. Относительно у уравнение принимает вид
1	2	1
у + — = 2,5<=>у -2,5у+1 = 0, откуда л = ~,У2 = 2 .Тогда или
У	2
J16z 1 16z	1	1
ПТГГ^Гй’г'=~5п’1'™
= 32,z2=2.
Ответ: z} = z2 = 2-
6.060. Hsx + 1 -V5X-12 = 1.
Решение.
Перепишем уравнение в виде ^5х + 7 = V5x-12 +1 и возведем обе части в куб:
5х + 7 = 5х-12+з(^5х-12У +3^5х-12+1<=>
«> (V5X-12)2 +V5x-12-6 = 0.
Пусть V5x-12 = t. Относительно t уравнение принимает вид t2 -1 - 6 = 0, откуда найдем Z, = -3 и t2 = 2.
Тогда или ^5х-12 = -3, 5х -12 = -27, х( = -3 , или V5x-12 = 2 , 5х-12 = 8, х2 = 4.
Ответ: х, = -3, х2 = 4.
6.061. 2Vx+5Vx-18 = 0.
Решение.
ОДЗ: х>0.
Обозначим Vx = у > 0 • Относительно у уравнение принимает вид 9	9
1уг +5^-18 = 0, откуда найдем я ---, у2 =2 ;	= -- <0 ие под-
ходит.
Тогда Vx = 2, х=26 =64-
Ответ: х = 64.
6.062. >/Зх2 +1+д/х2 +3 =7бх2 +10.
Решение.
Возведя обе части уравнения в квадрат, имеем
Зх2 +1+2<Дзх2 +1)(х2 +з)+х2 +3 = 6х2 +10 <=>
<=> 7(зх2 +lj(x2 +з) = х2 +3 =>
=> (зх2 + 1)(х2 + з)= (х2 + if. <=> (зх2 + 1)(х2 + з)- (х2 + з)* = 0 <=>
<=> (х2 +з)(зх2 +1-х2 ~з)=0<=> (х2 +з)(х2 -1)= 0;
х2+3^0,х2-1 = 0,х2 =1, х12=±1.
Ответ: х12 =±1.
Решение.
ОДЗ: 0<х*1.
Перепишем уравнение в виде
V7 +1	у/х +1 - 3Vx +3 л
-7-=----3 = 0, х * 1 <=>-——--------= О <=>
Vx-l	Vx-1
<=> -264х +4 = О о Vx = 2,х = 26 = 64.
Ответ: х = 64.
6.064. х+2 + л/Зх + 8 = >/2х + 6.
Решение.
х + 2^0,
ОДЗ:<Зх + 8>0,<=>х£-2.
2х + 6>0
Запишем уравнение в виде >/х+2 -л/2х+6 = -\/Зх + 8 и возведем обе его части в квадрат:
х + 2-2^/(х + 2)(2х + 6) +2х + 6 = Зх + 8<=>
<=> 7(х + 2)(2х + 6)=0,
откуда х + 2 = 0, Xj = -2, или 2х + 6 = 0, х2 = -3— не подходит по ОДЗ.
Проверкой убеждаемся, что х = -2 является корнем данного уравнения.
Ответ: х = -2.
6.065. V2x+5 +V5X + 6 =712х+25.
Решение.
ОДЗ:
2х + 5>0, 5х+6>0, <=>х>-—. 12х + 25>0	5
Возведя обе части уравнения в квадрат, имеем 2х+5 + 2Л/(2х + 5)(5х+6) + 5х+6 = 12х + 25» о 27(2х + 5)(5х+6) = 5х+14 => => 4(2х+5)(5х+6) = 25х2 + 140х +196 <=> 15х2 + 8х - 76 = 0, 38	,	38
откудаХ| = х2 = 2; Xi = не подходит по ОДЗ. Проверкой убеж-
даемся, что х = 2 является корнем уравнения.
Ответ: х-2.
6.066. х2 -4х-6 = >/2х2-8х + 12.
Решение.
Возведя обе части уравнения в квадрат, имеем
(х2-4х-бУ = 2х2 -8х + 12 <=> (х2 -4х-6^ -2(х2-4х-6 + 12)=0.
Пусть х2 - 4х - 6 = у, у > 0. Относительно у уравнение примет вид у2 -2у-24 = 0, откуда у1 = -4 , у2 = 6; у} = -4 не подходит.
Тогда х2 -4х-6 = 6<=> х2 -4х-12 = 0, Xj = -2, х2 = 6 . Проверкой убеждаемся, что это действительно корни исходного уравнения.
Ответ: Xj = -2, х2 = 6.
Решить системы уравнений (6.067—6.119):
6.067.
х + у = 0,9.
Решение.
Перепишем систему в виде
(х + 0,2)-+ (у + 0,3/ =1, х + 0,2 - 0,2 + у + 0,3 - 0,3 = 0,9
х + ОД = и, 7 + 0,3 = v.
Тогда •
и2 + v2 =1, и + v = 1,4
(w + v)2-2uv = l. и + v = 1,4
(1,4-2uv = 1,	fl,96-2uv = 1,	(uv = 0,48,
и + v = 1,4	[u + v = 1,4	[и + v = 1,4.
По теореме Виета возможны только следующие варианты: [и] =0,6,	[u2=0,8,
< Л или < [v! = 0,8 [vs = 0,6.
fx + 0,2=0,6,	[х + 0,2 = 0,8, fxj=0,4,	]х2=0,6,
Тогда	или <	<	_ или <
[у + 0,3 = 0,8	[^ + 0,3 = 0,6; |/i=0,5	[у2 =03.
Ответ: (0,4; 0,5), (0.6; 0,3>
6.068.
х3 + у3 =7, Х3у3 = -8.
Решение.
По теореме Виета возможны только следующие варианты:
или
х3=-1, (х2 =-1, /=8, Ы=2-
Ответ: (2; -1) (-1; 2)
6.069.
х-1 + у 1 =5, х~2 +у-2 =13.
Решение.
Перепишем систему уравнений в
виде *
1 + 1 = 5, х у
1	1	,,
2 + 2
X	У
ОДЗ:
х#0, у .* 0.
Приводя к общему знаменателю, получаем
х + у = 5ху, х2 + у2 =13х2у2
х + у = 5ху,	(х + у = 5ху,
(х + уУ - 2ху = 1 Зх2у2	[ху(бху -1) = 0.
Последняя система равносильна двум системам уравнений:
jx + y = 0, |ху = 0
*!=0,
Л =0-
Это решение не подходит по ОДЗ.
6.070.
х у 13 у X 6 х + у = 5.
Решение,
ОДЗ:
х*0, /*0.
Умножив левую и правую части первого уравнения на Ьху * 0, получим
б(х2 +^2)=13х^,б^хч-^)2 -2xj)=13x%\ху = 6,
х + у = 5	|х + у = 5	[х + >> = 5,
у2-5^4-6 = 0, 1*1=2, (х2=3, x + j> = 5,	/1=3, (/2=2.
Ответ: (2; 3 X (3; 2)
6.071.
х - у = 1, х3-/=7.
Решение,
Преобразуем второе уравнение системы
х-у = 1,	[х-у = 1,
(x-jj(x:2 +ху + _у2)=7	(х-у)2 +3х^ = 7
х-у = 1, [х-у = 1, <=>
1 + Зху = 7	|х>> = 2,
откуда
х2 =-1,
У2 = “2-
Ответ: (2; 1) (-1; -2)
6.072.
'J___1_ = J_
}> + 1 х’ /-х-5 = 0.
Решение.
1У ±1, °Д3: |х#0.
Преобразуем первое уравнение системы
ху + х-ху+х = у2 -1, у2 — х = 5
2х = у2-1, у2 -х = 5
у2 -х = 5
=> х = у2 - 5. Подставив это значение х в первое уравнение системы, получим 2(у2 -5)= у2 -1, у2 = 9, у, = 3, у2 = -3; тогда Xj = 4, х2 = 4 .
Ответ: (4;ЗЦ4;-3)
у2 -ху = -12, х2 - ху = 28.
Решение.
6.073.
(у(у-х)=-12, Из условия имеем	у) - 28
Разделив первое уравнение на второе, получим
Зх у=-’ х(х-у)=28.
х(х-у)=2%
х(х- у)=28
Зх
Подставив у = — из первого уравнения системы во второе, получим
Зх У~~’ х[х-—1=28
Ц 7 )
Отсюда:
Зх г о у =—, л
7 Ь1=-7 х = -7	1 1
Ответ: (- 7; - 3} (7; 3)
Зх у~~’
X2 =49.
1)
или
2)
Зх У~-
х = 7
У2 =3, х2 = 7.
у Л
6.074.
х + у + — = 9, У к±2>=20.
Решение, ОДЗ: у*0.
Пусть
х + у = и, f
|W + V=9.
х _ Имеем s	По теореме Виета возможны толь-
,У	”
ко следующие варианты:
Тогда
или
2)
и2 =5, v2 =4.
или
Х2 =4, ,У2 =1-
Ответ:
< х2у + ху2 =6, ху + х + у = 5.
6.075.
Решение.
fxy(x + y) = 6, Из условия имеем < z \ с
I ху = и, П*СТЬ U + , = v.
{uv = 6,
,, откуда по теореме w + v = 5
Виета находим и, = 2, и2 = 3 , V[ = 3, v2 = 2 .
ху = 2,	, Гху = 3,	]*> Ь
„ или <	, откуда 1_ 7 и
х + у = 3 [х + у = 2	{У1~^
х2 = 2, ,Уг =L
Ответ: (1; 2), (2; 1)
6.076. i
х2у3 + х3у2 =12, х2у3 -х3у2 =4.
Решение.
Из условия имеем
х2у2(у + х)=12, х2у2(у-х) = 4.
Разделив первое уравнение на второе, получим х2у2(у + х) 12 у + х _	,	,
,z,;----( = — <=>  -= 3 <=> у + х = 3у-3х <=> у = 2х.
х2у (у-х) 4 у-х
Из первого уравнения системы находим
х2(2х)3 +х3(2х)2 =12 <=> 8х5+4х5 =12 <=> х5 =1, х = 1.
Тогда у = 2.
Ответ: (1;2)
6.077.
х4+/ =82, ху = 3.
Решение.
Перепишем систему в виде
((х+у)2 -2xyf -2х2у2 =82, Rx+y)2 -6^ -18 = 82, ху = 3	[ху = 3
((х + у^-б/ =100, ху = 3.
Из первого уравнения (х + у)2 - 6 =10, откуда (х + у)2 =16 или
(х + у)2 = -4; (х + у)2 = -4 не подходит. Тогда
{х + у = 4, |х[=1, (х2 =3, ху = 3, 1/1=3, 1/2 =1
или
(х+у = -4, Гх3=-1, Гх4=-3, 2)|ху = 3,	[у3=-3, |у4=-1-
Ответ. (1;3)(3;1)(-1,-3)(- 3,-1)
6.078.
х3+у3 =35, х + у = 5.
Решение.
По формуле суммы кубов получаем
(х + у)(х2-ху + у2)=35,^ х + у = 5
(х + уд(х + у)2 - Зху)= 35, х + у = 5
|5(25-Зху)=35, (25-Зху = 7, Г ху = 6, |x + j> = 5	|х + у = 5	|х + у = 5.
[%! =2,	[х2=3,
По теореме Виета возможные варианты; < _ или «	_
Ответ: (2; 3} (3; 2)
6.079.
х3 +у3 =9, ху = 2.
Решение.
Перепишем систему в виде
х6 - 9х3 +8 = 0, где х * 0,
2
У = -• х
Из первого уравнения получаем х3 = 1 или х2 = 8, откуда Xj = 1, х2=2.Тогда ^=2, j2=l.
Ответ: (1; (2; 1)
6.080.
и2 + uv = 15, v2 +uv = 10.
Решение.
Ju(w + v) = 15, Перепишем систему в виде j / -ь v) = 10 и раЗД6™14 пеРвое уравне-
ние на второе:
u(w + v) 15	и	3	3v
v(w + v) 10	v 2	2
ж-r	3v
Подставив м= — во второе уравнение системы, получим
э 3v 5v
v2 + -у = 10 , -у = Ю, v2 = 4 , откуда Vj = -2, v2 = 2 . Тогда их = -3 ,
и2 =3 .
Ответ: (-3; -2\ (3;2)
6.081.
х3 + у3 =65, х2у + ху2 =20.
Решение.
Разложив левые части, представим систему в виде . (x + yk*2 -xf + /2)=65,(x + y^x + yf -Зху)=65, ху(х + j>) = 20	+ j)=20.
х + у = и, Тогда
ху = V.
u(w2 -3v)=65.
uv = 20
u(u2 -3v)= 65, 20
v = —.
и
„	( 2 а 2(Н
Из первого уравнения получаем и! и -3— I и
= 65, и3 = 125,отку-
20	х + у = 5,
да и = 5 . Тогда v = — = 4 и s А Отсюда 5	[ху = 4.
Ответ: (4; 1) (1; 4)
х2 + у4 = 5, ху2 = 2.
Решение.
Xi=4,	(х2 =1,
1И1 л [У1=1	[у2=4.
6.082.
2
Из второго уравнения системы х = — . Тогда из первого уравнения
У
2 получаем —
I У
+ у4 = 5 , j8 - 5у4 +4 = 0. Отсюда yf = 1 или у4 = 4 ,
Г-	Г-	2
откуда У!=-1, y2=U ^з=“^2, ^4=^2. Тогда х1>2=у = 2;
*3,4 =|=1.
Ответ: (2; Ц (2; -1^; 41) (1; - 41) 12(х + у^ + х = 2,5-у, б(х-у? +х = 0,125 + у.
Решение.
6.083.
Перепишем систему в виде
12(х + у^ + (х + у)-2,5 = 0, 6(x-yf + (х-у)-ОД 25 = 0.
Тогда первое уравнение будет квадратным относительно х + у, а второе относительно х - у. Решая указанные уравнения, получаем
-1±V1+12O =-1±11
24	24 ’
(* + Л,2
-1±2
Перебирая возможные варианты, имеем:
	f	1	3	[ 1	5
	х+у=~~,	Х' ~ ~ 8 ’	х+у=~~,	Х2~ 24 ’
1)-	1 <=>'	- 1-2)	1 <=>'	7
	Г^-4	П 8’	х-у =— 1	12 J	У2 24’
	Г	5	1	[	5	1
	х+у =—, 12 <=><	12 ’	х+^ = -.	Х4 4,
з)-	1	-1. ч	1	1
		3’	х-у = — 1 Л 12	Г4 = 6-
Ответ:
4’6 Д12 ’ 3 Д 24 ’ 24 Д 8’ 8J
6.084.
—+ —= 3, х 3
х	3	3
--1-  —
2	у	2
Решение.
[х#0, °да; Uo.
Приводя к общему знаменателю, получаем
6 + ху - 9х,
=> 9х - Зу = 0,
откуда у = 3х .Отсюдаполучаем — + — = 3, х2 -Зх + 2 = 0 при х # 0 , х 3
откуда X] = 1, х2 = 2 ; тогда = 3, у2 = 6 .
Ответ: (1; 3) (2; б)
6.085. 1
х2 + у2 _ 10
х + у	3 ’
х у 4
Решение.
х*0,
ОДЗ:
X * -у.
Перепишем систему в виде
з(х2 +/)=Ю(х+Я<=>, З^х + у)2 -2ху)=10(х + Я 4(х + у)~3ху	[4(х + у)=3х^.
(х + у = и,	Г 3u2 -10w-6v = 0,
Пусть I _ у Тогда в новых переменных *
4	7	(4 1	7
Отсюда v = -w и Зи -10и-6\-и =0, Зи -18w = 0, откуда 3	3
и{ = 0 , и2 = 6; тогда Vj = 0, v2 = 8.
Получили совокупность двух систем lx + j = 0,	(х + у = 6,
или2)Ь = 8.
1х!=2, 1х2 =4,
Решая эти системы, найдем 1 „	и]„
Ответ: (2; 4)l (4; 2)
(х-у/х2 - у2) =45,
6.086. Г А ' ’ х + у = 5.
Решение.
Перепишем эту систему в виде
< '(* - И* - уХ*+J>)= 45,	((х - у)2 (х+у)= 45,
х+у = 5	х+у = 5.
=» (х - yf -9, откуда х - у = -3 или х - у = 3 . Получили совокупность двух систем:
х-у = -3, |х-у = 3, 2) 1
х + у = 5, |х + у = 5.
Решая эти системы, найдем
xj =4, 7i=1
х2 =1, Л =4-
Ответ; (4;1}(1;4)
6.087.
х4-/=15, х3у-ху3 =6.
Решение.
Пусть t = —, тогда у = tx и система принимает вид
х4-/4х4 =15,	[х4(1-?)=15,
x4r-x4z3=6	x4(z-z3)=6.
1-“/^ 15
После деления получаем------ = — <=> 2z2 - 5/+2 = 0, откуда
t-r 6
1
А = 2’ г2=2-
При Zi из уравнения х4(1-/4)=15 имеем
X4fl- —L15»X4
I 16J
= 16
9
откуда Xj = -2 , x2 = 2 ; тогда yx = -1, y2 = 1.
При t2 = 2 имеем x4 (1 -1 б) = 15, x4 = -1, это решение не подходит.
Ответ: (-2; -1), (2; 1)
6.088.
*-2 = 2, у х б’
X2 - у2 =5.
Решение.
ОДЗ:
х * О, 7*0.
После преобразований первого уравнения, получим
Х ~У = 7ХУ> 5 с г 6
’	6	=> — ху = 5 <=> xj> = 6, у = ~.
2	2	<	Х
X -у = 5.
Из второго уравнения системы находим
х2 — —у-= 5 <=> х4 -5х2 -36 = 0 х
откуда х2 = -4 или х2 = 9; х2 = -4 не подходит, поэтому х, = -3 ,
х2 = 3; тогда у1 = -2 , у2 = 2 .
Ответ: (- 3; -2\ (3; 2).
Решение.
Из первого уравнения системы v3 = m -1 - и3. Подставив это значение v3 во второе уравнение, получим
u3(w-l-u3)=-/и <=> (w3)2-(w-l)u3-?и = 0,
откуда
з __	+	+4m m — 1 ±V/h2 —2m +1 + 4/И _
“u -	2	~	2
_ m-1 ±Jm2 +2m+l _ m -1 ±^/(w+l)2 _ zn-l±(m+l)
"	2	2	’>	2
ИЛИ 3 m~\ + m + \	— -
«2 =----------=;"J’ “2 = ^fn ’
тогда = m ,vx= >[m или	= m -1 -m = -1, v2 = -1-
Ответ: (-1; Vw) (Vm;-1)
6.090.
ax+— =2, У
b
—t-ay = 2ab.
.x
Решение.
(x *0, °д3: V#o.
„	(axy + b = 2y,	,
Перепишем систему в виде	=> 2у = 2аЬху у = abx.
\Ьл-аху = 2аЬх
Из первого уравнения системы получаем а2х2 -2ах + 1-0 (при/>*0)
или (ох-1)2 =0,откуда Xi =х2 = —.Тогда y = a b — = 6,где а^О. а	а
Ответ: если ab = 0 , то корней нет; если ab 0, то х = —, у-Ь. а
[(х-у)ху^30,
6-091, [(x + j) xj' = 120.
Решение.
После деления второго уравнения системы на первое получаем
(x+r)xv_120	3
(х - у)ху ~	И3 первого уравнения системы находим
3'3
х - ~ х к -х = 30, х3 = 53, откуда х = 5; тогда у = 3 .
Ответ: (5; 3)
6.092. i
х2 + у2 +6x + 2j> = 0, х + у + 8 = 0.
Решение.
Из второго уравнения системы у = -8 - х. Подставив это значение^ в первое уравнение системы, получим
х2 +(--8-х)2 +6х +2(-8- х)= 0 <=> х2 +1 Ох+ 24 = 0,
откуда Xj = -6 , х2 = -4; тогда = -2 , у2 = -4 .
Ответ: (- 6; - 2\ (-4; -4)
v-u = 1,
6.093. <>-v = l,

Решение.
Из первого уравнения системы найдем у = 1 + и. Подставив это значение v во второе и третье уравнения системы, имеем
w-(l + u) = l,	(w-u = 2,
(u-1)5 + (l + w-2)3 +(w-3)3 =3	(u-1)3 + (u-l)3 + (w —З)3 =3
и - и = 2,
г^-^+^-з^з.
Из первого уравнения последней системы найдем w = 2 + и . Подставив это значение и> во второе уравнение этой же системы, находим
2(и-1)3 + (2+и-3)3 =3<=>(м-1)3 = 1, откуда и = 2. Тогда w = 4, a v = 3.
Ответ: (2;3;4).
6.094.
х+у ' х-у 13 х-у х+у 6 ’ ху = 5.
Решение,
ОДЗ: х*+у.
Преобразовав первое уравнение системы, получим
6(х + у)2 +6(х-у)2 = 13(х-у)(х+у)<=>х2 = 25у2, откуда
=-5у,х2 =5у.
Из второго уравнения системы находим у1 = -1 (не подходит) или у1 = 1, откуда Д2 ~ *1- Тогда х12 = ±5.
Ответ: (5;1), (-5;-1).
3x+2y + 2z = 13,
6.095. s2x+3y + 2z = 14,
2x + 2y+3z = 15.
Решение.
Сложив все три уравнения, получим 7(x + y + z) = 42, откуда
х+у+ z = 6. Теперь будем последовательно вычитать это уравнение из каждого уравнения системы:
(3x + 2y+2z = 13,	, [2x+3y + 2z = 14,
<	<=>х = 1; <	<=>у = 2;
[x + y+z =6	[x+y + z = 6
|2x + 2y + 3z = 15, 1	<=>У = 3.
[х + у+ z = 6
Ответ:
6.096. i
хУ =16, =2.
Решение.
у
Деля первое уравнение системы на второе, получаем — = 8, у = 8х .
3	2	5	1
Из второго уравнения системы имеем х • 64х = 2, х = —, откуда
1
х = - ; тогда у = 4.
Ответ:
x + 2y + 3z = 3,
6.097. \3x + y + 2z = 7,
2х + Зу + z = 2.
Решение.
Будем преобразовывать систему по методу Гаусса, т.е. из второго и третьего уравнения системы вычтем первое, помноженное на соответствующее число
х + 2у + 3z = 3,	х+2у + 3z = 3,
Зх + у+2z = 7, <=> ’ - 5у - 7z = -2, <=> 2x + 3y + z = 2	-y-5z = -4
x + 2y + 3z = 3, у 4- 5z = 4,	<=>
-5y-7z = -2
x = 2, J=-l, z = 1.
Ответ: (2; -1;1)
X3 +/ =7, 6.098. 1/^4	0
|xy(x + jJ = -2.
Решение.
Перепишем систему уравнений в виде
(х + у/^-ху + у2^?,^ xy(x + y) = -2
(x + y)((x + y)2-3xy)=7, _xy(x + y)=-2.
IX 4- У = U, Пусть s	тогда система уравнений имеет вид
(ху = V,
u(u2 -3v)=7,	2
uv = -2	и
Из первого уравнения полученной системы найдем
и и2 + — |=7<=>и3 + 6 = 7> и3 и 1
= 1,
>ткуда и = 1. Тогда
2	9 П
= -у = -2 .Далее,
v
Ответ: (2; -1) (-1; 2)
6.099. 1
х2 + ху + у2 = 91, x + Jxy + у = 13.
Решение.
ОДЗ: ху>0.
Пусть <
тогда
X = и2
У = V2,
х2 = и4 У =v4.
Относительно и и v система уравнений принимает вид
м4 +u2v2 + v4 = 91, С2 +г2У -2u2v2 +u2v2 = 91, и +uv + v =13	u2+v2=13 — uv.
Из первого уравнения полученной системы имеем (13-mv)2-w2v2 =91, 169-26mv+m2v2-w2v2 =91, uv = 3. Из второго уравнения системы получим
u2+v2=13-3, (u + v)2-2uv = 10, (u + v)2 =10 + 2uv = 16, откуда
и + v = -4 или
u + v = 4•
Получили две системы уравнений:
[u + v = 4,
2) 1 Q
7 [uv = 3,
или
|uv = 3
откуда по теореме Виета находим
{Wi=-1, fu2 =-3, (и3 =1, Ju4=3, Vj = -3, [ v2 = -1, [v3 =3, [v4 = 1.
Тогда для <
[Xj =1, fVx=3,	f*2=9>
откуда	откуда <
bl =9> bb=l,	Ьг=1-
Ответ: (1; 9) (9; 1)
6.100.
л/w + v - Vu-v = 2,
и + v - -Ju — v = 8.
Решение.
[u + v>0, 0ДЗ: L-v>0.
Перепишем систему уравнений в виде
Складывая и вычитая уравнения системы, получаем
\Vu + v =6,
Vu + v = 3, Vu-v =1.
Отсюда
|« + v = 81, Ju=41, [u - v = 1, |v = 40.
Ответ: (41; 40)
6.101.
Решение,
Перепишем систему уравнений в виде
Если '
u> Ju + v = 6, v, TO |u v = 8.
J«2 =4, и™ |y2 =2.
По теореме Виета единственно возможные варианты
Гм, =2, |v,=4
Тогда
или •
|x +j? = 4, откуда
[x - у = 64
или
х2=12, Л =4-
и 1
*i = 34,
/,=-30,
x 4- у = 16, x-^ = 8, Ответ: (34;- 30^(12; 4)
6.102.
y]2x-y+l\ -^Зх+у-9 = 3, ^2х-у+11 +фх+у-9 = 3.
Решение.
Пусть "
$]2х-у + \ 1 = и > О, ^/Зх + у-9 = v > 0.
, Относительно и и v система принимает вид
и1 -у2 =3, J(u-vXw + y) = 3, (и-v = l,	(и = 2,
\ + v = 3 ^[u + v = 3	^tu + v = 3, откуда V = l.
Тогда «
ф.х-у+\1=2, фх+у-9=1
2x-j + ll = 16, <=>
Зх + у-9 = 1
2x-j = 5,
3x+j = 10,
откуда
[х = 3, |у = 1.
Ответ: (3;1}
у/5х + у + у]5х- у = 4.
Решение.
ОДЗ:
5х + у > 0,
5х - у > 0,
у>о.
Пусть = z > 0 . Тогда z - — = 1 или z1 - z - 2 = 0, где z*0 . От
сюда zl = -1, z2 = 2 ; Zj = -1 < 0 не подходит.
i У У
Тогда J— = 2,— = 45^ = 4х.Из второго уравнения системы имеем
л/5х + 4х + у/5х-4х = 4, у/9х + у[х = 4, 4-Jx =4, у[х = 1,откуданахо-дим х = 1. Тогда у = 4. Непосредственной проверкой убеждаемся, что это решение.
Ответ: (1;4)
ylxy[y +tfy>[x =12, 6.104.
ху = 64.
Решение.
(х >0, °Д3: [у > о. Перепишем систему в виде
.	= 12,<=>|Vx?V/(V7 + Vx)=12,
ху = 64	|xj = 64.
Пусть >Гх = и > 0, a tfy = у > 0. Тогда имеем
u2v2 (u + v) = 12,	[(«у)2 (м + у)=12,
м6у6=64	|иг = 2
[4(u + v)=12, fu + v = 3, <	<=> <
[uv = 2	[uv = 2,
fui =1,	fu2=2,
откуда <	или 5
h=2	|v2=l.
Тогда
откуда
Xi=l,	[x2=64,
< или 4
[^i=64	[у2=1-
Ответ: (1; 64), (64; 1)
6.105. i
^?=з.
Л’-г)2 =•
Решение.
Из условия имеем ’
|х + /| = 3, >-у|=1.
Из этой системы уравнений получаем
следующие четыре системы: [х+у = -3,	[х+у = -3,	[х+у = 3,	[х + у = 3,
1)	/2)	1	3)	/4) Л ,
=	|х-у = 1;	[х->у = 1;	[х->» = -1.
Складывая и вычитая уравнения каждой системы, найдем ее решения:
{Xi =~2, jx2=-l, Jx3 =2, Jx4=l, Л =4 V?=-2, |у3=1, V«=2-
Ответ: (-2; -1} (-1;-2\ (2; 1} (1; 2)
6.106. 1
и2 +v2 = uv+13,
u + v = Vuv +3.
Решение.
ОДЗ: uv>0.
Относительно x иу получаем систему
*4 +у4 =х2у2 +13,	(х2 +y2>f -2х2у2 -х2у2 +13,
х2 +у2 =ху + 3	[х2+/=х>- + 3
(х2 +у2У -Зх2>>2 -13 =0,
х2 + у2 -ху + 3.
Из первого уравнения системы имеем
(ху+З)2 - Зх2/ -13 = 0, х2у2 + бху + 9-Зх2у2 -13 = 0,
х2у2 -Зху+2 = 0,откуда ху = 2 или ху = 1 .Получили две системы уравнений:
1)
ху-2, (х+у)2 = 3ху+3
или
2)
ху = 1,
(х + у)2 = 3ху+3,
откуда находим
х2 =2, ,У2 =1-
Тогда
Ответ: (1; 4^(4; 1), (* - >/3; 2 + >/з ) (г + >/3; 2 - V3 )
1	1	4
ху = 9.
Решение.
Пусть <
где и > 0 и v > 0 .
Относительно и и v система уравнений примет вид
[114
- и v 3 u2v2 =9.
Учитывая, что и > 0, v > 0 , получаем
w+v 4	[	4
-----= —,	и + v = — uv, 4 uv 3 <=>	3	<=>
uv = 3 uv - 3
и + v = 4, uv = 3,
[uj =1, fu2 =3, откуда <	_ <	1
[vt=3; [v2=l.
Тогда <
yfx =l, fxj =l, 77 = 3. Vi=9;
x2
У2
= 9, = 1.
Ответ: (1; 9) (9; 1)
3b.-Jx-y) +\ob. + Jx + y\ =5.
6.Ю8.4 ;	'	,	'
4^-Jx-y) -Sfy + Jx+y) =3.
Решение.
Перепишем систему уравнений в виде
3	!	10
2-у[х-у 2+^х+у
2-у/х-у 2 + <Jx + y
х-у>0,
ОДЗ: <U + >’>0, х-у *4.
Пусть 4
Относительно и и v система уравнений прини-
мает вид
(3u + 10v = 5,
[4u-5v = 3.
Отсюда получаем и = 1; v = - . Тогда
2-Jx-y	2-y/x-y =1,	y/х-у =1,	(х-у = \,
1	_	[2 + ^х + у =5 |/г+7 = 3	1х+>' = 9’
2+yjx + y 5
откуда
|х = 5, [у = 4.
Ответ: (5; 4)
6.109.
Ifx+tfy =4, х+^ = 28.
Решение.
Пусть
Vx =и,
х = и3,
3 Относительно и и v система принимает вид У = V .
u + v = 4, fu + v = 4,
u3 + v3 = 28 (м + v)(u2 -uv + v1 )= 28
(u + v = 4,
=> <
i uv = 3,
откуда
{«1=1, Jw2=3, vt=3; [v2=l.
y[x=l, [x(=l, Тогда <	<=>•!
l[y = 3 th = 27;
Ответ: (1; 27), (27; 1)
Jtfx+y + yjx-y -4,
6.110. ] I---- I------ o
[у1х~^У ух~У =8.
Vx =3,
u + v = 4, ((м + v)2 -3uv)=7
x2 =27,
У2 =1-
Решение.
\х + у>0,
2
Пусть <
= V2.
Относительно и и v система примет вид u + v = 4, ju + v = 4, и2 -v2 =8<[(m + vXm-
u + v = 4, u-v = 2,
|w = 3, откуда 5	, Тогда <
I v = 1.
х+^ = 81, jx = 41, откуда
х - у = 1,	1л -
Ответ: (41; 40)
Решение.
°д3: V °-
Перепишем систему уравнений в виде <
и вве-
дем подстановку
и,	л
где и > 0 и v > 0. Тогда
ху = V,
2u = 3v, и2 -2v = 5
2и v =—,
3
tr-2v = 5
2и v~ 3 ’
2 о 2w и -2-----= 5
3
2и v = —,
3
Зи2 -4и-15 = 0.
6.111.
4	4
Из второго уравнения их =-у , и2 =3; их = - — не подходит. Тог
да v = 2 и
х+у = 5, ху - 4.
„	„	1*1=4, \х2 =1,
Используя теорему Виета, находим: <	•{
1л=1; (Л =4.
Ответ: (4; 1} (1; 4)
6.112.
Решение.
х>0,
ОДЗ: Ь>0.
Пусть
V* = и > О,
V7=v > о,
Относительно миг система имеет вид
и2 +V2 =10, u + v = 4
откуда
(m + v)2 -2uv = 10,	|wv = 3,
u+v = 4	|u+v = 4,
wi =1, yi =3;
m2 =3, v2 =1.
Тогда
$q =1, .^ = 3;
^/x7 = 3, |х(=1, $7=1 ° Vi =81;
Ответ: (l;81),(81;l)i
x2 =81, y2 =1.
6.113.
x + у = xy + a.
Решение.
ОДЗ: — >0.
У
Пусть ------= t, где t > 0. Относительно t уравнение принимает
1	7	7	IX + tf
вид r + - = 2, г -2г + 1 = 0, (г-1) = 0, откуда / = 1. Тогда J-------=1,
/	V У
-----= 1, откуда у = х + а. Из второго уравнения получаем
У
х + х + а = х(х + а) + а, х2 + (а - 2)х = 0,х(х + а - 2) = 0,
откуда X] = 0,х2 = 2 - а. Тогда = д,у2 = 2.
Ответ: если а * 0, то Х| = 0,	= а, х2 = 2-а, у2 = 2; если а = 0, то
х = у = 2.
6.114.
у42х - Ху/2у = 6, ху2 — х2 у = 30.
Решение.
ОДЗ:
х>0, у>0.
Перепишем первое уравнение в виде л/2(7ху2 -д/х2у) = 6 и поло-
/ Г I 2
жим уху = w, ух у = v, где и > 0, v > 0. Тогда система относительно и и v примет вид
< V2(u-v) = 6,^ L-v = 3V2, и2 -v2 =30	[(w-v)(u + v) = 30
и - v = 3 VI,
30 <=> и + V =--7=-
3J2
u-v = 3V2, и + v = 5>/2,
откуда и = 4>/2, v = V2.
Значит, <
ху2 - 32, х2у - 2.
Перемножив эти уравнения, получим х3у3 = 64, откуда ху = 4. Окон-
2	1	32 о
{ательно находим х = — = —,у = — = 8.
4 2	4
Ответ: (—; 8).
Решение.
Пусть
х = м
Относительно миг система принимает вид
u + v = 3,	и + v = 3,	u + v = 3,
и2 -uv+v2 =3	(u +v)2 -3wv = 3	З2 -3wv-3
и + v = 3, uv - 2,
{г	13/—	с
lu2=2,	Vx = l,	|*1=1’
< Тогда < откуда <
V1 =2;	[v2 =1.	1^7	= 2>	=8’
Их = 2,	[х = 8,
откуда <
34у = 1,	^=1-
Ответ: (1;8),(8;1).
6.116.
у/u +Hv =5.
Решение.
Г и >0, ОДЗ: I v > 0.
Пусть <
Относительно х и у система принимает вид
х2 + у2 =5
x-y = l,	|х-у = 1,	(x-y = l,
(x - + 2xy = 5 V + 2xy = 5	|xy = 2,
I Xi =-1, [х2 = 2, I Xi =-1<0, откуда 5	5	5	не подходит.
171=-2; Ь'2=»; bi=-2<o
Тогда *
Vm =2, (и = 16, VJ = 1	|v = l.
Ответ: (16; 1)
6.117.
х-у-^а1,
Решение.
ОДЗ: Vs0-
Перепишем систему уравнений в виде
1) При « = 0 имеем
[xi =0. откуда <
Vi = 0;
2) При а * 0 имеем
откуда <
х = Зя,
х2 =9я2, /2 =^2
при a > 0.
Ответ: если а = 0, то Xj =	= 0; если а > 0, то х2 = 9я2, у2 = a2 *>
если а < 0,0.
I 2	V 3
1* + У 1*-у -
[ 8	V 12
Решение.
ОДЗ:
х+у>0, х-у^О.
Обозначим
1х+у
. — - и,
V 2
---- гдеи>0иу^0. x-j
,---— - V,
V з
Относительно и и v система принимает вид
u + v = 14, и - v = 6,
ju = 10, т откуда < Тогда * v = 4.
^=10, 2
= 4
^’^„fx^-200,
х-у = 48,
[V=‘6
Jx = 124, откуда |J = 76 Ответ: (124; 7б)
6.119.
Vx - Vy = 0,5 yfxy, x + y = 5.
Решение.
fx^O, °Д3: [y>0.
Пусть
где и > 0 и v > О.
Относительно и и v система принимает вид
и - v = 0,5uv, и - v = 0,5uv,
и2 + v2 =5 /и-v)2 +2uv = 5
=> (0,5uv)2 + 2uv-5 = 0, 0,25(uv)2 +2uv-5 = 0,
откуда uv = -10 или uv = 2 ; uv = -10 < 0 не подходит. Тогда
u-v = 0,5uv,	fu —v = l,	[u = 2,
<=> < откуда <
uv = 2	[uv = 2,	[v = 1;
Vx=2, |x = 4, 77=1, V = L
Ответ: (4;1)
6.120.	He решая уравнения ax2 +bx + c = Q , найти xf2 + x£2, где x1 и x2 —корни данного уравнения.
Решение.
_2_?1	1 Х\ + х2 (х, + х-> )2 -2х, х?
1 +Х2“=— + — =
Х1 х2 х{х2	lVjX2X
По теореме Виета Xj +х2 = —, х1 х2 =— и а	а
*Т-2-
a j а _ а2 л _Ь2 -2ас а2 _ Ь2 -2ас
Ь2 -2ас
Ответ:----,--
1	1
6.121.	Составить квадратное уравнение с корнями и , если Х|	х2
Х| и х2 —корни уравнения ах2 +6х + с = 0.
Решение.
Пусть у1 + ру + q = 0 есть искомое уравнение с корнями У\ ~	,
_ 1
У2 - .Из условия по теореме Виета имеем х2
Тогда '
У1+?2 =“А
71 у 2 = <?-
а
с хгх2=-.
а
Отсюда
р = -(у\+у2) = -
xt + х2 _Ь с _Ь Х\Х2 а а с’
1
Ч = УгУг = —
*1
1 _ а
х2 с
Ь а
Получили уравнение у2 +—у+— = 0, ас*Ц , <=> су2 +Ьу + а = Ъ . с с
Ответ: су2 + by + a = Q при а .
6.122.	Составить уравнение второй степени, один из корней которого был бы равен сумме, а другой — произведению корней уравнения ах2 +bx + c = Q •
Решение.
Пусть у2 + ру + q = 0 — искомое уравнение с корнями у1 = х{ + х2, у2 = х, • х2. По теореме Виета имеем
b У\=х^х2= —, а
С и 5 у2=Х|-Х2=-	Ь1У2=^
Отсюда р = -(у1+^2)= —- —= -^—q = yty2	Получили
а а а	а2
уравнение
2 Ь~С be л 22	/»	\ t л
у +-----у—- = 0<=>a у + a\b-c)y-be = 0 .
a a2
Ответ: a2у2 + a(b-c)y-bc = 0.
6.123.	Составить уравнение второй степени, корни которого были
бы на единицу больше корней уравнения ах2 + Ьх + с = 0 .
Решение.
Пусть у2 + ру+q = 0 — искомое уравнение с корнями yi = Xj +1, У2 = х2 +1. Из условия по теореме Виета
b х\ + х2 = —, а тогда с
Х1 -х2 =“, а
У\ +У2 =xi + 1 + х? + l = Xj +х? + 2 = - —+ 2 = -р, а
У1 ' У2 = (*1 + 0(х? +1)=х1*2 + Х1 + х? + 1 = --- + 1 = <7, а а
Ь-2а Р =-----,
а
а-Ь + с 4 =-----
а
Получили уравнение
у ч-----уч--------= 0<=^ау +(Ь-2а)у + а-Ь + с = 0
а	а
Ответ: ау2 +(р-2а)у + а-Ъ + с = Ъ.
6.124.	Определить коэффициенты квадратного уравнения
х2 + px + q = 0
так, чтобы его корни были равны р и q.
Решение.
{p + q--p,	[2р + ^ = 0,
<=> 5 / х
Р4 = 4
Из второго уравнения системы имеем ^ = 0 или р-1 = 0. Тогда = 0,	= 0; р2 =1, ^2 =-2р2 = -2.
Ответ: рх = qx = 0; р2 = 1, q2 =	.
6.125.	Найти коэффициенты АиВ уравнения х2 + Ах + В = 0, если известно, что числа АиВ являются его корнями.
Решение.
По теореме Виета (я+в = -я,	[2Л+в = о,. (4=о,	(4=1
[ЛВ = В	|В(Л-1)=0 |5,=0	[В2=-2.
Ответ: Ах= = 0; А2 = 1, В2 = -2.
6.126.	При каком целом значении к один из корней уравнения 4х2 -(3Ar+2)x + (fc2 -1)=0 втрое меньше другого?
Решение.
Из условия по теореме Виета имеем
ЗА+2
*1+*2= —
Jt2-1 ^2 = —,
х2 = 3Xj
л ЗА:+2 4X1=—
Зл’=*^ 1	4
хг =3х.
ЗА+2
Х1=Лб-’ х2 = 3хь /ЗА+2? А2-1 3 16	4
где ке Z • Отсюда 31к2 -36Аг-76 = 0, к{ =2, к2 =-—Z (не подходит).
Ответ: к = 2.
6.127.	При каком целом значениир уравнения Зх2 -4х + р-2 = 0 и х2-2рх + 5 = 0 имеют общий корень? Найти этот корень.
Решение.
Пусть Xi — общий корень, тогда
Зх2 -4xj + р-2 = 0, Зх2 -4xt +р-2 = 0,
xf - 2рхх + 5 = 0 |3xf -6pxj +15 = 0
=» -4xi +6pxj + р-2-15 = 0, (6p-4)xi +р-17 = 0,
17-р ы
откуда х( =--— . Из второго уравнения системы имеем
6р-4
r17-p V
/
-2р
17-р
6р-4
+5 = 0,
12р3-31р2-138р+369 = 0,
12р3-36р2 + 5р2 -15р-123р+369 = 0, (12р3 -36р2)+(5р2 -15р)-(123р-369)=0,
12р2(р-3)+5р(р-3)-123(р-3) = 0, (р-з)^2р2+5р-12з)=0.
Отсюда р—3 = 0, Р] =3, или 12р2+5р-123 = 0, откуда Рг =~^2’ 41
Рз = 3; Рг =	не подходит. Таким образом, р = 3 , тогда х = 1.
Ответ: х = 1, р = 3 .
6.128.	Найти все значения а, при которых сумма корней уравнения х2 -2я(х-1)-1 = 0 равна сумме квадратов корней.
Решение.
{Х1 + х2 =2а,
Xi -х2 = 2а-1 Далее,
%! + х2 =х? +х2 =(х1 +хг)2 -2XjX2 <=> х, +х2 = (xj +х2)2 -2х{х2 . Используя значения хх+х2=2а и хгх2=2а-1, получаем 2а = (2а)2 -2(2а-1), откуда 2а2 -За+1 = 0 > а1 = | > а2 =1 •
Ответ:	, а2 = 1.
6.129.	При каком значении а уравнения х2+ах + 8 = 0 и х2 + х + а = 0 имеют общий корень?
Решение.
Пусть	— общий корень, тогда
*|2 х12
+аХ] + 8 = 0, +*! +а = 0
=> ах{ -Х| +8-а = 0,
*1
а-8 а-1
Из второго уравнения системы имеем
fe-8? м
(а-8
о,
а3-24а+72 (я-1)2
а3 -24а + 72 = 0,
а3+216-216-24а+72 = 0, (а3+21б)-24а-144 = 0, (а3 +63)-24(а+б)=0,
(а+б/а2 -6а+Зб)-24(а+б)=0,
(а+б)(а2-6а+12)=0,
откуда а = -6 . Для квадратного уравнения D < 0,0 .
Ответ: а = -6.
6.130.	В уравнении х2 -2х+с=0 определить то значение с, при котором его корни и х2 удовлетворяют условию 1х2	=47 .
Решение.
Из условия по теореме Виета имеем 4
%! + х2 = 2, Xi*x2=c, Отсюда 7х2 -4х! =47.
х2 =2-Х| и получаем
7(2 - X] )—4х| = 47	|Xj = -3.
Таким образом, с = -15.
Ответ: с = -15 .
6.131.	Не решая уравнения х2 -(2а +1)х+а2 +2 = 0, найти, при каком значении а один из корней в два раза больше другого.
Решение.
Из условия по теореме Виета имеем
		2а+1
х, +х2 =2а+1,	Зх, = 2а+1,	х,= 3 ,
х, -х2 =а2 +2, <=>•	2х,2 -а2 +2, <=>-	2 о2 +2 Xi =	 2
х2 = 2х.	х2 = 2х,	х2 =2х,.
Отсюда
2а+1А2 а2+2	4а2+4а+1 а2+2
----- =------<=>----------=------<=>
3 J 2	9	2
<=>а2 -8а +16 = 0 <=> (л-4)2 =0.
Таким образом, а = 4.
Ответ: л = 4.
6.132.	При каком значении р отношение корней уравнения
X2 + рх -16 = 0 равно -4 ?
Решение.
По теореме Виета и условию имеем систему
х,+х2= -р, ’ ХГХ2 =-16, <=>
— = -4
\|+х2 =-р, 'Х{-Х2 =-16, =>
/2 = -4х.
хх-4хх=-р, Х1(-4х,)=-16
-Зх, =-р,
-4х2 =-16
х -S-Х1’з’ х,2=4.
р2 .	г
Таким образом, — = 4, откуда р
= 36, или р1>2 = ±6.
Ответ: Р\2 = ±6.
6.133.	Не решая уравнения Зх2 - 5х - 2 = 0 , найти сумму кубов его корней.
Решение.
По теореме Виета и условию имеем систему
5
*1+*2 = P
2
X|X2 = ~3
и
Отсюда х*
з 5 f5Y ( 2A 215 + Xj =-	-	- —	=---.
2 3 3	3	27
V ' v '/
215
Ответ:
6.134.	При каком целом значении b уравнения 2х2 + (36-1)л -3 = О и 6х2 -(26-3)х-1 = 0 имеют общий корень?
Решение.
Пусть %! —общий корень. Тогда
2х(2 + (3 b - ifo - 3 = 0, |бх2 + (96 - 3> - 9 = 0, < 6х2 - (26 - 3>q -1 = 0 |бх2 -(2Ь-3>( -1 = 0 «(96-3)х + (26-3>-9+1 = 0, х = ——.
1 \Ь — 6
Из первого уравнения имеем
г[—— 1 +(зб-1{—^—)-з=о, ^116-6 )	\116-6 J
6, = -^-, Ьг =2;
1	99 2
99Z>2-1646-68 = 0,
к 34
bi = - — не является целым значением.
99
Ответ: Ь = 2.
6.135. При каком положительном значении с один корень уравнения 8х2 -6х + 9с2 =0 равен квадрату другого?
Решение.
По теореме Виета и условию имеем систему
3
2
Отсюда получаем с1 = -3 или с1 = —; с2 = -3 < 0 не подходит. Тог-
1 1
Да Q с2 = -
Cj = — <0 не удовлетворяет условию.
Ответ: с = ~.
Решения к главе 7
ЛОГАРИФМЫ. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ
ОСНОВНЫЕ СВОЙСТВА И ФОРМУЛЫ
Степени с действительными показателями
a0 al,	(7.1)
где 0° не имеет смысла;	
а~п а—(а^О) а”	(7.2)
где п - действительное число;	
О AI ^2, 1 * 1^2 in SI с Q	(7.3)
где т и п - натуральные числа;	
а°а₽=аа+₽,	(7.4)
— SaaH5 аР	(7.5)
	(7.6)
где а и Р —действительные числа.	
Показательная функция
Показательной функцией переменной х называется функция у = ах, где а - данное число.
Если а < 0, то функция аЛ определена только при целых и при дробных значениях л- (если знаменатель дробного показателя - нечетное число). Если а = 0, то выражение ОY определено при х > 0. Если а > 0, то функция ах определена при всех действительных значенияхх, причем при а = 1 имеем 1х -1, т.е. функция равна постоянному.
В дальнейшем показательную функцию ах будем рассматривать при а > 0 и а 1.
Основные свойства показательной функции у = ах при а>0,
1.	Показательная функция определена при всех действительных значениях х (хе R).
2.	Областью изменения показательной функции служит множество всех положительных действительных чисел, т.е. у е (0, + ©о).
3.	При а > 1 показательная функция строго возрастает, т.е. из неравенства д') <х2 следует неравенство ах' <аХ2 . Причем если хе (-©©;()), то уе(0;1);если х=0,то у = 1; если хе (0;©о), то уе (1; + ©©),т.е. если хе (-©о; + ©о), то уе (0; + ©©); у—>0 при х—>-©© и У -> +°° при х —> +©© .
4.	При а е (0; 1) показательная функция строго убывает, т.е. из неравенства X) < х2 следует неравенство лЛ| > а*2. Причем если х е (-©©; 0), то уе (1; + ©о); если Л-=0,то у = 1;если хе(0; + ©©),то уе(0;1),т.е. если хе (-©©; + ©©), то уе(0; + ©©);	при х—»-©© и ^—>0 при
X —> +©© .
5.	Характеристическое свойство: значение показательной функции от суммы равно произведению значений этой функции от слагаемых, т.е.
Логарифмы и их свойства
Логарифмом числа/? по основанию а называется показатель степени, в которую надо возвести числом, чтобы получить число b: 1 oga b = х, если ах = b, или
№=/>•	(7.7)
В дальнейшем основание логарифмов будем считать положительным и отличным от единицы (а > 0, а * 1).
Приведем некоторые свойства логарифмов (при любом положительном основании, отличном от единицы).
1.	Логарифм единицы равен нулю, т.е. loga 1 = 0.
2.	Логарифм основания равен единице, т.е. loga а = 1.
3.	Для любого положительного числа b существует, и притом только одно, такое действительное число а, что logа Ь = а.
4.	Из равенства logfl X! = loga х2 следует Xj = х2 (и наоборот).
Основные правила логарифмирования
1.	Логарифм произведения двух или нескольких положительных чисел равен сумме логарифмов этих чисел, взятых по тому же основанию, т.е.
\oga(bc) = \ogab + \ogac.	(7.8)
Замечание. Логарифм произведения нескольких чисел, если оно по-ложительно, равен сумме логарифмов модулей этих чисел, взятых по тому же основанию, т.е.
loga(Z>! b2...bn)s loga|6,| + loga|б2|+... +
+ loga|ft„| (Z>r/>2...6„ >0).	(7.9)
2.	Логарифм частного двух положительных чисел равен разности логарифмов делимого и делителя, взятых по тому же основанию, т.е.
loga = loga b - logfl с.	(7.10)
Замечание. Логарифм частного двух чисел, если оно положительно, равен разности логарифмов модулей делимого и делителя, взятых по тому же основанию, т.е.
loga-^sloga|Z>|-loga|c| (ЬоО).	(7.11)
3.	Логарифм степени положительного числа равен произведению показателя степени на логарифм ее основания (логарифмы взяты по тому же основанию), т.е.
logfl6c = eloga6.	(7.12)
Замечание. Логарифм положительной степени числа, отличного от нуля, равен произведению показателя степени на логарифм модуля ее основания, взятый по тому же основанию, т.е.
logoy=clogoH (У>о).	(7.13)
Формулы перехода от одного основания логарифма к другому
1.	Логарифм числа по данному основанию равен логарифму этого числа по новому основанию, деленному на логарифм данного основания по новому основанию, т.е.
,	_ _ log6 #
1оё<Л = —.	(7.14)
log* a	v '
1
Множитель |og а называется модулем перехода.
2.	Из формулы (7.14) при N = Ь получаем
<715>
3.	Часто в логарифмических преобразованиях пользуются тождествами
log? N = log|a| N (ak > о)	(7.16)
И
logi IN
U>0) (717)
Логарифмическая функция, ее свойства и график
Логарифмической функцией называется функция вида y = logox,
где а > 0, аФ\ их - независимая переменная.
По определению логарифма выражение v = log„ х означает то же, что и выражение ау - х , т.е. логарифмическая функция есть обратная функция по отношению к показательной.
Основные свойства логарифмической функции
1.	Логарифмическая функция определена при всех положительных действительных значениях х (нуль и отрицательные числа при положительном основании логарифмов не имеют).
2.	Областью изменения логарифмической функции служит множество всех действительных чисел у € (- <»; + <»).
3.	При а>0 логарифмическая функция возрастает, т.е. если 0<х1<х2,то loga Xj < loga х2. Причем если хе(0;1),то уб(-«>;0); если х = 1 ,то у = 0;если хе (1; + ©©),то уе (0;+<»),т.е.если хе (0; + <»), то уе (-°°;+оо); у ->-<» ПрИ х —>0 и у при х->+оо .
4.	При 0<я<1 логарифмическая функция убывает, т.е. если 0 < Xj < х2, то logaXj >loga х2 . Причем если хе (0; 1), то уе (0;+<»); если х = 1,то у = 0;еслихе (1;+<»),то уе (-©о; 0), т.е. если хе (0; + «>), то уе (-°°; + оо); у->-©о ПрИ х _»+оо и у —>+°° при х ->0<
5.	Характеристическое свойство: значение логарифмической функции от произведений двух положительных чисел равно сумме значений функции от каждого из чисел:
loge (х, • х2) = loge X) + loga х2.
Показательные уравнения
Показательным называется уравнение, содержащее неизвестное только в показателе степени.
Рассмотрим несколько типов показательных уравнений, решаемых методами элементарной математики.
Показательные уравнения рассматриваются в множестве действительных чисел. Проверка найденных значений неизвестного по условию уравнения при решении показательных уравнений в общем случае обязательна.
1. Уравнение вида
ах=Ь	(7.18)
называется простейшим показательным.
Рассмотрим уравнение (7.18) при а > 0 и а Ф1. Если b > 0, то уравнение имеет единственное решение х = loga b . Если Ь < 0, то уравнение решений не имеет.
2. Показательное уравнение вида
а/М = ь/гЫ,	(7.19)
где <7 > 0 a*l,Z>>0,6*l,a f\(x\f2(x)—заданные элементарные функ-ции, логарифмированием приводится к виду
/l(x)log£,a = /2(x)logf b.
Если последнее уравнение решается методами элементарной математики, го тем самым решается уравнение (7.19).
Логарифмические уравнения
Лога} ифмическим уравнением называется уравнение, содержащее неизвестные только под знаком логарифма.
Логарифмические уравнения, как и показательные, рассматриваются в множес тве действительных чисел. Проверка найденных значений неизвестного по условию уравнения в общем случае является обязательной.
1.	Ур шнение вида
logax = Z>,	(7.20)
где х - н ^известное, а а и b - заданные числа, называется простейшим логарифмическим.
Если а > 0 и а * 1, то такое уравнение при любом действительном значени i b имеет единственное решение
х = аь.	(7.21)
2.	Логарифмическое уравнение вида
loga/i(*)=1ogaZ>(x)	(7-22)
где а > 0 и а Ф1, после потенцирования приводится к виду /,(х)=/2(х).	(7.23)
Корнями уравнения (7.22) будут только те корни уравнения (7.23), при кот< рых j\ (х) > 0 и /2 (х) > 0, т.е. корни, принадлежащие к области определения уравнения (7.22).
3.	Ло арифмические уравнения вида
/(logev(x))=0,	(7.24)
где /(/) и у(х) — некоторые заданные функции, заменой loga у(х)= t приводятся к уравнению f(t)=O 
Показательно-логарифмические уравнения
Если неизвестное в уравнении входит в показатель степени и под знак логарифма или в основание логарифма, то такое уравнение называют показательно-логарифмическим.
Показательно-логарифмические уравнения чаще всего решают, логарифмируя обе части уравнения, и приводят их к логарифмическим уравнениям.
При решении систем показательных и логарифмических уравнений в основном применяются те же способы, что и при решении систем алгебраических уравнений (подстановки, алгебраического сложения, введения новых неизвестных и др.).
Упростить (7.001-7.015):
[ 1 1
7.001. *251086 5 + 49108,7 .
Решение.
I i 1	_____________ _______________
V 251086 5 4- 491088 7 = 7521°85 6 + 721087 8 — ^51°85 + 71087 & =
= 7б2+82 =10.
Ответ: 10.
1 4
36 +31087 9
Решение.
1	4	3	4	3
81log5’ +271О8»36 + 31О8’9 =з41°8з5 + 32108136 + 321083 7 =54+362+49 =
= 625+216+49 = 890.
Ответ: 890.
7.003. -log2log2M
Решение.
П=	1	1
-log2log2 Vv2 =-log2log228 =-log2-log22 = -log22 3 =3.
8
Ответ: 3.
7.002. 81 °85 3 +2710g9
7.004. -log3log3^.
Решение.
- log3 log3	= —log3 log3 3’ = —log3 ^log3 3 = —log3 3"2 = 2.
Ответ: 2.
7.005.
Решение.
Ответ: -11.
7.006. Зб10^5 +101 ~lg2 _^iog936 Решение.
36loe*5 +10l-le2 — 31069 36 =62log65 । Ю jiog^262 = 10Ig2
= 6i°g652 + 10 _3iog36 _52 +5-6 = 24.
2
Ответ: 24.
7.007.
814 2log’4 4-25108,23 8
^log72
Решение.
8>4 2log’4 +25log,2s8 »49log72
814 t 52Iogs323
Ответ: 19.
7.008.
409
з__
( /	\ 2
------125log236
Решение.
g2lOg9 5 +j31og3V6
409
</ ! \21og725	>
72	_g3Iogs26 _
---------X 409
625-216
409
Ответ: 1.
7.009.
i । ।
1У 1У 1У	(основания лога
рифмов представляют собой идущие подряд натуральные степени числа 2).
Решение.
№°82Л'	... ^°esi2^
is
= (у106' 2 • y108v4 . д^,ов№ ДГ,О8«5|2^5 —
= (2-4-8 -512)й = ^' -22 -23 -2’)^ = (г|т2+3+ +9)^.
Выражение Sn =1 + 2 + 3 + . .. + 9 является суммой членов арифметической прогрессии, где ах = 1, d = 1, ап = 9, п = 9. Тогда Sn = *--- п = = ^•9 = 45. Отсюда (г45р =23=8.
Ответ: 8.
гою. (г108*"
.[741og„a _50.51о?75о
Решение.
^21O84^W — 3lo82?(fl2+1) _2л^74Iog49а — 5°’51og^" _ j = ^2log2fl4 _з1оё?(^+1)_2^у ^7log7a2 -5log5fl-l^=
а -а-1
=	~а~^ (д2 +а + 1)=а2 +а + 1.
о2-а-1
Ответ: а2 + а+1.
70П loga A/a2-l log?/fl7«2-l logo2(a2-l)-log^Va2-l
Решение.
logaл/а2 -1 -logyfl 7а2 -1 2^°^и^а	“О
loge2 (а2 -1)- log.^ Va2 -1 1 lOge (а2 -1)-1 loga (а2 -1)
= I loga (a2 -1)= loga Ve2-1.
Ответ: loge -J a2 -1.
——+1	——+1
7.012. alo8*a	Ь-2аХоъ“A+1 • 6log*e+l + ablog“b .
Решение.
2	2
a'og»/ .ь-2а'°ьм .b'°ba+i +ab'°s‘b* =а-а2^ь Ь-
-2a aloe"b-b b'ot*a+a b b2'otta = a-alo8“*2 b-2abba + +a-b-b^ = ab2b-2a2b2 +aba2 = ab3 -2a2 b2 +aba2 =
= ab3 -2a2b2 + a3b - ab^2 - 2ab + a2 )= ab(b - a)2 =
= aZ>(a - i)2.
Ответ: ab(a-bf.
<	1	\	2
2521og4,25	,4 log34_a2
7.013. -------------------;------------------------•
1-a
Решение.
1	2
2521ogw25+21og21og21og2a21ob4 ,4 log,4_a2
.1_______________________________________=
1-a
^51o6549^ +2iog2log24 .(l210*3)-1 -a2 — ................. ..	./------------—
1-a
W +2108,2'1.9-'-а2	(7 + 2)-1-ог
= ---------------------= ——2--------= 1=2- = 1 + a.
1-a	1-a	1-a
Ответ: 1 + a.
12 M. И. Сканави, группа A
353
7.014. (loga b + log4 a + 2Xloga b - loga6 />)log4 a -1.
Решение.
(logo b + log* a + 2Xloga b - loga4 Z>)logz, a -1 = loga b +
1~4 + 2 x loga6 J
logaab Jlogab	log„b
logn6 ______1____1 =
logaa + logaZ> J loga A
= 5ogM.[, i-JofoLp_________________1 =
logab	l + loga6 JlogaZ>
(lOg^ + l)2	/	1	) 1 (iQgq^+lHl + lOg^-O
10ga b ° [ 1 + loga b Jloga b	(\ + \og„b)iogab
-1 = loga/> + l-l = logaZ>.
Ответ: loga b.
7.015.
________1-lOgqfe_______
(loga/> + log4a+l)loga D
Решение.
________1-logp _________
(loga b + log4 a + 0-loga b
Z>+l + loga/>Xl-logaZ>)
Ответ: logfl b.
7.016. Если logfl 27 = ft, то чему равен log^ y[a 1 Решение.
log jr y[a = — • 2 log3 a =---= —-— = -7.
6	53 31ogfl3 log, 27 ft
7.017. Показать, что при условии х>0 и у>0 из равенства х1 +4у2 = 12ху следует равенство lg(x+2y)-21g2 = 0,5(lgx + ig у)
Решение.
Из условия имеем: (х+2 у? - 2х • 2у = 12ху, (х+2yf = 1 бху.
Прологарифмировав обе части полученного равенства по основанию 10, получим:
\g(x + 2y? = lgl6xy, 21g(x + 2y)=lgl6+lgx + lgy, 21g(x + 2y)=41g2 + Igx + Igy, lg(x + 2y)-21g2 = 0,5(lgx + Igy)
7.018. Вычислить сумму 2х + 2~x, если 4 х +4-х =23.
Решение.
2 х +2~х =y[^x+2~xJ = 74х+4-х+2 = 723 + 2 = 725 = 5.
Ответ: 5.
7.019. Доказать, что если у = 2х* и z = 2У , то х = ±A/0,51og2 log2z , и указать все z, при которых х принимает действительные значения.
Решение.
По условию у > 0 и z > 0. Прологарифмировав обе части равенства по основанию 2, получим log2 у = log2 2Х?, log2 у = х2, откуда х = ±«Jlog2 У • Аналогично z = 2У => у = ^/log2z .
Таким образом, х = ±Jlog2 л/iogTz = ±70,51og2 log2 z . Отсюда log2 log2 z > 0, log2 z > 1, z > 2 .
Ответ: z^2.
Решить уравнения (7.020 - 7.046):
7.020. fl+—Ilg3 + lg2 = lg(27-3l/x).
\ )
Решение.
ОДЗ:
x*0, 27-3l/x >0.
Ig3 2x +lg2 = lg 27-3V
1+—
1g 2-3 2х
= lg 21-3х
1+— 1 1 1
2-3= 27-3Y, 3х +6-32v -27 = 0.
Это уравнение, квадратное относительно 32х; найдем 32х = -9, ко-
77	1
торое не подходит, и 32Л = 3, откуда х = —.
Ответ: -7. 2
7.021. 31og5 2+2-х = Решение.
ОДЗ: 3*-52-v >0.
log5 8 + 2log5 5 -log5(з x -25 • 5 X)=x a log5
откуда ~x $_x = 5 Y <=> 15х = 152. Таким образом, x = 2 .
Ответ: 2.
7.022. A/iog^x?-41og9V3^’ = l.
Решение.
ОДЗ:
x>0, log3x>0, х>1.
-Jlog3 x9 = 1 + 4log9V3x <=» ^9log3x = l + log33x <=>
<=> ^/91og3 x = 1 + log3 3 + log3 x <=> 791og3 x = 2 + log3 x.
Возведя обе части уравнения в квадрат, получим
9 log3 х = 4 + 4 log3 х + log3 х <=> log3 x - 5 log3 x + 4 = 0.
Решая это уравнение как квадратное относительно log3 х, имеем (log3 х), = 1, (log3 х), =4, откуда х, = 3, х2 = З4 = 81.
Ответ: 3; 81.
7.023. log|_x 3 - logbv 2 - 0,5 = 0.
Решение.
ОДЗ:
1 - x > 0, 1-х*1,0*х<1.
3	3 I-----	9	5
Из условия log|_x —= 0,5 <=> — = vl—х => — = 1-х, откуда х = -—.
Ответ:
4
7.024. 1g 5 + lg(x+10)=1 - lg(2x -1)+ lg(2 lx - 20)
Решение,
ОДЗ:
х + 10>0, 2х-1>0, 21х-20>0,
1g5 + lg(x +10)= Igl 0 - lg(2x -1)+lg(2 lx - 20) <=> lg5(x +10)=
= lg 10(21x-20)	5(% + J0)= 10(21x-20),
2x-l	2x-l
откуда 2x2 -23x + 30 = 0 . Решая это уравнение, имеем хх = 1,5; х2 = 10.
Ответ: 1,5; 10.
7.025. log2182 - 2 log2 V5^x = log2 (11 - х)+1.
Решение.
[5-х >0,
ОДЗ:
м [11-х>0,х<5.
log, 182 - log2 (5 - х) = log2 (11 - х)+ log2 2 => log2	= log2 (11 - х)- 2,
-^- = 2(11-х 5-х
откуда х2 -16х - 36 = 0, Х| = -2, х2 = 18; х2 = 18 не подходит по ОДЗ.
Ответ: -2.
7.026. log5 Vx-9 - log; 10 + log5 >]2x-\ = 0.
Решение. lx-9>0,
0ДЗ: [2x-l>0,x>9.
Из условия
.	J(x-9)(2x-l)	J(x-9X2x-l) .	/7—ттт-----
log5 2L1-------L = о <=> —---------- = 1 <=> уЦх - 9Д2х -1) = 10 =>
=>(x-9X2x-l)=100, 7	7
откуда 2x2 -19x-91 = 0, x, =13, x2 =—^', xi =~ не подходит по ОДЗ.
Ответ: 13.
7.027. lg(x+l,5)=-lgx.
Решение.
(x + l,5>0,
ОДЗ:	n
[x >0.
lg(x +1,5)+Igx = 0=>lg(x4-l,5)x = 0=>x2 4-1,5x-1 = 0,
откуда Xj = —, x2 = -2; x2 = -2 не подходит по ОДЗ.
л 1
Ответ: — •
2
7 028 52(,og52+T)-2 = 5 v+log52
Решение.
^x+iogs2 j2 _ jx+iogs2 _2 = 0; решив это уравнение как квадратное относительно 5 x+log52, найдем 5v+logs2 =-1 и 5v+log52 = 2; 5x+log52 =-1 не имеет решений.
Таким образом,
5x+,og52 =2=>log55A+1O8s2 =log52, x4-log52 = log52,
откуда x = 0 •
Ответ: 0.
7.029. 0,25log2 ^-W'ofct2-’) = ^2(7-x).
Решение.
x + 3 > 0,
ОДЗ:	x2-9>0, 3<x<7.
[7-x^O.
Из условия имеем
(2-гГ’_ ДТТТ) а 2,ОЬ(ЛПГ .2,ogj(.=-,) _
Следовательно, х2 -4х -5 = 0 при х > 3. => Xj = 5, х2 = -1; х2 = -1 не подходит по ОДЗ.
Ответ: 5.
7.030. xlgV55r?-lg25 = 0.
Решение.
2х-8	(2х-8>	2х2-8х
xlg5 5 = lg25, lg5 5 = lg52, 5 5 = 52,
откуда Xj = 5, x2 = -1.
Ответ: 5; -1.
7.031. log5(x-2)+log^(r3-2)+log0>2(x-2)=4.
Решение.
ОДЗ:	x-2>0,x>2.
Из условия имеем
log5(x-2)+21og5(r3 -2)-log5(x-2)=4, log5(x3-2)=2,
откуда x3 -2 = 25, x3 = 27. Тогда x = 3 •
Ответ: 3.
7.032.
2-lg4 + lg0,12 lg(j3x + 1 +4) -lg2x
Решение.
x>0,
ОДЗ: <3x + l>0, lg(73x + l +4)* lg2x,
Из условия
i inn i л i 1 (/->	7	-	1 100*0Д2 « >/Зх4-1+4
lg 100 - 1g 4 + 1g 0,12 = lg к/ Зх+1 + 4)- lg 2x => lg   = 1g  -
4	2x
3 = >/3x + l +4	73х+Т = 6х-4, 6x-4 >0 =>
2x
3x4-l = 36x2 -48x4-16, 6x-4>0
12x2 -17x4-5 = 0, 'Х>Л.
3
„	.	5	,	5
Корнями квадратного уравнения будут хх =—,х2 =1; xi =— не
подходит.
Ответ: 1.
7.033. xlg’x“51gx =0,0001.
Решение.
ОДЗ: 0<х*1. '
Логарифмируя обе части уравнения по основанию 10, получаем lgxIg x"5Igx = lg0,0001=> (lg3 x-51gx)lgx = ^, lg4 x-51g2 x+4 = 0.
Отсюда (igx^ = -1, (igx^ = 1, (igx)^ = -2, (lgx)4 = 2. Тогда Xj =	,
X2=10, Хз=Т5о’X4=100-
Ответ: 7—10; 100.
7.034. lg(?x -24-x)=2+0^51gl6-0^xlg4.
Решение.
ОДЗ: 3х-24-x >0.
Из условия
lg(3x-24-х)= lgl00+ lg2-lg2x => 18(зх-24-x)= lg*25Ll,
3* _2‘*-x — 200
” 2х '
Отсюда 6х = 216, откуда х = 3.
Ответ: 3.
7.035. log(81х +32x)=31og27 90.
Решение.
Из условия log3 (вIх + 32х )= log3 90, 92х +9* -90 = 0, откуда найдем 9х = -10, что не подходит, или 9х = 9, откуда имеем х = 1.
Ответ: 1.
7.036. 3x-log6 8х =log6(33x +х2 -9)
Решение.
ОДЗ: З3х + х1 - 9 > 0.
Из условия Зх = log6 8х +log6 (з3х + х2 -9) Зх = log6 8х (з3х + х2 ~9), откуда63х =8х(?3х +х2 -9) З3х =33х +х2 -9<=>х2 =9.Тогдахц =±3.
Ответ: -3; 3.
7.037. log6^3x2 +l^-log6^32-x2 +9j=log62-l.
Решение.
Из условия
logef3’2 +1У1о8б(з2-х2 +9l=log62-log66, log6 =log6
V )	\	)	32-х +9	6
ТА	V2
Решая это уравнение как квадратное относительно 3 , получим 3х = -1 (не подходит) или 3 х" = 3 , откуда х2 = 1, х1>2 = ±1.
Ответ: -1; 1.
7.038. Igf625^5*^®^” 1=0.
Решение.
x2-20.V4-55	X2-20x4-55
Из условия имеем 625-5	5	=1, 5	5	=5"4, откуда
х2-20x4-55 л 2
------------= -4, х2 -20х+75 = 0. Тогда х} = 5; х2 =15.
Ответ: 5; 15.
7.039. Ig^lO^2-21) j-2 = Igx -Ig25.
Решение.
ЛТТ_ х2 -21 >0,	/г?
ОДЗ: 1	x>V21.
|х>0,
Из условия имеем
1 ( 2	. ,ЛП 1	1 ос 1 х2-21 .. х х2-21 х
Iglx -21l-lgl00 = lgx-lg25, 1g-----= lg—, ------= —.
V ’ &	5	6 Б 100	6 25	100	25
Получаем квадратное уравнение х2-4х-21 = 0, корнями которого будут X] = 7 , х2 = -3; х2 = -3 не подходит по ОДЗ.
Ответ: 7.
7.040. Igp +l)=21g’‘(х2 +1)-1.
Решение.
ОДЗ: х*0.
lg(x2 +1)= ^2 +i)-l, lg2(х2 +l)+lg(x2 +1)-2 = 0.
Решая это уравнение как квадратное относительно lg(x2 +1), найдем lg(x2 +1)=-2 и lg(x2 + 1)=1. Отсюда х2 +1 = 0,01, х2 =-0,99,0 . х2 +1 = 10, х2 =9 .Тогда х12 =±3 .
Ответ: -3; 3.
7.041. igV5x(13'x)+lllg2 = ll.
Решение.
*(13-х)	х(13-х)	х(13 —х)
Отсюда имеем 5 2 •2||=10||,5 2	=5’'.Тогда-----------= 11,
х2 -13х+22 =0, откуда Х| =2; х2 =11.
Ответ: 2; 11.
7.042. x(lg5-l)=lg(2x+l)-lg6.
Решение.
x(lg 5 -lg 10)= lg(ix +1)-lg6, Xlg= lg—, 1U О
9х 4-1	9х 4-1
lg2-x=lg——, 2-x=——22x+2x-6 = 0. 6	6
Решив это уравнение как квадратное относительно 2х, найдем
2х = -3 (не подходит), 2х = 2 , откуда имеем х = 1.
Ответ: 1.
7.043. Ig^l Vs*2’8* ^=0.
Решение. ;—	?~8х	г2 _8г
Имеем81уЗх'~8* =1, 3 3 =3^,откуда—-— = -4, х2 -8х+12-0;
х, = 2 ; х2 = 6.
Ответ: 2; 6.
7.044. log* 9х2 ;log2 х = 4.
Решение.
ОДЗ:	0<х*1.
Имеем
log3 9х ]og2 х _ 4	9 + |og3 х2 )]og3 х _ 4 iog2 х + |og3 х _2 = 0.
log3x
Решая это уравнение как квадратное относительно log3 х, найдем
(logз х^ = -2 , откуда Л1 = ^ > 0°8з л')2 = 1 ’ 0ТКУДа хг = 3 • 1 _
Ответ: —;3.
7.045. log5 (Зх -11)+ log5 (х -27)=3 + log5 8.
Решение.
|3x-ll>0, ОДЗ: |«-27>О. *>27'
Имеем
log5 (Зх -11)+ log5 (х - 27) = log5125+log5 8,
log5 (Зх -11)- (х -27)= logj(125-8} (Зх -11Хх - 27) = 125 • 8,
Зх2 -92х-703 = 0,
19	19
откуда находим Xj =37 , ^2	—; х2 =—— не подходит по ОДЗ.
Ответ: 37.
7.046. lg(5-x)+21gV3-x =1.
Решение.
/5-х > 0,
°Д3: |з-х>ц х<3
Имеем lg(5 - х)+lg(3 - х) = 1, lg(5 - хХз - х) = 1, откуда (5 - хХз - х)=10, х2 -8х + 5 = 0. Тогда х, =4-Vn, х2 =4 + Vn ; х2 = 4 + Vn не подходит по ОДЗ.
Ответ: 4-л/ГТ.
7.047. Найти натуральное число п из равенства
-^2 ^5 ^8 ^З/i-l _27^
Решение.
32+54-8+...+3П-1 =315( 2 + 5 + 8 + ... + Зп-1 = 15.
В левой части уравнения имеем сумму членов арифметической про-с*	о , „ а 1 1 ак~а\ 1	3/7-1-2 ,
грессии Sk, где =2, rf = 3,	=3/2-1, к=—-----L + l =-----+1 = п.
п =
a}+ak 2-ьЗл-1 Зл2 +п
Тогда Зк -—  к =------------л =—-—, и уравнение принимает
Зл2 +п ., , j -л .
вид —-— = 15, Зл +л-30 = 0,откуда п = 3.
Ответ: 3.
Решить уравнения (7.048 — 7.127):
7.048. 0,5(lg(x2 - 55х+9о)- lg(x -Зб))= 1g Л.
Решение.
(х2 -55х+90>0,
[х-36>0.
Из условия
0,5(lg(x2 - 55х+9о)- lg(x - 36))= 0,5 lg2, lg*2~55* + 9° = 1 g2,
x-36
x2 -55X + 90 2
x-36
Имеем x2 -57x4-162 = 0 при x*36-Отсюда Х]=54, х2=3;
х2 = 3 не подходит по ОДЗ.
Ответ: 54.
7.049. lg(5-x)-|lg(35-x’)=0.
Решение.
ОДЗ:
5 - х > 0, 35-х3 >0,
x<V35.
Из условия имеем 31g(5-x)=lg(35-x3
lg(5-x)3 =lg(?5-x3), от-
куда (5-х)3 =35-х3, х2 -5x4-6 = 0 Тогда xt =2, х2 =3.
Ответ: 2; 3.
7.050. log2	4-log2 (г2 -25)= 0.
Решение.
ОДЗ: —7>0илихе (-«;-5)U(5;°°)
* х+5
Имеем log,	——— = 0, (х-5)2 = 1, откуда х-5 = -1 или
х + 5
х-5 = 1- Тогда Х| =4, х2 =6; Xj =4 не подходит по ОДЗ.
Ответ: 6.
7.0SL lgS-lg(x-5) = |
lg Vx + 7-lg2
Решение.
х-5 >0,
ОДЗ:^х + 7>0,	х>5.
л/х + 7 5*2,
Из условия
lg8-lg(x-5)= lg2-lgVx + 7, lg—= lg 2-—, x-5 Vx+7
- = -=£=, 4Vx + 7 = x-5, 16x + 112 = x2-10x+25,x>5.
x-5 Vx+7
Имеем x2 -26x-87 = 0 , откуда Xj =29 , x, =-3 ; x, =-3 не под-
ходит по ОДЗ.
Ответ: 29.
7.052. logo 5 4х + 1оё2	= 8-
О
Решение.
ОДЗ: х > 0.
Имеем
log2 4x + log, -—8 = 0, 8
log2 x + 61og2 х-1 = 0.
(log2 4+log2 x)2 + log, x2 —log2 8-8 = 0,
Решая это уравнение как квадратное относительно log, х , найдем (log2 х)| = -7, откуда х, = 2'7 =	, или (log2 х)2 = 1, откуда х2 = 2 .
12о
Ответ:
7.053. lg(lg x)+ lg(lg x3 - 2)= 0.
Решение,
Igx >0, ОДЗ:	,
Igx3 -2>0, Из условия имеем
31g2 x-21gx-l = 0.
Решая это уравнение как квадратное относительно 1g х, найдем
(lg x)i = -1, откуда х( =
-5	V1 v
не подходит по ОДЗ.
или (lg х\ = 1, откуда х2 = 10;
Ответ: 10.
7.054. log2 х + log4 х + log8 х = 11. Решение, ОДЗ: х > 0.
Имеем log2 х + 2. log2 х+i log2 х = 11, log2 х = 6, откуда х = 26 =64.
Ответ: 64.
7.055. log3(jx -8)=2-х.
Решение.
ОДЗ: У -8 >0.
По определению логарифма имеем 3Х-8 = 32-Х,
9 Зх-8 = —
32х - 8 • 3х - 9 = 0, откуда, решая это уравнение как квадратное отно
сительно 3х, найдем 3х = -1,0 ; или 3х = 9, откуда х = 2.
Ответ: 2.
7.056. 7lgx -5lgx+1 = 3-5lgx4 -13 • 7lgx-1.
Решение.
ОДЗ: х > 0.
Из условия
7lgx _5.5igx =2.5ig* -12.7^, 35-7lgx +65 7,gx =2b5lgx +175-5lgx, 5	7
( 7	( 7 V
100-7l8X =196-5lgx, -	= -
15 I 5
откуда Igx = 2 и x = 100-
Ответ: 100.
7.057. 5х+6 —3*+7 = 43-5x+4 -19 3x+s Решение.
( с V ( c \ J
Имеем 56-5х-43-54-5х = З7-3х-19-35-3х, — = — ,отку-l3 J t3 J
да x = -3.
Ответ: -3.
Решение.
7
ОДЗ: 2х-7>0,х>-.
Из условия
logs(V2x-7 +1)= |logs(V2x-7 + 7) log5p2x-7 +1)= logs^2x-l+l,
откуда
л?2х-7 +l = -JV2x-7 + 7 =>(>/2x-7)2 + 2<j2x-7+1 = V2x-7+7, (V2x-7j + V2x-7 -6 = 0.
Решив это уравнение как квадратное относительно >/2х-7 , найдем
V2x-7 = -3,0; или V2x-7 = 2, откуда х = 5,5.
Ответ: 5,5.
Решение.
ОДЗ: х>0.
I x 2+Jx+x	1 x 2+Jx+x
J2 . jl+Vx .3 2(1+Vx) _ j4 3 2 1+Vx 2(1+Tx) _
откуда
1 x 2 + yfx +x л
Решив это уравнение как квадратное относительно 4х 9 найдем 4х = -1,0 ; или 4х =9, откуда х = 81.
Ответ: 81.
7.060.	0,12= = 4^2.
Решение.
ОДЗ: х * 0.
Перепишем уравнение в виде
х £ -J_	1	*+*__!_	2+-
22 -23 -2 2х = 22 -23 22 3 2х =2 3
откуда х х 1	7	-
2 + з"2Гз’5*2-14*-3 = 0-
Тогда Xj = -у, х2 = 3.
Ответ: -у; 3. 5	1
7.061. -Л0^4'^+1° -16^=0.
Решение.
ОДЗ: х>0. Из условия j 5	2	1	5	2
22.2 4<Jx+io _2^+* 22 4V*+io =2^+1 откуда
= -Л- =.(ЛУ-зЛ-10.0,
2 477+10 77+1 v ’
Решая это уравнение как квадратное относительно 4* , х = -2, 0; или Vx = 5, откуда х = 25.
Ответ: 25.
х-3 J / Зх-1
7.062. 8^-7^0,25 х'*'1 =1.
Решение.
ОДЗ
7
3
Перепишем уравнение в виде
Зх-9 Зх-1	Зх-9 Зх-1
23х-7 «2 Зх-з = 2°, 23х~7 Зх-з =2°,
откуда
Зх-9 Зх-1 Л 5 -----------= 0 => х =
Зх-7 Зх-З	3
Ответ: —. 3
7.063. 2х2-3-5х2-3 =0,01 (10х’1)3.
Из условия 10х -3 = 103х-5, х2-3 = Зх-5, х2 -Зх + 2 = 0,
X] = 1, х2 = 2.
Ответ: 1; 2.
T25Y 12 ( 27 V
7.064. 0,6х —	= — .
V 9 ) U25J Решение.
Имеем
-2х2+х + 24 = 9,2х2-х-15 = 0,
найдем
откуда
5
откуда Х| = - —, х2 = 3.
л 5 , Oti'ieeiTi. , 3.

1 1
7.065. 5Х~& -0^ = ^25.
Решение.
QJ& 0<х*1. ।	1	2 I________!_	2
Изусловия 5Х~^ -5	= 53, 5х’77	=53 .
Отсюда —, 2^/х J2 + Vx - 6 = 0. Решив это уравне-х~^х у/х 3 ние как квадратное относительно Jx , найдем Jx = -2,0; или Jx 9 откуда х = —. 4 9 Ответ: — ♦ 4 1	1	77
7.066. 2^~{	=4х+л/*.
Решение. ОДЗ: 0< х*1. 1	_1	277	1___1	2 77
Имеем* 2^*4 *2	= 2*+77	77+1 =2*+77.
_	1	1 2л/х Г о л п
Тогда —/=-------j=— =-----т=г, х - V х -2 = 0. Решая это уравне-
Vx-1 Vx+1 x + vx
ние как квадратное относительно Jx , найдем Jx = -1,0; или Jx = 2, откуда имеем х = 4 *
Ответ: 4.
4+79^7
7.067. 2,5	0,41_,/5=х =510 ОД5.
Решение. ОДЗ: 9-х>0, х<9.
Перепишем уравнение в виде
Тогда
откуда X) = -7, х2 = 8.
Ответ: -7, 8.
7.068. 2х2-1 -З'2 =Зх2_| -2х2+2.
Решение.
2х ,2 3х ,2	9	,2	4	,2
ИмеемV + 4 2 “ + 3*, ~2Х = ^3Х 2	3	2	3
Тогда х2 = 3, откуда х, = —7з , х2=у[з .
Ответ: - 73; >/з.
7.069. log л (г - б)- logV5 (ix - 2)= 2.
Решение.
ОДЗ:-
4х-6 >0, 2х -2 >0.
4х -6 Имеем log -----= 2,
'Г52х-2
п2х —6
—-----= 5, 22х -5 -2 х +4 = 0. Решая это
22-2
уравнение как квадратное относительно 2 х, найдем (2 х J = 1, откуда имеем X] = 0, или (гх = 4, откуда имеем х2 = 2 ; х( = 0 не подходит по ОДЗ.
Ответ: 2.
7.070. 410g’x2 +log7J3 = 0>2(42+log’x-4log’x).
Решение.
ОДЗ: х > 0.
Перепишем уравнение в виде
42iog,x +21Og33 = 0^6-4lt>E’x -4log’x) 4210g’-v -3-410fox +2=0.
Решая это уравнение как квадратное относительно 4log’’c, найдем ^4log’x |=1, откуда (log9 х), = 0, X] = 1, или (4log’x = 2 , откуда (log9 х)2 = 1, х, = 3
Ответ: 1; 3.
7.071. 3-52х-1 -2-5х’1 = 0,2.
Решение.
Из условия 3-52х-2-5х =1, 3-52х-2-5х-1 = 0. Решая это уравнение как квадратное относительно 5 х, получаем 5 х = -1,0; или 5х =1, откуда х = 0.
Ответ: 0. 2	1	1
7.072. 10 х + 25х = 4,25-50х.
Решение.
ОДЗ: х * 0.
1	2	( L' •
Разделив обе части уравнения на 25 х, имеем 2 х -4,25 2 х +1 = 0,отку
да, решая уравнение как квадратное относительно 2х, получим 2 х
ч Л
4
откуда | — | = -2, х. = -—, или 2х
\х Л	2
1 1 k
Ответ: Х( = --; х2 =-.
7.073. 9х2-1 -36-3х"•’ +3 = 0.
Решение.
и Pl -2	1
= 4,откуда! ~ I х2 =-.
9х’	3х
Имеем-------36---+ 3 = 0,
9	27
З2'2 -12 -3х2 +27 = 0 . Решив это
2	2
уравнение как квадратное относительно 3 , получим 3х = 3, откуда х2 = 1, х|>2 = ±1, или 3? = 9, откуда х2 = 2 , *3,4 = ±з/2 .
Ответ: — V2; — 1; 1; V2.
7.074. 4х-10-2х’1-24 = 0.
Решение.
Из условия 21х - 5 • 2 х - 24 = 0. Решая это уравнение как квадратное относительно 2х, получим 2х = -3,0; или 2х = 8, откуда х = 3.
Ответ: 3.
7.075. (Vi)* +(^’10 =84.
Решение.	'
Перепишем уравнение в виде
+ Ж -84 = 0, 3 • $3$* +	-252 = 0 .
Решая уравнение как квадратное относительно (>/з)*, получаем (т/з)* = -—, 0 ; или = 9,310 = З2, откуда = 2, х = 20.
Ответ: 20.
7.076. 9^ -21 = 6-3^.
Решение.
ОДЗ: х-5>0, х>5.
З2^-6-3^ -27 = 0.
Решаем уравнение как квадратное относительно З^”* . Имеем 3^5 =—3 (не подходит) или 3'^ =9, откуда >/х-5 =2 , или х - 5 = 4. Тогда х = 9.
Ответ: 9.
7.077. 17.2^х-8 = 2-4'^х.
Решение.
ОДЗ: х2 -8х > 0, хе (-<»;0]ll[8;-н»)
Имеем 2-22л/х2’'‘х-17-2'/х2"®х+8 = 0. Решая это уравнение как
квадратное относительно 2^ 8х , получаем 2^х2~8х = 2 *, откуда >1х2 -8 = -1,0; или 2^x2~ix = 8, откуда д/х2 -8х = 3, х2 -8х = 9, х2 -8х-9 = 0, х, = -1, х2 = 9.
Ответ: -1; 9. 2 ix+i 7.078. 8х -2 х +12 = 0. Решение.
ОДЗ: х 0.
Перепишем уравнение в виде
2 х -23+* +12 = 0,
Решая это уравнение как квадратное относительно 2 х, получаем
( 3 > 2х
= 2, откуда
*1
(
= 3, или 2 х = 6 > откуда
< Д
( log22x
( 3 \	а
= log2 6 I — = log2 6 х2 = --------- = 31og6 2 = log6 8
’ (X L ’ log2 6
Ответ: 3; log6 8.
7.079. 21ogx27-31og27x = l.
Решение.
ОДЗ: 0<х*1.
Перейдем к основанию 27. Имеем
— -----3 log27 х — 1 = 0 => 3 log27 х + log27 х - 2 = 0.
log27 *
Решая это уравнение как квадратное относительно log27 х, получаем
1	2	-
(log27 х\ = -1, откуда х( = —, или (log27 х)2 = -, откуда х2 = 273 = 9.
1 27 3
Ответ:
7.080. lgL/6 + .v+e)—
1о8д10
Решение.
6 + х>0,
ОДЗ: <х>0,	0<х^1.
х*1,
Перейдем к основанию 10. Имеем
lg(j6+x +
lg(>/6 + x + б)= 1g х.
Тогда >/б+х + 6 = х,
л/б+ X = X - 6 => <
х2 -13x4-30 = 0, х >6,
откуда х = 10.
Ответ: 10.
7.081. log5 x + logx25 = ctg2 О
Решение.
ОДЗ: 0<х*1.
Перейдем к основанию 5. Имеем
1	2	((А	,	2	,
log5x+-----= ctg 4л+-	, log5x + ---= 3=>
log5x	6JJ	log5x
=> log2 x-31og5 х + 2 = 0.
Решая это уравнение как квадратное относительно log5 х, получаем (log5 x)t = 1 или (log5 х)2 = 2 , откуда х, = 5; х2 = 25.
Ответ: 5; 25.
lgx+5
7.082. х 3 =10s+lgJt.
Решение.
ОДЗ: 0<х*1.
Логарифмируя обе части уравнения по основанию 10, имеем
Igx 3 =lgl05+lgr, ^X^---lgx = (54-lgx)lgl0, lg2 x4-21gx-15 = 0.
Решая это уравнение как квадратное относительно Igx , получаем (Igx)! = -5, или(^х)2 = 3, откудаxj = 10"5,х2 =1000.
Ответ: 10”5; 103.
7.083. х10®4 х-2 = 23('og4
Решение.
ОДЗ:0<х*1.
Логарифмируя обе части уравнения по основанию 4, имеем
log4 x10g4 х“2 = log4 23(log4 хЧ), (log4 x - 2) log4 x = 3(log4 x -1) log4 2,
О	3	7
log4 x - 2 log4 x = — (log4 x -1), 2 log4 x - 71og4 x + 3 = 0.
Решая это уравнение как квадратное относительно log4х,найдем
/. ч 1
(log4x),=-,
2
(log4x)2 =3. Следовательно, =42 = 2,х2 =43 =64.
Ответ: 2; 64.
7.084.
2х+ 10	9
4	" 2х-2 ’
Решение.
Из условия
2^10=	9	2^10 = 36>22х+10.2Ж_144 = 0
4 2х -2“2	4 2х
Решая это уравнение как квадратное относительно 2х, найдем 2х = -18,0, или 2х =8,откуда х = 3.
Ответ: 3.
7.085. Ю1+х2 -10b? =99.
Решение.
г2 10	Ov2	г2
Имеем 1010х--------г-99 = 0=>10102х -99 10х -10 = 0. Решив
10х
U	г2 1
это уравнение как квадратное относительно 10 , получим 10 = -—, 0,
г2	7
или 10 =10, откуда х =1,х12=±1.
Ответ: - 1; 1.
'Ч'8А	1 л
7.086. х 3	--= = 0.
V100
Решение.
ОДЗ: 0<х*1.
1— IgA'2	j
Записывая уравнение в виде х 3	=  и логарифмируя обе
V100
части по основанию 10, получаем
i-rig* 1	(	2 А 1	о
Igx 3	= lg-==T, l--lgx lgx = --IglOO, 21g2 x-31gx-2 = 0.
V100 V 3	)	3
Решая это уравнение как квадратное относительно 1g х, находим
(lgx)| =-- или (lgx)2 =2,откуда х( =10 2 х2 = Ю2 =100.
Ответ: -Д=г;100.
V10
7.087. 7*(л/г)2*2"6=0.
Решение,
Из условия
7х-2х2-3 =7х-2"2х =>2хМ =2’2х, х2-3 = -2х, х2+2х-3 = 0, откуда %! = -3 , х2 = 1.
Ответ: -3; 1.
7.088. 3-41ое*2 -46-2log’2'1 =8.
Решение.
ОДЗ: 0 < х Ф 1.
Имеем 3 ♦ 221°8х2 - 23 • 2logx2 -8 = 0. Решая уравнение как квадратное относительно 2108x2, найдем 2108x2 = -у, 0 ; или 2108x2 = 8, откуда log* 2 = 3, х = yfl.
Ответ: у/1.
7.089. 91оВ|/3 (*+l) = 5log|/5	+1)
Решение.
ОДЗ: х + 1>0, х>-1.
Из условия
310g3(x+>r2 =5ЮЬ^+1Г t (x + i)”2 =^x2 +1)->,
1 _ 1 (x + 1)2 2x2+l
Решая это уравнение, имеем х, = 0, х2 = 2 .
Ответ: 0; 2.
7.090. 27lgx-7-9Igx-2L3lgx+27 = 0.
Решение.
ОДЗ: х > 0.
Имеем
331gx -7.32'1?* -21 • 3lgx +27 = 0, ^3lgx +27)-7-3lgx(?lgx +з)=0, (1lgx + 3^2lgx - 3 • 3lgx + 9)- 7 • 3lgx felgx + 3)= 0,
^lgx+3b21gx-10-3lgx+9 = 01
откуда 32 lgx -10 • 3lgx + 9 = 0. Решая это уравнение как квадратное относительно 3lgx, получаем (з1гх ) = 1 или (з1вх = 9, откуда (igx^ = 0 или (igx^ = 2. Отсюда X! = 1, х2 = 100.
Ответ: 1; 100.
7.091. log2^-3x —б)—log2^9x -б)=1.
Решение.
ОДЗ:
4-Зх-6>0, 9х-6 >0.
4.4х—А	4-4х—6
Имеем log2 —z--= 1, —z------ 2 => 32х - 2 • 3х -3 = 0. Решая
32х-6	32х-6
его как квадратное относительно 3х, найдем 3х = -1,0; или 3х = 3, откуда х = 1.
Ответ: 1.
7.092. 21og3(x-2)+log3(x-4)2 =0.
Решение.
ОДЗ: !Л 2 >	2 < х * 4.
|х-4 0,
Из условия 2 log3 (х - 2) 4- 2 log3 |х - 4| = О или log3 (х - 2) 4- log3 |х - 4| = 0. Имеем:
(2<х<4,	|2<х<4,
1) [1 °ёз (* “ 2)+ 1оёз (4 - х) = 0	(log 3 (х - 2Х4 - х) = О
2 < х < 4,
<=М 7
х~ - 6х 4- 9 = О,
откуда X, = 3 ;
2)
х>4,	|х>4,
log3 (х - 2)+ log3 (х - 4) = 0	1 og 3 (х - 2 Хх - 4) = 0
х >4,
х2 — 6х + 7 = 0,
откуда х2 = 34-72.
Ответ: 3;3 4-72.
9
7.093. log3 х • log9 х • log27 х • log81 x = -.
Решение.
ОДЗ: х>0.
Ill 2
Имеем log3x.-log3x -log3x -log3x = y, log3x = 16, откуда
(log3 x)j = -2 или (log3 x)2 = 2 . Отсюда , x2 = 9.
Ответ: —;9.
7.094. 4log5 ? -4log5X+1 4-41ое5ЛГ_| -1 = 0.
Решение.
ОДЗ: x>0.
Из условия 4'42|°85* -15 -4log5* -4 = 0. Решая это уравнение как
квадратное относительно 41о®5 х, найдем 4108’х = -—, 0; или 4,og5 х = 4, 4
откуда log5 х = 1, х = 5.
Ответ: 5.
7.095. 7logo х + 71о6х а = у •
Решение.
logo х > 0,
ОДЗ: -|0<а*1,
0 < х * 1.
Из условия
A/logox + ;   -^ = 0=»3(viogfl х)2 -Юд/logo X+ 3 = 0. 71оё<»х 3
Решая это уравнение как квадратное относительно -jloga х , получаем (jlpgex| = |, 0°ga *)i = у откуда х, = 94а , или Qlogax)2 = 3, (logo х\ = 9»откуда х2 = а9.
Ответ: >[а;а9, где 0 < а # 1.
7.096. lg(3x2 +12x + 19)-lg(3x + 4)=l.
Решение.
ОДЗ: Зх + 4 > 0, х > ~.
. Зх2+12х + 19 . Зх2+12х+19 л 2 10 о, л
Имеем 1g-------------= 1, ----------~ = 10, Зх -18х-21 = 0
Зх+4	Зх + 4
при Зх + 4 # 0. Отсюда X] = -1, х2 = 7.
Ответ: -1; 7.
7.097. logj (х - З)2 + log3 |х - 3| = 3.
Решение.
ОДЗ: х-3 Ф 0,х ф 3.
Из условия
21og3|x-3| + log3|x-3| = 3, 31og3|x —3| = 3, log3|x-3| = l,
откуда |x-3| = 3. Тогда (х-3)]=-3или (х-3)2 = 3. Отсюда Х]=0, Х2 =6.
Ответ: 0; 6.
7.098. lgVr^3+lgVTb3=2-0,51g625.
Решение.
^ттг» [*“3>0,
ОДЗ:< х>3.
|х+3>0
Имеем
lgVx-3+lgV* + 3 =lglOO-lg25, lg>/x2 -9 = lg4, 7x2 -9 =4, отку-
да x2 = 25,	= -5, x2 = 5, X] = -5 не подходит по ОДЗ.
Ответ: 5.
7.09	9. lg(3-x)-|lg(27-x3) = 0.
Решение.
ОДЗ: 3-х>0, х<3.
Перепишем уравнение в виде
31g(3-x) = lg(27-x3), lg(3-x)3 =lg(27-x3).
Тогда (З-х)3 =27-х3 =>х2-9х = 0, откуда Х[ =0,х2 =9;х2 =9 не подходит по ОДЗ.
Ответ.О.
7.100.	21gx-lg4 = -lg(5-x2).
Решение.
	x>0,
ОДЗ:-	э 0<x<y5. 5-x2>0,
Из условия
lgx2 +lg(5-x2) = lg4, lg(x2(5-x2)) = lg4, x2(5-x2) = 4,
x4-5x2+4 = 0.
Решая это уравнение как биквадратное относительно х, найдем х1 = -1, хг =1, х3.= -2, х4 =2; Xj = -1 и х3 = -2 не подходят по ОДЗ.
Ответ: 1; 2.
7.101.	lg8-lgVx + 6 = lgl6-lg(x-2)
Решение.
(х + 6>0,
°Д [х-2>0, Х>
Имеем
lg—L. = lg2L,	2>/х + 6=х-2, х2-8х-20 = 0,
>/х + 6	х-2 Vx + 6 * _2
откуда Xi = 10, х2 = -2; х2 = -2 не подходит по ОДЗ.
Ответ: 10.
7.102.	21gV4-x + lg(6-x)=l.
Решение.
[4-х > 0, °Д3:Ъ	х<4~
[6 - х > 0,
Перепишем уравнение в виде lg(4-x)+lg(6-x)=l, lg(4-xX6-x)=l,
откуда (4-хХб-х)=10, х2 +1 Ох-14 = 0.Следовательно,х, =5--ЛТ, х2 = 5 + л/ГТ; х2 = 5 + -УГГ не подходит по ОДЗ.
Ответ: 5 —>/11.
lg(2x-19)-lg(3x-20)_ / .	* •
Igx
Решение. • (2х-19>0,	19
°да:1з,-20>0, Х>2-Из условия lg(2x -19)- lg(3x - 20)=- 1g х, lg(2x -19)+ 1g x = !g(3x - 20) x(2x-19)=3x-20, x2-llx+10 = 0.
Отсюда %! = 10, х2 = 1; х2 = 1 не подходит по ОДЗ.
Ответ: 10.
7Л04- d^5)=1-
Решение,
ОДЗ:
х * 0,	5
6х - 5 > 0, 6
Имеем 1gх2 = lg(6x - 5), откуда х2 = 6х - 5, х2 - 6х + 5 = 0, отсюда X] = 5 и х2 = 1; х2 = 1 не подходит по ОДЗ.
Ответ: 5.
7.105.	loga у + logfl (у + 5)+logo 0,02 = 0.
Решение
у >0,
ОДЗ: 5у + 5>0,
0<а*1
у >0, 0 < а * 1.
Имеем
loga (у(у + 5)’ 0,02) = 0, 0,02/ + ОД у = 1, 0,02/ + 0,1у -1 = 0, откуда = 5 ; у2 = -10 не подходит по ОДЗ.
Ответ: у = 5 при 0 < а *1.
7.106.	log* 42 - log* 42 = log3 27 - log* (2х}
Решение.
ОДЗ: 0<х#1.
Перепишем уравнение в виде
-logx2--log2 2 = 3-logx2-1, log2 2-61ogv 2+8 = 0. 2	4
Решая это уравнение как квадратное относительно log* 2 , найдем log* 2 = 2, log * 2 = 4 , откуда х2 =2 или х4 =2. Тогда Xj=-V2, х2 = 42 , х3 = -42 , х4 = 42 ; = -42 и х3 = -42 не подходят по ОДЗ.
Ответ: 42; 42.
7.107.	(log2 x - 3)log2 x+2(log2 x + l)log2 ^2=0.
Решение.
ОДЗ: x > 0.
Из условия
log2V2 = log22|/3 =|, log2x-31og2x+|log2x+| = 0,
3 log2 x - 7 log2 x+2 = 0.
Решая уравнение как квадратное относительно log2 х, имеем (log2 х\ = или (log2 х\ = 2 , откуда Х1 = V2 , х2 = 4.
Ответ: V2; 4.
7.108.	ОД log2 (х - 4)- Ц log2 (х -4)+ 3,6 = 0.
Решение.
ОДЗ: х-4 >0, х>4.
Решая это уравнение как биквадратное относительно log2 (х - 4), имеем
(log2 (х - 4))j = -2; (10g2 (х - 4))2 = 2 ; (log2 (х - 4)), = -3; (log2 (х - 4))4 = 3 ,
17 о 33
откуда х, = —, х2 = 8, х3 = —, х4 = 12. 4	о
17 33
Ответ: j;y;8;12.
7.109.	5 2x4 + 22х -52х +22х+2 =0.
Решение.
Запишем уравнение в виде
—-52х =-22х-4-22х,	-52х =-5-22х
5	5
Ответ: 1.
13 М. И., Сканави, группа А
7.110.	log2(9-2x)=10l8(3-x).
Решение.
ОДЗ:
9-2л >0,
3 - х > 0,
х < 3.
Имеем log2(9-2x)=3-x, 9-2х=23’х, 22х-9-2х+8 = 0. Решив это уравнение как квадратное относительно 2х, имеем ^2Х ) = 1 или (2х )г = 8 , откуда х{ = 0, х2 = 3; х2 = 3 не подходит по ОДЗ.
Ответ: 0.
7.111.	|lg^271 + 32'/x^+lgl0=2.
Решение.
ОДЗ: х£0.
Изусловия | lg^271 + 32Л )+1 = 2, lg^271 + З2^ )=3.Тогда271+32,/х = = 1000, З2^ = З6, откуда -Jx = 3, х = 9.
Ответ: 9.
7.112.
Решение.
ОДЗ: х > 0.
Перепишем уравнение в виде 3
7
= 34 .Тогда
Зх2 -16х-140 = 0,
,Л 14	14	ЛТТ„
откуда X] = 10 , х2 = —— ; х2 = —— не подходит по ОДЗ.
Ответ: 10.
7.113.	xlgx =1000x2.
Решение.
ОДЗ: 0<х*1.
Логарифмируя обе части уравнения по основанию 10, получаем lgxlgx = lgl000x2, lgxlgx = lgl000 + lgx2, lg2 x-21gx-3 = 0.Решая это уравнение как квадратное относительно 1g х, получаем (lg х\ = -1 или (ig Д =3 , откуда %| = ОД, х2 = 1000.
Ответ: 0,1; 1000.
7.114.	lg(x(x+9))+lg-^-i^ = 0.
х
Решение.
ОДЗ: х(х + 9)> 0, хе (-оо; -9)U (0;
Имеем igX(x + 9Xx + 9) _ ц , откуда (х + 9J2 = 1 • Тогда (х + 9\ = -1, х( = -10 или (х + 9^ = 1, х2 = -8; х2 = -8 не подходит по ОДЗ.
Ответ: -10.
7.115.	1g2 (100х)+ 1g2 (10х)= 14 + 1g—. х
Решение.
ОДЗ: х > 0.
Логарифмируя, имеем
(iglOO+lgx)2 H-GglO + lgx)2 =14-lgx, 21g2 x + 71gx-9 = 0.
Решая это уравнение как квадратное относительно 1g х, получаем (lgx)i = или (lg х^ = 1, откуда х, =10~9/2, х2 = 10.
Ответ: 10”9^2;10.
7.116.	l + 21ogx21og4(10-x)= ——. log4x
Решение.
Переходя к основанию 2, имеем
1 + 1оё?^0-л) = 4—, log^ x + log2(10-x) = 4, log2 х(10-х)=4 => log2 х log2 X
=>х2 -10х + 16 = 0,
откуда л, = 2, х2 = 8 .
Ответ: 2; 8.
7.117.	210gvv2 •5log?x=400.
Решение.
ОДЗ: х > 0.
Из условия 4log’v .5log,A =400, 20|о8’л = 202, откуда log3x = 2, х = 9-
Ответ: 9.
7.118.	5log2^2-21^0,022 .25~0,5log2 V =1.
Решение.
ОДЗ: К21>0’ х >0,
Записываем
51об2(х2-21) 004------- 1 
25о’51°82 log2(x2 - 21)= 2 + log2 х,
-1 ^log2 (х2-21) _ $2+log2 х log2(x2 -21)=log2 4x,
откуда x2 -21 = 4x, x2 -4x-21 = 0, Xj =7, x2 =-3; x2 =-3 не подходит по ОДЗ.
Ответ: 1.
7.119.	421°8н(2л-2) . 025,og8(2x“3) = V16.
Решение.
[2х-2>0,	3
ОДЗ: i	х>-.
м [2х-3>0,	2
Имеем
421og«(2x-2) 4-1о&(2х-3) = 42/3	421og8(2x-2)-log8(2x-3) = ^2/3
у,	. А 2	,	(2Л--2)2	2	(2л-2)2	.
21og8(2x-2)-log8(2x-3)=-, log82---------— = -, —------— = 4,
3	2х-3	3	2х-3
х2-4х+4 = 0, (х-2)2 =0,
откуда х = 2 • Ответ: 2.
7.120.	log3|r ~|3х+28+-^ j=log5 0,2.
Решение.
Из условия
х2-13х+283х2-13х+28	_£	3х2-1 Зх+28 __J_
9)	’	93’	9’
3х2-13х+28 =3-2> х2 _13х + 28 = -2, х2-13х+30 = 0,
log3 3
откуда Xj = 3 , х2 = 10.
Ответ: 3; 10.
7.121.	log2(4r +4)=x + log2(2T+1 -З)
Решение.
ОДЗ: 2х+1-3>0.
Перепишем уравнение в виде
log2^2x +4)-log2(z-2x ~з)=х, log2 2 +.4 =х, 2-2 -3
7д-4	л
- ..tz_ = 2\ 22х-3-2Х-4 = 0.
2 -2х -3
Решая это уравнение как квадратное относительно 2 х, получаем 2х = -1,0 ; или 2х = 4, откуда х = 2 .
Ответ: 2.
7.122.	^275^ =3Х(^4)
Решение.
ОДЗ: х > 0.
Имеем 35Л=Зх^)^5^ = х(^-4) 7х=0, Xj=0, или (л/х)2 - 4>/х- 5 = 0 •
Решая это уравнение как квадратное относительно , получаем у[х = -1,0 ; ИЛИ Vx = 5 , X = 25.
Ответ: 0; 25.
7.123.	log6 7зх(|5’х) + 81og6 2 = 8.
Решение.
Из условия log6 зЛ(15"Л)/7 + iog6 28 = 8, log6 ^х05-*У7 • 28 )= 8. Отсюда 3х(15-хУ7 ,28 =68 3'(15-.г)/7=38 Тогда *(!.^х) = g х2-15Х + 56 = 0 , 7
откуда Xj = 7 , х2 = 8.
Ответ: 7; 8.
7.124.	log5(4x +144)-41og52 = l + log5(r’2 +1)
Решение.
Имеем
,	22х +144 ,	/2х J 22х +144 5&х+4)
log 5-------= log 5 5 —+1 , --------=
5	16	5	4	16	4
Ч 7 22х-20-2х +64 = 0.
• Решая это уравнение как квадратное относительно 2х, получаем =4 или (2*)г =16 , откуда х{ =2, х2 =4 .
Ответ: 2; 4.
7.125.	27x10g2’x =х10/3.
Решение.
ОДЗ: 0<х*1.
Логарифмируя обе части уравнения по основанию 3, имеем
log3 27xlog27X = log3 х10/3, 3+-^log3 x = ^log3 x,
log3 x-101og3 x + 9 = 0.
Решая это уравнение как квадратное относительно log 3 х, получаем (log3 x)j = 1 или (log3 х)2 = 9, откуда X! = 3 , х2 = З9.
Ответ: 3; З9.
7.126.	logx 9+logx2 729 = 10.
Решение.
x>0,
°дз: U±i,
0<x*l.
3	r~
Имеем logx 9+—log x 9 = 10, logx 9 = 4, откуда x4 = 9, x = V3 ,
x = —Уз не подходит по ОДЗ.
Ответ: -J1.
7.127.	log2(25x+3 -l)=2 + log2(5x+3 +1)
Решение.
ОДЗ: 25х+3-1>0, 25х+3>25°, х>-3.
Из условия
log2 (Z53 -25х -l)=log2 4(53 -5х +1) 253 -52х -1 = 4-53 -5х +4, 3125-52х-100 5х-1 = 0,
откуда, решая это уравнение как квадратное относительно 5 х, имеем
5х = -0; или 5х = 5"2, откуда х = -2.
Ответ: -2.
Решить системы уравнений (7.128 - 7.149):
7.128.
log? х + log* у = 2, х2 -у = 20.
Решение.
ОДЗ:
0<х*1,
0 < у * 1.
Из первого уравнения имеем:
log„x + -—J--2 = 0, log2 x-21og„x + l = 0,
logy x
(log^x-1)2 =0,
откуда logyx = l, х = у. Из второго уравнения системы имеем у2 - у - 20 = 0, откуда у( = -4 , у2 = 5; У| = -4 не подходит по ОДЗ. Тогда х = у = 5.
Ответ: (5; 5)
7.129.
10i+ig(*+y) _ jo, lg(* ~ у)+lg(* + у)=2 - lg5.
Решение.
ОДЗ:
х-у >0, х + у >0.
Имеем:
lgl01+1^) = ig 50,	fl + lg(x + y)= lg50,
lg(x2 - y2 )= lg20 |x2 - y2 = 20
x + y = 5,	jx + y = 5,
(x-yXx + y) = 20 |x-y = 4,
9	1
откуда x = -, у = -
Ответ:
(91
<2’2
7.130.
lg(x2+y2)=2-lg5, lg(* + y)+ lg(x - y)=lg Ц+1.
Решение.
[x + y >0, ОДЗ: |x-y>0. Из условия lg(x2 + у2 )= lg20, lg(x2-y2)= lgl2
x2+y2 =20, x2-y2=12.
Отсюда х2 = 16, откуда х1>2 = ±4. у2 = 4, у1>2 = ±2. Следовательно,
х( = 4, (х2 =4, .>'1=2; 1>>2=-2.
Остальные решения не удовлетворяют ОДЗ.
Ответ: (4; 2) (4; - 2)
7.131.
log4 х + log4 у = 1 + log4 9, х + у-20 = 0.
Решение.
ОДЗ:
х >0, у>0.
Имеем	ОТКуДа. х*
|х + у = 20,	3	[у, =18;
х2 =18, Л =2-
Ответ: (2;18)(18;2)
Зу-9х = 81,
7.132.	• , ч,
lg(y + xf -lgx = 21g3.
Решение.
х>0, °^Ux^0.
Из первого уравнения системы 3J+2x = З4, у+2х = 4, у = 4 - 2х.
(у + xY	(у + хУ
Из второго уравнения системы 1g —-— = 1g 9, откуда —-— = 9.
Тогда исходная система приобретает вид
у = 4-2х,	,
 v	=> х2 -17х + 16 = 0,
\у + ху =9х
откуда Х| = 1, х2 = 16. Тогда yt = 2, у2 = -28.
Ответ: (1; 2), (16; - 28)
7.133.	+
ху = 27. Решение.
Из первого уравнения системы имеем: 2 log2 х - 5 log}. х + 2 = 0, откуда, решая это уравнение как квадратное относительно log? х, най
дем (logj, х)( = у или (logy х)2 = 2 . Отсюда х{ = Jy , х2 = у2 .
Из второго уравнения системы найдем у3/2 =21,	= 9. Подстав-
ляя значение х2 = у2, найдем у2 = 27, у2 = 3.
Учитывая ОДЗ, имеем
X! =3,
Ji =9;
_'х2 =9, 72 =3.
Ответ: (3; 9), (9; 3)
7.134. i
32х -2У = 725, 3х -2у12 =25.
Решение.
Перепишем систему уравнений в виде
(зх -2у,2^х +2у/2)= 725, |зг +2У/2 = 29, |зх = 27, 3* -2у/2 =25	** |з* -2у/2' = 25 ** [2у/2 = 2,
[х = 3, откуда i = j Ответ: (3;2) 7.135. И!^!)=2.
log2 X-4 = log2 3-log2 у.
Решение.
|х>0, °дз: Ь>о.
Из первого уравнения системы уравнений имеем х2 + у2 = 100. Из
, х ,	3	х	3
второго уравнения системы найдем log7 — = log2 —, откуда — = —, * 16 у	16	у
'16
м
< У >
48
х~~  Далее получаем
+ у2 -100 = 0,
/-100/+2304 = 0,
откуда Д2 = ±6 ,	= ±8; у2 = -6 и у4 = -8 не подходят по ОДЗ.
Тогда jq = 8, х2 = 6.
Ответ: (8; б), (б; 8)
7.136.
З^’^ =81, igT*? »i+ig3.
Решение.
ОДЗ:
х >0, у >0.
Из первого уравнения системы имеем з^'Т? = 34,2>/х - -Jy = 4,
Ту = 2-Тх -4. Из второго уравнения системы получим Jxy = 30, 4х • Ту = 30. Система принимает вид
Ту =2л/х -4,
Тх • Ту = 30
(Тх)2-2Тх-15 = 0,
откуда Тх = 5 или Тх = -3 (не подходит). Тогда Ту = 6. Следовательно, х = 25, У = 36 .
Ответ: (25; Зб)
7.137.
2 2 +2 v =2,5, lg(2.v ->)+! = lg(y + 2x)+ 1g 6.
Решение.
ОДЗ:
2x-у > О, у + 2х > 0.
( £2?
2 2
Из первого уравнения системы получаем
X-V
-2,5-2~ +1 = 0.
х-у
Решая это уравнение как квадратное относительно 2 2 , найдем
'	( у-у
2 2	=2“1 или 2 2
= 2, откуда =-2 или (х-^)2 = 2.
к Л	k J2
Из второго уравнения системы получаем lgl0(2x- j)= lg6(y + 2x), от
куда 10(2х - у) = б(у + 2х), х = 2у. Таким образом, исходная система
эквивалентна системам уравнений:
Гх-_у = -2, [х-у = 2,
'>[Х = 2К 4-2,;
откуда:
х, =-4,	(х2 =4, I*] =-4,
1)5	2)5 2	1
|у!=-2;	[у2 =2;	(у, =-2 (не подходит по ОДЗ).
Ответ: (4; 2)
7.138.
х2/-' =5, х<+2 =125.
Решение.
ОДЗ:	0<х*1.
Логарифмируя первое и второе уравнения системы по основанию 5, получаем
log5 х2’’'4 = log5 5, fey2 - l)log5 х = 1,	1
,	=> 1 / ,	\	=> 1оё5 V =--5--•
logs xr'2 “logs 125	[(y2+2)log5X = 3	2у -1
Из второго уравнения системы имеем -Z—tA 2/-1
У = ±1. Тогда log, х = 1, т.е. х = 5 •
Ответ: (5; 1) (5; -1}
,Ъ-№ГУ = О,5?-3, log3 (х -2у)+log3 (Зх + 2у)= 3.
Решение.
fx-2v >0, °ДЗ: [Зх + 2у>0.
Имеем
7.139.
3+2^ = з-Л 2
(x-2/X3x + 2j)=27,
3+— 1 .2 2 =23Л
log3(x-2yX3x+2y) = 3
откуда, учитывая ОДЗ, получаем х = 3, У = -3 •
Ответ: (3; - 3)
7.140.
4Х+' =2У~Х,
4log^x=/-5.
Решение.
ОДЗ: х > 0. Из условия
2^х+2у _ 2У-Х л	—
210foX =/-5
2х+2у = у-х, 4	4 с
х = у -5
=> у = -Зх.
= 3, у2 = 1, откуда
х = -у, у2 =9,
Из второго уравнения х4 = (- Зх)4 - 5
1	3
ОДЗ, получаем х = - , у = - —.
4	1
х = —, откуда, учитывая
Г1._з
Ответ: К ’ 2
7.141.
log4 х - log2 у = 0, х2 -2/-8 = 0.
Решение.
lx >0,
ОДЗ: .п
[/>0.
Перепишем первое уравнение системы в виде
log4 X = log2 у2 => i log2 X = log2 У, log2 X = log2 у2, X = /.
Из второго уравнения системы имеем у4 - 2у2 - 8 = 0, откуда с учетом ОДЗ, у = 2. Тогда х = 4 •
Ответ: (4; 2)
7.142. 1
log2 х + log4 у = 4, log4x + log2 j = 5.
Решение.
Гх >0, 0ДЗ: Uo. Перейдем к основанию 2. Имеем
log2 X+| log2 у = 4,	р log2 х+10g2 у = 8
1.	.	.	|log2 x+21og2 у = 10
-log2x+log2 у = 5	1
log2x2y = 8, х2у = 28, log2 ху2 =10 ху2 = 210.
28
Из первого уравнения системы у = —у. Из второго уравнения х2
( ?8 Y
— =2*°,х3
kj
Ответ: (4; 1 б)
= 26, откуда х = 4 , У = 16.
7.143.
х+у х+у .2 3 + 2~ =6, х2 + 5у2 = 6ху.
Решение.
Из условия
f х+у Y х+у
2 6	+26 -6 = 0- Решая это уравнение как квад-
< >
х+у	х+у	х+у
ратное относительно 2 6 , имеем 2 6 =-3,0; или 2 6 =2, откуда
6
Из второго уравнения системы х2 -бух + 5>>2 = 0 , решая его как квадратное относительно х, имеем Xj = у, х2 = 5у. Исходная система эквивалентна двум системам:
нН4 2)f«^=6. e 0Ь=3-	2)b=5’
V = 5y	Vi=3;	Ьг=1-
Ответ: (3; 3), (5; 1).
7.144.
2х Зу =6, 3х -4У =12.
Решение.
Разделив второе уравнение заданной системы на первое, получим
3х-4^ _ 12 221-7 V-у-^у
2х-3Л	6’ 2х~1у
Это равенство возможно, когда
{х-у = 0,	, Л
=>х = ь 1 + у-2/ = 0, у = 1.
l + x-2j = 0
Тогда х = у = 1.
Ответ: (1; 1)
7.145.
y = l + log4x, х'=4б.
Решение,
ОДЗ: 0<х*1.
Логарифмируя второе уравнение системы по основанию 4, имеем log4 ху = log4 46, у log4 х = 6. Отсюда
1 , 1 + logj.x’=>(l + log4x)log4x = 6, log4x + log4x-6 = 0, [ylog4x = 6
откуда, решая это уравнение как квадратное относительно log4 х, найдем
(log4 х), = -3, (log4 х)2 = 2, Xj = х2 = 16. Тогда ух = -2, у2 = 3.
64
L (16; 3).
log^toO = 8,
7.146.
log3logi/9- = 0.
Решение.
ОДЗ:
О < х * 1, у >0,
log1/9->0=>0<-<1.
У У
Из первого уравнения системы ху = х4 или с учетом ОДЗ у - х3. Из
X	X	1
второго уравнения имеем logi/9 — = 1, — = —. Исходная система перепи-
У	У 9
сывается в виде 
У = х\	,
х 1
х 1 => —у = ~> откуда с учетом ОДЗ х = 3, у = 27. — = — xJ 9
у 9
Ответ*, (3; 27).
logXJ,(x-y)=l, logXJ,(x + y)=0.
Решение.
x-y >0,
ОДЗ: ^x + y >0,
0<xy*l.
Имеем
lx у xy,	_ J_x-(l-x)-x(l-x)=0, x2+x-l = 0,
[x + y = 1
-1-75	-1 + 75	3 + 75	3-75
откуда x, =—-—, x2=—-—, У1 =	2 , У2=—— •
_	-1 + 7?	3-7?
Тогда с учетом ОДЗ имеем x = —-—, у = —-—.
Ответ:
'-1 + 7?.3-7?'
2	’ 2
7.148.
(х + у)-!’’-2* = 6,25, (х + у)2х-у = 5.
Решение.
ОДЗ:
0<х + у #1, 2х-у *0.
Логарифмируя оба уравнения по основанию 10, имеем
lg(x+у). 2У~2х = Igf—Т,	!в(х+З’)* (У - 2х)182 = 20ё 5 “ 1821
l2J =»• lg(x + yk 1£5
lg(x + y)2x-y =lg5	I. 2x-J
Из второго уравнения системы получаем lg(x + у) = (2х - j)lg5 , тогда (2x-y)lg5 + (y-2x)lg2 = 2(lg5-lg2| (2x-yXlg5-lg2)=2(lg5-lg2} 2х-у = 2.
Исходная система принимает вид (2х-у = 2,	(2х-у = 2,
[lg(x+.y)=21g5, |х + у = 25,
fx=9, откуда |^_16
Ответ: (9;1б)
glog,(x-4y) _ I 7-149. !
_j.2x~2y
= 8.
Решение.
ОДЗ: х - 4у > 0.
Из условия
glog9(x-4y) _ g0
-7-2x-2-F-8 = 0.
Из первого уравнения системы имеем log9(x-4j>) = 0, откуда х -4у = 1. Решая второе уравнение системы как квадратное относительно 2х~1у, получаем 2х~1у = -1,0;	= 23, откуда х -2 у = 3 .
{х-4у = 1, [х = 5, х-2у = 3	[7 = 1-
Ответ: (5; 1)
Решения к главе 8
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
ОСНОВНЫЕ ФОРМУЛЫ
Соотношения между тригонометрическими функциями одного и того же аргумента
sin2 a + cos2 a = li	(81)
tga= sjna> a*5(2и + П neZ;	(8.2)
cosa 2
cosa	„
ctga =----, a*im, neZ;	(8.3)
sina
tgactga = l, a*-y-, neZ',	(8.4)
l + tg2a = —, а*-^(2и + 1^ neZ;	(8.5)
cos a 2
1 + ctg2 a = —, a * ли, n e Z.	(8.6)
sin2 a
(Здесь и в дальнейшем запись и g Z означает, что и - любое целое число.)
Значения тригонометрических функций некоторых углов
Для некоторых углов можно записать точные выражения их тригонометрических величин (табл. 8.1), а также знаки функций по четвертям (табл. 8.2).
Таблица 8.1
Аргумент (а, градусы, радианы)			Функция			
			sina	cosa	tga	ctga
0°(0)			0	1	0	оо (не определен)
15'[п]			Уз-i 242	242	2-43	2 + 45
,8“			45-1 4	15 + 45 242	45-1 110+245	110 + 245 4~5-1
Hi)			£ 2	45 2	1 4з	45
[j]			15-45 242	4	110-245 45+1	410-245
«•			1 42	1 42	1	1
54°	[10 J		4	^5-45 242	45+1 J10-245	110-245
6°’ [2]			4з 2	£ 2	45	1 45
75е	(5пу U2.		242	Уз-1 242	2 + 45	2-45
9°- [2]			1	0	оо (не определен)	0
Таблица 8.2
Четверть	Функции			
	sina	cosa	tga	ctg a
I	+	+	+	+
II	+	—	-	—
III	—	-	+	+
IV	—	+	—	—
Формулы сложения и вычитания аргументов тригонометрических функций
sin(a+p)=sinacosp + cosasin0;	(8.7)
sin(a - P)=sin acos p - cos asin p ;	(8.8)
cos(a + p)=cos a cos p - sin a smp;	(8.9)
cos(a - p)=cosacosp + sin a sinP;	(8.10)
tg(a + p)= tg(X + te	a,p,a + p*^ + 7cn, neZ- 1-tgatgp	" 2	(8.H)
tg(a-p)=-^^—a,p,a~P*-^ + 7tn, neZ-1 + tgatgp	2	(8.12)
ctg(a + p)= ctSactgP J	a,p,a + p*7w, neZ- ctga + ctgp	(8.13)
ctg(a p)= 8	, a,p,a P*tw, neZ. ctg a-ctg p	(8.14)
Формулы двойных и тройных аргументов sin2a = 2sinacosa;	(8.15)
cos2a = cos2 a-sin2 a = 2cos2 a-1 = 1-2sin2 a J (8.16) . „ 2tga п як , „ я tg2a =--:—, a* —+—,keZ,a^ — + nn,neZ.	ro i 7\
l-tg2a 4 2	2	’	I*-1 '>
ctg 2а =	1, а* — ,ке Z, а* ли, не Z- 2 ctg а	2	’	(8.18)
sin За = 3sina-4sin3 а > cos За = 4 cos3 а - 3 cos а 5	(8.19) (8.20)
_ . 3tga-tg3a	л/_ tg3a = — 	г—, а*-(2и + Цие2. l-3tg а	6	(8.21)
_ 3ctga-ctg3a	ли	„ ctg3a = —2	, a* —-,neZ l-3ctg2a	3	(8.22)
Формулы половинного аргумента
. э a 1-cosa sin — =	; 2	2			(8.23)
		2 a 1+cosa COS — =	; 2	2	’	(8.24)
tg2	a 2	1-cosa =	, а*я(2и + 1}ие Z; 1 + cosa	(8.25) 1
ctg2		> a 1 + cosa	,	„ — =	, а*2ли,neZ; 2 1-cosa	(8.26)
•4		sina 1-cosa	„	(8.27)
		1 + cosa	sina	
. a ctg у		1 + cosa sina	„ 	 —	-	 ry ITm MC / ‘	(8.28)
		sina 1-cosa	
Формулы преобразования суммы и разности тригонометрических функций в произведение
sina+sinP = 2sin^i^cos——- • 2 .	2 ’	(8.29)
. о _ а + Р . а-р sma-sinp = 2cos—-sin—- • 2	2	(8.30)
cosa + cosP = 2cos^-^cos——&; 2	2 ’	(8.31)
о _ . а+В . а-В _ . а+В . В-а cos а - cos р =-2 sin	-sin		 = 2sin -sinr • 2	2	2	2’	(8.32)
cos a + sin a = 41 cos(45° - a);	(8.33)
cosa-sina = %/2 sin(45° -a);	(8.34)
tga + tgp= 8*п(а + Р) а,р*—(2и-Цие Z; 6	H cosacosp	H 2' A tga-tgP= S—“ 21 а,Р* ^(2и-Цие Z; cosacosp	2V	(8.35) (8.36)
ctga+ctgP = —+а,р*яи, neZ; sin a sin p ctg a - ctgP = --P^ a). а,р*ли, neZ; sin a sin p tga+ctgP = cos(a ft\ a* — + nk,ke Z,^^rni,ne Z; cosasinp	2 tg a - ctg p = - cos(a±P), a* —+itk,kGZ,fi*itn,nG Z; cosasinp	2 .	.	2	m tga + ctga = -	, a*—, neZ; sin2a	2	(8.37) (8.38) (8.39) (8.40) (8.41)
tga-ctga = -2ctg2a,	”^Z;	(8.42)
,	2 «
1 + cosa = 2 cos — •
2 ’
1	о • 2«
1-cosa = 2sin —;
2
(8.43)
(8.44)
l+sina = 2cos2^45’-yj;	(8.45)
l-sina = 2sin2^45° -y);	(8.46)
sin(45’+a)	V2sin(45’+a)	л	„
1 + tga = —ь-----'- =-----ia* —+ Jtn, neZ; (8.47)
cos 45’cosa	cosa	2
.	sinks’-a)	>/2sm(45’-a)	я	_	.О.оч
l-tga = —i-------’- =------------a*- + 7tn, neZ; (8.48)
cos 45’cosa	cosa	2
1 + tgatgp =-CO—a —j, a,₽*—+ ЛИ, neZ;	(8.49)
cosacosp	2
l-tgatgP= cos(a + P), a,p# —+ лл, «eZ;	(8.50)
cosacosp	2
ctgactgp +1 = cos(a ~ P) a,p#7tn, neZ; (8.51) sin asm p
. , 2 cos2a	%_
l-tg2a = —-—, a* —+ Jtn, neZ;	(8.52)
cos a	2
1-ctg2 a = -cos^a, a* тог, neZ;	(8.53)
sin2 a
«,₽,! + 1И, ,5Z;	(8.54)
cos acos p	2
c.g^-ae;P = -sin(a^)si^-a>, 0,15^, .sZ;	(8.55)
sin asin p
tg2a-sin2a = tg2asin2a, a^j + яи, neZ; ctg2 a-cos2 a = ctg2 acos2 a, a*m, neZ;
Формулы преобразования произведения тригонометрических функций в сумму
sin a sin p = i (cos(a - p)- cos(a + p));
cos acos p = у (cos(a+p)+ cos(a - p)); sin a cos p = ± (sin(a + p)+ sin(a - p));
sinasinpsiny=
= - (sin(a+P -y)+sin(p+y- a)+sin(y+a - p)-sin(a+p+y));
4
sinacospcosy=
=—(sin (a+Р - у)- sin(p+ у - a)+ sin(y+a - р)+ sin(a+p + у)}, 4
sinasinpcosy=
= - (-cos(a+p - y)+cos(p+y- a)+ cos(y+a- p)-cos(a+p + y)); 4
cos acospcos у=
•^x (cos(a+p - y)+cos(p+y- a)+cos(y+a~p)+ cos(a+p+y)).
(8.56)
(8.57)
(8.58)
(8.59)
(8.60)
(8.61)
(8.62)
(8.63)
(8.64)
Формулы, выражающие тригонометрические функции через тангенс половинного аргумента
2tgy
sina =----—, а*л(2п + 1} neZ;
l + tg2“
1-tg2 у
cosa =-----a*Jt(2n + li neZ;
i+tg2y
(8.65)
(8.66)
2tgy tga =---
а,у*у(2и + 1), neZ;
(8.67)
i 2 &
1-tg у
ctga =-----а* ли, neZ.
2.4
(8.68)
Формулы приведения
sin —±a =cosa, sin (% ± a) = +sin a, I2 )
 (3 M }
sml — л±а =-cosa,
sin(2rc ± а) = ± sin а;
(8.69)
I Л ,	]	, •
cos — ±а = ±sina,
I2 J
(3	}
cos — л±а = ±sina,
I 2
cos(ic±a)=-cosa,
cos(2n±a)=cosa;
(8.70)
tl
+ctga, a*ли, neZ,
tg(x±a)=±tga, a*y(2n+l} neZ, f 3 A
tg-л±а =Tctga, a#ли, neZ,
tg(2n±a)=±tga,
(8.71)
a#j(2n+l| neZ;
ctg -±a = + tga, <2	7
ctgOt±a)=±ctga,
(з
ctg -л±а =Ttga, <2 J
ctg^±a)=±ctga,
а#^(2и+1} hgZ,
a # тот, и g Z, а^^(2и+1) hgZ, a * ли, и g Z.
(8.72)
ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Тригонометрическим называется уравнение, в котором неизвестное входит только под знак тригонометрических функций непосредственно или в виде линейной функции неизвестного, причем над тригонометрическими функциями выполняются только алгебраические действия.
Простейшие тригонометрические уравнения
Простейшими тригонометрическими уравнениями называются уравнения вида
sinx = /и,	(8.73)
cosx = w,	(8.74)
tg x = m,	(8.75)
ctgx = w,	(8.76)
где т - любое действительное число.
Решить простейшее тригонометрическое уравнение - значит найти множество всех углов (дуг), имеющих данное значение тригонометрической функции.
Рассмотрим решение простейших тригонометрических уравнений.
1.	sinx = т. Если |лп| < 1, то решения данного уравнения определяются формулой
х = (-1)" arcsin т + т, п е Z.	(8.77)
Если |ди| > 1, то уравнение (8.73) решений не имеет.
2.	cos х = т. Если |m| < 1, то решения этого уравнения определяются формулой
х = ±arccosт + 2ли, neZ.	(8.78)
Если |ди| > 1, то уравнение (8.74) решений не имеет.
3.	tgx = n?. При любом действительном ди
х = arctgди + ли, пе Z.	(8.79)
4.	ctgx = m. При любом действительном ди
х = arcctg ди + ли, и g Z.	(8.80)
В частных случаях при ди = -1, ди = 0, ди = 1 получаются следующие формулы:
Л _	'	„ шх = -1; х =— + 2ли, hgZ; 2	(8.81)
sinх = 0; х = пп, neZ;	(8.82)
sin х -1; х = — + 2ли, и g Z; 2	(8.83)
cosx = -l; х = л + 2ли, hgZ;	(8.84)
л cosx = 0; x = — + лн, hgZ; 2	(8.85)
cos x = 1; x = 2ли, n g Z;	(8.86)
tgx = -l; x = -— + ли, hgZ;	(8.87)
tgx = 0; х = ли, hgZ;	(8.88)
tgx = l; x = —+ лл, weZ;	(8.89)
4
ctgx = -l; x = -—4-тел, neZ;	(8.90)
4
ctgx = 0; х = у + ли, weZ;	(8.91)
ctgx = l; x = — + 7W, neZ.	(8.92)
4
Тригонометрические уравнения вида sin (ax + b) = m, cos(ax + b) = m, tg(ax + b) = t, ctg(ax + b) = 1, где ax + b — линейная функция, |w| < 1, a * 0, x, b —любые действительные числа, также относятся к простейшим и приводятся к уравнениям (8.73) - (8.76) заменой ах + b = у.
Тригонометрические уравнения, содержащие тригонометрические функции одинакового аргумента
Рассмотрим тригонометрические уравнения, рациональные относительно тригонометрических функций.
Пусть имеем
7?(sin х, cos х) = 0,	(8.93)
где R - рациональная функция относительно sin х и cos х .
Данное уравнение приводится к алгебраическому относительно тригонометрической функции одинакового аргумента. Затем, решая получившееся алгебраическое уравнение относительно этой функции, приводят данное уравнение к нескольким простейшим тригонометрическим уравнениям, из которых находят значения неизвестного и проверяют, какие из них являются решениями данного уравнения.
Если х # (2и + 1)л, где ц е Z, то каждое тригонометрическое уравнение вида (8.93) можно привести к рациональному уравнению отно-сительно неизвестного с помощью формул (8.65) - (8.68). Решая уравнение таким методом, можно потерять корни вида х = (2 п + 1)л, где
neZ, для которых tgy не имеет смысла. Поэтому необходимо проверить, являются ли числа х = (2л + 1)я, где ле Z, корнями исходного уравнения.
Если уравнение (8.93) или приводимое к нему при замене х на я - х не изменяется, то его имеет смысл приводить к рациональному относительно sin х.
Если уравнение (8.93) или приводимое к нему не изменяется при замене х на -х , то его имеет смысл приводить к рациональному относительно cosx.
Если уравнение (8.93) или приводимое к нему при замене х на я + х не изменяется, то его имеет смысл приводить к рациональному относительно tg х.
Однородные тригонометрические уравнения и уравнения, приводящиеся к ним
Тригонометрическое уравнение вида
а0 cos” x + tfj cos'1”1 xsinx + a2 cos"’2 xsin2 х + ... + ял sin" x = 0, (8.94)
где л0, ax,..., an — данные числа, ал — натуральное число, называется однородным уравнением относительно функций sin х и cos х . Сумма показателей у sinx и cosx во всех членах такого уравнения одинакова. Эта сумма называется степенью однородности уравнения или показателем однородности.
Уравнение (8.94) являетсяластным случаем уравнения (8.93) и делением обеих своих частей на cos'1 х ф 0 (или на sin" х * 0) приводится к целому рациональному относительно tg х (или ctg х):
а0 tg" х + ах tg"-1x + a2 tg"’2 х + ... +=0
или	_1
а0 ctg" х + ах tg" х + а2 tg" х + ... + ал =0;
при этом область определения уравнения сужается на значения х = у(2л + 1) (илина х = ял), где ле Z.
Умножением на тригонометрическую единицу (sin2 x + cos2 , где ке N , можно привести к однородному некоторые уравнения, не
являющиеся однородными. Так, к уравнению вида (8.94) сводится уравнение
а0 cos2" x + aj cos2""1 xsinx + fl2 cos""2 xsin2 x + ... + an sin" x = b.
Для этого нужно умножить Ь на тригонометрическую единицу:
b = Z>(sin2 х + cos2 xf, ке Z.
Уравнение вида a sin сох + b cos сох = с [а2 +Ь2 * о)
Это уравнение является частным случаем уравнения (8.93), следовательно, его можно решать с помощью универсальной подстановки, а также приводить к однородному.
Укажем еще один способ решения этого уравнения, так называемый способ введения вспомогательного угла. Пусть
asincox + Z>coscox = c ^z2+/>2*o).	(8.95)
Разделим обе его части на -Ja2 + Ь2 > тогда а	b	с
.  sin (ОХ + .  cos сох = , 	.
777F
Пусть <р — одно из решений системы
а
COS<P = -/ , —> у/a2 +Ь2 b sm ф = —=_____
JJTb2
Воспользовавшись этими равенствами, запишем уравнение в виде с sin сох cos ср + cos сох sm ср =	-.
4а2 + Ь2
Применив формулу sin (а + р) = sin а cos р + cos а sin р, получим урав-
нение sin(cox + <p) = .. Л.. =•, которое, как видно из проделанных yla2 +Ь2
выкладок, равносильно исходному уравнению. Если
а2 + Ь2 > с2, то уравнение имеет решение
сох + ф = (-1)" arcsin . С.	+ ял
у/a2 + Ь2
или
Если
ф ял со со
с у]а2 + Ь2
1, т.е. а2 + Ь2 < с2, то уравнение решений не имеет.
ле Z.
Уравнения, рациональные относительно выражений sinx±cosx и sinxcosx
Если левая часть тригонометрического уравнения /(х) = 0 содержит лишь одно из выражений sin х + cos х или sin х - cos х и функцию sin 2х (или произведение sin х cos х), то, вводя новое неизвестное t = sin х + cos х или t = sin х - cos х и учитывая, что sin 2х = (sin х + cos х)2 -1, sin 2х =
-1 - (sin х - cos х)2, приходим к уравнению относительно t.
СИСТЕМЫ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
При решении систем тригонометрических уравнений пользуются способом подстановки или сводят системы тригонометрических уравнений к системам алгебраических уравнений. В ряде случаев для решения системы тригонометрических уравнений ее преобразуют с помощью почленного сложения, вычитания, умножения, деления уравнений с целью, например, исключить одно из неизвестных, разложить полученное уравнение на множители и т.д. Решения системы записываются в виде упорядоченных пар (х; у).
Решить уравнения (8.001 - 8.175):
8.001. cos3x-sinx = V3(cosx-sin3x)
Решение.
1	л/з"
cos Зх - v3 cos х = sin х - V3 sin Зх, <=> — cos Зх+—sin Зх =
2	2
1 .	, V3	. л . , . я
=—smx+—cosx,<=> cos 3x cos—+sm3xsm— = 2	2	3	3
я . я .	л A ( tC\
= cos—cos x + sin—sinx, <=>cos3x— =cos x —
6	6 I 3 J < 6
- K I I Л ] Л О • <=>cos Зх— -cos x— = 0, <=>-2sin
I 3J
О я . K 3x---x + -xsin---------—
2
Тогда:
1) sin| 2x--^ |=0, I 4 I
-1я. 71
3*-3+*~6x 2
Л
— = 0<=>sin| 2x~—|sin[ x—— |=0. I 4 I I 12 J
2x]	= vk,
x!=£+^=£(4*+a kez-, о Z о
%
6
2) sinfx ——— |=0, x2—— = im, x2 = —+ nn =—(12л+11 neZ.
12 J 2 12	2 12	12v ' A
Ответ: x( =^(4Л + 1)х2 =-^-(12и + 1| k,neZ. o	12
8.002. 7 + 4sinxcosx + l^(tgx + ctgx)=0.
Решение.
ОДЗ-
sin x 0, cosx *0.
sinx j cosx^j q
cosx sinx J • 2	2
sm x+cos x
sinx cosx
7 + 4sinxcosx + l,5
<=> 7+4sinxcosx + l,5
L5	3
«=> 7+4sinxcosx + -— --= 0<=> 7+2sin2x+—---= 0.
smxcosx	sin2x
Отсюда получаем уравнение 2 sin2 2х + 7 sin 2х + 3 = 0, квадратное относительно sin2x  Таким образом, sin2x = -3,0, или sin2x = ~, откуда 2х = (-1)*f-^+кк, ке Z, х = (-1)*+1-^ + ^, ке Z.
6 )	12	2
Ответ: х = (-1)*+1 — + —, к е Z.
V 7 12 2
8.003. 4Ctg* 4-sin2 2x4-1 = 0.
14-ctg2x	z
Решение.
ОДЗ: sinx^O.
Из условия
4cosx
——4-sin2 2x4-1 = 0, <=> sin2 2x4-2sin2x4-l = 0 <=>
, cos2 x
1 + —~ sin X <=>(sin2x4-l)2 =0, sin2x = -l.
Тогда 2x = -— + 2idc, ke Z, x = -- + itk = -(4k-l\ keZ.
2	4	4.
Ответ: x = (4k -1} к e Z. 4
8.004.
sin2 2x-4sin2 x . - 2 —----------------+ l = 2tg x.
sin 2x4-4sin x-4
Решение.
ОДЗ: cosx * 0. Имеем
sin2 2x-4sin2 x +sin2 2x4-4sin2 х-4	_ 2
----------------------------------= 2 tg2 x <=> sin 2x4-4sin x-4
2sin22x-4 o 2 sin22x-2 + 2
—=----------5------= 2 tg2 x, —5------------= tg2 x <=>
sin 2x4-4sin x-4	sin 2x4-4sin x-4
sin22x-2 l-cos2x
<=>----------------=--------<=>
sin2 2x + 4sin2 x-4 l + cos2x
1-cos2 2x-2	l-cos2x 3- 2O л
1-cos2 2x + 2-2cos2x-4 l + cos2x cos2 2x(cos2x +1)= 0.
Отсюда:
1)cos22x = 0, cos2x = 0, 2x= — + nk, ke Z,
x =l + ^. = ^.(2k+l\ keZ;
1 4 2 4V A
2) cos2x+l = 0, cos2x = -l, 2x = it+2im, neZ,
x2 = — + JW = — (2и+Ц neZ.
я лет Ял,	„
Объединяя решения, получаем x = — +	+ Ц ш e Z.
Ответ: x = 4(2m +1) me Z.
4
8.005. sinzsin(60° -z)sin(60’ +z)=-.
8
Решение.
Из условия
sinz^sin(60° -z)sin(60° +z))=-^,<=>sinz^os2z-cosl20’>)=^<=>
<=> 2 sin z cos 2z + sin z = —, <=> - sin z + sin 3z + sin z = —, sin 3z =—.
2	2	2
Тогда 3z = (-!)*• 30°+1804, keZ, z = (-l)* 10° +604, ktZ.
Ответ: z = (-1)* 10° + 60°k, keZ.
-9	8
8.006. cos 2f-sin 2/ = -.
3
Решение.
ОДЗ:
cos2z 0, sin2z 0.
Перепишем уравнение в виде
1	1	8	_ cos2 2t-sin2 2t	8	n
--;-------j-----= 0, ----;----------+ —= 0, <=>
cos2 2/	sin2 2/	3 sin2 2/cos2 2/	3
cos4t 2	. cos4t	2..	2 . ,	. _ л
<=>—-— + —= 0, ------z— + — = 0, 2cos 4t-3cos4t-2 = 0.
sin2 2/ 3 l-cos24t 3
Решив это уравнение как квадратное относительно cos 4г, найдем cos4t =2,0;cos4/ = --^-,откуда 4t = ±-л+2лА:, keZ, t = +— +—, 2	3	6	2
ке Z.
тг тт]с
Ответ: t = + — +—, keZ.
8.007. tg3t-tgt-4sint = 0.
Решение.
fcos3t*0, ОДЗ;
[cost *0.
,	.	. о sin(a-B)
Использовав формулу tga - tgp = —-—, перепишем уравнение в cosacosp
sin2t	л™, о 2sintcost . Л - . fl-2cos3t3
виде—;-------4sinr = 0,-----------4smt = 0, <=> 2sintl---- = 0.
cos 3t cost	cos 3t cost	cos3t )
1 %
Отсюда sin t = 0,^=7^, ke Z ,или1-2со53г =0, cos3r = —, 3r = ±y+ 2яи ?
. я 2тсл
=± — +----, n e Z .
2	9	3
, п 2т ,	_
Ответ: t, = лк; t2 = ±- + -у, к, п G Z.
8.008. cos“l 3z-6cos3z = 4sin3/.
Решение.
ОДЗ: cos3z * 0.
Из условия
l-6cos2 3/-4cos3rsin3z = 0, cos2 3z + sin2 3/-6cos2 3r-4cos3rsin3z = 0, 5 cos2 3/ — sin2 3r+4cos3rsin3r = 0.
Разделив уравнение на-cos2 3z 0,имеем tg2 3z-4tg3z-5 = 0.Решив
это уравнение как квадратное относительно tg3z, получим (tg3/)] =-1 или (tg3/)2 =5, откуда 3/|=—+	+	=	keZ’’
,	<	. arctg5 ли _
3z2 = arctg5 + ли, t2 =—-— + —, neZ.
Ответ: /, =^(4Л-1}/2	+ k,neZ.
8.009. ctgt-sinz = 2sin2 —. 2
Решение.
ОДЗ: sin Г * 0.
COS t	л	. 2
-------sin t = 1 - cos t => cos t - sin t = sin t - sin t cos /, sin/
(cos t + sin t cos/)- ^in2 t + sin /)= 0, cos /(1 + sin t)-sin /(1 + sin /)= 0,
(1 + sin t Xcos t - sin t) = 0.
Отсюда 1) l + sin/ = 0 или2) cos/-sin/ = 0.Тогда:
l)sin/ = -l, /j = -— + 2tc£ = y(4£-l), fceZ;
2) cos/ = sin/<=>tg/ = l, /2 =“ + тш = — (4/1 + 1), ne Z.
Ответ: /j =~(4А-1^/2 = ^(4и + 1} k.neZ. 2	4
Решение.
Имеем
4 cos z (:os 2z+cos 120°)+1 = 0, 4 cos z cos 2z - 2 cos z +1 = 0 <=»
1	2
<=> 2 cos z + 2 cos 3z - 2 cos z +1 = 0, cos 3z = —, 3z = ±—л + 27^,
2	3
. 2 2nk . _ z = ±—Л +--, keZ.
9	3
,2 2тсЛ . _ Ответ: z = ±—тс + ——, keZ. 9	3
2
Решение.
ОДЗ: sin3x * 0. Из условия
cos2xctg3x-sin2x-72cos5x = 0 <=> (cos2xcos3x . _ ) [т ,
<=> ---:------sin2x -V2cos5x = 0,
cos2xcos3x-sin2xsin3x /т , Л
-------------------V2cos5x = 0<=>
sin3x
O^.^cos5x=0, c°^4-^sin3x) = [)
sin3x	sin3x
Отсюда:
l)cos5x = 0, 5x = —+ 7tZc, Xj = — + — = —(2&+1), keZ, 2	1 10 5	10 Л
или
2) I-V2sin3x = 0, sin3x = ^, 3x = (-1)" —+ ли, x2=(-l)"—+ —
2	4	12 3
ne Z.
Ответ: x} =— (2& + 1}x2 = (-1)”— + —, k, n& Z, 1 10	2	12	3
7C
8.012. sinxcos2x +cosxcos4x = sin —+ 2x 4
.	71	_
sin —3x 4
Решение.
Перепишем заданное уравнение в виде
71
-sinx + sin3x+cos3x + cos5x = cos5x-cos —х <=>
I2 >
<=>sin3x+cos3x = 0, sin3x = -cos3x, tg3x = -l,
откуда Зх =	+ Tin, х = ——+ —= —(4л-1)> weZ-
4	12	3	12
Ответ: х = —- (4и -1), п е Z.
. -	4 X . 4 X
8.013. sin2x = cos —sm —. 2	2
Решение. Имеем
( 2* -2*Y 2 X . 2 л
2sinxcosx- cos —- + sin — I cos — — sin •— = 0,
I 2	2 A 2	2 J
2sinxcosx-cosx = 0 <=> cosx(2sinx-l)=0.
Тогда:
1) cosx = 0, Xj =y + ял = у(2и + 1), ne Z; или
2)2sinx-l = 0, sinx = —, x2 = (-1)*+ nk, keZ. 2	6
Ответ:	=-^(2n+l}x2 =(-1)* y + n,keZ.
2	6
8.014. (1 + cos 4x)sin 2x = cos2 2x.
Решение.
Из условия
(14-1 —2sin2 2x)sin2x = l-sin2 2x, 2 sin3 2x-sin2 2x-2sin2x+l = 0, sin2 2x(2 sin 2x -1)- (2 sin 2x -1)= 0, (2 sin 2x -l)(sin2 2x -1)= 0.
Отсюда или
1) 2sin2x-l = 0, sin2x = —, 2x = (-l)fe —+ Я&, Xj = (-1)*+ 2	6	12 2
fceZ,
или
2) sin2 2x-1 = 0, sin2x = ±l, 2х = у + дл, x2 = ^ + ^ = ^(2и + Ц
ne Z.
Ответ: x} = (-1)*	x2 = у (2и +1} k,neZ.
12 2	4
8.015. sin2 2z + sin2 3z + sin2 4z + sin2 5z = 2.
Решение.
Перепишем уравнение в виде
(1 - cos 4z)+ j (1 -cos 6z)+(1 - cos 8z)+ у (1 - cos 1 Oz)=2,
(cos 4z + cos 6z)+ (cos 8z + cos 1 Oz)=0, <=► 2 cos 5zcos z+2 cos 9zcos z = 0,
2 cos z(cos 5z +cos 9z)=0.
Тогда:
1) cosz = 0,z! =y+Jtfc =y(2£ + l} keZ, или
2) cos5z+cos9z = 0, 2cos7zcos2z = 0, cos7z = 0, 7z = — + m,
2
z2 =77 + -т = гт(2п + Ц weZ; cos2z = 0, 2z = - + rcm,
14 7	14	2
it m n( x
z3 = —+-^- =—(2m+Ц me Z; zx входит в z2.
Ответ: z, = -Д- (2n + l)t z2 = (2m +1} n, m € Z.
14	4
8.016. ctg4 2z + sin-4 2z = 25.
Решение.
ОДЗ: sin2z*0.
Из условия
°08* 2z +—J---25 = 0 <=> cos4 2z+l-25sin4 2z = 0 «=>
sin4 2z sin4 2z
<=>(cos22z)2 +1-25sin4 2z = 0, (1 -sin2 2zf +1-25sin4 2z = 0«=> «=>12sin4 2z + sin2 2z-l = 0.
Решив уравнение как биквадратное относительно sin2z, получим sin2z = ±i откуда 2z = ±~ + iik, z = +^- + ^- = -^-(6k + l\ ke Z.
2	6	12	2	12
Ответ: z = -jy fck ± 1), к e Z.
8.017. tg2xcos3x + sin3x + V2sin5x = 0.
Решение.
ОДЗ:	cos2x * 0.
Перепишем уравнение в виде
sin2xcos3x . ~ /г . - л ----------+ sin3x + V2sin5x = 0<=>
sin2xcos3x+cos2xsin3x /т . -<=>----------------------+ V2 sin 5x = 0,
cos2x sin5x /г . c л ------+ V2 sin 5x = 0, cos2x
= 0.
cos2x
Отсюда или
l)sin5x = 0, 5x = Tcfc, X|=—, keZ,
ИЛИ
2) 1 + V2cos2x = 0, cos2x =-, 2x = ±—я+2ли,
2	4
x2 = ±—n+ял = —(8« ± 3), n € Z. О	о
Ответ: x{ =^-;x2 =^fan±3\ k,neZ.
5 о
8.018. ctS^“ + x j- tg2 x = (cos2x - l)cos“2 x. Решение, ОДЗ: cosx^O.
Имеем
A x 2 cos2x-1 sinx sin2x l-cos2x -tgx-tg2x =------—, -----+ ——  ----------<=>
cos x cosx cos X COS X
sinxcosx+sin2x l-bcos2x-ll . /	\ „ . 2 Л
<=>-------5-----= —E—5-------smx(cosx+sinx)-2sm x = 0,
cos x	cos x
sinx(cosx+sinx-2sinx)= 0, sinx(cosx-sinx)=0.
Тогда:
l)sinx = 0, х^тсЛ, fceZ, или
2) cosx-sinx = 0<=>tgx = l, x2 =—= —(4л+1| ле Z. 4	4
Ответ:	= лЛ; x2 = ^(4л + 1} к. пе Z.
8.019. cos—cos---sinxsin3x-sin2xsin3x = 0.
2	2
Решение.
Перепишем уравнение в виде
cos х+cos2x - cos2x + cos4x - cos x+cos 5x = 0 <=>
<=> cos4x+cos5x = 0, <=> 2cos—cos— = 0. 2	2
Тогда или
9x Л 9x л . л 2тсЛс я л,.	_
1) cos— = 0, — = —+ rcfc, Xi= — +--------= —(2Л + Ц keZ.
4	2	22	1 9	9	9 Л
или
2) cos у = 0,
— = —+ лл, x2 = л + 2ли = л(2и + 11 neZ 2 2
х2 вхо-
дит В Xj .
[X	x
8.020. 1 - sin 3x = sin — cos—
2	2
2
Ответ: х = (2Л +1)> ке Z.
\2
7
Решение.
Имеем
1	•	. 2 X _ . X X 2 X . -	.
1 ~ sin Зх = sin — 2 sin—cos — + cos; —, sm Зх - sin x = 0 <=> 2	2	2	2
<=> 2sinxcos2x = 0.
Тогда или
l)sinx = 0, Xj=7i«} neZ, или
2)cos2x = 0, 2x = —+ л£, x2 =^ + —= ^(2^ + 1), keZ. '	2	4 2	4
Ответ:
Xj = nn; x2 = (?k +1}
n,ke Z.
8.021. 2ctg2 xcos2 x + 4cos2 x-ctg2 x-2 = 0.
Решение.
ОДЗ: sinx^O.
Из условия 2cos2x(ctg2x + 2)-(ctg2x + 2)=0, или (ctg2x + 2zj>
x(jcos2 x-l = o), (ctg2x + 2)cos2x = 0. Так как ctg2x + 2*0,TO
cos2x = 0, 2x = — + idc, x = ^ + —= ^(2Л + 11 ke Z.
2	4	2	4
Ответ: x = (2fc + Ц к e Z.
4
8.022. 2sin3 x+2sin2 xcosx-sinxcos2 x-cos3 x = 0.
Решение.
Перепишем уравнение в виде
2sin2 x(sinx+cosx)-cos2 x(sinx+cosx)=0,«
«(sinx + cosx)^sin2 x-cos2 x)=0.
Тогда:
1) sinx+cosx = 0, или
2) 2sin2 x - cos2 x = 0.
Имеем:
1) tgx = -l или
2) tg2x = -,откуда X) =“ + лл= = 21(4л-1) neZ;
72
x23 = ± arctg+ ide, keZ.
Ответ: x, = (4л -1} x2 3 = ± arctg+ nk, n,ke Z.
8.023. sin 7x + sin 9x = 2 cos2 — - x - cos21 — + 2x
14 I 14
Решение.
Из условия
2sin8xcosx = l + cos—2х —I—cosl —+4х <=>
I2 J \2 J
<=> 2sin8xcosx = sin2x + sin4x <=>
<=> 2 sin 8х cos х - 2 sin Зх cos x = 0, <=> cos x(sin 8x - sin 3x) = 0. Тогда:
I) cosx = 0 или
2) sin8x-sin3x = 0,
откуда 1)х1 =~ + 1& = ^(2£ + 1) ке Z,2)2sin|-xcosy х = 0, sin-|x - 0,
5	2	11 л 11 я , я 2 ,
—х = яи , х-, = — тт, ns Z • cos—х = 0, —х = — + я/, х, =—+ — я/ =
2	’ 2 5	2	’ 2	2	’ 3 11 11
= уу(2/+1} IeZ.
Ответ: A'i = y(2fc + l}x2 = -пп;х3 = уу(2/ + Ц k,n,lsZ.
8.024. tg х + tg 2х - tg Зх = 0.
Решение.
cosx * о, ОДЗ: xcos2x * 0, cos3x * 0.
Используя формулу tg а - tg р = -8*-(а—, перепишем уравнение в виде cosacosp
sin3x sin3x _q<=> sin3x(cos3x-cosxcos2x)_ cosxcos2x cos3x	cosxcos2xcos3x
откуда:
1) sin3x = 0 или2) cos3x-cosxcos2x = 0.
Тогда:
1)3х = ли, X, =~> neZ;
2) 4cos3 x -3cosx - cosx(?cos2 x-l)=0 , cosx(:os2 x-l)= 0, cosx * 0,=> cosx = ±1, x2 = пк, ke Z; x2 входит в X!.
8.025. sin(150 +x)+sin(45° -x)=l.
Решение.
Имеем:
п . 15°+x+45’~x	15°+x-45°+x 1	( 1CO\ ,
2 sin------------cos-------------= 1, coslx -15 1=1.
2	2	v 7
Тогда x-15° =360%, x = 15°+360%, ktZ.
Ответ: x = 15° + 360°k, ke Z.
8.026. cos х + ctg Зх = ctg у -.
Решение.
ОДЗ:
cosx * 0, sin3x * 0,
• Зх Л sin— *0.
.	2
Из условия
if	3x 1	1
---+1 ctg 3x-ctg— 1=0 <=> cosx I	2
•	I a	3	I
sin 3x — x
Г	2	J
cosx	.	,	.3
sin 3x sm — x
2
. 3 sin —х
2
cos х . _ . 3 sin3xsin —х
2
= 0,
-1----b=o,
cos x sin 3x
sin3x-cosx _q cosx sin 3x
1
sin3x-cosx = 0,<=>sin3x-sin — -x |=0<=> 2
_ я	_ я
Зх+—x	Зх —+x
<=> 2 cos-----sin-------= 0,
2	2
( ТС I	I 7C ]
откуда: 1) cos x+4 = 0;2) sin 2x-- =0
Тогда:
1)х + —= —+ лЛ, Х| = — + пк = — (4А: +1), keZ;
4 2	4	4
2) 2x — = ля, x, = — + — = — (4n +11 и e Z.
'	4	2 8 2	8
Ответ: х, = у (4к + 1); х2 = (4и +1} к, п е Z. 4	о
8,027. sinxsin3x + sin4xsin8x = 0.
Решение.
Перепишем уравнение в виде
— (cos(x - Зх)~ cos(x + Зх))+ — (cos(4x - 8х)- cos(4x + 8х)) = 0, 2	2
о	л ~ . 2х+12х . 12х-2х л
cos 2х - cos 12х = 0 <=> 2 sin-sin----= 0,
sin7xsin5x = 0.
Отсюда:
1) sin7x = 0,
2) sin5x = 0,
7x = ЯЛ,
5x = лк,
x. =—, ne Z;
1	7
я£ i
x? =—, ke Z .
2	5
m лк
Ответ: -*i = —; x2 = —,
л, к g Z.
8.028. 2 tg3 x -2 tg2 x + 3 tg x - 3 = 0.
Решение.
ОДЗ: cosx * 0.
Из условия 2tg2 x(tgx-l)+3(tgx-l) = 0, (tgx-l)(2tg2 х + з)=0 .
Отсюда tgx-l = 0, tgx = l, х = ^ + im = ^(4n + l\ пе Z. 4	4
Ответ: х = ~ (4и + 1)^ п 6 Z.
л‘ (п . (к А . (Зя . ] f 7я _
8.029. cosxcos2x = sin —+ х sin —+ 4х +sin — + 4х cos--5х
14 I I 4 I 14 J I 4
Решение.
Перепишем уравнение в виде
(cos(x - 2х)+cos(x + 2х))=
=2 2
л л
(л	Я . 1 п . л . .
cos —+ х--4х |-cos —+ %+—+4х
14	4
4 ' ' 4 '.Гз, .
7я
2
. (Зя . 7я с ] . (Зя 7я , и sin —+4х-+ 5х +sin —+4х+-5х <=>
4	4
4
4
<	=> cos x+cos 3x = cos 3x - cos^y+5x	sin(jt - 9x)+ s*n^'| л - x J <=>
<	=> cos x = sin 5x - sin 9x+cos x, sin 9x - sin 5x = 0 <=>
.	9x+5x . 9x-5x
<	=> 2 cos-sm—-—
2	2
= 0,
откуда:
l)sin2x = 0, 2x = ltk, X|=—, keZ-
2)cos7x = 0, 7x = —+ лл, x2 = — + — = —(2л+ 1) «eZ.
2	14	7	14
Ответ: x( = x2 = •£• (2л + Ц к, n € Z. 2	14
8.030. 2 + tgxctgy + ctgxtg — = 0.
Решение.
cosx * 0, sinx * 0,
ОДЗ:
sin— *0, 2
cos— * 0. 2
_ .	x a l + cosa . a sina
По формулам половинного аргумента ctg у =	, tg — = ] + cosa >
поэтому
A sinx 1+cosx cosx sinx л „ 1+cosx cosx л 2+------------+-------------= 0 => 2+------+--------= 0,
cosx sinx sinx 1+cosx	cosx 1+cosx
4cos2 x+4cosx+l = 0, (2COSX+1)2 =0,
откуда cosx =-у, х = ±^л+2л£ = у^(3&±1} ke.Z.
Ответ: x =	(3k± 1), keZ.
8.031. sin2x + sin(rc-8x)= V2cos3x.
Решение.
Из условия
sin 2х+sin 8х - л/2 cos Зх = 0 <=> 2 sin	cos	_ ^2 cos Зх = 0,
2	2
2 sin 5хcos Зх - >/2 cos Зх = 0, cosЗх(г sin 5х - >/2 )= 0.
Отсюда:
l)cos3x = 0, Зх = —+ л£, X) = — + — = — (2fc + l) £eZ;
2	6	3	6
2) 2sin5x-V2 =0,sin5x = ^-,5x = (-l)" -4-лл, 2	4
=(->) Kz.
Ответ: *i = y(2fc + 0x2 = (-1)"+ ^-, k,ne Z. 6	20	5
8.032. 0,5(cos5x + cos7x)-cos2 2x + sin2 3x = 0.
Решение.
Перепишем уравнение в виде
cos 5х * cos -х •	(1 + cos4x)+(1 - cos 6х)= 0 <=>
<=> 2 cos 6х cos х -1 - cos 4х+1 - cos 6х = 0, 2 cos 6х cos х -
i л	\ Л . -I 4х+6х	4х-6х Л
-(cos4x+cos6x)=0«=>2cos6xcosx-2cos—-—cos—-— = 0, cos 6хcosх -cos 5xcos x = 0 <=» cos x(cos 6x - cos 5x) = 0.
Отсюда:
l)cosx = 0, Xj =y(2fc+0 k&Z;
2) cos6x -cos5x = 0, -2sin 6* + 5x	5x ~ 6x _
2
2
2лл ~ . х х , х? =-----, п е Z : sin — = 0, — = я/,
2	11	’	22
• И а И Тогда sin—x = 0, —x = m,
x3 = 2я/, I € Z; x3 входит в x2.
Ответ: xi = у(2& + 0x2 = k,n^Z.
8.033. 2(cos4x-sinxcos3x)= sin4x + sin2x.
Решение.
Имеем
2 cos 4x - 2 sin x cos 3x - sin 4x - sin 2x = 0, 2 cos 4x - sin (x - 3x)-- sin(x + 3x)- sin 4x - sin2x = 0, 2 cos 4x+sin 2x - sin 4x - sin 4x --sin2x = 0, 2cos4x-2sin4x = 0<=> tg4x = l,
откуда 4х = —+я&, x = —+— =—(4Л + 1), keZ.
4	16 4	16
Ответ: х = £(4Л+1} keZ.
16
8.034. sinxcosxcos2xcos8x = — sin!2x.
4 Решение.
Из условия
2(2sinxcosx)cos2xcos8x = sinl2x <=>2sin2xcos2xcos8x = sinl2x <=> <=> sin 4x cos 8x - sin 12x = 0	(sin(4x - 8x)+ sin(4x+8x ))- sin 12x = 0,
- sin 4x + sin 12x - 2 sin 12x = 0, sin 12x + sin 4x = 0 <=>
- . 12x+4x	12x-4x	. Л
<=> 2sin-----cos--------= 0, sin8xcos4x = 0.
2
2
Отсюда:
1) sin8x = 0,
2) cos4x = 0, ДИТ В X!.
8x = nfc, x, =—, keZ: 1	8
л ТС	7C 7Ut 7U	„
4x = — + im, x2 = — + — =—(2n+l| neZ;x2Bxo-
2	о	4	о
ilk
Ответ: x = —, к g Z. о
8.035. 3sin2 2x + 7cos2x-3 = 0.
Решение.
Имеем
з(1 - cos2 2x)+ 7 cos 2x - 3 = 0 <=> 3 cos2 2x - 7 cos 2x = 0, cos2x(3cos2x-7)=0.
Отсюда:
I)cos2x = 0, 2x = y + rcfc, Xj = -^ + -^ = ^(2fc + l) £gZ;
7
2) 3cos2x-7 = 0, cos2x = — >1-0.
Ответ: х = ^(2Л + 1) keZ.
4
8.036. sin2xsin6x-cos2xcos6x = y[2 sin3xcos8x.
Решение,
Из условия
(cos 2x cos 6x - sin 2x sin 6x)+ 72 sin 3x cos 8x = 0 <=>
<=> cos 8x + 72 sin 3x cos 8x = 0, cos8x|j + 41 sin 3x)= 0.
Отсюда:
1) cos8x = 0, 8x = — + ли, Xi = — + — = —(2и + 11 neZ;
7	2	1 16 8	16v л
2) 1+72 sin3x = 0, sin3x = -—, 3x = (-l)fef-— + я& = (-1/+1—+ rcfc.
2	I 4 J	4
X2 = (-1/** —+ —, keZ.
2	1 12	3
Ответ: X] =^(2л + 1}х2	+ n,keZ.
16	12	3
8.037. sin3xcos3x = sin2x.
Решение, Имеем
2sin3xcos3x-2sin2x = 0, <=> sin 6x-2sin2x = 0, sin 3(2x)- 2 sin 2x = 0, <=> 3 sin 2x - 4 sin3 2x - 2 sin 2x = 0, 4sin3 2x-sin2x = 0, sin2x(4sin2 2x-l)=0.
Отсюда:
itn l)sin2x = 0, 2х = яи, xt=—, wgZ;
2) 4sin22x-l = 0, sin22x = —, sin2x = ±—, 2x = ±—+ 7tfc, 7	4	2	6
x23 =±—+ —= —(6Л + Ц ke Z.
23	12	2	12v h
Ответ:	= -у; х2,з =	(6^ ± k € z-
8.038. cos2x-5sinx-3 = 0.
Решение.
Из условия l-2sin2x-5sinx-3 =0, 2sin2x + 5sinx+2 = 0. Решая это уравнение как квадратное относительно sinx, имеем
sinx =-2,0 ; или sinx = “, откуда х = (-1Уг+| — + л£, ке Z.
2	6
Ответ: х = (-1/+1 у + лЛ, к е Z. 6
8.039. 3sin2x+2cos2x = 3.
Решение.
Имеем
6sinxcosx+2(cos2 x-sin2 х)=з(со$2 x+sin2 х), 5sin2 x-6sinxcosx+cos2 x = 0,<=>5tg2 x-6tgx+l = 0.
Решив это уравнение как квадратное относительно tgx, найдем
(tg*)i
= -^ mni(tgx)2 =1,откудах( = arctg+ пк = arcctg5+пк, ке Z; э
х2 =—+ пп = — (4л + 1), neZ. 4	4
Ответ: х, = arcctg 5 + пк; х2 = — (4л+1), к, п е Z. 4
оллл . (Зл 'I t 2 . l + cos2x л
8.040. ctg--х I- ctg x +--------= 0.
(2 j	sin2 x
Решение.
[cosx*0,
ОДЗ: .
(sin x * 0.
Перепишем заданное уравнение в виде
х А 2	1 + 2COS2 Х-1 „	2	~	2
tgx-ctg х +------------= 0, <=> tgx-ctg x+2ctg х =0,
sin2 х
ctg2 х+—-— = 0, ctg3x = -l, ctgx = -l. ctgx
Тогда x = —л + я& = —(4£ + 3)> keZ.
4	4
Ответ: x = — (4k + 3) к e Z.
4
8.041. cos 9x - cos 7x + cos 3x - cos x = 0.
Решение.
Перепишем уравнение в виде
_ . 9x + 7x . 9x-7x	. Зх + х {. Зх-х л
- 2 sin------sin--------2 sin----sin-------= 0 <=>
2	2	2	2
<=> sin8xsinx + sin2xsinx = 0 <=> sinx(sin8x + sin2x)=0.
Отсюда:
l)sinx = 0, Xj =ли, weZ;
. _ л . 8x + 2x 8x-2x л 2) sin 8x + sin 2x = 0 <=> 2 sin-cos--= 0,
7	2	2
sin 5x cos Зх = 0
_ izk Тогда или sin5x = 0, 5x = nk, x2=—, £€7,или cos3x = 0,
3x = ^ + iun, x3 =- + —= -(2zn + l), meZ , x} входит в x2. 2	6	3	6
Ответ:	x2 = •— (2m + 1) k,me Z.
t i
8.042. 2 tg—1 =cosz. 2
Решение.
ОДЗ: cos|- * 0-Имеем
2-
. t sin-
——-1 t cos — 2
2 t . 2 f | л cos —sin - = 0<=>
2
J . t	t \
2 sin—cos-	z	4
I 2	2] ( t .
—*--------z- cos—sin— X
r	2	2
cos - V	J
2

2
(	'	• ' I л I • '	'
х cos- + sin- =0<=> sin—cos —
2	2	2	2
t
2
t cos-
. t t +sm-+cos-2
2
, t	t 2t
sin—cos— 2 + sin—cos—+ cos —
2	2 JI 2	2	2
t cos—
Отсюда:
1) sin—-cos —= 0; 2) 2+sin—cos—+ cos2 —= 0,0.
2	2	7	2	2	2
Из первого уравнения получим
tg— = 1, — = —+ ли, t = — + 2nn =—(4и + 1), n&Z,
*2	2 4	2	2
Решение,
Из условия
72	72 7з	7з
sin 3z-----cos 3z------ — <=> sin 3z cos 45° - cos 3z sin 45° = — <=>
2	2
<=> sin(3z - 45°) =
откуда 3z-45° = 60°+ 360% или 3z-45° = 120° + 360%. Отсюда zj = 35° + 120%, z2 = 55° + 120%, к e Z.
Ответ: zj = 35° + 120%,z2 = 55° + 120%,£ gZ.
8.044. V3sin2x + cos5x-cos9x = 0.
Решение,
Перепишем заданное уравнение в виде
гт . о ~ . 5х + 9х . 5х-9х Л
V3 sin 2х - 2 sm---sin-------= 0 <=>
2	2
<=> 7з sin 2х + 2 sin 7х sin 2х = 0 <=> sin 2х(Тз + 2 sin 7х) = 0. Отсюда:
1) sin2x = 0, 2х = яи, Xj =—, п eZ;
2) 7з+2sin7x = 0, sin7x = -—, 7х = (-1)*+| - + кк.
2	3
( iV+i Л . life ,	„
x2=H) Yi keZ' ли z u+i n itk .	_
Ответ: xl=—;x2=(-\J' ^[ + ~’ n>keZ-8.045. 2 cos2 x + 5 sin x - 4 = 0.
Решение.
Имеем2^-sin2 x)+5sinx-4 = 0 или 2sin2 x-5sinx + 2 = 0.Решив это уравнение как квадратное относительно sin х, получим sin х = 2, 0 ,
или sinx = —, x = (_ 1)* — +	ktZ,
2	6
Ответ: x = (-1)* — + кк, ke Z. . z	3z	1- n . 3z	z
8.046. sin - cos-sin 2z = sin—cos—.
2	2 V3	2	2
Решение. Перепишем уравнение в виде
If . (z 3z ] . I — sin------+sin
2	*	*
z 3z n sin2z
2 2 I Л
2 2
1 f . ( 3z z A . (3z z H n — sin------+sm—+— =0<=>
2^ ^2 2)	|^2 2))
. „ 2sin2z	• а л
<=>-sinz+sm2z---=----sinz-sin2z = 0 <=>
V3
sin z(>/3 + 2 cos z)= 0.
Отсюда:
1) sin z = 0, z, = wi, ne Z;
г-	у(3	5
2) V3+2cosz = 0, cosz =---, z2=±—n + 2nk, keZ.
2	6
Ответ: z, = iui;z2 = ±—л+2кк, n,keZ.
8.047. sin3 z cos z-sin z cos3 z =—.
8
Решение.
Из условия
- sin z cos zlcos2 z - sin2 z )= — <=> 2 sin z cos zlcos2 z - sin2 z )=---<=>
\	7	8	Г	/	4
<=> sin2zcos2z = —— <=> 2sin2zcos2z =-, sin4z = ——,
4	2	2
откуда 4z = (-1)*+1 + nk, z = (-1)*+1 ~ + “r> keZ. 4	16	4
Ответ: z = (-1)*+1	, keZ.
16	4
8.048. sinl -7 + 5x I 4
.In 1. % , sm — + x sm — - 6x
4	4
Решение.
Перепишем заданное уравнение в виде
if . (я , л „	. (п . л „
— sm —+5х--2х +sin —+5х + —+2х
2|14	4	)	^4	4
If (л	л , 1 f Л
— cos —+х—+6х -cos — 2	4	4	4
<=> sin Зх +
(тс ।	(тс 1
+ sin —+ 7х -cos7x+cos—5х =0<=>sin3x+cos7x-cos7x +
U	2
5х + 3х 5х — Зх + sin 5х = 0, sin Зх + sin 5х = 0 <=> 2 sin-cos— -= 0,
sin4xcosx = 0.
Отсюда:
l)sin4x = 0, 4х = тсл, х, =—, neZ; 1	4
2) cosх = 0, х2 = — + nk, ке Z ; х2 входит в х.
Ответ: х = —, п € Z. 4
f 3л
8.049. cos3x = 2sin — + x 2
Решение.
Перепишем заданное уравнение в виде 4cos3 х - 3cos х = -2 cos х, <=> 4 cos3 х - cos х = 0 <=>
<=^cosxi
Отсюда:
l)cosx = 0, Xj = +	= у(2Л + 1) fceZ;
7	1	я
2) 4cos x-l = 0, cosx = +—, x7 =±— + nn, neZ.
'	2	2	3 •
Ответ: Xj = ^(2Л +1} x2 = ±y + itn, k,ne Z.
8.050. 5(1 + cos x) = 2 + sin4 x - cos4 x.
Решение.
Из условия
5+5 cosx - 2 +(cos2 x - sin2 x)(cos2 x+sin2 x)= 0,
2cos2 x+5cosx+2 = 0.
Решив это уравнение как квадратное относительно cosx , получим 1	2
со8х = -2,0;или cosx = откуда х = ±-л + 2л&, ке Z . 2	3
•2
2
Ответ: х = ±—я + 2л&, keZ. 3
8.051. l + sin2x = (cos3x + sin3x)2.
Решение.
Имеем
1 + sin 2х = cos2 Зх + 2 sin Зх cos Зх + sin2 Зх, 1 + sin 2х = 1 + sin 6х, . ,	. л	6х + 2х . 6х-2х л	_	..
sin 6х - sin 2х = 0 <=> 2 cos-sm------= 0, cos 4х sm 2х = 0,
2	2
откуда:
1) cos4x = 0, 4x = y + Ttfc,
я	keZ
8	4	8 V A
2)sin2x = 0, 2х = тсл, х2=^р neZ.
Ответ:	= ^(2£ +1) x2 - k,neZ.
o	2
8.052. sin3x = 2cos — -х 2
Решение.
Перепишем уравнение в виде
3sinx-4sin3х =2sinx, 4sin3 x-sinx = 0, sinx^sin2} откуда:
l)sinx = 0, xl=itn, neZ;
2) 4sin2x-l = 0, sinx = ±—, x23=±— + ick, keZ.
2	’	6
Ответ: x, = itn; x2 3 = ±-^ + nk, n,k&Z.
6
8.053. cos4x + 2 sin2 x = 0.
Решение.
Перепишем уравнение в виде 2cos2 2x-l + l-cos2x = 0, cos 2x(2 cos 2x -1) = 0, откуда:
1) cos2x = 0, 2x = y+7t£,
2 cos2 2x -cos 2x = 0,
X'=7+V = Z(2*+1* keZ'> 4	2	4
2) 2cos2x-l = 0,cos2x =—, 2x = ± — + 2пп,x2 = ± — + itn,neZ. 2	3	2	6
Ответ: x, = — (2fc + l)x2 =±—+nn, k,neZ. 4	6
8.054. sin x + sin 7x - cos 5x + cos(3x - 2л) = 0. Решение, Из условия
(sin x+sin 7x)- (cos 5x - cos3x)= 0 фф 2 sin * +^X- cos *
_ . 5х + 3х . 5х-3х _ ' . л . . л
+ 2 sin------sm------= 0 <=> sm 4х cos х + sin 4х sin х = О,
2	2
sin 4x(cos Зх+sin х) = О,
откуда:
Ttlc
l)sin4x = 0, 4х = яЛ, х(=—, keZ;
2) cos3x+sinx = 0, 2cos[ х+— cos|2x-— =0.
I 4 J I 4 J
Полученное уравнение эквивалентно двум уравнениям:
\ I 7С j Л ТС ТС	ТС	«—
a)	cos х + — =0, х+— = —+ 7си, х2 = —+ лл, neZ;
4	4 2	2 4
б)	cosl 2х-^-1=0, 2х--^ = у + л/и, х3 =-^(4/и+3} те Z .
Решения х2 входят в X].
Ответ: х, =	, х2 = (4и + 3) к, п е Z.
.	,	25
8.055. cos 2x + 6cos 2х =— 16
Решение.
Имеем 16cos4 2х + 96cos2 2х - 25 = 0. Решив это уравнение как биквадратное относительно cos2х , получим cos2х = -, 2х = ± у + тсА:}
л лк
- + —,где ке Z. 6 2
Л	. л лк . _
Ответ: х = ±— + —, keZ. 6	2
8.056. 1 + cos/+ cos 2/+ cos Зг = 0.
Решение.
Перепишем заданное уравнение в виде l+cosz+2cos2 r-l + 4cos3 r-3cos/ = 0, 4 cos31 + 2 cos21 - 2 cos t = 0 <=> 2 cos cos21 + cos t -1)= 0.
Отсюда:
l)cos/ = 0, lt =у + л& = -^-(2&+1} keZ-,
2) 2cos21+cosz-l = 0.
Решив уравнение как квадратное относительно cos Г, получим (cos/)j =-!, t2 = л + 2ли, ле Z; (cos/)3 =i,	=±у + 2пт, те Z.
Объединив решения t2 и z3, получим t2 = у (2л + Ц п е Z .
Ответ:	=y(2A:+l)/2 =у(2л+1| k,neZ.
8.057. cos2x = (cosx — sinx)
Решение.
Из условия
cos2 x - sin2 x - >/2 (cos x - sin x)=0 фф
<=> (cosx-sinx)(:osx + sinx--j2}= 0.
Тогда:
1)	cosx-sinx = 0,
2)	cosx + sinx-72 =0.
Из первого уравнения tgx = 1, х, = — + пк ,к е Z .Из второго уравнения 4
•J2	у/2 ,	я . я
cosx----+sinx-----= 1 <=> cos х cos— + smxsm—
2	2	4	4
(	i
<=>cos х— =1,
I 4 .
откуда х - = 2тт, х2 = + 2 т, neZ . Объединив решения х} и х2, получим х = + пк, keZ .
Ответ: х = - + лА:, keZ, 4
8.058. l + cos7x= sin-cos—
I 2	2
Решение.
Имеем
.	_	. 2 Зх - . Зх Зх 2 Зх t	_
l + cos/x = sin-2sin—cos— + cos —, l + cos7x = l-sm3x,
2	2	2	2
f \	7x + —-3x
f Л I	7
cos 7x + sin 3x = 0, cos lx+cos — 3x = 0 <=> 2 cos---x
2	2
7x— + 3x /	\	\
2	/ч	71 I (r я I Л
xcos---------= 0, cos 2x + — cos 5x — = 0.
2 I 4 J I 4 J
Отсюда:
t\	I л	7C7C	л Л
I) cos 2x4-— = 0, 2x4-—= —4-яи, 2x = — 4- m ,
4 I 4 2	4
Л TZH Л /.	- \
Xj =-+ —= -(4и+Ц neZ;
o	2.	о
2) cos|5x-—|=0, 5x-— =—+itk 5x = —л + яЛ,
'	4J	42	’	4
x2 = — n + — = — (4k + 3\keZ
2 20	5	20
Ответ:
xi =7(4«+>^2 =^r(4k + 3\n,ke Z. o	ZU
8.059. 2 tg4 Зх - 3 tg2 Зх +1 = 0.
Решение.
ОДЗ: cos3x *0.
Решив это уравнение как биквадратное относительно tg3x, полу-у/2 гг	± arctg —
чим: 1) tg3x = ±—, х12 =-------—-4-—, keZ;2) tg3x = ±l,
2	3	3
, Л
Хз’4-±12+-3~ ’ пе^' .1	, -J1 пк . п пп ,	„
Ответ: х12 =±-arctg—+ у;х3>4 =+—+ у, k,n<=Z.
( Зл
8.060. sin 2х - sin Зх + sin 8х = cos 7х + — 2
2х + 3х
Решение.
Из условия 2x —Зх (sin2x-sin3x)+(sin8x-sin7x)=0,<=>2sin---cos
А
- . 8x-7x	8x + 7x	_ .x	5x	. x	15x	_
+2sin------cos------= 0, -sm—cos—+sm—cos-------= 0 <=>
2	2	2	2	2	2
. x( 5x 15xЛ <=>-sm— cos---cos--- =0<=>
2^	2	2 J
5x 15x	15x 5x
—— sin —-----— = 0 <=>
2	2
5.	n 2
4=>sin — -2sin— 2
X	j
<=> sin—sin 5x sin—x = 0. 2
Тогда:
1)	sin— = 0, — = ли, x. = 2itn, ne Z;
2	2
2)	sin5x = 0, 5х = лА:, x2 = —, AreZ;
5	5	2
3)	sin—x = 0, — x = таи, x3 = —	Z; Xj и х3 входят в x2.
2	2-	5
Ответ: x = —, keZ. 5
8.061. 4 tg2 3x - cos'2 3x = 2.
Решение.
ОДЗ: cos3x *0.
Имеем
----------1	2 = 0«4z£^)-1---2 = o, cos2 3x cos2 3x------------------------cos2 3x cos2 3x
4^-cos2 3x)-l-2cos2 3x = 0, cos23x = ^.
Отсюда cos3x = ±—3x = ±— + як, x = +—+—, k&Z.
2	4	12 3
л	. it nk
Ответ: x = ±—+—, *G z
8.062. cos3 x + cos2 x - 4 cos2 — = 0.
2
Решение.
Из условия
cos3x + cos2 x-4 — (l + cosx)=0, cos3 x+cos2 x-2cosx-2 = 0, <=> 2
« cos2 x(cos x +1)- 2(cos x +1)=0, <=> (cos x + l/cos2 x - 2 )= 0.
Тогда cosx + l = 0,cosx = -l,Xj =л+2ли =	Z ; cos2 x-2 ^0.
Ответ: x = я(2л + 1} n e Z.
8.063. sin 9x = 2 sin 3x.
Решение.
Переписав уравнение в виде sin 3(3х)~ 2 sin Зх = 0 и воспользовав-
шись формулой sin За = 3 sin а - 4 sin3 а, имеем 3sin3x-4sin3 3x-2sin3x =0, 4sin3 3x-sin3x =0, sin3x(4sin2 3x-l)=0.
Тогда
1) sin3x = 0, Зх = ли, Xi = —, ne Z;
1	3
2)4sin2 3x-l = 0,sin3x = ±-, Зх = ±- + л*5х2 =±—+ — keZ.
2	О	1 о 5
8.064. (sin ^H-cos 1 z)(sinz + cosz)+2 = 0.
Решение.
ОДЗ:
sinz^O, cosz * 0.
Перепишем уравнение в виде
1	1	/.	\ _ Л smz + cosz (.	\ и л
----+-----Msinz+cosz)+2 = 0,	(sinz + cosz)+2 = 0. sinz cosz )	sin z cosz
Отсюда
(sinz+cosz)2 + 2sinzcosz - 0, sin2 z + 2sinzcosz+cos2 z + 2sinzcosz =
= 0,4sinzcosz = -l, sin2z =	.
Тогда 2z = (-1)*+1 -+jtf, z = (-1)*+1—+—, к e Z. 6 v 7	12 2
Ответ-. z = (-l)*+l—+—, к eZ. 12 2
8.065» sin2z + cos2z = >/2sin3z.
Решение.
„ .	ГТ (Я
По формуле cos a + sm a = <2 cos — - a получаем
V-	( Я	|	Г"	( Я	|
2cos---2z = V2sin3zocos —2z -sin3z = 0o
И	J	И	)
<=> cos — - 2z j - cosl — - 3z I = 0, U )	12	)
Я ~ Я	о । о
---------------2z +-----------3z —2z — + 3z - 2 sin--------2-sin—-------2-----_ q
2	2
Тогда:
= 0.
. (5z	Зя^	Л 5z	Зя	5z	Зя
l)sm------=0,------------= яи, — = —
V 2	8 J 2	8	2	8
Z1 =
—я + —яи = —(8и+3), n eZ; 20	5	20
. (z	яА	Л z	я	. z	п	.
2) sin---=0,-----= яЛ, — = — + пк,
12	8J 2	8	2	8
г2=~ + 2яЛ = -(8* + 1),^€2;
4	4
Ответ*. z1 =t^(8>i + 3);z2 =^-(8£ + l), nJceZ.
8.066. 6sin2x + 2sin22x = 5.
Решение.
Перепишем это уравнение в виде
6~(l-cos2x) + 2(l-cos2 2х)-5 = 0 о 2cos2 2x+3cos2x = 0, cos 2х(2 cos 2х + 3) = 0.
Тогда
cos2x = 0, 2х = — + пп, л. =—+ — =—(2л+1), ne Z;
2	’*424
2cos2x + 3*0.
Ответ: х = -^ (2л + Ц л е Z.
8.067. sin Зх + sin 5х = 2(cos2 2х - sin2 Зх).
Решение.
Перепишем заданное уравнение в виде
2
_ . Зх + 5х Зх-5х	1	. \
2 sin—-—cos-------= 2 — (1+cos 4x1-
2	2	^2
2 sin 4x cos x = cos 4x+cos 6x <=>
_ . A - 4x + 6x	4x-6x
» 2 sm 4x cos x - 2 cos-cos---
2	2
<=> sin 4x cos x - cos 5x cos x = 0, cos x(sin 4x - cos 5x)=0.
Отсюда:
l)cosx = 0, х, = — + ли = — (2м+ 11 weZ; 2	2
4x-— + 5x	4x + —-5x
7	2
2) sin 4x - cos 5x = 0 <=> 2 sin---cos-------= 0,
2	2
9x Л ( sin--------cos
2 4
=0.
2 4
. f 9x %	Л	9x %	,	9x л .	я
Тогда или	sin ———	= 0,	——— = л£,	— = т + лк,	^2=77 +
12	4	1	2	4	2	4	1о
2 » л /.. «\ » п	(х л j _ х л я . х Зл
+-л/с = — (4fc +1), ke Z, или cos-------=0,---------=—+я/, — = — +
9	18	’	(2 4 J 2 4 2	2 4
3
+ л 9 х3 = —л+2л/, /е Z; х3 входит в х,.
Ответ:	= ^(2л+l) х2 = (4Л+Ц п,к e Z.
2	1 о
п ) э • -2
8.068. lS г+х hctgzx-sm
x(l + cos2x)=0.
Решение.
ОДЗ: sinx^O.
Из условия
-ctgх-ctg2 х + ^+^-С-^ Х—- = 0, -ctgх-ctg2 х + 2ctg2 x = О, sin2 x
ctg2 x-ctgx = 0, ctgx(ctgx-l)=O.
Отсюда:
l)ctgx = O, Xj =у + л/с = у(2Л + Ц keZ;
2)ctgx-l = 0, ctgx = l, x2 = —+ яи = —(4n + l| wgZ.
Ответ:	= ~ (2fc +1); x2 = (4л +1), к, n g Z.
8.069. 2sin3 x-cos2x-sinx = 0.
Решение.
Имеем
2sin3 x-l + 2sin2 x-sinx = 0, 2sin3 x+2sin2 x-sinx-1 = 0, 2sin2 x(sinx + l)-{sinx + l) = 0, (sinx+l)^sin2 x-l)=0.
Отсюда:
l)sinx + l = 0, sinx = -l, Xj =-~ + 2як = j(4fc-l| fceZ;
2) 2sin2x-l = 0, sinx = ±—; x2	—(2и+1) hgZ.
2	4 2	4
Ответ: x, =--(4Л-1)х2 = — (2и+Ц k,ns Z. 2	4
8.070. 3sin5z-2cos5z = 3.
Решение.
Из условия
3sin2| — z |-2cos2| — z |-3| cos2 —z+sin2 — z |=0<=> I 2 I 2 I I 2	2
15 M. И. Сканави, группа A
449
, . 5	5	7 5	. 7 5 ।	5
<=>6sin—zcos—z-2 cos — z-sin — z -3 cos —z+sin —z = 0<=>
2	2^2	2 J (	2	2 J
. 7 5	, . 5	5	.	2 5	„
<=>sin_ — z—6sin—zcos—z + 5cos —z = 0.
2	2	2	2
2 5
Разделив это уравнение на cos —z * 0, получим tg2|z-6tg|z + 5 = 0.
„	5
Решив уравнение как квадратное относительно tg—z, найдем
5	,5	л	, л 2
tg~^ = l, -г = - + л*, Z) = —+-лЛ, ке Z, 2	2	4	10 5
или
5.5 с	2 с 2
tg-z = 5 , —z = arctg5 + 7w , z2 =-arctg5+ -ли, weZ.
2	2	5	5
я 2 t 2	_ 2	.	_
Ответ: ^ = — + у я*; z2 = yarctg 5 + у ял, к, п е Z.
8.071. 4sin3z + —cos3z = 3. 3
Решение,
Перепишем уравнение в виде
. 3z 3z о 3z . 2 3z 2 3z A . 2 3z Л 24 sin—cos — + cos--sin----9 cos----9 sin — = 0 <=>
2	2	2	2	2	2
<=> lOsin2 — -24sin—cos — + 8cos2 — = 0.
2	2	2	2
3z Разделив это уравнение на 2 cos2 — ф 0, получим 5tg2y-12tg^ + 4 = 0;
3z	3z 2
решив уравнение как квадратное относительно tg —, найдем tg — = у,
3^	2	2	2	2	3~	3
— = arctg — + пп, Z| =-arctg—+ —ли, neZ; tg-^ = 2, —x = arctg2 +
2	5	3	5	3	2	2
2	2
=-arctg2 + -nfc, ke Z .
z 3	3
2_____2.2
(✓ZAIOC/Z*. ~1	3---C,	- 3
2	2 2	2
Ответ: zi = “ arctg у+у ял; z2 = у arctg 2 + у я*, к. п е Z.
8.072. (cos 6x - l)ctg 3x = sin 3x.
Решение.
ОДЗ: sin Зх * 0.
Имеем
(cos2(3x)-l)cos3x . , L 2, -Л ->	• 2i л
------—'— -------sin 3x = 0, 12 cos 3x - 2 Icos 3x - sin 3x = 0, sin 3x
-2^-cos2 3x)cos3x-sin2 3x = 0, 2sin2 3xcos3x + sin2 3x = 0, sin2 3x(2cos3x + l)=0.
1	2
Так как sin3x*0,TO 2cos3x + l = 0, cos3x = --, Зх = ±утс+2тс/:1 2	2
Х = ±9Я+3^’ keZ' 2	2
Ответ: х = +-к + -кк, keZ.
Решение.
ОДЗ:
cos —+ х h*0,
I4 J
(n л
cos —x pO. 14	)
Перепишем уравнение в виде
<=> l+cos2x-3(cos2x+0)=0,
„ 1 cos2x = —, 2
2x =+—+2nn, x = +— + nn, ne Z.
3	6
Ответ: x = ±—+л и, n e Z.
6
8.074. 1-cos^r + x)-sin^^X =0.
Решение.
Имеем
1 + cosa* + cos — = 0 <=> l + 2cos2 —-1 + cos — = 0, 2	2	2
-	2 X X л x(X Л л
2cos — + cos— = 0, cos— 2 cos — + 1 =0.
2	2	2^	2 J
Отсюда:
1) cos— = 0,
— = — + nk, Xi = л+ 2nk = л(2£ + 11 keZ: 2 2	1
>v	x 1 x 2	4
2	) 2cos — + 1=0, cos —= —, — = ± — л + 2ли, x2 =± —л + 4ли, 2	2	2	2	3	2	3
ne Z
Ответ: *i = nfa + Oi x2 = ± j л + 4ли, к, n e Z. 2
8	.075. 9C0SX =9sin Y . jcosx	,
ОДЗ: cos x * 0.
Решение.
Из условия
2	2sinjf| 2
32cosx =32sinx.3cosx <=>32cosx=3 S,nx+Cosx 2 COS X = 2 sin X +.
COSX
Отсюда
cos2 x-sinxcosx-l = 0, sinxcosx + l-cos2 x = 0, sin xcos x + sin2 x = 0, sin x(cosx + sin x) = 0.
Тогда:
1) sinx = 0, Xj = nn , ne Z;
.	л
2) cosx + sinx = 0 <=> tgx = l, x2 =~—+ лАг, ke Z
Ответ:
л .	. _
Xj = ли; x2 =	+ лк, и, к e Z.
8.076. sin x - sin 2x + sin 5x + sin 8x = 0.
Решение.
Имеем
(sinx-sin2x)+(sinx+sin8x)=0 <=> 2sin—cos—-— +
- . 5x + 8x 5x-8x л „ . x Зх - . 13x +2sm------cos------= 0 <=> -2 sin—cos—+2sm--x
2	2	2	2	2
Зх л „	3x( . x . 13xA л 3x
xcos— = 0<=>-2cos— sin—sin---- =0<=>cos—x
2	2	2	2 J 2
x 13x	x 13x
9	7	9	9	3x	7x
x2sin—--— cos—---— = 0 <=> cos—sin3xcos— = 0.
2	2	2	2
Отсюда:
Зх . Зх n , n 2 , n fa,	„
1) cos— = 0, — = —+nk, x, =—+—nk = — Qk+l\ keZ-
'	2	2 2	* 3 3 3V
2) sin 3x = 0, Зх = ял, x7 = —, 3
ле Z ;
3)cos—= 0,	=	x3=^ + ^ = ^(2/+ll /6Z;
2	2	2	7	7	7
X] входит в x2.
Ответ:
X|=y;*2=y(M n,leZ.
2
8.077. 2sinz-cosz = -.
Решение.
Переходя к половинному аргументу, находим
«2 Z	2 Z • 2 I	2	*2^1 л
20sm—cos—5 cos —sin — -2 cos — + sin — 1=0, 22^	2	2J<	2.2)
3sin2 —+20sin—cos—-7cos2 — = 0« 3tg2 —+20tg—-7 = 0, 2	2	2	2	2	62
z	z
решив это уравнение как квадратное относительно tg —, найдем tg — = -7,
- = -arctg7 + jtfc, zx =-2arctg7 + 2rc& , fceZ; ^f=3’ 7 = arctSy +
+z/, z2 =2arctgj+2Tt/ = 2arcctg3+2jc/, IeZ .
Ответ: zx =-2arctg7 + 2TtA:; z2 =2arcctg3 + 2n/, Z,
8.078. cos —+ 5x +siiix = 2cos3x.
I2 J
Решение.
Из условия
(sin5x-sinx)+2cos3x = 0 <=» 2cos—-——sin---— + 2cos3x = 0,
7	2	2
2sin2xcos3x + 2cos3x = 0, 2cos3x(sin2x + l)=0.
Отсюда:
l)cos3x = 0, Зх = —+ я£, X, = — + — = — (2^ + 1) ZceZ;
7	2	1 6	3	6 V Л
7C	7C
2)sin2x + l = 0, sin2x = -l, 2x = —+2ял, x3 =—+itn =
2	2	4
= ^(4и-1) n&Z.
Ответ: *1 = ^$k + l); x2 =-^(4л-1) к,ne Z. 6	4
/ K x \
8.079. (l + sinx)tg-----=cos-1 x-cosx.
4 2 I
Решение,
cosx^O, ОДЗ: cos
--- Uo. 4 2
Имеем
(1+sinx
• i я sin —
1 ------cosx, cosx
(1 + sin хХ1 - sin х) _ 1-cos2 x cosx	cosx
Отсюда 1 - sin2 х = 1 - cos2 х, sin2 х = cos2 х <=> tg2 х = 1, откуда
ТС	Я
tgx = ±1, т.е. xj = —+ л£ , ке Z, х2 =	+ тси, ne Z. Объединив Xj
л пк И/., а
и х2,получим х = — + — = — (2х + 1), ке Z.
4 2	4
Ответ: х = —(2А + 1} keZ.
4
8.080. cos х - л/з sin х = cos Зх.
Решение,
Из условия
(cosx-cos3x)-V3 sinx = 0 <=>-2sin	sin——— - л/з sinx =0,
2	2
2 sin 2х sin х - л/з sin x = 0, sin x(i sin 2x - VI )= 0.
Отсюда:
l)sinX = 0, Xj=TCH, hgZ;
2)	2sin2x-7з =0, 2sin2x = — 2x = (-l)* -^ + тсЛ, 2	3
(л\к тс Ttk .	_
-1Г — +—, ke Z '62
Ответ:
Xj = тси;х2 = (-1)* +
8.081. 6sin2 x + sinxcosx-cos2 x = 2.
Решение.
Имеем
6sin2 x + sinxcosx-cos2 x-2^in2 x + cos2 x)=0, 4sin2 x + sinxcosx-3cos2 x = 0 <=> 4tg2 x + tgx-3 = 0.
Решив это уравнение как квадратное относительно tg х, получим тс	3	3
tgx = -l, X. =—- + idc, ке Z; tgx = -, х2 = arctg-+тг, neZ-4	4	4
я	,	3	,	„
, Ответ: х( = — + юс; х2 = arctg—+пп, к,пе Z.
4	4
8.082. cos7x + sin8x = cos3x-sin2x.
Решение.
Имеем
(cos 7х - cos Зх) + (sin8x + sin 2x) = 0 <=> -2 sin
7x + 3x . 7x-3x
+ 2 sin +	cos ——— = 0,-2 sin 5x sin 2x + 2 sin 5x cos 3x = 0,
2	2
-2 sin 5x(sin 2x - cos 3x) = 0.
Отсюда:
l)sin5x = 0, 5x = ял, xj = n g Z;
2) sin 2x - cos 3x = 0 <=> sin 2x - sinI у - Зх I <=>
2x4- —-Зх	2x- —4-Зх	/_	/г
л о	( Я	х ]	.	( 5	я	л
<=> 2 cos-*--sin-----= 0, 2 cos-sin — х — = 0.
2	2	И	2J	U	4J
Отсюда:
ч (п х^ Гх я^ л х я я .	3
a)cos-----= cos-= 0,--= —4-я£, х9 = — it + 2nk =
U 2J 124)242	2 2
= -y+2rot = y(4*-l),*eZ;
б)	sin|—Х-— | = 0, — Х-— = nl, х3 =—+ —л/ = —(4/ + 1), I е Z.
<2 4J 2	4	3 10 5	10
Ответ: Х} = ™;х2 = ^(4к -1); х3 = ^(4/ +1), п, kJ е Z.
8.083. sin2x-2sinxcosx = 3cos2x
Решение.
Разделив обе части уравнения на cos2 х # 0, имеем tg2 х - 2 tg х - 3 = 0.
Решив это уравнение как квадратное относительно tg х, найдем
я
(tgx)j = -1, X] = — + пк, к e Z;(tg х)2 = 3; х2 = arctg 3 + лл, п 6 Z.
Ответ: Xj =	+пк, х2 = arctg 3 + пл, к, п е Z.
8.084. cos5x+cos7x = cos(n+6x) Решение.
Из условия _ 5х + 7х	5х-7х
2 cos-----cos-------
2	2
cos 6х(2 cos х +1)=0. Отсюда:
+ cos6x = 0, 2cos6xcosx+cos6x = 0,
Я l)cos6x = 0, 6х = —+ ТСЛ, Xj =
ТС ТС Л	ТС . \ п
—+— =—(2/14-11 neZ;
12	6	12
1	2
2) 2cosx4-l = 0, cosx =—, х, =±—л4-2л&, A:gZ.
7	2	2	3
Ответ: Xj =^-(2и4-1)х2 =±уЯ4-2лЛ, n,keZ.
8.085. 4sinxco;
i=l.
Решение,
По формулам приведения имеем
4sinxsinx-4sinxcosx+2cosxcosx-l = 0,
4sin2 x-4sinxcosx+2cos2 x-(:os2 x+sin2 x)=0,
3sin2 x-4sinxcosx+cos2 x = 0, 3tg2 x-4tgx+l = 0;
решив уравнение как квадратное относительно tg х, найдем (tg х)| = j, х{ = arcig-^ + тсА:, ке Z; (tgxl =1, х2 = ^+ли, neZ-
3	.	4
1	тс
Ответ: х{ = arctg— + лк; х2 = — + тел, Л, п е Z.
8.086. cos6x = 2sin—+2х
I 2
Решение.
ГЗтс	I
Представив уравнение в виде cos 3(2х)- 2 sin —+2х = 0 и приме-12	J
нив формулу cos За = 4 cos а - 3 cos а, имеем
4 cos3 2х - 3 cos2x 4-2 cos 2х = 0, 4 cos3 2х - cos2x = 0,
cos2x(4cos2 2х -1)= 0.
Отсюда:
l)cos2x = 0, 2х = — + пк, х. = —+— = —(2&+1) fceZ; 2	1 4 2 V л
2)	4cos22x-l = 0, cos2x = ±—, 2х = ±— + ял, 2	3
Х2 =
я пп
— +—, wgZ.
6 2
Ответ: х, = — (2& + 1)х2 =±— + —, MeZ. 1 4	2	6 2
8.087. 2 sin х cos^^" + * j- 3 sin(^ - x)cos x++ x jcos x = 0. Решение.
По формулам приведения
2 sin х sin х - 3 sin x cos x + cos x cos x = 0,
2sin2 x-3sinxcosx + cos2 x = 0 <=> 2tg2 x-3tgx + l =0;
решив уравнение как квадратное относительно tg х, найдем (tg х\ = ~,
X! = arctg+ ък , к е Z ; (tgx)2 = 1, х2 = + тт = (4л +1), п е Z.
Ответ: Xj = arctg + пк; х2 = (4л + 1) к, п g Z. 2	4
8.088. (sin4z + cos4z)2 = 16sin2zcos3 2z-8sin2zcos2z.
Решение.
Из условия
sin2 4z + 2sin 4rcos4/ + cos2 4/ = 8(2sin2/cos2t)cos2 2t - 4(2sin 2tcos 2t)<^>
<=» sin2 4t +2sin4rcos4f+ cos2 4r = 8sin4r ^(l + cos4/)-4sin4r, sin24/+ 2sin4rcos4z + cos24f = 4sin4/(1 + cos4r-1), sin24/ + 2sin4rcos4r + + cos24z =4sin4zcos4r, sin2 4/-2sin4zcos4z + cos2 4t = 0,
(sin 4z - cos 4t f =0, sin 4t - cos 4t = 0 <=> tg 4t = 1, 4z = — + nk,
4
r = 2L + ^ = 2L(4^ + Q keZ.
16 4	16
Ответ: t = — (4k + 1} keZ.
8.089. cosl
1
2cos 130
Решение.
Имеем
+ sml
cos 50’	'	' 2 cost 80°-50°)^
cos(zz -18° )sin 50° + sinfez -18° )cos 50° _	1
-2cos50'
sin(2z+32°)=-|.
cos 50° =>sm(2/-18’+5O°)=-|,
Отсюда:
1) 2/+ 32° =-30°+360%,
keZ, z, =-31° +180%;
2) 2z + 32° =210°+360%.
z2 =89 +180%, keZ.
Ответ: tx =-31° +180%; t2 =89° +180%, keZ.
8.090. tg^-ctgy + cos *^sin_Iy = l. Решение.
ОДЗ:
t Л cos—*0, 2
• 3z л sm— * 0.
2
Перепишем уравнение в виде
. Z 3Z sm—cos—	.	.	,,
2	2	1	, n . Z 5t z .
— -----£- +-----z--l = 0=> sm—cos-cos—sm
z . 3z	Z .	3z	2	2	2
cos-sm— cos—sm—
2	2	2	2
«sin|—|+l = 0,	-sinz+l = 0,	sinz = l.
k2 2 J
Отсюда z = —+2zt£ =—(4/r+11 keZ. 2	2
+1 = 0
Ответ: t = (4к +1) keZ.
8.091.
1_________1
л/З-tgr у/3 + tgt
= sin 2t.
Решение.
ОДЗ:
tg/ * ±г/з, cos / # 0.
Имеем
Ji.ig.-JS+.g. =sin2)| 2Js< in2,=()e
(73-tgr)(73+tgJ	3 18'
2 sin/
cos t . л	2 sin/cos2/	. ~ л
<=> —-------sin It = 0 <=>------------— - sin 2/ = 0 =>
3-sin-./	cos/pcos2 /-sin2 /)
cos2 /
=>2sin/cos/-2sin/cos/(3cos2 / -sin2 /)= 0,2 sin/cos/(1-3 cos2 / +sin2 /)=0, 2sin/cos/(sin2 / + cos2 /-3cos2 / + sin2 /)=0, -2sin/cos/(cos2 /-sin2 /)=0, sin/cos/cos2/ = 0.
Отсюда:
1) sin/ = 0, /j = nn, ne Z ;
_ л л 7C ,	71 itk 71 t \	,	_
2)cos2/ = 0, 2/= — + 7%, z2=—+— = —(2Zc + lJ keZ-9cost*0.
2	4	2	4
Ответ:
/j =яи; /2 =^-(2Zc + Q
n, к e Z.
8.092. cos(20o +x)+cos(100°-x)=si.
Решение.
Перепишем уравнение в виде
20°+х + 100°-л-	20°+х-100°+х 1 . ,ло/	1
2cos-------------cos-------------= -, 2cos60 lx-40 )= — ,
2	2	2	2
cos(x-40°)=-^.
Отсюда
x-40° =±60’ +3604, x1 =-20°+360%; x2 =100° +360%, keZ-
Ответ: x, = -20° + 360° k\ x2 = 100° + 360е к, к e Z.
8.093. coszsin —+6z +cos — -t Isin6z = cos6z+cos4z.
I2 J I2 J
Решение.
По формулам приведения cos t cos 6z + sin t sin 6z = cos 6z + cos 4/ <=>
/,	\ - 6z + 4z 6z-4z Л	c. c. . л
<=> cos(6z -Z l-2cos--cos-----= 0, cos5z -2cos5zcosZ = 0,
2	2
cos5z(l-2cosz)=0.
Отсюда:
l)cos5z = 0, 5z = — + як, z. =—+— =—(2/c + Q keZ; 2	1 10	5 IOV
2)1-2cosz = 0, cosz = — , z2=±—+2л/, leZ. ’	2	3
Ответ: Z] =^(2^+l|z2 = ±y+2itZ, k,leZ.
1-cosx „
8.094. ----— = 2-
sin—
2
Решение.
ОДЗ: siny^O.
Из условия
l-cos2 -у l-l+2sin2 —
12*	о а . х , х п Л ,
-----—= 2 <=>	— = 2 =ф sin— = 1, — =—+2кк, . х	. х--2	2 2
sin—	sin—
2	2
х = п + 4пк = п(4к + 1} к e Z.
Ответ: х = я(4А:+1Х keZ.
7х	Зх	х	5х
8.095. sin—cos — + sin—cos — + sin2xcos 7x = 0.
2	2	2	2
Решение.
Применив формулу
sin acos Р = у (sin (a - 0 j+ sin (a + p))
запишем
уравнение в виде
2
2
. ( 7х Зх sin---------
2	2
I . (7х Зх + sin-----1---
I 2	2
5х ] . (х 5х ] ] — +sin —+— +
2	2 2
+ (sin(2x - 7х)+ sin(2x + 7х))=О,
sin 2х + sin 5х - sin 2х+sin Зх - sin 5х+sin 9х = О,
9х д. 3 х	9х — Зх
sin 9х + sin Зх = 0 <=> 2 sin-cos-----= 0, sin 6х cos Зх = 0.
2	2
Отсюда:
1) sin6x = 0,
6х = ли,
пп
—, п 6 Z •
6
2) cos3x = 0,
Зх = — + 2
Я*, Х2="б+~’ *е > х2 ВХ°ДИТ В Х1 •
~	ли „
Ответ: х-—, neZ.
6
8.096. sin Зх + sin 5х = sin 4х.
Решение.
Перепишем заданное уравнение в виде
2 sin 3**5Х cos 3*—_ sin 4х = 0, 2 sin 4х cos х - sin 4х = 0, 2	2
sin 4х(2 cos х -1) = 0.
Отсюда:
l)sin4x = 0, 4х = ли, Xj=—, mgZ;
4
2)2cosx-l = 0, cosx = y, x2 =±у + 2яА: = у(бЛ:±1) keZ.
Ответ: Xj = ™ix: =у(б£±1)> n,ke Z.
8.097. sin z - sin2 * * * z = cos2 z - cosz. Решение.
sinz + cosz
z+cos2z)=0, sinz+cosz-l = 0,
. JZ 1 Jl) ( 1Z 2 Z А л ~  Z z 2 Z sin2 — +cos2 - - sin — + cos — =0, <=>2sin—cos—+cos —-2	2	2	2	2	2	2
-sin2 —-sin2 —-cos2 — = 0<=>2sin—cos—-2sin2 4 = 0<=> 2	2	2	2
z л
2 J
^„2 z _^2 z
- 2 — 2
„ , z( _ z
V, 2U”2
Отсюда:
<=>2sin— cos—sin— =0.
. Z л Z
1) sin— = 0, — = лл, 2	2
z{ = 2л», n e Z ;
2) cos—-sin—= 0 « tg—= 1, — = —+nk, z2 =^+2nfc = ^(4fc + l) 2	2	62	2 4	2 2	2
keZ.
Ответ: z( = 2л»; z2 = у (4fc + Ц n, к e Z.
8.098. sin z + sin 2z + sin 3z = cos z + cos 2z + cos 3z. Решение.
Перепишем заданное уравнение в виде
.	. z + 3z z-3z	. _	. z + 3z z-3z	.
2sin----cos-----+sin2z =2cos------cos----+cos2z &
2	2	2	2
2 sin 2z cos z+sin 2z	= 2 cos 2z cos z + cos 2z, sin 2?(2 cos z+1)-
-cos2z(2cosz+1)= 0,	(2cosz+lXsin2z -cos2z)= 0.
Отсюда:
12	2
l)2cosz+l = 0, cosz = -j, z, =±уЯ + 2лА: = ул(ЗА:±1), keZ;
2) sin2z-cos2z = 0<=>tg2z = l, 2z = —+ ли, z2 = — + — = —(4м+1}
4	2 8 2	8
ne Z.
A
Ответ:	=— я(3&±1) z2= —(4л + 1) ktneZ.
3	8
8.099. ctgx-tgx+2-
( I
ktgx + l
1 tgx-1
= 4.
Решение.
ОДЗ:
tgx * ±1, cosx # 0, sin x * 0.
Из условия
4 sinx
cosx _ sin2 x
cosx sinx sinx cosx
cos2 x
2cos2x 2sin2x .
---------------= 4,
sin2x cos2x
Отсюда 4x = — + tin, 4
cos2 x-sin2 x 4 sin xcos2 x sinxcosx cosxtsin2 x-cos"
cos22x-sin22x , cos4x , x A , -------------= 1, -----= 1, ctg 4x = 1.
2sin2xcos2x sin4x
7t UH 7C /.
— +— = —(4л + 11 neZ, 16 4 16V	Л
Ответ: x = тт (4и+0 ne Z. 16
8.100.	l-cos6x = tg3x.
Решение.
ОДЗ: cos Зх * 0,3x # — + ял, x # — (2л + Q n g Z. 2	6
Имеем
1-cos 6x —S*n	=0, (1 - cos 6xXl+cos 6x)— sin 6x = 0,
l+cos6x
1-cos2 6x-sin6x = 0, sin2 6x-sin6x = 0, sin6x(sin6x-l)=0.
Тогда:
1 \	• Z" z\ Z"	7C/1	/'ЧТТ’Э	Ttin
1)	sin6x = 0, 6x = тш, Xj = — ,носучетомОДЗ Xj = —,
6	3
m*2n + l, meZ;
2)	sin6x-l = 0, sin6x = l, 6х = -^ + 2тЛ, x2 = — + ~ = ]y(^ + 0,
keZ-
Ответ: *1	<x2 =^-(4fc+l) m,keZ.
8.101.	V? cos х ч-cos 2х + cos 4х = 0.
Решение,
Перепишем уравнение в виде
—	2х + 4х	2х-4х	г~
2 cos X 4- 2 cos - — cos = О » V2 cos X +
2	2
4- 2 cos Зх cos x = 0 <=> cos x( V2 4- 2 cos 3x) = 0, Отсюда:
1) cos x = 0, Xj = у 4- пк = у (2k 4-1), к e Z;
/-	42	3
2) V2 4-2cos3x = 0, cos3x =-, Зх = ±—я4-2ял,
'	2	4
x2 - ±—+—лл = — (8л ± 3), k,neZ,
2	4 3	12	7
Ответ: Xj = y(2£ +1); *2 = yy ± 3), k,n e Z. 8.102. sin4x4-cos4x = sin2x-0,5.
Решение,
Имеем
(sin2 x 4- cos2 x)2 - 2sin2 xcos2 x - sin 2x + 0,5 = 0 <=> 1 - ~sin2 2x -
1	7
- sin 2x 4- — = 0, sin 2x 4- 2 sin 2x - 3 = 0.
2
Решив это уравнение как квадратное относительно sin 2х, получим
sin 2х = -3,0, или sin 2х = 1, 2х = — 4- 2лл, х = — 4- пп = —(4л 4-1), n g Z.
2	4	4
п
Ответ: х = —(4л 4-1), л е Z.
4
8.103.	2cos2x4-2tg2x = 5.
Решение,
ОДЗ: cosx*0.
Перепишем уравнение в виде
2 cos 2х 4- ——- 5 = 0 => 2 cos 2х(14- cos 2х) 4- 2(1 - cos 2х) -14- cos 2х
- 5(14- cos 2х) = 0, 2 cos2 2х - 5 cos 2х - 3 = 0.
Решив это уравнение как квадратное относительно cos2x , найдем
cos2x = 3,0, или cos2x = -—, 2х = ±—л + 2л& 2	3
х = +у + л* = у(з*±1)> keZ.
Ответ: х = у (3£ ± 1) к е Z.
8.104.	sin2хsin6х = cosxcosЗх.
Решение.
Перепишем заданное уравнение в виде
у (cos(2x-6x)-
cos(2x + 6х))- у (cos(x - Зх)
+ cos(x + 3x))=0,
cos 4х - cos 8х - cos 2х - cos 4х = 0, cos 8х + cos2x = 0 <=>
2 cos------cos------= 0, cos 5x cos Зх = 0.
2	2
Отсюда:
I)cos5x = 0, 5x = —+	x, = —+ —= —(2Zc + l) keZ;
J	2	1 10 5	10V Л
2)cos3x = 0, Зх = —+ ли, x2 =^ + —= —(2« + l) neZ.
Ответ: Xj = -^-(2Zr+ 1) x2 =у(2л + 1) k,ne Z. 10	6
8.105.	sin4 2x + cos4 2x = sin2xcos2x.
Решение.
Имеем
(sin2 2x + cos2 2х^ -2sin2 2xcos2 2x-sin2xcos2x = 0,
1	- 2 sin2 2x cos2 2x - sin 2x cos 2x = 0 <=> sin2 4x + sin 4x - 2 = 0.
Решив это уравнение как квадратное относительно sin4x, найдем sm4x =-2, 0 , или sin4x = l, 4x = y + 27in, х = у+ —= у (4л+ 1), не Z •
Ответ: х = — (4и + 1} neZ. о
Решение.
Из условия
1
2cos210'
:-3O°Jsin3O’ 1
cos 30’	~ 2cos^80’+30’)
cos(jx-30’)cos30’ -sm^x-30’)sin30’______1_______
cos 30’	2cos^80’+30’)
cos(3x-30° +30’)	1	_	.	-	- rt
—--------------1+-------= 0 <=> 2cos3x+l = 0,
cos 30’	2 cos 30’
cos(jx-30‘
1	2	2я 2
откуда cos3x = —, 3x = ±—n+2nk, x = ±—+—itk, ke Z.
2	3	9 3
,2n 2 . . _ Ответ: х = ±-+-як, keZ.
8.107. 4 sin x + cos x = 4.
Решение.
Перепишем уравнение в виде
2 x ^„2 x
X
4sin2 — +cos2 — -4 cos—+sin — =0<=>8sin—cos — + 2
2
2	2
2”" 2
+cos2 --sin2 —-4cos2 —-4sin2 — = 0, 5sin2 —-8sin—cos—+
2	2	2	2	2	2	2
+ 3cos2 = 0, <=> 5tg2 — -8tg—+3 = 0.
2	2	2
~ 4 *
Решив последнее уравнение как квадратное относительно tg у, найдем
3	3
arctg — + лл, Xj =2arctg —+ 2ял, ие Z;
5	5
= 1,
у 1 =^ + nk> x2 = y+2nfc = y(4Ar+l), keZ.
Ответ: х, = 2 arctg +2ял; х2 = у (4& +1} п,ке Z.
8.108.	2sin2z + tg2z = 2.
Решение.
ОДЗ: cosz *0.
Из условия
_ . о sin2z Л ~ • 2 sin2z - Л 2sin z+—г—2 = 0 <=>2sinz +-----------—2 = 0=>
cos z	1—sin z
=> 2 sin2 z(l - sin2 z)+ sin2 z - 2^ - sin2 z)= 0, 2 sin4 z - 5 sin2 z+2 = 0.
Решив это уравнение как биквадратное относительно sinz , полу-
чим sinz = ±—, z = — + — = ~ (2£ + 1), keZ.
2	4 2 4V 7
Ответ: z = (2к +1} keZ.
4
8.109.	cos2x + cos6x + 2sin2 х = 1.
Решение.
Из условия
cos 2х + cos 6х - (1 - 2 sin2 х )= 0 <=> cos2х + cos 6х - cos 2х = 0, cos 6х = 0 .
,_L	, Л	Л ЛЛ	Л /_	,\	~
Тогда 6х = — + лл, х = —+—= —(2л + Ц, neZ.
2	12	6	12
Ответ: х = —(2л + 1) weZ.
8.110.	cos Зх cos 6х = cos 4х cos lx.
Решение.
Имеем
у (cos(3x - 6х)+ cos(3x + 6х))=(cos(4x - 7х)+ cos(4x + 7х))
cos Зх+cos 9х - cos Зх - cos 11х = 0, cos 9х - cos 11х = 0 <=>
_ . 9х + 11х . 9х-11х л • 1Л • л
» -2 sin-------sin------= 0, sin 1 Ox sin x = 0.
2	2
Отсюда:
l)sinl0x = 0, 10х = пл, Xi=—, weZ;
10
2) sin х = 0, х2 = пк, ке Z; х2 входит в Xj.
хч	Л Л
Ответ: х = —, п е Z.
Jy	1
8.111. sin3x +—sin5x + — cos5x = 0. 2	2
Решение.
Перепишем уравнение в виде
sin3x + cos30° sin5x+sin30’ cos5x = 0, sin3x+sin(30’ +5x)= 0 <=>
„ . 3x+30’+5x	3x-30’-5x n . (. t<A / n
e*2sin-----------cos----------= 0, sin^4x+15 )cospc+15 J=0.
Отсюда:
1) sin(4x + 15’)=0, 4x+ 15’=1804, xt=-^- + 45%, teZ; 2) cos(x + 15’)=0, x +15’=90’+1804, x2 = 75’+1804, ne Z. Ответ: x, = -3’45 + 45%; x2 = 75’ +180’ n, k,ne Z.
8.112. ctg3 x + sin“2 x-3ctgx-4 = 0.
Решение.
ОДЗ:	sinx^O.
Из условия
COS3X 1 3COSX . Л з .	-	* 2 a ‘ 3 f\
—-— + —--------:------4 = 0=» cos x+smx- 3cosx sin x -4sin x = 0,
snrx sin2 x sinx
cos3 x + sinx^in2 x+cos2 x)-3cosxsin2 x-4sin3 x = 0, cos3 x +
+ sin x cos2 x+sin3 x - 3cos x sin2 x - 4 sin3 x = 0, (cos3 x + sin xcos2 x)~
- 3 cos x sin2 x - 3 sin3 x = 0, cos2 x(cos x+sin x)- 3 sin2 x(cos x + sin x) = 0, (cosx + sin x)(cos2 x-3sin2 x)=0.
Отсюда:
1) cosx + sinx = 0;
2) cos2 x-3sin2 x = 0 => ctgx = -1, x, = — + m, ne Z;
4
Ctgx = ±у[3 , x2 =±—+ 7l/c , к G Z .
6
ЗтС	. 7C •	«
Ответ: Xj = — + Ttn; x2 = ±- + як, n,ke Z. 4	6
•у	у	О	3
8.113.	cos Зх + cos 4x + cos 5х = —. 2
Решение.
По формулам понижения степени получаем
111	3
— (1+cos 6х)+ — (1 +cos 8х)+—(1+cos 1 Ox) =—, cos 6x+cos 8x +
6x+10x	6x-10x	„ Л
+coslOx =0 <=> 2cos-cos-+cos8x = 0,
2
cos8x(2cos2x +1)=0.
2 2cos8xcos2x + cos8x = О,
Отсюда:
l)cos8x = 0, 8x = — + nk, Xi = — + — = —(2Л+1), keZ;
2	1 16 8	16
2)
2cos2x + l = 0, cos2x = -—, 2x = ±—n + 2nk, x2 =±—+ ля = —(Зи±11 2	3	2	3	3
я g Z.
Ответ: Xj = 77 (2 к +1) x2 = (Зи ± 0	n e z-
lo	3
8.114.	l + sinx-cos5x-sin7x = 2cos2 |-x.
Решение.
Перепишем заданное уравнение в виде
l+sinx-cos5x-sin7x = l+cos3x <=> (sinx-sin7x)-(cos5x + cos3x)=0 <=> <=> -2 sin Зхcos4x - 2cos4xcosx = 0, -2 cos4x(sin 3x + cosx) = 0.
Отсюда:
l)cos4x = 0, 4x = —+ nA:, x, = —+ —= —(2£ + l), fceZ;
'	2	1 8	4	8 V Л
(-	\	3x + y~x
--x
2
2) sin3x+cosx = 0 <=> sin3x + sin —-x =0, 2sin “2
Имеем
f	л It	7U /«	_
sinI x + — =0, x + —= лл, x2 = — + ли=—(4и-Ц weZ,
14	4	4	4
или
cosf2x-—1=0, 2х-—= —+ л/, х3=—л +—, leZ-4	4 2	3 8	2
х3 входит в х}.
Ответ: X! =-^(2& + 1) х2 = ^-(4л-1) к, neZ.
8.115.	-^^ = 2-ctgz.
1 + cosz Решение.
ОДЗ: Jsin2*0’ [cosz ^-1.
Из условия
—Ш—— 2 +	= 0 => sin2 z - 2 sin z(l + cos z)+ cos z(l+cos z)= 0
1 + cosz sinz
sin2 z-2sinz-2sinzcosz+cosz+cos2 z = 0, (l-2sinz)+
+ (cosz-2sinzcosz)=0, (l-2sinz)+cosz(l-2sinz)=0, (l-2sinzXl + cosz)=0.
Отсюда
l-2sinz = 0, sinz = —, z = (-1)* — + nk, 2	6
ke Z; 1+cosz * 0.
Ответ:
z = (-1)*^ + nk, keZ. 6
8.116.	sin^5°+x)+cos(45’+x)+| = 0.
Решение.
Имеем
sin^5° +x)+sin(90’ -45° -x)+^ = 0,
sin(l5° +x)+sin(45° -x)+
1 Л 0. 15° + x + 45°-x	15°+x-45°+x 1 _
+ - = 0 <=> 2 sin-------cos-------------+ — = 0,
2	2	2	2
2 sin 30° cos(x -15°)+ j = 0, cos(r -15°)=-^.
Отсюда
х-15° =±120° +360%,	=-105°+360%; х2 = 135° +360%, ке Z-
Ответ: xf = -105° + 360%; х2 = 135° + 360%, к е Z.
8.117.	1 + sin 2х = sinx + cosx.
Решение.
Перепишем уравнение в виде
sin2 x+2sinxcosx+cos2 x-(sinx+cosx)= 0, (sinx+cosx)2 -
- (sin x + cos x)= 0, (sin x+cos xXsin x+cos x -1)= 0.
Отсюда или sinx + cosx = 0, или sinx + cosx-1 = 0-Из первого
уравнения tgx =-1, х. = -—+ л£ = —(4&-1), ке Z. Второе уравнение 4	4
запишем в виде
2sin—cos—+cos2 --sin2 —-fcos2 —+sin2 — 1=0, 2sin—cos —-
22	2	2 {	2	2)	2	2
-2sin2 —= 0, 2sin—[cos—-sin—|=0.
2	2^2	2)
Отсюда
X	X
sin — = 0, — = nn, x, = 2ли, n e Z,
2	2	2
или
cos ——sin — = 0 <=> tg—= 1—= — + л/, x3 = —+2л/ = —(4/ + l|/e Z. 2	2	z 2 4	3 2	2
Ответ: x( = (4Л -1); x2 = 2лп; x3 = у (4/ +1| k,n,le Z.
8.118.	3(l-sinz)+sin41 = l+cos4t.
Решение.
Из условия
3-3sinl+sin4l-l-(;os2tj =0, sin4t-3sint+2-(l-sin2zy = 0<=>
<=>2sin2 z-3sin/+l = 0.
Решив последнее уравнение как квадратное относительно sinl, получим (sin/)] = |, t, =(-1^^ + пк, ке Z,
2	О
(sint)j =1, t2 =у+2ли = у(4л+1), ne Z.
Ответ: ^ = (-1^у+лЛ;Г2 =^(4n + l} k,neZ. О	2
8.119.	tg^^ + x^-3tg2 x = (cos2x-l)cos 2 x Решение. [cosx 0,
0ДЗ:
Имеем
.	2 cos2x-l 1	2 l-cos2x
- ctgx - 3 tgz X =--— <=>-----+ 3 tg X =  -<=>
cos x tgx	|(l+cos2x)
<=> —— + 3tg2 x-2tg2 x = 0, ——+tg2 x = 0=> tg3 x+l = 0, tgx	tgx
tgx = -l, x = ~— + itk = —(4Л-11 keZ. 4	4
Ответ: х = -^(4£-1} keZ. 4
8.120.	cos2 —+ cos2 - -sin2 2x-sin2 4x = 0. 2	2
Решение.
По формулам понижения степени
(1+cos х)+ (1+cos Зх)-у (1 -cos4x)- (1 -cos 8х)=0,
(cos х+cos Зх)+ (cos 4х+cos 8х)= 0 <=> 2 cos 2х cos х+2 cos 6х cos 2х = 0, 2 cos 2x(cos х+cos 6х)=0.
Отсюда:
l)cos2x = 0, 2х = — + як, Xi = — + — =—(2Л + 1| keZ;
’	2*424
_	. Л _	,х+6х	х-бх л 7х	5х .
2) cos х+cos 6х = 0 <=> 2 cos-cos-= 0, cos—cos — = 0 =>
2	2	2	2
a)	cos—= 0, — = —+ яи, x2 = — + — icn = — (2и + 11 neZ; 2222777VA
6)	cos— = 0, — = -+я/, х,=-+-я/ = -(2/ + 1} leZ. 2	22	3 5 5 5V Л
Ответ: x, =^-(2fc+l)x2 =y(2n+l)x3 =y(2/ + l} k,n,leZ.
8.121.
sin* 2 * * 5х-1 A 2 X
л ;,°18 у sin x-4cos —
2
Решение.
2 х л cos — * О,
ОДЗ: 2Х . 2 х	л 2 х л
sin----4cos — ^0.
I 2	2
Перепишем заданное уравнение в виде
sin2x-2 _ 1-cosx 1-cos2 х-2 1-cosx sin2 х-2(1 +cosx) 1+cosx 1-cos2 x-2-2cosx 1 + cosx cos2x + l	1-cosx л cos2x + l	1—cosx л
-----------------------= о,------------------= 0 => cos2 X + 2COSX + 1 1+COSX (1+cosx)2 1 + cosx => cos2 x + l-(l-cosxXl+cosx)=0<=>2cos2 x = 0, cosx = 0,
x = y + Л& = y(2£ + l) keZ.
Ответ: x = у (?k + 1) ke Z.
8.122. cos2 x + cos2 2x - cos2 3x - cos2 4x = 0.
Решение.
По формулам понижения степени
± (1+cos2x)+~ (1 + cos4x)- у (1 +cos 6х)- у (1 + cos8x)=0, (cos2x + cos4x)-(cos6x+cos8x)=0 <=> 2cos3xcosx-2cos7xcosx = 0,
2 cos x(cos 3x - cos 7x) = 0.
Отсюда или cos x = 0, или cos Зх - cos 7x = 0. Из первого уравнения имеем х1 = у + пк , к е Z . Второе уравнение эквивалентно следующему: sin5xsin2x = 0, откуда или sin5x = 0, 5х = ял, х2=^у, neZ, или8ш2х = 0, 2х = л/, х3 =у , ZeZ; Xj входитв х3.
Ответ: х, =—;х2=—, n,leZ.
5	2
8.123.	sin3x-4sinxcos2x = 0.
Решение.
Перепишем уравнение в виде
sin Зх -2(sin(x -2х)+ sin(x + 2х)) =0, sin Зх + 2sin х -2 sin Зх = 0, sin 3x-2sinx = 0.
Так как sin3a = 3sina-4sin3 а , то 3sinx-4sin3x-2sinx = 0, 4sin3 х - sin х = 0, sin x(l sin2 х -1)= 0.
Отсюда:
l)sinx = 0, хх=пп. neZ,
2)	4sin2 х-1 = 0, sinx = ±—, х2 = ±—+ л£ = —(б/с ±Q keZ.
2	6	6
Ответ:
X] = ли;х2 = —(б/с±1), 6
л, к е Z.
8.124.	tgx + ctgx = 2cos“l4x.
Решение.
cos х # 0, ОДЗ: -sinx^O, cos4x*0.
Из условия
sinx cosx 2 Л sin2x+cos2x 2
-----+------------= 0,--------------------= 1
cosx sinx cos4x sinxcosx cos4x
1	1	7
<=> -—---------— = 0 => 2 sin 2x+sin2x -1 = 0.
sm2x l-2sin22x
Решив это уравнение как квадратное относительно sin2x, най
дем (sin2x)j = -1,2xj = --|-+2лЛ, Xj = “+л£, ке Z ; (sin2x)2 ,
2х2 = (-1/ +л/, х2 = (-1/ ~ + ~, /•€ Z. Объединив решения х( и 6	12 2
л пк л /., ,\
х2, получим Х = —+ —= —(4*+1), keZ.
Ответ: х = — (4Л + 1) к е Z.
8.125.	sin^ + Зх j-sin(n-5x)= VJ (cos5x -sin3x)
Решение^
Перепишем заданное уравнение в виде
Л _	-	Л -	_
— + Зх - л + 5х	— + Зх + л - 5х
2	2
—-----------cos—------------
2	2
2 sin
1) sin|4x- — )=0, 4х-—= л&, 4х = —+ л&, Xj = — + —= —(41'+ 1)
4 j 4	4	1 16 4 16
A:gZ;
(Зл А ГТ . ( л^ ~ Зл . Зл .
2) cos---х +V3sin х + — =0<=>cos—cosx + sin—sinx +
4	4	4	4
ГТ .	Л	ГТ	Л	_	Л	.	. л
+ V3 sinхcos — + V3 cosxsin — = 0, -cosxcos— + smxsin— +
4	4	3	6
. Л	Л
+ sin x sin — + cos x cos— 3	6
л f	Л .	. Л
= 0«- cosxcos—sinxsin — +
3	3
+cosxcos— + sinxsin — = 0<=>-cos X + — + COS X— =0<=>
6	6 I 3 J I 6 J
л л
^sin---5----
2
Л Л
 x+3'x+6 „ - (
sin--------— = 0, sin x+— sin — = 0,
2	12	4
= 0, x2 =——+mi = — (12/j-l), neZ.
2	12	12
 I я sm x + —
I 12
Ответ: *i =	+1)x2 = -^(12n-l) k,neZ.
16	12
1	1	16
8.126.	:----- + —— = тт-
1+cos z 1 + srn Z 11
Решение.
Перепишем заданное уравнение в виде
1	|	1	16 Q 2	|	2	16_0
l+|(l+coS2z)+l+|(l-cos2z) 11	’ 3+cos2z 3-cos2z 11.
о 3	у/з л
=> cos 2z =	cos2z = ±—, 2z = ±— + лк,
4	2	6
z = ±—+— = — (6k±likeZ. 12 2	12v л
Ответ: Z =	(бк ± 1), к G Z.
tg—tgx+1
8.127.	—--------------------= 2Л
2tgyCOS J tgy + ctgx
Решение.
ОДЗ:
х л cos — ^0,
2 sinx Ф 0, tgy +ctgx^0.
Из условия получаем
. х .
sin —sinx
2
cosx
cos —cosx 2
2 sin —cos* 2 —
2	2
cos —
2
sm —
2 +cosx
x sinx cos —
2
sm — sm x+cos — cos x cos x 2	2
cos —sinx 2
sinx
cos —cosx 2
sin — sin x+cos—cos x 2	2
2	• 2
cosx sinx	cos x-sin x _2^
sinx cosx	sinx cosx
2	• 2
cos Х-sm X /Т - ГТ _ П . --------------= V3, ctg2x = V3, 2x= — + nk, 2 sin x cos x-6
7t	Tlk	7t ,'.	14	„
x = —+ — = —(6k +1), к e Z.
12	2	12
Ответ: х = у^-(6£ + ОД е 2.
8.128.	cos4xcos(n+ 2x)-sin2xcos —
V2 • л — sin4x.
2
Решение.
По формулам приведения
V2
-cos4xcos 2х-sin2xsin 4х----2sin2xcos2x = 0, cos4xcos2x +
2
cos 2х( 1 + V2 sin 2х) = 0.
Отсюда:
1)	cos2x = 0, 2х-~ + ли, X. = —+ —= —(2п + 1), и gZ;
7	2	1 4 2	4
2)	1 + V2sin2x = 0, sin2x = -—, 2х = (-l)*+I — + пк,
2	4
х2=(-1/+1^+уДег.
Ответ: X] =-^-(2л + 1);х2 = (-1)*+1-^+-?р n,keZ.
8.129.	sinx-sin3x-sin5x+sin7x = 0.
Решение.
Имеем
(sin х + sin 7х) - (sin Зх + sin 5х) = 0 <=> 2 sin
х + 7х	х-7х
-----cos	 2----2
- 2 sin -*—-5* cos ——— = 0, 2 sin 4х cos Зх - 2 sin 4х cos х = 0, 2	2
2 sin 4x(cos Зх - cos x) = 0.
Отсюда:
nk
1)	sin4x = 0, 4x = itk, х}=—, keZ;
2)	cos3x-cosx = 0 <=> 2sin?x+,y sin ——— = 0, -sin2xsinx = 0, 2	2
ткуда
a)sin2x = 0, 2х = пп, х2=^-, neZ,
б)	sinx = О, х3 = л/, /е Z; х2 и х3 входят в х{.
Л	л£ ,
Ответ: х = —, к € Z.
4
8.130.	sin3x-sin7x =-Уз sin2x.
Решение.
Перепишем заданное уравнение в виде
2 sin	7* cos	- 7з sin 2х = 0, -2 sin 2х cos 5х - V3 sin 2х = 0,
2	2
-sin2x(j cos5x + >/з )= 0.
Отсюда:
лАг
1) sin2x = 0, 2х = л£, %j=—, fceZ;
2) 2cos5x + V3 =0, cos5x = -—, 2
_	,5	iл 2
5x = ±—л+2лл, x2 =±—-+—ЛМ, 6	6 5
ne Z
nk
Ответ: xi=~j
л 2 — +—nn, 6 5
k,neZ.
Л
*3
Решение.
cos x Ф 0,
ОДЗ:
л ] л cos —x *0. I3 J Из условия
3
• I	л	1
Sin X + — -X
(	3	J
(
COS XCOS —-X
3
(~	Л ]	Л	,	(~	Л I	1	- л , л	_ ,
соя 2х—и-cos—= 1, соя 2х— =-, 2х— = ±—+2лк;
\	3 J	3	\	3 J	2	33
2хх=2пку x^Tdc, keZ; 2х2 = у+2л/, х2 =у + л/ = |(3/+1} /eZ.
Ответ: xi = л&; х2 = —(З/ + Q k,leZ.
8.132.	sin2 xcos^4 x-4tg2 x + 3cos~2 x-12 = 0.
Решение.
ОДЗ: cosx *0.
Имеем
sin2x 4sin2x 3 л 1-cos2 x 4-4cos2x j — - —-	j- -	12-0,	-	-	+
cos x cos x cos x	cos x cos x
3	A	9
+-----12 = 0=> 8cos x + 2cos2 x-1 = 0.
cos2 x
Решив это уравнение как биквадратное относительно cos х , полу-
чим cosx = ±у, х = ±~ + пк = у(3£±1), ке Z .
Ответ: * =	keZ.
8.133.	sin2 Зх + sin2 4х = sin2 5x + sin2 6x.
Решение.
По формулам понижения степени
i(l-cos6x)+y (1-cos 8x)=у (1-cos 10x)+y (1-cos 12x}
(cos 6x+cos 8x)- (cos 1 Ox+cos 12x) = 0 <=> 2 cos + cos 6* §x
,	10x + 12x	10x-12x
- 2 cos------cos---------
2	2
2cosx(cos 7x-cosl lx)=0.
= 0 <=> 2cos7xcosx-2cosl lxcosx = 0,
Отсюда:
l)cosx = 0, Х| =у+ лА: = у(2Л+0 keZ;
2) cos lx - cos 1 lx = 0 <=> 2 sin ?x+l — sin	= o,
2	2
sin9xsin2x = 0.
Отсюда:
a)sin9x = 0, 9x = m, x2neZ;
6)sin2x = 0, 2x = nl, хз=^ /e Z; X| входит в x3.
nl nn .	_
Ответ: xi - —> x2 =	l,ne Z.
8.134.	(sin2/-sin"I2/)2 +(x>s-I2/-cos2<)2 =1.
Решение.
[sin 2/ *0,
ОДЗ: 4
M |cos2f*0.
Имеем
sin22f-2+—---------------2+cos22r = l, -Ц—+—!r—
sin 2t cos 2/	sin 2t cos 2/
<=> cos2 2/ + sin2 2t = 4sin2 2zcos2 2t, sin2 4/ = 1, sin4r = ±1,
откуда 4/ = — + пк, / = + —= —(2fc+l| keZ. 2	8 4	8
Ответ: Z = — (2& + l) keZ. о
8.135.	sin4 x + cos4 x = cos2 2x + 0,25.
Решение.
Из условия
(sin2 xf +(cos2 xf = cos2 2x+0,25 <=»P cos2x A
rl + cos2x Y
O- J
= cos2 2x + 0,25 <=> 2cos2 2x-1 = 0 <=> cos4x = 0, 4x = — + ick,
2
£+^=”(2Л+1) keZ.
8 4 8V
Ответ: x = ~U keZ. о
8.136.	sin 2г - 4 cos 2z = 4.
Решение.
Перепишем заданное уравнение в виде 2sinzcosz-4(:os2 z-sin2 z)-4(cos2 z+sin2 z)=0, 2sinzcosz-8cos2 z = 0, 2cosz(sinz-4cosz)=0.
Отсюда:
l)cosz = 0, z( = ^ + nk = -j(2fc+l^ fceZ;
2)	sinz-4cosz = 0<=>tgz = 4, z2 =arctg4 + Kn, neZ.
Ответ: zi = у (2^+0 z2 = arctg4 + ли, к, n € Z.
8.137.	3 + 2sin2x = tgx + ctgx.
Решение.
|cosx*0, ОДЗ. [sinx^Q
Имеем
3 + 2 sin 2x - f S*n * + C0S* |=0 => 3 sin 2x+2 sin2 2x-2 = 0, ^cosx sinx I
2sin2 2x + 3sin2x-2 =0.
Решив это уравнение как квадратное относительно sin2x, найдем sin2x =-2,0 , или sin2x = i, 2х = (-1)* — + пк ; х = (-1)^	»
k<=Z-
Ответ: х = (-1)*	keZ.
 21 Я
!П-------1
8
8.138.	sin2[ — + t |=sinf + sin' I 8
Решение.
По формулам понижения степени
— 11-cosl — + 2г | =sint + — 11 —cosf — -2t ] , 2sinz +cos| — + 2t I-
2	14 J 2	14 J	I 4	1
k V 'J	\	\	J)	v /
Я Я	Я Я «
z x	—+2z + --2r	--2z----2t
(я)	4	4	.4	4
-cos —2t =0 <=> 2 sin/ + 2 sin—-----sin----------= 0<=>
4	2	2
« 2sin/-2sin^sin 2t = 0, 2sint-2^2 sin Г cos/ = 0,
2 sin z(l - >/2 cos r) = 0.
Отсюда:
1) sin t - 0, Zj = ял, n e Z;
2) 1 -5/2 cost = 0, cost =	, t2 =	+ 2nk = -^(&t ± 1), к e Z.
Ответ: = ял; t2 =	±n,keZ,
8.139. sin3 — - sin2 —cos—-3 sin—cos2 —+3cos3 — = 0. 3	3	3	3	3	3
Решение,
Перепишем уравнение в виде
sin 2 — | sin — - cos	- 3 cos 2 — f sin—- cos — | = 0,
3<	3	3)	3<	3	3)
f , X xY . 2 X „	2 X^ Л
sin — cos— sin	—3cos	— = 0.
к 3	3 Jk	3	3)
x	x Л	•	2 X	2х	л
Отсюда: sin — cos — = 0,	sm	— 3 cos — = 0.
3	3	3	3
Тогда:
l)tg- = l,- = -+KJl, я. =-л + Зл* = —(4*+l),*€Z;
3	3 4	*4	4
2) tg2y = 3, tgy = ±-Уз, у = ±у+л£, x2 = ±я + Зли = л(3и± 1), neZ.
Ответ: xx = ~^-(4k +1); x2 = л(3л.±.1), k,neZ.
8.140. tg(x-15°)ctg(x + 15°) = |.
Решение, Имеем
sin(x-15°)cos(x+150) _ £ =	sin(x-15o-x-15o)+sin(x-15o-bx + 15°)
cos(x-15°)sin(x+15°) 3	sin(x+15o-x+15o)+sin(x + 15o + x-15°)
1 n -sin30°+sin2x 1	. +sin2x ।
-- = 0,----------------= 0,	----------= 0:
3	sin 30’+sin 2x 3	—-+sin2x 3
2
2x = 90°+360%, x = 45’+180% = 45’(4£+U keZ.
Ответ: x = 45 ° (4fc + Ц к e Z.
8.141. cos(x +1 )sin 2(x +1) = cos 3(x + l)sin4(x + 1)
Решение.
Перепишем уравнение в виде i(sin(2x+2-x-l)+sin(2x+2 + x+l))-
- у (sin(4x + 4 - Зх - 3)+ sin(4x + 4 + Зх + 3)) = 0, sin(x +1)+ sin(x + 3)-
-sin(x + l)-sin(7x + 7) = 0, sin(3x + 3)-sin(7x + 7)=0 <=>
-	Зх +3 + 7х +7	Зх + З- 7х—7	/_	_\ . /_	_\
<=> 2 cos----------sin-----------= 0, cos(5x + 5 )sin(2x+2) = 0.
Отсюда:
О cos(5x + 5)=0, 5х + 5 = ~ + л&, х. =-1 + —+ —= — (2Zc+ 1)-1,
•	2	1	10 5	10v ’
keZ\
2) sin(2x + 2)=0,
2x + 2 =
ЛЛ, x2 = -
l+~
2
ле Z.
Ответ:	=~l+—(2£ + l}*2	+ k,n^Z.
8.142.	cos(4x + 2)+3sin(2x + l) = 2.
Решение.
Из условия
cos2(2x+1)+3sin(2x +1)-2 = 0 <=> 1 -2 sin2 (2x +1)+ 3sin(2x +1)-2 = 0, 2sin2(2x + l)-3sin(2x+l)+l = 0.
Решив это уравнение как квадратное относительно sin(2x +1), найдем (sin(2x + l)), =|, г^+М-^+л*, X! =(-l)^-|+-f ’ k&Z', (sin(2x+1)^ =1, 2х,+1 = у+2ли, х2 =-^-^ + 7гл = ^-(4л+1)-р neZ.
Ответ: х( = (—1/" -^-у+^;х2 = j(4n+l)-|, k,neZ. 12 2	2	4	2
8.143.	cos4x+2cos2 x = l.
Решение.
Имеем
cos2(2x)+2cos2 x-l = 0,«*2cos2 2x-l+cos2x = 0,
2cos2 2x+cos2x-l = 0.
Решив это уравнение как квадратное относительно cos2x , най-
дем (cos2x)!=-1, 2хх=п+2пк, х(= — + пк, keZ; (cos2x)2 = —,
2	2
2x2 = ±—ч-2лл , x2 =±—ч-тот , ne Z. Объединив Xj и x2, получим 3	6
я пк Ям» 1 \
- + —= -(2fc+l), fceZ.
O 3	0
Ответ: x = — (2fc ч-1} к e Z. 6
4	4	5
8.144.	sin хч-cos x = —. 8
Решение.
Представим уравнение в виде
(sin2 хч-cos2 xf -2sin2 xcos2 х-—= 0, 8-4(4sin2 xcos
8
3	Л/3	7C
3-4sin22x = 0, sin22x =—, sin2x = ±—, 2x = ±— + nk, 4	2	3
x = ±|+^ = £(M:±l) keZ. О z О
Ответ: x = у (3fc ± к е Z. 6
8.145.	cos х - cos 2х = sin Зх.
Решение.
Перепишем уравнение в виде
* . хч-2х . 2х-х .
2 sin----sin------sin Зх = 0,
2	2
_ . Зх . х _ . Зх	Зх Л
2 sin — sin — 2 sin—cos — = 0, 2	2	2	2
Зх	х	(Зх 1
2sin —sin—-sin2 — =0, 2	2	I2 J
- . 3x( . x	Зх^ Л
2sm— sin — cos— =0. 2.2	2
-cos— =0.
Отсюда:
Зх Зх	2
1) sin — = 0, у = яЛ, x}=^nk, k&Z-
x	тс 3x	x я Зх
	4»	 — 4-- ч . x Зх л ~ • 2	7-2-222
2) sin—cos — = 0 <=> 2 sin ——-—— cos ——-—— - 0,
7	2	2	2	2
я
4
я
4
x
2
sin x
cos
= 0.
Отсюда:
a)	sin| X-—j=0, X-—= я/, x2 = —+ я/ = —(4Z+1J ZgZ;
14 1	4	4	4
6)	cosf —	| = 0, - — + — = — + ял, x3 =я 4-2ял = — (4л-1)
^4 2 J 2 4 2	3	2	2
ne Z.
Ответ: Xj =|-я£;х2 =^(4Z + l);x3 = у (4л-1), к.Цпе Z.
8.146. tgx + tg50° +tg70° = tgxtg50° tg70°.
Решение.
ОДЗ: cosx * 0.
Из условия
sinx sin 50°	sin 70°	sinx sin 50° sin 70°	Л
cosx cos 50° cos 70° cosx cos 50° cos 70’ => ^inxcos50° cos 70° -sinxsin50° sin 70°)+ + (sin50° cosxcos70° +sin70° cosxcos50°)=0, sin x(cos 50° cos 70° - sin 50° sin 70°)+ +cos x^in 50° cos 70° + cos 50° sin 70° )= 0 <=> <=>sinxcos(50° +70°)+cosxsin(s0° + 70°)=0, sinxcosl20° + +cosxsin 120° =0, sin(x+120°)=0, -sin(x-60°)=0.
Отсюда x-60° =180’л , x = 60° +180°л , ле Z.
Ответ: x = 60°+180°л, neZ.
8.147. cosx-sinx = 4cosxsin2 x.
Решение.
По формулам понижения степени
cosx-sinx =2cosx(l-cos2x)«^2cosxcos2x-(cosx+sinx)=0,
2 cos x(cos x+sin xXcos x - sin x)- (cos x + sin x)=0, (cosx+sinx)(2cosx(cosx-sinx)-l)=0, (cosx+sinx)x x (2 cos2 x - 2 sin x cosx -1)= 0 <=> (cos x+sin xXcos 2x - sin2x)=0.
Тогда:
1) cosx+sinx = 0<=>tgx = -l, x, =-— + nk = — (4Л-1), fceZ;
4	4
2) cos2x-sin2x = 0 <=> tg2x = l, x2 = —+— = —(4л + Ц ne Z .
8 2	8
Ответ: x{ = ^(4fc-l)x2 = ^-(4л + 1} kfneZ.
8Л48. tg2xsin2x-3V3ctg2xcos2x = 0. Решение.
ОДЗ:
cos2x * 0, sin2x *0.
Имеем
sin2xsin2x 3-Уз cos2xcos2x _	. 3_	. rr 3^ л
	= 0 => sin 2x - 3V3 cos 2x = 0, cos2x	sin2x
tg32х = 3л/з, tg2x = V3, 2x = —+ яи,х = —+—= —(Зл+1)п€ Z.
3	6 2 6
Ответ: x = у(Зи + 1} ne Z.
6
8.149. cos x - cos 3x = sin 2x.
Решение.
Из условия
х + Зх	Зх-х
2 sin-----sin------sin 2х = 0, 2 sin 2х sin х - sin 2х = 0,
2	2
sin 2х(2 sin х -1)=0.
Отсюда:
пк l)sin2x = 0, 2х = лА:, x. =—, JteZ;
2
2) 2sinx-l = 0, sinx = —, x2 = (-1)" — + im, neZ-2	6
Ответ: xl=^-;x2 = (-1)" + nn, k,neZ. 2	о
8.150. >/2(1 + COS x)=Ctg-y.
Решение,
ОДЗ: sin у *0.
a 1 + cosa По формуле ctg— = —:---получаем
2 sina
/Г/.	\ 1 + COSX Л A / /Т 1 Л
V2(l + cosx)------= 0, (1+cosxl V2-----1=0.
sinx	sinx J
Отсюда:
l)l+cosx = 0, cosx = —1, Xj = л + 2лл = л(2л + 1} «eZ;
2)72-----— = 0, sinx = —, x2 =(-1/—+ n/c, keZ,
sinx	2	4
Ответ: Xj = л(2и +1) x2 = (-1У ~ + nk, n,ke Z.
-‘I
2
л , Зх-7л л-Зх 8.151. sin-----cos-------= cos
2	2
Решение.
Зх
ОДЗ: cos’^“ * 0-
Перепишем уравнение в виде
sin
n Зх^ (к ЗхА 1 — + — +cod------------—
2	2	12	2 I _ 3x
J \ J cos----------
2
Л Зх . Зх 1 = 0 <=> cos—+sin---—
2	2 Зх
cos—
2
cos2 —+sin—cos—-1 = 0 <=> cos 3x + sin 3x -1 = 0, 2	2	2
. „ л „ \ л . 3x 3x ~ . 2 Зх л sin 3x - (1 - cos 3x) = 0 <=> 2 sm—cos-2 sin — = 0,
2	2	2
Зх( 2 Отсюда:
Зх . Зх
2 sin— cos-sin— =0.
2	2
. 3x	3x	.
1) sm— = 0, — = nfc, 2	2
2яЛ , _ X| =——. xeZ;
_ Зх . Зх л
2) cos---sm — = 0,
2	2
л 2m n
X2 =-+—- = -(4n+l| neZ.
О 3 О
. Зх	Зх	Зх , Зх	л
sin — = cos—, tg— = 1, — = —+ яп, 2	2	2	2	4
Ответ: х\ = — > х2 = у (4л+1} к, п € Z. 3 о
8.152.	sin23x = 3cos23x.
Решение.
Разделив это уравнение на cos2 Зх ф 0, получим
tg2 3x = 3,tg3x = ±^,3x = ±y + K*,^ = ±|+y = |(3*±l),*6Z.
Ответ: х = (ЗЛ ±	к е Z.
8.153.	sin3x + sinx = 4sin3x.
Решение.
Поформуле sin3a = 3sina-4sin3 а получаем
3sinx-4sin3 x+sinx-4sin3 x =0, 8sin3 x-4sinx =0,
4sinx(zsin2 x-l)=0.
Отсюда:
l)sinx = 0, х{=кк, keZ;
2)	2sin2x-l = 0, sinx = ±—, x2 =—+ — = —(2л+1| neZ. 2	4 2 4
Ответ: xl=nk;x2 =—^.n+l), k,ns Z.
8.154.	sin6x + sin2x = ^tg2x.
Решение.
ОДЗ: cos2x * 0.
„ ,	ПА* a+P a“P
По формуле sin a+sinp = 2 sin—— cos —- получаем
_ . 6x+2x	6x-2x sin2x Л	~ sin2x Л
2 sm------cos--------------= 0, 2 sin 4x cos 2x---= 0,
2	2 2cos2x	2cos2x
4 sin 2x cos 2xcos 2x —S^n^X = 0 => 8 sin 2 x cos3 2x - sin 2x = 0, 2cos2x
sin2x(8cos3 2x-l)=0.
Отсюда:
< \	Л /4	ЛЛ
1)	sin2x = 0, 2х = ли, Xj=—, mgZ;
2)	8cos32x-l = 0, cos2x = — ,2x = ±—+2itk,x2 =±—+itk = -^(б& + 1}
2	3	6	6
keZ
Ответ: xi = ^xi = J(6fc±H n,keZ. L О	/
2cosGt + x)-5cos[ —л-х j 12	13
8.155.		7-----г *---------z = ~
I 3 j /	\	2
cos — л + х -costo-x)
Решение.
ОДЗ: sinx +cosx * 0.
По формулам приведения
-2cosx + 5sinx 3 n _ .	_ n .
---------------= 0 => 7sin x-7cosx = 0 <=> tgx = 1,
sinx + cosx 2
x = — + пк = ~ (4k + Ц keZ.
4	4
Ответ: x = — (4k +11 keZ. 4
8.156. (sin2x + >/3cos2x)2 = 2-2со^уЯ-xj.
Решение.
Имеем
/	Г- \2	,
11	v3	I	(2 A
4 —sin2x + —cos2x = 2-2cos — л-х ,
V2	2	J	U	)
/ \2 /o \
« Л Л	Z4 I .	I ~	I
2 sm—sin2x + cos—cos2x =l-cos -л-х <=>
I 6	6 J u )
_ 2l	л I «	। 2	i л
<=>2cos —2x — 1 + cos — л-х =0<=>
<6	) U	)
(n A A (2 Л <=> cos — 4x1 + cos — л - x I = 0 <=>
я A 2л я A 2n
---4x +------x--------4x------+ x
<=> 2 cos —-------------cos —------------= 0,
2	2
Отсюда:
„ . 5x _ 5x	2	_
1) sin — = 0, — = Tin, Xi = — ял, n € Z;
7	2	2	1 5
(Зх яА Л Зх я я .	2	2 . 2я/<5. ч
2) cos — + — =0,— = — + —+ яА:,Х2 =— я +—пк = — (ЗЛг + 1) 7	{26J	2	62	2 9	3	9
keZ.
2 2я
Ответ: Х] = у ял, х2 =—(3^ +1), n.keZ.
8.157. ctg х + tg 2х +1 = 4 cos2 х + S*n ^Х- - 2 cos 2х. sinx
Решение.
ОДЗ:
cos2x^0, sinx 7*0.
По формуле sin3a = 3sina-4sin3a запишем уравнение в виде
cosx sin2x , А 2 3sinx-4sin3x _
----+	+1 = 4 cos х +	2 cos 2х, sinx cos2x-----------------sinx
cos2xcosx + sin2xsinx , A 2 sinx(3-4sin2 x) -	_
------:-------------------------------+ 1 = 4 cos x +-----------------	- - 2 cos 2x <=> sinxcos2x----------------------------------------sinx
COS X	2	л • 2	/ч
<=>—-------+ l = 4cos x + 3-4sin x-2cos2x<=>
sinxcos2x
COSX 4/2	• 2 1	~ cosx A _
<=> —------= 4fcos x - sin x 1+ 2 - 2 cos2x <=»  ---= 4 cos2x +
sin x cos 2x	sin x cos 2x
- -	_	COSX	~ Л Л cosx
+ 2 -2 cos2x <=>--------2(cos2x +1) = 0,------------
sin x cos2x	sin x cos2x
- 2 (2 cos2 x -1 +1)= 0, —----4 cos2 x = 0,
sinx cos 2x
(	1 л	n
cosx-------------4 cosx 1=0,
sinx cos 2x	)
cosx(l-4sinxcosxcos2x) л /	. . \ л
------------------------- = 0, cos х(1 - sin 4x) = 0.
sinxcos2x
Отсюда:
l)cosx = 0, Xj =y + rcA: = y(2fc+l} fceZ;
4	_	.	. 7Г _	ТС ПП 7t /.
2)l-sin4x = 0, sin4x = l, 4x = — + 2 л л, x?=—+ — = — (4л+ Ц 2	2	2 8 2	8
ne Z.
Ответ:
X] = — (2Л+1)х2 =—(4л+1| к, neZ. 2	8
8.158.	tgxtg20° +tg20° tg40° +tg40° tgx = 1. Решение.
ОДЗ: cos x * 0.
По условию
sinx sin 20°	sin 20° sin 40°	sin 40° sinx , n
------------- ;----------+---------------1 = 0, cos x cos 20° cos 20° cos 40° cos 40° cos x
^in x sin 20° cos 40° + sin x cos 20° sin 40° )+
+(cosxsin20° sin40° —cosxcos20° cos40° )= 0,
sinx(sin20° cos40° +cos20° sin40°)-
- cos x(cos 20° cos 40° - sin 20° sin 40° )= 0 <=>
<=> sin x sin(20° + 40°)- cos x cos(20° + 40° )= 0, sin x sin 60° -
—cosxcos60° =0, -cos(x+60°)=0, x +60° =90°+180%, x = 30°+180%, k<=Z.
Ответ: x = 30° +180%, ke Z.
8.159.	2cos2 --I = sin3x. 2
Решение.
Имеем
( П „ А л . (п V л А cosx-cos —Зх =0<=>sin —х sin —2х =0, 2	4	4
л
4
п
. л
Отсюда:
sin x— sin 2x— 1=0.
4
1) sin[ Х-— 1=0, 4
— = nk, x, = —+ nfc = —(4fc+Q fceZ;
4	4 4V л
п ПП П (.	_
,= —+— =—(4л+11 neZ 2 8 2	8
Ответ: х, = у (4*+1) х2 = (4 п+1) к, п е Z. 4	8
2	2	9
8.160.	sin 2x + sin х =—.
16
Решение.
По формулам понижения степени
1 —cos2 2х + —(l-cos2x)- —= 0, 16cos2 2x + 8cos2x-15 =0. 2	16
Решая это уравнение как квадратное относительно cos2x, находи
5	3	3
cos2x = —,0,или cos2x = — 2х = ±arccos—+2пк
4	4	4
1	3
x = ±—arccos—+ лАг, k^Z‘ 2	4
Ответ: х = ±—arccos—+Ttfc, к g Z. 2	4
8 Л 61.3 cos2 х = sin2 x + sin 2x.
Решение.
Из условия sin2x + 2sinxcosx-3cos2x = 0. Разделив это уравнение на cos2 х*0, имеем tg2x + 2tgx-3 = 0. Решая уравнение как квадратное относительно tgx, находим (tgx)j = -3, xj = -arctg 3 + пк,
*тт	ТЕ
к gZ; (tgx)2 = 1, х2 = —+ лл = —-(4л + 1), л gZ.
Ответ'. Xj = -arctg 3+ яЛ, х2 = -^(4л +1), к,п g Z.
8Л62. 2(l-cos2x) = V3tgx.
Решение.
ОДЗ: cosx * 0.
Из условия
2(1 - cos 2х) - ^<1~cos2x) = 0, (1 - cos 2х) • f 2 ——'I = 0. sin2x	I sin2x,
Отсюда:
1) l-cos2x = 0, cos2x= 1, 2x = 2nk, xj = як, к g Z;
_. _	3 z\ •	n 3 — z , ч ft Л	z i \ л	Л Л
2)2——— = 0, sin2x = —,2x = (-l) -+nn, x2 = (-l) -+~^> sm2x	2	3	6	2
л gZ.
Ответ: xj
*2=(-0 -+y,^,«eZ.
8.163. acos2 — -(a + 2Z>)sin2 — = acosx-i>sinx; 6*0.
2	2
Решение.
По формулам понижения степени
^(l+cosx)-^^^(l-cosx)-acosx+ftsinx = 0,a+acosx-a-2b+ +(a + 2Z>) cosx-2a cosx+ 26 sinx = 0 <=> 26cosx + 26sinx-26 = 0, 6(cosx + sinx-l) = 0.
Так как 6 * 0, то получаем уравнение cos х + sin х -1 = 0;
U X ]	. J X 1	7 X . 2 X 1 л . X X ,2х л
cos2 — +sin2 — - cos — + sin — = 0<=»sin —cos—sin — = 0, |^2 J |^2 J 2	2 )	2	2	2
X (	X	X I
sin— cos—sin— =0.
2	2	2
Отсюда:
1)	sin — = 0, — = яи, x, = 2nn9 neZ-f 2	2	1
-.4 x . X „ X , X It ,	*	- »	Л/.,
2)	cos--sin—= 0 <=> tg—= 1, — =—+ itk, x, =—+2пк = — (4Л+Ц
2	2	2	2 4	2	2
keZ.
Ответ:	= 2ял; x2 = у(4fc+1) n,keZ.
8.164. sin 5x = cos4x.
Решение.
По формулам приведения
5x-—+4x	5x+—-4x
--------cos--------= 0, 2
sin 5x-sin — -4x =0<=>2sin 2
2
. (9х п । (х я) _ sm-----cos —+ — =0.
2 4 J ^2 4 J
Отсюда:
. (9x Л 9x п	я 2 я (.	_
1)	sin----=0,------= ял, Xi = — +—ял = — 14л + 11 neZ:
2 4	2 4	1 18 9	18' Л
>Ч\.	I	I /4	/4 >	f A f < \
2)	cos — + — =0, — + — = — + тгЛ,	= —+ 2тиЛ = —(4fc+ll ke Z .
’	2 4	2 4 2	2 2	2 ' Л
Ответ: *i =т^(4л+й*2	(4*+0 n,keZ.
Io	2
8Л65. 2tgx-2ctgx = 3.
Решение.
ОДЗ:
cosx 0, sinx Ф 0.
Имеем
l^cosx sinx J ’ sinxcosx 2 sin2x 4’
A ~	3 o	3	1	3 ял _
ctg2x = -—, 2x =-arcctg —+ ял, x =arcctg—+—, neZ.
1	3 m	_
Ответ: x = --arcctg-+—, n g Z. 2	4 2
8.166. 25sin2 x +100cosx = 89.
Решение.
Из условия
25^-cos2 x)+100cosx-89 = 0 , 25cos2 x-100cosx + 64 = 0.
Решив уравнение как квадратное относительно cosx, получим 16	4	4
cosx = —,0, или cosx = —, х = ± arccos у+2пк, keZ •
4
Ответ: х = ± arccos у + 2пк, к е Z.
8.167. cos2x + sin2 x + sin х = 0,25.
Решение.
Перепишем уравнение в виде 1 - 2 sin2 х + sin2 х + sin х - 0,25 = 0, 4 sin2 х - 4sin х - 3 = 0, Решив его как квадратное относительно sin х, получим sinx = —, 0 ; sinx =	, х = (-l)*+1 ~ + пк , ке Z .
2	2	6
Ответ: х = (-1/с+1-- + 7Л, keZ.
о
---------= 1 + COS4X.
l-tg22x
Решение.
cos2jc*0,
°Д3: [tg2x *±1.
2 a _ 1-cosa
По формуле tg — = :----
Y J 2 1+cosa
имеем
1 i л — 1 + cos 4x 1 + cos 4x , l-cos4x	i + cos4x=1+cos4x
1+cos4x	2cos4x
Так как I + cos4x Ф 0, to
1	<	Л	1 Л	X /X »
---------= 1, cos4x = —, 4x = ±—+2як, 2cos4x--2	3
x = ± —+ —= —(6fc±l} ke Z.
12 2	12v Л
Ответ: х = (бк ± 1} к 6 Z.
8.169. sinx + sin3x = 4cos3 х.
Решение.
Из условия
Л . х + Зх х-Зх л з Л 2 sin----cos-------4 cos х = 0,
2	2
<=> 2 cos x(? sin x cos x - 2 cos2 x)= 0,
Отсюда:
1) cosx = 0, X! =^ + nk = ~(2fc+l)
2) sinx-cosx = 0<=> tgx = l, x2 = —+1Ш =—(4n+l\ ne Z. 4	4
2 sin 2x cosx-4 cos3 x = 0 <=>
4cos2 x(sinx-cosx)= 0.
keZ\
Ответ: х, = (2к +1) х2 = ^(4л +0» к,п6 Z.
8.170. cos2x + 3sinx = 2.
Решение.
Имеем l-2sin2x + 3sinx-2 = 0, 2sin2 x-3sinx+ 1 = 0. Решив это уравнение как квадратное относительно sinx, получим (sinх)| = у ,
= (~1У £ + яЛ, fce Z; (sinx)2 =1, x2 = у+2ял = у(4л+1), neZ.
Ответ: x( = (- if — + itk;x2= —(4 л+1) к, л € Z. 6	2
8.171. cos2x = l-sin2x.
Решение.
По формулам двойного аргумента получаем
cos2 x-sin2 х =cos2 x+sin2 x-2sinxcosx, 2sin2 x-2sinxcosx = 0, 2 sin x(sin x - cos x)= 0.
Отсюда:
l)sinx = 0, Х]=тги, wgZ;
2) sinx-cosx = 0<=> tgx = l, x2 = -“•+ nk = -^(4/r + l), ke Z .
Ответ: X! = пл; x2 = — (4Л +1} n,keZ, 8.172. tg(?O° +x)+tg(20‘ -x)=2.
Решение.
ОДЗ:
cos(?0° cos(>00
+ x)^ 0, - x)^ 0.
_ ,	n sin(a + p)
По формуле tg a + tg p =--—— представим уравнение в виде
cosacosp
sin(70° +x+20° — x) _	sin 90°	- 2 =>
cos(70° + x)cos(20° -x)	cos(70° + x)cos(2(F- x)
2cos(70° + x)cos(i0o -x)= 1 <=> cos(?0° +x-20° +x)+ + cos(70°+x+20°-x)=l, cos(2x + 50°)=l, 2x + 50°=360%,
x =-25°+180%, keZ.
Ответ: x = -25° +180°Zc, keZ.
8.173. sin x +sin —= sin x + — я	nJ
Решение.
Перепишем уравнение в виде
1 1 х + — х —
= 0 <=>2sin--—cos-----—
2	2
Х + “
sinx + sin— -sin2- ---—
л ]	2
-2sin----—cos----— = 0,
2	2
1 x+—
2 sin-—
\	7
1 1 . 1 1 . X— x + — x + — x — x + -	---*- +----------5---*
<=> 2 sin-— • 2 sin —--2— sin —2-1— - о
2	2	2
1 x+-	x 1
sin--— sin—sin — = 0.
2	2	2л
Отсюда:
1 1 x + —	x + —	.
1) sin---— = 0, --— -лк, Xy — — + 2лЛ, keZ;
2	2	л .
2) sin — = 0, — = лп, x7 = 2ля, n g Z.
2	2	2
Ответ:	= - — + 2лк; x2 = 2ли, к, n g Z.
л
8.174. tg2 3x-2sin2 3x = 0.
Решение.
ОДЗ: cos3x*0.
sin2 3x _ . 2 /X • 2 о (	1
Имеем—т.—2sin 3x = 0’ sm 3x’ — cos 3x	^cos 3x
Отсюда:
лк
l)sin3x = 0, Зх = лЛ, x{=—, keZ-
2)---5---2=0, cos3x = ±—3x = — + —
cos2 3x	2	4 2
= ^(2«+!i n&Z.
-2 =0
л лп
—+—
12 2
лк л ,\ .
Ответ:	=— ;x2 =— (2и + 1) k,neZ.
8.175. 6ctg1 2 x-2cos2 x = 3.. Решение.
ОДЗ: sin x * 0.
Из условия
^P-2co?,-3.0»6(UC°s2x)-(H-co>2x)-3 = 0^ sin2 x	l-cos2x
=> 6(1 + cos2x)- (1 + cos2xXl -cos2x)-3(l -cos2x)= 0,
cos22x + 9cos2x + 2 = 0.
Решая это уравнение как квадратное относительно cos2x , имеем
-9-V73	-9 + V73
cos2x =------< -1,0 , или cos2x =-----, откуда
Л	-9 + V73 „ .	.1	-9 + V73 . . „
2х = + arccos-----+ 2л£, х = ±—arccos-------+ keZ.
4	2	2
1	V73-9
Ответ: х = ±—arccos-----+ ide, ке Z.
2	2
Решения к главе 9
НЕРАВЕНСТВА
НЕРАВЕНСТВА С ОДНИМ НЕИЗВЕСТНЫМ
Неравенства fx(x)> f2(x), /i(x)^ /2(х), f(х)< /2(х), _/;(х)< /2(х), где /, (х) и f2 (х) — заданные функции переменной х (одна из них может быть постоянной), называются неравенствами с одним неизвестным.
Переменная величина х называется неизвестной. Если/(х) и /2(х)— алгебраические выражения, то неравенство называется алгебраическим.
Решением неравенства с одним неизвестным называется такое значение неизвестного, при котором данное неравенство обращается в тождественное (истинное).
Решить неравенство с одним неизвестным — значит найти множество (совокупность) всех его решений или показать, что оно не имеет решений.
Областью допустимых значений неизвестного данного неравенства (ОДЗ) или областью определения неравенства называют множество всех значений неизвестного, при которых существуют обе части неравенства.
Равносильные неравенства и основные теоремы о равносильности неравенств
Так как рассматриваемые ниже понятия и свойства неравенств одинаковы для неравенств /(%)> /2(х), /1(х)- ЛЙ, /1(*)< /г(х)» f2(x) , то будем рассматривать только неравенства вида
Пусть даны два неравенства с одним неизвестным fM>f2[x),	(9.1)
gl(*)>g2(*)'
Неравенство (9.2) называется следствием неравенства (9.1), если все решения неравенства (9.1) есть решения неравенства (9.2) или неравенство (9.1) не имеет решений.
Два неравенства (с одним неизвестным) называются равносильными (эквивалентными), если каждое из них является следствием другого.
Если над обеими частями неравенства с одним неизвестным произвести тождественные преобразования, не меняющие области определения неравенства, то получим неравенство того же смысла, равносильное данному, т.е. если дано неравенство f\ (*) > /2 (*) с областью определения D и в результате тождественных преобразований получилось неравенство /з(х) > А(х) с той же областью определения, то они равносильны.
Если к каждой части данного неравенства прибавить одно и то же число или выражение, имеющее смысл при всех значениях неизвестного из области определения неравенства, то получим неравенство того же смысла, равносильное данному, т.е. если дано неравенство f\(x)> f2(x) с областью определения D и т(х) — число или выражение, имеющее смысл при всех значениях х из £>, то неравенство /i(x) + m(x)> > f2(x) + m(x) равносильно данному.
Члены неравенства можно переносить с противоположным знаком из одной части неравенства в другую.
Если обе части неравенства умножить на одно и то же положительное число или выражение, принимающее положительные значения при всех значениях неизвестного из области допустимых, то полученное неравенство того же смысла будет равносильно данному.
Если обе части неравенства умножить на одно и то же отрицательное число или выражение, принимающее отрицательные значения при всех значениях неизвестного из области допустимых, то получим равносильное данному неравенство противоположного смысла, т.е. если дано неравенство /1 (*) > /2 (х) и число или выражение т(х) < 0 при всех х из ОДЗ неравенства, то неравенство /\(х) т(х)< f2<x),m(x) будет равносильно данному.
Неравенство > 0 равносильно неравенству f\(x)f2(x) > О при /2W
/2(х)*0.
< 0 равносильно неравенству f\(х) • /2 (*)< 0 при /2W
/2(х)*0.
РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ С ОДНИМ НЕИЗВЕСТНЫМ
Решение неравенства первой степени с одним неизвестным
Неравенства вида
/1М>л(4
где /i(x) и /2(х) —линейные функции переменной х (одна из которых может быть постоянной), называются неравенствами первой степени с одним неизвестным.
Всякое линейное неравенство с одним неизвестным всегда можно привести к каноническому виду
ах + й>0-	(9.3)
Решение неравенства ах + й > О
Если а > 0, то после умножения обеих частей неравенства на — > О ь а получим равносильное данному неравенство х + — > 0, из которого
Ь	а
последует X > — . а Если а<0, то после умножения обеих частей данного неравен-
ства на — < 0 получим равносильное данному неравенство х 4- — < 0, а	а
b из которого следует х < — .
а
Если а = 0, то при b < 0 для любого действительного значения х неравенство обращается в неверное, т.е. решений не имеет, а при Ь > О данное неравенство верно при всех действительных значениях х , т.е. все действительные числа являются решениями неравенства.
Решение неравенств второй степени (квадратных) с одним неизвестным
Неравенство, обе части которого есть многочлены относительно неизвестного не выше второй степени, причем хотя бы один из них второй степени, называется неравенством второй степени с одним неизвестным.
Всякое неравенство второй степени с одним неизвестным (квадратное неравенство) можно привести к одному из его канонических видов:
ах1 + Ьх + с>$, ах1 4-Ьх 4- с >О,
ах2 + Ьх + с < 0, ах2 4- Ьх 4- с < 0, где х * 0 .
Решение неравенства ах2 + Ьх + с>$ (а Ф 0)
Если а > 0, то данное неравенство равносильно неравенству
2 Ь с Л
X 4- —Х4-—>0 а а или
Х24-рх4-#>0,	(9.5)
Ь	с
где Р = - , Я. а	а
Если а < 0, то данное неравенство равносильно неравенству
о Ь с Л X" 4- — Х+ — <0 а а
или
х2 4- рх 4- q < 0,	(9.6)
Ь	с
где р = — , Я = —. а	а
Другие неравенства вида (9.4) также приводятся к виду, аналогичному (9.5) или (9.6).
Исследование трехчлена х2 4- рх 4- q = 0
Рассмотрим трехчлен
х2 + рх 4- q.	(9.7)
1. Если D = р2 - 4q > 0, то трехчлен х2 + рх + q можно разложить на множители с действительными коэффициентами
х2 + px + q = {x-xx\x-x1\
I/ \2 р I р ]	р
где X!	J « *2 = ~ +
-q — корни трехчлена
(Xj <%,)•
Если х < jq < х2, то х - Xj < 0 и х - х2 < 0; тогда х2 + рх + q > 0.
Если Xj < х < х2, то х - Xj > 0, а х - х2 < 0; тогда х2 + рх + q < 0 .
Если х > х2 > Xj, то х - Xj >0 и х-х2 > 0; тогда х2 + рх + q > 0.
Вывод. Если D = р2 -4# > 0, то квадратный трехчлен х2 + рх + q положителен при значениях х , меньших меньшего корня и больших большего корня, и отрицателен при значениях х , лежащих между корнями.
2. Если D = р2 -4q = 0
, то трехчлен х
+ рх + q прини-
мает вид
2	2	Р I Р
х + px + q = х + рх 4-	= х 4- •—
р	р
и при всех х * будет положительным, а при х = равен нулю.
3. Если D = р2 -4q < 0, то трехчлен х2 + рх + q можно предста
вить в виде
2	( Р Y р2 -4q ( р Y 4q- р2
х +рх + а=Дх+—\ -i---= х + — +———.
2	4	2	4
Так как
> 0 при всех х , a 4q - р2 > 0 , то трехчлен
х2 + рх + q положителен при всех значениях х.
Решение целых рациональных неравенств с одним неизвестным
Целым рациональным алгебраическим неравенством с одним неизвестным называется такое неравенство, обе части которого есть многочлены относительно неизвестного.
Степенью целого рационального алгебраического неравенства с одним неизвестным называется большая из степеней многочленов, входящих в это неравенство.
Всякое целое рациональное алгебраическое неравенство и-й степени с одним неизвестным может быть приведено к одному из канонических видов
aQxn + а}хп~1 + а2хп~2 + ... + а„_2х2 + аяЧх + ал >0,	(9.8)
aQxn +а{хп~х + а2хп~2 + ... + ап_2х2 +апАх + ап >0	(9.9)
или
а$хп + а1х”’1 + а2хп~2 + ... + ап_2х2 +ап_1х + ап <0,	(9.10)
Oqx” ч-^х""1 + а2хп~2 + ... + ап_2х2 +ап_{х + ап <0	(9.11)
(ао * О) •
Метод интервалов
Чтобы найти решения неравенства
(х - X! X* - *2 Х*-*3 )•••(*-*/>)> °	(9-12)
или
(х “ X] Хх — Х2 Хх — Х3 )... (х Хп ) < 0 ,	(9.13)
достаточно нанести на числовую ось нули (корни) левой части неравенства Xj, х2, х3,..., хп, а затем проверить знак левой части неравенства на каждом из полученных интервалов путем подстановки любого числа из этого интервала. Тогда множеством всех решений неравенства (9.12)
(х-х1Хх-х2Хх-Хз)...(х-х„)>0
будет объединение всех промежутков, в которых поставлен знак плюс, а решением неравенства (9.13)
(х - Xj Хх- - х2 Хх - х3)... (х - х„) < 0
будет объединение всех промежутков, в которых поставлен знак минус.
При решении неравенств
(х-Х!Хх-х2Хх-Хз)...(х-хл)>0
и
(х-Х]Хх-х2Хх-х3)...(х-хл)<0	• 1
с помощью метода интервалов, кроме соответствующих интервалов зна-копостоянства левых частей неравенств, к их решениям надо относить и их нули (корни).
Обобщенный метод интервалов
Рассмотрим схему решения неравенства (9.8) аохл+а1хл-1 + а2хл-2 + ... + ал_2х2 + «л-1х + ал >0
Многочлен aQxn + а1хл“1 + а2хл'2 + ... + ал_2х2 + алЧх + ал в множестве действительных чисел можно представить в виде
аохл -ь^х”4 + а2хл”2 + ... + ал_2х2 + ал-1х + ал = = а0(*_*1X"1 ~*2У”2 ...(х-х*)т‘(х2 +р1х + ^У‘ ,..(х2 + р,х + <7,У', где Xj, х2,..., хк — действительные корни соответственно кратности zn1,zn2,...,mA., а трехчлены х2 + p}x + qt,...,x2 + р,х + ^, имеютотри-цательные дискриминанты, т.е. при всех х положительны.
Неравенство (9.8) можно переписать в виде
ao(x-xi)m'(*-x2>ri ...(х-х*.)'"4^2 + pix+qj' ... ...(х2 +р,х+<7,У' >0.
Так как квадратные трехчлены в этом неравенстве принимают положительные значения при всех действительных значениях неизвестного, то оно равносильно неравенству
a0(x-xl)'"l(x-x2)'"2 ...(x-xtX"* >0.
Множители левой части неравенства с нечетными показателями можно оставить в первой степени, а с четными - опустить, выписав те значения х, при которых они обращаются в нуль. Тогда неравенство примет вид
при а0 > 0 оно равносильно неравенству
(х-хДх-хл). ..(x-xyJ>0,
а при a0 < 0 — неравенству
(х-хДх-хл)...(х-х7- )<О.
Поел щнее неравенство решаем методом интервалов.
Дробно-рациональные неравенства
Неравенства вида
или
(9.14)
(9-15)
(а0 *0) и
где Рп(х) = аохп +а1хп 1 + а2хп 2 + ... + ял_2х2 + ап_хх + ап
QnAx)=boxm +М'"'1 +Ьгхт-1 +... + bm_1x1 +bm_lx + bm (Z>0 * 0) —мно-гочлены переменной х, называются дробно-рациональными неравенствами.
При решении таких неравенств пользуются следующими утверждениями:
1 п	Л(х) Л
I.	Неравенство -	> 0 равносильно неравенству
Qm W
p„(x)em(x)>o.
Р (х)
2.	Неравенство	> 0 равносильно системе неравенств
рл(х)ет(х)>о> ет(х)*о.
р (х)
3.	Неравенство —< 0 равносильно неравенству
Qm \х/
Л(Х)бт(Х)<°-
Р (х)
4.	Неравенство \ < 0 равносильно системе неравенств бДх)
рл(х)ет(х)<о) ет(х)*о.
Таким образом, решение дробно-рациональных неравенств сводится к решению целых рациональных неравенств.
При решении дробно-рациональных неравенств нужно придерживаться следующей схемы:
а)	перенести все члены неравенства в левую часть;
б)	привести все члены левой части нераве (ства к общему знаменателю;
в)	заменить дробные неравенства целыми;
г)	разложить левую часть полученного неравенства на простейшие множители;
д)	привести полученное неравенство к виду (9.12) или (9.13);
е)	найти решения полученного неравенства по методу интервалов.
РЕШЕНИЕ СИСТЕМ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ С ОДНИМ НЕИЗВЕСТНЫМ
Системой неравенств с одним неизвестным называется несколько неравенств, в которых под одной и той же буквой, обозначающей неизвестное, подразумевается одна и та же величина.
При решении системы неравенств с одним неизвестным обычно решают каждое из неравенств системы, а затем находят пересечение множеств полученных решений.
Решить систему неравенств с одним неизвестным - значит найти множество всех ее решений или показать, что система не имеет решений.
НЕРАВЕНСТВА С НЕИЗВЕСТНЫМ ПОД ЗНАКОМ АБСОЛЮТНОЙ ВЕЛИЧИНЫ
При решении неравенств, содержащих переменную под знаком абсолютной величины (модуля), используется определение абсолютной величины:
IfM-J /Мпри/(х)>0, |-/(х)при/(х)<0.
Кроме того, иногда бывает полезным применить геометрический смысл модуля числа, согласно которому |х| есть расстояние от точки х числовой прямой до начала отсчета, а |х - л| — это расстояние на числовой прямой между точками х и а.
Рассмотрим неравенство /(jx|)<g(x),	(9.16)
где /(х) и g(x) —некоторые функции.
Неравенство такого вида равносильно следующей совокупности двух систем неравенств:
fx<0,	Jx>0,
’> t/(-x)<Hx)ra“2,l/W<sM
Рассмотрим неравенство |/(x)|<g(x))	(9.17)
где /(х) и g(x) —некоторые функции. Неравенство такого вида рав-носильно следующей совокупности двух систем неравенств: fg(x)>0,	[g(x)<0,
|-g(x)</(х)< g(x)101,12) [хе 0.
Рассмотрим неравенство
|/(x)|>g(x),	(9.18)
где /(х) и g(x) —некоторые функции. Это неравенство равносильно
следующей совокупности двух систем неравенств:
1)
g(x)^0, r/W>«W lu„2JsW>0' , >
/(х) < -g(x)	' I* e	неравенства (9.18)
Рассмотрим неравенство

(9.19)
где /(х) и g(x)—некоторые функции. Это неравенство можно решить двумя способами. Во-первых, оно равносильно совокупности двух систем:
х >0,
или 2) jjy(х} < g(x).
Во-вторых, оно также равносильно двойному неравенству
Рассмотрим неравенство
где /(х) и g(x) — некоторые функции. Это неравенство можно решить двумя способами. Во-первых, оно равносильно совокупности двух систем:
х <0,
х>0,

[|/(-x)|>g(x)
Во-вторых, оно также равносильно совокупности двух неравенств /l|x|)>g(xl /(*|)< -g(x).
Рассмотрим неравенство
(9.21) где f(x) и g(x) — некоторые функции. Это неравенство решается при помощи разбиения области его допустимых значений на промежутки, каждый из которых является промежутком постоянства знака как функции /(х), так и функции g(x). Затем на каждом из этих промежутков решается неравенство без знака абсолютной величины. Объединив решения на всех промежутках, получим множество всех решений неравенства.
Некоторые неравенства вида (9.21) |/(х)| |g(x)| целесообразно ре
шать, перейдя к равносильному неравенству (/(х))2 > GKx))2, т.е. возведением обеих частей исходного неравенства в квадрат.
ИРРАЦИОНАЛЬНЫЕ НЕРАВЕНСТВА
Алгебраическое неравенство называется иррациональным, если его неизвестное входит под знак корня.
При решении иррациональных неравенств, как и иррациональных уравнений, корни четной степени рассматриваются только арифметические, а корни нечетной степени рассматриваются на всей числовой оси (при всех действительных значениях подкоренных выражений).
Если неравенство, обе части которого неотрицательны при всех значениях неизвестного из области допустимых, возвести в любук) натуральную степень, то получим неравенство того же смысла, равносильное данному, т.е. если дано неравенство
fl(x)> f2(x),
причем при всех х из ОДЗ (х) > 0 и /2 (х) > 0, то неравенство
ШУ >(Л(х)У
равносильно данному.
Если обе части неравенства возвести в нечетную натуральную степень, то получим неравенство того же смысла, равносильное данному, т.е. если дано неравенство
то неравенство (/’1(х))2л+| > (f2(x}fn+i равносильно данному. В частности, неравенство вида
(9.22)
равносильно системе 1 у<	а неравенство вида
(9.23)
равносильно неравенству f(x) < g(x); неравенство вида
(9.24)
равносильно системе « g(x) >0,	а неравенство вида
f(x)<(g(x)yn,
(9.25)
равносильно неравенству f(x) < (?(х)У”+1; неравенство вида
(9.26)
равносильно совокупности двух систем неравенств g(x)>0,
И*)<о, п или
а неравенство вида
ne N,
(9.27)
равносильно неравенству f(x) > (g(x)f”+1 •
ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА
При решении показательных неравенств используются следующие правила:
1)	Если а > 1, то неравенство
а/М<аЛМ	(9.28)
равносильно неравенству /((х)< /2 (х), а неравенство a/.W>aAW	(9.29)
равносильно неравенству /1(х)> f2(x).
2)	Если 0 < а < 1, то неравенство
.afM<afAx)	(9.30)
равносильно неравенству /t(x)> /2(х), а неравенство a/t(x)>aAW	(9.31)
равносильно неравенству fx(x)< f2(x).
3)	Если а > 1, то неравенство
loga /1(*) < loga fi (*)>	(9.32)
где (х) > 0, /2 (х) > 0, равносильно неравенству fx (х) < /2 (х), а неравенство
loga/iM>loge/2(x),	(9.33)
где /1(х)>0, /2(х)>0 , равносильно неравенству fx (х) > /2 (*) •
4)	Если 0 < а < 1, то неравенство
loga /1 («) < l°ge fi (Д	(9.34)
где /] (х) > 0, f2 (х) > 0, равносильно неравенству j\ (х) > /2 (х), а не-равенство
loga/iM>loge/2(x),	. (9.35)
где /|(х)>0, /2 (х) > 0, равносильно неравенству /!(х)< /2(х).
ТРИГОНОМЕТРИЧЕСКИЕ НЕРАВЕНСТВА
Тригонометрическим неравенством называется неравенство, в котором неизвестное входит под знак тригонометрических функций непосредственно или в виде линейной функции неизвестного, причем над тригонометрическими функциями выполняются только алгебраические действия.
К простейшим тригонометрическим неравенствам относятся:
1.	Неравенство sin х > а. Если а < -1, то решением неравенства будет любое действительное число. Если -1 < а < 1, то решениями неравенства будут
arcsina+2rcH <х< л-агс$тл+2лл, ne Z.	(9.36)
Если а > 1, то неравенство решений не имеет.
2.	Неравенство sin х < а. Если а < -1, то неравенство решений не имеет. Если -1 < а < 1, то решениями неравенства будут
л-агс8та+2ли<х<2л + агс$та + 2ли, ne Z .	(9.37)
Если а > 1, то неравенство верно при всех действительных значениях х,
3.	Неравенство cosx > а . Если а < -1, то неравенство верно при всех действительных значениях х . Если -1 < а < 1, то решениями неравенства будут
-arccos а+2лл <x<arccosa + 2Tcn, ne Z .	(9.38)
Если а > 1, то неравенство решений не имеет.
4.	Неравенство cos х < а . Если а < -1, то неравенство решений не имеет. Если -1 < а < 1, то решениями неравенства будут
агссо$а+2лл <х<2л-агссо5а+2лп, neZ .	(9.39)
Если а > 1, то неравенство верно при всех значениях х .
5.	Неравенство tg х > а , Это неравенство имеет решения при любых действительных значениях а, причем
л
arctg я + ти? < х < у + ля, neZ.	(9.40)
6.	Неравенство tgx < а. Это неравенство имеет решения при любых действительных значениях а, причем
-y + nn<x<arctga + nn, neZ.	(9.41)
7.	Неравенство ctg х > а. Это неравенство имеет решения при любых действительных значениях а, причем
лп < х < arcctgа + т, ne Z.	(9.42)
8.	Неравенство ctg х < а . Это неравенство имеет решения при любых действительных значениях а, причем
arcctgtf + ял <х< л + яи, neZ.	(9.43)
В случае нестрогих неравенств к решениям присоединяются соответствующие концы интервалов.
9.	001. Показать, что для всех положительных чисел а и b верно неравенство 4a+4b > 4а+ Ь •
Решение,
Возведя обе части данного неравенства в квадрат, имеем эквивалентное неравенство a+24ab+b> a + b&24ab >0«=> 4аЬ >0, а/>>0. Так как а>0и/>>0,то последнее неравенство очевидно, и тем самым справедливость равносильного ему исходного неравенства доказана.
2\fcb
9.0	02. Доказать, что если а>0 и £ > о, то	—т= ^чао
yja +\1Ь
Решение.
Так как 4а + 4b > 0, то получим
24ab <[4а +4b)4ab <=^24ab-[4a + 4b)4ab <0;
учитывая, что - Vad <0, найдем 4a-2^lab + 4b>Q<^ fya-tfbf > 0-
Полученное, а значит, и исходные неравенства истинны.
9.0	03. Доказать, что если р>0 и ? > 0, то (р + 2\q + 2\p + q)>16pq.
Решение.
Имеем
p2q + pq2 +2р2 + 2q2 + 4pq + 4p+4q >16? <=>
<=>p2q + pq2 +2р2 + 2?2 -12p? + 4p+4?>0«=>
<=> ^p2 -4pq+2q2)+ (p2q-2pq/pq + pq2 )+4(p-2y[pq + q)+
+ fapq-Jpq -ipq + iJpq)>0^2(p-qY +(pjq ~qjpf +
+ 4(у1^~4р\ +2y[pq(pq-4y[pq+4)>Q^
&2(р qf + (pjq-qjpf + 4(y[q-Jpf + 2jpq(4pq -if >0.
Полученное неравенство истинно, а значит исходное неравенство справедливо.
1 . 2
9.0	04. Доказать, что если а * 2 , то --7 > —5—“.
а -4а +4 а -8
Решение.
Перепишем данное неравенство в виде
1_________2	а2 + 2а + 4-2а + 4
(а-2)2 (а-2)(а2+2а+4)> ** (а-г^а2+2а+4)> **
Так как сг +8 > 0 при ае R ; (а-2)2 > 0 при а #2 и а2 +2а+4 > 0 при a g R , то это неравенство очевидно. Итак, исходное неравенство истинно.
9.0	05. Доказать, что если т , п и р представляют собой длины сторон некоторого треугольника, то т2 + п2 + р2 < 2{тп + тр + пр).
Решение.
Для всякого треугольника сумма двух сторон больше третьей:
?и + п> р,п + р> т,т + р> п.
Запишем неравенства в виде р-т < п,т-п < р,п-р <т.
Возведя каждое из этих неравенств в квадрат, получим
(p-mf <п2, р2-2тр + т2 <п2, (\2	2	2	2	2
т-п) <р ,<=>т -2тп + п <р ,
(\^	7	7	2	2
п-ру <т~ п -2пр vр <т .
Сложив левые и правые части этих неравенств, найдем
2т2 + 2н2 +2р2 -2(тп + тр + пр)< т2 + л2 + р2 <=>
<=> т2 + п2 + р2 < 2(тп + тр + пр\
что и требовалось доказать.
9.006. Доказать, что если т>0ил>0,то тп(т + п)<т3 +п3.
Решение.
Из условия
тп(т + п}< (т + п^п2 -тп+п2),
тп(т + п)~ (т + n)(pi2 -тп + п2)< 0,
(т + п^пп -т2 + >ил-л2)<0, -(т + и)^п2 -2аии + и2)<0,
-(m + nfcn-n¥ <0, (m + nfon-n^ >0.
Так как т + п > 0 по условию; (т - л)2 > 0, отсюда
(m + nfen-п? >0-
9.007. Доказать, что для любых действительных чисел х и у верно неравенство х2 + 2у2 + 2ху + 6у +10 > 0 .
Решение.
Имеем х2 + у2 +у2 +2ху+6.у + 10>0, (x + yf +(у2+6j + lo)>O-B полученном неравенстве (х + yf >0 для хе R и ye R,ay2 +6у + 10 >0 для уе 7?, так как Р = 36 - 40 < 0 ♦ Значит, и^ + ^у)2 +(у2 + бу + ю)> 0, что и требовалось доказать.
9.008. При каких значениях а оба корня уравнения х2 - (а + 1)х + а + 4 = 0 оказываются отрицательными.
Решение.
Используя теорему Виета, получаем, что оба корня отрицательны тогда и только тогда, когда их сумма Х| + х2 < 0, а произведение х} • х2 > 0.
Имеем систему неравенств х{ + х2 = а +1 < 0,	[а < -1,
- Х| • х2 = а +4 > 0, <=> ’ а > -4, 1) = я2-2л-15£0	[(я-5Хл + 3)> 0.
Методом интервалов получаем ае (- 4;-3].
-4	-3-15 а
Ответ: ае (-4;-3].
ab
9.009. Показать, что для любых двух положительных чисел произведение их суммы на сумму их обратных величин не меньше четырех.
Решение.
Пусть а > 0 и Ь > 0. Предположим, что
/	, \ Г 1 1 А (	,\а + Ь л Л a2 + 2ab + b2-4аЬ
(a + b)-1- + - >4 <=> (а + Ь)-
{а Ь) .	ab
a2-2ab + b2	Л
(а-Ь?
Так как (а-Ь? >0 и ab>0 при а >0 и Ь >0,то ——— ^0 инера-венство истинно, следовательно, и исходное неравенство справедливо.
9.010. Найти целые положительные значения х, удовлетворяющие 5х + 1 _	_
неравенству ——j- > 2х + 2 .
Решение.
Имеем
5х+1 7v 5х+1-2(х+1Х*-1) ------ZX > и --------------------
-2х2 +5х + 3
С помощью числовой прямой найдем, что х = 2 .
-1/2
-6 ф 1
-6-
3
х
Ответ: х = 2.
9.011. Найти целые решения системы неравенств
х —1 2х + 3 х - х + 5
	+ —<2	, 2	3-6	2
Решение.
Имеем
	+ 2 +	<( 2	3-6	2
, х + 5 4-х - , х+1 1------+----Зх+------<0
8	2	4
х<2,	7
7 <=> — <х<2.
х>-	9
9
Значит, х = 1 •
Ответ: х = 1.
9.012. Найти натуральные значения х , удовлетворяющие системе неравенств
log^ (х -1) < 4,
' х х-5 2х
----+-----<-----'
х-3 х 3-х
Решение,
Из условия
1 < х < 5, 4х2-8х + 15 п<=>
х(х - 3)
1 < х < 5,
4х2 -8х+15 > 0 при хе R,
х(х-3)<0.
С помощью числовой прямой находим решение системы х = 2 .
Ответ: х-2,
9.013. При каких значениях х функция у = V10 + x - V2-x принимает положительные значения?
Решение,
Учитывая ОДЗ, из условия имеем
Vio+x-TT^x >о, 10+х>0, 2-х>0
10 + х>4-4х+х2, х>-10,
х<.2
х1 -5х-6<0, х^-10,	<=>
х<2
-1<х <6,
х>-Г0,
х <2.
С помощью числовой прямой находим решения системы -1 < х < 2 .
Ответ: х е (-1; 2)
9.014. Найти множество целых значений х, удовлетворяющих системе неравенств
[—>2,
’ х+2
Решение.
Учитывая ОДЗ, решаем второе неравенство системы:
х+2
(х-4Х*+2)<0,
——-2>0, х+2
С помощью числовой прямой находим целые решения системы х, = 2; х2 = 3.
-21411	х
Ответ: хх = 2; х2 = 3.
9.015. При каких значениях т неравенство х2 -тх>— выполняется для любых X ?
Решение.
2
Имеем х2 - тх - — > 0. Неравенство выполняется для хе R, ког-
да Z) =	+—< 0 <=>————< 0, (m + ltm2-2m+4k <0. Так как
т	т
т2 _ 2т + 4 > 0 при т е R, то полученное неравенство равносильно неравенству (т + 2)т < 0 . Методом интервалов получаем -2 < т < 0.
> т
Ответ: те(-2;0)
Найти области определения функций (9.016 - 9.021):
9.016. У —
|х2-7х + 12
х2-2х-3 '
Решение.
D(y)-. Х\ 1х*П>0, fc-
х2 - 2х - 3	(х-ЗХх + 1)
(х - 3f (х -4Х*+1)^ 0, х-3#0, х+1^0.
Методом интервалов находим решение системы х < — 1 или х > 4.
Ответ: х g (-<»;- 1)U [4; оо}
V4-xz+---
9.017. у = 0,5	*-«.
Решение.
D(y): •
4-х2 £0, <=>
х-1#0
-2 £ х £ 2, х#1.
Ответ: хе [-2;l)(j(l;2].
к	х-1
9.018. y=Jlog0>3—-т.
V	х + 5
Решение.
х+5 *0
(х- 1Х* + 5)> 0, х + 5>0.
Методом интервалов находим решение системы х > 1 •
11	1	х+1
9.019. У = /log 1 10g3--.
V Й Х-1
Решение,
D(y}\ logj logj 0, 0<log3	1<—<3,
т х-1	Х-1	х-1
л+а-л+Чо,
*_| «
х + 1-Зх + З
х-1
х-^^’	|х-1>0,	|х > 1,
-2х + 4 <q	[(х-2Хх-1)>0 [(х-2Хх-1)>0.
. х-\
С помощью числовой прямой находим решение х > 2 •
Ответ: х G [2; <»)
9.020. у = .5-х--. V х
Решение.
D(y)'. 5-х-— >0,
Методом интервалов находим х < 0 или 2 < х < 3 .
Ответ: хе (-0)U[2;3J
9.021. У~
logo, (х-Г
V-x2 + 2x + 8
Решение.
bg0,3(x-l) >Q log03(x-l) log0,3(x-l)^0,
V-x2 +2x+8	-J-x2 +2x+8	- x2 + 2x + 8 > 0
x-l>l, x2-2x-8<0
x>2, -2<x<4
<=> 2 < x < 4.
Ответ: x 6 [2; 4)
Решить неравенства (9.022 - 9.095):
9.022. -^— + —^—<1.
2-х 2 + x
Решение.
Имеем
1	5 п 2 + х + 10-5х-4 + х2 л х2-4х + 8 п
2-х 2+х	’	(2-х)(2 + х)	’ (х-2Хх+2)
В полученном неравенстве х2 -4х + 8 > 0 ПРИ хе R, поэтому оно равносильно неравенству (х - 2Хх + 2) > 0. Методом интервалов находим х < -2 или х > 2 •
Ответ: х е (- <»; - 2)U (2; °?)
, Зх-1 ,
9.023. logi777<L
Решение.
Это неравенство равносильно неравенству
Зх-1 1 Зх-1 1 	9х-3-х-2 . 8х-5 п
х+2	3	х+2 3	3(х + 2)	х+2
(8х-5Хх+2)>0.
С помощью числовой прямой находим х > - или д < -2.
Ответ:
Зх-5
9.024. log3----<1.
х + 1
Решение.
Неравенство равносильно системе неравенств
Зх-5 х + 1 Зх-5 х + 1
Методом интервалов находим х
5
3
Ответ: хе —
I3 )
9.02S. log, (л + 27)-1ое_ (16-2х)< log, х.
Решение.
Из условия
logg
х + 27 16-2х
< log, х. Это неравенство равносильно, с
учетом ОДЗ системе неравенств
х+27 ------< х, 16-2х
•х+27>0, <=> 16-2х>0
х + 27	Л 	х<0, 16-2х	2х2-15х + 27>0 2х-16	> ’
х > -27,	<=> •	х > -27,	<=>
-2х>-16	х<8
.	.	.	9
С помощью числовой прямой находим 3 < х < —.
Ответ: х G
9.026. log0 з (Зх ~ 8) > log0 з (*2 + 4)
Решение.
Это неравенство равносильно системе неравенств
Зх-8>0, Зх-8<х2+4
х2 -Зх+12 >0.
Так как х2 - Зх +12 > 0 при х е R, то последняя система неравенств
8 эквивалентна неравенству х > -.
п (8
Ответ: хе Ь;»
9.027. (х + ОО-хХх-г)2 >0.
Решение.
Имеем
(x+lfr-SXx-Z^O. +
|х-2^0	[х^2.
Ответ: х е (-1; 2)U (2; 3)
9.028. -hx-x2 <4-х. Решение.
Данное неравенство равносильно системе неравенств
Зх-х2 <(4-хУ,	Ьх2 -11х + 16>0,
’ Зх-х2 >0,	« х(х-3)<0,
4-х>0	х<4.
Так как 2х2 -1 lx +16 > 0 при х g R, то полученная система нера-
(х(х-3)<0, венств равносильна системе 5 < Методом интервалов находим 0 < х < 3.
Ответ: хе[0;3}
9.029.
1
Зх-2 -х2
7х-4-Зх
Решение.
Перепишем данное неравенство в виде
3	1 Л 3	1
-------------п------> 0» -----7----Т “ 7 
Зх2-7х+4 х2-Зх+2	U-lX^-2)
Методом интервалов получаем х е (- «>; 1)U —; 2
Ответ:
xg (-°o;l)U
9.030. -Д- <-^-z х + 2 х-3
Решение.
Имеем
_J----!_<о^ -2х-9
х + 2 х-3 (х + 2)(х-3)
< 0 €> (2х + 9)(х + 2)(х -3) > 0.
Г 9	|
Методом интервалов получаем х е I -—;-2 IU (3;оо).
----±-----►
—9/2	-	3 х
9.031.
Решение.
Ответ: хе
Зх2-10х + 3 .
------->0
х-10х + 25
V-уЪ-З)
Из условия —-'—2--
(х-5)2
* 5/-3)>0’
х*5.
помощью числовой прямой получаем х е
-®;|]U(3;5)U(5;oo).
С
Ответ-. xe^-oo;-ijU(3;5)U(5;oo).
9.032. |2х2 -9х + 15|>20.
Решение.
Имеем 2х2 - 9х +15 > 0 при х g R, следовательно, исходное нера
венство равносильно неравенству 2х2 - 9х +15 > 20,2х2 - Эх - 5 > 0,
1
2(х-5]х + — >0. Отсюда х^-—или х>5.
2
Ответ: х е
9.033. |х2-5х|<6.
Решение.
Используя геометрический смысл модуля, получаем, что
С помощью числовой прямой получаем хе (-1;2)и(3;б).
Ответ: хе (-1;2)|_|(3;б)
9.034. 5х-20£х2 £8х.
Решение.
Перепишем это неравенство в виде системы неравенств
х2 -5х+20^0, х2-8х£0.
Так как х2 - 5х + 20 > 0 при х е R, то данное неравенство равносильно неравенству х2 - 8х 2 0, х(х - 8) £ 0. С помощью метода интервалов находим хе [0;8].
9.035.
4х2 -1
£0.
Решение,
logj 7	(1 - log7 3 )^ < 0, поэтому исходное неравенство равносильно следующему: 4х2 -1^0. Решив его, найдем х > или х <	.
Ответ: х е
9.036.
0.
Решение.
logo^ (1об2 5 -1) j < О, поэтому исходное неравенство равносильно следующему: (х“8Хх-2)>0.Отсюда х<2 или%>8.

8 х
2
Ответ: х е (- «>; 2)U (8; «>}
9-037. (оД^^фХб))"46.
Решение,
Преобразовав бесконечные десятичные периодические дроби в простые, найдем
(4У*’1 >ГбУ2+6 pY~
I?)	>|<9) ’ [з,
<=>х2 <8,-272 <х<2>/2.
2х2-2	/ \х2+6
>| —I <=>2х2 -2<х2 +6<=> 3
9.038.
Зх2-16х + 21
logo,з И + <)
Решение.
Выражение log0>3 (х2 +4)< 0 при xg R. Следовательно, исходнс неравенство равносильно неравенству
Зх2-16х + 21 >0, 3(х-3)|х-- |>0. 1	3
Методом интервалов получаем х е
J ]и(3;~).
Ответ: х е
9.039. —Ц*-------- < 0
4х2 — 16х Решение.
logs t2 +з)> о при хе R,поэтому 4х2 -16х<0, х(х-4)<0 . Ответ: х е (0; 4)
 - х~7	-<0.
з/4х2 -19х + 12
Решение.
Данное неравенство равносильно системе неравенств х-7<0, 4х2 -19Х + 12 >0.
9.040.
Методом интервалов получаем х е
|Vl(4; 7). 4
3/4
o^.wssss

4	7
9.041. х6-9х3+8>0.
Решение.
Пусть х3 = у. Тогда получаем у2 - 9у + 8 > 0. Решив это неравен-(х-2)(х2 +2х+4)>0,
ство, найдем
у > 8, . Тогда
х3 >8, з . т.е, _х <1,
Так как х2 +2х + 4>0 и х2 + х+1>0 при хе R, то последняя сово-х >2,
х - 2 > 0, купность неравенств равносильна совокупности
т.е.
Ответ: х е (- <»; 1)U (2; °°)i
9.042. 0,32+4+6+ '+2х > ОЗ72 (xeN}
Решение.
Данное неравенство равносильно неравенству 2+4 + 6+...+2х<72, где в левой части неравенства сумма членов арифметической прогрессии, у которой а{ = 2, d = 2, ап = 2х. Тогда получаем
2+2х	_
2	«<72,
2х-2
I 2
Отсюда имеем х2+х-72<0, -9<х<8• Так как x = neN, то л = 1,2,3,4,5,6,7.
Ответ: 1, 2, 3, 4, 5, 6, 7.
9.043. 7х2 -х-12 <х.
Решение.
Данное неравенство равносильно системе неравенств
п = х.
С помощью числовой прямой получаем х е [4; ©о).
ММ
-12 -3	0	4
Ответ: хе [4; °°).
9.044. -17 15* 2— > 0. х + 3
Решение.
17
2
Данное неравенство равносильно системе двух неравенств 17-15х-2х2 >0,	[2х2+15х-17<0,
х + 3 > 0	Iх>-3
Ответ: хе (-3; 1)
9.045. 79х-20 < х.
Решение.
Данное неравенство равносильно системе неравенств
9х-20>0, • х > 0,	<=>
9х-20<х2
х2 -9х+20>0,
х>0
х > 5, х<4,
20 9
Ответ:
хе у;4 jU(5;~)
9.046. 1 <
Зх2-7х + 8 х2 +1
Решение.
Перепишем данное неравенство в виде
Зх2-7х + 8 ,
----5----->1>
х2 +1
Зх2 - 7х + 8 » -	< 2
X2 +1
Так как х2 +1 > 0 >то получаем
2х2-7х + 7>0, х2 -7х + 6<0.
Здесь 2х2 - 7х + 7 > О при хе R, поэтому эта система равносильна неравенству х2-7х + 6<0, (х-1Хх-б)<0, 1<х<6.
Ответ: х е (1; б)
9.047.
х4 +х2 +1 Л —---------<0.
х2 - 4х - 5
Решение.
Так как х4 + х2+1>0 при х е R, поэтому имеем х2-4х-5<0> (х + 1Хх-5)<0, -1<х<5.
Ответ: х е (-1; 5)
4 — х 1
9.048. —у > — х-5 1-
Решение.
ОДЗ:	х *1, х
Из условия
4-х	1 Л (4-хХ1“*)“* + 5 л х2-6х+9
—	(x-5Xi-«) >0'F3Fr
Jx-5^-i) < °’ (х _	~ 5Х* - 0 < °-
Методом интервалов находим х е (1;3)U(3;5).
Ответ: х е (1; 3)U (3; 5) 9.049. lglOle^2+21^ > 1 + lgx. Решение.
ОДЗ: х > 0.
Получаем
lg(x2 +21)> lglO+lgx <=> lg(v2 +21)>lgl0x <=>
x2 +21>10x, x>0
x2-10x + 21>0,
Ответ: x e (O; 3)U (7; «J
x2 -3x + 2
9.050. -j—------
x + 3x + 2 Решение.
ОДЗ: x * -2, x Ф -1. Имеем
Методом интервалов находим х € (- оо' — 2)U(-l;0].
Ответ: х g (-<»;- 2)U (-1; О]
9.051.
1 \*2-2х
3
7
Решение.
ОДЗ:	х 0.
Из условия
х2-2х
Ы "I7
Ответ: xg (0;2j
ч°
г2
< 0,
.2
<0,
(х-2)х<0, х*0.
9.052. 21-2" <0Д25.
Решение.
ОДЗ:	х * 0.
Перепишем данное неравенство в виде
1	±±±11
21-2’<2~3 <=>1-2х <-3, Iх >4, 2х >22, —>2, --2>0, х х
--->0, ---<0, (2х-1д<0.
X	X
С помощью числовой прямой находим х е 10; — .
Ответ: х е0; —
I 2 J
9.053. х2-3х-3X+1 SO.
Решение.
Из условия х2-3х-3-3Х <0, Зх(х2 ~з)<0. Так как 3х >0 при х € R, то полученное неравенство равносильно неравенству х2 - 3 S 0, х2 <3> -7з SxsV3 •
Ответ: х е
9.054. 52л+1 >5Х +4.
Решение.
Имеем 5 - ($х J* - (з* )+ 4 > 0 ♦ Решив его как квадратное относитель-
4
но 5х , получим 55 < -у, 0, или 5х > 1, откуда х >0.
Ответ: х е (0; <»)
9.055. 0,5 х~2 > 6.
Решение.
Из условия
22"* >6, log222-x >log26<=>2-x>log22-3, х <2-1 -log2 3, х < l~log2 3.
Ответ: x g (- <»; 1 - log2 3)
lOgQjfc + l)
9-056- log03100-log03 9 < 
Решение.
ОДЗ: Имеем
bgo,3U + l)-logo,3 ---------------------9 <0
.	100
1оВо,з-£-
,^-i<o, ,	100
logo,3 —
100 где log0 з < 0 • Следовательно,
i (	1^1 ЮО л i ( й i 100
log0>3 U+1 J-log0,3 — > 0, log0>3 (x+1) > log0>3 — <=>
9-91<o,
100
9 ’<=>{ 100
91 9
I i 91 Ответ: x € ~ "9”
log, logz-j— 9.057.0,3 3	>1.
Решение.
Перепишем неравенство в виде
1°810g	3*+6	3*+6	3*+6
оз 3	>03u<=>log! log2-=—-<0, logz-y—>1, -J—>2,
з jc+2	xz+2	jr+2
3x + 6	n 3x + 6-2x2-4 л -2x2+3x + 2 2x2-3x-2
-z----2>0, ------------->0, -----5, ----------------<0.
x +2	x +2	x +2 x +2
,	1	1
Так как х2 + 2 > 0 , то 2х2 -Зх-2 <О, — < х <2 . 2
Ответ: xG|-^-;2|.
I 2 7 .	. 5х
iogo,4Xl0go,4V < 9.058. 2	2 >1.
Решение.
ОДЗ:	х>0.
Из условия logo 4 X’lOgo 4~“	п	$Х
2	2 >2° <=>iog04x-log04 — >0<=>
«log0>4 х| log04 х+log0(41 I > 0.
Отсюда
,	i 5
logo,4*>-log0,4-, z
logo,4 x<°
0<x<|,
Ответ: xg 0;j U (1; °°)l
9.059. 4*-22(x-i> + 83<* 2)>52.
Решение.
Имеем
4х-4X“*+4X-2 > 52, 4х-—+—>52, 4	16
13-4X >16-52,
4х > 43 <=> x > 3.
Ответ: x 6 (3; ©°),
9.060. 21og8(x-2)-log8(x-3)> |.
Решение. *
ОДЗ:	x>3.
Имеем
log8(x-2y -log8(x-3)> j,
1Og8 —
(x-2)2 x-3
2
2
3
х2-4х+4 . Л 	 	Л 'S 11	U-4
		 	*+ V,	
<=>•	х-3	<=>'	х-3
х>3	х>3
>0,
Ответ: х е (3; 4)U (4; <»)
х#4,
х>3.
9.061. 25х <6 5х-5.
Решение.
Записав неравенство в виде (5х Г - 6 рх)+ 5 < 0 и решив его как
квадратное относительно 5х, получим 1 <5х <5, откуда найдем 0 <х<1 •
Ответ: х € (0; 1)
\1о8о.25(<2-5х+8)
9.062. у	<2,5.
Решение.
ОДЗ: х е R.
Имеем
<=> х2-5х+4£0, 1£х£4.
2 \|о8о’5(*2-5*+8)
5
<=> х2-5х+8 <4 <=>
Ответ: х е [1; 4J
1-1	1-2
9.063. 4 х -2х -3<0.
Решение.
ОДЗ: х * 0.
2х
Из условия ----L-
4
-12<0, решим его
_1_	£
как квадратное относительно 2х . Получим 2 х >-3 , откуда найдем
х#0, или 2х <4, откуда найдем
— <2, — -2<0, ——<0,
(2х-1)х>0,
2*
Ответ:
2 хЗ(2х-7)	4х+1
у -12,25 2 >1.
Решение, Из условия
М(2*-7) г 49^
V
<=>3-(2х-7)^4х+1, х<И1.
Ответ: х е (- «>; 11J
9.064.
2 V(2x~7)
7 ,
2>.4х+!
7
4
15
9.065. ——----Г>1
4 + Зх-х
Решение,
Перенесем 1 в левую часть неравенства и приведем его к общему
„ х2-Зх + 11 Л	2	Л
знаменателю. Имеем —-z-------<0. Так как х -Зх+11>0 при
. х2-Зх-4
х€Я,тох2-Зх-4<0. Решив это неравенство, найдем -I < х < 4.
Ответ: х е (-1; 4)
9.066. 0,64 < Vo,8x(x-3) <1.
Решение.
Перепишем неравенство в виде х2 — Зх -——>0, 2
х2 — Зх ——<2 2
—Зх
(0,8)2<(0>8)-^-<(0,8Г^
х2 -Зло 0, х2 -Зх-4<0
С помощью числовой прямой получаем х е (- l;0)U(3;4)
-1	0	3	4 х
Ответ: х € (-1; 0)U (3; 4}
9.067. y + log9x-log35x>log|(x + 3)
2	з
Решение.
ОДЗ: х > 0.
Перейдем к основанию 3. Имеем
|+1 log3 х - log3 5х > -log3 (х+3) log3 .v-21og3 5x+21og3(x + 3)>-l <=>
log3 Л - log3 25x2 + log3 (x + з)2 > -1, log3 x(x+rf > _ 1
25x
Ответ: x e (O; «>)
9.068. |о8;и°-, >0 .v+5
Решение.
Переходя к основанию 0,3, получаем
Ответ: х е (1; <»)
9.069. (log0>2(x-l))2 >4.
Решение.
ОДЗ: х >1.
Переходя к равносильному неравенству, получаем |logo,2 (х ~ > 2 . Отсюда:
1) log02(x-l)>2<=>0<x-l<(0^)2 « 1 <х< 1,04;
2) log0,2(х-0< “2	х-1 > (0,2)'2, х > 26 .
Ответ: х € (1; l,04)U (26;«)
,	2х-8 Л
9.070. 10g15------ < 0.
х-2
Решение.
Данное неравенство равносильно системе двух неравенств
2х-8 х-2 2х—8 . х-2
С помощью числовой прямой получаем хе (4; б).
2	4	6 х
Ответ: х е (4; б)
9.071. log0>J(x2 -5х + 7)> 0.
Решение.
Данное неравенство равносильно системе двух неравенств
Ответ: х е (2;3)
9.072. х8 - 6х7 + 9х6 - х2 + 6х -9 < 0.
Решение.
Перепишем неравенство в виде
х6(х2 -6х + 9)-(х2 -6х+9)<0, (к6 - 1)(х2 -6х + 9)<0,
(х-З)2^3 - 1р +1)<0, (х-3)2 (х-1)(х2 + х + 1)[х + 1)(х2 -х + 1)<0.
В этом неравенстве выражение х2+х + 1>0 и х2 - х +1 > 0 при х е R, поэтому оно равносильно неравенству (х - З)2 (х - 1Хх +1) < 0. Методом интервалов получаем х g (-1; 1).
Ответ: xg(-1;1)
9.073. а4 + а3 - а -1 < 0.
Решение.
Группируя, получаем
а3(а + 1)-(л+ 1)< 0, (д + 1)(д3 -1)<0, (а + 1Хя - 1)(а2 +а + 1)<0.
В этом неравенстве а1 + а +1 > 0 при a g R , поэтому оно равносильно неравенству (а + 1Х« -1) < 0. С помощью числовой прямой получаем
Ответ: ае(-1;1)
9.074. т3 + т2 - т -1 > 0.
Решение.
Из условия
/n2(w + l)-(w+l)>0, (ж + 1)(/и2-1)>0, (w + 1Xw + 1Xw-0>0>
/	1Y2/ п |7и-1>0,	(т>1,
(w+1 г(/и-1)>0<=>	<=> ^	т>1.
'	|ет+1*0	|ет*-1,
Ответ: те (1;
°°^
9.075. log2 1 + log । x - log9 x < 1.
.	9
Решение.
Данное неравенство равносильно двойному неравенству 0 < 1 + log 1 х - log9 х < 2, -1 < log i х - log9 x < 1.
’ 1 9
Перейдем к основанию у . Имеем
—1 <log] x+log। х< 1, -l<21og1x<l, -i<log( x<i<=>
9	2	9	2
9
9
1 <=>-<x<3.
3
„	0 a
Ответ: xe —;3 3
log?* 4
Решение,
<№*>»• bfc.
Из условия x 2	>2, x 4 >2. Логарифмируя обе части нера-
венства по основанию 2, получаем lOgjX	.
log2x 4 >log22, °^2Х -log2x >1, log2x >4 «=>|log2 x| >2 =>
=^1) log2 x < -2, или 2) log2 x > 2 .
Отсюда: 1) 0 < x < — или 2) x > 4 .
4
Ответ: x 6 (0; — |U (4;
I 4 I
9.077. 2x+2 -2x+3 -2X+4 >5X+I -5x+2.
Решение.
Имеем
4-2x-8-2x-16-2x >5-5x-25-5x, -20-2x >-20-5x «
(2 Y . (2 y
<=> — <1, — • l5J w
Ответ: x g (O; <»)
2?
У , x>0.
9.078. 0,32х "3х+6 < 0,00243.
Решение.
Из условия
0,32х2-3х+6<035 <=> 2х2-Зх + 6 > 5, 2х2-Зх + 1 > 0,
Ответ: х е | - <»; - |U (1; оо)
I 27
— X2 + X — 1
9.079. --- 	 <0.
х + 8
Решение.
ОДЗ: х Ф —8.
х2(х-1)+(х-1) Л (х-1)(х2+1) Л
Перепишем неравенство в виде — --------- < 0,----—1 ь 0.
Так как х2 +1 > 0 при хе А,тополученноенеравенстворавносильносио [(х-1Хх + 8)<0, теме неравенств < (х * - 8.
Методом интервалов получаем х е (- 8; 1].
Ответ: х е (- 8; 1J
9.080.
х4-2х2-8 л ---------<0.
х2 +2х + 1
Решение.
ОДЗ:	х*-1.
Решив биквадратное уравнение х4 - 2х2 - 8 = 0, представим нера-(х2 +2Ух2 -4)
венство в виде	---‘<0. Так как х2+2>0 при хе R и
(х + 1)2
(х + 1)2 > 0 при х — 1, то это неравенство равносильно системе нера-
венств
(х-2Хх+2)<0, х*-1.
Ответ: х € (- 2; - 1)U (-1; 2).
9.081. log12(x-2)+logw(x + 2)< log12 5.
Решение.
ОДЗ: х > 2.
Имеем logl2(x-2Xx + 2)< logw 5. С учетом ОДЗ полученное неравенство равносильно системе неравенств
Ответ: х е (2;3)
Решение.
ОДЗ: х * -3, х * -2, х * -1. Имеем
(х-1Хх-2Хх-3)	-12х2-6	„
(х + 1Х«Т2Т+з)‘ ’ ~ (х + 1Хх + 2Х« + з)’° ~
2х2+1
Так как 2х2 +1 > 0 при хе R, то полученное неравенство равносильно неравенству (х + 1Хх + 2\х + 3) < 0. Методом интервалов находим х е (-«о; - 3)U (-2; -1).
<>-----<>
-1 х
Ответ: х е (-<»; -3)U (-2; -1)
’081
Решение.
ОДЗ: х # -1. Из условия
-------------< 0 «=> 3х+5 3-3Х-1
3-Зх-1-Зх-5 Л (зх + 5Ь-Г-1)< ’
2-Зх-6 л
(З^З Г-!^ ’
Так как 3х + 5 > О ПРИ хе R, то это неравенство равносильно нера-
2-Зх-6 венству -------
3-Зх-1
<0, (зх-3]3х-- |<0, З’1 <3Х <3, -1<х<1.
1	3
Ответ: хе(-1;1)
9.084. logx (log9 (зх - 9))< 1.
Решение.
ОДЗ:
хе (0;l)U(l; + ~l 3х-9 >1,
х€ (0; 1)U (1;+ °4 3х >10,
хе (log310; + оо}
Получаем следующую систему неравенств
x>log310,	[x>log310,
logx(log9(3' -9))< logx х ** [log9(зх -9)< x
x>log310,	x>log310,	x>log310,
log9(3x-9)<log99x [3х-9<32x	1^хУ-Зх+9>0<=>
[xe (log310;+oo} |xe R.
Отсюда x e I-Д-lg3
Ответ: x G
х2+2
9.085. 0,2	>25.
Решение.
ОДЗ:	х*±1.
Перепишем неравенство в виде
X2 +2	2	2
г’,*-. . .2 .. х +2>2 Л_!2+2<0, ’	2_1
х2+2+2х2-2 л
——<0-
.2
Зх2 J-7<0’
х*0,	[.
х2-1<0 Ответ: х е (-1; 0)U (О; 1)
х*0,
9.086. 52^ +5<5^+1 + 5^.
Решение.
( J~ V J— Jx
Представим данное неравенство в виде 5V*	+ 5<5-5VJt+5,
/ j- \2	j~
5 vx - 6 • 5 vx + 5 < 0. Решив это неравенство как квадратное относи-
тельно 5^,получим 1 <5^ <5, 0<Vx<l, 0<х<1-
Ответ: х е (0; 1)
9.087. |3-log2 х|<2.
Решение.
ОДЗ:	х > 0.
Данное неравенство равносильно неравенству
-2 <3 -log2 х <2, -5 < -log2 х < -1 <=> 1 < log2 х < 5, 2 < х < 32.
Ответ: х G (2; 32}
9.088. 5-0,2lgx >0,04lg2.
Решение.
ОДЗ:	х > 0.
Имеем
5-5”'8Х >5-2182, 5I-l8x >5’184 <=> 1-lgx>-lg4, lgx-lg4<l,
lg-<l<=»0<-<10, 0<x<40.
4	4
Ответ: x e (0; 40)
9.089. log2Iogl 1оё5*>0-
3
Решение.
Это неравенство равносильно неравенству
log j log5 х > 1 <=> 0 < log5 л < - <=> 1 < х < ^5. 3
Ответ: xe(l;Vs)
9.090.	+3Va--i _^Vx-2 <ц
Решение.
ОДЗ: х > 0.
Из условия 3^ 4--^—-^—<11,11-3^ <911,3^ <32 .Оно равносильно неравенству Vx<2,0^x<4.
Ответ: xe[0;4)l
9.091. о,5х < 0,25 х2.
Решение.
Имеем 0,5х <0,52х'<=> х>2х2, 2х2-х<0, х(2х-1)<0. Методом
интервалов получаем х е
> х
А 1 Ответ: хе 0; — . 2_
9.092. logo>5 х + log0 5 х - 2 < 0.
Решение.
ОДЗ:	х > 0.
Решив это неравенство как квадратное относительно log0,5 х»полу
чим -2 < log0 5 х < 1,0,5 < х < 4 .
Ответ: х е [0,5; 4J
1	*-2
log,--
9.093. 5 ’ * <1.
Решение.
x — 2 ОДЗ: =-=- > 0. x
x—2
Это неравенство равносильно неравенству log3------< 0, а после-
х
днее неравенство эквивалентно системе двух неравенств
Методом интервалов получаем х е (2; оо).
Ответ: х е (2; оо)
9.094. log3 х + log^j х + log j x < 6.
з
Решение.
ОДЗ: х > 0.
Перейдем к основанию 3. Получим log3 х + 21og3 х - log3 х < 6, 21og3x<6, log3x<3, 0<х<27-
Ответ: хе(0;27).
9.095. log4(x + 7)> log2(x + l}
Решение,
QR3-. х >-1.
Перейдем к основанию 2. Имеем
log2 (х 4- 7) > log2 (х + 1)<=> log2(x + 7)>21og2(x + l)<=>
<=> loga (^ + 7) > log2 (х +1)2.
Последнее неравенство равносильно с учетом ОДЗ системе неравенств
Ответ: хе(-1;2)
Решения к главе 10
ЗАДАЧИ ПО ПЛАНИМЕТРИИ
ОСНОВНЫЕ ФОРМУЛЫ
1. Произвольный треугольник (а, с —стороны; а, Р, Y — противолежащие им углы; р —полупериметр; Л —радиус описанной окружности; г — радиус вписанной окружности; S —площадь; ha — высота, проведенная к стороне а):
5 = |айа;	(ЮЛ)
S = — 6с sin а • 2	(10.2)
S = -Jp(p-a/p-b^j>-c);	(Ю.З)
S г = —. Р '	(Ю.4)
R^- 4S '	(Ю.5)
S - °2 2sin^4	(10.6)
а2 = b2 +с2 - 2bccos а (теорема косинусов);	(Ю.7)
а	b	с	, = .	= .	=2А (теорема синусов), sina sinp smy	(10.8)
2. Прямоугольный треугольник (а, Ь — катеты; с ас, Ьс — проекции катетов на гипотенузу):	— гипотенуза;
S = —ab- 2	’	(Ю.9)
s={chc’	(10.10)
a + b-c	(10.11)
r =	• 2	’	
/? = -; 2 ’	(10.12)
a2 +b2 - с2 (теорема Пифагора);	(10.13)
/	hc bc	(10.14)
ac	.	(10.15)
a c bc _b	
	(10.16)
b c	
a = csina = ccos|$ = Z>tga = i>ctgP.	(10.17)
3. Равносторонний треугольник:	
с_а2Л . •Э —	. 4	(10.18)
а-Ji	(10.19)
г =	; 6	
3	(10.20)
4. Произвольный выпуклый четырехугольник^ и d2	—диагона-
ли; ф —угол между ними; S —площадь):	
о	1 J J . S = —^i^2sin ф.	(10.21)
5. Параллелограмм (a и b —смежные стороны; a —	угол между
ними; ha — высота, проведенная к стороне а):	
S = aha =adsina = ~^i^2 sinep.	(10.22)
6. Ромб:	
S = aha =a2 sina = yJ1J2.	(10.23)
7.	Прямоугольник:
8.	Квадрат (J —диагональ):
S=a2=d2/2.	(10.25)
9.	Трапеция (а и b —основания; h —расстояние между ними;./ — средняя линия):
/ =	(Ю.26)
S = ^~h = lh.	(\Ь.2Т)
10.	Описанный многоугольник (р — полупериметр; г — радиус вписанной окружности):
S = pr.	(10.28)
11.	Правильный многоугольник (ап — сторона правильного «-угольника; R —радиус описанной окружности; г —радиус вписанной окружности):
а3 = Л-Л; а4 = Rj2 ; a6=R;	(10.29)
S = ^-	(Ю-ЗО)
12.	Окружность, круг (г —радиус; С —длина окружности; S — площадь круга):
С = 2яг;	(10.31)
5 = яг2-	(Ю.32)
13.	Сектор (/ —длина дуги, ограничивающей сектор; п —градусная мера центрального угла; а — радианная мера центрального угла):
/ = ^- = га;	(10.33)
180’
? о я о 7W* «	1 j	z«л а 1 \
s =------= -г2а.	(10.34)
360’	2
ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
1.	Три медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины треугольника.
2.	Длина медианы треугольника выражается формулой та = ^72t>2 +с2)-а2 , где а, Ь, с —длины сторон треугольника.
3.	Длина стороны треугольника выражается формулой a = |72(W*	>
где та, ть, тс —длины медиан треугольника.
4.	Биссектриса делит сторону треугольника на отрезки, пропорциональные двум другим его сторонам.
5.	Длина биссектрисы треугольника выражается формулой lc = y/ab-a^ ,
где а и Ь —длины двух сторон треугольника АВС; ах и Ьх —отрезки третьей стороны.
6.	Длина биссектрисы треугольника выражается через длины его сторон а , Ь и с по формуле
_ y]ab(a + £ + сХа + 6 - с) с	а + Ь
7.	Для всякого треугольника зависимость между его высотами ha , hb, hc и радиусом г вписанной окружности выражается формулой
1111 --+---4---= -ha hb hc г ‘
8.	Площадь S равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату ее высоты, т.е. S = h2 .
9.	Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим ее оснований.
Доказательство всех этих дополнительных соотношений можно найти в любом издании данного сборника задач последних лет.
10.	001. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найти катеты треугольника.
Решение.
По условию ЛЕ = 5 см,ЕЕ = 12 см (рис. 10.1). Обозначим через г—радиус вписанной окружности. BE = BP = 12 см, PC = г, ВС = PC + BP = 12 + г, AE = AF, CF = r, AC = CF + AF = г + 5, AB = AE + EB = 12 + 5 = 17. ЛАВС, ZC = 90°. Имеем AB2 = AC2 + BC2, (r + 12f+(rЧ-5)2 =289, r2 + 17r-60 = 0, r = 3 см.Следовательно, BC = \5 cm, AC = 8 cm.
Ответ: 8 см, 15 см.
10.	002. Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
Решение.
Так как AD —диаметр окружности (рис. 10.2), то OD = ОС = 10 см. Проведем CL1AD; тогда OL = 6 см и из ACLO находим
CL = 4ОС2 -OL2 = 8 (см).
Тогда из ДЛ£С и &CLD имеем
АС = -JCL2 + AL2 = V64 + 256 = (см)
И	__________
CD = -JCL2+LD2 = 764 + 16 = 4^5 (см).
Ответ: 4-Js и 8-^5 см.
Рис. 10.4
10.	003. В равнобедренной трапеции даны основания а = 21 см, b = 9 см и высота h = 8 см. Найти радиус описанного круга.
Решение.
Трапеция ABCD вписана в круг (рис. 10.3). Значит, &ABD —вписан.
21-9
ВС = 9 см, AD = 2\c^yBE^h = i см, АЕ = —; АЛЕВ, ХВЕЛ =90°.
2
Имеем
АВ = 764 + 36 = 10 см; ABED, ABED = 90°.
Имеем
ED = AD-АЕ = 2\-Ь = \5 см, ££> = 7225 + 64 =17 См.
Обозначим через R радиус описанного круга:
D ABBDAD 17 10 21
R =-----------= —-------= 10,625 см.
4 • — • 8 • 21
2
Ответ: 10,625 см.
10.004. Высота ромба, проведенная из вершины тупого угла, делит его сторону на отрезки длиной т и п. Определить диагонали ромба.
Решение.
Длина стороны ромба равна т + п . Из &АВК (рис. 10.4) находим ВК2 — (т + пУ - т2. В \BKD имеем
BD2 = ВК2 +п2 =(т + пУ -т2 +п2 = 2п(т + п),
т.е. BD = yl2n(m + п) •
Так как AC2 + BD2 = 4AD2 = 4(?и + и)2, то
А С2 = 4(/и + п)2 - 2тп - 2п2 = 4т2 + бши + 2п2, т.е АС = yl4m2 + 6тп + 2п2.
Ответ: BD = у]2п(т + и),ЛС = V4m2 + бтп + 2п2.
10.005. В прямоугольный треугольник с катетами а и Ь вписан квадрат, имеющий имеющий с треугольником общий прямой угол. Найти периметр квадрата.
Решение.
Обозначим сторону квадрата через х (рис. 10.5). Так как а Ь
ААСВ- &FEB, то — = ---. Имеем
х Ь-х
ab п . 4аЬ
х =----,Р = 4х =---.
а+Ь	а+Ь
Ответ: ---
а+Ь
10.006. Две окружности радиусов R = 3 см и г = 1 см касаются внешним образом. Найти растояние отточки касания окружностей до их общих касательных.
Решение.
Обозначим FM = x
R-r R+r ----=------, отсюда
(рис. 10.6). Из &О\ТО - &FMO имеем г(Я-г) „	r(R-r) 2Rr
R + r	R + r R+r
6 3 п . .
= — = — см. Если же в качестве общей касательной окружностей рассматривать прямую EF, то искомое расстояние равно нулю.
Ответ: 0 и — см.
2
Рис. 10.7
Рис. 10.8
10<007. Около окружности диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найти основания трапеции.
Решение.
По условию KQ = 15 см, АВ - CD = 17 см, ВС + AD = АВ + CD = 34. В ДСЕО Z.CED = 90°, СЕ = KQ (рис. 10.7) Имеем DE = V289-225 = 8 см, AD = 2ED +ВС = 16 +ВС, ВС + \6 + ВС = 34, ВС = 9 см, Л£> = 25 см. Ответ: 9 см; 25 см.
10.008. В равнобедренном треугольнике с боковой стороной, равной 4 см, проведена медиана боковой стороны. Найти основание треугольника, если медиана равна 3 см.
Решение.
Используя теорему косинусов, получим
х2 = 16 + 16-216cosa, т2 = 16 +4-2-8 cosa
=> х2 -2т2 = -8, х2 = 10, х = V10 (рис. 10.8).
Ответ: л/То см.
10.009. В равнобедренном треугольнике основание равно 16 см, а боковая сторона равна 10 см. Найти радиусы вписанной и описанной окружностей и расстояние между их центрами.
Решение.
SMBC = ^AC-BD, где BD = >IaB2-AD2 = 71O2 -82 = 6 (рис. 10.9), т.е. S^bc = 6-8 = 48(см2). Пусть Лиг— радиусы описанной и вписанной в треугольник окружностей. Тогда
„ АВВСАС 10 10 16 25, ч S 48 8, .
R =----------=--------=—(см), г = — = — = —(см),
4S 4-48	3	р 18 3
где р — полупериметр &АВС. Расстояние между центрами 0{02 = 02В-01В = 02В-(ВО-0}0) = В-(6-г) = К + г-6 =
25 8 . ,, , с
- —+—-6-11 — 6 = 5 (см).
8 25
Ответ: — и 5 см. 3 3
10.010. Каждая сторона правильного треугольника разделена на три равные части, и соответственные точки деления, считая в одном направлении, соединены между собой. В полученный правильный треугольник вписана окружность радиуса г = 6 см. Определить стороны треугольников.
Решение.
По условию AS = CS = AC, SB = BD = DC = MC = KM = AK = AF = ГГ rc .	/ 1Л1МС	FB + BM + FM 3FB
= FE- ES, r = 6 см (рис. lO.lO).*?^^ =------r = —• r.
S*™, = FB2—, т.е. FB = 12л/з см. В &AFM ZAFAM = 60°, AF =—, ил	д	2
AM = -| A C, FM 2 = AF2 + AM 2 - 2 • AF  AM  cos ZFAM (по теореме косинусов), откуда FM2 =^— + — AS2-2 — AS2 •—, FM2 = — 9	9	9	2	9
J<?	r-	r-r-
FM = —j=,AS = FM•>/3, FM = BF, AS = 12V3 • V3 = 36 cm.
V3
Ответ: 12>/з см и 36 см.
Рис. 10.12
10.011. Основание равнобедренного треугольника равно 4^/2 см>а медиана боковой стороны 5 см. Найти длины боковых сторон.
Решение.
Так как ДЛВС —равнобедренный, то высота BD является медианой (рис. 10.11); далее, точка пересечения медиан делит каждую из них
в отношении 2:1, откуда АО = — (см). Из AAOD получим
od = Jao2 -ad2
(е„).
т.е. BD = >/28 (см). Из &BDC имеем ВС = Л/^У+^У = 6 (см).
Ответ: ВС = 6 см.
10.012. Из точки А, не лежащей на окружности, проведены к ней касательная и секущая (рис. 10.12). Расстояние от точки А до точки касания равно 16 см, а до одной из точек пересечения секущей с окружностью равно 32 см. Найти радиус окружности, если секущая удалена от ее центра на 5 см.
Решение.
По условию ЛС = 32 см, ЕО = 5 см, ЛВ = 16 см, АВ2 = ACAD,
АС - AD 
256 = 32-AD, AD = 8 см, СЕ =---= 12 см,С0 = 725+ 144 = 13см.
Ответ: 13 см.
10.013. Дан треугольник со сторонами 12, 15 и 18 см. Проведена окружность, касающаяся обеих меньших сторон и имеющая центр на большей стороне. Найти отрезки, на которые центр окружности делит большую сторону треугольника.
Решение.
Используя теорему косинусов, из рис. 10.13 имеем:
АВ2 = ВС2 + АС2-2-ВС-AC-cosa =>
=> 122 = 152 +182 -2-15 18cosa, cosa = —, sina = Vl-cos2 a =	;
4	4
BC2 =AB2+AC2 -2- AB- ЛС-cosp =>
=> 152 =122 +182 -21218-cosp, cosp = ^, sinp =-Ji-cos2 p =	.
OM R . n OK R sina x 4
sm a =---=-------. sin p =-= — и —— =--------= —.
ОС 18-х АО х sin(3 18-х 5
5х = 72-4х, 9х = 72, х = 8, У = Ю. АО = Ъ см, ОС = Ю см.
Ответ: 8 и 10 см.
10.014. Хорда окружности равна 10 см. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Определить радиус окружности, если внутренний отрезок секущей равен 12 см.
Решение.
Проведем радиус в точку А ;таккак ,то ОА1ВС и BD = 6 см (рис. 10.14). Пусть О А = г, OD = х. Тогда AD = у1аВ2 -BD2 = 8, т.е. r + x = 8 (1). Но OD2 = OB2 -BD2 или г2-х2=36; так как
г2 - х2 = (г + хХг - х), то г - х = 36/8 = 9/2 (2). Решив систему уравнений (1) и (2), найдем г = 6,25 (см).
Ответ: 6,25 см.
10.015. Через концы дуги окружности, содержащей 120°, проведены касательные, и в фигуру, ограниченную этими касательными и данной дугой, вписана окружность. Доказать, что ее длина равна длине исходной дуги.
Решение.
Обозначим через г — радиус вписанной окружности, R — радиус
дуги. ААО{В = (Л°, АВАОХ =90° (рис. 10.15), значит, ААВОХ =30°. Из
ДВЛ Ох имеем ВО{ = ——— = 2R, из АВЕО2 /.ВЕО^ = 90°. Отсюда sin 30°
ВО2 = 2г, ОХО2 = 2(В-г). По условию получим, что О{О2 = R + r,
2(B-r)=B + r, B = 3r, г = у; таким образом, 1{ = 2к-г = ^^- —длина вписанной окружности, /2 = R. а = R • —. Следовательно, 1Х = /2, что и требовалось доказать.
10.016. В сектор АОВ с радиусом R и углом 90° вписана окружность, касающаяся отрезков ОАУ О В и дуги АВ (рис. 10.16). Найти радиус окружности.
Решение.
&0MF —равнобедренный (Z.MOB = Z.MFO = 45°). Отсюда МО = MF, OF = R^2 . Из AOigO ~ &OMF имеем — = Г , г = r{J2 -1).
R J2R	7
Ответ: в(л/2-1)
10.017. Дана точка Р, удаленная на 7 см от центра окружности радиуса 11 см. Через эту точку проведена хорда длиной 18 см. Каковы длины отрезков, на которые делится хорда точкой Р?
Решение.
Проведем диаметр CD через точку Р (рис. 10.17), которая разделит его на отрезки PD и СР длиной 11-7 = 4и11 + 7 = 18 (см). Пусть АР = х; тогда РР = 18-х. Так как ЯРРР = СРР£> = 418, то х(18-х) = 72 или х2 -18х + 72 = 0, откуда Xj = 12, Х2 = 6, т.е. хорда ЯР делится точкой Р на отрезки длиной 12 и 6 см.
Ответ: 12 и 6 см.
10.018. Найти длины сторон АВ и АС треугольника АВС, если ВС = 8 см, а длины высот, проведенью к АС и ВС, равны соответственно 6,4 и 4 см.
Решение.
По условию ЯС = 8 см, ЯР = 4 см, Р/С = 6,4 см (рис. 10.18).Из
&ВКС-&АЕС следует, что	; АС = 5 см. Из АЯЕС имеем
4 АС
СЕ = 725-16 =3 см, BE = 8-3 = 5 см; тогда из ДЯЕР находим ЯР = 716 +25 =74? см.
Ответ:	см, 5 см.
10.019. Площадь равностороннего треугольника, вписанного в окружность,равна Q2 (рис. 10.19). Доказать, что радиус окружности равен 2£?7з/3.
Решение.
По условию Smbc - Q2» АВ = ВС = АС. Пусть ВО = ОС = АО = В, тогда 3$д,ос =б2, 3fl2.l sinl20° = e2, ^Я2 =02,й = J-^02 = 2	4	у 3^/3
2(?^3	,
= —, что и требовалось доказать.
10.020. В пересечение двух равных кругов вписан ромб с диагоналями 12 и 6 см. Найти радиус окружности.
Решение.
По условию ABCD —ромб, BD = 12 см, А С = 6 см(рис. 10.20).0бозна-
АС
чим: ОХО = х , R — радиус окружностей. Тогда х = R------= R-3.
В ЩОВ ZOIOB = 90°, R2 = 36 + (/?-3)2, Л = —= —см.
6	2
Ответ: 7,5 см.
10.021. Медиана, проведенная к гипотенузе прямоугольного треугольника, равна т и делит прямой угол в отношении 1:2. Найти стороны треугольника.
Решение.
„	ЛВСО 2
По условию С0 = т> АО=ВО,------= -, АВ = 2т (О —центр
ЛА СО 1
описанной окружности) (рис. 10.21). Обозначим ЛАСО=х, ЛВСО = 2х,
х + 2х = 90°, х = 30°, ЛАСО = ЛСАО. В ЛАВС ЛАСВ = 90° , ВС = 2m-sin 30° = т , АС = ^4т2 -т2 = т4з .
Ответ: т ; ггь/з , 2т .
10.022. Определить острые углы прямоугольного треугольника, если медиана, проведенная к его гипотенузе, делит прямой угол в отношении 1:2.
Решение.
ЛВСО 2
АО=ОВ, —77-г(рис. 10.22). В &АВС ЛАСВ = 90 ; таким ЛАСО 1
образом, О —центр описанной окружности, значит, АО = ОВ = СО, &АОС —равнобедренный, ЛА = ЛОСА, ЛВ = ЛВСО. Обозначим
Рис. 10.23
ZOCA - х , значит, ZBCO = 2х, х + 2х = 90°, х = 30°, таким образом, Z^=30\ ZBCO = ZB = 60°.
Ответ: 30°, 60°.
10.023. Дан квадрат, две вершины которого лежат на окружности радиуса R, две другие — на касательной к этой окружности. Найти длину диагонали квадрата.
Решение.
Пусть х —сторона квадрата (рис. 10.23), в АОЕА ZOEA = 90°, ЕА2 = OA2-OE2,R2-(x-Rf =Z,Z + X2 =2xR;x = — -,AC = x>/2^ v ’	4 4	5
= — -4z=\£r41 .
5
Ответ: 1,6/?V2.
10.024. Длины параллельных сторон трапеции равны 25 и 4 см, а длины непараллельных сторон — 20 и 13 см. Найти высоту трапеции.
Решение.
По условию ДС = 4 cm, AD = 25 см, АВ = 20 см, CD = 13 см (рис. 10.24). Проведем BE1AD и CF1AD. Пусть BE = CF = h, АЕ = х, FD = у. Тогда из &АВЕ и ACFD находим Л2 = 202 - х2 = 132 - у2. Учитывая, что у = 25-4-х = 21-х, имеем 202 -х2 = 132-(21-х)2 или 42х = 672, откуда х = 16 (см). Итак, h = V202 -162 = 12 (см).
Ответ: 12 см.
10.025. Общая хорда двух окружностей служит для одной из них стороной вписанного квадрата, а для другой—стороной правильного вписанного шестиугольника. Найти расстояние между центрами окруж-
Рис. 10.25
ностей, если радиус меньшей из них равен г (рассмотреть два возможных случая расположения окружностей).
Решение.
1-й случай. По условию Ох А = г , CD = 2СЕ; &0{ЕС — равнобед-
л/2	г~	г~
ренный, ZOj£C = 90°, СЕ = г •—-, CD = rV2 , R = r<2 (рис. 10.25,a).
Обозначим
CD = a = rj2, O,E = - = — = r— • ACEO2, ЛСЕО2 =90’, 2	2	2
EO2 = C£ctg30° = —Л = — 7з=—, 2	5	2	2	2’
2-йслучай. OtO2 =EO2-EOt, CD = r j2, ЕО} EOi =г4б/2,
(\O2 =	(рис. 10.25,6).
_	г(4б+Л)
Ответ: —-------------
2	2
10.026. Из внешней точки проведены к окружности секущая длиной 12 см и касательная, длина которой составляет 2/3 внутреннего отрезка секущей. Определить длину касательной.
Решение.
2
По условию ЛВ = 12 см, АС = — DB (рис. 10.26). Обозначим BD = х,
<2
|х 1 = 12(12-х), х2 +27х-324 = 0, х = 9 см,
тогда AC2 = АВ- AD ,
2 AC = —9 = 6 см.
3
Ответ: 6 см.
10.027. Каждая из трех равных окружностей радиуса г касается двух других. Найти площадь треугольника, образованного общими внешними касательными к этим окружностям.
Решение.
Треугольник АВС —правильный (рис. 10.27); поэтому его площадь рав-а24з
на------, где а — сторона треугольника. Проведем ОК1АС  Так как
4
Z<X4/C = 30°,to AO = 2r, АК = г-Л , откуда а = 2г-Уз + 2г = 2г(л/з +1).
„	_ 4r2t+2V3+l)j3
Следовательно, о =---— --------— = 2г Ц-J3 +3).
Ответ: 2г2^>/3+з)
10.028. Основания равнобедренной трапеции а и Ь, боковая сторо-
на ее равна с, а диагональ равна d. Доказать, что d2 =ab + c2 . Решение.
По условию ВС = а, AC = d, CD = c, AD = b (рис. 10.28). В &CED
Рис. 10.29
ZCED = 90’, С£2=с2-|—1.В ЛАЕС ZA ЕС =90°, d2=c2-2
_b—2ab+a +b +2ba+a . j2 =/}.a + c^, что и требовалось доказать. 4	4
10.029. Общая хорда двух пересекающихся окружностей равна а и служит для одной окружности стороной правильного вписанного треугольника, а для другой—стороной вписанного квадрата. Определить расстояние между центрами окружностей (рассмотреть два возможных случая).
Решение.
1-йслучай. Поусловию AB = a = AN = NM = MB-BD = AD, ОХЕ = --,
Z.BO2E = 2ZEDB = 60’, О2Е = ЕВ ctg60° =	,
2V3
°i°2 =	+ 4 ~ 7 + (Рис- 1 °-29’а)-
2V3 2 о
2-й случай. О{О2 = О2Е - ЕО{, ЕОХ = у, ЕО2 = ЕВ • ctg60°
а
О{О2 = -^-- = -(з-Л) (рис. 10.29, б).
Ответ:	+ 7з )/б ,	- Л )/б ♦
10.030. На сторонах квадрата вне его построены правильные треугольники, и их вершины последовательно соединены. Определить отношение периметра полученного четырехугольника к периметру данного квадрата.
Решение.
Обозначим сторону квадрата через х , тогда периметр квадрата
Ро = 4х, bFBM — равнобедренный, zLFBM = 360° - 90° - 2 • 60° = 150°,
FM = yllx2 -2x2 cos 150° = х\2 + у/з (рис. 10.30). Таким образом,
Ответ:
>/б + >/2
2
10.031. В ромб, который делится своей диагональю на два равносторонних треугольника, вписана окружность радиуса 2. Найти сторону ромба.
Решение.
Пусть а —сторона ромба, a d} и d2 —его диагонали (рис. 10.31). Так как высота ромба равна диаметру окружности, то его площадь а. С другой стороны, S = 1 dxd2, откуда, учитывая, что dx = а , находим

2 а ., или а - — +16, т.е. а =---.
4	3
Ответ: 8->/з/3.
10.032» В треугольнике длины двух сторон составляют 6 и 3 см (рис. 10.32). Найти длину третьей стороны, если полусумма высот, проведенных к данным сторонам, равна третьей высоте.
6 ha+hb = 6	+ l =	2 I 1 = 12
hb АВ' 2hb АВ hb АВ ’ АВ ’
4 см.
Решение.
По условию А С = 6 см, ВС = 3 см. Обозначим через ha, hb, hc —
высоты. Тогда = hc. ЬВЕС ~ ЛАКС => - = AANC ~ 2	6 ha
~ АЛЕВ =>
ЯВ = 4см-
Ответ:
10,033. К окружности, вписанной в равнобедренный треугольник с основанием 12 см и высотой 8 см, проведена касательная, параллельная основанию. Найти длину отрезка этой касательной, заключенного между сторонами треугольника.
Решение.	__________
Найдем длину боковой стороны ВС (рис. 10.33): ВС = уВМ2 + МС2 = = 7б2 +82 = 10 (см). Учитывая, что АО — биссектриса &АВМ, имеем МО/ОВ = AMI АВ или г/(8 - г) = 6/10, откуда г = 3 (см). Так как DE^A С, то &DBE ~ &АВС , т.е. DE/AC-BN/BM или DE/12 = (8 -2г)/8, откуда £>£ = 3 см.
Ответ: 3 см.
10.034. Из одной точки проведены к окружности две касательные (рис. 10.34). Длина каждой касательной 12 см, а расстояние между точками касания 14,4 см. Определить радиус окружности.
Решение.
По условию А К = AN = 12 см, KN -14,4 см. В &АЕК ААЕК = 90°,
AE = Jl44-fytf =9,6 см, КЕ2=АЕ ОЕ, ОЕ = ^£ = 5,4 .В ЬКЕО
ЛКЕО = 90°, Л = ^51,84 + 294 6 = 9 см.
Ответ: 9 см.
10.035. Из точки А проведены две прямые, касающиеся окружности радиуса R в точках В и С так, что треугольник АВС — равносторонний. Найти его площадь (рис. 10.35).
Решение.
По условию ОВ = ОС = R, АВ = АС = ВС . Так как ДЛВС — рав-
носторонний, то S = ВС2 —; ZABO = 90е, ZABC = 60°, АСВО = 30°, 4
BC=2J? cos30 = V3 J?, S = 3R2 —.
4
л/з
Ответ: 3R2 —.
4
10.036. В прямоугольный треугольник с углом 60° вписан ромб со стороной, равной 6 см, так, что угол 60° у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника.
Решение.
В &FBD (рис. 10.36) катет FD = 6 см и лежит против угла в 30°, откуда FB = 12 см и, значит, ЛВ = 18 см. Далее, в &АВС имеем А С = А В/2 = 9 см. Наконец, ВС = >1аВ2 - АС2 = >/243 = 9>/з (см).
Ответ: 9,9>/з и 18 см.
Рис. 10.38
10.037. Дан правильный треугольник АВС (рис. 10.37). ТочкаХ'делит сторону Л С в отношении 2:1, а точка М—сторону А В в отношении 1:2 (считая в обоих случаях от вершины А). Показать, что длина отрезка КМ равна радиусу окружности, описанной около треугольника ЛВС.
Решение. у д 2
По условию —— = —;	= —. Пусть А М = х. Так как ДЛВС — пра-
Л М 1 КС 1
вильный, то /ВА С = 60° и КМ2 = AM2 + АК2-2 AM • ЛКсозбО0;
КМ2 =4х2 +х2 -4х2 cos60°, КМ2=Зх2\ КМ = х4зR = AB—;
3
3
Что и требовалось показать.
10.038. Периметр параллелограмма равен 90 см и острый угол содержит 60° (рис. 10.38). Диагональ параллелограмма делит его тупой угол на части в отношении 1:3. Найти стороны параллелограмма.
Решение.
/ABD 3
По условию 2ВС + 2СВ = 90 см, /.BCD = 60°, ~^ЬвС = Т ‘ Имеем BC + CD = 45, Z.AВС + ZBCD = 180°. Пусть ZCBD = x, ZABD = 3x, следовательно, Зх + х + 60° = 180° и х = 30°, ZABD = 90\B &ABD AB = AD cos60°, АВ = 4г- = ^~, AB = CD, ВС + — = 45, ЗВС = 90;
2	2	2
ВС = 30 CM. AD = DC = \5 см.
Ответ: 15 и 30 см.
10.039. Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом (рис. 10.39). Найти длины сторон трапеции, если ее площадь равна 12 см2, а длина высоты равна 2 см.
Рис. 10.39
Рис. 10.40
Решение,
~	90°
По условию SMBCD = 12 см2, BE = 2 см; /LOAD = /LODA = — = 45°,
BE _ AD AD _ 2	Г'ТЪ	DC ВС + Dr _ 1
	= АВЬ АВ = .— • 2 = 2V 2 = CD, АЕ — BE — 2,-* BE = 12, sin45°-------------------------------------------------------у/2	2
.?C + AD .2 = 12,ВС + AD = 12, тогда 2ВС + 2АЕ = 12, ВС + АЕ = 6,
2
ВС + 2 = 6, ВС = 4 см, AD = 4 + 4 = 8 см.
Ответ: 4 и 8 см; 2^2 и 2^2 см.
10.040. В прямоугольный треугольник вписана полуокружность так, что диаметр лежит на гипотенузе, а центр делит гипотенузу на отрезки длиной 15 и 20 см (рис. 10.40). Найти площадь треугольника и длину вписанной полуокружности.
Решение,
По условию АО = 20 см, OB = 15 см. Обозначим через г радиус полуокружности; &AFO ~ &ОЕВ, имеем — = , Г 	; 4^225-г2 = Зг;
>5
16(225 - г1) = 9г2, г2 = 9 • 16, г = 12 см; / = яг = 12я. В ДЛГО ZAFO = 90°,
А С=V400-144+12 = 28, ВС=л/225-144 +12 = 21, S== 294 см2.
2
Ответ: 294 см2,12лсм.
10.041. Величина одного из углов параллелограмма равна 60°, а меньшая диагональ 2>/з1см. Длина перпендикуляра, проведенного из точки пересечения диагоналей к большей стороне, равна 415/2 см. Найти длины сторон и большей диагонали параллелограмма.
Решение.
Проведем BN1AD (рис. 10.41); так как BN = 20М, то BN = V75 см. Учитывая, что в &ANB Z.ABN = 30“, имеем АВ = 2AN и, значит, 4AN2 =75 + AN1, откуда AN = 5 см и ЛВ = 10 см. Далее, из NBND получим ND2 = BD2 - BN2 = 124 - 75 = 49; следовательно, ND = 1 см и JD = 12 см. Наконец, из равенства АС2 + BD2 =2АВ2 + 2AD2 находим АС2 =200+ 288-124 = 364,т.е. АС = 2451 см.
Ответ: 12 ; 10 и 2^/91 см.
10.042. Один из углов трапеции равен 30°, а прямые, содержащие боковые стороны трапеции, пересекаются под прямым углом (рис. 10.42). Найти длину меньшей боковой стороны трапеции, если ее средняя линия равна 10 см, а одно из оснований 8 см.
Решение.
По условию Z.BCA- 30°, Z.ABC = 90°, О/= 10 см, D£ = 8 см, 8 4" /4 С7
—-— = 10, АС = 12 см (так как КМ — средняя линия). Так как
АВ AC x + DB 12 ,	х	1
ДДВЕ-ДЛВС.то —= —;-^- = -(гдеЛР = х)>х = РВ-.
В ZDBE = 90°, ^-BED = ЛВСА = 30°, DB = DE sin30° =8/2 = 4, значит, х = 4 ♦ — = 2 см.
2
Ответ: 2 см.
10.043. В окружность, диаметр которой равен V12 , вписан правильный треугольник. На его высоте как на стороне построен другой пра-
Рис. 10.43
вильный треугольник, в который вписана новая окружность. Найти радиус этой окружности.
Решение.
По условию R = 0,5-ЛТ. Сторона АВ правильного вписанного треугольника (рис. 10.43) равна R-J1, т.е. 0,5-J\2 • 7з = 3. Найдем сторону CD нового треугольника: а = д/з2 -1,52 = 1,5-х/з . Так как радиус г вписанной в него окружности равен а7з/б, то окончательно получим г = 1,573-7з/б = 3/4.
Ответ: 3/4.
10.044. В окружности проведены две хорды АВ = а и АС = Ь. Длина дуги А С вдвое больше длины дуги АВ. Найти радиус окружности.
Решение.
Обозначим /.ВОА = а, тогда ZACB = —, a2 = 2R2 -2R2 -cosa 2
(R —искомый радиус) (рис. 10.44). По теореме синусов а = —— = 2R, • a sina
sm—
2
sina = -^- , a2 =2R2 -2R2 — yl4R2 -b2 ,	= 1 - Jl-
2R	2R	’ 2R2 N 4R2
R2 =	°4	• В =	°
4а2 - Ь2 ’	у/4а2 -Ь2
а2
Ответ: / , . -Г’ 74а2 -Ь2
Рис. 10.46
10.045. Общая хорда двух пересекающихся окружностей видна из центров под углами 90° и 60°. Найти радиусы окружностей, если расстояние между их центрами равно л/з +1.
Решение.
Пусть г—радиус одной, R — радиус другой окружности. По условию ЛАОХВ = 90°,ZJO2£ = 60°, О{О2 = 73+1; АВ = rV2;
О^Е = АВ/2; О\Е = r^-, АВ = 2flsin30° = R^ZAO2E =	зна-
чщ R = rj2, EO2 = R^- = r-y, O,O2 =O{E+O2E =	=
= >/з +1, г(>/б + 72) = (л/з + 1)-2,г = 72;Я = л/2->/2=2 (рис. 10.45).
Ответ'. 2 и 41.
10.046. Окружность касается большего катета прямоугольного треугольника, проходит через вершину противолежащего острого угла и имеет центр на гипотенузе треугольника. Каков радиус окружности, если длины катетов равны 5 и 12?
Решение.
По условию АС = 5, СЯ = 12 (рис. 10.46). В ЬАВС ZC = 90°,
АВ = >/25 + 144 = 13. Имеем ЛА СВ ~ ЛОйВ => — =	Пусть OD = R
OB OD 3
— радиус данной окружности, тогда = и OB = \3-R, поэтому
13 —Л R 18
65
Ответ: — 
18
Рис. 10.47
Рис. 10.48
10.047. Периметр прямоугольного треугольника АВС (ZC = 90°) равен 72 см,, а разность между длинами медианы СК и высоты СМ равна 7 см (рис. 10.47). Найти длину гипотенузы.
Решение.
По условию СК - СМ = 7 см, РАВС
= 72 см, р = ?АВС = 36. Если г —
F 2
радиус вписанной окружности, то r = p- АВ, S = рг = р(р-АВ).
Обозначим АВ = х, К —центр описанной окружности, СК = АК = = КВ = ^- = ^; S = 36-(36-х); — -СМ = 7 (по условию) СЛ/= —-7;
2	2	2	2
2l2 J 4
Ответ: 32 см.
— = 362 -36х, х2 +130х-5184 = 0, х = 32 см. 2
10.048. В острый угол, равный 60°, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен г  Найти радиус большей окружности.
Решение.
По условию Z2?AC = 60°, <?,£ = г (рис. 10.48). В A/lCOj ZACOt =90°, О, С
ZO, А С = 30’; AOj = ——- = 2OiC = 2г . В \О2ЕА Z.O.EA = 90°; sin 30
ДЛ	л ^2Е 3r + R R 3r + R D ,
ЬО7ЕА ~ ДО.СЛ => —±— =------; — =-----; R = 3r.
ОКС 2г г 2г
Ответ: Зг.
19 М. И. Сканави, группа А
577
10.049. Точка на гипотенузе, равноудаленная от обоих катетов, делит гипотенузу на отрезки длиной 30 и 40 см. Найти катеты треугольника. Решение.
По условию Z-C - 90°, AD = 30 см, BD = 40 см (рис. 10.49). Пусть
АС = х,ВС - у. Так как точка, равноудаленная от сторон угла, лежит на его
X 30 4х Т1 2	2	2 16х2
биссектрисе, то — = —, т.е. у =—. Нох +у -Ай или х +-------=70,
у 40	3	9
2 откуда х = 1764. Итак, х = 42 (см), у = 56 (см). Ответ'. 42 и 56 см.
10.050. Найти радиус окружности, описанной около прямоугольного треугольника, если радиус окружности, вписанной в этот треугольник, равен 3 см, а катет равен 10 см. Решение.
Проведем радиусы OD, ОМ и ON в точки касания (рис. 10.50) Имеем OD = ОМ = СМ = CD и, следовательно, BD = 10 - 3 = 7 (см). Но BD - BN и AN = AM (касательные, проведенные из одной точки). Положим AN = х; тогда (х + 7)2 = (х + З)2 +102, откуда 8х = 60, т.е. х = 7,5 (см). Отсюда АВ = 14,5 (см) и получаем ответ: R = 0,5ЛВ = 7,25(см).
Ответ: 7,25 см.
10.051. Три окружности разных радиусов попарно касаются друг друга. Отрезки, соединяющие их центры, образуют прямоугольный треугольник. Найти радиус меньшей окружности, если радиусы большей и средней окружностей равны 6 и 4 см.
Решение.
Рис. 10.51
Рис. 10.52
Пусть г — радиус меньшей окружности. Тогда О1О2 = г + 4, ОХО3 = г + 6 (рис. 10.51). Так как О2О2 =^1^2 + 0|<?з , то ^2 = = (г + 4)2+(г + б)2, г2 + 10г-24 = 0, откуда г = 2 см (корень г = -12 не удовлетворяет условию).
Ответ: 2 см.
10.052. Окружность касается одного из катетов равнобедренного прямоугольного треугольника и проходит через вершину противолежащего острого угла. Найти радиус окружности, если ее центр лежит на гипотенузе треугольника, а катет треугольника равен а.
Решение.
По условию СВ = а, А С = СВ (рис. 10.52). Значит, ЛСАВ = АСВА = 45°
(таккак ZC = 90°) => АВ = а^2. ЬАСВ ~ WEB =>	=—,
aJ2-R R
Л = -^- = ^-Л).
V2 + 1
Ответ:
10.053. В параллелограмме ABCD высота, проведенная из вершины В тупого угла на сторону DA, делит ее в отношении 5:3, считая от вершины D (рис. 10.53). Найти отношение АС: BD , если AD: АВ = 2.
Решение.
AD	ED >
По условию — = 2, — = -; Л£> = 3х + 5х = 8х Ad	Ac. 3
8x
AB
AB=4x, BE = 716x2 -9x2 = хЛ , BD = ^25x2 +7x2 = х>/32 =4хЛ
(ABED, ABED = 90’). В ЛА FC AAFC = 90’, A C = tIfC2 +AF2 ;
AF = BE = xJl, FC = 3x + 8x = llx, AC = 7121x2 +7x2 = 8x^2 ;
ЯС_8хЛ _2
4x72
Ответ: 2:1.
10.054. На основании равнобедренного треугольника, равном 8 см, как на хорде построена окружность, касающаяся боковых сторон треугольника (рис. 10.54). Найти радиус окружности, если длина высоты, проведенной на основание треугольника, равна 3 см.
Решение.
По условию AB=BQ, AQ = 8 см, ВЕ = 3 см. АВ = 716 + 9 =5 см,
АЕ2=ВЕОЕ => ОЕ-3 = 16, ОЕ = -- AB2=BDBC> 3
25 = (Л + 3 + 1ШаМ R2 =625^9 = 400 r = 2*
I	3 J I 3 J 9	9	3
„	20
Ответ: — см.
10.055. В равнобедренный треугольник с углом 120° при вершине и
боковой стороной а вписана окружность (рис. 10.55). Найти радиус этой окружности.
Решение.
По условию АВ = ВС = а, Z.ABC = 120°, ЛВАС = ЛАСВ = 30°,
_ ОЛО я с»	АВ+ВС+АС	~	2а^/з гт
BE = a sin 30 -—,8 -г------------, АС = 2а ♦ cos 30 =-= aV3;
2	2	2
2	4	4	2	2
п a73(2-V3)
Ответ: -----------.
2
10.056. Доказать, что сумма расстояний от любой точки, взятой внутри правильного многоугольника, до всех прямых, содержащих его стороны, есть величина постоянная.
Решение.
Соединим любую внутреннюю точку Р со всеми вершинами многоугольника и опустим перпендикуляры на все стороны (или их продолжения). Пусть длины этих перпендикуляров равны d\, di* ...,dn. Нужно доказать, что сумма d\ +di +...+dn не зависит от Р: Площадь многоугольника 5 = 0,5а(d{ +	• + dn)’ гДе а — сторона многоугольника. Значит,
+^2 +— + dn = 28/а, т.е. эта сумма не зависит от выбора точки Р. Что и требовалось доказать.
10.057. Диагональ прямоугольной трапеции и ее боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см.
Решение.
По условию AD = 2 см; DB = ВС = 4 см (рис. 10.56). В &DAB
ZDA В = 90°, AB = -J\6-4=J\2, ВЕ = —= - = - = !, ВМ = — = 2. 2	2	2	2
В ABEMZBEM = 90°, ЕМ = 41^\=4з и NM = NE+ЕМ = АВ+ЕМ = = л/12+7з = Зл/3(см).
Ответ: З-ТЗсм.
Рис. 10.58
10.058. В правильный треугольник вписан квадрат, сторона которого равна т . Найти сторону треугольника.
Решение.
По условию EF = FN = NM = ЕМ = т (рис. 10.57); АВ = ВС = АС = х.
S Ху13	2х
Б0ЧХ ~~ MOC~*FNC =
т^Ц+з) 3
m(2V3+3)
Ответ: ----------.
3
10.059. В окружности радиуса г проведена хорда, равная г/2 . Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной (рис. 10.58). Найти расстояние между касательной и секущей.
Решение.
ОК - ОМ = г, КМ = -; по теореме косинусов КМ1 2 = OK2 +ОМ2 -2
г2	7	7
-2OK OM cosa, — = 2r2 -2r2cosa, cosa = - ОЕ = rcosa = r-4	8	8
7	1
{/.КОМ = Za). EK = КО-ЕО = r--r = -r , 8	8
1
Ответ: - г. О
10.060. Радиусы вписанной и описанной окружностей прямоугольного треугольника равны соответственно 2 и 5 см (рис, 10.59). Найти катеты треугольника.
Решение.
Поусловиюг = 2 см, А = 5 см. В ЬАСВ, СВ = 90°, ЛВ = 2В = 10, АК = АЕ,КВ = МВ,АС = АЕ + СЕ = АК + СЕ = АК + г,ВС=МВ+СМ = = KB + CM = r + KB, AC + CB = 2r + AB, AC+ СВ = 2(г+ В). Пусть АС-х, тогда СВ = 2(r + R)-x , СВ = 14-х . Так как АВ2=АС2 + + ВС2,то 100 = х2 + 196-28х + х2, ^=8, х2 =6.
Ответ: 6; 8 см.
10.061. Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15 см. Разность длин сторон параллелограмма равна 7 см (рис. 10.60). Найти длины сторон параллелограмма и его диагоналей.
Решение.
Поусловию АЕ = 6 см, ЕС = 15 см, ВС -АВ-1 см. Обозначим ВС = х, АВ = х-7.ВДВЕЛ Z.BEA=9tf => BE2 = х2 -14х + 49-36. В &ВЕС Z.BEC = 90° => BE2 = х2 -225. Отсюда х2 - 14х + 49 - 36 = х2 -225; х=17, значит, ВС = 17см, АВ = 17-7 = 10 см, АС = 6 + 15 = 21 (см); АО = —, ЕО=^-АЕ=^-6 = ~, В£ = 7289-225=8, BD = 2-.64+ —
2	2	2	2	V 4
(ЛВЕО, где ZBEO = 90’), BD = V337 .
Ответ: 10; 17; 21; >/з37 см.
Рис. 10.61	Рис. 10.62
10.062. В большем из двух концентрических кругов проведена хорда, равная 32 см и касающаяся меньшего круга (рис. 10.61). Определить длину радиуса каждого из кругов, если ширина образовавшегося кольца равна 8 см.
Решение,
По условию СВ = 8 см, Л5 = 32 см, ЕВ2-ВС • ВК . Так как £В = -^ = 16и ДАГ = ВС + 2г,то256 = 8-(8 + 2г)=> г = 12, R = ОС + СВ = = г+8 = 12 + 8 = 20 см.
Ответ: 12 и 20 см.
10.063. В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2:3. Диагонали ромба равны т и п (рис. 10.62). Найти стороны треугольника, содержащие стороны ромба.
Решение.
KD 3	Л	1т2 п2
По условию, BD = m, АС = п- Отсюда АВ = .-----+— =
DM 2	у 4	4
1	Г~г---Г	AD KD
= -'Jm + п . &KAD ~ &DCM => 777 = 7П7 и, так как АВ = ВС =
2	CM DM
/ 2	2 = DC = AD (поусловию), т +п = 3, см = СМ 5	/ 2	2	KD	АК + ВС = — ^т +п . Так как 	=	, то 6	DM	CD -4т2 +п2 , КВ=АК+АВ=—4т2 +п2 . 4	4 Ответ: у4т2 +п2 ; ^-4т2 +п2 . 6	4	/2	2 —-—, вм=см+ АК	3 И АК~ у/т +п z
10.064. Боковая сторона равнобедренного треугольника равна 10 см, основание 12 см. К окружности, вписанной в треугольник, проведены касательные, параллельные высоте треугольника и отсекающие от данного треугольника два прямоугольных треугольника. Найти длины сторон этих треугольников.
Решение.
Площадь треугольника находится по формуле (рис. 10.63):
5 = -Jptp-alp-blp-c) = д/16(16-10X16-10X16-12) = 48.
iS 48
Радиус вписанной окружности г = — = — = 3 (см); г = DH. НС = DC -р 16
-DH = 6-3 = 3 см; &BCD и &FCH подобные, поэтому =
ВС • НС 10*3
Отсюда FC =----------=-----= 5 см. Из №СН следует, что FC2 =
DC 6
= FH2 + НС2; FH = 4fC2-HC2 = 4$2 -З2 = 4 (см).
Ответ: 3 см, 4 см, 5 см.
10.065. В равносторонний треугольник вписана окружность. Этой окружности и сторон треугольника касаются три малые окружности. Найти сторону треугольника, если радиус малой окружности равен г•
Решение.
Пусть а — сторона треугольника, R — радиус вписанной в него ад/з
окружности; тогда R = —— . Проведем радиусы ОМ и ОХК в точки 6
касания (рис. 10.64). Из подобия треугольников АОМ и АОХК имеем
R АО	а4з
— = ~АО—~R— ’ Отсюда, учитывая, что А О = —— , получаем
6r
- aJ3 a-j3 3—
или --------г = 2г, т.е. а = 6гу/з .
6
Ответ: 6г>/з.
10.066. Один из катетов прямоугольного треугольника равен 15 см, а проекция другого катета на гипотенузу равна 16 см (рис. 10.65). Найти радиус окружности, вписанной в треугольник.
Решение.
Искомый радиус находится по формуле: г -	~; ЛАРС и
ВС DC ?
&BDC подобные, отсюда	. ВС = АС • DC. Из ЛАВС по-
лучаем АС2 ~ АВ2 = ЯС2. Отсюда: (16 4-х)2 -152 = 1б(1б4-х). Решая уравнение х2 +16х - 225 = 0, находим Xj = -25 см (не удовлетворяет решению задачи) или х2 = 9 см. АС = 94-16 = 25 см. ВС = V16 25 = 20 см. тя 15 + 20-25 с Итак, г =---------= 5 см.
2 Ответ: 5 см.
10.067. Внутри круга радиуса 15 см взята точка М на расстоянии 13 см от центра. Через точку М проведена хорда длиной 18 см. Найти длины отрезков, на которые точка М делит хорду.
Решение.
Проведем ОС1АВ (рис. 10.66). Тогда СВ = i АВ = 9 см. Из ДОВС
находим ОС = yloB2 - ВС2 = 12 (см), а из ЬОМС получим МС -- у1оМ2 - ОС2 = 5 (см). Следовательно, AM = 9 + 5 = 14 (см), МВ -= 9-5 = 4 (см).
Ответ: 14 и 4 см.
10.068. Длина основания треугольника равна 36 см. Прямая, параллельная основанию, делит площадь треугольника пополам. Найти длину отрезка этой прямой, заключенного между сторонами треугольника. Решение.
Обозначим искомую длину через х . Тогда из подобия треугольников АВС и LBM (рис. 10.67)имеем AC2 :х2 = S:(iS/2), где5—площадь ДЛВС. Отсюда АС2 = 2х2 и х = 18>/2 (см).
Ответ: 18>/2 см.
10.069. Радиус окружности, описанной около прямоугольного треугольника, равен 15 см, а радиус вписанной в него окружности равен 6 см. Найти стороны треугольника.
Решение.
По условию АВ = 2R = 2 • 15 = 30 (см) (рис. 10.68). Радиус вписанной a + b-с	_
окружности г = —-— . Отсюда 2г = а + b - с . Решая систему
2г = а + Ь- с,	12 = a + Z>-30,
а2 + Ь2 =с2 а2 +Ь2 = 900,
получаем =18 (см), Ьх =24 (см) или а2 =24 (см), Ь2 =18 (см). Ответ: 18; 24 и 30 см.
Рис. 10.69
10.070. В круговой сектор с центральным углом 120° вписан круг. Найти радиус вписанного круга, если радиус данного круга равен R.
Решение.
&О2АО\ — прямоугольный, ЛО\О2А - 60°, sin 60° =	= —-—;
R — r
— = —— (рис. 10.69). Отсюда г =	= Тз7?(2 — л/з).
2 R-r	2 + V3
Ответ: л/з/?(2-л/3).
10.071. Найти сторону правильного шестиугольника, равновеликого равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
Решение.
Так как AD — диаметр окружности (см. рис. 10.2), то OD = ОС = = 10 см. Проведем CL AD\ тогда OZ = 6 см и из ACZO находим CL = yloC2 -OL2 =8 (см). Тогда SABCD = 0,5(ВС + AD) CL = 0,5(12 +
+20) -8 = 128 (см2). Обозначив сторону правильного шестиугольника че-6л2>/з	2 128-2	16^3
рез х, имеем —-— = 128, откуда х	те- х = —j—•
п |6^3 Ответ:------
3
10.072. В равнобедренном треугольнике основание равно 30 см, а боковая сторона равна 39 см. Определить радиус вписанного круга.
Решение.
СМ.
Проведем BDLAC (рис. 10.70); так как &АВС—равнобедренный, то BD является и медианой. Имеем BD2 = АВ2 - AD2, откуда BD = 7з92 -152 =36 (см) и, значит, 5 = 1.30 • 36 = 540 (см2). Но S=рг = = 54г, откуда г = 10 см.
Ответ: 10 см.
Рис. 10.72
10.073* В квадрате, сторона которого 12 см, середины его смежных сторон соединены между собой и с противоположной стороной квадрата. Найти радиус круга, вписанного в образовавшийся треугольник.
Решение.
Найдем площадь треугольника NMD (рис. 10.71); S^md = ~= 0,5-6-6 = 18(см2); ^ДЛ/CZ)“0,5-6-12 = = 36 (см2); S^MD =144-2-36-18 = 54 (см2). Так как MD=DN= = 7122+62 =7180 =бТ5(см), ^ = 7б2+62 = 6-71 (см), то P&nmd = = 0,5(12д/5 +6>/2) = 65/5+ 3-72 (см). Тогда по формуле (10.4) получим
г =
54	18
&J5+3/1 245 + 42-
2л/5-л/2(см).
Ответ: 2 75 - 42 см.
10.074. Одна из двух параллельных прямых касается окружности радиуса R в точке Л, а другая пересекает эту окружность в точках В и С. Выразить площадь треугольника АВС как функцию расстояния х между прямыми.
Решение.
Пусть расстояние между параллельными прямыми равно х (рис. 10.72); тогда площадь S треугольника АВС равна 0,5ВС • х. Так как АМ1ВС, то ВМ = МС и ВМ • МС = АМ • MD = x(2R - х). Значит, 0,25ЯС2 = x(2R - х), откуда S - 0,5х• 2^2Rx-x2 = x^2Rx-x2.
Ответ: x^2Rx-x2.
10.075. Катеты прямоугольного треугольника равны 9 и 12 см. Найти расстояние между точкой пересечения его биссектрис и точкой пересечения медиан.
Рис. 10.73 и
Решение,
Выберем систему координат хОу, связанную с данным прямоу-.
гольным треугольником АО АВ, таким образом, как это показано на рис. 10.73. Тогда
А В = у10А2+0В2 = д/92 + 122 = 15,
S = -OAOB = 54 см2,
2
р = |(9 + 12 + 15)= 18 см
Точка пересечения биссектрис совпадает с центром вписанной в этот треугольник окружности — Q (3; 3). Найдем точку С2 пересече
ния медиан как точку пересечения прямых AD и В К . Составим урав
нение прямых AD и ВК. Пусть уравнение AD \ yt = k}x + b{) где Л(0; 12) и £>(%;о). Отсюда =12, 0 = ^Л1+12, кх = -•|. Значит,
AD: у = --х + 12 .
л 3
Пусть уравнение прямой В К : у2 -к2х + Ь2, где 2?(9; 0) и АГ(О; б).
Тогда Ь2 = 6, 0 = 9^ + 6, к2 = — . Получили, что уравнение ВК ’
2
У = -—х + 6. Координаты точки С2 находим из системы
у =—х + 6,
7	3
8
у =—х+12 3
x = V = 4,C2(3;4)
=>2х-6 = 0,
По формуле расстояния между двумя точками координатной плоскости имеем: СХС2 = ^(З-З)2 + (3-4)2 = 1 см.
Ответ: 1 см.
в
20-х
Рис. 10.74
Рис. 10.75
10.076. Найти отношение радиуса окружности, вписанной в равнобедренный прямоугольный треугольник, к высоте, проведенной к гипотенузе.
Решение.
Так как ДЛВС —равнобедренный и прямоугольный, то высота CD является биссектрисой, т.е. Z_DCA = Z?1 = 45O (рис. 10.74); поэтому AD = DC и AC = y/2DC • Но АС = AK + KC = DC + r (AK = AD как касательные, проведенные из одной точки), откуда г = y/2DC - DC, т.е. r/DC^Jl-X.
Ответ: у[2 -1.
10.077. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20 см. Найти биссектрису угда при основании треугольника.
Решение.
(рис. 10.75). Отсюда х = 4 (см). DC = х = 4 (см),
HD = = 20 - 4 = 16 (см). Длина биссектрисы
AD = JAC AB-BD DC = V20-5-416 = 6 (см).
Ответ: 6 см.
10.078. Катеты прямоугольного треугольника равны 6 и 8 см. Найти расстояние от центра вписанной в треугольник окружности до центра описанной около него окружности.
Решение.
АВ - >1аС2 + СВ2 = у]б2 +82 =10 (см) (рис. 10.76). Расстояние меж-ду центрами ОК = JoE2 + ЕК2; р = (АВ+ВС+АС)/2 = 12 (см). Радиус вписанной окружности г = р - АВ = 2 (см).
Получим
КЕ = АЕ-АК = AF - АК = 6-5 = 1 (см),
ОК = у1оЕ2 + ЕК2 =74 + 1=75.
Ответ: 4$ см.
10.079. Найти биссектрисы острых углов прямоугольного треугольника с катетами 24 и 18 см.
Решение.
DC BD	I—;----7	х 24-х
— = — (рис. 10.77); ЛС = у242 + 182 =30(см), — = —ГГ“ От-АС АВ	1б
сюда х= 15, CD = 15 (см), BD = 24-15 = 9 (см).
Биссектриса /ВАС: AD=<JAС- АВ-CD- BD=V30-18-15-9 = 9^5 (см).
ЯЛ£=Л« у =]8-у отсюда у = 10 (см), ЛЛ/ = 10(см), Л/В = 8(см). АС ВС 30	24
Биссектриса ZBCA :
СМ = -JАС-ВС-AM МВ = л/30-24-8 10 = 8-У10 (см).
Ответ: 9у/5 и 8-УГо см.
Рис. 10.78	Рис. 10.79
10.080. Доказать, что если в четырехугольнике (рис. 10.78) диагонали лежат на биссектрисах его углов, то такой четырехугольник есть ромб.
Решение.
ZBCA = ZDCA, ZBAС = ZDA С, ZABD = ZCBD, ZCDB = ZADB => => &BAD = bBCD. Отсюда Z.BAD = Z.BCD, ВС = АВ, DC - DA  AABC = AADC .Отсюда ZABC=ZADC, AB = AD, BC=DC. Получаем AB = BC = CD = DA. Так как &ABC — равнобедренный, то ВО — высота и медиана BD1A С. Что и требовалось доказать.
10.081. Площадь прямоугольника равна 9 см2, а величина одного из углов, образованного диагоналями, равна 120° (рис. 10.79). Найти стороны прямоугольника.
Решение.
CD = x- АО CD —равносторонний; AO=OC=CD=x; АС-2х.
1	1	>/з	/—
Площадь прямоугольника S' = — dld^ sin 60 =—2х • 2х • —, 9 = х2 -J3 .
о о4/4
Отсюда х=-> = ^— = 33/4 =^27 (см). ЛС = 2^7 (см).
V3 З*4
Из AACD:
AD2 =АС2-CD1 = 4^27= 3^27 ,
AD = ^27 =35/4 =3^3 (cm).
Ответ: ^27 и 3^/3 см.
10.082. Площадь равнобедренной трапеции, описанной около круга, равна S', а высота трапеции в два раза меньше ее боковой стороны (рис. 10.80). Определить радиус вписанного круга.
Решение.
CN = CD/2;AD+BC=AB + CD = = 4х. Площадь равнобедренной трапеции
S = ^(AD + BC)-CN = ^4xx = 2x2.
Отсюда х =	. Искомый радиус
D _ CW VS _ -J2S
’ 2	2^2	4
п Ответ: ------.
4
10.083. Сумма длин диагоналей ромба равна т , а его площадь рав
на S. Найти сторону ромба.
Решение.
AC+BD=m, АС = х, BD = у . S = ^dld2 (рис. 10.081). Решая си-
fx + y = т, стему|25 = ху)
получим х1 =
m + ylm2 — 8S 2
т- у/nr -8S
’У1 2
или
т-4 т2 -8S	т + Jm2 -8S
Х2 2	’ У2 2
Отсюда:
т + 4т2 -8S	т - ^т2 -8S
Г2 + Г2
, _ Vw2 -4S '	2 ~'
Л Vw2 -4S
Ответ: --------.
т2 -4S 4
Рис. 10.81
Рис. 10.82
10.084. Периметр ромба равен 2 м, длины его диагоналей относятся как 3:4. Найти площадь ромба.
Решение.
Искомую площадь найдем по формуле S = ^АС-BD = 2AOOB (рис. 10.81). В ЬАОВ АВ2=А01+В02, где ОВ = ^АО, ЛЛ=^=^(м). Тогда получим уравнение ± = АО2+-^АО2, откуда	т.е.
А О = 0,4 (м). Итак, S = 2 ♦ 0,4 • 0,3 = 0,24 (м2).
Ответ'. 0,24 м2.
10.085. В равнобедренную трапецию вписана окружность радиуса R. Верхнее основание трапеции в два раза меньше ее высоты. Найти площадь трапеции.
Решение.
CD~y\ED~x (рис. 10.82). Решим систему
/2у = (Я + 2х) + Я, «	От-
[х2+4Я2=/.
3
сюда получаем х- — 7?, тогда AD = R + 2x = R + 3R = 4R. Искомая пло-
1	1	9
шадь S = -(AD + ВС) • ЕС = —(R + 4R) • 2R = 5R2.
Ответ'. 5R2.
10.086. На каждой медиане правильного треугольника взята точка, делящая медиану в отношении 3:1, считая от вершины. Во сколько раз площадь треугольника с вершинами в этих трех точках меньше площади самого треугольника?
Решение,
EF = -AC; FD = -АВ; ED = -ВС (рмсЛ 0.S3). ЛАВС и &FDE — 2	2	2
подобные,	= к2 = 22 = 4. &FDE и &LK.M — подобные,
S&FDE
KL = -FD;KM = -ED;LM = -EF;^^- = k2 =4. Далее, &LKM и 2	2	2
ENRP — подобные и к - 2, т.е. = 4. Итак, ^вс = 4.4.4 = 64.
^ENRP	^tiNRP
Ответ: в 64 раза.
10.087. В равнобедренный треугольник вписан квадрат единичной площади, одна сторона которого лежит на основании треугольника. Найти площадь треугольника, если известно, что центры масс треугольника и квадрата совпадают (центр масс треугольника лежит на пересечении его медиан).
Решение.
BD — медиана, ВО : OD = 2 :1; OD = 0,5 (см), ВО = 1 (см), BD =
= OD + BO=1,5 (см) (рис.10.84). &BEF и &BDC — подобные,
Отсюда DC^————,	АС-2*
BE EF	BE	0,5
1	1	3 3 9
x DC = 3 (см), S^BC = 2 A C • BD = - • 3 • 1,5 = - - = - (кв. ед).
Ответ: — кв. ед. 4
Рис. 10.85
Рис. 10.86
10.088. В окружность радиуса R вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции.
Решение.
AD-2x-2R (рис. 10.85). Отсюда х = R. Искомая площадь
= ДС + ЯВ СЕ =^JCD2_ED2 =Ix2 =
2	V 4	2	2
R + 2R >/з Зл/З 2
Э —---------/С —---А .
2	2	4
Ответ: ^^-R2.
4
10.089. Найти площадь круга, описанного около равнобедренного треугольника, если основание этого треугольника равно 24 см, а боковая сторона 13 см.
Решение.
Площадь круга S = nR2 (рис. 10.86). Радиус описанной окружности R = _£*£_ где s --ACBD.
4SMBC ^ВС 2
Из ASDC получим BD = -JbC2-DC2 = 7132-122 =5 (см). Тогда Saabc =-24-5 = 60 (см2). Отсюда 7? = 1313 24 = 1^. (см). Итак, 2	4-60	10
2
5 = л = 285,61л (см2).
100
Ответ: 285,61л см2.
10.090. Расстояние от центра круга до хорды длиной 16 см равно 15 см. Найти площадь треугольника, описанного около круга, если периметр треугольника равен 200 см.
Решение.
Радиус окружности из &ОСВ: R = V152 +82 = 17 (см). Искомая пло-
щадь треугольника = R-p = \r	= 1700 (см2)(рис. 10.87).
Ответ: 1700 см2.
10.091. Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно а, а угол при меньшем основании равен 120°.
Решение.
В &CED Z.CDE = 60° и cos 60 = а	(рис. 10.88). Отсюда -—- = -,
2с	2с 2
а - b = с. Для описанной равнобедренной трапеции а + b = 2с.
Решая систему
л-/> = с,	2	•	2/?
, ~ получим с = — а. sin 60 = —. Отсюда а + /> = 2с,	3	с
п sin 60 с у/З у/з „	о п2 3 2 IM2
R =-------= — с = —а . Площадь круга о = лк = л—а = —- .
2	4	6	36	12
ла2
Ответ: ——.
12
10.092. В окружность радиуса R вписан треугольник с углами 15 и 60° (рис. 10.89). Найти площадь треугольника.
Решение.
ЛАВС = \№>°', ААВС = Ш° -— Z.AОС.Отсюда ZAОС = 150°.Зна-2
чит, ZOAC =\5°. Из &ADO находим AD = Rcosi5°,AC=2AD = = 2flcosl5°. Из АЛОВ (равнобедренного):
АВ2 =R2+R2-2R2cos 120° = 2Я2(1 + cos60°) = ЗЯ2; АВ = >/зЯ.
Площадь треугольника АВС:
S = -ABACsinl5° = -^3R-2Rcosl5°sinl5o =—R2. 2	2	4
л/з 7
Ответ: -----R.
4
10.093. Периметр прямоугольного треугольника равен 2р, а гипотенуза равна с. Определить площадь круга, вписанного в треугольник.
Решение.
ЛАВС — прямоугольный (рис. 10.90); АВ = х, ВС - у. Известно, что
2р = х + у + с. Отсюда х + у = 2р-с. Радиус вписанной окружности х + у —с
г =-------=---------= р- с. Искомая площадь круга находится по
формуле S = яг2 = п(р - с)2.
Ответ: п(р~с)2.
10.094. Найти площадь круга, вписанного в прямоугольный треугольник (рис. 10.90), если проекции катетов на гипотенузу равны 9 и 16 м.
Решение.
А С = AD + DC = 25 (м); AADB и ЛА ВС — подобные: — = —. Ог-АВ АС
сюда -=—,х2=9-25=225,х = 7225 = 15(м),ЛД=15(м). ABDCnAABC х 25
_ DC ВС	16 у 2 .>•
— подобные: -----=----. Отсюда — =—> у =16-25 = 400,
у = >/400 = 20 (м), ВС = 20 (м). Радиус вписанной окружности:
а + Ь-с 15+20-25 ,
г =-------=----------= 5 (м). Искомая площадь круга
S = кг1 = 25л (м2).
Ответ: 25л м2.
10.095. Площадь равнобедренного треугольника равна 1/3 площади квадрата, построенного на основании данного треугольника. Длины боковых сторон треугольника короче длины его основания на 1 см. Найти длины сторон и высоты треугольника, проведенной к основанию.
Решение.
1	2
По условию ВС2 =3 -^ВС-АН (рис. 10.91) или АН = — ВС. Но АН1 = АВ2 -f-Дс) и,значит,-ЯС2 =АВ2 -—ВС2 или АВ2 =^ВС2, ^2	)	9	4	36
т.е. АВ =—ВС. Тогда получим АВ = — (АВ + 1), откуда АВ = 5 (см).
О	6
Следовательно, ВС = 6 см, АН=4 см.
Ответ: 5; 6 и 4 см.
10.096. Площадь равнобедренной трапеции, описанной около круга, равна 32>/3 см2 (рис. 10.92). Определить боковую сторону трапеции, если известно, что острый угол при основании равен л/3.
Решение.	г-
2R	уЗ
&CED — прямоугольный и sin 60° =	. Отсюда 2R = —CZ),
CD = x => 2R = ^~-x . Площадь трапеции S= Л = 2Rx = ^-x2.
По условию — л
Ответ: 8 см.
2 = 64, х=8 (см).
в
10.097. Площадь прямоугольного треугольника (рис. 10.93) равна 2л/з см2. Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1:2.
Решение.
Z.ABD = 30°, Z.DBC = 60°. Площадь М.ВС находится по формуле
1	DC
S - — АВ-ВС. Из &BDC получаем ВС =-------. Из &ADB находим
2	sin 60°
АВ = — . Тогда 5 = ——DC	— = -^=DCAD. Так как &ADB и
sin30°	2 sin60°-sin30° <3
BD DC
&BDC —подобные, to ------=----. Отсюда BD2=AD-DC. Тогда
AD BD
S = ^=BD2 и В£> = л/З(см).
V3
Ответ: >/з см.
10.098. Прямая, параллельная основанию треугольника, делит его на части, площади которых относятся как 2:1. В каком отношении, считая от вершины, она делит боковые стороны?
Решение.
1’ SbABC = SAMNc+SbMBN = х + 2х = Зх;  _	= — (рис. 10.94).
bbBMN 2
Отсюда (=	= 4зх> МВ = VL; AM = (>/з-Л)х,
\ АВ)	3 АВ ]/ 3
AM V3-V2	1
2-	S^BC=SAMiNic+S^MlNl (рис. 10.94). Аналогично находим МХВ: АМХ =(>/з+1):2.
Ответ: (л/б + 2): 1 или (л/з +1): 2.
Рис. 10.95	Рис. 10.96
10.09	9. Площадь равнобедренной трапеции (рис. 10.95), описанной около круга, равна 8 см2. Определить стороны трапеции, если угол при основании содержит 30°.
Решение.
2R	с
Из &CED получим sin30° = —. Отсюда 2/?=—. Площадь трапе-с	2
с2	?
ции 5 = 2Rc - — = 8. Отсюда с = 16, с = 4 (см), CD = АВ = 4 (см). Име-2
ED	г~	я + b = 4,
ем cos30° = -—, ED = 2у/3 (см). Решим систему 7	_ Отсюда
CD	b = a+4>J3.
получим а = 4 - 2 , b = 4 + 27з.
Ответ: 4 - 2>/3; 4 + 2л/з ;4 и 4 см.
10.100.	Равносторонний шестиугольник ABCDEF состоит из двух трапеций (рис. 10.96), имеющих общее основание CF. Известно, что АС= 13 см, АЕ = 10 см. Найти площадь шестиугольника.
Решение.
АСКА —прямоугольный, АК = ± АЕ = 5 (см), СК = >]АС2 - АК2 = = 7132-52 =12(cM),cos<p=^|;sin<p=-^. Рассмотрим АСОВ (КСОВ = 5	5 12 120
= 90°): sin2(p = —и sin2<p = 2sin<pcos<p = 2-—• —= —Отсюда х = х	13 13 169
169-5 169	, СО .	2	• 2	144
=-------=----- (см), cos2<p =-----; cos2<p = cos <р — sin <р = ——-
120	24	х	169
25	119 л™ nn 1®
— --.Отсюда С0 = —
119 119
Liz = _ (ал), СО = KF, CF = СО + OF = 169 24
119 407
= СК + KF = 12 +	(см). Площадь искомого шестиугольника:
Sabcdef = 2Scdef =2.1(CF + ED).£* = ^ + ^|5 = 120 (см2).
Ответ: 120 см2.
10.101.	Найти площадь правильного треугольника (рис. 10.97), вписанного в квадрат со стороной а, при условии, что одна из вершин треугольника совпадает с вершиной квадрата.
Решение.
CD = a ; BE = FD = x ; AF = AE = a-x', СЕ = EF = CF = y . Ре
шим систему
у2 = а2 +х2
а2 +х2 =2(a-xf. Решая это уравнение,
получим х = а^->/з). Найдем у2 =а2 +a2fe-y/lf =.а2(8-4-Д)-
Площадь искомого правильного треугольника находится по формуле
4	4
Ответ: а2- з)
10.102.	Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции.
Решение.
По условию ЛВСА -ZACD (рис. 10.98). Но ЛВС А = Л-CAD, а зна-
Рис. 10.99
Рис. 10.100
чит, АЛ CD — равнобедренный и AD = CD. Имеем 3AD + ВС = 42; так как ВС = 3 см, то Л£> = 13 см. Проведем BK1AD; тогда АК = у (13-3)= 5 (см) и из ДАКВ находим ВК = V132 -52 = 12 (см). Итак, 5 = 1 (3 +13)-12 = 96 (см2).
Ответ: 96 см2.
10.103.	Найти площадь круга, вписанного в прямоугольный треугольник, если высота, проведенная к гипотенузе, делит последнюю на отрезки, тиной 25,6 и 14,4 см.
Решение.
Так как ДЛ2?С — прямоугольный и CD1AB (рис. 10.99), то АС2 = ЛВ ЛЛ = 40-25,6 иВС2 = ЛВ-В£> = 40 14,4,откудаЛС = 32 (см),
ВС = 24 (см) и S^BC =^'32 -24 = 384 (см2). С другой стороны, = рг = 48г . Следовательно, г = 8 и SKp = лг2 = 64л (см2).
Ответ: 64л см2.
10.104.	Периметр прямоугольного треугольника равен 24 см, Площадь его равна 24 см2. Найти площадь описанного круга.
Решение.
Гипотенуза треугольника с = 2R (рис. 10.100).
24 = х + у+ 2Я,
24 = — ху, получим х = 6 (ал), X2 + у2 =4Я2,
Реши (систему ’
р = х + у + 2Л3
х2 +у2 =4Я2
24 — х — у у = 8 (см). Радиус круга R =--—- = 5 (см). Площадь искомого
описанного круга S = лЛ2 = 25л (см2).
Ответ: 25л см2.
Рис. 10.102
10.105. Найти площадь равнобедренного треугольника (рис. 10.101) с углом 120°, если радиус вписанного круга равен V12 см.
Решение.
Из ABDCнаходим BD =ВС sin30°=	; DC =2?Csin60°= —ВС.
2	2
Полупериметр &ABC p = j (x +
Площадь ДЛБС: S = pr = х 1 +	t
'12 .
С другой стороны, S = ^AC BD = -jix  x2. Решим урав-
нение — х2 = х 1 + — >/12 . Получим х =
4
ЬАВС S =
—*----. Тогда площадь
<3
cm2).
Ответ: 2(7 + 4>/3) (см2).
10.106.	На сторонах равнобедренного прямоугольного треугольника с гипотенузой с вне этого треугольника построены квадраты. Центры этих квадратов соединены между собой. Найти площадь полученного треугольника.
Решение.
BE = КС = ^;EF = 2ВЕ = с (рис. 10.102). Четырехугольник ABCD —
квадрат. Отсюда А С = BD = с. Площадь искомого треугольника
1	1 , с2
S = —BDEF = —с2 =— .
2 г 2	
Ответ: —.
2
2
Рис. 10.103
10.107.	В квадрат вписан другой квадрат, вершины которого лежат на сторонах первого, а стороны составляют со сторонами первого квадрата углы в 60°. Какую часть площади данного квадрата составляет площадь вписанного?
Решение.
Пусть al = а, LB = b и LK = с (рис. РЗ103). Тогда площадь данного квадрата Si =(а + й)2 =а2 +2ab + b2-с2 +2аЬ. Так как ZBLK = 60°, то Z.BKL = 30°, откуда с = 2Ь , a = byf$ и, значит, S, =462+262>/з . Площадь вписанного квадрата S2 - с2 = 4/>2. Итак,
“I— * =4-2j5
S1 4/>2+26?V3 2 + V3
Ответ: 4-2>/з.
10.108.	Найти площадь квадрата, вписанного в правильный треугольник со стороной а.
Решение.
ВС ВК I---------------г
AJBKC и \ЕМС — подобные => — = —, BK = jBC2 -КС2 = .
ЕС ЕМ
| 2 а2 ауЦ	ЕС ВК (а-х)аЬ Л
= da-----=-----; ЕМ = х и х =------=----------. Отсюда 2ах =
V 4	2	ВС 2а 
= a-fi(а - х) • Решая уравнение, получим х =	• Площадь искомо-
го квадрата:
5 = х2 = 3а\=За2(7-4>/з).
Ответ: За2 (? - 4>/з )
Рис. 10.105
10.109.	На сторонах равностороннего треугольника вне его построены квадраты. Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если
сторона данного треугольника равна а.
Решение.
Площадь искомого шестиугольника (рис. 10.105)
Cl	1
Shkdefg - $ьавс + ^анкв + ^S^kbd = —— + За2 + 3 •—a2 sin 120 =
я2>/3 - 2 3 а22(0, пЛ
= —+	— = а P + V3).
Ответ: а2(з + >/з).
10.110.	Данный квадрат со стороной а срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника.
Решение.
Пусть АЕ-х (рис. 10.106). Тогда AB = 2AE + EF или2х + х>/2 = а, a db — >/2)
откуда х =----= = —-------. Следовательно, искомая площадь
2+Л	2
-о 4<г	4x2-„2 4а2Ц-4>/2+2)	-.//г
- SABCD ’-4одл£лг - а — - а--------------------- 2а \J2 -1).
Z	о
Ответ: 2a2(V2-l)
10.111.	Сторона правильного треугольника, вписанного в окружность, равна а . Вычислить площадь квадрата, вписанного в ту же окружность.
Решение.
Обозначим радиус описанной окружности через R. Тогда а = r4?> , откуда R = а/.Так как сторона вписанного квадрата равна R^l , то его площадь 5 = 2R2 = 2л2/3.
Ответ: 2л2/3.
10.112.	Вычислить отношение площадей квадрата, правильного треугольника и правильного шестиугольника, вписанных в одну и ту же окружность.
Решение.
Пусть R — радиус окружности. Тогда сторона правильного впи-D/r _ aj-A 3/?2Л _
санного треугольника а3 = л V3 и 53 =	— = —-— . Далее, сторо-
на квадрата а4 = ylS4=o.\ =2Л2 и, наконец, сторона правильно-_ с 6R24i 3r24i
го вписанного шестиугольника a6=R и э6 =—-— = —-—.
Следовательно, S4 : S3 : S6 = 8: 3>/3 : бТз .
Ответ: 8: 3>/3 : 6>/з.
. 10.113. Сторона равностороннего треугольника, вписанного в окружность, равна а. Вычислить площадь отсекаемого ею сегмента.
Решение.
Площадь сегмента АпВ равна разности площадей сектора АОВ и я/?2 о \ R aR &АОВ (рис. 10.107). Находим SCCKT/10B = ^—, $ьаов = 2	= "4~’
с л/?2 aR	п а
откуда о = —---------. Так как R = —=, то окончательно получим
3	4	^3
s=^6
Ответ: а2 (4л - 3>/3 Узб.
10.114.	Сторона квадрата, вписанного в окружность, равна а . Вы
числить площадь отсекаемого ею сегмента.
Решение.
Jq2 _|_д2
Площадь круга SKp = л/?2 . Радиус круга R =-----
— .От-2
сюда о кр =----. Площадь искомого сегмента:
10.115.	На диаметре 2R полуокружности построен правильный треугольник, сторона которого равна диаметру. Треугольник расположен по ту же сторону от диаметра, что и полуокружность. Вычислить площадь той части треугольника, которая лежит вне круга.
Решение.
&AOD , &DOE , ЬОЕС, &DBE —равносторонние со стороной R (рис. 10.108). Искомая площадь S = S^BE - ScerM. ScerM = у7?2 ~^r2 J о 4
5	-^-R2 S = -R2--R2+ — R2=R2(^^-
z^dbe " 4 K ’	4	6	4 I 6
Л п2(зТЗ-Л>|
Ответ: R ------- ,
6
10,116.	Круг радиуса R обложен четырьмя равными кругами, касающимися данного так, что каждые два соседних из этих четырех кругов касаются друг друга (рис. 10.109). Вычислить площадь од ного из этих кругов.
Решение.
В &ОХОО2 ЛОХОО2 = 90°. Решим уравнение 4х2 = 2(х+Т?)2. Найдем х =	+ 72), где х = г — радиус четырех равных кругов. Площадь
искомого круга S = яг2 = яЯ2 (l+T?)2 = яЯ2(? + 272).
Ответ: %R2 (з +141).
Рис. 10.111
10.117.	В точках пересечения двух окружностей с радиусами 4 и 8 см касательные к ним взаимно перпендикулярны. Вычислить площадь фигуры ОХАВО2 , где АВ — общая касательная к окружностям, а О, и О2 —их центры.
Решение.
ЪмкакОхА1ЛВ мО2В1АВ,тоOjЛ||О22? и,значит,фигураОХАВО2 — трапеция (рис. 10.110). Касательные в точке С взаимно перпендикулярны, а потому каждая из них проходит через центр другой окружности, т.е. О]С = 4 см, О2С = 8 см, откуда О}О2 = yjo^C2 +О2С2 = 4>/5 (см).Проведем О{ D\\ А В и из Д DO, найдем О{ D =	-O2D2 = >/80-16 = 8 (см).
Следовательно, 5О1/1Д(92 = 0,5(8+ 4)-8 = 48 см2.
Ответ: 48 см2.
10.118.	Определить сторону ромба, зная, что площадь его равна £, а длины диагоналей относятся как т: п .
Решение.
Запишем BD = mx \ АС = пх (рис. 10.111). Площадь ромба
с 1	2	т Di
S = — тпх , откуда х = J. Тогда Bi 2	У тп
-	1 Л 1 э
Сторона ромба ВС = -BD~ + -АС~ = 4	4
2S \2Srn \2Sn mJ— =J------; ЛС = J---.
У тп V п	Ут
2Sm 2Sn sinr+n2) ~ 477 4т 2тп
сюда ВС = J—----
V 2тп
Ответ:
10.119.	Периметр ромба равен 2р; длины диагоналей относятся как т.п . Вычислить площадь ромба.
Решение.
Используя рис. 10.111, имеем BD = mx,
nz-2	(AC''? (тх^
АС = пх. ВС=\— + ------ = — +
I 2 I I 2 I I 2 I
Рис. 10.112
ORO
О. к
пх V _ х2(ги2 +п
Т J "	4
Периметр
2р = 4ВС = 41х2Ьп2+п V 4
т2 + п2
р
Отсюда х = .-----1
ylm2 + л2
1	1	2
Площадь ромба S = — BD АС = — тпх
~	тпР2
Ответ:	г	—г-».
_ 1 mnp2 2 (w2 +n
10.120.	Две окружности радиуса R с центрами в точках О1 и О2 касаются друг друга. Их пересекает прямая в точках А, В , С и D так, что АВ = ВС = CD . Найти площадь четырехугольника OXADO2 .
Решение.
&АОХВ 9 &О{ВО , ДВОС, ДОСО2> &CO2D —правильные со сто
роной Я (рис. 10.112). Площадь AAOtB S^O^B =—-—. Площадь ис
комого четырехугольника O{ADO2 S = 5S^OiB = ——
Ответ: -----
4
Рис. 10.113
10.121.	Вычислить площадь
прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно а и большая боко-
вая сторона равна Ь •
Решение.
D	ь45
Высота трапеции равна ——,
а большее основание равно а + —.
Следовательно, ее площадь 5 = —
(	Ь}Ь>13 (4а+6>Тз
а+а+— ----=-------—
2 J 2	8
Ответ: (4а + Ь)ьЛ/%.
10.122.	Большее основание трапеции имеет длину 24 см (рис. 10.113). Найти длину ее меньшего основания, если известно, что расстояние между серединами диагоналей трапеции равно 4 см.
Решение.
АЕ = EC',DF = FB ,КЕ = DC/2,FT = DC/2\DC = х.КТ = 2KE + EF =
= х+4 . С другой стороны, КТ =
х+24	л х + 24
—-—. Решая уравнение х+4 = —-—
получим х = 16 (см).
Ответ: 16 см.
10.123.	Площадь равнобедренной трапеции, описанной около кру
га, равна S. Определить боковую сторону трапеции, если известно, что
острый угол при основании равен тс/6.
Решение.
Пусть х — длина боковой стороны; тогда высота трапеции равна ^х. Так как трапеция описана около круга, то сумма ее оснований равна сумме боковых сторон. Следовательно, площадь трапеции
S = --2х- — х , откуда x = ^2S.
2	2
Ответ: J2S.
10.124.	Трапеция разбита диагоналями на четыре треугольника (рис. 10.114). Доказать, что треугольники, прилегающие к боковым сторонам, равновелики.
Решение,
АО DO , Рассмотрим &AOD и АСОВ • Они подобные, —- = —— = к , Отсю-со ВО
да \DO = kBO’ s =-ВО AOsinZBOA = -BO k COsinZBOA, [AO = kCO.	2	2
S’acoc = |c0 0D sin ZCOD = | CO k BO sin ZCOD и ZBOA = ZCOD.
Отсюда следует, что 5^0A = S&C0D, что и требовалось доказать.
10.125.	* На большем катете треугольника как на диаметре построена полуокружность (рис. 10.115). Найти ее длину, если длина меньшего катета 30 см, а хорда, соединяющая вершину прямого угла с точкой пересечения гипотенузы и полуокружности, равна 24 см.
Решение,
Из &BDC получим DC = 4ВС2 -BD2 - V900-576 =18 (см). &BDC и &ADB —подобные. Отсюда BD2 =DC-DA => DA = BD2/dC = = 242/18 = 32 (см). Из ДЛДС имеем АВ = 4АС2 -ВС2 = 40 (см). Дли-на полуокружности I = лЛО = 20л (см).
Ответ: 20л (см).
10.126.	На диаметре полукруга построен правильный треугольник, стороны которого равны диаметру. Как относятся площади частей треугольника, лежащих вне и внутри полукруга?
Рис. 10.117
Решение.
Площадь части треугольника, которая лежит внутри полукруга:
$1 -25Д4ОР + SceKT
2Л2>/з л/?2 „гГзТз+л"
=--------1-----= к ----------
4	6	6
\	7
(рис. 10.116). Пло-
щадь части треугольника, которая лежит вне полукруга:
Отношение площадей: _2 — уУ =____ТС
S1 б^зЙ+л) ЗЙ+л
Ответ:
Зл/З-л 3-Уз + л
10.127.	В правильный треугольник со стороной, равной а, вписана окружность, в которую вписан правильный шестиугольник. Найти площадь шестиугольника.
Решение.
Радиус окружности, вписанной в правильный треугольник со сторо-л>/3
нои а , равен г =--. Сторона шестиугольника, вписанного в эту ок-
6
я>/3
ружность, равна радиусу: а6 = г =--, а радиус окружности, вписан-
6
а6	а6у/з а-у/З-у/з а
нои в этот шестиугольник, г = -----= —-— = ——— = —.
180°	2	62	4
2tg—
„	о 6а6г	ба^За а2у/з
Площадь шестиугольника о = —-— =	= —-—
2	2-6*4 о
а2>/3
Ответ: —-—.
10.128.	Около квадрата, сторона которого равна а, описана окружность, а около окружности — правильный шестиугольник. Опреде
лить площадь шестиугольника.
Решение.
Радиус описанной около квадрата окружности равен половине диа-
гонали квадрата г = —. Эта же окружность является вписанной для а6	ah yf3	а41 а6 V3
шестиугольника: г =---2—- =	— . Получим —— =	—, откуда
г	2tg “а
аб -	. Тогда площадь шестиугольника
2	2V3-2
Ответ:	.
10.129.	В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной т и п. Определить площадь трапеции.
Решение.
Пусть АК = т> КВ = п (рис. 10.117). Тогда КВ = ВМ = МС = п,
AK = AN = ND = m .
Найдем высоту трапеции:
h = ВН = у1аВ2 - АН1 = у1(т + пУ -(m-nf = 2<jmn .
Итак, S = ^(ВС + AD^h = (т + n)h = 14тп{т + и).
Ответ: 2у1тп (т + п).
10.130.	Сторона квадрата, вписанного в окружность, отсекает сегмент, площадь которого равна (2я - 4) см2. Найти площадь квадрата.
Решение.
tzR1
Пусть R — радиус круга. Тогда площадь сектора равна -, а
Рис. 10.118
R2 площадь треугольника равна — и, следовательно, площадь сегмента nR2 R2 Я2 (я-2) составляет —------— = —.
4	2	4
„	Я2(л-2) _	.
Имеем ---------= 2л-4, откуда
4
R = 2^2 (см). Итак, площадь квад-
рата равна 2R2 =16 (см2).
Ответ: 16 см2.
10.131.	В ромб с острым углом 30° вписан круг, площадь которого равна Q. Найти площадь ромба.
Решение.
Проведем радиусы ОК , OL , ОМ, ON в точки касания (рис. 10.118). ААВС = 180°-Z.BAD = 180°-30° = 150°.Таккакдиаго-
150°
нали в ромбе являются биссектрисами, то ЛАВО = —— = 75°. Значит,
on- К0 - КО	ВО	КО	2КО
ВО --------- ------- Тогда АВ =---------=-------------=------
sin75	cosl5	sinZO45 sinl5’cosl5° sin30°
= 4X€> = 4r. У ромба АВ = ВС = CD = AD-4г . Площадь ромба
S =/4B HDsin3Oe =16r2sin30°- Площадь круга Q = nr2, откуда
, О „	„ 80
г = —. Поэтому окончательно S =	.
л	л
Ответ: —• л
10.132.	В круговой сектор, дуга которого содержит 60°, вписан круг.
Найти отношение площади этого круга к площади сектора.
Решение.
Пусть В, D, Е — точки касания. Радиус окружности, из которой вырезан сектор, обозначим R, а радиус вписанной в сектор окружности—
г (рис. 10.119). Значит, ВО =DO -ЕО = r,a ВО-R. ОО =R-r-
DO =ОО sin30’-Этозначит,что г = у(/?-г),откуда R = 3г.Площадь
сектора S, =	=-^у—. Площадь вписанного круга S2 =лг2;
S2 :Si = лг2: — = 2:3.
2
Ответ: 2:3.
10.133.	Из точки м, находящейся на расстоянии а от окружности, проведена к этой окружности касательная длиной 2а. Найти площадь правильного шестиугольника, вписанного в окружность.
Решение.
Проведем радиус О А в точку касания (рис. 10.120) и обозначим радиус окружности через г. Тогда в КО А М имеем (2а)2 + г2 = (а + г)2
или 4а2 + г2 = а2 + 2аг + г2 , откуда г =	. Таким образом,
_ _ 6г2 V3 _ 27а2 V3
4	8	‘
27а2
Ответ: ------
Рис. 10.121	Рис. 10.122
10.134.	В равнобедренной трапеции одно основание равно 40 см, а другое 24 см. Диагонали этой трапеции взаимно перпендикулярны. Найти ее площадь.
Решение.
Площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату ее высоты: S = h2. С другой сторо-
а + Ь.	. а + Ь 40 + 24 „ , . .
ны, S =-----h , откуда h ----=-------= 32 (см). А площадь
2	2	2
S = 322 = 1024 (см2).
Ответ: 1024 см2.
10.135.	Основание треугольника равно 30 см, а боковые стороны равны 26 и 28 см. Высота разделена в отношении 2:3 (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Определить площадь полученной при этом трапеции.
Решение.
По условию АВ = с = 30 см, АС = Ь = 26 см, ВС = а = 28 см (рис. 10.121). Тогда р = 0,5(д+ /> + <?)=42 , р-л = 14, р —= 16 , р-с = 12 и по формуле Герона находим S^BC = >/42 • 14 ♦ 16 • 12 = 336 (см2). Так как ЛЛЖ ~ ДДВС , то 5д;ИЛ.с : SMBC =СК2: CD2 = 4/25 = ОД6. Отсюда определяем площадь трапеции:
$amnb = *^длвс ~ $&mnc = 336 — 0,16 • 336 = 282,24 (см2).
Ответ: 282,24 см2.
10.136.	В прямоугольном треугольнике биссектриса острого угла делит противоположный катет на отрезки длиной 4 и 5 см. Определить площадь треугольника.
Решение.	-----
Пусть ВС = х (рис. 10.122). Тогда АВ = у1^1 + х2 и -=	1 + *
4	5
Рис. 10.123
Рис. 10.124
(поскольку BD — биссектриса). Отсюда имеем 25х2 = 16(81 + х2), т.е.
х = 12 (см). Следовательно, S^BC = — ВС • АС = — * 12 • 9 = 54 (см2).
Ответ: 54 см2.
10.137.	Хорда АВ постоянной длины скользит своими концами по окружности радиуса R. Точка С этой хорды, находящаяся на расстояниях а и b от концов А иВ хорды, описывает при полном обороте окружность. Вычислить площадь кольца, заключенного между данной окружностью и окружностью, описанной точкой С.
Решение.
ЛАОВ —равнобедренный (рис. 10.123). Значит, ZBAO = ZABO .
Пусть ОС = г . По теореме косинусов г2 = R2 + a2 -2aRcosa. С другой стороны, г2 = R2 +b2 -2Wfcosa . Приравнивая, получим а2 -Ь2 =
= 2/?cos а(а-/>), откуда cos а =	Значит, г2 = R2 +b2 - 2bR -
2R	2R
= R2 -ab. Площади кругов Sj = nR2, S2 = nr2 = n^R2 - ab). Площадь
кольца S =	- S2 = nR2 - nR2 + nab = nab.
Ответ: nab.
10.138.	Три равные окружности радиуса г попарно касаются одна другой. Вычислить площадь фигуры, расположенной вне окружностей и ограниченной их дугами, заключенными между точками касания.
Решение.
Отрезки, соединяющие центры окружностей (рис. 10.124), образуют пра-w _ _	с 4г2 7з 2 /?
вильныи треугольник со стороной 2г. Его площадь: Sj = —-— = г V3 .
_	1	е ЯГ2 60° 7СГ2 _
Площадь 1-го сектора о2 = ——= ——. Так как секторов три, то пло-
щадь фигуры, расположенной вне окружностей и ограниченной их дугами, заключенными между точками касания, будет равна
Г2Д лг2 Г2(2>/3-л) 2	2
_	г2(2>/3-л)
Ответ: -----------.
2
10.139.	На сторонах ромба как на диаметрах описаны полуокружности, обращенные внутрь ромба. Определить площадь полученной розетки, если диагонали ромба равны а и Ь. Решение.
Площадь полученной розетки будет равна сумме площадей четырех заштрихованных (рис. 10.125) частей. Площадь каждой заштрихованной части равна разности площади полукруга и площади прямоугольного тре-
а Ь
угольника со сторонами — и — . Сторону ромба можно наити как гипоте
нузу: с = у л/л2 +£2. Тогда радиус полуокружности R = — с = — yja2 + Ь2.
Площадь полукруга S] =^nR2 = -^~(а2 + b2). Площадь прямоугольного
треугольника S2 =	Площадь розетки 5 = 4($1 -^2)=
2 2 2	8
/	\	2
.( Л . 2 > 2 -> а^> I л(д
= 4 —(<Г+/Г)----= ——
U2 8 )
+ b2)-4ab
8
л	л(а2 + b2) - 4ab
Ответ: —--------------.
8
10.140.	Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемого этими прямыми, в два раза больше площади данного четырехугольника.
Решение.
По условию (рис. 10.126), KL || АС|| NM, KN ||ЯЯ|| LM. Площадь параллелограмма KLMN равна
Рис. 10.127
$KLMN ~$ABCD +$АКВ + $BLC + $CDM +$AND •
Так как KB^AO и Х>ф?О,то КВОА —параллелограмм и АВ — его диагональ. Значит, SAKB -SABO . Аналогично SBLC = SB0C , $CMD - $COD » $DNA “ $DOA * Тогда
$KLMN ” $ABCD + \$BOC +$COD +&DOA + $АВо)-$АВСй +$ABCD - ^$ABCD>
что и требовалось доказать.
10.141.	Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны соответственно 8 см, 14 см и 44 см2.
Решение.
Пусть ВС = 8, AD = 14 (рис. 10.127). Проведем BL.LAD , CM1AD.
_ ВС + AD	2S лот .	_
SABCD ---2----’ Отсюда BL = де	(см). Условию
AD-LM _ у ч _
AB = CD> BL = CM .Значит, AL = MD =---= 3 (см). Тогда
АВ = у/bL2 + ЛЬ2 = V16 + 9 =5 (см).
Ответ: 5 см.
10.142.	В правильный треугольник вписана окружность, а в нее — правильный шестиугольник. Найти отношение площадей треугольника и шестиугольника.
Решение.
Пусть сторона правильного треугольника равна а. Тогда его пло-
с аЧЗ _	~	W3
щадь Si = —-—. Радиус окружности, вписанной в треугольник, г = ——.
Он будет равен стороне шестиугольника, вписанного в эту окружность:
а6 =-----. А радиус окружности, вписанной в этот шестиугольник:
6
«6
= 2.
_ 180°	2	4 '
2,g—
Площадь шестиугольника
С _ ^а5Г _ °2	. $! _ '
— — —------- *------
2	2	8 S2
Ответ: 2.
10.143.	Общей хордой двух кругов стягиваются дуги в 60° и 120°.
Найти отношение площадей этих кругов.
Решение.
Пусть АВ — общая хорда, , R2 — радиусы соответствующих
окружностей (рис. 10.128). По теореме косинусов
АВ2 = R2 + R2 -2А, A] cos 60° = A2 .
С другой стороны, АВ2 = R2 + R-2 — 2R2R2 cos 120° = 3R2. Значит,
А2 = ЗА2 . Площади кругов = лА2, S2 = лА2 •
Л	Si ЗА2 л 3
Отношение — =----г- = — .
S2 лА2 1
Ответ: 3:1.
10.144.	В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. Определить, на какие части делится пло-
Рис. 10.131
Рис. 10.130
щадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4 м.
Решение,
Пусть АК и DL — биссектрисы (рис. 10.129), AD = 4, ВА = 2, АКАВ = 45°, АВ = 90°, АВКА = 45°. Значит, ЛАВК — равнобедренный и АВ = ВК = 2 (м). Аналогично, КС = CD = 2 (м). Так как ВК + CL = 4 (м), то точки L и К совпадают. Имеем 5^^ = = l/iB.^ = 1.2-2 = 2(M2),SDCJ<=lc/f CD = l-2.2 = 2(M2), SAKD =
= SABCD~SABK ~SDCK = 2-4-2-2 = 4 (м2).
Ответ: 2, 2, 4 (м2).
10.145.	Высота ромба равна 12 см, а одна из его диагоналей равна 15 см. Найти площадь ромба.
Решение.
Пусть В/k = 12 (см), BD = 15 (см) (рис. 10.130). Из ЛВКО
ЬК 12	4	.2	1	10 J
sma=—=—=—;так как 0<а<9(г,то cosa = VI-sin а= 1---=—.
BD 15 5	V 25 5
а	OD BD	BD 15-5 75, ч
Из ЛА OD cos а  --=----, откуда AD =------=------- — (см).
AD 2AD J	2cosa 2-3	6
75	э
Площадь ромба S = AD • ВК = — • 12 = 150 (см2).
Ответ: 150 см2.
10.146.	Длина высоты, опущенной на основание равнобедренного треугольника, равна 25 см, а радиус вписанной окружности равен 8 см. Найти длину основания треугольника.
Рис. 10.132
Решение.
Пусть К, L,M—точки касания (рис. 131).
Тогда ВК = 25 (см), ОК = OL = ОМ = 8 (см). Значит,
BO = BK-OK = V1 (см),
ВМ = >1ВО2-ОМ2 = >/289-64 = 15 (см).
ОМ 8
Т огда tg а = —— = —. С другой старо-
ЬМ 13
8	40
АТ?	8	40
ны, tgа =	, откуда КС = ВКtga = 25 — = — (см). Значит,
ЯК	15	3
15	3
АС = 2КС = — (см).
80
Ответ: — см.
10.147.	В параллелограмме с периметром 32 см проведены диагонали. Разность между периметрами двух смежных треугольников равна 8 см. Найти длины сторон параллелограмма.
Решение.
Обозначим стороны параллелограмма через а и b. Тогда его периметр равен р = 2(а + b) = 32 . Периметр одного треугольника равен
Р\ =b+2 + 2' второго Рг параллелограмма. Разность
/А ^2 j j
= а + —+ —,где d\, d7 —диагонали 2	2
Р\~Рг =Ь-а = Я. Получили систему:
а = 4, 6 = 12.
Ja + 6 = 16, i, о Решая ее, найдем — а = о.
Ответ: 12 см, 4 см.
10.148.	Найти площадь равнобедренной трапеции, если ее высота равна h, а боковая сторона видна из центра описанной окружности под углом 60°.
Решение.
Так как центральный угол COD равен 60° (рис. 10.132), то вписан-
ный угол CAD равен 30°. Следовательно, h = у А С и из КАКС получим АК = 7 л с2 - СК2 = hjl . Находим площадь трапеции:
S = ^(BC + AD)h = (AE + EK)h = AKh = hj3h = h2j3.
10.149.	Круг, радиус которого равен R, разделен на два сегмента хордой, равной стороне вписанного квадрата. Определить площадь меньшего из этих сегментов.
Решение,
Обозначим сторону вписанного квадрата через а. Диаметр окружности является его диагональю. Это значит, что 2а2 = (2Z?)2, откуда а = R^2 • Площадь круга S, = nR2. Площадь квадрата S2 = а2 = 2R2. Площадь меньшего сегмента
3.1(3, 4	4	4
. Л2 (я-2)
Ответ: ---------.
4
10.150.	Определить площадь кругового кольца, заключенного между двумя концентрическими окружностями, длины которых равны Cj и
Решение,
п С, п С2 Длина окружности Cj = 2лЛ, С2 = 2nR2, откуда R\ = —, R2 = — .
2л 2л лС?^	С2	о2
Площадь большего круга	= —у- = -7-; S2 =	. Площадь.
4л	4л	4л
кольца S = S] -S2 = у-(с2 -С22).
4л
г»	С12 ~С2
Ответ: ----------.
4л
10.151.	Круг разделен на два сегмента хордой, равной стороне правильного вписанного треугольника. Определить отношение площадей этих сегментов.
Решение,
Пусть г — радиус круга, a Sj и S2 — площади сегментов. Тогда
S2 = nr2-St =лг2-^г2(47Г-3>/з)=^г2^л + 3>/з).
Д _4л-зТз
Значит, т- - --~гт .
’ *$2 8JU + 3V3
4Л-3>/3
Ответ: ~	”"7= •
87C + 3V3
10.152.	В правильный шестиугольник, сторона которого равна а, вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями.
Решение.
Радиус вписанной в шестиугольник окружности q =--- = ——.
Радиус описанной же окружности около шестиугольника г2 = а. Пло-
За2
щадь большего круга S2 = тел2, меньшего— S| = к-.
Площадь кольца S = S2 -	= тш2 - —= -~-
>
л тиг
Ответ: ------.
4
10.153.	Круг радиуса R разделен двумя концентрическими с ним окружностями на три равновеликие фигуры. Найти радиусы этих окружностей.
Решение.
Обозначим радиусы внутренних окружностей через R\ и R2. Пусть S — площадь самого малого круга; тогда nR2 = S’, tcR2 = 2S, nR2 = 3S • Сле-о2 лЯ2 —n2 2nR2	_ R _	_ [2
довательно, TtRr =--и tcR2 =------, откуда Ri = —= и R2 =RJ- .
1	3	3	Л V3
Ответ:
10.154.	Площадь кругового кольца равна S. Радиус большей окружности равен длине меньшей окружности. Определить радиус последней.
Решение.
Радиус большей окружности обозначим через R2, а меньшей — через Л,. Площадь кольца S = лТ?22 - л7?2. Так как R2 - 2nRx, то 5 = л-4л2Я12 -лЯ2 = W?!2(lrt2 -1).
<*з
I S
Откуда /?! = г •
Рис. 10.133
120
5
Ответ:
10.155.	В круге радиуса R по разные стороны от центра проведены две параллельные хорды, одна из которых равна стороне правильного вписанного треугольника, а другая—стороне правильного вписанного шестиугольника. Определить площадь части круга, содержащейся между хордами.
Решение.
Длина хорды, равная стороне вписанного правильного шестиуголь-37? г~
ника, а6 =7?, а треугольника а3 =-= = V37? (рис. 10.133). Площадь V3
сектора О АВ S, равна площади сегмента плюс площадь треугольника
е о е ЛЯ2-60° ЛЯ2
АОВ: S, =5^! +SA0B =	Откуда
360	6
„ лЯ2 1 _2 • ,л. nR2 Я27з
5сегм1=-7---— Я251п60 = —--------— .
6	2	6	4
Площадь сектора OCD S2 также равна сумме площадей сегмента и _ <, о о ля2 120° ля2 треугольника ODC: S2 = осеГм2 +^odc ----------= откуда
360	3
„ лЯ2 1 -2 • пл» пК2 л/зя2 _
оСегм2 = ~--2 К sm * 20 = — -------—. Площадь круга, содержа-
щаяся между хордами:
лЯ2 -J3R2 = Я2(я+>/з)
3 + 4	2
S — HR £Сегм1 *^сегм2 “
лЯ2 R2>
----+ ’ 6---4
Ответ:
Рис. 10.134
10.156.	В круг радиуса Л вписаны два правильных треугольника так, что при их взаимном пересечении каждая из сторон разделилась на три равных отрезка. Найти площадь пересечения этих треугольников.
Решение,
Фигура, образованная при пересечении таких треугольников, будет правильным шестиугольником. Сторона
3R г~
вписанного правильного треугольника равна а3 =	= J3R . Тогда
1 V3 сторона правильного шестиугольника равна а6 = —а3 - — R. Радиус
вписанной в него окружности г
а*, yfl _ л/з ♦ -J3R _ R
180°	Г2 У
2‘6—
_	„ 6a6r 6Я73Я J$R2
Площадь шестиугольника: S6 =	= —2—
л ^r2
Ответ: ------.
2
10.157.	Через точки R и Е, принадлежащие сторонам АВ и AD параллелограмма ABCD, и такие, что AR = (2/3)ЛВ, АЕ =, ^3)AD, проведена прямая. Найти отношение площади параллелограмма к площади полученного треугольника.
Решение.
Пусть h —высота параллелограмма A BCD, hx —высота треуголь
ника ARE (рис. 10.134).Тогда SABCD =AD h, S^RE =^AE /it. Но
h АВ 3	$abcd ADh AD h
— = = -. Следовательно, —--= ------= -—:-----z— = >.
Л, AR 2	S^RE \_A YlADlh
2	1 2 3	3
Ответ: 9.
10.158.	Три окружности радиусов =6 см, R2 = 7 см, R3 =8 см попарно касаются друг друга. Определить площадь треугольника, вершины которого совпадают с центрами этих окружностей.
Решение.
Отрезки, соединяющие центры этих окружностей, равны: a = Rx +/?! = 6 + 7 = 13 (см), b = R2 + Я3 =7 + 8 = 15 (см), c = Rx + /?3 = = 6 + 8 = 14 (см). Тогда площадь этого треугольника можно найти по
1	г"	а + b + с 13 + 15 + 14 z ч
формуле Терона, где р =------=-----------= 21 (см):
2	2
S = ylp(p-atp-b\p-c) = ^21(21-13X21-14)^1-15) = 84 (см2).
Ответ: 84 см2.
10.159.	Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, длины сторон которых равны.
Решение.
Пусть сторона правильного треугольника, квадрата, шестиуголь-
Т	с а2^ С 2 е	о
ника равна а. Тогда S3 =—-—, SA-a , 56 =—-—. Значит,
4	4
:S4 :S6 = ^^--.а2 :—а2 = 73:4:6>/з .
4	4
Ответ: 7з: 4:67з.
10.160.	В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон.
Решение.
Так как S = j(a + 6)ft, то ±(a + b)-22 = 594, откуда а + Ь = 54 . Из
]а + /> = 54, системы уравнений । а __ находим а = 30 (м), b = 24 (м).
Ответ: 30 м и 24 м.
10.161.	Через вершину прямого угла прямоугольного треугольника с катетами 6 и 8 см проведен перпендикуляр к гипотенузе. Вычислить площади образовавшихся треугольников.
Решение.
Пусть СК —перпендикуляр к гипотенузе АВ &АВС (рис. 10.135).
в
в
Рис. 10.135
Рис. 10.136
Тогда АВ = ^ВС2 +АС2 =10
(см); SABC =^ АС  ВС = 24 (см2);
(АВ^ ВС
&ВКС ~ &АСВ. Значит, $АСВ $вкс _5лсл ВС2 _ 24-64 _ --------------------ioF"15’36(CM)
. Найдем
Тогда SACK = 5авс ~$вкс =24—15,36 = 8,64 (см2).
Ответ: 15,36; 8,64 (см2).
10.162.	Вычислить площадь равнобедренного треугольника, если длина его высоты, проведенной к боковой стороне, равна 12 см, адлина основания равна 15 см.
Решение.
Пусть АК —перпендикуляр к боковой стороне ВС (рис. 10.136).Тог-да АК = 12 , АС = 15 (см); КС = -JaC2-AK2 = 7225-144 = 9 (см). Обо
значим АВ = ВС = х. Тогда АВ2 =АК2 + 13х2 или х2 = 144 + (х-9)2,
откуда х = у (см). Тогда SABc = “	‘ ВС = 12 ~ = 75 (см2).
Ответ: 75 см2.
10.163.	Стороны треугольника равны 13,14 и 15 см. Найти отношение площадей описанного и вписанного в этот треугольник кругов.
Решение.
Пусть г п R —радиусы вписанной и описанной окружностей. Тогда
S D abc
г = —, к =---. Найдем
р 4S
S = ylp(p-a\p-b^-c) =
= л/21-8-7-6 =84 (см2).
Следовательно/ = 4см, A = — см, 8
откуда получим искомое отноше-
nR2 (65 ?
ние площадей: —г- = — .
nr ^32 J
(65?
Ответ: тт
Рис. 10.137
ЮЛ64. Вычислить площадь трапеции ABCD (AD^BC), если длины ее оснований относятся как 5:3 и площадь треугольника ADM равна 50 см2, где М —точка пересечения прямых АВ и CD.
Решение.
Пусть ABCD —данная трапеция (рис. 10.137). AD .BC = 5:3 ;
SADM =50. ^ADM ~ АВ СЛ/, Значит,	• Тогда
$ВСМ	J
_SADMBC2 (ВС? /З?
BCM~~AD2	"5VJ
ABCD = $ADM ~$всм =50-18 = 32 (cm2).
Ответ: 32 см2.
10.165. В правильный треугольник вписана окружность и около него опйсана окружность. Найти площадь образовавшегося кольца, если сторона треугольника равна а.
Решение.
„ С Л	2	3	Яд	Л	2 2	7з	„ а3
Имеем Яд =— а , р --а, г- — = —а = —a, R =--------=
4	2	р	4 За	6 4ЯД
а3 43	__ 2	2	2(11^ ла2
= г- - = — а.ОгаодаЯ = лЯ -пг =па \---=-----.
,43а2 . 3	1^3 12 J 4 -
7Ш2
Ответ: ----.
10.166. Один из катетов прямоугольного треугольника равен 15 см, а радиус окружности, вписанной в треугольник, равен 3 см. Найти площадь треугольника.
Решение.
Пусть К. L, М — точки касания вписанной окружности (рис. 10.138). Тогда КО = LO = МО = 3 (см), СА = 15 (см). Отсюда СМ = КС = 3 (см), МА = СА - СМ = 15 - 3 = 12 (см). Значит, LA = = 12 (см). Обозначим ВК = BL = х. Тогда пл о-щадь треугольника S = 2SBKO + 2Sqla + $КОМС =
= 2~x-3 + 2-~12-3 + 3-3 = 3x+45. С другой сторо
ны, S = (x + 3)-15~ = —х + —. Тогда — х + — = Зх + 45, откудах = 5.
2	2	2	2	2
1	7
Итак, площадь треугольника S = 15 • 8 — = 60 (см ).
Ответ: 60 см2.
10Д76. Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
Решение.
Пусть точки К,М— середины непараллельных сторон АВ и CD (рис. 10.139), ML — перпендикуляр к стороне АВ, BN— перпендикуляр к AD. Из &ANB найдем sina=-^^. Из &KLM получим sina = -^-. Зна-
АВ	КМ
BN LM
чит,	гДе — средняя линия трапеции ABCD. Итак,
АВ КМ
АВ • LM = BN • КМ = S, что и требовалось доказать.
10.168.	Доказать, что если диаметр полукруга разделить на две произвольные части и на каждой из них построить как на диаметре полуокружность (внутри данного полукруга), то площадь, заключенная между тремя полуокружностями, равна площади круга, диаметр которого равен длине перпендикуляра к диаметру полукруга, проведенного в точке деления до пересечения с окружностью.
Решение.
Пусть R — радиус данного полукруга, аг — радиус одного из пост-
Рис. 10.139	Рис. 10.140
роенных полукругов (рис. 10.140). Тогда площадь заданной фигуры равна 0,5^гЛ2 - яг2 - я(Я - г)2 )= яг(Л - г) • Так как AADB = 90‘, то
CD2 =ACCB = 2r-2(R-r)=4r(R-r), откуда = яг(Я - г). Что 4
и требовалось доказать.
ЮЛ 69. В круг радиуса R вписан прямоугольник, площадь которого вдвое меньше площади круга. Определить стороны прямоугольника. Решение.
Пусть стороны прямоугольника равны а и Ь . Тогда диагональ его, являясь диаметром окружности, равна у/а2 + Ь2 , т.е. а2 + Ь2 = 4Я2.
Площадь круга лЛ2 = 2аЬ. Получим систему:.
а2+62=4Я2, лЯ2 = 2аЬ.
Откуда
„ R-Jn+4+Ryl4-n
Ответ: ----------------.
2
10.170.	Определить площадь круга, вписанного в сектор круга радиуса R с хордой 2а.
Решение.
Опустим радиусы вписанного круга в точки касания (рис. 10.141). Тогда из прямоугольных треугольников ЛА BD и ЛОКВ получаем
sina =
ОК ов
AD -----<=> АВ
г	а	п п	Ra
----= — <=> Rr = Ra-ra	г  	 R-r R	R+a
Рис. 10.142
Рис. 10.141
Ra V
---- —площадь вписанного круга. R + a I
Ответ: к
( Ra R + a
10.171.	Основания трапеции равны а и Ь, углы при большем основании равны я/6 и л/4. Найти площадь трапеции.
Решение.
Пусть BC^AD и АЛ = л/6, Z.D - л/4 . Опустим перпендикуляры ВК и CL на сторону AD (рис. 10.142). CL = BK обозначим через Л. Тогда tgrc/4 = -^-. Значит, LD = h. Тогда =	tg7u/6 = J^- =
LD	АК
Л 1 Л	. b-а _
=-------- , -т=г =---, откуда Л = -5=— . Площадь трапеции
b-a-h Ji b-a-h	V3+1
b-a _ (Тз -1)(б2 -а2)
2	2 Тз+1 4
Л (УЗ-lfe2 -а2)
Ответ: ------
4
10.172.	В ромб с острым углом 30° вписан круг, а в круг — квадрат.
Найти отношение площади ромба к площади квадрата.
К Рис. 10.144
A
D
Решение.
Пусть К, L, М, N —точки касания окружности и сторон ромба. ЛА = 30“ (рис. 10.143), АЛОВ ~ АОКВ . Значит, =	.
Обозначим KO-OL-OM -ON = r, АВ = ВС = DC = AD = a . Тог-r	«cosl5‘	a	.
да —. , „ =--------.откуда r = asinl5 cos 15 =— sin30 .Диаметр
asml5 a	2
окружности является диагональю вписанного в окружность квадрата, т.е. 2Ь2 = (2rf ,где5—сторона квадрата, тогда b = г>/2 = — V2 sin 30“. Пло-1	а1 1
щадь ромба S] = a2 sin 30“ = а1 • —. Площадь квадрата S2 = b2 = — • —.
£
Отношение =4.
Зд
Ответ: 4.
10.173.	Длины сторон прямоугольного треугольника образуют арифметическую прогрессию с разностью 1 см. Найти длину гипотенузы.
Решение.
Пусть с —длина гипотенузы. Тогда длины катетов равны с-1 и с-2.Имеем (с-1)2 + (c-lf -с1 или с2 -6с + 5 = 0 , откуда с = 5 (см) (второй корень уравнения не удовлетворяет условию).
Ответ: 5 см.
10.174.	Площадь равнобедренной трапеции, описанной около круга, равна 5. Определить радиус этого круга, если угол при основании трапеции равен 30°.
Решение.
Пусть ВС||ЛD, ЛА = 30° (рис. 10.144). Обозначим ВС = а , AD = Ь;
опустим перпендикуляр ВК на AD, обозначим его h , АВ = с . Так
, _	а + Ь тт
как окружность вписана в трапецию, то а + о = 2с или с = —-—. Из
. h 2h 2h 1	,	, _
ЬАВК найдем sin 30 = — =----,----- = — откуда а + Ь = 4Л . Значит,
с а+Ь а+Ь 2
S =	h=2h2; так как h = 2r, to S = 8r2, откуда r -
2S 4
„ J2S
Ответ: -----
4
10.175.	Найти площадь равнобедренного треугольника, если основание его равно а, а длина высоты, проведенной к основанию, равна длине отрезка, соединяющего середины основания и боковой стороны.
Решение.
По условию DK — средняя линия &АВС (рис. 10.145). Так
как BD = DK --ВС, то ZC = 30° и BC = 2BD& &BCD имеем 2
CD2 = ВС2 - BD2 или = 4BD2 -BD2 , откуда _	• Следо-
1	2 /¥
вательно, S = - А С BD = CD • BD = 2	12
Ответ: —-—.
12
10.176.	Доказать, что в параллелограмме ABCD расстояния от любой точки диагонали^ С по прямых ВС и CD обратно пропорциональны длинам этих сторон.
Решение.
Пусть К — произвольная точка диагонали АС (рис. 10.146). Опустим перпендикуляры КМ и KN на ВС и CD.
Из &КМС КС = -^_. Из АЛТУС sina
KN	sinp	KN
КС = .	. Это значит, что --—	=--.
sinp	sina	MK
Из АЛ CD по теореме синусов находим
CD AD
—---= и так как AD = ВС, то
sma sinp
sinp _ ВС sina CD
~	KN ВС
Это значит, что-=---= k
MK CD
k	k
или KN CD - k, MK • ВС = k. Отсюда KN =-----, MK =----, что и тре-
CD	ВС
бовалось доказать.
10.177.	Доказать, что отношение периметра треугольника к одной из его сторон равно отношению высоты, опущенной на эту сторону, к радиусу вписанной окружности.
Решение.
Так как площадь треугольника S’ = pr- 0,5aha ,ro2p/a = ha/r, что и требовалось доказать.
10.178.	Найти длины сторон равнобедренного треугольника АВС с основанием АС, если известно, что длины его высот AN и ВМ равны соответственно пит.
Решение.
\CMB~ &CNA (рис. 10.147), откуда = Отсюда АС = — ВС, AN АС	т
1	( А2
МС=-АС=—ВС. Из ДЯА/СВС2 = МВ2 +МС2,ВС2 = т2+ВС2\ — 2 2т	к 2mу
2т2	2тп
откуда ВС = .	, А С = -====-.
у14т2-п2	ч4т2—п2
Ответ:
2т2 2тп
114т2 ~п2 \l4rn2-п2
Рис. 10.148
10.179.	Ромб, у которого сторона равна меньшей диагонали (рис.
10.148)	, равновелик кругу радиуса Л . Определить сторону ромба. Решение.
Из условия &ABD —равносторонний, следовательно, ZB4D = 60°.
л/3
Площадь ромба: Sp = х2 sin 60° = —-х2 = nR2 =>
Ответ: R
10.180.	Вычислить площадь трапеции по разности оснований, равной 14 см, и двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность.
Решение.
Пусть ЯВ = 13, CD = 15 (рис. 10.149). Обозначим АЕ = х , FD = y. AD - ВС = 14, значит, х + у = 14; BE2 = АВ2 - х2 , CF2 = CD2 - у2 ,
откуда 132 - х2 = 152 - у2. Получили систему ’
х + ^ = 14, 132-х2=152-/,°Т‘
куда х = 5, У = 9 . Значит, BE = 12 , ВС + AD = АВ + CD = 28. Тогда
SABCD = (5С +	=28 • 6 = 168 (см).
Ответ: 168 см2.
10.181.	В квадрате со стороной а середины двух смежных сторон соединены между собой и с противоположной вершиной квадрата. Определить площадь внутреннего треугольника.
Рис. 10.151
Решение.
ПустьК,Ь—середины ЛИ и CD (рис. 10.150). Тогда
„	1 а а	а2 „	1	а а2
S) —• — —-----j Di — Q • ~ —
2 22 2	82	2	4
. Площадь квадрата So = a2 . Зна-
с» _ о с» Q с» ___ 2	__ Зб7
чит, о — »Sn — Oi — S^ S^ — ci ~	 — — —.
0,2	3	4	4	8	8
3a2
Ответ: ——.
8
10.182.	Около квадрата co стороной а описана окружность. В один из образовавшихся сегментов вписан квадрат. Определить площадь этого квадрата.
Решение,
Диагональ квадрата является диаметром окружности (рис. 10.151).
(2 7? У = 2а2, откуда R = >/2а. Пусть сторона меньшего квадрата рав-
на х . Тогда PM2 + РО2 = ОМ2, РМ = ~Ь РО = — + х. Значит, 2 f ч2 2	2	2
х (а	) а	а „
— + у + х = —, 0ТКуда Х = "5’ Площадь меньшего квадрата
25
а
Ответ: —.
25
10.183.	В равнобедренную трапецию вписан круг. Доказать, что отношение площади круга к площади трапеции равно отношению длины окружности к периметру трапеции.
В______________q	Решение.
/к	Обозначим основания трапе-
\	ции через а и Ь. Так как круг впи-
\	сан в трапецию, то a + 6 =2 с ,где
\ с — боковая сторона. Значит, \	а + ь т
\ с =--------. Тогда площадь трапе-
А К	L D 2
„ а + Ь .
ции S| =-----h, где h — ее вы-
Рис. 10.152	2
сота; периметр
рх = a + b + 2- a + b = 2(а + b),
^2
Площадь круга S2 = тег2 = л—. Длина окружности / = 2лг = лЛ, 4
S2 лй2 2 nh I TI
отсюда — = —7------r— = —7--г = —. Что и требовалось доказать.
Sj 4(а + б)-Л 2(а + б) р{
10.184.	Вычислить площадь трапеции, параллельные стороны которой содержат 16 и 44 см, а непараллельные — 17 и 25 см.
Решение.
Пусть В К и CL —перпендикуляры, опущенные на AD (рис. 10.152). ВС = 16 (см), ЛВ = 44 (см), JB = 17 (см), CD-25 (см). Обозначим АК = х, LD = у.Тогда АВ2-АК2=ВК2, CL2 =CD2 - LD2 . Это значит, что 172-х2=ВЛГ2, С1?=252 -у2- Получили систему J17 х -25 у , ОТКуДа x_g, j = 20 . Имеем CL = V625-400 =15, [х + у+ 16 = 44,
с ВС + AD гт 16 + 44	, 2\
S abcd _	2	—	2	5 — 450 (см ).
Ответ: 450 см2.
10.185.	В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции.
Решение.
Пусть основания трапеции равны а и Ь , высота — h • Тогда пло-
Рис. 10.153
« а + 6,	.у гч .	а + Ь ~
щадь $-------h. С другой стороны, S = h . Значит, Л =-= 5, откуда
2	2
5=25.
Ответ, 25.
10.186.	Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности, описанной около трапеции, если известно, что ее средняя линия равна высоте.
Решение,
Пусть ВС = 5к, AD = 12Л (рис. 10.153). Тогда BC*AD =h = l7,
\2к+5к _ j?, откуда к = 2. Значит, ВС = 10, AD = 24. Пусть CL ± AD, BK1AD, AK = LD= AD~BC = 7 (см); CD = ^CL2+LD2 = >/172 + 72 = = 13>/2, sina = -|^ = ^=. Из AALC найдем AC = ^CL2 +AL2 =
—	д с
172+172 =17л/2. По теореме синусов ---= 2R, следовательно,
sina
17>/2-13>/2 D D 1 *5 /	\
---------= R, R = 13 (см).
17-2
Ответ: 13 см.
10.187.	Высота, проведенная к основанию равнобедренного треугольника (рис. 10.154), равна Н и вдвое больше своей проекции на боковую сторону. Найти площадь треугольника.
Решение.
Пусть ВК = Н ,BL — проекция ВК на АВ.
2R-x/\j_
откуда АВ=2Н-Значит,
ак = 'Jab2 -вк2 = ^4н2-н2 = н&.
Рис. 10.155
Площадь
8 = -вкас = -н-2н4з=н2у[з.
2	2
Ответ: Н2 >/з.
10.188.	Радиус окружности, описанной около прямоугольного треугольника, относится к радиусу вписанной в него окружности как 5:2. Найти площадь треугольника, если один из его катетов равен a.
Решение.
Пусть R и г — радиусы вписанной и описанной окружностей, ВС = а (рис. 10.155). Положим BD = х; тогда BL = x (как касательные, проведенные из одной точки), LA-AK = 2R-x (так как &АВС —прямоугольный,то AB = 2R). Имеем АС2 + ВС2 = АВ2 или (г + 2R - х)2 + a2 = 4R2. Но R = 5r/2, х = а-г , и последнее уравнение примет вид (7г-а)2 +а2 =25г2 или 12г2 -1аг + а2 =0, откуда q = а/3 , г2 = а/4 . Этим корням соответствуют значения (ЛС)] = 4а/3 , (А = За/4. В результате получаем два решения:
с 1 4а 2а2 с 1 За За2
1 2	3	3	2 2	4	8
Л 2а2 За2
Ответ: ------ или--.
3	8
10.189.	В сегмент, дуга которого равна 60°, вписан квадрат. Вычислить площадь квадрата, если радиус круга равен 2л/з + >/17 .
Решение.
ОбозначимBC = CD = DA = ЛВ = х(рис. 10.156).Рассмотрим &ONC,
В N' С
Рис. 10.156	Рис. 10.157
AONC = 90’. Имеем ON2 + NC2 = ОС2, где ОС = А = 2-Уз + V17 . ON =
= OM + MN~OM + x , NC = -.B \OMF /-ОMF = 90’, ZMOF =
2
^EOF	о	л/3	л/З
—-— = 30° тогда ОМ = OF-------- R---, следовательно, ON =
2	2	2
Ry/3
2
f Я>/з
+ х . Таким образом, имеем + х
2
— = R . Решая квад-4
ратное уравнение, получим, чуо х = ^у(>/Г7-2>/з); SABCD = х2;
“ 1 > $ABCD ~ 1 •
5
Ответ: 1.
10.190. В треугольнике длины сторон относятся как 2:3:4 (рис. 10.157). В него вписан полукруг с диаметром, лежащим на большей стороне. Найти отношение площади полукруга к площади треугольника.
Решение.
По условию АВ: ВС: АС = 2:3:4 .Обозначим АВ = 2х, тогда ВС = Зх,
_ ВС АС .	,о„. 4х2-9х2-16х2 7
АС = 4х, длвс ~ х	sin£ВСА, cosZ.BCA--------——	—
2	-24х о
-24x2
sin £BCA
49 V15	3x2J\5 п
77 =	; smbc =-------• Пусть о —центрполукруга
04	о	4
с	АВ АО 2 АС , 4х 5
и ВО-биссектриса,тогда — = — ; - = — -1, — = -; ОС-
В ДОЕС Z.OEC = 90’. OE = R = OCsmZ.BCA~-~- = ^-
э о 1U
2,4л.
:Л5 ;
о	nR2 9л-15х2 27 2
о „„ =---=--------— =—их . Таким образом,
кр 2	100-2	40	н
с _27 2	4	_ 9л _ЗлЛ5
’ "'С 40 “ З^Л5=10Л5° 50
л Ответ: ------.
50
Решения к главе 11
ЗАДАЧИ ПО СТЕРЕОМЕТРИИ
ОСНОВНЫЕ ФОРМУЛЫ
1.	Произвольная призма (/— боковое ребро; р — периметр основания; S — площадь основания; Н — высота; Р^ч — периметр перпендикулярного сечения; Sce4 — площадь перпендикулярного сечения; 5бок	— площадь	боковой поверхности;	К	—	объем):
5б0к=^;	(пл)
v = sh;	(Н.2)
У = ^сеч1.	(11.3)
2.	Прямая призма:
S6oK=Pl.	(11.4)
3.	Прямоугольный	параллелепипед	(а,	Ь,	с	—	его	измере-
ния; d — диагональ):
5бок=РЯ;	(11.5)
V = abci	(П.6)
d2=a2+b2+c2-	(П.7)
4.	Куб (а — ребро):
V = a3;	(П.8)
d = ay(3.	(П.9)
5,	Произвольная пирамида (5 — площадь основания; Н — высота; JZ — объем):
у = \$н.	(п.ю)
6.	Правильная пирамида (р — периметр основания; / — апофема; S6oK — площадь боковой поверхности):
5eo«=|w;	(Н.П)
V = \sH.	(11.12)
7.	Произвольная усеченная пирамида (и S2 — площади оснований; h — высота; у — объем):
= j + S2 +	.	(11.13)
8.	Правильная усеченная пирамида (и Р2 — периметры оснований; Z — апофема; 5бок — площадь боковой поверхности):
$бок=|(^+^>.	(И14)
9.	Цилиндр (R — радиус основания; Н — высота; S6oK — площадь боковой поверхности; у — объем):
5бок=2яЯЯ;	(11.15)
V = nR2H-	(1116)
10.	Конус (R— радиус основания; Н — высота; Z — образующая; S6oK — площадь боковой поверхности; у — объем):
S6oK=^Z;	(11.17)
V = ^R2H.	(11.18)
11.	Шар, сфера (Л— радиус шара; 5 — площадь сферической поверхности; V — объем):
5 = 4лЯ2;	(И19)
К =	(11.20)
12.	Шаровой сегмент (R— радиус шара; h — высота сегмента; S —площадь сферической поверхности сегмента; у —объем):
S = 2nRh;
(11.21)
V = rii2\R--h
к 3
(11.22)
13.	Шаровой сектор (R— радиус шара; Л — высота сегмента; V —объем):
V = -nR2h.
3
(11.23)
ДОПОЛНИТЕЛЬНЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ПРИЗМЫ И ПИРАМИДЫ
1.	Пусть в пирамиде выполняется одно из следующих двух условий: а) все боковые ребра образуют с плоскостью основания равные углы; б) длины всех боковых ребер равны. Тогда вершина пирамиды проецируется в цёнтр окружности, описанной около основания пирамиды (эта же точка служит точкой пересечения серединных перпендикуляров к сторонам основания пирамиды).
2.	Пусть в пирамиде выполняется одно из следующих условий: а) все боковые грани образуют с основанием равные углы; б) длины
всех апофем боковых граней равны. Тогда вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды (эта же точка служит точкой пересечения биссектрис углов в основании пирамиды).
3.	Если в наклонной призме боковое ребро А{ВХ составляет равные углы со сторонами основания, образующими вершину Л, (рис. 11.1), то основание О высоты ВХО лежит на биссектрисе угла 4.
S
Рис. 11.2
Это же утверждение можно сформулировать так: если в трехгранном угле два острых плоских угла равны, то проекция их общего ребра на плоскость третьего плоского угла является его биссектрисой.
4.	Если высота треугольной пирамиды проходит через точку пересечения высот треугольника, лежащего в основании, то противоположные ребра пирамиды перпендикулярны. Справедливо и обратное утверждение.
5.	Если SO — высота пирамиды SABC и SA1BC, то площадь SAO1BC (рис. 11.2)
Доказательство указанных дополнительных соотношений можно найти в любом издании данного сборника задач последних лет.
11.001. В основании пирамиды лежит прямоугольный треугольник с гипотенузой, равной с и острым углом 30°. Боковые ребра пирамиды наклонены к плоскости основания под углом 45°. Найти объем пирамиды.
Решение,
По условию ZJCB = 90°, ZBZC = 30° (рис. 11.3); поэтому
С	сЛ	1	Сл/З^
вс = -, А С = —-, откуда 30СН = - А С ВС = —- . Проведем SO 2	2.	2	о
так, чтобы АО-ОВ^ Тогда О — центр описанной около ЬЛВС окружности, SO — высота пирамиды (см. «Дополнительные соотношения между элементами призмы и пирамиды», п. 1). В &ASO
с
имеем ZSAО = 45" и, значит, SO = АО = — . Итак, 2
V = -S.
3 *
Ответ:
48 ’
Рис. 11.4
11.002. Вычислить объем правильного тетраэдра, если радиус окружности, описанной около его грани, равен R .
Решение.
У тетраэдра ребра равны. Обозначим их через а . Радиус окружности, описанной около основания тетраэдра (а это правильный треугольник), равен R =	, откуда а = Rд/з . Высота тетраэдра
проецируется в центр описанной около основания окружности (рис. 11.4). Тогда SH = JSA2-AH2 = <Ja2-R2 = 7зЯ2-Я2 =r41. _	_ а27з З-УЗЛ2 _
Площадь основания о0СН = —-— = —-— . Тогда объем
_	R346
Ответ: —-—.
4
11.003. Сторона основания правильной треугольной пирамиды равна а, двугранный угол при основании равен 45°. Определить объем и полную поверхность пирамиды.
Решение.
У правильной треугольной пирамиды SA = SB = SC (рис. 11.5); SH — высота, причем Н — центр описанной окружности;/) — середина А С,
Рис. 11.5
это значит, что HD1A С (кдьДАВС —правильный). ZSDH = 45°  Пло
щадь основания SOCH = ——. Из &SDH имеем DH = S7/tg45° = SH.
С другой стороны, — радиус вписанной окружности — г = ——.
6
Это значит, что SH = ДД. Тогда апофема SD =	. Полу-
6	sin45° V6
3 периметр основания р = — а. Площадь боковой поверхности
5бок =SD р = —— . Полная площадь S = 50СН + S6oK =-J
а объем Р = |$Я50СН=^.
_ а3 п2Уз(1 + >/2)
Ответ: — ; ----*----L.
24	4
11.004. Определить объем наклонной треугольной призмы, у которой площадь одной из боковых граней равна S, а расстояние от плоскости этой грани до противолежащего ребра равно d •
Решение.
Через тачку К на ребре АА' = 1 (рис. 11.6) проводим сечение перпендикулярно к этому ребру. Тогда КМ1ВВ', т.к. ВВ'^АА'; KNLCC’, т.к. СС'\\АА' • В &KMN проведем высоту KD. KD1MN и KDi.CC', следовательно, KDIBB'C'C и KD = d  По условию площадь грани
ВВ'С’С равна S’. Тогда V = S£j:mnAA’ = ^KDMN-АА'= ^dal,
где MN = a, MNLCC' = l.
Далее, V = ^d. (a l)=^d(MN CC')=^dS.
Ответ: У = ^dS.
11.005. Плоский угол при вершине правильной треугольной пирамиды равен 90°. Найти отношение боковой поверхности пирамиды к площади ее основания.
Решение.
У правильной пирамиды АВ=ВС=АС=а (рис. 11.7).
ZZSC = 90°, SA = SC = SB* Это
значит, что z£4C = 45°> AD = DC -
Тогда из \SAC- SA = — — - = —— (так как ДЛ5С — равнобедрен-cos45° 2
ный). SD — апофема. Тогда SD = ZSsin45° = —. Боковая поверх-
„	з
носгь 5бок = p-SD, где р — полупериметр основания — р = - а;
с 3 а За2	а24з _
*^бок = 2°’J = Площадь основания	=—-—. Отношение
^бок = За2 - 4 =
*^осн 4а2 ♦ л/з Ответ: Л.
11.006. Диагональ прямоугольного параллелепипеда равна 13 см, а диагонали его боковых граней равны 4>/10 и 3>/Г7 см. Определить объем параллелепипеда.
Решение,
Обозначим стороны основания а и Ь, высоту параллелепипеда h»и пусть Ь > а • Диагональ основания параллелепипеда = То2 +й2 •
Диагональ боковой грани с ребрами ь и h равна Дх = Тй24-й2 = 4>/10 • Диагональ боковой грани с ребрами а и h равна d2 = Ja2+h2 = 3>/Г7 . Диагональ параллелепипеда d = ^d} + h2 =13 . Получим систему b2+h2 =(4л/1о)2,
• a2+h2	откуда д = 3, b = 4, h-\2-Объем к = айй = 144 см3.
a2 +b2 +h2 =132,
Ответ: 144 см3.
11.007. Найти отношение объема куба к объему правильного тетраэдра, ребро которого равно диагонали грани куба.
Решение.
У тетраэдра все ребра равны. Обозначим их через а. Радиус опи-
Дл/З
санной около основания тетраэдра окружности К = —у— . Основание высоты Н является центром описанной около &АВС окружности (см. рис. 11.5). Тогда Н = yla2 -R2 = и объем Vx = у SOCH Н •
2 /Т	^3
Так как ЛАВС правильный , то S0CH = —-—. Значит, Vx = -уу— • Пусть ребро куба равно Ь ♦ Диагональ куба равна £^2 • Она равна а3
а
ребру тетраэдра ь41 = а, откуда . Объем куба V2=b' =	.
а312 __2
Отношение 2у/2<Гу[2
Ответ: 3.
11.008. В прямом параллелепипеде стороны основания равны а и /?, острый угол между ними содержит 60°. Большая диагональ основания равна меньшей диагонали параллелепипеда. Найти объем параллелепипеда.
Решение.
Большая диагональ основания лежит напротив большего угла т.е. 180°-60° =120°. Отсюда, по теореме косинусов, dx = т1а2 +b2 -2aZ>cosl20° = у/a2 + b2 +ab • Меньшая диагональ основания параллелепипеда d2 = Va2 +Z>2 -2nZ>cos60° = yla2 + b2 -ab • По условию меньшая диагональ параллелепипеда равна dx. С другой стороны, d2 =h2 +d%, гдей — высота параллелепипеда. Это
значит, что h = ^d2 -d2 = ^2ab . Площадь основания
е г • хЛо «Лаб	, JbabJab
50СН = aftsin60 = -у—. Объем V = S0CH • h =-------.
Л 4баЬ>[аЬ
Ответ: ---------.
2
11.009. Центр верхнего основания правильной четырехугольной призмы и середины сторон нижнего основания служат вершинами вписанной в призму пирамиды, объем которой равен V. Найти объем призмы.
Решение.
Рис. 11.8
Пусть сторона основания призмы равна а (рис. 11.8). Тогда сторона а& основания пирамиды равна ——, а площадь этого основания рав-а2
на —. Обозначим объем призмы через Ух; имеем Vx = a h , где h —
высота призмы. Так как по условию объем пирамиды равен у, то 2
V = J ~ • h . Но a2h = Ух, откуда Vx = 6К .
Ответ: 6У .
Рис. 11.9
11.010. В кубе, ребро которого равно а, центр верхней грани соединен с вершинами основания. Найти полную поверхность полученной пирамиды.
Решение.
Из условия ясно, что высота пирамиды равна высоте куба, т.е. а
(рис. 11.9). К — середина AD,HHX — высота. Тогда НК- — \
HfK = ^нн^+нк2 =
ау/5
. Полупериметр основания
р = — 4а = 2а. Боковая поверхность 5бок -Н{К р =	• 2а = а2 V5 .
**	л
Площадь основания S0CH = а2. Полная поверхность
S = $бок +$осн = «2+Д2 V5 = <4 + 75).
Ответ: а2(1 + Т5)
11.011. Основанием правильной пирамиды служит многоугольник, сумма внутренних углов которого равна 720°. Определить объем пирамиды, если ее боковое ребро, равное /, составляет с высотой пирамиды угол 30°.
Решение.
По формуле суммы внутренних углов многоугольника узнаем вид многоугольника 720° =180°(«-2). Отсюда п = 6» т.е. получили
шестиугольник; так как угол между боковым ребром и высотой ра-
V3
вен 30°, то высота h = /cos30° =—/. Радиус описанной около шес
тиугольника окружности Я = / sin 30° = . Он равен стороне шести-
/
угольника а = 2 • РаДиУс окружности, вписанной в шестиугольник,
а	ZV3
равен г =----- = —— = —-. Значит, площадь основания
180	2	4
24—
_ баг bfil1 .	.. 1„	, З/3
5осн = — = —г—, а объем И = -$осн А = —.
Z 10	3	10
„	З/1
Ответ: —
16
11.012. Диагональ квадрата, лежащего в основании правильной четырехугольной пирамиды, равна ее боковому ребру и равна а. Найти полную поверхность пирамиды и ее объем.
Решение,
Обозначим сторону квадрата через Ь - Диагональ квадрата d = bjl • Она равна боковому ребру пирамиды а = Ь& (рис. 11.10).
2 а1
Площадь основания S0CH - b = —. Высота пирамиды, как видно
l I 2 Г d из рисунка, h = da -I—
, .	, L, (Ь'\ |з7
Апофема пирамиды / = J л +1 I =
а2 a<Jl
---^.Полуперв-
метр основания р = 2Ь =	. Боковая поверхность ^бок = / • р =
Рис. 11.11
Рис. 11.12
a a2-J7	а241 a2 a2 W7
- —2— • Полная поверхность S = 5б01с + 50СН = —-—+— = —
Объем Р = -5осн й = - —
3 осн 3 2
а^З _ а2 _ 43а2
Ответ:
а2(1 + У7) 43а2
2	’ 12
11.013. Центр верхнего основания куба с ребром, равным а, соединен с серединами сторон нижнего основания, которые также соединены в последовательном порядке. Вычислить полную поверхность полученной пирамиды.
Решение.
Так как ребро куба равно а, то сторона основания пирамиды
SABCD равна (рис. 11.11). Учитывая, что OK = ^AD =	>
найдем апофему пирамиды:
SK = -JsO2 +ОК2 = ja2+^- = 1 о 4
Значит, 5бок
л 1 «>/2 За-Jl За2 4----------------=-----
2	2	4	2
+ *^бок "	.
Ответ: 2а2.
11.014. Апофема правильной шестиугольной пирамиды равна h, а двугранный угол при основании равен 60°. Найти полную поверхность пирамиды.
Решение.
Так как Z_SKO = 60° (рис. 1112), то ОК -	= у. Основание
пирамиды — правильный шестиугольник, поэтому AKOD = 30° и
6РЕ27з а2Уз 2
KD-^OD. Тогда OK2 = OD2 -KD2 =4KD2 -KD2 =3KD2, т.е.
KD = ^-, DE = 2KD =	. Получаем: S0CH =
6	3
^бок =	• h — h л/з > ‘S'nOJlH = *$ОСН +‘S,60K —	2	*
4
_ зл27з
Ответ: —~—.
2
11.015. Найти полную поверхность правильной треугольной пирамиды, сторона основания которой равна а, а двугранный угол при основании равен 60°.
Решение.
Радиус вписанной в правильный
&АВС окружности равен г = —— 6
(рис. 11.13); SH — высота пирами-
ды, SK — апофема, к — середина
/_ Г С
I ----— -	. Боковая поверхность
Рис. 11.13
А С, Z.SKH = 60° • Апофема
$бок = Р ’ Л где Р — полупери-
За _	а>/3 За а2>/3 „ а27з
метр основания р = — .Тогда 5бок = — • — =	= ——
2	3	2	2	4
„	о о о а24з а2Л 3а2>/3
Полная поверхность 5 = о0СН + 5бок = —-— + —-— = —-—.
Л 3a2V3 Ответ: —-—.
4
11.016. Основание четырехугольной пирамиды — прямоугольник с диагональю, равной Ь, и углом 60° между диагоналями. Каждое из боковых ребер образует с плоскостью основания угол 45°. Найти объем пирамиды.
Решение.
По условию BD = 6, ZAOB = 60° (рис. 11.14);
отсюда АВ = — 2
AD = —^~. Значит, S0CH=JB JD =
---. Так как 4
ASAO = ASBO =
= ZSCO = ZSDO = 45°, то SO — высота пирамиды
ь и SO = —. Итак, 2
К=-$осн$О = —
3 осн 24
л ь34з
Ответ: • _ .
24
11.017. Сторона основания правильной треугольной пирамиды равна 1 см, а ее боковая поверхность составляет 3 см2. Найти объем пирамиды.
Решение.
Обозначим сторону основания правильной треугольной пирамиды че-
2	За
рез д, т.е. а = 1 (см); 56ок =3 (см ). Так как 5бок = р/, где р = — —
5	3
полупериметр основания, а / — апофема, то / = —— =--= 2 (см). Ра-
р 3/2
дуЗ диус вписанной в правильный треугольник окружности г =------
6
= —— (см). Тогда можно найти й =л//2 - г2 = А~~~Т" (так как
6	V 36 2уЗ
основанием высоты в правильной пирамиде является центр вписанной в треугольник основания окружности). Площадь основания
50сн =--------~ — (см2)- Тогда объем
4	4
г/ 1 с	д 1 V3 V47	У 47 . v
К= —5осн-й =----------------(см ).
3 °сн 3 4 2>/з	24 V 7
Ответ:	см3.
24
Рис. 11.14	Рис. 11.15
о
11.018. Основанием пирамиды служит треугольник со сторонами, равными а, а и Ь. Все боковые ребра наклонены к плоскости основания под углом 60°. Определить объем пирамиды.
Решение.
2 Ь2 По условию АВ - ВС = а (рис. 11.15); поэтому ВН -а-- —- =
4
= —yl^a2 — b2 . Отсюда 50СН = ~ А С • ВН =	-Ь2 . Проведем
высоту SO. Так как все ребра пирамиды одинаково наклонены к плоскости основания, то точка О — центр описанной около ЬАВС окружности. Пусть радиус этой окружности равен R . Тогда 2»	2
Гур _ р _ Д Р _ Д	SB
4$осн	в ^0В 0В^- -' ПОЭТОМУ
SO = y/sB2—ОВ2 = у/4ОВ2-ОВ2 = ОВу1з =	. Имеем
V4a2-62
' I	1 Ь^4а2-b2	a2-Jl _a2byli
3	3	4	у/4а2 -Ь2
_ a2W3 Ответ: —------.
12
11.019. Боковое ребро правильной треугольной пирамиды равно /, а высота равна h • Определить объем пирамиды.
Решение,
Обозначим AS = l, SH-h (см. рис. 11.5). Тогда
АН = -JaS2-SH2 = y/l2-h2  В правильной пирамиде АН является радиусом описанной около правильного &АВС окружности, т.е.
. „ D а4з ГЗ ау/з	Зу1 I2 -h2 [ГК Г2П
АН = R = —^~ или V/ -h - ——,откуда а =----------= yj3\l -h J.
Площадь основания S0CH =
. Тогда объем
а2>/3 _ 3>/з(/2-А2) 4	4
r = |SocH/' = |A
Узл(/2 - л2)
Ответ: -----21----L,
4
11.020. В основании наклонной призмы лежит параллелограмм со сторонами 3 и 6 дм и острым углом 45°. Боковое ребро призмы равно 4 дм и наклонено к плоскости основания под углом 30°. Найти объем призмы.
Решение.
Пусть АВ-3 (дм), AD-Ь (дм), АА{ =4 (дм)(рис. 11.16);4Я —
высота. Тогда АХН = ЛЛ, sin30° =2 (дм). Площадь основания
S0CH = АВ • Л/) sin 45° =	(ДМ2). Объем
V = $осн • А{Н = 9 V2 • 2 = 18>/2 (дм3).
Ответ: 18-J2 Дм3.
11.021. Каждое из боковых ребер пирамиды равно 269/32 см. Основание пирамиды— треугольник со сторонами 13, 14 и 15 см. Найти объем пирамиды.
Решение.
269
Пусть SA = SB = SC = -^- (см) (рис. 11.4), а ЯВ = с = 15 (см), ВС-а = \3 (см), AC = b = \4 (cm),SH — высота. Это значит, что ASHA = ASHB = AS НС. Тогда АН = ВН = СН (из равенства ДЛSH,
\BSH, &CSH). Значит, Н является центром описанной около ЬАВС окружности и R = ^^. Площадь &АВС можно найти по формуле Герона 5 = р(р ~ а)(р - Ь)(р - с), где р =	+ с -21 (см).
Тогда В = ^21(21 -13)(21 -14)(21 — 15) = 84 (см2). Вычислим радиус опи-
D 13-14-15 65 ч
санной окружности R = —— = — (см) и высоту пирамиды
Г—,------г If 269? f65? 69 Z ч
SH = у AS2 - АН2 = 111"з2’1 "lyl =32 (см)-
Объем К = - SOCH • SH = - • 84 • — = 60,375 см3. 3 осн 3	32.
Ответ: 60,375 см3.
11.022. Определить объем правильной четырехугольной призмы, если ее диагональ образует с плоскостью боковой грани угол 30°, а сторона основания равна а.
Решение,
Пусть АВ = ВС = CD =DA = a, B{D — диагональ призмы, Z.DB} А = 30° (рис. 11.17). Обозначим АВ} = Ь. Тогда b - -	= дТз. Высота
h = BB\ = >lb2 -а2 = а&  Объем V = S0CH • h . Так как ABCD — квад-
рат, то S0CH = а2 . Тогда V = а2 • а41 =а3^2 
Ответ: а3 ^/2
11.023. В правильной четырехугольной пирамиде сторона основания 6 дм, а высота 4 дм. Найти боковую поверхность усеченной пирамиды, отсекаемой от данной плоскостью, параллельной ее основанию и отстоящей от нее на 1 дм.
Решение.
Пусть AD = DC = ВС = АВ = а{ (6 дм), SH — высота, SH = 4 (дм) (рис. 11.18). По условию НН} =1 (дм). Из подобия &HES и AH^S
НЕ _ SH
(где £hEj —середины CD и CXD{ соответственно):	~ SH} ,но
4	9
SHi = SH - ННХ =4-1 = 3 (дм). Значит, нхЕх = НЕ — (дм). Зна-3 4
чит, A'Di = 2Я]Е, = | (ДМ). SEX = ^SH2 +НХЕ{ = J32 + [-1 = — (дм).
2	у ^4J 4
SE = JSH2+HE2 = V42 +32 = 5 • Тогда 5бок1 = рх  SEX, 56ок2 = р2 • SE,
где pi, р2 — полупериметры АХВХСХОХ и ABCD соответственно;
9	15 135
р2 = 2 • 6 = 12 (дм), рх = 2 • - = 9 (дм). Тогда 5бо1(1 = 9 • — = — (дм2);
S6ok2 =12-5 = 60 (дм2). Боковая поверхность усеченной пирамиды
£бок =5бок2-5бок1 = 60-^ = ~26,25 (ДМ2).
Ответ: 26,25 дм2.
11.024. Основаниями правильной усеченной пирамиды служат квадраты со сторонами ап Ь (а>Ь)> Боковые ребра наклонены к плоскости основания под углом 45°. Определить объем усеченной пирамиды.
Решение.
Пусть AD = DC = BC = АВ = а, А{В}= В}С{ =	= DXAX =b
(рис. 11.19), Z.DXDH = 45°, где^Я — высота усеченной пирамиды.
OOj|pD^, OH = O\I\. О,Dj =^BiDl = ^b>/2 . Аналогично OD = ^aj2.
Значит, HD = OD-OH = —(a-b). HDX = HZ»tg45° =^(a-i>); Z	z
SABCD = fl2 ’	= Ьг. Объем усеченной пирамиды
= ^Dx^abcd +^SABCDSAiBiCiDi +SAiBiCiD.^=-—(a-b^a2 +ab+b2)=
4^’)-
Ответ:	(fl3 ~ )
6
11.025. Боковые ребра правильной усеченной треугольной пирамиды наклонены к плоскости основания под углом 60°. Стороны нижнего и верхнего оснований равны соответственно а и Ь (а>Ь)-Найти объем усеченной пирамиды.
Решение.
Пусть ЛБ = БС = ЛС = я, ДА = ВХСХ =Q4 = b , ZJ^^ = 60°
(рис. 11.20). Так как М.ВС и АХВ£Х —правильные, то б? иЦ —центры
Рис. 11.20	Рис. 11.21
ь4з
описанных около них окружностей. Это значит, что А1О1 =	= -у-,
AO = R = ^,	. Значит, АН = АО-НО-R~RX =
Высоту АХН можно найти: А{Н = АН tg 60° =	(а - b)• 7з = (л - b).
Площадь SABC = —-—,	= —-— Тогда объем
лвс +^АВС$Л№ +SAiBlcJ-
?-Z>;
Ответ: — (а3-Ь3\ ш
12 v г
11.026. Основанием прямого параллелепипеда служит ромб. Плоскость, проведенная через одну из сторон нижнего основания и противоположную сторону верхнего основания, образует с плоскостью основания угол 45°. Полученное сечение имеет площадь, равную Q. Определить боковую поверхность параллелепипеда.
Решение.
Проведем RK\ DC (рис. 11.21), тогда BXK1DC также. Отсюда
Z.BKB' = 45’ и ВК = ВВ' = h , В'К = 4ih • Пусть стороны ромба рав-ны а. Тогда боковая поверхность
S
S6 = 4а ВВ, ~4ah = -^=a-42h = у/2
= 2-j2 CD B'K = 2j2Q, так как по условию площадь сечения AXBXCD равна Q.
Ответ: 2Q<j2.
11.027. Определить объем правильной четырехугольной пирамиды, если ее боковое ребро составляет с плоскостью основания угол 45°, а площадь диагонального сечения равна S.
Решение.
Рис. 11.22
Пусть АВ = ВС - CD = AD = а (рис. 11.22).Тогда АС = ajl. SH — о CLtH
высота, Z.SCH = 45’. SH = CH tg45 = ——. Площадь диагональ-
ного сечения
о 1 CU 41а а42-	I-- о
S = -ACSH = —---------— = — , откуда а = 42S  Зна
чит, SH = 4s • Площадь основания 5^ = а2 = 2S. Объем
v = -^оск • sh=2S • 4s  - = -s4s.
3 °сн	зз
Ответ: ^s4s.
11.028. Основанием пирамиды служит ромб с острым углом 30°. Боковые грани наклонены к плоскости основания под углом 60°. Определить объем и полную поверхность пирамиды, если радиус вписанного в ромб круга равен г.
Решение.
Пусть PABCD — данная пирамида (рис. 11.23), PH — высота,
HK1.CD , значит, PK1.CD , Z.PKH = 60°. ZBCD = 30°, НК = г ,
Z.CDH = 75° Из &HDK найдем DK =----------. Из \СКН КС =----------;
tg75°	tgl5°
nv vs, I 1	1 I	sin 90°	2r .
DC = DK +KC = л------+------- = r----------=--------= 4r
^tg75° tgl5°J sinl5°cosl5° sin30°
Площадь основания 5^ = ВС  DC sin 30° = 4r • 4r  — = 8r1 2 * * 5. Высота
IP
PH ИЗ ^PHK равна PH = HK tg60° = rV3 , a PK =-------------= 2r. Tor-
cos 60°
боковая поверхность
1	1	г“ Яг
да И = |5оснРЯ = |8г2г>/3=^
5бок = р  РК, где р — полупериметр основания р = 2 • 4г = 8г ; это
значит, что S6oi( = Sr 2г = 16г2. Полная поверхность
5 = 56oK+SOCH=16r2+8r2=24r2.
Ответ: —-—, 24г2 •
11.029. Объем правильной треугольной пирамиды, боковая грань которой наклонена к плоскости основания под углом 45°, равен 9 см3. Найти полную поверхность пирамиды.
Решение.
Пусть РАВС—данная пирамида (рис. 11.24), PH — высота, где Н— центр вписанной в ЬАВС окружности; НК1АС, значит, PKLAC, НК = г =	ZPКН =45°. Далее, PH = НКtg45° = —, РК = НК =
6	6 cos45°
а^Зу/2 а4б <,	_а24з г	с За
=-------=---; осн = —“—• Боковая поверхность ^бок = — • гл =
6	6	4	2
3 а4б а24б „ о р е а27з(1 + л/2)	„
= -а— = —Тогда S = 5бок +	Объем V =
Z О 4	4
= -50СНРЯ = —= 9, откуда а = 6 (см). Итак, 5 _ Збл/зО + л/!) _ 3	24	4
= 9>/з(1 + л/2) см2.
Ответ: 9л/3(1 + >/2) см2.
11.030. В основании прямого параллелепипеда лежит параллелограмм со сторонами 1 и 4 см и острым углом 60°. Большая диагональ параллелепипеда равна 5 см. Определить его объем.
Решение.
Пусть АВ = 1 (см), ВС = 4 (см) (рис. 11.25); Z.BAD = 60°, тогда ZADC-120°. Значит, АС можно найти по теореме косинусов: АС = = AD2 + DC2-2AD-DCcosl20° = 1 + 16+2-4ACt =5 (см).Значит, СС2 = АС?-АС2 =25-21 = 4 (см2). Тогда CCt=2 (см). Объем И = $осн'СС,; 5осн = ЛВ-ЛЙ8т60° = Ь4 ^ = 2>/з (см2). Тогда У = 243 -2 = 443 (см)3.
Ответ: 4^3 см3.
Рис. 11.25
Рис. 11.26
11.031. Центр куба, ребро которого равно а, соединен со всеми его вершинами. Определить объем и поверхность каждой из полученных пирамид.
Решение.
Так как при указанном построении образовалось 6 одинаковых дз
пирамид (рис. 11.26), то каждая из них имеет объем V = — и полную 6
поверхность SnoriH = а2 +4 • у а • ОК . Но ОК = >1оР2 +РК2 =	,
откуда 5П0ЛН = а2 + а2 Л = а2(1 + Vl).
11.032. Основание пирамиды — равнобедренный треугольник с основанием 6 см и высотой 9 см. Каждое боковое ребро равно 13 см. Вычислить объем пирамиды.
Решение.
Пусть АС = 6 (см), ВК = 9 (см) (рис. 11.27), PH — высота, РА = РВ = PC = 13 (см); из равенства \РНА = \РНВ = \РНС следует
Рис. 11.27	АН = НВ = НС , значит,// — центр
описанной около Д4ВС окружности.Тогда АК = КС = -^-- = 3 (см). Значит, ВС = АВ = JbK2+KC2 = >/81 + 9 = 3>/Й) .
Площадь основания S0CH = SABC =	• АС = -6♦ 9 = 27 (см2).
Тогда радиус описанной окружности
„ ав вс ас з-Ло-з-Ло-б . ( ч ~
А =-----------= —-----—----= 5 (см). Значит,
4S^C	4-27
PH = л1ра2-АН2 = 12 (СМ). Объем V =	• PH = |• 27 12 = 108 (см3).
Ответ: 108 см3.
11.033. В треугольной пирамиде боковые ребра взаимно перпендикулярны и имеют длины ^70, 799 и 7126 см. Найти объем и площадь основания пирамиды.
Решение.
По условию ZAPC = ЛАРВ = АВРС = 90° > АР = ТтО , РВ = 799 , PC = 7126 (рис. 11.28, а). По теореме Пифагора
АВ = у1рА2 +РВ2 =>/70 + 99=13. BC = -JpB2 +РС2 =>/99 + 126=15.
Рис. 11.29
AC = J РА2 +PC2 = V70 + 126 = 14 . Тогда площадь основания SABC можно найти по формуле Герона
SABC = д/21(21 -13X21 -14)(21-15) = 84 (см2). Для того чтобы найти объем пирамиды, перевернем ее так, чтобы основанием была грань РАВ (рис. 11.28, б). От этого ее объем не изменится. Тогда СР = V126 является высотой полученной пирамиды, т.к. &РАВ — прямоуголь-
ный, то его площадь
spab = |рЛР5 = |770 799. Объем
V = ^CP SPAB = |Т126 -ТтО-799 = 21755 (см3).
Ответ: 21^55 см3, 84см2.
11.034. Определить объем правильной шестиугольной призмы, у которой наибольшая диагональ равна d , а боковые грани — квадраты.
Решение.
V = 5 • Н. Обозначим DXD = х (рис. 11.29). Тогда имеем
Зх2>/3 АВ - ВС = CD = ED = FE = AF = DXD = x (по условию) S = —-—;
AD = 2x * В &ADDX, Z.ADDX = 90°; значит, ADX = ^AD2 +DXD2 ; (no
условию ADx=d). Имеем, что d = xj5', отсюда х = -^=-Н,
V = SH =
3d3J5 10>/5
3J3V3
ЫГ
11.035. Найти объем куба, если расстояние от его диагонали до непересекающегося с ней ребра равно d •
Решение.
Расстояние от ребра ААХ до диагонали BXD равно расстоянию от этого ребра до плоскости BBXDXD, т.е. длине отрезка АХЕ (рис. 11.30). Пусть ребро куба равно а; тогда из AAXEDX находим 2d2 = а1, откуда я = <л/2.Итак, р =а3 =2J3V2 .
Ответ: 2d3 41.
11.036. Определить объем октаэдра (правильного восьмигранника), ребро которого равно а .
Решение.
к = “5'я,гдея = 2 Л = 2-5О, 5 = а2
(рис. 11.31). В &SOC ZSOC = 90°,тогда SO2 = SC2-ОС2, где ОС = ^^-;
5<?2 = 2д2~а2 = —• Л = Л Н = ^
2	2 ’	>12’ V2 ’
и, таким образом,
Рис. 11.31
Ответ:
а3 41 3
Рис. 11.33
Рис. 11.32
11.037. Основание призмы— квадрат со стороной, равной а. Одна из боковых граней — также квадрат, другая — ромб с углом 60°. Определить полную поверхность призмы.
Решение.
5поли =4 sabcd +2 SBCC,Bt (рис. 11.32), SABCD=a2 (таккак ABCD — 1	Q2 л/З
квадрат и АВ = а\ SBCC& =-a2sin60° = (ВВХСХС— ромб, ВВх=а, АВХСХС = 60’), 5ПОЛН = 4а2 +а2Л = а2(4 +>/з).
Ответ: а2(4 + -/з)
11.038. Основанием параллелепипеда служит квадрат. Одна из вершин верхнего основания одинаково отстоит от всех вершин нижнего основания и удалена от плоскости этого основания на расстояние, равное Ъ • Сторона основания равна а. Определить полную поверхность параллелепипеда.
Решение.
S = 2Sосн + 5бок > где 5бок = ^ладв (рис. 11.33), 5ОСН = а2 (ABCD — a	П а2”
квадрат) и ЕО = — . В АЕОА{ АЕОАХ = 90°, тогда АХЕ = Jb2 +— ;
X	f
SAlABBt = AB AXE= a>‘4b^+a2- , s = 2fl2 + 2a J 4b2 + a2 •
Ответ: 2a( a + yjlb2 + a2
11.039. В кубе центры оснований соединены с центрами боковых граней. Вычислить поверхность полученного октаэдра, если ребро куба равно а.
Решение.
\ 2	2	[у
S = 8 • S^EC, где СЕ = — + — =	; СЕ = BE = ВС (рис. 11.34),
поэтому ZBEC = ZECB = ZCBE = 60° и
е 1 а41 а^2 . ,по ^двес ~ 2~2	2~Sm60
Ответ: а2 V3.
11.040. Основанием пирамиды служит треугольник с длинами сторон 6, 5 и 5 см. Боковые грани пирамиды образуют с ее основанием равные двугранные углы, содержащие по 45°. Определить объем пирамиды.
Решение.
V = ^S Н, S = у1р(р-б\р-5\р-5) ; Р = у = 8, поэтому 5 = 12;
S = p г; отсюда r = — = -.В ASOE, ZSOE = 90° (рис. 11.35), о Z
22 М. И. Сканави, группа Л
673
з
ZSEO = 45° (по условию) => ЕО = SO = - (так как ЕО = г), отсюда
Г = |12-| = 6 см3.
Ответ: 6 см3.
11.041. Определить объем прямоугольного параллелепипеда, диагональ которого равна / и составляет с одной гранью угол 30°, а с другой 45°.
Решение.
ЩВС (рис. 11.36) Z4^C = 90°;
а = ВС = 4C sin30° = 1-; А{В =	. В ЩС{С, ЛАХСХС = 90°;
„„ лг 	лп к 17^2------2	|3/2 2l2
С,С = с = АС• sin45 =-; AB = b = JA}B -с =J-----------=J—:
1	2 ’	3/1 V 4	4 V 4 ’
/3л/2 V = abc =
8
_	/3Л
Ответ: —
11.042. Определить объем правильной четырехугольной усеченной пирамиды, если ее диагональ равна 18 см, а длины сторон оснований 14 и 10 см.
Решение.
Искомый объем выражается формулой V = y(5t +52	)» гДе
51 = 196 (см2), S2 = 100 (см2). Найдем h = B\K (рис. 11.37). Имеем ВуК =
V2	2
B\D -KD . Так как BBXDXD— равнобедренная трапеция, то
= 0,5(5/)-5]^) = 0,5(14^2-10^2) = 2^2 (см) и KD = BD-BK =
= 12>/2 (см), т.е. h = -J182 -(12>/2)2 = 6 (см). Итак,
V = |(196 +100+140) = 872 (см3).
Ответ: 872 см3.
11.043.‘Основанием прямого параллелепипеда служит ромб, площадь которого равна Q. Площади диагональных сечений равны Sj и S2. Определить объем и боковую поверхность параллелепипеда.
Решение.
Имеем V = 50СНЛ, где 5^ = Q (по
Рис. 11.38
условию); таким образом, следует найти h. Так как ABCD — ромб, то =0,5ЛС-2?£> (рис. 11.38}; учитывая, что ЛСЛ = 51, S	S	S S
BDh = S2, находим АС = —Ц BD =—. Отсюда получаем 2Q = —— h	h	h h
i----- I------------------- ✓ X 7	✓ X 2
Л = Тогда V = Из ACOD: CD2 +f-^| V 20	V 2	I 2 ) t 2 )
+ f^2?|2 _ s\+s2 2h) A2aJ " 4Л2
Итак,
=4CDh = 4h-	= 2-Js2 + Si.
Ответ: ^SiS2Q/2\ 2^S2 + S2.
11.044. Боковое ребро правильной четырехугольной пирамиды равно / и наклонено к плоскости основания под углом 60°. Найти объем пирамиды.
Рис. 11.39
Решение.
V = \sH .В Д50С ZSOC = 90°. ZSCO = 60’. SC = 1 (рис. 11.39).
Отсюда имеем ОС = SC  cos 60° =
1_
2
H = SO = SC sin60° =^-l;
2
DC = AD = AB = ВС В ДЛРС ZD = 90° (по условию),
, 4 I2 I2
AD2 + DC2 = AC21 2AD2 = 4OC2; $ = AD =yy=y;
Ответ:
12
11.045. Наибольшая диагональ правильной шестиугольной призмы равна d и составляет с боковым ребром призмы угол 30°. Найти объем призмы.
Решение,
V = SH.K &ADDX (рис. 11.40) Z.A DDX = 90°, AADXD = 30°, ADX = d, Toraa# = ^Z> = Jcos30° =<А/з/2; AD = J sin 30° = d/2. Пусть BC = x,
AE sin 30е
AE = (^-x |:2 = 4-^, ZEBA = 30°;
V2 J 4 2
= 2AE J
_ 3d2 Ji dji _9d3
32	2	64 ’
Ответ:
64
11.046. Стороны основания прямоугольного параллелепипеда равны а и Ь- Диагональ параллелепипеда наклонена к боковой грани, содержащей сторону основания, равную Ь, под углом 30°. Найти объем параллелепипеда.
Решение.
V = SH, S = ab- В Ы\АВ ZDxAB = 90°, ^^ = 30° (рис. 11.41).Отсюда ADX =a ctg30° = ау/з, Н = ^AD2 - A^D2 =yjla2-b2 ;
V = SH = abj3a2-b2 
Ответ: abj3a2 -b2.
11.047. Стороны основания прямоугольного параллелепипеда равны а и Ь. Диагональ параллелепипеда наклонена к плоскости основания под углом 60°. Определить боковую поверхность параллелепипеда.
Решение.
В &BAD ZBAD = 9W, DB = yla2+b2 (рис. 11.42). В &D{DB
Z.DXDB = 90°, DjD = ВЛ • tg60° = л/з • л/а2 + b2 , S^ba = yfiayla2+b2 ;
Sbb^c = V36 • 7a2 +Z>2 ; S = ^Sa^Ba + $вв{\с) = 2л/з • yla2 +b2 (a + b).
Ответ: 2>/3 • yla2 +b2 (a + b).
11.048. Найти объем наклонной треугольной призмы, основанием которой служит равносторонний треугольник со стороной, равной а, если боковое ребро призмы равно стороне основания и наклонено к плоскости основания под углом 60°.
Решение.
Проведем АХК перпендикулярно плоскости АВС (рис. 11.43);тог-
^2 5/3
да V = SMBC  А\К, где SMBC = —-—. Учитывая, что АК = 60“,
а-/з	а2 Л а-]з За3
находим А,К = ——. Итак, V = —--------— = ——.
2	4	2	8
л За3
Ответ:
11.049. Найти объем правильной треугольной призмы, если сторона ее основания равна а и боковая поверхность равновелика сумме площадей оснований.
s
Решение.
V = S0CH H (рис. 11.44), 3S6oK =2 S0CH; S0CH =	, S6oK = За-H;
За Я = 2~; Я= —; Г =	—	.
4	6	4	6	8
Ответ: a3/i.
11.050. Найти боковую поверхность правильной шестиугольной пирамиды, высота которой равна h» а боковое ребро равно /.
Решение.
S6ok=6 S&fsa=6 ^-AF SK = 3AF-SK (рис. 11.45); ASOA, ZSOA = 90°, OA = Jl2-h2 =AF> SK = J/2 -l-^~ =	>
тогда S6oK =3-V/2-h2 • ^3/22+A2 =|7(Z2-h2\3l2 +h2).
Ответ: ^y/fy2 “^2^2 +A2).
11.051. Найти объем правильной треугольной пирамиды, у которой плоский угол при вершине равен 90°, а сторона основания равна 3 см.
Решение,
V =-SH (рис. 11.46); S = —у[3; ОС =	=	= у/з (так как
3	4	3	3
АВ = ВС=АС = а = 3 см); ЕО =	В AESC ZESC=90°, Н2 = ЕО*
6	2
9	9у/2
472	8
Ответ:	см3
8
11.052. В правильной треугольной призме площадь сечения, проходящего через боковое ребро перпендикулярно противолежащей боковой грани, равна Q. Сторона основания призмы равна а. Найти полную поверхность призмы.
Решение.
s = 2SOCH + ISbb^a (рис. 11.47); CD = АВ = ВС = СА = а;
Q-CDC^^-C.C-, c'c = ^; So^,
Sbw =ABBBl=ABCiC = ^a = ^. Ch/3 v3
S = ^-+2Q^3 = л/з(о,5а2 +2q).
Ответ: 7з(о,5а2 +2g)
11.053. Высота правильного тетраэдра равна h. Вычислить его полную поверхность.
Решение.
S = S0CH +35^ =4S^BC = 4~^ = АВ24з (рис. 11.48);
АО = АВ-Л/3, так как = AB = SB = BC-SC = АС (по уело-
вию); AAOS, ZJOS = 90°; AS2 =ОА2 +SO2 AS2 = -^- + h2;
3	2	2
_ зл27з
Ответ: —-—.
2
11.054. Каждое из боковых ребер пирамиды равно Ь • Ее основанием служит прямоугольный треугольник, катеты которого относятся как т: п, а гипотенуза равна с. Вычислить объем пирамиды.
Решение.
V = is-Н . Обозначим АВ-тх, ВС-пх (рис. 11.49). По условию АС = с, SC = b-B ЬАВС ZABC = 90°'> значит, с2 = т2х2 + п2х2, с2 _ с	_ 1	2 тле2 —
Чт2+л2 у1т2+п2	2	2{т2 +л2)
Рис. 11.49
Рис. 11.50
С -> d	-Jdh^ — е1
H = SO и АО = ОС = ВО = ~, тоН2=Ь2- —; Н = ——— (в &SOC 2’___________________________ 4_____________ 2
ZSOC = 90’); V =	 d^L =
3 2 (m2+n2)-2	12(т2+п2)
тпс2^4Ь2 - с2 12(/и2 + п2)
Ответ,
11.055. Центр верхнего основания куба соединен с серединами сторон нижнего основания. Образовался четырехгранный угол, каждый плоский угол которого равен а. Доказать, что 30° < а < 45°.
Решение.
I------------ Г2 Ji
Имеем АВ = J AM2 + МВ2 = .— + — =	(рИС. 11.50). Из CSOB
V 4	4	2
I	a2' а4$
находим SB = SA = J а2 + — =------. Пусть ZB SA = а; тогда в ASAB по
V	4	2
7	2
2	2	2	_ о 5а
теореме косинусов получим АВ = 2SB - 2SB cos а, или — - 2 —-5а2	4	42 4 7з
- 2 • —— cos а, откуда cos а = у. Очевидно, что < у <	» т.е., дей-
ствительно, 30° < а < 45°.
Рис. 11.51
Рис. 11.52
11.0	56. Диагональ прямоугольного параллелепипеда равна 10 см и образует с плоскостью основания угол 60°. Площадь основания равна 12 см2. Найти боковую поверхность параллелепипеда.
Решение.
Из &DXDB (рис. 11.51) находим BD = 5 см, DDX = 5>/з см. Боковая поверхность 5бок = 2(DDj • DC+ DDi • AD) = 2DD, (DC+ AD). Но DC2 + AD2 = = /?D2=25, а по условию DC-AD = 12. Значит, (DC + JD)2 = = DC2 + AD2 +2DC - AD = 25 + 24 = 49, откуда DC + AD = 7 (см). Итак, Sfon = 2 • 5• 7 = 70Л (см2).
Ответ: 70>/з см2.
11.0	57. Определить объем прямоугольного параллелепипеда, если его диагональ равна d, а длины ребер относятся как т : п : р.
Решение.
V = abc, DxB = d. Обозначим АВ = тх, ВС - пх,ВхВ~ рх (так как т .п :р = АВ:ВС:ВХВ) (рис. 11.52). В &DXDB ZDXDB = 90°, тогда Dj52 = D{D2+DB2. В \DAB Z.DA В = 90° и DB2 = AD2+AB2, поэтому DlB2 = DyD2 + AD2 + AB2, d2 = p2x2 +m2x2 +n2x2, значит, x = d
Jm2 +n2 + p2
5
Отсюда V = АВ  ВС • В,В = тпрх3 =	.
/ 2	2	2 г/2
,	\т + п+р ]
mnpd3
Ответ: ( ->	9	7 \з/2 ’
\т +пл + р£]
11.058. Определить объем правильной треугольной пирамиды, если высота треугольника, служащего ее основанием, равна h, а апофема пирамиды равна т .
Решение.
V = ^SH, MC = h> SM = m (рис. 11.53). АВ = ВС = АС, значит
ав4з ab = 2™=2!l s~ — abJ3 h СМ = — => АВ	и	Л/О = —= -.В
ЛВОМ Z.SOM = 90° Н = >ISM2-МО2 = ^т2= ^9т ~h .
.. 1 h2 yl9m2-h2 43 ,2 lQ 2 ,2
Отсюда	---3----~^lh ~h ’
Ответ:	h2 ylvm2 -h2 .
11.059. Площади боковых граней прямой треугольной призмы равны м у N и р. Боковое ребро ее равно /. Определить объем призмы.
Решение.
По условию SABiBA = М ,	= N , SAACCi -Р, ССХ = I
N М Р
(рис. 11.54). Тогда ВС = —; АВ = — ; АС = —;
TZ С гг С / / ЛГ + Л/ + Р (N+P-M\ (N + M-P\ (M + P-N\ K = s h = s /=/ j - I. - д — д——j
(по формуле Герона находим 5). Таким образом,
V = ^-yl(N + M + P/M + N-P\M + P-NlN + P-M).
Ответ: ^J(N + M + P^M + N-P\M + P-N\N + P-M).
11.060. Известны площадь основания Р и объем V правильной четырехугольной призмы. Вычислить ее полную поверхность.
Решение.
*5П =23’осн +^*^бок (рис. 11.55), где Р = S0CH и р = а2 (а — сторона
х	гт У
квадрата). V-P Н => # =
/— у
^бок = а ‘ Н = >1Р —. Отсюда
S = 2P+4V—
Р
4Г
Ответ:	^~^р
11.061. Найти боковую поверхность правильной треугольной призмы с высотой h, если прямая, проходящая через центр верхнего
Рис. 11.56
5
стороны нижнего основания, наклонена к
основания и середину плоскости основания под углом 60°.
Решение.
Обозначим сторону основания через а. Тогда S6oK = 3ah . Проведем высоту ОХО (рис. 11.56). В &DOOX имеем Z.OOXD = 30°, поэтому OXD = 2OD и 4О£>1 2 - OD2 = h2 , откуда OD = Л>/з/з. С другой стороны, OD - а4з)() и, следовательно, а = 2h . Итак, S6oK = 3 • 2h • h = 6h2.
Ответ: 6/z2
11.062. В основании пирамиды лежит квадрат. Две боковые грани перпендикулярны плоскости основания, а две другие наклонены к нему под углом 45°. Среднее по величине боковое ребро равно /. Найти объем и полную поверхность пирамиды.
Решение.
По условию SC = /, Z.SBC = 90°, Z.SCB = 45° (Рис- 11 -57)> ОТКУ“ /	1	р Jy
да SB - ВС = —,= , Имеем V = -ВС2  SB =------. Полная поверх-
V2	3	12
НОСТЬ *-*полн = S0CH +2S&SAB +^&SAD » ТаК как $bSAB = $&SBC >
1 if I Y I2
8&SAD = $&SCD  Ио S^AB = — AB SB = — I —j- I = —,
S&sad -—AD SA
Итак,
i34i /2(г+>/2) Ответ:	----L.
12	2
11.063. Найти объем и полную поверхность правильной четырехугольной пирамиды, сторона основания которой равна а, а угол наклона боковой грани к плоскости основания равен 60°.
Решение.
^ = |5осн где S0CH=a2 и Z_SEO = 60° (рис. 11.58). В bSOE
Z.SOE = 90° =» // = 5O = ~ tg60°	. Имеем К = ^->/3 . Далее,
Z	Z	о
S = Soch + 4*$б = а? +45б’ гДе	5Е = —^— = а, значит
£	2 cos 60
2
5б =	и S’ = За2 .
Ответ: За ; —— 6
11.064. Найти объем правильной треугольной пирамиды, высота которой равна h, а все плоские углы при вершине прямые.
Решение.
Проведем BD1AC (рис. 11.59). Пусть сторона основания будет а .
Так как пирамида правильная, то OD-^——, AD = DC =
6	2
SOch =——. Выразим а через Д.В ASAC имеем SA = SC9
5
S
a
Z.CSA = 90° > откуда Z.ASD = 45° и SD = AD = - . Тогда
________ 2 л 2
h = SO = JsD2-OD2 = J—=-^ => a = hjf>-
..	.. 1 _ , 1 а27з , 1 6Л2Л . Л37з
ИмеемГ = -S0CHA = y—-—h = -— ------=
Ответ:
11.065. Найти боковую поверхность правильной треугольной пирамиды, если плоский угол при ее вершине равен 90°, а площадь основания равна S'.
Решение.
а2^3
Пусть а — сторона основания; тогда 5 = —-—, откуда а -V J
Искомая боковая поверхность выражается так: S6oK =3 ^a-BD
а „	3?	3 4$ г
(рис. 11.60). Так как BD = DC = —, то ^бок -	~
Ответ: sj3.
Рис. 11.61
11.066. Найти объем правильного тетраэдра с ребром, равным а.
Решение.
Объем тетраэдра V ~^SH (рис. 11.61). Площадь основания на
ходится как 5=—-—.Рассмотрим &SDC (Z.SDC = 90° л
I а2 а
/ = Ля2-—=-л/3. Рассмотрим &SOD (ZSOD = 90°):
/2	2 IЗл^ 2
Я = \/ -г =	—г В ДЛВС радиус вписанной окружнос-
e-Уз	„ _ /За2 За2 _ 2а
ти г = ——. Тогда н -	----— - ~г=.
6	V 4	36 V6
Окончательно получаем: v “ у—‘	~
Ответ: ——
12
11.067. Правильная шестиугольная призма, боковые ребра которой равны 3 см, рассечена диагональной плоскостью на две равные четырехугольные призмы. Определить объем шестиугольной призмы, если боковая поверхность четырехугольной призмы равна 30 см2.
Решение.
Пусть АВ-а (рис. 11.62); тогда искомый объем V = 6 --—
h = 3 см — высота призмы. Найдем а. По условию боковая поверхность призмы ABCDA}B}€\D} равна 30 см2. Но S6oK = ($АВ + AD)h;
здесь AD = 2а (как диаметр окружности, описанной около правильного шестиугольника). Следовательно, 5л 3 = 30, откуда а-2 см.
22>/з г Итак, И = 6 ——-3 = 1873 см3. 4
Ответ: 18^3 см3.
11.068. По стороне основания, равной л, определить боковую поверхность и объем правильной четырехугольной пирамиды, у которой диагональное сечение равновелико основанию.
Решение.
Площадь боковой поверхности правильной четырехугольной пира-
миды находится по формуле 5бок =уР/ (рис. 11.63). Периметр основа-
2 1
ния равен р = 4л. Из условия SABCD = S,iSC . Отсюда а = —AC SO.
Из квадрата ABCD АС = а42 . Подставим и получим 2л2 = a&SO.
__________ 1 Г
Отсюда SO = а^2 . Из ASOE SE = ylSO2 + ОЕ2 = J2a2 + ^-- =	.
V 4	2
Подставим и получим
с 1 , Зл 2 А - с
^бок = 2	• — = Зл .А искомый объем находит-
ся по формуле V = “-$77 = ~^а2а42 =
Ответ:
Зл2;
а3 42
3
Рис. 11.63
Рис. 11.64
11,069. Боковое ребро правильной треугольной призмы равно высоте основания, а площадь сечения, проведенного через это боковое ребро и высоту основания, равна Q. Определить объем призмы.
Решение.
Искомый объем призмы находится как V = SH (рис. 11.64).
Площадь сечения DDXCXC Q-DC-CQ. Так как по условию /—	х2л/з
DC = ССХ, то DC = ССХ = y/Q . Площадь ДАВС : S’ = —-— . Из
_ х1 2	2	_ 0,Л> _ Q
&CDB 2 + —= х .Отсюда х = —.Тогда д - “/т и иска-4	3	3
мый объем
У.Ы1 л
Ответ: Q-JQ/3.
11.070. В прямом параллелепипеде стороны основания равны а и b и образуют угол 30°. Боковая поверхность равна S Определить объем параллелепипеда.
Решение.
Объем параллелепипеда находится по формуле И = 50СНЯ
(рис. 11.65). Площадь основания 50СН = Z?«sin3O° = —ab. Площадь боковой поверхности S = PH. Периметр основания Р = 2(а + Ь).
Отсюда Н “ 2^а + • Тогда получим объем параллелепипеда:
abS
4(а + b)'
abS
Ответ: ^ьу
11.071. Найти отношение объема правильной шестиугольной пирамиды к объему правильной треугольной пирамиды при условии, что стороны оснований этих пирамид равны, а их апофемы в два раза больше сторон основания.
Решение.
Объем шестиугольной пирамиды:	• Нх. Площадь основания
шестиугольной пирамиды	, а высота равна Нх = ф2 - г2 ,
За
где апофема / = 2а, а радиус вписанной окружности г\ -	. Тогда
H = ~V13. Подставим и получим Vx = ~а2у/з •—\^- = ^-а3>/39 .
2	3 2	2	4
Объем треугольной пирамиды И2 = ^S2H2. Площадь основания
этой пирамиды £•> = —— , а ее высота Н^ 4
, где радиус
ау]3	ГТ а /тут
вписанной окружности г2 - ——. Подставим и получим Н2 = --V141 .
6	6
TZ 1 аЧЗ V141
Тогда V2 = ~—--------—
3 4	6
Получаем отношение:
Ух = а3Уз9 46 = 3 62>/13 = 18-У1833 = 6>/1833
У2 4а3Л>/141	7141	141	47 ’
_ бЛвзз
Ответ: ———.
47
11.072. Стороны основания прямоугольного параллелепипеда относятся как т: п, а диагональное сечение представляет собой квадрат с площадью, равной Q. Определить объем параллелепипеда.
Решение.
Искомый объем V = Somh, где S0CH = А В • AD (рис. 11.66), h — высота параллелепипеда. По условию BBXD{D — квадрат и, значит, Л = y[Q .
Найдем АВ и AD. Так как АВ \ AD = m :n,io AD = — AB.B &ABD т
имеем АВ2 + AD2 = BD2, т.е. АВ2 +^-АВ2 = Q => АВ = гт2^- , м	>1т2 +п2
AD =	. Итак, V = AB AD h = mnQ>^.
>1т2+п2	т2+п2
тп г—
Ответ: —$-----
т +п
11.073. Измерения прямоугольного параллелепипеда равны 2, 3 и 6 см. Найти длину ребра такого куба, чтобы объемы этих тел относились как их поверхности.
Решение.
Объем прямоугольного парллелепипеда равен Ипар = 2-3-6 = 36 см3. Объем куба Кк =л3. Площадь полной поверхности прямоугольного параллелепипеда находится так: 5ПЯП =	+ 25nrH = PH + IS^ = 2(2 + 3) • 6 +
+2 • 3• 2 = 72 см2. Площадь полной поверхности куба SK = 6л2. Из усло-
^пар *^пар х-х	36	72
вия —- = —Отсюда — = —-. Получаем а = 3 см.
SK	а3 6а2
Ответ: 3 см.
11.074. Высота пирамиды равна 8 м. На расстоянии 3 м от вершины проведена плоскость, параллельная основанию. Площадь полученного сечения равна 4 м2. Найти объем пирамиды.
Решение.
Искомый объем пирамиды V = SH (рис. 11.67). Пирамида SABCDEF
SO 8 подобна пирамиде	с коэффициентом подобия к =---= —.
Тогда площади их оснований относятся как ^AB(^PEF- -^k2. Отсюда Sa^D^F,
Sabcdef = у •4 = ^ (см2). Значит, V = 1~-8» 75,85см3.
Ответ: «75,85 см3.
11.075. Доказать, что объем конуса равен объему цилиндра с тем же основанием и той же высотой минус произведение боковой поверхности этого цилиндра на 1/3 радиуса его основания.
Решение.
Пусть Кцил — объем цилиндра, Ккон — объем конуса, г — ра-
диус основания, h — высота; тогда
2	1	2	1
^ЦИЛ ~ ПГ ^КОН = у= '^^ЦИЛ-
1	2 2	2
Так как ^бок.цил “2tcz7i , то ‘^‘^'бок.цил^* ~~	^^цил • Отсюда
I/ — —	г — _1/ — I/
Г ЦИЛ j ‘“'ООК.ЦИЛ' J г цил — г кон •
Что и требовалось доказать.
11.076. Высота конуса равна диаметру его основания. Найти отношение площади его основания к боковой поверхности.
Решение.
Площадь основания конуса: S0CH=tlR2 (рис. 11.68). Площадь
боковой поверхности конуса S6oK = тМ, где
/ = >Ih2+R2 = -J4R2 +R2 = Rj5  Отсюда 56ок = nR2 . Оконча-
SOCH _ n^2 _ 1 _ Vs
тельно получим	_2 /7 -~fr ~T" •
o6oit iJCJS -J 5	5
Ответ:
y[5
5 '
11.077. Выразить объем конуса через его боковую поверхность S и расстояние г от центра основания до образующей.
Решение.
Объем конуса находится по формуле у = i SH = у nR2H (рис. 11.69).
Рассмотрим ЛОВА (ХОВА = 90°): sina = ^. Из &SOA (XSOA = 90° )’• лх г
Н = 1 sina = /~ . Площадь боковой поверхности 5бок = kRI. Окон-R
чательно запишем объем конуса:
V = -nR2H = -лЯ2 — = -KRlr = -S6r.
3	3 Я 3	3 6
Ответ:
11.078. Цилиндр образован вращением прямоугольника вокруг одной из его сторон. Выразить объем у цилиндра через площадь S' этого прямоугольника и длину С окружности, описанной точкой пересечения его диагоналей.
Решение.
Искомый объем цилиндра находится как V = nR2H (рис. 11.70). По построению R = а, Н = Ь- Площадь прямоугольника S' = а • Ь RH.
Рис. 11.71
Рис. 11.72
Длина окружности
а
С = 2яг , где г = -. Тогда
С =	= ita = nR.
2
Тогда окончательно получаем V = nR • RH = CS .
Ответ: CS.
11.079. Доказать, что если два равных конуса имеют общую высоту и параллельные основания, то объем их общей части составляет 1/4 объема каждого из них.
Решение.
Пусть радиус основания каждого из данных конусов равен R, а высота равна Н (рис. 11.71). Тогда объем каждого конуса

nR2H . Общая часть состоит из двух конусов; ее объем
__	2 2»
И2 = -пг h , где г — радиус основания, h — высота. Рассмотрим осе-
вое сечение фигуры. Так как ЛО{ОА ~ ЛО^СВ, то А О : ВС = Ofi :
„	. Н	R „
или R.r-H th Но Л = —, откуда следует, что г = у . Итак,
Г2=-л — — = — nR2H = -Vi. 2 3	4 2 12	4 '
Что и требовалось доказать.
11.080. На основаниях цилиндра с квадратным осевым сечением построены два конуса с вершинами в середине оси (цилиндра). Найти сумму полных поверхностей и сумму объемов конусов, если высота цилиндра равна 2а.
Решение.
По построению Н = 2R (рис. 11.72). Эти конусы одинаковые. Площадь полной поверхности одного конуса: = 5бок	= яЛ/+яЯ2 .
Из ЬАВС 2l = 2j2R- Отсюда / = 5/2Я- Так как 2Я = 2а, то Sj = ла2 71 +ла2. А сумма полных поверхностей S = 2na2\j2 4-1)-
Объем одного конуса Vx = лЯ2Я = j ла3 • А сумма объемов конусов
V = -7W3 .
3
Ответ: 2ла2(>/2 +1); j”0’ •
11.081. Около конуса с радиусом основания R описана произвольная пирамида, у которой периметр основания равен 2р. Определить отношение объемов и отношение боковых поверхностей конуса и пирамиды.
Решение.
Пусть общая высота конуса и пирамиды равна Н (рис. 11.73). Обозначим объемы конуса и пирамиды через Vx и V2, а их боковые
1	2
поверхности — через Sj и S2 ; тогда Vx = ~nR Н ,	= nRl, где / —
образующая конуса. Найдем V2 и S2 . Так как периметр основания пирамиды равен 2р, а основание конуса— вписанная в основание пирамиды окружность, то площадь основания пирамиды равна pR, откуда И2 = ^pRH , S2 = pl (высота любой грани равна /). Итак, ^- = ~tiR2H:^-pRH = —, ^- = nRl: pl = — .
v2 3	3 p S2	p
nR Ответ:	.
P
Рис. 11.73
Рис. 11.74
11.082. Высота конуса и его образующая равны соответственно 4 и 5 см. Найти объем вписанного в конус полушара, основание которого лежит на основании конуса.
Решение.
Из ASOA: ЛО = Л = V25-16 =3 см (рис. 11.74). Объем искомого полушара V =|-яг3. Из ASBO: г2 + (5-х)2 =16. Из ЛАВО: х2+г2 =9.
Решив систему
г2+(5-х)2 = 16, г2+х2 =9,
получим х =
|. Тогда г = л/9-х2 =
12	2 123	1152
= — (см). Окончательно получаем V = —л—у =------п (см3).
5	3	5	125
Л 1132	3
Ответ: ----л см .
125
11.083. Определить объем шара, вписанного в правильную пирамиду, у которой высота равна А, а двугранный угол при основании равен 60°.
Решение.
Проведем сечение правильной пирамиды через апофему АВ и высоту ВС = Л, на которой лежит центр шара, вписанного в пирамиду (рис. 11.75). Шар касается боковой грани в точке К апофемы АВ.
Рис. 11.75
Тогда л В АС = 60° > Z.ABC = 30° • Из ЛВКО имеем sin30° = — = -;
г 1	1 » -г.	„	4	з	4	,	з
•7— = r, 2r = h-r,	r = -h. Тогда	Иш	=-лг	=—^ .
/7 — / Z	3	3	01
4 з
Ответ: ~nh • о 1
11.084. Конус и полушар имеют общее основание, радиус которого равен R . Найти боковую поверхность конуса, если его объем равен сЗъему полушара.
Решение.
2
Так как объемы конуса и полушара равны, то V = —nR*; с дру
гой стороны, V = -nR2h, где h — высота конуса, т.е. h = 2R • Имеем
S6oK = nRl, где / = у/R2 + Л2 = R^5 . Итак, 5бок = nR2^5 .
Отв^т: itR2j5.
11.085. В цилиндре площадь сечения, перпендикулярного образующей. равна М, а площадь осевого сечения равна N. Определить поверхность и объем цилиндра.
Решение.
Площадь осевого сечения 5сеЧ1 = Н 2R = N. А площадь сече
ния, перпендикулярного образующей, Sce42 = nR2 = М. Площадь полной поверхности цилиндра находится так:
S = $бок + 2S0CH = 2nRH + 2nR2 = Nji + 2М. Объем цилиндра можно най-
титак: V = nR Н = МН. Радиус основания B = J—, а высота цилиндра
V л
У TvVrc
Н = — = —Находим искомый объем цилиндра:
2R 2у/М
Njn N 24м ~ 2
V = M-
Ул/л.
АГ /---
Ответ: Nn + 2M; —*4 Мп.
2
П.086. В конус, осевое сечение которого есть равносторонний треугольник, вписан шар. Найти объем конуса, если объем шара равен З2л/Зсм3.
Решение.
4 1 32
Объем шара Иш = у пг = — л (рис. 11.76). Отсюда г = 2 см. Объем
1	7
искомого конуса находится как Кк - — nRH. Так как AASB— равносторон-
аУз ~	12	/г
нии, то радиус вписанной окружности г =-. Отсюда а = -^ = 4<3 см.
6	уз
Радиус основания конуса Я=у = 2Уз см. Из tiSOBSO = H = = 7SB2 - OB2 = (4л/з)2 - (2л/з)2 =6 см. Окончательно получим: Кк = = |я(2>/з)2 -6 = 24л.
Ответ: 24л см3.
11.087. Доказать, что объем конуса равен 1/3 произведения боковой поверхности на расстояние от центра основания до образующей.
Решение.
Нужно доказать, что объем конуса
V = у*$бок г. Объем конуса
V = -пЯ2Н . Высоту конуса можно выразить как Н = Zsina из AS О А г	1г
(рис. 11.69). Рассмотрим &SOB; sina = — Тогда Н = — .Подста
вим в объем и получим
1 1г 1
V = -nR2 - = -nRlr . Но известно, что 3 R 3
*^бок =	• Тогда окончательно получим: V = у5бок г.
Что и требовалось доказать.
11.088, Даны шар, цилиндр с квадратным осевым сечением и конус. Цилиндр и конус имеют одинаковые основания, а их высоты равны диаметру шара. Как относятся объемы цилиндра, шара и конуса?
Решение.
*^оснц ^оснк j Нк ”	• Объем шара
4	,	4 з	1	2	2 з
Гш	= з‘я^ • Объем конуса Ук = Н = -kR , Объем ци-
линдра Кц = nR2H = 2яЯ3. Отсюда отношение:
Иц : Кш : Кк = 6:4 :2 = 3 :2 :1.
Ответ: 3:2:1.
11.089. Радиус основания конуса равен R , а угол при вершине в развертке его боковой поверхности равен 90°. Определить объем конуса.
Решение.
Объем конуса находится как: у = ^nR2H (рис. 11.77). Длина дуги
nla nl „ v	» л/
сектора, с =	= — .С другой стороны, с - 2nR . Отсюда 2хк = — и
получаем / = 4R, где / — образующая. Тогда Н = v^R)2 - R2 = 715R.
Подставим и получим V = -у k715R3 =
VI5 п3
Ответ: ——nR .
3
11.090. Вычислить поверхность тела, полученного от вращения ромба площадью Q вокруг одной из его сторон.
Решение.
Площадь искомого тела:
‘$ = -$бокц+25’бок,он (рис. 11.78). Пло-щадь боковой поверхности цилинд
Рис. 11.78
ра находится как Збокц = 2rcR# . Высота цилиндра Я = я , а радиус
цилиндра R = asina- Отсюда 5б0Кц = 2rca2sina. Площадь боковой поверхности конусов (они одинаковые) S6oKk = nRl, где R = asina, а I = а. Отсюда 5боКж = па2 sina. Площадь ромба Q = a2 sina ♦ Окончательно получаем S = 4ла2 sina = 4л0 .
Ответ: 4nQ.
11.091. На отрезке АВ как на диаметре построена полуокружность с центром в точке О, а на отрезках О А и ОВ построены две полуокружности, расположенные в той же полуплоскости с грани-
цей АВ, что и первая. Найти поверхность и объем фигуры, которая образована вращением вокруг АВ фигуры, ограниченной этими тремя полуокружностями, если АВ = 20 см.
Решение.
Объем искомой фигуры равен: К = КШ1-2КШ2
4 _з где
(рис. 11.79). Так как ЛВ = 20 см, то =10 см. Тогда получаем
TZ 4000
ИШ1 = ~ з~ '71 • Так как Rx =10 см
т/ 4 оз 500	TZ 4000
Кь	=— it. Тогда V = —j-Tt-
то R2 = 5 см. Отсюда
п = 1000л см3. Площадь
искомой фигуры равна: S'= ,5Ш1 +25Шг. Площадь большей сферической поверхности равна: $ш =4тсЛ12 = 400л. Площадь меньшей сферической поверхности равна: 5Ш? = 4л7?2 = Ю0гс. Тогда
S = 400л + 200л = 600л см2.
Ответ: 600л см2; 1000л см3.
11.092. Треугольник со сторонами 10, 17 и 21 см вращается вокруг большей стороны. Вычислить объем и поверхность полученной фигуры вращения.
Решение.
Из АЛОВ (ОВ = 2\-х) R2 = 172-(21-х)2 (рис. 11.80). Из ЛАОС
(ОС = х) R2 = Ю2 - х2 • Решая систему:
R2 = 172 -(21-х)2, ,	,	, полу-
|Я2 = 102-х2,
ним ОС = х = 6 см, а 05 = 21-6 = 15 см. Тогда R - V102 -62 =8 см. Площадь большего конуса S6oKi = itRlx = л8 -17 = 136л см2. Площадь меньшего конуса £бок^ = nRl2 = л8 10 = 80л см2. Тогда площадь поверхности искомой фигуры равна: £ = S6oK( + S6ol<2 = 216л см2. Объем
большего конуса Vx = ^nR2Hx = ^л64 15 = 320л см3. Объем меньше-
Рис. 11.80
см3. Тогда объем искомой
го конуса У2 = лЯ2Я2 = | л64-6 = 128л
фигуры равен: У = Ух + У2 = 448л см3.
Ответ: 448л см3; 216л см2.
11.093. Найти отношение поверхности и объема шара соответственно к поверхности и объему вписанного куба.
Решение.
Пусть радиус шара равен R, ребро куба равно а; тогда
2 fflY Я2	_ 2Л
R - — = —, откуда а - —jr . Обозначим объемы и поверхности k Z у Л	У1J
4 з шара и куба соответственно через Ух, У2 и Sj, S2 . Имеем У\ = у лЛ , tz з 8Л^	-	-	-	<-
У>=а	5'1=4л/Г, S2 = 6а2 = 8Я, откуда Г1:Г2=л73:2,
S. :52 = л:2
Ответ: п:2', пу[3 :2•
11.094. Найти отношение поверхности и объема шара соответственно к полной поверхности и объему описанного вокруг него конуса с равносторонним осевым сечением.
23 М. И. Сканави, группа А
705
Рис. 11.81
Рис. 11.82
Решение.
4 з	11
Объем шара = —пг , объем конуса Ук = -nR Н (рис. 11.81).
Так как сечение — равносторонний треугольник, то г = ——. Отсюда 6
а ~	= 2>/Зг. д радиус основания конуса = =	 Высота конуса
I ,	а2 Г~2------2	-	Еш- 4гоЛз _4
H = Ja-----= vl2г - Зг	= Зг.	Отсюда	отношение тг - , , 2	“ о	•
V 4	ик ЗпЗг  Зг 9
Площадь сферической поверхности £ш = 4лг2. Площадь полной по
верхности конуса
$к = 5б0К + S0CH = itRa + nR2 = njir • 2>/Зг + Зкг2 = 9кг2 . Отсюда отно-
_ 4w2 _ 4
ШеНИе: ST"9^"9-
-4
Ответ: у* ~ Sk ~
11.095. Около правильной треугольной призмы, высота которой вдвое больше стороны основания, описан шар. Как относится его объем к объему призмы?
Решение.
4 з
Объем шара равен: Уш =—nR (рис. 11.82). Объем призмы равен:
Уп = S H . Площадь основания призмы равна: S = —-—, а высота
।
призмыН = 2а .Отсюда Ип = —-—.Рассмотрим ДЛ ОБ: ОБ = -Н = а ;
AB = r = —у- (радиус описанной окружности для равностороннего
треугольника).
Тогда R - 4аВ2 +ОВ2 = Ja2	• ТогДа
V 9	3 V3
Кп - Jyj • Искомое отношение:
Кш _ 4 • 8д3л • 2 _ 64л
K"3-3V3a3V3 ~~ТГ'
64л
Ответ:
11.096. Определить поверхность шара, описанного около конуса, у которого радиус основания равен R, а высота равна Л.
Решение.
Поверхность шара равна: Sm = 4лг2 (рис. 11.83). Сечение конуса — равнобедренный треугольник. Для него радиус описанной окружности г =	• Для &АВС S = ^AC BD = ^2R h = Rh. Стороны
ЛВ = ВС = 7я2+A2 ♦ Отсюда r = —
тельно получаем = 4л“-------
4h
h2
——L. Оконча-2h
„ п\К+п)
Ответ: ——z—L~.
h2
11.097. В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности конуса к поверхности шара.
Решение.
Рассмотрим осевое сечение конуса, которое пройдет через центр шара. Так как диаметр основания конуса равен образующей, то в сечении получим правильный треугольник, вписанный в окружность (рис. 11.84)).
Пусть радиус шара равен R; тогда АВ = Rjl, AD = -у- • Обозна-
чим полную поверхность конуса через , а поверхность шара — через
S2. Имеем S, =	• /?7з +
2	2
9	>	,
=	, S2 = 4лЛ , откуда
:S2 =9:16.
9 Ответ: —• 16
11.098. Боковая поверхность конуса вдвое больше площади основания. Площадь его осевого сечения равна Q. Найти объем конуса. Решение.
Объем конуса VK = ^nR2H (рис. 11.85). Площадь осевого сечения
1 >
Q = —2RH = RH . По условию S6oK = 2S0CH. Отсюда nRl = 2nR2 и
l = 2R- Из рисунка I2 = H2 + R2 = 47?2. Отсюда Ц = д7з > а также
Н = . Тогда = Л-Уз и получаем R =	. Окончательно полу
1
чаем: К = -nRH  R =
* з з t/з
3
Ответ: ^4^ kQ-JQ-
11.099. Равнобедренная трапеция с основаниями 2 и 3 см и острым углом 60° вращается вокруг меньшего основания. Вычислить поверхность и объем полученной фигуры вращения.
Решение.
Искомый объем V = -2Ккон , а по-
верхность S' — +2SK0H, где , Ккон и 5’цил , 5К0Н — объемы и боковые поверхности цилиндра и конуса соответственно (рис. 11.86). Имеем Кцил=кг2й , где
Рис. 11.86
r = CK, h = AD = 3 см. Так как DK = j(AD-BC)=^ (см), а CD = 2DK = 1 (см), то СК = ylcb2 -DK2 =	(см)* Следовательно, Кщл = л • 3 = ^5 (см3), Икон = | п ~	(см3), отку-
да V = —,---- = 2л (см3).,Наконец, находим
4 4
S'tuvi =2itrh = 2л~*3 = 3л-/з (см2), SKOH = nrl = л*-^-*1 = ^^ (см2), откуда 5 = Зл>/з+л-Уз =4л-Уз (см2).
Ответ: 4я*Уз см2; 2л см3.
11.100. Высота конуса разделена на три равных отрезка, и через точки деления параллельно основанию проведены плоскости, разбивающие конус на три части. Найти объем среднего усеченного конуса, если объем данного конуса равен у.
Решение.
Иуск = |+ S2 + <jslS2);	= л/?!2, S2 = itR2 , тогда получим,
что Иуск = ^-Лл(А|2 +R2 + RlR2) (рис. 11.87). По условию имеем
н	зи	зк	V
h =	, где Я = — =	, следовательно, А = —у. Получим, что
3	о	nR	nR
^с.к=|^(л,2+л22+ал)=7
э R	3
В
А
ол-
С
Рис. 11.87
7л, У а,а2 La J La J r2
ДВС\Е ~ ДВОС, то имеем
££ = ^l. А._з_. A = l Tak
ос BO’ r н ’ а з’
как ABO2F ~ \BOC, to
A2 2/3 Я A^ = 2 A ~
. Так как
Н
_v_( уск-3 13
, D - , , тогда
К j
if 72V 2'
3) +9
IV
27 •
Ответ: —.
27
11.101. Боковая поверхность конуса развернута на плоскости в сектор, центральный угол которого содержит 120°, а площадь равна S. Найти объем конуса.
Решение.
Пусть радиус основания конуса равен г, а его образующая , т	с 1,2 2л л/2	, |3S
равна /. Тогда площадь развертки о = -I • — = -у-, откуда у~-
и, следовательно, г
конуса найдем
по формуле
V = :~nr2h где h - 4l2 -r2 = J~~Y“ =	• Итак,
3	V л Зл V3re
V = 1 2 1^ = 2Sy^
3 Зл V3n 27л '
Ответ: 2S>/6nS/(27л).
11.102. Из медной болванки, имеющей форму прямоугольного параллелепипеда размерами 80x20x5 см, прокатывается лист толщиной 1 мм. Определить площадь этого листа.
Решение,
Искомую площадь найдем по формуле S = К/й , где V — объем листа, h — его толщина (при этом форма листа значения не имеет). Так как объемы обоих тел равны, то V = 80-20-5 = 8000 (см3). Итак, 5 = 8000/0,1 = 80000 см2 = 8 м2.
Ответ: 8 м2.
11.103. Металлический шар радиуса R перелит в конус, боковая поверхность которого в три раза больше площади основания. Вычислить высоту конуса.
Решение.
4 з
Так как радиус шара равен R, то объемы тел равны уяЯ .
Пусть г — радиус основания конуса; тогда, по условию, 5бок = Зяг2 • С ДРУгой стороны, 5бок = кг/, где / — образующая
конуса. Поэтому / = 3Г, откуда А = J/2 _г2 = 2ri/2 > т е- г =	h •
1	12	1
Находим V = —лг2й = - л • —Л2 • h = — лй3. Из равенства 3	3	16	24
4 j 1	,3
улЛ =—лй получим h = 2RV4-
Ответ: 2Я^4.
11.104. В правильном тетраэдре построено сечение его плоскостью, проходящей через ребро АС и точку К, принадлежащую ребру SB , причем ВК : KS = 2:1. Найти объем отсеченной пирамиды КАВС, если ребро тетраэдра равно а.
Решение.
Vkabc - 'KN (рис. 11.88),
2ч/з
где S^bc =	♦ Так как ,
Рис. 11.88
TO BN .NO = BK :KS=2 A, откуда
BN = ^BO.\to BO = — ,r.e. 3	3
2а4з	„кт	dm2 /4л22а4б
BN = —-— и, значит, KN = vBK - BN = J—-— = —-— .
9	V 9	27	9
D
Рис. 11.89
Ответ:	л3л/2/18.
11.105. Ромб вращается вокруг своей большей диагонали, а затем вокруг меньшей диагонали. Доказать, что отношение объемов полученных фигур вращения равно отношению площадей их поверхностей.
Решение.
Пусть сторона ромба равна а 9
а его диагонали равны 2d{ и 2d2
(рис. 11.89). При вращении получается тело, состоящее из двух конусов. Обозначим объем и поверхность тела вращения вокруг диагона
ли АС через VAC и ВАС, а вокруг диагонали BD — через VBD и
2	2
SBd • Тогда Уде ~	’ $ас =	, Увя = уTtd2d\, SB£f = 2iuid2 .
Уде _ (2/3)tu/2J2 _	_ SAC
огда fafynd^di d2 SBD ‘
Что и требовалось доказать.
_______Решения к главе 12_ ЗАДАЧИ ПО ГЕОМЕТРИИ С ПРИМЕНЕНИЕМ ТРИГОНОМЕТРИИ
НЕКОТОРЫЕ СООТНОШЕНИЯ МЕЖДУ ЭЛЕМЕНТАМИ ФИГУР
1.	Площадь параллелограмма ABCD (рис. 12.1) можно вычислить по следующим формулам:
5 =
AC2-BD2 а
----~л--^А'’
4
(а)
Л Д2 — Л D2
S=“- tgZAOD,	(б)
где О —точка пересечения диагоналей АС и BD-
2.	Пусть известны длины Ь и с двух сторон треугольника АВС и угол А, образуемый ими (рис. 12.2). Тогда длина биссектрисы AD треугольника, проведенной из вершины этого угла, выражается
3.	Справедливы следующие соотношения между элементами шара и вписанного в него конуса:
/ = 2/?sina;	(а)
l2=2RH,	(б)
где R — радиус шара, / — длина образующей конуса, Н — его высота, a — угол между образующей и плоскостью основания.
Такие же соотношения справедливы и для вписанной в шар пирамиды, боковые ребра которой имеют длину / и составляют с плоскостью основания угол a.
4.	Пусть А& —боковое ребро пи
рамиды или призмы, АХО — его проекция на плоскость основания, ZB14<^ = a, Z(?44=P» ZBl4J2=y (рис. 12.3). Тогда справедливо равенство cosy = cosacosp.
Доказательство этих соотношений можно найти в любом издании данного сборника задач последних лет.
12.001. Сумма двух неравных высот равнобедренного треугольника равна 1, угол при вершине равен a. Найти боковую сторону.
Решение.
По условию АВ = А С , ААХ1ВС, ВВХ1А С, /ВАС = a, ААХ + ВВХ = /
(рис. 12.4). Пусть ВС = а . Из ЛАА1С имеем А 4 = у ctg у, А С =
а из ДВВ^С находим ВВ{ =asin[ — - — j = acos— . По условию
/	\	tg —
-ae-+a<x,s- = l. ^ctg^ l + 2sin^ =/, a =--2— Получили
2	2	2	2	V	l + 2sin5
I
l______
.Ina} о • л+а л-За sin--+sma 2 sm—-—cos—-—
12 2 J	4	4
_______I_______
Ответ: 2 sin	cos— —
4	4
12.002. Угол при основании равнобедренного треугольника равен a. Найти отношение радиусов вписанной и описанной окружностей.
Решение.
По условию АВ-ВС, ^ВАС-Z-BCA-a. Пусть АС = х, тог-
да из ДАЕО, ХАЕО-9^ имеем OE = r-— tg— (рис. 12.5), где 2 2
г — радиус вписанной окружности. Из &АЕВ ЛАЕВ = 90° име-
>4 F* у
ем, что АВ =------=-----. Рассмотрим ^ВК(\ , АВКО,-90\
cosa 2cosa
©л D ВК	п „ АВ х
ВО. =R =---——; в К =----=------ (Oi — центр описанной ок-
cosOq	2 4cosa 1
ружности). ЛАВЕ = 90°-а, тогда ВО. = Л =-----------7-----? =
4cosacos(90°-a)
х	г xtg~'2sin2a
=----------. Следовательно, — =---2----------= tg—• sin 2a.
4cosasina	R 2x	2
Ответ: tg у sin 2a.
12.003. В ромбе через вершину острого угла, равного a, проведена прямая, делящая этот угол в отношении 1:2. В каком отношении эта прямая делит сторону ромба, которую она пересекает?
Решение.
п	АЛВЕ 1	2	. ос
Пусть ZABC = а и = -, значит ХЕВС = -а, ХАВЕ = —, Z.2SjdC 2	э	э
ZDBC =	= - > ХЕВМ = ХЕВС - XDBC = --- = - (рис. 12.6).
2	2	3	2 6
Из подобия \ADO ~ &EDM следует ^p__DO_ Так как
ED DM
AD = ED + AE,то — = ^--1 .Обозначим АВ = ВС = CD = AD = х  ED DM
Из taCOD ZCOD = 90°, XODC = a/2, OD = DC cos^- = x cosy ,
BD=2DO = 2x"CoS'—. Из \BME , ZBME = 90°, EM = BM t&^ . 2	6
Рассмотрим дел/D, /ЕЛ/л=9П°. DA/= ЕЛ/ctg^, DA/=EA/tg—ctg^, 2	6	2
где BM=BD-DM, тогда DM = (BD-DM\i%-ctg-- Получили,
6	2
ЧТО ----i---
oc	a
tgvctg-
O	2
л»	ОС
2xcos—
=------
DM
BD-DM	1
------, где BD = 2x ♦ cos — . Тогда -
DM	2	<ctg^
О 2
DM =
_ a	a a
2xtg—ctg—cos—	AE * 1
----2---------к.. Следовательно, -
, , t a t a	ED
1 + tg-ctg-О 2
Рис. 12.6
Рис. 12.7
at.	а	а
х-cos-- 1 + tg-ctg-2 \	О	2
л а а 2xtg-ctg-О 2
, (х	а .а	а	. а	а
1-tg—ctg— sin— • cos sin— • cos—
_ i =	6	2	=	2	6	6	2 .
•cos— 2tg— ctg— 2sin—cos— 2	6	2	6	2
Ответ: cos—: cos—.
6	2
12.004. В квадрате ABCD через середину M стороны АВ проведена прямая, пересекающая противоположную сторону CD в точке N. В каком отношении прямая MN делит площадь квадрата, если острый угол AMN равен а? Указать возможные значения а.
Решение.
ABCD — кыщрп. М е АВ. МА = MB. ZAMN = а, Ne CD (рис. 12.7);
требуется найти S^MND:	Пусть АВ = а; тогда
е MA+ND a+2ND „ MB+NC ^+а~^ ^AMND------~ а-------7	°’ SBMNC~--Z-----а~-----~----а ~
2ND S~amnd _ а + 2ND ЦрОведем	низ &MEN име-
4 SBMNC За-2ND F	11
ем ME = a ctg а. Отсюда ND = МА - ME = — - a ctg а=-—2flCtga . Значит, 2	2
Samnd = а+ а-2аctga _ 1-ctga _ tga-1 $BMNC 3a-a + 2actga 1 + ctga tga + 1
л tga-tg—
4
«	.	. Л
1 + tgatg-
4
Наименьшее значение угла a достигается в случае совпадения точки Nс вершиной D\ тогда tg a = a: (а / 2) = 2. С другой стороны, a < л / 2. Итак, arctg 2 < a < л /2.
।	л)
Ответ: tg a— ; arctg2 < a< л/2. k J
12.005. Высота равнобедренной трапеции равна h, а угол между ее диагоналями, противолежащий боковой стороне, равен а. Найти среднюю линию трапеции.
Решение.
По условию в равнобедренной трапеции ABCD имеем: АВ = CD, BB{LAD, ВВ{ =h, ACC\BD = O, Z.COD = a (рис. 12.8). Так как ZCOD — внешний угол равнобедренного треугольника AOD, то Z.OAD = Z.ODA -= ^. Далее, имеем B}D = ED + B}E = ^AD + ^BC = ^(AD +ВС) = MN,
где MN—средняя линия трапеции. Из ABB^D получим B|D = S5jCtgy =
, <Х
= Actgy.
Ответ: Actgу.
12.006. В прямоугольном треугольнике даны его площадь S и острый угол а. Найти расстояние от точки пересечения медиан треугольника до гипотенузы.
Решение.
В прямоугольном треугольнике АСВ имеем: Z.ACB - 90°, Z.CAB = а,
SMBC =5’ АВ\ =В\С и АС\ =С1В, ВВ\ ПСС1 (Рис- 12*9)’
Рис. 12.8	Рис. 12.9
A
нужно найти расстояние от О до АВ. Проведем CD1AB и положим
__	h __ h h
CD = h Ai3AADC vt&CDB находим AC =-,CB = —----r =-----.
sina sin|?-a] cos“ j	A2	___ '
Так как 5 = - AC  ВС =	, to h = VSsin2a • Проведем OF^AB ,
OFf\AC = F, OFC\CB = E uOFQCD = K.Таккак ACKO ~ ДСРСр
_ ОС -	2	1 VSsin2a
to ~	“ j , откуда СК = -jCD, a KD = ~^CD =-j------это
и есть расстояние от О до АВ, поскольку О е ЕЕЦаБ .
Ответ:
-•JSsmla. 3
12.007. В прямоугольник ABCD (ЛВ||С1>) вписан треугольник AEF. Точка Е лежит на стороне ВС, точка F — на стороне CD • Найти тангенс угла EAF, если АВ: ВС = BE: ЕС = CF :FD = k  Решение.
По условию	= к (рис. 12.10). Обозначим AD = ВС - х,
ВС ЕС FD
ВС х тогда АВ = DC = кХ-ВС = ВЕ+ЕС = кЕС+ЕС'ОКЮдаЕС=——=——, 1+к 1+к
BE = -^~. DC = FC+DF = kDF+DF,тогда DF = ^-, FC = ^~. l+k	l + k	l+k
ZFAE = ZDAE - ZDAF , ZDAE = ZBEA (ВС||ЛР, AE — секу-щая), отсюда /FA e = /BE A - /DA F . Получили, что tgZF4E = = tg(z.BEA-ZDAF} = t&^BEA-tgZDAF Рассмотрим &ADF,
v	’ 1 + tg ZBEAtg ZDAF
ZA DF = 90° > tgZDAF = ^- = 7-^- = -^-H3 &ABE, ZABE = 90°> AD + l+/c
, . к
1 J. If __ tg ZBEA=	=1+к. Окончательно tgZFAE=-?—1±^— =
Ы)2 •
Л2+Л+1
12.008. В параллелограмме co сторонами а и Ь и острым углом а найти тангенсы углов, образуемых большей диагональю параллелограмма с его сторонами.
Решение.
Влвсв = a b sma (рис. 12.11)и SABCD =2 Ssacd = AC CD sinZACD; получили, что absina = a-ACsinZACD, ZADC = 180’-ct > AC2 = a2 +b2 -2ab cosZADC (по теореме косинусов). Отсюда AC = ->la2 +b2 +2af>cosa > b sin a = Va2 +Z>2 +2aZ>cos a sin ZACDi
_______dsina_____
sinZACD = ~ I 2 , ,2 7~7	• По
Va +b +2af»cosa
теореме косинусов находим, что
AD2 = AC2 +CD2 -2АС CD cosZACD
Рис. 12.12
cos ZACD =
2a2 +2aZ>cosa 2a-Ja2 +b2 +2ab •cosa
,Asina ya2 +b2 +2aAcosa Asina tg ZA CD = .	• -------------=--------
Va2 +b2 +2aAcosa a+Acosa a+Acosa
tg zbca=tg(zB/ip - zacd)= WAD~4^i) =
6	V	' 1 + tgZBADtgZACD
Asina
_ ga a+Acosa	asina
. , ^sina b+acosa'
1 + tga-----
a+Acosa
Asina	a sin a
Ответ: ----;----; -------.
a + Acosa A+acosa
12.009. Основание равнобедренного треугольника равно а, угол при вершине равен a. Найти длину биссектрисы, проведенной к боковой стороне.
Решение.
Имеем АВ=АС, ВС = а, ZBAC=a, ZABB{=ZBlBC
(рис. 12.12). Тогда ZABC = ZACB = у-у,	=
/ddt (к a п п За
- л-1 — - —+—I- — + — # Из ЬВВХС по теореме синусов
а acos-
находим ——- = —  ---------- , тх. ВВ^ = —т-
. f л а ]	. (л За)	c;JK.L3al
sin --—	sin —+—	sm Т+“Г
(2 2 J 14 4 J	И 4 J
Ответ:
a acos— _______2
• (	3a Y
sin 45 +—
k	4 )
в
Рис. 12.13	Рис. 12.14
12.010. Около круга радиуса R описана равнобедренная трапеция с острым углом а при основании. Найти периметр этой трапеции.
Решение.
По условию ABCD — трапеция, АВ = CD, О — центр вписанного в трапецию круга, OE1AD, OE = R, ABAD = а, а<л/2 (рис. 12.13); нужно найти PABCd = AD + 2AB + BC. По свойству описанного четырехугольника AD + ВС = 2АВ и PABCd =	• Проведем В£||ОЕ; тог-
да ВК = 2ОЕ = 2R. Из кВ КА находим АВ - и PABCd = “т—" • sina	sina
8Я
Ответ: ~— • sina
12.011. Доказать, что во всяком треугольнике разность между суммой квадратов любых двух его сторон и произведением этих сторон, умноженным на косинус угла между ними, есть для данного треугольника величина постоянная.
Решение.
Пусть АВ-с, ВС = а, А С = b. Соответственно ABAC = а, АВСА = у, ААВС = $. Обозначим dx-a2 +b2-ab cosy, d2 =а2 +с2-accosp, d3 = с2 + b2 - ей cos a . По теореме косинусов с2 - a2 +b2 -2abcosy, b2 = a2+с2-2accosp, а2 =с2 +b2 -2c6cosa- Тогда dx =с2 +aZ?cosy, d2 = b2 +accosp , d3 = a2 +bccosa, dx + d2 = b2 +c2 +tf(6cosy + ccosp)=
= b2 +c2 +a(CE + BE} = b2 +c2 +a2 (рис. 12.14). d2+d3-b2+a2 + + c(acos0 + frcosa)=/>2 +a2 + c(BF + AF}= b2 + a2 + c2, d3 +dt =a2 +c2 + + b(c cosa+a cosy) = a2 +c2 +b(CM+AM}=a2 +c2 +b2 . Следова
тельно, dt +d2 = d2 +d3 = d3 +d{. Откуда d{=d3, d3=d2, значит, dx =d2 = d3 = a2 +b2 +c2. Что и требовалось доказать.
1X012. Даны стороны а, Ь, с и d четырехугольника, вписанного в окружность. Найти угол, заключенной между сторонами а и Ь • Решение.
Так как ABCD — четырехугольник, вписанный в окружность, то ZB+ZD = ZA+ZC = 180°  Из ABCD по теореме косинусов
BD2 = а2 +b2 -2af>cosZC-H3 ABAD BD2=d2 +с2 -IdccosAA Orao-№ d2 + c2+2dccosC = a2+b2-2abcosC (рис. 12.15). 2(ab+dc)cosC =
= a2 + b2 - If/2 + c2), cosC=), AC=arcco: 2(ab+dc}
Ответ:
arccos
ZT2 _1_ A2 z72	^2
a +b —a —c
2(ab+dc)
12.013. Отношение площади прямоугольного треугольника к площади квадрата, построенного на его гипотенузе, равно к • Най
ти сумму тангенсов острых углов треугольника.
Решение.
В ДЛСВ Z.ACB = 9V  Пусть ZG4B = a, ZABC=p, тогда tga + tgp = ——а+^ =-------. (a+0=90°). Обозначим AB = BF =
cosacosp cosacosp
.	.	„ Saacb AC • BC
=EF=AE=x (ABFE — квадрат) (рис. 12.16).	= ——5—;
Sabfe 2xl
AC = ЛВ-cosa, CB = ЛВ-cosp, тогда ^св = *2 cos a • cos 0.	= k
$ABFE x '2 $ABFE
1 1
(по условию). Имеем, что - cosa.cosp ° Следовательно,
tga + tgp = -!-. 2k
Ответ: tga + tgp = —.
12.014. Площадь прямоугольной трапеции равна S’, острый угол равен a. Найти высоту трапеции, если ее меньшая диагональ равна большему основанию.
Решение.
По условию ZCB/4 = 90°, Z^Z>C = a, AC = AD- SABCD=S, o BC + AD t	, 2S	2S
тогда S =---------h , откуда h =--------=------------
2	BC + AD AD-ED+AD
(рис. 12.17). Из &CED, ZCED = 90°> ED = h ctga. Из ЛАЕС
ZAEC=9W, ZC/l£ = 180°-2a (AC = AD\ AC = -^—, тогда sin 2a
. 2S . 2 h . cosa ’ ---------------Л —-- 2 sina cosa sma
!2 = 2Ssinacosa>/i = ^^ sin2 a
Ответ: y/lSdga.
12.015. Общая внешняя касательная двух внешне касающихся окружностей составляет с линией центров угол a. Найти отношение радиусов этих окружностей.
Решение.
Пусть R, г — радиусы двух внешне касающихся окружностей, Z0p4C = a. R = O{E+EC, EC = r (О{С1АС, О2В1ЛС, О2Е1АС) (рис. 12.18). Из SO2OiE, Z.O2EOl=9tf, ZX\O2E = = ZOtAC =а; имеем О\Е = О{О2 sina, ЦО2=г+Л; тогда Q£ = (/?+r)sina, значит, £ = r+(A+r)sina, 7?(l-sina)=r(l+sina), R 1+sin a	2(n a A
r 1-sina	^4 2)
2( л a'I
Ответ: CU> I у I-
12.016. Две высоты параллелограмма, проведенные из вершины тупого угла, равны Л, и , а угол между ними равен a. Найти большую диагональ параллелограмма.
Решение.
По условию BF1.CD, BF = h1, BE1AD, BE = h{, Z.EBF = a. Тогда ZABF = Z.CFB = 90’ (ЛВ||С/)Х ZABE = 9Q°-а. Из АВЕА ZBEA = 90‘ • ^£ = A1tg(90’-a)=A1ctga (рис. 12.19). Из &BFC £BFC = 99°, CF = h2ctga, AB = CD = -^~, BC = AD = ^-, sina	sina
o i-r	^2 Л,+Л12 4-2A.A2 cosa
ZD = 180 -а- По теореме косинусов АС= —-------1,
sin a
+ Л,2 +2^*2 cosa следовательно, A C =	5.
sina
Л ч/й?+Й.2+2A|A,cosa
Ответ:	—2------12------.
sina
12.017. Диагональ прямоугольника равна d и делит угол прямоугольника в отношении т: п . Найти периметр прямоугольника. Решение.
По условию ABCD—прямоугольник, AC=d, = — (рис. 12.20). ЛА CD п
п	л л . . тп
Так как ZBCD = — , то тх + пх = — х = т/---\J ^АСВ = -?——т
2	2	2(т + п)	2\т + п)
ZZCD = > Ж--Л . Из ДАВС и ДА DC находим ВС = Jcos	ч ,
2(т + п)	2{т + п)
	1 ИЛ ~	т>	л! I /ИЯ I ия 1
DC = dcos—7--г. Отсюда Pabcd = 2 “COS77----г+«cos-?------v =
2(m + n)	ABCD V	2(т + л)	2(m + «)J
. , л л(т-п) Л гг, л(т-п)
= 4dcos—cos -7---( = 2yl2dcos -7-(.
4	4(m + n)	4(w + n)
_ rr , л(т-п}
Ответ: 24/2Jcos—у-----г.
4(т + и)
12.018. В равнобедренной трапеции, описанной около круга, отношение боковой стороны к меньшему основанию равно к . Найти углы трапеции и допустимые значения к .
A
Рис. 12.22
Рис. 12.21
Решение.
CD ,
По условию - Обозначим ZBAE = a (рис. 12.21). Имеем ВС
BC + AD = 2AB,a AD = ВС+2 АЕ, тогда ВС+АЕ=АВ, —+—= 1-АВ АВ
Из ДВЕ А {ХВЕА- 90’) имеем АЕ = АВ cosa, AB=CD, тогда
—+cosa = l, a = arccos-,
к	к
ZABC = ZBCD = я - a = л -
к-1 arccos----
к
Возможные значения к находим из системы
=> ЛИ-
Л-1	к-1
Ответ: arccos-— и я-arccos-—; jfc >1. К	К
12.019. Площадь равнобедренного треугольника равна S, а противолежащий основанию угол между медианами, проведенными к его боковым сторонам, равен а. Найти основание.
Решение.
Имеем АВ — АС > $&лвс —	— В^С, АС\ — С\В, ВВ^ ПCCf — О,
ZBOC = а (рис. 12.22). Тогда -Удвос =	, так как высо-
1
та ДВОС, проведенная из О, равна ~ высоты ДАВС, проведенной из а  Находим площадь ДВОС:
• I Ct |	| Л Ct ]	-л	Ci	r\	(V
BC sin —-— sm —-— BC2 cos2- BC2cos-
c _	2J \2 2J	2 _	2 _
~------------------------------=----------=
2sma	2sma A • a
4sm—cos —
2	2
BC2ctgy	BC2ctgy ,	4Stgy
	Итак, 	— = — S, откуда BC1 =-— =t>BC = 4------------------------------------------4-3	3
"4
3
Stg^
Ответ: 21-----
V з
12.020. В сегмент, дуга которого равна а, вписан правильный треугольник так, что одна его вершина совпадает с серединой дуги, а две другие лежат на хорде. Площадь треугольника равна S. Найти радиус дуги сегмента.
Решение.
По условию Z-АВС = ot (рис. 12.23). Пусть ЕМ = MF = EF = а, с с	е а24ъ L .лг, аЛ	Л 2Л
S&EMF - тогда 5 =---------; п = МО ------; отсюда а = —?=, значит,
S.i*22^=‘; R = BO+OM = R-cos-t-tA/sS, откуда R= .
3 4 V5	2	2sin22
4
Ответ: —------.
о ♦ 2 a 2 sin —
4
12.021. В равнобедренном треугольнике угол при основании равен а, радиус вписанного круга равен г. Через вершину угла при основании и центр вписанного круга проведена прямая. Найти отрезок этой прямой, заключенный внутри треугольника.
Решение.
Имеем АВ = АС, О — центр окружности, вписанной в ДЛВС, ZABC-a, ODLBC, OD = r, ВО НАС = (рис. 12.24). Так как
Рис. 12.23	Рис. 12.24
ВВХ —биссектриса ХАВС9 то ZJ?XBC = у, а АВВ^С = я-у1. Из &ODB
а
получаем ЯР = г ctg у. Так как D — точка касания основания ВС равно
бедренного треугольника АВС с окружностью, то ВС = 2BD = 2 г ctg у.
В &ВВХС по теореме синусов имеем
ВВХ 2rctg 2 sina . ( 3a sin я------------
I 2
т.е.
o . a .	.	2 a
2rctg —sina 4rcos —
ад =------\----=-------=-2-.
1	.3a	.3a
sin— sin—
2	2
A 2 Ct 4rcos —
Ответ: ----——
Рис. 12.25	Рис. 12.26
12.022. Найти угол треугольника, если известно, что стороны, заключающие этот угол, равны 1 и 3, а биссектриса угла равна 0,75>/з.
Решение.
В ЛЛ5С имеем: АС= 1,ВС=3, ЛАСС1=ЛВССХ, СС{ = 0,75л/3; тре-буется найти ZACB (рис. 12.25).
1	~ 1 2aftcos(C/2) ,
Воспользуемся формулой 1С =-----------(см. «Некоторые соотно-
а + Ь
С
шения между элементами фигур», с. 713). Выразив отсюда cos—, имеем
С 1Да + Ь) cos — = —----
2 2ab
или, после подстановки значений а = 1, b = 3, 1С = 0,75^3, находим
С зТз-4 л/з cos — =------= —.
2	4-21-3	2
С
Следовательно, у = 30°, откуда С= 60°.
Ответ'. 60°.
12.023. В равнобедренном треугольнике даны основание а и угол а при основании. Найти длину медианы, проведенной к боковой стороне.
Решение.
Имеем АВ = АС, ВС = а, ZABC = a, ABi=BlC (рис. 12.26). В
АС ВС
М.ВС по теореме синусов находим sin(X “ sinUQ» _2а] =*
a sin а а sin2а 2cosa'
Проведем AiBl ||ВС. Из ДВДД получаем
AiBl=^BC = ^, ВА,=^АВ = ^АС = —^—, ZB,A,B = 180°-а и по
2	2	2	2 4cosa 1 1
теореме косинусов
л2	л2	л2	/	\
ВВ% = —+—--------2—-—cos(180° -а =
4 16cos2a	8cosa	'	'
a2 a2 a2 a2 tacos2 а+1)
=---1-------1----= —-------- •
4 16cos2a 4 16cos2a
ВВХ =^l8+-L-=^y/9+tg2a.
4 V cos а 4
Отверг: —-J^ + tg2».
12.024. Найти отношение периметра трапеции, описанной около окружности, к длине этой окружности, если углы при большем основании трапеции равны аир.
Решение.
По условию ABCD — трапеция, описанная около окружности,
ZBAD-ql, ZCDA = $. Пусть R —радиус вписанной окружности.
Длина окружности / = 2лЯ (рис. 12.27). Р = БС + ЛЛ + ЛВ + С£>,
2©
bc+ad=ab+cd, 2(ab+cd)=p. Из ABFA ZBFA = 90°, АВ--
sma
Из bCED ZCED = 9O’> CD = -^~  Тогда P = 4/?|-Д-+-Д—j; sinp	Iosina smpj
. . a+p a-P
P 2(sina+sinp) 4sm—cos—
/ rcsinasinp rcsinasinp
. a+p a-p
4 • sm   cos ——
Ответ: -------2------2—.
я-sinasinp
12.025. В прямоугольном треугольнике АВС острый угол А равен а радианам. Дуга окружности с центром в вершине прямого угла С касается гипотенузы в точке D и пересекает катеты АС и ВС соответственно в точках Е и F. Найти отношение площадей криволинейных треугольников ADE и BDF.
Решение.
По условию в ЬАСВ ZACB = 90°, ZCAB = a (рис. 12.28). Обозначим АС = х Из &ADC, ZADC = 90°, CD = xsina, тогда SCed =-x2sin2a-f^-al (т.е. Z.ACD = —-а);	=	5	=
2	12 J	2	2
2 • 2 1 тс 1
„	э	x sin a--a
x2cosasina- c _c c -x cosasina	\2 J
=----------> °4Z>£ “	“ °C£D-------Z	Z	•
2	2	2
x2
Из ACDB, ZCDB = 9Q°, DB = xsinatga, S&CDB = — sin2atga,
о 1 2 • 2	„	„	„ x2sin2atga x2sin2aa
$CDF ~ 2 x Sln a ’a ’ $DFB ~ S&CDB ~ $CDF ~	»
sdfb _ sin2a(tga-a) tga-a ^AED sin2a| ctga-^+a | ctga-^+a • V 2	)	2
tga-a
Ответ: -----------•
ctga- —+a
Рис. 12.29
12.026. В параллелограмм со сторонами а и Ь (а<Ь) и острым углом а вписан ромб; две его вершины совпадают с серединами больших сторон параллелограмма, две другие лежат на меньших сторонах (или на их продолжениях). Найти углы ромба.
Решение,
Пусть DC = b, ВС = а, ZADC = a = ZAKO; NEFM — ромб,
КО = — = - (рис. 12.29), OF = — = —. Из ДЕОГ Z£O£ = 90°> 2	2	2	2
OF
tgZOEF = — .Uj \КЕО ХКЕО = 90° (Л/)||#Г, ЕО — секущая
ZFOE = ZKEO = 90'), EO = ^sina, значит, tgZOEF = ? 2 ;
2	2b sm a
FNEF = 2ZOEF = 2 arctg , a , Z.EFM = n - 2 arctg —~. bsina	bsina
a	a
Ответ: 2arctg——; л-2arctg——. bsina	bsina
12.027. Около круга радиуса R описана трапеция с углами а и р при большем основании. Найти площадь этой трапеции.
Решение.
Пусть BAD-a. ACDA = $, ОЕ-R (рис. 12.30). Тогда
$abcd =---2---* $abcd ~ (&С+AD)-R. Так как ВС+AD = AB+CD»
то BC + AD=2R —+-У (АВ = ^_, CD = — ). Тогда ^sina sinp)	sina sinp
Рис. 12.30
Рис. 12.31
1
4sina sinp
1
$ABCD - 2Л2
.d2 • a+B	a-B
2/?2(sina+sinp) 4R sin 2	2
sin a sin p	sin a sin p
ad2 . a+P a-p
4R  sm —_ - cos ——-
Ответ: ---------2------2—.
sin asinP
12.028. В равнобедренный треугольник с углом а при основании вписана окружность радиуса г • Найти радиус окружности, описанной около треугольника.
Решение.
По условию АВ = ВС, ЛВАС = ЛВС А = а, г — радиус вписанной окружности (рис. 12.31). Пусть АВ = АС = х, тогда АС = 7*2 • 2(1+cos 2a) = 2х • cos a; 5 = рг,где р —полупериметр
_	_	_ x _	x2sin2a
&ABC • Таким образом, о =—2xcosa sina =------------, значит,
x2sin2a (2x+2xcosa)r	2(l+cosa)r	BC	_
--------= ----------— и x= . ---------. Имеем -— = 2R (no
2	2	sin2a	sina
ч 2(l+cosa) r OD D_ (l+cosa)-r теореме синусов), тогда —------——=21с ;	; так как
sinasin2(x	sin asm a
a
a 1+cosa	Tctg—
ctg- = —------,то я =---2_
2	sina	sin 2a
x ос r ctg— Ответ: 2. sin2a
Рис. 12.32
Рис. 12.33
12.029. Площадь равнобедренного треугольника равна S, угол между высотой, проведенной к боковой стороне, и основанием равен а. Найти радиус круга, вписанного в треугольник.
Решение.
По условию SABC = S, АВ-ВС, ZEAC = а, ЛЕСА = 90° - а (рис. 12.32). Z/1BC = 180°-2(90°-а)=2а, так как АВ = ВС Имеем, что _2S
S = рг ,г~~,гре р —полупериметр SABC.Обозначим АС = х-Из
AABD ZBDA = 90°, BD = у ctga, тогда S = y*yCtga = -^-ctga, отсюда х = 2,/Stga , ВС = АВ =	~^а., р = i/Stgo +^5 tga;
S' sina -JStga cosa tga (sin a +1) (sina + 1)
= 4s^. sM"/2_z.y) 1	I
1+cos —a
I 2

Ответ: V^tga • tg^— - у J.
12.030. Равносторонний треугольник пересечен прямой, проходящей через середину одной из его сторон и составляющей с этой
стороной острый угол а. В каком отношении эта прямая делит площадь треугольника?
Решение.
Пусть АВ=ВС=АС=а, АМЕС = а, АЕ = ЕС(р»с. 12.33). Из ДЛ/АГЕ,
АМКЕ = 90°, ЕК = МК ctga. В \МКС, АМКС = 90’, КС =
1/ Г/’	(	1
= Aftfctg60° =-=- ЕС=ЕК+КС=МК ctga+4=
J3 ’	{	-J3
Л/jdctga+i =£; MK = -7----—S^CU=\-MK ЕС =
k	(	1	2
21 ctga+-^1
= “7	Г~\ • $АВМЕ - $ЬАВС “ S&ECM > $ЬАВС = ~7~ > ТОГДЯ ^ВМЕ.
8ctg(X+ *	4	s*cm
I V3j
1 ctga+-^=r
ctga + -J=
V3
= 2>/3ctga+l =
2д/з cosa+sina sina
Л 2V3cosa+sina
Ответ: ------:-------.
sina
12.031. В квадрат ABCD вписан равнобедренный треугольник AEF; точка Е лежит на стороне ВС, точка F — на стороне CD и АЕ = AF. Тангенс угла AEF равен 3. Найти косинус угла FAD .
Решение.
Имеем: ABCD — квадрат, AEF — равнобедренный треугольник, АЕ = AF. Ее ВС, F eCD, tgZAEF = 3 (рис. 12.34); требуется найти cosZ.FAD. Положим ZAEF = a, ^FAD = р;тогда z_EAF = 180° -2a• Так
как \АВЕ = &ADF (по катету и гипотенузе), то Р = ~(90° -180° +2а)= = а-45°. Отсюда cosP = cos(a-45e)=^(cosa + sina). Учитывая,
Рис. 12.34
Рис. 12.35
что tg а = 3, находим 1+9 = —5—, откуда cos а = -7=, sina = cos а	VIО
3	л/2	4	2л/5
= tgacosa = -j= cosB = —=-----------
716’	2 710 5 *
Ответ: ——.
12.032. В равнобедренном треугольнике угол между боковыми сторонами равен a, радиус вписанной окружности равен г • Найти площадь треугольника.
Решение.
По условию в Д4ВС АВ = ВС, ЛАВС = a, г — радиус вписанной окружности. Из ДО£С АОЕС = 90° (рис. 12.35), ЕС = г ctg Z.ECO-
= r-ctgl я/4-—I. Из &ВЕС, ZBEC = 90°, имеем
B£ = £Cctg| =
а	г, 2 2	21 л a] a
•ctg—.Тогда S = ctg 7-- <ctg“ =
2	2 I4 4 J 2
2 + 2f л-a) „ a = r ’ctg l"Y”J’ctg? ’
2 л-a^ a
Ответ: r ct8 I “I ctgy*
12.033. Около круга описана прямоугольная трапеция с острым углом а. Найти высоту трапеции, если периметр ее равен р.
Решение.
Пусть Z.CDA = a, ZABC = 90° > Р —периметр трапеции (рис. 12.36) (ВС||ЛЛ). Так как BC + AD = AB+CD, a P = BC + AD+AB + CD, р
то BC + AD = — = DC + AB. Обозначим АВ = СЕ = х-Из ACED,
X	Р X
Z.CED = 90°, CD = —— тогда — = х+—— и отсюда sina	2	sina
Psina _Р sina _ Psina
2(l + sina) 2 Г a	.	2(n
I siny+cos— I 4COS “ 2 J
Psina
Ответ: 4cos2|---|
И 2 J
12.034. В равнобедренном треугольнике угол при основании равен а. Найти отношение площади треугольника к площади описанного около него круга.
Решение.
По условию АВ = ВС, /.ВАС = a. Пусть R — радиус описанного круга, тогда 5кр = nR2 = пВО2 (рис. 12.37). Пусть АВ = ВС = х, /АВС = 180° - 2a, тогда ZOBC = 90е - a • Из ЬВЕО /ВЕО = 90°,
_л BE X	„ Itx2	1	2
в О = ----= —-----, получим, ЧТО	. 1— • ^ЛАВС =тАВ х
sina 2sina	р 4sm a	2
2	2	2
. /*пг х —>~ -т- $ьлвс 4 х sin2asin a х sin ZABC = — sin 2a. Тогда	=------------------
2	SKp	2лх2
_ 2sin2asin2a
Я
2sin2asin2a Ответ: --------------.
n
12.035. В треугольнике даны длины двух сторон а и Ь и угол а между ними. Найти длину высоты, проведенной к третьей стороне.
Решение.
По условию АВ = а, ВС = Ь, ХАВС = а (рис. 12.38), тогда
А С = у/a2 +b2 -2abcosa (по теореме косинусов), S^BC = а • b • sin а и
1	1	;-------- 2S
SMBC = -ACBE = -yla2+b2-2abcosaBE; BE = -—	-----
2	2	Vfl2+Z>2-2tf£>cosa
V02 +b2 -2aA cosa
, afesina
Ответ: Г2 ,2 _ ,	‘
у/a +o -2a6 cosa
12.036. Показать, что если в треугольнике отношение тангенсов двух углов равно отношению квадратов синусов этих же углов, то треугольник равнобедренный или прямоугольный.
Решение.
tg Л sin2 А
ЛАВС имеем —г = / 2 D tgB sin В
В
; требуется доказать, что треуголь
ник либо равнобедренный, либо прямоугольный. Из данного
равенства получим	sin A sin2 В cos В - cos Л sin В sin2 А = 0	или
sin Л sin ^(sin В cos В-cos ^4 sin Я) = 0. Ho зшЛ^О, sinB^O, так как
Лив —углы треугольника; следовательно, зт2В-8ш2Л = 0 или
2 соз(Л+B)sin(B - Л) = 0 , откуда
соб(Л+В)=0, sin(B- Л) = 0
Л+В = л/2, В-Л = 0.
Итак, либо С = п/2 , т.е. треугольник прямоугольный, либо Л = В > т.е. треугольник равнобедренный. Что и требовалось доказать.
12.037. В ромб ABCD и в треугольник ЛВС, содержащий его большую диагональ, вписаны окружности. Найти отношение радиусов этих окружностей, если острый угол ромба равен а.
Решение.
ABCD — ромб (рис. 12.39), ZBЛC = а (а<90°)> П — радиус
окружности, вписанной в ромб, г2 — радиус окружности, впи-
санной в ДЛВС . Пусть АВ = а • Проведем BE1AD . В &ВЕА
BE - 2rt = asin a, откуда q =
asina „ -----. Из ДЛВС по теореме косину-
сов имеем
Л С = ^2а2-2 а1 cos(l 80° - a) = 2а cos у
. Отсюда
a л 2 ос Р^авс =2a+2acosy = 4acos -j,
л 2 ОС
2 •	„ asina-4cos —
= 2^длвс = а sina = Д sin а и =______________4 =2cos2 —
' Р^вс 4acOs2“ 4cos2— r2 2asina	4
4	4
2 Ot Ответ: 2 cos —.
12.038. На меньшем основании равнобедренной трапеции построен правильный треугольник. Его высота равна высоте трапеции, а площадь в 5 раз меньше площади трапеции. Найти угол при большем основании трапеции.
Решение.
По условию AB=CD, ВЕ = ЕС = ВС, ЕМ=СО, Еевес=^^', тогда AD = ВС+2 • OD = ВС+2 • СО • ctgZCDO (рис. 12.40)- Из ДЕЛ/С
Уз
АЕМС = 90°. АМСЕ = 60°, ЕМ = СО = ВС—, тогда
•J3
AD = ВС+2 • ВС~ • clgACDO
Sabcd =	l+y-CtgZCj?Q ГС2
Уз
2 ’
2
S&BEC
а
sabcd=5Sebec (по условию), поэтому
V3 l+-y-ctgZCZ>0
5	г-
= -, ctgZCDO = УЗ , ACDO = 30° •
Ответ: зо°.
12.039. Высота BD правильного треугольника АВС продолжена за вершину в и на продолжении взят отрезок BF > равный стороне треугольника. Точка F соединена отрезком прямой с вер
шиной С. С помощью этого построения показать, что tgl 5° = 2 - Уз •
Решение.
По условию BF = АВ = ВС = А С • В \FDC AFDC = 90°,
ADFC + AFCD = 90° > ABFC + ADCB + ABCF = 90° > ABCF = ABFC так как BF = BC (по условию), тогда 2 • ABFC+60° = 90°> AB FC = 15°
(рис. 12.41). BE1FC, тогда BE = FE-tgl5° => tg 15° = —. Обозна
чим BF - AB = ВС = AC = x, тогда FC = ^2x2(1 -cosfl80’ -30°)) =
F
Рис. 12.41
Рис. 12.42
= xyj2 +у/З (по теореме косинусов). Из ЬВЕС /ПЕС = 90°,
BE = х2 -	= ^^2-у/з . Следовательно,
2X-J2-V3 „ гт
tgl5’=— ^=— = 2-v3
2х72+7з
Ответ: 2 - 4з.
12.040. Высота равнобедренной трапеции равна h • Верхнее основание трапеции из середины нижнего основания видно под углом 2а, а нижнее основание из середины верхнего — под углом 2р. Найти площадь трапеции в этом общем случае и вычислить ее без таблиц, если h = 2» а = 15°, Р = 75°.
Решение.
В трапеции ABCD имеем: АВ = CD, BC\\AD, Mg AD, AM = MD, NgBC, BN = NC, BE1AD, BE=h, ZBMC=2a, ZAND = 2$ (рис. 12.42). Так как ДАВМ = NCMD и NABN = NNCD (по двум сторонам и углу между ними), то ВМ = МС и AN = ND • Из &AMN и &BMN находим А М = h tgp. BN = Л tg а, отсюда SABCD = (АМ +BN)h = ,п п\ h2 sin(a + б)
= Л (tga+tgp)= CQsacosp • При Л=2, а = 15° и 0 = 75° имеем
Рис. 12.44
4sin90°	_	4	8 =1б
ABCD cos 15’cos 75° cos 15° sin 15’ sin 30°
A2sin(a+p)
Ответ: ---------z~; 16-
cosacosp
12.041. Даны две стороны b и с треугольника и его площадь, равная 0,46с. Найти третью сторону.
Решение.
По условию SMBC =0,4-6-с, где Ь = АС, с = АВ (рис. 12.43). Обозначим СВ = х, тогда SMBC = -Jp{p-c\p-b\p-x), где р = С+^+Х ,	,	„	.	„ Ic+b+x b+x-c Ь+с-х х+с-Ь
(по формуле Герона) и SMBC = J—-------------------------— =
= 1^?-(б2 ♦с2-*2)2 046с = ^Н^±И^1;
4	’	4
2,5662? = 462с2 -(б4 +2<?62 -2х2Ь2 +с4 -2с2х2 +х4), отсюда х4 -2х2({>2 + с2)+ b4 +с4 +0.5662? =0, D = 4b4 +862с2 + 4с4 -4Ь4 -4с4 -
, ,	, ,	2 2Ь2+2с2±2,4Ь с	г-.—------
-2^4Ь2с2 = 5,7662? > х =-----j------- Х = ^Ь +с ±1>26с'
Ответ: Jb2 +с2 ±l£bc.
12.042. Из точки, взятой на окружности радиуса R, проведены две равные хорды, составляющие вписанный угол, равный а ра-
Рис. 12.45
Рис. 12.46
дианам. Найти часть площади круга, заключенную внутри этого вписанного угла.
Решение,
По условию АС= АВ, АСАВ=а, R —радиус окружности (рис. 12.44). $слв = 2$ьсоа + $сов > $сов = 2 СО2 ’ ^сов, АСОВ = 2АСАВ — 2а > тогда $сов = 2	’2а = ^2 а, АСОА=^ ^а=180°-а . Имеем, что
•$дссм
= -Я2 2
•sin(180° -а)=
Л2
—sina; SCAB
= A2sina + 7?2a = /?2(a+sin а).
Ответ: R1 (а+sin а}
12.043. Через вершину А равнобедренного остроугольного треугольника АВС и. центр описанной около этого треугольника окружности проведена прямая, пересекающая сторону ВС в точке D . Найти длину AD, если АВ = ВС = b и ZABC = а 
Решение.
По условию АВ = ВС = b, ZABC = a, О — центр описанной
окружности. Рассмотрим \ВЕО, АВЕО = 90°, ВО = —-— = АО, 2 cos 5 a b a	2
ОЕ = BE • tgy = — tg— (рис. 12.45). А О = BO, значит, ABAO --ZABO = -, a+-+ZBDA = lW° и ZBDA = 180°~— . Из 2	2	2
„ OE
\OED, Z.OED = 90’, OD = . sm ABDA
. a
b bt^2
AD = AO+OD = —-—+------2_
_ a . . 3a
2 cos— 2sm—-
2	2
a b ^2 .
2  3a ’ sm— •
2
.3a . a A sm—+sm— __2____2 a . 3a cos—sm—
2	2 )
b
2
a sma-cos —
= b---------
___±!__ dsina
a . 3a ”. 3a ‘ cos—sin— sm— 2	2	2
b sin a
Ответ:
2
12.044. В прямоугольном параллелепипеде диагональ основания равна d и составляет со стороной основания угол a. Через эту сторону и противоположную ей сторону верхнего основания проведена плоскость, образующая с плоскостью основания угол ₽. Найти боковую поверхность параллелепипеда.
Решение.
По условию AC = d,AACD = a. , AA^DA-^ (рис. 12.46).
= 2SAiDyDA + 2SDlCiCD .Из AADC AADC = 90’ • AD = d sin a,
DC = dcosa- Из ДАА^), AAAfD = 90°, AAf =</sina tg₽ , тогда SAAtDtD =^D-4^ = </2sin2a tgP; S’ofi1c1c = rf2cosa sina tgp. Имеем S6 = 2d2 • tg P • sin a(sin a+cos a)=2-j2d2 • tg P • sin a^sin a •	+cosa •	j=
=2-j2d2 tgPsinal sina-cos—+cosa-sin— ]= \	4	4 J
= 2-j2d2 sina tgP sinl a+y I
$6 -
Ответ: 2-Jld2 sina-tgp-sin
Рис. 12.47
12.045. Разность между образующей и высотой конуса равна d, а угол между ними равен а. Найти объем конуса.
Решение.
Пусть SO — высота конуса, SA и SB — его образующие (рис. 12.47). По условию SA-SO = d, ZASO = а. Пусть ОА = R - Из
Л
AS О А находим SO = Rctga, SA = •	. Используя условие, имеем
R п /?(l-cosa) „ а .	D , ос
	Rctgа = — 	- = Rtg— = d, откуда R = dctg—. Получи-sm а--------------------sina-2	2
ЛИ икон = |nR2 • SO = | nR3 ctga = | nd3 ctg3 у ctga.
1	>3 з a
Ответ: -nd" ctg" у ctg a.
12.046. Основанием пирамиды служит правильный треугольник. Одно боковое ребро перпендикулярно плоскости основания и равно /, два других образуют с плоскостью основания угол a. В пирамиду вписана прямая призма; три ее вершины лежат на боковых ребрах пирамиды, три другие — на основании пирамиды. Диагональ боковой грани призмы составляет с плоскостью основания угол р . Найти высоту призмы.
Решение,
По условию АВ = ВС = AC. SA1AB, SA1AC, ZSBA^a = ZSCA, ZOAE = $.SA = l (рис. 12.48). Из bSAB (ZSAB = 90°): АВ = ВС = АС =
= I - ctga, SB = ——. Обозначим АЕ = FE = AF = х. тогда из &АЕО име-sina
ем OE = x tgP = A/H. Из Д5Л/0(23Л/0 = 90°): SM = xtga, SA = x-tga+
+x  tgP,x(tga+tgp)=I,x=----—-, OE = /tgP =-------z /sin^ —
tga+tgp tga+tgp / sina , smp \cosa cosP
/cosasinp sin(a + P)
Ответ:
/cosasinp sin(a+P)
12.047. Диагонали осевого сечения усеченного конуса точкой пересечения делятся в отношении 2:1. Угол между диагоналями, обращенный к основаниям конуса, равен а. Длина диагонали равна /. Найти объем усеченного конуса.
Решение.
Пусть ABCD — диагональное сечение
Рис. 12.49
(рис. 12.49). По условию, АК: КС = 2:1. Это значит, что
АК=—1, КС = -1. Из ЛАОК найдем АО. Так как ХАКО = — ,то 3	3	2
HO = HX-sin- = -/sin-. Из ЬСО'К: O,C = KCsm- = |/sin-. Вы-2 3	2	2	3	2
соту ОО{ найдем как сумму ОХК + КО. где ОХК = КС cos— =
1 , а л a 2, a _
= — Zcos—, КО = ЛК cos— = — /cos—. Тогда
3	2	2 3	2
00t = /cosy. Объем V = -nh{jtf +RlR2 +R%), где h = OO} = /cos—, 2	3	2
R, = A О = ^/sin^ , R2= O,C = -I sin— . Тогда 3	2	3	2
1 ,	a (4,2 . 2 <* 1 ,2 • 2 a 2 ,2 . 2
V = -n/cos— — I sin —+-/ sin —+-/ sin — =
3	2<9	23	23	2)
7 ,3 . 2 a	a	7 ,3 . .a
=—id sin —cos— =—id sin asm—.
27	2	2 54	2
л 7 >з •	«
Ответ: — я/ sin a sin у.
12.048. Найти угол при вершине осевого сечения конуса, если центральный угол в развертке его боковой поверхности равен a радианам.
Решение.
Обозначим образующую конуса через R, а радиус окружности, лежащей в основании конуса, через г (рис. 12.50). Длина сектора, полученного в развертке, равна / = Ra. С другой стороны 2лг = / • Ra
Это значит, что 2лг = Ra, откуда г = ——. Угол при вершине осевого 2л
. В г	a	о _ .а
сечения конуса обозначим 0. Тогда sin — = — = — и р = 2 arcsin —.
2 R 2л	2л
Л	А	ОС
Ответ: 2 arcsin —. 2л
о
12.049. Плоский угол при вершине правильной шестиугольной пирамиды равен углу между боковым ребром и плоскостью основания. Найти этот угол.
Решение.
Пусть OABCDEF — правильная шестиугольная пирамида, ОО}1(аВС), ZFOE = ZOFOl (рис. 12.51).Положим OF = l и ZFOE = a; тогда FE = -j2l2 -2/2cosa = 2/sin у. Учитывая, что OXF = FE, в
AOQF имеем cosa = —-2sin2^+l=2snw; 2sin2 ^+2sin^-l=0; 12	2’22
. а -1+7з a . 73-1	_	. л/З-1
sm — =-----; — = arcsin-; a = 2 arcsin-.
2	2	2	2 ’	2
Л о • V3-1
Ответ: 2 arcsin--.
2
12.050. Через вершину с основания правильной треугольной пирамиды SABC проведена плоскость перпендикулярно боковому ребру SA • Эта плоскость составляет с плоскостью основания угол, косинус которого равен 2/3. Найти косинус угла между двумя боковыми гранями.
Решение.
Пусть СКВ —данное сечение (рис. 12.52). Это значит, что KCLAS, KB1AS, L — середина ВС, Z.ALK = a- Необходимо найти Z.CKB = р. Обозначим АВ-ВС=АС=а кВ КС —равнобедренный, у него КВ = КС (т.к. CK1AS, KBLAS, АВ = АС, АК —
В LC
общая). Тогда tg— = ——. Из прямоугольного треугольника AKL 2, KL
(ведь KL1AS, т.к. KL лежит в плоскости КВС) найдем KL •
KL = /ILcosa, где AL — высота правильного kABC, AL = —— 
„ ajl aJ3 2 а4?>	В a-3 V3
Тогда KL, — cosa»^ з = — Тогда
‘-I 
Значение cos В =------.
i+2 ’
Ответ: у.
12.051. В основании прямой треугольной призмы лежит равнобедренный треугольник АВС , у которого АВ = ВС = а и ZBAC = a. Через сторону АС проведена плоскость под углом <р(ср < я/2) к основанию. Найти площадь сечения, если известно, что в сечении получился треугольник.
Решение.
Пусть ALC —данное сечение (рис. 12.53), LK — перпендикуляр к АС, значит, КВ1АС (по теореме о 3-х перпендикулярах), К — середина АС. Из ДАВК АК = ABcosa = acosa. AC = 2АК = 2acosa. „	„	1	~	?	a2sin2a
Площадь ДА ВС SABC= — ACAB = a cosasina =------------. Так как
Sa nr a2 sin 2a ДАВС является проекцией ДАЬС, то SALC =	-• = —-----.
costp 2coscp
a2 sin 2a
Ответ: ----------
2cos<p
Рис. 12.53
12.052. Треугольник АВС вращается вокруг прямой, лежащей в плоскости этого треугольника, проходящей вне его через вершину А и одинаково наклоненной к сторонам АВ и АС  Найти объем тела вращения, если АВ = а, АС = Ь и ZBAC = a.-
Решение.
Объем данного тела можем получить, если из объема усеченного конуса с диаметрами ВВХ и СС( в основаниях отнимем объемы конусов с вершиной в Л и диаметром в основании BBt и с вершиной в Л и диаметром в основании СС{ (рис. 12.54). Опустим перпендикуляры ВК
и CL на прямую /. Тогда
Z.KAB = Z.CAL = 18°. “ = 90’ - v • Тогда 2	2
КВ = ЛБвш) 90°	| = acos— а CL = ЛСвт) 90’	| = Z>cos— •
I 2 J 2’	I 2)	2 ’
АК - ЛВсо8^90’ —у) - a sin —, AL = bsin у. Высота усеченного ко
нуса KL = АК + AL = sin у (а+b). Объем усеченного конуса
V = | п  KL • (кВ2 + КВ • LC+LC2 )= | л sin у (а+ft)cos2 у (а2 + ab+Ь2).
Объем К,	=-ne3cos2—sin—. Объем V2=-n-ALLC2 =
3	3	2	2	3
1,3	2 ot . a
= —iu> cos у sin у. Тогда объем полученного тела вращения
У = У'-У -y	cos2 - sin - (a3 + 2a2 b+2ab2 +b3-a3-b
3	2 2V
2 d 2« • a л , /	, \ . a
=—пата+b Icos — sin— =—ama+b Ism acos—.
3	'	2	2 3	'	2
Ответ: —	) sin acos—.
3	2
12.053. Боковая поверхность правильной треугольной пирамиды в 5 раз больше площади ее основания. Найти плоский угол при вершине пирамиды.
Решение.
Пусть SABC — правильная треугольная пирамида, 5бок = 55^^ (рис. 12.55); требуется найти AASB♦ Пусть SA = I и Z.ASB = а; тог-
2
да ^бок=2^ s*na- Из AASB по теореме косинусов находим
АВ2 = 212 -212 cosa = 4Z2 sin2 у; тогда $мВС =---
9	01	3 9	9 Г~ f ос
= / V3sin у. Используя условие, имеем: у/ sin а = 5/ V3sin у;
, . a а с /г . 2 a V3 a V3 „ J3 3sin—cos—= 5V3 sin —; tg—= —; — = arctg—,т.е. a = 2arctg—.
2	2	2	25 2	5	5
V3
Ответ: 2 arctg—.
12.054. Высота конуса равна Н, угол между образующей и высотой равен а. В этот конус вписан другой конус так, что вершина второго конуса совпадает с центром основания первогд конуса, а соответствующие образующие обоих конусов взаимно перпендикулярны. Найти объем вписанного конуса.
Решение,
Пусть SO = H, ZLSO = a (рис. 12.56), SL1K0; &SOK — прямоугольный. Значит, КО = SOsina = Язта. Из &SOL AOLS = 90° -а • Тогда Z.LOK = а • Отсюда Х.ОхКО = ALOK = а (как внутренние на-
крест лежащие). Тогда ОХК = OK cos АОХКО = Н sin acosa = — Я sin 2a.
Из &ОХКО ООХ = OK sina = Нsin2 a. Объем
V = -пОхК2ООх = -лЯsin2a-#2 sin22a = —лЯ3 sin2 asin22a .
3	3	4	12
Ответ: — лЯ3 sin2 a sin2 2a.
12
12.055. Сторона большего основания правильной четырехугольной усеченной пирамиды равна а. Боковое ребро и диагональ пирамиды составляют с плоскостью основания углы, равные соответственно аир. Найти площадь меньшего основания пирамиды.
Решение.
Имеем, ABCDAiBxCxDx — правильная четырехугольная усеченная пирамида, АВ = а , ООХ1\АВС), ДЕЦДГЦОф , Z.DXDE = a,
AB{DE = p (рис. 12.57). Пусть ДВ, = х; тогда B,D, = х^2 , BD = aVI >
FD = OD-OF =	x^
2	2	2
ED = OD+OE =	+ Из дл p£) находим
2	2	2
D,F = FD tga = ——tga, а из AB,ED получим
B,E = EPtgP =	tgP. Так как D,F = B,E = ОО,, to
(a-x)tga = (a+x)tgP, x(tgP + tga)=a(tga-tgP), т.е.
asin(a-p) sin(a+p)
Получили SA)BiCiDi
a2 sin2(a-p) sin2 (a + p)
Ответ:
a2 sin2(a-p) sin2 (a+p)
12.056. Радиус круга, вписанного в прямоугольную трапецию, равен г, острый угол трапеции равен a. Эта трапеция вращается вокруг меньшей боковой стороны. Найти боковую поверхность тела вращения.
Решение.
Пусть KLMN — точки касания круга с трапецией, причем КО = ОМ = OL = ON = r, ZMDC = а (рис. 12.58). Пусть трапеция
вращается вокруг стороны В А — получим усеченный конус. Боковая поверхность его 5бок = л(Л,+Л2У , где — ВС,	— AD ь I — CD • Так
как OD — биссектриса Z.MDC и &OMD — прямоугольный, то г	(	а^
DM =-------- = rctga/2; AM = г> тогда AD = AM+MD = г 1+ctg— ;
tga/2	I	2)
/.BCD = 180°- ZADC = 180° - a • Тогда из ЬКСО,
KC = — = r tg* CB, BK+CK = r+rtg^. CD = l = ^~.
180°-a 2	2	sina
Тогда
n . a a . 2 a 2 a
_	\	2 2sin—cos—+ sin —+cos —
a a} 2r 2кг 2	2	2	2
r+rctg—+ r+ rtg—----------------~----------------
2	2 J sina sina	• a a
7	sin—cos—
2	2
4кг2 z. .	\
—7— (l+sina)= sin a
4rcr2 ( . к	А 8кг2 . я/2+a к/2-а
—=— sin— + sina 1 = —=—sin—-----cos—------
sin2 a V 2	J sin2 a 2	2
8кг2 sin2 a
8кг2 (к —<^7
sin a
. (к a А (к a^ sin —+— cos-------------=
1,4 2) И 2 J
к
4
a
2
8кг2
. 2 sin a
a
2 л cos —
14
8nr2 2(
Ответ: ~2 cos • sin2 a <4 2)
12.057. В основании прямой призмы лежит прямоугольный треугольник с острым углом а. Диагональ большей боковой грани равна d и образует с боковым ребром угол р. Найти объем призмы.
Решение.
Пусть ЬАВС — прямоугольный, ZC = 90е, ZBAC = a (рис. 12.59). По условию ВА{ =d , ZBAiA = ^. Тогда из ^BAiA высота призмы AAi = Jcosp, а АВ = t/sinP, так как дв — гипотенуза
ДАВС, то АС = i4Bcosa = t/sinpcosa. Площадь основания
Объем V = 5^ -/Ц =-rf3sin2pcosPsin2a = —rf3sinPsin20sin2a.
8	8
~	d 3 sin Р sin 2Р sin 2 a
Ответ'. -----------------.
8
12.058. Диагонали осевого сечения цилиндра пересекаются под углом, равным а, обращенным к основанию. Объем цилиндра равен V. Найти высоту цилиндра.
Решение.
Пусть АА\В\В — осевое сечение цилиндра, ZAOB-a (рис 12. 60).
Положим АА\ = Я; тогда,учитывая,что ZOAB = ZOBA = у-у, из &А\АВ
находим АВ = Н ctgf у - у I = Н tg у. Следовательно, V = л
rrx а Htg2
2
н=
J^ctg2^
------— , откуда Н = V--- I л
4
3 4Kctg2y
Ответ. ]-------—
I я
Рис. 12.61
12.059. Найти острый угол ромба, зная, что объемы тел, полученных от вращения ромба вокруг его большей диагонали и вокруг его стороны, относятся как 1: 2>/5 •
Решение.
Обозначим сторону ромба а, а острый угол а (рис. 12.61, а). Это значит, что Z.DAB = a, АС — большая диагональ. При вращении ромба вокруг большей диагонали получится тело, состоящее из 2-х
равных конусов (рис. 12.61, б). Объем каждого конуса V' = - 5'сн • h',
где Л' —высота конуса, равная АО, я. 50СН = пг2, где г = ВО- Из
кАВО
АО = acos— 2
ВО = asin—. Значит, 2
2я з . 1 a ос = —a sin — cos —
3	2	2
. Объем тела
V2, полученного при вращении
ромба ABCD вокруг стороны ВС, можно найти как объем цилиндра с центрами окружностей в основаниях К и L (ведь конусы с вершинами С и В равны). К2 = S'^.n • h", где h" = KL = CD = a • Пло
щадь основания S0CH = лЛ£2; т.к. AC — диагональ ромба, то
АС = 2acos— , а из \ALC AL = ЛС-sin— = 2asin —cos— . Тогда 2	2	2	2
^осн = я 4а2 sin2 у cos2 у = ла2 sin2 а. Тогда объем V2 = ла3 sin2 а.
По условию К,: К2 = 1: 2^/5 , это значит, что
_ з • 2 а а
2tw sin -cos- j	„ а /г
-----------------— = —=, откуда 3 cos — = V 5 . Значит ~ л з • 2 а 2 а 2V5	1 2
3• 4tuz sin —cos — J
2	2
а cos—=
2
/5 3
-	2 « 1	5 л I	I
cosa = 2cos —1 = 2-----I = -. Значит, a = arccos-
2	9	9	9
Ответ:
I arccos-.
9
12.060. Основанием пирамиды служит равнобедренный треугольник, у которого боковая сторона равна' а, а угол при вершине равен а. Все боковые ребра наклонены к плоскости основания под углом р . Найти объем пирамиды.
Решение.
По условию SABC — треугольная пирамида, АВ-ВС-а, ZABC = a, SO.1_(ABC), ZSAO = ZSBO = ZSCO = 0 (рис. 12.62). Так как &SOA = t^SOB = &SOC (по катету и прилежащему углу), то OA = ОВ = ОС , т.е. О — центр окружности, описанной около АЛВС. Пусть OA = R, тогда AB=2R$siZACB или
_. ( л а ]	а
a = 2/?sin---= 21? cos—
12 2 J	2
, a R = —----Из AS О А находим
2cos— 2
SO = —, откуда
2 cos—
2
Кпир = I$ллвс so = ^a2 sincc-atgft- = | a3 * * sin у tg0.
3	6 2cos— 6	2
2
1 з . а _
Ответ: ~а sin —tgp.
6	2
12.061. Основанием прямой призмы служит равнобедренная тра-
пеция, у которой основания равны а и Ь (а>Ь), а острый угол
равен а. Плоскость, проходящая через большее основание верхней
5
Рис. 12.62
Рис. 12.63
трапеции и меньшее основание нижней трапеции, составляет с плоскостью нижнего основания угол Р. Найти объем призмы.
Решение.
Пусть AD = а, ВС = b, ZADC = а (рис. 12.63). Проведем CKIA^, из точки К опустим перпендикуляр KL на AD, значит, CL1AD (по теореме о 3-х перпендикулярах); ZKCL = Р. В равнобедренной трапеции ABCD LD=-D~BC=^-.M3 &CLD CL = LD tga = tga.
2	2	2
_	„ a+b a+b a-b^
Тогда площадь основания	• CL - —-----— tg a =
= ^~ b tga. Из &CKL (ZCLK = 9Q°) AL = CL tgP = ^-^tga tgp. 4	2
Объем призмы V = tga ^y^tgatgp = ^—b^a ^tg2atgp.
Ответ:	—— tg2 a tg p.
8
12.062. Угол между диагоналями основания прямоугольного параллелепипеда равен а. Диагональ параллелепипеда составляет с плоскостью основания угол р. Найти высоту параллелепипеда, если его объем равен V .
Решение.
Объем параллелепипеда V =	• Н , где Н — высота (рис. 12.64).
, н
Из рисунка видно, что а -	. Так как в основании параллелепипе-
да лежит прямоугольник, то его диагонали равны, а площадь основа-
1	1 Н2
ния ^оси=т^ sina = -—г—sina. Подставляя все в формулу, полу-2	2 tg р
1	2ft	j 2V
чим: V =-----z— sin a. Откуда н3 =------—-, значит, Н = з—z---------.
2	tg2p	sina	Vctg psina
I 2У
Ответ: iL 2n •
V ctg p sin a
12.063. Каждое из боковых ребер четырехугольной пирамиды образует с высотой угол a. Основанием пирамиды служит прямоугольник с углом р между диагоналями. Найти объем пирамиды, если ее высота равна h •
Решение.
Так как каждое из боковых ребер четырехугольной пирамиды образует с высотой угол a, то вершина пирамиды проектируется в точку пересечения диагоналей прямоугольника, лежащего в основании
(рис.12.65). Таким образом, если d — длина диагонали, то у = A tga и
площадь основания
5 = 4-i у ^sin0=^</2sinP=2A2 tg2asm|J.
Объем пирамиды
r = l$./i = 12A3tg2asinp.
Ответ: yA’tg^asinp.
12.064. В основание конуса вписан квадрат, сторона которого равна а. Плоскость, проходящая через одну из сторон этого квадрата и через вершину конуса, при пересечении с поверхностью конуса образует равнобедренный треугольник, у которого угол при вершине равен а. Найти объем конуса.
Решение,
Пусть ABCD — данный квадрат со стороной а (рис. 12.66) и пусть секущая плоскость проходит через сторону AD. Тогда по условию Z>4S’Z) = a. Пусть £ — середина
AD. Это значит, что AL = — . Так как ЛАSD — равнобедренный, то
AS =
AL
. a sin—
2
окружности:
—-----Диагональ АС квадрата является диаметром
2sin—
2
2а2 = d2 • Откуда d = ayfl, АО = г = ^ = ^- . Тогда
высота SO = ^AS2 -АО2 = |-----------
J.. 2»	2
w4sin —
I 2
a2 1-2 sin2 — |	i-----
s 2 ) а V cos a
.. 2 a	• 2^
4sm —	2 sin —
2	2
Площадь основания конуса S0CH = яг2 =п^—. Тогда объем
1	1 па2
y=^sOCHso=~ —
7ta3Vcosa
Ответ: 12sin—
oVcosa _ na3Vcosa
2sin2—	12sin—
2	2
12.065. Боковое ребро правильной треугольной пирамиды равно / и составляет с плоскостью основания угол a. Найти объем пирамиды.
Решение,
Пусть SABC — правильная треугольная пирамида. SA-1 > SO1[ABC), Z.SAO = a (рис. 12.67). Из &SAO находим 50 =/sina, XO = /cosa, откуда АВ = А0^3= 1^3 cosa. Следовательно,
„	_ АВ2у/з _3-j3l2 cos2 а
Ьлмс -	j ;
tz 1 о ™ 1 Зу/з/2 cos2 a . .	/37з sin 2a cos a
^пиР = з Smbc SO = -----------/ sin a =------------.
_	134з sin 2a cos a
Ответ: --------------.
8
12.066. Через диагональ нижнего основания правильной четырехугольной призмы и противоположную вершину ее верхнего основания проведена плоскость. Угол между равными сторонами сечения равен а. Найти отношение высоты призмы к стороне основания.
Решение.
Обозначим сторону основания призмы а (ведь в основании призмы лежит квадрат, т.к. призма правильная). Диагональ квадрата d = ay/l (рис. 12.68). Так как сечение — равнобедренный треуголь-
ник со сторонами / и углом между ними a, то
, d . a
Z = —:sin~-2	2
d
2sin— 2
Тогда высота призмы
а /р	Г~2а*	~2
л = у/ —а = I--а —-------а
. L . 2 а J. . 2 « u4sin— il4sin —
1	2	12
• а 2sin—
2
2 1—sin
flV2cosa
2sin— 2
h >/2 cos a
Тогда отношение — =-------.
a ~ . a 2sin— 2
V2 cosa
Ответ: ------— •
2sin—
2
12.067. Основанием прямой призмы служит равнобедренный треугольник с углом а при вершине. Диагональ грани, противоположной данному углу, равна / и составляет с плоскостью основания угол р. Найти объем призмы.
Решение.
Пусть АВСА^Су — прямая призма, АС = СВ, ZACB = a, AiB = l, ZAiBA = fi (рис. 12.69), нужно найти Кщ, =*^длвс ’4^ • Из ДА1АВ находим ААХ =/sinp, y4B = /cosp, а из AADC имеем
Рис. 12.69
Z>C = i4Z)ctgy = ^/cospctgy.
Отсюда
FL, = /c°sP • -1 cospctg^ • I sinp = - /3 cos2 Pctg—sinP =	sin2Pcospctg^.
22	24	28	2
Ответ: |/3 sin2pcospctg^-. 8	2
12.068. Боковое ребро правильной треугольной пирамиды образует со стороной основания угол а. Найти угол между боковым ребром и высотой пирамиды и допустимые значения а.
Решение.
Обозначим сторону основания через а (рис. 12.70), а боковое ребро — через /. Тогда из равнобедренного треугольника, являю-
щегося боковой гранью пирамиды, найдем < = 2~c~^sa • Так как пи" рамида правильная, то основанием высоты является центр, описанной около треугольника-основания пирамиды окружности. А радиус а>/з	. о R aV3-2cosa 2cosa
этой окружности R = -у— . Тогда sinp = у =----~.
2 cos a
2 cos ос
Так как О<0<л/2,то O<sin0<l, т.е. 0<—^=—<1 или
V3
2cos a .
—j=—>0-
7з
Решая эту систему и учитывая, что 0 < а < тс/2 , получим, что
I я л ае — ; —
1б 2
Л	. 2 cos а п	п
Ответ: arcsm—j=—; — <а< —.
7з	6	2
12.069. Плоскость, проведенная параллельно оси цилиндра, делит окружность основания в отношении т: п . Площадь сечения равна S’. Найти боковую поверхность цилиндра.
Решение,
Пусть ABCD — данное сечение (рис. 12.71). Пусть длины дуг DLC и CKD относятся как т: п. Это значит, что DLC = mx, CKD = nx. Так как
Рис. 12.71
DLC+CKD = 2nR, где R = OD — радиус окружности лежащей в
основании цилиндра, то (т+и)х = 2 nR, откуда х= -	. Значит,
т + п
2nRm	2nRn
DLC =------, CKD =-----. С другой стороны, CKD = Ret, где а —
т + п	т + п
радианная мера центрального угла для дуги CKD* Это значит
2nRn _	2пп _	_
	= Ret, откуда а =	. Так как &DOC — равнобедренный, т+п-------------------т + п
то DC = 2Z)Osin—= 27?sin---.Площадь £ сечения
2	т + п
S = DC AD-2Rsin-----Н, откуда Н =--------. Длина всей
т+п	__ . пп
2/? sin-
т+п
S 2Rsin-т-т+п
окружности L = 2nR- Тогда S6oK=L H =
2nR =
nS
пп
sin----
т+п
Ответ: -------
пп
sin---
т+п
о
Рис. 12.72
Рис. 12.73
12.070. Боковые ребра правильной треугольной пирамиды попарно взаимно перпендикулярны. Найти угол между боковой гранью и плоскостью основания.
Решение.
По условию ZASC = ZCSB = ZASB = 90’ (рис. 12.72). Кроме того, AS = SB = SC, ДАВС — правильный; SK1PC, HKLBC, где Н — основание высоты. Так как ASCB — прямоугольный и равнобедренный, то ZSCB = 45’. Обозначим SC через а, тогда
•J2	г
SK = SC sin ZSCB = a sin 45’ = а—, а ВС = а->12 (как гипотенуза
ASCB); НК является радиусом вписанной в ДАВС окружности, а-Л-Тз -т-	НК ау/2-Л-2 Vi? Q
значит, нк = г = ———-  Тогда cosa =----=------т=— = — • Зна-
6	SK 6а>/2	3
7з чит, a = arccos—.
3 л/З Ответ: arccos—.
3
12.071. В полушар вписан конус; вершина конуса совпадает с центром окружности, являющейся основанием полушара; плоскости оснований конуса и полушара параллельны. Прямая, проходя
щая через центр основания конуса и произвольную точку окружности большого круга полушара, составляет с плоскостью основания конуса угол а. Найти отношение объемов полушара и конуса.
Решение.
Обозначим радиус круга, лежащего в основании полушара, через R, т.е. OK = R, а. в основании конуса — через г, т.е. 0{L = г, 40{К0 = а (рис. 12.73). Тогда высота О{О конуса будет равна h = КО • tga = R tga. С другой стороны, образующая конуса OL является радиусом полушара. Тогда LO2 = 01} - ОО2 или г2 = Я2 - Л2 >
Г2Ч 2 г» cos2 a-sin2 a n 7cos2a _ это значит, что г = JR -R tg a = Rj-----=----= R-------. Tor-
V cos2 a cosa
да объем конуса Кк =^-‘S'OCH h = -nr2h = -nR2 ^^ J?tga. Объем 3	33 cos a
rz 2 -3	Vn	2cos2 a
полушара Ип = — nR . Отношение — =-----------.
J	3	Ик	cos2atga
2 cos2 a
Ответ: ----z~—•
cos 2a tga
12.072. Основанием пирамиды служит прямоугольный треугольник с острым углом a. Высота пирамиды равна Н. Все боковые ребра составляют с плоскостью основания один и тот же угол, равный р. Найти объем пирамиды.
Решение.
Так как все боковые ребра наклонены под одинаковым углом к плоскости основания, то основанием высоты данной пирамиды будет являться центр описанной около основания окружности. Тщс как в основании лежит прямоугольный треугольник, то центром описанной около него окружности будет являться середина гипотенузы (рис. 12.74). Тогда SK = H, 4SCK = $, 4АСВ = Ю> 4САВ = a. Тогда из bSCK
СК = R = Я/tgP, гипотенуза АВ = 2R =	, АС = А В cos a =
tgp	tgp
Объем пирамиды	V = у S0CH Н , где	А В • А С sin a =
1 2Н 2tgP
2Hcosa _	.	.. №sin2a „ /73sin2a
---- —sina. Тогда объем V =----z H = :—
tgP	3tg2p 3tg2p
Ответ:
H3 sin 2a 3tg2p '
12.073. Образующая конуса равна а, расстояние от вершины конуса до центра вписанного шара равно b • Найти угол между образующей и плоскостью основания.
Решение.
По условию SM = а, SOX = b (рис. 12.75). Точка К — точка касания
конуса и шара. &SKO} ~ ASOM (ZS —общий, Z_SKOX -Z.SOM- 90°).
Тогда ZKO{S = a. Отсюда из &SKO{ г = КО{ = 6 cos а. Из ДЛ/SO
9,	2 a
sina =	= -+r. = ^_+cosa) =_2_, Учитывая, что sina=2sin^cos^,
МС а а	а	2	2
a	a 2Z>C°S у	a b	b
получим 2sin—cos— =-----. Откуда tg— = —, a = 2arctg—.
2	2a	2 a	a
Ответ: 2 arctg—.
a
Рис. 12.77
12.074. В конус вписан шар. Отношение радиуса окружности касания шаровой и конической поверхностей к радиусу основания конуса равно к . Найти косинус угла между образующей конуса и плоскостью основания.
Решение,
Из условия задачи радиус окружности касания шаровой и конической поверхностей будет КОХ, радиус основания конуса LO2 (рис. 12.76). ZSLO2 =а. Из рисунка видно, что &SKO ~ &SO2L, а &SKO ~ ЬКОХО, значит, АКООХ =Z.SLO2 - а. То^да из ЬКОХО КО - КО—. Из &LOO2 ОО2 = LO2 • tg^. Так как КО и ОО2 равны, since	2
КО, т „ а КО, а . . 2 а ,	. а /Г
то —L = LO2tg- . —i- = sinatg-=2sin - = к. Тогда sm- = J-.
since	2 LO2	l,	2	2*2
А значит, cosa = l-2sin2 — = 1-2—= l-fc . 2	2
Ответ: 1 - k,
12.075. Площадь основания цилиндра относится к площади его осевого сечения как т:п, Найти острый угол между диагоналями осевого сечения.
Решение,
Пусть радиус окружности, лежащей в основании цилиндра, ра
вен R, а высота Я (рис. 12.77). Тогда 50СН = лЛ2, Sce4 = 2RH. Так как
SOCH : Sce„ = лЛ2 : 2RH = т: п, то -^- =—. Так как tg— = ^-, то осн сеч	2Н Tin	2 Н
. а	4т	Лт	т	_
to — =--- т-г	„	4/И	,	т	71
ь ?	тги ’	Поскольку а — острый угол, имеем — < 1, т.е. — < — и
пп	п	4
о 4т _ т л 4т ,
а = 2 arctg	. Если же — > —, то-> 1 и искомым острым углом явки--------------------------------и 4 ли
о . пп
ляется a = 2arctg—.
4т
~	х 4т	т	п	пп	т	п
Ответ', а = 2 arctg- при — < —; а = 2 arctg- при — > —.
ли	и	4	4т	и	4
12.076. В основании прямой призмы лежит ромб с острым углом а. Отношение высоты призмы к стороне основания равно к. Через сторону основания и середину противоположного бокового ребра проведена плоскость. Найти угол между этой плоскостью и плоскостью основания.
Решение.
Пусть ABCDAXBXC}D} —прямая призма, A BCD — ромб, Z.BAD = a (а < 90°), ААХ : АВ = к, СХЕ = EC,ADEF— сечение призмы (рис. 12.78); требуется найти Z(ABC);(FAD). Пусть АВ = а; тогда ААХ = ка. Проведем BK1AD', тогда FK1AD (по теореме о трех перпендикулярах) и Z.FKB — линейный угол между сечением и основанием ABCD. Из ЕАКВ найдем
ВК = a sin а; так как E'F|| AD, то FB -^ВВХ -~^ка. Наконец, из &FBK
к
,	ка к	. к
получим tg Z.FKB =----=---------=-----, откуда Z.FKB = arctg —;-.
ВК 2а sin а 2 sin а	2 sin а
к
Ответ', arctg-----.
2sina
12.077. Стороны основания прямого параллелепипеда относятся как 1:2, острый угол в основании равен а. Найти угол между меньшей диагональю параллелепипеда и плоскостью основания, если высота параллелепипеда равна большей диагонали основания.
Решение.
Обозначим стороны основания параллелепипеда через а и Ь. Тогда а: b = 1:2. Большая диагональ основания
d2 = ^а2 + Z?2 -2aZ>cos(180°-a) = yja2 +Z?2+ 2aZ?cosa. Учитывая, что
Рис. 12.78
b = 2а, d2 = 75a2+4a2cosa • Меньшая диагональ основания rfj = Ja2 +b2 -labcvsa. = 75a2-4a2cosa * Так как высота
ft = = ^5а2 +4a2 cosa , to tgP (рис. 12.79) можно найти как
п h |5+4cosa
d{ V5-4cosa’
l5+4cosa
Ответ: arctg J -—-----.
V 5-4cosa
12.078. Отношение одной из сторон основания треугольной пирамиды к каждому из остальных пяти ее ребер равно ft . Найти двугранный угол между двумя равными боковыми гранями пирамиды и допустимые значения ft .
Решение.
АС АС АС АС
Пусть SABC — треугольная пирамида, — = — = — = — АВ ВС SA SB
=	= к <РИС- 12-80)- Так как AB = BC = SA = SB = SC = ——, ТО
SC	к
&ASB = ABSC (по трем сторонам). Проведем Л ЛIЛ7? и соединим
точки D и С . Тогда AASD = ASDC (SA = SC, сторона SD —
Рис. 12.81
общая и ZASD = ZDSC), откуда следует, что ZSDC = ZSDA = 90’ • Поэтому ZADC — линейный угол двугранного угла ASDC, т.е. искомый угол. Из AADC по теореме косинусов находим
,	,	,	.п SA-J3 АС&
AC2 =2AD2 -2AD2cosZADC , где AD = —^— =	, так как
ЗАС^
&ASB —равносторонний. Значит, АС2 =2——г—(1-cos ZZDC); 4к
1	2к2 т	2к2	. A A DC	[к2 ку/з
l-cosZADC =----; 2sin ----=---; sin----= J—=—.—;
3	2	3	2 V 3	3
У л	1	Г~
Z/WC = 2arcsm—y, где 0<—у<1,т.е. 0<к<у/3-
Ответ: 2 arcsin —у; о < к < 4з •
12.079. Плоскость квадрата составляет угол а с плоскостью, проведенной через одну из его сторон. Какой угол составляет с той же плоскостью диагональ квадрата?
Решение.
Пусть ABCD — квадрат, ABKL — данная плоскость, ВС1АВ, ВК1АВ) ЛСВК-а (рис. 12.81), КС —перпендикуляр к плоскости ABKL* АС — диагональ квадрата. Обозначим сторону квадрата а .
Из прямоугольного АВ КС КС = BCsina; искомый Z.KAC можно
КС
найти из Д/С4С* sinp = ——, где tfC = asina, AC = aJl- Тогда
. п asina sina	. sina
sinp = —. Откуда р = arcsin—7=-aV2 у/2	V2
. sina Ответ: arcsin—yr-. J2
12.080. Боковое ребро правильной треугольной призмы равно стороне основания. Найти угол между стороной основания и непересекающей ее диагональю боковой грани.
Решение.
Обозначим сторону основания призмы через а (рис. 12.82). Необходимо найти угол между АВХ и ВС, но т.к. ВС||ДС| , то этот
угол равен углу между АВХ и	Рис. 12.82
ВХСХ. Диагональ АВХ является
диагональю квадрата, т.е. АВХ = а&, аналогично АС[ = а^2 .
Тогда по теореме косинусов: А С2 = АВ2 +ВХС2 -2АВХ ВХСХ cosa или
1 V2
2а2 =2а2 +а2 -2a2V2cosa, откуда cosa = ^~ = —.
V2
Ответ: arccos—.
4
12.081. Диагонали боковых граней прямоугольного параллелепипеда составляют с плоскостью основания углы а и Р. Найти угол между диагональю параллелепипеда и плоскостью основания.
Решение.
Пусть стороны параллелепипеда будут а и Ь, а высота h (рис. 12.83). b _ tga
Тогда A = atga = 5tgP, откуда "^“"[gp* ’ Диагональ основания
Рис. 12.83	Рис. 12.84
-—- tgy=!h= atga = /g” = Ц” = tg<xtgp
+ Ь	d -Ja2 +b2 L.^_ L tg2 a -J^a + tg2^
i a2 N tg2₽
1 1
ctga ctgP ___________1______
1	!	1 7ctg2a + ctg2p
ctg2 a ctg2 p
или ctgy = 7ctg2a+ctg2 ₽ ♦
Ответ: arcctg 5/ctg2 a+ctg2 p.
12.082. Найти угол между непересекающимися диагоналями двух смежных боковых граней правильной четырехугольной призмы, если плоскость, в которой они лежат, составляет с плоскостью основания угол a.
Решение.
Так как призма правильная, то в ее основании лежит квадрат. Обозначим его сторону а (рис. 12.84). ВО1АС , ВХО1АС , Z.BXOB = a.
ВО
Из &ВХВО найдем В, О =------. Так как ВО — середина диагонали
cosa
BD,то ВО = — .Тогда В,О = -^^, ОС = ВО = ^. Из ЛАОС 2	2cosa	2
р ОС а41 2cosa _ Л _
tg~ =----=------— = cosa. Тогда Р = 2 arctgcos a.
2 BXO 2ay/2
Ответ: 2 arctg cos a.
12.083. Найти угол между апофемами двух смежных боковых граней правильной и-угольной пирамиды, если плоский угол при ее вершине равен а.
Решение.
Пусть SABC к — правильная и-угольная пирамида, A A SB = а, SM и SN — апофемы смежных боковых граней; требуется найти /.MSN (рис. 12.85). Проведем SOL(ABC) и соединим О с точками А, в, М и
Рис. 12.85
N. Имеем АЛОВ = —, Z.ABC =	. Пусть АВ = а. Из AAfSB
п
п
а а
найдем 5Л/ = —ctgy . Далее, из AMNB по теореме косинусов нахо-
1хаг2 л2’ л2	я(и-2) а2(1	(	2л
дим MN =-----cos—---- = — 1 — cosl п-=
22 п	2	v	п ))
= —fl+cos—1 = a2 cos2 -, а из AMSN получим MN2 = 2SM2 -
2 \ п )	п
-2SM2 cos Z.MSN = 2yctg2 у (1 - cos ZAfSAT) = a2 sin2	ctg2 у .
2	2 п 2-2 Z.MSN 2«	. /.MSN n a _
Отсюда a cos — = a sin —--ctg —; sin — --= cos—tg—. По-
n	2	2	2 n 2
лучили
i	It OL
ZMSN = 2 arcsin cos—tg— (	л	2
а
2
Ответ: 2 arcsin
cos—tg n
12.084. Найти косинус угла между апофемой и диагональю основания правильной четырехугольной пирамиды, у которой боковое ребро равно стороне основания.
5
Решение.
Обозначим сторону квадрата, лежащего в основании пирамиды через а; SK — апофема, АС — диагональ (рис. 12.86). Проведем
КМ^АС, КМ —средняя линия ДЛС£>, КМ = ~АС = ASAD
является правильным (у него AD = SA = SD = a)- Тогда SK =
Аналогично SM = —. Из AKSM найдем Z.SKM = а. По теореме
косинусов SM2 -KS2 + КМ2 -IKS КМ cosa или
За2 За2 а2 - а^З а& _	1	>/б
-4- = -^- + —-2-—-----— cosa. Откуда cosa = -^= = —.
Ответ:
Уб 6 
12.085. В конус вписана треугольная пирамида, у которой боковые ребра попарно взаимно перпендикулярны. Найти угол между образующей конуса и его высотой.
Решение.
Пусть SO —высота пирамиды (рис. 12.87). Боковые ребра пирамиды равны, значит, АО = ОВ = ОС = R, значит, пирамида SABC —пра-
п
вильная. Обозначим сторону основания пирамиды а. Тогда R = —
ZASC = 90° • Значит, ZSCA = ZSAC = 45’. Тогда SC из AASC равна
SC= - — - = -^.Из ASOC 2 cos 45° V2
куда
ZSCO = arcsin—
3
Ответ:
. V6 arcsin—-3
12.086. В грани двугранного угла, равного а, проведена прямая, составляющая
угол р с ребром двугранного угла. Найти угол между этой прямой и другой гранью.
Решение.
Рис. 12.88
По условию Yi А у2 ~ I > двугранный угол / равен а, АВ е yj, (/; АВ) = р; требуется найти (у2; АВ) (рис. 12.88). Проведем ЛО±у2 , А СИ 9 тогда ХАСО = а (как линейный угол двугранного угла
АВСО ), ZABC = Р. Так как ОВ — проекция АВ на у2, то ZABO —
искомый угол. Пусть АО = сГ, тогда АС = —— (из ЛАОС), а в sina
АС а
ЛАСВ имеем ЛВ = -—= —----------—. Наконец, из ЛАОВ находим
sinp sinasinP
sinZ/lBO =	= sinasinP. Получили ZABO = arcsin(sinasinp).
AB
Ответ: arcsin(sin a sin p).
12.087. Найти угол между образующей и высотой конуса, у которого боковая поверхность есть среднее пропорциональное между площадью основания и полной поверхностью.
Решение.
По условию задачи 5бок =	= 75осн(5бок +5осн) • Обозна-
чим образующую конуса /, радиус окружности основания R . Тог
да S6oK = nRl, S0CH = nR2, a sina = у, где a — искомый угол, по
этому R = I sin a • Тогда л/2 sin a = ^Ttl2 sina(rc/2lina +л/2 sin2 a), откуда sin2a + sina-l = 0. Решая это квадратное уравнение, полу-
-1±V5	А л	V5-1
чим sina = —-—. Так как 0<а<у,то sina = —-—.Тогда
Ответ: arcsin—-—.
2
12.088. Все боковые ребра треугольной пирамиды составляют с плоскостью основания один и тот же угол, равный одному из острых углов прямоугольного треугольника, лежащего в основании пирамиды. Найти этот угол, если гипотенуза треугольника равна с, а объем пирамиды равен у.
Решение.
Так как все боковые ребра пирамиды составляют с плоскостью основания равные углы, то основанием высоты является центр описанной около основания окружности. Так как ЬАВС — прямоугольный (ZB = 90°), то Центр этой окружности лежит на середине гипотенузы,
с
т.е. R = - (рис. 12.89). Обозначим АА = a. Тогда А В = А Сcosa = ccosa.
_	„	1 .„	.	1 7 .	c2 sin 2a „
Тогда 5^ = -AB ACsina = — c sinacosa = —-— . По условию
AC ctsa
ASAK = ABAC = a. Тогда высота SK = AK  tga = -j- tga =	—
s
Рис. 12.90
,, 1 „	„„ c2sin2a ctga	3.2 n
Объем V = -S0CH • SK  -------—, откуда 12K = c sin a. Зна-
3 0CH	12	2
/12Г ll2Vc JnPc чит, sina = ^-r = J—=—5-.
. V12Fc
Ответ: arcsin—5—. c
12.089. Диагональ прямоугольного параллелепипеда равна / и составляет с боковым ребром угол a. Найти объем параллелепипеда, если периметр его основания равен р.
Решение.
ABCDAXBXCXDX — прямоугольный параллелепипед, BxD = l, ZBxDDx=a, Pabcd^P (рис. 12.90). Из &BXDXD находим DDX = /cosa, а DXBX = DB = /sina. Положим AB = x, AD = у; тогда (2x+2y = P,	[x+y = P/2,	lx2 +2xy+y2 =P2/4,
|x2 + у2 = I2 sin2 a ]x2 + у2 = I2 sin2 a	x2 +y2 = I2 sin2 a.
P2-4/2sin2a
Вычитая из первого уравнения второе, получим ху =----------
О
Рис. 12.92
_	P2-4/2sin2a . l(p2 -4/2sin2a)cosa
Отсюда Гпар =-------------/cosa = -J-----------c----.
О	о
Ответ: |(p2 -4/2 sin2 a)/cos a.
О
12.090. Плоскость, проведенная через образующую цилиндра, составляет с плоскостью осевого сечения, содержащего ту же образующую, острый угол а. Диагональ прямоугольника, полученного в сечении цилиндра этой плоскостью, равна / и образует с плоскостью основания угол Р . Найти объем цилиндра.
Решение,
Объем цилиндра находится так: у - nR2 н . Высота цилиндра Н = G4 = /sinP (из ДСЛВ)(рис. 12.91). Из &САВ : АВ = /cosP. Рассмотрим &OFB (ZOFB = 90°)• ЛВ = |cosр. Радиус основа-
п	™ /cosp о
ния цилиндра равен: R-OB--------=------—. Подставим и оконча-
cosa 2 cos a
TZ /2cos2p . . Q nl3 sin2Pcosp
тельно получим: V = л ----z-/sinp =-------5----.
4cos a	8 cos a
_ rc/3sin2pcosP
Ответ: --------ч----•
8 cos a
12.091. Сторона ромба равна а, а его острый угол равен а. Ромб вращается вокруг прямой, проходящей через его вершину параллельно большей диагонали. Найти объем тела вращения.
Решение.
Объем тела вращения есть сумма объемов двух одинаковых фигур Кт вр =2К (рис. 12.92). Объем такой фигуры есть: V = Иуск -Ук. Объем усеченного конуса равен: Иуск =^^-(л2+г2+Лг). Радиус
большего основания Я = CZD = 2asin—. Радиус меньшего основания 2
_ _	. а	__ о л	a
г = ВС = asm у • Высота усеченного конуса: Н = ВА = a cos у . Подставим и получим:
т. Л а( . 2  2а 2 • 2® - 2 • 2®1 7 З.а.
KVCI[ = — acos— 4а sin —+а sin —+2а sin — =—ла sin—sina ус 3	2	2	2	2) 6	2
Объем конуса с меньшим основанием:
тл • 1 2 гг 1 з • 2 a al 3.a.	_
VK=-nr H = -ita sm — cos—=-тит sin—sma . Тогда объем тела 3	3	2	2 6	2
вращения равен:
7 З.а. 1 з.а. ^^з.а. - ла sm—sin а — ла sin—sin а = 2 ла sin—sin а 6	2	6	2	)	2
V = 2Г г т.вр * V ус.к
л	з а
Ответ: 2iur sm у sin а.
12.092. Объем шара равен V. Найти объем его сектора, у которого центральный угол в осевом сечении равен а.
Решение.
2	2
Объем сектора находится так: Ус = — nRh (рис. 12.93). Объем шара:
= 7^’.Отсюда л = з — .Из ЬОВС (Z.OBC = 90’)> BO = Rcos^.
J	V 4л	2
Тогда высота сегмента h = AB = R-BO = R\ 1-cos^ | = 2/fsin2^. k 2 у 4
Подставим и окончательно получим:
т, 4	2 <*	4 ЗК . 2 а т, • 2а
К = — nR sin — = — л — sin — = V sin2 — .
c 3	4 3 4л 4	4
_	t, • 2 а
Ответ: ^sin —.
4
12.093. Угол между высотой правильной треугольной пирамиды и боковым ребром равен а (а<л/4). В каком отношении делит высоту пирамиды центр описанного шара?
Решение.
Из А5ОЯ (равнобедренный: SO = ОА ) следует: OD1SA и SD = DA = ^ (рис. 12.94). Из ASDO SD = SOcosa; x = 2SOcosa-
Отсюда SO =———. Из ASO.A SO, = S4cosa = xcosa. Тогда 2cosa	1	1
„„ ел ел	х 2xCOS2(X-X _
ОО, = SO, -SO = xcosa-------=-----------. Отсюда:
2cosa	2cos a
00, i2xcos2a-x)2cosa _	2	<	->
—1 = JE--------<------=2 cos a -1 = cos 2a.
SO 2cosax
Ответ: cos 2a.
12.094. Основания двух конусов, имеющих общую вершину, лежат в одной плоскости. Разность их объемов равна V  Найти объем меньшего конуса, если касательные, проведенные к окружности его
Рис. 12.95
основания из произвольной точки окружности основания большего конуса, образуют угол а.
Решение.
Разность объемов конусов: VX-V2=V (рис. 12.95). Объем боль-
12	1	2
шего конуса V\ = j н • Объем меньшего конуса И2 = -nR2H. Из
а OB R	R
ЬАВО (Z.OBA = 90° > sin — = — =	. Тогда Rx = ——. Подста-
2 О A R\	а
1	sin—
/	\	2
вим: V = |ян(й,2-Я22)=|лН
*2 R2 sin — 2
1	2	2 Q
= -itHR2 ctg —. Отсюда 3	2
V	2 а
Н = —— = Ktg2- . .2 а 2 ctg -
2 ЗИ
R2 =--------. Тогда объем меньшего конуса
n/Zctg2y г, 1 ЗК V2 =-п--------
3
2 ОС Ответ: V tg
12.095. Боковая грань правильной усеченной треугольной пирамиды составляет с плоскостью основания острый угол а. Найти угол между высотой и боковым ребром пирамиды.
Решение.
Из &SOD (Z.SOD = 90°): SO-DOtga, a DO = —— (радиусвпи-6
санной окружности) (рис. 12.96). Отсюда SO = —~-tga. Из &SOA 6
(ZSOA = 90°) tgP = -—;	= (радиус описанной окружнос-
SO	3
ти). Тогда tgP =
= 2 ctg a, Отсюда p = arctg(2 ctg a).
Ответ: arctg(2 ctg а).
12.096. В конус вписан полушар: большой круг полушара лежит в плоскости основания конуса, а шаровая поверхность касается поверхности конуса. Найти объем полушара, если образующая конуса равна / и составляет с плоскостью основания угол а.
Решение.
2
Объем полушара равен: Кпш = -л/с (рис. 12.97). Из ДАВО
(ЛАВО = 90°) Я = <9B = O4sina. Из &SOA (ZSOA = 90°) OA = /cosa-
Подставим 7£ = /cosasina = ^sin2a. Тогда объем полушара равен
2 /3 . 3 I' • За = - л—sm 2a = — л sin 2a.
~ - 12
v =2-/3 -пш 3 ” 8 —-
Ответ: 4: л sin3 2a.
12
12.097. Стороны оснований правильной л-угольной усеченной пирамиды равны а и Ь • Боковая грань составляет с плоскостью основания угол a. Найти боковую поверхность пирамиды.
Решение.
Боковая поверхность пирамиды равна: 5бок = -(/} + Р2У ; Р\=пЬ\
Р2=па (рис. 12.98). Рассмотрим ДВСА (ZBG4 = 90°):
s
Рис. 12.98
AC = AO-BO}
(АО и BOX —радиу-
сы вписанных окружностей). Из
Подставим и получим:
ВВСЛ'ЛВ = 1 =/1~ = —° ь . cosa 2cosatgl^-п
a
n
£бок =|n(a+z>)--
2cosatg----
п
п\
п
4 cos а
п к-*)*™
Ответ: ______п
4cosa
12.098. В шар вписан конус. Площадь осевого сечения конуса равна S, а угол между высотой и образующей равен а. Найти объем шара.
Решение.
4 з
Объем шара равен: V =—nR . Площадь осевого сечения конуса
1	I 2S
равна: S = т< sin2a. Отсюда I = J \ • — . Справедливо следующее 2	V sin 2a
соотношение между элементами шара и вписанного в него конуса:
I = 2R sin(90° - а)= 2R cos а. Отсюда Л = —-— . Подставим и получим: '	'	2cosa
2S 4sin2acos2 a
D 2S „	f 4 2S
R = J--------— . Объем шара V = - л--------у—
V4sin2acos2a	3 4sin2acos a
2	S 725 sin 2a	1 V2Ssin2a
— — n ; т i — “z 5	*
3 2sm 2acos a 3 sin 2a cos a
Л 1 _ 725 sin 2a
Ответ: — ito —z------z—.
3 sin 2a cos a
12.099. Основанием четырехугольной пирамиды служит ромб со стороной а и острым углом а. Все боковые грани наклонены к плоскости основания под одним и тем же углом р. Найти полную поверхность пирамиды.
Решение.
Пусть SABCD —пирамида, ABCD —ромб, Z.BAD = а (а<90°)> АВ=а > {{sab) {abc))={{sbc)(авс))={{scd) {abc))={{sda){авс))=$, SOA.{ABC) (рис. 12.99). Проведем апофемы пирамиды SE, SF, SK, SL ; тогда ОЕ1АВ , OF1EC , OK1CD , OLLAD (по теореме о 3-х перпендикулярах) и, значит, ZSEO = Z.SFO = Z.SKO = ZS£O = p.
2 n	c. sabcd a sina
Далее имеем 5бок =---тг =-------
cosp
„ . Отсюда cosp
_ a2 sina 2 •
^полн =-----7Z~+a Slna =
cosp
a2sina(l+cosp) 2fl2sinacos2| cosp	cosp
~ 2 •	2 P
2a sin a cos -
Ответ:
cosp
2
12.100. В основании прямой призмы лежит равнобедренная трапеция, у которой диагональ равна а, а угол между диагональю и большим основанием равен а. Диагональ призмы наклонена к основанию под углом Р. Найти объем призмы.
Рис. 12.99
Рис. 12.100
Решение.
Объем призмы находится так: V = S H (рис. 12.100). Высота призмы находится из BXBD (ZB15Z) = 90°): Н = a-tgp. Площадь осно-
вания 5=	+ -ВЕ  Из &BED (Z.SE.D = 90°): 5E = asina, а
2
ED = acosa. Так как AD-EF+AE+FD = BC+2FD, то
AD + BC = 2BC+2FD = 2(BC + FD)=2(EF + FD)=2ED = 2acosa . Тогда
_ 2 a cos a	а2 . . Л
о = — ----a sin а =—sm2a. Окончательно получаем:
з
V = —sin2atg0.
аз
Ответ: — sin2atgP.
12.101. Сторона основания правильной четырехугольной призмы равна а. Угол между пересекающимися диагоналями двух смежных боковых граней равен a. Найти объем призмы.
Решение.
Пусть ABCDA^C^ — правильная четырехугольная призма, АВ = а, ZAiDCl = а (рис. 12.101). Имеем	= а42 • Пусть A\D = х;
Рис. 12.101
тогда DCX = х . Из ^AlDCl по теореме косинусов находим
гу	Q у 2
2а2 = 2х2 -2х2 cosa = 4х2 sin2 - , откуда х =--. Из &DDXAX имеем
z	2 sin —
__________ 2 J.
I---z--- a 2 1 - 2 sin —	------------
__	2a2	2	} \	2 J aV2cosa
DD} =---------a = —-----------r_ -------------. Отсюда
J , ♦ 2a	~ - a	~ a
v4sm —	2sin—	2sin —
12	2	2
v _ a3V2cosa
л a3V2cosa
Ответ: -----------.
2 sin —
2
12.102. Объем конуса равен V. В конус вписана пирамида, в основании которой лежит равнобедренный треугольник с углом a между боковыми сторонами. Найти объем пирамиды.
Решение.
Объем пирамиды равен: Кп - (рис. 12.102). Площадь осно-
АВ^ • СВ	сх
вания пирамиды 5 = ——— . Из ЛАВС СВ = 2 АВ sin у. Тогда
2AB3 sin	2x3 sin	2x3 sin—
V =2 ________2. Отсюда R =------------—. Объем конуса
4R 4R	45
1 ,	ЗК
V = -nR2H . Отсюда H-—-y
3	лЯ
Подставим в объем пирамиды:
1 S-3K1652 4PS3
K-[2x3sin— 1 rcx6sin2y
I 2 J	z
. С другой стороны, площадь осно-
1 2 •
вания равна: S = —x sina. Тогда окончательно получим:
2 a
' 2 2У .	2a
—— = — sm acos — л	2
rz 4Kx6sin3a к sina4sin2Icos:
У =---------=---------------£---
8Kx6sin2- 2я 2
• 2 a sm —
2
_	.	2 a
Ответ: —sin acos —. я	2
12.103.	Через две образующие конуса, угол между которыми равен a, проведена плоскость. Найти отношение площади сечения к полной поверхности конуса, если образующая конуса составляет с плоскостью основания угол Р.
Решение.
Площадь сечения равна = — SA2 sina (рис. 12.103), полная поверхности конуса равна 5П0Л =56oK + SoclI = 7cA/+7d?2	+ Из
ASOA (ZSOA = 90°) А О = SA cos р. Подставим: 5П0Л =7t£42(cosp+cos2p). Тогда окончательно получаем:
SCC4 £42sina	sina
5П0Л 2kSt12(cosP+cos2₽) 4jtcospcos2|‘
л	sina
Ответ: ------------х-.
4rccospcos2
Рис. 12.103
s
12.104.	Отношение боковой поверхности правильной треугольной пирамиды к площади ее основания равно к • Найти угол между боковым ребром и высотой пирамиды.
Решение.
По условию SABC — правильная треугольная пирамида, 5бок '-SbABC = SO.l(ABC); требуется найти AASO (рис. 12.104). Пусть SO = h и AASO = a, тогда в ASOA имеем AO = htga, отку-да АВ = АОу[з	, OD = |ОА = jЛtgа. Проведем SD1AC
и из ASOD найдем SD = >IsO2+OD2 = ^Л2 +^й2 tg2 a =^74+tS2a •
Следовательно,
s6., =|ля ТЦ,/4+Ч!а =
4	4
. Имеем уравнение
ЗЛ2 tga73(4+tg2 a)4 _ 4-3A2tg2 а-Тз
74+tg2a tga
= к; ^4 ctg2 а+1 = к ;
4ctg2 а = кг -1; ctga = 	1
откуда а = arcctg—-—
ylk1 -1
Ответ: arcctg—-—.
12.105.	Через две образующие конуса, угол между которыми равен а, проведена плоскость, составляющая с основанием угол р. Найти объем конуса, если его высота равна h •
Решение.
Объем конуса равен: И = -тгЛА2 (рис. 12.105). Из ДЛ СО (ХАСО = 90°) 3
R2 = АО2 = ОС2 + АС2 Из ASOC (ZSOC = 90°) 0С = ГТ’ Из tgP
ДДСЛ (Z.SCA = 90°) Л С = SC tg , а из &SOC SC =	. Подста-
2	sinp
.2 A2tg2— *2[cos2p + tg2y)
вим и получим: R2 =--------+------2_ =—. Оконча-
tg2 р sin2 Р	sin2 р
й3 Я тельно получаем: У-——
sin2p
яй3( COS2p + tg2 ~ 1
Ответ: -----
3sin2p
12.106.	Высота правильной треугольной пирамиды равна я, двугранный угол при основании равен а. Найти полную поверхность пирамиды.
Рис. 12.107
Решение.
Полная поверхность пирамиды равна: 5ПОЛ = S6oK + S0CH (рис. 12.106).
Площадь основания = Зг2 Л • Из ASOD (ZSOD = 90°) находим:
г = DO = Я ctga. Тогда	= 3-J3  Н2 ctg2 a. Площадь боковой поверх-
1	н
ноет равна: ^бок = -Р1. Из &SOD: l-SD = -7—. Сторона основания
АВ = -^ = 2ЛЯctga. тогда S6oK = бЛя2= зЛя2
V3	2 sina	sin a
Окончательно получаем:
2 з4з „2 cosa --=-----£1 -----
2
sm.=+з ctg2 а=зЛи= cosa(1:c°sa) = sin a	sin a
n 2 a cosa-2cos
=з-Ля2------------=-
A . 2 a 2 a 4sin —cos — 2	2
• 2 a sin —
2
Ответ:
зЛ „2 cosa ----£1 -------
2 a sin —
2
12.107.	Около шара описан усеченный конус, у которого площадь одного основания в четыре раза больше площади другого основания. Найти угол между образующей конуса и плоскостью его основания.
Решение.
По условию S2 = 45( (рис. 12.107). Отсюда nR% =4лЛ|2 => R2 =2R{
FD ВО
(АО = 2BOt). Искомый угол можно найти так: cos ACDO =	.
Известно,что CF2 = BCAD=2BOl-2AO=ZBO} .Из bCFD (ZCFD=90>) CF2 + FD2 = CD2  Отсюда CD = ^8BO2 +BO? = -j9BO2 = 3BO{.
Окончательно получаем: cos /.CDO = _^L = 1	/CDO = arccosf i .
3BO{ 3	\3)
Ответ:
fl] arccos - .
13 J
12.108.	Через сторону нижнего основания куба проведена плоскость, делящая объем куба в отношении т: п , считая от нижнего основания. Найти угол между этой плоскостью и плоскостью ос-
нования, если т < п •
Решение,
Рис. 12.108
По условию
Объем
*1 = SH = ^KP КО AD (рис. 12.108). Из ЬОКР (/.ОКРУЖУ-
OP = ^-,OK = OPsma = KPtga. AD = KP. Отсюда K|=^-AP3tga. cosa	2
Объем куба у = АВ3 = КР3 • Тогда V2 = V - у, = КР3 -^КР3 tga =
- AP3fl-—tga] Подставим в соотношение:
I””18” _ .g« .	.e«
” V.gap 2-‘8“	2-8“
2m	( 2m
да 2m-wtga = «tga ; tga =- => a-arctg — I
m + n	{m+nj
Ответ: arctg ----
\m + n
12.109.	Высота правильной треугольной призмы равна н . Плоскость, проведенная через среднюю линию нижнего основания и параллельную ей сторону верхнего основания, составляет с плоскостью нижнего основания острый двугранный угол а. Найти площадь сечения, образованного этой плоскостью.
Решение.
Пусть АВСА^С^ — правильная треугольная призма, ААХ = Н, AN = NB, ВМ = МС, ((АхСхМ)ХАВС)) = а. (рис. 12.109). Проведем ВЕ1АС и ££||ЛД; AFEB-а как линейный угол двугранного угла. Пусть BE П MN = О ; тогда F01MN (по теореме о 3-х перпендикулярах). Сечение A^NMC^ — трапеция, так как Л/ЛГ||ЛС . Из &FEO
FE Н
находим FO--— = —— ЕО-Нctgа, откуда B£ = 2#ctga.H3 sina sina
ЬВЕС получим ЕС = MN = BE ctg60° = 277ctga—=--
значит, А С = ДС\ = ^^ctga
с	AC + MN „г- Н Н243с1
SAinmc} =----;----F0 = Hyl3 ctSa ~— =-----•—
1	1	2	sina sina
7/V3ctga
Ответ: -----;----.
sina
12.110.	Найти боковую поверхность усеченного конуса, описанного около правильной треугольной усеченной пирамиды, зная, что острый угол трапеции, служащей боковой гранью пирамиды, равен а и что в эту трапецию можно вписать окружность радиуса г •
Рис. 12.109
Решение.
Боковая поверхность усеченного конуса равна 5бок = тг(т^ +Л2У
2г
(рис. 12.110). Высота трапеции A,F = 2г. Из A^FA: ДА = ——,
АГ - ~~~. Обозначим Afii = а, АС = b • Из трапеции ~a+77Z • Из-
_	_ 4г	о 4г о
вестно, что а-Ь - 4г = аг +а-Решая уравнение а +а---4г = 0,
tga	tga
„ fl+cosa)	fl-cosa^
получаем ft = -2л —:--- и а2 =2г —:------ ; а, — не подходит.
\ sma )	V slna /
_	, -fl-cosa) 4r . fl+cosa)
Тогда о = 2л------- +-----= 2л------ . Известно также, что
\ sina J tga V sina j
_	_ Ьу1з _
/?! = ——; R2 =-у-. Окончательно получаем
о Viz -Уз _ fl-cosa+1+cosa) 2г ъЛпг1 5бок =	+	= Я—2г -------;------ I--T— =	. .	.
3	3	\ sma ) sina 3sin2a
Ответ:
8>/Зяг2
3sin2a
12.111.	Сторона основания треугольной пирамиды равна а , прилежащие к ней углы основания равны а и Р. Все боковые ребра сослав? пот с высотой пирамиды один и тот же угол Ф • Найти объем пирамиды.
Решение.
Объем пирамиды V = ^SH (рис. 12.111). Из &SOA (Z.SOA = 9W)
Н-SO- . По теореме синусов: 2R = 2 АО = —? = tg9	sin(180-a-p)
а _	а _
=	Т°™а Н - 2tEq,sin(<x + P) "° ’еОР<:Ме С“"УС°В
СВ а	__ asinp „
—— = —7-------; => СВ = -г-?——г. Площадь основания
sinp sin(a+P)	sm(a+P)
е 1	„„ .	1 n2sinpsina Тл„„о
S = --aCBsina =------г-—т—• Тогда
2	2 sin(a+P)
У _ 1 аг sinPsina _ 1 a3sinPsinactg<p
3 4tg(psin2(a+p) 12 sin2(a+p)
Ответ:
a3 sinPsinactgtp 12sin2(a+p)
12.112.	Расстояние от центра основания конуса до его образующей равно d • Угол мевду образующей и высотой равен a. Найти
полную поверхность конуса.
Решение.
Полная поверхность конуса Sn0J1 = S6oK +	= nRl + nR2 (рис. 12.112).
Из ДОВЛ (2ОВЛ = 90°; ZBOA = ZASO = a.) R = OA =-. Из
cosa
&SOA (z SO А = 90°') SA = -^-;m SSBO SO = ~^—. Тогда cosa	sina
l = SA = —— ---. Отсюда
sinacosa
Рис. 12.111
<?
мпол
= л
d* I * 2
d2
•	2	2
sinacos a cos a
d2
1
= я—Г" ~— cos a \ sin a
= я
,2f	2 a a • a a . 2a
к тш cos — +2sin—cos—+sin —
<Z2(l+sina)	I 2	2	2	2 J
z	x2 " z	\ 2 z	\2
I	2« • 2 a i (	a . a 1 (	a • a ]
sina cos --sin — sinoq cos—-sin— cos—+sin —
I 2	2 J Д2 2 J I 2	2 J
nd2
nd2
. a
a .a) cos—+sm—
2	2)
sinaf	a	. a A f	a	. a)	( a	. a
cos—sm— cos—+sin— sina cos—sm—
I	2	2 И	2	2)	l2 2
.2 “
2 sin
nd2
T)	3
i a . a) cos—-sin— ‘I 2	2)
nd2
nd2
1	i V
1	a	1 . al
-7= cos——7=sin—
/2	2 Я 2
ltd2
. n a	я . a
sm—cos—cos—sm—
4	2	4	2
I2	. 2(n a
2smasm —
14 2
Ответ:
ltd2
A *	- 2 Л a
2 sin asm-------
14 2
Рис. 12.114
12.113.	Основанием пирамиды ABCD служит прямоугольный треугольник АВС (ZC = 90° )• Боковое ребро AD перпендикулярно основанию. Найти острые углы треугольника АВС, если Z.DBA = a и ZDBC = P (а<£).
Решение.
Пусть DABC —пирамида, АА СВ =90°, ADl(ABC), ZDBA = a, ZDBC = Р (а<р) (рис. 12.113). Пусть AD = h; тогда из &ADB на-
nn h
ходим ЛВ = Лс1еа, DB = ——. Так как БС_ЫС,то DC» ЯС и из sina
h cos В
&DCB получим ВС = Z)BcosP = —------. Итак, в ДЛВС имеем
sina
. ВС Acosp cosp	. cosp
sm	— —- -	—	- откуда ^A = arcsin----------
AB sina-A ctga cosa J	cosa
у» я ° cosp
ZB =— arcsin------ .
2 cosa
. cosВ	cosp
Ответ: arcsin------; arccos-
cosa	cosa
12.114.	В правильной шестиугольной призме плоскость, проведенная через сторону основания и середину отрезка, соединяющего центры оснований, составляет с плоскостью основания острый угол
a. Найти площадь сечения, образованного этой плоскостью, если сторона основания призмы равна а.
Решение.
(BE + AF I
Площадь сечения 5сеч = 2SBAFE =2l-----------РК I (рис. 12.114).
Радиус вписанной окружности в основании призмы: ОК = г =
Из \РОК (ЛРОК = 90°} РК =	. Радиус описанной
cosa 2 cos a
окружности R = BP = a Отсюда BE = 2а- Окончательно получаем:
Sce4 = (ВЕ + AF)PK = (2а+а)-^~
2 cos a
За2 4з Ответ: ---------.
2 cos a
12.115.	В конус вписан шар, поверхность которого равна площади основания конуса. Найти косинус угла при вершине в осевом сечении конуса.
Решение.
По условию 5Ш = (рис. 12.115).
Рис. 12.115
Отсюда 4лЯ£ -	=> RK -2Rai.
Рассмотрим ASCA . По теореме ко
синусов (2ЛО)2 = 2SA2 ~2SA2cosa = 2SA2(1-cosa). Отсюда
2SA2-2(rJ , 2R2
cosa =---—-г----= 1——у. &SOA и AS-SQ подобные:
2SA	SA
— = — => SA = SOl -^- = 2SOi. Из &SOA; SA2 = OA2 + SO2, а
BOi SOi	Лш
z	\2
SO = S(\+ Ofi = —+OjB. Подставим: £42 = OA2 + f+OtB j .
O'A2
SA2 =R2 +—^—+SA‘Rul +R^ =5Лщ +—— -vSA-R^. Решая уравнение
35Л* 2	2 n	cd	“6Л11 z
——----оЛ-Лщ-57^, =0, получаем: 1) SA = ——; 2) SA = —-— (не
ч	. 2-4/£-9 , 18	7
подходит). Тогда окончательно получаем: cosa = 1-^5— = 1-— = —.
100/^	25 25
7
Ответ: — •
25
12.116.	Основанием прямой призмы служит равнобедренный треугольник, у которого боковая сторона равна а, а угол между боковыми сторонами равен а. Найти объем призмы, если ее боковая поверхность равна S.
Решение.
Объем призмы V = 5ОСН • Н (рис. 12.116). Площадь основания рав-
1 2 •	5
на: S^^-a sina. Боковая поверхность S = PH, отсюда H = —
Обозначим A С = x♦ По теореме косинусов:
x1 = 2a2 -2a2cosa = 2a2(l-cosa)  Тогда x = 0^2(1-cos a) = 2 a sin “ .
Отсюда p = 2a +2asin— = 2a 1+sin I. Окончательно получаем: 2 I 2 J

17	1 2 ♦
V = ~a sina
2 n f. . a
2 л 1+sin —
I 2
a sin a
J i , . a 4 1+sin—
I 2
o . a a aS-2sin —cos — ______________2	2	; A(	2« . 2 a . . a	a
4 cos —+sin — +2sin —cos—
1	4	4	4	4
Г,	•	ос
/	\	aS	sin—
Л .	a1	a	.al	9
aS sin— cos—sm—'	2
2^4	4
Y a	°сЛ
2 cos—+sin — 14	4
. a( 2 a • 2 a sin — cos —“Sin —
2 V 4	4
/ \2 j	a	. a)
4 cos —+ sin—
V	4	4 J
• ос sin —
1—4-a
cos —
.____4 J =
• °с sin—
4
a cos —
4 7
Рис. 12.116
с • ah . a aSsinyll-tg-2f1 + tSj)
_ . ol n * a) aSsin— tg—-tg— „ z x
21 4	4 j aS . a (it a]
J, л	2	2 \4 4 J
21 + tsZt84
aS . a л-a
Ответ: -^-sinytg——.
12.117.	Основанием пирамиды, вписанной в конус, служит четырехугольник, у которого смежные стороны попарно равны, а угол между одной парой смежных сторон равен a. Найти отношение объема пирамиды к объему конуса.
Решение.
Объем пирамиды
V -'-S
Г П J ° осн
Н (рис. 12.117). Площадь основа-
ния пирамиды
Soc„=2Smbc=2 ^AB BC (z,4BC = 90’).H3 ЛАВС
AB=2OC sin^; а ВС=2Rcosy. Тогда 5^ =47?2cosysiny =27?2 sina.
Объем конуса Ик = л7?277. Тогда искомое отношение:
Ki _ ^осн Н _ 2R2 sina _ 2sina
VK л/?2 Н nR2 п
2 sin a Ответ: ---------.
л
26 М. И. Сканави, группа А	801
s
12.118.	Найти косинус угла между смежными боковыми гранями правильной четырехугольной пирамиды, у которой боковое ребро равно стороне основания.
Решение.
Из ДЛОС по теореме косинусов AC2 =2АО2-2АО2 cosa
2АО2-АС2
(рис. 12.118). Отсюда cosa =--------.Из ДЛВС (Z_ABC = 90°):
2 А О
_______	I 2
AC = yj2a2 =aj2 .Из MOB (ZAOB = 90°): AO = Ja2-— =-^-
2-3a2 , 2
-------2a ।
Тогда окончательно получаем: cosa = —-—=--------= —
За2 3
2
Ответ: — — •
12.119.	В конус вписан шар. Радиус окружности, по которой касаются конус и шар, равен г. Найти объем конуса, если угол между высотой и образующей конуса равен a.
Решение.
1 ?
Объем конуса равен: И = -гсЯкЯ (рис. 12.119). Из ААО^О
(Z^0i0 = 90°) OA = RV1~-; 0Ц = rtga. Из bS(\A
cosa
(Z-SOxA = 90°) SO{ =--. Высота конуса:
1	tga
Н = S0\ + О^О + Аш
1	1 I
-----+tga+---- = cosa-tgaj
(l+sina)sina+cos2a^ ~ fsma+1
-------L----------1 = 2r —----- I sin2a
cos a sin а
Из ASBC (ZStfC)
n Tr ( sina+1 ) sina (sina+1)
Кк = Htga = r  -----------= r----j— Тогда
Vsmacosa) cosa cos a J
T, 1 sma+П /ч (sina+1^ 1 v = -nr2\--r— -2r- —| = -лг‘
3 V cos a J V sm2a ) 3 з( 2a .2« a - a	a]
nr cos — +sin — +2sm—cos—
1	2	2	2 2 J
-*1 2)
»	2-1	2 а . л
3cos asmal cos y“sm
/	\3
31	a	. a)
лг cos—+sin—
I	2	2 J
з (sina+1)*	_
cos4 a sin a cos a
3i	a	. a
nr cos—+sm—
I	2	2 J
z	\3
о 2	• f 2»	• 2 И |
3cos asrna cos —sm —
I 2	2 J
^„3 nr
• a sin —
2
a cos —
2 /
/	\3
»	2-i a . a,
3cos asm a cos—sin —
^2	2 J 3cos2asina
. a sm— 1----2_
a cos—
2 J
/	\3	z
з| i А ос х я 1	з . 31 л а
nr 1 + tg—-tg—	,	яг ctg-----
t 6 2	4 J	nr3 1	U 2
2	. ( л aY 3 cos a sin a . з( л a| 3cos asma
3cos asinaltg—-tgy I
a
2
Ответ:
3 . 31 л ЛГ ctg -
14
3 cos2 a sin a
12.120.	Боковое ребро правильной четырехугольной пирамиды равно т и наклонено к плоскости основания под углом a. Найти объем пирамиды.
Решение.
Объем пирамиды И = ^50СНЯ (рис. 12.120). Из &SOA
находим:
АС
5(? = Я = wsina; ЛО = диcosa =. Отсюда ЛС = 2wcosa- Пло-
AC2 4zn2cos2a 2 т
щадь основания о’ =-------=----------= 2т cos a. Тогда
2	2
__	1 -	2	1	•	1	1
V = -2m cos a znsina = -7H cosasm2oc.
3	3
Ответ: - nr cos a sin 2a.
3
12.121.	Основанием пирамиды служит правильный треугольник со стороной а. Две боковые грани пирамиды перпендикулярны плоскости основания, а равные боковые ребра образуют между собой угол a. Найти высоту прямой треугольной призмы, равновеликой данной пирамиде и имеющей с ней общее основание.
Решение.
Пусть DABC — пирамида, АВС — правильный треугольник, (ABD)l(ABC), (BCD)1.(ABC), ZADC=a, АВ = а (рис. 12.121). Тре-буется найти высоту призмы с основанием, равным ЬАВС, причем Кпр = Ипир . Высота пирамиды совпадает с ребром db , так как перпендикуляр, опущенный из D на (ЛВС), должен принадлежать и
Рис. 12.120
(Я/?С),и (СЯО). Проведем DK1AC ', так как AADC —равнобед-а а ренный, то КА = КС  Из &DKC находим Z>^ = yCtgy, а из
J-> а а ctg-Г з„2 I ~ ------—------= -. /ctg2-3 .
4	4 2V 2
? а . a3 L( ? й _ ctg2—3 =— 3 ctg2 — -3 . Так как 2	24 V V 2	)
г~	1	3 .Г"7	\
a2V3 а -73 „ a J 2« ,1 ^пир = ^пР = —Н, то ~д-Я “ 24 ^|3[ctg 2 "3J ’ откУДа
1 а2-Л а Отсюда ^пиР=т—-—т н 3	4	2
Рис. 12.122
Рис. 12.123
12.122.	Найти объем конуса, если в его основании хорда длиной а стягивает дугу в а радианов, а высота конуса составляет с образующей угол 0. Решение.
Пусть SAK — конус, SO — его высота, ВК — хорда, ВК = а, <jBnK = a, Z.OSK = 0 (рис. 12.122). Так как \jBnK = a, то Z.BOK = a~ Пусть R — радиус основания конуса; тогда в S.OBK имеем а2 = 2Л2 --2R1 cosa = 4Я2sin2—, т.е. a = 2J?sin—, откуда 7?= Q . Из 2	2	2sin(a/2)
SSOK находим 50 = О/С ctg 0 =——С——. Итак, 2sin(a/2)
V =\яг so =1.
3	3	4	sin2—	2 sin—	24 sin3 —
2	2	2
~	7M3Ctgp
Ответ'. -----
_ . 3 a 24snr— 2
12.123.	Угол при вершине осевого сечения конуса равен 2а, а сумма длин его высоты и образующей равна а. Найти объем конуса.
Решение.
По условию SA + SO = a => SO = a-SA (рис. 12.123). Объем ко-
1 ,
нуса V = -tzR Я. Из &SOA SO = SA cos а. Тогда SXcosa = a-SA •
а yt ™ acosa	. asrna
SA = ------ и H = SO =----------, а AO = R = S?4sina = -------.
1+cosa	1+cosa	1+cosa
Тогда окончательно получаем: л . 2 а 2 a i	„з cosa-4sm —cos —
1 a sm a	a cos a .a	2	9
V = - n------rz- • 7------ = П------------=
3 (1+cosaf (1+cosa)- 3 f , aY
2 cos —
3 a » 2 ft 3	. 2 ft
a tccos a • 4 sin — a я cos a • sin —
2 =2
о 4 ft	X 4 ft
3-8cos —	6 cos —
лежит ромб с острым углом а	рис 12 124
и меньшей диагональю d , а
высота параллелепипеда в два раза меньше стороны основания. Решение.
Полная поверхность параллелепипеда 5П0Л =5бок +25^ (рис. 12.124). . АВ а
По условию АА{ = -у- = —. Периметр основания р = 4a, а высота
а	аг
Н = ~. Тогда 56ок =4— = 2а2. Из £	L
LABD по теореме косинусов
j2
DB1 = 2АВг -2АВ2 cosa; d2 = 2a2 -2a2 cosa. Тогда a2 = —r------г.
2(l-cosa)
12-	2 •
Площадь основания =25'Д4В2) =2—a sina = a sina. Оконча
тельно получаем:
„	. 2	2 •	2J* 2	2d2 sina 2rf2(l+sina)
•Snon = 2a + a sin a = —>-------;+—>-------; =------------- =
2(1-cosa) 2(1-cosa) 4sin2—
2
,2(	2«	. 2 a . . a	a
a cos —+sin — +2 sin —cos — у 2	2	2	2
2 sin2 — 2
'/ \2
\ a . a) cos — +sin— у 2	2)
. 2a sin —
2
1
,2	2[ я a
a cos —- —
<4 2
. 2 a sin —
2
z	\2
,2i	я	a	. it . a)
a I cos—cos— + sm—sin —
V	4	2	4	2)
2 a sin — 2 ,2	i( it a"!
J cos-------
n	14 2 J
Ответ: ----------------.
. 2« sin —
2
12.125. В правильной двенадцатиугольной пирамиде, ребра которой пронумерованы подряд, проведено сечение через первое и пятое ребра. Плоскость сечения образует с плоскостью основания пирамиды угол a, а площадь этого сечения равна S . Найти объем пирамиды.
Решение.
Пусть SAlA2A3... Л12 — правильная двенадцатиугольная пирамида, SAtA5 —сечение пирамиды плоскостью, ([SAiA5\(AtA2A3))=a, S (рис. 12.125). Проведем 5О1(4^2^з)° Пусть ОА^ —R; так
как ZAflAz = уу- = 30°, ZAiOA5 = 30° • 4 = 120°, то AtA5 — сторона правильного вписанного в окружность треугольника и А{А5 = R-J3 
Проведем OKIA^; тогда ZAiOK = 60°, ОК = у R . Из &SOK нахо-
OK R	1 n
дим oa =----= ----, SO = — Rtga, так как Z.SKO —линейный
cosa 2 cos a	2
Рис. 12.125
Рис. 12.126
угол двугранного угла между сечением и основанием. Имеем
с	w <• ’оН Л r2^	__2VScosa
Ядудл, = х44 SK,т.е. S = -Ry/3  -=  ---, откуда R---—.
’ 2	2 2cosa 4cosa	v3
Далее, = 125ДОу4|Л =12-|/?2sin30’ =ЗЛ2 = 12SJ»sa =45>/зcosa. Получили
tz 1 о ол 4Ss/3cosa 1 2VScosa t 45 sin aV5 cos a ^пир = 3  SOCH  SO  ----------^=— tg a =---------------=
_ 45^3 sin a-7 S'cos a
3	’
Л 45^3 .	r=.--
Ответ: —— sm av 5cos a.
12.126. Найти угол в осевом сечении конуса, если сфера с центром в вершине конуса, касающаяся его основания, делит объем конуса пополам.
Решение.
2	,
Объем сектора	=—nR^ • h (рис. 12.126). Объем конуса
VK = 7 лЛ2 • Н. По условию У„к =	; 7 лЛ^Л = nR2H. Высота ко-
3	2 3	6
нуса Н = Rm; высота сегмента h = R^ -SA. Из &SAB находим:
SA = Rm cos—. Отсюда h = Аш 1-cos— . Из &SOC находим: 2 J
a	2 „3 Л	cO 1 -3 2 a
R = OC = Rmtg — . Подставим:	~z =>
2	5	\	Z J о	Z
/1 а I 1 i
. 4 1-cos— =—z-------1;
2 J cos2 a/2
A 2°tfi	al (1	Mi	ОС
4cos — 1-cos— = 1-cos — 1+cos —
21	2J l	2Л	2
i 2« 1-COS —
_______2 .
2 a cos —
2
.	2 a , a
=> 4cos — = 1 + cos— .
2	2
. 2 a	a . Л	a л
4cos —cos—1 = 0. Обозначим cos—= Z.
2	2	2
Решая уравнение
4r2-z-l = 0, получаем Zj =
a 1+V17	а
сюда cos — =------ => — = arccos
2	8	2
1-V17
и 6 =------
2	2
1+V17
—-—. Тогда о
(не подходит). От-
o 1+V17
a = 2 arccos----
8
8
O 1 + V17
Ответ: 2 arccos------.
8
12.127.	Разверткой боковой поверхности цилиндра является прямоугольник, диагонали которого пересекаются под углом а. Длина диагонали равна d • Найти боковую поверхность цилиндра.
Решение,
Пусть ААХВХВ — развертка боковой поверхности цилиндра, ААх и ВВХ — его образующие, АВ и АХВХ — длины окружностей его оснований, ABx=d, ААОАх=а (рис. 12.127). Так как ААОАХ — а внешний угол равнобедренного треугольника АОВ, то АОВА = —.
a	a
Из	А В находим Ax A = d sin у, AB = d cos у. Получили
S6oK -2nRH - ABAAX = rf2sinycosy = |rf2 sina .
1	2
Ответ: —d sina. 2
12.128.	В конус, образующая которого равна /, вписана правильная шестиугольная призма с равными ребрами. Найти боковую поверхность призмы, если угол между образующей и высотой конуса равен а.
Решение.
Боковая поверхность призмы 5бок =Р Л (рис. 12.128). Пусть ребро призмы равно х. Тогда h = x и р = 6х-Из &SOA SO = 1 cosa- Из tiSOxB SO =	.Найдем SO = OO, +OiS = x + -?- = xl 1+-^- I. Решим
tga	tga V tga J
J i . 1 i 7	~ /cosasina ~	x 2
уравнение: x|l+---I =/cosa => x =-----------.Тогда =6x =
tga J	cosa + sina
6/2 cos2 a sin2 a _	3Z2cos2asin2a _ 3Z24cos2asin2a
3Z2 sin2 2a
4sin2f— + a И
Ответ:
3Z2 sin2 2a
A • 2 Я 4sin —+a
5
Рис. 12.129
Рис. 12.130
12.129.	Найти объем правильной четырехугольной пирамиды, если сторона ее основания равна а, а двугранный угол при основании равен а.
Решение,
Объем пирамиды К = -577 (рис. 12.129). Площадь основания:
S = a2- Высота пирамиды из &SOE
1 а3	а3
j z	о
SO = H = ^tga.
2
Отсюда
а
Ответ: —tga.
6
12.130.	Развертка боковой поверхности цилиндра представляет собой прямоугольник, в котором диагональ равна а и составляет с основанием угол a. Найти объем цилиндра.
Решение.
Объем цилиндра к = лЯ2/7 (рис. 12.130). Высота цилиндра из
М.ВС равна Н = CB = asina. Длина окружности основания
тт	-	п т- п a cos a
с = А В = a cos a. Но, с другой стороны, с = 2nR. Тогда R = —-.
2л
2	2	3	2-
a cos a	a cos asinot
Подставим и получим: И = л—-------a sin a =----------.
4л2	4л
Л	a3 cos2 a sin a
Ответ: -------------.
4л 812
________________Решения к главе 13___________________ ПРИМЕНЕНИЕ УРАВНЕНИЙ
К РЕШЕНИЮ ЗАДАЧ
13.001. Из данных четырех чисел первые три относятся между собой как 1/5:1/3:1/20, а четвертое составляет 15% второго числа. Найти эти числа, если известно, что второе число на 8 больше суммы остальных.
Решение.
Искомые числа таковы: Л/5; к/3; к/20; ОД 5 к/3 = к/20 . По усло-к к к к
вию у-8 = j +	+ откуда * = 240-
Ответ: 48; 80; 12; 12.
13.002. Сколько килограммов воды нужно выпарить из 0,5 т целлюлозной массы, содержащей 85% воды, чтобы получить массу с содержанием 75% воды?
Решение.
В целлюлозной массе содержится 0,85 -500 = 425 кг воды. Пусть выпарено х кг воды; тогда получим 425-х = 0,75(500-%), откуда х = 200 (кг).
Ответ: 200 кг.
13.003. В двух бидонах находится 70 литров молока. Если из первого бидона перелить во второй 12,5% молока, находящегося в первом бидоне, то в обоих бидонах будет поровну. Сколько литров молока в каждом бидоне?
Решение.
Пусть первоначально в первом бидоне х, а во втором 70-х литров молока. После переливания в первом бидоне осталось х-0,125х = 0,875х литров, а во втором стало 70-х + 0Д25х литров. По условию 70-х+0,125х = 0,875х, откуда х = 40 • В первом бидоне было 40 литров, во втором — 30 литров молока.
Ответ: 40 и 30 л.
13.004. Две бригады, работая одновременно, обработали участок земли за 12 ч. За какое время могла бы обработать этот участок каждая из бригад в отдельности, если скорости выполнения работы бригадами относятся как 3:2?
Решение
Пусть Зх — скорость выполнения работы первой бригадой, 2х — скорость выполнения работы второй бригадой. Первая бригада
1 1
выполнит всю работу за — часов; вторая — за — часов. Вместе
они выполнят всю работу за -——“-т- часов. По условию I	JA
^- = 12, откуда х = 60- Первая бригада выполнит всю работу за
—?— = 20 часов; вторая — за —!— = 30 часов.
3—	2 —
60	60
Ответ: 20 и 30 ч.
13.005. Сумма цифр двузначного числа равна 12. Если к искомому числу прибавить 36, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение.
Пусть искомое число имеет вид 10x+j>. Тогда по условию х + >> = 12 (1) и 10x+>> + 36 = 10j> + x, т.е. х-у+4=0 (2). Складывая (1) и (2), получим 2х = 8, откуда х = 4, а у = 8 .
Ответ: 48.
13.006. Тракторист вспахал три участка земли. Площадь первого равна 2/5 площади всех трех участков, а площадь второго относится к площади третьего как 3/2:4/3. Сколько гектаров было во всех трех участках, если в третьем было на 16 га меньше, чем в первом?
Решение.
Пусть площади участков равны х, У, х-16 (га). По условию
х = — (х+_у—16 + х) и у: (х-1 б)= 3/2:4/3, откуда у = “(х-1б). Имеем 5	о
х = - 2х-16+—х-18 <=> х = - —--34 I, х —-. Далее находим
51	8	)	51 8 J 5
9 (212
J-8l 5
216 D	544 216 ,.	, ч
-у-. Вся площадь составляет у- + -у--16 = 136 (га).
Ответ: 136 га.
13.007. Цену товара сначала снизили на 20%, затем новую цену снизили еще на 15% и, наконец, после пересчета произвели снижение еще на 10%. На сколько процентов всего снизили первоначальную цену товара?
Решение.
Пусть х — первоначальная цена товара. После первого снижения цена стала х - 0,2х = х(1 - 0,2); после второго — х(1 - 0,2/1 - 0,15); после третьего— х(1-0,2)(1-0Д5Х1-0Д) = 0,612х. Значит, всего пер
воначальную цену товара снизили на 1-0,612 = 0,388 = 38,8%.
Ответ: 38,8%.
13.008. Морская вода содержит 5% соли по массе. Сколько пресной воды нужно добавить к 30 кг морской воды, чтобы концентрация соли составляла 1,5%.
Решение.
Пусть х кг соли в 30 кг морской воды, х кг составляют 5%. Отсюда х = 1,5 кг, 30 кг— 100%. В разбавленной морской воде: 1,5 кг
соли составляет 1,5%, а кг— 100%, откуда а = 100 кг разбавленной морской воды. Значит, надо добавить 100-30 = 70 кг пресной воды.
Ответ: 70 кг.
13.009. В библиотеке имеются книги на английском, французском и немецком языках. Английские книги составляют 36% всех книг на иностранных языках, французские— 75% английских, а остальные 185 книг— немецкие. Сколько книг на иностранных языках в библиотеке?
Решение.
Пусть х —всего книг на иностранных языках. Английских книг — 0,36х; французских 0,75 • 0,36х ♦ По условию 0,36х+0,75 • 0,36х+185 = х, откуда х = 500-
Ответ: 500.
13.010. Насос может выкачать из бассейна 2/3 воды за 7,5 мин. Проработав 0,15 ч, насос остановился. Найти вместимость бассейна, если после остановки насоса в бассейне еще осталось 25 м3 воды.
Решение,
Пусть хм3 — вместимость бассейна. За 7,5 мин насос может вы
качать—х воды. За 0,15 ч = 9 мин насос выкачал
9-х 3
7,5
= 0,8х воды. В
бассейне осталось 0,2х воды. По условию 0,2х = 25, откуда х = 125.
Ответ', 125 м3.
13.011. Вследствие реконструкции оборудования производительность труда рабочего повышалась дважды в течение года на одно и то же число процентов. На сколько процентов возрастала каждый раз производительность труда, если за одно и то же время рабочий раньше вырабатывал изделий на 2500 руб., а теперь на 2809 руб.?
Решение,
Пусть за 8 часов работы рабочий изготавливал а деталей. Тогда
2500
расценка составляет-----руб. за деталь, а производительность труда
а
a w „
равна — деталей в час. После первого увеличения производительности о
Л/	а ха
нах% рабочий стал изготовлять — + деталей в час; после второго 8 100*8
а [ 1 х	х
увеличения производительности еще на х% — ~ I 1 + y^jy II 1 + ууу I дета-
/ I X ] лей в час. За 8 часов он стал изготовлять al 1 + уу^ I деталей и заработал
а 1+----------руб. Согласно условию, а 1+—-------------= 2809,
I 100 J а ™	>	I 100)	а
откуда х = 6%.
Ответ'. 6%.
13.012. Рабочий день уменьшился с 8 до 7 ч. На сколько процентов нужно повысить производительность труда, чтобы при тех же расценках заработная плата возросла на 5%?
Решение.
Пусть за 8 ч работы мастер изготовлял а деталей и зарабатывал Ь руб. Тогда расценка составляет b/а руб, за деталь, а производительность труда равна а/8 деталей в час. После увеличения
а ха производительности на х% мастер стал изготовлять — +	• •• де-
о о*100
1а ( х
талей в час. Поэтому за	7	ч он	изготовил	"g~l1 + ]oo I	деталей	и
_	1а Л x\b	IbL	х	_
заработал	— 1 + — —	= — 1+—	РУб.	Согласно	условию,
F	8 < lOOja	8 <	100J	J
T +T5o ]=1,05Z? ’ откуда x=20°/o ’
Ответ: 20%.
13.013. В январе завод выполнил 105% месячного плана выпуска готовой продукции, а в феврале дал продукции на 4% больше, чем в январе. На сколько процентов завод перевыполнил двухмесячный план выпуска продукции?
Решение.
Пусть х/2 — месячный план завода; х — двухмесячный план. В январе завод выполнил 0,05 х/2 сверх плана; в феврале — 0,04 0,05 -х/2 . За два месяца завод перевыполнил план на
0,05 у+0,04 0,05 у = 0,071х . Значит, завод перевыполнил двухмесяч
ный план выпуска продукции на 7,1%.
Ответ: 7,1%.
13.014. Найти три числа, если первое составляет 80% второго, второе относится к третьему как 0,5:9/20, а сумма первого и третьего на 70 больше второго числа.
Решение.
Пусть х — первое число, у — второе число, z — третье число.
Тогда, согласно условию,
х = 0,8у,
У 0,5
=	Решая систему, получим
z 9/20
x + z = >’ + 70.
х = 80; jp = 100; т = 90.
Ответ: 80, 100, 90.
13.015. Турист проехал расстояние между двумя городами за 3 дня. В первый день он проехал 1/5 всего пути и еще 60 км, во второй 1/4 всего пути и еще 20 км, а в третий день 23/80 всего пути и оставшиеся 25 км. Найти расстояние между городами.
Решение.
Пусть х км — расстояние между городами. Составим следующую таблицу:
День	Путь, пройденный за день
Первый	^х + 60 (км)
Второй	-х+20 (км) 4
Третий	23 — х+25 (км) 80
Пр условию -Х + 60+ —Х+20+—х+25 = х, откуда х = 400«
Ответ: 400 км.
13.016. Числители трех дробей пропорциональны числам 1, 2 и 3, а обратные величины соответствующих знаменателей пропорциональны числам 1, 1/3 и 0,2. Найти эти дроби, если их среднее арифметическое равно 136/315.
Решение.
Составим следующую таблицу:
Дробь	Числитель	Знаменатель
Первая	X	Уу
Вторая	2х	3/у
Третья	Зх	Wy
Первая дробь—ху\ вторая-ху, третья — 0,6 ху. Среднее арифме-
2
ху + — ху + 0,6ху тическое дробей ---------------
136	136 4 о
=----, откуда ху —-----= —. Значит,
315	238 7
первая дробь — вторая — —; третья — —.
Ответ:
А.Л.И 7’ 21’ 35
13.017. Найти сумму трех чисел, зная, что третье относится к первому как 18,48 : 15,4 и составляет 40% второго, а сумма первого и второго равна 400.
Решение.
„	гт	z 1848 6
Пусть х, у, z — указанные числа. По условию имеем: — =--= —,
х 1540 5
z = 0,4у, х + у = 400. Так как у = -|z и z = |-x, то у = 3х и х + Зх = 400=>
=> х = 100, Z = -х = 120. Тогда 5
S=x+y+z= 400 + 120 = 520.
Ответ: 520.
13.018. Вкладчик снял со своего счета в Сбербанке сначала 1/4 своих денег, потом 4/9 оставшихся денег и еще 640 руб. После этого у него осталось на сберкнижке 3/20 всех его денег. Как велик был вклад?
Решение.
Зх
Пусть вклад составляет х руб. Тогда первый остаток равен —; вто-4
рой остаток— — -— —-640 = —. Имеем — -—-— = 640, откуда 4 9 4	20	4 3 20
х = 2400 (руб.).
Ответ: 2400 руб.
13.019. На уборке снега работают две снегоочистительные машины. Первая может убрать всю улицу за 1 ч, а вторая — за 75% этого времени. Начав уборку одновременно, обе машины проработали вместе 20 мин, после чего первая машина прекратила работу. Сколько еще нужно времени, чтобы вторая машина закончила работу?
Решение,
Весь объем работы примем за 1. Производительность первой машины
3 4	1
равна 1 (за 1 ч), второй 1: — = — (за 1 ч). Работая вместе — ч, они выпол-4 3	3
1 , 1 4 7	.
нят — • 1 +--= — всей работы. Тогда на долю второй машины останется
3	3 3 9
2 с	с 2 4 1 , х
— работы, для чего потребуется —: у = — (ч).
Ответ', 10 мин.
13.020.Сумма первых трех членов пропорции равна 58. Третий член составляет 2/3, а второй — 3/4 первого члена. Найти четвертый член пропорции и записать ее.
Решение.
Пусть пропорция имеет вид — - —. По условию а+6 + с = 58; b d
2	3	3	2
с = — а: Ь = ~а. Значит, а +—а + — а = 58, откуда а = 24; с = 16; b = 18.
3	4	4	3
Ьс
Значит, d - — = 12.
а
„ М 16
Ответ: 12;— = —.
18 12
13.021. Одна бригада может убрать все поле за 12 дней. Другой бригаде для выполнения той же работы нужно 75% этого времени. После того как в течение 5 дней работала только первая бригада, к ней присоединилась вторая, и обе вместе закончили работу. Сколько дней работали бригады вместе?
Решение.
Пусть бригады работали вместе х дней. Производительность 1	1	1 гг
первой бригады — —; второй бригады — 12' 0~75 = *9* Условию
— 5+ — + --х = 1, откудах = 3 дня.
12 Ц2 9J
Ответ: 3 дня.
13.022. На вступительном экзамене по математике 15% поступающих не решили ни одной задачи, 144 человека решили задачи с ошибками, а число решивших все задачи верно относится к числу не решивших вовсе как 5:3. Сколько человек экзаменовались по математике в этот день?
Решение.
Пусть х человек всего экзаменовались. Не решили ни одной
0Д5х-5
задачи 0,15х человек; решили все задачи— —-— = и/эх чело-
век. По условию 0,15х+144+ 0,25х = х, откуда х = 240-
Ответ: 240.
13.023. Однотипные детали обрабатываются на двух станках. Производительность первого станка на 40% больше производительности второго. Сколько деталей было обработано за смену на каждом станке, если первый работал в эту смену 6 ч, а второй — 8 ч, причем оба станка вместе обработали 820 деталей?
Решение.
Пусть производительность второго станка х; тогда производительность первого — 1,4х деталей в час. Первый станок обработал в смену 1,4х-6 деталей; второй— х-8 деталей. По условию 1,4х-6 + х-8 = 820, откуда х = 50- Значит, первый станок обработал в смену 1,4-50-60 = 420 деталей; второй— 50-8 = 400 деталей.
Ответ: 420 и 400 деталей.
13.024. Тракторная бригада может вспахать 5/6 участка земли за 4 ч 15 мин. До обеденного перерыва бригада работала 4,5 ч, после чего остались невспаханными еще 8 га. Как велик был участок?
Решение.
Пусть х га — весь участок. До обеда бригада вспахала
4,5 —х 1$	15
4,25 ~ 17Х Га условию —х + 8 = х, откуда х = 68 га.
Ответ: 68 га.
13.025. От пристани в город отправилась лодка со скоростью 12 км/ч, а через полчаса после нее в том же направлении вышел пароход со скоростью 20 км/ч. Каково расстояние от пристани до города, если пароход пришел туда на 1,5 ч раньше лодки?
Решение.
Пусть х ч был в пути пароход. Тогда х + 0,5 +1,5 ч была в пути лодка. Пароход прошел 20 х км, а лодка 12(х + 2) км. Тогда 20х = 12(х+2), откуда х = 3 ч. Расстояние между городами и пристанью 20 • 3 = 60 км-
Ответ: 60 км.
13.026. Турист проплыл по реке на лодке 90 км и прошел пешком 10 км. При этом на пеший путь было затрачено на 4 ч меньше, чем на путь по реке. Если бы турист шел пешком столько времени, сколько он плыл по реке, а плыл по реке столько времени, сколько шел пешком, то эти расстояния были бы равны. Сколько времени он шел пешком и сколько времени плыл по реке?
Решение.
Пусть х ч турист шел пешком. Тогда он плыл на лодке (х + 4) ч.
10	,	90
Скорость туриста пешком — км/ч; на лодке —------ км/ч. Согласно
х	х+4
Ю /	90
условию, — (х+4) = + 4 х , откуда х = 2 ч.
Ответ: 2 и 6 ч.
13.027. Сумма квадратов цифр двузначного числа равна 13. Если от этого двузначного числа отнять 9, то получится число, записанное теми же цифрами, но в обратном порядке. Найти число.
Решение.
Пусть искомое число имеет вид 10х + ^. Согласно условию,
х2+.у =13
Л . Отсюда х=?3, ? = 2.
10х + у -9 = 10д> + х
Ответ: 32.
13.028. Числители трех дробей пропорциональны числам 1, 2, 5, а знаменатели пропорциональны соответственно числам 1, 3, 7. Среднее арифметическое этих дробей равно 200/441. Найти эти дроби.
Решение.
Искомые дроби имеют вид:
х 2х 5х
х 2х 5х
у Зу 7у _ 200
3	“ 441 ’
7; з7; 77 •По условию
х _ 4 2х откуда
8 5х
21’ 1у
20
49’
4 8 20
От“т
13.029. В штате гаража числится 54 шофера. Сколько свободных дней может иметь каждый шофер в месяц (30 дней), если ежедневно 25% автомашин из имеющихся 60 остаются в гараже для профилактического ремонта?
Решение.,
Пусть х свободных дней в месяц имеет каждый шофер. Тогда рабочих дней — 30-х. По условию (30-х)-54 = 60 0,75-30, откуда х = 5.
Ответ: 5.
13.030. Три бригады рабочих сделали насыпь. Вся работа оценена в 325 500 руб. Какую зарплату получит каждая бригада, если первая состояла из 15 человек и работала 21 день, вторая — из 14 человек и работала 25 дней, а число рабочих третьей бригады, работавшей 20 дней, на 40% превышало число рабочих первой бригады?
Решение.
Пусть х руб. получит один человек за один день работы. Тогда первая бригада получитх • 15 *21 руб.; вторая —х • 14 -25 руб.; третья — х • 1,4 - 15 • 20 руб. По условию 15 • 21х 4- 14 • 25х + .1,4 * 15 • 20х = = 325 500, откуда х = 300. Значит, первая бригада получит 15-21 • 300 = = 94 500 руб.; вторая — 14 - 25 • 300 = 105 000 руб.; третья — 1,4 • 15 х х 20 • 300 = 126 000 руб.
Ответ: 126 000, 105 000 и 94 500 руб.
13.031. Группа студентов во время каникул совершила поход по Подмосковью. Первые 30 км они прошли пешком, 20% оставшейся части маршрута проплыли на плоту по реке, а затем опять шли пешком, пройдя расстояние в 1,5 раза больше того, которое проплыли по реке. Остальной путь проехали за 1 ч 30 мин на попутном грузовике, который шел со скоростью 40 км/ч. Какова длина всего маршрута?
Решение.
Пусть х км — длина всего маршрута. Тогда студенты проплыли на плоту (х - 30) • 0,2 км, затем прошли пешком еще 1,5(х-30) 0,2 км. По условию 30 + (х-30)0,2 + 1,5(х-30) 0,2+40 1,5 = х, откуда х = 150 км.
Ответ: 150 км.
13.032. За 3,5 ч работы один штамповочный пресс может изготовить 42% всех заказанных деталей. Второй пресс за 9 ч работы может изготовить 60% всех деталей, а скорости выполнения работы на третьем и на втором прессах относятся как 6 : 5. За какое время
будет выполнен весь заказ, если все три пресса будут работать одновременно?
Решение.
Пусть х деталей — весь заказ. Тогда скорость работы первого прес-
0,42х	0,6х	6 0,6х
са — “ЧТ” дет/ч; второго — —— дет/ч; третьего — - • —— дет/ч. Зна-
чит, все три пресса, работая одновременно, выполнят весь заказ за
—-----—------------ = 3,75 (ч) = 3 ч 45 мин.
0,6х 0,42х 6 0,6х	’ v 7
—-----+ -2--+-------’--
9	3,5	5 9
Ответ: за 3 ч 45 мин.
13.033. Каждая из двух машинисток перепечатывала рукопись объемом 72 страницы. Первая машинистка перепечатывала 6 страниц за то же время, за которое вторая перепечатывала 5 страниц. Сколько страниц перепечатывала каждая машинистка в час, если первая закончила работу на 1,5 ч быстрее второй?
Решение.
Пусть х страниц в час перепечатывала первая машинистка,
5	72
тогда вторая— — х . Первая машинистка работала — часов; вто-6	х
72	72	72
рая--------часов. По условию — = -z-----1,5, откуда х = 9,6 (стр/ч);
5	х
-х	-х
6	6
вторая перепечатывала -7-9,6 = 8 стр/ч.
6
Ответ: 8 и 9,6 стр/ч.
13.034. В магазин для продажи поступили учебники по физике и математике. Когда продали 50% учебников по математике и 20% учебников по физике, что составило в общей сложности 390 книг, то учебников по математике осталось в три раза больше, чем по физике. Сколько учебников по математике и сколько по физике поступило в продажу?
Решение.
Пусть в продажу поступило х учебников по математике, у учеб
ников по физике. Продали 0,5х+0^^ = 390 учебников. Осталось
0,5х учебников по математике, 0,8^ учебников по физике. По усло-
°,5х . n
зию ~ = i . Решив систему 0,8у
0,5х +0^ = 390
0,5х _ 3	, получим х = 720;
0,8у ”
у = 150.
Ответ: 720 и 150.
13.035. Обувная фабрика за первую неделю выполнила 20% месячного плана, за вторую произвела 120% количества продукции, выработанной за первую неделю, а за третью неделю — 60% продукции, выработанной за первые две недели вместе. Каков месячный план выпуска обуви, если известно, что для его выполнения необходимо за последнюю неделю месяца изготовить 1480 пар обуви?
Решение.
Пусть х — месячный план выпуска обуви. За первую неделю фабрика выпустила 0,2х пар обуви, за вторую— Ц0,2х; за третью— 0,б(0,2х+1,2 0,2х) пар. По условию
0,2х+1,2 0,2х+0,б(0,2х+1,2 0,2х)+1480 = х, откуда х = 5000 пар.
Ответ: 5000.
13.036. Свежие грибы содержат по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
Решение.
Пусть х кг сухих грибов получится из 22 кг свежих. Тогда воды в сухих грибах — ОД 2х. По условию х - 0,12х = 22(1 - 0,9); 0,88х = 2,2 . Откуда х = 2,5 кг.
Ответ: 2,5 кг.
13.037. Одна мельница может смолоть 19 ц пшеницы за 3 ч, другая — 32 ц за 5 ч, а третья — 10 ц за 2 ч. Как распределить 133 т пшеницы между этими мельницами, чтобы, одновременно начав работу, они окончили ее также одновременно?
Решение.
Пусть х ч — время работы мельниц. Первая мельница смелет за
19	32	Ю
это время —х ц пшеницы; вторая— —х ц; третья— — х ц. По 3	5	2
19	32	10
условию — х+—х + —х = 1330, откуда х = 75 ч. Значит, первая
10	32
мельница смелет — 75 = 475 ц; вторая— — -75 = 480 ц; третья —
— 75 = 375 ц.
Ответ: 475, 480 и 375 ц.
13.038. В трех секциях спортивной школы было 96 спортсменов. Число членов конькобежной секции составляло 0,8 числа членов лыжной, а число членов хоккейной секции составляло 33-% сум-
марного числа членов двух первых секций. Сколько спортсменов было в каждой секции?
Решение.
Пусть х чел. — число членов лыжной секции; 0,8х чел. — конь-
Зз|
кобежной секции; —-(х + 0,8х) чел. — хоккейной секции. По усло-100
(х + 0,8х)=96, откуда х = 40 чел. в лыжной сек-
вию х+0,8х +—-100
ции. В конькобежной секции 0,8-40 = 32 чел.; в хоккейной — 96-40-32 = 24 чел.
Ответ: 40, 32 и 24 чел.
13.039. За первый квартал автозавод выполнил 25% годового плана выпуска автомашин. Число машин, выпущенных за второй, третий и четвертый кварталы, оказалось пропорционально числам 11,25, 12 и 13,5. Определить перевыполнение годового плана в процентах, если во втором квартале автозавод дал продукции в 1,08 раза больше, чем в первом.
Решение.
Пусть х — годовой план автозавода. За первый квартал завод выполнил 0,25х плана, за второй квартал завод выпустил 11,25>> машин, что составило 1,08 • 0,25х плана: 11,25у = 1,08 - 0,25х = 0,27х , отсюда у = 0,024х. За третий квартал завод выполнил 12у = 12-0,024х = 0Д88х плана, за четвертый— 13,5у = 0,324х пла
на. За весь год завод выполнил 0,25х + 0,27x4- 0,288х + 0,324х = 1,132% плана, т.е. он перевыполнил план на 0,132 = 13,2%.
Ответ: 13,2%.
13.040. Трое сотрудников получили премию в размере 2970 руб., причем второй получил 1/3 того, что получил первый, и еще 180 руб., а третий получил 1/3 денег второго и еще 130 руб. Какую премию получил каждый?
Решение.
Пусть х руб. — премия первого сотрудника. Тогда — х +180 руб. —
второго; —х + 180 | + 130 руб. — третьего. По условию
3<3	)
х+-х + 180 + -| —х + 180 | + 130 = 2970, откуда х= 1800руб. — премия
3	3<3	)
первого сотрудника; ^ 1800 + 180 = 780 руб. — премия второго;
^•780 + 130 = 390 руб. — третьего.
Ответ: 1800, 780 и 390 руб.
13.041. Смешали 30%-ный раствор соляной кислоты с 10%-ным и получили 600 г 15%-ного раствора. Сколько граммов каждого раствора было взято?
Решение.
Пусть взяли х г 30%-ного раствора соляной кислоты и (600 - х) г — 10%-ного раствора. Масса соляной кислоты в 30%-ном растворе составляет 0,Зх г; в 10%-ном — 0,1(600 -х) г. В полученном 15%-ном растворе масса соляной кислоты составляет 0,15 • 600 = 90 г. По условию 0,Зх 4- 0,1(600 - х) = 90, откуда х = 150 г 30%-ного раствора; 600 - 150 = 450 г 10%-го раствора.
Ответ: 150 и 450 г.
3 5 3
13.042. Площади трех участков земли относятся как 2 —: 1 —: 1—. Из-
вестно, что с первого участка собрано зерна на 72 ц больше, чем со второго. Найти площадь всех трех участков, если средняя урожайность составляет 18 ц с 1 га.
Решение.
Пусть х , У , z — площади участков. Тогда х/у = 6/4, y/z •- 4/3, откуда х = 6к, У = 4к, z = Зк • По условию (б£-4А?)-18 = 72, к = 2 и площадь всех трех участков составляет х 4- у + z = 2(б+4 + 3)=26 (га).
Ответ: 26 га.
13.043. Расстояние между Москвой и Смоленском по железной дороге равно 415 км. На этом пути расположены города Можайск и Вязьма. Расстояние между Москвой и Можайском относится к расстоянию между Можайском и Вязьмой как 7:9, а расстояние между Можайском и Вязьмой составляет 27/35 расстояния между Вязьмой и Смоленском. Найти расстояния между каждыми двумя соседними городами.
Решение.
Пусть х км — расстояние между Можайском и Вязьмой. Тогда
км— расстояние между Москвой и Можайском;
35
— х км —
_ 7 35
между Вязьмой и Смоленском. По условию -- х + х + — х = 415, отку-
У	2.7
да х = 135 км. Между Москвой и Можайском —
7-135 = 105 КМ; 9
между Вязьмой и Смоленском — — 135 = 175 км.
Ответ: 105, 135 и 175 км.
13.044. В магазин привезли сахар и сахарный песок в 63 мешках, всего 4,8 т, причем мешков с сахарным песком было на 25% больше, чем с сахаром. Масса каждого мешка с сахаром составляла 3/4 массы мешка с сахарным песком. Сколько привезли сахара и сколько сахарного песка?
Решение.
Пусть привезли х мешков сахара; 1,25х мешков сахарного песка. По условию х + 1,25х = 63, откуда х = 28 мешков сахара; 1,25 -28 = 35 мешков сахарного песка. Теперь пусть всего У т сахар-
у
ного песка; 4,8т— сахара. Тогда — т— масса одного мешка
сахарного песка;
4,8-у
28
т— масса мешка сахара. По условию
~	- , откуда у = 1,8 т сахарного песка; 4,8 -1,8 = 3 т сахара.
Ответ: 1,8 и Зт.
13.045. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Решение.
Первоначально в сплаве 36 0,45 = 16,2 кг меди. Пусть добавили х кг меди. Тогда масса нового сплава 36+ х кг, масса меди в нем 16,2 + х кг. По условию 16,2 + х = (36 + х) 0,6, откуда х = 13,5 кг.
Ответ: 13,5 кг.
13.046. Охотничий порох состоит из селитры, серы и угля. Масса серы должна относиться к массе селитры как 0,2:1,3, а масса угля
должна составлять массы серы и селитры вместе. Сколько
пойдет каждого из веществ на приготовление 25 кг пороха?
Решение.
02
Пусть х кг— масса селитры. Тогда — х кг— масса серы;
02	V1!	02	(	0,2 А 1	„
— X   КГ—угля. По условию х+—х+ х+—х — = 25, 13	) 100	13	I	13 ) 9
02	1
откуда х = 19,5 кг селитры. Тогда уу-19,5 = 3 кг серы; (3+19,5)-= 2,5 кг
угля.
Ответ: 3 кг серы; 19,5 кг селитры; 2,5 кг угля.
13.047. Музыкальный театр объявил конкурс для поступления в оркестр. Первоначально предполагалось, что число мест для скрипачей, виолончелистов и трубачей распределится в отношении 1,6:1:0,4. Однако затем было решено увеличить прием, и в результате скрипачей было принято на 25% больше, а виолончелистов на 20% меньше, чем ранее намечалось. Сколько музыкантов каждого жанра было принято в оркестр, если всего приняли 32 человека?
Решение.
Пусть предполагалось набрать 1,6х скрипачей, х — виолончелистов, 0,4х трубачей. Тогда набрали 1,25 • 1,6х скрипачей, (1 - 0,2)х виолончелистов, 0,4х трубачей. По условию 1,25 1,6х + (1-0,2)х + 0,4х = 32, откуда х = 10. Значит, набрали 1,25 • 1,6 • 10 = 20 скрипачей; 0,8 • 10 = 8 виолончелистов; 0,4 • 10 = 4 трубача.
Ответ: 20 скрипачей, 8 виолончелистов, 4 трубача.
13.048. Длина Дуная относится к длине Днепра как 19/3 : 5, а длина Дона относится к длине Дуная как 6,5 : 9,5. Найти протяженность каждой из рек, если Днепр длиннее Дона на 300 км.
Решение.
Пусть х км — длина Дуная. Тогда длина Днепра —
5 ----х км, длина 19/3
Дона— -^-х км‘ П°условию у^у-х--^-х = 300, откуда х = 2850 км —
длина Дуная. Тогда длина Днепра — — -2850 = 2250 км, длина Дона —
—2850 = 1950 км.
9,5
Ответ: 2850, 2250 и 1950 км.
13.049. Первое из неизвестных чисел составляет 140% второго, а отношение первого к третьему равно 14/11. Найти эти числа, если разность между третьим и вторым на 40 единиц меньше числа, составляющего 12,5% суммы первого и второго чисел.
Решение.
г.	1	и
Пусть х — первое число, Тогда — х — второе число, — х — третье
число. По условию 11 х - А. х + 40 = 0,125^х + -j^ х J откуда х = 280. Вто-
рое число----— = 200; третье — — • 280 = 220.
Ответ: 280, 200, 220.
13.050. Заработные платы рабочего за октябрь и ноябрь относились как 3/2 : 4/3, а за ноябрь и декабрь как 2:8/3. За декабрь он получил на 450 руб. больше, чем за октябрь, и за перевыполнение квартального плана
рабочему начислили премию в размере 20% его трехмесячного заработка. Найти размер премии.
Решение.
Пусть х руб. — заработная плата рабочего за ноябрь. Тогда за октябрь
ГЗ 4Л 9	с (8	4	„
она составляет —: — х = —х руб.; за декабрь — -:2 х = -х руб. По
А2 3J 8	<3 J 3
4	9
условию — х = — х + 450, откуда х = 2160 руб. — заработная плата за но-3	8
ябрь; -—2160 = 2430 руб. — за октябрь; —♦ 2160 = 2880 руб.—за декабрь.
8 '	3
Тогда размер премии — (2160 + 2430 + 2880) • 0,2 = 1494 руб.
Ответ*. 1494 руб.
13.051. По наклоненной доске длиной 6 м катятся два цилиндра, у одного из которых длина окружности равна 3 дм, а у другого 2 дм. Можно ли увеличить длины окружностей обоих цилиндров на одну и ту же величину так, чтобы на том же пути один из них сделал на 3 оборота больше другого?
Решение.
Допустим, что длины окружностей можно увеличить на х дм. Тогда
60	-	60 „
первый цилиндр сделает ---- оборотов, второй--------. По условию
3 + х	2+х
60	-	60	2	1 Л Л ть
----+ 3 = ---’ 0ТКУда х + 5х-14 = 0. Решив это уравнение, получим,
что длины окружностей можно увеличить на х = 2 дм.
Ответ*, можно увеличить на 2 дм.
13.052. Искусственный водоем имеет форму прямоугольника с разностью сторон 1 км. Два рыбака, находящиеся в одной вершине этого прямоугольника, одновременно отправились в пункт, расположенный в противоположной вершине. При этом один рыбак поплыл напрямик по диагонали, а второй пошел пешком вдоль берега. Определить размеры водоема, если каждый рыбак передвигался со скоростью 4 км/ч и один из них прибыл к месту назначения на 30 мин раньше другого.
Решение.
Пусть х км — длина меньшей стороны водоема, х+1 км — длина второй стороны (рис. 13.1). Тогда первый рыбак проплыл -у/х2 + (х+1)2 км, а второй прошел х + х+1 км. По условию
(х + х+1)/4 - 0,5 = -Jx2 + (х +1)2 Д, откуда х = 3 км.
Ответ: 3x4 км.
13.053. Кристалл, находясь в стадии формирования, равномерно наращивает свою массу. Наблюдая формирование двух кристаллов, заметили, что за год первый кристалл увеличил свою первоначальную массу на 4%, а второй— на 5%, в то время как прирост массы первого кристалла за 3 месяца оказался равным приросту массы второго кристалла за 4 месяца. Каковы были первоначальные массы этих кристаллов, если известно, что после того как каждая из них увеличилась на 20 г, отношение массы первого кристалла к массе второго кристалла достигло числа 1,5?
Решение.
Пусть а — первоначальная масса первого кристалла; Ь — второго; и пусть х — прирост массы первого кристалла за 3 месяца. За год прирост массы первого кристалла составляет 4х; второго кристалла— Зх. По условию л+4х = 1,04л, b + 3x = 1,05ft. По условию
а +20 также -—— ft+20
а + 4х = 1,04а
= 1,5. Решив систему ft+ 3х = 1,05ft находим, что а +20 = 1,5(6+20),
а = 100 г; ft = 60 г.
Ответ: 100 и 60 г.
13.054. Один фермер получил средний урожай гречихи 21 ц с 1 га, а другой, у которого под гречихой было на 12 га меньше, добился среднего урожая 25 ц с 1 га. В результате у второго фермера было собрано на 300 ц гречихи больше, чем у первого. Сколько центнеров гречихи было собрано каждым фермером?
Решение.
Составим следующую таблицу:
Фермер	Площадь, га	Урожайность, ц/га	Масса, ц
Первый	X	21	21х
Второй	х-12	25	25(х-12)
По условию 25(.v-12)-21.v = 300, откуда х = 150. Тогда 21х = 3150 (U). а 25(л--12)=3450 ц.
Ответ: 3150 и 3450 ц.
13.055. На вагоноремонтном заводе в определенный срок должно быть отремонтировано 330 вагонов. Перевыполняя план ремонта в среднем на 3 вагона в педелю, на заводе уже за две недели до срока отремонтировали 297 вагонов. Сколько вагонов в неделю ремонтировали на заводе?
Решение.
Пусть х вагонов в неделю ремонтировали на заводе, а должны были ремонтировать по плану— (х-3). Тогда срок выполнения пла-
330	f 330
па — ------ недель. По условию------2 Lv = 297. Отсюда х = 33.
х	х—3 J
Ответ: 33.
13.056. На расстоянии j км 1*рузовой автомобиль расходует бензина на а л больше, чем легковой. Расходуя 1 л бензина, грузовой автомобиль проходит по той же дороге на b км меньше, чем легковой. Каков расход бензина каждого из этих автомобилей па расстоянии s км?
Решение.
Пусть л л бензина на s км расходует грузовой автомобиль. х-а л — легковой. Тогда, расходуя I л бензина, грузовой автомо
биль проходит — км, а легкгвой— —— КМ’ Условию
.г , л	. ->	, л	ab + ^a2b2 +4sab
—+b =----. Отсюда hx" -abx-sa = 0, откуда х =----------л
х х-а	2Ь
бензина расходует грузовой автомобиль па 5 км.
ab + >la2b2 + 4sab	~ab+>la2h2 +4sab
Ответ: -------------- и---------------- л.
2b	2b
13.057. Две силы приложены к одной точке и направлены под прямым углом. Модуль одной из них на 4 Н больше модуля другой, а модуль равнодействующей на 8 Н меньше суммы модулей данных сил. Найти модули данных сил и их равнодействующей.
Решение.
Пусть л* Н — модуль одной силы, а*+ 4 Н— второй. Тогда модуль равнодействующей силы— x+.v + 4-8 Н. Из рисунка 13.2 внд-
но, что х24-(х4-4)2 =(х4-х4-4-8)2, откуда х = 12 Н. Модуль второй силы— 16 Н, модуль равнодействующей силы — 20 Н.
Ответ: 12, 16 и 20 Н.
13.058. В лаборатории измеряется скорость, с которой распространяется звук вДоль стержней, сделанных из разных материалов. В первом
опыте оказалось, что весь путь, состоящий из трех последовательно соединенных стержней, звук проходит за время а с, а путь, состоящий из второго и третьего стержней, звук проходит в два раза быстрее, чем один первый стержень. В другом опыте второй стержень заменили новым, и тогда последовательное соединение из трех стержней звук прошел за время b с, а соединение из первого и второго стержней вдвое медленнее, чем один третий стержень. Найти скорость распространения звука в новом стержне, если его длина / м.
Решение.
Пусть Zj, t2, t4 соответственно — это время прохождения звука вдоль 1-го, 2-го, 3-го, нового стержней. .Четвертый стержень — это новый, которым мы заменяем второй во втором опыте. По условию в первом опыте:
/| 4-t2 4" /3 — а,	2.
во втором опыте
Zj4-/44-/3=6,	„ Л
=> 3/j 4-3/4 = 26; /14-/4=2/3,
Тогда скорость распространения звука в новом стержне _ I _ 3/
V~ t4~l(b-a}w'c^b>a.
31
Ответ:	м^с’ имеет смысл при Ь> а .
13.059. По обе стороны улицы длиной 1200 м лежат прямоугольные полосы земли, отведенные под участки, одна — шириной 50 м,
а другая — 60 м. На сколько участков разбит весь поселок, если более узкая полоса содержит на 5 участков больше, чем широкая, при условии, что на узкой полосе каждый участок на 1200 м2 меньше, чем каждый участок на широкой полосе?
Решение.
Пусть х участков на широкой полосе, х + 5 участков — на узкой, ум — ширина участка на узкой полосе, у + 1200 м — на широкой.
Г(х + 5)у = 1200-50,
По условию j j	12QQ эд "ешив системУ> находим х = 20 учас-
тков на широкой полосе. Значит, на узкой — 25 участков. Всего 20 + 25 = = 45 участков.
Ответ: на 45.
13*060. Груз массой 60 кг давит на опору. Если массу груза уменьшить на 10 кг, а площадь опоры уменьшить на 5 дм2, то масса, приходящаяся на каждый квадратный дециметр опоры, увеличится на 1 кг. Определить площадь опоры.
Решение.
Пусть х дм2 — площадь опоры. Тогда — кг/дм2 — масса, при-х
ходящаяся на 1дм2 опоры. После уменьшения массы груза и площа-
50	7	50	60
ди опоры эта масса равна ----кг/дм . По условию------1=—, от-
х-5	х-5 х
кудах = 15.
Ответ: 15 дм2.
13.061. Для оплаты пересылки четырех бандеролей понадобились 4 различные почтовые марки на общую сумму 84 коп. Определить стоимость марок, приобретенных отправителем, если эти стоимости составляют арифметическую прогрессию, а самая дорогая марка в 2,5 раза дороже самой дешевой.
Решение.
Пусть х коп. — стоимость самой дешевой марки, x + J, x + 2J, х + 3d — стоимости остальных марок. По условию
fx + x + d + x + 2d + x + 3d = 84,
1 п о с	откуда х = 12; d = 6. Стоимости ма-
[х + За =2,5х,	7
рок: 12 коп., 18 коп., 24 коп, 30 коп.
Ответ: 12 коп., 18 коп., 24 коп, 30 коп.
13.062. Ученик токаря вытачивает шахматные пешки для определенного числа комплектов шахмат. Он хочет научиться изготавливать ежедневно на 2 пешки больше, чем теперь; тогда такое же задание он выполнит на 10 дней быстрее. Если бы ему удалось научиться изготовлять ежедневно на 4 пешки больше, чем теперь, то срок выполнения такого же задания уменьшился бы на 16 дней. Сколько комплектов шахмат обеспечивает пешками этот ученик, если для каждого комплекта нужно 16 пешек?
Решение.
Пусть токарь обеспечивает пешками х комплектов шахмат. Он выполняет задание за у дней. По условию
— + 2 (у-10) = 16х, У Л
—+ 4|(^-16) = 16л,
. У J
откуда х = 15.
Ответ: 15.
13.063. В зрительном зале клуба было 320 мест, расположенных одинаковыми рядами. После того как число мест в каждом ряду увеличили на 4 и добавили еще один ряд, в зрительном зале стало 420 мест. Сколько стало рядов в зрительном зале?
Решение:
320
Пусть в зрительном зале было х рядов;---- число мест в одном
х
ряду. После того как число мест в ряду увеличили на 4 и добавили
Г 320 А
один ряд, всего мест в зале стало -+ 4 (х +1) = 420, откуда х = 20.
V х )
Значит, в зрительном зале теперь имеется 21 ряд.
Ответ: 21.
13.064. Запас сена таков, что можно ежедневно выдавать на всех лошадей 96 кг. В действительности ежедневную порцию каждой лошади смогли увеличить на 4 кг, так как две лошади были проданы. Сколько лошадей было первоначально?
Решение.
Пусть первоначально было х лошадей. Ежедневная порция
96
каждой лошади была — кг. Так как две лошади были проданы дру
гому колхозу, то их стало х-2, а ежедневная порция каждой лоша-
ди стала —+4 кг. По условию + 4 |(х-2)=96, откуда х = 8-
X	\х )
Ответ: 8.
13.065. Сочинение писали 108 экзаменующихся. Им было роздано 480 листов бумаги, причем каждая девушка получила на один лист больше каждого юноши, а все девушки получили столько же листов, сколько все юноши. Сколько было девушек и сколько юношей?
Решение,
Пусть х было девушек, Ю8-х — юношей. Юноши получили
по У листов, а девушки — по у+1 листов. По условию »
(х(у+1)+(108-х)у = 480,
1х(}’+1)=(108-х)у	откуда х = 48• Девушек было 48, юношей —
108-48 = 60-
Ответ: 48 и 60.
13.066. На машиностроительном заводе разработали новый тип деталей для генераторов. Из 875 кг металла изготовляют теперь на три детали нового типа больше, чем деталей старого типа изготовляли из 900 кг. Какова масса детали нового и старого типов, если две детали нового типа по массе меньше одной детали старого типа на 0,1т?
Решение.
Пусть х кг— масса детали нового типа, у кг— старого. По
875
условию у-2х = 100. Из 875 кг изготовляют —деталей нового
875 900
~	~ ~ 3. Решив систему
АЛА	900
типа, из 900 кг изготовляли - деталей старого типа. По условию
У
875 9ОО 3
х у ’ находим х = 175 кг, у-2х = 100,
7 = 450 кг.
Ответ: 175 и 450 кг.
13.067. В первый день спортивных соревнований не выполнили зачетные нормы и выбыли из дальнейшей борьбы 1/6 часть состава
команды юношей и 1/7 часть состава команды девушек. В течение остального периода соревнований из обеих команд выбыло из-за невыполнения норм одинаковое количество спортсменов. Всего к концу соревнований не выполнили зачетные нормы 48 человек из команды юношей и 50 человек из команды девушек, но из общего количества спортсменов, выполнивших зачетные нормы, девушек оказалось вдвое больше, чем юношей. Какова была первоначальная численность команд?
Решение'.
Пусть зачетные нормы выполнили х юношей и 2х девушек. Тогда первоначальная численность команд составляет х + 48 юношей и 2х + 50 девушек. По окончании первого дня соревнований выбыло -^-(х + 48) юно
шей и — (2х + 50) девушек. Позже еще выбыло из обеих команд одинако-
вое количество спортсменов, поэтому 48 — (х + 48) = 50—(2х + 50), от-6	7
кудах = 24. Итак, первоначальная численность команд — 72 и 98 человек.
Ответ: 72 юноши и 98 девушек.
13.068. Рабочий час мастеров Я и В оплачивается неодинаково, но оба мастера работали одинаковое число часов. Если бы А работал на один час меньше, а В — на пять часов меньше, то А заработал бы 720 руб., а В — 800 руб. Если бы, наоборот, А работал на пять часов меньше, а В — на один час меньше, то В заработал бы на 360 руб. больше, чем А. Сколько заработал каждый мастер в действительности?
Решение:
Пусть мастера работали х часов. Если бы А работал на 1 час
720	с с
меньше, то он зарабатывал бы --- руб. в час; если бы В работал на
х-1
5 часов меньше, то он зарабатывал бы
800
х-5
руб. в час. По условию
800	720
	(х-1)	(х-5) = 360, откудах = 25. В действительности Л за-х-5---------х-1
720	800
работал ——--25 = 750 руб., В заработал -^-*25 = 1000 руб.
Ответ: 750 и 1000 руб.
13.069. В одном бассейне имеется 200 м3 воды, а в другом — 112 м3. Открывают краны, через которые наполняются бассейны. Через сколько часов количество воды в бассейнах будет одинаковым, если во второй бассейн вливается в час на 22 м3 больше воды, чем в первый?
Решение.
Пусть количество воды в бассейнах станет одинаковым через х часов. Пусть У м3 вливается воды в первый бассейн в час, у+22 м3 — во второй. По условию 200+ху = 112+х(у +22), откуда х = 4-
Ответ: через 4 ч.
13.070. Через час после начала равномерного спуска воды в бассейне ее осталось 400 м3, а еще через три часа — 250 м3. Сколько воды было в бассейне?
Решение.
Пусть х м3 воды было в бассейне. За 1 час спуска из бассейна вылили (х-400) м3; за 4 часа спуска — (х-250) м3. По условию
х-250
х -400 = —-—, откуда х = 450 -
Ответ: 450 м3.
13.071. Для перевозки 60 т груза из одного места в другое затребовали некоторое количество машин. Ввиду неисправности дороги на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, поэтому было дополнительно затребовано 4 машины. Какое количество автомашин было затребовано первоначально?
Решение.
Пусть х машин было затребовано первоначально. Одна маши-60
на может перевозить — т груза. Ввиду неисправности дороги зат-
,	л	(60
рсбовали х+4 машины, а на одну машину грузили---------0,5 т
V х )
<60 Y к
груза. По условию I---0,5 Их+4)= 60. Отсюда х = 20-
Ответ: 20.
13.072. Город С, расположенный между пунктами А и В, снабжается газом из этих пунктов, расстояние между которыми 500 км. Из резервуара А в каждую минуту откачивается 10000 м3 газа, а из
резервуара В — на 12% больше. При этом утечка газа в каждой магистрали составляет 4 м3 на километр трубы. Зная, что в город С газ поступает из резервуаров АиВ поровну, найти расстояние между городом С и пунктом А .
Решение.
Пусть х км — расстояние между А и С, 500-х км — между С и В • Учитывая утечку газа, из А в С поступает Ю000-4х м3 газа, из В в С поступает 10000 1,12-4(500-х) м3 газа. По условию 10000 - 4х = 1,12 Ю000-4(500-х), откуда х = 100-
Ответ: 100 км.
13.073. Имеются два куска кабеля разных сортов. Масса первого куска равна 65 кг; другой, длина которого на 3 м больше длины первого и масса каждого метра которого на 2 кг больше массы каждого метра первого куска, имеет массу 120 кг. Вычислить длины этих кусков.
Решение.
Пусть хм— длина первого куска кабеля, х+3 м— второго.
65
Масса каждого метра первого куска кабеля — — кг. По условию масса второго куска кабеля— (х+3)^^ + 2^ = 120, откуда х = 5 м или х = 19,5 м. Длина второго куска кабеля 8 м или 22,5 м.
Ответ: 5 и 8 м или 19,5 и 22,5 м.
13.074. В швейный цех поступило три кипы бельевого материала, всего 5000 м. В первой кипе количество материала было в три раза меньше, чем во второй, а в третьей — 22% всего количества. Из материала первой кипы сшили 150 простыней и 240 наволочек. Для изготовления одной простыни требовалось на 3,25 м больше материала, чем для изготовления одной наволочки. Из скольких метров материала шьется одна наволочка?
Решение.
Пусть х м материала было в первой кипе, Зх м — во второй, 5000 • 0,22 = 1100 м — в третьей. По условию х + Зх +1100 = 5000 , откуда х = 975 м — в первой кипе. Пусть одна наволочка шьется из У м материала, а простыня — из 3,25 + у м. На простыни всего израсхо
довали (3,25 +у)-150 м материала, на наволочки — 240_у м. По условию 150(3^5+у)+240^ = 975 , откуда у = 1,25.
Ответ: из 1,25 м.
13.075. Двое рабочих за смену вместе изготовили 72 детали. После того как первый рабочий повысил производительность труда на 15%, а второй — на 25%, вместе за смену они стали изготовлять 86 деталей. Сколько деталей изготовляет каждый рабочий за смену после повышения производительности труда?
Решение.
Первоначально рабочие изготовляли за смену х и 72-х деталей, азатем 1,15х и 1,25(72-х) деталей. По условию 1,15х+90-Ц5х = 86; 0Дх = 4; х = 40; 1,15-40 = 46.
Ответ: 46 и 40 деталей.
13.076. Сбор кукурузы с полей животноводческой фермы составлял 4340 ц. На следующий год запланировано получить 5520 ц кукурузы за счет увеличения площади на 14 га и повышения урожайности на 5 ц с 1 га. Определить площадь, занятую под кукурузу, и урожайность в центнерах с 1 га (урожай был меньше 40 ц с 1 га).
Решение.
4340
Пусть х га— площадь, занятая под кукурузу, ------- ц/га —
х
урожайность. На следующий год площадь х+14 га, а урожай-
4340	(4340	Y	\
ность ----+ 5 ц/га. По условию ------+5 их+14) = 5520, откуда
х	V х	J
4340
х = 98 га или х = 124 га. Урожайность ——«44,3 ц/га или
4340 _ , ---- = 35 ц/га.
124
Ответ: 124 га; 35 ц с 1 га.
13.077. Старший брат на мотоцикле, а младший на велосипеде совершили двухчасовую безостановочную поездку в лес и обратно. При этом мотоциклист проезжал каждый километр на 4 мин быстрее, чем велосипедист. Сколько километров проехал каждый из братьев за 2 ч, если известно, что путь, проделанный старшим братом за это время, на 40 км больше?
Решение.
Пусть .v км проехал младший брат, х+40 км — старший. Млад-120	120
ший брат проезжал 1 км за мин, старший за мин. По
120 л 120
условию------4 = —-—, откуда д = 20 •
X 40+х
Ответ: 20 и 60 км.
13.078. Турист ехал на автомобиле 5/8 всего пути, а остальную часть— на катере. Скорость катера на 20 км/ч меньше скорости автомобиля. На автомобиле турист ехал на 15 мин дольше, чем на катере. Чему равны скорость автомобиля и скорость катера, если весь путь туриста равен 160 км?
Решение.
5
Турист проехал на автомобиле 160 -= 100 км, а на катере о
160-100 = 60 км. Пусть х км/ч—скорость катера, 20+ х км/ч —
„	,	100	60
автомобиля. Турист ехал на автомобиле ч, на катере — — ч.
По условию —--------= 0,25, откуда х = 60 или х = 80.
20+х х
Ответ: скорость автомобиля 100 или 80 км/ч; скорость катера 80 или 60 км/ч.
13.079. Первый турист, проехав 1,5 ч на велосипеде со скоростью 16 км/ч, делает остановку на 1,5 ч, а затем продолжает путь с первоначальной скоростью. Спустя 4 ч после отправки в дорогу первого туриста вдогонку ему выезжает на мотоцикле второй турист со скоростью 56 км/ч. Какое расстояние они проедут, прежде чем второй турист догонит первого?
Решение.
График движения изображен на рис. 13.3. Пусть t — время (в часах), за которое второй турист догонит первого. Так как vBC/1 =16 км/ч,
vM0T = 56 км/ч, то 5ВСЛ = (2,5+/)16, SM0T = 56/. Отсюда 56/ = 16/+40,
т.е. / = 1 (ч). Итак, S = 56 км.
Ответ: 56 км.
13.080. Из поселка, расположенного в 60 км от города, сегодня должен приехать отец студентки, который хотел посетить воскресную лекцию. Однако лекция перенесена на другой день. Чтобы
предупредить отца об этом, дочь поехала по шоссе ему навстречу. При встрече выяснилось, что отец и дочь выехали на мопедах одновременно, но средняя скорость дочери была вдвое большей. Возвращаясь после встречи, каждый из них увеличил первоначальную скорость на 2 км/ч, и дочь прибыла в город на 5 мин позже, чем отец в поселок. С какой средней скоростью отец и дочь ехали первоначально?
Решение.
Пусть х км/ч — первоначальная скорость отца, 2х км/ч — дочери. До встречи отец проехал у км, дочь— 60-у км. По условию
Z -	, откуда у = 20 км проехал отец, 40 км проехала дочь. На
х 2х
20	40
обратный путь отец затратил--- ч, дочь — т--- ч. По условию
х + 2	2х+2
40	20	1
-----------= —, откуда
2х + 2 х+2 12
х = 14-
Ответ: 14 и 28 км/ч.
13.081. Мотоциклист отправился из пункта А в пункт В , отстоящий от А на 120 км. Обратно он выехал с той же скоростью, но через час после выезда должен был остановиться на 10 мин. После этой остановки он продолжал путь до А, увеличив скорость на 6 км/ч. Какова была первоначальная скорость мотоциклиста, если известно, что на обратный путь он затратил столько же времени, сколько на путь от А до В1
Решение.
По условию АС = CD (рис. 13.4). Имеем АС = — , где х — пер-
л 1 120-х	120 7 120-х
воначальная скорость; С£> = 1 + —+----— => ----= — +-----7“ >
6	х + 6 х	6	х+6
откуда х = 48 (км/ч).
Ответ: 48 км/ч.
13.082. Две группы туристов должны идти навстречу друг другу из турбаз А и В, расстояние между которыми 30 км. Если первая группа выйдет на 2 ч раньше второй, то они встретятся через 2,5 ч после выхода второй группы. Если же вторая группа выйдет на 2 ч раньше, чем первая, то встреча произойдет через 3 ч после выхода первой группы. С какой средней скоростью идет каждая группа?
Решение.
Пусть х км/ч — скорость первой группы, у км/ч — скорость второй. Если первая группа выйдет раньше второй, то 2,5 у+(2,5+2)х = 30. Если вторая группа выйдет раньше первой, то 3х+(3+2)у = 30. Ре-
|2,5^+4,5х = 30, шив систему <	_	находим х = 5 км/ч, у = 3 км/ч.
[Зх + 5^ = ЗО,
Ответ: 5 и 3 км/ч.
13.083. Товарный поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда.
Решение.
Пусть скорость поезда до задержки равна х км/ч, а после нее — (х+15) км/ч. Тогда (рис. 13.5) АВ = у, СЕ = 60, CZ> = 60-y, X	%
60-- 4П	60	~	/-л
пп -_____5. ХЕ =------. Так как BD - АЕ, то-----2. ------ от-
х	х + 15	х х+15
куда х = 60 (км/ч).
Ответ: 60 км/ч.
13.084. Из пунктов А и В , расстояние между которыми 120 км, вышли одновременно навстречу друг другу два автобуса. В пути первый сделал остановку на 10 мин, второй— на 5 мин. Первый автобус прибыл в В на 25 мин раньше, чем второй прибыл в А.
Можно считать, что скорости движения автобусов были постоянными, причем скорость первого автобуса превышала скорость второго автобуса на 20 км/ч. Сколько времени продолжалась поездка пассажиров каждого из этих автобусов между пунктами А и В?
Решение.
Пусть х км/мин скорость вто
рого автобуса,
км/мин —
первого. Первый автобус был в
120	.	120 с
пути ----+10 мин; второй------+ 5 мин. По условию
1	х
х+з
120 с —+5-
= 25. Отсюда х = 1 км/мин. Первый автобус был в
“*+10
v+3
пути “““+10=100 мин = 1 ч40 мин; второй— ^+5=125 мин = 2ч 5 мин.
1+з
Ответ: 1 ч 40 мин и 2 ч 5 мин.
13.085. Два брата взяли свои велосипеды и одновременно тронулись в путь с намерением проехать 42 км. Старший брат на всем пути сохранял одну и ту же скорость* а младший брат каждый час отставал от старшего на 4 км. Но так как старший брат отдыхал в пути целый час, а младший— только 20 мин, то к финишу они прибыли одновременно. Сколько времени продолжалась поездка?
Решение.
Пусть х км/ч— скорость старшего брата, тогда (х-4) км/ч —
42 скорость младшего. Старший брат был в пути время	=—+1, а
младший — время /мл = ——- + - . По условию zCT = rMJ1, то есть
42	42	1	1 42 J
— + 1 =--т+т, отсюда х = 18 и ' = ! + —= 3т.
х х-4 3	18	3
Ответ: 3 ч 20 мин.
13.086. Задумано целое положительное число. К его записи присоединили справа цифру 7 и из полученного нового числа вычли квадрат задуманного числа. Остаток уменьшили на 75% этого остатка и еще вычли задуманное число. В окончательном результате получили нуль. Какое число задумано?
Решение.
Пусть задумано число х. Рассмотрим числа Юх + 7, 10х + 7-х2 и
остаток -^-(10^+7-х2). Тогда 7(10х + 7-х2)-х = 0, х2-6х-7 = 0=> 100;	4
=» х = 7-
Ответ: 7.
13.087. Задумано целое положительное число. К его записи присоединили справа цифру 5 и из полученного нового числа вычли квадрат задуманного числа. Разность разделили на задуманное число, а затем вычли задуманное число и в результате получили единицу. Какое число задумано?
Решение.
Пусть х — задуманное число. Тогда новое число можно пред-
ставить в виде Юх+5 • По условию-------------х = 1, отсюда х = 5 •
Ответ: 5.
13.088. На рис. 13.6 изображена окружность, касающаяся двух взаимно перпендикулярных осей Ох и Оу, и прямая АВ, касающаяся окружности в точке Р . Радиус окружности R = 10 см, а площадь треугольника ОАВ равна 600 м2. Найти координаты точек А , В , Р , учитывая, что О А > ОВ .
Решение.
Пусть а и b — длины катетов; тогда а-10+д-10 — длина гипотеку-зы. Отсюда (а + b- 20)2 -а2 +Ь2	= 600, откуда а = 40 (см),
Ь = 30 (см), т.е. Л(40; 0), В(0; 30). Находим угловой коэффициент прямой 3	3
АВ: к = -—. Значит, уравнение прямой АВ имеет вид у =—х + 30, а 4	4
уравнение окружности — вид (х-10)2 +(у-10)2 = 100. Решение системы этих уравнений дает координаты точки Р: Р(\6; 18).
Ответ: Л(40; 0), Я(0; 30), Р(16; 18).
13.089. Некоторое расстояние поезд прошел со скоростью 120км/ч. После этого расстояние, на 75 км большее, он прошел со скоростью 150 км/ч, а остальное расстояние, на 135 км меньшее пройденного, — со скоростью 96 км/ч. Как велик весь путь, если средняя скорость поезда оказалась равной 120 км/ч?
Решение.
Участок	Расстояние	Скорость	Время
Первый	х км	120 км/ч	X 	 ч 120
Второй	75 +хкм	150 км/ч	75+х 	 ч 150
Третий1	2х - 60 км	96 км/ч	2х-60 	ч 96
Весь путь равен х + 75 + х + 2х - 60 = 4х +15, все время равно х 75 + х 2х-60 43х-150 _	4х + 15
-и'	CpCT™c»pocn,„o«K	1^
1200
Отсюда х = 100 км. Весь путь составит: 4 • 100+ 15 = 415 км.
Ответ: 415 км.
13.090. Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы полученный новый сплав содержал 40% меди?
Решение.
Первоначально в сплаве было 12 * 0,45 = 5,4 кг меди. После добавления олова эти 5,4 кг меди составляют 40%. Значит, масса всего кус-
54
ка сплава -13,5 кг. Итак, надо добавить 13,5 - 12 = 1,5 кг олова.
0,4
Ответ'. 1,5 кг.
13.091. Имеющиеся на складе 300 кг товара проданы в неравных количествах двум организациям по цене 37,5 руб. за 1 кг. Первая организация перевозит купленный товар на расстояние 20 км, а вторая — на 30 км. Перевозка 10 кг товара обходится в 1,5 руб. за 1 км пути. Зная, что вторая организация заплатила за покупку и перевозку товара на 2700 руб. больше первой, определить, сколько килограммов купила каждая организация и какую сумму она заплатила за товар и его перевозку.
Решение.
Используя условие задачи, составим таблицу
Организация	Товар (кг)	Стоимость (руб)	Перевозка (руб.)	Общая стоимость (руб.)
№ 1	X	37,5х	Зх	40,5х
№2	300-х	37,5(300 - х)	4,5(300-х)	42(300 — х)
По условию задачи имеем 42(300-х)-40,5х = 2700, откуда х = 120 (кг), 300-х = 180 (кг); 40,5х = 4860 (руб.), 42(300 - х) = = 7560 (руб.).
Ответ'. 120 кг и 4860 руб.; 180 кг и 7560 руб.
13.092. Денежная премия была распределена между тремя изобретателями: первый получил половину всей премии без 3/22 того, что получили двое других вместе. Второй получил 1/4 всей премии и 1/56 денег, полученных вместе двумя остальными. Третий получил 30000 руб. Как велика была премия и сколько денег получил каждый изобретатель?
Решение.
Пусть х руб. — премия первого изобретателя, у руб. — второго. По условию вся премия равна х + у + 30000 руб. Тогда
X = 1(х+у+30000) - -^(у+30000),
1	1	откуда х = 40000, у = 25000. Вся
у =	+ у + 30000) +—(х + 30000),
4	56
премия 40000 + 25000 + 30000 = 95000 руб.
Ответ: 95000 руб.; 40000, 25000 и 30000 руб.
13.093. Сплав меди с серебром содержит серебра на 1845 г больше, чем меди. Если бы к нему добавить некоторое количество чистого серебра, по массе равное 1/3 массы чистого серебра, первоначально содержавшегося в сплаве, то получился бы новый сплав, содержащий 83,5% серебра. Какова масса сплава и каково первоначальное процентное содержание в нем серебра?
Решение.
Пусть х г — масса серебра, х - 1845 г — масса меди. Тогда 2х - 1845 г — масса всего сплава. После добавления серебра его
1	о ю.г 1	1
масса станет х + -хг, а масса сплава — 2х-1845 + — х г; х + — хг 3	3	3
составляют 83,5%. Значит, масса сплава ^х + ^-х^: 0,835. Тогда (x+-jX^:0,835 = 2x-1845 + yx, откуда х = 2505 г — масса серебра. Масса всего сплава 2-2505-1845 = 3165 г; 3165 г составляют 100%, 2505 г серебра составляют у%; 2122-12® отсюда у «79,1 %.
2505 у
Ответ: 3\65 г; «79,1%.
13.094. В 500 кг руды содержится некоторое количество железа. После удаления из руды 200 кг примесей, содержащих в среднем 12,5% железа, в оставшейся руде содержание железа повысилось на 20%. Какое количество железа осталось еще в руде?
Решение.
200 12,5
В 200 кг примесей железа будет х =—	=25 кг. Пер-
воначально z кг железа составляло в 500 кг руды у%, т.е.
500 у	/	\
z= = 5у кг. В оставшейся руде (5^-25) кг железа составляет
(у+20)%. Таким образом, 25 = У+20 2jp = 85, у = —. В F 300	100	2
425
руде останется железа 5^-25 = ---25 = 212,5-25 = 187,5 кг.
Ответ: 187,5 кг.
13.095. На ровной горизонтальной площадке стоят две мачты на расстоянии 5 м друг от друга. На высоте 3,6 м от площадки к каждой мачте прикреплено по одному концу куска проволоки длиной 13 м. Проволока натянута в плоскости расположения мачт и прикреплена к площадке, как показа-
но на рис. 13.7. На каком расстоянии от ближайшей мачты нахо-
дится точка прикрепления проволоки к площадке? Решение.
Обозначим искомое расстояние через х . Из &АВС получим:
ЛБ2+ВС2=ЛС2; ас = У, (х+5)2+3,62 =у2 • Из &AED получим:
АЕ1 + ED2 = AD2^ AD = z- х2 +3,62 = z2 - По условию: z+y = 13. Ре-
(х+5)2 +3,62 = J2,
шив систему:
< х2 + 3,62 = z2,	находим, что х = 2,7 м.
z + j> = 13,
Ответ: 2,7 м.
13.096. Велосипедист каждую минуту проезжает на 500 м меньше,. чем мотоциклист, поэтому на путь в 120 км он затрачивает времени на 2 ч больше, чем мотоциклист. Вычислить скорость каждого из них.
Решение.
Пусть х км/ч — скорость мотоциклиста. Мотоциклист затратил
120	120 о _
на весь путь — ч, а велосипедист	+2 ч. Скорость велосипеде	х
/120 А
диета— (х-0,5-60) км/ч. По условию (х-0,5-601—+2 1 = 120, от-
сюда х = 60 км/ч — скорость мотоциклиста. Скорость велосипедиста— 60-30 = 30 км/ч.
Ответ: 30 и 60 км/ч.
13.097. Расстояние от А до В по железной дороге равно 88 км, а по реке оно составляет 108 км. Поезд из А выходит на 1 ч позже теплохода и прибывает в В на 15 мин раньше. Найти среднюю скорость поезда, если известно, что она на 40 км/ч больше средней скорости теплохода.
Решение.
Пусть х км/ч — скорость поезда, %-40 км/ч — скорость тепло
хода. Поезд был в пути — ч, а теплоход —
108	88	1	Х
---тт---= 1 + ~, откуда х = 88-
х-40 х	4
108 х-40
ч. По условию
Ответ: 88 км/ч.
13.098. Пешеход и велосипедист отправляются одновременно навстречу друг другу из городов А и В , расстояние между которыми 40 км, и встречаются спустя 2 ч после отправления. Затем они продолжают путь, причем велосипедист прибывает в А на 7 ч 30 мин раньше, чем пешеход в в • Найти скорости пешехода и велосипедиста, полагая, что они все время оставались неизменными.
Решение.
Таблицу значений скорости, пути и времени заполним в порядке, указанном цифрами (1), (2), ..., (12):
Турист	До встречи			После встречи		
	скорость, км/ч	время, ч	путь, км	скорость, км/ч	время, ч	путь, км
Пешеход	(1)Х	(3)2	(5) 2х	(7)х	(11) 40-2х X	(9) 40-2х
Велосипедист	(2) 20-х	(4)2	(6) 40-2х	(8) 20-х	(12) 2х 20-х	(Ю) 2х
По условию--------------= — , откуда х = 4 (км/ч).
х 20-х	2
Ответ: 4 и 16 км/ч.
13.099. Расстояние между поселками А п В равно s км. Из Л отправились в В одновременно по одной и той же дороге два автотуриста, которые должны были прибыть в В в одно и то же время. В действительности первый турист прибыл в В на п ч раньше срока, а второй на Зп ч опоздал, так как последний проезжал за каждый час в среднем на г км меньше первого. Определить среднюю скорость каждого автотуриста.
Решение.
5	5
Пусть t —время, V, и v2 —скорости; тогда “z ~ п, (1)	= t + Зл,
V1	v2
(2)	Vj-v2=r. Вычитая (1) из (2), получим
lv2 vx)
=> (vj - V2)s = 4hV|V2
sr
=> vi v2 ”	• Решением системы
4л
Vj+(-V2)=r,
4(_^)=_2L,
2	sr Л
являются корни Zj = vx и z2 =-v2 квадратного уравнения z -rz- — = 0.
Получаем ответ:
nr+Jnr(nr+s)	-nr + Jnr(nr + s)
----—1--------- или-------------км/ч.
2л	2л
Ответ:
пг + <jnr(nr + s)	-ИГ+ y]nr(nr + s)
2п И 2л
13.100	. Определить целое положительное число по следующим данным: если его записать цифрами и присоединить справа цифру 4, то получится число, делящееся без остатка на число, большее искомого на 4, а в частном получится число, меньшее делителя на 27.
Решение.
_	_	10х + 4	л
Пусть х — искомое число. По условию ---= х + 4 -27, отку-
х+4
да х = 32.
Ответ: 32.
13.101	. В один и тот же час навстречу друг другу должны были выйти А из поселка М и В из поселка N. Однако А задержался и вышел позже на 6 ч. При встрече выяснилось, что’ А прошел на 12 км меньше, чем В . Отдохнув, они одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате А пришел в N через 8 ч, а В пришел в М через 9 ч после встречи. Определить расстояния Л/W и скорости пешеходов.
Решение.
Пусть х км — расстояние от М до места встречи; х+12 км — расстояние от дг до места встречи. Тогда расстояние между М и N равно 2х+12 км. Пусть у км/ч — скорость пешехода A, z км/ч —
х х+12 х — =-----4-6,
У ?
скорость пешехода в • Тогда
Решив систему, нахо-
дим:
х = 36 км, у = 6 км/ч, z = 4 км/ч. Тогда весь путь равен
2-36+12 = 84 км.
Ответ: 84 км, 6 и 4 км/ч.
13.102	. Даны два двузначных числа, из которых второе обозначено теми же цифрами, что и первое, но написанными в обратном порядке. Частное от деления первого числа на второе равно 1,75. Произведение первого числа на цифру его десятков в 3,5 раза больше второго числа. Найти эти числа.
Решение.
' Представим первое число в виде 1 Ох+у, тогда второе — 10у + х.
По
10х + у
условию: slOy + x
= 1,75,
(1 Ох+у )х = 3,5(1 Оу+х).
Решив систему, находим х = 2,
у = 1. Искомые числа 21 и 12.
Ответ: 21 и 12.
13.103	. От станции железной дороги до турбазы можно пройти по шоссе или тропинкой, причем тропинкой ближе на 5 км. Два
товарища условились, что один пойдет по шоссе, строго выдерживая намеченную скорость v км/ч, а второй — тропинкой со скоростью 3 км/ч. Второй пришел на турбазу раньше первого на 1 ч. Найти расстояние от станции до турбазы по шоссе и скорость v первого товарища, если известно, что v — целое число.
Решение.
Пусть х км—расстояние от станции до турбазы по шоссе, х-5 км — х х-5	2v
по тропинке. По условию-------— = 1, откуда х =	* Выражение
имеет смысл при v> 3 • Подбором находим: при v= 4 км/ч х = 8 км. Остальные решения этого уравнения не удовлетворяют условию х-5>0-
Ответ: 8 км, 4 км/ч.
13.104	. Длина автобусного маршрута 16 км. В часы «пик» автобус переходит на режим экспресса, т.е. значительно уменьшает число остановок, вследствие чего продолжительность поездки от начала до конца маршрута сокращается на 4 мин, а средняя скорость автобуса увеличивается на 8 км/ч. С какой скоростью идет автобус в режиме экспресса?
Решение.
Пусть х км/ч — скорость автобуса в режиме экспресса. Тогда ( 16 И
время поездки в этом режиме будет ------ч- По условию
\ х — О 1 э J
( 16	1 А
-----	* = 16, откуда х = 48 км/ч.
lx-8 15 J
Ответ: 48 км/ч.
13.105	. По одной из трамвайных линий начали курсировать трамваи новой конструкции. Рейс протяженностью 20 км продолжается теперь на 12 мин меньше, так как средняя скорость трамвая новой конструкции на 5 км/ч больше средней скорости трамвая устаревшей конструкции. Сколько времени затрачивает на рейс трамвай новой конструкции и какова его средняя скорость?
Решение.
Пусть х км/ч — средняя скорость трамвая новой конструкции.
20
Тогда время, которое он затрачивает на рейс, — — ч. По условию
20	20	1	20 4
— =------ ~ , откуда х = 25 км/ч, и время — — - ~ ч = 48 мин.
х х-5 5	25 5
Ответ: 48 мин, 25 км/ч.
13.106	. Самолет должен пролететь 2900 км. Пролетев 1700 км, он сделал вынужденную посадку на 1 ч 30 мин, после чего полетел со скоростью, на 50 км/ч меньшей, чем раньше. Найти первоначальную скорость самолета, если известно, что он прибыл на место через 5 ч после вылета.
Решение.
Пусть х км/ч — первоначальная скорость самолета. До посадки
1700	1200
он был в воздухе --- ч, после посадки — ----— ч. По условию
1700
1200 '
—— = 5, откуда находим х = 850 км/ч. х-50
Ответ: 850 км/ч.
13.107	. Две бригады, работая вместе, должны отремонтировать заданный участок шоссейной дороги за 18 дней. В действительности же получилось так, что сначала работала только одна первая бригада, а заканчивала ремонт участка дороги одна вторая бригада, производительность труда которой выше, чем у первой бригады. В результате ремонт заданного участка дороги продолжался 40 дней, причем первая бригада в свое рабочее время выполнила 2/3 всей работы. За сколько дней был бы отремонтирован заданный участок дороги каждой бригадой отдельно?
Решение.
Пусть х — скорость работы первой бригады, у — второй. Рабо
тая вместе, бригады отремонтируют участок за
1
да. По усло-
вию -----= 18. Производительность первой бригады —; второй —
Х + у	X .
~ . По условию - — + —= 40. Решив систему f , У J	3 х 3 у	2111
---+--- 3 х 3 у
находим: — = 45 дн.; “-30 да. или — =24 да., —-72 дн. Учиты-х	У	х	У
вая условие задачи, окончательно: — = 45 да, —-30 дн Значит,
первая бригада отремонтирует весь участок за 45 дн., вторая — за 30 дн.
Ответ: 45 и 30 дней.
13.108	. На полях, выделенных агролаборатории для опытов, с двух участков собрали 14,7 ц зерна. На следующий год после применения новых методов агротехники урожай на первом участке повысился на 80%, а на втором — на 24%, благодаря чему с этих же участков было собрано 21,42 ц зерна. Сколько центнеров зерна собирают с каждого участка после применения новых методов агротехники?
Решение.
Пусть х ц зерна собирают с первого участка после применения новых методов, у ц— со второго участка. По условию х+у = 21,42.
X	у
Первоначально с первого участка собрали ц, со второго — ц.
По условию
1,8 +1,24
= 14,7. Решив систему
х + у = 21,42
х у . находим —+^— = 14,7,
[1,8 1,24
х = 10,26 ц; у = 11,16 ц.
Ответ: 10,26 и 11,16 ц.
13.109	. Два велосипедиста выехали одновременно навстречу друг другу из двух мест, расстояние между которыми равно 270 км. Второй проезжает в час на 1,5 км меньше, чем первый, и встречается с ним через столько часов, сколько километров в час делает первый. Определить скорость каждого велосипедиста.
Решение.
Пусть х км/ч— скорость первого велосипедиста, х-1,5 км/ч — второго. До встречи первый проехал х • х км, а второй х(х -1,5) км. По условию х2+х(х-1,5) = 270, откуда х = 12 км/ч; 12-1,5 = 10,5 км/ч.
Ответ: 12 и 10,5 км/ч.
13.110	. Два поезда отправляются из пунктов А и В навстречу друг другу. Они встретятся на половине пути, если поезд из А выйдет на 2 ч раньше, чем поезд из В . Если же оба поезда выйдут одновременно, то через 2 ч расстояние между ними составит 1/4 расстояния между А и В. За какие промежутки времени каждый поезд проходит весь путь?
Решение.
Пусть первый поезд проходит весь путь за х ч, второй — за у ч; расстояние между А В равно а км. Тогда скорость первого
а .	а . „
поезда— — км/ч; второго— — км/ч. Первый пройдет половину х	У
пути за
х	-у
= — ч; второй— за —
2 F	2
ч.
х у
По условию =
Выйдя одновременно, поезда пройдут за 2
а а ] 3
—+— ~"7а км =>
х У) 4
ч 2
1 1
—+—
х у
3
4
Решив систему, находим: х = 4 ч, у = 8 ч.
—+2 = —.
.2	2
Ответ: 4 и 8 ч.
13.111	. Поезд был задержан на t ч. Увеличив скорость на т км/ч, машинист на перегоне в s км ликвидировал опоздание. Определить, какую скорость должен был иметь поезд на этом перегоне, если бы не было задержки.
Решение.
Пусть тх км/ч — скорость поезда, если бы он шел без задержки;
Zj ч — время движения поезда в этом случае. По условию тх = 5. Двигаясь быстрее со скоростью т{ +т км/ч, поезд был в пути (fj -z) ч.
Тогда 5 = (тх + mfa - z). Отсюда
Msfa+*W,
S h=— т\
Решив систе-
JtmUs+tm)-tm му, находим тх =-------------.
2z
Л	Jt m\4s + tm) - tm
Ответ:  --------—---- км/ч.
2z
13.112	. Два тела движутся навстречу друг другу из двух мест, расстояние между которыми 390 км. Первое тело прошло в первую секунду 6 м, а в каждую следующую проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/с и начало движение спустя 5 с после первого. Через сколько секунд после того как начало двигаться первое тело, они встретятся?
Решение.
Пусть t с— время движения первого тела до встречи; /-5 с —
П “	а/2	6/2
второго. Первый прошел до встречи — = — = Зг км; второй —
12(1-5) км. По условию 3/2+12(/-5)=360, откуда / = ю с.
Ответ: через 10 с.
13.113	. В отверстие трубы вошла одна материальная частица, а спустя 6,8 мин в то же отверстие вошла вторая частица. Войдя в трубу, каждая частица немедленно начинает поступательное движение вдоль трубы: первая частица движется равномерно со скоростью 5 м/мин, а вторая в первую минуту пробегает 3 м, а в каждую следующую минуту на 0,5 м больше, чем в предыдущую. Через сколько минут вторая частица догонит первую?
Решение.
Пусть t — время (в минутах), за которое вторая частица догонит первую. Расстояние, пройденное второй частицей, равно сумме t членов арифметической прогрессии, у которой ах = 3, d = 0,5;
2^+J^-l)	6+0,5(z-l)
следовательно, s =----------* =---------t. То же расстояние,
пройденное первой частицей, составит 5(б,8+г)=34 + 5/. Итак, 6+0,5G-l) „ ,	z ч
----—----1 = 34 + bt, откуда t = 17 (мин).
Ответ: 17 мин.
13.114	. Расстояние между двумя городами равно а км. Два автомобилиста, выехав из этих городов навстречу друг другу, встретятся на полпути, если первый выедет на t ч раньше второго. Если же они выедут одновременно друг другу навстречу, то встреча произойдет через 2t ч. Определить скорость каждого автомобиля, если считать, что скорости постоянны на всем пути.
Решение.
Пусть х км/ч — скорость первого автомобиля, у км/ч — второ-
a	_a_
го. Первый проедет полпути за — ч; второй — за . По условию
a a	f
~ + За 2t ч они проедут 2t(x + y)=a км. Решив систему
-a-4ia<a т
5 а а находим *1 - ------t—, х2 =------<0. Тогда
— + ' = —>	4/	4t
2х 2у
~ a^-Js) я(л/5-1)	.
Ответ: —-------L и —к—-‘ км/ч.
4r	4г
13.115	. Турист А отправился из города М в город N с постоянной скоростью 12 км/ч. Турист В, находившийся в городе N, получив сигнал, что А уже проехал 7 км, тотчас выехал навстречу ему и проезжал каждый час 0,05 всего расстояния между М и N. С момента выезда В до его встречи с А прошло столько часов, на сколько километров в час продвигался В . Найти расстояние между городами Л/ и ДГ, если оно не меньше 100 км.
Решение.
Пусть х км — расстояние между М и N. Тогда скорость туриста В — 0,05х км/ч. До встречи А проехал 7+0,05x12 км; В проехал (0,05хУ км. По условию Т+О.ОЗх-П + ^.Обх)2 =х, от-куда х,=20 км; х2=140 км. Учитывая, что х>100 км, находим х = 140 км.
Ответ: 140 км.
13.116	. Выйдя со станции с опозданием в 20 мин, поезд покрыл перегон 160 км со скоростью, превышающей скорость по расписанию на 16 км/ч, и пришел к концу перегона вовремя. Какова по расписанию скорость поезда на этом перегоне?
Решение.
Пусть х км/ч— скорость поезда на перегоне по расписанию. Двигаясь со скоростью (х+1б) км/ч поезд прошел перегон за t ч.
Значит, (х + 1б)г = 160; двигаясь со скоростью х км/ч, поезд прохо-
(х + 16> = 160,
(. П 1 сл откуда х = 80 км/ч. х г+- =160,
I 3J
1
дит перегон за / + - ч. Отсюда «
Ответ: 80 км/ч.
13.117	. Велосипедист проехал 60 км из пункта А в пункт в • На обратном пути он первый час проехал с прежней скоростью, после чего сделал остановку на 20 мин. Начав движение снова, он увеличил скорость на 4 км/ч и поэтому потратил на путь из в в А столько же времени, сколько и на путь из а в в • Определить скорость велосипедиста на пути из а в в •
Решение.
Пусть х
км/ч — скорость велосипедиста на пути из а в В • На 60	_	,1 60-х
В он затратил — ч; на путь обратно — 1 + з+ 7х+4~ ’
путь из я в
По условию
60 , 1 60-х
— = 1+- +-------, откуда х = 20 км/ч.
х 3 х + 4
Ответ: 20 км/ч.
13.118.	Два автобуса одновременно выехали с фабрики и отправились в зону отдыха, к озеру. Расстояние между фабрикой и озером 48 км. Первый автобус прибыл к озеру на 10 мин раньше второго, причем средняя скорость второго меньше средней скорости первого на 4 км/ч. Вычислить скорости автобусов.
Решение.
Пусть х км/ч — скорость первого автобуса, х - 4 км/ч — второ-
„	48	„	48
го. Первый автобус приехал к озеру за — ч, второй — за ——- ч.
48	48 1
По условию -------= 7, откуда х = 36 км/ч, 36-4 = 32 км/ч.
х-4 х 6
Ответ: 32 и 36 км/ч.
13.119.	Произведение цифр двузначного числа в три раза меньше самого числа. Если к искомому числу прибавить 18, то получится число, написанное теми же цифрами, но в обратном порядке. Найти это число.
Решение.
Представим искомое число в виде 10х + у. Тогда
(10x + y = 3xy
«{	Решив систему, находим v = 2 > v = 4. Иско-
(10х+у+18 = 10у + х.
мое число — 24,
Ответ: 24.
13.120.	Мотоциклист остановился для заправки горючим на 12 мин. После этого, увеличив скорость движения на 15 км/ч, он наверстал потерянное время на расстоянии 60 км. С какой скоростью он двигался после остановки?
Решение.
Пусть х км/ч — скорость мотоциклиста после остановки; t ч — время, за которое мотоциклист прошел бы 60 км со скоростью х -15 км/ч; t -0,2 ч — время, за которое мотоциклист прошел 60 км со скоростью , т	Г(/-0,2> = 60 „
х км/ч. Тогда < / v ’ Решив систему, находим х = 75 км/ч. |у(х-15) = 60.
Ответ: 75 км/ч.
13.121.	При испытаниях на дальность самолет пролетел от заводского аэродрома до заранее намеченного пункта всего 5 км, затратив на это /| ч. Затем он повернул обратно и за время t2 ч возвратился на аэродром (/| <t2)‘ В полете туда и обратно истинная скорость самолета (скорость относительно неподвижной массы воздуха) сохранялась одной и той же, а неравенство г, < t2 объясняется влиянием ветра, сначала попутным, а затем встречным. Найти истинную скорость v самолета, скорость ветра vB и путь $ист = vB(r2 -rt), пройденный самолетом относительно неподвижной массы воздуха.
Решение.
От аэродрома до намеченного пункта самолет летел со скорос-S	S
тью — = v+ vB км/ч, а обратно — со скоростью — = v- vB. Решив zi	f2
_ s(z2 ~Z|) vb —	~ „

_s(t2 + /J
Ответ: v~ ll\l2
„ - S^2 ~'l) о ^S(l2-ty B 2tlt2 ; ист 2t{t2
13.122.	Два брата имели билеты на стадион, расположенный в 20 км от их дома. Чтобы добраться до стадиона, они решили воспользоваться своим велосипедом и договорились, что отправятся одновременно, один на велосипеде, а другой пешком; проехав часть пути, первый оставит велосипед, а второй, дойдя до места, где будет оставлен велосипед, дальше поедет на нем и догонит первого у входа на стадион. Где должен оставить велосипед первый брат и сколько времени уйдет на дорогу, если каждый из братьев будет идти равномерно со скоростью 4 км/ч, а ехать в 5 раз быстрее?
Решение,
Пусть х км пройдет второй брат. На этот путь он затратит — ч.
Оставшиеся 20-х км он проедет за
20-х
ч. Все время движения
второго брата — — +
20-х	„	х
Ш ч. Первый брат проедет х км за — ч и
пройдет (20 - х) км за
20-х	х 20 - х
—ч. В пути он будет — + —-— ч. По
х 20___х х 20—х
условию — +	— = — -I—-—, откуда х=10 км. На всю дорогу
X 20-х 10 20-10 , и+—=	ч'
Ответ: на середине пути; 3 ч.
13.123.	Мотоциклист задержался у шлагбаума на 24 мин. Увеличив после этого свою скорость на 10 км/ч, он наверстал опоздание на перегоне в 80 км. Определить скорость мотоциклиста до задержки.
Решение.
Пусть х км/ч — скорость мотоциклиста до задержки, х +10 км/ч — на перегоне. Не задерживаясь, мотоциклист проехал бы 80 км за t ч,
но он прошел 80 км со скоростью х+10 км/ч за z-0,4 ч. Тогда
J(x+10)(r-0(4)=80> |х/ = 80,
Ответ: 40 км/ч.
13.124.	Из порта одновременно вышли два теплохода, причем один из них пошел на юг, а другой на восток. Через 2 ч расстояние между ними составило 174 км. Найти среднюю скорость каждого теплохода, если известно, что один из них в среднем за каждый час проходил на 3 км больше, чем второй.
Решение.
откуда х = 40 км/ч.
х+3 км/ч
Рис. 13.8
Пусть х км/ч — скорость второго теплохода, х + 3 км/ч — первого. За 2 ч первый прошел 2(х + 3) км, а второй 2х км. Из прямоугольного
треугольника (рис. 13.8) по теореме Пифагора (гх)2 +(2(х+3))2 = 1742, откуда х = 60 км/ч.
Ответ: 60 и 63 км/ч.
13.125.	Скорости пассажирского и товарного поездов относятся как а: b • Пассажирский поезд вышел со станции А на 0,5 ч позже товарного, а прибыл на станцию в на 0,5 ч раньше его. Найти скорости поездов, если расстояние между А и В равно s км.
Решение.
Пусть ах км/ч — скорость пассажирского поезда, Ьх км/ч — то-
варного. Пассажирский поезд был в пути — ч, товарный — — ч.
S	S По условию — = — + 0,5 + 0,5 Ьх ах s(a-b} пассажирского поезда —		 b	-sb + sa , откуда х =	. Тогда скорость ab s(a-b) км/ч; товарного —	км/ч. а
	s\a-b) s\a-b)
Ответ:	v --- и 		км/ч. b	а
13.126.	По двум окружностям равномерно вращаются две точки. Одна из них совершает полный оборот на 5 с быстрее, чем другая, и поэтому успевает сделать в 1,мин на два оборота больше. Сколько оборотов в минуту совершает каждая точка?
Решение.
Пусть первая точки делает оборот за х с; вторая — за х + 5 с. В
60	60
минуту первая точка делает — оборотов, а вторая — * — . По
60	60 .
условию — =------+2, откуда х = 10- Первая точка делает в мину
ту — = 6 оборотов, вторая— — = 4 оборота.
Ответ: 4 и 6.
13.127.	По сигналу дрессировщика два пони одновременно побежали равномерно вдоль внешней окружности арены цирка в противоположных направлениях. Первый пони бежал несколько быстрее второго и к моменту встречи пробежал на 5 м больше чем второй. Продолжая бег, первый пони подбежал к дрессировщику, оставшемуся на том месте, от которого начали бежать пони, через 9 с после встречи со вторым пони, а второй— через 16 с после их встречи. Каков диаметр арены?
Решение.
Пусть х м пробежал до встречи второй пони, х + 5 м — первый.
Тогда длина всей арены nd = 2х + 5 • Скорость первого пони — м/с,
второго —
х + 5 16
,	Лх + 5 х
м/с. По условию 9---= 16----, откуда х = 15 ,
х х + 5
I
I = nd = 35 м. Отсюда d = — «11 м. я
Ответ: «11м.
13.128.	Над пунктом А вертолет был в 8 ч 30 мин. Пролетев по прямой 5 км, вертолет оказался над пунктом в • Продержавшись в воздухе над пунктом в 5 мин, вертолет пошел обратным курсом по той же трассе. К пункту а он вернулся в 10 ч 35 мин. От а к В он летел по ветру, а обратно против ветра. Скорость ветра все время была постоянной. Найти скорость ветра, если собственная скорость вертолета также все время постоянна и при безветрии равна v км/ч.
При каком соотношении между заданными величинами задача имеет решение?
Решение.
Пусть х ч занял путь от Л к В, У ч — от В к Л. По условию
__	S
х +у = 2 . Скорость вертолета от Л к В была v+ vB = — , а на обрат-
х + ^ = 2,
_ S	_ 5
ном пути— v-vb-—. Решив систему	’ находим
У	х
S
v-vB=-,
Г-1---V	У
vB = V v(v- s) км/ч при v> s .
Ответ:	v(v- s) км/ч при v> s .
13.129.	В 9 ч самоходная баржа вышла из а вверх по реке и прибыла в пункт в;2ч спустя после прибытия в в эта баржа отправилась в обратный путь и прибыла в а в 19 ч 20 мин того же дня. Предполагая, что средняя скорость течения реки 3 км/ч и собственная скорость баржи все время постоянна, определить, когда баржа прибыла в пункт в • Расстояние между А и в равно 60 км.
Решение.
Пусть v км/ч — собственная скорость баржи. Из А в в баржа
60	60	60	60	1Л1
плыла------ ч, обратно —---- ч. По условию--- +2 +--- = 10-
v-3 F v+3	7	v-3 v+З 3
откуда v=15 км/ч. Баржа прибыла в В в 9+	=14 ч.
z	15-3
Ответ: в 14 ч.
13.130.	Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по той же трассе через 5 ч с момента отплытия. Весь рейс составил 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем им требовалось столько же времени, сколько на каждые 3 км по течению. Найти скорость течения, время проезда туда и время проезда обратно.
Решение.
Пусть v км/ч—собственная скорость лодки, vT км/ч—скорость тече-
3
ния. По условию
v- vT v+vT	5 t 25	.
5	5 откуда vT = — км/ч; v= — км/ч.
-----+------= 5, v-vT v+vT
Время проезда туда 25 5	3 ч, обратно — 2 ч.
12 "12
Ответ:	км/ч; 3 и 2 ч.
13.131.	Бакенщик, инспектируя свой участок реки, в обыкновенной весельной лодке поднялся вверх по реке на 12,5 км, а затем по той же трассе вернулся на прежнее место. В этом рейсе он преодолевал каждые 3 км против течения и каждые 5 км по течению в среднем за одинаковые промежутки времени, а всего в пути находился ровно 8 ч. Найти скорость течения и время рейса бакенщика вверх по реке.
Решение.
Пусть икм/ч — собственная скорость лодки, vT км/ч — скорость тече-
	3	5 v-vT v+vT	5	20
ния. По условию ’	ис	откуда vT=- км/ч, V=— км/ч. 12,5	12,5 Л	об 		—+—:— = 8 , v- vT v+ vT
т> -	U5 с
Время рейса бакенщика вверх по реке — ——- = 5 ч.
т~6
Ответ: - км/ч; 5 ч. о
13.132.	В лабораторной установке некоторая жидкость поступает в сосуд через три входных крана. Если открыть все краны одновременно, то сосуд наполнится за 6 мин. Если же наполнять сосуд только через второй кран, то на это потребуется 0,75 того времени, за которое может наполниться сосуд только через один первый кран. Через один третий кран этот сосуд наполняется на 10 мин дольше,
чем через один второй кран. На какое время надо открывать каждый кран в отдельности для наполнения сосуда?
Решение.
Пусть первый кран надо открыть на х мин, второй — на у мин, третий— на z мин. Если все краны открыть одновременно, то
— +	По условию >> = 0,75х; z = ^ + 10. Решив систему
х у z 6
X у Z 6 « у = 0,75х, z = j> + 10>
56
находим х = — мин; У = 14 мин; z = 24 мин.
Ответ:
на —, 14 и 24 мин.
13.133.	Бассейн для плавания имеет три трубы разного сечения для отвода воды с помощью равномерно откачивающего насоса. Через первую и вторую трубы вместе при закрытой третьей трубе наполненный бассейн опорожняется за а мин, через первую и третью вместе при закрытой второй— за Ь мин, а через вторую и третью трубы при закрытой первой— за с мин. За какое время наполненный бассейн опорожняется через каждую трубу в отдельности?
Решение.
Пусть через первую трубу бассейн опорожняется за х мин; через вторую — за У мин; через третью — за z мин. По условию:
fill
х у а
1 1	1	2abc	2abc
откуда х = —-—---- мин, у =-:------ мин,
х	z	b	ab+bc-ac	ac	+	bc-ab
1	1	1
- + - =
у	Z	с
2 abc Z = —-----— МИН.
ab + ac-bc
2abc 2abc	2аЬс
Ответ: за —— ------, --------- и —-----— мин.
ab + bc-ac ac + bc-ab ab+ac-bc
13.134.	Согласно программе, два станка на поточной линии должны за а ч обработать по одинаковому числу деталей. Первый станок выполнил задание. Второй станок оказался не вполне исправным, работал с перебоями, вследствие чего за то же время обработал на п деталей меньше, чем первый. На обработку одной детали на втором станке затрачивалось в среднем на Ь мин больше, чем на первом. Сколько деталей обработал каждый станок?
Решение.
Пусть х деталей обработал первый станок, х - п деталей — второй. На г	а
обработку одной детали на первом станке затрачивалось — ч, на втором х
а „	а а Ь
-------ч. По условию----= — н--, откуда
х-л	х-ихбО
bn + y/b2n2 +240аЬл	- Ьп + у] b2n2 + 24Qabn
х =------------------; х - п =---------------.
2b	2Ь
~ Ьп + у Ь2п2 + 240аЬл	- bn + 4b2п2 + 240д/м
Ответ:------------------и-------------------- деталей.
2b	2Ь
13.135.	Бригада слесарей может выполнить некоторое задание по обработке деталей на 15 ч скорее, чем бригада учеников. Если бригада учеников отработает 18 ч, выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение 6 ч, то и тогда будет выполнено только 0,6 всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения этого задания?
Решение.
Пусть х ч необходимо ученикам для выполнения задания; х - 15 ч —
бригаде слесарей. За 18 ч ученики выполнят ~18 всего задания, за 6 ч х
6	„	18	6
слесари выполнят ----— всего задания. По условию — +----— = 0,6,
откуда х = 45 ч.
Ответ: 45 ч.
13.136.	От пристани отправился по течению реки плот. Через 5 ч 20 мин вслед за плотом с той же пристани отправилась моторная лодка, которая догнала плот, пройдя 20 км. Какова скорость пло
та, если известно, что скорость моторной лодки больше скорости плота на 12 км/ч?
Решение.
Пусть х
км/ч — скорость плота, х + 12 км/ч — скорость лодки.
20	20	„
пройдет за — ч, лодка— за —ч. По условию
20 км плот
20	20
16
—, откуда х = 3 км/ч.
х х + 12 3
Ответ: 3 км/ч.
13.137.	Три машины разных систем выполняют некоторую счетную работу. Если всю работу поручить только одной второй или одной первой машине, то одна вторая машина затратит на выполнение всей работы на 2 мин больше, чем одна первая. Одна третья машина может выполнить всю работу за срок, вдвое больший, чем одна первая. Так как части работы однотипны, то всю работу можно поделить между тремя машинами. Тогда, работая вместе и закончив работу одновременно, они выполнят ее за 2 мин 40 с. За какое время может выполнить эту работу каждая машина, действуя отдельно?
Решение.
Пусть первая машина может выполнить работу за х мин, вто
рая — за у мин, третья — за z мин. По условию
у = х+2,
z = 2x,
1113
—।—ь— = —»
х у z 8
откуда х = 6 мин, ^ = 8 мин, Z = 12 мин.
Ответ: за 6, 8 и 12 мин.
13.138.	Двое рабочих, из которых второй начал работу на 1,5 дня позже первого, работая независимо один от другого, оклеили обоями несколько комнат за 7 дней, считая с момента выхода на работу первого рабочего. Если бы эта работа была поручена каждому отдельно, то первому для ее выполнения понадобилось бы на 3 дня больше, чем второму. За сколько дней каждый из них отдельно выполнил бы эту же работу?
Решение.
Пусть первый рабочий выполнил бы всю работу за х дн., вто-
7
рой — за х-3 дн. За 7 дн. первый выполнил — всей работы, за
a 1 <	< с	-	5,5	_	_	7	5,5	,
7 - 1,5 = 5,5 дн. второй сделал - работы. Тогда — +—•— = 1, отку-
х-3	х х-3
дах= 14 дн.
Ответ: за 14 и 11 дней.
13.139.	Найти двузначное число, частное отделения которого на произведение его цифр равно 8/3, а разность между искомым числом и числом, написанным теми же цифрами, но в обратном порядке, равна 18.
Решение.
Представим искомое число в виде Юх + у. Тогда по условию
10x + j;_8
< ХУ 3	откуда х = 6, у = 4. Искомое число — 64.
10x + ^ = 10^ + x + 18,
Ответ: 64.
13.140.	На одном из двух станков обрабатывают партию деталей на 3 дня дольше, чем на другом. Сколько дней продолжалась бы обработка этой партии деталей каждым станком в отдельности, если известно, что при совместной работе на этих станках втрое большая партия деталей была обработана за 20 дней?
Решение.
Время (г), количество работы, выполняемой в единицу времени, т. е. производительность (FF), и весь объем работы (V) связаны соотношением V = Wt. Примем V = 1 и заполним следующую таблицу:
Станок	Время, дни	Объем работы	Производительность
Первый	X	1	2 X
Второй	х-3	1	1 х-3
Оба вместе	20	3	3 20
Так как при совместной работе станков их производительности 1	1	3
складываются, то —+---- = —, откуда х = 15 •
х х-5 20
Ответ: 15 и 12 дней.
13.141.	Было задано целое число. Требовалось увеличить его на 200 000 и полученное число утроить. Вместо этого приписали к цифровой записи заданного числа справа цифру 2 и получили правильный результат! Какое число было задано?
Решение.
Пусть х — искомое число. Приписав к этому числу справа цифру 2, получим число Юх+2- По условию 10х+2 = 3(х+200000), откуда х = 85714 •
Ответ: 85714.
13.142.	Чан наполняется двумя кранами А и В. Наполнение чана только через кран А длится на 22 мин дольше, чем через кран В . Если же открыть оба крана, то чан наполнится за 1 ч. За какой промежуток времени каждый кран отдельно может наполнить чан?
Решение.
Пусть чан наполняется только через кран В за х мин, через А — „ 111
за х+22 мин. По условию — + —— = — .откуда х = 110 мин.
X X । OU
Ответ: за 132 и 110 мин.
13.143.	Некоторую работу А выполняет в срок, на а дней больший, чем В, и на Ь дней больший, чем С. Работая вместе, А и В выполняют эту работу за столько же дней, что и С. Определить время, за которое каждый выполняет эту работу отдельно. При каком соотношении между заданными величинами задача имеет решение?
Решение.
Пусть А выполняет работу за х дн., В —за х-а дн., С —за _	111	п-----с
х-b ДН. По условию - + —— = —- откуда х = b+y]b(b-a) дн.;
При ь>а, x-a = b-a + -Jb(b-a) дн.; x-b = -Jb(b-a) дн.
Ответ: b+-Jb{b-a); b-a+Jb(b-a); Jb(b-a) дней; задача имеет решение при Ь>а-
13.144.	Сумма всех четных двузначных чисел разделилась на одно из них без остатка. Полученное частное отличается от делителя только порядком цифр, а сумма его цифр равна 9. Какое двузначное число являлось делителем?
Решение.
Представим делитель в виде 10а + Ь. Тогда по усло-
вию
2430 10а+6
= 10£ + а,
а + Ь = 9,
откуда а = 4, b = 5. Искомое число — 54.
Ответ: 54.
13.145.	Сначала катер шел 10 км по течению реки, а затем вдвое большее растояние — по озеру, в которое река впадает. Весь рейс продолжался 1 ч. Найти собственную скорость катера, если скорость течения реки 7 км/ч.
Решение.
Пусть v км/ч — собственная скорость катера. По течению реки
10	20	„	10	20 ,
катер шел —-ч, по озеру--------ч. По условию ------+— = 1, откуда
v + 7	v	v + 7 v
v2 - 23v -140 = 0, т. е. v = 28 (км/ч).
Ответ: 28 км/ч.
13.146.	Найти три числа, из которых первое больше второго во столько раз, во сколько второе больше третьего. Если из первого числа вычесть сумму двух других, то получится 2, а если к первому прибавить полуразность второго и третьего, то получится 9.
Решение.
Пусть х, у, z — искомые числа. По условию
У
x-(y + z) = 2, откуда
2z£ = 9, 2
х = 8, = 4, z = 2 или х = - 6,4; у = 11,2; z = -19,6.
Ответ: 8; 4; 2 или - 6,4; 11,2; -19,6.
13.147.	Имеется лист жести в форме прямоугольника, у которого отношение длины к ширине равно 2:1. Из этого листа изготовлена открытая сверху коробка таким образом, что по углам листа вырезано по квадрату со стороной 3 см, и получившиеся края загнуты. Определить размеры листа жести, если объем коробки оказался равным 168 см3.
Решение.
Пусть 2а см — длина листа, а см — его ширина. Длина коробки (2а-г б) см, ее ширина — (а-б) см, а высота — 3 см. Объем коробки равен 3(а- бХ2а - б)= 168, откуда а = 10 см — ширина листа, 20 см — его длина.
Ответ: 10x20 см.
13.148.	Фотокарточка размерами 12x18 см вставлена в рамку постоянной ширины. Определить ширину рамки, если ее площадь равна площади самой карточки.
Решение.
Пусть х см— ширина рамки (рис. 13.9). Тогда ее площадь равна 2 12х+2(18+2х)х см. По условию 2-12х + 2(18+2х)х = 12‘18, от
12x18
Рис. 13.9
куда х = 3 см.
Ответ: 3 см.
13.149.	Найти два числа, сумма которых равна 44, причем меньшее число отрицательно. Процентное отношение разности между большим и меньшим числами к меньшему числу совпадает с меньшим числом.
Решение.
Пусть х и У — искомые числа ( у < 0 ). Т огда
х+у = 44,
^100 = у °т-. У
куда х = 264, у = -220.
Ответ: -220 и 264.
13.150.	В рукописи задачника по арифмсггике был написан пример, в котором- данное число надо умножить на 3 и от полученного результата отнять 4. В типографии допустили опечатку: вместо
знака умножения поставили знак деления, а вместо минуса — плюс. Тем не менее конечный результат от этого не изменился. Какой пример предполагали поместить в задачнике?
Решение.
Пусть х — данное число. Тогда предполагаемый пример имеет
вид— Зх-4, а напечатанный— у+4 . По условию Зх-4 = у+4,
откуда х = 3-
Ответ: 33-4-
13.151.	Кошка, гнавшаяся за мышкой вдоль длинного коридора, догнала ее через а с после начала погони. Первоначальное расстояние между ними / м. Если при таком же начальном расстоянии мышка с перепугу побежала бы не от кошки, а навстречу ей, то была бы схвачена через Ь с. Полагая, что в том и в другом случае кошка и мышка прилагали бы максимальные усилия, найти средние скорости каждой из них.
Решение.
Пусть х м/с — скорость мышки, У м/с — скорость кошки. За а с
_	/ + ах _
кошка пробежала / + ах м, значит,--= а . Во втором случае за Ь с
У
кошка пробежала 1-Ьх м, и -—= Ь . Решив систему У
1+ах ----= а,
У
1-Ьх ---- — Ь 9
У
l(a-b) l(a + b) находим х = --	; у= ,
2аЬ	2ао
Ответ:	,
2аЬ
l(a + b) l\a-b) ------ И	:— М/С. 2аЬ
13.152.	Участок прямоугольной формы обнесен изгородью. Если от него отрезать по прямой некоторую часть так, что оставшаяся часть окажется квадратом, то при этом его площадь уменьшится на 400 м2, а изгородь умень шится на 20 м. Определить первоначальные размеры участка.
Решение.
Пусть хху м — первоначальный размер участка (х <у). Тогда первоначальная плопг.адь участка— ху м2. По условию
ху = х2 + 400 (рис. 13.10). Длина изгороди 2(х + у) = 4х + 20. Решив
систему
х-у = х2 +400,
2(х + у) = 4х + 20,
находим х = 40 м, у = 50 м.
У
	400 м2
Рис. 13.10
Ответ: 40 х 50 м.
13.153.	Для спортплощадки отвели участок в форме прямоугольника с диагональю, равной 185 м. При выполнении строительных работ длину х каждой стороны уменьшили на 4 м. При этом прямоугольная форма была сохранена, но площадь оказалась уменьшенной на 1012 м2. Каковы действительные размеры спортплощадки?
Решение.
Пусть х — длина, а у — ширина площадки. По теореме Пифагора х2+у2 =1852. Кроме того, (х-4) (у-4) = ху-1012, откуда ху-4(х + у) =
= ху-1028; х + у = 257; у = 257-х. Решив квадратное уравнение х2 + (257-х)2 -1852 =0, находим xj = 104, х2 = 153.
Ответ: 100 х 149 м.
13.154.	3а 1 кг одного продукта и 10 кг другого заплачено 20 руб. Если при сезонном изменении цен первый продукт подорожает на 15%, а второй подешевеет на 25%, то за такое же количество этих продуктов будет заплачено 18 руб. 20 коп. Сколько стоит килограмм каждого продукта?
Решение.
Пусть х руб. — цена одного продукта, у руб. — другого. По условию х + 10у = 20. При сезонном изменении цен цена 1 кг первого продукта будет стоить 1,15хруб.,а 1 кг второго — 0,75у руб. Тогда 1,15х + 10 • 0,75у = 18,2.
[1,15х +0,75 Юу = 18,2,
Решив систему s	находим х = 8 руб., у = 1,2 руб.
I X 1 О
Ответ: 8 руб. и 1 руб. 20 коп.
13.155.	В первую неделю отпускного путешествия друзья израсходовали на 60 руб. меньше, чем 2/5 количества взятых с собой денег; во вторую неделю 1/3 остатка и еще на билеты в театр 12 руб.; в третью неделю 3/5 нового остатка и еще на морские прогулки 31 руб. 20 коп., после чего у них осталось 420 руб. Сколько денег было израсходовано за три недели путешествия?
Решение.
Пусть первоначально было х руб.
Неделя	Израсходовали	Остаток
Первая	2 уХ-60 (руб.)	уХ + 60 (руб.)
Вторая	—| —х + 60 | + 12 = —х + 32 (руб.) 3\5	)	5	2 у х + 28 (руб.)
Третья	3 f 2	А	1 - —х + 28 + 31—х = 5^5	)	5 = — х + 48 (руб.) 25	-х + 28-—х-48 = 5	25 4 = — х-20 (руб.)
По условию - 20 = 420, откуда х = 2750 руб. За три недели было израсходовано 2750 - 420 = 2330 (руб.).
Ответ: 2330 руб.
13.156.	Моторная лодка, обладающая скоростью движения 20 км/ч, прошла расстояние между двумя пунктами по реке туда и обратно, не останавливаясь, за 6 ч 15 мин. Расстояние между пунктами равно 60 км. Определить скорость течения реки.
Решение.
Пусть vT км/ч — скорость течения реки; 60 км туда лодка прошла за
60	60	60	60
------ч, а обратно за------ч. По условию —-----+—-------= о,2э, от-20 + vT н 20-vT J 20 + vT 20-vT
куда vT = 4 км/ч.
Ответ: 4 км/ч.
13.157.	Найти двузначное число такое, что если его разделить на произведение цифр, из которых оно составлено, то в частном получит
ся 16/3, а если вычесть из него 9, то разность будет также двузначным числом, которое отличается от искомого числа только порядком следования цифр.
Решение.
Пусть 10х + у — искомое двузначное число. Тогца
С 10x4-у _ 16
5 ху 3 откуда х = 3, у = 2. Искомое число — 32.
[10х + у-9 = 10у + х,
Ответ*. 32.
13.158.	В магазин привезли яблоки 1-го сорта на сумму 228 руб. и яблоки 2-го сорта на сумму 180 руб. При разгрузке привезенные яблоки случайно перемешались. Подсчет показал, что если теперь продавать все яблоки по одной цене — на 90 коп. ниже цены килограмма яблок 1-го сорта, то будет выручена ранее намеченная сумма. Сколько килограммов яблок привезено, если известно, что яблок 2-го сорта было на 5 кг больше, чем 1-го сорта?
Решение.
Пусть в магазин привезли х кг яблок первого сорта и х + 5 кг яблок второго сорта. Всего привезли яблок 2х + 5 кг. Килограмм яблок 1-го
228	(228
сорта стоит ---руб. Новая цена яблок —---------0,9 руб. Сумма,
X	к X	)
(228
вырученная за продажу всех яблок, —------0,9 (2x4-5). По условию
I х )
------0,9 (2x4-5) = 228 4-180, откуда х = 40 кг. Всего привезли яблок к х J
2 • 40 + 5 = 85 кг.
Ответ: 85 кг.
13.159.	От трех кафедр института поступили заявки на приобретение дополнительного оборудования для лабораторий. Стоимость оборудования в заявке первой кафедры составляет 45% от заявки второй кафедры, а стоимость оборудования в заявке второй кафедры — 80% от заявки третьей. Стоимость оборудования в заявке третьей кафедры превышает заявку первой на 640 тыс. руб. Какова общая стоимость оборудования в заявках всех трех кафедр?
Решение.
Пусть х, у, z тыс. руб. — стоимость оборудования в заявках первой,
второй и третьей кафедр соответственно. По условию
х = 0,45у, у = 0,8z, от-z - х + 640,
куда х = 360 тыс. руб., у = 800 тыс. руб., z = 1000 тыс. руб. Общая стоимость оборудования в заявках всех трех кафедр — 360 + 800 + + 1000 = 2160 (тыс. руб.)
Ответ*. 2 млн 160 тыс. руб.
13.160.	Если двузначное число разделить на сумму его цифр, то в частном получится 4 и в остатке 3. Если же это число разделить на произведение его цифр, то в частном получится 3 и в остатке 5. Найти это число.
Решение.
Пусть искомое число есть 10х + у. Тогда по условию имеем систему
(10х + у-3 = 4(х + у),
<	=>х = 2, у = 3.
[10х + у-5 = Зху
Ответ: 23.
13.161.	Перевозка тонны груза от пункта М до пункта N по железной дороге обходится на b руб. дороже, чем водным путем. Сколько тонн груза можно перевезти от М до N по железной дороге на сумму а руб., если водным путем на эту же сумму можно перевезти на к т больше, чем по железной дороге?
Решение.
Пусть х т груза можно перевезти по железной дороге, (х + к) т — водным путем. Перевозка тонны груза по железной дороге стоит
— руб., водным путем----— руб. По условию —-----— = Ь, откуда
х	х + к	х х + к
-bk + yl b2k2 + 4abk 2Ь
-bk + ^b2k2 + 4abk Ответ: -----------------т.
2Ь
13.162.	Некоторый товар был куплен осенью и за него было уплачено 825 руб. Килограмм этого товара осенью на 1 руб. дешевле, чем весной, и поэтому на ту же сумму весной было куплено на 220 кг меньше. Сколько стоит 1 кг товара весной и сколько его было куплено осенью?
Решение,
Пусть осенью было куплено х кг товара. Весной на ту же сумму было
825
куплено х-220 кг товара. Стоимость 1 кг осенью—-руб., а весной —
х
825	825	825
	руб. По условию-= 1, откуда* =550 кг. Стоимость 1 кг х-220--------------------------------х-220	х
товара весной--------= 2 руб. 50 коп.
550-220
Ответ: 2 руб. 50 коп.; 550 кг.
13.163.	При уборке урожая с каждого из двух участков собрано по 210 ц пшеницы. Площадь первого участка на 0,5 га меньше площади второго участка. Сколько центнеров пшеницы собрано с 1 га на каждом участке, если урожай пшеницы на первом участке был на 1 ц с гектара больше, чем на втором?
Решение,
Пусть х га — площадь первого участка, (х + 0,5) га — площадь второ-
го. С 1 га на первом участке собрано --ц пшеницы, на втором —
х
210	„	210	210	,
+ 05 ц. По условию------+0~5 = ’ откУдах = Ю га. С 1 га на первом
210
участке собрано = 21 ц пшеницы, со второго — 20 ц.
Ответ: 21 и 20 ц.
13.164.	Стоимость 60 экземпляров первого тома и 75 экземпляров второго тома составляет 2700 руб. В действительности за все эти книги уплатили только 2370 руб., так как была произведена скидка: на первый том в размере 15%, а на второй — в размере 10%. Найти первоначальную цену этих книг.
Решение,
Пусть х и у руб. — первоначальная цена первого и второго томов соответственно. По условию 60х + 75у = 2700. После скидки цена
первого тома стала 0,85х руб., второго — 0,9у руб. По условию 60 • 0,85х 4- 75 ♦ 0,9у = 2370. Решив систему
160x4-75у = 2700,	,Л ,	о л cz
4	находим х = 20 руб., у = 20 руб.
[60 • 0,85x4-75 0,9у = 2370,
Ответ'. 20 руб.
13.165.	Имеется 140 банок двух вместимостей. Объем банки большей вместимости на 2,5 л больше объема банки меньшей вместимости. Общий объем больших банок равен общему объему малых банок и равен 60 л. Определить количество больших и малых банок.
Решение.
Пусть х — количество больших банок, (140-х) — малых, ул — объем
|х(у 4-2,5) = 60, меньшей банки, (у 4- 2,5) л — большей. По условию <
[(140-х)у = 60, откуда х = 20 — количество больших банок и 140 - 20 = 120 малых банок.
Ответ: 20 и 120.
13.166.	Ученику надо было найти произведение числа 136 на некоторое двузначное число, в котором цифра единиц вдвое больше цифры десятков. По рассеянности он поменял местами цифры двузначного числа, отчего и получил произведение на 1224 больше истинного. Чему равно истинное произведение?
Решение.
Пусть искомое число — 10х 4- 2х. Число, записанное в обратном порядке, — (20х 4- х). По условию 136(20х + х) - 136(1 Ох 4- 2х) = 1224, откуда х = 1. Искомое число — 10 + 2 = 12, а истинное произведение равно 12- 136= 1632.
Ответ: 1632.
13.167.	Моторная лодка и парусник, находясь на озере в 30 км друг от друга, движутся навстречу и встречаются через 1 ч. Если бы моторная лодка находилась в 20 км от парусника и догоняла его, то на это потребовалось бы 3 ч 20 мин. Определить скорости лодки и парусника, полагая, что они постоянны и неизменны в обоих случаях.
Решение.
Пусть х км/ч — скорость лодки, у км/ч — парусника. По условию х14-у-1 = 30. Во втором случае за 3 ч 20 мин лодка прошла бы
3^+20^,
3|у+2О км. Тогда
Решив систему
х+у = 30, - 31УЧ-20 «3 «J
находим % = 18 км/ч, у = 12 км/ч.
Ответ'. 18 и 12 км/ч.
13.168.	Однозначное число увеличили на 10 единиц. Если полученное число увеличить на столько же процентов, как в первый раз, то получится 72. Найти первоначальное число.
Решение.
Пусть х — искомое число, которое увеличили на у-100 %. Тог-
Л	х+10 „	/ 1Л\ х+10	*
да х+10 = ух, откуда у =-----. По условию (x+10J—-— = 72,
откуда х = 2-
Ответ: 2.
13.169.	Кристалл, находясь в стадии формирования, равномерно наращивает свою массу. Наблюдая формирование двух кристаллов, заметили, что первый из них за 3 мес. дал такой же прирост массы, как второй за 7 мес. Однако по истечении года оказалось, что первый кристалл увеличил свою первоначальную массу на 4%, второй — на 5%. Найти отношение первоначальных масс этих кристаллов.
Решение.
Пусть годовой прирост массы х равен а; тогда по условию
Зд	Зд
годовой прирост массы у равен — . Имеем а = 0,04.x, — = 0,05 =>
4 х
5‘7"3
=> х:у = 35:12.
Ответ: 35:12.
13.170.	Одна тракторная бригада вспахала 240 га, а другая — на 35% больше, чем первая. Ежедневно первая бригада обрабаты* вала на 3 га меньше, чем вторая, но закончила работу на 2 дня раньше второй. Сколько гектаров обрабатывала каждая бригада за рабочий день, если известно, что намеченная ежедневная норма 20 га перевыполнялась обеими бригадами?
Решение.
Вторая бригада вспахала 240 1,35 = 324 га. Пусть х га ежедневно обрабатывала первая бригада, (х+3) га — вторая; У дней рабо
тала первая бригада, (у+2) дня— вторая. По условию
(х-у = 240,
[(х+3)(у+2)=324, 0ТКУда * = 24 га.
Ответ'. 24 и 27 га.
13.171.	В семье отец, мать и три дочери; всем вместе 90 лет. Разница в возрасте у девочек — 2 года. Возраст матери на 10 лет больше суммы возрастов дочерей. Разность лет отца и матери равна возрасту средней дочери. Сколько лет каждому члену семьи?
Решение.
Пусть х лет — возраст младшей дочери. Тогда возраст средней — х+2 года, старшей — х + 4 года, матери — х + х+2 + х+4+10 = Зх+16 лет, отца Зх+16 + х+2 = 4х + 18 лет. По условию х + х+2+х+4 + Зх+16+4х + 18 = 90, откуда х = 5 лет — возраст младшей дочери, 5+2 = 7 лет— средней, 5 + 4 = 9 лет — старшей, 3-5 + 16 = 31 год—матери, 4-5+18 = 38 лет — отца.
Ответ'. 38, 31, 5, 7 и 9.
13.172.	Два сосуда с раствором соли поставлены для выпаривания. Ежедневно выпариваемые порции соли постоянны для каждого сосуда. Из первого сосуда получено 48 кг соли, а из второго, стоявшего на 6 дней меньше, — 27 кг. Если бы первый сосуд стоял столько же дней, сколько второй, а второй столько, сколько первый, то из обоих растворов получилось бы одинаковое количество соли. Сколько дней стоял каждый раствор?
Решение.
Пусть х дней стоял первый раствор, У дней — второй. Ежедневно
48 выпариваемая порция для первого сосуда — кг соли, для второго —
27
~ кг. По условию
48	27
— 'У =---х,
X	у	откуда
у-х-6,
х = 24 дня, у = 18 дней.
Ответ'. 18 и 24.
13.173.	Если неизвестное двузначное число разделить на число, изображенное теми же цифрами, но в обратном порядке, то в частном получится 4 и в остатке 3. Если же искомое число разделить на сумму его цифр, то в частном получится 8 и в остатке 7. Найти это число.
Решение.
Пусть
10х + у — искомое число. Тогда
10х + у = (10у+х)*4+3, 10х + у = (у +х)-8 + 7,
откуда х = 7, у = 1. Искомое число — 71.
Ответ: 71.
13.174.	В четырех ящиках лежит чай. Когда из каждого ящика вынули по 9 кг, то во всех вместе осталось столько же, сколько было в каждом. Сколько чая было в каждом ящике?
Решение.
Пусть в каждом ящике было по х кг чая, осталось по (х-9) кг. По условию 4(х - 9) = х, откуда х = 12 кг.
Ответ: 12 кг.
13.175.	Катер отошел от причала одновременно с плотом и прошел вниз по реке 40/3 км. Не делая остановки, он развернулся и пошел вверх по реке. Пройдя 28/3 км, он встретился с плотом. Если скорость течения реки 4 км/ч, то какова собственная скорость катера?
Решение.
40_28
Катер и плот были в пути -3---3_ _। ч. Пусть v км/ч — соб-
4
40
ственная скорость катера. Вниз по реке катер шел —3— ч, а вверх — 4 + v
28	40	28	68 z
ч. По условию	) = 1,0ТЖУДа v=y км/ч.
Ответ: 68/3 км/ч.
13.176.	Общая вместимость трех цистерн составляет 1620 л. Две из них наполнены керосином, а третья пустая. Чтобы наполнить ее, нужно использовать либо все содержимое первой цистерны плюс 1/5 содержимого второй, либо все содержимое второй плюс 1/3 содержимого первой. Найти вместимость каждой цистерны.
Решение.
Пусть х л — вместимость первой цистерны, у л — второй, z л —
третьей. По условию
л'+г + г = 1620,
1
<г = л + ^у, откуда л-= 540 Л, >> = 450 л,
z = 630 л.
Ответ: 540, 450 и 630 л.
13.177.	Планом было предусмотрено, что предприятие на протяжении нескольких месяцев изготовит 6000 насосов. Увеличив производительность труда, предприятие стало изготовлять в месяц на 70 насосов больше, чем было предусмотрено, и на один месяц раньше установленного срока перевыполнило задание на 30 насосов. На протяжении скольких месяцев было предусмотрено выпустить 6000 насосов?
Решение.
Пусть было предусмотрено выпустить 6000 насосов за х меся-6000
цев. В месяц предприятие должно было изготовлять —— насосов, а
6000
изготовляло ——+ 70 насосов. Работая х-1 месяц, предприятие выпустило 6030 насосов. Значит, р^^ + 7о)(х-1)=6ОЗО, откуда х = 10 месяцев.
Ответ: десяти.
13.178.	Два парка общей площадью НО га разбиты на равное количество участков. Участки каждого парка по площади равны между собой, но отличаются от участков другого. Если бы первый парк был разбит на участки такой же площади, как второй, то он имел бы 75. участков, а если бы второй был разбит на такие же участки, как первый, то он содержал бы 108 участков. Определить площадь каждого парка.
Решение.
Пусть S — площадь парка, п — число равновеликих участков, Q — площадь участка. Тогда S: п = Q . Данными и искомыми значениями заполним таблиц} в последовательности, указанной цифрами (1), (2), ..., (12):
Парк	Первоначально			При новом разбиении		
	S	И	Q	5	п	Q
Первый	(7) х	110-х	(9) ПОх 108	(1) х	(3) 75	(5) X 75
Второй	(8) 110-х	(12) 75(110-х) X	(Ю) X 75	(2) 110-х	(4) 108	(6) 110-х 108
108х	75(110-х)
По условию —-----=--------, откуда х = 50 ♦
НО-х х
Ответ: 50 и 60 га.
,13.179. Отец хочет разделить 36 яблок между пятью своими детьми. Половину всех яблок он отдает сыновьям, которые делят их поровну, а другую половину отдает дочерям, которые тоже делят их поровну. Оказалось, что каждая дочь получила на 3 яблока больше, чем каждый сын. Сколько у отца было сыновей и дочерей?
Решение.
Пусть у отца было х сыновей и 5-х дочерей. Каждая дочь 18 с	w	18 с
получила ----- яблок, а каждый сын— — яблок. По условию
18	18 о
7-------= 3, откуда х = 3
5-х х
Ответ: 3 сына и 2 дочери.
13.180.	Одна из двух дробей вдвое больше другой. После возведения каждой из дробей в квадрат и сложения этих результатов получается некоторая сумма. Та же сумма получается после возведения каждой из дробей в куб и сложения этих результатов. Найти данные дроби.
Решение.
Пусть х — первая дробь, 2х — вторая. По условию
х2 +4х2 = х3 + 8х3, откуда х = | — первая дробь, 2 | = у — вторая.
Ответ'.
5	10
9 И 9 ’
13.181.	Бригада рабочих должна была изготовить за смену 7200 деталей, причем каждый рабочий делал одинаковое количество деталей. Однако в бригаде заболело трое рабочих и поэтому для выполнения всей нормы каждому из оставшихся рабочих пришлось сделать на 400 деталей больше. Сколько рабочих было в бригаде?
Решение.
Пусть х рабочих было в бригаде. Каждый рабочий делал -----------
деталей. После того как в бригаде стало х-3 рабочих, каждый стал делать по +400 деталей. По условию |	+400 |(х-3)= 7200,
х	\ х )
откуда х = 9-
Ответ: 9.
13.182.	В два сосуда одинаковой массы налита вода, причем масса сосуда А с водой составляет 4/5 массы сосуда В с водой. Если воду из сосуда В перелить в сосуд А , то масса его вместе с водой станет в 8 раз больше массы сосуда В . Найти массу сосудов и количество воды в них, зная, что в сосуде В содержится воды на 50 г больше, чем в сосуде А .
Решение.
Пусть х г — масса сосудов. Масса сосуда В с водой у г, сосуда А
4	Г4	\
с водой —у г. Масса воды в сосуде А — I I г, в В— (у-х) г.
По условию
4 уу+у-х=8х, y-x-f^y-x j = 50,
откуда х = 50 г, у = 250 г. В сосуде
А — 150 г воды, в В — 200 г.
Ответ'. 50, 150 и 200 г.
13.183.	В зале клуба имеется 500 стульев, расположенных рядами, причем каждый ряд содержит одинаковое количество стульев. После реконструкции зала в каждом ряду оказалось на 5 стульев больше, чем было, но зато число рядов уменьшилось на 5. В результате общее число мест в зале уменьшилось на 1/10 прежнего количества стульев. Сколько рядов было в зале и сколько стульев было в каждом ряду?
Решение.
Пусть х рядов было в зале, у стульев в каждом ряду. Всего мест в зале было х-.у = 500. После реконструкции зала мест стало
, у \ 9	|х-у = 500,
(у + 5)(х-5)= — -500. Решив систему Ъ ,v	находим
10	Пу+5|х-5)=450,
х = 20, J = 25.
Ответ: 20 рядов по 25 стульев в каждом.
13.184.	Если бы ученик правильно перемножил два написанных на доске числа, то получил бы в произведении 4500. Но, переписывая с доски сомножители, в одном из них ученик вместо последней цифры 5 написал цифру 3 и после умножения в результате получил 4380. Какие числа должен был перемножить ученик?
Решение.
Пусть Юх+5 —первое число, У —второе. Тогда
(10х+5)у = 4500, ' (10х+3)у = 4380,
откуда х = 7, первое число 10-7+5 = 75; >’ = 60.
Ответ: 75 и 60.
13.185.	При испытании двух двигателей было установлено, что первый израсходовал 300 г, а второй 192 г бензина, причем второй работал на 2 ч меньше, чем первый. Первый двигатель затрачивает в час на 6 г бензина больше, чем второй. Какое количество бензина в час расходует каждый из двигателей?
Решение.
Пусть х г бензина в час расходует второй двигатель, (б + х) г в
300	192
час — первый. Первый двигатель работал ---- ч, второй — — ч.
х+6	X
300 192
По условию х+6--------= 2 > откуда х = 24 г в час расходует бензина
второй двигатель, 24+6 = 30 г в час—первый.
Ответ: 30 и 24 г.
13.186.	Бригада каменщиков взялась уложить 432 м3 кладки, но в действительности на работу вышло на 4 человека меньше. Сколько всего каменщиков в бригаде, если известно, что каждому работавшему каменщику пришлось укладывать на 9 м3 больше, чем первоначально предполагалось?
Решение.
Пусть всего в бригаде х каменщиков. Каждый каменщик уклады-432
вает ---- м3 кладки. Т.к. работало х-4 каменщика, то каждому при-
шлось укладывать по---+9 м3 кладки. Значит, --+ 9 |(х-4)=432,
х \ х )
откуда х = 16-
Ответ: 16.
13.187.	Бригада рабочих должна была изготовить 8000 одинаковых деталей в определенный срок. Фактически эта работа была окончена на 8 дней раньше срока, так как бригада делала ежедневно на 50 деталей больше, чем было намечено по плану. В какой срок должна была быть окончена работа и каков ежедневный процент перевыполнения плана?
Решение.
Пусть работа должна была быть окончена за х дней. Ежедневно к	'8000	(*™°+501
бригада должна была делать дет., а делала I х дет. и
работала всего (х-8) дней. Значит, [ ^^+50 |(х-8)=8ООО, откуда
х = 40 дней. В день бригада должна была делать по
8000 40
= 200
дет.,
а делала 200+50=250, У = ——— = 125%. Значит, ежедневный
процент перевыполнения плана 125-100 = 25%-
Ответ: 40 дней; 25%.
13.188.	На обработку одной детали рабочий А затрачивает на к мин меньше, чем рабочий В. Сколько деталей обрабатывает каждый из них за t ч работы, если А обрабатывает за это время на п деталей больше, чем В ?
Решение.
Пусть В обрабатывает х дет., А — х + л дет. На обработку 1 дет.
t „ t „	t t к
А затрачивает---- ч, В — — ч. По условию---------= —, откуда
х + л	х	х х + л 60
-kn + ^k2n2 +240tkn 2k ’
-kn + 'j k2n2 + 240/Ьа	kn + y/k2n2 + 240/foi
-----------------------+ n =	 2k---------------------2k
i	______
Ответ: (-kn + 7k2n2 + 240/Ли)!(2k) и (kn+ylk2n2 + 240zto)/(2£).
13.189*	Сумма квадратов корней уравнения х2 -Зах+а2 =0 равна 1,75. Найти значение а.
Решение.
Решим уравнение относительно х: х - Зах + а = 0;
_ Л 2 а 2	2 3a-aV5	За + ау5
D - 9а 4а - 5а . Xj -	, х2 -	2 ‘По условию
^-(3 - V5)2 + ^-(3 + V?)2 = 1,75, откуда а2 = -, а = ±0,5.
4	4	4
Ответ: ±0,5.
13.190.	Кусок платины, плотность которой равна 2,15 Л О4 кг/м3, связан с куском пробкового дерева (плотность 2,4 • 102 кг/м3). Плотность системы равна 4,8-102 кг/м3. Какова масса куска дерева, если масса куска платины составляет 86,94 г?
Решение.
Обозначим массу куска дерева как х кг, объем куска дерева как У} м3, а объем куска платины как у2 м3. Объем куска платины
S 694 * 10 2 кг	а 1
у,  -------------= 4,044-10“” м . Теперь можно составить систему
2,15-Ю4 кг/м3
уравнений
— = 2,4-102;
У1
^^94J0:2 4>8.1о2
у,+ 4,044-10“”
Решив ее, находим
х = 8,694 • 10“2 - 4,8 • 102 • 4,044 -10"6 « 85 г.
Ответ: «85 г.
13.191.	К материальной точке приложены две силы, угол между которыми равен 30°. Модуль одной из приложенных сил в 7^3 раза больше модуля другой, а модуль равнодействующей силы на 24 Н больше, чем модуль меньшей силы. Определить модуль меньшей силы и равнодействующей силы. Решение.
Пусть х Н— модуль меньшей силы (рис. 13.11). По теореме косинусов: (24+х)2 =х2 +fyj3xf -2x-7>/3x cos(1800 - 300). откуда
х = 2 Н — модуль меньшей силы; 24 + 2 = 26 Н — модуль равнодействующей силы.
Ответ'. 2 и 26 Н.
13.192.	Имеются три сосуда, содержащих неравные количества жидкости. Для выравнивания этих количеств сделано три переливания. Сначала 1/3 жидкости перелили из первого сосуда во второй, затем 1/4 жидкости, оказавшейся во втором сосуде, перелили в третий и, наконец, 1/10 жидкости, оказавшейся в третьем сосуде, перелили в первый. После этого в каждом сосуде оказалось 9 л жидкости. Сколько жидкости было первоначально в каждом сосуде?
Решение.
Составим таблицу:
Сосуд	Первоначальное количество жидкости	После первого переливания	После второго переливания	После третьего переливания
1	х л	2 зхл	2 зхл	е; z- '' — | сП + — | тг + ^72 и ГЧ | СП
2	У л	1 У+уХ л	»=: И ' Г- |<<) 4-m | тг	з( 1 А 4С зх]л
3	Z л	Z л	1 ( 1 Z + — у+ -х л 4V 3 J	9 (	if	1 	 Z+— У+-Х л 10t 4(	3 ))
Решив систему
находим х = 12 л;
у = 8 л; z = 7 л.
Ответ: 12, 8 и 7л.
13,193.	На учениях разведывательный катер подошел к головному кораблю эскадры и получил приказание произвести разведку впереди эскадры по направлению ее движения на расстоянии 70 км. Определить, через какое время катер вернется к головному кораблю эскадры, продолжающей идти вперед, если известно, что скорость катера 28 км/ч, а эскадра должна двигаться со скоростью 14 км/ч.
Решение.
Пусть катер вернется к головному кораблю через х ч. За это время эскадра пройдет 14х км. Значит, катер должен пройти 70 + 70 - 14х км. По
условию 140 - 14х = 28х, откуда х = ч.
Ответ: через 3 ч 20 мин.
13.194.	Переднее колесо движущейся модели на протяжении 120 м делает на 6 оборотов больше, чем заднее. Если окружность переднего колеса увеличить на 1/4 ее длины, а окружность заднего — на 1/5 ее длины, то на том же расстоянии переднее колесо сделает на 4 оборота больше, чем заднее. Найти длины окружностей переднего и заднего колес.
Решение.
Длина окружности колеса С, число оборотов п и расстояние s связаны формулой Сп - s. Таблицу значений этих величин заполним в порядке, указанном цифрами (1), (2),..., (12):
Колесо	До изменения			После изменения		
	С	S	п	С	5	п
Переднее	(1)х	(3) 120	(5)12° X	(Т> — 4	(9) 120	(И)23О1 5х
Заднее	(2) У	(4) 120	(б)^ У	(8)^ 5	(10) 120	(12)2201
По условию, имеем систему
Ответ: 4 и 5 м.
120 120
х у
96 100
у
откуда х = 4 (м), у = 5 (м).
13.195.	Бригада монтеров могла окончить электропроводку в 4 ч дня, прокладывая в час по 8 м. После выполнения половины всего задания один рабочий выбыл из бригады; в связи с этим бригада стала прокладывать в час по 6 м и закончила запланированную на день работу в 6 ч вечера. Сколько метров провода было проложено и за сколько часов?
Решение.
Пусть было проложено х м провода. Прокладывая по 8 м элект
1
ропроводки в час, бригада могла бы проложить -х м провода за
х	х	Г л*	]	1
ч.	Но она работала —+2 ч. По условию '°“7х * отку-2-8	16	\1о	)	L
да х = 96 м. Всего бригада работала
х	х	96	.
—I------ь2 =------1-2 = 14 ч.
16 16	8
Ответ. 96 м, за 14 ч.
13.196.	Через два часа после выезда с фабрики шофер посмотрел на спидометр и заметил, что проехал только 112 км. Он прикинул мысленно, что если и дальше поедет с той же скоростью, то на 30 мин опоздает с доставкой груза на станцию. Поэтому шофер увеличил скорость и прибыл на станцию даже на 30 мин раньше срока. Определить начальную и последующую скорости движения автомобиля, если расстояние от фабрики до станции по спидометру составляет 280 км.
Решение.
112
Первоначальная скорость автомобиля -— = 56 км/ч. Всего шо-
280 , л „
фер был в пути----1 = 4 ч. Пусть он увеличил скорость на х км/ч.
56
С этой скоростью он ехал 2 ч и проехал 280-112 = 168 км. Значит,
2(56 + х) = 168, откуда новая скорость автомобиля 84 км/ч.
Отвепг. 56 и 84 км/ч.
13.197.	В кинозале имеется две двери, широкая и узкая. Через обе двери после сеанса зрители выходят из зала в течение 3 мин 45 с. Если зрителей выпускать через одну широкую дверь, то выход из зала займет времени на 4 мин меньше, чем в том случае, если зрителей выпускать только через одну узкую дверь. Сколько времени требуется для выхода зрителей из кинозала через каждую дверь в отдельности?
Решение.
Пусть х мин необходимо, чтобы выпустить зрителей только через широкую дверь, (х+4) мин — только через узкую. В одну мину-
1 1
ту через широкую дверь выходит — чел., через узкую — —— чел.
1 1 1
По условию: — + * + = уу, откуда л = 6 мин.
J 4
Ответ\ 6 и 10 мин.
13.198.	Некоторое вещество впитывает влагу, увеличивая при этом свою массу. Чтобы впитать 1400 кг влаги, требуется взять нераздробленного вещества на 300 кг больше, чем раздробленного. Сколько процентов от массы вещества составляет масса впитанной влаги в случае раздробленного вещества и в случае нераздробленного, если во втором случае это число процентов на 105 меньше, чем в первом?
Решение.
Пусть надо взять х кг раздробленного вещества, (х + 300) кг — нераздробленного.
х кг составляет 100%
1400 кг —	%
х + 300 кг составляет 100%
1400 кг —	у2 %.
Отсюда
140000
Л =------’
х
_ 140000 > решив систему, находим у, = 280 %:
2 х + 300
Я =j^2+105.
^2=175 %.
Ответ: 280 и 175 %.
13.199.	На пути от села до поля колесо грузовика делает на 100 оборотов меньше, чем колесо велосипеда, и на 150 оборотов больше, чем гусе-нйца трактора. Найти расстояние между селом и полем, если известно, что длина окружности колеса грузовика составляет 4/3 длины окружности колеса велосипеда и на 2 м короче гусеницы трактора.
Решение.
Пусть хм — расстояние между селом и полем, у м — длина окружно
4
сти колеса велосипеда; —у м — грузовика,
м — трактора.
Колесо грузовика делает —— оборотов; велосипеда-оборотов; гусе-
4	у
—у
3Л
ница трактора —	— оборотов. По условию < Г+2	о О' «п + §	7 1	4 ч И |	I m II	II * |тГ 1 m * |тГ 1 сп
куда х = 600 м.
Ответ'. 600 м.
13.200.	Две шкурки общей стоимостью в 22500 руб. были проданы на аукционе с прибылью в 40%. Каковоа стоимость каждой шкурки, если от первой было получено прибыли 25%, а от второй — 50%?
Решение.
Пусть х руб. — стоимость первой шкурки, 22 500-х руб. — стоимость второй. Первая шкурка была продана за 1,25х руб., вторая — за 1,5(22 500 - х) руб. По условию 1,25х +1,5(22 500 - х) = 1,4 • 22 500, откуда х = 9000 руб.
Ответ: 9000 и 13500 руб.
13.201.	Спортивная площадка имеет форму прямоугольника, длина которого на b м больше ширины. Площадка окаймлена дорожкой одинаковой ширины вам. Каковы размеры спортивной площадки, если ее площадь равна площади окаймляющей ее дорожки?
Решение.
Пусть х м — ширина площадки, Ь+х м— ее длина (рис. 13.12).
Площадь площадки — x(x + Z>) м. Площадь дорожки —
2ах+2(b+х+2а)а, откуда х =
>lb2+32а2 -Ь+4а 2
м;
_	4a+b+>lb2+32а2
b+x =--------------
2
м.
Ответ:
13.202.	Две машинистки должны перепечатать рукопись, состоящую из трех глав, из которых первая вдвое короче второй и втрое длиннее третьей. Работая вместе, машинистки перепечатали первую главу за 3 ч 36 мин. Вторая глава была перепечатана за 8 ч, из которых 2 ч работала только первая машинистка, а остальное время они работали вместе. Какое время потребуется второй машинистке для того, чтобы одной перепечатать третью главу?
Решение,
Пусть х — скорость работы первой машинистки, у — второй.
По условию------= 3,6 — время, за которое была перепечатана пер-
х+у
вая глава. За 8 ч работы первая машинистка перепечатала 8х вто-
рой главы, вторая за 6 ч —
10x + j> = 3(x + j>)+7
77	По условию
х +у -ху = 10х + у,	1
8х + бу' = 2 . Решив систему
—— = 3,6,	v 1 _
х + у	находим у = -. Третью гла-
8х + 6у = 2,	9
1 a
ву вторая машинистка может перепечатать за / = — = 3 ч. У
Ответ: 3 ч.
13.203.	Расстояние между двумя селами равно 10 км. Два человека выходят одновременно из одного села в другое, причем первый идет со скоростью, на 3 км/ч большей, чем второй, и приходит к месту назначения на 3 ч раньше. С какой скоростью идет каждый из них?
Решение.
Пусть х км/ч — скорость второго, х + 3 км/ч — скорость первого
человека. По условию у = 7, откуда х = 2 км/ч.
Ответ: 2 и 5 км/ч.
13.204.	Двое рабочих, работая вместе, выполняют некоторую работу за 8 ч. Первый из них, работая отдельно, может выполнить всю работу на 12 ч скорее, чем второй, если тот будет работать отдельно. За сколько часов каждый из них, работая порознь, может выполнить работу?
Решение.
Пусть х — скорость работы первого рабочего, У — второго. По
условию
1	1 ш
- = -+12 ,
х у
откуда — = 24, — = 12 . Первый рабочий может
выполнить всю работу за 24 ч; второй — за 12 ч.
Ответ: 12 и 24 ч.
13.205.	Если двузначное число разделить на сумму его цифр, то в частном получится 3 и в остатке 7. Если затем взять сумму квадратов цифр этого числа и вычесть из нее произведение тех же цифр, то получится первоначальное число. Найти это число.
Решение.
Пусть 10х+у — искомое число. По условию
10х + у = 3(х+у)+7,
х2+/-ху=-10х + у, откуда х = y = 1 ’ Искомое число —37.
Ответ: 37.
13.206.	Трехзначное число оканчивается цифрой 2. Если ее перенести в начало записи числа, то полученное число будет на 18 больше первоначального. Найти это число.
Решение.
Пусть искомое трехзначное число имеет вид 100х + 1 Оу + 2; тогда после перенесения цифры 2 оно примет вид 200 + 10х + у (1). По условию, 200 + 10х + у - (ЮОх + 1 Оу + 2) = 18, откуда 10х + у = 20. Подставив это выражение в (1), получим 200 + 20 = 220. Итак, первоначальное трехзначное число есть 202.
Ответ: 202.
13.207.	Экспресс проходит путь от Москвы до Санкт-Петербурга на 3 ч 30 мин быстрее пассажирского поезда, так как за 1 ч он проходит на 35 км больше. Сколько километров в час проходит каждый)из них, если расстояние между Москвой и Санкт-Петербургом принять с округлением равным 650 км?
Решение.
Пусть х км/ч — скорость пассажирского поезда, х + 35 км/ч — ско-
„	650	650 о с	z
рость экспресса. По условию------------ 3,5, откуда х = 65 км/ч.
х х + 35
Ответ: 65 и 100 км/ч.
13.208.	Некоторое двузначное число в 4 раза больше суммы и в 3 раза больше произведения своих цифр. Найти это число.
Решение.
Пусть 10х +у — искомое число. По условию
10х + у = 4(х + у),
10х + у = 3лу,
куда х = 2, у = 4. Искомое число — 24.
Ответ: 24.
13.209.	Два тела одновременно начали прямолинейное движение навстречу друг другу. Одно из них проходит в каждую минуту 7 м, другое в первую минуту прошло 24 м, а в каждую последующую проходит на 4 м меньше, чем в предыдущую. Через сколько минут оба тела встретятся, если первоначальное расстояние между ними было равно 100 м?
Решение.
Пусть тела встретятся через t мин. За это время первое тело пройдет It м. Скорость второго тела — (24 - 4(/ -1)) м/мин, и за t мин оно пройдет 0,5((2 • 24 - 4(Г - 1))Г м. По условию (24 - 2(t -1))/ + 7 = 100, откуда t=4 мин.
Ответ: через 4 мин.
13.210.	На сколько процентов следует увеличить длину радиуса круга, чтобы площадь круга стала больше на 96%?
Решение.
Пусть радиус круга надо увеличить на х. Тогда г}=г+х, 5, =1,96 5, З^тц2. Значит, 1,96г2 =л(г+х)2 • Отсюда находим, что х = 0,4г . Значит, радиус круга надо увеличить на 40 %.
Ответ: на 40 %.
Приложение
Действия над числами
Законы	Сложения	Умножения
переместительный	а+д=д+а	а • b=b•а
сочетательный	(а+Ь)+с=а+(Ы-с)	(а • Ь) • с=а • (Ь • с)
распределительный закон умножения относительно сложения	(а+Ь) ♦ с=ас+Ьс	
Проценты
1 % — один процент	1 : 100 = 0,01
1 % от числа А	— = 0,01А 100
b % от числа А	В = Ь — = Ь0,01А 100
Отношение числа А к числу В, выраженное в процентах	b = —100 в
Нахождение числа А, если b % его равны В	А = —100 b
Арифметическая и геометрическая прогрессии
Формула четных чисел	ап = 2м;м g Z
Формула нечетных чисел	ап = 2п +1; п е Z
Формулы n-го члена арифметической прогрессии	а=а ,+d; П	п-1 ап = а, + J(n-1); ne N,d e R
Свойство n-го члена арифметической прогрессии	a _ an-\ +ал+1 . e jy "	2
Формулы суммы п первых членов арифметической прогрессии	5л=^±^-и; "	2 „	2a,+d(n-l) Sn = —!	*	^n.n e N "	2
Формулы n-го члена геометрической прогрессии	Ьп=Ьп-х Ч- •' bn = b\ qn~'', n e N,q e R,q 0
Свойство n-го члена геометрической прогрессии	bn=4bn-xb„^
Формула суммы п первых членов геометрической прогрессии	1-?
Формула суммы бесконечной геометрической прогрессии	V -C 1 II
Числовые промежутки
отрезок	а< х<Ь	[а;д]	a	b
интервал	а<х<Ь	(а;&)	a	b
полуинтервалы	а<х<Ь	[а;6)	a'	b
	а<х<Ь	(а;&]	a	b
Логарифмы
Определение логарифма числа x по основанию а	Если logax=d, то аь=х, х>0,а>0, а ^1
Основное логарифмическое тождество	х=а1°ёаХ; а>0, а ^1, х>0
Свойства логарифмов	logea=l, logal-Q; a>Q, а ^1 logaxy=\ogax+\ogay loga — =logaX-logay У logaXk=k • logax 1 logak X=— • logax a>0, x>0, y>0, a ^1, k ^1
Переход к другому основанию в логарифмах	log* a , 1 logaX- , log, a a>0, a #1, x>0, x #1, 6>0, b ^1.
Решение линейного уравнения
Уравнение	а	ь	Корни	Графическое решение
ах+Ь=0	а ^0	Ь gR	ь х—— а	к А jdJoj о '
	а=0	ь=о	х eR	
	а=0	Ь #0	0		>х
Решение линейных неравенств
Неравенство	а	b	Равносильное неравенство	Множество решений	Графическое решение
ах+Ь<0	а>0	6gR	*O| Q 1 V н	,	b 4 xg(-o° ;— ) a	a
ах+b < 0	а>0	beR	1Л 1 a 1	XG(-oo	] a		>x "a
ах+Ь<0	а<0	bcR	»-b-a	/ b 4 xg(—	) a	.Й a
ах+b < 0	а<0	beR	:>-b a	г b	X x e [—	) a	.Й a
ах+6<0	а=0	b<0	—	xeR	
ах+Ь<0	а=0	b<Q	—	xgR	
Неравенство	а	b	Равносильное неравенство	Множество решений	Графическое решение
ах+Ь<0	а=0	Ь>0	—	0	
					
ax+b^0	а=0	Ь>0	—	0	
					
ах+&>0	а>0	beR	н V 1 s Ю	x e ( —; oo) a	
					rx a
ах+Ь0	а>0	beR	a	r b . xg[ —; <*>) a	ft _й a
ах+Ь>0	а<0	beR	x<-b-a	Z xe(-oo; —) a		>x “a
ах+b - 0	а<0	beR	a	z	Ьл xg (-oo; —J a	"a
ах+&>0	а=0	b>0	—	xeR	
ax+b-Q	а=0	o-IV О	—	хе R	
					
ах+&>0	а=0	о VI •о	—	0	
					
ах+b-0	а=0	b<0	—	0	
					
Простейшие выражения с модулем
а	Выражение	Равносильное выражение		Множество решений	Графическое решение
а>0	|х|=а	J х = а [х = -а		{-а;а}		h-Ч	 -а	а
	|х| <а		х<а х>-а	хе (-а;а)	»х -а	а
	|х|<а		х<а х>-а	хе [-а;а]		 -а	а
	|х| >а		х>а х<-а	хе (—оо;-а) (а;оо)	-а	а
	|х| а		х>а х<-а	ле (-оо;-а]’~’ [<Чоо)	-а	а
а=0	|х| -0	х = 0		{0}	——•—►X 0
	М <о	—		0	— '	» X
	И>0	х*0		хе (ftoo)	0
	lf«	—		хе R	X
а<0	|^а	—		0		*>х
	|х|^а	—		хе R	
Решение квадратного уравнения
Квадратное уравнение	D-62-4ac	Корни	Графическое решение	
ах2+Ьх+с=0, а^О	D>0	-Ь-Jd Xi =	 2a -ь+Jd X2= 2a	У1	
			0	Xi	
	D=0	b *1=*2	~ 2a	У'	\ /
			0	
	D<0	0	У1	1
			0	
Теорема Виета
ах2+Ьх+с=0	b
а*0, D>0	Х1+х2=	 а
«1 и «2 — корни квад-	с
ратного уравнения	Xi • х2— а
Решение показательного уравнения
а*=Ь равносильно а,=а1о«.*; а>0, a# 1
b	Ь>0		Ь <0	
Графическое решение		и 	1	А — у	У 	1	J
	0	logab	0	ь	~
Корни	x=loga6		0	
Определение тригонометрических функций угла
а sm а = - с b cos а = — с а tga =-г ь ь ctg а = — а	c a /	 Be	Л	
Если точка А получена поворотом начальной точки Ао единичной окружности на угол a, то ординату точки А называют синусом угла а, абсциссу точки А — косинусом угла (X. Отношение синуса угла а к косинусу угла а называют тангенсом угла a , а обратное отношение косинуса угла а к синусу угла а называют котангенсом угла a: sina	cosa tg a =	; ctg a = . cosa	sina	У‘ 1	I A (cosa; sina)
		Xa ;
	-1	h 5
X	к 2+a	M IЯ 1 R	n+a	тс-a	3 -л + а	3 2я °	2я + а	2л-a
sin х	cos ОС	cos ОС	-sin ОС	sin ОС	-cos ОС	-cos ОС	sin ОС	-sin ОС
COS X	-sina	Sina	-cos a	-cos a	sin a	-sin a	сое a	cos a
tg*	-ctg a	ctg a	tg a	-tg a	-ctg a	ctg a	tg a	-tg a
ctg X	-tga	tga	ctg a	-ctg a	-tg a	tg a	ctg a	-ctg a
Выражение одних тригонометрических функций через другие
	Функция — аргумент			
Функция	sina	cosa	tga	ctg a
sina	sina	±71-cos2 a	± tga Ji+tg2a	± I	— jl + Ctg ОС
cosa	±71-sin2 a	cosa	** 71+(g2a	± ctga ,jl+ctg2a
tga	+ sina 71-sin2a	+71-cos2a cosa	tga	1 cfga
ctg a	+Vl-sin2a ~ sina	cosa	1 tga	ctg a
		71-cos2a		
Формулы сложения и вычитания аргументов тригонометрических функций
sin (а + Р) = sin acos Р + cos asin Р sin (а - Р) = sin acos р - cos asin p cos (a + p) = cos acos P - sin asin p cos (a- P) = cos acos p + sin asin p
tg (a + P>- *	, a, H, a + P * (2»+l), n eZ
tg(a~ P) = -p——а» P> a~P ~(2n+l), n gZ ________1 + tgatgp__________________2____________
ctg (a + P) = c*gactgP *, a, p, a+ p # лп, n r ctga + ctgP
a. p.
ctga-ctgP
Формулы преобразования произведения тригонометрических функций в сумму
sin a sin /3 =	^(cos(a - /3) - cos(a + /?))
sina cos P =	(sin(a - /3) + sin(a+/?))
cos a cos P =	(cos(a - P)+cos(a + Д))
Основные соотношения для треугольников
Треугольник АВС (Д АВС) А, В, С — вершины ДАВС ZA, ZB, ZC — углы ДАВС АВ=с, ВС=а, АС=Ь — стороны ДАВС	в с/ а/	\с ь	
Первый признак равенства треугольников: если а=а\у b=bi, ZA=ZAi, то Д АВС= Д A^Ci	В	В! Ab С A, b. С,	
Второй признак равенства треугольников: если &=&i, ZA=ZA!» ZC=ZCi, то ДАВС=ДА1ВхС1	В	в. Ab С A, bt С,	
Третий признак равенства треугольников: если a=ai, b—by, e=Ci, то ДАВС=ДА1В1С1	В	Вг Ab С A, b, С,	
BDJ_AC => BD — высота Ль» проведенная из вершины В на сторону Ь. АК=КС => ВК — медиана проведенная из вершины В на сторону b	/	К
	A D Б К " С	
Содержание
Решения к главе 1................................. 3
Решения к главе 2. Тождественные преобразования алгебраических выражений........................25
Решения к главе 3. Тождественные преобразования тригонометрических выражений.................. 137
Решения к главе 4. Прогрессии....................242
Решения к главе 6. Алгебраические уравнения......263
Решения к главе 7. Логарифмы. Показательные и логарифмические уравнения......................343
Решения к главе 8. Тригонометрические уравнения..403
Решения к главе 9. Неравенства...................501
Решения к главе 10. Задачи по планиметрии.........551
Решения к главе 11. Задачи по стереометрии........645
Решения к главе 12. Задачи по геометрии с применением тригонометрии..................................713
Решения к главе 13. Применение уравнений к решению задач..........................................813
Приложение.......................................899
АВТОРСКИЙ КОЛЛЕКТИВ
Егерев Виктор Константинович Зайцев Владимир Валентинович Кордемский Борис Анастасьевич Маслова Тамара Николаевна Орловская Ираида Федоровна Позойский Роман Исаевич Ряховская Галина Сергеевна Сканави Марк Иванович Суходский Андрей Матвеевич Федорова Нина Михайловна
ТВОРЧЕСКИЙ КОЛЛЕКТИВ
Профессор кафедры высшей математики Белорусского Государственного Университета Информации и Радиоэлектроники Карпук Андрей Андреевич
Профессор кафедры высшей математики Белорусского Государственного Университета Информатики и Радиоэлектроники Жевняк Ростислав Михайлович
Кандидат физико-математических наук Брмолиц-кий Александр Александрович
Учебное издание
ПОЛНЫЙ СБОРНИК РЕШЕНИЙ ЗАДАЧ ПО МАТЕМАТИКЕ
для поступающих в вузы
Труппа А
Под редакцией М. И. Сканави
Подписано в печать с готовых диапозитивов заказчика 18.10.2011. Гарнитура «Таймс». Бумага газетная. Печать офсетная.
Формат 60x90‘/l6. Усл. печ. л. 57,00. Доп. тираж 3000 экз. Заказ 1047.
Общероссийский классификатор продукции ОК-005-93, том 2; 953005 — учебная литература
ООО «Издательство «Мир и Образование». 115193, Москва, ул. 5-я Кожуховская, д. 13, стр. 1. Тел./факс: (495) 742-43-51, 742-43-54.
E-mail: mir-obrazovanie@onyx.ru
ООО «Издательство Астрель». 129085, Москва, пр-д Ольминского, д. За.
Издание осуществлено при техническом содействии ООО «Издательство АСТ».
Издано при участии ООО «Харвест». ЛИ № 02330/0494377 от 16.03.2009. Республика Беларусь, 220013, Минск, ул. Кульман, д. 1, корп. 3, эт. 4, к. 42.
E-mail редакции: harvest@anitex.by
ОАО «Полиграфкомбинат им. Я. Коласа». ЛП №02330/0150496 от 11.03.2009.
Республика Беларусь, 220600, Минск, ул. Красная, 23.