Комплекс учебников из 21 выпуска
Под редакцией В. С. Зарубина и А. П. Крищенко
I. Введение в анализ
И. Дифференциальное исчисление функций
одного переменного
III. Аналитическая геометрия
IV. Линейная алгебра
V. Дифференциальное исчисление функций
многих переменных
VI. Интегральное исчисление функций
одного переменного
VII. Кратные и криволинейные интегралы.
Элементы теории поля
VIII. Дифференциальные уравнения
IX. Ряды
X. Теория функций комплексного переменного
XI. Интегральные преобразования
и операционное исчисление
XII. Дифференциальные уравнения
математической физики
XIII. Приближенные методы математической физики
XIV. Методы оптимизации
XV. Вариационное исчисление и оптимальное управление
XVI. Теория вероятностей
XVII. Математическая статистика
XVIII. Случайные процессы
XIX. Дискретная математика
XX. Исследование операций
XXI. Математическое моделирование в технике

С.А. Агафонов, А.Д. Герман, Т.В. Муратова
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Под редакцией
д-ра техн. наук, профессора B.C. Зарубина
и д-ра физ.-мат. наук, профессора А.П. Крищенко
Издание третье, стереотипное
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Москва
Издательство МГТУ имени Н.Э. Баумана
2004

УДК 517.9@75.8)
ББК 22.161.6
А23
Рецензенты: доц. Э.Р. Розендорн, проф. A.M. Седлецкий
А23 Агафонов С.А., Герман А.Д., Муратова Т.В. Диффе-
Дифференциальные уравнения: Учеб. для вузов / Под ред. B.C. Зару-
Зарубина, А.П. Крищенко. - 3-е изд, стереотип. -М.: Изд-во МГТУ
им. Н.Э. Баумана, 2004. - 352 с. (Сер. Математика в техниче-
техническом университете; Вып. VIII).
ISBN 5-7038-1649-1 (Вып. VIII)
ISBN 5-7038-1270-4
Изложены основы теории обыкновенных дифференциальных уравне-
уравнений (ОДУ) и даны основные понятия об уравнениях с частными про-
производными первого порядка. Авторы стремились объединить строгость
изложения теории дифференциальных уравнений с прикладной направлен-
направленностью ее методов. В связи с этим приведены многочисленные примеры
из механики и физики. Отдельная глава посвящена линейным ОДУ вто-
второго порядка, к которым приводят многие прикладные задачи. Главу,
посвященную изложению численных методов, следует рассматривать как
вводную.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов и вузов. Может быть по-
полезен интересующимся прикладными задачами теории дифференциальных
уравнений.
Ил. 60. Табл. 1. Библиогр. 41 назв.
Выпуск книги финансировал
Московский государственный технический
университет им. Н.Э. Баумана
УДК 517.9@75.8)
ББК 22.161.6
© С.А. Агафонов, А.Д. Герман,
Т.В. Муратова, 2000
© Московский государственный
технический университет
ISBN 5-7038-1649-1 (Вып. VIII) им' НЭ' Баумана> 2°°°
7ПЧЯ 197П 4 © Издательство МГТУ
-7038- U7U-4 им R g Ваумана> 2000

ПРЕДИСЛОВИЕ
Этот выпуск серии учебников „Математика в техническом
университете" посвящен изложению теории, методов решения и
качественного исследования обыкновенных дифференциальных
уравнений (ОДУ). Цель издания — помочь студентам в осво-
освоении теории и приобретении практических навыков решения
ОДУ, широко используемых при описании явлений и процессов
в различных областях естествознания и техники.
С развитием науки и техники узкоспециальные знания име-
имеют тенденцию к быстрому устареванию. Поэтому для решения
постоянно возникающих новых задач инженеры должны обла-
обладать хорошей подготовкой в области таких фундаментальных
наук, как математика, физика, механика. Такая подготов-
подготовка служит базой для быстрого усвоения и овладения новыми
перспективными научными и техническими направлениями. В
связи с этим авторы сконцентрировали внимание на постанов-
постановке и решении приводящих к ОДУ задач из механики и физики,
достаточно часто встречающихся в инженерной практике.
Содержание учебника полностью охватывает программу
курса „Обыкновенные дифференциальные уравнения" для тех-
технических университетов и вузов с углубленной программой
изучения математики. Помимо изложения основ теории ОДУ
в учебнике приведены краткие сведения об уравнениях с част-
частными производными первого порядка.
Этот выпуск тесно связан с предыдущими выпусками серии
„Математика в техническом университете". При использова-
использовании в этом выпуске сведений и понятий из других выпусков
даны соответствующие ссылки. Например, [II, 4.1] означает
ссылку на первый параграф четвертой главы второго выпуска.
Выделение в тексте какого-либо термина светлым курсивом
указывает на то, что в данном параграфе он отнесен к ключе-

ПРЕДИСЛОВИЕ
вым словам и читателю для понимания излагаемого материала
должно быть известно значение этого термина. Читатель мо-
может уточнить это значение, найдя при помощи предметного
указателя, помещенного в конце книги, необходимую страницу,
на которой используемый термин строго определен или опи-
описан (на этой странице он выделен полужирным курсивом).
Следует иметь в виду, что в предметный указатель все тер-
термины входят в алфавитном порядке (по существительному в
именительном падеже). Если в предметном указателе против
термина стоит римская цифра, то это означает, что данный
термин введен и описан в выпуске с соответствующим номе-
номером. В таком случае светлым курсивом указана страница этой
книги, содержащая некоторые пояснения.
Ссылки в тексте на номера формул и рисунков набраны
обычным шрифтом (например, A.2) — вторая формула в пер-
первой главе, (рис. 4.1) — первый рисунок в четвертой главе),
тогда как (см. 2.3) отсылает читателя к третьему параграфу
второй главы, а (см. Д. 12.1) — к первому дополнению двена-
двенадцатой главы этой книги.
Большинство используемых в этой книге обозначений вве-
введено в [I]. Они помещены в следующем за предисловием пе-
перечне, где^ наряду с их краткой расшифровкой дана ссылка,
позволяющая найти более подробное объяснение по каждому из
обозначений. В конце перечня даны написание и русское про-
произношение входящих в формулы букв латинского и греческого
алфавитов. Список рекомендуемой литературы помещен перед
предметным указателем в конце книги.
Перед чтением этого выпуска целесообразно в целях само-
самоконтроля выполнить следующие несложные задания. В конце
каждого задания римской цифрой отмечен номер того выпуска,
в котором при возникновении затруднений можно найти все не-
необходимые сведения. Значения терминов, выделенных в тексте
этих заданий прямым полужирным шрифтом, далее будем
считать известными (в основном тексте книги эти термины не
выделены и не входят в предметный указатель).

Задания для самопроверки
1. Запишите при помощи символов включения связь
между множествами С комплексных чисел, К действи-
действительных чисел, Z целых чисел и N натуральных чисел.
Что такое абсолютное значение действительного числа
и модуль комплексного числа? [I]
2. Дайте геометрическую интерпретацию неравенства
треугольника. [I]
3. Какие из промежутков числовой прямой R имеют
общие точки: отрезок [а, 6], интервал (Ь,с), полуинтер-
полуинтервал (а, с], бесконечный интервал (—оо, Ь) и бесконечный
полунтервал [Ь, -Ьоо)? Есть ли общая точка у всех этих про-
промежутков? При помощи символа принадлежности укажите,
какие из этих промежутков содержат точку с. [I]
4. Что называют критерием некоторого утверждения? [I]
5. Из каких этапов состоят доказательства от против-
противного и по методу математической индукции? [I]
6. Укажите область определения (существования)
и область значений и постройте графики однозначных
ветвей многозначной действительной функции у2 = 1/х
одного действительного переменного х. [I]
7. Сформулируйте определения предела, производной
и дифференциала скалярной функции действительного
переменного в точке. Всякая ли функция, непрерывная в
точке, является дифференцируемой в этой точке? Каковы
свойства функции, непрерывной на отрезке? [I], [II]
8. При выполнении каких условий у функции у = f(x) су-
существует дифференцируемая обратная функция х = f~l(y)
и как связаны между собой производные этих функций? Как
вычислить производную сложной функции и функции, за-
заданной параметрическим способом? [I], [II]
9. Изобразите годограф двумерной вектор-функции
r(t) скалярного аргумента t, если ее координатными
функциями являются x(t) = t и y(t) = t2. [II]

8 ПРЕДИСЛОВИЕ
10. Как вводят в n-мерном евклидовом (векторном)
пространстве W1 декартову систему координат? В
каком случае совпадают координаты точки и вектора в
этом пространстве? Что такое радиус-вектор? [II], [IV]
11. Запишите выражение для линейной комбинации п
векторов и сформулируйте определения линейно зависимой
и линейно независимой системы векторов. [III], [IV]
12. Перечислите основные свойства определителя ква-
квадратной матрицы. Запишите выражение для производной
определителя, элементы которого являются действительными
функциями одного действительного переменного. [II], [III]
13. Как задать матрицу линейного преобразования?
Что называют собственным вектором, собственным зна-
значением и характеристическим уравнением такого пре-
преобразования? [IV]
14. При каком условии однородная система линейных
алгебраических уравнений (СЛАУ) имеет ненулевое реше-
решение? Как найти решение такой СЛАУ? [III]
15. Сформулируйте критерий Сильвестра знакоопре-
знакоопределенности квадратичной формы. [IV]
16. Каковы условия существования и дифференцируемости
неявной векторной функции векторного аргумента?
Что такое частная производная этой функции? [V]
17. Как направлен вектор градиента скалярной функции
векторного аргумента по отношению к ее поверхности или
линии уровня? [V]
18. Что называют неопределенным интегралом? Напи-
Напишите формулу Ньютона — Лейбница. Чему равна произ-
производная определенного интеграла по переменному верхнему
пределу? [VI]
19. Сколько нулей имеет многочлен степени п? Каким
числовым множествам могут принадлежать эти нули? В чем
различие между простым и кратным нулем? [I]

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
<4 и > — начало и окончание доказательства
# — окончание примера или замечания
а € А, А Э а — элемент а принадлежит множеству А (множе-
(множество А содержит элемент а) I, 1.1
аф А — элемент а не принадлежит множеству А (множество
А не содержит элемент а) 1,1.1
А = {а, Ь, с} — множество А состоит из элементов а, Ь, с I,
1.1
А = {х: ...} — множество А состоит из элементов х, обладаю-
обладающих свойством, указанным после двоеточия I, 1.1
А С В, В D А — подмножество А включено в множество В (В
включает А) 1,1.2
АС В, В 2 А — подмножество А включено в множество В или
совпадает с ним 1,1.2
N — множество натуральных чисел 1,1.3
Z — множество целых чисел I, 1.3
Q — множество рациональных чисел 1,1.3
R — множество действительных чисел 1,1.3
R — расширенная числовая прямая 1,1.3
[а, 6] — отрезок с концами в точках аи Ь 1,1.3
(а, Ь) — интервал с концами в точках а и b 1,1.3
[а, Ь), (а, Ь] — полуинтервалы с концами в точках а и b 1,1.3
\х\ — абсолютное значение числа х 1,1.3
+оо, —оо — бесконечные точки расширенной числовой пря-
прямой I, 1.3
оо — объединение бесконечных точек +оо и —оо I, 1.3

10 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
(—оо, +оо), (—со, а), (Ь, +оо) —бесконечные интервалы 1,1.3
(—оо, а], [Ь, +оо) — бесконечные полуинтервалы 1,1.3
% — мнимая единица (г2 = —1) I, 4.3
С — множество (поле) комплексных чисел I, 4.3
Re z — действительная часть комплексного числа z I, 4.3
Imz — мнимая часть комплексного числа z I, 4.3
argz — главное значение аргумента комплексного чис-
числа z I,4.3
z — число, комплексно сопряженное числу z I, 4.3
и(жо) — окрестность точки хо I,1.3, 5.2
и(жо, е) — ?-окрестность точки xq I,1.3, 5.2
A\JВ —объединение множеств А и В 1,1.4
АГ)В — пересечение множеств А и В 1,1.4
А\В — разность множеств А и В I,1.4
Зх:... — существует такое #, что ... 1,1.5
3! х:... — существует единственное х, такое, что ... 1,1.5
$х:... — не существует ж, такого, что ... 1,1.5
Vx — для любого х 1,1.5
у = /(?) — йеременное у — функция переменного t I, 2.1, 3.1
f(a) — значение функции f(t) в точке t = а I, 2.1, 3.1
D(f) — область определения (существования) функции
f(x) 1,2.1,3.1
R(f) — область значений функции }{х) I, 2.1, 3.1
х = f~l(y) — функция, обратная к функции у = f(x) I, 2.3,
3.3
g(f(x)) — композиция функций у = f(x) и д(у) (сложная функ-
функция аргумента х) I, 2.4, 3.3
М(х\ у) — точка М плоскости с координатами х (абсцисса) и
у (ордината) I, 2.5
(*о; хо) — точка с координатами to (абсцисса) и xq (ордина-
(ордината) на плоскости tOx

11
X x Y — произведение (декартово) множества X на множе-
множество Y 1,2.5
Rn — произведение (декартово) п множеств действитель-
действительных чисел I, 2.5
п
^2 ак — сумма п слагаемых ai, ..., a*;, ..., ап I, 2.6
к=\
п\ — произведение всех натуральных чисел от 1 до п
включительно 1,2.6
к = 1, п — число к принимает последовательно все значения из
множества натуральных чисел от 1 до п включи-
включительно I, 2.6
Рп(х) — многочлен степени п Е N I, 3.6, 4.4
{хп} — бесконечная последовательность элементов хп I,
6.2
lim{rrn} — предел последовательности {хп} I, 6.3
х -» а — переменное х стремится к точке а I, 7.1
lim f(x) — предел функции f(x) в точке а (при х —> а) I, 7.1
х—>а
f(a + 0) — предел справа функции f(x) в точке а I, 7.2
f(a — 0) — предел слева функции /(#) в точке a I, 7.2
еж, ехрх — экспоненциальная функция (экспонента) аргу-
аргумента х I, 7.8
lnx — натуральный логарифм числа х (по основа-
основанию е) 1,7.8
shrr, chx, thrr, cthx — гиперболические синус, косинус, тан-
тангенс и котангенс аргумента х I, 7.8
Ах и Ду = Af(x) — приращения аргумента х и функции у =
= /(*) 1,9.1
/(ж) = О(з(#)) — функции /(ж) и з(я) одного порядка при
Х~*а х-*а 1,10.1
f(x) = о(д(ж)) — функция f(x) более высокого порядка малос-
малости по сравнению с функцией д(х) при х-+ а 1,10.1

12 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
f(x) ~ g(x) — функции f(x) и д(х) эквивалентны при
х~*а х->а 1,10.2
у(п)(а) — значение n-й производной функции y(t) в точке
t = a
у'(х), у'х, dy/dx, у1 — производная функции у = f(x) II, 1.3
/'(a), df/dx\x-a — значение производной функции f(x) в точ-
точке а II, 1.3
dx и dy = df(x)\x-a — дифференциалы аргумента х и функ-
функции у = f(x) в точке а II, 3.1
/"(а) и /'"(а) — производные второго и третьего порядков
функции f(x) в точке а II, 4.1
/(п)(а) — производная n-го порядка (n-я производная) функ-
функции /(ж) в точке a II, 4.1
t/n)(a), dny/dtn\t-a — значение n-й производной функции y(t)
в точке t = a
dxn и dny = dnf(x) — дифференциалы n-го порядка аргумен-
аргумента х и функции y = f{x) 11,4.5
r(t) — вектор-функция скалярного аргумента t II, 9.1
г, j, fc — орты (единичные векторы) ортонормированного ба-
аиса {г, j, к) II, 9.1
г'(to) —производная вектор-функции r(t) в точке to П,
9.1
Г = {г (t), te [a, b]} — векторное представление кривой Г II,
9.2
Г = {xi(t), г = 1, n; t G [a, Ь]} — координатное представление
интегральной кривой Г в расширенном фазовом
пространстве Rn+1 11,9-2
р и (р — полярные координаты (полярный радиус и поляр-
полярный угол) точки на плоскости I, 4.3; II, 9.3; III,
3.6
а, \а\ — вектор и его длина III, 1.1,1.2
|| а || —длина n-мерного вектора а 9.1

13
О — нулевой вектор III, 1.1
га
— линейная комбинация векторов а\,..., а^,..., ат с
к=г коэффициентами ai,... ,а&,... ,am III, 1.5
Oxy (Oxyz) — правая прямоугольная система координат на
плоскости (в пространстве) III, 3.1
(ai,..., а&,..., ап) — точка фазового пространства W1 с коор-
координатами аь (fc = l,n) 1.2
(t,ai,...,a&,...,ttn) — точка расширенного фазового простран-
пространства Rn+1 с координатами t и a& (fc = l,n) 1.2
/(ж) — векторная функция векторного аргумента ж 1.2
/(?, ж) — векторная функция скалярного t и векторного ж
аргументов 1.2
a = (ai,..., а&,..., ап)т — координатное представление векто-
вектора в n-мерном векторном пространстве IV
/(?,ж) = (/х(?,ж),...,/п(?,ж))т — координатное представление
векторной функции в n-мерном векторном про-
пространстве 1.2
grad/^) — вектор градиента скалярной функции /(ж) век-
векторного аргумента ж V, 8.1
df(t,x)/dx, fx(t,x) — частная производная функции /(t, x)
по переменному х V, 2.2
f(t)dt — неопределенный интеграл от подынтегральной
функции /(?) по переменному интегрирования t
t VI, 1.1, 3.1
f(r) dr — определенный интеграл от подынтегральной функ-
to ции f(t) в пределах от io до t VI, 2.1, 5.1
t
I

14
ОСНОВНЫЕ ОБОЗНА ЧЕНИЯ
Буквы латинского алфавита
Начертание
А а
В b
С с
D d
Б е
F f
Gg
Н h
I i
Jj
К к
L 1
M m
A a
В b
С с
D d
E e
F f
G g
H h
I i
J j
К к
L I
M m
Произно-
Произношение
a
бэ
ЦЭ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
О о
Рр
Qq
R г
S s
Т t
U u
V v
W w
X х
Yy
Z z
N п
О о
Р р
Q я
R г
S s
Т t
U u
V v
W w
X х
Y у
Z z
Произно-
Произношение
эн
о
пэ
ку
эр
эс
тэ
у
вэ
дубль-вэ
икс
игрек
зэт
Представлен наиболее употребительный (но не единствен-
единственный) вариант произношения (в частности, вместо „йот" иногда
говорят „жи").
Буквы греческого алфавита
Начер-
Начертание
А а
В Р
Г 7
Д S
Е е
z С
Н п
/~\ Q /\
С I/ U
Произно-
Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта
Начер-
Начертание
I i
К х
Л Л
М /i
N v
s i
О о
П 7Г
Произно-
Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи
Начер-
Начертание
р р
S a
Т т
Т v
Ф tp
х х
ф ф
п и
Произно-
Произношение
ро
сигма
тау
ипсилон
фи
хи
пси
омега
Наряду с указанным произношением также говорят „лямб-
„лямбда", „мю" и „ню".

1. ОБЩИЕ СВЕДЕНИЯ
О ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЯХ
1.1. Основные понятия и определения
При рассмотрении всевозможных физических явлений часто
не удается непосредственно найти зависимость между величи-
величинами, характеризующими эволюционный, т.е. изменяющийся во
времени, процесс. Аналогичные трудности могут возникнуть
и в ситуациях, когда в качестве независимого переменного вы-
выступает одна из координат точки или иная переменная величи-
величина. Однако во многих случаях можно установить связь между
искомыми характеристиками изучаемого явления (функциями)
и скоростями их изменения относительно других переменных,
т.е. найти уравнения, в которые входят производные неизвест-
неизвестных функций. Такие уравнения называют дифференциаль-
дифференциальными.
Если неизвестные функции зависят от одного независимо-
независимого переменного (аргумента), то говорят об обыкновенных
дифференциальных уравнениях (ОДУ), иначе — о диф-
дифференциальных уравнениях с частными производными.
Ограничимся (в основном) рассмотрением свойств и методов
решения ОДУ.
Обозначив независимое переменное, производная по кото-
которому от искомой функции входит в состав ОДУ, через <t, а эту
искомую скалярную функцию через x(i), запишем ОДУ в виде
-* <">
Порядок п Е N старшей производной в A.1) называют поряд-
порядком дифференциального уравнения. Таким образом, A.1)

16 1. ОБЩИЕ СВЕДЕНИЯ
является обыкновенным дифференциальным уравнением
п-го порядка.
Определение 1.1. Решением обыкновенного диффе-
дифференциального уравнения A.1) в некотором промежутке Т С
С R числовой прямой R называют п раз непрерывно диффе-
дифференцируемую в этом промежутке функцию x(t), удовлетворя-
удовлетворяющую при любом t ? Т этому уравнению.
Если в A.1) п = 1, то имеем обыкновенное дифференци-
дифференциальное уравнение первого порядка F(ty х, dx/dt) = 0. Во
многих случаях его удается записать в виде
f = /(*,*). A-2)
Тогда его называют обыкновенным дифференциальным
уравнением первого порядка, разрешенным относи-
относительно производной. При п > 1 получаем обыкновенное
дифференциальное уравнение высшего порядка.
В A.1) и A.2) входит одна искомая функция x(t). В тео-
теории ОДУ рассматривают также системы уравнений, которые
состоят из п обыкновенных дифференциальных уравнений и
такого же числа искомых функций. Если система ОДУ пер-
первого порядка разрешена относительно производных:
^х. ,
-± = fi(t, хи ..., хк, ..., хп), г = 1, п, A.3)
то ее называют нормальной системой ОДУ. В этом случае
число п уравнений, входящих в A.3), называют порядком
нормальной системы ОДУ. Если правые части в A.3) не
зависят явно от t (dfi/dt = O, i = 1, п), то имеем автономную
нормальную систему ОДУ.
Рассматривая Xi(t) (i = l,n) как координатные функ-
функции, введем вектор-функцию скалярного аргумента x(t) =
), ..., xn(t))T. Аналогично, считая
fi(t, x) = /i(t, хи • • •, xk, ..., жп), г = 1, п,

1.1. Основные понятия и определения 17
координатными функциями векторной функции, представим ее
в виде /(?, х) = (/i(t, ж), ..., /п(?, х))т. Тогда A.3) можно
записать в векторной форме
^ = f(t,x). A.4)
Определение 1.2. Решением нормальной системы
A.4) ОДУ в некотором промежутке TCR называют вектор-
функцию ж(?), определенную и непрерывно дифференцируе-
дифференцируемую в этом промежутке и при любом t E T удовлетворяющую
этой системе.
Обыкновенное дифференциальное уравнение n-го порядка
dnx / dx dn~lx\ K.
^t J A.5)
разрешенное относительно старшей производной, можно свести
к нормальной системе. Действительно, обозначив x(t) =xi(i),
dx/dt = dxi/dt = z2(t), • • • j dn~lx/dtn-1 = dxn-i/dt = a;n(t), полу-
получим dnx/dtn = dxn/dt, и A.5) примет вид
A.6)
eft
Процесс нахождения решения ОДУ обычно называют ин-
интегрированием дифференциального уравнения. Если ре-
решение ОДУ можно получить при помощи конечного числа опе-
операций интегрирования и дифференцирования и выразить через
элементарные функции, то иногда говорят, что решение диф-
дифференциального уравнения получено (или выражено) в квадра-
квадратурах.

18
1. ОБЩИЕ СВЕДЕНИЯ
Следует отметить, что ОДУ имеют обычно бесконечное
множество решений. Например, нетрудно проверить подста-
подстановкой, что при любом значении постоянного числа а функция
х(г)=аег — 1 является решением ОДУ первого порядка
1.2. Геометрическая интерпретация
решения ОДУ. Поле направлений
Всякое решение X{(t), teT (г = 1,п) нормальной системы
A.3) ОДУ в интервале Т можно интерпретировать геометри-
геометрически как кривую Г с координатным представлением
в (п + 1)-мерном пространстве Rn+1, точки которого име-
имеют координаты ?, х\, ..., #п. Это пространство называют
расширенным фазовым пространством, а кривую Г —
интегральной кривой. Фазовым пространством назы-
называют n-мерное пространство Шп с координатами х\, ..., хп
точек (жх, ..., хп) € Мп, а проекцию на него интегральной кри-
кривой — фазбвой траекторией (рис. 1.1). Эта траектория
является годографом вектор-
функции x(i). Координа-
Координаты точек (#i, ..., хп) € Кп
иногда называют фазовыми
переменными. В частном
случае п = 2 фазовым про-
пространством будет фазовая
плоскость, а фазовой тра-
траекторией — плоская кривая.
В каждой точке некоторой
области D С En+1 расширенного фазового пространства си-
система A.3) определяет направление, характеризуемое вектором
з = A, /i,..., /п)т- Первая составляющая этого вектора рав-
Рис. 1.1

1.3. Задачи, приводящие к решению дифференциальных уравнении 19
на единице, поскольку для первой координаты t точки (?, х)
расширенного фазового пространства dt/dt = 1. Построив в
каждой точке (?, х) Е D вектор s, получим в области D мно-
множество векторов, называемое векторным полем. В каждой
точке (i, х) ? D вектор з задает направление касательной
к проходящей через эту точку интегральной кривой системы
A.3), множество которых называют полем направлений.
Интегрирование системы A.3) ОДУ можно рассматривать
как процесс нахождения кривых, у которых в каждой точке
направление касательной совпадает с направлением вектора 5
(см. рис. 1.1).
1.3. Задачи, приводящие к решению
дифференциальных уравнений
Простейшие обыкновенные дифференциальные уравнения
(ОДУ) рассматривали в своих работах еще И. Ньютон и
Г. Лейбниц. Именно Г. Лейбниц ввел в 1676 г. термин „диф-
„дифференциальные уравнения". Задачу решения ОДУ И. Ньютон
трактовал как обратную по отношению к нахождению произ-
производной для заданной функции, а вычисление неопределенного
интеграла он считал частным случаем этой задачи. Для Нью-
Ньютона как создателя основ математического естествознания та-
такой подход к восстановлению функции по зависимости между
функцией и ее производными был вполне логичным, поскольку
большинство известных в науке закономерностей может быть
выражено в форме дифференциальных уравнений.
Пример 1.1. Тело массой т падает под действием силы
тяжести тд (д — ускорение свободного падения) и силы
сопротивления FTp = — kv, пропорциональной скорости г;, где
к — коэффициент сопротивления. Найти зависимость скорости
движения тела от времени t.

20 1. ОБЩИЕ СВЕДЕНИЯ
Используя второй закон Ньютона, составим ОДУ, описыва-
описывающее движение тела:
т— = mg — kv.
at
Имеем ОДУ первого порядка, разрешенное относительно про-
производной dv/dt, имеющей механический смысл ускорения дви-
движения рассматриваемого тела. Можно проверить подстанов-
подстановкой, что решением этого ОДУ является совокупность функций
где С — произвольная постоянная. Если в момент времени
t = 0 тело начинает падение с начальной скоростью v@) = vo,
то С = vo — mgjfk, и тогда
Кроме того, это ОДУ имеет, очевидно, решение Vqq = mg/k, к
которому стремятся при t -» +00 все решения вне зависимости
от значения г>о.
Пример 1.2. Из точки О под углом а к горизонту бро-
бросают с заданной начальной скоростью vq тело массой т так,
что оно падает под прямым углом
на наклонную плоскость, проходящую
через точку О и образующую с го-
горизонтом заданный угол (р. Считая
углы а и ср острыми (рис. 1.2), най-
найти угол а.
Поместим в точку О начало пря-
прямоугольной декартовой системы координат, направив ось аб-
абсцисс Ох вдоль наклонной плоскости. Согласно второму зако-
закону Ньютона, уравнения движения тела имеют вид
d2x . <Ру
т—2- = -mgsin<^, m-jp=-mg cos (p. A.7)

1.3. Задачи, приводящие к решению дифференциальных уравнении 21
Это ОДУ второго порядка, разрешенные относительно стар-
старшей производной. Они имеют решение
^sm<p + Cit + C2, y(t) cos<p + C3t + C4. A.8)
Z JL
В A.8) входят четыре произвольных постоянных С% (г =
= 1,4). Поэтому р,ля выбора из бесконечного множества
возможных решений единственного решения, описывающего
действительное движение рассматриваемого тела, необходимо
использовать сведения о положении и скорости этого тела в на-
начальный момент времени t = О, однозначно определяющие эти
произвольные постоянные. Так как при t = О тело находится в
начале координат, т.е. х = у = 0, то, согласно A.8), С<2 = С\ = 0.
Дифференцируя A.8), получаем
dx du
— = -gtsincp + Cu -77 = -gtcostp + Сз.
at at
С учетом заданного при t = 0 значения vq скорости тела
имеем
С\ = uocos(a — </>), Сз = i>osin(a — ср).
Подставляя найденные выражения для произвольных посто-
постоянных в A.8), запишем
x(t) = —— simp + VQtcos(a - ip),
al (L9)
y(t) = —— cosip + votsin(a-(p).
Полученное решение содержит пока еще неизвестное значение
угла а. Это значение можно найти, приняв во внимание, что
тело падает на наклонную плоскость под прямым углом, т.е.
в момент t = t\ падения у = 0 и проекция скорости тела на
координатную ось Ох равна нулю (dx/dt = 0). Учитывая A.9),
из последнего условия имеем
dx
~dt
— (л) = 0, или U =
t=h - - ¦ -
— ip)

22
1. ОБЩИЕ СВЕДЕНИЯ
а из первого условия, используя полученное выражение для t\,
имеем
gt2
= —^-—~2 [cos<p • cos(a — (р) — 2sin(a — ф) • sin<p] = 0.
Поскольку по смыслу задачи cos (a — ф) ф 0, то равно нулю
выражение в квадратных скобках:
cosy? • cos(a — (р) — 2sin(a — <р) • sin<p = 0.
Отсюда после тригонометрических преобразований получаем
tga =
или а =
Пример 1.3. Человек, находящийся в точке Q, движется
вдоль оси ординат Оув положительном направлении и тя-
тянет тяжелый предмет, расположен-
расположенный в точке Р, за веревку постоян-
постоянной длины а (рис. 1.3). Пусть на
плоскости хОу в начальный момент
времени точка Q находится в на-
начале координат, а точка Р имеет
координаты (а; 0). Составим ОДУ
* траектории точки Р.
Обозначим через у = у(х) урав-
уравнение искомой траектории точки Р.
Из условия задачи следует, что PQ является касательной к
этой траектории в точке Р с координатами (х\ у). Длина
отрезка AQ (см. рис. 1.3) равна у/а2 — х2, a tga = у/а2 — х2/х.
Принимая во внимание геометрический смысл производной [II],
т.е. dy/dx = tgGr — a) = — tga, получаем ОДУ первого порядка
О
X
Рис. 1.3
dy
dx
X

Вопросы и задачи 23
разрешенное относительно производной. Одним из решений
этого ОДУ является функция
. f
у=аЫк
а~Т у \л а/ \ /о о
которая задает хорошо известную плоскую кривую — трак-
трактрису.
Вопросы и задачи
1.1. Три черепахи А, В и С в начальный момент вре-
времени расположены в вершинах равностороннего треугольни-
треугольника со стороной а (рис. 1.4) и начина-
начинают движение с постоянной скоростью v
каждая по направлению к черепахе, на-
находящейся справа, сохраняя направление
движения на эту черепаху. Составить
дифференциальное уравнение траекто-
Л Рис. 1.4
рии черепахи А.
1.2. Человек и собака находятся в начальный момент време-
времени в точках А и В из. расстоянии L друг от друга. Человек
уходит от собаки со скоростью v по дороге, перпендикуляр-
перпендикулярной к отрезку АВ, а собака бежит по направлению к человеку
со скоростью 2v. Составить ОДУ траектории собаки.
1.3. Свет распространяется в атмосфере с переменной плот-
плотностью р = poe~kh (ро и к — постоянные, a h — высота
над поверхностью Земли) согласно закону преломления Снел-
лиуса nsina = const, где п = ар — коэффициент преломления
(а = const), а — угол между направлением луча и вертикалью.
Составить ОДУ траектории луча, испускаемого под углом «о
к вертикали точечным источником света, находящимся на вы-
высоте Н (кривизну поверхности Земли не учитывать).

2. ТЕОРЕМА СУЩЕСТВОВАНИЯ
РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
2.1. Постановка задачи Коши.
Интегральное неравенство
Из рассмотренных выше примеров следует, что обыкновен-
обыкновенное дифференциальное уравнение (ОДУ) первого порядка может
иметь бесконечное множество решений. Чтобы выделить из
этого множества решение, которое нас интересует, необходи-
необходимо иметь дополнительные данные, например знать начальное
значение искомой функции.
Задачу Коши для ОДУ первого порядка
dx
— = /(«,*), *,i€R, B.1)
формулируют так: найти решение x(t) уравнения B.1), такое,
что
x(to)=xo, B.2)
где д?о> to — заданные числа. Условие B.2) называют на-
начальным условием, или условием Коши, а функцию х(?),
удовлетворяющую ОДУ B.1) и начальному условию B.2), —
решением задачи Коши.
Пусть х = x(t) — решение ОДУ B.1), определенное в ин-
интервале (to — <J, to + 5), S > 0. Интегральной кривой ОДУ B.1)
будет график функции х = x(t). Можно, следовательно, задачу
Коши сформулировать так: найти интегральную кривую ОДУ
B.1), проходящую через заданную точку (to, xq) (рис. 2.1).
Возникает вопрос о существовании решения задачи Коши и
его единственности. Ответ на поставленные вопросы дает од-

2.1. Постановка задачи Копт. Интегральное неравенство
25
на из центральных теорем в теории ОДУ — х,
теорема Коши, которая будет сформулиро-
сформулирована и доказана далее. Здесь же докажем х°
интегральное неравенство Гронуолла,
которое весьма полезно при доказательстве
ряда утверждений и которое будет нами не-
неоднократно использовано в дальнейшем.
Теорема 2.1. Пусть скалярные функции u(t) и v(t) непре-
непрерывны и неотрицательны на отрезке, ограниченном точками t
и to. Если для них выполнено неравенство
О
Рис. 2.1
to
B.3)
где А = const
Гронуолла
0, то справедливо интегральное неравенство
B.4)
to
(здесь и далее ехр? обозначает экспоненциальную функцию е^
аргумента ?).
< Пусть сначала А > 0 и t^t$. Опуская в неравенстве B.3)*
знак модуля и умножая неравенство на v(t), получаем
u(t)v(t)
<«(*)•
B.5)
to
Так как, согласно теореме о дифференцировании интеграла по
верхнему переменному пределу [VI],
to

26
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
то, интегрируя B.5) в пределах от to до t (to < t), находим
t t
to
to
t
или
t0 to
Учитывая B.3), имеем
t t
to
to
to
Aexp | fv
to
т.е. неравенство B.4) справедливо. Оно справедливо и при
А > 0, t < to, поскольку при t < to B.3) принимает вид
t0 t
и, следовательно, в соответствии с рассматриваемым случаем
= Лехр /ti
Если A = 0, то u(t) = 0. Действительно,
t
to

2.2. Теорема Копш 27
для любого е > 0. На основании B.4) имеем
to
При е -> +0 получаем u(t) < 0, но, по условию, u(t) ^ 0.
Значит, u(t) = 0. >
2.2. Теорема существования
и единственности решения (теорема Коши)
Определение 2.1. Функция /(?, #), определенная в обла-
области (?, удовлетворяет условию Липшица в б? относительно #,
если существует такое число L > 0, называемое постоянной
Липшица, что для любых двух точек (<, я) и (*, у) из С?
выполнено неравенство
\f(t,x)-f(t,y)\^L\x-y\.
Замечание 2.1. Функция /(i, ж), имеющая в замкнутой
ограниченной области G непрерывную частную производную
df/dx, удовлетворяет условию Липшица в G относительно
х. Это следует из теоремы Лагранжа о конечном приращении
функции [V]:
/(*, хг) - /(t, x2) = (хг - x2)f'x(t, xi + X(x2 - a?i)), A G @, 1).
Действительно, если fx{t, x) непрерывна в G, то и ограничена
в этой области. Значит, существует такая постоянная L > 0,
что |/?(?, х)\ < L V(t, ж) Е -D. Тогда для любых двух точек
(?, xi) и (t, х2) из jD будем действительно иметь

28
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
Теорема 2.2 (теорема Коши). Пусть функция f(t,x)
определена и непрерывна в прямоугольной замкнутой области
= {(*, х): \t-tQ\^a, |ж-жо|<6}
B.6)
и удовлетворяет в этой области условию Липшица относительно
х. Тогда существует единственное решение x(t) задачи Коши
B.1), B.2), т.е. решение обыкновенного дифференциального
уравнения (ОДУ) первого порядка dx/dt = f(t,x) с начальным
условием x(to) = яо. Это решение определено при \t — to\ < Л,
где h = min{a; b/M}, М= max {\f{t, х)\}.
(t,x)€D
Перед доказательством теоремы дадим геометрическую ин-
интерпретацию ограничения \t — *о| ^ h на область определения
функции x(t). Так как |/(?, х)\ < М, то интегральная кри-
кривая х = x(t), проходящая через точку (to, а?о)> должна лежать
внутри заштрихованного на рис. 2.2 участка области D и
не может пересекать прямые, описываемые уравнениями х =
= хо ± M(t — to) (иначе в окрестности точки пересечения
было бы \dx/dt\ > М, что противоречит ОДУ B.1)). Если
Ма ^ Ь, то указанные прямые пересекают границу области
D в углах» прямоугольника или по его вертикальным сторо-
сторонам, а интегральная кривая гарантированно определена при
I* — *о| ^ в? т.е. h = а. Если же Ma > b (как изображено
на рис. 2.2), то точки пере-
пересечения прямых с границей
области D лежат на гори-
горизонтальных сторонах прямо-
прямоугольника и имеют абсциссы
to ± Ь/М. В этом случае ин-
интегральная кривая гаранти-
1 рованно определена лишь при
\t — to\ < b/M, т.е. h = b/M.
xo-b
Рис. 2.2
M Прежде всего убедимся, что если непрерывная функция
x(t) удовлетворяет при всех t E [to — /i, to + h] неравенству

2.2. Теорема Копт 29
\x(t) — #о| ^ Ь и интегральному соотношению
t
{) B.7)
to
то она является решением указанной задачи Коши. Инте-
Интеграл в B.7) существует на отрезке [to — Л, to + Л], так как
подынтегральная функция /(?, #(?)) на этом отрезке непре-
непрерывно зависит от переменного интегрирования ? [VI] (фун-
(функция х(?) непрерывна на [to — Л, to + Л], а функция /(?, х)
непрерывна в прямоугольнике D (см. рис. 2.2) по условию те-
теоремы, причем h^a). Из B.7) непосредственно следует, что
x(to) = #о, т.е. функция x(t) удовлетворяет начальному усло-
условию B.2). Поскольку подынтегральная функция непрерывна
при ? G [?о — Л, to + Л], то интеграл в B.7) является на этом от-
отрезке дифференцируемой функцией верхнего предела t [VI],
причем ее производная равна /(?, х) Vt € [to — /i, to + /i]. Следо-
Следовательно, и функция x(t) дифференцируема на этом отрезке.
Тогда, дифференцируя B.7) по t, получаем dx/dt = /(t, ж), т.е.
непрерывная функция x(t) удовлетворяет и ОДУ B.1).
Следующим этапом является доказательство существования
непрерывной функции rr(t), удовлетворяющей B.7). Для этого
рассмотрим функции xo(t) = жо,
to to
Покажем методом математической индукции, что график
функции xn(t) лежит в области D, если \t — to| < h (в
противном случае построение элементов последовательности
незаконно, поскольку функция /(t, x) определена лишь в D
и для нахождения значений /(t, xn(t)) необходимо, чтобы
\xn(t) - хо\ ^ Ь Vt е [t0 - Л, t0 + Л]).

30
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
При п = 0 утверждение очевидно. При п = 1, согласно
оценке абсолютного значения определенного интеграла [VI]
t
J
(p(r)dr <
to 't0
справедливой и при t ^ to, получаем
t
to
B.8)
т.е. график функции x\(t) расположен в области D.
Предположим, что для некоторого п 6 N график функции
xn(t) расположен в области JD, т.е. |жп(<) — xq\ ^ Ь. Тогда
to
to
т.е. график функции rcn+i(*) также лежит в области D. Таким
образом, для любого натурального п имеем |жп(<) — жо| ^6
при te [to-h,to + h].
Далее убедимся, что при любом фиксированном значении
t G [to — Л, to + h] соответствующая числовая последователь-
последовательность {xn(t)} имеет конечный предел, который обозначим
x(t), т.е.
lim xn(t) = x(t) e К. B.9)
fi—ЮО

2.2. Теорема Копт 31
Для этого также методом математической индукции докажем
справедливость неравенства
При п = 1 имеем
to
Пусть неравенство B.10) справедливо для некоторого n E N.
Докажем справедливость этого неравенства для п + 1. Исполь-
Используя условие Липшица и оценку B.8) для абсолютного значения
определенного интеграла, получаем
to
t
to
to
to
Полагая \t — *o| ^ Л и обозначая ип = MLn~lhn/n\, находим
^ n!
Покажем, что un ^ C/2n, где С = const и не зависит от п.
Обозначив ап = 2пип, имеем an+i/an = 2Lh/(n + 1) —>• 0 при

32 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
п —> оо. Следовательно, существует такое uq Е N, что ап+1 < ап
при п > по, т.е. начиная с некоторого номера п > по последо-
последовательность {ап} является убывающей и ограниченной, т.е.
а>п ^С Vn > по- Поэтому глп < С/2п, т.е. |#п(?) — #n_i(?)| <
^С/2п при |*-«0|<Л-
Теперь докажем, что {xn(t)} удовлетворяет критерию Ко-
Коши сходимости последовательности (см. утверждение 6.3 [I]).
При N > по, опуская обозначение аргумента ?, имеем
- XN+2 + .. - + XN+p-1 — XN+p\
p с с p i с
т.е. |жлг@ — xjv-f.p| -> 0 при iV —> оо. Это означает, что число-
числовая последовательность {xn(t)} является, согласно определе-
определению 6.4 [I], фундаментальной и в силу критерия Коши имеет
конечный предел B.9) при выполнении условия \t — ?о| ^ h.
В предпоследней части неравенства B.11) стоит сумма р
членов геометрической прогрессии со знаменателем q = 1/2,
равная (см. пример 7.1 [I])
sp =
где а\ = 1/2 — первый член этой прогрессии. Тогда вместо
B.11) запишем
Переходя в этом неравенстве к пределу при р-^оо и учитывая,
что в силу справедливости B.9)
lim

2.2. Теорема Коши 33
получаем
\xN{t) — x{t)\ ^ -zjf • B.12)
Так как предел B.9) существует при всех t E [to — Л, to + Л],
то x(t) является функцией, определенной на этом отрезке.
Покажем, что она непрерывна на [to — /i, to + Л], а ее график
содержится в D. Для этого рассмотрим разность xn{t\) —
— #71(^2) при любых t\ и t2, принадлежащих этому отрезку.
Используя аддитивность определенного интеграла и оценку
B.8) его абсолютного значения, имеем
\xn{ti)-xn{t2)\ =
t\ t2
to to
t2 t2
Переходя в этом неравенстве к пределу при п -» оо и учитывая,
что правая часть этого неравенства от п не зависит, получаем
\x(ti)-x{t2)\^M\tl-t2\.
Отсюда следует, что бесконечно малому приращению аргумен-
аргумента t отвечает также бесконечно малое приращение функции
tf(t), т.е. в силу определений 9.3 и 9.9 [I] функция x(i) непре-
непрерывна на отрезке [to — Л, to + h].
Уже доказано, что неравенство |xn(t) — жо| ^ Ь выполняется
при t E [to — Л, to + h]. Переходя в этом неравенстве к пределу
при п —> оо, получаем \x(t) — хо\ ^ Ь. Следовательно, график
функции x(t) содержится в D при tE[to — h,to + h].
На этом этапе осталось доказать, что непрерывная функция
x(t) удовлетворяет B.7) при всех t E [to — Л, to + h]. Справед-
2 - 9306

34 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
ливо соотношение
J f(bxn-1(O)dZ = x0 + J f(b
хп(ъ) = жот
t0 t0
t0 t0
а так как при п -> оо
/Г
J
to t0
поскольку с учетом оценки B.8) абсолютного значения опреде-
определенного интеграла, условия Липшица и B.12) при п —> оо
to
to
то функция x(t) удовлетворяет B.7).
Таким образом, при любом t Е [*о — К *о + h] существует
функция х(?), являющаяся решением задачи Коши B.1), B.2).
Наконец, методом от противного докажем единственность
этого решения. Пусть существуют два решения x\(t) и x2(t)^
удовлетворяющие ОДУ B.1) и одному и тому же начально-
начальному условию B.2), причем их графики содержатся в ?), но
xi(t) ф x2(t) при некотором значении t E [to — /i, to + h]. Тогда
dt
dx2{t)
dt ./ v">~'v//> X2(t0) =X0.

2.2. Теорема Коши 35
Из этих равенств следует, что xi(to) — #2(*о) = 0 и
dt
Проинтегрировав последнее равенство, получим
t
xi(t)-x2{t) =
to
С учетом B.8) и условия Липшица справедлива оценка
t
1 <
t0 t0
т.е.
to
Если теперь применить интегральное неравенство B.4) Гро-
нуолла при u(t) = \x\ (t) — д;2(*)| ^ 0, v(t) =L>0 и Л = 0, то
получим u{t) = 0, или х\ (t) = o?2(t), что доказывает единствен-
единственность решения. >
Замечание 2.2, Пусть правая часть ОДУ B.1) определена
в некоторой области Df. Будем говорить, что для ОДУ B.1)
выполнены условия теоремы Коши в области Df, если для лю-
любой точки (to 5 #o) G D* существует прямоугольная замкнутая
область D С D\ в котором выполнены условия теоремы 2.2. #
В качестве примера, иллюстрирующего теорему Коши, рас-
рассмотрим ОДУ dx/dt = t2 + х2 с начальным условием х@) = 0.
Зададим область
? = {(*,*): 1*1 <1. W<2>.

36 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
В этой области М = max(t2 + х2) = 5. Так как а = 1, 6 = 2,
то h = min{a; b/M} = 0,4. Правая часть ОДУ удовлетворяет
условию Липшица, причем
df
max
(t,x)<=:D
дх
= 2 max \x\ = 4,
т.е. L = 4. Значит, согласно теореме 2.2, существует единствен-
единственное решение этой задачи Коши, по крайней мере, для 11 | ^ 0,4.
Невыполнение условия Липшица для функции /(?, х) при-
приводит, вообще говоря, к нарушению единственности решения
задачи Коши.
Рассмотрим ОДУ dx/dt = 2v/jxf, т.е. /(?, я) = 2^/|ж[. Усло-
Условие Липшица не выполнено в прямоугольниках, содержащих
точки координатной оси Ot, так как иначе при х\ ф Х2 имело
бы место неравенство
Но при Х2 == 0 и a:i -> 0 получаем 2/y|xi| —>• оо. Непосред-
Непосредственной подстановкой можно проверить, что уравнение имеет
два различных решения, удовлетворяющих одному и тому же
начальному условию x(to) = xq = 0: x\(t) = 0 и
-(<-*oJ,
Теорема Коши гарантирует существование и единствен-
единственность решения ОДУ B.1) с начальным условием B.2) в области
где h = min{a; b/M}, M = max |/(t, x)|. Возникает вопрос:
(tx)e?>
что же происходит с решением задачи Коши B.1), B.2) вне
указанной области?
Рассмотрим замкнутую область G, причем D\ С G. Имеет
место теорема, которую приведем без доказательства.

2.3. Оценка разности решении двух уравнений 37
Теорема 2.3. Пусть функция f{t,x) определена и непре-
непрерывна в замкнутой области G и удовлетворяет условию Лип-
Липшица в G по #, a x(t) — решение ОДУ B.1) с начальным
условием B.2). Тогда решение x(t) продолжаемо либо нео-
неограниченно, либо вплоть до границы 6G области G, и это
продолжение единственно. #
Неограниченная продолжаемость означает, что решение
x(t) определено при любом t ? R. Например, ОДУ dx/dt =
= 1/A + ?2), х@) = 0, имеет решение x(t) = arctgt, опреде-
определенное при всех значениях t Е К. Продолжаемость вплоть до
границы означает следующее. Пусть x(t) — решение, опре-
определенное при to ^ t < t* < оо. Тогда предел функции x(t) в
точке t = t* существует, причем он может быть как конечным,
так и бесконечным. В первом случае этот предел существует
и конечен. Это реализуется, например, для ОДУ dx/dt = 1 в
области G, представляющей собой некоторый прямоугольник
на плоскости tOx. Для ОДУ dx/dt = ж4/3 с начальным усло-
условием х@) = 1 реализуется второй случай, так как для решения
x(t) = 1/v^l — t этого ОДУ имеем x(t) —> оо при t -> 1 (здесь
t* = 1, причем интегральная кривая имеет вертикальную асим-
асимптоту t — 1).
2.3. Оценка разности решений двух уравнений.
Непрерывная зависимость решения
от начальных условий и параметра
Рассмотрим задачу Коши для каждого из двух обыкно-
обыкновенных дифференциальных уравнений (ОДУ) первого порядка с
соответствующими начальными условиями:
dx dxi
h(t) (t) ^
= h(t,x), x(to)=xo; ^ = /2(*,У), у(*о)=Уо. B.13)
Пусть x(t),y(t) — решения задачи Кошщ определенные
на отрезке [^ —/г, to +/i], где h — число, фигурирующее в
формулировке теоремы 2.2 Коши. Функции /i(?, ж), /2B, у)

38
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
непрерывны и удовлетворяют в прямоугольной области
где и равно х или у, условию Липшица по х или у соот-
соответственно. Обозначим
Д= max l/i(*,u)
Из B.13) следует
dx dy
— = f 1 (^> *&) — j2v^j 2/)j *^(^o) — 2/(^0) = 3*0 — 2/о*
dt dt
Отсюда интегрированием в пределах от to до * получаем
t
«w - y(t) - (хо -1»)=у (л (е,
, у(о))«=
to
Тогда с учетом неравенства треугольника, линейности опреде-
определенного интеграла и оценки B.8) его абсолютного значения, а
также условия Липшица
\f2(t,x)-f2(t,y)\^L\x-y\
имеет место оценка t
ИО-у(*I<1и>-*о|-
to
to
Если теперь применить интегральное неравенство B.4) Грону-
олла при u(i) = \x(t) — y(t)\ ^ 0, v(t) = L > 0 и А = \xq — уо| +

2.3. Оценка разности решении двух уравнении 39
+ ЛД ^ 0, то будем иметь
ь1*-*°1 < (\xo-yo\+hA)eLh. B.14)
Это неравенство позволяет сформулировать важные след-
следствия, но предварительно дадим ряд определений.
Определение 2.2. Решение ОДУ B.1) непрерывно зависит
от начальных условий, если для любого е > О существует такое
6(е) > 0, что при |хо — уо| < 8 для любого t E[to — Л, to + h]
будет выполнено неравенство \x(t)— y(t)\ <e, где ж(?) и y(t)—
решения задач B.13) Коши в случае /х = /2 = /.
Определение 2.3. Решение задачи Коши B.1), B.2) непре-
непрерывно зависит от правой части ОДУ B.1), если для любого
е > 0 существует такое 6(е) > 0, что при Д < 6(е) для любого
t G [to—hj to+h] будет выполнено неравенство \x(t) — y(t)\ < е
(здесь x(t) и y(t) — решения задач B.13) Коши в случае
яо = Уо)-
Предположим, что правая часть ОДУ зависит от параметра
Л Е Л (Л — некоторый отрезок числовой прямой R):
dr
— = f(t,x,\), B.15)
а х(?, А) — решение B.15), удовлетворяющее начальному усло-
условию
n?(to,A)=a:o. B.16)
Определение 2.4. Решение x(t, А) задачи B.15), B.16)
Коши непрерывно зависит от параметра А, если для любого
е > 0 существует 6(е) > 0, такое, что при всех |ДА| < 6(е)
для любого t G [to — /i, *o + h) будет выполнено неравенство
\x(t, А + ДА) - x(t, А)| < г, где x(t, А + ДА) — решение задачи
B.15), B.16), соответствующее /(?, ж, А + ДА) в правой час-
части B.15).
Применим B.14) к исследованию свойств решений ОДУ,
удовлетворяющего условиям теоремы 2.2 Коши.

40 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
Следствие 2.1. Решение ОДУ B.1) непрерывно зависит
от начальных условий, если правая часть B.1) удовлетворяет
условиям теоремы Коши.
< Пусть в B.13) функции Д и /2 совпадают с функцией
f{t,x) в правой части B.1). Тогда в прямоугольнике D\ имеем
А = 0 и с учетом B.14) получаем
\*{t) - V(*)l < l*o ~ !/o|eLh \ft e [to - Mo + h].
Если для любого е > 0 выбрать 5(е) = ee~Lh, то при условии
|#о — Уо| < S(e) будем иметь \x(t) — y(t)\ < е, т.е. в силу опреде-
определения 2.2 решение ОДУ B.1) непрерывно зависит от начальных
условий. >
Следствие 2.2. Решение задачи Коши B.1), B.2) непрерыв-
непрерывно зависит от правой части ОДУ B.1), если она удовлетворяет
условиям теоремы Коши.
<4 Пусть в B.13) xq =уо- Тогда из B.14) имеем
\x(t)-y(t)\^hAeLh.
Если для любого е > 0 выбрать 5(е) = ee~Lh/h, то при условии
Д < 5(е) получаем \x(t) — y(t)\ < с, т.е., согласно определе-
определению 2.3, решение задачи Коши B.1), B.2) непрерывно зависит
от правой части ОДУ B.1). >
Следствие 2.3. Решение x(t, А) задачи Коши B.15), B.16)
непрерывно зависит от параметра Л, если при Л G Л правая
часть /(?, х, Л) ОДУ B.15) удовлетворяет условиям теоремы
Коши и df/d\(t,x,\) непрерывна в D.
< Рассмотрим два различных значения параметра Л = Ai и
А = Аг. Оценим разность |/(t,x,A2) — /(t,s,Ai)|, используя
теорему Лагранжа о конечных приращениях функции, спра-
справедливой в силу непрерывной дифференцируемости функции
по А:
§? А2 —Ах|,

2.3. Оценка разности решении двух уравнений 41
где 0 < 0 < 1. Поскольку переменные t и х принадлежат
замкнутой области J9, то существует постоянная А > О, для
которой |c?//dA(?,a;, Ai + 0(А2 — Ai)) | ^ А. Поэтому справедли-
справедлива оценка
В силу выполнения условия Липшица по х существует L > О,
такое, что
Из этих неравенств, согласно B.14), следует, что
Если для любого е > О выбрать 5(е) = ee~Lh(Ah)~1, то
при условии |А2 — Ai| < 5(e) получим \x(t, A2) — ж(*, Ai)| < e,
т.е. в силу определения 2.4 решение задачи Коши B.15), B.16)
непрерывно зависит от параметра А € Л. В начальном условии
B.15) параметр А принимает значения Ai и А2. >
Пример. Рассмотрим задачу Коши для ОДУ dx/dt = — х +
+ Ах3 с начальным условием х@) = 1. Правая часть ОДУ
непрерывно зависит от параметра А € Е. Поэтому, согласно
следствию 2.3, решение этой задачи Коши должно непрерывно
зависеть от А. В частности, это решение при А —> 0 должно
стремиться к решению x(t) = е~г задачи Коши с тем же на-
начальным условием, но для ОДУ dx/dt = —ж, которое следует
из исходного ОДУ при значении А = 0. Действительно, не-
непосредственной подсталовкои можно проверить, что решением
исходной задачи Коши будет
B-А)е2*'
причем

42 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
Вьшолнение условий теоремы Коши гарантирует существо-
существование и единственность решения задачи Коши B.1), B.2), на-
называемого также частным решением ОДУ B.1) первого
порядка, удовлетворяющим начальному условию B.2). Зафик-
Зафиксируем to и будем считать начальное значение xq переменным
параметром, принимающим различные числовые значения, не
выходящие за область D B.6), в которой выполнены условия
теоремы Коши, т.е. условия, накладываемые на правую часть
ОДУ B.1). Обозначим xq = С, где С — некоторая постоянная.
Определение 2.5. Решение ОДУ B.1) вида х = x(t, С)
называют общим решением этого ОДУ первого порядка
в области D, если для любой точки (?*,?*) Е D существует
значение параметра С = С*, которое удовлетворяет равенству
х* = x(U, С*), и # = х(?, С*) — частное решение ОДУ B.1)
с начальным условием B.2) в виде x(U) = ж*. Если общее
решение не разрешено явно относительно я, т.е. имеет вид
соотношения Ф(?, #, С) = 0, обращаемого в тождество в любой
точке (ж*,?*) Е D выбором некоторого значения параметра
С = С*, то такое соотношение называют общим интегралом
ОДУ B.1) первого порядка в области D.
Пример 2.1. Рассмотрим ОДУ dx/dt = 1 + х2. Его правая
часть зависит только от х. Она определена, непрерывна и име-
имеет непрерывную производную по х при всех значениях х Е К,
т.е., согласно теореме 2.2 Коши (с учетом замечания 2.1), через
любую точку плоскости tOx проходит единственная интеграль-
интегральная кривая этого ОДУ.
Непосредственной подстановкой можно убедиться, что фун-
функция x(t, С) = tg(t + С) при любом значении произвольной
постоянной С удовлетворяет этому ОДУ, т.е. является его ре-
решением. Согласно определению 2.5, эта функция будет общим
решением данного ОДУ, поскольку для любой точки (?*, х*) Е
Е К2 существует значение С* = arctgrr* — ?*, такое, что ж* =
= x(U, С*) = tg(?* + С*). Так как через эту точку проходит
только одна интегральная кривая рассматриваемого ОДУ, то

2.3. Оценка разности решений двух уравнений 43
график функции x(t) = tg(i + С*) и является именно этой ин-
интегральной кривой. Следовательно, функция x(t, С) = tg(< + С)
представляет все решения данного ОДУ в области R2. Инте-
Интегральные кривые в виде тангенсоид, сдвинутых вдоль оси Ot
на произвольное расстояние С, заполняют всю плоскость tOx.
Соотношение Ф(?, х, С) = arctgx — t — С = 0 является общим
интегралом рассматриваемого ОДУ в области R2. Действи-
Действительно, из этого соотношения для любой точки (?*,ж*) Е R2
также можно найти значение С* = arctgx* — ?*, удовлетворя-
удовлетворяющее частному решению a;(t, С*) = tg(t + С*) данного ОДУ с
начальным условием x(U) = z*. Уравнение arctga; — t — С* = О
в неявном виде задает функцию x(t), график которой являет-
является интегральной кривой этого ОДУ, проходящей через точку
(UjX*)eR2.
Пример 2.2. Правая часть ОДУ
?=*>-!, B.17)
как и в примере 2.1, не зависит от ?, определена, непрерывна
и имеет непрерывную производную по х при всех значениях
жЕМ. В силу замечания 2.1 и теоремы 2.2 Коши через лю-
любую точку плоскости tOx проходит единственная интегральная
кривая ОДУ B.17).
Значения х = ±1 обращают правую часть ОДУ B.17) в
нуль. Поэтому x\(t) = l и X2(t) = — 1 являются его решениями.
Кроме того, несложно проверить, что функция
удовлетворяет ОДУ B.17) при любом значении постоянной С,
т.е. является решением этого ОДУ. При С = 0 из B.18) следует
решение x\(t) = 1. Интегральные кривые ОДУ B.17), описы-
описываемые с помощью B.18), при С < 0 заполняют в плоскости
tOx полосу — 1 < х < 1, а при С > 0 — полуплоскости х > 1 и
х<-1 (рис. 2.3).

44
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
Рис. 2.3
Действительно, если записать B.18) в виде (х — 1)/{х +1) =
= Се2*, то в силу неотрицательности экспоненциальной функ-
функции e2t равенство при С < О возможно лишь для значений
х Е (—1, 1). Точкам в полуплоскости х > 1 отвечает условие
Ce2t < 1, или С < e~2t, а точкам в полуплоскости х < — 1 —
Ce2t > 1, или С > e~2t. Но не существует значения С € К,
которое, будучи подставленным в B.18), соответствовало бы
решению я?2(*) = — 1-
Таким образом, B.18) не является общим решением ОДУ
B.17) в области R2 в смысле определения 2.5, поскольку для
любой точки (?*,—1)еМ2 не существует такого значения
параметра С* G М, которое бы удовлетворяло равенству —1 =
= A + С*е2**)/A — С*е2**). Это равенство можно выполнить
лишь в случае перехода в его правой части к пределу при

2.4.' Изоклины и их использование 45
С* —>• оо. Вместе с тем B.18) является общим решением ОДУ
B.17) в области D = R2 \ {(*, -1): t e R}, т.е. в плоскости tOx,
из которой удалены точки прямой х = — 1.
Отметим, что функция x(t) = {С\ + е2ь)/(С\ — e2t) также
удовлетворяет ОДУ B.17) при любом значении постоянной С\,
а при значении С\ = 0 включает и решение X2(t) = —1, но
не включает решения x\{t) = 1. Следовательно, эта функция
также не является общим решением ОДУ B.17) в области R2.
2.4. Изоклины и их использование
для приближенного построения
интегральных кривых
Обыкновенное дифференциальное уравнение (ОДУ) B.1)
первого порядка каждой точке (?, х) G D прямоугольной обла-
области D B.6) ставит в соответствие определенное значение
dx/dt = /(?, х) = tga, где a — угол между касательной к ин-
интегральной кривой и координатной осью Ot. Таким образом,
в каждой точке области D определено некоторое направле-
направление, т.е. имеем поле направлений, которое можно предста-
представить на плоскости tOx, поместив в соотвествующих точках
области D отрезки, образующие с координатной осью Ot
углы arctg/(t, x). Это поле направлений можно представить
также при помощи плоских кривых, описываемых уравнением
/(?, х) = к (к = const) и называемых изоклинами (от грече-
греческих слов шоС^ — равный и кХьии — наклоняю). Для кривой с
некоторым фиксированным значением к в каждой ее точке ка-
касательная к интегральной кривой, проходящей через эту точку,
имеет одинаковое направление, задаваемое углом а = arctgfc.
Чтобы приближенно построить интегральную кривую, не-
необходимо начертить достаточное количество изоклин, а затем
изобразить кривую, которая в точках пересечения с изокли-
изоклинами, описываемыми уравнениями f(t,x) = k\, f(t, x) = &2, • • •>
имеет касательные с угловыми коэффициентами соответствен-
соответственно fci,fc2,...

46
2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
Пример, а. Для ОДУ dx/dt = t2 + х2 уравнение изоклин
имеет вид t2 + х2 = fc, т.е. они представляют собой семейство
концентрических окружностей радиуса VT, к ^ 0. Некоторые
изоклины и интегральные кривые для этого ОДУ изображены
на рис. 2.4.
Рис. 2.4
б. Пусть правая часть ОДУ dx/dt = /(?, ж) имеет вид
/(*,*) =
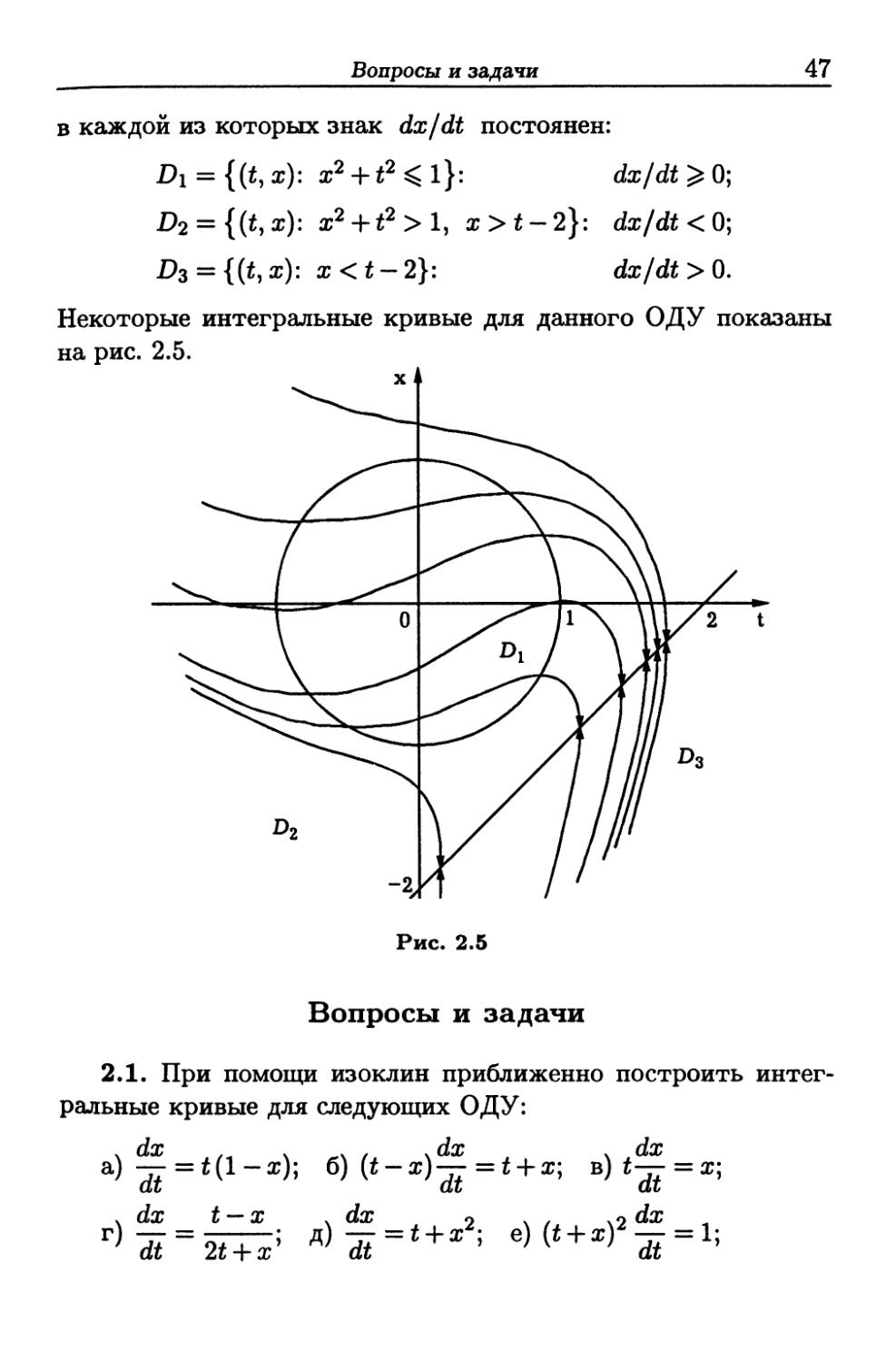
Эта функция разрывна на прямой х = t — 2, а в точках окружно-
окружности х2 +12 = 1 выполнено равенство dx/dt = 0. Таким образом,
в точках пересечения интегральной кривой с этой окружностью
касательная параллельна координатной оси Ot. Эти прямая и
окружность разбивают плоскость Юх на три области (рис. 2.5),

Вопросы и задачи
47
в каждой из которых знак dx/dt постоянен:
?>! = {(*, ж): x2 + t2^l}: dx/dt ^ 0;
D2 = {(t,x): x2 + t2>l, x>t-2}: dx/dt<0;
D3 = {(t,x): x<t-2}: dx/dt > 0.
Некоторые интегральные кривые для данного ОДУ показаны
на рис. 2.5.
Вопросы и задачи
2.1. При помощи изоклин приближенно построить интег-
интегральные кривые для следующих ОДУ:
dx dor
а) -? =t(l-ar); 6) (t-x)—=
dx t — x
dx
dcr
; в)*— = х;
-

48 2. ТЕОРЕМА СУЩЕСТВОВАНИЯ РЕШЕНИЯ ОДУ
ч dx 9 9 ч dx x — t2
ж) ш**, э>^ .
2.2. Установить области существования и единственности
решения для следующих ОДУ:
2.3. Пользуясь теоремой Коши, оценить область существо-
существования решения следующих ОДУ:
dx
а) — = x + t2, s@)=0, D = {(t,x): |t| < 1, |а;|<2};
б) ^- = te , ж@) = 1, 2? = {(*,ar): |<| < 2, |х-1|<1}.
2.4. Является ли функция ж(?) = 1/(С — t) общим решением
ОДУ dx/dt = х2 в области Е2? В каких областях эту функ-
функцию и функцию sci(i) = Ci/A — Ci?) можно считать общими
решениями данного ОДУ в смысле определения 2.5?

3. ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
ПЕРВОГО ПОРЯДКА
В этой главе рассматриваются специальные виды ОДУ пер-
первого порядка, решения которых удается найти в квадратурах.
Предполагается, что обсуждаемые ОДУ удовлетворяют усло-
условиям теоремы Коши.
3.1. Дифференциальные уравнения
с разделяющимися переменными
Обыкновенное дифференциальное уравнение (ОДУ) первого
порядка вида
^ *) C.1)
называют ОДУ с разделяющимися переменными. Будем
предполагать, что функции /i(<), /2B) непрерывны в ин-
интервалах (^1,^2) и (а,Ь) соответственно, и пусть /2B;) Ф О
Ух Е (а, Ь). При этих предположениях для ОДУ C.1) в области
?> = {(?, x)\ *i < t < ^2, a<x<b}
выполнены условия теоремы Коши (см. замечание 2.2).
Умножив ОДУ C.1) на dtlh{x), получим уравнение
= /i(t)<ft, C.2)
h{x)
в котором левая и правая части зависят от разных переменных.
Преобразование C.1) к виду C.2) называют разделением пе-
переменных. Зафиксируем какую-либо точку (?о,Ж)) в области

50 3. ОДУ ПЕРВОГО ПОРЯДКА
D и введем в рассмотрение определенные в D функции
X t
J(x) = |-щ, G(t) = jh(t)dt. C.3)
Xq to
С помощью теоремы о неявной функции [V] покажем, что
уравнение
J(aO-G(t)=0 C.4)
определяет х как неявную функцию *, являющуюся частным
решением ОДУ C.1), проходящим через точку (?о>#о)'
Рассмотрим функцию F(t, x) = J(rc) — G(t). Прежде всего
отметим, что F(to, яо) = J{%o) — G(*o) = 0. В силу теоремы о
дифференцируемости определенного интеграла по переменно-
переменному верхнему пределу [VI] функции J(x) и F(t) непрерывны и
дифференцируемы по своим аргументам соответственно в ин-
интервалах (а,Ь) и (ti,*2)) так как в этих интервалах непрерыв-
непрерывны подынтегральные функции 1//2(#) и fi(t) в интегралах
C.3). Поэтому функция F(t, x) непрерывно дифференцируема
в D. Так как i^(i, х) = J'(x) = 1//2(я), производная F^(t,x)
в D не обращается в нуль и, в частности, F^(io,#o) ^ 0.
Таким образом, выполнены все условия теоремы о неявной фун-
функции [V]: функция F(t, x) непрерывно дифференцируема в
окрестности точки (to? #o) и удовлетворяет в самой точке со-
соотношениям -F(t(b жо) = 0) Fxfoi xq) ф 0. Значит, уравнение
F(t, х) = 0 C.4) в окрестности точки (to, xq) задает диффе-
дифференцируемую функцию х = х(?), такую, что #(?о) = хо и
) _ G'(t)
Отсюда следует, что функция x(t) является частным ре-
решением ОДУ C.1), удовлетворяющим начальному условию
x{to) = Xq.

3.1. ОДУ с разделяющимися переменными 51
Поскольку точка (?о,жо)Е1? была выбрана в области
D произвольно, то C.4) описывает все решения ОДУ C.1),
определенные в этой области. Наряду с C.4) для задания
функции x(t) как решения ОДУ C.1) можно использовать
равенство
C-5)
Переход от равенства C.2) к соотношению C.5) называют
интегрированием этого равенства. Вычисление неопределен-
неопределенных интегралов в C.5) приводит к равенству*
J(x)-G(t) = C,
которое представляет собой общий интеграл ОДУ C.1) в
области D.
Замечание 3.1. При переходе к равенству C.2) предпола-
предполагалось, что /2(я) ф 0. Если это условие нарушено, то как C.4),
так и C.5) не дают всех возможных решений ОДУ C.1). В
самом деле, из C.1) непосредственно следует, что все значе-
значения я*, для которых /г(х*) = 0, дают дополнительные решения
ОДУ C.1) вида x(t) = х*. В этом случае для получения всех ре-
решений ОДУ C.1) к множеству функций ж(?), задаваемых при
помощи C.4) или C.5), необходимо присоединить все такие по-
постоянные решения. #
Пример, а. Рассмотрим ОДУ
—
at
* Вместо ранее введенных функций J(x) и G{t) можно взять любые
первообразные функций 1//2(х) и f\(t).

52 3. ОДУ ПЕРВОГО ПОРЯДКА
Разделив переменные, получим ОДУ вида C.1):
dx 1 х — 1
причем в данном случае fi(t) = 1/t2 и /2B) = (ж — 1)/х2.
Используя C.5), находим
?Ь C.6)
Это решение определено на всей числовой прямой R, кроме
точки t = 0. Для любой точки (?*, ж*) области D\ = R\ @; 1)
существует единственное значение
х2 1
С + +1|1| +
удовлетворяющее частному решению данного ОДУ с х(**) = х*.
Поэтому, согласно определению 2.5, C.6) задает общее решение
данного ОДУ в области D\.
Однако этому ОДУ удовлетворяет и решение x(t) = 1,
обращающее в нуль функцию /2(х) (см. замечание 3.1). Это
решение было „потеряно" при разделении переменных в силу
предположения, что /2B) Ф 0. Чтобы получить все решения
заданного ОДУ, необходимо к решениям, описываемым при
помощи C.6), присоединить решение x(t) = 1.
б. Если ОДУ dx/dt = еь~х привести к виду C.1) dx/dt =
= е*е~х, то будем иметь fi(t) = е* и /2B;) = е~х. В данном
случае /2B:) ф 0 Vx G R. Поэтому, разделяя переменные
(ех dx = e* dt) и интегрируя
fexdx= feldt,
находим все решения этого ОДУ:

3.1. ОДУ с разделяющимися переменными
53
Полученные интегральные кри-
кривые изображены на рис. 3.1.
При С Ф О они имеют право-
правостороннюю наклонную асимп-
асимптоту х = ?, которая являет-
является интегральной кривой, соот-
соответствующей значению С = 0.
Кроме того, при С > 0 они
имеют горизонтальные асимп-
асимптоты х = 1пС, а при С < 0 —
вертикальные асимптоты t =
-2
Любой точке (<*, х*) 6 R2 отвечает единственное значение
= ех* —
е**, выделяющее частное решение x(t) = ln(e*
+ ех* — etm) исходного ОДУ с начальным условием x(t*) = ж*,
т.е., согласно определению 2.5, соотношение x(t) = ln(e* + С)
является общим решением данного ОДУ в области R2, а
Ф(?, ж, С) = ех — ег — С = 0 — его общим интегралом в этой
области.
Пример 3.1. Шарик, масса которого т, нанизан на гори-
горизонтальную проволочную круговую петлю радиуса г (рис. 3.2).
Зная коэффициент трения /,
определить, какую начальную
скорость vq нужно сообщить
шарику р,ля того, чтобы он
сделал один полный оборот по
проволоке и остановился.
На шарик действуют четы-
четыре силы (см. рис. 3.2): сила
тяжести Р с абсолютным значением Р = тд (д — ускорение
свободного падения), центробежная сила N\ инерции с абсо-
абсолютным значением N\ = mv2/r (v — скорость шарика), сила
N реакции проволоки и направленная против его движения си-
сила F трения. Сила реакции проволоки уравновешивает силу
Рис. 3.2

54 3. ОДУ ПЕРВОГО ПОРЯДКА
тяжести и центробежную силу инерции, поэтому абсолютное
значение этой силы
\ г / г
Следовательно, абсолютное значение силы трения
/го
г
Согласно второму закону Ньютона, запишем уравнение движе-
движения шарика в виде
mdt "" ~" г
Поскольку г; = ds/dt, где 5 — расстояние, пройденное шариком
после начала движения, то можно написать
dv __dv ds __ dv
eft ds (it ds
В итоге получаем уравнение движения шарика в виде
ds
Это ОДУ с разделяющимися переменными. После разделения
переменных и интегрирования находим
vdv
I
Интеграл в левой части этого равенства подстановкой v2 = х
можно свести к табличному интегралу, тале что приходим к
соотношению
gr

3.2. Однородные и квазиоднородные уравнения 55
По условию, v = О при s = 2тгг. Отсюда С = 2nf. Начальную
скорость vq шарика найдем из условия v = vq при 5 = 0, т.е.
ы
2 gr
или (после решения биквадратного уравнения относительно
е4тг/ _ е-4тг/
Характерно, что значение vo и движение шарика не зависят
от его массы.
3.2. Однородные и квазиоднородные уравнения
Функция <р(?, х) является однородной функцией степе-
ни fc, если для всякого Л > 0 выполнено равенство </?(А?, А#) =
= \k<p(t, х). При А: = 0 имеем <р(А?, Хх) = у>(?, #), т.е. получаем
однородную функцию нулевой степени.
Например, t2 + х2 — tx является однородной функцией
второй степени, tk~lx + xk — однородной функцией fc-й степе-
степени, a Bt — x)/(t + x) — однородной функцией нулевой степени.
Обыкновенное дифференциальное уравнение (ОДУ)
первого порядка
называют однородным, если f(t,x) — однородная функция
нулевой степени (к = 0), т.е. /(At, Хх) = /(t, x). Если в этом
равенстве положить А = 1/?, то получим тождество /(t, ж) =
= /A,ж/?). Таким образом, если ОДУ C.7) является одно-
однородным, то его правая часть будет функцией лишь одного
аргумента x/t. Обозначив эту функцию через <р, запишем C.7)
в виде
Иг
f = <Р(Ф). C.8)

56 3. ОДУ ПЕРВОГО ПОРЯДКА
Сделаем замену искомой функции
x = ty. C.9)
Дифференцируя C.9) и подставляя результат в C.8), полу-
получаем ОДУ с разделяющимися переменными
Разделив переменные и проинтегрировав, найдем
dy
I
ч>{у) - у
= ln|*|. C.11)
В силу замечания 3.1 помимо решений C.11) ОДУ C.10) может
иметь решения вида у = уо> где Уо — корни уравнения <р{у) = у.
Решению у = уо ОДУ C.10) соответствует решение х = уо*
ОДУ C.8).
Пример. Уравнение
dx _tx + x2e-Vx
dt ~ t2
является однородным ОДУ. Замена x = ty приводит его к виду
или, после разделения переменных,
dt
После интегрирования и возврата к исходным переменным
получим е*/х + 1п|?| = С. При разделении переменных было
потеряно решение у = 0, которому соответствует решение
х = 0 исходного уравнения. #

3.2. Однородные и квазиоднородные уравнения 57
К однородным уравнениям заменами x = y + v и t= r + u
можно привести ОДУ вида
dx _ / ax + bt + c \
dt ~~" )
Смысл этих замен состоит в избавлении от постоянных сла-
слагаемых в числителе и в знаменателе аргумента функции /.
Постоянные u, v являются решением системы линейных алге-
алгебраических уравнений (СЛАУ)
u + c = 0; ( .
0 C ]
При аЪ\ — aib = 0, т.е. когда СЛАУ C.12) не имеет единствен-
единственного решения, следует применить подстановку у = ах + bt.
Пример. Рассмотрим ОДУ
cfa; /
dt \
х +
После замены переменных # = у — 1, t = r + 3 получаем
Это однородное ОДУ можно привести к ОДУ с разделяющими-
разделяющимися переменными заменой z = у/т:
dz z + z3
+ О
После разделения переменных и интегрирования находим

58 3. ОДУ ПЕРВОГО ПОРЯДКА
или 2Te2arctg2; = G, где С = ±eCl. Возвращаясь к исходным
переменным, получаем
При разделении переменных мы потеряли решение z(r) = О
(см. замечание 3.1), или, в исходных переменных, x(t) =
= —1. В самом деле, нетрудно убедиться, что в постоянная
функция x(t) = — 1 действительно является частным решением
исходного ОДУ и в общем решении соответствует константе
/~Ч ^^ Г\ II
О — U. Чг
ОДУ C.7) первого порядка называют квазиоднородным,
если для всех Л > 0 справедливо равенство
JIА Г, A X) — A J ye, X), (tj.Xo)
где a, /3 e E. Заменой ж = yt^la квазиоднородное ОДУ можно
преобразовать к ОДУ с разделяющимися переменными. Дока-
Докажем справедливость этого утверждения.
Полагая в C.13) Л = V 'Q, имеем /A, x/t^'a) = t "'af(tj ж),
или /(?, х\= t^/a/(l, x/tP/a). Учитывая это представление и
проводя в C.7) замену х = yt^la, запишем
+ yt r/(i, у).
at a
Отсюда и следует ОДУ с разделяющимися переменными
Некоторые ОДУ первого порядка можно привести к од-
однородным заменой х = уш, где т — число, подлежащее опре-
определению. Например, ОДУ

3.3. Уравнения в полных дифференциалах 59
после замены х = ут принимает следующий вид:
at
Оно будет однородным в случае равенства степеней всех его
членов: 4 + 2т — 1 = Am = 6. При т = 3/2 эти равенства спра-
справедливы, поэтому замена х = у3/2 приводит к однородному
ОДУ вида
Решал конкретные уравнения при помощи замен вида х =
= У^а? # = у"\ следует обращать внимание на знаки перемен-
переменных. Так, выражение ут при у < 0 и иррациональном m не
определено.
3.3. Уравнения в полных дифференциалах.
Интегрирующий множитель
Обыкновенное дифференциальное уравнение (ОДУ) первого
порядка dx/dt = f(t,x) иногда бывает удобно записать в
форме
M(t, x) dt + N(t, x) dx = 0. C.14)
В случае выполнения равенства
dN(t,x) dM(t,x)
dt dx
C.15)
тождественно (на всей плоскости tOx или в некоторой ее обла-
области D) C.14) называют ОДУ в полных дифференциалах.
Если функции М(<, ж) и ЛГ(?, х) непрерывно дифференци-
дифференцируемы в некоторой области Z), то условие C.15) обеспечивает
для любой точки (to,a?o) G -D в некоторой ее окрестности су-
существование такой функции W(t, ж), полный дифференциал
которой является левой частью C.14), т.е.
M(t, x) dt + N(t, x)dx = dW(t, x). C.16)

60 3. ОДУ ПЕРВОГО ПОРЯДКА
Тогда C.14) принимает вид dW(t, ж) = 0, откуда находим
W(t, я) = С, где С — произвольная постоянная. Функцию
W(t, х), удовлетворяющую условию C.16), можно представить
следующим образом [VII]:
t х
W(t,x) = J M(r,xo)dT + J N(t,t)dt. C.17)
t0 XQ
Действительно, используя правило дифференцирования инте-
интеграла по параметру [VI] и условие C.15), получаем
ХО XQ
= M(t, х0) + Af (t, х) - M(t, s0) = M(t, x) C.18)
и dW/dx = JV(t, x), т.е. функция VF(t, ж) удовлетворяет усло-
условию C.16).
Итак, решение ОДУ C.14) в полных дифференциалах в неяв-
неявной форме можно задать в виде общего интеграла W(t, x) = С.
Пример. Рассмотрим ОДУ
(Зх2 + 2xt + 2t) dt + (Ш + t2 + 3)dx = 0.
Это ОДУ в полных дифференциалах, так как в данном случае
t, х) = Зх2 + 2xt + 2t, N(t,x) = 6xt + t2 + 3 и
{З2 + 2t + 2t) 6 + 2t
— {Зх2 + 2xt + 2t) =6x + 2t;
ox ot
т.е. во всех точках плоскости tOx выполнено условие C.15).
Вычисляя интегралы в C.17), положив to = 0 и xq = 0, находим
W(t, ж) = 3x2f + xt2 +12 + Зх. Следовательно, общим интегралом
исходного уравнения будет
ЗхН + xt2 + t2 + 3x = C = const. #

3.3. Уравнения в полных дифференциалах 61
Конечно, не всякое ОДУ вида C.14) удовлетворяет условию
C.15). Если это условие не выполнено, то иногда все же удается
привести C.14) к ОДУ в полных дифференциалах умножением
на некоторую не равную нулю функцию /i(?, ж), называемую
в таком случае интегрирующим множителем. При этом
вместо C.15) получаем
dt дх
или
_ __ _ dN\
dt dx \ dx dt i
Найти функцию /i(?, x) из этого дифференциального уравнения
с частными производными в общем случае не удается. В ряде
частных случаев оно упрощается, например в случае, когда
интегрирующий множитель \х зависит только от одного из
переменных. Так, если /л = //(?), то имеем ОДУ
_ 1 (дМ dN\
Ясно, что для существования интегрирующего множителя /i,
не зависящего от ж, необходимо и достаточно, чтобы правая
часть этого уравнения была функцией только t.
Пример. Рассмотрим ОДУ
Здесь M(t,x)=ex + t и N(t,x) = 2tex. Так как дМ/дх = ех
и dN/dt = 2ex, то очевидно, что условие C.15) не выполнено:
dN/dt ф дМ/дх. Однако выражение
dN\ _ 1
не зависит от х. Тогда для интегрирующего множителя
будем иметь ОДУ с разделяющимися переменными
din И _ 1
dt " It

62 3. ОДУ ПЕРВОГО ПОРЯДКА
Одним из решений этого ОДУ является функция /x(t) =
= 1/<У1*[, t Ф 0. Итак, интегрирующий множитель найден в
области D = {t^0}.
Рассмотрим случай t > 0. Умножив исходное ОДУ на
интегрирующий множитель //(?) = 1/\Д, запишем
Покажем, что в области {t > 0} это ОДУ в полных дифферен-
дифференциалах. В самом деле, нетрудно убедиться, что теперь условие
C.15) будет выполнено, если принять M(ty х) = (ех + г)/уД и
Vi. Тогда
е^ dN ех
дх ~ y/i1 dt уД'
т.е. dN/dt = dM/dx.
Подставляя принятые выражения для М(?, х) и iV(t, x) в
C.17), интегрированием находим функцию W(t, x), положив
для простоты *о = 1 и #о = 0:
t х
1 0
Следовательно, общим интегралом исходного ОДУ будет
где С — произвольная постоянная, а общее решение этого ОДУ
можно записать в виде
С

3.4. Линейные ОДУ первого порядка 63
Случай t < О рассматривается аналогично. При этом
интегрирующий множитель будет иметь вид /i(<) = 1/y/^i.
Отметим, что у ОДУ первого порядка в форме C.14) пе-
переменные ?, х равноправны и каждое из них можно рассма-
рассматривать как функцию другого. Если независимым переменным
является ж, а роль функции играет ?, то уравнение C.14) имеет
решение t(x) = 0, теряющееся при интегрировании ОДУ.
3.4. Линейные дифференциальные уравнения
первого порядка.
Уравнения Бернулли и Риккати
Обыкновенное дифференциальное уравнение (ОДУ) первого
порядка вида
C.19)
a(t)
где правая часть является линейной функцией #, a a(t) и b(t)
непрерывны в некотором интервале изменения ?, называют
линейным ОДУ первого порядка.
Если b(t) = 0, то C.19) примет вид
dx
-? = a(t)x. C.20)
Это уравнение называют однородным линейным ОДУ пер-
первого порядка, соответствующим C.19), в отличие от уравне-
уравнения C.19) с b(t) ^ 0, называемого неоднородным.
Существует ряд методов решения ОДУ C.19). Изложим
здесь два из них.
1. Метод Бернулли. Будем искать решение ОДУ C.19)
в виде x(t) = u(t)v(t). Подставляя x(t) в C.19) и опуская
обозначение аргумента ?, получаем
du dv
v — + и — = auv + Ь,
at at

64 3. ОДУ ПЕРВОГО ПОРЯДКА
или
/dv \ du __
\dt aV)U V dt"
Выберем в качестве v(t) одно из отличных от тождественного
нуля решений ОДУ dv/dt — av = 0. Это ОДУ с разделяющимися
переменными; после разделения переменных и интегрирования
находим v(t) = еА^\ где A(t) — одна из первообразных
функции a(t). Тогда u(t) должно удовлетворять ОДУ
Ье
dt '
после интегрирования которого имеем u(t) = Со + B(t), где
B(t) —первообразная функции b{t)e~A^\ а Со —произволь-
—произвольная постоянная. В итоге решение ОДУ C.19) примет вид
C.21)
В качестве примера рассмотрим ОДУ dx/dt = х + е*. В
данном случае a(t) = 1, A(t) =f и b(t) = е*, B(t) = t. Согласно
C.21), находим
2. Метод Лагранжа. Однородное ОДУ C.20), соответ-
соответствующее неоднородному линейному ОДУ C.19), представляет
собой уравнение с разделяющимися переменными и имеет об-
общее решение
x(t) = CeA{t\ C.22)
Решение ОДУ C.19) будем искать в виде
C.23)
где C{t) — функция, подлежащая определению. Дифферен-
Дифференцируя C.23) и подставляя полученный результат в C.19), при-

3.4. Линейные ОДУ первого порядка 65
ходим к ОДУ
dC(t)
dt
Отсюда интегрированием находим
C.24)
и, подставляя C(t) в C.23), получаем итоговое выражение
идентичное C.21).
Таким образом, с помощью этого метода решение про-
произвольного линейного неоднородного ОДУ удается свести к
операции интегрирования, причем функция C(t) в C.23) со-
совпадает с функцией u(t), используемой в методе Бернулли.
Найдем решение ОДУ C.19), удовлетворяющее начальному
условию x(to) = хо- Полагая в C.23)
t t
A(t) = Ja{№ B(t) =
t0 t0
и используя начальное условие, получаем
= Со,
так как при таком выборе функций A(t) и B(t) имеем
A(to) = B(to) = 0. Таким образом, частное решение ОДУ C.19),
удовлетворяющее начальному условию x(to) = хо, имеет вид
3 - 9306

66 3. ОДУ ПЕРВОГО ПОРЯДКА
Замечание 3.1. В ряде учебников общее решение ОДУ
C.19) записывают в виде
Сехр fa{t)dt + I 1
6(t)exp (- Ia(t)dt) dt\ exp /a(t)dt,
подразумевая под содержащимися в формуле неопределенными
интегралами соответствующие первообразные. Но неопреде-
неопределенный интеграл — это все множество первообразных, а не
отдельно взятая первообразная, так что такое использование
понятия неопределенного интеграла неточно и является "жар-
"жаргонным". В современной математической литературе такая
неточность допускается, так как приведенная формула удобна
для приложений, тем более что смысл, в котором использует-
используется символ неопределенного интеграла, легко определяется и к
путанице не приводит. #
Решим методом Лагранжа, иногда называемым методом
вариации постоянной, линейное неоднородное ОДУ
at
»
В данном случае а(?) = — cost и b(?) = e~sint. Соответствую-
Соответствующее этому ОДУ однородное уравнение dx/dt + x cos t = 0 имеет,
согласно C.22), решение
x(t) = Ce~sint.
Полагая С = C(t) и подставляя в исходное уравнение, а затем
интегрируя, находим
и окончательно получаем
x(t) = de-sint + te~8int

3.4. Линейные ОДУ первого порядка
67
Рис. 3.3
Пример 3.2. Сосуд, наполненный жидкостью, вращают
с угловой скоростью и вокруг оси Оу. Жидкость в сосу-
сосуде образует воронкообразную полость
(рис. 3.3), границей которой являет-
является поверхность вращения некоторой
кривой, которая описывается уравне-
уравнением у = у(х). Найдем форму этой
поверхности.
Рассмотрим частицу на поверхно-
поверхности полости, имеющую массу т и ко-
координаты (#, у(х)). Во вращающейся
вместе с жидкостью системе координат Оху частица покоит-
покоится. В этом случае равнодействующая F силы тяжести Р и
центробежной силы инерции N\ с абсолютными значениями
соответственно тд и тиР'х ортогональна поверхности вра-
вращения. Тогда
тиJх о х
= аГ-.
тд д
Но в силу геометрической интерпретации производной yf(x)
как углового коэффициента касательной к графику функции
у(х) имеем tg(p = dy/dx, и поэтому
dx g
Решая это линейное однородное ОДУ с начальным условием
= 0, получаем
т.е. границей полости является параболоид вращения. #
В некоторых случаях ОДУ, в котором независимым пере-
переменным является <, а искомой функцией — ж(?), можно пре-
преобразовать в линейное, если, наоборот, считать х аргументом,

68 3. ОДУ ПЕРВОГО ПОРЯДКА
at — искомой функцией. Например, уравнение
записанное в форме
dt Ъ(х) _ с(х)
dx a(x) а(х)'
представляет собой линейное неоднородное ОДУ.
Уравнением Бернулли называют ОДУ вида
dx
— = a{t)x + b{t)xa, C.25)
где а € К, а ^0,1. Подстановка у = х1~а приводит C.25) к
линейному неоднородному ОДУ
которое можно решить изложенными выше методами. Другой
вариант — отыскание решения ОДУ C.25) в виде x(t) =
= u(t)v(t), используемом при решении линейного ОДУ методом
Бернулли.
Пример. Решим двумя указанными способами уравнение
Бернулли
dx х х2 _
I способ. Выполнив подстановку у = 1/х (х ф 0), получим
У2 " dt + yt ~ yH Ш*'
ИЛИ
dt t~ tlnt'

3.4. Линейные ОДУ первого порядка 69
т.е. линейное неоднородное ОДУ. Соответствующее ему од-
однородное ОДУ имеет решение y(t) = Ct. Решая неоднородное
уравнение методом Лагранжа, получаем ОДУ
после интегрирования которого находим
и
Возвращаясь к исходному переменному, в итоге запишем
1 1
x(t) =
y(t) l + Cit + \nt'
При выполнении подстановки могло быть потеряно решение
х = 0. Проверка показывает, что действительно x(t) = 0
является решением исходного ОДУ.
II способ. Полагая x(t) = u(t)v(t) и подставляя в исходное
ОДУ, имеем
du dv uv u2v2,
Приравняв нулю коэффициент при n(t), получим ОДУ
dv/dt + v/t = 0, в качестве частного решения которого возьмем
v(t) = 1/t. Тогда ^ля нахождения u(t) имеем ОДУ с разделяю-
разделяющимися переменными
1 du и2_
Учитывая возможность потери решения u(t) = 0 при разделе-
разделении переменных, после интегрирования этого ОДУ запишем
Окончательно получаем
^ и X(t)=0. #

70 3. ОДУ ПЕРВОГО ПОРЯДКА
Уравнением Риккати по имени итальянского математи-
математика и инженера Я.Ф. Риккати A676-1754) называют ОДУ вида
W/t»
— = c(t) + b(t)x + a(t)x2, C.26)
at
где а(?), b(t), c(t) — функции, непрерывные в некотором ин-
интервале изменения t. Это ОДУ содержит в себе частные
случаи уже рассмотренных ранее уравнений: если a(t) = 0, то
C.26) — линейное неоднородное ОДУ, а если c(t) = 0 — урав-
уравнение Бернулли с а = 2.
К сожалению, решение уравнения Риккати в общем случае
не удается свести к операции интегрирования. Однако если
известно одно частное решение ОДУ C.26), то его общее
решение можно найти при помощи двух последовательных
операций интегрирования. Действительно, пусть х = x(i) —
частное решение C.26). Выполнив подстановку у = x(t) — x(t),
получим
^ + Щ = c(t) + b(t)y + b(t)x(t) + a{t)y2 + 2a(t)x(t)y + a(t)x2{t).
at at
»
Так как x(t) — решение ОДУ C.26), то окончательно имеем
Это уравнение Бернулли с а = 2. Заменой у = 1/z его мож-
можно свести к линейному неоднородному ОДУ, для нахождения
общего решения C.21) которого достаточно выполнить после-
последовательно две операции интегрирования.
Пример. Уравнение Риккати
^ + x2-tx = l C.27)
at

3.5. Особые точки и особые решения ОДУ первого порядка 71
имеет частное решение x(t) = t. Замена х = t + у приводит
C.27) к уравнению Бернулли
Положим y(t) =u(t)v(t). Тогда можно записать
du dv о о
v — + и — + u v* + tuv = 0.
at at
Приравняв нулю коэффициент при и, получим ОДУ dv/dt +
+ tv = 0, имеющее частное решение v(t) = e~*2/2. Теперь ОДУ
для нахождения u(t) принимает вид
dt
Разделяя переменные и интегрируя, получаем с учетом поте-
потерянного решения u(t) = 0
где G(t) — первообразная функции е~* /2. В итоге уравнение
Риккати C.27) имеет решения
и
3.5. Особые точки и особые решения
ОДУ первого порядка
Если в обыкновенном дифференциальном уравнении (ОДУ)
первого порядка dx/dt = f(t,x) правая часть /(*, х) не-
непрерывна в некоторой области D и удовлетворяет условию
Липшица по х, то через каждую точку (?q, #о) € D этой
области проходит, согласно теореме 2.2 Кошщ единственная

72 3. ОДУ ПЕРВОГО ПОРЯДКА
интегральная кривая. Такую точку интегральной кри-
кривой называют обыкновенной. Точку (?(ь#о)> не являющу-
являющуюся обыкновенной, называют особой точкой ОДУ dx/dt =
= /(?, х). Через особую точку, вообще говоря, не проходит ни
одна интегральная кривая или же проходят по крайней мере
две интегральные кривые.
Нарушение условий теоремы 2.2 Коши в точке (?(ь#о)
является лишь необходимым условием того, что эта точка
является особой. Например, для ОДУ dx/dt = x/t точка
(?(b#o) = @, 0) будет особой, поскольку через нее проходит
бесконечное множество интегральных кривых x(i) = Ct, где
С — произвольная постоянная. Напротив, через особую точку
(*(Ь #о) = @, 0) ОДУ dx/dt = — t/x не проходит ни одной
интегральной кривой х2 +12 = С (С > 0).
Особым решением ОДУ называют такое решение ОДУ
B.1), которое во всех своих точках не удовлетворяет свойству
единственности, т.е. в окрестности каждой точки (?, х) осо-
особого решения существуют по крайней мере две интегральные
кривые, проходящие через эту точку. Теорема Коши дает до-
достаточные условия для того, чтобы в некоторой области не
существовали особые решения. Таким образом, для существо-
существования последних необходимо, чтобы условия этой теоремы были
нарушены. Если, например, /(*, х) непрерывна в некоторой
области, то особые решения могут проходить только через те
точки, в которых не выполнено условие Липшица.
Пример, а. Рассмотрим ОДУ dx/dt = ж2/3. Интегрируя
его, находим общее решение x(t) = (? + СK/27 (рис. 3.4). Кро-
Кроме того, это ОДУ имеет особое решение x(t) = 0, проходящее
через точки, где не выполнено условие Липшица (см. рис. 3.4).
Действительно, если бы условие Липшица было выполнено для
правой части /(?,х) = х2^ этого ОДУ, то при хфу было
справедливо неравенство

3.5. Особые точки и особые решения ОДУ первого порядка 73
где L — постоянная Липшица. Но при у = О и х -> О левая
часть этого неравенства стремится к бесконечности.
Xi
ooj
(Г
jc=o |c<o
f '
Рис. 3.4
б. Найдем особые решения ОДУ
и построим интегральные кривые.
Выполним в этом уравнении подстановку у =
чим ОДУ с разделяющимися переменными
— t и полу-
dt
C.28)
Функция Зу1/3/2 не удовлетворяет условию Липшица при у =
= 0. Очевидно, что y(t) = 0 является решением и, следова-
следовательно, может быть особым. Найдем другие решения ОДУ
C.28). Разделяя в C.28) переменные и интегрируя, получа-

74
3. ОДУ ПЕРВОГО ПОРЯДКА
С>0
Рис. 3.5
ем y(t) = ±(t-CK/2. При * = *о
условию у (to) = 0 удовлетворя-
удовлетворяют по крайней мере два реше-
решения: y(t)=O и y(t) = (i-foK/2.
Поэтому у(?) = 0 — особое ре-
решение ОДУ C.28).
Решением исходного ОДУ яв-
являются x(t) = t+(t- Cfl2 и
x(i) = ?, причем x(t) = t — его
особое решение. Интегральные
кривые изображены на рис. 3.5.
3.6. Уравнения, не разрешенные
относительно производной
Обыкновенное дифференциальное уравнение (ОДУ) первого
порядка, не разрешенное относительно производной, имеет вид
"('•*• i)=°-
C.29)
Допустим, ОДУ C.29) можно разрешить относительно
dx/dt (пусть и неоднозначно), т.е. можно получить г соот-
соотношений
И/Г
C.30)
— = /*(*,*), г = 1,2,...,г.
Тогда к каждому из г ОДУ C.30) можно применять методы
интегрирования, изложенные выше. Но приведение к виду
C.30) не всегда возможно. Поэтому решение ОДУ C.29) часто
приходится искать, используя параметр, например р = dx/dt.
Рассмотрим ряд частных случаев.
Предположим, что C.29) можно разрешить относительно #,
т.е. записать в виде х = f(t,p). Вычислим полный дифферен-
циал dx = — сЙ+ тг~Ф- Поскольку dx =pdt, то его можно
ot op
представить в виде ОДУ М(?, р) dt + iV(t, p) dp = 0, интегрируя

3.6. Уравнения, не разрешенные относительно производной 75
которое (если это возможно), найдем общее решение t = ?(p, С),
С = const. Тогда общее решение исходного ОДУ C.29) в пара-
параметрической форме будет иметь вид
Г t = t(p,C);
1 x = f(t,p).
Пример. В уравнении
Л dx . dx
laTt+smTt=t
положим dx/dt = p и запишем t = \np + sinp. Так как dx=pdt,
то имеем dx = р{1/р + cosp) dp и, интегрируя, получаем общее
решение исходного ОДУ в параметрической форме
{t = lnp + sinp;
х = р + cosp + psinp + С, р > О, С = const. #
Рассмотренным методом решают, в частности, уравнения
Лагранжа и Клеро.
Уравнением Лагранжа называют ОДУ вида
где ip(p) и ф(р) — непрерывно дифференцируемые функции,
причем (р(р) ф р.
Поскольку dx =pdt и dx = <р(р) dt + t(pf (p) dp + ф1 (р) dp, то
можно записать
C.32)
Так как ОДУ C.32) линейно относительно ?(р), то его можно
проинтегрировать по р. После интегрирования получим t =
= ?(р, С), С = const. Подставив t = t(p, С) в C.31), запишем

76 3. ОДУ ПЕРВОГО ПОРЯДКА
общее решение уравнения Лагранжа в параметрической форме:
Пример. Рассмотрим ОДУ
dx
Это уравнение Лагранжа. Обозначим p = dx/dt
ф(р) = -р). Тогда ОДУ C.32) примет вид
dt 2 1
+t
dp p-1 p{p-I)'
Решая его, получим
p-lnp + C
5
х = tp2 — р, р > О, С = const.
Частным случаем уравнения Лагранжа является уравнение
Клеро
dx
(ззз)
названное по имени французского математика и астронома
А.К. Клеро A713-1765). Применим ту же процедуру, что и
при решении уравнения Лагранжа:
dx = pdt + tdp + V>'
а так как da; =pdt, то

3.6. Уравнения, не разрешенные относительно производной 77
т.е. либо р — С = const, либо t = —ifc'ip). В первом случае в
соответствии с C.33) имеем общее решение уравнения Клеро
в виде x(t) = Ct + ф(С), а во втором — особое решение этого
ОДУ в параметрической форме
I У h C.34)
(последнее будет обосновано после формулировки варианта
теоремы Когии существования и единственности ре-
решения ОДУ первого порядка, но вида C.29), т.е. ОДУ, не
разрешенного относительно производной).
Теорема 3.1 (теорема Коши). Пусть функция F(t, я,р),
где p = dx/dt, в окрестности точки М(?о,#(ъРо) непрерывна
по всем переменным и непрерывно дифференцируема по ж и р.
Пусть, кроме того, F(M) = 0 и в точке М dF/dp Ф 0. Тогда
существует единственное решение х = x(t) задачи Коши для
ОДУ C.29), удовлетворяющее начальному условию x(to) =xq.
Из этой теоремы следует, что особые решения ОДУ C.29),
если таковые существуют, удовлетворяют системе уравнений
0F(t,x,p) C.35)
Для отыскания особого решения необходимо из системы
C.35) исключить р. Полученное после этого соотношение
Ф(?, х) = 0 определяет так называемую дискриминантную
кривую. Каждую ветвь этой кривой необходимо проверить,
чтобы узнать, соответствует ли она решению ОДУ C.29), и
если соответствует, то это решение, вообще говоря, особое.
Для уравнения Клеро dF/dp = 0 при t = —ф'(р), и си-
система C.35) дает решение C.34), которое является особым.
Действительно, касательная к интегральной кривой C.34) в

78 3. ОДУ ПЕРВОГО ПОРЯДКА
точке, соответствующей фиксированному значению параметра
р, имеет уравнение х =pt + ф(р), т.е. входит в семейство пря-
прямых, задаваемых решением x(t) = Ct + ip(C), причем угловой
коэффициент касательной в этой точке, согласно правилу диф-
дифференцирования функции, заданной параметрически [II], равен
,_р__ф(р)рф(р)ф(р)_
* t'P -Пр) Р'
Вместе с тем при значении параметра С = р эта точка лежит
как на прямой x(t) = Ct + ip(C), так и на интегральной кривой
C.34). Следовательно, решение C.34) особое, а интегральная
кривая является огибающей однопараметрического семейства
прямых x(t) = С? + ф{С).
Пример. Решим уравнение Клеро х = txf + xf2/2. Здесь
ф(х') = xf2/2. Согласно изложенному выше, общим решением
этого ОДУ будет x(t) = СЧ + С2/2, а C.34) задает особое ре-
решение, причем t = —il>f(p) = — Р) а х = —p^'(p) + ф(р) = —р2/2.
Таким образом, особое решение исход-
исходного ОДУ принимает вид t = — р, х =
= —р2/2 или, после исключения р, x(t) =
= — ?2/2, т.е. интегральная кривая осо-
особого решения как огибающая семейства
прямых x(t) = Ct + C2/2 будет парабо-
Рис. 3.6 лой (рис. 3.6).
Дополнение 3.1. Особенности составления
дифференциальных уравнений
в прикладных задачах
Необходимым этапом решения любой прикладной задачи
является построение математической модели изучаемого объ-
объекта или процесса. Обыкновенные дифференциальные уравне-
уравнения (ОДУ) первого порядка составляют основу сравнительно

Д.3.1. Особенности составления ОДУ в прикладных задачах 79
простых, но весьма распространенных математических моде-
моделей, применяемых в самых разных областях науки и техники.
Причина состоит в том, что многие законы физики, меха-
механики, химии и других фундаментальных наук, используемые
для количественного описания реальных объектов и процессов,
устанавливают связь между величинами и их бесконечно ма-
малыми приращениями, т.е. дифференциалами. Иными словами,
применяемые при решении прикладных задач фундаменталь-
фундаментальные законы часто предопределяют структуру используемых
соотношений между зависимыми и независимыми переменны-
переменными, близкую или совпадающую со структурой ОДУ.
Однако формальное использование известных законов в
прикладных задачах обычно не дает желаемого эффекта. Дело
в том, что каждая прикладная задача имеет свои особенности,
требующие осмысления и, как правило, обоснованного упро-
упрощения и выделения основных влияющих факторов прежде, чем
удается применить тот или иной закон для построения матема-
математической модели. Поскольку цель решения прикладной задачи
состоит в установлении соотношений между конечными значе-
значениями зависимых и независимых переменных, то желательно,
чтобы ОДУ, входящие в математическую модель, допуска-
допускали интегрирование и представление решения в элементарных
функциях. Это условие далеко не всегда выполнимо, но поиск
разумного компромисса между сложностью реального объекта
или процесса и желаемой простотой их описания является лейт-
лейтмотивом математического моделирования — одного из наибо-
наиболее перспективных направлений прикладной математики.
Таким образом, составление входящих в математическую
модель ОДУ требует сочетания знаний в конкретной приклад-
прикладной области и достаточно высокой математической культу-
культуры. После получения решения прикладной задачи важно уметь
осмыслить и проанализировать полученный результат, дать
ему практическую интерпретацию и попытаться сделать полез-
полезные выводы, направленные на совершенствование рассматрива-
рассматриваемого объекта или процесса.

80 3. ОДУ ПЕРВОГО ПОРЯДКА
Несмотря на то что математическое моделирование — это,
по существу, применение математики к решению прикладных
задач, формализовать все его этапы и указать исчерпываю-
исчерпывающие правила составления ОДУ и построения математических
моделей не удается. Успех здесь зависит от творческого подхо-
подхода, изобретательности, интуиции и приобретаемых практикой
навыков.
Рассмотрим на примерах некоторые особенности состав-
составления ОДУ первого порядка и построения математических
моделей применительно к достаточно простым прикладным
задачам.
Пример 3.3. Известно, что электрический конденсатор
емкостью С, будучи заряженным некоторым количеством Q
электричества, постепенно теряет этот заряд. Это приводит к
тому, что разность потенциалов ДС/ на обкладках конденса-
конденсатора, изолированного от других элементов электрической цепи,
постепенно уменьшается. Причиной являются несовершенство
электрической изоляции и утечка заряда через окружающую
среду. Вместе с тем в любой текущий момент времени t оста-
остается в силе известное соотношение AU(t) = Q(t)/C, которое в
данном случае можно рассматривать как линейную математи-
математическую модель конденсатора в конечной форме.
При количественном анализе быстропротекающих процес-
процессов в электрических цепях обычно не учитывают потери заря-
заряда и используют идеализированную линейную математическую
модель конденсатора в дифференциальной форме
C'36)
Здесь / — сила электрического тока, проходящего при измене-
изменении ДС/ в цепи, содержащей последовательно включенный кон-
конденсатор. Возникает естественный вопрос: можно ли учесть
утечки заряда и оценить их влияние на протекающие процес-
процессы, уточнив эту модель, но не слишком усложняя ее ?

Д.3.1. Особенности составления ОДУ в прикладных задачах 81
Если предположить, что сила тока 7* утечки пропорцио-
пропорциональна текущей разности потенциалов Д?/(?), то это равно-
равносильно предположению, что конденсатор обладает некоторым
конечным внутренним сопротивлением Д* (рис. 3.7) в отличие
от модели C.36), в которой такое сопротивление считают бес-
бесконечно большим. Согласно закону баланса
токов в разветвлениях цепи (первому зако-
закону Кирхгофа, названному по имени немец-
немецкого физика и математика Г.Р. Кирхгофа
A824-1887)), имеем / + Д=0. Отсюда с
учетом C.36) и закона Ома находим Рис- 3-7
с
Таким образом, математическая модель, учитывающая (в
рамках принятого предположения) утечки заряда конденсато-
конденсатора, включает ОДУ с разделяющимися переменными, которое
также можно рассматривать как линейное однородное ОДУ
первого порядка. После интегрирования получаем
где С\ — произвольная постоянная. Если в момент времени
t = О конденсатор был заряжен от внешнего устройства до
разности потенциалов Д?/о, а затем это устройство было
отключено, то в этом случае С\ = Д?/<ь и в итоге соотношение
Д17(*) = ДС/ое~*/(/г*с) C.38)
устанавливает зависимость изменения разности потенциалов
AU(t) на обкладках конденсатора от времени t. Аналогичной
будет зависимость от времени заряда конденсатора: Q(t) =
= Яое~~г^К*С\ где Qo = CAUq — заряд в начальный момент
времени t = 0.
Уточненная математическая модель электрического конден-
конденсатора в виде ОДУ C.37) или в конечной форме C.38) (ино-
(иногда говорят о модели в интегральной форме, поскольку такую

82 3. ОДУ ПЕРВОГО ПОРЯДКА
модель получают интегрированием ОДУ) содержит параметр
Я*, который не входит в паспортную характеристику конденса-
конденсатора. Поэтому перед применением таких моделей необходимо
найти способ оценки значения этого параметра, т.е. провести
идентификацию математической модели (от латинско-
латинского слова identifico — отождествляю). Оценить значение Я*
теоретическим путем достаточно сложно из-за большого чис-
числа трудно поддающихся количественному описанию факторов,
влияющих на это значение (тип и качество применяемого в кон-
конденсаторе диэлектрика, особенности технологии изготовления
и условий работы конденсатора и т.п.). В таком случае более
реальным и более надежным является способ, связанный с ис-
использованием экспериментальных данных.
Если в момент времени U измерить разность потенциалов
на обкладках конденсатора, предварительно заряженного до
начальной разности потенциалов ДС/io, то по полученному
значению AU(U) = AU\ из C.38) несложно найти
R* = CHAUo/AUiY C-39)
Однако использование одного измерения, вообще говоря,
недостаточно для надежной идентификации рассматриваемой
уточненной модели. Дело в том, что при измерениях возникают
неизбежные погрешности, связанные с ограниченной чувстви-
чувствительностью измерительных приборов. Кроме того, предполо-
предположение о пропорциональной зависимости силы тока /* утечки
от AU(t) может оказаться достаточно грубым. Наконец, ре-
результаты измерения, проведенного на одном конкретном кон-
конденсаторе, могут быть не характерны для партии конденсато-
конденсаторов равной емкости, изготовленных по одинаковой технологии
из одних и тех же материалов. Короче говоря, в общем случае
следует ожидать некоторого разброса значений Я*, вычислен-
вычисленных из C.39) по данным измерений на одном конденсаторе для
различных моментов времени U и для начальных значений

Д.ЗЛ. Особенности составления ОДУ в прикладных задачах 83
Д?/о, а также по результатам измерений на нескольких конден-
конденсаторах равной емкости. Если такой разброс мал по сравнению
с требованиями по точности, предъявляемыми к математичес-
математической модели, то говорят, что модель адекватна (от латинского
слова adaequatus — приравненный) реальному объекту, и ее
можно использовать для количественного анализа. В против-
противном случае ее необходимо уточнять или вообще отказаться от
тех предположений, которые были приняты при ее построении.
Пусть приемлемое значение Д* в C.37), C.38) найдено.
Остановимся на применении уточненной математической мо-
модели конденсатора.
В изображенной на рис. 3.8 электрической цепи при левом
положении ключа К происходит заряд конденсатора емкостью
С с внутренним сопротивлением Д* от внешнего источника с
постоянным напряжением U* через резистор с сопротивлени-
сопротивлением i?i, а при правом положении ключа — разряд конденсатора
через резистор с сопротивлением i?2-
Изменение во времени t напряжения
U(t) на одной обкладке конденсато-
конденсатора при заземлении другой обкладки
можно описать при помощи ОДУ вида
C.37), если в правую часть этого ОДУ
добавить слагаемое, которое, соглас-
согласно первому закону Кирхгофа, учиты- ~
вает ток заряда или разряда: Рис. 3.8
C
При левом положении ключа I = (U* — U)/R\, а при правом
/ = —C//i?2- Для этих положений ключа интегрированием C.40)
находим соответственно
Ux(t) = U{ + Cie-*/<AlC>, U2(t) = С2е-г'^с\ C.41)
где Щ = U*k, Rx = Rxk, R2 = R2K к = 1/A + Л2/Д*)- Отме-
Отметим, что при левом положении ключа и любом начальном на-

84 3. ОДУ ПЕРВОГО ПОРЯДКА
пряжении С/о на конденсаторе U\(t) -+Щ <U* при t -> +00,
т.е. сколь бы долго не происходил заряд неидеального конден-
конденсатора, напряжение на нем не достигает напряжения внешне-
внешнего источника (в случае идеального конденсатора R* -> оо и
Ui(t)->U* при *->+оо).
Постоянные С\ и Съ в C.41) найдем из следующих усло-
условий. Пусть в начальный момент времени t = О ключ К нахо-
находится в левом положении (см. рис. 3.8) и 17@) = С/о < Щ. При
достижении напряжением U\{t) значения U\ (Uq <U\ <U*)
ключ мгновенно переходит в правое положение и начинается
разряд конденсатора. Тогда Ci = — C/j* + С/о, а из выражения
Ui(t) = U{ - {U{ - ио)е-*К&1С\ C.42)
описывающего изменение напряжения на конденсаторе при
заряде, найдем момент времени, соответствующий условию
Теперь из второго соотношения C.41) получим
С2 = и^НЪ^ и U2(t) = Uxe-l'-bMbC). C.43)
Ясно, что U2(t) —> 0 при t —> +00, причем темп разряда
будет более высоким по сравнению с идеальным конденсатором,
поскольку R,2<R2-
Добавим еще одно условие: пусть при разряде конденсатора
напряжение С/г(*) падает до значения С/г @ < С/2 < C/i), a
затем ключ мгновенно переходит в левое положение и снова
начинается заряд конденсатора, а далее процесс переключений
повторяется. Тогда из C.43) и условия 1/г(*г) = ^2 находим
момент времени перехода ключа в левое положение

Д.3.1. Особенности составления ОДУ в прикладных задачах 85
а из первого соотношения C.41) и условия Uifa) = U2 — новые
значение постоянной С[ = — (J7f — U2)et2^RlC^ и зависимость
Ux(t) = U{ -
C.44)
описывающую изменение напряжения на конденсаторе при
заряде. Теперь условие U\(t) = U\ будет выполнено в момент
времени
Далее длительности заряда и разряда конденсатора в ка-
каждом цикле будут неизменными и равными соответственно
Начиная с момента времени t\ (а при условии Щ^ЩК
<U\ — с момента времени t = 0) изменение напряжения
на конденсаторе будет описывать составная периодическая
функция времени с периодом Т = Т\ + Т?,, график которой имеет
пилообразную форму (рис. 3.9).
и*
и
о t{ t2 t[ t
Рис. 3.9
Пусть теперь ключ К (см. рис. 3.8) постоянно находится
в левом положении, а напряжение внешнего источника изме-
изменяется во времени t по закону U*(t) = U*sinujt с круговой

86 3, ОДУ ПЕРВОГО ПОРЯДКА
частотой и, причем в начальный момент времени t = О на-
напряжение на конденсаторе U@) = 0. Тогда придем к задаче
Когии
для линейного неоднородного ОДУ первого порядка. Его общим
решением, будет
Щ.) = (|L/(e*p/ « ) т) мр(. / « ) .
x V W
0 0 0
RiCJ V 1 + МхСJ
ч
U*R R~^
+ К-1— (sino;* - uRiCcosut). C.45)
о
Первое слагаемое в правой части C.45) со временем умень-
уменьшается по абсолютному значению, и изменение напряжения на
конденсаторе начинает определять второе слагаемое, которое
можно запивать в виде
U(t) = A(u)U* sin {u)t — <р(ш)),
где
/? С1
А(ш) = 1 =, <p(w) = arctg
В данном случае А(ш) и <р(ш) — амплитудно-частотная и
фазочастотнал характеристики рассматриваемой элек-
электрической цепи, отличающиеся от характеристик цепи с иде-
идеальным конденсатором лишь благодаря учету внутреннего со-
сопротивления Я* конденсатора, которое входит в выражение
для Дь

Д.3.1. Особенности составления ОДУ в прикладных задачах 87
При достаточно высокой частоте изменения напряжения
на конденсаторе из-за неидеальности диэлектрика возникают
потери: часть электрической энергии переходит в тепловую и
необратимо рассеивается в окружающую среду. Эти потери
также можно учесть в пределах уточненной математической
модели, соответствующей схеме на рис. 3.7. При этом, чем
значение Д* больше, тем потери меньше. Величину uR*C
называют добротностью конденсатора, a tgS = l/(uR*C) —
тангенсом угла диэлектрических потерь.
Рассмотренный пример показывает, что даже ОДУ первого
порядка позволяет построить уточненную математическую мо-
модель, существенно расширяющую наши представления о таком
известном и казалось бы простом объекте, как электрический
конденсатор.
Пример 3.4. В рамках теории пределов ([I], пример 7.14)
выведена известная формула Циолковского
vK = t;o + K;ln— C.46)
mK
для идеальной скорости ракеты, движущейся в пустоте вне по-
поля тяготения, где ио и то — начальные значения скорости
и массы ракеты, тк — масса ракеты в конце работы ракет-
ракетного двигателя, w — скорость истечения продуктов сгорания
топлива. Эта формула непосредственно следует из закона со-
сохранения количества движения в системе, состоящей из ракеты
и отбрасываемых продуктов сгорания и не испытывающей воз-
воздействия внешних сил.
Рассмотрим два состояния этой системы. Первое состоя-
состояние характеризуют значения массы т и скорости v ракеты,
так что количество движения системы равно mv. После от-
отбрасывания массы Am1 продуктов сгорания со скоростью w
относительно ракеты в направлении, противоположном скоро-
скорости v, ракета массой т — Am! получает приращение скорости
Av. При этом во втором состоянии системы количество дви-
движения отброшенной массы будет Am! {v — w), а количество

88 3. ОДУ ПЕРВОГО ПОРЯДКА
движения ракеты — (т — Дт') (v + Av). Из закона сохране-
сохранения количества движения в рассматриваемой системе следует
mv = Amf(v -w) + {m- Am') (v + Av). C.47)
Раскрыв скобки, получим
mAv = wAmf + Am'Av. C.48)
При переходе системы из первого состояния во второе масса
ракеты получила приращение Дт = — Дт'. Поэтому вместо
C.48) можно записать
тДг> = — wAm — AmAv.
После деления обеих частей этого равенства на Дт и
перехода к пределу при Дт ->• 0, учитывая, что Av -> 0 при
Дт -» 0, придем к ОДУ с разделяющимися переменными
m-^- = -w, C.49)
dm
в котором в качестве независимого переменного выступает
переменна* масса т ракеты. Интегрирование C.49) при
начальном условии v(mo)=vo дает
v(m)=vo + wln—. C.50)
m
Отсюда при т = тк получаем C.46).
Значение тк включает массу т* полезного груза (напри-
(например, спутника или космического корабля) и массу т* кон-
конструкции ракеты. Разность то — тк составляет массу из-
израсходованного топлива. Совершенство конструкции ракеты
и ракетного двигателя можно характеризовать отношением
Л = m*/(mo — m*), причем, чем это отношение меньше, тем при
прочих равных условиях больше значение vK. Тогда запишем
тк = т* + т* =m* +A(mo — т*) = Ато + A — Л)т*

Д. 3.2. Особенности составления ОДУ в прикладных задачах 89
и вместо C.46) получим
A-А)т*'
Отсюда следует, что наибольшего значения
C.51)
Л
идеальной скорости можно достичь при условии га* = 0, т.е.
при отсутствии полезного груза. Современные конструкци-
конструкционные материалы позволяют создавать ракеты, для которых
0,05 < Л < 0,1, а для современных ракетных топлив может быть
получена скорость w истечения продуктов сгорания, несколь-
несколько превышающая 4 км/с. Таким образом, при vq = 0 в идеаль-
идеальных условиях можно было бы говорить о достижении скорости,
близкой к так называемой параболической (или второй кос-
космической) скорости около 11 км/с, позволяющей удалиться от
Земли на бесконечно большое расстояние. Но влияние атмо-
атмосферы Земли и сил тяготения уменьшает реально достижимую
наибольшую скорость до значения, сопоставимого со значени-
значением круговой (или первой космической) скорости около 8 км/с,
достаточной лишь для выведения конструкции ракеты на око-
околоземную орбиту.
Подчеркнем, что приведенные оценки относятся к случаю
га* = 0, а наличие полезного груза приводит к дополнительному
уменьшению скорости ракеты. Как можно преодолеть возни-
возникающие ограничения ?
Математическая модель, включающая ОДУ C.49), учиты-
учитывает изменение массы ракеты только за счет отбрасываемых
продуктов сгорания топлива. При этом наряду с ускорени-
ускорением полезного груза вплоть до достижения конечной скорости
и* приходится тратить энергию топлива на ускорение всей
конструкции, часть которой становится бесполезной по мере
расходования топлива. Поэтому естественной является идея

90 3. ОДУ ПЕРВОГО ПОРЯДКА
сконструировать ракету так, чтобы можно было избавляться в
процессе полета от ненужной части конструкции.
Сначала рассмотрим гипотетическую конструкцию раке-
ракеты, позволяющую по мере непрерывного расходования топлива
также непрерывно отбрасывать пропорциональную по массе
часть конструкции, но с нулевой относительно ракеты скоро-
скоростью. Тогда суммарное приращение Дга < 0 массы ракеты
будет состоять из массы —АДт отбрасываемой части кон-
конструкции, имеющей количество движения — АДгаи, и массы
— A —А)Дт продуктов сгорания, имеющих количество дви-
движения —A — A)Am(v — w). Теперь вместо C.47) из закона
сохранения количества движения следует
mv = (т + Am)(v + Av) — XAmv — A — X)Am(v — w).
После преобразований, аналогичных проведенным выше, полу-
получим ОДУ
интегрирование которого при прежнем начальном условии
г; (m0) = v0 дает
»
v(m) = v0 + A - X)w In —. C.52)
га
Принципиальное отличие C.52) от C.50) состоит в том, что
теперь конечная масса ракеты после расходования всего топли-
топлива просто совпадает с массой га* полезного груза, поскольку к
этому моменту времени вся масса конструкции уже отброшена.
Тогда вместо C.46) будем иметь
vK = tto + (l-A)ii;ln—. C.53)
га*
Отсюда следует, что при vq = 0 и заданных значениях А, ги,
гао полезному грузу можно сообщить любую нужную скорость,
хотя, чем больше эта скорость, тем меньше допустимая масса

Д.3.1. Особенности составления ОДУ в прикладных задачах 91
т* полезного груза. Так, при Л = 0,1 и ги = 4 км/с парабо-
параболическую скорость можно достичь в идеальных условиях при
то/т* «22,5, тогда как, согласно C.51), при принятых зна-
значениях г>о, A, w и отсутствии полезного груза наибольшая
возможная скорость v* « 9,2 км/с.
Конечно, рассмотренная гипотетическая конструкция раке-
ракеты не осуществима. Но к такой схеме отбрасывания ненуж-
ненужных частей конструкции можно приблизиться, создавая ракету
из отдельных ступеней и отбрасывая каждую ступень после
выработки в ней топлива. В этом состояло существо идеи
пкосмического поезда", выдвинутой создателем отечественной
теоретической космонавтики К.Э. Циолковским A857-1935).
Эта идея реализована в современной ракетно-космической тех-
технике.
Пример 3.5. Пусть жидкость, находящаяся в сосуде, выте-
вытекает через отверстие в его дне, имеющее площадь /. Известно,
что скорость истечения жидкости через отверстие пропорцио-
пропорциональна квадратному корню из высоты уровня жидкости над
отверстием, а количество жидкости, вытекающее в единицу
времени и называемое расходом, можно представить в виде
Q(z) = iify/2gz, где /i — коэффициент гидравлического сопро-
сопротивления, g — ускорение свободного падения, z — текущая
высота уровня жидкости в сосуде, отсчитываемая от дна сосу-
сосуда.
Примем, что площадь F(z) горизонтального сечения сосу-
сосуда является известной функцией расстояния z этого сечения
от дна сосуда. Пусть в некоторый момент времени t уровень
жидкости находится на высоте z. Тогда за достаточно малый
промежуток времени At через отверстие вытечет количество
жидкости QAt = [j,fy/2gzAt, что вызовет понижение уровня
жидкости на — Az = Q(z)At/F(z) (считая, что Az > 0). Та-
Таким образом, имеем
AQ()/ r—
V9
At" F(z)~ F(z)

92
3. ОДУ ПЕРВОГО ПОРЯДКА
и после перехода в левой части этого равенства к пределу при
At —» О получаем ОДУ с разделяющимися переменными
dz
F(z)
C.54)
Если в начальный момент времени t = О высота уровня жид-
жидкости была Н, т.е. начальное условие имело вид z@) = Н, то,
разделяя в C.54) переменные, можно записать
я
C.55)
Рассмотрим несколько форм сосудов. Цилиндрический
сосуд с вертикальной образующей имеет постоянную площадь
Fq горизонтального сечения. В этом случае из C.55) следует
или зависимость уровня от времени
z[t) =
Рис. 3.10
Вся жидкость вытечет из такого сосуда
за время Т, соответствующее условию
z(T) = 0, т.е. Г = F0,j2Hfi/(nf).
Цилиндрическая цистерна длиной L
с круговым поперечным сечением ради-
радиуса R (рис. 3.10) и плоскими днищами
имеет площадь горизонтального сечения
F(z) = 2LV2Rz-z2. Тогда из C.55) получаем

Д.3.1. Особенности составления ОДУ в прикладных задачах 93
и зависимость уровня жидкости от времени
Для опорожнения цистерны понадобится промежуток времени
3/ V V V 2R
Из полностью заполненой цистерны (Н = 2R) вся жидкость
вытечет за время То = 8RLy/R/g/Cfj,f).
Если стенка сосуда имеет форму параболоида вращения,
который описывается уравнением z = а(х2 + у2), то имеем
F(z) = kirz, где к = а, и из C.55) находим
2Ьг
и изменение уровня жидкости во времени
Время полного опорожнения этого сосуда будет
2ктгН [Ш
Т =
3/i/ V 9
В древности чашу, в дне которой было небольшое отвер-
отверстие, использовали в качестве водяных часов для того, чтобы
ограничивать время выступлений ораторов. Ее форма позво-
позволяла добиться постоянной скорости понижения уровня воды в
чаше. Если стенку чаши рассматривать как поверхность вра-
вращения, то зависимость радиуса г горизонтального сечения
такой чаши от высоты z уровня воды можно найти следующим
образом. Обозначим через с постоянную скорость понижения

94
3. ОДУ ПЕРВОГО ПОРЯДКА
уровня, т.е. с= —dz/dt. Тогда, учитывая, что F(z) = тгг2(г),
вместо C.54) запишем
с =
тгг2(г)
После возведения в квадрат обеих частей этого равенства и
замены г2 = х2 + у2 получаем уравнение поверхности вращения
Теперь рассмотрим два сообщающихся сосуда цилиндри-
цилиндрической формы с вертикальными образующими и площадями
горизонтальных сечений соответственно F\ и i<2 (рис. 3.11).
Отверстие в общей для сосудов стенке имеет площадь /, а на-
начальная разность уровней жидкости
в сосудах равна ho. Расход жидко-
жидкости через отверстие Q = fify/2gh, где
h — текущая разность уровней жид-
жидкости в сосудах. Найдем время Т, за
которое уровни жидкости в сосудах
станут одинаковыми.
Для определенности примем, что
Рис. 3.11 в начальный момент времени t = О
уровень жидкости в первом сосуде с площадью основания F\
выше, чем во втором. Пусть в момент времени t разность
уровней равна h(t). Тогда за достаточно малый промежуток
времени At по соединяющей сосуды трубе пройдет объем
жидкости
AV(t) = Q(t)At = nfy/2gh(t) At
Это приведет к понижению уровня в первом сосуде и повыше-
повышению его во втором соответственно на
—
AV(t)
и
Ah2 =
F2

Д.3.1. Особенности составления ОДУ в прикладных задачах 95
так что за этот промежуток времени разность уровней изме-
изменится на величину
ДМ*) = -(ДМ*) + ДМ*)) = -
Отсюда
Переходя к пределу при At -> 0, получаем ОДУ
dh
с разделяющимися переменными. Его интегрирование дает
dh F1+F2
I Vh~
F\F2
или
Постоянную С найдем из начального условия h@) = ho- В
итоге зависимость от времени t разности уровней в сосудах
примет вид
Из условия h(T) = 0 находим искомое время
г FXF2
Отметим, что полученный результат не зависит от того, в
каком из сосудов был выше начальный уровень жидкости.

96 3. ОДУ ПЕРВОГО ПОРЯДКА
Пример 3,6. Работающая по замкнутому циклу косми-
космическая энергетическая установка помимо источника энергии
должна иметь устройство для охлаждения рабочего тела. Для
этой цели может быть использован ленточный излучатель, со-
состоящий из вращающегося барабана 1 (рис. 3.12), внутренняя
поверхность которого омывается охлаждаемым рабочим телом
или промежуточным теплоносителем, движущейся тонкой ме-
металлической ленты 2 и прижимного устройства 3. Двигаясь без
проскальзывания
в контакте с бара-
барабаном, лента на-
нагревается, отби-
рая теплоту у ра-
Рис. 3.12 бочего тела, а по-
после выхода из зоны контакта участки ленты излучают тепловую
энергию в окружающее пространство. В условиях невесомости
петля ленты при постоянной скорости v движения принима-
принимает некоторую неизменную форму, определяемую равновесием
центробежных сил инерции и сил упругости ленты.
Для тонкой металлической ленты температуру Т ее любо-
любого участкам можно считать однородной по толщине и зависящей
при установившемся режиме работы излучателя лишь от те-
текущего положения участка относительно барабана. При этом
допустимо пренебречь передачей теплоты вдоль ленты.
После вступления некоторого фиксированного участка лен-
ленты в контакт с барабаном, имеющим известную постоянную
температуру Т*, через единицу площади контакта за проме-
промежуток времени At в ленту поступает количество теплоты
где а — коэффициент контактного теплообмена, зависящий
от шероховатости контактирующих поверхностей и усилий, со-
создаваемых прижимным устройством. Это количество теплоты

Д.3.1. Особенности составления ОДУ в прикладных задачах 97
вызывает приращение
cph
температуры участка ленты (сир — удельная массовая
теплоемкость и плотность материала ленты, h — толщина
ленты). Из этих двух равенств следует
-**~ /*у
у
At cph
После перехода к пределу при At -> 0 получаем ОДУ
dt cphv ;
с разделяющимися переменными, общим решением которого
будет выражение
Обозначим через Го температуру рассматриваемого участ-
участка ленты в момент t = 0 его вступления в контакт с барабаном,
т.е. начальное условие имеет вид Г@) = Го. Используя это на-
начальное условие, находим значение постоянной С = Го — Г* и
в итоге имеем
Если длина дуги контакта ленты с барабаном равна /, то при
скорости v движения ленты время контакта ее фиксирован-
фиксированного участка будет tK = Z/v. Тогда в момент схода с барабана
температура этого участка составит
Т. = T(tK) =Т*- (Т* - То) ехр ( - -^-). C.56)
Аналогично можно составить ОДУ, описывающее измене-
изменение температуры фиксированного участка ленты после его схо-
схода с барабана. С единицы площади этого участка с двух сторон
4 — 9306

98 3. ОДУ ПЕРВОГО ПОРЯДКА
его поверхности за промежуток времени At, согласно закону
Стефана — Больцмана, в окружающее пространство рассеива-
рассеивается количество теплоты
Qp = 2еа0Т4 At,
где е — коэффициент излучения поверхности ленты; <то =
= 5,67 • 10~8 Вт/(м2 • К4) — постоянная Стефана — Больцмана.
Тепловые потери вызывают отрицательное приращение
% = 2^
cph cph
температуры участка. Отсюда после деления на At и перехода
к пределу при At -> 0 получаем ОДУ
dt cph
интегрированием которого находим
T\t)~cph^^-
Так как в момент времени tK схода участка ленты с барабана
Т(*к)=Т„то
и окончательно для свободной от контакта части ленты
щг)-тгб?й{*-*к)- C>57)
Чтобы при очередном вступлении в контакт с барабаном
фиксированный участок ленты имел температуру То, проме-
промежуток времени свободного движения этого участка должен
составить в силу C.57)
cph
То3

Д. 3.1. Особенности составления ОДУ в прикладных задачах 99
а длина свободной части ленты должна быть
„58,
При этом условии возможен установившийся режим работы
ленточного излучателя, который на единицу длины барабана
(или ширины ленты) будет рассеивать мощность
W = cphv(T*-T0),
или, учитывая C.56),
Приведем это соотношение к безразмерному виду:
а/(Г*-Го) ?
При заданном значении комплекса параметров al (Г* — Го)
функция /(?) характеризует эффективность ленточного излу-
излучателя. В интервале @, +оо) эта функция монотонно убывает
и /(?) —> 1 при ? -> +0. Таким образом, при прочих равных
условиях для повышения эффективности излучателя целесо-
целесообразно увеличивать значение комплекса параметров cphv, но
следует иметь в виду, что в силу C.58) это приведет к увели-
увеличению длины ленты и к росту массы излучателя.
Пример 3.7. Подводная лодка массой то из неподвиж-
неподвижного положения при нулевой плавучести начинает погружение
за счет заполнения водой балластных цистерн. Сопротивление
воды поступательному вертикальному движению лодки можно
принять пропорциональным текущей скорости v погружения
(коэффициент пропорциональности к > 0). Необходимо за ми-
минимальное время провести погружение на глубину Н так, что-
чтобы на этой глубине лодка имела нулевую плавучесть. Скорость

100 3. ОДУ ПЕРВОГО ПОРЯДКА
заполнения водой балластных цистерн не может превышать
т+, а скорость ее вытеснения — га_, причем для определен-
определенности примем т_ < к/2.
Если спроектировать на вертикаль действующие при погру-
погружении на лодку силы, то, согласно второму закону Ньютона в
форме теоремы об изменении количества движения, получим
линейное неоднородное ОДУ первого порядка
{mv) + kv + P(t) = 0, C.59)
at
где P(t) — переменная во времени t плавучесть лодки,
равная разности архимедовой силы и силы тяжести тд (га —
текущая масса лодки, д — ускорение свободного падения).
Архимедова сила для лодки постоянного объема постоянна и
в начальный момент времени t = 0 при нулевой плавучести
лодки уравновешена силой тяжести тод. Поэтому
о
где подынтегральная функция га(?) равна скорости изменения
массы лодки за счет заполнения или опорожнения балластных
цистерн. Наиболее рациональная стратегия в данном случае
состоит в заполнении цистерн в течение пока неизвестного
периода времени Т+ с наибольшей возможной скоростью, т.е.
rh(t) = га+ Vt Е [О, Т+], а затем в вытеснении воды также с
наибольшей возможной скоростью, т.е. га = —га_ при t > Т+.
На первом этапе в процессе заполнения балластных цистерн
масса лодки изменяется по закону m(t) = гао + га+?, а плаву-
плавучесть — по закону P(t) = —m+gt. Тогда из C.59) следует
(гао + га+?) — + (к + га+) v — m+gt = 0,
at
или
dv k + ra+ m+gt
dt 771q

Д.3.1. Особенности составления ОДУ в прикладных задачах 101
Общим решением этого ОДУ будет (см. замечание 3.2)
v(t) =
+ exp(-
+ rh+t J
(k + rh+)dt
h+)dt\ Г rh+gtdt Г
m+t ) J mo + m+t J
G\ gt (mo+m+t)g
l + k/m+ (l + fc/m+)(fc+2m+)'
Используя начальное условие v@) = 0, из C.60) находим
rn0
2+k/rh+
и в итоге на первом этапе погружения
V( ' = A +
" l J
В конце первого этала (t = Т+) масса лодки ш+ = то +
Ч-т+Т^., ее плавучесть Р(Т+) = —m+gT+ и скорость погру-
погружения
9T+(mo + m+r+)g
На втором этапе погружения при вытеснении воды из
балластных цистерн масса лодки изменяется по закону m(t) =
— m+ — m_ (t—T+), а плавучесть — по закону P(t) = — m+gT+ +
+ ih-g(t-T+). Из условия Р(Т)=0 в момент времени < = Г

102 3. ОДУ ПЕРВОГО ПОРЯДКА
завершения второго этапа погружения получим — т+дТ+ +
-T+) = 0, или
Из C.59) для второго этапа имеем
или
dv к — m_ "г+2+ ~ rh-t
++ rht
~dl~~m+-m-(t-T+)V m+-m-(t-T+)9'
Интегрирование этого ОДУ аналогично C.60) и дает
«(*) = C2f(t) +
f{m+T+-m-(t-T+))gdt f (k-m.)dt
y m+-m-(t-T+) ехрУ m+-m-(t-T+)-
7?;-gt C.64)
(fc-m_)(fc-2m_) ' v ;
где
Используя условие v(T+) = v+, из C.64) получаем

Д.3.1. Особенности составления ОДУ в прикладных задачах 103
так что скорость на втором этапе погружения будет
v+{m+-m-(t-T+)y '
«(*) =
ту
т+Г+-т_(*-Т+) ,
fc^hl 9+
(fc-m_)(Jfc-2rh_) ¦
Примем во внимание, что скорость лодки v = dh/dt, где
— текущая глубина погружения лодки. Тогда из C.61)
интегрированием по t в пределах от t = 0 до t = Т+ по-
получим глубину погружения в процессе заполнения балластных
цистерн:
Л 1 \
\ A + т+Г+/тп0)*/Л+/
gT^/2 (mo + m+r+/2)gr+
l + fc/m {l + k/rh){k + 2mY { }
Аналогично интегрированием C.65) от Т+ до Т с учетом
C.63) и равенств т+ - rh-{T -Т+) = то и h(T) = Я найдем
то+тН+Т+Л I
, 1\/ , m+m-
1" )nT +
k(k-m.) V
(m+T+Jg (mo + m+T+/2)th+T+g
2m_(fc-m_). (k-th-)(k-2m.) '
Это уравнение в общем случае не удается разрешить отно-
относительно искомого значения Т+ и приходится использовать
численные методы решения [II]. По вычисленному значению Т+
затем из C.63) можно найти полное время Г погружения, а из
C.65) — скорость в конце погружения v(T).

104 3. ОДУ ПЕРВОГО ПОРЯДКА
Пример 3.8. Скорость химической реакции характеризу-
характеризуют скоростью образования конечного продукта реакции. Со-
Согласно закону действующих масс, эта скорость при постоянной
температуре пропорциональна произведению текущих концен-
концентраций реагирующих веществ. Пусть для получения х молекул
конечного продукта X требуется х молекул вещества А и х/2
молекул вещества В, т.е. уравнение реакции можно записать в
виде
2А + В = 2Х.
В момент времени t = 0 начальные концентрации веществ А
и В, определяемые количеством молекул этих веществ в объ-
объеме химического реактора, равны соответственно а и 6, а
концентрация конечного продукта х@) = 0. В силу закона
действующих масс в этот момент времени начальная скорость
реакции пропорциональна произведению а 6, а в некоторый
момент времени t > 0 при концентрации x(t) конечного про-
продукта получим ОДУ
Ы /V* / /у» Ч
C.67)
с разделяющимися переменными, где fci > 0 — константа
скорости рассматриваемой реакции в данных условиях. После
разделения переменных и интегрирования получим
л 2b-x{t)
In
a-x{t)
26-а
Используя начальное условие х@) = 0, найдем постоянную С =
= 1пB6/а) и запишем
2b-x(t)
a-x(t)
= — exp—— = — eHt, x=—±-. C.68)
a ^26-a a 26-a v ;
Если известно, что в момент времени t\ > 0 концентрация
конечного продукта x(t\) = a?i, то это позволяет при помощи

Д.3.1. Особенности составления ОДУ в прикладных задачах 105
C.68) вычислить константу скорости реакции
Исходя из уравнения протекающей реакции ясно, что в
рассматриваемых условиях хтгх = min{a; 26}. Следовательно,
|BЬ — х)/(а — х)\ ^ 0 и C.68) можно записать в виде
ext — I I — e~Ht
x(t) = 2a6——; = 2a6— т. C.69)
Из C.67) следует, что если количество конечного продукта ре-
реакции ограничено начальной концентрацией а вещества А, то
скорость реакции тем выше, чем выше начальная концентрация
6 вещества В. При условии 26 > а имеем х > 0, и знаменатель
дроби в правой части C.69) положителен при t ^ 0. Если же
2 6 < а, то скорость реакции уменьшается, н < 0, и C.69) в этом
случае целесообразно записать в виде
Отсюда ясно, что знаменатель также положителен при t ^ 0.
Особый случай соответствует условию 26 = а, т.е. так на-
называемому стехиометрическому соотношению начальных кон-
концентраций реагирующих веществ. В этом случае теоретически
должны полностью прореагировать все молекулы исходных ве-
веществ, а вместо C.67) скорость реакции будет подчиняться
ОДУ
- = к2{а-х)\
Решением этого ОДУ с учетом начального условия х@) =0
будет
Отметим, что во всех случаях полному завершению реакции
соответствует условие t —> +оо.

106 3. ОДУ ПЕРВОГО ПОРЯДКА
Пример 3.9. Одна из простейших математических моделей
эволюции биологической популяции основана на предположе-
предположении, что численность х популяции и скорость dx/dt измене-
изменения численности во времени t пропорциональны, т.е.
dx
-=гх. C.70)
Коэффициент г можно трактовать как разность коэффициен-
коэффициентов Ъ и d — соответственно рождаемости и смертности. Если
считать коэффициент г = b — d постоянным, то решением ОДУ
C.70) будет зависимость
где #о — численность популяции в момент времени t = 0.
Однако такой вариант математической модели малоинфор-
малоинформативен и не позволяет проанализировать влияние на эволюцию
популяции среды обитания. Действительно, при г > 0 числен-
численность популяции неограниченно растет, что нереально в силу
ограниченности средств существования, а при г < 0 числен-
численность уменьшается до нуля, т.е. популяция вымирает. Частный
случай г =*0 соответствует стабильной численности, т.е. она
не изменяется во времени.
Если влияние среды обитания удается отразить зависимо-
зависимостью коэффициента г от времени, т.е. введением функции
г == /(*)> т0 решение ОДУ C.70) при том же начальном усло-
условии х@) = xq > 0 примет вид
Однако подобрать функцию /(?), учитывающую реальное вли-
влияние среды обитания, достаточно трудно.
Рассмотрим иной путь учета этого влияния, связанный с
введением понятия максимальной численности х*, при которой

Д.3.1. Особенности составления ОДУ в прикладных задачах 107
популяция еще может обеспечить себя средствами существо-
существования. Тогда коэффициент 1 — х/х* будет мерой неисполь-
неиспользованных популяцией ресурсов, допускающих увеличение ее
численности, т.е. вместо C.70) будем иметь ОДУ
С учетом начального условия х@) = xq оно имеет решение
x(t) =
x*ert
x* + xo{ert-l)
+ (ж* — xo)e~rt'
C.72)
r>0
включающее не представляющее интереса тривиальное реше-
решение x(t) = 0, соответствующее условию хо = 0, и решение
x(t) = х* при теоретически возможном совпадении значений
xq и х*. В остальных случаях C.72) описывает эволюционный
процесс изменения во времени численности популяции. Рассмо-
Рассмотрим эти случаи.
При г < 0 и t -> +оо имеем x(t) —> 0, т.е. популяция
обречена на вымирание. Однако
модель адекватно описывает эво-
эволюционный процесс лишь при усло-
условии xq < х* (рис. 3.13). В случае
г > 0 численность x(t) популяции
во времени монотонно возрастает,
если xq < ж*, и монотонно убывает,
если xq > ж*, но при t -> +oo стре-
стремится к одному и тому же пределу, Рис. 3.13
равному х*.
Несложно установить, что при xq < х* функция #(i),
задаваемая соотношением C.72), имеет точку перегиба U =
= A/гIп(ж*/#о -~ 1)> которой отвечают ордината #* = x(t*) =
= х*/2 точки перегиба графика этой функции и наибольшая
по абсолютному значению скорость изменения численности

108 3. ОДУ ПЕРВОГО ПОРЯДКА
популяции. График этой функции называют логистической
кривой. При сочетаниях параметров г > 0, хо > х*/2 или г <
< 0, хо < х*/2 имеем t* < 0, т.е. точка перегиба логистической
кривой лежит на ее продолжении в область отрицательных
значений t.
Логистическая кривая описывает многие эволюционные
процессы, на протекание которых влияют конкурирующие или
ограничивающие факторы. Помимо биологических и экологи-
экологических приложений математические модели, связанные с этой
кривой, находят применение в экономике. В частности, модель,
включающая ОДУ C.71), описывает процесс распространения
рекламной информации о некотором товаре среди его потен-
потенциальных покупателей, максимально возможное число которых
равно х*. Пусть в момент времени t = 0 были даны реклам-
рекламные объявления о товаре в печати, по радио и телевидению и
об этой информации узнали лишь xq (xq < x*) потенциальных
покупателей. В последующем передача рекламной информации
происходит лишь за счет общения потенциальных покупателей,
причем скорость распространения этой информации пропор-
пропорциональна как числу х осведомленных, так и числу х* — х
неосведомленных покупателей, а отношение г/х* > 0 являет-
является коэффициентом пропорциональности.
Дальнейшее уточнение моделей рассматриваемого типа свя-
связано с учетом влияния на скорость dx/dt эволюционного про-
процесса не только текущего значения х(?), но и значений x(t — г)
в один или несколько предшествующих моментов времени (в
частности, промежуток времени т можно интерпретировать
каик период биологического цикла размножения). Уравнения
вида
входящие в такие модели, относят к типу дифференциальных
уравнений с отклоняющимся аргументом.

Д.3.2. Ортогональные и изогональные траектории 109
Дополнение 3.2. Ортогональные
и изогональные траектории
Рассмотрим одну из геометрических задач, решение кото-
которой можно свести к составлению и интегрированию обыкно-
обыкновенного дифференциального уравнения (ОДУ) первого порядка.
Семейство линий уровня функции F(t, х) описывается урав-
уравнением F(t, х) = а, где а — параметр. Предположим, что
функция F(?, x) непрерывно дифференцируема по перемен-
переменным t и х в некоторой области их изменения. Обозначим
частные производные этой функции соответственно dF/dt =
= Fi(t,x) и dF/dx = F2(t,x).
Напомним, что вектор градиента n= (Fi(t, x), i<2(?, x))T
в точке (?, х) ортогонален проходящей через эту точку ли-
линии уровня функции F(t, x). Угловой коэффициент прямой,
параллельной вектору градиента, равен k\ = 2*2 (*? #)/-Fi(*? #)>
а угловой коэффициент касательной к линии уровня в этой
точке fc = — 1/fci = —Fx(t,x)/F2(t,x), поскольку угловые ко-
коэффициенты перпендикулярных прямых обратны по величине
и знаку [III]. Согласно геометрическому смыслу производной
[II], k = dx/dt, где x(t) — функция, график которой является
линией уровня функции F(t,x). Таким образом, приходим к
ОДУ первого порядка
cte _ Fi(t,x)
Л" y
интегральными кривыми которого будут линии уровня функ-
функции F(?, x).
Поле направлений, соответствующее ОДУ C.73), в каждой
точке плоскости Юх повернем на угол тг/2. Полученное таким
образом поле направлений будет соответствовать ОДУ
)
y [ '
Интегральные кривые этого ОДУ пересекают линии уровня
функции F(?, x) под прямым углом, так как в каждой точке
(?, х) касательная к интегральной кривой ОДУ C.74) ортого-

1103. ОДУ ПЕРВОГО ПОРЯДКА
нальна касательной к линии уровня F(?, х) = а, проходящей
через эту точку. Интегральные кривые ОДУ C.74) назы-
называют ортогональными траекториями семейства линий
F(t, x) = а.
Пусть F(?, х) = t2 + x2. Тогда уравнение F(t, х)=а зада-
задает семейство концентрических окружностей с общим центром
в начале системы координат Otx. Радиус каждой окруж-
окружности зависит от значения параметра а > 0 и равен у/а. В
данном случае dF/dt = Fi(t, x) = 2t и dF/dx = F2(i, x) = 2я,
а C.74) принимает вид ОДУ с разделяющимися переменны-
переменными dx/dt = x/t. Интегральными кривыми этого ОДУ будут
прямые х = Ct, С = const, которые проходят через нача-
начало той же системы координат и, оче-
очевидно, являются ортогональными тра-
траекториями семейства концентрических
окружностей (рис. 3.14). Ясно, что, в
свою очередь, концентрические окруж-
t ности будут ортогональными траекто-
траекториями пучка прямых, проходящих че-
через общий центр этих окружностей.
Таким образом, ортогональные траек-
•о о - А тории семейства линий и сами эти ли-
Рис. 3.14 г
нии обладают свойством взаимности.
Линии, пересекающие все линии семейства F(t, x) = а под
одним и тем же углом а, называют изогональными тра-
траекториями (от греческих слов шоС, — равный и ^/uuta —
угол) этого семейства. В частном случае а = тг/2 изогональ-
изогональные траектории переходят в ортогональные. В любой точке
(t, x) плоскости tOx касательная к линии семейства F(t, x) = a,
проходящей через эту точку, и касательная к изогональной
траектории образуют заданный угол а. Если угловой коэф-
коэффициент касательной к изогональной траектории обозначить
через &2, то
kk

Д.3.2. Ортогональные и изогональные траектории 111
где к = —1*1 (*, rr)/F2(*, ж) — угловой коэффициент касательной
к линии уровня F(t, #) = а, проходящей через точку (*, #).
Отсюда
fc + tgg =F2(t,g)tga-Fi(t1a?)
2 1 - fc tga F2(i, x) + Fi(t, ж) tga'
С учетом геометрического смысла производной получаем ОДУ
первого порядка
dx _ Fafoafltga-FifcaQ f
Интегральные кривые этого ОДУ и будут изогональными
траекториями семейства линий F(t, х) = а.
Пример. Найдем изогональные траектории, пересекающие
под углом а пучок прямых х = Ct (С = const), проходящих
через начало системы координат Otx. В данном случае
F(t, x)=x — Ct, F\ = —С = —re/*, i*2 = 1 и после подстановки
в C.75) приходим к ОДУ
d* *-
При помощи соотношений
t и
'
перейдем в C.76) к полярным координатам р и <р, выбрав
полюс полярной системы координат в начале прямоугольной
декартовой системы координат Otx и направив полярную ось
по octz atfcijucc Ot. Тогда находим
d* = cosipdp — р sin<pd</>, dx = p costpdtp + sinepdp
и после тригонометрических преобразований вместо C.76)
получаем
dp
-=pctga.

112
3. ОДУ ПЕРВОГО ПОРЯДКА
Это ОДУ с разделяющимися переменными. Его интегриро-
интегрирование дает
Inp{(p) =<pctga + Cu или р((р) = С*е*^, С* > О,
где fc* = ctga, С* = expCi = const. Таким образом, изого-
изогональными траекториями пучка прямых являются логарифмиче-
логарифмические спирали (рис. 3.15). В технике свойство логарифмической
спирали пересекать пучок прямых под постоянным углом ис-
используют при профилировании режущих кромок вращающихся
ножей и фрез. При этом по
всей режущей кромке угол ре-
резания тг/2 — а между каса-
касательной к ней и направлени-
направлением резания остается постоян-
постоянным, что обеспечивает наи-
наилучший технологический ре-
режим процесса резания и спо-
способствует равномерному из-
изнашиванию режущего инстру-
инструмента. #
Изогональные траектории
Рис. 3.15 рассматривают не только на
плоскости. На поверхности
вращения изогональные траектории меридианов называют
локсодромиями (от греческих слов Ао?о? — косой и Spofio^ —
путь). Если а = тг/2, то локсодромия на поверхности враще-
вращения переходит в ортогональную траекторию — линию широты.
При а Ф 7г/2 локсодромия на замкнутой поверхности враще-
вращения образует бесконечное множество витков вокруг каждого
из полюсов, неограниченно приближаясь к ним. Штурманы ко-
кораблей, прокладывая курс, часто используют дуги локсодромий
на земной сфере. Путь по дуге локсодромии не является крат-
кратчайшим между двумя точками на земной сфере, но по такой
дуге удобно двигаться, выдерживая курс по компасу.

Вопросы и задачи 113
Вопросы и задачи
3.1. Решить следующие уравнения:
ч dx ж1/2 . dx 2tx ч dx
г) ^ + Y^ = 1; Д) A + x2)dt + Bt
е) Ct2 + 2tx + x3)dt + (t2 + Ztx2 + cosx) dx = 0;
ж) cos{t + x)dt+ (cos(t + aj) —2isin2a;)dx = 0;
da; el/x dx _ xchi + sht
з) = И) = ;
dt ' —' ''dt
dx 1 + y/W^i dx _ A -12 - x2)t
dt ~ лЛ2~ГТ ' а' dt~
^ = x + t(i + e); n)B<xt)^
ai at
a;^ + a:2 + 4t(< + l)=0; c) (t2x- 1)^ +x2t- 1 = 0;
ai at
. dx dx .
+ )
3.2. При каких р и g ОДУ dx/dt = a?p + 6#9 является
квазиоднородным?
3.3. Найти уравнение кривой, проходящей через точку A; 1)
и обладающей следующим свойством: расстояние от любой
касательной к этой кривой до начала координат равно абсциссе
точки касания.
3.4. Зеркало отражает лучи, выходящие из фиксирован-
фиксированной точки, параллельно заданному направлению. Определить
форму зеркала.

114 3. ОДУ ПЕРВОГО ПОРЯДКА
3.5. Для следующих уравнений Риккати найти частное
решение и проинтегрировать эти уравнения:
a) t2^+tx+t2x2 = 4; б) ^-2tx+x2 = 5-t2; в) 3^+s2 = -|;
at at at tz
г) t^-Bt + l)x + x2 = -t2; д) ^
at at
3.6. Показать, что ОДУ dx/dt = f(at + bx + c), где a,byc —
постоянные, подстановкой у = at + bx + c можно привести к
ОДУ с разделяющимися переменными.
3.7. Предположим, что ОДУ dx/dt = f(x) имеет частные
решения х = а и х = b (/(а) = /(Ь) = 0), причем функция
f(x) непрерывно дифференцируема на отрезке [а, Ь]. Пусть
f(x) > 0 (f{x) < 0) Уж G (а, 6). Доказать, что любое решение
x(t) этого ОДУ с начальным условием х@) = #о € (а, 6) при
?-»+оо стремится к 6 (стремится к а).
3.8. Используя результат задачи 3.7, построить интеграль-
интегральные кривые ОДУ dx/dt = х A — х).
3.9. Пуля пробивает плоскую стену толщиной h перпен-
перпендикулярно Ьоверхности стены. Сопротивление движению пули
в стене пропорционально квадрату скорости v пули (коэффи-
(коэффициент пропорциональности к). Найти время движения пули в
стене, если она попала в стену со скоростью t>o, а вылетела из
нее со скоростью vi.
3.10. Цилиндрический резервуар (радиус основания Д, вы-
высота Н) заполнен жидкостью. На дне образовалось круглое
отверстие радиуса г. Считая скорость истечения жидкости
пропорциональной высоте ее уровня, определить время истече-
истечения всей жидкости.
3.11. Может ли уравнение Риккати C.26) иметь особое
решение ?

4. СИСТЕМЫ ОБЫКНОВЕННЫХ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
4.1. Задача и теорема Коши
Рассмотрим нормальную систему обыкновенных дифферен-
дифференциальных уравнений (ОДУ) вида
D.1)
где функции fi определены в некоторой области G С Rn+1
(п + 1)-мерного расширенного фазового пространства Rn+1
системы D.1).
Задачу Кохии для нормальной системы ОДУ D.1)
формулируют так: задана точка (to, х\,..., х^) ? D\ требует-
требуется найти определенное в окрестности точки to G К решение
х\ = xi(t), ...,#n = xn(t) нормальной системы D.1), удовле-
удовлетворяющее при t = to условиям
*i(*o)=*i, x2{t0) = xl ..., xn{t0)=x°n, D.2)
которые называют начальными условиями для данной си-
системы ОДУ,ъ, to, #§,..., х^ — начальными значениями.
Определение 4.1. Векторная функция /(t, ж), t € R,
ж G Mn, удовлетворяет в области G G En+1 условию Липшица
относительно х = (a?i,..., жп), если для двух произвольных
точек (t, ж), (t, у) G G ее координатные функции /i(t, ж) удов-

116 4. СИСТЕМЫ ОДУ
летворяют неравенствам
= 1, п,
где L > О — постоянная Липшица.
Замечание 4Л. Если функции /Д?, ж), г = 1,п, ж =
= (xi,..., яп), определены в замкнутой ограниченной области
?> = {(*, ал,..., жп): |t-to|<a, |a?i-a:?|<6, г = Т^} D.3)
и имеют в D непрерывные частные производные по пере-
переменным rci, ..., жп, то для для векторной функции f(t,x) =
= (/i(?, ж),..., /n(?, bfx))) условие Липшица в D будет выпол-
выполнено. Чтобы убедиться в этом, рассмотрим две произвольные
точки М(О),МAN А где М@) = (*,уь ...,уп) и МA) =
= (t,si,...,a;n). Все точки М(А) = (t, &(A), .-.,fn(A)), где
6(А) = Уг + Нх{ - yi), г = 1, п, А б @,1), D.4)
также принадлежат области D, поскольку с учетом D.3) и
неравенства треугольника
Воспользуемся формулой Лагранжа для скалярной функ-
функции fii
fi(t, x) - fi(t, у) = 2^ о^; \xi ~ Уз) > D-5)

4.1. Задача, и теорема Коши 117
где х = (Ж1,...,яп); у = (уь ...,yn); #6@,1). Поскольку
частные производные dfi/dxj непрерывны в замкнутой огра-
ограниченной области D, они ограничены в этой области. Следова-
Следовательно, существует такое число L > О, что в D выполняются
неравенства \dfi/dxj\ < L, г, j = 1, п. Тогда из D.5) с учетом
неравенства треугольника получаем
D.6)
и, согласно определению 4.1, функции /j(?, ж), i = 1,п, удов-
удовлетворяют условию Липшица. #
Сформулируем теорему существования и единственности
решения нормальной системы ОДУ, также связанную (как и
все теоремы такого рода) с именем О. Коши.
Теорема 4.1 (теорема Коши). Пусть в замкнутой об-
области D D.3) функции fi(t, x\j..., xn), i = 1, n, определе-
определены, непрерывны и удовлетворяют условию Липшица относи-
относительно переменных х\, ..., жп. Тогда на некотором отрезке
[*о-Мо + Л], гДе
/i = min(a, Ь/М), М = max max |/j(i, ж)|,
ж = (rci, ...,rrn), существует, и притом единственное, решение
#1 = si(i),..., хп = xn(t) задачи Коши для нормальной системы
ОДУ D.1), удовлетворяющее начальным условиям D.2).
Доказательство этой теоремы, осложненное наличием п
ОДУ в системе D.1), аналогично доказательству теоремы
Коши для одного ОДУ (см. 2.2).

118
4. СИСТЕМЫ ОДУ
4.2. Частное и общее решения системы
дифференциальных уравнений
Рассмотрим нормальную систему обыкновенных дифферен-
дифференциальных уравнений (ОДУ). Существование частного реше-
решения нормальной системы ОДУ, удовлетворяющего началь-
начальным условиям D.2), утвер-
утверждает теорема 4.1. Геомет-
Геометрически это означает, что
существует, и притом един-
единственная, интегральная кри-
кривая, проходящая через точ-
ку (<0,x?,^,...,4)^Rn+1
(рис. 4.1).
Будем считать <о задан-
заданным, а #5, • ••»#? переменными параметрами, которые могут
принимать различные числовые значения из области, где вы-
выполнены условия теоремы 4.1 Коши. Введем следующие обо-
обо\ = Сг,..., х„ = Сп.
Рис. 4.1
значения: х\ =
Определение 4.2. Решение
г =
D.7)
системы D.1) будем называть общим решением нормаль-
нормальной системы ОДУ в области D, если для любой точки
(to, х\, #2> • • • ? хп) € D существует совокупность значений па-
параметров С\ = С{, C<i = С?!, ..., Сп = С?, определяемая путем
решения системы уравнений
З.-.cs). i =
D.8)
и при этих значениях С?, j = 1, п, система функций D.7)
является решением задачи Коши для нормальной системы ОДУ
с начальными значениями to, х*, х%,..., ж*.

4.3. Оценка разности двух решений 119
4.3. Оценка разности двух решений
Рассмотрим две нормальные системы обыкновенных диф-
дифференциальных уравнений (ОДУ), которые запишем в вектор-
векторной форме вида A.4):
D.10)
где х = (a?i,..., хп)Т и у = (уь ..., уп)т принадлежат п-мер-
ному фазовому пространству Шп.
Введем обозначения
му фазовому простр
Введем обозначения
Покажем, что из условия Липшица для каждой из функций /j
относительно a?i, ..., хп с общей постоянной L:
t(t,x)-fi(t,у)| <
следует неравенство
\\f(t,x)-f(t,y)\\^nV2L\\x-y\\. D.11)
Из неравенства Коши — Буняковского
п . 2 п . п
i=l i=l г=1
при 6i = 62 = • • • = Ьп = 1 следует, что
2
i=i i=i

120 4. СИСТЕМЫ ОДУ
если а{ > 0, г = 1, п. Учитывая неравенство
п о
0
г=1 г=1
которое можно доказать, например, при помощи метода мате-
математической индукции, получаем
п
\2 ^
<(*, х) - Л(«, у))
г=1
что эквивалентно D.11).
Предположим, что функции /(t, х) и g(t, у) в области D
D.3) удовлетворяют всем условиям теоремы 4.1 Коши, a x(t)
и y(t) являются решениями нормальных систем ОДУ D.9) и
D.10) соответственно, определенными на отрезке [to — /i, to + Л],
где Л — число, фигурирующее в формулировке этой теоремы.
Проинтегрируем системы D.9) и D.10) от to Д° t:
D.12)
«о
V(to)=[9{Z,v@)dZ, D.13)
to
где
f f{ZMO)dt= (j fi{(MO)d?,-, f MtMO)dt) D.14)
V /
to Vto t0

4.3. Оценка разности двух решений
121
и аналогично записывается интеграл от функции g(t, y{t)).
После вычитания D.13) из D.12) запишем:
t
x(t) - y(t) = x(to) - у (to) + / (/(?, *@) - /«, у (О)) « +
I D.15)
to
С учетом неравенств \\а + Ь\\ ^ ||а|| + ||Ь|| и
t
имеем
to
to
\\x(t)-y(t)\\^\\x(tQ)-y(to)
t
to
<\\x(to)-y(to)\\+n3^L
+ ЛД. D.16)
Если применить теперь к D.16) интегральное неравенство
B.4) Гронуолла при u(t) = ||ж(<) -y(t)|| > 0, v(i) = Пу/nL > 0 и
Л = ||ж(г0) ~ 2/(^о)II + /iA > 0, то получим
N*) -У(*)Н < (ll*(«u) -y(«d)|| +hA)en^Lh. D.17)
При помощи D.17) можно получить ряд важных следствий.

122 4. СИСТЕМЫ ОДУ
Следствие 4.1. Если нормальная система ОДУ вида D.9)
удовлетворяет в области D D.3) всем условиям теоремы 4.1
Коши, то решение этой системы непрерывно зависит от на-
начальных условий в смысле, аналогичном определению 2.2.
<4 Пусть в D.9), D.10) / = #. Тогда Д = 0 и неравенство D.17)
принимает вид
\Ш - У(*)Н< Ы*о) -y(to)\\enVELh.
Положим x(to) = (#5,..., #^)T, где to? #5,..., х^ — начальные
значения, входящие в начальные условия для нормальной систе-
системы ОДУ D.9). Если для любого е > 0 выбрать S = ee~n^L\
то при условии \\x(t0) - у(t0) || < S будем иметь \\x(t) - y(t)|| <
< ?, т.е. решение x(t) системы D.9) непрерывно зависит от
начальных значений, определяющих ее начальные условия. >
Следствие 4.2. Если нормальная система ОДУ вида D.9)
удовлетворяет в области D D.3) всем условиям теоремы 4.1
Коши, то решение этой системы непрерывно зависит от правой
части D.9) в смысле, аналогичном определению 2.3.
< Пусть x(to) = y(to). Тогда из D.17) имеем
Если для любого е > 0 выбрать S = ee~nv^L/l//i, то при условии
Д < S получим \\x(t) — y(t)\\ < ?, т.е. решение системы D.9)
непрерывно зависит от ее правой части. >
Рассмотрим случай, когда правая часть в D.9) непрерывно
зависит от некоторого скалярного параметра Л 6 Л (Л —
некоторый отрезок числовой прямой R), и пусть этот параметр
принимает два значения Ai и Лг- Тогда мы будем иметь две
системы
^ ,Xx); D.18)
,X2). D.19)

4.3, Оценка разности двух решении 123
Обозначим через ж(?, Ai) и ж(?, А2) решения систем D.18) и
D.19), определенные на отрезке [to-- Л, to + h] и удовлетво-
удовлетворяющие одинаковым начальным условиям ж(?(ь Ai) = sc(io, A2).
Пусть функция df/d\(t, ж, А) непрерывна в области D. Тогда
для каждой координатной функции /*, г = 1, га, имеет место
теорема Лагранжа о конечных приращениях функции
Для всех точек (?,#), принадлежащих замкнутой области D,
можно найти А > О, такое, что |с?//9А(?, #, А)| ^ А, г = 1, п.
Тогда верна оценка
Суммируя эту оценку по всем координатным функциям, полу-
получим
В силу выполнения условия Липшица по х существует L > О,
такое, что
, *(*,А2), А2) - /(«, х(«,Ах), Ai)|| < n3/2L||x(t, A2) -x(i,
Это позволяет и в данном случае применить D.17) и получить
неравенство
||x(t9 Ax) - *(t, A2)|| < A|Ai ~ A2|/ien^Lh.
Если для любого е > 0 выбрать 5 = ee~ny^Lh/(Ahy/n)y то при
условии |Ai — А2| < S получим ||ж(?, Ai) — ж(?, А2)| < е. Таким
образом, справедливо следующее утверждение.

124 4. СИСТЕМЫ ОДУ
Следствие 4.3. Решение x(t, А) нормальной системы
ОДУ D.18) непрерывно зависит от параметра Л в смыс-
смысле, аналогичном определению 2.4, если при Л G Л правая
часть /(t, ж, Л) этой системы удовлетворяет условиям тео-
теоремы Коши и df/d\(t, х, А) непрерывна по Л в области D,
АеЛ.
В ряде случаев требуется, чтобы решение задачи Коши для
нормальной системы ОДУ было дифференцируемой функцией
параметра А и начальных значений to, #?,..., х^. Сфор-
Сформулируем без доказательства теорему о дифференцируемости
решения этой задачи по параметру.
Теорема 4.2. Пусть в некоторой области изменения пара-
параметра А и переменных t и ж векторная функция /(t, ж, А)
имеет непрерывные частные производные по всем аргументам.
Тогда решение ж(?, А) задачи Коши для нормальной системы
ОДУ вида D.18) является непрерывно дифференцируемой век-
векторной функцией t и А.
Покажем теперь, что исследование зависимости решения
задачи Коши для нормальной системы ОДУ от начальных
значений можно свести к анализу зависимости этого решения
от параметра. Выполним в D.9) подстановки т = t — to и
и = х — жо, где жо = (#5,..., ж^)т, и представим задачу Коши в
виде
«/(т + *о,и + жо), ii@) = O. D.20)
Начальные значения to, x®,..., ж^, являющиеся аргументами
в правой части этой системы ОДУ, играют роль параметров.
Если векторная функция /(t, ж) в правой части D.9) диф-
дифференцируема в области D D.3), то правая часть в D.20)
удовлетворяет условиям теоремы 4.2, т.е. решение ж(^ ^,жо)
задачи Коши для нормальной системы ОДУ вида D.9) является
непрерывно дифференцируемой функцией независимого пере-
переменного t и начальных значений to, ж?,..., х%.

4.4. Теорема Коши о существовании и единственности 125
4.4. Теорема Коши о существовании
и единственности решения уравнения высшего
порядка. Случаи понижения порядка
Обыкновенное дифференциальное уравнение (ОДУ) п-го по-
порядка, разрешенное относительно старшей производной, имеет
вид
dnx _ / dx dn"lx\
~№ " V V**' Л"''''' ~dt^)' ( }
Обозначим для краткости записи
(") d(n~l)x
х = (ж(°\ ..., х(п~1)) . Введем в рассмотрение область
= О77^Т}, D.22)
где Xq ^ = x(k\to)] a, b — некоторые постоянные.
Решением ОДУ D.21) п-го порядка на отрезке / =
= [to — a, to + о] называют функцию x(t), удовлетворяющую
следующим условиям:
1) функция x(t) непрерывно дифференцируема п раз на
отрезке /;
2) подстановка функции x(t) в ОДУ D.21) обращает его в
тождество.
Задачей Коши для ОДУ D.21) п-го порядка называют
задачу нахождения функции rc(t), удовлетворяющей уравнению
D.21) и начальным условиям
4°\ 41} = 4П~г\ D-23)
где Xq , гго ,..., ^о ~ — задалные числа.

126 4. СИСТЕМЫ ОДУ
Теорема 4.3 (теорема Коти). Бели функция <р не-
непрерывна в области D D.22) и удовлетворяет условию Лип-
Липшица по переменным х(°\ ..., х^п^:
то в этой области существует единственное решение ОДУ
D.21), удовлетворяющее начальным условиям D.23).
Условия теоремы 4.3 будут выполнены, если, в частности,
функция ip(t, ж(°>,..., х^)) непрерывна в D и имеет ограни-
ограниченные частные производные по х^°\ ..., х^"). Для этого до-
достаточно, чтобы частные производные дер/дх^ (А; = 0, п—1)
были непрерывны в области D (см. замечание 4.1).
Функцию х = ж(?, Ci,..., С*,..., Сп), где С{ — произволь-
произвольные постоянные, называют общим решением ОДУ D.21)
п-го порядка в области D D.22), если эта функция имеет
непрерывные производные по t до n-го порядка включитель-
включительно и для любой точки (to* #q , #q ,..., Xq ) ? D существует
конкретный набор значений Ci~Cf (i = 1, п), удовлетворяю-
удовлетворяющих равенствам
»
г = Т7^, D.24)
для которых функция х = х(?, С?,..., С®) является решением
ОДУ D.21).
Если в общем решении х = х(?, Ci,..., Ci,..., Сп) придать
постоянным Ci, ..., Сп конкретные числовые значения, то
получим частное региение ОДУ D.21) п-го порядка.
Укажем типы ОДУ высшего порядка (п > 1), допускающих
его понижение, т.е. интегрирование этих уравнений можно
свести к интегрированию ОДУ меньшего порядка. Будем
исходить из формы записи ОДУ, когда оно не разрешено
относительно старшей производной, т.е.
dX ^=0. D.25)

4.4. Теорема Копт о существовании и единственности 127
1. ОДУ D.25) не содержит функции х и некоторого
количества последовательных производных:
При помощи подстановки у = dsx/dts ОДУ D.26) можно при-
привести к ОДУ (n — s)-ro порядка:
Например, подстановка у = cPx/dt2 в ОДУ
приводит его к ОДУ с разделлющгышсл переменными:
Разделяя переменные и интегрируя, получаем
Левая часть этого равенства является обратной гиперболиче-
гиперболической функцией — ареасинусом аргумента у, обозначаемым
Arshy. Тогда имеем y = sh(i + Ci) и с учетом выполненной
подстановки
Интегрируя, последовательно находим
dx
—
at

128 4. СИСТЕМЫ ОДУ
2. ОДУ D.25) не содержит явно независимого переменно-
переменного t:
•(«.§••••¦?)-* <**>
К ОДУ такого типа достаточно часто приводят прикладные
задачи. Так, при составлении дифференциального уравнения,
описывающего процесс, развивающийся во времени ?, могут
быть использованы те или иные физические законы, в соот-
соотношения для которых время может не входить в явном виде
(например, законы сохранения таких субстанций, как масса,
импульс, энергия, электрический заряд).
Сделаем в D.27) замену dx/dt = у, где у = у(х) — но-
новая искомая функция, а ж — новое независимое переменное.
Покажем, что такая замена приведет к понижению порядка
уравнения D.27) на единицу. Используя правило дифференци-
дифференцирования сложной функции, имеем
d2x __dy __ dy dx _ dy
<Px^_dj dy\_dy_ dy d_ /dy_\ dx_ _ (^У\2 , 2<1?У.
dt* ~~dtVdx)~ dt' dx Уdx\dx) dt ~V\dx) У dx2''
dtn
где h — известная функция соответствующих аргументов.
Подстановка этих выражений в ОДУ D.27) приводит к ОДУ
(п — 1)-го порядка относительно у.
Пример 4.1. Найдем изменение во времени t длины x(i)
конца тяжелой цепи, сползающего с горизонтального стола,
в то время как не вступившая еще в движение часть цепи
свернута в клубок у самого края стола (рис. 4.2). Пусть р —

4.4. Теорема Ковш о существовании и единственности
129
масса единицы длины цепи, g —
ускорение свободного падения.
Особенность рассматриваемой
задачи состоит в том, что масса
рх движущейся части цепи пере-
переменна во времени и, как следствие,
на эту часть цепи действует на-
направленная вертикально вниз переменная сила тяжести рхд,
вызывающая изменение количества движения px(dx/dt) цепи.
Согласно второму закону Ньютона в форме теоремы об изме-
изменении количества движения, запишем
d { dx
Рис. 4.2
После дифференцирования левой части этого равенства будем
иметь ОДУ второго порядка
d2x
"~1~ D.28)
Выполнив в D.28) замену dx/dt = у (ж), получим
dy 2
ху-=дх-у
ИЛИ
т.е. придем к уравнению Бернулли вида C.25) при а = —1,
которое подстановкой z = yl~a = у2 приводится к линейному
ОДУ первого порядка
— = -2-
ах х
D.29)
Решим это ОДУ методом Лагранжа, записав для соответству-
соответствующего однородного уравнения решение z(x) = С/х2. Решение
неоднородного ОДУ D.29) будем искать в виде z(x) = С(х)/х2.
Тогда для нахождения С(х) имеем ОДУ dC(x)/dx = 2gx2, ре-
решая которое, получаем
5 — 9306

130 4. СИСТЕМЫ ОДУ
В итоге, имея в виду, что z = у2 = (dx/dtJ, запишем
Постоянную С\ можно найти из начальных условий. На-
Например, если в момент времени t = to цепь неподвижна, а длина
свешивающегося со стола конца цепи x(to) = яо? т0 ^ля ОДУ
D.29) начальное условие можно записать в виде z(xq) = 0, по-
поскольку y/z = у = dx/dt имеет смысл скорости. Тогда из D.30)
следует, что С\ = — 2дх\/Ъ.
Разрешая D.30) относительно производной и учитывая, что
dx/dt ^ 0, получаем ОДУ с разделяющимися переменными
3"" ¦ О '
решение которого можно записать в виде
xdx
I
= t+c2.
Интеграл Ь левой части этого равенства в общем случае не
удается выразить через элементарные функции [VI].
3. ОДУ D.25) является однородным относительно я, dx/dt,
(Px/dt2,..., dnx/dtn со степенью однородности, равной fc, если
для любого А > 0
Покажем, что заменой
можно понизить на единицу порядок однородного относитель-
относительно ж, dx/dt,..., dP'x/dt4 ОДУ со степенью однородности т.

4.4. Теорема Коши о существовании и единственности 131
Имеем
ах
D.32)
du
где Л — вполне определенная функция соответствующих аргу-
аргументов. Подставив D.32) в D.25), получим ОДУ
которое распадается на два уравнения: алгебраическое хт = О,
или x(t) = 0, и ОДУ (п — 1)-го порядка
относительно и. Если известно общее решение этого ОДУ: и =
= n(t, Ci,C2,..., Cn-i), то, подставляя это решение в D.31) и
интегрируя, находим
я(<) = Сп expU(t, Си С2>..., C«_i), D-33)
где С/ — одна из первообразных функции w(i, Ci, C2,.. -, Cn_i);
Cij ^2» •••> C'n — произвольные постоянные. Отметим, что
решение x(t) = 0 следует из D.33) при Сп = 0.
4. ОДУ D.25) называют обобщенно-однородным, если
для любого Л > 0 и некоторых fe, m имеет место равенство
Хкх А* — А*""—^ - АтаФ^ х —
Замены
t = ет, ж = ue*r (если t < 0, то t = -er) D.34)

132 4. СИСТЕМЫ ОДУ
приводят обобщенно-однородное уравнение к ОДУ, не содержа-
содержащему независимое переменное т, а следовательно, к типу, рас-
рассмотренному в п. 2.
Преобразование производных при заменах D.34) происхо-
происходит по формулам
dx dx r (du kr _ кт\ T (du , \ (k i\_
— = — e~T = 1 — ekT + kuekT 1 e"T = (— + ku 1 e(fc)r;
dt dr \dr ) \dr )
dnx ( du
Подставив эти выражения и D.34) в D.25) и сократив на emr,
приходим к ОДУ вида
du
которое не содержит явно независимое переменное т.
Пример. Можно показать, что ОДУ
является обобщенно-однородным с fc = 1 и т = 3, причем
замены D.34) приводят его к виду
сРи /du\Z du
Вопросы и задачи
4.1. Решить следующие ОДУ:
d2x dx Л ^ (Рх dx ч о
+0 6)+4 )

Вопросы и задачи
133
#х 1 1 dx сРх dzx
сРх
dx
dx / с^жч . <Рх
^=exp(t--^); к) ^з- =
ч d2x/dx\2 о
)Ы
dx
4.2. Решить следующие задачи Коши:
dx
t -
dx
J) d*
t=l
= 4;
da;
t=2
dx
= 5;
= 2.
t=0
4.3. Показать, что ОДУ
era; _ / da;V
является однородным со степенью однородности к = 2. Сделав
замену D.31), понизить его порядок. Указать тип полученного
при этом ОДУ первого порядка и найти общее решение исход-
исходного ОДУ.
4.4. В примере 4.1 рассмотреть частный случай С\ = О
и найти закон движения цепи. Какому начальному условию
соответствует этот случай ?

5. СИСТЕМЫ ЛИНЕЙНЫХ
ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
5.1. Определения и основные свойства решений
Нормальной системой линейных обыкновенных диф-
дифференциальных уравнений (ОДУ) называют нормальную си-
систему ОДУ вида
* =
E.1)
где Xi(t) — неизвестные функции, подлежащие определению;
dij(t) и gi{t) — известные функции аргумента t€T, непре-
непрерывные в некотором промежутке ТсЕ числовой прямой R.
Для линейной системы E.1) в области D = TxRn выполнены
все условия»теоремы 4.1 Коши существования и единственности
решения. Действительно, для любого номера г правая часть в
E.1) имеет непрерывные в промежутке Т частные производ-
производные по любому из аргументов Xj (j = 1, п), что, согласно заме-
замечанию 4.1, равносильно выполнению для правой части системы
ОДУ E.1) условия Липшица относительно всех аргументов Xj
(j = l,n) при любых значениях t ? Т.
Запись системы в виде E.1) можно упростить, если восполь-
воспользоваться матричными обозначениями:
; A(t)=
fan(t) ...
021 (*) -
\ani(t) ... ann(t)J
92(t)

5.1. Определения и основные свойства решении 135
Здесь x(t) и g(t) — вектор-функции; A(t) — квадратная
матрица, называемая матрицей системы ОДУ. Над вве-
введенными матрицами можно проводить известные алгебраиче-
алгебраические операции [III], а также операции предельного перехода,
дифференцирования [V] и интегрирования [VII]. В частности,
напомним, что при дифференцировании или интегрировании
матрицы надо просто продифференцировать или проинтегри-
проинтегрировать все ее элементы.
С учетом введенных обозначений систему E.1) перепишем
в виде
/Уд*
— = A(t)x + g(t). E.2)
Если g(t) = 0 в Т, то
^ . E.3)
Систему E.3) называют нормальной однородной системой
линейных ОДУ, соответствующей системе E.2). При g(t) ф О
в Т система линейных ОДУ будет неоднородной.
Приведем теоремы, устанавливающие основные свойства
однородных и неоднородных систем ОДУ.
Теорема 5.1. Линейная комбинация решений однородной
системы E.3) также является решением этой системы.
< Пусть х\(i), X2{t) — решения системы E.3), т.е.
Рассмотрим линейную комбинацию этих решений
x{t) = axi{t)+Px2(t), a, /3 G M.
Имеем
т.е. ax\(t) + /3x2(t) также является решением системы E.3). >

136 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Теорема 5.2. Разность любых двух решений неоднородной
системы ОДУ E.2) есть решение однородной системы E.3).
Ч Пусть xi(t), X2(t) — решения системы E.2), т.е.
= A(t)xl+g(t), ^f- = A(t)x2 + g(t).
Вычтем из первого равенства второе и получим
d{xi(t)-x2(t)) , .
-^ — L = A(t)(xi(t)-x2(t)),
т.е. xi(t) — X2{t) — решение однородной системы E.3). >
Аналогично можно доказать и следующую теорему.
Теорема 5.3. Сумма решения неоднородной системы E.2)
и решения соответствующей ей однородной системы E.3) есть
решение неоднородной системы E.2).
Теорема 5.4. Если x\(t) и X2(t) — решения нормальных
систем линейных ОДУ соответственно
^ = A(t)x + g(t) и — = A(t)x + f(t),
то x(t) = x\(t) + X2(t) является решением нормальной системы
линейных ОДУ
Her
—
<4 Действительно, имеем
f{t) = A(t)x + g(t) + f(t),
что доказывает утверждение теоремы. >

5.1. Определения и основные свойства решений 137
Рассмотрим вектор-функции
*i(t), ..., х{Ц), ..., xn(t), E.4)
необязательно являющиеся решениями систем E.2) или E.3).
Определение 5.1. Систему вектор-функций E.4) на-
называют линейно зависимой в некотором промежутке ТСК
числовой прямой R, если существует такая система чисел
Аь ..., Ai, ..., AneR,
что имеет место тождество
Xixi(t) + ... + \iXi(t) +... + An»n(«) = 0 Vt 6 Т. E.5)
Если же такой системы чисел не существует, то систему
вектор-функций E.4) называют линейно независимой в про-
промежутке Т.
Любая система вектор-функций, включающая вектор-функ-
вектор-функцию, тождественно равную в промежутке Г нулевому вектору
0, является, согласно определению 5.1, линейно зависимой. Дей-
Действительно, выбирая в E.5) коэффициент при такой функции
отличным от нуля и полагая коэффициенты при остальных
функциях равными нулю, приходим к тождеству для любых
teT.
Система вектор-функций линейно независима в каком-либо
промежутке Т, если она линейно независима в меньшем про-
промежутке Т\ С Т. Если система линейно зависима в Г, то ее
линейная зависимость будет сохранена ив Т\ С Т, но обрат-
обратное, вообще говоря, неверно. При рассмотрении конкретного
набора вектор-функций часто для краткости опускают слово
„система" и говорят о линейных зависимости или независимо-
независимости этих вектор-функций.

138 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
5.2. Определитель Вронского.
Фундаментальная система решений.
Формула Остроградского — Лиувилля
Пусть задана система п вектор-функций
определенная в некотором промежутке Т С Ш числовой прямой
R. В этой записи первый индекс у скалярной функции Xik(t)
означает, как и в E.1), номер координатной функции вектор-
функции хк, а второй — номер этой вектор-функции.
Определитель
xn(t) ... xin(t)
'•• Х2п^ E.6)
... xnn{t)
называют определителем Вронского системы вектор-функ-
вектор-функций х 1 (?),..., xn(t) по имени польского математика Ю. Вронь-
ского A776-1853). Сформулируем в виде теорем некоторые
свойства этого определителя.
Теорема 5.5. Если система вектор-функций
Xk(t) = {xik(t), • • •, Xnk(t))T, к = 1, n, E.7)
линейно зависима в некотором промежутке TCR, то опреде-
определитель Вронского W(t) = О V* € Т.
Л Если вектор-функции xk(t) {к = 1, п) линейно зависимы в
промежутке Т, то, согласно определению 5.1, хотя бы один из
коэффициентов в E.5) отличен от нуля (например, Xj ф 0). То-
Тогда вектор-функция Xj(t) будет линейной комбинацией осталь-
остальных вектор-функций:
cn(t) Vt6Tf

5.2. Фундаментальная система решений 139
где а\ = —Ai/Aj,..., an = —Xn/\j, В этом случае j'-й столбец
определителя W(t) является линейной комбинацией остальных
столбцов и поэтому W(i) = О V* € Т. >
Теорема 5.6, Если определитель W(t) для системы век-
вектор-функций E.7), являющихся в промежутке TCR решения-
решениями однородной системы линейных ОДУ E.3), равен нулю хотя
бы в одной точке to € ?\ то эта система вектор-функций ли-
линейно зависима в промежутке Т.
^ Пусть PF(to) = O. Тогда векторы a?i(to), ...,xn(to) линейно
зависимы [IV] и, следовательно,
Рассмотрим вектор-функцию
Согласно теореме 5.1, эта вектор-функция является решением
однородной системы E.3), причем ж(*о) = 0- Система E.3)
имеет, очевидно, решение x(t) = 0 Vt G Г, которое удовле-
удовлетворяет качальнолеу условию ж(*о) = 0. Так как система E.3)
удовлетворяет всем условиям теоремы 4.1 Коши существования
и единственности решения, то начальному условию ж (to) = 0 в
промежутке Т отвечает единственное решение x(t) = 0. Та-
Таким образом,
что, согласно определению 5.1, доказывает утверждение тео-
теоремы. >
Из теоремы 5.6 вытекает следствие, которое приведем без
доказательства.

1405. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Следствие 5.1. Если определитель W(?), составленный из
вектор-функций, являющихся решениями однородной системы
линейных ОДУ E.3) в некотором промежутке Г, равен нулю в
одной точке <о € Г, т.е. W(to) = 0, то он тождественно равен
нулю в этом промежутке (W(t) = 0 Vi € Т).
Одним из важнейших понятий в теории однородных систем
линейных ОДУ является понятие фундаментальной системы
решений.
Определение 5.2. Линейно независимую в промежутке
ТСЕ систему из п вектор-функций вида E.7), каждая из
которых является в нем решением однородной системы п ли-
линейных ОДУ E.3), называют фундаментальной системой
решений для E.3) в этом промежутке.
Теорема 5.7. Фундаментальные системы решений сущест-
существуют.
<4 Пусть г, к = 1, п и п2 чисел
-{? Я
образуют единичную матрицу Е = (Ь^) размера п, определи-
определитель которой detJS —1. Рассмотрим п решений
{.., xnk(t))T, к = Vn,
однородной системы E.3), которые определены в некотором
промежутке ГСЕ числовой прямой Е и в точке to ET
удовлетворяют начальным условиям х\ \to) = 6^? t, fc = 1, п.
Тогда получим W(to) = det E = 1 ф 0, т.е. W(t) ф 0 в проме-
промежутке Т. На основании теоремы 5.5 и определения 5.1 отсюда
следует, что эти решения линейно независимы в промежутке Т
и, согласно определению 5.2, образуют в нем фундаментальную
систему решений для E.3). >

5.2. Фундаментальная система решений
141
Запись в виде E.3) соответствует нормальной однород-
однородной системе линейных ОДУ с переменными коэффи-
коэффициентами, поскольку элементы a^(t) (г, j = l,n) матрицы
A(t) этой системы являются функциями независимого пере-
переменного t. Такие системы удается проинтегрировать и по-
получить решение в виде аналитической зависимости лишь в
исключительных случаях. Однако существует одна замечатель-
замечательная формула, связывающая между собой решения произволь-
произвольной однородной системы E.3) ОДУ с переменными коэффи-
коэффициентами.
Вычислим производную по t от определителя Вронского
E.6), составленного из решений Xk(t) =
к = 1,п, системы ОДУ E.3):
dxn
dW
dt
dt
dt
ъпп
xn
dt
dt
dt
xnn
xn
#21
#22
dx
ni
dxn
E.8)
dt dt
В E.8) использовано правило вычисления производной от
определителя квадратной матрицы размера п [II]. Так как
определитель представляет собой сумму п! слагаемых с соот-
соответствующими знаками, а каждое слагаемое есть произведение
п элементов, то, используя правило дифференцирования про-
произведения п функций [II], приходим к записи E.8). Вектор-
функция Xk(t) является решением однородной системы E.3),
т.е.
dxjk
dt

142
5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
#21
#22
Поэтому первый определитель в правой части E.8) имеет вид
= an(t)W.
Здесь использовано правило сложения определителей, а также
то, что определитель, имеющий две одинаковые строки, равен
нулю.
Аналогично второе, третье и т.д. (вплоть до последнего)
слагаемые в E.8) равны:
#11
#ln
dt dt
dt
xn
= ann(t)W.
i_ dxn2 dxnn
dt dt '" dt
С учетом этих выражений E.8) принимает вид
dW „A
г=1
E.9)
Отсюда следует, что определитель Вронского удовлетворяет
линейному однородному ОДУ первого порядка с разделяющими-
разделяющимися переменными. Разделяя переменные и интегрируя, получаем

5.2. Фундаментальная система решений 143
соотношение
t n
W(t) = W(to)exp( [Y,aa(t)dt). E.10)
которое называют формулой Остроградского — Лиувил-
ля (Ж. Лиувилль A809-1882) — французский математик и
механик, а о русском математике и механике М.В. Остроград-
Остроградском A801-1861) см. Краткий исторический очерк [I]).
Пример. Рассмотрим нормальную систему ОДУ
dx\
=х
где p(t) — произвольная функция, непрерывная в некотором
промежутке TCR. Матрица этой системы
«<>=(-:,<> :)¦
2
Отсюда следует, что ^2au(t) = 0, и формула Остроградско-
Остроградского — Лиувилля принимает вид
xn(t) xn(t)
где С = W{to) = const.
Итак, для двух произвольных решений
xi{t) = (a?n(t), x2i(t))T, x2{t) = )
рассматриваемой системы справедливо E.11). Отметим, что
E.11) можно использовать для контроля точности получаемых
решений системы ОДУ при ее численном интегрировании.

144 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
5.3. Теоремы о структуре общего решения
однородной и неоднородной систем
Выше отмечалось, что решение однородной системы линей-
линейных обыкновенных дифференциальных уравнений (ОДУ) вида
E.3) с переменными коэффициентами в общем случае не уда-
удается получить при помощи операции интегрирования. Однако
можно указать структуру общего решения как системы E.3),
так и системы линейных неоднородных ОДУ вида E.1), кото-
которую также называют нормальной неоднородной системой
линейных ОДУ с переменными коэффициентами.
Важно подчеркнуть, что, согласно определению 4.2 общего
решения нормальной системы из п ОДУ, это решение включа-
включает п произвольных постоянных Ck (fc = l,n). Следующая
теорема позволяет не только указать структуру общего ре-
решения однородной системы вида E.3), но и установить, что
в случае задачи Коши для системы линейных ОДУ эти посто-
постоянные определены однозначно.
Теорема 5.8. Если вектор-функции
• xk(t) = (xik{t), ..., xnk(t))T, k = T7n,
определенные в промежутке Г числовой прямой Е, образуют
в нем фундаментальную систему решений однородной системы
линейных ОДУ E.3), то общее решение этой системы имеет вид
E.12)
k=l
с некоторыми постоянными коэффициентами Ск (к = 1, п).
М Рассмотрим частное решение x(t) системы E.3), удовлетво-
удовлетворяющее при toET условию x(to) = жо. Согласно теореме 4.1
Коши, условия которой, очевидно, выполнены для системы
E.3), такое решение существует и единственно.

5.3. Структура общего решения системы ОДУ 145
Векторы Xk{to) {к = 1, п) линейно независимы в силу ли-
линейной независимости в промежутке Т фундаментальной си-
системы решений (см. определение 5.2), и их можно рассматри-
рассматривать как базис евклидова (векторного) пространства Rn. В
базисе разложение вектора
k=l
единственно в том смысле, что коэффициенты линейной комби-
комбинации E.13) определены однозначно [IV].
Вектор-функция
А;=1
будучи линейной комбинацией решений системы E.3), согласно
теореме 5.1, является решением этой системы, которое удовле-
удовлетворяет условию x*(to) = x(to) = Хо- В силу единственности
решения системы E.3), удовлетворяющего этому условию, име-
имеем x*(t) = ж(?) и, учитывая E.14), получаем E.12).
Таким образом, E.12) верно при фиксированных to Е Т и
хо Е Кп, причем в этом случае коэффициенты С* (к = 1, п)
определены однозначно. Поскольку точка (?о, #о) ? D = TxW1
может быть выбрана произвольно, то E.12) определяет струк-
структуру любого решения в этой области, причем каждому такому
решению отвечает конкретный набор коэффициентов С&. В
этом смысле линейная комбинация E.12) определяет структуру
общего решения однородной системы E.3) в области D как
совокупности всех частных решений, так как из E.3) можно
получить любое частное решение в этой области, вычислив по
заданным to и жо коэффициенты С*. >
Нетрудно заметить, что совокупность решений однородной
системы E.3) образует n-мерное линейное пространство. Лю-
Любая фундаментальная система решений служит базисом в этом
пространстве.

146 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Теорема 5.9. Общее решение неоднородной системы E.2)
есть сумма общего решения соответствующей ей однородной
системы E.3) и частного решения неоднородной системы E.2):
E.15)
Здесь x*(t) — частное решение неоднородной системы E.2),
определенное в промежутке Т; ajfc(i), к = 1, п, — фундамен-
фундаментальная система решений соответствующей однородной систе-
системы E.3), определенных в том же промежутке; Cfc, к = 1, п, —
некоторые постоянные коэффициенты.
< На основании теоремы 5.3 E.15) является решением неод-
неоднородной системы E.2). Наоборот, если x(t) — какое-либо
решение неоднородной системы E.2), то, согласно теореме 5.2,
x(t) — x*(t) — решение однородной системы E.3), которое мож-
можно представить в виде E.12), т.е.
Отсюда непосредственно следует утверждение теоремы. Для
любого частного решения неоднородной системы E.2), удо-
удовлетворяющего при произвольном to ? Т условию x(to) = жо,
значения коэффициентов С* (А; = 1, п) могут быть найдены
однозначно при разложении вектора xq — ж*(to) в базисе, обра-
образованном линейно независимыми векторами Xfc(to). В этом
смысле E.15) определяет структуру общего решения неодно-
неоднородной системы E.2) как совокупности всех частных решений
этой системы. >
Несмотря на достаточно общий характер теорем 5.8 и 5.9,
они не только играют важнейшую роль в теории ОДУ, но и
указывают путь решения систем линейных ОДУ с переменными
коэффициентами.

5.4. Метод вариации постоянных 147
5.4. Метод вариации постоянных
Покажем, что интегрирование неоднородной системы ли-
линейных обыкновенных дифференциальных уравнений (ОДУ) E.2)
с переменными коэффициентами можно свести к нахожде-
нахождению фундаментальной системы решений соответствующей од-
однородной системы ОДУ E.3). Иными словами, если известна
фундаментальная система решений, то общее решение неод-
неоднородной системы можно получить при помощи операции ин-
интегрирования.
Пусть xi(t),..., Xjfe(t),..., xn(t) — фундаментальная систе-
система решений однородной системы E.3), определенных в некото-
некотором промежутке TCR числовой прямой IR, причем
xk(t) = (я 1*(*),..., xik{t),..., xnk{t))T, k = I7n,
где Xik(t) — координатные функции вектор-функции Xk(t).
Каждое из решений, составляющих фундаментальную систему
решений, удовлетворяет системе E.3), т.е.
Введем в рассмотрение матрицу
xn{t) ... xln(t)
E.16)
E.17)
xni(t) ... xnn(t)J
Бе называют фундаментальной матрицей. Дифференци-
Дифференцируя ее по t и используя E.16), получаем
ТйГ= {% ¦ • ¦' if) = {A{t)Xb • • •'A{i)Xn) = A{t)x- E18)
Будем искать решение неоднородной системы E.2) в виде
*(*) = Ci(t)xi + ... + Ck{t)xk{t) + ...+
n(t)xn = X(t)c(t), E.19)

148 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
где c{t) = (Ci(t),..., Ck(t),..., Cn(t))T, a Ck(t) — подлежащие
определению координатные функции вектор-функции c(t).
Подставив E.19) в E.2), запишем
или, учитывая E.18),
dc
X
= g(t). E.20)
Определителем фундаментальной матрицы X(t) является
определитель W(t) Вронского для системы вектор-функций,
образующих рассматриваемую фундаментальную систему ре-
решений однородной системы E.3). В силу определения 5.2 фун-
фундаментальной системы эта система вектор-функций линейно
независима в промежутке Г. Поэтому W(t) ^ О Ш ? Т, так
как если хотя бы в одной точке этого промежутка определи-
определитель Вронского будет равен нулю, то, согласно теореме 5.6,
система вектор-функций будет линейно зависимой в Т, что
противоречит исходному условию.
Таким образом, detX(t) ^0 Vt ? Т, т.е. в каждой точке t
промежутка Г можно построить матрицу X-1(t), обратную
фундаментальной матрице X(t). Умножая слева обе части
E.20) на Х~1 и интегрируя в промежутке Т от to E T до
?, получаем
t
c(t) = / X (т)д(т) dr + со, E.21)
to
где со = c(to) — вектор, равный значению в точке to G Т
искомой вектор-функции с(?), т.е.
, ki-'-i^n) ^ ^Л — bk\tQ), /С — 1,П.

5.4. Метод вариации постоянных 149
При построении общего решения неоднородной системы
E.2) вектор со можно выбрать произвольно. Действительно,
подставив E.21) в E.19), найдем
t
x{t)=X(t)co + X{t) [х~1(т)д(т)Aт. E.22)
to
Если выбрать cq = 0, то получим частное решение систе-
системы E.2)
t
x*(t)=X(t)Jx-\T)g(T)dT. E.23)
to
Поскольку X{t)c0 = C$xi(t) + ... + C%xn(t), то E.22) с учетом
E.23) можно записать также в виде
E.24)
В силу теоремы 5.9 E.24), а следовательно, и E.22) дают общее
решение неоднородной системы E.2).
Если решать задачу Коши для системы E.2) при начальном
условии x(to) = жо, то, полагая в E.22) t = <о> получим хо =
= X(to)co, или со = -Х>~1(<о)а*о- Тогда решение задачи Коши
для системы E.2) можно записать в виде
г
x(t) = X(t)X-l(to)xo + X(t)f X-1 (т)д(т) dr.
to
Изложенный метод нахождения решения неоднородной си-
системы E.2) называют методом вариации постоянных, или
методом Лагранжа неопределенных коэффициентов.

150 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Пример. Найдем общее решение неоднородной системы
двух линейных ОДУ (п = 2)
dx\ . _ _t
— =4xi-3x2 +e ,
dx2
—¦
at
Исходной системе соответствует однородная система
dxi
— = 4xi- 3x2;
?<5-25)
Непосредственной проверкой нетрудно убедиться, что вектор-
функции x\(t) = (e*, 3e2t)T и X2(t) = (e*, 2e2t)T удовлетворя-
удовлетворяют системе E.25) и являются линейно независимыми на всей
числовой прямой. Согласно определению 5.2, они образуют
фундаментальную систему решений системы E.25), а фунда-
фундаментальная матрица и обратная ей матрица размера п = 2
имеют вид
Так как в данном случае g(t) = (е"*,0)т, то X" (*)#(?) =
= (—2е~2*, e"t)T. Положив to = 0 и со = 0 и использовав
E.23), вычислим сначала интеграл
to 0
а затем найдем частное решение
/
to

5.5. Система ОДУ с постоянными коэффициентами 151
исходной неоднородной системы. При построении ее общего
решения положим со = (С?, С^У и, согласно E.24), запишем
его в виде
x(t) = (xi(t), x2(t))T = x,(t)
или
5.5. Система линейных дифференциальных
уравнений с постоянными коэффициентами.
Характеристическое уравнение системы
Пусть все коэффициенты а^ в нормальной системе линей-
линейных обыкновенных дифференциальных уравнений (ОДУ) E.1)
постоянны. Иначе говоря, постоянны все элементы матрицы
A(t) системы: aij= const, г, j = l, п. Такую систему называют
нормальной системой линейных ОДУ с постоянными
коэффициентами. При этом, если g(t) ^0 в некотором про-
промежутке Т числовой прямой Е, в котором рассматривают
решение этой системы ОДУ, то систему называют неодно-
неоднородной, а в противном случае — однородной. Среди систем
линейных ОДУ система ОДУ с постоянными коэффициента-
коэффициентами — один из немногих случаев, допускающих интегрирование.
При выяснении вопроса об интегрировании в силу сказанного
в 5,4 можно ограничиться рассмотрением однородной системы
линейных ОДУ с постоянными коэффициентами, которая мо-
может быть записана в матричной форме
~dt=Ax> E'26)
где А — заданная матрица, а х = x(t) — искомая вектор-
функция.

152 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Будем искать не равное тождественно нулю решение систе-
системы E.26) в виде
x(t)=aex\ E.27)
где aGKn (а^О), AGK подлежат определению. Продиффе-
Продифференцировав x(t) как вектор-функцию: — (aeAt) = Хае , под-
подставим в E.26): Xaext = A(aext). В этом матричном уравне-
уравнении ext представляет собой ненулевой скалярный множитель,
на который можно сократить. Получим матричное уравнение
Аа = Ха. С помощью единичной матрицы Е уравнение можно
преобразовать к виду
= 0. E.28)
Это уравнение показывает, что искомый вектор а является
собственным вектором матрицы А [IV]. В координатной
форме уравнение E.28) имеет вид
(an - A)ax + ai2a2 + ... + ainan = 0;
- A)a2 +... + a^nOLn = 0;
+ о>п2<*2 +... + (апп - Х)ап = 0.
Мы получили однородную систему линейных алгебраиче-
алгебраических уравнений (СЛАУ). Для того чтобы она имела ненулевое
решение a Е Мп, необходимо и достаточно, чтобы равнялся ну-
нулю ее определитель [III]:
п\\ — X сь\2 •.. ain
~Л •¦• °2п =0. E.30)
Раскрытие определителя приводит E.30) к алгебраическому
уравнению n-й степени относительно А. Его называют харак-
характеристическим уравнением матрицы А, а в теории дифферен-
дифференциальных уравнений — характеристическим уравнением
системы ОДУ E.26).

5.6. Нахождение фундаментальной системы решении 153
5.6. Нахождение фундаментальной
системы решений в случае различных
корней характеристического уравнения
Пусть все корни Ai, ..., Ап характеристического урав-
уравнения E.30) действительны и различны. Выбрав из них Xj
и подставив его в E.29), получим однородную систему ли-
линейных алгебраических уравнений (СЛАУ) с определителем,
равным в силу E.30) нулю. Среди решений такой СЛАУ есть
ненулевое решение, являющееся собственным вектором aj =
= (aij,..., otnjY матрицы А системы ОДУ E.26), соответ-
соответствующим собственному значению Xj этой матрицы А [III].
Таким образом, выбранному корню Xj отвечает решение
однородной системы линейных обыкновенных дифференциаль-
дифференциальных уравнений (ОДУ) E.26) с постоянными коэффициентами,
которое с учетом E.27) можно записать в виде вектор-функции
*,(«) = а,-еА'*. E.31)
Поскольку такая запись справедлива для каждого из корней Aj
(j = 1, п) характеристического уравнения E.30), то E.31) сле-
следует рассматривать как совокупность из п решений системы
E.26). Покажем, что эти п решений образуют фундаменталь-
фундаментальную систему решений однородной системы E.26).
Прежде всего напомним, что система собственных векторов
матрицы А, отвечающих различным собственным значениям
Xj (j' = 1, п), линейно независима [IV]. Поэтому определитель
матрицы, составленной из собственных векторов, отличен от
нуля, т.е. det(otij) ф 0. Умножение всех элементов любой стро-
строки определителя на некоторый одинаковый множитель рав-
равносильно умножению на этот множитель всего определителя.
Учитывая это, получаем для определителя Вронского системы
вектор-функций Xj(t), j = 1, п, выражение
п
W(t) = exp (t ^ Ai) det (a^ фО V< G R.
t=i

154 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Следовательно, эта система на основании теоремы 5.5 и опре-
определения 5.1 является линейно независимой, причем на всей чи-
числовой прямой R. Так как каждая из вектор-функций Xj(t) —
решение однородной системы E.26), то они, согласно опреде-
определению 5.2, образуют фундаментальную систему решений этой
однородной системы.
В силу теоремы 5.8 о структуре общего решения однородной
системы линейных ОДУ с переменными коэффициентами в
частном случае системы E.26) с постоянными коэффициентами
для построения общего решения можно использовать E.12) в
виде
x(t) = ?С,-*;(*) = ^С^-еЧ E.32)
i=i i=i
где Cj — произвольные постоянные, или в координатной
форме
Cj-atnj-e^*. E-33)
3=1 J=l
Пример. Найдем общее решение системы ОДУ
Матрица А и характеристическое уравнение E.30) системы
ОДУ в данном случае имеют вид
¦G О-
X"A 2 =0
2 1 - A U'
Раскрывая определитель, получаем квадратное уравнение А2 —
— 2А — 3 = 0, имеющее два действительных различных корня

5.6. Нахождение фундаментальной системы решении 155
дг =3, Л2 = —1. Они являются собственными значениями мат-
матрицы А.
Найдем собственные векторы матрицы А, отвечающие этим
собственным значениям. При А = Ai = 3 система (А — \Е)а =
= 0 имеет одно решение, например ац = а2\ = 1, т.е. значению
Ai = 3 соответствует собственный вектор а\ = A,1)т.
При А = А2 = — 1 система (А — \Е)а = О имеет, например,
решение ai2 = l, 0*22 = —1, т.е. собственному значению Ai = — 1
отвечает собственный вектор а2 = A, —1)т.
Таким образом, записанные в соответствии с E.31) вектор-
функции
образуют фундаментальную систему решений рассматривае-
рассматриваемой системы ОДУ и в силу E.32) и E.33) позволяют построить
общее решение этой системы ОДУ в векторной форме
или в координатной
xi(t) = Сгезг + С2е'\ x2(t) = Cxeu - С2е"*,
где С\ и С2 — произвольные постоянные. #
Пусть среди простых корней характеристического уравне-
уравнения есть комплексные. Такие корни разделяются на пары ком-
комплексно сопряженных корней А = а + г6, А = а — гЬ (г2 = — 1),
поскольку характеристическое уравнение E.30) является урав-
уравнением n-й степени с действительными коэффициентами [I].
Каждому комплексному корню А = а + г b соответствует ком-
комплексное решение СЛАУ E.29) вида a = p + iq, p, q € Rn. Для
полученных А и а рассмотрим комплекснозначную вектор-

156 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
функцию x(t) = aext = (p + iq)e^a+tb^t. Используя формулу
Эйлера
e^cosi + isin*, E.34)
преобразуем функцию x(t) к виду
х (t) = (р + г q) eat (cos bt + г sin bt) =
= eat (p cos bt - q sin bt) + i eat (qcosbt + p sin bt),
или x(t) = u(?) + iv(?), где
гх (t) = eat (p cos 64 - q sin 6t), v (t) = ea* (g cos bt + p sin bt).
Используя правило дифференцирования комплекснозначных
вектор-функций действительного аргумента
(u(t) + iv{t))' = u'(t)+iv'(t)9
можно показать, что (аел*)' = a\ext и, следовательно, вектор-
функция x(t) = aeAt, для которой А — комплексный корень
характеристического уравнения, а вектор а является решени-
решением соответствующей СЛАУ, удовлетворяет системе ОДУ E.26).
Если a = p + iq — решение СЛАУ E.29), соответству-
соответствующее корню А = а + гЬ характеристического уравнения, то
комплексно сопряженному корню А = а — г b будет соответство-
соответствовать комплексно сопряженное решение^ a = p — iq. При этом
комплекснозначная функция x(t) = aext будет удовлетворять
системе ОДУ E.26). В силу линейности системы ОДУ E.26) ей
будут удовлетворять и вектор-функции u(t) = 0,5(x(t) + x(t))
и v(i) = 0,5i (x(t) — x(t)), принимающие лишь значения в Rn.
Таким образом, вектор-функции u(t) и v(t), будучи дей-
действительной и мнимой частями комплекснозначной функции
x(t) = аел*, являются решениями системы ОДУ E.26).

5.6. Нахождение фундаментальной системы решении 157
Отметим без доказательства, что функции u(t) и v(t)
линейно независимы в R. Значит, паре простых комплексно
сопряженных корней А = а ± г Ь характеристического уравне-
уравнения соответствует пара действительных линейно независимых
решений системы ОДУ.
Пример. Найдем общее решение системы ОДУ
—
Для этой системы матрица А и характеристическое уравнение
имеют вид
А =
4-А -1
5 2-Л
= 0.
Раскрывая определитель, приходим к квадратному уравнению
А2 — 6А + 13 = 0 с комплексно сопряженными корнями AiJ = 3±
±2г. Корню Ai=3 + 2i соответствует решение oti = A,1 — 2г)т
СЛАУ E.30), а корню А2 = 3 - 2г — решение а2 = A,1 + 2г)т.
Выделяя действительную и мнимую части в
получим
cos2< A 3t
3t
Функции u(t) и v(t) образуют фундаментальную систему
решений для рассматриваемой системы ОДУ. Общее решение
этой системы можно представить в виде
x(t) = Ciu(t) + C2v(t), Си С2 е Е. #

158
5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Рассмотрим общий случай простых корней характеристи-
характеристического уравнения E.30), среди которых выделяются пары
комплексно сопряженных корней Ai, Ai, ..., Am, Am и не-
некоторое количество простых действительных корней Агш+ъ
..., Ап. Каждой паре комплексно сопряженных корней Aj,
Aj, j = 1,га, соответствует пара линейно независимых вектор-
функций tij(t), Vj(t), являющихся действительной и мнимой
частями комплекснозначной функции оуел'*, где оу — реше-
решение СЛАУ E.29) при А = Aj. Каждому действительному корню
A», г = 2га+ 1, га, соответствуют собственный вектор щ мат-
матрицы А и решение системы ОДУ E.26) вида Xi(t) = aje*»*.
В рассматриваемом случае фундаментальную систему ре-
решений системы ОДУ E.26) образуют функции txi(t), vi(t),...,
^m@> vm(?)> ^2m-fieA2m+1 *,..., aneXnt. Общее решение систе-
системы ОДУ можно записать при помощи этой фундаментальной
системы решений в виде
x(t) =
C2t;i(t)
i=2m+l
Пример. Найдем общее решение системы ОДУ
dt
dt
dx\ _
~dt =
Характеристическое уравнение системы имеет вид
4-А -5
1 -4-А
-4
0
7
9
5-А
= 0.

5.6. Нахождение фундаментальной системы решений 159
Раскрыв определитель, найдем корни уравнения: Ai = 1, А2 =
= 2 + Зг, Аз = 2 — Зг. Собственному значению Ai = 1 соответ-
соответствует собственный вектор а\ = A, 2,1)т, являющийся реше-
решением СЛАУ (А — Х\Е)а = 0. Комплексному корню А2 = 2 + Зг
соответствует комплексное решение а2 = C — Зг, 5 — Зг, 4)т
СЛАУ (А — \2Е)а = 0, а комплексно сопряженному корню
Аз = 2 — Зг — комплексно сопряженное к а2 решение аз =
= C + Зг,5 + Зг,4)тСЛАУ (A-A3#)a = 0.
Решение системы ОДУ, соответствующее собственному
значению Ai, имеет вид
X1(t) = a1ex>t=l 2 Je*.
Два других решения u(t) и v(t) системы получим, выделив
действительную и мнимую части комплекснозначнои функции
a2eX2t:
/3cos3* + 3sin3A /-3cos3i + 3sin3t\
u{t)= I 5cos3t + 3sin3t j e2*, v{t) = I -3cos3t + 5sin3i I e2t
\ 4cos3t / \ 4sin3t
Общее решение системы будет иметь вид
). #
В прикладных задачах представляет интерес нахождение
частного решения неоднородной системы линейных ОДУ, удо-
удовлетворяющей нулевым начальным условиям. Если соответ-
соответствующая ей однородная система имеет постоянные коэффи-
коэффициенты, то для нахождения такого решения можно применить
изложенный выше способ, воспользовавшись операцией инте-
интегрирования. Но если неоднородность представляет собой ли-
линейную комбинацию синусов и косинусов, то частное решение
можно найти более простым путем, представив его в виде такой
же линейной комбинации, хотя этот прием иногда и не приме-
применим (подробнее об этом см. в 6.6, а здесь лишь рассмотрим
характерный пример).

160 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Пример 5.1. По горизонтальной плоскости без трения мо-
могут перемещаться два тела массой mi и т2, причем тело мас-
массой mi связано с неподвижной стенкой пружиной, жесткость
которой &i, а с телом массой т2 — пружиной с жесткостью
к2. На тело массой mi действует сила с периодически из-
изменяющейся горизонтальной
составляющей F = Fosincjf,
Fo = const (рис. 5.1). Соста-
Составим уравнения движения и
V///////////////////////// х найдем их частное решение,
отвечающее нулевым началь-
начальным условиям.
Обозначим через xi,x2 перемещения масс тел массой mi
и т2 соответственно. На основании второго закона Ньютона
запишем
+ к2(х2 - xi) +
E.35)
Заметим, что систему ОДУ E.35) можно записать в форме
E.2), если ввести дополнительные переменные х$ = dxi/dt,
х\ = dx2/dt. Будем искать частное решение системы E.35) в
виде
xi(t) = asino;*, x2(t) = 6sincj?. E.36)
Подставив E.36) в E.35) и сократив на sina;?, получим два
уравнения для определения амплитуд а и Ь:
(ki — miu2 + к2)а — k2b = Fo, (k2 — т2ш2) Ь — к2а = 0.
Отсюда находим
F0(k2-m2u2)
а =
+ k2 — mia;2) (к2 — т2и2) — к2'
Fpk2
+k2 — miw2) (к2 — т2и2) — Щ

5.7. Структура фундаментальной системы решений 161
Частное решение E.36) имеет смысл лишь для тех значений
ы, для которых (к\ + А?2 — тпхш2) (&2 — ГП2Ш2) Ф fc|. Пусть cj2 =
= ^2/^2- В этом случае а = 0, 6 = — -Ро/^2 и xi(t) = 0, Я2(*) =
= — (F0//C2) sincttf. Иными словами, при таком значении частоты
и; изменения вынуждающей силы тело массой mi, к которому
приложена эта сила, остается неподвижным.
Обнаруженный эффект носит название антирезонанса
(значения о;, обращающие знаменатель в выражениях для ам-
амплитуд в нуль, соответствуют резонансу). На практике эффект
антирезонанса используют при конструировании динамических
гасителей колебаний.
5.7. Структура фундаментальной системы
решений в случае кратных корней
Для завершения анализа систем линейных обыкновенных
дифференциальных уравнений (ОДУ) с постоянными коэффици-
коэффициентами осталось рассмотреть случай наличия кратных корней
характеристического уравнения системы ОДУ.
Пусть характеристическое уравнение E.30) имеет кратные
корни. Будем нумеровать каждый кратный корень столько раз,
сколько линейно независимых собственных векторов матрицы
системы ОДУ E.26) ему отвечает. Например, если какому-
либо значению кратного корня отвечают собственные векторы
а^ ,..., с*!, то будем писать Ai, A2,..., Ап (при этом Ai =
= А2 = ... = АГ1). Итак, имеем всего s ^п корней Ai,..., А5,
каждому из которых отвечает собственный вектор.
Наиболее важный результат в теории ОДУ, касающийся
структуры фундаментальной системы решений, основан на
следующей теореме, которую приведем без доказательства.
Теорема 5.10. Существует система из п линейно незави-
независимых векторов l^ {jk = 1,..., gjk, k = 1, s), удовлетворяющих
6 - 9306

1625. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
соотношениям
E.37)
где сумма <&, отвечающих одинаковым А&, равна кратности
этого корня. #
Векторы 1к ,..., 1к называют присоединенными век-
векторами, порожденными собственным вектором rk . Напом-
Напомним, что корни Xk при разных А; могут быть одинаковыми.
Рассмотрим корень А&. Ему отвечает решение хк =
= 1к ^еЛ/г*. Оказывается, ему отвечают еще (% — 1) решений,
что утверждает следующая теорема, которую также приведем
без доказательства.
Теорема 5.11. Каждому корню А& отвечает q^ решений
вида
E.38)
Таж каж каждому А^, к = 1, в, отвечает qk решений вида
E.38), то всего имеется q\ + 92 + • • • + Я$ = л решений:
E.39)
Теорема 5.12. Решения E.39) образуют фундаментальную
систему решений однородной системы линейных ОДУ E.26).

5.7. Структура, фундаментальной системы решений
163
Поскольку
= /<
/
(jfc =
при t = О
и, согласно теореме 5.10, векторы /^ ,...,/^ в количестве
91 + 92 + • • • + 4s = n линейно независимы, то определитель
Вронского при t = 0 отличен от нуля: И^@) ^ 0, что в
силу теоремы 5.5 и определения 5.1 доказывает линейную
независимость решений E.39). >
При практическом построении фундаментальной системы
решений можно воспользоваться их выражениями E.38), пред-
предварительно найдя все собственные и присоединенные векторы.
Однако для системы с небольшим числом ОДУ проще посту-
поступить следующим образом.
Пусть среди корней характеристического уравнения систе-
системы ОДУ есть кратные действительные корни. Если кратному
собственному значению А соответствует столько собственных
векторов c*i, ..., а*;, какова его кратность, то для этого соб-
собственного значения мы имеем к линейно независимых решений
a\ext, ..., ockext системы ОДУ.
Пример. Решим систему
dx3
Характеристическое уравнение системы имеет вид
= 0.
Раскрывая определитель, приходим к уравнению А3 — ЗА — 2 =
= 0, корнями которого будут Ai = 2, Аг,з = — 1. Корню Ai = 2
соответствует собственный вектор оц — A,1,2)т, решением
-А
1
1
1
-А
1
1
1

164 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
системы будет Xi(t) = aieAl* = A,1, 2)Te2t. Кратному корню
Л2,з = — 1 отвечает СЛАУ (А + Е)а = 0, имеющая два линей-
линейно независимых решения, например а2 = @,0, — 1)т и аз =
= @,1,1)т. Каждому из этих решений соответствует одно
решение системы ОДУ:
(°\ f°\
X2(t) = a2eX2>3t = I 0 I e~\ x3(t) = a3eA2'3< = 1 e~*.
Три решения x\(t), x2(t), xs(t) линейно независимы и
образуют фундаментальную систему решений рассматривае-
рассматриваемой системы ОДУ. Общее решение имеет вид
x(t) = Cixi(t) + C2x2{t) + C3x3(t) =
Если действительному собственному значению Л кратно-
кратности к соответствует только т (т<к) линейно независимых
собственных векторов, то решения системы ОДУ, отвечающие
собственному значению А, можно искать в виде произведения
векторного многочлена степени к — т на ext:
x(t) = (a0
Чтобы найти векторы ao, ..., cxk-mi надо подставить
функцию x(t) указанного вида в систему. После сокращения
на общий множитель ext мы получим систему алгебраических
уравнений, причем каждое из уравнений будет представлять
собой равенство двух многочленов переменного t. Приравняв
коэффициенты в каждом уравнении при одинаковых степенях
?, получим систему уравнений для определения координат
векторов а0, ..., ак-т-

5.7. Структура фундаментальной системы решений 165
Пример. Найдем общее решение системы ОДУ
Характеристическое уравнение системы
= 0
3-А 1
-1 1-Л
имеет один корень Ai?2 = 2 кратности, равной двум. Ранг ма-
матрицы СЛАУ (А — Xii2E)a = 0, соответствующей этому кор-
корню, равен единице. Решение будем искать в виде
*(*) =
Подставим это выражение в систему ОДУ, сократим на е2* и
в результате получим
fbi+ 2(ai + ht) = 3(ax + bxt) + a2 + b2t\
\b2 + 2(a2 + b2t) = -01 - bit + a2 + b2t.
Приравняв коэффициенты при одинаковых степенях ?, полу-
получим однородную систему четырех линейных уравнений с че-
четырьмя неизвестными ai, 61, а2, Ь2, имеющую два линей-
линейно независимых решения. Решению oi = 1, bi = 0, а2 = — 1,
&2 = 0 СЛАУ соответствует решение xi(t) = A, —l)Te2t сис-
системы ОДУ. Взяв в качестве второго решения СЛАУ ai = 1,
&i = 1, а2 = 0, &2 = "~1? получим второе решение системы ОДУ:
= A +1, —t)Te2t. Общим решением системы ОДУ будет
x(t) = Cixi(t) + C2x2(t) = Сг ( \ ) e2t + C2( J +Л e2t. #

166
5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Пример. Найдем общее решение системы ОДУ
dx\
dt
dxo
_—2*!-*»;
~Ж
Матрица системы имеет вид
собственные числа равны Ai = 2, Л2,з = 1. Собственному значе-
значению Ai = 2 соответствует собственный вектор а\ = A, —2,2)т.
Ранг матрицы А — А2,з-Е равен единице, и решения системы
ОДУ, соответствующие собственному значению А2,з> следует
искать в виде x\(t) = (ai + М)е*, X2(t) = (аг + &2*)е*, xs(t) =
= (аз + fatye1. Подставляя эти выражения в систему ОДУ и
сокращая на е*, а затем приравнивая коэффициенты при оди-
одинаковых степенях t, получаем
62 = -2a2-
k C2 =
Ранг матрицы этой системы равен четырем, в качестве сво-
свободных неизвестных можно взять, например, oi и 6i. Тогда
множество решений системы ОДУ, отвечающих собственному

5.7. Структура фундаментальной системы решений 167
значению А2,з? можно записать в виде
Два линейно независимых решения можно получить, полагая
ai = 1, b\ = 0 и ai = 0, &i = 1. При этом общее решение
системы ОДУ будет иметь вид
Если характеристическое уравнение системы ОДУ имеет
комплексный корень А кратности fc, той комплексно сопря-
сопряженное число А будет корнем характеристического уравнения
кратности к. В этом случае можно найти 2к линейно неза-
независимых решений системы ОДУ. Для этого достаточно рас-
рассмотреть комплекснозначную функцию в виде произведения
векторного комплексного многочлена степени к — m (m —
количество линейно независимых комплексных решений СЛАУ
Подставив эту функцию в систему ОДУ и сократив затем
на общий множитель ел*, получим СЛАУ с комплексными
коэффициентами. Разделив на действительные и мнимые
части уравнения системы, придем к СЛАУ с действительными
коэффициентами относительно неизвестных oti и /%. Эта
СЛАУ даст к линейно независимых решений, что приведет
к к различным функциям xx(t), ..., Xk(t). Выделяя у
этих функций действительные и мнимые части, получим 2к
решений системы ОДУ.

168 5. СИСТЕМЫ ЛИНЕЙНЫХ ОДУ
Вопросы и задачи
5.1. Решить системы уравнений:
v Г dxi/dt = — Ъх\ — 4х2; ^ Г dx\/dt = xi + bx2\
*' { dx2/dt = 2хх+х2\ \ dx2/dt =-2xi-x2;
v Г dx\/dt = x2; v Г dx\jdt = —x\ — 2x2\
В^ \ ^2/Л = 2ж1+ж2; Г^ \ dx2/dt = 2xi-х2\
Г dx\jdt =—Ьх\—х2\ v Г
\ dx2/dt = 3xi-х2; ^ \
dx\/dt = х\ + 2х2\
=-4a?i - Зя?2;
{ = х\ + х2 - ж3;
dx2/dt = —х\ + 2х2 — жз;
= 2х\ —х2
5.2. Методом Лагранжа найти общее решение систем урав-
уравнений:
dxi/dt = 2х\ +х2 + sint;
+ 3cost.
Г dxi/dt = — xi +Ах2 + ег; . Г
5.3. Найти частное решение систем уравнений:
. Г dxi/dt = 2x!+X2 + t; . Г с1х1/(И = 2х2 + гег;
&) \ dx2/dt = xi+ 2х2 +1 + е~1; ' \ dx2/dt = 2xi.

6. ЛИНЕЙНЫЕ
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ВЫСШИХ ПОРЯДКОВ
6.1* Сведение к линейной системе.
Определитель Вронского и структура
общего решения однородного уравнения
Линейное обыкновенное дифференциальное уравне-
уравнение (ОДУ) п-го порядка имеет вид
где функции ai(t), ...,an(t) и g(t) определены и непрерывны
в некотором промежутке TCR числовой прямой R.
Пусть функция y(t) имеет в промежутке Г непрерывные
производные по крайней мере до (п — 1)-го порядка включи-
включительно. Введем функции
xi(t) = y{t)t x2(t)=y'(t), ...,
^i(*)=y(i-1)W, .... xn(t) = y(n-1)(t). F.2)
Тогда ОДУ F.1) можно записать в виде нормальной системы
линейных ОДУ:
dx\
dt -**'
F.3)
dt
dxn
dt
= -an(t)xi - an-i(t)x2 ... - ai(t)xn + g(t).

170
6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
В матричной форме система F.3) имеет вид
где x =
A(t) =
0
0
—
1
0
F.4)
и
О
1
о
о
о
0
an-2(t)
1
a\{t))
F.5)
Таким образом, если y(t) — решение ОДУ F.1), то сово-
совокупность функций F.2) служит решением системы ОДУ F.4).
Справедливо и обратное утверждение.
Задача и теорема Коши для ОДУ n-го порядка были
сформулированы в 4.4. Не повторяясь, отметим лишь, что
условия теоремы Коши о существовании и единственности ре-
решения соответствующей задачи заведомо выполнены в области
D для ОДУ F.1) (см. теорему 4.1), если функции di(t) (г = 1, n)
непрерывна в промежутке Т.
При g(t) ф 0 в Т уравнение F.1) называют линейным
неоднородным ОДУ п-го порядка. Если же g(t) =0
в Т, то из F.1) следует соответствующее F.1) линейное
однородное ОДУ п-го порядка
dny
F.6)
которое путем введения функций F.2) можно свести к линейной
однородной системе ОДУ, совпадающей с F.3) при условии
g(t) = 0 в Т. В матричной форме такая система примет вид
§
F.7)

6.1. Сведение к линейной системе 171
Введем ряд необходимых далее понятий, непосредственно
связанных с аналогичными понятиями для систем ОДУ (см. 5.1
и 5.2).
Определение 6.1. Систему функций yi(t), ..., у*(*)> ••• ?
ym(t) называют линейно зависимой в некотором промежут-
промежутке Т С R числовой прямой R, если существует такая система
чисел
ль ..., а*, ..., хтеш,
что
+... + \kVk(t) +. • • + \mVm(t) =0 Vt € Т. F.8)
Если же такой системы чисел не существует, то эту систему
функций называют линейно независимой в промежутке Т.
Определение 6.1 почти дословно повторяет определение 5.1
аналогичных понятий для системы вектор-функций. Как и
в случае системы вектор-функций, система функций линейно
независима в каком-либо промежутке Т, если она линейно
независима в некотором промежутке Т\ С Т. Если же она
линейно зависима в Т, то ее линейная зависимость будет
сохранена ив Т\ С Т, но обратное, вообще говоря, неверно.
Замечание 6.1. Любая система п функций, включающая
функцию yj(t) = 0 Vt € Т, будет, согласно определению 6.1, ли-
линейно зависимой. В самом деле, выбрав в F.8) коэффициент
Xj при такой функции отличным от нуля и положив коэффи-
коэффициенты при остальных функциях равными нулю, приходим к
тождеству F.8).
Пример 6.1. Покажем, что система функций 1, i, t2, *3
линейно независима на всей числовой прямой. Предположим
обратное. Тогда, согласно определению 6.1, в R должно быть

172 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
справедливо тождество
4
*2 + А4*3 0 53 А? * °
Ах + X2t + A3*2 + А4*3 = 0, 53 А?
j=i
Последнее невозможно, так как в левой части стоит многочлен
не выше третьей степени, который может обращаться в нуль
не более чем в трех точках. Следовательно, система функций
1, ?, ?2, ?3 является линейно независимой в любом непустом
промежутке числовой прямой. #
При рассмотрении конкретного набора функций часто для
краткости опускают слово „система" и говорят о линейных
зависимости или независимости этих функций.
Покажем, что две функции /i(t) и /2(?) линейно независи-
независимы в промежутке Т тогда и только тогда, когда их отношение
Л(*)//2(*) в этом промежутке не равно константе. Предпола-
Предполагается, что f2{t) ф 0 Vt Е Т.
Пусть f\(t) и f2(t) линейно независимы. Это означает,
что тождество \ifi{t) + \2f2{t) = 0 возможно только при Ах =
= Л2 = 0. Отсюда следует, что их отношение fi(t)/f2{t) не
может быть постоянной функцией.
Обратное утверждение докажем от противного. Допустим,
что f\(t) и J2{t) линейно зависимы, т.е. существуют такие
Ах и А2, А? + А|^О, что Ai/i(t) + A2/2(t)=0 Vt 6 Т. Для
определенности пусть Ai ^0. Тогда fi(t)/f2(t) = — А2/А1, т.е.
отношение функций представляет собой постоянную функцию,
а это противоречит допущению. Следовательно, функции Д (t)
и f2(t) линейно независимы.
Если есть точки t G Т, в которых /2(?) = 0, но fi(t) ф 0
VtET, то можно взять отношение /2(?)//i(?) и для него
провести те же рассуждения.
Пример 6.2. Согласно доказанному утверждению функции
/х(?) = sint и f2{t) = cost линейно независимы на любом про-
промежутке Т С К, так как их отношение fi(t)/f2(t) = sin?/cost =
= tgt не является постоянной функцией.

6.1. Сведение к линейной системе 173
Определение 6.2, Линейно независимую в промежутке
TCR систему из п функций yk(t) (fc = l,n), каждая из
которых является в нем решением линейного однородного ОДУ
F.6) гс-го порядка, называют фундаментальной системой
решений этого уравнения в указанном промежутке.
Рассмотрим совокупность п функций yk{t) (&
имеющих при t&T непрерывные производные по крайней мере
до (п — 1)-го порядка включительно. Определитель
W(t) =
yx{t) V2(t) ... Vn(t)
y[{t)
F.9)
назовем вронскианом системы п функций, непрерывно диф-
дифференцируемых п — 1 раз в промежутке Г (в отличие от
аналогичного по структуре определителя Вронского E.6) си-
системы вектор-функций).
Теорема 6.1. Если система п функций yk{t) (fc = l,n)
линейно зависима в промежутке Т, то ее вронскиан W(t) = О
VteT.
< Согласно определению 6.1, для линейно зависимой системы
функций хотя бы один из коэффициентов в F.8) отличен от
нуля (пусть для определенности Ап ф 0). Тогда функция yn(t)
будет линейной комбинацией остальных функций:
Vn{t) = am(t) + a2y2{t) +... + ап-гУп-гЦ) Vt G T, F.10)
где «i = -Ai/An,..., an-i = -An_i/An. Продифференцировав
F.10) последовательно n — 1 раз, подставив результаты вместо
последнего столбца в F.9) и опустив обозначение аргумента ?,

174 б. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
получим определитель
Ух Уч •••
У\ У2 •••
(п-1) (п-1) (п-1) , (п-1) , . (п-1)
У1 } У2 ••• <*1У +<*2У ; + +«1У
в котором последний столбец при всех t€T является линейной
комбинацией остальных столбцов. Поэтому записанный опре-
определитель равен нулю, что доказывает утверждение теоремы. >
Если функция yk(t) является решением однородного ОДУ
F.6) в промежутке Г, то она, согласно определению 1.1 ре-
решения ОДУ, п — 1 раз непрерывно дифференцируема в этом
промежутке. Тогда в промежутке Г можно ввести совокуп-
совокупность функций вида F.2), являющихся координатными функ-
функциями вектор-функции
t4<\ F.11)
которая будет решением однородной системы F.7).
Пусть система функций
yi(*), ..., Ук{1), ..., yn(t) F.12)
является решением однородного ОДУ F.6) в промежутке Г.
Тогда система вектор-функций #*(?), fc = l,n (см. F.11)),
будет решением однородной системы ОДУ F.7) в том же
промежутке.
Вронскиан F.9) системы функций F.12) в промежутке Г
тождественно совпадает, очевидно, с определителем Вронского
E.6) системы вектор-функций F.11), т.е.
VteT. F.13)

6.1. Сведение к линейной системе 175
Поэтому для вронскиана в промежутке Т справедлива форму-
формула E.10) Остроградского — Лиуеилля в виде
- fai(r)dr\ F.14)
to
так как сумма элементов, стоящих на главной диагонали
матрицы A(t) F.5) однородной системы ОДУ F.7) равна
—ai(t). Из F.14) следует, что если W(to)j^O в некоторой точке
t0 G Т, то И^(^) ^ 0 Vt е Т, и наоборот, при W(t0) = 0 имеем
Если функции F.12) составляют фундаментальную систе-
систему решений однородного ОДУ F.6), то соответствующие им
вектор-функции F.11) будут составлять фундаментальную си-
систему решений однородной системы ОДУ F.7), и наоборот, т.е.
обе системы могут быть линейно независимыми в промежутке
Т только одновременно. Убедимся в этом, рассуждая от про-
противного.
Пусть функции 2/fc(?), fc = l,n, линейно зависимы в Т. Тог-
Тогда на основании теоремы 6.1 и с учетом F.13) W(t) = W(t) =
= 0 V? Е Т, что означает, согласно теореме 5.6, линейную
зависимость системы вектор-функций F.11) в Т. Если же
линейно зависимы в Т вектор-функции #*;(*), к = 1,п, то в
силу определения 5.1
Xixi(t) + ... + Xkxk{t) + ... + Xnxn{t) = 0 Vt € Г,
где хотя бы один из коэффициентов Л^ отличен от нуля. Запи-
Записав это векторное равенство в координатной форме, для первых
в F.11) координатных функций у*(?) (к = 1, п) получим F.8),
т.е., согласно определению 6.1, система функций F.12) линейно
зависима в Т.
Итак, рассматриваемые системы функций и вектор-функ-
вектор-функций могут быть линейно зависимыми или линейно независи-
независимыми, а также составлять фундаментальные системы решений

176 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
однородных соответственно ОДУ F.6) и системы ОДУ F.7)
только одновременно. Поскольку из теоремы 5.7 следует, что
существуют фундаментальные системы решений однородной
системы вида F.7), то существуют и соответствующие фун-
фундаментальные системы решений однородного ОДУ F.6).
Установленная связь между фундаментальными системами
решений однородного ОДУ F.6) и однородной системы ОДУ
F.7) позволяет в дальнейшем использовать результаты, изло-
изложенные в гл. 5 применительно к системам линейных ОДУ.
Теорема 6.2. Если yi(t), ...,yfc(t), ...,уп(*) — фундамен-
фундаментальная система решений ОДУ F.6) в промежутке Г, то любое
решение y(t) в нем этого ОДУ имеет вид
А:=1
где С\,..., С*,..., Сп — постоянные.
< Прежде всего убедимся, что F.15) является решением ОДУ
F.6) при любых значениях постоянных С& (& = 1,п). Для этого
подставим F.15) в F.6) и запишем
A;=l
Так как по условию теоремы функции yk(t) (fc = l,n) являют-
являются решениями ОДУ F.6), то каждая из них при t ? Г обращает
в нуль соответствующее слагаемое записанной суммы. Следо-
Следовательно, левая часть этого выражения равна нулю при t€T,
а F.15) есть решение ОДУ F.6).
При некотором to E Т зададим произвольные начальные
условия y(to)=yly'(to)=yl...,y{i-1)(to)=yl...,y(n-14to) =
= у{|, которым в силу теоремы 4.2 Коши удовлетворяет един-
единственное решение ОДУ F.6). Такое решение может иметь
вид F.15) и быть единственным только в том случае, если по

6.2. Общее решение неоднородного уравнения 177
заданным начальным значениям можно однозначно найти по-
постоянные Ck (к = 1, п).
Если, дифференцируя F.15) необходимое число раз, подста-
подставить результаты при значении t = to в начальные условия, то
получим систему из п линейных алгебраических уравнений
(СЛАУ)
°(^о) = уг0, г = М, F.16)
с п неизвестными значениями постоянных С*, fc = l,n (в
этой записи при i = 1 использовано обозначение yjj. '(to) =
= 2/fc(?o)). Определитель этой СЛАУ является вронскианом
W(to) фундаментальной системы решений ОДУ F.6) в про-
промежутке Т, совпадающим с определителем W(?o) Вронско-
Вронского фундаментальной системы решений однородной системы
ОДУ F.7), для которой в силу теоремы 5.6 W(t) ^0 VteT.
Таким образом, определитель СЛАУ отличен от нуля и она
имеет единственное решение, что доказывает утверждение
теоремы. >
Эта теорема является аналогом теоремы 5.8 и устанавли-
устанавливает структуру общего решения линейного однородного
ОДУ F.6) п-го порядка в виде F.15).
6.2. Общее решение неоднородного уравнения.
Метод Лагранжа вариации постоянных
Аналогом теоремы 5.9 о структуре общего решения неодно-
неоднородной системы F.4) линейных обыкновенных дифференциаль-
дифференциальных уравнений (ОДУ) является следующая теорема.
Теорема 6.3. Общее решение линейного неоднород-
неоднородного ОДУ F.1) п-го порядка есть сумма общего реше-
решения соответствующего однородного ОДУ F.6) п-го порядка и

178 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
частного решения уравнения F.1):
F.17)
k=l
Здесь у*(?) — частное решение неоднородного ОДУ F.1),
определенное в некотором промежутке TCR; Vk{t) — фунда-
фундаментальная система решений соответствующего однородного
ОДУ F.6), определенных в том же промежутке; Ck — некото-
некоторые постоянные коэффициенты (к = 1, п).
<4 Пусть y*(t) — какое-либо частное решение, a y(i) — произ-
произвольное решение неоднородного ОДУ F.1) в промежутке Т.
Введем функцию z(t) в соответствии с формулой
z(t)=y(t)-y*(t) F.18)
и, подставив F.18) в F.1), убедимся, что z(t) должно удовле-
удовлетворять соответствующему однородному ОДУ F.6), т.е. z(t)
можно выбрать в виде F.15), и тогда F.18) совпадет с F.17).
Функция y(t) F.17), содержащая п произвольных посто-
постоянных Cfc, *fc = 1, п, является решением неоднородного ОДУ
F.1) в промежутке Т, что легко проверить, подставив вы-
выражение F.17) в ОДУ. Это решение будет общим только в
том случае, если для произвольно заданных при некотором
t0 е Т начальных условиях y(t0) = yj, y'(?0) = 2/2> • • • > У^г~1Ч*о) =
== У?> • • • > j/71)(^о) = Уп> которым в силу теоремы 4.2 Коши удо-
удовлетворяет единственное решение y(t) ОДУ F.1), постоянные
Ck можно найти однозначно. Покажем это. Продифференци-
Продифференцировав F.15) необходимое число раз и подставив результаты при
значении t = to в начальные условия, придем к системе из п
линейных алгебраических уравнений (СЛАУ)
= у? - yt'
k=l

6.2. Общее решение неоднородного уравнения 179
с п неизвестными значениями постоянных С^, fc = l,n (в
этой записи при г = 1 использованы обозначения yjj, '(to) =
= У*(*о) и yj '(to) = у*(to)). Определитель этой СЛАУ равен
значению вронскиана W(to) фундаментальной системы реше-
решений ОДУ F.6) в точке to Е Т и совпадает с определителем
СЛАУ, рассмотренной при доказательстве теоремы 6.2, т.е.
отличен от нуля. Таким образом, и в данном случае СЛАУ
имеет единственное решение, что доказывает утверждение те-
теоремы. >
Покажем, что если в промежутке Т известна фундамен-
фундаментальная система решений у*(*), fc = l,n, однородного ОДУ
F.6), то решение неоднородного ОДУ F.1) можно представить
в виде
F.19)
где функции Ck{t) (к = 1, п) должны удовлетворять неодно-
неоднородной системе линейных ОДУ
F.20)
Здесь c(t) = (Ci(t),..., Ck(t),..., Cn(t))T, вектор-функция g(t)
определена при записи системы ОДУ F.4), а матрица Y(t)
имеет вид
/ Vl (*) V2(t) ... Vn(t) \
Y(t) =
F.21)
Действительно, так как вектор-функции Xk(t) F.11) соста-
составляют фундаментальную систему решений однородной систе-
системы ОДУ F.7), соответствующей неоднородной системе F.4),

180 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
а матрица Y(t) в этом случае совпадает с фундаментальной
матрицей X(t) E.17), то F.20) и E.20) идентичны и реше-
решение неоднородной системы F.4), как это следует из 5.4, можно
представить в виде E.19):
Записав это векторное равенство в координатной форме, для
первых в F.11) координатных функций yk(t) (к = 1, п) полу-
получим F.19).
Определитель матрицы Y(t) F.21) является вронскианом
W(t) фундаментальной системы решений однородного ОДУ
F.6) в промежутке Т, и поэтому W(t) ^ 0 VtET, т.е. матрица
Y(t) имеет обратную матрицу Y~l(t) \/t G Г. Умножая слева
обе части F.20) на Y~l(t)} запишем
или, используя формулы Крамера,
dCk(t) = Wk(t)
dt W{t) '
= l,n, F.22)
где И^(?) — определитель, полученный из вронскиана заменой
в нем А;-го столбца столбцом @,0, ...,g(t))T. Интегрируя
F.22) в промежутке Т от to G Т до ?, получаем
t ~
Ck(t)= №^dr + Cl F.23)
J W(r)
to
где С% = Ck(to) — постоянные, равные значениям в точке
to E T искомых функций Ck(t), k = 1, п.
При построении общего решения неоднородного ОДУ F.1)
значения С? (А; = 1, п) можно выбрать произвольно. В самом

6.2. Общее решение неоднородного уравнения 18 i
деле, подставив F.23) в F.19), найдем
|Щ^ ?? F.24)
Взяв Су. = О (к = 1, п), получим частное решение неоднородно-
неоднородного ОДУ F.1)
^^*. F-25)
Тогда F.24) с учетом F.25) можно записать в виде F.17), т.е.
в силу теоремы 6.3 F.24) дает общее решение неоднородного
ОДУ F.1).
При решении для ОДУ F.1) задачи Коши с начальными
условиями y(%~~l)(to) = у® (г = 1, п), полагая в F.24) t = to,
придем к СЛАУ вида F.16) относительно постоянных С% (к =
= 1, п), которая, как показано при доказательстве теоремы 6.2,
имеет единственное решение.
Описанная процедура нахождения решения неоднородного
ОДУ F.1) предложена Ж. Лагранжем. Она аналогична ме-
методу вариации постоянных построения решения неоднородной
системы ОДУ вида F.4) (см. 5.4). Чтобы отличать эту проце-
процедуру от указанного метода, назовем ее методом Лагранжа
вариации постоянных.
Пример. Найдем методом Лагранжа вариации постоянных
общее решение ОДУ
с переменными коэффициентами, определенными и непрерыв-
непрерывными при ?ER\{0}.
Несложно проверить, что функции

182
6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
являются решениями соответствующего однородного ОДУ в
промежутках Т\ = (—оо, 0) и Тг = @, +оо). Убедимся, что
эти функции образуют фундаментальную систему решений
однородного ОДУ в указанных промежутках. Действительно,
вронскиан
W(t) =
l/l(«)
y[(t)
=
t
1
0
t2
2t
2
t*
Zt2
6t
VtGK\{0}.
Заменяя столбцом @, 0, t/(l + y/t)T последовательно столбцы
вронскиана, получаем
Vt'
yft
Для нахождения C*(<) (fc = 1,2,3), согласно F.22), имеем три
дифференциальных уравнения
dCxjt)
dt
dC2(t)
dt
t
dCz(t)
dt
1
Интегрирование этих ОДУ дает
21n(l
C2°;
Общее решение исходного неоднородного ОДУ примет вид

6.3. Понижение порядка линейного ОДУ 183
6.3. Понижение порядка линейного
дифференциального уравнения
В некоторых случаях порядок линейного однородного обык-
обыкновенного дифференциального уравнения (ОДУ) F.6) может
быть понижен.
1. Предположим, что известно частное решение у = (p(t)
ОДУ F.6) в промежутке Т. Выполним в этом ОДУ под-
подстановку у = ip(t)z(t) и вычислим в преобразованном ОДУ
коэффициент при z(t). Так как
dky dkip
где х —выражение, содержащее только производные от z(t),
то искомый коэффициент будет
teT-
Учитывая, что (p(t) — решение ОДУ F.6), заключаем, что этот
коэффициент в промежутке Т равен нулю. Поэтому ОДУ для
z(t) можно записать в виде
dnz dn~^z сГ*"~*2 dz
+b{t)++b{t)++b{tH
где функции bj(t) (j = 1, n — 1) можно выразить через функ-
функции a,i(t) (i = l, n) в F.6) и известное решение (p(t). Порядок
этого ОДУ можно понизить подстановкой и = dz/dt. Если
п = 2, то при этом получим ОДУ первого порядка с разделя-
разделяющимися переменными.
Для ОДУ второго порядка (п = 2) найти второе решение,
линейно независимое с <р(?), можно с помощью формулы Остро-
Остроградского — Лиувилля, которая в данном случае имеет вид
v>(t) v(t)
?>'(*) !/(*)
to
= W(tQ).

184 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
После раскрытия определителя и преобразований получаем
линейное неоднородное ОДУ первого порядка для неизвестного
решения y(t):
to
2. Линейное однородное ОДУ F.6) можно свести подстанов-
подстановкой w = у1/у к ОДУ (п — 1)-го порядка, но уже нелинейному.
Последовательно вычислим
dy d?y (dw
т.е. все производные от y(t) имеют вид
dky ( dw dk~l
где Fk — известные функции указанных аргументов. Если
подставить эти выражения для производных в ОДУ F.6), то
придем, вообще говоря, к нелинейному ОДУ (п — 1)-го порядка
dw (p-l
не разрешенному относительно старшей производной.
Пример. Подстановкой w = у1/у линейное однородное
ОДУ второго порядка

6.4. Линейные ОДУ с постоянными коэффициентами 185
можно привести к уравнению Риккати C.26)
или
-^ + аг (t)w + w2 + а2 (t) = О,
at
которое можно проинтегрировать, если известно какое-либо
его частное решение.
6.4. Линейные дифференциальные уравнения
с постоянными коэффициентами.
Случай различных корней
характеристического уравнения
Если в линейном неоднородном обыкновенном дифферен-
дифференциальном уравнении (ОДУ) F.1) n-го порядка все функции
ai(t) = const (i = 1, п), то ОДУ
а;ЕМ, F.26)
называют линейным неоднородным ОДУ п-го порядка с
постоянными коэффициентами.
Ему соответствует однородное ОДУ с постоянными
коэффициентами
Заметим, что условия теоремы Коши о существовании и един-
единственности решения соответствующей задачи Коши для ОДУ
F.27) заведомо выполнены на всей числовой прямой.
В 6.2 было показано, что, зная общее решение однородного
ОДУ вида F.27), путем интегрирования можно найти общее

186 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
решение неоднородного ОДУ вида F.26). Поэтому сосредото-
сосредоточим внимание на методе нахождения решений для однородного
уравнения F.27).
Введем символический оператор р = d/dt дифферен-
дифференцирования по f и представим производные y^{t) (г = 0, га)
как символические произведения ргу степеней оператора р и
дифференцируемой функции у(?), считая, что при % = О такое
произведение равно этой функции. Тогда левую часть F.27)
можно записать в виде
где L(p) = pn + a\pn l + ... + щр71 l + ... + an — многочлен
степени п от оператора р. При таком обозначении вместо
ОДУ F.27) будем иметь уравнение
L(p)y = 0. F.28)
Частное решение этого уравнения будем искать в виде
y(t) = ext. F.29)
Подставляя F.29) в F.28), получаем
L(p)ext = (рп + alPn~l + ... + а{рп~{ + ... + о») ext =
= (Лп + (ц\п-1 + ... + аг\п~г + ... + ап) ext = L(X) ext = 0.
Если А — корень алгебраического уравнения L(X) = 0, где
L(X) = Хп + сцХ71-1 + ... + сц\п-* +... + ап,
то y(t) = ext — решение ОДУ F.28).
Уравнение L(A) = 0 называют характеристическим
уравнением ОДУ п-го порядка.
Рассмотрим случай, когда все корни характеристического
уравнения L(X) = 0 действительны и различны: А& ф Aj, k ф j,

6.4. Линейные ОДУ с постоянными коэффициентами
187
j, к = 1, п. Им соответствуют п решений у*(<) = ел**. До-
Докажем, что эти решения образуют фундаментальную систему
решений ОДУ F.28). Вычислим вронскиан F.9):
W(t) =
„Ait
п
i=l
1 ...
Ах ...
лп-1
1
А,
\fi-
, F.30)
где в средней части равенства стоит определитель Вандермон-
(?а, равный произведению всевозможных разностей A& — \j при
условии 1 ^ j < к ^ п (в данном случае все эти разности отлич-
отличны от нуля).
Так как вронскиан отличен от нуля, то эти решения обра-
образуют фундаментальную систему решений (см. 6.1). Общее
решение ОДУ F.28) в этом случае имеет вид
F.31)
к=1
Если характеристическое уравнение имеет простые ком-
комплексные корни, то они входят парами комплексно сопряжен-
сопряженных чисел \ = a + iP, A = a~i/3, так как коэффициенты ха-
характеристического уравнения действительны [I].
Для комплексного корня А = а + i($ характеристическо-
характеристического уравнения рассмотрим комплекснозначную функцию y(t) =
= ext. Эта функция дифференцируется по обычным правилам:
(еЛ*) = АеЛ* (см. 5.6). Продолжая последовательно диффе-
дифференцировать, находим, что (exty' = A*eAt, k = 1,п. Непо-
Непосредственной проверкой убеждаемся, что функция y(t) = ext
удовлетворяет ОДУ F.27). Функция y(t) = еЛ*, соответствую-
соответствующая комплексно сопряженному корню А характеристического

188 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
уравнения, также удовлетворяет этому ОДУ. В силу свойств
линейности функции
u(t) = 0,5(y(t) + y(t)), v(t) = 0,5г(у(<) -y(t)), F.32)
представляющие собой соответственно действительную и мни-
мнимую части у(?), также удовлетворяют ОДУ F.27), т.е. являют-
являются его решениями.
Так как u(t)/v(t) = ctgCt=? О, решения u(t) и v(t) линейно
независимы (см. 6.1).
Рассмотрим более общую ситуацию. Пусть характеристи-
характеристическое уравнение среди п корней имеет т пар различных
комплексно сопряженных Ai, Ai, ..., Am, Am, \j = aj+i/3j,
j = 1, m, а остальные n — 2m корней А2т+ь • • • > ^n действи-
действительные и тоже различные. Каждой паре простых комплексно
сопряженных корней Aj, Aj соответствует пара решений ОДУ
F.28)
Uj(t) =
Vj(t) = ImeA^ = e^sinfijt, j = T7m, F.33)
а каждому простому действительному корню А* — одно реше-
решение этого ОДУ
y(t) = eXi\ i = 2т + 1, п. F.34)
В итоге имеем п решений вида F.33) и F.34) для одно-
однородного ОДУ F.28). Докажем, что они линейно независимы на
всей числовой прямой К, т.е., согласно определению 6.2, образу-
образуют фундаментальную систему решений этого ОДУ. Составим
их линейную комбинацию
deXit F.35)
j=l i=2m+l
и покажем, что она не равна тождественно нулю в М, если
хотя бы один из коэффициентов Aj, Bj (.7 = 1,771) или С{

6.4. Линейные ОДУ с постоянными коэффициентами 189
(г = 2га + 1,га) отличен от нуля, т.е. в силу определения 6.1
является линейно независимой системой функций.
Согласно формуле Эйлера
cos
jt = 0,5(е^ + е"^'*); sinjfyi = 0,5г (е~*№ - е'^*).
Подставив эти выражения в F.35), после преобразований за-
запишем
?Л*<, F.36)
где Cfc = 0,5(ilj-tSj), Afc = AjnpH k = 2j-l и С* = 05(А
А& = Aj при k = 2j, j = I, m. Если в F.35) отличен от нуля
хотя бы один коэффициент, то в F.36) будет отличен от нуля
хотя бы один коэффициент Cfc. Поскольку нумерация корней
произвольна, примем без ограничения общности, что Сп Ф 0.
Предположим, что правая часть F.36) тождественно равна
нулю, т.е. рассматриваемая система решений линейно зависима.
Поскольку eXkt фО V? G М (ив случае, когда показатель экспо-
экспоненциальной функции является комплексным числом), то после
деления правой части F.36), по предположению тождественно
равной нулю, на еЛ1Ь получим
k=2
Дифференцируя это тождество по ?, снова получаем тождество
поделив которое на ехр ((А2 — Ai)t) ф 0, запишем новое тожде-
тождество
С2(А2 - Ai) + ?С*(А* - А!)е^-Л2)* = 0

190 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
и после его дифференцирования по t придем к тождеству
= 0.
Повторив описанную процедуру еще п — 2 раза, на послед-
последнем этапе получим тождество
Сп(Хп - А1)(А„ - Аа) ¦ • ¦ (Ап - Хп^х^х^г = 0,
которое невыполнимо, так как в его левой части все сомножи-
сомножители отличны от нуля. Полученное противоречие доказывает,
что рассматриваемая система решений линейно независима, т.е.
является фундаментальной системой решений, а F.35), соглас-
согласно теореме 6.2, дает общее решение однородного ОДУ F.28) с
постоянными коэффициентами, выраженное через элементар-
элементарные действительные функции.
Пример. Найдем общее решение ОДУ
у'"-8у = 0.
В данном ^случае характеристическое уравнение А3 — 8 = 0
имеет корни Ai = 2 и Аг,з = 1 ± *л/3. Принимая во внимание
F.33) и F.34), имеем фундаментальную систему решений этого
ОДУ, состоящую из функций yi(i) = e2*, j/2(<) = e*cosv^* и
у3(?) = etsiny/3t1 так что общее решение можно записать в виде
y(t) = aie2t + et(C2cos\/3< + C3sinv/3t).
6.5. Формула сдвига. Случай кратных
корней характеристического уравнения.
Уравнения Эйлера, Лагранжа, Чебышева
Если среди корней характеристического уравнения L(X) =
= 0 есть кратные, то рассмотренное выше построение фун-
фундаментальной системы решений ОДУ F.28) не годится, так

6.5. Формула сдвига 191
как при этом в F.30) W(t) = 0 Vt G R. Это указывает на то,
что решения yk(t) (fc = l,n) линейно зависимы. Прежде чем
построить в случае кратных корней фундаментальную систему
решений, докажем справедливость формулы сдвига
ад [/(*) ext] = extL(p + A) [/(*)]. F.37)
Эта запись означает, что многочлен L(p) степени п от опе-
оператора дифференцирования р = d/dt действует на выражение,
заключенное в квадратные скобки.
Доказательство проведем методом математической индук-
индукции по степени многочлена п для случая L(p) =pn. При п = 1
имеем
p[f(t)ext] = |е* +А/(«)е* = е%
Пусть F.37) справедливо при п = г — 1, т.е.
At]=e> + A)' [/
Тогда при п = г имеем
= eAt(p + А)(р + АГ^/С*)] = eAt(p + A)l[/(f)]. F.38)
Итак, формула F.37) сдвига доказана для L(p) =pn. По-
Поскольку многочлен
L(p) = pn + aip71-1 +... + агрп"^ +... + ап F.39)
является линейной комбинацией степеней рг (i = 0, п), то,
умножая левую и правую части F.38) на an-i и полагая,
что а0 = 1 при i = n и pz[/(t)eAt] = extf(t) при г = 0, после
сложения полученных выражений придем к F.37) для общего
случая L(p) в виде F.39).

192 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
Пусть Ai — действительный корень кратности к\ харак-
характеристического уравнения L(X) = 0, т.е.
Докажем, что ему соответствует ровно к\ решений: у\ =
= eAl*, j/2 = teXl\..., ykl = tkl~leXlt. Подставим yr = treXlt (r =
= 0, k\ — 1) в F.28) и применим формулу F.37) сдвига:
[] ], F.40)
где
п п
L(p + Ai) = 53oi(p + Ai)i = 53b№<. F.41)
г=0 г=0
Полагая в F.41) р = 0, получим 6о = ?(^i) = 0. Последователь-
Последовательно дифференцируя по р F.41), находим
=L'(A!)=0;
р=0
Теперь можно записать
I(p + Ai) = ЬлУ1 + 6fcl+ipfcl+1 +... + ЪпРп.
Так как г < к\% то отсюда следует, что L(p + \\)tr = 0, а
согласно F.40) делаем вывод, что L(p)[treAl<] =0. Таким
образом, ух = eAl*,..., у^ = tkl~leXlt — решения однородного
ОДУ F.28).
Рассмотрим теперь общий случай: пусть характеристиче-
характеристическое уравнение L(X) = 0 имеет т < п различных действи-
действительных корней Ai,..., Am. Кратности этих корней обозначим
через fci,..., кт. Тогда функции
Vi(t) = eAlt, y2(t) = te^\...,ykl(t) = t^-V1';

6.5. Формула сдвига 193
будут решениями однородного ОДУ F.28). Поскольку fci +... +
+ кт = п, то имеем ровно п функций $/&(?), к = 1, п. Остает-
Остается показать, что они образуют фундаментальную систему
решений этого ОДУ.
Допустим, что эти решения линейно зависимы, т.е., согласно
определению 6.1, между ними существует тождественное по t
соотношение
r=l
m
= ^Рг(*)еЛг< = 0, F.43)
r=l
где ар = const, причем хотя бы один из этих коэффициентов
отличен от нуля. Без ограничения общности предположим,
что хотя бы один не равный нулю коэффициент является
коэффициентом многочлена Рш(?), т.е. Рт(?) ф 0. Разделив
F.43) на eXlt Ф 0, запишем
т
Pi(t) + ^Pr(t)e(A^Al^ = 0. F.44)
г=2
Поскольку степень s\ многочлена P\{t) не превьппает
к\ — 1, после si-кратного дифференцирования тождества F.44)
по t получим новое тождество
0, F.45)
г=2
где Qr(t) — многочлены тех же степеней, что и Pr{i). По-
Поскольку Pm(t) ф 0, то и Qm(t) ф 0.
Сумма в F.45) в отличие от F.43) содержит на одно
слагаемое меньше. Повторяя описанную процедуру, придем в
итоге к тождеству
7 — 9306

194 б. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
что невозможно, так как е^Хт"Хт-1^ Ф О, а многочлен Sm(t) ф
ф О, поскольку он имеет хотя бы один отличный от нуля
коэффициент.
Следовательно, в силу определения 6.1 система решений
F.42) линейно независима и, согласно определению 6.2, пред-
представляет собой фундаментальную систему решений ОДУ F.28).
Тогда на основании теоремы 6.2 общим решением этого ОДУ
будет
где Ck (А; = 1, п) — постоянные.
Пусть характеристическое уравнение L{\) = 0 имеет ком-
комплексный корень \ = a + i/3 кратности к. Тогда комплексно
сопряженный корень Л имеет ту же кратность к. Комплекс-
нозначные функции
Vi(*) = eAt, 2/2W=teAt, ..., yk{t) = tk-lext, F.47)
удовлетворяют ОДУ F.27). Действительные iti(t), ..., Uk(t) и
мнимые vi(<), ..., Vk(t) части этих функций также удовлетво-
удовлетворяют этому ОДУ в силу их представления, аналогичного F.32).
Итак, комплексному корню Л кратности к и его комплексно
сопряженному А соответствует 2к линейно независимых ре-
решений
'tii(t) = Reyi(t) = e^ cos fit]
v\(t) = Imyi(t) = eatsmCt]
F-48)
uk(t) = Reyfc(t) = ^"Vcos/ft;
Рассмотрим случай, когда характеристическое уравнение
L(X) = 0 имеет только пары комплексных корней Xj = otj + iCj
и Xj кратностей kj, j = l,m, 2k\ +... 4-2km = п. Для каждой
пары корней Xj, Xj мы имеем Ikj решений

6.5. Формула сдвига 195
ОДУ F.27), что в совокупности дает нам п решений этого
ОДУ. Можно показать что выбранная система функций обра-
образует фундаментальную систему решений ОДУ F.27).
Пример. Найдем общее решение ОДУ
yVI-4yv + 8yIV-8y'" "
Корни характеристического уравнения А6 — 4Л5 + 8А4 —
- 8А3 + 4А2 = 0 этого ОДУ равны Ai,2 = О, А3,4 = 1 + h A5,e =
= 1 — г. Поэтому фундаментальную систему решений образуют
функции 1, ?, e*cos?, e*sin<, ?e*cosi, ?e*sin?. Общее решение
уравнения имеет вид
y(t) = С\ + C2t + el (Oncost + C^sint + C5tcosi + C^tsint).
Пример, а. Для однородного ОДУ третьего порядка
характеристическое уравнение А3 — А2 — А + 1 = 0 имеет корни
Ах = Х2 = 1 и Аз = — 1. Общее решение
б. Линейное однородное ОДУ второго порядка с
постоянными коэффициентами
^ ^| = 0, n^O, w>0, F.49)
описывает изменение во времени t отсчитываемого от поло-
положения равновесия у = 0 перемещения у материальной точки
массой т = 1 под действием пропорциональной у упругой
силы и пропорциональной скорости dy/dt точки силы трения
Bп является коэффициентом трения, а и имеет смысл часто-
частоты собственных колебаний точки в частном случае отсутствия

196
б. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
трения, когда п = 0). Для этого ОДУ характеристическое
уравнение A2 + 2raA + cj2 = 0 имеет корни Ai^ = — га ± \/га2 — с*;2.
Если п > о>, то они действительные и различные, причем оба
отрицательные. Тогда общее решение ОДУ F.49) имеет вид
При га = ш корни кратные: Ai = A2 = —га, что приводит к
видоизменению общего решения:
В рассмотренных случаях (га > и и п = uj) движение точки
носит апериодический характер (рис. 6.1, а): в зависимости от
начальных условий при t = 0 материальная точка приближает-
приближается к положению равновесия (у = 0) из начального положения
либо монотонно, либо немонотонно с изменением или без изме-
изменения знака перемещения.
Рис. 6.1
При 0 < п < и корни будут комплексно сопряженные: Ai =
= — п + ш\ и А2 = — п — го>1, где и>\ = \fuP- — п2, а общее решение
в виде действительной функции аргумента t
y(t) = e~nt(CriCosa;i^ + C2sina;it)
описывает затухающие колебания точки около положения
равновесия (рис. 6.1, б), называемые так потому, что их ампли-
амплитуда (наибольшее отклонение точки от положения равновесия)
стремится к нулю при t -> -Ьоо.

6.5. Формула сдвига 197
Если трение отсутствует (п = 0), то общее решение являет-
является периодической функцией
y(t) = C\ cosutf + C<i smut
с периодом Т = 2тг/сдЛ Описываемые такой функцией колеба-
колебания точки относительно положения равновесия происходят с
постоянной амплитудой (рис. 6.1, в), и их называют гармони-
гармоническими.
Систему (не обязательно механическую), процесс в которой
описывает однородное ОДУ вида F.49) при условии 0 ^ п < ш,
принято называть линейным осциллятором (от латинского
слова oscillo — качаюсь). В случае п = 0 осциллятор
является гармоническим. #
Изложенные результаты позволяют заключить, что линей-
линейные однородные ОДУ с постоянными коэффициентами можно
всегда проинтегрировать и получить общее решение в элемен-
элементарных функциях. Такая возможность делает заманчивыми
попытки так преобразовать ОДУ других типов, чтобы свести
их к уравнениям с постоянными коэффициентами. Однако эти
попытки оказываются удачными лишь для некоторых линей-
линейных однородных ОДУ с переменными коэффициентами. Один
из приемов состоит в подборе соответствующей замены неза-
независимого переменного t. Рассмотрим некоторые характерные
случаи.
1. Уравнение Эйлера имеет вид
t=^ F-50)
где a,i = const, г = 1,п. Замена t = еТ (при t > 0) приводит
ОДУ F.50) к линейному однородному ОДУ с постоянными ко-
коэффициентами. Но решение уравнения Эйлера можно искать
и непосредственно в виде y(t) = ?Л, причем нахождение значе-
значения Л удается свести к решению алгебраического уравнения,
которое и в этом случае называют характеристическим.

198 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
Поясним сказанное на примере. Рассмотрим однородное
ОДУ
§ + |=0> *^*о>О, F.51)
которое допускает механическую интерпретацию: оно описы-
описывает движение маятника, на который действует сила, возвра-
возвращающая маятник в положение равновесия и обратно пропорци-
пропорциональная квадрату времени t.
Решение ОДУ F.51) будем искать в виде у = *Л. Последо-
Последовательно вычислим
dt~ ' dt*
Подставив выражения для у и cPy/dt2 в F.51), после сокра-
сокращения на <Л~2 получим квадратное уравнение
А2-А + 1 = 0,
из которого найдем Ai,2 = 1/2 ±г\/3/2.
Используя равенство <Л = еЛ1п*, пару независимых частных
решений уравнения F.51) можно записать в виде
Общее решение уравнения F.51) имеет вид
y(t) =
Заметим, что ОДУ F.51) остается неизменным при замене
t на — t. Поэтому при рассмотрении случая t < 0 нужно в вы-

6.5. Формула сдвига
199
-CVt
ражениях для решений заменить t
на |?|. График решения y*(t) при
начальном условии yi(?o) = уо < О
представлен на рис. 6.2.
Рассмотренный пример пока-
показывает, что, хотя действующая на
маятник сила всегда направлена к
положению равновесия у = О, ам-
амплитуда колебаний растет по закону СуД. Если ввести понятие
мгновенной частоты u(t) = >/3lnt/Bt), то с увеличением вре-
времени t эта частота будет уменьшаться и стремиться к нулю
при t —> оо.
2. Уравнение Лагранжа п-го порядка записывают в
виде
Рис. 6.2
_i {at + b)^
= 0, F.52)
где а, Ь, ai (i = 1, n) — постоянные коэффициенты. Если Ь = О
и а = 1, то F.52) переходит в уравнение Эйлера. Подстановка
at + b = eT приводит F.52) к линейному однородному ОДУ с
постоянными коэффициентами.
3. Уравнением Чебыгиева называют ОДУ
F.53)
A -12) ^| -1^ + n2y = 0, п - const.
Сделаем замену t = cosr (при \t\ < 1). Тогда
dy _ 1 dg/ _ 1 dy
dt
d?V_ = _d_ /J_ tdy\J_t±
d2 d i d
sinr dr
(J_ dy\ =
\sinr dr/
cosr dy
d
1
sin3r dr sin2r dr2'

200 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
Подставляя найденные выражения для производных в ОДУ
F.52), получим с учетом соотношения t = cost
= O. F.54)
Поскольку корнями соответствующего характеристического
уравнения Л2 + п2 = 0 являются комплексно сопряженные чи-
чисто мнимые числа (Ai,2 = ±i, г2 = — 1), то общее решение ОДУ
F.54) будет таким:
у (г) = С\ cos пт + C<i sin пт.
Возвращаясь к переменному ?, получаем
y(t) = C\ cos(n arccost) + C2sin(n arccosi).
Если n — целое, то частное решение y(t) = cos(narccosi)
оказывается многочленом степени п относительно t [II], для
которого принято обозначение Tn(t) = cos(narccost). Напри-
Например, T0(t) = l, Ti(t) = «, T2(t) = 2t2-1, T3(i) = 4t3~3t, T4(t) =
= 8tA — 8^2. Справедливо рекуррентное соотношение
Эти многочлены введены П.Л. Чебышевым в 1854 г. в связи
с решенией им задачи о центробежном регуляторе равномер-
равномерности вращения вала паровой машины и носят его имя (более
точно их называют многочленами Чебышева первого ро-
рода). Они находят широкое применение как в теоретических
исследованиях, так и при решении прикладных задач (подроб-
(подробнее см. [II]).
6.6. Структура частного решения
уравнения с постоянными коэффициентами
и специальной правой частью
Пусть правая часть линейного неоднородного обыкновенно-
обыкновенного дифференциального уравнения (ОДУ) F.26) п-го порядка с
постоянными коэффициентами имеет вид g(t) = Pr(?)e^, где

6.6. Структура частного решения неоднородного ОДУ 201
Pr(t) — многочлен степени г, \х Е Ш. Сформулируем без дока-
доказательства теорему о структуре частного решения ОДУ F.26)
с такой правой частью.
Теорема 6.4. Если /i не является корнем характеристи-
характеристического уравнения
Ап + а1Ап~1+... + ап = 0, F.55)
соответствующего ОДУ F.26) обморочного уравнения F.27), то
ОДУ F.26) имеет частное решение вида
y*(*) = Qr(*)e<", F.56)
где Qr{t) — многочлен той же степени г, что и многочлен
Pr(t).
Если же /i — корень кратности к характеристического
уравнения F.55), то частное решение имеет вид
y*(t) = tkQr(t)^. # F.57)
Общий прием нахождения неизвестных коэффициентов мно-
многочлена Qr(t) состоит в подстановке F.56) или F.57) в исход-
исходное ОДУ F.26) и приравнивании (после сокращения на е/4* Ф 0
Vi € IR) коэффициентов при одинаковых степенях t.
Пусть правая часть ОДУ F.26) имеет вид
g{t) = eat (Pr{t) cos Ct + Qs(t) sin/%),
где Pr(t), Qs{t) —многочлены степеней г, 5 соответственно.
Сформулируем, не доказывая, теорему о виде частного реше-
решения с такой правой частью.
Теорема 6.5. Если число a + i/З не является корнем
характеристического уравнения F.55), то ОДУ F.26) имеет
частное решение вида
y*(t) = e

202 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
где Ri и 5/ — некоторые многочлены степени /, J = max{r, s}.
Если же число a + ifi является корнем характеристического
уравнения кратности &, то уравнение имеет частное решение
вида
у* (t) = tkeat (Ri (t) cos fit + Si (t) sin fit).
Пусть правая часть ОДУ F.26) имеет вид
Зная частное решение уравнения с правой частью <?&(?), к =
= 1,т, мы можем построить частное решение уравнения с
правой частью g(t).
Теорема 6.6. Если y*i(t)> •••» V*m(*) —частные решения
ОДУ F.26), соответствующие правым частям gi(t), ..., ffm(<),
то
является частным решением ОДУ с правой частью g(t).
< Так как y*k{t) является решением ОДУ с правой частью
gk(t): L(p)y*k(t) = 9k(t), то
171 171 7П
Hp)y.(t) = L(p) (?>*(<)) = ^I(p)^(<) = ^5*(<) = g(t),
т.е. y*(t) — решение ОДУ с правой частью g(i). >
Если правая часть ОДУ F.26) имеет вид
г=1

6.6. Структура частного решения неоднородного ОДУ 203
где Pri (t) — многочлен степени т^, то частные решения строят
для каждого слагаемого этой суммы: y*i(t), ...,t/*m(t). Тогда
в силу линейности ОДУ F.26) сумма
также будет его частным решением (правило, позволяющее
рассматривать итоговый результат как сумму независимо най-
найденных частных результатов, принято называть принципом
суперпозиции (от латинского слова superpositio — наложе-
наложение)).
Пример, а. Для ОДУ второго порядка
корнями характеристического уравнения Л2 + 1 = 0 являются
комплексно сопряженные чисто мнимые числа Ai,2 = ±i. В
соответствии с изложенным выше, частное решение ищем в
виде y*(t) = (at + Ь)е*, так как \х = 1 не является корнем
характеристического уравнения. Последовательно вычисляя
% = (at + a + b)e,
at at
и подставляя y*(t) и <Py*/dt2 в исходное ОДУ, получаем
(at + 2a + b) el + (at + b) el = 4te*,
или после сокращения на е1:
Ba-4)t + 2a + 26 = 0.
Ясно, что это равенство будет выполнено при любых t € М, если
a = 2 и b = —2. Тогда частным решением рассматриваемого
ОДУ будет

204 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
а его общее решение примет вид
y(t) = C\ cost + C2 sint + Bt - 2)eK
б. Найдем частное решение ОДУ второго порядка
d2y
+y
Характеристическое уравнение А2 + 1 = 0 этого уравнения
имеет корни Ai = г, \2 = —г. Общее решение соответствую-
соответствующего однородного уравнения имеет вид
y(t) = C\ cos t + C*i sint.
Так как в данном случае для правой части уравнения а = 0,
/3=1, а число /х = г является корнем характеристического
уравнения кратности т = 1, частное решение у*(?) следует
искать в виде y*(t) = t(acost + bsint). Последовательно вычи-
вычислим
—- = acost + bsint + i(-asini + bcost);
at
—?- = —2asint + 2bcost + t(—acost — bsint).
Подставляя rf2y*/dt2 и у* в исходное ОДУ, получаем
—2a sint + 2bcost +1(—acost — bsint) + t(acos t + bsint) = 4sint.
Это равенство должно быть выполнено для любого t, что
возможно, если коэффициенты при подобных членах будут
равны нулю, т.е. (—2а — 4)sint = 0 и 2bcost = 0. Отсюда
следует а = —2 и 6 = 0. Итак, для исходного ОДУ получаем
частное и общее решения соответственно в виде
уф(<) = —2tcost, y(t) = С\ cos t + С2 sin t — 2t cost.

6.6. Структура частного решения неоднородного ОДУ 205
в. Найдем общее решение ОДУ второго порядка
^ 2^ + 2у = е-1 sint. F.58)
Характеристическое уравнение А2 + 2А + 2 = 0 имеет комплекс-
комплексно сопряженные корни Лх = —1 + г, А2 = — 1 — г. Общее реше-
решение соответствующего исходному ОДУ однородного уравнения
будет
y(t) = е~1(С\ cost + C2smt).
В данном случае ^ = — 1 и /9 = 1, a /i -Н/3 = — 1 + i = Ai, т.е.
совпадает с одним из корней характеристического уравнения.
Поэтому частное решение исходного уравнения ищем в виде
где А, В — постоянные, подлежащие определению. Для на-
нахождения последних необходимо подставить y*(t) в исходное
уравнение и после сокращения на е~1 приравнять коэффици-
коэффициенты при cost и sint. В результате получим В = 0, А = —1/2.
В итоге общее решение ОДУ F.58) имеет вид
y(t) = е~ь(С\ cost + C2 sint) — -e^cost.
г. Найдем общее решение ОДУ
Характеристическое уравнение А2 + 4 = 0 имеет корни
Ai = 2г, А2 = —2г. Общее решение соответствующего однород-
однородного уравнения имеет вид
y(t) = CiCos2t + C2sin2t.
Правая часть неоднородного ОДУ представляет собой сумму
двух функций специального вида. Для 9\{t) = t частное
решение неоднородного ОДУ ищем в виде y*i(t) = At + В.
Подставляя в ОДУ, находим AAt + AB == t, откуда, приравнивая

206 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
коэффициенты при одинаковых степенях i, находим А — 1/4,
В = 0. Частное решение y*2(t), соответствующее второму
слагаемому g2(i) = e2tcost, ищем в виде у*2(*) = e2t(Ccosi +
+ Dsint). Подставляя в ОДУ и сокращая на е2*, находим
{1С + 42?) cos t+{7D- AC) sint = 0.
Приравниваем коэффициенты при cost и sint нулю (напри-
(например, в силу линейной независимости этих функций) и получаем
из системы двух уравнений с двумя неизвестными С = 7/65,
D = 4/65. На основании теоремы 6.6 делаем вывод, что част-
частным решением рассматриваемого ОДУ будет
1 e2t
V*(t) = V*i(t) + y*2{t) = 4*+65 Gcost + 4sint)-
В итоге общее решение ОДУ имеет вид
1 e2t
y(t) = C\ cost + C*i sint + -t + — Gcost + 4sint).
Пример 6.З. Колебания линейного осциллятора, на ко-
который действует периодически изменяющаяся вынуждающая
сила, описывает линейное неоднородное ОДУ второго
порядка с постоянными коэффициентами
т—% + h-^- + ky = qcosu>t. F.59)
aV at
Здесь t — время; у — перемещение материальной точки мас-
массой m; h — коэффициент сопротивления движению, пропор-
пропорционального скорости dy/dt точки; к — жесткость упругой
связи; и и q — частота изменения и амплитуда вынуждаю-
вынуждающей внешней силы. Выясним, существует ли частное решение
ОДУ F.59) в виде периодической функции, и если существует,
то попытаемся найти его.
В силу принципа суперпозиции искомое решение будет
действительной частью функции y(t), удовлетворяющей неод-

6.6. Структура частного решения неоднородного ОДУ 207
нородному ОДУ
^ ^ + ky = qe^. F.60)
Замена по формуле Эйлера тригонометрических функций экс-
экспоненциальной функцией в ряде случаев оправдана и приводит
к менее громоздким вычислениям. Будем искать функцию y(t)
в виде
у(<)=У*е^'. F.61)
Продифференцировав F.61) дважды, подставив выражения для
функции и ее производных в F.60) и сократив на отличный от
нуля при любых t E R множитель егш*, находим
У* =
к — mo;2 — ihu
где
к — mo;2 hu
(fc - ma;2J + /i2cj2 ' (Jfe - ma;2J + h2u2'
Подставив теперь у* в F.61) и выделив действительную часть,
получаем решение ОДУ F.59) в виде периодической функции
Rey(t) = Re(q(c-id)eiwt) =
= Re(q(c —id) (cos ut + isinut)) =
= q(ccosut + dsinut) = A cos(a> t —<p),
где
Найденное решение имеет тот же период Т = 2тг/а>, что и
вынуждающая сила.
Зависимости А и у? от о; являются амплитудно-частот-
амплитудно-частотной и фазочастотной характеристиками линейного осцилля-
осциллятора и для различных значений коэффициента сопротивления
h схематично изображены на рис. 6.3, а, б соответственно.

208
6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
о
Рис. 6.3
Характеристики изображены для значений h<i > h\ > ho = О
коэффициента h.
Вопросы и задачи
6.1. Найти частное решение неоднородного ОДУ, если
известно общее решение x(t) соответствующего однородного
уравнения:
dPx dx I -f" t
a) -j^- + 2—tgt-x = -,
at? at cos i
a^ at
6.2. Найти общее решение ОДУ, если известно одно из его
частных решений x*(t):
a.)
d х dx
+2
dx
It

Вопросы и задачи 209
6.3. Найти общее решение ОДУ:
d4x _ d3x
2
6.4. Составить линейное однородное ОДУ с постоянными
коэффициентами, зная его общее решение:
а) x(t) =
б) x(t) =
в) x(t) =
г) *(t) = Cxe-2t + C2te'2t
6.5. Найти общее решение ОДУ:
а) —=¦ + я: = tsint; б) -трг - 5 — + 4х = 17sint + Зе*;
atz atz at
ч d2x dx + ч d2x
LdF+3a:=ie; r^
dx Л * ч d2a; Л dx + Л +
^+:с=3е ; е^+2^+ж=3<е +2е ;
d x dx
ж) -7T + 5-r
acz at
6.6. Решить уравнения Эйлера:
Л

210 6. ЛИНЕЙНЫЕ ОДУ ВЫСШИХ ПОРЯДКОВ
6.7. Шарик массой т может скользить без трения в труб-
трубке, вращающейся с угловой скоростью ш вокруг вертикальной
оси (рис. 6.4). На шарик действует упругая сила со стороны
пружинки жесткостью А;, равная ну-
нулю, когда шарик занимает положение
^ЛЛ/v*yyг [J » х = жо. Найти закон движения x(t)
шарика во времени t при начальных
Рис. 6.4 условиях: х@) = ж0, я'@) = 0.
6.8. Решить ОДУ
и построить график решения. Как ведет себя мгновенная
частота во времени t ?
6.9. Для ОДУ F.49) найти соотношения между начальными
значениями ? = 0, у@) и у'@), соответствующие каждому из
трех типов интегральной кривой, изображенной на рис. 6.1, а.
6.10. Найти общее решение ОДУ
+ 9xf = 5t + 8cost- sin*.

7. НУЛИ РЕШЕНИИ
ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ ВТОРОГО ПОРЯДКА
7.1. Приведение уравнения к двучленному виду
Рассмотренные в 6.5 уравнения Эйлера, Лагранжа п-го
порядка и Чебышева удается привести к обыкновенному диф-
дифференциальному уравнению (ОДУ) с постоянными коэффициен-
коэффициентами, однако эта возможность является скорее исключением,
чем правилом. В общем случае даже при п = 2 нельзя записать
решение линейного однородного ОДУ второго порядка
в явном виде. В то же время эти уравнения обладают рядом
свойств, позволяющих сделать качественные выводы о поведе-
поведении их решений, что может быть весьма полезно при решении
прикладных задач.
Объектом исследования будет линейное однородное ОДУ
второго порядка с переменными коэффициентами
^ G.1)
где функция a\(t) непрерывно дифференцируема, а функция
o,2(t) непрерывна в некотором промежутке Г числовой пря-
прямой R. Покажем, что G.1) при помощи замены
y(t) = <p(t)z(t), G.2)
где z(t) — новая искомая функция, можно привести к виду,
не содержащему первой производной dz/dt, если должным
образом выбрать функцию (p(t). Подставив G.2) в G.1) и
опустив обозначение аргумента t, запишем
4 = °- G-3)

212 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
Если в G.3) приравнять нулю коэффициент при производной
dz/dt, то получим ОДУ первого порядка с разделяющимися
переменными
частным решением которого будет
ai(r)dr). G.4)
Тогда вместо G.2) можно написать
ч* t
y(t) = z(t) exp ( -±Jai(T)dTy G.5)
to
Подставляя G.4) и равенства
dip __ 1 d2(p ^ a\ dip ip da\ /a\ 1 da\\
dt 2 ' d^2 2 dt 2 dt V 4 2 dt J
в G.3), получаем
или, обозначив
приведем исходное ОДУ G.1) к так называемому двучленному
виду
+ q(t)z = Q. G.7)
Ясно, что функция q(i) определена и непрерывна в проме-
промежутке Г.

7.1. Приведение уравнения к двучленному виду 213
Пример. Сопоставляя ОДУ
d2y dy
dt2 dt
с G.1), устанавливаем, что в данном случае a\(t) =? и a2(t) =
= ?2/4 — 1/2. Эти функции определены и непрерывно диффе-
дифференцируемы на всей числовой прямой R. Используя G.4), при
to = 0 находим
<p(t) = ехр ( - \fr dr) = exp ( - ?) = е~^\
to
Для приведения исходного ОДУ к двучленному виду при
помощи G.6) вычислим
и, согласно G.7) запишем
Общее решение этого линейного однородного ОДУ второго
порядка с постоянными коэффициентами будет
o-t
а исходного уравнения (с учетом G.2) и найденного выражения
для функции ip(t)) —
2/1et + C2e-i). #
Отметим, что ОДУ G.7) можно также проинтегрировать в
элементарных функциях, если q(t) = k/t2, где k = const. В этом
случае G.7) является частным случаем уравнения F.50) Эйлера
при п = 2 и an_i = а\ = 0, а2 = к.

214 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
Каждому из уравнений G.1) и G.7), очевидно, удовлетворя-
удовлетворяет тождественно нулевое региение ОДУ, которое обычно на-
называют тривиальным (от латинского слова trivialis — обык-
обыкновенный). Если же решение ОДУ в некотором промежутке Т
тождественно не равно нулю, то такое региение будем назы-
называть нетривиальным в этом промежутке. Применительно к
ОДУ G.7) в двучленном виде нас будут интересовать нетриви-
нетривиальные решения.
7.2. Нули решений. Теорема
о конечности числа нулей на отрезке
Напомним, что значение U аргумента t функции z(t),
которое обращает данную функцию в нуль, т.е. z(t*) = 0, назы-
называют нулем этой функции. Если функция z(t) в некотором про-
промежутке TCR числовой прямой R является решением какого-
либо обыкновенного дифференциального уравнения (ОДУ) п-го
порядка, то она в этом промежутке имеет производные zW (t)
{k = 1, п) ив окрестности точки U ? Т может быть прибли-
приближенно представлена многочленом Тейлора
При z'(t*) ф 0 точка U будет простым нулем этого мно-
многочлена, в противном случае — кратным (при п ^ 2). Под
нулем решения z(t) ОДУ в дальнейшем будем понимать
такую точку U Е Г, что z(t*) = 0, но z'(U) ф 0. Если **
является внутренней точкой промежутка Т, то существует
окрестность этой точки, в которой решение z(t) меняет знак.
Будем считать, что заменой G.5) линейное однородное ОДУ
G.1) второго порядка с переменными коэффициентами уже
приведено к двучленному виду G.7). Если в промежутке Т,

7.2. Нули решении. Теорема о конечности числа нулей на отрезке 215
где определена и непрерывна функция д(?), решение ОДУ
G.7) имеет не более одного нуля, то его называют неколеблю-
неколеблющимся в этом промежутке, а в противном случае — колеб-
колеблющимся.
Функция (p(t) G.4) отлична от нуля при любых t Е К.
Поэтому в промежутке Г С Е в силу G.5) нули решения z(t)
ОДУ G.7) и решения y(t) ОДУ G.1) совпадают.
Для любого ненулевого решения ОДУ G.7) справедлива
следующая теорема.
Теорема 7.1. Всякое нетривиальное на отрезке [а, Ь]
решение ОДУ G.7) может иметь на этом отрезке не более
конечного числа нулей.
<4 Доказательство проведем методом от противного. Допу-
Допустим, что нетривиальное решение z(t) имеет на [а, Ь] бес-
бесконечное множество нулей ?п, т.е. z(tn) = О, п Е N. Так
как последовательность {tn} ограничена, то, согласно теореме
Больцано — Вейерштрасса [I], из нее можно извлечь подпосле-
подпоследовательность {tkn}, сходящуюся к конечному пределу, т.е.
на отрезке [а, Ь] существует предельная точка t* последова-
последовательности {?п}, или
Не ограничивая общности, можно считать, что tn -> f* при
п —? оо. Так как z(tn) = 0, то вследствие непрерывности
функции z(t) как решения ОДУ G.7) имеем z(t*) = 0. Из
равенства z(tn) = z(tn+i) =0 на основании теоремы Ролля [II]
следует, что в интервале (?п, ?п+1) найдется точка ?^, такая,
что для дифференцируемой в этом интервале функции z(t)
будет выполнено равенство dz/dt = 0. Поскольку tfn -» t*
t=tn
при п-»оо, то dz/dt

216 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
Таким образом, в некоторой точке t* Е [а, Ь] отрезка име-
имеем z(U) = 0, zf(t*) = 0. Но таким начальным условиям в
силу теоремы 4.2 Коши о существовании и единственности ре-
решения ОДУ n-го порядка, условия которой выполнены для
уравнения G.7), соответствует только тривиальное решение
z(t) =0 этого ОДУ. Полученное противоречие и доказывает
теорему. >
7.3. Теорема о чередовании нулей.
Теоремы сравнения и Кнезера
Пусть z\{t) и Z2{t) — линейно независимые в некотором
промежутке TCR, а значит, и нетривиальные в этом про-
промежутке (см. замечание 6.1 и определение 6.1) решения линей-
линейного однородного обыкновенного дифференциального уравнения
(ОДУ) G.7) и пусть хотя бы одно из этих решений, например
z\(t), является в Т колеблющимся, т.е. имеет в нем не менее
двух нулей. Эти решения не могут иметь в Т общих нулей. В
самом деле, если в некоторой точке U eT z\(U) = Z2(U) = 0,
то вронскиан F.9) этих решений в ней равен нулю и, согласно
формуле F.14) Остроградского — Лиувилля, он равен нулю во
всем промежутке Т, что противоречит линейной независимо-
независимости решений Z\(t) И Z2(t) В Т (СМ. 6.1).
Теорема 7.2 (о чередовании нулей). Если z\(t) и
Z2{t) — линейно независимые решения ОДУ G.7) в промежутке
Т и одно из них колеблющееся, то их нули чередуются, т.е.
между двумя нулями одного решения лежит нуль другого
решения.
Л Пусть 2Ti(ti) = 2Ti(t2) = 0 и *i(t)^0 при te(tut2)GT,T.e.
t\ и t<i — соседние нули решения z\{t). Покажем, что решение
Z2{t) имеет нуль ?* Е (*i, *2)«
Предположим противное, т.е. Z2(t) Ф 0 при t E (*i, *г)»
и рассмотрим непрерывно дифференцируемую в интервале

7.3. Теорема о чередовании нулей. Теоремы сравнения и Кнеэера 217
1,*г) функцию u(t) = zi(t)/z2(t). Вычислим с учетом F.9)
z2{t)
z[(t) z'2(t)
W(t)
du
~dt
так как вронскиан для двух линейно независимых решении
линейного однородного ОДУ второго порядка отличен от нуля.
В то же время u(ti) = u(t2) = 0, и, согласно теореме Рол-
ля [II], найдется точка ? € (<i, t2), такая, что uf(?) = 0. Полу-
Полученное противоречие означает, что решение z2(t) обращается
в нуль в интервале (*i, *г)- При этом в (*i, *г) может быть
только один нуль этого решения. Действительно, если а\ и
ol2 — соседние нули z2 (?), причем t\ < а\ < а2 < ?, то, повторив
проведенные рассуждения для интервала (ai,a2), но поменяв
ролями решения z\(t) и z2(t), придем к противоречию. >
Например, функции zi(?)=cos?, z2(t) = sint линейно неза-
независимы на всей числовой прямой (см. пример 6.2) и являются ре-
решениями ОДУ d2z/dt2 +
+ z = 0. Нули этих ре-
решений чередуются: меж-
между соседними нулями Z\(t)
лежит один нуль z2(i), и
наоборот (рис. 7.1). Рис. 7.1
Теорема 7.3 (сравнения). Пусть даны два ОДУ вида G.7)
d2zx
dt2
+ 91 (*)*i= 0,
d2z2
dt2
q2(t)z2 =
G.8)
с непрерывными в некотором промежутке ГсК функциями
91 (*), 92(*), такими, что qi(t)^q2{t)* 4te[tut2]CT. Тогда
между любыми двумя соседними нулями нетривиального в Т
*Мы предполагаем, что функции qi(t) и q2(t) могут совпадать в
отдельных точках промежутка Т, но не равны тождественно ни на каком
интервале в промежутке Т.

218 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
решения z\ (t) первого ОДУ лежит по крайней мере один нуль
любого нетривиального в Т решения Z2(t) второго ОДУ.
М Пусть t\ < t2 — соседние нули решения z\(t), т.е. z\(ti) =
= z\(t2) = 0. Подставим в оба ОДУ G.8) решения соответствен-
соответственно zi(t) и Z2{t), умножим первое из полученных тождеств на
Z2(?), а второе — на —z\(t) и после сложения результатов за-
запишем
= | (z[(t)z2(t)-z'2(t)zl(t)) ^
te(tut2).
Учитывая, что zi(ti) = zi(t2) = 0, проинтегрируем среднюю и
правую части этого тождества от t\ до t2 :
. G.9)
Примем для определенности, что z\(t) > 0 W E (<i, ?2). Тогда,
так как zi(?i) = ^1(^2) = 0, будем иметь ^i(^i) > 0 и z[(t2) < 0.
Последующие рассуждения проведем от противного. Пред-
Предположим, что решение z2(t) не имеет нулей на интервале
(*1» *г)- В этом случае, считая, что z2(t) >0 VtG (?1,^2M за-
заключаем, что левая часть G.9) неположительна (^2(^1) ^ 0 и
^2(^2) H в силу непрерывности z2(t)), тогда как интеграл в
правой части G.9) в силу сделанного предположения положите-
положителен. Возникшее противоречие неустранимо и в случае, когда
z2{t) < 0 Vt G (*i, ?2). Это противоречие доказывает, что при
z\(t) > 0 V? G (<i, ?2) решение ^(t) должно менять знак в ин-
интервале (ti, ^2), т.е. иметь в этом интервале хотя бы один нуль.
Аналогично можно убедиться, что, приняв z\(t) <0 при
t€ (*ь*2)? снова придем к противоречию в тождестве G.9),
если предположить отсутствие в интервале (*i, *г) нулей реше-
решения z2(t). >

7.3. Теорема о чередовании нулей. Теоремы сравнения и Кнезера 219
Понятие о колеблющемся решении было введено француз-
французским математиком Ж. Штурмом A803-1855), а теоремы 7.2 и
7.3, доказанные им, носят названия соответственно первой и
второй теорем Штурма.
Следствие 7.1. Если в ОДУ G.7) функция q(i) непре-
непрерывна и неположительна при t E К*, то любое решение этого
ОДУ может иметь не более одного нуля, т.е. является неколеб-
неколеблющимся.
<4 Применим теорему 7.3 сравнения. Пусть в G.8) q\{t) = q(t) ^
^0 и <й(*) = 0 VtElR. Допустим, что решение z\(t) первого
ОДУ G.8) имеет два нуля в точках t\ и t*i: z\(t\) = zifa) = 0.
Но тогда в интервале (<i, ?2) обязано обратиться в нуль любое
решение уравнения d?Z2/dt2 = 0, а это неверно, например, для
решения Z2(t) = 1. >
Пример 7.1. Применим теорему 7.3 сравнения для каче-
качественного описания поведения решения уравнения Эйри
Это ОДУ находит применение в различных приложениях, на-
например в квантовой механике. Возьмем произвольное доста-
достаточно малое число а > 0. Сравним уравнение Эйри с ОДУ
одно из частных решений которого
Z\ It) = Sin
a
является периодической функцией с периодом 2а. Нули это-
этого решения расположены равномерно на числовой прямой R,
*Но не равна нулю тождественно ни на каком интервале, см. предыдущее
примечание.

220 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
причем расстояние между соседними нулями равно а. Если
t > (тг/аJ, то в силу теоремы сравнения между соседними ну-
нулями решения z\ (t) должен лежать хотя бы один нуль любого
решения z(t) уравнения Эйри, т.е. расстояние между соседни-
соседними нулями решения уравнения Эйри не превышает 2а. При
возрастании t в неравенстве t > (тг/аJ можно выбирать все
меньшие значения а, так что при t -» +oo соседние нули лю-
любого решения уравнения Эйри неограниченно сближаются.
Теорема 7.4 (теорема Кнезера). Пусть ^ля непрерывной
в промежутке [*о, +оо), to > 0, функции q(t) выполнено усло-
условие 0 < q(t) ^ l/Dt2)*. Тогда любое решение z(t) ОДУ G.7)
имеет в этом промежутке не больше одного нуля, т.е. являет-
является неколеблющимся. Если же q(t) > A + e)/Dt2) Vt Е [?о> +oo)
при е > 0, то z(t) имеет бесконечное множество нулей, т.е.
является колеблющимся.
М Доказательство проведем методом от противного. Пред-
Предположим, что при q(t) < 1/D?2) Vt € [to, +oo) решение z(t)
ОДУ G.7) имеет больше чем один нуль, т.е. существуют точки
*ь h € [*(h +oo), в которых z(ti) = z(t2) = 0. Наряду с ОДУ G.7)
рассмотрим уравнение F.50) Эйлера при п = 2, an_i = а\ = 0,
п2 = const ф 0, t > 0
и применим теорему 7.3 сравнения, в силу которой любое реше-
решение x(t) этого уравнения при а2 = 1/4 должно иметь нуль в
интервале (ti, ?2). Однако функция #(?) = y/i, являясь решени-
решением уравнения Эйлера при а2 = 1/4, не имеет нулей на (<i, ?2).
Это противоречие доказывает первую часть утверждения тео-
теоремы.
Пусть теперь q(t) > A + ?)/D?2) (е > 0) в промежутке
[to, +00). Покажем, что любое решение z(t) ОДУ G.7) имеет
*При этом q(t) ф 1/D?2) ни на каком интервале в промежутке [to, +00).

7.3. Теорема о чередовании нулей. Теоремы сравнения и Кнезера 221
бесконечное множество нулей. Заменой t = ет (см. 6.) при-
приведем G.10) к линейному однородному ОДУ второго порядка с
постоянными коэффициентами
сРх dx . ' ' ,_ Л л ч
____ + a2Z==0. G.11)
Его характеристическое уравнение А2 — А + о>2 = 0 имеет при
п2 > 1/4 комплексно сопряженные корни
г2 = -1.
Это означает, что любое решение х(т) ОДУ G.11) является
колеблющимся, имеющим на числовой прямой бесконечное мно-
множество нулей. При этом бесконечное множество нулей этого
решения будет и в промежутке / = [то, +оо), где то = Into, & в
соответствующий / промежуток [to, +oo) попадет бесконеч-
бесконечное множество нулей решения x(t) ОДУ G.10), если п2 > 1/4.
Выбрав а>2 так, чтобы 1/4 < п2 < A + е)/4, получим
| G.12)
При выполнении условия G.12) между каждой парой соседних
нулей решения x(t) уравнения G.10), а таких пар бесконечное
множество, будет лежать, согласно теореме сравнения, нуль
любого решения z(t) ОДУ G.7). Это доказывает вторую часть
утверждения теоремы. >
Заметим, что при a<i < 1/4 уравнение Эйлера G.10) не
имеет колеблющихся решений, так как все решения этого
уравнения являются линейными комбинациями решений
Xl(t) =
Теорема 7.4 была доказана немецким математиком А. Кне-
зером A862-1930) и носит его имя,

222 7. НУЛИ РЕШЕНИЙ ОДУ ВТОРОГО ПОРЯДКА
Дополнение 7Л. О нулях решений
нелинейных дифференциальных уравнений
Исследование расположения нулей решений обыкновенных
дифференциальных уравнений (ОДУ) является составной ча-
частью качественного анализа этих уравнений. Изложенные в
7.3 результаты о нулях решений линейного однородного ОДУ
второго порядка стали к настоящему времени классическими
и вошли во многие учебники по дифференциальным уравнени-
уравнениям. Однако не следует думать, что анализ расположения нулей
решений ограничен рамками линейных ОДУ.
В качестве примера рассмотрим нелинейное ОДУ второго
порядка
Предположим, что функция д(х) удовлетворяет условию Лип-
Липшица и неравенству хд(х) > 0 при х ф 0. Заметим, что при
д(х) = п2Х {п2 = const) получаем частный случай G.10) урав-
уравнения F.50) Эйлера. В 7.3 было показано, что любое реше-
решение ОДУ G.10) является при п2 > 1/4 колеблющимся, а при
п2 < 1/4 — неколеблющимся. В случае а>2 = 1/4 у этого ОДУ
наряду с неколеблющимся решением x\(t) = \Д существует
еще решение X2(t) = \/* 1п?, которое является также неколеблю-
неколеблющимся. Поскольку x\{t) is X2(t) образуют фундаментальную
систему решений уравнения G.10) Эйлера, то любое решение
x(t) = (C\ + C2lnt)\/t этого ОДУ будет неколеблющимся при
а,2 = 1/4. Таким образом, значение п2 = 1/4 является в опре-
определенном смысле критическим.
Приведем формулировки теорем, относящихся к нетриви-
нетривиальным решениям ОДУ G.13).
Теорема 7.5. Все нетривиальные решения ОДУ G.13)
являются колеблющимися, если при е > 0 неравенство
х *" 4 1п|#|

Вопросы и задачи 223
выполнено для всех |х| > М, где М — достаточно большое
положительное число.
Теорема 7.6. Все нетривиальные решения ОДУ G.13)
являются неколеблющимися, если при 0 < е < 1/4 неравенство
х ^ \1п|я|
выполнено для всех \х\ > М, где М — достаточно большое
положительное число.
В частности, из теоремы 7.5 следует, что все решения ОДУ
it Т Ф
отличные от тривиального решения x(t) = 0, являются коле-
колеблющимися, поскольку неравенство х2 ^ 1/4 + s/ In | x \ выпол-
выполнено для всех | х | > М, где М > 0 — достаточно большое число.
Вопросы и задачи
7.1. Описать качественное поведение решений следующих
ОДУ:
. &х /9 Ь
б) -^2-
в) S+i^0'<>o-
Для уравнения а) рассмотреть случаи b > 0 и Ь < 0.

8. ПЕРВЫЕ ИНТЕГРАЛЫ
8.1. Основные понятия и определения
Запишем нормальную автономную систему обыкновенных
дифференциальных уравнений (ОДУ) в векторной форме:
где x(t) = (#i(?), ..., xn(t)) — вектор-функция скалярного
аргумента t с координатными функциями Xi(t), определен-
определенными в некотором промежутке Т С Ш числовой прямой М,
a f(x) = (/i(x), ..., fn(&)) — векторная функция векторно-
векторного аргумента х с координатными функциями /i(as), г = 1, п,
определенными и непрерывно дифференцируемыми в некото-
некоторой области D СШп n-мерного фазового пространства W1.
Отметим, что любую нормальную систему ОДУ вида A.3)
можно свести к автономной вида (8.1), если обозначить t =
= жп+ъ т-е- увеличить число неизвестных функций на единицу.
Естественно, такой прием приведет к увеличению на единицу
и порядка системы ОДУ.
Рассмотрим некоторое решение x(t) = g(t) системы ОДУ
(8.1) и непрерывно дифференцируемую в расширенном фа-
фазовом пространстве скалярную функцию п(?, х). В точ-
точках (?, #i,..., хп) Е Rn+1, принадлежащих интегральной кри-
кривой, соответствующей решению x = g(t), значения функции
u(t, x) будут зависеть только от значений аргумента ?, т.е.
u(t, g(t)) = v(t). Продифференцируем это тождество по ?, учи-
учитывая, что х = g(t) — решение системы (8.1), и запишем
dv = (du Эй dx\\ =(<fo + <fof(
dt \dt dx dt) \x=g(t) \dt dxjy

8.1. Основные понятия и определения 225
или в скалярном виде
dv
(8.2)
г=1 ""'"
Выражение
Ant r\nt До i
(8.3)
называют полной производной по t функции u(t, x) в
силу системы (8.1). Если и = гх(ж), то du/dt = 0 и (8.3)
принимает вид
¦г? = У2 7Г" Л(жь • ¦ ¦, «п) = (gradu(x), /(ж)), (8.4)
где (а,Ь) обозначает стандартное скалярное произведение а
иЬвК" [IV].
Определение 8.1. Функцию и(х) = w(rri,..., хп), опреде-
определенную и непрерывную вместе со своими частными производ-
производными в некоторой области D изменения фазовых переменных
zi,...,xn, называют первым интегралом системы (8.1) в
области D, если при подстановке в и(х) произвольного ре-
решения х = g (t) этой системы, траектория которого целиком
расположена в D, получим постоянную относительно t вели-
величину.
Иными словами, функция u(g(t)) зависит только от выбора
решения д(<), но не от независимого переменного t.
Теорема 8.1. Для того чтобы функция и(х) была первым
интегралом системы (8.1), необходимо и достаточно, чтобы она
удовлетворяла в области D соотношению
EOU» / \
8 — 9306

226
8. ПЕРВЫЕ ИНТЕГРАЛЫ
А Пусть и(х) — первый интеграл системы (8.1). Рассмотрим
произвольную точку а?о € D, Если x(t) = g(t) — решение
системы (8.1), удовлетворяющее начальному условию g{to) =
= жо G D, то, согласно определению 8.1, v(t) = u(g(t)) = const и
dv/dt = 0. В соответствии с (8.2) производная dv/dt совпадает
с полной производной по t функции и(х) в силу системы (8.1)
на решении g(t). Поэтому в точке xq
du
dt
X—XQ
dv
dt
= 0,
t=to
т.е. в области D выполнено равенство (8.5).
Докажем обратное утверждение. Пусть выполнено (8.5)
и x(t) —git) — решение системы (8.1), фазовая траектория
которого лежит в D. Тогда с учетом (8.5) имеем
d
Jt
т.е. u(g(t)) не зависит от t и, следовательно, в соответствии
с определением 8.1 и(х) — первый интеграл системы (8.1). >
Условие (8.5) имеет простой геометрический смысл. В
любой точке ж* Е D вектор gradu(sc*) градиента скаляр-
скалярной функции и(х) ортогона-
ортогонален к ее поверхности уров-
уровня 5, задаваемой ураВНеНИ-
Ш ilyJu J — UyX*j L J" \"*^/
следует, что в каждой точке
ж* Е S вектор /(ж*) каса-
касается этой поверхности. По-
Поэтому фазовая траектория 7?
проходящая через точку ж* Е
Рис S1 E 5, лежит на поверхности S
(рис. 8.1).
Пример, а. Покажем, что система уравнений
dx\ о ¦ dx2
——• = —Жо + sina?i; —г- = —X2cosxi
dt dt

8.1. Основные понятия и определения 227
имеет первый интеграл u(xi, Х2) = 3x2sinxi — х\. Используя
(8.4), вычислим
at at at
=0,
что отвечает определению 8.1 первого интеграла системы. Ра-
Равенство du/dt = 0 означает, что вдоль любой фазовой траек-
траектории для данной системы функция и(х\,Х2) сохраняет посто-
постоянное значение.
б. Известно, что движение материальной точки массой m
в потенциальном поле можно описать, согласно второму закону
Ньютона, уравнением
<Рх _ <Ш
m~dfi-~fa'
Здесь t — время; Щх) — потенциал поля, зависящий в данном
случае только от положения материальной точки, определяе-
определяемой ее координатой х. Сила, действующая на точку, равна
—dU/dx и при отрицательном значении производной направ-
направлена в сторону возрастания координаты х. Вводя скорость
v = dx/dt материальной точки, исходное ОДУ можно свести к
нормальной автономной системе
dx dv dH /Л ЛЧ
Первый интеграл этой системы имеет вид
V2
u(x, v) = m — + Щх) = const
и отражает закон сохранения энергии: сумма кинетической и
потенциальной энергии материальной точки в потенциальном
поле постоянна. В самом деле, с учетом системы (8.6) получаем
du dv dU dx ( dv dU\
— =rnv — + —• —= vim— + —1=0,
dt dt dx dt \ dt dx)
т.е. в силу определения 8.1 функция u(x, v) является первым
интегралом системы (8.6).

228 8. ПЕРВЫЕ ИНТЕГРАЛЫ
8.2. Теорема о локальном существовании
системы первых интегралов
Пусть правая часть f(x) нормальной автономной системы
(8.1) обыкновенных дифференциальных уравнений (ОДУ) опре-
определена в некоторой области D CW1 изменения фазовых пере-
переменных х\,...,хп.
Определение 8.2, Точку й = (ui,..., й»,..., ап) Е D назы-
называют положением равновесия системы (8.1), если x(t) = a
является частным решением этой системы.
Для любого положения равновесия а системы (8.1) выполня-
выполняется равенство /(а) = 0, и наоборот, если /(а) = 0 в точке
а, то эта точка будет положением равновесия системы.
Отметим, что элемент арифметического пространства Еп
может рассматриваться и как вектор в линейном простран-
пространстве [IV], и как точка в метрическом пространстве [I], a
это приводит к различным его обозначениям: вектор оЕК
записывают в виде матрицы-столбца а = (ai,..., ai,..., an)T,
а точку aEK записывают в виде матрицы-строки а =
= (ai,..., а«,..., ап). В дальнейшем будем использовать оба
варианта обозначений элементов арифметического простран-
пространства, выбирая в конкретной ситуации наиболее удобное.
Предположим, что известно несколько первых интегралов
щ(х), г^2(ж),..., щ(х) системы (8.1), определенных в неко-
некоторой окрестности точки х = a G D, не являющейся положе-
положением равновесия системы (8.1), т.е. /(а) Ф 0.
Определение 8.3. Первые интегралы
системы (8.1), определенные в окрестности точки a G D
(f(a) т^О)) называют независимыми в этой точке (или про-
просто независимыми), если матрица Якоби {дщ/дх^)\х=а (i =
= 1, fc, j = 1, п, А; < п) размера кхп имеет ранг, равный числу
первых интегралов к. Если первые интегралы независимы в
каждой точке области D, то их называют независимыми в
этой области.

8.2. Теорема о локальном существовании первых интегралов 229
В силу определения 8.1 в качестве первого интеграла лю-
любой системы вида (8.1) можно взять произвольную константу,
т.е. выражение для первого интеграла не будет содержать фа-
фазовых переменных. Несложно проверить, что, согласно опре-
определению 8.3, среди независимых первых интегралов не должно
быть интегралов вида u = const. Необходимо отметить, что
непостоянные (т.е. отличные от констант) первые интегралы
встречаются достаточно редко. Их отсутствие связано с тем,
что в общем случае фазовые траектории системы вида (8.1)
не лежат целиком на поверхностях уровня какой-либо одной
функции. Однако локально, в окрестности точки, не являющей-
являющейся положением равновесия системы (8.1), фазовые траектории
устроены просто и непостоянные первые интегралы существу-
существуют. Это обстоятельство отражено в следующей теореме.
Теорема 8.2. Пусть точка а ? D не является положением
равновесия системы (8.1), т.е. /(а) ф 0. Тогда в окрестности
этой точки существует п — 1 независимых первых интегралов
системы (8.1). #
Покажем, что условие /(а) ф 0 в формулировке теоре-
теоремы 8.2 существенно.
Пример. Рассмотрим систему ОДУ
2*1
dt ZXU dt
и покажем, что в окрестности положения равновесия х\ = х2 =
= 0 этой системы не существует первого интеграла, отличного
от интеграла вида и = const. Общее решение этой системы
ОДУ имеет вид xi{t) = Cie2*, x2(t) = С2е4*, где Ci и С2 —
произвольные постоянные. Исключая из этих решений ?,
получим уравнение х2 = Сх\ (С = С2/С\) семейства фазовых
траекторий. Первый интеграл и{х\,х2) постоянен на любой
кривой этого семейства. Но каждая такая кривая при малых х\
и х2 оказывается в произвольно малой окрестности положения
равновесия х\ = х2 = 0, а в совокупности все эти кривые

230 8. ПЕРВЫЕ ИНТЕГРАЛЫ
(с учетом двух фазовых траекторий на оси Оу) покрывают
такую окрестность. Из непрерывности функции и{х\,Х2) в
положении равновесия следует, что она постоянна в некоторой
окрестности этого положения равновесия.
Вместе с тем в любой не содержащей точку @; 0) области
D С R2 \ {@,0)} фазовой плоскости R2 первый интеграл
существует и имеет вид и(х\, Х2) = ff2/#i> либо и(х\,Х2) =
= х\/х2. #
Заметим, что теорема 8.2 носит достаточный характер. В
окрестности положения равновесия системы первые интегралы
могут как существовать, так и не существовать.
Пример. Система ОДУ
dx\
имеет, в отличие от предыдущего примера, первый интеграл
u(xi, X2) = х\ + х\, определенный в R2, включая положение
равновесия х\ = х2 = 0 этой системы.
8.3. Понижение порядка системы
дифференциальных уравнений
при помощи первых интегралов
Ограничимся рассмотрением нормальной автономной си-
системы третьего порядка
dx-
-J7 = fi(xu *2, *з), i = 1, 2, 3. (8.7)
at
Пусть u(#i, а?2, жз) — первый интеграл системы (8.7) в области
DCR3, Чтобы решить задачу Коши для этой системы,
необходимо задать начальные условия жх(?о) = #?> xz(to) = ^2»
x3(to) = Ж3. Рассмотрим поверхность уровня первого интеграла
и(х\, ГГ2, х$) = С. Для заданных начальных условий постоянная
С принимает фиксированное значение Cq: u(x\,X2, #з) = Со-

8.4. Симметричная форма записи системы ОДУ 231
Предположим, что уравнение u(x\, x<i, x$) = Со можно
разрешить в некоторой области G С D относительно одной
из фазовых переменных, например х$: х$ = <р(#ъ Х2), где
tp(xi, X2i Co) — непрерывно дифференцируемая функция пере-
переменных Ii И 12-
Подставив функцию х$ = <р(#ъ Х2, Со) в первые два ОДУ
системы (8.7), получим систему двух ОДУ
^ , ж2, Со)); -^ = /2(хь ж2> <р(хих2, Со)).
Решение xi(t,Co), ^2(t,Co) задачи Коши для полученной
системы позволяет представить решение задачи Коши для
исходной системы (8.7) в следующем виде:
Таким образом, при помощи первого интеграла порядок систе-
системы (8.7) удается понизить на единицу.
Формально такой способ понижения порядка можно распро-
распространить и на систему (8.1) произвольного порядка п. Если
известен первый интеграл системы (8.1), то он позволяет све-
свести ее к системе (п — 1)-го порядка.
8.4. Симметричная форма записи
нормальной автономной системы
дифференциальных уравнений
Перейдем от векторной формы нормальной автономной си-
системы (8.1) обыкновенных дифференциальных уравнений (ОДУ)
к записи в координатной форме вида A.3):
Если теперь представить каждое из ОДУ (8.8) в виде
fi(xu ..., хп)

232 8. ПЕРВЫЕ ИНТЕГРАЛЫ
и приравнять правые части этих соотношений для всех значе-
значений г, то придем к так называемой симметричной форме
записи системы ОДУ
dxi dx2 dxn (8g)
/i(rri,...,xn) /2(^1,..., xn) '¦' fn(
Симметричная форма записи удобна для нахождения первых
интегралов исходной системы ОДУ. При этом часто использу-
используют свойство равных дробей: если а^, bj, г = 1, п, таковы,
что ai/&i = 02/62 = ... = an/bn, то имеет место равенство
CL\ 0,2 Q>n X\Cb\ + A2U2 "Ь • • • "
bi-fc—-Ь>-^ ¦*¦¦ • ¦-' (8Л0)
где AiEM (г = 1,п).
Пример, а. Систему ОДУ
dx\ dx2
dt dt dt
запишем в симметричной форме:
(8.11)
Из первого равенства имеем dx\jx\ = dx2/x2- Интегрируя,
получаем х\/х2 = Ci, где С\ — произвольная постоянная.
Для нахождения другого первого интеграла используем
свойство (8.10) равных дробей, предварительно умножив чи-
числитель и знаменатель первой дроби в (8.11) на Х2, а второй —
на х\. Тогда, положив в (8.10) Ai = A2 = 1, запишем
Х2 dx\ Х\ dX2 Х2 dx\
или
d(xix2)
Отсюда после сокращения на xi^2 интегрированием находим
+х\ = С2, где С2 — также произвольная постоянная.

8.4. Симметричная форма записи системы ОДУ 233
Итак, два первых интеграла исходной системы таковы:
б. Симметричная форма системы ОДУ
dx\ . dx2 9 9 9
имеет вид
dx2 _ dx3
10. X.L)
— ТулТу
2х\х2 x^ — xf — х\
Приравнивая левую и правую части (8.12), после интегрирова-
интегрирования получаем х\ = С3Х3. Затем, умножив числители и знамена-
знаменатели дробей в (8.12) соответственно на 2rci, x2, 2жз, запишем
— х\ —
В силу свойства (8.10) равных дробей при Ai = A2 = A3 = 1
находим
2d 2x2 dx2
2х2(х\
или после сокращения на 2х2
d{x\ + х\
х\ \ \ $
Интегрирование этого выражения дает х\ + х\ + х\ = С4Ж3.
Таким образом, исходная система ОДУ имеет два первых
интеграла
?i х\±4±4 #
Семейство фазовых траекторий нормальной автономной
системы третьего порядка вида (8.7) можно найти без интегри-
интегрирования ОДУ этой системы, если известны два ее независимых
первых интеграла и\(х\,х2,хз) и и2(х\,х2,хз). Действитель-
Действительно, рассмотрим поверхности, задаваемые уравнениями
u\{xi, х2, хз) = Си и2(хи х2, хз) = С2, (8.13)

234 8. ПЕРВЫЕ ИНТЕГРАЛЫ
где С\ и С2 — произвольные постоянные. Если для любой
точки (ж5,Ж25жз) в области JD, где определены первые ин-
интегралы системы, из (8.13) вычислить значения постоянных
С® = и\{х\, #2, #3), С2 = и2{х\, #2» жз)> т0 система уравнений
щ(хи х2, х3) = С°, и2{хи х2, х3) = С° (8.14)
будет задавать фазовую траекторию, проходящую через эту
точку. В самом деле, вдоль фазовой траектории, проходя-
проходящей через точку (х^х^ #j$), первые интегралы постоянны.
Следовательно, фазовая траектория должна находиться на по-
поверхностях уровня первых интегралов, которые описываются
уравнениями (8.14). Однако для нахождения движения по фазо-
фазовой траектории необходимо интегрировать одно из уравнений
системы (8.7). Например, разрешив систему уравнений (8.14)
относительно х2 и хз и подставив в первое уравнение си-
системы (8.7), получим ОДУ первого порядка с разделяющимися
переменными.
Вопросы и задачи
8.1. Найти первые интегралы и, понизив порядок системы
ОДУ, найти ее решение:
. dx\ _ 1 dx2 _ 1 v dx\ __ х\ dx2 __
ч dx\ dx2 dx$ ч dx\ dx2
B) тп—- = — = —; r) 3—3 - —
д)
e)
2X2-Жз ^2 ЯЗ Щ-Щ Х3 Х2
dx\ dx2
(^3 ""^2) ^2(^2 — ^1) Ж
dx\ dx2
ч dxi dx2
ж)
~~ xl ^1+^2 + X3 X\ —
dx2

9. ЭЛЕМЕНТЫ ТЕОРИИ
УСТОЙЧИВОСТИ
9.1. Основные определения и понятия
Возникновение математической теории устойчивости дви-
движения связано с именем гениального русского математика
и механика Александра Михайловича Ляпунова A857-1918).
Основы этой теории были разработаны A.M. Ляпуновым более
100 лет назад, когда им было опубликовано знаменитое сочине-
сочинение „Общая задача об устойчивости движения" A892). Однако
лишь с начала 30-х годов теория устойчивости получила интен-
интенсивное развитие. Частично это объяснимо бурным развитием
в эти годы науки и техники, которые ставили новые, ранее
не известные задачи. К настоящему времени теория устой-
устойчивости по Ляпунову является общепринятой и применяется
во многих областях естествознания. Например, в механике ее
используют при анализе устойчивости полета снаряда, стабили-
стабилизации движения спутника, устойчивости механических систем
с вращающимися массами (роторами), движения твердых тел
с упругими элементами и полостями, содержащими жидкость,
и т.д. В последнее время теорию устойчивости начали приме-
применять также при решении задач химической кинетики, экологии,
экономики и др.
Дадим основные понятия и определения, а также приведем
примеры использования этой теории.
Рассмотрим нормальную систему обыкновенных дифферен-
дифференциальных уравнений (ОДУ), записанную в векторной форме
вида A.4):
где t — время; у = (уь ...,уп)т; / = (/ь ••, /п)т.

236 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Естественным предположением относительно системы (9.1),
является требование существования и единственности ее реше-
решения. Теорема 4.1 Коши гарантирует это на некотором отрезке
[to — /i, to + h], 0 < h < oo. В определениях, сформулированных
ниже, предполагается, что решение этой системы определено
при любом t ^ to? т.е. решение может быть продолжено на весь
промежуток [to, +оо). Однако всех условий в теореме Коши,
вообще говоря, не достаточно для того, чтобы решение систе-
системы (9.1) было определено во всем этом промежутке. Приведем
формулировки двух теорем, в которых гарантирована опреде-
определенность решений системы (9.1) для любого t Е Ш.
Теорема 9.1. Пусть функции /* (х = 1,п) определены
и непрерывны при t Е R, у ЕШп. Тогда, если функции fi
(i = 1, п) обладают свойством
то решения системы (9.1) определены при любом t E К. #
Напомним, что свойство /j(t, у) = O(w) при гу —> сю озна-
означает существование ненулевого конечного предела
w
Обозначим
г = \\y\\ =
Теорема 9.2. Если существует непрерывная при г ^ О
функция L(r), такая, что несобственный интеграл I является
расходящимся, a |/j| < L(r) (i = 1, п), то решения системы (9.1)
определены при любом t E Ш. #

9.1. Основные определения и понятия
237
Например, для линейной системы dy/dt = A(t)y условия
обеих теорем будут выполнены, если предположить, что элемен-
элементы матрицы A(t) являются непрерывными и ограниченными
функциями t. В дальнейшем будем предполагать, что для си-
системы (9.1) выполнены условия одной из этих теорем.
Определение 9.1, Решение y*{t) = g{t) системы (9.1),
определенное при t ^ to> называют устойчивым по Ляпу-
нов у, если для любого достаточно малого е > О существует
такое число S = J(e, to) > 05 что все решения y(t) этой систе-
системы, удовлетворяющие условию \\y{to) — g{to)\\ < S, определены
при t ^ to и для них выполнено неравенство
\\y(t)-g(t)\\<e, t>t0.
(9.2)
Определению 9.1 можно дать следующую геометрическую
интерпретацию: решение y^{t) —g{t) системы (9.1) устойчи-
устойчиво по Ляпунову, если график
функции y{t) = ||y(t)||, соот-
соответствующий любому решению
y(t) этой системы, достаточ-
достаточно близкому к y*(t) при t =
= to, целиком заключен в сколь
угодно узкой полосе шириной
2б, построенной вдоль графи-
графика функции g(t) = ||flf(t)|| (на
рис. 9.1 такая полоса заштри-
хована).
Определение 9.2. Решение y*(t)=g(t) системы (9.1) на-
называют асимптотически устойчивым, если оно устойчиво
по Ляпунову и, кроме того, при \\y(to) — ff(to)|| <5(e,to) выпол-
выполнено условие
tKmJy(t)-g(t)\\=0. (9.3)
Дополнительное условие означает, что любые решения си-
системы (9.1), мало отклоняющиеся от g(t) в начальный момент
времени to, с ростом t неограниченно приближаются к g(t).
Рис. 9.1

238 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Определение 9.3. Решение y+{t) = g(t) системы (9.1)
называют неустойчивым по Ляпунову, если для некоторых
е > О и to и любого 8 > О существуют решение у = G(t) этой
системы и момент времени t\ = *i((J, e) > to, такие, что
Геометрически это означает, что если решение g(t) систе-
системы (9.1) неустойчиво по Ляпунову, то среди всех решений этой
системы найдется хотя бы одно даже достаточно близкое при
* = *о к g(t) решение, которое в момент времени t\>to пере-
пересечет стенку трубки (см. рис. 9.1) с выбранным фиксированным
радиусом е и выйдет за ее пределы.
Пример. Частным решением ОДУ dy/dt = ку (к = const),
удовлетворяющим начальному условию y(to) == Уо = 0> будет
тривиальное решение y*(t) = #(*) =0 Vt G К. Если же уо Ф 0,
то решением этого ОДУ будет y(t) = уоек(г~~г°\
При А: < 0 решение ^(t) = 0 будет, согласно определе-
определению 9.1, устойчивым по Ляпунову, так как при t^to и |уо| <
Отметим, что в данном случае значение 8 зависит лишь от
выбранного значения е и не зависит от to.
Если к < 0, то
lim |yo|e*(*-*o)=0,
и в силу определения 9.2 решение g(t) = 0 асимптотически
устойчиво.
При к > 0 для некоторого фиксированного значения е > 0
и любого 8, 0 < 8 < 2е, можно указать такой момент времени
1 2е
h tzto + -\n-j >t0,
что при 8/2 ^ |уо| < 8 рря решения y(t) = уое*^~*°^ будет
выполнено неравенство |y(ti)| ^ е. В самом деле,
\ • Ц = е.

9.1. Основные определения и понятия 239
Таким образом, при А: > 0 решение g(t) = 0 рассматриваемого
ОДУ, согласно определению 9.3, будет неустойчивым по Ляпу-
Ляпунову. #
Для исследования устойчивости решения ym(t) = g(t) систе-
системы (9.1), которое имеет координатные функции <7i(?),..., <7п(*)>
целесообразно преобразовать ОДУ этой системы к новым
переменным х\(t) = у\(t) -g\(?),..., xn(t) = yn(t) -gn{t), являю-
являющимся координатными функциями векторной функции x(t) =
= (xi(?),..., xn(t)) . Такое преобразование равносильно замене
в (9.1)
y(t) = x(t) + g(t). (9.4)
Подставляя (9.4) в (9.1) и учитывая, что у» =g(i) — решение
системы (9.1), получаем
Обозначая F(t, х) = /(?, х+g{t)) — /(<, #(?)), окончательно име-
имеем
^=F{t,x). (9.5)
Входящие в нормальную систему (9.5) ОДУ называют урав-
уравнениями возмущенного движения. Они имеют очевид-
очевидное решение ж*(?) = 0. Решение y*(t) = g(i) системы (9.1),
устойчивость которого подлежит анализу, называют невозму-
щенным движением, а переменные х\,...,хп — возмуще-
возмущениями.
Отметим, что устойчивость по Ляпунову решения y*(t) =
= g(t) системы (9.1) равносильна устойчивости решения
x*(i) = 0 уравнений возмущенного движения. Составление
уравнений возмущенного движения — первый этап при анализе
устойчивости невозмущенного движения.

240 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Пример. Нормальная система второго порядка
dy\
—гг = -2/1 + sint + cost;
Т" = 2/12/2 — 2/1 cost — у2 sin t + sint -cost — sint
at
имеет решение yi{t) = sint, 2/2(*) = cost. Примем его за
невозмущенное движение
y,(t) = (yi(t), y2(t))T = (sint, cost)T.
Сделав в исходной системе замену переменных у\ = х\ +sint,
2/2 = a;2 + cost, получим, согласно (9.4) и (9.5), систему уравне-
уравнений возмущенного движения
dx\
Пример 9.1. Движение математического маятника длиной
/ в однородном поле сил тяжести при постоянном значении
ускорения д свободного падения описывает ОДУ второго
порядка
d? a
s
где <р — угол отклонения маятника от вертикали.
Запишем уравнение движения в виде системы (9.1), обозна-
обозначив (р = у\:
$ f ,9.7)
Эта система имеет решения
y 0; (9.8)
(9.9)

9.2. Устойчивость системы линейных ОДУ 241
Если за невозмущенное движение принять решение (9.8), то
уравнениями возмущенного движения являются сами уравнения
движения (9.7).
Если же за невозмущенное движение принять решение (9.9),
то после замены переменных у\ = х\ + тг, у2 = #2 получаем
(с учетом равенства sin(a;i + 7г) = — sin^i) уравнения возму-
возмущенного движения
dx\
X
9.2, Устойчивость системы линейных
дифференциальных уравнений
Рассмотрим нормальную неоднородную систему
^ f1(t) (9.10)
из п линейных обыкновенных дифференциальных уравнений
(ОДУ) с переменными коэффициентами и соответствующую ей
однородную систему ОДУ
-? = A(t)x. (9.11)
Будем предполагать, что элементы матрицы A(t) размера п
и вектор-функция fi{t) непрерывны при любом t ^ to.
Определение 9.4. Нормальную неоднородную систе-
систему (9.10) линейных ОДУ с переменными коэффициен-
коэффициентами называют устойчивой (неустойчивой), если все ее
решения y(t) устойчивы (неустойчивы) по Ляпунову.
Определение 9.5. Нормальную неоднородную систе-
систему (9.10) линейных ОДУ с переменными коэффициента-
коэффициентами называют асимптотически устойчивой, если все ее
решения y(t) асимптотически устойчивы.

242 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Замечание 9.1. Поскольку нормальная однородная система
(9.11) линейных ОДУ является частным случаем неоднородной
системы (9.10), то определения 9.4 и 9.5 применимы и в этом
частном случае.
Теорема 9.3. Для устойчивости нормальной неоднородной
системы (9.10) линейных ОДУ с переменными коэффициентами
необходимо и достаточно, чтобы было устойчивым тривиаль-
тривиальное решение ж* = О соответствующей ей однородной системы
(9.11).
Ч Сначала докажем необходимость. Согласно определению 9.4,
если система (9.10) устойчива, то все ее решения устойчивы
по Ляпунову. Пусть y*{t) = g(t) — одно из таких решений.
В силу определения 9.1 это означает, что для каждого е > 0
существует 6 > 0, такое, что для любого другого решения
y(t) системы (9.10) справедливо при t ^ <о неравенство (9.2)
\\y(t) -g(t)\\ < е, если только ||у(«о) -&(*о)|| < <*• Но в соот-
соответствии с теоремой 5.2 разность y(t) — g(t) = x(t) является
решением однородной системы (9.11), и предпоследнее нера-
неравенство эквивалентно неравенству ||ж(?)|| < е при t ^ to, если
только ||ж(?о)|| < S. А это и означает, согласно определению 9.1,
устойчивость тривиального решения x*(t) = 0 однородной си-
системы (9.11).
Докажем теперь достаточность условия теоремы. Пусть
тривиальное решение x*(t) = 0 однородной системы (9.11)
устойчиво по Ляпунову. Тогда в силу определения 9.1 для лю-
любого е > 0 существует такое S > 0, что для любого решения
x(t) этой системы при ||ж(?о)|| <^ справедливо неравенство
||ж(<)|| < е Vf ^ ?о- Следовательно, если y*(t) = g(t) — некото-
некоторое решение неоднородной системы (9.10), a y(t) — произволь-
произвольное решение этой системы, такое, что y(t) = x(t) +g{t), то из
неравенства ||аз(<о)|| = ||у(^о) — ff(*o)|| < 8 будет вытекать нера-
неравенство \\y(t) — g{t)\\ < е Уг ^ to. Это означает,, что решение
y+(t) =ff(t) устойчиво и в силу определения 9.4 неоднородная
система (9.10) устойчива. >

9.2. Устойчивость системы линейных ОДУ 243
Замечание 9.2. Теорема 9.3 устанавливает критерий устой-
устойчивости нормальной неоднородной системы (9.10) для любой
непрерывной при t^to вектор-функции /i(t). Поскольку при
fi(t) = О Vt ^ to система (9.10) переходит в соответствующую
ей однородную, то этот критерий справедлив и для системы
(9.11). Аналогичный критерий имеет место и для асимптоти-
асимптотической устойчивости таких систем: для этого необходимо и
достаточно, чтобы тривиальное решение x*(t) = 0 однородной
системы было асимптотически устойчивым. #
Таким образом, при исследовании устойчивости любой нор-
нормальной неоднородной системы линейных ОДУ достаточно
рассматривать лишь соответствующую ей однородную систе-
систему. Однако анализ решений однородной системы вида (9.11) с
точки зрения их устойчивости по Ляпунову и асимптотической
устойчивости является при произвольной матрице A(t) далеко
не простой задачей.
Ограничимся рассмотрением нормальной однородной си-
системы линейных ОДУ с постоянными коэффициентами
-А-, (9Л2)
где А = (o,ij) — матрица размера п с действительными
постоянными элементами ац = const, г, j = l,n. Для такой
системы справедлива следующая теорема.
Теорема 9.4. Для асимптотической устойчивости нормаль-
нормальной однородной системы (9.12) из п линейных ОДУ с посто-
постоянными коэффициентами необходимо и достаточно, чтобы лю-
любой из т различных корней Ai,...,Am характеристического
уравнения det(A — ХЕ) = 0 этой системы имел отрицательную
действительную часть, т.е.
T7m. (9.13)
< Докажем сначала достаточность условия теоремы. Пусть
для корней Ai,..., Am (m ^ п) характеристического уравнения
выполняется условие (9.13).

244 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Любое решение этой системы в общем случае кратных
(в том числе комплексно сопряженных) корней Xj = ay +ifij
(ay, /3j Е R, j = 1, m, i2 = —1) на основании теорем 5.11 и 5.12
и с учетом формулы Эйлера имеет вид
га
x(t) = $^ea''*(Pj(t) cosfyt + Qjit) sinfijt), (9.14)
i=i
где Pj(t), Qj(t) — вектор-функции, координатные функции
которых — многочлены степеней, меньших кратности qj
корня Aj, причем q\ + ... + q3; + ... + qm = п. Из (9.14) с учетом
неравенства треугольника имеем
Тогда
поскольку при условии (9.13) в виде ReAj = aj < 0 (j = I, m)
каждое слагаемое в правой части (9.15) стремится к нулю при
t -» оо. Таким образом, согласно определению 9.2, выполнение
условия (9.13) достаточно для асимптотической устойчивости
системы (9.12).
Условие (9.13) является также и необходимым. Предполо-
Предположим, что хотя бы один из корней \s = а + i /3 (a, E G R) ха-
характеристического уравнения имеет положительную действи-
действительную часть, т.е. ReA5 = a > 0. Тогда система (9.12) имеет
решение вида
x(t) = ea*(acos/ft+ bsin/ft), a, be Rn,
причем ||a|| + ||Ь|| ф 0. Отсюда следует, что ||ж(*)|| заведомо
не стремится к нулю при t -> +oo, что противоречит определе-
определению 9.2 асимптотической устойчивости тривиального решения
«*(*) = 0.

9.3. Теоремы Ляпунова об устойчивости по йервому приближению 245
Допустим теперь, что хотя бы один корень Xs = г/х (/х G К),
т.е. Re As = 0. Тогда система (9.12) имеет решение
x(t) = (acosfit + Ьsin/it), a, be Rn, ||а|| + ||6|| ф 0.
Как и в предыдущем случае, ||ж(?)|| не стремится к нулю при
t -> +oo, что также противоречит определению 9.2 асимптоти-
асимптотической устойчивости решения x*(t) = 0.
Этим доказана необходимость условия (9.13). >
9.3, Теоремы Ляпунова об устойчивости
по первому приближению
Рассмотрим случай, когда правые части п уравнений воз-
возмущенного движения, составляющих систему (9.5), не зависят
от времени ?, т.е.
^ = F(x), F@) = 0, (9.16)
причем векторная функция
F(x) = {Fl(x),...,Fi(x),...,Fn(x))T (9.17)
дважды непрерывно дифференцируема по фазовым перемен-
переменным xi,..., хп в некоторой окрестности точки х = @,..., 0)
фазового пространства Шп. В соответствии с условием диф-
ференцируемости функции F(x) представим ее в окрестности
точки х = @,..., 0) в виде
где Ах — линейная часть приращения функции (А — матрица
Якоби, элементы этой матрицы вычислены в точке х = 0), а
F*(x) представляет собой совокупность членов более высокого
порядка малости, т.е.
lim —[г—-— = 0.
IMI-ю ||ж||

246 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Тогда система (9.16) примет вид
dx
Ax + F*(x). (9.18)
at
Если в (9.18) отбросить слагаемые F*(x), то получим си-
систему (9.12), которую в данном случае называют системой
уравнений первого приближения. Приведем формулиров-
формулировки двух основных теорем, установленных A.M. Ляпуновым и
получивших название теорем Ляпунова об устойчивости по
первому приближению.
Теорема 9.5. Если все корни характеристического уравне-
уравнения det(A — ХЕ) = 0 системы уравнений первого приближения
(9.12) имеют отрицательные действительные части Re Л < 0, то
невозмущенное движение x*(t) = O асимптотически устойчи-
устойчиво, каковы бы ни были слагаемые F*(x) в (9.18). #
Теорема 9.6. Если среди корней характеристического
уравнения системы уравнений первого приближения (9.12) име-
имеется хотя бы один с положительной действительной частью, то
невозмущенное движение ж*(?) = 0 неустойчиво независимо от
вида слагаемых F*(as) в (9.18). #
При выполнении условий этих теорем анализ асимптотиче-
асимптотической устойчивости невозмущенного движения можно провести
по уравнениям первого приближения. Однако эти теоремы
оставляют невыясненными случаи, когда характеристическое
уравнение системы первого приближения, не имея корней с
положительными действительными частями, имеет корни с
действительными частями, равными нулю, т.е. когда корни
являются чисто мнимыми числами или равны нулю. Такие
случаи анализа устойчивости названы A.M. Ляпуновым
критическими в том смысле, что для них устойчивость и
неустойчивость не могут быть выяснены рассмотрением урав-
уравнений первого приближения. Исследование устойчивости в
критических случаях представляет собой сложную задачу. К

9.3. Теоремы Ляпунова об устойчивости по первому приближению 247
настоящему времени в решении этой проблемы достигнут боль-
большой прогресс, однако до полного завершения исследований еще
далеко.
Вернемся к теоремам 9.5 и 9.6 Ляпунова об устойчивости
по первому приближению. Характеристическое уравнение
det(A — \Е) = 0 можно привести к виду
ab...,ane:
(9.19)
Условия, при которых действительные части корней характери-
характеристического уравнения (9.19) отрицательны, выражает следую-
следующая теорема, названная по имени английского математика и
физика Э. Рауса A831-1907) и немецкого математика А. Гур-
вица A859-1919).
Теорема 9.7 (теорема Рауса — Гурвица). Действи-
Действительные части всех корней уравнения (9.19) отрицательны то-
тогда и только тогда, когда положительны все главные диаго-
диагональные миноры матрицы Гурвица
i 1 0 0 0 0 ... 0 \
з a2 ai 1 0 0 ... 0
5 fl4 fl3 fl2 al 1 ••• 0
V о о о о о о ...
т.е. когда
Дх = ох > 0;
аз
1
о2
a5
1
а4
«3
# (9.20)
Условия (9.20) называют условиями Рауса — Гурвица.
Квадратная матрица Гурвица размера п построена так.
На ее главной диагонали стоят по порядку п коэффициен-
коэффициентов ai,..., ап характеристического уравнения (9.19); в каждой

248 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
строке при движении влево от диагонального элемента номер
т коэффициента ат последовательно возрастает на единицу,
причем если га > п, то ат = 0, а при движении вправо от диа-
диагонального элемента этот номер последовательно уменьшается
на единицу, причем если га = 0, то clq = 1, и если га < 0, то
Пример. Для характеристического уравнения второй сте-
степени А2 + а\Х + 0,2 = 0 условия Рауса — Гурвица имеют вид:
Ai=ai>0; Д2 =
аг
О а2
или а\ > О, п2 > 0. #
> 0,
В качестве иллюстрации теорем Ляпунова об устойчивости
по первому приближению рассмотрим ряд примеров.
Пример, а. Исследуем устойчивость тривиального реше-
решения x\{t) = X2{t) = 0 системы уравнений возмущенного движе-
движения
dx\ t ч dx2 2
4sina; + ln(l + х); х + Х + х
L ,-1пA + ж2); ~-rr=xi+x2'
at at
Составим уравнения первого приближения
dx\
~df'
и соответствующее им характеристическое уравнение
4~А * =0, или А2-5А + 3 = 0.
1 — Л
Корни этого уравнения Ai^ > 0. На основании теоремы 9.6
невозмущенное движение x\(t) = X2(t) = 0 неустойчиво.

9.3. Теоремы Ляпунова об устойчивости по первому приближению 249
б. Нормальная система обыкновенных дифференциальных
уравнений (ОДУ)
= -sin(xi
at
7^ = sinx3 а?2 sina^; (9-21)
at
dxi
at
очевидно, имеет тривиальное решение x\(t) = X2(t) = #з(?) = 0.
Запишем систему уравнений первого приближения
dx\
at at at
характеристическое уравнение которой A3 + ЗА2 + 4A + 2 = О
имеет корни Ai = —1, Аг,з = —1 ±t. Действительные части
всех корней отрицательны, т.е. Re Xj < О, j = 1, 2,3. В силу
теоремы 9.5 невозмущенное движение x\(t) = X2(t) = #з(*) = О
асимптотически устойчиво.
Пример 9.2. Три электрических заряда А, В и С величи-
величиной 4g, 4q и —g соответственно расположены как показано
на рис. 9.2. Заряды А и В занимают фиксированное поло-
положение на оси Ох, а заряд С
может перемещаться вдоль этой
оси, и его положение характери-
характеризует координата х. Найти поло- А ОС В
жение х* равновесия заряда С
Риг О 1
и исследовать это положение на
устойчивость.
Полная энергия взаимодействия зарядов, определяемая на
основе закона Кулона,
м
• 
r0 -

250 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Согласно второму закону Ньютона, уравнение движения заряда
С, масса которого принята равной единице, запишем в виде
d?x dU d?x ло 2 х
или 1б
dt2 dx dt2 (rg-z2J
Обозначим х\ = ж, Х2 = dx/dt и приведем ОДУ второго
порядка к нормальной системе:
Эта система имеет тривиальное решение x\(t) = х2(t) = 0,
соответствующее ее положению равновесия, которое, в свою
очередь, отвечает положению равновесия заряда С в начале
координат (см. рис. 9.2) на одинаковом расстоянии от зарядов
А и В. Отметим, что x2(t) = О означает, что в положении
равновесия {х\ = 0) скорость х2 = dx/dt заряда С равна
нулю.
Исследуем устойчивость положения равновесия системы,
приняв указанное тривиальное решение за невозмущенное дви-
движение. Тогда система (9.22) будет состоять из уравнений
возмущенного движения, а система уравнений первого прибли-
приближения примет вид
dx\ dx2 ^q2
Характеристическое уравнение этой системы
щУ4 Л =0' MH a2-16^ = 0'
имеет положительный корень X = 4q/y/rQ. На основании те-
теоремы 9.6 Ляпунова об устойчивости по первому приближению
невозмущенное движение неустойчиво, т.е. неустойчиво най-
найденное положение ж* = 0 равновесия заряда С. #

9.4. Функции Ляпунова 251
Полученный в этой несложной задаче результат справед-
справедлив для любой системы электрических зарядов, в которой не
действуют никакие силы, кроме сил электрического взаимо-
взаимодействия. Неустойчивыми являются все статические модели
атомов, в которых ядра и электроны неподвижны. В связи
с этим для построения устойчивой модели атома была пред-
предложена „планетарная модель", в которой электроны движутся
вокруг ядер.
9,4. Функции Ляпунова. Теоремы Ляпунова об
устойчивости и асимптотической устойчивости
Для исследования устойчивости A.M. Ляпунов разработал
два метода. Первый метод Ляпунова основан на ин-
интегрировании системы уравнений возмущенного движения.
Второй, или прямой, метод Ляпунова не связан с возмож-
возможностью интегрирования этой системы, а приводит к отысканию
функций, обладающих определенными свойствами, и его часто
называют также методом функций Ляпунова. Изложим
основные понятия этого метода.
Пусть система из п уравнений возмущенного движения
имеет вид (9.16). Рассмотрим некоторую скалярную функцию
V(x) векторного аргумента х = (#i,..., хп) при условии
А < н = const > 0, (9.23)
считая в (9.16) время t^O. Будем полагать функцию V(x) не-
непрерывной вместе со своими частными производными
(i = 1, п) в области U, определяемой условием (9.23) и предста-
представляющей собой замкнутый шар радиуса у/Н в фазовом про-
пространстве Rn (центр шара находится в точке @, 0,..., 0)).
При х = 0 функция V(x) обращается в нуль: V@) = 0.
Наряду с функцией V(x) будем рассматривать ее полную
производную по t б силу системы (9.16) уравнений возмущен-

252 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
ного движения:
^ ^T. {),F(x)), x€U. (9.24)
Введем ряд определений.
Функцию V(x) называют знакоопределепной (опре-
(определенно-положительной или определенно-отрицательной), если
она во всей области U за исключением точки х = О принимает
значения одного знака (положительные или отрицательные),
Vxeu\{o}.
Функцию V(x) называют знакопостоянной (постоян-
(постоянно-положительной или постоянно-отрицательной), если она
принимает в области U значения одного знака, но может
обращаться в нуль и при х ф О, т.е. V(x) ^ 0 (V(x) ^ 0)
Например, функция V(x\, Х2) = х\ + 2х\ определенно-поло-
определенно-положительная, а У = [х\ —Х2J постоянно-положительная, так как
она обращается в нуль на всей прямой х\ = Х2-
Функцию V(x) называют знакопеременной, если она
в области U может принимать как положительные, так и
отрицательные значения.
Теорема 9.8 (теорема Ляпунова об устойчивости).
Если для системы уравнений возмущенного движения (9.16)
возможно найти знакоопределенную функцию V(x), полная
производная которой dV/dt в силу этой системы есть знако-
знакопостоянная функция противоположного с V знака или тожде-
тождественно равная нулю, то невозмущенное движение x*(t) = О
устойчиво. #
Пример. Рассмотрим систему уравнений возмущенного
движения
^ = х2 + Ъх\х\ - 4xf;

9.4. Функции Ляпунова 253
считал, что невозмущенное движение x\(t) = X2(t) = 0. В каче-
качестве функции V(x) примем определенно-положительную функ-
функцию V(x\, X2) = (х\ + Ж2)/2. Вычислим полную производную в
силу системы (9.25):
dV dx\ dxo
X+X
xi -xl + x\x2) = -Bx1 ~ xlJ < 0-
Функция dV/dt является постоянно-отрицательной. На осно-
основании теоремы 9.8 Ляпунова об устойчивости невозмущенное
движение x\(t) = X2{t) = 0 устойчиво.
Теорема 9.9 (теорема Ляпунова об асимптотической
устойчивости). Если для системы уравнений возмущенного
движения (9.16) возможно найти знакоопределенную функцию
V(x), полная производная которой dV/dt в силу этой системы
есть знакоопределенная функция со знаком, противоположным
знаку V, то невозмущенное движение x*(t) = 0 асимптотиче-
асимптотически устойчиво.
Пример. Рассмотрим систему уравнений возмущенного
движения
^ = 2x1-4; ^. = -Х1-4, (9.26)
имея в виду, что невозмущенное движение x\(t) = x2(t) = 0. В
качестве функции V(x) примем определенно-положительную
функцию V(xi,x2) = (xf+ ^2)/2 и вычислим полную произ-
производную в силу системы (9.26):
dV dx\ ft 3 dx2
x+2x
= xi{2x1 - xi) + 2ж2(~ж1 - xl) = "A - 2x\ < 0.
Таким образом, функция dV/dt является определенно-отрица-
определенно-отрицательной, т.е. ее знак противоположен знаку функции V(x\, x2).

254 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Поэтому на основании теоремы 9.9 Ляпунова об асимптотиче-
асимптотической устойчивости невозмущенное движение xi(t) = #2(*) = О
является асимптотически устойчивым. #
Удовлетворяющие условиям теорем 9.8 и 9.9 функции V(x)
называют функциями Ляпунова.
9.5. Теоремы Четаева
и Ляпунова о неустойчивости
Пусть дана функция V(x), xGU, где U — область, опре-
определяемая условием (9.23). Совокупность значений переменных
х = (#i,...,хп) из области U, удовлетворяющая неравенству
V(x) > О, называют областью V > О, а поверхность V(x) = О —
границей области V > 0.
Функцию W(x) называют определенно-положительной в
области V > 0, если во всех точках этой области она поло-
положительна и в нуль может обратиться только на границе этой
области или вне ее.
Теорема 9.10 (теорема Четаева). Бели система уравне-
уравнений возмущенного движения (9.16) такова, что возможно найти
функцию V(x), для которой существует область V > 0, и ес-
если полная производная dV/dt в силу этой системы является
определенно-положительной в области V > 0, то невозмущен-
невозмущенное движение х = 0 неустойчиво.
Функции, удовлетворяющие условию теоремы 9.10, называ-
называют функциями Четаева — по имени отечественного мате-
математика и механика Н.Г. Четаева A902-1959).
Пример. Покажем, что невозмущенное движение x\(t) =
= X2(t) = 0, соответствующее системе уравнений возмущенного
движения
-^ = х\ + 2*1*1; -|г = *1*2, (9.27)
неустойчиво.

V>0
9.5. Теоремы Четаева и Ляпунова о неустойчивости 255
Рассмотрим функцию V(x\,X2) = х\ — х\. Полная произ-
производная в силу системы (9.27) будет равна dV/dt = xf. Область
V > 0 можно задать неравенством х\ >
> #2 (рис. 9.3). В этой области функция 2
dV/dt определенно-положительна. Та-
Таким образом, выполнены условия теоре- Q
мы 9.10 Четаева, т.е. выбранная функция
V(x\,X2) является функцией Четаева,
невозмущенное движение x\{t) = X2(t) =
Рис 9 3
= 0 неустойчиво. #
Теорема Четаева о неустойчивости является обобщением
двух теорем о неустойчивости движения, доказанных A.M. Ля-
Ляпуновым. Приведем формулировку одной из них.
Теорема 9.11 (первая теорема Ляпунова о неустойчи-
неустойчивости). Если система (9.16) уравнений возмущенного движе-
движения такова, что существует функция V(x), полная производная
которой dV/dt в силу этой системы является знакоопределен-
ной, а сама функция V(x) в окрестности точки х = 0 может
принимать значения одного знака с функцией dV/dt, то невоз-
невозмущенное движение x(t) = 0 неустойчиво.
Обобщение Н.Г. Четаева заключается в том, что он ослабил
условия, налагаемые на функцию dV/dt: требуется только
определенная положительность в области V > 0, в то время
как в теореме 9.11 требуется знакоопределенность во всей
окрестности точки х = 0.
Пример. Покажем, что невозмущенное движение x\(t) =
= X2{t) = 0, соответствующее системе уравнений возмущенного
движения
-^ = ххх\ + х\х2 + х\\ ^ = х\ - х\, (9.28)
неустойчиво.

256 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
Рассмотрим функцию V = {х\ + х^)J. Ее полная произ-
производная в силу системы (9.28) будет dV/dt = х\х\ + х\ + Х2>0.
Следовательно, выполнены все условия теоремы 9.11 и невозму-
невозмущенное движение x\(t) = X2(t) = 0 неустойчиво. #
В заключение отметим, что применение прямого метода Ля-
Ляпунова основано на использовании функции V(x), однако к
настоящему времени не известен общий способ построения фун-
функции Ляпунова, удовлетворяющей соответствующим теоремам.
Поэтому не следует пренебрегать имеющейся информацией об
исследуемой системе. Особенно полезны первые интегралы си-
системы, так как их можно использовать для отыскания функций
Ляпунова или для исключения части переменных и уменьшения
порядка системы.
Для нормальной однородной системы (9.12) линейных ОДУ
с постоянными коэффициентами функцию Ляпунова следует
искать в классе квадратичных форм: V(x) = хТВх, где матри-
матрица В является искомой. Полная производная в силу системы
(9.12) в таком случае будет
Потребуем теперь, чтобы квадратичная форма V(x) удовле-
удовлетворяла уравнению dV/dt = W, где W(x) = хтСх — заданная
квадратичная форма. Для нахождения матрицы В запишем
матричное уравнение
АТВ + ВА = С. (9.29)
Исследование уравнения (9.29) представляет большой инте-
интерес, поскольку оно позволяет по заданной полной производной
функции V(x) в силу системы (9.12) найти эту функцию в виде
квадратичной формы. Справедливо следующее утверждение:
если корни характеристического уравнения системы (9.12) та-
таковы, что Xj + \ьт?О ни при каких j, k = 1, п, то, какова бы
ни была наперед заданная квадратичная форма W(x) = xTCx,
существует единственная квадратичная форма V(x) = xTBx,

Д.9.1. Библиографический комментарии 257
удовлетворяющая уравнению dV/dt = W. Заметим, что если
все Re Aj < 0, j = 1, п, то условие \j + A& ^ 0 будет заведомо
выполнено.
Дополнение 9.1. Библиографический
комментарий
В этой главе даны лишь основные сведения о теории устой-
устойчивости: приведены основные определения, понятия и форму-
формулировки основных теорем. Поэтому ее можно рассматривать
как вводную. Читателю, который хотел бы более углубленно
ознакомиться с этой теорией, рекомендуем следующие книги.
В качестве учебного пособия для первоначального знаком-
знакомства хороша книга Д.Р. Меркина. В этой книге акцент сде-
сделан на прикладной характер теории устойчивости: разобрано
большое количество прикладных задач из различных областей
естествознания. В ней читатель найдет доказательства теорем
9.8 — 9.11. В книге Б.П. Демидовича систематически изложе-
изложены основы теории устойчивости решений ОДУ. Упор сделан на
математическую сторону вопроса, следствием чего являются
точность формулировок и строгость доказательств. Приложе-
Приложения теории затронуты весьма незначительно. В этой книге
читатель найдет доказательства теорем 9.5 — 9.7.
Наряду с указанной учебной литературой имеется ряд пре-
прекрасных книг монографического характера. В первую очередь
сюда можно отнести книгу Н.Г. Четаева. Однако чтение этой
книги требует от читателя определенной подготовки. В ней,
в частности, изложены основные критические случаи, исследо-
исследованные A.M. Ляпуновым: пара чисто мнимых корней и один
нулевой корень у характеристического уравнения. Детальный
анализ ряда других критических случаев читатель найдет в
книге И.Г. Малкина. И та, и другая книги содержат решения
многих прикладных задач.
Обобщению классических теорем Ляпунова и Четаева, а
также проблеме существования функций Ляпунова посвящена
книга В.В. Румянцева и А.С. Озиранера. В ней также излага-
9 — 9306

258 9. ЭЛЕМЕНТЫ ТЕОРИИ УСТОЙЧИВОСТИ
ется материал по применению дифференциальных неравенств
в теории устойчивости. Теория иллюстрируется примерами из
механики и примерами математического характера.
Вопросы и задачи
9.1. Используя теоремы Ляпунова об устойчивости по пер-
первому приближению, исследовать на устойчивость невозмущен-
невозмущенное движение x\(t) = X2(t) = О, соответствующее следующим
системам уравнений возмущенного движения:
б)
dt
( dx\ _ о 2
в)
Лъ(\ + х\х2)-Ъх\ + х\.
9.2. Построением функций Ляпунова показать, что асимп-
асимптотически устойчиво невозмущенное движение x\(t) = X2(t) =
= 0, соответствующее следующим системам уравнений возму-
возмущенного движения:
а) { Ц ' Xl Xl Ж181ПЖ2' б) ' dt
9.3. Построением функций Ляпунова показать, что невоз-
невозмущенное движение x\(t) = X2(t) = 0, соответствующее системе
уравнений возмущенного движения
—- = -бж^г; -? = -Щ
at at
устойчиво (в данном случае функцию Ляпунова следует искать
в виде многочлена от фазовых переменных х\ и

10. ОСОБЫЕ ТОЧКИ
НА ФАЗОВОЙ ПЛОСКОСТИ
10.1. Фазовый портрет системы
Рассмотрим нормальную автономную систему, состоящую
из двух обыкновенных дифференциальных уравнений (ОДУ)
—^ = Р(хъ х2);
dl2
-f = Q(xi,x2).
Здесь P, Q — функции, непрерывно дифференцируемые в
некоторой области D изменения фазовых переменных х\ и
Х2\ t — время.
Системе A0.1) присущи три типа фазовых траекторий на
фазовой плоскости xiOx2i точка, замкнутая кривая и неза-
незамкнутая кривая. Точкам соответствуют положения равновесия
системы, т.е. такие решения системы, при которых фазовые
переменные х\,Х2 не изменяются во времени ?, т.е. x\{t) =
= х\, X2(t) = х\, xv X2 = cons^- Замкнутые кривые на фазовой
плоскости изображают решения, описываемые периодическими
функциями x\(t) =xx(t + Ti), X2(t) = X2(t + T2) с периодами Т\
и Тг соответственно, удовлетворяющими условию raTi= пТ2,
m, n G N. Такие решения называют периодическими. Не-
Незамкнутые кривые на фазовой плоскости изображают решения
системы A0.1), которые не являются периодическими.
Основная задача при качественном исследовании системы
A0.1) — установление структуры разбиения фазовой плоско-
плоскости на траектории. Картина, которую образуют фазовые

260 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
траектории на плоскости xiOx2, носит название фазового
портрета системы A0.1). Каждая из фазовых траекторий
является годографом вектора
x(t) = (xl(t),x2(t))T A0.2)
решения системы A0.1), если начало этого вектора зафиксиро-
зафиксировать в начале системы координат Ох\х2 на фазовой плоско-
плоскости, т.е. считать A0.2) радиус-вектором. При таком условии
x(t) называют фазовым вектором.
Обратимся к случаю, когда A0.1) является однородной
системой линейных ОДУ с постоянными коэффициентами:
dx\
—- = anxi+ai2X2;
f A0.3)
dX2
¦— =a2\Xi+U22X2'
at
Если пцп22 — a>viQ>2\ Ф 0, то система A0.3) имеет единственное
положение равновесия в начале координат, т.е.
Xl = Х2 = 0. A0.4)
Этой точке фазовой плоскости отвечает тривиальное решение
системы A0.3) x*(t) = 0, которое можно рассматривать как
невозмущенное движение.
Замечание 10.1. Часто понятия устойчивости и асимпто-
асимптотической устойчивости системы, введенные определениями 9.4
и 9.5, переносят на невозмущенное движение и непосредствен-
непосредственно на соответствующее ему положение равновесия системы и
говорят об устойчивости или асимптотической устойчивости
положения равновесия. #
Характер поведения фазовых траекторий системы A0.3) на
фазовой плоскости xi 0x2 определяют корни Х\ и Л2 харак-

10.1. Фазовый портрет системы 261
теристического уравнения
ац — Л а\2
«21 «22 ~"'
A0.5)
Эти корни могут быть либо действительными (Ai,A2ER),
причем простыми (\\ ф А2) или кратными (Ai = A2), либо
комплексно сопряженными (А^АгЕС, A2 = Ai). Рассмотрим
каждый из этих случаев.
1. Корни действительные простые. В этом случае
общее решение системы A0.3) в векторной форме имеет вид
x(t) = (xi(t), x2(t))T = CleXltal+C2eX2ta2, A0.6)
где С\ и C2 — постоянные; а\ и а2 — собственные векторы
матрицы системы ОДУ. Векторы а\ и а2 линейно незави-
независимы, поскольку отвечают различным собственным значениям
Ai и А2 этой матрицы и, следовательно, образуют базис на
фазовой плоскости. Тогда
Ш = Схем, Ш = С2ех* A0.7)
являются координатными функциями вектор-функции x(t) в
этом базисе.
В общем случае направления векторов а\ и а2 не совпада-
совпадают с направлениями координатных осей Ох\ и 0x2 и система
координат O?i?2> вообще говоря, не является прямоугольной.
Однако для наглядности удобно использовать переменные ?i,
?2 как прямоугольные координаты другой плоскости и изобра-
изображать поведение системы на этой плоскости в прямоугольной
системе координат O?i?2. В такой системе координат фазовую
траекторию в параметрической форме задают соотношения
A0.7), причем роль параметра играет время t. Если положение
точки на фазовой траектории характеризовать значением ?, то

262 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
при помощи A0.7) можно проследить за ее движением по фазо-
фазовой траектории, так что именно в этом смысле оправдано ис-
использование термина „траектория" (от латинского trajectus —
передвижение). В этом случае движущуюся точку называют
изображающей.
Ясно, что координаты х\,Х2 и ?i,?2 одной и той же точки
фазовой траектории связаны линейным преобразованием, кото-
которое несколько видоизменяет фазовый портрет при переходе от
одной системы координат к другой, но сохраняет его основные
особенности. Эти особенности существенно зависят от знаков
корней Ai и А2.
Рассмотрим возможные варианты.
а. Пусть Ai < 0, А2 < 0. Положим для определенности
Ai > A2.
Из A0.7) следует, что ?i -> 0 и & ->• 0 при t -> +оо, т.е.
изображающая точка по любой фазовой траектории стремит-
стремится к началу координат, но начало координат формально при-
принадлежит лишь одной фазовой траектории (при С\ = С2 = 0),
которая вырождается в точку и соответствует положению рав-
равновесия A0.4). Если С\ ф0, С2 = 0, то, согласно A0.6) и A0.7),
в системе координат O?i?2 фазовая траектория — полуось оси
O?i (sgn?i = sgnCi), а если С\ =0, С2 Ф 0, то фазовая траек-
траектория — полуось оси О?2 (sgn^2 = sgnC2).
Любой фазовой траектории, задаваемой соотношениями
A0.7) в первом квадранте плоскости ?iOf2 при конкретных
значениях С\ > 0 и С2 > 0, отвечают еще три фазовые траек-
траектории: симметричная относительно оси O?i при смене знака
постоянной Сг, симметричная относительно оси О& при сме-
смене знака С\ и симметричная относительно начала координат
при смене знаков С\ и С2 одновременно. Следовательно, что-
чтобы представить фазовый портрет системы A0.3) в плоскости
?i0f2> достаточно построить ее фазовые траектории в первом
квадранте этой плоскости.

10.1. Фазовый портрет системы
263
Исключив при С\ > 0 и С2 > О из A0.7) время t, получим
?2 = c?f, где с = const и a = Л2/А1 > 1. Таким образом, фазовые
траектории в плоскости ?iO^2 имеют вид ветвей парабол.
Если к ним присоединить начало координат, то в нем они будут
иметь общую касательную — ось О?\.
Фазовый портрет в переменных ?i,?2 и х\,Х2 изображен
на рис. 10.1 и 10.2 соответственно.
Рис. 10.1
Рис. 10.2
При отрицательных значениях корней Ai и Аг в силу тео-
теоремы 9.4, определения 9.5 и замечания 9.1 линейная однородная
система ОДУ A0.3) асимптотически устойчива, так как все
решения этой системы, согласно определению 9.2, асимпто-
асимптотически устойчивы, что позволяет, согласно замечанию 10.1,
говорить в данном случае об асимптотической устойчивости
положения равновесия системы. На фазовой плоскости оно
отвечает началу координат, куда по каждой из фазовых тра-
траекторий стремится изображающая точка при t -> +00. В
данном случае положение равновесия называют устойчивым
узлом.

264 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
б. Пусть Ai > 0 и Л2 > 0, причем Ai < A2. В этом случае,
рассуждая аналогично случаю отрицательных корней, придем
к выводу, что фазовые траектории имеют ту же форму. Од-
Однако при t -> +00 движение изображающей точки по фазовой
траектории происходит от начала координат. Поэтому фазо-
фазовый портрет совпадает с изображенным на рис. 10.1 и 10.2, но
стрелки направлены в обратном направлении. Решение ж* (t) =
= 0 системы A0.3), а значит, и положение равновесия в нача-
начале координат при положительных корнях характеристического
уравнения будут в соответствии с теоремой 9.4 и определени-
определением 9.4 неустойчивыми по Ляпунову. В этом случае говорят,
что положение равновесия в начале координат, называемое не-
неустойчивым узлом, не является устойчивым.
в. Корни Ai и А2 имеют разные знаки. Пусть для опреде-
определенности Ai < 0, а Аг > 0. В случае С\ = 0, Сгф§ получим
6 =0, & = С2вЛ2* и & -> оо при t -* +00, т.е. фазовая траек-
траектория — полуось оси О& (sgn?2 = sgnC^), а движение изобра-
изображающей точки происходит от начала координат. Если С\Ф§
и <?2 = 0, то имеем ?2 = 0, fi = C\eXlt и ?1 -» 0 при t -> +00
(фазовая траектория — полуось оси <9?i (sgn?i = sgnCi), a
движение изображающей точки происходит к началу коорди-
координат). При С\ ф 0, С2ФО уравнение фазовой траектории, по-
полученное исключением из A0.7) времени t, будет ?2 = c?f > где
с = const и а = А2/А1 < 0, т.е. фазовые траектории имеют вид
гипербол, для которых оси О?\ и О?г являются соответствен-
соответственно горизонтальной и вертикальной асимптотами. Фазовый
портрет в переменных ?i,&2 и х\,Х2 изображен на рис. 10.3
и 10.4 соответственно.
Положение равновесия в начале координат, соответствую-
соответствующее невозмущенному движению x*(t) = 0, в этом случае назы-
называют седлом. Седлу соответствует невозмущенное движение
x(t) = 0, которое в силу определения 9.2 не будет асимптотиче-
асимптотически устойчивым решением системы A0.3). Поэтому, согласно
замечанию 10.1, седло не является асимптотически устойчивым
положением равновесия.

10.1. Фазовый портрет системы
265
Рис. 10.3
Рис. 10.4
г. Один из корней равен нулю (пусть для определенности
Ai ф О, а Л2 = 0). В этом случае из A0.7) имеем ^(^) = Сг =
= const. Это тождество задает в плоскости ?iO%2 семейство
прямолинейных фазовых траекторий, параллельных оси О?\.
Направление движения по ним изображающей точки зависит
от знака корня Ai. Если Ai < 0, то ?i —>• 0 при t -> +оо и
ее движение происходит в направлении к оси О&2- Если же
Ai > 0, то ?i -> оо при t —> +оо, и ее движение происходит в
противоположном направлении.
Из характеристического уравнения A0.5) следует, что один
из корней будет равен нулю при условии пцпю — ^12^21 = 0, т.е.
когда матрица А системы ОДУ A0.3), записанной в виде
dx
fan а\г\
V°2i а22/
A0.8)
является вырожденной. В этом случае однородная система
Ах = 0 линейных алгебраических уравнений (СЛАУ) имеет
бесконечное множество решений, которым в силу определе-
определения 8.2 положения равновесия системы ОДУ соответствует
бесконечное множество ее положений равновесия. Действи-
Действительно, всякая точка оси 0^2? т.е. прямой ?i = 0, является в

266 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
данном случае положением равновесия системы A0.8). Соот-
Соответствующие положениям равновесия решения системы A0.8)
и отвечающие им невозмущенные движения, согласно определе-
определениям 9.1 и 9.2, при Ai < 0 являются устойчивыми по Ляпунову,
но не будут асимптотически устойчивыми, а при Ai > 0 — не-
неустойчивыми по Ляпунову.
2. Корни действительные кратные. Обозначим Ai =
= А2 = А. В этом случае могут возникнуть два существенно
различных варианта в зависимости от значений коэффициентов
а\2 и a2i в правой части A0.3).
а. При а\2 = ^21 =: 0 система A0.3) является, по существу,
совокупностью двух независимых линейных однородных ОДУ
первого порядка с решениями
xi(t) = dean\ x2(t) = C2ea22t, A0.9)
причем ац = <*22 = ^ Тогда, исключив из A0.9) время ?, по-
получим уравнение С2Х1 — C\x<i — 0 пучка прямых в плоскости
xi 0X2, проходящих через начало координат, которое следует
рассматривать как положение равновесия A0.4) такой системы.
Каждая полупрямая, не содержащая начало координат, будет
фазовой траекторией, а изображающая точка будет прибли-
приближаться по ней к началу координат, если А < 0, и удаляться от
него, если А>0 (случай А = 0 рассмотрим особо). Фазовый
портрет для случая А < 0 изображен
на рис. 10.5.
Положение равновесия в начале ко-
координат называют дикритическим
узлом. Такое положение равновесия
в соответствии с замечанием 10.1 яв-
является асимптотически устойчивым
Рис. 10.5 при А < 0 и не будет устойчивым при
А>0.
Частный случай А = 0 возможен, если все коэффициенты
в правой части системы A0.3) равны нулю. Тогда любая точ-
точка {х\, х%) фазовой плоскости является положением равновесия

10.1. Фазовый портрет системы 267
такой системы, а соответствующее ему невозмущенное дви-
движение x(t) = жо = (ж?, #2)т> согласно определениям 9.1 и 9.2,
устойчиво по Ляпунову, но не является асимптотически устой-
устойчивым.
б. Пусть хотя бы один из коэффициентов а\2 и а,2\ в пра-
правой части A0.3) не равен нулю. Положим для определенности,
что а\2 7^0. Исключим из системы A0.3) переменное #2- Для
этого продифференцируем первое уравнение этой системы:
d?x\ dx\ dx2
__=au_+Ol2__
Подставляя в это соотношение вместо dx2/dt правую часть
второго уравнения системы A0.3), находим
d2x\ dx\
a
p jT + a12^21^1 + 0,12A22X2-
Выразив ai2#2 через переменное х\ при помощи первого урав-
уравнения системы A0.3), подставляем в последнее соотношение.
Получим линейное однородное ОДУ второго порядка с посто-
постоянными коэффициентами
(лХл dx]
-^2- - (an + a22) -?- + (aiia22 - ai2a2i) xx = 0,
A0.10)
характеристическое уравнение которого, естественно, совпада-
совпадает с A0.5) и имеет в рассматриваемом случае кратные корни
Ai = A2 = А. Общее решение ОДУ A0.10), согласно F.46), будет
xi(t) = (Ci + C2t)ext, Си С2 = const. A0.11)
Подставив A0.11) в первое ОДУ системы A0.3), найдем
X2(t) = —— (Ci + C2t) ext + —C2ext. A0.12)
^12 «12
Используя A0.11) и A0.12), общее решение системы A0.3)
в случае корня А кратности q = 2 запишем на основании
теоремы 5.11 в виде

268
10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
где ?i(t) = (Ci + C2t)ext и &(*) = C2ext — координатные
функции вектор-функции x(t) в базисе, образованном линейно
независимыми векторами
аг = A, (Л - an)/ai2)T и а2 = @, l/ai2)T.
При С\ = С2 = 0 имеем положение равновесия системы
в начале координат. Если С\ Ф 0, а Сг = 0, то фазовые
траектории являются полуосями оси O?i (sgn?i = sgnCi). При
С2ФО имеем t = (I/A) In 1^2/^21 и в системе координат
получаем уравнение фазовой траектории в виде
= (С + - In | ?> |) 6, С = const.
В случае Л < 0 при ? -> +оо как ?i -» 0, так и ?2 -> О,
т.е. изображающая точка по каждой из фазовых траекторий
неограниченно приближается к положению равновесия A0.4) в
начале координат, но не достигает его. Фазовый портрет ^ля
этого случая в переменных ?i,&2 и х\^Х2 (при произвольной
ориентации линейно независимых векторов а\ и 02) показан
на рис. 10.6.
Рис. 10.6
В случае Л > 0 фазовый портрет аналогичен, но направле-
направление движения изображающей точки противоположно. Поло-
Положение равновесия в обоих случаях называют вырожденным
узлом. В соответствии с замечанием 10.1 оно асимптотически
устойчиво при А < 0 и не является устойчивым при А > 0.

10.1. Фазовый портрет системы 269
В случае А = 0 координатные функции принимают вид
Прямолинейные фазовые траектории параллельны оси O?i, все
точки которой являются положениями равновесия. Направле-
Направление движения изображающей точки по фазовой траектории
зависит от знака постоянной С2-
3. Корни комплексно сопряженные. Условием возник-
возникновения комплексно сопряженных корней характеристического
уравнения A0.5) является выполнение неравенства
(аи + а22J < 4(аца22 - ai2«2i),
или
-01 = (аи - а22J + 4ai2a2i < 0.
Отсюда следует, что коэффициенты ai2 и a2i должны быть
отличны от нуля и иметь разные знаки. Тогда Ai^ = /х ± г/3
(г2 = -1), причем /i = (an + a22)/2.
Действительное решение ОДУ A0.10), соответствующего
системе A0.3), можно записать в виде (см. 6.4)
Xl(t) = (Ci cos fit + C2 sin/ft^', Cu C2 = const. A0.14)
Подставив A0.14) в первое ОДУ системы A0.3), получим
X2(t) = м " fln (Ci cos^f + С2siafit) ef*+
«12
+ —(C2cos/3«-Cisin/3t)e^*. A0.15)
«12
Используя A0.14) и A0.15), общее решение системы A0.3) в
случае комплексно сопряженных корней запишем в виде A0.13),
но теперь координатными функциями вектор-функции x(t) в
базисе линейно независимых векторов
oi = @, /3/ai2)T и a2 = (l, (/1 - an)/ai2)T

270
10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
являются
Ы*) = (C2cos/?t-Ci sin/ft) е"', &(*) = (Cicos/?t + C2 sin/ft) e"<.
A0.16)
Вместо A0.16) можно написать
ро = \JC\ + С2, tg7 = С\/С2- Рассмотрим возможные
частные случаи.
а. Если в A0.3) ац = — а22 (в частности ац = а22 = 0), то
/i = 0 и корни характеристического уравнения A0.5) являются
чисто мнимыми числами Лх = г/3 и Л2 = —г/3. Исключая в этом
случае из A0.17) время ?, получаем уравнение фазовой траек-
траектории ^i+^2=P2' Таким образом, в плоскости ?i0&2 фазовые
траектории являются семейством концентрических окружно-
окружностей с центром в начале координат, которые в плоскости xiOx2
переходят в семейство эллипсов (рис. 10.7), т.е. фазовые тра-
траектории замкнуты, что свидетельствует о том, что решение
системы периодическое.
Рис. 10.7
При выбранных координатных функциях ?i(?), ?2(*) и ори-
ориентации координатных осей в плоскости fiOf2 направление
движения изображающей точки по фазовой траектории проис-
происходит против движения часовой стрелки. В плоскости xiOx2

10.1. Фазовый портрет системы
271
это направление зависит от взаимного расположения векторов
а\ и а2.
Начало координат соответствует значениям С\ = Сг = О
(р = 0) и является положением равновесия системы A0.3). Его
в этом случае называют центром. Оно в соответствии с
замечанием 10.1 устойчиво, хотя и не асимптотически.
б. Комплексно сопряженные корни имеют отрицательную
действительную часть (ц < 0). Тогда соотношения A0.17)
будут в параметрической форме задавать фазовые траектории
в виде логарифмических спиралей, по которым изображающая
точка будет стремиться при t —> +оо к началу координат
(рис. 10.8). В данном случае начало координат является
асимптотически устойчивым положением равновесия системы
A0.3) и его называют устойчивым фокусом.
Рис. 10.8
в. Если комплексно сопряженные корни имеют положитель-
положительную действительную часть (/л > 0), то фазовый портрет ана-
аналогичен, но направление движения изображающей точки по
фазовой траектории противоположно, поскольку при t —> -foo
как ?i —> оо, так и ?2 —> оо. Положение равновесия в начале ко-
координат в этом случае не является устойчивым и его называют
неустойчивым фокусом.

272 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
Этим исчерпаны все возможные случаи сочетания корней
характеристического уравнения A0.5).
Заметим, что систему A0.3) можно свести к одному урав-
уравнению, исключив время t:
dx\ сьцХх +CL12X2
Интегральные кривые этого ОДУ первого порядка являются
фазовыми траекториями системы A0.3), положение равновесия
х\ = Х2 = 0 которой называют особой точкой ОДУ A0.18).
Таким образом, проведенный выше качественный анализ фа-
фазовых портретов системы A0.3) можно рассматривать как
исследование структуры интегральных кривых ОДУ A0.18) в
окрестности его особой точки.
Фазовые траектории можно изображать сразу в плоскости
xi 0x2, не находя направлений осей Ofi и Of2 в этой плоско-
плоскости. Однако в случаях узла, седла и вырожденного узла нужно
найти фазовые траектории, которые лежат на прямых, прохо-
проходящих через начало координат. Эти прямые всегда направлены
вдоль собственных векторов матрицы А системы A0.8), но их
можно определить и иначе.
Пример. Для линейной однородной системы ОДУ
характеристическое уравнение А2 + 7А +10 = 0 имеет действи-
действительные простые корни Ai = —2, А2 = —5. Следовательно,
положение равновесия х\ = Х2 = 0 представляет собой устой-
устойчивый узел.
Прямые, содержащие фазовые траектории системы, будем
искать в виде Х2 = xxi, я = const, подставив Х2 = >сх\ в ОДУ
Х\— 4X2
2х2'

10.2. Система нелинейных дифференциальных уравнений 273
которое можно получить исключением времени t из исходной
системы ОДУ. Тогда придем к квадратному уравнению 2х2 +
+ X— 1 = О, КОРНЯМИ КОТОРОГО будут Xi = — 1 И Х2 = 1/2.
Таким образом, искомыми прямыми в плоскости ххОхг бу-
будут Х2 = —х\ и Х2 = xi/2. Остальные фазовые траектории,
если к ним присоединить начало координат, будут иметь в
нем касательную с уравнением
X2 = #i/2 (рис. 10.9), посколь-
поскольку параллельный этой касатель-
касательной собственный вектор а\ =
= B, 1)т матрицы исходной си-
системы соответствует большему
собственному значению Ai =
= -2 (Ai > А2). Рис. 10.9
10.2. Система нелинейных
дифференциальных уравнений
Вернемся к нормальной автономной системе A0.1) второго
порядка, состоящей из нелинейных обыкновенных дифференци-
дифференциальных уравнений (ОДУ). Положение равновесия этой систе-
системы, согласно определению 8.2, должно удовлетворять системе
уравнений
Р(хъх2) = 0] Q(xux2) = 0. A0.19)
Система A0.19) может иметь, вообще говоря, несколько
решений. Пусть (х®, х^) — одно из них. Без уменьшения
общности предположим, что х\ = х\ = 0. В противном случае
можно сделать замену переменных щ = х\ — х\, иг = #2 — ^2-
Тогда система A0.1) примет вид

274 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
Положению равновесия х\ = х\, Х2 = х\ исходной системы
отвечает равновесие щ = щ = 0 преобразованной, и наоборот.
Считая функции Р(х\,Х2) и Q{x\,X2) непрерывно диффе-
дифференцируемыми в рассматриваемой области изменения перемен-
переменных х\ и #2, запишем систему A0.1) в виде
d/Хл
f
A0.20)
ах2
—- = CL2\Xi + 0,22*2
at
где Fi(x\, X2) (i = 1, 2) — бесконечно малые при (#i, X2) —* @, 0)
порядка выше первого относительно \/х\ +х\. Отбросив эти
слагаемые, придем к линейной системе A0.3), которая является
системой уравнений первого приближения для исходной систе-
системы ОДУ A0.1).
Если корни характеристического уравнения, составленно-
составленного для системы A0.3), простые и имеют отличные от нуля
действительные частщ то положение х\ = х\ = 0 равновесия
системы A0.20) имеет тот же тип, что и положение равновесия
системы A0.3) в следующем смысле. Фазовые траектории си-
системы A0.20) в окрестности этого положения равновесия слегка
деформированы относительно соответствующих фазовых тра-
траекторий системы A0.3). Это легко объяснить при помощи
теорем 9.4 и 9.5 Ляпунова об устойчивости по первому при-
приближению.
В случае чисто мнимых корней характеристического урав-
уравнения положение х\ = х\ = 0 равновесия системы A0.3) являет-
является центром. Однако наличие нелинейных слагаемых в правой
части A0.20) может, вообще говоря, изменить тип равновесия.
С точки зрения устойчивости здесь имеет место критический
случай: анализ устойчивости нельзя проводить исходя из урав-
уравнений первого приближения. Поясним это на примере системы
+xl). A0.21)

10.2. Система нелинейных дифференциальных уравнений 275
Здесь axi(x\ + х\) = Fi(rcbx2); ax2(x\ + x\) = F2(xu ж2), а =
= const 7^ 0. Характеристическое уравнение системы уравнений
первого приближения, соответствующей A0.21), имеет пару
чисто мнимых корней Ai,2 = ±* (г2 = — 1). Поэтому, согласно
изложенному в 10.1, положение х\ = х2 = 0 равновесия для
системы уравнений первого приближения в данном случае
является центром.
Исследуем устойчивость этого положения равновесия для
системы A0.21), введя знакоопределенную (определенно-поло-
(определенно-положительную) функцию Ляпунова V = (х\ + х2)/2. Вычислив
полную производную в силу системы A0.21), получим
— = а(х\+х22J.
Если а < 0, то положение х\ = х2 = 0 равновесия системы
A0.21), согласно теореме 9.9 Ляпунова об асимптотической
устойчивости, является асимптотически устойчивым, а при
а > 0 в силу теоремы 9.11 (теорема Ляпунова о неустойчивости)
оно неустойчиво. Фазовые траектории имеют вид спиралей, и
изображающая точка в случае а < 0 стремится к положению
равновесия, а при а > 0 бесконечно удаляется от него.
В качественной теории дифференциальных уравнений та-
такой тип положения равновесия называют сложным фокусом.
Надо заметить, что все сказанное выше следует отнести к
так называемому локальному анализу системы A0.20). В ря-
ряде отдельных случаев удается решить и глобальную задачу,
т.е. установить поведение фазовых траекторий на всей фазо-
фазовой плоскости. Однако в общем случае эта задача является
достаточно сложной.
Пример, а. Рассмотрим систему ОДУ
-^ = -а?! + хгх2; -Jj? = -z2 + 2zis2. A0.22)
Эта система имеет два положения равновесия: х\ = х2 = 0 и
х\ = 1/2, х2 = 1, которые представляют собой все решения

276
10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
системы уравнении
—Х\
= 0;
= 0,
составленной по правым частям ОДУ A0.22).
Исследуем поведение фазовых траекторий вблизи этих по-
положений равновесия. В случае х\ = Х2 = 0 система уравнений
первого приближения имеет вид
dx\
Для этой системы положение равновесия х\ = Х2 = 0 является
дикритическим узлом, так как корни характеристического
уранения Ai = Л2 = —1 < 0.
Выполнив подстановку щ = х\ — 1/2, U2 = Х2 — 1, линеа-
линеаризуем затем систему A0.22) в окрестности положения равно-
равновесия г*1 = U2 = 0. В результате получим систему уравнений
первого приближения
1
du2
Рис. 10.10
б. Система ОДУ
dx\
Для этой системы корни характеристи-
характеристического уравнения Ai = 1, А2 = — 1, а
собственные векторы а\ = A, 2)т и а>2 =
= (—1, 2)т. Следовательно, положение
равновесия является седлом. Фазовый
портрет системы A0.22) представлен на
рис. 10.10.
х\
A0.23)
имеет два положения равновесия: xi = X2 = 0 и х\ = 4, ^2 = 0.
Легко показать, что эти положения равновесия для системы

10.2. Система нелинейных дифференциальных уравнений 277
уравнений первого приближения являются соответственно цен-
центром и седлом. Чтобы для системы A0.23) найти уравнения
фазовых траекторий, необходимо исключить из нее время t.
Получающееся при этом ОДУ
dx\
легко проинтегрировать. Разделяя переменные и интегрируя,
получаем
*2=6*1-:
A0.24)
где С — постоянная интегрирования. Отметим, что выраже-
выражение u(x\, X2) =х1 + Х2~ #?/6 является первым интегралом си-
системы A0.23). Фазовые траектории, которые проходят через
седло, называют сепаратрисами. Для нахождения уравнения
сепаратрисы подставим в A0.24) координаты х\ = 4, Х2 = 0
положения равновесия системы A0.23), соответствующие сед-
седлу, и вычислим С = 16/3. Тогда из A0.24) получим уравнение
сепаратрисы
Фазовый портрет системы A0.23) изображен на рис. 10.11.
Изображающая точка стремится по сепаратрисе 7 K по-
положению х\ = 4, Х2 = 0
равновесия при t —> ±00.
В области, ограниченной
сепаратрисой, все траек-
траектории являются замкну-
замкнутыми и окружают поло-
положение равновесия х\ =
= Х2 = 0. Рис. 10.11

278 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
Дополнение 10.1. Математическая
модель сосуществования двух популяций
Нормальная система нелинейных обыкновенных дифферен-
дифференциальных уравнений (ОДУ) вида
dx dv
— = -ах + Ьху; ^ = СУ ~ hxV^ A0-25)
где а, 6, с, h — положительные коэффициенты, была исполь-
использована итальянским математиком В. Вольтерра A860-1940)
в качестве математической модели эволюции двух сосуще-
сосуществующих биологических популяций, особи одной из которых
являются кормом для особей другой. При помощи этой модели,
называемой в математической литературе моделью п хищник —
жертва", В. Вольтерра объяснил колебания уловов различных
видов рыбы в Адриатическом море, имеющих одинаковый пе-
период, но сдвинутых по фазе.
В A0.25) х — количество рыб-хищников, питающихся
рыбами-жертвами, количество которых обозначено через у.
Слагаемое Ьху характеризует зависимость скорости роста ко-
количества рыб-хищников от численности рыб-жертв. При от-
отсутствии рыб-жертв эта скорость была бы отрицательной с
коэффициентом пропорциональности —а < 0, что привело бы
в итоге к вымиранию рыб-хищников (см. пример 3.9). Наобо-
Наоборот, при отсутствии рыб-хищников скорость роста количества
рыб-жертв, имеющих достаточно корма в окружающей среде,
была бы положительной с коэффициентом пропорциональности
с > 0, что вызвало бы неограниченный рост их численности.
Но слагаемое —hxy, пропорциональное числу встреч жертвы
и хищника, заканчивающихся в пользу последнего, уменьшает
эту скорость.
Для удобства анализа приведем систему ОДУ A0.25) к
безразмерному виду
fjUoffo-1); ^=,A-0, A0.26)

Д. 10.1. Математическая модель сосуществования двух популяций 279
где ? = hx/c, rj = by/a, а = а/с > 0, а переменное г = ct явля-
является безразмерным временем. Из A0.26) следует, что ? = г) =
= 1 является положением равновесия этой смсгаелш. Системе
уравнений первого приближения соответствует характеристи-
характеристическое уравнение, имеющее чисто мнимые корни Х\^ = ±i
(г2 = — 1), т.е. это положение равновесия является центром для
системы уравнений первого приближения.
После деления первого ОДУ в A0.26) на а и сложения
полученного результата со вторым ОДУ находим
1 « + *»-„ р
По смыслу рассматриваемой математической модели ? > 0 и
г) > 0. Разделив первое ОДУ в A0.26) на а?, второе ОДУ на г\
и почленно сложив результаты, запишем
J_.* + !.*»=„_<
Два последних равенства дают уравнение
а? dr 7} dr a dr dr '
после интегрирования которого придем к равенству
- ln? + In г/ - ~ - г? = const. A0.27)
Таким образом, первый интеграл системы A0.26) можно запи-
записать в виде
Из A0.27) следует, что
^-^a, С = const,

280
10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
причем в силу положительности г\ и ? постоянная С > 0.
На рис. 10.12 для частного случая а = 2 представлены гра-
графики функций Y(r)) = е77/^ и Х(?) = л/?е~~^/2, связанных со-
соотношением У =
Функция Y (гу) дости-
достигает минимального зна-
значения Ymin = e при 77 =
= 1, а функция Х(?) —
максимального значе-
значения Хтах = е~х1а при
Рис. 10.12
Пусть в некоторый
момент времени t = to численности рыб-хищников и рыб-
жертв были хо и уо соответственно. Тогда безразмерному
значению то = с to времени отвечают значения ?(то) = fo =
= hxo/c и r/(ro) = ?7о = Ьуо/а. Эти значения являются координа-
координатами точки Мо в фазовой плоскости ^Otj и однозначно опре-
определяют постоянную С как угловой коэффициент прямой, про-
проходящей через начало координат и точку Mq (см. рис. 10.12).
Если точка Мо совпадает с положением равновесия М*, то
прямая будет проходить через точку Ml и Стах = 1/еA+а^а.
При помощи прямой, проходящей через точку Мо, неслож-
несложно построить фазовую траекторию, которая, как оказывается,
будет замкнутой кривой, целиком расположенной в первом ква-
квадранте плоскости ?Ог). Из A0.26) следует, что движение
изображающей точки по фазовой траектории будет происхо-
происходить по ходу часовой стрелки.
Итак, численности рыб-
хищников и рыб-жертв явля-
являются периодическими функ-
функциями времени. Характер за-
зависимостей f и 7) от г по-
показан на рис. 10.13. При ко-
т лебаниях численности попу-
Рис. 10.13 ляций рост количества рыб-

Вопросы и задачи 281
хищников запаздывает по фазе относительно роста количе-
количества рыб-жертв. Из-за ограниченности корма численность
рыб-хищников достигает некоторого максимума и затем идет
на убыль, что спустя некоторое время приводит к очередно-
очередному росту численности рыб-жертв, и цикл вновь повторяется.
Чем далее от положения равновесия М* находится точка Mq
(см. рис. 10.12), тем больше размах колебаний численности обе-
обеих популяций рыб.
Вопросы и задачи
10.1. Исследовать поведение фазовых траекторий систем
обыкновенных дифференциальных уравнений и сделать эскизы
фазовых портретов:
, 6)
=x1 + 2x2;
dx\ ( dx\
10.2. Определить типы положения равновесия для следую-
следующих систем обыкновенных дифференциальных уравнений:
dxi о i 4 ( dx\
а) < ,dt б)
СбЖ2 о 3 I ^-^2 9
dt X 2 12» ^^—12-

282 10. ОСОБЫЕ ТОЧКИ НА ФАЗОВОЙ ПЛОСКОСТИ
(х2)(Зх+х5); [ = х
= (х22)(Зх1+х25); [
в) { dt г) I dt
10.3. Изобразить в плоскости ?iO^2 фазовый портрет
системы A0.3) для случаев, когда корни характеристического
уравнения этой системы: a) Ai =0, Л2 > 0; б) Ai = Л2 = 0,
«21 Ф 0; в) Ai = А2 = 0, аи = а2\ = 0.
10.4. Построить эскизы фазовых портретов для обыкновен-
обыкновенного дифференциального уравнения F.49), сведя его к системе
второго порядка, и указать типы положений равновесия
следующих сочетаний параметров:
а) и > п ^ 0; б) п > ш ^ 0; в) п > и > 0; г) п = и.

11. КРАЕВЫЕ ЗАДАЧИ
ДЛЯ ДИФФЕРЕНЦИАЛЬНОГО
УРАВНЕНИЯ
11.1. Постановка краевой задачи
Напомним, что постановка задачи Коши для обыкновенно-
обыкновенного дифференциального уравнения (ОДУ) п-го порядка (п ^ 2)
или для нормальной системы ОДУ, имеющей тот же порядок,
включает п начальных условий, заданных для некоторого од-
одного значения to независимого переменного t. Если для этих
ОДУ или системы известно общее решение, содержащее п про-
произвольных постоянных Ck {к = 1,п), то начальные условия
позволяют найти значения постоянных. Но п условий для на-
нахождения значений постоянных можно задать не обязательно
при одном значении t = to- В этом случае из общего решения
необходимо выделить такое частное решение, которое будет
удовлетворять в сумме п дополнительным условиям, но задан-
заданным при нескольких значениях независимого переменного *.
Задачу отыскания такого частного решения принято называть
краевой задачей для ОДУ п-го порядка или для нор-
нормальной системы ОД У соответственно.
Более подробно рассмотрим постановку краевой задачи для
ОДУ второго порядка
§-'(¦¦* !)• <»•»
где у — искомая функция; х — независимое переменное; / —
функция, определенная и непрерывная в некоторой замкнутой
области D изменения своих аргументов. Общее решение тако-
такого ОДУ содержит две произвольные постоянные. Если для их

284
11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
нахождения задать при х = xq значения у(хо) искомой фун-
функции у(х) и ее производной у'(хо)? то придем к постановке
задачи Коши для ОДУ A1.1) с двумя начальными условиями.
Если же потребовать, чтобы искомое решение у(х) удовлетво-
удовлетворяло также двум условиям
У{о) = Уа, У(Ь) = У&,
A1.2)
но в двух различных точках х = а и х = 6, то получим одну из
возможных постановок краевой задачи, называемую двух-
двухточечной. Соотношения вида A1.2) называют краевыми
условиями данной задачи. Геометрически постановка зада-
задачи с краевыми условиями A1.2) означает, что требуется найти
такую интегральную кривую у(х) ОДУ A1.1), которая прохо-
проходит через точки А(а,уа) и В(Ь,уь) (рис. 11.1).
Возможно видоизменение постановки краевой задачи: най-
найти такое решение y=zy(x) ОДУ A1.1), чтобы в точках # = а и
х = b были выполнены краевые условия для производной фун-
функции у (х):
у'(а)=Уа, У'(Ъ)=у1 A1.3)
где у1 (а) = dy/dx\x_ и yf(b) = dy/dx\ .. Такая постановка
краевой задачи с геометрической точки зрения соответствует
поиску интегральной кривой у(х) ОДУ A1.1), пересекающей
прямые х = а и х = Ь под заданными углами тг/2 — а и
тг/2 — /3 (рис. 11.2), где, согласно геометрическому смыслу
производной функции у (ж), a = arctgy^ и /3 = arctgy?.
В
У i
Ь х
Рис. 11.1
Рис. 11.2

11.1. Постановка краевой задачи 285
Условия A1.2) и A1.3) принято называть краевыми усло-
условиями первого и второго рода соответственно. Очевидно,
имеет смысл и постановка смегианной двухточечной кра-
краевой задачи, когда в точках х = а и х = Ь заданы краевые
условия разного рода.
Необходимо отметить, что в отличие от задачи Коши, для
которой теорема 4.2 Коши гарантирует при выполнении опре-
определенных условий существование и единственность решения
ОДУ, краевая задача для того же ОДУ может не иметь реше-
решения или иметь несколько решений (в том числе и бесконечное
множество решений).
Пример 11.1. Так, для линейного однородного ОДУ вто-
второго порядка
g y = O A1.4)
общее решение имеет вид у(х) = С\ cos a; + C^sinx. Если в точ-
точке xq = 0 задать начальные условия у@) = уо и у'@) = j/q,
то по этим условиям единственным образом находим значения
произвольных постоянных Ci=yo и С2 = Уо, так что соответ-
соответствующая этим условиям задача Коши имеет единственное ре-
решение у(х) = уо cosх + Уо sinx. Теперь зададим краевые условия
в точках х = 0 и х = Ь: у@) = 0 и у(Ь) = у&. Подставив общее
решение ОДУ в первое краевое условие, найдем С\ = 0, а из вто-
второго краевого условия следует, что Съ = уь/sinb. Казалось бы,
удалось получить единственное решение у(х) = (уь sinx)/ sin b
краевой задачи. Но при уъф® и 6 = тг решения не существу-
существует, а при уь = 0 и Ь = тг этим краевым условиям и ОДУ A1.4)
удовлетворяют бесконечное множество решений у(х) = Csinrr,
где С — произвольная постоянная. #
Из этого примера должна быть понятна необходимость
выяснения вопроса о существовании и единственности решения
краевой задачи прежде, чем искать методы нахождения этого
решения.

286 11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
Для ОДУ n-го порядка
краевую задачу (не обязательно двухточечную) формулируют
следующим образом: найти решение у(х) этого ОДУ, та-
такое, что значения функции у(х) и ее производных dy/dx,
...jd№y/dx№ (p^n —1) в точках Xj (j = l,ra, m ^ 2) удо-
удовлетворяют п независимым краевым условиям Ф^ = О (г =
= 1,п), причем аргументами каждой из функций Ф» могут
быть значения у(х) и ее производных в любых точках Xj. Ана-
Аналогично можно сформулировать краевую задачу и для системы
ОДУ. Например, краевая задача определения траектории ма-
материальной точки массой т, находящейся в момент времени
t = to в точке с радиус-вектором r(to) = т*о и попадающей в
момент времени t\ > to в точку с радиус-вектором r(ti) = ri,
имеет вид
dv\
= F(t,r,—y r(to) = rOj rit^^n. A1.5)
11.2. Линейная краевая задача.
Сведение ее к задаче Коши
Рассмотрим линейное неоднородное обыкновенное диффе-
дифференциальное уравнение (ОДУ) второго порядка
у = /(*), xe[a,b). A1.6)
Функции р(х), q(x), f(x) предполагаем непрерывными на
отрезке [а, 6]. Требуется найти на этом отрезке решение у(х)
ОДУ A1.6), удовлетворяющее краевым условиям
/Зоу(Ь) +C1У'(Ъ) = В. A1.7)

11.2. Линейная краевая задача 287
Здесь с*о, ot\, А, /?о, Ри В — постоянные, причем |ao| + |ai | ф О,
|А)| + |/?i| 7^ 0- Этот вариант краевых условий является линей-
линейной комбинацией краевых условий первого и второго рода, и
его принято называть краевыми условиями третьего ро-
рода. В частном случае ао = /?о = 1 и ai = /?i = 0 соотношения
A1.7) переходят в краевые условия A1.2) первого рода, а при
ад = Д) = 0 и а\ = /?i = 1 — в краевые условия A1.3) второго
рода.
Постановка двухточечной краевой задачи в виде A1.6),
A1.7) включает линейное ОДУ второго порядка и линейные
относительно значений искомой функции и ее производных
краевые условия. В таком случае говорят о линейной двух-
двухточечной краевой задаче. Ее называют однородной, ес-
если f(x) = 0 и А = В = 0, и неоднородной — в противном
случае.
Однородная краевая задача всегда имеет тривиальное ре-
решение у(х) = 0. Однако в прикладных исследованиях часто для
однородной задачи представляют интерес решения у(х) ф 0. В
этом случае в ОДУ или краевые условия A1.7) вводят пара-
параметр, изменяя который можно добиться, чтобы при некоторых
его значениях однородная краевая задача помимо тривиаль-
тривиального имела решение, отличное от тождественно нулевого. В
некоторых случаях такой параметр уже присутствует в ис-
исходной формулировке краевой задачи и имеет вполне опреде-
определенный физический, механический или геометрический смысл
(см. 11.3). Эти исключительные значения параметра, при ко-
которых однородная краевая задача имеет решение, отличное от
тривиального, называют собственными значениями, а отвеча-
отвечающие им решения — собственными функциями этой задачи.
Нахождение собственных значений и собственных функций со-
составляет содержание так называемой задачи на собствен-
собственные значения, или задачи Штурма — Лиувиллл.
Краевую задачу A1.6), A1.7) можно свести к задачам Коши
для того же ОДУ A1.6) второго порядка и соответствующего

288 П. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
ему однородного ОДУ
d и du
u = O. A1.8)
Для этого решение краевой задачи будем искать в виде
у(х) = /j,u(x) + v(x), /i = const, A1-9)
где и = и{х) — нетривиальное решение однородного ОДУ
A1.8), a v(x) — решение неоднородного ОДУ A1.6). Ясно, что
A1.9) как линейная комбинация решений неоднородного ОДУ и
соответствующего ему однородного уравнения также является
решением ОДУ A1.6).
Потребуем, чтобы первое из краевых условий A1.7) было
выполнено для у(х) при любом значении //. Подставив A1.9)
в это краевое условие, запишем
fiaou(a) + aov(a) + /j,aiuf (a) + a\vf(a) = А.
Это равенство будет выполнено при любом значении /i, если
приравнять нулю коэффициент при /i, что приведет к двум
равенствам
(а) + ot\ v!{a) = 0; aov(a) + а\ v'(a) = А,
для выполнения которых достаточно, например, положить
и(а) = с*ь и1 (а) = -а0; A1.10)
г/(а)=0, ао^О. A1.11)
В случае ао = 0 вместо A1.11) положим
v(a)=0, v'(a)=A/au «i Ф 0. (П-12)
Таким образом, и(х) есть решение задачи Коши для од-
однородного ОДУ A1.8), удовлетворяющее начальным условиям
A1.10), а v(x) — решение задачи Коши для неоднородного

11.2. Линейная краевая задача 289
ОДУ A1.6), удовлетворяющее начальным условиям A1.11) или
A1.12). При этом для любого /i функция у(х) = fj,u(x) + v(x)
удовлетворяет первому из краевых условий A1.7) (при х = а).
Постоянную /i выбирают так, чтобы функция у(х) удовле-
удовлетворяла второму из краевых условий A1.7) (при х = 6), т.е.
ц {C0u(b) + fa u'(b)) + pov(b) + ft v'(b) = В. A1.13)
Если выполнено неравенство
то из A1.13) находим
В-0оу(Ь)-ЛуГ{Ь)
'(Ь) • ( ]
Итак, краевая задача A1.6), A1.7) сведена к двум задачам
Коши относительно функций и(х) и v(x) для однородно-
однородного A1.8) и неоднородного A1.6) ОДУ соответственно. Эти
ОДУ удовлетворяют всем условиям теоремы 4.3 Коши о су-
существовании и единственности решения задачи Коши, т.е. су-
существует единственное решение и(х) ОДУ A1.8), удовлетво-
удовлетворяющее начальным условиям A1.10), и единственное решение
v(x) ОДУ A1.6), удовлетворяющее начальным условиям A1.11)
или A1.12). Поэтому при выполнении неравенства A1.14) су-
существует решение рассматриваемой линейной краевой задачи
A1.7), A1.8).
Отметим, что если исходное ОДУ A1.6) будет однородным,
т.е. f(x) = 0, и в A1.7) А = 0, то в силу начальных условий
A1.11) или A1.12) имеем v(a) = 0 и vf(a) = 0, и поэтому
v(x) = 0. Тогда при выполнении неравенства A1.14) получим
где и(х) — решение ОДУ A1.8), удовлетворяющее начальным
условиям A1.10).
Ю — 9306

290 П. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
В примере 11.1 была рассмотрена краевая задача для одно-
однородного ОДУ A1.4) с краевыми условиями первого рода, т.е.
ого = /?о = 1 и <*1 = /?i = 0. Этому ОДУ и заданному в точке
х = 0 условию и@) = 0 удовлетворяет решение и(х) = sina;.
Так как u(b) = sinb ф 0 при Ьфктт (к € Z), то в этом случае
неравенство A1.14) будет выполнено и, согласно A1.16), при
В = уь имеем у(х) = y&sinx/sinb, что совпадает с полученным
в примере 11.1 результатом. Но два других варианта краевых
условий, рассмотренных в этом примере, для которых принято
6 = 7г, обращают левую часть A1.14) в нуль. Решение краевых
задач с этими краевыми условиями изложенным методом найти
нельзя. Отметим, что в одном случае решение не существует,
а в другом существует, но не единственно.
11.3. Прикладные примеры
решения краевой задачи
Необходимость в рассмотрении и поиске решения краевых
задач для обыкновенных дифференциальных уравнений (ОДУ)
часто возникает при проведении прикладных исследований в
различных областях науки и техники. В большинстве встреча-
встречающихся на практике случаев удается ограничиться постанов-
постановкой и решением краевой задачи для ОДУ второго порядка на
некотором отрезке изменения независимого переменного.
Пример 11.2. Рассмотрим металлический трубопровод
тепловой магистрали, покрытый кольцевым слоем теплоизо-
теплоизоляции, имеющим внутрений радиус Rq и внешний радиус R
(рис. 11.3). Стенка трубопровода нагрета до постоянного зна-
значения температуры То, а на внешней поверхности теплоизо-
теплоизоляции происходит теплообмен с окружающей средой, имеющей
постоянную температуру Гс. Интенсивность теплообмена ха-
характеризует коэффициент а = const. При таких условиях в
слое теплоизоляции возникнет постоянное во времени, но меня-
меняющееся вдоль отсчитываемой от оси трубопровода радиальной

12.3. Прикладные примеры решения краевой задачи
291
Рис. 11.3
темпе-
координаты г распределение темпе-
температуры Т(г). Нахождение этого рас-
распределения важно для оценки рассеи-
рассеиваемого в окружающую среду коли-
количества теплоты и суждения об эф-
эффективности применяемой теплоизо-
теплоизоляции, для выбора внешнего радиуса
Д, обеспечивающего допустимые те-
шюпотери.
Из курса физики известно, что
вектор q плотности теплового по-
потока, передаваемого путем теплопро-
теплопроводности в веществе при неравномерном распределении
ратуры Т, пропорционален ее градиенту gradT:
q = -AgradT,
где А — коэффициент теплопроводности вещества. Это соот-
соотношение называют законом Фурье — по имени французского
математика и физика Ж.Б.Ж. Фурье A768-1830). В данном
случае для трубопровода достаточно большой длины l^> R
в силу осевой симметрии градиент температуры имеет лишь
радиальную составляющую dT/dr, т.е. тепловой поток распро-
распространяется только в радиальном направлении.
В слое теплоизоляции рассмотрим две цилиндрические по-
поверхности радиусов г и r + Дг (Дг > 0) и одинаковой длины /.
Через эти поверхности в радиальном направлении проходят
тепловые потоки соответственно
Qr = -2тг/Л0(г) и Qr+Ar = -2тг/Ав(г + Дг), A1.17)
где в (г) = r(dT/dr). При установившемся распределении тем-
температуры на основании закона сохранения энергии эти тепло-
тепловые потоки должны быть равны, т.е. Qr = Qr+Ar5 или после
сокращения на 2тг/АДг ф 0
О(г + Дг)-в(г)
Дг
= 0.
A1.18)
ю*

292 11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
Предполагая, что распределение температуры Т(г) дважды
дифференцируемо по г, и переходя в A1.18) к пределу при
Аг —> О, в силу определения производной [II] получаем
т.е. приходим к линейному однородному ОДУ второго порядка
с переменным коэффициентом при первой производной
На внутренней поверхности слоя теплоизоляции радиуса
До? прилегающей к стенке трубопровода, примем T(Rq) =
= То. На внешней поверхности радиуса R тепловой поток,
поступающий из слоя теплоизоляции, равен тепловому потоку,
воспринимаемому окружающей средой, т.е.
2nRl = a(T(R) -TcJnRl,
r=R
или, сокращая на 2ttRI, имеем aT(R) + XTf(R) =aTc. Таким
образом, краевые условия можно представить в виде
Т(До) = То; olT(R) + \T'(R) = aTc. A1.21)
Отметим, что в данном случае при г = Rq имеем краевое
условие первого рода, а при г = R — третьего рода, т.е.
линейная двухточечная краевая задача A1.20), A1.21) является
смешанной.
Вместо поиска решения ОДУ A1.20) последовательно про-
проинтегрируем второе равенство в A1.19):
dT dT C\ ( .
dr ' dr r
Для нахождения произвольных постоянных С\ и C<i подста-
подставим Т(г) в A1.21) и получим систему двух алгебраических

11.3. Прикладные примеры решения краевой задачи 293
уравнений
d In До + С2 = То; aCi In R + aC2 + ъСг = aTc.
JrC
Отсюда находим
Г°~Гс Го~Гсд 1пДо-
лд лд
- + aln— - + aln —
гС ito it rto
В итоге решение краевой задачи имеет вид
Г(г)=Г0- лГ°~Гсд 1п^. A1.22)
График зависимости Т(г) показан на рис. 11.3.
Рассеиваемый с внешней поверхности теплоизоляции тепло-
тепловой поток будет
QR = 2nRla(T{R) -Тс) = 2nlX f°~TcR - (И.23)
—г+ln-—
aR До
Отметим, что к тому же результату можно прийти более
простым путем, не выводя ОДУ A1.20) второго порядка. Ис-
Используя закон сохранения энергии, запишем первое равенство
A1.17) в виде —27rrl\dT/dr = Q = const и после разделения пе-
переменных и интегрирования получим
Г = С - -% lnr, С = const. A1.24)
27uA
Подставляя A1.24) в краевые условия A1.21), придем к системе
двух алгебраических уравнений

294 П. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
из которых после исключения С получим для Q выражение,
совпадающее с A1.23).
Интересно, что с возрастанием радиуса Д при фиксиро-
фиксированных значениях остальных параметров функция Qr(R) в
A1.23) может не быть монотонной, хотя, казалось бы, с уве-
увеличением толщины слоя теплоизоляции теплопотери должны
уменьшаться. В самом деле, производная
dR ~ ""'" ( Л . , R\*\ aB?' R
равна нулю при R = Д* = А/а (Д* — это критический радиус
слоя теплоизоляции), причем меняет знак с плюса на минус, что
в силу теоремы 8.5 [II] является достаточным условием того,
что в точке Д* функция Qr(R) имеет локальный максимум
в интервале @, +оо). Следовательно, монотонное убывание
теплопотерь с возрастанием радиуса Д возможно лишь при
Д ^ Д*. Если Д* ^ До, то выбор толщины кольцевого слоя те-
теплоизоляции, такой, что R&R*, является нерациональным, так
как теплопотери при этом близки к максимальным. Обеспе-
Обеспечить снижение теплопотерь можно либо выбором R*5> R*, т.е.
увеличением толщины слоя теплоизоляции, либо применением
более эффективной теплоизоляции с меньшим значением коэф-
коэффициента теплопроводности А, что приведет к уменьшению
значения Д*. Признаком рационального выбора теплоизоля-
теплоизоляции является выполнение условия Д* < До-
Пример 11.3. При создании конструкций, нагруженных
сжимающими усилиями, часто возникает необходимость расче-
расчета сжатых прямолинейных стержней. Впервые подобная задача
была рассмотрена Л. Эйлером.
Пусть стержень длиной Z с круговым поперечным сечени-
сечением, имеет неизменную по длине жесткость Е J на изгиб, где Е
и J — соответственно модуль упругости материала и геоме-
геометрический момент инерции сечения стержня, и нагружен посто-

11.3. Прикладные примеры решения краевой задачи 295
янной сжимающей силой Р, направленной вдоль оси Ох, про-
проходящей через концевые шарнирные опоры (рис. 11.4). Будем
предполагать, что под действием силы Р возможно, искривле-
искривление первоначально прямолинейной оси стержня, описываемое
функцией у (ж), имею-
имеющей смысл зависимо-
сти от координаты х
прогиба стержня в по-
поперечном направлении Рис. ц.4
вдоль оси Оу.
В любом сечении искривленного стержня сила Р созда-
создает изгибающий момент М = —Ру(х), направленный при у > О
(см. рис. 11.4) против хода часовой стрелки и уравновешива-
уравновешиваемый моментом, создаваемым в этом сечении напряжениями,
возникающими при изгибе стержня. Из курса сопротивления
материалов известно, что уравновешивающий момент равен
произведению жесткости Е J на изгиб и кривизны оси стерж-
стержня. При условиях \у(х)\ <§; /, [у'(х)] <Cl VxG [О, I] кривизну
плоской кривой, задаваемой функцией у(х), приближенно при-
принимают равной у"(х). Таким образом, в любом сечении стерж-
стержня условием равновесия является равенство EJy" = —Ру (в
случае у(х) > О при выбранной на рис. 11.4 системе координат
Оху имеем у" (х) < 0). Это равенство можно записать в виде
линейного однородного ОДУ
= 0 A1.25)
второго порядка с постоянными коэффициентами, где и2 =
= P/(EJ). Шарнирные опоры стержня запрещают поперечное
смещение его сечения, так что краевыми условиями будут
у@)=уA)=0. A1.26)
Краевая задача A1.25), A1.26) является однородной и имеет
тривиальное решение у(х) = 0, которое соответствует прямо-
прямолинейному стержню. Выясним, существует ли хотя бы одно

296 11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
значение силы Р, входящее в параметр о;, при котором воз-
возможно искривление стержня. Математически ответ на этот
вопрос сводится к определению значения (или значений) о;, при
котором (или при которых) краевая задача A1.25), A1.26) име-
имеет решение у(х) ф 0.
Соответствующее A1.25) характеристическое уравнение
А2 + и2 = 0 имеет комплексно сопряженные чисто мнимые
корни Х[ 2 = ±ш. Тогда на основании теоремы 6.2 о структуре
общего решения однородного ОДУ для уравнения A1.25) общее
решение можно записать в виде (см. 6.4)
у(х) = С{ coswz + С\ sincjz, A1.27)
где С\ и С% — произвольные постоянные.
Подставляя A1.27) в краевые условия A1.26), находим С{ =
= 0 и C2sina;J = 0. Если в последнем равенстве принять С%=0,
то придем к тривиальному решению. Но это равенство можно
выполнить, если при С?фО положить sina;/ = 0, т.е. ш^1 = кп
(к 6 Z). Тогда каждому значению и^ как собственному зна-
значению данной краевой задачи будет с учетом A1.27) соответ-
соответствовать ее собственная функция
^ A1.28)
которую можно задать с точностью до произвольного множи-
множителя С%- В связи с этим считают, что одинаковым по абсолют-
абсолютному значению к отвечает одна и та же собственная функция,
поэтому отрицательные значения к можно исключить из рас-
рассмотрения. Значению к = 0 соответствует u$ = 0, и A1.28)
дает уже упомянутое тривиальное решение у(х) = 0.
Итак, бесконечное множество решений данной краевой
задачи, отличных от тривиального, можно описать при помощи
A1.28), считая, что k E N. Каждому из таких решений
соответствует значение сжимающей силы
fc€N, A1.29)

11.3. Прикладные примеры решения краевой задачи 297
при котором может существовать форма равновесия стержня,
отличная от прямолинейной. Из структуры A1.29) видно, что
выбор к из множества Z целых чисел не дает новых значений
сжимающей силы по сравнению с выбором к из множества
N натуральных чисел, за исключением, естественно, значения
Ро = 0, соответствующего ненагруженному стержню.
При к = 1 из A1.29) получаем наименьшее значение Рх* =
= тг2EJ/12 сжимающей силы, которое может вызвать искривле-
искривление прямолинейного стержня, называемое в механике потерей
устойчивости стержня, или потерей устойчивости его прямо-
прямолинейной формы равновесия. Значение Рх* называют первой
критической силой для данных условий закрепления стержня,
но часто это значение именуют эйлеровой силой.
Несмотря на соответствие проведенного анализа изложен-
изложенным в 11.2 теоретическим положениям, его результаты долж-
должны вызвать некоторое недоумение. В самом деле, из получен-
полученного решения следует, что при Р = Р? (к Е N) возникает кри-
криволинейная форма равновесия стержня, а при Р? < Р < Р/*+1
стержень снова должен стать прямым, что явно не соответ-
соответствует действительности. Причина состоит в том, что в ОДУ
A1.25) кривизна оси стержня приближенно заменена второй
производной у"(х), что вполне допустимо при малых значениях
|у(ж)|, но вносит большие погрешности и искажает механиче-
механический смысл результатов анализа, когда при искривлении оси
стержня значения \у{х)\ возрастают. Если использовать точ-
точное выражение для кривизны плоской кривой, то вместо A1.25)
следует рассматривать краевую задачу для нелинейного ОДУ
второго порядка
dx2
и краевых условий A1.26). Решение такой задачи не удает-
удается выразить через элементарные функции, однако это решение
подробно исследовано и установлено, что изменение конфигу-

298
11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
рации оси стержня непрерывно зависит от изменения значения
сжимающей силы.
Пример 11.4. Покажем, что на собственные значения и
собственные функции краевой задачи существенно влияют кра-
краевые условия, т.е. в случае рассмотренного в примере 11.3
сжатого стержня — условия закрепления его концов. При
х = 0 заменим шарнирную опору жесткой заделкой (рис. 11.5),
запрещающей не только поперечное смещение стержня,
но и поворот его сечения, т.е. касательная к искривленной
оси стержня в точке
х = О горизонталь-
горизонтальна. Следовательно,
при х = О у@) = О
и у'@) =0, т.е. вме-
вместо A1.26) краевые
условия примут вид
Рис. 11.5
у(О)=у'(О)=О;
= 0.
A1.31)
Для того чтобы удовлетворить этим трем краевым условиям,
общее решение ОДУ должно содержать три произвольные
постоянные.
Принципиальное отличие рассматриваемого случая закреп-
закрепления стержня от описываемого краевой задачей A1.25), A1.26)
состоит в том, что теперь искривленная ось стержня, описы-
описываемая функцией у(#), будет иметь хотя бы одну точку В
перегиба, не лежащую на оси Ох (см. рис. 11.5), так как в силу
необходимого условия существования точки перегиба дважды
дифференцируемой функции для этой точки искривленной оси
уп(х) = 0, т.е. равен нулю изгибающий момент. Но это воз-
возможно, если в точке А на стержень помимо сжимающей силы
Р действует еще и поперечная реакция R шарнирной опоры,
такая, что равнодействующая этих сил направлена по прямой
АВ. Тогда условием равновесия сечения стержня с коорди-
координатой х будет равенство EJy" = — Ру + R(l — ж), которое

11.3. Прикладные примеры решения краевой задачи 299
приведет к линейному неоднородному ОДУ второго порядка с
постоянными коэффициентами
Таким образом, имеем линейную неоднородную краевую за-
задачу для ОДУ A1.32) с краевыми условиями A1.31). Несложно
проверить, что функция
ту
является частным решением ОДУ A1.32). На основании те-
теоремы 6.3 о структуре общего решения неоднородного ОДУ,
учитывая A1.27), запишем общее решение уравнения A1.32) в
виде
R
у(х) = 9__(г - х) + С[coswa; + C'2smu)x. A1.33)
Это решение содержит три постоянные Д, С[ и С2,
которые следует подобрать так, чтобы удовлетворить краевым
условиям A1.31), т.е.
у@)=0:
У'(О)=О: --*- + С-и, = О; (И-34)
уA) = 0: С[ cosul + O2 smul = 0.
Ясно, что эта однородная система линейных алгебраических
уравнений (СЛАУ) имеет относительно искомых постоянных
нулевое решение R = С[ = С2 = 0, которое соответствует три-
тривиальному решению у(х) = 0 (стержень остается прямолиней-
прямолинейным). Чтобы эта СЛАУ имела ненулевые решения, необходимо
и достаточно равенство нулю ее определителя [III], т.е.
l/(u2EJ) 1 0
-l/{u2EJ) 0 и
0 cosujI
= 0.

300
11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
Раскрывая определитель, получаем
tg/i = /i, fi = u;l = h —
A1.35)
Уравнение A1.35) служит для нахождения /х и имеет беско-
бесконечное множество корней /хп, п = 0,1,2,... (рис. 11.6), ко-
которому принадлежит и корень ^о = 0, соответствующий зна-
значению Ро = 0, т.е. тривиальному
решению у(х) = 0, при котором
стержень прямолинеен. Осталь-
Остальным корням соответствуют зна-
значения
Р -
п€,
A1.36)
Рис. 11.6
сжимающей силы.
•Наименьший положительный корень уравнения A1.35) ц\ «
«4,493 соответствует наименьшему значению u>i=/ii// па-
параметра о;, при котором краевая задача A1.32), A1.31) имеет
решение, отличное от тривиального. Тогда Pi = fifEJ/l2 —
наименьшее значение сжимающей стержень силы, вызываю-
вызывающее искривление его оси при рассматриваемых условиях его
закрепления. Сравнивая Р\ с эйлеровой силой Рх*, видим,
что для того же стержня первая критическая сила благодаря
более жесткому закреплению стержня возросла в (/ii/тгJ «
« 2,045 раза.
Каждому значению корня /in (n Е N) отвечает значение
параметра ь)п = цп/1, которое будет входить в бесконечное
множество собственных значений краевой задачи. В свою оче-
очередь, каждому собственному значению шп соответствует соб-
собственная функция, содержащая одну произвольно выбираемую
постоянную и определяющая форму искривленной оси стерж-
стержня при значении сжимающей силы Рп = cj^EJ. Действительно,
исключая из A1.33) при помощи A1.34) и A1.35) две из трех

11.3. Прикладные примеры решения краевой задачи 301
постоянных, получим для собственных функций выражение
ГУ
Уп(х) = ^EJ (un(l -x)- conl cosu)nx + smunx). A1.37)
К тем же результатам можно прийти и более формальным
путем, рассматривая однородную краевую задачу. Предпола-
Предполагая, что искомая функция у(х) имеет на отрезке [0, /] не-
непрерывные производные до четвертого порядка включительно,
дважды продифференцируем ОДУ A1.32) и получим линейное
однородное ОДУ четвертого порядка с постоянными коэффи-
коэффициентами
которому соответствует характеристическое уравнение Л4 +
+ и>2\2 = 0, имеющее действительные кратные корни Х\ = Х2 =
= 0 и комплексно сопряженные чисто мнимые корни Аз, 4 =
= ±го;. Общее решение ОДУ A1.38) имеет вид (см. 6.4, 6.5)
у(х) = С\ + С2х + С3 coso;x + C4 sinwz, A1.39)
где Сг, г = 1, 4, — произвольные постоянные.
Для нахождения этих постоянных необходимо дополнить
краевые условия A1.31). Отметим, что шарнирная опора
стержня при х = Z (см. рис. 11.5), запрещая поперечное сме-
смещение стержня, т.е. уA) = 0, допускает поворот его сечения.
Так как сжимающая сила Р и реакция R опоры не создают
момента относительно сечения стержня в точке х = Z, то кри-
кривизна оси стержня в этой точке равна нулю и у"A) = 0. В итоге
краевые условия для ОДУ A1.38) с учетом A1.31) примут вид
1/@) = j/@) = 0; уA) = у"A) = 0. A1.40)
Итак, имеем однородную краевую задачу A1.38), A1.40),
для которой у(х) = 0 является тривиальным решением, соот-
соответствующим прямолинейному стержню. Подстановка A1.39) в

302 11. КРАЕВЫЕ ЗАДАЧИ ДЛЯ ОДУ
первое соотношение A1.40) приводит к уравнениям С\ + Сз = 0,
С2+С0С4 = 0, с учетом которых вместо A1.39) получим
у(х) = С\{1 — coscjx) + C2 — {шх — sina;x). (И-41)
Подстановка этого выражения во второе соотношение A1.40)
дает еще два уравнения для определения постоянных:
С\и)A — cosul) + (^2@;/ — sincjl) = 0;
A1.42)
С\и cosul + Casino;/ = 0.
Эта СЛАУ имеет ненулевые решения при условии
A —cosu;/) u)l — sinujl _
и cos u)l sin о;/
Раскрыв этот определитель, получим уравнение A1.35) для
определения собственных значений краевой задачи A1.38),
A1.40), совпадающих с собственными значениями ип краевой
задачи A1.32), A1.31). Выразив при помощи A1.35) из второго
уравнения A1.42) C<i через С\ (С2 = —С\/1) и подставив в
A1.41), запишем выражение для собственной функции краевой
задачи A1.38), A1.40)
уп(х) = —^т (ипA - х) - unl cosLJnx + sinu;nx),
которое с точностью до постоянного сомножителя совпадает с
A1.37).
Общий вывод таков: существует бесконечный набор кон-
конфигураций стержня, каждая из которых возможна лишь при
вполне конкретном значении силы Р, получаемом путем ре-
решения уравнения A1.35). При других значениях сжимающей
силы краевая задача A1.38), A1.40) имеет только тривиаль-
тривиальное решение у(х) = 0. Если использовать точное выражение
для кривизны плоской кривой, то и в данном случае придем к
нелинейной краевой задаче, решение которой устанавливает не-
непрерывную зависимость изменения конфигурации оси стержня
от изменения значения сжимающей силы (см. пример 11.3).

Вопросы и задачи
303
Вопросы и задачи
11.1. Дать геометрическую интерпретацию решения линей-
линейной краевой задачи A1.6), (И.7).
11.2. Для однородной краевой задачи
у@)=у'@)=0,
найти наименьшее положительное значение параметра а, при
котором существует решение, отличное от тривиального.
11.3. Для однородной краевой задачи
_0
У"A)=У'"A)=О
найти уравнение для определения таких значений параметра /3,
при которых существует ненулевое решение.
11.4. Найти все значения силы Р (рис. 11.7), при которых
имеет решение неоднородная краевая задача
где / — длина стержня; EJ —
его жесткость на изгиб; / —
заданное смещение линии дей-
действия силы Р относительно оси
Ox; R — реакция опоры, опре-
определяемая из дополнительного
граничного условия.
Я
Рис. 11.7

12. ПРИБЛИЖЕННЫЕ МЕТОДЫ
РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
12.1. Интегрирование дифференциальных
уравнений при помощи степенных рядов
В общем случае нахождение точного решения обыкновенно-
обыкновенного дифференциального уравнения (ОДУ) первого порядка его
интегрированием невозможно. Тем более это неосуществимо
для системы ОДУ. Это обстоятельство привело к созданию
большого числа приближенных методов решения ОДУ и их си-
систем. Среди приближенных методов можно выделить три груп-
группы: аналитические, графические и численные. Разумеется,
подобная классификация в известной мере условна. Например,
графический метод ломаных Эйлера лежит в основе одного из
способов численного решения дифференциального уравнения.
Интегрирование ОДУ при помощи степенных рядов являет-
является приближенным аналитическим методом, применяемым, как
правило, к линейным уравнениям не ниже второго порядка.
В изложении метода использованы некоторые сведения из те-
теории рядов [IX]. Ограничимся для простоты рассмотрением
линейного однородного ОДУ второго порядка с переменными
коэффициентами
*»+.(,) 4+tW,_0. A2.!)
Замечание 12.1. Достаточно широкий класс функций f(t)
можно представить в виде
Jfc=0

12.1. Интегрирование ОДУ при помощи степенных рядов 305
где Д, to — некоторые постоянные. Это выражение называют
степенным рядом. Если его значения равны соответствую-
соответствующим значениям функции f(t) для любого t из интервала
(to — Т, to +T), то такой ряд называют сходящимся в этом ин-
интервале [IX]. #
Предположим, что функции a(t), b(t) можно разложить в
сходящиеся в интервале (to — Т, to + Т), Т > 0, ряды:
оо
-to)fc, b(t) = 5^bjb(*-*o)*. A2.2)
fc=0
Имеет место следующая теорема (опуская доказательство, при-
приведем лишь ее формулировку)*.
Теорема 12.1. Если функции a(t),b(t) имеют вид A2.2),
то любое решение y(t) ОДУ A2.1) представимо в виде сходя-
сходящегося при \t — to| < Т степенного ряда:
У(«) = !>(*-'°)*. # A2.3)
А;=0
Эта теорема не только дает возможность представить ре-
решение в виде степенного ряда, но и, что самое главное, обосно-
обосновывает сходимость ряда A2.3). Для простоты положим в A2.2)
и A2.3) to = 0 и будем искать решение ОДУ A2.1) в виде
оо
y(t) = !>**• A2.4)
А;=0
Подставив A2.4) в A2.1), получим равенство
A2.5)
k=2 k=0 *=1 ^
* Доказательство теоремы см. в книге Коддингтон Э.А., Левинсон Н.
Теория обыкновенных дифференциальных уравнений. М.: Изд-во иностр.
лит., 1958.

306 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Для выполнения A2.5) необходимо, чтобы коэффициент при
каждой степени t был равен нулю. Из этого условия получаем
бесконечную систему линейных алгебраических уравнений
ЬоУо + aoj/i + 2j/2 = 0;
hyo + (bo + ai) ух + 2а0у2 + 6у3 = 0;
+ (fc + i)(fc + 2)yfc+2 = 0;
m=l
из которой можно последовательно найти уг, уз, •.., если задать
значения уо и yi (в случае задачи Коти для ОДУ A2.1) они
входят в начальные условия у@) = уо, у'@) = yi).
Если функции а(?), b(t) являются рациональными, т.е.
a(t) = ai(t)/ao(t), Ь(?) = bi(t)/bo(t)^ где fli(t), ao(^)> bi(t),
Ьо(?) — многочлены, то в окрестностях точек, в которых
ao{t) = 0 или Ьо(?) = 0, решение в виде степенного ряда может
не существовать, а если и существует, то может расходиться
всюду, за исключением точки t = 0. Это обстоятельство
было известно еще Л. Эйлеру, который рассмотрел уравнение
первого порядка
dy у 1
Этому уравнению удовлетворяет степенной ряд
Нетрудно, однако, видеть, что этот ряд расходится при любом
t ф 0. Решение ОДУ в виде расходящегося степенного ряда
называют формальным.
Пример. Решение уравнения Эйри
0 A2.6)

12.1. Интегрирование ОДУ при помощи степенных рядов 307
будем искать в форме степенного ряда A2.4). Тогда равенство
A2.5) принимает вид
Приравняем нулю коэффициент при каждой степени t. Ко-
Коэффициент при нулевой степени t равен 2у2- Следовательно,
У2 = 0. Из равенства нулю коэффициента буз + уо при t на-
находим уз = — уо/6. Коэффициент при tk~2 равен укк(к — 1) +
+ у^_з- Отсюда
Ук-г
Ук к{к-\у
Из этой формулы получаем
— Узр-з Узр-6
УЗр" Зр(Зр-1)^Зр(Зр^1)(Зр-3)(Зр-4)"
Аналогично находим
(-1)р
УЗр+1"(Зр+1)Зр---4-3Уь
(-1)р
УЗр+2 =
Коэффициенты уо и у\ остаются неопределенными. Для
нахождения фундаментальной системы решений положим вна-
вначале уо = 1, у\ = 0, а затем наоборот. В первом случае имеем
а во втором
На основании теоремы 12.1 эти ряды являются сходящимися
всюду на числовой прямой Ш.

308 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Функции у1 (?), ?/2 М называют функциями Эйри. При
больших значениях t асимптотическое поведение этих функ-
функций описывают формулы
Графики этих функций изобра-
Ух@ j/2@ жены на рис. 12.1. В примере 7.1
при помощи теоремы 7.3 сравнения
было показано, что при неограни-
8 t ченном увеличении t нули всяко-
всякого решения уравнения Эйри нео-
граниченно сближаются, что видно
и из асимптотического представле-
представления этих решений, но совсем не очевидно из представления
функций Эйри в виде сходящихся степенных рядов. Отсюда
следует, что способ поиска решения ОДУ при помощи ряда,
вообще говоря, малопригоден при решении прикладных задач,
а само представление решения в виде ряда затрудняет анализ
качественных свойств полученного решения.
12.2. Метод последовательных приближений
Этот метод, имеющий в основном теоретическое значение,
изложим сначала применительно к задаче Коши
^ =/(*,*), *(«о) = хо A2-7)
at
для обыкновенного дифференциального уравнения (ОДУ) перво-
первого порядка. Предполагаем, что функция /(?, х) удовлетворяет
всем условиям теоремы 2.2 Коши о существовании и единствен-
единственности решения задачи Коши.
Идея метода последовательных приближений изложена, по
существу, в самом доказательстве этой теоремы. Пусть x(t) —

12.2. Метод последовательных приближений 309
решение ОДУ в A2.7). Подставив это решение в A2.7),
после интегрирования с учетом начального условия получим
равенство
t
f{Z,x{Z))dt. A2.8)
to
Далее, заменив в подынтегральном выражении неизвестную
функцию x(t) на жо, найдем первое приближение
to
Аналогично находим второе приближение
t
to
и т.д. Для n-го приближения будем иметь
t
/(f,a;n-i(O)df, n = l,2,... A2.9)
to
В ходе доказательства теоремы 2.2 Коши установлено, что при
каждом t ? [to — Л, to + h] последовательность {xn(t)} имеет
пределом решение x*(t) задачи Коши A2.7), т.е.
lim xn{t) = x*(t).
п—>оо
Метод последовательных приближений можно также приме-
применить и к задаче Коши
/(*,«), x(to) = xo A2.10)
для нормальной системы ОДУ вида A.4). Нулевое приближение
соответствует а?о, & последующие приближения (п = 1, 2,...)

310
12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
находят по формуле
ъ
f
to
При этом под интегралом от векторной функции f(t, x(t))
понимают матрицу-столбец вида D.14).
Этот метод применим и к задаче Коши для ОДУ п-го
порядка, если это уравнение предварительно представить в
виде нормальной системы ОДУ.
12.3. Метод ломаных Эйлера
Пусть дана задача A2.7) Коши для обыкновенного диффе-
дифференциального уравнения (ОДУ) первого порядка, причем t €
Е[?о,Т]. Разобьем отрезок [?о,Т] на N одинаковых отрезков,
концы которых обозначим через tn = to + nh (n = 0, N), где
h = (Т — to)/N, а значение x(tn) функции x(t) в каждой из
этих точек — через хп. Кроме того, обозначим f{tn,xn) = fn.
Конечное множество, содержащее iV + 1 точек tn (n = 0, N),
называют обычно сеткой, эти точки — узлами сетки, а
одинаковую для всех отрезков [tn, tn+i] (n = 0, JV — 1) длину
h — шагом сетки.
Искомую интегральную кривую x(t) ОДУ в A2.7), про-
проходящую через точку Ао(?о»#о) (рис. 12.2), приближенно за-
заменим ломаной A$A\A2-..An с пока еще неизвестными вер-
вершинами в точках An(tn,xn) (n = l,N). Наклон каждого зве-
звена АпАп+\ этой ломаной, назы-
называемой ломаной Эйлера, при-
примем равным угловому коэффи-
коэффициенту fn касательной к ин-
интегральной кривой, проходящей
через точку An(tn,xn). Наклон
звена AqA\ известен благода-
благодаря заданию начальных условий в
О
Рис. 12.2

12.3. Метод ломаных Эйлера, 311
задаче Коши A2.7) и равен /о = /(?(ъ#о)- Это позволяет
из уравнения прямой х — xq = fo(t — to), имеющей угловой
коэффициент /о и проходящей через точку Ао(?о> #о)> найти в
узле ?i значение
хг=х0 + /o(*i - *о) = ^о + М,
т.е. вычислить ординату ближайшей к Aq вершины А\ ло-
ломаной Эйлера. Далее, повторяя описанную процедуру, можно
последовательно вычислить значения
Xn + fnh, n = l,iV-l, A2.11)
и найти ординаты всех остальных вершин этой ломаной.
Изложенный способ приближенного построения интеграль-
интегральной кривой для задачи Коши вида A2.7), называемый мето-
методом ломаных Эйлера, предложен Л. Эйлером в 1768 году.
Помимо представленной геометрической интерпретации этому
методу можно дать и другую трактовку. Записав A2.11) в виде
^ = /„, п = б^\П=Т, A2.12)
нетрудно установить, что это выражение соответствует при-
приближенной замене в ОДУ, входящем в A2.7), значения произ-
производной dx/dt в узле tn правой конечной разностью, иногда
называемой конечной разностью вперед.
Возникающую при такой замене погрешность можно умень-
уменьшить, если уменьшить шаг сетки /г, т.е. для заданного отрез-
отрезка [to,T] увеличить число N частичных отрезков [?
(п = 0, N — 1) разбиения заданного отрезка [io??1]- Но при этом
возрастет необходимый объем вычислений, что приведет к
накоплению большей вычислительной погрешности, возникаю-
возникающей, например, за счет округления чисел при их представлении
в ЭВМ хотя и с большим, но конечным числом разрядов. При
этом создается ситуация, аналогичная влиянию ошибок округ-
округления при численном дифференцировании.

312 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Существует несколько модификаций метода ломаных Эй-
Эйлера, позволяющих уменьшить погрешность вычислений. Ос-
Основная идея модификации состоит в более точном вычислении
интеграла на каждом частичном отрезке [?n, ?n+i]- По анало-
аналогии с A2.8) запишем
tn+h
I (К A2.13)
Если ^ля вычисления интеграла использовать квадратурную
формулу левых прямоугольников, то придем к A2.11). Вместе с
тем известно [VI], что более точными являются квадратурные
формулы трапеции и прямоугольника.
Но если применить, например, формулу трапеции непо-
непосредственно к A2.13), то получим, вообще говоря, нелинейное
уравнение
xn+i =xn + -(fn + /(*п+ъ xn+i)) A2.14)
относительно искомого значения хп+\. Чтобы избежать не-
необходимости решать такое уравнение, вычисления проводят в
два этапа. Сначала прогнозируют при помощи A2.11) ожидае-
ожидаемое значение жп+ъ а затем уже используют формулу трапеции
длякоррекции этого значения. В итоге рабочая формула при-
принимает вид
xn+i = хп + j (/n + /(*n+i. Xn + hfn)). A2.15)
Она характеризует метод Эйлера — Коши.
Аналогичная идея лежит в основе усовершенствованно-
усовершенствованного метода ломаных. В этом методе сначала прогнозируют
ожидаемое значение жп+1/2 = ж(*п+1/2) = хп + fnh/2 в проме-
промежуточной точке tn+i/2 = in + Л/2, а затем используют формулу
прямоугольника
= Хп

12.3. Метод ломаных Эйлера
313
так что рабочая формула имеет вид
xn+i = xn + /(^n+V2' Хп ~^~ fnh/2)h, A2.16)
Пример. Применим метод ломаных Эйлера и его модифи-
модификации для численного решения задачи Коши
dx
— = 2tx, я@) = 1, «6 [0,1], A2.17)
имеющей точное аналитическое решение
x(t) = el\ A2.18)
В данном случае благодаря линейности ОДУ A2.17) удобно
использовать и A2.14), принимающее вид
l + h2n
xn+i = хп —
Результаты расчетов при h = 0,1 (N = 10) представлены в
табл. 12.1.
Таблица 12.1
tn
од
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
Рабочая формула
A2.11)
1,00000
1,02000
1,06080
1,12445
1,21440
1,33584
1,49615
1,70561
1,97850
2,33463
A2.14)
1,01010
1,04102
1,09468
1,17450
1,28577
1,43624
1,63700
1,90390
2,25958
2,73660
A2.15)
1,01000
1,04070
1,09399
1,17319
1,28347
1,43236
1,63059
1,89345
2,24260
2,70906
A2.16)
1,01000
1,04060
1,09367
1,17253
1,28228
1,43038
1,62749
1,88870
2,23546
2,69843
A2.18)
1,01005
1,04081
1,09417
1,17351
1,28403
1,43333
1,63232
1,89648
2,24791
2,71828
Из таблицы видно, что модификации позволяют уменьшить
погрешность вычислений метода ломаных Эйлера.

314 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
12.4. Метод Рунге — Кутты
Построение метода численного решения задачи A2.7) Коши
для обыкновенного дифференциального уравнения (ОДУ) перво-
первого порядка можно провести формальным путем. Рассмотрим
один из частичных отрезков [tn, tn+\) (n = О, N - 1) разби-
разбиения отрезка [to, Г] на N равных частей с шагом сетки
h = (Т — to)/N. Предположим, что известна ордината хп =
= x(tn) точки искомой интегральной кривой x(t) для задачи
A2.7) Коши в узле сетки tn = to + n/i, являющемся левым кон-
концом частичного отрезка [tn,tn+i]. Будем искать приближенное
значение ординаты, соответствующей правому концу этого от-
отрезка в узле ?п+ъ в виде
т т
xn+i = x(tn+i) = хп + h^2^ikh Yl^k = 1> A2.19)
г=1 k=l
где
h = f{tn,xn)\
km = f (tn + a
A2.20)
m-l
Число m?N и коэффициенты а^,/3у,7^ (г = 2, m, j = l,m — 1,
k = 1, m) выбирают, руководствуясь различными соображени-
соображениями, но одно из основных соображений связано с желанием
повысить точность рабочей формулы A2.19). Эта формула
характеризует метод, названный по имени немецких матема-
математиков К.Д.Т. Рунге A856-1927) и В. Кутты A867-1944) ме-
методом Рунге — Кутты.
Пусть x(t) — точное решение задачи A2.7) Кошщ а хп+\ —
приближенное значение ординаты интегральной кривой для

12.4. Метод Рунге — Кутты 315
ОДУ в A2.7), проходящей через точку (?о,жо), найденное из
A2.19) в узле tn+i при условии, что хп = x(tn), т.е. по точному
значению ординаты этой кривой при tn. Ясно, что в этом
случае разность
= x(tn+i) -
га
= ?(*п + /0-?(*п)-ЛУЧл| , . A2.21)
fr^ \xn-x{tn)
называемая погрешностью метода на шаге, будет функ-
функцией шага h.
Предположим, что функция f(t,x) в A2.7) дифференциру-
дифференцируема 5 + 1 раз в области изменения своих аргументов. Тогда,
согласно A2.20) и A2.19), столько же раз можно продифферен-
продифференцировать по h и функцию <p{h). Представим ее в окрестности
точки /i = 0 формулой Тейлора с остаточным членом в форме
Лагранжа
6,@,!). A2.22)
В этой записи принято, что при к = 0 <р(°)@) = <р@) и 0! = 1,
а также обозначено </?^@) = dktp/dhk\h:_Q.
Задачу подбора коэффициентов а^, ^j, 7fc (i = 2, m, j =
= l,77i — 1, fc = l,m), обеспечивающего повышение точности
рабочей формулы A2.19) теперь можно сформулировать так:
при заданном т € N найти такое сочетание значений этих
коэффициентов, чтобы при наибольшем возможном s E N в
A2.19) было выполнено условие (р@) = <р'@) = ... = (р^@) = 0.
В этом случае погрешность метода на шаге будет определять
в A2.22) лишь остаточный член, пропорциональный сомно-
сомножителю Л5+1. Степень s + l этого сомножителя называют
порядком точности метода на шаге. Поскольку погреш-
погрешность возникает на каждом шаге, то при N вычислениях на

316 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
отрезке [to, T] суммарная погрешность будет пропорциональ-
пропорциональна Nhs+l = (Г — to)hs, т.е. порядок s точности метода
на отрезке будет на единицу меньше, чем на шаге.
Ясно, что при т = 1 A2.19) переходит в A2.11), т.е. метод
ломаных Эйлера можно рассматривать как частный случал
метода Рунге — Кутты. В этом случае, согласно A2.19) —
A2.21), имеем 71 = 1 и
(p(h) = x(tn + h)-x(tn)-hf(tn,x(tn)).
Отсюда при h = 0 получаем ср(О) =0 и, учитывая, что
dx/dt\t=tn=f(tn,x(tn)),
dh /1=0 L dt
а также
W(n,(n))l =0,
t-tn+h J/i=o
dt2
•l = i
t=tn+h
Поскольку в общем случае ??"@) = x"(tn) ф 0, то в соответствии
с A2.22) устанавливаем, что метод ломаных Эйлера имеет
второй порядок точности на шаге и первый порядок точности
на отрезке, причем погрешность этого метода на шаге будет
<p(h)=x(tn + eh)h2/2, ве @,1).
При ш = 2 из A2.19) и A2.20) с учетом условия 71 +72 = 1
следует
xn+i=xn + h (A-72)^1 +72^2); П2 23)
h = f{tn, xn), k2 = f(tn + a2h, xn + fohk)
В этом случае, согласно A2.21), будем иметь
x(tn + h) -x(tn) - A -

12.4. Метод Рунге — Кутты 317
Обозначив
трижды продифференцируем функцию (fi(h):
<p'(h) = x'(tn + h)-(l- 72) /n - 72 f(t, x) -
- J2hoi2fl(t, x) - 7
<p"{h) = x"(tn + h)- 272 {a2fl(i, x) + (hxf'x{t, x) fn) -
-42h{alp;t{t, x) + 2a2fati'x(l x) fn
- 372 («!/«(<, x) + 2a2lhiftx(l x) U + РУХХA x)fl) + O(h),
где использованы обозначения
Jt dV Jx dx" Jtt dt2' Itx dtdx' Jxx
dt2' Itx dtdx' Jxx dx2'
Учитывая, что для ОДУ в A2.7)
подставим в выражения для функции ip(h) и ее производных
значение h = 0 и получим
p"(h) = A - 272а2) f[(tn, xn) + A - 272/?2i)/z(tn, xn) /„;
/^(tn, ?n) + 2A - b2CX2/hl)f?x(tn, Xn)fn +
ll)f?x(tn, Xn)fl + fx(tn, Xn)x"(tn).
Равенство <^"@) = 0 имеет место для произвольной диффе-
дифференцируемой функции f(t, x) при условиях
1-272а2 = 0 и l-272A>i=0. A2.24)

318 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Выполнение условий A2.24) обеспечивает при использовании
A2.23) третий порядок точности на шаге и второй — на
отрезке.
Если принять 72 = 1/2> то из A2.24) найдем е*2 = /hi = 1?
что соответствует рабочей формуле A2.15) метода Эйлера —
Коти. Если же взять 72 = 1? то получим ol<i = /З21 = 1/2,
т.е. придем к рабочей формуле A2.16) усовершенствованного
метода ломаных. Таким образом, эти методы имеют второй
порядок точности на отрезке.
Задавая различные значения параметра 72? можно постро-
построить так называемое однопараметрическое семейство методов
Рунге — Кутты, имеющих второй порядок точности на отрез-
отрезке. Увеличить порядок точности при т = 2 путем выполнения
равенства iptn@) = 0 в общем случае не удается. Например,
для ОДУ dx/dt^x при любых значениях 72? &2 и $21 имеем
<рш@) = 1. Поскольку главная часть погрешности этого семей-
семейства методов, согласно A2.22), равна <p//;@)/i3/6, в некоторых
конкретных случаях эту величину можно уменьшить, пользуясь
полученным выражением для <рш@). Так, если для некоторого
класса ОДУ мала величина fxxh\ то целесообразно подобрать
коэффициенты так, чтобы помимо выполнения условий A2.24)
в выражении для <р/п@) обратились в нуль первые три слагае-
слагаемых, т.е. были бы выполнены равенства
1 - 372^2 =0, 1 - 372<*2/321 =0, 1 - 372$! = 0.
Несложно убедиться, что всем этим условиям удовлетворяют
значения 72 = 3/4, a<i = /З21 = 2/3, что приводит к рабочей
формуле
Xn+i =хп + ^ (/п + 3/(*п + 2Л/3, хп + 2Л/„/3)).
Аналогично рассмотренному случаю т = 2 можно постро-
построить семейства методов Рунге — Кутты для т ^ 3. При т = 3
в общем случае s < 3, т.е. удается обеспечить третий порядок

12Л. Метод Рунге — Кутты 319
точности на отрезке, причем одной из наиболее употребитель-
употребительных рабочих формул является
хп + т (h + 4fc2 + fa);
и
Из семейства методов четвертого порядка точности на отрезке,
получаемых при га = 4, наиболее часто используют вариант,
приводящий к рабочей формуле
+ -(k1 + 2k2 + 2ks + k4);
2 = f(tn + h/2,xn + hkl/2), A2-25)
, xn + hk2/2), k4 = f{tn + h, xn + hk3).
Отметим, что если правая часть ОДУ в A2.7) не зависит от
ж, то обе последние рабочие формулы переходят в формулу
Симпсона
для отрезка длиной /г, имеющую пятый порядок точности на
шаге и четвертый — на отрезке длиной Т — to = Nh.
Если применить A2.25) к решению задачи A2.17) Коши, то
при h = 0,1 результаты будут отличаться от приведенного в
табл. 12.1 точного решения A2.18) не более чем на 10~5.
Рабочие формулы при га > 5 используют достаточно редко
ввиду их громоздкости. В случае необходимости повысить точ-
точность и количественно оценить погрешность получаемого при-
приближенного решения можно при га ^ 5 применить метод Рунге
двойного пересчета. Аналогичный подход используют при раз-
разработке ЭВМ-программ с автоматическим выбором шага для
обеспечения заданной точности е. Приведем соотношения так

320 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
называемого пятиэтапного метода Рунге — Кутты, которые
обычно используют в таких программах:
= Хп + g (ki+4kA+k5), <+1 = хп + - (&1/2-ЗА;з/2+2А;4);
h = f(tn + Л/3, хп + hki/6 + hk2/6),
В качестве приближенного решения на шаге берут значение
жп_|_1, а значение ж*+1 используют для контроля точности.
Если Л = 1x^+1 — #n+i|/5 > e, то далее шаг уменьшают вдвое,
если е/64 < А ^ ?, то его оставляют прежним. При А ^ е/64
шаг увеличивают вдвое.
Рабочие формулы метода Рунге — Кутты несложно запи-
записать применительно к решению задачи Коши для нормальной
системы ОДУ. Для этого систему следует представить в виде
A.3) и использовать выбранную рабочую формулу для каждого
из уравнений.
12.5. Метод Чаплыгина
Приближенное аналитическое решение задачи Коши для
нормальной системы обыкновенных дифференциальных уравне-
уравнений (ОДУ) можно получить методом Чаплыгина, предло-
предложенным в 1919 году отечественным математиком и механиком
С.А. Чаплыгиным A869-1942). Для простоты изложим этот
метод применительно к задаче A2.7) Коши для ОДУ первого
порядка.
Идея метода состоит в построении двух аппроксимирующих
точное решение x(t) последовательностей функций {un(t)},
{vn{t)} {un(t) ^ x(t) < vn(t) Vt G [to, T]) с начальными условия-
условиями un(to) = vn(to) =x(to) = XQ. Эти последовательности таковы,
что последовательность {vn(t) — un(t)} равномерно сходится
по t на отрезке [to, T] к нулевому пределу при п —> оо [IX].

12.5. Метод Чаплыгина
321
Геометрически этот метод можно интерпретировать следу-
следующим образом: интегральная
кривая x(t) ограничена свер- х
ху и снизу графиками функций
vn(t) и un(t) (рис. 12.3). Он
основан на теореме Чаплыги- х0
на о дифференциальных нера-
неравенствах. Введем обозначение о t0 г ~t
J(w) = dw/dt — /(?, w). Если
x(t) — решение ОДУ в A2.7), Рис. 12.3
то J(x) = 0.
Теорема 12.2 (теорема Чаплыгина). Бели функции
u(t), v(t) (to < t < T) удовлетворяют неравенствам J(u) < 0,
J(v) ^ 0, то для любого t G fahT1] имеют место неравенства
u{t) < x(t) ^ v(t) (ix(*o) = v(*o) = x
Алгоритм построения аппроксимирующих последовательно-
последовательностей {un(t)} и {vn(t)} состоит в следующем. Эмпирически
выберем две функции щ = щ(г) и vq = vo(t) (щ < ^о) так,
чтобы uo(to) = vo(to) = я?о, uo(t) < ^o(t), t E [to, T], и
A2.26)
J(tio) = -ao(«) < 0, J(«o) = /%(t) ^ 0.
В качестве исходных примем функции г^о(^), щ{Ь). Положим
щ (t) = щ (t) + /i0 (*), v\ (t) = v0 (t) -1/0 (t), причем функции /i0 (t),
^o(^) (mo(^o) = ^o(^o) = 0) удовлетворяют линейным ОДУ пер-
первого порядка
где
A2.27)
dt
Po(t) =
дх '

322 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Решеньями ОДУ A2.27) при начальных условиях /хо(*о) =
= 0 являются функции
aoit) exp(-fpo@<K) df
t0 / t0
t
f
to I to
Так как на основании A2.26) ao(t)^O и /?о(*) ^ 0, то в силу не-
неотрицательности определенного интеграла от неотрицательной
подынтегральной функции [VI] имеем для решений ОДУ A2.27)
/iO(*)^O и vo{t)>Q Vt€[t<bT].
Бели предположить, что d2f/dx2 сохраняет постоянный
знак в области существования решения задачи Коши, то можно
показать, что J{u\) ^ 0, J(vi) ^0 Vt 6 [to, T] (это утвержде-
утверждение оставляем без доказательства). Следовательно, используя
метод математической индукции, для произвольного п € N
имеем JK) = -an(<K0, J(«n)=A»(*)>0.
Положим теперь un+i(t) = un(t) + /хп(*), vn+i(t) = vn(t) -
~-Vn(t)- Функции nn(t) и vn(t), определяемые из ОДУ
A2.28)
при начальных условиях /in(*o) = ^«(^о) = 0, неотрицательны
Vte[tQ,T]. В A2.28) обозначено:
fl/fotin) m f(t,vn)-f(t,un)
Описанная процедура в принципе позволяет построить не-
неубывающую {un(t)} и невозрастающую {vn(t)} последова-
последовательности, причем можно показать, что искомое решение x(t)

12.5. Метод Чаплыгина 323
задачи Коши A2.7) расположено между любыми элементами
этих последовательностей:
x{t)^vn{t) VneN.
Анализ метода Чаплыгина показал, что
Kn^ (vn(t) - un(t)) = О Vt G [t0, T].
Если для заданной допустимой погрешности е > 0 прибли-
приближенного решения найдено такое п, что vn(t) — un(t) < 2e
Vt G [t0, Т], то полагают z(t) «
Пример. Построим методом Чаплыгина первое приближе-
приближение к решению задачи Коши
В данном случае /(?, х) = t + x2, J(w) = dw/dt — t — w2.
Положим щ(г) = 0 и vo(t) = t. Тогда J{uq) = —t, ()
= 1 — ? — t2 и, следовательно, c*o(?) = i, /?0(t) = 1 — i — *2. Так
как J(^o) = 0 при Г = (\/5 — l)/2 « 0,618, то искомое первое
приближение будет иметь смысл лишь на отрезке [0, Т].
Вычислим
ox
и запишем ОДУ вида A2.27)
Их решение с учетом начальных условий /io(O) = ^о(О) = 0
таково:

324 12. ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ОДУ
Тогда
ui(t) = uo(t) +iio{t) = *2/2, vi(t) = vo(t) - M*) = e<2/2
На основании найденного первого приближения примем
Оценим погрешность полученного приближения по значе-
значению
a tfl(*)"~Ul(*) 1 / *2/о t2\
Д = max = - max [е ' — 1 .
t€[to,TJ 2 2t€[«o,T]V 2/
Значение Д « 0,019 отвечает правому концу отрезка [0, Г].
Вопросы и задачи
12.1. Для следующих задач Коши найти решение в виде
степенного ряда:
dx
а) — + xsint = sin21 + cost, ж@)=0;
at
fi т fii* finr
б) ^2- + -^rsint + a; = sin2i, x@) = 2, —
at* at at
d2x dx t dx\
в)+е ж=1 *@) = 1 L
=0;
12.2. Методом Чаплыгина построить первое приближение к
решению задачи Коши, взяв за начальное приближение uo(t) =
= 0 и vo{t)=t:
dx
а) _=х + 3*, х@)=0, 0 < * < 1/4;
at
б) ^=ж2 + ^2, я?@)=0, 0 < *

13. ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
13.1. Линейное дифференциальное уравнение.
Уравнения характеристик. Задача Коши
Линейным неоднородным дифференциальным урав-
уравнением (ДУ) первого порядка с частными производны-
производными называют уравнение
...,хп)- \-a2\x\, ...,хп
\a2\x\, ...,хп)(...+
ап(хи ..., хп)-^г = b(xu ..., хп), A3.1)
где ai(x\, ...,жп) (г = 1,п) и b(xi,...,хп)—заданные функ-
функции п независимых переменных хi,..., хп, непрерывно диф-
дифференцируемые в некоторой области D С Еп; и{х\,..., хп) —
искомая функция.
Если в A3.1) b(xi,..., хп) = 0 во всех точках (o?i,...,a:n)
области D, то будем иметь линейное однородное ДУ пер-
первого порядка с частными производными
ч ди
) + +
=0, A3.2)
соответствующее A3.1). Решением ДУ A3.1) и A3.2) в об-
области D будем называть непрерывно дифференцируемую в
D функцию, которая обращает эти уравнения в тождества в
любой точке (x\j ...,#n) € D.

326 13. ДУ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Рассмотрим сначала однородное ДУ A3.2) и поставим ему
в соответствие систему обыкновенных дифференциальных урав-
уравнений (ОДУ)
-^=аг(хи...,хп), г = 1,п. A3.3)
Поскольку dt = dxi/ai, i = 1, п, то систему A3.3) можно пред-
представить в симметричной форме записи
dx\ dx2 dx{ dxn
a\ п2 a>i an
Систему A3.3) называют системой уравнений характери-
характеристик для однородного ДУ A3.2), а ее фазовые траектории —
характеристиками.
Теорема 13.1. Функция и(х\,..., хп) является решением
ДУ A3.2) в области D тогда и только тогда, когда она есть
первый интеграл системы A3.3) уравнений характеристик в
этой области.
< Действительно, если функция и(х\,..., хп) является реше-
решением ДУ A3.2) в области D, то ее полная производная в силу
системы A3.3)
du v^ ди dxk v^ ди _
gg0
Это означает, что функция u(xi, ...,хп) вдоль каждой из
характеристик сохраняет постоянное значение, т.е. является
первым интегралом системы A3.3) в D.
Если, наоборот, функция u(xi,...,?n) является первым
интегралом системы A3.3) в ?>, то ее полная производная в
силу системы A3.3) равна нулю, т.е. справедливо равенство
A3.4). А это означает, что функция u(xi, ...,xn) является
решением ДУ A3.2) в области D. >

13.1. Линейное дифференциальное уравнение. Задача Копт 327
Пусть <pj(xi,..., xn), j = 1, п — 1, — первые интегралы си-
системы A3.3), и при этом они являются независимыми в обла-
области D (см. определение 8.3). Приведем формулировку теоре-
теоремы, устанавливающей структуру общего решения однородного
ДУ A3.2).
Теорема 13.2. Любое решение однородного ДУ A3.2) в
области D имеет вид
...,?>„_1), A3.5)
где щ(х\,...,#n), j = l,n—1, — первые интегралы систе-
системы A3.3) в области ?>, а Ф — функция, непрерывно диффе-
дифференцируемая в этой области.
Иными словами, формула A3.5) описывает все множество
решений ДУ A3.2) в области D.
Задача Коши для ДУ A3.2) ставится так: найти такое реше-
решение этого ДУ, которое на заданной поверхности S совпадает
с заданной функцией.
Пример. Найдем решение и(х\,Х2) задачи Коши для од-
однородного уравнения
ди ди л
удовлетворяющее условию пA, #2) = х\. Это условие означает,
что искомое решение уравнения в точках прямой х\ = 1 долж-
должно совпадать с функцией <р(х\, Х2) = х\.
Соответствующая этому ДУ система уравнений характери-
характеристик в симметричной форме записи имеет вид
dx\
Отсюда интегрированием находим первый интеграл этой си-
системы
/S7 l|| = С = const,

328 13. ДУ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
который на каждой из характеристик сохраняет постоянное
значение. Общее решение, согласно теореме 13.2, имеет вид
и = ФЫ, где z = д/?Г + 1П1#2|- Выделим из общего реше-
решения частное решение, удовлетворяющее условию гхA, х2) = х\.
Из первого интеграла при хх = 1 получаем \п\х2\ = С-1 и
^A яо) = х2 = е2^с~~1\ Выражая в последнем равенстве посто-
постоянную С через первый интеграл, находим решение исходного
ДУ в виде о о г о
J2^2 #
Перейдем теперь к рассмотрению неоднородного ДУ A3.1).
Его решение будем искать в неявном виде
W(xu...,xn,u) = 0. A3.6)
В силу правила дифференцирования неявно заданной функ-
функции [V] имеем
du dw/dXi
Подставляя A3.7) в неоднородное ДУ A3.1), получаем
dW
n)— + a2(xu..-,xn)— + ...+
dW dW
+ b(..,xn)-^=O. A3.8)
Уравнение A3.8) является линейным однородным ДУ от-
относительно искомой функции W и включает частные произ-
производные этой функции по (п + 1)-му независимому переменно-
переменному xi,..., хп, и. Этому ДУ соответствует система уравнений
характеристик
dxi dx2 _dxi _ _ dxn _ du
= 5= ... — -— — ... — -- — —.
ai a2 a% an о

13.1. Линейное дифференциальное уравнение. Задача Коши 329
Пусть функции <Pi(xi,..., жп, гх), г = 1, п, являются в области
Dl = {(xu...,xn,u): (xu...,xn)?D}CRn+1
независимыми первыми интегралами системы A3.9). Тогда
общее решение однородного ДУ A3.8) в силу теоремы 13.2
имеет вид
где Ф — произвольная непрерывно дифференцируемая в обла-
области D\ функция, такая, что дФ/du^O в области D\. Из
A3.6) следует, что равенство
-..,?>п) = 0 A3.10)
задает искомое решение и ДУ A3.1) как неявную функцию
независимых переменных rci,..., хп.
Задача Коши для неоднородного ДУ A3.1) ставится так же,
как и для однородного ДУ A3.2).
Пример. Найдем решение задачи Коши для неоднородного
линейного ДУ
2 ди ди
#1
дх\ ОХ2
удовлетворяющее условию u@, х%) = х\. Запишем в симметрич-
симметричной форме систему уравнений характеристик вида A3.9):
2 Х\
Из равенства левой и средней частей A3.11) после интегриро-
интегрирования получаем а?! — #? = Gi, а из равенства средней и правой
частей находим 1п|ж2| — и = С2- Таким образом, первые ин-
интегралы системы A3.11) таковы:
(fl = х\ - х\, (р2 = 1П | Х2 | - U.
Тогда, согласно A3.10), равенство
Ф{х1-х\, 1п|ж2|-г0=0

330 13. ДУ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
задает искомое решение и исходного ДУ как неявную функ-
функцию независимых переменных xi, х2. Если удастся разрешить
это равенство относительно и, то будем иметь и(х\,х2) =
= 1п|х2| + Ф(#2 "" х\ )> гДе Ф — произвольная непрерывно диф-
дифференцируемая функция. Так как в силу заданного условия
г* = #2 ПРИ ^1=0, то Ф(#2) =^2 — lnlo^^U ИЛИ
В итоге искомое решение принимает вид
Фи х2) = 1п|я?2| + А - х\ - - 1п|ж1 -х\|.
13.2. Квазилинейное дифференциальное уравнение
Квазилинейным дифференциальным уравнением (ДУ)
первого порядка называют ДУ с частными производными
..., хп, и) — + а2[xi,..., хп, и) — + ... +
+ ап(хи ..., хп, и)-— = Ъ(хи ..., хп, и), A3.12)
дхп
где ai(xi,...,xn,u) (г = 1,п) и Ь(хи ...,жп, w) — заданные
функции, непрерывно дифференцируемые в некоторой области
D\ С Rn+1 изменения п переменных Х{ (г = 1, п) и искомой
функции г*. Подчеркнем, что, в отличие от ДУ A3.1), коэф-
коэффициенты ai (i = 1, п) и правая часть 6 в A3.12) зависят от
искомой функции и.
Процесс нахождения общего решения ДУ A3.12) аналогичен
нахождению общего решения неоднородного ДУ A3.1). Приве-
Приведем основные этапы этого процесса.
Система уравнений характеристик для квазилинейного ДУ
по форме полностью совпадает с системой A3.9) для неодно-
неоднородного ДУ A3.1). Интегральные кривые этой системы называ-
называют характеристиками квазилинейного ДУ A3.12). Если

13.2. Квазилинейное дифференциальное уравнение 331
в области D\ найдены п первых независимых интегралов
<Pi(xi,..., хп, и) (г = 1, п) системы уравнений характеристик,
то все решения ДУ A3.12) можно получить из равенства A3.10),
в котором Ф — произвольная непрерывно дифференцируемая
функция.
Постановка задачи Коши для квазилинейного ДУ аналогич-
аналогична постановке этой задачи для однородного линейного уравне-
уравнения A3.2). При практическом решении этой задачи необходимо
руководствоваться следующими правилами.
Пусть решение и(х), х = (х\,...,жп)т, ДУ A3.12) долж-
должно удовлетворять условию и(х) = Ф(ж) на поверхности 5,
которая задана уравнением /(xi,..., хп) = 0. После нахожде-
нахождения первых интегралов <pi(x, и) (г = 1, п) системы уравнений
характеристик вида A3.9), исключив из системы уравнений
(Рг(х,и) = ъ, г = Т7п; /(х)=0; и = Ф(ж),
переменные х\, ..., #п, щ получим равенство F(ci,C2, ...,Cn) =
= 0, в которое следует подставить с* = <Рг(ж, г*), г = 1,п. Тогда
получим
(ж, и), ??2(ж, и),..., <рп(ж, п)) = 0.
Одно из решений и(х) этого уравнения и будет искомым.
Пример. Решим задачу Коши
h() + 2 на 5: 2xi +3ж2 = 0.
ОХ\ ОХ2
Постановка задачи допускает геометрическую интерпретацию:
найти уравнение поверхности и = u(xi, #2), проходящей через
кривую, заданную уравнениями х^ = 2u, ^i + 2^2 = и.
Составим систему уравнений характеристик
*!. A3.13)
гх Ж2

332 13. ДУ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Интегрируя равенство средней и правой частей A3.13), нахо-
находим и2 — х\ = с\. Далее, используя свойство равных дробей,
запишем равенство
d( ) _ dx\
X2 + U Х\
и после его интегрирования получим Х2 + и = с^х\. Таким
образом, имеем два первых интеграла системы A3.13):
2 2 X2+U
lfl=U -Х2\ <Р2 = •
XI
Составим систему уравнений
2 = ci; u = xi + 2x2; 2xi+3x2 = 0.
Из этой системы уравнений необходимо исключить переменные
xi, Ж2, и и найти зависимость между параметрами ci и С2.
Исключая и, получим систему из трех уравнений
(xi + 2х2J -x\ = ci\ Зх2 = (с2 - l)xi; 2х\ + Зх2 = 0.
Из последних двух уравнений имеем (с2 + 1)х\ = 0. Так как
xi ф 0 (в противном случае и Х2 = 0), то с2 = — 1. Таким
образом, решением задачи Коши является функция и{х\,Х2) =
= —xi — Х2.
Пример 13.1. Квазилинейное ДУ вида
|+ ,(,)g= 0 A3.14)
описывает изменение плотности р(х, t) газа при его изотерми-
изотермическом (т.е. при постоянной температуре) одномерном течении
в канале. Здесь v(p) — скорость течения газа в направлении
оси Ох, заданная известной функцией от плотности р.
Построим решение задачи Коши для ДУ A3.14) с начальным
условием р(х, 0) = ро(#)> заданным в момент времени t = 0.
Запишем уравнение характеристик для этого ДУ:
dt dx dx . ч ( ч
Tt=v{p)- A3Л5)

13.2. Квазилинейное дифференциальное уравнение 333
С учетом A3.15) полная производная функции p(x,t) равна
dp _ dp dp dx dp dp
Вытекающее из A3.14) равенство этой производной нулю озна-
означает, что плотность р(ж, t) остается постоянной на характе-
характеристиках, каждая из которых имеет в плоскости tOx посто-
постоянный угловой коэффициент k = dx/dt =
= v(p) = const, т.е. представляет собой пря- t ,
мую. Это позволяет для произвольных зна-
значений х\ и t\ следующим образом най-
найти плотность газа. Через точку M(x\,t\) OL
(рис. 13.1) проходит прямолинейная харак-
характеристика Рис* 13#1
x = xi+v(p)(t-ti).
Эта прямая пересекает координатную ось Ох в некоторой
точке
xo=xi-v{p)ti.
В этой точке, согласно начальному условию, известно значение
плотности р(хо,О) = ро(#о)- Таким образом, значение xq
является решением уравнения
Предположим, что это уравнение удалось явно разрешить
относительно жо, т.е. xq = ф(х\^ t\). Тогда плотность газа
в произвольно выбранной точке M(x\,t\) будет
В за1слючение сделаем замечание о существовании и един-
единственности задачи Коши для ДУ с частными производными
первого порядка на примере п = 3.

33413. ДУ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ
Бели поверхность S задается уравнением /(жь #2? #з):= О,
то достаточным условием однозначной разрешимости зада-
задачи Коши является неортогональность в каждой точке на по-
поверхности S векторов grad/(x) и а = (ai(x), а2(ж),аз(ж))т,
где а^, i = 1,2,3, — правые части системы A3.3) для п = 3:
),a(»))^0, xeS.
Вопросы и задачи
13.1. Решить следующие дифференциальные уравнения с
частными производными:
ч ди ди о о ^ч 1 ди 1 ди и
а) х2 т— + xi -?— = х{ + х\\ б) — +
дх\ 3X2 Х
? = х{ + х\\ б) г
3X2 Х\ ОХ\
ди Л ди о ди
+ 2+
13.2. Решить задачу Коши для следующих дифференциаль-
дифференциальных уравнений с частными производными:
. ди ди п ди п
) + + 2 ° 1
. ди ди о о х\
9г/ 9u 1 2
В) #1 — h Х2 ~X := 14 — Х\Х2ч U = 1 -\- Xi При #2 == 2.
13.3. Найти уравнение гх = u(xi,X2) поверхности, удовле-
удовлетворяющее квазилинейному ДУ
ди ди
+
+ X\U
ОХ\ ОХ2
при условии, что поверхность проходит через кривую, задан-
заданную уравнениями
х\ = 1; Ж + 2 1

СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособия
Агафонов С.А., Зарубин B.C., Яковенко М.Г. Прикладные методы и
задачи в разделе „Дифференциальные уравнения". М.: Изд-во МВТУ, 1988.
68 с.
Амосов А.А., Дубинский Ю.А., Копчено в а Н.В. Вычислительные ме-
методы для инженеров. М.: Высш. шк., 1994. 544 с.
Арнольд В.И. Обыкновенные дифференциальные уравнения. М.: Нау-
Наука, 1984. 272 с.
Барбашин Е.А. Функции Ляпунова. М.: Наука, 1970. 240 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.:
Наука, 1987. 600 с.
Бугров Я.С, Никольский СМ. Высшая математика: Дифференци-
Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного
переменного. М.: Наука, 1981. 448 с.
Демидович Б.П. Лекции по математической теории устойчивости. М.:
Наука, 1967. 472 с.
Калиткин Н.Н. Численные методы. М.: Наука, 1978. 512 с.
Карташев А.П., Рождественский Б.Л. Обыкновенные дифференци-
дифференциальные уравнения и основы вариационного исчисления. М.: Наука, 1986.
272 с.
Лизоркин П.И. Курс дифференциальных и интегральных уравнений с
дополнительными главами анализа. М.: Наука, 1981. 384 с.
Матвеев Н.М. Дифференциальные уравнения. Минск: Вышэйш. шк.,
1968. 348 с.
Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука,
1987. 312 с.
Петровский И.Г. Лекции по теории обыкновенных дифференциальных
уравнений. М.: Наука, 1970. 280 с.
Пискунов Н.С. Дифференциальное и интегральное исчисления: В 2 т.
Т. 2. М.: Наука, 1985. 560 с.

336 СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Пономарев К.К. Составление и решение дифференциальных уравнений
инженерно-технических задач. М.: Учпедгиз, 1962. 184 с.
Понтрлгин Л. С. Обыкновенные дифференциальные уравнения. М.:
Наука, 1970. 332 с.
Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. 425 с.
Степанов В.В. Курс дифференциальных уравнений. М.: Наука, 1958.
468 с.
Тихонов А.Н., Васильева А.В., Свешников А.Г. Дифференциальные
уравнения. М.: Наука, 1980. 232 с.
Федорюк М.В. Обыкновенные дифференциальные уравнения. М.: Нау-
Наука, 1985. 448 с.
Хартман Ф. Обыкновенные дифференциальные уравнения / Пер. с
англ. М.: Мир, 1970. 720 с.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчи-
исчисление. М.: Наука, 1969. 424 с.
Campbell S.L. An introduction to differential equations and their applica-
applications. New York; London: Longman, 1986. 563 p.
Derrick W.R., Grossman S.L. Elementary differential equations with appli-
applications. Addison — Wesley series in mathematics. New York; London: Reading
(Mass), 1976. 538 p.
Etgen G., Morris W.L. An introduction to ordinary differential equations.
New York; London: Harper and Row cop., 1977. 512 p.
Leipholz H. Stability Theory. An introduction to the stability of dynamic
systems and rigid bodies. Stuttgart: John Wiley and Sons, 1987. 359 p.
Miller R.K, Michel A.N. Ordinary differential equations. New York; Lon-
London: Acad. press, 1982. 460 p.
Справочные издания и монографии
Александрова Н.В. Математические термины: Справочник. М.: Высш.
шк., 1978. 190 с.
Амелькин В.В. Дифференциальные уравнения в приложениях. М.:
Наука, 1987. 160 с.
Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Наука,
1981. 568 с.
Баутин Н.Н., Леонтович Е.А. Методы и приемы качественного иссле-
исследования динамических систем. М.: Наука, 1990. 488 с.

337
Бронштейн И.Н., Семендлев К.А. Справочник по математике для
инженеров и учащихся втузов. М.: Наука, 1986. 544 с.
Воднев В.Т., Наумович А.Ф., Наумович Н.Ф. Математический словарь
высшей школы / Под ред. Ю.С. Богданова. Минск: Вышэйш. шк., 1984.
528 с.
Герасимович А.И., Кеда Н.П., Сугак М.Б. Математический анализ:
Справочное пособие для студентов втузов и инженеров: В 2 т. Т. 2. Минск:
Вышэйш. шк., 1990. 272 с.
Еругин Н.П. Книга для чтения по общему курсу дифференциальных
уравнений. Минск: Наука и техника, 1979. 744 с.
Малкин И.Г. Теория устойчивости движения. М.: Наука, 1966. 532 с.
Математический энциклопедический словарь / Гл. ред. Ю.В. Прохоров.
М.: Сов. энциклопедия, 1988. 848 с.
Румянцев В.В., Озиранер А. С. Устойчивость и стабилизация движения
по отношению к части переменных. М.: Наука, 1987. 256 с.
Четаев Н.Г. Устойчивость движения. М.: Наука, 1987. 204 с.
Задачники
Задачи и упражнения по математическому анализу для втузов / Под
ред. Б.П. Демидовича. М.: Наука, 1970. 472 с.
Матвеев Н.М. Сборник задач и упражнений по обыкновенным диффе-
дифференциальным уравнениям. Минск: Вышэйш. шк., 1987. 320 с.
Михайленко В.М., Антонюк Р.А. Сборник прикладных задач по выс-
высшей математике. Киев: Выща шк., 1990. 168 с.
Самойленко A.M., Кривошея С.А., Перестюк Н.А. Дифференциальные
уравнения. Примеры и задачи. М.: Высш. шк., 1989. 383 с.
Сборник задач по математике для втузов: Специальные разделы
математического анализа / Под ред. А.В. Ефимова, Б.П. Демидовича: В
3 т. Т. 2. М.: Наука, 1981. 368 с.
Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. М.:
Наука, 1985. 128 с.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсцисса точки 1-78, 28
Аддитивность определенного
интеграла VI, 33
Антирезонанс 161
Аргумент функции 1-70, 1-106, 15
Ареасинус VI, 127
Асимптота вертикальная 1-256, 31
- горизонтальная 1-255, 53
- наклонная правосторонняя 1-377,
53
Базис III, IV, Ц5, 261
Вектор фазовый 260
Векторы присоединенные 162
Величина переменная 1-215, 15
Вид уравнения двучленный 212
Возмущения 239
Вронскиан 173
Выражение подынтегральное VI,
309
Гипербола 1-107, 264
Движение невозмущенное 239
Диагональ матрицы главная III, 247
Дифференцирование численное II,
311
Задача Коши для нормальной
системы ОДУ 115
ОДУ п-го порядка 125
первого порядка 24
Задача краевая двухточечная 284
линейная 287
неоднородная 287
однородная 287
смешанная 285
- для нормальной системы ОДУ
283
ОДУ п-го порядка 283
- на собственные значения 287
- Штурма — Лиувилля XII, 287
Значения начальные 115
- собственные XII, 287
Идентификация математической
модели 82
Изоклина 45
Интеграл несобственный
расходящийся VI, 236
- общий ОДУ первого порядка 42
- первый системы 225
- табличный VI, 54
Интегралы первые независимые в
области 228
точке 228
Интегрирование ОДУ 17
Касательная II, IP
Колебания гармонические 197
- затухающие 196
Координаты полярные HI, 111
Корни действительные II, 153
- комплексно сопряженные II, 155
Коэффициент угловой III, 45

339
Кривая дискриминантная 77
- замкнутая (замкнутый контур)
II, 259
- интегральная 18
- логистическая 108
- плоская II, 18
Кривизна плоской кривой в точке
II, 295
Линейность определенного
интеграла VI, 38
Линии уровня функции V, 109
Ломаная Эйлера 310
.Максимум функции локальный II,
294
Матрица вырожденная III, 265
- ГУрвица 247
- единичная III, Ц0
- обратная III, Ц8
- системы ОДУ 135
- Якоби V, 228
Матрица-столбец III, 310
Метод Бернулли 63
- вариации постоянных 149
- Лагранжа 64
- вариации постоянных 181
- неопределенных коэффициентов
149
- ломаных усовершенствованный
312
-- Эйлера 311
- Ляпунова второй (прямой) 251
- первый 251
- Рунге И, 319
- Рунге — Кутты 314
- функций Ляпунова 251
- Чаплыгина 320
- Эйлера — Коши 312
Миноры главные диагональные III,
247
Многочлен Тейлора II, 214
Многочлены Чебышева первого
рода 200
Множество бесконечное 1-43, 18
- конечное 1-43, 310
Множитель интегрирующий 61
Модель математическая II, 18
Начало координат 1-77, 20
Неравенство интегральное
Гронуолла 25
- Коши — Буняковского IV, 119
Нуль решения ОДУ 214
- функции 1-345, 214
Область V, 21
Огибающая однопараметрического
семейства V, 18
Окрестность точки 1-51, 1-182, 28
Оператор дифференцирования 186
Определитель Вандермонда III, 181
- Вронского 138
Ордината точки 1-78, 101
Осциллятор гармонический 197
- линейный 197
Ось абсцисс III, 20
- координатная 1-46, 36
- ординат III, 22
- полярная III, 111
Отрезок разбиения частичный VI,
311
Парабола 1-107, III, 18
Параболоид вращения III, 93
Параметр 1-115, 39
Переменное интегрирования VI, 29

340
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Переменные фазовые 18
Период функции 1-121, 85
Плоскость фазовая 18
Поведение функции
асимптотическое 1-355, 308
Погрешность метода на шаге 315
Подпоследовательность 1-243, 215
Поле векторное 19
- направлений 19
Положение равновесия системы 228
Полюс полярной системы
координат III, 111
Портрет фазовый 260
Порядок системы ОДУ нормальной
16
- точности метода на отрезке 316
шаге 315
- уравнения дифференциального 15
Последовательность
невозрастающая (неубывающая)
1-218, 322
- ограниченная 1-219, 32
- сходящаяся равномерно на
отрезке IX, 320
- убывающая 1-218, 32
- фундаментальная 1-232, 1-314, 32
Постоянная Липшица 27
Предел функции в точке
бесконечный 1-257, 31
конечный 1-257, 31
Представление кривой
координатное II, 18
Принцип суперпозии 203
Приращение аргумента в точке
1-326, 33
- функции в точке 1-326, 33
Произведение скалярное
стандартное в Rn IV, 225
Производная функции полная V,
333
в силу системы 225
Пространство 1-177, 18
— фазовое 18
— расширенное 18
Разделение переменных 49
Разложение вектора III, IV, Ц5
Размер матрицы III, Ц0
Разность конечная правая (вперед)
II, 311
Ранг матрицы III, 165
Решение ДУ с частными
производными первого порядка
линейного неоднородного 325
однородного 325
— задачи Коши 24
— нормальной системы ОДУ общее
(частное) 118
— ОДУ 16
-- колеблющееся 215
— неколеблющееся 215
— нетривиальное 214
— п-го порядка 125
неоднородного общее 177
общее 126
однородного общее 177
частное 126
-- особое 72
— первого порядка общее 42
частное 42
— тривиальное 214
-- формальное 306
— периодическое 259
— системы неустойчивое по
Ляпунову 238
-- ОДУ нормальной 17
— устойчивое асимптотически 237

341
Решение системы устойчивое по
Ляпунову 237
Ряд степенной IX, 305
- сходящийся в интервале IX, 305
Свойство равных дробей 232
Седло 264
Сепаратриса 277
Сетка 310
Сила эйлерова 297
Система вектор-функций линейно
зависимая 137
независимая 137
- координат полярная III, 111
- линейных ОДУ нормальная 134
неоднородная 135
однородная 135
с переменными
коэффициентами нормальная
неоднородная 144
устойчивая
асимптотически 241
устойчивая
(неустойчивая) 241
однородная 141
постоянными
коэффициентами нормальная 151
неоднородная 151
однородная 151
- ОДУ 16
- нормальная 16
автономная 16
- решений фундаментальная 140,
173
- уравнений первого приближения
246
-- характеристик 326
- функций линейно зависимая 171
независимая 171
Случаи анализа устойчивости
критические 246
Соотношение рекуррентное 1-87,
200
Спираль логарифмическая II, 112,
211
Теорема Коши существования и
единственности решения ОДУ
первого порядка 27
не разрешенного
относительно производной 77
Точка изображающая 262
- интегральной кривой
обыкновенная 72
- множества внутренняя 1-184, 2Ц
- ОДУ особая 72, 272
- перегиба графика функции II,
107
-- функции И, 101
- последовательности предельная
1-242, 215
Траектория изогональная 110
- ортогональная 110
- фазовая 18
Трактриса II, 23
Узел вырожденный 268
- дикритический 266
- неустойчивый 264
- сетки 310
- устойчивый 263
Уравнение алгебраическое II, 152
- Бернулли 68
- дифференциальное 15
-- обыкновенное (ОДУ) 15
в полных дифференциалах 59

342 ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Уравнение дифференциальное Уравнение Лагранжа 75
обыкновенное второго порядка — п-го порядка 199
линейное неоднородное с - матричное III, 256
постоянными коэффициентами - Риккати 70
206 - характеристическое ОДУ п-го
однородное 211 порядка 186
с постоянными -- системы ОДУ 152
коэффициентами 195 - Чебышева 199
высшего порядка 16 - Эйлера 197
п-го порядка 16 - Эйри 219
линейное 169 Уравнения возмущенного движения
неоднородное 170 239
однородное 170 Условие Коши (начальное) 24
с постоянными - Липшица 1-208, 21
коэффициентами неоднородное - начальное 24
185 Условия краевые 284
однородное 185 -- второго рода 285
однородное 130 -- первого рода 285
первого порядка 16 — третьего рода 287
квазиоднородное 58 - начальные для системы ОДУ 115
линейное 63 - Рауса — ГУрвица 247
неоднородное 63
однородное 63 Фокус неустойчивый 271
однородное 55 - сложный 275
разрешенное относительно - устойчивый 271
производной 16 Форма записи системы ОДУ
с разделяющимися симметричная 232
переменными 49 Формула квадратурная VI, 312
— первого порядка квазилинейное - Лагранжа II, 116
330 - прямоугольника VI, 312
— с отклоняющимся аргументом - прямоугольников левых VI, 312
108 - сдвига 191
частными производными 15 - Симпсона VI, 319
первого порядка линейное - Тейлора с остаточным членом в
неоднородное 325 форме Лагранжа II, 315
однородное 325 - трапеции VI, 312
- квадратное Н-350, 154 ~ Эйлера 156, 189
- Клеро 76 Формулы Крамера III, 180

Функции гиперболические
обратные VI, 127
- Ляпунова 254
- собственные XII, 287
- тригонометрические 1-128, 207
- Четаева 254
- Эйри 308
- элементарные 1-131, 17
Функция энакоопределенная 252
- знакопеременная 252
- знакопостоянная 252
- линейная 1-132, 63
- неявная II, 50
- однородная степени к 55
- периодическая 1-121, 85
- разрывная 1-191, 46
- составная 1-110, 85
- экспоненциальная 1-288, 25
343
Характеристика
амплитудно-частотная 86
- фазочастотная 86
Характеристики 326
- квазалинейного ДУ 330
Центр 271
- шара 1-179, 251
Числа комплексно сопряженные
1-150, 187
Число чисто мнимое 1-150, 200
Шаг сетки 310
Шар замкнутый 1-179, 251
Элемент матрицы III, 135
- диагональный III, 248
Эллипс III, 270

ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 9
1. Общие сведения о дифференциальных уравнениях 15
1.1. Основные понятия и определения 15
1.2. Геометрическая интерпретация решения ОДУ. Поле
направлений 18
1.3. Задачи, приводящие к решению дифференциальных
уравнений 19
Вопросы и задачи 23
2. Теорема существования решения дифференциально-
дифференциального уравнения первого порядка 24
2.1. Постановка задачи Коши. Интегральное неравенство 24
2.2. Теорема существования и единственности решения (те-
(теорема Коши) 27
2.3. Оценка разности решений двух уравнений. Непрерыв-
Непрерывная зависимость решения от начальных условий и пара-
параметра 37
2.4. Изоклины и их использование для приближенного по-
построения интегральных кривых 45
Вопросы и задачи 47
3. Дифференциальные уравнения первого порядка 49
3.1. Дифференциальные уравнения с разделяющимися пере-
переменными 49
3.2. Однородные и квазиоднородные уравнения 55
3.3. Уравнения в полных дифференциалах. Интегрирую-
Интегрирующий множитель 59
3.4. Линейные дифференциальные уравнения первого по-
порядка. Уравнения Бернулли и Риккати 63
3.5. Особые точки и особые решения ОДУ первого порядка 71
3.6. Уравнения, не разрешенные относительно производной 74
Д.3.1. Особенности составления дифференциальных уравне-
уравнений в прикладных задачах 78

345
Д.3.2. Ортогональные и изогональные траектории 109
Вопросы и задачи 113
4. Системы обыкновенных дифференциальных уравне-
уравнений 115
4.1. Задача и теорема Коши 115
4.2. Частное и общее решения системы дифференциальных
уравнений 118
4.3. Оценка разности двух решений 119
4.4. Теорема Коши о существовании и единственности ре-
решения уравнения высшего порядка. Случаи понижения
порядка 125
Вопросы и задачи 132
5. Системы линейных дифференциальных уравнений 134
5.1. Определения и основные свойства решений 134
5.2. Определитель Вронского. Фундаментальная система
решений. Формула Остроградского — Лиувилля . . 138
5.3. Теоремы о структуре общего решения однородной и
неоднородной систем 144
5.4. Метод вариации постоянных 147
5.5. Система линейных дифференциальных уравнений с
постоянными коэффициентами. Характеристическое
уравнение системы 151
5.6. Нахождение фундаментальной системы решений в слу-
случае различных корней характеристического уравнения 153
5.7. Структура фундаментальной системы решений в слу-
случае кратных корней 161
Вопросы и задачи 168
6. Линейные дифференциальные уравнения высших по-
порядков 169
6.1. Сведение к линейной системе. Определитель Вронского
и структура общего решения однородного уравнения 169
6.2. Общее решение неоднородного уравнения. Метод
Лагранжа вариации постоянных 177
6.3. Понижение порядка линейного дифференциального
уравнения 183
6.4. Линейные дифференциальные уравнения с постоянны-
постоянными коэффициентами. Случай различных корней харак-
характеристического уравнения 185

346 ОГЛАВЛЕНИЕ
6.5. Формула сдвига. Случай кратных корней характери-
характеристического уравнения. Уравнения Эйлера, Лагранжа,
Чебышева 190
6.6. Структура частного решения уравнения с постоянны-
постоянными коэффициентами и специальной правой частью . 200
Вопросы и задачи 208
7. Нули решений дифференциального уравнения вто-
второго порядка 211
7.1. Приведение уравнения к двучленному виду 211
7.2. Нули решений. Теорема о конечности числа нулей на
отрезке 214
7.3. Теорема о чередовании нулей. Теоремы сравнения и
Кнезера 216
Д.7.1. О нулях решений нелинейных дифференциальных урав-
уравнений 222
Вопросы и задачи 223
8. Первые интегралы 224
8.1. Основные понятия и определения 224
8.2. Теорема о локальном существовании системы первых
интегралов 228
8.3. Понижение порядка системы дифференциальных урав-
уравнений при помощи первых интегралов 230
8.4. Симметричная форма записи нормальной автономной
системы дифференциальных уравнений 231
Вопросы и задачи 234
9. Элементы теории устойчивости 235
9.1. Основные определения и понятия 235
9.2. Устойчивость системы линейных дифференциальных
уравнений 241
9.3. Теоремы Ляпунова об устойчивости по первому при-
приближению 245
9.4. Функции Ляпунова. Теоремы Ляпунова об устойчиво-
устойчивости и асимптотической устойчивости 251
9.5. Теоремы Четаева и Ляпунова о неустойчивости . . . 254
Д.9.1. Библиографический комментарий 257
Вопросы и задачи 258

347
10. Особые точки на фазовой плоскости 259
10.1. Фазовый портрет системы 259
10.2. Система нелинейных дифференциальных уравнений 273
Д.10.1. Математическая модель сосуществования двух популя-
популяций 278
Вопросы и задачи 281
11. Краевые задачи для дифференциального уравнения 283
11.1. Постановка краевой задачи 283
11.2. Линейная краевая задача. Сведение ее к задаче Коши 286
11.3. Прикладные примеры решения краевой задачи .... 290
Вопросы и задачи 303
12. Приближенные методы решения дифференциальных
уравнений 304
12.1. Интегрирование дифференциальных уравнений при по-
помощи степенных рядов 304
12.2. Метод последовательных приближений 308
12.3. Метод ломаных Эйлера 310
12.4. Метод Рунге — Кутты 314
12.5. Метод Чаплыгина 320
Вопросы и задачи 324
13. Дифференциальные уравнения первого порядка с
частными производными 325
13.1. Линейное дифференциальное уравнение. Уравнения
характеристик. Задача Коши 325
13.2. Квазилинейное дифференциальное уравнение .... 330
Вопросы и задачи 334
Список рекомендуемой литературы 335
Предметный указатель 338

Учебное издание
Математика в техническом университете
Выпуск VIII
Агафонов Сергей Алексеевич
Герман Анна Дмитриевна
Муратова Татьяна Владимировна
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Редактор Е.Н. Ставицкал
Художник С. С. Водчиц
Корректор Е.В. Аеалова
Подписано в печать 05.12.2003. Формат 60x88 1/16.
Печать офсетная. Бумага офсетная.
Усл. печ. л. 22. Уч.-изд. л. 21,12.
Тираж 2000 экз. Заказ №9306
Издательство МГТУ им. Н.Э. Баумана,
105005, Москва, 2-я Бауманская, 5.
Отпечатано в полном соответствии
с качеством предоставленного оригинал-макета
в ППП «Типография «Наука»
121099, Москва» Шубинский пер., 6
ISBN 5-7038-1649-1
985703"81
93