Текст
московскийrОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ
имени М.В. ЛОМОНОСОВА
Механико"математический факультет
Кафедра вычислительной математики
к.ю. Боrачев
Практикум на ЭВМ.
Методы прибли)Кения функций
Москва 2002 rод
S<::ANNED ВУ: DMVN I::ORP.
THANX то: А. VORDNTSDV
ББК 22.193
Б 30
УДК 517.97
к.ю. БО1'ачев. Практикум на ЭВМ. Методы приближения
функций. З е изд., перераб. и доп. М.: Изд во ЦПИ при
механико математическом ф те Mry, 2002, 192 с.
Настоящее пособие содержит описания ал1'оритмов, предла1'а
емых к реализации на ЭВМ студентам механико математическо
ro факультета Mry на занятиях по "Практикуму на ЭВМ". ДЛЯ
всех ал1'оритмов приводится необходимое теоретическое обосно
вание, соответствующие расчетные соотношения и рекомендации
по их практическому осуществлению на ЭВМ.
ДЛЯ студентов и аспирантов, изучающих и применяющих Me
тоды вычислительной математики, и преподавателей, проводя
щих практические занятия.
Первое издание ВЫШЛО в 1998 1'., второе в 1999 1'. и 2000 1'.
(дополнительный тираж). В третьем издании исправлены заме
ченные опечатки и неточности, изменено и дополнено изложение
ряда разделов.
Рецензент: академик РАН Н.С. Бахвалов
@ БО1'ачев к.ю.
1998 2002 1'1'.
Оrлавление
Оrлавление
ПРЕДИСЛОВИЕ........................ 9
u
rJIaBa 1. МЕТОДЫ ПРИБЛИ:Ж:ЕНИЯ ФУНКЦИИ
U u
ОДНОИ ПЕРЕМЕННОИ . . . . . . . . . . . . .. 11
91. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОЙ ИНТЕР
П ОЛЯЦИИ . . . . . . . . . . . . . . . . . . . . . . .. 11
з 2 . ОБУСЛОВЛЕННОСТЬ БАЗИСА . . . . . . . . . '. 15
з3. ИНТЕРПОЛЯЦИОННЫЙ мноrОЧЛЕН ЛАrРАН
ЖА . . . . . . . . . . . . . . . . . . . .. ..... . 16
4. РАЗДЕЛЕННЫЕ РАЗНОСТИ . . . . . . . . . . . .. 19
95. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА 26
96. ИНТЕРПОЛЯЦИЯ "ДВИЖУЩИМИСЯ" MHOrO
ЧЛЕНАМИ . . . . . . . . . . . . . . . . . 28
з7. ОЦЕНКИ поrРЕШНОСТИ ИНТЕРПОЛЯЦИОН
HOI1 ФОРМУЛЫ НЬЮТОНА. . . . . . . . . 31
з8. РАЗДЕЛЕННЫЕ РАЗНОСТИ С КРАТНЫМИ УЗ
ЛАМИ . . . . . . . . . . . . . . . . . . . . . . . . . .. ЗЗ
з9. ИНТЕРПОЛЯЦИЯ С КРАТНЫМИ УЗЛАМИ ... 34
з 1 О. ВЫЧИСЛЕНИЕ ПРОИЗВОДНЫХ мноrОЧЛЕ
НА ЛАrРАНЖА В ФОРМЕ НЬЮТОНА ...... 41
fil1. мноrОЧЛЕНЫ ЧЕБЫШЕВА ............ 46
g12. МИНИМIIЗr\ЦИЯ поrРЕШНОСТИ ИНТЕРПО
ЛЯЦИИ ЗА СЧЕТ ВЫБОРА УЗЛОВ. . . 50
fi13. РАЗЛОЖЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫШЕВА 53
з 1 3.1. Постановка задачи линейной интерполяции . 53
lЗ.2. Ал1'ОРИТМ построения разложения . . . . . .. 58
.
3
Оrлавление
913.3. Оценка количества арифметических операций 59
913.4. Связь разложения по lvIНО1'очленам Чебышева
и интерполяции . . . . . . . . . . . . . . . . .. 60
914. ПРЕИМУЩЕСТВА кУсочно мноrОЧJIЕННОЙ
АППРОКСИМАЦИИ .............. 64
915. КУСОЧНО ЛИНЕЙНАЯ ИНТЕРПОЛЯЦИЯ . . .. 65
16. КУСОЧНО ЛИНЕЙНАЯ АППРОКСИМАЦИЯ ME
ТОДОМ НАИМЕНЬШИХ !(ВАДРАТОВ . . . . . .. 67
916.1. Постановка задачи линейной интерполяции . 68
916.2. Вычисление матрицы системы задачи линей
ной интерполяции .. ........ .... 70
916.3. Свойства приближающей функции ...... 74
916.4. Вычисление правой части системы задачи ли
нейной интерполяции ..... ........ 77
17. АППРОКСИМАЦИЯ мноrО"(IЛЕНАМИ "(IЕБЫ
ШЕВА МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ 83
917.1. Интеrральные свойства 1\1ноrочленов Чебышева 84
917.2. Постановка задачи линейной интерполяции . 86
917.3. Вычисление коэффициентов разложения . 88
917.4. Алrоритм вычисления коэффициентов разло
жения ..................... . 94
917.5. Оценка количества арифметических операций 94
918. КУСО"(IНО ЛИНЕЙНАЯ ИНТЕРПОЛЯЦIIЯ HEf ЛАД
КИХ ФУНКЦИЙ НА СПЕЦИАЛЬНЫХ СЕТКАХ . 95
з19. ИНТЕРПОЛЯЦИЯ КУСОЧНО КУБИЧЕСКИМИ
ФУНКЦИЯМИ . . . . . . .. ........ 98
919.1. Общая CXe1\1a ............ . . .. 98
919.2. Ал1'ОРИТМ вычисления коэффициентов MHO
1'очлена P i . . . . . . . . . . . . . . . . . . . .. 99
919.3. I(усочная интерполяция кубичеСКИ1\1И MHoro
членами Эрмита ................. 100
4
Оrлавление
19.4. Кусочная интерполяция кубическими MHoro
членами Бесселя . . . . . . . . . 102
19.5. Кусочная интерполяция кубическими MHo1'o
членами Ivlетодом Акимы ........... 103
919.6. Кусочная интерполяция кубическими MHoro
членами с использованием разделенных раз
настей . . . . . . . . . . . . . . . . . . . 105
919.7. Интерполяция кубическими сплайнами . . . . 106
919.8. Определение недостающих rраничных условий 108
919.8.1. Определение недостающих rранич
ных условий по известным значени
ям первой производной функции В
I'раничных узлах. . . . . . . . . . . . l09
19.8.2. Определение недостающих rранич
ных условий по извеСТНЫ1vl значени
ям второй производной функции В
rраничных узлах. . . . . . . . . . . . l09
919.8.3. "Естественные" rраничные условия . 111
919.8.4. Условие "отсутствия узла" в приrра
ничных узлах. . . . . . . . . . . . . . 112
з19.8.5. Дополнительный узел в ПРИ1'ранич
ных узлах . . . . . . .. ....... 115
919.8.6. Экстраполяция в ПРИ1'раничных узлах117
э2О. ИНТЕРПОЛЯЦИЯ ПАРАБОЛИЧЕСКИМИ СПЛАЙ
НАМИ . . . . . . . . . 11 7
20 .1. Общая схема ................ 117
920.2. Ал1'ОрИТМ вычисления коэффициентов MHO
1'очлена P i . . . . . . .. ..... . . . . 118
920.3. Интерполяция параболическими сплайнами . 119
920.4. Определение недостающих 1'раничных условиj1122
5
Оrлавление
920.4.1. Определение недостающих 1'ранич
ных условий по известным значени
ям первой производной ФУНКЦИИ В
rраничных узлах. . . . . . . . . . . . 123
920.4.2. Определение недостающих rранич
ных условий по известным значени
ям второй производной функции В
rраничных узлах . . . . . . . 127
920.4.3. НЕстественные" rраничные условия 127
920.4.4. Условие "отсутствия узла" Б приrра
ничных узлах. . . . . . .. .... 128
920.4.5. Дополнительный узел Б приrранич
ных узлах . . . . . . . . .. .... 132
з20.4.6. Экстраполяция в приrраничных узлах132
u
rлава 11. МЕТОДЫ ПРИБЛИЖЕНИЯ Функции
мноrих ПЕРЕМЕННЫХ ........... 133
1. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ мноrих ПЕРЕ
МЕННЫХ ТЕНЗОРНЫМИ ПРОИЗВЕДЕнияrvlИ . 133
1.1. Постановка задачи интерполяции тензорны
ми произведениями И теорема корректности 134
91.2. Оценка числа арифметических операций .. 136
91.3. Ал1'ОрИТМ интеРПОЛЯI ИИ тензорными произ
ведеНИЯ!\1И . . . . . . . . . . . . . . . . . . . . . 137
з1.4. ПРО1'раммная реализация алrоритма ... . . 138
91.5. Интерполяция тензорными произведениями в
случае мноrочленной аппроксимации . . . . . 140
91.5.1. Интерполяционный МНОI'очлен Ла
rранжа ............. 140
91.5.2. Разделенные разности для функции
МНОI'их переменных . . . . . . . . . . 142
91.5.3. Ин'rерполяционная формула Ньютона143
6
Оrлавление
1.5.4.
Интерполяция "движущимися" MHO
1'очленами. . . . . . . . . . . . . . . . 144
Интерполяция с кратными узлами . 144
Разложение по МНО1'очленам Чебы
91.5.5.
91.5.6.
шева . . . . . . . . . . . . . . . . . . . 144
Sl.5.7. Аппроксимация МНО1'очленами Че
бышева методом наименьших KBaд
ратов .................. 146
1.6. Интерполяция тензорными произведениями в
случае КУСОЧНО МНО1'очленной аппроксимации 149
1.6.1. Кусочно линейная интерполяция .. 149
1.6.2. Кусочно линейная аппроксимация Me
тодом наименьших квадратов . . . . 152
1.6.3. Кусочно кубическая интерполяция . 153
1.6.4. Кусочно квадратичная интерполяция 158
2. ПРИБЛИЖЕНИЕ ФУНКЦИЙ MHOrl1X ПЕРЕ
IvlEHHbIX МЕТОДОМ КОНЕЧНЫХ ЭЛЕl\1ЕНТОВ 162
S2.1. Постановка задачи линейной интерполяции . 162
S2.2. Способы построения трианrуляции области . 164
S2.3. Приближение функций в треУ1'ольнике . . . . 165
s2.3.1. Постановка задачи линейной интер
ПQЛЯЦИИ .. .. . . . . . . . . . . . 165
g2.3.2. Приближение функций в прямо
уrольном треУ1'ольнике . . . . . . . . 166
g2.3.3. Приближение линейными функциями 168
s2.3.4. Приближение квадратическими функ
циями . . . . . . . . . . . . . . . . . . 1 72
g2.3.5. Приближение ку6ичеСКИIvlИ функци
ями ................... 1 76
2.4. Приближение функций методом наименьших
квадратов . . . . . . . . . . . . . . . . . . . . .. 180
7
Оrлавление
92.4.1. Постановка задачи линейной интер
ПQЛЯЦИИ . . . . . . . . . . . . . . . . .
92.4.2. Вычисление системы задачи линей
ной интерполяции
181
проrРАММА К"УРСА
ЛИТЕРАТУРА .....
182
184
191
8
ПРЕДИСЛОВI'IЕ
Предисловие к первому изданию
Настоящее пособие содержит описания алrоритмов, предлаrа
емых к реализации на ЭВМ студентам механико математическоrо
факультета Mr T на занятиях по "Практикуму на ЭВМ". ДЛЯ
всех ал1'оритмов приводится необходимое теоретическое обосно
вание, соответствующие расчетные соотношения и рекомендации
по их практическому осуществлению на ЭВМ (орrанизация про
цесса вычислений, хранения данных и результатов в памяти ЭВМ
и т.п.).
МНО1'ообразие ал1'оритмов объясняется, с одной стороны,
необходимостью обеспечить преподавателей достаточным набо
ром задач для проведения занятий, а с друrой стороны, жела
нием продемонстрировать различные подходы к решению задачи
приближения функций. Алrоритмы имеют разную точность, дa
ют разную rладкость приближающей функции, имеют разную
чувствительность к ПО1'решностям во входных данных. ft CaMoro
лучшеrо"метода приближения не существует, и выбор ал:rорит
ма зависит от конкретной задачи. Этот выбор будет различным,
например, для аппроксимации аналитически заданной функции
сложноrо вида и ДЛЯ обработки результатов измерений физиче
ской величины.
Подбор алrоритмов для Практикума диктовалСЯ, в ОСНОВНОМ,
возможностью реализации их студентами при сущеСТВУЮll ИХ ре.-
сурсах времени на ЭВМ, что привело к отказу от рассмотрения
усложненных подходов. Часть описанных алrоритмов BЫTeCHe
на из широкой вычислительной практики более эффективными
(и более сложными) ал1'оритмами, рассмотреть которые в KYP
се "Практикум на ЭВМ"не представляется возможным. Te не
9
ПРЕДИСЛОВИЕ
менее, эти ал1'оритмы представляют интерес для решения опре
деленноrо Kpyra задач и включены в пособие.
Форма отчетности студентов по Практикуму призвана сти"
мулировать как развитие практических навыков решения MaTe
матических задач с помощью компьютера, так и создание опре
деленноrо круrозора в области существующих методов решения
поставленной задачи. Поэтому в рамках Практикума студентам
предла1'ается как разработать ПРО1'рамму на ЭВМ, реализующую
заданный ал1'оритм, так и письменно ответить хотя бы на по
ловину вопросов из предложенноrо варианта, составленноrо из
вопросов, приведенных в конце пособия.
В основе настояще1'О пособия лежат материалы лекций, ЧИ"
тавшихся автором в течении 4..х лет в рамках Факультативноrо
курса "Практикум на ЭВМ". В электронном варианте оно уже 60"
лее 5 ти лет используется при проведении занятий со студентами
в дисплейном классе.
Предложения, замечания и отмеченные опечатки просьба co
общать автору на кафедру вычислительной математики.
Предисловие ко второму изданию
Первое издание предла1'аемоrо пособия вышло в свет в 1998 r.
и e1'o тираж к настоящему времени уже разошелся. Это потребо..
вало BToporo издания, в котором также исправлены замеченные
опечатки инеточности.
Предисловие к третьему изданию
Второе издание пособия было издано Б 1999 r. Дополнитель..
ный тираж был допечатан в 2000 1'. В TpeTbe1vf издании исправ
лены замеченные опечатки и неточности, изменено и дополнено
изложение ряда разделов.
10
rлава 1.
мЕтодыI ПРИБЛИЖЕНИЯ
ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ
u u
1. ПОСТАНОВКА. ЗАДАЧИ ЛИНЕИНОИ
ИНТЕРПОЛЯЦИИ
Пусть задана. функция j : Х У, j Е F(X, У) HeKOTO
рому функциональному пространству, набор функций 91,. . · , 9n ,
gi : Х У, gi Е F(X, }""), и набор линейных Функциона.il0В
Лl,. .., Л m на пространстве F(X, У). Требуется построить ап
проксимацию Р f функции f вида
n
Р! == ЕЙj9j
j==1
(1)
такую, чтобы были выполнены линейные условия интерполяции
>\i(Pf) == Лi(f), i == 1,... ,т.
(2)
Задача построения такой Р f называется зада'Ч,ей л'Uнейной и'Н,
mерnоляцuи.
Пример 1. Интерполяция по набору мноrочленов.
Х == (а, Ь], У == R 1 , F(X, У) == С([а, Ь]), 9i(X) == xi, i == 1, . . . , n.
11
rлава 1. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕННОЙ
Пример 2. Поточечная интерполяция.
Х == [а, Ь], У == R 1 , F(X, У) == С([а, Ь]), Лi(f) == f(Xi),
rде Х1, . . . ,Х т набор точек на [а, Ь].
Пример з. Х == [а, Ь], У == R 1, Р(Х, У) == L 1 ([а, Ь]), Лi(f) ==
Xi+l
f f(x) dx, {'де Xl,'. ., Х т набор точек на [а, Ь].
Xi
Определение. Задача линейной интерполяции называется
корректной, если ее решение (т.е. набор коэффициентов Qi) cy
ществует и единственно ДЛЯ ВСЯКОЙ функции f Е F( )(, У).
Обозначим
С(Х, У) == (gj)j==l....,n == t O:jgj : о: == (O:j)j==l,...,n Е Rn } ,
j==1
А(Х, У) == (>'i)i==l,...,m == if1 13i>'i : 13 == (13i)j==-i,...,m Е R m } ,
а(х, У) С Р(Х, У), Л(Х, У) С Р*(Х, У). Если функции
91, . · . ,9n линейно независимы и функционалы Лl".., Л m ли
нейно независимы, т.е. образуют базисы пространств С(Х, У)
и А(Х, У) соответственно, то задача линейной интерполяции
может быть поставлена в эквивалентной форме: для заданной
f Е F(X, У) найти 9 == Р! Е С(Х, У) такую, что л(f) == л(g)
для всех л Е Л(Х, У).
Теорема 1. Пусть фУН'I'b'Ции 91,..., 9n линейно 'Независи.м/Ьt
и фУU'l'bцио'Н,аЛ'Ьt лl,. . . , л m .линей'Н,о независи.м'ы.
1. ТО2да зада'Ч,а линейной интерполяции 'Коррех;т'На в то-м и
толь'l'bО в том с.лу'Чае, 'КО2да m == n и -матрица
А == (лi (g j ) ) , i == 1, . . . , т, j == 1, . . . , n
(3)
обратима.
12
91. ПОСТАНОВКА ЗАДАЧИ ЛИНЕЙНОЙ ИНТЕРПОЛЯЦИИ
2. Ес.ли зада'Ча .линеuноu интерполяции 'Корре'Ктна, то иH
терnолиРУЮ'lцая фу'Н'Кц'Ия представляется в виде
n
Р! == Lajgj,
j==l
zae
Q ( О: . ) . 1 A l ( ( Л . (f)) . 1 )
з з== ,...,n t t== ,...,n .
(4)
3. Если зада'Ча линейной интерполяции 'Корре'l'bтна, то one
ратор Р : Р(Х, У) а(х, У) является иaeMnOтeHfflH'btM (т.е.
р2 == Р и, следовател'Ьно, 1т Р n Kef Р == О, Р f == ! для всех
jEG(X,Y)).
Доказательство.
n
1. Из (1), (2) следует, что Р! == Е lXjgj является решением
;==1
задачи линейной интерполяции тоrда и только тоrда, коrда
Лi ( t a jgj ) == Лi(f) для всех i == 1, . . . , т,
)==1
или
n
L QjЛi(gj) == )\i(f) ДЛЯ всех i = 1,. . ., т.
j==l
Друrими словами
11
L aijaj == Лi(f) для всех i == 1,..., т,
;==1
1'де aij == Лi(gj), А == (aij), Т.е.
Ао: == (Лi(!))i==l,...,m,
(5)
1'де Q == (а; )j==l,...,n. Следовательно, задача линейной интер
поляции корректна тоrда и только тоrда, коrда система ли
нейных уравнений (5) имеет единственное решение ДЛЯ всякой
13
rлава 1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l..Й ПЕРЕМЕННОЙ
f Е F(X, У). Следовательно, матрица А осуществляет биектив
ное соответствие между множеством
{(Лi(I))i==l,...,m : f Е Р(Х, У)} С R m
и множеством
{а : й решение (5)} С R n .
Как известно из курса математическо1'О анализа (или курса aJI
rебры) это означает m == n и существование A l.
(Для полноты изложения дадим доказательство этоrо факта.
Пусть А необратима. Если m > n, то существует нетриви
альная линейная комбинация столбцов (п х m) матрицы А, paB
иая нулю, Т.е. существует Q =1 о такое, что Ай == О. Так как
n
{9j}j:=1,...,n линейно независимы, то 9 == Е Qjgj i- О. Следо
j==l
вательно, для f = о задача линейной интерполяции имеет два
решения: 9 и О. Это противоречит ее корректности.
Если т < n, то существует нетривиальная линейная ком:бина
ция строк (11,хт) матрицы А, равная нулю, 1.'.е. существует а =1 о
такое, что (x t A t == о. Так как {Лi}i==l,...,m линейно незаВИСИ?vfЫ,
m
то Л == Е QiЛi =1 О. Из равенства Qt At == О получаем
i==l
m m
л(gj) == L ЙiЛi (9j) == L Oiaij == О
i==l i==l
для всех j == 1,... , n. Поскольку л ненулевой функционал на
Р(Х, У), то существует f Е F(X, У) такая, что л(l) :/= о. Тоrда
для этой функции f задача линейной интерполяции не имеет
решения, так как л{l) =1= о == л(gj) для всех j == 1, . . . , n.)
2. Второе утверждение теоремы следует из (5).
3. Пусть 9 == Р 1, 1'де 1 Е С(Х, У). Поскольку {gj }j==l,...,п
n n
базис С(Х, У), то f == Е ajgj, 9 == Р f == Е {3jgj, причем по
' 1 j==1
14
з2. ОБУСЛОВЛЕННОСТЬ БАЗИСА
доказанному свойству (4)
{3 == A l (>ч(J» == A l (Л i ( с чgj ) )
== A l ( tО'.jЛi(gj» ) == A l ( tO'.ja ij ) == A l (Аа) == а,
з 1 з 1
т.е. fJ == Q; и потому 9 == f. Поэтому Р! == ! и р2 = Р, так как
Р! Е а(х, У) ДЛЯ всех! Е Р(Х, У).
9 2. ОБУСЛОВЛЕННОСТЬ БАЗИСА
При вычислении коэффициентов {а; } У 1 разложения Функ
цИИ Р! Е Р(Х, У) по базису {gj} j 1 пространства а(х, У) С
n
F(X, У) , 9 == Р f == Е Qjgj неизбежны вычислительные по
j==1
rрешности. Их влияние на результат функцию 9 характеризу
ется ЧИС.ilОl\1 обусловленности.
11YCTb в подпространстве С(Х, У) С F(X, У) введена норма
11 . IIG, а. в пространстве Rn зафиксирована некоторая норма 11.
IIRn . Введем
n
"" a. g .
L, з з
3==1
т == mln
aERn
G
,
м == шах
aERn
n
Е ajgj
j==l
G
IIQllRn
IIQllRn
ТО1'да ДЛЯ всяко1'О а Е Rn
n
mllallRn < L: Qjgj
j==1
< MllallRn.
(1)
G
15
rЛ8В8I. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕННОЙ
Пусть вместо ТОЧНО1'о вектора коэффициентов разложения а
получен приближенный а == а + С. Следовательно, вм:есто ФУНК
ППп
ции 9 == Е ajgj будем иметь 9 == Е (Qj + ej)gj == Е CY.jgj +
j==1 j==1 j==l
n n
Е Cjgj = 9 + Уе, 1'де Уе == Е Cj9j. Из (1) имеем
j==1 j==1
mlfellRn < IIgellC < MllellRn,
mllollRn < IIgllc < MllallRn.
Отсюда
т IlellRn < Ilge IIG < М lIellRn .
м l/allRn IIglIG m IlallRn
Определение. Числом обусловленности базиса {gj } У 1 Ha
зывается
м
cond(gj) == .
т
С использованием 3'1'01'0 определения и соотношений y€ == 9 9 и
......
С == СУ. СУ. последнее неравенство перепишется в виде
1 Ila allRn < 119 911G < d ( . ) "а ollRn
cond(gj) llaIIR"& IIglIG con Уз 1ICY.IIRn .
Это неравенс'1'ВО устанавливает связь между О'fJ1'Носител'Ь'Нои no
u 119 оНа
2решносmью интерnолирующеи фуюсции 11911G и oтHocи
11& allRn
тельной nО2решностью 'К:оэффициентО6 разложения lIallRn .
Чем больше число обусловленности базиса, 1 1 ем хуже он с вычис
лительной точки зрения.
3 3.
u
интЕрполяционныIи lVIноrОЧЛЕН
ЛАrРАНЖА
в общей схеме линейной интерполяции (см. 1) рассмотрим
случай: Х == [а, Ь], У == R 1, Р(Х, У) == С([а, Ь]).
16
3. ИНТЕРПОЛЯЦИОННЫЙ мноrОЧЛЕН ЛАrРАН)f(А
Пусть заданы точки а == Xl < Х2 < . . . < х n == Ь (называемые
узлами интерполяции) и известны значения f{Xl),. . . , !(х n )' Bы
n X X'
берем функции gi(X) li(X) == П :J , i == 1,. . . , n (назы
j==1,j=li Xi Xj
ваемые элементарными мноrочленами Лаrранжа) и Функциона
лы )ч(!) == f(Xi), i == 1,..., n. ТО1'да задача линейной интерполя
ции примет вид: для заданноЙ (в точках Xi, i == 1, . . . , n) функции
n
f найти L(x) == (Pf)(x) == Е aili(x) такую, что L(Xi) == f{Xi)
i==1
для всех i == 1,. . . , n .
Проверим, что функции l1,.'" ln линейно незаВИСИ!\1Ы и
функционалы Л1, . . . , Л N линейно независимы. Действительно, ec
n
ЛИ существует такое а Е Rn, Q f:. о, что Е Gili(X) == О ДЛЯ всех
i==l
n
Х Е [а, Ь), то Е aili{Xj) == о для всех j == 1,...,11,. Поскольку
i==l
li(Xj) == дiз, то отсюда получаем а; == О для всех j == 1,..., N,
Ч'I'О противоречит Q 1:- О. Анало1'ИЧНО, если существует такое
11-
а Е Rn, а -# О, что ЕаiЛi(f) == о ДЛЯ всех f Е С([а,Ь]), то
i==l
n
Е о'iЛi (lj) == о для всех j == 1,...,11,. Поскольку Лi (lj) == <Sij, то
i:::: 1
отсюда получаем aj == О для всех j == 1,..., n, что противоречит
G о.
Таким образом, применима теорема 1.1. !\1атрица (1.3) еди
ничная (А == 1), поскольку Лi(lj) == дij. Следовательно, зада
ча линейной интерполяции корректна, и ее решение в силу (1.4)
представляется в виде
ппп
L(x) == L !(Хi)Цх) == L f(xi) П :. ;. · (1)
i==l i==l j==] t J .
j=l-i
По теореме 1.1 построенный МНО1'очлен L единственный из
(li)i=:l,...,n, удовлеТВОРЯЮll ИЙ условиям интерполяции. ПОК(:1жем,
17
rлава Т. ПРИБЛИ)l(ЕНИЕ Функций l Й ПЕРЕМЕННОЙ
что L единственный из всех мноrочленов степени n 1, удо--
влеТБОРЯЮЩИЙ условиям интерполяции.
"
Действительно, пусть L Е pп ] пространству МНО1'очленов
""
степени n 1 и удовлетворяет условиям интерполяции: L(Xi) ==
f(Xi), i == 1, . . . , n. Тоrда L L Е Pn 1 И L(Xi) L(Xi) == f{Xi)
f(Xi) == О для всех i == 1,..., n, т.е. имеет n нулей в точках
"
Хl, . . . , Х п . Следовательно, L L = о.
Лемма 1. (Без доказательства). Обусловленность базиса из
элеМ,ентариъtх миО20'Членов Л а2ра'Нжа в слу'Чае рав'Н,о.мерио рас..
nреде./l,е'Н/нъtх то'Че Xi не М,енее const е п / 2 .
Оценка числа арифметических операций
Оценим число арифметических операций, требуемых на BЫ
числение значения мноrочлена Ла1'ранжа в точке Х по форму..
ле (1). На вычисление каждоrо из li(X) требуется 2(n 1) опе..
раций вычитания, 2(п 2) операций У 1ножения и одна операция
деления. Таким образом, для вычисления [1 (х),. .., ln(x) требу
ется 2n(n 1) операций сложения, 2n(n 2) операций умножения
n
И п операций деления. Для вычисления L(x) == Е f(xi)li(x) Tpe
i==1
буется еще (n 1) операций сложения и п операций умножения.
Общее число операций: 2п 2 + О(п) (п (0) адцитивных и СТОЛЬ
ко же мультипликативных операций.
Число арифметических операций, требуемых на вычисление
значения МНО1'очлена Ла1'ранжа в точке х по формуле (1), может
быть леrко уменьшено в два раза.
1
1. Вычислим yi == f(Xi) n
П (Xi Xj)
.i==1,j#i
(Yi можно хранить на месте f(Xi)). На это требуется п(п 1)
аддитивных и столько же мультипликативных операций.
ДЛЯ всех i == 1,..., п
18
4. РАЗДЕЛЕННЫЕ РАЗНОСТИ
п
2. Вычислим <р(х) == П (х Xi). На это требуется n адцитив
i==l
ных И n 1 МУJlЬТИПЛИкативных операций.
'n у:.
3. Вычислим L(x) == ср(х) Е . На это требуется n
i== 1 Х Х i
1 аддитивных и п + 1 мультипликативных операций. (Из этой
формулы также видно, что yi можно не запоминать, а вычислять
по мере необходимости).
Общее число операций: п 2 + О(п) (T (0) адцитивных и
столько же мультипликативных операций.
Вычисление по формуле (1) (и первым, и вторым способами)
требует БОЛЫIIИХ вычислительных затрат и приводит к появле
нию большой вычислительной поrрешности. Поэтому были раз
работаны друrие способы вычисления интерполяционно1'О MHoro
члена Ла1'ранжа.
з4. РАЗДЕЛЕННЬIЕ РАЗНОСТИ
Пусть заданы точки а == Xl < Х2 < ... < Х п == Ь, функция
f Е С([а, Ь]) и известны значения f(Xl),'.., f(xn).
Определение. Разделе'Н'Ной разиостъю функции f нулевоrо
порядка называется f(Xi) == f(Xi), разделенной разностью l 1'o
f(x.) f(Xi) u
порядка называется f (Xi; Х j) == J , разделеннои раз
Xj Xi
ностью k 1'o порядка называется
f( . ) f(Xi+l;...;Xi+k) f(Xi;,.,;Xi+k l)
Xi, . . . ; Xi+k == ·
Xi+k Xi
(1)
19
rлава 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕАJЕННОЙ
Свойства разделенных разностей
Лемма 1. Справедливо представление
i+k
f(Xi;...;Xi+k) == L
j==i
f(Xj)
i+k
П (Xj XI)
l==i
li=j
(2)
Доказательство. При k == О равенство (2) имеет вид f(Xi) ==
f{Xi) И потому верно. При k == 1 равенство (2) имеет вид
f( '." ) !(Xi) + !(Xi+l) !(Xi+l) f(Xi)
X t , Xt+l
Xi Xi+l Xi+l Xi Xi+l Xi
и верно в силу определения (1) разделенной разности.
Пусть равенство (2) верно при нек.отором k. Покажем, что оно
верно при k + 1 (тем самым лемма будет доказана. по индукции).
В силу определения (1) разделенной разности
f( ) f(Xi+l; ...; Xi+k+l) f(Xi;...; Xi+k)
Xi; · · . ; Xi+k+l := ==
Xi+k+l Xi
1
i+k+l
L
j==i+l
i+k
f(Xj) '"'
i+k+l
п (Xj XI) j==i
l==i+l
l#j
f(Xj)
i+k
П (Xj XI)
l==i
l=#=j
Xi+k+l Xi
Вычислим коэффициенты при f(Xi), f(Xj), j == i + 1,..., i +
k, f(Xi+k+l), И покажем, что они совпадают с соответствующими
коэффициентами в равенстве (2).
20
з4. РАЗДЕЛЕННЫЕ РАЗНОСТИ
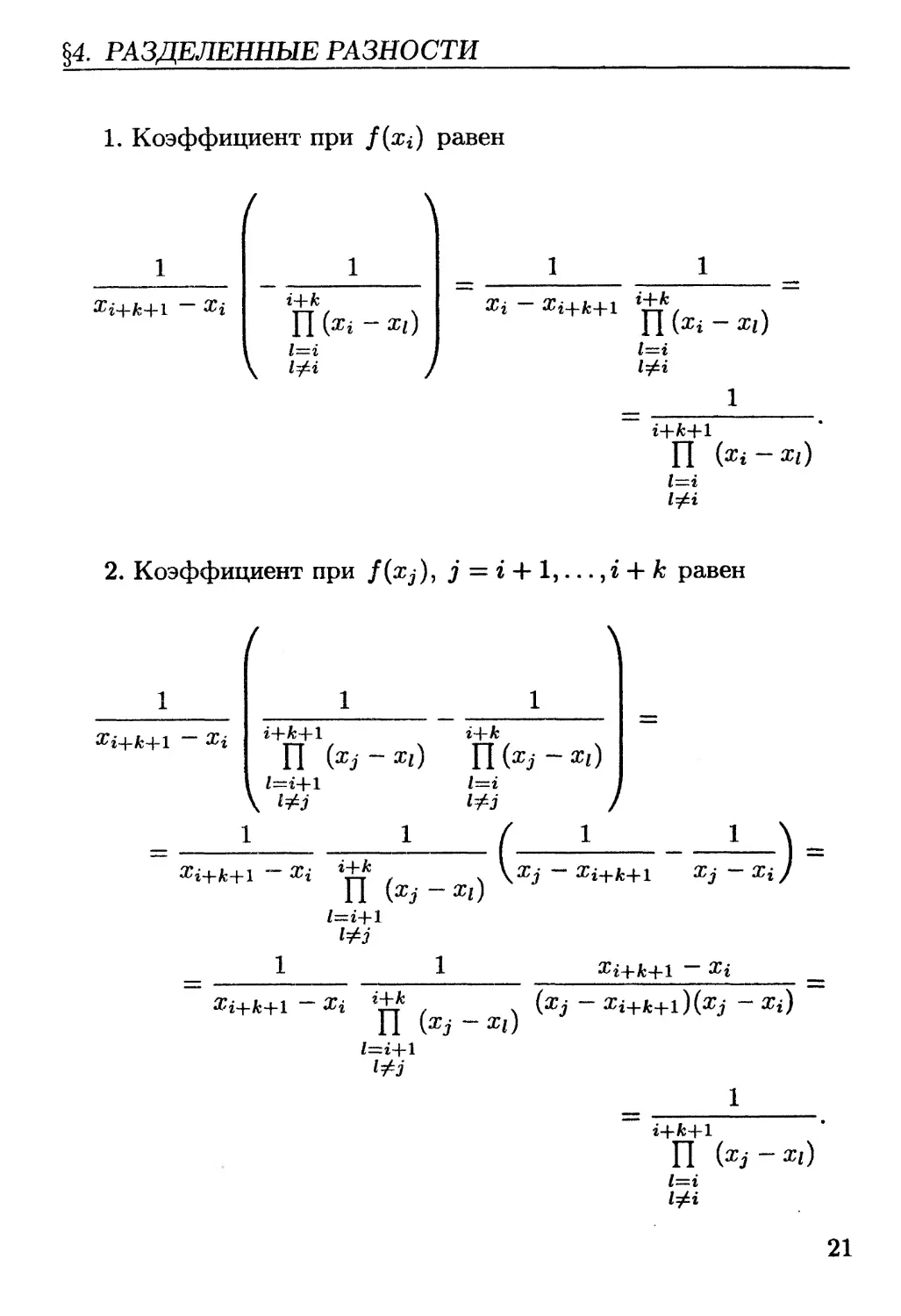
1. Коэффициент при f(Xi) равен
1
1
Xi+k+l Xi
i+k
П(Хi Хl)
l==i
lj;i
1
1
Xi Xi+k+l i+k
П (Xi Xl)
l==i
l#;i
1
i+k+l
П (Xi XI)
l==i
l#;i
2. Коэффициент при f(Xj), j == i + 1, . . . ,i + k равен
i+k
П (Xj Xl)
l==i
lj;j
i+k 1 ( Xj i+k+l
П (Xj ХЕ)
l==i+l
l#;j
1 Xi+k+l Xi
i+k (Xj Xi+k+l)(Xj Xi)
П (Xj Xl)
l=i+l
l:f:j
1
1
Xi+k+l Xi
i+k+l
П (Xj XI)
l==i+l
l#j
1
Xi+k+l Xi
1
Xi+k+l Xi
1
Xj xJ =
1
i+k+l
П (Xj Xl)
l==i
l#i
21
rлава 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕМЕННОЙ
3. Коэффициент при f(Xi+k+l) равен
111
Xi+k+l Xi
i+k+ 1
П (Xi+k+l Xl)
l==i+l
l#i+k+l
i+k+ 1
П (Xi+k+l Xl)
l==i
l#i+k+l
Таким образом, коэффициент при f(Xj), j == i,...,i + k + 1
равен
1
i+k+l
П (Xj Xl)
l==i
l#j
и потому
i+k+l
f{Xi; · ..; Xi+k+l) == L
з==
f(Xj)
i+k+l
П (Xj Xl)
l==i
l#i
Лемма доказана.
Лемма 2. Разделенная разност'Ь f(Xi;...; Xi+k) .являетСJl
си.мметри'Чной фУН'х;цией своих аР2у.ментов.
Доказательство вытекает из равенства (2).
Лемма 3. Для всех i < s, r < i + k, s f:. r справедливо paвeH
ство
f(Xi; . . . ; Xi+k) ==
f(Xi;...; XT 1; Х т +l;...; Xi+k) f(Xi;...; XB 1; Х в +l;'.'; Xi+k)
ХВ Х Т
Доказательство. Без О1'раничения общности будем считать,
что r < s. Обозначим
Yi == Х т , Yj+l == Xj, j == i,...,r 1, Yj == Xj, j == r + 1,..., s 1,
Yj == Xj+l , j == в, . . . , i + k 1, Yi+k == Хв.
22
4. РАЗДЕЛЕННЫЕ РАЗНОСТИ
Индексы точек У получаются из индексов точек Х путем дей
ствия перестановки
( i i+l ... T 1 r т+l
i+l i+2 ..0 r i т+l
8 1 8 8+1
8 li+k s
i +k )
i+k 1
(подходит любая обратимая перестановка, такая, что Yi == Х Т И
Yi+k == Х в ). В силу симметричности разделенной разности и опр&
деления (1)
f(Xi; . . . ; Xi+k) :::: f(Yi; . . . ; Yi+k) ==
f(Yi+l;...; Yi+k) f(Yi;...; Yi+k l)
Yi+k Yi
f{Xi;.. о ;XT l;XT+l;". ;Xi+k) f(Xi;... ;XB l;XB+l;". ;Xi+k)
ХВ х т
Лемма доказана.
Лемма 4. Разделенная разносrnъ f (Xi; . . . ; Xi+k) является
лuнеUН'Ьt-м, Фун'Кцuонало-м, от f, т. ео для всяких а, {3 Е R 1
(о:! + (3g)(Xi; о . . ; Xi+k) == af(Xi; . . . ; Xi+k) + (3g(Xi; . . . ; Xi+k)'
Доказательство вытекает из равенства (2).
Обозначим через Lm интерполяционный мноrочлен Лаrран
жа (для функции f), построенный по точкам Хl,. . . , Х т (степени
т 1).
Лемма 5. Справедливо представление
Lk+l (х) == Lk(X) + f(Xl; . . . ; Xk+l)(X Xl) . . . (х Xk). (3)
Доказательство. Рассмотрим Р(х) == Lk+l (Х) Lk(x) МНО"
rочлен степени ko Поскольку P(Xi) == Lk+l(Xi) Lk(Xi) == f(Xi)
f{Xi) == О для всех i = 1,. о . ,k (т.е. Хl,.'., Xk есть (все) корни
23
rлава 1. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
мноrочлена Р степени k), то Р(х) == А(х Хl) . . . (х xk), А
постоянная, значение которой может быть определено из условия
A(Xk+l Хl) ... (Xk+l Xk) == P(Xk+l) ==
== L k + 1 (Xk+l) Lk(Xk+l) == f(Xk+l) Lk(Xk+l) ==
k k
'"'"' П Xk+l Х.
= !(Xk+l) L.Jf(Xj) Х. Х. 'l =
j==l i==l J 'l
i#j
k k
= f(Xk+l) + " f(Xj) xk+l x.i П Xk+l Xi ==
L.J X. Xk + l X. X.
j==l J i==l J 'l
i#j
k
k П (Xk+l Xi)
== f(Xk+I) + L f(Xj) i k l
j==l П (Xj Xi)
i::= 1
i#j
1 k 1
!(Xk+l) k + L: f(xj) k+l Х
П (Xk+l Xi) j==l П (Xj Xi)
i==l i==l
i=l-i
k k+l f(xj) П k
Х П (Xk+1 Xi) == L k+1 (Xk+1 Xi) ==
i==l j==l П (Xj Xi) i==l
i==l
i#j
== f(Xl; . . . ; Xk+l)(Xk+l Хl) . . . (Xk+l Xk)
(в последнем равенстве мы использовали лемму 1). Из этоrо ypaB
нения находим: А == !(Xl;...;Xk+l). Следовательно, Lk+l(X)
Lk(X) == !(Хl;... j X k+l)(X Хl).'. (х Xk)'
24
4. РАЗДЕЛЕННЫЕ РАЗНОСТИ
Будем обозначать (коrда. это не ПРИВОДИТ к путанице) через
Lk интерПQЛЯЦИОННЫЙ мноrочлен Лаrранжа степени k 1, по
строенный по k точкам Xi,.. . , Xi+k l . Тоrда лемма 5 может быть
записана в виде:
Lk+l(X) == Lk(X) + f(Xi;... ;Xi+k)(X Xi)... (х Xi+k l), (4)
{'де Lk+l интерполяционный мноrочлен Лаrранжа степени k, по--
строенный по k + 1 точке Xi," . , Xi+k .
Лемма 6. Пусть
Уl == min{Xi,'.', Xi+k}, У2 == maX{Xi"", Xi+k}
и f Е C(k) ([Уl, У2]). Tozaa существует Е [Уl, У2] такое, 'Что
f(k) ( )
f(Xi;...;Xi+k)== k! .
Доказательство. ПОСТРОИlVl для функции f(x) интерполяци
онный МНО1'очлен Lk+l(X) степени k по k + 1 точке Xi,..., Xi+k
(т.е. Lk+l (Xj) == f(Xj), j == i, i + 1, . . . , i + k), для чеrо воспользу
емся (5):
(5)
Lk+l (х) == Lk(X) + f(Xi;. . .; Xi+k)(X Xi) . . . (х Xi+k l), (6)
1'де Lk интерполяционный мноrочлен Лаrранжа степени k 1,
построенный по k точкам Xi"", Xi+k l . Для функции
<р(х) == f(x) Lk+l (х)
(7)
И1vlеем в силу построения Lk+l для всех j == i, i + 1, . . . , i + k
<p(Xj) == f(Xj) Lk+l (Xj) == f(Xj) f(Xj) == О,
т.е. <р имеет не менее k + 1 нуля на отрезке [Уl, У2] .
По теореме Ролля производная <р' имеет не менее k нулей
на отрезке [Уl, У2]' По теореме Ролля, примененной к функции
25
Тлава 1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
<р', функция <.р" имеет не менее k 1 нуля на отрезке [Уl, У2] .
Продолжая так и дальше, находим, что функция <p(k) имеет по
крайней мере один нуль на отрезке [Уl, У2]. Обозначим e1'O €:
<p(k) ( ) == О, Е [Уl, У2]. в силу (7)
<p(k) ( ) == f(k) ( ) L l ( ) == О,
в силу (6)
L l ( ) == k!f(Xi; . . . ; Xi+k)
(так как k я ПРОИЗБодная МНО1'очлена Lk степени k 1 paB
на нулю, а k я производная мноrочлена Lk+l степени k равна
ero старшему коэффициенту, уr.лноженному на k!). Из последних
двух равенств получаем
f(k) ( ) = k! f(Xi; . . . ; Xi+k),
откуда вытекает требуемое равенство (5).
s 5. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА
НЬЮТОНА
Пусть требуется построить Ln(x) интерПОЛЯЦИQННЫЙ MHO
rочлен Лаrранжа степени n 1 ПО точкам Хl, . . . , Х N . Представим
ero в виде
Ln(x) == Ll(X) + (L2(X) Ll(X)) +... + (Ln(x) Ln l(X)
и применим здесь в каждом слаrаемом лемму 4.5. Получим
Ln{x) == !(Хl) + f(Xl; Х2)(Х Xl)f
t... + f(Xl;... ;Хп)(Х Xl)... (х Xn 1).
(1)
Такая запись интерполяционноrо МНО1'очлена Лаrранжа называ
ется u'Нтерnолл/цио'Н/ной формулой Ньютона.
26
5. ИНТЕРПОЛЯЦИОННАЯ ФОРМУЛА НЬЮТОНА
Равенство (1) часто записывают в виде
n
Ln(x) == 2::(х Xl)'.' (х Xi l)f(Xl;'.'; Xi), (2)
i==l
i l
rде (х Хl)... (х Xi l) == П (х Xj) считается 1, если i == 1.
j==l
Алrоритм вычисления интерполяционноrо мноrочлена в
форме ныоонаa
1. Вычисление разделенных разностей f(Xl;...; Xi), i =
1, . . . , n, участвующих в представлении (2) интерполяционно1'О
МНО1'очлена в форме Ньютона.
Пользуясь определением (4.1) разделенных разностей, запол
няем таблицу
f(Xl )
\
f(Xl; Х2)
../
\
f(X2; хз)
../
\
!(хз; Х4)
./
\
!(Х2)
f(хз)
!(Х4)
\
f(Xl; Х2; хз)
./
\
f(X2; хз; Х4)
../
\
\
f(Xl; Х2; Хз; Х4)
../
\
. . . \
f(Xl;... ;Х n )
. . ../
f(Xn l)\ f(xn 2; Xn l; Хn)
f(Xn l; Х п )../
f(x n ) .('
Столбцы вычисляются слева направо, элементы столбца вычис
ляются снизу вверх, стрелки указывают ячейку памяти, в KOTO
рую ПО ..1ещается результат. По окончании вычислений на месте
f(Xi) будет лежать f(Xl;..'; Xi).
27
rлава 1. ПРИБЛИ)l(ЕНИЕ Функций l Й ПЕРЕМЕННОЙ
2. Вычисление значения интерполяционноrо MHoro
члена (Pf)(x) в точке осуществляется по схеме ropHepa:
(Р f)(x) == f(Xl) +(х Хl )(f(Xl; Х2)+
+(х Х2)(!(Хl; Х2; хз) + · . . +
+(Х Xn 2)(f(Xl; . . . ; Xn 1)+ (3)
+(х Xn l)f(Xl;'..; Х n »)...)'
n l
Оценка числа арифметических операций
1. На вычисление всех f(Xl;...; Xi), i == 1,. . . , п по изложен
ному выше алrоритму надо вычислить п(п 1)/2 разделенных
разностей (элементов таблицы). Соrласно их определению (4.1)
для вычисления каждой требуется 2 вычитания и 1 деление.
Общее количество операций: п(п 1) вычитаний и п(п 1)/2
делений.
2. Вычисление значения интерПQЛЯЦИОНlIоrо МНО1'очлена в
точке по формуле (3) требует (п 1) умножений, (n 1) BЫ
читаний и (п 1) сложений.
Отметим, что если требуется вычислить несколько значений
интерполяционно1'О мноrочлена (2) в различных точках, то разде
ленные разности f(Xl;"'; Xi), i == 1,..., n вычисляются только
один раз. Значение мноrочлена в точке вычисляются затем по
формуле (3).
3 6. ИНТЕРПОЛЯЦИЯ "ДБИЖУЩИМИСЯ"
мноrОЧЛЕНАМИ
Пусть заданы точки а == Хl < Х2 < ... < Х п == Ь, значе
ния f(Xl),...,f(xn} И целочисленный параметр 1 < k < n 1.
Интерполирующая функция Р f строится таким образом, что на
каждом отрезке [Xi, Xi+l], i == 1, . . . ,n k она совпадает с MHoro
членом P i степени k, таким, что Pi(Xj) == f(Xj), j = i,...,i+k
28
96. "ДВИ)КУЩИЕСЯ" мноrОЧЛЕНЫ
(т.е. P i интерполяционный мноrочлен Ла1'ранжа степени k, по
строенный по точкам Xi,..., Xi+k ). На отрезке [Xn k, Х n ] интер
полирующая функция Р! совпадает с Pn k интерполяцион
ным МНО1'очленом Ла1'ранжа степени k, построенным по точкам
Xn k, . . . , Х п .
По интерполяционной формуле Ньютона
i+k
Pi(X) == L:(x Xi)... (х Xj l)f(Xi;'.. ;Xj). (1)
i==i
Коэффициенты P i , i == n k, n k 1,. . . , 1 вычисляются с
использованием таблицы разделенных разностей:
f(Xl) \
f(Xl; Х2) \
f(X2) / f(Xl; Х2; ХЗ) . ..\
\
f(Х2;ХЗ) / . . .f(Xl ; . . . ; Xk+l)
\
f(хз) / f(X2; хз; Х4) . . /
\
f{хз; Х4) /
\
f(X4) /
\
f(Xn k lХ
f(Xn k l; xn k
f(Xп k) ( f(Xn k l;Xn k;Xn k+l)"'\
f(Xn k; Xn k+lX .. .f(Xn k l;".; Xn 1)
f(Xn k; Xn k+l; Xn k+2)' . <
.. . f(Xn k; .. . ; Хn)
. . /
f(Xn l) (
f(Xn l; Х n )
f(xn) /
f(Xn 2;Xn 1;Xn)
/
Вначале вычисляются коэффициенты мноrочлена Pn k:
f (Xn k), f(Xn k; Xn k+l), . . . , f(Xn k; . . . ; х n ).
29
rлава 1. ПРИБЛИ)l(ЕНИЕ Функций l Й ПЕРЕМЕННОЙ
за k(k + 1) вычитаний и k(k + 1)/2 делений (поскольку Pn k
интерполяционный мноrочлен, построенный по k + 1 точке
Xn k, . . . , Х п ). Затем таблица заполняется по диаrонали:: вычис
ляются
f(Xn k l), f(Xn k l; Xn k), · . . , !(Xn k l; . . . ; Xn 1)
ПО формулам
f(Xn k l; . . . ; Xn k+i) ==
f(Xn k; . . . ; Xn k+i) f(Xn k l; . . . ; 'Xn k+i l)
Xn k+i Xn k l
i := О, . . . , k 1
за 2k вычитаний и k делений (эту процедуру называют ал1'о
ритмом сдвиrа представления МНО1'очлена в форме Ньютона), и
далее
f(Xn k 2 ),
f(Xn k 2; Xn k l),
. . . ,
f(Xn k 2; . . . ; Xn 2),
f(Xl),
f(Xl;X2),
. . . ,
f(Xl; . . . ; Xk+l).
Bce1'o надо заполнить n k 1 диаI'оналей. На это потребуется
2k(n k 1) вычитаний и k(n k 1) делений. Общие затраты
на вычисление всех коэффициентов: k(k + 1) + 2k(rL k 1) ==
2kn k(k+l) вычитаний и k(k+1)/2+k(n k 1) == kn k(k+l)/2
делений.
Вычисление значения интерполирующей функции Р f
в точке х осуществляется по следующему а.i1:rоритму. Опреде
ляем i из условия Х Е [Xi,Xi+l]. Если i > n k, то полаrаем
i == n k. ТО1'да (Pf)(x) = Pi(X), Вычисление значения MHoro
члена (1) степени k в точке х осуществляется по схеме ropHepa
Pi(X) == f(Xi) +(Х xi)(f(Xi; Xi+l)+
+(х Xi+l)(!(Xi; Xi+l; Xi+2) + . . . +
+(Х Xi+k 2)(f(Xi; . . . ; Xi+k l)+
30
97. ОЦЕНКИ поrРЕШНОСТИ ФОРМУЛЫ НЬЮТОНА
+(х Xi+k l )f(Xi; . . · ; Xi+k) ) . . .)
k l
с затратой k вычитаний, k сложений и k умножений.
3 7. ОЦЕНКИ поrРЕШНОСТИ
ИНТЕРПОЛЯЦИОННОЙ ФОРМУЛЫ
НЬЮТОНА
в этом разделе мы получим оценки поrрешности интерполя
ции с помощью интерполяционно1'О МНО1'очлена Ла1'ранжа, запи
caнHoro в форме Ньютона.
Теорема 1. Если! Е С([а, Ь]) и {Xi} i 1 последователь..
'Ностъ mо'Че'К: 'На [а, Ь], то для вся'Х:оео Х Е R 1
f(x) = Ln(x) + (х Хl) . . . (х xn)f(Xl;..'; Х n ; х), (1)
n
еде Ln(x) == Е (х хl)... (х Xi l)f(Xl;...; xi).
i==l
Доказательство. Без О1'раничения общности можно считать,
что Х -# Х j, j == 1,..., n, поскольку в точках х j поrрешность
интерполяции равна нулю и это соответствует (1).
При n == 1 равенство (1) имеет вид
f(x) == !(хl) + (х Хl)!(Хl;Х)
и справедливо в силу определения (4.1) разделенной разности.
Пусть равенство (1) доказано при n == k:
f(x) ::;; Lk(X) + (х Xl)'" (х Xk)f(Xl;...; Xk; х). (2)
в силу леммы 4.3
f ( ) f ( х 1 ; . . . ; х k ; Х) ! ( х 1 ; . . . ; Х k ; Х k+ 1 )
Xl;...;xk;xk+l,X = .
Х ...... Xk+l
31
rлава 1. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l..Й ПЕРЕ1\tIЕННОЙ
Отсюда имеем
f (х 1 ; . . . ; Х k ; х) ==! ( Х 1 ; . . . ; Х k ; Х k+ 1 ) +
+ (Х Х k+ 1) f (х 1 ; . . . ; Х k ; Х k+ 1; х).
Подставим (3) в (2), получим
f(x) = Lk(X)+(X Xl)". (х Xk)f(Xl;...; Xk+l)
+(Х Хl)." (х Xk+l)f(Xl;...; Xk; Xk+l; х).
В силу леммы 4.5 справедливо представление (4.3)
(3)
(4)
Lk(X) + f(Xl;'.. ;Xk+l)(X Хl)." (х Xk) == Lk+l(X)
и потому (4) принимает вид
f(x) == Lk+l(X) + (х Хl)..' (х Xk+l)!(Xl;... ;Xk;Xk+l;X),
Т.е. равенство (1) справедливо для n == k + 1. Тем самым теорема
доказана по индукции.
Теорема 2. Если f Е с(n) ([а, Ь]) и {Xi} f 1 nоследователъ
ностъ то'Че на (а, Ь], то для вСЯ-КО20 Х Е (а, Ь] существует
== (x) Е [Yl, У2] (zae Уl == Уl (х) == min{Xl,..., Х n , х}, У2 ==
У2 (х) == mах{ хl, . . . , Х n , х}) та'К:ое, 'Что
. f(n)( )
f(x) :::: Ln(x) + (х Хl) . . . (х Х n ) " (5)
n.
n
zae Ln(x) == Е (х Xl) ... (х Xi l)f(Xl;.'.; xi).
i==l
Доказательство. По теореме 1
f(x) == Ln(x) + (х Хl) . .. (х xn)f(Xl;'.., Х n ; х). (6)
По лемме 4.6 существует == (x) Е [Yl,Y2] (rде Уl == Уl(Х)
min{x},... ,хn,х}, У2 == У2(Х) == maX{Xl'..' ,Хn,Х}) такое, что
f(n) ( )
f(Xl;'..;Xn;X) == .
n.
32
з8. РА3ДЕJIЕННЫЕ РАЗНОСТИ С КРАТНЫМИ УЗЛАМИ
Подставляя это в (6), получаем требуемое равенство (5).
э 8. рАздЕлЕнныIE РАЗНОСТИ С
крАтныIии УЗЛАМИ
Определение. Пусть задан набор точек Xi".., Xi+k (не обя
зательно различных). РазделеН'Nои раЗ'Nостью функции f нуле
Bo1'o порядка называется f(Xi) == f(Xi), разделенной разностью
k 1'o порядка называется
!(Xi;...;Xi+k) ==
:! f(k) (Xi), если Xi == . . . == Xi+k И f Е C(k) ,
f{Xi;...; Xr l; Х т +l;.,.; Xi+k) f(Xi;...; Хэ 1; Xs+l;...; Xi+k)
Ха Х Т
если существуют Ха i=- Х т ,
(1)
(это определение корректно, Т.е. не зависит от выбора точек Х Т и
Ха, в силу симметрии разделенной разности по своим aprYMeHTaM,
доказательство см. лемму 4.3).
Лемма 1. Если f Е C(k) , то f(Xi; . . . ; Xi+k) является пenpe
pbtBHOи фу'Нх;цией своих k + 1 ар2у.ментов Xi,. . . , Xi+k .
Доказательство. При k == О разделенная разность f(Xi) COB
падает с f{Xi), которая непрерывна по условию.
Пусть лемма доказана для разделенных разностей порядка
k 1. Рассмотрим произвольную точку (Xi;..'; Xi+k) Е Rk+l.
Если существуют i < s, r < i + k такие, что Ха :/= Х т , то В силу
определения (1) разделенная разность f(Xi;...; Xi+k) непрерыв
на как линейная комбинация непрерывных (по предположению
индукции) функций:
f(Xi; . . . ; Xi+k) ==
f(Xi; . . . ; Xr l; Xr+l; . . . ; Xi+k) f(Xi; . . . ; Xs l; Ха+l; · . . ; Xi+k)
Ха Х Т
33
rлаваI. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
Если Xi == . . . == Xi+k , то по определению (1)
f(x .' · х . k) f (k) (x ' )
, . . ., + k ! .
Поскольку по условию f(k) непрерывна, то для всякоrо € > О
существует fJ == д(€) > о такое, что ДЛЯ всех , IXi I < fJ
If(k) (Xi) f(k) ( )I < Е.
Пусть (X ;...; x +k) Е Rk+l произвольная точка, такая, что
Ixj Xil < д, j == i, i + 1,.. ., i + k. В силу леммы 4.6 существует
Е [Уl, У2] (rде Уl == min{x ,..., X +k}' У2 == max{x ,..., X +k})
такое, что
j(k)(f.)
f(x ; . . . ; X +k) == k! ·
Так как по выбору (xi;...; x +k) Е Rk+l [Уl, У2] С (Xi д, xi + д),
то
1 1
If(Xi;... j Xi+k) f(X j... j x +k)1 == k! If(k)(Xi) f(k)( )1 < k! е,
что и означает непрерывность разделенной разности порядка k
f(Xi; . . . ; Xi+k) в точке (xi;...; Xi+k).
9 9. ИНТЕРПОЛЯЦИЯ С крАтныIии
УЗЛАМИ
Пусть заданы точки а == Хl < Х2... < Х п == Ь и значения
f(i) (Xj), i == О,..., mj 1, j == 1,..., n. Требуется построить
n
интерполяционный МНО1'очлен Lm == Р f степени m 1 == L mi
i==l
1 такой, что
L (Xj)==f(i)(Xj), i==O,...,mj l, j==l,...,n. (1)
34
9. ИНТЕРПОЛЯЦИЯ С КРАТНЫМИ УЗЛАМИ
Этот мноrочлен называют u'НmерnОЛЯЦUО'Н/Н'Ьtм' м''НО20'Ч,л'е'Ном' с
t;;paтH'btMU узлаJvfЛl, а числа тl,..., т Т }, 1Сраm'Ност.я.мu узлов
Хl,...,Х п соответственно.
Такой мноrочлен единственнен среди всех мноrочленов степе
ни m 1. Действительно, если Qm мноrочлен степени т 1,
удовлетворяющий условию (1), то их разность Lm Qm имеет
точку Xj нулем кратности mj, j == 1, . . . , n. Следовательно, MHO
п
rочлен Lm Qm степени не выше m 1 имеет Bcero Е mi == m
i==l
нулей (с учетом кратности). Поэтому Lm Q111 == о.
Теорема 1. Инmерnоляцuон'Н/ый М'ИО20'Чле'Н. Lm, удовлетво
ряющий условия-м (1), .мо:жет быть представлен в виде
m
Lm{x) == Е(х Уl)'.' (х Yi l) !(Уl;...; Yi), (2)
i==l
2де
Уl == ... == Утl == хl, Утl+1 == ... == Утl+ т 2 ==
== Х2, . . ., Y n 1 т-+l == . . . == Ут == Хn.
.L...,. i := 1
(3)
оказательство. Положим
(Е) ( . 1)
X ij == Xj + 1, е,
i==l,...,mj, j==l,...,n,
(4)
1'де О < Е < Ео, Ео такое, что все точки {x j)} различны ДЛЯ
всех € Е (О,Ео). Построим по m точкам {X ;)} интеРПОJIЯЦИОННЫЙ
МНО1'очлен в форме Ньютона L ) степени m 1 так, что
L )(X j) == f(x j) для всех i == 1,. .., mj, j == 1,..., n, О < Е < ео.
(5)
в силу единственности TaKoro мноrочлена
m
L (e) { ) "'"' ( (е» ) « Е) ) f( (Е). . (Е» )
m х L...J Х Уl . .. Х Yi l Уl' · · · , Yi ,
i==l
(6)
35
rлаваI. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
ДЛЯ всякоrо способа перенумеровать набором y c),. . . , y ) набор
{х};>}. Поэтому нам достаточно доказать, что соотношения (1)
выполнены для точки Х1.
Положим
(е) (е) (е) (е) (1:) (е) (1:)
У1 Х 1 ,1' .., , Утl Х т1 ,1' Утl +1 Х 1 ,2' , Yml +т2
(е) (е) (е) (е) (е) (7)
Х т 2'...' Y E n l Х 1 n' ... , У т Х т n.
2, т'+1' n'
i==l t
Из (7), (4), (3) вытекает, что liт у)Е:) == У; дЛЯ всех j == 1,. . . , т.
I:----tО
В силу непрерывности разделенных разностей (лемма 8.1) в pa
венстве (6) можно перейти к пределу по е ----+ О (ПОЛУЧИБШИЙСЯ В
результате мноrочлен обозначаем Lm):
m
Lm(x) == L:(x У1)'.. (х Yi l) !(У1;...; Yi) ==
i==l
тl
== L(x X1)i 1 f(Xl; . . . ; Xl)+
' 1
== i раз
m
+ (х Хl)т 1 L (х Yml+l) .. . (х Yi 1)f(Y1;. ..; Yi)
i==ml + 1
Используя определение (8.1) разделенной разности с кратными
узлами, получаем:
тl f(i l) (х ) ,
Lm(x) == (i 1) (х Xl). l+
==1
m
+ (х Xl)m 1 L (х Yml+1) ... (х Yi 1)f(Y1;'.'; Yi)
i==ml +1
(8)
Из этоrо представления следует
L (Xl) == j(i)(Xl) i = О,...,тl 1
36
99. ИНТЕРПОЛЯЦИЯ С КРАТНЫМИ УЗЛАМИ
(поскольку производные до порядка тl 1 включительно BTOp
1'0 слаrаемоrо в (8) равны нулю в точке Xl). Тем самым доказано,
что МНО1'очлен вида (2) удовлетворяет условиям (1) в точке Хl.
Определение. Задаваемый равенствами (2), (3) МНОI'очлен
называется uиmерnОЛЯЦUО'Н/I-t'Ьt-м 'ИО20'Члено-м с 'KpamH'bt-мu узла
-ми в форме Ньютона.
Теорема 2. Если f Е с( т )([а, Ь]), ( т == . тах mj) и {Xi} i 1
з==l,...,п
последовательность то'Че'К на (а, Ь], то для вСЯ'КО20 Х Е R 1
f(x) == Lm(x)+ (х Хl)т 1 ... (х хп)т п Х
Xf(Xl;...;Xl; ,хn;...;Хп;Х), (9)
".."..
тl т п
2де Lm(x) задается равенства-ми (2), (3).
Доказательство. Запишем равенство (9) в эквивалентной
форме
f(x) == Lm(x) + (х Уl) .. . (х Ут)!(Уl;'." Ут; х), (10)
{'де точки Уl,. . . ,Ут задаюr.rся (3), и будем доказывать вместо (9)
равенство (10). При этом можно считать, что х f. Yj, j ==
1, . . . , т, поскольку в точках Yj поrрешность интерполяции равна
нулю и это соответствует (10). Далее доказательство повторяет
доказательство теоремы 7.1.
При m == 1 равенство (9) имеет вид
f(x) == f(Yl) + (х Yl)f(Yl;X)
(11)
и справедливо в силу определения (8.1) разделенной разности.
Пусть равенство (9) доказано при m == k:
f(x) == Lm(x) , (х Уl) . . . (х Yk)!(Yl; . . . , Yk; х). (12)
37
rлава 1. ПРИБЛИ)КЕНИЕ Функций l Й ПЕРЕМЕННОЙ
в силу леммы 4.3
f С . .. ) f СУ1; · · · ; у k ; Х) f (Yl; . . · ; у k; У k+ 1 )
Yl,...,Yk,Yk+l,X .
х Yk+l
Отсюда имеем
!(Уl;...; Yk; х) == !(Уl;...; Yk; Yk+l)+
+(х Yk+l)!(Yl;... ;Yk;Yk+1;X).
(13)
Подставим (13) в (12), получим
f(x) == Lk(X)+(X Уl)'" (х Yk)!(Yl; _..; Yk+l)
+(х Уl)'.' (х Yk+l)!(Yl;... ;Yk;Yk+l;X).
(14)
в силу теоремы 2 справедливо представление
Lk(X) + f(Yl;...; Yk+l)(X Уl)". (х Yk) == Lk+1(X)
и потому (14) принимает вид
f(x) == Lk+l (х) + (х Уl) . . . (х Yk+l)!(Yl; . . .; Yk; Yk+l; х),
Т.е. равенство (10) справедливо ДЛЯ rп == k+ 1. Тем самым теорема
доказана по индукции.
Теорема 3. Если f Е с(т)([а, Ь]) и {Xi} r l nоследовател'Ь
'Ност'Ь то'Ч,е'Х: 'На [а, Ь], то для вСЯ'Х:О20 х Е (а, Ь] существует
== (X) Е [ 1, 2] (2де l == l(X) = min{xl,"',X n ,x}, 2 ==
2(X) = тах{ Хl, . . . ,Х n , х}) та'Х:ое, 'Ч,т.о
f С ) L ( ) ( ) т 1 С ) тп f( т) ( )
Х m Х + Х Хl . .. х Х п "
т.
(15)
еде Lm(x) задается равенствами (2), (3).
38
99. ИНТЕРПОЛЯЦИЯ С КРАТНЫМИ УЗЛАМИ
Доказательство. Введем как в теореме 1 точки X ;) , по KO
торым построим интерполяционный мноrочлен в форме Ньютона
L ) степени m 1 , удовлетворяющий (5) и имеющий вид (6) (rде
точки y e) задаются (7». По теореме 7.2 для всякоrо х Е [а, Ь]
существует €(e) == (e) (х) Е [ e), e)] (rде e) == E) (х) ==
. { (е) (е) } t"(e) с(е) ( ) { (Е) (Е) })
Шlп Уl ,..., Ут , Х , 2 == 2 Х == шах Yl ,..., Ут , х такое,
что
f(m) (€(e»
f(x) == L )(x) + (х У1 е »... (х y » " (16)
т.
Как показано в теореме 1, lim L )(x) == Lm(x) (rде Lm(x)
e.-....tО
задается равенствами (2), (3». в силу непрерывности f(m)
Нт о f(m,) ( (E» == f(m) ( ), rде € == Нт о (e), причем Е [ 1, {2] ,
e.-....t e.-....t
rде в силу (3) 1 == l(X) == min{xl,"',X 11 ,x}, (2 == (2(Х) ==
таХ{Хl,'. . , Х п , х}). ПОЭТОМ.У, переходя в (16) к пределу при е
О, получаем требуемое равенство (15).
Алrоритм вычисления интерполяционноrо мноrочлена с
кратными узлами
.Д.лrоритм вычисления интерполяционно1'О мноrочлена с KpaT
ными узлами Lm(x) вида (2), (3) тот же самый, что для интер
поляционноrо мноrочлена в форме Ньютона без кратных узлов
(см. Э 5), только пересчет элементов таблицы разделенных разно
стей осуществляется по определению (8.1) разделенной разности
с кратными узлами.
Пример. Пусть в n точках Хl, . . . , Х п заданы значения функ
ции f(x): f(Xl),'.', f(x n ) И значения ее производной f'(x):
f'(Xl),"" f'(x n ) (т.е. Б постановке (1) задачи интерполяции с
кратными узлами тl == ... == т п == 2). ТО1'да таблица разДf7
39
rлава 1. ПРИБЛИ)l(ЕНИЕ Функций l Й ПЕРЕМЕННОЙ
ленных разностей имеет вид
!(Xl)
!(Xl)
/(Х2)
!(Х2)
\
l' (Хl)
./
\
!(Xl;X2)
./
\
f'(X2)
./'
\
\
!(Xl;Xl;X2)
./
\
f(Xl; Х2; Х2)
./
\
f(X2; Х2; хз)
\
I(Xl; Xl; Х2; Х2)
-/
\
f(Xl; Х2; Х2; хз)
./
\
f(Xn l)( f(Xn l;Xn l;Xn)(
f(Xn l;Xn)( f(Xn l;Xn l;Xn;Xn)
f(xn) \ f(Xn l; Х n ; Х n ) .,/
/' (Х n ) ./
f(x п ) ./'
Столбцы вычисляются слева направо, элементы столбца ВЫЧИС
ляются снизу вверх, стрелки указывают ячейку памяти, в KOTO
рую помеПJ.ается результат. По окончании вычислений на месте
/ (Yi) будет лежать f (у!; . . . ; Yi), {'де Yi задаются (3).
Оценка числа арифметических операций, необходи
мых для построения интерполяционноrо мноrочлена Lrn(x) ви
да (2), (3), следует из оценки числа операций, необходимых для
построения интерполяционно1'О МНО1'очлена степени т 1 без
кратных узлов (см. 9 5): требуется не более т(т 1) вычита
ний и т(т 1)/2 делений (количество операций будет меньше
этих величин из за Toro, что час'rь разделенных разностей BЫ
числяется через заданные значения производных функции).
40
10. ПРОИЗВОДНЫЕ мноrОЧЛЕНА ЛАrРАН)КА
3 10. БыIислЕниЕE производныIx
мноrОЧЛЕНА ЛАrРАНЖА в ФОРМЕ
НЬЮТОНА
Пусть Ln(x) МНО1'очлен Лаrранжа функции f, построенный
по точкам Хl,..., Х п :
n
Ln(x) == L(x хl) . · · (х Xi l)f(Xl; . . . ; Xi).
i==l
Для HeKoToporo k > О требуется найти L k)(y) k ю производ
ную Ln в некоторой точке у.
в силу единственности мноrочлена Ln(x) степени n 1,
принимающеrо в заданных точках хl,.. . , Х п заданные значения
f(Xl), ..», f(x n ), мноrочлен Ln(x) совпадает с интерполяцион
ным мноrочленом для функции Ln(x) (caMoro себя):
n
Ln(x) == L(x хl)... (х Xi l)Ln(Xl;...; Xi). (1)
i==l
в силу единственности интерполяционноrо мноrочлена Ln(x)
степени n 1, он совпадает с интерполяционным МНО1'очленом,
принимающим в точках y,+l,.'.,Xп l значения Ln(y), L n (Xl),
..., Ln(Xn l). По интерполяционной формуле Ньютона этот MHO
1'очлен имеет вид
n 1
Ln(x) == Ln(y) + (х у) Е(х хl)... (х Xi l)Ln(y; хl;...; Xi).
i==l
(2)
ТО1'да
n 1
L (x)lx==y == E(Y Xl)...(Y Xi l)Ln(y;xl;...;Xi) (3)
i==l
и тем самым вычислена 1 я производная в точке у.
41
ТлаваI. ПРИБЛИ)КЕНИЕ ФУНКlfИЙ l Й ПЕРЕМЕННОЙ
Алrоритм вычисления значения L (y) в форме (3). Нам Tpe
буется по известным значениям
Ln{y), L n (Xl), L n (Xl;X2),
, Ln(Xl;.'.; Xn 1)
вычислить
Ln(y; Хl), Ln(y; Xl; Х2),
, Ln(y; Хl;..'; Xn 1)
Используем для 3TOI'O алI'ОРИТМ СДВИI'а представления МНО1'очле
на в форме Ньютона (см. 6). Добавим точку у и значение Ln(y)
в таблицу разделенных разностей и заполним по определению
разделенной разности
L ( ) Ln(Xl;...;Xi) Ln(Y;Xl;",;Xi l)
n у; Хl ; . . . ; Xi == ,
Xi У
i == 1, . . . , n 1, эту таблицу:
Ln{y)
f(Xl}
f(X2)
f(ХЗ)
f(X4)
\
Ln{y; Хl)
.,/
\
f(Xl; Х2)
.,/
\
f{X2; хз)
.,/
\
f(ХЗ;Х4)
.,/
\
\
Ln (у; Xl; Х2)
.,/
\
f(Xl; Х2; ХЗ)
./
\
!(Х2j Х Зj Х 4)
.,/
\
(4)
\
Ln(y; Хl; Х2; ХЗ)
./
\ 00\
f(Xl; Х2; ХЗ; Х4)
.,/
\
Ln (у; Xl ; . . . ; Xn 1)
.,/
..\
f(Xl;'.' ;Хn)
. о /'
f(Хn lЛ f(Xn 2;Xn 1;Xn)
f(Xn l; ХnУ
f(Xn) .,/
Трудоемкость вычисления L (y):
1. На вычисление n 1 разделенных разностей по формуле (4)
требуется 2(n 1) вычитаний и n 1 делений.
42
910. ПРОИЗВОДНЫЕ мноrОЧЛЕНА ЛАrРАН)КА
2. На вычисление L (y) по формуле (3) по схеме rориера
L (y) = Ln(y; Хl) +(у xl)(L n (y; Хl; Х2)+
+(у x2)(L n (y; Хl; Х2; хз) + . · . +
+(у хn з)(Ln(у; Хl; . . . ; Xn 2)+
+(у xn 2)Ln(y; Хl;' а.; Xn 1))".)
n 2
требуется n 2 вычитаний, n 2 сложений и n 2 умножений.
Bcero требуется 4(n 1) 2 а,пдитивных операций и 2(n 1) 1
мультипликативных операций.
Для вычисления L (у) аналоrично продолжаем.
В силу единственности интерполяционно1'О МНО1'очлена Ln(x)
степени n 1, он совпадает с интерполяционным МНО1'очленом,
ПрИНИ lающим в точках у, Хl , . . . , Xn 2 значения Ln (у), Ln (Хl) ,
..., Ln(Xn 2), а в точке у имеющим производную, равную L (y).
По интерполяционной формуле Ньютона с кратными узлами этот
МНО1'очлен имеет вид
Ln(x) == Ln(y) + (x y)Ln(y; у)+
n 2
+ (x y)2 Е (x xl)" а (X Xi l)Ln(Y;Y;Xl;..' ;Xi) ==
i==l
== Ln(y) + (х y)L (y)+
n 2
+ (х у)2 Е (х Xl)." (х Xi l)Ln(Y;Y;Xl;... ;Xi).
i==l
(5)
ТО1'да
n 2
L (x)lx==y == 2! L:(y хl) ... (у Xi l)Ln(y; у; хl;".; Xi) (6)
i==l
и тем самым вычислена 2 я производная в точке у.
Алrоритм вычисления значения L (y) в форме (6). Нам Tpe
буется по известным значениям
Ln(y), Ln(y; хl), Ln(y; хl; Х2),
, Ln(y; Хl;.. а; Xn 2)
43
rЛ8ваI. ПРИБЛИЖЕНИЕ ФУНКЦИl1 l Й ПЕРЕМЕННОЙ
вычислить
Ln(y; у; Хl), Ln(y; у; Хl; Х2),
, Ln(y; у; Хl;" . ; Xn 2)'
Как и выше используем для ЭТО1'о ал1'ОРИТМ СДВИ1'а представле
ния МНО1'очлена в форме Ньютона (СМ. 6). Добавим точку у и
значение Ln (у) в таблицу разделенных разностей и заполним по
определению разделенной разности
L ( ) Ln (у; Хl; . . . ; Xi) Ln (у; у; Хl; . . . ; Xi l)
n У; У; Xl; . . . ; Xi = ,
Xi У
(7)
i == 1, . . . , n 2, эту таблицу:
Ln(y)
Ln{y)
f(Xl)
f(X2)
!(ХЗ)
!(Х4)
\
L (у)
./
\
Ln(y; Хl)
./
\
!(Хl; Х2)
./
\
!(Х2;ХЗ)
.,/
\
!(ХЗ;Х4)
./
\
\
Ln{y; у; Хl)
.,/
\
Ln{y; Хl; Х2)
./
\
f(Xl; Х2; хз)
./
\
f(X2; Хз; Х4)
.,/
\
\
Ln(y; у; Хl; Х2;)
.,/
\
Ln (у; Хl; Х2; хз) Ln(y; у; Хl; . . . ; Xn 2)
.,/ ..../
\ \
!(Хl;Х2;ХЗ;Х4) L n (y;Xl;... ;Xn 1)
,/ ...../
\ \
f(Xl;'" ;Хn)
..../
f(Xn l f(Xn 2; Xn 1; Жn)
!(Xn 1; хnУ
f(x n ) ./
Трудоемкость вычисления L (у) :
1. На вычисление n 2 разделенных разностей по формуле (7)
требуется 2(п 2) вычитаний и n 2 делений.
2. На вычисление L (y) по фОР lуле (6) по схеме rориера
L (y) == 2!(Ln(y; у; Хl) +(у Xl)(L n (y; У; Х1; Х2)+
44
10.. ПРОИ3ВОДНЫЕ мноrОЧЛЕНА ЛАrРАН)l(А
+(у x2)(L n (y; у; Хl; Х2; хз) + . .. . +
+(у xn 4)(Ln(y; у; Х1;.' .; Xn 3)+
+(у хn з)Ln(у; У; Хl; . . . ; Xn 2) ) . . .) )
n З
требуется n 3 вычитаний, n 3 сложений и n 3 умножений..
Bce1'o требуется 4(n 2) 2 аддитивных операций и 2(n 2) 1
мультипликативных операций.
Рассмотрим общий случай. После l, 1 == О, . . . , k 1 шаrов
описанно1'О выше процесса мноrочлен имеет ВИД
1 1 LW) (у ) .
Ln(x) == Е ., (х y)J+
j ==0 J .
n l
+(х y)l Е(х хl).... (ж Xi l) Ln(y;... ;у;Хl;..... ;Xi)
. 1
t== 1
и может быть вычислена
n '
L ){y) == l! Е(у Хl)... (у Xi l) Ln(y;...; у; хl;.... ;Xi).
. 1
z== 1
Для перехода к очередному ша1'У надо вычислить
Ln(y; . . . ; у; Xl; . . . ; Xi), i == 1, . . . , n l 1
1+1
по формулам
Ln (у; . .. .. ; у; Xl; . . . ; Xi) ==
1+1
== (Ln(y;....; у; Хl;..'.; Xi) Ln{y;....; у; Хl;... ;Xi I»/(Xi у),
l l+1
i == 1, . . . , n l 1,
(8)
45
rлава 1. ПРИБЛИ)КЕН1IЕ Функций l Й ПЕРЕМЕННОЙ
а затем
n E l
L +1)(y) == (l+l)! L (Y Xl)...(Y Xi 1)Ln(Y;".;Y;X1;...;Xi).
. 1
t= 1+1
(9)
Трудоемкость вычисления L + 1) (у) :
1. На вычисление n l 1 разделенных разностей по Форму
ле (8) требуется 2(п 1 1) вычитаний и n 1 1 делений.
2. На вычисление L +l)(y) по формуле (9) по схеме rориера
L +1) (у) == (l + 1)!(Ln(y; . . . ; у; Х1)+
1+1
+(у Xl)(L n (y;. . .; у; Х1; Х2)+
[+1
+(у X2)(Ln(y;. ..; у; Хl; Х2; хз) + ... +
1+1
+(у Хn l з)(Ln(у;...; у; хl;".; Xn I 2)+
1+1
+(у Xn I 2)Ln(y;...; у; Х1;"'; Xn l l) )...) )
1+1 n I 2
требуется n 1 2 вычитаний, n 1 2 сложений и n 1 2
умножений.
Bcero требуется 4(n 1 2) 2 аддитивных операций и 2(п
1 2) 1 мультипликативных операций.
s 11. мноrОЧЛЕНЬI чЕБыIЕвАA
Определение. Мноrочленами Чебышева называют MH01'o
члены т n (х) степени n > О, задаваемые следующими peKKypeHT
ными соотношениями:
То(х) == 1,
Т1(Х) = х,
(1)
46
{ ,
11. мноrОЧЛЕНЫ ЧЕБЫIПЕВА
Tп+l(x)==2xTп(x) Tn 1(X) при п>О. (2)
Коэффициент при старшем члене МНО1'очлена Тn+1 (х) полу
чается из CTapmero члена мноrочлена Тп(х) умножением на 2.
Следовательно, старший член lноrочлена Тп(х) при n > О есть
2n 1xп.
Поскольку для всяких Q И {З COS Q COS (3 == (СОS(Q+,В)+СОS(Q
(3) ), то при любом f}
cos( (n + 1)0) == 2 cos О cos( пО) cos( (n 1)0).
Положив О == arccos х, получим при х Е [ 1, 1]
cos ( (n + 1) afCCOS х) == 2х COS ( n arccos х) COS ( (n 1) arccos х) ,
Т.е. функция 'Рn (х) == cos( п arccos х ) удовлетворяет соотноше
ниям (2) для всех n > О и х Е [ 1, 1]. Так как 'Ро(Х) ==
cos(O afCCOS х) == 1, ер1 (х) == cos(l arccos х) == х при х Е [ 1, 1],
Т.е. она удовлетворяет (1), то Тп(х) = <;?n(Х):
Тп(х) == cos(narccosx), n > О, х Е [ 1, 1]. (3)
Из представления (3) вытекают следующие свойства MHoro
членов Чебышева:
1)
ITn(x)1 < 1 при х Е [ 1, 1].
2) Точки экстремума МНО1'очлена тn(х) на [ 1, 1], т.е. точки
Х т , IТn(Хт)1 == 1 есть
"" ( 7rffi )
Х т == COS '
m == О, 1, . . . , n,
причем
Тn(Х т .) == сов 7rffi == ( 1)т.
3) Нули МНО1'очлена Тп(х) на [ 1, 1] есть
( п(2m 1) )
х т == COS 2п '
т == 1, 2, . . . , n.
47
Тлава 1. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕННОЙ
Поскольку найдены n нулей МНО1'очлена Тn(х) степени n, тодру--
rих нулей у He1'o нет и
Тn(х) == 2n 1(x хl)... (х х п ).
Определение. Введем
т n(Х) = 2n 1 тn(х) == х n + . . .
Лемма 1. Если Рп(х) == х n + . .. м,НО20'Член степени n со
старшим оэффи'Цие'Нто.м, рав'Н/ы.м 1, то
1
шах 'Рn(х)' > шах IT n(х)' == 2 1 '
XE[ lJl] xE[ l,l] n
Доказательство. Предположим противное, т.е. существует
такой МНО1'очлен Рn(х) == х n + . .. степени n со старшим коэф--
1
фициентом, равным 1, что IPn(x)1 < 2п 1 для всех х Е [ 1, 1].
Рассмотрим Qn l (х) == Т n(х) Рn(х) мноrочлен степени не BЫ
ше n 1, поскольку Т n(х) == х n +. . ., Рn(х) == х n +. ... Вычислим
знак МНО1'очлена Qn l в точках Х т , m == О, 1, . . . , n:
signQn l(Xm) == sign( T n(xm) Рn(Хт» = sign ( 1)т 2nl 1 )
== sign ( 1)т 2nl 1 ) == ( l)т
(поскольку IPn(xm)1 < 2nl 1 )' Подчеркнем, что Qn l(Xm) f: О,
m == О,1,...,п. Таким образом, на отрезке (Xm,Xm+l], m ==
0,1,..., n 1 функция Qn l (х) меняет знак и поэто:му имеет KO
рень, принадлежащий интервалу (Х т , Х т +l), m == О, 1, . . . , n 1.
Следовательно, МНО1'очлен Qn l степени не выше n 1 имеет
n различных корней и потому Qn l = о. Однако, по доказан
ному Qn l (Х т ) -:F О, m == О, 1, . . . , n. Полученное противоречие
доказывает лемму.
48
11. мноrОЧЛЕНЫ ЧЕВЫПIЕВА
Определение. МНО1'очлен Т n (х) называется МНО1'очленом
степени п, 'Н,аименее У'к;лои.пющ'Uмсл от нуля на отрезке [ 1, 1] .
Пусть [а, Ь] есть заданный отрезок.
Определение. Введем отображения
х : [а, Ь] [ 1, 1J,
у(х)== (a+b)+(b a)x ,
2
х(у) == 2y (b+a)
b a
(4)
у : [ 1,1] [а,Ь],
и М/ttоzо'Ч.лсn Чеб'Ышсва 'На отреЗ1f,е [а, Ь]
,... ( 2У (Ь + а) )
Тп(У) == Тп(х(у)) = Т п Ь а .
Нули мноrочлена Тп(у) (все принадлежат отрезку [а, Ь]) есть
а + ь Ь.... а 7r(2m ......1)
Ут == У (х т) == 2 + 2 cos 2п ,т == 1, 2, . . . , n. (5)
....... ( 2 ) п 22n 1
Старший коэффициент Тп(у) есть Ь а 2n 1 == (Ь а)п .
Определение. Положим
т ( ) == (Ь а)п т ( ) == (Ь а)n т-. ( 2 У (Ь + а) ) .
n У 22n 1 n у 22n 1 n Ь а
Лемма 2. Мноео'Член Тn (у) является .мНО20'Члено.м, Haи
менее у'К.ло'Няющи.мс.я от 'НУЛЯ, т. е. для вс.я-К;О20 .м'НО20'Чле'На
р n (у) == уn +. .. степени n со старшим 'КоэффициентО.Аt, paeH'btM
1,
(b a)n
шах IPn(y)1 > шах ITn(y)1 == 22 1 ·
уЕ[а,Ь] уЕ[а,Ь] n
Доказательство. Утверждение вытекает из леммы 1 путем
замены переменной.
49
rлаваI. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
э 12. МИНИМИ3АЦИЯ поrРЕШНОСТИ
ИНТЕРПОЛЯЦИИ ЗА СЧЕТ выIорАA
"УЗЛОВ
Минимизируем поrрешность интерполяции функции f на OT
резке [а, Ь] с помощью интеРПОЛЯЦИОННОl'О МНО1'очлена Лаrранжа
Ln степени n 1 за счет выбора узлов интерполяции Хl,..., Х п .
По теореме 7.2
f(n) ( )
f(x) Ln(x) == 1 (х Xl)... (х х n ), (1)
n.
rде Хl,.. . , х п , Х Е [а, Ь], Е [а, Ь]. Следовательно,
I f(n)
111 LnIIC([a,b]) < II(x хl) . . . (х xn)IIC([a,b]), (2)
I n. С([а,Ь])
{'де
IlgIIC([a,b]) == шах Ig(x) 1.
хЕ[а,Ь]
Минимизируем правую часть, выбрав мноrочлен Рп(х) == (х
хl) ... (х х n ) наименее уклоняющимся от нуля на отрезке [а, Ь],
Т.е. с минимальной нормой IIPnI!C([a,b]). Бозьмем
(b a)n ( 2X (b+a» )
Рп(х) == (X Xl)," (X Xп) == Тп(х) == 22n 1 Т п Ь а .
Из ЭТО1'о paBeHCTB вытекает, что точки Xl,.'., Х п являются HY
лями мноrочлена тn(х) на отрезке (а, Ь]. Б силу (11.5)
а + ь ь а п(2т 1)
х т == Ут == 2 + 2 cos 2n ' т == 1,2, . · . , n. (3)
По лемме 11.2 при таком: выборе узлов
(b а)n
IIPnIIC([a,b]) == 22n 1
50
12. МИНИМИ3АЦИЯ ПОТРЕIПНОСТИ ИНТЕРПОЛЯЦИИ
и оценка (2) имеет вид
11 L 11 < I lf (n) 11 (Ь а)n
f n С([а,Ь]) --- n! С([а,Ь]) 22п 1 ·
(4)
Полученная оценка (4) неулучшаема.
n
Действительно, возьмем f(x) == апх n + . .. + аО == L атх т
т==О
мноrочлен степени n. Тоrда f(n)( ) == апn! и оценка поrрешно--
сти (1) примет вид
f(x) Ln(x) == ап(х хl) . . . (х Х п ) == апРп(х)
rде Рn(Х) мноrочлен (на отрезке (а, Ь]) со старшим коэффици
ентом, равным 1. По лемме 11.2 получаем
(Ь а)п
111 LnIIC([a,b) == lanIlIPnIIC([a,b]) > lanl 22n 1
11 (n) 11 (Ь а)n
п! f С([а,Ь]) 22n 1 '
что и означает неулучшаемость оценки (4).
Итак, для минимизации поrрешности в качестве узлов интер
поляции Хl,..., х п надо брать нули (3) мноrочлена Чебышева
тn(х) .
Такой выбор улучшает также качественное поведение поrреш
ности при n 00.
Пример (без доказательства). Рассмотрим функцию f(x) ==
1
1 + 25х 2 и отрезок (а, Ь] == [ 1, 1]. Для равномерно распреде
ленных на отрезке [а, Ь] точек хl,'.', Х п (т.е. Xi == а + (i l)h,
b a
h == n l ' i == 1,..., n) поrрешность интерполяции 11I
LnIIC([ l,l]) 00 при n 00. Для точек Хl,..., Х п HY
лей (3) мноrочлена Чебышева Тn(Х) поrрешность интерполяции
11I LnIIC([ l,l]) О при n ----t 00.
51
rлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННО.Й
Точную характеристику поведения П2rрешности интерполя
ции по нулям мноrочлена Чебышева Тn(х} дают следующие
утверждения.
Теорема 1. (без до'Казател'Ьства). Обусловле'Нност'Ь базиса
n х X.
из элеме'Н,тар'Н,ъtх м'Ноzо'Члеuов Л а2ра'Нжа li (Х) == П J при
j==1 Xi Xj
j#i
2
Х т == Ут из (3) не nревъtшает ln n + 1.
7r
Теорема 2. Поzреш'Н,ост'Ь f Ln nриблuж;е'Ния фу'Н'Кции f
и'Нmерnол.я/цио'Н,'НъtМ М'НО20'Членом Ла2ра1tЭlCа Ln степени n 1,
nocтpoeHH,'btM по нулям (3) М1tО20'Члена Ч еБыlева,, удовлетворя
ет нераве'Нства.м
distc(f, Pn l) < 111 LnIlC([a,b]) < (2 + ln п ) distc(f, Pn l)
2де Pn 1 пространство ,мНО20'Ч.леuов стеnеии n 1,
distc(f, Pn 1) == inf 111 Pn lIlC([a,b]).
Pn lEPn l
Теорема 3 (Джекеона). Если f Е С<Т)[а,Ь] и n> т+l, то
. 6 (Зе ) r ( Ь а ) r ( ( r ) Ь а )
dlstc(f, Pn l) < 1 + r п 1 (;.) f ; 2(п 1 т) ·
дe
w(g; h) == sup{ Jg(x) у(у)' : х, у Е [а, Ь) , Ix yl < h}
ест'Ь одул'Ь Henpepbt6Hocmu ФУU1Сции.
Пример. Рассмотрим функцию f(x) == Ixl a , Q Е (0,1) на
отрезке [ 1,1]. Тоrда w(f;h) == h a . По теореме 3 при r == О,
n > 1 получаем
. ( 2 ) 6
dlstC(f, Pn l) < 6(;.) f; 2(п 1) = (п 1)0: '
52
13. РА3ЛО)КЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫШЕВА
По теореме 2
111 LnIIC([ l,l]) < (2 + ln n) (n 1)<1 '
Например, для f(x) == V'fXТ
( 2 ) 6 lnn
111 LnIlC([ l,l]) < 2 + 1r ln n (n 1)1/2 n 1 / 2
при n ---+ 00.
з 13. РАЗЛОЖЕНИЕ по мноrОЧЛЕНАМ
чЕБыIЕвАA
Пусть n заданное целое число, (а, Ь] заданный отрезок,
Хl, . . . , Х п различные точки, принадлежащие отрезку [а, Ь] . Вне..
дем в пространстве С([а, Ь]) дискретное "скалярное" произведе..
ние: для всяких f, 9 Е С([а, Ь]) положим
n
(f,g)n == L f(xm)g(xm).
т==1
(1)
13.1. Постановка задачи линейной интерполяции
Рассмотрим задачу построения разложения
n 1
Pf(x) == L a{ri(x)
i==O
(2)
функции f Е С([а, Ь]) по мноrочленам Чебышева на отрезке
[а, Ь] :
Ti(X)=Ti( 2x :a» ), i=O,1,...,n 1, (3)
53
rлава 1. ПРИБЛИЖЕНИЕ функций l...Й ПЕРЕМЕННОЙ
так, чтобы были выполнены линейные условия интерполяции:
(Ti,Pf)n == (Ti,f)n, i == O,1,...,n 1. (4)
"" -л.. -л..
Лемма 1. МНО20'Чле'Н/ы То, Т 1 , . . . , Tn l линейно независи.м'Ьt,
фу'н,'/щио'На.л'Ы лi (1) == (Ti' f ) n .ли'Н,ей'Н,о 'Н,езависим'Ы.
Доказательство. Предположим, что МНО1'очлены То, Т 1 , . . .,
-л..
Tn 1 линейно зависимы, Т.е. существует а Е Rn, Q 1= о Ta
n l ""
кое, что Pn 1(X} == Е aiTi(X} == О для всех Х Е [а,Ь]. Так
i==O
........
как degT i == i, то старший коэффициент мноrочлена Pn l(X) ==
n 1 ........ ........
Е QiTi(X) равен старшему коэффициенту мноrочлена Tj(X) (1'де
i==O
j == max{j : aj =f. О} ), умноженному на O:j. Поскольку МНО1'очлен
Pn 1 (х) = О, то e1'o старший коэффициент равен О. Следователь
но, а] == О, что противоречит тому, что j == max{j : O:j =f. О} . По
лученное противоречие доказывает первое утверждение леммы.
Предположим, что функционалы лi (1) == ( T i , f ) n линей
но зависимы, Т.е. существует Q Е R n, Q -1 о такое, что
n 1 n 1 / )
л == i аiЛi == О. Друrими словами, л(1) == i ai \ T i , f n
/n l )
\ i aJ:;i, f n == О ДЛЯ всякой f Е С([а, Ь]). Возьмем f(x)
n Х X.
lk(X) == П . Поскольку lk (Хз) == дkj, то
i==l Xk Xi
ii=k
о == л(lk) == ( aiTi,lk ) == t aiTi(xj)lk(Xj) ==
1.==0 n з==1 ==o
n n 1 n l
== L L a/Ti(xj)tSkj == L Qi11(xk)
j l i==O i==O
54
з13. РА3ЛО)l(ЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫШЕВА
для всех k = 1, 2, . . . , n. Следовательно, мноrочлен Pn 1 (х) ==
n 1
Е a/Ti(x) степени не выше n 1 имеет n нулей и потому
i==O
n 1
Pn l(X) О, T e. Е a/ri(x) == о для всех х. В силу доказан
i==O
"" "" ""
ной выше линейной независимости МНО1'очленов То, Т 1 ,. . . , Tn 1
получаем Q == о. Полученное противоречие с предположением
а i= о доказывает второе утверждение леммы.
Теорема 1. (без до-казате.льства). Обусловле'Н'Ность баз'Uса
из .м'НО20'Ч./I,е'Нов Чебышева То, Тl, . . . , Tn l 'Не nревышает V2n.
Из леммы 1 и теоремы 1.1 вытекает, что если матрица
А == (Щj), aij == ('ri,Tj) n' i,j == О,1,...n 1 (5)
обратима, то задача линейной интерполяции по мноrочленам Че
бышева (3) корректна и ее решение имеет вид (2), {'де коэффи
циентыразло)Кения
а == А 1 ( ( (Ti' f) J i==O.l.....n J ·
(6)
Подберем точки Xl".., Х n так, чтобы матрица А была леrко
обратима.
Лемма 2. Пусть
а+Ь b a 7r(2m 1)
Х т == Ут == 2 + 2 cos 2п ' m = 1, 2, · · · , n (7)
.......
нули М,'НО20ftJ,леuа ЧеБЪtшева Т п степени n. ТО2да
(Ti,Tj)n = о при i i:j, (Tj,Tj)n = ; npuj i: О, (то, ТО)n = N.
55
rлава 1. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕННОЙ
........ ( 2х (Ь + а) )
Доказательство. Так как Tj(X) == сов j arccos
b a
ДЛЯ всех х Е [а, Ь], то
n
(Ti' T j ) n == L Ti(Xm)Tj(xm) ==
т==1
( . (2т 1)7r ) ( . (2т 1)7r )
== L..J сов z 2 сов J 2 ·
т==l n n
1
Воспользуемся формулой сов Q сов J3 :;;:; 2 (cos(a (3) + СОВ(й + {З)):
( ,..", ......... ) 1 ( (2т 1)1t" )
T i , Т; n == 2 !;;;:1 сов (i j) 2n +
+ сов ((i + j) (2т2 1)71" ) == F(i j) + F(i + Л,
(8)
rде
F(k) == ! t сов ( k (2т 1)п ) ==
2 т==1 2п
( { . k(2m 1)7r } { . k(2rп 1)7r })
2 1;;:1 2 ехр z 2n + ехр z 2n
1 { ik(2m 1)7r } { ik(2( (m 1)) 1)1l" }
== ехр +ехр ==
4 т==] 2п 2п
! { ik(2m 1)7r }
4 ехр 2п
т== (n 1)
1 { 'k } n ( { 'k }) т
== 4 ехр z2: Е ехр z n7r ==
т== (n 1)
56
13. РАЗЛОЖЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫШЕВА
1 { 'k } ( { .k }) п 2п ( { 8k }) т
== 4 ехр 2: ехр n7r ехр n7r
Поскольку
2п {
qm ==
q2n 1
q
q l
2п
при
q#l
q==l
при
то при k i= о
F(k) 1 { ik7r } { 8 k } { ik7r } ехр {2ik7r} 1
== exp ехр z 7r ехр 8
4 2п п { Zk7r } 1
exp
n
== О,
так как ехр {2ikn} == 1 ДЛЯ всех k. При k == О q == ехр { i 7r } == 1
и
1 n
F(O) == 4 . 1 . 1 . 2п == "2.
Итак,
{ Опри k =1= о
F(k) == n
2 при k == О
Подставляя это значение в (8), получаем
(Ti,Tj)n ==0+0==0
(Ti' T i ) n == ; + о == ;
(То, То ) n == ; + ; == n
Лемма доказана.
Из леммы 2 получаем, что при выборе точек Хl,..., Х п как
В (7) матрица А в (5) есть
А == diag [n, ; , . .. , ; ] (9)
при i f:. j
при i f:. о
57
rлава 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕМЕННОЙ
и искомое разложение (2), (6) имеет вид
n 1
Р f(x) == L a/ri(x),
i==O
(Ti' f)
Qt / ) n, i == О, 1, . . . , n 1. (10)
. \Ti,T i п
13.2. Алrоритм построения разложения
Запишем выражения (10) ДЛЯ Qi в виде таблицы
1 " ,..... .......
аО == (TO(Xl)f(Xl) +T O (X2)f(X2) + . . . +To(xn)f(xn) )
n
2 " ....... .......
аl == (T 1 (Xl)!(Xl) +Т 1 (Х2)!(Х2) + . . . +Т 1 (xn)f(x n ) )
n
2 ....... ....... ""
а2 == (Т 2 (Хl)!(Хl) +Т 2 (Х2)!(Х2) + . · · +T2(X n )f(x n ) )
n
2 "" "" ""
an 1 == (Tn 1 (xl)f(Xl) +Tn 1 (Х2)!(Х2) + . . . +Tn 1 (xn)f(x n ) )
n
(11)
Из реккурентных формул (11.1), (11.2) для МНО1'очленов Че
бышева Т п на отрезке [ 1, 1] заменой переменных (11.4) по
лучаются реккурентные формулы для мноrочленов Чебышева
Тп(х) == Т п ( 2Х : а» ) на отрезке [а, Ь}:
то(х) == 1, Тl(Х) == 2х (Ь+ а)
b a
"" 2х (Ь + а) " "
тn+l(х) == 2 Ь а тn(х) Tn l(X) при n > о.
(12)
Пользуясь этими формулами, буде!\.1 вычислять в суммах (11)
столбцы слева направо, а каждый столбец сверху вниз.
Обозначим ДЛЯ i ::::: О, . . . n 1, j == 1, . . . , n
gi,j == T i (Xj) !(Xj),
7r(2j 1)
Z j == 2 cos 2 .
п
58
41
913. РАЗЛОЖЕНИЕ по мноrОЧЛЕНАJ\1 ЧЕБЫШЕВА
По формулам (12) для всех j == 1,2, . . . , n вычисляются
1 1
gO,j == f(xj), gl,j == 2 Zjf(Xj) == 2 ZjgO,j, (13)
9i,j == Zjgi l,j gi 2,j, i == 2, . . . , n ..... 1.
Эти формулы позволяют вычислять элементы таблицы (11) по
столбцам (слева направо), при этом каждый столбец заполняется
сверху вниз. Как только очередной столбец таблицы вычислен,
он прибавляется к сум:ме предыдущих столбцов:
Qi :== Qi + gij, i == О, . . . , n 1.
(14)
После вычислений по формулам (13), (14) для всех j ==
1,2,.. ., n вычисляются коэффициенты Qi:
1
(};о :== ao,
n
Q:i : == 2 й1, i == 1, 2, . . . , n 1.
n
(15)
После Toro, как коэффициенты ai вычислены, значение при-
n 1
ближающеrо мноrочлена в точке Pf(x) == Е l1:iTi(X) БЫЧИСЛЯ
i==O
ется с использованием формул (12)
,А... ,.А..
То(Х) == 1, тl(х) == z/2,
" " "
Ti(X) == Z Ti l (х) Ti 2(X),
....... ,.А..
Pf(x) == аоТо(х) + аI Т l(Х)
Pf(x) :== Pf(x) + a/ri(x)
i == 2, . . . , n 1.
(16)
2 2х (Ь + а)
{'де z Ь .
a
э 13.3. Оценка количества арифметических операций
Для всех j == 1,2,..., n нам требуется произвести вычисления
1. По формулам (13). На это требуется n + 0(1) мультипли
кативных и столько же адцитивных операций.
59
rлаваI. ПРИБЛИ)КЕНИЕ Функций l Й ПЕРЕМЕННОЙ
2. По формулам (14). На это требуется n + 0(1) а,пдитивных
операций.
Общее количество операций для вычислений по формулам (13)
и (14) для всех j == 1,2,...,n-: п 2 +О(п) мулътипликативных и
2п 2 + О(п) аддитивных операций.
Для вычисления коэффициентов Gi по формулам (15) требу
ется еще п + 0(1) мультипликативных операций.
Следовательно, суммарное количество операций, необходи
мых для вычисления коэффициентов ai, равно п 2 + О(п) h-1УЛЬ
типликативным и 2п 2 + О(п) адцитивным операЦИЯtv1.
На вычисление значения приближающе1'О мноrочлена Р f в
точке по фОрZVIулам (16) требуется 2n+O(I) МУЛЬ1'ИПЛИкативных
и столько же адцитивных операций.
13.4. Связь разложения по мноrочленам Чебышева и
интерполяции
При построении мноrочлена Р f не требовалось, чтобы он COB
падал с функцией f в ка.ких бы то ни было точках (требов8ЛОСЬ
лишь выполнение линейных условий интерполяции (4)). Однако,
оказывается, что построенный выше приближающий МНО1'очлен
р f можно рассматривать как интерполяционный МНО1'очлен.
Лемма 3. ПостроеUН'ЬtU в'ыше М/НО20'Ч,.лен (10) по mО'Ч'lCа.м (7)
является u'НтерnОЛЯЦUО'Н'Н/Ьt-М .м'НО20'Чле'Но.м с узлами в этuх
то'Ч'К:ах, т. е.
(Р f)(xm) == f(xm), m == 1,2,. . . , п
(17)
и, следовател'Ь'Но, совпадает с и'Нmерnоляцuо'Н'Н'Ы-м, м/ноео'Ч.ле'Но.м
""
Ла2ра'Нжа, nocтpoeHH'btM по 'Нулям М'НО20'Ч.ле'На ЧеБЪtшева Т п .
60
913. РА3ЛО)l(ЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫП1ЕВА
Доказательство. Вычислим мноrочлен (10) в точках Х т ,
т==1,2,...,п:
n 1 (Tj,f)
(Р Л(Хт) == Е ( ) Tj(x m ) ==
з==О Тз, Тз
n
n 1 n
1 ..... "
== ( ....... ......... ) L..tTj(xi)f(xi)Tj(xm) ==
з==О Тз, Тз i==l
n
n n 1
'" '"' 1 ......... .........
== {;;; f(Xi) f::o (T j , Т; ) n Т; (xi)T j (Хт)
Таким образом, для доказательства (17) (а значит, и леммы) нам
достаточно показать, что
n 1
1 ......... .........
L.J ( ......... ..... ) Tj(Xi)Tj(xm) == дim
з==О Tj, Tj
n
т.е.
1 n l 2 ......... .......
+ Е Tj(xi)Tj(xm) == dim
n . 1 n
з==
или
n 1
".................. n 1
L.J Tj(Xi)Tj(x m ) == 2 дim + 2 .
j==O
(18)
Имеем
n 1 n 1 ( )
......... ......... 2i 1 1r 2т 1 1r
2: Tj(Xi)Tj(xm) == 2: cos / 2) cos ( j ( ) ) .
. О . о п 2п
з= з==
61
rлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
1
Воспользуемся формулой cos а cos {J == 2 (cos( Q {3) + cos( а + (3)) :
n 1 ( . )
n 1 ............ 1 "(z m)7r
?: Tj(Xi)Tj(x m ) == 2 L cos J +
1=0 j O n
1 ( "(i + m 1)7r )
+ 2 cos J ==
. n
1==0
== S(i т) + S(i + m 1)
(19)
1'де
1 n l ( 'k ) 1 n 1 ( { ..k } { '"k })
S(k)== 2 H COS J n п == 4 Н \ех р ZJ n 7f +ехр Z 7f ==
1 ( n 1 { "k })
== 4 1 + j f l) ехр ZJ n 7f ==
1 ( . { i j k1r })
== 4 1 ехр {zk7f } +. ехр ==
з;;;;;; (n 1)
== (1 ( l)k + ехр { ik7f( 1) } 2 l (ех р { i 7f }) j)
Поскольку
2n 1. { q2n 1
Eq3:= q l
з==О 2n
при q f 1
при q -= 1
то при k =1= о
S(k) == 1 ( I)k + ехр { ik7f(: 1) } eXP{2; } 1
ехр 1
. n
== (1 ( I)k)
62
..
g13. РА3ЛО)КЕНИЕ по мноrОЧЛЕНАМ ЧЕБЫIПЕВА
{ 1fik }
так как ехр {27rik} == 1 для всех k. При k == О q == ехр == 1
и
1 n
8(0) == (1 1 + 2п) ==
4 2
Итак,
{ !(I ( I)k)
S(k) ==
2
при k f:. о
при k == О
Подставляя это значение в (19), получаем при i :f. т
n 1 ........ ........ 1.
L Tj(Xi)Tj(Xm) == S(i т) + S(i + т 1) == 4 (1 ( 1)' т) +
j==O
+ ( 1 ( l)i+m l) == ! +! == 1
4 4 4 2
(поскольку числа i m и i + m 1 имеют разную четность). При
",==т
n 1
L Tj (xi)T j (Хт) == S(i т) + S(i + m 1)
j==O
n 1 ( 2i 1 ) n 1
== + 1 ( l) == + .
2 4 2 2
Тем самым формула (18) (и вместе с ней лемма) доказана.
Все рассмотренные выше аппроксимации Р f функции f име
ли вид: на отрезке [а, Ь] функция f приближается МНО1'очленом
Р f == Lm степени т. Сравним этот способ со следующим: разде--
лим отрезок (а, Ь] на k частей и на каждой из них приблизим
мноrочленом Ln степени n. Такая аппроксимация называется
кусочно МНО1'очленной.
63
rЛ8В8I. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l--Й ПЕРЕМЕННОЙ
э 14. ПРЕИМУЩЕСТВА
кУсочно мноrОЧЛЕННОЙ
АППРОКСИМАЦИИ
Оценки поrрешности всех рассмотренных ранее методов име
ют вид
11I р Illc < const(n) distc(f, Pl1 l),
(rде Р f аппроксимация мноrочленом степени n 1, Р n 1
пространство мноrочленов степени n 1). По теореме Джекеона
(см. теорему 12.3) при n > r + 1
. ( ь а ) r ( 1') Ь а )
dlStc{f, Pn l) < const(r) n 1 VJ 1 ; 2(n 1 т) ·
Следовательно, оценка поrрешности
( b a ) T ( ( ) b a )
111 р 1IIc < const(n) const(r) n 1 VJ 1 т ; 2(n 1 т) .
Увеличение точности при фиксированной величине модуля
непрерывности функции 1(1') может быть достиrнуто либо YBe
личением n, либо У 1еньшением Ь а; разбиение отрезка [а, Ь] на
k частей дает тот же эффект, что и использование МНО1'очленов
степени kn. Преимущества разбиения отрезка перед увеличением
степени МНО1'очлена:
1. Требуется решать (в общей схеме задачи линейной интер
поляции) k систем размера n вместо одной размера kn.
2. С ростом степени мноrочлена n растет обусловленность ба
зиса, а при разбиении отрезка она не меняется, так как
размерность базиса n (степень мноrочлена на каждом из
отрезков разбиения) не изменяется с ростом количества OT
резков разбиения k.
64
15. КУСОЧНО tJТ[lfНЕЙНАЯ ИНТЕРПОЛЯЦИЯ
u
3 15. КУСОЧНО..ЛИНЕИНАЯ
ИНТЕРПОЛЯЦИЯ
Пусть на отрезке (а, Ь] заданы точки а == Хl < Х2 < ... <
Х п == Ь и значения f(Xl), f(X2),' . . , f(x n ) некоторой функции
f Е С([а, Ь]). Требуется построить приближение функции J
кусочно линейной функцией 1 2 f, совпадающей с f в точках Xi,
i == 1,2,.. . , n. Друrими словами, требуется построить функцию
121 такую, что для всех i == 1,2,..., rt 1 на отрезке [Xi, Xi+l]
функция 121 является линейной функцией, значения которой в
точках Xi и Xi+l совпадают со значениями f(Xi) и f(Xi+l) функ
ции f в этих точках.
По интерполяционной фОРI\1уле Ньютона для всех х Е
[Xi,Xi+l], i == 1,2,...,n 1
f(X-+l) f(x-)
12f(x) == I(Xi)+(X Xi)f(Xi;Xi+l) == f(Xi)+(X Xi) l
Xi+] Xi
(1)
Лемма 1. Если f Е С 2 ([а, Ь]), то справедлива следующая
оце'Н'К;а nоzрешности 'Кусо'Ч'Но ..ли1tеЙ1tОЙ интерполяции
11I 1 2 f1IС([а,ь]) < h211/"IIC([a,b])
zae
h == _ шах (Xi+l Xi).
l==l ,2,_ _ _ ,n 1
Доказательство. По теореме 7.2 получа.еI\1
IIf PfIIC([Xi,Xi+l]) < 2 \ [ шах ] I(X Xi)(X Xi+l)1 Jl/"IIС([Хi,Жi+l1)'
. хЕ Xi,Xi+l
(2)
Функция у(х) == (х Xi)(X Xi+l) == х2 (Xi + Xi+l)X + XiXi+l < О
ДЛЯ всех Х Е [Xi,Xi+l] и имеет нуль производной (Xi + Xi+l)/2,
65
rлаваI. ПРИБЛИ)l(ЕНИЕ функций l Й ПЕРЕМЕННОЙ
принадлежащий отрезку [Xi, Xi+l]. Поскольку g(Xi) == g(Xi+l) ==
о, то
( Х'+Х'+1 )I
шах Ig(x)1 == 9 t 2 1 ==
XE[Xi,Xi+l] I
1 2
== (Xi+l Xi) .
4
Xi+l Xi Xi Xi+l
2 2
Подставляя это в (2), получаем
111 р fllc([Xi,Xi+l) < (Xi+l Xi)2 111"IIС([Жi,ЖiН])'
Следовательно,
111 1 2 f1IС([а,ь) == i==l,Т, n 1 111 р flIС([Жi,Жi+l) < h 2 111"IIC([a,b])'
Лемма доказана.
Определение. Обозначим через 82 линейное пространство
непрерывных ломаных линий на отрезке [Хl, Х n ] == [а, Ь] с изло..
мами Х2 < Хз < . . . < Xn 1
Лемма 2. Если f Е С([а, Ь]), то справедлива следующая
оце'Н'Х:а n02peulnocтu усо'Ч'Но .л/u'Неи'Ноi1 интерполяции
distc(f,8 2 ) < 111 1 2 fIlC([a,b}) < 2distc(f, 82).
Доказаr.rельство. В силу единственности интерПQляционноrо
мноrочлена на каждом из отрезков [Xi, Xi+l] , i == 1,2,..., n 1
получаем для всякой f Е 82
1 2 ! == f
(3)
Очевидно, что
11I 1 2 fIIC([a,b]) > in s f 11I пIIC([a,b]) == distc(f, 82).
gE 2
66
16. МЕТОД НАИМЕНЫПИХ КВАДРАТОВ
в силу линейности 1 2 ! на [Xi, Xi+l]
1I 1 2fIlC'([a t b]) = . шах I(I 2 f)(xi)1 == шах If(Xi)1 < IlfIIC([a,b])'
==1 ,2,.. .,n ==1 ,2,.. .,n
т.е. для всякой 1 Е С([а, Ь])
III 2 fIIC([a,b]) < IlfIIC([a,b]).
(4)
Имеем ДЛЯ всякой 9 Е 82
111 1 2 fIIC([a,b]) == 11(1 у) + (у 1 2 1)IIC([a,b])'
Используя (3) и линейность [2, продолжаем
111 1 2 fIlC([a,b]) = 11(/ у) 12(1 g)IIC([a,bJ) <
< 11(1 g)IIC([a,b]) + 1112(/ g)IIC([a,b])'
с помощью (4) находим
111 1 2 fIIC([a,b]) < 11(1 g)iIC([a,b]) + 11(1 у)IIС([а,ь])
== 211(1 g)IIC([a,b])
для всякой 9 Е 82. Следовательно,
11I 1 2 /11С([а,ь]) < inf 11(1 g)IIC([a,b]) = 2distc(f, 82).
gES2
Лемма доказана.
э 16. КУСОЧНО..ЛИНЕЙНАЯ
АППРОКСИМАЦИЯ МЕТОДОМ
НАИМЕНЬШИХ КВАДРАТОВ
в предыдущем разделе мы построили кусочно линейную
функцию, совпадаЮЩУIО с функцией 1 в заданных точках. OДHa
ко, если ее значения известны с неко'rорой поrрешностью, то это
67
rлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
может дать приближение плохоrо качества. В описываемом ни
же аЛ1'оритме близость функции и ее приближения измеряется в
интеrральной норь,1е, И, следовательно, приближающая функция
будет менее чувствительной к выбросам в значениях приближа
емой функции.
16.1. Постановка задачи линейной интерполяции
Пусть требуется построить приближение функции f кусочно
линейной функцией L 2 f Е 82 такое, что
11I L 2 /I1 L 2([a,b]) -+ min
Т.е.
111 L 2 fIIL 2 ([a,b]) == in s f 111 gIIL 2 ([a,b]),
уЕ 2
(1)
1'де
ь
IIgIlL2([a,b) == (Y,Y) [a,Ь)' (u,v)L2([a,b) == J u(x)v(x)dx.
а
Введем базис пространства 82
Hj Е 82, Hj(Xi) == дij, i == 1,2,. .., п, j == 1,2,. . ., п. (2)
Всякая 9 Е 82 раскладывается по этому базису слеДУЮIЦИМ об
разом
n
у(х) == L g(Xj)Hj(X).
j=l
(3)
n
Действительно, в силу (2) имеем: для п(х) == Е g(Xj)Hj(X):
j==l
g(Xi) == g{Xi), i == 1,2,...,п. Следовательно, у(х) == 129
кусочно линейная интерполирующая функция. По доказанному
в лемме 15.2 ДЛЯ 9 Е 82 выполнено (15.3). Следовательно, 9 == g.
68
16. МЕТОД НАИlVIЕНЫПИХ КВАДРАТОВ
Таким образом, задача (1) может быть сформулирована в сле
дующем виде: найти (Оз)з==1.2,...,n такие, что функция
n
(L 2 f)(x) == L OjHj(x)
J==l
(4)
удовлетворяет соотношению
n I
1 LQjH j
j==l
== 9i 2 11/ gIlL2({a,b])'
1.12 ([ а,Ь])
(5)
Известно, что в евклидовом пространстве (в нашем случае
L 2 ([a, Ь]» минимум (5) реализуется на функции (4), являющейся
проекцией функции f на подпростраНСТБQ 82. Следовательно,
элемент 1 L 2 ! ортоrонален подпространству 82. Поскольку
{ H i .} i 1 составляют базис 82, то условие ОРТО1'ональности 82 эк
вивалентно условию ортоrональности всем H i , i == 1, . . . , n :
(1 L 2 j, H i ) L 2 ([a,ь]) == О, для всех i == 1, . . . , n,
т.е.
(L 2 1, H i ) Е2([а,Ь}) == (1, H i ) L 2 {[a,b]) , i == 1, . . . , n. (6)
Условия (6) представляют собой линейные условия интерпо
ляции, которым должна удовлетворять приближающая функ
цня (4).
Из (6) и (4) находим:
n
L (Hj, H i ) L2([a,b]) aj == (1, H i ) L2([a,b) , i == 1, . . . , n
j==l
или
n Ь Ь
! Н; (X)Hi (х) dx · а; == ! /(x)Hi(x) dx, i == 1, . . . , n. (7)
J==la а
69
Тлава 1. ПРИБЛИЖЕНИЕ функций l..Й ПЕРЕМЕННОЙ
ТОТ же результат (7) может быть получен из условия
2
n
F(a) == f L QjHj
j=l
L 2 ([а,Ь])
( 1 t Ci.jHj , 1 t Ci.jH j ) ----+ min
з==1 з==1 L2([a,b])
путем дифференцирования функции Р(а):
( ( 1 tO: jHj ) ,1 tO: jHj ) +
1==1 з==1 L2([a,b])
+ ( 1 t o.jHj, :0: ( 1 t O: jH j ) )
1==] 1==1 L2([a,b])
== ( 2Hi' 1 t Ci.jH j )
з==1 L2([a,b])
дР
И приравнивания к нулю производной д Б точке минимума:
ai
дР
Ba.i
BF == О, . 1
z == ,..., n.
Bai
16.2. Вычисление матрицы системы задачи линейной
интерПОЛЯЦИI'I
Вычислим матрицу системы (7). Так как
Бирр H i == [Xi l, Xi+1]
Бирр Н 1 == [Xl, Х2],
при i == 2,3, . . . , n 1,
БиррН n == [Xn l'Xn],
70
916. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
то
(Hj, H i ) L 2 ([a,b]) == О при li jl > 1.
Поэтому в i OM уравнении системы (7) отличны от нуля не более
3 x коэффициентов:
(Hi 1, H i ) L2([a,b]) при (}i l И i == 2,3, . . . , n,
(H i , H i ) L 2 ([a,b]) при ai И i == 1,2, . . . , n,
(Hi+l' H i ) L 2 ([a,b]) при (}i+l И i == 1, 2, . . . , n 1.
1. Вычислим для i == 1, 2, . . . , n 1
(H i , H i + 1 ) L 2 ([a,b]) ==
J
Hi(X)Hi+l (х) dx =
supp Hi nsupp Hi+l
Xi+l
== J Hi(X)Hi+l(X) dx.
Xi
Так как H i , Hi+l Е 82 кусочно линейные и Hi(Xi) 1,
Hi(Xi+l) == о, Hi+l (Xi) == О, Hi+l (Xi+l) == 1, то
Hi(X)
Х Xi+l
при Х Е [Xi, Xi+l]
Xi Xi+l
X X'
Hi+l (х) == при Х Е [Xi, Xi+l]
Xi+l x.i
Следовательно,
Xi+l
(H i , Hi+l)L 2 ([ a Ь ]) == ( 1 )2 J (х Xi)(Xi+l х) dx ==
, Xi+l Xi
Xi
Xi+l
1 J (х Xi)«Xi+l Xi) + Xi х) dx ==
(Xi+l Xi)2
Xi
71
rлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
Xi+l
1 J (Xi+l Xi)(X Xi) (х Xi)2) dx ==
{Xi+l Xi)2
Xi
1
(Xi+J Xi)2
( 1 з 1 З ) 1
"2 (Xi+l Xi) 3 (Xi+l Xi) == 6 (Xi+l Xi)
2. Заменой индексов i :== i 1, i + 1 :== i в предыдущей фор
муле получаем для i == 2,3, . . . , n
1
(Hi l, H i ) L 2 ([a,b]) == 6 (Xi Xi l)
з. Вычислим для i == 2, з, . . . , n 1
Xi+l Xi Xi+l
(H i ,H i )L2([a,b]) == J H;(x)dx == J H;(x)dx+ J H;(x)dx.
Xi l
Xi l
Xi
Имеем:
X J i l H'f(x) dx = J Xi ( Х Xi l ) 2 dx == (Xi Xi l)
Xi Xi l 3
Xi X& l
Xi+l
J H'f(x)dx=
X J i+l ( Х Xi+l ) 2 d
Xi Xi+l Х
Х,
Х'&
1 1 ( 3 ) 1
== (Xi Xi+l) ==== (Xi+l Xi)
(Xi Xi+l)2 3 3
Следовательно,
1 1 1
(H i , Hi)L 2 ([a,b]) = 3 (Xi Xi l) + 3 (Xi+l Xi) == 3 (Xi+l Xi l)
4. Вычислим
J X2 2 J X2 ( Х Х2 ) 2 1
(H 1 , H 1 )L2([a,b]) == Н 1 (x)dx = Xl Х2 dx == з(Х 2 хl)
Xl Xl
72. .
916. МЕТОД НАИМЕНЫПИХ КВАДРАТОВ
5. Вычислим
х"
(H n ,H n )L2([a,bj)= / H (x)dx=
Xn l
= / х п ( х Xn 1 ) 2 dx = 3 1 (хn Xn l)
Х п Xn l
Xn l
Итак, система (7) имеет вид:
Х2
1 1 /
3 (Х2 xl)al + 6 (Х2 Хl)а2 == Н 1 (x)f(x) dx
Хl
111
6 (Xi xi l)ai l + з(Хi+l xi l)ai + 6(Xi+1 xi)ai+l ==
Xi+l
= / Hi(X)f(x)dx, i==2,З,...,n 1
Xi 1
Х"
1 1 /
6 (х n Xn 1)an 1 + з(х n Xn 1)an == Hn(x)f(x) dx
Xn 1
Если положить Ха == Хl, Хn+l == Х n , то эту систему можно запи
сать в более компактном виде
111
6 (Xi Xi l )ai l + 3 (Xi+l Xi l )ai + 6 (Xi+l xi)ai+l ==
Xi+l
== f Hi(X)f(x) dx, i == 1,. . . , n
(8)
Xi l
(ао и а п +l входят сюда с нулевыми коэффициентами).
73
rлаваI. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
Определение. Матрица А == (aij) Е М N называется матри
цей с диаеонаЛ'ЬН'Ьt-М преобладанием, если
n
I аи I > L: I aij 1, i == 1, 2, . . . , n.
j==l
j:j;i
Матрица системы (8) является трехдиаrональной с диаrональ
ным преобладанием. Системы с такими матрицами можно pe
шать обычным методом raycca без выбора rлавноrо элемента.
э 16.3. Свойства приближающей функции
Лемма 1. Если! Е С([а, bJ), то для приближающей фу'Н,,
ции L2! справедлива априорная о'Цен?Са
IIL 2 fIlC([a,b]) < 3I1fIlC([a,b])'
Доказательство. Так как Hj(Xi) == дij, то для кусочно
линейной функции (4)
n
IIL 2 fIIC([a,b]) == . шах I(L 2 !)(Xi)1 == . шах L ajHj(Xi)
==1,...,n 1.==1,.. .,n
j==l
== . шах IЙil.
1.== 1,. . . ,n
Обозначим
IЙjl == . шах IЙil == IIL 2 fIIC([a,b]).
1.== 1 , . . . , n
(9)
"Умножим j oe уравнение системы (8) на 6 , полу
Xj+l Xj l
чим
Xj+1
')'j laj l + 2а; + '')'jHajH == 6 f Hj(x)f(x) dx, (10)
, Xj+1 Xj l
Xj l
с
74
916. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
rде
Xj Xj l
,j l == ,
Xj+l Xj l
Х "+1 Х'
"v J J
lj+l
Xj+l Xj l
'Уз 1 + ')'З+l == 1.
(11)
Из (10) имеем
6
21aj I <
Xj+l Xj l
Xj+l
! Hj(x)J(x) dx + l')'j laj l + ')'j+1aj+1l.
Xj l
(12)
Рассмотрим
l,j l аз 1 + ,j+1 aj+ll < "Yj 1 k j 11 + "Yj+1Iaj+ll.
В силу (9)
Ifj l аз 1 + 'Уз+1 aj+11 < ')'j 1IQj I + fj+1laj I =: ('Уз 1 + 1';+1 )Iaj I
в силу (11)
Ifj laj 1 + I'j+1 a j+ll < lajl.
Подставляя это в (12), находим
6
21аз' <
Xj+l Xj l
Xj+l
! Hj(x)J(x) dx + lajl.
Хз ]
Отсюда получаем
ХЗ+l
laj I < 6 ! Н; (х) dx · IIfIIС([х , . l,Ж-i+l])' (13)
ХЗ+l Xj 1 "
Xj- l
Поскольку
Xj+l Х; Xj+l
! Hj(x) dx == ! х Хз 1 dx + ! х Х;+l dx ==
Xj Xj 1 Xj Xj+l
Xj l Xj l Х;
1 1 1
== 2 (Х; Xj l) + 2 (Xj+1 Xj) == 2 (Xj+l Хз 1),
75
rлава 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕМЕННОЙ
ТО из (9) и (13) получаем
JlL 2 fIlC([a,b]) == fc j I < 31IfIIС([Жj 1'Жi+1J) < 31IfIIC([a,b]).
Лемма доказана.
Лемма 2. Если f Е С([а, Ь]), то справедлива следующая
оцеН7Са nО2реш'Ности 7Сусо'ч/н,о ли'Нейно'Й аnnро'К:си.мации методом
наименьших квадратов
distc(f,8 2 ) < 111 L 2 fIlC([a,b]) < 4distc(f, 82),
Доказательство. Так как проекция элемента из подпр
странства на это подпространство равна этому элементу, то
L 2 f == f для всех 1 Е 82.
(14)
Очевидно, что
111 L 2 /1IC([a,b]) > in s f 111 gIJC([a,b]) == distc(f, 82).
уЕ 2
Имеем для всякой 9 Е 82
11/ L 2 fIIC([a,b]) == 11(1 в) + (g L 2 !)IIC{[a,b])'
Используя (14) и линейность L 2 , продолжаем
111 L 2 fIIC([a,b]} == 11(1 g) L 2 (/ g)JlC([a,b]) <
< 11(1 g)IIC([a,b]) + IIL 2 (1 g)IIC([a,b]).
с помощью леммы 1 находим
11I L 2 /1IC([a,b]) < 11(1 g)IIC([a,b]) + 311(/' g)IIC([a,b])
== 411 (1 у) IIC([a,b])
ДЛЯ всякой 9 Е 52. Следовательно,
11I L 2 f1IC([a,b)) < NJt2 411С! g)IIC([a.b]) == 4distc(f, 82),
Лемма доказана.
76
16. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Лемма 3. Если f Е с(2) ([а, Ь]), то сnраведлuва следующая
о'ЦеН7Са nО2реШ1-tости 'Х;УСО'Ч1iо ли'Ней'Ной аnnРО7Сси.мации -методо-м
наи-меu'Ьших 7Свадратов
111 L 2 f1IC([a,b]) < h2111"I!C([a,b]),
zae
h ==. шах (Xi+l Xi).
z== 1,2,. .., n 1
Доказательство. В силу леммы 15.2
distc(f,8 2 ) < 11I 1 2 fIlC([a,b])'
По лемме 15.1
distc(J,8 2 ) < 111 1 2 111С([а,ь]) < h2111"IIC([a,b])'
в силу ле1vIМЫ 2
111 L 2 f1IC([a,b]) < 4distc(J, 82) < h2111"IIC([a,b])'
Лемма доказана.
s 16.4. Вычисление правой части системы задачи
u u
линеинои интерполяции
Для вычисления правой части системы (8) требуется Y1vIeTЬ
вычислять интеrралы вида
Xi+l
! Hi(X)J(x) dx, i == 1,2,..., n.
Xi l
Обычно описанный выше а.тrrоритм применяют в следующей си
туации: заданы точки а == Уl < У2 < ... < YN == Ь И известны
77
rлаваI. ПРИБЛИ)l(ЕНИЕ функций l Й ПЕРЕМЕННОЙ
значения функции f в этих точках: f (Уl ), f (У2), . . . , f (у N ) , здесь
N > n. Тоrда пола1'ают, например,
Xi+l Xi+l
/ Hi(X)f(x) dx / Hi(X) (12 f) (х) dx i == 1,2, . . ., n, (15)
Xё 1
Xi l
1'де 1 2 ! кусочно линейная интерполирующая функция, постро
енная по точкам Yl, У2, . . . , у N. Интеrралы в правой части при
ближенно1'О равенства (15) вычисляются аналитически посколь
ку подынте1'ральная функция представляет собой МНО1'очлен не
выше второй степени.
ПО1'решность, вносимая при замене левой части (15) на пра
вую, может быть оценена с пQмощыo леммь] 15.1:
lZl Иi (Х)f(Х) dx xZ1Hi(X)(I2f)(X) dx < h2I1f"IlC([a,b])Ci,
rде
Xi+l
C i == / Hi(x) dx == (XHl Xi l) < h
Xi l
и
h ==. шах (Xi+l Xi).
==1.2,...,n ]
Поэтому
lZl Hi(X)f(x) dx XZ 1Hi (x)(I 2 f) (х) dx < h3I1f"IIC([a,b])
Покажем, что условие N > n важно. Предположим, что
N == n, Т.е. о функции f нам известны ЛИIIIЬ ее значения
f(Xl), f(X2),.", f(x n ) В точках Хl, Х2",., Хn.
78
916. МЕТОД НАИМЕНЬПIИХ КВАДР.4.ТОВ
1. Вычислим для i == 1,2, . . . , n 1
Xi+l
! Hi(X)f(X) dx.
(16)
Xi
Приблизим функцию f на отрезке [Xi, Xi+l] линейной функцией
интеРПОЛЯЦИОННЫ 1 мноrочленом Лаrранжа L i) первой степе
ни, построенным по точкам Xi и Xi+l :
(i) !(Xi+l) f(Xi)
L 2 (х) == f(Xi)+(X Xi)f(Xi; Xi+l) == f(Xi)+(X Xi) .
Xi+l Xi
При этом в силу теоремы 7.2 ДЛЯ всех х Е [Xi, Xi+l] справед
ЛИВО равенство
f(x) L i)(x) == ;! (х Xi)(X Xi+l) f"( (x»
{'де (x) Е [Xi, Xi+l]' Следовательно,
Xi+l Xi+l
! Hi(X)f(x) dx / Hi(X)L i) dx <
Xi
Xi
Xi+l
< ! ;! (X Xi)(X Xi+l)f"( (x»dx <
Xi
Xi+l
< Ilf"IIС([х;,:Щl]) ! (х Xi)(Xi+l х) dx.
Xi
Поскольку
Xi+l
! (х Xi)(Xi+1 х) dx =
Xi
79
rлава 1. ПРИБЛИ)КЕНИЕ функций l Й ПЕРЕМЕННОЙ
Xi+l
/ (х Xi)«xHl Xi) (х Xi)) dx =
Xi
1 3 1 3 l ( 3
== 2 (Xi+l Xi) 3 (Xi+l Xi) == 6 Xi+l Xi) ,
(17)
то
Xi+l Xi+l
/ Hi(X)f(X) dx / Hi(X)L i) dx <
Xj
Xi
< 112 (Хн! Xi)311f"IIC([Xi'X'+l)). (18)
Поэтому мы можем приблизить интеrрал (16) следующим спосо
бом:
Xi+l Xi+l
/ Hi(X)f(x) dx / Hi(X)L i) (х) dx (19)
Xi
Xi
с ошибкой (18).
Имеем
Xi+l Xi+l
/ Hi(X)L i) dx = /
х Х'+l
Z (f(Xi) + (х xi)f(Xi; Xi+l)) dx ==
Xi Xi+l
Xi
Xi
( f(x i ) X / i+l(Xi+1 х) dx+
Xi+l Xi
Xi
Xi+l )
+ f(Xi; хнl) ! (х Xi)(Xi+l х) dx
1
с помощью (17) продолжаем:
Xi+l
/ Hi(X)L i) dx = 1 ( f(X i ) 2 1 (Xi+l ..... Xi)2+
Xi+l Xi
Xi
('
80
16. МЕТОД НАИМЕНЬП1ИХ КВАДРАТОВ
+ J(X H1 ) f(Xi) 1 (ХН1 хi)з )
Xi+l Xi 6
== (ХН1 Xi) ( J(Xi) + (f(Xi+1) J(Xi»)
1
== б (Xi+l xi)(2f(Xi) + f(Xi+l)).
Итак, в силу (19), (18) получаем:
Xi+l
f д(х)f(х) dx (ХН1 xi)(2f(Xi) + f(Xi+1»' (20)
Xi
с ошибкой
Xi+l 1
1 Hi(X)f(x) dx б-(Х i + 1 xi)(2f(Xi) + f(Xi+1)) <
< 112 (ХН1 хi)з IIP'llc([x. .''''+1])'
(21)
2. Аналоrично вычислим для i == 2,3, . . . , n
Xi
f Hi(X)J(x)dx (x> Xi 1)(2J(Xi) + J(Xi l)), (22)
Xi l
с ошибкой
Xi 1
X.{l Hi(X)f(x) dx б (х. Xi 1)(2f(Xi) + f(Xi l» < (23)
< 112 (Xi Хi l)Зllf"IIС([Хi I'Х'])'
Вычислим правую часть системы (8):
Х2
1. Формулы для f Н 1 (x)f(x) dx получаются из (20), (21) при
Хl
i == 1.
81
rлава 1. ПРИБЛИ)l(ЕНИЕ Функций l..Й ПЕРЕМЕННОЙ
2. Вычислим для i = 2,3,... ,n 1
Xi+l
(H i , 1)L2([a,b]) == ! Hi(X)f(x) dx ==
Xi l
Xi Xi+l
== ! Hi(X)f(X) dx + ! Hi(X)f(X) dx.
Xi l
Xi
в силу (20), (21), (22), (23)
(H i , f)L 2 ([a,b])
1 1
6 {Xi+l xi)(2f(Xi) + f(Xi+l)) + 6 (Xi Xi 1)(2f(Xi) + f(Xi l))
1 1 1
== B(Xi Xi l)f(Xi l)+ 3 (Xi+l Xi l)f(Xi)+ 6 (Xi+l Xi)!(Xi+l)
с ошибкой
(Hi, 1) L2([a,b]) ( (Xi Xi l)f(Xi l)+
1 1 )
+ 3 (Xi+l Xi l)!(Xi) + 6(Xi+l xi)f(Xi+l) <
< 112 (Хн 1 Xi)3I/f"IIC([Xi,Xi+l]) + 112 (Xi Xi l )31If"I/C([XH,Xi]) <
< 11 2 1If "IIC([XH,Xi+l]) (XHl Xi)3 + (Xi Xi l)3)
Х N
3. Формулы для J Hn(x)f(x) dx получаются из (22), (23)
Xn l
при i == n 1.
Если положить Ха = Хl, Х 71 +1 == Х n , то формулы для правой
части системы (8) можно записать в более компактном виде:
1 1
(H i , 1) L2([a,b]) б (Xi Xi l )f(Xi l) + з (XHl Xi l )f(xi) +
1
+ 6 (Xi+l Xi)f(Xi+l), (24)
82
fi17. МЕТОД НАlfМЕНЬП1ИХ КВАДРАТОВ
rде ошибка приближения
(H i , 1) L2([a,b]) ( (Xi Xi 1)f(Xi 1)+
1 1 )
+ 3 (Xi+l Xi l)!(Xi) + 6 (Xi+l Xi)!(Xi+l) <
< 112 {(ХН1 Xi)3 + (Xi Xi 1)3) IIfI/IIС([Хi l"Щl])
Если обозначить
(25)
h ==. шах (Xi+l Xi),
==1 ,2,.. .,n 1
то ошибку (25) можно записать в виде
(H i ,1) L 2([a,b]) ( (Xi Xi 1)f(Xi 1)+
1 1 )
+з(Хi+1 Xi l)f(Xi) + в(Хi+l Xi)!(Xi+l) <
< h3 1If " ll
6 C([Xi 1 ,Xi+l])
Из вида системы (8) и ее правой части (24) получаем, что
Qi == l(xi) , т.е. приближение по методу наименьших квадратов
совпадает с приближением, построенным кусочно линейной ин..
терполяцией: L 2 ! == [21 .
(26)
э 17. АППРОКСИМАЦИЯ
мноrОЧЛЕНАМИ чЕБыIЕвАA МЕТОДОМ
НАИМЕНЬШИХ КВАДРАТОВ
Задача построения приближающей функции Р! Е Pn 1, наи
более близкой к заданной функции f в норме L 2 (т.е. миними
зирующей Функционал 111 р !IIL2) является сложной с вычис
лительной точки зрения. Однако, задача минимизации функцио
нала 11I р 111*, rде 11.11* норма пространства L 2 с некоторым
весом, может быть решена достаточно леrко.
83
rЛ8В8I. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
17.1. Интеrральные свойства мноrочленов Чебышева
""
Лемма 1. МНО20'Ч,лен'ы Чеб'Ьtшева То, Т 1 ,.. ., Tn 1 1-ta отрез
"е [а, Ь] (см. (13.3» образуют баз'Uс пространства Pn l .мH020
'ЧЛенов степени n 1.
Доказательство. Линейная независимость мноrочленов То,
;о..
Т 1 , ..., Tn 1 доказана в лемме 13.1.
Пока)l(ем, что всякий мноrочлен Pn 1 Е Pn 1 может
быть представлен в виде линейной комбинации мноrочленов
"" ""
То, Т 1 , · . . , Tn 1 .
Определим по точкам (13.7) дискретное "скалярное" произ
ведение (1з.1) и построим разложение (1з.10) по tvlНОI'очленам
"" ........
Чебышева То, Т 1 , . . . , Tn 1 ДЛЯ функции f == Pn 1' В силу лем
мы 13.3 Pn 1 (Xi) == Р f(Xi), i == 1,2,..., n. Поскольку Pn 1
И р f являются мноrочленами степени не выше n 1 и COB
падают в n точках, то P71 1 = Р f. Итак, всякий МНО1'очлен
Pn 1 Е Pn l представлен в виде линейной комбинации MHoro
членов То, Т 1 ,. . . , Tn 1 (причем коэффициенты разложения BЫ
числены нами явно, см. (1з.10».
Лемма доказана.
Лемма 2. МНО20'ЧлеН'Ьt Чеб'Ьtшева То, Т 1 , . . . , Tn 1 'На отрез
х:е [а, Ь] удовлетворяют СОО1пношенu.я.м:
ь ........ ........
I Ti(y)Tj(Y) d 1r А..
У 2 и з,
yI (b у)(у а)
а
Ь ""
I Тб(У) d
yI {b y){y a) у==п.
а
i 2 + j2 =1= о,
84
917. МЕТОД НАИМЕНЫПИХ КВАДРАТОВ
Доказательство. Докажем вначале, что мноrочлены То, Т 1 ,
. .., Tn 1 на отрезке [ 1, 1] удовлетворяют соотношениям:
1
/ Ti ( Х ) Tj ( х) dx == 1r 8.. i 2 + З . 2 ...J. О ,
\/ 1 х 2 2 З' r
1
1
/ Тб(Х) dx == 11:. (1)
у l х 2
1
И1\л:еем:
1 1
/ TjX)Tj( ) dx == / v 1 cos(iarccosx) cos(jarccosx) dx.
1 х 2 1 х 2
1 1
Сделаем здесь замену х == cos (), () Е [О, п]:
1 О
/ Ti(X)Tj(X) dx == / () cos(iO) cos(jO)( sinf) d8 ==
-J l х 2 Sln
1
1т
== / cos(iO) cos(jO) dO ==
о
п п
== / cos«i ЛО) dO + / cos«i + ЛО) dO ==
о о
== (I(i j) + I(i + Л),
rде
1т
I(k) == / cos(kO) dO ==
о
i sin(kO) ' == О, k 1: о
11< 1 dO == 11:, k == О
== 1rбk,о.
Следовательно,
1
/ Ti(X)Tj(x) d 1:.. ! . . { 1rbij, i 2 + j2 f О
/1 х 2 Х 2 1rU ,J + 2 1rU1,, J
V 1f', i == j == О
1
85
rлаваI. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
Сделаем здесь замену переменных (11.4): х == х(у), х
2у (Ь + а)
(а,Ь] [ 1,1], х(у) == b а :
1 Ь
J Ti(X)Tj(x) dx == J 1 Ti(y)Tj(Y) 2 dy
l V l х 2 а J 1 ey :a) ) 2 ь а
Так как
J l ( 2Y (b+a) ) 2== 1 v(b a)2 (2y (b+a))2 ==
b a b a
1
== Ь а V (b а (2у (Ь + а)))(Ь а + 2у . (Ь + а)) ==
1 2
== Ь а V (2b 2у)(2у 2а) == Ь а V (b у)(у а)
ТО
1 Ь
J Ti(X)Tj(x) dx == J T i (y)Tj (у) dy
v l х 2 V (b у)(у а)
l а
Из (1) получаем требуемый результат.
Лемма доказана.
э 17.2. Постановка задачи линейной интерполяции
Введем скалярное произведение
ь
[и, v] == J u(y)v(y) dy,
v (b у)(у а)
а
норму
,i Ilull* == [и, и]l j 2
86
17. МЕТОД НАИМЕНЫПИХ КВАДРАТОВ
и пространство
L; ([а, Ь]) == { 1 Ilfll* < 00 }.
в силу
ь
! dy < 00
vI (b у)(у а)
а
имеет место включение С([а, Ь]) С L;([a, Ь]).
По методу наименьших квадратов для функции 1 Е L;([a, Ь])
требуется построить приближение Р f Е Pn 1 такое, что
11I Pfll* == il1f 11I gll*.
YEPn l
в силу леммы 1 можно искать Р f в виде
71 l
РI == L GjT j .
j==O
(2)
Следовательно, надо найти {Йj} j J такие, что
n 1
111 L GjT j "* == inf 11I 911..
. yEPn l
з==0
в евклидовом пространстве L 2 [a, Ь] минимум 11I Р 111* pea
лизуется на функции Р 1, являющейся проекцией f на подпро-
( ) n 1
странство Pn l == Tj. . Следовательно, элемент f Pf OpTO
з==О { } n 1
rонален IIDдпространству Р n 1 . Так как Tj. базис Р n 1 ,
з==О
то условие ортоrональности Pn 1 эквивалентно ортоrональности
.......
T i , i == О, 1, . . . , n 1 :
[! Р J, T i ] == О, i == О, 1, .. . ,n 1,
87
ТлаваI. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕIIНОЙ
т.е.
[P/,1'i] == [/,1' i ] , i ==O,1,...,n 1.
(3)
Условия (3) представляют собой линейные условия интерп
ляции, которым должна удовлетворять приближающая ФУНК
цИЯ (2).
Из (3) и (2) находим:
n l
L [T j , T i ] О!; := [/, T i ], i := О, 1, .. . , n 1. ( 4)
j=O
в силу леМl'v1Ы 2
[T j , Ti] ;;;;; bij [T i , T i ] i,j == О, 1,..., n 1,
поэтому из (4) получаем
Qi=
[/, Ti]
[Ti' T i ]
i = 0,1,..., n..... 1,
т.е.
О!О == [/,1'0], O!i:= [/,1' i ] ,
i == 1,2, . . . , n 1,
(5)
17.3. Вычисление коэффициентов разложения
Для вычисления коэффициентов разложения (5) требуется
вычислять интеrралы
Ь /'о..
[ f' i ] == f /(y)1'i(Y) dy.
J(b у)(у а)
а
88
s.z 7. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Сделаем здесь замену переменных (11.4): У == У (х), У : [ 1, 1] -----+
[ Ь] ( ) (а + Ь) + (Ь а)х .
а, , у х 2 .
1 '"
[1 Т ......... ] ! f(x)Ti(X) d
, v _Х'
1 х2
1
1'де f(x) == f«(a + Ь) + (Ь а)х)/2). Пусть значения функции f
известны в точках а = УО < Уl < ... < YN == Ь (например, У; ==
b a ........
а + jH, Н == N ' j == 0,1,..., N, N > О). Тем самым f задана
в точках 1 == ХО < Хl < . . . < XN == 1, Xj == (2Yj (Ь+ а))/(Ь а),
j == О, 1, . . . , N. Тоrда
N l Xj+l",
[! т. ] == " ! f(x)Ti(X) dx
, z V l х2
з О Х.
J
(6)
Приблизим функцию f на отрезке [Xj,Xj+l] линейной функцией
интерполяционным мноrочленом Лаrранжа L j) первой степе
ни, построенным по точкам Xj и Xj+l :
(j) ........ . ........ ........ [( Х j + 1 ) !( Х j )
L 2 (х) f(xj)+(x Xj )f(xj; Xj+l) == f(xj )+(X Xj) .
Xj+l X;
При этом в силу леммы 15.1 справедливо неравенство
111 L j)llc([xj,Xi+l]) < (Xj+1 Xj)21If'IIC([Xj,Xi+l])'
Следовательно, поскольку ITi(x)1 < 1 для всех Х Е [ 1, 1],
Х j + 1 '" Х j + 1 (j)
! f(x)Ti(X) dx ! L2 Ti(X) dx <
V l х 2 y' l х2
ХЗ
х.
J
89
Тлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l..Й ПЕРЕМЕННОЙ
Xj+l
1 2 11 /' 11 / ITi(X)1
< '8 (Xj+1 Xj) f C([X;,XHl]) v'1 х2 dx <
Х'
J
< (хн! Х; )21If'IIC([x; ,Xj+1])C j ' (7)
l Xj+l 1
rде С ; = v' dx. Поэтому мы можем приблизить ин
Х . 1 х 2
J
l Xj+l [(х)Т'(х)
теrрал v" dx следующим способом:
Х . 1 х 2
J
X / Hl !(X)Ti(X) dx X / Hl L j)Ti(X) dx
y' l х 2 V l х 2
Х; Х;
с ошибкой (7). Подставляя это в (6), находим
N 1 Xj+l (j)
[1 т. ] / L2 Ti(X) dx
, V l 2
j==O Х. Х
J
(8)
с ошибкой
N 1 Xj+l (j)
[1 т. ] / L2 T i (х) d <
, /1 2 Х
j==O Х. Х
J
N l
< L (хн} Xj)21If'IIC([xj,XHl))C j <
i==O
N l
1 11 /' 11 2 """' Ь а 2 11 " 11
< 8 f C([ l,l]) h С ; < 16 С h f С([а,Ь)
j==O
(9)
rде
1
h == шах (Xj+l Xj), С == / 1 dx == 1r.
з==О,l,...,N 1 j V l х 2
1
90
917. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Вычислим
Х / Н 1 L j)Ti(X) dx
V l х 2
х.
J
Xj+l "'" ........
/ (f(xj) + (х Xj)f(Xj;Xj+l))Ti(X) dx ==
\1' 1 х 2
Х.
J
Xj+l
"'" .".... / Ti ( Х )
(f(Xj) XjJ(Xj; XjH» \1'1 х2 dx +
Х'
3
Xj+l
"'" / xTi(X)
+f(XjjXj+l) \1' 2 dx
l x
х'
J
(10)
с помощью замены х == cos 8, 8 Е [O,7r] находим:
/ Ti(X) dx == / cos(i arccos(x)) dx == / cos(i8) d8 ==
у 1 х 2 у l х 2
== { t sin(i8), i:f. о } == { sin(i arccos(x)), i -1 О }
fJ, i == О arccos(x), i == О
и аналоrично
/ XTi(X) d / xcoS(iarccos(x)) d / fJ ( . 8)dfJ
x x cos COS'l
у l х 2 у l х 2
== { J ( cos ( (i 1) О) + cos ( (i + 1) fJ)) d(}, i =J о } ==
sin«(}), i =: О
( i 2 1 sin«(i 1) arccos(x)) + i l sin«i + 1) arccos(x))),
i > 1
(arccos(x) + sin(2 arccos(x)) , i == 1
sin(arccos(x)), i == О
Определение. Мноrочленами Чебышева BToporo рода назы
вают мноrочлены Un(Х) степени n > О, задаваемые следующими
реккурентными соотношениями:
Uо(Х) == 1,
U 1 (х) == 2х,
(11)
91
rлава 1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
и п + 1 (Х) == 2хU п (х) Uп l(X) при n > О. (12)
Также, как в S 11, проверяется, что мноrочлены Uп(х) удовле
ТБОРЯЮТ на отрезке [ l, 1] равенству
U (х) = sin«n + 1) arccosx) О [ ]
N , n > , Х Е 1 , 1 .
у1 х2
(13)
Следовательно,
J Ti(X) dX== { t v' 1 x2Ui 1(X), if;O } (14)
V/ l х2 arccos(x), i == О
и
J XTi(X) dx ==
v' l х 2
V l X2( i 1 Ui 2(X) + i l Ui(x)), i > 1
! (arcco s(x) + ! vl 1 х 2 Ul(Х))) , i == 1
у l х2 uо(х), i == О
(15)
Обозначим
Xj+l
a i . = J Ti(X) dx,
1 v 1 х 2
Х;
Xj+l
b i . == J XTi(X) dx,
J VI1 х2
Х;
(16)
1'де интеrралы вычисляются, используя формулы для первооб
разных (14) и (15). Продолжим вычисление (10):
Xj+l (j)
J L2 T i (х ) ,.... ,.... . '"' .
v dx== (f(Xj) XjJ(Xj;Xj+1»aj + J(Xj;Xj+1)bj ==
1 х2
х'
J
== a i<xj) + (b ajxj)!(Xj;Xj+l)) =
. 1 ....... ( . ) + (b i i X . ) i<Xj+l) !(Xj)
аз х) . а. з
J З Xj+l Xj
92
17. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
( b i i " ) b i i "
i j ajx)".... j ajXJ"""
== aj f(xj) + f(Xj+l) ==
Xj+l Х) Xj+l Xj
i b i b i i
а .Xj+l .".... . а 'Xj
== J J f(xj) + J J f(Xj+l),
ХЗ+l Х) Xj+l Х)
Обозначим
i b i
i a j Xj+l j
с.
J ХЗ+l Xj ,
b i i
i j ajxj
d.
J Xj+l Xj
(17)
Тоrда
3;j+l (j)
f L2 T i (х) . ".... . ""
.j dx == cj/(xj) + dj/(xj+1)'
1 х2
х.
J
Подставляя это в (8), находим
N l
[/,1Ч L (c j(Xj) +d i(xj+1)) ==
):=0
N l
== c l(xo) + L (c + d l)j(Xj) + d lf(XN).
j==1
Обозначим
и i C i
О о'
и j == c + dj 1, j == 1, . . . , N 1,
i d i
иN N l.
(18)
Тоrда
N
D:i == [1:1\] 'Е и j(Xj)
з==О
(19)
с ошибкой (см. (9))
N
[ ] '"'" ( ) ь а 2 11 " 11
f, T i 'и ! Xj < 16 7r h 1 С([а,Ь])'
з==О
(20)
93
rлава 1. ПРИВЛИ)КЕНИЕ Функций l Й ПЕРЕМЕННОЙ
17.4. Алrоритм вычисления коэффициентов
разложения
Нам требуется ДЛЯ всех i == О, 1, . . . , n 1 вычислять коэф
фициенты разложения (5), используя представление (19), rде KO
эффициенты задаются выражениями (18), (17), (16). Запишем
выражения для ai в виде таблицы
1 о" + и l(Xl) +U i(XN) )
ао == (uof(xo) +
7r
2 1" + uil(xl) + + U}yj(XN) )
аl == (uof(xo)
7r
2 2" 2"" + + U f(XN) )
а2 == ( ио!(хо) + u 1 f(Xl)
7r
"'"
+ uN l f(XN) )
(21)
Будем вычислять в суммах (21) столбцы слева направо, а каж
дый столбец сверху вниз. Для вычислений в (16) используе:м
представления (14) и (15), 1'де значения мноrочленов Чебыше
ва 2 ro рода в точках Xj, j == О, 1, . . . , N будем определять по
реккурентным формулам (12).
2 n 1 "'"
an 1 == ( и о f(xo)
1r
+ u li(Xl)
+
17.5. Оценка количества арифметических операций
Для всех j == О, 1, . . . , N нам требуется произвести вычис
ления столбца коэффициентов и;, i = О, 1, . . . , n 1 в форму
лах (21). Соrласно выражениям (18), (17), (16), (14), (15) это
осуществляется за линейное по n число арифметических опера
ций: О(п). Еще 2п операций потребуется для умножения и; на
"'"
значение функции в точке f(Xj) == f(Yj) и послеДУЮIцеrо сумми
рования полученных значений с текущим значением Qi. Следова
тельно, суммарное количество арифметических операций, необ
ходимых для вычисления коэффициентов ai, равно O(Nn).
94
,.
18. lIНТЕРПОJIЯЦИЯ HEr ЛАДКИХ ФУНКЦИЙ
u
З 18. КУСОЧНО..ЛИНЕИНАЯ
ИНТЕРПОЛЯЦИЯ HEr ЛАДКИХ ФУНКЦИЙ
НА спЕциАльныIx СЕТКАХ
Справедлива следующая теорема:
Теорема 1. (без доказательства). Пусть
1. f Е с(2) ((а, Ь)) (т.е. 2ладкост'Ь функции 1 в тО'Ч'lCах а u Ь
'Не требуется);
2. функция 1/" (х) I .монотонна при х ----+ а+ и х ----+ b ;
ь
3. J 11" ( х ) 11/2 dx < 00;
а
4. то'Чки а == хl < Х2 . . . < Xn 1 < Х п == Ь въtбранъt так, 'Что
Xi Ь
j lf//(x)1 1 / 2 dx := i 1 j l/"(X)1 1 / 2 dx, i == 2,..., n 1.
n ]
а
а
ТО2да nО2реИl/ность интерполяции функции 1 кусо'ч,'но линейно'Й
фун'Х:цuей [2 f, совпадающей с f в то'Чх;ах xl, Х2, . . . , х п , удовле
творяеm. соотношению
11I 1 2 fIlC([a,b]) == o(n 2) (n ----+ (0).
Мы докажем эту теорему в частном случае функции I(X) ==
V1XТ и отрезка [а, Ь] == [0,1]. Проверим выполнение условий Teo
ремы для этой функции.
1 1
1. f'(x):= 2 x 1/2, f"(X) := 4 x 3/2 непрерывны на (0,1);
1
2. f/l(x):= 4 x 3/2 монотонна на (0,1);
95
rлава 1. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
111
/ 1 / 1 х 1 / 4
3. 11" (х) 11/2 dx == 2 x 3/4 dx == 2" 1/4 о == 2 < 00;
о о
Xi
/ 1/2 1/4 i 1
4. из условия Ij"(x)1 dx == 2x i == n 1 2 получаем Xi ==
а
( . 1 ) 4
: -=- 1 ' i == 2,3, · · · , n 1, хl == а == О, х п == Ь == 1.
Найдем
11I 1 2 /11С[а,ь] == шах I/(x) (I 2 /)(x)1 =
хЕ[а,Ь]
( f(X'+1) f(X') )
=. шах шах f(x) f(Xi) + (х Xi) t z
t==1,2,...,n 1 XE[Xi,Xi+l] Xi+l Xi
(1)
Обозначим
9i(X) == f(x) ( f(Xi) + (х Xi) f(XiH) f(Xi) ) .
Xi+1 Xi
Поскольку 9i(Xi) == о, 9i(Xi+l) == О, rro максимум 19i(X)1 ДОСТИ
1'ается в точке 9 (X) == О, принадлежащей отрезку [Xi,Xi+l] (по
теореме Ролля такая точка существует). Из уравнения
у'(х) == р(х) f(XiH) f(Xi) == О
Xi+1 Xi
находим
{(х) == j( X i+l) f(Xi) .
Xi+l Xi
Для функции f(x) == JiXТ имеем
VXi+1 VXi 1
2ф Xi+l Xi yXi+l + VXi
96
18. ИНТЕРПОЛЯЦИЯ НЕrtЛАДКИХ Функций
1 ) 2
Отсюда х == 4 (.VXi+1 + JXi , Т.е. нуль у'(х) единственнен. Так
как по теореме Ролля существует нуль g'(x) Е [Xi, Xi+l], то этот
нуль и есть найденное значение. Вычислим
( VfXi+l VXi )
g(x)==VX VXi+(X Xi) ==
Xi+l Xi
1
== ( y'Xi+l + JXi)
2
( VXi + ( ( v/Xi+l + JXi)2 4X i ) 1 ) ==
4 V Xi + 1 + fti
1
== 2 ( V X i+ 1 JXi)
1 1
( v/ X i+l JXi) ( v/ X i+l + ЗJXi)
4 V Xi + 1 + fti
== ( yl X i+1 JXi) ( 2 VfXi+l + З VXi ) == (VfXi+l VXi) 2
4 V Xi + 1 + fti 4 y" X i+l + fti
Итак,
I ( ) . 1 ( V Xi + 1 VXi)2
шах g Х I == .
XE[Xi,Xi+l] 4 y" X i+l + VXi
( . 1 ) 4
При Xi == получаем
n 1
1 ( ( n 1 ) 2 ( ) 2) 2
тах Ig(x)1 == 2 2
XE[Xi,Xi+l] 4 ( i ) + ( i 1 )
n 1 n 1
1 (i2 (i 1)2)2
4 (п 1)2 i 2 + (i 1)2
1 1 (2i 1)2
4 (п 1)2 i 2 + (i 1)2
97
rлаваI. ПРИБЛИ)l(ЕНИЕ функций l Й ПЕРЕМЕННОЙ
== ! 1 ( 2 1 ) < 1
4 (п 1)2 i 2 + (i 1)2 4 (п 1)2
Подставляя это в (1), получаем
1 1
11I 1 2 f1IC[a,b] < 4 (п 1)2 '
т.е. поrрешность порядка O(n 2). Теорема доказана.
Замечание 1. Поrрешность f L 2 приближения функции
f == М интеРПОЛЯЦИОННЫfvl мноrочленом Лаrранжа L 2 степе
ни 1, nOCTpoeHHbIl'vl по нулям (12.3) :м:ноrочлена Чебышева, имеет
порядок O(n 1/2) (см. при мер из 12).
э 19. ИНТЕРПОЛЯЦИЯ
КУСОЧНО..КУБИЧЕСКИМИ ФУНКЦИЯМИ
Рассм:отрим задачу интерполяции кусочно кубическими фун"
кциями.
19.1. Общая схема
Пусть заданы точки а == Хl < Х2 < ... < Х п == Ь и значения
f(Xl), !(Х2) .. ., !(Х 11 ). Интерполирующая функция Р f строится
таким образом, что на каждом отрезке [Xi, Xi+l], i == 1, . . . , п 1
она является мноrочленом P i степени 3, таким, что
Pi(Xi) == !(Xi),
Р/ (Xi) == d i ,
Pi (Xi+l)
Р/ (Xi+l)
I(Xi+l) }
d i + 1
i==1,...,n 1
(1)
1'де d i , i == 1, . . . , n свободные парам€тры, тот или иной способ
выбора которых определяет метод кусочной интерполяции куби..
чески ми мноrочленами. Полученная функция Р! совпадает с !
98
19. КУСОЧНО КУВИ-ЧЕСКИЕ ПРИБЛИJКЕНИЯ
в точках Xi, Z 1,..., n и ДЛЯ люБОI'О набора параметров d i
р f Е C(l) ([а, Ь]).
19.2. Алrоритм вычисления коэффициентов
мноrочлена P i
Коэффициенты мноrочлена P i , записанноrо в фОрIvlе
Pi(X) == al,i + a2,i(X Xi) + аз,i(Х Xi)2 + a4,i(X Xi)2(X Xi+l)
MorYT бы'ть вычислены по интерполяционной формуле Ньютона с
кратными узла 1И (СМ. определение (4.1) разделенных разностей):
f{Xi)
\
d i
\
\
f(Xi; Xi+l) d i
f(Xi)
Xi+l Xi
\
d i + d i + 1 2f(Xi; Xi+l)
(Xi+l Xi)2
!(Xi+l) (
d i + 1
!(Xi+l) ./
f{Xi; Xi+l) (
d i + 1 f(Xi; Xi+l) ./'
Xi+l Xi
.,/
Столбцы вычисляются слева направо, элементы столбца вычис
ляются снизу вверх, стрелки указывают ячейку памяти, в KOTO
рую помещается результат. Отсюда получаем
al,i
:= f(Xi)
аз,i
== d i
f{Xi; Xi+l) di
Xi+l Xi
d i + d i + 1 2f(Xi; Xi+l)
(Xi+l Xi)2
a2,i
a4,i
Для представления в виде
Pi(X) == Cl,i + C2,i(X Xi) + Сз,i(Х Xi)2 + C4,i(X Xi)3 (2)
99
rлава 1. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕННОЙ
запишем
(х Xi)2(x Xi+l) = (х Xi)3 (Xi+l Xi)(X Xi)2
откуда получаем
Cl,i == al,i == f(Xi)
Сз,i
= а2 i == d i
,
( ) 3f(Xi; Xi+l) 2d i di+l
== аз,i a4,i Xi+l Xi ==
Xi+l Xi
d i + d i +l 2f(Xi; Xi+l)
== а4 i ==
, (Xi+l Xi)2
(3)
C2,i
C4,i
9 19.3. Кусочная интерполяция кубическими
мноrочленами Эрмита
Пусть в точках а == Хl < Х2 < ... < Х п == Ь И3
вестны значения функции: f(Xl),".' f(xn) И ее производной
f'{Xl),.' ., f'(x n ). Тоrда параметр d i в общей схеме интерполя
ции кусочнcrкубическими функциями полаrается равным
d i == l' (Xi),
i == 1,2,. . . , n.
(4)
Основные свойства приближающей функции Р f :
1. Р f является кусочно мноrочленной функцией, значения
которой зависят только от JIокальноrо поведения функции
f и 1', И1-1енно: значения Р! на отрезке [Xi,Xi+l] зависят
только от значений функции f и ее производной l' В точках
Xi И Xi+ 1 .
2. Метод приближения является линейным: Р(! + у) == Р! +
Ру, P(af) == аР/.
100
19. КУСОЧНО КУБИЧЕСКИЕ ПРИБЛИ)l(ЕНИЯ
Лемма 1. Если 1 Е С(4)([а,Ь]), то справедлива следующая
оце'Н/ка nО2реш'Ности аnnро'Кси.мации 'Кубu'Чесtcu.ми М'НО20'Чле'На.мu
Эр.мита
1 1 4 (4)
11I р IIIC([a,b]) < 4! 24 h 111 IIC([a,b])'
2де
h ==. шах (Xi+l Xi).
t==1,2,...,n 1
(5)
Доказательство. По теореме 7.2 получаем
11I р IIIC([x"X,+l]) <
< 4 1, шах I(x Xi)2(X XiH)2111/(4)IIC«(Xi,:",+1])'
. XE[Xi ,Xi+l]
(6)
Функция у(х) == (х Xi)(X Xi+l) == х2 (Xi + Xi+l)X + XiXi+l < О
для всех х Е (Xi,Xi+l] и имеет нуль производной (Xi + Xi+l)/2,
принадлежащий отрезку [Xi, Xi+l]. Поскольку g(Xi) == g(Xi+l) ==
О, то
9 ( Xi + 2 Xi+l ) 2
тах Ig(x)12 ==
XE[Xi,Xi+l]
2 1
xi+l Xi Xi Xi+1
2 2 == 42 (XiH Xi)'t.
Подставляя это в (6), получаем
111 р IIIC([xi. x i+l]) < ! 214 (Xi+1 Xi)4 11/(4) IIC([Xi.Xi+t])'
Следовательно,
11I р IIICC[a,b]) == i==l n l 111 р fIlС([Хi,Жi+l])
1 1 4 (4)
< 4! 24 h 111 IIC([a,b]).
Лемма доказана.
101
rлаваI. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
s 19.4. Кусочная интерполяция кубическими
мноrочленами Бесселя
Пусть в точках а == Хl < Х2 < ... < Х N == Ь известны значе
ния функции !(Хl),'.., f(xn). Параметр d i , i == 2, З, . . ., n 1 в
общей схеме интерполяции кусочно кубическими функциями по
лаrается равным значению в точке Xi производной мноrочлена
P(i) второй степени, совпадающеrо с f в точках Xi l, Xi, Xi+l .
По интерполяционной формуле Ньютона
P(i) (х) == f(Xi l) + (х Xi l) f(Xi l; Xi)+
+(Х Xi l)(X Xi)f(Xi l; Xi; Xi+l)
и
P(i) (Xi) == f(Xi l;Xi) + (Xi Xi l)!(Xi l;Xi;Xi+l) =:
f( . . " ) + ( " . ) f(Xi; Xi+l) f(Xi l; Xi)
X'L 1, Х'l X't X't 1
Xi+l Xi l
(Xi+l xi)f(Xi l;Xi) + (Xi Xi l)f(Xi;Xi+l)
Xi+l Xi l
Следовательно,
d . Р ' ( . ) (Xi+l X'i)!(Xi l; Xi) + (Xi Xi l)f(Xi; Xi+l)
't ( " ) Х?,
't Xi+l Xi l '
i == 2,3,.. .,n 1.
(7)
Недостающие значения d 1 и d n в r'раничных узлах выбираются,
исходя из той или иной дополнительной информации о функции
! (см. ниже).
Основные свойства приближающей функции Р f :
1. Р f является кусочно мноrочленной функцией, значения
которой зависят только от локальноrо поведения функции
f, именно: значения Р f на отрезке [Xi, Xi+l] зависят только
от значений функции! в точках Xi 1,Xi,Xi+l,Xi+2.
102
919. КУСОЧНО КУБИЧЕСКИЕ ПРИБЛИ)КЕНИЯ
2. Метод приближения является линейным: Р(! + у) = Р f +
Ру, P(af) == aPf.
Лемма 2. (без доказательства). Если f Е С(З) ([а, Ь]), то
справедлива следующая оценка nО2решиости аппроксимации KY
би'Чесх;ими .мНО20'Члеиа.ми Вессе-ля
"! р fIlC([X2)Xn l]) < const h311/1IC(3)([a,b])'
2де h определяется равеиство.м (5).
ПО1'решность аппроксимации на отрезках [Хl, Х2] и [Xn 1, Х n ]
зависит от способа выбора значений d 1 и d n .
Замечание 1. Если точки Xi распределены на отрезке [а, Ь]
равномерно: Xi == a+(i l)h, h == (b a)/(n 1), то формулы (7)
приобретают особенно простой вид:
1 f(Xi+l) f(Xi l)
di == 2" (f(Xi l; Xi) + f(Xi; Xi+l)) == 2h '
i == 2, 3, . . . , n 1.
19.5. Кусочная интерполяция кубическими
мноrочленами методом Акимы
Этот метод прибли)кения используется для борьбы с выброса
ми приБJlижающей функции, которые появляются, если значения
функции в точках заданы снекоторой поrрешностью.
Пусть в точках а == Хl < Х2 < ... < Х п == Ь известны значения
функции f(Xl),.", f(xn).
В силу леммы 4.6 разделенная разность f(Xi l, Xi) является
приближением к f'(Xi) слева, а f(Xi, Xi+l) является приближени
ем к f'(Xi) справа. в методе Акимы эти приближения усредняют
ся с весами, которые тем больше, чем меньше rладкость функции
на соседнем отрезке. Окончательная формула для определения
103
rЛ8В8I. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
параметра d i в общей схеме интерполяции кусочно кубическими
функциями имеет вид
Wi+l f(Xi l; Xi) + Wi l f(Xi; Xi+l)
Wi+l + Wi l
при WT+l + W; l =1- О
d i ==
(Xi+l Xi)f(Xi l; Xi) + (X'i Xi l)f(Xi; Xi+l)
(8)
Xi+l Xi l
при Wi+l == Wi l == О
rде i == 3, 4, . . . , n 2 и
Wj == If(xj; Xj+l) f(Xj l; Xj )1.
Недостающие значения d 1 , d 2 И dn 1, d n в ПРИ1'раничных узлах
выбираются, исходя из той или иной дополнительной информа--
ции о функции f (см. ниже).
Основные свойства приближающей функции Р f :
1. р f является кусочно мноrочленной функцией, значения
которой зависят только от локальноrо поведения функции
f, именно: значения Р f на отрезке [Xi, Xi+l] зависят только
от значений функции f в точках Xi 2, Xi l, Xi, Xi+l , Xi+2,
Xi+3 .
2. Метод приближения не является линейным: P(f+g) 1: Pf+
Ру, хотя Р(а!) == аР/.
Лемма 3. (без доказательства). Если f Е С(2) ([а, Ь]), то
справедлива следующая оце'Н'Ка nО2реш'Носmи аnnрох;си.мации 'X;y
бu'Чес'Кuми М'НО20'Члеиа.ми методом А'КUМъt
11/ р fIIС([ХЗ'Хn 2]) < const h21IfIIC(2){[a,b]),
zae h определяется раве'Нством (5).
Поrрешность аппроксимации на отрезках [Хl, ХЗ] и [Xn 2, Х n ]
зависит от способа выбора значений d 1 , d 2 И dn l, d n .
104
19. КУСОЧНО КУБИ"{IЕСКИЕ ПРИБли.жЕНИЯ
19.6. Кусочная интерполяция кубическими
u
мноrочленами с использованием разделенных разностеи
Этот метод приблиясения используется для получения при
ближающей функции Р 1, первая и вторая производная которой
оrраничены разделенной разностью функции f (т.е. приближе
нием к 1'). Небольшие требования к rладкости приближаемой
функции f позволяют использовать этот метод в том случае,
КО1'да значения функции в точках заданы с некоторой ПО1'реш
ностью.
Пусть В точках а == Хl < Х2 < ... < Х п == Ь известны зна
чения функции f(Xl),..., f(xn). Параметр d i , i == 2,3,. . . , n 1
в общей схеме интерполяции кусочно кубическими функциями
полаrается равным
signf(Xi; xi+l).min {11(Xi l; xi)l, If(Xi; Xi+l)I},
d i == если sign f(Xi l; Xi) == sign f(Xi; Xi+l)
о
иначе
(9)
Случай signf(xi l;Xi) "# signl(Xi;Xi+l) соответствует ситу
ации, коrда в точке Xi приближение f(Xi l;Xi) к l' слева ro
БОрИТ, что функция возрастает (убывает) на отрезке [Xi l, Xi], а
приближение f(Xi; Xi+l) к l' справа утверждает, что функция
соответственно убывает (возрастает) на отрезке [Xi, Xi+l]. Следо
вательно, на отрезке [Xi l, Xi+l] происходит изменение характера
Ivl0НОТОННОСТИ функции и мы полаrаем f'(Xi) d i == О.
в случае signf(xi l;Xi) == signl(Xi;Xi+l) характер MOHOTOH
насти функции на отрезке [Xi l, Xi+l] не изменяется и в качестве
d i выбирается приближение к l' с наименьшим модулем.
Недостающие значения d 1 и d n в rраничных узлах выбирают
ся, исходя из той или иной дополнительной информации о функ
ции f (см. ниже).
Основные свойства приближающей функции Р f :
1. Р 1 является КУСОЧНО МНО1'очленной функцией, значения
105
rлава 1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕнноii
которой зависят только от локальноrо поведения функции
1, именно: значения Р f на отрезке [Xi, Xi+l] зависят только
от значений функции f в точках Xi 1,Xi,Xi+l,Xi+2'
2. Метод приближения не является линейным: P(f+g) f= Р f+
Ру, хотя P(af) == аР f.
Лемма 4. (без доказательства). Если f Е С(2) ([а, Ь]), то
справедлива следующая оценка nО2решности аnnро'Х;си.мации x;y
бu'Чес'Х;uми МНО20'Членами с исnолъзова'Н/lLем разделенн'ых раз'Но
стей
111 р fIIC([X2,Xn lJ) < const h21IfIIC(2)([a,b])'
2де h определяется равенством (5). При этом сnравед.ливЪt 'Нepa
ве'Нства:
II(Pf)'IIC([a,b]) < i==l n llJ(Xi;XHl)1
IJ(P f)IIJ1C([a,b]) < 6 _ шах шах { X +2 . Xi I!(Xi; Xi+l)1 2 ,
z 2,3,...,n 2 Xz Xz l
Xi+l Xi l I f( .. . _ )1 2 }
Xt l, Xz
Xi Xi l
ПО1'решность аппроксимации на отрезках [Xl,X2] и [Xn l'Xn]
зависит от способа выбора зна.чений d 1 и d n .
19.7. Интерполяция кубическими сплайнами
Пусть в точках а == Xl < Х2 < ... < х n == Ь известны значения
функции f(Xl)"", f(x n ).
Определение. Сплайном порядка m называется функция,
которая на каждом отрезке [Xi, Xi+l], i == 1,2,..., n 1 совпа
дает с мноrочленом P i степени m и является функцией класса
c(m l) ([Хl, Х n ])'
Интерполяция кубическими сплайнами (т == 3) используется
для получения наиболее rладкой приближающей функции Р f в
рассматриваемом классе кусочно кубических мноrочленов.
106
19. КУСОЧНО КУБИЧЕСКИЕ ПРИБЛИЖЕНИЯ
Параметры d i , i == 1,2,..., n Б общей схеме интерполяции
кусочно кубическими функциями выбираются из условия Р f Е
с(2) ([а, Ь]), т.е.
P/ l (Xi) == Р/' (Xi),
i == 2,З,...,n 1.
(10)
Из представления мноrочлена P i в виде (2) находим
PI l (Xi) == 2СЗ,i 1 + 6C4,i 1 (Xi Xi l),
PI' (Xi) == 2СЗ,i. (11)
Подставляя эти значения в (10), имеем
2СЗ,i 1 + 6C4,i 1 (Xi Xi l) == 2СЗ,i,
i =: 2, 3, . . . , n 1.
с помощью (3) находим
Зf(Хi l; Xi) 2di 1 d i 3( ) di l + d i 2f(Xi 1; Xi)
+ Xi Xi l =
Xi Xi l (Xi Xi 1)2
Зf(Хi; Xi+l) 2d i d i + 1
Xi+l Xi
Т.е.
(Xi+l Xi) (3f(Xi 1; Xi) 2di 1 d i + 3di 1 + Зd i 6f(Xi 1; Xi)) ==
== (Xi Xi 1)(3f(Xi; Xi+l) 2d i d i + 1 )
Преобразуем это равенство:
(Xi+l xi)(di l + 2d i 3f(Xi 1; Xi) ==
== (Xi Хi l)(Зf(Хi; Xi+l) 2d i d i + 1 ),
или
(Xi+l xi)di l +2(Xi+l xi)di+2(Xi Xi 1)di+(Xi Xi 1)di+l ==
== Зf(Хi l; Xi)(Xi+l Xi) + 3f(Xi; Xi+l)(Xi Xi l)
107
rл а 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕМЕННОЙ
Следовательно,
(Xi+l xi)di l + 2(Xi+l Xi l)di + (Xi Xi l)di+l ==
== 3f(Xi 1; Xi)(Xi+l Xi) + 3f(Xi; Xi+l)(Xi Xi l)
i == 2,3,...,n 1.
(12)
Это система из n 2 линейных уравнений относительно n неиз
вестных d 1 , d 2 , . . . , d n . Для ее замыкания требуется еще два ypaB
нения, которые строятся, исходя из той или иной дополнительной
информации О функции f (см. ниже).
Система (12) является системой уравнений с трехдиаrональ
ной матрицей с (строrим) диаrональным преобладанием и ее
можно решать методом raycca без выбора rлавноrо элемента.
Основные свойства приближающей функции Р f :
1. Р f является нелокальной кусочно мноrочленной функци
ей, значения которой зависят от поведения функции f в
каЖДОЙ точке Хl, Х2"." Х п .
2. Метод приближения является линейным: Р(! + g) == Р! +
Ру, P(Qf) aPf.
Поrрешность аппроксиl\tIации кубическими сплайнами (в си
лу нелокальности сплайна) зависит от выбора дополнительных
уравнений ДЛЯ замыкания систеl\tIЫ (12) и составляет от O(h 2 ) до
O(h 4 ), rде h определяется равенством (5).
19.8. Определени:е недостающих rраничныx условий
В методах, изложенных в 19.4 и З 19.6, требуются два дo
полнительных условия для определения параметров d 1 и d n , в
методе из Э 19.5 требуются четыре дополнительных условия для
определения napal\tIeTpOB d 1 , d 2 И dn 1, d n . В методе приближения
кубическими сплайнами ( 19.7) требуются два дополнительных
уравнения для замыкания системы линейных уравнений. Исполь
зуются несколько методов построения дополнительных условий,
108
19. кусоqНО КУБиqЕСКИЕ ПРИБЛИЖЕНИЯ
которые выбираются в зависимости от Toro, :какая дополнитель
ная информация известна о приближаемой функции.
з 19.8.1. Определение недостающих rраничных условий
по известным значениям первой производной функции
в rраничных узлах
Пусть известны значения f'(Xl) и f'(xn) производной f'
функции f в rраничных узлах хl и Х п . ТО1'да пола1'аем
d 1 == j'(Xl)'
d n == l' (Х n ).
(13)
в :м:етодах, изложенных в S 19.4, S 19.5 и S 19.6, равенства (13)
дают недостающие значения параметров d 1 и d n . В методе при
ближения кубическими сплайнами (9 19.7) равенства (13) являют
ся двумя недостающими уравнениями, которые для сохранения
трехдиаrональности системы (12) надо сделать соответственно
первым и послеДНИ11 уравнениями этой системы.
Интерполяция кубическими сплайнами с использованием это
1'0 способа выбора rраничных условий дает сплайн Р f, который
называют ФундаментаJIЬНЫМ сплайном. Неулучшаемые oцeH
ки ero ПО1'решности
11I pflIC([a,b]) < 3 4 h411/(4)IIC([a,b]),
11/' (Р f)'IIC([a,b]) < 2 h З 11/(4) IIC([a,b]),
1'де h определяется равенством (5).
э 19.8.2. Определение недостающих rраничных условий
по известным значениям второй производной функции
В rраничных узлах
Пусть известны значения j"(Xl) и j"(x n ) производной f"
функции f в rраничных узлах Хl и Х п . Тоrда потребуем от при
ближающей функции Р f
(Pf)"(Xl) == j"(Xl), (Pf)"(x n ) == j"(x n ),
109
rлава 1. ПРИБЛИЖЕНИЕ Ф НКЦИЙ l--Й ПЕРЕМЕННОЙ
т.е.
P{'(Xl) == /"(Xl),
Из (11) находим
P:: l (Х п ) == /" (Х п ).
(14)
Р{' (Xl) == 2СЗ,1,
P:: l (Х п ) == 2СЗ,п 1 + 6C4,п 1(Xn Xn 1).
Подставляя эти значения в (14), имеем
2СЗ,1 = /"(Xl),
2СЗ,n 1 + 6C4,n l (Х 71 Xn l) == jf1(x n ).
с помощью (3) находим
2 3 ЛХ 1 ;Х 2 ) 2d 1 d 2 = Р'(Хl)'
Х2 Хl
2 3ЛХn 1; х n ) 2dn 1 dn +3(dn 1 +d n 2ЛХn 1; х n )) = f"(x n ).
Х N Xn 1
Т.е.
2 3 ЛХ 1 ; Х2) 2d 1 d 2 = f"(Xl),
Х2 Хl
2 dn 1 + 2d n 3f(Xn l;Xn) = f"(x n ).
Х п Xn l
Запишем эти выражения в виде
2d 1 + d 2 = 3f(Xl; Х2) f"(Xl)(X2 Xl),
dn l + 2d n = 3f(xn 1;Xn) + f"(xn)(xn Xn l)
В методах, изложенных в 19.4 и 19.6, равенства (15) поз
воляют определить недостающие значения параметров d 1 и d n ,
поскольку параметры d 2 и dn l известны (СМ. соответственно (7)
или (9».
В методе Акимы (9 19.5), rде требуются 4 параметра d 1 ,d 2 и
dn l, d n , равенства (15) представляют собой связь между этими
(15)
110
19. КУСОЧНО КУБИЧЕСКИЕ ПРИБЛИ)КЕНИЯ
параметрами. Если, например, известны еще и значения f'(Xl) и
f'(x n ), от d 1 И d n опредеЛЯIОТСЯ из равенств (13), а d 2 и dn l
находятся из уравнений (15).
В методе приближения кубическими сплайнами (э 19. 7) paBeH
ства (15) являются двумя недостающими уравнениями, которые
для сохранения трехдиа1'ональности матрицы системы (12) надо
сделать соответственно первым и последним уравнениями этой
системы.
9 19.8.3. "Естественные" rраничные условия
Этот метод используется, коrда никакой дополнительной ин..
формации о приближаемой функции f нет.
ТО1'да потребуем от приближающей функции Р 1
(Pf)"(Xl) == О,
(Р 1)" (х п ) == О,
т.е.
Р{' (Xl) == О,
P:: l (Х п ) == о.
Из уравнений (15) при f"(Xl) == О и f"(xn) == О получаем
2d 1 + d 2 == Зf(Хl; Х2)
dn l + 2d 11 == Зf(Хn l; Х n )
Эти уравнения используются так же, как уравнения (15).
Если у приближаемой функции f"(Xl) -# О или f"(x n ) =1= О, то
произвол в выборе rраничных условий приводит к повышенной
поrрешности в приrраничных узлах (порядка O(h 2 )), что особен
но плохо отражается на приближении сплайнами, rде в силу ero
нелокальности эта поrрешность будет во всех точках отрезка.
111
rлава 1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ 1 11 ПЕРЕМЕННОЙ
з 19.8.4. Условие "отсутствия узла" в приrраничных
узлах
Этот метод используется, коrда никакой дополнительной ин
формации о приближаемой функции f нет.
Тоrда потребуем от приближающей функции Р f
р} Р2, Pn 2 = Pn 1,
(16)
т.е. мноrочлен Рl = Р2 интерполирует f на [Хl, Хз] по точ
кам Хl, Х2, хз: Рl (Xl) == !(Хl), P 1 (Х2) == f(X2), P 1 (Хз) == !(хз)
и Р{(Хз) == d з , а мноrочлен Pn 2 Pп l интерполиру
ет f на [Xn 2,Xn] по точкам Xn 2,Xn 1,Xn: Pn 1(Xn 2) ==
f(Xn 2), Pn 1 (Xn 1) == f(Xn l), Pn 1 (Х п ) == f(x n ) И P l (Xn 2) ==
dn 2' Следовательно, мноrочлен Рl = Р2 строится как интерпо
ляционный мноrочлен третьей степени, ПРИНИl\1ающий в точках
Хl, Х2, ХЗ значения !(Хl), !(Х2), !(Хз) и Иlvfеющий в точке хз
производную, равную d з ; мноrочлен Pn 1 = Pn 2 строится как
интерполяционный мноrочлен третьей степени, ПрИНИl\fающий в
точках Xn 2,Xn 1,Xn значения !(Xn 2),!(Xn 1),!(Xn) и имею
щий в точке Xn 2 ПрОИЗБОДНУЮ, равную dn 2.
Таким обраЗОlvf, Bl\1eCTO n 1 мноrочлена P i , i == 1,2..., n
1 и n параlvfетров d i , i == 1, 2, . . . , n имеем n 3 мноrочле
на Рl = Р2, Рз, Р4,. . . , Рп З, Pn 2 = Pn l И n 4 параметра
d з , d 4 , . . . , dn 2 .
Тем самым проблема rраничных условий в методах, изло
женных в З 19.4, 19.5 и 19.6, снята, поскольку параметры
d i , i == 3, 4, . . . , n 2 определяются по приведенным в методах
формулам (см. (7), (8), (9)).
В методе приближения кубическими сплайнами (3 19.7) воз
можны два подхода.
1. Из условия Р f Е с(2) ([а, bJ) получаем
P; l (Xi) == Р;' (Xi),
i == З,4,...,n 2
n 4 уравнения относительно n 4 неизвестных d з , d 4 ,..., dn 2'
Уравнения для i == 4, 5, . . . , n 3 совпадают с выписанными ранее
112
19. КУСОЧНО КУВИЧЕСКИЕ ПРИБЛИЖЕНИЯ
уравнениями (12), уравнения дЛЯ
Р{' (хз) p ' (хз) == p ' (хз),
Р:: з (Xn 2) == P:: 2(Xn 2) = P:: l (Xn 2)
изменятся в силу измеНИВJlIе1'ОСЯ вида мноrочленов Р 1 = Р2,
Pn 2 Pn l .
2. Будем задавать Рl, Р2, . . . , Pn 1 как раньше набором d] , d 2 ,
. . ., d n . Выполнения условия (16) добьемся, потребовав непрерыв
ности (Р f)'" В точках Х2 И Xn 1, Т.е.
Р} /" (Х2) == О 2 ''' (Х2)' Р /" ( ) Р '" ( )
r. n 2 Xn 1 == n 1 Xn 1
(17)
(условия (16) и (17) эквивалентны для мноrочленов третьей CTe
пени, поскольку в силу (10) у P 1 и Р2, Pn 2 И Pn 1 совпадают
все производные от нулевоrо до TpeTbero порядка включительно).
Соотношения (17) дают два недостающих для замыкания си
стемы (12) уравнения.
Из представления мноrочлена Pi в виде (2) находим, что co
отношения (17) эквивалентны
С4,1 == С4,2, C4,n 2 == C4,n l
(18)
а) Рассмотрим первое уравнение (18). С помощью (3) находим
d 1 + d 2 2f(Xl; Х2)
(X2 Xl)2
d 2 + d з 2f(X2; хз)
(хз Х2)2
или
(хз X2)2d 1 + (хз X2)2d 2 (Х2 Xl)2d 2 (Х2 Хl)2d з ==
== 2f(Xl; Х2)(ХЗ Х2)2 2f(X2; ХЗ)(Х2 Хl)2,
Т.е.
222
(хз ..... Х2) d 1 + (хз Хl)(ХЗ 2Х2 + Хl) d 2 (Х2 Хl) d з ==
== 2f(Xl; Х2)(ХЗ Х2)2 2f(X2; ХЗ)(Х2 Хl)2,
113
rлава 1. ПРИБЛИ:ЖЕНИЕ Функций l Й ПЕРЕ!\tlЕННОЙ
Если добавить это уравнение к системе (12), то нарушится ее
трехдиаrОНaJIЬНQСТЬ. Поэтому прибавим к этому уравнеНИIО пер
вое уравнение системы (12) (т.е. при i == 2):
(хз x2)d 1 + 2(хз xl)d 2 + (Х2 Хl)d з ==
== 3f{Xl; Х2)(ХЗ Х2) + Зf{Х2; ХЗ){Х2 Хl)
умноженное на (Х2 Хl), получим
(ХЗ Х2)(ХЗ Х2+Х2 Хl)dl +(ХЗ Хl)(хз 2Х2+Хl +2(X2 Xl»d2 ==
== f(Xl; Х2)(ХЗ Х2)(2(хз Х2) + З(Х2 Xl) + f(X2; ХЗ)(Х2 Xl)2,
или
(хз x2)d 1 + (хз xl)d 2 ==
f(Xl; Х2)(ХЗ Х2)( 2х з + Х2 ЗХ1) + f(X2; ХЗ)(Х2 Xl)2
Хз Х1
Это уравнение добавляется к систеrvlе (12) в качестве перБоrо.
б) Рассмотрим второе уравнение (18). С помощью (3) находим
dn 2 + dn l 2f(xn 2; Xn l)
(Xn l Xn 2)2
dn l + d n 2f(Xn 1; х n )
(х n Xn 1)2
или
(Хn Xn 1)2dn 2 + (х n X1t 1)2dn 1
(Xn l Xn 2)2dn 1 (xn l Xn 2)2dn ==
== 2f(xn 2; Xn l)(Xn Xn 1)2 2f(xn 1; Xn)(Xn l Xn 2)2,
т.е.
(х n Xn 1)2dn 2 + (х n Xn 2)(Xn 2Xn 1 + Xn 2)2dn 1
(Xn 1 Xn 2)2dn ==
== 2f(xn 2; Xn l)(Xn Xn 1)2 2f(xn 1; Xn)(Xn l Xn 2)2,
114
19. КУСОЧНО..КУБИЧЕСКИЕ ПРИБЛИЖЕНИЯ
Если добавить это уравнение к системе (12), то нарушится ее
трехдиаrОНaJIЬНОСТЬ. Поэтому вычтем это уравнение из послед
Hero уравнения системы (12) (т.е. при i == n 1):
(Х п xn 1)dn 2 + 2(Х п , xn 2)dn 1 + (Xn 1 xn 2)dn ==
== 3f(xn 2; Xn l)(Xn Xn 1) + 3f(xn 1; Xп)(Xп l Xn 2)
уl\tlноженноrо на (х n . xn l), получим
(Хn Xn 2)(2(Xll Xn 1) (Хn 2Xn l + xn 2»dn 1 +
+(Xn l Xn 2)(Xп Xn 1 (Xn 1 xn 2)dn ==
== f(Xn 2; Xn l)(Xn Xn 1)2+
+ f(Xn l; Xn)(Xn l Хn 2)(З(хn Xn 1) + 2(х n Xn 2»),
или
(Х n xn 2)dn 1 + (Xn 1 xn 2)dn == (f(xn 2; Xn l)(Xn Xn 1)2+
+ f(Xn l; Xn)(Xn l Хn 2)(Зхn Xn 1 2Xn 2) /(х n Xn 2)'
Это уравнение добавляется к систеrvlе (12) в качестве последнеrо.
s 19.8.5. Дополнительный узел в приrраничных узлах
Этот метод используется, коrда никакой дополнительной ин
формации о приближаемой функции f нет.
Введем дополнительные точки ХО < Хl И хn+l > Х N И значе..
иия приближаемой функции f(xo) и f(X n +l) В этих точках.
Тем самым проблема 1'раничных условий в методах, изложен
ных в 19.4 и 19.6, снята, поскольку параметры d i , i == 1,2,. . . , n
теперь определяются по приведенным в методах формулам (см.
(7), (9)).
в методе приближения кубическими сплайнами ( 19.7) воз..
IO:}KHЫ несколько подходов.
1. Два дополнительных уравнения есть
Рl (хо) = f(xo),
Pn 1 (Х n +l) == f(X n +l).
115
Тлаваl. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
Из представления (2) МНОI'очлена P i и вида (3) e1'o коэффици
ентов видно, что В эти уравнения ВХОДЯТ соответственно d 1 , d 2 И
dn l, d n . Следовательно, эти уравнения можно добавить к систе
ме (12) в качестве первоrо и последнеrо уравнений с сохранением
ее трехдиаrональноrо вида.
2. Мноrочлен P 1 интерполирует f на [хо, Х2] по точкам
ХО, Хl, Х2: P 1 (хо) == f(xo), P 1 (Xl) == f(Xl), Р 1 (Х2) == !(Х2) и
Р{ (Х2) == d 2 , а мноrочлен Pn 1 интерполирует f на [Xn 1, Х n +l]
по точкам Xn 1, х n , х n +l: Pn 1 (Xn 1) == f(Xn l), Pn 1 (х n ) ==
f(x n ), Pn 1 (х n +l) == !(х n +l) и P l (Xn 1) == dn l' Следова
тельно, мноrочлен Рl строится как интерполяционный rvlHo1'o
член третьей степени, принимающий в точках Хо, Хl, Х2 значения
f(xo), f(Xl), f(X2) И имеющий в точке Х2 ПрОИЗБDДНУЮ, равную
d 2 ; мноrочлен Pn 1 строится как интерполяционный мноrочлен
третьей степени, принимающий в точках Xn l, Х n , хn+l значения
f(Xn l), f(x n ), f(X n +l) и имеющий в точке Xn l ПРОИЗБОДНУЮ,
равную dn l.
Таким образом, вместо n парам:еТРОБ d i , i == 1,2, . . . , n имеем
и n 2 параметра d 2 , d з , . . . , dn l .
Из условия Р f Е с(2) ([а, Ь]) получаем
P: l (xi) == Р:' (Xi),
i == 2, 3, . . . , n 1
n 2 уравнения относительно n 2 неизвестных d 2 , d з , . . . , dn l .
Уравнения для i == 3,4, . . . , n 2 совпадают с выписанными ранее
уравнениями (12), уравнения дЛЯ
Р{'(Х2) == P /(X2)' P:: 2(Xn 1) == P:: l (Xn 1)
изменятся в силу изменившеrося вида мноrочлеиов.
3. Вычисляем приближение к j'(Xl) и f'(x n ) аналоrично при
ближеНИIО кубическими МНО1'очленами Бесселя (см.э 19.4). Дpy
rими словами, мы вычисляем d 1 и d n по формулам (7) при i == 1
и i == n. Эти уравнения добавляются к системе (12) в качестве
первоrо и последнеrо уравнений с сохранением ее трехдиаrональ
Horo вида.
116
20. ПАРАБОЛИЧЕСКуIЕ СПЛАЙНЫ
Значения f(xo) и f(X n +l) MorYT находиться из соображений
периодичности, четности и т.п.. Если никакой дополнительной ИН
формации о приБЛИ)i<аемой функции f нет, то можно использо
вать экстраполяцию, например, линейную:
хо == Xl (Х2 хl),
хn+l == х n + (Х п Xn 1),
f(xo) == !(Хl) (f(X2) f(Xl»,
f(Xn+l) == f(x n ) + (f(x n ) f(Xn l»).
9 19.8.6. Экстраполяция в приrраничных узлах
Этот метод используется, КО1'да никакой дополнительной ИН
формации о приближаемой функции f нет.
в качестве приближенноrо значения f' (хl), f' (Х п ), либо
f" (хl), f" (х п ) берутся значения Q (хl), R (х п ), либо Q (хl),
R (Xn), rде Qk(X) интерполяционный мноrочлен Ла1'ранжасте
пени k 1, построенный по точкам хl, Х2, . . . , х k, Rk (х) интер
поляционный мноrочлен Лаrранжа степени k 1, построенный
по точкам Xn k+l, Xn k+2, . . . , х n , k > 3. Полученные значения
l' или 1" в точках Хl И Х N используются как указывалось BЫ
те (см. построение rраничных условий по значениям первой или
В'l орой производной функции В rраничных узлах).
3 20. ИНТЕРПОЛЯЦИЯ
u
ПАРАБОЛИЧЕСКИМИ СПЛАИНАМИ
Рассмотрим задачу приближения кусочно квадратическими
функциями.
g 20.1. Общая схема
Пусть заданы точки а == Хl < Х2 < ... < Х п == Ь и
значения f(Xl), f(X2) . .., f(x n ). Введем дополнительные точки
1, 2, . . . , n+l так, чтобы
1 < а == Хl < 2 < Х2 < 3 < ХЗ < . . . < Xn 1 < n < Х п == Ь < n+l.
117
Тлава 1. ПРИБЛИЖЕНИЕ Функций l Й ПЕРЕМЕННОЙ
Например, можно положить
с. Xi l + Xi
,
2
i == 2, 3, . . . , n.
Интерполирующая функция Р f строится таким образом, что на
каждом отрезке [ i, i+l], i == 1, . . . , n она является мноrочленом
P i степени 2, таким, что
Pi(Xi)
Pi( i)
== f(Xi),
== Vi, Pi( i+l)
== Щ+l }
i=l,...,n
(1)
rде Vi, i == 1,2,..., n + 1 свободные параметры, ТОТ или иной
способ выбора которых определяет метод кусочной интеРПОJIЯ
ции параболическими МНО1'очленами. Полученная функция Р f
совпадает с f в точках Xi, i == 1,..., n и ДЛЯ любоrо набора
парамеТРОБ Vi Р f Е С([а, Ь]).
20.2. Алrориr.rм вычисления коэффициентов
мноrочлена P i
Коэффициенты Мноrочлена P i , записанноrо в форме
Pi(X) == al,i + a2,i(X i) + a3,i(X i)(X Xi)
MorYT быть вычислены по интерполяционной формуле Ньютона
(см. определение (4.1) разделенных разностей):
Vi
\
f(Xi) Vi
Xi i
\
.,/ 1
f(Xi) \ Hl i
Vi+l f{Xi) ./
i+l Xi
Vi+ 1 .,/
( Vi+l f (Xi) ...... f (Xi) Vi )
i+l Xi Xi i
118
920. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
Столбцы вычисляются слева направо, элементы столбца ВЫЧИС
ляются снизу вверх, стрелки указывают ячейку памяти, в KOTO
рую помещается результат. Отсюда получаем
al,i
= Vi
a2,i
f{Xi) Vi
Xi i
== 1 ( Vi+l f(Xi) f(Xi) Vi )
i+] i i+l Xi Xi i
аз,i
Для представления в Биде
Pi(X) == Cl,i + C2,i(X i) + C3,i(X i)2
(2)
запишем
(X i)(X Xi) == (X i)(X i+ i Xi) == (X..... i)2 (Xi i)(X i),
откуда получаем
Cl,i == al,i == Vi
C2,i == a2,i (Xi i)аз,i ==
Xi i ( Vi+l f{Xi) f(Xi) Vi )
Xi i i+l i {i+l Xi Xi i
== аз,i == 1 ( Vi+l f{Xi) f(Xi) Vi )
i+l i i+l Xi Xi i
f(Xi) Vi
(3)
СЗ,i
20.3. Интерполяция параболическими сплайнами
Интерполяция параболическими сплайнами используется для
получения наиболее 1'ладкой приближающей функции Р f в pac
сматриваемом классе кусочно квадратичных мноrочленов.
Параметры Vi, i == 1, 2, . . . , n + 1 в общей cxervle интерполя
ции кусочно квадратичными фУНКЦИЯ1vlИ выбираются так, чтобы
119
rлзва 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
приближающая функция Р f была сплайном 2 ro порядка т.е.
р f Е С(l) ([а, Ь)) или
P: l ( i) == Р: ( i),
i == 2, 3, . . . , n.
(4)
Из представления 1\1ноrочлена P i в виде (2) находим
P: l ( i) =: C2,i 1 + 2( i i l)Сз,i l'
С ПОМОЩЬЮ (3) ВЫЧИСЛИМ
Р! ( i) == C2,i. (5)
f(Xi) Vi Xi 'i ( Vi+1 f(Xi) f(Xi) Vi )
i
, Xi i i+1 i i+l Xi Xi i
== ( 1 + Xi i ) f(Xi) Vi Xi 'i Vi+1 f(Xi)
i+l i Xi i 'i+l i i+1 Xi
( 1 1 ) Xi i
== Vi + Vi+l +
Xi i i+1 i ( i+l i)( i+1 Xi)
f ( ) ( 1 1 Xi i )
+ Xi + +
Xi i i+1 i ((i+1 (i)( i+l Xi)
( 1 1 ) ( 1 1 )
== Vi + Vi+l +
Xi i (i+1 i (i+l Xi i+1 (i
( 1 1 )
+ f(Xi) + ,
Xi i i+1 Xi
а также
Сз i == 1 ( Vi+l f{Xi) f(Xi) Vi ) =
, i+l i i+l Xi Xi i
1 ( 1 1
== Vi + Vi+l
(i+1 i Xi i i+l Xi
( 1 1 ))
f(Xi) + .
Xi -i i+1 Xi
и
C2,i + 2( i+l i)Сз,i ==
120
920. ПАРАБОJIИЧЕСКИЕ СПJIАЙНЫ
== Vi ( 1 + 1 ) Vi+l ( 1 1 ) +
Xi i i+l i i+l Xi i+l i
+ f(Xi) ( 1 + 1 ) +
Xi i i+l Xi
+2 ( Vi 1 +Vi+l 1 f(Xi) ( 1 + 1 )) =
Xi i i+l Xi Xi i i+l Xi
== Vi ( 1 1 ) + Vi+l ( 1 + 1 )
Xi i i+l i i+l Xi i+l i
f(Xi) ( 1 + 1 )
Xi i i+l Xi
С помощью этих равенств и (5) находим
P[( o) ;;; Vi ( Х. . + 0+11 .)
( 1 1 )
..... v. + 1 ..... +
t i+l Xi i+l i
( 1 1 )
+ f(Xi) + ,
Xi €i Ci+l Xi
(6)
и
P: l( i) == Vi l ( 1 1 ) +
Xi l i l i i l
( 1 1 )
+ Vi +
i Xi l €i i l
( 1 1 )
f(Xi l) +
Xi l i l i Xi l
Подставляя (6) и (7) в (4), получаем для всех i == 2,3,.. ., n
(7)
( 1 1 )
Vi l +
Xi l {i l i i l
( 1 1 1 1 )
+ + + + Vi +
i Xi l i i l Xi i i+l i
121
rлаваI. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
( 1 1 )
+ Vi+l ==
'i+l Xi i+l i
( 1 1 )
+ f(Xi l) +
Xi l i l i Xi l
+ ( 1 + 1 ) f{Xi)
Xi i i+l Xi
Это система из n 1 линейных уравнений относительно n + 1
неизвестных Vl, V2, . . . , v n + 1. Для ее замыкания требуется еще
два уравнения, которые строятся, исходя из той или иной дo
полнительной информации о функции f (см. ниже).
Систе?v18 (8) является системой уравнений с трехдиаrон&пьной
матрицей с (строrим) диаrоналЬНЫ?vl преобладанием и ее можно
решать методом raycca без выбора rлавноrо элемента.
Основные свойства приближающей функции Р f :
(8)
1. Р f является нелокальной КУСОЧНО ?vlноrочленной Функци
ей, значения которой зависят от поведения функции f в
каждой точке Хl, Х2, . . . , Хn'
2. Метод приближения является линейным: Р(! + у) == Р! +
Ру, P{af) == aPf.
Поrрешность аппроксимации параболическими сплайнами (в
силу нелокальности сплайна) зависит от выбора дополнительных
уравнений для замыкания системы (8) и составляет от O(h 1 ) до
O(h 3 ), rде h определяется равенством (19.5).
20.4. Определение недостающих rраничных условий
Используются несколько методов построения двух дополни
тельных уравнений для замыкания системы (8), которые выбира
ются в зависимости от Toro, какая дополнительная информация
известна о приближаемой функции.
122
20. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
20.4.1. Определение недостающих rраничных условий
по известным значениям первой производной функции
в rраничных узлах
Пусть известны значения f'(Xl) и f'(xn) производной f'
Функп ии 1 в rраничных узлах хl и х n ' Возможны два экви
валентных подхода.
1. Два дополнительных уравнения получаются из условий
Р{ (х 1) == f' ( Х 1 ) ,
p (х n ) == l' (Х n )'
Вычислим
Р; (Xi) == C2,i + 2(Xi i)Сз,i ==
( 1 1 )
v' +
Xi i i+l i
( 1 1 )
V'+l +
i+l Xi i+l i
( 1 1 )
+ f(Xi) + +
Xi i {i+l Xi
Xi {i ( 1 1
+ 2 Vi + Vi+l
i+l i Xi i i+l Xi
( 1 1 ))
f(x-) +
Xi {i {i+l Xi
Поскольку
Xi i 1 1 1
i+l . i i+l Xi €i+l Xi €i+l €i '
Xi i ( 1 + 1 ) Xi.... i i+ 1 ..... i
i+l i Xi Ci Ci+l Xi Ci+l Ci (Ci+l Xi)(Xi i)
1
--- ,
i+l Xi
ТО
Р! (Xi) == Vi ( 1 f- 1 )
t Xi €i €i+l €i
123
ТлаваI. ПРИБЛИ)l(ЕНИЕ Функций l Й ПЕРЕМЕННОЙ
( 1 1 )
V.+l +
'l i+l Xi i+l i
( 1 1 )
+ f(Xi) + +
Xi i i+l Xi
1 ( 1 1 )
+ 2v. + 2V'+1
'l i+l i. 'l i+l Xi i+l i
1
2f(Xi)
i+l Xi
( 1 1 ) ( 1 1 )
== Vi + Vi+l +
c;i+l i Xi c;i i+l Xi i+l i
( 1 1 )
+f(Xi)
Xi i i+l Xi
Два дополнительных уравнения получаются из условий
P:(Xi) == j'(Xi),
i == 1, n.
Эти равенства являются двумя недостающими уравнениями, KO
торые для сохранения трехдиаrональности системы (8) надо сде..
лать соответственно первым и последним уравнениями этой си
стемы.
2. Выбираем i == Xl, п+l == Х п . ТОl'да в систему ypaBHe
ний (8) Vl и Vn+l не войдут, а Р 1 и Р п строятся по интерполя..
ционной формуле Ньютона с кратными узлами: мноrочлен
P 1 (х) ::::: Cl,l + (х Xl)C2,1 + (х Хl)2 сз ,1
строится из условий
Р 1 (Xl) == f(Xl), Р{ (Хl) == f'(Xl), Рl ( 2) == V2,
что дает
CI,l = f{Xl), С2,l == j'(Xl), СЗ 1 == 1 ( V 2 Л Х l) fl(Xl» ) ;
, 2 Xl 2 Xl
124
20. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
аналоrично, мноrочлен
Рn(х) == Сl,n + (х n)C2,n + (х {n)2 сз ,n
строится ИЗ условий
Pn( n) == V n , Рl (х п ) == f(x n ), Р{ (х n ) == f' (х n ),
что дает
Сl,п == V n ,
2 / (х n ) V n f ' ( )
С2, п С Х п ,
Х N n
1 (/ ' ( ) I(x n ) vn )
Сз,n х n
Х N n х п п
Из условия Р 1 Е с(1) ([а, Ь]) получаем
Р; 1 ( i) == Р; ( i) , i == 2, 3, · . . , n.
n 1 уравнения относительно n 1 неизвестных V2, Vз, . . . , V N .
Уравнения ДЛЯ i == 3,4,..., n 1 совпадают с выписанными ранее
уравнениями (8), уравнения для
Р{ ( 2) == P ( 2),
P l ( n) == p ( n)
изменятся в силу изменившеrося вида мноrочленов Р 1 и Pn 1.
1. Выпишем новое первое уравнение системы (8). Имеем
P{( 2) == C2,1 + 2( 2 хl) == I'(xl) + 2 ( V2€ f(Xl) P(Xl» ) ==
2 хl
== 2 V2 f(Xl) P(Xl),
2 Хl
выражение для P ( 2) получаем из (6) при i == 2:
I ( 1 1 ) ( 1 1 )
P2( 2) == V2 + vз +
Х2 2 3 2 3 Х2 3 2
+ f(X2) ( 1 € + € 1 ) .
Х2 2 3 Х2
125
rлаваI. ПРИБЛИ)l(ЕНИЕ функций l Й ПЕРЕМЕННОЙ
Следовательно, уравнение имеет вид
( 2 1 1 ) ( 1 1 )
V2 + + + Vз ==
2 Хl Х2 2 з 2 3 Х2 з 2
=j(Xl) 2 +f( X 2) ( 1 + 1 ) +j'(Xl).
2 Хl Х2 2 3 Х2
2. Выпишем новое последнее уравнение системы (8). Имеем
Р ' ( С ) == == 2 !(Х n ) V n f ' ( )
n п С2,n с Х п ,
Х п n
выражение для P1 1 ({n) получаем из (7) при i == n:
P l ( n) == Vn l ( 1 ) +
Xn 1 n 1 n n 1
( 1 1 )
+ v n +
n Xn 1 n n 1
( 1 1 )
f(Xn l) +
Xn 1 n 1 n Xn 1
Следовательно, уравнение имеет вид
( 1 1 )
Vn l +
Xn 1 €n 1 €n €n 1
( 1 1 2 )
+ + +
€n Xn 1 €п <n 1 Х п <n
== f(Xn l) ( 1 + 1 ) + f(x n ) 2 { j'(x n ).
Xn 1 n 1 n ..... Xn 1 Х п --- n
126
20. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
э 20.4.2. Определение недостающих rраничных условий
по известным значениям второй производной функции
В rраничных узлах
Пусть известны значения f"(Xl) и f"(x n ) производной 1"
функции f в 1'раничных узлах Хl и хn' Тоrда потребуем от при
ближающей функции Р f
(Pf)"(Xl) == f"(Xl),
(Р 1)" (Х п ) == f" (Х п ),
т.е.
Р{'{Хl) == f"{Xl),
Из (2) находим
Р:: (Х п ) = j" (Х п ).
" ( ) 2 ( 1
P i Xi == 2СЗ,i == Vi +
i+ 1 i Xi i
+щн 1 f(Xi) ( 1 + 1 ) ) .
i+l Xi Xi i i+l Xi
Тоrда дополнительные уравнения
(9)
PI' (Xi) == 1" (Xi),
i==l,n.
Эти равенства являются двумя недостающими уравнениями, KO
торые для сохранения трехдиаrональности системы (8) надо cдe
лать соответственно первым и последним уравнениями этой си
стемы.
20.4.3. "Естественные" I'раНllчные условия
Этот метод используется, КО1'да никакой дополнительной ин...
формации о приближаемой функции f нет.
Тоrда потребуем от приближающей функции Р f
(Р f)" (Xl) == О,
(Р f)" (Х п ) == О,
Т.е.
Р{' (Xl) == О,
Р:: (Х п ) == О.
127
rлава 1. ПРИБЛИЖЕНИЕ ФУ/IКЦИЙ l Й ПЕРЕМЕННОЙ
Из соотношений (9) получаем два дополнительных уравнения
PI' (Xi) == О,
i == 1, n.
Эти равенства являются двуr..1Я недостающими уравнениями, KO
торые для сохранения трехдиаrональности системы (8) надо cдe
лать соответственно первым и последним уравнениями этой си
стемы.
Если у приближаемой функции f"(Xl) f:. О или f"(x n ) i- О, то
произвол в выборе rраничных условий ПРИБОДИТ К повышенной
ПОI'решности в ПрИI'раничных узлах.
з 20.4.4. "Условие "отсутствия узла" в приrраничныx
узлах
Этот метод используется, КОI'да никакой дополнительной ин
формации о приближаемой функции f нет.
Тоrда потребуем от приближающей функции Р f
Рl ..... Р 2 , Pn 1 Р п ,
(10)
Т.е. МНОI'очлен Рl = Р2 интерполирует f на [ l' 3] по точкам
Хl, Х2: Рl (Хl) == f(Xl), Рl (Х2) == !(Х2) и Рl ( з) == vз, а МНОI'очлен
Pn l = Рn интерполирует f на [ n l, €n+l] по точкам Xn l, Х N :
Pn(Xn l) == f(Xn l), Рn(Х n ) == f(x n ) И Pn( n 1) == Vn l. Следо
вательно, МНО1'очлен P 1 - Р2 строится как интерполяционный
мноrочлен второй степени, принимающий в точках Хl, Х2, {з зна
чения !(Хl), f(X2)' vз; мноrочлен Р п = Pn 1 строится как интер
поляционный мноrочлен второй степени, принимающий в точках
€n 1, Xn 1, Х N значения Vn l, f(Xn l), f(x n ).
Таким образом, вместо 1 МНО1'очленов P i , i == 1,2 . . . , n и n+ 1
параметров Vi, i == 1,2,..., n + 1 имеем n 2 МНО1'очлена P 1 =
Р2, Рз, Р4,. . . , Pn 2, Pn 1 = Рn И n 3 параметра Vз, V4,. . . , Vn l .
В методе приближения параболическими сплайнами возмож
ны два подхода.
128
20. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
1. Из условия р f Е C(l) ([а, Ь]) получаем
P: l ( i) == Р: ( i),
i == 3, 4, . . . , n 1
n з уравнения относительно n 3 неизвестных vз, V4,..' , Vn l.
Уравнения для i == 4, 5, . . . , 11 2 совпадают с выписанными ранее
уравнениями (8), уравнения для
Р{( з) = Р ( з) == P ( 3)' P 2( n 1) == .P l( n l) = P ( n 1)
изменятся в силу измеНИВIIlеrося вида МНО1'очленов Р 1 = Р2,
Pn l Рn.
а). Быпишеrvf новое первое уравнение системы (8). По интер
ПQЛЯЦИОННОЙ формуле IIьютона
Рl (х) == аl,l + (х xl)a2,1 + (х хl )(х Х2)аз,1
rде
аl,l == !(Хl), а2,l == f(Xl; Х2),
1 ( v з !(Х2) f( . ))
аз 1 == с Хl, Х2 .
, €з хl з Х2
Поэтому
Р{ ( з) == а2,l + (2 з Хl Х2)аЗ,1 ==
f( . ) 2 з Хl Х2 ( v з !(Х2) f( . ))
Xl , Х2 + с с Xl, Х2
3 Xl 3 Х2
( 1 1 ) 3 Х2
== + (: (vз f( X 2)) Л Х l; Х2).
з Хl 3 Х2 3 Хl
Выражение для P ( 3) получаем из (6) при i == 3:
I ( 1 1 ) ( 1 1 )
Рз( з)== Vз' + V4 +
хз 3 4 3 4 ХЗ 4 з
+ f(хз) ( 1 + 1 ) .
ХЗ З 4 ХЗ
129
Тлава 1. ПРИБЛИЖЕНИЕ функций l Й ПЕРЕМЕliНОЙ
Следовательно, уравнение имеет вид
( 1 1 1 1 )
vз + + + +
з Хl з Х2 ХЗ з 4 3
( 1 1 ) ( 1 1 )
+V4 == !(Х2) + +
4 ХЗ 4 з з Хl з Х2
( 1 1 ) 3 Х2
+!(ХЗ) + + . j( X lj X 2)'
ХЗ 3 4 ХЗ 3 Хl
б). Выпишем новое последнее уравнение системы (8). ПО ИН
терПQЛЯЦИОННОЙ формуле Ньютона
Рn(х) == аl,n + (х...... n 1)a2,n + (х ..... n 1)(x...... Хn l)аз,n
{'де
f(Xn l) Vn l
al,n == Vn l, а2,n:;'::; ,
Xn 1 .... n 1
1
аз.п == (f(Xn l; х п ) а2.п) .
х n Тt l
Поэтому
P ( n 1) == а2.n + ( n 1 ...... Хn 1)аз.n =
Xп 1 n 1 ( ( ) )
== а2,'/1 ! Xп l j Х п а2,п =
Х п п l
Xn 1 + Х п 2 п 1 Xn 1 €n 1 f( . )
с а2,n t Xn 1,Xп
Х п n 1 Х п n 1
== ( 1 + 1 ) (f(Xn l) Vn l)
Xn 1 n l Х Т1 n 1
Xп l n 1 f( )
с Xn 1; Х п ·
Х п n 1
Выражение для P 2 ( n 1) получаем из (7) при i == n 1:
, ( ) ( 1 1 )
Pn 2 (n 1 == Vn 2 +
Xn 2 n 2 n l (n 2
130
20. ПАРАБОЛИЧЕСКИЕ СПЛАЙНЫ
( 1 1 )
+ Vn l +
n 1 Xn 2 n 1 n 2
( 1 1 )
f(Xn 2) +
Xn 2 n 2 n 1 Xn 2
Следовательно, уравнение имеет вид
( 1 1 )
Vn 2 +
Xn 2 n 2 n 1 n 2
( 1 1 1 1 )
+vn 1 + + + ==
п l Xn 2 n l n 2 Xn 1 n 1 Х п n 1
( 1 1 )
== f(Xn 2) + +
Xn 2 n 2 п l Xn 2
( ) ( 1 1 ) Xп 1 n 1 ( )
+fXn l + fXn l;Xn.
Xп l п l Х N n 1 Х п n 1
2. Будем задавать Р 1 , Р 2 , . . . , Р п как раньше набором Vl, V2,
. . ., V n +l. Выполнения условия (10) добьемся, потребовав непре
рывности (Р f)" в rrочках 2 И п, Т.е.
P{'( 2) == P '(€2), P:: l ( n) == P::( n)
(11)
(условия (10) и (11) эквивалентны для мноrочленов второй CTe
пени, поскольку в силу (4) у Рl и Р2, Pn 1 И Рn совпадают все
производные от нулевоrо до BToporo порядка включительно).
Соотношения (11) дают два недостающих для замыкания си
стемы (8) уравнения.
Из представления мноrочлена P i в виде (2) находим, что co
отношения (11) эквивалентны
Сз,l == СЗ,2, Сз,n l == Сз,п
(12)
131
rлава 1. ПРИБЛИЖЕНИЕ ФУНКЦИЙ l Й ПЕРЕМЕННОЙ
9 20.4.5. Дополнительный узел в приrраничных узлах
Этот метод используется, коrда никакой дополнительной ин
формации о приближаемой функции 1 нет.
Введем дополнительные точки ХО < Хl И Хn+l > Х п и зна
чения приближаемой функции f(xo) и f(X n +l) в этих точках.
ТО1'да пола1'аем 1 == Хо И n+l == хn+l
Vl == f( l),
V n +l == f( n+l).
Эти равенства являются двумя недостаЮIЦИМИ уравнениями, ко...
торые для сохранения трехдиа1'ОНальности системы (8) надо cдe
лаrrь соответственно первым и последни!v! уравнениями эrrой си
стемы.
20.4.6. Экстраполяция в приrраничных узлах
Этот метод используеrrся, КО1'да никакой дополнительной ин
формации о приближаемой функции f нет.
в качестве приближенноrо значения f'(Xl), f'(x n ), либо
j"(Xl), j"(xn) берутся значения Qk(Xl), R (xn), либо Q (Xl),
R (xn), 1'де Qk(X) интерполяп;ионный МНО1'очлен Лаrранжа CTe
пени k 1, построенный по точкам х 1 , Х 2, . . . , Х k, Rk ( Х) интер
поляционный мноrочлен Лаrранжа степени k 1, построенный
по точкам Xn k+l, Xn k+2, . . . , Х п , k > 2. Полученные значения
l' или f" в точках Хl И Х п используются как указывалось BЫ
те (см. построение 1'раничных условий по значениям первой или
8ТОрОЙ ПрОИЗ80ДНОЙ функции в rраничных узлах).
132
rлава 11.
мЕтодыI ПРИБЛИЖЕНИЯ
ФУНКЦИЙ мноrих ПЕРЕМЕННЫХ
IIнтерполяция функций f : n с Rn "'""4 R 1 укладывается в об
щую схему задачи линейной интерполяции. Но эта схема требует
обращения матрицы (1.1.3) и потому для одномерноrо случая BЫ
ше был предложен ряд методов, в которых эта матрица не более,
че:f\Л: трехдиа1'ональна.
Для MHOf'OMepHbIX областей построение хорошо обратимой
матрицы (1.1.3) ПрОИ3БDДИТСЯ, в основном, двумя методами:
1. интерполированием тензорными произведениями,
2. приближением ме'l'ОДОМ конечных элементов.
s 1. ИНТЕРПОЛЯЦИЯ ФУНКЦИЙ
мноrих пЕрЕмЕнныIx тЕн30рныIии
ПРОИЗВЕДЕНИЯМИ
Этот Iv1етод интерполяции позволяет наиболее просто свести
задачу интерполяции функции мноrих переменных, заданной в
параллелепипеде, к задаче интерполяции функций одной пере-
менной.
lЗЗ
Тлава 11. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
9 1.1. Постановка задачи интерполяции тензорными
произведениями и теорема корректности
Пусть задана ФУНКЦИЯ f : Z == Х х У R 1 , f Е F(Z, Rl)
некоторому функционал:ьному npocrrpaHCTBY, наборы функций
иl, . . . , и п , tli : Х R 1 , Ui Е Р(Х, R 1) И Vl, . . . , V m , Vi : у 4 R 1 ,
Vi Е Р(У, R 1) И наборы линейных функционалов А1,.'.' Л N на
пространстве F(X,R 1 ) и J.-Ll,... ,J.-Lm на пространстве F(Y,R 1 ).
Требуется построить аППРОКСИ Iацию Р f функции f вида
n m
Р ! == 'if. .w. .
L...J L...J ' ,З ,з
i==l j==l
такую, чтобы были выполнены линейные условия интерполяции
Vi,j(Pf) == Vi,j(!), i == l,...,n, j == 1,...,т, (1)
rде
Wi,j == tli 0 Vj, т.е. Wi,j(X, у) == tli(X)Vj(Y),
Vi,j == Лi J.Lj, т.е. vi,j(f) == >"i(J.Lj (fx (у)) == J.-tj(Лi(fу(х»),
fx(Y) == f(x,y) Е F(Y,R 1 ), fy(x) == f(x,y) Е F(X,R 1 ),
f Е F ( Z, R 1 ) , i == 1, . . . , n, j == 1, . . . , rп, х Е .J , У Е У.
Обозначим
и == (Ui) 1 == { t O'iUi : О' Е Rn } , V == (Vj) 7 1 '
z== 1
. == (Лi) l' М == (J.-tj) ; 1 '
W == и Q9 V == {w == и Q9 v : и Е И, v Е V} .
Теорема 1. Пусть
1. ФУН'к;ции иl, . . . , и n линей'Н,о 'Н,езависи.м'Ы, ФУ'Н,'lCцuо'Н,ал'ы Лl ,
. . ., Л N линейно 'Н,езависu.м'Ьt и матрица
А ( А. ( и . » . . 1
Z J 'l,J== ,...,n
(2)
134
/
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
обрати-ма;
2. функции Vl, . . . , V m ли'Неuuо uезависи-М'Ьt, фуu'Кцuо'Налы J.Ll ,
. . ., Рт .ли'Н,ейно независим'Ы и .матрица
в ( H' ( V' ») .. 1
r't J 't,J== ,...,т
(3)
обратима.
ТО2да
1. Фун'Х:ции Wij == Ui 0 Vj составляют базис пространства
W == и Q9 v и, следовател'Ьно, размер'Ност'Ь W равна пт.
2. Зада а линейной 'llнmерnо.ляции -к;орре-к;тна.
3. Интерполирующая Фун-к;ция представляется в виде
n m
Р f == L L 1'i,jU'i,j
i= 1 j = 1
(4)
2де
1 ( ) ( t ) 1
r ('Yi,j)(i=l,p.,'1l,j=l,...,m) A (Vi,j(!))(i=l,...,n,j=l,...,m) В .
(5)
Доказательство. Всякий элемент w Е W == и @ v представ
ляется в виде
n m
W = L L ri,jWi,j
i==l j==l
Действительно, w Е U@V есть w == и0v, Т.е. w(x,y) = u(x)v(y).
Так как иl,..., и п составляют базис и и Vl,..., V m составляют
базис V, ТО
n
и(х) == L ЙiUi(Х),
i:::::l
m
v(y) == L: (JjVj (у).
j==1
Поэтому
n rrL
w(X, у) == L: L: Ui,8j U i(X)Vj(Y),
i=1 i=l
135
rлава 11. ПРИБЛИЖЕНИЕ функций 2 X ПЕРЕМЕННЫХ
Проверим, что это представление единственно (это и будет 03Ha
чать, что Wij == Ui @ Vj образуют базис и @ V). Рассмотрим
Vkl(W) == P'k 01-L1)(w) == (Лk 01-L1) ( 'Yi,jUi 0 Vj)
n m n m
== Е Е 'Yi,jAk(Ui)J.tI(Vj) == Е Е 'Yi,jakib'j
i l j l i lj l
n m
== Е Е aki''fi,jb 1j == (Ar Bt)kl
i==l j==l
По условию матрицы А и В обратимы, следовательно
r A l ( v ( ш )) ( Bt ) l
kl k==l,...,n,l==l"..,m
(6)
Отсюда вытекает, что коэффициенты ')'ij однозначно определя
ются функцией ш, т.е. Wij базис w.
Из (1) и (6) вытекают второе и третье утверждения теоремы.
Теорема доказана.
1.2. Оценка числа арифметических операций
Оценим трудоемкость вычислений по формуле (5).
1. С помощью, например, LU разложения мы можем вычис
лить A l С затратой О(п 3 ) арифметических операций.
2. С помощью, например, LU разложения 1Ы можем вычис
лить B l С затратой О(т З ) арифметических операций.
З. Матрица Т == A l(Vkl(f)) вычисляется по опре,целеНИIО
произведения маТрИI с затраrl'ОЙ О(п 2 т) арифметических
операций.
4. Матрица r == T(Bt) l вычисляется по определению произ
ведения матриц с затратой О(пт 2 ) арифметических опера
ций.
136
1. ИНТЕРПОЛЯЦFIЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
Таким образом, общее количествО арифметических операций,
требуемых для проведения вычислений по формуле (5), равно
О(п З + п 2 т + пт 2 + тЗ).
Замечание 1. Непосредственное определение коэффициен
тов r ('Yi,j) из системы
n m
Е Е Лk(Ui)JLI(Vj)1'ij == Vkl(!), k == 1,2,.. ., n, 1 == 1,2,..., т
i==l j==l
из n. m линейных уравнений относительно n. m неизвестных 1'ij
2
требует 3 (п . т)3 сложений и столько же умножений по методу
raycca. Например, при п == т это дает О(п 6 ) арифметических
операций, в то время, как формуле (5) О(п З ).
з 1.3. Алrоритм интерполяции тензорными
произведениями
11з теоремы 1 вытекает следующий алrоритм вычисления ис
комых коэффициентов r == ("Yi,j )(i:=l,...,n, j=:l,...,m) функции Р f .
Обозначим fkl == Vkl(!), fl == (!11,..., !nl)t вектор из эле
ментов fkl, F == [11,.." 1т] n х т матрица, составленная из
векторов fk. Тоrда формула (5) утверждает, что
r == А 1 F(Bt) l.
Рассмотрим матрицу
т == А 1 F == А 1 [11 , . . . , f т] == [А 1 f 1 , . . . , .l4 1 f т] .
в силу результата (1.1.4) теоремы (1.1.1) если Ь == (Ь 1 ,..., bn)t
произвольный вектор, то вектор С == A lb есть вектор коэф
n
фициентов интерполирующей функции и == Е CiUi такой, что
i==l
137
Тлава 11. ПРИБЛИ)l(ЕНИЕ функций 2 X ПЕРЕМЕННЫХ
Лk(и) == b k , k == 1,2,...,п. Следовательно, k й'столбец матри
цы т есть вектор коэффициентов интерполирующей функции,
построенной по k MY столбцу /k матрицы F.
Рассмотрим матрицу
r == T(Bt) 1 == (B lTt) t .
Если обозначить T t == [t 1 ,..., t n ] столбцы t i Е R m матрицы
r t , то B IT == [B ltl,"., B ltn]. В силу результата (11.4) Te
оремы (1.1.1) если Ь == (Ь 1 ,..., bm)t произвольный вектор, то
вектор с == B lb есть вектор коэффициентов интерполирующей
m
функции и == Е CjUj такой, что JLI(и) == bl, 1 == 1,2,..., т. Сле
j==:1
довательно, 1 ая строка матрицы r есть вектор коэффициентов
интерполирующей функции, построенной по [..ой строке tl MaT
рицы Т.
Матрицы Т и r обычно хранятся на месте матрицы F . В этом
случае описанный выше алrоритм может быть сформулирован в
следующем виде.
1. Для всех k == 1,2,..., n заменить k й столбец fk MaT
рицы F на вектор O'.k коэффициентов интерполирующей
n
функции U == Е GkiUi такой, что Лi(!k) == fik == Лi(и},
i==l
i == 1,2,...,п.
2. Для всех 1 == 1, 2, . . . ,т заменить 1 ую строку tl матрицы
F на вектор fЗI коэффициентов интерполирующей функции
т
V == Е {3'jVj такой, что JLj(tl) == tjl == J.Lj(и) , j == 1,2,..., т.
j==1
1.4. Проrраммная реализация алrоритма
Пусть ПОДПрО1'рамма INTERP X(LU, N, ALPFA) по вектору
LU == ((>\i (и» (i==l,...,N»)
138
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
значений функционалов Лi на некоторой функции и Е F(X,R 1 )
строит вектор ALPFA == (ai) (i=:l,...,N) коэффициентов интерпо
лирующей функции Рхи == E 1 o'iUi по некоторому методу 1
линейной интерполяции функций из F (Х, R 1 ) .
Пусть ПОДПРОI'рамма INTERP Y(MV, М, ВЕТА) по вектору
МУ == (щ( v)) (j==l,...,M))
значений функционалов /li на некоторой функции v Е F(Y, R 1 )
строит'вектор ВЕТА == «(3i) (j=:l,...,M) коэффициентов интерпо
лирующей функции Pyv == E 1 {3jVj по некоторому методу 2
линейной интерполяции функций из F (У, R 1 ) .
Пусть f Е Р(Х х У, Rl). Обозначим N х М матрицу
NF == ( «>'i 0 /ч)(1) ) (i==l,...,N, ,==1,...,М) )
Искомая N х М матрица коэффициентов G АММА == r ФУНК
цИИ Р!
N М
(Pf)(x,y) == L L 1'i,j U i(X)Vj(Y)
i==l j==l
вычисляется следующим алrоритмом
1. Для i == 1, N выполнять
INTERP Х(i й столбец NF, N, i й столбец GAMMA)
2. Для j == 1, М выполнять
INTERP У(j я строка GAMMA, 1\1, j я строка GAMMA)
Если метод 1 или 2 требуют ДЛЯ CBoero провед€ния обраще...
иия некоторой матрицы, то эта матрица будет одной и той же при
каждом вызове ПОДПРО1'раммы INTERP X и INTERP У. Следо
вательно, при первом обращении к подпроrрамме INTERP Х
139
rлава 11. ПРИБЛИЖЕНИЕ ФУНКI ИЙ 2 X ПЕРЕМЕННЫХ
или INTERP У 10ЖНО построить, например, LU разложение
этой матрицы и сохранить это разложение до следующеrо BЫ
зова подпроrраммы во ВСПОМО1'ательном массиве.
Н зависимости от используемоrо языка проrраммирования ли
бо пункт 1 либо пункт 2 этоrо алrоритма может быть осуществлен
без дополнительных ВЫЧИСJIительных затрат на вызов подпро
rpaMM интерполяции по переменной Х или У. НаПРИ11ер, на язы
ке FORTRAN, в котором массивы хранятся по столбцам, первый
пункт алrоритма можно записать в виде
DO I==1,N
CALL INTERP X( NF(l,I), N, GAMMA(1,I) )
ENDDO
На языке С, в котором l\1ассивы хранятся по строкам, второй
пункт алrоритма можно записать в виде
for( j O; j < М; j++ )
INTERP У( GAMM.A.[j], М, GAMMA[j] );
1.5. Интерполяция тензорными произведениями в
u
случае мноrочлеНIIОИ аппроксимации
Пусть f == f(x,y) функция двух переменных, заданная на
ПРЯМОУ1'ольнике [а, Ь) х [с, dJ. Пусть также заданы точки а == Хl <
Х2 < . . . < Х п == Ь и с == Уl < У2 < . . . < Ут == d, и известны значе
ния f (х i, У j), i == 1, 2, . . . , n, j == 1, 2, . . . , m функции f в точках
(Xi, Yj). Продемонстрируем применение теоремы 1 для paCCMOT
ренных ранее методов приближения.
1.5.1. Интерполяционный мноrочлен Лаrранжа
IIYCTb каждый из методов приближения по переменным х и у
является аппроксимацией мноrочленом Лаrранжа (см. 3 1.3). При
ближающая функция (по каждой из переменных) вычисляется по
формуле (1.3.1).
140
1. ИНТЕРПОJIЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведениями объекты. Базисные Функ
I ИИ:
11
П Х Xk
Ui(X) == ,
х' X k
k==l ,k-j:.i.J .J
i == 1, 2, . . . , n,
тn
П У YI
Vj (у) == ,
l==l,I=I=j Yj YI
j == 1,2,...,т.
Функционалы
Лi (и) == U ( Х i ) , i == 1, 2, . . . , n, J.L j ( V) == V (У j ) , j == 1, 2, . . . , m.
(7)
Матрицы А в (2) и В в (3) единичные. Базис в пространстве
функций тензорных произведений:
n m
П П Х Xk У Yl
Wij(X,y) == Ui(X)Vj(Y) == ,
k==l ,k=l=i 1==1 ,I#j Xi Xk Yj У,
i == 1, 2, . . . , n, j == 1, 2, . . . , т.
Базис в пространстве функционалов теНЗ0РНЫХ произведений:
Vij(f) == Лi(/-lj(f») == !(Xi, Yj) i == 1,2,..., n, j == 1,2,..., т.
По теореме 1 приближающая функция имеет вид (4), rде коэф
фициенты rij ВЫЧИСJIЯЮТСЯ в (5). В силу A l == 1, B l == 1
имеем: rij == Vij (f). в итоrе приближающая функция имеет вид
n m
n
m
LL П П X Xk Y YI
Pf== f(Xi,Yj) .
. . -J..' -J.. . Xt Xk Yj Yl
t=:l 3==1 k==l,k..,....'l l==l ,l..,....3
141
rлава 11. ПРИБЛИЖЕНИЕ функций 2 X ПЕРЕМЕННЫХ
s 1.5.2. Разделенные разности для функции мноrих
переменных
Разделенные разности, введенные в 9 1.8, являются (по дoкa
занному в S 1.8) линейными непрерывными функционалами. Мы
можем рассмотреть их тензорное произведение:
f(Xi;" .; Xi+k, Yj;. . .; Yj+l) ==
== (f(Xi;.. .; Xi+k))(Yj;... ; Yj+l) == (f(Yj;...; Yj+I))(Xi;...; Xi+k).
Равенство здесь справедливо в силу представления (1.4.2).
Это. определение эквивалентно следующему аналоrу определе
ния (1.8.1).
Определение. Пусть задан набор точек
Xi, . . . , Xi+k, Yj,..., Yj+l
(не обязательно различных). Разделенной разностью функции f
нулевоrо порядка называется f(Xi, Yj) == f(xi, Yj), разделенной
разностью (k + l) ro порядка называется
f ( Х i; . . . ; Х i+ k , У j; . . . ; У j +' )
1 akf
k! oxk (Xi, Yj; · · · ; YHl), если Xi == · · . == xHk И f Е C(k+1} ,
(f(Xi;...; XT 1; Х т +l;."; Xi+k, Yj;"'; Yj+l)
f(Xi;...; XB 1; Хв+l;.' .; Xi+k, Yj;.'.; Yj+l»)/(X s Х Т )
если существуют хв -.:J Х т ,
1 8 If (x .. . х - k У - ) если У - У . 1 И f Е C (k+l)
l! ayl t, . · ., z+ , 1 , 1 . . . 1 + ,
(f(Xi;...; Xi+k, Yj;'..; YT 1; Ут+l;.'.; Yj+l)
f ( Х i; . . . ; Х i+ k , У j; . . . ; У s 1 ; У s + 1 ; . . . ; У j +1) ) / (у 8 Ут)
если существуют Ув #- Ут,
142
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИЗВЕДЕНИЯМИ
1.5.3. Интерполяционная формула Ньютона
Пусть каждый из методов приближения по переменным х и у
является аппроксимацией мноrочленом Лаrранжа, который BЫ
числяется по формуле Ньютона (СМ. 1.5). Приближающая функ
ция (по каждой из переменных) вычисляется по формуле (1.5.2).
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведениями объекты. Базисные функ
ции:
i l
Ui(X) == П (х Xk), i == 1, 2,. . . , n,
k==l
j l
V j (у) == п (у Yl), j == 1, 2, . . . , m
l==1
(здесь считается, что произведение равно 1, если верхний предел
меньше нижнеrо). Функционалы задаIОТСЯ в (7). Однако, удобнее
рассмотреть друrую систему функционалов, которая дает ту же
приближающую функцию. В силу (1.10.1) в качестве функциона
лов можно взять
Лi ( и) == U ( Х 1 ; . . . ; Х i) , i == 1, 2, . . . , n,
J-tj(v) == V(Yl;."; Yj), j == 1,2,..., т.
Для этой системы функционалов матрицы А в (2) и В в (3)
единичные. Базис в пространстве функций тензорных произве
дений:
i l j l
Wij(X,y) == Ui(X)Vj(Y) == П П (х Xk)(Y Yl)
k==ll==l
i == 1,2,..., n, j == 1,2,..., т.
Базис в пространстве функционалов тензорных произведений:
Vij (/) == Лi (J-tj (/)) == 1 (Хl ; . . . ; Xi, Уl; . . . ; Yj)
i == 1, 2, . . . , n, j == 1, 2, . . . , т.
143
Тлава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
По теореме 1 приближающая функция имеет вид (4), rде коэф
фициенты 'Yij вычисляются В (5). В силу A l == 1, B l == 1
имеем: 'Yij = lJij (f). в ИТО1'е приближающая функция имеет вид
n m i lj l
Pf(x,y) == LLf(X1;...;Xi,Y1;...;Yj) П П(Х Хk)(У Yl)
i==l j=l k==l l::::l
(8)
Вычисление разделенных разностей осуществляется соrласно
1.4 применением алrоритма из З 1.5 по каждой из переменных х
и у.
1.5.4. Интерполяция "движущимися" мноrочленами
Пусть каждый из методов приближения по переменным х и у
является интерполяцией "движущимися" мноrочленами (СМ. 1.6)
степени k и 1 соответственно. Эти методы являются на каждом
из отрезков [Xi, Xi+l], i == 1,2, . . . , n k 1, [Xn k, Х n ] и [Yj, Yj+l],
j == 1,2,..., т 1 1, [Ym l, Ут] аппроксимацией интерполяци
онным мноrочленом Лаrранжа, записанным в форме Ньютона.
Поэтому приближающая функция строится так же, как в преды
дущем разделе.
1.5.5. Интерполяция с кратными узлами
Пусть каждый из методов приближения по переменным х и
у является аппроксимацией мноrочленом JlarpaH)J(a с кратными
узлами (см. Э 1.9). Теорема 1.9.1 позволяет рассматривать такую
аппроксимацию анало1'ИЧНО описанной выше без кратных узлов.
з 1.5.6. Разложение по мноrочленам Чебышева
Пусть каждый из методов приближения по переменным Х и
у является аппроксимацией мноrочленами Чебышева (СМ. 1.13).
Приближающая функция (по каждой из переменных) ВЫЧИСJIЯ
ется по формуле (1.13.10).
144
1. ИНТЕРПОЛЯЦИЯ ТЕНЗОРНЫМИ ПРОИ3ВЕДЕНИЯМИ
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведениями объекты. Базисные Функ
ции:
Т.(Х) ( ) == . ( 2Х (Ь + а) )
z х t Ь '
a
T Y)(y) == Tj ( 2 У (d + С» ) ,
3 d c
i O,1,...,n 1,
(9)
j == О, 1, . . . , т 1,
Функционалы задаются в (1.13.4):
( "'(х) ) (Х)
Лi ( и) == T i , U n '
J.Lj ( v) == (T i ( у) , v ) :) ,
i == О, 1, . . . , n 1,
j==O,l,...,m l,
rде
n
</, y} X) == L f(Xi)g(Xi),
i==l
m
<f,g) ) == Lf(Yj)g(Yj).
j==l
Для этой системы функционалов матрицы А в (2) и В в (3)
диаrональные (см. (1.13.9»:
А == diag [n, ; ,..., ; ] Е М n , В == diag [т, ; ,..., ; ] Е М т .
Базис в пространстве функций тензорных произведений:
"'(х) .....(у)
Wij(X, у) == Ui(X)Vj(Y) == T i (x)T j (у),
i == О, 1, . . . , n 1, j == О, 1, . . . , m 1.
(10)
Базис в пространстве функционалов тензорных произведений:
п т
Vij(f) == Лi(/lj(!)) == L L Wij(Xi, Yj)f(Xi, Yj) (Wij, f) )
i==l j==l
i == О,1,...,n 1, j == О,1,...,т 1,
145
Тлава 11. ПРИБЛИ)l(ЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
rде
n m
(f,g) ) == L L f(Xi,Yj)g(Xi,Yj).
i==1 j==1
Из леммы 1.13.2 получаем
(Wij, Wkl) ) == о
< ) (ху) nт
Wij, Wij nт
при i 1= j и k 1= 1,
при i 1= о и j 1= о,
4
( W" W. . ) (х у ) nт
1 , 1 nт 2
( ) (ху)
Woo, Woo nт == nт,
при i =1 о, j == о или i == О, j -1- о,
т.е. базис Wij ОРТО1'онален относительно скалярноrо произве
дения (., .)(х у ). По теореме 1 приближающая функция имеет
вид (4), rде коэффициенты 1'ij вычисляются В (5). В силу ви
да матриц А и В имеем:
Vij (f)
/ij = ( )
( W" w.. ) ху
"') , '1,1 nт
( f} (XY)
Wij, nт
(w .. w. . ) (ху).
'l,J , "') nт
в итоrе приближающая функция имеет вид
Pf( ) (W'ij, f) ) ..
х (жу) W'l,J'
i==O з==О (Wij, Wij ) nт
Вычисление коэффициентов разложения осуществляется соrлас..
но 1.4 применением алrоритма (1.13.11) по I<ажДоЙ из перемен
ныххиу.
з 1.5.7. Аппроксимация мноrочленами Чебышева
методом наименьших квадратов
Пусть каждый из методов приближения по переменным х и
у является аппроксимацией мноrочленами Чебышева, построен
ной методом наименьших квадратов (см. 1.17). Приближающая
146
1. ИНТЕРПОЛЯЦИЯ ТЕНЗОРНЫМИ ПРОИЗВЕДЕНИЯМИ
ФУНКЦИЯ (по каждой из переменных) вычисляется по форму
ле (1.17.2) с коэффициентами (1.17.5).
Введем все участвующие в постановке задачи линейной интер
поляции теНЗ0РНЫМИ произведениями объекты. Базисные функ
ции: (9). Функционалы задаются в (1.17.3):
Лi(и) == [и, (X)] (Х), i == О, 1, .. . ,n 1,
J..tj(v) == [v, Т}У)] (У), j == 0,1,..., m 1,
rде
ь d
[f, g](x) == / f(x)g(x) dx, [1, g](Y) == / f(y)g(y) dy.
v C b х)(х а) V (d у)(у с)
а с
Для этой системы функционалов матрицы А в (2) и В в (3)
диаrональные (см. лемму 1.17.2):
А == diag [п, ; , .. . , ; ] Е М п , В == diag [п, ; ,.. . , ; ] Е М т .
Базис в пространстве функций тензорных произведений: (10).
Базис в пространстве функционалов тензорных произведений:
Vij (Л == Лi (щ (Л) == [Ti(X)T}Y) , f] (ху) == [Щj, 1](ХУ)
i == 0,1,. . ., n 1, j == О, 1, . . ., m 1,
rде
ь d
[f, у](ХУ) J J f(x, y)g(x, у) dxdy.
V (b х)(х a)(d у)(у с)
а с
Следовательно, приближающая функция Р! Е Pn l(X) @
Pт l(Y) удовлетворяет следующим линейным условиям интер
поляции:
[ Р ! T X)T Y) ] (ХУ) == [1 T X)T Y) ] (:су)
, t J ' J '
147
Тлава 11. ПРИВЛИ)l(ЕНИЕ Функций 2..Х ПЕРЕМЕННЫХ
i == O,l,...,n 1,j == O,1,...,т 1,
которые являются МНО1'омериым аналоrом условий (1.17.з). В си
лу доказанноrо в 3 1.17 это означает, что приближающая функция
Р/ Е Pn l(X) 0Pт l(Y) реализует минимум
11I р /11: = [/ Р /, f р f](XY) ---7 min
в пространстве всех ФУНКЦИЙ Р! Е Pn l(X) Q9Pm l(Y).
Из леммы 1.17.2 получаем
[ ] (ху) О
Wij, Wkl
п 2
[Ш .. Ш .. ] (ху)
13 , '1,3
4
1Т 2
при i 1: j и k i= 1,
при i =1- о и j 1= о,
[ Ш.. Ш. . ] (х у )
'lJ , 13 2
[ ] (ху) 2
WOO, WOO 1[' ,
при i =J. о, j == о или i = О, j # о,
Т.е. базис Wij ортоrонален относительно скалярноrо произведе
иия [ ., .] ( Х У) .
По теореме 1 приближающая фУНКЦИЯ имеет вид (4), rде KO
эффициенты 'Yij вычисляются В (5). В силу вида матриц А и В
имеем:
Vij (f) [Wi,j, f](XY)
'Yij ==
[ W.. W. . ] (ху) [ 'lv.. Ш. . ) (ху) .
13 , 13 13 , 13
В итоrе приближающая функция имеет вид
n 1 т 1 ( .. f](xy)
Pf(x) == L L W-з, (ху) Щjо
i==O j==O [Wij, Wij J
Вычисление коэффициентов разложения осуществляется соrлас
но 3 1.4 применением алrоритма (1.17.21) по каждой из перемен
ных х И у.
j
148
1. ИНТЕРПОЛЯЦИЯ ТЕНЗОРНЫАIИ ПРОИЗВЕДЕНИЯМИ
1.6. Интерполяция тензорными произведениями в
u
случае кусочно мноrочленнои аппроксимации
в случае, коrда каждый из методов интерполяции по пере
менным х и У является кусочно мноrочленны,, описанный BЫ
те алrоритм интерполяции тензорными произведениями может
быть значительно упрощен.
Пусть f == f(x,y) функция двух переменных, заданная на
прямоуrольнике [а, Ь] х [с, d]. Пусть также заданы точки а == Хl <
Х2 < ... < Х п == Ь и с == Уl < У2 < ... < Ут == d, и каждый из
методов интерполяции по переменным х и у таков, что интерпо
лирующая функция на каждом из отрезков [Xi,Xi+l], [Yj,Yj+l]
строится независимо (от друrих отрезков [Xk,Xk+l], [Yl,Yl+l],
k 1= i, l 1= з). Тоrда матрицы A l и B l В (5) будут блочно
диаrональными, и из теоремы 1 вытекает, что интерполирую
щая функция на прямоуrольнике [Xi,Xi+l] х [Yj,Yj+l] строится
независимо (от друrих прямоуrольников [Xk, Xk+l] Х [Yl, YI+l],
k f. i, 1 i j). Поэтому Teopervry 1 можно применять незави
симо на каждом из прямоуrольников [Xi, Xi+l] Х [Yj, Yj+l]. Это
обстоятельство позволяет также расширить область примени
мости алrоритма: функция f может быть задана не только на
прямоуrольнике [а, Ь] х [с, d], а и на любой области, представи
мой в виде объединения неперекрывающихся прямоуrольников
U ([Xi, Xi+l] Х [Yj, Yj+l]) .
i,j
э 1.6.1. Кусочно--линейная интерполяция
Пусть каждый из методов приближения по переменным х и У
является кусочно линейной интерполяцией (см. 1.15). СОI'ласно
сказанному выше достаточно рассмотреть приближение на пря
МОУI'ольнике [Xi, Xi+l] Х [Yj, Yj+l]. Приближающая функция (по
каждой из переменных) вычисляется по формуле (1.15.1).
Введем все участвующие в постановке задачи линейной интер--
поляции тензорными произведениями объекты. Базисные Функ
149
rлава 11. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ 2 X ПЕРЕIvIЕННЫХ
ции:
Х Xi+l
Ui,l (х) := ,
Xi Xi+1
У У '+1
Vj,l (у) == З ,
Yj Yj+l
Х Xi
Ui,2(X) := ,
Xi+l Xi
У у'
Vj,2 (у) := 3 ,
Yj+l Yj
Х Е [Xi, Xi+1],
у Е [Yj, Yj+l].
Функционалы:
Лi,l(U) == U{Xi),
Jlj,l (V) == V(Yj),
Лi,2{и) == U{Xi+l),
Jlj,2(V) == V(Yj+l)'
Матрицы А в (2) и В в (3) единичные. Базис в пространстве
функций теН30РНЫХ произведений:
Wij,kl(X,y) == Ui,k(X)Vj,l(Y), k,l == 1,2.
Базис в пространстве функционалов тензорных произведений:
Vij,kl(!) == )\i,k(/lj,l(!)), k,l == 1,2,
т.е.
Vij,11 (f) == f(Xi, Yj), Vij,12(!):= f(Xi, Yj+l),
Vij,21 (f) == f(Xi+l, Yj), Vij,22 (f) == f(Xi+l, Yj+l).
По теореме 1 приближающая функция имеет вид (4):
2 2
Р f == L L 1'ij,kl W ij,kl,
k==l l==1
{'де коэффициенты 'Yij,kl вычисляются В (5). В силу A l == 1,
B l == 1 имеем:
')'ij,kl == Vij,kl (f).
150
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
в ИТО1'е приближающая функция имеет ВИД
Pf==f(Xi,Yj) X Xi+1 Y Yj+1 +
Xi Xi+1 Yi Yi+l
Х Xi+l У ..... Yi
+ !(Xi, Yi+1) +
Xi Xi+l Yi+1 Yj
Х Xi У Yi+l
+!(Xi+l,Yj) +
Xi+l Xi Yj Yi+l
Х Xi У ..... Yi
+ !(Xi+l, Yi+l)
Xi+l Xi Yj+1 Yj
Построенную приближающую фУНКЦИЮ часто называют би.ли
uейuой.
В случае кусочно линейной интерполяции тот JКe результат
можно получить, при меняя теорему 1 на всей области определе
ния функции !.
Определение. Обозначим через S X) линейное пространство
непрерывных ломаных линий на отрезке [Хl, Хn] == [а, Ь] с изло
мами Х2 < ХЗ < ... < Xn l; а через s y) линейное пространство
непрерывных ломаных линий на отрезке [Yl, Ут] == [с, d] с изл
мами У2 < Уз < · . . < Yт 1 .
Введем базисы пространств B X), S Y) (см. (1.16.2»
Hi(X) Е s x),
H Y) Е в(у)
J 2'
н}х) (Xk) == б ik , i, k == 1,2, . . ., n,
HJY)(Yl) == б jl , j,l == 1,2,..., т.
Всякая и Е S x) и всякая V Е S y) раскладывается по этому
базису следующим образом (СМ.( 1.16.3)):
n
и(х) == L и(xk)H x)(x),
k==l
m
V(Y) == L v(yl)H,(Y) (У).
l==1
в качестве функционалов выбираем Ai(U) == U(Xi), i
1,2,...,п, J..Lj(V) == V(Yj) , j == 1,2,...,т. ТО1'да матрицы А в (2)
151
rЛ8В8 11. ПРИБЛИ)l(ЕНИЕ функций 2 X ПЕРЕМЕННЫХ
и В в (3) единичные; базис в пространстве функций TeH
u ( ) Н (х) { )н {у) ( ) . 1 2
зорных произведении: Wij х, У i Х j ,У, == , ,..., n,
j == 1, 2, . . . , т; базис в пространстве функционалов тензорных
произведений: Vij(f) == f(Xi, Yj), i == 1,2,..., n, j == 1,2,..., т.
По теореме 1 приближающая функция имеет ВИД (4), rде коэф
фициенты 'Yij вычисляются в (5). В силу A l ::: 1, B l == 1
имеем: 'Yij == Vij (f). в ИТО1'е приближающая функция имеет вид
n m
Р! == LLf(x.i,Yj)Hi(x)(x)HJy)(y).
i==l j==l
9 1.6.2. Кусочно"линейная аппроксимация методом
наименьших квадратов
Пусть каждый из методов приближения по переменным х и
У является кусочно линейной аппроксимацией, построенной Me
тодом наименьших квадратов (СМ. 1.16). В ЭТО 1 случае удобнее
применять теорему 1 на всей области определения функции f.
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведениями объекты. Базисные Функ
ции (см. определения в предыдуще 1 разделе):
Ui(X) = Н}Х)(х), i == 1,2,... ,n, Vj(Y) HJy)(y), j = 1,2,... ,т.
ФункционалЬI:
Лi(и) == ( и, Н}Х» ) , i == 1,2, . . . , n,
L2([a,b])
II з " ( v ) == ( V, н{У) ) , З " == 1, 2, . . . , т.
r j L2([c,d])
Матрицы А в (2) и В Б (3) трехдиаrОНaJ1ьные, см. (1.16.8).
Базис в пространстве функций 'l'ензорных произведений:
Wij(X,y) == иfх) (x)HJy) (у), i == 1,2,...,n, j == 1,2,...,т.
152
1. ИНТЕРПОЛЯЦИЯ ТЕНЗОРНЫМИ ПРОИЗВЕДЕНИЯМИ
rде
1
о
о
о
о 1 О О
A l(h)== 3 2 3 1
h 2 h h 2 h
2 1 2 1
h 3 h 2 h 3 h 2
Таким образом, Ai 1 == А l (Xi+l Xi), в;l == А 1 (Yj+l Yj).
(Друrими словами, коэффициенты a:i == (a:i,k)t==l...4 Е R4 при
4
ближающей функции Ри == L D:i,kUi,k, удовлетворяющей ли
k==l
нейным условиям интерполяции >Ч,k(РU) == Лi,k(U), вычисляются
как ai == A 1(Xi+l Хi)Лi(U), rде Лi(U) == (Лi,k(U))k==1...4 Е R4.
Коэффициенты {Зj == ({Зj,l)f==l...4 Е R 4 приближающей функции
4
Pv == L (3j,lVj,l, удовлетворяющей линейным условиям интер
1==1
поляции Mj,1 (Pv) == J..Lj,l (v), вычисляются как {3; == А 1 (Yj+l
Yj)J..Lj(v), rде J..Lj(v) == (J..Lj,I(V»)1==1...4 Е R 4 ).
Базис в пространстве функций теНЗ0РНЫХ произведений:
к.." t--1
Wij Ilt.t(K) )" иi.,II.()() ;tM:= ()( )tj) ('!- j) ) к,е = !.2,з, 't.
Базис в пространсr,::'ве функционалов тензорных произведений:
Vij,kl (f) == Лi,k (Mj,l (f)), k, l == 1, 2, 3,4. (11)
По теореме 1 приближающая функция имеет вид (4):
4 4 4 4
Р f == L L rij,klWij,kl == L L 'Yij,kl (х Xi)k l (у У; )1 1 ,
k==11==1 k==11==1
rде коэффициенты 'Yij,kl вычисляются в (5). В силу Ai 1
А 1 (Xi+l Xi), в;l == A l (Yj+l Yj) имеем:
r ij == A 1(Xi+1 xi)Fij(A l(Yj+l Yj)t,
155
rЛ8ва 11. ПРИБЛИЖЕНИЕ функций 2 X ПЕРЕМЕННЫХ
1'де r ij
M 4 (R) .
(')'ij,kl)k,l==1...4 Е M 4 (R), Fij (Vij,kl(!»k,I==1...4 Е
Вычисление функционалов тензорных произведений
В случае кусочной интерполяции кубическими мноrочленами
Эрмита (см. 3 1.19.3) матрица F ij имеет вид
f(Xi,Yj) 8f(Xi,Yj) f(Xi, Yj+l) а f(Xi, Yj+l)
ду ду
Bf(Xi,Yj) 82 f(Xi, Yj) 8f(Xi, Уз+l) 82 f(Xi, Yj+l)
8х дхду ах [)х[)у
f(Xi+l, Yj) B!(Xi+l,Yj) f(Xi+l, Yj+l) 8!(Xi+l, Уз+l)
ау ау
а f(Xi+l' Yj) 82 f(Xi+l, Yj) 8!(Xi+l, Уз+l) 82 f(Xi+l, Yj+l)
8х дх8у дх 8х8у
т.е. в каЖДОЙ 'точке (Xi, Yj), i == 1,2,..., n, j == 1,2,..., m (быть
может, за исключением rраничных) ДОЛЖНЫ быть заданы значе
f( ) а f(Xi, yj) 8 f(Xi, Yj) а 2 f(Xi, Yj)
ния Xi, У j, ах ' 8у , 8х8у .
В случае кусочной интерполяции кубическими мноrочленами
Весселя (см. 3 1.19.4), кусочной ИН'l'ерполяции кубическими MHO
rочленами методом Акимы (см. 9 1.19.5), кусочной интерполя
ции кубическими мноrочленами с использованием разделенных
разностей (см. Э 1.19.6), интерполяции кубическими СПJIайнами
(см. 1.19.7) выражения (1.19.7), (1.19.8), (1.19.9), (1.19.12) (допол
ненные соответствующими rраничными условиями, см. 3 1.19.8),
можно рассматривать как системы уравнений для определения
коэффициентов d i (в первых трех методах "система" имеет диа
rональную матрицу). Обозначим через с(х) (при Xi :== Xi) и, co
ответственно, с(у) (при Xi :== Yi), матрицу, выражающую реше
ние системы (1.19.7), (1.19.8), (1.19.9) или (1.19.12) через BeK'l'Opa
F(X) == (!(Xi)i==1,2,...,n (соответственно, F(Y) == (f(Yj)j=1,2,...,m),
так, что п(Х) == с(х) Р(Х) , п(у) == а(У) р(у) , rде D(X) == (d i )i==1,2,...,n
при Xi :== Xi, пСУ) == (d j )j:=1,2,...,m ри Xi :== Yi. Матрица с(х)
156
91. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИЗВЕДЕНИЯМИ
Базис в пространстве функционалов тензорных произведений:
Vij(f) = }.i(щ(f)) = (/, HIx) HjY») L2([a,b]x[c,d]) ,
i == 1,2,...,п, j == 1,2,...,т.
Следовательно, приближающая функция Р f = L 2 ! Е B X) Q9 B Y)
удовлетворяет следующим линейным условиям интерполяции:
( L f H X) H Y» ) == (1 H X) H Y» )
2, t J ) t J '
.L2([a,bJ) L2{[a,b)
i O,1,...,n 1,j == О,l,...,т 1,
которые являются MHo1'oMepHbIM анало1'ОМ условий (1.16.6). В си
лу доказанноrо в 9 1.16 это означает, что приближающая функция
Р! == L 2 f Е S x) 0 s Y) реализует минимум
111 L 2 fIlL2([a,b]x[c,d]) ----t min
в пространстве всех функций L 2 ! Е B X) Q9 B Y) .
По теореме 1 приближающая функция имеет вид (4), 1'де KO
эффициенты rij вычисляются в (5). При этом применяется ал
1'оритм из S 1.4, а для ускорения вычислений для матриц А и В
строятся их LU разложения.
э 1.6.3. Кусочно--кубическая интерполяция
Пусть каждый из методов приближения по переменным х и
у является кусочно кубической интерполяцией (СМ. 1.19). CO
rласно сказанному выше достаточно рассмотреть приближение
на прямоуrольнике [Xi, Xi+l] Х [Yj, Yj+l]. Приближающая функ
ция (по каждой из переменных) вычисляется по формуле (1.19.2),
rде коэффициенты задаются (1.19.з).
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведениями объекты. Базисные Функ
ции:
Ui,k(X) == (х Xi)k l, k == 1,2,3,4, х Е [Xi, Xi+l],
153
rлава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
Vj,l (у) == (у УЗ )' 1 , 1 == 1,2, З, 4, У Е [Уз, Уз+l].
ФункционалЬI:
Лi,l (и) == U{Xi),
Лi,З (и) == и(Xi+l),
Jlj,l(V) == v(Yj),
/-Lj,3 (v) == V(Yj+l),
Лi,2 (и) == d i (и) ,
Лi,4(и) == di+1(и),
/-Lj,2(V) == dj{v),
Jlj,4(V) == d j + 1 (v),
1'де величины d i , d j определяются выбранным меТОДОl\1 интерпо
ляции, см. (1.19.4), (1.19.7), (1.19.8), (1.19.9), (1.19.12) (в последнем
случае величины d i получаются в результате решения системы
линейных уравнений).
Формулы (1.19.3) представляют собой выражения для матриц
Ai 1 в (2) и B;l в (3). Действительно, выражения (1.19.3) можно
записать в виде (обозначив h i == Xi+l Xi)
Cl,i == f(Xi)
C2,i == d i
Сз,i == i ( :i (J(Xi+I) f(xi» 2d i di+l) ==
3 2 3 1
== h; f(Xi) h i d i + h; f(xi+I) h i d i + 1
C4,i == (d i + d i + 1 i (J(Xi+I) f(Xi») ==
212 1
== h f(Xi) + h d i h f(Xi+l) + h d i + 1
'1 t
Следовательно,
Ci = (Cl,i, C2,i, СЗ.i, C4,i)t == A l (h i ) (f(Xi), di, !(Xi+l), di+1)t
154
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
Соrласно сказанному выше достаточно рассмотреть прибли
[ I:(X) I:(X) ] [ с(у) с(У) ] П б
жение на прямоуrольнике i , i+l Х j , j+l. ри лижаю
щая ФУНКЦИЯ (по каждой из переменных) вычисляется по фор
муле (1.20.2), rде коэффициенты задаются (1.20.3).
Введем все участвующие в постановке задачи линейной интер
поляции тензорными произведеНИЯ!vlИ объекты. Базисные функ
ции:
( ) ( c(x» ) k l
Ui,k Х Х i ,
Vj,I(Y) == (у ;Y»)l l,
k == 1, 2, 3,
1 == 1, 2, З,
[ с(Х) с(х) ]
Х Е i , i+ 1 ,
У Е [ c Y) c y) ]
З ' з+l.
Функционалы
Лi,l (и) == V X), Лi,2(и) == и(Xi), Лi,з(и) = vl ,
J-lj,l(V) == v;y) , JLj,2(V) == v(Yj), J-lj,з(V) == V) l.
ФОРlv1УЛЫ (1.20.3) представляют собой выражения для матриц
Ai 1 в (2) и Bjl В (3). Действительно, (СМ. вычисления в 1.20.3)
выражения (1.20.3) можно записать в виде (обозначив h i == Xi i,
Zi == i+l Xi, h i + Zi = i+l i)
Cl,i == Vi
C2,i == Vi ( + 1 ) + f(Xi) ( + ) Vi+l ( 1 )
h i hi + Zi h i Zi Zi J'ti + Zi
1 1 1 ( 1 1 ) 1 1
Сз,i == Vi f(Xi) + + Vi+l
h i + Zi h i h i + Zi h i Zi h i + Zi Zi
Следовательно,
Ci (СI,i,С2,i,сз,i)t == A l(hi,Zi) (Vi,!(Xi),Vi+l)t
159
rлава 11. ПРIIБЛИ)l(ЕНИЕ Функций 2 X ПЕРЕМЕННЫХ
1'де A l(h,z) ==
1
( + h:Z )
1 1
h+zh
о
о
( + )
( .!. + )
h+z h z
( h:Z )
1 1
h+zz
б A l A l ( с(х) с(х) ) B l
аким о разом, i Xi i , i+l Xi, j
А 1 (Yj )y) , ) 1 Yj). (Друrими словами, коэффициенты Qi ==
4
(Оi,k) ==l...з Е RЗ приближающей функции Pi(X)и == Е Oi,kUi,k,
k==l
удовлетворяющей линейным условиям: интерполяции (12) вида
Лi,k(Р(Х)и) == Лi,k(и), вычисляются как Qi == A l(Xi €ix),€i
Хi)Лi(и), rде Лi(и) == (Лi,k(и»k==l...З Е R3. Коэффициенты [3з ==
3
('вj,l)f==l...З Е R3 приближающей функции Pj(Y)v == Е (3j,lVj,l,
1==1
удовлетворяющей линейным условиям интерполяции (12) вида
(р (у) ) ( ) fЗ A l ( с(у) с(у)
J-Lj,l j V J-Lj,l V , ВЫЧИСЛЯIОТСЯ как j Yj ) , j+l
Yj)J-Lj(V), rде J1j(v) == ({tj,l('U»l==l...з Е RЗ).
Базис в пространстве функций теНЗ0РНЫХ произведений:
Wij,kl(X,Y) == Ui,k (X)Vj,l (У) == (x 1X))k 1(y )Y))l 1, k,l == 1,2,3.
Базис в пространстве функционалов тензорных произведений:
lIij,kl (f) == Лi,k (J1j,l (f»), k, l == 1, 2, 3.
(14)
По теореме 1 приближающая функция имеет вид (4):
3 3 3 3
Р f == L L 'Yij,kIWij,kl == L L 'Yij,kl (х {iX»)k l (у {)Y»)I l ,
k 11 1 k ll l
160
1. ИНТЕРПОЛЯЦИЯ ТЕНЗОРНЫМИ ПРОИ3ВЕДЕНИЯМИ
имеет размер n х п, а(У) размер т х т, и учитывает COOTBeT
ствующие rраничные условия.
Теперь мы можем сформулировать алI'ОРИТМ вычисления
функционалов Vij,kl{!) в (11). Пусть F == (!ij) обозначает п х т
матрицу значений f (Xi, У j ). Вычислим (один раз):
n х m матрицу р(х) == (fi X») = G(x) Р,
n х m матрицу F(V) == (Ji<Y») = F(G(y»)t,
n х т матрицу F(XY) == (fi xv») a(x)p(G(y»)t.
Значения функционалов F ij == (Vij,kl (f) )k,I==1,2,з,4 В (11):
!i,j f Y) fi,j+l !i(, 1
1, ,}
f X) f X.Y) 1(Х) j(XY)
F ij == ,} 1,} i,j+l i,j+l
f(Y) 1(У)
fi+ 1,j i+ 1 ,j !i+l,j+l i+l,j+l
/(Х) I(XY) j(X) f(XY)
i+ 1 ,j i+ 1 ,j i+l,j+l i+l,j+l
Орrанизация хранения данных в памяти ЭВМ
Хранение информации о функции и ее приближении удоб
но осуществить следующим образом. Входные данные значе
пия функционалов (Vij,kl(!)) , i == 1,2,...,п, j == 1,2,...,т,
k,l == 1,2,3,4, размещаются в 3 x мерном массиве F == (!ijk),
i == 1, 2, . . . , n, j == 1, 2, . . . , т, k == 1, 2, 3, 4 размера (n х т х 4),
1'де
!ij,l == Vij,11(!) == f(Xi,Yj), !ij,2 == Vij,12(!),
fij,3 = Vij,21 (f), fij,4 == l/ij,22 (f).
Матрица F ij выше получается из элементов 4 x мерных BeKTO
рОБ Fi,j, F i + 1 ,j, F i ,j+l , F i + 1 ,j+l . Коэффициенты приближающей
функции ('Yij,kl), i == 1,2,...,п, j:= 1,2,...,т, k,l == 1,2,3,4,
вычисляются один раз и хранятся в 4 x мерном массиве r ==
157
rлава 1/. ПРИБЛИ)КЕНИЕ Функций 2 X ПЕРЕ!vIЕННЫХ
(rijkl), i == 1, 2, . . . , n, j == 1, 2, . . . , т, k, l
(n х m х 4 х 4), rде 'Yijkl == 'Yij,kl .
1,2,3,4 размера
1.6.4. Кусочно"квадратичная интерполяция
Пусть каждый из методов приближения по переменным Х и
у является кусочно квадратичной интерполяцией (см. 9 1.20), rr.e.
введены точки
с(х) с(Х) .t(x) Ь с(Х)
1 < а == Хl < 2 < Х2 < · . . < Xn 1 < n < Х N == < n+l'
и
с(у) < < С(У) < « < с(у) < d < с(у)
1 С Уl 2 У2 . . . Yт 1 т, Х т т+l'
и интерполирующая функция одной переlvlенной р(х) j (р(у) j)
строится таким образом, что на каждом отрезке [ X), )1]' i ==
1,2, . . . , n ([ )y), ) 1]' j == 1,2, . . . ,т) она является МНО1'очленом
P i ( Х ) (Р} у») степени 2, таким, что
J}(X) (Z l 8) J( t.) )
Pi(X) ( lX») == v x), Pi(X) ( l )l) t X )
V i + 1
(12)
или, соответственно,
pJY) (Yj) == f(Yj), } j == 1, 2, . . . , m
pJY) ({;у») == v;Y) , pJY) ({; 1) v(y)
j+l
(13)
(х) . 1 2 1 (у) . 1 2 1 б
l' де v i , 't , ,..., n + , V j , J , ,..., m + сво одные па
раметры, тот или иной способ выбора которых определяет метод
кусочной интерполяции квадратичными МНО1'очленами. В leToдe
интерполяции параболическими сплайнами эти параметры полу
чаются как решение системы линейных уравнений (1.20.8).
158
1. ИНТЕРПОЛЯЦИЯ ТЕН30РНЫМИ ПРОИ3ВЕДЕНИЯМИ
{'де коэффициенты 'Yij,kl вычисляются В (5). В силу Ai 1 ==
A l ( ,"(Х) с(Х) ) B l A l ( с(у) с(у) )
Xi i , i+l Xi, j У) j , j+l Yj имеем.
r A l ( с(Х) с(Х) ) "D (A l ( с(у) с(у) » t
ij А. Xi i , i+1 Xi rij А. У] } , "'j+1 У] ,
rде r ij == (,ij,kl)k,l==l...з Е Мз{R), F ij == (Vij,kl(!))k,l==l...з Е
Мз(R) .
Вычисление функционалов теНЗ0РНЫХ произведений
Входными даННЬПvIИ ал1'оритма являются значения f(Xi, Yj) ==
Лi,2(/-Lj,2(!)), i == 1,2,..., n, j == 1,2,..., т, и те или иные краевые
условия (c:rv1. fi 1.20.4). Для построения интерполирующей функ
ции требуется вычислить все остальные значения функционалов
Vij,kl(!) в (14).
Обозначим в (12) /(X) == (V x»)i==1,2,...,n+l Е Rn+l, р(х) ==
(f(Xi) )i:=l ,2,...,n Е R n, И В (13) vCy) == (v}Y) )j==1,2,...,m+l Е R т+l ,
р(у) == Cf(Yj ))j:=1,2,...,m Е R m . Система (1.20.8), дополненная Kpa
евыми условиями, представляет собой связь между между BeK
торами V(x) и р(х} (при Xi :== Xi, :== (x»), а также между
векторами /(Y) и р(у) (при Xi :== Yi, :== (y»). Обозначим че
рез с(х) и, соответственно, с(У), матрицу, выражающую реше
ние системы (1.20.8) Iерез вектора Р(Х) (соответственно, р(у»),
так, что V(x) == а(Х) р(х), vCY) == а(у) р(у). Матрица а(Х) име
ет размер (n + 1) х n, а(У) размер (т + 1) х т, и учитывает
соответствующие rраничные условия.
Теперь мы можем сформулировать ал1'оритм вычисления
функционалов l/ij,kl (f) в (14). Пусть Р == C!ij) обозначает n х т
матрицу значений f(Xi,Yj). Вычислим (один раз):
(п t- 1) х т матрицу р(х) == (fi X») = а(Х) Р,
п х (т + 1) матрицу F(Y) == (fi ») = F(G(y»)t,
(п + 1) х (т + 1) матрицу F(xy) == (fi XY)) = G(X)P(G(y»)t.
161
rлава 11. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
Значения функционалов Fij == (Vij,kl (f) )k,l==1,2,З в (14):
f X.Y) f X.) f(XY)
,1 %,) i ,} + 1
P ij == f Y) fi,j fi<,j 1 (15)
'1, ,]
f(XY) j(x) j<XY)
i+ 1 ,] i+ 1 ,] i+l,j+l
Орrанизация хранения данных в памяти ЭВМ
Хранение информации о функции и ее приближении удобно
осуществить следующим образом. Входные данные значения
функционалов (Vij,kl (f)), i == 1, 2, . . . , n, j == 1, 2, . . . ,т, k, l ==
1,2, З, хранятся в четырех введенных выше fатрицах F Е Мn,т,
Р(Х) Е М n + 1 ,т, р(у) Е М n ,т+l, Р(ХУ) Е Mn+,m+l. Матрица
P ij = (Vij,kl(!))k,I==1,2,з получается СО1'ласно (15). Коэффициенты
приближающей функции (rij,kl), i == 1,2,. .., n, j == 1,2,..., т,
k, 1 == 1, 2, З, вычисляются один раз и хранятся в 4 x мерном
массиве r == (,ijkl), i == 1,2,...,п, j == 1,2,...,т, k,l == 1,2,3
раЗ fера (п х m х 3 х 3), {'де /ijkl == rij,kl .
u
З 2. ПРИБЛИЖЕНИЕ ФУНКЦИИ мноrих
пЕрЕмЕнныIx МЕТОДОМ конЕчныIx
ЭЛЕМЕНТОВ
Этот метод интерполяции позволяет приблизить функции
fНО1'ИХ переменных, заданные в областях сложной формы. Для
простоты мы будем рассматривать только функции двух пере
менных.
9 2.1. Постановка задачи линейной интерполяции
Пусть задана функция f : D R 1 , rде D с R 2 О1'рани
ченная область с достаточно 1'ладкой 1'раницей, f Е F(D, Rl)
некоторому функциональному пространству,
162
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
Представим область D в виде объединения конечноrо числа
треуrольников D..k С D, не имеющих общих внутренних точек:
N
п' = U D..k С D. Построение TaKoro набора треуrольников (Ha
k==l
зываемоrо трuа'Нzуляцuеи области D) в общем случае является
очень сложной задачей и для ее решения существует большое чис
ло методов. Ниже мы рассмотрим несколько самых простейших
из них.
Далее, на каждом треУ1'ольнике Llk функция f приближается
тем или иным методом, т.е. строится функция Pkf, удовлетво
ряющая тем или иным линейным условиям интерполяции. При
ближающие функции в соседних треуrольниках должны быть c
rласованы: если (х, У) Е д'kl n D..k2 точка общей rраницы Tpe
У1'ольников, то Plk 1 (X,y) == P/ k2 (X,y). Значение приближающей
функции РI в точке (х,у) Е п' вычисляется следующим обра
зом: определяется k, такое, что (х, У) Е Дk, И по определению
полаrается Р 1 (х, у) == Pk 1 (х, у). Этот подход является обобще
нием КУСОЧНО МНО1'очленной аппроксимации на случай функций
МНО1'их переменных.
Возможен друrой способ построения приближаlощей функ
ции. На области D' определяют набор базисных функций <PI (Х, у)
и приближающую функцию ищут в виде их линейной комбина
ции. Базисные функции <PI(X, У) обычно выбирают так, чтобы
их носитель содержал как можно меньше треу1'ОЛЬНИКОВ D..k.
Например, выбирается точка (XI,YI) Е D' и базисная функция
'PI(X, у) полаrается равной мноrочлену заданной степени в каж
дом из треу1'ОЛЬНИКОВ D..k, таких, что (Xl, YI) Е D..k. В остальных
треу1'ОЛЬНИках <PI (х, У) полаrается равной нулю. Если функциона
ль! ЛI в задаче линейной интерполяции есть значения функции в
точке: ЛI (1) == f(XI' YI), то при таком ПОС'l'роении базисных функ
ций сужение приближающей функции Р f на треуrольник Ll k и
описанная выше функция P k ! совпадают.
163
rлава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ 2 X ПЕРЕАIЕННЫХ
s 2.2. Способы построения трианrуляции области
Ниже мы опишем несколько простейших способов построения
трианrуляции оrраниченной области D с достаточно rладкой rpa
ницей.
1) Область D оrраничена, поэтому существует ПрЯ МОУ1'ольник
[а, Ь] х [с, d], такой, что D с (а, Ь] х (с, d]. Каждая из сторон 3'1'01'0
ПРЯМОУ1'ольника разбивается на равные части точками Xi == а +
ih x , i == О,1,...,п, hx == (b a)/n, УЗ == a+jhy, j == О,l,...,т,
hy == (d c)/m. k является треуrольником с вершинами в точках
Qk,l, Qk,2, Qk,3, если Qk,l Е п, 1 = 1,2, 3 и выполнено одно из
четырех условий:
1. Qk,l == (Xi,Yj), Qk,2 == (Xi+l,Yj), Qk,3 == (Xi+l,Yj+l);
2. Qk,l == (Xi, Yj), Qk,2 == (Xi, Yj+l), Qk,3 == (Xi+l, Yj+l);
3. Qk,l == (Xi, Уз)' Qk,2 == (Xi+l, Уз)' Qk,3 == (Xi, Уз+l);
4. Qk,l == (Xi+l, Yj), Qk,2 == (Xi+l, Yj+l), Qk,3 == (Xi, Yj+l).
(1)
Условие Дk С D может быть не выполнено в ПРИ1'раничных Tpe
уrольниках. Полученная трианrУЛЯI ИЯ будет точно аппроксими
ровать область (т.е. D == U D.k), если D является мноrоуrольни
k
ком с вершинами в точках (Xi, УЗ), стороны KOToporo либо парал
лельны осям координат, либо состаВЛЯIОТ с ними уrол 7r /4.
2) Выполняем описанную в пункте 1) трианrуляцию. Для по
вышения точности аппроксимации области рассмотрим все пря
моуrольники Пk с/.. D с вершинами Qk,l == (Xi, Yj), Qk,2 ==
(Xi+l,Yj), Qk,З == (Xi+l,Yj+l), Qk,4 == (Xi,Yj+l), такими, что хо--
тя бы одна из точек Qk,l Е D. СДВИ1'анием точек Qk,l ------t Q ,l'
1 == 1,2,3,4 на наименьшую воз:можную величину по направле
нию к rранице 8D области D добиваемся Toro, чтобы либо все
новые точки Q ,l f/:. п, либо для какой либо тройки Q ,l (или
двух троек) было выполнено одно из условий (1)'. Треуrольники
с такими вершинами Q 1 Е D добавляем к трианrуляции. По
,
лученная трианrуляция будет точно аппроксимировать область
164
92. ИНТЕРПОЛЯЦliЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
(т.е. D == U Дk ), если D является мноrоуrольником с вершинами
k
в точках (Xi, Yj).
3) Предположим, что можно построить преобразование (rлад
кое и без особых точек), переводящее область а, для которой
мы умеем строить трианrуляцию (например, прямоуrольник), в
рассматриваемую область п. Тоrда вершины треуrольников три
анrуляции области D MorYT быть получены как образы вершин
трианrуляции области G при этом преобразовании.
4) Предположим, что область D можно разрезать прямыми
линиями на подобласти, в каждой из которых мы можем постро
ить трианrуляцию. Если вершины треуrольников, лежащие на
линиях разрезов, в каждой из трианrуляций соответственно COB
падают, то объединение этих трианrуляций дает трианrуляцию
всей области п.
2.3. Приближение функций в треуrольнике
Рассмотрим задачу приближения функции f == f(x, у), задан
ной в треуrольнике д.
з 2.3.1. Постановка задачи линейной интерполяции
Пусть каждая сторона треуrольника Д разбита на l равных
частей, и через точки разбиения (включая вершины треуrольни
ка) проведены прямые, параллельные ero сторонам. Обозначим
через т множество, состоящее из точек пересечения этих пря
мых, лежащих в замкнутом треуrольнике . Число этих точек
1+1
равно n == L k == (1 + 1)(1 + 2)/2. Будем обозначать их через
k==l
Ql(Xl,Yl), ..., Qn(xn,yn).
Рассмотрим задачу построения мноrочлена Р f степени 1
Pf(x,y) == L aijXiyj,
i+j l
(2)
165
rлава 11. ПРИБЛИЖЕНИЕ Функций 2 X ПЕРЕМЕННЫХ
принимающеrо в точках Qk(Xk,Yk) заданные значения
P!(Xk,Yk) == !(Xk,Yk), k == 1,2,...,п.
(3)
Условия (3) представляют собой n линейных условий интерпо
ляции. Поскольку число неизвестных коэффициентов aij также
равно n, то соотношения (3) образуют систему из n уравнений с
n неизвестными. Если задача линейной интерполяции корректна,
т.е. эта система разрешима, то из нее можно найти коэффициенты
aij.
Искомый мноrочлен Р f можно выписать явно и в paCCMOT
рениом выше общем случае. Однако, это выражение достаточно
сложно и на практике используется редко. Ниже мы выпишем вид
мноrочлена Р f в случае, коrда треуrольник Д ПРЯ 10уrольный
со сторонами, параллельными осям координат, а также для слу
чаев l == 1, 2, 3.
s 2.3.2. Приближение функций в прямоуrольном
треуrольнике
Решим поставленную выше задачу линейной интерполяции в
случае, коrда треуrольник d прямоуrольный со сторонами, па
раллельными осям координат. Пусть ero вершинами являются
точки (а, с), (Ь, с), (а, d) (т.е. треуrольник образован делением
прямоуrольника (а, Ь] х [с, d] ero диаrональю). Пусть
а == Хl < Х2 < . . . < Xn 1 < Х N == Ь,
с == Уl < У2 < . . . < Yт ] < Ут == d,
'и'известны значения функции f в точках (Xi,Yj) Е Д. Требуется
построить приближающую функцию Р f вида (2), удовлетворя
ющую условиям
Pf(Xi,Yj) == f(Xi,Yj), (Xi,Yj) Е д.
(4)
Эта постановка является более общей, чем описанная в предыду
щем разделе, которая получается при равномерно распределен
ных точках Xi, Yj И m == n.
166
S2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
Для целей вывода алrоритма приближения мы будем счи
тать, что известны значения функции f в точках (Xi,Yj) д
(например, будем считать f равной нулю в этих точках). Тоrда
для функции f применимы алrоритмы аппроксимации тензор
ными произведениями в прямоуrольнике [а, Ь] х [с, d]. Нам удоб
но использовать приближение интерполяционным мноrочленом
Лаrранжа в форме Ньютона, Т.е. приближающую функцию (1.8),
которую мы запишем Б следующем виде
р f(x, у) ==
+
i l j l
L f(Xl; . . . ; Xi, У1; . · . ; Yj) П (х Xk) П (у YI)+
i,j: (Xi ,Yj) E k==1 1==1
i 1 j l
L f(X1;..' ;Xi,Yl;... ;Yj) П (х Xk) П (у YI)
i,j:(Xi,Yj) k==1 l==1
(5)
(здесь Ll считается замкнутым множеством). По построению, эта
функция удовлетворяет условию Р f(Xi, Yj) == f(Xi, Yj) для всех
(Xi, Yj) Е [а, Ь] х (с, d]. Заметим, что
i 1 j l
П (х Xk) П (У YI) == о
k==1 [==1
для всех ( х, У) == (х р, у q ) , р == 1, 2, . . . , i 1, q == 1, 2, . . . , j 1.
Следовательно, вторая сумма в (5) равна О для всех (х, у)
(xi, Yj) Е Д. (поскольку для всяких (Xi, Yj) rI:. д, (ХР' Yq) Е Д
выполнено либо Xi > Хр, либо У; > Yq). Поэтому функция
i l j l
Pf(x,y) == L f(Xl;...;Xi,Yl;...;Yj) П(Х Хk) П(У Уl)
i,j : (Xi ,Yj) E k==l 1==1
(6)
удовлетворяет условиям (4), Т.е. является решением задачи ли
ней ной интерполяции. Поскольку Xi > Xk при i > k и Yj > Yl
167
Тлава 11. ПРИБЛИЖЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
при j > 1, то все разделенные разности f(Xl;...; Xi, Yl; . . . ; Yj)
в (6) вычисляются только через значения функции f в точках
(Хi,Уj)ЕД.
При m == n выражение (6) можно записать в виде
i l j l
Pf(x,y) == L f(Xl;..' ;Xi,Yl;... ;Yj) П (х Xk) П (у Yl)
i+j n+1 k==l 1==1
2.3.3. Приближение линейными функциями
Рассмотрим описанную выше задачу линейной интерполяции
в частном случае l == 1 в (2), т.е. приближение линейной Функ
цией.
Приближение на треуrольнике
Обозначим вершины треуrольника Д через (Хl, Уl), (Х2, У2),
(Хз, Уз). Нам требуется построить приближающую функция вида
Pf(x,y) ==ах+{3у+"
удовлетворяющую условиям
Р f(Xk, Yk) == f(Xk, Yk), k == 1,2, З.
(7)
Коэффициенты а, (J , , MorYT быть получены из уравнения плос
кости, ПрОХGдящей через три точки (Xk,Yk,!(Xk,Yk»), k == 1,2,3.
Однако, для дальнейшеrо изложения нам удобнее ввести базис
ные функции задачи линейной интерполяции и построить Р f как
их линейную комбинацию.
Обозначим
L( Ul ,Vl ),( и2 ,V2) (Х, у) ==
х иl У Vl
и2 иl V2 Vl
(8)
== (х U1)(V2 Vl) (У Vl)(U2 иl)
168
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
линейная функция, обращающаяся в нуль на прямой, проходя
щей через точки (Ul, Vl) и (и2, V2). Введем также функции
'Фl (х, у) == L(Х2,У2),(ХЗ,УЗ) (х, у),
'Ф2 ( х, у) == L ( х 1 , У 1 ) , ( х З , уз) ( х, у ) ,
фз(х, у) == L(Xl,Yl),(X2,Y2) (х, у),
т.е.
х Х2 У У2
Ф1 (х, у) = Х Х У У
З 2 3 2
== (х Х2)(УЗ У2) (у У2)(ХЗ Х2),
Х Хl У Уl
Ф2(Х, у) ==
хз Xl Уз Уl
== (х Хl)(УЗ Уl) (у Уl)(ХЗ Хl),
Х Хl У Уl
'Фз ( Х, у) == Х Х У У
2 1 2 1
== (х Xl)(Y2 Yl) (у Уl)(Х2 Хl),
а также
( ) 'Фi (х, У) . 1 2 3
'PiX,y ==nk ( . . ) ' "'== ".
«f/ X , y
(9)
Имеем:
<{Ji(Xj,Yj) == дij, i,j == 1,2,3.
Функции 'Pi(X,Y), i == 1,2,3 возьмемвкачествебаЗИСНЫХБзадаче
линейной интерполяции, т.е. приближающую функцию Р f будем
искать в виде
з
р f(x, у) == L Qi<Pi(X, у),
i==l
rде коэффициенты Qi определяются из условий (7). Так как
матрица (1.1.з) задачи линейной интерполяции единичная, то
169
rлава [1. ПРИБЛИ)КЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
Gi == !(Xi,Yi), i == 1,2,3 и приближающая функция имеет вид
з
р f(x, у) == L f(Xi, Yi)'Pi(X, у).
i==l
Значения приближающей функции Р f на стороне треуrоль
ника (например, [(Xl,Yl),(X2,Y2))) определяются только значе
ниями функции f в точках, лежащих на этой стороне (в нашем
примере (Хl, Уl) И (Х2 , У2) ). Следовательно, если треуrольни
ки Дl И Д2 имеют общую сторону, то значения приближающих
функций, построенных в каждом из них, совпадают в точках этой
общей стороны. Это позволяет строить из приближающих функ
ций Pk f, определенных в треуrольниках k, кусочно линейную
N
аппроксимацию Р f, определенную на трианrуляции U Ak, по
k==l
правилу: Pf(x,y) == Pkf(x,y) при (х,у) Е Дk.
Приближение на трианrуляции
Построенную выше приближающую функция Р f , определен
N
ную на трианrуляции D' == U Дk, можно получить также сле
k==l
дующим способом.
Определение. Обозначим через V 1 (D') линейное простран
ство непрерывных в D' функций, являющихся линейными в каж
N
дом треуrольнике Дi С D' == U Дk.
k==l
Введем базис пространства V 1 (п') :
cp l) Е V 1 (D'),
(1) (
lfJi Xj, Yj) bij,
i,j == 1,2,...,А1 1 ,
(10)
{'де {(Xj, Yj)}j==1,2,...,M 1 множество вершин треуrольников D.,k С
D' . Функции <p 1) часто называют фУН'lCцuя.мu Куранта. Анали
тически функцию Ч? 1) можно задать следующим образом. Пусть
Ak, , 1 == 1,2, . . . , ni треуrольники, имеlощие точку (xi, Yi) в Ka
честве вершины. Обозначим через <Pk, (х, у) линейную функцию,
170
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
определенную в треуrольнике Il k" равную 1 в точке (Xi, Yi) И о
в остальных вершинах Дk, . Такие функции мы построили ранее,
см. (9). Тоrда
'P 1) (Х, У) ==
О,
пi
если (Х, У) f/:. U Il kl
1==1
<t'kl(X,y), если (х,у) Е Il kl
Всякая 9 Е V 1 (D') раскладывается по базису из функций
{cp l) (Х, у) }i==1,2,...,M 1 следующим образом:
Мl
у(х, У) == L g(Xi, Yi)'P}l) (Х, у).
i==l
Мl (1)
Действительно, для функции у(х, У) == 2: g(Xi, Yi)<Pi (х, У) в си
i==l
лу (10) имеем: g(Xj, Yj) == g(Xj, Yj), j == 1, 2, . . . , М 1 . Следова...
тельно, у(х, У) является в каждом треуrольнике Дk линейной
интерполирующей функцией. В силу корректности задачи ли
ней ной интерполяции интерполяционный мноrочлен единствен...
нен. Следовательно, 9 == 9 в каждом треуrольнике Дk, И, значит,
N
в D' == U Дk.
k==]
Рассмотрим задачу нахождения приближающей функции
Р! Е V 1 (D') , совпадающей с функцией f в точках {(Xj,Yj)}:
Pf(xj,Yj) == f(xj,Yj), j == 1,2,...,М1. (11)
Функцию Р f будем искать в виде
Мl
Р f(x, У) == L Qi<P l) (Х, у),
i==1
{'де коэффициенты Qi определяются из условий (11). В силу (10)
матрица (1.1.3) задачи линейной интерполяции единичная. По
этому D:i == f(Xi, Yi), i == 1,2, . . . , М 1 И приближающая функция
171
rлава 11. ПРИВЛИ)l(ЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
имеет вид
Мl
Р f(x, у) =: L f(xi, Yi)tp l) (х, у).
i:=l
2.3.4. Приближение квадратическими функциями
Рассмотрим описанную выше задачу линейной интерполяции
в частном случае l == 2 в (2), т.е. приближение квадратической
функцией.
Приближение на треуrольнике
Обозначим вершины треуrольника Д через (Xl,Yl), (Х2,У2) ,
(Хз, Уз), середины ero сторон через
(Х4, У4) = (Хl,2, Уl,2), (Х5, У5) = (Х2,з, У2,з), (Хв, У6) = (Хl,З, Уl,з),
rде Xk,l == (Xk +xl)/2, Yk,l == (Yk +YI)/2. Нам требуется построить
приближающую функцию вида (2), удовлеТВОрЯЮJЦУЮ условиям
Pf(Xk, Yk) == f(Xk, Yk), k == 1,2,...,6. (12)
Построим базисные функции задачи линейной интерполяции.
Введем (см. рис. 11.1) точки Pk == (Xk,Yk), k == 1,2,...,6 и
функции
'Фl (Х, у) == L Р 2 ,Рз (х, У) , Ф2 ( Х , у) == L P 1 , Р з (Х, у ) ,
'Фз(Х,У) == Lpl,P2(X,y), Ф4(Х,У) == LР 4 ,Рб(Х'У)'
'Фб (Х, У) == Lp4,P5 (Х, у), 'Фв(Х, у) == Lp5,P6 (Х, у),
({'де функции L определены в (8)), а также
1]1 (Х, У) == 'Фl (Х, У )Ф4 (Х, у),
1]З(Х, У) == 'Фз(Х, у)'Фв(Х, У),
'Тl5 ( Х, У) == Ф2 ( Х, У) Фз ( Х, у),
1]2(Х, У) == Ф2(Х, У)Ф5(Х, У),
1/4 ( Х, У) == Фl (х, У) 'Ф2 ( Х, у),
'Тl6 (Х, У) == 'Фl (Х, У )'I/'З (х, у).
172
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
'Фl
'Ф2
1/1з
Рис. 11.1. Схема построения базиса для интерполяции квадрати
ческими функциями
Положим
( ) 1Ji ( х, У) . 2 6
<Pi Х, У == ( ) , z == 1, ,..., .
7Ji Xi, Yi
(13)
Имеем:
'Pi(Xj, Yj) == дij, i,j == 1,2,...,6.
Функции 'Pi(X, у), i == 1,2,...,6 возьмем в качестве базисных
в задаче линейной интерполяции, Т.е. приближающую функцию
р f будем искать в виде
6
Pf(x,y) == LQi'Pi(X, у),
i==l
rде коэффициенты Qi определяются из условий (12). Так как
матрица (1.1.3) задачи линейной интерполяции единичная, то
Qi =- f(Xi, Yi), i == 1,2, . . . ,6 и приближающая функция имеет вид
6
Р f(x, У) == L f(Xi, Yi)VJi(X, У).
i==l
173
rЛ8В811. ПРИБЛИЖЕНИЕ Функций 2 X ПЕРЕМЕННЫХ
Значения приближающей функции Р f на стороне треуrоль
ника (например, [( Хl , Уl), (Х2, У2)]) определяются только значе
ниями функции f в точках, лежащих на этой стороне (в Ha
шем примере (Хl,Уl), (Х2,У2) и (Хl,2,Уl,2)). Следовательно,
если треуrольники 1 и Д2 имеют общую сторону, то значе
иия приближающих функций, построенных в каждом из них,
совпадают в точках этой общей стороны. Это позволяет строить
из приближающих функций Pk f , определенных в треуrольниках
k , кусочно квадратическую аппроксимацию Р f , определенную
N
на трианrуляции U Дk, по правилу: Pf(x,y) == Pkf(x,y) при
k==l
(х,у) Е Дk.
Приближение на трианrуляции
Построенную выше приближающую функция Р f , определен
N
иую на трианrуляции D' == U д'k, можно получить также сле
k==l
дующим способом.
Определение. Обозначим через V 2 (D') линейное простран
ство непрерывных в п' функций, являющихся квадратическими
N
в каждом треуrольнике Дi С D' == U Дk.
k==l
Введем базис пространства V 2 (D'):
4? 2) Е V 2 (D'),
(2) )
4?i (Xj, Yj == 6 ij ,
i,j == 1,2,...,Л1 2 ,
(14)
rде {(Xj,Yj)}j==1,2,...,M2 множество вершин и средних точек CTO
рон треуrольников Дk С D' .
Аналитически функцию <p 2) можно задать следующим об
разом. Пусть д'k" 1 == 1, 2, . . . ,ni треуrольники, такие, что
(Xi, Yi) Е D:..k , . Обозначим через 4?k, (Х, у) квадратическую функ
ЦИЮ, определенную в треуrольнике Дk, , равную 1 в точке (Xi, Yi)
174
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
и О в остальных вершинах и серединах сторон д'k, . Такие Функ
ции мы построили ранее, см. (13). Тоrда
'Pk, (х, у), если (х, У) Е д'k,
'P 2)(x,y) ==
О,
ni
если (х, У) U д'k,
1==1
Всякая 9 Е V 2 (D') раскладывается по базису из ФУНКЦИЙ
{<p 2) (х, У) }i==1,2,...,M 2 следующим образом:
М2
у(х, У) == L g(Xi, Yi)<p 2) (х, у).
i==l
"... М2 (2)
Действительно, для у(х,у) == Е g(Xi,Yi)'{Ji (х,у) В силу (14)
i==1
имеем: g(Xj,Yj) == g(Xj,Yj) , j == 1,2,...,М 2 . Следовательно,
у(х, у) является в каждом треуrольнике Дk квадратической ин
терполирующей функцией. В силу корректности задачи линей
ной интерполяции интерполяционный мноrочлен единственнен.
Следовательно, 9 == 9 в каждом треуrольнике д'k, и, значит, в
N
D' == U Дk.
k==l
Рассмотрим задачу нахождения приближающей функции
Р f Е '-'2 (п'), совпадающей с функцией f в точках {(Xj, Yj)} :
Pf(Xj,Yj) == f(xj,Yj), j == 1,2,...,М2. (15)
Функцию Р f будем искать в виде
М2
Pf(x,y) = L Q i'Pi 2 )(x,y),
i==l
{'де коэффициенты Qi определяются из условий (15). В силу (14)
матрица (1.1.3) задачи линейной интерполяции единичная. По
этому Qi == f(Xi, Yi), i == 1,2,..., М 2 И приближающая функция
175
rЛ8В8 П. ПРИБЛИЖЕНИЕ ФУНКЦИЙ 2 X ПЕРЕМЕННЫХ
имеет вид
М2
Р f(x, у) == 2: f(Xi, Yi)<p 2) (х, у).
i==l
2.3.5. Приближение кубическими функциями
Рассмотрим описаННУIО выше задачу линейной интерполяции
в частном случае l == 3 в (2), т.е. приближение кубической Функ
цией.
Приближение на треуrольпике
Обозначим вершины треуrольника Д через (Xl,Yl), (Х2,У2),
(хз, Уз), точки, делящие ero стороны на три равные части, через
(Х4, У4) = (Xl,2,1, Yl,2,l),
(Х6, У6) = (Х2,З,1, Y2,3,l),
(Ха,ув) = (Хl,з,l,Уl,З,l),
(Х5, У5) (Xl,2,2, Уl,2,2),
(Х7,У7) = (Х2,3,2,У2,З,2),
(Xg, yg) = (Хl.З,2, Уl,З,2),
rде Xk,l,s == «3 S)Xk + SХI)/З, Yk,l,s == {(З S)Yk + SУ1)/З, S == 1,2
центр тяжести треуrольника через
(ХI0, У10) (Х1,2,з, Уl,2,з),
{'де Хl,2,з == (Х! +Х2+ Х З)/3, Уl,2,з == (У! +У2+УЗ)/3. Нам требуется
построить приближающую функцию вида (2) удовлетворяющую
условиям
Р f(Xk, Yk) == f(Xk, Yk), k == 1,2, . . . , 10. (16)
Построим базисные функции задачи линейной интерполяции.
Введем (см. рис. 11.2) точки P k == (Xk, Yk), k == 1,2,...,10 и
функции
1/11 (Х, У) == L р2 ,рз (Х, У), 'Ф2(Х, у) == LР1,РЗ (Х, у),
'Фз (Х, у) == L p1 ,Р2 (х, У), 'Ф4 (Х, у) == Lp4,PS (Х, у),
176
92. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫJ\,fИ ЭЛЕМЕНТАМИ
Фl
1/;2
Фз
Рис. 11.2. Схема построения базиса ДЛЯ интерполяции кубически--
ми функциями
'Ф5(Х, у) == L p5 ,P9 (х, у), Ф6(Х, у) == L P5 ,P6 (х, у),
'Ф7(Х,У) = L p4 ,P7(X,y), 1/;в(х,у) == L p7 ,P9(X,y),
'Ф9 (х, у) == Lрб,рs (х, у),
(rде функции L определены в (8)), а также
r]1 (х, у)== 1/;1 (х, У ) )4 (х, У )1/;5 (х, у), r]2 (х, у) == 1/;2 (х, У )'Ф6 (х, У )1/;7(Х, у),
'ТJз(х, у)=='l/Jз(х, у)'Фs(х, у)'Ф9(Х, у), 1]4(Х, у) ==1/;1 (х, у)'Ф2(Х, У)Ф5(Х, у),
1}5(Х, у)=='ФI (х, у)'Ф2(Х, у)'Ф7(Х, у), 'Тl6(X, у) =='Ф2(Х, у)'Фз(х, у)'Ф7(Х, у),
1}7 (х, у)== 'Ф2 (х, У )'Фз (х, у )фg (х, у), 'Т/8 (х, у) = 'Фl (х, У )Фз (х, у )'Ф5 (х, у),
1J9(X, у)=='Фl (х, у)'Фз(х, у)'Ф9(Х, у), 'Т/lо(Х, у)=='Фl (х, у)'Ф2(Х, у)Фз(Х, у).
Положим
( ) 1Ji ( Х, у)
VJi Х, у = ( ) , i = 1, 2, . . . , 1 О.
1Ji Х i , У i
(17)
Имеем:
'.{Ч(Хj,Уj) == 8 ij , i,j == 1,2,...,10.
177
Тлава 11. ПРИБЛИЖЕНИЕ функций 2..Х ПЕРЕМЕННЫХ
Функции <Pi(X,y), == 1,2,...,10 возьмем в качестве базисных
в задаче линейной интерполяции, т.е. приближающую функцию
Р! будем искать в виде
10
Pf(x,y) == LGi<t'i(X,y),
i==l
rде коэффициенты Cti определяются из условий (16). Так как
матрица (1.1.3) задачи линейной интерполяции единичная, то
Qi == f(Xi, Yi), i == 1,2,..., 10 и приближающая функция имеет
вид
10
Р f(x, У) == L f(Xi, Yi)<Pi(X, У).
i==I
Значения приближающей функции Р f на стороне треуrоль
ника (например, [(Xl, YI), (Х2, У2)]) определяются только значе
ниями функци ! в точках, лежащих на этой стороне (в нашем
при мере (XI,YI), (Х2,У2), (XI,2,I,Y1,2,I) И (Xl,2,2,YI,2,2)). Сле
довательно, если треуrольники Дl и 2 имеют общую сторону,
то значения приближающих функций, построенных в каждом из
них, совпадают в точках этой общей стороны. Это позволяет CTpO
ить из приближающих функций P k !, определенных в треуrоль
никах д'k, кусочно кубическую аппроксимацию Р f, определен
N
ную на трианrуляции U Dak, по правилу: Р f(x, у) == Pkf(x, у)
k==1
при (х,у) ЕДk'
Приближение на трианrуляции
Построенную выше приближающую функция Р f , определен
N
ную на трианrуляции п' == U Дk, мо}кно получить также сле
k==l
дующим способом.
178
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТААIИ
Определение. Обозначим через Vз(D') линейное простран
еТБО непрерывных в п' функций, являющихся кубическими в
N
каждом треуrольнике D:.. i С п' == U д.k.
k==l
Введем базис пространства Vз(D'):
<р З) Е vg(D'), <р З)(Хj,Уj) == Jij, i,j == 1,2,...,М з , (18)
rде {(Хj,Уj)}j==1,2,...,Мз множество, состоящее из выбранных
ДЛЯ интерполяции точек треуrольников k С D' (т.е. множе
ство построенных выше точек (Xl, Yl) Е д == Дk, l == 1, 2, . . . , 10,
k==1,2,...,N).
Аналитически функцию <pi 3 ) можно задать следующим об
разОМ. Пусть D:..k" l = 1,2,..., ni треуrольники, такие, что
(Xi, Yi) Е k,. Обозначим через Ч'k, (х, у) кубическую функцию,
определенную в треуrольнике 6,k" равную 1 в точке (Xi, Yi) И о
в остальных выбранных ДЛЯ интерполяции точках (Xj,Yj) Е Ak,.
Такие функции :мы построили ранее, см. (17). Тоrда
<р З)(х,у) ==
О,
ni
если (х,у) U D:..kl
1==1
C{Jk, (Х, у), если (х, у) Е kl
Всякая 9 Е Vз(D') раскладывается по базису из ФУНКЦИЙ
{<р З) (х, у) }i==1,2,...,Мз следующим образом:
Мз
и(х, у) == Е g(Xi, Уi)<Р З) (х, у).
i==l
...... Мз (3)
Действительно, для у(х,у) == Eg(Xi,Yi)<Pi (х,у) В силу (18)
i==l
имеем: g(Xj, УЗ) = у(хз, Yj), j == 1,2,..., М з . Следовательно,
о(х, у) является в каждом треуrольнике Ak кубической интер
полирующей функцией. В силу корректности задачи линейной
179
rлава 11. ПРИБЛИЖЕНИЕ Функций 2 X ПЕРЕМЕННЫХ
интерполяции интерполяционный мноrочлен единственнен. Сле
довательно, 9 == 9 в каждом треуrольнике t:.. k , и, значит, в
N
D' =: U dk.
k==l
Рассмотрим задачу нахождения приближающей функции
Р! Е Vз(D'), совпадающей с функцией f в точках {(Xj,Yj)}:
Pf(Xj,Yj) = f(xj,Yj), j == 1,2,...,М з . (19)
Функцию Р f будем иска'l'Ь в виде
М з
Pf(x,y) = LQi<P 3)(x,y),
i=l
rде коэффициенты D:i определяются из условий (19). В силу (18)
матрица (1.1.3) задачи линейной интерполяции единичная. По..
этому D:i == f(Xi, Yi), i == 1,2,.. . , М з и приближающая функция
имеет вид
М з
р f(x, у) == L f(Xi, Уi)<Р З) (Х, у).
i==l
2.4. Приближение функций методом наименьших
квадратов
В предыдущем разделе (см. 9 2.3) мы построили приближа
ющую функцию, заданную на трианrуляции { k }r==l области
N
п' = U Llk С D, являющуюся мноrочленом степени 1, l == 1,2,3
k==l
на каЖДО 1 из треуrольников D.k и совпадающую с функцией f в
выделенных точках (Xi, Yi), i == 1,2,..., М , этих треуrольников.
Такими выделенными точками являются:
. для 1 == 1 вершины треуrольников Дk (СМ. 2.3.3);
. для l == 2 вершины и середины сторон треуrольников D.k
(см. Э 2.3.4);
180
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
. для 1 == 3 вершины и центры тяжести треуrольников Дk,
а также точки, делящие их стороны на три равные части
(СМ. S 2.3.5).
Однако, если значения функции f известны с некоторой поrреш
ностью, то этот ПОДХОД может дать приближение плохоrо каче
ства. В описываемом ниже алrоритме близость f и ее прибли
жения измеряется в интеrральной норме, и, следовательно, при
ближающая функция будет менее чувствительной к выбросам в
значениях приближаемой функции.
2.4.1. Постановка задачи линейной интерполяции
Обозначим через \Ii == \Ii(D') линейное пространство непре
рЫБНЫХ Б п/ функций, ЯБЛЯЮЩИХСЯ мноrочленом степени l,
N
l == 1, 2,3 в каждом треуrольнике i С D' == U k.
k==l
Пусть требуется построить приближение функции f функци
ей 11/ Е V[(D') такое, что
111 l'tIIlL2(D') == gEi fD') 111 gIIL2(DI), (20)
rде
IIgI!L2(D') == (g, g) DI)' (и, V)L 2 (D') == ! и(х, y)v(x, у) dxdy.
D'
Введем базис пространства Vl(D')
4? ') Е vl (D'), <p ') (х j, Yj) = Oij, i, j == 1, 2, . . . , М" (21)
rде (Xi, Yi), i == 1,2,..., М, выделенные точки треуrольников
t:1 k (см. выше), функции <p O построены для 1 == 1,2, 3 COOTBeT
ственно в 2.3.3 (см. (10), 2.3.4 (см. (14), 2.3.5 (см. (18».
Всякая g Е Vl(D') раскладывается по этому базису следующим
181
rлава 11. ПРИБЛИЖЕНИЕ функций 2 X ПЕРЕlvIЕННЫХ
образом
М,
у(х, у) == L g(Xj, Yj)CPY) (Х, у)
j==l
(см. доказательство для 1 = 1,2,3 соответственно в 9 2.3.3, 9 2.3.4,
2.3.5).
Таким образом, задача (20) может быть сформулирова.на в
следующем виде: найти (aj)j==1,2,...,M , такие, что функция
(22)
м,
(Ilf)(x, у) == L ajcp l) (х, у)
j==l
(23)
удовлетворяет соотношению (20). Как было показано ранее (см.,
например, Э 1.16) в евклидовом пространстве Vi(D') с базисом
{cp I)} ' l минимум (20) реализуется на функции (23), удовлетво
ряющей условиям
(li /, <p l)) L2(D') == (/, <p l») L2(D') ,
Условия (24) представляют собой линейные условия интер
поляции, которым должна удовлетворять приближающая функ
ция (23).
Из (24) и (23) находим:
i == 1, . . . , М[ .
(24)
Ml j
(1) (1) (1)
<Pj (X,y)<Pi (x,y)dxdy.aj== j/(x,y)<P i (x,y)dxdy,
3==1 п' D'
i==1,...,Ml.
(25)
2.4.2. Вычисление системы задачи линейной
интерполяции
Сделаем несколько замечаний, упрощающих вычисление си
стемы (25). Заметим, что носитель функции 'P)l) (х, у) состоит
182
2. ИНТЕРПОЛЯЦИЯ КОНЕЧНЫМИ ЭЛЕМЕНТАМИ
только из треуrольников, которым принадлежит точка (Xj,Yj).
Поэтому произведение <p)I)(X,y)<p l)(x,y) отлично от нуля толь
ко на треуrольниках, которым одновременно принадлежат точки
(Xj, Yj) и (Xi' Yi). Следовательно, система (25) может быть запи
сана в виде
м,
L L f r.p)l)(х,у)r.p l)(х,У)dxdУ'Щ
j==l . { (Xj ,У; )E6 Jc il k
k. (aii,Yi)E k
L J f(x, y)<p !) (х, у) dxdy, i == 1,..., М,.
Дk : (Xi ,Yi) ЕДII; 1:111;
(26)
в i й строке матрицы этой системы столько ненулевых элемен
тов, сколько имеется выделенных точек (Xj,Yj) в треуrольниках,
которым принадлежит точка (Xi, Yi). Отметим, что для получе
ИИЯ ленточноrо вида матрицы системы важен способ нумерации
точек (Xi,Yi), i == 1,2,...,М , .
В левой части системы (26) стоят интеrралы от мноrочленов
степени не выше 21, которые вычисляются аналитически. Для
вычисления правой части функция f на каждом треуrольнике
Дk приближается мноrочленной функцией степени 1 + 1 либо
(чаще) степени l, но построенной по точкам, не совпадающим
ни с одной из точек (Xi,Yi), i == 1,2,...,М, (о причинах TaKoro
выбора интерполирующей функции в одномерном случае было
сказано в 3 1.16.4).
183
проrРАММА КУРСА
проrРАММА КУРСА
1. Постановка задачи линейной интерполяции (ЗЛИ). Теорема
о корректности зли. Представление решения ЗЛИ
2. Обусловленность базиса. Оценка относительной поrрешности
линейной комбинации элементов базиса через относительную
поrрешность коэффициентов этой линейной комбинации.
3. Интерполяционный мноrочлен Лаrранжа. Ero единствен
ность. Оценка числа арифметических операций, необходимо
ro для вычисления значения интерполяционноrо мноrочлена
Лаrранжа в точке.
4. Определение разделенных разностей. Формула для непосред
cTBeHHoro представления разделенной разности через зна
чения функции. Симметричность разделенной разности как
функции своих aprYMeHToB. Линейность разделенной разно
сти как Функционала.
5. Вычисление интерполяционноrо мноrочлена Лаrранжа, по
cTpoeHHoro по k точкам, через интерполяционный мноrочлен
Лаrранжа, построенный по k 1 точке. Интерполяционная
формула Ньютона.
6. Алrоритм вычисления коэффициентов интерполяционноrо
мноrочлена в форме Ньютона. Орrанизация процесса вычис"
лений и хранения промежуточных результатов. Оценка числа
арифметических операций. Алrоритм вычисления значения
интерполяционноrо мноrочлена в форме Ньютона в точке.
Оценка числа арифметических операций.
184
проrРАММА КУРСА
7. Интерполяция "движущимися" мноrочленами (алrоритм сдви
ra представления интерполяционноrо мноrочлена в форме
Ньютона). Оценка числа арифметических операций.
8. Оценка поrрешности интерполяционной формулы Ньютона с
представлением остаточноrо члена в виде произведения раз
деленной разности и фиксированноrо мноrочлена.
9. Оценка поrреmности интерполяционной формулы Ньютона с
представлением остаточноrо члена в виде произведения про
изводной функции В некоторой точке и фиксированноrо MHO
rочлена.
10. Представление разделенной разности через производную
функции. Определение разделенных разностей с кратными
узлами. Непрерывность разделенной разности как функции
своих aprYMeHToB.
11. Постановка задачи интерполяции с кратными узлами. Един
ственность интерполяционноrо мноrочлена. Теорема о по
строении интерполяционноrо мноrочлена в форме Ньютона.
12. Оценка поrреmности интерполяции с кратными узлами с
представлением остаточноrо члена в виде произведения раз
деленной разности и фиксированноrо мноrочлена.
13. Алrоритм вычисления коэффициентов интерполяционноrо
МНОI'очлена с кратными узлами. Орraнизация процесса BЫ
числен ий и хранения промежуточных результатов. Оценка
числа арифметических операций. Алrоритм вычисления 3Ha
чения интерполяционноrо мноrочлена с кратными узлами в
точке. Оценка числа арифметических операций.
14. Алrоритм вычисления значений производных мноrочлена в
форме Ньютона в точке. Оценка числа арифметических опе
раций.
185
ПРОТРАММА КУРСА
15. Мноrочлены Чебышева. Реккурентная формула. Аналитиче
ская форма, нули мноrочленов, экстремумы. Теорема о MHO
rочлене, наименее уклоняющемся от нуля.
16. Минимизация поrрешности интерполяции за счет выбора уз
лов интерполяции. Интерполяция по нулям мноrочленов Ч
бышева. Неулучшаемость оценки поrрешности в рассматри
ваемом классе' оценок остаточноrо члена. Оценка снизу и
сверху поrрешности интерполяции по нулям мноrочленов Че
бышева через поrрешность наилучшеrо paBHOMepHoro. при
ближения (без доказательства). Теорема Джекеона (без дo
казательства) .
17. Разложение по мноrочленам Чебышева с использованием дис
KpeTHoro скалярноrо произведения. Ортоrональность MHoro
членов Чебышева по этому скалярному произведению.
18. Алrоритм вычисления коэффициентов разложения по MHoro
членам Чебышева. Орrанизация процесса вычислений и xpa
нения промежуточных результатов. Оценка числа арифмети
ческих операций. Алrоритм вычисления значения аппрокси
мирующеrо мноrочлена в точке. Оценка числа арифметиче
ских операций.
19. Теорема о совпадении интерполяционноrо мноrочлена, по
CTpoeHHoro по нулям мноrочленов Чебышева, с аппроксими
рующим мноrочленом, полученным разложением по MHoro
членам Чебышева с использованием дискретноrо скалярноrо
произведения.
20. Преимущества кусочно мноrочленной аппроксимации. Ky
сочно линейная интерполяция. Оценка поrрешности. OцeH
ка поrрешности через поrрешность наилучшеrо paBHolvIepHoro
приближения в классе непрерывных ломаных линий.
186
ПРОТРАММА КУРСА
21. Кусочно линейная аппроксимация по методу наименьших
квадратов. Построение базиса, постановка задачи, вычисле
иие матрицы системы.
22. Оценка поrрешности кусочно линейной аппроксимации по ме...
тоду наименьших квадратов через поrрешность наилучшеrо
paBHoMepHoro приближения в классе непрерывных ломаных
линий.
23 Аппроксимация мноrочленами по методу наименьших KBaд
ратов в пространстве со специальным скалярным произведе
нием. Построение базиса из мноrочленов Чебышева, ero ор...
тоrональность относительно этоrо скалярноrо произведения,
вычисление коэффициентов аппроксимирующей функции.
24. Теорема о кусочн линейной интерполяции неrладких функ...
ций на специальных сетках (без доказательства). Доказатель...
ство теоремы. в случае функции М на отрезке [ 1, 1] .
25. Общая схема кусочной интерполяции кубическими мноrочле
нами. Алrоритм вычисления коэффициентов интерполирую..
щих кубических мноrочленов.
26. Кусочная интерполяция кубическими мноrочленами Эрмита.
Выбор параметров. Простейшие свойства приближающей фу...
нкции. Оценка поrрешности (без доказательства).
27. Кусочная интерполяция кубичеСКИl\1И мноrочленами Бесселя.
Выбор параметров. Простейшие свойства приближающей фу--
нкции. Оценка поrрешности (без доказательства).
28. Кусочная интерполяция кубическими мноrочленами методом
Акимы. Выбор параметров. Простейшие свойства приближа..
ющей функции. Оценка поrрешности (без доказательства).
29. Кусочная интерполяция кубическими мноrочленами с ис
пользованием разделенных разностей. Выбор параметров.
187
проrРАММА КУРСА
Простейшие свойства приближающей функции. Оценка по
rрешности (без доказательства).
30. Определение сплайна. Интерполяция кубическими сплайна..
ми. Выбор параметров, построение матрицы системы. Про
стейшие свойства матрицы системы и приближающей функ...
ции. Оценка поrрешности (без доказательства).
31. Определение недостающих для кусочно кубической интерпо-.
ляции rраничных условий по известным значениям первой
либо второй производной функции в rраничных узлах, eCTe
ственные rраничные условия. Определение недостающих па...
раметров в случае кусочной интерполяции кубическими MHO
rочленами и построение дополнительных уравнений в случае
интерполяции кубическими сплайнами.
32.. Определение недостающих для кусочно",кубической интерпо...
ляции rраничных условий из условия "отсутствия узла" в при
rраничных узлах. Определение недостающих параметров в
случае кусочной интерполяции кубическими мноrочленами
и построение дополнительных уравнений в случае интерпо...
ляции кубическими сплайнами.
33. Определение недостающих для кусочно кубической интерпо
ляции rраничных условий при ПОМОIЦи введения дополни
тельноrо узла рядом с rраничными узлами либо экстрапо
ляции в приrраничных узлах. Определение недостающих па
раметров в случае кусочной интерполяции кубическими MHO
I'очленами и построение дополнительных уравнений в случае
интерполяции кубическими сплайнами.
34. Общая схема кусочной интерполяции параболическими MHO
I'очленами. Алrоритм вычисления коэффициентов интерпо
лирующих квадратичных мноrочленов.
188
проrРАММА КУРСА
35. Определение сплайна. Интерполяция параболическими сплай
нами. Выбор параметров, построение матрицы системы. Про...
стейшие свойства матрицы системы и приближающей функ...
ЦИИ. Оценка поrрешности (без доказательства).
36. Определение недостающих для интерполяции параболичес..
кими сплайнами уравнений по известным значениям первой
производной функции в rраничных узлах.
37. Определение недостающих для интерполяции параболичес..
кими сплайнами уравнений по известным значениям второй
производной функции В rраничных узлах, естественные rpa
ничные условия.
38. Определение недостающих для интерполяции параболичес..
кими сплайнами уравнений из условия "отсутствия узла" в
приrраничных узлах.
39. Определение недостающих для интерполяции параболически...
ми сплайнами уравнений при помощи введения дополнитель
Horo узла рядом с rраничными узлами либо экстраполяции в
приrраничных узлах.
40. Интерполяция тензорными произведениями. Построение ба
зиса из тензорных произведений в пространстве функций и
в пространстве функционалов. Постановка задачи линейной
интерполяции теНЗ0РНЫМИ произведениями. Теорема о KOp
ректности. Алrоритм интерполяции тензорными произвед
ниями.
41. Интерполяция теНЗ0РНЫМИ произведениями мноrочленов. Ин
терполяционный мноrочлен Лаrранжа, разделенные разности
и интерполяционная формула Ньютона для функции 2 x пе
ременных.
42. Аппроксимация тензорными произведениями кусочно"линей
ных функций. Интерполяция и метод наименьших квадратов.
189
проrРАММА КУРСА
43. Интерполяция тензорными произведениями кусочно куби
ческих функций. Вычисление функционалов теНЗ0РНЫХ
произведений. Орrанизация хранения данных в памяти ЭВМ.
44. Интерполяция тензорными произведениями кусочно квадра
тических функций. Вычисление функционалов теНЗ0РНЫХ
произведений. Орrанизация хранения данных в памяти ЭВМ.
45. Постановка задачи линейной интерполяции функций 2 x пе
ременных методом конечных элементов. Способы построения
трианrуляции области.
46. Постановка задачи линейной интерполяции ФУНКЦИЙ 2 x П
ременных, заданных в треуrольнике. Приближение функций
в прямоуrольном треуrольнике.
47. Приближение функций 2 x переменных конечным:и элемента
ми l ro порядка. Построение приближения в треУI'ольнике и
на трианrуляции в целом.
48. Приближение функций 2..х переменных конечными элемента..
ми 2 ro порядка. Построение приближения в треуrольнике и
на трианrуляции в целом.
49. Приближение функций 2 x переменных конечными элеl'.1ента
ми 3 I'o порядка. Построение приближения в треуrольнике и
на трианrуляции в целом.
50. Приближение функций 2 x переменных конечными элемента
ми методом наименьших квадратов. Постановка задачи ли
нейной интерполяции, вычисление матрицы системы.
190
ЛИТЕРАТУРА
1. Н.С. Бахвалов, Н.П. Жидков, r.M. Кобельков. Численные Me
тоды. М., "Наука", 1987.
2. К. Де Бур. Практическое руководство по сплайнам. М., "Pa
дио и связь", 1985.
3. ю.с. Завьялов, Б.И. Квасов, в.л. Мирошниченко. Методы
сплайн Функций. М., "Наука", 1980.
4. С.Б. Стечкин, Ю.Н. Субботин. Сплайны в вычислительной
математике. М., "Наука", 1976.
191
'у чебное издание
Боrачев Кирилл Юрьевич
Практикум на ЭВМ.
Методы приближения функций
Издание третье,
переработанное и дополненное
М.: Издательство ЦПИ при механико математическом
факультете Mry, 2002. 192 с.
Подписано в печать 04.03.2002 {'.
Формат 60 х 90 1/16. Объем 12 п.л.
Заказ 10. Тираж 400 экз.
Издательство ЦПИ при механик математическом
факультете Mry
{'. Москва, Воробьевы {'оры.
Лицензия на издательскую деятельность ид В 04059,
от 20.02.2001r.
Отпечатано с ОрИI'инал макета на типоrрафском
оборудовании механико-математическоrо факультета и
Франко русскоrо центра им. А.М. Ляпунова.