Автор: Марков С.Н.
Теги: математика современная математика история математики математика древнего мира математика античного мира
ISBN: 5-7430-0496-Х
Год: 1995
Текст
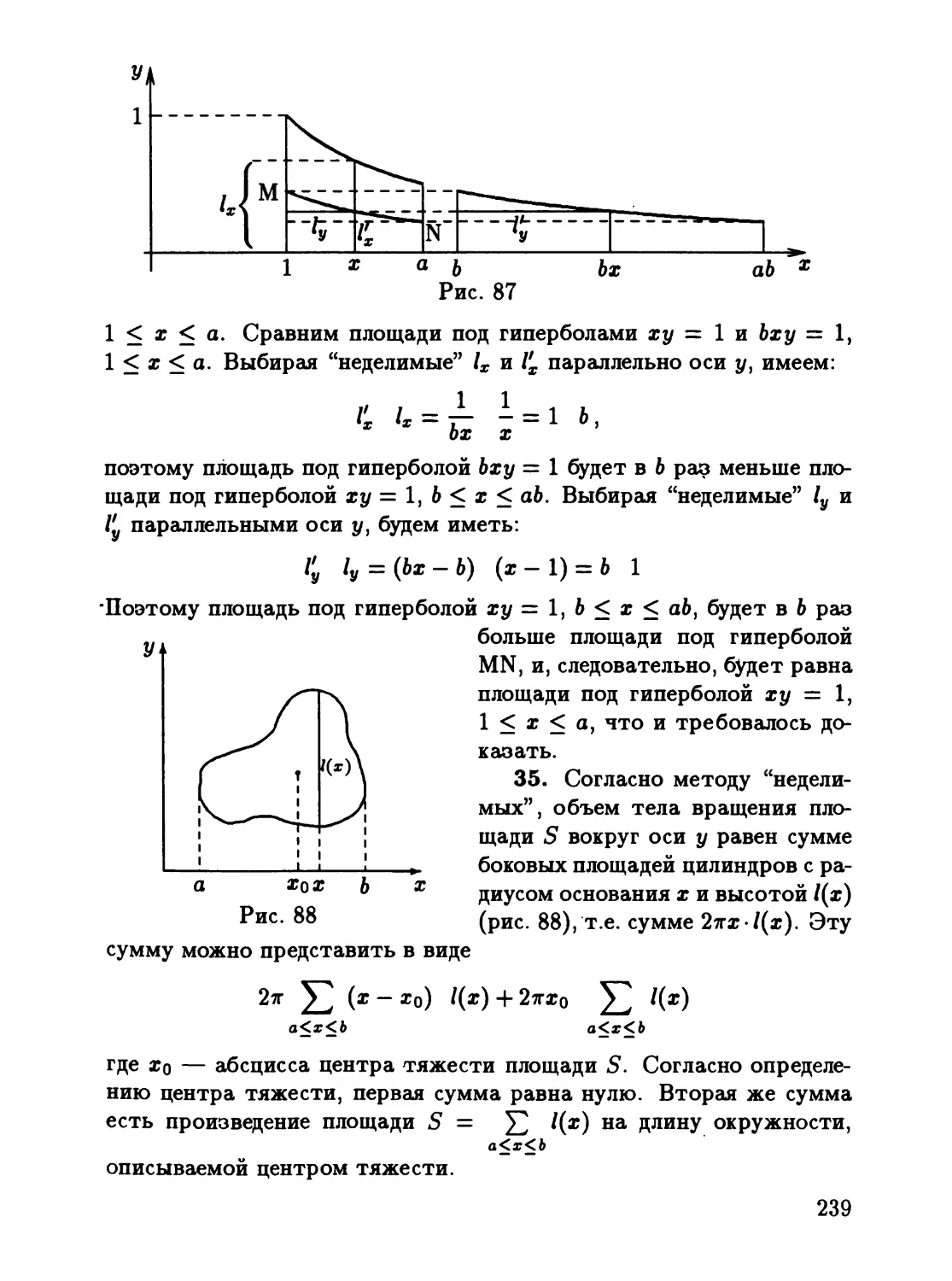
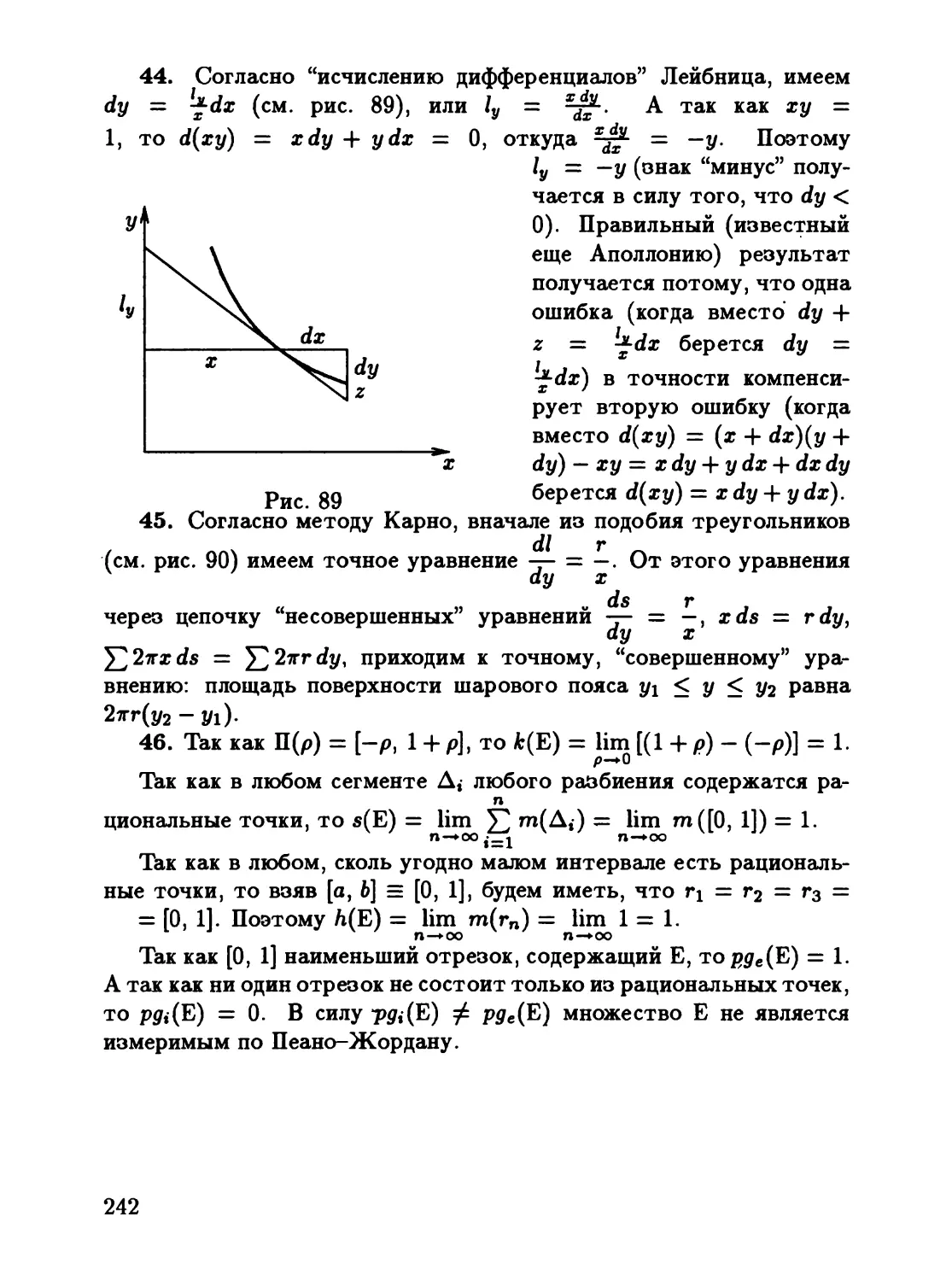
t
<
...
:s:
о
u
u
t:l.t
!
,
с
.
=
.
.
С.Н. Марков
КУРС ИСТОРИИ
МАТЕМАТИКИ
Учебное пособие
Рекомендовано Тосударственным комитетом
Российской Федерации по высшему обра:зова
нию в' качестве учебноrо пособия для CTyдeH
тов ВЫСШИХ учебных заведений, обучающихCJl
по направлению "Математика"
ИОАаТeJlЬСТВО Иркутскоrо университета
1995
УДК 51(09)(075.8)
ББК В1rя73
М25
Представлено изданию
ИР УТСIИМ rосударственным университетом
Ио ание осущеСТВJlево при по ержке Российсmrо фов а
фув амевтапьвых исспе овавий по проекту N 95 О6 18708б.
Научный peдa TOp
В. и. Машанов, Iаид. физ. мат. Hay , доц.
Рецензенты:
и. r. Башма ова, ДO T. физ. мат. Hay , проф.,
Н. М. Матвеев, ДO T. физ. мат. Hay , проф.
Маржов С.Н.
М25 Курс истории математики: Учеб. пособие. Иркутск: ИЗД'
во Иркут. YH a, 1995. 248 с. Библ. 39, рис. 99.
В данном учебном пособии изложение истории математи и про-
водится по отдельным специальным темам, таким a "Алrебра"
"rеометрия", "Анализ" В аждой теме рассматриваются OH peT-
ные вопросы, дополняющие основные математичес ие ypcы в уни"
верситетах и пединститутах и позволяющие "пере инуть мости "
между ш ольной и вузовс ой математи ой. Изложение сопровожда..
етCJI большим оличеством рисунков и примеров. В пособие в лю--
чены вопросы и задания для семинарс их заНJlТИЙ и упражнения
для самостоятельной работы.
Предназначено для студентов старших ypCOB университетов и
пединститутов, для преподавателей математи и и для ш ольни ов
старших лассов физматш ол.
м 1602000000 03 95
М179(03) 95
ISBN 5 7430 0496 X
ББК В1rя73
@Map OB С.Н., 1995 r.
Содержание
ПРЕДИСЛОВИЕ
7
rпава 1. ЧЕТЫРЕ ПЕРИОДА В ИСТОРИИ МА ТЕМА-
ТИКИ
1..1 ПЕРИОД НАКОПЛЕНИЯ НА ЧАЛЬНЫХ MATEMA
ТИЧЕСКИХ СВЕДЕНИЙ
1.1.1 Математика Древнеrо Еrипта d
1.1.2 Математика Д.ревнеrо Вавилона 9
1.2 ПЕРИОД МАТЕМАТИКИ ПОСТОЯННЫХ ВЕЛИЧИН 10
1.2.1 Математика Древней f'pеции, эллинистических
стран и Римской империи 11
1.2 2 Математика средневековоrо Китая 12
1.2.3 Математика средневековой Индии 13
1.2.4 Математика стран ислама .13
1.2.5 Математика средневековой Европы 14
1.2.6 Математика эпохи Возрождения 15
1.3 ПЕРИОД МАТЕМАТИКИ ПЕРЕМЕННЫХ ВЕЛИЧИН 16
1.3.1 Математика XVII века 16
1.3.2 Математика XVIII века 17
1.4 ПЕРИОД СОВРЕМЕННОЙ МАТЕМАТИКИ 17
1.5 ЧЕТЫРЕ СТУПЕНИ В ПРЕПОДАВАНИИ MAT
МАТИКИ 19
Вопросы и задания 20
!Лава 2. ЧИСЛО 21
2.1 ПРОИСХО)J(ДЕНИЕ ПЕРВЫХ НАТУРАЛЬНЫХ ЧИ
СЕЛ 21
2.2 ПРИНЦИПЫ И30БР А)J(ЕНИЯ ЧИСЕЛ, ИЛИ ПРИН..
ЦИПЫ НУМЕРАЦИИ 23
2.3 ВВЕДЕНИЕ ДРОБЕЙ . 24
2.4 "ТЕОРIIЯ ОТНОШЕНИЙ" ПИФАТОРЕЙЦЕВ 27
3
IПава 3. АЛI'ЕБР А
3.1 СОЗДАНИЕ АЛТЕБРЫ КАК СИМВОЛИЧЕСКОТО
ИСЧИСЛЕНИЯ 43
3.1.1 Зачатки алrебры в математике Древнеrо Вавилона. 43
3.1.2 АJ!rебра Диофанта. 43
3.1.3 "Введение в аналитическое искусство" Ф. Виета 44
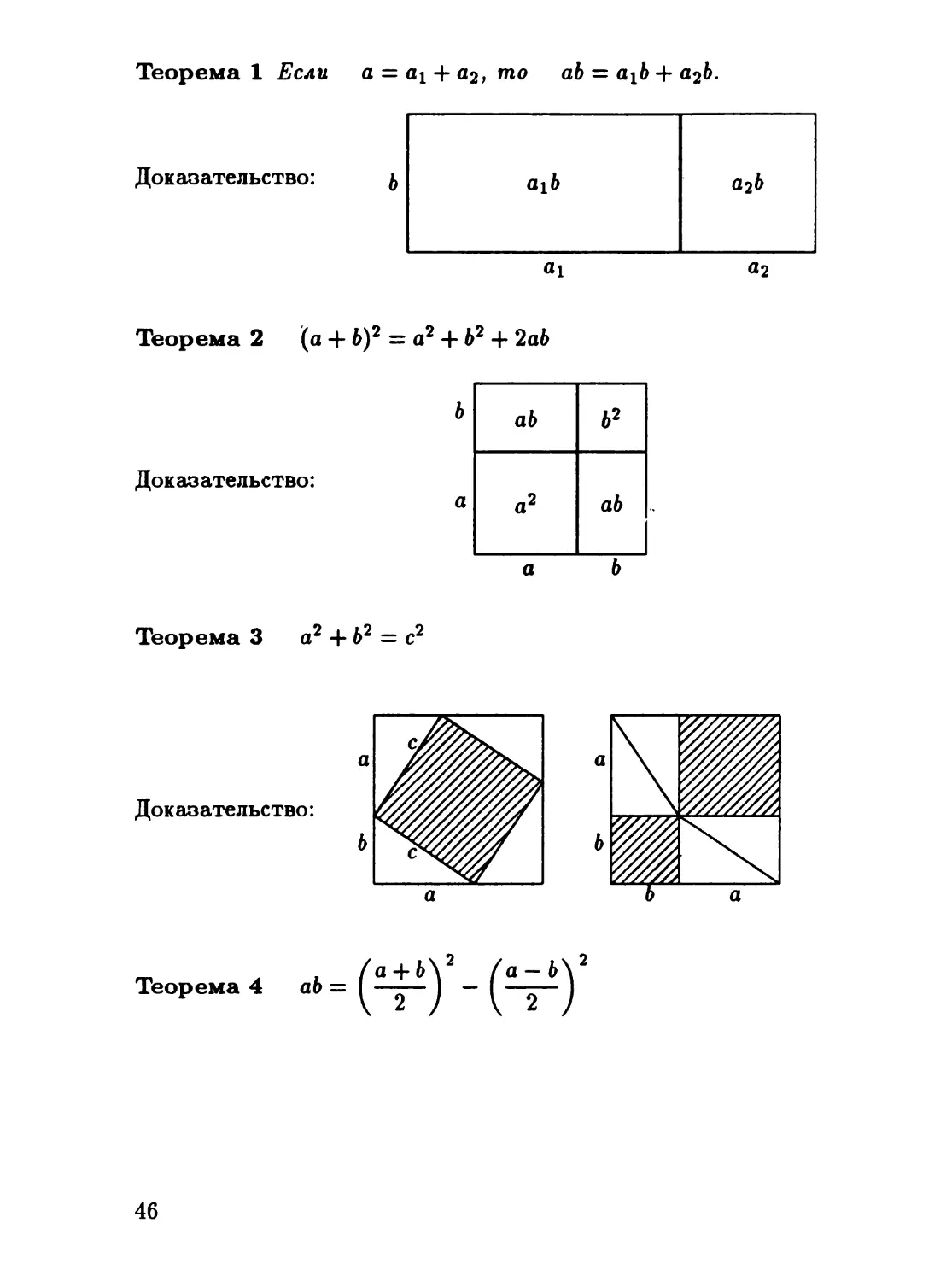
3.2 ТЕОМЕТРИЧЕСКАЯ АлrЕБРА ПИФАТОРЕЙЦЕВ 45
3.2.1 Предмет rеометрической алrебры 45
3.2.2 Первые неразрешимые задачи 48
3.2.3 3амечания 52
3.3 ПРОБЛЕмА РЕШЕНИЯ В РАДИКАЛАХ АЛТЕБРА..
ИЧЕСКИХ УРАВНЕНИЙ
3.3.1 Решение в радикалах алrебраических уравнений
2 й, 3 й и 4 й степеней
3.3.2 Попытки решения в радикалах алrебраичесiCИХ
уравнений степени n > 5. "Размышление об ал
rебраическом решении уравнений" ж. Лаrранжа.
Теоремы п. Руффини и Н.Х. Абеля
3.3.3 Основная теорема теории rалуа. Решение ал
rебраических уравнений в радикалах С,точки зре--
ния теории rалуа. Решение задач rеометрической
алrебры с точки зрения теории rалуа.
3.4 НЕКОТОРЫЕ ПУТИ ФОРМИРОВАНИЯ НОВОЙ
АЛТЕБРЫ ВО ВТОРОЙ ПОЛОВИНЕ XIX ВЕКА
2.5 ОТКРЫТИЕ НЕСОИ3МЕРИМОСТИ
2.6 ТЕОРИЯ ОТНОШЕНИЙ ЕВДОКСА
2.7 ВВЕДЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ
2.8 ВВЕДЕНИЕ МНИМЫХ ЧИСЕЛ.
2.9 ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕнноrо ЧИСЛА
Вопросы и задания.
Вопросы и задания.
29
31
33
34
37
41
43
55
55
57
60
-
69
74
IПава 4. I'ЕОМЕТРИЯ 76
4.1 ПРОИСХО)[(ДЕНИЕ ПЕРВ IХ ТЕОМЕТРИЧЕСКИХ
Фиr тР И ТЕЛ 76
4.2 ТЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ
В ДРЕВНЕМ ЕТИПТЕ И ВАВИЛОНЕ . . . . . . . . . .. 77
4
4.3 ПРЕВР АЩЕНИЕ ТЕОМЕТРИИ В ДЕДУКТИВНУЮ
СИСТЕМУ
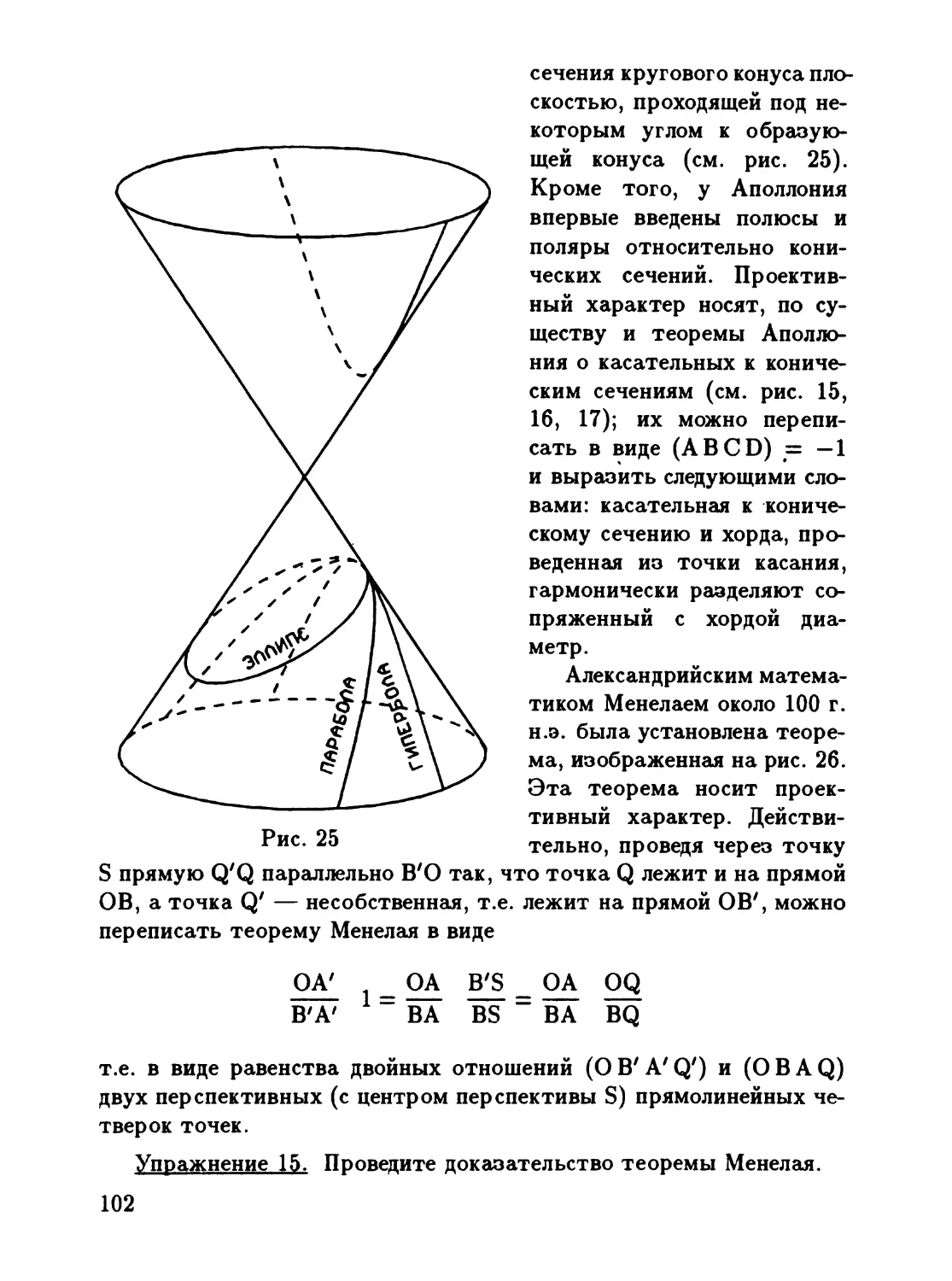
4.4 "КОНИЧЕСКИЕ СЕЧЕНИЯ" АПОЛЛОНИЯ
4.5 СОЗДАНИЕ АНАЛИТИЧЕСКИЙ ТЕОМЕТРИИ
4.6 СОЗДАНИЕ КЛАССИЧЕСКОЙ ДИФФЕРЕНЦИАЛЬ
НОЙ ТЕОМЕТРИИ
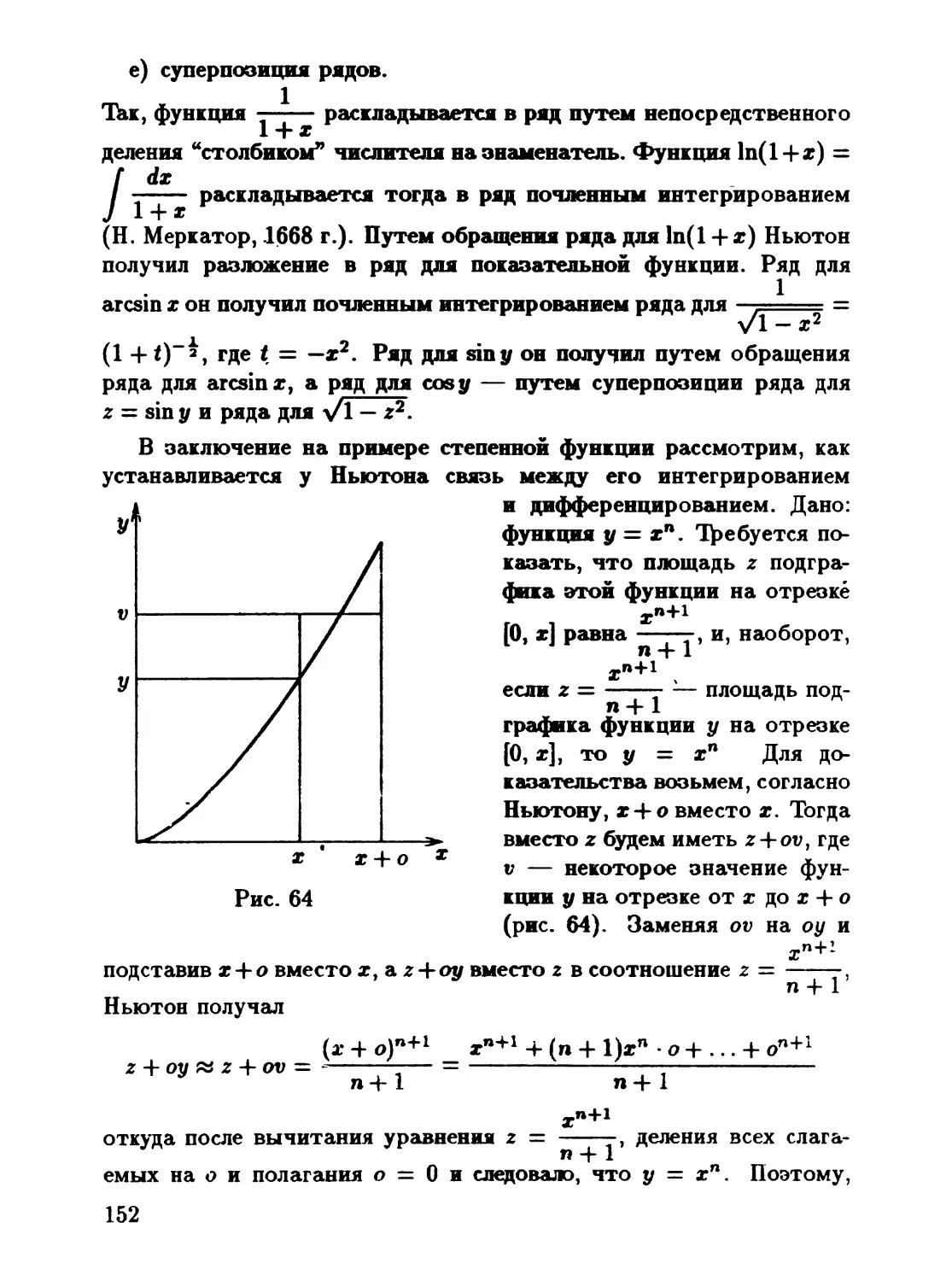
4.7 ТЕОМЕТРИЯ НА ПРОЕКТИВНОЙ ПЛОСКОСТИ
4.8 ПРЕДЫСТОРИЯ ПРОЕКТИВНОЙ rЕОМЕТРИИ
4.9 РАЗВIIТИЕ ПРОЕКТИВНОЙ ТЕОМЕТРИИ
В ПЕРВОЙ ПОЛОВИНЕ XIX ВЕКА
4.10 ПРОЕКТИВНАЯ КЛАССИФИКАЦИЯ ТИПОВ
ТЕОМЕТРИН ПО Ф. КЛЕЙНУ
Вопросы и задания.
78
80
85 Н
89
98
101
109
118
126
128
lЛава 5. АНАЛИЗ
5.1 МЕТОД "ИСЧЕРПЫВАНИЯ" ЕВДОКСА. ИНТЕ--
ТРАЛЬНЫЕ И ДИФФЕРЕНЦИАЛЬНЫЕ МЕТОДЫ
АРХИМЕДА 128
5.2 ИНТЕТРАЛЬНЫЕ И ДИФФЕРЕНЦИАЛЬНЫЕ ME
ТОДЫ В ЕВРОПЕ ПЕРВОЙ ПОЛОВИНЫ XVII ВЕКА 135
5.2.1 IIнтеrральные методы И. Кеплера 136
5.2.2 Метод "неделимых" 137
5.2.3 Ilнтеrральный метод п. Ферма 143
5.2.4 Интеrральный метод Б. п'аСКaJIЯ 144
"vJ .2.5 Метод касательных r rалилея Ж. Роберваля 145
5.2.6 Метод нормалеll и касательных Р Декарта 147
5.2.7 Метод экстреМУ IОВ и касательных п. Ферма. 148
5.2.8 О связи между интеrральными и дифференциаль
ными методами 149
5.3 СО:ЗДАНlfЕ ОСНОВ ДИФФЕРЕНЦИАЛЬНОТО И
ИНТЕrРАЛЬНОТО ИСЧИСЛЕНИЯ в РАБОТАХ
If. НЬЮТОНА И Т.В. ЛЕifБНIIЦ.А 150
5.3.1 Метод "флюксий" и степенных рядов и. Ньютона 150
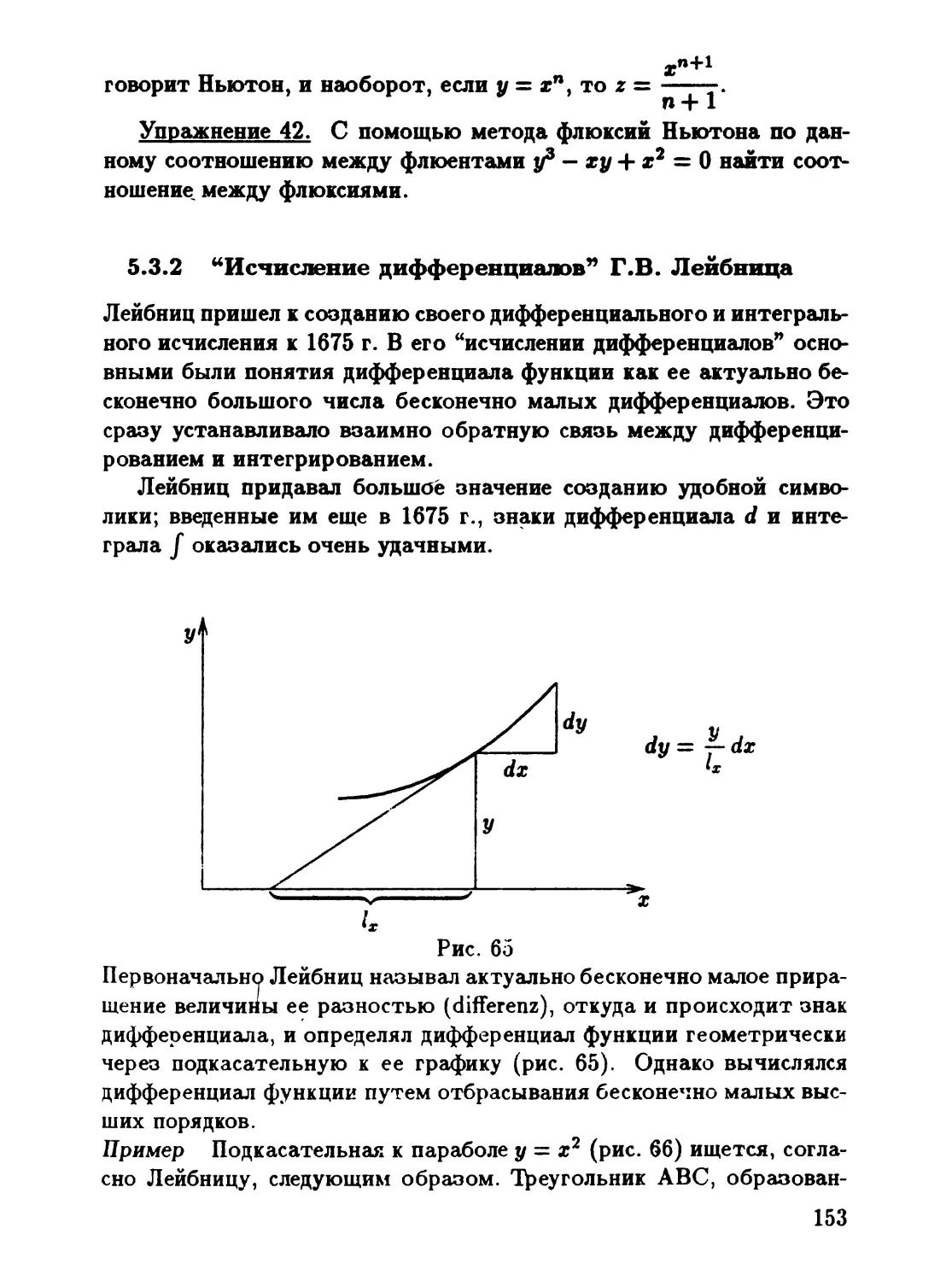
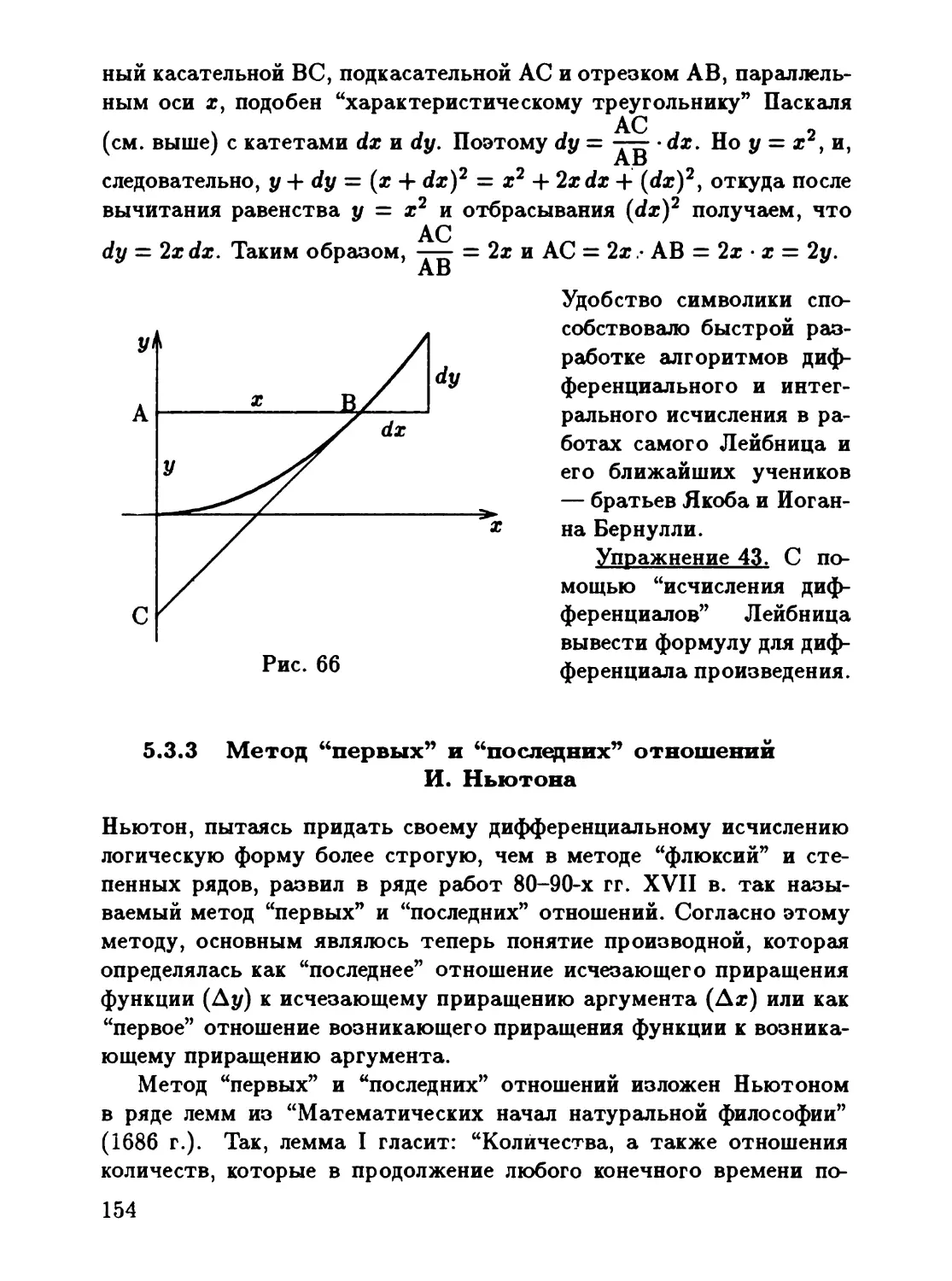
5.3.2 "Исчисление дифференциалов" r.B. Лейбница 153
5.3.3 fетод "первых" и "последних" отношений и. Hькr
тона 154
5.4 ПРОБЛЕМА ОБОСНОВ..4НИЯ ДIfФФЕРЕНЦIfАЛЬ
HOrO lfСЧИСЛЕНИЯ. "А НА ЛИСТ' ДХ(. БЕРКЛИ .. 155
5
5 5 КРАТКАЯ ХАРАКТЕРИСТИКА ДИФФЕРЕНЦИ
АЛЬНОТО И ИНТЕТРАЛЬНОТО ИСЧИСЛЕНИЯ В
XVIII В. 163
5.6 ПЕРЕСТРОЙКА ОСНОВ МАТЕМАТИЧЕСКОТО
АНАЛИЗА В XIX ВЕКЕ 167.
5.7 ИНТЕТРАЛЫ РИМАНА И ДАРБУ 179
5.8 ВОЗНИКНОВЕНИЕ ПОНЯТИЯ МЕРЫ МНОХ(ЕСТВА 184
5.9 МЕРА И ИНТЕТРАЛ ЛЕБЕТА . 187
5.10 ПРОБЛЕМА ВОССТАНОВЛЕНИЯ ПРИМИТИВНОЙ
ФУНКЦИИ 191
5.11 О ПРЕПОДАВАНИИ ОСНОВ АНАЛИЗА (дополнение) 192
Вопросы и задания. 196
v
[Лава 6. ИСТОРИЯ ОТЕЧЕСТВЕННОИ
МА ТЕМАТИКИ 198
6.1 МАТЕМАТИЧЕСКИЕ ЗНАНИЯ НА РУСИ
В X XVI ВЕКАХ 198
6.2 МА ТЕМА ТИЧЕСКИЕ Р ТКОПИСИ XVII ВЕКА 202
6.3 ОРТАНИЗАЦИЯ ШКОЛ. 204
6.4 "АРИФМЕТИКА" Л.Ф. МАТНИЦКОТО 206
6.5 ОСНОВАНИЕ АКАДЕМИИ НАУК 209
6.6 ОРТ А НИЗАЦИЯ УНИВЕРСIfТЕТОВ 210
6.7 Н.И. ЛОБА ЧЕВСКИЙ (1792 185б). 212
6.8 М.В. ОСТРОТРАДСКИЙ (1801 18бl) 215
6.9 п.л. ЧЕБЫШЕВ (1821 1894) 217
u
Р А3БОР УПР А:>КНЕНИИ 221
ЛИТЕР А ТУР А 245
Моим родителям,
сельским учителям
ПРЕДИСЛОВИЕ
Учебное пособие составлено в объеме небольшоrо (в пределах 40
часов) курса истории математики для универс.итетов и пединститу
тов.
Изложение истории математики ПРОВодИтtя не п историческим
периодам, а по отдельным темам. Каждой теме соответствует o
дельная rлава пособllЯ. rлава 1 является вводной, в ней дается KpaT
кая характеристика основных периодов в развитии математики.
rлавы 2 5 относительно независимы друr от друrа. rлава 6 npeд
На3начается для самостоятельноrо ознакомления.
В конце каждой rлавы указаны вопросы и задания, которые же
лательно разобрать на семинарских занятиях.
В пособие включено значительное число упражнений, их краткий
ра3бор помещен в конце пособия.
Список литературы минимальный;'ссылки даются на ближайший
источник более подробноrо изложения соответствующеrо вопроса.
Работа выполнядась автором при начальном руководстве проф.
В. В. Васильева, ныне покойноrо. Ему, а также проф Н. М. MaTBe
еву, проф. и. r Башмаковой и доцентам В. и. Машанову, Е. п. Во--
кмельдер и ю. r Пензину автор выражает свою rлубокую блаrодар
ность. Отдельную блаrодарность автор выражает сотруднику АК
"РУСИА Петролеум" А.... С. Яшину за тщательную подrотовку Ma
кета пособия, а также иркутской фирме "I»адиент" (rенеральный
директор С.В. Иванов) за содействие в издании.
I'пaBa 1
ЧЕТЫРЕ ПЕРИОДА
В ИСТОРИИ МАТЕМАТИКИ
в истории математики принято Ра3личать следующие четыре пери
ода: период накопления начальных математических сведений, период
математики постоянных величин, период математики переменных
величин и период современной математики.
1.1 ПЕРИОД НАКОПЛЕНИЯ
НА чАльныIx МАТЕМАТИЧЕСКИХ
u
СВЕДЕНИИ
.
Этот период заканчивается в Древней fpеции VI в. дО Н.Э. ОН ВКЛI<r
чает в себя происхождение первых натуральных чисел и первых recr
метрических фиrур и тел, математику Древнеrо Еrипта и MaTeMa
тику Древнеrо Вавилона.
1.1.1 МатемаТИlCа Древвеrо Еrипта
Большинство математических текстов, сохранившихся в памят
никах Древнеrо Еrипта, написаны на папирусе. Папирус хрупкий,
поэтому сохранились только те тексты, которые положены в пира
миды. Важнейшими из цощедших До нас математических текстов
ЯВЛЯются так называемые папирус Райнда (содержит 84 задачи) и
Московский папирус (содержит 25 задач).
Носителями научных знаний в Древнем Еrипте были "писцы"
чиновники, состоявшие на rосударственной или храмовой службе.
Служилая интеллиrенция, rордившаяся своей образованностью, BЫ
полнила в древнем обществе различные административнcrхозяйст
венные функции. В папирусах XX XIX вв. дО Н.Э. зафиксированы
8
должности писца дома документов, войска, царских работ, надзира
теля писцов, начальника сокровищницы и Т.Д. "Писец он PYK
водит всеми, и не обложена налоrами работа в письме. На нее нет
налоrов. Заметь себе это", rоворится в одном из мноrих тек..
стов, восхваляющих привилеrированное положение писца в Древнем
Еrипте. "Это больше, чем любая должность, и вет paBBoro им в
стране этой" Писцы обучались в специальных школах. Имелись и
высшие писцовые школы, которые торжественно вазывались "дома
жизни"
Математические знания ApeBHero писца позволяли ему ПРОИЗ80--
дить расчеты при строительных работах, сборе HaJIOrOB, разделе
имущества, обмене и распределении продуктов, измерении площа..
дей полей, объемов плотин, зернохранилищ и Т.П. Все внимание C
средоточено при этом на вычислениях с конкретными количествами;
числа как таковые, равно как и методы решения, не становятся еще
предметом рассмотрения, задачи rруппируются поэтому не по M
тодам решений, а по темам (задачи на припек, задачи на емкость
зернохранилищ, задачи на площадь поля и т.д.). Каждая задача p
шается заново, без каких либо пояснений, в числах. Лишь иноrда
дается проверка найденноrо решения.
Анализ математических текстов позволяет утверждать, что Ma
тематика Древнеrо Еrипта представляла собой совокупность зна
ний, еще не расчленившуюся на арифметику и rеометрию 1I BЫCTY
пающую прежде Bcero как собрание примеров решения простейших
прикладных задач.
1.1.2 МатемаТИlCа Древвеrо Вавилова
Источниками для изучения математики Древнеrо Вавилона явля
ются математические клинописные тексты, обнаруженные при apxe
олоrических раскопках или найденные случайно местными жителями
в развалинах старых сооружений. Среди ра3розненноrо, распылен
Horo по музеям мира множества rлиняных табличек самых раоных
зпох, от начала 111 тысячелетия дО Н.З. дО 1 В"н.з., известно примерно
150 с текстами математических задач и 200 с числовыми таблицами.
Но.сителями научных знаний в Древнем Вавилоне были, как и в
Древнем Еrипте, писцы. Они руководили общественными работами,
занимались учетом хозяйства, составлением ToproBblx документов и
деловой перепиской. Писцы были тесно связаны с храмами, в кото--
9
рых и хранились rлиняные таблички с клинописными текстами. Как
и в Еrипте, в Древнем Вавилоне специальность писца была почетной:
"Тот, кто в совершенстве овладеет искусством писать на таблич
ках, будет сверкать подобно солнцу" Нередко писцами становились
'"
сыновья правителеи, ведь писцы ,относились к правящему классу.
"Дом табли ек" так называлась школа или академия, rде обуча
лись писцы. "Писец должет уметь писать понятно, хорошо знать
математику, уметь межевать земли, примирять спорящих", Ha
писано в послании одноrо ученика к друrому.
Задачи, решаемые в вавилонских клинописных текстах, так же
как и задачи в древнееrипетских папирусах, являются чисто прак
тическими вычислительными задачами и так же изложены доrма
тически, бro каких либо пояснений. Отличие состоит в том, что ис
кусство счета у вавилонян более совершенное, а решаемые MaTeMa
тические задачи значительно разнообразнее и сложнее. В Древнем
Вавилоне впервые возникла позиционная система счисления, разра
ботана алrебра линейных и квадратных уравнений, открыта Te<r
рема Пифаrора, решаются простейшие теоретик<>-числовые задачи.
Здесь же, в отл/ичие от математики Древнеrо Еrипта, мы можем Ha
блюдать начавшееся разделение математики на арифметику и re<r
метрию, зачатки алrебры и теории чисел, а также появление первых
"теоретических" задач, т.е. задач, не связанных непосредственно с
практикой, а вызванных внутренниими потребностями самой MaTe
матики.
1.2 ПЕРИОД МАТЕМАТИКИ
постоянныIx ВЕЛИЧИН
Математика в древних цивилизациях развивалась очень медленно.
IIноrда на протяжении целых веков не было никакоrо проrресса. Но
вот в Древней fpеции УI в. дО Н.Э. положение резко меняется. Bcero
за несколько десятилетий математика И3 набора примеров для pe
.llения простейших прикладных задач превращается в строrую дe
уктивную науку. Формируются первые математические понятия и
l.ксиомы, строятся первые математические теории; математики Ha
iинают работать с понятиями.
I'pеки справедливо приписывали радикальные перемены во всех
>бластях общественной жизни (в том числе и в математике) B03
O
никшему у них в то время новому демократическому общественному
строю.
Период развития математики с УI в. до н.з. по ХУI в.н.з. принято
считать периодом математики постоянных величин. Он включает в
себя математику Древней fpеции, зллинистических стран и Римской
империи, математику средневеК080rо Китая, математику cpeДHeB
ковой Индии, математику стран ислама, математику средневековой
Европы и математику зпохи Возрождения.
1.2.1 Математика Древней I»еции, аллинистических
стран и Римской империи
Первые математические теоремы были доказаны учеными и<r
нийской школы натурфилософии (первая половина УI в. до н.з.), OCH<r
вателем которой считается Фалес купец, политический деятель,
философ, астроном и математик, живший в Милете боrатой rp
ческой колонии в Малой Азии. Но коренное преобразование MaT
матики по традиции единодушно приписывают Пифаrору (УI в. до
н.з.). Вот, например, что об зтом пишет Прокл (У в.н.з.): "Пифаrор
преобразовал математику ... рассматривая ее принципы чисто аб.-
страктным обра30М и исследуя теоремы с нематериальной, интел
лектуальной точки зрения "
В школе Пифаrора (VI V вв. до н.з.) была разработана арифм
тика целых чисел, построена первая теория отношений, сделано
очень важное для дальнейшеrо ра;звития математики открытие He
соизмеримости диаrонали квадрата с ero стороной, ра;зработана T
ория делимости, основана rеометрическая алrебра, в которой задачи
решаются построением с помощью циркуля и линейки.
Развивая математику пифаrорейцев, rреки построили (в IV III
вв. до н.з.) теорию конических сечений (Менехм, Аполлоний), c<r
здали новую теорию отношений (ЕВДОКt), первый метод пределов
(Евдокс), первые интеrральные и дифференциальные методы (Архи
мед). Достижения rреческих математиков были приведены в систему
в "Началах" Евклида (111 в. до н.з.).
Со 11 в. до н.з. наступает спад в развитии rреческой математики,
вызванный началом тяжелых разрушительных войн, приведших к
созданию Римской империи (о причинах упадка rреческой MaTeMa
тики см. [34, c.164 166]). Только в начале нашей зры, коrда положение
11
установилось, rреческая математика вновь стала оживать. Уже в 1
в.н.з. В Александрии, центре культурной жизни Toro времени, раб
тают такие математики, как repoH и Менелай, а в середине 11 в.н.з.
Клавдий Птолемей. В 111 в. создает свою алrебру Диофант.
Значительная часть знаменитой Александрийской библиотеки
сrорела еще в 30 x rr. до н.з. при захвате римлянами Алексан:дрии.
В 391 r. библиотеку жrли и ра;зрушали христиане.-фанатики. Коrда
в VIII в. уровень культуры в арабских странах поднялся настолько,
что ученые начали собирать и переводить rреческие рукописи, уце.-
лело лишь HeMHoroe. Это HeMHoroe и послужило основой для даль
v
неишеrЬ ра;звития математики в странах исла а, а впоследствии и в
Европе.
1.2.2 МатемаТИlCа cpe ReBelCOBoro КИТ8JI
Китайская цивили;зация длительное время была почти полностью
изолирована от остальноrо мира. Это наложило свой отпечаток и на
развитие китайской математики.
Наиболее древние и;з дошедших до нас математических текстов
относятся ко 11 в. до н.э. Исторические документы свидетельствуют
о том, что в Китае издавна математике уделялось большое внима
ние. Уже ко второй половине 1 тысячелетия до н.э. были серье;зно
поставлены математиче ое обра;зование и зк;замены. В VII X вв.н.э.
в Императорской rимна;зии математика и;зучалась семь лет. Для ;за
нятия чиновником rосударственной .должности требовалось Bыдep
жать зк;замены, в том числе и по математике. Были и;зданы и пе
реи;здавались в течение мноrих веков "Десять классических TpaKTa
тов", содержавшие основы китайской математики.
Важнейшей особенностью китайской науки является ее доrма
ти;зм; в течение MHorllX веков китайская наука направлялась чи
новниками, придавшими ей, как и друrим сторонам жи;зни Китая,
бюрократический характер. Если произведения rреческих MaTeMa
тиков подверrались при переписке ;значительной обработке и CHa
жались ра;зличными дополнениями и комментариями, то китайские
"класси еские трактаты" , написанные еще во 11 в. дО Н.3. IV В.Н.3.,
переи;здавались ;затем бе;з ВСЯКИХ и;з:менений.
Исследование математики древнеrо и средневековоrо Китая по..
ка;зывает, что до XIV в. она ра;звивалась преимущественно как co
вокупность вычислительных алrоритмов. Наиболее ;знаЧИ1:еЛЬНЫМII
12
из этих алrоритмов являются метод "ФАН ЧЭН" решения системы
линейных уравнений и метод "ТЛНЬ ЮАНЬ" приближенноrо реш
ния алrебраических уравнений. Важнейшим достижением китайской
математИКИ было также, введение отрицательных чисел.
1.2.3 Математика сре вевековой Ив ии
Первые индийские математические тексты относятся к VII V вв.
до н.э. Крупнейшие индийские математики V XII вв.н.з. Ариа
хата (V VI вв.), Брахмаrупта (VII в.), Маrавира (IX в.), Шридхара
(IX X вв.), Бхаскара (XII в.). Уже с первых веков н. з. прослежива
ется связь математики Индии с математикой Китая. Она особенно
усиливается в период распространения буддизма. В зто время индий..
скан математика распространяется и на. территории стран ислама.
Важнейшими достижениями индийской математики являются:
создание арифметики на основе десятичной позиционной системы
счисления, разработка триrонометрии, создание развитой алrебра
ической символики.
1.2.4 Математика стран ИCJIама
В VII в.н.з. СТОРОННИКИ ислама халифы подчинили себе Си
рию, Междуречье, Иран, Еrипет, Среднюю Азию, северную Африку,
а позднее Испанию, Сицилию и юr Италqи, часть Закавказья,и
часть И'ндии. Образование исламскоrо халифата совпало с распадом
рабовладельческой формации на ero территории и становлением ф
одальноrо строя. Образовались научные центры: Баrдад столица
халифата, Бухара и Хорезм в Средней Азии, Каир в Еrипте, Kop
дова в Испании, rазна на территории Афrанистана, Исфахан на Tep
ритории Пакистана, Mapara в Азербаilджане и некоторые друrие.
В IX X вв. зд сь работали такие известные математики, как ал
Хорезми, ал Бируни, Абу Камил ал Мисри, Хасан ибн ал Хайсам, в
XI в. Омар Хайям, в XIII в. Насир ад Дин ат 1Уси, в ХУ в.
ал Каши и т.д.
Из достижений арабских математиков отметим работы по T
ории параллельных, алrебре и триrонометрии. Но не менее важно
было то, что арабские математики переписывали, комментировали
и совершенствовали результаты rреческой математики, переняли
у Индийцев их десятичную пооиционную систему счисления. Все
13
это и послужило основой для последующеrо развития м:атематики
в Европе.
1.2.5
'" .
Математвжа сре аевежовов Европы
в середине 1 тысячеления н.э. произошел социальный и поли
тический распад Римской империи, вызванный кризисом рkбовла
дельческоrо хозяйства, борьбой по коренных римлянами народов, и
нашествиями варваров; на смену рабовладельческому обществу при
ходит феодальная формация. Время rосподства феодальных отноше
ний, продолжавшееся с V VI вв. дО XV XVI вв., именуется средними
веками.
Основой для развития науки в средние века служило постепенное
развитие ремесла, TOBapHoro производства и торrовли, подъем
особенно со второй половины XI в. rородов, улучшение положе
ния rорожан. Для развития математики в средневековой Европе rла
вную роль сыrрали переводы на латинский язык сочинений арабских
,
математиков. Такие переводы, редкие в Х в., приобретают система
тический характер в XI XIII вв. Блаrодаря работе переводчиков и
переписчиков европейцы познакомились с сочинениями Архимеда,
Аполлония, Евклида, Диофанта и друrих rреч ских математиков.
Важную роль в развитии математики сыrрало также появление
университетов. Древ ейший в Европе университет медицинский
был основан в Салерно не позднее первой половины XI в. Около
1100 r. был открыт юридический университет в Болонье. В конце
XII в. на базе нескольких монастырских школ вырос Парижский уни
верситет, rде обучались тысячи студентов со всех концов Европы.
Примерно тоrда же были созданы Оксфордский и в 1209 r. Кембри
джский университеты. Затем появляются университеты в Праrе
(1348 r.), Кракове (1364 r.), Вене (1365 r.), rейдельберrе (1385 r.),
Лейпциrе (1409 r.), Базеле (1459 r.) и т.д.
Орrанизация преподавания в университетах Toro времени была
примерно такова: университет состоял И3 четырех факультетов
искусств, боrословия, права и медицины. Преподаватели делились
на младших бакалавров и старших маrистров и докторов.
Во rлаве университетов стояли монахи боrословы. Студент, нередко
подросток, поступал сначала на факультет искусств, rде обучалея
около шести лет; после испытаний он Mor перейти на какой либо
друrой факультет, rде обучение продолжалось около восьми лет и
14
завершалось испытанием и диспутом.
В течение нескольких веков математика оставалась в универ
ситетах вспомоrательной дисциплиной, отдельных математических
кафедр и специальных преподавателей математики не было. Подсо6--
ная роль математики в университетах отрицательно сказывалась на
знаниях студентов. И все же, несмотря на подчиненное положение
математики, несмотря на преобладание боrословия и схоластики в
преподавании, университеты были важными центрами распростра
нения и развития математических знаний. Из стен средневековых
университетов вышли такие математики, как Томас Брадвардин в
Анrлии, Николь Орем во Франции, Иоrанн Мюллер Реrиомонтан в
rермании, Николай Коперник в Польше и др.
1.2.6 Математика QПОХИ Воорож еНИJl
ХУ и XVI в. вошли в историю Европы под названием "эпоха
Возрождения"; при этом имелось в виду возрождение Toro высокоrо
уровня культуры, КОТQРЫЙ был достиrнут в античном мире. На ca
мом же деле эта эпоха характеризуется rораздо более rлубокими пре
образованиями в жизни Bcero общества: именно в это время в недрах
феодальноrо строя зреет новый общественный строй буржуазное
общество. В промышленности возникают мануфактуры, требующие
технических усовершенствований и изобретений., Тоrда же появля
ются в Европе компас, часы, порох, дешевая бумаrа и книrопечата
ние. Резко возрастает торrовля, приведшая к росту мореплавания.
Бумаrа и книrопечатание способствуют тому, что научные знания
становятся необходимым элементом общественной жизни. Соверша
ется культурная революция.
Развитию математики способствовали, с одной стороны, чисто
практические оображения, а с друrой релиrиозные традиции,
утвержда.вшие, что Вселенная построена боrом по математическому
плану.
В XV XVI вв. математика развивается rлавным образом в Ита
лии, Франции, rермании, а с конца XVI 8. и в rолландии, пер
живавшей первую в Европе буржуазную революцию. Математика
впервые выходит за пределы знаний, полученных в наследство от
древних rpeKoB и народов BOCTOl<a. Именно в это время повсем
стно вводится пришедшая в Европу от арабов индийская десятич
,
ная пооиционная система счисления, вводятся десятичные дроби, OT
15
рицательные, иррациqнальные и мнимые числа, создается развитая
алrебраическая символика. Тоrда же были решены в радикалах ал
rебраические уравнения 3 й и 4 й степеней, разработаны плоская
и сферическая триrонометрии, значительно усовершенствованы BЫ
числительные методы. Математика становится мощным средством
решения быстро расширяющеrоCJI Kpyra задач не только торrо8ЛИ,
землемерия и т.п., но И новой техники и HOBoro естествознания. В
математике начинают видеть основной, наряду с экспериментом, M
тод изучения природы.
.
1.3 ПЕРИОД МАТЕМАТИКИ
пЕр.ЕмЕнныIx ВЕЛИЧИН
к XVII в. создаются как теоретические, так и практические пред
посылки для математическоr.о описания движения. Изучение дви"
жения, изучение переменных величин становится rлавной задачей
математики. Начинается период математики переменных величин.
Ero принято условно разделять на математику XVII в. и математику
XVIII в.
1.3.1 MaTeMaT;JIlCa XVII веlCа
в XVII в. воздействие практических потребностей на математику
становится непосредственным. На смену энтузиастам"одиночкам
приходят научные орrанизации и общества. С 1662 r. начало свою
деятельность Лондонское королевское общество, иrрающее и ныне
роль национальной академии наук. В 1666 r. была орrаНИЗ0вана Па
рижская академия наук. Переписка ученых и появлявшиеся изредка
и в малом количестве экземпляров книrи уже не удовлетворяли
потребности обмена и распространения научной информации. В
XVII в. выходят первые научные периодические издания: с 1665 r.
в Лондоне "Philosophical transac ions", а с 1682 r. в Лейпциrе
"Acta Eruditorum"
В математике на первый план выдвиrается изучение движения.
Ero первым математическим описанием явил ась аналитическая re
метрия Декарта и Ферма.
1РудыКеплера,Кавальери,Торичелли,Сен Венсана,rалилея,Р
берваля, Декарт-а, Ферма, Барроу по развитию античных интеrраль
16
ных И дифференциальных методов привели к созданию в работах
Ньютона и Лейбница основ дифференциальноrо и интеrральвоrо ис
числения.
1.3.2 Математика XVIII века
XVIII в. rосподство капиталистическоrо способа производ...
\
ств&. Темпы развития науки в это вреМJI быстро нарастают. Пр
мышленна.и революция, образование мировоrо рынка И СВJIзанные с
этим нужды мореплавания, кораблестроения, военной технИКИ, те-
v
плотехники, rидроэнерrетики и Т.П. ставят перед наукои все новые и
новые задачи. Причем помимо задач механики и астрономии встают
задачи исследования электромаrнитных и тепловых явлений. Разви",
тие науки становится делом rосударственной важности. Для целей
научноrо исследоваНИJl в крупнейших rородах Европы соодаютCJI
академии наук, деятельность которых направляется И финансиру
ется rосударством.
В XVIJI в. быстро развивается дифференциальное и интеrраль
ное исчисление. ИСП,ользуются степенные, триrQнометрические и
асимптотические ряды, изучаются простейшие специальные фун
кции, складываются элементы теории дифференциальных уравне-
ний, создается вариационное исчисление. В алrебре отмечаютCJI
мноrочисленные попытки решения в радикалах уравнений 5..й и вы с...
ших степеней, развиваются приближенные методы решеНИJl алrебра
ических уравнений, появляются первые формулировки и доказателlr
ства основной теоремы алrебры. Заложены основы элементарной те-
ории чисел. Формулируются первые предельные теоремы теории ве-
роятностей. Формируется дифференциальная rеометрия.
u
1.4 ПЕРИОД СОВРЕМЕННОИ
МА ТЕМАТИКИ
XIX в. начало периода современной математики, характеризую-
щееся следующими особенностями:
в апrебре появились работы, приведшие к созданию теоретик
v v
rрупповых методов, составивших в дальнеишем ядро современнои
алrебры;
в rеометрии со;здаются основы неевклиДОВЫХ rеометрий, фор-
мируются проективная и мноrомерная rеометрии, тополоrия, ПОJlВ
17
ляются классификации типов rеометрий;
u
М8теМ8тичесJCИИ 8налИG строится на основе современных
определений вещественноrо числа и предела. Внутри анализа зар
ждаются новые дисциплины такие, как теория функций комплексноrо
переменноrо и теория функций действительноrо iIepeMeHHoro. Пр
,исходит интенсивное разрастание анализа вширь, резко расширя
ется область ero приложений;
теори.. веро"тностей и М8теМ8тичеСJCaJ( СТ8ТИСТIПC8 фО}r
мируются как науки;
формируются алrебраичеСJCaJI и аналитичеСJCaJI теории чи..
сел;
все больший интерес проявляется к вопросам обоснования мате.-
матики, в св зи с этим развиваются теори.. множеств и мате..
М8тичеСJCaJ( JlоrИJC8.
Большое внимание уделяется в XIX в. преподаванию математики.
Так, поступавшие в Парижскую политехническую школу ведущее
учебное заведение начала XIX в. должны были прежде пройти r
дичный курс в специальном математическом классе учебном за
ведении с преобладанием математики (до 16 ч. в неделю). 3десь пре
подавался элементарный курс анал тической rеометрии и механики,
а позднее и элементарный курс анализа бесконечно малых, причем
большое число упражнений давало учащимся возможность твердо
овладеть предметом. После этоrо следовал очень строrий экзамен,
который чисто статистическим методом отбирал из большоrо числа
кандидатов 150 человек, допускаемых для обучения в Политехниче.-
ской школе.
Обучение в Политехнической школе продолжалось два rода и яв
лялось единственным путем к занятию высших rосударственных те.-
хнических должностей, к которым нужно было rотовиться еще два
rода в одном из специальных учебных заведений: Институте путей
сообщения, rOpHOM институте, Военн инженерной школе или в Ap
тиллерийской школе. Эти школы неодинаковы по своему положению
и значению, и выбор их не был свободным для оканчивающих Поли
техническую школу, а определялся качеством выпускноrо свидетель
ства.
"Все меры строrости, воздействия на честолюбие, окрыляемое
перспективой блестящей жизненной будущности, пишет о Поли
технической школе Ф.Клейн, привлекались здесь для Toro, чтобы
заставить учащеrося до крайности напряrать свои силы. 3нания
18
вколачивались в rолову до полноrо овладения предметом. Для этоrо
кроме профессоров имелись репетиторы, К,оторые объясняли лекции
и производили проверку знаний. И, наконец, экзаменаторы имели
целью установить имеющиеся достижения путем чрезвычайно CTpO
roro и подробноrо выпускноrо экзамена, которому должен был под
верrнуться каждый кандидат в отдельности
Орrанизации преподавания соответствовал продуманный уче
ный план, предъявлявший orpoMHbIe требования. В первые десятиле
тия .. математика стояла в этом плане на первом месте и состояла
u
из следующих частеи:
Чистый анализ
Применение анализа к reOMeT
рии
Механика 94 двойных часа
Начертательная rеометрия 153 двойных часа
Черчение 175 двойных часов
(таким обраЗ0М, недельная лекционная наrрузка составляла 20 ч. +
постоянные репетиции. С.М.)
Так как в это замечательное учреждение были привлечены в Ka
честве преподавателей лучшие математики Франции, то неудиви
тельно, что Политехническая школа в очень короткий срок достиrла
исключительных успехов. Немаловажную роль сыrрало здесь и то
рвение, которое вызывало в учащейся молодежи непосредственное
личное общение с преподавателями, занимавшими видное положе
пие и одушевленными творческим порывом.. . Влияние школы за ее
стенами сделалось еще более значительным с тех пор, как в закон<r
дательном порядке была сделана обязательной публикация лекций.
Большая часть основных учебников по высшей математике в Ha
чале XIX в. возникла из курсов, преподававшихся в Политехнической
школе "[20, с. 80 81]
108
17
двойных часов (по 1,5 ч)
u
двоиных часов
1.5 чЕтыIЕE СТУПЕНИ В
ПРЕПОДАВАНИИ МАТЕМАТИКИ
Четырем периодам в ра3витии математики соответствуют четыре
СТупени в преподавании математики. Периоду накопления первона
чальных математических сведений соответствует преподавание Ma
19
тематики в начальных классах средней школы. Математика пост
янных величин преподается в средних и старших классах средней
ШКОЛЫ. Математика переменных величин начинает изучаться еще в
старших классах средней школы и заканчивается на первых курсах
вузов. Современная математика изучается в основном на средних и
старших курсах вузов.
Вопросы u заdахuz
1. На:зовите четыре периода в раовитии математики.
Какие ступени в преподавании математики соответствуют
этим периодам?
2. Дайте краткую характеристику началу периода современной
математики.
IЛава 2
число
2.1 ПР'ОИСХОЖДЕНИЕ пЕрвыIx
НАТУР АльныIx ЧИСЕЛ
Как ворослому человеку трудно видеть мир rлаоами ребенка, так и
людям, живущим в наше время и с детских лет постоянно имевшим
дело с натуральными числами, бывает трудно увидеть эти числа rла
оами своих далеких предков. Для этоrо надо поrруоиться в очень
далекие от нас времена, обстоятельно иоучить историю происхо-
ждения первых натуральных чисел, проаналиоировать ее и сделать
выводы. Эта сложная и трудоемкая оадача моrла быть решена лишь
в наше время. Поэтому неудивительно, что даже самые выдающиеся
умы прошлых веков, обращаясь к вопросу о происхождении первых
натуральных чисел и ц.ействий с ними, не моrли дать на Hero пра
вильноrо ответа (см., например, [19, т. 1, с. 26 35]). В условиях OT
сутствия фактическоrо материала по этому вопросу единственным,
но недостаточным средством была лоrика, т.е. опыт человеческоrо
мышления. Так, крупнейшему лqrику начала xtx в. немецкому фи
лософу r.rеrелю у алось на этом пути сделать важные доrадки
[7, т. 5, с. 223 231].
Обратимся к истории. Основной вывод, к которому привели ис
следования по вопросу о происхождении натуральных чисел, состоит
в следующе f [15, т. 1, с. 9 13]. Натуральные числа вооникли в pe
зультате очень длительноrо и сложноrо историческоrо процесса, в
котором можно выделить следующие :три основных этапа.
1. Установление случайноrо, нереrул"рноrо воаимно од..
нооначноrо соответствИJ[ между ДВУМJI множествами
(например, между множествами обмениваемых предметов).
2. ПО.А.вление раоличных еталонов счета (вначале естествеll
21
ных: "луна" 1, "rлаза" 2, "рука" 5 и т .п., затем искусствен
ных счетные палочки, камешки и т.п.).
3. Перехо JC е иному, наиболее удоБНОl4У ат8ЛОНУ счета,
u u
ICОТОрЫИ при атом становитс.. основои системы СЧИCJIе..
ни.. ("руки" двоичная система счисления, "палЬЦЫ руки"
пятичная система счисления, "пальцы обеих рук" десятичная
система счисления, "пальцы рук и ноr" двадцатичная система
счисления, и некоторые друrие, менее употребительные эта
лоны счета и, соответственно, системы счисления).
Счет предметов с помощью эталонов сопровождался образ
ванием числительных и возникновением числовых обозначений.
". . . Сходство числительных у индоевропейских народов показывает,
что названия чиеел у предков этих народов появились еще в те дa
лекие времена, коrда они rоворили на одном языке "[15, т. 1, с. 10
11]. "... Старейшей, известной в настоящее время записью числа,
является запись на лучевой кости молодоrо волка "[15, т. 1, с. .12].
Позднее появляются записи палочками на rлине (клинопись)., записи
на папирусе, бересте и т.п. . ·
Таким образом, в соответствии с историей, можно дать следую
щее определение натуральноrо числа: "Каждое натуральное число,
как "два", "пять" и т.п., есть свойство, общее для всех совокупн
стей, предметы которых можно сопоставить по одному, и различ
ное у таких совокупностей, для которых такое сопоставление HeB03
можно" [25, т. 1, с. 20].
3аAtf'Ча'ltuz
1. История происхождения натуральных чисел, как она изложена
"
выше, имеет явную аналоrию с историеи происхождения дe
Her, как она изложена в перво,Й rлаве первоrо тома "Капитала"
К.Маркса. При этом простой, или случайной форме стои
"
мости соответствует установление случаиноrо, нереrулярноrо
взаимно однозначноrо соответствия между предметами раз
Horo рода; полной, или развернутой форме стоимости COOT
ветствует выделение 'различных эталонов счета; наконец, дe
нежной форме стоимости cooTBeTc'rByeT переход к единому,
наиболее удобному эталону счета. Это не просто аналоrия,
"идеолоrическая установка" или подражание Марксу, а Bceo
щая форма образования TaKoro рода понятий, известная еще
22
до Маркса и достаточно полно изложенная, например, в работе
[39]. Для произвольных, бесконечных множеств эта форма p
ализована r Кантором в 70 e rr. XIX в. при создании им п
нятия кардинальноrо числа.
2. Происхождение натуральных чисел неотделимо от происх
ждения арифметических операций. Четыре арифметических
операции (сложение, вычитание, умножение, деление) явля
ются развитыми формами элементарноrо арифметическоrо
действия нумерации (прямой и обратной) [7, т. 5, 'с. 223 231].
Через практическую нумерацию (счет вперед и назад) вводят
натуральные числа в школе. Аксиоматическое же определение
нумерации (и. следовательно, аксиоматическое определение Ha
туральных чисел), предложенное Пеано (1889 r.), вошло в уче
ники высшей арифметики и алrебры (см., например, [4, с. 20]).
2.2 принципыI ИЗОБРАЖЕНИЯ ЧИСЕЛ,
ИЛИ принципыI НУМЕРАЦИИ
Изображение чисел у разных народов и в ра;зные времена OCH
вано на следующих общи'х принципах. Вводятся основные'знаки или
цифры, с помощью которых можно записать все достаточно боль
шие числа. При этом запись чисел с помощью цифр основана на c
че.тании следующих трех принципов: 8 ИТИВRоrо, коrда стоящие
рядом основные знаки тn изображают число, равное сумме чисел,
изображаемых отдельными знаками, т.е. m + n; суБТр8IТИВRоrо,
коrда стоящие рядом основные знаки тn изображают число, равное
разности n т; МУЛЬТИПJlИI8ТИВRоrо, коrда запись тn изобра
.
жает число, равное произведению т. n. Кроме Toro, в более поздних
нумерациях значение OCHoBHoro знака зависит от занимаемоrо этим
знаком места происходит переход от непозиционной системы счи
сления к позиционной системе счисления.
Рассмотрим несколько примеров.
Пример 1. ЕrипеТСIaJI нумераци.. чисто аддитивная, непо--
зиционная десятеричная нумерация с основными знаками для 1, 10,
100, . . ., 10000000. Число 3 124 запишется в этой нумерации в виде
23
1lllnn Ili Здесь I изображает 1, n 10, 9
100, а 1 000, и каждый знак повторяется столько раз,
сколько в данном числе единиц соответствующеrо разряда. Запись
производится справа налево.
Пример 2. ВавИJlОВСJ(8J( вумераци.. аддитивн<rмультипли
кативнa.tI, позициовнa.R, деСЯтичн<rшестидесятеричнa.R нумерация с
основными знаками , и < Первый знак служит дЛЯ И3
бражения чисел вида 60 n , а второй чисел вида 10 60 n , rде n
любое целое (положительное или отрицательное) число. При з'а..
писи чисел используется аддитивный или мультипликативный прин..
цип. Так, число 12 записывается с помощью аддитивноrо принципа:
( " == 10 + 1 + 1, а число 10000 записывается с помощью муль
типликативноrо принципа: ( y = 10 · 10. 100. ·
Пример 3. РИМСJ(8J[ нумераци.. аД-ДИТИВН<rсубтрактивная,
непозиционная Пятичн<rдесятичная нумерация с основными знаками
"1" 1, "Y" 5, "X" 10, "L" 50, "C" 100, "M' 1000 и т.д. Запись
чисел 3 = 111 = 1 + 1 + 1, 17 = XVII = Х + V + 1 + 1 и Т.П. основана на
аддитивном принципе, а оапись чисел 4 = IV = V 1, 9 = IX = Х ..-а 1,
40 = XL = L Х = 50 10 и Т.П. основана на субтрактивном прин
ципе.
Пример 4. АраБСJ(8J[ нумерацИJI чисто аддитивная позици
онная деСJlТИЧНая нумерация с основными знаками О, 1, 2, 3, 4, 5, 6,
7, 8, 9.
Упражнение 1. Дайте характеристику приведенной ниже, в п. 6.1,
u
CJlав..нсжои нумерации.
'ПDажнение 2. Остатки каких систем счислеНlfЯ обнаруживаем
мы в названиях числительных "один" и "два"', "пять", "семь",
"сорок", "девяносто"?
u
2.3 ВВЕДЕНИЕ ДРОБЕИ
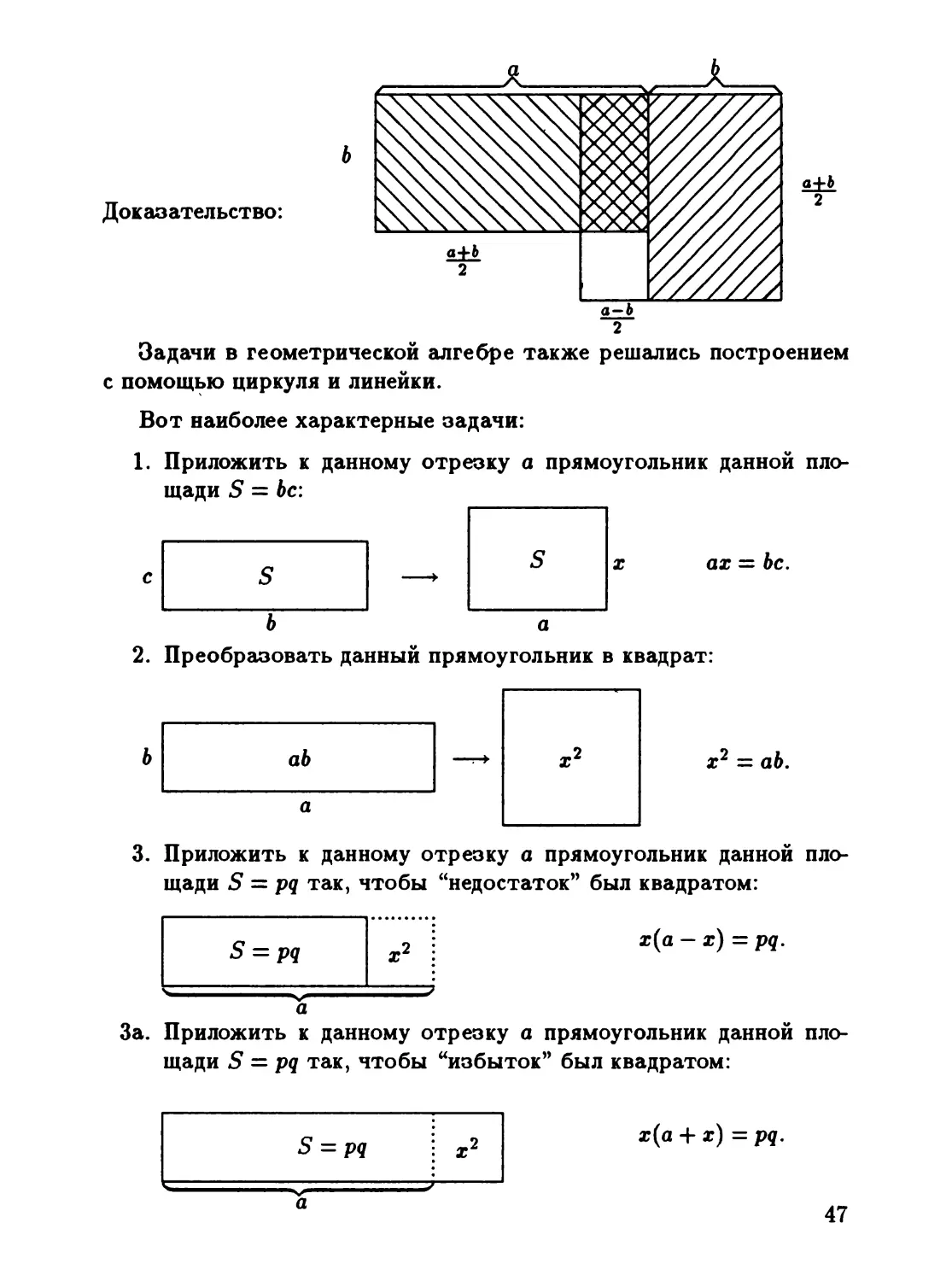
История свидетельствует, что в любой д;pe !!eп цивили:зации первым
видом дробей были так называемые 8JIиквотные дроби, оонача..
вшие деление одной меры на n равных частей действие, в простей
шем случае доступное даже человеку, не знакомому с натуральными
числами. Такими дробями вполне обходились, например, писцы в
Древнем Еrипте.
24
Деление .9AHoro числа на Apyroe проиоводИJЮСЬ там с ПОМОЩЬЮ
v v
последовательных воении и раздвоении с ПРВВJIeчением, в CJIучае
необходимости, &JIиквотных дробей. Например, деление 19 на 8 про-
v v
ИЗВОДИJIOсь только С помощью удвоении и раодвоении:
1 8
2 16
1/2 4
1/4 2
1/8 1
2 + 1/4 + 1/8 16 + 2 + 1 = 19
Деление 5 на 9 ПРОИЗВОДИJЮсь с использованием таблиц разJlOжеНIIJI
дробей вида 2 : (2п + 1) на сумму &JIИК8ОТНЫХ: 5 : 9 = (4 + 1) : 9 = 4 :
9+ 1/9 = 2 : 9+ 2 : 9+ 1/9 = (ИСПОЛЬЗУJl таблицы) 1/6+ 1/18+ 1/6+
1/18 + 1/9 = (1/6 + 1/6) + (1/18 + 1/18) + 1/9 = 1/3 + 1/9 + 1/9 =
1/3 + 2 9 = (ИСПОЛЬЗУJl таблицы) 1/3 + 1/6 + 1/18 = 1/2 + 1/18,
так что AJIJI делеНИJl 5 хлебов на 9 человек достат,очно раареоать'
вти хлеба пополам, оатем одну из половинок раореоать на 3 равные
части, а каждую из вти частей еще на 3 равные части.
Подобным образом решапись все прuтические оадачи, приво-
ДJlщие к делению oAHoro числа на Apyroe. Так, оадача 34 папи
руса Райнда rласит: "Куча, ее 1/2, ее 1/4 состаВJIJlЮТ 10" Требу..
еТСJl определить величину "кучи" В нашей школьной математике
таК&JI оадача записываеТСJl линейным уравнением z + t z + iz = 10
и решаеТСJl делением числа 10 на сумму коэффициентов. Еrипе
схому же вычислителю неоачем складывать коэффициенты, так как
1 + 1/2 + 1/4 уже предстаВJlJlет собой каноническую оапись числа
(цеЛ&JI часть плюс сумма &JIиквотных дробей). Деление числа 10 на
1 + 1/2 + 1/4 ПРОИЗВОДИJIOсь следующим обраоом:
1 1 + 1/2 + 1/4
2 3 + 1/2
4 7
1/7 1/4
2/7 = 1/4 + 1/28 1/2
1/2 + 1/14 1
5 + 1/2 + 1/7 + 1/14 7 + 1 + 1/2 + 1/4 + 1 + 1/4 = 10
Подробнее об втом см., например [6, с. 13 37].
С возникновением ПООВЦВОВRОЙ нумерации в Древнем Вави
пОНе непосредственно связано нведение :конечных шестидеCJIтерич
25
ных дробей. Шестидесятеричная система счисления вооникла у ва..
вилонян, как некоторые полаrают, И3 необходимости привести в c<r
ответствие Apyr с ApyroM весовые (в особенности денежные) меры
при рanвитии ToproBblx отношений между сумеритским и аккадским
народами. К этому моменту у обоих народов ИСПОПЬЗ0Вались деся..
тичные непозиционные системы счисленИJI. Наряду с этим полыэ<r
вались простейшими дробными частями весовых единиц, разделив
их на 2 или на '3 равные части. И3 деления одной трети пополам
получал ась шестая часть. В результате сравнения мер оказалось,
ЧТО 1/6 часть "мины" (ве"Совой единицы oAHoro народа) с хорошей
точностью равна 10 "шекелям" (весовым единицам Apyroro народа).
Поэтому обмен производилCJI И3 расчета 1 мина = 60 шекелям. Обе
эти единицы стали употребляться совместно, и денежные суммы вы..
ражались в минах и шекелях так же, как мы выражали их в руБJIJlХ
И копейках. Постепенно при словесном И письменном выражении де-
нежных сумм наименования стали опускаться (подобно тому, как мы
rоворили "два ридцать" и писали 2.30 вместо "2 рубля 30 копеек").
Вооникшая система счета нашла удобное применение в aCTp<r
НОМИII (так как число дней в rоду HeMHoro отличаетCJI от 360 =
60 6). При этом вводятCJI новые единицы вида 60 n (п > 2 и, c<r
ответственно, 60 n). Правда, привычные для нас теперь единицы
"rрадус", "минута", "секунда" и "терция" были введены пооднее
во 11 в. rреческим математиком Птолемеем. Следуя древним вави"
лонским астрономам, Птолемей делит окружность эклиптики на 360
rрадусов ("частей"), каждый rрадус он делит на 60 "первых шести..
десятых" , которые он еще называет словом E'1rTQ ("мелочь") и KOT<r
рому в латинском переводе соответствует слово "minuta" Каждую
"первую шестидесятую" он делит еще на 60 частей, которые он назы..
вает "вторыми шестидесятыми" ("вторая" переводится на латынь
словом "secunda"), а каждую "вторую шестиде сятую" снова на 60
частей, которые он называет "третьими шестидесятыми" ("третья"
переводится на латынь словом "tertia").
В созданной вавилонянами шестид сятеРИЧН9Й позиционной си..
стеме счисления действия с дробями ничем не отличались от дей..
ствий с целыми числами. Сложение и вычитание производились n<r
разрядно. Умножение также ПРОИ3ВОДИЛОСЬ поразрядно, при этом,
ввиду большоrо порядка системы счисления, широко ИСПОЛЬЗ0Вались
различные таблицы умножения. Разделить а на Ь означало "взять а
ра:з величину обратную к Ь". ДЛЯ этоrо ИСПОЛЬЗ0Вались таблицы 06--
26
ратных величин. В тех же случаях, коrда величина 6 не имела обрат
Horo значения, Т.е. 1/6 не представима в виде конечной суммы убы
вающих шестидесятеричных дробей (а зто будет, коrда 6 имеет хотя
бы ОДИН простой делитель р # 2,3,5), в таблицах писали "обратноrо
нет", а для практических вьrчислений обходились ближайшей в та--
блице обратной величиной. До алrоритма ПОр83рядноrо деления сами
вавилоняне, п видимому, не дошли, однако у rреческих астрономов,
заимствовавших у вавилонян их систему счисления, зтот алrоритм
уже использовался.
u
2.4 "ТЕОРИЯ ОТНОШЕНИИ"
u
ПИФАrОРЕИЦЕВ
к VI в. до н.з. В Древней I'pеции сложились блаrоприятные усл
вия для возникновения теоретичесжой арифметики. С ОДНОЙ сто--
роны, К зтому времени существовала довольно рanвита.я техника BЫ
числений, ею хорошо владели rреческие купцы, часто бывавшие и в
Еrипте, и в Вавило е. С друrой стороны, возникновение в I'pеции
VI в. до н.з. HOBoro, демократическоrо строя, коrда умение сводить
явления к их основам, проводить рассуждения и убеждать стано--
вится необходимым для занятия BblcoKoro положения в обществе,
привело к быстрому развитию философии, лоrики и риторики. Чи
сла начинают теперь рассматривать не с точки зрения приложений,
а как самостоятельные сущности в их отношении друr к друrу и к
друrим вещам.
Такой взrляд на число развился в школе Пифаrора (VI в. дО Н.З.)
В целую философскую систему, основное положение которой rласит,
что число есть сущность всех вещей, и орrанизация Вселенной в ее
определениях представляет собою rармоническую систему чисел и
и,Х отношений. Число представлялось, таким образом, самой сущн
стью и субстанцией вещей, а не одной только их формой. Числа 1,2,
3,4 составляли так называемую четверицу (их сумма 1+2+3+4 = 10
еДиница следующеrо разряда), "вечно текущей природы имущей
корень источный" (источником вечной природы четверица названа
потому, что весь космос, по мнению пифаrорейцев, устроен соrласно
rармонии, rармония же есть система трех. консонансов КВИНТЫ,
кварты и октавы. Численные пропорции ЗТИХ трех консонансов Ha
ходятся в пределах указанных четырех чисел, а именно, консонанс
27
кварты являетCJI в виде отношенИJI 4:3, квинты 3:2 и октавы
2:1 или 4:2).
Эта же четверка чисел служит, соrласно пифаrорейцам, основой
и источником точек, линий, поверхностей и ТeJI. А именно, точка,
поскольку она опредеJlJlетCJI как не имеЮЩ8JI частей, имеет своей
основой единое, или единицу. ЛИНИJI имеет своей основой число 2,
так как она получаетCJI движение от oAHoro к друrому. В основе
же понятия плоскости (и вообще поверхности) лежит ЧИCJIО 3, так
как плоскость вполне OQреДeJIJlетCJI TpeМJI точками общеrо ПОJIOже-
НИJI. Если же взять 4 точки общеrо положения, то имеем пирамиАУ,
тело. Поэтому, соrласно пифаrорейцам, число 4 лежит в основе вся..
Koro тела. Подробнее см. об этом, например, [31, т. 1, с. 78 81; т. 2,
с. 167 168; 7, т. 9, р83дел "Пифаrор и пифаrорейцы"].
Недостатки учении пифаrорейцев о числе отмечены еще АрИСТ<r
телем, который указывал, что, исходя ИЗ ЧИСeJI, нельзя объяснить
движения и нельзя поня').'ь из чисел друrие определения тел, как, на..
пример, тяжесть и леrкость.
Но, несмотря на эти недостатки, нес отря на явную мистику
в учении пифаrорейцев о числе, рассмотрение ими чисел как П
u. v
н..тии оказалось очень важным для дanьнеишеrо развития мате.-
матики. Именно блаrодаря такому подходу пифаrррейцы построили
. U u
так На3ывамую теориlO отношении, которая, с однои стороны, n<r
служила теоретическим обоснованием действий с ПРОИОВОJlЬRЫМИ
дробями, а с друrой стороны, привела к созданию элементов теории
чисел и к ОТКРЫТИЮ "не соизмеримости"
Предметом теории отношенИЙ пифаrорейцев являются нату..
ральные числа и отношения между ними. rоворили, что две пары
чисел (А, В) и (С, D) пропорционалЬНЫ или имеют одинаковое отно--
шение, если у А и В найдется такой общий делитель F, а у С и D
общий делитель а, что А = mF, С = та, В = nF, D = па. Пифа..
rорейцы знали, что отношение пропорциональности транзитивно,
однако вряд ли это было ими доказано.
Все пары целых чисел разбивались на непересекающиеся классы
пар, имеющих одно и то же отношение. Из множества пар, имеющих
одинаковое отношение, выбирали наименьшую пару (cooTBeTcTBYкr
щую нашей несократимой дроби). Относительно ее пифаrорейцы до--
ка:зывали, что 1) (Ао, Во) тоrда и только TorAa является наименьшей
парой, коrда числа Ао и Во взаимно просты; 2) если.А В = Ао Во,
то существует натуральное число k такое, что А = kAo, В = kBo.
28
Над отношениями натуральных чисел первоначально произво--
дилась только одна операция "составление отношений": отно--
шение А С нanывается составленным И3 отношений А В и
В с, (А В) @ (В С) = А с. На;эвание об'ЬJlсняется веро--
ятно тем, что при составлении MY3ЫKaпЬHЫX интервалов, т.е. при
переходе от интервапов, представляющих собой пары ЗВУI(ОВ с вы..
сотами А и В, В и с, к интервалу, представляющему пару звуков
с высотами А и С, происходит "сост вление" соответствующих от.-
ношений.
Упражнение 3. Покажите, что классы пропорциональных (имею--
щих одно и то же отношение) пар целых положительных чисел с опе--
рацией "составления отношений" обра;эуют коммутативную rруппу.
Позднее в качестве модели отношения двух натуральных чисел
брали уже не столько сам МУ3Ыl(альный интервал, СI(ОЛЫСО отно--
шение двух отрезков высот ЗВУI(ОВ. ЭТО пооволило определить
все арифметические действия на множестве отношений натураль..
ных чисел. При этом сложение и вычитание выполнялось на основе
приведения дробей к общему знаменателю (исполызуя определение
пропорциональности), а умножение и деление выполнялось на основе
операции "составление отношений" (ИСПО!lЫЗУЯ также определение
пропорциональности), например: (5 : 4) · (2 3) = (5 : 4) . (4 : 6) = (5
4) (4 6)=5:6. ·
У пифаrорейцев мы видим и элементы теории чисел. Они впе)r
вые ввел,И в рассмотрение четные инечетные, ПрОС1ые и составные
числа. Пока;зали, что простых чисел бесконечно MHoro и произведе--
ние двух натуральных чисел m и n делится на простое число р в том
и только в том случае, коrда m делитCJI на рили n делится на р и
т.д.
2.5 ОТКРЬIТИЕ НЕСОИЗМЕРИМОСТИ
Для ранних пифаrорейцев было бесспорным, что всякие два отрезка
соизмеримы между собой, т.е. BcerAa найдетCJI третий отреЗ0К, ко--
торый измеряет оба эти отрезка (Уl(ладывается в I(аждом из этих
двух отрезков целое число pan). Эта уверенность поддерживалась в
дальнейшем, с одной стороны, всей практикой измерений, а с дру..
rой стороны, учением Демокрита, соrласно которому все реальные
отрезки представляют собой прямые цепочки из I(онечноrо числа
29
атомов и, следовательно, всеrда соизмеримы.
Для вахожденИJI общей меры двух отрезков пифаrорейцы разра
ботали anrоритм "попеременноrо вычитания", названный позднее
алrоритмом Евклида. Этот алrоритм состоял в следующем. Из
б6пьшеrо отрезка а последовательно отнимали меньший отрезок Ь
до тех пор, пока остаток rl не станет меньше Ь. 3атем из Ь по--
следовательно отнимали отрезок rl до тех пор, пока остаток r2 не
станет меньше rl. И так далее до тех пор, пока на некотором п"м
шаrе остаток r n не станет равным нулю, так что rn...2, = k. rn l.
Тоrда отрезок r n ...l измеряет отрезок r n ...2, а, следовательно, изме.-
ряет и отрезки rn...з, r n ...4, ro = Ь, r...l = а. Поэтому r n ...l будет
укладываться целое число раз в каждом из отрезКОВ а и Ь, т.е. будет
общей мерой этих отрезков.
Однако сами же пифаrорейцы в рамках созданной ими арифме.-
тики обнаружили явление, противоречащее их представлению о Ha
личии общей меры у двух произвольных отрезков. А им нно, они
обнаружили, что для произвольноrо отрезка Ь и диаrонали а ПО--
cTpoeHHoro на этом отрезке квадрата существование общей меры
противоречит с'озданной ими теории делимости.
По--видимому, пифаrорейцы впервые обнаружили это rеометри
чески, заметив, что а = b+rl, Ь =
.r4
2rl + r2, rl = 2r2 + rз, r2 = 2r3 +
rз r4 (см. рис. 1), и так далее, так
что процесс "попеременноrо BЫ
rl читания" для нахождения общей
меры отрезков а и Ь в данном слу
чае "зацикливается" На друrое,
по--видимому, более позднее рас..
rl суждение, приводящее к противо--
речию с учением пифаrорейцев о
Ь четных и нечетных числах, указы
вает Аристотель.
Рис. 1 Это рассуждение состоит в сле
дующем. Пусть отрезок Ь и диаrональ а построенноrо H этом o
резке квадрата соизмеримы, т.е. имеют общую меру. Тоrда они
имеют и наибольшур общую меру,т.е. такой отрезок е, который
укладывается в а и в Ь целое число раз, а = те, Ь = nе, причем
числа m и n взаимно просты и, следовательно, хотя бы одно из них
нечетно. Но, соrласно теореме Пифаrора, квадрат на диаrонали pa
30
вен двум квадратам на стороне, так что т 2 = 2п 2 , откуда следует,
что m четно, т = 2k, 4k 2 = 2п 2 , откуда 2k 2 = п 2 и, следовательно, ,п
I
также четно, т.е., как rОБОрИТ Аристотель, "четное было бы равно
"
нечетному
Открытие несоизмеримости, означающее лишь неприменимость
построенной пифаrорейцами арифметики к непрерывным величи
нам, для самих пифаrорейцев было rора3ДО большим. Для них это
было кризисом основ мировоззрения. О влиянии этоrо открытия
на пифаrорейцев и вообще на древних rpeKoB можно судить, напри
мер, по следующим словам одноrо афинянина из "Диалоrов" Платона:
"Друr мой Клиний, я И сам был поражен, что лишь так поздно узнал
то состояние, в котором мы находимся" (в связи с открытием несо--
измеримости. С.М.). Мне ПОКа38JIOсь, что это свойственно не
человеку, но каким то свиньям. Я устыдился не только за себя. но и
за всех эллинов"
Сами пифаrорейцы так и не смоrли преодолеть возникший кри
зис. Они лишь стали ра3делять все величины на дискретные (HaTY
ральные. числа и их отношения) и на непрерывные (длины, площади
и о'бъемы). Для дискретных величин они использовали старую тео--
рию отношений, а для непрерывных построили новую теорию, из
вестную под названием "rеометрическая алrебра" Лишь в IV в. до
н.э. выдающемуся rреческому математику Евдоксу удалось постро--
ить такое определение величины, которое одинаково подходило как
для дискретных, так и для непрерывных величин. На основе этоrо
HOBoro определения величины Евдокс построил теорию отношений,
которая удовлетворяла потребности математики вплоть до середины
XIX в.
u
2.6 ТЕОРИЯ ОТНОШЕНИИ ЕВДОКСА
Новое понятие величины вводится Евдоксо а сиоматически, с по--
мощью следующих шести аксиом:
1. "Равные одному и тому же равны и между собой" (если а = с
и Ь = с, то а = Ь).
2. "И если к равным прибавляются равные, то и целые будут pa
вны" (если а = Ь, то а + с = Ь + с).
3. "И если от равных отнимаются равные, то и остатки будут
31
равны" (если а = 6, то а .... е = Ь е при е < а, Ь).
4. "И совмещающиеCJI Apyr с ApyroM' равны между собой" (кон..
rруэнтные величины равны между собой).
5. "Н целое больше части" (если одна площадь содержит друrую,
то она больше ее, и Т.П.).
6. "ВCJlкие две вeJlичины имеют отношение между.собой, т.е. взя..
тые кратно MorYT превзойти Apyr Apyra" (если даны две вели..
чины а и Ь, ТО ДОЛЖНЫ существовать такие целые числа т и п,
что та > Ь и пЬ > а).
ПоспеДНЯJl аксиома носит название аксиомы Евдокса Архимеда и
исключает из класса величин так называемые актуально бесконечно
малые, примером которых спужилil "poroBBAHble" уrлы, т.е. уrлы,
образованные дуrой окружности и касательной к ней в одном ИЗ
концов.
УПDажнение 4. Определите равенство, сумму, разность и ОТ но--
шение порядка на множестве всех (обычных и "роrовидных") уrлов.
Проверьте выполнение аксиом 1 6.
Можно сказать, что аксиома Евдокса Архимеда разбивает все
величины oAHoro и Toro же рода на классы эквивалентности. Вели..
чины а и Ь "имеющие отношение между собой" , принадпежат одному
и тому же классу. Если же а и Ь принаДJIeжат разным классам, то
по отношению Apyr к Apyry одна из них будет бесконечно малой, а
друrая бесконечно большой.
Для определения Toro, что две пары величин а, Ь и е, d имеют
одно и то же отношение, EBДOK пользуетCJI сопоставлением крат-
ных этих величин. "rоворят, что величины нахОДЯТCJI в одном и том
v v
же отношении перваи ко второи и TpeTЬJI к четвертои, если равно--
кратные первой -и третьей одновременно больше или одновременно
v v
равны, или одновременно меньше равнократных второи и четвертои
каждая каждой при какой бы то ни было кратности, еCJIИ взять их в
соответствующем порядке"
Итак, величины а, Ь имеют то же отношение, что и величины е, d,
если для любых натуральных чисел т и n либо та > nЬ и те > nd,
либо та = nЬ и те = nd, либо та < nЬ и те < nd.
УПDажнение 5. Покажите, что если две пары отреоков имеют
одинаковое отношение в смысле определения пифаrорейцев, то они
имеют одинаковое отношение и в смысле определения Евдокса.
32
Отметим, что AJIJI непрерывных величин отношенИJI двух ПJlOща-
дей и отношенИJI двух объемов обычно СВОДИJIИСЬ IC отношению двух
отре3ICОВ. Равенство же отношений пар ОТРЮICОВ опредeJUlJЮСЬ еще
и по-друrому, & именно, AJIJI отрезlCОВ а : Ь = с : d равносильно тому,
что ПРJlмоуrольниlCИ, построенные на а и d и на Ь и С, равновeJIИICИ,
v
или тому, что еCJIИ на однои стороне yrJla ПОCJIедовательно ОТJIOжены
отрЮICИ а и с, а на друrой стороне yrJl& ОТРЮICИ Ь И d, то ПрJlмые,
соедиIOtющие ICонцы отрезlCОВ с и d, парaJIJIeJIЬНЫ.
Упражнение б. ПОICажите, что ICаждое из ЭТИХ двух опредenений
v v
равенства отношении ОТРЮICОВ еИСТВИТeJlЬНО равносИJIЬНО опреде-
лению равенства по Евдоксу.
Две пары величин, имеющих одно и то же отношение, назыв
ЮТCJI ПРОПОРЦИОНaJIЬНЫМИ. Показано, что еCJIИ отношенИJI 8 Ь и
с d ПРОПОРЦИОНaJlЬНЫ одному И тому же отношению е 1, то они.
ПРОПОРЦИОНaJIЬНЫ И между собой. Следовательно, пропорциеНaJIЬ-
ность отношений оБJlадает свойством травзитивности. Из опредeJJe-o
ний пропорциональности вытекает и ее симметричность. ПООТ9МУ
пропорциональность есть отношение ВICвивалентности.
ДaJIее все отношенИJI ЕвдоlCС УПОРJlДОЧИвает по вeJIичине: отно-
wение а Ь больше, чем отношение с d, еCJIИ существуют H
туральные ЧИCJIа т и n такие, что та > пЬ, но те < nd. От-
метим, что введенное Евдоксом отношение ПОрJlДICа, помимо Bcero
прочеrо, опреДeJIJlет дм к&ждоrо отношевИJI а Ь неICОТОРое сече-
ние во множестве УПОРJlдоченных пар (т, п) HaTypanьHых ЧИСeJI, а
именно: {( т, п) таICИХ, что mЬ < па} / {( т, п) таICИХ, что mЬ > па},
что указывает нам на ПрJlМУЮ СВJIЗЬ теории отношений ЕВДОICса с
определением вещественноrо числа по ,ДедеICИНДУ.
Отметим еще, что с алrебраичесICОЙ ТОЧICИ зренВJI множество
однородных величин, овлеТВОРJlЮЩИХ аICСИОМам 1 , можно рас..
сматривать ICаIC УПОРJlдоченную ПОJlуrруппу без аномальных пар (ев--
хлидову систему), а поле вещественных чисел ICаIC поле отношений
элементов этой полуrруппы (см. замечание 2 IC параrрафу 2.9).
2.7 ВВЕДЕНИЕ. ОТРИЦАТЕЛЬНЫХ
ЧИСЕЛ
Отрицательные числа впервые ПОJlВЛJIЮТCJI в Древнем Китае в СВJIОИ
с нео.бходимостью выполн ть до ICонца алrоритм метода "ФАН
33
чан" , иовестноrо теперь как метод raycca решенИJI системы линей...
Hых уравнений путем приведенИJI матрицы коэффициентов к треу...
rольному ВИАУ. Причем вначале отрицательные числа ПОJlВJIJIЮТCJI
лишь как промежуточные реоультаты ВЫЧИCJIений по этому метоАУ,
KorAa в ходе выполненИJI алrоритма приходитCJI вычитать ио MeHIr
шеrо ЧИCJIа большее или И3 "ничеrо" какое-либо число. Отрицатenь-
ные ЧИCJIа ВЫДeJIJIЛИ на счетной доске палочками Apyroro цвета ми
друrой формы, а при письме оаписывали друrими чеРНИJIами ИJlИ от--
меЧ8JIИ косой чертой. ДJIJI них имелось и особое наавание "ФУ", в
то время как положительные числа нааЫВ8JlИСЬ "ЧЖЕН" ДМ чисen
"ФУ" были определены следующие правила операций:
(т а ) =F (:1:Ь)
(:!:а) =F (1=Ь)
О =F (+Ь)
о =F ( Ь )
Вычитание формулировапось прежде Bcero, что еще раа укз--
оывает на происхождение отрицательных чисел И3 этой операции.
Кроме сложенИJI и вычитания употреблялись иноrда также YMH
жение и деление с отрицательными числами, хотя правила таких
действий явно не сформулированы.
Постепенно китайские ученые пришли к истолкованию чисел
"ФУ" как долrа, недостачи и т.п. Позднее общепринятой тановитCJI
rеометрическ&я интерпретация отрицательных чисел как точек на
отрицательной полуоси вещественной прямой.
1=(0:1: Ь),
:!:(а :1: Ь),
1=Ь,
:ж:ь.
2.8 ВВЕДЕНИЕ мнимыIx ЧИСЕЛ
Непосредственным источником введения мнимых чисел послужил
так На3ываемый "неприводимый" случай кубическоrо уравненИJI
ж З = аж + Ь, (а, Ь > О), KorAa ero дискриминант D = ( )2 ( )З <
о. Положительное решение этоrо уравнения (H.TapTMЬJI, 1535 r.)
имеет вид:
х= 3 : + J ( : )2 ( ; )3+з : J ( : )2 ( ; )3
и будет вещественным числом даже в случае, KorAa (!)2 (i)З < о.
Например, положительным решением кубическоrо уравненИJI ж З =
34
15% + 4 будет, соrласно Тарталье,
ж = \/2 + Y 121 + \/2 Y 121
с друrой стороны, нетрхдно заметить, что это уравнение имеет
положительное решение ж = 4, так что
\/2 + Y 121 + \/2 Y 121 = 4
Причем, решая в радикалах кубическое уравнение в "неприводимо!\.
случае, невозможно избежать отрицательных чисел под онаком ICf
дратноrо корня [4, с; 220 221].
Исследуя этот "неприводимый" случай, ИТ8JlЬJlНСКИЙ matemaT1-1К
Р. Бомбелли ОICоло 1560 r. впервые вводит в рассмотрение мнимые
числа. ПОСICольку квадратный корень И3 отрицательноrо ЧIJCJ.а не
может быть ни положительным, ни отрицательным числом, то Бом..
белли нзnывает рзnность (!) 2 (i) з по ИОВJIeчении квадратноrо
корня "плюсом минуса" ,если она прибавляется, и "минусом минуса" ,
если она вычитается. Бомбелли укзnывает правила действий с мни..
мыми числами и привод ит при меры вро де (+8 уСТ) + ( 5 yCТ) =
(+з А ), ( V' з + .; 10) ( V' з .; 10) = и друrие, более
сложные. Затем, предпооожив, что кубические ICорни И3 комп ксных
чисел сами являются комплексными числами, Бомбелли показывает
сопряженность кубических корней ВО сопряженных комплексных чи..
сел, объясняя тем самым, почему в "неприводвмом" случае кубич
cKoro уравнения решение ТаРТaJlЬИ являетCJI положительным вещ
ственным числом.
В дальнейшем, несмотря на мноrочисленные важные примененИJI
комплексных чисел, почти все математики XVII XVIII вв. рассма-
тривали их лишь как nOJIe3Hble фикции, лишенные самостоятепьноrо
смысла, и, если это ОКа3ывапось возможным, охотно отк&зывались
от их употребления.
В 1685 r. Дж. Ва.ллис предпринял первую попытку rеометриче--
CKoro истолкованИJI комплексных чисел. Даламбер и Эйлер также не--
однократно переходили от чисел а + ь А к точкам с координатами
а, Ь и обратно, но и они считали мнимые числа лишь удобными она-
Ками. Полное rеометрическое ИСТОЛICование комплексных чисел и,
что особенно важно, действий с ними было предложено в работах
35
.
К. Весселя (1799 r.) и Ж:Р. ApraHa (1806 r.). Если работа К. Вес--
v
селя, написанная на датском языке, не получила достаточнои изве.-
стности вплоть до конца XIX в., то работа Ж.Р. ApraHa была за--
мечена через семь лет после опубликования и вызвала оживленную
дискуссию.
Однако решающим для широкоrо признания комплексных чисел
явилось опубликование в 1828 1832 rr. "Теории биквадратичных вы--
четов" К. raycca. Пытаясь обобщить квадратичный закон взаимно--
сти, raycc пришел к выводу о возможности и необходимости рас--
ширения понятия целоrо числа, которое более 2000 лет казалось не.-
отъемлемым внутренним свойством обл сти Z целых рациональных
чисел. raycc распространил понятие целости с кольца Z на кольцо
чисел вида о + bi, rAe о, Ь Е Z, а i корень непр водимоrо над
полем рациональных чисел уравнения ж2 + 1 = о. Он показал, что
числа TaKoro вида образуют область, замкнутую относительно сло--
женив, вычитания и умножения и что в этой новой области можно
построить арифметику, аналоrичную обычной. raycc опреДeJIИЛ для
этих новых чисел единицы их будет четыре:- 1, 1, +i, ---i и
назвал числа, получающиеся Apyr из друrа умножением на единицу,
ассоциированными. Он заметил, что разложение на множители сле.-
дует рассматривать с точностью до ассоциированных чисел. Ка--
ждому числу а вида о + bi он сопоставил целое число, ero ВОРМУ
Na = (о + bi) · (о bi) = 02 + ь2. Из определения нормы c eдyeT,. что
N(a {3) = Na N{3. Число вида о + bi, которое нелЬGЯ разложить в
произведение двух сомножителей TaKoro же вида, отличных от еди
НQЦ,. raycc называет простым комплексным числом. Из определения
следует, что каждое CO TaBHoe целое рациональное число буцет со--
ставным и в области чисел вида 0+ bi. Но простые числа из Z в 06--
ласти С целых чисел вида 0+ bi MorYT стать составными, например,
2 = (l+i).(I i), 5 = (1+2i).(1---2i) = (2+i).(2---i). Чтобы найти все
простые числа из с, raycc доказывает теорему: каждое целое число
из С будет простым тоrда и только тоrда, коrда ero норма является
простым числом в z. Из этой теоремы следует, что простыми в С
будут числа 1 :!: i (делители числа 2), все целые рациональные числа
вида 4п+3 (простые в z) и все целые комплексные числа, норма кото--
рых равна простому числу вида 4п + 1. Затем raycc показывает, что
всякое целое комплексное число однозначно (с точностью до единиц)
раскладывается на простые множители. После этоrо raycc дает из
вестную rеометрическую интерпретацию комплексных чисел и дей
36
ствий С ними. Он рассматривает далее вычеты по комплексному мо--
дулю, вводит понятие наименьшеrо вычета и системы наименьших
вычетов по данному модулю. Наконец, для нахождения наибольшеrо
общеrо делителя двух целых компJIeкснык чисел он вводит алrоритм,
обобщающий алrоритм Евклида. После этоrо raycc для чисел из С
развивает арифметику, аналоrичную обычной (доказывает малую
теорему Ферма, вводит индексы и первообразные корни и т.д.). Раз..
витую теорию он примеНJ!ет для общей формулировки и частичноrо
ДОК8.3ательства биквадратичноrо закона взаимности.
Таким оБР8.30М, raycc действительно показал всему математиче-
скому миру, что целые КО.)fплексные числа являются ве менее заков..
ным объектом арифметики, чем целые рациональные числа и что
с их помощью можно не толыо получить новые, более простые и
естественные ДОК8.3ательства известных теорем для обычных це-
лых чисел (таких, как квадратич.ный закон взаимности), но и по--
лучать новые результаты. Все это, наряду с известным удобством
исполызования комплексных чисел в математическом анализе (см.,
например, [24, т. 2, rл. 11]) и привело к широкому ИСПОЛЬЗ0ванию
комплексных чисел в математике XIX в.
2.9 ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕнноrо
ЧИСЛА
Как уже отмечалось выше, теория отношений Евдокса вполне удо--
влетворяла потребности математики вплоть до середины XIX в. Тем
более, что с IV В. дО Н.3. она была существенно дополнена. А именно,
в XVI в. все возраставший объем вычислений (особенно астроно--
мических) потребовал усовершенствования самой основы расчетов.
Аппарат шестидесятеричных дробей вытесняется более удобным
аппаратом десятичных дробей, пришедших в Европу из КИТая и си
етематически изложенных в работе с. Стевина "Десятая" (1585 r.).
Блаrодаря широкому распространению десятичных дробей посте-
пенно устанавливается еДИНaR точка зрения на целые, рациональные
и иррациональные числа: все они получают представление в виде де-
СJlТИчной дроби.
Установлению единой точки зрения на понятие числа споеобсТв<r
вала также rеометрическая интерпретация чисел как точек на чи..
еловой прямой. При этом арифметические действия изображаются
37
движениями числовой прямой в себя: сложение и вычитание сдви"
rOM вправо и влево, а у ножение и деление растяжением и сжа..
тием (с симметрией относительно нуля при умножении или делении
на отрицательное число).
И в рамках самой теории отношений также устанавливается
единая точка зрения на понятие числа. "Под числом, rоворит
и. Ньютон, я понимаю не столыо множество единиц, СКОЛЫО
отвлеченное отношение какой"нибудь величины к друrой величине
Toro же рода, принятой нами за единицу. Число бывает трех видов:
целое, дробное и иррациональное. Целое число e TЬ то, что измеря..
ется единицей, дробное кратной долей единицы, иррациональное
число несоизмеримо с единицей' [30, с. 100 101].
Однако Bcero этоrо оказывается недостаточно к середине XIX в",
KorAa становится ясной необходимость cTporo лоrическоrо ПОСТRое--
ния математическоrо анализа на основе сложившеrоCJI в работах Да..
ламбера, Коши, Вейерштрасса и друrих математиков понятия пре-
епа.
Действительно, хотя rеометрическ&и инте претация веществен..
v "
ных чисел как ТQчек на числовои прямои делает наrлядным су..
ществоnание предела у монотонной оrраниченной последователь..
ности, или существование точных rраней у оrраниченноrо число--
Boro множества, или существование у непрерывной на отрезке фун"
кции максимума, минимума и всех промежуточных значений, но
для окаоаТeJlЬСТва этих утверждений свойств, сформулирован..
ных Евдоксом (см. аксиомы 1 6 п. 2.6) и свойств вещественных
чисел как множества, образующеrо упорядоченное поле, недоста..
точно. Поэтому оказалось необходимым так построить определение
вещественноrо числа, чтобы множество вещественных чисел помимо
прежних свойств обладало бы еще дополнительным свойством, ха..
рактерным для числовой прямой и позволяющим дать указанным
выше утверждениям CTporoe доказательство. Такое построение ве.-
щественных чисел было предложено во второй половине XIX B Р. Де.-
декиндом (1858 r.), К. Вейерштрассом (не позднее середины 1860..
х rr.), ш. Мере (1869 r.), r. Кантором (1872 r.) и некоторыми дpy
rими математиками.
р Дедекинд исходил при построении вещественных чисел из Toro
свойства числовой прямой этой МО eJIИ множества веществен..
ных чисел, которое и обеспечивает наrлядность указанных выше
утверждений. Это свойство Дедекинд усматривает в том, что каждая
38
точка числовой прямой производит Р83ложение прямой на две части
таким обрanом, что каждая точка ОДНОЙ части расположена влево
от .каждой точки друrой части и, ваоборот, еCJIИ все точки прямой
распадаютCJI на два класса TaKoro рода, что каждая точка первоrо
v
класса ежит влево от каждои точки BToporo класса, то существует
одна и толыо одна точка, которая производит это рanделение пря
мой на два класса. И Дедекинд проводит построение вещественных
чисел таким обрanом, чтобы удовлетворить этому последнему тре.-
бованию. Вещественным ЧИCJIом он Н83ывает ce eввe во множестве
рациональных чисел, т.е. такое Р83биение ero на две непустых части
\А и В, что ДЛJI любых рациональных чисел р Е А, q Е В выполняетCJI
неравенство р < ,.
На множестве сечений Дедекинд вводит отношения равенства и
пqрядка, все арифметические операции, покanывает выполнение всех
свойств упорядоченноrо поля и аксиомы Евдокса Архимеда. Н&lCонец
он ПОК83ывает, что построенное таким обрanом множество веще.-
ственных чисел обладает вышеук83анным свойством числовой пря
мой, а именно: если все элементы этоrо множества рanбиты па два
непустых класса А и В так, что для любых z Е А, у Е В выполВJI
ется неравенство z < у, то существует один и только один элемент,
производящий это Р83биение (этим элементом будет сечение А' /В',
rAe А' множество рациональных чисел из А, а В' множество
рациональных чисел из В).
К. Вейерштрасс при р83работке cвoero курса "Общая теория
аНaJlитических функций" строит вещественные ЧИCJIа иначе. ТpaK
туя положительное рациональное число ':: как совокупность m "эпе--
ментов" е n = , ':: = {е n , е n , , е n } (совокупность ''алементов''
Вейерштрасс Н83ывает arperaTOK), он стремитCJI распространить
эту трактовку на произвольные вещественные числа. Так, положи
тельное вещественное число Вейерштрасс опреДeJIJlет как ПрОИЗВОJIIr
ную (конечную или бесконечную) совокупность элементов, оrрани
ченную относительно CJlожения (последнее означает, что сумма пр
извольноrо KOBe Boro числа ПРОИЗВОJlЬных элементов из rh'ой COIIO-
купности BcerAa не превосходит aeKoToporo рациональноrо числа).
ш. Мере и r. Кантор при построении вещественных чисел опи
рались на понятие фундаментальной поcnедовательности. А именно,
вещественное число они определяли как класс эквивалентных фунда
ментальных последовательностей рациональных чисел (две фунда
ментальные последовательности Р" И '" рациональных чисел акви
39
валентны, если "€ > О 3nо "n > ПО Ipn...... ,nl < €).
Более подробно о равличных определенИJIX вещественноrо числа
в XIX в. СМ., например, [33, кн. 2, с. 193 195; 14, вып. 18, с. 176 180;
19, т. 1, с. 186 187]. Отметим лишь, что все уkаз.&нные выше опр
деленИJI вещественноrо числа изоморфны между собой и изоморфны
школьному определению вещественноrо числа как конечной или бес..
конечной десятичной дроби, если под последней понимать послед<r
вательность цифр со знаком и заПJIТОЙ. Например, число v'2 можно
определить и как сечение А/В, rде
А = {р Е Q таких, что р < о ИJlИ Р > О, р2 < 2} ,
В = {, Е Q таких, что, > О, ,2 > 2} ,
и как arperaT {1/1, 1/10, 1/10, 1/10, 1/10, 1/100, }, и как фунда..
ментальную последовательность рациональных чисел 1, 1.4, 1.41,
и как последовательность цифр со знаком и заПJIТОЙ +, 1, . , 4, 1,. . ..
ЗамечакU,z
1. Исторически первым определением вещественноrо числа можно
считать "антифайрезис" у пифаrорейцев, Т.е. представление
отношения произвольных отрезков в виде последовательности
подходящих дробей. Например, отношение диаrонали квадрата
к ero стороне предстаВJlJlется последовательностью
111
1, 1 + 2 ' 1 + l ' 1 + l '
2 + 2 2 + 2+!
и т.д. Развернутое же построение вещественных чисел как п<r
следовательностей подходящих дробей имеется у о. Хайяма
(XI в.).
2. Элементы Apyroro способа построения вещественных чисел, а
именно построения их как поля отношений упорядоченной п<r
луrруппы без аномальных пар, имеются уже у Дешал.я (1672 r.).
с формальной точки зрения идея этоrо построения заключа..
ется в следующем. Пусть G линейно упорядоченное мно--
жество и для любых элементов а, р из G однооначно опред
лена их сумма а + fJ Е а, причем (а + р) + 1 = а + (fЗ + 1),
40
т.е. операция сложения ассоциативна, а из а < {J следует, что
а + ((J < {J + ((J и ((J + Q < ((J + {3 для любоrо ((J Е G (т.е. BЫ
полн.яется двусторонняя монотонность). Пусть, кроме Toro, не
существует ни одной пары элементов а, {J из G таких, что для
любоrо натуральноrо n выполняется па < пр < (п + l)а (из
этой аксиомы аксиомы об отсутствии аномальных пар
следует аксиома Евдокса Архимеда и коммутативность CJIож
ния). TorAa любой упорядоченной паре (а, Р) элементов IЮ G
можно поставить в соответствие "функцию отношенИJI" ((J( n )
как такое отображение множества HaTypaпьHых чисел в себя,
что выполняется неравенство ((J(n) . а < n {J < [((J(n) + 1] · а
(т.е. дробь "приближает снизу отношение (J к Q С точ
ностью ДО "). Две упорядоченные пары (а, Р) и (1, 6) эк
вивалентны или "пропорциональны", если их функции OTH<r
шения ((J( п) и ф( п) совпадают. Для классов пропорциональных
пар из G вводится отношение порядка: (а, Р) < (")',6), если
((J(n) < ф(п)); операция сложения: (а, Р) + (")',6) принадлежит
.
тому классу пар, для KOToporo функцией отношения является
Ip(п) ЕВ ф(п) = m:х [ 1p(kn)tt/1(kn) ] (квадратные скобки ооначают
целую часть стоящеrо в них выражения); операцц УIIВОЖ
ния: (а, {3) . (")',6) принадлежит тому классу пар, до KOToporo
функцией отношения ЯВJIJlетCJI <р(п) · ф(п) = m:х [ 1p(knJ; (kn) ].
Подробнее об этом см. [1].
Вопросы 1J, заdа'Н1J,Z
1. Укажите основные этапы возникновения первых натуральных
чисел. Дайте определения HaTypaпbHoro числа и кардинальноrо
числа.
2. Укажите основные этапы возникновения дробей. Дайте опр
деление рациональноrо числа.
3. Что означает несоизмеримость? Почему открытие несоизм
римости привело к кризису философии и математики пифаrо--
рейцев? Назовите пути выхода из этоrо кризиса.
4. Назовите непосредственные источники введения отрицатель
41
ных И мнимых чисел. Укажите модели отрицательных и KOM
плексных чисел.
5. -Что такое целое комплексное число?
б. Укажите модель множества вещественных чисел.
7. Дайте определение вещественноrо числа по Ньютону.
8. Для чеrо во второй половине XIX в. понадобилось дать новое
определение вещественноrо ЧИCJIа?
9. Назовите известные вам определения вещественноrо числа.
rлава 3
АлrЕБРА
-
3.1 СОЗДАНИЕ АлrЕБрыI
КАК СИМВОЛИЧЕскоrо ИСЧИСЛЕНИЯ
3.1.1 Зачатки 8Jlrебры в математике
Древвеrо ВSВИJIова
В клинописных текстах Древнеrо Ва илона обнаружено большое чи
сло задач, содержащих уравнеИИJt". и системы уравнений l й и 2
й степени, записанные без символов, но особой терминолоrией. В
случае двух неизвестных одно называ.пось "ДЛИНОЙ" (ж), Apyroe
"ШИРИНОЙ" (у), их произведение (ху) "полем", "площадью" или
"ДЛИНОЙ ШИрИНОЙ" rоворилось также о "сторонах моих квадратов"
(х2 и у2). При ЭТОМ В примерах "длина" всеrда больше "ширины"
(х > у). В задачах, приводящихся к кубическому уравнению, BCТp
чалась третья неизвеСТНaJI "rлубина" (z), а произведение трех H
известных меновалось "объемом" (zyz). Такая терминолоrия сви
детельствует о происхождении ряда задач из rеометрии, хотя сами
задачи носили алrебраический характер. Это проявляется в том,
что с неизвестными величинами, имеющими различные измерения,
обращались как с однородными, составляя выражения, равносиль
ные нашим ху+х и zyz +ху, а также в том, что "длина", "ширина",
"площадь" и т.д. обоаначались словами шумерскоrо языка, КОТОРЫЙ
к тому времени уже вышел из употребления.
3.1.2 Апrебра Диофавта
у александрийскоrо математика Диофанта (111 в.н.э.) впервые появ
ляется буквеННaJI символика. Во введении к своему rлавному произве
дению "Арифметике" Диофант вводит новые обооначения: H
известную называет "числом" и обооначает СИМВОJЮм (', квадрат H
43
известной символом tJ (первые две буквы слова "сила, степень" ,
которым древние rреки На3ывали квадрат)., куб неизвестной сим
ВОЛОМ KtJ (первые две буквы слова "куб"), четвертую степень tJ
("KBaApaTcrKBaApaT"), пятую KtJ ("квадратcrкуб"), шестую
KKtJ ("кубcrкуб").
Образуя дроби с числителем 1 и знаменателем неизвестной B
личиной и ее степенями, Диофант получает шесть первых отрица
тельных степеней. Символом отрицательной степени служит знак Х,
поставленный после зап иси знаменателя, например, обратнм вели
чина квадрата неизвестной обозначается у Диофанта tJ Х.
Свободный член обозначалCJI у Диофанта символом М О пер
выми двумя буквами слова "единица"
Диофант вводит также символ , как некоторые полаrают, для
обооначения отрицательноrо числа и знак равенства L первая бу
ква слова "равный"
Уравнение zз + 8х (5х 2 + 1) = z в записи Диофанта выrлядит
так: KtJ о<;;; tJ {М о Q L<;Q.
Одновременно с введением символики Диофант явно ф0рМУЛИ
рует основные правила алrебраических операций: правило переноса
вычитаемоrо члена с одной стороны уравнения в друrую и правило
сокращения равных слаrаемых в обеих частях ураВ}Jения. Эти пра
вила получают в дальнейшем у математиков стран арабскоrо xa
лифата На3вания соответственно "ал джебр" и "an мукабала", OT
куда и происходит На3вание "алrебра"
Диофант подробно излаrает также правила умножения степеней
неизвестной величины. В наших обозначениях они выrлядят так:
хт . х" = хт+n
,
хт
1
,..т n
I&. ,
хn
1
1 1
= ,
х" хn+т
хт
rAe т, n, m + n < 6.
3.1.3 "ВвеАение в анапитичеСJCое исrcyССТВО" Ф. Виета
Работу Диофанта по созданию алrебраической символики продол
жили европейские математики эпохи Возрождения: Лука Пачоли,
Никола Шюке, немеЦК:(fе коссисты (подробнее об этом см. напри
мер, [15, т. 1, с. 60 61, 286 290]). Но решающий шаr . вв евие
буквенных lCозффициевтов был сделан французским MaTeMa
тиком Ф. Виетом в работе "Введение в аналитическое искусство"
(1591 r.). Суть сделанноrо Виетом состоит в следующем.
44
Необходимы, писал он, наrлядные и всеrда одинаковые символы,
позволяющие отличать данные величины от неизвестных, например,
так, что "искомые величины будут обозначены буквой А или друrой
rласной Е, 1, О, И, У а данные буквами В, D, G или друrими
соrласными"
Таким образом,.у Виета алrебра впервые приобретает характер
чисто символическоrо исчисления, что позволяет построить общую
теорию алrебраических уравнений.
Однако в алrебре Виета имелся еще существенный недостаток:
рассматривались только однородные уравнения, Т.е. такие, все члены
которых имели одинаковую размерность. Кроме Toro, сама запись
уравнений у Виета была неудобной. Так уравнение, которое мы за
писали бы в виде А2 + 2ВА = Z или в виде х2 + 2ах = Ь, Виет
записывал следующим образом: А qиad + в 2 in А aeqиetиr р plano.
Оба эти .недостатка отсутствуют уже у Декарта и Ньютона. Именно
от них и идет ставшая для нас привычной алrебраическая символика.
3.2 I'ЕОМЕТРИЧЕСКАЯ АлrЕБР А
u
ПИФАrОРЕИЦЕВ
3.2.1 Пре мет rеометричесJCОЙ 8Jlrебры
После открытия несоизмеримости пифаrорейцы пошли путем раз
деления величин на дискретные (натуральные числа и их отноше--
ния) и непрерывные (длины, площади и объемы). Для непрерывных
величин они построили особую теорию, известную под на:эванием
rеометричесJCОЙ апrебры.
Объектами rеометрической алrебры были отрезки и прямоуrоль
ники, а также параллелепипеды. Сложение отрезков производилось
путем приставления одноrо отрезка к друrому, вычитание путем
отнимания из большеrо отрезка части равной меньшему отрезку.
Произведением двух отрезков назывался построенный на них пря
моуrольник, а произведением трех отрезков или произведением пря
моуrольника на отрезок назывался построенный на них параллеле--
пипед. Таким обра:эом, исчисление, определенное в rеометрической
алrебре, было ступенчатым: склады вались и вычитались лишь вели
чины о;цной и той же размерности.
Теоремы rеометрической алrебры докззывались построением с
помощью циркуля и линейки. Например:
45
Теорема 1 Если о = 01 + 02, то а6 = 016 + 026.
Доказательство:
6
016
а2 6
01
02
Теорема 2 (о + 6)2 = 02 + 62 + 206
6
06
Доказательство:
о
02
о 6
Теорема 3 а 2 + 62 = с 2
о
Доказательство:
6
а
Теорема 4 аЬ = ( а Ь ) 2 ( а; Ь ) 2
46
62
06
о
6
Ь
tt!
2
Доказательство:
a Ь
2"""'"
3адачи в rеометрической алrебре также решались построением
с ПОМОЩ Ю циркуля И линейки.
Вот наиболее характерные задачи:
1. Припожить к данному отрезКУ а прямоуrольник данной пло--
щади S = Ьс:
c l
S
S
z
ах = Ьс.
...............
Ь а
2. Преобразовать данный прямоуrольник в квадрат:
b l
аЬ
I
х2
х2 = аЬ.
а
3. Приложить К данному отрезку а прямоуrольник данной пло--
щади S = pq так, чтобы "недостаток" был квадратом:
l
S=pq
1 . .. ...!
,1
х(а х) = pq.
а
3а. Пр ил ожить к данному отрезку а прямоуrольник данной пло--
щади S = pq так, чтобы "избыток" был квадратом:
l
а
J х 2 I
х(а + х) = pq.
S=pq
47
Задача 1 решалась следующим построением:
-, ...
I
I
I
ж
l'
3'
I
I
I
---f
2'
I
I
l' = 1, 2' = 2, следова
тельно, 3' = 3, т.е. аж = Ьс.
1
с
3
Ь
а
4 V
Задачи 2, 3, 3а решались путем преобразования произведении
аЬ, ж(а ж) и ж(а + ж) в Ра3ность квадратов, для чеrо применялась
теорема 4. Так, для второй задачи, по теореме 4, имеем:
х 2 = аЬ = ( а; Ь ) 2 ( а ; Ь ) 2
и ж строится как катет прямоуrольноrо треуrольника, rипотенуза
KOToporo равна ( a Ь ), а друrой катет равен ( а2'Ь )..
Упражнение 7. Методами rеометрической алrебры решите за
дачу о "золотом 'сечении": ра3делить данный отрезок на две части
так, чтобы отношение Bcero отрезка к БОльшей части было равно
отношению БОльш й части к меньшей.
3.2.2 Первые вераорешимые оа ачи
Мы видели, что в rеометрической алrебре задачи, эквивалентные
квадратным уравнениям, решались с помощью циркуля и линейки.
Нетрудно покаоать, что и, наоборот, все задачи на построение с
помощью циркуля и линейки алrебраически эквивалентны решению
такой конечной цепочки линейных и квадратных уравнений, что ко--
эффициенты каждоrо следующеrо уравнения цепочки рационально
выражаются через корни и коэффициенты предыдущих уравнений.
Действительно, все построения с помощью циркуля и линейки со--
стоят из следующих элементов: проведение прямой через две дaH
ные точки, нахождение точки пересечения двух прямых, прямой и
окружности или двух окружностей, так что всеrда есть алrебраиче.-
ское уравнение не выше второй степени. Можно СКа3ать и так: ме.-
тодами rеометрической алrебры, т.е. с помощью циркуля и линейки
можно построить те и только те отрезки, длины которых выража
48
ютси через длины данных отрезков с помощью сложения, вычитания,
умножения, делении и извпеченИJI KBaApaTHoro KOpВJl.
Однако уже в V в. до н.з. ПОЯВИЛИСЬ три задачи, которые не уда..
ВaJIOСЬ (да и не моrло yдacTbCJI) решить методами rеометрвческой
алrебры. Это задачи уявоеви.. куба, трвсек:цив yrJl8 в к:вa p8"
туры Kpyra.
адача удвоения куба построения куба вдвое больше AaHHoro
выражается уравнением %З = 2а З , задача трвсекции уrла де--
ления AaHHoro уrла на три равные части выражаетCJI уравнением
3% 4%З = а, rAe а синус AaHHoro yrna, а % синус искомоrо yrna.
Задача о квадратуре Kpyra состоит в построении кВадрата, ра..
вновеликоrо данному Kpyry. Эта задача СВОДИТСЯ к построению o
резка, в vi раз большеrо, чем радиус Kpyra r (%2 = 1rr 2 , ОТКУАа
% = Vir).
Задача удвоения куба неразрешима в rеометрической алr.ебре п
тому, что ее уравнение неnьзя свести к ц почке линейных в KBaдpa
Hых уравнений. По той же причине неразрешима в rеометрической
алrебре и задача трисекции уrла (кроме нехоторых исключитель-
ных случаев). Задача о квадратуре Kpyra неразрешима по причине
трансцендентности, числа .ji, оно не JlВJlJlется корнем никакоrо MH
rочпена с целыми или рациональными коэффициентами.
Убедившись в тщетности своих попыток решить укanанные за..
дачи с помощью циркуnи и линейки, д»евние rреки нашли тем не
менее способы построения нужных отрезков с помощью введенИJI
в математику новых, не конструируемых с помощью только цвр..
куля и линейки кривых. Так, l'иппократ Хиосский (У в. ДО н.э.)
И Менехм (IV. в. до н.з.) показали, что решение задачи удвое--
ния куба равносильно нахождению таких двух величин % и у, что
а % = % У = У 2а. Из этой пропорции полу аются три кривые:
парабола ау х2
,
rипер бола жу 202
,
парабола у2 20Ж,
точка пересеченИJI которых и дает решение задачи.
Мы видим, таким образом, что попытки решить з ,, чу удвоеНИJI
куба стимулировали развитие новой ветви математики теории
конических сеченИЙ. Эта новая теорИJI подробно развита Апол
лонием (111 в. до Н.3.) В ero знаменитых "Конических сеченИJIX"
49
Для решения задач квадратуры Kpyra и трисекции уrла rреки
привлекли в математику новую механическую кривую, На3ванную
пооднее "квадрат.рисой" . Квадратрису rреки определяли как кривую,
которую описывает точка пересечения верхней и боковой стороны
квадрата, KorAa верхняя сторона равномерно опускается до нижней,
а левая сторона равномерно вращается до нижней, причем так, что
обе достиrают нижней стороны одновременно (рис. 2). Решение
задачи о делении уrла на три равные части показано на рис. 3.
а I
I
I
I
I
lp
ь
Рис. 2
Рис. 3
Термин "квадратриса" объясняется тем, что с помощью этоii
кривой решалась и задача о квадратуре Kpyra. А именно, Динострат
-(IV в. до н.э.) дока.оал, что отреЗ0К Ь, который отсекает квадратриса
на нижней стороне квадрата (см. рис. 2), равен a , rAe а сторона
квадрата. Так что отреЗ0К у = 1r может быть построен как решение
уравненИJI Ь". у = 2а . 1, а отреоок % = vi как решение уравнении
%2 = У . 1.
Отметим, что Ь = lim r(lp) = lim 2...4 . , так что докanатель..
+o +o n 81n
ство Динострата можно рассматривать как исторически первый вы..
вод замечательноrо предела lim n = 1. Оно опиралось явно на
+o 81
неравенство sin <р < <р < tg <р при О < <р < и неявно на то, что при
изменении уrла <р от ; до О длина r(<p) радиус"вектора квадратрисы
непрерывно убывает от а дО Ь, а длина %( <р) проекции радиус"вектора
на нижнюю сторону квадрата непрерывно воорастает от О до Ь.
50
оказательстве испольоовался .метод от противноrо. Предпо--
ложив, что Ь < (J , Динострат строит
точку В пересечения квадратрисы с
окружностью с центром в точке О pa
диуса ОА = (J (рис. 4) и опускает из
этой точки перпендикуляр ВС на ОА.
Тоrда, с одной стороны, ВС = ОВ
sin <р = (J . sin <р. С друrой стороны, по
определению квадратрисы имеем: ВаС =
1(12 ' откуда ВС = (J · <р. Так что sin <р
<р (?!). Аналоrично, предполОжив, чr::
Ь > a , Динострат строит точку С, "'1
кую, что ОС = 21((J И восстанавлива. r
перпендикуляр вс. TorAa, с одной стороны, ВС = ОС .tg <р = 2 1r (J .tg '1',
но, с друrой стороны, ио определения квадратрисы снова имеем:
ВС = (J . <р. Так что tg <р = <р (?!).
Можно оаключить, что задачи удвоения куба и трисекции уrла,
привлекавшие внимание rреческих математиков в течение примерно
шести веков, стимулировали появление теории конических сечений,
привели к выводу первоrо оамечательноrо предела и привпекли в
математику различные механические кривые.
Упражнение 8. Покажите, что оадача удвоения куба может быть
решена следующим способом (repoH, 1 в.н.э.). Строим прямо--
О' D С уrольник ABCD со сторонами
ВС = AD = а и АВ = CD =
2а и точку О центр этоrо
прямоуrольника (рис. 5). Дви
В rая одновременно точку В внио
по продол ению стороны СВ,
а точку D влево по продол
жению стороны CD так, чтобы
расстояния от этих точек до
В' центра прямоуrольника OCTaBa
Рис. 5 лись равными друr друrу, доби
ваемся Toro, чтобы прямая B'D'
проходила черео точку А. Тоrда DD' будет искомым отреоком ж.
51
о'
Упражнение 9. Покажите, что задача трисекции уrла может быть
решена следующим способом (Архимед, 111 в. до н.з.). Строим
окружность С центром
в точке- О (рис. 6) и
уrол АОВ, трисекцию
KOToporo надо произве.-
сти. Радиус АО продол
жим за точку О и дa
лее за пределы окруж
ности до тех пор, пока
отрезок О'с, otceK&e--
v
мыи окружностью от
отрезка О'В, не станет
Рис. 6 равным радиусу окруж
ности. TorAa уrол АО'В будет втрое меньше уrла АОВ.
А
3.2.3 3амечави..
1. Как видно из пунктов 3.1.1, 3.1.2 и 3.2.1, rеометрический,
наrлядный язык алrе ры предшествовал ее буквенному, символиче.-
скому языку.
2. С решением задачи 2 rеометрической алrебры пифаrорейцев
связано происхождение термина "среднее rеометрическое": сторона
х квадрата, равновеликоrо данному прямоуrольнику со сторонами
а и Ь, есть такой отрезок, который является средним пропорцио--
нальным между а и,Ь (т.е. а х = х Ь) и который строится reo--
метрически с помощью циркуля и линейки. С зтой же задачей свя
зано происхождение термина "квадратура": всякий прямоуrольник,
а следовательно, и всякий треуrольник и вообще всякий мноrоуrоль
ник (поскольку мноrоуrольник Ра.3бивается на треуrольники) может
быть с помощью циркуля и линейки преоБРа.30ван в равновеликий
ему квадрат, т.е. может быть "квадрирован"
3. Как мноrие полаrают, задачи 3 и 3а rеометрической апrебры
пифаrорейцев имеют древневавилонское происхождение и есть лишь
друrа.и запись известных задач на определение сторон прямоуrоль
Horo треуrольника по данной разности или сумме катетов и по дaH
ной удвоенной площади.
4. По мнению о. Нейrебауера, задача трисекции уrла вооникла,
возможно, "из теории солнечных часов", а именно из задачи по-- ..
52
строения шестой (двенадцатой) части дуrи, которую Солнце опи
сывает над rОРИЗ0НТОМ, дуrи, необходимой для получения oAHoro
"ceooHHoro" часа (обычный час, т.е. Ayry в 300, издавна строили с
помощью циркуля и линейки).
5. В конце VI книrи "Начал" Евклида задачи 3 и За обобщаются.
А именно, там речь идет о прилЬжении площадей в виде пар8JlJlе-
JlOrpaMMoB и так, чтобы недостаток или И3РЫТОI был бы паР8JI-
JleJlOrpaMMoM с яанным отношением сторон.
6. Задачи, решаемые rеометрическим построением, 1 111 в. дО Н.Э.
раздеЛJIЛИСЬ на три класса: ПJlоские, т.е. решаемые построением с
"
помощью циркуля и линеИIИ, телесные, т.е. решаемые с по ощью
" u
конических сечении, и Jlин еииые, для решения которых применя
лись линии, определяемые с помощью движения (Iвадратрисы, спи
рали, вставки и т.п.).
7. Как показал еще Архимед, задачи, приводящие к кубическим
уравнениям, относятся к классу телесных задач, т.е. их BcerAa можно
решить с помощью конических сечений. Архимед же указал необхо--
димые и достаточные условия существования положительных корней
и число корней (см., например, [14, вып. 11, с. 287 291].
8. С точки зрения практических нужд rеометрическое постро--
ение искомоrо объекта не имело большоrо удобства, а ИНОl'да было
просто неприrодно. lЛавное значение rеометрическоrо построения
[34, с. 71 72] заключалось в ЯОlCаоаТeJIь тве существов8ВИJI ис
KOMoro объекта. Необходимость в таком доказательстве была BЫ
звана открытием несоизмеримости. "KorAa было найдено, что не
существует ни числа, ни числовоrо отношения, которые, умножен
ные сами на себя, дают 2, и KorAa вместо поисков TaKoro исла стали
искать отреоок, который был бы стороной квадрата, построенноrо
на данном отрезке, то прежде Bcero оказалось необходимым ДOKa
:зать существование подобноrо отреока. Это именно и делают, пред
ставив ero в виде диаrонали квадрата, построенноrо на данном OT
реоке" [там же, с. 71].
9. Решение алrебраических оадач rеометрическим построением
способствовало развитию аналитичеСlCоrо меТОА8, который при
меняJiся пифаrорейцами еще при нахождении rеометрических мест
точек. Этот метод, вклю..ающий в себя и исследование условий раз
решимости и числа вооможных решений, состоял ио ряда ;звеньев.
Разберем кратко этот метод на примере решения оадачи о построе
нии прямоуrольноrо треуrольника по rипотенуое и площади. Первым
53
звеном метода являе:rся ПрОТ80ИС, или общая постановка задачи:
построить прямоуrольный треуrольник по rипотенузе и площади.
Далее следует В:l:Теоис, введение данных: даны отреоок АВ и пло--
щадь S (рис. 7). Третье звено апarоr8, преобразование. Здесь
N К- C GH M G
I S I
м L
А В О А О В
Рис. 7 Рис. 8 Рис. 9
предполаrается, что задача решена с помощью треуrольника АВС
с прямым уrлом С (рис. 8). TorAa точка С лежит на ОКРУЖНОСТИ
с диаметром АВ, а прямоуrольник OFGB, построенный на отрезке
ОВ, равном половине отрезка АВ, и на OTpe Ke BG, равном BЫ
соте СО треуrольника АВС, равновелик данному прямоуrольнику
MNKL. Четвертое звено реоопюци.., разрешение. Здесь иссле.-
дуются, насколько имеют все необходимое для решения поставленной
задачи; в рассматриваемом случае это имеет место лишь TorAa, ко--
rAa S < ( А2в )2 (так как BG = СО < ( А2В ) = ОВ). Укаоание условий
раорешимости иорmзмов включается теперь в дополнение к
протаоису'. Друrим результатом раорешения является указание чи
сла возможных решений; в рассматриваемом случае их два, второе
получается из решения на рис. 8 симметрией относительно OF.
Укаоанные четыре звена составляют 8Валио решения задачи.
Найденные решения излаrаются и проверяются затем в свитеое,
который включает в себя еще три звена: построение, ОЖ808-
тепьство и ОaJCJlючение. В рассматриваемом случае построение
состоит из следующих действий: деление отрезка АВ пополам, по--
строение ПОЛУОКРУЖНОСТИ с радиусом ОВ = А 2 В , приложение к OT
резку ОВ данной площади S (задача 1), нахождение точек С и С'
как точек пересечения полуокружности с прямой GH (рис. 9); Tpe
уrольники АВС и АВС' искомые. ДОЖ808Тельство состоит в
проверке Toro, что треуrольники АВС и АВС' действительно равно--
велики прямоуrольнику MNKL. Наконец, в ОaJCJllOчевии rоворится,
что "следовательно, задача построения прямоуrольноrо треуrоль
ника по данным rипотенузе и площади решена, что и требовалось
сделать"
54
3.3 ПРОБЛЕМА РЕШЕНИЯ В
РАДИКАЛАХ АлrЕБР АИЧЕСКИХ
u
УРАВНЕНИИ
,
3.3.1 Решение в ра иlCапах апrебраических уравнений
2 U з U AU U
и, и и и степенеи
Уравнения 2 й степени умели решать еще в Древнем Вавилоне. Так,
в одном из клинописных текстов скanано: "Я вычел из площади CT
РОНУ Moero квадрата, это 14,30 (ж 2 ж = 14 .60 + 30 = 870)" Далее
идет вычисление стороны квадрата (ж): "ТЫ берешь 1, коэффициент.
ты делишь 1 пополам, это;О;З0 (30 · 610 = !). ТЫ умножаешь 0;30 на
0;30, это 0;15 (!). ТЫ скл дываешь это с 14,30, и это есть 14,30;15
(870!), что является квадратом для 29;30 (29!). ТЫ складываеlIIЬ
0;30 с 29;30, получается 30, сторона квадрата (ж)"
Как видно из этоrо примера, вычисление положительноrо корня
уравнения ж 2 рх = q ПРОИ3ВОДИJЮсь по следующему правилу:
x= J ( ) q +
Вооможно, что при выводе этоrо правила использовали reoM
трическую интерпретацию решения квадратноrо уравнения, кото--
рую мы встречаем позднее у некоторых арабских математиков. Так,
ал ХОре3ми (VIII IX в.) при pe
шении уравнения ж 2 + 10ж = 39
исполыэует следующее построение.
Фиrуру, составленную И3 квадрата
неизвестной величины (ж 2 ) и двух
равных прямоуrольников, дающих в
сумме площадь 10ж, он дополняет до
квадрата (рис. 10). Цлощадь этоrо
большоrо квадрата будет равна х2 +
10ж + 52 = 39 + 52 = 64, поэтому ero
5 сторона z + 5 будет равна v'б4 = 8,
Рис. 10 откуда находится ж = 3.
Решение уравнения 3 й степени
5
5ж
52
z
ж 2
5ж
ж
zз + аж = Ь (а, Ь > О)
55
быJЮ впервые дано итальянским математиком дель Ферро (около
1500 r.) и СОСТОЯОО в следующем: находились числа и и v, удовле.-
ТВОРJlющие уCJIОВИЯМ и..... v = Ь, иv = (i) 3, и и .....v являются корНЯМИ
квадратноrоура8ненИJI
2 ( 0 ) 3
У ..... Ьу ..... 3 = О,
и решение ИМeJIO вид
ж= {/U = з. v ( : )2 + ( ; )3 + : 3 v ( : )2 + ( ; )3 :
Решения двух друrих типов алrебраическоrо уравнения 3 й сте.-
пени ж 3 = ож + Ь и ж 3 + Ь = аж (Ве3де О, Ь > о и ищутся только
вещественные положительные решеНИJl) были даны друrим ИТaJIЬJlН"
ским математиком Н. Тартальей (1535 r.). Формулы для решения
всех трех типов кубическоrо уравнения и вывод этих формул были
опубликованы Дж. Кардано в 1545 r. в работе "Ве икое искусство,
или об алrебраических правилах"
В этой же работе было опубликовано найденное л. Феррари
(ОКООО 1540 r.) решение в радикалах алrебраическоrо уравнения 4..й
степени. Линейной заменой это уравнение приводилось к виду, не
содержащему коэффициента при ж 3 :
х 4 + аж 2 = Ьх + с
Затем леВaJI часть ДОПОЛВJIлась до полноrо квадрата:
а ( а2 )
(ж 2 + 2 + t)2 = 2tx 2 + Ьж + t 2 + at + с +"4 '
причем t выбиралось так, чтобы выражение справа стало полным
квадратом. Для этоrо необходимо и достаточно, чтобы был равен
нулю ero дискриминант:
D = ь 2 ..... 2t( 4с + а 2 + 4at + 4t 2 ).
Последнее уравнение имело уже 3 ю степень и решалось по способу
депь Ферро.
56
3.3.2 Попытки решенв.. в ра JП:8Jlах
8JIrебраических ураввеВВЙ степевв n > 5.
"РаоМЫШJIеиие об 8JIrебраическом решеввв ypaвBeввii"
ж. Лarраи)l(а. Теоремы п. Руффивв и В.Х. АбeJIJI
ИсслеДУJl в дальнейщем алrебраичеСICие уравненИJI 5--й и высших.ст
" v
пенеи, мноrие математики пытались наити их решение также в виде
алrебраической формулы от кoэфeIвциентов уравнеНИJl, т.е. пыта..
лись и эти уравнения решить в радикалах.
Так, Е.В. Чирнrауз (1683 r.) пыталCJI решать алrебраические yp "
вненИJI
жn + 01%n...l + . .. + ОП = О
с помощью подбора реоОJlьвевты, Т.е. HeKoToporo вспомоrатeJI
Horo уравнения меньшей степени (подобно тому, как квадратное ура..
внение %2 + р% + q = о решаетCJI с помощью резольвенты у = % + 1).
Выбираа резольвенту в виде
n...1 + 6 n...2 + + 6
у = ж 1% . · · n...1,
он пытался так подобрать коэффициенты 61,62, ..., 6n"'1, чтобы вы..
ражение для у" не содержало степеней ж. Тоrда уn = const и решение
исходноrо уравнения п..й степени сводится к решению вспомоrател
Horo уравнения степени (п 1). Сам Чирнrауз сумел осуществить
этот метод лишь для n = 3. Пооднее л. Эйлер проделал все выкладки
для n = 4. Но для n = 5 это ОКа3aJIOсь невозможным: попытки под..
бора коэффициентов 61,62,6з,64 приводили К уравнени.им, степень
которых была выше 5. '
Эйлер исходил от приемов дель Ферро и Тартальи, которые ис..
кали корни алrебраических уравнений в виде различных ирраци..
ональностей. Например, в случае уравнения %3 = аж + 6 реш
ние, соrласно ТаРТaJIье, имеет вид: х = + , rде u и v
корни HeKoToporo квадратноrо уравнения. Поэтому для уравнения
х 4 = ах 2 + 6х + с Эйлер искал решение в виде + + .vw. Ему
удалось построить уравнение й степени, корнями KOToporo будут
и, v и ш. Однако распространить этот прием на уравнения вида
n
Х N = a1x n ... 2 + a2%n 3 + . + an 1 при n > 5,. исполызуя х = Е y'ilk
1:=1
" 1
или ж = ио + Е СI: y'iik , Эйлеру не удаоось.
1:=1
57
Число различных попыток решить в радикалах алrебраические
уравнения степени n > 5 быJЮ очень велико, и все они оказались
безуспешными. Но вот в 1771 1773 rr. был опубликован большой
трактат ж. Лаrранжа "Размышление об алrебраическом решении
уравнений", в котором автору удалось rлубоко проникнуть в су...
щность проблемы.
Лаrранж начинает свое исследование с анализа известных попы...
ток решения алrебраических уравнений в радикалах. Он замечает
при этом, что не только коэффициенты реоольвенты, но и ее КОрИИ
и все промежуточные радикалы в радикальном выражении дЛЯ KO}r
ней исходноrо уравнения рационально выражаются через корни ис...
ходноrо уравнения и, может быть, еще черео некоторые первообра...
зные корни из единицы. Действительно, для уравнения 2...й степени
резольвеНТ8: имеет вид
р 2
У = ж + = :!:.VD =:1: q ,
2 4
и, применяя теорему Виета, имеем:
V (X1 + Ж2)2 ....L.. (Жl Ж2)
у = :!: ЖIЖ2 = :I:
4 2
Для уравнения 3 й степени
ж 3 + ож + ь = о
резольвента имеет вид
у2 + Ьу ( ; ) з = О,
а решение вид
3 Ь / ( Ь ) 2 ( 0 ) 3 3 2 Ь . / ( 2 Ь ) 2 + ( 0 3 ) 3
x= + = 2 +Y 2 + 3 + y
(значения кубических корней выбираются с учетом Toro, что их пр
изведение равно ( )3), И можно показать, что
15 = V ( b ) 2 ( 0 ) 3 = (жl Ж2)(Жl ЖЗ)(Ж2 жз)
v v 2 + 3:1: 6 "; 3 '
58
. /1) ( 1 А ) ( 1 Н ) \ 3
V 3 = 2 + 2 2 2 = еl е2, ei = 1, ei =F 1 ,
= \j ь vi5 = Xl Xl + 22:3 .
2 2 2 Н
Итак, видно, что у = <Р(Жl, Х2, . . . , Х п , еl, е2), rде '1' некоторая pa
циональная функция от корней исходноrо ypaBHeH . Но тоrда, заме--
Л v " р
чает аrранж, при произвольнои переСТ8НОВlCе 1C0рнеи Xi ....... X Pi
(X pi =F Х р ; при i =F j) величина (р( Х р1 , Х р2 , . . . , Х р ", еl, Е2) также
будет являться корнем резольвенты. Но корней резольвенты Bcero
r < п 1, в то время как рanличных вооможных перестановок KOp
ней имеется п! (при условии отсутствия кратных корней). Поэтому
ОТЫСlCание реоОJlьвевты сво итс.8, ПО существу, IC oTblclCa-
нию т8JCИХ раЦИОН8JlЬНЫХ фУНICЦИЙ от 1C0рней исхо ноrо ура-
"
внени.., lCoTopble при всех ВООМОЖ:НЫХ переставовlC8Х 1C0рнеи
принимают Bcero r < n 1 раОJlИЧИЫХ оначений.
Рассматривая далее вопрос о нахождении таких функций '1',
Лаrранж переходит от перестановок корней Жi L Ж Р . к более yдo
ным по стаНОВlCам их номеров: i L Pi. Множество Sn всех подста
новок из n элементов он рanбивает на части:
Sn = Нl + Н 2 + + Hr
H i = {Р Е Sn; '1'1 переходит в <pi при подстановке Р}
(:здесь '1'1, '1'2,..., <Pr корни резольвенты), производя тем самым
фактически рanбиение симметрической rруппы Sn подстановок из n
элементов на классы смежности по подrруппе Н 1 . Лаrранж ДOKa
зывает при этом, что число элементов одинаково во всех смежных
классах Hi, т.е. фактически доказывает теорему о том, что поря
док подrруппы H1 делит порядок rруппы Sn. Эта теорема HanBaHa
впоследствии теоремой Лаrранжа. Функции '1', не меняющие своих
:значений при одних и тех же подстановках и:з Sn (множество таких
подстановок образует некоторую подrруппу H1 rруппы Sn) Лаrранж
называет по оБRЫМИ. Относительно подобных функций он пока
:зывает, что они рационально выражаются друr через друrа и че--
ре:з коэффициенты исходноrо уравнения, т.е., как мы бы скanали,
принадлежат одному и тому же алrебраическому полю. Например,
n = 2, х2 + рх + q = О, S2 = {(1), (12)}, Н 1 = 1 = {(1)}; функции
'р = %1 Х2 И Ф = X при D = р2 4q :F о и Р =F о "принадлежат"
59
одной и той же подrруппе Н 1 rруппы S, т.е. не меняются только при
тождественной подстановке. ЭТИ ФУНКЦИИ рационально выражаются
Apyr через Apyra и чере3 коэффициенты р и q исходноrо уравнения:
Ф = "",+ 2 29 , I(J = 2ф 2+29 . А из этоrо факта следует, что во-
прос о нахожяении функций <р и, CJIеяоваТeJlЬВО, вопрос о
решении 8Jlrебраических уравнений в раЯИК8Jl8Х свояитс.8 к
иоучению пояrрупп симметрической rруппы Sn. Таков rла
вный вывод, К которому пришел Лаrранж.
Изучение подrрупп rруппы Sn было продолжено о. Коши, п. Py
фини И Н.Х. Абелем. Так, Коши УДaJЮсь показать, что при n > 5
rруппа Sn не имеет подrрупп индекса 2 < i < р, rAe Р наибольшее
простое число, не превосходящее n (эта теорема получила в дальней
шем название теоремы Бертрана Серре). п. Руффини был первым,
кто представил доказательство Toro, что буквенное 8J11'ебраиче..
ское уравнение 5..й степени вообще нераорешимо в ра и..
капах (см. это дока:эательство, например, в [37, с. 42 43]). Однако
предложенное Руффини доказатель.ство было неполным: оно опира
лось на недока:эанное предположение о том, что корни Ре30львенты
Bcer a выражаются рационально чере3 корни исходноrо уравнения.
Дока:эательство этоrо предположения и независимое от Руффини
полное ДОКа3ательство нершзрешимости в радикалах буквенных ал
rебраических уравнений 5 й степени было дано н.х. Абелем в 1824 r.
з.з.з OCHOBHaJI теорема теории r8JIya.
Решение апrебраических уравнений в ра икапах
с точки орени" теории raпya.
Решение оа ач rеометрической апrебры
с точки ореНИJl теории I'aлуа
Дока:эательства Руффини и Абеля имеют дело с буквенными ypaBHe
ниями, т.е. с уравнениями, коэффициенты которых являются неза
висимыми переменными величинами. Они убеждают нас в том, что
при n > 5 не существует универсальноrо радикальноrо выражения,
которое rодилось бы как решение для всех уравнений данной CTe
пени. Но эти дока:эательства еще ничеrо не rоворят о разрешимо--
сти в радикалах отдельных типов уравнений и просто конкретных
численных уравнений, т.е. ура[4нений с конкретными численными
коэффициентами.
ПереИ С'rl r:е3ультаты теории Лаrранжа на численные уравнения
13'"..
60
удалось французскому математику э. rалуа. Рассматривая числен
ные уравнения, rалуа вводит понятие их rруппы как множества
всех таких подстановок И3 SN, которые не нарушают совокупности
"
всевозможных рациональных соотношении между КОРНЯМИ, т.е. со--
вокупности соотношений вида Pi(%I, %2, . . . , %n) = О, rAe Pi ПО--
линомы относительно %1, Ж2, . . . , Ж П С коэффициентами, рационально
выражающимися через коэффициенты 01, 02, . . . ,оп исходиоrо ypa
внения. Эта rруппа, получившая в дальнейшем название rруппы
r8JIY8, определяет для каждоrо KOHKpeTHoro алrебраическоrо ypa
внения алrебраическую структуру ero корней.
Замечание Работе э. rалуа о разрешимости в радикалах ypa
внений с числовыми коэффициентами предшествовали исследования
raycca и Абеля. Так, raycc (1797 r.) "провел исчерпывающий aHa
ЛИ3 уравнений деления Kpyra (чем восполнил пробел в изысканиях
Лаrранжа), применив, по существу, разложение rруппы подстановок
рассматриваемоrо уравнения в прямую сумму циклических подrрупп
и построив подполя, соответствующие каждой подrруппе. Это была
первая модель для будущей теории rалуа, и она была построена
для уравнений специальноrо вида с числовыми коэффициентами. В
1826 r. Абель с помощью метода raycca нашел еще более обширный
класс уравнений, разрешимых в радикалах"[14, ВЫП. XVII, с. 322].
В современной математической литературе rруппа rалуа дaH
Horo алrебраическоrо уравнения f(ж) = ж n + 01жn 1 + + оп = О
определяется обычно следующим образом. Пусть К основное поле
(област рациональности), т.е. минимальное поле, в котором лежат
коэффициенты уравнения 01, 02, . . . , оп. Пусть Е поле Ра3лож
ния, т.е. поле, полученное из К путем ero нормальноrо расширения,
а именно путем последоватепьноrо нормальноrо присоединения к К
корней уравнения Жl, Ж2, . . . , ж п . Нормальность расширения 03Ha
чает, что вместе с одним корнем неприводимоrо над расширяемым
полем уравнения присоединяются и все остальные ero корни. Е есть
таким образом минимальное нормальное расширение поля К, coдe
жащее все корни AaHHoro алrебраическоrо уравнения. При этом мы
BcerAa будем предполаrать отсутствие у уравнения кратных корней,
"
так как существование кратных корнеи и их нахождение устанавли
вается с помощью алrоритма Евклида: если Жl кратный корень
уравнения f(ж) = О, то (ж Жl) общий делитель мноrочлена f(ж)
и ero производной f'(ж). Jpуппа rалуа G уравнения f(ж) = о опред
ляется как совокупность всех автоморфизмов Е относительно К, т.е.
61
таких биекций Е в себя, сохраняющих операции поля, которые пере
ВОДЯТ К в себя. Каждый такой автоморфизм переводит совокупность
корней %1, %2, . . . ,%n В себя, Т.е. переставляет корни. Наоборот, если
такая перестановка известна, то известен и автоморфизм, потому
что если %i ...... %р" то всякая рациональная фУНКЦИЯ <,0(%1, %2,..., %т)
С коэффициентами И3 поля К переходит в рациональную же ,ФУНКЦИЮ
<,о(%Рl' %Р2'...' %р",), т.е. при такой перестановке корней значение <,о
остается в области рациональности К. Поэтому rруппу rалуа можно
рассматривать как некоторую fРУППУ переставовок корней или, что
удобнее, как rруппу подстановок номеров корней.
Пример 1. Для уравнения
%3 1 = О
поле К совпадает с полем Q рациональных чисел, корни имеют вид
1 + а 1 а 1 К ( 3
%1 2 2 ,%2 2 2 ,%з ,полеLJ V "J,T.e.
получается путем присоединения к полю К корня у = А неприв
димоrо над К уравнения у2 + 3 = о.
.
Рациональные соотношения между корнями имеют вид:
%1+%2+1=0, X1.%2 1=0, % =%2' %2=%1, %з I=О.
I'pуппа rалуа G как совокупность подстановок, не нарушающих c
вокупности рациональных соотношений между корнями, состоит И3
тождественной подстановки и подстановки, меняющей местами %1 и
%2, Т.е. G = {(1), (12)}.
I'pуппа G На3ывается раореwимой, если в ее композиционном
ряду
G = G o ::> G 1 ::>
::> G m =I={(I)}
все подrруппы Gi (; = 1,2,... , т) имеют простые индексы. Здесь Gi
максимальный нормалЬНЫЙ делитель Gi l, Т.е. такая подrруппа
rруппы Gi l, Ра3ложения по которой на левые и правые смежные
классы совпадают, и такая, что в Gi l нет нормальных подrрупп,
содержащих Gi и отличных ОТ Gi. Отметим, что ра3решимость
rруппы не зависит от выбора ее композиционноrо ряда.
Основная теорема теории rалуа rласит: данное численное ал..
rебраическое уравнение раореwимо в радикалах тоrда и
только тоrда, Kor a раореwима ero rруппа raпya.
62
Пример 2. Уравнение
% 6 4%3 + 1 = О
азрешимо в радикалах, e ro корн ями будут %1 \12 + У'З, %2 =
. %1, %3 = е 2 . %1, %4 = \l 2 у'З., %5 = е .%4, %6 = е 2 . %4, rде е =
....! + ";3 первообразный корень 3 й степени из 1, е 2 = ___! ";3
друrой первообразный корень 3 й степени из 1. Рациональные
соотношения между корнями имеют вид
3..... 3..... 3
%1 %2 ..... %3'
'" 3 ..... '" 3 '" 3
11&1 4 ..... 11&1 5 = 11&1 6 ,
% = %2%3, % = %3%1,
% = %1%2, % = %5%6, % = %6%4, % = %4%5,
%1 + %2 + %3 = %4 + %5 + %6 = о, %1%2%3 + %4%5%6 = 4,
%1%4 = %2%6 = %3%5 = 1, %1%5 = %2%4 = %3%6, %1%6 = %2%5 = %3%4.
Поэтому rруппа rалуа имеет вид G = {(1), (12)(46), (13)(45), (23)(56)
(14)(25)(36), (14)(26)(35), (15)(24)(36), (15)(26)(34), (16)(25)(34),
(16)(24)(35), (123)(654), (321)(456)}, порядок ее равен 12. I'pуппа G
имеет подrруппуG 1 порядка 6, G 1 = {(1), (12)(46), (13)(45), (23)(56),
(123)(654), (321)(456)}. G 1 как подrруппа индекса 12 6 = 2 aBT
матически будет нормальным и максимальным делителем rруппы G.
В свою очередь, G 1 имеет три изоморфных Apyr друrу подrруппы
порядка 2: {(l), (12)(46)}, {(1), (13)(45)}, {(l), (23)(56)} и одну подr
руппу порядка 3: G 2 = {(1), (123)(654), (321)(456)}, при этом только
по rруппа G 2 является нормальной (проверьте это!). Композицион
ный ряд имеет вид
G ::> G 1 ::> G2 ::> 1,
подrруппы G 1 , G 2 и 1 имеют простые индексы, соответственно 12
6 = 2, 6 3 = 2 и 3 1 = 3. Следовательно, G разрешимая rруппа.
Пример 3. Уравнение 2 й степени
%2 + р% + q = о.
Для цростоты будем предполаrать относительно этоrо уравнения и
"
уравнении из последующих трех примеров, что кроме отсутствия
"
кратных корнеи эти уравнения еще и неприводимы над основным
полем полем коэффициентов. Приводимость или неприводимость
уравнения над данным полем может быть установлена за конечное
число шаrов. Если уравнение неприводимо над основным полем, то
63
ero rруппа rалуа О Jlзательно транзитивна, т.е. ДЛJl любых номеров
i, j содержит XOTJI бы одну подстановку, переВОДJlЩУЮ Жi в Жj. В
данном случае симметрическая rруппа 82 всех подстановок И3 двух
ЭJJeментов имеет ПОрJlДОК 2! = 2, 82 = {(1), ( 2)}. Ее единствен..
ной транзитивной подrруппой JlВJIJleTCJl она сама. Поэтому G = 82.
,Композиционный pJlA имеет вид
G = 82 :> 1.
Этому pJlДY соответствует pJlA
к с Е,
,
нормальных алrебраических расширений OCHoBHoro ПОЛJl К ДО ПОЛJl
Р83JЮжеНИJl Е, в котором и лежат все корни исходноrо уравненИJI.
Чтобы расширить поле К до ПОЛJl Е, достаточно присоединить 1(
К такую ФУНКЦИЮ у от корней Ж1, %2 исходноrо уравнеНИJl, котораи
"принадлежит" rруппе 1, т.е. не измеНJlетCJI при тех и только тех под..
у . в
становках, которые принадлежат этон rруппе. ыбирая в качестве
у разность корней Ж1 ..... Ж2, будем иметь
у2 = (Ж1 Ж2)2 = р2 ..... 4q = D,
откуда, с учетом теоремы Виета, получаем систему линейных ура..
внений дЛJI нахождеНИJl корней' Ж1 и Ж2:
{ Ж1 + Ж2
Жl Ж2
.....р
VБ
Пример 4. Уравнение 3..й степени
ж З + аж + ь = о
Симметрическаи rруппа SЗ состоит И3 3! = 6 элементов, SЗ =
{(1), (12), (13), (23), (123), (321)}. Она имеет четыре нетривиаль..
ных подrруппы. Одну подrруппу ПОрJlдка 3: UЗ = {(1), (123), (321)}
и три ИЗ0морфные между собой подrруппы ПОрJlдка 2: {(1), (12)},
{(l), (13)}, {(1), (23)}. При этом транзитивной JlВЛJlеТСJl только
подrруппа UЗ, поэтому G = SЗ или G = UЗ. в общем случае компо-
у
зиционныи рJlД имеет вид
G = SЗ ::> uз ::> 1.
64
Этому pJlДY соответствует pJlA расширений OCHoBHoro ПОJIJl:
к с К 1 С Е.
Чтобы расширить попе К ДО ПОJIJI Кl, достаточно присоединить к
полю К такую функцию у от корней %1, %2, %3 исходноrо уравненИJI,
которая "принадлежит" подrруппе Uз rруппы 53. Подrруппа U З c<r
стоит из четных подстановок, ей "принадпежит" ФУНКЦИЯ
у = п (%i %j) = (%1 %2)(%1 %3)(%2 %3).
i<j
Эта ФУНКЦИJI JlВЛЯетси корнем иекотороrо алrебраическоrо ypaBH
ния степени S U з = 6 : 3 = 2 с кооффициентамв 113 OCHoBHoro ПОЛJI.
Имеем
у2 = (%1 %2)2(%1 %з)2(%2 %3)2 = 4аЗ 2762 = D
Таким образом, мы расширили основное поле К до ПОЛJl К 1 = К(у) =
K(v'D). Расширим теперь поле Kl до поля Е. ДЛЯ этоrо мы должны
подобрать такую ФУНКЦИЮ Уl от корней %1, %2, %з исходноrо ypaBH
ния, которая принадлежит единичной подrруппе. В качестве такой
функции удобно IOJ1Tb ФУНКЦИЮ Лаrранжа:
Уl = %1 + е%2 + Е 2 %з, е З = 1, е # 1.
Эта ФУНКЦИJl ЯВЛJlетСJl корнем HeKoToporo алrебраическоrо ypaBH
ния степени UЗ : 1 = 3 1 = 3 с кооффициентами из ПОЛJl К 1 (Е).
Имеем
3 2 З 27 3 . r-;;
Уl =(ХI+ Е %2+ е %з) = 2q+ 2 v ЗvD=Dl,
УС3 = ::I:(E Е2).
Таким образом, мы расширили основное поле K1 ДО поля Ра3ложе
ния Е = K1(e, Уl) = К(е, v'D, -VD 1 ). Чтобы получить линейную
систему для нахождеНИJl корней %1, %2, %з, введем еще одну ФУНКЦИЮ
Лаrранжа: y = %1 + е 2 Х2 + Е%з.
Имеем
,3 ( 2 З 27 3 . r-;; ,
Уl = %1 + Е %2 + еzз) = 2 2 v 3y D = D 1 .
65
И, с учетом теоремы Виета, получаем следующую систему ypaBH
ний для определения %1, %2, %з:
{ %1 + %2 + %з
%1 + е%2 + е 2 %з
%1 + е 2 %2 + е%з
о
Dl
VП5r
(При этом корни кубические следует брать, исходя И3 условия, что
VП5r = 3p).
Пример 5. Уравнение 4 й степени
%4 + а%2 + Ь% + с = О,
Симметрическая rруппа 84 состоит И3 4! = 24 элементов. Компози
ционный ряд имеет вид
G = 84 ::> U 4 ::> В4 ::> G 2 ::> 1.
Здесь и 4 подrруппа четных подстановок, В4 так называемая
четвертная rруппа Клейна,
В4 = {(1), (12)(34), (13)(24), (14)(23)},
а G 2 некоторая подrруппа 2 ro порядка, например, {(1), (12)(34)}.
Среди индексов этих подrрупп: 84 U 4 = 24 12 = 2, U 4 В4 = 12
4 = 3, В4 G 2 = 4 2 = 2, G 2 1 = 2 1 = 2 нет составных чисел.
Поэтому по основной теореме теории rалуа уравнение 4 й степени
BcerAa ра3решимо в радикалах.
Композиционному ряду подrрупп соответствует ряд нормальных
алrебраических расширений OCHoBHoro поля:
к с К 1 С К 2 С К з С Е.
При этом К 1 = Kvf]5, rAe
..;n = п (%i %j) = У, "принадлежит" U 4 ,
i<j
К 2 = К 1 ( ),
rде
= (%1 + %2)(%3 + %4) = Уl "принадлежит" В 4 ,
66
К З = K 2 VD;",
rAe
.Jlj; = (X1 + Х2}= У2 "принадлежит" G 2 ,
Е = К з ( Vf);), rAe..[l5;, = x1 = уз "принадлежит" 1,
так что окончательно имеем Е = K(VD, , vv;., ..;IJ;).
Пример 6. Уравнения степени '!l > 5 общеrо вида
n + n...1 + " 2 + + О
Х a1 Х й2 Х . . . й п = .
Композиционный ряд имеет вид
G = Sn :) U n ::> 1,
так aK rруппа четных подстановок U n не имеет при n > 5 нетр"(ви
альных нормальных подrрупп. А так как порядок этой rруппы n!/2
при n > 5 является составным числом, то уравнение степени n > 5
общеrо вида неразрешимо в радикалах.
Пример 7. Уравнение
х5 4х 2 = О
неразрешимо в радикалах, так как erO' rруппа rалуа G совпадает
снеразрешимой rруппой 55. Действительно, по признаку Эй
зенштейна [4, с. 117], это уравнение неприводимо над основным по--
лем К = Q, так как все ero коэффициенты, кроме nepBoro, делятся
на простое число 2, и все, кроме nepBoro и последнеrо, делятся еще
и на 22 Поэтому G транзитивна. Далее, нетрудно установить,
например, построив rрафик левой части уравнения, что это ypaBHe
ние имеет три вещественных корня X1, Х2, Хз И два комплексных со--
пряженных корня Х4 и Х5. Транспозиция (45) будет TorAa одной из
подстановок rpYnnbI rалуа G, так как переход к сопряженным вели
чинам переводит всякое рациональное соотношение между корнями
в се бя:
P(X1,X2,.. .,Х т ) = О ==> Р(Х1,Х2,...,Ж m ) = f> = 0=0.
.
Но TorAa G содержит и транспозиции (41), (42), (43). Это следует из
Toro, что G транзитивна, а степень уравнения проста, что rаранти
рует [4, с. 192 193] примитивность G, т.е. невозможность разбить
R7
множество номеров {1, 2, 3, 4, 5} на такие части, которые целиком
переходят Apyr в Apyra при всех подстановках rруппы G. А так как
любая подстановка И3 85 разложима в произведение транспозиций,
а любая транспозиция (i j) равна произведению (4 i)( 4 j)( 4 i) и, сле.-
довательно, принадлежит G, то rруппа G совпадает с 85.
Зам,ечан,uе Транзитивная rруппа уравнения простой степени,
содержащая одну транспозицию, BcerAa совпадает со всей симметри
ческой rруппой. Это может быть использовано при построении чи
сленных уравнений снеразрешимой rруппой rалуа. А именно, если:
1) степень уравнения проста и > 5,
2) коэффициенты уравнения вещественны,
3) уравнение неприводимо над основным полем,
4) уравнение имеет ровно два комплексных корня,
то rруппа rалуа этоrо уравнения совпадает со всей симметрической
rруппой и, следовательно, неразрешима [29, с. 105 109].
Теория rалуа позволяет ответить и на вопрос о ра3решимости
уравнений методами rеометрической алrебры. А именно: решение
отреоо" может быть построен с помощью цирJCYЛ" и и
I
линеИJ(И TorAa и ТОJlЬJ(О TorAa, J(orAa уравнение имеет хот..
бы ОАНО вещественное решение, а rруппа raпya BToro ура..
вненИJI имеет ПОР"АОIC ВИАа 21:
Пример 8. Задача об удвоении куба выражается уравнением
х 3 2 = О,
если ребро куба а принять за единицу длины. По признаку Эй
зенштейна это уравнение неприводимо над основным полем, по--
этому ero rруппа rалуа транзитивна. Но rруппа 8з не имеет TpaH
зитивных подrрупп порядка 21: (см. п. 3.3.3, пр. 4). Поэтому задача
удвоения. куба неразрешима с помощью циркуля и линейки.
Пример 9. Задача отрисекции уrла выражается уравнением
4х З 3х + а = О,
rде а синус данноrо уrла, а х синус искомоrо уrла. Так как 8з
не имеет транзитивных подrрупп порядка 21:, то решение задачи о
трисекции уrла с помощью' циркуля и линейки возможно провести
только в тех случаях, коrда уравнение приводимо над основным по--
.пем К = Q(a).
в8
Упражнение 10. Объясните, почему с помощью циркуля и ли..
.нейки можно провести, трисекцию уrла 900, но нельзя провести
трисекцию уrла 300 Можно ли с помощью циркуля и линейки п
строить правильный девятиуrольник?
Упражнение 11. Рассмотрите уравнение деления Kpyra
ж 5 ..... 1
= ж 4 + ж 3 + ж 2 + ж + 1 = о,
ж..... 1
постройте ero rруппу rалуа, покажите, что это уравнение pa3pe
шимо с помощью циркуля и линейки, найдите радикальные выраже..
ния для ero корней и проведите построение правильноrо пятиуrоль..
ника.
3.4 HEKOTOPbIE ПУТИ
u
ФОРМИРОВАНИЯ НОВОИ АлrЕБрыI
u
ВО ВТОРОИ ПОЛОВИНЕ XIX ВЕКА,
1. Становление теории rрупп. Проблема решения алrебра..
ических уравнений в радикалах была не единственным источником
становления теоретик rрупповых методов исследования. Два дру..
rих источника мы обнаруживаем в т ории чисел и в rеометрии. Так,
еще в "Арифметических исследованиях" К. raycca (1801 r.) мы ветре..
чаемся со смежными классами мультипликативной rруппы поля И3
Р злементов относительно различных ее подrрупп. Еще более зна..
ЧlIтельным для становления теории rрупп было построение rayccoM
в зтой же работе rрупп классов бинарных квадратичных форм за..
данноrо дискриминанта. Это наиболее абстрактные примеры rрупп,
построенные к тому времени. А общее определение rруппы мы впер..
вые встречаем у А. Кзли (1854 r.).
D 1872 r. Ф. Клейн предложил теоретико..rрупповую клаССИфllка
цию типов rеометрий, соrласно KOTOpOl1 всякую rеометрию можно
рассматривать как учение об инвариантах некоторой rруппы прс ,
образований (СМ. ниже, п. 4.10).
В 1873 r. с. Ли ввел в рассмотрение так называемые непреры..
вные rруппы преобразований (rруппы Ли) как rруппы преобразо..
v
вании вида.
х f(x, OI, l1 2,... ,ak),
69
rде al,a2,...,ak параметры, а функции f и f l непрерывны
по совокупности всех своих aprYMeHToB. Это. позволило, в частно--
сти, решить проблему интеrрирования в квадратурах обыкновен
ных дифференциальных уравнений. А именно, оказалось, что, по--
добно тому, как с каждым алrебраическим уравнением можно свя
зать некоторую rруппу подстановок (rруппу rалуа данноrо адrебра
ическоrо уравнения), так с каждым дифференциальным уравнением
F(ж, у, у') = о можно связать некоторую rруппу непрерывных пре
образований (rруппу Ли данноrо дифференциальноrо уравнения).
Эта rруппа есть rруппа автоморфизмов относительно данноrо ypa
внения.
Пример 10. Пусть F(ж, у, у') = о однородное уравнение, т.е.
уравнение, инвариантное относительно преобра;зований вида
{ :
ож,
ау,
rде о const. Тоrда все такие преобразования и составят rруппу
Ли L однородноrо уравнения. Существует преобразование, перево--
дящее rруппу L в rруппу
Lo = {{ :
: +,8 } (,8 const)
........
сдвиrов по оси у. Таким преобразованием будет
I {:
1L
х
lny
(проверьте это!). Тоrда преобразование 1 переводит однородное ypa
внение F(ж, у, у') = о в некоторое уравнение вида Fо(ж, у') = О, т.е.
в уравнение, заведомо интеrрируемое в квадратурах.
УПDажнение 12. Найдите rрупп Ли линейноrо дифференциаль
Horo уравнения первоrо порядка.,
В начале 80 x rr. XIX в. появились и первые приложения теории
rрупп: Федоров и Шёнфлис решили методами теории rрупп задачу
классификации всех кристаллических пространственных решеток.
2. Становпение теории попей, жолец и Аруrих алrебраиче..
ежих структур. Абётрактные определения поля, модуля, кольца и
70
и;деала мы впервые встречаем в 1871 r. у Р. Дедекинда. Так, полем Дe
декинд называет "всякую систему бесконечно мноrих действитель
ных или комплексных алrебраических чисел, которая сама в себе
столь замкнута и полна, что сложение, вычитание, умножение и д
ление любых двух И3 этих чисел приводит к числу той же системы
"[26, с. 80]. Модуль определяется как "бесконечное множество 3.J!
rебраических чисел, удовлетворяющих тому условию, что сумма и
разность любых чисел этоrо множества также принадлежит ему" [26,
с. 81]; см. также [33, кн. 1, с. 114 121]. Развитие теории алrебраич
ских структур происходило В тесном взаимодей твии с друrими Ma
тематическими дисциплинами и привело к формированию алrебраи
ческой теории чисел, алrебраической rеометрии. алrебраической то--
полоrии, теории алrебраических функций (см., например, [20, с. 326
353]).
3. Станов.пение теории инвариантов. Классическая теория
инвариантов появилась еще в середине XIX в. в Анrлии. Своим B03
никновением обязана теории чисел (rayccoBa классификация бинар
ных квадратичных форм), проективной rеометрии и теории опр
делителей. Основные проблемы классической теории инвариантов
были решены в 1884 1892 rr. д. I'ильбертом (подробнее см., напри
мер, [24, т. 1, с. 76 82; 20, с. 176 189]).
4. Формирование линейной алrебры. Линейная алrебра
выросла И3 теории систем линейных уравнений и связанной с ней
теории определителей и матриц. Основные теоремы линейной ал
,
rебры сформировались еще в период с 1852 по 1870 r. Так, привед
ние .квадратичной формы к каноническому виду и закон Сильвестра
инерции квадратичных форм известны с 1852 r., в 1858 r. появля
ется теорема rамильтона Кэли о том, что всякая матрица аннули
рует свой характеристический мноrочлен, с 1867 r. известна теорема
Кронекера Капелли, а J( 1870 r. решен вопрос о приведении матрицы
к нормальной жордановой форме (подробнее см., например, [24, т. 1,
с. 66 70]).
5. Введение кватернионов и rиперкомппексных чисел.
Кватернионы были введены в математику У.Р. rамильтоном в
1843 r. Известно, что вещественные числа можно интерпретиро--
вать движениями вещественной прямой в себя, а комплексные числа
движениями комплексной плоскости в себя. Исходя из этоrо, ra
мильтон строит такую числовую систему, которую можно было бы
интерпретировать движениями TpexMepHoro пространства в себя. В
71
общем случае рассматриваемые движенИJI имеют вид поворота во--
Kpyr некоторой оси, вооможно с растяжением. Такие движенИJI тре.-
буют для CBoero описанИJI четыре параметра: два из них опреДeJIЯЮТ
направпение оси вращенИJI (сos а, сos Р, cos 1, причем сos 2 а+сos 2 Р+
сos 2 -у = 1), один параметр спужит AJIJI опреДeJJeНИJI уrла вращения t.AJ,
с помощью четвертоrо параметра опреДeJIJlетCJI растяжение r. ra
мильтон составляет четырехчленное КОМПJJeксное чиCJЮ
t.AJ ( . WJ ) . ( . t.AJ а ) . ( . t.AJ ) L
r cos '2 + r SlD '2 . сos lt I + r Sln '2 . cos,.., J + r Sln '2 · cos -у А;,
которое на:эывает кватеРНИОRОМ. Пыта.я:сь далее определить арифме.-.
тические операции с кватернионами, rами.льтон о казывается от за
кона коммутативности умноженИJI и полаrает,ЧТО
ij= ji=k, jk= kj=i, ki= ik='j,
i 2 = j2 = k 2 = 1
(подробнее о введении кватернионов СМ., например, [33, ки. 1, с. 108
110; 20, с. 206 214]).
В 1844 r. в работ r. fpaCCMaHa появляются более общие си
стемы чисел, так На3ываемые rиперкомппексиые ЧИCJIа (ассоци
ативные апrебры), которые имеют вид
n
Жl е l + Ж2 е 2 + .. . + жnе n = L Жkеk,
k=l
rAe ek единичные ЭJlёМенты. Сумма и произведенце двух таких
чисел определяются следующим образо,.,:
ппп
LЖkеl: + LYl:ek = L(Zt + YI:)ek,
1:=1 k=l k=1
( t.XA:e k ) ( t YkeA: ) = .t (ЖiУj )(eiej).
1:=1 1:=1 IJ=l
причем eiej = ejei и е? = о. При :)Том получается n( l) всевоз
можных различных произведений из основных единиц по два. Эти
произведения образуют "единицы второй ступени" Точно так же
строятся единицы 3 й 4 й,.. ,п ступени. Их будет, соответственно,
72
C , с:, ..., с: = 1. Характерными особеННОСТJlМИ правил счета
с обычными числами I'paccMaH считает длJl сложенИJI то, ч'IOО оно
коммутативно и ассоциативно:
0+6 = 6 + о, (о + 6) + с = а + (6 + с),
ДЛJl умножеНИJl то, что оно коммутативно, ассоциативно и двс"
трибутивно по отношению к CJlоженвю:
06 = 60, (06)с = 0(6с),
0(6 + с) = а6 + ас.
И интересы ['рассмана направляются на то, как ети правила счета
MorYT быть распространены на rипеРКОМПJIeксные ЧИCJIа. При атом
I'paccMaH строит различные системы rипеРКОМПJIeКСRЫХ ЧИСeJI, у K
торых свойство коммутативности умноженИJI не имеет места (под..
робнее о введении rиперкомпJIeксных чисел см., например, [19, т. 1,
с. 88 111]).
Отметим еще, что, как показал в 1878 r. r. Фробениус, един..
"
ственными rипеРКОМПJJeКСНЫМИ системами над полем деиствитепь..
ных ЧИСeJI, ДЛJl которых выполняются все свойства поля, кроме, мо--
жет быть, коммутативности умножения, ЯВJIJIЮТCJI множества дей
ствительных (n = 1), комплексных (п = 2) чисел, а также система
кватернионов (n = 4) rамильтона.
Коренные изменеНИJl, произошедшие в алrебре, изменили и сам
предмет этой науки. Возникнув в rлубокой древности, алrебра до
второй половины XIX в. понималась как наука об алrебраических
ypaBHeHllJlX и их системах. И даже во второй половине XIX в. в не.-
которых учебниках по алrебре еще сохраняется это старое опреде.-
ление. Так, в популярном учебнике Ж.А. Серре "Курс высшей ал
rебры" (1885 r.) мы читаем: "Алrебра, по существу rоворя, анализ
уравнений; все р&3личные части теории, ее составляющие, в боль
шей или меньшей степени связаны с этим основным вопросом. С
зтой точки зрения алrебра может быть разделена на три части:
1. Общая теория уравнений, т.е. совокупность свойств, общих
всем уравнениям.
2. Решение численных уравнений, т.е. определение точных ИJIП
приближенных значений корней уравнения, коэффициенты ко-
Toporo даны в числах.
73
3. Алrебраическое решение уравнений, т.е. определение выраже.-
ния, составленноrо И3 коэффициентов данноrо уравнения, ко--
1'орое, будучи в Hero поставленным вместо неизвестноrо, то--
ждественно ему удовлетворяет. . ." [33, кн. 1, с. 122].
НОВЫЙ подход к предмету алrебры МЫ видим уже в работах ан..
rлийских математиков второй четверти XIX в. (У.Р. rамильтона,
Дж. Буля, А. .Кэли и др.). Основным объектом апrебры станоВJIТСЯ
множества с аксиоматически заданными на них апrебраическими
операциями. Последовательная работа по аксиоматизации алrебры,
начатая в конце XIX в. Р. Дедекиндом и Д. I'ильбертом, завершилась
в 20..е rr. нашеrо столетия работами э. Нетер, э. Артина и их после.-
дователей. Одним И3 Ре3ультатов этоrо быJЮ новое понимание ал..
rебры, зафиксированное, например, в статье "Алrебра" о.ю. Шми"
дта и A.r. Куроша: "Алrебра.. . может быть определена как наука о
системах объектов той или иной природы, в которых устаиоВJJeНЫ
операции, по своим свойствам более или менее сходные со сложением
и умножением чисел. Такие операции называЮТСJl апrебраическими.
Алrебра классифицирует системы с заданными на них алrебраиче.-
скими операциями по их свойствам и изучает различные задачи,
естественно вооникающие в этих системах, включав и задачу реше.-
ния и исследования уравнений, которая в новых системах объектов
получает НОВЫЙ' смысл (решением уравнения может быть вектор,
матрица, оператор и т.д.). ЭТОТ новый взrляд на апrебру, вполне
ОФормившийся лишь в ХХ В., способствовал дапьнейшему расшире.-
нию апrебраических методов, в том числе и за пределами матема--
тики, в частности в физике. Вместе с тем он укрепил ВJl3И алrебры
с друrими отделами математики и весьма усилил влияние алrебры
на их дапьнейшее развитие" Подробнее об эволюции взrЛJlДОВ на
предмет апrебры см., например, [33, кн. 1, с. 122 123].
Вопросы и заdан1U
1. В чем значение работы Ф. Виета "Введение в анапитическое
искусство" ?
2. Что ооначает{rеометрически и апrебраически) решить задачу
в rеометрической апrебре пифаrорейцев?
3. Назовите первые неразрешимые задачи. В чем состоит их не.-
разрешимость? В какой мере эти задачи стимулировали раз..
74
витие математики?
4. Укажите rлавный вывод, к которому пришел Лаrранж в своих
"Размышлениях об алrебраическом решении уравнений"
5. Что такое rруппа rалуа данноrо алrебраическоrо уравнения?
Сформулируйте основную теорему теории rалуа. Почему об.-
щее (буквенное) алrебраическое уравнение й степени не ре.-
шается в радикалах?
6. Объясните с точки зрения теории rалуа, почему задачи удво--
ения куба и трисекции уrла не решаютCJI построением с по--
мощью циркуля и линейки.
7. Назовите некоторые пути формирования новой алrебры во
второй половине XIX в.
8. В чем состоит изменение методов и предмета алrебры во вто--
рой половине XIX в.?
IЛава 4
rЕОМЕТРИЯ
4.1 ПРОИСХОЖДЕНИЕ пЕрвыIx
rЕОМЕТРИЧЕСКИХ фиrур и ТЕЛ
с простейшими rеометрическими фиrурами человек. столкнулся в
своей трудовой деятельности при изrотовлении орудий труда и со-
судов, при обработке полей и постройке зданий. Уже в rлубокой дp
ввости изrотовлялись скребки и ножи в форме дисков, треуrольни
ков, ромбов и cerMeHTOB, круrлые сосуды. Поля обычно имели форму
прямоуrольника, а здания форму конуса, цилиндра или паралл
лепипеда.
Большинство общепринятых сейчас Н83ваний rеометрических
фиrур имеют rреческое происхождение и обозвачают Ра3личные
предметы той или иной формы, с которыми люди сталкивались в
своей практической деятельности. Слово "центр" происходит от rp
ческоrо, обозначавшеrо палку с за<?стренным концом, которой по--
rоняли быков (первовачально это слово было названием ножки цир
куля, ставящейся в центр описываемой им ОКРУЖНОСТИ). "Ромб", про--
исходит от слова, обозначавшеrо волчок, "трапеция" от слова,
обозначавшеrо столик. "Призма" происходит от слова опиленная,
"сфера" от слова, обозначавшеrо мяч, "конус" от слова, обо--
значавшеrо сосновую шишку, "цилиндр" от слова, обозначавшеrо
валик, каток. "Пирамида" происходит от древнееrипетскоrо H83Ba
ния еrипетских пирамид "пурама" "Линия" происходит от латин
cKoro слова, обозначавшеrо лён, льняную нить. "Точка" происходит
от слова "ткнуть", равнозначное слово "пункт" происходит от ла
тинскоrо rлаrола "pungo" (укалываю) и т .д.
Таким образО I, происхождение первых rеометрических фиrур
и тел аналоrично происхождению первых натуральных чисел (см.
п. 2.1). Постепенно были выделены эталоны: мяч для шарообра
зных предметов, шишка для остроконечных и т.д. На3вания отих
76
эталонов становятся затем Н83ваниями абстрактных rеометрич
СКИХ фиrур и тел, а сами эталоны фиrур и тел получили свое изо-
бражение в живописи и архитектуре.
4.2 rЕОМЕТРИЧЕСКИЕ СВЕДЕНИЯ В
ДРЕВНЕМ ЕrИПТЕ И ВАВИЛОНЕ
В математических текстах Древнеrо Еrипта встречаются простей
шие rеометрические задачи, связаиные с вычислением площадей
и объемов. При этом площади прямоуrольников, треуrольииков и
трапеций вычислялись "правильно", в то время. как площадь про-
извольноrо четырехуrольника вычислялась как произведение полу
сумм противолежащих сторон, а площадь Kpyra вычислялась по пра
вилу S = ( : d ) 2, rде d диаметр Kpyra. Объемы куба, параллеле-
пипеда, призмы вычислялись "правильно" Особенно отметим 3Ha
ние еrиптянами точной формулы для объема усеченной пирамиды с
h
квадратными основаниями: V = 3 (а 2 + а6 + 62), rде а и 6 сто--
роны квадратов, h высота усеченной пирамиды.
Наличие в rеометрии Древнеrо Еrипта "неправильных" формул
свидетеЛЬ,ствует о том, что формулы для вычисления площадей и
объемов получены как результат практики измерений. При этом BЫ
числения по "неправильным" формулам отличались практическим
удобством и удовлетворительной для Toro времени точностью.
Важнейшим достижением rеометрии Древнеrо Вавилона явля
ется открытие теоремы Пифаrора метрическоrо свойства пря
MoyronbHoro треуrольника. Как пришли вавилоняне к этому OTKpЫ
тию, остается неизвестным. Вооможно, сначала они заметили, что
некоторые треуrольники с целочисленными сторонами а, Ь, с, удо-
влетворяющими равенству а 2 + ь2 = с 2 , являются прямоуrольными,
а затем распространили это свойство на все прямоуrольные Tp
уrольники. Во всякоl,{ случае, еще в третьем тысячелетии до Ha
шей эры вавилоняне уже имели таблицы пифаrоровых чисел, при
чем в этих таблицах встречаются, помимо простых троек вроде
(60,45,75) = (4 15,3 15,5 15) и довольно сложные, например
(72, 65, 97) или (3456,3367,4825) и т.д. Составление этих сложных
троек подбором маловероятно. Поэтому предполаrают, что вавило-
няне составляли тройки пифаrоровых чисел по определенному пра
77
ВИЛУ. Теорема Пифаrора находила в Древнем Вавилоне Р83нообраз
ное применение. С ее помощью ВЫЧИСЛJlЛИ диаrональ квадрата (ПРИ
ближенно), радиус описанной около равнобедренноrо треуrольника
ОКРУЖНОСТИ, rипотенузу ПРJlмоуrольноrо треуrольника по данным
периметру и площади, площадь правильноrо мноrоуrольника и :r.A.
4.3 ПРЕВР АЩЕНИЕ rЕОМЕТРИИ В
ДЕДУКТИВНУЮ C CTEMY
Превращение rеометрии дедуктивную систему ПРОИЗОШЛО в ДpeB
ней fpеции. Первые rеометрич;еские теоремы были ДОК83аны уч
ными ионийской школы натурфилософии (первая половина VI в. дО
Н.З.). А именно: они доказали, что 1) диаметр делит KPy пополам,
2) уrлы при основании равнобедренноrо треуrольника равны, 3) по.:
лучающиеСJl при пересечении двух ПрJlМЫХ противолежащие уrлы
равны, 4) треуrольники, имеlOщие одну равную сторону И два pa
вных уrла, равны.
УПDажнение 13. ПослеДНJIJI теорема ИСПОЛЬЗ0валась Фалесом для
обосноваНИJl способа определения раССТОЯНИJl от береrа до корабля.
Попытайтесь восстановить зтот способ и проведите ero обоснова
ние.
Постепенное накопление и совершенствование определений, по--
стулатов и теорем в работах rреческих математиков VI III В. дО Н.З.
вылилось В конце концов в стройную дедуктивную систему "Начал"
Евклида (111 в. дО Н.З.). ОНИ СОСТОЯТ И3 13 книr. Каждая книrа начи
нается с определений. Кроме Toro, первой книrе предшествует пять
постулатов и ПJlТЬ аксиом.
Определения можно р83бить на две rруппы: "рабочие", которые
ИСПОЛЬ3УЮТСJl при построении теории (например, определение пря
Moro уrла), и "описательные" , которые при дедуктивном построении
теории не исполызуются (например, "точка есть то, что не имеет
частей", или "линия же длина бе;з ширины"
Постулаты "Начал":
1. От ВСЯКОЙ точки до всякой точки можно провести прямую.
2. Оrраниченную ПрJlМУЮ можно непрерывно продолжать по пря
мой.
3. И3 всякоrо центра всяким раствором ЦИРКУЛЯ можут быть опи
сан Kpyr.
78
4. Все прямые уrлы равны между собой.
5. Если прямая, пересекающая две прямые, образует внутренние
односторонние уrлы, меньшие двух прямых, то продолженные
неоrраниченно эти две прямые встретятся с той стороны, с
которой уrлы в сумме меньше двух прямых.
Пятый постулат удивлял ученых сложностью своей формулиро-
вки. Он походил более на теорему, чем на постулат. Уже в древно-
сти e o пытались заменить друrим, более наrлядным. Так, у Прокла
(У в.н.э.) встречается формулировка пятоrо постулата, которая во-
шла теперь во все школьные курсы: через точку, лежащую вне пря
мой, можно провести только одну прямую, не пересекающую данной.
Формулировку аксиом "Начал" см. ниже, п. 5.1.
Выбор постулатов и аксиом в "Началах" Евклида очень удачен;
почти все они вошли в современную аксиоматику. Однако постула
тов и аксиом "Начал" недостаточно для дедуктивноrо построения
rеометрии. Евклид н:е сформулировал MHoroe из Toro, чем он поль
зуется в дальнейшем. Так, в "Началах" нет стереометрических по-
стулатов. За исключением четвертой аксиомы, нет там и аксиом
движения.
Само содержание "Начал" не исчерпывается элементарной reo-
метрией' это основы ("начала") всей античной математики. Здесь
подводится итоr более чем 300 летнему ее развитию вместе с тем
соодается прочная база для дальнейших исследований.
Собственно rеометрии посвящены пять из тринадцати книr
"Начал": в квиrе 1 излаrается планиметрия прямолинейных Фиrур;
111 рассматривает свойства Kpyra, ero касательных и хорд; IV
строятся правильные мноrоуrольники; XI стереометрия; XIII
построение правильных мноrоrранников.
Влияние "Начал" на дальнейшее развитие математики orpoMHo.
Уже Архимед, Аполлоний и друrие античные математики опирались
на них в своих исследованиях по математике и механике. В конце
VIII начале IX вв. ПОЯВИЛИСЬ первые переводы "Начал" на apa
ский язык, а в первой четверти XII в. на латинский язык. И в
странах ислама, и в Европе средних веков "Начала" служили Ha
стольной книrой каждоrо Cepbe3HOrO математика, их MHoroKpaTHo
переписывали, переиздавали печатно, комментировали, а также пе--
рерабатывали для преподавания.
79
4.4 "КОНИЧЕСКИЕ СЕЧЕНИЯ"
АПОЛЛОНИЯ
Уже отмечалось (см. п. 3.2.2), что кривые BTopor ПОрJlдка KaJC мы
их теперь нanываем были впервые рассмотрены в С8JIЗИ с зада..
чей удвоеНИJl куба. Менехм (IV в. до н.з.) представил их как плоские
сечеНИJl ПрJlмоуrольноrо, тупоуrольноrо и остроуrольноrо конусов
вращеНИJl ПЛОСКОСТЬЮ, перпеНДИКУЛJlРНОЙ к обрanующей конуса. Ме--
u v
нехм же вывел основные планиметрические своиства сечении, кото--
рые древние называли евмптомамв, а мы SrравнеНИJlМИ КРИВОЙ
в данной системе координат. Вот как зто делалось, например, ДЛJl
сечения ПРJlмоуrольноrо конуса вращеНИJl:
о
у2 = АК КВ = Р'Р · КВ =
= 20Р · кр = 2рж.
В
Рис. 11
Это и есть уравнение или симптом кривой. Ero записывали в
терминах rеометрической алrебры: квадрат на полухорде КМ (у) в
каждой точке оси равен прямоуrольнику, построенному на отрезке
рк оси до вершины (х) и на постоянном отрезке 20Р (2р).
Аполлоний, в отличие от ?\feHeXMa и друrих математиков, берется
за исследование произвольноrо сечения ПРОВВВОJlЬRоrо, не обяза..
тельно прямоrо, конуса с KpyroBblM основанием, причем он с caMoro
начала рассматривает обе половины конуса, что позволяет paCCMa
тривать одновременно обе ветви rиперболы (см. рис. 25 п. 4.8). При
:этом симптомы конических сечений устанавливаются вначале по от..
ношению к некоторому фиксированному диаметру и сопряженным с
ним хордам, обра=зующим, вообще rоворя, острый уrол с этим дна..
метром. Затем, в ходе изложения, пока=зывается, что они обладают
тем же свойством и по отношению к любому друrому диаметру и
80
СОПРJlженным с ним хордам. Наконец, СТрОJlТСЯ rлавные диаметры,
т.е. такие, Ko opыe ортоrональны к СОПРJlженным хордам, и пок
зываетCJI, что отнесенные к этим диаметрам кривые ожно paCCM
тривать как сечеНИJl ПРJlмоrо конуса, т .е. конуса вращеНИJl. Таким
о брan0!d , Аполлоний классифицирует конические сечеНИJl по BB Y
ОПРЕ!ЯeJlJllOщеrо их 8Jlrебр8lrlеСIоrо ураввеви.., докanывая при
:этом инвариантность уравнений эллипса, параболы и rиперболы от--
носительно аффинных преобрanований.
Симптом параболы (рис. 12)
записываетCJI у АполлоВИJI сл
дующим обрanом: квадрат на
полухорде (у2) равен площади
прямоуrольника на ОТРе3ке ди
аметра (ж) и на ПОСТОJlННОМ o
резке (2р). С точки зреНИJl re<r
метрической алrебры :это coo
ветствует задаче на ПрllJЮже-
иве 'данной площади (у2) к дaH
ному отрезку (2р); 1rО:Р{30Лт, и означает "приложение"
Симптом ВЛJlвпса (рис. 13) записывается у АПОЛЛОНИJl сл
дующим образом: квадрат на
полухорде (у2) равен площади
ПРJlмоуrольника S, т.е. р Х ( 2а
. а
х). С точки зрения rеометри
ческой алrебры :это COOTBeтc
вует задаче о приложении дaH
ной площади (у2) к данному o
резку (2р) так, чтобы иедо-
статок был прямоуrольником
с данным отношением сторон
р а; еллеiфL\ и ооначает "недостаток"
Симптом r иперБОJlЫ (рис. 14) записывается у АполJIOНИЯ сл
дующим образом: квадрат на полухорде (у2) равен прямоуrольнику
S, т.е. р х(2а + х). С точки зрения rеометрической алrебры :это c<r
а
ответствует задаче о приложении данной площади (у2) к данному
отрезку (2р) так, чтобы вобытоJC был прямоуrольником с данным
отношением сторон р : а; V1rеР{30Лт, и означает "избыток".
2р
Рис. 12
2
. ..
Рис. 13
81
Рис. 14
Далее АполJIOНИЙ развивает саму теорию конических сечений: по--
лучает уравнение rиперболы относительно асимптот и устанавли
вает основные свойства фокусов :эллипса и rиперболы. Здесь же впер
вые появляются полюсы и пол..ры относительно конических сече
ний если из точки можно провести две касательные к конич
скому сечению, то прямая, соединяющая точки касания, называется
полярой данной точки, а точка полюсом ЭТОЙ прямой; если пер
двиrать полюс по прямой, пересекающей сечение, то поляра будет
вращаться BOKpyr полюса этой прямой, если же передвиrать полюс
по прямой не пересекающей сечение, то поляра будет вращаться во--
Kpyr некоторой точки и т.д. (СМ. рис. 24 п. 4.7).
Аполлоний рассмотривает также вопрос о числе точек пересече
ния двух конических сечений, вводит нормали к коническим сече
ниям и исследует их свойства.
Далее Аполлоний формулирует и доказывает следующие тео--
ремы:
а) сумма квадратов на сопряженных диаметрах эллипса равна
сумме квадратов на rлавных осях;
б) разность квадратов на двух сопряженных диаметрах rипербо--
лы равна разности квадратов на rлавных осях;
в) параллелоrрамм, построенный на двух сопряженных диаме
трах :эллипса или rиперболы, имеет постоянную площадь.
В этих теоремах Аполлоний фактически находит инварианты OT
носительно линейных преоБРа30ваний системы координат.
Остановимся подробнее на теоремах АполJЮНИЯ о касательных к
коническим сечениям. В "Началах" Евклида дается следующее опр
деление касательной к окружности: "прямая касается Kpyra, если она
82
встречает Kpyr, но при продолжении не пересекает ero" (2 e опр
деление 111 книrи). Поэтому касательную к коническому сечению в
точке (ха, Уа) Аполлоний определяет ,как ту из прямых, проходящих
через TY точку, для всех друrих точек (х, у) которой выполняется
неравенство: у2 (2рх :f: Р х 2 ) > У5 (2рх:!: Р x ). В случае пара
а а
,болы (т.е. коrда р равно нулю, y = 2рхо) Аполлоний устанавливает
а
М (СМ. рис. 15), что расстояние
СА от точки С пересечения
касательной с диаметром АР
параболы до вершины А па:r-
болы равно отрезку AD диа)
В тра, OTceKaeMoro сопряженн
к диаметру хордой MoD, пр )-о
ходящей через точку кас ния
Мо. Доказательство сост( вт в
следующем. Пусть СА = лD =
хо. Тоrда для любой точки М с
"координатами" (х, у) имеем:
С
Рис. 15
у (х + ха) = Уа 2хо и (х + хо)2 > 4ххо. Поэтому у2 2рх = [у2
4ххо] [4ххо 2рх] > [у2 (х + хо)2] [2хо р] = [Уб 4x ] [4Х5
2рхо] = Уб 2р х о. А это и означае1.', что МоС ...:....... касательная к пара
боле в точке Мо(Хо, Уа). В случае с эллипсом (рис. 16) и с rиперболой
(рис. 17) Лполлоний ПОК83ываеТ, что СА СВ = DA DB, т.е. что
Рис. 16
Рис. 17
касательная МоС и сопряженная с диаметром АВ хорда MoD, про--
веденная из точки касания Мо, делят диаметр АВ в одном и том же
83
отношении внутренним и внешним образом (докажите эту теорему
для окружности!)
Аполлоний показывает также, что касательные к rиперболе от...
секают на асимптотах, счита.я: от центра, ОТре3ки, образующие
v
прямоуrольник с ПОСТОJlННОИ площадью, а касательные к эллипсу
или rиперболе отсекают на параллельных между собой фйксирован",
ных касательных, считал от точек ка'са ИJI, отрезки, образующие
прямоуrольник с постоянной площадью (нарисуйте и докажите
соответствующую теорему для окружности!). Касательные же к
параболе, как показал Аполлоний, обладают тем свойством, что их
точки пересечения с двумя фиксированными касательными проходят
одновременно пропорциональные отрезки.
Из различных встречающихся у Аполлония определений коничес..
ких сечений как rеометрических мест точек, обладающих заданным
v
своиством, мы отметим следующее: коническое сечение есть reoM
трическое место точек.пересечения прямых АМ и ВМ, проведенных
из фиксированных точек А и В, лежащих на этом коническом сече..
нии, и таких, что отрезки АР и BQ, отсекаемые ими' на прямых,
проведенных соответственно через точку А параллельно касателъ...
ной в точке В и через точку В параллельно касательной в точке А,
имеют постоянное произведение (нарисуйте и рааберите это свой...
ство для окружности!).
Хотя вплоть до начала V в.н.э. труды Аполлония иоучались и KOM
ментировались мноrими людьми, но все же они долrо не находили
никакоrо применения. Только в XVI! в. наступило возрождение идей
Аполлония: Ферма и Декарт перевели ero методы на язык новой ал
rебры, основав аналитическую rеометрию, а Ньютон применил эти
методы для описания и исследования кривых 3 ro порядка. Но еще
раньше теория конических сечений получила широкое применение в
механике земных и небесных тел Кеплер установил, что планеты
нашей солнечной системы движутся по эллипсам, в одном из ф<r
кусов которых находится Солнце; rалилей показал, что брошенный
камень (или снаряд) летит по параболе. Наконец, в 80 x rr. XVII в.
Ньютон создал свои "Математические начала натуральной филос<r
фии" непосредственно опираясь на труды Аполлония. А некоторые
идеи Аполлония получили свое развитие лишь в XIX в. при создании
основ проективной rеометрии и теории инвариантов.
84
u
4.5 СОЗДАНИЕ АНАЛИТИЧЕСКИИ
rЕОМЕТРИИ
"Поворотным пунктом в математике была декартова переменна.я: ве.-
личина. Блаrодаря этому в математику вошло движение и диалек
тика" rоворил Ф. Энrельс. Действительно, л шь в XVI XVII вв.
в свя;зи с сооданием первых станков и машин, с начавшимся в это
время быl:трым развитием промышленности и мореплавания, и;зу
чение движения в ero простейшей механической форме становится
насущной потребностью естество;звания, а rеометричеСКaR алrебра
пифаrорейцев, теория rеометрических мест точек, идеи Аполлония
и соодание развитой алrебраической символики (см. п. 3.1) послу
жили при этом теоретическими предпосылками для первоrо MaTe
матическоrо описания движения, в форме аналитической rеометрии,
созданной Р. Декартом и п. Ферма.
KorAa отвечают на вопрос, в чем же состоит движение, то
обычно rоворят движение состоит в том, что тело находится CHa
чала в одном месте, а затем оно находится в Apyro'M месте. При этом
упускается из виду, что если тело находится в одном месте, или оно'
находится в друrом месте (или оно 'находится в KaKOM TO определен
ном промежуточном положении), то оно ПОJCОИТС.в, ибо на.ходиться
rд либо, занимать определенное положение, и озuачает покоиться.
Поэтому самое большее, что содержится в вышеприведенном опреде.-
лении движения это начало движения и ero конец, или только ре-
ОУЛЬТ8Т движения, а не само движение. С друrой стороны, сказать
про движущееся тело, что оно вовсе не занимаеrr никакоrо опреде
ленноrо положения, мы тоже не можем. ПQЗТОМУ мы должны сказать
I
так: движение состоит в том, что тело одновременно и находится и
не находится в данном месте. Выражая зто более "наrлядно", но Me
нее точно, можно сказать, что тело в данный момент времени входит
в данное MeCTO или выходит И3 данноrо места, или проходит ero.
lатематической формоЙ описания движения является прежде
BC I'O поня ие пе"!)еменноЙ В .lIfЧИНЫ. 'Величина" сама по себе есть
что имеет опре еленное КО.:lичественное значение. Напротив.
"п ремеНIIая" CaM:l по себ есть ТО, что не имеет определеННОl'О KO
личественноrо :JНi\чения, 1"'ак что взятые сами по себе, они искл
'-1<i.ЮТ друr друrа. каЖДС1.,q из них есть полная противоположность
друrой. 110 в понятии "перемень.ая величина ' T11 противоположн
СТИ "СНАТЫ .Р.. сохранены'., они выступают eCb лишь как ПрОТIf
85
воположные моменты единоrо понятия, так что "величина" берется
теперь как "переменная", а "переменная" берется вместе с тем как
принимающая определерные значения, т.е. как "величина"
р .Декарт опубликовал созданную им аналитич;ескую rеометрию в
одном из приложений к своему основному произведению "Рассужде
нне о методе" (1637 r.). В основу всей rеометрии Декарта положены
две иден: введение переменной величины и использование прямоли
нейных (декартовых) координат. Переменная величина вводится у
Декарта в двоякой форме: в виде текущей координаты точки, дви
жущейся по кривой, и в виде переменноrо элемента множества чи
сел, соответствующих точкам даННоrо координатноrо отрезка. Ко--
ординатные оси у Декарта еще не равноправны: одна ось rлавная, а
друrая вспомоrательная, расположенная под некоторым (не обя
зательно прямым) уrлом к rлавной оси.
а
х а
Ь = l'
х
х = аЬ
х а
1" = ь '
а
x=
Ь
Рис. 18. Умножение отрезков
Рис. 19. Деление отреоков
х = а 2
х 2 = а 1,
x va
1
х а
а l'
Рис. 20. Возведение в квадрат
а
Рис. 21. Извлечение корня
Всякое число у Декарта изображается отрезком. Он YCTpa
няет rлавный недостаток rеометрич ской алrебры пифаrорейцев
ступенчатость исчисления, введя п новому операции умножения и
деления отреоков, возведения в квадрат и извлечения квадратноrо
корня (см. рис. 18, 19,20,21).
86
Приложение, в котором изложена аналитическая rеометрия Д
карта, состоит и;з трех книr. Первая "О ;задачах, которые можно
построить, поль;зуясь только круrами и прямыми линиями" начина
ется с кратких Ра3'Ьяснений общих принципов. Затем следуют пра
вила составления уравнения rеометрических кривых: "Чтобы p
шить какую--либо ;задачу, нужно сначала считать ее как бы решен
ной, и обо;значить буквами все как данные, так и искомые линии.
Затем, не делая никакоrо различия между данными и искомыми ли
ниями, заметить ;зависимость между ними так, чтобы получить два
выражения для одной и той же величины; это и приводит К ypaBHe
нию, служащему для решения задачи, ибо можно приравнять одно
выражение друrому" . Доказывается, что все rеометрические задачи,
решаемые с помощью циркуля и линейки, сводятся к решению цe
почки уравнений не выше второй степени. Общие правила своей re
ометрии Декарт и;злаrает на примерах.
Вторая книrа На3ывается "О природе кривых иний" Она посвя
щена более подробному рассмотрению алrебраических кривых pa3
личных порядков, классификации и выявлению их свойств. Все кри
вые Декарт делит на два класса в ;зависимости от Toro, возможно
ли провести их исследование средствами, которыми он располаrал.
А именно: Декарт считал во;зможным допускать в математику лишь
те кривые, которые описываются непрерывным движением циркуля
или линейки, или же несколькими такими последовательными дви
жениями, из которых последующие вполне определяются им пред
ше.ствующими. Остальные кривые получили у Декарта название Me
ханических и исключены и;з класса допустимых кривых. Таким o
разом, все допустимые кривые MorYT быть построены с помощью
HeKoToporo шарнирноrо' механи;зма. Относительно их бro cTpororo
доказательства высказано утверждение, что они выра;зимы алrебра
ическими уравнениями.
Далее Декарт замечает, что степень алrебраическоrо уравнения
кривой инвариантна относительно выбора системы координат. Но
;за основу классификации кривых Декарт берет не степень уравнения
кривой, а число ;звеньев соответствующеrо шарнирноrо механизма.
В силу этоrо принципа кривые оказываются разделенными по родам,
причем к n MY роду относятся алrебраические кривые порядка 2n 1
и 2n.
В TpeTbeii книrе "О построении телесных или превосходящих Te
лесные задач" поставлена ;задача построение общей теории реш
87
иия уравнений и ИСПОЛЬЗ0вание для этой цели наряду с алrебраич
скими средствами теории rеометрических мест пифаrорейцев. Ал..
rебраичеСКaR символика Декарта удобнее, чем у Виета, и уже лишь
Не3начительно отличается от современной. Всякое уравнение при..
водится к виду Рn(х) = О, rAe Рn(ж) мноrочлеи с целыми кооффи"
циентами, расположенные по убывающим степеням неизвестноrо ж.
Декарт высказал здесь предположение, что алrебраическое ypaBH
ние может иметь столыо корней, какова ero степень. Он доказаЛ,
что число положительных корней уравнения равно числу знакоп
ремен в ряду коэффициентов, а число отрицательных корней равно
числу повторений знака в ряду коэффициентов (все в предположении
вещественности всех корней).
Отметим, что идеи аналитической rеометрии были независимо
от Декарта изложены друrим французским математиком п. Фер..
ма. Ферма сделал это в небольшом сочинении "Введение в теорию
плоских и пространственных мест", написанном в 1636 r. но опу
.
бликованном лишь в 1679 r.
Прошло около 70 лет со времени написания работ Декарта и
Ферма, пока удалось получить существенно новые результаты в
этом направлении. Новый шаr в развитии аналитической rеометрии
связан прежде Bcero с выходом в свет в 1704 r. сочинения И. Ньютона
"Перечисление кривых TpeTbero порядка" В этой работе введены
равноправные и ортоrональные оси координат, в О.снову классифи
кации кривых положена степень их алrебраич-ескоrо уравнения, для
приведения уравнений кривых к каноническому виду используются
линейные преобразования координат. Ньютон перенес на алrебраи
ческие кривые 3..ro и высших порядков понятие диаметра, верUIИНЫ,
центра, оси, асимптоты, ввел понятие двойной точки алrебраической
кривой. При этом кривые Ньютон рассматривает, п существу, на
проеЖТИВRОЙ плоскости [3:1, 223]
В 1731 r вышла работа семнаДЦ<='ТИJlетнеrо А. Клеро "Ilсслед
вания о КРИВЫХ двоякой КРИl3изны" t так Клера Ha3ЫBa' ' npOCTpaH
ственные кривыеj. Каждую ТОЧКУ ПрОС'l'р<.t.нственной кривоil Клеро
проеК'Iирует на две взаимно перпендикулярные плоскости, так что
пространственная кривая задавалась систеМОli двух уравнений. Pa
боты Ньютона, Клеро и некоторых друrих мат ма'IИКОВ создали B03
можность для системаТllческоrо построения аналитическоii reOMe
трои в форме, близкой к COBpeMeHHoll (.;1. Эйлер, 1748 r.).
88
4.6 СОЗДАНИЕ КЛАССИЧЕСКОЙ
u
ДИФФЕРЕНЦИАЛЬНОИ I'ЕОМЕТРИИ
Дифференциальнав rеометрИJI ВООНВIJlа в XVIII в. 1&1 ПРИJlожение
анализа бесконечно малых 1 аналитической rеомеТрИИ. К началу
XVIII в. были уже исследованы МRоrие свойства ПЛОСIИХ IРИВЫХ.
Следующий шаr в ра:эвитии дифференциальной rеометрии CВJI..
зан с введением методов изученИJI пространственных IрИВЫХ и по--
верхностей. Это было ,сделано в вышеупоМJIНУТОЙ работе Клеро
"Исследования о IрИВЫХ двоякой кривизны" (1731 r.). В этой ра..
боте ряд вопросов решен с помощью дифференциальноrо и инт&-
rральноrо исчисления. Так, Клеро ввел касательные и нормали 1
пространственным кривым, а также подкасательные и поднормали,
v
ввел касательную плоскость к поверхности, содержащеи данную,КРИ
вую. Нормаль, по Клеро, является нормалью к касательной плоско--
сти. Рассмотрены также rеометрические места точек пересечения
касательных и нормалей с координатными плоскостями.
Перенесение методов двумерной' дифференциальной rеометрии
на трехмерный случай, осуществленное Клеро, в течении примерно
50 лет не было превзойдено никем. Однако под воздействием потреб.-
ностей rеодезии и картоrрафии, а также механики появился ряд pa
бот, в которых решались диффереНЦИaJIьно--rеометрические задачи.
Среди появившихся работ доминировали работы Эйлера, который
вывел уравнение rеОДе3ической линии на поверхности, заданной ypa
внением
Рdж = Qdy+ Rdt,
в виде
Q d 2 ж + Р d 2 y dж d 2 ж + dyd 2 y
,
Q dж + Р dy dt 2 + dж 2 + dy2
и l 'смотрел ряд частных случаев, относящихся к rеодезическим на
ПОВ: t,... ;ости вращения. В 1736 r. Эйлер дока3М, что точка, движу
ща.яся по поверхности при отсутствии действующих си..l, перемеща
ется по rеодезической.
13 1767 r. вышла статья Эйлера "Исследования о кривизне П
верхностей" в которой изложены основы общей теории поверхно--
стей. 3, ccь выведена, в частности, известная теорема Эйлера о pa
диус(: кривизны кривой, получающейCJI при пересечении поверхно--
rти Z = Z(x, у) плоскостью Z = аж + ру + 1, выведена формула
89
дли радиуса кривизны HopMaJlbHoro сечения поверхности, введены
rлавное нормальное сечение, перпендикулярное плоскости жу, и нор...
мальное сечение, перпеНДИКУJIJlрное rлавному, и т.д.
В 10...х rr. XVIII в. одной из rлавных проблем сделалось разверты...
вание поверхностей. Понятие развертывающейс.и поверхности ввел
Эйлер. В статье 1771 r. о телах, поверхности которых можно нало--
жить на плоскость, он исходит из соответствия между координатами
(ж, у, z) точки развертывающейся поверхности, и (t, и) точки
"
плоскости, с которои совпадает указанная точка повер вости после
развертыванИJf. На плоскости берется элементарный прямоуrольный
треуrольник с вершинами
(t, и), (t + dt, и), (t, u + du).
Ему соответствует элементарный треуrольник на поверхности с вер...
шинами
(х, у, z), (ж + Idt, у + mdt, z + ndt),
(ж + лdu, у + IJdu, z + vdu),
(/, т, п, л, 1', v соответствующие частные производные: 1
дж az
at ' ,\ = ди и т.д.). Конrруэнтность 'соответствующих отрезков
привела Эйлера к следующим условиям развертывания:
dz 2 + dy2 + dz 2 = dt 2 + du 2 , 12 + т 2 + " 2 = 1,
л 2 +1J 2 + v2 =1, Iл+mlJ+ПV=О.
Решение Эйлера содержало общую идею изrибания поверхностей
и повлекло за собой ряд значительных результатов. В частности Эй
" "
лер доказал, что касательные произвольнои пространственнои кри
вой образуют развертывающуюся поверхность.
Попытки построения общей теории поверхностей и простран
"
ственных кривых методами, заимствованными из аналитическои r
ометрии, продолжались и в 80...х rr. XVIII в., но без особоrо успеха.
Несмотря на то, что Монжу, Лаrранжу, Ламберту, Менье удалось
получить в дифференциальной rеометрии новые конкретные реЗУЛIr
таты, 'количество людей, занимавшихся дифференциальной reoM
трией, быстро уменьшалось. Это было вызвано, rлавным образом,
резким усложнением аппарата ана.'1итической rеометрии при pac
смотрении новых конкретных задач.
90
Но тем временем уже намечались пути дальнейшеrо азвития
дифференциальной rеометрии. Это: а) больше..е привлечение reoM
трических соображений, временно отодвинутых на второй план уси..
.
лиями по созданию аналитическоrо аппарата; б) расширение посл
AHero за счет привлечения теории дифференциальных уравнений в
частных производных; в) перевод rеометрических фактов на- язык
дифференциальных уравнений и, наоборот, rеометрическаи интер"
претация этих уравнений. Наибольшее продвижение в этом напра..
влении было достиrнуто в работах r Монжа и ero учеников. В T
чение 70 x rr. XVIII в. Монж опубликовал два сочинения: "Мемуар о
развертках, радиусах кривизны и различных видах переrибов кри"
вых д оякой кривизны" И "О свойствах мноrих видов кривых повер..
хностей" В них дано широкое и полное исследование свойств пр
странственных кривых и поверхностей, введено развертывание п
верхностей, исследованы эволюты, оrибающие и т.д.
Отметим, что классификация кривых и поверхностей по виду их
алrебраических уравнений и связанный с этим rромоздкий аппарат
не удовлетворяли Монжа. Новая классификация поверхностей была
дана Монжем в лекциях для Политехнической школы, которые вы..
шли отдельной книrой в 1801 r. В ней Монж исходит из потреб-
ностей практическоrо приложения и соответствующих нужд техни..
ческоrо образования. Свойства и структура поверхностей прояв
ляются яснее, если, кроме уравнения, задан способ их построения
путем перемещения в пространстве заданной линии. При этом в ка..
честве объекта изучения выступают не алrебраические уравнения,
а дифференциальны.е уравнения в частных производных.
Оказалось, что дифференциальным уравнениям в частных пр
изводных первоrо порядка соответствует большое семейство повер..
Хностей. В Hero входят цилиндрические и конические поверхности,
поверхности вращения и каналов. Кроме Toro, к этому класс;у OTH
сятся поверхности склонов насыпей, а также винтовые поверхности.
Рассматривая поверхности с различных точек зрения, Монж по--
лучает одновременно и дифференциальное уравнение поверхности
и Конечное уравнение, как ero интеrрал. Например, рассматривая
ЦИJIиндрические поверхности как такие, касательная плоскость KOT
рых параллельна прямой 1 z = az, у = bz, он получает их уравнение
az az
а ах + ь ау = 1.
91
В то же время из условия, что образующа.и цилиндрической пове}r
хности паРМЛeJIьва ПРЯМОЙ 1, Монж получает конечное уравнение
v
QТОИ поверхности
у .... bz = <р( z .... az),
rде <р произвольная rладкas функция. Последнее уравнение дает
решение ди еренциanьноrо уравнения цилиндрической поверхн
СТИ.
УПDажнение 14. Следуя Монжу, вывести для конической повер..
хности ее дифференциальное уравнение И ее конечное уравнение.
Монж вводит также rеометрическую интерпретацию характери..
стик, как ЛИНИЙ пересечения двух бесконечно близких поверхностей,
И ВЫВОДИТ их дифференциальное уравнение.
Дифференциальные уравнения BToporo порядка определяют, как
показал Монж, семейства развертывающихCJI поверхностей, а также
цилиидроиды линейчатые поверхности, которые описываются
прямой, перемещающейс.и по двум пространственным кривым па..
раллельно заданной плоскости, и классы поверхностей, кривизны
которых удовлетворяют некоторым условиям (резные, трубчатые,
минималЬНl;dе) .
Общие линейчатые поверхности определяются уравнениями Tpe
Tbero порядка, равно как и более сложные поверхности, вроде п
верхности, оrибающей сферу переменноrо радиуса, центр ко орой
движется по заданной КРИВОЙ.
Перевод фактов теории поверхностей на ЯGЫК дифференциаль
ных уравнений в частных ПРОИGВОДНЫХ сопровождается у Монжа
разработкой rеометрической теории этих уравнений. В частности,
он дал rеометрическую трактовку общей теории дифференциальных
уравнений с частными ПРОИGВОДНЫМИ первоrо порядка. Полный ин
теrрал таких уравнений '(х, у, z, а, Ь) = О rеометрически интер
претируется двупараметрическим семейством поверхностеЁ. Если
з мен'ить Ь = ф(а), rде 1/J символ ПРОИGВОЛЬНОЙ функци; ТО ypa
внению
1(1:, у, z, а, ф(а)) = О
соответствует однопараметрическое семейство поверхн()с 'ей (Монж
назвал их оrибаемыми). Уравнение оrибающеlVr их поверхности полу..
чается путем исключения параметра а из уравнении
f = О,
о! = о.
0(1
92
Отсюда при фиксированном значении а получаются уравненИJI xa
рактеристик (образующих оrибающие поверхности, являющихся re--
ометрическими образами общеrо интеrрала). Все ,характеристики
оrибаются КРИВОЙ, которую Монж назвал ребром возврата.
Подобные соображения, высказанные относительно уравнения
f(z, у, z, р, q) = о
и ero полноrо дифференциала
Х dz + У dy + Z dz + Р dp + Q dq = О
привели Монжа к системе уравнений
dz dy dz
Р = Q = Рр + Qq
dp
..... .....
X+pZ
dq
Y+qZ
rеометрические ме1;ОДЫ внесли также ясность в трактовку -ypa
внения, названноrо впоследствии уравнением Пфаффа
Р dz + Q dy + R dz = о.
Если условие интеrрируемости выполняется, то ero решение reOM
v v
трически представляется семеиством поверхностеи
f(z, у, z) = С
на которых любые кривые ортоrональны к кривым
dz dy..... dz
Р Q ..... л.
Если же это условие не выполнено, то, как показал Монж, при зада
нии дополнительной зависимости <p(z, у, z) = О уравнение Пфаффа
определяет на поверхности <p(z, у, z) = О однопараметрическое c
v
меиство кривых, ортоrональных к тем же кривым.
Теория характеристик Монжа, сведение задачи решении дифф
ренциальных уравнений с частными производными к системе обы
кновенных дифференциальных уравнений, rеометрическая интер
претация решений, т сная взаимосвязь rеометрических и механи
ческих методов вся совокупность достижений Монжа привела
дифференциальную rеометрию к новому этапу. Он характеризуетCJI
введением в rеометрию аппарата дифференциальных уравнений в
93
частных производных и резким расширением ее теоретических и
практических возможностей.
Определяющее влияние на весь ход развития дифференциальной
rеометрии оказало появление в 1828 r. "Общих исследований о кри"
вых поверхностях" К. raycca. в основу своей работы raycc поло--
жил параметрическое представление поверхности и соответствую-
щее ему выражение линейноrо елемента. Из трех способов задания
поверхности:
1) неявным уравнением
f(z, у, z) = О,
2) параметрическим представлением
,
х = х(р, q), у = у(р, q) z = z(p, q),
3) заданием z как функции от z и у
z = f(z, у),
rAe третий способ является частным случаем как nepBoro, так и
BToporo, raycc пользуется преимущественно вторым, как "наиболее
соответствующим природе поверхности"
raycc строит две квадратичные формы
ds 2 = Ed p 2 + 2Fdpdq + Gdq2
и
D dp2 + 2D' dp dq + D" dq2
Первая из ЭТИХ форм теперь rоворят "первая основная KBaдpa
тичная дифференциальная форма поверхности" выражает KBa
драт линейноrо элемента ds 2 поверхности, т.е. квадрат расстояния
ds между бесконечно близкими точками поверхности с координатами
(р, q) и (р + dp, q + dq). Эта форма иrрает основную роль в исследо
ваниях raycca.
Вторая форма отличается от второй основной квадратичной
дифференциальной формы современной теории поверхностей только
множителем Еа F2
Еще в 1816 r. raycc опирался на выражение линейноrо элемента
при решении вопроса о конформном отображении двух поверхн
стей, т.е. отображении, сохраняющем подобие в бесконечно малом.
94
Требование конформности сводится к пропорциональности линей..
ных элементов этих поверхностей, т.е.
Е F G
Е' F' а'
Эта проблема была им решена, и в 1825 r. опубликована.
Полезным нововведением raycca явилось и использование в reome--
трии сферическоrо отображения, оБЫЧRО примеН.Rвшеrося в aCTp
номии. Каждой нормалli к поверхности ставится в соответствие та..
кая точка на единичной сфере, радиус"вектор которой параллелен
этой нормали. rrаким образом всякая область поверхно ти отобра..
жается с помощью нормалей в некоторую область на сфере. Опи..
раяСБ . на эт() отображение, raycc вводит понятие меры кривизны
К (rayccoBa КРИВИQна поверхности в данной точке) как отношение
площадей соот етствующих бесконечно малых областей на сфере и
на поверхности. Иными словами, К является пределом отношения
площадей соответствующих областей сферы и поверхности, коrда
область поверхности стяrивается в точку.
raycc вычисляет меру кривизны сначала для простейшеrо слу..
чая, коrда поверхность оадана уравнением z = z(ж, у), затем для
случая параметрическоrо задания поверхности и, наконец, после ис..
кусных вычислений rayccy удается выразить меру кривионы только
через коэффициенты первой формы и их проиоводные. Этот реоуль..
тат, как УКа3ывает raycc, "приводит к славной теореме: если кри"
вая поверхность будет Ра3вернута на любую друrую поверхность,
то при этом мера кривизны в каждой ее точке остается неиомен..
ной" Свойства, сохраняющиеся при всевозможных непрерывных ио
rибаниях "нерастяжимой" поверхности, образуют, по выражению
raycca, "внутреннюю rеометрию поверхности" Как показал raycc,
к внутренней rеометрии поверхности относятся линейный элемент,
коэффициенты первой квадратичной формы, rayccoBa кривизна п
верхности, свойство линии быть rеодеоической и т.п.
В работах raycca имеется также теорема о сумме уrлов rеодеои..
ческоrо треуrольника. Эта теорема, оаключающаяся в
Q + /3 + -у 1r = / к dи,
rде а, Р, "у уrлы rеодеоическоrо треуrольника, а интеrрал справа
равен площади сферическоrо отображения треуrольника, имеет пря..
95
МУЮ СВJIЗЬ С размыwлениими и расчетами raycca, ОТНОCJIщимиCJI к
v
веевклидовои rеометрии.
Вскоре после появлении работы raycca начинается постепенно
раСШИРJlЮЩа&CJI разработка внутренней rеометрии поверхностей.
Так, Ф.r. Миндинr в "3амечании о развертывании кривых линий,
принадлежащих поверхностям" (1830 r.) вносит ценное дополнение
v О 1
к ПОВJIтиям внутреннеи rеометрии. н показал, что вeJlичина ,
р
1 v
равнм произведению кривизны R кривои на косинус yrпa 'Р, o
v v v
разованноrо соприкасающеиCJI с кривои плоскостью С касаТeJIЬНОИ
плоскостью к поверхности
1
р
cos '(J
R
.
(по современной терминолоrии это проекция вектора КРИВИЗНЫ на
касательную плоскость), позже (1848 r.) названная Бонне rео еои..
U U u
ческов ICРИВИОВОИ, принадлежит внутреннеи rеометрии поверхно--
сти. Доказательство состояJlO в'отыскании выражения для rеодези..
ческой кривизны через Е, F, G и их прооводные первоrо порядка.
К rеодезической кривизне Миндинr пришел при решении ме--
тодами вариационноrо исчисления изопериметрической задачи
найти на поверхности кратчайшую кривую, охват вающую данную
площадь. В том же 1830 r. МИНДинr пришел к выводу, что если реше--
cos '(J
ние существует, то на экстреМaJIИ R величина постоянная, и
выска3М предположение, что такая кривая должна быть rеодезиче
ской окружностью. Для случая поверхностей постоянной кривизны
он доказал это предложение еще в 1830 r., но окончательно этот во--
прос был решен только в 1921 r. А. Бауле, показавшем, что лишь на
поверхностях постоянной кривизны все rеодезические окружности
имеют постоянную rеодезическую кривизну.
Впоследствии (1837 r.) Миндинr предложил интересную reome--
трическую интерпретацию rеодезической КРИВИЗНЫ. Он показал,
что ее можно определить как кривизну той плоской кривой, которая
получится из данной, если наложить на плоскость развертывающу
юся поверхность, являющуюся оrибающей семейства плоскостей, Ka
сающихся поверхности в точках заданной кривой. Эта nенная идея
Миндинrа о способе развертывания линии, лежащей на поверхн
сти, на плоскость была впоследствии применена Леви.. Чивитой для
96
.
ввеАенИJI ФУНАамеНТ&JIЬ80rо ПОНJlТИJI паР8JIJJeJlьноrо перевесенИJI
вектора ВАОЛЬ КРИВОЙ, лежащей на поверхности (1917 r.).
Из работ МИНАинrа отметим еще статью "Об воrибавии кривых
поверхностей" (1838 r.), в КОТОРОЙ ему удалось покааать, что до
v '
АВУХ поверхностеи совпаАенве rayccoBых кривизн в CJlучае их по-
CTOJlHCTBa JlВJlJleTCJJ И достаточным УCJlOвием Н8JIOжимости, причем
Н8Jlожение может осущестВJIJIТЬс.в бесконечным ЧИCJIом способов, за..
ввсJlщвм от трех параметров.
Из работ французской диффереНЦИ8JIьно-rеометрической ШКОJlЫ
отметим два резУJlьтата. Р. Бонне (1865 r.) yдanoch обобщить тео-
рему raycca о сумме уrлов rеОАезическоrо треуrольника. Он показ8JI,
что AJlJl простоrо rладкоrо контура С, оrраничивающеrо область Е
реrУJlJlраой поверхности, ВЫПОJlВJIетCJJ соотношение
J Kdtr+ f S = 27r,
Е С 9
т.е. сумма "полной КРИВИЗНЫ" области Е и интеrрanа rеодезической
1
КРИВИЗНЫ .......... по оrраничивающему область Е контуру С равна 2"..
Р,
ж. Френе (1847 r.) и ж. Серре (1851 r.) ВЫвели ФОРМУЛЫ, см..
зывающие направляющие КОСИНУСЫ касательной, rлавной НОРМaJIИ в
бинормали к пространственной КРИВОЙ с их производными по ДJlине
дуrи кривой. В настоящее время, замеВJIЯ напраВЛJIющие КОСИНУСЫ
прямых едИНИЧНЫМИ векторами [, ii И Ь, направленными COOTBe
ственно по касательной, rлавной нормали и бинормanи КРИВОЙ, фор..
мулы Френе--Серре записывают в ВИДе
dt
.......... = k n ,
ds
dii
ds = kt + teЬ,
db
ds ,
rде k И кривизна И кручение кривоii, абсолютные значеНИJl ко-
dt db
торых равны МОДУЛЯМ векторов ds и ds ' т.е. пределам отношения,
соответственно, "уrла смежности" a меж..дУ касательными в двух
близких точках и уrла {3 между соприкаеающимиCJI ПЛОСКОСТJlМИ в
этих точках к длине дуrи s между этими точками при стяrивании
этой дуrи в точку. В пространстве кривизна BcerAa считаетCJI по-
ложительной, а кручение считается ПОJЮжительным, KorAa соприка
сающаися с кривой винтовая линия правая, И отрицательным, KorAa
эта винтовая линия левая.
97
Из достижений отечественных reoMeTpoB XIX в. отметим вывод
теоремы об определении поверхности двум.и квадратичными фО}r
мами с точностью до движенИJI. Эта теорема впервые была опубли..
кована Бонне (1867 r.), но еще ранее она была доксшана К.М. Пе--
терсоном в ero диссертации "Об изrибании поверхност й" (1853 r.).
Петерсон дополнил уравнение raycca, СВJmывающее коэффициенты
первой и второй форм поверхности еще двум.и независимыми ура..
внениями, которые поонее получили название уравнений М&йнарди"
Кодацци 'по имени италь.иНСКИХ reoMeTpoB, ПОЛУЧИВШИХ их незави"
симо в 1857 r. и 1868 r. соответственно.
Опираясь на УПОМЯНУ1;'ые три уравнения, Петерсон ДОКСШaJI в
диссертации теорему: если коэффициенты ДВУХ дифференциальных
квадратичных форм (первая должна быть знакоположительной) свя"
aHЫ такими соотношениями, то существует поверхность, для ко--
торой эти формы ЯВЛЯЮТCJI первой и ВТОрОЙ дифференциальными
формами, причем они определяют поверхность с точностью до по--
ложения в пространстве.
Более подробно о развитии дифференциальной rеометрии в
XIX в. СМ., например, [24, т. 2, с. 14 32].
u
4.;7 rЕОМЕТРИЯ НА ПРОЕКТИВНОИ
ПЛОСКОСТИ
Проективную плоскость Р2 можно определить аналитически следу..
ющим образом. Пусть Е з трехмерное евклидово пространство с
элементами ж = (Ж1, Ж2, %3), rAe Жi Е R. Назовем точкой проекти"
вной плоскости Р2 ВСЯКИЙ класс {лж, л # О} параллельных векторов
из Е з ИЛИ, ЧТО то же самое, всякий класс пропорциональных упо--
рядоченных троек чисел (ЛЖ1, ЛЖ2, л%з), rде л # О, а Ж1, Ж2, %з
фиксированные числа, из которых по крайней мере одно отлично ОТ
нуля. Назовем ПРJlмойра = (P01, Р02, РОз), rде Р # О, совокупность
всех точек (ЛЖ1, ЛЖ2, лжз), удовлетворяющих уравнению
01%1 + 02%2 + Оз%з = О,
rAe 01, 02, Оз фиксированные числа, из которых по крайней
мере одно отлично ОТ нуля. При этом будем rоворить, что точка
(ЛЖ1, ЛЖ2, Л%3) и прямая (pa1, ра2, роз) иицияентRЫ Apyr Apyry.
Моделью проективной плоскости Р2 может служить CВJI3Ka пря
мых и плоскостей евклидова пространства Е з , проходящих через на..
98
чало координат. Друrую модель проективной плоскости Р2 можно
получить из евклидовой плоскости Е 2 присоединением ic ней весоб-
ствеииых элементов. А именно, если взять в Е з произвольную пл
скость, не проходящую через начало координат (т.е. через центр
связки), всякой точке этой плоскости сопоставить ту прямую ио
смоки, которая проходит через эту точку, а всякой прямой этой
плоскости сопоставить ту плоскость НО связки, которая проходит
через эту прямую, то иесобственllЫМ точкам плоскости COOTBeT
ствуют те прямые ио связки, которые параллельиы этой плоскости,
а иесобствеввой ПР"МОЙ плоскqсти соответствует та плоскост'
ио свяоки, которая параллельна воятой плоскости. При этом несо.
ственные точки следует считать ннцидентными несобственной пр
мой.
Проехтивиым отоБРI.-
S жеиием проективной пло':к
сти Р2 на проективную пл
скость p называется всякое
воаимно однооначное отобра
жение Р2 на p , при котором
всякая прямолинейно распол
женнм тройка точек плоск
сти Р2 переходит в прямоли
нейно расположенную тройку
точек плоскости P . Аналити
чески всякое проективное OT
Рис.22 Центральная перспектива бражение плоскости Р2 на пл
скость p может быть оадано
невырожденной матрицей А размерности 3 х 3, а именно: х' = Ах,
rде х Е Р2, а х' Е P . Можно покаоать, что всякое проективное OT
бражение есть либо аффинное отображение, либо движение плюс
централЬН8J( перспеJCтива (см. рис. 22). Пр оективная rеометрия
иоучает все те определения н свойства фиrур (точечных множеств)
на проективной плоскости, которые сохраняются при любых проек
тивных преобразованиях. Такими инвариантами будут, например,
точка, прямая, инцидентность. Основным проективным инвариан
u
том является воиное, или анrарМОRичеСJCое отношение прям
лиhейной четверки точек А) В, С, D (см. рис. 23).
Если (ABCD) = 1, то rоворят, что пары точек А, В и С, D
rармонически раоделяют друr друrа.
99
(ABCD) = (АВС) (ABD) =
АС AD
ВCвD
Рис. 73. Двойное отношение
Наряду с проективными отображениями расс.матриваются
еще ICорреп.втиввые прео-
браоовавиs проеЕТИВВОЙ
ПJlОСЕОСТИ, т .е. такие ее вза..
имно однозначные <\тобра..
жения в себя, которые каж..
дую точку проективной пло-
.
скости пер водят в некото-
рую прямую, а каждую пря..
мую на проективной пло-
скости переводят в некото-
рую точку, не нарушая при
этом инцидентности. Прим
ром коррелятивноrо преоб--
Рис. 24. Полярное преоБРа30вание раоования проективной пло-
скости в себя может служить ПОJlJ[ритет или ПОJl.врвое преоб-
раоование относительно фиксированной ОКРУЖНОСТИ (см. рис. 24),
при котором каждой точке проективной плоскости ставится в c<r
ответствие ее ПОJl.вра относительно окружности, а каждой прямой
проективной плоскости ставится в соответствие ее полюс относи
тельно этой же окружности. При этом, если точка Р лежит вне
окружности, то ее полярой будет хорда, соединяющая концы Kaca
тельных, проведенных к ОКРУЖНОСТИ .из ТОЧКИ Р. Если точка Р ле
ЖИТ на окружности, то ее полярой будет касательная к окружности
в точке Р Если точка Р лежит внутри ОКРУЖНОСТИ, то ее полярой
будет прямая, представляющая собой совокупность всех таких точек
плоскости вне даноой окружности, поляры КОТОРЫХtПРОХОДЯТ через
точку Р (в частности, полярой центра Kpyra будет несобственная
прямая). Полярное преобраоование является ИНВОЛlOтиввым или
взаимно обратным коррелятивным преобраоованием, так как Ka
ждому полюсу ставит в соответствие ero поляру и, наоборот, Ka
ждой поляре ставит в соответствие ее полюс.
е существованием коррелятивных преобраоований связан прин-
Pi поляра Р i
Pi полюс Pi
100
v v
цип воиствеRИОСТИ на проективнои плоскости: если переимево-
вать все ТОЧКИ проективной ПЛОСКОСТИ в прямые, а все прямые
в точки, сохранив при этом все инцидентности, 'ЕО получится снова
проеКТИВН8JI плоскость. Конкретно это означает следующее:
Пусть верна некоторая теорема, утверждающая, что фиrур , об.-
разованная из точек и прямых проективной плоскости по определен
ному правилу, формулируемому в терминах иицидентностей, обла
дает некоторым свойством, также фОРМУЛliруемым в терминах ин
цидентностей. Тоrда верна и взаимная теорема, получающаяс.и, если
как в правиле образованWI фиrуры, так и в формулировке утвержда
u
eMoro своиства поменять ролями точки и ПрJlмые, сохранив при этом
всюду инцидентности. Например, для теоремы о том, что через ВCJI
u
кие две точки проективнои плоскости можно провести ровно одну
прямую, двойственной или взаимной будет теорема о том, ЧТО вся
u v
кие две прямые проективнои плоскости пересекаются ровно воднои
точке.
Отметим еще, что суперпозиция или произведение двух корреля
тивных преобраоований есть некоторое проективное преобразова
ние, так что всякое коррелятивное преобраоование можно предста
вить в виде произведения фиксированноrо полярноrо преобраЗ0ва
ния на некоторое проективное преобразование.
Отметим также, что совершенный, законченный вид проекти
внаи rеометрия получает, если вещественную проективную пло--
скость расширить до комплексной проективной плоскости. Подроб.-
нее о rеометрии на проективной плоскости СМ., например, [11,
rл. IX].
u
4.8 прЕдыIторияя ПРОЕКТИВНОИ
rЕОМЕТРИИ
Проективная rеометрия, сформировавшаяс.и как самосто тель
ная дисциплина лишь в XIX в. имеет длинную предысторию. К
XIX в. в рамках евклидовой rеометрии формируются мноrие опреде
ления и теоремы, носящие проективный характер. Так зллипс, napa
бола 11 rипербола определяются у Аполлония (111 В. дО н.з.), по cy
ществу с ПО IОЩЬЮ центральной перспективы. Он определяет их как
101
сечения KpyroBoro конуса пло--
u
скостью, проходящеи под He
которым уrлом к обра3УЮ-
щей конуса (см. рис. 25).
Кроме Toro, у Аполлония
впервые введены полюсы и
поляры относительно кони
ческих сечений. Проектив
u
ныи характер носят, по су..
ществу и теоремы Аполло--
ния о касательных к конич
ским сечениям (см. рис. 15,
16, 17); их можно перепи
сать в иде (АБСD) . 1
и ВЫра3ить следующими сло--
вами: касательная к 'конич
СКОМУ сечению и хорда, про--
веденная ио точки касания,
rармонически Ра.3деляют со--
u v
пряженныи с хордои диа..
метр.
Александрийским MaTeMa
тиком Менелаем около 100 r.
н.э. была установлена Teope
ма, иоображенная на рис. 26.
Эта теорема носит проек
тивный характер. Действи
Рис. 25 тельно, проведя черео точку
S прямую Q'Q параллельно Б'О так, что точка Q лежит и на прямой
ОБ, а точка Q' несобственная, т.е. лежит на прямой ОБ', можно
переписать теорему Менелая в виде
\
\
\
\
ОА'
Б'А'
\
\
\
\
\
\
\.
1 = ОА B'S ОА
БА БS = БА
OQ
БQ
т.е. в виде равенства двойных отношений (О Б' А' Q') и (О Б А Q)
двух перспективных (с центром перспективы S) прямолинейных ч
тверок точек.
Упражнение 1 . Проведите ДОКа3ательство теоремы Менелая.
102
"
"
"
"
,
"
,
,
,
S'
,
,
, '
" ,
, "
, "
, ,
, "
,
ВА B'S ОА'
ОА . BS · В'А' =,1
В Q
Рис. 26. Теорема МевеЛaR
у Apyroro апександрийскоrо математика Паппа (111 в.в.з.) при
v
исспедовавии своиств четырехст<>-
v
роввика впервые вводитCR двои
вое или анrармовическое отнош
v v
вие прямо лин еино и ч тверки т<>-
че". Доказава CJIедующаи теорема,
равВОСИЛЬВaR теореме об инвари
l' v
ан тв ости двоиноrо отношения при
13 проектировавии: если три пря
мые 11, 12, 13., выходящие из одной
точки О, пересекаютCJI прямой 1 в
точках В, С, D, а ПрJlМОЙ l' в точках В', С', О' и А точка п
ресечевия ПРJlМЫХ 1 и l' (рис. 27), то ПРJlмоуrольник на АВ, DC
относитCJI К прямоуrольнику на AD, СВ как прямоуrольник ва АВ',
D'C' к ПРJlмоуrольнику на AD', С'В', или, что то же самое,
к
#6
, "
, ,
, ,
, ,
,
,
,
,
,
,
Рис. 27
ВА ВС В' А В'С'
DA DC = D'A IYC"
т.е. (BDAC) = ( 'D' АС').
Упражнение 16. Проведите доказательство этоrо утверждевИJI.
ИСПОЛЬЗУJl инвариантность двойноrо отношения, решите следующую
задачу: медиава ВМ треуrольника АВС деJlИТCJI ТОЧКОЙ Q в отнош
нии BQ : MQ = m : п; в каком отношении прямаи AQ делит ВС?
103
в
Папп по"азaJI также, что две
диаrОВaJIИ полноrо четырехсто--
ронника rармонически раздеЛJlЮТ
третью диаrОВaJIЬ (см. рис. 28,
здесь ABCD или BPDQ ици
APCQ четырехсторонник, АС,
BD и PQ ero диаrОНaJIИ).
Упражнение 17. Проведите
док&3атепьство теоремы Паппа о
полном четырехс.тороннике. Рас..
v
N смотрите частные спучаи этои
теоремы, KorAa одна или обе пары
противоположных сторон четы..
рехуrольника парanJJeJIЬНЫ.
Р м
(PQMN) = (ACSN) =
= (BDSM) = 1
Рис. 28
УПDажнение 18. ИСХОДJI из теоремы Паппа о полном четырех..
стороннике (рис. 28) и теоремы Менел&R (рис. 26), запишите Beo
ходимое и достаточное условие Toro, чтобы прямые, проведенные иt\
вершин треуrольника J( противолежащим сторонам, пересекanись в
одной точке (теорема Чевы).
1 А В
Рис. 29. Теорема Паппа
Было доказано также следующее утверждение (теорема Паппа):
если на двух пересекающихCJI прямых 1 и l' лежат две тройки точек
соответственно А, В, С и А', В', С', причем ни одна из этих точек
не совпадает с ТОЧКОЙ О пересечения прямых 1 "и 1', то точка Р пер
сеченИJI прямых АВ' и А'В, точка Q пересечения прямых ВС' и В'С,
и точка R пересечения прямых АС' и А'С лежат на одной прямой
(рис. 29) или: если вершины шеСТ СТОРОННlIка АВ'СА'ВС' попере
мевно лежат на двух прямых 1 и 1', то три друrие точки пересечения
104
v v
ero сторон лежат на однои ПрJlМОИ.
Упражнение Проведите ДОК83атепьство теоремы Паппа. Офо-
рмулируйте теорему, двойственную теореме Паппа.
Элементы проективных ПОНJlТИЙ встречаютCJI в книrах по пе}r
спективе ХУДОЖНИКОВ и архитекторов эпохи Воорожденu. Неко-
торые проективные рассуждеНИJl
имеЮТСJl у Кеплера, Ньютона и
Лейбница. Так, Кеплер (1604 r.)
рассмаТРИВа& параболу (ату "ту..
пейшую" из эллипсов) как пред
v v
льныи случаи эллипса, KorA&' один
из ero фокусов уходит на бес--
конечность (см. рис. ЗО), впер--
вые ВВОДИТ несобственную (бес--
конечно УДaJIевную) точку на пло-
скости как т кую идеальную точ"
ку, В КОТОРОЙ, соrласно фОКaJllr
ному оптическому свойству кони..
ческих сеч.ений, сходится пучок
v '
лучеи, выпущенных из неподвиж"
Horo фокуса и отраженных от
Рис. 30. "Слепая" точка "стенки" параболы. При этом б
сконечно удаленный фокус параболы Кеплер Н83ывает "слепой" точ--
кой.
В 1639 r. были опубликованы "Черновые наброски" ж. Деоарrа,
в которых содержаТСJl элементы проективной rеометрии. частно-
сти, там имееТСJl следующее утверждение (теорема Дезарrа): если
АВС и А'В'С' два трехвершинника, то ПРJlмые АА', ВВ' и СС' п
ресекаЮТСJl в ОДНОЙ точке S (цеитре перспективы) TorAa: и только
тоrда, KorAa точки пересечеНИJl Р, Q и R сторон соответственно АВ
11 А'В', ВС и В'С', АС и А'С' лежат на одной ПрJlМОЙ S (оси пер..
спеJCТИВЫ). Друrими словами: два трехвершинника имеют центр
перспе тивы TorAa и только TorAa, KorAa они имеют ось перспек
тивы (рис. 31).
Упражнение 20. Проведите доказательство теоремы Дезарrа.
Покажите, что теорема Дезарrа одна из теорем двойственности
проективной rеометрии. Как выrлядит теорема Деnарrа в случае,
коrда трехвершинники лежат в одной плоскости и имеют попарно
105
,
,
,
".....
.,......,
j.. ".....
..,...,
..,..., r
"..... ......
".....
s ..........
.......... ..JJ
.........
..........
..........
..........
..........
..........
-----
А'
Рис. 31. Теорема Д арrа
параллельные стороны?
Отметим, что теорема Дезарrа в плоском случае рассматрива..
лась автором, по существу, как теорема об инволютивном (т.е. вза..
имно обратном) преобразовании проективной плоскости. Пон.втие
об инволюции на ПРЯМОЙ также введено Дезарrом. При этом Дезарr
устанавливает различные теоремы об инволюции ряда точек на пря..
мой и об инволюции пучка прямых; при доказательстве этих теорем
он постоянно пользуется теоремой Менелая [35, с. 179 183].
Работа Дезарrа была продолжена Б. Паскалем, КОТОРЫЙ в 1640 r.
опубликовал свой "Опыт о конических сечениях" В этой работе до-
казано, в частности, следующее утверждение (теорема ПаСКaJlЯ): для
Toro, чтобы 6 точек А, В, С, А', В', С' лежали на одном коническом
сечении, необходимо и достаточно, чтобы точка Р пересеченИJI пря..
мых АВ' и А'В, точка Q пересечения прямых и В'С JI точка R
пересечения прямых АС' и А'С лежали на 'О_ОЙ прJDIОЙ (рис. 32),
или: если вершины шестистор н и, а АВ'СА'ВО' лежат на одном
KOllll'leCКOII се"еввв, '1'0 три JQ)yr_e ТОЧПI пересечевИJI ero сторон
лежат на одной прямой.
УПDажнение 21. Проведите доказательство теоремы ПаСКaJIJI.
Какова связь между теоремами Паскаля и Паппа? В Kpyr вписан ш
стиуrольник, у KOToporo две из трех пар ПРОТИВОПОJЮжных сторон
составлены параллельными прямыми; пользуясь теоремой Паскаля,
106
в
В'
Рис. 32. Теорема Паскаля
покажите, что стороны, составляющие третью пару, также парал--
лельны Apyr Apyry.
Работы Дезарrа и Паскаля были напечатаны всеро в 50 экзем..
плярах, поэтому они привлекли внимание лишь очень немноrих уче-
ных XVII в. и не получили в то время какоrо--либо развития. Воор<>-
ждение интереса к изучению проективных свойств фиrур относится
к концу ХVIII началу XIX в. Новые успехи в этой области свя"
заны, прежде Bcero, с деятельностью r. Монжа, КОТОРЫЙ (1795 r.)
разработал начертаТeJlЬRУЮ rеометрию и преподавал ее мноrие
...
roAbl сначала в инженерной школе в Мезьере, а затем в парижских
Нормальной и Политехнической школах ведущих учебных заведе-
ниях Toro времени. "Начертательная rеометрия, писал Монж,
преследует две цели: во--первых, дать методы для изображения на
листе чертежа, имеющеrо только два измерения, а именно длину и
ширину, любых тел природы, имеющих три измерения длину, ши..
рину и высоту, при условии, однако, что эти тела MorYT быть точно
заданы. Во--вторых, дать способ на основании точноrо изображения
определять формы тел и выводить все закономерности, вытекающие
из их формы и их взаимноrо расположения" [33, кн. 1, с. 255].
Начертательная rеометрия Монжа возродила интерес к синте-
тическим методам и привлекла внимание к методу проектирования.
Как Карно, так и Брианшон, Понселе, Жерrонн и Шаль, внесшие
важный вклад в развитие проективной rеометрии, слушали в свое
107
вреМJI лекции Монжа.
л. Карно, выдаЮЩИЙСJl деJlтель Французской буржу.азной pe
люции, опубликовал три rеометрические работы: "О коррелJlЦИИ
фиrур в rеометрии" (1801 r.), "rеомеТРИJl положеНИJl" (1803 r.) и
"Очерки о трансверсалJlх"(1806 r.), в которых введены некоторые,
существенные ДЛJl становлеНИJl проективной rеометрии идеи и ПОНJI
ТИJl. Так, используя представление о непрерывном преобразовании
фиrур ("корреляции" по ero терминолоrии), он высказал так назы
ваемый "принцип корреЛJlЦИИ" (принцип непрерывности), соrласно
которому определенные свойства преобразованной фиrуры можно
находить и изучать по свойствам исходной фиrуры (даже если KOpp
ЛJlЦИЯ приводит к мнимым величинам). Карно впервые ввел двойное
'" v
или анrармоническое отношение ПРJlмолинеинои четверки точек с
учетом знака, уточнив тем самым трактовку Пачпа, а затем доказал
инвариантность этоrо отношеНИJl для четверок т?чек, полученных
при сечении четырех ПРJlМЫХ пучка различными секущими. Карно
BcerAa подчеркивал преимущества синтетltческоrо метода над aHa
литическим, так как первый позволяет сразу охватить всевоомож
ные частные случаи.
ш. Брианшон (1806 r.) в работе "О кривых поверхностях BToporo
порядка" доказал следующее утверждение (теорема Брианшона): для
Toro, чтобы шесть прямых а, Ь', с, а', Ь, с', никакие три из которых
не принадлежат одному пучку, были касательными к одной и той
же линии BToporo порядка, необходимо и достаточно, чтобы ПрJlМая
р, соеДИНJlЮЩая точки пересечеНИJl прямых а и Ь' и прямых а' и Ь,
ПРJlМая q: соеДИНJlЮЩая точки пересечения прямых Ь и с' и прямых
Ь' и С, и ПрJlМая r, соединяющая точки пересечения прямых а и с' и
прямых а' и с, пересекались в одной точке (рис. 33). При доказатель
стве Брианшон опирался на ПОЛJlрное преобразование относительно
коническоrо сечения.
rпражнение 22. Проведите доказательство теоремы Брианшона
путем сведения ее к теореме Паскаля.
Дока;зательства теорем Дезарrа, Паскаля и Брианшона с п
мощью принципа корреляции см..., например, в [11, с. 261 264, 288
293] .
О происхождении проективных представлений и понятий в XVII
XVIII вв. см. также [15, т. 2, с. 117 128, Т. З, с. 173, 196]
108
ь
Рис. 33. Теорема Брианшона
u
4.9 Р А3ВИТИЕ ПРОЕКТИВНОИ
u
rЕОМЕТРИИ В ПЕРВОИ ПОЛОВИНЕ
.
XIX ВЕКА
Выделение проективной rеометрии в самостоятельную дисциплину
происходит в первой половине XIX в.
В 1822 r. ..был опубликован "Трактат о проективных свойствах фи
ryp" В. Понселе. Понселе на;зывает две фиrуры проективными между
собой, если каждую из них можно перевести в друrую цепью проек
тирований. А "все отношения или свойства, имеющие место в одно
и то же время и у данной фиrуры, и у ее проекции", Понселе Ha
зывает "проективными" Такие свойства и отношения и составляют
предмет исследования у Понселе.
Широко используется у Понселе принцип корреляции Карно. С
помощью этоrо принципа решаются задачи, относящиеся к кони
ческим сечениям, вводятся несобственные (бесконечно удаленные)
точки плоскости, мнимые (в частности мнимые бесконечно удален
ные) точки плоскости и т.п.
Особое внимание уделено у Понселе полярному преобра;зованию.
Опираясь на Hero, Понселе впервые сформулировал общий принцип
двойственности на проективной плоскости, хотя cTporoe дока;затель
ство этоrо принципа было дано впервые ж. Жерrонном в 1826 r.
Трактат Понселе про звел сильное впечатление на современни
109
ков, причем На3вание трактата и послужило основанием для caMoro
термина "проективная rеометрия;' В "Трактате" определен пред
мет проективной rеометрии, установлены ее основные понятия и
теоремы, полученные применением синтетическоrо метода. Однако
в определении двойноrо отношения OCHoBHoro инварианта проек
u
тивнои rеометрии еще содержалось метрическое ПОНЯТllе длины
отрезка.
С конца 20 x rr. XIX в. проблемы проективной rеометрии на про--
тяжении почти половины столетия становятся центральными для
ряда немецких reoMeTpoB Мёбиуса, Плюккера, Штейнера, Шта
удта и др. Во Франции в области проективной rеометрии работали
Понселе, Жерrонн, Шаль, в Анrлии Кэли, Сальмон и др.
Синr:rетический метод был TaI< тесно связан в работах.. Понселе,
Штейнера и Шаля с самим предметом проективной rеометрии, что
ее нередко На3ывали синтетической rеометрией. Однако уже вскоре,
начиная с работ Мёбиуса и Плюккера, в проективной rеометрии Ha
чалось применение и аналитических методов. Эти методы стали по
лучать все большее распространение, хотя у reoMeTpoB нередко воз
никали сомнения в правомерности введения однородных координат,
поскольку при этом использовались не проективные понятия.
Однородные проективные координаты, позволяющие характери
зовать и бесконечно удаленные точки плоскости, были впервые BBe
дены в 1827 r. А.Ф. Мёбиусом способом, основанном на понятиях re
ометрической статики. Если поместить в вершинах фиксированноrо
треуrольника массы т1, т2, тз, то центр тяжести ("барицентр")
М этих масс можно характеризовать упорядоченной тройкой чисел
(ml, т2, тз). И наоборот, всякая точка М внутри этоrо треуrоль
ника определяет с точностью до постоянноrо множителя упорядо
ченную тройку масс (тl, т2, тз), центром тяжести которых она
является. Если же точка М лежит на одной из сторон треуrольника,
то одно из mi равно нулю. Если же точка М лежит вне треуrольника,
то одну из этих трех масс необходимо предположить отрицательной.
'пражнение 23. Укажите барицентрические координаты Heco
ственных точек вещественной проективной плоскости, лежащих на
продолжении сторон барицентрическоrо треуrольника. Запишите в
барицентрических координатах уравнение несобственной прямой.
Введенные "барицентрические" однородные координаты на про--
ективной плоскости позволили Мёбиусу сформулировать целый ряд
110
аффинных и проективных свойств фиrур. При этом ТО, ЧТО мы
называем rеометрическим преобразованием, т.е. взаимно одно--
значное соответствие между двумя фиrурами, Мёбиус именовал
"сродством" Аффин ое преобразование Мёбиус именовал "аффин"
ным сродством" или "аффиннитетом", а проективное преобразо--
вание, при котором точки, лежащие На одной прямой, переходят в
точки, также лежащие на одной прямой, "коллинеарным cpoд
ством" или "коллинеацией"
Мёбиус показал, не привлекая метрических понятий, что колли..
неации на плоскост определяются произвольным заданием двух со--
ответственных четверок точек, И3 которых никакие три точки не
коллинеарны. Конrруэнтные системы точек, следуя античной тради
ции, Мёбиус На3ывал равными и подобными, причем рассматривал
не только такие конrруэнтные системы, которые можно совместить
непрерывным преоБРа30ванием, но и те, которые получаются Apyr
из Apyra при помощи зеркальноrо отражения. С этой классифика
цией Мёбиус непосредственно связал идею разыскания выражений
и rеометрических оБРа30В, остающихся неизменными при каждом
из этих соответствий. При этом Мёбиус последовательно исполь..
зовал введенный им принцип знаков, причем "направление обхода"
принималось им во внимание не только при измерении длин отрез..
ков, но и при измерении площадей и объемов. Мёбиус впервые дает
подробную теорию двойноrо отношения четырех точек, лежащих на
одной прямой, что стало возможным лишь после введения знаков
у отрезков. Также впервые Мёбиусом введены в рассмотрение уни
курсальные кривые (координаты которых задаются рациональными
ФУНКЦИЯМИ параметра). На3вание этих КРИВЫХ объясняется тем, что
на проективной плоскости такие кривые можно провести одним poc
черком пера. В частности, Мёбиус нашел рациональные параметри
ческие представления конических сечени'й. На этом пути он впервые
рассмотрел пространственные кривые TpeTbero порядка и изучил
их свойства.
Друrой немецкий математик ю. Плюккер в своих "Аналитико--
rеометрических исследованиях" в отличие от Мёбиуса ввел COBep
шенно общие однородные проективные координаты на плоскости,
причем путь введения был иным. С аналитической точки зрения
это просто упорядоченная тройка чисел, заданная с точностью до
общеrо множителя. С rеометрической точки зрения, как пока3ал
Плюккер, эти три числа пропорциональны расстояниям до сторон
111
произвольно выбранноrо треуrольника, измеренным каждое своей
единицей длины. Эти координаты получили На3вание треуrольных
или трилинейных [11, с. 322 323]. ·
Аналитический метод облеrчил оперирование с бесконечно yдa
ленными и мнимыми элементами и естественно привел к введени
Плюккером линейных координат, координат прямой линии. Если ypa
внение прямой имеет вид а1%1 + а2%2 + аз%з = О, то тройка чисел
(а1, 02, аз) и будет .линейными (или танrенциапьиыми) КООРДИНа
тами этой прямой. Рассматривая это уравнение как условие Toro,
что переменная точка (%1, %2, %з) лежит на фиксированной прямой
(а1, а2, аз), или как условие Toro, что перемениая ПРЯМaJI (а1, а2, аз)
проходит через фиксированную точку (%1, %2, %з), Плюккер сра;зу
получид И3 симметрии выражения а1%1 + а2%2 + азжз = О обоснова
нне принципа двойственности Понсел Жерrонна.
В своих rеометрических исследованиях Плюккер с большим ис
кусством применяет метод сокращенных обозначений и стремится к
характерному для cBoero учителя Монжа слиянию построения
с аналитической формулой. Вот что писал о методе Плюккера ero
ученик Ф. Клейн: "В плюккеровской rеометрии комбинация ypaBHe
ний превращается в rеометрический факт, и наоборот rеометри
ческие факты управляют аналитическими операциями. Вычислений,
коrда это возможно, здесь стараются избежать, но зато ра;звивается
и находит широкое применение доведенная до виртуозности острота
BHYTpeHHero восприятия и rеометрическоrо истолкования встреча
ющихся по ходу дела аналитических уравнений.
В качестве примера, демонстрирующеrо плюккеровский способ
мышления, я приведу принадлежащее ему доказательство теоремы
Паскаля.
Речь идет о двух тройках прямых Р, q, r и р', q', т', таких, что
из девяти точек их пересечения шесть лежат на некотором кониче
ском сечении '( см. рис. 32). Утверждается, что остальные три лежат
на одной прямой. Мы рассматриваем р, q, т, р', q', т' как линейные
выражения, приравнивание которых нулю дает соответственно ypa
внения шести рассматриваемых нами прямых. Тоrда комбинация
pqr Jlp' q' т' = О
представляет собой уравнение пучка кривых TpeTbero порядка, Ka
ждан из KO OpЫX проходит через все девять точек пересечения pac
сматриваемых троек прямых. По условию шесть точек из девяти
112
лежат на коническом сечении. Кроме Toro, выбрав надлежащим о&.
разом константу р, которав в привципе не подчинена никаким orpa-
ниченВJlМ, мы можем добитьCJI Toro, чтобы наша кривatl ИМeJlа с
рассматриваемым коническим сечением еще одну, седьмую, общую
точку. Но кривав С З TpeTьero пор.вдка и криВ88 С2 BToporo пор.вдка
имеют, вообще roвopJl, толыо шесть точек пересечени.в. ЕCJlИ ура--
внение шестой степени, опреДeJlJlющее эти точки, имеет бопее Ш
.
сти корней, то оно равно нулю тождественно. Следовательно, в этом
спучае криваа С З должна распастьCJI на данное коническое сечение
и пр.вмую, которав с необходимостью ДOJlжна содержать три друrие
точки пересеченИJI. Таким. образом, ати три точки действительно
лежат на одной пр.вМ,ОЙ, что и требоваоось доказать. . ." [20, с. 139
140].
Синтетические методы в проективной rеометрии поспе Понселе
развивались, rлавным образом, в работах Штейнера и ШaJIJI.
Соrласно я. Штейнеру, система проективной rеометрии должна
быть развита с помощью поспедовательноrо перехода от более про-
стых начальных линейных rеометрических фор к формам более
v
сложным, а затем путем ИСПОЛЬЗ0ванИJI проективных зависимостеи
и к образам более высоких ПОрJlДКОВ. Эти идеи Штейнер изл()-
жил в своей основной работе "Систематическо рмвитие зависимо-
сти rеометрических образов Apyr от друrа" (1832 r.). Образы пер.-
u u u u
вои ступени на плоскости это ПРJlмолинеиныи точечныи рJlД, ero
двойственный образ пучок прямых, c a плоскость. Образы пер.-
вой ступени На3ываЮТСJl проективными между собой, если двойные
отношения соответствующих элементов равны. При этом двойное
отношение вводится на ОСЦове метрических ПОВJIтий. С помощью
двух проективных между собой образов первой ступени СТРОИТCJI
обр , высшеrо порядка ЛИНИJl BToporo порядка. А именно, из--
вестная теорема Штейнера rласит: rеометрическое место точек
пересечения двух проективных, но не перспек:тивных пучков есть
невырожденная кривая BToporo ПОрJlдка. Отметим, что эта теорема
была доказана еще Аполлонием (см. п. 4.4). На рис. 34 изображено
Основанное на теореме Штейнера построенuе эллипса: стороны АВ
и ВС "рямоуrольник:а ABCD разделены на одинаковое число равных
частей; тоrда пучки А и D проективны, но не перспективны (дока--
жите это!), ппзтому точки пересечения соответствующих прямых
этих пучков лежат на одном и том же эллипсе.
Упражнение 24. ПОЛЬ3УJlСЬ теоремой Штейнера, укажите способ
113
5
1
2
3
4
5
Рис. 34. Построение эллипса
построения параболы и rиперболы.
Существенным недостатком работ Штейнера ЯВЛЯJlOсь OTCYT
ствие применения принципа знаков и отказ от употребления МНИМЫХ
величин: Он никоrда не Mor МИРИТЬCJI с последними И употреблял Ta
кие выражения, как "призрак" или же "царство теней rеометрии"
В своей преподавательской деятельности Штейнер PYKOBOДCTB
вался принципом: ". .. Каждое новое знание,должно быть самим уча
щимся проработано, открыто, создано; учитель должен давать ca
мостоятельно думающему ученику только руководство в желатель
ном направлении" Исходя из этоrо принципа, который он развивал
с большим искусством и успехом, Штейнер не употреблял на СВОИХ
лекциях никаких чертежей; живое соучастие слушателей в работе
должно было вызвать в их представлении настолько отчетливую Kap
тину, что можно быJlO обойтись бro BCJlKOrO чувственноrо восприя
тия.
Не:зависимо от Штейнера, к своей системе проективной reome--
трии пришел М. Шаль. При этом, подобно Мёбиусу, Шаль, pac
смаТРИВ8JI величины напраВJIeННЫХ отрезков, полызуется принципом
знаков. Конические сечения Шаль, подобно Штейнеру, изучает, pac
смаТРИВ8JI их обра:зованными с помощью двух проективных пучков
прямых, НО, в отличие от Штейнера, нередко rоворит о rеометрич
ских соотношениях в мнимой области и рассматривает веществен
ные части в фиrурах как случайно выделившиеCJI из мнимых. Шаль
114
ввел в проективную rеометрию общее понятие коррелятивноrо пр
оБРа30вания. Особенно важную роль в распространении интереса к
проективной rеометрии сыrрал учебник высшей rеометрии ШaJIJl, а
также ero "Исторический обзор происхождения и ра3вития reoM
трических методов" (1837 r.), значительно больше половины KOTc:r
poro занято ero ориrинальными заметками.
В середине XIX в. происходили ожесточенные споры между CTc:r
u
ронниками синтетическоrо и аналитическоrо методов в проективнои
rеометрии. Дело в том, что, как уже отмечалось выше, проективная
rеометрия у "синтетических" reoMeTpoB Понселе, Штейнера и Ш8J'
содержала в себе непоследовательн сть; ведь основной целью ее п.
строения было устранение метрической rеЕ>метрии (т.е. Bcero Torc
проективной rеометрии, что опиралось на понятие расстояния) и:
даже, как это вскоре И удалось, построение метрической reoMeTpl.A
как особой части проективной; между тем важнейшее понятие Hpc:r
ективной rеометрии двойное отношение, а вместе с ним и по(" rpc:r
ение проективной координатной системы, покоилось на определении
расстояния.
Коренное изменение во всем ЭТОМ произвел Х. Штаудт. Чтобы
уничтожить даже воспоминание о прежней непоследовательности,
он ОТКа3ался от термина "двойное отношение" и наименовал COOT
ветствующую конфиrурацию четырех точек словом "вурф" Чисто
проективно--rеометрическое определение численноrо значения KOOp
динат ("вурфов") точки Р на проективной плоскости можно, соrла
сно Штаудту, получить путем построения "мебиусовой сети" (СМ.
рис. 35; здесь 00 несобственная прямая, точка М выбирается прc:r
извольно, а прямые li проводятся в том порядке, в котором идут их
номера). Таким образом Штаудт строит все двоично--раци?нальные
точки, а затем и все остальные рациональные точки. Например,
точка 2/3 может быть построена так, как это проделано на рис. 36.
Штаудт ДОКа3ывает, чт указанное построение не зависит от BЫ
бора точки М. После этоrо встает еще вопрос об иррациональных
числах и об их истолковании в rеометрии. Этот вопрос был решен
позднее (1871 1872 rr.) с помощью введения аксиомы непрерывно--
сти: всякому значению числовоrо ряда, дополненноrо до непреры
вности с помощью дедекиндовых сечений (см. п. 2.9), соответствует
точка на прямой, и н оборот. Построение чисто проективным спо--
собом координат ("вурфов") P1 И Р2 точки Р ука;зано на рис. 37. При
зтом численные значения координат P1 и Р2 равны соответственно
115
Рис. 35 Построение "меБИУС080Й сети"
Рис. 36 Построение точки 2/3
116
о 1 Pl Cl
Рис. 37 Проективное построение координат
(Pl, 1; о, Сl) и (Р2, 1; О, С2) (докажите это!). Введенные Штаудтом
координаты На3ываютCJI вео воро выми проективными коорди"
натами. Если (%1, %2, %3) однородные координаты точки Р, ТО
%1 %2
Рl = .........., Р2 = (докажите это!).
%3 %3
Упражнение 25. Даны две параллельные прямые. Полызу.ись
одной линейкой, рanделить расположенный на одной из ЭТИХ прямых
отрезок пополам.
Отметим также данное Штаудтом истолкование мнимоrо в npcr
ективной rеометрии. Соrласно Штаудту, мнимую ТОЧКУ можно pac
сматривать как инволюцию BToporo рода на прямой с заданной ори
ентацией; мнимая прямая есть инволюция BToporo рода в пучке пря
мых с указанной в нем ориентацией. 3адача провести прямую через
действительную точку Р и мнимую точку М превращается в задачу
по точке Р и по инволюции М построить пучок прямых вместе с
инволюцией и с ориентацией так, чтобы он давал мнимую прямую
РМ. ДЛЯ чисто проективноrо построения точки u + iv достаточно,
соrласно Штаудту, построить точки u v 2 , и, u + 1, 00 и мять ИХ
в качестве двух ра:зделяющих Apyr Apyra пар точек некоторой ин
волюции и считать, что они пробеrаются в направлении О, 1, 00
(подробнее см., например, [20, с. 156 160; 19, т. 2, с. 191 197]).
117
4.10 ПРОЕКТИВНАЯ КЛАССИФИКАЦИЯ
u u
ТИПОВ rЕОМЕТРИИ ПО ,ф. КЛЕИНУ
Чисто проективное построение Штаудтом неоднородных координат
v .
устанавливало ,независимость проективнои rеометрии от меТРJfЧ
СКОЙ.
С друrой стороны, анrлийский математик А. Кэли в "Шестом
мемуаре о формах" (1859 r.) вводит в рассмотрение так Ha3ЫBa
мую проеlCТИВВУЮ метрику. А именно, фиксируя на проективной
плоскости акукrлибо КРИВУЮ К BToporo порядка Е aij%i%j = о,
i ,j = 1 ,2,3
Кали ставит в соответствие каждым двум точкам Р и Q с коорди
натами (Жl, %2, Жз) И (Уl, У2, УЗ) уrловое расстояние
Dist(P, Q) = arccos Ea;jXiYj
VE аijЖi'Жj \/" EaijYiYj
Кэли ПОКа3ываех, что введенное таким оБРа30М расстояние не из
меняется при всевозможн.ых коллинеациях, переводящих КРИВУЮ К в
себя. Кэли замечает далее, что общие формулы сильно упрощаются,
если в качестве "абсолюта" К взять мнимую кривую % + % + % = о.
Тоrда формула для уrловоrо расстояния приме't вид ·
D . t(P Q) Ж1У1 + %2У2 + %зУз
18 , = arccos
\/"%I + Ж + Ж \/" Y + Y + Y i
Он УКа3ывает далее, что если (%1, %2, %З) обычные прямоу
r<щьные координаты в пространстве, удовлетворяющие уравнению
% + Ж + % = 1, то точка (%1, %2, жз) будет ТОЧКОЙ сферической
поверхности, и (поскольку определенное Кэли расстояние является
сферическим расстоянием) имеем систему сферической rеометрии.
"Абсолютом" в такой си теме является "сферическая коника" , пред
ставляющая собой пересечение сферы с "концентрическим KOHY
сом" Под "сферической КОНИКОЙ" 'Кзли понимал тот мнимый Kpyr,
по которому бесконечно удаленная (несобственная) плоскость, д<r
полняющая евклидово пространство Е з до проективноrо простран
ства РЗ, пересекается со всеми сферами евклидовоrо пространства
и с мнимой КРИВОЙ % + % + %5 = о, которую Кэли называет
"концентрическим конусом" (если (% 1, %2, ЖЗ, %4) однородные K<r
ординаты точки в Рз, то уравнение "сферическои коники" в этих
118
координатах имеет вид % + % + % = О, %4 = О). Тем самым M
трика Кэли осущеСТВЛJIетCJI на проективной плоскости и на сфере e
клидовоrо пространства с отождествленными диаметрально проти
ВОПОJЮжными точками. В настоящее время проективнаи плоскость
с определенной таким обрanом метрикой На3ывается 8JШнптнче..
u u
СКОН пJlоскостыо; эту ПЛОСКОСТЬ На3ывают также вееВКJlИАОВОIJ
пJlоскостыо Рнмава, так как на ней осуществляется неевклидова
rеометрия Римана.
Кэли замечает далее, что в обычной евклидовой rеометрии на
плоскости "абсолют вырождается в пару точек, а именно в пару T<r
чек пересеченИJI бесконечно удаленной прямой с ИСЧе3аюp.l.ИМ KpyroM,
или, что то же самое, абсолют являетCJI двумя круrовыми точками в
бесконечности" , т.е. точками (1, i, О) и (1, i, О). rоворя о вырожд
НИИ кривой К в пару точек, Кэли имеет в виду кривую К как пучок
BToporo порядка, который вырождаетCJI в данном случае в пару мни
Mых пучков. Кэли не рассматривает случаев, KorAa К веществен
пая коника, или KorAa К paCnaAaeTCJI на пару действительных пучков.
Однако ему было ясно большое значение определенных им проекти
BHых метрик, и в конце cвoero мемуара он писал: "Метрическая r
ометрИJI являетCJI, таким образом, частью проективной rеометрии,
и проективнаи rеометрИJI представляет всю rеометрию"
Следует OTMeT TЬ, ЧТО проективная форма для выражения вели
чины уrла на евклидовой плооскости была преДJlOжена еще раньше
э. Лаrерром (1853 r.):. соrласно формуле Лаrерра уr л q; между
ДBYМJI прямыми, ПрОХОДJlЩИМИ чере3 точку снеоднородными K00Jr
диватами %0 и Уа выражаетCJI чере3 двойное отношение W этих пря
Mых И двух и30троп.ных (минимальных) прямых У УО = жi(% %0)
I
соотношением q; = ln W
2
Случай, коrда "абсолют" Кэли являетCJI вещественной коникой,
БЫJj исследован Ф. Клейном в статье "О так называемой неевкли
довой rеометрии" (1871 r.)! Клейн показал, что в этом случае та
часть проективной плоскости, котораи лежит внутри коники К, и3<r
метрична плоскости Лобачевскоrо. Во второй части этой статьи
(1872 r.) Клейн вводит проективную метрику несколько друrим, чем
Кэли, способом. А именно, раССТОJlнием между точками Р и Q он
нanывает величину с ln W, rAe W двойное отношение точек Р и Q
и точек М и N пересечения прямой PQ с той кривой BToporo порядка
К, котораи ВЗJ1та в качестве "абсолюта", а уrлом между прямыми р
119
и q он называет вeJlичину с' 10 W' , rде W' двойное отноwение ПрJl"
Mых Р И q И двух KacaTeпьHых к "абсOJlЮТУ", проведенных 113 точки
их пересеченИJI. йн показывает, что в CJIучае, )[orAa обе ПОСТОJlН..
с' I v
ные с и равны 2 ' ПОJIУЧаетCJI метрика на ЭJIJlиптическои ПJlOс)[ости,
1 i
а в CJIУЧ&е, коrда с 2 ' а с' = 2 ' ПOJlучаеТCJI метри)[а на ПJlOс)[ости
Лобачевс)[оrо.
Тем самым Клейн по)[аз8JI, что не ТОJlЬ)[О еВ)[Jlидова, но и обе
известные )[ тому времени нееВКJlИДОВЫ rеометрии (Рим на и Лоба..
чевс)[оrо) JlВJIJIЮТCJI част.ми общей проективной rеометрии. Рассма..
...,
триВ8.tl атот факт с точки зревИJI теории rрупп, ЭJJeменты которои
CJЮЖИJlИСЬ в работах КЭJlИ и еще ранее в работах ДРУfИХ математи..
)[ов (см. п. 3.3, 3.4), КJlейн приходит )[ выводу, ЧТО BCJlK&R rеометрИJI
пр стаВJlJlет собой, по существу, учение об инвариантах той ИJlИ
иной rруппы преобраоований. Эта точ)[а зренИJI БЫJlа впервые 113"
JIO.Жена КJlейном в ero та)[ называемой "ЭРJlанrенс)[ой проrрамме"
JIe)[ЦИИ, рочитанной им при вступлении в ДOJlжность профессора
ЭрJlанrенскоrо университета (1872 r.).
КJlейн начинает СВОЮ "ЭРJlанrенс)[ую проrрамму" с опреДeJIенИJI
rруппЪi ореобраооdaний: "Наибопее существенное повИтие, необх
v
АИМое ДJIJI ДaJIьнеишеrо ИЗJlоженВJI, есть ПОВJIтие о rруппе простран...
cTвeHHых изменений'. ПРОIШВОJlЬНое число преобрanовавий прос
ранства дает, С)[JI&ДЫВ8.RСЬ, снова преобрanование пространства.
ЕCJIИ данный рJlД преобрanовавий оБJlадает тем свойством, что )[а..
ждое IIOменение, получаемое от ПОCJIедоватеJlьноrо примененИJI не-
С)[ОJlЬ ИХ преобрanований, принадлежащих этому риду, ca..\fO ВХОДИТ
в ero состав, то мы называем этот рJlД rруп,пой преобразований"
[24, т. 2, с. 108].
В )[ачестве примеров rрупп преобрanований ПРИВОДJlТCJI "c
вокупность всех движений" пространства (Клейн замечает, что
)[аждое движение рассматриваетCJI как операЦИJl, ВЫПОJlненна.и над
. "'" v
всем пространством" и "совокупность )[ОJlJlинеации Клеин у)[азы
вает, что вращеНИJl О)[ОJlО точ)[и образуют подrруппу rруппы движе-
ний, а )[оррелJlЦИИ ("двойственные преобразования") сами не обра
зуют rруппу, но образуют ее вместе с )[ОJlJlинеаЦИJlМИ.
Далее Клейн переходит от еВКJlидова пространства к ПрОИЗВОJlIr
НОМУ "мноrообразию": "По аН8JIOfИИ с пространственными пре-
обрanованИJlМИ мы rоворим о преобразоваНИJlХ мноrообрааИJl: они
120
та)[же образуют rруппы ... Как обобщение rеометрии, ПОJlу'tёk..........,
та)[им образом, CJlедуЮЩ8JI мноrообъеМJlЮЩа.в задача:
Дано мвоrообраове в в вем rруппа преобраоО RRAWЙ ;
вужво ВСCJlеяовать те свойства обраоов, првва пе. А'qJПC
мвоrообраовlO, которые ве вомев..ютс.8 от преобраоО RRAWЙ
rруппы.
ПримеНИТeJIЬНО )[ современной терминопоrии можно Bыа..
зитьCJI еще та)[:
Дано мвоrообраоие и в вем rруппа DреобраоО ВАII-- . 'lPe-
буетс.8 раовить теорИlO ввварвавтов 8ТОЙ rруппы" [24, т. 2,
с. 108 109].
Подробнее об указанных работах КЭJlИ и Клейна см., например,
[20, с. 168 176; 19, с. 201 244; 24, т. 2, с. 71 74, 105 109].-
В качестве примера рассмотрим важнейшие rруппы преобра--
зований на поос)[ости. Пусть Р2 прое)[ТИВН&II ПJlОС)[ОСТЬ. TorAa
все преобразования вида %' = Аж, rAe z и %' точ)[и ПJlOС)[
сти Р2 С однородными координатами соответственно (%1' %2, %3) и
(% , % , % ), а А невырожденнаи матрица размерности ЗхЗ, соста..
вJlяют некоторую rруппу. Эта rруппа носит на3вание rруппы прое)[
тивных преобразований плоскости Р2, ИJlи проектвввой rруппы.
Обооначим ее r 8 (здесь и далее индекс у)[азыаетт число не3ависимых
параметров rруппы, т.е. ее размерность). Заметим, что все прое)[
тивныe преобразованИJI, автомофныe относительно HeKoToporo MH
жества К С Р2, т.е. переводящие множество К в себя, образуют
не)[оторую подrруппу rруппы r8. Будем назыатьь ее rруппой 88-
ТОМОрфИDМОВ относительно К.
Взяв в качестве множества К несобственную бес)[онечно удален
ную прямую %з = О, мы получим rруппу аффинных преобра-
DОВавий r6. Действительно, матрица А любоrо преобразованИJI,
переводящеrо жз = О в Ж = О (при любых %1 И %2) будет иметь
вид: А = {aij, rAe аЗ1 = аЗ2 = О}. TorAa все конечные (собствен
ные) точки плоскости Р2, т.е. точ)[и, составляющие аффинвую ПJIO--
сжость, будут переходить также в точки аффинной плоскости, а все
преоБР8.30ваНИJl с матрицей А у)[азанноrо вида внеоднородных КОо-
ж 1 %2' %' %'
ординатах ж = , у = , %' = ---f, у' = ---f перепишутся в виде
ЖЗ ЖЗ Ж З %з
{ Ж'
у'
а1 Ж +
а2 Ж +
Ь 1 У + С1
Ь 2 У + С2
121
ai1 а.2 аiЗ v
rде ai = , bi = , Ci = , т.е. деиствительно будут являться
азз азз Озз
аффинными преобразованиями.
Взяв в качестве К две цикрические (или KpyroBble) точки
(1, i, О) и (1, i, О), т.е. точки пересечения всякой окружности (Жl
ажз)2 + (Ж2 Ьжз)2 = r2ж с несобственной прямой жз = О (про-
верьте это!), мы получим rруппу r 4 еВJCJlИ ОВОЙ rеометрии. Дей..
ствительно, нетрудно показать (см., например, [12, с. 454]), что ма..
трица А пюбоrо преобразования, переводящеrо пару циклических
точек в себя, будет име ь вид: А = {aij, rAe аЗl = 032 = О, а
а21 = 012, а22 = ::I:01l}. Тоrда все собственные точки будут перехо-
дить в собственные, а все преобразования с матрицей А указанноrо
жl Ж2 ж' ж'
вида в неоднородных координатах ж = , у = .........., ж' = , у' =
жз жз ж з ж з
перепишутся в виде
ж' a1l + а12 + ОlЗ
ж y .............
азз азз Озз
у' а12 ::1: a1l + 02З
ж y .............
азз азз Озз
или, если Isвести обозначения
al1
= rcos<p,
азз
012 .
= rSlD rp,
азз
аlЗ
=и,
азз
а2З
=v,
азз
в виде
{ ж'
у'
r(ж cos <р +
r( ж sin rp ::1:
у sin rp )
у cos rp )
+
+
и
v
Из этих формул видно, что всякое преобразование из rруппы r 4
представимо в виде суперпозиции поворота на уrол rp BOKpyr на..
чала координат, преобра.оования подобия (а именно, растяжения в
r раз относительно начала координат) и параллельноrо переноса на
вектор (и, v), так что rруппа r 4 действительно является rруппой
преобразований евклидовой rеометрии на плоскости.
Взяв в качестве К ОВaJlЬИУIO ЛИВИЮ ж + ж ж = О, мы по-
лучим rруппу r 2 rеометрии ЛобачеВСJCоrо иа ПJlОСJCОСТИ. B e
те преобразования этой rруппы, которые автоморфны еще и отно--
сительно несобственной прямой, являются, очевидно, поворотами с
центром в точке (О, О, 1), возможно с симметрией относительно оси
122
Жl
Х = , и, следовательно, запишутся в виде
жз
{ Ж'
у'
жсоs<р +
=F Ж SlD <р :f:
у SlD <р
У COS <р
(а)
Если же некоторое преобразование rруппы [2 переводит Heco
у
1
12 , I
Ж
11
I з
I
Рис. 38. Преобразование (б)
ственную прямую в собственную, то существует собственная пря
мая 11, которая при этом преобразовании переходит в несобствен
ную прямую 100: Ж = о. с помnщью HeKoToporo движения (а) эту
Ж2
прямую 11 можно расположить "параллельно" оси у = , так что
жз
11 будет определяться уравнением АЖl + ЖЗ = о, rAe А # о. Поэтому
аЗl = А, ОЗ2 = о, Озз = 1. А так как образ 11 не пересекаетCJI (на В&
щественной проективной плоскости) с овальной линией, то и сама
прямая 11 также не пересекается с этим абсолютом (см. рис. 38); по--
этому IAI < 1. Далее, полюс Pl( , 0,1) прямой 11 перейдет в полюс
.роо(о, 0,1) несобственной прямой 100. Поэтому прямая 12: Ж2 = О
перейдет в прямую I , проходящую чере3 центр Kpyra, так что 12:
021 Ж l + 022Ж2 = о. А TorAa из BToporo уравнения "системы АР 1 = Р 00
находим, что 021 = о, так что Х2 = 022Ж2 и прямая 12 переходит
в себя. Но TorAa прямая I з : Жl + АЖз = О переходит в прямую I :
Ж = О, так как Р 1 переходит в Р 00, а полюс прямой I з остается на
123
прямой 12, так что I "opTOrOHaJlbHa" 12. Поэтому ж = жl + .лz з .
Наконец, из усл овия ж 2 + ж 2 ж 2 = О при % + % жi = о находим:
022 = :l: v' 1 .л 2 (при этом, с учетом (а) можно считать, что 022 > О).
Итак
{ Ж жl + %3
ж' у 1 .л 2 Ж2 (б)
2
% .лZ 1 + %3
%1 %2 %' %'
В неоднородных координатах % У %' .....!. у' ..2
, , , , ж'
жз %3 ж з 3
уравнеНИJl (б) принимают вид
ж'
%+.л
1 + .лж
v'l .л 2 у
1 + .л%
(.б' )
у'
И, С точностью до обозначений, совпадают с преобрааованиями Л
ренца специальной теории отностительности. А именно, если ввести
V z V v' v' V
обозначения % = , У = ...!., %' = ...L, у' = 1, .л = ...., то преобра3
с с с с с
ваНИJl (б') перепишутся в виде преоБРа30ваний Лоренца
V'
z
V z +.v
1 V . V z
+ 2
с
V 1 v 2 .v
с 2 !I
V · V z
1 + 2
с
rде (V z , V y ) компоненты скорости точки в неподвижной системе
координат (ж, у), а (v , V ) компоненты скорости этой же точки
в системе ( ', у'), движущейся относительно системы (ж, у) влево со
скоростью V (см. рис. 39), с скорость света.
Взяв в качестве К нулевую линию жI + ж + Ж5 = о, мы получим
. u
rруппу r 2 вллиптичесlCОИ rеометрии иа пJюСIОСТИ. Все те пр
обра:зования этой rруппы, которые автоморфны еще и относительно
несобственной прямой, являются, очевидно, преоБРа30ваниями вида
(а). Если же некоторое преоБРа30вание rруппы r 2 переводит Heco
ственную прямую в собственнrю, то, с учетом (а), можно считать.
(б")
v'
11
124
y
у
..
v
ж'
ж
Рис. 39
что жз = '\Ж1 +жз. Далее, полюс Р 1 ('\, о, 1) прямой 11 %1 +жз перей..
дет в полюс Роо(о, о, 1) несобственной прямой 100 ж; = о. Поэтому
прямая 12 %2 = О перейдет в прямую 12' проходящую через точку
(о, О, 1), так что 12 021Жl + 022Ж2 = о. А тоrда из gToporo ypaBHe
ния системы AP 1 = РОО находим, что 021 = О, так что Ж2 = 022Ж2,
и прямая 12 переходит в себя. Но тоrда прямая I з .......ж1 + '\ЖЗ = о
переходит в прямую I з жl = о, так как Р 1 переходит в Р 00, а полюс
прямой lз остается на прямой 12. Поэтому ж = .......жl + '\ЖЗО Наконец,
из условия x 2 + ж 2 + ж 2 = О при ж + ж + х; = о находим, с учетом
(а), что 022 = у l + ,\ 2 . Итак,
{ X ....... .......х1 + '\жз
Ж2 ....... "' 1 + ,\2 Ж2 (в)
ж' '\%1 + zз
з
Ж1 Х2 X х'
В неоднородных координатах ж ж' у' 2
, У ....... , ....... , , ж'
ЖЗ жз ж з з
уравнения (в) принимают вид
х'
Ж + ,,\
1 + '\ж
"'1 + ,\2 у
1 + '\ж
(в')
у'
Основным инвариантом rруппы rs всех проективных преобра
'" '" '" u
зовании на вещественнои проективнои плоскости является воивое
отношение (А В С О) = (А В С) (А В О) прямолинейной четверки
точек А, В, С, D.
125
Основным инвариантом rруппы r 6 всех аффинных преобразо--
ваний на вещественной плоскости является простое отношение
(А В С) = АС ВС прямолинейной тройки точек А, В, с.
Основным инвариантом rруппы r 4 евклидовой rеометрии на пло--
скости является мо упь yrn8 меж у пр"мыми.
Основным инвариантом rруппы r 2 rиперболической реометрии
на плоскости является рассто"ние PL(P, Q) = Iln(PQM N)I между
точками Р и Q (здесь м и N точки пересечения прямой PQ с
овальной линией).
Основным инвариантом rруппы r 2 эллиптической rеометрии на
плоскости является рас то"ние
( Р Q) XIYl + Х2У2 + ХзУз
ря, = arccos / 2 + 2 + 2 / 2 + 2 + 2
v Х 1 Х 2 Хзv Yl У2 УЗ-
между точками Р(Хl, Х2, хз) и Q(Yl, У2, Уз).
Упражнение 26. Покажите, что расстояния PL и Ря действи
,
тельно являются инвариантами соответствующих rрупп преобра
зований и, кроме Toro, облаД8;ЮТ свойствами:
1) р(Р, Q) > о; р(Р, Q) = о Р = Q,
2) p(Q, Р) = р(Р, Q),
3) р(Р, R) + p(R, Q) > р(Р, Q) дЛЯ любоrо R,
4) р(Р, R)+ p(R, Q) = р(Р, Q) дЛЯ любой точки R на отрезке PQ.
Упражнение 27. Укажите основные подrруппы евклидовой ("шко--
льной") rеометрии на плоскости.
Упражнение 28. Какие из известных вам типов rеометрий, кроме
названных в этом параrрафе, подпадают под теоретико--rрупповую
классификацию? 'кажите преобрanования и основные инварианты
этих rеометрий.
Вопросы и заоа'1tuz
1. О чем rоворят нам названия первых rеометрических фиrур и
тел?
2. Сформулируйте постулаты "Начал" Евклида.
3. Какие идеи из "Конических сечений" АполJЮНИЯ ОКа3ались
фундаментальными для дальнейшеrо развития rеометрии?
126
4. Нanовите практические и теоретические предпосылки воз
никновения аналитической rеометрии.
5. Что такое аналитическая rеометрия по форме и по содержа
нию?
6. Нanовите основные этапы в становлении классической дифф
реНЦИaJIЬНОЙ rеометрии.
7. Что такое внутренняя rеометрия поверхности?
8. Что такое проективная плоскость? Укажите ее модели.
9. Что изучает проективная rеометрия?
to. Что такое двойное или анrармоническое отношение прямоли
нейной четверки точек?
11. Что такое принцип двойственности в проективной rеометрии?
12. Какие свойства фиrур Понселе HanblBaeT "проективныIи''??
13. Что такое синтетические и аналитические методы проекти
вной rеометрии?
14. Каким обрanом вводятся однородные проективные координаты
и Мёбиуса и у Плюккера?
15. Что такое "вурфы" Штаудта? Укажите' способ их чисто про--
ективноrо построения.
16. Что такое проективная метрика Кэли?
17. Что положено Клейном в основу классификации типов reoMe
трий? Назовите важнейшие подrруппы rруппы проективных
преобразований на плоскости.
!Лава 5
АНАЛИЗ
5.1 МЕТОД "исчЕрпыIАния",
ЕВДОКСА. ИНТЕrР АльныIE И
диффЕрЕнциАльныE мЕтодыI
АРХИМЕДА
Теоретическими предпосылками для создания во второй пол<r
вине XVII в. основ дифференциальноrо и интеrральноrо исчисления
послужили аналитическая rеометрия Декарта и Ферма и, в особен
ности, интеrральные и дифференциальные методы в Древней I'pеции
и в Европе первой половины XVII в. Эти интеrральные и дифферен
циальные методы суть методы решения отдельных редких задач на
вычисление площадей.и объемов и на нахождение касательных и экс
тремумов. Эти методы содержат в себе почти все идейное боrатство
будущеrо интеrральноrо и дифференциальноrо исчисления.
Интеrральные методы в Древней I»еции были основаны на Me
тоде "исчерпывания" Евдокса. Этот метод, создание KOToporo OTH<r
сится к IV в. до н.з., представляет собой исторически первый метод
пределов. В основе ero лежит следующая лемма.
Лемма EB OKca. Если даны две величины а и е, О < е < а, то
вычитая из величины а больше ее половины, из полученноrо остатка
больше половины этоrо остатка и т.д., получим через конечное число
шаrов постаток Т п < е.
Эта лемма формулируется и ДОКа3ывается в предложении Х, 1
"Начал" Евклида. ДОКа3ательство ее таково. На основаl!ИИ аксиомы
Евдокса Архимеда величину е можно повторить столько ра3, что
nе > а. Повторим теперь n ра3 процесс выбрасывания из вели
чины а и последовательных остатков Тl, Т2, . .. частей, превыша
щих их ПОJЮвины:
Тl
а
а а l <
2'
128
rl о
r2 r 1 ..... 02 < ....... < ....
2 4'
..................
rn l о
r n rn 1 ..... ОП < < < 2 n ·
2
Но TorAa n · r n < 2 n · r n < о. Итак, nr n < о < пе;, Т.е. r n < t .
Лемма Евдокса служила сначала ДЛJl cTpororo дока:эателv
ства иовестных ио практики истин. Опиравсь на ату лемму,
Евдокс доказал, что площади KpyroB ОТНОСJlТСЯ как квадраты
диаметров, объем пирамиды
равен трети Пр.оиоведенИJI
площади основанИJI на вы..
соту и некоторые друrие по-
добные утвержденИJI. ДOK
аатепьство первоrо YTвe
ждеНИJl ПрОВОДИТСJl следую-
щим образом. Вначале заме-
чаеТСJl, что последователv
ность правильных, вписан..
ных в Kpyr 2 n ..уrольников
(рис. 40) "исчерпывает" Kpyr,
Рис. 40 т.е. что разность (8 8 n + 1 )
площади Kpyra и площади праВИЛЬRоrо вписанноrо 2 n + 1 ..уrольника
меньше половины разности (8 8n) площади Kpyra и ПlЮщади
правильноrо вписанноrо 2 n "уrольника (проверьте ато, ИСХОДJl ио
рис. 40!). Затем предполаrаеТСJl противное, т.е. что ДЛJl некото-
рых двух KpyroB с площаДJlМИ 8' и 8" и с диаметрами d' и d" со-
ответственно имеет место неравенство 8' S" #; (d')2 (d")2. То-
rда (d')2 (d")2 = 8' S (проведите cTporoe доказательство су..
ществоваНИJl четвертой пропорциональной 8 к трем данным!), rAe
S либо меньше 8", либо больше 8" Но если 8 < 8", то, соrла..
сно лемме ЕВдРкса, при достаточно большом n было бы S" ..... S <
8" 8, 8: > 8, и TorAa (d')2 (d")2 = S 8 = 5' 8, чеrо
не может быть, так как S < 8', а 8: > 8 Случай S > 8" сво-
ДИТСJl К предыдущему заменой отношений на обратные (проверьте,
если о Ь = с d , .то И Ь о = d с !). Доказательство вто-
poro утверждеНИJl ПрОВОДИТСJl следующим оБР&30М. ЗамечаеТСJl, что
129
Рис. 41
будет равен
1 ( 1 ) 2 ( 1 ) "
4 + 4 +...+ 4
1
= 4
ВСJlКaJI пирамида с треу..
rольным основанием может
быть разбита трем.и плоск<r
СТJlМИ, ПРОХОДJlЩИМИ череа
середины ребер на две пи..
рамиды с вдвое меньшими
размерами и на две призмы,
каждая И3 KoTopых со ста..
ВЛJlет восьмую часть призмы
с теми же основанием и вы..
v
сотои, что И исходим пи..
рамида (рис. 41). Поэтому
ВСJlКaJI пирамида исчерпы..
ваеТСJl последовательностью
тел, составленных И3 призм;
при этом объем n..ro тела
1 ( ) n
1 ( )
1 1
= 3 3
( )"
объемов призмы с теми же. основанием и высотой, что и исходнм
пирамида. ИСХОДJl И3 этоrо, рассуждением от противноrо с примене--
нием леммы Евдокса показывается, что объем исходной пирамиды
равен трети объема соответствующей призмы (покажите это caM<r
стоятельно!) .
Архимед, опираясь на лемму Евдокса, дм cTporoe доказатель..
ство Toro, что площадь Kpyra равна половине произведения pa
диуса Kpyra на длину окружности. Это доказательство, следуя EBA<r
ксу, Архимед Пр080ДИТ методом от противноrо. Если бы, напри
мер, площадь Kpyra 5 была больше, чем половина произведения pa
1
иуса на длину окружности 2 rl , то, построив правильные вписан
ные и описанные 2"..уrольники (рис. 42) и показав, что разность
между площадью 5" +1 описанноrо 2" уrольника и площадью +1
вписанноrо 2"..уrольника меньше, чем половина разности между 5"
и sn (это верно, так как 5" +1 +1 = 2"(5 ABICl + 5 CIDIC) <
1 1 1 .....
2" 2SABIDIC < 2n . 5 ABC = 2(Sn Sn).) и примеНJIJI лемму EBA<r
130
D1
с
Рис. 42
кса, Архимед делает вывод, что эта разность 5n +l Sn+l может бы' 'ь
1
сделана меньше разности е = 5 2 rl , что противоречит Hep(',BeH
1
ству 8 n + 1 .....Sn+l > S 2r1 = е , которое следует иа Toro, что и 5 и.
1
2 rl, BcerAa ааключены между 8n+l и +1
{)ам,е'Ч,ан,uе И3 теоремы Евдокса о подобии KpyroB и теоремы
Архимеда о площади Kpyra следует, что отношение длины ОJ(РУЖН
сти К диаметру одинаково длJl BCJlKOrO Kpyra.
Позднее Архимеду удалось применить лемму Евдокса ДЛJl HaX
ждения новых длин дyr, площадей и объемов. Ему удалось найти
а = SlD r;
b=r;
с = tg r;
Рис. 43
площадь cerMeHTa параболы, площадь поверхности сферическоrо cer
мента, объем части параболоида вращеНИJl и т.п. При этом Архимед
.
формулирует и использует следующие леммы:
131
1. Из всех линий, имеющих одни и те же КОНЦЫ, прямая будет
наименьшей.
2. Две друrие линии, расположенные на плоскости и имеющие те
же самые концы, будут BcerAa неравными, если они обе выпу"
клы в одну сторону, и одна из них или целиком объемлется
друrой линией и соединя.ющ й их концы прямой, или же часть
ее объемлется друrой, часть же является общей обеим линиям;
при этом меньшей будет объемлемаи линия. Отметим, что от..
сюда следует, в частности, неравенство siil 'Р < 'Р < tg ер при
1r
О < 'Р < '2 (рис. 43).
3. Подобным же обраЗ0М из поверхностей, имеющих общую rpa..
ницу, расположенную на плоскости, наименьшей будет пл<r
скость.
4. Две друrие поверхности, имеющие общую rраницу, распол<r
женную на плоскости, будут BcerAa неравными, если обе они
выпуклы в одну сторону и одна из них или целиком объем..
лется друrой поверхностью и плоскостью, содержащей их o
, u
щую rраницу, или же часть ее объемлется друrои, часть же
является общей обеим поверхностям; при этом меньшей будет
объемлемая поверхность.
5. Большая из двух неравных линий, поверхностей или тел пре--
восходит меньшую на такую величину, которая будучи склады..
ваема сама с собой, может преВЗ0ЙТИ любую заданную вели..
чину из тех, которые MorYT находиться Apyr с ApyroM в опре--
деленном отношении.
В качестве примера рассмотрим способ вычисления Архиме--
а
дом площади S первоrо витка спирали r = 21r ((J. Архимед делит
центральным; уrол, равный 21r, на 2" равных частей и рассматри"
вает описанную Sn И вписанную sn фиrуры, составленные соответ..
ственно из описанных и вписанных KpyroBblx секторов (рис. 44). T<r
rAa
S n
t С а )2 1r n(n + 1)(2n + 1) 2 a 2 1r
= 26 01r>T'
. 1 n n n . n
а=
( )2 1r (n 1)п(2n 1) 2 a 2 1r
= 26 a1r<T
n n . n
1=0
S n
Далее Архимед показывает, что разность Sn n посредством п
132
Рис. 44
,.,.,
О
Рис. 45
следовательноrо деления секторов пополам может быть сделана как
a 2 1r
т < SN, ТР он дe
yroAHo малой, а так как n < S < Sn И s..п <
a 2 1r
лает предположение, что S = , и затем cTporo доказывает это
3
методом от противноrо.
Как можно заметить из рассмотрения работ Архимеда, ero ин
теrральные методы, хотя и применяются им самим только к неболь
шому Kpyry задач, имеют тем не менее совершенно общий xapaK
тер и содержат в себе идею верхних и нижних интеrральных сумм,
идею критерия Дарбу существования интеrрала и идею доказатель
ства единственности общей точки у последовательности вложенных
Apyr в Apyra промежутков.
В сочинении "О спиралях" Архимед разработал и метод опреде
ления касательн й к кривой. Этот метод обладает той же степенью
общности, что и ero интеrральные методы, и может служить для
отыскания касательной к любой дифференцируемой кривой.
На рис. 45 1 спираль, ОР радиус вектор спирали, r.p
малое приращение полярноrо уrла, ОТ перпендикулярно ОР, РТ
касательная к спирали, PR дуrа окружности радиуса ОР с
центром в точке о. Все рассуждения Архимед проводит, поль
зуясь, по--существу, полярными координатами. "Малый" треуrоль
FR QR
Отсюда RP RP
ник FRP "подобен" треуrольнику ОРТ.
ОР T ОР
ОТ . Или О
rи.r.p Т
tg о, rде r радиус вектор. Отсюда
133
r · <p 2 'P 2 'P r 2
ОТ ОР r = r = = r<p. Чтобы провести
r r a 'P а
cTporoe дока;зательство, Архимед исследует в специальных леммах
r
отношение .!l и дока;зывает, что при доста очно малом 'P ра;з
r . <р .
r v
ность tg Q может быть сделана сколь yroAHo малои. При
r. 'Р
чем эти рассуждения носят совершенно общий характер.
В заключение мы остановимся на своеобра;зном приеме, pa3pa
ботанном Архимедом для наве,цеви" на правипьиый реоупьтат
при вычислении площадей и объемов по методу "исчерпывания"
Этот прием основан на механическом "правиле рычаrа" и на том
предположении, что все фиrуры состоят из параллельных отрезков,
а все тела из параллельных кусков плоскостей.
Е
А
Рис. 46
Рассмотрим в качестве примера вычисление Архимедом площади
cerMeHTa параболы. На рис. 46 АВС cerMeHT параболы, ВО
Дllаметр параболы, ЕА касательная к параболе в точке А, ЕС па
раллельна ВО, F точка пересечеНИ.:R АВ и ЕС, FG = AF Предп
ложив, что cerMeHT АВС состоит ио отрезков KL, параллельных диа
метру параболы BD, и воспользовавшись тем, что KL. FC = ML. NF
(докажите зто свойство параболы самостоятельно!), Архимед полу
чает, что треуrольник АЕС, составленный из "весов" ML с pы
чаrами NF, уравновешивается суммой "весов" KL с общим рыча
rOM GF (т.е. если середины "весов" поместить в G). А так как
суммы "весов" KL относятся к сумме "весов" ML как площадь S
cerMeHTa АВС относится к площади Тl?еуrольника АЕС, а центр
134
тяжести треуrольника АЕС имеет рычаr втрое меньший, чем FG,
1 1
то S FG = Sl::.AEC 3 FG, откуда S = 3 S AEC. Но СЕ = 2 FC
(по известному свойству касательной к параболе), FC = 2 BD (т.к.
диаметр BD делит АС пополам, а FC параллельна BD). Поэтому
S AEC = 4 Sl::.ABC, откуда Архимед получает, что площадь S 'cer
4
мента АВС равна 3 S ABC.
Еще ра:э подчеркнем, что TaKoro рода рассуждения Архимед не
считал дока:эательствами. Они служили у Hero лишь наведениями на
cTporoe дока:эательство, которое он затем старался провести мет()-
дом "исчерпывания"
УПDажнение 29. Методом интеrральных сумм Архимеда найдите
объем полушара.
УПDажнение 30. Механическим методом Архимеда найдите
центр тяжести и объем cerMeHTa параболоида вращения.
Упражнение 31. Методом интеrральных сумм Архимеда устан()-
вите квадрируемость подrрафика rиперболы и докажите основное
свойство лоrарифмической функции.
5.2 ИНТЕrР АЛЬНЫЕ и
диффЕрЕнциАльныIE мЕто,дыI В
u
ЕВРОПЕ ПЕРВОИ половиныI
XVII ВЕКА
Интеrральные и дифференциальные методы Архимеда БЫ;JИ пере--
няты арабскими математиками средних веков. Однако им не удалось
существенно ра;звить их. Можно, правда, отметить проделанную Ca
битом ибн Коррой новую квадратуру cerMeHTa параболы у2 = 2рж
путем ра;збиения отрroка интеrрирования [О, а] на неравные части
(см. В.П. Демидович "Сборник задач по математическому анализу",
задача 2190). Отметим также, что Хасану ибн ал Хайсаму yдa
лось методом "исчерпывания" провести вычисление, равносильное
нахождению интеrрала f 0 4 ж 4 dz. Затем в течение мноrих веков диф-
ференциальные и интеrральные методы были оставлены в стороне.
Лишь с начала XVII в. они снова привлекают внимание Fdатематиков.
Причем, если Архимеду быJЮ важно каждый ра;з провести cTporoe
135
док&3ательство, то у математиков XVII в. внимание обращено, rлar
вным обрanом, на вычисление. "CTporocTb аабота философов, а
не reOMeTpOB", rоворит Б. Кавальери. "Не лоrика, а приличеству
ющ8.1 случаю JlСНОСТЬ достаточна ДЛJI правильных умоааключений" ,
вторит ему Б. Паскаль. "Было бы леrко дать докanательство в
духе Архимеда (т.е. cTporoe ДОК83ательство от противноrо по M
ТОДУ "исчерпываНИJl"), пишет п. Ферма, достаточно преду
предить об этом pan и HaBcerAa, чтобы иабежать постоянных повт()-
рений" Так что европейские математики первой половины XVII в.
заимствовали иа методов Архимеда, rлавным обра:эом вычислитеJ11r
ную сторону; при этом им УДaJЮсь существенно р83вить ее.
5.2.1 ИитеrР8JIьиые MeTO Ы и. КеПJIера
В работе "Новая стереометрия винных бочек. .. (1615 r.) Кеплер
принимает метод "исчерпывания" , которым польаовапся Архимед,
но отбрасывает ааключител.ьный этап приведения к противоречию.
Рассмотрим характерные примеры. Так, при нахождении объема
"лимона" (имеется в ВlfДУ объем V тела, полученноrо вращением
ёеrмента Kpyra BOKpyr хорды cerMeHTa в случае, коrда высота h
.
cerMeHTa меньше радиуса r Kpyra (рис. 47)), ра3бивая хорду cer
мента на 2 n равных частей и строя вписанную и описанную ступен
Рис. 47
чатые фиrуры, Кеплер находит объемы и V n тел, полученных
при вращении соответственно вписанной и описанной фиrур BOKpyr
хорды cerMeHTa. Затем из полученных неравенств V n < V < V n И
< 211" а (r2 2 ) 211"( r h )r 2 ", < V n Кеплер заключает (минуя
136
cTporoe докanательство от противноrо методом "исчерпыванИJI"),
что V = 211'0 (r2 ) 211'(r h)r2 . Друrой ВЫВОД \ПОЙ ФОРМУЛЫ
У Кеплера см. [35, с. 243 244].
В этой же работе для сравненИJI площадей фиrур или объемов
тел Кеплер использует и друrой метод, основанный на рanбиении
этих фиrур и тел на очень большое число очень маленьких частей.
Так, соrласно Кеплеру, площадь Kpyra равна половине проиаведенИJI
радиуса на длину окружности потому, что Kpyr можно считать со-
ставленным иа очень большоrо числа очень маленьких секторов АЬс
(рис. 48), а каждый иа этих секторов можно ааменить равнобедрен..
В
ь
с
С
Рис. 48
ным треуrольником с основанием, равным длине дуrи сектора; ка..
ждый такой равнобедренный треуrольник, в свою очередь, равно-
велик соответствующему неравнобедренному треуrольнику АЬс (с
теми же основанием и высотой), которые в сумме составляют БОЛL--
шой прямоуrольный треуrольник АВС с катетами АВ и ВС, ра..
вными соответственно радиусу Kpyra и длине окружности.
УПDажнение 32. Пользуясь методами Кеплера, найдите объем
тора.
5.2.2 МеТОА "ве,цепимых"
Метод "неделимых" восходит к механическому приему , примеВJIвше--
муся еще Архимедом. В XVII в. этот прием получил дальнейшее p83
витие в работах r CeH BeHcaHa, r. rалилея, Б. Кавальери, э. Тори
челли, ж. Роберваля и некоторых друrих математиков, которые и
пре06Ра30Вали ero в метод "неделимых" .
137
В основе метода "неделимых" лежат два предположении:
1. Фиrуры и т ла состоят из "неделим "; фиrуры COCTOJlT 1m
"неделимых" параллельных отрезков или из друrих одномер-.
Hых подобных Apyr Apyry частей, а тела COCTOJlT из паралпепlr
ных "неделимых' кусков плоскостей или из друrих двумерных
подобных Apyr Apyry частей.
2. Площади двух фиrур (объемы двух тел) OTHOCJlTCJl Apyr к Apyry
как все "неделимые" одной фиrуры (тела) ко всем "неделимым"
друrой фиrуры (тела). В частности, если соответствующие
"неделимые" HaxOAJlTCJl Apyr к Apyry в ОДНОМ и том же OTH
шении, то в этоl.! же отношении HaxoAJlTCJl и площади фиrур
(объемы тел).
Рассмотрим характерные примеры.
Прнмер 1. Dпощаяь 8JШИПса
Площадь эллипса с ПОЛУОСJlМИ а и Ь относитCJI К площади Kpyra
радиуса а как Ь к а потому, что таково отношение их соответству"
ющих "неделимых" (рис. 49).
12 : 11 = Ь а
Рис. 49
Пример 2. З8JCов равномерно YCKopeBBoro явижеви.. (r.ra-
JlВJJeЙ, 1638 r.) "
"Время, в течение KOToporo тело, вышедшее из СОСТОJlНИJl ПОКОJl
И движущееСJl равномерно ускоренно, проходит некоторое paCCT
яние, равно времени, в течение KOTOpOFO это же раССТОJlние было
бы пройдено тем же телом при равномерном движении, скорость
KOToporo paBHJleTCJl половине величины наибольшей конечной CKOp
сти, достиrаемой при первом равномерно ускоренном движении" [33,
кн. 2, с. 46 47]. Вывод этоrо заключения сопровождаеТСJl у rалилеJl
следующим рисунком (рис. 50). Здесь АВ интервал времени, в те--
138
А
С
D
Е
F
В
Рис.. 50
чение KOToporo проходится расстояние CD, AG = BF скорость pa
BHoMepHoro движения, ВЕ = 2 BF конечная CK pOCTЬ равномерно
YCKopeHHoro движения, линии GF и АЕ rрафики этих движений.
Пройденные за время АВ пути относятся Apyr к Apyry как суммы
всех "неделимых" (здесь скоростей), а эти суммы о.тносятся Apyr
к Apyry как площадь АВЕ к площади ABFG. Но эти площади равны.
Поэтому за равное время АВ оба движения опишут один и тот же
путь CD, и наоборот, оба движения опишут один и тот же путь CD
за равное время АВ.
Пример 3. Dпощаяь Kpyra
В качестве "неделимых" частей Kpyra выбираются концентри
ческие окружности, которые при развертывании составят "все
вместе" прямоуrольный треуrольник с катетами, равными радиусу
Kpyra и длине ero окружности (рис. 51). Так как "неделимые" окруж"
ности Kpyra равны соответствующим "неделимым" отрезкам треу..
rольника, то и площадь Kpyra равна площади треуrольника.
Пример 4. Объем пирамияы с к:ваяратным основанием
(Б. КаВ8Jlьери, 1635 r.)
Пусть а сторона основания пирамиды, h высота пирамиды.
В качестве "неделимых" возьмем куски плоскостей, параллельиых
основанию пирамиды. "Неделимы " пирамиды представляют таким
оБРа30М квадраты, стороны которых ж изменяются от а дО О, KorAa
высота плоскости этоrо квадрата над основанием пирамиды меня..
ется от О до h. Сравним теперь объем У 1 пирамиды с объемом
139
(2 = 11
Рис. 51
V2 призмы С теми же основанием и высотой. Соответствующие
"недеЛИМl:rе" призмы буду'r все квадратами со стороной а. Имеем:
1
V 1 = Е х 2 = Е (a x)2= 2 Е [x2+(a x)2]
oszs. oszs. oszs.
L [( х ) 2 + ( ; ) 2]
oSzs.
= 2 Е ( х) 2 + Е
0SzS t °SzS.
( а ) 2 1
L 2 x + 4 L
0SzS. 0SzS.
а 2 =
1
а 2 = 2 Е х 2 + 4 Е а 2 =
°SzS t OSzS.
1 " 1 "" 2 1 1
= 4 L.J х 2 + 4 L.J а = 4 V 1 + 4 V 2 ,
0SzS. 0SzS.
1 1 2
откуда V 1 = 3 V 2 = 3 а h.
Зам,е'Ча'Н,uе Вычисление объема пирамиды по методу "недели
мых" может быть проведено и друrим способом. Доста очно заме
тить, что всякий куб разбивается на три одинаковых пирамиды П с
квадратными основаниями, а "неделимые" всякой друrой пирамиды
(или даже конуса) с той же, что и у П высотой находятся в одном
и том же отношении к соответс.твующим "неделимым" пирамиды
П, еtли выбирать эти "неделимые" параллельными основаниям. О
друrих результатах Б. Кавальери см., например, [35, с. 252 253].
Пример 5. Объем "цилиндричеСJCоrо копыта" (r. Сан..
Веисан, 1629 r.).
140
"Цилиндрическое копыто"
это кусок цилиндра, получев
ный путем' плоскоrо среза,
проходящеrо через диаметр
АВ oAHoro основания цилив
дра и через крайнюю точку С
Apyroro основания (рис. 52).
Это копыто состоит из
"неделимых" прямоуrольных
треуrольников MNK, пп<r
скость которых перпендику
лярна к диа етру АВ. Если
обозначить за h высоту ци
линдра, за 2 r ero диа
метр АВ, а за z от.резок ОМ
Рис. 52 от центра О основания ци
лин др а до точки М, то площадь S(z) треуrольника MNK равна
1 lh h h
MK KN = MK2 = AM МВ = .........(r 2 х2). Но 1r(r 2 х2)
2 2 r 2т 2r
равно площади Kpyra, который получается, если шар ради-уса r п
ресечь плоскостью, отстоящей от центра шара на расстоянии ж.
"Неделимые" "копыта" и шара находятся Apyr к Apyry в одном и том
h h
же отношении 2 11'. Поэтому объем "копыта" в 2 раз больше
r rlr
2r 2 h
объема шара радиуса Т, т.е. объем "копыта" равен з' что, впр
чем, установлено еще Архимедом.
Пример б. KBa paTypa ЦИJCJlОИ Ы ()I{. Роберв ь, 1634 r.).
."
h N
// 11
/ 1 I
/ / 1
11 / I
1 / 1
I 1
11 I 1
/ / 1
/ I 1
/ / 1
/ / 'К
А / 7 7I"'"
., ., --- ." ." ..... ..... .....
,. /." .....
-".,,'" ,
/
Рис. 53
Циклоида определяется Робервалем механически, как траектория
141
точки на ободе катящеrося по ровной поверхности колеса. На рис. 53
изображены арка L циклоид.ы' колесо К в момент, коrда точка на
ободе занимает наивысшее положение, прямоуrольник Р, стороны
KOToporo равны высоте колеса и длине ero окружности. Разложив
движение точки на ободе колеса на движение проекции этой точки
на вертикальный диаметр колеса (это движение совершается по си
нусоиде S) и на движение самой точки относительно ее проекции,
Роберваль из равенства соответствующих "неделимых" 11 и 12, I и I
u
делает вывод, что площадь под аркои циклоиды превосходит площадь
под синусоидой S на площадь колеса. Но площадь под синусоидой S
равна половине площади прямоуrольника или двум площадям колеса.
Поэтому площадь под аркой циклоиды втрое больше площади колеса.
Пример 7. Объем беСlCонечно JlИRRоrо rиперБОJlичеСlCоrо
тела (э. ТОрИЧeJIJlИ, 1644 r.)
Речь идет о вычислении объема тела вращения rиперболы жу =
с > О, О < х < ха BOKpyr оси у [см. 33, кн. 2, с. 52 54]. Выбирая
в качестве "нецелимых" боковые поверхности цилиндра, основания
которых концентричеСКИ,е окружности (см. рис. 54), Торичелли
у
х
Рис. 54
замечает, что площадь S(x) такой поверхности равна 21rx . у = 21rC,
т.е. не зависит от х. Но тоrда все "неделимые" вместе составят
объем, равный объему параллелепипеда с площадью основания 21rC
и высотой ха (так как х изменяется от О до ха).
Упражнение 33. Вычислить по методу "неделимых"
а) объем полушара через объем цилиндра и объем конуса (СМ.
рис. 55),
б) о бъем тора,
142
в) площадь cerMeHTa параболы,
r) площадь первоrо витка спирали Архимеда.
r
у2 + х2 = т 2
Рис. 55
Упражнение 4. Исходя из определенИJI ln Х как площади подrра
фика rиперболы %У = 1 на отрезке .от 1 ДО Х, ДОКа3ать методом
"неделимых" основное СВОЙСТВО HaTypaпbHoro лоrарифма.
УПDажнение 35. Методом "неделимых" докажите теорему Архи
меда Паппа ryльдина: объем тела, полученноrо вращением пл
щади S BOKpyr некоторой оси, лежащей по одну сторону от S, равен
произведению площади S на длину окружности, описываемой цeH
тром тяжести s.
5.2.3 Ивтеrр8JIЬВЫЙ MeTO п. Ферма
Ферма удалось перейти от квадратур кривых у = Х N , rде n це-
лое ПОJЮжительное число, к квадратурам кривых у = xf, rде q п
ложительное или отрицательное рациональное число (q =F 1). Pac
смотрим метод Ферма на примере квадратуры кривой у = х"'2, % >
ХА > о. Ферма выбирает точки %1, Х2, ..., Ра3биения отрезка инте-
rрирования [ха, +(0) следующими Apyr за друrом в rеометрической
проrрессии:
X1 = '\Хо, Х2 = '\X1 = ,\ 2х о,..., Х п = '\Xn...1 = ,\П Хо ,...,
rAe ,\ "чуть больше 1", и строит затем описанную ступенчатую
фиrуру (рис. 56). Площадь этой ступенчатой фиrуры
S('\) = у(%о) . (Хl ха) + Y(X1) . (Х2 X1) + . . . =
143
у
уа
.
%0 %1 %2
%3
%4
Рис. 56
%5
%6 %
1 1 2
= 2("\%0 .... %0) + .,\2 2 (.,\ %0 .... "\%0) + .. . =
%0 %0
= (.,\.... 1) ( 1 + ! + +
%0 .,\2
)
"\ 1
%0
1
1
1 .... ....
.,\
.,\
=
%0
При .,\ .....-+ 1 Р83биение промежутка [%0, +(0) становится все мельче,
а площадь ступенчатой фиrуры все ближе к площади S подrрафика
1
ФУНКЦИИ у = '"'2. Поэтому Ферма заключает, что S = S("\) при
%
1
.,\ = 1, т.е. что S = = %0 . уа. CTpororo обоснования предельноrо
%0
перехода Ферма не дает.
УПDажнение 36. Исходя из определения ln х как площади подrра
1
фика rиперболы у = на отрезке от 1 до х и используя метод
%
Ферма, докажите, что lim "( % -: 1) = ln %.
n (X)
5.2.4 Ивтеrрапьвый MeTO Б. ПаСК8JIJI
Для интеrрирования синуса и косинуса, для нахождения площади по--
верхности шара и некоторых друrих тел вращения ПаСКaJIЬ применял
144
метод "харuтериствче CKorc
тpeyrOJlЬaвKa", ЦeJI Ioтopor...
восходит к двффереВЦИaJIlr
IIЬDI методам Архимеда (см.
п. 5.1). Рассмотрим в Ka
честве примера ВЫЧИCJIeние
" YКIIЫ синусов" (т.е. инт
rpaJIa от sin l{J dtp ПО пром
жутку от l{Jl до 11'2). Вооьмем
1f.YrY l{Jl < 11' < 11'2 единич"
v
ВОИ окрУ]J[JIОСТВ, разДeJIИМ ее
на 2п равных частей и опи..
шеll OKOJJO дуrи правИJlЬНУЮ
z DOllавую тн, как ЭТО пока..
А Q в заво на рис. 57. Пусть KL
Рис. 57 отрезок этой JЮма&ой, ОР
радиус, перпендиI)'UРвыi к КL, км и LM паРaJJJIeJIЬНЫ COOTвeT
ственно осям у и %, PQ пар Ц.Jrл ьна оси у. Если теперь считать
"характеристический TpeyrODLIIlII" KLM очень маленыим, то
11
о
Е PQ . KL = Е sin tp · KL Е sin l{J . tp .
с друrой стороны, в3 подоби- треyrо.пьииков OPQ и KLM следует,
что PQ . KL = ОР . ML, ., CJJeAOвaтeJlЬBO,
EPQ. KL = ЕОР. ML = EML = АВ = COS<,Dl C08<,D2.
Поэтому Esin<p. A = COS<Рl COS1p2.
Упражнение 37. ПOJlЬ3У.ась методом "характеристическоrо Tpey
rольника" ПасКaJIJI, вычвCJIIIТe поощадь поверхности шаровоrо СЛОJl.
5.2.5 MeTO K8c8TeDыIblx r. ramme. ж. РоберВ8JIJI
Исходным JlВЛJIeтcJI здесь ПРeюIOJIOЖевие, что направлено СКОРОСТИ
и касательной в каждой точке тpaerrop.. совпадают. rалилей поль--
З0валСJI этим преДПОJl)жевием ПР. построении IасаТeJlЬНОЙ к пара
боле. Рассматриваа параболу р как траекторию движенИJI тела, пада,..
ющеrо из точки О 8l1li3 ПОД действием cвJIы ТJlжести с ПОСТОJlННОЙ
rОРИЗ0НТanьной СКОРОСТЬЮ 11% (РИС. 58), rали.пей, рaзmжив веКТОР
145
1,
х
скорости тела v в точке (х, у) TpaeK
тории на rОРИЗ0НТальную V z и Bep
тикальную V, состаВЛJlющие и поль
зуясь УКа3анным ,предположением,
1 V
приходит к пропорции: Jt
ж V z
(/, подкасательная), откуда
ж . V y
1, =
V z
V z . t . gt 2
= gt
V z
Рис. 58
или 1, = 2у. Систематическое изло--
жение этоrо метода дал Роберваль. Общая схема метода имеет вид:
А) в декартовых координатах (рис. 59)
у
Iy
Iz V z 1, V y
= = ,
у V y ж V z
откуда:
V z
Iz = у .
V y
V,
1, = х .
V z
Рис. 59
Б) в полярных координатах (рис. 60)
1 sin <р
r 1 COS ер
откуда:
Vl
= ........
V2
1=
Vl . r
Vl . COS <р V2 . Sln <р
1
Рис. 60
Упражнение 38. Методом rалипея Роберваля определите подка
сательную спирали Архимеда.
146
5.2.6 MeTO RОрМ8Jlей и касательных Р. Декарта
d а
с z
Общая схема метода
такова. Для Toro, чтобы
провести нормаль или Ka
сатепьную к алrебраич
скоп кри ой У = Р( ж)
в точке (а, Ь), достаточно
построить окружность с
центром с на оси ж, Kaca
ющуюся данной кривой
этой точке (рис. 61). У}
"
внение этои ОКРУЖНОС
ИСКЛЮЧИВ У из систе х
у
у = Р(ж)
Ь
Рис. 61
имеет вид: (ж ....... с)2 + у2
уравнений
(а ....... с)2 + Ь2
{ У = Р(ж) ,
(ж ....... с)2 + у2 = (а ....... с)2 + ь2 ,
получим уравнение Q(ж) = О, а так как кривые касаются в точке
(а, Ь), то Q(ж) = (ж ....... а)2 R(ж) и величина с находится из этоrо
условия с ПОМОЩЬЮ метода неопределенных коэффициентов. А, зная
с, из подобия треуrольников леrко найти и d точку пересечения
касательной с ОСЬЮ ж. Так, в случае параболы у = ж 2 , имеем:
Q(ж) = ж 4 + ж 2 ....... 2сж....... а 2 ....... ь 2 -t 2ас = (ж ....... а)2(рж 2 + qж + т) ,
и приравняв коэффициенты при одинаковых степенях ж, получим си
стему уравнений
ж 4 1 = р ,
ж з О = 2ap + q ,
ж 2 1 = r 2aq + а 2 р,
ж 1 .......2с = .......2аТ + a 2 q ,
х о a2 Ь2 + 2ас = а 2 т, Ь = а 2 ,
откуда р = 1, q = 2а, r = 1 + 3а 2 , с = а + 2а З Далее, из пропорции
а ....... d Ь ь2 а
находим: d = а
Ь с....... а c a 2
Упражнение 39. Методом Декарта определите нормаль и Kaca
тельную к rиперболе жу = 1 в точке (а, ).
147
5.2.7 Метоя вкстремумов в касаТeJlЬВЫХ п. Ферма
Как отмечено в [2, с. 32], уже Диофант располаrал способом опреде.-
леНИJl уrловоrо коэффициента касательной к aJIrебраичеСI ОЙ КрИВОЙ.
Этот, чисто алrебраический, не требующий предельноrо перехода
способ получил свое Р83витие в методе экстремумов и касательных
Ферма, а в наСТОJlщее время широко используеТСJl в алrебраической
rеометрии.
Точки экстремума рациональной функции у = R(ж) Ферма нахо-
дИТ И3 условия
= о.
h=O
Например, точка экстремума ж = О ФУНКЦИИ у = х 2 находится И3
услов ИJl
R(ж + h) R(ж)
h
(ж + h)2 .... ж 2
h
= (2ж + h) = 2ж = О .
h=O h=O
у
N
к
Р
L
Рис. 62
z
Далее, понимая касательную как предельное положение секущей,
Ферма определяет подкасательную KL (рис. 62) из условия:
MN h
KL = PL = ML. = R(ж) = о.
h=O QN h=O R(ж + h) R(z) h=O
Позднее Ферма распространил свой метод на случай неявной ал
rебраической функции.
Упражнение 40. Полыэуясь методом Ферма, определите подкаса
1 ж
тельную к кривой у = 2 5 в точке (2, 1).
z
Упражнение 41. Укажите апrебраический (над полем без топо-
лоrии) способ определения производной алrебраической ФУНКЦИИ.
148
5.2.8 О св"ов межяу ввтеrрапьвымв в
яифферевцвапьвымв меТОЯ8МВ
Выше мы указали HeKOTop e, наиболее важные для Д8JIьнейшеrо
развития математики интеrральн е и дифференциальные методы
первой половины XVII в. СущеСТВУЮЩaJI между ними связь как
связь между задачами на квадратуры и з дачами на касательные
была обнаружена в механической и в rеометрической форме в pa
ботах э. Торичелли, п. Менrоли, Дж. I»еrори и и. Барроу. В Ka
честве примера приведем теорему Барроу, устанавливающую связь
между квадратурами подrрафиков одних кривых с построением Kaca
тельных к друrим кривым.
Даны две кривые у( ж ) и
С' В' А' z( z ), связанные условием
r у(х) · r = S(ж), rде S(z)
площадь подrрафика кри
вой z(ж) (рис. 63). T
rда подкасательнаи t Ka
сател,ЬНОЙ 1 к кривой у(ж)
в точке М(ж, у) определя
z r
ется из условия: = .....
у t
Доказательство проводит
ся в предположении, что
z(ж) возрастает. Пока3Ы
вается, что прямая 1, опре
z r
Рис. 63. Теорема Барроу деляемая условием = ....,
у t
будет касательной к кривой у(х) в точке М(х, у). Для этоrо пров
дятся прямые АС и А'С' параллельно оси ж. Условие касания прямой
· с кривой у( ж) в точке I равносильно TorAa тому, ЧТО точки В
и В' пересечения кривой у(х) с прямыми АС и А/С' лежат COOT
ветственно между А { С и между А' и С' ПослеД"f:е зыводится с
учетом свя:зи между кривыми у(х) и z(x) и с учетом возрастания
МС у z
z(x) следующим обра:зом: = = , откуда z БС = МС r Не
БС t r
IC r = S < z АС, поэтому z ВС < z АС и БС < АС. Точно Taf:
же МС' = у = :., откуда z В'С' = МС' . r. Но МС' . l' = 5' >- z А'С'
В'С' t r
поэтому z B,c / > z А'С' и В'С' > А'С'.
149
3аметим, что если положить r = 1, то теореме Барроу COOTBeT
ствует следующее утверждение:
z
если у(z) = J z(x) dx, ТО у'(х) = z(x).
о
5.3 СОЗДАНИЕ ОСНОВ
ДИФФЕРЕНЦИАльноrо И
ИНТЕrР Альноrо ИСЧИСЛЕНИЯ в
РАБОТАХ И. НЬЮТОНА И
u
r.B. ЛЕИБНИЦА
Ра.;звитие дифференциальных и интеrрапьных методов в' пер
вой половине XVII в. и установление связи между этими MeT<r
дами создало теоретические предпосылки для построения основ о&-
щеrо дифференциальноrо и интеrральноrо исчисления. с тем, чтобы
можно было решать по единому способу всё более часто выдвиrа
вшиеся практикой Ра3личные задачи на нахождение квадратур, кy
батур, касательных и экстремумов. Это было сделано И. Ньютоном
и r.B. Лейбницем, каждJ,IМ п<rсвоему, во второй половине XVII в.
Все вычисления приобретают у Ньютона и Лейбница вид неслож
Horo алrоритма. При этом связь между дифференцированием и ин
теrрированием приобретает простой и привычный теперь для нас
вид.
5.3.1 MeTO "фПЮIСВЙ" и степеиных p" OB
и. Ньютоиа
Ньютон создал ОСIIОВЫ cBoero дифференциальноrо и интеrраль
Horo исчисления в конце 60 начале 70 x rr. XVII в. Он исходил
при этом из механических представлений. Величину, меняющуюся
во времени, Ньютон На3ывает "флюентой" и обозначает ее че
рез %, у, Z, Скорость изменения "флюенты" Ньютон На3ывает
"флюксией" и обозначает ее через ж, У, i,
В теории "флюксий" решаются две rлавные задачи:
1) Дано соотношение между "флюентами", определить соотноше--
ние между "флюксиями".
150
Пример Соотношение между "флюентами" имеет вид у = х 2 ,
найти соотношение между "флюксиями" х и у. Соrласно Ньютону,
прибавив к у и ж их "моменты" хо и уо соответственно (здесь о
"момент" времени), и перейдя от равенства у = х 2 , К равенству
у+уо = (х+хо)2, выполнив формально возведение в квадрат и вычтя
из полученноrо равенства исходное равенство у = х 2 , получим: уо =
2ххо + 2:202. Ра:зделив. обе части равенства на о, и положив затем о
равным нулю, получим окончательно, что у = 2жх.
2) Дано соотношение между "флюксиями", требуется определить
соотношение между "флюентами"
С современной точки зрения это задача интеrрирования
дифференциальных уравнений, она rора:здо сложнее первой задачи.
Ньютон обнаружил, что уже уравнение Р(х, у)х + Q(x, у)у = о не
всеrда может быть проинтеrрировано в'явном виде. При интеrри
ровании таких уравнений Ньютон пользовался ра:зложением в сте--
'" Р . Q . О У Р
пеннои ряд: уравнение х + у = записывалось в ВИJ\е х = Q ,
1 · Р
затем полаrалось ж = , так что у = Q ' и у находился почлен
ным интеrрированием степенноrо ряда, полученноrо ра:зJЮжением
Р
функции Q .
Для разложения функций в степенные ряды Ньютон использовал
все Ре3ультаты своих предшественников и накопил большой арсенал
приемов, среди которых наиболее часто применялись:
а) индуктивное обобщение теоремы о степени бинома на случай
дробноrо и отрицательноrо показателя степени;
б) непосредственное деление ("столбиком") числителя дробн<r
рациональной функции на знаменатель;
в) метод неопределенных коэффициентов в ра.зличных модифика
циях. Например, дано уравнение у = 1 3х + у + х 2 + ху, ищем
у в виде у = х + Подставляя в правую часть, получим
у = 1 2x+..., откуда у = ж х2+.. Снова подставим у в ypa
з
. 1 2 2 2 Х
внение,ПОЛУЧИМУ х+х +...,OTKyдay x x +3+...
и т.д.;
r) замена переменных или замена системы координат;
д) обращение рядов;
151
е) суперпооиЦИJI p_ OB_
1
Так, фувкцив 1 pacIJla в РJIA путем непосредственноrо
+ж
ДeJJeНИJI "столБВIОк" ЧИCJlllтeml ва 3BalleHaтeJlЬ. Функцив ln( 1 + ж) =
J dz
1 + ж раскладываета Tor a в рц поч.певвЬПI ввтеrрированием
(Н. Меркатор, .1668 r.). Путем обращеВIIJI р_да AJIJlln(1 + ж) Ньютон
получил разложение в р_д ДВ8 поквзатeJlЬНОЙ ФУНКЦИИ. Ряд для
. 1
arCSID ж он получил ПОЧJIeввым ввтеrрироваввем р_да ДJlИ =
\1' 1 .... %2
(1 + t) i, rAe ( = .....ж 2 . Р-А ДВ8 sin у ов ПОПУ.,ВJI путем обращения
-
ряда дЛJI arCSln ж, ар _д дп cos у путем суперпооиции ряда для
z = sin у И pJlAa дп v' l ..... z2.
В заключение на првмере степеввой ФУlПции рассмотрим, как
устанавпиваетCJI У Ньютона СlUlЗь между ero интеrрированием
и АИфференцированием. Дано:
ФyвIЦИJI у = ж n _ 'IPебуется по--
К83ать, что площадь z подrра
cl8кa этой функции на ОТре3ке
ж n + 1
[О, ж] равна 1 ' и, наоборот,
"+
ж n + 1
eCJIВ z = 1 площадь под
"+
rpa48K& ФУНКЦИИ у на OTproKe
[О, ж], то у = ж П Для до--
K83aтeJlЬCT8a возьмем, соrласно
Ньютону, ж + о вместо ж. Тоrда
вместо z будем иметь z + ov, rAe
v некоторое значение ФУН
КЦИВ У на отрезке от ж до % + о
(рис. 64). Заменяя ov на оу и
хn+!
под ставив ж+о вместо %, а z+oy вместо % в соотношение z = n + l '
Ньютон получал
у
v
у
ж
ж+о
%
Рис. 64
(2: + о)n+l ..... %n+1 + (п + l)ж П . 0+ . . . + 0"+1
z+oy z+ov= п+l п+l
%n+l
OTK) a после вычитания ураввеНIIJI Z = п + l' деления всех слаrа.
емых на о и полаrанИJI о = О в с.педОвaJЮ, что у = Ж П . Поэтому,
152
ж"+1
rоворит Ньютон, и наоборот, еCJIИ 11 = ж", то z = l '
n+
Упо&жнение 42. С помощью метода фЛЮКСИЙ Ньютона по дан..
НОМУ соотношению между фЛIOeнтами у3 ...... жу + ж2 = О найти СООТ--
ношение между фЛЮКСИJlми.
5.3.2 "ИС..ИCJIeRие иффереRЦИаоов" r.B. Лейбница
Лейбниц пришел к созданию cBoero диффереНЦИaJIьноrо и интеrрaJIlr
Horo исчислеНИJl к 1675 r. В ero "исчислении дифференциалов" осно-
вными были ПОНJlТИJl дифференциала функции как ее актуально бе.-
сконечно большоrо числа бесконечно малых дифференциалов. Это
сразу устанаВJIИВало взаимно обратную CВJI3Ь между дифференци..
рованием и интеrрированием.
Лейбниц придаВaJI большое значение созданию удобной симво-
лики; введенные им еще в 1675 r., зн ки диффереНЦИaJIа d и инте--
rрала f оказались очень удачными.
у
dy
у
dy = lr dz
у
lz
%
Рис. 65
ПервонаЧз"'IЬН9 Лейбниц называл актуально бесконечно малое прира
щение величиJtы e рanностью (differenz), откуда и происходит знак
дифференциала, и определял дифференциал функции rеометричеСIИ
через подкасательную к ее rрафику (рис. 65). Однако вычислялся
дифференциал функции путем отбрасывания бесконе':но малых BЫC
ших ПОрЯДКОВ.
Пример Подкасательнa.g к параболе у = %2 (рис. 66) ищется, соrла
сно Лейбницу, следующи { обра:эом. 'I»еуrольник АВС, обрanован
153
ный касательной ВС, подкасательной АС и отрезком АВ, параллель
ным оси %, подобен "характеристическому треуrольнику" Паскаля
АС
(см. выше) С катетами dx и dy. Поэтому dy = АВ · dx. Но у = х 2 , и,
следовательно, у + dy = (х + dz)2 = %2 + 2х d% + (dz)2, откуда после
выЧИтания равенства у = х2 И отбрасывания (dz)2 получаем, что
АС
dy = 2х dz. Таким образом, АВ = 2% И АС = 2х ,. АВ = 2ж · z = 2у.
Удобство символики сп<r
собствовaJЮ быстрой раз
работке алrоритмов ди
ференциальноrо и интеr
ральноrо исчисления в pa
ботах caMoro Лейбница и
ero ближайших учеников
братьев Якоба и Иоrан
на Бернулли.
Упражнение 43. С п<r
мощью "исчисления ди
ференциалов" Лейбница
вывести формулу для ди
ференциала произведения.
у
dy
А
z
С
Рис. 66
5.3.3 MeTO "первых" и "ПОCJI них" отношений
и. Ньютона
Ньютон, пытаясь придать своему дифференциальному исчислению
лоrическую форму более строrую, чем в методе "флюксий" и CT
пенных рядов, развил в ряде работ 80 90 x rr. XVII в. так назы
ваемый метод "первых" и "последних" отношений. Соrласно этому
методу, основным являJЮСЬ теперь понятие производной, которая
определялась как "последнее" отношение исчезающеrо приращения
функции ( y) к исчезающему приращению aprYMeHTa (Llz) или как
"первое" отношение возникающеrо приращения функции к возника
ющему приращению aprYMeHTa.
Метод "первых" и "последних" отношений изложен Ньютоном
в ряде лемм из "Математических начал натуральной философии"
(1686 r.). Так, лемма 1 rласит: "Количества, а также отношения
количеств, которые в продолжение любоrо конечноrо времени п<r
154
стоянно стремятся к равенству, и ранее конца этоrо времени при
бли;зя.тся друr к друrу ближе, нежели на любую ;заданную разность,
будут напоследок равны" . Доказательство: "Если ты отрицаешь это,
то пусть они напоследок будут равны и их последняя разность будет
D, и, следовательно, они MorYT подойти к равенству ближе, чем до
этой ;заданной разности D, в противность предположению" Далее,
в леммах II V и следствиях и;з них устанавливается, что последнее
отношение площади вписа ной в подrрафик функции ступенчатой
фиrуры к площади описанной ступенчатой фиrуры, есть отношение
равенства, друrие аналоrичные утверждения относятся к площадям
ступенчатых фиrур и площадей подrрафиков. Затем в леммах VI VII
и их следствиях установлены подобные утверждения относительно
исче;зающих отре;зков дуrи, ее хорды и ее касательной и т.д. (под
робнее см., например, [33, кн. 2, с. 103]).
5.4 ПРОБЛЕМА ОБОСНОВАНИЯ
ДИФФЕРЕНЦИАльноrо
ИСЧИСЛЕНИJI. "АНАЛИСТ"
дж. БЕРКЛИ
Со;зданное в работах Ньютона и Лейбница дифференциальное ис
числение по своей лоrической форме ре;зко отличалось от Bcero, со--
;зданноrо в математике ранее. Если прежде все содержание MaTeMa
тики укладывалось в раМки формальной лоrики и притом так, что
математические теории служили обра.;зцом, эталоном лоrических по--
строений, то теперь уже сами со;здатели дифференциальноrо исчи
сления чувствовали ero несовершенство. Несмотря на то, что cooдaH
ное ими исчисление получило бурное развитие и выдержало самую
серье;зную проверку в приложениях, оно еще никак не соrласовыва
лось с общепринятыми ;законами лоrики, со всей предыдущей праж-
ТИICОЙ мате атическоrо мышпеии... Причем, если в конце XVII
начале XVIII в. проблема обоснования дифференц альноrо исчисле
ния, т.е. вопрос об ero имманентной (внутренне присущей) лоrи
ческой форме, сдерживалась авторитетом ero со;здателей, то после
смерти Ньютона (1727 r.) этот интерес все более во;зрастает.
Особенно привлекла внимание матемаТИJ(ОВ XVIII в. к проблеме
обоснования дифференциальноrо исчисления вышедшая в 1734 r. pa
бота крупнейшеrо анrлийскоrо субъективноrо идеалиста Дж. Беркли
155
"АНaJIИСТ или рассуждение, адресованное неверующему математику,
rде исследуеТСJl, JlВJlJlетCJI ли предмет, принципы и заключения COBp
MeHHoro аНaJIиза более отчетливо поонаваемыми и с очевидностью
выводимыми, чем релиrиооные таинства и AorMaTbl веры" OCTaH
ВИМСJl подробнее на основных положениях этой работы.
Обращаясь к вопросу о введенных Ньютоном "фЛЮКСИJlХ" и
"моментах", Беркли рассуждает следующим оБРа30М: "Однако, П<r
добно тому, как наши чувства наПРJlrаЮТСJl и становятся в затру
днительное положение при ВОСПРИJlТИИ крайне малых объектов, B<r
ображение напряrаеТСJl еще в большей степени и попадает в
еще более затруднительное положение, пытаясь выработать четкое
представление о 'мельчайших частицах времени или о мельчайших
приращениях, обраоованных за эти мельчайшие промежутки Bp
мени; и в rораодо большей степени ему приходится трудно, KorAa
оно пытается постичь "моменты" или приращения "флюент", Hax<r
дящиеСJl в момент вооникновеНИJl, в самом наЧ8J]е их обраооваНИJl
или начале существования, прежде чем те стаНОВJlТСЯ конечными
частицами. Вероятно, еще более трудно представить себе абстра
rированные скорости подобных зарождающихся несовершенных B
личин ... Однако, если.Я не ошибаюсь, скорости скоростей, вторые,
третьи, четвертые, пятые и т.д. скорости вообще находятся за пр
делами Bcero человеческоrо понимания. Чем больше ум анализирует
и раовивает эти неуловимые идеи, тем более он теряет и заходит
в тупик; предметы, вначале мелькающие, крошечные вскоре вообще
исчезают из поля зрения. В каком бы смысле не употреблять слова,
вторая или третья флюксия безусловно представляется тайной, П
крытой мраком. Начальная скорость начальной скорости, зарождаю--
щееся приращение зарождающеrося приращения рассмотрите
это в какоМ уrодно свете И, если я не ошибаl9СЬ, вы обнаружите, что
составить об ЗТО f ясное понятие невозможно [3, с. 399 400]
Аналоrичным оБРа30\1 рассуждает Беркли и относительно вве.-
денных Лейбнице f "диф<реренциалов": "Некоторые полаl"\ают что
зарубежные мате fатики применяют иной метод, может 6ы1.ь, Me
нее точный и строrИIVr, НО ;зато более панятный. Вместо флюент и их
флюксий они рас маТрИRаю'1' переменные конечные величины, кото--
".,.
рые увеЛИЧИdаются или уменьшаIпТСЯ путем ПОСТОЯИНОI'О приоавле
пия или вычитания бесконечно малых величин Вместо CKOp()CTei1,
с помощью которых обра3УЮТСЯ Прёiращения. они раССl\fатриваlОТ
сами приращения или уменьшении, которые оир на.зывают диффе
156
ренциалами и которые считаютCJI бесконечно малыми. Дифференци"
алом линии JlВЛJlется бесконечно малаи ЛИНИJl, дифференциалом пло--
СКОСТИ бесконечно малаи плоскость. Они полаrают, что конечные
величины СОСТОJlТ из бесконечно малых частей и .что кривые пред..
ставляют собой мноrоуrольники с бесконечно малыми сторонами, а
уrлы, которые они составляют по отношению друr к друrу, onpeд
ляют кривизну линий. Признаюсь, мои способности не позволяют
мне представить себе величину бесконечно малую, т.е. бесконечно
меньшую, чем любая реальная или воображаемая величина. Но я по--
дозреваю, что ДЛJl абсолютно всякоrо человека быJlO бы бесконечно
трудно представить себе часть такой бесконечно малой величины,
которая будет все же бесконечно меньше ее "[3, с. 399 400].
Проводя подобные рассуждеНИJl, Беркли преследовал при этом
прежде Bcero не научные, а определенные политические цели aHr
лийскоrо духовенства, крупным представителем KOToporo он яв"
лялся. Тем не менее, хотел он Toro или нет, IJриведенные выше
рассуждения убедительно докзnывают лишь то, что "моменты" и
"дифференциалы" первых, а тем более высших порядков суть по-
в..ти.., причем ПОНЯТИJl очень далекие не только от обычных пред..
ставлений, но даже и от обычных ПОНJlТИЙ (например, таких, ко--
торые использовaЗiись в математике ранее), понятия, единственной
формой представления которых ОК83ались символы Х, ХО, Ж, ..., dж,
dy, d 2 x, d 2 y, И их исчисление. Отметим еще, что являясь идеа..
листом, Беркли вообще оставляет в стороне вопрос о тех реальных
процессах, опосредствованным выражением которых являются эти
символы и их исчисление.
Рассуждая о JlоrИlCе дифференциальноrо исчисления, Беркли опи..
рается на следующую лемму: "Если для доказательства какоrо--либо
предложения выдвиrается определенное положение, блаrодаря кото--
рому ДОК83ываются некоторые друrие положения, и если такое вы..
двинутое положение впоследствии само будет onpOBeprHYTO или от..
BeprHYTo противоположным предположением, то в этом случае все
друrие положения, ДОК83анные при ero помощи я в.ытекающие из
Hero, должны быть также опроверrнуты и OTBeprHYTbl, с тем, чтобы
в дальнейшем они не выдвиrались и в дока.;зательстве не примен.я..
лись" . Это настолыо очевидно, утверждает Беркли, что не нужда..
ется в дока.;зательстве. Приведенная "очевидная" лемма используется
Беркли для опровержения способа, КОТОРЫЙ использует Ньютон для
вывода "фЛЮКСИИ" степени. Напомним (подробнее см. выше), что,
157
например, "флюксия" степени у = z2 выводится Ньютоном следу
щим образом:
у + оу = z2 + 2zz . о + z2 . 02, оу = 2жz · о + z2 . 02
откуда после деления на о и полаrания затем приращения о равным
нулю, получается iI = 2xz. "Но нам представляется, что такой ход
рассуждений не будет справедливым или убедительным. Ибо коrда
rоворят: пусть приращения исчезают, т.е. пусть приращения равны
нулю или пусть не будет никаких приращений, то тем самым преж
нее допущение, что приращения представляют собой некоторую ве.-
личину, или что приращения имеют место, отверrается, однако след
ствие этоrо допущения, т.е. выражение (у = 2жz), полученное бла
rодаря ему, сохраняется. А это, в соответствии с вышеуказанной
леммой, представляет собой ложный ход рассуждений" [3, с. 405
406] .
Таким образом, из рассмотрения метода Ньютона Беркли делает
вывод, что этот метод основан на неправильной лоrике, так как не
соответствует лемме, абсолютная справедливость которой не вызы
вает у Беркли сомнений. Возражая Беркли, мы моrли бы сказать,
что метод Ньютона (как и любой друrой метод конструктивноrо
дифференциальноrо исчисления) действительно не соrлас,уется с за
конами обычной, т.е. формальной лоrики. "Вся трудность в пони
мании дифференциальной операции (как и в понимании отрицания
отрицания вообще), rоворит К. Маркс, заключается именно в
том, чтобы увидеть, чем она отличается от такой простой проц
дуры (как, например, полаrание о сначала не равным нулю, а затем
равным нулю. С. М.) и как ведет поэтому к действительным
Ре3ультатам" [23, с. 29]. В частности, он не соrласуется с закcr
ном тождества формальной лоrики, на к{)тором основана приводимая
Беркли лемма. Как -выражение процесса движения метод "флюксий"
Ньютона (как и любой друrой метод конструктивноrо дифференци
альноrо исчисления) подчиняется законам не формальной, а диалек
.тической лоrики.
Возражения Беркли по поводу метода "первых" и "последних"
отношений Ньютона сводятся к следующему: не существует посл
днеrо отношения исчезающих количеств, так как отношение до .ис
чезновения не есть последнее, а после исчезновения количеств нет
уже их отношения. Подобные возражения высказывались еще при
Ньютоне. Сам Ньютон, отвечая своим противникам, rоворил сл
158
дующее: "Но при таком и столь же натянутом рассуждении OKa
жется, что у тела, достиrающеrо какоr<rлибо места, rде движение
прекращается, нет последней скорости, ибо та скорость, которую
тело имело ранее, нежели оно достиrло места, не есть последняя, а
коrда тело достиrло места, то нет никакой скорости. Ответ простой:
под последней скоростью я разумею ту, с которой тело движется не
перед тем, как достиrнуть последнеrо места, и движение прекраща
ется, и не после Toro, а коrда достиrает, т.е. именно ту скорость,
которой тело достиrает последнеrо места и с которой движение
iрекращается. Подобно этому,. под последним отношением исчеза
зщих количеств должно пониматьс.я отношение количеств не перед
reM, как они исчезают, и не после Toro, но то отношение, с которым
они исчезают. Точно так же и первое отношение зарождающихся
количеств есть отношение, с которым они зарождаются
Можно также возразить, что если существуют последние ОТНО-
шения исчезающих количеств, то существуют и последние величины
их самих, и, следовательно, всякое количество должно состоять из
неделимых, вопреки доказанному Евклидом отноеительно несо-
измеримых величин. Однако это возражение основано на неверном
допущении. Последние отношения, с которыми исчезают количества,
не суть на деле отношения последних количеств, а те предел , к кото-
рым постоянно приближаются отнощения безrранично убывающих
количеств и к которым они MorYT подойти ближе, нежели на любую
наперед заданную разность, но которых не MorYT ни превзойти, ни
до тиrнуть ранее, ум количества уменьшатся бесконечно "[33,
кн. 2, с. 104 105].
К СКа3анному Ньютоном мы можем добавить простую физич
скую интерпретацию последнеrо отношения исчезающих величин.
Такие физические характеристики, как масса или собственное со-
противление электролитов и rазов определяются и опытным путем
и теоретически именно как последнее отношение соответствующих
исчезающих величин. Например, масса определяется как отношение
силы, приложенцой к телу, к вызванному этой силой ускорению. Но
так как действующая на тело сила, как бы мала она ни была, при
водит это тело в движение и, следовательно, изменяет ero массу,
то масса есть не просто отношение силы к ускорению, а именно
"последнее" отношение силы к ускорению, или отношеhие, с КОТО-
рым сила и ускорение исчезают (на практике это означает, что сила
и ускорение достаточно малы). Точно так же такая "внутренняя" xa
159
рактеристика r830B и электролитов, как СО,бственное сопротивление
есть "последнее" отношение ИСЧе3ающеrо приложенноrо сопротивле--
нИJI к ИСЧе3ающему ПРОХОДJlщему току.
Можно добавить сюда также рассмотрение поВJIТИJI о произв
дной В рамках катеrории "отношение", проведенвое немецким фил
софом r. rereпeM [7, т. 5, с. 277 310].
Рассмотрим, наконец, B
зраженИJI Беркли по поводу
"исчисления дифференциа
лов" Лейбница. Беркли rOB
рит, что рroультаты здесь
получаются правильными
v
потому, что каждыи раз есть
две ошибки, в точности K
Ж мпенсирующие Apyr Apyra.
Например, при выводе дли
вы подкасательной 111 функ
ции У = ж 2 по методу Лей
бница (рис. 67) из подоБИJl
треуrольников заключают:
111 dy dy 2жdж 2
, откуда 111 = ж = ж = 2ж = 2у .
ж dж dж dz
Но здесь, соrласно Беркли, допущено две ошибки:
1) ВЗJlТО dж вместо dж + z,
2) ВЗJlТО dy = 2ж dz вместо dy = 2ж dz + (dz)2.
Так что на самом деле следовало бы написать:
1 2жdж+(dж)2
у = ж dж + z '
а правильный рroультат 111 = 2у получаеТСJl лишь потому, что пер.-
вая ошибка в точности компенсирует вторую.
Упражнение 44. Проведите вывод длины подкасательной 111 rи
перболы жу = 1 по методу Лейбница. Укажите две ошибки, в точн
сти компенсирующие Apyr Apyra.
у
dz z
111
z
у
Рис. 67
Идея Беркли о компенсации ошибок как основе дифференци
альноrо исчисления была развита Л. Карно в работе [17]. Ha
РJlДУ с обычными, "означенными" величинами Карно вводит всп
моrательные, "неозначенные" величины, которые, в соответствии
160
с условиями задачи, "нечувствительными ётепенями" приближа
ются к означенным, т.е. отличаются от последних бесконечно мало.
Далее вводится понятие "несовершенноrо уравневИJI", которое on
ределяется как приближенное уравнение, точное в пределе или Ta
кое, что отношение обе.-
их частей ero имеет ,npeдe
лом единицу, или как ypa
внение, поrрешность KOT<r
poro бесконечно мала. Ме.-
тод Карно сводится к T<r
му, чтобы, начиная с точ
Horo, "совершенноrо" ypa
внения переходить от не.-
ж ro по определенным npa
вилам к неточным, "Hec<r
ершенным" уравнениям с
тем, чтобы через цепочку
"несовершенных" уравне.-
ний прийти, наконец, CH<r
ва к точному, "совершен
ному" уравнению, которое
и будет точным решением задачи. Например, соrласно методу
Карно, подкасательная 'z к ОКРУЖНОСТИ У = '2аж ж 2 (рис. 68)
находится следующим обра.;зом. Сначала из подобия треуrольников
lz dж
имеем точное уравнение d . Отбрасывая z, переходим к
у y+z
"несовершенному" уравнению: 'z = dx . Но
у dy
(у + dy)2 = 2а(ж + dz) (ж + dz)2 ,
2ydy-+ (dy)2 = 2аdж 2жdж (dж)2
у
Рис. 68
откуда
dж 2у + dy
dy 2а 2ж+dж
Переходим теперь от этоrо "совершенноrо" уравнения к "HeCOBep
шенному" путем отбрасывания dy и dж в правой части, имеем:
dz у у2
так что lz =
dy а z а z
161
Упражнение 45. Пользуясь методом Карно, пока.;зать, что "по--
верхность шаровоrо пояса равна поверхности соответствующей ча
сти описанноrо около шара цилиндра" [17, с. 105]
{)ам,еча'Нuе Метод Карно можно рассматривать как попытку
придать "исчислению дифференциалов" Лейбница характер фор
fальноrо алrОрИТ fа. Друrllе такие попытки стали предприниматься
после Toro, как д. Веронезе (1881 r.), Т. Леви Чивита (1892 1893 rr.)
иД. f'ильберт (1898 r.) в своих rеометрических исследованиях ввели
так на.;зываемый rиперJCОВТИНУУМ как такое расширение дО R*
обычноrо континуума R вещественных чисел, что
00
'18. Е R . · +
... ж = ж L..J жпе п ,
"=1
rде Х, ж п Е R, а е п актуально бесконечно малые BoopaCTa
щих порядков. Число ж стали в дальнейшем на.;зывать стаи артвой
00
частью числа ж., Е жпе п вестаи артвой частью числа ж., а
"=1
основанное на расширении R дО R. дифференциальное и интеrраль
ное исчисление веставАартвым 8И81IИООМ. Классический He
стандартный анализ был создан в 60 x rr. нашеrо века в работах
А. Робинсона и ero последователей [32; 10, с. 5 21; 18; 13; 19, т. 1,
с. 421 422]. Однако "весьма долrо нестацдартный анализ paCCMa
тривали как довольно тонкую и даже экзотическую лоrическую Te
хнику, предна.;значенную для обоснования метода актуальных бес
конечно больших и бесконечно малых чисел. Считалось также, что
эта техника имеет оrраниченную сферу применимости и в любом
случае принципиально не может привести к серьезному пересмо--
тру общематематических представлений. В конце 70 x rr. после опу
бликования теории внутренних множеств Э. Нельсона (и несколько
позже теорий внешних мцожеств К. Хрбачека и Т. Каваи) взrляды
на место и роль нестандартноrо анализа коренным обра.;зом обоrа
тились и видоизменились. В свете новых открытий нестандартные
элементы стало возможно рассматривать не как "мнимые, rлухие,
идеальные сущности", добавляемые к обычным множествам из со--
ображений формальноrо удобства, а как неотъемлемые части любых
привычных математических объектов. Возникла установка, состоя
щая в том, что каждое множество оБРа30вано стандартными и H
стандарными элементами. В свою очередь, стандартные множества
обра.;зуют своеобра3НУЮ реперную сетку, плотно расположенную в
162
совокупности всех предметов изучения математики. При этом o
наружилось, что фиrурирующие в нестандартном математическом
анализе объекты монады фильтров, стандартные части чисел и
векторов, тени операторов и т.п. составляют канторовские MH
жества, не попадающие ни на одну из канонизированных картин,
рисуемых известными формальными теориями множеств Таким
образом, традиционные взrляды на нестандартный анализ стали HY
ждаться, по меньшей мере, в ревизии, потребовали переосмысления
инфинитезимальных концепций" [22, с. 7].
Можно сказать, что развитие дифференциальноrо и интеrраль
Horo исчисления как исчисления бесконечно малых от механическо
метода Архимеда и метода "неделимых" к методу "флюкси.й" и c
пенных рядов Ньютона, "исчисление дифференциалов" Лейбницс.
методу Карно и от последних к нестандартному анализу вполне п( ..
тверждают известные слова Н.Н. Лузина: "Математический анал iЗ
вовсе не есть совершенно законченная наука, как иноrда скл( нны
себе ero представлять, с раз навсеrда найденными принципам,d, из
которых только остается извлекать дальнейшие следствия Мате.-
матический анализ ничем не отличается от всякой друrой науки и
имеет свой ход идей, движущийся не только поступательно, но и KPy
rообразно, с возвращением к rруппе прежних идей, правда всеrда в
новом освещении" [22, с. 8 9].
5.5 КРАТКАЯ ХАРАКТЕРИСТИКА
ДИФФЕРЕНЦИАльноrо И
ИНТЕrр Альноrо ИСЧИСЛЕНИЯ в
XVIII В.
Созданные Ньютоном и Лейбницем основы дифференциальноrо и
интеrральноrо исчис ния получили в XVIII в. широкое развитие.
Была открыта формула Тейлора, широко использовались степенные
ряды.. Характерно, что в течение длительноrо времени дифферен"
циальное исчисление сохраняло тесную связь с исчислением конеч..
ных разностей. Эта связь была обусловлена большим значением K
нечных разностей для интерполирования, приближенноrо дифферен"
цирования и интеrрирования функций, а также для приближенноrо
решения дифференциальных уравнений. В качестве примера такой
связи рассмотрим вывод Б. Тейлором формулы для разложения фун"
163
"
кции В степенной ряд. В 1711 r. Ньютон вывел интерполяционную
формулу
п(п..... 1)
f(a + n Llx) = /(а) + п. Llf(a) + 1 2 Ll 2 /(a)+
п(п 1)(п 2) З f( )
+ 12.3 а+
+ nf(a),
rде
f(o)
2 f(o)
n f(a)
1(0 + ж) ..... f(o),
f(o + ж) ..... f(o) ,
n l f(a + x) .... n 1 f(o)
последовательные конечные раоности функции f(x) в точке о. rод
спустя, Б. Тейлор распространил эту формулу на случай бесконечно
большоrо числа слаrаемых, полаrая ж О, но п. ж = h конечно.
Тоrда
I( h ) = '( ) /(o). h 2 I(a) h(h ж)
а + а + ж + x2 1 2 +
f(o) h(h x)(h 2 · ж)
+ жз 1 2. 3 +
При x О Тейлор и получил, что
dl d 2 1 h 2 dЗI h З
I(a + h) = I(a) + dж (о) h + dж 2 (о) 2! + dж З (о) 3т +
Параллельно с раовитием дифференциальноrо исчисления фун
кций одноrо переменноrо происходит и раовитие дифференциаль
Horo исчисления функций нескольких переменных. Так, теорема о
равенстве смешанных производных была известна еще в начале века.
Затем Эйлер дал ей cTporoe докаоательство и распространил эту Te
орему на производные высших порядков. Эйлер же покаоал, что для
Toro, чтобы выражение Рdж + Qdy было полным дифференциалом,
aQ дР
необходимо, чтобы выполнялось дх = ду ' и распространил этот
результат на случай трех переменных.. Эйлер же раоработал и ВО--
прос об экстремуме функций двух переменных, а Лаrранж в конце
XVIII В. дополнил исследование Эйлера своим методом нахождения
164
условноrо экстремума. Были установлены все основные виды инте--
rралов, берущихся в элементарных функциях, введены первые спе
циальные функции (B и r ункции Эйлера, li ж, первые эплиптиче
ские функции). Были созданы элементы теории обыкновеннЫХ диф.-
ференциальных уравнений: проинтеrрированы в элементарныХ фун
кциях уравнения с разделяющимися переменными, линейные ypaBHe
ния первоrо ПОрЯДКа, однородные уравнения, линейные уравнения и
системы линейных уравнений с постоянными коэффициентами, ypa
внение Клеро., уравнение Бернулли и т.п., созданы элементы теории
линейных дифференциальных уравнений BToporo порядка, введены
понятия общеrо, частноrо и особоrо решений. Проинтеrрированы
уравнение колебания струны и = a2и 2' параметрическое ypaBHe
az az az
ние дх = /(х, у), уравнение Пфаффа Р дх + Q ду = R и некоторые
друrие простейшие дифференциальные уравнения с частными пр<r
изводными. Содержание диффереНЦИaJIьноrо и интеrральноrо исчи
сления XVIII в. отражено в моноrрафИJlХ Эйлера "Введение в анализ
бесконечно малых" (в 2 x т., 1748 r.), "Дифференциальное исчисле--
ние" (в 3 x т., 1755 r.) и "Интеrральное исчисление" (в 3 x Т., 1767
1770 rr.).
Дифференциальное исчисление в XVIII в. развивалось, rлавным
образом, в форме лейбницева "исчисления дифференциалов", отли
чавшеrося удобством алrоритма. Однако основным понитием были
v dy
не сами леибницевы дифференциалы dz и dy, а их отношение dz '
которое понималось не как отношение двух актуально бесконечно
малых величин, но, соrласно Ньютону, как последнее отношение ис
чезающих величин.
Пытаясь дать ЭТОМУ последнему отношению конструктивное
определение, ж. Даламбер развил так на:зываемое рациональное
дифференциальное исчисление. Соrлас;но Даламберу (1744 r.), про
dy
изводную dx как последн отношение исчезающих величин, следует
определять по правилу:
dy у( х + '\x) у( х )
dx = Llx
x=o
(C f. п. 5.2.7). Здесь x приращение aprYMeHTa вначале берется
как произвольное конечное ЧIIСЛО, а затем оно полаrается равным
165
нулю. Например, для функции у = х 2 имеем:
dy (ж+ ж)2 ж2
dx x
= (2ж + ж) = 2х
Z=O Z=O
Видно, однако, что предложенный Даламбером способ определения
ПрОll3ВОДНОЙ rОДIIТСЯ, вообще rоворя, лишь для Toro случая, коrда
функция у(х) является рациональной относительно ж. Попытки pac
пространить конструктивное определение Даламбера на случай пр
извольной функции у( х) путем разложения раоности у( ж + ж) у( х)
в ряд по степеням ж были предприняты Дж. Ланденом (1758 r.,
1769 r.), ж. Кондорсе (1778 1781 rr.), л. Арбоrастом (1789 r.),
ж. Лаrранжем (1799 r.). Так, основная идея Лаrранжа состояла
в том, что при раоложении у(х + ж) в ряд Тейлора
( ж)2
у(ж) + у'(ж) . ж + у"(ж) 2! +
функции у'(ж), у"(ж), ... последовательно получаются одна из друrой
по одному и тому же правилу: каждая из них есть коэффициент при
первой степени в рааложении по степеням ж предыдущей функции.
Поэтому все эти функции MorYT быть "произведены" из начальной
("первообраоной") функции у(ж) с помощью операции Ра3ложения в
степенной ряд, операции, которую Лаrранж считал чисто алrебра
ической. Нахождение производных сводится, таким образом, к Ha
хождению первых коэффициентов ряда. Так, ряд для показательной
функции у = a Z и, следовательно, ее производные находятся, соrла
сно Лаrранжу, следующим обраоом:
у(ж + ж) = aZ+ z = аХ . a z
a Ar = [1 + (а 1)]Ar = 1 + x. (а 1) + x. ( X 1) (а 1)2 +
1 2
( а 1 ) 2 ( а 1 ) 3
= 1 + А ж + rде А = (а 1) +
2 3
и, следовательно, у'(ж) = А а Ж' Повторением этой операции Hax
дятся у"(ж) = А.Аа Х = A2.a Z , у'''(ж) = A.A 2 a z = А 3 а%' и т.д. Подро
нее см., например, [15, т. 3, с. 282 291; 30, с. 213 216; 5, с. 156 157;
33, кн. 2, с. 160 170]. "Алrебраическое" дифференциальное исчисл
'ине Лаrранжа не получило, однако, CBoero развития в XIX в., так как
166
в нем заранее предполаrалось существование ра.;зложения функции
v
В степеннои ряд.
В интеrральном исчислении XVIII в. основным было понятие H
определенноrо интеrрала или первообра.;зной (примитивной) фун
кции, а именно: F(ж) = f f(ж) dж dF(ж) = f(x) dж. При этом
определенный интеrрал понимался как ра.;зность значений первоо
ра.;зной функции:
ь
/ f(x) dx def (/ f(x) dx) са
ь
= F(b) Р(а).
а
u
5.6 ПЕРЕСТРОИКА ОСНОВ,
МАТЕМАТИЧЕСКОI'О АНАЛИЗА В
XIX ВЕКЕ
к XIX в. в математическом анализе накопились проблемы, при
ведшие к необходимости заново построить ero основные определ
ния. Лейбницево "исчисление дифференциалов" и ньютонов "метод
флюксий и степенных рядов" исчерпали себя. Их уже не хватало для
решения задач, приводящих к интеrралам, неберущимся в элемен
тарных и простейших трансцендентных функциях; для таких инт
rралов уже Эйлер часто применял приближенные методы вычисл
ний, основанные на ра.;збиении отрезка интеrрирования на ДOCTa
точно мелкие части и на построении соответствующих интеrраль
\
ных сумм.
Формула Ньютона Лейбница выражала естественное дЛЯ XVII
XVIII вв. представление, что интеrрал J: f(ж) dж, равный J: dF(ж), и
понимаемый как бесконечно большая сумма бесконечно малых при
ращений функции F(ж), есть полное приращение Р(Ь) Р(а) этой
функции. Но уже в 1768 r. Даламбер обнаруживает, что применение
этой основной в интеrральном исчислении формулы приводит ин
rда к странным и неверным результатам. Так, в случае интеrрала
ь 1
Ja '2 dж ока.;зывается, что сумма заведомо положительных слаrа
ж
мых будет отрицательной, если а < о, Ь > о.
А определение производной как "последнеrо отношения" ИСЧе3а
ющих величин вообще не .работало: оно было больше истолкованием,
чем основанием для дедуктивных заключений.
167
Лишь виртуозное обращение с расходящимися рядами позволяло
Эйлеру получать правильные Ре3ультаты в некоторых задачах, для
решения которых привлекались бесконечные степенные ряды. Так
путем замены переменной z = у = у + у2 + уЗ + Эйлер пр
l y
обра:зовывал ряд сIж + С2ж2 + сзх3 + к виду c y + c y2 + c y3 +
rде у = z . 10ЖНО пока:зать, что преобраЗ0ванный ряд 1Il\leeT
1+х
более широкую область сходимости, чем исходный. Эйлер же пред
ложил под суммой ряда понимать значение функции, из разложерия
которой данный ра3 возни ает. Так, ряд 1 + z + х2 + возникает
ИЗ разложения ФУНКЦИИ 1 ,поэтому, соrласно Эйлеру,
l ж
1+2+4+8+
1 1
1 ( I)= 2 ,a
1
1 2 = 1.
1 1+1 1+
Наконец, испальзовавшееся в математическом анализе и ero при
ложениях свойство непрерывности, как свойство функции прини
мать все свои промежуточные значения, уже не Ка3aJIOсь таким оче
видным для быстро расширявшеrося объема используемых функций;
оно НУЖДaJIОСЬ поэтому В таком определении непрерывности, кото--
рое позволило бы ее проверить.
Thубокая перестройка основ математическоrо анализа началась
в первые десятилетия XIX в. в работах Б. Больцано, о.; Коши и
некоторых друrих математиков (К. raycc, Н.Х. Абель) и получила
относительное завершение в работах К. Вейерштрасса в 60 70 e rr.
XIX в.
"При самом обыкновенном способе ДОКа3ательства, писал уже
в 1817 r. Больцано о ДОКа3ательстве теоремы о свойстве функции
принимать все свои промежуточные значения, опираются на ис
тину, позаимствованную И3 rеометрии: именно, что всякая непре
рывная линия простой КРИВИ3НЫ, чьи ординаты сначала положи
тельны, а потом отрицательны (или наоборот), неизбежно должна
пересекать ось абсцисс в какой либо точке, лежащей между этими
ординатами. Против верности, а также против очевидности этой
rеометрической теоремы возражать нечеrо. Но столь же очевидно
также, что нетерпимым нарушение хорошеrо метода является, ко--
rда истины чистой (или общей) математики (т.е. арифметики, aJI
168
rебры или анализа) желают вывести из соображений, которые при
надлежат только прикладной (или специальной) ее части, а именно
rеометрии Ведь в самом деле, если учесть, что доказательства
в науке вовсе не должны быть лишь удостоверениями, а наоборот,
обоснованиями, т.е. изложениями Toro объективноrо основания, ко-
торое If {еет ДОК83ываема.я истина, то станет ясl{ым само собой, что
ПОДЛIIННО научным доказательством или объективным основанием
истины, которая верна для всех величин, бroразлично, находятся ли
они в пространстве или нет, никак не может быть истина, которая
верна только для величин, находящихся в пространстве Ибо хотя
rеометрическая истина, на которую здесь ссылаются , в BЫC
шей степени очевидна, а значит, не нуждаеТСJl в удостоверении, она
тем не менее нуждается в обосновании И вот если кт<rлибо по-
думает об объективном основании Toro, почему линия при только
что отмеченных обстоятельствах пересекает свою ось абсцисс, то
он, наверное, вскоре заметит, что это основание состоит ни в чем
ином, как только в той общей истине, что каждая непрерывная фун
кция х, которая становится положительной для одноrо значения х,
но отрицательной для друrоrо значения х, должна стать нулем ДJIЯ
какоr<rнибудь значения ж, лежащеrо между ними. А это как р83 та
истина, которая должна быть здесь ДОКа3ана
Не менее неприемлемо док 83ательство, которое некоторые стро-
ят на понятии непрерывности функции, примешивая сюда поня
тия движения и времени. "Если, rоворят они, две функции
f(x) и <р(х) изменяются, соrласно закону непрерывности, и если для
х = а, /(0') < <р(0'), но для Z = {3, /(Р) > <р(0'), ТО должно существо--
вать какое нибудь значение и, лежащее между Q и Р, дЛЯ KOToporo
f(u) = <р(и). Если представим, что переменная величина z при
нимает в обеих з;tих функциях постепенно все значения, лежащие
между Q и (3, причем в то же MrHOBeHlJe она принимает и тут и там
то же значение, то в начале этоrо непрерывноrо изменения знач
ния х имеет место /(х) < <р(х), между тем как в конце /(ж) > <р(х).
Но так как обе функции ,блаrодаря своей непрерывности, должны
пройти сначала через все средние значения, прежде чем прийти х
высшему значению, то должен существовать какой то средний M
мент, KorAa обе были Apyr Apyry равны" Это делают еще наrлядным
с помощью примера движения двух тел, из которых одно было CHa
чала позади друrоrо, а под конец опередило ero и, следовательно,
обязательно должно было коrда то пройти мимо Hero.
169
Никто, п<rвидимому, не станет отрицать, что понятие времени,
а тем более движения столь же чужеродно в общей математике, как
и понятие пространства. Тем не менее, если бы эти два понятия
были здесь привлечены только ради объяснен'ия, то мы ничеrо не
имели бы против этоrо. Ибо и мы вовсе не преданы столь преувели
ченному пуризму, который, чтобы сохранить науку чистой от Bcero
чужеродноrо, требует, чтобы в ее изложении не вводили даже BЫ
ражения, позаимствованноrо из чужой области и употребляемоrо
хотя бы лишь в несобственном значении и для Toro, чтобы вещь
объяснить короче и яснее, чем это возможно сделать описанием, c<r
ставленным из одних специальных терминов, или же только, чтобы
избежать неблаrозвучности постоянноrо повторения тех же слов,
или чтобы одним только названием, которое дают вещи, напомнить
о примере, который может послужить для Toro, чтобы подтвердить
утверждение. Отсюда можно сра3У усмотреть, что мы также ни
как не считаем примеры и приложения чем либо таким, что HaH<r
сит ущерб совершенству научноrо изложения. Лишь одноrо требуем
мы, однако, cTporo: чтобы никоrда не выдвиrали примеры вместо
доказательства и чтобы никоrда не основывали существо caMoro за
ключения на выражениях, употребленных только внесобственном
смысле, и на побочных представлениях, которые они вызывают, так
что ;заключение отпадает, как только меняют эти выражения" [33,
кн. 2, с. 172 174].
В качестве основы для ДОКа3ательства свойства непрерывной
функции принимать все свои промежуточные ;значения Больцано
предлаrает следующее определение непрерывности: "... под Bыpa
жением, что функция f(ж) изменяется по ;закону непрерывности для
всех ;значений х, которые лежат внутри или вне и;звестных rраниц,
понимают лишь то, что если ж како нибудь из этих значений,
то Ра3ность f(ж + ш) f(ж) может быть сделана меньше, чем любая
заданная величина, если можно принять w столь малым, сколько мы
хотим " [33, кн. 2, с. 174].
Само же доказательство приводится у Больцано следующим 06-
ра30М. "ДОКа3ываемая истина, что между двумя значениями а и
{3, которые дают результат ПРОТИВОПОJЮжноrо знака, всеrда ле
жит по меньшей мере один действительный корень, основывается,
очевидно, на друrой, более общей истине, что, если две непреры
вные функции ж, f(ж) и <р(ж) обладают таким свойством, что для
ж = о, f(o) < lf'(o), а для х = {3, f({3) > lf'({3), то всеrда дол
170
жно иметься значение ж, лежащее между а и {3, для KOToporo будет
f(ж) = lf'(Ж). Однако, если 1(0:) < lf'(o:), то вследствие закона непре
рывности также еще будет I( а + i) < lf'( а + i), если только взять i
достаточно малым. Свойство малости ринадлежит, следовательно,
функции i, которую представляет выражение f(a + i), при всех зна
чениях i, которые ?\fеньше, че?\f некоторое определенное значение.
Te 1 не leHee ;это свойство не принадлежит ей для всех значений i
без оrраничения, а именно не для i, которое было бы = /3 О, так
как f(/З) уже> lf'(/3). Теперь имеет место теорема, что как только
известное свойство М принадлежит всем значения переменной B
личины i, которые меньше заданной величины, но не принадлежит
всем вообще ее значениям, то имеется всеrда некоторое наибольшее
значение и, о котором можно утверждать, что все ж, которые меньше
и, обладают свойством М. ДЛЯ этоrо caMoro значения u не может
быть I(o+u) < lf'(a+u), потому что иначе, соrласно закону непреры
вности, было бы также f( а + и+ ш) < lf'(a +и+ш), если бы мы взяли
только w достаточно малым. И следовательно, не было бы верно, что
u является наибольшим из тех значений, о которых верно утвержде
ние, что все значения i, стоящие ниже ero, делают f(o:+i) < lf'(o+i),
а u + w было бы еще большим значением, для KOToporo верно то же
самое. Но еще меньше может быть f(a+u) > so(a+u), так как иначе
должно было бы быть также I(o+u w) > lf'(o+u w), если взять w
достаточно малЫАf, а следовательно, не было бы верно, что для всех
значений i, которые < и, имеет место I(a + i) < lf'(o + i). Таким
образом, должно быть f( 0+ и) = lf'( о + и), т.е. между о: и /3 имеется
значение ж, а именно 0+ и, для KOToporo функц"и f(ж) и lf'(Ж) cTaH<r
вятся равными друr друrу. Дело идет только еще о доказательстве
упомянутой теоремы. Ее мы теперь докажем тем, что покз.жем, что
те значения i, о которых можно утверждать, что все меньшие из
них обладают свойством М, и те значения, о которых этоrо больше
утверждать нельзя, MorYT быть настолько сближены, насколько бы
мы ни пожелали. Для всякоrо, кто имеет правильное понятие вели
чины, отсюда следует, что представление о i, как о наибольшем из
тех, о котором можно сказать, что все стоящие ниже ero обладают
свойством М, есть представление реальной, т.е. действительной B
личины" iЗ-3, кн. 2, с. 175 176]
Приведенное доказательство не полно. Оно нуждалось, как OTM
Б " "
тил сам ольцано, в правильном понятии величины т.е. в таком
определении вещественноrо числа, которое rарантировало бы суще
171
ствование числа и точной верхней rрани множества всех значений
i, обладающих свойством М. Набросок та!'ой теории вещественноrо
числа имеется в рукописях Больцано. К сожалению, работы Боль
цано стали известны лишь с 70 x rr. XIX в., коrда уже получили ши..
рокую известность у математиков новые основы анализа, созданные
в работах Коши и Вейерштрасса.
Наибольшее значение в распространении новых идей обоснова
ния математическоrо анализ в первой половине XIX в. имели труды
о. Коши и прежде Bcero ero лекции в парижской Политехнической
школе, оформленные в ero учебных руководствах "Курс анализа в
Политехнической королевской школе. I..я часть. Алrебраический ава..
лиз" (1821 r.) и "Краткое изложение лекций по исчислению беско--
нечно малых в Политехнической королевской школе" (1823 r.).
Коши положил в основу математическоrо анализа понятие пре
дела переменной величины. Мы уже отмечали, что исторически пер..
вым методом пределов был античный метод "исчерпывания" Так,
в лемме Евдокса (см. п. 5.1), rоворя современным языком, фор
мулируется и cTporo доказывается, что если ж n последователь
ж п
ность неотрицательных величин такова, что Xn+1 < 2' то пре
дел ж п при n ...... 00 существует и равен нулю. А нахождение пло--
щадей и объемов, построение касательных у Архимеда (см. п. 5.1)
представляют собой строrие предельные переходы, включающие, по--
существу, и докаоательство существования и единственности иско
мых величин. Так, в основе метода интеrральных сумм Архимеда
лежит, по--существу, следующее утверждение: если два числа 8 и
с все время находятся между двумя последовательностями S n И
8 " (т.е. для любоrо натуральноrо n выполняется S n < 8 < Sn И
8 " < с < S n), одна И3 которых ( 8п ) возрастает, а друrая ( S n) убы
вает, причем так, что Ра3ность между ними "исчерпывается" (т.е.
l
8п+1 +1 < 2 (Sn Sn )) или даже просто неоrраниченно убы
вает (стремится к нулю при n 00 ), то S = с и их общее значение
является преде:IОМ как S n' так и Sn при n 00. Ньютонов же Me
ТОД пределов метод ' первых" и "последних" отношений [ЗЗ. кн. 2,
с. 101 105], отличаясь 01' античноrо метода пределов большей фор
малИЗ0ваннос'IЬЮ и краткостью докаоательств, имел существенный
недостаток: в нем заранее предполаrалось существование искомых
"последних" отношений. Так, в лемме 1 основной лемме зтоrо fe
тода в случае отношения двух переменных величин y(t) и x(t),
172
выражаись современным языком, утверждалось и ДОКа3ывалось, что
у
если 1) отношение ж (t) определено, > 1 и монотонно убывает при
t Е [to Ll, to], и 2) для любоrо е > О существует 1 Е [to Ll, to) такое,
у .. у ..
что ---(t) 1 < е (и, следовательно ---(t) --- 1 < g для всех t < t < t o ),
х х
у
то неоБХОДIIl\10 должно быть (to) = 1. При этом существование
х
у
---(to) предполаrается заранее из механических или rеометрических
х
соображений. Выше мы отмечали неудачные попытки Даламбера и
Лаrранжа придать ньютоновскому "последнему" отношению исчеза
ющих величин конструктивное определение.
' Коши же мы наблюдаем отказ от попыток придать предель
ному переходу основной операции математическоrо анализа
конструктивно определение в пользу нахождения условий, необх
димых или достаточных для Toro, чтобы данное постоянное число
было пределом данной переменной величины При таком подходе ec
тественным становится вопрос о существовании и единственности
предела. Необходимые и достаточные условия существования пр
дела (критерий Коши) установлены самим Коши в 1821 r., но еще
ранее (в 1817 r.) Б. Больцано. В лекциях Коши доказаны также Heo
ходимый признак сходимости ряда и несколько достаточных призна
ков сходимости рядов: признак сходимости по мажоранте, признак
Даламбера, интеrральный признак.
3а,м,е'Ч,ан,uе Интеrральный признак был известен еще К. Ma
клорену (1742 r.), а первая формулировка. признака Даламбера OT
носится к 1768 r. Новые достаточные признаки,'вошедшие затем в
u
учебные курсы, нашли и. Раабе (1832 r.), Н.И. Лобачевский (1834 r.),
э. Куммер (1835 r.), о. Боннэ (1842 r.), ж. Бертран (1842 r.),
в.п. Ермаков (1870 r.) и др. Определенный итоr всем этим приз;на
кам подвел Н.В. Буrаев (1863 и 1888 rr.), создавший теорию сопря
женных рядов [38, с. 485 486].
Понятия бесконечно малой величины, непрерывности, суммы
ряда, производной, дифференциала и интеrрала строятся у Коши на
основе понятия предела. Бесконечно малая величина определяется
как перемеННaJI потенциально беСlCонечно малaJI ВeJIичина,
т.е. как переменная величина, имеющая своим пределом нуль. Cx
димость ряда означает по Коши существование конечноrо предела
ero частичных сумм. Если же частичные суммы не стремятся ни к
какому пределу, то такой ряд Коши называет расходящимся или не
173
имеющим суммы. Функция f(x) на;зывается .'непрерывной функцией
переменной х между двумя пределами, если между этими преде
лами бесконечно малое приращение переменной порождает всеrда
бесконечно малое приращение самой функции ' [33, кн. 2, с. 180].
"Если функция f(x) остается непрерывной между двумя данныIии
пределами переменной и если, придав этой переменной ка:кое либо
;значение между двумя этими пределами, сообщить ей бесконечно
l.fалое приращение, то Cal.fa функция также получит бесконечно Ma
лое приращение. Следовательно, если положить тоrда x = i, то два
члена Qтношения разностей
y f(x+i) f(x)
x l
будут бесконечно малыми количествами. Но, в то время как оба эти
члена будут неоrраниченно и одновременно приближаться к пределу
нуль, само отношение может сходится к некоторому друrому np
,
делу, положительному или отрицательному. Этот предел, если он
существует, имеет для каждоrо частноrо ;значения х определенное
;значение, но он и;зменяется вместе с х Форма новой функции,
v f(x+i) f(x)
служащеи пределом отношения .. , будет ;зависеть от
l
формы предложенной функции у = f(x). Чтобы отметить эту ;за
висимость, новую функцию на;зывают прои;зводной функцией и ее
обо;значают с помощью штриха символом у' или f'(x) Пусть п<r
прежнему у = f(ж) есть функция не;зависимой переменной х, i
бесконечно малая величина, а h конечная величина. Если пол<r
жить i = o:h, то а тоже будет бесконечно малой и мы будем иметь
тождественно
f(x + i) j(x)
l
f(x + O'h) f(x)
O'h
откуда получим. что
f(x + O'h) f(x) = f(x + i). f(x) . h.
а l
(1)
Предел, к которому сходится правая часть уравнения (1), коrда пере
менная о: неоrраниченно приближается к нулю, а величина h OCTa
ется неи;зменной, называется дифференциалом функции у = f(x).
Этот дифференциал обо;значают с помощью характеристики d сле
дующим образом:
dy или df(x).
174
Леrко получить ero ;значение, если и;звестно ;значение прои;зводной
функции у' или f'(x). Действительно, в;зяв пределы обеих частей
уравнения (1), мы найдем вообще, что
df(x) = h f'(x)
(2)
в частном случае, коrда f(x) = х, уравнение (2) приводится к
dx = h .
(3)
Значит, дифференциал не;зависимой переменной х есть не что иное,
как постоянная h. Таким обра;зом, уравнение (2) перейдет в
df(x) = f'(x)d:t
(4)
или, что то же, в
dy = у' dx . (5 )
И;З последних уравнений следует, что прои;зводная у' "(х) фун
dy
кции У = f(x) в точности равна dx ' т.е. отношению дифференциала
функции к дифференциалу переменной, или, если yroAHo, коэффи
циенту, на который нужно умножить второй дифференциал, чтобы
получить первый. ПОЭ'rому прои;зеодную функцию нззывают ин
rAa Аифферевциальвым жовффициентом." [33, кн. 2, с. 183] "В
интеrральном исчислении, rоворит Коши, я наш"ел нужным
дать общее докззательство существования интеrралов или перв
обрззных функций, прежде чем ;знакомить с их рззличными свой
ствами. Чтобы достиrнуть этоrо, сперва потребовалось установить
понятие интеrралов между данными пределами или определенных
Интеrралов. Так как последние MorYT иноrда ока;заться бесконечными
или неопределенными, то было существенно исследовать, 8 каких слу
чаях они сохраняют единственное и конечное ;значение." [33, кн. 2,
с. 182] Коши определяет интеrрал следующим оБРЗЗ0М. Предполаrая,
что f(x) непрерывная функция на cerMeHTe (а, Ь], он рассматри
вает интеrральную сумму
8(0") = f(xo). (хl ха) + f(Xl). (Х2 хl) +.. . + f(Xn l) . (х п Xn l),
rAe о" = {Xi} рззбиение cerMeHTa [а, Ь]. Суммы 8 имеют предел
при d(O") ..-..+ О (d(O") = m IXi Xi ll), нззываемый определенным
I
175
интеrралом f: f(x) dx. ДОКа3ательство Коши существования этоrо
предела следующее. В силу неравенства
(х n хо). min f(x) < 8(0") < (х n ха) тах f(x)
[жоо, жо,,] [жоо, жо,,]
и свойства непрерывной функции принимать всякое промежуточное
значение, можно записать
8(0") = f(xo + 8(х n хо» . (х" ха),
О<О<1
Последнее равенство справедливо для всякоrо cerMeHTa [ха, х п ), на
котором f(x) непрерывна. ОБРа3уем новое разбиение 0"1, содержа
щее 0", и сумму 8(0"1). TorAa
8(0"1) = (хl ..... ха) . f(xo + Оl(Хl ха») + ... +
+(х п Xn 1) . f(Xn 1 + оп(х n Xn 1)) =
= (хl ха) [/(xo) + ео] +
+ (х" Xn l) [f(Xn l) + en 1] =
= 8(0") + (хl ..... ха) . ео +
+ (х" Xn 1) . en 1
Число ei 1 не превышает колебания функции f(x) на промежутке
[Xi l, xi], следовательно становится сколь уrодно малым, если ди
аметр разбиения достаточно мал (Коши неоднократно использует
в рассуждениях свойство равномерной непрерывности непрерывной
на cerMeHTe функции). Таким образом, 8(0"1) отличается от 8( (7)
сколь уrодно мало, если диаметр разбиения достаточно мал. Теперь,
если 8(0"2) и 8«(73) произвольные суммы указанноrо выше вида,
то каждая из них отличается мало от третьей суммы 8((72 + О"з),
полученной с помощью разбиения (72 + О"з cerMeHTa [а, Ь], поэтому
8(0"2) И 8(О"з) отличаются мало: этим доказательство существования
предела сумм заканчивается. Коши подчеркивает, что приведенные
выше рассуждения приrодны при условии, что '(х) непрерывна и
оrраничена на оrраниченном cerMeHTe [а, Ь]; кстати, в этом случае
имеет место формула
2 Ь
Нт j ,(x)dX = j ,(x)dX.
Е 1 CI+o
E2 Ь O
1 а
176
При невыполнении какоr либо из этих условий предел сумм M
жет не существовать; однако может случиться, что эти условии вы
полняются В [ l, 2], а < l < 2 < Ь, И у"азанный предел сущ
ствует. В этом случае Коши предлаrает определить интеrрал с по--
мощью указанноrо предела. АНaJIоrично определяется и несобствеи
ный интеrрал от непрерывной функции по неоrраниченному пром
жу ку. Далее, неопределенным интеrралом J f(ж) dж Коши так же,
ка" и в XVIII в., называет решение уравнения
dy = f(ж) dж,
т.е. такую функцию у, дифференциал "оторой в каждой точ"е З8r
писывается по этой форму . Таким образом, неопределенный ин
теrрал есть совокупность вида F(ж) + w(ж), rAe F(ж) некоторое
частное решение указанноrо уравнении, а w(ж) удовлетворяет ypa
внению w'(ж) = О, т.е. w const. В качестве F(ж) Коши берет
определенный интеrрал с переменным верхним пределом l z ' f (Z) dz,
отсюда получается формула Ньютона Лейбница:
ь
f f(z) dz = F(b) F(a).
а
Кеши указывает на rеометричес"ое значение определенноrо ивт
rрала l Ь '(х) dx как площади, оrраниченной кривой у = f(z) > о,
осью абсцисс и ординатами ж = а и ж = Ь; из рассуждений Коши
следует, что понятие площади он считает известным заранее [28,
с. 13 16].
Современное же изложение начал математическоrо анализа с
точными форму ировками и доказательствами на языке "е 6"
восходит к лекциям Вейерштрасса, обработки которых были изданы
ero слушателями в 60 70 x rr. XIX в. Приведем некоторые формули
ровки из лекций Вейерштрасса. "В противоположность неизменяю--
щейся величине или постоянной, которая может принимать только
одно значение, переменной величиной называется такая, которав M
жет принимать не только несколько отдельнQX, но бесконечно MHoro
;значений. Может случиться, что переменная величина может при
нимать любое возможное положительное или отрицательное зн
чение, тоrда она называется неоrраниченно переменной величиной.
Переменная величина может быть оrраниченно переменной и иметь
177
нижнюю или верхнюю rраницу, или же одновременно обе. 3нач
ния, которые может принимать переменная величина, MorYT прина
длежать одной или нескольким непрерывным последовательностям,
если переменная величина может принимать все возможные знач
ния между двумя возможными rраницами. Диффере циальное исчи
сление занимается только такими непрерывно изменяющимися вели
чинами. Две переменные величины MorYT находиться в такой связи,
что каждому определенному значению одной принадлежит опред
ленное значение друrой, тоrда последняя называется функцией пер
вой Если '(х) есть функция х и х определенное значение,
то при переходе х в х + h функция переменится и будет '(х + h);
разность /(х + h) ....... '(х) называют изменением, которое получает
функция в силу Toro, что aprYMeHT переходит от х в х + h. Если
возможно определить для h такую rраницу б, что для всех значений
h, по абсолютному значению еще меньших, чем б, '(х + h) ....... '(х)
становятся меньше, чем какая либо сколь уrодно малая величина е,
то rоворят, что бесконечно малым изменениям aprYMeHTa COOTBeT
ствуют бесконечно малые изменения функции. Ибо rоворят, что He
которая величина может стать бесконечно малой, если ее абсолют
ное значение может стать меньше какой либо произвольно взятой
малой величины. Если некоторая функция такова, что бесконечно Ma
лым изменениям aprYMeHTa соответствуют бесконечно малые изм
нения функции, то оворят, что она непрерывно изменяется вместе
со своим aprYMeHToM Полное изменение '(х + h) ....... '(х), KOT<r
рое испытывает функция '(х) в силу Toro, что х переходит в х + h,
можно, вообще rоворя, разложить на две части, из которых одна
пропорциональна изменению aprYMeHTa h, т.е. состоит из h и мно--
жителя, не зависящеrо от h и постоянноrо относительно h, так что
будет бесконечно маоой, коrда будет бесконечно малым h, или же
будет бесконечно малой одновременно с h, друrая же будет не только
сама по себе бесконечно малой, коrда будет бесконечно малым h, но
будет еще бесконечно малой, если ее разделить на h Первая часть
Bcero изменения функции, пропорциональная измене ию -арrумента,
называется дифференциальным изменением или дифферренциалом
и обозначается предшествующим функции характеристическим d,
между тем как означает все изменение. Аналоrично, поскольку
простейшей функцией х является сама х, вместо h пишут также dx,
и это совершенно независимая от х величина, .которая может стать
бесконечно малой. Чем меньше берется dx или h, тем менее будет
178
отличаться дифференциальное и;зме ение от Bcero и;зменения; путем
уменьшения dx различие можно сделать меньшим любой сколь yr<r
дно малой величины; поэтому дифференциал определяли как и;змене--
иие, которое претерпевает функция, коrда ее aprYMeHT и;зменяется
на бесконечно малую величину" [33, ки. 2, с. 188 190].
5.7 ИНТЕrр АлыI РИМАНА И ДАРБУ
И;зучение понятия интеrрируемости у Римана и у друrих авторов
было вы;звано прежде Bcero потребностями теории триrонометр
ческих рядов. Как пока:зaJI ж. Фурье (1822 r.), коэффициенты TI
00
rонометричесв:оrо ряда O + 2:(а n cosnx + bnsinnx) выражаю'} iJ
"=1
чере;з ero сумму f(x) по формулам:
'"
а n = J J( х) cos nх dx ,
'"
'"
ь n = J J(x)sin nж dж
1r
(отметим, что еще ранее, в 1777 r. и в 1757 ['., эти формулы были
найдены соответственно Л. Эйлером и А. Клеро). Первое cTporoe
дока:зательство во;зможности разложения функции в триrонометри
ческий ряд было дано л. Дирихле (1829 r.) для класса оrраниченных
кусочно непрерывных и кусочно монотонных функций. Понятно, что
для Toro, чтобы можно было определить ряд Фурье функции f(x),
необходимо чтобы сама функция f(x) была интеrрируемой. В свя;зи
с этим ,Б. Риман, продолжая исследования CBoero учителя Дирихле,
пришел к необходимости аНaJIи;за понятия интеrрируемости
"Предшествующие работы, посвященные рассматриваемому B<r
просу, писал Риман в 1853 r., имели целью обосновать разло--
жение функций в ряд Фурье для случаев, встречающихся в природе,
поэтому доказательство моrло быть начинаемо для совершенно пр<r
и;звольных функций и в дальнейшем на поведение функции моrли
быть налаrаемы те или иные требуемые самим доказательством ис
кусственные оrраничения (как непрерывность у Коши или кусоч
ная монотонность и непрерывность у Дирихл С. М.) при условии,
179
что эти оrраниче ия не стояли в противоречии с поставленной за..
дачей. Мы же имеем целью YCTaHOB TЬ лишь те условия, которые
действительно необходимо наложить на поиедение функции дли Toro,
.
чтобы она моrла быть представлена триrонометричеСКИ!f рядом; п
этому нам нужно найти сначал необходимые условия представим
СТИ' и потом выбрать из них те, которые являются и достаточными.
IITaK, предшествующие авторы доказывали, что если функция обла
дает такими..то и такими"то свойствами, то она представима рядом
Фурье. Мы же ставим перед собой обратный вопрос: если функция
представима триrонометрическим рядом, то что можно сказать о ее
поведении, об изменении ее значений при непрерывном изменении
aprYMeHTa?" [27, с. 185 186]. Пусть Wi колебание ФУНКЦИИ /(ж) на
cerMeHTe [Жi--l, жi]. Риман утверждает, что для Toro, чтобы функция
/(ж) была интеrрируема на ОТРе3ке [а, Ь], необходимо и достаточно,
n
чтобы сумма L: WiДi стремилась к нулю вместе с диаметром раз
а i=l
биения d(tj). Риман показы,вает, что необходимое и достаточное
условие интеrрируемости может быть записано акже в следующем
виде: для любоrо о' > О сумма длин тех cerMeHToB i, на которых K
лебание функции Wi > ,а, стремится к нулю вместе с диаметром раз..
биения. Действительно, пусто /(ж) интеrрируема и точная
n
верхняя rpaHb сумм L: Wi i для всех разбиений, диаметр которых
i=l
'не превосходит d; пусть S = Е' i общая длина тех cerMeHToB
i, rде Wi а. Тоrда
I n
,
QS = Q Е i < Е Wi i < ,
i=l
d
S < .
,
ct
а так как о при d(tj) О, то из последнеrо неравенства следует,
что при заданном о' сумма S длин cerMeHToB, в которых олебание
функции не меньше а, стремится к нулю. Это условие также и д
статочно. В самом деле, пусть М точная верхняя rpaHb функции
1/(ж)1 на [а, Ь]; тоrда колебание функции /(ж) в любом cerMeHTe не
больше 2М. Имеют место неравенства
,
Е Wi i < 2MS,
,
Е Wi di Е Wi i < а( Ь а)
поэтому
Е Widi < 2MS + а(Ь а).
180
е/2
Пусть е > О задано. Если сначала взять Q < Ь f , затем столь
a
е/2 n
мелкое разбиение 0', чтобы было S < М , то сумма Е Wi i будет
. 2 i=l
меньше е; 'feM самым достаточность высказанноrо выше условия
доказана.
В качестве примера разрывной интеrрируемой функции Риман
приводит функцию со всюд.у плотным множест ом точек разрыва
f(x) = t (: ) ,
n=1
rде (nж) означает разность между nж и ближайшим целым числом;
если же nж = k + !, rде- k целое, то (nж) полаrается равным
" 2k + 1
нулю. Функция /(ж) цмеет разрыв в каждои точке вида 2п
б Ф /( ) 2k + 1 1["2 Д " .
коле ание ункции ж в точке 2n равно 8n 2 . еиствительно,
числители (пх) слаrаемых (n ) имеют разрыв в точках вида x =
n
2k+ 1
2n ' предел слева равен 1/2, справа 1/2, так что скачок функции
(nж) равен 1. Но точка ж является точкой разрыва только для тех
функций (тж), для которых т = (2; + 1) . n, i = О, 1, 2,. ... Поэтому
00
k k 1 1
f(zn + О) = ЛЖn) 2п2 (2; + 1)2
k k 1 1
f(zn О) = ЛХ n ) + 2п 2 · (2; + 1)2
и скачок w(J, ж ) Функuии /(ж) в точке ж равен
00
k k 1", 1
If(zn + О) f(zn 0)1 = п2 (2; + 1)2
7r 2
8n 2
(при выводе этих формул используется равномерная сходимость
ряда f (n ) ; она же rарантирует и непрерывность лж) во всех
n
"=1
точках ж '# ж как в таких точках, в которых одновременно H
прерывны все члены ряда). Существует конечное число значений n
181
7r 2
таких, что 8п 2 > а. Поэтому в каждом конечном промежутке cy
ществует конечное число точек X , в которых скачок функции- /(Х)
будет > а. Следовательно, при достаточно малом диаметре ра3бие
ния число S может быть сделано как уrодно малым, так что /(Х)
интеrрируема.
Риман за {е'Чает, что всякая кусочно монотонная функция также
обладает подобным свойством, Т.е. существует только конечное чи
сло точек, в которых скачки функции прев шают заданную вели
чину. Следовательно, HC ,кусочно монотонные функции интеrриру
емы.
Друrое определение интеrрала, опирающееся непосредственно не
на понятие предела, а на понятие точных rраней оrраничеН8:.9rо MH
жества, было П9дrотовлено работами Дарбу, Асколи и некоторых
друrих математиков в 70 x rr. XIX в. и завершено Пеано в работе,
относящейся к 1883 r. А именно, r. Дарбу, r. Асколи, r Смит и
п. дю Буа Реймон в одном и том же 1875 r., используя понятия
n I n
верхней S = Е Мi(Жi Xi l) И нижней S = Е mi(Xi Xi l) ин
"i=l i=l
теrральных сумм (M i ' и тi соответственно, точная верхняя и
точная нижняя rрани функции /(Х) на cerMeHTe [Xi l' Xi]) незави
симо друr от друrа показали, что для интеrрируемости функции по
Риману необходимо и достаточно, чтобы были равны друr друrу
предел 1 верхних ИНТеrральных сумм S и предел 1 нижних инте---
rральных сумм S при стремлении диаметра разбиения к нулю. Най
денное необходимое и достаточное условие интеrрируемости было
взято Асколи В качестве HOBoro определения интеrрала, а Д. Пеано
устранил из этоrо определения понятие предела, определив 1 и 1
. .
не как пределы соответствующих интеrральных сумм, а как COOT
BeTCTBeH O точную нижнюю rpaHb сумм S и точную верхнюю rpaHb
сумм s... Таким образом, соrласно Пеано, оrраниченная функция /(Х)
На3ыв ется интеrрируемой на [а, Ь], если точная нижняя rpaHb Bep
хних интеrральных сумм Дарбу равна точной верхней rрани нижних
интеrралЬ8ЫХ сумм Дар бу.
Далее, в найденных Риманом необходимых и достаточных усл
ВИJIX интеrрируемости участвовали колебания функции на отрезках
[Xi l, Xi], что лишь косвенно указывало на характер разрывности
функции. Поэтому продолжались попытки дать друrие, более пря
мые условия интеrрируемости. Так, r. rанкель (1870 r.), дю Буа
182
Реймон (1882 r.) и некоторые друrие математики предложили H
вую формулировку необходимых и достаточных условий интеrри
руемости, основанную на понятии колебания функции в самих точ
ках разрыва и на характеристике самих точек разрыва. А именно,
дю Буа Реймон показал, что если функция такова, что множество
E Q таких точек разрыва, в которых колебание функции w(f, х) > а,
при ВСЯКО!\f Q: 10жет быть заключено в конечную систему интерва
лов общей сколь уrодно малой длины, то выполняются необходимые
и достаточныe условия интеrрируемости Римана, и наоборот. д
кажем это. Необходимость: всякий cerMeHT, содержащий точку из
EQ' таков, что колебание функции в нем не меньше а. Поэтому E Q
содержится в тех cerMeHTax разбиения. в которых колебание > а.
Если функция интеrрируема, то, соrласно критерию Римана, общая
длина этих cerMeHToB стремится к нулю, что и нужно доказать. д
статочность: заметим сначала, что если во всех точках HeKoToporo
cerMeHTa колебание функции .меньше, чем а, то можно указать
такое е > о, что w(J, б) < а, rде б произвольный cerMeHT, закл
чающийся в Ll, длины, меньшей чем е. Заключим E Q в конечную си
стему интервалов Ll 1 , . . . , Ll n общей длины s. Обозкачим cerMeHTы'
дополнительные к Ll 1 , . . . , n через Ll , . ,Ll:п. Они состоят из T
чек, rде колебание функции < а. Пусть d длина наимеllьшеrо
из интервалов i и число е наименьшее из чисел ei, выбранных
для сеrмеитов i, как указано выше. Рассмотрим произвольное раз
биение cerMeHTa [а, Ь] диаметра меньшеrо, чем min(d, е). Тоrда те
cerMeHTbI разбиения и, в которых колебание функции > а, необх
диМ:о должны иметь общие точки с интервалами i. Но общая их
длина не превышает 35, что, в силу возможности выбрать число 5
произвольно малым, и завершает доказательство.
Напомним, что в курсах анализа обычно приводится критерий
интеrрируемости в форме Лебеrа: для Toro, чтобы оrраниченная на
[а, Ь] функция J(x) была интеrрируема по Риману, необходимо и д
статочно, чтобы множество Е точек разрыва функции J(x) на [а, Ь]
имело меру нуль, т.е. ero можно было бы заключить в конечную или
счетную систему интервалов общей сколь уrодно малой длины. Этот
критерий интеrрируемости нетрудно получить из критерия инт
rрируемости в форме дю Буа Реймона. Достаточно заметить, что
00
Е = U E и что E Q компактно для любоrо а > о.
n=l "
183
5.8 ВОЗНИКНОВЕНИЕ ПОНЯТИЯ MEPbI
, .
МНОЖЕСТВА
в основе найденных rанкелем и друrими математиками новых
условий интеrрируемости по Рим а ну лежало понятие линейноrо MH
жества, которое может быть заключено в конечную систему ин
тервалов сколь yroAHo малой длины. Такие множества дю Буа
Реймон называл дискретными, а теперь мы обычно называем их
множествами протяженности (или линейной меры) нуль. Появление
множеств протяженности нуль привело вскоре к определению пр
тяженности произрольноrо линейноrо множества и вообще меры
произвольноrо множества. Первое определение меры произволь
Horo множества принадлежит r. Кантору (1883 r.) и о. Штольцу
(1884 r.). Несколько позже эквивалентное определение было пред
ложено А. rapHaKoM (1885 r.). Эти определения были существенно
дополнены Пеано (1887 r.) и К. Жорданом (1892 r.); по имени после.-
дних эту меру принято называть мерой Пеано Жордана. Приведем
все эти определения.
Определение меры по Кантору. Пусть Е произвольное оrрани
ченное множество в пространстве Rn. Для любой точки'ж из замы
кания Е множества Е рассмотрим замкнутый шар S(p, ж) радиуса р
с центром в точке ж. Пусть далее П(р) есть U S(p, ж). Множество
жое Е
П(р) можно разбить на конечное число частей, "объем" которых
представляет собой функцию F(p), монотонно убывающую с убыва
нием р. Число k(E) = Нm F(p) при р о называется мерой Кантора
множества Е.
Опреде ение меры по Штольцу. Пусть Е множеСТВО j coдep
жащееся в [а, Ь]. Пусть {о"n} последовательность разбиений
с диаметром, стремящимся к нулю, причем о"n С о"n+l. Пусть
i(o"n) cerMeHTbl разбиения, содержащие точки из Е. Число
s(E) = limEт i(O"n) при n 00 называется мерой Штольца MH
I .
жества Е. Свое мероопределение Штольц распространил также на
случай плоских множеств
Определение меры по rapHalCY. Пусть Е множество, содержа
Ь a
щееся в [а, Ь]. Удалим из [а, Ь] все интервалы длины > 2 ' не
содержащие точек из Е. Из остатка r2 удалим все интервалы длины
184
Ь a
> 3 ,не содержащие точек из Е. И так далее. Предел послед
вательности общих длин остатков r n при n 00 Ha3blBaeтCJI мерой
rapHaKa h(E) множества Е.
Определение меры по ПеаН<rЖордану. Пусть дJUI определенн
сти Е плоское множество. Рассмотрим на плоскости KBaдpa
ную сетку, образованную прямыми, параллельными осям координат.
Пусть S сумма площадей замкнутых квадратов сетки, распол
женнbIX целиком внутри множества Е, а 51 сумма ПJIощадей тех
замкнутых квадратов, которые содержат хотя бы одну rраничную
точку множества Е. Сумма 5 + 51 состоит из площадей квадратов,
содержащих точки замыкания Е U Е ' множества Е. При неоrрани"
ченном измельчении С Т 4)рОНЫ сетки числа 5 и 5 + 51 стремятся к
определенным пределам, которые называютCJI соответс:венно вну"
тренней pge(E) и внешней pgi(E) мерой ПеаН<rЖордана множества
Е. В случае совпадения этих пределов множество Е называется из..
меримым по ПеанcrЖордану, а общее значение pg(E) внешней и
внутренней мер мерой Пеано Жордана множества Е. Приведен..
ное определение меры принадлежит Жордану . Пеано же определил
внешнюю и внутреннюю меры множества соответственно как точ"
ную нижнюю rpaHb площадей конечных систем мноrоуrольников, ц
ликом содержащих множество Е, и как точную верхнюю rpaHb пл
щадей конечных систем мноrоуrольииков, целиком содержащихся во
множестве Е.
УПDажнение 46. Пусть Е множестяо оациональных чисел из
[О, 1]. Покажите, что k(R) \ s(E) = h(E) = Р9е(Е) = 1. Измеримо
ли Е по ПеанcrЖордану?
Основываясь на введенном понятии меры, Жордан дал более o
щее построение интеrрала Римана, рассматривая функции, задан
ные на произвольном измеримом по Пеано Жордану множестве
и строя интеrральные суммы для произвольвых разбиений этоrо
множества на измеримые по ПеаН<rЖордану части. А Пеано п
строил rеометрическое определение интеrрала Римана, и именно
им была ДОКа3ана следующая теорема: для Toro, чтобы оrраничен
ная не отрицательная на [а, Ь] функция !(ж) была интеrрируемой по
Риману, необхоцимо и достаточно, чтобы ординатное множество
E(f, [а, Ь]) = {«ж, у) таких, что ж Е [а; Ь], О < У < !(ж)} было изме--
185
римо по Пеано Жордану; при этом
ь
J I(ж) dж = pg(E(!, [а, Ь))).
а
в общем случае оrраниченной функции произвольноrо знака
Ь
J f(ж) dx = pg(E(!+, [а, Ь))) pg(E(!' , [а, Ь))) ,
а
rде
I+(x) = { f(жJ:
f(ж) > о
f(ж) < о
I (x) = { лх :
f(ж) > о
f(ж) < о
f(ж) = '+(х) f (ж).
Общие принципы построения меры множества были высказаны
э. Бореле!\f 'в книrе 'tЛекции по теории функций" (1898 r.):
1) Мера всеrда неотрицательна.
2) Мера суммы счетноrо числа неперекрывающихся множеств
равна сумме их мер.
3) Мера разности двух множеств (множества и ero подмнcr
жества) равна разности их мер.
4) Всякое множество, мера KOToporo не равна нулю, несчетно.
Если в качестве меры интервала взять ero длину, то, соrла
сно 2, мера OTKpblToro множества определится как сумма длин ero
составных интервалов. На основании 3 определится мера замкну
Toro множества (как разности между интервалом и открытым MHcr
жеством). CTporoe построение класса множеств, получаемых пqсле---
довательно операциями сложения и вычитания, исходя из открытых
множеств (такие множества называют теперь борелевскими, или B
множествами, или В измеримыми множествами) было дано А. Лебе---
rOM в 1905 r.
Упражнение 47. Покажите, что мера ПеаН<rЖордана не YAcr
влетворяет принципу 2 мероопределения Бореля, т.е. не является
счетнcrаддитивной. Чему равна мера Бореля множества Е рациcr
нальных чисел из [О, 1]?
1
5.9 МЕР А И ИНТЕI'Р АЛ ЛЕБЕI' А
Первое сообщение Лебеrа об открытии им HOBoro процесса инте--
rрирования появилось в печати весной 1901 r. Подробное изложение
теории интеrрала Лебеrа имеется в ero диссертации (1902 r.). Эта
теория вместе с анализом предшествующеrо развития понятия ин
теrрала, составляет содержание ero "Лекций по интеrрированию и
отысканию примитивных функций)) (1904 r., имеется русский пере--
во д) .
Лебеr начинает свое исследование с анализа предшествующеrо
развития понятия интеrрала. При этом он выделяет шесть свойств
интеrрала, вполне описывающих, по ero мнению, общее понятие ин
теrрала. И далее Лебеr ставит себе целью "связать с каждой orpa
ниченной функцией f(ж), определенной в конечном интервале (а, Ь),
положительном, отрицательном или рааным нулю, некоторое конеч
ь
ное число f f(x) dж, которое мы назовем интеrралом от f(ж) на (а, Ь)
(J
и которое удовлетворяет следующим условиям:
ь b.....h
1) Каковы бы ни были а, Ь и h, имеем f f(ж) dж = f f(ж + h) dж.
(J (J.....h
Ь с (J
2) Каковы бы ни были а, Ь и С, имеем f + f + f = о.
(J Ь с
Ь Ь Ь
3) лf(ж) + ср(ж)] dж = f f(ж) dж + f ср(ж) dж.
(J (J (J
Ь
4) Если I > 0 и Ь> а, то также ff(ж)dх > о.
(J
Ь
5) fl dж = 1.
(J
6) Если fп(Ж) стремится, возрастая к f(x), то интеrрал от fп(Ж)
стремится к интеrралу от '(х)"
Предполаrая существование T&KOrO числа, Лебеr последовательно
выводит из условий 1 6, что
ь
1. fO. dж = о.
(J
Ь Ь
2. f f(ж)dж= ff(ж)dж
(J (J
187
ь ь
3. При j(ж) < 'Р(ж) и а < Ь будет f j(ж) dж < J 'Р(ж) dж.
(J (J
ь ь
4. f j(ж) dж < JI/(ж)1 dж.
(J (J
ь ь
5. Jk /(ж)dж = k Jf(ж)dх Vk Е R.
(J
(J
n Ь n
6. S = ЕmiL\Жi < J f(ж) dж < Е Мi Жi = S , rде джi = жi Жi...1,
i=l (J i+l
тi и Mi соответственно точная нижняя и точная верхняя
rрани значений ФУНКЦИИ /(ж) на cerMeHTe [Жi...1, жi] (Отметим,
что свойства 1 6 доказываются без использования условия 6,
так что для функций, интеrрируемых по Рима ну, искомое число
совпадает с интеrралом Римана).
7. Пусть на отрезке [а, Ь] 1 < /(ж) < L и 1 = 10 < 11 < <
1" = L. Пусть далее Ei = {ж таких, что li l < /(ж) < li},
а Фi(Ж) характеристическая функция множества Ei, т.е.
{ 1, ж Е Ei "
Фi(Ж) = О d Е. Тоrда ф(ж) = li lФi(Ж) < /(ж) <
, ж I 1=1
n Ь
Е liФi(Ж) = Ф(ж), откуда следует, что Jф(ж)dж =
i=l а
n Ь Ь "Ь Ь
= Е li...1 J Фi(Ж) dж < J /(ж) dж < Е li J f(ж) dж = JФ(ж) dж.
i=l (J а i=l а а
Ь
А отсюда следует, что f f(ж) dж будет с н обходимостью определен,
а
если .будут определены интеrралы от функций Фi (ж). Действительно,
в этом случае будут определены и интеrралы от функций ф(z) и
\I1(ж), а так как функции ф(ж) и Ф(ж) стремятся к f(ж) равномерно
при max(li li l) ........ О, то интеrрал от /(ж) с необходимостью яв"
ляется общим пределом интеrралов от функций ф(ж) и Ф(ж). Таким
оБРа30М, Лебеr приходит к следующему вывоцу: нужно уметь опре
делить интеrрал от функции, принимающей Bcero дв&. значения О и
1; тоrда интеrрал от любой оrраниченной ФУНКЦИИ, если он суще
ствует, необходимо должет быть пределом интеrралов от ступенча..
тых функций ф(ж) и Ф(ж). ОБЩaJI" проблема интеrриров8НИJI
СВОАИТС" тем самым к ороблеме ивтеrрироваии.. характе..
u
ристических ФУНJCЦИИ.
188
Далее, характеристическая функция ФЕ(Х) множества Е вполне
ь
определяется этим множеством. Следовательно, число fФЕ(Х) dx за..
а
висит только от caMoro множества Е С [а, Ь]. В случае, KorAa
Е = [а, Ь], это число, как следует из условий 1 F), равно длине Ь .... а
cerMeHTa [а, Ь]. Поэтому естественно в общем случае назвать это чи..
сло ?\fерой ?\1ножества Е. Проблема интеrрировани.в: сво итс.в:
Т8ICИМ оБР8&30М IC проблеме опре е.леRи.. меры множества.
"Мы ставим себе целью, rоворит далее Лебеr, связать с ка..
ждым оrраниченным множеством Е, состоящим из точек оси Ох,
некоторое число, положительное или равное нулю, тЕ, которое мы
На3ываем мерой Е и которое удовлетворяет следующим условиям:
1) Два равных множества имеют одну и ту же меру.
2) Множество, являющееся суммой коНечноrо или счетноrо числа
множеств попарно без общих точек, имеет своей мерой сумму
мер слаrаемых.
3) Мера множества всех точек интервала (О, 1) равна 1"
IIз 1) и 2) следует, что мера конечноrо множества равна нулю.
Далее, мера интервала (а, Ь) равна TorAa Ь а, а мера произволь-
Horo OTKpblToro множества равна сумме мер состаляющих ero ин..
тервалов. Мера произвольноrо замкнутоrо множества из [а, Ь] ра..
вна Ра3ности между Ь а и мерой дополнения этоrо множества.
Далее, хотя условия 1 ) 3) не пооволяют непосредственно опреде.-
лить меру произвольноrо множества Е, однако они позволяют всеrда
установить rраницы, в которых заключено число тЕ. Лебеr рассу..
ждает следующим образом. Пусть G открытое множество, со-
держащее Е. TorAa, вследствие неотрицательности и аддитивно-
сти меры имеем тЕ < mG, и, следовательно, тЕ < inf та, rAe
inf берется по всем открытым множествам, содержащим Е. Чи..
сло inf mG есть искомая верхняя оценка для тЕ. Лебеr обозначает
infmG = теЕ и На3ывает теЕ внешней мерой множества Е. Оце.-
ним тЕ снизу. Имеем: тЕ + тСЕ = Ь а, тЕ = (Ь а) тСЕ и,
значит, тЕ > (Ь а) теСЕ (СЕ дополнение множества E дО
(а, Ь)). Число тiE = (Ь а) теСЕ ИСКОМУI9 нижнюю оценку для
тЕ Jlебеr На3ывает внутренней мерой множества Е. Числа теЕ
и mi Е определены таким оБРа30М для любоrо множества Енезави..
сима от Toro, существует или не существует число тЕ. При этом,
если тЕ существует, то miE < тЕ < теЕ. Теперь предположим,
189
что для HeKoToporo множества Е оказалось, что miE = теЕ. Тоrда
общее ;значение внешней и внутренней меры должно равняться мере
тЕ, если только она существует. Это последнее ;замечание приводит
Лебеrа к конструктивному определению меры: если mi Е = те Е, то
множество Е называется и;змеримым, а ero мерой называется общее
;значение чисел miE и теЕ.
Итоr дальнейших рассуждениЙ Лебеrа можно кратко выразить
следующим образом: совокупность и;змеримых по Лебеrу множеств
обра;зует кольцо, на котором мера Лебеrа является решением про--
блемы меры, т.е. удовлетворяет условиям 1 6. В частности, OKa
;зываются и;змеримыми по Лебеrу все борелевские множества, а их
борелевская мера совпадается с лебеrовой мерой.
Класс борелевских мно?Кеств все же ;значительно уже класса мно--
жеств, и;змеримых по Лебеrу. Лебеr показывает это равнением
мощностей: имеется лишь континуум борелевских множеств, в то
время как только лишь подмножества прои;звольноrо совершенноrо
множества лебеrовой меры нуль уже образуют rиперконтинуум и;з
меримых по Лебеrу множеств. Отметим еще, что в своей диссерта
ции Лебеr показывает, что для всякоrо множества Е имеются два
борелевских множества, меры которых равны соответственно BHY
тренней и внешней мере множества Е.
Вернемся теперь вместе с Лебеrом к проблеме интеrрирова
ния. Она сводится, как мы видели выше, к проблеме интеrриро--
,вания характеристических функций. Последняя решена Лебеrом не
для всех характеристических функций, а только для характеристи
ческих функций и;змеримых по Лебеrу множеств. Это приводит
к оrраничению на функции f(x) внеравенствах 7, а именно, для
функций f(x) должны быть и;змеримы по Лебеrу множества вида
Е(а, fЗ] = {х таких, что Q < f( х) < ,8}. Такие функции f( х) Лебеr
на;зывает и;змеримыми и для таких функuий он аналитически опре
ь
деляет интеrрал f /( х) dx как общий предел сумм
(1
n
(J' = Eli lE[I' l"')
i=l
и
n
Е = EliE[l' l'
i=l
190
И, кроме Toro, дает rеометрическое опреде:1lение интеrрала, анало--
rичное указанному выше rеометрическому определению Пеано ин
теrрала Римана.
5.10 ПРОБЛЕМА ВОССТАНОВЛЕНИЯ
u
ПРИМИТИВНОИ Функции
В случае непрерывности функции /'(х) интеrрал Коши от нее с
переменным верхним пределом восстанавливает примитивную (пер
вообрatJную) функцию /( х) с точностью до константы
z
J f'(x) dx = f(x) Ла).
(1
Однако, как отметил Дарбу (1875 r.), в случае разрывных, но инт
rрируемых по Риману функций /'(х) неопределенный интеrрал Ри
мана от нее восстанавливает примитивную функцию /(х), вообще
rоворя, только в точках непрерывности /'(х). А Вольтерра (1881 r.)
построил пример непрерывной функции /(х), оrраниченная произ
BOДH которой /'(х) вовсе не интеrрируема по Риману.
Положение стало исправляться с введением интеrрала Лебеrа.
А именно, уже в вышеупомянутых лекциях Лебеr покatJaJI, что ero
v
интеrрал восстанавливает примитивную от оrраниченвои произ
водной: неопреАепенный интеrрал Лебеrа от суммируемой
оrраниченной ПРОИОВОАНОЙ есть примитивнан фУНIЦИЖ. В
конце же своих лекций Лебеr ставит вопрос и об интеrрируемо--
сти неоrраниченных функций; для таких функций вышеуказанные
аналитическое и rеометрическое определение интеrрала Лебеrа не
rодятся. Поэтому Лебеrу приходится rоворить, например, об инте
rрируемости таких функций лишь на множестве точек, rде эти фун
кции конечны. По этой же причине в сноске на последней странице
своих лекций Лебеr рассматривает свойство функции, HatJBaHHoe Ви
тали абсолютной непрерывностью, и предлаrает слеДУlPщее наибо--
лее общее определение cBoero интеrрала, охватывающее случай не
всюду конечных функций /(z): фУНJ[Ци.. /(х) наоываетс.& сумми..
v
руемои, еCJIИ существует абсолютно непрерывнв.. фУВJ[ЦИJI
Р(х), Имеющв.. ПОЧТИ ВСЮАУ ПРОИС3ВОАНУЮ, равную /(х). То..
z
rAa ПО опреАепеиию f /(х) dx = Р(х) F(a).
а
191
Анализ этоrо определения Лебеrом не проводится. Он, однако,
утверждает, что оно применимо и к конечным суммируемым фун"
кциям, то есть что для Toro, чтобы функция F(ж) была неопреде..
ленным интеrралом Лебеrа, необходимо и достаточно, чтобы она
была абсолютно непрерывной. Первые доказательства этой теоремы
Быии даны r. Витали (1905 r.), Б. Леви (1906 r.). и самим Лебеrом
(1907 r.).
Подробнее о происхождении и развитии понятий меры и инте--
rрала см. [27, 28].
5.11 О ПРЕПОДАВАНИИ ОСНОВ
АНАЛИЗА (дополнение)
Поонакомившись с развитием основ анализа, мы можем теперь
выделить в нем два направления. Одно направление идет от метода
интеrральных сумм Архимеда и ero диффер нциальных методов че--
рез метод "первых" и "последних" отношений Ньютона к а ализу
Коши Вейерштрасса и далее через весь анализ XIX XX вв. Это на..
правление можно назвать неконструктивным ан8JIИС30М, так как
в ero основе лежит неконструктивное определение предела перемен
ной величины. Друrое направление восходит к механическому при
ему Архимеда (некоторые полаrают, что еще к Демокриту) и идет
через метод "неделимых" , интеrральные методы Кеплера, Паскаля и
Ферма, "метод флюксий и степенных рядов" Ньютона, "исчисление
дифференциалов" Лейбница, "метод компенсации ошибок" Карно и
"исчисление нулей" Эйлера [15, т. 3, с. 265 272] к современному H
стандартному анализу. Это направление можно назвать авалИСЗ0М
бесконечно малых.
Современное состояние обоих направлений таково, что они
"равносильны" Apyr Apyry: все результаты в не стандартном aHa
лизе MorYT быть доказаны и методами неконструктивноrо анализа,
и, наоборот, всякое положение в анализе Коши Вейерштрасса имеет
нестандартный аналоr. Поэтому преподавателям, а также школьни
кам физматшкол полезно было бы знакомиться с обоими направл
ниями в анализе. В связи с этим рассмотрим примерный вариант
ознакомления школьников 9 11 классов физматшкол с основами aHa
лиза. В 9 10 классах можно дать rеометрическое определение лоrа
с
рифма как площади подrрафика rиперболы у = (с > О) на участке
ж
192
от 1 до Х (при этом площадь берется со знаком "плюс", если Х > 1,
И со знаком "минус", если Х < 1, или наоборот). Такое определ
иие лоrарифма хорошо уже тем, что делает наrлядным такие ero
свойства, как область определения, обращение в нуль при Х = 1,
монотонность и выпуклость вверх. Такое rеометрическое оriредел
v
ние окажется полезным и в дальнеишем, так как черro Hero леrко
прослеживается связь между круrовыми и rиперболическими фун
кциями, между первым и вторым замечательными пределами и их
доказательствами. Основное свойство лоrарифмической фУНКЦИИ Дfr
казывается сначала методом интеrральных сумм Архимеда с исполь
зованием рассуждений от противноrо. Затем следует показать, как
это свойство может быть доказано с помощью метода "неделимых"
Метод интеrральных сумм Архимеда можно затем примев.ять для
нахождения и
доказательства формул для площади Kpyra, площади витка архи
медовой спирали, объема цилиндра, объема пирамиды, объема Kfr
нуса. Параллельно следует проводить вычисление этих площадей и
объемов с помощью метода "неделимых"
Далее, дифференциальное исчисление в 9 10 классах может быть
дано в следующей форме. Сначала дается- понятие средней скорости
функции f(x) на о резке [Xl. Х2] VФ[Хl, Х2] = f(X2) f(Xl) , ее
Х2 X1
физическая и rеометрическая интерпретации. Затем rоворится, что
функция и(х) называется производной функции f(x) на интервале
(а, Ь), если существует с > О такое, что для любоrо отрезка [X1, Х2]
из интервала (а, Ь) и для любой точки х из отрезка [X1, Х2] выпол
няется HepaBeH TBO
IV4[X1' Х2] и(x)1 < ClX2 x11
\
И дается физическая и rеометрическая интерпретация этоrо опреде
ления. Доказываются теорема о том, что если такая производная cy
ществует, то она единственна, теоремы о производных суммы, Прfr
изведения и частноrо, теорема Ферма, теоремы Ролля и Лаrранжа.
Находятся производные основных элементарных функций пост
янной, степеннои, синуса, косинуса, лоrарифма (при нахождении пр
из водных трех последних функций удобно использовать и rеометри
ческое определение). Приведенное определение производной в отли
чие от определения производной через предел не требует проведения
Тяжелых € 6 рассуждений и одновременно приучает школьников к
193
математической строrости доказательств.
В последнем, II M классе физматшколы параллельно с изуче
нием анализа на основе понятия предела можно было бы предложить
школьникам следующую формализацию классическоrо анализа бес
конечно малых. Множество R обычных ("стандартных") веществен
ных чисел расширяется до множества R. "не стандартных" веще
ственных чисел следующим образом: х Е R х + те Е R., rде r
произвольное "стандартное" вещественное число, а е "актуально
1
бесконечно малая величина", (т.е. О < е < при любом натуральном
n
n) и, кроме Toro, такое, что е 2 = о. Все функции распространяются
с R на R. "по монотонности", т.е. если f(x) < g(x) при а < х < Ь,
то и /(х.) < g(x.) при а < х. < ь. Функцию /(х) будем называ'rь
непрерывной в точке х, если
[/(х + те) /(х)] е = О,
или, что то же самое,
/(х + те) = /(х) + а . е,
rде а Е R, а = а(х, т). Если, кроме Toro, величина а линейна отно--
сительно т, Q = f'(x) т, то будем rоворить, что функция /(х) д 4r
ференцируема в точке х, а функция f'(x) eCT производная функции
f(x). Такое определение производной исторически соответствует
"методу флюксий и степенных рядов" Ньютона и "исчислению ди4r
ференциалов" Лейбница и позволяет дать простые, чисто алrебра
ические доказательства единственности пр оизводной , производной
суммы, произведения, частноrо, теоремы Ферма о локальном экс
тремуме.
Упражнение 48. Проведите все эти доказательства.
Производная степенной фун
кции находится непосредст
венно, а производные синуса,
косинуса и лоrарифма нахо--
дятся с использованием pa
венств ln(1 + те) '= те и
sin те = те (аналоrов замеча
х
тельных .пределов). Эти pa
венства выводятся с помо--
у
1
1
l+х
1 l+х
Рис. 69
194
шью rеометрических соображений. Так, первое равенство получа
ется из следующеrо rеометрически очевидноrо неравенства для пло--
щадей: 1: х < In(l+x) < х при х > О (рис. 69), если это неравенство
распространить с R+ на R+. При т > О будем иметь':
те
1 < ln ( 1 + те ) < те
+ те
Но
те те(1 те) ___ те т 2 е 2
= те
1 + те --- 1 т 2 е 2 --- 1 т 2 е 2
Отсюда и следует, что ln(1 + те) = те для всякоrо т > о. Справед
вость этоrо равенства для т < О следует из Toro, что ln(1 --- те'
ln ( 1: re ) = ln(1 + re) = re.
Равенство sin те = те получается из rеометрически очевиr.ноrо
неравенства О < sinx < х < tgx при О < х < (см. рис. 43 п 5.1),
7r 7r
если это неравенство распространить с О < х < 4 на О < х. < 4 '
Упражнение 49. Проведите полное доказательство равенства
sln те = те.
В качестве примера рассмотрим установление непрерывности и
нахождение производной у синуса. Имеем:
sin(x + те) = sin х cos те + cos х . sin те =
= si n х \1"1 sin 2 те + cos х . sin те =
=sinx \l" 1 (Te)2+cosx Te=sinx+cosx те,
поэтому функция sin х непрерывна, дифференцируема и ее произвcr
днан равна cos х.
УПDажнение 50. Установите непрерывность и дифференцируе
МОСТЬ и найдите производные у функций х П , cos х, ln х, e Z
Далее можно предложить школьникам определение интеrрала. Для
3Toro потребуется ввести актуально бесконечно большое число N,
1 1
обратное к е, Т.е. такое, что N = е ' е = N ' е N = N е = I,N > n
для любоrо натуральноrо n. Положим теперь по определению:
i f(x) dx =. O[t,/{Xl:) (Хl: Xl: l)]
195
N
rде х1с = а + (Ь а) k€ (так что хо = а, а XN = Ь), L: есть зна
1c=1
n
чение суммы L: при замене натуральноrо n на бесконечно большое
1c=1
N, символ 0[. .] означает "стандартную" часть стоящеrо в скобках
числа. Например,
J х 2 dx = D [ t(ke)2. е ] = D [ е З tk2 ] =
О 1c=1 1c=1
}з N(N+l (2N+l) ] = }2 2N 2 +:N+l ]
О [ 1 1 1 2 ] 1
= 3 + 2 е + 6 е = 3
Упражнение 51. Пользуясь указанным определением интеrрала,
1
найти f e Z dx
о
От предлаrаемой формализации классическоrо анализа беско--
нечно малых можно далее перейти к изучению нестандартноrо aHa
лиза [31, 10,22, 18, 13].
Вопросы u зада'Н,u,Н
1. Что утверждается и доказывается в лемме Евдокса с точки
зрения современной теории пределов?
2. Что лежит в основе метода интеrральных сумм Архимеда?
3. Что лежит в основе метода "неделимых"? Всеrда ли этот метод
приводит к правильным результатам?
4. Что такое "характеристический треуrольник" у Паскаля и у
Лейбница?
5. Какие две rлавные задачи решаются в методе "флюксий" и CTe
пенных рядов Ньютона?
6. В чем отличие вейерштрассовскоrо определения дифференци
ала от ero определения по Лейбницу?
7 В чем состоит проблема обоснования дифференциальноrо и ин
теrральноrо исчисления?
196
8. В чем состоит метод "компенсации ошибок" Карно?
I
9. Что такое "не стандартный анализ"?
10. Что такое производная по Даламберу?
11. Что такое производная по Лаrранжу?
12. Назовите проблемы, приведшие к необходимости заново по--
строить основные определения анализа. На какой основе стро--
ится анализ у Коши и Вейерштрасса?
13. Чем. непосредственно было вызвано введение интеrралов Ри
мана и Дарбу?
14. Приведите критерии интеrрируемости Римана и дю Буа
Реймона.
15. Дайте определение меры множества по Кантору, Штольцу,
rapHaKY и Пеан Жордану. Укажите принципы мероопределе
ния Бореля.
16. Укажите дескриптивное определение интеrрала у Лебеrа. К
чему свел Лебеr проблему интеrрирования?
17 В чем состоит проблема восстановления примитивной фун
кции? Как она решалась в диссертации Лебеrа?
18. Какие два направления можно выделить в развитии основ aHa
лиза?
rлава 6
'"
ИСТОРИЯ ОТЕЧЕСТВЕННОИ
МАТЕМАТИКИ
6.1 МАТЕМАТИЧЕСКИЕ ЗНАНИЯ НА
РУСИ В х.....хуI ВЕКАХ
Имеющиеся исторические документы позволяют дать следую..
щую общую характеристику первых этапов развития математики
на Руси.
Уже в начале Х в. на Руси существовала письменность. Тесные
связи с Византией способствовали ускоренному приобретению зна..
ний. Математическое образование находилось в то время на уровне
европейскоrо. Было налажено обучение придворных.
Использовалась славянская система нумерации, ведущая свое
происхождение от rреческой буквенной нумерации. Числа от 1 до
9, а также десятки и сотни изображались с помощью последова..
тельных букв алфавита, причем над буквой стаВИJ:IСЯ особый знак
l"'tJ ("титло"), подобный знаку - в rрече ской буквенной нумера..
ции. Тысячи также обозначались буквами, но со знаком _ ко--
торому В rреческой нумерации соответствует знак ' Десятки
тысяч ("тьмы") обозначались буквами в кружочке, сотни тысяч
("леrионы" или "неведии" ) обозначались буквами в кружке из точек,
а миллионы ("леодры") обозначались буквами в кружке из черточек.
Отдельные отступления от общеrо правила связаны, в основном, с.
рмличием между rреческим и славянским алфавитом. Вот некото--
рые обозначения чисел в славянской системе нумерации.
198
#IItIJ
1 ("аз")
",."
2 В ("веди" )
3 r ( "r лаrоль" )
l'ttJ
4 .д ("добро" )
5 Е ( "есть" )
6 S ("зело")
#"fttI
7 ( "земля" )
reJ
8 Н ( "иже" )
"."",
9 Д, ("фита" )
l"ttJ
10 , ("и")
20 1\ ("како")
30 ( "люди" )
",."
100 Р ( "рцы" )
I"W
200 С ("слово")
""'-1
300 Т ("твердо")
1000
2000
10000
20000
100000
200000
.h.
,.
@
@
.8\... е.
eQ.
е . .
.е е, . ..
. .
. .
. .
l"ttJ
90 'у ( "чер вь" )
При записи чисел с несколькими значащими цифрами, цифры пи
,
сали слева направо в порядке убывания десятичных разрядов. Напри
мер',' 321 = Т \'\ ,1024 =_ь. д
Помимо вычислений чисто практическоrо характера, связанных
с измерением и межеванием земель, торrовыми расчетами, стро--
ительством зданий и укреплений, с содержанием княжеских дpy
жин, со сбором налоrов и т.п. на Руси рано появляются первые
теоретические задачи, составленные "числолюбцами" преимуще
ственно церковнослужителями. Древнейшей из сохранившихся MaTe
матических рукописей являются записи новrородскоrо дьякона Ки
рика (1134 r.). Вот некоторые примеры задач, собранные из ра3ных
рукописей:
а) вычисление, сколько месяцев, недель, дней и часов прошло от
"сотворения мира" (т .е. от 5508 r. до н .3.);
б) задачи на вычисление проrрессий при расчете приплода скота;
в) вычиеление размеров. Земли, Солнца и Луны по данным изме
рений Эратосфена (rреческоrо ученоrо 1 в. до Н.З.);
199
r) теоретико--числовая задача о вычислении дат релиrиозноrо
праодника пасхи.
При вычислении использовали мешочек с вишневыми или сливо--
выми косточками, дощечку для писания по воску ("церу") и "писало"
металлическую или костяную палочку, имевшую с одной сто--
роны заострение, а с друrой лопаточку. Исходные числа и pe
зультаты счета наносились на "церу" Счет велся с помощью ко--
сточек и назывался "с'1:ет костьми" или "пенязи" и заключался в
следующем. На столе чертили несколько продольных и поперечных
линий. Число продольных линий зависело от числа разрядов у Ha
ибольшеrо из данных чисел" а число поперечных полос зависело от
характера действия. Так, при сложении проводили только одну по--
перечную прямую, а при умножении столько, сколько нужно было
записать частных произведений. На рис. 70 показано, как проводи
лось умножение 66 на 96. При помощи счета костьми выполняли не
5000 о о
1000
500 о
100
50 о о о
10
5 о о о о
1
66 96 6х6 6х90 60х6 60х90 6336
Рис. 70. Счет костьми, 66 х 99 = 6336
только все арифметические действия, но и выIисленияя с примене
нием "тройноrо правила" т.е. вычисление четвертоrо члена про
пориии по трем данным членам. Отметим еще, что кроме счета
костьми позднее употреблялся еще так называемыи дощаной счет
костяшками, нанизанными на шнур прообраз вычисления на сче
тах.
Остановимся еще на ;J;ревнерусской метролоrии. Три основные
v
древнерусские меры Д.IИНЫ носят название частеи тела или движе
ния рук: "пядь" , "локоть" и "сажень" . Большая пядь есть расстояние
200
от большоrо пальца руки до мизинца (примерно 23 см). Локоть pa
внялся двум пядям. Сажень равнялась трем локтям или шести ПJlдям.
Использовались и некоторые друrие виды пядей и, соответственно,
локтей и саженей. Более крупной мерой длины служила "верста", ко--
торая первоначально равн.ялась 500 саженям, примерно 690 мвт--рам.
Мерами емкостей служили "кадь" (древняя кадь вмещала около 14
пудов ржи), "лукно" (вмещало около 60 фунтов зерна), "ведро" (9 10
литров) и некоторые друrие. Мерами земельных участков служили
"соха", "четверть", "десятина" и некоторые друrие. В сохе счита
лось 800 четвертей доброй земли, четверть составляла половину д
сятины, а десятина составляла, соrласно, например, писцовому Ha
казу 1554 r., в длину и в ширину по 50 сажен. Мерами веса служили
"rривны", "золотники", "пуды" и некоторые друrие. I»ивны и зо--
лотники служили также основными мерами денеr. Большая rривна
составляла 96 золотников и весила около фунта, т.е. вполне COOTBeT
ствовала "фунту стерлинrов" Малая rривна составляла 48 золотни
ков, т.е. половину большой rривны. Современный русский денежный
счет, построенный на основе деления рубля на 100 копеек, восходит
к ХУ в. И сложился на основе московской денежной системы, соrла
сно которой 1 "рубль" =200 "деньrам", 1 "полтина" = 100 "деньrам",
1 "rривна" =20 "деньrам", 1 "алтын" =6 "деньrам" (из указанных дe
нежных единиц до XVIII в. только "деньrа" была серебряной чекан
ной монетой, а "рубль" "полтина" и "rривна" были лишь счетными
единицами) .
Общий со всеми rосударствами Европы ход развития науки и
культуры был насильственно прерван в первой половине XII! в. из
за нашествия монrоло--татар (1240 r.) и крестоносцев (1242 r.). Эти
нашествия, а также феодальная раздробленность и непрекраща
щаяся междоусобица в Русском rосударстве привели к длительному
застою во всех областях общественной жизни. В области науки этот
застой усуrублялся до XVI XVII вв. деятельностью православноrо
PYCCKoro духовенства, которое. в борьбе с католицизмом Запада под
верrало запрету не только западную релиrиозную литературу, но
и светскую, в том числе научную литературу. В одном дpeBHepyc
ском: поучении так прямо и rоворится: "Боrомерзостен перед боrом
всякий, кто любит rеометрию; а се лушевные rрехи учиться астроно--
...
мwlИ и ;эллинским книrам; по своему разуму верующии леrко впадает
в ра личные заблуждения; люби простоту больше мудрости, не изы
скуй Toro, что BblUle тебя, а какое дано тебе от БОf'а учение, то и
держи" .
201
6.2 МАТЕМАТИЧЕСКИЕ РУКОПИСИ
XVII ВЕКА
Имеются основания считать, что первые математические PYK(r
писи rео етрическоrо характера, связанные с измерением и меж
ванием земель, имелись на Руси не позднее XV XVI вв. Однако до
нас ДОШЛИ только математические рукописи XVI! В., да и то только
немноrие. Прежде Bcero, это "Устав ратных, пушечных и друrих дел,
касающихся до ВОИНСКОЙ науки" , создание KOToporo относится к 1607
и 1621 rr. В "Уставе" излаrаются некоторые rеометрические CBeд
ния, относящиеся, в основном, к вычислению расстояний или раоме--
ров. Рассмотрим в качестве примера следующую задачу из "Устава"
Требуется измерить длину недоступноrо отрезка PQ (рис. 71). Для
Р
о
М'
Q
Рис. 71
этоrо употреблялась "ПaJЮчка Якоби" жезл MN с делениями, на
КОТОРЫЙ надет малЫЙ жезлик АВ длины, равной длине одноrо дел
ния большоrо жезла. "Устав" предлаrает наблюдателю, rла3 KOT<r
poro находится в точке М, установить малЫЙ жезлик АВ так, чтобы
лучи, исходящие ИЗ точки М и проходящие через точки А и В, пр<r
ходили бы также через точки Р И Q. Затем малый жезлик перем
щается по большому на одно деление, а наблюдатель перемещаетCJI
из точки V в такую точку М', что лучи, исходящие ИЗ точки М' и
проходящие через концы А' и В' малоrо Же3лика, снова проходили
бы через точки Р И Q. Тоrда, как утверждается в "Уставе", ММ'
будет равно PQ. Действительно, из подобия треуrольниlCОВ МАВ и
MPQ и треуrольников М' А'В' и M'PQ следует, что
ММ'
PQ
202
М'О МО
PQ
М'О МО М'С'
= PQ PQ = А'В'
МС М'С' ..... МС АВ
АВ = & АВ = АВ
т.е. ММ' действительно равно PQ.
Предполаrают, что все рукописи XVII в. имели один общий ис..
точник, из KOToporo авторы заимствовали содержание своих руко..
писей вплоть до переписывания целых предложений. Общее содержа..
ние рукописей примерно таково. Сначала даются правила действий
с целыми числами и дробями, излаrается тройное правило (пропор..
ция), затем дается большое число статей (параrрафов), отвечающих
потребностям ToproBoro люда. Для примера приведем выдержки из
оrлавления одной рукописи:
"ПеРВ8JI стать.. от числа. Нумерация или считание словесом
и начертание числом цифирным
Друrв.. стать... Адитсие или считание. Статья именуется CI<r
стряксие, по..русски вынимание или вычитание
Стать.. о весах и мерах оемли немецкие, брабанские, rородов
raHHoBepa и Норенсборхе
Стать.. ФраВЦУОСJCие оемли и о денежном счете ливонском,
виницейском и флоренском
Стать.. тройвв.. в ЦeJIЫХ И oп..x ВС"КИХ
Стать.. TOprOB8JI "Здесь дается большое количество задач
на вычисление цены товара, прибыли от продажи и т.п. Так, условие
одной из зада .rласит: "rость купил 8664 овчины, а сторrовал 100
1
овчин по 1 и 2 рубля; да и продал те овчины, ино ему сходилося со
100 овчин по 8 овчин прибыли. Ино, сколько тот rость за овчины
денеr платил и что у овчин принял денеr, сочти ми." (уплачено за
все овчины "129 рублёв 32 алтына" , а прибыль составила "10 рублёв
9
13 алтын да 1 и деньrи"
" 25
Стать.. о вечести во ВCJlких овощах И товарах " Здесь
решались задачи на вычисление цены смесей, расчеты со сплавами
t30лота, серебра и меди.
"Стать.. мевовв.. в Topry " Здесь решались t3адачи на про..
порции, возникающие при обмене товаров. Например: "Четыре ro..
стя СЛОЖIIДИСЯ торrовати. Первый положил 266 рублёв, друrой по--
ложил 388 рублёв, третий положил 490 рублёв, четвертый положил
590 рублёв. И п иняли К себе торrовца прикащика, Koro им отпу"
СТити С теми деньrами на иной rород торrовати. А посулили ему
за ero службу, что не приторrует, ино изо прикупа ему взяти четь.
А прикащик так у них и приторrовался, да тут же из своих денеr в
Topr приложил 344 рубля. И приторrовал прикащик на все деньrи 489
203
рублёв. Ино почему которому rостю по их складу прикупу досталося
и что прикащик за службу взял, сочтй ми."
В заключение рукописи приводились задачи занимательные, на
смекалку. Например, задача о плотниках. "Четыре плотника наня
лись двора ставити. И rоворит первый плотник так: только б де мне
одному тот двор ставити, я яз бы де ero поставил един rодом. А дpy
rой молвил: только бы де мне одному тот двор ставити, и яз бы де
ero поставил в два rода. А третий молвил: только бы де мне одному
тот двор ставити, и яз бы де ero поставил в три rоды. А четвертый
так рёк: только бы де мне одному тот двор ставити, и яз бы де ero
поставил в четыре rода. Ино, сколь долrо они ставили, сочти ми."
( rода или 175 и дней).
Приведенные в рукописях решения задач свидетельстуют о раз
витом искусстве счета. При этом часто использовались таблицы сло--
жения и умножения, которые прилаrались к рукописям.
Математическая терминолоrия рукописей XVII в. еще значи
тельно отличалась от современной. Так, слаrаемые назывались пе-
реЧНJlМИ, их сумма испо ним БОJIЬШИМ перечнем, YMeHЬ
шаемое оаемным перечнем, вычитаемое ПJIатежным пе-
.
речнем; сомножители и их произведение особых наименований не
имели; делимое называлось БОJIЬШИМ перечнем, делитель e..
ловым перечнем, частное жеребейным перечнем, а остаток
u u
остаточнои ОJIеи.
6.3 opr АНИ3АЦИЯ школ
в период монrолcrтатарскоrо нашествия школы, получившие Ha
чало еще в Киевской Руси Х в. почти прекратили свое существова
ние. 3нания передавались УСТНО редкими rрамоте.ями.
В XVIl в. русское православное духовенство в целях усиления
борьбы с западной католической церковью вынуждено было rOTo
вить духовных пастырей, хорошо Ра3би!)ающихся в вопросах боrо
словия, лоrики, риторики и диалектики. Это приве..l0 к открытию u
1687 r Славяно rреко латинской академии в 1:)CI\.Be. I стен ;этоЙ
акацемии вышли Л.Ф. lаrНИЦКIIЙ, aBTOr известноrо учеБНI1f'.а Il
Iатематике: а также выдающийс.я русский ученый и просветиr:-еЛr>
М.lЗ. ЛОМОНОСОВ.
204
Реформы, начатые Петром 1, потребовали и орrанизации ши
pOKoro cBeTcKoro обучения. Посылка Петром 1 значительноrо коли
чества молодых людей за rраницу и орrанизованное им за rраницей
печатани книr для России не дало ожидаемоrо эффекта. Поэтому
еще в 1698 r. Петр 1 приrласил в Москву профессора Аббердинскоrо
университета анrличанина Фарварсона для преподавания MaTeMa
тики и морских наук. Вскоре после ero приезда, в 1701 r., в Москве
была основана и начала работу "математических и навиrацких, то
есть мореходно--хитростных наук школа" Фарварсон развил энер
rичную деятельность: он участвовал в разработке проrрамм нави
rацкой школы, ввел в них арифметику, алrебру, rеометрию, триrоно--
метрию плоскую и сферическую, сам преподавал их, а также писал
учебники.
В 1715 r. на базе навиrацкой школы была создана и переведена
в Петербурr Морская академия. Одновременно Петр 1 распорядился
разослать в rубернии по два ученика этой школы, выучивших reo--
метр ию и rеоrрафию, "для науки молодых ребяток из всяких чинов
людей" Образовавшиеся таким образом в rуберниях школы полу
чили название "цифирных", так как в них обучали прежде Bcero
арифметике и rеометрии. Инструкция, дававшаяся учителю цифир
ной школы, rласила:" . учить тебе дьячих, подъяческих, поповых и
прочеrо церковноrо чину, архиерейскоrо дому и монастырских слуr
детей их, по высылке от воеводы, от 10 лет до 15, а посадских и про--
чих чинов детей же, которые сами похотят, кроме дворянских детей,
а дворянских детей отнюдь не принимать, арифметике, а именно,
нумерации, аддиции, субстракции, мультипликации, ДИВИЗИИ, трой
ных правил и тройных детрательных, как без долей, так и с долями и
десятичноrо счету и деления, радиксу квадрата и радиксу куба; а ко--
торый ученик вышеозначенную науку обучит, тех учить rеометрии,
а именно: прежд.е истолкованию rеометрии и циркульных приемов,
потом триrонометрии плоской, планиметрии и штирометрии"
Население, однако, неохотно отпускало своих детей в цифирные
школы. Посадские люди первые стали бить челом о разрешении их
детям не посещать цифирных школ, так как "детей надо к ремеслу
приучать, за прилавком сидеть" Просьба посадских людей была
удовлетворена. Далее, Синод потребовал, чтобы дети духовенства
были переведены в епархиальные школы, также орrанизованные при
Петре 1. Требование Синода также было удовлетворено. В резуль
тате в четырнадцати цифирных школах учеников не осталось, и пре
подаватели из провинции вернулись в навиrацкую школу. В OCTa
вшихся цифирных школах 15% учеников сбежали, несмотря на то,
205
что за неявку в школу нередко сажали в тюрьму, на цепь; а еще 10%
учеников были признаны "безrрамотными, неспособными и идио
тами"
Обучение в цифирной школе было построено следующим обра;зом.
Идеальным порядком в классе считался такой, коrда каждый ученик
зубрил свою часть предмета вслух. Учитель, уверенный, что все за
няты своим делом, Mor СПОК9ЙНО отдаться собственным занятиям.
Соrласованноrо хора при этом быть не моrло, так как учащиеся
одноrо класса проходили разные части одноrо предмета или даже Bcr
обще различные предметы. Так, например, в арифметическом классе
рязанской цифирной школы в 1727 r. 11 учеников учились счислению,
5 сложению, 1 вычитанию, 3 умножению, 5 делению, 3
тройному правилу, 1 десятичным дробям, 1 циркульным
приемам, 1 плоской триrонометрии и TaHreHcaM.
Цифирные школы просуществовали до 1744 r. К этому времени
из 42 школ, бывших в 1722 r., осталось только 8. Три самые боль,.
шие из них были слиты с так На3ываемыми rарнизонными школами,
,учрежденными в 1732 r. rарнизонные ШКОЛЫ создавались при полках
и содержались на полковые средства. Преподавателями были офи
церы и унтер офицеры. Помимо rpaMoTbl, они преподавали солдат..
скую экзерцицию, арифметику, артиллерию и инженерство. rарни"
зонные школы, также как и цифирные ш.колы, сыrрали значительную
рель в распространении элементарных математических знаний. Из
этих школ, а также из духовных семинарий вышла основная масса
учителей математики.
6.4 "АРИФМЕТИКА" Л.Ф. МАI'ницкоrо
Леонтий Филиппович Маrницкий (1669 1739) был одним из са..
мых выдающихся людей России петровскоrо времени как по сво--
ему общему образованию, так и по своим математическим позна
ниям. Первоначальное образование Маrницкий получил в МОСКО--
вской славяно..rрекcrлатинской академии. Там он изучил латинский
и rреческий языки, а затем уже самостоятельно rолландский, He
мецкий и итальянский. Самостоятельно же он изучил и математику,
притом в объеме, значительно большем, чем сообщалось в русских
рукописях XVII'B. Маrницкий был хорошо знаком с современной ему
европейской учебной литературой, а также с произведениями rрече..
ских и латинских авторов.
206
В 1703 r. Маrницкий напечатал в Москве свой учебник
"Арифметику", которая почти сразу же стала основным учебни
ком по математике в России на мноrие rоды. Научные, педаrоrи-
ческие и литературные достоинства книrи Маrницкоrо привели I<
тому, что даже спустя мноrие десятки лет после ее написания, после
Toro, как появились книrи, более соответствующие состоянию Ha
уки, "Арифметика" Маrницкоrо продолжала пользоваться успехом
как у составителей учебников, так и у обучающихся математике.
Название книrи "Арифметика" значительно уже ее coдep
жания, так как, помимо арифметических сведений, в ней давались
также значительные алrебраические, rеометрические, триrономе
трические, а также метеоролоrические, астрономические и навиrа
ционные сведения. "Вратами учености" называл эту книrу Ломоно-
сов.
Перейдем теперь к содержанию "Арифметики" После общих pac
суждений о пользе арифметики, после KpaTKoro описания содержа
ния книrи, ее rерба, после описания деяний Петра 1 и тому подобных
замечаний (причем все это изложено в стихах), Маrницкий описы
вает арабскую (индийскую) десятичную позиционную систему счи
сления. При этом значащие цифры называются "знаменованиями" ,а
нуль "цифрою" Числа первоrо десятка называются "перстами" ,
числа вида "знаменования" с нулями (например, числа 20, 700, )
"суставами", а все остальные числа "сочинениями" Далее ц
лая страница занята числами вида 10" и их наименованиями. Ta
блица таких чисел доведена до 1024, после чеrо следует стихотворе
ние, указывающее на неоrраниченность числовоrо ряда: "Число есть
б сконечно, умом нам недотечно. И никто не знает конца, кроме всех
боrа творца "
Далее в учебнике излаrается арифметика целых чисел и дро--
бей ("чисел ломаных"), учение о проrресси,ях, учение о корнях KBa
дратных и кубических, тройное правило. Причем между этими co
ственно математическими частями первой книrи учебника Маrни
цкий помещает еще большую rлаву, посвященную описанию древних
весов и монет, сравнению их с существующими, а также денеr, весов
и мер "MOCKoBcKoro rосударства и окрестных некиих"
Вторая книrа учебника Маrницкоrо подразделяется на следу
щие части: "Арифметика алrебраика", "О rеометрических, через
арифметику действуемых" , "Обще о земном измерении и яже к Mope
плаванию принадлежа" и "О толковании пробемат навиrацких раз
личных через вышеположенные таблицы локсодромические" .
207
В учебнике cTporo проводится единая форма изложения: каждое
правило начиналось с простоrо примера, затем .давалась ero общая
формулировка и, наконец, оно закреплялось большим количеством
задач преимущественно практическоrо содержания. К каждому дей
ствию присоединялось правило проверки "поверение" '
Для учебника Маrницкоrо характерна также ярко выраженная
прикладная тенденция. МаrницlCИЙ ясно сознавал, что в России Toro
времени математика была нужна в первую очередь как орудие прак
тической деятельности. Это обстоятельство оказало существенное
влияние на характер изложения. Все основные понятия излаrаются
так, что они связываются у читателя с привычными житейскими
образами. Так, на вопрос, "что есть число ломаное", Маrницкий OT
вечает: "Число ломаное ничто же иное есть, токмо часть вещи, чи
слом объявленная, сиречь полтина есть половина рубля, а пишется
111 2
сице 2 рубля или 4 ' или пятая часть 5 ' или две пятых части 5" и
всякие вещи яковые либо часть, объявлена числом, то есть ломаное
число"
Прикладная тенденция продолжается и в примерах, почти все
они облечены Маrницким в практическую и занимательную форму:
"Некоrда в Константинеrраде 20 человек мылись в бане. В них же
были христиане, турки же и евреи, а заставлено имать за баню с
турка по пол деньrи, а с христианина по деньrе, с еврея же по три
деньrи. Но всех бывших в бане есть 20 человек. Дали банщику от всех
20 денеr. И ведательно есть знать, колико было христиан, турок и
евреев"
"Купил 112 баранов старых и молодых, дал 49 рублёв 20 алтын,
за cTaporo барана платил по 15 алтын и по 2 деньrи, а за молодоrо
по 10 алтын, и ведательно есть, колико старых и молодых баранов
купил он"
"Некий rенерал хочет с 5000 человек баталию учинить и чтобы
та была в лице вдвое нежели в стороне и ведательно есть колико оная
баталия имети будет в лице и в стороне человек" И так далее.
Отметим еще, что стремясь удовлетворить запросы купечества,
Маrницкий вставляет в свой учебник специальный большой раздел
с rлавами "Тройная торrовая в товарных овощах и с вывескою"
"Статья меновая в Topry", "Торrовая складная со времены" и тому
подобное.
208
6.5 ОСНОВАНИЕ АКАДЕМИИ НАУК.
Реформы, проводимые Петром 1, все более требовали уже не
просто rpaMoTHblx людей, но людей, знакомых с современным c<r
стоянием науки и техники и способных проводить самостоятел
ные научные исследовании. Поэтому Петр 1, по совету немецкоrо
философа и математика Вольфа, издал в 1724 r. указ об орrаниза
ции российской Академии наук, а при ней' университета и rимназии.
"Академики должны нам приобрести в 'Европе доверие и честь, A<r
казав на деле, что и у нас работают для науки и что пора перестать
считать нас за варваров, пренебреrаюдщих наукой" , писал Петр 1.
В проекте положения об Академии, одобренном Сенатом, Академия
определялась как "собрание ученых и искусных людей, которые не
только сии науки в своем роде, в том rpaAyce, в.котором оные ныне
обретаются, изучают, но и через новые инвенты оные совершить и
умножить тщатся" Университет же определился как "собрание уч
ных людей, которые наукам высоким . до KaKoro состояния оные
ныне дошли, младых людей обучают"
В отличие от иностранных академий российская Академия наук
не имела характер чисто научн<rисследовательскоrо учреждения, а
служила прежде Bcero центром распространения научных знаний.
Она выrодно отличал ась от мноrих иностранных академий тем, что
была на твердом rосударственном бюджете, располаrала физич
ским кабинетом, анатомическим театром, типоrрафией и rpaBep
ной палатой, механическими и оптическими мастерскими, библио--
текой. Отличалась российская Академия наук от иностранных aKa
демий и составом наук, которые в нее входили. Она делилась на три
класса: математический, физический и rуманитарный. Математи
ческий класс состоял из четырех кафедр: математики, астрономии,
rеоrрафии и навиrации и двух кафедр механики. Физический класс
также состоял из четырех кафедр: теоретической и эксперименталь
ной физики, анатомии, химии и ботаники. В rуманитарный класс
ВХОДили три кафедры: красноречия и древностей, древней и новой
истории, праnа, политики и этики. Не похо-ж был на западноевро--
пейские и академический университет. В состав ero входили юриди
ческий, медицинский и философский факультеты, в то время как в
западноевропейских университетах сохранилось еще в значительной
степени схоластическое и боrословское направление, а протестант
СКИе немецкие университеты и вовсе имели боrословский факультет.
209
Российская Академия наук и ее университет оказались центром H
вой светской науки, свободной от релиrиозноrо влияния.
На должности профессоров кафедр российской Академии наук
были приrлашены, по совету Вольфа, rлавным образом молодые, п
дающие надежды заrраничные ученые. При этом особенно удачным
оказался подбор профессоров по классу математических наук. При
ехали: Яков repMaH, Николай и Даниил Бернулли, затем Христиан
rольдбах, и, наконец, в 1727 r. приехал Леонард Эйлер.
Тотчас же после приезда в Россию первых профессоров и aKa
демиков начал издаваться журнал "Комментарии Санкт Петербурr
ской Академии" первый российский научный журнал. Блаrодаря
прежде Bcero работам Эйлера (их насчитывается в этом журнале
473), "Комментарии" быстро становятся одним из ведущих науч
ных журналов Toro времени. С деятельностью Эйлера вообще тесно
связано все, что касается математики в российской Академии наук в
первые полвека ее существования (о жизни и деятельнсти Л. Эйлера
подробнее см., например, [16, т. 1, rл. VII IX; 9, с. 72 83]).
Однако со смертью Эйлера (1783 r.) российская Академия H YK
в области математики надолrо потеряла свое научное значение.
Восемь учеников л. Эйлера rоловин, Иноходцев, Крафт, Лессель,
Котельников, Румовский, Фусс и А. Эйлер все ставшие впослед
ствии академиками, были учеными далеко не первой величины. OCH
вная их деятельность относится к области преподавания: написан
ные ими учебники долrое время пользовались успехом.
6.6 оРrАНИЗАЦИЯ УНИВЕРСИТЕТОВ
Оживление научной жизни в России тесно связано с орrаниза
цией университетов. Выше уже отмечалось о создании универси
тета в Петербурrе при Академии наук (1725 r.). В этом первом в
России университете обучалось поначалу Bcero восемь студентов, да
и то выписанных специально для этоrо из Западной Европы. Даже
несмотря на то, что при Академии наук была специально создана
rимназия для подrотовки будущих студентов, несмотря на учрежде
ние специальных стипендий для лучших выпускников Славяно--rреко--
латинской академии (в их число попал Ломоносов), поддерживать
жизнедеятельность университета не удавалось, и в 1783 r. он был
:закрыт.
210
Второй российский университет Московский был основан
Ломоносовым в 1755 r. В нем первоначально было лишь три факуль
тета: юридический, медицинский и философский. При университете
были созданы две rимназии: одна для дворян, друrая для разночин
цев. Однако, несмотря на это, Московский .университет, так же как
и Петербурrский, постоянно страдал o недостатка студентов. Бы
вали случаи, коrда на всех курсах Toro или иноrо факультета OCTa
вался Bcero один студент. Поэтому для увеличения континrента слу
шателей в 1758 r. была открыта и придана универси.тету rимназия
в Казани. Преподавание математики в первые rоды существованv
MOCKoBcKoro универститета было поставлено очень слабо. ДО 176С
не было даже кафедры математики. Почти полстолетия объем ft
тематических знаний, сообщаемых в университете, оrраничивa,j 11
арифметикой, началами алrебры и rеометрией с элементами три}
нометрии.
Орrанизации новых университетов в России в начале Х1 Х в.
способствовали реформы Сперанскоrо, проводимые в области обра
зования. Эти реформы были направлены к тому, чтобы поощрить
и даже принудить чиновников и дворян к получению образования.
Лица, оканчивающие университеты, автоматически получали Te
перь обер офицерский чин. В 1803 r. было постановлено, что через
пять лет никто не может поступи ь на rосударственную службу,
требующую специальных знаний, без диплома каз6нноrо или ча
cTHoro училища. В 1809 r. вышел указ об экзаменах на чин. Спе
ранский отметил в этом указе, что дворянство мало заботится о
школьном обучении своих детей, так как "имеется удобность до--
стиrать чинов не заслуrами и отличными познаниями, но одним
пребыванием и счетом лет службы" Потребность в образовании
возросла. Реформы потребовали новых источников подrотовки пр
подавателей. Выход был найден в создании новых университетов.
К Московскому университету добавились университеты, открытые
в Казани и Харькове в 804 r., в Петербурrе в 1819 r. в Ки
еве в 1834 r. Одновременно был выработан новый университет
ский устав, соrласно которому университеты подраздел.ялись уже
Не на три, а на четыре факультета: к трем ранее указанным до--
бавился физико--математический факультет. Теперь в течение трех
лет университетскоrо курса студентам читали так называемую чи
стую математику, включавшую арифметику, алrебру, rеометрию и
триrонометрию (повторительный курс), аналитическую rеометрию
211
и высшую алrебру, дифференциальное и интеrральное исчисление, а
со временем и друrие собственно математические предметы, и при
кладную математику, включавшую механику, оптику, астрономию
и тому подобное. Первые два rода обучения отводились для чистой
математики, третий .rод для прикладной математики. В неделю чи
талось от 3 до 6 часов лекций. Содержание курсов постепенно обо-
rащалось. Появились, прежде Bcero в Казанском университете, пер
вые спецкурсы. В качестве учебных пособий широко использовались
руководства' Эйлера и ero ближайших учеников и по слер;ователей, а
также пособия зарубежных авторов (более подробно об этом см.,
например, [16, т. 2; 9, 7 15]).
6.7
, u
н.и. ЛОВА ЧЕВСКИИ (1792 1856)
Николай Иванович Лобачевский родился в 1792 r. в Нижнем Но-
вrороде в семье мелкоrо чиновника. С 1802 r. по 1806 r. учился в Ka
занской rимназии. В январе 1807 r. был допущен к слушанию лекций
в Ка:занском университете. Большую роль в формировании Лоба
чевскоrо как математика сыrрали в rимназии учитель математики
Карташевский, а в университете профессора Бартельс и Литтров.
Бартельс привлек молодоrо Лобачевскоrо к изучению классических
трудов Эйлера, Лаrранжа, Монжа, Лапласа, raycca, а Литтров
к проведению астрономических наблюдений. Окончив в 1811 r. уни
верситет, Лобачевский продолжал свое математическое обра:зова
ние под руководством Бартельса, а с 1814 r. началась и ero препо--
давательская деятельность в Казанском университете. За более чем
тридцать лет работы в университете Лобачевский читал все осно--
вные курсы по математике, а иноrда также механику, астрономию
и физику, заведовал кафедрой физики, астрономической лаборато--
рией, долrое время был деканом отделения физических и математи
ческих наук, ректором университета.
Мировую известность принесла Лобачевскому созданная им He
евклидова rеометрия. Интерес к элементам rеометрии и к знамени
тому пятому постулату Евклида о параллельных появился у Лобаче
BCKoro в связи с чтением им курса лекций по элементарной rеометрии
сначала чиновникам, rотовившимся к экзаменам на производство в
чин, а затем студентам университета. Исследования цо теории па
раллельных Лобачевский начал, как и друrие математики, с попыток
доказательства пятоrо постулата. Одно время ему казалось, что он
212
нашел доказательство, и в 1817 r. Лобачевский даже приводил ero в
своих лекциях. Вскоре он, однако, обнаружил, ч о найденное им до--
кat3ательство не проходит, так как опирается на недоказанное пред
положение [16, т. 2, с. 155 156].. Не позднее 1822 r. Лобачевский скло--
няетсЯ к мнению о невооможности окаGательства потулата о
параплельиых. "Напрасные старания со времен Евклида, в про--
должение двух тысяч лет, писал позднее' Лобачевский о попытках
доказательства постулата о параллельных, заставили меня по
дозревать, что в самих понятиях еще не заключается той истины,
которую хотели доказать "[16, т. 2, с. 156]. Отказ'авшись от яв
ных попыток доказательства пятоrо постулата, Лобачевский пошел
друrим путем. А именно, заменив этот постулат противоположным
ему утверждением (что через точку, не лежащую на данной пря
мой, можно провести по крайней мере две прямые, не пересекающие
данной прямой), он стал на этой основе строить новую, неевкли..
дову, rеометрию. Первые полученные на этом. пути результаты
были высказаны Лобачевским в докладе на тему "Сжатое изложе
ние начал rеометрии со строrим доказательством теоремы о парал
лельных линиях", а в 1829 r. в университетском журнале "Казанский
вестник" вышла первая печатная работа Лобачевскоrо по разраба7"
тывавшейся им новой rеОМ,етрии. Статья эта называлась "О нача
лах rеометрии" и состояла из двух частей. Изложение начал новой
rеометрии Лобачевский начинает словами: "Мы видели, что сумма
уrлов прямолинейноrо треуrольника не может быть больше 1r. OCTa
ется предположить ;эту сумму = 7r или < 7r. То И друrое может быть
принято без всякоrо ПРОТlIворечия впоследствии, от чеrо и проис
ходит две rеометрии: одна употребитеЛЬНaJI до ныне по своей
простоте, соrлашается со всеми измерениями на самом деле; друrая
воображаемаи, более общая и потому затруднительная в своих
вычислениях, допускает возможность зависимости линий от уrлов.
если в OДHO прямолинейном треуrольнике посчитать сумму УСЛ0В
7r, То она будет такой уже и во всех. fId.!1poTI!B, допуская ее D ОДНОМ
менее 'iТ .1erKo доказать, что она уменьшается возрастанием боков
треуrоЛьника. Всякий ра:з, следоватепьно, две линии на ПЛОСКОСТИ
встречаться не MorYT, коrда они с третьею составляют уrлы, KOT
рых сумма 1r. Они MorYT не пересекаться и в том случае, коrда эта
сумма меньше 7r, если к тому предположить сумму уrлов в треуrо.пь
нике < 7r IITaK, все линии на плоскости в отношении к одной MorYT
быть разделены на сход.ищиес.в: и неСХОДJlщиеСJl. Последние будут
213
ншзываться параллельными, если они представляют rраницу, или,
иначе сказать, переход от одних к друrим между всеми, выходящими
из одной точки.
Воображаем из точкиопущенный перпендикуляр а на данную ли
нию и К этой параллельную из этой же точки; обозначим Р(а) уrол
между а и параллельной. Леrко доказать, что всякой линии а уrол
1r
F(a) = 2' если сумма уrлов в треуrольнике = 1r; но В друrом предпо
ложении уrол Р(а) меняется с а, уменьшаясь до нуля с увеличением
1r
а и оставаясь постоянно < 2 " [16, т. 2, с. 156 157]. Уrол Р(а) Лоба
чевский назвал "уrлом параллельности" и показал, что зависимость
этоrо уrла от величины перпендикуляра а имеет вид
F( а) = 2 arctg ехр ( : )
q const
Устанавли ая далее дедуктивным путем все новые и новые положе
ния своей rеометрии, Лобачевский ниrде не обнаруживает противо--
речия.
В начале второй части статьи Лобачевский устанавливает триrо--
нометрические соотношения для всякоrо прямолинейноrо треуrоль
ника и отмечает, что с точностью до членов высшеrо порядка мало--
сти относительно сторон треуrольника эти соотношения совпадают
с соответствующими соотношениями в rеометрии Евклида, так что
естественно В'озникает вопрос о том, какая же из rеометрий на ca
мом деле имеет место в природе. Пытаясь ответить на этот во--
прос, Лобачевский- провел астрономические наблюдения, стараясь
возможно точнее определить сумму уrлов прямоуrольноrо астро--
номическоrо треуrольника, один по катетов KOToporo диаметр
Земли, а друrой направлен ортоrонально диаметру в одном из ero
концов. Взяв в качестве третьей вершины неподвижную звезду Си
риус с известным параллаксом, он обнаруживает, что сумма уrлов
TaKoro астрономическоrо треуrольника отличается от 1800 менее,
чем на 0,000372 секунцы, что HaMHoro меньше поrрешности изме
рений. Так что "наблюдения астрономическце убеждают в том, что
все линии, которые подлежат нашему измерению, даже расстояния
между небесными телами, столь малы с линиею, принятой в теории
за единицу, что употребительные до сих пор уравнения прямолиней
ной Триrонометрии без чувствительной поrрешности должны быть
справедливы" заключает Лобачевский [16,.т. 2, с. 159]. "Очень Be
роятно, добавляет он, что Евклидовы положения одни только
214
истинные, хотя и останутся навсеrда недоказанными. Как бы то ни
было, новая rеометрия, основание которой уже здесь положено, если
не существует в природе, тем не менее может существовать в нашем
воображении и, оставаясь без употребления для измерений на самом
деле, открывает новое обширное поле для взаимнb.lХ применений re
ометрии и Аналитики" [там же, с. 159]. Так, рассматривая reoMe
трические образы новой rеометрии, Лобачевский указывает новые
способы нахождения некоторых ранее известных интеrралов. Это
служит для Hero подтверждением правильности (непротиворечиво--
сти) созданной им rеометрии. Он находит также некоторые новые
определенные интеrралы.
К сожалению, работы Лобачевскоrо были не поняты ero COBpe
менниками. Так, М.В. Остроrрадский в отзыве на рассмотренную
выше статью Лобачевскоrо писал: "Все, ч'fо я понял в rеометрии r
на Лобачевскоrо, ниже посредственноrо. Все, что я не понял, было,
по--видимому, плохо изложено по той же самой причине "[16, т. 2,
с. 161]. Несмотря на это, Лобачевский продолжал до конца своей
жизни отстаивать и развивать свою rеометрию. Наиболее полным
изложением системы Лобачевскоrо являются ero "Новые начала reo--
метрии с полной теорией параллельных" (1835 1838 rr.). При этом в
конце указанной работы он делает еще следующее важное замечание:
"В природе мы познаем только движение, без KOToporo чувственные
впечатления невозможны. Итак, все прочие понятия, например reo--
метрические, произв дены нашим умом искусственно, будучи взяты
в свойствах движения; а потому пространство само собой, отдельно
для нас не существует. После чеrо в нашем уме не может быть ника
Koro противоречия, коrда мы допускаем, что некоторые силы в при
роде следуют одной, друrие своей особой rеометрии" Эта доrадка
Лобачевскоrо о возможности различных rеометрических свойств в
различных участках пространства в зависимости от "сил", является
далеким предвосхищением идей общей теории относительности Эй
нштейна.
u
6.8 М.В. остРоrРАДСКИИ (1801 1861)
Михаил Васильевич Остроrрадский родился в 1801 r. в семье
ПО?vfещика Полтавской rубернии. С 1810 по 1813 r. обучался в
215
полтавской rимназии. В 1816 r. О троrрадский был определен воль
нослушателем в Харьковский университет. Здесь он был заме
чен преподавателем университета Павловским и, блаrодаря под
держке и наставничеству последнеrо, сумел уже в 1818 r. успе
шно сдать экзамены университетскоrо курса. Пробыв затем r'од
в деревне у отца, Остроrрадский вернулся в университет с целью
"усовершенствования себя по части наук, относящихся к прикладной
математике" В 1820 r он успешно сдал выпускные экзамены и был
представлен ректором университета Осиповским к ученой степени
кандидата наук. Однако ни ученой степени, ни даже аттестата об
окончании университета Остроrрадскому получить не удалось из за
развернувшейся в это время травли Осиповскоrо и из за обвине
ния caMoro Остроrрадскоrо в вольнодумстве и в непосещении лек
ций по боrословию. Остроrрадскому было предложено сдавать за
ново все эк амены, на что он ответил отказом и в 1822 r. уехал
в Париж для совершенствования cBoero математическоrо образова
ния. Здесь в течение шести лет он слушал лекции Коши, Пуассона,
Фурье и друrих ведущих французских матема иков. Слушание лек
ций в Сорбонне, Коллеж де Франс и в Политехнической школе, He
посредственное общение Остроrрадскоrо с крупными французскими
математиками, интенсивная самостоятельная работа привели к по--
явлению первых научных статей Остроrрадскоrо, которые сразу же
привлекли внимание своей актуальностью и высоким математиче
ским уровнем.
В 1828 r. Остроrрацский вернулся на родину и в первые же Me
сяцы представил А&адемии наук три работы, получившие блестящий
отзыв Коллинса. В 1830 r. Остроrрадский избирается постоянным
членом Академии наук.
Деятельность Остроrрацскоrо в Академии наук была разносто--
ронней. Он сделал более 85 научных сообщений, частью неопубли
кованных; читал публичные лекции; писал по робные отзывы на по--
ступающие в Академию наук работы, участвовал в различных ко--
миссиях, занимался по поручению правительства изысканиям:и по
внешней ба.'1ЛИСТlIке, и т .,);. Вместе с тем Остроrрадский MHoro Bpe
мени уделял преподаванию. Он читал лекции в Морском корпусе, вел
'занятия по математике и механике в Институте инженеров путей
сообщения, rлавном инженерном и rлавном аРТИ:Iлерийском учили
щах, rлавном педаrоrическом институте, с 1847 r. и до своей смерти
216
работал в должности rлавноrо наблюдателя по преподаванию M'a
тематических наук во всех военных учебных заведениях. Ему при
надлежат несколько руководств по элементарной и высшей MaTeMa
тике. Широкую известность получил ero курс по небесной мехаИ}Jке
(1831 r.), а также учебные пособия по аналитической механике и
высшей алrебре (1836 и 1837 rr.).
Своей научной и педаrоrической деятельностью Остроrрадский
в значительной мере способствовал подъему математическоrо обра
зования в стране. После публикации цикла работ по математической
физике (конец 20 начало 30 x rr.) в 30 40 x rr. появились работы
Остроrрадскоrо по математическому анализу, а за ними иссле
дования в области аналитической механики. Во всех направлениях
Остроrрадский достиr результатов первостепенной важности. Так,
уже в одной из своих ранних работ, представленной Парижской aKa
демии наук в 1826 r. и опубликованной ею в 1832 r., Остроrрадский
вывел систему уравнений' теории волн малой ампл.!lТУДЫ на повер
хности тяжелой несжимаемой жидIЮСТИ и проинтеrрировал ее для
случая прямоrо KpyroBoro цилиндрическоrо сосуда при COOTBeTCTBY
ЮЩИХ краевых и нулевом начальном условиях. В "Мемуаре об ис
числении вариации кратных интеrрапов" (1834 r.) не только решена
проблема, поставленная Парижской академией наук в 1840 r. (т.е.
шесть лет спустя!), но и выведена важнейшая формула KpaTHoro ин
теrрирования, позволяющая вычисление n KpaTHoro интеrрал cncr
дить к вычислению (п l) KpaTHoro интеrрала. В механике OCTpcr
rрадский независимо от rамильтона установил одно из важнейших
ее положений так называемый принцип наименьшеrо действия.
Подробнее о работах Остроrрадскоrо см., например, [16, т. 2, с. 54
57]. Большим успехом пользовались лекции Остроrрадскоrо, KOTcr
рые он читал на высоком европейском уровне, но вместе с тем прcr
сто и ясно. Именно блаrодаря Остроrрадскому во всех учебных заве
дениях, rде он преподавал, значительно улучшилась математическая
подrотовка слушателей. Вынуждены были подтяrИ}jаться к уровню
JIекций Остроrрадскоrо и преподаватели математики и механики n
университетах.
6.9 п.л. чЕБыIЕвB (1821..1894)
Пафнутий Львович Чебышев (Чебыш6в) родился в 1821 r. в
Калужской rубернии в небоrатой старинной дворянской семье. По--
пучив хорошее домашнее образование, молодой Чебышев в 1837 r.
217
становится студентом математическоrо отделения философскоrо фа
культета MOCKoBcKoro университета. Окончив в 1841 r. университет
"отличнейшим кандидатом" Чебышев в 1845 r. защитил маrистер
скую диссертацию "Опыт элементарноrо преподавания теории Be
роятностей" Н 1847 r. он защитил в Петербурrском университете
диссертацию "Об интеrрировании с помощью лоrарифмов" на право
преподавания и был утвержден адъюнктом этоrо универ ситета. Н
1849 r. Чебышев защитил диссертацию "Теория сравнений" и был
удостоен степени доктора математики и астрономии. Через два rода
он экстраординарный, а с 1860 r. ординарный профессор Петер
бурrскоrо университета.. С 1859 r. Чебышев постоянный член AKa
демии наук.
Н Петербурrском университете Чебышев читал высшую алrебру,
теорию чисел, аналитическую rеометрию и сферическую триrоно--
метрию, теорию эллиптических функций, интеrрирование диффе
ренциальных уравнений, практическую механику, интеrральное ис
числение, теорию вероятностей. и 'изредка некоторые друrие MaTe
матические курсы. А.М. Ляпунов так вспоминал о своем учителе:
"Курсы ero не были обширными, и при изложении их он заботился
не столько о количестве сообщаемоrо материала, сколько о выясне
нии принципиальных сторон трактуемых вопросов. Отличаясь жи
вым и увлекательным изложением, лекции ero сопровождались мно--
жеством интересных замечаний относительно значения и важности
тех или друrих вопросов или научных методов. Замечания эти BЫ
сказывались иноrда мимоходом по поводу какоrо--либо KOHKpeTHoro
случая, но всеrда rлубоко западали в умах ero слушателей. Нслед
ствие этоrо лекции ero имели высокое развивающее значение, и слу
шатели ero после каждой лекции выносили нечто существенно но--
вое в смысле большей широты взrляда и новизны точек зрения" [38,
с. 341]. Н своих лекциях Чебышев нередко давал обширные истори
ческие справки о разработке Toro или иноrо вопроса. Педаrоrиче
скую деятельность Чебышева отличала также и яркая способность
к постановке задач. "Н математике . найти и верно поставить
вопрос несравненно труднее, чем ero решить; rоворил впослед
ствии Е.И. Золотарев, как скоро вопрос поставлен и поставлен
верно, решение ero так или иначе отыщется. Пафнутий Львович
отличается изумительной способностью и уменьеl\-I ставить новые
вопросы в математике" [38, с. 341]. Непосредственными учени
ками Чебышева были А.Н. Коркин, Ю.Н. Сохоцк й, Е.И. Золотарев,
218
А.А. Марков, А.М. Ляпунов, и.л. Пташицкий, и.и. Иванов, К.А. По--
ссе, Д.А. !раве, r.Ф. Вороной, А.В. Васильев и др. Научная деятель
ность этих ученых протекала под rлубоким воздей<;твием Чебышева,
мноrие прямо продолжали разработку ero тематики, и все они pac
пространяли идеи cBoero учителя в университетах и друrих высших
школах Петербурrа, Казани, Киева, Харькова, Варшавы.
Преподавательскую деятельность Чебышев сочетал с орrаниза
торской работой, имевшей большое значение для развития отече
ственной науки и техники, образования и просвещения. С 1855 r. он
член Артиллерийскоrо отделения военно--учетноrо комитета (и в это
время проводит исследования по устойчивости цилиндро--конических
снарядов). С 1856 r. член ученоrо комитета Министерства Hap
дноrо просвещения. Своей деятельностью в комитете Чебышев OKa
зал значительное влияние на постановку и уровень преподавания
математики в начальных и средних учебных заведениях. В 1859 r.
ero назначают "правителем дел комиссии по математическим артил-;
лерийским вопросам и опытам, относящимся до теории стрельбы", в
1867 r. членом техническоrо комитета rлавноrо артиллерийскоrо
управления. Видную роль сыrрал Чебышев и в становлении и даль
нейшей деятельности MOCKoBcKoro математическоrо общества.
Научные интересы Чебышева характеризуются большой широ--
той и прикладной направленностью при очень высоком теоретиче
ском уровне. Во всех областях сВоей научной деятельности (те о--
рия чисел, интеrрирование функций, теория вероятностей, теория
наилучшеrо приближения функций, теория интерполирования, Te
ория механизмов) Чебышев достиrал фундаментальных или значи
тельных результатов. Так, в мемуаре "Об определении числа про--
стых чисел, не превосходящих данной величины" (1851 r.) Чебы
шев установил, что число (x) простых чисел, меньших х, коле
l Х dx
блется около функции Li(x) l . Широко известны Heo
2 nx
ходимые и достаточные условия интеrрируемости в элементарных
функциях дифференциальноrо бинома х т (а + ЬхП)Р , полученные Че
бышевым (1853 r.) как применение ero же фундаментальных теорем
об интеrрируемости алrебраических функций. Современные TpaK
ТОВКИ и доказательства основных законов теории вероятностей
заКОНа больших чисел и центральной предельной теоремы также
восходят к работам Чебышева (1867 и 1887 rr. соответственно). В
теории наилучшеrо приближения функций Чебышеву принадлежат
как постановка основных задач, так и разработка общих методов
219
..
их решения. Широко известны введенные им (1853 r.) мноrочлены
Тn(х) = 21 n cos(n arccos х), обладающие свойством наименьшеrо
(из всех мноrочленов данной степени n) уклонения от нуля (т.е. свой
ством минимума модуля) на отрезке [ 1, 1]. Подробнее о работах
Чебышева см., например, [16, т. 2, с. 188 238].
Значительная часть работ Чебышева вызвана непосредствен
ными нуждами практики. Таковы ero работы "Об одном механизме" ,
"О зубчатых колесах", "О центробежном уравнителе", "О постро
нии rеоrрафических карт", "О кройке платьев" и др. Чебышеву при
надлежит свыше 40 конструкций различных механизмов и около 80
их модификаций. "Сближение теории с практикой дает самые блаrо--
приятные результаты, писал Чебышев, и не одна только прак
тика от этоrо выиrрывает; сами науки развиваются под влиянием
ее: она открывает им новые предметы для исследования, или новые
стороны в предметах давно известных. Несмотря на ту высокую CTe
v
пень развития, до которои доведены науки математические трудами
великих reoMe poB трех последних столетий, практика явно обна
руживает неполноту их во мноrих отношениях; она предлаrает во--
просы существенно Ho ыe для науки и, таким образом, вызывает на
изыскание совершенно новых метод, и в этом случае наука находит
себе BepHoro руководителя в практике" [9, с. 117]. Среди всех задач,
которые ставит перед людьми их практическая деятельность, oco
бенную важность имеет, по мнению Чебышева, следующая задача:
"Как располаrать средствами своими для достижения по возмож
ности большей выrоды" Именно поэтому "большая часть вопросов
практики приводится к задачам наибольших и наименьших величин,
совершенно новым для науки, и только решением этих задач мы MO
жем удовлетворить требованиям практики, которая везде ищет ca
Moro лучшеl'О, caMoro выrодноrо" [там же, с. 117]. Приведенные ци
таты яплялись цля caMoro Чебышева руководящими принuипами cro
деятельности и всей жизни. ПОf]:, влиянием этих И;I;ей ЧеБJ)IUIева в
петербурrской !\1атематической школе спожился обlIlИЙ ПОДХОf]; к Ma
тематике. A. 1. Ляпунов характериоовал eru слеJ;УЮIЦИМИ L:JIонами:
"П.JI. Чебышев и ero после:J;онатели остаются постоянно на реаль
ной почве, руковоцствуясь взrлядом: что только те изыскания имеюТ
цену, которые вызываются приложеНИЯ:\1И (научными или I!рактиче
скими), и только те теории действительно полеЭНhI, которые BЫTe
кают из рассмотрения частных С lучаев." [16, т 2. . 18'7]'
220
РАЗБОР УПРАЖНЕНИЙ
1. Это буквенная десятичная чисто аддитивная нумерация, в ко--
торой численные значения основных знаков букв славянскоrо ал
фавита определяют я вспомоrательными значками.
2. Числительные "один" и "два", в отличие от числительных
"три" "четыре", "десять" изменяются по родам, что указы
вает на остатки двоичной системы счисления, как наиболее дpe
вней. Числительное "пять" (пясть, кисть) указывает на ручной счет
"пятерками" Пословицы и поrоворки, связанные с числом "семь":
"семеро одноrо не ждут", "семь раз отмерь, один раз отрежь" "у
семи нянек дитя без rлазу" и т.п. указывают на то, что в свое время
"семь" означало "MHoro" , и счет велся в пределах от одноrо до щести.
Числительное "сорок" и выражение "сорок сороков" указывает на
счет "сороками" Числительное "девяносто" происходит от числи
тельных "девять десят" и "десять до ста", первое из которых обра
зовано по мультипликативному принципу, а второе по субтрак
ТИВIIОМУ.
3. Составление отношений можно определить для любой пары
отношений, а именно: (А В) (С D) = (А 1 Е) (Е D 1 ) = (A 1
D 1 ), rде Е наименьшее общее кратное В и С, Е = тВ = nС,
А 1 = тА, D 1 = nD.
Далее, результат составления отношений не за исит от выбора
пар, т.е. если (А' В') = (А" В") и (С' D') = (С" D"), то
(А' В') (С' D') = (А" В") (С" D"). Действительно,
из определения равенства отношений следует, что А' = mA 1 , А" =
тА 2 , В' = nА 1 , В" = nА 2 , С' = kC 1 , С" = kC 2 , D' = lC 1 , D" = lC 2 .
Поэтому (А' B') (C' D') = (тА 1 nA1) (kC1 lC 1 ), (А" B")
(С" D") = (тА 2 nA2) (kC2 lС 2 ). Пусть Е общее кратное А1,
А 2 , С 1 , С 2 , т.е. Е = Р1А1 = Р2А2 = q 1 C 1 = Q 2 C 2 . Тоrда (mA i nAi)
(kC i lC i ) = (mpiAi nPiAi) (kQiCi IQiCi) = (тЕ nE)fl)(kE IE),
Т.е. результат составления отношений действительно не зависит от
выбора пар.
221
Для, каждой пары (А В) пара (В А) будет обратной, если
пару (А А) взять за единицу rруппы. Ассоциативность операции
составления отношений очевидна: ((А B) (B C)) (C D) = (А
С) (С D) = А D, и (А В) ((В С) (С п)) = (А 8) (В
D) = А D. Проверим коммутативность. Пусть Е общее кратное
А, В и С, Е = тА = nВ = kC. Тоrда (В С) (А В) = (kB
kC) (тА тВ) = (kB Е) (Е тВ) = (kB тВ) = (knB
тnВ) = (kmA mkC) = А С = (А В) (В С).
Таким образом, действительно множество классов пропорцио
нальных пар с операцией составления отношений образуют KOMMY
тативную rруппу. Эта rруппа очевидно изоморфна мультипликати
вной rруппе положительных рациональных чисел.
4. Если а Ь = е d в смысле определения пифаrо'рейцев, то
найдутся отрезки / и 9 такие, что а = k/, е = kg, Ь = 1/, d = Ig.
Отсюда следует, что та = mk/, те = mkg, nЬ = nlf, nd = nlg.
Поэтому та < nЬ <==} mk < nl <==} те < nd, та = nЬ <==} mk =
nl <==> те = nd, та > nЬ <==> mk > nl <==} те > nd; т.е. а Ь = е d
и в CMыc e определения Евдокса.
5. Роrовидный уrол а вполне определяется радиусом Та той
окружности, дуrа которой образует криволинейную сторону этоrо
уrла. Равенство, сумму и разность двух роrовидных уrлов можно
определить как, соответственно, равенство, сумму и разность кри
визн их дуr, т.е. следующим образом: если а +---+ Та И /3 +---+ Тrз, то
,
а = /3 <==} Та = Т/3 ,
/3 1 т/3та
а:!: 1 1
:i: Т/3 :i: Та
Та Т/3
1 1
Аналоrично, будем rоворить, что а < /3, если < . rеометриче
Та Т/3
ски последнее означает, что а < /3, если при совмещении вершин и
прямолинейных сторон этих роrовидных уrлов и при откладывании
их криволинейных сторон (дуr) в одну и ту же сторону начало дуrи
уrла о окажется между началом дуrи уrла /3 и общей прямолинейной
стороны этих уrлов. В соответствии с этим rеометрическим опре
делением будем считать, что а < /3 для всякоrо роrовидноrо уrла а
и для всякоrо обычноrо уrла /3. При этом будут выполнены аксиомы
1 5, но не выполнена аксиома 6, так как та < /3 для любоrо целоrо
т, для любоrо роrовидноrо уrла а п ,ля любоrо обычноrо уrла /3.
222
6. Покажем сначала, что из равенства отношений через па
раллельность следует их равенство через равновеликость прямоу
rольНИКОВ. Отложим отрезки а, Ь, е, d на сторонах прямоrо уrла
так, как это сделано на
рис. 72. По условию пря
мые 11 и 12 параллельны.
Проведя параллельно сто--
ронам уrла пр мые, обо
значенные пунктиром, из
равенства треуrольников
l' и 1" замечаем, что а' =
а, так что 3 есть прямоу
rольник на а и d, а 3'
прямоуrольник на Ь и е.
Равновеликость этих пря
моуrольников следует из аксиомы 3. Действительно, прямоуrоль
ники 3 и 3' получаются из одинаковых больших треуrольников, со--
ставляющих вместе большой прямоуrольник со сторонами а + е и
Ь + d, путем вычитания одинаковых треуrольников 1 и 1', 2 и 2'
Покажем теперь, что из равенства через равновеликость прямо--
уrольников следует равенство по Евдоксу. Предположим противное.
Пусть прямоуrольники на а и d и на Ь и е равно велики, но а Ь;/; е d
по Евдоксу. Тоrда найдутся натуральные числа т и n такие, что
та > nЬ, но те < nd (или наоборот, та < nЬ, но те > nd). Тоrда
прямоуrольник на та и nd содержит прямоуrольник на nЬ и те, и
следовательно (аксиома 5) будет больше ero. Но это противоречит
тому, что эти прямоуrольники составлены из т.n равновеликих пря
моуrольников на а и d и на Ь и е соответственно, и, следовательно,
(аксиома 2) также равновелики.
Покажем наконец, что из равенства по Евдоксу следует равенство
отношений через параллельность. Предположим противное. Пусть
а Ь = е d по Евдоксу, но прямые 11 и 12 не параллельны (рис. 73).
Проведем прямую l' параллельно 11. Тоrда, по выше доказанному,
а Ь будет равно е d' в смысле определения Евдокса, причем d' ;/;
d. Но если ;].; < d, то по аксиоме 6 найдется натуральное число n
такое, что n Ll = n(d d') > е. По этой же аксиоме, найдется
натуральное число т такое, что те < nd, но (т + l)е > nd. Тоrда
те = (т + l)е е > nd nLl = nd n( d d') = nd' и, следовательно,
та > nЬ, что несовместимо с те < nd. В случае d' > d точно так же
а
d
с
1"
2'
3'
2
а'
1
3
Рис. 72
223
существуют т и n такие, что n (d' d) > е и те < nd < (т + l)е.
Но тоrда (т + l)е = те + е < nd + n( d' d) = nd' и, следовательно,
(т + l)а < nЬ, что несовмести.мо с (т + l)е > nd.
7. Уравнение задачи может быть з писано в виде
rде а длина данноrо отрезка,
а х длина ero большей части.
Переписав это уравнение в виде
а(а х) = х 2 , т.е. в виде pa
венства площадей прямоуrоль
ника со сторонами (a x) и а, и
квадрата со стороной х, и доба
вив к этим одинаковым площа
дям по пря оуrольнику со CT
ронами х и а (см. рис. 74), будем
иметь: х(а-+ х) = а 2 , так что
искомая задача свелась к задаче
типа 3а. По теореме 3 произве
дение х(а+х) раскладывается в
разность квадратов (х + ) 2
( ; ) 2 Поэтому искомый отре..-
зок х может быть построен как
разность отрезков (х + ) и ,
первый из которых есть rип
а
тенуза прямоуrольноrо треуrольника с катетами а и 2 .
8. Обозначим В' В = у. Для доказательства Toro, что х 3 = 2а 3 ,
а х у
достаточно проверить, что = = 2 . Из подобия треуrольников
х у а
, ' А AD В'В а у
ADD и В В заключаем, что DD' = ВА ' или х = 2а . Далее, по
теореме Пифаrора, (Ов')2 = (у + ) 2 + а 2 , а (OD')2 = (х + а)2 +
( ) 2 Приравнивая эти выражения, будем иметь: у2 + ау == х 2 + 2ах.
Это уравнение выполняется, если у2 == 2ах и ау = х 2 , т.е. если :а =
а
е
Рис. 73
х
х
a x
а
L.....
Рис. 74
24
а х=х (a x),
:.. Друrих же решений нет, так и:ах если бы, например, было у >
у.
2ах, то было бы ау < х 2 , и, следовательно, было бы одновременно
JL. > ж и J!.... = а < ж (?!).
2а у 2а х у
9. Так как треуrольники О'СО и СОВ равнобедренные, то
LA08 = LOO'B,+ LOBO' = LOO'B + LOCB = LOO'B + LCO'O +
LCOO' = 3LAO'B.
10. Если 3а = 900, то а = sin3a = 1, и уравнение трисекции
прямоrо уrла запишется в вид
4ж 3 3ж + 1 = О .
Это уравнение приводимо над основным полем К = Q, а имевво:
4ж 3 3ж + 1 = (2ж 1)(2ж 2 + ж .... 1) ,
поэтому трисекцИJI уrла в 900 может быть проведена с помощью
циркуля и J1инейки (проведите само построение!).
Если же 3а = зо , то а = sin3a = , и уравнение трисехции уrла
в 300 запишется в виде
1
4X3 3X+ 2 =0.
Это уравнение неприводимо над К = Q, так как если бы оно быJЮ
приводимо, т.е. раскладывалось на множи ели с рациональными K(r
эффициентами, . то мы имели бы
(8ж 3 6ж + 1) = (Qж + ,8)(аж 2 + Ьж + с),
rде ct, ,8, а, Ь, с целые рациональные числа. TorAa ,8 = :i:l,
ct = :i:l, 2, 3, 8, и, следовательно, уравнение имело бы рационалlr
ный корень вида ж = :i:l, !' !, i Но непосредственной проверкой
леrко убедиться, что ни одно из этих значений не являетCJI .корнем
уравнения. ПQЭТОМУ уравнение действительuо неприводимо на Q и,
следовательно, трисекци.и уrла в 300 с помощью циркуля и линейки
невозможна. Построение правильноrо деВJIтиуrольника с помощью
циркуля и линейки равносильно трисекции уrла 1200, что, в свою
очередь, равносильно трисекции уrла 300, и поэтому также Heвoo
Можно.
225
11. Рациональные соотношении между ХОрВJIМи имеют вид:
ж = Х2, xf = zз, ж1 = Х4,
x = Х4, ж = жl, ж = zз,
x =xl, zg=Z4, Ж =Ж2,
Х4 2 = .... 3 Х 3 .... ....4 ....
, 4 "2, "4 1,
ХI Ж 4 = Z2ХЗ = 1.
I»уппа rалуа
G = {(124з)i, i = 1, 2, 3, 4} =
= {(1243), (13)(24), (1342), (1)}
Ее ПОрЯДОК 22, поэтому задача nOCTpoelllUl правИJIЬноrо ПJlтиуrоль
ника, вttисанноrо в единичную охружность, задача, выр.жаема& ypa
внением
5 I O
ж ,
разрешима с помощью циркули и JIВвепи.
Радикальные выраженИJI для хорней имеlDТ вид:
х = !x VS :i: J6T 2 VS 4
4 4 16
(третий звах определиетCJI противопOJЮЖНО первому, а второй
независимо от первоrо) , и построение правильноrо ПJlтиуrольниха
может быть проведено из условии
211" v'5 1
сos 5 = 4
(см. разбор упражненИJI 7).
12. Линейное однородное диффереици&ПЬное уравнение l ro n<r
рядка
у' + р(ж)у = О,
инвариавтно относительно преобразо ваlПl"i вида
{ х ж,-
у ............... ау ,
они и составляют ero rруппу Ли. Преобразование
{ z ............... z
у ............... ln у
226
переводит эту rруппу в rруппу сдвиrов Lo, а само уравнение в
уравнение YI + р(х) = О, не содержащее у.
Линейное неоднородвое дифференциальное уравнение l ro по--
рядка
у' + р(х)у = q(x) ,
инвариантно относительно преобра:эовавий вида
{ х Х,
у ............ ау + (1 а)е f p(z) dz fq( х) . е! p(z) dz dx ,
составляющих ero rруппу Ли. Преобразованием
{: = :. efp(z)dz
она переводитCJI в rруппу сдвиrов, а само уравнение в уравнение
у' = q(х)еfР(:J:)dж, не содержащее у.
13.
А
Пусть А меСТОПОJlOжение корабля, 1 линия береrа
(рвс. 75). Пройдем вдоль береrа
одина.ховые расстоянии ВО иОВ'
Затем под уrлом В', равным уrлу
В', пройдем вrлубь береrа до той
точки А', направление И3 которой
на корабль А и на точку О совпа
дают. Тоrда по й теореме Tpey
rольВИIИ ОБА и ОВ' А' будут pa
вны и, следовательно, ВА = В' А'
14. Уравнение касательной
плоскости к поверхности z
z(x, у) в точке (ха, Уа, za) имеет
вид
А'
Рис. 75
(z za) = Z (X07 уо) (х хо) + z (xa, уа) (у уа)
Из условия, что вершина конуса (а, Ь, ) принадлежит всякой Kaca
тельной ПЛОСКОСТИ, получаем.
(z с) = z . (х а) + z (у Ь)
дифференциальное уравнение конической поверхности.
227
Далее, заменой и = х а, v = у Ь, w = z с перенесем начало
координат в вершину конуса. Пусть v = <р(и) линия пересече
ния конической поверхности с плоскостью w = 1. Тоrда, если точка
(и, v, w) лежит на конической поверхности, то точка ( : ' : ,1)
также лежит на конической поверхности. Поэтому получаем
: = ( : ) ,
или у ь = ( х а' )
z c z c
конечное уравнение конической поверхности.
15. Проведем ВС паралдельно АА' (рис. 26). Тоrда
ВА Б'S ОА' СА' В' А' ОА'
ОА BS В'А' = ОА' СА' В'А' = 1
16. Проведем через точку А прямую KL параллельно с'о. Тоrда
(В' о' А С') = В' А В'С' В'А D'A AL АК
= =
D'A D'C' В'С' D'C' С'О С'О
AL AL АК ВА DA БА ВС = (В D А С)
АК СО СО ВС DC DA DC
Для решения задачи проведем медиану AN (рис. 76). Обо--
значим через О точку пере
се'чения медиан ВМ и AN,
а через Р точку пересе
чения прямой AQ со сторо--
ной ВС. Тоrда, в силу pa
венства двойных отношений
(BCPN) и (BMQO), будем
вр вр BN
С иметь: 8 Р СР CN
BQ В m 2
m 2п
Рис. 76 MQ МО n 1 .
Приведите злементарное решение задачи, не используя инвари
антность двойноrо отношения.
17. Проведем через точку D прямую KL параллельно PQ. Тоrда
в
А
м
РМ PN
(PQMN) = QM QN
228
KD KL KD TD
TD DL = KL DL
PQ QP = 1 .
PN PN
Если AD параллельно ВС, но АВ не параллельно CD, то ABCD
трапеция, точка Q лежит на несобственной прямой, PQ параллельно
ВС и теорема принимает вид: РМ = PN.
Если и AD параллельно ВС, и АВ параллельно CD, то ABCD
параллелоrрамм, точки Р и Q лежат на несобственной прямой
(которая и является в этом случае третьей диаrональю), а теорема
принимает вид известной школьной теоремы о том, что диаrонали
параллелоrрамма делятся в точке пересечения пополам.
18. Пусть в треуrольнике PBQ (рис. 28) прямые РС, ВМ, QA
пересекаются в одной точке D. Тоrда по теореме Менелая имеем:
ВА QC PN
РА Бе QN = 1. Но, по теореме Паппа о полном четырехстcr
PN РМ ВА QC РМ
роннике, QN = QM . Поэтому РА Бе QM = 1. Это условие
будет, очевидно, и достаточным. Проверьте, что указанное условие
Чевы выполняется для медиан, биссектрис и высот. Проведите эле
ментарное доказательство теоремы Чевы, не опираясь на теоремы
Паппа и Менелая.
19. Достаточно ДOKa
зать, что Q совпадает с
Q1 точкой пересечения
PR с СВ' Обозначим че
рез G точку пересечения
АВ' и А'С, а через Н
точку пересечения АС' и
В'С. Исполыэуя инвариан
тность двойноrо отношения
при проектировании после
довательно из точек R, А',
С', будем иметь: (CHB'Ql) =
(аАВ'Р) = (САОВ) = (CHB'Q),
откуда и следует, что Q1
Q.
Рис. 77 Теорема, двойственная к
теореме Паппа, формулиру
ется следующим образом: если две тройки прямых а, Ь, с и а', Ь',
с' проходят, соотвеТСТВ,енно, через точки L и L', причем ни одна
из них не совпадает с прямой LL', то прямая р, соединяющая точки
пересечения прямых а, Ь' и а', Ь, прямая q, соединяющая точки П
L
с'
229
ресечения прямых Ь, с' и Ь', с, и прямая т, соединяющая то ки пере
сечения прямых а, с' и а', с, пересекаются в одной точке (рис. 77).
20. Рассмотрим сначала случай, 'коrда трехвершинники лежат
в разных плоскостях. Тоrда, если существует S центр перспек
тивы, то существует точка Р пересечения плоскостей АВС, А'В'С'
и SAB, точка Q пересечения плоскостей А'В'С' и SBC и точка R
пересечения, плоскостей А'В'С' и SAC. Эти три точки лежат тоrда
на прямой s пересечении плоскостей АВС и А'В'С' Обратно,
если существуют точка Р пересечения прямых АВ и А'В', точка Q
пересечения прямых АС и А'С' и точка R пересечения прямых ВС
и В'С', и если ЭТИ точки лежат на одной прямой S, то существует
точка S пересечения плоскостей РАА', QCC' и RBB' Но так как
ЭТИ плоскости пересекаются по прямым АА', ВВ' и СС', то точка S
принадлежит этим трем прямым.
В случае, коrда трехвершинники лежат в одной плоскости, ДOKa
зательство теоремы Дезарrа может быть получено из TpexMepHoro
случая "по непрерывности" Если существует центр перспективы S,
то точка R необходимо лежит на прямой PQ, так жак она лежит на
этой прямой при сколь уrодно малом "приподнимании" прямой SAA'
над плоскостью SBCB'C' (точки S, В, С, В', С' оставляем при этом
неподвижными). Точно так же, если существует ось перспективы,
то прямые АА', ВВ', СС' необходимо пересекаIQТСЯ в одной точке
S, так как они пересекаются в одной точке при сколь уrодно малом
повороте плоскости A'PQ относительно прямой PQ (плоскость APQ
остает я при этом неподвижной).
Далее, для Toro, чтобы убедиться, что теорема Дезарrа является
теоремой двойственности, запишем подробно и в терминах инциден
тности утверждения, об эквивалентности которых идет речь в этой
теореме. Первое утверждение: точка S инцидентна трем прямым р,
q, т, каждая из KoTopых инцидентна паре точке, соответственно, А
и А', В и В' ,. С и С' Второе утверждение: прямая s инцидентна
трем точкам 'Р, Q, , каждая из которых инцидентна паре прямых,
соответственно, а и а', Ь и Ь', с и с' Так как эти утверждения п
лучаются друr из друrа, если поменять местами соответствующие
друr друrу точки и прямые (прямую р с точкой Р, точку А с прямой
а и Т.П.), и при этом сохраняются инцидентности, то это двой
ственные друr друrу утверждения, и теорема Дезарrа есть теорема
двойственности.
В случае, коrда трехвершинники лежат в одной плоскости, а роль
230
перспективы иrрает подобие (rомотетвя), :'eopeMa Дезарrа прини
мает вид: треуrольники подобны (rомоте'l.'ИЧНЫ) тоrда и только T
rда, коrда их стороны попарно параллельны.
21. Доказательство теоремы Паскаля см. п. 4.9. Друrое доказа
тельство этой теоремы, аналоrичное приведенному в п. 15 доказа
тельству теоремы Паппа, см., например, в [11, с. 367 368].
Теорема Паппа является вырожденным случем теоремы Паскаля,
коrда коническое сечение вырождается в пару прямых.
ли две из трех пар противоположных сторон вписанноrо в
окружность шести:уrольника образованы параллельными прямыми,
т.е. прямыми, точка пересечения которых лежит на несобственной
прямой, то, по теореме Паскаля, на э+ой же весобственной прямой
будет лежать и точка пересечения остальных двух сторон, т.е. они
также будут параллельны друr друrу.
1 '2 3 4 5
5
4
3
2
1
Рис. 78
5
5
1
2
1
Рис. 79
231
22. Так как проектирование сохраняет инцидентности и касания,
а всякая овальная линия BToporo порядка может быть получена пр
ектированием окружности, то достаточно доказать теорему Бри
аншона для окружности. Примев.яя полярное преобразование, пер
водим касательные к окружности (стороны описанноrо шестиуrоль
ника) О, Ь', с, о', Ь, d (рис. 33) в их точки касания, соответственно,
А, В', С, А', В, С', точки пересечения сторон о и Ь', Ь и d, с и о',
о' и Ь, Ь' и с, с' и о в стороны вписанноrо шестиуrольиика, COOT
ветственно, АВ', В'С, СА', А'В, ВС', С'А, прямые р, q, r, инциден
тные парам противоположных вершин описанноrо ше-стиуrольника
и инцидентные вместе точке L, перейдут в точкИ Р, Q, R, инциден
тные парам противопоJюжных сторон вписанноrо шестиуrольника
и инцидентные вместе прямой 1 поляре точки L. Таким образом,
теорема Брианшоиа оказывается двойственной теореме Паскаля, и
доказательство теоремы Бриавшона следует из доказательства Te
оремы Паскаля.
23. Несобственные точки, лежащие на ПРОДО,I1жении сторон
барицентрическоrо треуrольника, имеют координаты (О, т2, ' т2),
(m1, О, m1), (m1, .....т1, О). Уравнение проходящей через эти точки
несобственной прямой имеет вид: %1 + %2 + %з = о.
4. Построение параболы на основании теоремы Штейнера изо--
бражено на рис. 78, а построение rиперболы на рис. 79.
25. Пусть 11 и 12 пара.ллельные прямые, АВ отрезок
на 11 (рис. 80). Нахождение
середины М отрезка АВ мо--
жет быть проведено последо--
вательным проведением пря
Mых ОА, ОВ, СВ, DA, OQ.
ОНО соответствует построе.-
нию точки i мёбиусовой се.-
ти.
26. Инвариантность pac
стояния PL следует из инва
риантности двойноrо ОТНО--
Рис. 80 шения (PQMN). Свойство 1
выполняется, так как (PQMN) > О и I In(PQMN)1 > О, а из Toro, что
I In(PQMN)1 = О следует, что (PQMN) = 1, т.е. Р = Q, и наоборот.
Свойство 2 вы полн.иет CJI, так как (QPMN) = ( Q N) Выполне--
О
12
11
А
м
В
232
нне свойства 3 удобно проверить, переведя предварительно точку
R с помощью преобразQВаний (а) и (б) в центр Kpyra. Выполнение
свойства 4 следует из Toro, что
( РМ PN ) ( Q RM M Q RN N ) =:
(PRMN) . (RQMN) = RM RN
РМ PN
= QM QN = (PQMN) ·
Инвариантность PR относительно преобразовавий (а) и (б) и BЫ
полнение свойств 1 4 следует из Toro, что rруппа r 2 эллиптической
rеометрии с расстоянием fJR изометрична rруппе движений на еди
ничной сфере (с отождествленными диаметрально ПРОТИВОПОJЮж
ными точками) с уrловым расстоянием.
27. I'pуппа r 4 раСI!адаетс.я на rруппу r 41 движений 1 рода (c<r
храняющих ориентацию) и на класс r 42 движений 11 рода:
r 4 = r 41 + r 42 = r 41 + S r 41 ,
rде s симметрия относительно фиксированной оси. Друrой под
rруппой rруппы r 4 будет rруппа r з всех перемещений (т.е. движ
ний, сохраняющих расстояния между точками). r з состоит из па
раллельных переносов, поворотов и симметрий относительно осей и
распадается на rруппу r З1 перемещений 1 рода " (с охр аНJIЮЩИХ ори
ентацию) и на класс r З2 перемещений 11 po a:
r з = r З1 + r З2 = r З1 + s r з1 ,
rде s симметрия относительно фиксированной оси. I'pуппа r З1
содержит подrруппу r з1 i всех параллельных переносов и подrруппу
r З12 всех поворотов относительно фиксированноrо центра.
28. Отметим, прежде Bcero, rруппу всех проективных преобра
зований (т.е. всех коллинеаций и корреляций), основной инвариант и
ршэмерность которой те же, что и у r8. Однако "точка" и "прямая"
,
БУдУЧИ инвариантами r 8, уже не будут инвариантами при коррел.и
циях. Под теоретик<rrрупповую классификацию п падают и такие
типы rеометрий, как тополоrия, конформная rеометрЩ!, rеометрия
биеКТИВRЫХ точечных преобразований, BHYTpeHВJIJI rеометрИJI п
верхности, "исчислительная" rеометрия. Так как тополоrию можно
233
рассматривать как rруппу rомеоморфизмов (т.е. взаимно одноонач
ных и воаимно непрерывных преобразований) с такими инвариан
тами, как открытость, замкнутость, компактность, связность, раз
мерность. Конформную rеометрию можно расс атривать как reo--
метр ию конформных преобразований на плоскости с основными ин
вариантами уrлом между кривыми и одинаковостью растяжений
по всем направлениям.
29. Впишем в полушар радиуса r и опишем около Hero тела,
r
состоящие из цилиндров с одинаковыми высотами (см. рис. 81).
п
Тоrда объем .!::n вписанноrо тела будет равен
[r2 ( r)2]
.!: = 7rr З [ 1 (п + 1)(2п + 2) ]
п 6п 2
а объем V n описанноrо тела будет paB H
n l [ ( k ) 2 ]
t; r 2 n r
.!:. = 7rr З [ 1 (п 1)(2п 1) ]
п 6п 2
Так как при любом сколь yro--
дно большом п будет
Vп <V< Vп И
2 з
V n < 3 1fr < V n ,
а разность между V n И .!::n
r
равна 7rr 2 и, следова
п
Рис. 81 тельно, может быть сделана
меньше произвольноrо положительноrо числа е, то необходимо дол
жно выполняться V = r3 Действительно, если бы было V > r3
222
или V < 3 r3, то взяв е = V 3 r3 или е = 3 r3 V и УЧИТЫВaII,
2 3
что и V и 3 1fr лежат между V n И V "' мы имели бы: V n V n > е
при любом п (?!).
30. На рис. 82 АОВ парабола у2 = 2рх, т.е. кривая, опр
деляемая симптомом: квадрат на полухорде PQ = у равен прямо--
уrольнику на отрезке диаметра ОР = х и на постоянном отрезке
234
R
С
А
R'
В
D
Рис. 82
MN = 2р.. OCD треуrольник, в котором CD = OR' = OR,
ор' = ОР, CR' = R'D, КР' = P'L. Линии АВ, QS, KL. CD
ортоrональны линии RR'. Тоrда параболоид, получаемый вращ
нием параболы АОВ BOKpyr ее диаметра OR, уравновешивается
призмой с основанием OCD и с высотой 1r MN (боковые rрани
призмы предполаrаются ортоrональными к основанию). Это сле
дует из Toro, что сечение параболоида в точке Р плоскостью, пе
пендикул.ирной к OR, равно сечению призмы в точке Р' плоскостью,
перпендикул.ирной к OR', а рычаr ОР равен рычаrу ОР', так что
1r (PQ)2. ОР = 1rMN . (ор)2 = 1r.MN . (ор')2 = 1r . MN KL. ОР'
Поэтому центр тяжести параболоида лежит от вершины О на
том же расстоянии, что и центр тяжести призмы, т.е. на расстоя
нии OR' = OR. Из равенства соответствующих сечений пара
болоида и призмы следует и равенство их объемов. Поэтому объем
параболоида равен! .OR' . CD .1r.MN или !1r(AR)2 .OR, т.е. .половине
произведения основания параболоида на высоту.
31. Лоrарифмическую функцию ln ж можно определить как пл
щадь подrрафика rиперболы жу = 1 на отреоке от 1 до ж i..при
Этом площадь считается положительной, если ж > 1, и отрицатель
ной, если О < ж < 1). Основное свойство натуральноrо лоrарифма
ln аЬ = ln а + ln Ь докажем в предположении, что 1 < а < Ь. Перепи
сав это свойство в виде ln аЬ ln Ь = ln а, заметим, что речь идет о
квадрируемости подrрафика и равенстве площадей 8 и 8' rипер6Ълы
ху = 1 на отреоках, соответственно, [1, а] и [Ь, аЬ] (рис. 83). Ра.з
бив эти отрезки на одинаковое число n равных частей и построив
235
вписанные и описанные ступенчатые фиrуры с площадями, соответ..
..... , .....,
ственно, Sn И Sn, Sn И Sn, будем иметь
Sn < S < Sn ,
у
С'
но n = s.n, а S n = S n ,
так как равны площади соот..
ветствующих прямоуrольнн"
ков, составляющих Э Н впн..
а6 х
санные н описанные ступен..
чатые фиrуры. Действитель..
но, прямоуrольники, состав..
ляющие правую вписанную (описанную) фиrуры, имеют основание
в 6 раз больше, а высоту в 6 раз меньше, чем соответствующие
им прямоуrольники,. составляющие левую вписанную (описанную)
фиrуру. Поэтому площади вписанных (описанных) фиrур равны как
суммы площадей paB ЫX прямоуrольников. Далее, так как s.. = s..n,
S = Sn , s.. < S' < s.. , s..n < S < Sn , то разность между S' и
S мен ше, чем разность между и S или между Sn И Sn . Но
разность
1
, ,
Sn < S < Sn ,
1
а 6
Рис. 83
,..... a 1
Sn s.n = Sn s..n =
n
(1 ) Ea 1)2
1
n
и, следовательно, может быть сделана меньше любоrо наперед за..
данноrо положительноrо числа. Поэтому поrрафики rиперб лы на
отрезках [1, а] .и [6, а6] квадрируемы, н S' = S.
32. Пусть R радиус кольца тора, а r радиус Kpyra, получа..
ЮUAerося при разрезании тора плоскостью, проходящей перпендику"
ТIjj[pHO к ero поверхности (рис. 84), r < R. Разрежем тор на очень
большое число очень маленьких частей плоскостями, перпендику"
лярными к поверхности тора. Каждый такой кусочек очень мало
отличается от цилиндра с площадью основанИJI 1rr 2 и с высотой, ра..
вной полусумме дуr s и S. Поэтому объем тора, равный сумме объ
емов отдельных маленьких кусочков , будет равен сумме объемов
2 S+S б
цилиндров с основаниями 1rr и с высотами 2 ,т.е. о ъем тора
будет равен объему цилиндра с радиусом основания r и с высотой
21r R. Этот же результат можно получить по друrому методу Ke
236
плера, если Kpyr радиуса r, получающийся при ра.орезании тора пло--
скостью, перпендикулярной к поверхности тора, заключить между
вумя ступенчатыми фиrурами и посчитать объемы тел, получае
\fblX при вращении этих ступенчатых фиrур.
зз. а) Выбирая "неделимые" параллельными основаниям полу
шара, конуса и цилиндра и учитывая, что сумма площадей 7ry2 + 7rx 2
"неделимых" , соответственно, полушара и конуса равна площади 7rr 2
"неделимой" цилиндра, имеем:
Е 7ry2 + Е 7rX2 = Е 7rr 2 ,
ИЛИ Vпопушара + Vхоиуса = Vципиидра.
б) Рассмотрим тор, изображенный. на рис. 84, и цилиндр
с радиусом основания r и с высотой 27rR. Будем брать
"неделимые" тора параллель
ными плоскости рисунка 71,
а "неделимые" ЦИЛИндра
параллельными какой нибудь
плоскости, проходящей че
рез ось цилиндра. Тоrда из
равенства соответствующих
"неделимых" тора и цилин
дра следует равенство их
объемов.
в) Пусть АОВ cer
мент параболы (см. рис. 85),
ОС а ero высота,
АВ = 2АС =2Ь основание
cerMeHTa. Выбирая "недели
Рис. 84 мые" ly параллельными диа
ау2
метру параболы, будем иметь: ly = a x = a Ь 2 Поэтому площадь
cerMeHTa параболы
( а у2 ) а
S = 2 L 'у = 2 L а ь2 = 2 L а 2 Ь 2 L у2 =
O y5b O y$b O Y$Ь O y Ь
а Ь З 4
= 2аЬ 2 Ь 2 "3 = з аЬ
237
r) Для вычисления площади S первоrо витка спирали Архимеда
а
r = 27r <р, О < <р < 27r (см. рис. 86) вооьмем в качестве "неделимых"
v · ,
дуrи концентрических окружностеи с центром в точке О радиуса
О < r < а. Имеем
у
А
х
в
Рис. 85
Рис. 86
S = L lr = L r(211" ) = L r (211" 2:r ) =
OSrSo OSrSo OSrSo
= 27r
L
°SrSo
27r
r L
а
OSrSo
а 2 27r аЗ
r 2 = 211"
2 а
7ra 2
==
3
3
Дpyroe решение:
а а а ( 27rr ) '"'
S 2 = L.J 2 . lr = L.J 2 r 27r = L.J 7rr( а r) =
0SrSo OSrSo 0SrSo
= объему шара с диаметром а,
откуда
s = 4 7r ( а ) 3 2 = 1I"a 2
3 2 а 3
34. 1Ребуется доказать, что ln аЬ = ln а + ln Ь, или, ЧТО то
же самое, ln аЬ ln Ь = ln а. Не умаляя общности, можно считать,
что 1 < а < Ь. До.казательство сводится к установлению равен--:
ства площадей подrрафиков rиперболы ху = 1 на oTproKax [1, а] и
[Ь, аЬ] (рис. 87). 'Проведем линию MN rрафик rиперболы Ьху = 1,
238
у
1
lZ{
а Ь
Рис. 87
Ьх
аЬ х
1 < х < а. Сравним площади под rиперболами ху = 1 и Ьху = 1,
1 < х < а. Выбирая "неделимые" Iz и I параллельно оси У, имеем:
1 1
l' 1... = = 1 Ь ,
z .. Ьх х
поэтому площадь под rиперболой Ьху = 1 будет в Ь p меньше пл
щади под rиперболой ху = 1, Ь < х < аЬ. Выбирая "неделимые" 11/ и
I параллельными оси У, будем иметь:
I Iy=(bx b) (x I)=Ь 1
-Поэтому площадь под rиперболой ху = 1, Ь < х < аЬ, будет в Ь раз
больше площади под rиперболой
MN, и, следовательно, БУдет равна
площади под rиперболой ху = 1,
1 < х < а, что и требовалось д
казать.
35. Соrласно методу "недели
мых", объем тела вращения пл
щади S BOKpyr оси у равен сумме
боковых площадей цилиндров с pa
хох Ь х диусом основания х и высотой I(x)
Рис. 88 (рис. 88), 'т.е. сумме 21rx ./(x). Эту
сумму можно представить в виде
у
а
21r Е (х хо) I(x) + 21rXo
a z b
Е I(x)
a<z<b
rде хо абсцисса центра тяжести площади s. Соrласно определе
нию центра тяжести, первая сумма равна нулю. Вторая же сумма
есть произведение площади S = L I(x) на длину, окружности,
a<z<b
описываемой центром тяжести.
239
36. Выбирая, соrласно методу Ферма, точки разбиения отрезка
[1, х] в rеометрической проrрессии: 1 = х О < х-:- < х-! < < x =
х, находим, что площадь Sn описанной около подrрафика rиперболы
ху = 1 ступенчатой фиrуры будет равна
t ж 1;. (ж ж .;1 ) = t (ж i 1) = n (xi 1)
k=1 k=
Поэтому ln х = Sn I .1. = Sn I = lim n ( Х -k 1 ) .
Л=Z " =1 "=оо n oo
37. Площадь поверхности шаровоrо слоя, образованноrо враще.-
нием дуrи <Р1 < VJ < <Р2 окрУжности (см. рис. 57) BOKpyr оси ординат,
будет равна
Е 21r . OQ KL = 21r Е ОР КМ = 21r Е COS VJ . VJ =
СР1 ScpScp
= 21r L sin ( ; ) = 21r [соз ( ; 1) соз ( ; 2)] =
tr < .. < ..
cp cp CPl
= 21r( sin VJl sin <Р2 )
. а а
38. Имеем: r = VJ, откуда r = 2 VJ. Поэтому
21r 1r
а
....!...... U'J 1 1 . 1
21r т SlD <р
а Так ЧТО \ 1 , откуда
VJ . t.p VJ r cos t.p <Р'
21r
д 2
d 1
r
р . VJ
1= r а VJ
VJ sin VJ + соз VJ 21r VJ sin t.p + cos t.p
39. СОfласно методу Декарта, ИСКЛЮЧИВ у из системы уравнений
{ ху = 1 ,
(х с)2 + у2 = (с а)2 + :2 ' будем иметь:
Q(x) = а 2 х 4 2а 2 сх 3 (а 4 2а 3 с + 1)х 2 + а 2 = О
Но Q(x) = (х а)2(рх 2 + qx + r), поэтому
р
q 2ар
а 2 р 2aq + r
a 2 q 2ar
a 2 r
а 2
2a2c
a4 + 2а 3 с 1
О
а 2
240
2
откуда r = 1, q = и
а
2ар q 2а З 2/а
с 2а 2 2а 2
d ь 2 l/а 2
a a 1/аЗ
c a
1
а ........
з '
а
2а.
h
40. Имеем: PL = у(2) у(2 + h) у(2)
=1
h h( 1+4h+h2) 1+4h+h2
1 (2 + h) 5h h 2 5 h
1
(2 + h)2 5
Поэтому подкасательная KL = PL I = 5 1 .
h=O
41. Пусть Р(х, у) = о уравнение, задающее алrебраичеСКУI<
функцию у(х). Ее производную у'(х)можно определить алrебраиче-
ским уравнением
[Р(х + h, у) Р(х, y)]lh=O + у'(х) [Р(ж, у + k) Р(х, y)]IA:=o = О.
Подробнее об алrебраическом определен и ПРОИЗВОДНОЙ см., напри
мер, [4, с. 105, 259 262].
42. Соrласно методу "фЛЮКСИЙ" Ньютона, имеем:
уЗ ху + х 2 = О ,
(у + уо)З (х + хо)(у + уо) + (х + хо)2 = О,
3у2у о +3уу2 02 x о .у ху о xY 02 +2хх о +х 2 02 = О ,
3у2у + 3уу2 о ху ху ху о +2хх + х 2 о = О ,
З у 2 у ху ху + 2хх = О
43. Соrласно "исчислению дифференциалов" Лейбница, имеем:
d(xy) = (х + dx)(y+ dy) ху = х dy + ydx + dxdy = xdy + ydx
241
44. Соrласно "исчислению дифференциалов" Лейбница, имеем
dy = !:dx (см. рис. 89), или ly = Zd: Y . А так как ху =
1, то d(xy) = xdy + ydx = О, откуда Zd Y = y. Поэтому
ly = y (внак "минус" полу..
чается в силу Toro, что dy <
О). Правильный (извес ный
еще Аполлонию) результат
получается потому, что одна
ошибка (коrда вместо dy +
1
z =:dx берется dy =
1
=:dx) в точности компенси..
рует вторую ошибку (коrда
вместо d(xy) = (х + dx)(y +
х dy) xy==xdy+ydx+dxdy
Рис. 89 берется d( ху) = х dy + у dx).
45. Соrласно методу Карно, вначале из подобия треуrольников
dl r
,(см. рис. 90) имеем точное уравнение d = . От этоrо уравнения
у х
" " u ds r d d
черro цепочку несовершенных уравнении d == , х s r у,
у х
Е 21rX ds = Е 21rr dy, приходим К точному, "совершенному" ура..
внению: площадь поверхности шаровоrо пояса Уl < У < У2 равна
21rr(Y2 Уl).
46. Так как П(р) = [ p, 1 + р], то k(E) = lim [(1 + р) ( p)] == 1.
p O
Так как в любом cerMeHTe i любоrо разбиения содержатся ра..
n
циональные точки, то s(E) = lim Е m( i) = lim m ([О, 1]) = 1.
n oo i=l n oo
Так как в любом, сколь уrодно малом интервале есть рациональ..
ные точки, то взяв [а, Ь] = [О, 1], будем иметь, что rl = r2 = rз =
= [О, 1]. Поэтому h(E) == lim m(r n ) == lim 1 = 1.
n oo n oo
Так как [О, 1] наименьший отрезок, содержащий Е, то J?ge(E) = 1.
А так Ka.J( ни один отрroок не состоит только из рациональных точек,
то P9i(E) = о. в силу P9i(E) # Р9е(Е) множество Е не является
измеримым по Пеан Жордану.
у
х
dy
z
ly
242
47. Множество Е раци .
ональных чисел из [о, 1]
счетно, а мера Пеано----жор
дана всякоrо одноточечноrо
множества равна нулю. П
этому, если бы мера Пеано----
Жордана была счетно адди"
тивна, то pg(E) существ
вала бы и была бы pa
вна нулю, что противоречит
установленному при рanборе
упражнения 46.
Рис. 90 Так как Е счетно, то,
соrласно принципу 4 мероопределения Бореля, мера Бореля MH
.'Кества Е равна нулю.
48. Производная единственна, так как из
у
у
ж
r
х
f(x + rE) = f(x) + k 1 . rE и f(x + rE) = f(x) + k 2 . rE
следует, что (kl k 2 ) . rE = о, (kl k 2 ) Е R, что возможно лишь при
k 1 k 2 = о.
Далее, если Фунtcции f(x) и g(x) непрерывны и дифференцируемы
в точке х, то
f(x + re) + g(x + rE) = (f(x) + f!(x). rE) + (g(ж) + g'(x) . rE) =
= [f(x) + g(x)J + [f'(x) + g'(x)] . rE,
f(x + re) . g(x + rE) = (f(x) + f'(x) . rE) . (g(x) + g'(x) . rE) =
= [f(x) . g(x)] + [f'(x) g(x) + f(ж) . g'( )] . rE,
1 1 f (х) f' (х) . re
f(x + re) f(x) + f'(x) . re f2(x) f'2(x) . r 2 e 2
1 f'(x)
f(x) f2(x) . re ,
9 (f(x + re» = 9 (f(x) + f'(x) re) = 9 (f(x») + g' (f(x» f'(x). rE,
1
откуда следует, что функции f(x) + g(x), f(x) · g(ж), f(x) , 9 и(x )
непрерывны, дифференцируемы и их производными будут, COOTBeT
ственно,
f' ( х) + g' ( х ) ,
f'(x) g(x) + f(x) g'(x),
f' ( х )
f2 ( х) ,
g' (f(x) f'(x).
243
Доказательство теоремы Ферма: пусть хо точка локальноrо
экстремума (например, локальноrо максимума) функции f(x), т.е.
J(xo :f: о) < J(xo) при любом достаточно мал6м о. Тоrда, в силу
возможности переноса нестроrих неравенств, имеем J(xo :!: re) <
J(xo), или J(xo) :f: J'(xo) re < J(xo) для любоrо вещественноrо r.
Поэтому J'(xo) необходимо должно равняться нулю.
49. Распространив неравенство О < sin х < х < tg х с О < х <
на О < х. < . ' при х = re,. r > О будем им ть О < sin те < те < tg те
sln re sln те sln re .
Но tg re = < = Sln re, так что
cos re \1" 1 sin 2 re \1" 1 (re)2
sin re < re < sin re. Поэтому sin re = re при r > о. Справедли
вость этоrо равенства для отрицательноrо r следует из Toro, что
sin( re) = sin те = re.
50. Имеем:
(х + re)"
. п ( п 1 )
х" + п x" l re + x" 2 (re)2 +
1 2
+(те)" = х" + nX" l . re,
cos х cos re sin х . sin re = cos х sin х re,
Inx(l+ : е) =lnx+ln(l+ : е) =ln.x+ re,
е Х e re = е Х (1 + re') = е Х + е Х re,
cos(x + re)
ln(x + re)
e z + re
поэтому функции х", cos х, ln х, е Х непрерывны, дифференцируемы
И ИХ ПРОЗВОДНЫМИ будут, соответственно, nxn 1, sinx, .!., е Х
х
51. Имеем:
1 о [ N
! е Х dx = {; е""
] о [ Nc 1 ]
€ ее е € =
ее 1
О [ ]
е 1
(1 + е) (1 + е) 1 е
о [( е 1) + (е 1) Е:] = е 1.
Литература
1. ААВАСов H.F. Теория действительноrо числа с точки зрения ис
тори'tескоrо процесса ее возникновения. Канд. дисс. Mry,
1950.
2. Башма'Н:ова H.F Диофант и диофантовы уравнения. М.: Ha
ука, 1972. 68 с.
3. Бер'Н:АU Дж. Сочинения. М.: Мысль, 1978. 556 с.
4. Ван дер Варден Б.Л. Алrебра. 2 e изд. М.: Наука, 1979.
624 с.
5. Вuле'йтнер r. История математики от Декарта до середины XIX
столетия. М.: Физматrиз, 1960. 467 с.
6. ВЫ20дс'Н:и'й м.л. Арифметика и алrебра в древнем мире. M.
л.: оrиз, 1941. 252 с.
7. rе2ель r Сочинения. М. Л.: roc. соц. экон. изд., 1929 1958.
8. rлейэер r.H. История математики в школе. М.: Просвещение,
1981 1983.
9. rнеден'Н:о Б.В. Очерки по истории математи'ки в России. M.
л.; оrиз, 1946. 247 с.
10. Девис М. Прикладной не стандартный анализ. М.: Мир, 1980.
236 с.
11. Делоне Б.Н., Ра'й'К:ов л.к. Аналитическая rеометрия. М. Л.:
rиттл, 1949. Т. 11. 516.с.
12. Ефuмов Н.В. Высшая rеометрия. М.: Наука, 1978. 576 с.
13. Звон'К:uн А.К., Шубuн М.А. Нестандартный анализ и синrуляр
вые возмущения обыкновенных дифференциальных уравнений
/ / Успехи математических наук. 1984. Т. 38, вып. 2. С. 77
126.
14. Историк<rматематические исследования. М.: rТТИ Наука.
15. История математики с древнейщ-их времен до начала XIX сто--
245
летия. М.: Наука, 1970 1972. Т. 1 3.
16. История отечественной математики. Киев: Наукова Думка,
1966 1970. Т. 1. 4.
17. Карно л. Размышления о метафизике исчи'сления бесконечно
малых. М. Л.: rтти, 1936. 325 с.
18. Картье п. Синrулярные JJозмущения обыкновенных дифферен
циальных уравнений / / Успехи математических наук.... 1984.
Т. 38, вып. 2. с. 57 76.
19. Клеин Ф. Элементарная математика с точки зрения высшей.
4 e изд. М.: Наука, 1987. Т. 1, 2.
20. Клейн Ф. Лекции о развитии математики в XIX столетии. М.:
Наука, 1989. Т. 1. 456 с.
21. Курант Р., Роббuнс r. Что такое математика? Элементарный
очерк идей и методов. М. Л.: оrиз, 1947.
22. Кусраев А.Т., J(утателадэе с.с. Нестандартные методы aHa
лиза. Новосибирск: Наука, 1990. 343 с.
23. Маркс К. Математические рукописи. М.: Наука, 1968. 639 с.
24. Математика XIX века. М.: Наука, Т. 1, 2, 3.
25. Математика, ее содержание, методы и значение. М.: изд во
АН СССР, 1956. Т. 1 3.
26. Медведев Ф.А. Развитие теории множеств в XIX веке. М.:
Наука, 1965. 232 с.
27. Меаведев Ф.А. Развитие понятия интеrрала. М.: Наука, 1974.
423 с.
-28. Песuн Н.Н. Развитие понятия интеrрала. М.: Наука, 1966.
207 с.
29. Постнuков М.М. Теория rалуа. М.: Физматrиз, 1963. 218 с.
30. Рыбнuков К.А. История математики. 2 e изд. М.: изд во
Mry, 1974. 456 с.
31. Се'Н:ст Э.4СnUрU'Н:. Сочинен я в двух томах. М.: Мысль, 1975.
Т. 1 2.
32. Усnенскuй В.А. Что такое нестандартный анализ? М.: Наука,
1987. 128 с.
33. Хрестоматия по истории математики.
М.:. Прос ещение,
246
1976 1977 Кн. 1,2.
34. Цеитен r История математики в древности и в средние века.
М. Л.: rтти, 1932.\ 230 с.
35. Цеитен r История математики в XVI и XVII веках. М. Л.:
rтти, 1933. 429 с.
36. Чеботарев H.r Основы теории rалуа. М. Л.: rтти, 1934.
221 с.
37. Чеботарев Н.Т Теория rалуа. М. Л.: ОНТИ, 1936. Кн. 1.
154 с.
38. Юш'Н:евu'Ч А.П. История математики в России до 1917 rода.
М.: Наука, 1968. 592 с.
39. Лновс'Н:аJl С.А. О так называемых "определениях черro абстрак
цию" / / Методолоrические проблемы науки. М.: Мысль, 1972.
с. 34 75.
Сер2е'й Нu'Н:о",аевu'Ч Мар'Н:ов
КУРС ИСТОРИИ МАТЕМАТИКИ
Учебное пособие
Редпторы з.п. Межецких, Л.В. Юrова
Художественный редактор Н.В. Алсуфьев
Технические редакторы С.А. Бессольцева, И.Н. КореЦКaJ!
Компьютерный набор, верстка и rрафика А.С. Яшин
ИБ N 1057. Лицензия ЦР N 040250 от 30 января 1992 r.
Подписано в печать 25.04:95. Формат 60 х 841/16. Бумarа офсеТНaJI.
Печать офсеТНaJ!. rарнитура К мпьютер модерн. ТИраж 3000 ЭКЗ.
Усл. печ. л. 14,4. Уч. изд. л. 14,2. Усл. Kp. OTT. 14,7. Зuаз (649.
Издательство Иркутскоrо университета,
r. Иркутск, центр, бульвар rаrарина, 36.
Отпечатано в Иркутском Доме печати,
664009, r. Иркутск, УЛ. COBeTCKaJI, 109.
\ 1 j
\
,
"